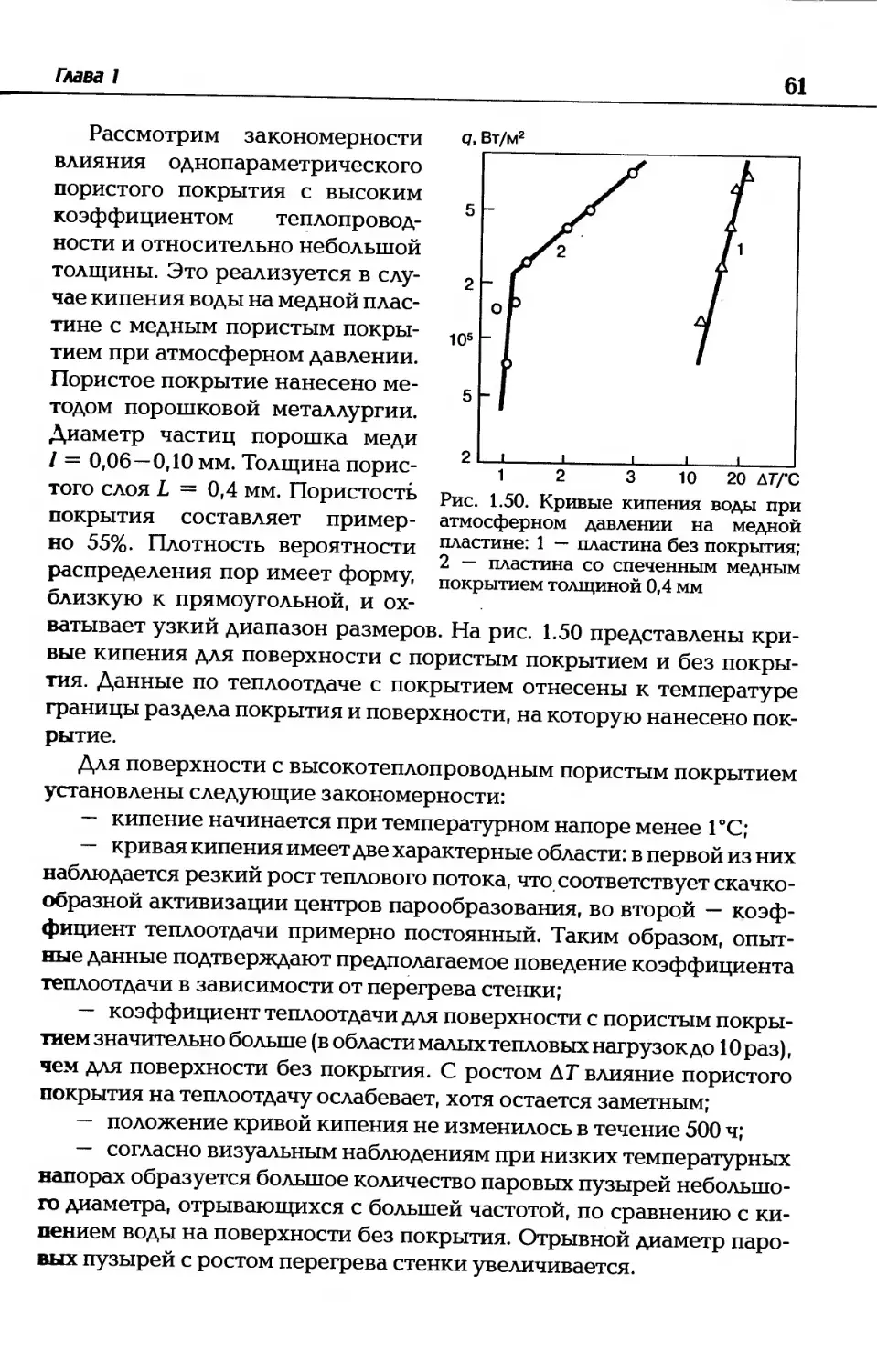
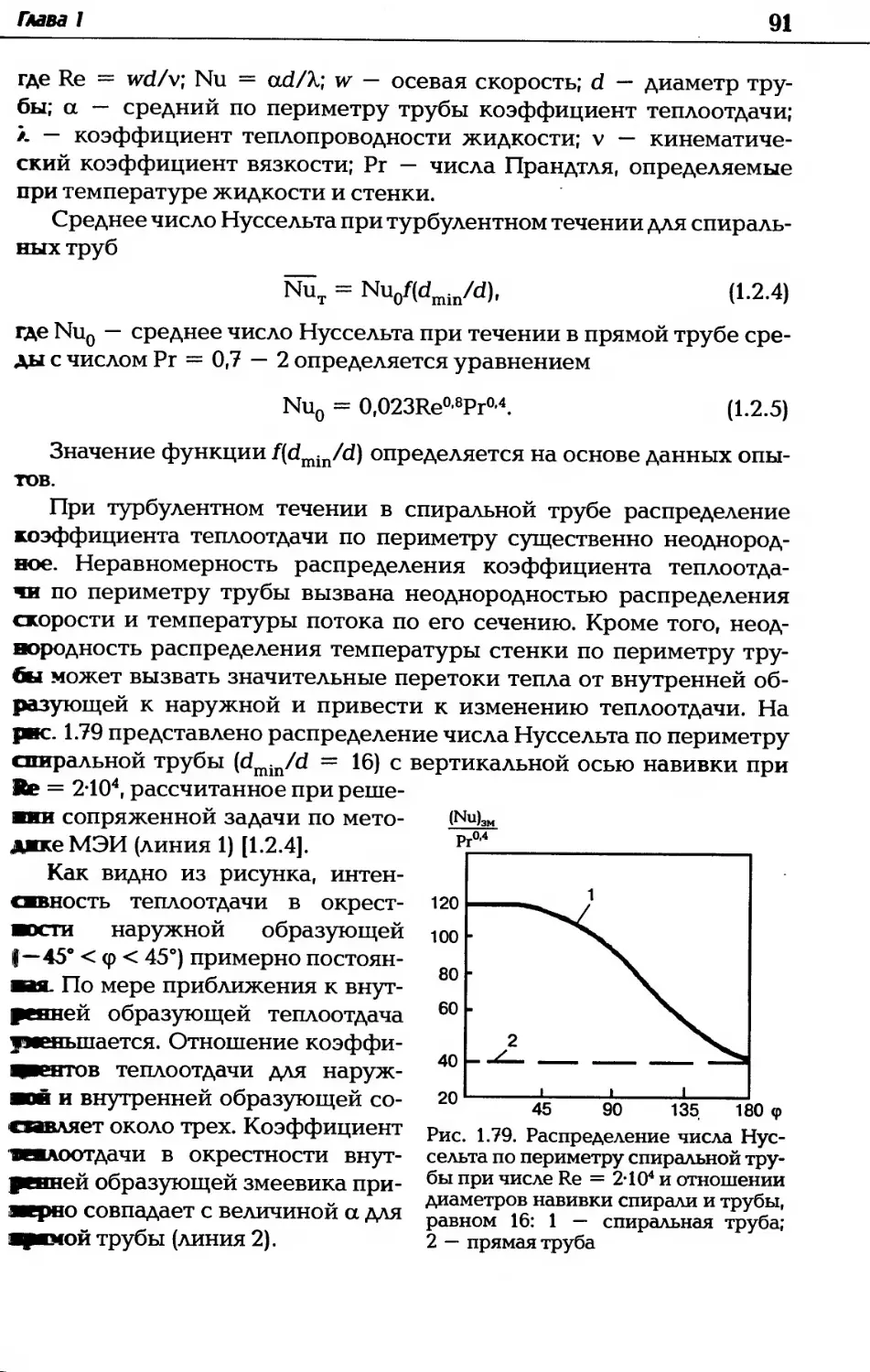
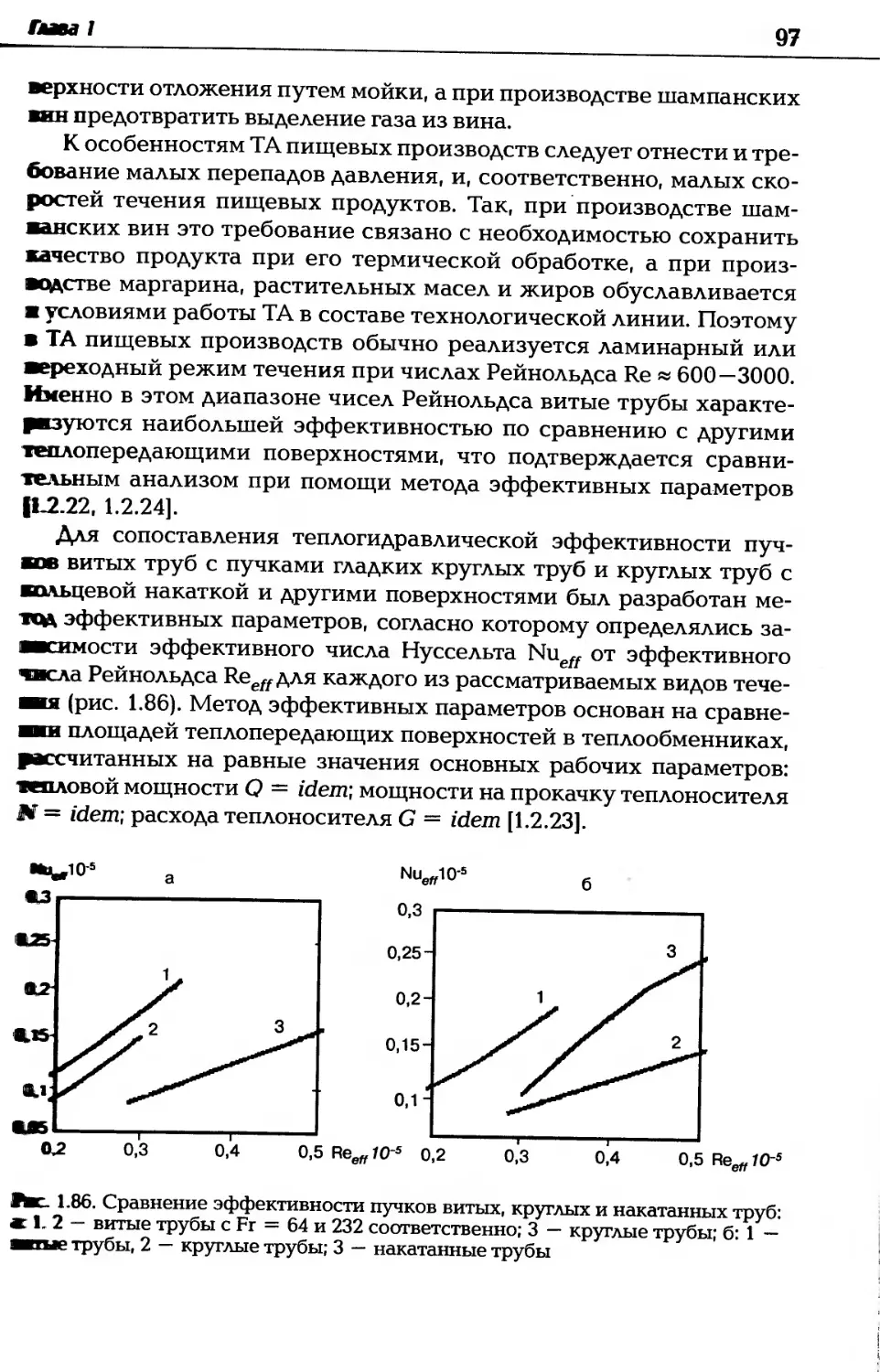
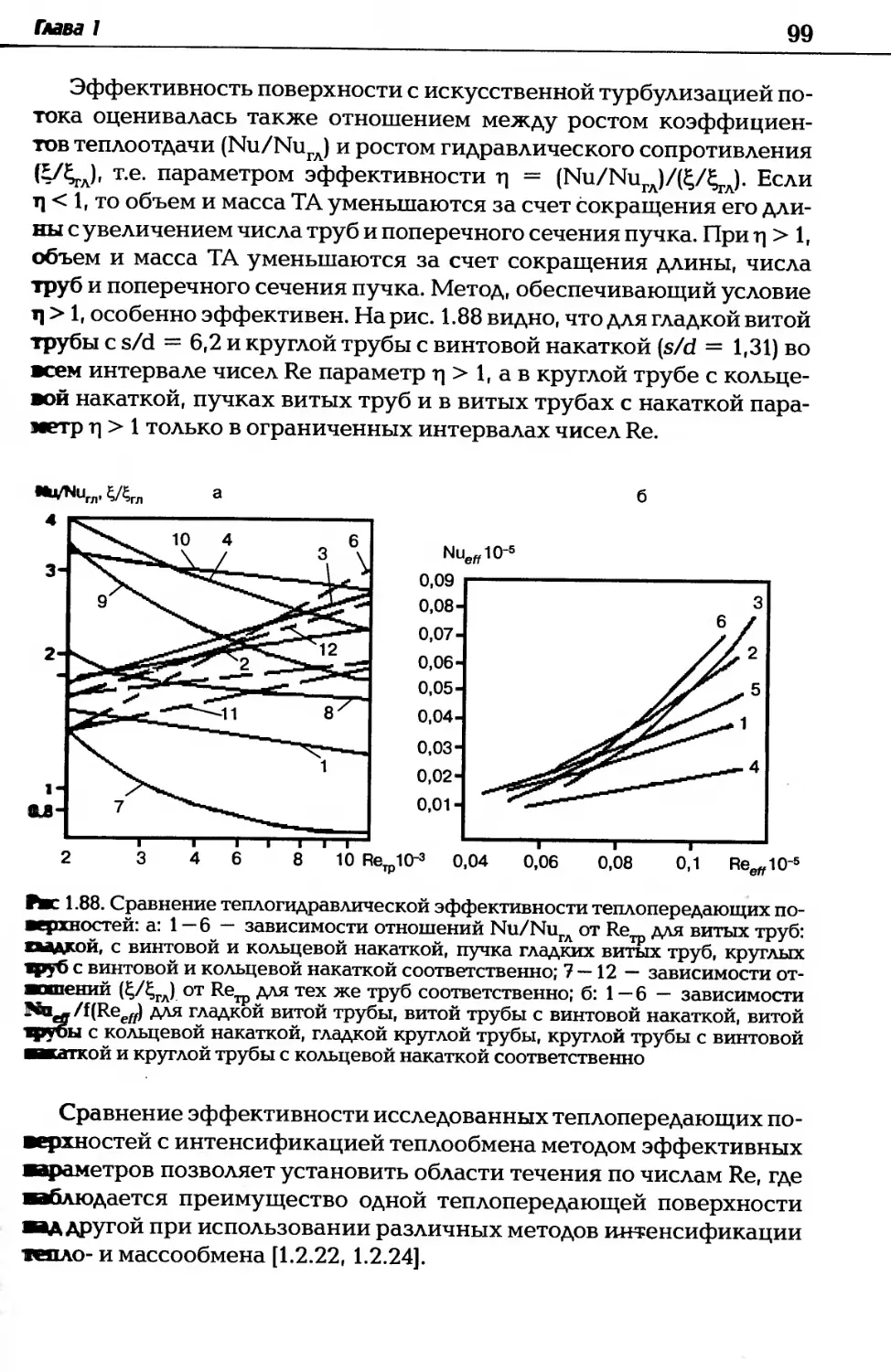
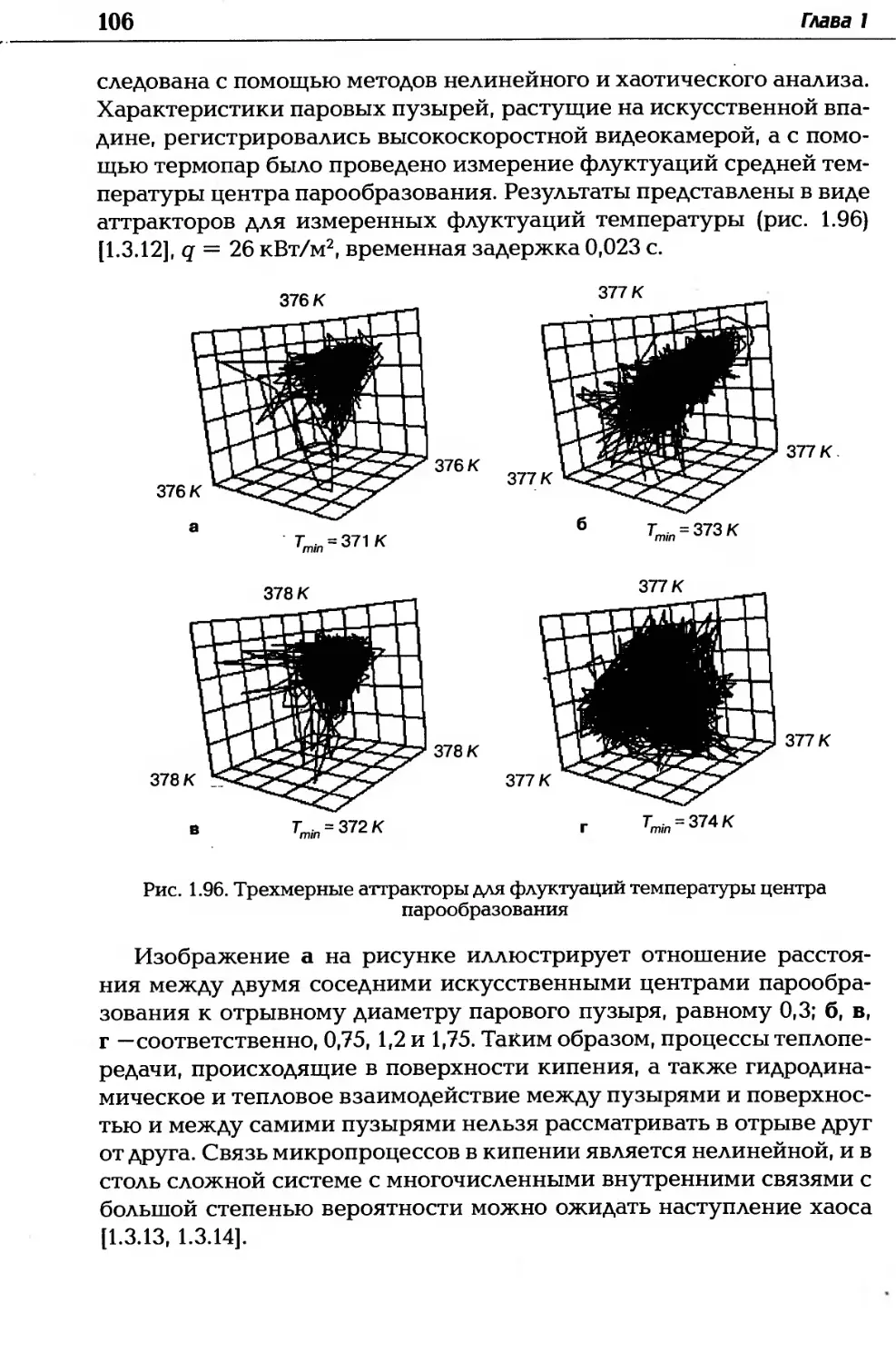
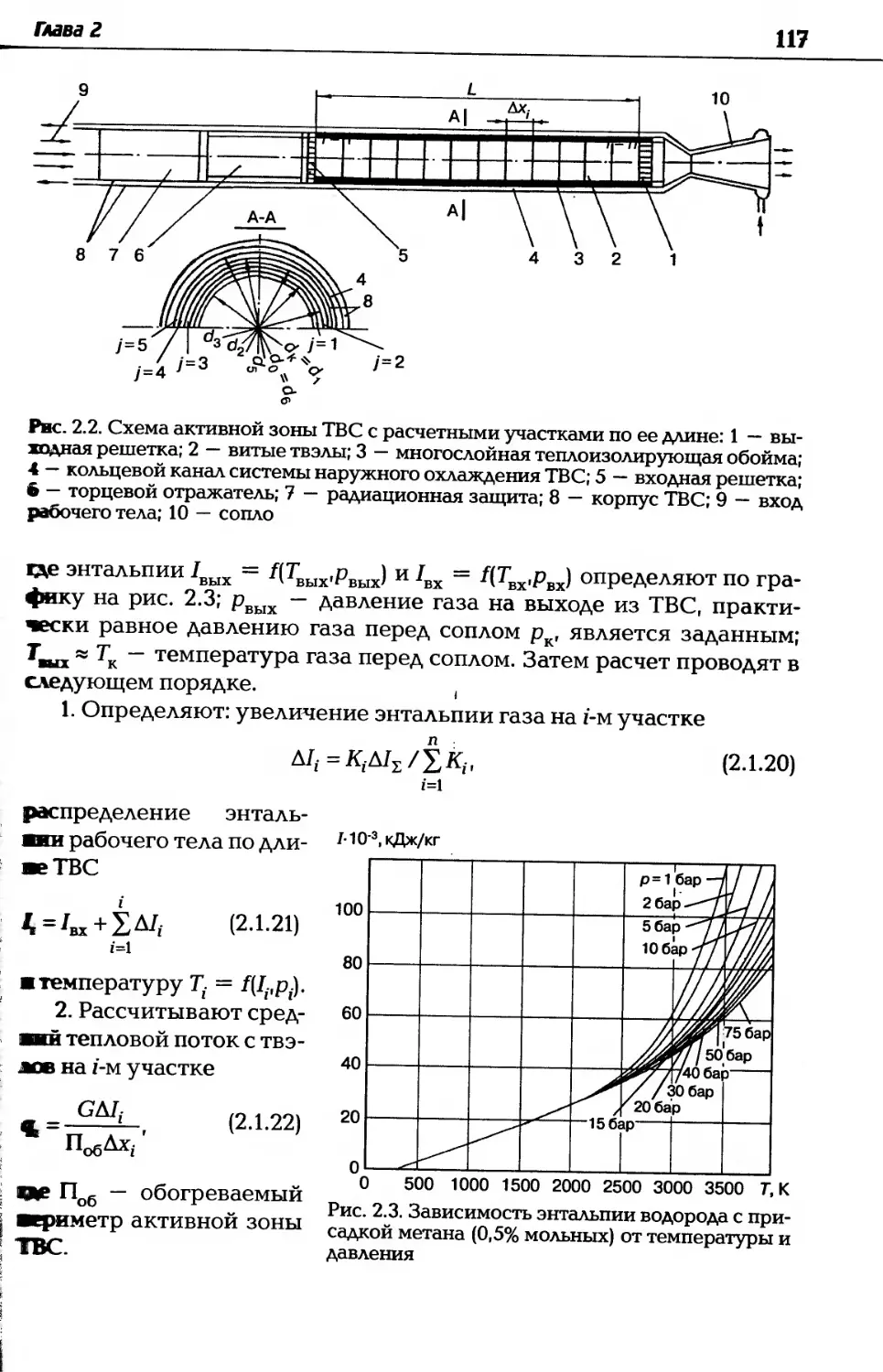
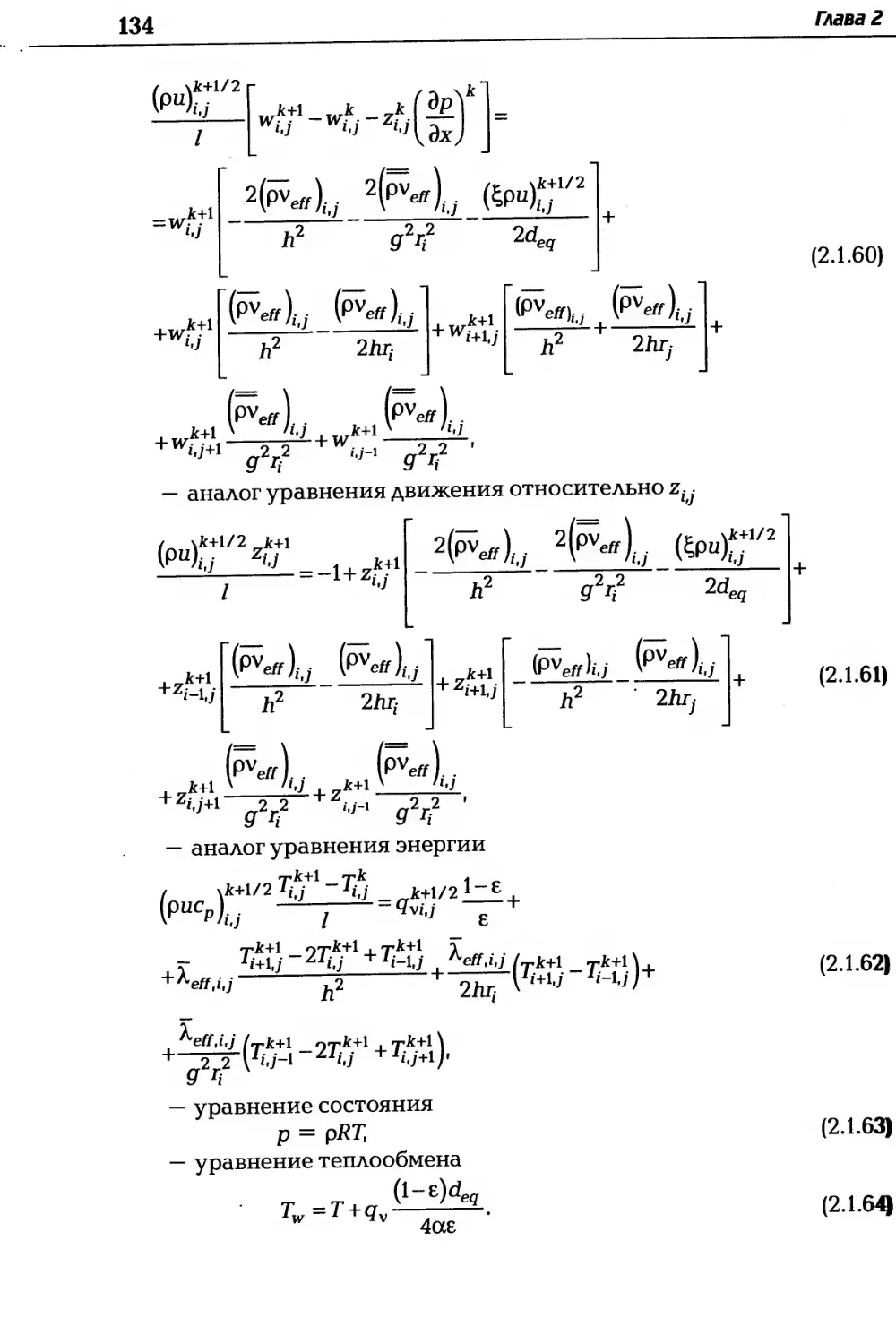
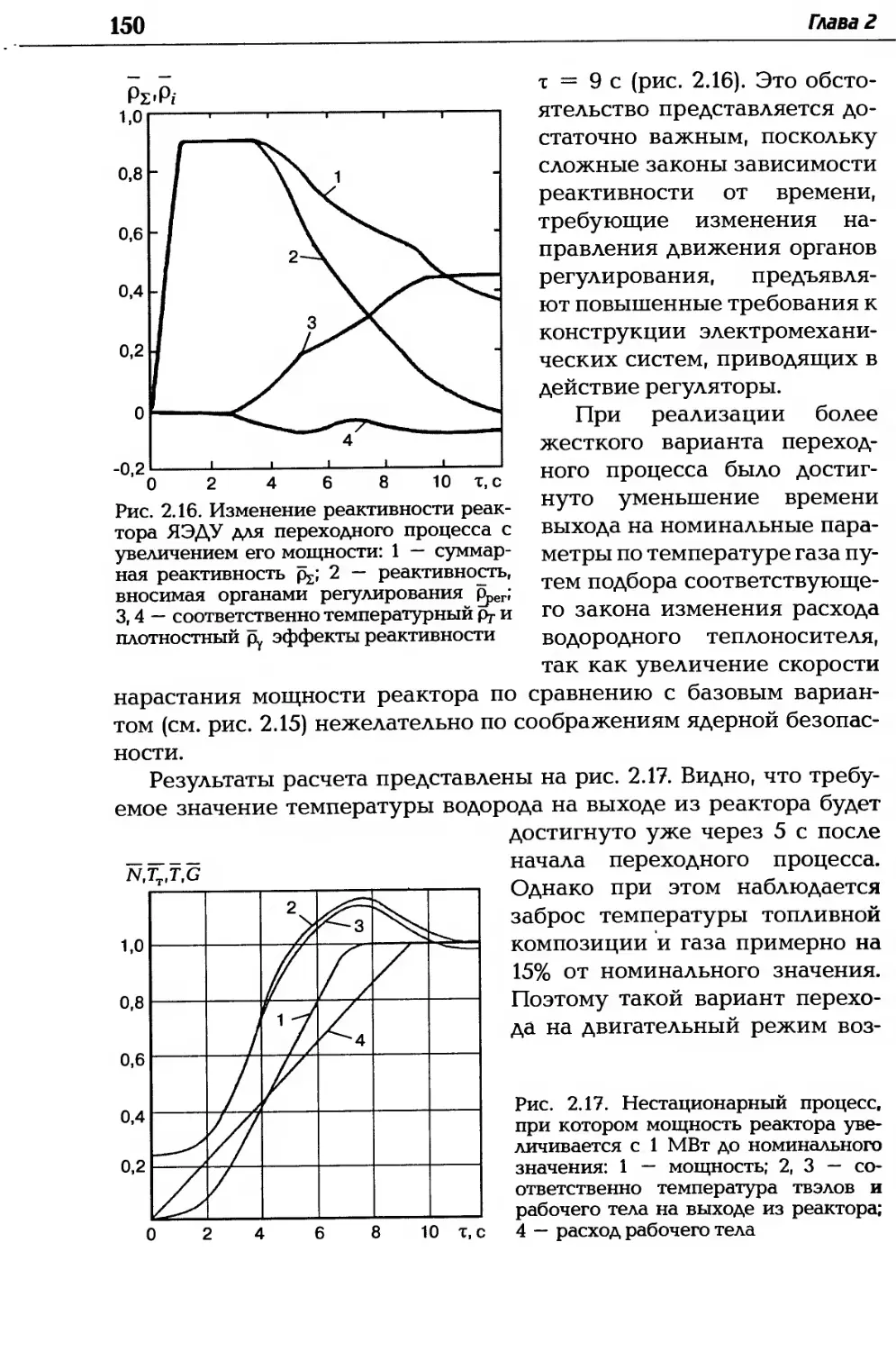
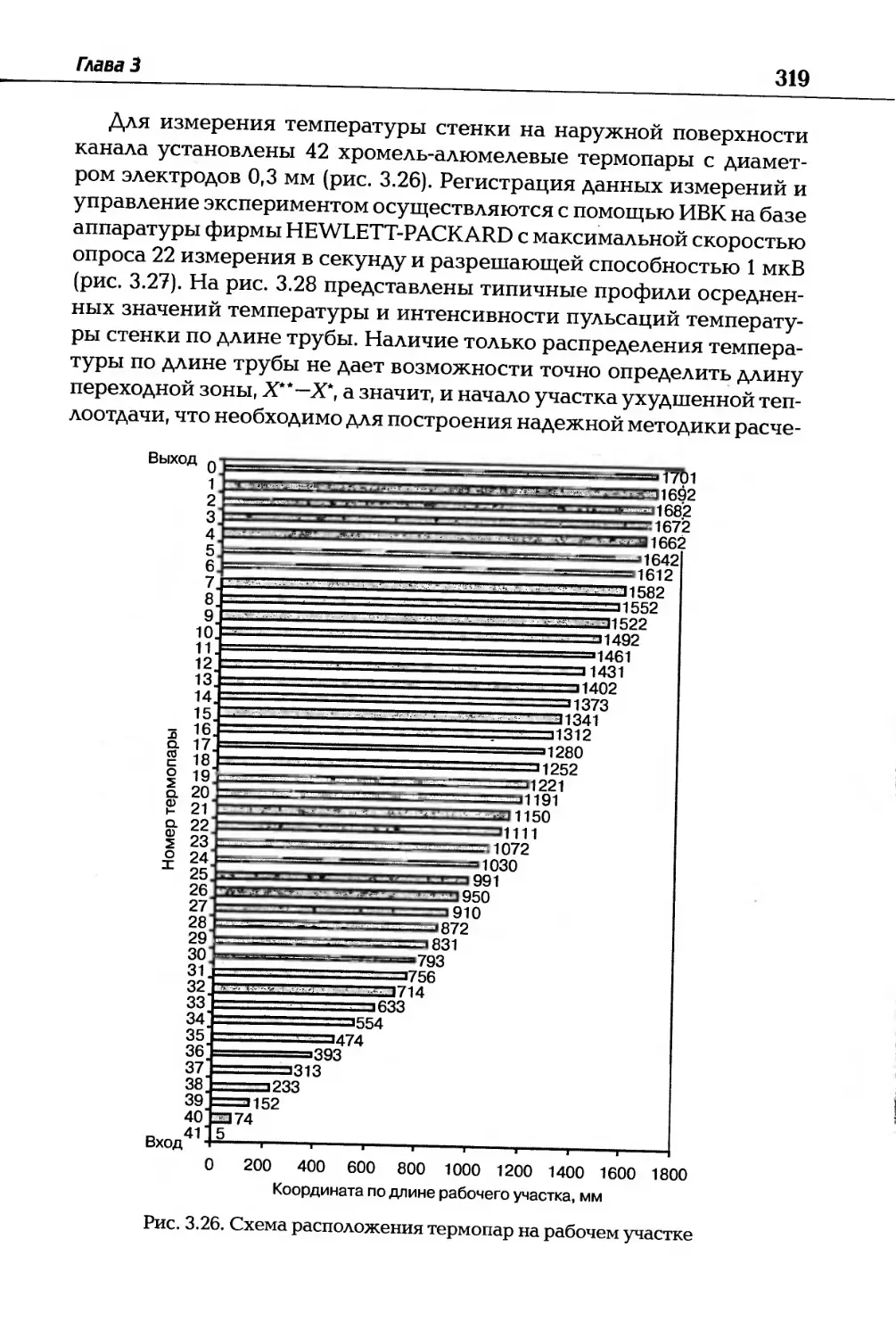
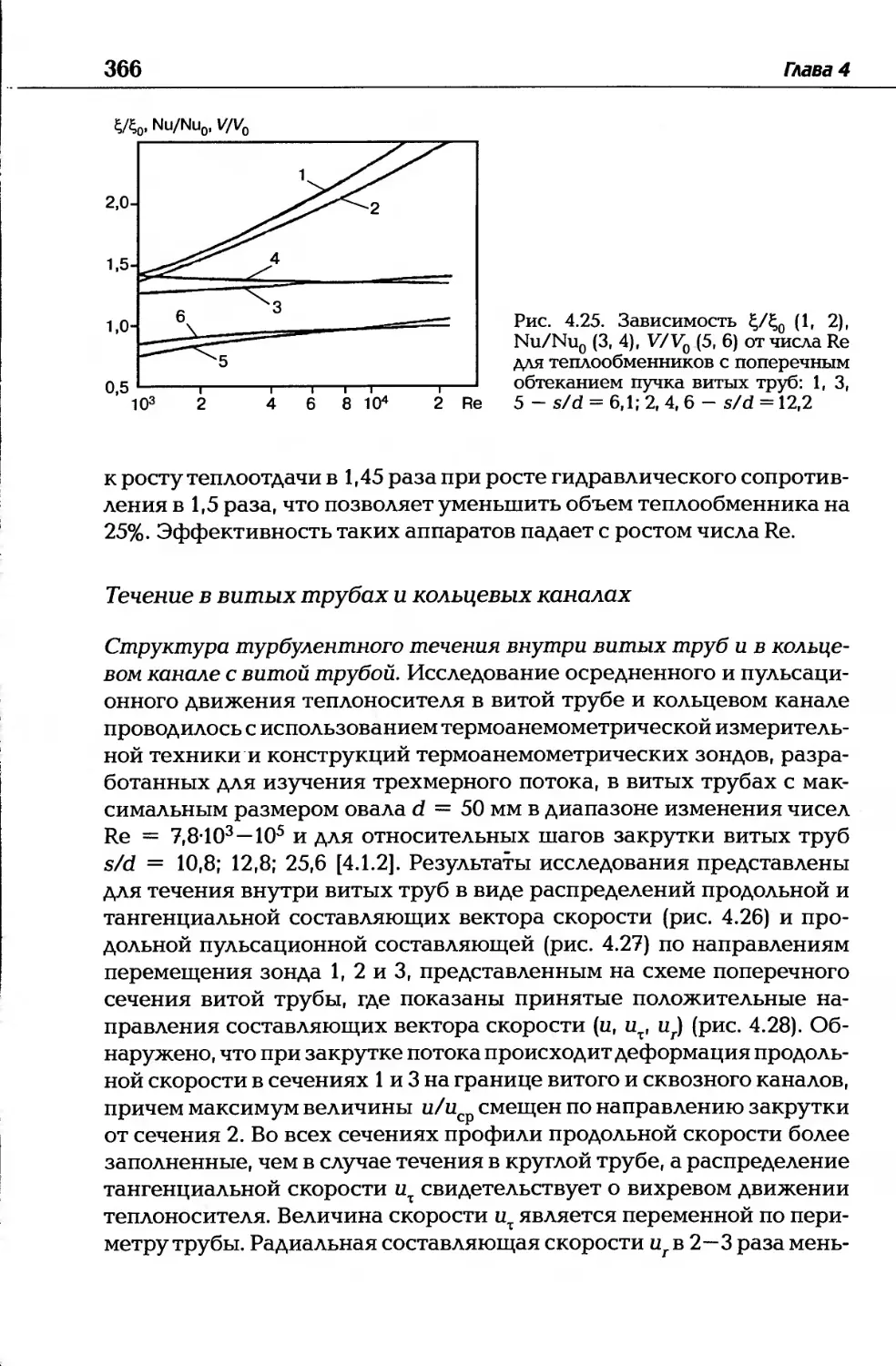
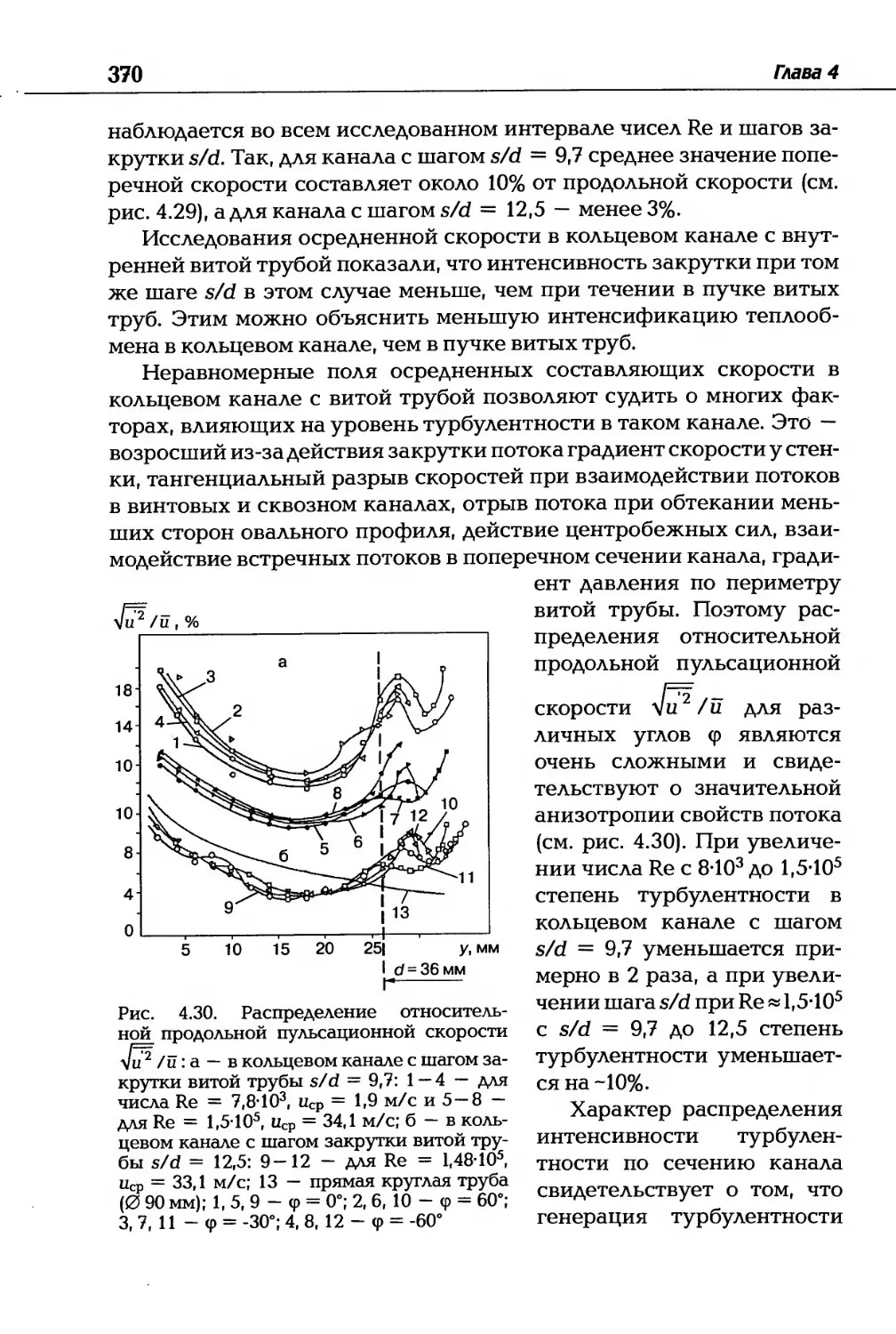
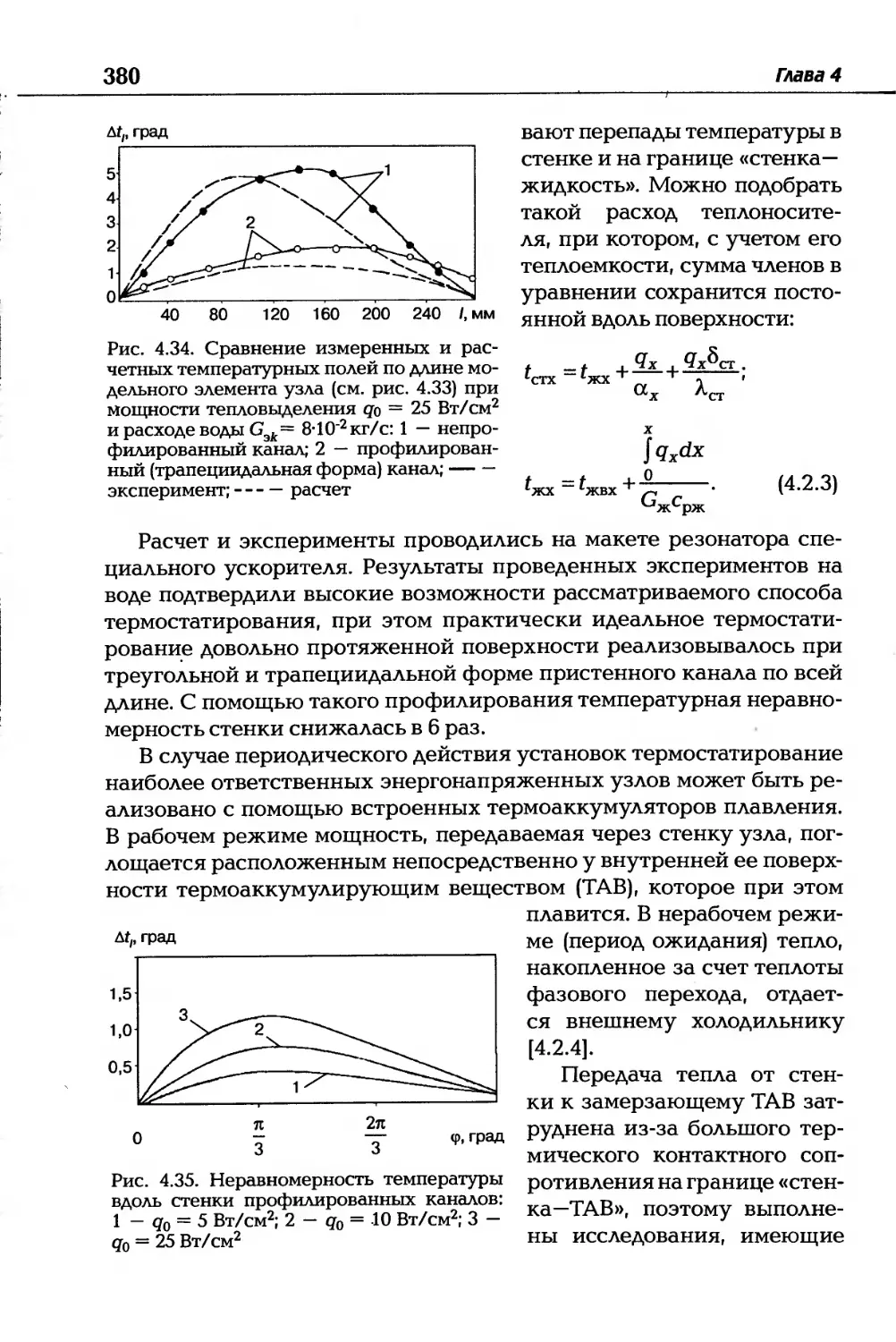
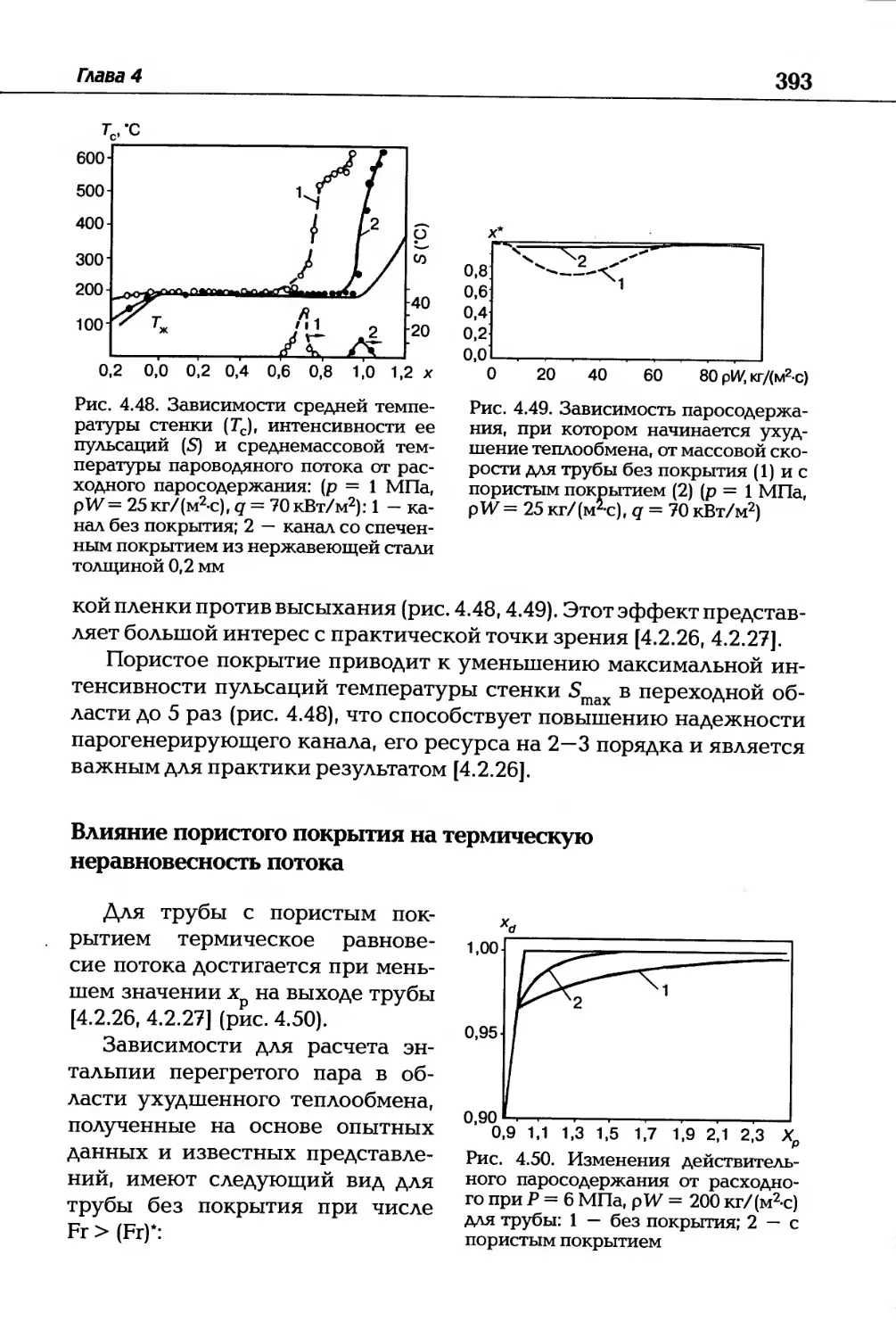
Интенсификация тепло и массообмена на макро, микро и наномасштабах - Дзюбенко Б.В., Кузма-Кичта Ю.А., Леонтьев А.И., Федик И.И., Холпанов Л.П.

Автор: Дзюбенко Б.В. Кузма-Кичта Ю.А. Леонтьев А.И. Федик И.И. Холпанов Л.П.
Теги: физика математическая физика атомная физика издательство цнииатоминформ
ISBN: 5-87911-166-0
Год: 2008
Похожие
Теплообменные аппараты ТЭС
Справочник по теплообменным аппаратам
Теплообменные аппараты холодильных установок
Развитые поверхности теплообмена.
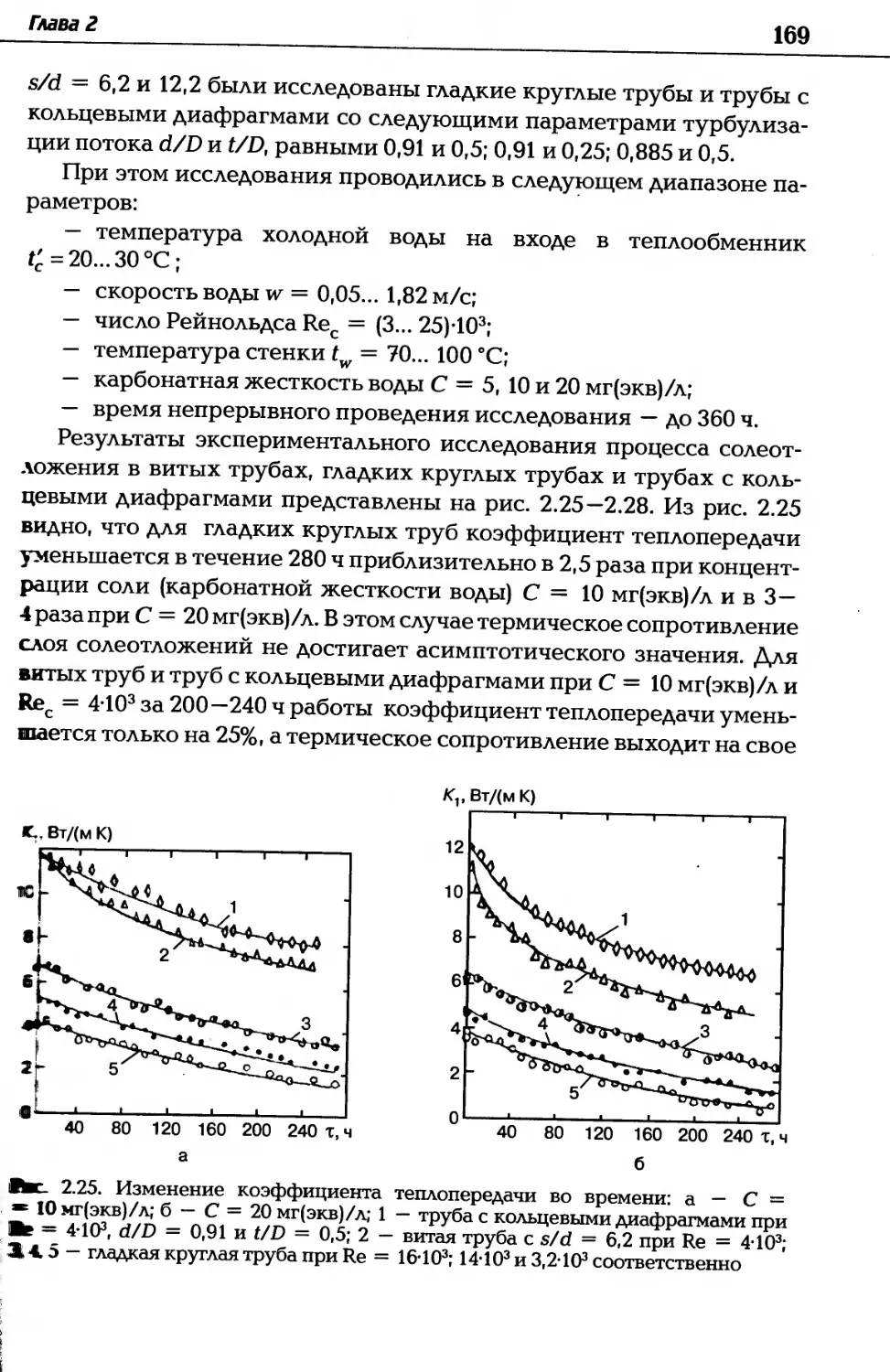
Текст
                    Б.В. Дзюбенко, Ю.А. Кузма-Кичта, А.И.Леонтьев,
И.И. Федик, Л.П. Холпанов
ИНТЕНСИФИКАЦИЯ
ТЕПЛО- И МАССООБМЕНА
на макро-, микро- и наномасштабах
Дзюбенко Борис Владимирович,
профессор, доктор технических наук
Кузма-Кичта Юрий Альфредович,
профессор, доктор технических наук
Леонтьев Александр Иванович,
профессор, академик РАН,
доктор технических наук,
заслуженный деятель науки и техники РФ,
член Инженерной академии США
Федик Иван Иванович,
член-корреспондент РАН,
профессор, доктор технических наук,
заслуженный деятель науки и техники РФ,
президент Ядерного общества России
Холпанов Леонид Петрович,
профессор, доктор технических наук
Б.В. Дзюбенко, Ю.А. Кузма-Кичта, А.И. Леонтьев,
И.И. Федик, Л.П. Холпанов
Интенсификация
тепло- и массообмена
на макро-, микро-
и наномасштабах
Под редакцией профессора,
доктора технических наук
Ю.А. Кузма-Кичты
Москва
ФГУП «ЦНИИАТОМИНФОРМ:
2008
ККЭ5ЛЗ
WG6J0l5-23
Инг 73
Дзюбенко Б.В., Кузма-Кичта Ю.А., Леонтьев А.И.,
Федик И.И., Холпанов Л.П.
Инт73 Интенсификация тепло- и массообмена на макро-, микро-
и наномасштабах. - М.: ФГУП «ЦНИИАТОМИНФОРМ», 2008,
с цв. вкладкой.
ISBN 5-87911-166-0
Представлены результаты теоретических и экспериментальных исследо-
ваний интенсификации тепло- и массообмена на макро-, микро- и наномасш-
табах в одно- и двухфазных средах, колебаний поверхности раздела фаз, се-
парации гетерогенных систем. Исследования, проведенные в целях повыше-
ния безопасности и эффективности энергетических установок, позволили
разработать новые методы интенсификации тепло- и массообмена, сфор-
мировать новые научные направления, создать новые аппараты, математи-
ческие модели процессов и инженерные методы их расчета. Дополнитель-
но рассмотрены энергодвигательные установки космических аппаратов для
пилотируемой экспедиции на Марс и используемые в них методы интенси-
фикации теплообмена, методы расчета тепломассообмена в условиях со-
леотложений при течении в витых трубах и трубах с кольцевыми диафрагма-
ми, расчет гидродинамики многофазных гетерогенных сред в центробежном
поле, представлены результаты исследования влияния поверхности рельефа
на теплообмен при кипении на сфере, обобщения данных по влиянию закру-
ченной ленты на критическую тепловую нагрузку. Представлены результаты
сравнения характеристик трубчатых и пластинчатых теплообменников с ин-
тенсификаторами теплообмена, характеристики теплообменных аппаратов
с витыми трубами, исследования интенсификации тепломассообмена при
конденсации водяных паров из уходящих дымовых газов котлов.
Для специалистов, занимающихся разработкой энергетического обору-
дования.
ББК35.113
ISBN 5-87911-166-0
© Авторы, 2008
© ФГУП «ЦНИИАТОМИНФОРМ», 2008
3
ВВЕДЕНИЕ
К началу 21 -го столетия методы интенсификации тепло- и массооб-
мена широко применяются в элементах оборудования в энергетике.
Наиболее распространенные методы интенсификации тепло- и
массообмена при конвекции — использование эффекта начально-
го участка, искусственная турбулизация потока, осуществляемая в
пристенном слое или по всему сечению потока с помощью кольцевых
или спиральных канавок, лунок, оребрения поверхности, закручен-
ных лент, шнеков, спиральных труб [1—8], струйное натекание теп-
лоносителя на поверхность, пористые и щеточные вставки [9—13],
колебания расхода [14], воздействие ультразвуковых колебаний [15],
электрического поля [16]. Влияние пристенных интенсификаторов
теплосъема на теплоотдачу при ламинарном течении исследовано в
работе [17].
•Для интенсификации теплообмена при кипении широко исполь-
зуются пористые покрытия [18—21], менее эффективны в этом случае
методы искусственной турбулизации потока.
Интенсификация теплообмена при конденсации осуществляется
за счет создания капельной конденсации, и в случае пленочной кон-
денсации для интенсификации теплообмена применяются накатка,
оребрение, изменение наклона поверхности [22].
Комбинированные методы интенсификации теплоотдачи основа-
ны на использовании, по крайней мере, двух методов повышения ин-
тенсивности теплосъема. Например:
—	использование искусственной шероховатости поверхности и
закрученной ленты;
—	использование спиральной трубы и пористого покрытия;
—	использование кольцевой накатки и закрутки потока в витых
трубах.
Интенсификация тепло- и массообмена позволяет существенно
улучшить характеристики оборудования. Например, интенсификация
теплообмена в пучках стержней с интенсификаторами-завихрителя-
ми способствовала повышению мощности реактора кипящего типа.
В работе [23] предложено совместить функции дистанционирующей
решетки и интенсификатора теплообмена. Разработанные и исследо-
ванные на полномасштабных стендах решетки-интенсификаторы осе-
вой закрутки внедрены на первом и втором блоках Игналинской АЭС.
Внедрение в конструкцию ТВС решеток-интенсификаторов позволи-
ло увеличить мощность каждого энергоблока в 1,5 раза.
4
Введение
Проблемы при разделении гетерогенных систем рассмотрены в
работах [24, 25].
В России сформировались авторитетные научно-производствен-
ные центры специалистов по теплофизике и химической гидроди-
намике, внесших заметный вклад в выдающиеся достижения нашей
страны в вышеназванных направлениях. К числу таких центров отно-
сятся ФГУП «НИИ НПО «Луч» (г. Подольск), Институт проблем хи-
мической физики РАН (г. Черноголовка), технические университеты
МАИ, МЭИ, МВТУ им. Баумана. Специалисты этих организаций и со-
ставляют авторский коллектив данного издания.
Приведены результаты известных и собственных теоретических
и экспериментальных исследований интенсификации тепло- и массо-
обмена в одно- и двухфазных средах, колебаний поверхности раздела
фаз и сепарации гетерогенных систем. Эти исследования проведены
в целях повышения безопасности и эффективности энергетических
установок. Выполненные исследования позволили разработать новые
методы интенсификации тепло- и массообмена, сформировать новые
научные направления, создать новые аппараты гидроциклонного типа,
математические модели процессов и инженерные методы их расчета.
В новом издании представлен обзор исследований в области ин-
тенсификации теплообмена на макро-, микро- и наномасштабах. Под-
робно рассмотрены имеющиеся исследования теплообмена и гидро-
динамики для поверхностей с луночным рельефом, моделирование и
визуализация смерчевой интенсификации теплообмена в канале с по-
лусферическими лунками, модернизация теплообменника для тепло-
снабжения за счет использования витых труб.
Рассмотрены известные представления о термогидродинамике на
микро- и наномасштабах: теплообмен при конденсации на макро- и
микрорельефах, теплообмен при кипении на поверхностях с порис-
тыми покрытиями и выступами, образующими однородный рельеф,
теплообмен при конвекции в микроканалах, возникновение проскаль-
зывания на стенке при течении жидкости по ультрагидрофобной по-
верхности, влияние сформированных на поверхностях молекулярных
слоев поверхностно-активных веществ на гидравлическое сопротивле-
ние трубопроводов.
Проанализированы методы расчета тепломассообмена в услови-
ях солеотложений при течении в витых трубах и трубах с кольцевы-
ми диафрагмами, расчет гидродинамики многофазных гетерогенных
сред в центробежном поле, представлены результаты исследования
влияния луночного рельефа на теплообмен при кипении на сфере,
обобщения данных по влиянию закрученной ленты на критическую
тепловую нагрузку.
Введение
5
Рассмотрены энергодвигательные установки космических аппа-
ратов для пилотируемой экспедиции на Марс и используемые в них
методы интенсификации теплообмена.
Анализируются характеристики трубчатых и пластинчатых теп-
лообменников с интенсификаторами теплообмена. Приведены ре-
зультаты исследования интенсификации тепломассообмена при кон-
денсации водяных паров из уходящих дымовых газов котлов.
О материалах, представленных в первом издании, положи-
тельно отзывались академик РАН, лауреат Нобелевской премии
А.М. Прохоров, академик РАН Г.Г. Девятых, академик РАН Г.А. Фи-
липпов. А.М. Прохоров отмечал, что материалы, содержащиеся в
монографии, представляют собой энциклопедический обзор мето-
дов интенсификации тепло- и массообмена на различных масшта-
бах в одно- и двухфазных средах в элементах энергетического обо-
рудования. В монографии описаны уникальные теплофизические и
испытательные стенды, оригинальные датчики и методики экспери-
ментальных исследований, разработанные при участии авторов, ко-
торые позволяют на высоком научном уровне проводить теплофи-
зические исследования не только в лабораторных условиях, но и на
головных образцах в натурных условиях работы реакторных, элект-
рофизических и лазерных установок.
Выполненные исследования направлены на решение следующих
проблем:
—	надежное охлаждение при высоких тепловых нагрузках
(1 кВт/см2 и выше) и «затягивание» кризиса теплообмена при кипе-
нии теплоносителя в энергонапряженных конструкциях;
—	термостатирование и минимизация термического деформиро-
вания теплонапряженных конструкций с интенсивным и неравно-
мерным энерговыделением;
—	организация высокоэффективных теплообменных процессов
с помощью жидких металлов;
—	создание и испытание конструкций различных интенсифика-
торов тепло- и массообмена при течении газовых и жидких теплоно-
сителей и плавлении теплоаккумулирующих фаз;
—	детальное изучение структуры турбулентных потоков в глад-
ких и шероховатых каналах и пористых средах с разной струк-
турой;
—	разработка теоретических моделей и обобщающих критери-
альных зависимостей для расчета и прогнозирования интенсивно-
сти тепло- и массообмена;
—	разработка и испытание энергетических установок с интенси-
фикаторами тепло- и массообмена;
6
Введение
—	концептуальное проектирование перспективных физико-энер-
гетических установок с интенсивными процессами тепло- и массооб-
мена;
—	повышение эффективности разделения гетерогенных систем в
тепло- и массообменных аппаратах.
Благодаря тесному сотрудничеству с ведущими академическими и
отраслевыми научными центрами, разработанные авторами методы
интенсификации тепло- и массообмена внедрены в различные энер-
гетические установки. Это позволило обеспечить их массогабарит-
ные и удельные параметры, а также безопасность и эффективность
на уровне лучших мировых образцов. В частности, результаты иссле-
дований авторов использованы в проектировании и создании таких
уникальных энергетических установок, как газоохлаждаемые ядер-
ные реакторы с витыми твэлами из карбидов тугоплавких металлов,
термоэмиссионные ядерные реакторы-преобразователи с жидкоме-
таллическим охлаждением, прошедшие испытания в космосе, мише-
ни и резонаторы для ускорительных установок, охлаждаемые зерка-
ла для мощных лазерных комплексов и приемников инфракрасного
излучения, высокоэффективные гидроциклоны для химической, гор-
норудной и металлургической промышленности, компактные тепло-
обменники различного назначения, испарители для обессоливания
воды, абсорбционные и компрессионные холодильники, охладители
жидкостей, кондиционеры и др. Авторы внесли также большой вклад
в разработку отечественных концептуальных проектов инерциаль-
ных термоядерных реакторов со струйным жидкометаллическим
бланкетом и реакторов-лазеров с пленочным ядерным топливом.
Настоящая монография является расширенным, дополненным и
переработанным изданием книги «Интенсификация тепло- и мас-
собменав энергетике», вышедшей в 2003 г. [26].
В новом издании сохранены разделы, представленные в первом
издании и написанные Кутеповым А.М., Свириденко И.П. и Харито-
новым В. В.
Введение
7
Список литературы
1.	Мигай В.К. Повышение эффективности современных теплообменников. Л.:
Энергия, 1980.
2.	Калинин Э.К., Дрейцер Г.А., Копп И.З., Мякочин А.С. Эффективные по-
верхности теплообмена. М.: Энергоатомиздат, 1998.
3.	Щукин В.К. Теплообмен и гидродинамика внутренних потоков в полях мас-
совых сил. М.: Машиностроение, 1970.
4.	Каменьщиков Ф.Т., Решетов В.А., Рябов А.А., Поляков В.К., Емель-
янов А.И. Вопросы механики вращающихся потоков и интенсификация теп-
лообмена в ЯЭУ. М.: Энергоатомиздат, 1984.
5.	Жукаускас А.А. Конвективный перенос в теплообменниках. М.: Наука,1982.
6.	Субботин В.И., Ибрагимов М.Х., Ушаков П.А. и др. Гидродинамика и теп-
лообмен в атомных энергетических установках. М.: Атомиздат, 1975.
7.	Кикнадзе И.А., Олейников В.Г. Самоорганизация смерчеобразных вих-
ревых структур в потоках газов и жидкостей и интенсификация тепломассо-
обмена: Препринт Института теплофизики Сибирского отделения АН СССР
№ 227-90. Новосибирск, 1990.
8.	Холпанов Л.П., Шкадов В.Я. Гидродинамика и теплообмен с поверхностью
раздела. М.: Наука, 1990. 271 с.
9.	Поляев В.М., Майоров В.А., Васильев Л.Л. Гидродинамика и теплообмен
в пористых элементах конструкций летательных аппаратов. М.: Машиностро-
ение, 1988.
10.	Мегерлин Ф.Е., Мерфи Р.В., Берглес А.Е. Интенсификация теплообмена
в трубах с помощью сетчатых и щеточных вставок//Теплопередача. 1974.
№ 2. С. 30-38.
11.	Аполлонов В.Б., Быстров П.И., Гончаров В.Ф. и др. Перспективы исполь-
зования пористых структур для охлаждения элементов силовой оптики//
Квантовая электроника. 1979. Т. 6, № 12. С. 2533-2545.
12.	Зейгарник Ю.А. и др. Теплообмен и термические деформации в охлаждае-
мых многослойных системах. М.: Изд-во ИВТАН СССР, 1982.
13.	Петухов Б.С., Алексеев В.А., Зейгарник Ю.А. и др. Проблемы тепло-
обмена в охлаждаемых зеркалах технологических лазеров/ДВТ. 1985. Т. 23,
№6. С. 1200-1210.
14.	Гапицейский Б.М., Рыжов Ю.А., Якуш Е.В. Тепловые и гидродинамические
процессы в колеблющихся потоках. М.: Машиностроение, 1977.
15.	Накоряков В. Е., Бурдуков А. П., Болдарев А. М., Терлеев П. Н. Теплообмен
и массообмен в звуковом поле. Новосибирск, 1970.
16.	Назмеев Ю.Г. Интенсификация теплообмена при ламинарном течении. М.:
МЭИ, 1971.
17.	Болога М.К., Смирнов Г.Ф., Дидковский А.Б., Климов СМ. Теплооб-
мен при кипении и конденсации в электрическом поле. Кишинев: Штиинца,
1987.
18.	Ковалев С.А., Соловьев С.Л. Испарение и конденсация в тепловых трубах.
М.: Наука, 1989.
8
Введение
19.	Мапышенко С.П., Андрианов А.Б. Неравновесные фазовые переходы
при кипении на поверхностях с пористыми покрытиями: Препринт ИВТАН.
№ 1-293. М., 1990.
20.	Красноухов Ю.В., Федорович Е.Д. Гидравлическое сопротивление винто-
вых змеевиков при движении однофазных и двухфазных потоков//Повыше-
ние эффективности теплообмена в энергетическом оборудовании. Л.: Наука,
1981.
21.	John R. Thome. Enhanced boiling heat transfer. Hemisphere Publishing
Corporation. N.-Y., 1990.
22.	Будов B.M., Дмитриев C.M. Форсированные теплообменники ЯЭУ. М.:
Энергоатомиздат, 1989.
23.	Aden V.G., Asmolov V.G., Blagovestova T.I., Kapustin V.A., Kobzar L.L.,
Kudriavtzev Y.V., Osmachkin V.S., Riabov AN., Philippov V.N. Study of heat
exchange enhancement in models of fuel elements bundles at the coolant boiling.
VI Inter.Heat Transfer Conf., Toronto, Canada, 1978.
24.	Поваров А.И. Гидроциклоны. M.: Госгортехиздат, 1961.
25.	Поваров А.И. Гидроциклоны на обогатительных фабриках. М.: Недра, 1978.
26.	Дзюбенко Б.В., Кузма-Кичта Ю.А., Кутепов А.М., Свириденко И.П.,
Федик И.И., Харитонов В.В., Холпанов Л.П. Интенсификация тепло- и
массообмена в энергетике. М.: ФГУП «ЦНИИАТОМИНФОРМ», 2003. С. 232.
Глава /
ВЫБОР И ОБОСНОВАНИЕ МЕТОДОВ ИНТЕНСИФИКАЦИИ
ТЕПЛООБМЕНА
1.1. ИНТЕНСИФИКАТОРЫ ТЕПЛООБМЕНА МАКРО-, МИКРО-
И НАНОМАСШТАБОВ
Интенсификаторы теплообмена макромасштаба при конвекции
Распространенные методы интенсификации теплообмена в кана-
лах с однофазным теплоносителем — искусственная турбулизация по-
тока, осуществляемая с помощью кольцевых или спиральных канавок,
оребрения поверхности, спиральных или витых труб, шнеков, закру-
ченных лент [1.1.1 — 1.1.14], организация теплообмена на начальном
участке, струйного натекания теплоносителя на поверхность [1.1.6].
На эффективность теплообмена при течении однофазных сред
оказывают влияние колебания расхода, и при резонансе с собствен-
ными колебаниями контура коэффициент теплоотдачи увеличива-
ется [1.1.7].
Поверхность с регулярной шероховатостью
Шероховатость поверхности — это отклонения рельефа реаль-
ной поверхности от идеально гладкой. Высота этих отклонений мо-
жет быть соизмерима с толщиной вязкого подслоя и промежуточного
слоя. Поэтому воздействие шероховатости поверхности сосредоточе-
но в сравнительно тонком пристенном слое и не приводит к возник-
новению вторичных течений, охватывающих весь поток, что харак-
терно для спиральных ребер, закрученных лент или шнеков.
Шероховатость поверхности характеризуется высотой и формой
ее элементов, их плотностью (числом на единицу поверхности) и вза-
имным расположением. Структура течения и перенос теплоты вблизи
шероховатой поверхности зависят от большого количества факторов.
Течение в трубах с шероховатостью, образованной плотно при-
мыкающими друг к другу одинаковыми элементами — зернами пес-
ка, наклеенными на поверхность трубы, исследовал Д. Никурадзе. В
10
Глава 1
этом случае шероховатость характеризуется одной величиной — вы-
сотой элемента песочной шероховатости к. Сопротивление и тепло-
обмен будут зависеть лишь от одного дополнительного параметра —
относительной шероховатости к/г.
Высоту элемента шероховатости можно представить и в другой
безразмерной форме, используя тот же масштаб длины (у), что и в
универсальной координате т| = (V*y/V), т.е. величину V7V*.
Тогда безразмерная высота элемента песочной шероховатости
примет вид
К = Vk/V =-ReT^/8	(1.1.1)
d
и ее удобно сравнивать с такими характерными величинами, как без-
размерная толщина вязкого подслоя (8V*/V)=5 или промежуточного
слоя (8V*/V)=30, где 8 — толщина пограничного слоя, V* — динамиче-
ская скорость, V — кинематическая вязкость жидкости.
Теплоотдача в шероховатой трубе может быть как выше, так и
ниже, чем в гладкой трубе. Это определяется формой, высотой, вза-
имным расположением элементов шероховатости и числами Re и Рг.
Выступы с прямоугольным и плавным профилями, расположен-
ные на одинаковом расстоянии друг от друга, приведены на рис. 1.1.
Шероховатость с прямоугольными выступами характеризуется
высотой элементов к, шагом I и шириной впадины Zr На рисунке ил-
люстрируется картина течения вдоль стенки с прямоугольными эле-
ментами. В результате отрыва потока за выступом возникает вихре-
вая зона, протяженность которой до точки присоединения составляет
примерно 8к (см. рис. 1.1, а). За этой зоной формируется поле скоро-
сти, аналогичное полю в гладкой трубе. Перед следующим выступом
также возникает неболь-
шая вихревая область про-
тяженностью (1—2)к. Если
расстояние между высту-
пами составляет пример-
но 4к, то вихревая зона за-
полняет всю впадину (см.
рис. 1.1, б). Срыв потока на
выступах шероховатости
Рис. 1.1. Поверхность с высту-
пами, имеющими прямоуголь-
ный (а, б) и плавный (в) про-
фили
Глава 1
11
ведет к усилению турбулентного переноса у верхней границы вих-
ревой зоны и в окрестности точки присоединения. В результате теп-
лоотдача в этих зонах улучшается. Застойные зоны во впадинах при-
водят к снижению теплоотдачи иногда до уровня более низкого, чем
в гладких трубах.
Таким образом, по длине впадины теплоотдача распределена не-
равномерно. В застойных зонах она понижена, вблизи точки присо-
единения максимальна, а вдали от выступа, где влияние вихревой
зоны ослабевает, снова уменьшается. Длина впадины, соответству-
ющая максимуму средней по поверхности теплоотдачи, составляет
(10- 12)к.
Рациональная высота элемента шероховатости соизмерима с тол-
щиной пристенного слоя, в котором сосредоточена основная доля
термического сопротивления и которая зависит от числа Рг. Так, при
числах Рг, равных 1,5,50, относительная высота шероховатости к* со-
ставляет, соответственно, 250, 50, 10.
При рациональных характеристиках искусственной шерохова-
тости можно повысить коэффициент теплоотдачи в два—три раза.
Однако важно, чтобы рост теплоотдачи сопровождался не слиш-
ком большим увеличением гидравлического сопротивления. Поэто-
му нерациональны элементы двумерной шероховатости с острыми
кромками. Возникающие за ними мощные вихревые зоны и высокое
сопротивление формы ведут к большим потерям энергии. Выгоднее
элементы шероховатости с плавными очертаниями (см. рис. 1.1, в),
для которых характерны меньшие потери энергии. В трубах с плав-
но очерченными выступами шероховатости при оптимальном отно-
шении l/к увеличение теплоотдачи сопровождается меньшим ростом
гидравлического сопротивления, чем в случае шероховатости, имею-
щей острые кромки.
При достаточно большой относительной шероховатости опреде-
ленный вклад в увеличение теплоотдачи вносит «эффект оребрения»,
т.е. увеличение поверхности шероховатой стенки по сравнению с
гладкой. Конечно, при условии, что элементы шероховатости имеют
хороший тепловой контакт со стенкой. В случае так называемой нало-
женной шероховатости, например проволоки, расположенной у стен-
ки и не припаянной к ней, эффект «оребрения» отсутствует.
Для расчета теплообмена в шероховатых трубах^ имеются эмпи-
рические и полуэмпирические зависимости. Полуэмпирические за-
висимости основываются на двух-, трех- и даже четырехслойных мо-
делях течения вдоль шероховатой стенки. Для каждого слоя подбира-
ются эмпирические зависимости для коэффициентов турбулентного
переноса.
12
Глава 1
Для расчета теплоотдачи в трубах с естественной и искусствен-
ной однородной шероховатостью, элементы которой имеют различ-
ную форму (проволоки, сферы, пирамиды, цилиндры и др.) и близко
расположены друг к другу, так что течение между ними определяется
их размерами и формой, в работе [1.1.8 ] предложено уравнение
Nu =------------------V^RePr--------- -----------
2,121п(г/к) + 0,55(Рг2/3-0,2)^)1/Ч10-(р-^уу+ 6,6,Д78
(1.1.2)
гдеЫи = ad/л; a — коэффициент теплоотдачи, отнесенный к поверх-
ности гладкой трубы с диаметром d = 2г, взятым во впадине.
Коэффициент сопротивления определяется по формуле Д. Нику-
радзе для песочной шероховатости. Высота песочной шероховатости,
эквивалентная заданной действительной шероховатости, находится
по таблице или экспериментально. Уравнение (1.1.2) справедливо для
100 < К < 4000, т.е. для режима с полным проявлением шероховатости
при достаточно больших числах Re в диапазонах к/г от 0,005 до 0,18
и чисел Рг от 0,7 до 9. Для указанных условий независимо от формы
элементов шероховатости отклонение измеренных чисел Nu от рас-
считанных не превышает 10%. Хотя уравнение получено для гранич-
ного условия первого рода, им можно пользоваться также при гра-
ничном условии второго рода.
Гидродинамика и теплопередача в винтообразно
профилированных трубах
Винтообразно профилированная труба представляет собой тру-
бу с прямолинейной осью, на стенках которой образованы винто-
вые выступы. Винтовая накатка может иметь различное число заходов.
Рис. 1.2. Винтообраз-
но профилированная
труба
На рис. 1.2 показана труба с двухзаходной накат-
кой. Внутри трубы с винтообразной канавкой
образуется выступ, закручивающий поток.
В результате закрутки теплоносителя умень-
шается термическое сопротивление конвектив-
ному переносу тепла через пограничный слой.
Вследствие этого теплообмен интенсифициру-
ется, но одновременно возрастает гидравличе-
ское сопротивление. Винтообразно профили-
рованные трубы в теплообменниках передают
значительно больше тепла, чем круглые гладкие
трубы. Такие трубы позволяют создать само-
Глава 1
13
очищающиеся поверхности нагрева и поддержать постоянным зна-
чение коэффициента теплоотдачи.
На рис. 1.3 представлено изображение поля скоростей, получен-
ное в работе [1.1.9].
Скоростное поле воспроизведено по измерениям в 78 точках вы-
ходного сечения винтообразно профилированной трубы. Труба име-
ет шаг двухзаходной винтовой накатки — 640 мм, радиус выступа
(для внутренней поверхности трубы) — 10 мм. Длина опытного участ-
ка трубы составляет 4817 мм. Поле скоростей замерялось при сред-
ней скорости потока 22,2 м/с, что соответствует значению числа Рей-
нольдса 54000. По значениям скорости в точках замера в плоскости
поперечного сечения винтообразно профилированной трубы прове-
дены изотахи.
По расположению изотах видно, что поле скоростей в поперечном
сечении трубы с двухзаходной винтовой накаткой растянуто по на-
правлению закрутки потока S-образно. На рис. 1.3 направление за-
крутки показано пунктирной линией А-В.
На основе анализа направлений векторов скорости установле-
но, что поток закручивается по всему сечению трубы неравномерно,
если не считать небольшую область в непосредственной близости от
продольной оси трубы.
Теплоотдача от внешней поверхности трубы с винтообразной на-
каткой исследовалась в аэродинамической трубе. Шаг накатки со-
ставлял 145 мм при наружном диаметре ненакатанной трубы 18 мм.
Площадь поверхности трубы в результате накатки не изменилась.
Опыты проводились также и с гладкой
круглой трубой с наружным диаметром
18 мм и внутренним 16 мм, изготовлен-
ной из того же материала, что и винтооб-
разно профилированная.
Скорость воздуха изменялась от 1,9
до 16,2 м/с, что соответствовало числам
Рейнольдса от 2230 до 18430. Температу-
ра стенки труб поддерживалась в преде-
лах от 83 до 90 °C, а температура возду-
ха — от 22 до 29 °C.
При расчете чисел Рейнольдса и Нус-
сельта за определяющую скорость при-
нята скорость потока воздуха w, под-
считанная в самом узком поперечном
сечении аэродинамической трубы, т.е. в
плоскости продольной оси трубки.
Рис. 1.3. Поле скоростей в
плоскости поперечного сече-
ния винтобразно профилиро-
ванной трубы
14
Глава 1
В качестве характерного размера d для обеих труб бралась вели-
чина наружного диаметра гладкой трубы. При увеличении числа за-
ходов и глубины накатки, а также при уменьшении ее шага вводи-
лась поправка на изменение миделева сечения.
В результате обработки данных эксперимента для гладкой круг-
лой трубы получена следующая зависимость:
Nu = O,2ORe0,61,	(1.2.3)
которая практически совпадает с рекомендациями А. А. Жукаускаса.
Для исследованной винтообразно профилированной трубы зависи-
мость имеет следующий вид:
Nu = O,27Re0'60.	(1.1.4)
Как установлено, даже при относительно невысокой температуре
стенки трубы поправкой на излучение пренебрегать не следует.
Анализ показал, что теплоотдача для трубы с винтовой накаткой
примерно на 25% выше, чем для гладкой трубы.
На рис. 1.4—1.7 показаны эффективности винтообразно профи-
лированных труб с одноходовой, трехходовой, двухходовой накаткой
с различным радиусом закругления профиля [1.1.9] . Эффективность
профилированных труб увеличивается с уменьшением скорости теп-
лоносителя. Так, например, коэффициент теплоотдачи для трубы № 1
(см. рис. 1.4) с относительным шагом одноходовой накатки f/d3 = 2,26
при одинаковых затратах удельной мощности, No = 5 Вт/м2, на переме-
щение теплоносителя, отнесенных на 1 м2 поверхности, на 50% выше,
чем для гладкой трубы (01). Для трубы № 2 (t/d3 = 1,72) с двухходовой
накаткой коэффициент теплоотдачи при одинаковых с гладкой трубой
затратах удельной мощности, No = 10 Вт/м2, примерно на 70% выше, чем
для гладкой трубы, а при No = 20 Вт/м2 — выше на 30% (см. рис. 1.6).
Рис. 1.4. Теплогидродинамическая эффективность труб
с одноходовой винтовой накаткой
Глава 1
15
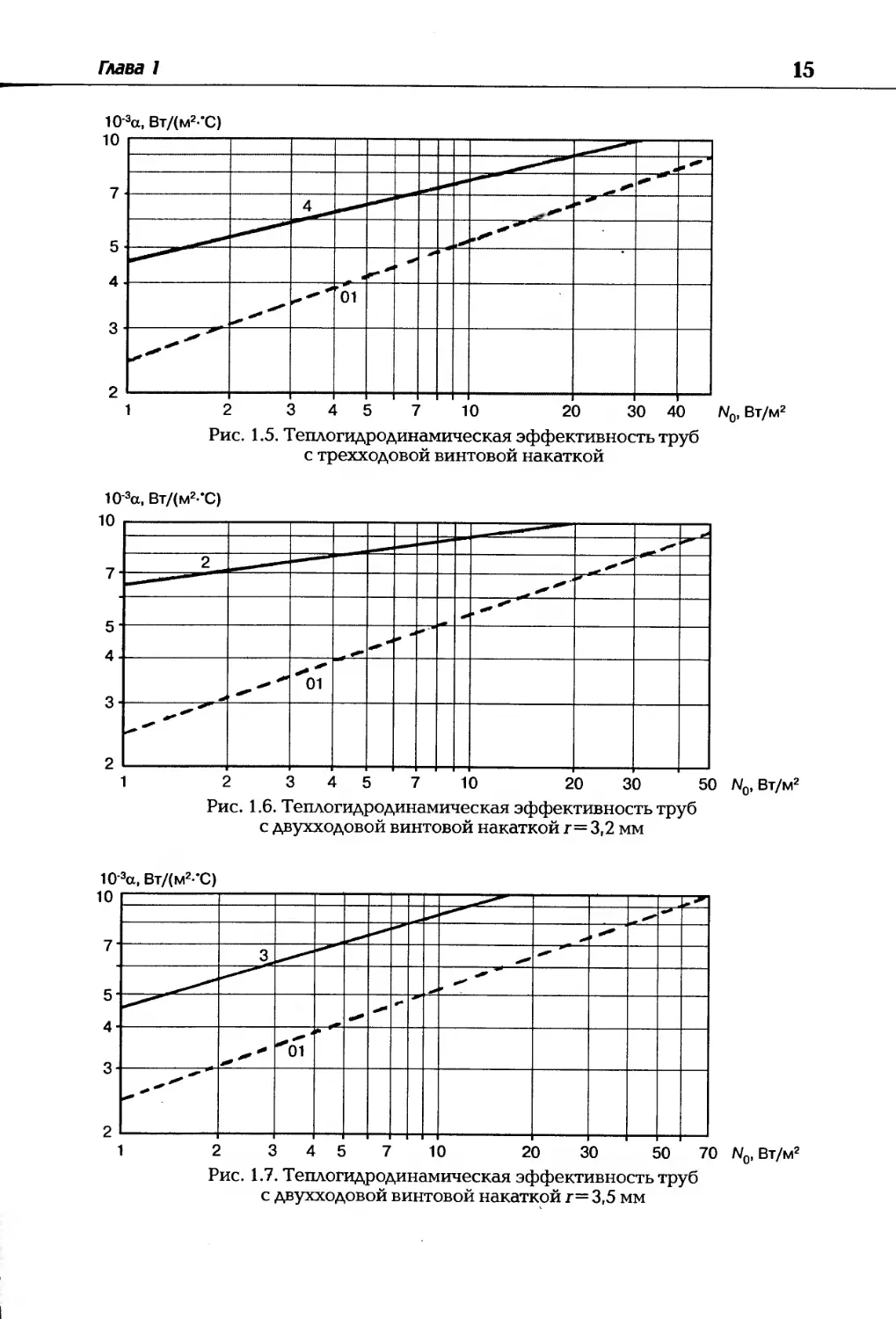
Рис. 1.5. Теплогидродинамическая эффективность труб
с трехходовой винтовой накаткой
Рис. 1.6. Теплогидродинамическая эффективность труб
с двухходовой винтовой накаткой г=3,2 мм
Рис. 1.7. Теплогидродинамическая эффективность труб
с двухходовой винтовой накаткой г= 3,5 мм
16
Глава 1
Для трубы с трехходовой накаткой (см. рис. 1.5) (t/d3 = 3,72) при
N0=2 Вт/м2 (Re=104) коэффициент теплоотдачи а в 1,7 раза выше, чем
для гладкой трубы.
Теплоотдача зависит от профиля накатанной канавки. Сравнива-
лась теплоотдача в трубе с двухходовой накаткой с радиусом высту-
па внутри трубы 3,2 и 3,5 мм. При небольших числах Re коэффици-
ент теплоотдачи выше внутри труб с меньшим радиусом выступа, то
при больших скоростях эффективнее оказались трубы с г = 3,5 мм
(см. рис. 1.6 и 1.7)
Опыты по определению теплоотдачи в поперечном потоке воздуха
на внешней поверхности трубы диаметром 18 мм, имеющей двуххо-
довую винтовую накатку с шагом t = 145 мм, показали, что при оди-
наковой с гладкой трубой площади поверхности коэффициент теп-
лоотдачи для профилированной трубы примерно на 25% выше, чем
для гладкой трубы. С увеличением числа Рейнольдса эффективность
профилированной трубы уменьшается. Результаты опытов с гладкой
трубой практически совпали с данными А. А. Жукаускаса.
Гидравлическое сопротивление при течении воздуха и воды ис-
следовалось для 35 винтообразно профилированных труб с одно-,
двух- и трехходовой накаткой. Относительный шаг накатки t/d3 на-
ходился в диапазоне 1,7—32,9. Трубы — стальные, бесшовные с внут-
ренним диаметром ненакатанной части, равным 16 мм. Большее со-
противление создавали трубы с меньшим шагом накатки.
Для диапазона чисел Re от 7000 до 30000 экспериментальные дан-
ные для труб с одноходовой винтовой накаткой аппроксимированы
уравнением
-4 = 1.81g
Re
Re0,72 '
t/d3
(1.1.5)
8 +
Для приближенных расчетов предложена более простая формула:
£ = 0,452Re'°'24 + ——.	(1.1.6)
t/d3
Данные, полученные из опытов с двух- и трехходовой накаткой,
обобщены видоизмененной формулой Колбрука:
1
~^ = "219
2,5
(1-1.7)
где К — переменная величина, характеризующая условную шерохо-
ватость труб, зависит как от относительного шага накатки, так и от
числа Re. Для t/d3>3,5 в пределах чисел Рейнольдса от 9403 до 3,2404
для определения величины К предложены зависимости:
Глава 1
17
1-^lgRe
(1.1.8)
Значения коэффициентов для исследованных труб приведены в
табл. 1.
Таблица 1
Значения коэффициентов для исследованных труб
Коэффициент	Количество заходов накатки z			
	2		3	
	3,5<f/d3<10	t/d>lO	t/d3<ll	t/d3>l 1
а	0,36	0,17	0,35	0,093
b	0,022	0,006	0,025	0,0019
Теплоотдача внутри винтообразно профилированных труб иссле-
дована как при охлаждении воздуха, так и при нагреве воды.
Гидродинамические и тепловые процессы внутри винтообразно
профилированных труб можно рассматривать как результат дейст-
вия закрутки потока в каналах некруглого сечения.
Для труб с накаткой в диапазоне чисел Рейнольдса 15-103—50403
для воздуха опытные данные по теплоотдаче в работе [1.1.9] аппрок-
симированы соотношением:
Nu = O,O32Re0'76.	(1.1.10)
В числах Нуссельта и Рейнольдса за определяющий размер при-
нят эквивалентный диаметр d3 = 0,038 м.
Из формулы (1.1.10) видно, что значения коэффициента теплоот-
дачи для воздуха в исследованном диапазоне чисел Рейнольдса в про-
филированной трубе выше, чем в гладкой трубе. Однако ввиду того,
что показатель степени при числе Re равен 0,76, тогда как для глад-
кой трубы он равен 0,80, тепловая эффективность профилированной
трубы несколько уменьшается с повышением числа Re.
Установлено, что применение профилированных труб эффектив-
нее при нагреве теплоносителя, чем при охлаждении.
При нагреве исследовалась область чисел Рейнольдса от ЗТО3 до
28-103. Температурный напор составлял 5—27°С, тепловая нагрузка —
8 — 64 кВт/м2.
18
Глава 1
Данные обработаны в виде
K = CRe?d,
(1.1.11)

Рг/0'43
Pff
Prw
(1.1.12)
Трубы с одноходовой накаткой эффективнее труб с двух- и трех-
ходовой накаткой. Для трубы с одноходовой накаткой t/d3= 2,25 при
Re = 10000 коэффициент теплоотдачи примерно в 2,2 раза выше,
чем для круглой трубы. Стабилизация зависимости K(Ref,d) для труб
с меньшим значением t/d3 наступает при меньших значениях Re
по сравнению с круглой ненакатанной трубой или трубами с боль-
шим значением t/d3. Так, например, для труб с относительным ша-
гом накатки t/d3< 6 развитый турбулентный режим наступает при
Re = (7—8) 103, в то время как для труб с t/d3 >10 — при Re > 9-103.
Установлено, что на вид кривой K(Re) существенно влияет фор-
ма накатанной канавки (выступа внутри трубы). При меньшем ради-
усе выступа г показатель степени п в уравнении выше, поэтому с из-
менением числа Рейнольдса коэффициент теплоотдачи изменяется
больше, чем в трубах с большим радиусом выступа. По этой причине
результаты исследования теплоотдачи внутри труб с двухходовой на-
каткой представлены отдельно для двух групп — для труб с г = 3,2 мм
и для труб с г > 3,3 мм.
В результате аппроксимации зависимости n(t/d3) с помощью ин-
терполяционной формулы Чебышева для труб с одноходовой накат-
кой в диапазоне t/d3 от 2,3 до 21,4 получена зависимость
n=0,001(t/d3)2 —0,025(t/d3) + 0,78.
(1.1.13)
Вначале, с увеличением t/d3 примерно до 12, значения п уменьша-
ются, после чего — вновь увеличиваются.
Для труб с двух- и трехходовой накаткой характерно уменьшение
значения п до t/d3 = 12—15, после чего оно стабилизируется, достигая
0,8. Это означает, что при указанном значении t/d3 меняется режим
потока. Об этом свидетельствуют также результаты изучения гидро-
динамики изотермических потоков в винтообразно профилирован-
ных трубах.
Рациональная интенсификация теплообмена
Она характеризуется условием
' Nu >f
< (^игл ) J Re-idem v ^гл J Re=idem
(1.1.14)
Глава 1
19
где Nu, % — число Нуссельта и коэффициент гидравлического сопро-
тивления для каналов с турбулизаторами; NurA, %гл — число Нуссель-
та и коэффициент гидравлического сопротивления для идентичных
по геометрии каналов с технически гладкой поверхностью.
Получение опережающего роста теплоотдачи относительно гид-
равлического сопротивления считалось невозможным. Основани-
ями для этого служили допущения, согласно которым выполняется
аналогия Рейнольдса и турбулентное число Прандтля равно едини-
це или по крайней мере постоянно по потоку, и опытные данные для
сред с низкими числами Прандтля.
Однако в работе [1.1.1] показано, что для турбулентных течений с
отрывами вихревые зоны служат источником дополнительной тур-
булизации потока и интенсификации теплообмена, и представлены
экспериментальные подтверждения соотношения (1.1.14).
Теоретическое и экспериментальное обоснование соотношения
(1.1.14) явилось предметом научного открытия со следующей фор-
мулой: установлена неизвестная ранее закономерность изменения
теплоотдачи на стенках каналов с дискретной турбулизацией пото-
ка при вынужденной конвекции, заключающейся в том, что в опре-
деленном соотношении размеров и расположений турбулизаторов
рост теплоотдачи больше роста гидравлического сопротивления по
сравнению с аналогичным гладким каналом [1.1.10].
Теплоотдача и сопротивление в каналах с кольцевой накаткой
Накатка — эффективный метод интенсификации теплоотдачи в
трубчатых теплообменных аппаратах. При этом на наружной повер-
хности трубы образуются периодически расположенные кольцевые
канавки, а на внутренней — кольцевые выступы с плавным профилем
(рис. 1.8).
Этот метод разработан Э.К. Калининым, Г. А. Дрейцером, Е.В. Дуб-
ровским, С.А. Ярхо, Г.И. Ворониным [1.1.1, 1.1.10].
Трубы с кольцевыми канавка-
ми достаточно просто изготовить,
возможна накатка труб с произво-
дительностью до 9 м/мин. В тру-
бах с кольцевыми турбулизатора-
ми образуется меньшая толщина
слоя отложений. Именно в трубах
с накаткой была обнаружена но-
вая закономерность — опережа-
ющий рост коэффициента теп-
t
Рис. 1.8. Труба с кольцевой накаткой:
t — шаг накатки; h — высота выступа;
d — внутренний диаметр трубы; d} —
минимальный диаметр трубы в зоне
выступов
20
Глава 1
лоотдачи по сравнению с увеличением гидравлического сопротив-
ления. Эта закономерность, которая была признана в качестве науч-
ного открытия, наблюдается в определенном диапазоне размеров и
расположений турбулизаторов.
При анализе эффекта накатки выделены три области:
—	Re < ReKp, где теплоотдача для трубы с накаткой может быть
больше или меньше, чем для трубы с технически гладкой поверхно-
стью, в зависимости от числа Рг и параметров накатки;
-	ReKp< Re Re‘- где аш >:> агл;
—	Re > Re*, где аш /агл > 1 = const.
Во второй области наблюдается повышение теплоотдачи до двух —
трех раз в результате более раннего перехода к турбулентному тече-
нию. Более эффективными оказываются турбулизаторы сравнительно
большой высоты. С увеличением числа Re (третья область) турбулент-
ный обмен в ядре усиливается и термическое сопротивление сосре-
дотачивается полностью в тонком пристенном слое. Толщина слоя
становится соизмеримой с высотой турбулизатора. Пока высота тур-
булизатора меньше толщины слоя жидкости, имеющего основное тер-
мическое сопротивление, рост чисел Re и Рг сопровождается повыше-
нием интенсивности теплообмена. Таким образом, в области слабо
развитой турбулентности наиболее эффективными оказываются вы-
сокие турбулизаторы.
При развитом турбулентном течении применение высоких тур-
булизаторов нецелесообразно, так как увеличение переноса теплоты
вдали от стенки не дает существенного увеличения теплоотдачи, но
Рис. 1.9. Изменение отношения чисел
Нуссельта (1) и коэффициентов гид-
равлического сопротивления (2) для
трубы с накаткой и без нее от относи-
тельной высоты турбулизатора при те-
чении воздуха
вызывает большой рост гидравли-
ческого сопротивления.
На рис. 1.9 показаны измене-
ния отношения Num/NurA (1) и
£,ш/£,гл (2) от относительной вы-
соты турбулизатора при тече-
нии воздуха в трубе с накаткой
[1.1.10]. В случае малых высот ди-
афрагмы повышение коэффици-
ента гидравлического сопротив-
ления и теплоотдачи примерно
одинаковое. В случае больших
высот накатки рост гидравличе-
ского сопротивления опережает
рост теплоотдачи.
Шаг расположения турбули-
затора существенно влияет на
Глава 1
21
теплоотдачу и гидравличе-
ское сопротивление. Коэф-
фициент теплоотдачи в зави-
симости от отношения шага
расположения турбулизатора
к его высоте достигает макси-
мума при t/h х 10. Отношение
коэффициентов гидравличе-
ского сопротивления £,ш/£,гл
примерно постоянно до значе-
ний t/h < 10, далее с ростом t/h
оно уменьшается.
£
101
10-2
10 4
Рис. 1.10. Зависимость коэффициента гид-
равлического сопротивления от числа Re
для технически гладкой трубы (1) и труб
с турбулизаторами плавной (2) и прямо-
угольной (3) формы
Коэффициент гидравлического сопротивления существенно зависит
от формы турбулизатора. Зависимости %(Re) для трубы с турбулизатора-
ми различной формы и без турбулизаторов представлены на рис. 1.10
[1.1.10]. Величина £ в случае турбулизатора с плавным очертанием су-
щественно меньше, чем с прямоугольным профилем. С ростом числа Re
до 5-105 различие между £,ш и £,гл увеличивается и достигает трех раз.
Механизм интенсификации теплоотдачи в каналах
с шероховатой поверхностью
Интенсификация теплоотдачи в случае искусственной шерохова-
тости обусловлена следующим:
1.	В результате создания отрывных зон и вихревых структур уве-
личивается интенсивность турбулентных пульсаций. Одним из рас-
пространенных средств образования вихревых структур являются
поперечные выступы, канавки на поверхности нагрева.
2.	При ступенчатом расширении канала размеры вихревой зоны
больше и интенсивность генерации турбулентности ниже, чем при
плавном изменении сечения канала.
3.	Наибольшая генерация турбулентности происходит на верх-
ней границе вихря, где наибольшие градиенты осредненной скоро-
сти и наибольшие касательные напряжения и пульсации скорости. В
этой зоне генерация турбулентности больше диссипации энергии. У
стенки диссипация энергии преобладает над генерацией турбулент-
ности. Известные методы расчета теплоотдачи для канала с турбули-
заторами используют аналогию Рейнольдса. Эта аналогия не спра-
ведлива в зоне отрывных течений. В зоне отрыва потока и вблизи нее
нет подобия профилей скорости и температуры. Для часто располо-
женных элементов шероховатости вне вихрей эта аналогия прибли-
женно соблюдается и теплоотдачу можно рассчитывать по гидравли-
ческому сопротивлению.
22
Глава 1
Влияние интенсификации теплоотдачи на солеотложения
в трубах
В технике часто необходимо наряду с интенсификацией теплоот-
дачи обеспечить предотвращение или снижение интенсивности рос-
та солеотложений на поверхности теплообмена. Образование отложе-
ний зависит от таких факторов, как солевой и ионный состав воды и
концентрация в ней солей, тепловая нагрузка, температура и скорость
движения жидкости, свойства материала поверхности нагрева.
Перечисленные факторы определяют состав, структуру, интенсив-
ность, термическое сопротивление отложений.
Существующие методы борьбы с солеотложением сводятся в ос-
новном к предварительной обработке воды, чаще всего химическими
реагентами. Эти методы непригодны в случае, если требуется обрабо-
тать большое количество воды. Кроме того, неприемлемы и такие спо-
собы борьбы с накипеобразованием, как контактная стабилизация,
добавление зернистых присадок, ультразвуковая, магнитная и радиа-
ционная обработка воды. Применение полимерных покрытий затруд-
нено ввиду их малой стойкости к уносу, сложности нанесения и боль-
шого термического сопротивления.
Представляет интерес исследование возможности снижения соле-
отложений на поверхностях теплообмена за счет искусственной тур-
булизации потока.
Как показали экспериментальные исследования, применение тур-
булизаторов позволяет значительно уменьшить солеотложения в теп-
лообменниках [1.1.1]. Термическое сопротивление отложений R* на
этих поверхностях, в отличие от гладких, изменяется асимптотически
от времени. В этом случае имеется возможность эксплуатации тепло-
обменника длительное время без специальных мероприятий по удале-
нию отложений (естественно, в случае приемлемой величины R* при
времени т—>°°).
Особенности образования отложений на стенке
с интенсификаторами теплосъема
При взаимодействии потока со стенкой происходит не только от-
ложение осадков, но и их унос из верхнего слоя отложений. При уве-
личении скорости потока w затрудняется образование отложений,
поэтому наблюдаются меньшие значения R*. Очевидно, что турбули-
зация потока пристенными интенсификаторами теплосъема затруд-
няет образование отложений на стенке.
Скорость уноса отложений с поверхности раздела определяется
действием потока (касательными напряжениями) на слой отложе-
Глава 1
23
ний, зависит от концентрации примесей, толщины слоя отложений.
Очевидно, что на поверхностях с турбулизаторами при той же скоро-
сти потока касательные напряжения больше, чем на гладкой поверх-
ности, и унос отложений также больше.
Влияние облунения поверхности на теплоотдачу
и гидравлическое сопротивление
В работе [1.1.15] дан обзор исследований интенсификации тепло-
обмена с помощью полусферических лунок.
Одно из первых исследований влияния полусферических лунок
на теплообмен и гидродинамику выполнено в 1961 г. [1.1.16] и содер-
жало результаты измерения гидравлического сопротивления и теп-
лоотдачи в плоских щелевых каналах с чередующимися рядами сфе-
рических лунок и выступов.
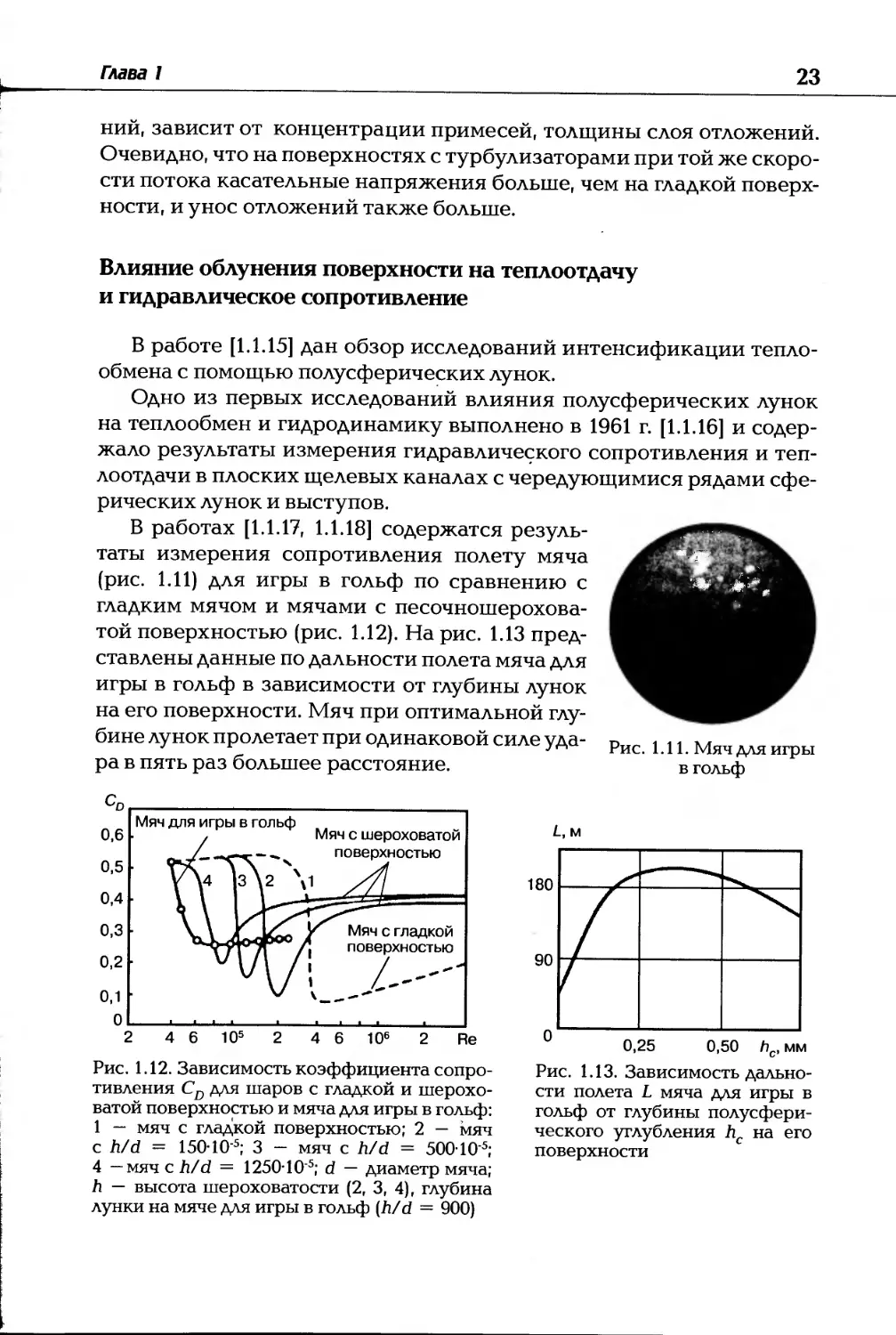
В работах [1.1.17, 1.1.18] содержатся резуль-
таты измерения сопротивления полету мяча
(рис. 1.11) для игры в гольф по сравнению с
гладким мячом и мячами с песочношерохова-
той поверхностью (рис. 1.12). На рис. 1.13 пред-
ставлены данные по дальности полета мяча для
игры в гольф в зависимости от глубины лунок
на его поверхности. Мяч при оптимальной глу-
бине лунок пролетает при одинаковой силе уда-
ра в пять раз большее расстояние.
Рис. 1.11. Мяч для игры
в гольф
Рис. 1.12. Зависимость коэффициента сопро-
тивления CD для шаров с гладкой и шерохо-
ватой поверхностью и мяча для игры в гольф:
1 — мяч с гладкой поверхностью; 2 — мяч
с h/d = 150-105; 3 - мяч с h/d = 500-10‘5;
4 —мяч с h/d = 1250-10’5; d — диаметр мяча;
h — высота шероховатости (2, 3, 4), глубина
лунки на мяче для игры в гольф (h/d = 900)
Рис. 1.13. Зависимость дально-
сти полета L мяча для игры в
гольф от глубины полусфери-
ческого углубления hc на его
поверхности
24
Глава 1
При обтекании облуненной поверхности выделены два режи-
ма обтекания лунки: безотрывное и отрывное. Полусферические
лунки, имеющие относительную глубину h/d = 0,1—0,2, обтекают-
ся практически безотрывно (рис. 1.14) (где h — глубина, d — диаметр
лунки), что подтверждено измерениями в работе [1.1.19]. Измерения
профиля статического давления в продольном направлении пока-
зали, что в передней половине лунки по ходу потока возникает по-
ложительный градиент давления, а в задней — отрицательный. В
лунке, подобно диффузорно-конфузорным каналам, могут сущест-
вовать нестационарные микроотрывы. Они появляются, если при
скруглении кромки лунки протяженность выпуклого участка скруг-
ления меньше глубины лунки h. При наличии острой кромки микро-
отрыв возможен, если угол между касательной к поверхности лун-
ки в области кромки и исходно гладкой поверхностью превышает
0,1 рад. Кроме того, на вогнутой поверхности лунки могут существо-
вать продольные микровихри, подобные микровихрям Тейлора—Гер-
тлера. Нестационарные микроотрывы на передней кромке сфериче-
ской лунки и продольные пристеночные микровихри могут привести
к интенсификации теплообмена.
Обтекание полусферических лунок с относительной глубиной
h/d > 0,1...0,2 происходит в условиях отрыва потока.
При этом, как установлено в ряде работ, например [1.1.20—1.1.29],
в лунке наблюдается самоорганизующееся смерчеобразное вихре-
вое течение. Вихревые структуры перемещаются в поперечном на-
правлении из одного дискретно-стационарного положения в другое
и обратно. Оси вихревых структур наклонены по отношению к на-
правлению внешнего набегающего потока.
Рис. 1.14. Картина течения в полусферической лунке:
а — при безотрывном обтекании (h/d <0,1 ...0,2): 1 — микроотрыв на пере-
дней кромке лунки; 2 — продольные вихри; б — при отрывном обтекании
(h/d >0,1 -0,2)
Глава 1
25
Исследование структуры течения в одиночной полусферической
лунке (h/d = 0,5) выполнено в работе [1.1.26]. Установлено, что эпи-
центр вихря перемещается из левой половины полусферы в правую
и обратно. Несмотря на нестабильность смерчеобразных вихревых
структур, определены координаты точек, где эпицентры вихрей диск-
ретно существуют. Эти точки расположены под углами + 45° и — 45° по
отношению к продольной плоскости симметрии лунки и на расстоянии
(0,25 — 0,3)h от дна лунки.
В работе [1.1.26] показано также, что осредненная скорость воз-
вратного течения составляет примерно 0,41^. Выходящий из полу-
сферической лунки вихрь образует «газодинамическое тело», от-
тесняющее от лунки внешний набегающий поток. Циркуляционное
течение в лунке образует замкнутый контур: часть поступающего в
лунку потока возвращается снова в лунку, а часть выносится во внеш-
ний набегающий поток.
По данным различных исследований [1.1.30, 1.1.31] область присо-
единения вихрей расположена на расстоянии примерно (0,5—2,5)d от
центра лунки вниз по потоку. При этом, как показано в [1.1.31], об-
ласти присоединения вихревых структур не соответствуют зонам с
максимальной теплоотдачей за лункой. Выходящие из лунки смерче-
образные вихри оказывают возмущающее воздействие на структуру
течения за лункой на расстоянии (3—5)d вниз по потоку.
Данные по гидравлическому сопротивлению в каналах со сфериче-
скими лунками получены в работах! 1-1-16, 1.1.21 — 1.1.24, 1.1.32 —1.1.48].
Приведенные в работе [1.1.32] результаты экспериментов пока-
зывают, что зависимость £, = f(Re) более пологая, чем по закону Бла-
зиуса. В работах [1.1.33, 1.1.38, 1.1.39] показано, что практически для
всех каналов в выражении
£ = ARen	(1.1.15)
показатель степени п = -0,25, что соответствует турбулентному по-
граничному слою в гладком канале. Лишь в канале с двухсторонним
расположением лунок, имеющих острые кромки, п = —0,23. Значе-
ние п = —0,25 получено также в работах [1.1.23, 1.1.35 — 1.37].
Согласно работе [1.1.43], коэффициент гидравлического сопро-
тивления изменяется в зависимости от числа Re в соответствии с со-
отношением
= 0,364 Re018.	(1.1.16)
Согласно работе [1.1.44], при Re = 7-103...2,2-104 наклоны зависи-
мостей £= f(Re) для гладкого канала и канала с лунками совпадают.
Так, для канала с лунками получено уравнение
Е, = 0,242 Re016.	(1.1.17)
26
Глава 1
Рис. 1.15. Влияние плотности расположения
лунок на относительный коэффициент со-
противления: 1 — h/d = 0,5; H/d = 0,2 —0,7;
2 - h/d = 0,5; H/d = 0,1; 3 - h/d = 0.1;
H/d = 0,1
Таким образом, согласно
многим исследованиям влия-
ние числа Рейнольдса на гид-
равлическое сопротивление
каналов с полусферическими
выемками описывается урав-
нением, в котором показатель
степени п = —0,25.
По данным различных
исследований, с увеличени-
ем глубины и плотности рас-
положения выемок, а также
стесненности канала коэф-
фициент гидравлического со-
противления возрастает. На
рис. 1.15 представлены резуль-
таты работ [1.1.33, 1.1.38, 1.1.39]
по влиянию относительной плотности расположения лунок на отно-
сительный коэффициент гидравлического сопротивления.
Скругление кромок приводит к снижению гидравлического со-
противления каналов с полусферическими лунками. Рекомендации
по радиусу скругления кромок даны в работе [1.1.46].
По результатам исследований [1.1.37] в коридорном пучке попе-
речно обтекаемых трубок с лунками гидравлическое сопротивление
снижается на 25%, а в шахматном пучке — на 35% по сравнению с
пучком гладких трубок.
В работах [1.1.20-1.1.23] получена эмпирическая зависимость гид-
равлического сопротивления от относительной глубины лунок и
плотности их расположения на поверхности, найденная при обра-
ботке данных для различных вариантов плоского щелевого канала с
лунками (h/d = 0...0.5):
^гл = 1 + 6,5fsin[3,14(h/d)].	(1.1.18)
В нестесненных каналах, в которых H/d > 0,7, для «безотрывных»
лунок (h/d < 0,1...0,2) по данным [1.1.35] и [1.1.36] коэффициенты гид-
равлического сопротивления для гладкого канала и канала с лунка-
ми практически не отличаются. Для стесненного канала (H/d = 0,1)
по данным работ [1.1.33, 1.1.38, 1.1.39] увеличение f от 0 до 0,7 приво-
дит к возрастанию относительного коэффициента гидравлического
сопротивления до 1,5 раз. Для глубоких лунок (h/d = 0,5) в стеснен-
ных каналах с увеличением f от 0 до 0,7 относительный коэффициент
гидравлического сопротивления возрастает до трех раз.
Глава 1	27
В работах [1.1.24, 1.1.41, 1.1.42] получено увеличение относитель-
ного коэффициента гидравлического сопротивления до трех раз при
увеличении f от 0 до 0,7 в неглубоких лунках с h/d = 0,13 в диапазоне
H/d от 0,16 до 1,0.
В работе [1.1.48] обсуждаются результаты продувок в аэродинами-
ческой трубе пластин с нанесенными на обеих сторонах полусфери-
ческими лунками. Получено, что некоторые пластины имеют коэф-
фициент аэродинамического сопротивления, превышающий всего
на (8—10)% его величину для гладкой пластины.
Для ламинарного обтекания пластин с полусферическими лунка-
ми относительной глубиной h/d — 0,14...0,18 при числе Re = 30...100 в
работе [1.1.49] получено уменьшение коэффициента гидравлическо-
го сопротивлениядо 18% по сравнению с гладкой пластиной.
Конвективный теплообмен
В работе [1.1.32] получена зависимость с показателем степени п в
формуле (1.1.19), равным 1,07:
Nu = ARen.	(1.1.19)
По данным работ [1.1.33, 1.1.38, 1.1.39], для каналов с односторон-
ним расположением лунок показатель степени в указанной зависи-
мости п = 0,8, а с двухсторонним — п = 0,76.
В работах [1.1.21—1.1.23, 1.1.34, 1.1.36, 1.1.37 ] получена зависимость
с показателем степени п = 0,8:
Nu = ARe0,8.	(1.1.20)
В работе [1.1.43] предложена зависимость
Nu = ARe0-74	(1.1.21)
для f= 0,78, h/d = 0,1 и H/d = 0,33...1.
В работе [1.1.44] при Re >7-103 получено соотношение
Nu = 0,04 Re°'8Pr°’4,	(1.1.22)
и при Re = З-Ю3... 7-103
Nu = 0,0068 RePr0-4.	(1.1.23)
Таким образом, согласно многим работам теплоотдача для каналов
с полусферическими лунками описывается зависимостью (1.1.20).
Влияние на среднюю теплоотдачу относительной глубины
лунок, относительной высоты канала, плотности
расположения и радиуса скругления кромок лунок
В работах [1.1.33, 1.1.38, 1.1.39] исследовано влияние параметров
h/d и H/d на теплоотдачу при одностороннем и двухстороннем распо-
28
Глава 1
ложении лунок с острыми и скругленными кромками. Исследовались
стесненные каналы (H/d < 0,4) с максимальной плотностью лунок
(f = 0,69). При этом был реализован односторонний подвод теплоты
к каналу. Полученные данные показывают, что в каналах с полусфе-
рическими лунками интенсивность теплоотдачи повышается до 4—6
раз. Из полученных данных также следует, что независимо от того,
скруглены кромки или нет, влияние относительной глубины лунок на
среднюю теплоотдачу одинаково. С увеличением h/d двухсторонний
рельеф лунок становится более предпочтительным.
Анализ изменения коэффициента теплоотдачи и гидравличе-
ского сопротивления при обтекании лунок с острыми и скруглен-
ными кромками показал, что скругление кромок для h/d = 0,5 при-
водит к снижению коэффициента гидравлического сопротивления
примерно на 20—30% и коэффициента теплоотдачи примерно на
10-15%.
Большинство имеющихся исследований посвящено изучению об-
текания неглубоких лунок в условиях, когда относительная высота
канала H/d практически не влияет на интенсификацию теплоотдачи
(H/d > 0,7).
Как следует из работы [1.1.37], в которой исследовали теплоотда-
чу в коридорном пучке поперечно обтекаемых трубок, интенсифи-
кация теплообмена имеет место только для первого ряда трубок. Для
глубинного ряда трубок небольшая интенсификация теплоотдачи
наблюдалась при Re > 104. Для шахматного пучка трубок отмечена
интенсификация теплоотдачи не только для первого ряда, но и для
глубинных рядов. Рост теплоотдачи в этом случае составлял пример-
но 20% по сравнению с пучком гладких трубок.
Данные по влиянию геометрических параметров на интенсифи-
кацию теплообмена полусферическими лунками приведены в рабо-
тах [1.1.24,1.1.41,1.1.42]. Некоторые из этих результатов приведены на
рис. 1.16.
В работе [1.1.26] получено распределение местных коэффициен-
тов теплоотдачи в полусферической лунке для h/d = 0,5. Это распре-
деление неравномерно и имеет минимум в донной области. Коэффи-
циент теплоотдачи больше в части лунки, расположенной ниже по
потоку. Этот факт качественно подтвержден опытами [1.1.31].
Исследования [1.1.29,1.1.50] теплоотдачи за одиночной лункой
(h/d = 0,5) не обнаружили каких-либо эффектов, которых можно
было ожидать в случае присоединения за лункой смерчеобразной
вихревой структуры. В работе [1.1.31] зафиксированы периодиче-
ские перемещения эллипсообразных областей с повышенной тепло-
отдачей с одной половины на другую поверхности между лунками.
Глава 1
29
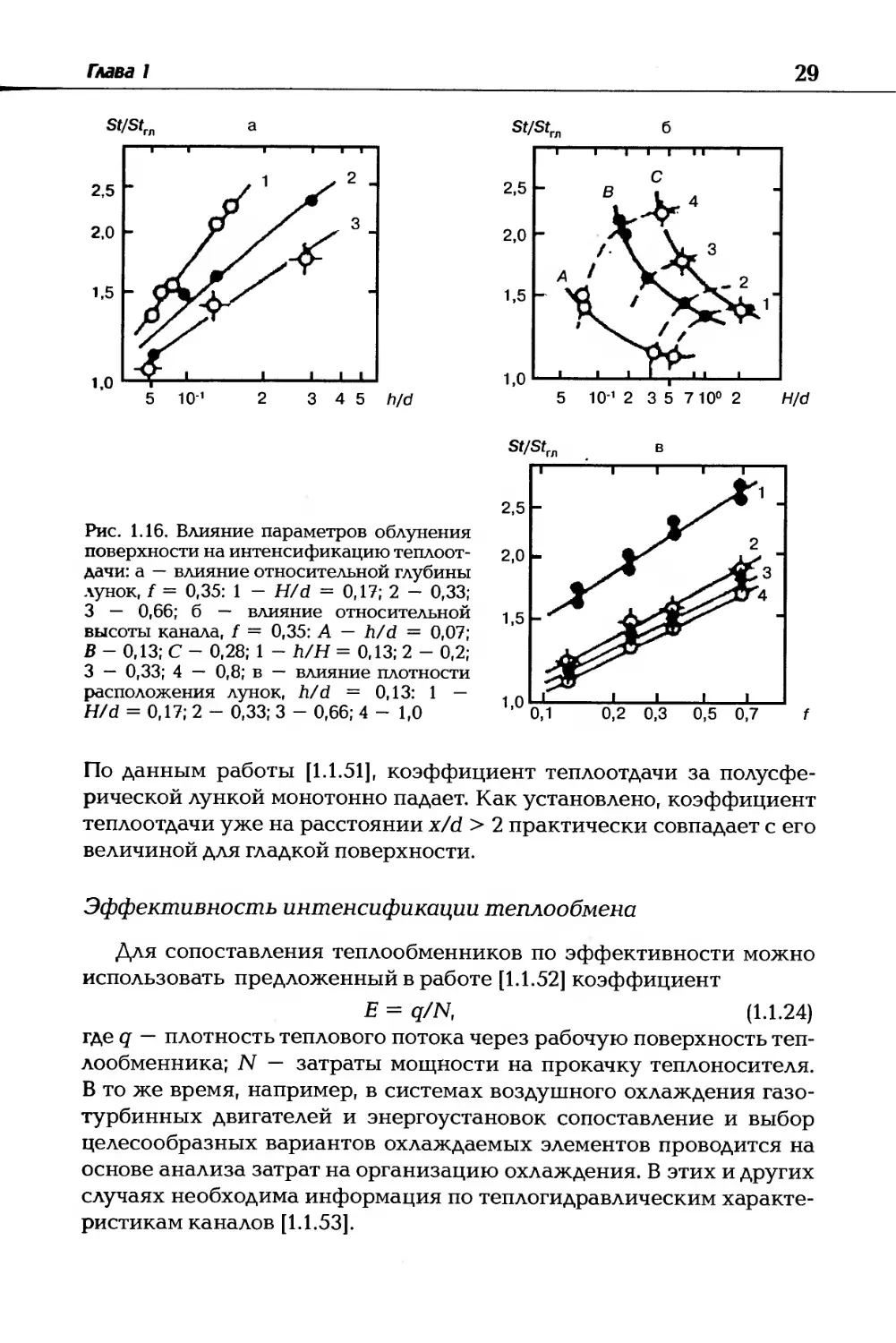
Рис. 1.16. Влияние параметров облунения
поверхности на интенсификацию теплоот-
дачи: а — влияние относительной глубины
лунок, f = 0,35: 1 - H/d = 0,17; 2 - 0,33;
3 — 0,66; б — влияние относительной
высоты канала, f — 0,35: А — h/d = 0,07;
В - 0,13; С - 0,28; 1 - h/H = 0,13; 2 - 0,2;
3 — 0,33; 4 — 0,8; в — влияние плотности
расположения лунок, h/d = 0,13: 1 —
H/d = 0,17; 2 - 0,33; 3 - 0,66; 4-1,0
По данным работы [1.1.51], коэффициент теплоотдачи за полусфе-
рической лункой монотонно падает. Как установлено, коэффициент
теплоотдачи уже на расстоянии x/d > 2 практически совпадает с его
величиной для гладкой поверхности.
Эффективность интенсификации теплообмена
Для сопоставления теплообменников по эффективности можно
использовать предложенный в работе [1.1.52] коэффициент
Е = g/N,	(1.1.24)
где q — плотность теплового потока через рабочую поверхность теп-
лообменника; N — затраты мощности на прокачку теплоносителя.
В то же время, например, в системах воздушного охлаждения газо-
турбинных двигателей и энергоустановок сопоставление и выбор
целесообразных вариантов охлаждаемых элементов проводится на
основе анализа затрат на организацию охлаждения. В этих и других
случаях необходима информация по теплогидравлическим характе-
ристикам каналов [1.1.53].
30
Глава 1
Ниже сопоставлены результаты исследования влияния сфериче-
ских лунок на относительные коэффициенты теплоотдачи и гидрав-
лического сопротивления, отражающие эффективность интенсифи-
кации теплообмена:
Nu/NurA = f(^rA).	(1.1.25)
Здесь £ и £,гл — коэффициенты гидравлического сопротивления
для канала с лунками и без лунок соответственно.
В качестве характерного линейного размера в числа Re и Nu вхо-
дит гидравлический эквивалентный диаметр D3 = 4Г/П (F — пло-
щадь поперечного сечения канала, П — его периметр). В случае кана-
ла с лунками гидравлический диаметр определялся по «смоченному
периметру», т.е. с учетом увеличенной поверхности за счет лунок.
Таким образом обрабатывались опытные данные в работах [1.1.16,
1.1.33, 1.38, 1.39] для глубоких лунок.
На рис. 1.17 заштрихованной областью показаны результаты из-
вестных экспериментальных исследований теплообмена и гидрав-
лического сопротивления в каналах с полусферическими лунками
[1.1.33, 1.38, 1.39].
Приведенные данные охватывают широкий диапазон измене-
ния параметров, а именно кольцевые коаксиальные и плоские кана-
лы с относительной глубиной лунок — h/d = 0,07...0,5; относитель-
ной высотой канала H/d = 0Д...1; плотностью расположения лунок
f — 0,16...0,78; при размещении лунок с острыми или скругленными
кромками в шахматном и коридорном порядке.
Как видно из рис. 1.17, несмотря на
значительный разброс опытных дан-
ных, выполняется соотношение
Nu/NurA=^rA. (1.1.26)
Лишь в области больших значе-
ний Nu/NurA и £>/^гл наблюдается
опережающий рост теплоотдачи по
сравнению с увеличением гидрав-
лического сопротивления. Этот ре-
зультат, полученный в работах [1.1.34,
1.1.38, 1.1.39], относится лишь к стес-
ненным каналам с относительно глу-
бокими лунками. Кроме того, в этих
работах показано, что каналы с лун-
ками на одной стороне энергети-
чески более выгодны, чем на двух.
Причем наиболее эффективный ва-
Рис. 1.17. Эффективность интенси-
фикации теплообмена полусфе-
рическими лунками по данным
различных исследований
Глава 1
31
риант — с односторонним расположением лунок и скругленными
кромками, а наименее эффективный — с двухсторонним расположе-
нием лунок и острыми кромками.
Анализ имеющихся работ показал, что большинство исследова-
ний гидродинамики и теплообмена проведено в случае неглубоких
полусферических лунок. Основной массив точек в этом случае кон-
центрируется около линии Nu/NurA=^/^rA.
Ниже сопоставлены два способа интенсификации теплообме-
на: с помощью полусферических лунок и поперечных кольцевых выс-
тупов.
На рис. 1.18 заштрихованной областью отмечены данные для на-
иболее выгодных диапазонов изменения геометрических парамет-
ров каналов с поперечными кольцевыми выступами применитель-
но к газам: относительный шаг поперечных кольцевых выступов
t/D = 0,25...1,0; отношение внутреннего диаметра трубы в области
выступов к внутреннему диаметру гладкой трубы d/D — 0,90...0,95
(для t/D = 1 значения d/D = 0,90...0,93).
Из сопоставления рассмотренных данных можно заключить сле-
дующее. Поперечные кольцевые выступы в области рациональных
значенийгеометрическихпараметровпозволяютобеспечиватьравен-
ство Nu/NurA = £>/£>гл. Имеется даже некоторое опережение роста теп-
лоотдачи по сравнению с ростом сопротивления. Область равенства
(Nu/NurA) и (£>/£>гл) располагается в диапазоне изменения £>/£>гл от 1,0
до 1,9—2,0. В этой области оба сопо-ставляемых способа интенсифи-
кации теплообмена имеют одинаковую эффективность. Интересно
отметить, что как раз в эту область
попадают данные для мелких лунок.
Дальнейшее увеличение теплоот-
дачи при (Nu/NurA) > 2 с помощью
поперечных кольцевых выступов
сопровождается опережающим уве-
личением гидравлического сопро-
тивления. При использовании же
полусферическихлунок удается обес-
печить одинаковый рост теплоотда-
чи и сопротивления до значительно
большего значения относительного
числа Нуссельта.
Значит, можно констатировать,
что если предельный уровень интен-
сификации теплообмена для попереч-
ных кольцевых выступов составляет
Рис. 1.18. Эффективность интенси-
фикации теплообмена поперечны-
ми кольцевыми выступами в круг-
лом канале
32
Глава 1
(Nu/NurA) = 1,9...2,0, то для сферических лунок — более 4. В послед-
нем случае реализуется смерчевой механизм интенсификации теп-
лообмена, характерный для глубоких лунок.
Таким образом, результаты исследований указывают на то, что на-
несение на теплообменную поверхность полусферических лунок яв-
ляется эффективным способом интенсификации теплообмена. Сле-
дует отметить, что анализ полученных данных свидетельствует о том,
что, по-видимому, существует оптимальная геометрия профилирован-
ной поверхности, обеспечивающая максимально выгодные условия
теплообмена при минимальных энергетических затратах.
Влияние внешних условий
Влияние внешних условий на интенсификацию теплообмена ис-
следовали на одиночных полусферических лунках.
Влияние внешней турбулентности на теплоотдачу в полусфери-
ческой лунке исследовали в работе [1.1.26]. Относительная глубина
лунки h/d составляла 0,5; число Red = (18,2...33,1) 104. Результаты ис-
следований показали, что турбулизация внешнего потока влияет на
теплоотдачу от лунки. Увеличение степени турбулентности набега-
ющего потока приводит к уменьшению частоты перемещения смер-
чеобразного вихря в полусферической лунке, и положение, вихря ста-
билизируется в той или другой половине полусферы.
Влияние продольного градиента давления на воздействие полу-
сферической лунки исследовано в работах [1.1.54, 1.1.55]. Лун-
ка относительной глубиной h/d = 0,5 имела острую кромку. Число
Re = 9,2-104...3,7-105; формпараметр F изменялся от 0 до — 2-10'3, па-
раметр ускорения К от 0 до 540’6. Показано, что с возрастанием сте-
пени конфузорности потока средняя теплоотдача в полусфериче-
ской лунке увеличивается по закону, близкому к линейному. Так, при
К = 5-106 средняя теплоотдача в ней возрастает примерно в два раза
по сравнению со случаем безградиентного течения. При этом осо-
бенно интенсивно теплоперенос возрастает в области эпицентров
вихря.
По данным работы [1.1.30], продольный градиент давления влия-
ет на частоту перемещения эпицентра вихря. С увеличением поло-
жительного продольного градиента давления частота перемещения
уменьшается, а с увеличением отрицательного градиента частота
возрастает по сравнению с безградиентным течением.
Таким образом, из анализа следует, что уровень турбулентности,
а также величина и знак продольного градиента давления внешнего
течения изменяют как гидродинамику, так и теплообмен в лунке.
Глава 1
33
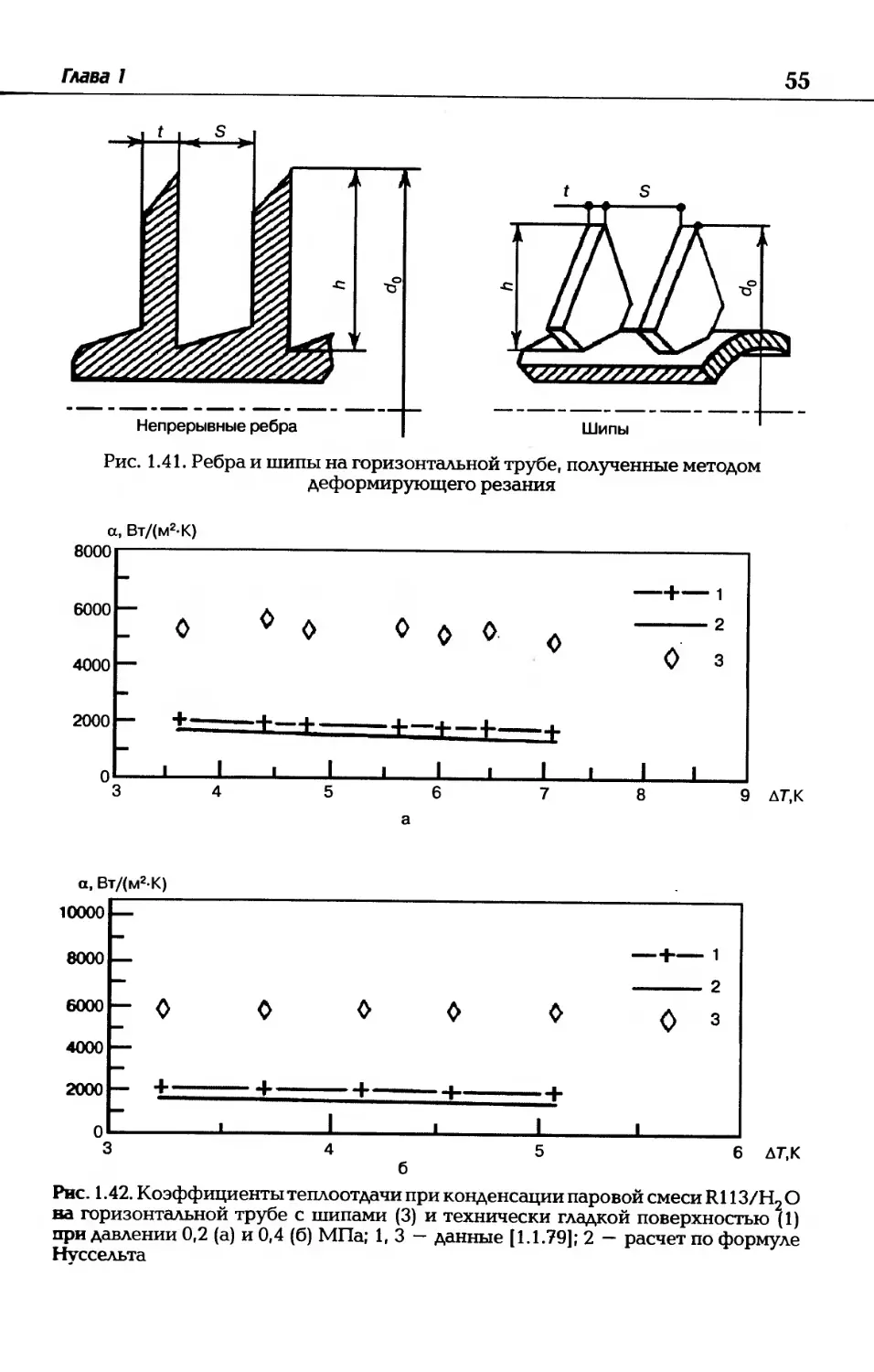
В работе [1.1.74] исследована интенсификация теплоотдачи в теп-
лообменнике типа труба в трубе. Для повышения теплоотдачи ис-
пользовано облунение внутренней трубы. Опыты проведены в диа-
пазоне чисел Re (7,5-103) — (5,2-104). Температура воды йа входе 68 °C.
Исследованы шесть труб с различным облунением и одна труба
без облунения. Обнаружено повышение теплоотдачи от 25 до 137%
при постоянном числе Re. Отношение коэффициента теплоотдачи к
коэффициенту трения для облуненной и гладкой трубы изменяется
от 0,93 до 1, 16.
В работе [1.1.57] проведен анализ самоорганизации смерчеобраз-
ных струй на основании:
—	визуальных наблюдений за обтеканием лунок;
—	результатов исследований гидродинамики и тепломассообмена
при обтекании одиночных лунок й рельефов;
—	решений нестационарных уравнений Навье-Стокса и нераз-
рывности, описывающих эволюцию смерчеобразных потоков вязкой
жидкости.
При анализе использовались видеозапись и фотографии, сделан-
ные совместно с В.Б. Хабенским и М.И. Рабиновичем в Институте
прикладной физики РАН в Нижнем Новгороде. В работе высказано
мнение, что самоорганизация смерчеобразных вихрей при обтека-
нии рельефов TLT обусловлена действием на жидкость в лунке сил,
возникающих при обтекании криволинейной поверхности. Эти силы
и создают условия для самоорганизации смерчеобразных струй по
мере увеличения скорости.
Циркуляционное движение приводит к возникновению в углуб-
лении трехмерного пограничного слоя, состоящего из вихрей типа
вихрей Гертлера или их ансамблей. Эти мелкомасштабные вихри вы-
полняют роль мелкодисперсной структуры.
Для выполнения прандтлевского условия прилипания вторич-
ной вихревой структуры к криволинейной поверхности углубления
во всем диапазоне исследованных чисел Re (103 < Red < 2-105) необ-
ходимо, чтобы в торцах вихря возникало малодиссипативное тече-
ние не только при ламинарном, но и при турбулентном обтекании
рельефов, когда азимутальная скорость вихря в лунке достаточно
высока и составляет, согласно измерениям, » (0,3—0,4)V,. Герт-
леровские вихри связывают торцы вихрей с поверхностями углуб-
лений и обеспечивают выполнение условий «прилипания». Герт-
леровский вихрь действует как колесо, катящееся по поверхно-
сти углубления, всегда имея скорость Vw = 0 на поверхности лун-
ки, а в остальных точках — скорость среды в торце вихревой струк-
туры. Вихревая структура в углублении при своей эволюции ис-
34
Глава 1
пользует гертлеровские вихри в качестве вихревого подшипника.
Другими словами, смерчеобразный вихрь «катается» на гертлеров-
ских вихрях по поверхности лунки, удовлетворяя условиям «прили-
пания» Л. Прандтля [1.1.57].
Формирование в углублениях вторичных вихревых структур во
всем диапазоне режимов их обтекания и трехмерного пограничного
слоя из вихрей Гертлера следует из анализа материалов визуализации
течения как при ламинарных, так и при турбулентных режимах.
Изложенные представления о роли вихрей Гертлера в формиро-
вании пограничного слоя на криволинейной поверхности и смерче-
вых структур и описание эффектов, сопровождающих это явление,
важны, потому что попытки использовать для этого известные ха-
рактеристики пограничного слоя не дают адекватного объяснения
наблюдаемых фактов. Взаимодействие между вихревыми структу-
рами в углублениях, пространственная ориентация и динамичность
вихревых структур на рельефах, а также данные по снижению тре-
ния и интенсификации тепло- и массообмена не находят объяснения
в рамках традиционных представлений гидродинамики и тепломас-
сообмена. Исследование взаимодействия смерчеобразного закручен-
ного потока с обтекаемой поверхностью в торце вихря, проведенное
М. А. Гольдштиком в 1960 г., показало, что такой вихрь сшивается с по-
верхностью лишь в одной точке, вращаясь вокруг нее подобно волч-
ку. Попытки связать торец вихря с обтекаемой поверхностью по всей
его площади приводят, как показал М.А. Гольдштик, к разрушению
закрученного потока. Этот важный результат указывает на непри-
менимость жесткого условия прилипания Л. Прандтля к вихревым
структурам в общем случае и смерчеобразным вихрям на рельефах.
Таким образом, самоорганизация вихревых структур в углубле-
ниях приводит к непрерывной генерации гертлеровских вихрей на
криволинейных поверхностях углублений, а также к их непрерыв-
ному отсосу смерчеобразной закрученной струей. Отсос гертлеров-
ских вихрей приводит к наполнению ими ствола вихря, выносяще-
го эту массу в основной поток, и обновлению вихревого подшипника
в торцах вихревых структур. Что касается внешней границы смер-
чеобразного вихря, то она встроена в основное течение и имеет та-
кую же скорость Vm. В ламинарных режимах обтекания рельефов,
когда вихревые структуры в углублениях замыкаются своими тор-
цами на боковые по потоку скаты лунок, это приводит к возникно-
вению поверхностей раздела между вихревыми структурами в лун-
ках и основным течением. Поверхности раздела, возникающие там,
где вектор азимутальной скорости вихревой структуры не сов-
падает с вектором скорости основного потока V*, неустойчивы, и
Глава 1
35
достаточно малого возмущения в основном потоке, чтобы вызвать
их разрушение. Процесс разрушения приводит к большей разно-
сти скоростей между основным потоком и вихрем в лунке, причем
эта разность может возрастать в одних местах и уменьшаться в дру-
гих, нарушая симметрию вихревых структур. Нарушение симмет-
рии происходит даже в том случае, когда пульсации составляют
0,05 % от средней скорости VM. Даже в таком потоке, судя по кад-
рам видеозаписи, не удается наблюдать стационарную симметрич-
ную структуру в лунке. Истекающая струя, как за «веревочку»,
тянет вихревую структуру, сопряженную с поверхностью лунки по-
средством «подшипников» из вихрей Гертлера, за собой, поворачивая
ее на небольшой угол относительно мидельного сечения углубления.
Однако, учитывая, что в лунке происходит поворот всей структуры,
необходимо принять, что происходит перенос массы среды внутри
вихревой структуры от одного ее торца к другому, это прослеживает-
ся при просмотре видеозаписи. Такой процесс не стационарен в свя-
зи с наличием в потоке, движущемся со скоростью V., различных по
амплитуде и направлению пульсаций скорости V/ [1.1.57].
Изложенный выше механизм описывает формирование вихревых
структур в углублениях рельефа. При увеличении скорости основно-
го течения повышается азимутальная составляющая скорости
вихревой структуры в лунке. Увеличение V , в свою очередь, вызыва-
ет уменьшение давления в стволе вихря, пропорциональное V 2 В свя-
зи с этим возрастает разность давлений во внешнем потоке и в ство-
ле вихревой структуры в лунке, что увеличивает расход среды через
вихрь, обеспечивая повышение радиальной VR и продольной Vz ком-
понент вихревой скорости в цилиндрических координатах.
Снижение давления внутри вихревой структуры приводит к вы-
равниванию давления во внешнем потоке и стволе вихря. Повыше-
ние скорости натекающего потока приводит к сжатию вихря в лун-
ке. На циркулирующий в лунке вихрь со стороны основного потока
действует подъемная сила. Эта сила стремится оторвать вихрь от по-
верхности лунки. Однако отрывается лишь один торец вихря, через
который происходит истечение среды из лунки в основной поток и ко-
торый связан с поверхностью углубления слабее, чем всасывающий
торец вихря. Наблюдения потока позволили проследить его эволю-
цию, сжатие вихря и изменение вихревой структуры в углублении.
Необходимо отметить, по крайней мере, две особенности обтекания
лунки и формирования закрученного течения. Одна из них связана с
возникновением достаточно четкой границы вихря, что свидетельст-
вует об отсутствии обмена средой между внешним течением и вих-
рем через его боковую поверхность. Обмен происходит лишь через
36
Глава 1
Рис. 1.19. Модель головного вагона
межконтинентального экспресса
ICE в 1/20 натуральной величины
с рельефом TLTна обтекаемой по-
верхности
торцы вихря. Вторая особенность со-
стоит в том, что всасывание среды в
вихрь происходит лишь из тонкой
пристенной области вблизи границы
сопряжения лунки с исходно гладкой
поверхностью.
Рельефы были нанесены на по-
верхность модели головного вагона
скоростного межконтинентального
экспресса, и полное сопротивление
модели уменьшилось примерно на
17% по сравнению с моделью, име-
ющей гладкую поверхность [1.1.57].
На рис. 1.19 показана эта модель с рельефом на обтекаемой поверх-
ности.
На рис. 1.20 [1.1.57] зафиксирована структура течения в лунке и
вокруг нее, соответствующая обтеканию поверхности потоком воды
при комнатной температуре при числе Red«2-105, определенном по ди-
аметру лунки dc « 50-Ю’3 м. Фотография получена с помощью мельчай-
ших пузырьков газа, подаваемых в поток воды специальным элект-
рохимическим приспособлением. Поток двигался слева направо. В
левой части фотографии, т.е. выше по потоку, видны газовые пузырь-
ки. Этот участок течения отмечен стрелкой с цифрой 1. На выпуклой
части углубления, сопрягающей исходно гладкую поверхность с вог-
нутой частью лунки, в поток встраиваются струйки, образуется трех-
мерный пограничный слой, состоящий из вихрей типа вихрей Герт-
лера. Эта зона течения обозначена стрелкой с цифрой 2. Стрелка с
цифрой 3 направлена на область, со-
стоящую из вихрей вторичного за-
крученного потока, истекающего из
лунки. Ствол вихря, обозначенный
стрелкой с цифрой 4, наполнен струй-
ками, втекающими в углубление по
его выпуклым скатам и генерируемы-
ми в торце вихря на криволинейной
поверхности вогнутой части углубле-
ния. Темный участок в закрученной
струе за пределами углубления в пра-
вой части фотографии рядом со стрел-
кой 4 свидетельствует о повороте вих-
ревой струи, истекающей из лунки
под углом -45° к направлению основ-
Рис. 1.20. Структура смерчеоб-
разной струи, истекающей из
углубления, визуализированная
с помощью мелких газовых пу-
зырьков
Глава 1
37
ного течения, и подстройке вектора скорости вихревой струи к век-
тору скорости основного потока. Стрелка с цифрой 5 указывает на
вихри, снесенные на нижние по потоку скаты углубления. Эти вихри
также всасываются смерчеобразным вихрем и переносятся в основ-
ное течение.
Эксперименты по визуализации обтекания углублений дали воз-
можность определить структуру поля скоростей в самоорганизу-
ющейся смерчеобразной вихревой струе. Считается, что вихрь состо-
ит из совокупности ni тонких слоев, для каждого из которых выполня-
ется условие:
R^Zi =const.	(1.1.27)
Уменьшение толщины пограничного слоя на рельефах по сравне-
нию с гладкой поверхностью подтверждено прямыми измерениями
профилей скорости в основном потоке.
В работе проведены измерения поля давлений на поверхности
лунки диаметром dc » 40-10'3 м и при глубине hc « 10’3 м и вокруг нее в
канале (рис. 1.21) [1.1.57].
В работе [1.1.61] приводятся результаты экспериментального ис-
следования обьемных флуктуаций потока за «мелкими» (h/D < 0,1)
одиночными, а также установленными в ряду сферическими и ци-
линдрическими углублениями. Исследование выполнено в услови-
ях ламинарного потока перед углублением (или рядом углублений),
когда влияние пристенной турбулентности отсутствует. Изучены
как одиночные углубления,
так и установленные в одно-,
двух- и трехрядной конфигура-
циях. Частота флуктуаций за
углублением определялась по
материалам видеосъемки. По-
лученные видеофильмы преоб-
разовывались в цифровой фор-
мат с последующей обработкой
при уменьшенной скорости вос-
произведения. Для визуализа-
ции потока перед углублением
и внутри него выполнялись по
пять отверстий диаметром 1 мм,
через которые подавалась под-
крашенная жидкость пяти раз-
личных цветов. Форма углубле-
Рис. 1.21. Безразмерное поле давления
на поверхности углублений. Измере-
ния проведены в 45 точках относитель-
но локального давления PQ в выбранной
точке на исходно-гладкой поверхности
38
Глава 1
ния, скоростьпотока, относительнаятолщинапограничного слояперед
углублением играют существенную роль в формировании флуктуа-
ций потока за ним, причем увеличение толщины пограничного слоя
подавляет флуктуации. Эксперименты выполнены в водяной трубе
Военно-воздушной академии США (г. Колорадо-Спрингс), работаю-
щей в интервале входной скорости от 0,05 до 0,5 м/с. Число Рей-
нольдса ReD, вычисленное по диаметру углубления, составляло от
3200 до 24500.
Экспериментальный участок (рис. 1.22) представлял собой плас-
тину из пластика толщиной 19 мм, в которой выполнялись одиночные
цилиндрические или полусферические углубления, а также один, два
или три ряда поперечных углублений с «шахматным» расположени-
ем [1.1.61].
Пластина имела эллиптическую переднюю кромку для обеспе-
чения безотрывного течения, длина пластины — 1220 мм, а шири-
на — 381 мм. Углубления имели диаметр 50,8 мм, глубину 5,08 мм или
2,54 мм.
Цилиндрические углубления получены с помощью сверления и
преобразовывались в сферические углубления заполнением полос-
ти отверстия твердеющим пластиком. Экспериментальный участок
располагался в испытательной секции таким образом, чтобы неста-
ционарные вихревые структуры могли наблюдаться через прозрач-
ное дно с помощью наклонной зеркальной поверхности, установлен-
ной под испытательной секцией. Поэтому углубления располагались
на нижней поверхности экспериментального участка. Две цифровые
видеокамеры SONY-DSR VX2000 использовались для записи образу-
ющихся вихревых структур в реальном масштабе времени.
Зависимость числа Струхаля от числа Рейнольдса для одиночных
углублений имеет максимум (рис. 1.23) [1.1.61]. Существует корреля-
ция между отрывом потока внутри углубления и переходом к турбу-
Направление
потока
Рис. 1.22. Экспериментальный участок
Цилиндрическое
углубление
Сферическое
углубление
Глава 1
39
Число Рейнольдса, ReD
Рис. 1.23 . Флуктуации потока за одиночным
цилиндрическим (0,0) и сферическим (А) уг-
лублениями: О — h/D = 0,1; О — h/D = 0,05;
А - h/D = 0,10
лентному режиму за ним.
Возникновение турбулен-
тности наблюдалось толь-
ко в пристенной области, а
большая часть профиля со-
храняла форму при лами-
нарном течении. Вследст-
вие этого объемные флук-
туации потока за углубле-
нием при визуализации
представляли собой лами-
нарновихревые структу-
ры. Сравнение интенсив-
ности флуктуаций для одиночного цилиндрического и сферического
углублений показывает, что геометрическая форма углубления игра-
ет важную роль в формировании нестационарных флуктуаций пото-
ка. Что касается максимальной интенсивности флуктуаций, цилинд-
рическое углубление предпочтительно в области ReD = 8000... 11000,
а сферическое — при Rep >12500. В области ReD <7500 геометри-
ческая форма углубления не оказывает влияния на величину чис-
ла Струхаля. При ReD > 9500 для x/D = 4,7 и при ReD >11000 для
x/D = 8,36 одиночное сферическое углубление генерирует более ин-
тенсивные объемные флуктуации потока, чем цилиндрическое.
За цилиндрическим и сферическим углублением во втором ряду
обьемные флуктуации потока уменьшаются по сравнению с флукту-
ациями в первом ряду при сохранении числа Рейнольдса, соответст-
вующего максимуму числа Струхаля (рис. 1.24). При Rep < 14000 ци-
линдрическое углубление
во втором ряду генерирует
более интенсивные флук-
туации, чем сферическое.
Общий вывод состоит в
том, что для цилиндриче-
ского и сферического уг-
лублений флуктуации по-
тока во втором и третьем
рядах меньше, чем в пер-
вом. Это связано с тем, что
флуктуации первого ряда
генерируют внешнюю тур-
булентность для второго и
третьего ряда углублений.
Рис. 1.24. Флуктуации потока за углублением
во втором ряду цилиндрических и сфери-
ческих углублений: О — х/£>=2,96. Цилинд-
рическое углубление во втором ряду; А —
х/£>=2,96. Сферическое углубление во вто-
ром ряду
40
Глава 1
Особенно заметно это проявляется для цилиндрического углубле-
ния в третьем ряду, которое располагается в «следе» за углублением
первого ряда. Для сферического углубления флуктуации в третьем
ряду меньше флуктуаций во втором ряду только при ReD >12500, т.е.
геометрическая форма углубления играет заметную роль в характе-
ре подавления флуктуаций в нижележащих рядах углублений.
Обоснование опережающего роста теплоотдачи от стенки канала
с полусферической лункой по сравнению с увеличением гидравли-
ческих потерь исследовано в работе [1.1.76, 1.1.77]. Вихревая интен-
сификация теплообмена путем нанесения на стенки канала луночных
рельефов оказывается более привлекательной по сравнению с други-
ми способами генерации вихрей (например, с помощью выступов или
наплывов) из-за возможности получения опережающего роста коэф-
фициента теплоотдачи по сравнению с гидравлическими потерями. В
принципе вполне благоприятной можно считать ситуацию, когда тем-
пы роста теплоотдачи и гидравлических потерь оказываются близки-
ми даже при опережении последних. Ведь для наплывов теплогидрав-
лическая эффективность, определяемая как (Nu/NupZ)/(£,/£,p/), гораздо
меньше единицы (здесь — коэффициент гидравлических потерь
тракта с периодическими наплывами).
Как отмечалось ранее, в экспериментальных работах 4 определя-
ется по перепаду статического давления между выбранными сечени-
ями. Однако в отрывных и в особенности пространственных течени-
ях существенный вклад в £, должна вносить неравномерность полей
скорости во входном и выходном сечениях, которая не учитывается в
физических измерениях, но может достаточно легко быть оценена в
численных расчетах. Тем не менее до сих пор это не было сделано ни
в одной из процитированных работ.
Роль сглаживания или скругления кромок сферической лунки
представляется чрезвычайно важной, и это подчеркивается в ис-
следованиях Г.А. Кикнадзе и им вводится определение поверхности
двойной кривизны, имея в виду радиус кривизны вогнутости и ради-
ус скругления кромки.
В работе [1.1.76] рассматривается влияние радиуса скругления г
сферической лунки (А = 0,28,6 = 0,15) в прямоугольном канале (Н>3;
Re = 104) на характеристики теплоотдачи и сопротивления Nu/Nup/,
£>/£,р/и (Nu/NupZ)/(^/y участка, окружающего лунку (рис. 1.25). Пред-
ставлены также результаты исследования теплообмена при турбу-
лентном обтекании поверхности с трансистентными траншейными
лунками.
Как и для сферических лунок, увеличение глубины траншейной
лунки сопровождается интенсификацией самоорганизующегося в
Глава 1
41
ней смерчевого потока.
При умеренной глуби-
не лунки отрывная зона
занимает большую пло-
щадь лунки и внутри ее
образуется закручен-
ное струйное течение,
наклоненное по отно-
шению к набегающему
потоку под углом уста-
новки траншейной лун-
ки. Далее с ростом Д от-
рывная зона охватывает
всю площадь лунки, т.е.
линия присоединения
потока практически сов-
падает с границей лунки.
Рис. 1.25. Влияние радиуса скругления г сфериче-
ской лунки (Д = 0,28, 5 = 0,15) в прямоугольном
канале (Н> 3; Re = 104) на значения Nu/Nup/, £/£р/
и (Nu/Nup/)/(£/£p;) участка, окружающего лунку
И, наконец, начиная с некоторой глубины, за лункой образуются вто-
ричные отрывные зоны.
Анализ картин изолиний относительных чисел Нуссельта показы-
вает, что на наветренной стороне траншейной лунки при всех глуби-
нах тепловые потоки меньше, чем на плоской стенке. По мере роста Д
увеличивается площадь наветренной части лунки, на которой наблю-
дается рост теплоотвода. Однако главное достоинство лунок как вихре-
генераторов состоит в интенсификации теплообмена в следе за ними.
При анализе теплогидравлической эффективности участка с тран-
шейной лункой на плоской стенке размером 3x2 (рис. 1.26) по мере
заглубления лунки от-
мечается опережающий
рост относительного ко-
эффициента теплоотда-
чи по сравнению с уве-
личением гидравличе-
ских потерь, причем в ди-
апазоне больших глубин
(от 0,18 до 0,34) значения
Nu/Nup/ и растут ли-
нейно от Д [1.1.76, 1.1.77].
Однако следует отметить,
что рост коэффициен-
та теплоотдачи сочетает-
ся с низкими гидравличе-
Рис.1.26. Влияние глубины траншейной лунки на
относительные характеристики теплоотдачи и со-
противления Nu/NUp,, £Др/ и (Nu/Nup/)/(£/S,p/)
42
Глава 1
скими потерями, что предопределяет локальный максимум тепло-
гидравлической эффективности (Nu/NupZ)/(^/^pZ) при А порядка 0,06.
Второй локальный максимум, примерно вдвое превышающий пер-
вый, имеет место при больших глубинах лунки. Для А >0,34 гидрав-
лические потери для участка с траншейной лункой превышают ко-
эффициент относительной теплоотдачи и, таким образом, глубина
траншейной лунки, равная 0,34, представляется оптимальной по теп-
логидравлической эффективности и по эффекту интенсификации
теплообмена.
Ориентация траншейной лунки оказывает существенное вли-
яние на теплоотвод от поверхности с лункой. Для умеренной глубины
лунки установлено, что при угле (р ее наклона по отношению к набега-
ющему потоку, равному 60°, коэффициент относительной теплоотда-
чи максимален. На рис. 1.27 приведены некоторые из результатов по
теплогидравлической эффективности лунок при изменении <р от 30
до 90°, т.е. до положения лунки, при котором она ориентируется попе-
рек набегающего потока [1.1.76, 1.1.77].
В целом, подтверждаются ранее сделанные выводы для лунок
умеренной глубины. Угол наклона, равный 60°, является предпочти-
тельным по максимуму относительной теплоотдачи и наибольшей
теплогидравлической эффективности. Минимум £/£pZ соответствует
ср =75°. Тепловая эффективность Nu/NupZ рельефа с оптимальным
углом ориентации траншейной лунки больше на 10%, чем при по-
перечном ее расположении.
Траншейные лунки в узком канале сравниваются по теплогид-
равлической эффективности с полусферическими. Смена режимов
обтекания от двухъячеистой структуры к моносмерчевой проис-
Рис. 1.27. Влияние ориентации траншейной лун-
ки (L= 1; Д = 0,22; г= 0,1) на отношения Nu/Nu z,
^р/и (Nu/NupZ)/(^/y. Re= 104
ходит под воздействием
возмущений. В рассмат-
риваемом случае располо-
жения лунки на стенке в
широком канале переход
к моносмерчевому режи-
му обтекания происходит
при больших глубинах.
Полусферическая лунка с
безразмерным радиусом
окружности по кромке
0,5 продуцирует доволь-
но протяженную, но уз-
кую зону повышенных
(по сравнению с плоской
Глава 1
43
стенкой) тепловых потоков в следе. В то же время такая же зона за
траншейной и эквивалентной лунками заметно шире. В работе сде-
лан вывод, что траншейная лунка по теплоотводу представляется
предпочтительнее эквивалентной.
Влияние на течение и теплообмен плотности и расположения
полусферических лунок на стенке узкого канала
Конструирование луночных рельефов, составленных из сфери-
ческих лунок, в основном сводится к их расположению на стенке в
коридорном или в шахматном порядке. Заданные шаги между цент-
рами лунок в продольном (по потоку) и поперечном направлениях
могут быть сведены к одному интегральному параметру у, характе-
ризующему плотность нанесения лунок на поверхности и определя-
емому отношением площади лунок к площади прямоугольного участ-
ка, на котором они расположены. В этом случае необходимо задать
топологию луночного рельефа, т.е. определить взаимное положение
лунок относительно друг друга. Первый тип, обозначенный А, пред-
ставляет собой конфигурацию лунок с расположением ближайших
центров в виде равностороннего треугольника. Второй тип Б пост-
роен на квадратной сетке из центров лунок с расположенными в сере-
дине квадратов дополнительными лунками. Продольные ряды лунок
в таких пакетах обычно ориентируются по потоку. В работе [1.1.78]
задаются близкими расстояния между центрами лунок в поперечных
рядах независимо от типа луночного пакета (1,4 для А и 1,6 для Б). Тог-
да плотность луночного пакета для A-типа равна 0,4, а для Б-типа — 0,6.
Турбулентный режим обтекания луночных рельефов рассчитывается
при Re = 104, степени турбулентности и температуре набегающего по-
тока 1,5% и 293К. Стенка с лунками нагрета др температуры 373К.
Для рельефа A-типа из 25 лунок глубиной 0,22 с радиусом скругле-
ния кромок 0,1 при толщине пограничного слоя в окрестности участ-
ка с лунками 5 = 0,5 на рис. 1.28 демонстрируется формирование в
пристеночном слое асимметричных согласованных вихревых струк-
тур, обеспечивающих интенсификацию теплообмена порядка 18%. В
пристеночном слое возникает самоорганизующееся упорядоченное
вихревое движение — вихревой слой, покрывающий рельеф. Имен-
но благодаря ему реализуется интенсификация теплообменных про-
цессов по сравнению с неупорядоченным вихревым движением в ок-
рестности плоской стенки. Анализ распределений относительных
чисел Нуссельта Nu/Nup/ в окрестности полусферических лунок в па-
кете показывает, что конфигурации зон повышенных тепловых пото-
ков в пределах лунок и в следе за ними такие же, как для уединенных
лунок на плоской стенке.
44
Глава 1
б
Рис. 1.28. Картины растекания (а) и распределений относительных чисел Нуссель-
та Nu/Nup/ (б) для рельефа с 25 полусферическими упорядоченными лунками глу-
биной 0,22 с плотностью пакета 0,46. Re = 104; 8 = 0,5; г = 0,1. Оцифрованные
линии соответствуют изолиниям: 1 — Nu/Nup/ = 0,2; 2 — 0,5; 3 — 1,25; 4 — 1,4;
5 — 2; 6 — 3. Штриховыми линиями нанесены края лунок
На рис. 1.29 приводится сравнение полей относительных тепло-
вых потоков и продольных распределений осредненных поперек по-
лосы пакетов типа А и Б из 18 глубоких (0,28) полусферических лунок
в каналах. Кромки лунок сглажены незначительно — г = 0,05.
Несмотря на существенное различие в плотности луночных паке-
тов, картины локальных относительных чисел Nu/NupZ весьма схо-
жи. Это сходство в тепловых полях у стенок подчеркивается и корре-
ляцией максимумов распределений осредненных по ширине полосы
с лунками отношения чисел Nu/NupZ. Для пакета типа Б минимумы
отношений Nu/NupZ заметно выше, чем в случае А.
С увеличением у коэффициент относительной теплоотдачи рас-
тет. Оценка относительных гидравлических потерь дает не-
сколько неожиданный результат — их превышение над Nu/NupZ. В
итоге теплогидравлическая эффективность рельефов с луночными
пакетами на стенке оказывается меньше 1 (порядка 0,9). Правда, сле-
дует отметить, что кромки полусферических лунок скруглены очень
мало, а это приводит, как отмечалось ранее, к высоким гидравличе-
ским потерям при обтекании такого рельефа.
В работе [1.1.76, 1.1.78] представлены результаты исследований
вихревой интенсификации теплообмена при ламинарном обтекании
пакетов лунок (типа Б). Число Рейнольдса равно 103. Глубина лунок —
Глава 1
45
а
б
Рис. 1.29. Сравнение распределений относительных чисел Нуссельта Nu/Nup/ для
пакетов из 18 сферических лунок (Д = 0,28; г = 0,1) на стенке канала с плотностя-
ми пакетов А — у — 0,46 (а) и Б — у — 0,6 (б). Re= 104; 8 =0,175. Оцифрованные ли-
нии соответствуют изолиниям: 1 — Nu/Nup/ = 0,3; 2 — 0,99; 3 — 1,5; 4 — 2; 5 — 4
0,28, радиус скругления — 0,05. Толщина пограничного слоя на вхо-
де в канал варьируется в сочетании с высотой канала. Следует отме-
тить, что интерес к ламинарным режимам обтекания лунок возрастает
в связи с многообразием технических приложений, в которых требу-
ется создать интенсификацию теплообмена в мини- и микромасштаб-
ных областях.
Несмотря на сравнительно малый прирост теплоотдачи в каналах,
за счет существенного снижения гидравлических потерь достигается
значительная теплогидравлическая эффективность. И еще один важ-
ный вывод: интенсификация теплообмена в ламинарном режиме на-
иболее предпочтительна применительно к узким каналам.
Траншейные лунки (£ = 1; ср = 45°) при глубинах 0,1< А <0,38 гене-
рируют устойчивые смерчеобразные вихри, обуславливающие высо-
кий уровень относительной теплоотдачи. Отношение чисел Nu/Nup/( А)
от участка с лункой возрастает почти линейно и быстрее, чем £/£,р/(А).
При А = 0,06 гидравлические потери предопределяют локальный мак-
симум теплогидравлической эффективности, отличающийся почти
вдвое от максимума при А = 0,34. Глубина лунки А = 0,34 представ-
ляется также предпочтительной по наибольшему теплоотводу
Nu/Nup/.
46
Глава 1
Наклон глубокой траншейной лунки (Д = 0,22) под углом 60° к набе-
гающему потоку является предпочтительным по максимумам Nu/Nup/
и (Nu/Nup/)/(^p/). При <р = 75° наблюдается минимум £/£р/. По теп-
ловой эффективности Nu/Nup/ рельеф с оптимальным углом наклона
траншейной лунки оказывается на 10% лучше, чем при ее поперечном
расположении.
Численно подтверждено предположение Г.И. Кикнадзе о самоорга-
низации в пристеночном слое при обтекании луночного рельефа упо-
рядоченного струйно-вихревого движения, обладающего преимущест-
вом по сравнению с неупорядоченным переносом жидкости вблизи
плоской стенки в отношении интенсификации теплообменных про-
цессов. На примере обтекания 25 сферических лунок глубиной 0,22
демонстрируется синхронизация вихревых структур в лунках, обус-
лавливающих тепловую эффективность относительных чисел Nu/Nup/
порядка 20%.
Сравнение упорядоченных рельефов лунок подтверждает, что уве-
личение плотности пакета у от 0,4 до 0,6 приводит к двукратному (от 40
до 80%) возрастанию Nu/Nup/. Однако теплогидравлическая эффек-
тивность из-за опережающего роста гидравлических потерь оказыва-
ется порядка 0,9.
При ламинарном обтекании рельефа сферических лунок по-
казано, что несмотря на сравнительно малый прирост теплоотда-
чи в каналах за счет существенного снижения гидравлических
потерь достигается значительная теплогидравлическая эффектив-
ность.
Теплообмен и структура потока при турбулентном течении
вблизи пластины с лунками
В работе [1.1.60] рассмотрено влияние лунок на поверхности на
теплообмен и структуру потока при различных конфигурациях об-
лученных каналов. Исследованная облуненная поверхность показа-
на на рис. 1.30, а схема мгновенной структуры потока при ее обтека-
нии — на рис. 1.31.
Исследование воздействия мелкого полусферического углубления
на структуру потока и теплообмен показывает, что поток обычно явля-
ется симметричным и возникает стабильная циркуляция. Поток дви-
жется вдоль подковообразной вихревой линии, и при этом формиру-
ется спиралевидное течение.
Для каждого Y/H нормальные напряжения растут с увеличением
глубины лунок. Нормальные напряжения Рейнольдса также растут с
уменьшением Y/H в диапазоне Y/H< 0,5.
Глава 1
47
На рис. 1.32 и 1.33 показаны резуль-
таты [1.1.60], иллюстрирующие влияние
глубины лунок в канале на число Нуссель-
та и коэффициент трения. На рис. 1.32
изображено отношение локального чис-
ла Нуссельта облуненного канала к чис-
лу Nu0 для гладкого канала в зависимо-
сти от Х/D вдоль центральной продоль-
ной линии поверхности Z/D = 0. Соглас-
но данным, отношение чисел Нуссельта
уменьшается, затем возрастает. Наиболь-
шее локальное значение Nu/Nu0 отмече-
но у внешней кромки лунки. Отношение
чисел Нуссельта для величины 5/D = 0,3
выше приблизительно на 25%, чем для
d/D = 0,2, и выше приблизительно на
50%, чем для 6/D = 0,1.
Отношение средних чисел Нус-
сельта является практически посто-
(б)
Направление потока
Форма
лунки
Рис. 1.30, Схема облуненной
поверхности (размеры даны
в сантиметрах)
Рис. 1.31. Схема мгновен-
ной структуры потока. От-
ношение высоты канала
к диаметру лунки — 0,5,
а отношение глубины к
диаметру лунки — 0,2. Чис-
ло Рейнольдса, определя-
емое по высоте канала, рав-
но 1250
янным при возрастании числа ReH (см. рис. 1.33). Для всех чисел ReH
данные, приведенные на рис 1.33, свидетельствуют об увеличении
отношения чисел Нуссельта с ростом &/D.
На рис. 1.34 показано отношение локального числа Nu для облу-
ненного канала к Nu0 для плоского канала в зависимости от попереч-
ной координаты Z/D, измеренной при различных H/D в 11 ряду лунок
вдоль постоянной линии Х/D, равной 8,50. Области с наибольшим зна-
чением Nu/Nu0 представлены при различ-
ных значениях Z/D. Показано, что области с
малыми отношениями чисел Нуссельта ме-
няются незначительно с изменением Z/D,
когда H/D — различно. Напротив, отноше-
ние чисел Нуссельта возрастает с уменьше-
нием H/D для плоской поверхности между
лунками.
На рис. 1.35 представлено отношение
осредненных чисел Нуссельта в зависимо-
сти от отношения коэффициентов трения.
В случае вихревой камеры получено на-
ибольшее повышение теплообмена. В ряде
случаев оребренные поверхности показы-
вают сопоставимые с вихревой камерой
отношения чисел Нуссельта. Однако поте-
48
Глава 1
Рис. 1.32. Отношение локального числа Нуссельта облуненного канала к числу
Nu0 для гладкого канала в зависимости от Х/D вдоль центральной продольной ли-
нии поверхности Z/D = 0:	• — область лунки
0	20000 40000 60000 80000 ReH
Рис. 1.33. Отношения осредненных чисел Нуссельта (а) и коэффициентов трения
(б) для облуненного и плоского канала в зависимости от числа Рейнольдса для
различных отношений глубины лунки к диаметру лунки 6/D
0
20000 40000 60000 80000 ReH
Рис. 1.34. Отношение локального чис-
ла Nu для облуненного канала к Nu0
для плоского канала в зависимости от
поперечной координаты Z/D, изме-
ренной при различных Н/D в 11 ряду
лунок вдоль постоянной линии X/D,
равной 8,5:
Nu/Nu0
0 4-------1----—।-------1--------1------1—
-1,35 -0,85 -0,35 0,15 0,65	1,15 Z/D
	H/D	ReH	Т /Т or W	X/D
О	0,20	9,800	0,93	8,50
д	0,25	8,800	0,92	8,50
о	0,50	10,200	0,94	8,50
□	1,00	10,300	0,92	8,50
Глава 1
49
Рис. 1.35. Отношение осредненных чисел Нусселъта в зависимости от отноше-
ния коэффициентов трения: х — для оребренной поверхности; А — поверхности
с выступами;  — вихревой камеры; • — облуненной поверхности с плоскими
участками; А — облуненной поверхности с выступами; О — полностью облунен-
ной поверхности; -I- — шероховатой поверхности; □ — гладкого канала
ри давления у оребренных поверхностей и вихревой камеры также
достаточно велики.
На рис. 1.36 представлено сравнение эффективности различных
интенсификаторов теплосъема. Наибольшая эффективность тепло-
отдачи получена для облуненной поверхности с плоскими участками,
а наименьшая — для оребренной поверхности.
Рис. 1.36. Сравнение эффективности различных интенсификаторов теплосъема:
х — оребренная поверхность; ▲ — поверхность с выступами;  — вихревая каме-
ра; • — облуненная поверхность с плоскими участками; А — облуненная поверх-
ность с выступами; О — полностью облуненная поверхность; + — шероховатая
поверхность; □ — гладкий канал
50
Глава I
В целом, эти результаты показывают, что облуненные поверхно-
сти являются эффективным и важным средством интенсификации
теплообмена при сравнительно небольшом повышении потерь дав-
ления.
Применение результатов исследований теплоотдачи
и гидродинамики для облуненных поверхностей на практике
Полусферические лунки в качестве интенсификаторов тепло-
обмена использованы при охлаждении турбинных лопаток [1.1.24].
Интенсификация теплообмена полусферическими лунками реали-
зована в авиационных газотурбинных двигателях четвертого и пя-
того поколений. Рельеф в виде полусферических лунок выполнялся
на поверхности охлаждающих трактов профильной части лопатки,
удлиненной ножки и замковой области рабочих лопаток турбин вы-
сокого и низкого давления. Плотность размещения лунок на поверх-
ности лопатки составила 0,4—0,5, относительная глубина h/d = 0,135.
Отмечено, что опыт эксплуатации лопаток с лунками дал положи-
тельные результаты. Во-первых, по сравнению с интенсификацией
теплообмена поперечными выступами (имеющими относительный
продольный шаг t/h = 12,5 и относительную высоту h/D = 0,156, где
D — эквивалентный гидравлический диаметр канала) уменьшилось
гидравлическое сопротивление и увеличилась пропускная способ-
ность охлаждающих трактов лопаток примерно на 25%. Во-вторых,
при сохранении располагаемого перепада давления охлаждающего
воздуха теплосъем в охлаждающих каналах увеличился примерно
на 30%, а долговечность лопатки возросла в 3—4 раза. В-третьих, при
одном и том же расходе охладителя теплосъем возрос на 10%, а ре-
сурс лопатки увеличился вдвое.
При использовании системы полусферических лунок в воздухо-
распределительных каналах рабочих лопаток турбины высокого дав-
ления удалось увеличить теплосъем на 20% и уменьшить температу-
ру стенки в условиях эксплуатации на 20—25 К [1.1.24]. Наряду с этим
удалось устранить неравномерность температурного поля на участ-
ках, где интенсификация теплообмена совсем не применялась.
Исследование интенсификации теплообмена полусферическими
лунками применительно к различным техническим устройствам
проведено в работах [1.1.15; 1.1.16; 1.1.23; 1.1.24; 1.1.26—1.1.51; 1.1.53—
1.1.78].
Метод интенсификации теплообмена с помощью полусфериче-
ских лунок нашел применение в системах охлаждения мощных полу-
проводниковых пребразователей энергии [1.1.72, 1.1.73].
Глава 1
51
Нетрадиционный способ использования полусферических лунок
в топках предложен в работе [1.1.30]. Здесь анализируется возмож-
ность реализации эффективного теплообменника-водонагревателя,
в котором полусферические лунки используются в различных целях:
в одном случае осуществляется сжигание газовоздушной смеси и от-
вод тепла от горячего газа к «холодному» теплоносителю, в другом —
только отвод тепла. Важно отметить, что в первом случае смерчевой
эффект, кроме интенсификации теплообмена, обеспечивает устой-
чивую стабилизацию пламени. Во втором случае происходит интен-
сификация конвективного теплообмена.
Интенсификаторы теплообмена макромасштаба
при конденсации
Для интенсификации теплообмена в конденсаторах поверхност-
ного типа используется создание капельной конденсации, оребре-
ние труб, вибрация поверхности, расположение трубного пучка под
наклоном [1.1.1].
В отличие от оребрения накатка позволяет интенсифицировать теп-
лоотдачу как на наружной, так и на внутренней поверхностях трубы.
Вибрация поверхности интенсифицирует теплоотдачу на обеих по-
верхностях трубы и предотвращает их загрязнение. Возможны как ис-
кусственная вибрация поверхности, так и регулирование естественной
вибрации. Однако вибрация может привести к разрушению труб.
Расположение трубного пучка под наклоном позволяет устранить
заливание конденсатом части поверхности труб, уменьшить паровое
сопротивление, улучшить деаэрацию конденсата.
В повышении теплопередачи в конденсаторах большую роль иг-
рает теплоотдача к охлаждающей воде, ее также необходимо увели-
чивать. Следует заметить, что пристенные турбулизаторы на внут-
ренней поверхности конденсатора не только интенсифицируют
теплоотдачу, но и уменьшают отложения на стенке.
При пленочной конденсации на наружной поверхности труб с ка-
навками интенсификация теплообмена обусловлена действием поверх-
ностного натяжения на пленку кон-
денсата. В результате пленка стекает в
канавки труб и ее толщина на осталь-
ных участках трубы уменьшается.
Этот эффект усиливается при
уменьшении относительного шага
канавок, а также в случае волново-
го профиля трубы (рис. 1.37). Пере-
менное сечение трубы с плавными
Рис. 1.37. Профилированная гори-
зонтально расположенная труба
52
Глава J
Рис. 1.38. Коэффициенты теплоотда-
чи при конденсации водяного пара
на горизонтальной латунной трубе
без накатки (1) и с накаткой (2)
переходами приводит к стеканию
конденсата в канавки. В результате
уменьшается толщина конденсатной
пленки на выступах трубы и ее тер-
мическое сопротивление. Стекание
конденсата в канавки снижает устой-
чивость пленки и приводит к ее сры-
ву. Перераспределение конденсата
по длине трубы ведет к росту средне-
го коэффициента теплоотдачи.
Коэффициенты теплоотдачи при
конденсации водяного пара на гори-
зонтальной трубе из латуни с накат-
кой (линия 2) и без накатки (линия 1),
полученные Г.А. Дрейцером, пред-
ставлены на рис. 1.38. Наружный
диаметр трубы 18,3 мм. Для трубы с
накаткой: dH/DH = 0,893; t/DH= 0,37;
R/DK= 0,76;Ro/DK= 0,062. Давле-
ние водяного пара (0,157 — 0,323)
МПа, температура стенки (75,2 — 98,3) °C; скорость пара менее 5 м/с;
RenA = 25— 150. Как установлено, коэффициент теплоотдачи для тру-
бы с накаткой растет больше, чем в два раза.
Рост коэффициента теплоотдачи тем больше, чем больше глубина
канавок, чем меньше их шаг и радиус закругления выступающих час-
тей труб.
Полученные опытные данные описаны зависимостью [1.1.1]
Г /7
-S- = 2,47(l-jfi-)(l-0,387*-)exp 3,65(1-^)
ЧГл	^Ат
(1.1.28)
н
ТА	Н
в диапазонах dH/DH= 0,89—0,95; t/DK= 0,283—0,37; R/DH= 0,5 — 1.
Теплоотдача для гладкой горизонтальной трубы описывается
уравнением
агл = 0,73^(r)3p3gr/(n'(/H-tc)DH ),	(1.1.29)
полученным для пленочной конденсации пара на горизонтальной
трубе. Свойства величин, входящих в уравнение (1.1.29), определя-
ются по температуре насыщения.
Трубы с накаткой испытаны в подогревателе сетевой воды, со-
стоящим из 214 труб длиной 4 м, диаметром 16 мм, толщиной стенки
0,85 мм. Ориентация труб горизонтальная. Параметры накатки: сна-
Глава 1
53
ружи трубы — dH/DH = 0,932, t/DH = 0,31; внутри трубы — d/D = 0,932,
t/D = 0,357. Испытания подогревателей проведены при одинаковых
давлениях греющего пара. При использовании труб с накаткой теп-
ловая мощность и коэффициент теплопередачи в подогревателях
увеличиваются более чем в два раза.
Интенсификация теплоотдачи при вертикальном расположении
трубы проявляется слабее, чем при ее горизонтальном расположе-
нии. Влияние накатки на теплоотдачу растет с увеличением RenA,
глубины накатки и уменьшением ее шага (рис. 1.39). При RenA < 400
снижение t/h меньше 8 не сопровождалось дальнейшим ростом от-
ношения чисел Нуссельта для труб с накаткой и без накатки. Это
объясняется удерживанием конденсата в канавках силами поверх-
ностного натяжения.
Для расчета средней теплоотдачи в трубе с накаткой получено
уравнение
д/з'
Nu
NurA
„	5400
1 +----7--
Кепл
(1.1.30)
гдеКепл= Суд/ц'= 40—3000; Суд— удельный расход конденсата;
= 0,925 Re" 3 [1+0,04 Re^+2,23-10"3 Rejf
Нс
и'
1/8
Визуальные наблюдения и фотосъемка процесса конденсации
пара на трубе с кольцевыми канавками показали, что при RenA< 500—
700 рост теплоотдачи вызван крупномасштабными изменениями
пленки конденсата — срывом с частотой до 1 Гц конденсата в виде со-
литонов протяженностью 50—100 мм. При высоких числах Рейнольд-
Рис. 1.39. Влияние накатки на
теплоотдачу при конденсации
на вертикальной трубе:
	d /D и и		ДЛОН	
•	0,933	0,37	0,5	0,092
о	0,931	0,283	0,5	0,095
л	0,910	0,37	0,5	0,093
X	0,927	0,53	1,0	0,053
А	0,913	0,32	0,5	0,094
54
Глава 1
Рис. 1.40. Труба с нака-
танными кольцевыми
канавками
са (RenA> 700) наблюдаются повышенная тур-
булентность, вихреобразование пленки.
При незначительном наклоне трубы (3—5°)
интенсификация теплоотдачи за счет канавок
на поверхности усиливается. Эта особенность
использована в трубах с накатанными коль-
цевыми канавками (рис. 1.40). Канавки распо-
ложены параллельно одна другой под углом,
меньшим 90° к оси трубы.
Расстояние между канавками равно их ут-
роенной ширине, глубина канавок определя-
ется из выражения
h = [ЗСкг/(^рдг5та)]1/3,
где GK — расход конденсата, образующегося
на поверхности трубы между двумя соседними канавками. Между
канавками могут быть расположены несообщающиеся с ними ребра
или канавки, ориентированные параллельно оси трубы. Это улучша-
ет стекание конденсатной пленки и способствует большей интенси-
фикации теплоотдачи.
На теплоотдачу при конденсации может оказать влияние материал
стенки. Механизм этого влияния — неоднородное распределение тем-
пературы стенки в случае низкого коэффициента теплопроводности.
Введение безразмерного комплекса \8с/(Хплс?э), где Хс, Хпл — коэф-
фициенты теплопроводности материала стенки и пленки; 5с —толщи-
на стенки; d3 — эквивалентный диаметр кольцевого канала, позволя-
ет обобщить данные по теплоотдаче при конденсации паров бензина
и воды в кольцевом канале единой зависимостью:
= 1 + 0,5 5 (АА)О,629 (1,196 - 0,79t / DH) х
^гл	^пл.э
(J
1-у^-
( 1.1.31)
Уравнение справедливо в диапазонах
ХД/(Х d) = 2,576-8,514; t/D = 0,25-0,44; d /D = 0,876-0,938.
Теплоотдача при конденсации паровой смеси R113/H2O на го-
ризонтальных оребренных трубах исследована в МЭИ [1.1.79]. На
рис. 1.41 показаны ребра и шипы на горизонтальных трубах, полу-
ченные методом деформирующего резания, который разработан в
МГТУ им. Баумана.
На рис. 1.42 представлены данные по теплоотдаче, полученные при
конденсации паров исследованной смеси на горизонтальной трубе с
Глава 1
55
Рис. 1.41. Ребра и шипы на горизонтальной трубе, полученные методом
деформирующего резания
Рис. 1.42. Коэффициенты теплоотдачи при конденсации паровой смеси R113/Н2 О
на горизонтальной трубе с шипами (3) и технически гладкой поверхностью (1)
при давлении 0,2 (а) и 0,4 (б) МПа; 1,3 — данные [1.1.79]; 2 — расчет по формуле
Нуссельта
56
Глава 1
шипами на наружной поверхности. На нем же представлены рассчи-
танные коэффициенты теплоотдачи при конденсации чистого фре-
она-113 и смеси R113/H2O на гладкой трубе диаметром 16 мм, из кото-
рой изготавливались трубы с шипами.
Увеличение коэффициента теплоотдачи для трубы с шипами, не
связанное непосредственно с развитием поверхности, оказалось до-
статочно большим и составило 1,5 и 1,7 для давлений 0,2 и 0,4 МПа.
Для трубы с ребрами и шипами обнаружена особенность, состоящая в
том, что коэффициент теплоотдачи слабо изменяется с ростом темпе-
ратурного напора.
Согласно методике определения коэффициента теплоотдачи при
конденсации на горизонтальных оребренных трубах бинарных сме-
сей паров, образующих несмешивающиеся жидкости, развитая по-
верхность трубы разделяется на две зоны — залитую и незалитую
конденсатом. Предложенная методика тестируется путем сравнения
с имеющимися опытными данными.
Интенсификаторы теплообмена макро- и микромасштаба
при кипении
На теплоотдачу при кипении оказывают влияние характеристики
поверхности (шероховатость, смачиваемость жидкостью, теплофи-
зические свойства стенки и жидкости, пористые покрытия, рельеф),
состояние теплопередающей среды (кипение в условиях свободной и
вынужденной конвекции), закрутка жидкости, электрическое поле.
Влияние шероховатости поверхности
Рис. 1.43. Кривая кипения хладона-113
в большом объеме при атмосферном
давлении: 1 — поверхность, обработан-
ная крупной наждачной шкуркой; 2 —
поверхность, обработанная мелкой
наждачной шкуркой
С ростом шероховатости стен-
ки до определенного предела на-
блюдается увеличение теплоот-
дачи. Как показано на рис. 1.43
[1.1.8], для поверхности, обрабо-
танной грубой наждачной шкур-
кой, кривая пузырькового кипе-
ния хладона-113 при атмосферном
давлении сдвигается влево (кри-
вая 1) по сравнению с поверхнос-
тью, обработанной мелкой на-
ждачной шкуркой (кривая 2). Для
активизации центров парообра-
зования в крупных порах требу-
ется меньший температурный на-
пор, чем в мелких порах.
Глава 1
57
Влияние резервуарных впадин на поверхности
На рис. 1.44 представлены известные данные по влиянию на теп-
лоотдачу при кипении искусственных впадин резервуарного типа.
Как установлено, для поверхности с впадинами резервуарного типа
уменьшается ДГНК, повышаются теплоотдача и устойчивость кипе-
ния.
На рис. 1.45 показаны положения границы раздела фаз при обра-
зовании парового пузыря в резервуарной впадине. Внутри резервуар-
ной впадины радиус кривизны границы раздела фаз отрицательный
(J?<0) и капиллярное давление компенсирует давление жидкости. В
этом случае давление в паре может быть меньше давления в жидкос-
ти, и пар может существовать во впадине при температуре, меньшей
температуры насыщения. При повышении тепловой нагрузки темпе-
ратура стенки растет, увеличиваются температура пара, его объем,
граница раздела фаз перемещается вверх. Чтобы пузырек пара вы-
шел из впадины, должно быть Тс > Т.
Рис. 1.44. Кривая кипения натрия в боль-
шом объеме: 1 — поверхность со впа-
динами резервуарного типа; 2 — поверх-
ность со сварными швами; 3 — зеркаль-
но-гладкая поверхность
Рис. 1.45. Положения границы
раздела фаз при возникнове-
нии парового пузыря в резерву-
арной впадине
Влияние пористых покрытий на теплоотдачу при кипении
Исследование кипения на поверхности с резервуарными впади-
нами предшествовало разработке чрезвычайно эффективного мето-
да интенсификации теплоотдачи с помощью пористого покрытия.
В 1970 г. инженер В. Мартин (фирма «Линде», ФРГ) предложил
способ интенсификации теплоотдачи при кипении — нанесение спе-
канием на поверхность нагрева покрытий, который оказался очень
эффективным. В этом случае резко уменьшается температурный на-
пор начала кипения (до 1 К) и повышается коэффициент теплоотда-
58
Глава 1
чи (до 10 раз). Это было объяснено возникновением большого коли-
чества пор, различных по форме и размерам, что привело к резкому
увеличению плотности активных центров парообразования. После
этого были разработаны самые различные технологии изготовления
пористых покрытий и проведено большое количество исследований.
На рис. 1.46, 1.47 приведены фотографии шлифов спеченного пок-
рытия, изготовленного по технологии, предложенной в работе [1.1.80].
Видно, что частицы покрытия практически не деформированы. Рас-
пределение пор по размерам (рис. 1.48) таково, что имеются мелкие
поры, по которым подтекает жидкость, и крупные поры, по которым
выходит пар [1.1.81].
Рис. 1.46. Фотография шлифа
спеченного покрытия
Рис. 1.47. Поверхности с пористым покрытием: а — инконель-600; б — сталь (уве-
личение в 100 раз)
Глава 1
59
Рассмотрим закономерности влияния пористых покрытий на теп-
лоотдачу при кипении.
На рис. 1.49 приведены зависимости д(ДТ) при кипении фреона-
22 (Ts = 283 К) для трубы без покрытия, с оребрением и различными
покрытиями: напыленным покрытием из нержавеющей стали (по-
ристость 40%), спеченным покрытием из нержавеющей стали (порис-
тость 50%), напыленным покрытием из бронзового порошка [1.1.82].
Наибольшая интенсификация теплообмена достигнута в случае
бронзового напыленного покрытия, и превышение коэффициента
теплоотдачи по сравнению с поверхностью без покрытия составляет
около 10 раз.
Рис. 1.49. Кривые кипения фре-
она-22 при температуре насыщения
283 К: 1 — поверхность без покры-
тия; 2 — поверхность с оребрени-
ем; 3 — поверхность с напыленным
покрытием из нержавеющей стали
(пористость 40%); 4 — поверхность
со спеченным покрытием из нержа-
веющей стали (пористость 50%); 5 —
поверхность с напыленным покры-
тием из бронзы
Рис. 1.48. Распределение частиц по раз-
мерам в пористом покрытии из инко-
нель-600
Классификация пористых покрытий
В работе [1.1.83] предложена классификация пористых покрытий
при кипении. Классификация распространена на покрытия, элемен-
ты которых контактируют между собой и с поверхностью, на кото-
рую они нанесены, и имеют характерный внутренний размер I, соиз-
меримый с радиусом критического зародыша при парообразовании
в названной системе.
В качестве основных параметров выбрана величина, равная отно-
шению характерного внутреннего размера слоя (например, диаметр
поры ///) к внешнему характерному размеру /I/ (толщина слоя)
60
Глава 1
L* = — ,k эффективная пористость £Эф. Последняя характеризует сте-
пень искривления и деформации пор, наличие замкнутых пустот. Ве-
личина эффективной пористости определяется из выражения
( е Y71-еэл)2 ДРэЛ
---эф =----эф,	(1.1.32)
^эф J < 1 — ^э.с у	Д^э.с
где £эс — пористость эталонного слоя, полученного без объемной
усадки и имеющего такие же характерные внутренний и внешний
размеры, как исследуемое покрытие; ДРЭф, АРЭ с “ паДение давления
при течении жидкости с одинаковым расходом через исследуемый и
эталонный пористые слои.
Согласно классификации, пористые покрытия разделены на
одно- и двухпараметрические. Механизм переноса теплоты при ки-
пении на поверхностях с однопараметрическими покрытиями {L* < 1)
принципиально такой же, как и на поверхности без покрытия. Осо-
бенности обусловлены специфичностью формы и распределения по
размерам готовых центров парообразования и термическим сопро-
тивлением покрытия.
Если форма впадин покрытия близка к резервуарной и распреде-
ление способных к активизации впадин охватывает узкий диапазон
размеров, то зарождение и развитие кипения происходит следующим
образом. Сначала в узком интервале перегревов стенки происходит
резкая активизация центров парообразования и коэффициент тепло-
отдачи резко возрастает, а затем с увеличением температурного на-
пора плотность центров слабо увеличивается и коэффициент тепло-
отдачи практически остается постоянным. Для этого типа пористых
покрытий обнаружены значительные эффекты по теплоотдаче.
Двухпараметрические покрытия (Z/L « 1) в зависимости от эф-
фективной пористости могут быть непроницаемыми, полупроница-
емыми и проницаемыми. Отвод теплоты от стенки с проницаемым и
полупроницаемым покрытиями осуществляется теплопроводностью
через пленку жидкости в основании покрытия с последующим испа-
рением и уносом образующегося пара через покрытие, а также теп-
лопроводностью через каркас пористой структуры.
В случае двухпараметрических пористых покрытий обнаруже-
но явление гистерезиса кривой кипения, исследованное детально
С.А. Ковалевым и С.Л. Соловьевым [1.1.84] и С.П. Малышенко [1.1.85].
При значительной толщине покрытия растет сопротивление выходу
пара и возникает внутрислойный кризис теплообмена. Теплоотдача
может быть ниже, чем для поверхности без покрытия.
Глава 1
61
Рис. 1.50. Кривые кипения воды при
атмосферном давлении на медной
пластине: 1 — пластина без покрытия;
2 — пластина со спеченным медным
покрытием толщиной 0,4 мм
Рассмотрим закономерности
влияния однопараметрического
пористого покрытия с высоким
коэффициентом теплопровод-
ности и относительно небольшой
толщины. Это реализуется в слу-
чае кипения воды на медной плас-
тине с медным пористым покры-
тием при атмосферном давлении.
Пористое покрытие нанесено ме-
тодом порошковой металлургии.
Диаметр частиц порошка меди
/ = 0,06 — 0,10 мм. Толщина порис-
того слоя L = 0,4 мм. Пористость
покрытия составляет пример-
но 55%. Плотность вероятности
распределения пор имеет форму,
близкую к прямоугольной, и ох-
ватывает узкий диапазон размеров. На рис. 1.50 представлены кри-
вые кипения для поверхности с пористым покрытием и без покры-
тия. Данные по теплоотдаче с покрытием отнесены к температуре
границы раздела покрытия и поверхности, на которую нанесено пок-
рытие.
Для поверхности с высокотеплопроводным пористым покрытием
установлены следующие закономерности:
—	кипение начинается при температурном напоре менее ГС;
—	кривая кипения имеет две характерные области: в первой из них
наблюдается резкий рост теплового потока, что соответствует скачко-
образной активизации центров парообразования, во второй — коэф-
фициент теплоотдачи примерно постоянный. Таким образом, опыт-
ные данные подтверждают предполагаемое поведение коэффициента
теплоотдачи в зависимости от перегрева стенки;
—	коэффициент теплоотдачи для поверхности с пористым покры-
тием значительно больше (в области малых тепловых нагрузок до 10 раз),
чем для поверхности без покрытия. С ростом АТ влияние пористого
покрытия на теплоотдачу ослабевает, хотя остается заметным;
—	положение кривой кипения не изменилось в течение 500 ч;
—	согласно визуальным наблюдениям при низких температурных
напорах образуется большое количество паровых пузырей небольшо-
го диаметра, отрывающихся с большей частотой, по сравнению с ки-
пением воды на поверхности без покрытия. Отрывной диаметр паро-
вых пузырей с ростом перегрева стенки увеличивается.
62
Глава 1
Проблема заноса пористых покрытий
С течением времени может происходить занос пористых покры-
тий вследствие образования отложений и уменьшение коэффициен-
та теплоотдачи. Этот процесс проявляется в меньшей мере при ки-
пении криогенных жидкостей и в большей мере при кипении воды
и хладонов. Ряд особенностей кипения на поверхности с пористым
покрытием приводит к уменьшению интенсивности образования от-
ложений. К ним относятся понижение температурных напоров, при
которых происходит парообразование, уменьшение отрывных диа-
метров и рост частоты отрыва паровых пузырей.
Проявление этих особенностей приводит к самоочистке порис-
тых покрытий при кипении. В настоящее время известны данные ре-
сурсных испытаний, которые свидетельствуют о стабильности эф-
фекта интенсификации теплоотдачи со временем.
Кипение на поверхности с микрорельефом
В работе [1.1.86] на основе анализа факторов, влияющих на тепло-
отдачу при кипении, предложена поверхность для получения высо-
кой теплоотдачи.
На рис. 1.51 представлена микрофотография поверхности со
столбчатым рельефом. Данный рельеф был получен с помощью элект-
роосаждения металла на поверхности.
Характеристики кипения на гори-
зонтальной трубке с предложенной
поверхностью при кипении в большом
объеме показаны на рис. 1.52 [1.1.86].
Кривые кипения получены для раз-
личных участков трубки. В верхней
части трубки перегрев стенки прак-
тически не зависит от теплового по-
тока. Снижение перегрева стенки с
ростом теплового потока объясняет-
ся протыканием пузыря элементами
теплоотдающей поверхности. Как ус-
тановлено, для гладкой трубы проис-
ходит рост перегрева стенки с ростом
теплового потока, перегрев структу-
рированной поверхности наоборот
остается почти постоянным в области
развитого кипения вследствие того,
Рис. 1.51. Микрофотография по-
верхности с микростолбчатым
рельефом
Глава 1
63
Рис. 1.52. Теплоотдача при кипении
фреона на трубке с нанесенным
микростолбчатым рельефом (О, □,
А) и без рельефа на поверхности
Ж А) : А, ▲ — верхняя образу-
ющая; □, 	— боковая образу-
ющая; О, •	— нижняя образу-
ющая
что растущий пузырь взаимодействует с несколькими элементами
микро столбчатой поверхности.
Интенсификаторы теплообмена микро- и наномасштабов
при конвекции
В настоящее время известны следующие методы снижения гид-
равлического сопротивления:
— изменение свойств жидкости (например, путем введения в нее
полимерных добавок),
— изменение рельефа поверхности (рис. 1.53) [1.1.87].
Рис. 1.53. Различные виды рельефа поверхности: а — жидкость проникает в про-
странство между выступами; б — жидкость не проникает в пространство между
выступами; в — фотография листа лотоса
64
Глава 1
Рис 1.54. Микрофотография поверх-
ности с ультрамалой шероховатостью
двойной кривизны
Капли скатываются с листа ло-
тоса при крайне малом угле накло-
на вследствие особенности релье-
фа его поверхности. Структура
листа лотоса состоит из комбина-
ции двух масштабов: один — 10 нм,
другой — 100 нм. Кроме того, лист
покрыт воском. Комбинация
рельефа поверхности и покрытие
воском создают супергидрофоб-
ность листа лотоса.
В работе [1.1.88] исследовано
гидравлическое сопротивление
при течении воды в канале с поверхностью с ультрамалой шерохова-
тостью двойной кривизны (рис. 1.54). Такая поверхность была изго-
товлена с использованием литографии и ионного травления и имела
покрытие.
На рис 1.55 показана зависимость коэффициента гидравличе-
ского сопротивления от числа Re для гладкой поверхности и поверх-
ности с микрошероховатостью двойной кривизны без покрытия и с
покрытием. Установлено, что коэффициент гидравлического сопро-
тивления в трубах с шероховатостью двойной кривизны и покрыти-
ем ниже, чем в гладких трубах. Для поверхности с высотой шерохо-
ватости 5 мкм и покрытием получено снижение сопротивления на
10% при числе Re = 65000. Снижение сопротивления на 8 % получено
также для мембраны из политетрафторэтилена с порами размером
0,8 мкм при числе Re = 60000.
Рис. 1.55. Зависимость коэффициента гидравлического сопротивления от числа
Re для гладкой поверхности(1); поверхности с микрошероховатостью двойной
кривизны без покрытия (2) и с покрытием (3)
Глава 1
65
В работе [ 1.1.89] исследовано влияние микро- и нанорельефа повер-
хности на краевой угол. Исследованы различные рельефы поверхнос-
ти: микролинейчатый, микростолбчатый, наностолбчатый (рис. 1.56).
Рис. 1.56. Различные рельефы поверхности: а — микролинейчатый; б — микро-
столбчатый; в — наностолбчатый
В работе показано, что увеличение краевого угла на поверхности с
наностолбчатым рельефом составило более 90%. Увеличение угла сма-
чивания на микролинейной поверхности составило 30 — 60% и 60% на
поверхности с микростолбчатым рельефом (рис. 1.57).
Для создания гидрофобных поверхностей в работе [1.1.90] пред-
ложен метод формования плотноупакованных упорядоченных моле-
кулярных слоев ПАВ на внутренней поверхности трубы. Формование
молекулярных слоев осу-
ществляется за счет адсор-
бции ПАВ на поверхности
металла из водных раство-
ров (рис. 1.58).
Измерение углов сма-
чивания поверхности без
покрытия и поверхности,
покрытой слоем ПАВ, по-
казало, что для исследу-
емых образцов смачивание
оказалось минимальным и
не зависящим от величины
исходной шероховатости.
В трубе с адсорбированны-
ми ПАВ на внутренней по-
верхности проведены из-
мерения гидравлического
сопротивления (рис. 1.59).
1 мм
1 мм
тефлон, 0 = 120’
микролинейная
структура, 0= 150*
наностолбчатая
структура, 0 = 160*
микростолбчатая
структура, 0 = 160*
Рис. 1.57. Фотографии капель жидкости на по-
верхностях с различным рельефом
66
Глава 1
Рис. 1.58. Схема расположения
молекул ПАВ на металлической
поверхности при формирова-
нии плотноупакованного гид-
рофобного слоя
В работе показано изменение во времени относительной величи-
ны гидравлического сопротивления в результате сорбции молекул
ПАВ на поверхности трубы. Верхняя кривая на рис. 1.59 соответству-
ет изменению гидравлического сопротивления трубопроводов без
дозирования ПАВ, нижняя — при наличии в потоке молекул ПАВ.
Таким образом, данные свидетельствуют о резком снижении гид-
равлического сопротивления трубопровода при сорбции ПАВ на его
внутренней поверхности. По мнению авторов [1.1.90], сорбция про-
Рис. 1.59. Изменение относительной величины гидравлического сопротивления
в трубах при сорбции молекул ПАВ: ♦ — без дозирования;  — с дозированием
ПАВ
Глава J
67
исходит вплоть до появления упорядочен-
ных слоев ПАВ, сравнимых по толщине с
величиной шероховатости исходной по-
верхности. Предложенный в работе спо-
соб позволяет снизить гидравлическое
сопротивление трубопроводов более чем
на 20 % , при этом он является простым и
экономически выгодным.
В работах [1.1.91, 1.1.92] исследовано
взаимодействие потока жидкости с про-
филированной стенкой (рис. 1.60) и пока-
Рис. 1.60. Взаимодействие
воды с ультрагидрофобной
поверхностью
зано, что при обтекании микропрофилированной поверхности воз-
можно локальное проскальзывание на стенке (рис. 1.61).
Рис. 1.61. Измеренный профиль ско-
рости при обтекании микропрофили-
рованной поверхности
Теплообмен и гидродинамика в мини- и микроканалах
В настоящее время большое внимание уделяется исследованиям
гидродинамики и тепломассопереноса в мини- и микроканалах. Это
связано с тем, что на практике требуется передать большие тепловые
потоки в ограниченном пространстве и объеме.
В каналах с поперечным размером, равным и меньшим капилляр-
ной постоянной, капиллярные силы и стесненность оказывают су-
щественное влияние на течение и теплообмен. При кипении жид-
кости в мини- и микроканалах поперечный размер канала становится
сопоставимым с размером центра парообразования, отрывным ди-
аметром парового пузыря, диаметром капель жидкости. Поэтому за-
кономерности теплообмена, кризиса кипения, структуры потока бу-
дут иными, чем в большом объеме или в обычных каналах. Приклад-
68
Глава 1
ные аспекты рассматриваемой проблемы связаны с перспективой
применения каналов малого и сверхмалого диаметра в промышлен-
ности для интенсификации тепломассопереноса в испарителях-кон-
денсаторах энергетических устройств, новых паровых котлах, тепло-
вых насосах и других устройствах.
В работе [1.1.93] предлагается следующее разделение каналов по
гидравлическим диаметрам:
—	обычные каналы — <2г>3мм;
—	миниканалы — 200 мкм < dr < 3 мм;
—	микроканалы — 10 мкм < dr < 200 мкм;
—	" наноканалы — dT< 10 мкм.
По сравнению с каналами большого размера в каналах малого ди-
аметра заметную роль могут приобретать силы поверхностного натя-
жения и шероховатость поверхности, характерный размер которой
в некоторых случаях становится соизмеримым с диаметром канала.
Эти два фактора могут оказывать заметное влияние на гидродина-
мические и теплообменные процессы в каналах малых размеров.
В работе [1.1.94] исследована гидродинамика в канале кругло-
го сечения диаметром 100 мкм и длиной 64,5 мм. Опыты прове-
дены при течении воды при давлении на входе в рабочий участок
0,2; 1,4; 3,4; 13,7 МПа. Массовая скорость воды изменялась в диапазо-
не от 20 до 4000 кг/(м2-с).
Полученные экспериментальные данные по коэффициенту гид-
равлического сопротивления для воды хорошо согласуются с рас-
считанными по классическим соотношениям (рис. 1.62). Как видно
из графика, переход от ламинарного к турбулентному режиму тече-
ния происходит при Re = 1900—2000. 100 _ I I 111||||	I I 11||||-	I I 11||||	I I I lij't - £ = 64/Re 10 = = 1 = Е	X ^ = 0,3164Re-0 25 |Е 0,1 = \ 0,01 I I I 11 Illi 	Ill	1 1 iiiiiI | ,11.111.11 1	10	100	1000	10000 Re	Рис. 1.62. Зависимость ко- эффициента гидравличе- ского сопротивления от числа Re
Глава 1
69
В работе [1.1.95] измерены потери давления при течении воды в
каналах круглого сечения с гидравлическим диаметром от 50 до
254 мкм, изготовленных из нержавеющей стали и плавленого кварца
(см. таблицу). Эксперименты проводились при условиях: р = 0,1 МПа;
Т = 20°С.
Размеры рабочих участков
Материал РУ	Диаметр канала, мкм	Длина короткого РУ, мм	Длина длинного РУ, мм
	63	30	55
	101	40	61
Нержавеющая	130	42	81,5
сталь	152	48	80
	203	35	61
	254	50	88
	50	28,5	53
	76	32	59
	80	37	63
Плавленый	101	33	62
кварц	150	34	64,5
	205	32	61
	250	31	62
Характерный размер шероховатости — 1,75 мкм			
Экспериментальные данные [1.1.95] в виде зависимости коэффи-
циента гидравлического сопротивления от числа Рейнольдса приведе-
ны на рис. 1.63. Как видно, для значений Re < 500 наблюдается хорошее
совпадение с классической теорией. В интервале чисел Рейнольдса от
500 до 1800 наблюдается переходный режим течения, а при Re > 1800
имеет место развитое турбулентное течение, что подтверждается
согласованием с соотношением Блазиуса. Столь раннее начало пере-
хода от ламинарного к турбулентному режиму течения авторы объяс-
няют заметным влиянием шероховатости поверхности.
Влияние диаметра канала на гидродинамику потока воды изуча-
лось в работе [1.1.96]. Эксперименты проводились в каналах, изготов-
ленных из полированного стекла и кремния. Все экспериментальные
точки хорошо согласуются с формулой Пуазейля. Переход от лами-
нарного к турбулентному режиму течения в микроканалах происхо-
дит при Re = 2000-5-2300, что подтверждает вывод о влиянии на него
шероховатости поверхности.
70
Глава 1
Рис. 1.63. Зависимость коэффициента гидравлического сопротивления для пото-
ка воды в гладких микроканалах
Влияние размеров канала на перепад давления в газожидкост-
ном потоке исследовали в работе [1.1.97]. Рабочие участки были из-
готовлены из плавленого кварца с каналами круглого сечения ди-
метрами 75; 100 и 251 мкм и, соответственно, длиной 60, 85 и 135 мм.
Эксперименты проводились на газожидкостной смеси азота и вод-
ного раствора этанола различной концентрации, а также азота и
дистиллированной воды. Для однофазного потока числа Рейнольд-
са изменялись в диапазоне от 2 до 2000, для газожидкостной смеси
скорость газа — 0,01—7,6 м/с; жидкости — 0,01—1,0 м/с. Для однофаз-
ного потока данные описываются классическими соотношениями.
Ранний переход от ламинарного к турбулентному течению в работе
не наблюдался.
В работе [1.1.98] изучалось течение воды и водовоздушного ади-
абатного потока в прямоугольных каналах шириной 20 мм, высотой
от 0,4 до 2 мм и длиной 230 мм. Для однофазного потока наблюдалось
согласование экспериментальных данных с классическими соотно-
шениями для ламинарного и турбулентного течений. Для двухфазно-
го потока экспериментальные данные с точностью до 20% описыва-
лись моделью, предложенной для труб большого размера.
Режимы течения двухфазного потока фреона R134a в трубе ди-
аметром 2,01 и 4,26 мм при различных давлениях (0,6; 1,0; 1,4 МПа)
Глава 1
71
исследованы в работе [1.1.99]. Выделены шесть режимов течения:
дисперсно-пузырьковый, пузырьковый, снарядный, эмульсионный,
кольцевой и дисперсный. Таким образом, структура двухфазных по-
токов в канале, согласно [1.1.99], соответствует известным представ-
лениям. С уменьшением диаметра канала возрастает влияние сил по-
верхностного натяжения, что приводит к смещению границ режимов
и исчезновению дисперсного режима течения для канала диаметром
2,01 мм.
Результаты исследования режимов течения водовоздушного по-
тока в прямоугольных каналах высотой 1,0; 0,6; 0,3 мм, шириной 12 мм
и длиной 260 мм представлены в работе [1.1.100]. Для первых двух ка-
налов наблюдались такие же режимы течения, как и в обычных тру-
бах: пузырьковый, снарядный, эмульсионный и кольцевой; однако
переходы между режимами течения начинались раньше. При те-
чении же в канале высотой 0,3 мм пузырьковый режим течения не
наблюдался.
В работе [1.1.101] исследовано течение фреонов Р134а и R245fa в
канале диаметром 0,5 и 0,8 мм и выделены четыре режима течения:
пузырьковый, снарядный, эмульсионный и кольцевой. Влияния диа-
метра канала на режимы течения не обнаружено.
В работе [1.1.102] проведено исследование теплообмена при лами-
нарном течении дистиллированной воды в каналах трапецеидально-
го сечения с гидравлическими диаметрами 62,3; 63,1; 114,5; 168,9 мкм.
Диапазон чисел Рейнольдса составлял от 100 до 1500. Удовлетвори-
тельного описания экспериментальных данных численной моделью
удалось добиться, лишь при учете шероховатости поверхности.
Экспериментальное исследование гидродинамики и однофазно-
го теплообмена проведено в работе [1.1.103]. Использовались рабочие
участки с тремя диаметрами: 520; 290 и 172 мкм, в качестве рабоче-
го тела выбрана вода. Диапазон чисел Рейнольдса составлял от 200
др 6000. Полученные экспериментальные данные сравнивались с из-
вестными соотношениями. При ламинарном течении для чисел Рей-
нольдса, меньших 900, наблюдается согласование, для больших Re
экспериментальные данные лежат несколько выше расчетных. При
турбулентном течении экспериментальные данные для всех диамет-
ров находятся в удовлетворительном согласии с известными соотно-
шениями.
Экспериментальное исследование теплообмена при течении в
прямоугольном канале размерами 0,3x12,7x200 мм проведено в работе
[1.1.104]. В качестве рабочей жидкости использовались вода и этанол.
Опыты проведены при следующих параметрах: массовая скорость от
50 до 500 кг/(м2-с), плотность теплового потока до 400 кВт/м2, давле-
72
Глава 1
Рис. 1.64. Изменение коэффициента теплоот-
дачи при течении воды в микроканале длиной
25 мм при изменении его поперечного размера
ние на выходе из рабочего
участка 0,1 МПа. Как обна-
ружено, эксперименталь-
ные данные согласуются с
известными соотношени-
ями.
В работе [1.1.105] ис-
следован теплообмен при
течении воды в прямо-
угольном канале размера-
ми 0,8x2,0x330 мм при мас-
совых скоростях от 50 до
1000 кг/(м2-с) и атмосфер-
ном давлении на выходе из
рабочего участка. Для одно- и двухфазного потока эксперименталь-
ные данные удовлетворительно согласуются с известными соотноше-
ниями в диапазоне чисел Рейнольдса от 700 до 2000.
Экспериментальное исследование гидродинамики и однофазно-
го теплообмена при течении воды в микроканалах проведено в ра-
боте [1.1.107]. На рис. 1.64 и 1.65 представлены полученные данные по
влиянию на теплоотдачу и потери на трение поперечного размера ка-
нала длиной 25 мм при массовых скоростях от 56 до 1170 кг/(м2-с).
Как обнаружено, с уменьшением поперечного размера канала ко-
эффициент теплоотдачи резко увеличивается, и коэффициенты тепло-
отдачи при поперечных размерах, равных 1 мм и 0,06 мм, отличаются
в 20 раз. Потери давления
Рис. 1.65. Потери давления по длине микрокана-
ла при различных тепловых нагрузках
с уменьшением величины
зазора также сильно воз-
растают.
Экспериментальные
данные по теплообмену
при кипении Я318С при
массовых скоростях от 200
до 900 кг/(м2-с) и давлении
0,8 МПа в кольцевом ка-
нале длиной 400 мм и за-
зором 0,95 мм получены в
работе [1.1.108]. Обнару-
жено удовлетворительное
согласование с известны-
ми зависимостями. В этой
же работе приводятся экс-
Глава 1
73
периментальные данные по кипению фреона 7?21 в прямоугольном
канале размерами 1,6x6,3x290 мм. Эксперименты проводились при
давлении 0,25 МПа и массовой скорости 50 кг/(м2 с). В этом случае эк-
спериментальные данные лежат существенно выше расчетных зави-
симостей. Повышение значений коэффициента теплоотдачи объяс-
няется авторами влиянием капиллярных сил.
Анализ и обобщение данных по кипению в миниканалах пред-
ставлены в работе [1.1.106]. Анализировались данные, в которых гид-
равлический диаметр каналов составлял от 400 до 2970 мкм, массовая
скорость — от 50 до 1600 кг/(м2-с), плотность подводимого теплово-
го потока — от 5 до 600 кВт/м2, в качестве теплоносителей исполь-
зовались фреоны ЛИ, Л12, ЛИЗ, Л123, Л124, Л134а, Л141Ь и FC-84. Для
анализа использовалось соотношение Kandlikar, разработанное для
труб большого размера. На основе анализа были сделаны следующие
выводы: для каналов с гидравлическим диаметром, превышающим
1 мм, достигается согласование соотношения с экспериментальными
данными. Для меньших диаметров экспериментальных данных не-
достаточно для анализа и обобщения.
В работе [1.1.109] исследовано кипение в одиночных микроканалах
с различной формой поперечного сечения, но одного гидравлическо-
го диаметра: круглый микроканал диаметром 210 мкм и квадратный
микроканал с поперечным сечением 214 мкм х 214 мкм (рис. 1.66). Тон-
кая пленка оксидов индия и олова нанесена на внешней поверхности
трубок для прямого джоулевого нагрева.
В квадратном микроканале схема изменения структуры потока
более простая: больше ядер зарождения пузырьков и больший коэф-
фициент местного теплообмена при более низком паросодержании.
Это достигается благодаря углам квадратного микроканала, которые
служат центрами образования пузырьков. Углы также способству-
Рис. 1.66. Схема рабочего участка
74
Глава 1
Рис. 1.67. Зависимость ко-
эффициента теплоотдачи
от паросодержания для
квадратных (□) и круглых
(О) каналов при кипении
HCFC123 и массовой скоро-
сти pw = 400 кг/(м2с)
ют формированию жидкостной пленки и образованию контактной
линии (линии стыка) между жидкостью и стенкой, которые стабили-
зируют поток. Местные коэффициенты теплоотдачи снижаются при
повышении паросодержания (рис. 1.67).
На рис. 1.68 показана зависимость числа центров парообразова-
ния от числа кипения для исследованных микроканалов. В квадратном
микроканале число центров нуклеации возрастает с повышением чис-
ла кипения. В круглом микроканале на зависимости количества цент-
ров нуклеации от числа кипения имеется максимум.
На рис. 1.69 показано изменение потерь давления во времени для
квадратных и круглых микроканалов. Обнаружены большие флук-
туации потерь давления как в круглых, так и в квадратных микрока-
налах. Амплитуда колебаний потерь давления составляет примерно
10—15 кПа, что происходит вследствие изменения структуры потока
в микроканалах.
Рис. 1.68 Зависимость числа центров
парообразования от числа кипения для
круглых и квадратных микроканалов:
□ — 214 мм; О — 0,21 мм
Рис. 1.69. Изменение потерь давле-
ния во времени в квадратных (1, 3)
и круглых (2) микроканалах при ки-
пении НС123 и массовой скорости
pw = 400 кг/(м2-с): 1 — q = 39 кВт/м2;
2 — q = 37 кВт/м2; 3 — q = 25 кВт/м2
Глава I
75
Щелевые каналы
Теплосъем при высоких тепловых нагрузках (q > 1 — 2 кВт/см2)
жидкими теплоносителями становится проблематичным из-за огра-
ничений, накладываемых кризисом кипения. Вот почему предложены
способы сохранения гидродинамической устойчивости двухфазно-
го пограничного слоя, исходя из имеющегося запаса по предельному
метастабильному состоянию жидкостей [1.1.110—1.1.112]. Сохранить
эту устойчивость удалось, подвергнув пристенный слой жидкости
воздействию дополнительных сил. Это было достигнуто увеличением
кинетической энергии жидкости за счет принудительной подачи ее
непосредственно в пристенный слой, что существенно ослабило дина-
мический напор пара, вытесняющий жидкость из пограничного слоя.
Анализ этих сил показал, что таким образом может быть достиг-
нут ускоренный отрыв и унос паровых конгломератов от теплооб-
менной поверхности.
При вынужденной конвекции принудительная подача жидкости
осуществляется через щелевую интенсифицирующую вставку, ус-
тановленную на расстоянии от поверхности теплосъема, примерно
равном толщине двухфазного слоя. Щелевые каналы подачи жидко-
сти в ней чередуются со щелевыми каналами отвода двухфазной сре-
ды. Для сведения к минимуму неравномерности, обусловленной дис-
кретностью обтекания поверхности струями из щелевых каналов,
размеры каналов и промежутки между ними выбираются соизмери-
л и I
мыми с величиной капиллярной константы Лапласа b - —------г ,
VtP'-Pj
так как она определяет размер паровых образований у стенки (для
воды b = 2,5 мм). При этом щелевые каналы подачи жидкости выпол-
няются несколько уже, чем значение Ь, а каналы отвода парожидкост-
ной смеси — несколько шире.
В случае кипения фреона-ИЗ на горизонтальной поверхности в
условиях естественной конвекции теплообменная поверхность раз-
бивалась на микроучастки с характерным размером в несколько ка-
пиллярных постоянных (рис. 1.70) [1.1.111]. На каждом таком участ-
ке близко к теплообменной поверхности расположен капиллярный
канал размером поперечного сечения, большим Ь. Образующийся на
теплообменной поверхности пар поступает в расположенные выше
капиллярные каналы, которые объединяются в общий парожидкост-
ный канал. Жидкость опускается к теплообменной поверхности сна-
ружи парожидкостного канала и распределяется вдоль нее между ка-
пиллярными каналами. Таким образом, в режиме кипения устанав-
ливается направленная циркуляция жидкости, причем скорость этой
76
Глава 1
Капиллярная сборка
Рис. 1.70. Влияние капиллярной сборки на критический тепловой поток
циркуляции зависит от разности плотностей жидкости и парожидкост-
ной смеси, а также высоты парожидкостного канала. В результате воз-
никшей циркуляции паровые конгломераты отрываются от теплооб-
менной поверхности и уносятся через капиллярные каналы.
В экспериментах при вынужденном движении воды удалось от-
вести тепловые потоки плотностью до 2,5 кВт/см2, при этом скорость
воды в щелевых каналах была -14 м/с, а давление -3 кг/см2. Тепло-
вая нагрузка на исследуемую поверхность (медное донышко 0 14 мм)
создавалась дуговым плазмотроном. Предварительно с помощью
каллориметрического датчика исследовалось радиальное распреде-
ление теплового потока, которое перед экспериментом было получе-
но также расчетным путем.
При кипении в большом объеме жидкого азота и фреона отводи-
мые от исследуемой поверхности тепловые потоки в 3 и 10 раз, со-
ответственно, превысили критические значения для гладких повер-
хностей.
Таким образом, описанный способ затягивания кризиса теплооб-
мена позволяет увеличить критические тепловые нагрузки в 10 и бо-
лее раз [1.1.111—1.1.112]. Этот способ нашел применение при охлаж-
дении силовой электроники. Он может быть успешно применен при
охлаждении мишеней сильноточных ускорителей, а также в тепло-
вой защите диверторов термоядерных реакторов.
Пористые и микроканальные вставки
Выбор метода интенсификации теплообмена в лазерных зерка-
лах диктуется требованиями к минимизации термического дефор-
мирования отражающей поверхности. В работах [1.1.113—1.1.115]
Глава 1
77
получен исключительно важный для термомеханики лазерных
зеркал и редкий для теории термоупругости результат — найдено
точное решение осесимметричной задачи термоупругости для ко-
нечного цилиндра, нагреваемого и охлаждаемого с торцов. Это ре-
шение позволяет определить термические напряжения и деформа-
ции в дисковых зеркалах, широко применяемых в технологических
лазерах. Из точного общего решения следует ряд принципиальных
и заранее неочевидных выводов, подтвержденных эксперименталь-
но [1.1.115], а именно: для зеркал мощных лазеров, где поглощаемые
тепловые потоки велики, систему охлаждения необходимо разме-
щать не снаружи, а внутри зеркала максимально близко к отража-
ющей поверхности с целью существенного снижения проникающе-
го в жесткую основу зеркала теплового потока. В связи с этим охлаж-
даемое зеркало структурно представляет собой трехслойную конст-
рукцию, состоящую из тонкого отражающего слоя, охлаждаемого
слоя с многоканальной (пористой) структурой и жесткой массивной
основой (рис. 1.71, 1.72).
Рис. 1.71. Многослойные и многозаходные системы охлаждения лазерных зеркал
 мишеней электрофизических установок: а — струйное охлаждение в цилинд-
рических ячейках; б — пористое охлаждение с прямоугольными коллекторами;
в — с цилиндрическими коллекторами
Рис. 1.72. У по ряд очные (регулярные) структуры пористого охлаждаемого слоя
зеркала или мишени
78
Глава 1
К системе охлаждения зеркала предъявляется ряд противоречи-
вых требований: обеспечить высокую теплоотдачу и механическую
жесткость охлаждаемого слоя, а также минимизировать проникно-
вение тепла в толстую основу Разработаны технологии изготовления
охлаждаемого слоя в виде упорядоченной структуры (компланарная,
щелевая, щеточная, вафельная и др.) и хаотической структуры (спе-
ченные порошки, сетки, пружины, порометаллы и др.). Поперечные
размеры каналов для теплоносителя в указанных системах охлажде-
ния могут быть от нескольких миллиметров до долей миллиметра в
зависимости от мощности и назначения установки. В качестве мате-
риалов зеркал используют медь, бериллий, молибден, вольфрам, кар-
бид кремния, инвар и др. [1.1.113, 1.1.114, 1.1.116—1.1.124].
ОБОЗНАЧЕНИЯ:
D f h ReD Rexo Sh sx	—	диаметр углубления, м; —	частота обьемных флуктуаций за углублением, с1; —	глубина углубления, м; —	число Рейнольдса для углубления, V^D/v; —	число Рейнольдса перед углублением, V^/v; —	число Струхаля, fD/Vj —	шаг между углублениями в продольном направле- нии, м;
Sz	— шаг между углублениями в поперечном направле- нии, м;
Tu K,	—	интенсивность пульсаций, %; —	скорость потока перед экспериментальным участ- ком, м/с;
X	— расстояние от передней кромки пластины, продоль- ная координата, м;
8	— толщина пограничного слоя, м;
V A, r, L, H	— кинематическая вязкость потока, м2/с. — глубина лунки; радиус скругления кромки, длина цилиндрической вставки и высота канала;
Nu, Re, Pr Cp	—	числа Нуссельта, Рейнольдса и Прандтля; —	давление и трение, отнесенные к удвоенному ско- ростному напору;
Y <P	—	коэффициент гидравлических потерь; —	плотность пакета лунок; —	угол наклона траншейной лунки.
Глава 7
79
Нижние индексы:
О — параметры потока перед углублением;
00 — параметры потока на плоской пластине;
pl — параметр на стенке.
Список литературы
1.1.1.	Калинин Э.К., Дрейцер Г.А., Копп И.З., Мякочин А.С. Эффективные
поверхности теплообмена. М.: Энергоатомиздат.1998.
1.1.2.	Ашмантас Л.-В.А., Дзюбенко Б.В. Проблемы теплообмена и гидроди-
намики в ядерных энергодвигательных установках космических аппара-
тов. Вильнюс: Pradai, 1997.
1.1.3.	Поляев В.М., Майоров В.А., Васильев Л.Л. Гидродинамика и тепло-
обмен в пористых элементах конструкций летательных аппаратов. М.:
Машиностроение, 1988.
1.1.4.	Справочник по теплообменникам. Т.1.: Пер. с англ./Под ред. Б.С. Петухо-
ва, В.К. Шикова. М.: Энергоатомиздат, 1987.
1.1.5.	Стырикович М.А., Полонский В.С., Циклаури Г.В. Тепломассообмен
и гидродинамика в двухфазных потоках атомных электрических станций.
М.: Наука, 1982.
1.1.6.	Исаченко В.П., Кушнырев В.И. Струйное охлаждение. М.: Энерго-
атомиздат, 1984.
1.1.7.	Галицейский Б.М., Рыжов Ю.А., Якуш Е.В. Тепловые и гидродинами-
ческие процессы в колеблющихся потоках. М.: Машиностроение, 1977.
1.1.8.	Петухов Б.С., Генин Л.Г., Ковалев С.А. Теплообмен в ядерных энерге-
тических установках. М.: Энергоатомиздат, 1986.
1.1.9.	Савельев П.А. Исследование гидродинамики и теплообмена потоков
в винтообразно профилированных трубах: Автореф. дис.... канд. техн,
наук. Рига, 1971.
1.1.10.	Калинин Э.К., Дрейцер Г.А., Ярхо С.А. Интенсификация теплообмена
в каналах. М.: Машиностроение, 1990.
1.1.11.	Ибрагимов М.Х., Номофилов Е.В., Субботин В.И. Теплоотдача и гид-
равлическое сопротивление при винтовом движении жидкости в трубе//
Теплоэнергетика. 1961. № 7. С. 57.
1.1.12.	Каменьщиков Ф.Т., Решетов В.А., Рябов А.А., Поляков В.К., Емель-
янов А.И. Вопросы механики вращающихся потоков и интенсификация
теплообмена в ЯЭУ. М.: Энергоатомиздат, 1984.
1.1.13.	Мигай В.К. Повышение эффективности современных теплообменни-
ков. Л.: Энергия, 1980.
1.1.14.	Kuzma-Kichta Yu.A. Coiled tube (flow and pressure drop and heat transfer
in)//lnt. Encyclopedia Heat and Mass Transfer. New York: CRS Press. 1997.
P. 167-170.
80
Глава 1
1.1.15.	Щукин А.В. и др. Интенсификация теплообмена сферическими выем-
ками//Изв. РАН. Энергетика. 1998. № 3.
1.1.16.	Федоров И.Г., Щукин В.К., Мухачев Г.А., Идиатуллин Н.С. Теп-
лоотдача и гидравлическое сопротивление щелевых каналов со сфе-
рическими выштамповками//Изв. вузов. Авиац. техника. 1961. № 4.
С. 120-127.
1.1.17.	Bernman P.W., Haivey I. К. Golfball aerodynamics//Aeronautical Quarterly.
1976. V. 27. Pt. 2. P. 112-122.
1.1.18.	Piesser K.H. Empirische Gleichungen zur Berechnung der Stoff - und
Waermeuebertragung fuer den Spezialfall der abgenssenen Stroemung//
Int. J Heat and Mass Transfer. 1972. V. 15. P. 2447-2471.
1.1.19.	Афанасьев B.H., Чудновский Я.П. Экспериментальное исследование
структуры течения в одиночной впадине//Вестник МГТУ. Сер. Машино-
строение. 1993. № 1. С. 85-95.
1.1.20.	Кикнадзе Г.И., Гачечиладзе И.А., Олейников В.Г. и др. Механиз-
мы смерчевой интенсификации тепломассообмена//Тр. 1-й Рос. нац.
конф, по теплообмену. М.: Изд. МЭИ. 1994. Т. 8. С. 97-106.
1.1.21.	Кикнадзе Г.И., Краснов ЮЖ., Подымако Н.Ф. и др. Самоорганиза-
ция вихревых структур при обтекании водой полусферической лунки//
ДАН СССР. 1986. Т. 291, №6. С. 1315-1318.
1.1.22.	Гачечиладзе И.А., Кикнадзе Г.И., Краснов ЮЖ. и др. Теплообмен
при самоорганизации смерчеобразных структур//Тр. Минского между-
нар. форума. Проблемные доклады. Секция 1-2. Минск: Наука и техни-
ка, 1988. С. 83-125.
1.1.23.	Кикнадзе Г.И., Олейников В.Г. Самоорганизация смерчеобразных
вихревых структур в потоках газов и жидкостей и интенсификация теп-
ло- и массообмена: Препринт № 227. Ин-т теплофизики СО АН СССР,
1990.45 с.
1.1.24.	Нагога Г.П. Эффективные способы охлаждения лопаток высокотемпе-
ратурных газовых турбин. М.: Изд. МАИ, 1996.100 с.
1.1.25.	Снидекер Р., Дональдсон К. Исследование течения с двумя устой-
чивыми состояниями в полусферической каверне//Ракетная техника и
космонавтика. 1966. № 4. С. 227-228.
1.1.26.	Кесарев В.С., Козлов А.П. Структура течения и теплообмен при обте-
кании полусферического углубления турбулизованным потоком возду-
ха//Вестник МГТУ. Сер. Машиностроение. 1993. № 1. С. 106-115.
1.1.27.	Громов П.Р., Зобнин А.Б., Рабинович М.И., Сущик М.М. Рождение
уединенных вихрей при обтекании сферических углублений//Письма в
ЖЭТФ. 1986. Т. 12, №21. С. 1323-1328.
1.1.28.	Леонтьев А.И. Современные проблемы теплопередачи//Вестник
МГТУ. Сер. Машиностроение. 1993. № 1. С. 54-59.
1.1.29.	Волчков Э.П., Калинина С.В., Матрохин И.П. и др. Некоторые ре-
зультаты экспериментального исследования аэродинамики и теплооб-
мена на поверхности с полусферическими кавернами//Сиб. физ.-техн,
журн. 1992. Вып. 5. С. 3-9.
Гн»? 7
81
1Л.30. Chudnovsky Ya.P., Kozlov A.P., Schukin A.V. et al. Combustion
enhancement and flame stabilization due to vortex generation//AFRC Intern.
Symp. «Combustion Technologies for Improving Productivity and Product
Quality», Sept. 21-24, Chicago, USA. 1997.
1-1-31. Езерский А.Б., Шехов В.Г. Визуализация потока тепла при обтекании
уединенных сферических углублений//Изв. АН СССР МЖГ. 1989. № 6.
С. 161-164.
1-1.32. Александров А.А., Горелов Г.М., Данильченко В.П., Резник В.Е.
Теплоотдача и гидравлическое сопротивление при обтекании поверх-
ностей с развитой шероховатостью в виде сферических углублений//
Пром, теплотехника. 1989. Т. 11, № 6. С. 57-61.
1-1.33. Амирханов Р.Д. Теплообмен и гидродинамика в щелевых каналах с по-
верхностными интенсификаторами: Автореф. дис. ... канд. техн. наук.
Казань, 1996. 16 с.
1-1.34. Арсеньев Л.В., Везломцев С.К., Носов В.В. Интенсификация про-
цесса теплоотдачи в щелевых каналах с генераторами вихрей в систе-
мах кондиционирования воздуха//Сб. Охрана труда и охрана окружа-
ющей среды. Николаев: НКИ, 1988. С. 14-20.
1.1-35. Афанасьев В.Н., Чудновский Я.П. Теплообмен и трение при без-
отрывном обтекании сферических углублений турбулентным пото-
ком воздуха//Вестник МГТУ. Сер. Машиностроение. 1991. № 4. С. 15-
25.
1.1.36. Беленький М.Я., Готовский М.А., Леках Б.М. и др. Эксперименталь-
ное исследование тепловых и гидравлических характеристик теплооб-
менных поверхностей, формованных сферическими лунками//Тепло-
физика высоких температур. 1991. Т 29, № 6. С. 1142-1147.
1-1.37. Беленький М.Я., Готовский М.А., Леках Б.М. и др. Интенсифика-
ция теплообмена при использовании поверхностей, формованных сфе-
рическими лунками//Тез. докл. конф. «Тепломассообмен ММФ-92».
Минск: ИТМО. АНБ, 1992. Т. 1. Ч. 1. С. 90-92.
1-1.38. Гортышов Ю.Ф., Амирханов Р.Д. Теплообмен и трение в каналах со
сферическими углублениями//Сб. «Рабочие процессы в охлаждаемых
турбомашинах и энергетических установках». Казань: КГТУ, 1995. С.
87-90.
1.1-39	. Гортышов Ю.Ф., Олимпиев В.В., Амирханов Р.Д. Расчетное и опыт-
ное моделирование теплообмена и сопротивления в каналах со сфе-
рическими выемками на стенках//Тез. докл. конф. «Тепломассообмен
ММФ-96». Минск: ИТМО АНБ, 1996. Т. 1. Ч. 2. С. 137-141.
1-1.40	. Шанин Ю.И., Афанасьев В.А., Шанин О.И., Емельянов О.С. Интен-
сификация теплоотдачи посредством сферических лунок на стенках ка-
налов//Г1роблемы теплофизики в ядерной энергетике. М.: МИФИ, 1991.
С. 62-66.
1.1.41.	Нагога Г.П., Ануров Ю.М. Результаты модельных и натурных иссле-
дований интенсификации «смерчевым» способом//Тез. докл. 2-й Рес-
публ. конф. «Совершенствование теории и техники тепловой защиты
энергетических устройств». Киев: Наукова думка, 1990. С. 25-26.
82
Глава 1
1.1.42.	Нагога Г.П., Рукин М.В., Ануров Ю.М. Гидравлическое сопротивле-
ние в плоских каналах со сферическими углублениями//Сб. Охлаждае-
мые газовые турбины двигателей летательных аппаратов. Казань: КАИ,
1990. С. 40-44.
1.1.43.	Почуев В.П., Луценко Ю.Н., Мухин А. А. Теплообмен в охлаждае-
мых лопатках высокотемпературных газовых турбин//Тр. 1-й Рос. наци-
ональной конф, по теплообмену. М.: МЭИ, 1994. Т. 8. С. 178-183.
1.1.44.	Туркин А.В., Сорокин А.Г., Брагина О.Н. и др. Интенсификация теп-
лообмена при помощи лунок в плоском канале при низких скоростях
движения воздуха//Тез. докл. конф. «Тепломассообмен. ММФ-92».
Минск: ИТМОАНБ, 1992. Т. 1.4. 1.€. 18-21.
1.1.45.	Афанасьев В.Н., Леонтьев А.И., Чудновский Я.П. Трение и теплооб-
мен на поверхностях, профилированных сферическими углублениями:
Препринт № 1-90. М.: МГТУ им. Н. Э. Баумана.
1.1.46.	Streamlined Surface. Международная заявка PCT/RU92/00106, номер
международной публикации WO 93/20355, 14 1093, Россия. 9 с.
1.1.47.	Козлов А.П., Щукин А.В., Агачев Р.С. Гидродинамические эффекты
от сферических углублений на поверхности поперечно обтекаемого ци-
линдра//Изв. вузов. Авиац. техника. 1994. № 2. С. 27-34.
1.1.48.	Afanasiev V.N., Chudnovsky Ya.P., Kozlov A.P. et al. Hydrodynamic
and heat transfer in case of streamlining of plate surfaces with hemispheric
cavities//lnt. Symp. Heat Transfer Enhancement in Power Machinery.
Moscow, Russia, 1995. Pt. 1 . P. 87-90.
1.1.49.	Клешканов В.И. Технологические способы повышения надежности
и долговечности авиационных гидроагрегатов: Автореф. дис. ... канд.
техн..наук. М., 1989. 16 с.
1.1.50.	Терехов В.И., Калинина С.В., Мшвидобадзе Ю.М. Конвективный
теплообмен на поверхности в области за каверной сферической фор-
мы//Теплофизика и аэромеханика. 1994. Т. 1. № 1. С. 13-18.
1.1.51.	ЩукинА. В., Козлова. П., Дезидерьев С. Г. и др. Конвективный теп-
лообмен за полусферической выемкой в диффузорном канале//Изв.
вузов. Авиац. техника. 1994. С. 24-30.
1.1.52.	Кирпичев М.В., Михеев М.Л. Моделирование тепловых устройств.
М.: Изд-во АН СССР. 1936. 320 с.
1.1.53.	Арсеньев Л.В., Везломцев С.К., Носов В.В. Исследование струк-
туры потока при течении в щелевом канале с генераторами вихрей//
Судостроительная промышленность. Промышленная энергетика,
охрана окружающей среды, энергосбережение судов. 1991. № 5. С. 25-
29.
1.1.54.	Щукин А.В., Козлов А.П., Дезидерьев С.Г. и др. Теплообмен в сфе-
рической выемке//Изв. вузов. Авиац. техника. 1996. № 3. С. 22-26.
1.1.55.	Щукин А.В., Козлов А.П., Дезидерьев С.Г. и др. Влияние положи-
тельного градиента давления на теплообмен в сферическом углубле-
нии//Там же. 1991 № 4. С. 74-78.
1.1.56.	Чудновский Я.П. Интенсификация теплообмена генерацией вихрей:
Автореф. дис.... канд. техн. наук. М., 1990. 170 с.
Глава 1
83
1.1.57.	Кикнадзе Г.И., Гачечиладзе И.А., Алексеев В.В. Самоорганизация
смерчеобразных струй в потоках вязких сплошных сред и интенсифи-
кация теплообмена, сопровождающая это явление. М.: Изд-во МЭИ,
2005. 84 с.
1.1.58.	Веселкин В.Ю. Исследование механизма интенсификации теплооб-
мена на профилированных сферическими углублениями поверхностях:
Автореф. дис.... канд. техн. наук. М., 1995. 199 с.
1.1.59.	Bungov V.V., Isaev S.A., Dilevskaya E.V. Numerical simulation of steady
turbulent flow and transfer in the channel with boundaries covered by
cavities//Heat Transfer Enhancement in Machinery. Int. Symp. Moscow,
Russia, 1995. Pt. 1. P. 130-131.
1.1.60.	Ligrani P. M. Dimple Array Effects on Turbulent Heat Transfer and Flow
Structure Turbulence, Heat and Mass Transfer 5 K. Hanjalic, Y. Nagano and
S. Jakirlic (Editors), 2006. Begell House, Inc.
1.1.61.	Халатов A.A. Теплообмен и гидродинамика околоповерхностных уг-
лублений (лунок). Киев, 2005. 76 с.
1.1.62.	Быстров Ю.А., Исаев С.А., Кудрявцев Н.А., Леонтьев А.И. Числен-
ное моделирование вихревой интенсификации теплообмена в пакетах
труб. СПб: Судостроение, 2005. 398 с.
1.1.63.	Исаев С.А., Леонтьев А.И., Баранов П.А., Усачов А.Е. Бифуркация вихре-
вого турбулентного течения и интенсификация теплообмена в лунке//
Докл. РАН. 2000. Т. 373, № 5. С. 615-617.
1.1.64.	Гачечиладзе И.А., Кикнадзе Г.И., Королев Г.Л. и др. Расчет обте-
кания трехмерных вогнутостей//Совр. проблемы газодинамики и теп-
лообмена и пути повышения эффективности энергетических установок.
Тез. докл. 8-й школы-семинара. М., 1991. С. 38-39.
1.1.65.	Afanasiev V.N., Leontiev A.I., Chudnovsky Ya.P. et al. Measurement
and numerical simulation vortex turbulent flow and heat transfer in spherical
cavity//Refined Flow Modelling and Measurements. Proc. 5th Int. Symp.
Paris, France, 1993.
1.1.66.	Исаев C.A., Чудновский Я.П. Численное исследование теплообмена
и механизмов вихревой динамики при обтекании сферических углубле-
ний//Интенсификация теплообмена. Тр. 1-й Рос. нац. конф, по теплооб-
мену. М.: Изд-во МЭИ, 1994. Т. 8. С. 80-85.
1.1.67.	Исаев С.А., Леонтьев А.И., Усачев А.Е., Фролов Д.П. Численное
исследование струйно-вихревого механизма интенсификации тепло-
массообмена в окрестности сферической лунки на плоскости при об-
текании ее потоком несжимаемой вязкой жидкости с учетом влияния
асимметрии формы, естественной конвекции и нестационарных про-
цессов//2-я Рос.нац. конф, по теплообмену. М., 1998. Т.6.
1-1.68. А.с. 1538190. СССР. Тонкостенная оболочка тепловыделяющего эле-
мента контейнерного типа ядерного реактора/Ю.В. Чушкин, Г.И. Кик-
надзе, О.Е. Коляскин//Б.И. 1990. № 3.
1.1.69.	А.с. 1570181 СССР. Способ обработки цилиндрической поверхности
деталей теплообмена/Кирсанов Г.Н., Ласточкин С.С., Чушкин Ю.В. и
др.//Б.И. 1988. №2.
84
Глава 7
1.1.70.	Кикнадзе Г.И. Запустите смерч в теплообменник//Энергия. 1991. № 6.
С.29-31.
1.1.71.	Кикнадзе Г.И., Крючков И.И., Чушкин Ю.В. Кризис теплоотдачи при
самоорганизации смерчеобразных вихревых структур в потоке теп-
лоносителя: Препринт ИАЭ. № 4841/3. М.: ЦНИИатоминформ, 1989.
29 с.
1.1.72.	Дилевская Е.В., Чудновский Я.П., Михайлов С.Н. Интенсификация
теплообмена на поверхностях охладителей силовых полупроводнико-
вых приборов//Тр. 1-й Рос. нац. конф, по теплообмену. М.: Изд-во МЭИ,
1994. Т. 8. С. 70-75.
1.1.73.	Dilevskaya E.V., Chudnovsky Ya.P., Mikhailov S.N. New method of
augmentation of heat transfer on the surfaces of power semiconductor
devices coolers//Proc. 10th Int. Heat Transfer Confer. Brighton. UK. 1994.
1.1.74.	H. Mueller-Steinhagen etal. Heat transfer enhancement in dimpled tubes//
App. Ther. Eng. 2001. N 21. P. 535-547.
1.1.75.	Кузма-Кичта Ю.А. Методы интенсификации теплообмена. М.: Изд-во
МЭИ, 2001.
1.1.76.	Исаев С.А., Леонтьев А.И., Баранов П.А. и др. Численный анализ
вихревой интенсификации теплообмена в канале с пакетом глубоких
сферических лунок на одной из стенок//Докл. РАН. 2002. Т. 386, № 5.
С. 621-623.
1.1.77.	Исаев С.А., Леонтьев А.И., Кудрявцев Н.А., Баранов П.А., Жуко-
ва Ю.В. Интенсификация вихревого теплообмена в пакете поперечных
труб с упорядоченными траншеями//ИФЖ. 2005. Т. 78, № 1. С. 112-
122.
1.1.78.	Исаев С.А., Леонтьев А.И., Кикнадзе Г.И. и др. Сравнительный ана-
лиз вихревого теплообмена при турбулентном обтекании сферической
лунки и двумерной траншеи на плоской стенке//То же. № 4. С. 1-12.
1.1.79.	Анисимов С. В., Рыжова Е.И., Смирнов Ю.Б. Теплообмен при кон-
денсации азеотропной паровой смеси R-113/H2O на горизонтальных
трубах с ребрами и шипами сложной формы//Тр. 2-й Рос. нац. конф, по
теплообмену. М. 1998. Т. 6.
1.1.80.	А.с. 1237310.1984. Способ получения покрытия на внутренней по-
верхности трубы и устройство для его осуществления/А.С. Комен-
дантов, Ю.А. Кузма-Кичта, Ю.Г. Хасанов, Б.А. Штутман, В.А. Леньков,
А.Т. Воронцов, В.Д. Ляховский//Б.И. 1966. № 22.
1.1.81.	Kuzma-Kichta Yu.A., Komendantov A.S., Bakunin V.G., Bartsch G.,
Goldschmidt R., Stein M. Enchancement of Heat Transferat Boiling with
porous coating Surface//Proc. 3 Europ. Thermal Science Conf. 2000.
Ueidelberg. P. 809-814.
1.1.82.	Гоголин A.A., Данилова Г.Н., Азарсков B.M., Медникова М.Н. Ин-
тенсификация теплообмена в испарителях холодильных машин. М.:
Легкая и пищевая промышленность, 1982.
1.1.83.	Алешин А.А., Кузма-Кичта Ю.А., Москвин В.Н., Сорокин Д.Н. Ис-
следование теплообмена при парообразовании на поверхности с по-
ристым покрытием//ТВТ. 1980. Т. 18. № 5. С. 1098-1101.
Глава 1
85
1.1.84.	Ковалев С.А., Соловьев С.Л. Испарение и конденсация в тепловых
трубах. М.: Наука, 1989.
1.1.85.	Малышенко С.П., Андрианов А.Б. Неравновесные фазовые перехо-
ды при кипении на поверхностях с пористыми покрытиями: Препринт
ИВТАН N1-293. М., 1990.
1.1.86.	Mitrovic J. How to create an efficient surface for nucleate boiling?//lntern.
J. of Thermal Sciences. 2006. № 45. P. 1-15.
1.1.87.	Xue-Mei Li, Reinhoudt D., Crego-Calama M. Whot do we need for
superhyd rophobic surface? A review on the recent progress in the preparation
of superhydrophobic surfaces//J. Chemical Society Reviews. 2007. DO
1:10.1039/b602486f.
1.1.88.	Kazufumi Kaneko and others. Drag Reduction on Ultra Small-Scale
Concave-Convex Surface//Transactions of the Japan Society of Mechanical
Engineers. 2000. № 4.
1.1.89.	Kim J. and Kim C.-J. Nanostructured Surfaces for Dramatic Reduction of
Flow Resistance in Droplet-based Microfluids//Technical Digest, IEEE Conf,
on MEMS, Las-Vegas, Jan. 2002.
1-1-90. Рыженков B.A., Седлов A.C., Рыженков A.B. О возможности сниже-
ния гидравлического сопротивления трубопроводов систем теплоснаб-
жения// Энергосбережение и водоподготовка. 2007. Окт. № 5(49).
1.1-	91. Chang-Hwan Choi, Johan К., Westin A. and Kenneth S. Breuer. Apparent
slip flows in hydrophilic and hydrophobic microchannels//Physics of fluids.
2003. V. 15, N 10.
1132. Jia Ou, Rothstein J. P. Drag Reduction and PIV Measurements of the flow
past Ultrahydrophobic Surfaces//Phys. Fluids, 2005. V. 17.103606.
HI-93. KandlikarS. Fundamental issues related to flow boiling in minichannels
and microchannels//Experimental Thermal and Fluid Science. 2002. N 26.
P. 389-407.
11-94. Kawahara A., Chung P., Kawaji M. Investigation of two-phase flow pattern,
void fraction and pressure drop in a microchannel//lnt. J. Multiphase Flow.
2002. N 28. P. 1411-1435.
1.1-95. Mala Gh., Li D. Flow characteristics of water in microtubes//lnt. J. Heat and
Fluid Flow. 1999. N 20. P. 142-148.
1.1-96. Guo Z. Characteristics of microscale fluid flow and heat transfer//! MEMS.
In: Proceedings of the Int. conf, on Heat Transfer and Transport Phenomena
in Microscale, Banff, Canada, 2000. P. 24-31.
1.1-97. Kawahara A., Sadatomi M., Okayama К., Kano K. Pressure drop for
gas-liquid two-phase flow in microchannels - effects of channel size and
liquid properties//3rd Int. Symposium on Two-Phase Flow Modelling and
Experimentation, Pisa, 22-24 Sept., 2004.
1.1.98.	LeeH., LeeS. Pressure drop correlationsfortwo-phaseflowwithin horizontal
rectangular channels with small heights//lnt. J. Multiphase Flow. 2001. N 27.
P. 783-796.
UI-99. Chen L., Tian Y., Karayiannis T. R134A flow patterns in small diameter
tubes//3rd Int. Symposium on Two-Phase Flow Modelling and Expe-
rimentation, Pisa, 22-24 Sept., 2004.
86
Глава 1
1.1.100.	Qu J. Experimental study on gas-liquid two-phase flow regimes in rectangu-
lar channels with mini gaps//lnt. J. Heat and Fluid Flow. 1999. N 20. P. 422-
428.
1.1.101.	Revellin R., Thome J. Experimental investigation of R-134a and R-245fa
two-phase flow in microchannels for different flow conditions//!bid. 2007.
N 28. P. 63-71.
1.1.102.	QuW., MalaGh. M., Li D. Heat transfer for water flow in trapezoidal silicon
microchannels//lnt. J. Heat and Mass Transfer. 2000. N 43. P. 3925-3936.
1.1.103.	Bucci A., Celata G., Cumo M., Serra E., Zummo G. Fluid flow and single-
phase flow heat transfer of water in capillary tubes//First Int. Conf, on Mic-
rochannels and Minichannels, Rochester, New York, USA. April 21-23, 2003.
1.1.104.	Diaz M., Schmidt J. Experimental investigation of transient boiling heat
transfer in microchannels//lnt. J. Heat and Fluid Flow. 2007. N 28. P. 95-102.
1.1.105.	Shuai J., Kulenovic R., Sobierska E., Mertz R., Groll M. Flow boiling
heat transfer in a vertical narrow channel//3rd Int. Symposium on Two-Phase
Flow Modelling and Experimentation, Pisa, 22-24 Sept., 2004.
1.1.106.	Kandlikar S., Steinke M. Flow Boiling Heat Transfer Coefficient in Mini-
channels - Correlation and Trends//12th Int. Heat Transfer Conf. Grenoble,
France. Aug. 2002. P. 1178.
1.1.107.	Satish G., Kandlikar S., William J. Grande Evaluation of Single Phase
Flow in Microchannels for High Heat Flux Chip Cooling—Thermohydraulic
Performance Enhancement and Fabrication Technology//Heat Transfer
Engin. 2004. V. 25(8). P. 5-16.
1.1.108.	Накоряков B.E., Кузнецов В.В. Тепломассообмен при фазовых пе-
реходах и химических превращениях в микроканальных системах/Др.
РНКТ-4. 2006. Т. 1. С. 33-37.
1.1.109.	Tzu-Hsiang Yen, Masahiro Shoji et al. Visualization of convective boiling heat
travsfer in single Micro-conduits with different Shapes of cross sections//
Intern. Confer, on Microchannels and Minichannels. June 13-15, 2005.
Toronto, Ontario, Canada.
1.1.110.	Свириденко И.П. и др. Разработка конструкции интегральной линейки
лазерных диодов с использованием для жидкостного охлаждения ка-
пиллярно-пористой структуры//Докл. на Минском межд. семинаре «По-
лупроводниковые лазеры и системы на их основе», 22-24 июня 1999 г.
1.1.111.	Свириденко И.П. и др. Способы затягивания кризиса теплообмена в
большом объеме и при вынужденном движении/Др. 1-й Российской
нац. конф, по теплообмену. Т. IV. 1994. С. 214.
1.1.112.	Свириденко И.П. и др. Тепло- и гидравлические исследования жид-
кометаллической пористой тепловой защиты энергонапряженных
конструкций/Др. VI Всероссийской конф. «Инженерные проблемы тер-
моядерных реакторов». Спб., 1997. С. 163 .
1.1.113.	Харитонов В.В. Теплофизика лазерных зеркал. М.: МИФИ, 1993.152 с.
1.1.114.	Субботин В.И., Колесов В.С., Кузьмин Ю.А., Харитонов В.В. и др.
Точное решение пространственной задачи термоупругости для конеч-
ного цилиндра//Докл. АН СССР. 1988. Т. 301, № 6. С. 1380-1384.
1.1.115.	Харитонов В.В. и др. Термические деформации охлаждаемых диско-
вых зеркал технологических лазеров: измерение и расчет/ДВТ. 1996.
Т. 34, №3. С. 419-422.
Глава 1
87
1.1.116.	Харитонов В.В. Температурная зависимость критериев стабильности
лазерных зеркал//Физика и химия обработки материалов. 1984. № 2.
С.139-141.
1.1.117.	Кузьмин Ю.А., Харитонов В.В. и др. Предельная мощность локально-
го источника тепла на поверхности многослойной стенки с внутренним
охлаждением/ДВТ. 1986. Т. 24, № 5. С. 948-956.
1.1.118.	Харитонов В.В. и др. Сравнение точного и приближенного выражений
для расчета осесимметричных термических перемещений конечного
цилиндра//Инж.-физ. журн. 1989. Т. 56, № 5. С. 857.
1.1.119.	Кузьмин Ю.А., Плаксеев А.А., Харитонов В.В. и др. Нестационар-
ный термический изгиб многослойных пластин с внутренним охлажде-
нием/Дам же. 1989. Т. 57, № 6. С. 1005-1010.
1.1.120.	Субботин В.И., Харитонов В.В. Теплофизика охлаждаемых лазерных
зеркал/ДВТ. 1991. Т. 29, № 2. С. 365-375.
1.1.121.	Харитонов В.В. Теплоотдача оребренной мишени при локальном на-
гревании мощным электронным пучком//Изв. АН СССР. Энергетика и
транспорт. 1991. № 4. С. 144-151.
1.1.122.	Тарутин Д.Ю., Харитонов В.В. Точные выражения для термических
деформаций охлаждаемых зеркал при осесимметричном освещении//
Оптико-механич. пром. 1991. № 12. С. 6-9.
1.1.123.	Харитонов В.В. и др. Тепловые режимы охлаждаемых медных мишеней
при интенсивном локальном нагреве/ДВТ. 1991. Т. 29, № 5. С. 941-948.
1.1.124.	Харитонов В.В. и др. Расчетная оптимизация микроканальной си-
стемы охлаждения силовых лазерных зеркал/Дам же. 1993. Т. 31, № 1.
С. 69-72.
12.	ЗАКРУТКА ПОТОКА В ТРУБАХ И ПУЧКАХ ТВЭАОВ И ТРУБ
Интенсификация теплоотдачи с помощью закрученной ленты
При закрутке потока лентой в поперечном сечении происхо-
дят перетекания от периферии к центру в результате градиен-
та давления (рис. 1.73). Жидкость из пограничного слоя проника-
ет (показано стрелками) в ядро потока. Эти
движения приводят к возникновению че-
тырех вихревых областей, которые способ-
ствуют усилению обмена и совместно с действи-
ем центробежных сил уменьшают толщину пог-
раничного слоя. Кроме того, вихревое смешение
(вводит к возникновению турбулентного тече-
кя при меньших числах Re.
Таким образом, повышение теплоотдачи при
закрутке потока с помощью ленты обусловлено
«зедующим:
—	увеличением пристеночной скорости;
Рис. 1.73. Схема об-
разования вторичных
течений в трубе с за-
крученной лентой
88
Глава 1
—	перестройкой потока и появлением вторичных течений и
вихрей;
—	повышением турбулентности потока.
Закрутку потока можно также осуществить с помощью при-
стенных завихрителей. При использовании пластинчатых спираль-
ных завихрителей турбулентность в пристенном слое повышается
вследствие закрутки и срыва потока. Оптимальные размеры плас-
тинчатых завихрителей составляют l/d = 3,5—4; h/d = 0,2.
Рассмотрим закономерности влияния закрученной ленты, уста-
новленной плотно в трубе, на теплоотдачу и гидравлическое сопро-
тивление. В работе [1.2.1] установлена зависимость отношения числа
Nu в случае закрутки потока воды к числу Nu0 для прямолинейного
потока от величины, обратной коэффициенту закрутки ленты. Рабо-
чий участок — труба с внутренним диаметром 12 мм. Площадь сече-
ния ленты 12x1 мм2. Коэффициент закрутки ленты у равен отноше-
нию длины участка /, на котором происходит поворот ленты на 360°, к
внутреннему диаметру трубы d. В качестве определяющей выбрана
средняя температура воды. В числе Nu за определяющий размер взят
гидравлический диаметр канала. Установлено, что закрутка потока
приводит к повышению теплоотдачи на 33% при у = 8 по сравнению
с прямолинейным течением.
Для расчета теплоотдачи предложена зависимость
Nu = Nu0K,	(1.2.1)
где
Nu0 = 0,021 Re0,8 Рг0-43 (Pr/PrJ0-25;
К = l+5652Re0,5d/Z.
Формула (1.2.1) справедлива в диапазоне 0 < D/1 < 0,125.
Повышение теплоотдачи на 33% сопровождается ростом гидрав-
лического сопротивления на 70—80%.
В работе [1.2.1] установлена зависимость коэффициентов гидрав-
лического сопротивления в случае закрученного и прямолинейно-
го потока от величины, обратной коэффициенту закрутки ленты (у).
При (1/у) < 0,05 гидравлическое сопротивление не зависит от закрут-
ки потока. При увеличении 1/у гидравлическое сопротивление воз-
растает и его можно определить по формуле
= ^(1+2,ЗОу’4),	(1.2.2)
где Ёф — коэффициент гидравлического сопротивления для прямоли-
нейного потока.
Конвективный теплообмен в канале с закруткой потока определя-
ется двумя составляющими. Одна связана с трением, другая с вихре-
вым смешением вследствие тангенциальной составляющей скорости.
Глава 1
89
Влияние закрученной ленты на
теплоотдачу и гидравлическое соп-
ротивление при числе Re = 34О4 по
данным различных исследований
иллюстрируется рис. 1.74 [1.2.2]. Ко-
эффициент К характеризует зак-
рутку потока:
I = 3,14.
(nd//)2
к -----------у , где
l+(7id//)2
По вертикали на рис. 1.74 отло-
жены отношения чисел Нуссельта
и коэффициентов гидравлического
Рис. 1.74. Зависимость отношения
чисел Нуссельта в случае закручен-
ного и прямолинейного потока от
коэффициента К, характеризующе-
го закрутку потока, по данным раз-
личных исследований
сопротивления для закрученного и
прямолинейного потока. С ростом К
отношение чисел Nu увеличивается,
при К = 0,5 теплоотдача увеличивается на 25 — 75%, коэффициент гид-
равлического сопротивления — в два—три раза. Разброс данных по
теплоотдаче и гидродинамике вызван тем, что в различных исследова-
ниях могли быть различными длина
участка стабилизации потока, ше-
роховатость трубы и лент, шаг скру-
ченной ленты.
На рис. 1.75 сравниваются харак-
теристики различных закручива-
ющих устройств в виде отношения
чисел Nu (1, 2, 3) и коэффициентов
гидравлического сопротивления (4,
S. 6) для каналов с интенсификато-
ром теплосъема и без него. Кривые
1 и 4 соответствуют использованию
спиральной накатки, кривые 2, 5 —
закрученной ленты, кривые 3, 6 —
пластинчатого завихрителя [1.2.3].
Как показывает сравнение,
наибольшее повышение теплоотда-
Рис. 1.75. Изменение отношения чи-
сел Нуссельта (1, 2,3) и коэффициен-
тов гидравлического сопротивления
(4,5,6) от числа Re: 1,4 — спиральная
накатка; 2, 5 — закрученная лента; 3,
6 — пластинчатый завихритель
чи получено для пластинчатого завихрителя, однако при наибольшем
росте коэффициента гидравлического сопротивления.
Особенности гидродинамики в змеевиках
Змеевики обеспечивают существенную интенсификацию тепло-
отдачи по сравнению с прямыми трубами и компактность теплооб-
иенных поверхностей.
90
Глава 1
Ось змеевика
Рис. 1.76. Вторичное
течение в спираль-
ной трубе
Течение жидкости в криволинейных кана-
лах, в частности в спиральных трубах, происхо-
дит под действием сил инерции, направленных
перпендикулярно оси потока. На более быстрые
частицы, движущиеся в середине трубы, дейст-
вует большая центробежная сила, чем на ме-
нее быстрые частицы жидкости вблизи стенки.
В результате жидкость в центральной части тру-
бы движется к наружной образующей, а вблизи
стенки — вдоль нее по направлению к внутренней
образующей. Таким образом, в трубе возникает
вторичное течение в виде пары симметричных
вихрей в поперечном сечении (рис. 1.76). На рис. 1.77 и 1.78 представле-
ны рассчитанные распределения скоростей при Re = 2-105; dmin/d = 24
(d — диаметр трубы, равный 0,03 м; dmin — диаметр спирали). Распре-
деление относительной скорости осевого течения w* = w/wQ, где w —
Рис. 1.78. Распределение относительной
скорости вторичных течений при числе
Re = 2105 и отношении диаметров на-
вивки спирали и трубы, равном 24
Рис. 1.77. Распределение отно-
сительной скорости осевого
течения при числе Re = 2-105 и
отношении диаметров навивки
спирали и трубы, равном 24
локальная продольная скорость; v/Q — продольная скорость на оси
трубы) в спиральной трубе характеризуется тем, что максимум w‘ на
кривой находится вблизи наружной образующей. Относительная ско-
рость вторичных течений v* = v/ v0 (v — локальная скорость вторичных
течений, v0 — скорость вторичных течений на оси) в ядре потока пос-
тоянная, и основное изменение v* происходит вблизи стенки.
Теплоотдача в спиральной трубе
Средняя теплоотдача при ламинарном течении в спиральной тру-
бе рассчитывается по формуле
№л = 0,06Re07Pr043(P^/Prc)0,25(dmin/d)018,	(1.2.3)
Глава 7
91
где Re = wd/v; Nu = ad/X; w — осевая скорость; d — диаметр тру-
бы; a — средний по периметру трубы коэффициент теплоотдачи;
л — коэффициент теплопроводности жидкости; v — кинематиче-
ский коэффициент вязкости; Рг — числа Прандтля, определяемые
при температуре жидкости и стенки.
Среднее число Нуссельта при турбулентном течении для спираль-
ных труб
NUT = Nuof(dmin/d),	(1.2.4)
где Nu0 — среднее число Нуссельта при течении в прямой трубе сре-
ды с числом Рг = 0,7 — 2 определяется уравнением
Nu0 = 0,023Re°’8Pr0'4.	(1.2.5)
Значение функции f(dmin/d) определяется на основе данных опы-
тов.
При турбулентном течении в спиральной трубе распределение
коэффициента теплоотдачи по периметру существенно неоднород-
ное. Неравномерность распределения коэффициента теплоотда-
чи по периметру трубы вызвана неоднородностью распределения
скорости и температуры потока по его сечению. Кроме того, неод-
нородность распределения температуры стенки по периметру тру-
бы может вызвать значительные перетоки тепла от внутренней об-
разующей к наружной и привести к изменению теплоотдачи. На
рис. 1.79 представлено распределение числа Нуссельта по периметру
спиральной трубы (d . /d = 16) с вертикальной осью навивки при
Re = 2-104, рассчитанное при реше-
нии сопряженной задачи по мето-
дике МЭИ (линия 1) [1.2.4].
Как видно из рисунка, интен-
сивность теплоотдачи в окрест-
ности наружной образующей
45е < ср < 45°) примерно постоян-
ная. По мере приближения к внут-
ренней образующей теплоотдача
уменьшается. Отношение коэффи-
циентов теплоотдачи для наруж-
ной и внутренней образующей со-
ставляет около трех. Коэффициент
НЕНлоотдачи в окрестности внут-
ренней образующей змеевика при-
мерно совпадает с величиной а для
римой трубы (линия 2).
Рис. 1.79. Распределение числа Нус-
сельта по периметру спиральной тру-
бы при числе Re = 2-104 и отношении
диаметров навивки спирали и трубы,
равном 16: 1 — спиральная труба;
2 — прямая труба
92
Глава I
Механизм интенсификации теплоотдачи в спиральной трубе
Анализ имеющихся представлений [1.2.2—1.2.5] показывает, что
интенсификация теплоотдачи вследствие закрутки потока в змееви-
ке обусловлена:
—	повышением градиентов скорости около стенки трубы;
—	перетеканием более горячего теплоносителя с меньшей плот-
ностью в результате возникновения вторичных течений в централь-
ной зоне потока. Этот эффект интенсифицирует теплоотдачу при
нагреве теплоносителя и ухудшает ее при охлаждении;
—	возникновением и развитием вихревых структур, зоны с дву-
мерными и трехмерными вихрями с противоположным направле-
нием вращения под воздействием центробежных сил в криволиней-
ных каналах. Это приводит к дополнительной турбулизации всего по-
тока, росту теплоотдачи и гидравлического сопротивления. Наличие в
потоке макровихрей, охватывающих все течение, приводит к сущест-
венной неравномерности распределения теплоотдачи по периметру
канала.
Интенсификация теплообмена в витых трубах
Рис. 1.80. Труба с трех-
ходовой винтовой на-
Метод интенсификации теплообмена в витых трубах деталь-
но исследовал Б.В. Дзюбенко [1.2.5]. Для усиления эффекта интен-
сификации теплообмена предложено использовать витые трубы
трехлопастного профиля, имеющие большую жесткость (рис. 1.80).
Витая труба трехлопастного профиля может рассматриваться как
круглая труба с трехходовой винтовой накаткой. При этом высту-
пы внутри трубы наряду с закруткой допол-
нительно турбулизируют поток за счет вих-
реобразования в тонком пристенном слое.
По существу, в витой трубе сочетаются пре-
имущества двух методов интенсификации
теплообмена, а именно закрутки потока и на-
катки.
При течении в витых трубах с интенсифи-
каторами теплосъема коэффициент гидрав-
лического сопротивления растет за счет об-
разования в пристенном слое периодических
областей отрывного течения. Уменьшение ко-
эффициента гидравлического сопротивления
в. витых трубах по сравнению с круглыми (как
гладких, так и с интенсификаторами тепло-
Глава J
93
съема) при Re>5000 связано с тем,
что на выпуклых и вогнутых частях
профиля витой трубы возникают
области с повышенной и понижен-
ной скоростью.
Теплогидравлическую эффек-
тивность поверхностей с интен-
сификаторами теплосъема можно
оценить, рассмотрев соотношения
между ростом теплоотдачи и коэф-
фициента гидравлического сопро-
тивления (рис. 1.81). При этом от-
ношение чисел Нуссельта растет с
уменьшением числа Re. Витая труба
с винтовой накаткой (линия 2) поз-
воляет интенсифицировать тепло-
обмен по сравнению с гладкой ви-
той трубой примерно в 1,9 раза при
Re = 10000. Однако с уменыпени-
Рис. 1.81. Изменение отношения
чисел Нуссельта (1, 2, 3) и коэффи-
циентов гидравлического сопро-
тивления (4, 5, 6) при течении воды
в витой трубе: технически гладкой,
с винтовой и кольцевой накаткой
ем числа Re этот эффект ослабляется. Витая труба с кольцевой на-
каткой (линия 3) позволяет увеличить интенсивность теплообмена в
2,2 раза по сравнению с гладкой витой трубой. Труба с винтовой на-
каткой (трехлопастная витая труба) (линия 5) благодаря движению
потока в пристенном слое по винтовым траекториям имеет меньшее
гидравлическое сопротивление, чем труба с кольцевой накаткой (ли-
ния 6). Для круглой трубы с кольцевой накаткой получен наибольший
рост теплоотдачи при Re = 10000 (отношение чисел Нуссельта рав-
но 3) при отношении коэффициентов гидравлического сопротивле-
ния 2,65.
Пучки витых твэлов и труб
Выбор метода интенсификации теплообмена определяется при-
кладными целями и условиями и базируется на изучении структуры
турбулентного потока в конкретных типах каналов и ее направлен-
ном изменении. Такая постановка задачи диктуется необходимо-
стью создания теплообменных аппаратов, к которым предъявляют-
ся высокие требования по массогабаритным характеристикам и за-
тратам мощности на прокачку теплоносителя. Важной проблемой яв-
ляется надежное дистанционирование труб или тепловыделяющих
стержней в теплообменных аппаратах и устройствах, а также хоро-
шее перемешивание потока в межтрубном пространстве для вырав-
94
Глава 1
Рис. 1.82. Теплообменный аппарат с
продольным обтеканием витых труб:
1 — витая труба; 2 — трубная доска;
3 — кожух; 4 — днища
нивания неоднородностей темпе-
ратур и скоростей при его нагреве.
Одновременное решение этих про-
блем, наряду с интенсификацией
теплообмена, может быть достиг-
нуто при продольном и поперечном
обтекании плотноупакованных
пучков витых труб (рис. 1.82—1.84),
поперечное сечение которых име-
ет овальную форму или форму
прямоугольника со скругленными
углами [1.2.6—1.2.16]. В этих пучках
возникают упорядоченные вих-
ревые структуры, приводящие к
струйному натеканию теплоноси-
теля на поверхность теплообмена и дополнительной турбулизации
потока, а возникающие вихревые структуры и конвективные потоки
существенно интенсифицируют тепло- и массообмен между сосед-
ними ячейками и в масштабе пучка витых труб [1.2.17—1.2.22].
Использование метода интенсификации тепло- и массообмена пу-
тем закрутки потока позволило решить проблему создания высоко-
температурных тепловыделяющих сборок (ТВС) газоохлаждаемого
гетерогенного ядерного реактора, предназначенного для энергодви-
гательной установки (ЯЭДУ) космических аппаратов [1.2.22, 1.2.23].
Твэлы и ТВС реактора ЯЭДУ должны обладать высокой надежностью
и способностью работать длительное время при высоких температу-
рах и плотностях теплового потока в водородной среде при много-
кратных сменах режима работы с двигательного на энергетический
Рис. 1.83. Теплообменный аппарат с поперечным обтеканием витых труб: 1 — ви-
тая труба; 2 — трубная доска; 3 — щелевой канал между трубами; 4,5 — коллекто-
ры подвода и отвода теплообменивающихся сред
Глава /
95
и обратно. Для обеспечения темпе-
ратуры теплоносителя на выходе
из ТВС на уровне 3000—3100 К твэ-
лы изготавливаются из карбидов
тугоплавких металлов [1.2.23]. Для
частичного выравнивания поля
энерговыделения осуществляется
концентрационное профилирова-
ние загрузки урана-235 по радиусу
и длине ТВС, для чего твэлы дела-
ются разрезными по длине. Витые
твэлы упираются торцами друг в
друга и размещаются в теплоизо-
лированной обойме с опорной (вы-
ходной) решеткой и системой вы-
равнивающих решеток на входе.
Перед нагревными секциями (ак-
Рис. 1.84. Теплообменный аппарат
с закрученным пучком витых труб:
1 — кожух; 2 — трубная доска; 3 — за-
крученный пучок витых труб; 4 — ви-
тая труба; 5 — прямой круглый конец
трубы; 6,7 — патрубки; I —IV — ряды
труб в пучке
тивной зоной ТВС) размещаются элементы торцевого отражателя и
радиационной защиты, малая пористость которых приводит к нате-
канию потока теплоносителя на пучок твэлов в виде системы струй
малого диаметра (рис. 1.85). Неравномерности полей скорости и тем-
пературы, сформированные входными узлами ТВС и неравномер-
ным полем тепловыделения, выравниваются при обтекании потоком
теплоносителя пучков витых твэлов за счет межканального переме-
шивания и выравнивающего действия гидравлического сопротивле-
ния пучка.
Требования технологичности, безопасности, надежности и удобс-
тва в эксплуатации являются определяющими при выборе методов
интенсификации тепло- и массобмена, в том числе и метода закрут-
ки потока.
Проведенное численное моделирование переходных процессов
в реакторе ЯЭДУ позволило определить оптимальные законы изме-
нения реактивности реактора для обеспечения быстрого перехода с
энергетического к двигательному режиму работы и обратно при ус-
ловии выполнения ограничения по ядерной безопасности и термо-
прочности витых твэлов из карбидов тугоплавких металлов [1.2.21,
1.2.22].
Выполненные экспериментальные и теоретические исследования
полей скорости и температуры позволили выбрать варианты проточ-
ной части ТВС ЯЭДУ, при которых обеспечивается благоприятный
теплосъем с твэлов всех секций при обеспечении заданных выход-
ных параметров теплоносителя (рис. 1.85).
96
Глава 1
Рис. 1.85. ТВС с витыми стержневыми твэлами:
а — схема ТВС: 1 — радиационная защита; 2 — отражатель; 3,12 — решетки; 4, И,
13 — корпус; 5 — витые твэлы; 6, 9 — пружины; 7, 10 — фиксаторы блоков актив-
ной зоны; 8 — тепловая изоляция;
б — поперечное сечение пучка твэлов с вытеснителями: 1 — 3 — номера зон с раз-
личной концентрацией урана-235;
в — поле энерговыделения по радиусу ТВС: 1 — 3 — поля энерговыделения для
входных, центральных и выходных нагревных секций (пучков) соответственно;
4 — расчетное поле энерговыделения
Применение витых труб в теплообменных аппаратах (ТА) поз-
воляет существенно уменьшить их массу и габариты и, следова-
тельно, металлоемкость и стоимость изготовления, а за счет гаран-
тированного взаимного касания витых труб в плотных пучках (см.
рис. 1.82) — существенно снизить вероятность возникновения вибра-
ций и повысить надежность. Кроме того, интенсификация массооб-
мена в пристеночном слое потока внутри витых труб и в межтрубном
пространстве пучка позволяет существенно снизить интенсивность
образования отложений на теплопередающих поверхностях и расхо-
ды на периодическую очистку ТА. ТА с витыми трубами для пищевых
производств имеют преимущество перед ТА с трубами, оснащенны-
ми интенсификаторами теплообмена в виде выступов или канавок
различной формы, поскольку пучки витых труб имеют гладкую теп-
лопередающую поверхность и постоянную по длине ТА площадь про-
ходного сечения, что позволяет легко удалять с теплопередающей по-
Глава 1
97
ерхности отложения путем мойки, а при производстве шампанских
вин предотвратить выделение газа из вина.
К особенностям ТА пищевых производств следует отнести и тре-
бование малых перепадов давления, и, соответственно, малых ско-
ростей течения пищевых продуктов. Так, при производстве шам-
панских вин это требование связано с необходимостью сохранить
качество продукта при его термической обработке, а при произ-
водстве маргарина, растительных масел и жиров обуславливается
ж условиями работы ТА в составе технологической линии. Поэтому
в ТА пищевых производств обычно реализуется ламинарный или
ереходный режим течения при числах Рейнольдса Re « 600—3000.
Именно в этом диапазоне чисел Рейнольдса витые трубы характе-
ризуются наибольшей эффективностью по сравнению с другими
теплопередающими поверхностями, что подтверждается сравни-
тельным анализом при помощи метода эффективных параметров
|1_2.22, 1.2.24].
Для сопоставления теплогидравлической эффективности пуч-
ов витых труб с пучками гладких круглых труб и круглых труб с
вальцевой накаткой и другими поверхностями был разработан ме-
тод эффективных параметров, согласно которому определялись за-
висимости эффективного числа Нуссельта Nueff от эффективного
числа Рейнольдса КееЯдля каждого из рассматриваемых видов тече-
ния (рис. 1.86). Метод эффективных параметров основан на сравне-
нии площадей теплопередающих поверхностей в теплообменниках,
рассчитанных на равные значения основных рабочих параметров:
тепловой мощности Q = idem', мощности на прокачку теплоносителя
М= idem; расхода теплоносителя G = idem [1.2.23].
Вас. 1.86. Сравнение эффективности пучков витых, круглых и накатанных труб:
«12- витые трубы с Fr = 64 и 232 соответственно; 3 — круглые трубы; б: 1 —
вне трубы, 2 — круглые трубы; 3 — накатанные трубы
98
Глава 1
При этом эффективные числа Рейнольдса и Нуссельта вводятся в
виде:
1
4 Nu <£„
(1.2.6)
Nue//=Nu——,
^eq
(1.2.7)
где р — произвольная постоянная с размерностью длины, которую
удобно выбрать равной 1 м. Выражения (1.2.6) и (1.2.7) позволяют срав-
нивать теплогидравлическую эффективность теплопередающих по-
верхностей на основе зависимостей Nue// от Ree//, которые можно
получить в результате обработки экспериментальных данных, пред-
ставленных в произвольной форме Nu = Nu(Re), = ^( Re). Тогда ра-
венство эффективных чисел Рейнольдса будет означать равенство
основных рабочих параметров (G, Q, N — idem), а отношение эффек-
тивных чисел Нуссельта будет обратно пропорционально отноше-
нию площадей теплопередающих поверхностей. Чем выше значение
эффективного числа Нуссельта при заданном значении эффективно-
го числа Рейнольдса, тем выше теплогидравлическая эффективность
рассматриваемой теплопередающей поверхности.
Как видно из рис. 1.86, в области малых чисел Ree//(Ree/f< 5-Ю4),
соответствующей области малых Re, пучки витых труб характери-
зуются большей теплогидравлической эффективностью по сравне-
Рис. 1.87. Влияние закрутки потока на теп-
логидравлическую эффективность при тече-
нии внутри витых труб: 1 — 3 — витые трубы с
s/d = 6,2, 8,2 и 12,2; 4 — круглая труба
нию с гладкими круглыми
трубами и круглыми тру-
бами с накаткой. При этом,
чем больше закрутка пото-
ка (чем меньше шаг закрут-
ки труб s/d и число Frm), тем
больше теплогидравличе-
ская эффективность пучка
витых труб. Оценка тепло-
гидравлической эффектив-
ности при течении внутри
витых труб с использова-
нием зависимостей (1.2.6) и
(1.2.7) показала, что эффек-
тивность витых труб также
выше, чем эффективность
круглых труб (рис. 1.87).
Глава /
99
Эффективность поверхности с искусственной турбулизацией по-
тока оценивалась также отношением между ростом коэффициен-
тов теплоотдачи (Nu/NurA) и ростом гидравлического сопротивления
(1/^.J, т.е. параметром эффективности ц = (Nu/Nu^/^/^J. Если
т] < 1, то объем и масса ТА уменьшаются за счет сокращения его дли-
ны с увеличением числа труб и поперечного сечения пучка. При ц > 1,
объем и масса ТА уменьшаются за счет сокращения длины, числа
труб и поперечного сечения пучка. Метод, обеспечивающий условие
Л > 1, особенно эффективен. На рис. 1.88 видно, что для гладкой витой
трубы с s/d = 6,2 и круглой трубы с винтовой накаткой (s/d = 1,31) во
всем интервале чисел Re параметр ц > 1, а в круглой трубе с кольце-
вой накаткой, пучках витых труб и в витых трубах с накаткой пара-
метр т| > 1 только в ограниченных интервалах чисел Re.
«МЧЖл а
2	3	4	6	8	10 ReTp10~3 0,04	0,06	0,08	0,1	Ree„105
₽Вс 1.88. Сравнение теплогидравлической эффективности теплопередающих по-
верхностей: а: 1—6 — зависимости отношений Nu/NurA от Re^ для витых труб:
емдкой, с винтовой и кольцевой накаткой, пучка гладких витых труб, круглых
1руб с винтовой и кольцевой накаткой соответственно; 7 — 12 — зависимости от-
жжпений (£/£гл) от Re^ для тех же труб соответственно; б: 1 — 6 — зависимости
>fin^/f(Reeff) для гладкой витой трубы, витой трубы с винтовой накаткой, витой
хртоы с кольцевой накаткой, гладкой круглой трубы, круглой трубы с винтовой
мягкой и круглой трубы с кольцевой накаткой соответственно
Сравнение эффективности исследованных теплопередающих по-
верхностей с интенсификацией теплообмена методом эффективных
араметров позволяет установить области течения по числам Re, где
наблюдается преимущество одной теплопередающей поверхности
ад другой при использовании различных методов интенсификации
тепло- и массообмена [1.2.22, 1.2.24].
100
Глава 1
Список литературы
1.2.1.	Ибрагимов М.Х., Номофилов Е.В., Субботин В.И. Теплоотдача и гид-
равлическое сопротивление при винтовом движении жидкости в трубе//
Теплоэнергетика. 1961. № 7. С. 57.
1.2.2.	КаменьщиковФ.Т., Решетов В. А., Рябов А. А., ПоляковВ.К., Емелья-
нов А.И. Вопросы механики вращающихся потоков и интенсификация
теплообмена в ЯЭУ. М.: Энергоатомиздат, 1984.
1.2.3.	Мигай В.К. Повышение эффективности современных теплообменников.
Л.: Энергия, 1980.
1.2.4.	Kuzma-Kichta Yu.A. Coiled tube (flow and pressure drop and heat transfer
in)//lntern. Encyclopedia Heat and Mass Transfer. New York: CRS Press.
1997. P. 167-170.
1.2.5.	Ашмантас Л.-В.А., Дзюбенко Б.В. Проблемы теплообмена и гидроди-
намики в ядерных энергодвигательных установках космических аппара-
тов. Вильнюс: Pradai, 1997.
1.2.6.	Дзюбенко Б.В. и др. Энергетические спектры турбулентности в теп-
лообменнике с закруткой потока//Изв. АН СССР. Энергетика и транс-
порт. 1983. №4. С. 125-133.
1.2.7.	Дзюбенко Б.В. и др. Нестационарное перемешивание теплоносителя в
теплообменнике с витыми трубами//Там же. № 3. С. 125-133.
1.2.8.	Дзюбенко Б.В. Теплообмен на начальном участке в теплообменнике с
закруткой потока//ИФЖ. 1982. Т. 42, № 2. С. 230-235.
1.2.9.	Дзюбенко Б.В. Гидравлическое сопротивление в теплообменнике с за-
круткой потока//Там же. 1983. Т. 44, № 3. С. 357-362.
1.2.10.	Дзюбенко Б.В. Влияние различных факторов на коэффициент гидрав-
лического сопротивления в теплообменнике с закруткой потока//Меж-
вуз. сб. науч, трудов «Современные проблемы гидродинамики и тепло-
обмена в элементах энергетических установок и криогенной технике».
М.: ВЗМИ, 1982. Вып. II. С. 70-77.
1.2.11.	Дзюбенко Б.В., Ашмантас Л.-В.А. Тепломассообмен в пучках ореб-
ренных стержней//ИФЖ. 1984. Т. 47, № 3. С. 357-363.
1.2.12.	Дзюбенко Б.В. и др. Перемешивание теплоносителя в теплообменнике
с закруткой потока/Дам же. 1981. Т. 40. № 5. С. 773-779.
1.2.13.	Дзюбенко Б.В. и др. Межканальное перемешивание теплоносителя в
пучке витых труб/Дам же. 1983. Т. 45, № 1. С. 26-31.
1.2.14.	А.с. 761820 СССР. Дзюбенко Б.В., Вилемас Ю.В. Кожухотрубный теп-
лообменник//БИ. 1980. № 33. С. 194.
1.2.15.	А.с. 840662 СССР. Дзюбенко Б.В., Дрейцер Г.А., Вилемас Ю.В. и др.
Кожухотрубный теплообменник/Дам же. 1981. № 23. С. 178.
1.2.16.	А.с. 937954 СССР. Дзюбенко Б.В., Вилемас Ю.В., Варшкявичюс Р.Р.,
Дрейцер Г.А. Кожухотрубный теплообменник/Дам же. 1982. № 23. С. 189.
1.2.17.	Данилов Ю.И., ДзюбенкоБ.В., ДрейцерГ.А., АшмантасЛ.-В.А. Теп-
лообмен и гидродинамика в каналах сложной формы. М.: Машинострое-
ние, 1986.
1.2.18.	Дзюбенко Б.В., Дрейцер Г. А, Ашмантас Л.-В.А. Нестационарный теп-
ломассообмен в пучках витых труб. М.: Машиностроение, 1988.
Яша J
101
1L2-19. Вилемас Ю.В., Дзюбенко Б.В. и др. Интенсификация теплообмена.
Успехи теплопередачи. Ч. 2. Вильнюс: Мокслас, 1988.
1-2.20. Дзюбенко Б.В., Ашмантас Л.-В.А., Сегаль М.Д. Моделирование ста-
ционарных и переходных теплогидравлических процессов в каналах
сложной формы. Вильнюс: Исток, 1994.
1-2^1. Дзюбенко Б.В., Сакалаускас А.В., Ашмантас Л.-В.А., Сегаль М.Д.
Турбулентное течение и теплообмен в каналах энергетических устано-
вок. Вильнюс: Исток, 1995.
1-2.22. Ашмантас Л.-В.А., Дзюбенко Б.В. Проблемы теплообмена и гидроди-
намики в ядерных энергодвигательных установках космических аппара-
тов. Вильнюс: Исток, 1997.
1-2-23. Федик И.И. и др. Обобщение опыта реакторной отработки стержневых
карбидныхтвэлов ЯРД и ЯЭДУ на стендовом комплексе «Байкал-1» и раз-
вития прикладных технологий//Сб. докл. 5-й отраслевой конф. «Ядерная
энергетика в космосе». Подольск, 1999. С. 49-60.
1-2.24. Дрейцер Г.А., Дзюбенко Б.В., Якименко Р.И. Интенсификация теп-
лообмена и анализ методов сравнения теплогидравлической эффектив-
ности теплопередающих поверхностей//Тр. 2-й Рос. нац. конф, по тепло-
обмену. М.: МЭИ, 1998. Т. 6. С. 99-102.
1-3. КОЛЕБАНИЯ ПОВЕРХНОСТИ РАЗДЕЛА ФАЗ
Существующие зависимости для расчета теплоотдачи при пле-
ночном кипении на горизонтальном цилиндре [1.3.1; 1.3.2] получены
в предположении, что тепло передается теплопроводностью через
ленку пара, толщина которой во времени не меняется. Однако это
допущение не соответствует имеющимся данным.
Методика лазерного зондирования процесса кипения
Впервые колебания границы раздела фаз при пленочном кипении
фреона-113 на горизонтальном цилиндре в окрестности нижней об-
разующей были зафиксированы
вработе [1.3.3]. Согласно разрабо-
танной в ней методике (рис. 1.89),
пучок лазерного излучения на-
правляется близ горизонталь-
ной трубки, которая нагрева-
ется за счет пропускания через
её переменного электрическо-
го тока. Перемещение трубки в
горизонтальном и вертикальном
вправлениях осуществлялось
с помощью микрометрического
Рис. 1.89. Схема измерения колебаний
толщины паровой пленки при пленоч-
ном кипении
102
Глава 1
устройства. После прохождения пучка излучения вблизи рабочего
участка, на котором устанавливается пленочное или пузырьковое
кипение, его интенсивность изменялась, что фиксировалось с помо-
щью фотоприемника.
Пленочное кипение. Толщина паровой пленки
На рис. 1.90 представлено изменение толщины паровой пленки
при пленочном кипении фреона-113 в большем объеме при атмосфер-
ном давлении на горизонтальном цилиндре в окрестности нижней
образующей [1.3.4]. Как установлено, колебания толщины паровой
пленки в окрестности нижней образующей цилиндра при пленоч-
ном кипении жидкости представляют собой случайный гауссовский
процесс.
В 1982 г. на Международной конференции по теплообмену был
представлен доклад Тода и Мори [1.3.5], исследовавших колебания
толщины паровой пленки при пленочном кипении воды на сфере
и проволоке. Тода и Мори воспроизвели разработанную методику
лазерного зондирования [1.3.4] и подтвердили полученные законо-
мерности колебаний толщины паровой пленки при пленочном ки-
пении.
В работе [1.3.6] впервые при квазистационарном пленочном кипе-
нии получены взаимные спектры колебаний толщины паровой плен-
ки и давления. Обнаружено, что наибольшая корреляция наблюда-
ется в диапазоне 0,5—2 кГц. С ростом недогрева жидкости пик на
взаимном спектре смещается в сторону низких частот.
В работе [1.3.7] колебания толщины паровой пленки учтены при
моделировании пленочного кипения. Согласно модели, предполага-
лось, что толщина паровой пленки меняется во времени по синусои-
дальному закону, и рассчитаны локальная плотность теплового пото-
ка, средняя толщина паровой пленки, а также амплитуда колебаний
границы раздела фаз.
5, мм
0,05	0,10	0,15 т, с
Рис. 1.90. Колебание тол-
щины паровой пленки в
окрестности нижней обра-
зующей трубки d = 2 мм
[1.3.4]
Глава I
103
Пузырьковое кипение. Колебания парового пузыря
В кипении фундаментальным вопросом является взаимосвязь
между теплопередачей и образованием пузырей. В работе [1.3.8] для ис-
следования колебаний парового пузыря, растущего на стенке, усовер-
шенствована методика [1.3.3]. Пучок излучения вырезается диафраг-
мой, имеющей характерный размер, превышающий диаметр парового
пузыря (рис. 1.91).
Рис. 1.91. Схема исследования колебаний парового пузыря при его росте на стен-
е (а); сигнал фотоприемника в опыте (б); калибровочная кривая (в)
Возникновение пузырей влияет на теплообмен при кипении через
образование и испарение в основании пузыря микро- и макрослоя,
испарение и конденса-
цию на поверхности пу-
зыря и теплообмен, вы-
званный конвекцией,
возникающей вблизи
ншреваемой поверх-
ности. Поэтому законо-
мерен интерес к изуче-
нию динамики паровых
пузырей при кипении.
J^hthtto по динамике
врового пузыря, рас-
тущего на стенке, пред-
ставлены в работе [1.3.8]
IRC. 1.92).
R, мм
Рис. 1.92. Колебания растущего парового пузыря:
Р = 0,1 МПа, вода, ДТ = 9,2 К
104
Глава 1
М. Шоджи и др. [1.3.9] изучали движение жидкости, вызванное
растущим паровым пузырем, используя анемометр с горячей прово-
локой, расположенной вблизи поверхности нагрева. Рабочим учас-
тком являлся нагреватель в виде диска диаметром 2 мм. Экспери-
менты проводились при кипении воды в состоянии насыщения при
атмосферном давлении. По данным измерений вычислялись спектр
Фурье и показатель Ляпунова. Как выяснилось, показатель Ляпу-
нова всегда получался положительным. Этот результат совместно с
широкополосными энергетическими спектрами показывал, что об-
разование парового пузыря является хаотическим процессом.
В работе [1.3.10] был использован комбинированный оптико-акус-
тический метод исследования динамики паровых пузырей при кипе-
нии жидкого гелия. Были получены фотографии растущего парового
пузыря на поверхности нагревателя (рис. 1.93) и зарегистрированы
колебания давления в жидкости с большой амплитудой, вызванные
его ростом и схлопыванием. Давление в опытах соответствовало тем-
пературе насыщения 1,9 К для гелия-2.
Также построены аттракторы (рис. 1.94) по измеренным флук-
туациям давления в жидкости и вычислены значения показателей
Ляпунова [1.3.10]. Максимальный и средний показатели оказались
положительными величинами, что свидетельствует о хаотической
природе колебаний давления в жидкости, вызванных ростом и ос-
цилляциями единичного парового пузыря.
Колебания давления наблюдаются в широкой полосе частот (от 2
до 300 Гц) со степенным законом спада интенсивности по спектру.
Указано, что колебания растущих и схлопывающихся паровых пузы-
рей сопровождаются значительными механическими вибрациями и
слышимым шумом. Причины подобных колебаний, однако, в работе
не указаны.
Рис. 1.93. Рост (а) и схлопывание (б) парового пузыря гелия-2
Жидкий Не-2
Паровой
пузырь
Поверхность
нагрева
Глава I
105
Рис. 1.94. Аттрактор, построенный по экспериментальным данным для
флуктуаций давления и его проекции на плоскости фазового пространства
При исследовании кипения воды с недогревом при давлении на-
сыщения 40 кПа комбинированным методом [1.3.11] с помощью гид-
рофонов были получены данные по колебаниям давления, вызван-
ным ростом единичного парового пузыря, при недогревах от 5 до 20К.
Одновременно использовалась скоростная киносъемка для измере-
ния радиуса единичного парового пузыря в зависимости от времени.
Эти данные приведены на рис. 1.95. Частоты колебаний, приведен-
ные в работе [1.3.11], согласуются с данными работы [1.3.8].
В работе [1.3.12] был использован теневой фотографический ме-
тод для исследования кипения метанола при атмосферном давлении
с недогревом. Показано, что при недогревах жидкости около 20К на
поверхности парового пузыря в определенный момент его роста на-
блюдается выброс тепла в виде струи в окружающую жидкость, а
граница раздела фаз испытывает колебания.
Связь процессов, происходящих на поверхности кипения, меж-
ду собой, а также их связь с динамикой паровых пузырей была ис-
Вк_ 1.95. Радиус парово-
го пузыря и соответству-
гонжй ему сигнал гидро-
Радиус пузыря, мм
106
Глава 1
следована с помощью методов нелинейного и хаотического анализа.
Характеристики паровых пузырей, растущие на искусственной впа-
дине, регистрировались высокоскоростной видеокамерой, а с помо-
щью термопар было проведено измерение флуктуаций средней тем-
пературы центра парообразования. Результаты представлены в виде
аттракторов для измеренных флуктуаций температуры (рис. 1.96)
[1.3.12], q = 26 кВт/м2, временная задержка 0,023 с.
Рис. 1.96. Трехмерные аттракторы для флуктуаций температуры центра
парообразования
Изображение а на рисунке иллюстрирует отношение расстоя-
ния между двумя соседними искусственными центрами парообра-
зования к отрывному диаметру парового пузыря, равному 0,3; б, в,
г —соответственно, 0,75, 1,2 и 1,75. Таким образом, процессы теплопе-
редачи, происходящие в поверхности кипения, а также гидродина-
мическое и тепловое взаимодействие между пузырями и поверхнос-
тью и между самими пузырями нельзя рассматривать в отрыве друг
от друга. Связь микропроцессов в кипении является нелинейной, и в
столь сложной системе с многочисленными внутренними связями с
большой степенью вероятности можно ожидать наступление хаоса
[1.3.13, 1.3.14].
Глава 1
107
Список литературы
1.3.1.	Кутателадзе С.С. Теплоотдача при конденсации и кипении. М., 1949.
1.3.2.	Bromley L.A. Heat transfer in stablefilm boiling//Chem. Eng. Progr. 1950.
V. 46, p. 221.
1.3.3.	Ковалев C.A., Жуков B.M., Кузма-Кичта Ю.А. Методика исследова-
ния колебаний границы раздела фаз при плёночном кипении жидкости с
помощью оптического квантового генератора//ИФЖ. 1973. Т. 25. №. 1.
1.3.4.	Petukhov B.S., Kovalev S.A., Zhukov V.M., Kuzma-Kichta Yu.A.
Investigation of the mechanism of heattrasfer upon film boiling of liquid//Proc.
5th Int. Heat Transfer Conf. Tokyo. 1974. N 4. P. 96.
1.3.5.	Toda S., Mori M. Proc. 7th Int. Heat Transfer Conf. Munich. 1982. P. 173-
176.
1-3.6. Кузма-Кичта Ю.А., Молошников A.C., Нигматулин Б.И. и др. Иссле-
дования колебаний границы раздела фаз при пленочном кипении. 1-я
часть//ТВТ. 1994. Т. 32. № 2. С. 255-260.
1-3.7. Кузма-Кичта Ю.А., Молошников А.С., Нигматулин Б.И. и др. Иссле-
дования колебаний границы раздела фаз при пленочном кипении. 2-я
часть//Там же. 1995. Т. 33. № 2. С. 273-278.
1.3.8.	Кузма-Кичта Ю.А., Зудин Ю.Б., Бакунин В.Г., Устинов А.А. и др.
Исследование колебания границы раздела фаз с помощью лазерной
диагностики/XII школа-семинар молодых ученых и специалистов под
руководством акад. РАН А.И. Леонтьева «Проблемы газодинамики и теп-
ломассообмена в энергетических установках». М., 25-28 мая 1999.
1.3.9.	Masahiro Shoji, Yuto Takagi. Bubbling features from a single artificial
cavity//lnt. J. Heat and Mass Transfer. 2001. N 44.
13-10. Zhang P., Murakami M-, Wang R.Z. Investigation of chaotic pressure
fluctuations induced by the vapor bubble oscillations in the film boiling of
superfluid helium//Heat and Mass Transfer. 2003. V. 39. P. 477-482.
13.11.	Schroeder J.J., Bode A. Pressure Pulse Generation by Single Bubbles in
Subcooled Pool Boiling/ Boiling-2000 Phenomena & Emerging applications
Conf., Anchorage, Alaska, 2000, April 30-May 5. V. 1. P. 81-99.
13-12. Boming Yu., Ping Cheng. A fractal model for Nucleate Pool Boiling Heat
Transfer/J. Heat Transfer. Dec. 2002. V. 124.
13-13. Шустер Г. Детерминированный хаос. Введение. М.: Мир, 1988. 240 с.
13.14. Устинов А.А. Исследования колебаний границы раздела фаз при кипе-
нии. Дис. канд. техн. наук. М.: Моск, энерг. ин-т. 2005.
Глава 2
ТЕОРЕТИЧЕСКИЕ МЕТОЛЫ ИССЛЕЛОВАНИЯ
ИНТЕНСИФИКАЦИИ ТЕПЛО- И МАССООБМЕНА
2.1. ПУЧКИ ВИТЫХ ТВЭЛОВ И ТРУБ
Метод интенсификации тепло- и массообмена путем закрут-
ки потока в каналах сложной формы, образованных пучками ви-
тых тепловыделяющих элементов (твэлов), первоначально полу-
чил применение в конструкциях тепловыделяющих сборок (ТВС)
ядерного ракетного двигателя (ЯРД) [2.1.1]. В каналах, образован-
ных пучками витых твэлов и труб овальной формы наблюдается
сложное пространственное течение теплоносителя с закруткой
потока. Поэтому возникла задача исследования турбулентной
структуры потока в пучках витых труб и твэлов и разработки ма-
тематической модели течения, описываемой системой уравне-
ний, поддающейся численному решению, а также методов расче-
та стационарных и нестационарных теплогидравлических задач.
В разработанной модели течения гомогенизированной среды
[2.1.1—2.1.4] течение в реальном пучке витых стержней замене-
но потоком двухфазной среды с неподвижной твердой фазой, в
котором источники объемного тепловыделения qv и гидравличе-
ского сопротивления %pu2/2deq распределены по определенному за-
кону (% — коэффициент гидравлического сопротивления). Эффект
гомогенизации учитывается введением в уравнение энергии мно-
жителя (1—е)/е, где £ — пористость пучка по теплоносителю, опре-
деляемая с учетом толщины вытеснения пограничного слоя. Прини-
мается, что вектор скорости потока параллелен оси пучка, градиент
давления в поперечном сечении пучка равен нулю, а диффузион-
ные члены в уравнениях энергии и движения учитывают влияние
различных механизмов переноса в пучке витых твэлов или труб.
При этом система уравнений теплообмена и гидродинамики, опи-
сывающая стационарное в среднем течение гомогенизированной
среды имеет вид:
_£_Э_|\ эД
+ г2Э(р( ett Э<р?
ЭТ 1-е	1 Э < _ ЭТА
РисРЧ~ =---
и Эх	8	г ЭД Эг)
(2.1.1)
Глава 2
109
др 1 Э (	ди] 1 д (	ЭиЛ е ри2
r = T+“r rf'v="r +“r PVetfX- -<
дх дх гдг\	дг J г оф<	Эф J 2deq
2л
G = 8 J J purdztftp,
о о
(2.1.2)
(2.1.3)
р = pRT.
Граничные условия задачи:
u(r,ф,0) = ивх(г,ф); Т(г,ф,0) = Твх(г,ф); р(0) = рвх,
и(г,ф,х) = и(г,ф 4- 2тс,х); Т(г,ф,х) = Т(г,ф 4- 2п,х).
(2.1.4)
(2.1.5)
(2.1.6)
(2-1.7)
Задача (2.1.1) —(2.1.4) с граничными условиями (2.1.5)—(2.1.7) ре-
шалась численными методами (методом установления и методом
матричной факторизации) [2.1.3, 2.1.4].
Система уравнений, описывающая турбулентное течение в пуч-
ках витых твэлов с учетом влияния межканального перемешивания
теплоносителя и эффектов нестационарности на поля температур
теплоносителя и витых твэлов (твердой фазы) при использовании
двухтемпературной модели течения гомогенизированной среды в
предположении, что возмущения параметров, определяющих про-
цесс течения невелики, а их длительность значительно превосходит
время распространения звуковой волны по длине пучка, для неста-
ционарной осесимметричной задачи имеет вид [2.1.1, 2.1.3—2.1.14]:
dTs
4СС8
(Ts -т)
1 д(.
+ — — fk,
г дг\ ‘
‘sr
дТЛ д	дТЛ
dr ) Эх< дх J
(2.1.8)
дТ	дТ 4а z	. Эр 1 Э ( .
рс₽3-+рисрТ- = 7~(^"Т) + Т"+~ЗГ гХ<
Эт	дх dPrT	' Эт г ЭН
эт
eff дг
Э ( дТ}
(2.1.9)
ди др е pu2 1 Э .
3	+ prVeffТ"
дх дх 2dpn г дг\ дг
Эи^
э7;’
гк
G(t) - 2я J Epurdr,
о
(2.1.10)
(2.1.11)
р = pRT.	(2.1.12)
Система уравнений (2.1.8—2.1.12) позволяет рассчитать поля тем-
ератур при нестационарных теплогидравлических процессах как
в моделях пучков витых труб (стержней) при их нагреве электриче-
ским током, так и в ТВС с витыми твэлами при математическом мо-
110
Глава 2
делировании переходных процессов в гетерогенном ядерном реакто-
ре, который в этом случае заменяется на эквивалентный гомогенный
реактор, к которому затем применяется диффузионная теория. К
этой системе уравнений присоединяются уравнения, описывающие
кинетику реактора с учетом запаздывающих нейтронов и обратных
связей по температурному и плотностному эффектам реактивности.
Граничные условия задачи:
х = 0:
и = ивх(г-т)- Р = РвхМ- т = ГвхМ, Ts = Tsbx(t,t),
Г = 0:
=()
Эг г=0
(2.1.13)
(2.1.14)
ЭТд(г,х,т)
ЭТ(г,х,т)
ЭТ5(г,х,т) =() ЭТ(г,х,т)
Эх Х=1	' Эх
ди(г'х^ =0,	(2.1.15)
дг г=гк
(2.1.16)
При т = 0 распределения температур Ts(r,x) и Т(г,х) являются за-
данными. Задача (2.1.8) —(2.1.12) с граничными условиями (2.1.13) —
(2.1.16) решалась в два этапа: решение уравнений теплообмена и сов-
местное решение уравнений движения и неразрывности, которые
затем увязывались через уравнение состояния и итерационные цик-
лы. Уравнения теплопроводности и энергии решались методом пере-
менных направлений при записи численных аналогов уравнений по
неявной схеме и использовании метода прогонки. Уравнения газовой
динамики решались методом прогонки с помощью подстановки Си-
муни. Сходимость процесса контролировалась по температуре теп-
лоносителя.
Эффективные коэффициенты турбулентной теплопроводности
Хе//и вязкости ve/f входящие в уравнения энергии (2.1.1), (2.1.9) и дви-
жения (2.1.2), (2.1.10) и используемые для замыкания систем уравне-
ний (2.1.1) —(2.1.4) и (2.1.8), (2.1.12), определялись для стационарного
течения и для каждого из рассматриваемых типов нестационарнос-
ти. При этом предполагали, что турбулентные числа Прандтля и Лью- >
иса равны единице, т.е. Pr/J; = pveffcp/Xe{{ = 1, Lem = pDef{cp/\ff = 1. ,
а опытные значения безразмерного эффективного коэффициента i
Глава 2
111
турбулентной диффузии К = Deff/udeq. Тогда искомые значения ко-
эффициентов ХеЯ и veff в каждый момент времени и для каждой точки
потока определялись по зависимостям Xeff — Kpucpdeq, veff = Kudeq.
Коэффициент К описывает переносные свойства турбулентного по-
тока во времени, но является неизменным для всей области течения в
фиксированный момент времени т, а параметры р, и и ср зависят как
от времени, так и от пространственного положения расчетной ячей-
ки. При этом предполагается, что в каждый фиксированный момент
времени коэффициенты переноса Л(>я и veff зависят от производных
некоторых эффективных средних значений температур и скоростей
в потоке с закруткой потока, где существенна диффузия турбулент-
ности и ее конвективный перенос осуществляется со средней скоро-
стью потока. Этот метод замыкания системы исходных уравнений с
помощью экспериментально определяемых коэффициентов X /f и veffl
основанный на использовании гипотезы о локальном подобии и фор-
мально-математическом подходе, был обоснован экспериментально.
При стационарных режимах безразмерный эффективный ко-
эффициент турбулентной диффузии в пучках витых стержней яв-
ляется функцией критериев подобия, характеризующих особен-
ности течения в ТВС Kqs = K(Frjn,Re,£), где критерий Frm = s2/ddeq
характеризует действие закрутки потока на его переносные свойст-
ва; Re = umde(p/p — критерий Рейнольдса, который при Re > 8403
фактически не влияет на коэффициент Kqs; £ — пористость пучка по
теплоносителю. В случае нестационарного протекания теплогидрав-
лических процессов в пучке витых твэлов эффективный коэффици-
ент турбулентной диффузии Кип зависит также от критерия Фурье
Р°Ь = V ^pPtX ) и безразмерного параметра G2/Gv представля-
ющего собой отношение расхода теплоносителя после внесения воз-
мущения G2 к первоначальному расходу теплоносителя Gr через пу-
чок стержней: Кип = К(Ргет, Fob, Re, G2/Gp£). При обобщении опытных
данных по коэффициенту Кип использовался относительный коэф-
фициент перемешивания к = Kun/Kqs = f(Fob, G2/Gp Frm).
Задачи эксперимента для метода интенсификации тепло- и мас-
«ообмена путем закрутки потока витыми твэлами или трубами были
сформулированы следующим образом:
—	экспериментальное обоснование модели течения гомогенизи-
рованной среды, ее математического описания и методов расчета пу-
мм сопоставления теоретически рассчитанных и экспериментально
жямеренных полей температур и скоростей теплоносителя и иссле-
дования структуры потока;
—	получение замыкающих экспериментальных зависимостей
в критериальной форме для расчета коэффициентов теплоотдачи,
112
Глава 2
гидравлического сопротивления и эффективного коэффициента
турбулентной диффузии, а также определение областей изменения
режимных и геометрических параметров, где обеспечивается мак-
симальная эффективность от применения метода интенсификации
тепло- и массообмена путем закрутки потока в пучках витых твэлов
и труб овального профиля;
—	комплексные испытания пучков витых твэлов на электромо-
делирующих установках при моделировании неравномерного поля
тепловыделения в поперечном сечении пучка;
—	натурные петлевые реакторные испытания пучков витых
стержневых твэлов при нагреве водорода до максимально возмож-
ных температур;
—	испытания натурных ТВС с витыми твэлами ЯРД в составе кон-
кретных изделий [2.1.15, 2.1.16].
Методы теплогидравлического расчета тепловыделяющих
сборок с витыми твэлами
В настоящее время в качестве одного из вариантов энергодвига-
тельного обеспечения марсианской экспедиции в XXI веке может
рассматриваться ядерная энергодвигательная установка (ЯЭДУ) с
твердофазным ядерным реактором [2.1.17]. Этот гетерогенный га-
зоохлаждаемый реактор содержит высокотемпературные тепло-
выделяющие сборки (ТВС) с пучками витых твэлов двухлопастного
профиля и замедлитель из гидрида циркония, в котором размеща-
ются с определенным шагом эти ТВС. ЯЭДУ работает по определен-
ной циклограмме то на двигательном, то на энергетическом режиме
при изменении тепловой мощности реактора и расхода теплоносите-
ля — водорода на несколько порядков. При этом число Рейнольдса из-
меняется также в широком диапазоне, охватывающем переходную и
турбулентную области течения.
Особенности газодинамики и теплообмена в пучках витых твэлов
или труб связаны с особенностями трехмерного закрученного по-
тока, формируемого этими пучками. Прежде всего, закрутка пото-
ка при продольном обтекании таких пучков существенно расширяет
область ядра потока с примерно одинаковой скоростью и образует
тонкий пристенный слой, где составляющие осредненной скорости
изменяются от нуля на стенке до максимального значения на внеш-
ней границе пограничного слоя. При этом интенсифицируются про-
цессы тепломассообмена также и за счет обмена порциями жидкости
между пристенным слоем и ядром потока, вызванного распределени-
ем составляющих скорости в поперечном сечении канала, образован-
Глава 2
113
ного пучком витых стержней или труб [2.1.18, 2.1.19]. Такой характер
течения позволил путем введения понятия средней толщины при-
стенного слоя в качестве определяющего размера обобщить данные
по теплообмену и гидравлическому сопротивлению в определенном
диапазоне изменения параметров для геометрически неподобных
мучков витых твэлов или труб, введя новый критерий подобия, учи-
тывающий интенсивность закрутки потока [2.1.4].
Наряду с таким представлением данных, в монографии рассмат-
ривается метод анализа и обобщения, основанный на использовании
в качестве определяющего размера эквивалентного диаметра пучка,
что позволяет наглядно продемонстрировать эффект интенсифика-
ции теплообмена по сравнению с теплообменом в круглых трубах.
Для определения характера перехода от ламинарного к турбулентно-
жу режиму течения в пучках витых стержней был исследован коэф-
фициент гидравлического сопротивления для стержней малого ди-
аметра различной формы, изготовленных из различных реакторных
материалов (графита, карбидов тугоплавких металлов и нержаве-
нцей стали). Данные этих исследований обобщаются с использова-
нием в качестве характерного размера средней толщины пристен-
ного слоя и эквивалентного диаметра, а также в форме многочленов
второго порядка в логарифмических координатах, что позволяет
обобщить опытные данные единой зависимостью для переходной и
турбулентной областей течения.
Концепция ЯЭДУ, которая может быть применена для пилотиру-
емого марсианского комплекса и при решении других транспортных
авдач в космосе, базируется на использовании отдельных модулей,
чмо повышает надежность установки, так как при неисправности мо-
држь может быть отделен от космического корабля. Каждый модуль
представляет собой самостоятельную двигательно-энергетическую
установку, в состав которой входят ядерный реактор и замкнутый
егур с турбомашинным циклом преобразования теплоты в элект-
рмескую энергию. Эта концепция является одной из перспектив-
кх концепций, поскольку в этом случае один ядерный реактор ис-
мжьзуется и для получения тяги и для выработки электроэнергии.
Цри работе на двигательном режиме максимальная температура во-
|ррода на выходе из реактора может достигать 2900...3100К, а макси-
ильная температура рабочего тела (смеси гелия и ксенона) перед
турбиной при работе на энергетическом режиме — 1200К.
Наиболее теплонапряженным элементом ЯЭДУ является высо-
втемпературный ядерный реактор, содержащий тепловыделяю-
е сборки с витыми твэлами, поэтому для обеспечения надежной
работы реактора и установки, которая должна эксплуатироваться в
114
Глава 2
космосе в течение нескольких лет, необходимо провести комплекс
детальных исследований теплообмена и гидродинамики, теплогид-
равлических и реакторных испытаний при стационарных и нестаци-
онарных режимах и разработать надежные методы теплогидравли-
ческого расчета ТВС и ядерного реактора.
При разработке ядерных реакторов для транспортных энергодви-
гательных установок, в том числе и космического назначения, возни-
кает необходимость в выборе наиболее эффективного метода интен-
сификации тепломассообмена, который учитывал бы особенности
работы высокотемпературного газоохлаждаемого ядерного реакто-
ра. Таким методом интенсификации тепломассообмена является ме-
тод интенсификации процессов турбулентного переноса тепла, мас-
сы и количества движения путем закрутки потока в каналах сложной
формы, образованных пучками витых тепловыделяющих элементов
(твэлов) различного профиля (овального, крестообразного и др.). При
продольном обтекании плотноупакованных пучков витых твэлов
возникают вихревые структуры, дополнительно турбулизирующие
поток, и конвективные течения в поперечном сечении пучка, кото-
рые существенно интенсифицируют межканальное перемешивание
теплоносителя и тепломассообмен.
Этот метод интенсификации позволяет создать компактный ядер-
ный реактор, в котором при эквивалентном гидравлическом диа-
метре пучка витых твэлов deq& 1... 2 мм и большом числе твэлов >151,
благодаря интенсивному межканальному поперечному перемешива-
нию теплоносителя, сводится к минимуму неблагоприятное влияние
допусков на геометрические размеры канала, присущее изолирован-
ным каналам с малыми диаметрами d = deq = 1... 2 мм и приводящее
к снижению средней выходной температуры теплоносителя на не-
сколько сот градусов. В то же время для космической ядерной энер-
годвигательной установки (ЯЭДУ) для полета к Марсу в 2011—2018 гг.,
чтобы обеспечить удельный импульс тяги на двигательном режиме
-9500 м/с, требуется нагреть теплоноситель (водород) до среднемас-
совой температуры на выходе из реактора -3000К.
В настоящее время такие выходные параметры ЯЭДУ можно
обеспечить только при использовании ядерных реакторов с виты-
ми стержневыми твэлами фасонного профиля, изготовленными из
твердого раствора карбидов урана, ниобия, циркония или тантала.
При этом одновременно обеспечивается безопасная работа ЯЭДУ на
различных режимах при ее многоразовых запусках. В ядерных ре-
акторах с витыми твэлами для частичного выравнивания неравно-
мерностей полей энерговыделения осуществляется также концент-
рационное профилирование загрузки урана-235 по радиусу и длине
Глава 2
115
ТВС, для чего твэлы делаются разрезными по длине. Витые твэлы
упираются торцами друг в друга и размещаются в теплоизолирован-
ной обойме с опорной (выходной) решеткой и системой выравнива-
ющих решеток на входе. Перед нагревными секциями (активной зо-
ной ТВС) размещаются элементы торцевого отражателя и радиаци-
онной защиты, малая пористость которых приводит к натеканию
потока теплоносителя на пучок твэлов в виде системы струй малого
диаметра (рис. 2.1).
Для теплогидравлического расчета ТВС с витыми стержневыми
твэлами может быть использовано одномерное описание течения
теплоносителя, если предположить, что поле энерговыделения по
радиусу и азимуту реактора и ТВС является равномерным. Этот теп-
логидравлический расчет ТВС по средним параметрам практически
равноценен модели течения в системе параллельных каналов, кото-
рые имеют диаметр, равный эквивалентному диаметру пучка — deq с
мгновенным выравниванием неравномерностей всех параметров по
радиусу и азимуту ТВС. Эта модель течения используется для сведе-
ния теплового баланса и баланса давлений на ТВС и реакторе, для оп-
ределения перепада давлений на длине ТВС и определения распреде-
ления давлений по ее длине при проведении теплового расчета ТВС и
гидравлического расчета ядерного реактора при его настройке с по-
мощью сменных шайб [2.1.17], а также для увязки схемы ЯЭДУ. Кроме
того, если путем радиального профилирования можно обеспечить
равномерное поле энерго-
ыделения по радиусу ТВС
^коэффициент неравномер-
ности Кт » 1,0) и получить
равномерное поле энерговы-
деления по радиусу реакто-
ра (коэффициент неравно-
мерности KR« 1,02...1,03), то
тогда можно ограничиться
теплогидравлическим рас-
четом по средним парамет-
рам при одномерном описа-
нии течения в ТВС [2.1.20].
Однако реальный прото-
чит гетерогенного реактора
•ЭДУ) с 3-зонным профи-
лированием U-235 по ра-
ЛМусу ТВС и с барабанной
«□темой регулирования
энерговыделения по длине ТВС: 1 — расчет
с учетом торцевых отражателей; 2 — за-
кон синуса (qVCD = smnx); 3 — эксперимент
[2.1.22]
116
Глава 2
имеет существенную неравномерность энерговыделения по радиусу
и азимуту ТВС и ядерного реактора [2.1.17]. Поэтому для определения
трехмерных полей температур теплоносителя и стенки твэлов разра-
ботан теплогидравлический расчет ТВС по локальным характерис-
тикам потока и энерговыделения [2.1.3, 2.1.19].
Разработанные методы теплогидравлического расчета ТВС с ви-
тыми твэлами по средним и локальным параметрам позволили оп-
ределить температурное состояние витых твэлов при испытании
модельных ТВС в исследовательском графитовом реакторе (ИГР)
и предельные уровни теплового потока, характеризующие термо-
прочность твэлов из карбидов тугоплавких металлов, и выполнить ва-
риантные расчеты ТВС ЯЭДУ с учетом межканального перемешивания
теплоносителя и эффектов нестационарности [2.1.3, 2.1.19, 2.1.21].
Метод теплогидравлического расчета тепловыделяющих
сборок с витыми твэлами по средним параметрам
Метод теплогидравлического расчета ТВС с витыми твэлами по
средним параметрам при одномерном описании течения позволяет
определить распределение среднемассовой температуры рабочего
тела и распределение давления по длине ТВС. При этом предполагает-
ся, что распределения загрузки урана-235 и относительного нейтрон-
ного потока по длине ТВС являются заданными [2.1.22] (см. рис. 2.1).
Тогда, разбивая активную зону ТВС по длине на i участков длиной
Дхг- (рис. 2.2) можно определить распределение относительного теп-
ловыделения по длине ТВС:
gv. = P'^fcP = 2L_ i = 1, 2,.п,	(2.1.17)
2L Pi Qvicp S
i=l	i=l
где Qvicp =fep/<7vmaxcP; Р/ “ загрузка урана-235 на z-м участке ТВС.
Расчет проводят методом итераций в два этапа. Сначала при рас-
чете не учитывают потери тепла через теплоизоляционную обойму
ТВС. Тогда для пучка твэлов с заданными геометрическими размера-
ми и формой твэлов можно определить интегральную толщину при-
стенного слоя [2.1.23]:
5 = 0,5deg (l+3,6Frm0'357)’4,	(2.1.18)
а зная температуру рабочего тела на входе в ТВС и на выходе из нее,
можно вычислить прирост энтальпии при нагреве газа в ТВС без уче-
та потерь тепла:
= 'вых^вх'	(2.1.19)
Глава 2
117
О-
СР
Рис. 2.2. Схема активной зоны ТВС с расчетными участками по ее длине: 1 — вы-
ходная решетка; 2 — витые твэлы; 3 — многослойная теплоизолирующая обойма;
4 — кольцевой канал системы наружного охлаждения ТВС; 5 — входная решетка;
6 — торцевой отражатель; 7 — радиационная защита; 8 — корпус ТВС; 9 — вход
рабочего тела; 10 — сопло
1де энтальпии /вых = ДТвых,рвых) и ZBX = f(TBX,pBX) определяют по гра-
фику на рис. 2.3; рвых — давление газа на выходе из ТВС, практи-
чески равное давлению газа перед соплом рк, является заданным;
Твых ~ Тк — температура газа перед соплом. Затем расчет проводят в
следующем порядке.	(
1.	Определяют: увеличение энтальпии газа на i-м участке
(2.1.20)
i=i
распределение энталь-
ии рабочего тела по дли-
яеТВС
+	(2-1.21)
1=1
 температуру Т- = Д/рР,-).
2.	Рассчитывают сред-
жий тепловой поток с твэ-
жж на i-м участке
GMj
ПобЛх,
(2.1.22)
цме Поб — обогреваемый
ериметр активной зоны
ТВС
Рис. 2.3. Зависимость энтальпии водорода с при-
садкой метана (0,5% мольных) от температуры и
давления
118
Глава 2
3.	Определяют среднюю температуру рабочего тела на i-м
участке
Гср,- =0,5(Ти + 7}).
4.	Задавая в первом приближении распределение температуры
стенки твэлов Tw;- по участкам, например Twi = доп, определяют
методом итераций температуру Twi, используя закон теплообмена в
пучке твэлов [2.1.23] в виде:
где	NuSml. = 0,020Re^ Pr°f,	(2.1.23) ReSm'=7?~'A'	(2L24) Nu. . = ^Prffi.L_	(2.1.25) 5mi (I .-Мн .
В формулах (2.1.23) —(2.1.25) в качестве определяющей температу-
ры используется средняя температура в пристенном слое на твэлах:
^ = 0-5(7;.+ Twi),
(2.1.26)
при которой определяют динамический коэффициент вязкости
= f(Tm;) (рис. 2.4) и число Prm. = Рг(ТП11). Напор энтальпий в при-
стенном слое на выходе из z-ro участка Iwi — L = AJcpi определяют ис-
пользуя уравнение (2.25), т.е.
Л Г =
с₽/ " Ыибпн.Ип„.
(2.1.27)
5.	Распределения энтальпий и температур стенки определяют по
формуле
^=Г/+Чр,-	(2.1.28}
Twi = fUwi'Pi> ~ по графику на рис. 2.3.
Рис. 2.4. Зависимость коэффициента вязко-
сти водорода с присадкой метана (0,5% моль-
ных) от температуры
Далее находят относи-
тельную ошибку при опре-
делении температуры стен-
КИ Twi
Т -Т'
т
л WI
которую сравнивают с за-
данной величиной е (на-
пример, принимается, что
£ = 10'4). При достижении
этой точности итерации
прекращают.
Глава 2
119
6.	Определяют коэффициенты теплоотдачи от газа к стенке теп-
лоизолирующей обоймы ТВС:
q — NUSmiHmi'A^cpi	^2 1 29)
ДТср,Ргт,8 
»еДГср. = Twi~ Ti’
а также потери тепла через теплоизоляцию на i-м участке ТВС:
г).=яАу1(А~Гохл1)	(2.1.30)
-^-+Е~7-1п-^-+-------—
7=1^7	^7	®охл1*^0
хде Тохл/ — температура теплоносителя в кольцевом канале системы
охлаждения ТВС; с?к — диаметр пучка твэлов (внутренний диаметр
обоймы); Л., (у = 1, 2,..., т) — коэффициент теплопроводностиу-го слоя
многослойной теплоизоляционной обоймы; аохл/ — коэффициент
теплоотдачи к потоку теплоносителя в рубашке охлаждения ТВС;
djg — наружный диаметр металлического корпуса ТВС (внутренний
диаметр кольцевого канала охлаждения ТВС). При этом наиболее це-
лесообразно для теплоизоляции использовать высокопористые мате-
риалы из карбидов тугоплавких металлов (карбоволокниты, пенокар-
биды, пирографиты и др.). Коэффициент вычисляют при средней
температуре по толщине каждого слоя j = 1, 2,..., т.
1. Определяют суммарные потери тепла через теплоизоляцию
п
ТВС: X Он и суммарную тепловую мощность ТВС:
1=1
п
Qz=G^ + ^Qni.	(2.1.31)
1=1
На втором этапе расчета ТВС по средним параметрам (при одно-
мерном описании течения) рассчитывают параметры рабочего тела с
учетом потерь тепла через теплоизоляционную обойму ТВС в следу-
хцем порядке:
— определяют напор энтальпии при условии, что температура пе-
ред реактивным соплом Тк = Твых:
ДАп=Ч +
Д/Е G
Ош.
G '
(2.1.32)
— рассчитывают энтальпию газа
i
Ап - Азх + S
1=1
(2.1.33)
120
Глава 2
и находят Т.п = f(/zn,pz);
— определяют распределение теплового потока по длине ТВС с
учетом потерь тепла
<7,„=-^-;	(2.1.34»
поДХг-
—	методом итерации уточняют температуру стенки Twin, исполь-
зуя выражения:
N1W. = 0,020Re^,n Pr°£,	(2.1.35J
„ G5	Т	(2.1.36)
"пИлгш	т ' ЛШ1П	
(2.1.37)!
NUgminMinm	j
= 0-5(Г1П + Twiny,	(2.1.38)
—	рассчитывают энтальпию рабочего тела при температуре на
стенке твэлов: Iwin = Iin + Д/ср-п и определяют по графику (см. рис. 2.3)
температуру Twin = f(Iwin,Pi).
Затем определяют относительную ошибку £ = (Twin — Twi)/ Twin, и
после достижения заданной точности £ = 10’4 полученная температу-
ра Twin стенки считается окончательной.
Для определения температуры на внутренней поверхности теп-
лоизоляционной обоймы расчет проводят в следующем порядке:
—	вычисляют плотность теплового потока на i-м участке:
9о(=<?п(/(П0Лх(),	(2.1.39)
где По = 7ido — периметр обоймы;
—	рассчитывают средний напор энтальпий на стенке обоймы:
АТ _Т _Т _ Яо1 РГдП $	(2.1.40)
MJoi •‘in 1woi NT	'
UgfljjnHnnn
где числа Nu5mzn и Re5mfn определяют по формулам (2.1.35) и (2.1.36)
при характерной температуре Tmoi = 0,5(Twoi + TJ;
—	определяют энтальпию рабочего тела при температуре стен-
ки обоймы: Iwoi = Iin — AIoi, а затем и температуру стенки обоймы
^woi ^woi’ Р^'
По предложенной методике была составлена программа расче-
та (рис. 2.5), которая состоит из массива начальных данных и собст-
венно программы счета. Массив начальных данных включает в себя:
расход рабочего тела — G, давление и температуру перед соплом рк
и Тк, диаметр твэла — d, площадь проходного сечения ТВС— S, шаг
закрутки твэлов — deq, периметр обоймы — По, длину z-ro участка —
Глава 2
121
Рис. 2.5. Блок-схема программы теплового расчета ТВС
при одномерном описании течения
122
Глава 2
тела по длине активной зоны ТВС при номи-
нальном двигательном режиме работы
Ах., значение Frm = s2/ddeqt
длину активной зоны ТВС-1,
температуру рабочего тела
на входе в ТВС — Твх, тем-
пературу газа в системе ох-
лаждения ТВС — Тохл, рас-
пределение давлений по
длине активной зоны ТВС
(рис. 2.6). Кроме того, зада-
ны распределения величины
Kt = pzgvicpl геометрические
характеристики входной и
выходной решеток и вход-
ных узлов ТВС и геомет-
рические характеристики
слоев теплоизоляционной
обоймы ТВС. Известны так-
же местные коэффициенты гидравлического сопротивления по про-
точному тракту ТВС и графики зависимости I = 1(Т,р) и ц = ц(Т) для
рабочего тела (см. рис. 2.3, 2.4).
Распределение температуры рабочего тела по длине ТВС, рас-
считанное по представленной методике теплового расчета (рис. 2.7),
является исходным для проведения гидравлического расчета ТВС
в предположении, что поток теплоносителя стационарный, а газ —
идеальный, т.е. применимо уравнение состояния в виде: р = pRT. Кро-
ме того, предполагается, что отбор и вдув газа по длине ТВС отсутст-
Рис. 2.7. Распределение среднемассовой тем-
пературы рабочего тела по длине активной
зоны ТВС: 1 — для расчетного распределения
qv; 2 — для закона синуса; 3 — для расчетно-
го распределения qv = const (х) и теплоемко-
сти ср = const(x)
вуют, т.е. ри = const, по-
скольку возможные протеч-
ки теплоносителя в высоко-
пористой волокнистой теп-
лоизоляции ТВС и в зазоре
между обоймой и металли-
ческим корпусом пренебре-
жимо малы. Принимается
также, что давление и тем-
пература газа по длине рас-
четного участка изменяются
линейно, а давление газа пе-
ред соплом равно давлению
на выходе из ТВС. Измене-
ние числа Re по длине ТВС
представлено на рис. 2.8.
Глава 2
123
Результаты теплогидрав-
лического расчета по из-
ложенной методике для
ТВС, работающей на 40%
мощности от номиналь-
ного режима, представле-
ны на рис. 2.9.
Расчет распределений
давлений по длине ТВС
проводится по тем же рас-
четным участкам (см. рис.
£2), что и при тепловом
Рис. 2.8. Распределение чисел Рейнольдса по
длине активной зоны ТВС: 1, 2 — при рп =
= 370 кг/(м2-с) и температурах Твх = 450 и 300К
соответственно; 3 — то же при ри = 148 кг/(м2-с)
и Твх = 300К
расчете, начиная с выход-
ного сечения ТВС (z = п),
методом итераций. В от-
личие от теплового рас-
чета гидравлический рас-
чет проводится не только для активной зоны ТВС, но и для выходных
я входных узлов ТВС (см. рис. 2.2). Поэтому для расчета потерь давле-
ния необходимо знать, наряду с коэффициентами гидравлического
сопротивления, характеризующими линейные гидравлические по-
тери, и коэффициенты местного сопротивления, которые учитыва-
®т резкое изменение сечения и формы канала. Эти коэффициенты
местных потерь могут быть взяты из соответствующих справочни-
ов при известных геометрических размерах элементов проточного
хракта ТВС или определены экспериментально при гидравлических
испытаниях натурных ТВС.
Рассмотрим методику расчета гидравлических потерь в ТВС при
известных коэффициентах гидравлического сопротивления. Тог-
зная параметры рабочего тела перед соплом (Тк, рк) и принимая
Вас. 2.9. Результаты теп-
аагадравлического рас-
чета при одномерном
течении водорода в ТВС
С витыми твэлами при
КМ = 148 кг/(м2-с)
124
Глава 2
рвыхр = Рк' опРеДелим перепад давления на выходной решетке в пер-
вом приближении
РТК
2р/
(2.1.41)
и давление на входе в решетку рвхр - рк + Др'.
Затем определим Др" во втором приближении
АРр ^вых р
vFnJp
RTK { G ] RTK
2Pbx p \ Jp Pk
RTK '
Рвхр ,
(2.1.42)
и давление pBX p = pK + App и т.д. до получения повторяющихся резуль-
татов. Определенное таким образом давление на входе в выходную
решетку ТВС рвх будет равно давлению на выходе из активной зоны
ТВС (из расчетного участка i = п согласно схеме на рис. 2.2). Расчет
перепада давления на каждом расчетном участке при известном дав-
лении на выходе из него (р2;) ведется также методом последователь-
ных приближений начиная с участка i = п (рис. 2.2). При этом:
— определяется перепад давления в первом приближении
Др;	А(Т Г ),	(2.1.43)
2p2i	Pli
давление на входе в z-й участок = p2i + и среднее давление
Рср;
Pli + Pli .
2	'
— определяется перепад давления во втором приближении
АР/=51
Дх/ G?RTcpf
^eqi V Ji 2рсрг-
р£
Pu >
(2-1.44) ]
<Fn)i Pli <
давление р1г-
л ”	” Plz + P2z
р2/ + Ар, и рср/ = ——~ и т.д. до получения повторя-
ющихся результатов.
В уравнениях (2.1.43) и (2.1.44) коэффициент гидравлического со-
противления пучка витых твэлов может быть определен по формуле;
приведенной в работе [2.1.23]:
0,266
Re0'25'
ке5Л
(2.1.45)
Глава 2
125
где Re5/l = G5/(Ffii[icp), p./f определяется на расчетном участке Ах;. при
средней температуре потока Tfcp = 0,5(Tf_1 4- Г.) (ц для водорода не за-
висит от давления (см. рис. 2. 4)).
Поскольку ТВС с витыми твэлами является, по-существу насып-
ной конструкцией, которая состоит из нескольких нагревных сек-
ций (НС), размещенных между входной и выходной решетками (см.
рис. 2.2), то на границах расчетных участков, где твэлы соседних НС
упираются торцами друг в друга, необходимо учитывать потери дав-
ления на стыках между НС. При этом расчет проводится по форму-
лам:
— для первого приближения
/?ТВХ;-
G
bp'd =Q
•^nJc ^Pbxi
— для второго приближения
РвЫХ1-1 РвХ! + ДрС1 |
(2.1.46)
АЙ =4
R jQXI-
< /с 2рвь1Х1-1
RT^xi
Рвх1
| Pbxi
Рвых/-1?
(2.1.47)
Рвьш-1 = Pbxi + Арй и Т-А-	(2.1.48)
После определения давления на входе в активную зону ТВС
|ва входе в первую НС) рассчитывают потери давления на вход-
ной решетке, а затем — на торцевом отражателе нейтронов и
а радиационной защите (рис. 2.10—2.12) по формулам (2.1.41) и
1X1.42), используя известные коэффициенты гидравлических соп-
ротивлений этих узлов ТВС (рис. 2.13, 2.14), а также полученные из
редыдущих расчетов значения давлений на входе в них. При этом
ринимается, что температура рабочего тела на элементах радиаци-
онной защиты, торцевого отражателя и входных решеток равна тем-
пературе газа на входе в активную зону ТВС (на входе в первую на-
ревную секцию).
В результате гидравлического расчета ТВС определяются сум-
марные потери давления на всех элементах ТВС:
1-п	к-т
bps = X АР/ + X ДРмА-	(2.1.49)
1=1	к=1
г- т — число местных сопротивлений узлов ТВС. Тогда давление
а на входе в ТВС будет равно
Рвхтвс = Рк + APz-	(2.1.50)
Результаты теплогидравлического расчета ТВС с витыми твэла-
при работе ядерного реактора на мощности, составляющей 40%
ве номинального значения, представлены на рис. 2.9, а результаты
126
Глава 2
Рис. 2.10. Проточный тракт ТВС с витыми твэлами (вариант 1):
1 — входной и выходной узлы; 2 — радиационная защита; 3 — отражатель и вход-
ная решетка; 4 — нагревные секции с промежуточными решетками; 5, 6 — соот-
ветственно промежуточная и выходная решетки
Глава 2
127
F= 177 мм2
d= 15 мм
031
Fn = 297 мм2
d__ = 1,138 мм
eq
100
600
Рис. 2.11. Проточный тракт ТВС с витыми твэлами (варианты 2-4):
Я — узел входа; 2 — радиационная защита; 3 — отражатель; 4 — система входных
|рвиветок № 1 и № 2 для вариантов 2 — 4; 5 — нагревные секции без промежуточ-
их решеток
128
Глава 2
Рис. 2.12. Проточные тракты радиационной защиты (1) и отражателя (2) ТВС с
витыми твэлами (вариант 5) при системе входных решеток по варианту 3 и при
нагревных секциях по вариантам 2 — 4
оценки вклада составляющих гидравлических потерь на отдельных
узлах ТВС в суммарные потери давления ТВС на различных режи- '
мах работы при давлении водорода на входе в сопло рк = 4,9 МН/м2 и ;
Тк = 3050К приведены в таблице 2.1.1.
Полученные данные по потерям давления позволяют оценить на-
грузку на витые твэлы для определения их работоспособности при
высоких температурах, что позволяет избежать явления ползуче-
Рис. 2.13. Зависимость коэффициента гидравли-
ческого сопротивления радиационной защиты от
числа Re для различных вариантов конструкции
ТВС с витыми твэлами
сти материалов твэлов.
При этом надо учитывать
предварительное поджа-
тие пружиной активной
зоны ТВС с торцевым
отражателем с усилием
примерно 10 кгс.
Коэффициенты мест-
ных сопротивлений для
различных вариантов
конструкций, их зависи-
мости от числа Рейнольд-
са для радиационной за-
щиты (^р з) и для торцево-
го отражателя с сис темой
решеток Котр+р) приведе-
ны на рис. 2.13 и 2.14.
Глава 2
129
Таблица 2.1.1
Результаты оценки вклада составляющих гидравлических потерь
а отдельных узлах ТВС в ДрЕ для различных вариантов конструкции
(см. рис. 2.10—2.12)
1 Вариант конструкции входных узлов	1			2	3
J Расход газа, кг/с	0,1045	0,1045	0,0418	0,1045	0,0418
Температура Гвх, К	450	300	300	450	300
Давление на входе в ТВС рвх, МН/м2	9,6	9,05	5,87	8,9	5,745
Jpv. МН/м2	4,7	4,15	0,97	4,00	0,845
|-4.3/APz	0,224	0,177	0,186	0,112	0,086
Г^Ротр + вх.р /APl	0,0966	0,073	0,073	0,094	0,0697
	0,524	0,570	0,606	0,615	0,697
Г^Рвых.р /^Рг	0,1585	0,179	0,124	0,186	0,149
Г^Рн.с ^Ротр + вх.р /^Рг	0,6206	0,6430	0,679	0,709	0,767
Шотери, связанные с ускорением |жутокаДруск/Дрх	0,0667	0,0752	0,053	0,0765	0,0661
Коэффициенты С,рз
 являются сум-
^спр + р	/
тарными коэффициен-
тами сопротивления.
Эго связано с тем, что
форма гидравлическо-
го тракта этих узлов
весьма сложная и раз-
йктъ его на отдельные
таементы не представ-
лялось возможным.
Результаты экспери-
ментального определе-
тая местных сопро-
•иилений для различ-
ных вариантов конст-
рукции ТВС представ-
лены в таблице 2.1.2.
>отр+р
											
											
											
											
											
											
											
									▲ - eapi • - вари	1ант4 ант 5	
											
2	3	456789105	2	3 Re
7
6
5
4
3
2
Рис. 2.14. Зависимость коэффициента гидравличе-
ского сопротивления отражателя с системой реше-
ток от числа Re для вариантов 4 и 5 конструкции
130
Глава 2
Таблица 2.1.2
Коэффициенты местных гидравлических сопротивлений
для различных вариантов конструкций (см. рис. 2.10—2.12)
Наименование узлов и элементов	Вариант конструкции				
	1	2	3	4	5
Узел входа	—	1,35	1,35	1,35	1,35
Радиационная защита	5.4	13,5	13,5	13,5	35,5
Отражатель	0,47	—	—	—	4
Входная решетка	1,85	—	—	—	2,2
Отражатель вместе с системой входных решеток	—	5,5	5,6	5,6	6,2
Промежуточные решетки	1,3... 1,9	—	—	—	—
Стык между нагревными секциями	—	0,2...0,3	0,2...0,3	0,2...0,3	0,2...0,3
Выходная решетка	1,65	1,65	1,65	1,65	1,65
Варианты конструкции решеток 2—5 обладают общим недостат-
ком, связанным с перекрытием периферийного ряда твэлов, что при-
водит к появлению в этой зоне циркуляционного течения и участка
выравнивания неравномерностей скорости по длине первой нагрев-
ной секции. Однако этот недостаток не сказывается на работоспо-
собности конструкции ТВС этих вариантов [2.1.17].
Методы расчета ТВС по локальным параметрам
Эти методы основаны на использовании модели течения гомо-
генизированной среды, в которой течение в реальном пучке витых
стержней заменено потоком двухфазной среды с неподвижной твер-
дой фазой, где по определенному закону распределены источники
объемного тепловыделения qv и гидравлического сопротивления
E,pu2/2deq. В случае нестационарного протекания процесса модель те-
чения гомогенизированной среды описывается системой уравнений,
содержащей, наряду с уравнениями энергии, движения, неразрывно-
сти и состояния для теплоносителя, и уравнение теплопроводности
для «твердой фазы» — витых труб. При этом решается сопряженная
задача: учитываются краевые эффекты и используются понятия ко-
эффициента теплоотдачи и эффективного коэффициента турбулент-
ной диффузии, зависящих от граничных условий [2.1.3].
Глава 2	131
Для численного решения стационарных задач тепломассообмена
в пучках витых труб были использованы различные методы. В слу-
чае асимметричной неравномерности тепловыделения в поперечном
сечении пучка наиболее приемлемым методом расчета является ме-
тод матричной факторизации, развитый Г.И. Марчуком примени-
тельно к решению уравнений параболического типа. Этот метод был
обобщен для случая течения гомогенизированной среды, которое
описывается системой параболических уравнений с нелинейностя-
ми и коэффициентами, зависящими от решения [2.1.3]. Для записи
численных аналогов исходных уравнений использовалась неявная
конечно-разностная схема. Для осесимметричной неравномерно-
сти тепловыделения расчет стационарных полей температур может
проводиться также методом сеток с использованием явной схемы и
методом установления, основанным на замене стационарной задачи
нестационарной задачей и доведении решения до момента, когда оно
перестает меняться во времени [2.1.3].
Для численного моделирования нестационарных задач был раз-
работан метод расчета, основанный на раздельном решении урав-
нений энергии и теплопроводности и уравнений гидродинамики с
увязкой их через уравнение состояния и итерационные циклы. Урав-
нения энергии и теплопроводности решались методом переменных
направлений как для осесимметричной, так и асимметричной нерав-
номерностей тепловыделения. При этом численные аналоги исход-
ных уравнений расписывались по неявной схеме и решались мето-
дрм прогонки, изложенным в работах А. А. Самарского, Г.И. Марчука
н Н.Н. Яненко. При решении уравнений движения и неразрывности,
записанных в квазистационарном приближении, для их решения ис-
пользовали метод прогонки с помощью подстановки Симуни [2.1.24].
Расчет стационарных режимов ЯЭДУ. Для расчета полей тем-
ператур и скоростей в пучках витых твэлов на стационарном ре-
жиме использовали метод матричной факторизации и на его осно-
ве строили алгоритм решения. Этот метод был обобщен на случай
решения нелинейной системы уравнений в цилиндрических ко-
ординатах [2.1.3]. Вся область определения искомых функций раз-
вивалась на т секторов по азимуту, п концентрических колец по
радиусу и h слоев по длине. Поскольку решали уравнения парабо-
лического типа, то число слоев по длине не ограничивали, так как
а каждом последующем слое по длине решение строили на осно-
вании результатов расчета предыдущего. Расчетные точки были по-
вицены в узлах пространственной сетки, нулевая точка — на оси
рассчитываемой ТВС, а граница ТВС — в середине последнего рас-
путного интервала по радиусу. Согласно этому методу все произ-
132
Глава 2
водные заменены конечно-разностными соотношениями по класси-
ческой неявной конечно-разностной схеме, обладающей абсолютной
устойчивостью при решении линейных уравнений.
Для расчета градиентного течения в цилиндрическом канале мето-
дом Л.М. Симуни вводилась некоторая дополнительная функция, не
имеющая физического смысла, но позволяющая расщепить уравнение
движения (2.1.2.) на два уравнения и находить градиент давления из со-
отношения для расхода теплоносителя, значение которого задано и не
изменяется по длине канала, так как отношение dp/dx в рамках приня-
той постановки задачи является функцией только одной переменной.
Этот прием для трехмерной задачи был обобщен в работе [2.1.3].
Трехмерное уравнение движения записывается в конечно-разно-
стном виде:
д^к+lk+l , л тк+1 „к+1 , пк+1 „к+1 , /~)к+1 „к+1 ,
+ ^i+ij^+ij + Л-,у-1^’./-1+ 4j+iu< j+i +
/ . чк+1
+C^lu^'=D^ + E^'\^\ ,	(2.1.51)
где z, у, к — индексы расчетных узлов по радиусу, азимуту и длине со-
dp	„	~
ответственно; —— — продольный градиент давления. Все величины
. dx
с индексом к полагаем известными из расчета предыдущего слоя по дли-
к+1
не, а коэффициенты при неизвестных величинах ц- • также извест-
ны. Если предположить, что решение уравнения (2.1.51) имеет вид
(2.1.52)
то исходное уравнение (2.1.51) после подстановки в него (2.1.52) мож-
но разбить на два: одно относительно , другое относительно z^:
+	= D*, (2.1.53)
+ "Дц4ц + CZ“ + +Ci.J 'Z-.J1 =<	<21-54»
Решив эти уравнения, получим величины и zf., которые затем
будем использовать для нахождения искомого градиента давления.
Интегрируя уравнение (2.1.52) и используя выражение для расхода
теплоносителя в интегральной форме, получим:
2я гк
G-eJ J pwrdrcfcp
/^„>к+1
^+1=^+1+zk+1
IdxJ
е J J pzrdrdcp
о о
Глава 2
133
С учетом принятого разбиения области определения искомых
функций можно получить выражение для определения градиента
давления при численном нахождении двойных интегралов в форму-
ле (2.1.55):
dp
dx
„ I 7th2 « 2ih2'
G'E ~7~Powo + X
I 4________
'jth2 "2ih2:
E ~rPozo + Z
ч	»=1
'7Г т
т j=l
71 S	Л
т м	)
(2.1.56)
TT	-
Нелинейные выражения типа pu— линеаризуются и представ-
ляются в виде:	х
3	,-k+l „к
du ( чк+1/2 ui,j ~ui,j
ри— = (ри).. —-------------—,
н дх V	I
(2.1.57)
причем индекс к 4- 1/2 означает, что величина берется в «полуцелой»
точке по длине.
Коэффициенты, находящиеся под знаками дифференциалов,
осредняются по шести точкам в соответствии с направлением диф-
ференцирования, после чего они выносятся из-под знаков диффе-
ренциала.
1 д ди
Например, выражение Veff7" в линеаРизованном виде за-
писывается так:
1 д (	ди\	1 с) f	/о л го»
“У Р^Г— =PVetf-T- Ь	(2Л>58)
гдг\	dr J	г дг\ дг)
причем средняя величина pve// по радиусу определяется уравне-
нием
(-	? РУ*Х + 2ру.У +PVJHJ +Pvf-i,j +2р< +PVM.J	(2.1.59)
eff i.i	8
а средняя величина (pv)e// по азимуту уравнением
—	_ (pv)*/-i+2(pv)‘,H + (pv),^! + (pv),yJ + 2(pv)^ + (pv)?J+1 (2 J 59a)
(pVeff)j.	-	. (	•
С учетом изложенных преобразований численный аналог исход-
ят системы уравнений имеет вид:
— аналог уравнения движения относительно w{.
134
Глава 2
(	\к+\/2
2(р^),;у 2Ы„,- (М;1'2
h2 g2r2 2deq
(2.1.60)
— аналог уравнения движения относительно zt-
, J 2(М.У 2(М, (м*;|/2
I	+ZiJ h2 g2r2 2deq
(P^effkj
h2
Л+1
Pveff)..	PM-.
!____'ч . 7k+\ 2_____22.
g2r2	g2r2
— аналог уравнения энергии
'т’к+1 тк	.
(г.	\k+i/2 li,i li,i _ ^к+1/2 1 ~ £
\Р UCp\,j	I qvi'j е
'7’if + l ryrk+1 , 'Т’к+1
г- ‘J+IJ ^^i,j +	^eff,i,j
2hr;
(2.1.61)
(2.1.62)
2 2
g ъ
-k+l Q'T’/c+l
i,j-l Z1i,j
— уравнение состояния
р = pRT,
— уравнение теплообмена
(1-E)deg
'	^=T + (?v	.2-g
4осе
(2.1.63)
(2.1.64)
Глава 2
135
Уравнения (2.1.60) —(2.1.64) дополняются соотношением для на-
хождения градиента давления (2.1.56).
В матричной форме записи численные аналоги исходных уравне-
ний упрощаются. Обозначим значения искомых функций w, z и Т на
I-м радиусе искомого слоя по длине через W^,Tf, индекс принад-
лежности данных функций к искомому слою АН-1 по длине опустим,
а величины, известные из расчета предыдущего слоя, будем обозна-
чать верхним индексом «*». Векторная форма записи означает, что
все азимутальные значения искомой функции на данном радиусе яв-
ляются элементами столбца.
Например:
(2.1.65)
Аналогичная форма записи выполняется и для величин V^.,Zf,qvf.
Затем каждый из численных аналогов исходных уравнений приво-
дят к виду:	л л	_>
(2.1.66)
иде At,Bi,Ci — матрицы, составленные из коэффициентов исходных
уравнений; — неизвестная функция; f. — величина, известная из
расчета предыдущего слоя.
Матрицы Ai и Ci — однодиагональные и имеют вид:
— для уравнений относительно W^Z,:
(2.1.67)
136
Глава 2
— для уравнения энергии:
^-+^1,0...о
h2 Ни-
g g heffijn [ heffi,m
....... h2 2hrt
(2.1.68)
heff i,l _ ^effi,\ л
~P ~2h^' .................
h2 2hrf
Матрица Bi формируется таким образом, чтобы можно было на
каждом радиусе искомого слоя удовлетворить условие периодично-
сти искомых функций по радиусу:
4444г	(2.1.69)
Условие периодичности выполняется, если ввести в матрицу Bi
угловые элементы, при этом сама матрица должна быть трехдиаго-
нальной. Для уравнений движения относительно w и z матрица Bt
имеет вид:
2ЮЫ. м;2. >4... нт Ы,.0 0 KI
g2r2 2deq h2 I ' g2r? ' ...................... g2r2
(ЯД2 2(Rff),2.	2(^ff),2 , (pu)iy Ы,.2
ff2r,2 ’ g2//2	t? I • g2r^ ............
(2.1.70)
KL n n KL 2KI+(^pC+2KL+(pC
2 2 -°- —-°- —~2^~’ ~?~2	—+ Г2 + 'j—
и для уравнения энергии соответственно:
Глава 2
137
2Лед;., (pucp),,i Kttu XeffM
h2 g2r? I ' g2r?.............................g2r?
^eff i 2 2Xe/fl2
2 2 ’	Г2 2 2
9 rf h
X.- 9
—— 0
2 2 ,v'
9 li
(2.1.71)
K,m n n Km 2Km K,m ^UCp\,m
g rf g^i h g*rf I
Еде g = 2п/т, а осреднение величин veff, Xeff проводится в соответст-
вии с направлением дифференцирования. Порядок всех матриц и
столбцов равен т — числу секторов по азимуту принятой пространст-
венной сетки.
Источник ff в правой части уравнения (2.1.66) для величины Wf-
редставляет собой суперпозицию величин, известных из расчета
предыдущего по длине слоя:
(2.1.72)
Для уравнения относительно zf источник записывается в виде
столбца порядка т, состоящего из минусовых единиц, а для уравне-
ния энергии величина ff представляет собой суперпозицию источ-
ника тепловыделения qv и величин температуры в соответствующих
уздах расчетной сетки, полученных на предыдущем по длине расчет-
ном слое:
.1/2 1~£
1 с (рПСр)1/2
„1 /2 1-£ . V	рЛ,1	т*
Qvi.i +	1	А’,1
е	I
(2.1.73)
\1/2
I
i,m
1/2 1-е
Таким образом, численные аналоги исходных уравнений (2.1.60) —
®1_64), в которых искомая функция в каждом узле расчетной сетки
138
Глава 2
определялась через значения в пяти соседних узлах, сведены к более
простым трехточечным соотношениям.
При решении уравнений методом матричной факторизации для
каждой z-й точки можно записать следующую систему уравнений:
АЛЛА
₽,.+1=С1+1(В,-₽(Г',	(2.1.74)
ё,+1=^+1(ё,+Л).	(2.1.75)
*;=С^+1Ф,+1+0/+1).	(2.1.76)
причем	С = А~' С, В = А~' В, F = A~' f.	(2.1.77)
Видно, что, определив совокупность значений вспомогательных
функций Pp0f во всех точках по радиусу, можно найти и всю сово-
купность значений неизвестной функции У,- и, тем самым, решить
задачу. При этом значения функций	вычисляются с помо-
щью уравнений (2.1.74) —(2.1.76), связывающих эти значения в двух
соседних по радиусу точках. Эта процедура носит название прямой
прогонки. При этом величины Рр©, находим в порядке возрастания
индекса z, т.е. от левой границы (оси теплообменника) к правой (пря-
мая прогонка), а искомая функция Фг, наоборот, — от внешней гра-
ницы теплообменника к оси с использованием граничных условий
по радиусу (обратная прогонка). Рассмотрим более подробно реше-
ние каждого из трех уравнений.
При решении уравнения движения относительно для нахож-
дения начальных значений вспомогательных функций р. и 0, не-
обходимо воспользоваться выражением, определяющим величину
W. на оси канала, которое в векторно-матричной форме записыва-
ется в виде [2.1.3]:
где Е — полная единичная матрица порядка т. С другой стороны, из
уравнения (2.1.76), записанного для z = 0, получаем соотношение, свя-
зывающее величины W, и Wo:
W0=C^,(^W1+§1).	(2.1.791
Приравнивая соответствующие члены в выражениях (2.1.78) 
(2.1.79), получим соотношения для определения начальных значение
Глава 2
139
Р; и 0г, необходимых для проведения прямой прогонки и нахож-
дения всей совокупности значений этих величин вплоть до точки
i — п:
(2.1.80)
Чтобы найти последнее по радиусу значение величины Wn и осу-
ществить обратную прогонку, используют граничное условие на
внешней границе ТВС (теплообменника) (см. уравнение 2.1.6), кото-
рое в конечно-разностном виде с учетом, что внешняя граница рас-
считываемой области помещена в середине последнего интервала по
радиусу, имеет вид:
W„_1=Wn.	(2.1.82)
Из уравнения (2.1.76) при i = п — 1 имеем:
W„_I=C;I(pJ1Wn+en).	(2.1.83)
Тогда из выражений (2.1.82) и (2.1.83) можно получить формулу для
определения Wn, т.е.
W„=0n(Cn-₽„r.	(2.1.84)
и осуществить обратную прогонку для определения всей совокуп-
ности величин W,- вплоть до значений Wt и Wo. Аналогичным спо-
собом решаем уравнение движения относительно Z,. Величина р в
этом случае совпадает с аналогичной величиной уравнения (2.1.80), а
находим по формуле
где D — столбец из единиц порядка т.
(2.1.85)
140
Глава 2
Для решения уравнения энергии используются векторно-матрич-
ная форма для записи значения Ti на оси и уравнение (2.L76) для
i = 0, чтобы получить выражения для определения величин и 0г:
4а2/	* £
m(4a2/+h2) ' ’
(2.1.86)
ё =	//12дУ02(1-е)	' Tph2
1’[е[(риСр)1;2Л2 + 4/^2] 4а2/+Л2
Q2 _ ^еДр('~Е)
е(р«ср)0 '
(2.1.87)
(2.1.88)
Для определения Тп используется граничное условие на внешней
границе ТВС в конечно-разностном виде:
Atfn-,/2., Tn,i = «п-1/2,/	(2.1.89)
Выражение (2.1.89) представляет собой систему алгебраических
уравнений с коэффициентами теплопроводности и теплоотдачи
а, которые могут меняться по периметру внешнего канала охлажде-
ния ТВС так же, как и температура окружающего потока TQx в систе-
ме охлаждения корпуса ТВС.
Применяя векторно-матричную форму записи и учитывая, что
Twj может быть определена как полусумма значений Тп- и Тп1-, пере-
пишем уравнение (2.1.89) в виде:
~	(Тп ~ Тп-i) ~ А (Тп + Тп-i— 2Tqx ),	(2.1.90)
причем матрицы л и А — однодиагональные порядка ш
	^еЯп-1/2'0...,0		an-l/2-0,...,0	
				
л =		, А =		(2.1.91)
	0,..., 0,	/ 2,щ		0,..., 0,	
Используя уравнение (2.1.90)и уравнение (2.1.76), записанное для
i = п — 1, и исключая вектор Tn_lf получим выражение для определения
Тп, чтобы провести обратную прогонку и найти все значения вектора Tf:
(2.1.92)
Глава 2
141
Температуру теплоносителя на оси вычисляют по формуле со-
гласно работе [2.1.3]
4^1/2/(1-е)
э /	\к+1/2
eh (pucp)o
4X*%Z2/(l-e) ” к+1,
,7/
emh (pucp)o 7-1
<?vo1/2/(»-e) t
/	\k+l/2+J0
e(pucp)0
(2.1.93)
Таким образом, задача нахождения значений температуры и ско-
рости во всех точках выбранной радиально-азимутальной сетки на
данном расчетном слое по длине полностью решена.
Рассмотренная расчетная методика использует метод матричной
факторизации совместно с итерационными циклами по нелиней-
ностям, учитывающими зависимости коэффициентов, входящих в
уравнения, и граничные условия от искомых температуры и других
параметров. В то же время метод матричной факторизации приме-
ним только к решению линейных уравнений с постоянными коэф-
фициентами. Поэтому возникает следующий алгоритм реализации
расчетной методики. Первым (известным) слоем считается вход в
ТВС, где заданы радиально-азимутальные поля скоростей и темпе-
ратур, а также давление теплоносителя. По этим параметрам можно
рассчитать все коэффициенты уравнений, полагая для первой ите-
рации равенство величин в полуцелых по длине точках соответству-
ющим величинам на первом слое. Имея набор коэффициентов, мож-
но решить систему уравнений (2.1.60) —(2.1.64) и получить всю сово-
купность значений	в каждом узле пространственной сет-
ки для второго слоя по длине.
Предположив, что давление на втором слое равно давлению на
первом (известном слое), можно отыскать распределение плотностей
р/;. газа по рассчитанному на втором слое распределению темпера-
тур. При известном распределении плотности газа и известных зна-
чениях величин и определяют градиент давления по форму-
ле (2.1.56), давление и распределение скорости газа на втором слое по
длине из соотношений:
p2 = p‘+f^fh,	(2.1.94)
\dxj
2
(2.1.95)
2	2	2 (dp
dx
142
Глава 2
и проводят уточненный расчет распределения плотности теплоноси-
теля на втором слое с использованием полученного значения давле-
ния р2.
Затем определяют все искомые величины на оси [2.1.3] по фор-
мулам (2.1.78) — для и z0, по формуле (2.1.93) — для То и темпера-
туру «твердой фазы» в гомогенизированной постановке по формуле
(2.1.64).
Поскольку температура Tw определяется с помощью коэффициен-
та теплоотдачи, зависящего не только от параметров потока и физиче-
ских свойств теплоносителя, но и от температурного фактора (Tw/Tf),
то неизбежно появление еще одного итерационного цикла внутри
процедуры вычисления температуры «твердой фазы».
Таким образом, после проведения первой итерации имеются все
рассчитываемые параметры второго слоя по длине теплообменника,
и можно вновь уточнить значения коэффициентов, входящих в урав-
нения, в первую очередь, в полуцелых точках. С этими значениями
коэффициентов проводят новый расчет для получения второго при-
ближения и далее до сходимости.
Сходимость итерационного процесса необходимо оценивать по
всей совокупности значений искомых функций. Однако для систем
уравнений, описывающих течение в ТВС с теплообменом и с пере-
менными физическими свойствами жидкости, давление является
необходимым и достаточным критерием сходимости итерационного
процесса. Численное значение этого критерия было определено при
достаточно широкой вариации параметров, определяющих режим
течения и соотношения шагов расчетной пространственной сетки
[2.1.3]. При этом учитывались требуемая для инженерной практики
точность расчета полей температур теплоносителя и затраты машин-
ного времени. Установлено, что приемлемым условием сходимости
итерационного процесса является отличие значений давления теп-
лоносителя для двух последовательных итераций не более чем на
0,01%.
Расчет нестационарных режимов ЯЭДУ. Рассмотрим алгоритм ре-
шения нестационарной задачи (2.1.8) —(2.1.12) с граничными услови-
ями (2.1.13) —(2.1.16). При этом уравнения теплопроводности (2.1.8) и
энергии (2.1.9) записываются согласно классическому методу пере-
менных направлений.
Все коэффициенты в уравнениях, зависящие от решения исход-
ной системы, осредняются по времени и пространству. Конечно-раз-
ностные аналоги уравнений (2.1.8) и (2.1.9) имеют вид:
направление х:
Глава 2
143
/«T’V+1/2___qt’V+1/2 , «T’V+1/2
^sy+l Z11sij
(2.1.96)
-rV+1/2 «pV	«pV «pV+1/2	.
о v	v	^0	У“1	I'rV-i
2pcn ————+pucn —---------------------=------
P p At	p Ax dea' slJ
v+l/2
Pij+1-Pij
At
Ku VftV T<-ij)	/ v
-27;;+^)+
, ^eff /«pV+1/2	o'T’V+1/2 , -pV+1/2
A?' 0+1 ij /7-1
(2.1.97)
направление r:
T’V+l _«T’V+1/2
2(pscs)^4^=gv7/2
К (Га|-+/ r»f-v ) К iTv
rt 2Дг Д?^я+1у
4oiE	/«t’V+I _ y v+l \ ,
(l-e)de/ s" «
К
Ax2
hV+1/2___q«t’v+l/2 . «T’V+1/2 \
sij+1 £1sij 'isij-l J’
(2.1.98)
rp>y
2Pcp ——------------+Puc .
p At	p Ax
"V+l___«T’V+1/2
ij
«T’V+1/2	«pV+1/2
1ij
—	/«T’V+I _ «T’V+I \
d \ sii У I
ueq
^V+l „V
Pij Pij
At
^eff
rV+l
i+1;
2Ar
nV+1 _Q«pV+l
i+lj
Ax2
r v+l/2 o«pV+l/2
y+1 -ZJy
(2.1.99)
где i, j, v — индексы расчетного узла по радиусу, длине и времени со-
ответственно.
Суть метода переменных направлений заключается в том, что на
каждом направлении решается уравнение параболического типа с
источником, которое может быть записано с помощью трехточечной
схемы в виде:
144
Глава 2
^i,j"
(2.1.100)
Это уравнение решается методом прогонки, изложенным достаточ-
но подробно в работах А.А. Самарского, Г.И. Марчука и Н.Н. Яненко.
В качестве примера использования граничных условий для пост-
роения алгоритма решения рассмотрим граничное условие сим-
метрии на оси рассматриваемой области. Оно используется для на-
хождения прогоночных коэффициентов и 0j для осуществления
«прямой» прогонки.
Система уравнений для нахождения прогоночных коэффициен-
тов и искомых функций имеет вид:
'+' В,-₽,
0,+1=3,+1(е,+Л).	(2.1.101)
г,=(₽,+1г,+1+ем)/с,+1.
Запишем численный аналог уравнения теплопроводности в точ-
ке г = 0, где имеется особенность, согласно правилу Лопиталя. Тогда
уравнение в этой точке будет иметь вид:
Pscs^ = <?v + 2Asr^4+Xsx-^4.	(2.1.102)
s 5 Эт v sr dr2 Эх2
Используя условие симметрии в точке г — 0, означающее, что
Tf. = Ttj (i — индекс по радиусу;; — индекс по длине), получим конеч-
но-разностное выражение, связывающее значение искомой функ-
ции Т на оси канала и в первой точке по радиусу:
r.V+1 _ yV+1 / Ps^s ,
so =z?* aJ
(2.1.103)
где Ar — шаг разбиения расчетной сетки по радиусу; f — член,, вклю-
чающий в себя объемное энерговыделение, величину Т^, известную
из расчета предыдущего слоя по времени, и величину л —у-, извест-
дхЛ
ную из расчета по направлению х. Имея условие связи величин 7^ и
TS1 из уравнения (2.1.101), записанного для i = 0, легко найти значе-
ния прогоночных коэффициентов pt и ®р а значит, и всю совокуп-
ность прогоночных коэффициентов и значений искомой функции 7^
от i = 1 до i = N, где N — число разбиений по радиусу.
Аналогичным образом решается уравнение энергии с той лишь
разницей, что в уравнении энергии присутствует конвективный
член, записанный с помощью разностей «против потока».
Глава 2
145
Уравнение движения расщепляется на два уравнения в соответст-
вии с методом расчета градиентного течения в цилиндрическом кана-
ле, предложенным Л.М. Симуни, и определяется градиент давления из
соотношения для расхода теплоносителя. Этот метод подробно рас-
смотрен при решении стационарной задачи в ТВС в начале раздела.
Поскольку для ТВС ЯЭДУ характерное время изменения парамет-
ров, определяющих теплогидравлические процессы, значительно
превосходит время распространения слабых возмущений по длине
пучка твэлов, то в этом случае система уравнений газовой динами-
ки была упрощена и записана в квазистационарном приближении
(уравнения (2.1.10) — (2.1.11)), что подтверждается оценкой порядковых
членов, выполненной при использовании в качестве базового време-
ни для обезразмеривания исходных уравнений величины тб = — (где
Ц,
I — длина пучка твэлов (/ < 1 м), иь — скорость распространения воз-
мущений, равная скорости звука).
Действительно, если характерное время изменения основных па-
раметров значительно превышает транспортное время, то в ряде слу-
чаев можно воспользоваться квазистационарным приближением не
только для уравнений газовой динамики, но и для уравнения энер-
гии. Однако для данной задачи целесообразно ограничиться случа-
ем, когда характерное время значительно превышает величину 1/иь,
и с помощью квазистационарной модели исследовать теплогидрав-
лические процессы, в которых возмущение основных параметров
происходит за время, много большее 0,1 с.
В качестве граничных условий для уравнений движения и нераз-
рывности, заменяемого уравнением расхода (2.1.11), задается значе-
ние расхода теплоносителя в зависимости от времени и статического
давления на входе в канал р = ръх(т) согласно уравнению (2.1.13).
При численном расчете переходных процессов в ядерных реакто-
рах космических энергодвигательных установок [2.1.17, 2.1.19] к си-
стеме уравнений (2.1.8) — (2.1.12) необходимо добавитьу равнения нейт-
ронной кинетики, описывающей изменение мощности реактора во
времени:
Tz^- = (pz-1)N + N- аТ	(2.1.104)
= \	i=l, 2,... 6,	(2.1.105) (2.1.106)
ewe
Глава 2
"fee т, — среднее время жизни одного поколения нейтронов деле-
ния с учетом наличия запаздывающих нейтронов, отнесенное к ре//;
£0. — доля запаздывающих нейтронов от числа нейтронов деления
(Ь,ля реактора на тепловых нейтронах т, « 0,1 с); N,N — соответс-
твенно мощность реактора и мощность, обусловленная делениями за
' Ьчет запаздывающих нейтронов; — постоянная распада i-й груп-
пы запаздывающих нейтронов; рх — суммарная реактивность ре-
актора, отнесенная к эффективной доле запаздывающих нейтронов
6
(pZ =P/Peff) J Peff =
i=l
К системам уравнений (2.1.8) —(2.1.12) и (2.1.104) —(2.1.106) для уче-
та влияния изменения теплогидравлических параметров на свойства
размножающейся среды и мощность реактора добавляется также со-
отношение для эффектов реактивности:
[„рдау JvPr5ydV
JvdV + f vdV
Рх=Р|.<гЙФ +
(2.1.107)
а для учета зависимости энерговыделения от р-, у-распада накопивших-
ся в реакторе осколков деления — формула Антермайера — Вайлса
= No+10) °'2 -0,87(ts +2-1O7)-0'2 -
/	\-0,2	/	7\-0,2
-(ts+tNo+10)	+0,87(ts +tNo +2-107)	].	(2.1.108)
В формулах (2.1.107) и (2.1.108) приведены параметры: 8Ф— смеще-
ние регулирующих органов от начального положения; 8Тт, бу — со-
ответственно изменение температуры материала активной зоны и
плотности теплоносителя; No — мощность реактора на режиме номи-
нальных параметров до выключения; ts — время, прошедшее после
останова реактора; tn — время работы реактора на режиме номи-
нальных параметров.
Физический смысл эффектов реактивности заключается в том,
что повышение температуры материалов активной зоны приводит к
изменению эффективного коэффициента размножения в результа-
те изменения геометрических характеристик реактора при тепловом
расширении. Существуют и более тонкие эффекты, обусловленные
изменением физики процесса замедления и поглощения нейтронов.
Значение температурного эффекта реактивности рт = /(Тт) получа-
ют путем нейтронно-физических расчетов.
Аналогично температурному эффекту реактивности определя-
ют и плотностный эффект реактивности ру , обусловленный исполь-
зованием в качестве теплоносителя водорода, являющегося эффек-
тивным замедлителем нейтронов. Заполнение реактора водородом
Глава 2
147
приводит к заметному увеличению эффективного коэффициента
размножения нейтронов.
Кроме того, реактивность системы изменяется в результате пере-
мещения регуляторов (5Ф) (см. формулу 2.1.107).
Система уравнений динамики реактора должна быть дополнена
уравнением (2.1.108), описывающим зависимость энерговыделения
от р-, у-распада накопившихся в реакторе осколков деления, посколь-
ку этот процесс играет очень важную роль в определении теплового
режима реактора после его останова. В отличие от энергоустановок,
использующих энергию химических реакций, ядерный реактор не
может быть мгновенно остановлен. После перевода в подкритиче-
ское состояние реактор еще долгое время выделяет энергию в резуль-
тате распада накопившихся в нем осколков деления. Уровень мощ-
ности этого «остаточного тепловыделения» в первые минуты после
останова составляет несколько процентов от мощности на рабочем
режиме.
Учет остаточного тепловыделения исключительно важен для
ядерных энергетических установок, а также при анализе различных
аварийных ситуаций, сопровождающихся экстренным переводом
реактора в подкритическое состояние.
Необходимость учета зависимости энерговыделения от р-, у-рас-
пада накопившихся в реакторе осколков деления можно обосновать
примером. Предположим, что реактор ЯЭДУ пилотируемого мар-
сианского комплекса проработал 1 час в двигательном режиме на
мощности 300 МВт. Согласно формуле (2.1.108), через 100 с после вы-
ключения реактора его мощность составит -6000 кВт, а через 1 час
-900 кВт соответственно. Поскольку замкнутый энергетический
контур рассчитан на предельную мощность 200 кВт, то все излишнее
тепло должно быть снято водородным теплоносителем и сброшено
в Космос. Этот процесс необходимо поддерживать до тех пор, пока
мощность остаточного тепловыделения не станет равной мощности
энергетического режима.
Для завершения математического описания задачи необходимо
добавить некоторые ограничения на основные параметры, характе-
ризующие переходные процессы.
Так, если математическая модель, описывающая динамику реак-
тора, используется для выбора способа реализации переходного про-
цесса от энергетического режима к двигательному, то из условий со-
хранения целостности конструкционных элементов активной зоны
и ядерного горючего необходимо, чтобы темп нагрева, абсолютные
значения температуры и тепловых потоков с поверхности тепловы-
деляющих элементов не превосходили предельно допустимых вели-
148
Глава 2
чин. Аналогичные ограничения должны быть сформулированы и при
реализации переходного процесса от двигательного режима к энер-
гетическому: термические удары при резком уменьшении мощности
реактора могут разрушить тепловыделяющие элементы.
Полная система уравнений вместе с ограничениями решалась
численными методами и реализована в виде программ расчета на
компьютере. Для решения системы уравнений нейтронной кинети-
ки использовался алгоритм, предложенный Я.В. Шевелевым в работе
[2.1.25].
Необходимо отметить, что одной из целей изучения переходных
процессов в энергонапряженных ядерных реакторах (ЯР) является
определение во времени термопрочностных характеристик конст-
рукционных материалов ТВС и карбидных твэлов. Очевидно, что при
реализации того или иного переходного процесса нельзя превышать
предельных для данного материала значений рабочих температур,
темпов нагрева или охлаждения, а также допустимых тепловых по-
токов, определяющих величины термических напряжений в элемен-
тах конструкции.
При этом следует иметь в виду, что при быстром разогреве ядер-
ного реактора влияние эффектов нестационарности на коэффици-
ент теплоотдачи (на тепловой поток) может быть весьма значитель-
ным, причем нестационарное значение коэффициента теплоотдачи
может как превышать квазистационарное значение коэффициента
теплоотдачи в несколько раз, так и быть меньше этого значения. Ана-
логичная картина наблюдается и для безразмерного эффективного
коэффициента турбулентной диффузии (перемешивания). Быстрое
изменение тепловой мощности или расхода теплоносителя приводит
к большим изменениям этих коэффициентов по сравнению со значе-
ниями, вычисленными при квазистационарном приближении. Наи-
более сильно этот эффект проявляется в пучках витых твэлов при
спиральной закрутке потока.
Рассмотрим результаты вариантных расчетов нестационарных
полей температур для двух типов переходных процессов: с увеличе-
нием мощности реактора с витыми твэлами на несколько порядков
(переход от энергетического режима к двигательному) и с уменьше-
нием мощности при переходе от двигательного режима к энергети-
ческому. И первый и второй процессы желательно провести доста-
точно быстро и с максимальной эффективностью с точки зрения
использования водородного теплоносителя, запас которого на бор-
ту ограничен. При этом для первого процесса весьма существенным
ограничением является максимальная величина вводимой реактив-
ности и скорость ее введения. Действительно, в реакторе со спект-
Глава 2
149
ром нейтронов, имеющих время жизни т,« 10‘5 с и характерных для
быстрого реактора, введение реактивности, превышающей величи-
ну эффективной доли запаздывающих нейтронов, приводит к вы-
ходу цепной реакции из-под контроля и к разгону реактора на мгно-
венных нейтронах. Поэтому одной из целей теплогидравлического
расчета было определение оптимального закона изменения реактив-
ности, с точки зрения ядерной безопасности и ограничений по тер-
мопрочности топливной композиции для реализации быстрого пере-
ходного процесса, с увеличением мощности.
В результате проведения численных расчетов при широкой вари-
ации законов изменения реактивности и подачи расхода теплоноси-
теля был выбран основной вариант переходного процесса, представ-
ленный на рис. 2.15. Согласно этому варианту, необходимо линейно
вводить положительную реактивность до величины ~0,9реЯсо скоро-
стью не более 1 ₽ef/c, а расход теплоносителя линейно за 3 с довес-
ти до номинального значения. При реализации такого переходного
процесса требуемое значение
температуры водородного
теплоносителя на выходе из
реактора (-2900К) достигается
примерно через 10 с после на-
чала перемещения регулято-
ров, а уровень мощности дви-
гательного режима (300 МВт)
примерно через 9 с при стар-
товом уровне мощности (уров-
не энергетического режима)
-200 кВт. Процесс происходит
достаточно плавно без пере-
регулирования мощности или
температуры.
Температура топливной
оппозиции нигде не превы-
шает допустимую. Что касается
закона изменения реактивно-
сти во времени, обусловлен-
ного перемещением регулято-
ре». с учетом и температурно-
о и плотностного эффектов
реактивности, то он представ-
ят т собой плавную кривую с
небольшим перегибом в точке
Рис. 2.15. Нестационарный процесс,
при котором мощность реактора увели-
чивается с 10 кВт до номинального зна-
чения: 1 — мощность; 2, 3 — температу-
ра соответственно твэлов и теплоноси-
теля на выходе из_реактора;_4 — расход
рабочего тела; N = N/N0,G = G/G0 —
мощность и расход, отнесенные к их
значениям на номинальном режиме;
7-г.вых ~ ^т.вых /^т.вых0' ^вых ~ ^вых /^вых0' ^т.выхд
и Твыхо — температура твэлов и теплоноси-
теля на выходе из реактора на номиналь-
ном режиме его работы (те же обозначе-
ния на рис. 2.17 —2.19 и рис. 2.21)
150
Глава 2
Рис. 2.16. Изменение реактивности реак-
тора ЯЭДУ для переходного процесса с
увеличением его мощности: 1 — суммар-
ная реактивность р^; 2 — реактивность,
вносимая органами регулирования Ррег;
3,4 — соответственно температурный Рг и
плотностный эффекты реактивности
т = 9 с (рис. 2.16). Это обсто-
ятельство представляется до-
статочно важным, поскольку
сложные законы зависимости
реактивности от времени,
требующие изменения на-
правления движения органов
регулирования, предъявля-
ют повышенные требования к
конструкции электромехани-
ческих систем, приводящих в
действие регуляторы.
При реализации более
жесткого варианта переход-
ного процесса было достиг-
нуто уменьшение времени
выхода на номинальные пара-
метры по температуре газа пу-
тем подбора соответствующе-
го закона изменения расхода
водородного теплоносителя,
так как увеличение скорости
нарастания мощности реактора по сравнению с базовым вариан-
том (см. рис. 2.15) нежелательно по соображениям ядерной безопас-
ности.
Результаты расчета представлены на рис. 2.17. Видно, что требу-
емое значение температуры водорода на выходе из реактора будет
достигнуто уже через 5 с после
начала переходного процесса.
Однако при этом наблюдается
заброс температуры топливной
композиции и газа примерно на
15% от номинального значения.
Поэтому такой вариант перехо-
да на двигательный режим воз-
Рис. 2.17. Нестационарный процесс,
при котором мощность реактора уве-
личивается с 1 МВт до номинального
значения: 1 — мощность; 2, 3 — со-
ответственно температура твэлов и
рабочего тела на выходе из реактора;
4 — расход рабочего тела
Глава 2
151
ложен только в том случае, если существующий запас термопрочно-
сти топливной композиции позволяет выдерживатьподобные кратко-
временные тепловые воздействия.
Разработанная математическая модель и программа расчета
Р-1.19] позволили осуществить изучение еще одного на сегодняшний
день мало исследованного процесса, связанного с формированием
температурных полей в топливной композиции и теплоносителе при
подаче холодного газа в разогретую активную зону реактора. Знание
особенностей такого процесса представляет практический интерес
как для разработчиков ядерных космических энергоустановок, так
 для разработчиков энергетических установок, использующих в ка-
честве теплоносителя криогенные жидкости. Расчеты показали, что
этот процесс зависит от скорости подачи теплоносителя, скорости
нарастания мощности во времени, а также определяется величина-
ми характерных времен теплового внутреннего, внешнего и транс-
портного запаздывания т-, те, xfr [2.1.19].
На рис. 2.18 показано изменение во времени температуры топ-
ливной композиции и газового теплоносителя на выходе из реактора
при мгновенной подаче теплоносителя в активную зону, прогретую
др 2000К, с расходом, равным
поминальному. При этом од-
новременно начинается про-
цесс увеличения мощно-
сти реактора по закону, изоб-
раженному на рис. 2.17 и 2.18,
 формируется температур-
ная волна, характеризующая-
ся чрезвычайно большими (до
1500—2000К/с) производны-
ми температуры, имеющими
к тому же разные знаки в раз-
личные моменты времени (см.
рис. 2.18). По-видимому, такие
производные температуры мо-
1ут привести к термическому
разрушению топливной ком-
позиции.
На рис. 2.19 изображен ва-
риант расчета, когда расход
теплоносителя подается по ли-
нейному закону. В этом случае
также формируется темпера-
Рис. 2.18. Нестационарный процесс, при
котором мощность реактора увеличивает-
ся (с предварительно разогретой активной
зоной) до температуры Гт = 2000К при
мгновенной подаче расхода теплоносите-
ля: 1 — мощность; 2, 3 — соответственно
температура твэлов и теплоносителя на
выходе из реактора; 4 — расход рабочего
тела
152
Глава 2
Рис. 2.19. Нестационарный процесс, при
котором мощность реактора с предвари-
тельно разогретой активной зоной уве-
личивается до температуры Гт = 2000К
при изменении расхода по линейному
закону: 1 — мощность; 2, 3 — соответ-
ственно температура твэлов и теплоно-
сителя на выходе из реактора; 4 — рас-
ход рабочего тела
турная волна, но производная
температуры не превышает по
абсолютной величине 1000К/с.
Таким образом, в принци-
пе, возможен способ организа-
ции переходного процесса, ког-
да происходит интенсивный
разогрев реактора в безрасход-
ном режиме благодаря кратко-
временному перерегулирова-
нию по мощности, а далее следу-
ет подача расхода по линейному
закону (с учетом ограничений по
допустимым значениям произ-
водной температуры топливной
композиции и элементов конст-
рукции).
Ключевым, с точки зрения
экономии рабочего тела, явля-
ется процесс расхолаживания
реактора при переходе от двига-
тельного режима к энергетиче-
скому Как следует из зависимости Антермайера—Байлса, мощность
реактора непосредственно после перевода его в подкритическое со-
стояние может составлять до 3—5% от того уровня, на котором он
эксплуатировался. Абсолютная величина этой мощности зависит от
длительности периода эксплуатации и определяется энерговыделе-
нием от р-, у-распада накопившихся продуктов деления. Этот про-
цесс не поддается регулированию, а зависимость энерговыделения
от времени подчиняется закону NOCT ~ т-0,2 (см. формулу (2.1.108)).
Если мощность реактора на энергетическом режиме составляет ~10-1
от соответствующей мощности на двигательном режиме, то процесс
расхолаживания должен длиться несколько часов. При этом вся вы-
деляющаяся тепловая энергия должна быть снята теплоносителем,
который затем выбрасывается в космическое пространство. С точки
зрения экономии рабочего тела целесообразно использовать эту энер-
гию для создания дополнительного импульса тяги. С наибольшей эф-
фективностью это можно сделать, если поддерживать в течение всего
процесса расхолаживания температуру истекающего теплоносителя
на уровне номинального значения температуры рабочего тела на дви-
гательном режиме, т.е. расход теплоносителя должен изменяться во
времени в соответствии с темпом уменьшения мощности.
Глава 2
153
Однако с учетом сложности в
технической реализации подобно-
го процесса на основании числен-
ных расчетов был выбран вариант
перехода от двигательного режи-
ма к энергетическому, согласно
которому с помощью органов ре-
гулирования реактор переводит-
ся в подкритическое состояние
таким образом, что его тепловая
мощность уменьшается до 10% от
номинального значения пример-
но за 5 с (рис. 2.20). При этом одно-
временно с началом перемещения
регуляторов начинает уменьшать-
ся расход теплоносителя до ве-
личины, равной 30% от значения
расхода на двигательном режиме,
как это изображено на рис. 2.21.
К 10-й секунде процесса расхола-
живания удается сэкономить -60%
массы теплоносителя по сравне-
нию с расхолаживанием при со-
хранении номинального расхода.
При этом ступенчатое снижение
расхода позволит избежать слиш-
ком резкого захолаживания топ-
ливной композиции, возможной
воломки и разрушения тепловыде-
ляющих элементов.
Что касается дальнейшего
протекания процесса, то по мере
уменьшения мощности в резуль-
тате 0- и у-распада накопивших-
ся продуктов деления необходи-
мо уменьшать и расход. При этом
длительность «ступеней» будет
возрастать, поскольку темп умень-
иения мощности замедляется со
временем. Весьма интересным
Составляется вопрос о мини-
чьно возможном значении рас-
Рис. 2.20. Изменение реактивно-
сти реактора ЯЭДУ для процес-
сов с уменьшением его мощности:
1 — суммарная реактивность р^;
2 — реактивность, вносимая орга-
нами регулирования ррег; 3, 4 — со-
ответственно температурный р?. и
плотностной ру эффекты реактив-
ности
Рис. 2.21. Нестационарный процесс,
при котором мощность реактора
уменьшается, а расход рабочего тела
ступенчато снижается: 1 — мощность;
2, 3 — соответственно температура
твэлов и теплоносителя на выходе из
реактора; 4 — расход рабочего тела;
5 — температура твэлов на рассто-
янии 100 мм от входа в активную
зону
154
Глава 2
хода теплоносителя. Если уровень мощности энергетического режи-
ма составляет 10‘3 от двигательного, то расход при расхолаживании
должен быть не меньше 10’3 от номинального, что составляет -10 г/с.
Если в реакторе имеется всего 10 каналов, то расход через канал дол-
жен быть -1 г/с. При таких параметрах течения процессы теплоотда-
чи и перемешивания недостаточно интенсивны, что может привес-
ти к локальному расплавлению топливной композиции и элементов
конструкции. Поэтому, несмотря на возможный проигрыш в массе
теплоносителя на расхолаживание, необходимо увеличить мини-
мальное значение расхода теплоносителя через реактор. Оконча-
тельный ответ на этот очень важный вопрос может дать, наряду с
численным расчетом процесса расхолаживания, экспериментальное
изучение особенностей теплообмена и перемешивания при реализа-
ции так называемых вялых, или ползучих, течений с малыми числа-
ми Рейнольдса.
В заключение отметим, что для приведенных параметров дли-
тельность процесса расхолаживания составляет около 3 часов. Если
верхняя граница значения расхода теплоносителя составляет 1% от
номинального (-100 г/с), то для расхолаживания необходимо -1 т во-
дорода, если же — 0,5%, то — 600 кг.
Таким образом, предложенная постановка задачи позволила вы-
брать оптимальные законы изменения реактивности реактора при
быстрых переходах с двигательного на энергетический режим ра-
боты и обратно при условии ограничений по ядерной безопасности
и термопрочности карбидных материалов витых твэлов при нагреве
водорода до температур, равных 2900—3100К.
Надежность рекомендаций, полученных при численных тепло-
гидравлических расчетах тепловыделяющих сборок ЯЭДУ была под-
тверждена при моделировании теплогидравлических процессов в
натурных условиях в испытательном графитовом реакторе (ИГР) на
моделях ТВС [2.1.17]. При испытаниях в таком реакторе моделей теп-
ловыделяющих сборок с витыми твэлами ЯЭДУ реализовывались ре-
жимы с одновременным ростом мощности и уменьшением расхода
теплоносителя, когда эффекты нестационарности, характерные для
случаев N = var при G = const и G = var при N = const, накладыва-
ются, резко увеличивая коэффициенты перемешивания теплоноси-
теля Кип и теплоотдачи а в первые моменты времени. Так, с ростом
мощности N расход G уменьшался, что способствовало поддержа-
нию постоянного перепада давлений на ТВС, а эффекты нестаци-
онарности суммировались. При этом интенсивность турбулентности
потока в пучке витых твэлов и коэффициенты теплоотдачи и пере-
мешивания росли по сравнению с их квазистационарными значени-
Глава 2
ОШ
ями. Типичные режимы испытаний модельныхсТВСшри резкам (рос-
те мощности представлены на рис. 2.22,а, а режимыфасхолажйва-
ния — на рис. 2.22,6. Максимальные параметры при испытания^ мо-
дельных ТВС достигали следующих значений: мощность N = 142...
...275 кВт, температура теплоносителя на выходе из ТВС Tmax t =
= 3600...3650К,массоваяскоростьтеплоносителяри = 100...186кг/(м2с),
средняя плотность теплового потока qmean = 8... 18 МВт/м2 и
(г)тЛ	(
—	= 250... 450 К/с. При расхолаживании ТВС: —	= (-150)...
Углах	Углах
... (-778) К/с.
Отсутствие принудительного охлаждения активной зоны испыта-
тельного графитового реактора и ограничение интегрального энер-
говыделения максимальной температурой активной зоны, которая
аккумулирует тепло при работе реактора благодаря своей теплоем-
кости, ограничивали время
испытания ТВС десятками
секунд (см. рис. 2.22). Усло-
вия испытания модельных
ТВС, в которых использо-
вались пучки из 7 твэлов
четырехлопастной формы,
выполненных из карби-
дов тугоплавких металлов
с шагом закрутки s/d — 30
(Frm = 4300), были близки
к натурным условиям по
уровню нейтронного по-
тока и концентрации 235U,
Рис. 2.22. Изменение расхода и
температуры теплоносителя во
времени: а — при росте мощ-
ности; б — при расхолаживании
модельных ТВС (для различных
режимов испытания): 1 —4 — рас-
ход, отнесенный к расходу при
т = 0 для режимов 1 — 4 соот-
ветственно; 5 — 8 — температу-
ра для тех же режимов соответ-
ственно; Go, То — значенияСиТ
при т = 0; Ттах — максимальная
температура рассматриваемого
рабочего режима в соответствии
с табл. 2.1.3
G Т
156
Глава 2
а также по использованию водорода с ингибирующей углеводород-
ной присадкой.
Кроме того, при этих испытаниях были достигнуты максималь-
но возможные температуры теплоносителя на выходе из ТВС и плот-
ности теплового потока. При этом в начальные моменты времени
при запуске реактора ИГР для рассматриваемого типа нестационар-
ности коэффициент теплоотдачи и плотность теплового потока в не-
сколько раз превышали свое квазистационарное значение. При этом
У mean max ~ (2- 3) Я mean (таблица 2.1.3), ЧТО ДЛЯ некоторых КраткОСрОЧ-
ных режимов испытания могло приводить к растрескиванию твэлов
из твердого раствора карбидов урана и циркония (UC-ZrC). Однако
для рассмотренных в статье режимов испытания (т = 20 и 30 с) ТВС с
витыми твэлами сохранили свою работоспособность при многократ-
ных испытаниях.
Таблица 2.1.3
Максимальные параметры испытаний ТВС в испытательном
графитовом реакторе
Параметр	Номер режима			
	1	2	3	4
(дТ/дт)тах, К/с (на рабочем режиме)	380	280	250	450
(<П7Эт)	, К/с (на режиме расхолаживания)	-340	-150	-250	-778
т	к 1 max out1	3600	3600	—	3650
ри, кг/(м2-с)	186	133	—	100
Чтеап max' МВт/м	18	8	—	9
Выполненные исследования показали, что для оценки величины ко-
эффициента перемешивания теплоносителя кцп при одновременном
изменении мощности и расхода могут быть использованы критери-
альные зависимости для расчета этого коэффициента при изменении
во времени лишь одного параметра: мощности или расхода, с учетом
наложения действия различных эффектов в ту или иную сторону.
Нестационарные режимы работы ЯЭДУ могут повлиять на ее ра-
ботоспособность, в основном, в первые моменты времени при резком
изменении мощности и расхода теплоносителя, когда коэффициен-
ты теплоотдачи и турбулентного переноса в потоке теплоносителя
также резко изменяются из-за нарушения баланса между энергией,
подведенной к турбулентному потоку, ее диссипацией, турбулент-
ной диффузией и конвекцией турбулентных молей. При переходе
Глава 2
157
на новый режим работы этот баланс постепенно восстанавливается
благодаря перестройке температурных полей теплоносителя и дейст-
вию механизмов, компенсирующих первоначальное возмущение
турбулентности и связанных с закруткой потока витыми твэлами и
тепловой инерцией системы.
Теплогидравлический расчет теплообменных аппаратов
с витыми трубами
Методы теплогидравлического расчета теплообменных аппара-
тов (ТА) с витыми трубами как с продольным, так и с поперечным об-
теканием пучка витых труб, аналогичны методам теплогидравличе-
ского расчета ТА с гладкими круглыми трубами и отличаются только
использованием критериальных уравнений теплоотдачи и гидрав-
лического сопротивления, учитывающих эффект закрутки потока
витыми трубами при течении в них теплоносителей и в межтрубном
пространстве с такими трубами.
Наиболее распространенным в инженерной практике констру-
ирования ТА является метод, согласно которому проводится сначала
тепловой расчет для определения площади теплопередающей повер-
хности и других геометрических размеров каналов и ТА, а затем —
гидравлический расчет, и определяются потери давления ТА, кото-
рые не должны превышать заданной величины этих потерь.
Для расчета ТА необходимо прежде всего задать исходные дан-
ные. Так, для теплообменника, представленного в работе [2.1.18], ис-
ходными данными для теплогидравлического расчета являются сле-
дующие.
1. Характеристика теплообменного аппарата: ТА трубчатый,
противоточный; трубы витые овального профиля с круглыми кон-
цами, заделанными в трубные доски; внутри труб протекает горя-
чий теплоноситель; в межтрубном пространстве нагреваемый теп-
лоноситель продольно обтекает пучок витых труб; размещение труб
в пучке — шахматное с взаимным касанием труб. Материал труб и
других элементов ТА — нержавеющая сталь 12Х18Н10Т.
2. Геометрические размеры ТА и витых труб: максимальный
размер профиля витой трубы задается в зависимости от исходно-
го диаметра круглой трубы, учитывая, что для сварки прямых кон-
цов витой трубы с трубной доской требуется определенное рас-
стояние между осями труб, равное dH = l,23dKpH (dB = l,23dKpB);
dH и dB — максимальные размеры овала с наружной и внутрен-
ней стороны трубы; dB = dK — 28 (где 8 — толщина стенки трубы;
dKp.H' dKP.B ~ Диаметры исходной круглой трубы); s — шаг закрутки
158
Глава 2
профиля трубы; deqx = —— — эквивалентный диаметр пучка витых
Пх	р
труб (межтрубного пространства); ех =	— пористость пучка
труб по нагреваемому теплоносителю (где — суммарная площадь
поперечного сечения теплообменника; Fnx, Fn г — площади проход-
ных сечений ТА по холодному и горячему теплоносителям:
far = ^+(d„-dOr)dOr = 4ab+(rc-4)b2,	(2.1.109)
где dOr — минимальный размер витой трубы по горячей стороне
(внутри канала); а и b — максимальный и минимальный радиусы
овального профиля внутри витой трубы соответственно: a = dB/2 и
b = d0r/2; ПгиПх - омываемые периметры труб и пучка.
Для расчета геометрических размеров овального профиля витой
трубы необходимо иметь в виду что под термином «овальный про-
филь» понимается плоский канал со скругленными концами по мак-
симальному размеру профиля dB. Тогда эквивалентный диаметр ви-
той трубы (по горячей стороне) будет равен:
= 4fn.r = Ttd0r+3 4(dB-d0i )d0r = 8аЬ+2(я-4)Ь2	„ t uo)
едг Пг	jtd0r + 2(dB-d0r)	2а+(я-2)Ь
Минимальный размер проходного сечения внутри витой трубы
(ширина плоского канала) — dOr определяется из условия, что внут-
ренний периметр витой трубы равен внутреннему периметру круг-
лой исходной трубы — 7tdKp в, из которой изготовлена витая труба пу-
тем протягивания через фильеру:
ndKn в - 2dB jrdKD в - 4a
= — к^в---в = —кр^----= 2Ь
Ог п-2	п-2
7idKnB -4a
при b = —.	(2.1.111)
F 2(п-2)
3. Заданные параметры:
— Gr и Gx — расходы горячего и холодного теплоносителей;
— Тг и Тт — среднемассовые температуры горячего теплоноси-
теля на входе и выходе соответственно;
— рт — давление горячего теплоносителя на входе в теплообмен-
ник;
— Дрг — потери давления по горячей стороне;
2
159
теплофизические свойства горячего и холодного теплоноси-
—	Тх — среднемассовая температура нагреваемого теплоноси-
1ля на входе в ТА ;
—	рх и Дрх — соответственно давление на входе и допустимые
утери давления по нагреваемому теплоносителю.
В результате расчета определяют коэффициенты теплоотдачи аг
о^, коэффициент теплопередачи К, поверхность теплообмена So6,
юло труб N, площади проходных сечений по горячему Fn и нагре-
*емому Fn х теплоносителям, габаритные размеры теплообменника.
Расчет теплообменника при одномерном описании течения теплоно-
гтеля проводится в следующей последовательности. Определяются:
—	тепловая мощность теплообменника
Q = GTcpT(TT-TT),	(2.1.112)
срг — средняя изобарная удельная теплоемкость теплоносителя,
/кг К, определяемая при Тт = 0,5(тт +Т^;
—	среднемассовая температура нагреваемого газа на выходе из
ктрубного пространства
"	> Q
''рх'“’х
срх — средняя изобарная удельная теплопроводность газового
лоносителя, определяемая при Тх = 0,5(тх' + ТХ"
—	среднелогарифмический температурный напор для противо-
(2.1.113)
• •• ।
Т -Т
In Л *
Т -Т
—	число Рейнольдса при течении внутри витых труб
Rer=A^L;
^п.г Мт
—	число Нуссельта внутри труб рассчитывается
< 7-103 по формуле
(2.1.114)
(2.1.115)
при числах
3,0384
(s/d)0'97
— коэффициент теплоотдачи в витых трубах
NurXr
ct =---—— ’
Г rl '
aeqr
Nur= 0,0486 1+
Re0,698 Рг0'4:
(2.1.116)
(2.1.117)

160
Глава 2
—	число Рейнольдса при течении нагреваемого теплоносителя в
межтрубном пространстве теплообменника с витыми трубами
Rex=^Sl;
Льх Их
—	число Нуссельта в межтрубном пространстве определяется по
формуле
(2.1.18)
Nux = 6,0540S 6 * ВFr"2’494+0’235IgFrn’ -Rex+aIgRCx
T
Prf’4, (2.1.119)
где п = _i(575Fr9-01661-°-043731gFr-; a = О^бОРг^0149-0’0104^^;
—	коэффициент теплоотдачи в межтрубном пространстве ТА с
витыми трубами
NuxXx
a =—
&eqx
— коэффициент теплопередачи, отнесенный к средней поверхно-
сти теплообмена витых труб по формуле для плоской стенки
к=-1—л
ССГ ^х
—	потребная поверхность теплообмена (по среднему диаметру
исходных круглых труб)
S —5—
06 Д7-срК’
— суммарная потребная длина пучка витых труб
Lz= S°6
^ср^ср^
(2.1.120)
(2.1.121)
1 ’
(2.1.122)
(2.1.123)
где dcp = кр'н -кр— — для исходной круглой трубы; N — число труб
в пучке.
В случае модульной конструкции аппарата выбирают длину од-
ной секции (модуля) и определяют необходимое число секций.
Далее проводится гидравлический расчет теплообменника при
заданных давлениях горячего и холодного теплоносителей на входе в
ТА и перепадах давлений для каждой из сторон ТА. Обычно оговари-
вается, чтобы этот перепад давления был не более определенной ве-
личины для ТА, устанавливаемых в технологических линиях различ-
ных производств и в энергетических установках. Если же перепад
давления будет меньше необходимой величины, то его можно всегда
Глава 2
161
компенсировать установкой дополнительного регулировочного гид-
равлического сопротивления или путем уточнения геометрических
параметров ТА в повторном расчете.
Общие потери давления в витых трубах определяются как сумма
потерь давления на трение в каналах (&Pfriction) и потерь давления на
локальных сопротивлениях (Лр1г):
ДРг = ^Pfnction + АР/г =	(2.1.124)
deqr 2	<=1	2
где pr=f(pr,Tr) — средняя плотность горячего теплоносителя;
Тг =(тг + Гг)/2 — средняя температура; рг =р'г + (Дрг/2) — среднее
давление.
В формуле (2.1.124) коэффициент гидравлического сопротивле-
ния 2, в витых трубах определяется при Re < 7-103 по формуле
с 4,804	3,0384
^Re°’632|_ (s/d)0'97
(2.1.125)
или по формулам работы [2.1.19] для чисел Re > 7-103.
Коэффициенты местного сопротивления д. берут из справочни-
ков для мест с резким сужением и расширением канала, для поворо-
та потока на 180° и других видов местного сопротивления, связанных
с особенностями проточной части конструкции ТА.
В межтрубном пространстве ТА общие потери давления при тече-
нии в пучке витых труб равны
Дрх=5-А-й^х+^,Т2&;	(2.1.126)
deqx 2	2
где px=f(px,Tx) “ средняя плотность холодного теплоносителя;
Тх = (тх + Тх)/2 и рх = рх + (Дрх /2) — соответственно средние тем-
пература и давление по холодной стороне. Коэффициент гидравли-
ческого сопротивления пучков витых труб определяется по форму-
лам:
для Frm > 100 и Re = З Ю3... 5-Ю4
0,3164<	3,6 '
Re0'25 ( Fr0'357J’
для Frm = 63,6 и Re = 2103... 5104
= 89,4Re’1,2322+0,121gRe
для Frm = 232 и Re=2103... 5104
= 156Re’1,4323+0,13761gRe
(2.1.127)
(2.1.128)
(2.1.129)
162
Глава 2
для Frm = 1052 и Re = ЗЮ3... 4-Ю4
— Д 67'103Re"2,2431+0,23981gRe
для Frm = 63,6... 1052 и Re = 104
= 10,5Fr”1,6181+0,263lgFrm ,
(2.1.130)
(2.1.131)
для Frm < 100
0,3164
Re0,25
4 3,110е
1ч--------
г; 3,38
(2.1.132)
В качестве примера рассмотрим результаты теплогидравличе-
ского расчета по представленной методике кожухотрубного ТА с ви-
тыми трубами, предназначенного для охлаждения вина в техноло-
гической линии производства шампанского производительностью
2000 литров в час на Московском комбинате шампанских вин. Тече-
ние теплоносителей в ТА организовано по схеме противотока: вино
течет внутри труб, а охлаждающая среда — водный раствор хлорис-
того кальция (СаС12) — в межтрубном пространстве. Температура
рассола СаС12 на входе в ТА равна (— 6±2) °C. Вино поступает в теп-
лообменник с температурой (+12±2) °C и охлаждается до темпера-
туры (—2±1) °C. Перепад давления на длине ТА должен быть менее
5-Ю4 Па. Теплообменный аппарат с витыми трубами заменил тепло-
обменник с прямыми круглыми трубами, который ранее использо-
вался в линии производства вина и имел внутренний диаметр труб
21 мм, общую длину труб 522 м и массу 1500 кг. Низкий коэффициент
теплопередачи К = 55 Вт/(м2К) при ламинарном течении в таком ТА
Рис. 2.23. Схема противоточного теплооб-
менного аппарата с витыми трубами для ох-
лаждения шампанского: 1 — 8 — модули ТА;
9 — патрубки; 10, 11 — соответственно вход
и выход виноматериала; 12 — выход рассола
СаС12; 13 — вход рассола СаС12
не обеспечивал охлаждение
вина с заданным расходом
до заданной температуры.
Для облегчения разбор-
ной мойки . ТА в процессе
эксплуатации при разработ-
ке нового ТА с витыми тру-
бами была выбрана модуль-
ная схема, представленная
на рис. 2.23. Новый ТА со-
стоит из 8 модулей, соеди-
ненных последовательно
при помощи патрубков. Мо-
дули смонтированы на тех-
нологической раме. Внутри
кожуха каждого из моду-
Глава 2
163
лей размещен пучок из 7 витых труб овального профиля, закреп-
ленных прямыми круглыми концами в трубных досках. Взаимное
касание витых труб обеспечивает высокую вибростойкость конст-
рукции ТА [2.18]. Теплогидравлический расчет аппарата с витыми
трубами проводился по изложенной методике с использованием
приведенных в методике критериальных зависимостей для расче-
та теплообмена и гидравлического сопротивления. Так, для течения
вина внутри витых труб расчет числа Nud/ и коэффициента £ про-
водился соответственно по формулам (2.1.116) и (2.1.125). Для расче-
та числа Nudf при течении рассола СаС12 в межтрубном пространст-
ве пучка витых труб использовалась зависимость (2.1.119) с учетом
поправки на особенности течения в пучке с числом витых труб мень-
ше 19, а для расчета коэффициента £ — формула (2.1.127). Теплофи-
зические свойства пищевых продуктов определялись по справочным
данным. Результаты расчета представлены в таблице 2.1.4.
Таблица 2.1.4
Теплогидравлические характеристики теплообменного аппарата
с витыми трубами (d = 24,6 мм; 5 = 200 мм; s/d=8,1; N-29 кВт)
Расчетные параметры	Течение вина внутри труб	Течение рассола СаС12 в межтрубном пространстве
Расход, кг/с	0,539	1,093
Скорость потока, м/с	0,4375	0,5560
Число Рейнольдса	1702	2947
Число Нуссельта	19,4	33,2
Коэффициент теплоотдачи, Вт/(м2К)	670	1051
Потери давления на длине аппарата, Па Коэффициент теплопередачи, Вт/(м2К) Расчетная площадь теплопередающей поверхности, м2 Расчетная длина аппарата, м	17169	26020 400 9,4 22,38
Длина одного модуля теплообменного аппарта была выбрана рав-
ной 3 м, что при числе модулей, равном 8, соответствует суммарной
длине аппарата 24 м и площади теплопередающей поверхности 10 м2.
Габариты ТА — 3300x700x360 мм. С учетом массы труб, кожухов, пат-
рубков, рамы и других элементов конструкции суммарная масса из-
готовленного ТА с витыми трубами, определенная экспериментально
путем взвешивания, составила около 350 кг, что в 4,3 раза меньше, чем
масса старого ТА с круглыми трубами. Таким образом, интенсифика-
ция теплообмена путем закрутки потока привела к существенному
164
Глава 2
выигрышу по массе. При этом ТА с витыми трубами позволил охла-
дить вино с температурой на входе (+12±2) °C до температуры -4 °C,
более низкой, чем охлаждает ТА с круглыми трубами (-1... -2 °C). Па-
раметры ТА с витыми трубами, представленные в таблице 2.1.4, были
подтверждены экспериментально при его испытании в составе тех-
нологической линии с использованием штатной измерительной си-
стемы на Комбинате шампанских вин.
Выполненные теплогидравлические расчеты ТА для охлаждения
шампанского и оценка его массогабаритных характеристик показа-
ли, что применение витых труб в аппарате позволяет путем интен-
сификации существенно уменьшить их массу и габариты и, следо-
вательно, металлоемкость и стоимость изготовления, а благодаря
гарантированному взаимному касанию витых труб в плотных пуч-
ках существенно снизить вероятность возникновения вибраций и
повысить надежность. Кроме того, интенсификация массообмена в
пристеночном слое потока пищевого продукта внутри витых труб
и в межтрубном пространстве пучка витых труб позволяет сущест-
венно снизить интенсивность образования осадков на теплопереда-
ющих поверхностях и операционные расходы на их периодическую
очистку.
Тепло- и массообмен при солеотложепиях
Для изучения влияния закрутки потока на уменьшение солеот-
ложений при течении внутри витых труб было проведено экспери-
ментальное исследование процесса минеральных отложений при
нагревании воды с большим содержанием минеральных солей мето-
дом теплообмена типа «труба в трубе» [2.1.26]. Этот метод исследо-
вания был ранее использован для изучения отложений солей снару-
жи труб с кольцевой накаткой [2.1.27]. При этом было обнаружено,
что использование интенсификаторов на поверхностях труб позво-
ляет значительно уменьшить загрязнения в теплообменниках и что
термическое сопротивление слоя загрязнения на поверхностях труб
асимптотически стремится с течением времени к постоянному зна-
чению этого сопротивления [2.1.28]. Такое поведение термического
сопротивления загрязнения в каналах с интенсификаторами тепло-
обмена позволяет обеспечить работоспособность теплообменных ап-
паратов в течение длительного периода их эксплуатации без очистки
поверхности от загрязнений, что невозможно для аппаратов с глад-
кими круглыми трубами.
Целью выполненного исследования было также получение обоб-
щающих зависимостей для расчета термического сопротивления
Глава 2
165
загрязнений в широком диапазоне изменения режимных и геомет-
рических параметров для витых труб, труб с кольцевой накаткой и
круглых гладких труб.
Управление процессами загрязнения поверхности теплообмена
при использовании охлаждающей воды, содержащей соли времен-
ной жесткости, является весьма важной проблемой. При использова-
нии такой воды, температура которой растет в направлении потока,
на поверхностях теплообмена образуются отложения солей. Поэто-
му необходимо либо предотвратить интенсивность роста загрязне-
ний на теплообменных поверхностях, либо ее уменьшить.
В последнее время большой интерес проявлялся к проблеме
уменьшения солеотложений на поверхностях теплообмена путем ис-
кусственной турбулизации потока [2.28, 2.27]. Уменьшение солеот-
ложений в каналах с дискретной турбулизацией и закруткой потока
связано с интенсивным обменом порциями жидкости между при-
стенным слоем и ядром потока в этих каналах. При этом современ-
ные концепции механизма солеотложений на гладких поверхностях
[2.1.29—2.1.33] могут быть использованы при построении качествен-
ной модели, описывающей процесс солеотложения на поверхностях
с искусственной турбулизацией потока и позволяющей получить
структурную форму для эмпирических зависимостей, которые наи-
более полно учитывают влияние различных факторов на процесс со-
леотложения и хорошо обобщают опытные данные.
Толщина слоя загрязнений на теплообменной поверхности зави-
сит от геометрических параметров канала, времени с начала работы
ТА, температуры потока теплоносителя и стенки, скорости течения,
давления и концентрации присадок в охлаждающей воде (ее жест-
кости). В опытах обнаружено, что рост скорости потока препятству-
ет образованию слоя загрязнений на стенке трубы как при закрутке
потока, так и при дополнительной турбулизации потока кольцевы-
ми диафрагмами. Экспериментально было также показано, что рост
термического сопротивления загрязнений на этих поверхностях со
временем значительно уменьшается и после достижения некоторой
величины термическое сопротивление становится независимым от
времени (по истечении некоторого времени с начала процесса). Та-
кой закономерности не наблюдается на внутренних поверхностях
гладких круглых труб. Таким образом, при закрутке потока в витых
трубах и при турбулизации потока кольцевыми диафрагмами терми-
ческое сопротивление отложений описывается экспоненциальной
зависимостью:
Rfoui = RfouiJ - ехр(-₽т)1	(2.1.133)
где Rfoui„ — термическое сопротивление отложений при т
166
Глава 2
Дело в том, что при отложениях происходят два одновременных
процесса: солеотложение и вынос из пристенного слоя осадков, не
осевших на стенке:
__ л dRfoul _	„
, Pfoul^foul j ^dep '^'car'
ат	ат
(2.1.134)
где &car — скорость выноса солеотложений с поверхности.
Скорость отложений &dep пропорциональна концентрации солей
С в потоке жидкости
®dep Pfoul^“foul^l
' с
1/Kp+1/KR^
-KDCW,
(2.1.135)
где Kv Кр, KRI KD — коэффициенты, зависящие от скорости течения,
температуры и геометрических параметров канала. Процесс выпа-
дения осадков определяется процессом массообмена из-за разности
концентрации солей и процессом протекания химических реакций
на границе раздела фаз.
Скорость выноса солеотложений с поверхности раздела фаз оп-
ределяется поверхностной силой, с которой поток воздействует на
слой отложений и которая возрастает с увеличением толщины слоя
отложений, т.е. с ростом Rfoul. В трубах с кольцевыми диафрагмами и
витых трубах при одной и той же скорости течения касательные нап-
ряжения больше, чем в гладких круглых трубах, и скорость выноса
солеотложений также более существенна:
®car K^wRfoul	Rfoul'
(2.1.136)
где£ = вт^/pw2 — коэффициент гидравлического сопротивления; К2
иК3 — коэффициенты.
Подставляя в (2.1.134) значения ®dep и ®car из выражений (2.1.135) и
(2.1.136), можно получить путем интегрирования выражения (2.1.134)
(с граничными условиями: при т = О Rfoul = 0, при т —> <=° RfouJ = Rfoulco)
уравнение (2.1.133) [2.1.26].
Тогда зависимость для расчета термического сопротивления слоя
отложений можно представить в виде:
Уравнение (2.1.137) отражает влияние скорости течения, кон-
центрации присадки в охлаждающую воду, параметров закрутки и
турбулизации потока на термическое сопротивление отложений. В
уравнении (2.1.137) коэффициент К3 зависит от скорости и геометри-
Глава 2
167
ческих параметров турбулизаторов на поверхности трубы и закрут-
ки потока.
Таким образом, при обобщении опытных данных необходимо оп-
ределить зависимости термического сопротивления слоя отложений
от следующих параметров:
—	для витых труб
Rfoui=t^C'C^^' s/dl	(2.1.138)
—	для труб с кольцевыми диафрагмами
Rfoui=f(RGc'C' d/D, t/D),	(2.1.139)
Pwde(J
где Rec =---- — число Рейнольдса; D — внутренний диаметр тру-
M-f
бы; deq — эквивалентный диаметр канала витой трубы; d — диаметр
кольцевой диафрагмы и максимальный размер овала витой трубы;
s — шаг закрутки витой трубы; t — шаг кольцевой накатки.
Схема экспериментальной установки для изучения процесса соле-
отложений внутри витой трубы с относительными шагами s/d = 6,2
и 12,2 была аналогична схеме установки для изучения солеотложе-
ний снаружи труб с кольцевой накаткой (рис. 2.24) [2.1.27]. Отличие
состояло только в том, что греющий теплоноситель — хлопковое мас-
ло — подавалось в кольцевой канал теплообменника типа «труба в
трубе», а нагреваемая соленая вода протекала внутри витой трубы
овального профиля и труб с кольцевыми диафрагмами. Теплооб-
менник работал по противоточной схеме. Хлопковое масло предва-
рительно нагревалось до температуры 110—115 °C. Холодная вода с
Рис. 2.24. Схема установки для изучения процесса солеотложения в каналах с ин-
тенсификацией теплообмена: 1 — баллон с СО2; 2 — бак с соленой водой; 3 — ро-
таметр; 4 — расходный бак; 5, 15 — насосы; 6 — резервуар с водой, содержащей
соли заданной концентрации; 7,8 — теплообменник типа «труба в трубе»; 9, 12 —
термометры; 10 — холодильник; 11 — расходомер; 13 — бак для хлопкового масла;
14 — электронагреватель; 16 — смесительная камера; 17 — термопара
168
Глава 2
заданным солесодержанием обладала карбонатной жесткостью до
20 мг(экв)/л. В ходе экспериментов заданная карбонатная жесткость
воды поддерживалась путем добавления в циркулирующую холод-
ную воду некоторого количества воды с более высокой жесткостью
из специального резервуара (см. рис. 2.24). В опытах измерялась тем-
пература на входе и выходе из теплообменника для греющего и хо-
лодного теплоносителей, а также их расход.
При заданных параметрах жидкостей на входе в теплообменник
опыты продолжались до момента времени, когда прекращалось вре-
менное изменение термического сопротивления солеотложений.
Этот- момент времени зависел от скорости течения w, температуры,
концентрации примесей и геометрических параметров, определя-
ющих эффект интенсификации тепломассообмена в исследуемых
каналах.
Исследуемые трубы имели внешний диаметр Dout = 10,4 мм (исход-
ный диаметр витой трубы) и внутренний диаметр D = 10 мм. Трубы
были изготовлены из нержавеющей стали. Внутренний диаметр внеш-
ней трубы теплообменника типа «труба в трубе» составлял 26 мм,
а ширина кольцевого канала — 5 мм. При этом эквивалентный ди-
аметр кольцевого канала deq =10 мм. Длина теплообменника Z = 2,5 м.
Методика эксперимента позволяла определять изменения термиче-
ского сопротивления в зависимости от роста слоя солеотложений. По
результатам определения линейных коэффициентов теплопередачи
в начальный и конечный моменты времени:
кю = О0/(^Т0),	(2.1.140)
Klx = Q/(nlbT)	(2.1.141)
определялся линейный термический коэффициент слоя солеотло-
жений:
п _ 1____________* _ foul
Ifoul if if У Г)
Л/0 ^fou!U
(2.1.142)
в предположении, что процесс солеотложений не влияет на коэффи-
циенты теплоотдачи снаружи и внутри исследуемой трубы. Терми-
ческое сопротивление внутри трубы
(21143)
где Rlfoul рассчитывается по уравнению (2.1.142). Необходимо заме-
тить, что эта методика определения Rfoul исключает необходимость
измерять температуру стенки трубы, значительно упрощая экспе-
римент. Знание коэффициентов теплоотдачи на горячей стороне поз-
воляет выполнить точные расчеты этой температуры. Помимо двух
витых труб овального профиля с относительным шагом закрутки
Глава 2
169
s/d = 6,2 и 12,2 были исследованы гладкие круглые трубы и трубы с
кольцевыми диафрагмами со следующими параметрами турбулиза-
ции потока d/D и t/D, равными 0,91 и 0,5; 0,91 и 0,25; 0,885 и 0,5.
При этом исследования проводились в следующем диапазоне па-
раметров:
—	температура холодной воды на входе в теплообменник
1'= 20... 30 °C;
—	скорость воды w = 0,05... 1,82 м/с;
—	число Рейнольдса Rec = (3... 25)-103;
—	температура стенки tw = 70... 100 °C;
—	карбонатная жесткость воды С = 5, 10 и 20 мг(экв)/л;
—	время непрерывного проведения исследования — до 360 ч.
Результаты экспериментального исследования процесса солеот-
ложения в витых трубах, гладких круглых трубах и трубах с коль-
цевыми диафрагмами представлены на рис. 2.25—2.28. Из рис. 2.25
видно, что для гладких круглых труб коэффициент теплопередачи
уменьшается в течение 280 ч приблизительно в 2,5 раза при концент-
рации соли (карбонатной жесткости воды) С = 10 мг(экв)/л и в 3—
4 раза при С = 20 мг(экв)/л. В этом случае термическое сопротивление
слоя солеотложений не достигает асимптотического значения. Для
витых труб и труб с кольцевыми диафрагмами при С = 10 мг(экв)/л и
Rec = 4-103 за 200—240 ч работы коэффициент теплопередачи умень-
шается только на 25%, а термическое сопротивление выходит на свое
toe 2.25. Изменение коэффициента теплопередачи во времени: а — С =
ж 10 мг(экв)/л; б — С = 20 мг(экв)/л; 1 — труба с кольцевыми диафрагмами при
в = 4-103, d/D = 0,91 и t/D = 0,5; 2 — витая труба с s/d = 6,2 при Re = 4-103;
Ж 4 5 - гладкая круглая труба при Re = 16-Ю3; 14-Ю3 и 3,2-Ю3 соответственно
170
Глава 2
Рис. 2.26. Изменение коэффициен-
та теплопередачи в зависимости от
безразмерного времени т/т^ при
С = 10 мг(экв)/л и Re=104 (тм =
= 250 ч): 1, 2, 3 — трубы с кольце-
выми диафрагмами при d/D = 0,91
и t/D = 0,5; d/D = 0,91 и t/D = 0,25;
d/D = 0,935 и t/D = 0,5 соответ-
ственно; 4, 5 — витые трубы при
s/d = 6,2 и s/d = ^^соответствен-
но; 6 — гладкая круглая труба
асимптотическое значение. При
концентрации С = 20 мг(экв)/л ко-
эффициент теплопередачи для труб
с интенсификацией уменьшается
на 40—50%, что значительно мень-
ше, чем для гладких круглых труб.
Таким образом, коэффициент теп-
лопередачи в витых трубах и трубах
с кольцевыми диафрагмами при со-
леотложении превышает значения
этого коэффициента в гладких тру-
бах в начальный момент времени,
когда отложения отсутствуют.
Эффективность труб с интен-
сификаторами и закруткой потока
при солеотложений увеличивается
по сравнению с эффективностью
гладких круглых труб. Это видно
из рассмотрения рис. 2.26. Если в
начальный момент процесса соле-
отложения (т = 0) отношение ко-
эффициента теплопередачи труб с
кольцевыми диафрагмами и витых
труб к коэффициенту теплопереда-
чи гладких труб составляет K/Klsm = 2,5... 3, то прит/тто — 1 отноше-
ние К/К[8т = 3,5... 5.
На рис. 2.27 показано влияние концентрации соли на термическое
сопротивление слоя солеотложений
для труб с кольцевыми диафраг-
мами с различными параметрами
турбулизаторов потока для момен-
та времени, когда т —> °о Обнаруже-
но, что с увеличением высоты ди-
афрагм величина Rfoul уменьшается.
Так, для d/D = 0,91 и t/D = 0,5 тер-
Рис. 2.27. Зависимость термического со-
противления солеотложений Rfoul от жес-
ткости холодной воды С при Re = 14-103:
1 — гладкая круглая труба; 2, 3, 4 — трубы
с кольцевыми диафрагмами при d/D =
0,935; 0,91; 0,91 и t/D = 0,5; 0,25; 0,5 соот-
ветственно
Глава 2
171
мическое сопротивление слоя солеотложений в 4—5,3 раза меньше,
чем в гладкой круглой трубе.
Результаты экспериментального исследования процесса солеот-
ложения в трубах с закруткой потока и с кольцевыми диафрагмами
были обобщены зависимостями вида (2.1.138) и (2.1.139) для расчета
термического сопротивления слоя солеотложений [2.1.26]. Для труб с
кольцевыми диафрагмами экспериментальные данные хорошо опи-
сываются степенной зависимостью:
( \0-129/ .х 0,701	.
RfouI = ll,81Re^'29C°’214 —	—	(0,062+1,2-10"3—), (2.1.144)
\DJ	D
которая справедлива для = 250 ч и следующего диапазона измере-
ния параметров: d/D = 0,91... 0,94; t/D = 0,25... 0,5; Rec = (4... 25)-103;
С = 5... 20 мг(экв)/л.
Для витых труб опытные данные по солеотложению в условиях
закрутки потока хорошо обобщаются следующей зависимостью
Rfoul
0,204Re^1227
£0,36
/ х 0,236 ,	0,447
Т	|S|
^oj	IdJ
(2.1.145)
полученной в диапазоне изменения параметров: s/d = 6,2... 12,2;
Rec = (3,2... 25)-103; С = 5... 20 мг(экв)/лпри = 250 ч. В зависимостях
(2.1.144) и (2.1.145) термическое сопротивление слоя солеотложений
Rfoul измеряется в (м2К)/Вт.
В результате экспериментального исследования процесса соле-
отложения было показано, что искусственная турбулизация потока
внутри витых труб и труб с кольцевыми диафрагмами позволяет су-
щественно уменьшить солеотложения на их внутренних поверхно-
стях (рис. 2.26 и 2.27).
Влияние солеотложений на коэффициент теплопередачи учиты-
валось введением величины термического сопротивления солеотло-
жений в выражение, определяющее этот коэффициент для цилинд-
рической стенки:
1	1	1 , Dout п 1
--- --------*--л--In-------R-lfoul "I-------
К, atD 2Х„ D ы a2Dout
(2.1.146)
где Oj и «2 - коэффициенты теплоотдачи внутри и снаружи трубы;
Дьо/ — линейное термическое сопротивление слоя солеотложений
ва внутреннем диаметре трубы.
При постоянном расходе холодной воды в исследованных каналах
рост солеотложений во времени приводит к увеличению гидравли-
ческого сопротивления. Из рис. 2.28 видно, что за 240 ч относительный
прирост во времени гидравлического сопротивления из-за солеотло-
172
Глава 2
Рис. 2.28. Изменение во вре-
мени гидравлического^ сопро-
тивления труб при различных
числах Рейнольдса и солеот-
ложениях с жесткостью хо-
лодной воды С = 20 мг(экв)/л:
1 — труба с кольцевыми ди-
афрагмами (d/D = 0,91 и
t/D = 0,5); 2 — витая труба
(s/d = 6,2); 3 — гладкая круг-
лая труба
жений при различных числах Рейнольд-
са составляет примерно 100% для глад-
ких круглых труб и 30—50% для витых
труб и труб с кольцевыми диафрагмами.
В то же время абсолютный прирост пе-
репада давления Д р за 240 ч в трубах с
кольцевыми диафрагмами в 2 раза пре-
вышает абсолютный прирост перепада
давления в витых трубах и гладких круг-
лых трубах при одинаковых значениях
числа Рейнольдса. Это объясняется тем,
что в трубах с кольцевыми диафрагма-
ми потери давления можно разделить на
потери на трение и местные гидравличе-
ские потери на диафрагмах. При этом
из-за отрывных течений на диафрагмах
толщина солеотложений различна по
длине канала на гладких участках тру-
бы в направлении течения, и это разли-
чие увеличивается с течением времени,
увеличивая долю перепада давлений на
местных сопротивлениях в суммарном
значении перепада давлений. В витых
трубах имеет место только линейное
гидравлическое сопротивление, и тол-
щина солеотложений распределена по
поверхности трубы достаточно равно-
мерно, что приводит к меньшему абсо-
лютному приросту перепада давлений в
витых трубах, а интенсивный вынос отложений с границы раздела
фаз в поток существенно уменьшает относительный прирост пере-
пада давлений по сравнению с гладкими круглыми каналами.
Выполненные исследования показали, что закрутка потока внут-
ри витых овальных труб и турбулизация потока кольцевыми ди-
афрагмами позволяют значительно интенсифицировать тепломас-
сообмен в этих каналах и уменьшить благодаря этому солеотложения
на внутренних поверхностях. При этом обнаружено, что с течени-
ем времени термическое сопротивление слоя солеотложений внут-
ри этих труб асимптотически приближается к своему постоянному
значению, что не наблюдается на внутренних поверхностях гладких
круглых труб. Интенсификация тепломассообмена в трубах позво-
ляет уменьшить минеральные отложения на внутренней поверхно-
Глава 2
173
сти примерно в 5 раз по сравнению с гладкими круглыми трубами.
При этом замена гладких круглых труб витыми трубами или трубами
с кольцевой накаткой позволяет обеспечить надежную работу труб-
чатых теплообменных аппаратов без специальной очистки их поверх-
ностей от солеотложений.
ОБОЗНАЧЕНИЯ:
a	— коэффициент температуропроводности, м2/с;
ср	— удельная изобарная теплоемкость, Дж/(кг-К);
С — концентрация солей в воде, мг(экв)/л;
Deff — эффективный коэффициент турбулентной диффузии,
м2/с;
D — внутренний диаметр трубы, м;
d — максимальный размер овала, м;
deq — эквивалентный диаметр, 4Ff/Hwet, м;
Ff — площадь проходного сечения пучка, м2;
Fob - критерий Фурье, V/fCpP^d2,,^);
Frm — модифицированный критерий Фруда, s2/(ddeq);
G — массовый расход теплоносителя, кг/с;
I — энтальпия, Дж/кг;
К — коэффициент теплопередачи, Вт/(м2К) (безразмерный
эффективный коэффициент турбулентной диффузии,
KD — коэффициент массообмена на поверхности раздела фаз,
м3/с;
К1 — линейный коэффициент теплопередачи, Вт/(мК);
Кр — коэффициент массообмена солей в воде, м3/с;
KR — постоянная химической реакции образования солей на
поверхности, м3/с;
Кип — нестационарный коэффициент перемешивания тепло-
носителя (эффективный коэффициент турбулентной
диффузии);
I	—	длина, м;
Le	—	критерий Льюиса, pc^)eff/Xe^
М	—	число Маха;
т	—	величина отложений на единице поверхности, кг/м2;
N	—	мощность, Вт;
— мощность, выделяющаяся за счет z-й группы запаздыва-
ющих нейтронов, Вт;
174
Глава 2
Nu Р Рг Q Чщеап Чу г Гк — bundle R К foul	—	критерий Нуссельта, adeg/X; —	давление, Н/м2; —	число Прандтля, срр/Х; —	тепловой поток, тепловая мощность, Вт; —	средняя плотность теплового потока, Вт/м2; —	плотность объемного тепловыделения, Вт/м3; —	радиальная координата; —	радиус пучка витых труб, м; —	удельная газовая постоянная, Дж/(кг К); —	термическое сопротивление слоя отложений, м2К/Вт;
Re S ^об S Т t и	—	число Рейнольдса, udeq/v; —	площадь поверхности теплообмена, м2; —	обогреваемая площадь поверхности, м2; —	шаг закрутки, м; —	температура, К; —	шаг турбулизаторов, (кольцевой накатки) м; —	продольная скорость, м/с;
w	— среднерасходная скорость, кг/с;
X a Peff Pi	—	продольная координата; —	коэффициент теплоотдачи, Вт/(м2-К); —	эффективная доля запаздывающих нейтронов; —	доля запаздывающих нейтронов i-й группы;
5	— интегральная толщина пристенного слоя, м; тол- щина стенки тубы, м;
Sfoul AT	— толщина отложений, м; — перепад температур, К;
e к	—	пористость пучка по теплоносителю, e=Ff/FT; —	относительный коэффициент нестационарного перемешивания, Kun/Kqs;
X	— теплопроводность, Вт/(м-К);
Ц V £ P P Pl	—	динамический коэффициент вязкости, Па-с; —	кинематическая вязкость, м2/с; —	коэффициент гидравлического сопротивления; —	смоченный периметр пучка, м; —	плотность, кг/м3; —	реактивность реактора; —	суммарная реактивность реактора, отнесенная к Peff'
Глава 2
175
Рг р,	—	температурный эффект реактивности твэлов; —	плотностной эффект реактивности теплоносите- ля;
Ррег	— эффективность регулирующих органов реактора, отнесенная к ре//;
Т V	— время, с; — среднее время жизни одного поколения нейтро- нов, с;
Ъ	— время, прошедшее после остановки реактора, с.
Индексы:
в	—	внутренний;
вх —	входные параметры;
вых —	выходные параметры;
г	—	горячий;
гл	—	гладкая;
и	—	режим испытаний ТВС;
к	—	корпус; камера;
кк —	кольцевой канал;
кр н	—	круглая; наружный;
о	—	обойма;
п	—	проходное течение;
р тр	— х	—	режим расхолаживания ТВС; труба; холодный;
ср ъ bundle d eff	среднее значение; среднемассовый; пучок; определено по deq; эффективный;
eq f foul — I	эквивалентный; жидкость; отложение; линейный;
m	—	среднее по толщине пристенного слоя;
max —	максимальный;
out —	внешний диаметр; выходной параметр;
176
Глава 2
р	— при давлении р — const;
qs	— квазистационарный;
г	—	по оси г;
s	—	твердая фаза;
sm	—	гладкая;
ип	—	нестационарный;
w	—	стенка;
1	— параметры до внесения возмущения в систему;
2	— параметры после завершения переходного процесса;
5	— определено по толщине пристенного слоя;
S	— суммарное значение параметра на длине ТВС;
Список литературы
2.1.1.	Дьяков Е.К., Нежевенко Л.Б., Подладчиков Ю.Н., Федик И.И. Ре-
зультаты разработки и испытаний ТВС активных зон реакторов ЯРД/Тру-
ды 3-й межд. конф. «Ядерная энергетика в космосе. Ядерные ракетные
двигатели». Подольск, 1993. Т. 1. С. 27-32.
2.1.2.	Паршин Н.Я., Попов Е.В., Федоров Э.М. Расчетно-теоретическое
обоснование работоспособности ТВС реакторов ЯРДДруды 3-й межд.
конф. «Ядерная энергетика в космосе. Ядерные ракетные двигатели».
Подольск, 1993. Т. 1. С. 143-149.
2.1.3.	Дзюбенко Б.В., Ашмантас Л.-В.А., Сегаль М.Д. Моделирование ста-
ционарных и переходных теплогидравлических процессов в каналах
сложной формы. Вильнюс: Исток, 1994.
2.*1.4	. Дзюбенко Б.В. Теплообмен при турбулентном течении в пучках витых
стержней и проблема замыкания системы уравненийДруды 2-й Россий-
ской национальной конф, по теплообмену. М.: МЭИ, 1998. Т. 6. С. 83-86.
2.1.5.	Дзюбенко Б.В., Дрейцер Г.А., Ашмантас Л.-В.А. Нестационарный
тепломассообмен в пучках витых труб. М.: Машиностроение, 1988.
2.1.6.	Дзюбенко Б.В., Сегаль М.Д., Ашмантас Л.-В.А. Нестационарное пе-
ремешивание теплоносителя в теплообменнике с витыми трубами/Изв.
АН СССР. Энергетика и транспорт. 1983. № 3. С. 125-133.
2.1.7.	Дзюбенко Б.В. Теплообмен на начальном участке в теплообменнике с
закруткой потока//ИФЖ. 1982. Т. 42, № 2. С. 230-235.
2.1.8.	Дзюбенко Б.В. Гидравлическое сопротивление в теплообменнике с за-
круткой потока/Дам же. 1983. Т. 42, № 3. С. 357-362.
2.1.9.	Дзюбенко Б.В., Вилемас Ю.В., Ашмантас Л.-В.А. Перемешивание
теплоносителя в теплообменнике с закруткой потока/Дам же. 1981. Т. 40,
№ 5. С. 773-779.
Глава 2
177
2.1.10.	Дзюбенко Б.В., Ашмантас Л.-В.А., Богдановичюс А.Б. Нестационар-
ное перемешивание при увеличении расхода теплоносителя в пучке ви-
тых труб/Дам же. 1988. Т. 55, № 3. С. 357-363.
2.1.11.	Дзюбенко Б.В., Ашмантас Л.-В.А., Богдановичюс А.Б. Закономер-
ности нестационарного перемешивания при уменьшении расхода тепло-
носителя в пучке витых труб/Дам же. 1989. Т. 56, № 1. С. 5-11.
2.1.12.	Дзюбенко Б.В., Ашмантас Л.-В.А., Богдановичюс А.Б. Нестационар-
ное перемешивание при уменьшении расхода теплоносителя в пучке ви-
тых труб//Изв. АН СССР. Энергетика и транспорт. 1989. № 2. С. 102-114.
2.1.13.	Дзюбенко Б.В., Ашмантас Л.-В.А., Богдановичюс А.Б. Межканальное
перемешивание теплоносителя при периодическом изменении расхода
во времени в пучках витых труб // ИФЖ. 1991. Т. 60, № 5. С. 724-729.
2.1.14.	Дзюбенко Б.В., Богдановичюс А.Б., Калятка А.В., Ашмантас Л.-В.А.
Нестационарный тепломассообмен при одновременном изменении мощ-
ности тепловой нагрузки и расхода теплоносителя/Дам же. 1992. Т. 62,
№ 3. С. 349-355.
2.1.15.	Приймак С.П., Федик И.И. Особенности метрологического обеспече-
ния измерений температуры термоэлектрическими преобразователя-
ми в условиях интенсивного реакторного облучения/Друды 3-й межд.
конф. «Ядерная энергетика в космосе. Ядерные ракетные двигатели».
Подольск, 1993. Т. 3. С. 327-334.
2.1.16.	Федик И.И. и др. Измерение высоких температур термопреобразова-
телями на основе тугоплавких металлов и карбидов//Преобразователи и
приборы для измерения температуры. Киев: Знание, 1978. С. 6-7.
2.1.17.	Ашмантас Л.-В.А., Дзюбенко Б.В. Проблемы теплообмена и гидроди-
намики в ядерных энергодвигательных установках космических аппара-
тов. Вильнюс: Pradai, 1997. 370 с.
2.1.18.	Дзюбенко Б.В., Вилемас Ю.В. Кожухотрубный теплообменник//Ав-
торское свидетельство СССР № 761820. М.: Бюллетень изобретений,
1980. №33. С. 194.
2.1.19.	Дзюбенко Б.В., Сакалаускас А.В., Ашмантас Л.-В.А., Сегаль М.Д.
Турбулентное течение и теплообмен в каналах энергетических устано-
вок/Под ред. Б.В. Дзюбенко. Вильнюс: Pradai, 1995. 300 с.
2.1.20.	Дзюбенко Б.В. Методика теплогидравлического расчета тепловыделя-
ющих сборок с витыми твэлами ядерной энергодвигательной установки.
М.: Изд-во МАИ, 2003. 24 с.
2.1.21.	Данилов Ю.И., Дзюбенко Б.В., Дрейцер Г. А., Ашмантас Л.-В.А. Теп-
лообмен и гидродинамика в каналах сложной формы/Под редакцией
В.М. Иевлева. М.: Машиностроение, 1986. 200 с.
2.1.22.	Проблемы нейтронной физики и ядерной безопасности реактора ЯРД
минимальных размеров/В.А. Коновалов, Г.В. Конюхов, Ю.В. Мамаев и
др.//Труды 3-й отраслевой конференции «Ядерная энергетика в космо-
се. Ядерные ракетные двигатели». Семипалатинск, 1992. С. 29-30.
2.1.23.	Дзюбенко Б.В., Иевлев В.М. Теплообмен и гидравлическое сопротив-
ление в межтрубном пространстве теплообменника с закруткой потока//
Известия АН СССР. Энергетика и транспорт. 1980. № 5. С. 117-125.
178
Глава 2
2.1.24.	Симуни Л.М. Численное решение задачи о неизотермическом движении
вязкой жидкости в плоской трубе.//ИФЖ. 1966. Т. 10, № 1. С. 86.
2.1.25.	Крамеров А.Я., Шевелев Я.В. Инженерные расчеты ядерных реакто-
ров. М.: Энергоатомиздат, 1984.736 с.
2.1.26.	Dreitser G. and Dzyubenko В. Decrease of Salt Depositions in Channels with
Discrete Turbulence Promoters and Flow Swirling//Proc. ECI conf, on Heat
Exchanger Fouling and Cleaning: Challenger and Opportunities, June 5-10,
2005, Kloster Irsee, Germany, 6 p.
2.1.27.	Dreitser G.A., Dubrovskiy Ye.V., Dzyubenko B.V., lyevlev V.M., Kali-
nin E.K., Simonis V.M., Slanciauskas A.A., Vilemas J.V., Voronin G.I.,
Zakirov S.G., Zukauskas A.A. and Yarkho S. A. Heat transfer: Soviet reviews,
Vol. 2. Enhancement of heat transfer, eds. A.A. Zukauskas, E.K. Kalinin, and
J. Taborek, Hemisphere, New York, 1990.
2.1.28.	Kalinin E.K. and Dreitser G.A. Heat Transfer Enhancement in Heat
Exchangers, Advances in Heat Transfer, Academic Press, New York, 1998,
Vol. 31, pp. 159-332.
2.1.29.	Chan S.H. Heat and mass transfer in fouling, in Annular Review of Heat
Transfer, Hemisphere Publishing, New York, 1992, Vol. 4, pp. 363-402.
2.1.30.	Knudsen J.G. and Roy B.U. Influence of fouling in heat transfer, Proc. 7 th
Int. Heat Transfer Conference 1982, Hemisphere, New York, 1982, Vol. 2, pp.
289-300.
2.1.31.	MQIIer-Steinhagen H. Fouling: The ultimate challenge for heat exchanger
design, Transport Phenomena in Thermal Engineering, Begell House, Inc.
Publishers, New^York, 1993, Vol. 2, pp. 811-823.
2.1.32.	Kim M.-H. and Webb R.L. Particulate fouling inside tubes having a re-shaped
two-dimensioned roughness by a flowing suspension of aluminium oxide in
water. Proc. 9th Int. Heat Transfer Conference 1990, Hemisphere, New York,
1990, Vol. 5, pp. 139-144.
2.1.33.	Pinhero J. Fouling of heat transfer surfaces, In Heat Exchangers-Thermal
Hydraulic Fundamentals and Design, eds. S. Kakas, A.E. Bergles, and
F. Meinger, McGraw-Hill, New York, 1981, pp. 1013-1035.
2.2. ГИДРОДИНАМИКА МНОГОФАЗНЫХ ГЕТЕРОГЕННЫХ
СРЕД ПРИ ДЕЙСТВИИ ЦЕНТРОБЕЖНЫХ СИЛ
Одним из наиболее перспективных методов интенсификации тех-
нологических процессов является проведение этих процессов в цент-
робежном поле при тонкослойном режиме течения. Указанный ме-
тод реализуется в различных центробежных аппаратах, таких, как
роторно-пленочные аппараты, центрифуги, гидроциклоны, жидкост-
ные тарельчатые сепараторы. Расчет таких аппаратов требует знания
гидродинамических характеристик течений с учетом особенностей,
возникающих в результате протекающего в аппарате конкретного
технологического процесса.
Глава 2
179
В работе [2.2.1] изучается ламинарное установившееся осесим-
метричное течение слоя многофазной гетерогенной среды по поверх-
ности вращающихся насадок. Рассматривается также напорное те-
чение во вращающейся щели; учитываются явления расслоения и
сгущения среды, а также наличие гидродинамического начального
участка течения; реологическое уравнение состояния неоднородной
среды описывается степенной моделью.
Пусть по поверхности вращающейся криволинейной насадки те-
чет слой многофазной гетерогенной среды со свободной поверхно-
стью. Вращающаяся насадка представляет собой поверхность враще-
ния, которая задана уравнением z = f(r). Течение рассмотрим в орто-
гональной системе координат (х,у,ср), координата х которой совпадает
с образующей ротора. Коэффициенты Ламе равны: Нх — 1, Н2 — 1,
Н3 = г. Тогда упрощенные уравнения механики многофазных сред
запишутся в виде:
Э|шй) + Э(фЩ = а	, = -
дх ду
dU, r, dU, W,2 Эг
I дх ду г дх
е
-X ^ijx +РЛХ;
7=2
W,2 Эг др Л _	_
Г ду ду j=2 Jy У
(2.2.2)
(2.2.3)
	f aw, aw,				)r, wm aY		
Pl	Г1 ax +v* ay +		r	Эх г Эу?			
	j__a_ г2 dy	r3mE" L	wY		e X Fijq> +PiA 7=2	Ф’	(2.2.4)
Pi	(„ dU,- TZ Э1/, W? di 1 Эх	оу г Эл			J	=-aI^+E^x+p2^x- (7X y=1 i^j		(2.2.5)
—?+£%+₽,-fy.	<2-2-6)
г ду ду j=i Jy у
180
Глава 2
А Г Г dW^17 dw2^w2U2 drW2V2 Эг |
dx dy r dx r dy J
e	__
= Х^Ф+РЛр. z = 1-6;
j=i
i^j
(2.2.7)
где E =
f dWiV Гец fl2
---- + ----
v Эу J { dy J
интенсивность скоростей деформации.
Приведенная система уравнений должна решаться при следу-
ющих граничных условиях, учитывающих фильтрационный отток
жидкости через проницаемую поверхность:
у = 0: U,=0, Уп=-А£_Р“ ш=0;
’	'	1 v d
Массовая сила складывается из центробежной силы, силы Кори-
олиса и гравитации
= (со2г — 2(oWI)sinp — pcosp,
Fiy = (со2/- — 2соИА)со8Р — gsinp,
Fi(f) = 2cot7fsinp — 2coVfcosp.
Решение уравнений механики гетерогенных сред с учетом ука-
занных особенностей течения и граничных условий вызывает боль-
шие трудности из-за нелинейности дифференциальных уравнений
в частных производных. Одним из перспективных методов решения
таких уравнений является метод поверхностей равных расходов.
Преимущество данного метода заметно возрастает в случае исследо-
вания процессов, протекающих в гетерогенных средах, поскольку он
позволяет непосредственно определять траектории частиц составля-
ющих фаз [2.2.2—2.2.5].
В соответствии с этим методом введем в поле течения суспензии
индивидуальные поверхности равных расходов (линии тока) для каж-
дой z-й фазы: у* = у*(х), к = l,Nif z = 1,8 и обозначим Uk = Ц [х,у* (х)],
V,* = [х,у* (х)], Wk = Wt [х,у* (х)], где Uk (х), Vk (х), Wk (х) - ком-
поненты скорости z-й фазы для k-го слоя в направлении координат
х,у,<р. Здесь Nt — количество введенных линий для z-й фазы (N — NJ.
Причем линия у- совпадает с поверхностью течения, а линия у/7 —
со свободной поверхностью.
Глава 2
181
Сведем задачу о развитии течения слоя суспензии к численному
определению полей скоростей и линий тока. Обозначим изменение
расхода z-й фазы между линиями у*"1 и у* через Ф^(х). По опреде-
лению интегральное условие сохранения имеет вид:
я у*	__ ________
Ф*(х) =— J 2TtraI-[7Idy1 / = 1,0, k = 2,Nf.	(2.2.8)
dx v*~i
Ji
Определим введенные функции Ф*(х) в предположении, что мас-
сообмен отсутствует. Для чего запишем интегральное условие сохра-
нения количества z-й фазы в пленке суспензии
h	х
f 2лгаД^у+ J 27irV1(0)dx =
0	xH
 продифференцируем no x
d h
— f 271га, 17. dy =27trVi(O).
dx J
Аналогичным образом записываются балансовые соотношения
для каждого слоя [у*-1 .у*]. Очевидно, что при отсутствии массо-
•бмена расход сплошной фазы может изменяться из-за фильтрации
жидкости через проницаемую поверхность и поэтому
Ф?(х) = 271га, УДО),
Ф^(х) = 0, z = lj, к = ЗЛ-.
Уравнения движения фаз записываются на своих линиях тока и
^результате приводятся к следующим обыкновенным дифференци-
альным уравнениям:
kdU*	дг Р1ЧF .1 = tv ' dx	г дх М	J 7=2 „idW*	W,kf кдг РА ,1 = Pl 1 dx	г	Эд j=2	dp*	, , ,dyk “* dx	dx + +P1F*,	(2.2.9) ,rk ЭгА эГ „„..aw.*" dyj Эу |_	Эу (2.2.10)
182
Глава 2
р1и'~г7=~р1-
dx
6	7	/
” E Ад * PiFix '
J=2
dr dPi т / i dYi
-— а.	+ a.Jz (х, у	-
*Ч	I у	I I \	* J f _Т
дх dx	dx
(2.2.11)
, dWl_ W{_[ , Эг , Эг) °	,
P‘Ui dx ~ Pl r (U‘ dx V' ду)	P,Fi9'	(2’2Л2)
e .	____ _______ • ___
где Jt(x,y) = Xp,F*, k = 2,Nt, / = 2,N„ 1 = 2,6.
J=1
В этих уравнениях присутствуют слагаемые, содержащие част-
ную производную дрк/дх. Для вычисления этого градиента давления
интегрируем на интервале [у*-1, у* ] и затем продифференцируем по
переменной х
dpk-i dPk д У,с vf Pj№j)2 dr 'I	——
=	J J T+PjFjy dY< k = Nit2.
dx dx dx k-i i=1 r dy J J)
V; J 1\	J
(2.2.13)
у.
Поскольку среда представляется как взаимопроникающий конти-
нуум с общим давлением, градиент давления для разных фаз вычисля-
ется по общей формуле, но на своих индивидуальных линиях тока у*.
Для дисперсных фаз эти рекуррентные вычисления имеют особен-
ности. В зоне [hf,h], где i-я фракция частиц отсутствует, при вычисле-
ниях градиента давления используются линии тока сплошной фазы.
После вступления в область присутствия i-й фазы рекуррентные вы-
числения проводятся по линиям тока данной фракции.
Чтобы воспользоваться рекуррентными соотношениями общей
формулы, нужно задавать значение dpN/dx. Экспериментальные и
теоретические исследования течений по вращающимся поверхно-
стям показывают наличие входного участка, где происходит разгон
пленки и стабилизация полей скоростей. На малых радиусах вход-
ного участка не вся поступающая жидкость может быть увлечена во
вращательное движение. В результате наблюдается захлебывающий-
ся режим, когда поверхность пленки имеет значительное искривле-
ние в виде локального максимума. На начальном участке таких тече-
ний давление Лапласа ра может оказаться существенным, поэтому
нужно принять dpN/dx= dpa/dx.
Давление, обусловленное продольной и поперечной кривизнами,
определяется известными формулами как функция от h, h', h". Поскольку
в полученных уравнениях эта сила присутствует в составе градиента дав-
Глава 2
183
ления, порядок производных повышается на единицу. При каждом вы-
числении правых частей уравнений эти производные вычисляются чис-
ленно.
Уравнения для поверхностей равных расходов записываются сле-
дующим образом:
dyl = dy{ 1 +	2УД0) g_ у/-у/ 1 х
dx dx аДСГ/' + с//"1) 2 ra^U!+U/~l)
x ra.-—-+ra,-
' dx
dU! dU! 1 TTi da{ rr»-idaf
——!— + tjj —l-+rU! —-
dx dx dx
rri dr rri~l dr
+a.U—+оШ/ —
1 1 dx 1 1 dx
/ = 1,0.
(2.2.14)
Здесь значения верхних индексов j, равных к (k = 2,Nt) и I
у = 2,Nit i = 2ДЭ), указывают соответственно на сплошные и дисперс-
ные фазы.
Скорости осаждения фракций УДО),/= 2,0 определяют из систе-
мы алгебраических уравнений (2.2.6). При этом скорость сплошной
фазы УДО) находят отдельно через скорость фильтрации, поэтому
при решении этой системы алгебраических уравнений она счита-
ется известной. Кроме того, чтобы воспользоваться рекуррентными
соотношениями (2.2.14), нужно задавать значение dyf/dx.
Для вычисления слагаемых, представляющих в уравнениях
движения изменения тензора вязкого напряжения, а также ско-
ростей между линиями тока, сеточные решения L7* = Ц [х,ук (х)],
W* = Wj [x,yk (х)] представим в виде разложения в ряд по полной си-
стеме базисных функций:
N{
Ц = Д.Дх)+ X Ау(х)Т(/.(х,у),	(2.2.15)
7=2
N,
WJ- = Bfl(x)+ X ВуДх^Дх.у),	(2.2.16)
>2
W 4<(x, у) — полная система базисных функций, удовлетворяющая
соответствующим граничным условиям для скоростей Ц., Wv Для
степенной реологической модели среды они выбираются исходя из
вда профиля течения в стабилизированном участке.
Потребуем, чтобы скорости, определяемые из этих двух уравне-
ний, совпали с Ц*(х), И^-*(х) на линиях у*(х). Тогда для нахождения
коэффициентов А~(х), В~(х) получим систему алгебраических урав-
нений:
184
Глава 2
Nf	__ ____
A1W+ Е А,(х)^(х,у) = ^; A = 1,N,; 1 = 1,1;	(2.2.17)
7=2
Nf	__ _
Вп(х)+ S В^х^х.у) = wf',. к = l,Nf; i = и.	(2.2.18)
J=2
Определив значения А^(х), В^(х) из этой системы уравнений и про-
дифференцировав соотношения (2.2.15) —(2.2.16), можно найти ком-
поненты тензора вязкого напряжения.
Линии тока z-й фазы вычисляют с помощью рекуррентных со-
отношений (2.2.14) снизу вверх, а градиент давления, согласно
(2.2.13), — сверху вниз. Поэтому для вычисления правых частей си-
стемы уравнений (2.2.9) —(2.2.12), (2.2.14) необходимо использовать
процедуру прогонки. Эта система построенных обыкновенных диф-
ференциальных уравнений позволяет моделировать работу осади-
тельных и фильтрующих центрифуг.
В режиме разделения среды с расслоением фаз необходимо учи-
тывать наличие слоя осадка. В центробежных аппаратах непрерыв-
ного действия осажденная масса непрерывно выносится из рабочей
зоны. Изменения толщины 6 текучего осадка можно описать с помо-
щью дифференциального уравнения (см. работу [2.2.4])
л б	е
a»—ft/2ody=Ia.v;(O).	(2.2.19)
d*o	i=2
Система (2.2.9) —(2.2.12), (2.2.14), (2.2.19) должна решаться при на-
чальных условиях:
х = хн : Ui = UiH (у), у* = у£, 5 = 0, где 6 - толщина.
На участке напорного фильтрования фильтрующей центрифуги
происходит сгущение неоднородной среды. Изменение средней кон-
центрации многофазной неоднородной среды, аср может быть опре-
делено с помощью дифференциального уравнения, приведенного в
работе [2.2.5]
darn	/?
—— = ~acprVI(O)/frUcpdy.	(2.2.20)
ax	/0
Это уравнение решается совместно с уравнениями (2.2.9)—(2.2.12),
(2.2.14) при начальных условиях:
х — хн . Uf — t^IH(y)f Yi — YiHi ocCp — ^cp|H •
Форма вращающейся насадки описывается уравнением z — f(r),
выраженным через тригонометрические функции:
Глава 2
185
sin 0=1/yjl+fdz/dr)2 ,
cos 0 = (dz/dr)Iy[l+(dz/dr)2 .
Угол p в общем случае является функцией относительно криволи-
нейной координаты х. Поэтому в полученных соотношениях присут-
ствуют производные от тригонометрических функций sinp и cosp.
Для выбранной поверхности течения необходимо установить
связь между продольной координатой х и радиусом г. Координата х
при заданном радиусе определяется, по сути, длиной дуги:
х = ^1+(dz/dr)2dr.
о
Кроме того, в уравнениях движения (2.2.9) присутствует произ-
водная дг/дх и для каждой конкретной формы насадки нужна соот-
ветствующая формула для ее вычисления. Для решения построен-
ной системы обыкновенных дифференциальных уравнений все эти
величины должны быть определены [2.2.5].
Использованный выше метод поверхностей равных расходов мо-
жет быть успешно применен при математическом моделировании
напорных течений. Рассмотрим течение гетерогенной среды во вра-
щающейся осесимметричной щели, образованной двумя поверхно-
стями вращения произвольной формы z = f(r). Такое течение реа-
лизуется, например, в межтарелочном зазоре жидкостных тарель-
чатых сепараторов. Течение рассматривается в ортогональной си-
стеме координат (х,у,ф) с коэффициентами Ляме 1, 1, г, координата х
которой совпадает с образующей тело вращения. Радиус г для про-
извольной точки межтарелочного зазора вычисляется по формуле
г = г0(х) — ycos0, где г0(х) — расстояние от текущей точки поверхно-
сти тарелки (у — 0) до оси вращения. Тогда упрощенные уравнения
сохранения массы и импульсов для тонкослойного течения запишут-
ся в виде (2.2.1) —(2.2.7).
Применим для решения этих уравнений метод поверхностей рав-
ных расходов и введем в поле течения индивидуальные линии тока
для каждой i-й фазы. Пусть поверхность у? совпадает с нижней та-
релкой, а — с поверхностью верхней тарелки. Изменения расхо-
да между линиями у, и yf определяются с помощью балансовых
соотношений (2.2.8). Положения поверхностей равных расходов оп-
ределяются из дифференциальных уравнений (2.2.14). Преобразо-
ванные уравнения движения, записанные на своих индивидуальных
линиях тока, имеют вид (2.2.9)—(2.2.12). Для вычисления вязкостно-
186
Глава 2
го члена, а также скоростей фаз между линиями тока, используются
разложения (2.2.14)—(2.2.15).
Трудности интегрирования этих уравнений для напорных тече-
ний связаны с определением падения давления по длине канала. Из-
менение давления вызывается затратой энергии на трение между
средой и стенкой, а также изменением кинетической энергии потока
вследствие перестройки профиля скорости. Вычисление градиента
давления на основе балансовых соотношений, дифференциальные
формы которых записаны в виде (2.2.14), позволяет учитывать все на-
званные источники потери давления.
При решении системы (2.2.14) для сплошной фазы положения
двух поверхностей равного расхода из N введенных уравнений
считаются известными, поскольку они совпадают с поверхностями
вращения, ограничивающими область течения. Так как эта систе-
ма для сплошной фазы состоит из N — 1 дифференциальных урав-
нений, одно уравнение освобождается для определения градиента
давления dp/dx.
Приведем некоторые результаты численных расчетов течения
слоя неоднородной среды со свободной поверхностью по коническо-
му ротору. Особенно интересные результаты получены для входного
участка, где одновременно происходят два процесса. С одной сторо-
ны, на начальном участке происходит развитие радиального тече-
ния от заданного начального профиля до параболического. С другой
стороны, возникает явление отставания текущей среды от враща-
ющейся поверхности под воздействием силы Кориолиса. При расче-
тах были использованы различные виды начального профиля: рав-
номерный, треугольный, параболический. Во всех случаях профиль
радиальной скорости развивался до некоторого установившегося
Рис. 2.29. Линии тока на поверхностях рав-
ных расходов при к = 0, со = 30 с1, Wj = 0,
Р = 45°, Re/Fr = 72:----без учета отстава-
ния, -----с учетом отставания
вида, который не зави-
сит от выбора начального
профиля.
На рис. 2.29 показа-
ны линии тока, характер-
ные для вращающихся
насадок. Они не имеют
асимптоту и непрерывно
растекаются по поверх-
ности ротора. Зависимо-
сти продольных скоро-
стей на поверхностях рав-
ных расходов от продоль-
ной координаты показаны
Глава 2
187
на рис. 2.30. Поскольку каса-
тельное напряжение по на-
правлению от стенки к сво-
бодной поверхности убывает,
кривые ближе к свободной
поверхности сгущаются. Раз-
витие тангенциальной ско-
рости показано на рис. 2.31.
Скорость отставания имеет
явно выраженный максимум.
Влияние отставания замет-
но на рассмотренных графи-
ках линии тока и продольных
скоростей. Графики отноше-
ния скорости на свободной
поверхности к вычислен-
ной средней скорости облада-
ют ярко выраженной асимп-
тотой. Полученные результа-
ты хорошо согласуются с из-
вестными в литературе дан-
ными. Как видно из рис. 2.32,
при отсутствии фильтрации
отношение скорости на по-
верхности к средней скоро-
сти имеет асимптоту в окрест-
ности 3/2. Для проницаемой
стенки асимптота не наблю-
дается.
Изменение средней кон-
центрации среды в режи-
ме фильтрования без обра-
зования осадка показано на
рис 2.33. С ростом скорости
вращения растет скорость
фильтрации, что приводит к
ускорению роста концентра-
ции частиц. На рис. 2.34 при-
веден характерный вид изме-
нения толщины образован-
ного осадка. С уменьшением
коэффициента консистенции
Рис. 2.30. Радиальные скорости налиниях
тока при к = 0, со = 30 с4, И<| =0, р = 45°,
Re/Fr = 72:------без учета отставания,
— — с учетом отставания
Рис. 2.31. Тангенциальные скорости на
линиях тока при к = 0, со = 30 с4, Re/Fr
= 72, р = 45°:_ИЛ|н =0, _ _ _ И/|н = сот
Рис. 2.32. Зависимость отношения
скорости на поверхности к средней
скорости от продольной координаты
при к = 0, со = 10 с4, р = 45°: кривая
1 — Re/Fr = 6,45; Re = 1,614; кривая
2 — Re/Fr = 51,64; Re = 3,228; кривая
3 — Re/Fr = 174,28; Re = 4,814; кривая
4 - Re/Fr = 413,1; Re = 6,455
188
Глава г
Рис. 2.34. Влияние консистенции
осажденной массы на толщину слоя
осадкаприкн = 1О‘4,Л1 = 0,01 (кг-сп'2)/м;
ОсР|н =0,01; а20 = 0,6; 0 = 45°;
со = 30 с1: кривая 1 — с = 50 (кг-сп'2)/м;
кривая 2 — с = 40 (кг-сп'2)/м; кривая
3 — с = 30 (кг-сп 2)/м
Рис. 2.33. Влияние скорости вращения
на изменение концентрации дисперс-
ной фазы при к = 4.54-10’3, 0 = 45°,
Re =	1,61: кривая 1 — со	=	30	с1;
Re/Fr	= 58,09; кривая 2	—	со	=	40	с1;
Re/Fr	= 103,3; кривая 3	—	со	=	50	с1;
Re/Fr	= 161,4; кривая 4	—	со	=	60	с1;
Re/Fr = 232,4
уменьшается интенсивность роста слоя, поскольку растет скорость
продольного движения осадка. Полученные результаты согласуются
с физической картиной рассматриваемых процессов.
ОБОЗНАЧЕНИЯ:
с	— коэффициент консистенции осадка, кг-ся’2/м;
d	— толщина проницаемой стенки, м;
Fjx ,Fiy ,'F[	— проекции на оси х,у,ср вектора ускорения массовых
сил, действующего на i-ю фазу, м/с2;
FiJX ,РуylFiJ(p — проекции на оси х,у,<р вектора силы взаимодействия
между i-й и j-й фазами, кг/(м2-с2);
h	— толщина пленки смеси, м;
к	— коэффициент проницаемости, м2;
т	— коэффициент консистенции гетерогенной среды,
кг-сп‘2/м;
п	— реологический коэффициент нелинейности среды;
N-	— количество поверхностей равных расходов для i-й
фазы;
Ра’ Р& Р ~ Давление, соответственно, атмосферное, Лапласа и
в пленке смеси, Н/м2;
Ц-, Vi,Wi — компоненты скорости i-й фазы смеси в направле-
нии координатх,у,<р (м/с);
Сэд	“ скорость движения осадка в направлении коорди-
наты х, м/с;
ос	— объемная концентрация i-й фазы;
Глава 2
189
/
аср = У а, — средняя концентрация дисперсных частиц в смеси;
а20 1=2	— доля дисперсных частиц в осадке;
р	— угол наклона образующего конуса;
5	—	толщина осадка, м;
§2	—	дельта-функция;
0	—	количество фаз;
рг	—	плотность z-й фазы, кг/м3;
о)	—	скорость вращения, с1;
Т	—	эквивалентная вязкость, кг-сп‘2/мп;
Re = рйц U| /т — число Рейнольдса;
Fr =	L /~ число фРУАа-
Индексы:
а	—	атмосферное;
н	—	начальное значение;
ср	—	среднее значение;
z	—	номер фазы или фракции;
к, I — номера поверхностей равных расходов для сплошной и
дисперсной фаз;
20	— осадок.
Список литературы
2.2.1.	Kholpanov L.P., Ibyatov R.l. Calculation the multiphase heterogeneous
medium hydrodynamic in a centrifugal field. Heat Trasfer Research. 2006.
V. 37. N 4. P. 307-320.
2.2.2.	Ибятов Р.И. Методы расчетов гидродинамических процессов при фильт-
ровании и центрифугировании суспензий: Автореферат, дис. на соиска-
ние ученой степени д-ра техн. наук. Казань: Казанский государственный
технологический университет. 2005.38 с.
2.2.3.	Холпанов Л.П., Ибятов Р.И., Ахмадиев Ф.Г., Фазылзянов Р.Р. Мате-
матическое моделирование гидродинамики на проницаемых поверхно-
стях//ТОХТ. 2003. Т. 37. № 3. С. 227-237.
2.2.4.	Ибятов Р.И., Холпанов Л.П., Ахмадиев Ф.Г. Течение многофазной
среды по проницаемой поверхности с образованием осадка//ИФЖ. 2005.
Т. 78. № 2. С. 65-72.
2.2.5.	Ибятов Р.И., Холпанов Л.П., АхмадиевФ.Г., Фазылзянов Р.Р. Мате-
матическое моделирование течений гетерогенных сред по вращающим-
ся проницаемым поверхностям//ТОХТ. 2003. Т. 37. № 5. С. 479-492.
190
Глава 2
2.3. ВОЛНООБРАЗОВАНИЕ В ТОНКОЙ ПЛЕНКЕ ЖИДКОСТИ
Массообмен при волнообразовании
Теоретические основы массообмена в тонкой пленке жидкости
при волнообразовании подробно описаны в работах [2.3.1—2.3.8], где
предложен механизм массообмена при волнообразовании. Механизм
переноса вещества при волновом режиме представлен в виде следу-
ющей модели. От некоторой точки в седловине волны с концентраци-
ей на межфазной поверхности ср начинает развиваться диффузион-
ный слой. Под диффузионным слоем будем понимать то расстояние
от поверхности раздела фаз, на котором концентрация распределя-
емого вещества отличается на 1% от концентрации в ядре потока. По
толщине пленки концентрация распределяемого вещества на неко-
тором начальном участке, равном длине волны, меняется от ср на меж-
фазной границе до нуля на границе диффузионного слоя 5. В конце
этого участка вследствие существования вихрей происходит полное
перемешивание жидкости. В результате этого концентрация распре-
деляемого вещества выравнивается по толщине пленки и становится
равной с1. Таким образом, концентрация на границе диффузионного
слоя меняется от 0 при х = 0 до с1 при х = X, где X — длина волны. На
последующем участке, также равном длине волны, опять происходит
рост диффузионного слоя, но с той разницей, что концентрация на
его границе становится равной с1. Поэтому на втором участке необ-
ходимо решать задачу с граничными условиями с — ср на поверхно-
сти раздела и с = с1 на границе диффузионного слоя. Решение, полу-
ченное с этими граничными условиями, качественно не изменится
от решения, найденного на первом участке. Однако количество ве-
щества, перешедшего из газа в жидкость на втором участке, будет не-
сколько меньше, чем на первом, за счет уменьшения движущей силы
процесса, т.е. Дс = ср — 0 > ср — с1.
Достаточным условием, позволяющим проводить решение урав-
нения конвективной диффузии на длине волны, доказано с помощью
результатов расчета гидродинамики пленочного течения [2.3.2] и ис-
следования нелинейных динамических систем (рис. 2.35, 2.36).
Количество вещества Q, перешедшего из газовой фазы в жидкую
на длине волны:
л
О = РжДспс?р$,	(2.3.1)
о
где Рж — коэффициент массоотдачи; d — диаметр трубки; ds —
элемент поверхности. С другой стороны:
Глава 2
191
х
Q = nd J j^ds,	(2.3.2)
о
где Д — плотность диффузионного потока на
длине волны. Откуда
х
jhds
₽ж=-е-г-.	(2.3.3)
Acfds
о
Таким образом, в случае полного переме-
шивания волн в седловинах задача сводится к
определению величины диффузионного слоя
на расстоянии вдоль поверхности массообме-
на, равном первой длине волны. Эту величину
определим из решения уравнения конвектив-
ной диффузии
дс дс дс _ д2с	п Q ,4
^7 + VxV- + Vy4- = Or-2	(2-34>
dt дх у ду ду
с граничными условиями
с = ср при у=угр= а0[1 + asinn(x-cot)],
фазовой скорости от
амплитуды: сплошная
линия — расчет по
нелинейной теории
[2.3.4]; точки — экспе-
риментальные данные
работы [2.3.11].
(2.3.5)
с = 0 при у-> 0 (вдали от поверхности раздела).	(2.3.6)
Рис. 2.36. Зависимость относительной фазовой скорости
от относительной амплитуды [2.3.12]
Е	f = 9, Re = 90	7=7, Re = 125	7 = 9, Re = 200	7=8, Re = 400
2,5	1	5	9	13
7,5	2	6	10	14
12,5	3	7	И	15
15,0	4	8	12	16
192
Глава 2
(2.3.7)
Особенность постановки данной задачи состоит в том, что кон-
центрация распределенного вещества (условие (2.3.5)) задается на
искомой волновой поверхности пленки. Эта нелинейность приводит
уравнение (2.3.4) также к нелинейному по переменным уравнению.
В уравнении (2.3.4) их, иу являются функциями х, у, t. При парабо-
лическом распределении скорости в пленке [2.3.2] имеем:
(	2 Л
— У У
и = Зи -—,
a 2a2
_	Un - co	.	....
гдеи = со + ----------—, a = ao[l+acp(n(x-cot))].
l+acp(n(x-cot))
Разделим второй член последней формулы на соотношение
[1 + a<P(^)].
В результате получим формулу, составленную из суммы скоро-
стей для гладкой пленки и возмущения скорости, возникшего из-за
наличия волн на поверхности пленки
u = 3uq 7^-775- +3(w-Uo)aq)©[l-aq>fi)]
I ho 2/iq)	l^ho 271q
= и+и',	(2.3.8)
V A) 2h0>
где a0 — средняя толщина пленки; co = voz — фазовая скорость;
n = 2я/Х — волновое число; и0 — средняя скорость жидкости. Если
известна компонента скорости их, то значение иу определяется из ус-
ловия неразрывности:
J-7^dy-
о dx
Из выражения (2.3.8) следует формальное представление актуаль-
ной скорости в виде осредненной и пульсационной, напоминающее о
турбулентном характере переноса количества движения. Однако, как
будет показано, этот формальный признак не является полной харак-
теристикой турбулетного переноса. Эргодический характер в явлении
переноса допускает существование периодических составляющих.
При решении уравнения (2.3.4) значения составляющих скоро-
стей их и иу возьмем на поверхности раздела, т.е. при у — угр. Это оп-
равдано тем, что процесс переноса осуществляется в диффузионном
слое, непосредственно примыкающем к поверхности раздела. Под-
ставляя значения их и иу при у — угр в уравнение (2.3.4), получим:
дс	.	..
—+аполПл cosn(x - cot) х
1+a sin n(x - cot) J dx
1-z
дс 3
dt + 2
в,
1-z
х 0,5z+l,5
1+a sin п(х - cot) J ду
дс _ d2c
dp'
(2.3.9)
Глава 2
193
Переходя к новым переменным ц = у — угр, £ = п(х — (Dt), х = xv
приведем уравнение (2.3.9) к виду:
*\2 л
(l+asin£)K—-^--|(d+esin^)-—-(g + hsin£) = 0,	(2.3.10)
Эц Э£	dxj
где к = D/von; е = 0,5za; d — 1,5— z; g = 1,5/n; h = l,5za/n.
Будем искать решение уравнения (2.3.10) в виде ряда Фурье
c = c0(T],x) + c10(T],x)sin^+c11(T],x)cos^+
+c20(T],x)sin2£+c21(T],x)cos2£-l-...	(2.3.11)
Для коэффициентов ряда Фурье получим систему уравнений
ксс.. е Эсп 1 , Эсщ л
кс0 +—По + “И i-о———h—— = 0,
0 2 10 2 11 У Эх 2 Эх
..	..	,	. Эсп	Эс1П
кас0 +кс0 +dcn-h—g—= О,
дх	дх
Эс
Kc0-dc10-g—— = 0.
Эх
(2.3.12)
Решим эту систему уравнений методом интегральных соотноше-
ний. В этом случае коэффициенты ряда Фурье ищем в виде полино-
мов:
2	3
ц	ту	ту
с0 ~с01 + с02 т + Соз Т2 + с04 ТУ,
О	о	о
Ц	Т]2	Т]3
С10 -С101 +С10 2 7Г + С10 3Т7 + С10 4—з-'
о	5	8
2	3
Т]	Tf	ТГ
С11 -Сц 1+Сп 2 х +Сц з~2+с11 4Тз"»
о	8	8
в которых коэффициенты и 8 являются функциями х. Граничные
условия (2.3.5) и (2.3.6) в новых переменных запишутся как:
л = 0 с0=ср
т) = -5 с0 = О
сю ~ ci i - 0>
сю =си
(2.3.13)
Для гладкости функций с- потребуем, чтобы ц = — 8, тогда:
дс/дц = 0, где i = 0, 10, И.
Проинтегрируем каждое уравнение системы (2.3.12) по ц от 0 до
—8. После несложных преобразований получим систему нелиней-
ных дифференциальных уравнений относительно Д = 82(х):
194
Глава 2
-Зк-С102
кос е _
----+----с112
2 24 112
А +
gd&
8 dx
h А dcl02 сю2 dA
— д--------+-------
241 dx 2 dX;
d
12
hdA
8 dx
g(dc102 c102 dA^
12^ dx 2 dx>
(2.3.14)
_ dCiQ2&
KCi 12
112	12
g(.dcl02 ci02 dA^
12^ dx 2 dx>
где c102-c102/c0, c112-c112/c0.
Запишем нелинейную систему уравнений (2.3.14) в виде, более
удобном для численного интегрирования:
^ = F.
dx
dc1I2	р _	12
-----~	Q19 н	А,
dx----2Д	дД
dx Al h 2 102J
24
Л-А
где
F = 8(f2h - 2flg)/(h2 -2g2), fi =3k+c102^-^Ac112;
d_ A ,	_ dA_
f2 - 3Kd + KC102	f3 - Kc112 +	c102-
(2.3.15)
Для x = О начальное условие A = 0, а для c112, c102 начальные ус-
ловия находили на основании системы (2.3.15) с учетом уравнений
(2.3.13) и А = 0 при х = 0. Поскольку для системы уравнений (2.3.15)
имеется неопределенность при А = 0, решение начинали со значения
х ф 0. Для этого функции А, с102, с112 разлагали в ряды, причем ко-
эффициенты рядов находили обычным способом. Полученное чис-
ленное решение нелинейной системы (2.3.15) аппроксимировалось
формулами, пригодными для инженерных расчетов: выражение для
относительной амплитуды и величины диффузионного слоя имеют
соответственно вид:
Iga =-0,71g—+0,91;
К
(2.3.16)
5(х) = >/кехр(1,5-0,71пос) 1-ехр -а^
\ I Л,
\1/2
(2.3.17)
Глава 2
195
где
A =f9c'
D
дп
(2.3.18)
сх-0 ,57 п о
а =-------2,3 при 0,6 < а,
0,01 F
а-0,39
а =------2,3 при 0,6 > а.
0,097
Определим плотность диффузионного потока на длине волны:
। дс л дс л дс дс
= — cos(nx)+—— cos(ny) = — cos 6 - — SinG,
т]=о	дУ	dy dx
где 0 = arctgdy/dx.
Переходя в этом выражении для диффузионного потока от пере-
менных х, у к переменным хр т), получим:
А • de	е дс дс^ дс _
^- = sm0   a0ancos£— + п—	cosO.
D	dr) dtj Эт]
Подставляя в формулу (2.3.19) вместо производных их значения
после усреднения по периоду, получим соотношение
2 " з
1+-(аоап)2 ,
А
D
дс
(2.3.19)
Пр ОСП
2
А = 2£
Дс 6(х)
где 5(х) дано выражением (2.3.17), записанным с учетом уравнений
(2.3.18). Для определения Рж подставим в формулу (2.3.13) значение
]\/Ас и, проинтегрировав по х от 0 до X, получим:
— 1+—(арап)2 ехр(0,71па-1,5) 1+*—ехР( . (2.3.21)
4 J	L а
Величина 1п(4 — ехр(—а))/а во многих случаях составляет 1—2%,
поэтому для простоты расчетов ее не учитываем. Без учета этого чле-
на формула (2.3.21) после несложных вычислений может быть пред-
ставлена в следующем виде:
₽Ж=7’5Й
5
4
1-
(2.3.20)
(2.3.22)
г voz
где I = —--частота волны; z — безразмерная фазовая скорость.
Л
Как отмечалось выше, формулы (2.3.21) и (2.3.22) получены при
условии существования вихревой когерентной структуры при вол-
нообразовании.
Однако, если предположить, что перемешивание раствора от-
сутствует, а величина диффузионного слоя постепенно растет по
всей длине трубки, то зависимость с(х) = Д/к от числа волн t = х/Х
описывается формулой
196
Глава 2
Hx) = AW-(1,6~a2)*
1 ’ к 0,017 Л’
откуда величина диффузионного слоя
(2.3.23)
1,6-а2 Щ
0,034л у
В этом случае баланс вещества для всей длины трубки можно со-
ставить следующим образом:
L	L
(ЗжЛспс? J ds - rcdj j[ds,
о	о
ад=
(2.3.24)
(2.3.25)
откуда
р = ° Дс-
Рж L
jds
о
Подставляя в эту формулу значение диффузионного потока
(2.3.20) и учитывая выражение (2.3.23), получим:
о i-96
(2.3.26)
1+НооОл)2
Руо
L
(2.3.27)
Таким образом, на основе решений уравнений переноса количест-
ва движения и вещества (см. формулы (2.3.21) и (2.3.22)) ясна сущ-
ность этого механизма при волнообразовании. Она состоит в том,
что массообмен происходит порциями по длине, почти «квантами»
только с позиций макрокинетики. Он назван «спиновым массообме-
ном». Массообмен при волнообразовании, согласно предложенному
механизму, определяется когерентной волновой самоорганизуемой
структурой, а характерным размером в этом случае является длина
волновой структуры, а не размер контактного устройства (напри-
мер трубки), как это принималось ранее. Длина волны когерентной
структуры, ее характерный размер намного меньше длины контакт-
ного устройства (например длины трубки).
В то же время, как это следует из формул (2.3.21), (2.3.27), харак-
терный размер находится в обратной зависимости в выражении для
расчета эффективности, то есть
р, = 1,673а0'7. или Рх = 1,673а0,7./—,	(2.3.28)
V л	V z
р1=.	--7^71,
VI, 6 -а2
(2.3.29)
Глава 2
197
где а — амплитуда волны; X — длина волны; L — длина контактно-
го устройства; и0 — средняя скорость; D — коэффициент диффузии;
f = —— — частота волны; z — безразмерная фазовая скорость. Из со-
Л
отношений (2.3.28) и (2.3.29) видно, что при волновом пленочном
течении эффективность массообмена повышается. При этом коге-
рентная структура, рассчитанная по формуле (2.3.28), намного пре-
вышает повышение интенсивности массообмена, определенной из
уравнения (2.3.29). Это превышение можно оценить по следующему
соотношению:
(2.3.30)
При параметрах: а =0,6, X = 2 см, L = 100 см, часто встречающих-
ся в процессах, согласно формуле (2.3.30), массообмен при волно-
образовании будет теоретически повышен до 5 раз. На самом деле,
практически интенсивность массообмена при волнообразовании
повышается в 2—4 раза в зависимости от числа Рейнольдса, что мож-
но объяснить неполным перемешиванием в седловине волны.
Пленочный режим в условиях волнообразования широко исполь-
зуется в высокоэффективных тепломассообменных аппаратах при
организации различных процессов: абсорбции, теплообмене, в том
числе с фазовыми переходами (конденсации, испарении), массооб-
мен при режимах восходящего прямотока интенсифицируется на
порядок.
Теоретическая зависимость, представленная формулой (2.3.30),
носит предсказательный характер при создании искусственно коге-
рентных структур в самоорганизующихся системах. Такие явления
имеют место в процессах тепломассообмена при создании искусст-
венной шероховатости, а также при использовании в тепломассооб-
менных аппаратах различного рода вставок и завихрителей с опре-
деленным шагом.
Предсказательный характер формулы (2.3.28) преследует цель со-
здания регулярной структуры, обеспечивающей при минимуме гид-
равлического сопротивления высокую интенсивность тепломассо-
обмена.
Таким образом, уравнение конвективной диффузии при волнооб-
разовании допускает два решения при малых и сравнительно боль-
ших числах Рейнольдса. Представим эти решения в безразмерном
виде:
Sh 1,96	11 бряайЛ2 М1/2
Sh0 5/1,6-а2 X J _\6у
(2.3.31)
198
Глава 2
^ = l,21a°'’f-'l .	(2.3.32)
Sh0	W
Формулы (2.3.31) и (2.3.32) получены делением формул (2.3.28) и
(2.3.29) соответственно на одну из известных формул, применяемых
для расчета пленочного массообмена в гладкую пленку, например на
формулу Левича [2.3.13]:
1/2
Sh
Re1/2
, где Re = q/v.
(2.3.33)
0 D ImJ
Из формул (2.3.31) и (2.3.32) следует, что если при массообмене, со-
ответствующем непрерывному росту диффузионного слоя, увеличе-
ние массообмена возможно на несколько процентов, то при когерент-
ном переносе скорость массообмена может возрастать в несколько
раз (формула (2.3.30)).
Следует еще раз обратить внимание на формулу для диффузион-
ного слоя при когерентном режиме массообмена. Она отражает но-
вый тип массообмена, обусловленный существованием продольно-
го пограничного слоя. Физически это означает, что при когерентном
массообмене существует продольная область, в которой происходит
основное изменение концентрации (до этого были известны области,
в которых основное изменение концентрации происходило в попе-
речном направлении). Это создало такие понятия, как пограничные
слои: гидродинамический, тепловой и диффузионный. Из теорети-
ческого исследования когерентного массообмена впервые получена
величина продольного пограничного слоя, указывающая на область
основного изменения концентрации в продольном направлении, сов-
падающем с направлением течения. Это, по существу, является те-
оретическим объяснением применения различных турбулизаторов
для интенсификации процесса тепломассообмена.
Отметим еще одну особенность гидродинамики и массообмена
при пленочном течении. Обратим внимание на характер распределе-
ния скорости, представленный формулой (2.3.8). Он вносит сущест-
венные коррективы в природу уравнения конвективной диффузии
для волновой пленки. На самом деле, если первый член этого урав-
нения по форме напоминает уравнение переноса вещества в гладкой
жидкой пленке (при a -> 0), то его второй член, имеющий пульсаци-
онную природу, характеризует волновую природу массообмена.
При волновом течении пленки жидкости и массообмене в ней
формально соблюдаются основные внешние признаки турбулент-
ности — добавка к осредненной скорости пульсационного движения
(2.3.8), как это имеет место при турбулентном движении. Однако эти
Глава 2
199
добавки не носят случайный характер. Об этом также свидетельст-
вует наличие периодической составляющей в зависимости корре-
ляционной функции от частоты. Спектральная плотность для это-
го случая показывает наличие доминирующей частоты. Показатели
Ляпунова имеют отрицательные значения [2.3.4].
Все это указывает на вероятность проявления эргодичности дви-
жения в фазовом пространстве. Поскольку для такого движения без-
различно, является траектория системы случайной или периоди-
ческой, то наличие в распределении скоростей двух составляющих
(средней и пульсационной) не противоречит проявлению когерент-
ных структур при пленочном волновом течении.
К тому же, при пленочном волновом течении проявляются дина-
мические свойства системы, отвечающие закономерностям возник-
новения самоорганизации и турбулентности [2.3.3; 2.3,4; 2.3.9; 2.3.10].
Именно в этих работах доказано, что условием возникновения тур-
булентности (хаоса) в неустойчивых системах является нелинейная
зависимость фазы (для распределенных систем) либо частоты (для
нераспределенных систем) от амплитуды возмущений. Необходи-
мым условием возникновения самоорганизации является линейная
зависимость фазы (частоты) от амплитуды. Естественно, возможны
и случаи вырождения этой зависимости: равенство нулю углового
или свободного члена в зависимости фазы (частоты) от амплитуды
возмущения. Как следует из рис. 2.35 и 2.36, действительно имеет
место линейная зависимость фазовой скорости от амплитуды, что
характерно для процессов, характеризуемых возникновением само-
организации. Эта зависимость следует как из решения нелинейного
уравнения Навье — Стокса [2.3.3; 2.3.4; 2.3.9; 2.3.10], так и из экспери-
ментальных данных работы [2.3.11].
Из сказанного следует, что возмущение, накладываемое на основ-
ное движение, может оказывать двоякое воздействие. При малой ам-
плитуде в уравнении поверхности пленки жидкости в виде периоди-
ческой функции влияние возмущения на характер движения будет
незначительным (рис. 2.37,а). В этом случае решение уравнения для
конвективной диффузии будет мало отличаться от решения уравне-
ния для гладкой пленки (некоторое увеличение вызвано увеличени-
У
ем поверхности контакта).	/	\
На рис. 2.37,а указаны значения функции тока у —	, изме-
У
няющиеся по длине волны и по толщине пленки жидкости [здесь
е 2я,	„
£ =—(x-cof)], рассчитанные по нелинейной теории течения тон-
Л
ких слоев жидкости при волнообразовании [2.3.2, 2.3.4]. Точ-
ки равных расходов в пленке жидкости соединены линиями. Как
200
Глава 2
Рис. 2.37. Мгновенная картина течения в пленке жидкости [2.3.2 —2.3.4]: а — при
Л = 0,095, Ga = g/i^/v2 = 18,193, ReL = 3g/v = 20,365; б — прит] = 0,165, Ga = 62,5,
ReL = 87,45
показано на рис. 2.37,а, в седловине волны функция тока име-
ет положительное значение по всей длине волны, т.е. в седлови-
не волны отсутствует перемешивание. Незначительное повышение
коэффициента массообмена обусловлено увеличением поверхности
контакта фаз; второй член уравнения (2.3.8) мало влияет на резуль-
тат решения. Формула (2.3.29) для коэффициента массоотдачи прак-
тически совпадает с формулой для гладкой пленки.
С увеличением амплитуды возмущение может изменить харак-
тер движения, а следовательно, и массообмен в пленке. Функция
тока V
на линиях равного расхода принимает отрицательное
значение в седловине волны (см. рис. 2.37,6). В этом случае второй
член уравнения (2.3.8) приобретает существенное значение. Форму-
ла (2.3.28) для коэффициента массоотдачи качественно отличается от
формулы (2.3.29).
Следует отметить, что рис. 2.36 и рис. 2.37 доказывают необходи-
мость решения уравнения конвективной диффузии на длине волны,
т.е. по модели полного перемешивания на длине волны.
В таблице 2.3.1, как пример, показано сопоставление результатов
расчета по формулам (2.3.28) и (2.3.29) с экспериментальными данны-
ми работы [2.3.14]
Следует отметить, что уже при Re£ = 4q/v = 35 данные расчетов
по формуле (2.3.29) становятся меньше экспериментальных данных Р'.
Начиная примерно с этих чисел ReL, в седловинах волн функция тока
Глава 2
201
Таблица 2.3.1
Сравнение коэффициента массоотдачи,
полученного экспериментально [2.3.14] и коэффициентов,
рассчитанных по формулам (2.3.28) и (2.3.29)
Re£	Коэффициент массоотдачи, м/ч		
	Р'	Р"	Р'"
	0,13	0,084	0,136
	0,115	0,077	0,12
	0,17	0,0965	0,167
04	0,154	0,0886	0,148
Примечание. В числителе — при десорбции О2, в знаменателе — при абсорбции СО2; Р' —
экспериментальные данные работы [2.3.14], Р" рассчитан по формуле (2.3.29), Р'" — по фор-
муле (2.3.28).
принимает отрицательное значение (см. рис. 2.37,6), то есть rotv =/- 0,
что указывает на завихренность течения. Пульсационная составля-
ющая (второй член в формуле (2.3.8)) возрастает, профиль скорости
становится более заполненным в седловинах волн. Отрицательное
значение функции тока в седловине волны указывает на существо-
вание когерентного характера переноса вещества при волнообразо-
вании в пленочном течении, что способствует интенсификации мас-
сообмена, поскольку в этом случае в качестве характерного размера
выступает длина волны, а не длина контактного устройства, напри-
мер трубки.
В табл. 2.3.2 приведены результаты сравнения коэффициен-
тов массоотдачи, рассчитанных по формуле (2.3.28) и полученных
экспериментально [2.3.63] на длинных трубках на расстоянии
2386 мм от верхнего среза трубы для системы О2—Н2О при 20 °C,
*>о2-н2о = 19-10’mVc.
Таблица 2.3.2
Сравнение коэффициентов массоотдачи,
рассчитанных по формуле (2.3.28) и полученных экспериментально
Re£ = 4q/v	а	Z	f, с1	Ррасч105- м/с	Рэксп105- м/с
60	0,40	1,95	3,30	4,98	4,7
100	0,49	1,65	3,60	6,53	6,1
200	0,53	1,60	5,09	8,44	8,4
400	0,574	1,51	5,966	10,09	10,0
800	0,643	1,36	6,85	12,03	10,3
1200	0,643	1,36	7,50	12,57	11,02
1600	0,643	1,36	7,50	12,57	11,09
202
Глава 2
Следует отметить, что до Re£ = 60 на интенсивность массообмена
существенную роль оказывает поверхность пленки, а не новая форма
организации интенсивности массообмена, связанная с его когерент-
ной структурой и использующая в качестве характерного размера
длину волны. Выше Re£ = 1600 существенную роль в интенсивности
массообмена начинают оказывать турбулентные пульсации и про-
цесс массообмена.
Интенсификация тепло- и массообмена на стенках аппаратов
с регулярной шероховатостью
Однофазная задача. Подобный подход был применен при исследо-
вании процессов тепломассообмена на стенках аппаратов с регуляр-
ной шероховатостью [2.3.2].
На основе теоретических решений уравнений переноса количест-
ва движений и вещества получено выражение для интенсивности
массообмена в пленке жидкости, текущей по шероховатой поверх-
ности:
₽S = J^-[1+O,6(anho)2^(a),	(2.3.34)
2тс
где S — расстояние между выступами шероховатости; п = — — вол-
Л
новое число; hQ —средняя толщина пленки жидкости;
ф(а) = 1,22 — 0,23а при а < 0,4;
ф(а) = 1,1 при а >0,4;
а = ——— (к — высота выступа).	(2.3.35)
к + 2/?0
Заметим, что формулы (2.3.28) и (2.3.34) идентичны по своей
структуре. В формуле (2.3.28) когерентная структура создается са-
мим течением, а в формуле (2.3.34) — регулярной шероховатостью. В
обоих случаях интенсивность массообмена обратно пропорциональ-
на длине регулярной структуры, которая в несколько раз превышает
длину контактного устройства, обеспечивая тем самым повышение
интенсивности массообмена.
Как видно из формулы (2.3.34), коэффициент массоотдачи зави-
сит также от геометрических характеристик регулярной шерохова-
тости, т.е. от расстояния между выступами шероховатости и высоты
самого выступа. Тогда зависимость, характеризующая повышение
интенсивности пленочного массообмена на стенке с регулярной ше-
роховатостью, например при а = 0,6, будет иметь вид:
Глава 2	203
|s.=0,685А	(2.3.36)
Pl »Ь
Для реальных конструктивных и расчетных параметров шерохо-
ватости при оптимальном режиме процессов массообмена в пленке,
текущей по стенке с регулярной шероховатостью, оптимальный ре-
жим реализуется при соотношении S/к = 6... 8, причем в этом случае
волновое течение повторяет структуру шероховатости, т.е. S = X. При
таком же соотношении реализуется режим оптимального тепломас-
сообмена при пленочном течении на пластине с регулярной шерохо-
ватостью. Расчет по формуле (2.3.34) показывает, что использование
при пленочном массообмене контактных устройств с регулярной ше-
роховатостью приводит к повышению интенсивности массообмена
примерно в 2 раза и более.
Результаты сравнения расчетов по формуле (2.3.34) с опытны-
ми данными работы [2.3.15] приведены в таблице 2.3.3. Как следует из
этой таблицы, с возрастанием числа Рейнольдса наблюдается улучше-
ние сходимости расчетных и экспериментальных данных. Отклонение
между расчетами и экспериментом при низких значениях чисел Рей-
нольдса связано, возможно, с тем, что расчетная формула получена без
учета установления оптимального гидродинамического режима.
Таблица 2.3.3
Сравнение значений коэффициентов массоотдачи, полученных
экспериментально [2.3.15] и рассчитанных по формуле (2.3.34)
	ReM = q/v	Толщина пленки h0, см	Рж40'2, см/с	
			экспериментальный	рассчитанный по формуле (2.3.34)
	170	0,046	1.9	2,46
	400	0,072	2,7	3,1
	700	0,095	3,5	3,74
	1000	0,12	4,0	4,31
	1500	0,14	4,8	4,9
Помимо всего прочего коэффициент массоотдачи при наличии
искусственной шероховатости существенно отличается от коэффи-
циента массоотдачи для гладкой поверхности при соблюдении про-
чих равных условий.
На основе теоретических исследований массообмена в аппаратах
с контактными устройствами с регулярной шероховатой поверхно-
204
Глава 2
2	6 Ю2 2	6 1 03 2	6 1O*Re
Рис. 2.38. Зависимость коэффициента мас-
соотдачи Рж от числа Re = q/v при абсорбции
СО2: сплошные линии — эксперименталь-
ные данные, приведенные в работе [2.3.15]
при различных отношениях расстояния
между выступами (S) к высоте выступа (к);
о° — данные, соответствующие массоотдаче
в гладкую пленку (6 = 24°56'); пунктирная
линия 1 — расчет по формуле (2.3.34) для оп-
тимального соотношения S/к = 6,7; штрих-
пунктирная линия 2 — расчет по формуле из
работы [2.3.15]
ке с регулярной шероховатостью, при различных отношениях S/k.
стью были разработаны
новые поколения аппара-
тов и систем кондициони-
рования воздуха. При этом
был отмечен эффект, свя-
занный с опережающим
ростом тепломассообмена
по сравнению с гидравли-
ческим сопротивлением,
отмеченный ранее при ис-
следовании массообмена в
пленке жидкости при вол-
нообразовании [2.3.16].
На рис. 2.38 представле-
но сопоставление резуль-
татов расчета по формуле
(2.3.34) с опытными данны-
ми работы [2.3.15]. Сопо-
ставление проведено с ко-
эффициентом массоотдачи
при абсорбции СО2 пленкой
жидкости, текущей по стен-
Двухфазная задача. Рассмотрим двухфазный массообмен при ус-
ловии, что сопротивление массопередаче остается в пленке жидкос-
ти. Влияние газа на массообмен в этом случае учтено касательным
напряжением на границе раздела пленки: жидкость — газ. Такая
постановка задачи при решении уравнений гидродинамики впервые
была предложена в линейной [2.3.1—2.3.3] и нелинейной [2.3.4—2.3.8]
постановках. В этих работах было получено выражение функции
тока для течения волновой пленки жидкости по гладкой поверхности
в спутном потоке газа в линейной и нелинейной постановках зада-
чи. Строго говоря, к данной задаче эта функция тока не применима,
так как в ней не учтено наличие шероховатости. Но если учесть, что
процесс массопередачи сосредоточен в тонком слое вблизи свобод-
ной поверхности, а отличие течений по гладкой и шероховатой по-
верхностям наблюдается в слое, примыкающем к стенке, то с боль-
шой степенью точности можно использовать формулы для скорости
течения около свободной поверхности.
Выражение для скоростей на поверхности раздела с учетом каса-
тельного напряжения на поверхности раздела, согласно полученной
в работах [2.3.4—2.3.8] функции тока, имеет вид:
Глава 2
205
Гз 1
1
u = Uq----------+—T(l+asinnx) ;
[_21+asinnx 4	J
U Г3 1 Um  Л
\) = nhGUQ cos nx-------+ -T(1+asinnx) ,
_21+asinnx 4
(2.3.37)
(2.3.38)
где T = Toho/p.uo — безразмерное касательное напряжение; n = 2ti/X;
u0 — средняя скорость; a — амплитуда волны; hQ — средняя толщина
пленки.
При этих предположениях механизм массоотдачи в пленке жидко-
сти, текущей по стенке с регулярной шероховатостью, можно счи-
тать частным случаем модели массопереноса в пленке жидкости при
волнообразовании, предложенной ранее.
Коэффициент массоотдачи рассчитывают по формуле
S	S
^=fjsdl/^dl,	(2.3.39)
О	о
где величина диффузионного потока определяется, в свою очередь,
из решения уравнения конвективной диффузии
дс дс д2с	[п о дгп
и— + O—- = D--Z-	(Z.J.4U)
Эх Эу Эу2
с граничными условиями
с = ср при у = угр = Йо(1 + asinnx),	(2.3.41)
с -> 0 при у —> 0 (вдали от поверхности раздела).
Несмотря на то, что уравнение (2.3.40) и граничные условия (2.3.41)
для двухфазной задачи формально совпадают с уравнениями и гра-
ничными условиями для однофазной задачи, данные уравнения су-
щественно отличаются между собой, так как в уравнение (2.3.40) сле-
дует вставить распределение скоростей из формул (2.3.37) и (2.3.38),
полученное с граничным условием
ди
И Эу = Т° ПРИ У = Угр'	(2.3.42)
учитывающим касательное напряжение т0 на границе раздела плен-
ки: жидкость—газ.
С учетом формул (2.3.37) и (2.3.38) уравнение (2.3.40) примет вид:
ЦрГ 6
4 1+asinnx
+ Т(1+asinnx)
Эс	Эс"1	Э2с
—+nh0acosnx— = D—т.
Эх	OyJ	Эу
(2.3.43)
Отметим, что при Т = 0 (отсутствует взаимодействие газа с плен-
кой жидкости) уравнение (2.3.43) переходит в уравнение для случая
гравитационного стекания пленки жидкости, текущей по стенке с
регулярной шероховатостью.
206
Глава 2
С введением новых переменных л = у — угр, угр = Ло(1 + asinnx),
хг = их уравнение (2.3.43) и граничные условия (2.3.41) приводятся к
виду:
6+Т(1+asinxj2 дс	д2с	толлх
пил-------------— -— = D—-,	(2.3.44)
4(14-a sin xj dxj Эт)2
с = ср прит] = 0, с = 0 прит| —> —оо.	(2.3.45)
Опуская промежуточные выкладки, которые аналогичны при ре-
шении однофазной задачи, приведем выражение для коэффициента
массоотдачи в жидкой фазе для случая двухфазной задачи [2.2]:
j 1+(anhQ cos (2тсх1) )2
₽Ж =	1--------—------------.	(2-3.46)
J1+(anhQ cos (2 Tuq) )2dxj
о
где
0 4t
t// 4(l+gSinx) х
o 64-T(14-asinx)
Аппроксимировав результаты численных решений интегралов в
уравнение (2.3.46), получим окончательную формулу для коэффици-
ента массоотдачи в жидкой фазе в условиях регулярной шерохова-
тости при наличии газового потока:
₽Ж =7Duo/A[l+O,6(anho)2K(7-),	(2.3.47)
где
f(T) = 1,1 + 0,113Т при Т<4,
ДГ) = 10,04л/Т/(14-5,97>/Т) при Т>4.	(2.3.48)
При X = S формула (2.3.47) принимает вид
₽ж =7Duo/S[l+O,6(anho)2]f(7’).	(2.3.49)
Величину амплитуды волны определяем по формуле из работы
[2.3.2]:
a (^тах ^minJ/^max + ^minb
причем это соотношение получено из условия сохранения расхода, а
именно, толщина пленки жидкости над выступом шероховатости та-
кая же, как и средняя толщина пленки. В этом случае
a = к/(к + 2Л0),	(2.3.50)
где к — высота выступа.
Глава 2
207
В табл. 2.3.4 сопоставлены экспериментальные данные для коэф-
фициентов массоотдачи, полученные в работе [2.3.25], с расчетными
данными по формуле (2.3.49) с учетом уравнений (2.3.48) и (2.3.50).
Расчет проведен для случая оптимального соотношения S/к = 6,7... 8,5
при различных нагрузках по жидкости и газу.
Из таблицы следует, что при числах Яеж = 693... 1128 и скорос-
тях газа до 30 м/с (до турбулентной области) наблюдается замет-
ное превышение расчетных данных над экспериментальными
(см. № 1—17). При этих числах Яеж заметное влияние оказывают
входные эффекты. При числах Иеж, соответствующих волновому
режиму, наблюдается удовлетворительное согласие теории и экс-
перимента (см. № 4—6, 20, 21, 23, 24, 26, 27, 29). При скоростях газа
более 30 м/с и числах Яеж, соответствующих переходу в турбулент-
ную область, турбулизация пленки жидкости возрастает, и это ска-
зывается на отклонениях расчетных и экспериментальных данных
(см. № 22, 25, 28, 30).
Совпадение расчетных и экспериментальных данных для режи-
ма, при котором наблюдаются на поверхности пленки стоячие вол-
ны, указывает на то, что выбранная математическая модель удовлет-
ворительно описывает сложный режим двухфазного массообмена
в пленке жидкости, текущей по стенке с регулярной шероховато-
стью.
Отклонение расчетных данных от экспериментальных для ре-
жимов, при которых необходимо учитывать либо входные эффек-
ты, либо развитую турбулентность, указывает на один из возмож-
ных подходов для теоретического исследования этой сложной проб-
лемы.
Надо полагать, что при рассмотрении вопроса массопередачи
в волновую пленку, движущуюся по поверхности с рёгулярной
шероховатостью, а также в условиях ее взаимодействия с газо-
вым потоком, при снятии предположения о наличии стоячих волн,
вид формул (2.3.34) и (2.3.49) сохранится. Тогда, заменяя в этих
формулах u0/A, = Uq/S = f/z (где f — частота волн; z — безразмер-
ная фазовая скорость), получим обобщенную зависимость для
коэффициента массоотдачи в пленку жидкости на регулярной ше-
роховатости:
Р, =В,4Шг,
где для i = 4 (однофазная задача) В4 = [1 + O,6(anho)2](p(a),
а <р(а) представлена функциями (2.3.35), и для i = 5 (двухфазная за-
дача) В5 = [1 + O,6(anho)2]/(T) (где f(T) представлена формулами
(2.3.48)).
208
Глава 2
Таблица 2.3.4
Десорбция кислорода водой в трубке с элементами шероховатости
прямоугольного профиля при восходящем движении
двухфазного потока
Номер по пор.	пг. м/с	<7, см2/с	Др, мм вод. ст.	к, мм	р, см/с		Иеж = 4q/v
					рассчитан- ный по фор- муле(2.3.49)	опытные данные [2.3.25]	
		Высота выступа к			= 0,3 мм		
1	20,31	1,733	88	2	0,15£3	0,0960	693
2	24,79	1,733	120	2	0,1705	0,1200	693
3	28,56	1,733	146	2	0,1798	0,1445	693
4	31,85	1,733	178	2	0,1879	0,1663	693
5	34,80	1,733	202	2	0,1946	0,1926	693
6	39,99	1,733	260	2	0,2200	0,2120	693
7	20,30	1,733	92	2,5	0,1357	0,1050	693
8	24,77	1,733	128	2,5	0,1465	0,1330	693
9	31,80	1,733	190	2,5	0,1620	0,1830	693
10	39,39	1,733	276	2,5	0,1770	0,2400	693
		Высота выступа к =			= 0,25 мм		
И	20,17	1,733	82	2	0,1500	0,0900	693
12	24,66	1,733	110	2	0,1600	0,1160	693
13	34,61	1,733	186	2	0,1836	0,1784	693
14	39,77	1,733	232	2	0,1939	0,2180	693
15	42,06	1,733	256	2	0,1983	0,2355	693
16	20,09	2,82	ИЗ	2	0,1728	0,1360	1128
17	24,53	2,82	218	2	0,1840	0,1726	1128
18	31,48	2,82	218	2	0,2090	0,2380	1128
19	39,43	2,82	312	2	0,2183	0,3200	1128
		Высота выступа к			= 0,3 мм		
20	20,16	3,74	166	2	0,1946	0,1750	1496
21	24,52	3,74	320	2	0,2101 	0,2246	1496
22	31,35	3,74	182	2	0,2300	0,3080	1496
23	20,23	3,74	182	2,5	0,1930	0,1861	1496
24	24,55	3,74	242	2,5	0,2100	0,2394	1496
25	31,36	3,74	350	2,5	0,2264	0,3212	1496
26	20,09	4,6	198	2	0,2090	0,2240	1840
27	24,44	4,6	266	2	0,2234	0,2637	1840
28	31,20	4,6	390	2	0,2419	0,3601	1840
. 29	20,05	4,6	216	2,5	0,2044	0,2276	1840
30	24,35	4,6	280	2,5	0,2182	0,2885	1840
Примечание: иг — скорость воздуха в трубке; q — плотность орошения; Др — перепад дав-
ления в трубке; = 16,8 мм; I = 150 мм; Гводы = 20 °C; 1водывх = 19,9 °C; £водывых = 19,7 °C.
Глава 2
209
Совместный тепло- и массообмен в многокомпонентных,
многофазных и струйных системах
Совместный расчет тепло- и массообмена базируется на решении
следующей системы уравнений и граничных условиях:
	^(pv)+V(pw) = pf+Vn..;	+V(pv) = 0.	(2.3.51) dt	Ч	dt Эс —+(v-V)c = £)VVc+F(c).	(2.3.52) dt ^+|vV)T = aVVT + O(T).	(2.3.53) ot f dv- ч	ч dx - dx- \ J 1J
На входе:	Т = Т0Й; c = c0(?).	(2.3.54)
Вдали от поверхности раздела:
	дс T = Tw{r)- — = 0.	(2.3.55) w	on
На поверхности раздела:
	1	f	дТ	/Гу П c = dT + b; —= 	 —.	(2.3.56) dn \AHDJdn
Пленка, капля, струя:
	₽,тм = ₽Л	(2.3.57) aiTM = az^2'	(2.3.58) /j =l(l-Ka/VLu);	f2 =l(l-VLu/Ka).	(2.3.59)
Здесь Lu = a/D — число Льюиса; Ка = AHd/pcp — число Кутателадзе;
ср — теплоемкость; d, b — параметры, характеризующие равновесие
между концентрационными и тепловыми полями.
На основе теоретических решений этих уравнений, описыва-
ющих совместный перенос, количество движения, вещества и энер-
гию применительно к течениям по шероховатой поверхности, в систе-
мах, состоящих из совокупности капель или пузырей, в многокомпо-
нентных системах, при пленочном и струйных течениях в различных
гидродинамических режимах (ламинарном и турбулентном), уста-
новлена общая закономерность [2.3.2], представленная формулами
(2.3.57—2.3.58).
210
Глава 2
Сущность этой закономерности в том, что она определяется про-
изведением двух членов: один член является общим для всех ти-
пов (для многокомпонентного массообмена он имеет векторный вид
[2.3.2]), другой член соответствует каждому из рассмотренных типов
тепло- и массообмена.
В формулах (2.3.57) и (2.3.58) pf, af. — коэффициенты абсорбции
и теплоотдачи для изотермических процессов. Они соответствуют
каждому из рассмотренных типов тепло- и массообмена. В то время
как f. и f2 являются общими функциями, они сохраняют свое пос-
тоянное значение в различных гидродинамических режимах и ус-
ловиях и имеют вид, представленный формулами (2.3.59). Данные
закономерности обобщают работы, проводимые под руководством
академика В.Е Накорякова.
Отметим, что вид добавочных множителей f\ и f2 в формулах ана-
логичен, полученному ранее в работах [2.3.46—2.3.47].
Таким образом, для того чтобы рассчитать коэффициенты массо-
отдачи (теплоотдачи) при неизотермической абсорбции, достаточно
провести расчет коэффициентов абсорбции (теплоотдачи) при изо-
термических условиях и полученное выражение умножить на или
f2. Например, формула для коэффициента массоотдачи в волновую
пленку при неизотермической абсорбции (по модели полного пере-
мешивания) имеет следующий вид:
Ртм -^>5
ехр (0,7 In а-1,5Ц,
(2.3.60)
где fj дана формулой (2.3.59).
На рис. 2.39 проведено сопоставление результатов расчета по фор-
муле (2.3.60) с опытными данными работ [2.3.46—2.3.47].
Рис. 2.39. Зависимость эффективности тепло-
массообмена при неизотермической абсорб-
ции водяного пара растворами бромистого
лития (•) и хлористого кальция (4-) от соотно-
шения Re-Pr(h0/X):
1 - Nu = l,673a017(l+(an)2^y-^V(l-Ka/^);
2 - Nu = l,673a0,7(l+(an)2 Re1/2 Рг1/2х
где Nu = P/Iq/Д Ка = &Hd/pc ; с = dT + b;
Lu = a/D; Re = UQhQ/v
Глава 2
211
Результаты теоретического и экспериментального исследования
процессов совместного тепло- и массообмена использованы при раз-
работке солнечной системы охлаждения и кондиционирования воз-
духа [2.3.16].
Гидродинамика в волновой пленке
Уравнения количества движения, переноса массы и энергии, яв-
ляющиеся предметом исследования нелинейной гидродинамики,
имеют вид:
^-(pv) + p(vV)v = pf + Vm-;	(2.3.61)
dt	J
-^+V(pv) = 0;	(2.3.62)
dt
где f — объемная сила;
ПУ = ~Pij + MdUi/dXj + diij/dxJ - (2/3)^(дик/дхк);
i,j,k= 1...3.	(2.3.63)
Граничными условиями являются:
—	прилипание на твердой поверхности
у = О, U = V = 0;
—	отсутствие влияния газового потока на течение пленки жидко-
сти, т.е. пленка жидкости стекает под действием силы тяжести
У = Л, тху = 0.
Течение тонких слоев в условиях волнообразования описывает-
ся системой уравнений (2.3.61)—(2.3.62), которую с помощью безраз-
мерных переменных: £ = (п/й0)(х — cof), ц = y/(hQh) (где со — фазовая
скорость, п = 2яй0/Х —волновое число; hQ, h — средняя и локальная
толщина пленки, х, у — продольная и поперечная координаты) сов-
местно с граничными условиями можно записать, согласно моногра-
фии [2.3.2], в виде:
А=-
Эт]
з
G ---д- + Н h +
.3
Эй
dh	Эу	Э2у (Эу
zh-^+zhu]—^------
д£>	Эт]	Эт)2


г
-й zh
Э2у Эу Э2у Эу Э2у^
Эт)Э£ Vr) Эт]Э£ + Э£ Эт]2
(2.3.64)
212
Глава 2
при Г) = 0: ig = O, Эу/Эц = О;
*~\2
при Т] = 1: —у = О, — (\g-zh) = O.
0Т]
(2.3.65)
Коэффициенты Е, G и Н выражаются через определяющие пара-
метры следующим образом:
Е = 3/(Re-n); G = 9n2y-Gal/3 / Re2; п =	/X;
Re = 3uo/lo/v; H = 9Ga/(Re2-n);	(2.3.66)
Y = op-1(gv4)-1/3; (0=21/0; Ga = gift /v2.
Решение нелинейного уравнения (2.3.64) с граничными условия-
ми (2.3.65) подробно рассмотрено в монографии [2.3.2]. В частности,
получена полная информация о течении волновой пленки (распреде-
ление скоростей, изолиний функций тока) и ее характеристиках (ам-
плитуде, длине волны, фазовой скорости и т.д.) Результаты расчета
удовлетворительно согласуются с известными экспериментальными
данными.
При изменении физико-химических свойств жидкой пленки (на-
пример вязкости) на несколько порядков (у = 2850... 1,7) расхождение
результатов расчета и эксперимента для амплитуды волны а колеб-
лется в пределах нескольких процентов (рис. 2.40).
Как следует из рисунка, кривые, представляющие собой зависи-
мость амплитуды волны от числа Рейнольдса, различаются по пара-
метру у.
Рис. 2.40,а. Сравнение теоретических и экс-
периментальных данных для зависимости
амплитуды волн оптимального режима а
от числа Рейнольдса: кривые 1—5 — рас-
считанные амплитуды волн для у = 2850 (1),
200 (2), 20 (3), 6,9 (4) и 1,7 (5); эксперименталь-
ные данные (точки) при у = 2850 и v =1,4 сСт
[2.3.11]; у = 700 и v = 1,6 сСт [2.3.11]; у = 6,9
иу = 59сСт [2.3.11]; у = 1,7 и v = 168 сСт
Это связано с тем, что
для течений с поверхно-
стью раздела существу-
ют два характерных числа:
Re и у = op’2(gv4)1/3, ответ-
ственных за смену гидро-
динамических режимов
(переход от ламинарного
режима течения пленки к
турбулентному).
Факт перехода ламинар-
ного режима течения плен-
ки в турбулентный в зави-
симости от чисел Re и у был
установлен эксперимен-
тально [2.3.86, 2.3.87].
Глава 2
213
Используя сочетание ука-
занных чисел, можно пост-
роить единую зависимость
(рис. 2.40,6), которая обобщает
экспериментальные данные в
широком интервале изменения
физико-химических свойств.
Для практического расчета ре-
комендованы следующие соот-
ношения:
а = 0,094(Re/y3711)1-74;
Re/y3711^ 1,26;
а = (Re/y3711)/(l,44 Re/у3711 + 5’;
l,26<Re/y3/n;
а = 0,505 + 2,05-10'3Re/y3711;
Re/у3711 >Ц,
Рис. 2.40,6. Обобщенная зависимость ам-
плитуды а от параметра Re/y3/11: сплошная
линия — результаты численного расчета;
пунктирные линии — теоретические за-
висимости (2.3.85): 1 — a = 0,l(Re/y3/11)1-83;
2 — а = 0,29; экспериментальные точ-
ки — см. рис. 2.40,а
где а = (hmax — ^min)/(hmax +	— относительная амплитуда; h —
толщина пленки.
Показана особенность течения волновой пленки жидкости, за-
ключающаяся в том, что зависимость толщины пленки от расходных
параметров проходит через экстремальное значение [2.3.2].
Отметим, что методы, применяемые при решении системы урав-
нений, описывающей нелинейные колебания, могут быть с успехом
использованы для других нелинейных колебательных систем.
Синфазность в процессах переноса
Процессы переноса вещества и энергии, как правило, проходят в
интенсивных гидродинамических режимах. Это и понятно, так как в
уравнения переноса входят конвективные члены, зависящие от гид-
родинамической обстановки. Но сама обстановка неоднородна и ею
можно управлять, например геометрией единичного тела или сис-
темы тел, взаимодействующих со средой. Все сказанное указывает
на возможность существования определенных соотношений меж-
ду гидродинамическими, концентрационными полями и геометри-
ческими характеристиками контактных устройств, в том или ином
виде взаимодействующими с потоками сплошной среды. Эти соот-
ношения должны обеспечить максимальный перенос вещества или
высокоэффективный массообмен. Одним из таких способов интен-
сификации процессов переноса является его проведение в режиме
214
Глава 2
синфазности геометрических, гидродинамических и концентраци-
онных полей.
Синфазность может быть организована на телах, пассивно влия-
ющих на сплошную среду, а также на телах или системе тел, активно
взаимодействующих со сплошной средой.
Примером проявления синфазности на телах, пассивно взаимо-
действующих со сплошной средой, является массообмен в волновую
пленку жидкости (1-й случай), стекающую по гладкой поверхности
под действием силы тяжести. Автоколебательная система, какой яв-
ляется волновая пленка, создает когерентную структуру. Перенос
вещества происходит в сплошной среде с когерентной структурой,
и при отсутствии сдвига фаз в геометрических и концентрационных
колебательных полях создаются условия, приводящие к повышению
интенсивности массообмена. Это имеет место в массообмене при на-
личии волнообразования, когда массоотдача определяется когерент-
ной структурой сплошной среды.
Примером проявления синфазности на телах, активно взаимо-
действующих со сплошной средой, является массообмен:
—	в волновую пленку, стекающую по стенкам канала с регуляр-
ной шероховатостью (2-й случай). В результате такого взаимодействия,
при определенных геометрических соотношениях между длиной ре-
гулярной шероховатости и ее высотой и длиной волны при пленоч-
ном течении по стенкам с регулярной шероховатостью, наступает ре-
жим, при котором сплошная среда повторяет структуру регулярной
шероховатости. В этом случае синфазность гидродинамических и
концентрационных полей достигается только при определенных со-
отношениях геометрических характеристик контактируемой среды
(формула (2.3.35), а именно, оптимальный режим реализуется при со-
отношении S/к = 6... 8, где S — расстояние между выступами, причем
в этом случае волновое течение повторяет структуру шероховатости,
т.е. S = X, к — высота этих выступов;
—	в аппарате с дискретно расположенными вдоль потока телами
различной геометрической формы (3-й случай) [2.3.32—2.3.33].
В отличие от синфазности, организуемой при течении пленки
жидкости по поверхности с регулярной шероховатостью, активно
взаимодействующей со сплошной средой, в данном случае синфаз-
ность организована системой тел, дискретно расположенных вдоль
потока сплошной среды, образуя эффективное контактное устройст-
во. Если при обтекании одиночного тела, образуемая при опреде-
ленных значениях числа Рейнольдса дорожка Кармана постепен-
но размазывается по потоку сплошной среды, то в случае дискретно
расположенных по потоку тел последующие тела способствуют со-
Глава 2
215
хранению дорожки Кармана, организуя когерентную структуру по
ходу расположения всей гирлянды тел.
Общим для рассмотренных случаев является наличие оптималь-
ных значений на зависимостях между гидродинамическими, массооб-
менными характеристиками и геометрическими размерами как самих
тел, так и расстояниями между ними. В первом случае (течение плен-
ки в условиях волнообразования) наблюдается оптимальная зави-
симость между числом Рейнольдса и длиной волны при постоянной
толщине пленки (наличие оптимальных расходов [2.3.1]. Во втором
случае наблюдается оптимальная зависимость коэффициента мас-
соотдачи пленки жидкости от расстояния между выступами шеро-
ховатости на стенке с регулярной поверхностью. В третьем — имеет
место оптимальная зависимость гидравлического сопротивления от
шага дискретно расположенных тел. Различие этих трех случаев со-
стоит в способах организации когерентных структур.
Данное явление нашло применение в процессах интенсификации
тепло- и массообмена, особенно при решении экологических проблем.
Математическое моделирование турбулентного массообмена
при пленочном течении
При гравитационном течении пленки жидкости уравнение пере-
носа пленки имеет вид
r_du _ди'
р u—+v —
I Эх ду)
Эр Э
дх ду
, .ди
Эу J
ди ди
дх ду
_Эс — дс д
дс
(D+Dt)— ,
оу ду [ ду
(2.3.67)
(2.3.68)
где р — плотность; и , с — осредненные скорости и концентрации
распределяемого компонента; ц, pf и D, Dt — коэффициенты динами-
ческой вязкости и диффузии при молекулярном и турбулентном пе-
реносе.
В общем случае коэффициенты переноса являются функцией
f(o, р, hQ, е). Впервые такая зависимость была предложена Левичем:
капиллярное давление, противостоящее динамическому напору, со-
ответствует тому усилию, которое гасит турбулентное движение,
уменьшая масштаб турбулентности. Эта сила препятствует выходу
турбулентных пульсаций за пределы поверхности пленки. Позже
216
Глава 2
авторы Prasher B.D., Fricke A.L. придали этой модели вероятностный
характер: коэффициенты турбулентной диффузии являются прояв-
лением двух независимых событий, совершающихся вблизи поверх-
ности пленки жидкости. Одно из них обусловлено капиллярными
силами, другое — диссипацией энергии вследствие интенсивного ха-
рактера мелкомасштабных движений. Таким образом,
/ 33
a = Go£	.	(2.3.69)
nt gv J
Расчеты по этим моделям мало различаются между собой, но по-
следнее соотношение подтверждает наличие двух характерных па-
раметров при течении систем с поверхностью раздела, что было нами
теоретически и экспериментально доказано. Особенность формулы
(2.3.69) состоит в том, что она имеет размерность. Поэтому в дальней-
шем принято, что Oq = a'o / 4птим - где 4птим — постоянное значение оп-
тимальной частоты волновой пленки, соответствующее доминиру-
ющей величине спектральной плотности волнового течения.
Отметим, что пленка имеет две поверхности раздела: стенка —
пленка жидкости и пленка жидкости — газ (пар). Этим объясняется
тот факт, что коэффициент турбулентности достигает своего макси-
мального значения в объеме пленки жидкости (крупномасштабные
турбулентные пульсации, зародившиеся в объеме пленки жидкости,
постепенно затухают, приближаясь к поверхности раздела и транс-
формируясь при этом в мелкомасштабные пульсации). Математиче-
ски это выражается следующими уравнениями:
уэф / V = 1+(VT / V) = 1+ге(Ло-По):
Взф/D = 1+(Г>г /D) = 1+ЩПо -По)-	(2.3.70)
где ТВ = абр / v; TD = ТВРг; ц0 = у/6р. Для расчета параметра а исполь-
зовалась функциональная зависимость (2.3.67).
Системы уравнений (2.3.67), (2.3.68) вместе с выражениями (2.3.69)
и (2.3.70) решены с учетом длины входного участка методом, изложен-
ным выше. Величина входного участка была получена при различных
значениях величины характеризующей отклонение рассчитанного
профиля скорости и толщины пленки от их стационарных значений
b = ZBX = тк2Ър Re£ = З.бЬпбрПо / v,	(2.3.71)
где т, к2 — коэффициенты пропорциональности; т = 0,3 при = 0,02
(рассчитанный профиль скорости и толщина пленки жидкости отли-
чались на.2% от их стационарных значений); т = 1, к2 = 3,61 при =
= 0,0002; 6р = 5,3-10’4 м при Re£ = 4qr/v = 1500, т.е. за величину 5р прини-
Глава 2
217
мали значение, равное предельной толщине пленки, соответствую-
щей переходу к турбулентному режиму.
В результате аппроксимации численных решений системы урав-
нений (2.3.65), (2.3.66) получена формула (2.3.69), которая зависит от
длины входного участка.
Входной участок:
^/D1/2 =
l,37+2,28oj/25p
rUohoy/4'U/2
I v J b1/2'
(2.3.72)
где oj/2 = 0-055 , a b = lBX дано формулой (2.3.69).
Подставляя в уравнение (2.3.70) зависимость (2.3.69), получим:
.,1/2
P2/D1/2=A^— + В| Re2/4,	(2.3.73)
8Р к о )
А = 1,32, В = 2,85-Ю*2 при Re L = 4q/v = 1500 и 6 = 5,310‘4.
Стабилизированный участок:
Формулы (2.3.72) и (2.3.73) позволяют рассчитывать массообмен в
турбулентную пленку в канале конечной длины с учетом входного
участка. При бесконечном удалении от оросителя, что практически
означает проведение массообмена в канале достаточно большой дли-
ны, концентрация распределяемого компонента становится зависи-
мой только от поперечной координаты и независимой от продольной.
В этом случае система уравнений сохранения количества движений
и вещества упрощаются. Турбулентный перенос описывается урав-
нением
у|1+ТО(у-у2)]^ = 0,
dy	dy
где TD = ТВ Рг; ТВ = aft2 /D; q =
/ о о х 1/2
ti$E3
(2.3.74)
(2.3.75)
a^2=2,5ctf2, aj/2 =0,055, Oqi =1,8940"2.
Таким образом, вид зависимости (2.3.75) такой же, как и на на-
чальном участке (2.3.69), однако коэффициент пропорциональности
может быть другим.
Граничные условия следующие:
с = ср при у = 0 (на поверхности);	(2.3.76)
с = Cj при у = 1 (на стенке)	(2.3.77)
либо
с = q при у —> (вдали от поверхности).	(2.3.78)
218
Глава 2
Для решения уравнения (2.3.74) достаточно двух граничных усло-
вий: одно задается на поверхности пленки жидкости (например ус-
ловие (2.3.76)), другое — на некотором характерном расстоянии от
поверхности раздела. В частности, таким характерным расстоянием
может быть орошаемая поверхность канала, на которой задано гра-
ничное условие в виде, например, соотношения (2.3.77). Тогда реше-
ние дифференциального уравнения (2.3.74) с граничными условиями
(2.3.76) и (2.3.77) предполагает, что диффундирующее вещество рас-
пределено по всей толщине пленки жидкости и, по существу, пред-
ставляет одну из возможных моделей массопереноса.
Если же задается граничное условие на достаточно большом удале-
нии от поверхности раздела, что означает использование граничных
условий (2.3.76) и (2.3.78), то в такой постановке предполагается су-
ществование диффузионного пограничного слоя, в котором происхо-
дит основное изменение концентрации распределяемого компонента.
В этом случае решение задачи (2.3.74) с граничными условиями (2.3.76)
и (2.3.78) представляет другую модель массопереноса вещества.
Проведенный расчет показывает, что окончательный результат
практически одинаков для обеих моделей и имеет вид
₽3/О,/2 = Д
I р
11 а.
1/2Г/1о3£зу/4
< ffv ,
(2.3.79)
или, выражая в этой формуле энергию диссипации через среднюю
скорость течения пленки жидкости (Е = ди0), получим:
л\1/2	h \3/4
(ffV)1/2(^	,
a; I v J
^/Dl/2=Ai
/	\1/2
Р3 /Г>1/2 = 3,1 -10-21	I (ReL)3/4,
V о )
(2.3.80)
где Д = 0,63aJ(2; aj{2 = 2,5aJ/2; aj/2 = 0,055; Д = 0,63aJ{2 = 8,бб40"2;
ReL = 4q/v.
Как уже упоминалось, значение толщины пленки 6р принимается
равной предельной толщине — 0,053 см, соответствующей переходу к
турбулентному режиму. Это соответствует ReKp L = Re£ = 4q/v = 1500.
Если турбулентную пленку жидкости hQ определить по известной
формуле из работы [2.3.28]:
1 Гзу2У/3Г<Г|8/15
4001/\ д J I vj
(2.3.81)
то, подставляя это значение h0 в формулу (2.3.80) и проведя необходи-
мые расчеты для водяной пленки жидкости, получим:
Глава 2
219
ZBX = 4,996(q/v)7/15.	(2.3.82)
Из формулы (2.3.81) следует, что величина входного участка при
турбулентном течении пленки жидкости отличается от величины
входного участка при ламинарном течении (2.3.120), (2.3.121) не толь-
ко коэффициентом перед числом Re, но и показателем степени при
Re. Показатель степени при числе Re для турбулентного выражения
равен 0,75, для ламинарного — 1,0, то есть развитие всех величин
(скорости, толщины пленки и т.д.) при турбулентном течении гра-
витационной пленки жидкости происходит медленнее, чем при ла-
минарном. Это объясняется особенностью турбулентного течения
в пленке жидкости. На входе в канал пленка жидкости приобретает
ускорение. Так как ускоренное течение более устойчиво против раз-
личных возмущений, то на входе в канал образуется участок, на ко-
тором масштаб турбулентности имеет порядок всей толщины плен-
ки, так называемый участок с внешним масштабом турбулентности.
И только пройдя этот участок, в пленке жидкости в полной мере раз-
вивается турбулентность с Колмогоровским масштабом турбулент-
ности, иногда называемым «внутренним масштабом турбулентно-
сти» [2.3.29]. Обычно расчет турбулентного массообмена проводится
с учетом только внутреннего Колмогоровского масштаба турбулент-
ности, а следовательно, не учитывается зависимость турбулентных
переносных свойств от продольной координаты х, что невозможно
объяснить влияние длины орошаемого канала на коэффициент мас-
соотдачи в турбулентную пленку. Вот почему при расчете турбулент-
ного массообмена в пленку жидкости необходимо учитывать зависи-
мость коэффициентов турбулентного переноса от продольной коор-
динаты, что и сделано при использовании зависимостей (2.3.70). Этим
и объясняется более высокое значение величины входного участка
при турбулентном течении пленки жидкости.
Расчет с учетом длины канала (трубки)
1	.При/0Х</
₽ср=₽2^+₽з^-	(2-3.83)
2	. Если ZBX > Z, то ZBX = Z (расчет следует проводить по формуле
(2.3.72).
Эти два положения очевидны. Действительно, если входной учас-
ток занимает всю длину трубки (Z), то он, естественно, и будет харак-
терным линейным размером, т.е. ZBX =Z. Второе положение, записан-
ное в формуле (2.3.83), означает, что когда входной участок занимает
только часть трубки Z и, следовательно, ZBX < Z, то существует длина
220
Глава 2
трубки, в которой массообмен определяется формулой для началь-
ного участка (2.3.73), а за пределом этой длины массообмен — форму-
лой (2.3.80) для стабилизированного участка трубы (канала). Тогда
коэффициент массоотдачи для этого случая будет определяться фор-
мулой (2.3.83).
Результаты расчета длины входного участка и приведенного коэф-
фициента массоотдачи р^О/Рпри абсорбции СО2 турбулентной пленкой
жидкости (0 = (v2/qr)1/3, £>СО2 = 1,77-10'5 см2/с, t = 20 °C) для турбулент-
ного течения при разных числах ReL = 4q/v представлены в табл 2.3.5.
Таблица 2.3.5
Результаты расчета длины входного участка и приведенного
коэффициента массоотдачи
Re, = 4g/v	1600	3000	5000	8000	10000
ZBX, см	81,79	109,68	139,2	172,55	191,45
Z, = 57 см, Р10/Г>	4,658	7,388	11,132	16,543	20,082
Z2 = 250 см, рсре/£>	3,421	5,213	7,311	9,945	11,400
Z3 = 600 см, Рср0/£>	3,278	5,136	7,400	10,337	12,070
Видно, что уже при числах Re£ = 1600 величина входного участка
становится значительной. При изменении числа ReL почти на целый
порядок входной участок изменился только в 2 раза.
На рис. 2.41 сопоставлены расчетные коэффициенты массоотда-
чи (сплошная линия) и результаты
работы [2.3.30] (штрихпунктир-
ная линия), в которой обобщены
практически все известные экспе-
риментальные данные, полученные
при исследовании массоперено-
са в турбулентную пленку жидко-
сти, стекающую под действием
Рис. 2.41. Сопоставление теоретических
и экспериментальных данных коэффи-
циента массоотдачи:-расчетные дан-
ные, полученные решением уравнений
(2.3.72), (2.3.83) в зависимости от длины
входного участка; — — — эксперимен-
тальные данные работы [2.3.30]; тонкой
кривой обозначена зона разработки дан-
ных
Глава 2
221
силы тяжести. Как следует из рисунка, наблюдается удовлетвори-
тельное совпадение расчетных и экспериментальных данных.
Массоперенос в режиме восходящего прямоточного течения
В работе [2.3.4] проведено исследование механизма массоперено-
са и его расчет в турбулентной пленке жидкости при наличии газово-
го потока или градиента поверхностного натяжения на основе реше-
ния уравнений переноса количества движения и вещества с учетом
входных эффектов и при условии, что турбулентный перенос изме-
няется по длине пленки жидкости. Поверхность пленки жидкости
при этом была искомой величиной. Получено общее выражение для
коэффициента массоотдачи
р =	(1+1,66л/ТБ)4/2>/*
(2.3.84)
где x = b/8pRePr; b = 3,61n?82uo/v = l,2998pReI/15/0; 6 = (v2/g)’/3
т = 0,3; ТБ = об2 / V, б = 5,ЗЮ'4 м; Re = 48 un/v = 4q/v;
lgA0 = (0,88B1/4 + 0,33)/(3,92 - 1,53В1'4), при В » 0,12;
Ло= 1,88 при 0< В <0.12, В = 8рт0/рэффи0.	(2.3.85)
Суммарная энергия диссипации двухфазного потока в режиме
спутного течения может быть представлена в следующем виде:
е = guo +rgurA/o/g(p-pr)//i0,
(2.3.86)
где у — коэффициент пропорциональности.
Подставляя это соотношение в формулу (2.3.84), получим:
В	А,	/ i \3/4 z , X1/2
^ = 0,9624/2^+1,124/24/2(3	х
xRe^/4 1+у-Ю2
_____Мт __________
(d — 211q )Мж
О
д(р-Рг)
-13/4
(2.3.87)
где а0 = 2-Ю'2; у = 1,22; d — диаметр трубки; Rer = ur(d — 2h0)/vr;
цг,	— динамическая вязкость газа и жидкости. Выражение для
Ао = 1,88 дано формулой (2.3.85).
Коэффициент пропорциональности найден по эксперименталь-
ным данным работы [2.3.31]. Первым членом в правой части формулы
(2.3.87) можно пренебречь вследствие его малости. В этом случае эта
формула принимает вид:
222
Глава 2
-^ = 0,4 • 4/24/2 (^1/2 Re3/4 х
х l + Y-102
______Hr ___________
(^ ~ 2/1q ) Цж В.еж
^(Р-Рг)
(2.3.88)
или, вычисляя коэффициенты, приведенные в уравнении (2.3.8), по-
лучим:
-^Е5- = 7,76-10‘2(^) Re3/4x
D1/2	I о )
х 1+у402------PrRei-----
(с?-2Ло)|1хжКеж
-13/4
д(р-Рг)
(2.3.89)
Результаты расчета по формулам (2.3.87) и (2.3.89), представлен-
ные на рис. 2.42, достаточно хорошо согласуются с эксперименталь-
ными данными работы [2.3.31].
рхЮ3, м/с
4 -
3 - •
2 
1 ’
10	20	30	40	ц., м/с
Рис. 2.42. Зависимость коэффициента
массоотдачи р в турбулентной пленке
жидкости от скорости газа иг в условиях
восходящего прямотока;-----расчет
по формуле (2.3.85); (2.3.87); *, о, + — экс-
периментальные данные работы [2.31]
Особенности энергетики индукционных полей
в не сильно проводящих движущихся средах
В технологических процессах, где необходимо использовать теп-
ловую энергию, неизбежно встает вопрос оптимального ее получе-
ния из электрической. Так, наиболее эффективным способом элект-
рическогонагреваявляетсяиндукционныйнагревпеременнымэлект-
ромагнитным полем, когда электрическая энергия преобразуется в
тепло (Джоулева тепловая диссипация) непосредственно внутри не-
которого приповерхностного слоя (скин-слоя) нагреваемого тела.
Причем ширина этого слоя зависит от частоты внешнего индукци-
онного поля и электромагнитных характеристик нагреваемого тела.
Например, индукционный нагрев сверхвысокочастотными (СВЧ) по-
Глава 2
223
лями, как правило, является поверхностным ввиду малости ширины
(порядка миллиметров и менее) скин-слоя даже для не сильно про-
водящих тел. По мере перехода к более низким частотам, скажем по-
рядка промышленной частоты 50 Гц, ширина скин-слоя возрастает,
тем более, если проводимость тела оказывается невысокой.
Химически превращающиеся жидкогазофазные системы, за-
нимающие ведущее место в химической технологии при отсутст-
вии поляризации и наличии весьма умеренных электропроводя-
щих свойств, зачастую обладают слабо выраженными магнитными
свойствами. Тем самым поля промышленной частоты здесь могут зна-
чительным образом проникать внутрь среды, что, помимо более рав-
номерного распределения тепловой Джоулевой диссипации, делает
значимым и характер распределения пондеромоторного воздействия
поля, усиливающего (или инициирующего) перемешивание (турбо-
лизацию) жидкогазофазной системы внутри скин-слоя. Причем ши-
рина скин-слоя в этом случае может достигать нескольких десятков
сантиметров.
Еще одним весьма важным обстоятельством для многих химико-
технологических процессов является наличие движения самой ре-
агирующей системы (например в проточных реакторах), причем со
скоростью, несравнимо малой со скоростью света.
Тем самым для проведения практических расчетов тепловой ди-
намики химически активных жидкогазофазных систем, слабо дви-
жущихся в индукционном электромагнитном поле, востребованы
методы анализа моделей теории квазистационарных электромагнит-
ных полей в медленно движущихся средах.
Эта теория успешно развивается уже более века, но вплоть до на-
стоящего времени она не содержит описания энергообмена между
индукционным полем постоянной частоты и медленно движущимся
полупроводящим неполяризующимся полупространством с непод-
вижной внешней границей (границей втекания среды).
Судя по всему, причин этому несколько. Выделим две из них, на
наш взгляд, наиболее главные. Первой и, наверное, самой главной яв-
ляется то обстоятельство, что ранее эта задача просто не была вост-
ребована ни в теории, ни на практике. По сравнению, например, с
такими объектами магнитогидродинамики, как магнитные жидко-
сти или плазма, эффекты, связанные с внешним индукционным по-
лем в средах, которые имеют электромагнитные свойства, подобные
вышеотмеченным свойствам реагирующих химических жидкогазо-
вых систем, будут иметь куда более слабо выраженный характер.
Второй, безусловно, тоже решающей, явилась разработка универ-
сальных методов решения электродинамических задач, имеющая бо-
224
Глава 2
лее чем вековую историю. Даже простой перечень имеющихся здесь
результатов потребовал бы куда больше места, чем формат насто-
ящей работы. Поэтому принято считать, что во всяком случае мето-
дическая база имеется и для рассматриваемой задачи.
В настоящее время оба указанных момента являются уже несо-
стоятельными. Главным недостатком приложений всех имеющих-
ся методов к рассматриваемой задаче является их исключительная
опора на конструкцию распространения электромагнитных волн в
среде. Для СВЧ-нагрева такой подход физически оправдан ввиду ма-
лости длин возникающих волн по сравнению с шириной скин-слоя.
Однако в применении к движущейся жидкогазофазной реагиру-
ющей смеси СВЧ-нагрев далеко не всегда является не только опти-
мальным, но и просто неприменимым, так как часто чреват иници-
ацией интенсивного фазового превращения жидкости в газ в очень
узком приповерхностном слое, например у границы входа в систему.
Поля промышленной частоты в данном случае оказываются предпоч-
тительней. Но именно для таких полей метод распространения элект-
ромагнитных волн теряет физическую наглядность, так как длины
волн в этом случае на порядки превышают ширину скин-слоя. Бо-
лее того, описание энергообмена поля и среды (который и представ-
ляет основной интерес для приложений в химической технологии),
опирающееся на электромагнитные волны (распространяющиеся
со скоростями, близкими к скорости света), имеет пространственно-
временные масштабы, не сочетающиеся с масштабами химико-тех-
нологических задач.
В работе [2.3.88] предложен нетрадиционный метод расчета энер-
гообмена поля постоянной частоты со со средой, имеющей постоян-
ные электромагнитные характеристики и движущейся, начиная
с некоторой плоскости входа в систему, с постоянной скоростью и.
Особенность предлагаемого метода состоит в том, что в результате
замены неизвестных в уравнениях Максвелла, предложенной в рабо-
те [2.3.89], удается сразу уйти от промежуточного этапа вычисления
электрической и магнитной составляющих поля к его энергетиче-
ским составляющим, на которые раскладывается вектор Пойтинга. В
отличие от работы [2.3.89], где исследовался вопрос энергетики волн
применительно к задачам оптики, в предлагаемом методе вообще не
рассматривается объект типа электромагнитной волны, а строится
физически наглядная картина стационарных колебаний индуциро-
ванного поля как вращения вокруг оси его энергетических составля-
ющих.
Исследование рассматриваемой задачи возможно с помощью чис-
ленного анализа, аналитического и комбинацией обоих этих подхо-
Глава 2
225
дов. В работе [2.3.88] авторы остановились на третьем, указав, с од-
ной стороны, точные формулы для полного аналитического решения
выделенной ими канонической задачи, а с другой — проведя числен-
ное исследование полученного решения, сделав его максимально на-
глядным с помощью графических средств. Проведенный анализ поз-
волил по-новому взглянуть на вопрос о глубине проникновения поля
в среду и привел к некоторым нетривиальным выводам, имеющим
общий характер. Представленные в работе формулы легко позволя-
ют построить численные алгоритмы для более общих случаев (на-
пример, с зависящими от пространственной координаты скоростью
и электромагнитными характеристиками) стационарно движущих-
ся систем. В работе [2.3.88] получено решение уравнения Максвелла
применительно для не сильно проводящих неполяризующихся дви-
жущихся систем.
Новая форма аналогии между количеством движения,
вещества и энергии
В основу новой формы аналогии положено понятие о вихревых
силах сопротивления в сплошных средах, причем возникновение
вихревых сил рассматривается как результат нелинейных взаимо-
действий. Установлена аналогия между гидродинамическими, теп-
ловыми и диффузионными процессами в системах, находящихся в
условиях взаимодействия различных силовых полей (гидродинами-
ческих, электрических, магнитных, скрещенных электрических и
магнитных). Для подтверждения этой формы аналогии использован
практически весь известный экспериментальный материал, накоп-
ленный в мировой практике [2.3.48].
Предложенный новый тип аналогии между количеством движе-
ния, вещества и энергии [2.3.48] может быть использован в расчетах
при разработке новых типов высокоэффективных контактных уст-
ройств в случае ограниченных экспериментальных данных в экстре-
мальных условиях.
Для того чтобы пояснить вывод нового типа аналогии, представим
уравнение равновесия единицы объема жидкости в следующем виде
[2.3.48]:
p£=_p,+^+^+£4±£Fj> (2390)
I э 1=1	1=1
где Р' — отнесенная к единице объема движущая сила; I — физи-
чески обоснованный характерный размер: гидравлический ди-
226
Глава 2
аметр канала и щели (dr = 4со/%) или эффективный диаметр частицы
(с?Эф =y/bV/п);к — коэффициент формы, например для сферы А: = 18,
для обтекаемого кругового цилиндра к = 8, для диска, установлен-
ного поперек потока, к = 10,2 [2.3.48]; о — средняя скорость потока;
j
— отнесенные к единице объема суммарные силы, вызывающие
м	/
(подавляющие) внутренние течения жидкости; 1ч — отнесенная к
1=1
единице объема равнодействующая внешних сил.
Для внутренней гидродинамической задачи Р' = ДР/L, а для внеш-
ней — Р' = Р/V, где Р — сила лобового сопротивления; V — объем тела.
Если в качестве характерного размера в уравнении (2.3.90) при-
нять параметр -ЛГ = y/l2/к , то уравнение для установившегося тече-
ния примет вид:
=	Л-	(2.3.91)
к \кк i=i i=i
Параметр л/k7 для данной системы (трубы, канала, сферы, ци-
линдра и др.) представляет собой соотношение гидравлического ди-
аметра и коэффициента формы в степени 1/2. Для пористых сред (см.
работу [2.3.48]) квадрат этого параметра является ни чем иным, как
коэффициентом проницаемости этой среды.
Преобразуем уравнение (2.3.91) в безразмерный вид, вводя обоз-
начения
P'J7
к =	(2.3.92)
ро
Re = P^.	(2.3.93)
П
Запишем уравнение (2.3.91) в виде:
X = 1/В,	(2.3.94)
где В назовем обобщенным критерием гидродинамического подобия
[2.48]:
Re
В =---------—-------:---.	(2.3.95)
n	ifik YFtk
l + ~7==Re+ —--------
y/k цо цо
Комплекс (2.3.95) характеризует соотношение силы инерции к
сумме сил, препятствующих движению, и учитывает все гидроди-
Глава 2
227
намические особенности течения. Если знаменатель этой формулы
равен единице, то коэффициент сопротивления будет обратно про-
порционален числу Рейнольдса, что имеет место при ламинарном те-
чении без учета вихревых сил сопротивления. Наличие вихревых
сил сопротивления изменяет выражение для коэффициента сопро-
тивления. Второй член в знаменателе этой формулы ответственен за
проявление сопротивления, возникающего при турбулентном тече-
нии. Коэффициент п можно определить аналитически, зная харак-
тер распределения давления в жидкости при безвихревом течении,
или получить из известных эмпирических зависимостей гидроди-
намического сопротивления от числа
Рейнольдса. Последний член в знамена-
теле представляет проекцию внешних
сил на ось движения.
В работе [2.3.48] показано, что зави-
симость (2.3.94) обобщает практически
весь накопленный в мировой практике
материал по гидравлическому сопро-
тивлению в системах, находящихся в
условиях взаимодействия различных
силовых полей: гидродинамических,
электрических, магнитных, скрещен-
ных электрических и магнитных.
В качестве примера на рис. 2.43
обобщены опытные данные по течению
жидкостей и газов в различных систе-
мах согласно зависимости (2.3.94).
На рис. 2.44 представлены резуль-
таты обобщения различных опытных
данных по течению жидкости и тепло-
обмену с помощью предложенной ана-
логии гидродинамических и тепломас-
сообменных процессов.
Эта зависимость имеет вид:
12Nu3
Re2Prd/£
Л = ув,
(2.3.96)
где критерий В представлен формулой
(2.3.95).
Зависимость (2.3.96) — это анали-
тический вид новый формы аналогии
между гидродинамическими, тепловы-
Рис. 2.43. Обобщение опытных
данных по течению жидкости с
помощью уравнения (2.3.94): 1 —
ньютоновская жидкость в пря-
мой гладкой трубе; 2 — жидкий
металл в трубе в продольном
магнитном поле; 3 — неизотер-
мический поток воды в горизон-
тальной трубе; 4 — газожидкост-
ная смесь в вертикальной трубе;
5 — поток жидкости и газа через
кипящий слой твердых частиц
неправильной формы; 6 — сус-
пензия в вертикальной трубе;
линии 1—6 смещены: 1 — вверх
на ЮЛ.; 2 — вверх на Ю2Л,; 3 — на
ЮЛ; 4 — не смещена; 5 — вниз
на 102Л. и вправо на Ю3В; 6 — не
смещена
228
Глава 2
Рис. 2.44. Обобщение опытных
данных по течению жидкости на
основе предложенной аналогии
гидродинамики и теплообмена
с помощью уравнения (2.3.96):
1 — жидкий металл в прямой тру-
бе; 2 — гидродинамический стаби-
лизированный поток газовоздуш-
ной смеси в прямой гладкой трубе;
3 — вода в прямой вертикальной
трубе; 4 —газографитовая смесь в
вертикальной трубе; 5 — галлий в
круглой трубе в продольном маг-
нитном слое; 6 — кипящий слой
в вертикальном аппарате; линии
2 — 6 смещены: 2 — вверх на 10у;
3 — вправо на 10В; 4 — вправо на
10В; 5 — вверх на Ю2/; 6 — вниз на
105/ и вправо на 104В
вались, для каждого
ми и диффузионными процессами.
От известных она отличается тем,
что учитывает вихревую природу
течения. Отметим, что аналитиче-
ские формы аналогии, получаемые
из законов сохранения количества
движения вещества и энергии, спра-
ведливы только при равенстве еди-
ницы тепловых и диффузионных
чисел Прандтлд. Другие формы ана-
логии не затрагивают природу тече-
ния, как это получено при представ-
лении уравнения (2.3.9).
Зависимости у = f(B), построен-
ные по уравнению (2.3.96), являют-
ся аппроксимацией опытных дан-
ных для случая теплообмена жидких
металлов в прямых трубах, для мас-
сопереноса в прямых трубах, для
теплообмена при движении воды в
вертикальных трубах, для теплооб-
мена между стенкой трубы и газо-
графитовой взвесью, для теплооб-
мена при течении галлия в трубе и
для теплообмена между стенкой вер-
тикального цилиндрического аппа-
рата и кипящим слоем.
Опытные данные рис. 2.44 обобще-
ны соответствующей линией, удов-
летворяющей уравнению (2.3.96). Для
того чтобы точки на графике не сли-
случая линии 2 — 6 сдвинуты по координатным
осям, на что даны поясняющие ссылки в подрисуночной подписи.
Уравнение (2.3.96) может быть использовано, очевидно, и для дру-
гих, по-видимому любых, систем.
При этом появляется возможность существенного упрощения
расчетов в заданной системе: потерь энергии и коэффициентов кон-
вективного тепло- и массопереноса при известных геометрических
параметрах системы и физических свойствах среды.
Расчет величины обобщенного критерия гидродинамического по-
добия (2.3.95) обеспечивает оценку коэффициентов сопротивления,
а также коэффициентов тепло- или массопереноса. В то же время
Глава 2
229
если для системы определен один из упомянутых коэффициентов, то
из формулы (2.3.96) следует, что известны и два других коэффициен-
та и, кроме того, обобщенный критерий гидродинамического подо-
бия (см. уравнение (2.3.95)).
Для неизученных систем можно, в частности, определять: коэффи-
циент п, соотношение к* = P/к; для процесса теплопередачи при извест-
ных характеристиках системы и физических свойствах жидкости —
температурный напор, т.е. температуру поверхности частиц в слое (ста-
ционарном или кипящем), стенок и элементов теплообменника и др.
Анализируя гидродинамические или тепломассообменные харак-
теристики аппаратов, можно выявить действие неизвестных ранее
силовых полей, вызывающих внутренние течения в этих системах, и
оценить величину этих сил.
Влияние входных гидродинамических эффектов
на эффективность тепло- и массообмена
Существование известных пограничных слоев: гидродинамиче-
ского, теплового и диффузионного в гидродинамических и тепломас-
сообменных процессах обусловлено наличием малых параметров
при старших производных в уравнениях переноса.
При решении уравнений переноса в полной постановке они про-
являются автоматически. Если длина контактного устройства намного
превышает длину входного гидродинамического слоя, на котором эф-
фективность тепломассообмена выше, чем на гидродинамически ста-
билизированом участке, то это превышение остается вне поля зрения
исследователя. Для тепломассообмена с поверхностью раздела при пле-
ночном, струйном течении, в том числе с фазовыми превращениями,
влияние входного гидродинамического участка на превышение тепло-
массообмена становится заметным, особенно если длина контактного
устройства соизмерима с величиной самого входного участка.
Расчет тепломассообмена с учетом входного участка (эффектов)
является сложной математической задачей, так как величина разви-
тия поверхности, соответственно и длина входного участка, является
искомой величиной.
В качестве примера приведем расчет массообмена с учетом вход-
ных эффектов при ламинарном режиме течения пленки жидкости и
формулы для расчета массообмена при турбулентном режиме, пре-
следуя цель — раскрыть существо метода.
Разнообразные случаи расчета тепломассообмена в различных
гидродинамических режимах, в том числе с фазовыми превращени-
ями, рассмотрены в монографии [2.3.2].
230
Глава 2
Ламинарный режим
Интерес к пленочному течению на входном участке за последнее
время возрос. Помимо применения результатов исследования гид-
родинамики и массообмена на входном участке в пленочных тепло-
массообменных аппаратах, результаты ускоренного течения пленки
жидкости на вертикальной и наклонной поверхностях могут быть
использованы при исследованиях гидродинамики и массообмена
в насадочных колоннах, в которых движется пленка жидкости по
элементам насадки (рис. 2.45).
В местах соприкосновения элементов насадки равномерность те;
чения нарушается. В результате потери части кинетической энергии
скорость падает, а в силу сохранения расхода толщина пленки меня-
ется в своих размерах. Миновав этот участок, пленка вновь приобре-
тает ускорение, которое происходит на безволновом участке, так как
ускоренное течение весьма устойчиво против различных возмуще-
ний. Как показано в монографии [2.3.2], турбулентное течение может
вновь стать ламинарным, если оно подвержено ускорению.
При изучении гидродинамики в пленке жидкости на входном
участке применяются различные методы решения, в которых дости-
галась разная точность. Исследование массообмена в пленке жидко-
сти на входном участке не проводили из-за сложности решения
задачи. Между тем развитие профиля скорости и толщины пленки
на входном участке непременно должно сказаться на дальнейшем
формировании пленочного течения и массообмена в ней. К тому же
на основании результатов экспериментальных исследований извест-
но, что на входном участке пленочного аппарата пленка жидкости
остается гладкой даже при больших числах Рейнольдса. Поэтому
Рис. 2.45. Течение пленки жидко-
сти на входе: а — плоский ороша-
емый канал, б — элементы насад-
ки, в — одиночные волны
исследования гидродинамики и мас-
сообмена на входном участке имеют
как научный, так и практический ин-
терес.
Наиболее плодотворным и эффек-
тивным методом для исследования
гидродинамики и тепломассообме-
на на входном участке оказался ме-
тод поверхностей равных расходов
[2.3.2]. Применим этот метод к иссле-
дованию гидродинамики и тепломас-
сообмена при пленочном течении по
гладкой поверхности в трубе или ка-
нале.
Глава 2
231
Система уравнений Навье-Стокса, уравнения конвективной диф-
фузии на входном участке в слое жидкости переменной толщины 5(х)
при ламинарном течении (случай, когда сопротивление массопереда-
чи сосредоточено в жидкой пленке) имеют вид:
Эи	ди	1 др	д2и
и—+т>— = gsincq —-^+V—у;	(2.3.97)
Эх	ду	р Эх	Эу
Эи Эн _
^-+3“ = 0:
дх ду
дс дс _ Э2с
дх ду ду
(2.3.98)
у = 0, и = в = 0, с = 0; х = 0, с = 0;	(2.3.99)
у = 5(х), ди/ду = 0, с — сг	(2.3.100)
Граничное условие (2.3.99) предполагает «прилипание жидкости»
к твердой поверхности канала; на входе в канал подается жидкость,
в которой отсутствует распределяемый компонент. Решение задачи
не изменяется, если на вход в канал подается жидкость с постоянной
концентрацией распределяемого компонента.
Граничное условие (2.3.100) предполагает отсутствие касатель-
ного напряжения на поверхности раздела; ускоренное стекание
гладкой пленки жидкости переменной толщины, величина которой
определяется из решения системы уравнений (2.3.97)—(2.3.100), про-
исходит только под действием сил гравитации и сил давления. В ряде
случаев силами давления, ввиду их малости по сравнению с силами
гравитации, можно пренебречь. Концентрация на поверхности плен-
ки жидкости принимается постоянной и равной сг
Обезразмеривание скоростей и и в и поперечной координаты у в
системе уравнений (2.3.95) и (2.3.96) можно проводить двояко:
—	текущую скорость можно относить к скорости в начальном се-
чении, а поперечную координату — к размеру щели Н(0), из которой
истекает жидкость;
—	текущую скорость можно относить к скорости на устано-
вившемся участке, а поперечную координату — к толщине пленки
на нем.
Обезразмеривание уравнений (2.3.97) и (2.3.98) и граничных усло-
вий (2.3.99) и (2.3.100) проведено по второму способу:
u = UqU, x = 6pRex, у = 6ру, c = qc,
(2.3.101)
232
Глава 2
1/3
/ \
где un — средняя скорость жидкости; 8„ = 3v2 / psinc^ р Re
L v	dx 7
толщина пленки жидкости; Re = (u05p)/v; Рг = v/D; Re = u08p/D.
Система уравнений и граничные условия (2.3.97)—(2.3.100) в без-
размерных переменных (2.3.99) примут вид:
_дй _Эй	Э2й
и —+ V— = 3 + —у;
Эх	Эу	Эу2
(2.3.102)
Эи Эн _ _Эс _Эс 1 Э2с
—+ — = 0; и — + D— =-------т;
Эх ду дх ду Рг Эу2
у = 0, и = о = 0, с = 0; х = 0 с = 0;
у = 8(х)/8р Эй/Эу = О, с=1.
(2.3.103)
(2.3.104)
В дальнейшем для простоты написания черточки в уравнениях и
граничных условиях (2.3.102) —(2.3.104) опущены.
Для решения задачи применим метод равной поверхности [2.3.2].
С этой целью представим профиль скорости и(х,у) в виде:
uk = YAj(x)Ujk[(yk(x)],	(2.3.105)
j=i
где N — номер приближения; Ujk(yk) — полная система функций по-
верхностей ук(х), через которые не проходит поток жидкости.
Введем в поле течения пленки жидкости линии ук = ук(х) и обоз-
начим
ик(х) = и[х, ук(х)], ик(х) = и[х, ук(х)], ск(х) = с[х, ук(х)],
где ик(х), нк(х) — компоненты скорости на поверхности ук(х) в направ-
лении координат х и у в условиях стационарного течения, рассматри-
ваемого в настоящей главе. Поставим цель — свести задачу о разви-
тии течения в пленке жидкости и массообмена в ней к численному
определению полей скоростей uk(x) и ък(х) и концентрации ск(х), а
также межфазной поверхности 8(х).
Из определения ук(х) как линии равного расхода, а также из усло-
вия сохранения расхода и уравнения неразрывности следует:
vk=uk^-.	(2.3.106)
Эх
Из постоянства расхода по длине массообменного аппарата сле-
дует:
д у*
( udy = 0.	(2.3.107)
Эх v
Ук-1
Глава 2
233
После замены интеграла конечно-разностным выражением полу-
чим уравнение для линий постоянного расхода
dyk
~^ = Fk,	(2.3.108)
dx
р _ dYk-i У к ~Ук-1 { duk du*x А
dx ик-ик_х\ dx dx J
Уравнение (2.3.102) с учетом условий (2.3.106), (2.3.107) примет вид
Uk*k=3A
dx ду2к
(2.3.109)
Чтобы рассчитать правые части в двух последних уравнениях, не-
обходимо иметь производные скорости по у, для вычисления которых
воспользуемся представлением профиля скорости через полные си-
стемы функций Цк[ук(х)]. Согласно соотношению (2.3.105), эта систе-
ма может быть представлена различными полиномами: ортогональ-
ными полиномами Чебышева, Лежандра и полиномами вида:
\YnJ
\YnJ
(2.3.110)
где yN(x) — поверхность пленки.
Полиномы Чебышева в полной системе функций Ujk применялись
в виде:
2
Ujk(y*) = r,+i(z*)-7)+i(O)-[7)(zt)-Ty(O)]4^-,	(2.3.111)
гдегк = yk(x)/yN(x).
Отметим, что существенного различия в результатах расчета при
применении полиномов (2.3.110) и (2.3.111) не наблюдалось, однако
требуемая точность при применении полиномов Чебышева дости-
галась меньшим числом членов. Выбор полиномов Чебышева обус-
ловлен еще и тем, что, во-первых, сходимость этих полиномов самая
сильная, во-вторых, погрешности в этих полиномах распределены
наивыгоднейшим образом, а именно равномерно по всему интервалу.
Поэтому в дальнейшем все расчеты проведены, в основном, с исполь-
зованием полиномов Чебышева. При вычислении коэффициентов
многочлена Чебышева использовалось рекуррентное соотношение
^}+JzJ ~ ^ZkTj^Zl) ~
Потребуем, чтобы скорость, определяемая по формуле (2.3.105),
совпала со скоростью ик(х) на линиях ук(х). Тогда коэффициенты Ак(х)
определим из системы алгебраических уравнений:
N
Б AjUjk [у* (х)] = Ui(x), 4=1,2.N.	(2.3.112)
/=1
234
Глава 2
После этого по формуле (2.3.105) найдем производные скорости
по ук. Системы уравнений (2.3.108), (2.3.105) и (2.3.112) решаем одно-
временно.
В сечении х = 0 должны быть заданы начальные условия. Мож-
но задавать профиль скорости и по заданному начальному профилю
определять А.-, можно также задавать коэффициенты А. и по ним оп-
ределять начальный профиль скорости в сечении пленки жидкости.
Зададим в начальном сечении профиль скорости, причем использу-
ем в расчетах как постоянный профиль, так и параболический. Сет-
ку линий по сечению пленки жидкости при х = 0 можно задавать как
переменной, так и равномерной (в расчетах применялась равномер-
ная сетка расчетных линий прих = 0: yk(0) = k/(N — 1), где N — номер
приближения).
При расчете массоотдачи в жидкую фазу уравнение конвектив-
ной диффузии с учетом соотношения (2.3.106) преобразовывалось к
виду, удобному для интегрирования:
dck _ 1 д2ск
Uk dx Рг дук '
где
dck = дск । дск дук .
dx дх дук дх '
N
ск(х,у)= ЁА1уМд(Ук(х)).
М
Концентрацию распределяемого вещества, подобно скорости,
разложим на полную систему функций Nljk. При расчете правой час-
ти уравнения (2.3.113) концентрация распределяемого вещества, вы-
раженная через полную систему функций, может быть представле-
на различными полиномами. В расчете применялись ортогональные
полиномы Чебышева, которые с учетом граничных условий (2.3.104)
имели вид:
My*(zt) = L+1(zt)+7)+i(0)(2zl-zt-l).	(2.3.116)
Система уравнений (2.3.108), (2.3.109), (2.3.113) с граничными ус-
ловиями (2.3.104) решаем методом Рунге-Кутта с постоянным и ав-
томатическим шагом. Для гладких решений шаг имеет порядок 0,02;
для случаев, когда перед второй производной стоит существенно
малый параметр, шаг, как показали расчеты, имеет порядок 0,005.
(В некоторых случаях удобно ввести безразмерную переменную вида
х = 8рРех1, где Ре = RePr, тогда в уравнении (2.3.103) исчезает малый
параметр при старшей производной.)
(2.3.113)
(2.3.114)
(2.3.115)
Глава 2
235
Изложенный алгоритм применен
для расчета на входном участке полей
скоростей и концентраций в зависи-
мости от ширины щели Н и числа Re,
толщины пленки по длине орошаемо-
го канала, касательного напряжения
на стенке, коэффициента массоотда-
чи в жидкую пленку, что дало возмож-
ность получить полную информацию
о течении ламинарной безволновой
пленки на входном участке.
На рис. 2.46 показана зависимость
локальной толщины пленки (как
конструктивного параметра колон-
ного аппарата) от безразмерной дли-
ны входного участка при различных
отношениях щели к толщине пленки
жидкости, рассчитываемой по форму-
ле Нуссельта. Существенное влияние ширины щели на ускоренное
течение пленки жидкости наблюдается до отношения Н/5р = 3. При
Н/бр > 3 ширина щели влияет незначительно на ускоренное течение
пленки жидкости (кривые 3, 4). На этом рисунке проведено сравне-
ние расчетных данных, найденных по предложенному алгоритму, с
экспериментальными данными [2.3.26], относящимися к ускоренно-
му течению пленки в орошаемом канале. Согласование теоретиче-
ских и экспериментальных данных, как видно из рисунка, можно
считать удовлетворительным. Фор-
мула для локальной толщины пленки,
полученная аппроксимацией числен-
ных решений на ЭВМ, для Н/5р » 1,1
имеет вид:
6(х) = 6р (Я / 6р ,	(2.3.117)
где x = x/5pRe.
На рис. 2.47 построена зависи-
мость локальной поверхностной ско-
рости от безразмерного расстояния от
входа. Показано, что профиль безраз-
Рис. 2.46. Изменение толщины
пленки жидкости на входном
участке: кривая 1 — Н/6р = 1,0;
кривая 2 — Н/8 = 1,5; кривая 3 —
Н/8Р = 3,0; кривая 4 — Н/8р = 10,0;
кривая 5 — Н/6Р = 0,5; • — экс-
периментальные данные [2.3.26]
для Н/5Р = 0,47
Рис. 2.47. Изменение поверхност-
ной скорости на входном участ-
ке: кривая 1 — Н/6р = 1,0; кривая
2 — Н/8 = 1,5; кривая 3 — Н/8Р =
= 3,0; кривая 4 — Н/8р = 10,0
мерной поверхностной скорости су-
щественно зависит от безразмерной
ширины входной щели до Н/бр = 3.
При Н/6р > 3 это изменение незначи-
236
Глава 2
тельно. Формула для поверхностной скорости, полученная аппрок-
симацией численных решений на ЭВМ для Н/8р » 1,1, имеет вид:
и(1)/п0=Ал/^+В,	(2.3.118)
где
А = ехр(2,ЗН1/(4,35Н1+21,5)); В = 0,33 + 0,44/у[Н^; Нх = Н/\. (2.3.119)
За длину активного гидродинамического участка принималось
расстояние от входа, на котором рассчитанные профиль скорости на
поверхности пленки жидкости и толщина пленки жидкости отлича-
лись на величину е от аналогичных, рассчитанных для случая стаби-
лизированного течения (решение Нуссельта). При G = 0,02 (это от-
личие составляет 2% от решения Нуссельта) длина входного участка,
полученная аппроксимацией численного решения на ЭВМ, выража-
ется формулой
/вх =exp(2,3H1/(20-28H1))5pRe;	(2.3.120)
при G = 0,0002
ZBX =2ехр(-2,ЗН1/(28Н1 -20))5pRe.	(2.3.121)
Другой важной характеристикой пленочного течения является
касательное напряжение на стенке орошаемого канала. (Авторам не-
известно о таких расчетах, проведенных ранее, несмотря на то, что
величина касательного напряжения связана с локальным градиен-
том скорости и перепадом давления и с ее помощью можно опреде-
лять гидравлические потери в пленочных аппаратах.)
На рис. 2.48 представлена характерная зависимость касательно-
го напряжения на входе в орошаемый канал при различных величи-
нах безразмерной ширины щели. Как видно из рисунка, наблюдает-
Рис. 2.48. Изменение касательного напряжения на входе в орошаемый канал: а —
Н/8Р = 0,5;.б — Н/8Р = 1,0 (кривая 1); Н/6Р = 1,5 (кривая 2); Н/5Р = 3,0 (кривая 3);
Н/8р = 10 (кривая 4)
Глава 2
237
ся резкое изменение касательного напряжения по длине орошаемого
участка, причем для < 1 оно падает, а для Hr > 1 — возрастает, при
этом падение касательного напряжения на стенке при Н{ < 1 обус-
ловлено ростом толщины пленки, а его возрастание — уменьшением
толщины пленки по длине орошаемого канала.
На рис. 2.49 проведено сравнение расчетных безразмерных тол-
щин пленок (а) и безразмерных касательных напряжений (б) при раз-
личных размерах щели с экспериментальными результатами работы
[2.3.26]. Как следует из рисунка, участки стабилизации для пленки
жидкости и касательного напряжения совпадают. Этот факт впер-
вые экспериментально отмечен в работе [2.3.26]. Последнее обстоя-
тельство, вероятнее всего, является условием сохранения расхода:
незначительное изменение профиля скорости, а соответственно, и
касательного напряжения на стенке орошаемого канала вызывает
изменение и в толщине пленки жидкости. И только при большой ста-
билизации профиля скорости (касательного напряжения) наблюда-
ется полная стабилизация пленки жидкости при условии сохране-
ния расхода.
Аппроксимация численного решения для касательного напряже-
ния на стенке орошаемого канала имеет следующий вид (для » 1,1):
1g—= -1/(А1х + 2),
тр
(2.3.122)
где
At = exp(2,3Hi/(0.73HJ-0,26)); х = х/6рRe.
сосредоточено в пленке жидко-
Как было отмечено, при расчете массообмена предполагалось,
что сопротивление массопередаче
Рис. 2.49. Сравнение теоретических и экспериментальных данных: а — по толщине
пленки; б — по касательным напряжениям; кривая 1 — Re = q/v = 75, Н/8Р = 3,7;
кривая 2 — Re = q/v = 455, Н/5Р = 1,0; кривая 3 — Re = q/v = 1805, Н/8Р =1,3
238
*»
Глава 2
сти. Для расчета коэффициента массоотдачи в ней использовано ра-
венство
( йсУ
D —
vdyj
d УР
= 7Г / ис<1У-
dx 0
(2.3.123)
Y=Yn
Это равенство может быть получено после интегрирования урав-
нения конвективной диффузии для пленки переменной толщины с
учетом кинематического условия на поверхности раздела (2.3.106),
выражающего тот факт, что поверхность пленки жидкости является
линиями тока.
Усреднив выражение (2.3.123) по продольной координате на участ-
ке с характерной длиной Ь, получим*:
1 d yN
dx = — — j (uc)dy dx.
Y=Yn Ь
После усреднения обеих частей равенства (2.3.124) по поверхно-
сти контакта, вычисления интеграла в правой части с учетом гранично-
го условия (2.3.114) и приведения к безразмерному виду х = 5р RePr^
получим:
1 Yn
₽ч>=г J исаУ =
ь о
На рис. 2.50 построена зависимость безразмерной величины HR2
от безразмерной координаты x^x/SpRePr при различных чис-
лах Рг. Линия 1 соответствует расчету HR2 в зависимости от х{ для
Рг = 300, линия 2 — для Рг = 1000. Параллельные линии, находящие-
ся между прямыми 1 и 2, отличаются одна от другой числом Рг. Выше
числа Рг = 1000 все расчетные линии в интервале от 1000 до 2500 сов-
пали с линией 2. Как видно из этого рисунка, влияние числа Рг на
величину отрезка, отсекаемого на оси HR2, незначительно. В частно-
сти, в интервале чисел Рг от 500 до 1000, где наблюдается различие в
расчете HR2 в зависимости от числа Рг, величина отсекаемого отрез-
ка колеблется от 0,98-10'2 до 1-Ю'2. Для этого интервала формула для
отсекаемого отрезка имеет вид:
br = ехр(—2,ЗРг/(0,5013Рг - 1,3)).	(2.3.126)
Зависимость nR2 от безразмерной длины выражается формулой
nR = 7155xi + b.	(2.3.127)
de
1 о
bo ((1У)
uo5pci 7	.
—-— j uedy
о
b
d УГ
dx 'о
(2.3.124)
-X!=b/5pRePr
.	(2.3.125)
* Градиент концентрации необходимо рассчитывать по нормали к поверхности пленки, то
есть j = D(dc/dn). Расчеты в связи с этим усложнялись, однако существенной разницы в ко-
нечных результатах не наблюдалось, так как dc/dy » dc/dx. Поэтому в дальнейшем сред-
ний коэффициент массоотдачи Рср рассчитывался по соотношению (2.3.125).
Глава 2
239
Формула для среднего коэффициента
массоотдачи в жидкую фазу с учетом урав-
нений (2.3.126) и (2.3.127) принимает вид
ц2'5р0'5 | bi6DPe
Pq, =₽2Ь = 125=2^-J1+0,65^-2—, (2.3.128)
где Ре = RePr.
Поскольку изменение в широком ин-
тервале изменения числа Рг незначительно,
в дальнейшем принято, что = 10’2. С уче-
том этого формула (2.3.128) принимает вид:
Рсп=1,254^[1+0,65Ь1
ср V b 1
SpPe"
b ,
(2.3.129)
ПЯ2 отхр а — Рг = 300 (ли-
ния 1); Рг — 1000 (линия 2);
б — форма волны, разви-
вающейся с расстоянием
где b — некоторый параметр длины.
Если за характерный параметр принять
длину входного участка, то b = Ьг Это соот-
ветствует случаю массообмена, при котором длина контактного уст-
ройства соизмерима с длиной входного участка. Такой случай имеет
место в насадочных аппаратах или в аппаратах с приставками, тур-
булизаторами. Если они намного меньше длины колонны, то их от-
ношение будет характеризовать ускорение массообмена. Если дли-
на орошаемого участка намного больше длины входного участка, а
осреднение коэффициента массоотдачи проводится на всю длину
орошаемого участка, то за характерный размер принимается длина
орошаемого канала, т.е. b = /. И формула (2.3.129) для гладкой пленки
с учетом входного участка принимает вид:
n	6-Ре^1
ft =1,25 р- 1+0,65^-^—
V 1 I 1 )
(2.3.130)
Формула (2.3.130), учитывающая развитие течения во вход-
ном участке, отличается от известных формул добавочным членом
^1+0,65^ (5рРе) / /, учитывающим массообмен на входном участке.
Влияние этого члена на коэффициент массоотдачи в жидкой фазе
возрастает с увеличением чисел Re.
В работе [2.3.27] исследовано гравитационное течение волновой
пленки жидкости и определены ее параметры. В частности, найдены
волны, имеющие относительную амплитуду а =	ПОрЯДка
240
Глава 2
единицы и длину волны Ход = 30,5 см в интервале чиселКе^ = (4U0h0)/v
от 900 до 6000. По форме волна имела вид, показанный на рис. 2.50, б.
Это — одиночная волна, развивающаяся с расстоянием. По виду она
схожа с ускоренным течением пленки жидкости на входном участ-
ке, что дает основание предполагать о возможном сходстве также и
в процессе массопереноса. В этом случае коэффициент массоотдачи
будет изменяться по зависимости (2.3.129).
В качестве характерного параметра используется длина волны.
Формула для массопередачи в жидкую фазу при этом предположе-
нии примет вид:
и?*5!)0'5 I	SDPe
p2=l,25^	1+0,65b,^—,	(2.3.131)
^од v	^°д
где Лод — длина волны [2.3.27], равная 30,5 см.
Ранее для расчета массоотдачи в жидкую пленку при волнообра-
зовании она имела вид [2.3.22]:
Рж = Р1Ь = 1,673a07 y/of7z.	(2.3.132)
Поскольку массообмен проходит при одновременном проявлении
входного участка и волнообразовании, имеющем место после вход-
ного участка, то общий коэффициент массообмена при волнообразо-
вании с учетом входного участка должен принимать вид:
Робщ =Р1Р2Ь +Р2р1ь»	(2.3.133)
где ₽2Ь = ₽/•
В формуле (2.3.133) коэффициенты массоотдачи при волнообра-
зовании с учетом входного участка входят со своими весовыми ко-
эффициентами, причем их сумма равна единице. Этим, вероятно,
можно объяснить тот факт, что ускорение массообмена при волнооб-
разовании отличается от действительного, поскольку длина входного
участка больше длины волны. А как было показано, эффективность
массообмена находится в обратной зависимости от этих величин.
В первом приближении весовые коэффициенты можно принять в
расчетах равными, т.е. pt = р2 = 0,5.
Моделирование гетерогенных сред
Моделирование нелинейного теплообмена дисперсной смеси при
пленочном течении. В монографии [2.3.49] предложена замкнутая
система уравнений механики гетерогенных сред. Здесь же приведе-
ны методы решения этой системы уравнений применительно к раз-
личным теплофизическим и химико-технологическим процессам.
Решим эту систему с использованием метода, изложенного в работе
Глава 2
241
[2.3.8],	на примере решения системы уравнений движения и энергии
дисперсной смеси для случая двухфазного пленочного течения.
Отметим, что течение дисперсной смеси при пленочном течении
находит применение в различных отраслях химической и нефтепе-
рерабатывающей промышленности. Дисперсной средой может быть
система пузырей, капель, а сплошной — жидкость с различной рео-
логией.. Решение данной задачи связано, например, с переработкой
тяжелой пиролизной смолы, которая образуется при производстве
этилена на комплексе Э-200. Пиролизная смола в этом случае пред-
ставляет собой монодисперсную двухфазную эмульсию. Сплошную
фазу составляют углеводы, дисперсную фазу — вода. В настоящей
статье метод поверхностей равного расхода применен для решения
нелинейного тепломассообмена дисперсной смеси при пленочном
течении.
Уравнения движения и энергии дисперсной смеси [2.3.49] для слу-
чая двухфазного пленочного течения имеют вид (z = 1 — сплошная
среда, i = 2 — дисперсная фаза):
VpiVi - 0, Vp2V2 - 0;	(2.3.134)
Р'1- a1Vp+Vn< dt	(2.3.135)
1 = a2Vp + f12+p2g2; dt	(2.3.136)
^- = -Vg1+O21+KIf12(V1-V2); dt	(2.3.137)
= -Vg2 + Q12+K2f12(V, - V2), dt	(2.3.138)
где: Vlr V2 —скорости соответственно дисперсной и сплошной фаз; ир
и2, otp «2 — соответственно их свободные энергии и концентрации;
Tj1 — тензор напряжений в i-й фазе; f12 — сила межфазного взаимо-
действия; q. — приток тепла за счет теплопроводности i-й фазы; Q- —
контактный приток тепла от j-й фазы к i-й фазе; ф / dt = Э / dt + VJ"Vn.
Уравнения (2.3.134) —(2.3.138) в проекциях на оси х и у имеют вид
(рр р2 = const, стационарный режим, погранслойное приближение):
Эг1у dviy	0v7y dv2y
——+—- = 0;	—— = 0;
Эх	Эу	Эх	Эу
(2.3.139)
9vlv Эг1г <Xi Эр Э , Эг^ „ ,
Р1,^Г ,2/р,+£71: ( Л40)
242
Глава 2
-«14^-42=0;	(2.3.141)
Эу
V2X^+''2y^L=-—^-+fn/P2 + g2.	(2.3.142)
дх у ду р2 дх
••|Е-/12/р2 = 0;	(2.3.143)
Рг «У
00<	00t	. д Г. 00^
vix~^~ + viyЧ““(1/Р1ср1)ч“	+<^12/ср1Рп	(2.3.144)
дх у ду р Эу^ ду)
002	Э02 л/ . д Л 0O2^	/о о 1 игл
v2x ^7 + У2у	= (1 /Р1ср2) эД Z2	+ 012 /ср2Р2- (2.3.145)
Граничными условиями для системы уравнений (2.3.139) —(2.3.145)
в плоскости х, у (где х — координата, совпадающая с направлением
силы тяжести, у — координата, перпендикулярная ей) являются сле-
дующие соотношения:
х = о 4 = 4°; ог=О1°;
дТ	d
У = ВД Лфф1 — =р(ДН,— J uixdy, где i = 1, 2. (2.3.147)
ду	dx 0
Для решения указанной системы уравнений применим метод по-
верхностей равных расходов [2.50]. В соответствии с этим методом
скорости сплошной и дисперсной фаз представим в виде VJx,yk(x)]
где уА(х) — линия тока. Для сплошной фазы полный дифференциал
равен:
^Щх _ 0ц1х । ^Ук
dx дх ду dx
Заменив в уравнении (2.3.140) частную производную си1х/дх, со-
гласно формуле (2.3.148), получим:
dvlx dv,	dyA
, (yiy vix , )~
dx	dy	7 dx
(2.3.148)
др d
дх dy
— -WPi+ffi-
Представим давление в виде:
dp 0р | др dyk
dx дх ду dx
(2.3.149)
(2.3.150)
Глава 2
243
и заменим в формуле (2.3.149) др/дх через — из формулы (2.3.150) с
dx
учетом уравнения (2.3.141). Тогда:
dvlx dvlx .	dyk ч	,	. „ dp
vlx	Л (Vly " Vlx = - «1 /Р1 ~
dx ду 3 dx	dx
-й2/р1) 1+4^+?1+1г
\ dx) ду
, i . dv,-
Эу
(2.3.151)
Второй член в левой части формулы (2.3.151) выразим следующим
образом:
— J vi*dy= J-JT
dx о о Эх
dx
= - J ~?Ldy+vix = ~viy +vix	(2.3.152)
0 оу	dx r dx
Учитывая последнее соотношение и изменение расхода по длине
пленки между линиями ук и ук+1, имеем:
d
— / Ри*<*у = Ф(х);
dx У к
выражение для скорости vlx приведем к виду:
vix	=^ф(*-1)-(“1/Р1)^-(А2/Pi)f 1+^-1+
dx ду	dx	V dx J
+31+x~ (P/P1)
Эу _
(2.3.153)
Э+1Х
ЭУ .
Аналогично можно получить выражение для дисперсной фазы и
для распределения температур сплошной и дисперсной фаз. Опус-
кая промежуточные выводы, приведем окончательные выражения
для k-го слоя:
V2x^' = ^i<I>(j£''1)_(“2/P2)dx+(/12/p2)0+^) + ff2: (2'ЗЛ54)
^1=эе1ф(к_1)+(1/ э_Г	(23155)
dx ду	р Эу^ ду J	р
V2x	=“^'Ф(^“1) + (1/Р2ср2)^'	“^12/Ср2Р2-	(2.3.156)
Уравнение для поверхности пленки определим из уравнения
(2.3.152), для чего представим интеграл по одной из формул числен-
ного интегрирования и затем продифференцируем полученную раз-
244
Глава 2
костную формулу по х. Если проинтегрировать уравнение (2.3.152) по
формуле трапеции, то уравнение для определения формулы поверх-
ности примет вид:
<?У* . fot-i ! 2Ф yjt-yt-T , duk-iY
dx d uk + ukA uk + uk_{ у dx dx J'
^ = o	(2-3.157)
dx
Система уравнений (2.3.153), (2.3.154)—(2.3.157) вместе с гранич-
ными условиями (2.3.146), (2.3.147) представляют замкнутую систему,
решить' которую при известных правых частях можно одним из чис-
ленных методов решения обыкновенных дифференциальных урав-
нений, например методом Рунге-Кутта.
Для определения выражения в правых частях представим реше-
ние щ(х, ук(х)), еДх, ук(х)) в виде:
<рА(х)= £ Л(х)Ук(У*(х))-	(2.3.158)
Jt=i
где <рк(х) = и((х, ук(х)), 0;(х, ук(х)), причем полиномы <рк(ук (х)) считаются
заданными функциями.
Расчет этой системы изложен в работе [2.3.2]. При расчете следует
иметь в виду, что 04 + 02= 1; f12 — сила межфазного взаимодействия;
Q- — контактный приток тепла от j-й фазы к i-й. Их значения можно
найти, например, в монографии [2.3.49].
Данный метод нашел применение для решения различных задач
при пленочном течении [2.3.51—2.3.55].
Математическое моделирование гидродинамики
на проницаемых поверхностях
В работе [2.3.2] были показаны широкие возможности примене-
ния метода поверхностей равных расходов для решения сложных не-
линейных задач гидродинамики и тепломассообмена при пленочном
течении как в ньютоновской, так и в неньютоновской жидкостях. В
работе [2.3.8] данный метод распространен на исследования нели-
нейной гидродинамики и тепломассообмена дисперсной смеси при
пленочном течении. В основу были положены уравнения сохране-
ния движения и энергии, предложенные в монографии [2.3.49]. При
этом в качестве дисперсной среды исследовалась система пузырей,
капель, твердых частиц, а в качестве сплошной — жидкости с раз-
личными реологическими свойствами.
Глава 2
245
Для расчета движения гетерогенной среды по поверхности порис-
того тела произвольной формы при наличии фильтрации применим
метод поверхностей равных расходов [2.3.52].
В тепломассообменных аппаратах контактные устройства с про-
ницаемыми поверхностями широко применяются для интенсифика-
ции многих технологических процессов. При расчете таких аппара-
тов возникают как внутренние, так и внешние гидродинамические
задачи. Внутренние задачи связаны с напорными течениями в раз-
личных каналах и трубах; внешние — с действием массовых сил на
движение рабочей среды со свободной поверхностью. Изучение и
выявление закономерностей таких течений представляет как теоре-
тический, так и практический интерес, поскольку эти процессы име-
ют различные технологические приложения: при разделении или
сгущении гетерогенных сред в фильтрующих аппаратах, при реали-
зации интенсивного тепломассопереноса в пленочных течениях, при
управлении пограничным слоем.
Постановка задачи и метод решения. Пусть по поверхности порис-
той пластины произвольной геометрической формы, имеющей посто-
янную толщину 5, происходит течение гетерогенной среды. При те-
чении гетерогенных сред по проницаемым поверхностям сплошная
фаза просачивается через стенку, а дисперсная фаза задерживается
в рабочей зоне. При этом возможны два случая. В первом случае при
значительных касательных напряжениях на стенке, создаваемых
потоком разделяемой среды и массовыми силами, частицы, задер-
жанные на поверхности, увлекаются потоком. В этом случае проис-
ходит фильтрование без образования осадка или сгущение разделя-
емой среды с изменением средней концентрации по длине аппарата.
Во втором случае при недостаточных касательных напряжениях на
стенке происходит фильтрование с образованием осадка.
Расчет течения гетерогенных сред без образования осадка. Урав-
нения сохранения массы и движения гетерогенной среды для случая
стационарного двухфазного течения имеют вид [2.49]:
VpjVj = 0, Vp2V2 = 0,	(2.3.159)
Pi(viv)vi = -«iVp+VTj -F12 +PtF,	(2.3.160)
p2(V2V)V2 =-a2Vp + Fi2 +p2F,	(2.3.161)
где F (Fv F2, F3) — вектор массовых сил и его компоненты в направле-
нии координат хр х2, х3; F12 — вектор силы межфазного взаимодейст-
вия; V/ (Ц, V., ИЛ) — вектор скорости z-й фазы и его компоненты в на-
246
Глава 2
правлении координат xv х2, х3, м/с; af — объемная концентрация z-й
фазы; Р;°, р,- = cc;pz°, Р = Pi + Р2 ~ соответственно плотность z-й фазы,
приведенная плотность и плотность смеси, кг/м3; тк1 — компоненты
тензора вязких напряжений.
В условиях слабой скоростной неравновесности, когда локальная
скорость относительного движения фаз мала по сравнению со сред-
необъемной скоростью потока, можно принять квазигомогенную
модель течения [2.49]. Уравнение сохранения среды в этом случае по-
лучается путем суммирования соответствующих уравнений
VpV = О,
p(W)V = -Vp+VT+pF.	(2.3.162)
В том случае, когда размеры включений и разности плотностей зна-
чительны, относительное движение фаз может существенно искажать
динамику движения неоднородной гетерогенной двухфазной смеси.
Для этого случая необходимо решать систему уравнений (2.3.159) —
(2.3.161). Рассмотрим методом поверхностей равных расходов [2.3.2],
примененным для расчета гидродинамики и тепломассообмена в не-
однородных гетерогенных средах [2.52 — 2.53], оба случая.
Выберем ортогональную систему координат, у которой одна из
координатных поверхностей х} = const совпадает с поверхностью те-
чения, а координатные линии (поверхности) х2 = const составляют
семейство нормалей к ней. Для оценки членов системы уравнений
(2.3.162) используем безразмерные переменные:
x,=x,/L, х2 = х2/Н, V = V/V., U = U/U., p = p/(pU?);
6 = H/L = V-/U., Re = HU-/v, Fr,=l7?/(H/<),	(2.3.163)
где V,, U., L — характерные скорости и размер области течения; Н —
начальная толщина слоя.
Тогда в ортогональной системе координат уравнение (2.3.162) с
учетом формул (2.3.163) преобразуется к виду (черточки опущены):
( U dU V dU UV днЛ з V2 дН2
<Н1	Н2 дх2 НГН2 дх2 J	НГН2 дх{
£2	1 ЭН2^зтп т22 дН2 ।
Re^H^Hg dxj НХН2 дхх
1	3 f Э(У/Н2)^
Н*Н2Н3дх2{	Эх, ))
1	1 Э f Н±Нз Э(1//Н1)'| е Эр 1
Re Н?Н2Н3 Эх2 ( Н2 Эх2 J Ht Эх, Fr,'
(2.3.164)
Глава 2
247
2 и av v av uv эн2 и2 эн,
Эхх H2 Эх2 HXH2 dXi J HiH2 dx2
£	1	Тц dHi [
' тЦ НХН2Н3	Эх2 НГН2 дх2
+2 \—//Н1Н2Н3 Э(У/Н1)Т| +
Н^НзЭхД	Эх2 ))
Е3 1 а Гн2н3 д(у/н2)}____i__ap_ i
Re HrH2H3 3xt [ Hr axj J H2 dx2 Fr2'
(2.3.165)
где Frf. — число Фруда, определяемое компонентом массовой силы,
направленной по координате xf.; Re — число Рейнольдса; Н. — коэф-
фициенты Ламе.
Полагая для тонкослойных течений малым параметр е и пренеб-
регая слагаемыми, величина которых на порядок меньше, чем масш-
таб градиента давления, получим:
„ ( и ди V ди UV днЛ
Ree —— +—-—+-----------!• =
<	Н2 ®^2	^1^2 ^^2
1 Э ГН,3Н3 Э(и/Н1)"| Ree др Re
н2н2н3 Эх2 k н2 Эх2 ? н{ axt Frt ’
и2 _______1 Эр 1
НХН2 дх2 Н2 дх2 + Fr2 ’
(2.3.166)
(2.3.167)
Произведение Ree дает число Рейнольдса, определяемое по скоро-
сти, нормальной к поверхности течения:
Rev = eRe = HV/v.	(2.3.168)
На начальном участке слагаемые с коэффициентами eRe должны
всегда учитываться. В области установившегося течения для непро-
ницаемой границы Rev -» 0; поэтому в уравнении (2.3.166) конвектив-
ными членами и градиентом давления можно пренебречь. Однако в
условиях фильтрации на участке установления скорость V. по поряд-
ку величины совпадает со средним значением скорости протекания
на границе. Следовательно, число Рейнольдса Rev определяется ин-
тенсивностью фильтрации. Поэтому вышеназванные слагаемые в
общем случае должны быть учтены.
С учетом приведенных оценок уравнения сохранения механики
гетерогенных сред (2.3.159) —(2.3.161) в ортогональной системе коор-
динат запишутся в следующем виде:
248
Глава 2
Э(Н2Н3р,и,) , Э(Н,Н3р,У,) = 0.
cbq	Эх2
Pl	ЭЦ У, ЭН, u,v, эн/ < Hi	H2 Эх2 HiH2 dx2;	=	
= -	_ eg Эр	1 ЭНрН3т12 _ Hi dxi HiH2H3 Эх2	^bxj +PiA«	(2.3.170)
U? ЭН, a! Эр P1 HjH2 Эх2 H2 dx2 12X2	1 2'			(2.3.171)
Э(Н2НзР2П2) + Э(Н,НзР2У2) = 0; Эх2			(2.3.172)
p2	'иг ди2' v2 du2! U2V2 dHt' < Hi 3xt H2 Эх2 HiH2 dx2		
= -	a2 Эр _ rr 2 +^12X1+P2^1> Hi dxi	1		(2.3.173)
U2 dHi a2 Эр _ —p2 —— —-1 = —-z^+Fl2x2 4 2 H{H2 Эх2 H2 Эх2 12		P2^2-	(2.3.174)
Движущими силами процесса фильтрации являются разность
давлений и массовая сила. Когда толщина пористой пластины на-
много меньше ее продольного размера, для расчетов можно при-
нять модель одномерной фильтрации. Уравнения неразрывности и
фильтрации в ортогональной системе координат в этом случае при-
мут вид:
дН,Н3У0 _
Uj
Эх2
цДН2Эх2
(2.3.176)
При фильтрации сплошной фазы имеет место сгущение среды,
сопровождающееся изменением концентрации твердой фазы. Для
того чтобы это учесть, представим при математическом моделиро-
вании изменение концентрации твердой фазы как функцию про-
дольной координаты 02 = a^Xj). Построим уравнение для ее опреде-
ления.
Количество твердой фазы остается неизменной. Тогда
02(х1) =	= const.	(2.3.177)
Глава 2
249
Расход жидкой фазы меняется из-за фильтрации согласно соот-
ношению
Q|x,) = Q(xte)+ J j‘a10V0(6)H1H3dx3dx1,	(2.3.178)
х1п х3п
где Vo — скорость фильтрации в направлении координаты х2, м/с;
5 — толщина пористого тела, м.
Дифференцируем эти два соотношения по х{
a2(xi№i)+a2(xi)O'(x1) = 0;
О'(х,) = J*a10V0(8)H|H3dx3,
*3n
найдем изменение концентрации дисперсной фазы
/ ОСо
= ~ J «iovo(8)WlH3dx3.	(2.3.179)
Граничные и начальные условия для решения системы уравне-
ний (2.3.169) —(2.3.176), (2.3.179), а также условия сшивания по коорди-
нате Xj следующие:
при	х2 = 0 р0 = рв, Ц=0;	(2.3.180)
при	х2 5 р0 р,	(2.3.181)
при	х2 = h(x) р = рА, т12 = 0;	(2.3.182)
при	xi ~ хщ ^2 ~— ^\п' h ~ Н,	(2.3.183)
где xin, xik — начальное и конечное значения z-й координаты; ain —	
объемная концентрация z-й фазы на входе.
Следует отметить, что, когда толщина пористого тела незначи-
тельна, уравнения фильтрации (2.3.175) —(2.3.176) заменяются гра-
ничными условиями на проницаемой стенке и решается система
уравнений (2.3.169) —(2.3.174). Граничные условия (2.3.180) —(2.3.181)
заменяются условиями:
♦
к
при х2=0 р0=рв, Ц=0,	V1=-----(Р-Рв);	(2.3.184)
Р1
а условия (2.3.182) —(2.3.183) остаются в силе.
Вначале определим параметр фильтрационного течения в порах
пористого тела. Скорость фильтрации жидкости находим из уравне-
ния (2.3.175)
V0=^l,	(2.3.185)
H1H3
где С — постоянная интегрирования.
250
Глава 2
Из уравнения (2.3.176) с учетом выражения (2.3.185) находят зави-
симость для давления
PO=-T-CHX1)J2(X1-X2)-P?^1(X1-X2) + C2(X1)-
к
где Ji(Xi,x2) = $H2F2dx2l J2(xvx2) = f-^-dx2.
Определив из граничных условий (2.3.180) —(2.3.181) с учетом
уравнения (2.3.170) постоянные интегрирования CJXj) и С2(х{), полу-
чим выражение для полей давления и скорости
Ро = Рв +	^7*'^’[ft “Рв+Р1 (Л(х1.8)-Л(х1.°))]+
J2(x1,0)-J2(x1,5) l	j
+pf(J1(x1,0)-Jl(x1,x2));	(2.3.186)
к Pj-pB+pflJilXpSl-J^XpO))
Vn —------------------------“----•	IZ.J.lorl
0 И1 H1H3(J2(x1,0)-J2(x1,5))
В этих формулах давление на стенке рг является искомой вели-
чиной.
Определим поля скоростей для слоя (h—6), где происходит движе-
ние гетерогенной среды. Уравнения движения (2.3.170), (2.3.173) обра-
зуют систему нелинейных дифференциальных уравнений в частных
производных, которые в квадратурах не интегрируются. Нелиней-
ную систему (2.3.169)—(2.3.174) решаем методом поверхностей рав-
ных расходов [2.2]. В работах [2.50] —[2.53] показана возможность
применения этого метода при математическом моделировании раз-
личных процессов в гетерогенных средах.
В соответствии с этим методом введем в поле течения суспензии
линии тока ук = y^xj и представим компоненты скорости i-й фазы для
k-го слоя в виде Uf =Ut xr,ук(xt)], V* = Vrf[x1,yJt(x1)]. Здесь k = l,N,
где N — количество введенных линий тока. Причем линия у{ совпада-
ет с поверхностью пористого тела х2 = 6, а линия yN — со свободной
поверхностью. Сведем задачу о развитии течения слоя суспензии к
численному определению полей скоростей и линии тока.
Для сплошной фазы полный дифференциал равен
А=^ц+ эц H2d&	(23188)
Н^х{ Hfixi Н2дук H^dXi
Заменив частную производную дГ^/дх^ согласно выражению
(2.3.188), получим:
Глава 2
251
H2dyky _
1	1 HydXy
(2.3.189)
(2.3.190)
pM dUy _ C4 Эр р1ЭС71
Ну dxy Ну Эху Н2Ъх2
РАУ, эн, эн2н3т12
Н,Н2 Эх2 Н,2Н2Н3Эх2 ,2х' Р1 '
Второй член правой части выразим через расход между линиями
тока. Расход сплошной фазы через произвольное сечение Ху за еди-
ницу времени определится соотношением
f / CLyUy[Xy,x2,x3)H2H3dx3dx2.
5x3n
Рассмотрим гидродинамическое течение без массообмена. Оче-
видно, что при отсутствии массообмена изменение расхода сплошной
фазы может происходить из-за фильтрации жидкости через прони-
цаемую поверхность. Предположим, что система координат выбрана
так, что величины ар 5, h, Uv Vt не зависят от координаты х3 и обоз-
начим Z = Н3(х3к — х3п). Тогда интегральное условие сохранения коли-
чества сплошной фазы для произвольного сечения запишется в виде:
jayZUyH2dx2 + J a10Z|V^(8)|H1dx1 = Qln. (2.3.191)
5 Х1П
При раскрытии модуля скорости нужно учитывать направление
фильтрации относительно оси х2. Продифференцируем соотноше-
ние (2.3.191) по Ху
d h
—— $ayZUyH2dx2 = oc10ZVr0(5).
8
Обозначим величину изменения расхода первой фазы для всей
пленки гетерогенной среды через OJxJ. По определению [2.3.2]
d л
Ja,Zt7,H2dx2 = Ф,(х,).
HjClXi б
Соответственно величина изменения расхода между линиями ук
и ук+1 составит:
—J a1ZUlH2dx2=0f(x1).
Сравнивая уравнения (2.3.192) и (2.3.193), получим
<t>i(x,) = a10ZV0(8).	(2.3.195)
Если соотношения (2.3.191) записывать для расхода между лини-
ями yt = 5 и у2, то после выполнения аналогичных выкладок получим
такое же выражение, т.е.
Ф,(х,) = а1огуо(5).
(2.3.192)
(2.3.193)
(2.3.194)
(2.3.196)
252
Глава 2
(2.3.197)
Это означает, что, когда изменение расхода происходит только из-
за фильтрации, выполняются соотношения:
Ф1(х)) = Ф1(х,)=а102У0(8)1
ф{с(х1) = 0, к = 2,77-1.
Применим правило Лейбница для дифференцирования интегра-
ла (2.3.194)
^к 1 у*,+1 Эа^ЦНо ,	.	dyjt+i , ^тт x dYk
Ф1 I -------4 dx2 + (ai^i^2)k+i773^_^ai^i^2)k773~-
yk dxr	H{dx{	HidXi
Интеграл в правой части полученного соотношения вычисляют с
учетом уравнения неразрывности, и тогда
Ф* = a,zf Vtk -U? ^Ук
-atZ V/
£+1 _	H2dyk+1
1 1
Hxdx}
Отсюда, с учетом кинематического условия на свободной поверх-
ности и соотношений (2.3.197), получим:
.к fytyk
1 Htdxt
a{Z Vf-U\
= 0, k = 2,N;
(2.3.198)
4
1 Hxdxx
=ф‘.
(2.3.199)
к

oqZ У/-Ц1
Отметим, что подстановка формулы (2.3.196) в соотношение
(2.3.199) подтверждает выполнение граничного условия (2.3.181).
На основе полученных соотношений можно сделать вывод, что на
линиях тока второй член правой части уравнения (2.3.189) пропадает.
Представим давление в виде (2.3.188) и выразим частное произ-
водное по Xj через полный дифференциал
дРк _ dPi<$Рк	(2.3.200)
Htdx{ H\dxr Н2дук H{dx{
Из суммы уравнений (2.3.171) и (2.3.174) находим
= pF2 + Plt7|2+P2t/2	(2.3.201)
HiH2 дх2
Интегрируя это уравнение на интервале [уА, ук+1], имеем:
Pk+i-Pk=Mk, k = lN^i,	(2.3.202)
гдеМк(х!)= J J(xltx2)dx2, J(xvx2) = H2pF2 +
и1 дХ2
дРк
Н1дук
Глава 2
253
Отсюда:
dpM dpk . dMk
(2.3.203)
(2.3.204)
(2.3.205)
k = l,N-l.
(2.3.207)
dxx dxi dxi
Учитывая, что pN = pat, рекуррентное соотношение (2.3.202) мо-
жет быть приведено к виду:
Рк=Ро1-1'мк. к=1УП.
Х=к
Дифференцируем полученное соотношение
dpk= NfldM^
dxi £к dxY '
Заменив дрк/дх} в уравнении (2.3.189) согласно (2.3.200) с уче-
том выражений (2.3.201) и (2.3.202), а также используя соотношение
(2.3.198), определим распределение скорости
рА*	, dyk
Ht dx, H,£idx, 1	" 2 H,dx,
ЭН, ЭнЗНоТ^о k	---
- 1 1	- + - 9~	—+P1F1- k = 2,N.	(2.3.206)
HiH2 dx2 H2H2H3dx2 12X1 H 1	1 J
Аналогично можно получить уравнения для дисперсной фазы.
Опуская промежуточные выводы, приведем окончательное выраже-
ние для распределения скорости U2 :
p2U2 dU2 a2NJdMk „	dyk
dXl	Hlktk dx{	211
p9UnV2 dH k	--
--2 2 2	- + Д2Х + P2^2- k = 2,N.
H{H2 dx2 12X1 K2 2
Если размер включений и разность плотностей фаз имеют неболь-
шие значения, относительное движение фаз может оказаться незна-
чительным. Тогда можно пользоваться квазигомогенной моделью.
В квазигомогенном приближении линии тока вводятся вполне одно-
значно для некоторой эффективной среды с переменными по про-
дольной координате характеристиками p(a2(Xj)), pfa^Xj)). Преобра-
зованное уравнение движения эффективной среды можно получить,
сложив уравнения (2.3.206) и (2.3.207), т.е.
P^dU^+P£ldUl = ±Ny'dMk+J х dy,
Н{ dx{ Hl dxx Hlk^k dx{ ° 2 H^Xi
Эх2 H?H2H3dx2 1 ''
н,н2
254
Глава 2
Когда U = Ц ® U2 и V = Vj« V2, последнее уравнение примет вид:
pUdU 1 N^dMk ri ч dyk
Н.	dx. H.£k dx.	2’H.dx.
puv dH, ЭН?Н3т*2
------  1 x----------1- OFi .
H.H2 dx2 H.H2H3dx2
(2.3.208)
Уравнения для поверхностей равного расхода определим из выра-
жения (2.3.194). Для этого, представив интеграл по одной из формул
численного интегрирования, продифференцируем полученную раз-
ностную формулу по хг Если проинтегрировать указанное выраже-
ние по формуле трапеций, то уравнение для определения поверхно-
сти будет иметь вид:
dyk+i = dyk t 2Н.Ф. $к yk+i -ук dAk ,
dx. dx. Дк	ДА dx.	(2.3.209)
^- = 0, k = 2JV,
dx.
где Д^ = (a.H2ZU.)k + (о^Н^Ц^+г
На реологию среды ограничения не накладывались. Несмотря на
это, можно считать, что для тонкослойных течений тензор вязкого
напряжения определяется градиентом dU./dx2. Для вычисления про-
изводных пох2 в уравнениях (2.3.206) сеточные решения представим
в виде разложения в ряд по полной системе базисных функций, удов-
летворяющих граничным условиям (2.3.182):
U=lAj(x.)Ukj(x.).	(2.3.210)
Систему базисных функций можно выбрать в виде [2.2]:
либо
(2.3.211)
(2.3.212)
где Tj — полиномы Чебышева первого рода;
j = UV; k = lN.
П*(Х1) =
УИ*|).
У1у(*1)’
Потребуем, чтобы скорость, определяемая из уравнения (2.3.210),
совпала с U.(x.) на линиях yjxj. Тогда коэффициенты Aj(x.) опреде-
лим из системы алгебраических уравнений:
Глава 2
255
XA;(x1)l/J[.[yJt(x1)] = <71i(x1), k = lN,	(2.3.213)
7=1
затем найдем производные скорости по х2 и вычислим правые час-
ти системы уравнений (2.3.206) или (2.3.209). Система уравнений
(2.3.179), (2.3.206)—(2.3.208) или (2.3.209) и граничные условия (2.3.183)
представляют замкнутую систему уравнений, решение которых при
известных правых частях можно получить одним из численных мето-
дов решения обыкновенных дифференциальных уравнений.
a- N~ldM\
Нетрудно заметить, что слагаемое — у---------—, входящее в пра-
х=к dx{
вые части системы (2.3.206) —(2.3.209), содержит искомую величину
dyN/dxv поэтому вычисление правых частей системы состоит из два
этапа:
1.	вычисление прогоночных коэффициентов и расчет по ним не-
известного dyN/dXp
2.	вычисление собственно правых частей.
Для этого необходимо представить искомые функции dyk/dxi в
виде прогоночных соотношений
(2.3.214)
(2.3.215)
^ = AJy»+Bk, к = ^.
dx, dx, к
Подставляя эти выражения в уравнения (2.3.206) —(2.3.209) и счи-
тая, что Ak V Вкл известны, получим явные выражения прогоноч-
ных коэффициентов. После их вычисления из уравнения системы
(2.3.214) определяем
йУы _ BN
dx{ l-AN
После этого обратной прогонкой вычисляем значения правых
частей системы дифференциальных уравнений (2.3.206) —(2.3.208).
Находить явные выражения прогоночных коэффициентов целесооб-
разно после конкретизации области течения и определения коэффи-
циентов Ламе: Нр Н2, Н3. Рассмотрим несколько примеров течения
гетерогенной среды без образования осадка.
Течение по поверхности плоской пористой пластины. Рассмотрим
течение гетерогенной среды по поверхности наклонной плоской по-
ристой пластины единичной ширины. Выберем декартовую систему
координат (х, у, z) с коэффициентами Ламе: Нг = 1, Н2 = 1, Н3 = 1. Для
этого течения не только коэффициенты Ламе, но и компоненты мас-
совых сил являются постоянными, поэтому:
F^gsirnp, F2=-grcosq), J(x,y) = pF2, Z = l,
Л(х.У) = /72У. Л(*.У) = У. Mk=pF2(yM-yk).
(2.3.216)
256
Глава 2
С учетом этих выражений уравнения для полей давления и скоро-
сти в порах пористого тела примут вид:
Ро=Рв + РА-Рв-^-^-у-.	(2.3.217)
О
Vo = -Af ~Рв ~P^<h~5Lp«F2l	(2.3.218)
Mil 8	J
Для давления в слое гетерогенной среды из соотношения (2.3.204)
получим:
Рк = Ра -Р^2(Л"У)«	(2.3.219)
Слагаемые, учитывающие в уравнениях (2.3.206) —(2.3.208) пере-
пад давления, примут вид:
dMk . dyk _ Г, .dp dyN ’
У1У-У*)-Т~+Р Я 
к=к dx	dx L dx dx J
Тогда дифференциальное уравнение (2.3.208), позволяющее опре-
делять скорость среды для плоской пластины на линиях равных рас-
ходов, принимает вид:
pl/‘^ = F r(y у )^P+p^Nl+|Ea+pF (2.3.220)
dx L dx dx J oyk
Система (2.3.209) для пластины единичной ширины (Z = 1) запи-
шется в виде:
dyk+i = ЛУк , 2аО1Уо Ьк
dx dx ai(Uk+Uk+l) 1
aJC^ + C^dxL	J
^ = 0,	k = 2,N.
dx
Изменение концентрации дисперсной фазы определяется из диф-
ференциального уравнения
dO2 =_а2ао.1.Уо	(2.3.222)
dx Q2
Приведем к безразмерному виду выражения (2.3.218), (2.3.220) —
(2.3.222) с помощью следующей подстановки:
х = HRex, у = Ну, 8 = Н8,
U _	9_	(2.3.223)
ц = Vo=—Vo, к = Н2к,
Глава 2
257
где U. — средняя скорость в начальном сечении; Н — величина щели,
из которой истекает смесь; Re = САН/v; Rez = и-Н/\\; Frz = СА2/(Н/<);
vo = Mi/Р? J vi = М/Р' = Безразмерное уравнение движе-
ния для случая ньютоновского реологического закона в новых пере-
менных примет вид (черточки опущены):
dx
(Ук-Ук)
Др da2
р dx
dx
1 d2Uk Re
---Ч 5~ + ,
Fr2 Эу2 Fij
dyk = ЛУк-i t 2а01У0	_
dx dx ai(Uk +Uk~l) 1
Ук-Ук-i d[ai(C/ +uk !)]	(2.3.224)
a{(Uk+Uk~l) dx
da2 а^оЛо
dx a2n
V0=kRef-Re1^-+-^-yN~S+^- .
t 1 S Fr2 5 Fr2 J
Для вычисления правых частей методом прогонки первые два
уравнения этой системы приведем к виду:
Ук ~ У к-1 + ^к^к-1 + ^к^к ~ ^к<
Uк — Dk +	,
ч _ Ук-Ук-1 п _ 1 (Р'Ун-Ук , 32Ut , Re'
* Uk+Uky к уДр Fr2 Эу2 FrJ'
С* = У Fr ' £jf = а (У +У )&* +Sk^k+Uk->hA (2-3-225)
Здесь номера поверхностей расходов (в обозначениях скорости)
для удобства даны в нижнем индексе, а штрихи означают производ-
ные по безразмерной координате х.
Представим искомую функцию у'к в виде прогоночного соотно-
шения
Ук=АкУы+Вк	(2.3.226)
и подставим его в уравнение (2.3.225). После несложных преобразо-
ваний получим явные выражения прогоночных коэффициентов в
виде следующих рекуррентных соотношений:
Ак = ^k-l ~ ^к^к-1~ Sk^k’
Bk=Bk.i-SkDk_l-SkDk + Ek.	(2.3.227)
258
Глава 2
Из условия Фк = ^Щ- = 0 и из системы уравнений (2.3.225) нахо-
dx dx
дим значения прогоночных коэффициентов при к = 2
А2 = -S2C2, В2 = Е2 -S2D2.	(2.3.228)
Остальные коэффициенты при k = 3,N вычисляем по соотноше-
ниям (2.3.227). При к = N из уравнения (2.3.226) имеем:
о
y'N=T^--	(2-3.229)
Далее, обратной прогонкой вычисляем значения правых частей
системы дифференциальных уравнений (2.3.225).
Течение по внутренней поверхности вращающегося конического
пористого ротора. Применим построенную систему дифференци-
альных уравнений (2.3.179), (2.3.208) —(2.3.209) для расчета процесса
сгущения гетерогенной среды в фильтрующей центрифуге. Выбе-
рем коническую систему координат х{ = х, х2 = у, х3 = ср с коэффи-
циентами Ламе: = 1, Н2 — 1, Н3 — г. Массовая сила определяется
компонентами вектора центробежного ускорения:
Tj = (02nsin<p, F2 = -(o2rcos(p, r = xsin<p. (2.3.230)
Кроме того,
^i=yF2« ^2=У/г- J = PF2- Z = 2nr, Mk=pF2(yk+l-yk). (2.3.231)
В общем случае, поля давлений и скорости в порах пористого ро-
тора определяются из соотношений (2.3.217) — (2.3.218). Однако, когда
толщина материала ротора незначительна, скорость фильтрации оп-
ределяется из граничного условия (2.3.184). В фильтрующих центри-
фугах разделение смесей происходит за счет центробежной силы, и на
практике перепад давления в разных сторонах фильтрующей перего-
родки не создается (рА = рв). С учетом сказанного для скорости филь-
трации несущей фазы из выражений (2.3.184) и (2.3.219) получим:
Vo=— phF2.	(2.3.232)
Hi
Дифференциальные уравнения для поверхностей равных расхо-
дов, скоростей и концентрации принимают вид:
ГТ dUk d(pF2).	.	„ dyN Эт^2
Put~r- = -^- Ум"У* +Р^-г!1+-у1+РЛ
dx dx	dx ayk
= dy* +—?Wo—5*-------Ук+1-Ук----—[ra(Uk +Uk+I)],
dx dx at(Uk+Uk+l) 1 rat(Uk+Uk+l)dxl K K+‘ 1 (2.3.233)
da2 _ 27tra2a01V0
dx Q2
Глава 2
259
Исключим размерность в системе уравнений (2.3.232) —(2.3.233)
с помощью подстановки выражения (2.3.223). Кроме того, учтем, что
к = Нк и Q2 = 2nrna2nU-H (к' — коэффициент проницаемости стен-
ки, м). После перехода к безразмерным переменным получим (чер-
точки опущены):
dx
. Apda2 dyN yN-yk
p dx dx x
1 d2Uk Re
—н—;
Fr2 dy2 Frt
dyk . dyk_, ,	2a01V0	yt-yt_, d[ra,(t/* H-t/*'1)]
dx dx а{(ик+Uk~l) 1 ta{(Uk +Uk~l) dx
da2 = alaolVo x .
dx a2n xn'
(2.3.234)
к Re2 h
Fr2
Искомая величина y'N в правой части этой системы уравнений
определяется методом прогонки. Для этого система приводится к
виду (2.3.225), где
n _ 1 Гум-УкЛр<*«2 , Ук’}'!, J’4
—  -----------------1-------1--—_ -|-
Fr2 Р dx xFl2 9y2 Fr1?
Ek =	2a°1V°	8*
a,(l7k + l7k_,)

(2.3.235)
atdx )'
а зависимости Sk, Ck по форме остаются неизменными. Вычисления
прогоночных коэффициентов и собственно правых частей системы
выполняют по формулам (2.3.225)—(2.3.229).
Системы обыкновенных дифференциальных уравнений (2.3.224)
и (2.3.234) с начальными условиями (2.3.185) решены численно мето-
дом Гира.
Обсуждение результатов численного решения. Рассмотрим случай
непроницаемой стенки. Задача решена методом Рунге-Кутты с авто-
матическим выбором шага. Характерная зависимость толщины по-
верхностей равных расходов от продольный координаты представ-
лена на рис. 2.51.
При течении среды по плоской пластине толщина пленки выходит
на постоянную величину. Результаты расчетов при различных значе-
ниях отношения чисел Рейнольдса и Фруда показаны на рис. 2.52.
При течении смеси по внутренней поверхности вращающего-
ся конического ротора с частотой вращения (о, с*1) толщина плен-
260
Глава 2
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 х
Рис. 2.51. Зависимость безразмерной
толщины поверхностей равных расхо-
дов от безразмерной продольной коор-
динаты для непроницаемой стенки при
Re/Frx = 8,5
ки не имеет асимптоту, посколь-
ку текучая среда растекается по
увеличивающемуся периметру.
Характерный вид поверхностей
равных расходов в случае тече-
ния по коническому ротору по-
казан на рис. 2.53.
В случае течения по проница-
емой поверхности объем среды
под нижней поверхностью тока
будет убывать из-за фильтрации
жидкости. Когда нижняя поверх-
ность тока достигнет проница-
емой стенки (у2 = yj, происхо-
дит уменьшение степени разло-
жения в ряд сеточного решения
(формула (2.3.210)). Изменение аппроксимации скорости вносит воз-
мущение в числовое значение .тензора вязкого напряжения и, следо-
вательно, в слагаемое &Uk/dy2. Резкое изменение отдельных членов
уравнения сохранения импульсов уравновешивается изменением
гидродинамических параметров. В результате этого числовое реше-
ние yN(x) терпит локальное искривление. Расчеты показывали, что
одношаговый метод Рунге-Кутты, как правило, не в состоянии пре-
одолевать такие пикообразные участки. Для преодоления этой осо-
бенности был применен метод Гира, предназначенный для решения
жесткой системы обыкновенных дифференциальных уравнений.
Рис. 2.52. Зависимость безразмерной
толщины пленки смеси от безразмер-
ной продольной координаты для непро-
ницаемой стенки: кривая 1 — Re/Fr* =
= 8,5; кривая 2 — Re/Frx = 3,4; кривая
3 - Re/Frx = 2,l
1,0
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 х
Рис. 2.53. Зависимость безразмерной
толщины поверхностей равных расхо-
дов от безразмерной продольной ко-
ординаты для непроницаемого ротора
при входном Re/Frx = 1,01 и (О = 10 с*1
Глава 2
261
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 х
Рис. 2.54. Зависимость безразмерной
толщины поверхностей равных рас-
ходов от безразмерной продольной
координаты для проницаемой стенки
npnRe/Frx = 8,5; к = 7,57-10*
Для случая проницаемой стен-
ки характерный вид зависимо-
сти толщин поверхностей равных
расходов от продольной координа-
ты показан на рис. 2.54—2.56. Из
этих рисунков видно, что при ис-
чезновении нижнего слоя, осталь-
ные линии имеют пикообразные
возмущения (рис. 2.55). Причем,
чем меньше остается введенных
поверхностей равных расходов,
тем заметнее становится локаль-
ное возмущение решения. В рас-
четах вначале были введены семь
поверхностей равных расходов
(N = 7). Из рис. 2.54 следует, что
возмущения, вносимые в расчеты при исчезновении первых четырех
поверхностей, незначительны. В точке х = 0,56, после исчезновения
пятой линии тока, числовое решение имеет заметное возмущение.
Следующее пикообразное изменение решения наблюдается после
исчезновения шестой, предпоследней линии тока. Подобное поведе-
ние числового решения было получено и для других режимов тече-
ния. Отсюда можно сделать вывод, что в разложении (2.3.210) коли-
чество слагаемых должно быть больше двух (N> 3).
Рис. 2.55. Зависимость безразмерной
толщины поверхностей равных рас-
ходов от безразмерной продольной
координаты для проницаемой стенки
при Re/Frx — 0,085; к — 1,9310 5
Рис. 2.56. Зависимость безраз-
мерной толщины пленки смеси от
безразмерной продольной коор-
динаты для проницаемой стенки:
кривая 1 — Re/Frx = 8,5; кривая 2 —
Re/Frx = 3,4; кривая 3 — Re/Frx = 2,1;
к =1,13-10-8
262
Глава 2
Рис. 2.57. Зависимость безразмер-
ной толщины пленки смеси от без-
размерной продольной координаты
для проницаемой стенки: кривая 1 —
Re/Frx = 0,085; кривая 2 — Re/Frx =
= 0,034; кривая 3 — Re/Frx = 0,021;
к = 1,93-10'5
Результаты расчетов толщины
пленки в плоском течении для
проницаемого ротора при раз-
личных отношениях гидродина-
мических параметров показаны
на рис. 2.57—2.59. Наиболее су-
щественное влияние на характер
течения оказывает отношение
числа Рейнольдса к числу Фру-
да (см. рис. 2.57) при значениях
этого отношения, меньших еди-
ницы. С увеличением этого отно-
шения различия нивелируются
(рис. 2.59).
На рис. 2.58 показан характер-
ный вид поверхностей равных
расходов для проницаемого рото-
ра. Увеличение скорости вращения ротора приводит к уменьшению
толщины пленки (см. рис. 2.59).
Характерный вид изменения напряжения по продольной коорди-
нате для проницаемой стенки и вращающегося ротора показан на
рис. 2.60—2.61. В обоих случаях энергия диссипации вблизи от входа
затрачивается на развитие профиля скорости, причем для пластин-
ки продольная скорость увеличивается, прижимаясь к поверхности
0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55 х
Рис. 2.58. Зависимость безразмерной тол-
щины поверхностей равных расходов от
безразмерной продольной координаты
для проницаемого ротора при входном
Re/Frx = 1,01; к =3,0340-6; со = Юс*
Рис. 2.59. Зависимость безразмер-
ной толщины пленки от безраз-
мерной продольной координаты
для проницаемого ротора при
к = 3.03-10'7; а2 = 0; кривая 1 —
Re/Frx = 9,ll,co = 10 с1; кривая 2—
Re/Frx = 20,5, (О = 20 с1; кривая
3 — Re/Frx = 36,4, со = 30 с‘
Глава 2
263
Рис. 2.60. Зависимость напряжения
от безразмерной продольной коор-
динаты для проницаемой стенки:
кривая 1 — Re/Frx = 8,5; кривая 2 —
Re/Frx = 3,4; кривая 3 — Re/Frx = 2,1,
к =1,13-10-8
Рис. 2.61. Зависимость напряжения от
безразмерной продольной координа-
ты для проницаемой стенки: кривая
1 — Re/Frx = 0,085; кривая 2 —
Re/Frx = 0,034; кривая 3 — Re/Frx =
= 0,021; к = 1.9310-3
Рис. 2.62. Зависимость концентрации
а2 от безразмерной продольной ко-
ординаты для проницаемой стенки:
кривая 1 — Re/Frx = 8,5; кривая 2 —
Re/Frx = 3,4; кривая 3 — Re/Frx =2,1;
к = 1,93107
пленки (см. рис. 2.60), для ротора, наоборот, — уменьшается, прижи-
маясь к его поверхности (см. рис. 2.61). Характерный вид увеличения
концентрации второй фазы от продольной координаты показан на
рис. 2.62.
Математическое моделирование динамики дисперсной фазы
Преобразуем векторное уравнение движения в Лагранжевой си-
стеме координат в систему двух скалярных уравнений для опреде-
ления модуля относительной скорости частицы и ее направления.
Полученную систему, записанную в коэффициентах Ламе, решим
совместно с уравнениями движения сплошной среды в эйлеровой
системе координат. На примерах покажем течение неоднородной
смеси между проницаемыми параллельными стенками и гетероген-
264
Глава 2
ной среды неньютоновского реологического поведения по поверх-
ности ротора осадительной центрифуги.
К вопросу моделирования динамики многофазных сред можно
подойти двумя путями.
В первом из них основным объектом исследования является
сплошная среда, а дисперсная фаза учитывается как дополнитель-
ное явление. Математическое моделирование среды основывается
на уравнениях типа Навье-Стокса, в которых влияние дисперсных
включений учитывается через концентрацию фаз, силы их взаимо-
действия и так далее. В этом направлении имеются существенные
достижения [2.3.49]. Однако использование для каждой из фаз пол-
ной системы уравнений сохранения, записанных в эйлеровой систе-
ме координат, вызывает трудности реализации решения. Кроме того,
определение химико-физических коэффициентов требует дополни-
тельной информации.
Во втором подходе «центр тяжести» ложится на дисперсную сре-
ду. При этом расчет движения частицы обычно базируется на урав-
нении динамики материальной точки, записанном в лагранжевой
системе координат. При этом предполагается, что траектория час-
тицы совпадает с траекторией средней скорости основного потока,
а влияние сплошной среды определяется через коэффициент сопро-
тивления частицы в неоднородной среде, определяемый из опыта. В
уравнениях сплошной среды такие частицы учитываются через эф-
фективную вязкость.
В действительности траектория частицы не может совпадать с
траекторией средней скорости основного потока, поскольку локаль-
ные компоненты тензора напряжений для двумерного вихревого по-
тока, влияющие на траекторию частицы, неоднородны. К тому же
такой подход не может воспроизвести полную картину траектории
частицы в вихревом потоке. В этом состоит существенный недоста-
ток второго подхода.
Достаточно привлекательным и перспективным является ком-
бинация этих двух подходов, когда векторное уравнение движения
дисперсной частицы в лагранжевой системе координат решается
совместно с уравнением движения сплошной среды в эйлеровой си-
стеме координат. С этой целью векторное уравнение для дисперсной
частицы [2.3.56]—[2.3.57] запишем в виде
= -kw2e + F,	(2.3.236)
где к = 0,75Cpj/(p2d); e=(e1,e2,e3) = cosa-7’ + sina-J+0-£ — единичный
вектор направления относительной скорости частицы VOT. Посколь-
Глава 2
265
ку задача рассматривается в двумерной
постановке, поэтому е3 = 0. Положение
этого вектора задается углом а, равным
значению угла поворота от орта i коор-
динаты Xj до вектора ё (рис. 2.63).
Положительным направлением угла
поворота будем считать, как это приня-
то в тригонометрии, направление про-
тив часовой стрелки. Тогда изменение
угла а от тс до 2тс соответствует осажде-
нию, а от 0 до тс — всплытию дисперс-
ной частицы (см. рис. 2.63). Вектор ус-
корения массовых сил F определяется
суммой векторов внешней силы и подъ-
емной силы Архимеда.
всплытие, б — осаждение час-
тицы
Скорость дисперсных частиц представим в виде суммы скорости
сплошной фазы и относительной скорости V2 = + VOT. Компоненты
скорости сплошной фазы обозначим через (U, V), а относительную
скорость выразим через модуль относительной скорости w = |VOT| и
угла а
Кт = cos ос, w since) = we.
Тогда
dV2 dV,	de dw _
dt	dt	dt dt
и уравнение (2.3.236) движения частицы принимает вид:
de dVx
dw . 2^1- de dVi -
—+ kw e + w— =-------------+F.
dt
dt dt
(2.3.237)
В этом уравнении учтена скорость движения сплошной среды в
той же точке.
Для полной производной несущей среды имеем:
dt dt \dt J
Так как частица находится на траектории движения сплошной
среды, можно положить dr/dt = V2. Отсюда для стационарного случая
получим:
^ = (V,-V)V1 + (VOT.V)V1.	(2.3.238)
Правую часть этого уравнения с помощью коэффициентов
Ламе запишем в криволинейной ортогональной системе координат
266
Глава 2
(хр х2, х3) и выразим его через векторные функции. Из векторного
анализа известно, что [2.3.58]:
grad(a • b) = (а • V)b + (b • V)a + a • rot b + b • rot a,
rot (a • b) = -(a • V)b+(b • V)a + adiv b - bdiv a.
Сумма этих уравнений будет равна
2(b-V)d = grad(d-b)+rot(d-b)-a-rotb-b-rotd-
-adiv b + bdiv a.	(2.3.239)
Если в этом равенстве предположить a = b = , то с учетом несжи-
маемости сплошной фазы имеем
(Vt • V) Vi = grad( V2 / 2) - Vi • rot Vj.
Поскольку
Vi2=C72 + V2,
1 f dH2V
HiH2( dXi
rot Vi =0-z +0-j +
ЗЩ7
3x9
к,
запишем векторные функции в правой части этого равенства в орто-
гональных координатах:
grad
Yl
2
Hi axi	axi ?
ox2	3x2 ?
ViXrotVi =
V (дН2У 3HjlfU U (dH2V dH^
HjH2 k dxi 3x2 , H{H2 k dxi 3x2 ,
Отсюда получим
(Vi • V)Vi = P(r) = Pi -Г+P2 J,	(2.3.240)
где:
p ~	U dU i V	dU i UV dHj	V2 dH2
1"	Hj 3X1	H2	3x2	HiH2 3x2	HiH2 3xi '
n	U 3V	V	3V	UV dH2	и2 ЭН1
2	Hi 3xi	H2	3x2	HiH2 3xi	HiH2 3x2 v	1
Теперь примем a = Vp b = VOT, тогда зависимость (2.3.239) с учетом
условия divVi = 0 запишется в виде
(Vot • V)V1 = [grad(Vi • VOT)+rot(VfVOT)-Vyrot VOT -
- VOT -rot Vi - Vjdiv VOT ]: 2.
(2.3.242)
Глава 2
267
Так как
Vj VOT = Uw cos a+Vw sin a,
VOT = 0* +0j + (Uw sin a - Vw cos a)k,
rotVOT = 0z + 0j +
1 ( 3H2wsina
dH{w coso?
Эх2 ,
^1^21
то несложно получить
grad(V1VOT) =
d(Uw cos a + Vw sin a) - d(Uw cos a + Vw sin a) -
H{dx{	H2dx2
-	_ ЭН3 (Uw sin a - Vw cos a) - dH3 (Uw sin a - Vw cos a) -
rot,v'v-)=—й^ —'	й^ }’
VJrotV^ =
V ГdH2wsma dHjVvcosc?
H^H2 0X|	0X2 у
dH2wsina dHjWcosoc^-
0Xj
dx2
VOTrotVi =
wsincc rdH2V _ дН^ - v^cosa r dH2V dHft'
HXH2 djq dx2 J HrH2 3xj Эх2 ?
Кроме того,
Vj divVOT = C/divVOTr+VdivVOTJ,
-	1	(dH2H3wcosa SHiHoWsinc?
где divVnT =-------------------+—i— -------- — скалярная ве-
H\H2H31 9xt	Эх2 J
личина.
Подставляя полученные выражения в уравнение (2.3.242), найдем
= Ё(г) = ДГ+B2J,	(2.3.243)
где
1 3(L/wcosa + Vwsina)	1 dH3(Uw sina-Vwcosa)
Hi	3xt	H2H3	dx2
w sin ar dH2V dH{U
^1^2 k dxi Эх2
V Г 3H2wsina ^H{w cqscC
H1H2 0X|	^-^2 у
U Г dH2H3wcosa
H!H2H3(
dH{H3w sin a
Эх2
(2.3.244)
268
Глава 2
1 3(LWcosoc + VW sin а)	1 3H3(LWsina-VWcosa)
H2 dx2	#iH3
wcosocf dH2V дНЛ}'
+------ —--------4—
HlH2 < 3-Xj ^x2 >
U ( dH2w sin а
#1^2 < dXi
dll\w cos a
Эх2
V Г dH2H3wcosa ^дР^Н^жьтс^
Hj/f2H3 <	dx2 }
Компоненты Fp F2 массовой силы определим после выбора систе-
мы координат с учетом условия проведения процесса в конкретном
аппарате.
С учетом выражений (2.3.238), (2.3.240) и (2.3.243) уравнение
(2.3.237) перепишем так:
(^L+kw^\e + w— = -P(r)-E(r) + F.	(2.3.245)
V dt J dt
Умножим скалярно обе части этого уравнения на вектор ё, а за-
тем — на de/dt. Вследствие ортогональности ё и de/dt получим:
^-+kw2 = -P(r)e - E(r)e + F e,
dt
( de
dt
2	_ _______ _____
-_х de	de - de
= -Р(г)—-Е(г)—+Р—.
dt	dt dt
(2.3.246)
W
После вычисления скалярных произведений соответствующих
векторов уравнения (2.3.246) принимают вид:
= -kw2 -(Д + Еу - Д )cosoc-(Р2 + Е2 -F2)sin а;	(2.3.247)
da /п . гт t-xsina /	xcosa
— = (Pi+Ei-Fi]--------(P2+E2-F2) .
dt v 17 w v	7 w
(2.3.248)
Таким образом, вместо исходного векторного уравнения (2.3.236)
получили систему двух скалярных уравнений (2.3.247) и (2.3.248) для
определения модуля относительной скорости частицы и ее направ-
ления. Полученные уравнения содержат компонент полей скоростей
несущей фазы и его дифференциальных характеристик. Поэтому,
для того чтобы определить движение дисперсной частицы в потоке
несжимаемой жидкости, необходимо решить совместно систему ска-
лярных уравнений и систему уравнений движения несущей среды.
Отличительной особенностью такого подхода к описанию дви-
жения гетерогенных сред является возможность раздельного реше-
ния соответствующих уравнений сохранения сплошной и дисперс-
Глава 2
269
ной фаз. Практическая ценность такого разделения определяется не
только облегчением решения системы дифференциальных уравне-
ний, но и наличием огромного количества решенных гидродинами-
ческих задач для сплошной среды. С помощью полученной системы
скалярных уравнений, записанной в коэффициентах Ляме, многие
решения могут быть обобщены на случай течения гетерогенной сис-
темы. Приведем несколько примеров.
В работе [2.3.59] рассматривается начальный участок течения «сте-
пенной» жидкости по наклонной плоскости. Решение получено в виде:
п+1
2п+1 Q
п+1 h v h)
Alh2~2n -h3
h' = —---------
^2
(2.3.249)
2п+1
п
где Ax =
n m „ A 2(2n+l) Q2
I ---rtf ; A2=—----------о - расход жидко-
pg smp	3n + 2 gsm[3
сти, m2/c; h — толщина пленки, м.
С учетом уравнения (2.3.249) из уравнения неразрывности нахо-
дим поперечную скорость жидкости
V = —yh'.	(2.3.250)
h
Из уравнений (2.3.249) и (2.3.250) легко определить дифференци-
альные характеристики течения, необходимые для решения систе-
мы скалярных уравнений, т.е.
ди = 2п+1дГ уАй ди_= (
ду п Л21 h) ' дх +УЭу]й'
ЭУ_ 31/ XL
ду дх ' дх
V ду 7 /г h
h„ 2A,(l-n)h|-Zn-3h2 ,
А2
(2.3.251)
При известных полях скоростей несущей фазы и их дифференци-
альных характеристиках с помощью скалярных уравнений (2.3.247) —
(2.3.248) можно вычислить траектории дисперсных частиц в движу-
щемся слое «степенной» жидкости.
В работе [2.3.60] решение уравнения (2.3.249) обобщается на слу-
чай, когда жидкая среда стекает по поверхности пористого тела про-
извольной формы при наличии фильтрации. Полученные результаты
также могут быть использованы совместно со скалярными уравне-
ниями при расчете траектории дисперсных включений.
270
Глава 2
В работе [2.3.61] рассматривается течение жидкости между про-
ницаемыми параллельными стенками, движущимися в своих плос-
костях с заданными постоянными скоростями. Уравнения Навье-
Стокса с соответствующими граничными условиями решаются с
помощью преобразования Лапласа. Окончательные формулы для
полей скоростей и давления получены в виде бесконечной суммы
элементарных функций, которые легко дифференцируются по про-
дольным и поперечным координатам. В частности, учитывая первые
два члена разложения, получены следующие предельные формулы
для расчета гидродинамики течения на достаточно большом удале-
нии от входа:
3/7 f v2Vr,	A Wi~Wn	Ш + Ж
U =	1-^2 Y-sh(kx/h)-B2ch(kx/A) + 1	2y+ 1	2,
4	/2 \	/ Zn	Z
,3
v =	2__y bBiCh(Xx//i)-B2Xsh(Xx/12)),
4 3/r h J
3B2C7„u	«	... BiUj,	.	.
P = P^+ —2 H - sh(Xx / h) —ch(Xx / h),
2Л.Л	2k
где В, = KP1U„ (B2 -2B3); B2 = (W, - W>)/C7H -2; B3 = Ap/ftt/2; Л = ЗцК/h;
Др — разность давлений; Wv W2 — скорости движения стенок, м/с;
h — полурасстояние между стенками, м.
Отсюда дифференциальные характеристики течения находим
без проблем:
— = Щ/1 _Z_Y^ch(kx/B)-^sh(Xx/h)];
Эх 4 I h Ik h	h	)
dU 3UHy(Bi	..Л Wi~W2
эг=-^Tsh,Xx/71)-B2Ch(Xx/h,J+"^~:
ЭУ 3U„( у3 у Y В,	... В2Л2 '
---= ——	— sh/x/Л)—-—ch/x/й)
Эх 4 ^ЗВ3 АД*	Л ')
дУ
Эу
зц/ у2
4В Л2
1 [B1ch(>x/B)-B2/sh(>.x/ft)J
7
Следовательно, с учетом системы скалярных уравнений (2.3.247) —
(2.3.248), решение, изложенное в работе [2.3.61], можно обобщить на
случай течения многофазной неоднородной среды.
Глава 2
271
Численный расчет траектории частиц покажем на примере реше-
ния уравнений (2.3.249) —(2.3.251). В декартовой системе координат
компоненты Рр Е;, Ff. скалярных уравнений примут следующий вид:
дх ду	дх ду
А
Г	dU . ЭсЛ
= w cosa——+sina— ,
I	Эх ду)
г,	dv . av]
E7=w coscct—+sina— ;
l Эх Эу J
(2.3.252)
^I=g(l-p?/p2)sinp,
F2=-g(l-p1%2)cosp.
С помощью подстановки
eReL* _	_	_
t =———t, x = ERe£*x, y = hHy, d = hHd, U-U^U,
V* _	hV.
V =w = utWi	e = -^- =—	(2.3.253)
ERe	£* U*
перейдем к безразмерным переменным. Полученные выражения
(2.3.253) позволяют уравнения (2.3.247) — (2.3.248), решения (2.3.249) —
(2.3.251) и соотношения (2.3.252) привести к виду (черта сверху опу-
щена)
---= -Rekw2 -(Pj +Ei -F1)cosa-(P2 + E2 -F2)sina; (2.3.254)
da , r- c\sina / n , с c\cosa
— = (p+F -F)---------(P2+B2-F2--------;
dt	w	w
dh 3n + 2 f2n + lA ,2-2n „ 3
— =-------- ------- h2 -Eh3 ,
dx 2(2n+l) V n J	1
(2.3.255)
(2.3.256)
n TTdU	dU „ U dv V dv
где Pi=L7—+V—P2=——+——,
dx	dy Re dx Re dy
f	Э17	ЭС7)
= w cosa——+Resin a— ;
4	ox	dy J
„ f cosa dV .
E2 = w----—-+sma—- ;
Re Эх	Эу J
Re
Re „ pi . n
1 = f7 sin₽:
P27
Fr
Frl P2,
cosp;
2n + l
n+1 h
V=u^—, —
hdx' Эх
^dh
h dx'
272
Глава 2
ди 2n+l 1 Л yAn dV Г auAyfdhV у d2h
— =-----7II--I , — = - 2СГ + у—рУ— +U-—тг;
ду п h2\ h) дх	Jdyjh2\dx) hdx2
dV dU d2h Зп+2 (2п+1\п	«_2п 3 ^2 dh
dy dx dx2 2n+l v n J	2 dx
Выражение (2.3.256), в отличие от уравнений (2.3.254) и (2.3.255),
содержит производную искомой функции по координате х. Перей-
дем к производным по времени, а также построим уравнение для
расчета траектории дисперсной частицы. Изменения ее координат
за время At в безразмерных обозначениях определим следующими
соотношениями:
x(t + At) - x(t) = U At + w cosa At,
у(t + At) - у(t) = V At + Re w sin a At.
Отсюда, при At -> 0 получим:
— = [7 + wcosa;
dt
dy
— = V + Rewsina.
dt
(2.3.257)
(2.3.258)
Последнее уравнение позволяет рассчитать траекторию частиц
по времени и с учетом выражения (2.3.257) оно приводится к виду:
dh
dt
Зп + 2 (2п + 1Л ,2-2п
-------- ------- Л zn
2(2n+l) V п J
-Fih3 (U + wcosa).
(2.3.259)
Таким образом, задача сводится к численному интегрирова-
нию системы дифференциальных уравнений (2.3.254) —(2.3.255),
(2.3.258) —(2.3.259). Для расчета траектории относительно продоль-
ной координаты можно перейти к производным по переменной х с
помощью выражения (2.3.257). В этом случае уравнение (2.3.256) ре-
шается совместно с уравнениями:
dw _	1 dw
dx U+wcosa dt ’
da _	1 da
dx U+wcosadt'
dy _V + Re w sin a
dx	U + wcosa
Глава 2
273
Уравнение (2.3.255) при w = 0 имеет свою особенность. Вместе с
тем за начальное условие для относительной скорости следует при-
нимать wH = 0. Для раскрытия неопределенности в начальном сече-
нии разобьем уравнение (2.3.255) на две части:
da Ei sin ос Eicosa
— = _1-----+ _------(
dt w w
[(P1-E1)sina-(P2-E2)cosa]|H =0.
Тогда неопределенность в этом уравнении раскрывается в виде:
^cosocBV . dVy
+ smoc——
Эу
da
It
. (	dU „ . ЭсЛ
= sma cosa——+Resina—
н I.	Эх	ду)
+ cosa-----—
k Re Эх
н
н
а начальное значение ан находим из соотношения
tgaH =
P2-F2
(2.3.260)
Причем ан выбираем так, чтобы (dw/dt) | >0. Зависимость (2.3.260),
в свою очередь, позволяет существенно упростить уравнения для от-
носительной скорости (2.3.254), которое с учетом wH = 0 преобразует-
ся к виду:
dw _ Ei -Р{
dt н cosa н
Некоторые результаты численного решения безразмерных уравне-
ний (2.3.254) — (2.3.255), (2.3.258) — (2.3.259) приведены на рис. 2.64 — 2.69.
Как показал анализ полученных результатов, интенсивные изменения
модуля относительной скорости w и угла а происходят на начальном
участке течения. Этот участок соответствует режиму ускоренного дви-
жения частицы. Затем, когда сила сопротивления среды уравновесится
массовыми силами, функции w и а выходят на асимптоту. При этом час-
тица движется равномерно, с постоянной скоростью. Предельные зна-
чения этих функций зависят от множества параметров.
На картину течения сильно влияют реологические характеристи-
ки несущей среды. При уменьшении коэффициента консистенции
т модуль относительной скорости w и угол а растут (см. рис. 2.64,а
и б). В результате интенсивность осаждения частицы возрастает. На-
пример, при изменении коэффициента т от 0,02 до 0,005 второе сла-
гаемое Rewsina в правой части уравнения (2.3.258), подсчитанное по
предельным значениям w и а (кривые 1 и 3 на рис. 2.64,а и б), увели-
чивается более чем в три раза: от 2,17 до 6,74. Траектории осаждения
частицы при различных значениях коэффициента консистенции по-
274
Глава 2
Рис. 2.64. Результаты численного решения безразмерных уравнений: а — за-
висимость w от t; б — зависимость а от t при различных т для О = 0,0002 м2/с,
h = 0,002 м, Р =30°, п = 0,8, р° = 1000 кг/м3, р° = 3000 кг/м3, d = 0,002 м,
Fr = 0,5; кривая 1 - т = 0,02 (кг-сЛ‘2)/м, Re = 21,8; кривая 2 - т - 0,01 (кгсЛ'2)/м,
Re = 43,7; кривая 3 — т = 0,005 (кг-сл’2)/м, Re = 87,5
казаны на рис 2.65,а, б, в. Направление влияния реологического ко-
эффициента нелинейности среды п такое же, т.е. его уменьшение вы-
зывает рост значений функций ж и а (рис. 2.65,6 и в).
Рис. 2.65. Траектории осаждения частиц: а — за-
висимость h (сплошные линии) и у (пунктирные
линии) от t при различных т для Q = 0,0002 м2/с,
йн = 0,002 м, р = 30°, п = 0,8, р? = 1000 кг/м3,
р° = 3000 кг/м3, d = 0,002 м, Fr = 0,5: кривая
1 — т = 0,02 (кг-сЛ'2)/м, Re = 21,8; кривая 2 —
т = 0,01 (кг-сЛ’2)/м, Re = 43,7: кривая 3 —
т = 0,005 (кг-сЛ'2)/м, Re = 87,5; б и в — зави-
симости соответственно ю а от f при различ-
ных п для Q = 0,0002 м2/с, йн = 0,002 м, р = 45°,
т = 0,005 (кг-сЛ'2) /м, р? = 1000 кг/м3,
р° = 2000 кг/м3, d = 0,0025 м, Fr = 0,5: кри-
вая 1 — л = 0,6, Re = 191; кривая 2 — л = 0,8;
Re = 87,5; кривая 3 — л = 1,0; Re = 40; кривая
4 - л = 1,2, Re = 18
Глава 2
275
Рис. 2.66. Влияние диаметра частицы на параметры w и а на интенсивность осаж-
дения: а — зависимость w от t при различных d для О = 0,0002 м2/с, hK = 0,002 м,
Р = 45°, т = 0,005 (кг.сп2)/м, п = 0,8, pf = 1000 кг/м3, = 2000 кг/м3, Re = 87,5,
Fr = 0,5: сплошная линия — ун = hH; пунктирная линия — ун = hH/2; кривая 1 —
d = 0,002 м, кривая 2 — d = 0,0005 м, кривая 3 — d = 0,0001 м; б — зависимость h
(сплошная линия) и у (пунктирные линии) от t при различных d для Q = 0,0002 м2/с,
hH = 0,002 м, р = 45°, т = 0,005 (кг-сп’2)/м, п = 0,8, р° = 1000 кг/м3, р° = 2000 кг/м3,
Re = 87,5, Fr = 0,5; кривая 1 — d = 0,002 м, кривая 2 — d = 0,0005 м, кривая 3 —
d = 0,0001 м
Как и ожидалось, при уменьшении диаметра частицы наблюда-
емые параметры wn а, а также интенсивность осаждения, уменьша-
ются. На рис. 2.66,6 приведены траектории частиц, которые начина-
ют осаждаться от свободной поверхности слоя. Соответствующие
этим траекториям значения w показаны на рис. 2.66,а сплошными
линиями. Поскольку дифференциальные характеристики сплош-
ной среды по толщине слоя изменяются, значения угла осаждения
и относительной скорости на начальном участке зависят от началь-
ной координаты частицы. Для частиц с одинаковыми диаметрами и
разными начальными координатами ун эти характеристики со вре-
менем выходят на общую асимптоту
В зависимости от отношения плотностей сплошной фазы и дис-
персных включений может наблюдаться как осаждение, так и всплы-
тие частиц. Когда р?/р5 <1,, уменьшение этого отношения вызывает
рост относительной скорости и угла осаждения частицы (рис. 2.67,а).
При этом время осаждения до поверхности течения уменьшается
(рис. 2.67,6). В случае Р?/р2>1 при уменьшении отношения плот-
ностей угол а и время всплытия частицы растут, а предельное значе-
ние w падает. Время всплытия или осаждения зависит от начального
местоположения частицы (см. рис. 2.67,6). От исходного положения
частицы зависят значения функций w и а, которые на участке рав-
276
Глава 2
а	б
Рис. 2.67. Влияние отношения плотностей сплошной фазы и дисперсных включе-
ний на траектории частиц: а — зависимость а от t; б — зависимость h (сплошная
линия) и у (пунктирные линии) от t при различных р° > Pi для Q = 0,0002 м2/с,
h = 0,002 м, 0 = 30°, т = 0,005 (кг.сп'2)/м, п = 0,8, р° = 1000 кг/м3. d = 0,0005 м,
Re = 87,5, Fr = 0,5; кривая 1 — р° = 2000 кг/м3, у = hH, кривая 2 — р^ = 6000 кг/м3,
ун = hH, кривая 3 — р° = 2000 кг/м3, ун = йн/2, кривая 4 — р° = 6000 кг/м3,
у“ = hH“/2
номерного движения стремятся к своим предельным значениям. Что
касается выхода кривых на общую асимптоту, то, как показано на
рис. 2.67,а, она связана с достижением частицей границы течения и
завершением относительного
Рис. 2.68. Зависимость а от t при раз-
личных U. для h = 0,002 м, Р = 30°,
т = 0,005 (кг-с)/м, п = 1, р? = 1000кг/м3,
р° = 3000 кг/м3, d = 0,0005 м; кривая
1 — U. = 0,1 м/с, Re = 40, Fr = 0,5;
кривая 2 — U. = 0,2 м/с, Re = 80,
Fr = 2,0; кривая 3 — U. = 0,4м/с, Re = 160,
Fr = 8,2; кривая 4 — U. = 0,6 м/с,
Re = 240, Fr = 18,3
движения в направлении оси у.
При этом относительное движе-
ние частицы в продольном на-
правлении с постоянной скоро-
стью сохраняется.
При постоянных физико-
химических свойствах фаз из-
менение расхода на динамику
частицы влияет через гидроди-
намические характеристики не-
сущей среды. Характерная тол-
щина слоя на входе Лн и средняя
скорость подачи U,, которые оп-
ределяют расход жидкости Q, на
характеристики осаждения вли-
яют по-разному. Например, при
увеличении U. число Re и угол а
возрастают (рис. 2.68), отноше-
ние Re/Fr и относительная ско-
рость w уменьшаются.
Глава 2
277
Траектории частиц приведены на рис. 2.69. На характер кри-
вых влияет способ обезразмеривания переменных. Из выражения
(2.3.253) следует, что безразмерная скорость V пропорциональна ха-
рактерной толщине hw, а безразмерное время обратно пропорцио-
нально квадрату этой толщины (Т = (v/h£)t, V = (hH/v)V, U = U/U^.
Поэтому при увеличении Лн безразмерное время осаждения резко
падает (см. рис. 2.69,6). Безразмерные Vh t от выбора U. не зависят, а
безразмерная скорость U обратно пропорциональна U., поэтому при
увеличении скорости подачи наблюдается относительно небольшой
разброс траектории частиц (см. рис. 2.69,а). Как видим, при росте ско-
рости подачи среды безразмерное время осаждения уменьшается.
Расчеты показали, что при росте отношения Re/Fr безразмерная тол-
щина слоя уменьшается (см. рис. 2.65,а; 2.69,а и б).
Отметим, что при анализе предельных значений угла осажде-
ния а необходимо учесть, что координатная ось Ох с горизонтальной
линией составляет угол 0. Приведенные результаты численных рас-
четов качественно согласуются с реальной картиной течения. Дан-
ный подход может быть успешно применен для расчета динамики
дисперсных частиц при моделировании различных гидромеханиче-
ских процессов.
Безусловно, область применения векторного уравнения (2.3.236),
преобразованного в систему (2.3.247) —(2.3.248), не ограничивается
модернизацией уже полученных решений. Подход может быть ус-
Рис. 2.69. Зависимость h (сплошные линии) и у (пунктирные линии) от t: а —
при различных [/. дляЛ = 0,002м: кривая 1 — U. = 0,1 м/с, Re = 40, Fr = 0,5; кривая 2 —
U. = 0,2 м/с, Re = 80, Fr = 2,0; кривая 3 — U. = 0,4 м/с, Re = 160, Fr = 8,2;
кривая 4 — U. = 0,6 м/с, Re = 240, Fr = 18,3; б — при различных hH для
[/. = 0,1 м/с: кривая 1 — hH = 0,002 м, Re = 40, Fr = 0,5, кривая 2 — hH = 0,004 м,
Re = 80,Fr = 0,25; кривая3 — hH = 0,012м,Re = 240,Fr = 0,085(0 = 30°,m = 0,005(кг.с)/м,
n = 1, p° = 1000 кг/м3, p° = 3000 кг/м3, d = 0,0005
278
Глава 2
пешно использован при математическом моделировании различных
гидромеханических процессов с гетерогенными рабочими средами.
Поскольку в обозначениях выражений (2.3.241) и (2.3.244), входящих
в уравнения (2.3.247) и (2.3.248), присутствуют не только поля ско-
ростей, но и дифференциальные характеристики течения несущей
фазы, эта особенность должна быть учтена при разработке или мо-
дернизации соответствующего численного метода.
Один из перспективных методов, позволяющий учитывать слож-
ную геометрию течения и нелинейную реологию среды, — это ме-
тод поверхностей равных расходов [2.3.2], [2.3.52], [2.3.53]. Он дает
возможность численно находить как поля скоростей и давления, так
и дифференциальные характеристики различных гидродинамиче-
ских процессов. Покажем особенности применения метода поверх-
ностей равных расходов в сочетании с уравнением (2.3.236), то есть с
системой (2.3.247) —(2.3.248).
В соответствии с методом поверхностей равных расходов введем в
поле течения среды линии тока ук = ук (xt), к = 1,N. Положения вве-
денных линий определяются с помощью дифференциальных урав-
нений [2.3.53]
^УкЦ йУк , 2HiZV0 yttl -yt dAt. k=2jj.
dx} dxx &k	&k dx{
^ = 0;	(2.3.261)
dx{
rAe	= (alH2ZU)k +(a1^2^^)k+l-
Распределение скоростей несущей среды на линиях тока опреде-
ляется из преобразованного уравнения движения, которое записыва-
ется в виде системы обыкновенных дифференциальных уравнений
Рик dUk=J_N^ldMx+J{	}_dYk—?UkVkdHi+Tk
Ъ dxx Hx£k dxx 7Hxdxx HXH2 dx2
(2.3.262)
где
Уа+i	orj2 др-г
Мк(х{) = f J(xi,x2)dx2,	J(x1,x2) = H2pF2+—^—1
y>	°X2
m
H? дх2 V J
^2 ^X2
Для вычисления производных по поперечной координате х2 пред-
ставим сеточные решения в виде разложения в ряд по полной систе-
ме базисных функций:
Глава 2
279
N
l/=EA7(x1)4'lg[yt(x1)].
J=i
Вид базисных функций, удовлетворяющих соответствующим
граничным условиям, выбирают исходя из геометрии области и ус-
ловия течения [2.3.2].
После интегрирования системы (2.3.261) —(2.3.262) с помощью од-
ного из численных методов решения обыкновенных дифференци-
альных уравнений определяют положения поверхностей равных
расходов ук и значения скоростей Uk на них. При известных значе-
ниях производных dUk/dxv которые вычисляются как правые части
дифференциальных уравнений (2.3.262), частные производные нахо-
дят по формулам:
дик dUk dVkdyk' к = —
dxx дук dx{ '
Согласно уравнению неразрывности, имеем:
дНхН3Ук^ дн2н3ик
Эх2	Э*!
(2.3.263)
(2.3.264)
Кроме того, из определения ук как линии равного расхода следует:
vk=uk— - k =	(2.3.265)
dx{
Отсюда
dUk , тт „ , —
3-L = ^-i-yi+t/tyl. * = 2,N.	(2.3.266)
vX| C/Xj
В этом соотношении значения ук определяют из уравнения
(2.3.261), а вторые производные — расчетным путем:
у№1)=У*-<-ХУ-^)-2У*^)+У*(х» + Ах1).	(2.3.267)
ДХ1
Анализ структуры последней формулы показывает, что коорди-
наты начального положения дисперсной частицы должны задаваться
в сечении х1н + Дхг
Поскольку траектории частиц отличаются от положения поверх-
ностей равных расходов, возникает необходимость вычисления ком-
понентов скоростей несущей фазы и их дифференциальных харак-
теристик между линиями тока. Поэтому, исходя из полученных зна-
чений искомых величин на линиях тока, на каждом шаге вычислений
решается задача аппроксимации. Полученные характеристики несу-
щего потока используются в уравнениях (2.3.247) и (2.3.248) для рас-
чета траектории движения дисперсных частиц.
280
Глава 2
В качестве примера рассмотрим течение гетерогенной среды не-
ньютоновского реологического поведения по поверхности ротора
осадительной центрифуги. Выберем коническую систему координат
= х, х2 = у, х3 = <р с коэффициентами Ламе: Нг = 1, Н2 = 1, Н3 = г,
у которой координата х совпадает с образующей ротора. Компонен-
ты векторов Р и Е вычисляются по формулам (2.3.252). Массовую
силу определяем следующими составляющими вектора центробеж-
ного ускорения:
Ft = со2х sin2 р, F2 = -со2х sin р cos Р.
Для определения динамических характеристик несущего потока
применим метод поверхностей равных расходов. В конической си-
стеме координат уравнения (2.3.261) и (2.3.262) запишутся в виде:
&Ук+1 _&Ук Ук+1~Ук Ук+1~Ук (и )
dx dx х (Uk +Uk+i) dx k k+l
dUk CD2sinPf 4 . o dyN\
=	-- (yw-yJsmP-xcosP—+
dx Uk <	dx J
ac/J"
дУ ,
m d
4----——
p(7t Эу
2	• 2
CO xsin ф
~Uk
Алгоритм решения данной системы приведен в работе [2.3.62]. Ос-
тальные характеристики потока определяются из формул (2.3.263)—
(2.3.267).
Закономерности возникновения самоорганизации
и динамического хаоса
Интенсивные тепломассообменные процессы в химико-техноло-
гических и теплообменных устройствах сопровождаются развитием
неустойчивых режимов в отдельных подсистемах: ламинарные ре-
жимы течения жидких пленок переходят в волновые и турбулентные
течения, в барботажных аппаратах развивается неустойчивость Тей-
лора, на поверхности жидкой фазы в массообменных аппаратах воз-
никает неустойчивость Марангони, в неоднородно-обогреваемых
емкостях образуются конвективные токи. Предотвратить развитие
неустойчивости в большинстве случаев невозможно, а в некоторых
случаях и нецелесообразно, так как возникающие неустойчивости
интенсифицируют тепломассообменные процессы.
Развитие неустойчивости приводит к появлению самоупорядо-
ченных монохроматических, маломодовых хаотических и многомо-
довых турбулентных режимов [2.3.64—2.3.66].
Глава 2
281
Для хаотических и турбулентных режимов характерны значи-
тельные разбросы гидродинамических и тепломассообменных пара-
метров. Вероятность выхода системы на аварийный режим работы
при хаотической неустойчивости выше, чем при других видах неус-
тойчивости.
Монохроматические режимы сочетают высокую интенсивность
тепломассообменных процессов, обусловленную упорядоченным
конвективным движением жидкости, с незначительными разбросами
тепломассообменных параметров и устойчивостью к возмущениям.
В целях предотвращения аварийных ситуаций в высокоэффек-
тивных процессах целесообразно использовать самоорганизующие-
ся режимы, для чего необходимо исследовать условия возникнове-
ния и закономерности долговременного развития неустойчивых ре-
жимов, провести их классификацию и найти условия перехода хао-
тических и турбулентных режимов в самоорганизующиеся.
Современная нелинейная динамика переживает радикальные
изменения. В нелинейных динамических системах, описываемых
нелинейными уравнениями с регулярными (неслучайными) коэф-
фициентами, совершающих колебания под действием регулярных
внешних сил периодической и особенно непериодической природы,
возникают непредсказуемые и хаотические на вид случайные коле-
бания. Иными словами, решения этих уравнений сильно зависят от
начальных условий. Другое свойство хаотических колебаний — они
«забывают» о начальных условиях. Хаотическая динамика (или ди-
намический хаос), свойственная всем нелинейным явлениям нежи-
вой и живой природы, вызвала в современной нелинейной динамике
революцию. До этого были известны три типа динамического движе-
ния: равновесное, периодическое (или предельный цикл) и квазипе-
риодическое. Эти состояния динамических систем на фазовой плос-
кости получили название «аттракторы», поскольку при затухании
движения или в случае потери устойчивости система «притягивает-
ся» к одному из перечисленных состояний. Хаотические колебания
и их нелинейные взаимодействия создали новый тип движения, свя-
занный с состоянием, получившим благодаря работам Рюэля, Такен-
са, Лоренца название «странный» аттрактор.
Возникновение аттракторов различной формы связано с нели-
нейным взаимодействием эволюционирующих возмущений. Извест-
ны модели (Гинзбурга-Ландау, Свифта-Хоэнберга, Ньюэлла-Уайхе-
да-Сегеля, Ван-дер-Поля), описывающие бифуркационные процессы
в нелинейных системах. Однако эти модели оставляют еще много не-
решенных вопросов, связанных с учетом различных видов нелиней-
ных взаимодействий возмущений.
282
Глава 2
Общее нелинейное параболическое уравнение (ОНПУ)
Большой класс неустойчивых теплофизических, физико-хими-
ческих, химически реагирующих, электрохимических, физических,
биологических и гидродинамических нелинейных процессов опи-
сывается известными системами нелинейных дифференциальных
уравнений в частных производных [2.3.67]:
?^(ф)+1о1(Ф)^4м,у(ф)-^ = 0.	(2-3.268)
dt /=1 dXi ij=i J дх,дх}
где ф = Цфр..., фп||Г — вещественный вектор, определенный в области
D = {(£, ххх2 )|t > 0, - оо < Xi < оо}; N = ||Nj,..., Nn ||Г; Q, М - матрицы пхп;
^12 = ^21’
Первые два слагаемых уравнения представляют собой известные
уравнения кинетики и биофизики, а при соответствующей конкре-
тизации вида коэффициентов — уравнения кинетики реакций типа
Белоусова-Жаботинского. Первое, второе и четвертое слагаемые
описывают те же реакции с диффузией, а также теплопроводность
с нелинейными источниками (стоками) энергии. В полном виде урав-
нения типа (2.3.268) характеризуют различные гидродинамические
явления и могут быть преобразованы в систему квазилинейных диф-
ференциальных уравнений с Источниковыми (стоковыми) членами,
исследованную в работе [2.3.68]. В общем случае данная система мо-
жет описывать совмещенные процессы, например конвективный
тепломассообмен, поскольку на вектор N не накладываются ограни-
чения на природу субстанции.
Пусть уравнение (2.3.268) допускает стационарное решение ф = ф0,
которое в открытой системе в результате внешнего воздействия либо
случайным образом при некоторых значениях параметров теряет ус-
тойчивость. В закритической области, согласно этому уравнению,
возбуждаются и растут возмущения, принадлежащие непрерывной
полосе спектра волновых чисел.
Зададим возмущенное решение уравнения (2.3.268) в виде:
ф =ф0 + ф.	(2.3.269)
Задача о нелинейном развитии возмущений из непрерывной по-
лосы спектра волновых чисел решается с помощью волновых паке-
тов [2.3.69-2.3.74]:
_	^20 +
ф = J J	F(kl,k2)expi(klxl + к2х2-а)1)с1к^к2 + к.с., (2.3.270)
к10-Д*! jc20-m2
Глава 2
283
где к10, к20 — центры волнового пакета по осям хр х2 соответственно;
Дкр Дк2 — ширина волнового пакета по осям хр х2 соответственно;
со = cor + zcOp к.с.— комплексно-сопряженные величины.
При допущениях:
= 0(e);	= 0(e);	= 0(e); (Зсо£/3 k)/co/=s0 = 0(e); е «1 (2.3.271)
к20 Фо
спектрально узкий волновой пакет может быть представлен в виде
квазимонохроматической волны
_ kjo+Akj к20+Дк2
ф= f J F(k1,k2)expz(k1x1 + k2x2-cot)dk1dk2 + K.c.=
ki0-Aki к20-Дй2
= Aexpz(kioxj +k20x2-co(klo,k2O)t)+K.c.=
= a(EtfE2t,Ex1,Ex2)expzO(Et)xexpz(klox1 + к2х2) + к.с.,	(2.3.272)
где
Akt AA2
A= J f F(k10+8k1,k2+8k2)expz(8k1x1 + 8k2x2-
-Akt -Дк2
' do/
if a2co
2l 3k2
= A(x11,x21,x12,x22,t1,t2)+0(E3).
8к^-
' 3co л
3k7i
я. < 1
6k2t— —-
2 2( 3 k,
32co
3kp3k:
(5k2)2t-
(5ki)2t-
6 kfi k2t) 38^38^ + 0(e3 ) =
(2.3.273)
Из формул следует, что сумму т гармоник, принадлежащих спект-
рально узкому волновому пакету, можно представить в виде квазимо-
нохроматических волн, причем амплитуда а и фаза 0, как видно из фор-
мулы (2.3.273), являются функциями медленных переменных (st, ex):
tg — t; tj — Et; t2 = E t; x^ — x^q; x2 = x2q; Хц = exp x2j — ex2;
x12 = e2xp x22 = e2x2 .	(2.3.274)
Введем разложение
Ф = Фо + £ X expz'ZfkjXjo + k2x20 -corto)+K.c.,
j=i /=-«
(2.3.275)
а также следующие операторы, учитывающие тот фактор, что про-
цессы протекают на многих масштабах:
284
Глава 2
д	д	Э	2	Э
---=----+ е--+ е -—;
dxj	Эх10	Эг)1	Эх12
Э	д	д	2	д
— = -—+Е-—+е -—;
дх2	Эх2о	vT]2	дх22
д	д	Э(йг Э	Эсог Э	2 д
dt dt0	Эк.! Эщ	дк2 Эт]2 dt2'
Л1=£(Xi-1sr^; Л2=е(Х2”1^)'А'7)
(2.3.276)
(2.3.277)
где а!// — вектор, комплексно-сопряженный с Aj;\
Таким образом, редукция уравнения (2.3.268) к уравнению для амп-
литуды нелинейного возмущения проводится комплексно: с использо-
ванием волновых пакетов (2.3.270), методов многих масштабов (2.3.276),
модификацией метода Мандельштама, согласно которому т гармони-
ческих волн с различными волновыми числами и частотами преобразу-
ются к виду квазимонохроматических волн с нелинейными амплитудой
и фазой, зависящими от медленных переменных. Эта идея была исполь-
зована при преобразовании спектрально узкого волнового пакета (фор-
мулы (2.3.272), (2.3.273)). Наконец, было использовано преобразование
(2.3.277), учитывающее групповую скорость огибающей волны, что ха-
рактерно для реальной нелинейной диспергирующей среды.
Нелинейная система дифференциальных уравнений в частных
производных в е-м приближении, полученная после подстановки
разложения (2.3.275) в систему (2.3.268) с учетом уравнений (2.3.276)
и (2.3.277), становится несовместной. Для ее разрешимости требует-
ся, чтобы правая часть полученной системы была ортогональна лю-
бому решению однородной сопряженной системы, как это было ра-
нее проведено [2.3.69—2.3.72]. Эта трудность преодолена с помощью
другого метода, изложенного в работах [2.3.67, 2.3.73, 2.3.74].
С учетом уравнений (2.3.276) и (2.3.277) в системе дифферен-
циальных уравнений, полученной после подстановки выражения
(2.3.275) в уравнение (2.3.268), выделим линейную часть, обозначив
ее матричным оператором через L, оставшуюся нелинейную часть —
также матричным оператором той же системы через V. Тогда полу-
(2.3.278)
(2.3.279)
ченную систему уравнений можно представить в виде:
Глава 2
285
Умножим левую и правую части этой системы на сопряженную
матрицу L*, получим:
L‘LX = L‘V.	(2.3.280)
Разложим эти матрицы по малому параметру в:
L = Lo + eLj + e2L2 + e3L3;
X = Xo + eXt + e2X2 + e3X3;
L =L0 + eL1 + e2L2 + e3L3;
V = Vo + еУ + £2 V2 + e3 V3.
Соберем члены при одинаковых ск, к = 0, 1, 2, 3.
при Е° : L0L0X0 = Vo;
при е1 : (LqL! +L1Lo)Xo +L LqX.| = Vp	(2.3.281)
при E2 : (L0L2 + LjLj + L2L0 )Xo + (ЬдЦ + LjL0 )Xj + L0L0X2 = V2
ит.д.
Последовательно исключая секулярные члены различных при-
ближений в системе (2.3.281), выделим секулярные члены третьего
приближения. Такая процедура позволила получить уравнение для
амплитуды огибающей волны в третьем приближении
0t2 дк^ Эх12
zY Э2сог _Э2со,
’А Э*Г+'Эк?) Эп?
/ Э2сог 32coz- 4
\ Э^Э^
ЭД) l Эсог дА$ Эсог ЭД)	i Эсо, dA$ i dcoz ЭД)
Эк2 Эх22 tdki Этц еЭ£2 Эт]2
if d2cor + . Э2сог Э2 Д
Ч Эк^ +Z J Эг|2
311'^- + (₽1+'₽2)|A)|2A)=0,
Э&1Эк2 у оГ|1Эт]2
(2.3.282)
где Рр Р2 — константы Ландау, причем Pj характеризует нелиней-
ное затухание возмущений, р2 — нелинейную дисперсию. Эти кон-
станты могут быть найдены из предыдущего приближения.
Подставляя в полученную формулу амплитуду волны Ао в виде:
Д = А+ exp z 8ksxs +	8ks + - ~ 8ks8kt 11 ,
+	s s s 2dks^kt s J
где повторяющиеся индексы в 8ksxs указывают на суммирование,
и переходя от переменных масштаба t2, х12, х22 к переменным t2,
Эсо	Эсог х
Л12 = х12 —^22 = х22“T7“f2 ' для амплитуды А. волнового па-
oki	ок2
286
Глава 2
кета, центр которого смещен на 6кр 6к2 от кривой нейтральной ус-
тойчивости, получим общее двумерное нелинейное параболическое
уравнение в виде:
z г Эсо,- ЭА.
E^d/q Эщ Эк2 Эт)2 2
. d2O)i Э2А+ .Г
|2 k дкхдк2
ЭА+
8t2
Эсо. ЭаЛ if Э2сог
2^ дк}
Ч ., Э2ш,2
,Э2соЛ Э2А
И Э со
2 Эк2 Эк2 J Эт)2
=	-(₽! +'’Р2)|Л|2 А
Е
Запишем в безразмерных переменных
ЧЧ drft
'l ЭЧ
Эк^ J Эт^Эпг
(2.3.283)
Лю=Л1

Тогда
ЭА / ЭА
ЧГ + г «31
2со,-
Е2
Э2СО;-
"akf
А = А
' Л20 ~ Л2
е2₽;
со,-
ЭА
+о22 -----
дТ]1О ^20
(	^2(Oi
+ sgn------1-
дт
д2А
о---^'«12	9
Эк2 ) Эт]20
2со,
Э2со,-
2 О СО;
г
(2.3.284)
где
( ^2coj •
+ sgn—f-zan
k dki
. ч Э2д
xr-^ih—ч—:
д2А

(2.3.285)
_эЧ/э*2. „ _Ч/< „ _₽2.
“’аЧ/Эк2'	12 эЧМ2' 2 ₽,'
Эсо,-
«31 =^—~
31 Э^
а
2____
d2COz
2 *>Ч
дкгдк2
эЧ
Ч
эЧ
Ч
Эсо.-
«32=—L
«/ =
2
Эк2
2 Э2со;-
Эк^к2
Э2сог-
Эк?
Э2соу

дк%
(2.3.286)
Глава 2
287
Анализ численных решений ОНПУ. Безразмерные комплексы
(2.3.286), являющиеся критериями динамических нелинейных си-
стем, имеют простой физический смысл: а^. характеризует отноше-
ние дисперсии групповой скорости в j-м направлении к дисперсии
инкремента, a3j- — отклонение центра волнового пакета в j-м направ-
лении от гармоники максимального инкремента; а2 — нелинейную за-
висимость фазы (частоты) от амплитуды, т.е. нелинейную дисперсию.
Уравнение (2.3.285) описывает эволюцию огибающей волны, по-
явившейся в результате нелинейного взаимодействия возмущений,
заданных в виде волнового пакета. Из этого уравнения получаются,
как частные случаи, известные уравнения, приведенные в работах
[2.3.75-2.3.76].
Для характеристики поведения динамических систем использова-
лись показатели Ляпунова, энтропия Колмогорова-Синая и отображе-
ние Пуанкаре. Например, для консервативных систем физики плаз-
мы, нелинейной оптики и гидродинамики идеальной жидкости при
сог = Р; = 0 уравнение (2.3.285) приводится к хорошо известному нели-
нейному параболическому уравнению Шредингера [2.3.75 — 2.3.76].
Количественной характеристикой аттрактора являются показа-
тели Ляпунова, определяемые для нелинейных динамических сис-
тем по методу, изложенному в работе [2.3.77]. Для системы (2.3.285)
показатели Ляпунова находились в пространстве ап, 0П:
1
МапоЛо)=Ит-1п||и(т,апО,0пО)||,
Т—»оо Т
где п(т, ап0, 0лО) — вектор функций чувствительности (касательный
поток). Причем, если все показатели Ляпунова отрицательны, то
система сжимается по всем направлениям ап, 0п и аттрактором в про-
странстве ап, 0п является устойчивый узел или устойчивый фокус. Об-
ращение в нуль одного из показателей Ляпунова (при отрицательном
значении всех остальных) свидетельствует о наличии предельного
цикла. Равенство нулю показателей Ляпунова п при отрицательных
значениях остальных показателей соответствует существованию
n-мерного тора. Появление положительных показателей указывает
на возникновение стохастического аттрактора.
Для характеристики динамического хаоса была также исполь-
зована энтропия Колмогорова-Синая. Этот метрический инвариант
динамических систем впервые был введен Колмогоровым [2.3.78].
Впоследствии это направление развито Синаем [2.3.79]. Мерой раз-
вития турбулентности являлась положительность метрического ин-
варианта динамических систем, приводящая к разбеганию экспо-
ненциально фазовых траекторий.
288
Глава 2
Наконец, для характеристики поведения динамических систем
использовалось также отображение Пуанкаре на плоскости.
Комплексное исследование этих положений для количествен-
ной и качественной характеристики нелинейных динамических
систем позволило проследить качественные изменения траекторий
этих систем при изменении параметров уравнения (2.3.286) при чис-
ленном решении общего нелинейного параболического уравнения
(2.3.285), т.е. исследовать бифуркацию.
При этом на разных стадиях эволюции нелинейного взаимодейст-
вия возмущений проявлялись известные последовательности би-
фуркаций, приводящих к странному аттрактору, к перемежаемости,
к удвоению периода по Фейгенбаумому, к рождению и разрушению
трехмерного тора, и, наконец, последовательность, приводящая к го-
моклиническому контуру.
На основе численного решения уравнения (2.3.285) [2.3.67,2.3.69—
2.3.74] установлено, что все управляющие безразмерные параметры
ау азу а2' названные нами критериями нелинейных динамических
систем, влияют на характер возмущения, но доминирующую роль
в перестройке возмущений, определяющих появление либо самоор-
ганизации, либо хаоса (турбулентности), играет о^. Учет влияния
и других критериев уравнения (2.3.286) на характер взаимодействия
и развития возмущений позволил установить следующие закономер-
ности возникновения самоорганизации и турбулентности (хаоса)
и перехода между ними в гидродинамических, теплофизических,
физических, химически реагирующих и биологических системах
[2.3.67, 2.3.73, 2.3.74]:
I.	Линейная зависимость фазы для распределенных систем или
частоты для нераспределенных систем от амплитуды возмущения
является необходимым условием самоорганизации. Возможны и вы-
рожденные случаи этой линейной зависимости: равенство нулю уг-
лового коэффициента или свободного члена либо того и другого од-
новременно.
Увеличение дисперсии способствует возникновению самоорга-
низации.
II.	Основным условием возникновения турбулентности (хаоса) яв-
ляется нелинейная зависимость фазы для распределенных систем или
частоты для нераспределенных систем от амплитуды возмущения.
III.	В хаотических, неупорядоченных системах самоорганизация,
когерентные структуры, порядок возникают в результате нелиней-
ного взаимодействия возмущений и наоборот.
IV.	Переход от одного вида нелинейного взаимодействия к друго-
му, а также возникновение структуры или явления сопровождаются
Глава 2
289
изменением распределения энергии по спектру, т.е. сужением (само-
организация) либо расширением (турбулентности) энергии по спект-
ру Возможно промежуточное состояние.
Указанные закономерности получены на основе анализа числен-
ных решений уравнения (2.3.285) и могут быть использованы для уп-
равления явлениями самоорганизации и турбулентности (хаоса).
Физическое представление явления самоорганизации и хаоса
(турбулентности) можно пояснить с помощью рис. 2.70. На этом ри-
сунке дано модельное представление самоорганизации и хаоса как
режимов, получившихся в результате нелинейного взаимодействия
возмущений в закритической области после потери устойчивости.
Режим 1 соответствует самоорганизации; режим 2 — явлению пере-
хода от самоорганизации к хаосу; режим 3 — хаосу.
Режим 1
i
i
Hmm®
»©©©©©©©©
Кельвинские кошачьи глазки
Многорукавные спиральные волны в сре-
де с реакцией Белоусова-Жаботинского.
Интервал между кадрами 15 с
Режим 2
!>©
|©©@© ©@>©|
te© ®@@@
»©©©©©©©©«
I ©>©©	©®в)(В1
Режим 3
Неупорядоченное поле капиллярных волн
Рис. 2.70. Модельное представление самоорганизации и хаоса (турбулентности)
290
Глава 2
Как следует из рисунка, возникшая структура характеризуется
постоянной амплитудой и фазой для огибающей волны; элементы
структуры можно опоясать периодической линией. Такой же лини-
ей можно опоясать и более сложные структуры, как, например, кель-
винские кошачьи глазки и многорукавные спиральные волны в сре-
де с реакцией Белоусова — Жаботинского. В обоих случаях имеем
огибающую волну с постоянной амплитудой и фазой. Для возникно-
вения самоорганизации необходимо выполнение пунктов I, II,III. По-
нятно, что такую огибающую периодическую волну нельзя постро-
ить для режимов 2 и 3, для которых необходимо выполнение пунктов
II, Ш, IV.
е
Рис. 2.71. Самоорганизация случайного поля
возмущений амплитуды (а—е) и фазы (ж —к)
в среде без дисперсии (ап = а12 = а2 — 0) в
результате самоорганизации во всех точках
пространства значения а и 0 постоянны
Такое упрощенное тол-
кование явлений самоор-
ганизации и хаоса вытека-
ет из сложных теорети-
ческих расчетов, изложен-
ных выше, и закономер-
ностей, представленных
пунктами I—IV, для различ-
ных видов сценарий, при-
водящих к бифуркации.
В качестве численного
анализа решений ОНПУ
приведем характерные
примеры, характеризу-
ющие возникновение са-
моорганизации либо тур-
булентности.
Развитие случайного
поля возмущений амплиту-
ды и фазы в среде без дис-
персии (ан = а12 = а2 = 0),
приводящее к самоорга-
низации, представлено
на рис. 2.71. В начальный
момент (т = 0) выбрано слу-
чайное поле возмущений
амплитуды и фазы из таб-
лицы случайных чисел. В
процессе развития исполь-
зовано условие I. Характе-
ристики волнового пакета
Глава 2
291
(амплитуда и фаза волны) эво-
т = 8,0 т=14,0
т = 4,0
Рис. 2.72. Сужение волнового пакета при
возникновении самоорганизации в сре-
де без дисперсии (ап = а12 = а2 = 0)
люционировались к монохро-
матической огибающей волне,
полученной в результате нели-
нейного взаимодействия воз-
мущений (условия I, III).
В этом случае непрерывный
спектр волновых чисел волно-
вого пакета сужается. Волновой
пакет эволюционирует к моно-
хроматической волне — усло-
вие IV (рис. 2.72).
В случае нелинейной зави-
симости фазы (частоты) от амплитуды график зависимости амплиту-
ды возмущения а принимает вид острых клиньев (рис. 2.73).
При многомодовой неустойчивости возбуждаются и растут воз-
мущения, принадлежащие широкой полосе спектра волновых чисел.
Происходит расширение волнового пакета при развитии многомо-
довой турбулентности (см. рис. 2.74). Амплитуды, симметричные от-
носительно центра волнового пакета, не равны друг другу. Энергия
возмущения достаточно равномерно распределена по спектру воз-
бужденного волнового пакета.
Траектории первоначально близких систем расходятся экспонен-
циально. В системе развивается многомодовая турбулентность.
Из рис. 2.73 и 2.74 следует, что первоначально в процессе име-
ло место моногармоническая волна. Затем с помощью тех или иных
взаимодействий, вынужден-
ных или естественных, флук-
туационных, выполнялось ус-
ловие II, а именно, фаза (либо
частота) нелинейно зависела
от амплитуды. В этом случае,
как видно из рис. 2.74, происхо-
дит расширение спектра вол-
новых чисел. Произошел пе-
реход к турбулентности, о чем
свидетельствуют все извест-
ные критерии для динамиче-
ских систем, характерные для
этого режима.
Таким образом, условие IV
является обязательным для
Рис. 2.73. Эволюция огибающей волны
при возникновении турбулентности
292
Глава 2
Рис. 2.74. Расширение волнового пакета
при развитии многомодовой неустойчи-
вости в среде с а2 * О
всех переходов, характеризу-
ющих качественные измене-
ния траектории динамических
систем, т.е. переход системы к
самоорганизации сопровож-
дается сужением спектра, а
переход турбулентности —
расширением спектра. В обо-
их случаях переход сопровож-
дается переносом энергии по
спектру (см. рис. 2.72, 2.74).
Предотвратить возникно-
вение многомодовой турбу-
лентности можно увеличени-
ем линейной дисперсии или уменьшением нелинейной зависимости
частоты от амплитуды. Увеличение дисперсии способствует образо-
ванию типа когерентных структур. В течениях несжимаемой жидко-
сти увеличение дисперсии волн Толлмина-Шлихтинга может быть
получено изменением состава движущейся среды, введением в
жидкость высокомолекулярных соединений. Изменить характер не-
линейного взаимодействия волн можно также уменьшением длины
периода L или значительным увеличением амплитуды начального
монохроматического возмущения, что может приводить к увеличе-
нию дисперсии. Расчеты уравнения (2.3.285) показали, что в линейно
недиспергирующей среде с сильной зависимостью фазы от амплиту-
ды воздействие белого шума на многомодовый турбулентный режим
может привести к установлению в системе упорядоченного монохро-
Рис. 2.75. Развитие амплитуды несущей
волны в среде при = 0; a2 = 3; a3 = 0;
кривая 1 — при отсутствии шума, кривая
2 — при действии «белого» шума
магического режима или пре-
дельного цикла.
На рис. 2.75 показана эво-
люция амплитуды несущей
волны в системе с au = a31 = 0,
a2 = 3, L = 50 при отсутствии
шума (кривая 1) и при нали-
чии «белого» шума (кривая 2).
Самоорганизация хаотиче-
ских режимов под действием
«белого» шума объясняется
тем, что в недиспергирующих
системах, наряду с предель-
ными циклами и хаотически-
ми аттракторами, существуют
Глава 2
293
устойчивые узлы, соответствующие монохроматическим режимам.
«Белый» шум способствует попаданию системы в область притяже-
ния устойчивого узла.
Скорость распространения фронтов локализованного волнового
пакета в диспергирующих средах выше, чем в недиспергирующих,
в результате дисперсионного расплывания волнового пакета. С рос-
том амплитуды волнового пакета изменяется фаза, в результате чего
растет отличие локальных волновых чисел на фронтах волнового па-
кета от волнового числа несущей волны, что вызывает самосжатие
волнового пакета, аналогичное самосжатию в консервативных си-
стемах. Самосжатие, проявляющееся в резком возрастании ампли-
туды в окрестности гребня огибающей волны, приводит к появле-
нию узких иглообразных волновых пакетов с большой амплитудой.
Большие градиенты амплитуды на фронтах иглообразных волновых
пакетов вызывают рост градиентов фазы, приводящих к появлению
локальных декрементов и затуханию иглообразных волновых паке-
тов. Эволюция огибающей волны в системах с < О определяется
динамикой возникновения, роста и затухания иглообразных волно-
вых пакетов, в которых сосредоточена основная часть энергии волно-
вого движения. В системах с > О монохроматическое экспонен-
циально растущее решение неустойчиво. Развитие неустойчивости
сопровождается появлением отдельных пиков большой амплитуды.
В последующем при разрушении этих пиков образуются турбулент-
ные пятна, распространяющиеся на весь волновой пакет. Отдельные
стадии образования иглообразного волнового пакета, приводящего
к возникновению турбулентного пятна, а также перенос энергии по
спектру приведены на рис. 2.76—2.78. Отметим, что возникновение
турбулентного пятна аналогично известному 6-слою [2.3.68]. Отли-
чие состоит в том, что явление возникновения турбулентных пятен,
как следует из рис. 2.76, 2.77, свойственно как живой, так и неживой
природе. Картина развития нескольких турбулентных пятен приве-
дена на рис. 2.78.
Классификация закритических режимов является одной из цент-
ральных проблем теории диссипативных структур [2.3.74]. Она поз-
воляет выделить отдельные существенные стороны объекта либо яв-
ления и определить условия перехода между ними.
Классификация закритических режимов, в которых на многих
масштабах кратные и некратные гармоники могут существенно вли-
ять на картину поведения нелинейных систем на аттракторе, про-
ведена по виду волны огибающей, по пространственным спектрам
волновых чисел, по временным частотным спектрам амплитуд и фаз
отдельных гармоник [2.3.74].
294
Глава 2
Рис. 2.76. Стадия развития турбулентного пятна из иглообразного волнового
пакета при модуляционной неустойчивости
Рис. 2.77. Эволюция спектра волновых чисел в процессе образования иглообраз-
ного волнового пакета и турбулентного пятна в среде с линейным затуханием
n
Рис. 2.78. Самосжатие волнового пакета, при-
водящее к появлению иглообразных волно-
вых пакетов — системы турбулентных пятен
Глава 2
295
Механизм возникновения турбулентности. Как было отмечено,
огибающая волна является топологическим отображением нелиней-
ного взаимодействия возмущений. Для многомодовой турбулентно-
сти огибающая волна разбивается на клиновидные волновые пакеты
с достаточно большими пространственными и частотными спектра-
ми. В среде возникает неоднородность по групповой скорости. Груп-
повая скорость коротких волн, входящих в волновой пакет, выше
групповой скорости самой несущей волны, в результате чего корот-
кие волны обгоняют несущую волну и концентрируются на перед-
нем фронте волнового пакета. Групповая скорость длинных волн
меньше групповой скорости несущей волны, поэтому длинные вол-
ны находятся в задней части волнового пакета. Поскольку нелиней-
ное долговременное развитие возмущений методом волновых паке-
тов исследовано в закритической области для непрерывной полосы
спектра волновых чисел, то по разные стороны несущей волны об-
разуются волны различной природы. Каждый вид волн в результа-
те нелинейного взаимодействия образует аттракторы, в том числе и
«странные» аттракторы. Между «странными» аттракторами проис-
ходит взаимодействие.
Естественные возмущения являются волновыми пакетами [2.3.81],
содержащими десятки мод, а число эффективно взаимодейству-
ющих мод, возникающих при комбинированных волновых числах при
возбуждении двух мод, равно (при нелинейной зависимости фазы,
частот) десяткам, сотням мод. Число мод возрастает в геометриче-
ской прогрессии, поэтому заполнение спектра волновых чисел про-
исходит очень быстро.
Таким образом, турбулентность есть результат взаимодействия
достаточно большого количества «странных» аттракторов. Этот вы-
вод согласуется с ранее высказанным предположением о механиз-
ме возникновения турбулентности [2.3.82, 2.3.83] и с результатами
экспериментальных исследований турбулентности в круглой трубе
[2.3.84].
Предложенный механизм не противоречит известным моделям,
согласно которым крупномасштабные возмущения (длинные вол-
ны в задней части волнового пакета) оказываются неустойчивыми,
создавая возмущения с мелким масштабом (короткие волны на пе-
реднем фронте волнового пакета). Поскольку концентрация волн
на границах волнового пакета есть нечто материальное, то это так-
же согласуется с выводами работ [2.3.82, 2.3.83], что при возникно-
вении турбулентности существенную роль играют «квазичастицы»,
составляющие «газ» турбулентности.
296
Глава 2
ОБОЗНАЧЕНИЯ:
F12 д к к*	—	вектор силы межфазного взаимодействия, Н; —	ускорение свободного падения, м/с2; —	коэффициенты Ламе; —	коэффициент удельного сопротивления, м2; —	коэффициент проницаемости стенки, м;
р0, Pv Ра< Рв’ Р ~ давление соответственно в порах осадка, на
поверхности пористого тело, атмосферное, за по-
Q oin Vp и., v., wt	ристым телом, в пленке жидкости, Н/м2; —	поток среды, м3/с; —	поток на входе, м3/с; —	вектор скорости i-й фазы и его компоненты в направлении координатхр х2, х3 соответственно, м/с;
Vo	— скорость фильтрации в направлении координа- ты х2, м/с;
xi Xin'Xik	— ортогональные координаты, м; — соответственно начальное и конечное значение хР м;
ai ain aoi 5 5? M. Hl	—	концентрация i-й фазы; —	концентрация i-й фазы на входе, об. доля; —	порозность пористого тела; —	толщина пористого тела, м; —	дельта-функция; —	эффективная вязкость дисперсной фазы и дис- персионной среды соответственно, Па-с;
V	— кинематическая вязкость, м2/с;
р9 r р. = cczp°, р = Pi + Р2 ~ соответственно плотность i-й фазы, при-
веденная плотность и плотность смеси, кг/м3;
Тк1 С d q (ер е2, е3)	—	компоненты тензора вязких напряжений; —	коэффициент сопротивления; —	диаметр частицы, м; —	единичный вектор направления относительной скорости частицы и его компоненты;
F(F„F2)	— вектор ускорения массовых сил, Н, и его компо- ненты в направлении координат xv х2, м/с2;
Глава 2
297
h	— толщина пленки смеси или полурасстояние между
стенками, м;
i, j, к	—	орты координатных осей xv х2, х3;
L	—	размер области течения;
т	—	коэффициент консистенции, кг-сп'2/м;
п	—	коэффициент нелинейности;
t	—	время, с;
V()	—	скорость фильтрации в направлении координаты
х2, м/с;
Wp W2	—	скорости движения стенок, м/с;
w	—	модуль относительной скорости, м/с;
Z	—	ширина области течения, м;
а	— угол между вектором ё и осью 0хр
Р	—	угол наклона;
О)	—	скорость вращения, с1;
Fr = U2 / (дЛц)	— число Фруда
Re = U?”п	/ т — число Рейнольдса.
Индексы:
i = 1	—	дисперсионная среда;
i = 2	—	дисперсная фаза.
н	—	начальное значение;
от	—	относительное значение;
— характерный размер.
Список литературы
2.3.1.	Холпанов Л.П., Шкадов В.Я., Малюсов В.А., Жаворонков Н.М.
О массообмене в пленке жидкости при волнообразовании. Теор. основы
хим. технол. 1967. Т. 1. № 1. С. 73-79.
2.3.2.	Холпанов Л.П., Шкадов В.Я. Гидродинамика и тепломассообмен с по-
верхностью раздела. М.:Наука. 1990. 271 с.
2.3.3.	Холпанов Л.П., Запорожец Е.П., Зиберт Г.К., Кащицкий Ю.А. Мате-
матическое моделирование нелинейных термогидрогазодинамических
процессов. М.: Наука. 2002. 605 с.
2.3.4.	Холпанов Л.П. Физико-химические и гидродинамические основы нели-
нейных процессов химии и химической технологии. Известия АН. Серия
химическая. 1996. № 5. С. 1065-1090.
298
Глава 2
2.3.5.	Холпанов Л.П., Кениг Е.Я., Малюсов В.А. Многокомпонентный теп-
ломассообмен при турбулентном течении пленки жидкости. ИФЖ. 1989.
Т. 57. №1.С. 16-22.
2.3.6.	Холпанов Л.П. Методы расчета гидродинамики и тепломассообмена в
системах с подвижной поверхностью раздела. Теор. основы хим. технол.
1993. Т. 27. № 1. С. 18-28.
2.3.7.	Холпанов Л.П. Турбулентный двухфазный массообмен в пленке
жидкости. Теор. основы хим. технол. 1997. Т. 31. №2. С. 131-139.
2.3.8.	Холпанов Л.П. Математическое моделирование нелинейных процес-
сов. Теор. основы хим. технол. 1999. Т. 33. № 5. С. 466-484.
2.3.9.	Холпанов Л.П. Самоорганизация и динамический хаос. Теор. основы
хим. технол. 1998. Т. 32. № 4. С. 355-368.
2.3.10.	Холпанов Л.П. Самоорганизация и динамический хаос в химико-тех-
нологических и теплообменных устройствах. Проблемы и задачи. Инж.-
физ. журн. 2001. Т. 74. № 4. С. 5-13.
2.3.11.	Капица П.Л. Волновое течение тонких слоев жидкости//Журн. экспе-
рим. и теорет. физики. 1948. Т. 18. № 1. С. 81; 1949. Т. 19. № 2. С. 3.
2.3.12.	Макареев С.М. Дис. канд. техн. наук. Моск. ин-т. хим. машиностроения.
Москва. 1990.
2.3.13.	Левин В.Г. Физико-химическая гидродинамика. М.: Гос. изд-во физ-мат.
литературы. 1959.700 стр.
2.3.14.	Дытнерский Ю.И., Борисов Г.С. Исследования тепломассообмена в
жидкой фазе//Процессы химической технологии. Гидродинамика, теп-
ло- и массопередача. М.: Наука, 1965. С. 266-284.
2.3.15.	Devies J.T., Warner K.V. The effect of large-scale roughness in promoting
gas absorption//Chem. Eng Sci. 1969. V. 24, N 2. P. 231.
2.3.16.	Холпанов Л.П., Квурт Ю.П., Дорошенко A.B., Корнилов В.Х., Кон-
цова М.М. Солнечные системы охлаждения и кондиционирования воз-
духа//Математическое моделирование ресурсосберегающих эколо-
гически безопасных технологий. Сб. науч. Статей под редакцией акад.
А.М. Кутепова и профессора А.Д. Баранова. М.: МГУИЭ. 1998. С. 26-49.
2.3.17.	Kholpanov L.P. The wavy flow of thin liquid films on vertical planes//lntern.
Chem. Eng. 1965. V. 5, N 4. P. 633.
2.3.18.	Kholpanov L.P. The theory of the two-phase film mass transfer in the
absence of body forces//!bid. P. 720.
2.3.19.	Холпанов Л.П. К вопросу волнового течения тонких слоев жидкости по
вертикальной плоскости//Инж.-физ. журн. 1965. Т. 8. № 4. С. 488.
2.3.20.	Холпанов Л.П., Шкадов В.Я., Малюсов В.А., Жаворонков Н.М.
К учету касательных сил при нелинейном расчете волновых течений
пленки жидкости/Деорет. основы хим. технологии. 1972. Т. 6, № 2.
С. 204.
2.3.21.	Холпанов Л.П., Шкадов В.Я., Малюсов В.А., Жаворонков Н.М. Вли-
яние газового потока на течение тонких слоев жидкости при волнообра-
зовании/Деорет. основы хим. технологии. 1973. Т. 7, № 5. С. 788.
2.3.22.	Холпанов Л.П., Малюсов В.А., Жаворонков Н.М. Расчет волновых
параметров волновой пленки жидкости в режиме нисходящего течения
фаз/Деорет. основы хим. технологии. 1975. Т. 9, № 6. С. 877.
Глава 2
299
2.3.23.	Холпанов Л.П., Шкадов В.Я., Малюсов В.А., Жаворонков Н.М.
Исследование течения волновой пленки жидкости, взаимодейству-
ющей с газовым потоком, в нелинейной постановке//Тр. Всесоюз. со-
вещ. «Математические методы в химии». Новосибирск, 1973. Т. 1.
С. 199.
2.3.24.	Kholpanov L.P., Shkadov V.Ya., Malyusov V.A., Zhavoronkov N.M.
The effect of gas flow rate on the flow of thin liquid films at wave formation//
IV Intern. Congr. Chem. Eng. Chem. Equipment Design and Automation.
CHISA. Csechoslovac, 1972. P. 18.
2.3.25.	Харин В.Ф. Гидродинамические закономерности и массообмен при
пленочном течении жидкости по шероховатой поверхности: Автореф.
дис.... канд. техн. наук. Казань, 1972. 24 с.
2.3.26.	Исследование турбулентных течений двухфазных сред/Под ред.
С.С. Кутателадзе. Новосибирск: Ин-т теплофизики СО АН СССР, 1973.
2.3.27.	Telles A.S., Durler А.Е. Statistical characteristics of thin vertical wave liquid
film//lnd. end Eng. Chem. Fundam. 1970. V. 9, N 3. P. 412.
2.3.28.	Brauer H. Stromung und Warmeubergang bei Rieselfilman//VDI-
Forschungsh. 1956. Bd. 457. S. 180.
2.3.29.	БреховскихЛ.М., Гончаров В.В. Введение в механику сплошных сред.
М.:Наука. 1982.333 с.
2.3.30.	Bin А.К. Mass transfer into a turbulent liguid film//lnt. J Heat transfer. 1983.
V. 26, N 7. P. 981.
2.3.31.	Харин В.Ф., Кабанов Г.П., Николаев H.A. Определение коэффициен-
тов массоотдачи в пленке жидкости//Известия вузов. Сер. Химия и хи-
мическая технология. 1977. Т. 20. № 6. С. 936-942.
2.3.32.	Петин В.Ф., БалабековО.С., Холпанов Л.П. Явление последователь-
ного взаимодействия вихрей при обтекании потоком газа или жидкости
систем дискретно расположенных вдоль него тел .//В сб. Интенсифика-
ция техники производства фосфора и термической фосфорной кис-
лоты. Материалы научн.-техн. комиссии при АН СССР. Чимкент, 1991.
С. 2-4.
2.3.33.	Петин В.Ф.,Балабеков О.С. Явление последовательного взаимо-
действия вихрей в регулярно расположенной насадке массообменных
аппаратов/ДОХТ.1994. Т. 28. № 4. С. 328.
2.3.34.	Запорожец Е.П., Холпанов Л.П., Зиберт Г.К., Артемов А.В. Иссле-
дование вихревых и кавитационных потоков в гидродинамических си-
стемах/ДОХТ. 2004. № 3. С. 243-352.
2.3.35.	Зельдович Я.Б. Теория разрыва жидкости//Журнал. эксперим. и те-
орет. физики. 1942. Т. 12. С. 525.
2.3.36.	Raleigh. On the pressure developed in a liquid during the collapse of a
spherical cavity//Phil. Mag. 1917. V. 34. P. 94.
2.3.37.	Майер В.В. Кумулятивный эффект в простых опытах. М.: Наука. 1968.
2.3.38.	Перник А.Д. Проблемы кавитации. Л.: Судостроение. 1966.
2.3.39.	Исаченко В.П. Теплообмен при конденсации. М.: Энергия. 1977.
2.3.40.	Новиков И.И., Воскресенский К.Д. Прикладная термодинамика и теп-
лопередача. М.: Атомиздат. 1977.
2.3.41.	Абрамович Г.Н. Прикладная газовая динамика. М.: Наука. 1991. Т. 1.
300
Глава 2
2.3.42.	Кнэпп Р., Дейли Дж., ХэммитФ. Кавитация. М.: Мир. 1975.
2.3.43.	Советский энциклопедический словарь. М.: Сов. Энциклопедия. 1990.
С. 286.
2.3.44.	Taleyarkhan R.P., West C.D., Cho J.S., Lahey R.T., Nigmatulin R.I.,
Block R.C. Evidence for Nuclear Emissions During Acoustic Cavitation//
Science 2002, V. 295. P. 1868.
2.3.45.	Жаворонков H.M., Нехорошее A.B., Гусев Б.В., Баранов А.Т., Хол-
панов Л.П., Щербак С.А., Мустафин Ю.И. Свойство коллоидных си-
стем генерировать низкочастотный переменный ток//ДАН СССР. 1983.
Т. 270. № 1.С. 124-128.
2.3.46.	Григорьева Н.И., Накоряков В.Е. Точное решение задачи о совмест-
ном тепломассопереносе при пленочной абсорбции//Инж.-физ. журн.
1977. Т. 50. №5. С. 893.
2.3.47.	Кутателадзе С.С., Накоряков В.Е. Тепломассообмен и волны в газо-
жидкостных системах. Новосибирск: Наука. 301 с.
2.3.48.	Витков Г.А., Холпанов Л.П., Шерстнев С.Н. Гидравлическое сопро-
тивление и тепломассообмен. М.: Наука. 1994. 280 с.
2.3.49.	Нигматулин Р.И. Динамика многофазных сред. М.: Наука, 1987. Т. 1.
463 с.,Т. 2. 358 с.
2.3.50.	Kholpanov L.P., Ibyatov R.l. Calculation the multiphase heterogeneous
medium hydrodynamic in a centrifugal field. Heat Transfer Research. 2006.
V. 37. No. 4. P. 307-320.
2.3.51.	Ибятов Р.И. Методы расчетов гидродинамических процессов при филь-
тровании и центрифугировании суспензий. Автореферат, дис. на соис-
кание уч.ст. д-ра техн. наук. Казань. Казанский государственный технол.
ун-т. 2005.38 с.
2.3.52.	Холпанов Л.П., Ибятов Р. И., Ахмадиев Ф.Г., Фазылзянов Р.Р. Ма-
тематическое моделирование гидродинамики на проницаемых поверх-
ностях/ДОХТ. 2003. Т. 37. № 3. С. 227-237.
2.3.53.	Ибятов Р.И., Холпанов Л.П., Ахмадиев Ф.Г. Течение многофазной
среды по проницаемой поверхности с образованием осадка//ИФЖ.
2005. Т. 78. № 2. С. 65-72.
2.3.54.	Ибятов Р.И., Холпанов Л.П., Ахмадиев Ф.Г., Фазылзянов Р.Р. Мате-
матическое моделирование течений гетерогенных сред по вращающим-
ся проницаемым поверхностям/ДОХТ. 2003. Т. 37. № 5. С. 479-492.
2.3.55.	Ибятов Р.И., Холпанов Л.П., АхмадиевФ.Г., Бекбулатов И.Г. Мате-
матическое моделирование течения многофазной гетерогенной среды
по проницаемой поверхности/ДОХТ. 2005. № 5. С. 1-9.
2.3.56.	Kholpanov L.P., Ismailov B.R., Vlasek Р. Modelling of multiphase flow
containing bubbles, drops end solid particles//Engineering Mechanics 2005.
V. 12.N6.C. 1-11.
2.3.57.	Холпанов Л.П., Ибятов Р.И. Математическое моделирование динами-
ки дисперсной фазы/ДОХТ. 2005. Т. 39. № 2. С. 206-215.
2.3.58.	Кочин Н.Е. Векторное исчисление и начала тензорного исчисления. М.:
Наука, 1965.
2.3.59.	Шульман З.П., Байков В.И. Реодинамика и тепломассообмен в пле-
ночных течениях. Минск: Наука и техника, 1979.
Глава 2
301
2.3.60.	Ахмадиев Ф.Г., Ибятов Р.И. Гидродинамика пленки жидкости на по-
верхности движущегося пористого тела//Теор. основы хим. технол.
1998. Т. 32. №1.С. 5.
2.3.61.	Бабаджанян Г.А., Даниелян Л.Е., Мнацаканян Р.Ж. Развитие тече-
ния жидкости в плоском канале с подвижными проницаемыми стенками
фракцией//Инж.-физ. журн. 1997. Т. 70. № 2. С. 200.
2.3.62.	Ибятов Р.И., Холпанов Л.П., Ахмадиев Ф.Г., Фазылзянов Р.Р. Рас-
чет течения гетерогенных сред неньютоновского поведения по проница-
емым поверхностям//Инж.-физ. журн. 2003. Т. 76. № 6. С. 80-87.
2.3.63.	Кулов Н.Н., Максимов В.В., МалюсовВ.А., ЖаворонковН.М. Массо-
отдача в стекающих пленках жидкости// Теор. основы хим. технол. 1983.
Т. 17. №3. С. 406.
2.3.64.	ДжозевД. Устойчивость движений жидкости. М.:Мир,1981.
2.3.65.	Гершуни Г. 3., Жуховицкий Е. М. Конвективная устойчивость несжи-
маемой жидкости. М.: Наука, 1972. 392 с.
2.3.66.	Хакен Г. Синергетика. М.: Мир, 1980. 404 с.
2.3.67.	Холпанов Л.П. Самоорганизация и динамический хаос в химико-техно-
логических и теплофизических устройствах//Инж.-физ.журн. 2001. Т. 74.
№ 4. С. 5-13.
2.3.68.	Самарский А.А., Галактионов В.А., Курдюмов С.П., Михайлов А.П.
Режимы с обострением в задачах для квазилинейных параболических
уравнений. М.: Наука, 1987. 477 с.
2.3.69.	Елюхин В.А., Холпанов Л.П., Малюсов В.А. Возникновение многомо-
довой турбулентности в гидродинамической и химически реагирующих
системах//Докл. АН СССР, 1984.Т. 278. № 5. С. 1188-1191.
2.3.70.	Елюхин В.А., Холпанов Л.П. Неустойчивые режимы в автоколебатель-
ных реакциях с диффузией//Журн. физ. химии, 1986. Т. 60. С. 1274-
1288.
2.3.71.	Елюхин В.А., Холпанов Л.П. Развитие и взаимодействие возмущений
в неустойчивых гидродинамических и химически реагирующих систе-
мах: В сб. Механика неоднородных и турбулентных потоков/Под редак-
цией акад. В.В. Струминского. М.: Наука, 1989. С. 132-142.
2.3.72.	Елюхин В.А., Холпанов Л.П. Условие самоорганизации неустойчивых
процессов химической технологии: В сб. Молекулярная газодинамика и
механика неоднородных сред/Под редакцией акад. В.В. Струминского.
М.: Наука, 1990. С. 131-137.
2.3.73.	Холпанов Л.П. Физико-химические и гидродинамические основы нели-
нейных процессов химии и химической технологии//Изв. Академии наук.
Серия химическая, 1996. № 5. С. 1065-1090.
2.3.74.	Холпанов Л.П. Самоорганизация и динамический хаос//Теор. основы
хим. технологии. 1998. Т. 32. № 4. С. 355-368.
2.3.75.	Карпман В.И. Нелинейные волны в диспергирующих средах. М.: Наука,
1973.
2.3.76.	Тахтаджян Л.А., Фаддеев Л.Д. Гамильтонов подход в теории солито-
нов. М.: Наука, 1986.
2.3.77.	Froeschle С. The Lyapunov characteristics exponent and applications//Proc.
Roy. Soc. 1954. Vol. 22A. P. 1161-1175.
302
Глава 2
2.3.78.	Колмогоров А.Н. Новый метрический инвариант транзитных динами-
ческих систем и автоморфизмов пространства. Докл. АН СССР, 1958.
Т. 119. №5. С. 861-865.
2.3.79.	Синай Я.Г. О понятии энтропии динамических систем. Докл. АН СССР,
1959. Т. 124. №4. С. 768-772.
2.3.80.	Николис Г., Пригожин И. Самоорганизация в неравновесных системах.
М.: Мир, 1979.
2.3.81.	Качанов Ю.С., Козлов В.В., Левченко В.Я. Возникновение турбулент-
ности в пограничном слое. Новосибирск: Наука, 1982.
2.3.82.	Струминский В.В. Аэродинамика и молекулярная газовая динамика.
М.: Наука, 1985. 240 с.
2.3.83.	Струминский В.В., Скобелев Б.Ю. Странные аттракторы и турбулент-
ность: В кн. Механика неоднородных и турбулентных потоков/Под ред.
акад. В.В. Струминского. М.: Наука, 1989. С. 164-173.
2.3.84.	Sieber М. Experiments on the attractor - dimension for turbulent pipe flow//
Phys. Let. - A. 1987. V. 122. N 9. P. 467-473.
2.3.85.	Javdani S.L. Goren. Finite-amplitude wavy flow of thin film.//Progr. Heat and
Mass Transfer, 1972. V. 6. P. 253-262.
2.3.86.	Квурт Ю.П., Холпанов Л.П., Малюсов B.A., Жаворонков Н.М. О за-
кономерногсти пленочного течения в каналах с регулярной шерохова-
тостью//ДАН СССР. 1984. Т. 274. № 4.С. 882-884.
2.3.87.	Квурт Ю.П., Холпанов Л.П. О некоторой закономерности смены гид-
родинамических режимов при пленочном течении жидкости: В сб. Моле-
кулярная газодинамика и механика неоднородных сред/Под редакцией
акад. В.В.Струминского. М.: Наука, 1990. С. 224-231.
2.3.88.	Закиев С.Е., Холпанов Л.П. Особенности энергетики индукционных
полей в несильно проводящих движущихся средах/ДОХТ. 2008 Т. 42.
№4. С. 1-11.
2.3.89.	KristenssonG., RicteS.J. Math. Phys., V. 34. N4, 1995. P.1339.
2.4. ИНТЕНСИФИКАТОРЫ ТЕПЛООБМЕНА
МАКРО- И МИКРОМАСШТАБОВ
Теплопроводные пористые среды с различной структурой нахо-
дят все большее применение в технике для интенсификации охлаж-
дения теплонапряженных конструкций, когда заданы жесткие
ограничения на температуру теплопередающих поверхностей при
высоких тепловых нагрузках (выше 1 кВт/см2). Пористая структура
играет роль своеобразного оребрения стенки канала. Для описания
конвективного теплообмена в таких каналах [2.4.1—2.4.9] использова-
на система дифференциальных уравнений в так называемом прибли-
жении пористой среды, когда пористый твердый каркас и движущая-
ся сквозь него жидкость рассматриваются как однородные взаимно
проникающие среды, обменивающиеся теплом и характеризующие-
ся собственными теплофизическими параметрами (свойствами) и
Глава 2
303
распределениями температур TK(x,z,t) и T^(x,z,t). Практически, — это
единственный метод анализа макротечения в теплообменном обору-
довании, в ядерных и химических реакторах, в системах охлаждения
зеркал.
При одностороннем нагреве канала (как, например, в лазерных
зеркалах) обычно предполагается, что тепло от стенки канала пере-
носится в глубь пористого слоя (вставки) теплопроводным каркасом и
передается жидкости за счет объемной теплоотдачи. При невысокой
теплопроводности каркаса значительная доля тепла от стенки канала
отводится непосредственно жидкостью, движущейся в пристенных
порах, и переносится внутрь пористой вставки благодаря эффектив-
ной (турбулентной) теплопроводности жидкости, обусловленной пе-
ремешиванием в сообщающихся порах. В достаточно общих случаях
простейшие двумерные уравнения нестационарного теплопереноса
по каркасу и жидкости принимают вид:
Ск——^-ау(Тк-Тж);
к dt к dz2 V 7
f дТж	dTL^i _ d2TL	/_ _ v
Сж —-——~-+oty \Т — Т\
V dt	dz J dz2	V 7
(2-4.1)
Здесь t — время от начала нагревания стенки канала (z = 0 — теп-
ловой поток направлен вдоль оси z); Ск и Сж — теплоемкости каркаса и
жидкости в расчете на единицу объема пористой среды; Дж/(м3К);Хк
и Хж — коэффициенты теплопроводности гомогенизированных кар-
каса и жидкости соответственно; Вт/(м К); и — средняя скорость жид-
кости в порах вдоль оси х, м/с (рис. 2.79).
Интенсивность охлаждения стенки канала (z = 0) характеризует-
ся коэффициентами «местной» (в сечении х) и «эффективной» (сред-
ней) теплоотдачи:
а (х)=_____2Й)_____
Гк(х,0)-Тж(х)'
a q -
эф Гк(0)-Гж'
Здесь q — плотность тепло-
вого потока в стенку канала,
Вт/м2.
Приведенные коэффици-
енты тем удобны для анализа,
что в силу линейности исход-
Местная
теплоотдача в ячейке
Эффективная
теплоотдача в ячейке
Рис. 2.79. Схема к расчету интенсифи-
кации теплообмена в каналах с тепло-
проводными пористыми вставками при-
менительно к охлаждаемым лазерным
зеркалам и мишеням ускорителей
304
Глава 2
Рис. 2.80. Влияние теплопроводности по-
ристого каркаса и гидравлического диа-
метра пор на долю тепла, отводимого твер-
дым каркасом от стенки (а), и на мест-
ную теплоотдачу стенки (б) при охлажде-
нии зеркала водой комнатной темпера-
туры
них уравнений они не за-
висят от теплового потока и
целиком определяются гео-
метрией канала, его струк-
турой и свойствами теплоно-
сителя и каркаса, что важно
для оптимизации конструк-
ции охлаждаемого оборудо-
вания.
Из решений уравнений
конвективного теплообмена
в пористом слое следует ряд
важных асимптотических
пределов интенсификации
охлаждения стенки канала.
Так, максимальный вклад
каркаса (оребрения) в теп-
лоотдачу стенки составляет
ак	,т.е. определяется
объемной теплоотдачей и
теплопроводностью карка-
са. Величина ак быстро рас-
тет с увеличением удельной
смоченной поверхности кар-
каса, т.е. с уменьшением раз-
мера пор (рис. 2.80).
На некотором расстоянии от входа в канал устанавливается стаби-
лизированный режим теплоотдачи, где местная теплоотдача не зави-
сит от продольной координаты и определяется следующим выраже-
нием (при Хж = 0)
1 h 1
	—	1	.
(Ху------------ЗХК-Titty
(2-4.2)
Отсюда следует, что существует оптимальная толщина канала
й=л/ЗХк/ау , при которой местная теплоотдача максимальна.
Подробный анализ результатов расчета теплоотдачи в каналах
с пористыми вставками для различных практически важных случа-
ев показал, что теплоотдача стенки канала с пористой теплопровод-
ной вставкой (интенсификаторами) в 5—10 раз превышает теплоот-
дачу того же канала без пористой вставки (при том же расходе
жидкости).
Глава 2
305
Термогидродинамическая аналогия в пористых средах
К числу наиболее важных закономерностей теплообмена в пря-
мых гладких каналах (трубах) относится термогидродинамическая
аналогия Рейнольдса, согласно которой коэффициент теплоотдачи
прямо пропорционален коэффициенту гидравлического сопротив-
ления (трения). В пористых средах (сложных каналах), в отличие от
труб, потери давления зависят от суммы поверхностных интегралов
от касательных напряжений (трения) и нормальных напряжений (дав-
ления), причем последние могут значительно превышать трение. На
основе полуэмпирической теории турбулентности [2.4.10—2.4.14] об-
наружена важная, ранее не известная, закономерность. Оказалось,
что зависимость коэффициента теплоотдачи элементов пористой
среды от ее гидравлического сопротивления (или от скорости дис-
сипации энергии потока, равной мощности на прокачку жидкости)
с приемлемой погрешностью (±20%) описывается единой функцией
для разных структур пористой среды (шаровых засыпок, сетчатых,
спиральных и зернистых материалов, поперечно обтекаемых пучков
труб различного поперечного сечения и т.п.):
а = KZ(2W/v3)1/4 Рг1/3 или Nu = ad/X = X(^Re3)1/4 Рг1/3,	(2.4.3)
где а — коэффициент теплоотдачи, Вт/(м2-К); W — мощность на про-
качку жидкости, Вт/кг; £ — коэффициент гидравлического сопро-
тивления.
Числовой коэффициент К достаточно консервативен и изменяет-
ся в узких пределах: К = 0,1... 0,2 при изменении в широком диапа-
зоне чисел Рейнольдса Re = 102... 107, чисел Прандтля Рг = 0,7... 2000,
пористости 14—80%, гидравлического диаметра d — 0,2... 150 мм для
разнообразных пористых сред. Для грубых оценок достаточно поло-
жить в приведенных формулах К = 0,145 (рис. 2.81).
Не исключено, что сам факт существования универсальной за-
висимости подтверждает одно из важнейших положений синергети-
Рис. 2.81. Зависимость коэффициента К (см. формулу (2.4.3)) от числа Рейнольд-
са, по экспериментальным данным разных авторов, для поперечно обтекаемых
шахматных 1 и перекрестных 2 пучков круглых и витых 3 труб, шаровых засыпок
4, охлаждаемых воздухом, углекислым газом, водой и маслом
306
Глава 2
ки: самоорганизующиеся структуры, в данном случае турбулентное
течение, есть свойство жидкости, а конкретная пористая структура
лишь определяет условия появления турбулентности.
Обнаруженная закономерность позволяет с приемлемой для прак-
тики точностью предсказывать коэффициенты теплоотдачи в кана-
лах с пористыми вставками на основе опытных данных по гидрав-
лическому сопротивлению, тем самым сводя к минимуму затраты на
проведение дорогостоящих, сложных и не отличающихся высокой
точностью измерений коэффициентов теплоотдачи на поверхностях
элементов сложных систем охлаждения [2.4.12—2.4.20].
Список литературы
2.4.1.	Харитонов В.В. Теплофизика лазерных зеркал. М.: МИФИ, 1993.
2.4.2.	Харитонов В.В., Плаксеев А.А. Предельные тепловые нагрузки в ла-
зерных зеркалах с охлаждаемой пористой подложкой/ДВТ. 1982. Т. 20.
Вып.4. С. 712-717.
2.4.3.	Харитонов В.В., Кошелев С.Б. О термоупругой устойчивости охлаж-
даемых лазерных зеркал//Инж.-физ. журн. 1983. Т. 45, № 4. С. 640-646.
2.4.4.	Субботин В.И., Харитонов В.В., Плаксеев А.А. Теплообмен в порис-
той подложке охлаждаемых лазерных зеркал//ТВТ. 1983. Т. 21. Вып. 6.
С.86-91.
2.4.5.	Харитонов В.В., Кошелев С.Б. Температурная зависимость критериев
стабильности лазерных зеркал//Физика и химия обработки материалов.
1984. №2. С. 139-141.
2.4.6.	Кошелев С.Б., Субботин В.И., Харитонов В.В. Составляющие тепло-
отдачи при струйном течении воды в ограниченном пространстве//ТВТ.
1985. Т. 23, № 3. С. 542-548.
2.4.7.	Гордеев В.Ф., Кошелев С.Б., Субботин В.И., Харитонов В.В. Тепло-
отдача оребренных стенок при струйном охлаждении//Изв. АН СССР.
Энергетика и транспорт. 1986. №2. С. 134-141.
2.4.8.	Кузьмин Ю.А., Харитонов В.В. Предельная мощность локального ис-
точника тепла на поверхности многослойной стенки с внутренним охлаж-
дением//ТВТ. 1986. Т. 24, № 5. С. 948-956.
2.4.9.	Субботин В.И., Харитонов В.В., Федосеев В.Н. Теория теплопере-
дачи в компактных теплообменниках в приближении модели пористого
тела//Изв. АН СССР. Энергетика и транспорт. 1989. № 4. С. 107-117.
2.4.10.	Кокорев Л.С., Федосеев В.Н., Харитонов В.В. Новый подход к расче-
ту теплоотдачи в пористых средах: Препринт МИФИ, № 24-86. М., 1986.
2.4.11.	Харитонов В.В., Плаксеев А.А., Федосеев В.Н., Воскобойников В.В.
Влияние перемешивания жидкости на теплообмен в каналах с пористы-
ми вставками/ДВТ. 1987. Т. 25, № 5. С. 954-961.
Глава 2
307
2.4.12.	Кокорев Л.С., Субботин В.И., Федосеев В.Н., Харитонов В.В. О вза-
имосвязи гидравлического сопротивления и теплоотдачи в пористых
средах/Дам же. № 1. С. 92-96.
2.4.13.	Федосеев В.Н., Субботин В.Н., Харитонов В.В. Универсальная зави-
симость теплоотдачи от градиента давления в пористых средах/Депло-
энергетика. 1987. № 6. С. 61-64.
2.4.14.	Плаксеев А.А., Федосеев В. Н., Харитонов В.В. Взаимосвязь теплоот-
дачи, интенсивности перемешивания теплоносителя и гидравлического
сопротивления в пористых средах//Изв. АН СССР. Энергетика и транс-
порт. 1988. № 6. С. 106-113.
2.4.15.	Кошелев С.Б., Плаксеев А.А., Харитонов В.В. Нестационарный теп-
лообмен в шаровых засыпках при вынужденной конвекции/Деплоэнер-
гетика. 1989. № 4. С. 64-65.
2.4.16.	Харитонов В.В., Федосеев В.Н. Обобщение экспериментальных дан-
ных о теплоотдаче в поперечно обтекаемых пучках витых труб/ДВТ. 1990.
Т. 28, №2. С. 180-182.
2.4.17.	Харитонов В.В., Киселева В.П., Атаманов В.В., Зейгарник Ю.А.,
Иванов Ф.П. Обобщение результатов интенсификации теплообмена в
каналах с теплопроводными пористыми вставками/Дам же. 1994. Т. 32,
№ 3. С. 433-440.
2.4.18.	Харитонов В.В., Федосеев В.Н. Интегральный метод измерения по-
перечной теплопроводности и диффузии в турбулентном потоке жидко-
сти//Измерительная техника. 1994. № 7. С. 51-53.
2.4.19.	Атаманов В.В., Харитонов В.В., Якутии Н.В. Взаимосвязь теплоотда-
чи и диссипации энергии потока в шаровых засыпках/ДВТ. 1996. Т. 34,
№4. С. 590-596.
2.4.20.	Харитонов В.В., Кокорев Л.С., Дельвин Н.Н. О роли коэффициента
аккомодации в контактном теплообмене//Атомная энергия. 1973. Т. 35.
Вып.б.С. 360-361.
Глава 3
ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЙ
ИНТЕНСИФИКАЦИИ ТЕПЛО- И МАССООБМЕНА
Для исследования интенсификации тепло- и массообмена раз-
работаны методы эксперимента, системы измерения и управления,
созданы оригинальные стенды и установки. В задачи эксперимента
входили: определение зависимостей подобия для расчета коэффи-
циентов теплоотдачи, гидравлического сопротивления, эффектив-
ных коэффициентов диффузии и др., решение проблемы замыкания
систем уравнений, которые описывают теплообменные процессы в
каналах с искусственной турбулизацией потока; обоснование разра-
ботанных моделей течения, описывающих их систем уравнений, ме-
тодов расчета, изучение структуры потока.
Для решения этих задач в ряде случаев потребовалось разрабо-
тать новые и усовершенствовать известные методы эксперименталь-
ного исследования теплообменных процессов и структуры потока, а
созданные установки оснастить автоматизированными системами
управления, измерения, сбора и обработки опытных данных, отвеча-
ющими требованиям быстродействия и малой инерционности. При
этом в ряде случаев разработаны новые методики измерений. Ниже
дано описание ряда экспериментальных установок и стендов, а так-
же методов исследований, использованных при изучении интенси-
фикации тепло- и массообмена.
3.1. ПУЧКИ ВИТЫХ ТРУБ
Методы исследования и экспериментальные установки для изу-
чения процессов теплообмена и гидродинамики в пучках витых труб
имеют ряд специфических особенностей. Так, для исследования
структуры потока в пучках витых труб в условиях стесненного про-
странства и высокой интенсивности турбулентности методом тер-
моанемометра постоянной температуры возникает необходимость
уточнить термоанемометрическое уравнение, настроить аппаратуру
на более широкий спектр частот, а также разработать специальную
конструкцию термоанемометрических зондов [3.1—3.7].
Глава 3
ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЙ
ИНТЕНСИФИКАЦИИ ТЕПЛО- И МАССООБМЕНА
Для исследования интенсификации тепло- и массообмена раз-
работаны методы эксперимента, системы измерения и управления,
созданы оригинальные стенды и установки. В задачи эксперимента
входили: определение зависимостей подобия для расчета коэффи-
циентов теплоотдачи, гидравлического сопротивления, эффектив-
ных коэффициентов диффузии и др., решение проблемы замыкания
систем уравнений, которые описывают теплообменные процессы в
каналах с искусственной турбулизацией потока; обоснование разра-
ботанных моделей течения, описывающих их систем уравнений, ме-
тодов расчета, изучение структуры потока.
Для решения этих задач в ряде случаев потребовалось разрабо-
тать новые и усовершенствовать известные методы эксперименталь-
ного исследования теплообменных процессов и структуры потока, а
созданные установки оснастить автоматизированными системами
управления, измерения, сбора и обработки опытных данных, отвеча-
ющими требованиям быстродействия и малой инерционности. При
этом в ряде случаев разработаны новые методики измерений. Ниже
дано описание ряда экспериментальных установок и стендов, а так-
же методов исследований, использованных при изучении интенси-
фикации тепло- и массообмена.
3.1. ПУЧКИ ВИТЫХ ТРУБ
Методы исследования и экспериментальные установки для изу-
чения процессов теплообмена и гидродинамики в пучках витых труб
имеют ряд специфических особенностей. Так, для исследования
структуры потока в пучках витых труб в условиях стесненного про-
странства и высокой интенсивности турбулентности методом тер-
моанемометра постоянной температуры возникает необходимость
уточнить термоанемометрическое уравнение, настроить аппаратуру
на более широкий спектр частот, а также разработать специальную
конструкцию термоанемометрических зондов [3.1—3.7].
Глава 3
309
Для исследования перемешивания теплоносителя в пучке витых
труб разработан метод зонного нагрева, который заключался в на-
греве части труб для создания неравномерного поля тепловыделения
и измерении сформированных им полей температуры теплоносите-
ля с последующим сопоставлением с теоретически рассчитанными
полями температур [3.8—3.12].
Метод диффузии теплоты от точечного источника, который ис-
пользовался для определения эффективного коэффициента диффу-
зии, усовершенствован с учетом особенностей конструкции пучка
витых труб [3.13, 3.14]. Диаметр источника диффузии выбран рав-
ным диаметру витой трубы, чтобы учесть все механизмы переноса,
действующие на индикаторный газ, вдуваемый в основной поток.
При этом круглая труба, по которой подавался индикаторный газ,
была надвинута на центральную витую трубу пучка и могла переме-
щаться относительно выходного сечения пучка, где измерялись поля
температур на различном расстоянии от подвижного источника диф-
фузии.
Исследования теплообмена при зонном нагреве пучка витых
труб велись методом локального подобия. Коэффициент теплоот-
дачи определялся по измеренным локальным температурам стен-
ки, температурам теплоносителя, скоростям потока на внешней
границе пристенного слоя и плотностям теплового потока [3.15 —
3.18]. Для проведения исследований использовались следующие
установки:
— Установка для исследования структуры потока и межканально-
го перемешивания методом диффузии теплоты от точечного источ-
ника в пучках витых труб (рис. 3.1-3.4). Основные параметры: макси-
мальный размер овального профиля 36—52 мм, длина труб 1000 — 1500
и 3000 мм, шаг закрутки 300—900 мм, число труб в пучке 7,19 и 37, дви-
жение теплоносителя горизонтальное и вертикальное (снизу вверх),
скорость воздуха 3—70 м/с (Re = 4,5-103- 1,1-Ю5), давление, близкое к
атмосферному, температу-
ра основного потока 280 К,
температура индикатор-
ного газа 340 К. Исполь-
зовался оригинальный
термоанемометрический
Рис. 3.1. Установка для иссле-
дования структуры потока и
межканального перемешива-
ния теплоносителя
310
Глава 3
Рис. 3.2. Выходное сечение пуч-
ка витых стержней установки для
исследования структуры потока и
межканального перемешивания теп-
лоносителя
Рис. 3.3. Витые стержни различного
профиля установки для исследова-
ния структуры потока и межканаль-
ного перемешивания теплоносителя
вращающийся датчик с наклонной нитью для измерения составля-
ющих скорости в трехмерном потоке и стесненном пространстве
пучка витых труб. Измерения проводились в двух взаимно перпен-
дикулярных плоскостях с поворотом датчика вокруг продольной оси.
Вместе с датчиком смонтирована трубка полного напора (рис. 3.5).
На рис. 3.6 и 3.7 представлены конструкции экспериментальных
участков с пучками витых труб для исследований структуры потока,
а на рис. 3.8 — блок-схема аппаратуры, использованной для этих ис-
следований.
Рис. 3.4. Принципиальная схема
экспериментальной установки
для исследования структуры по-
тока и межканального перемеши-
вания в пучке витых труб:
1 — ресивер; 2 — запорный кран;
3 — фильтр; 4 — рабочий редук-
тор; 5 — командный редуктор; 6 —
подогреватель; 7 — дросельный
расходомер; 8 — входной узел;
9 — экспериментальный участок;
10 — витая труба; И — термопара;
12 — трубка полного напора (тер-
моанемометрический датчик);
13 — координатный механизм;
14 — дифференциальный мано-
метр; 15 — сварочный трансфор-
матор; 16 — подвижная труба
Рис, 3.21. Криостат для исследова-
ния теплообмена в большом
объеме при испарении и кипении
жидкого азота
Рис. 3.22. Фрагмент литиевого
стенда для отработки элементов
космических ЯЭУ
Рис. 3.23. Экспериментальный
участок с плазменной горелкой
(N — 500 кВт) для исследований
при сверхвысоких тепловых на-
грузках
Рис. 3.24. Барокамера для тепло-
физических исследований маке-
тов акгивных зон высокотемпе-
ратурных малогабаритных ЯЭУ,
охлаждаемых сплавом Na-K
Рис. 6.23. Элементы конструкции тепловыделяющих сборок ядерного ракетного
двигателя из карбидов тугоплавких металлов
Рис. 6.24. Исследовательский реактор с витыми твэлами
Рис. 6.25. Охлаждамые лазерные зеркала с отражающей поверхностью из моно-
кристаллического молибдена
Рис. 6.26. Охлаждамые лазерные
зеркала и их конструктивные эле-
менты из карбида кремния
Глава 3
311
— Установка для комплексного
исследования стационарной теп-
лоотдачи, гидравлического сопро-
тивления и межканального переме-
шивания методом диффузии тепла
от группы линейных источников
(рис. 3.9, 3.10). Основные парамет-
ры: максимальный размер овала
труб 12,3 мм, толщина стенки труб
из стали 1Х18Н10Т 0,2—0,3 мм, шаг
закрутки 75—330 мм, длина труб
500—1500 мм, число труб в пучке
37 и 151, движение теплоносителя
горизонтальное и вертикальное
(снизу вверх), скорость воздуха до
60 м/с (Re = 2-103—5-104), давление,
близкое к атмосферному, тем-
пература воздуха на входе 280—
290 К, температура воздуха на
выходе 450—650 К, тепловая мощ-
ность до 30—90 кВт.
Схемы и конструкции экспери-
ментальных участков для исследо-
вания межканального перемеши-
вания и теплоотдачи в пучках вить
и 3.12.
Рис. 3.5. Термоанемометрические
датчики с наклонной и прямой ни-
тью, смонтированные на одной дер-
жавке (а). Связь составляющих век-
тора скорости с положением датчика
(б): 1, 2 — корпус; 3 — центрирующая
втулка; 4 — скоба; 5 — державка
: труб представлены на рис. 3.11
— Установка для исследования перемешивания теплоносителя
при нестационарных режимах работы в пучках витых труб методом
диффузии тепла от группы линей-
ных источников (рис. 3.13—3.17).
Основные параметры: максималь-
ный размер овала труб 12,3 мм,
толщина стенки труб 0,2 мм, шаг
закрутки труб 75—152 мм, длина
труб 500 мм, число труб в пучке —
Рис. 3.6. Экспериментальный участок
для исследования структуры потока: 1 —
кассета; 2 — витая труба; 3 — входная ка-
мера; 4 — переходный фланец; 5 — на-
кидной фланец; 6 — кольцо крепления
координатника; 7 — поворотная плат-
форма; 8 — координатник
312
Глава 3
Вид А Вид Б
Рис. 3.7. Крупномасштабный
экспериментальный участок:
1 — витая труба; 2 — кассе-
та; 3 — входная камера; 4 —
переходный фланец; 5 — на-
кидной фланец; 6 — кольцо;
7 — входной патрубок
Рис. 3.8. Блок-схема аппаратуры, использован-
ной для исследований структуры потока: 1 —
дифференциальный датчик давления фирмы
«Геттингер и Балдвин», ФРГ; 2 — эксперимен-
тальный участок; 3 — прибор для фиксации по-
ложения датчика; 4 — прибор давления фир-
мы «Геттингер и Балдвин», ФРГ; 5 — вольт-
метр; 6,15 — вольтметры фирмы «ДИСА», Да-
ния; 7,10 — квадратичные вольтметры фир-
мы «ДИСА», Дания; 8,11 — фильтры фирмы
«ДИСА», Дания; 9,12 — анемометры фирмы
«ДИСА», Дания; 13 — магнитофон фирмы «Ли-
рекс», Франция; 14 — анализатор Фурье фир-
мы «Гюли Паккард», США; 16 — вычислитель-
ный комплекс ИВК-14; 17 — вычислительный
комплекс ИВК-2
Рис. 3.9. Схема эксперимен-
тальной установки для иссле-
дования теплоотдачи, гидрав-
лического сопротивления и
межканального перемешива-
ния в пучке витых труб: 1 — 7 —
см. рис. 3.4; 8 — входной узел;
9 — экспериментальный учас-
ток; 10 — сварочный трансфор-
матор; 11 — пучок витых труб;
12 — термопара; 13 — коорди-
натник
Глава 3
313
Рис. 3.10. Установка для исследования теплообмена, гидравлического сопротив-
ления и межканального перемешивания теплоносителя методом зонного нагрева
в пучках витых труб (число труб — 37)
Рис. 3.11. Схема экспериментального участка с горизонтальной ориентацией пуч-
ка: 1 — витые трубы; 2 — кожух; 3 — коллектор; 4 — штуцер отбора статисти-
ческого давления; 5 — датчики статистического давления; 6 — уплотняющая про-
кладка; 7 — электроизолирующее покрытие из А1203; 8 — выходной токоподвод;
9 — входное устройство; 10 — конический рассекатель потока; 11 — выравни-
вающие сетки; 12 — гермоввод; 13 — провода для подвода электрического тока;
14 — теплоизоляционный чехол; 15 — датчики температуры и скоростного напо-
ра; 16 — координатный механизм; 17 — термоэлектрические датчики температу-
ры стенки витых труб
314
Глава 3
0640
Рис. 3.12. Экспериментальный участок с вер-
тикальной ориентацией пучка: 1 — координат-
ный механизм; 2 — токоподводы; 3 — кожух; 4 —
датчик статистического давления; 5 — входная ка-
мера; 6 — сопло; 7 — входной патрубок; 8 — сетка;
9 — штекерный разъем; 10 — токоподводящая
трубка; И — витая труба
Рис. 3.13. Установка для исследова-
ния нестационарного тепло- и массо-
обмена в электронагреваемых моде-
лях ТВС с витыми твэлами
Рис. 3.14. Координатный механизм с
гребенкой термопар и трубками Пито
(фрагмент установки)
Рис. 3.15. Схема устройства, изменяющего расход: 1 —
лепестки; 2 — корпус устройства; 3 — пневмокамера;
4 — пневмораспределитель; 5 — линия подачи сжато-
го воздуха в пневмокамеру; 6 — линия сброса сжатого
воздуха; 7 — рычаг; 8 — шток
Глава 3
315
Рис. 3.16. Принципиальная схема экспериментальной установки: 1 — экспе-
риментальный участок; 2 — отбор давления; 3 — координатник с термопарами;
4 — датчики давления; 5 — генератор постоянного тока; 6 — термопары на входе
в пучок; 7 — сопло для измерения расхода; 8 — управляющий пневмопривод; 9 —
задвижка; 10 — холодильник; И — автоматически регулируемые задвижки; 12 —
редуктор; 13 — рессивер; 14 — компрессор; 15 — фильтр; 16 — турбокомпрессор,
17 — устройство для изменения расхода
Рис. 3.17. Установка для исследования теп-
ло- и массообмена в ТВС с витыми твэлами
(число витых труб — 151)
151, движение теплоносителя вертикальное, расход воздуха 0,085—
0,46 кг/с, давление, близкое к атмосферному, температура воздуха на
выходе до 650 К. Стенд оснащен автоматизированной системой уп-
равления, измерения, сбора и обработки опытных данных, которая
позволяет изменять мощность генератора скачкообразно или по экс-
поненциальному закону от нуля до 90 кВт. Данные измерений в циф-
ровой форме вводились в ЭВМ с частотой 10 кГц.
— Установка для исследования структуры потока в круглой и ви-
той трубе и кольцевом канале с внутренней витой трубой (рис. 3.18).
Основные параметры: внутренний диаметр круглой трубы 90 мм,
длина трубы 4 м, максимальный размер овала витой трубы d = 36 мм,
относительный шаг закрутки s/d = 9,7—25,6, длина витой трубы 2 м,
скорость набегающего потока 1,9—34,1 м/с, температура воздуха на
входе 280—290 К. Витая труба размещалась центрально в круглой
трубе.
316
Глава 3
Рис. 3.18. Экспериментальный участок для тарировки датчиков и исследования
структуры потока в трубе: 1 — хонейкомб; 2 — сопло; 3 — труба; 4 — фланец для
крепления координатника; 5 — съемный конфузор
— Установка для исследования теплообмена и гидравлического со-
противления при течении внутри витых труб и в кольцевом канале с
внутренней витой трубой (рис. 3.19, 3.20). Основные параметры: мак-
симальный размер овала витой трубы d = 14,76 мм, толщина стен-
ки d = 0,6 мм, относительный шаг закрутки s/d = 6,2, длина 1,495 м,
наружный диаметр круглой трубы 18 мм и толщина стенки 0,7 мм,
расход воды (18—77)103 кг/с внутри трубы и в кольцевом канале,
температура горячей воды в кольцевом канале на входе (64—92) °C
и на выходе (49—66) °C, температура холодной воды в витой трубе
на входе (17—18) °C и на выходе (31—48) °C, тепловая мощность (1,8—
5,6) кВт. Теплообменные аппараты (ТА) типа «труба в трубе» из ста-
ли 12Х18Н10Т работали по противоточной схеме. На этой установке,
кроме ТА с витыми трубами, исследованы ТА с круглыми трубами:
Рис. 3.19. Принципиальная схема экспериментальной установки и систе-
мы измерений: 1 — теплообменник типа «труба в трубе»; 2 — турбинные
датчики расхода; 3 — дроссельные краны; 4 — термопары; 5 — электриче-
ский нагреватель; 6 — коммутатор; 7 — частотомер
Глава 3
317
Рис. 3.20. Экспериментальный участок для исследования теплообмена при тече-
нии воды в кольцевом канале с внутренней витой трубой методом теплообменни-
ка: 1 — витая труба овального профиля; 2 — внешняя круглая труба кольцевого
канала; 3, 6 — входной и выходной штуцеры для подвода и отвода горячей воды из
кольцевого канала; 4, 7 — выходной и входной штуцеры для отвода и подвода хо-
лодной воды в витую трубу; 5 — дистанционирующие стержни; 8 — круглые кон-
цы витой трубы; 9 — дистанционирующий стержень, закрученный по винтовой
линии при замене витой трубы на круглую прямую трубу
гладкой и кольцевой накаткой, а также витой трехлопастной трубой
и витой трубой овального профиля, имеющей либо кольцевую, либо
винтовую накатку.
3.2. ИНТЕНСИФИКАТОРЫ ТЕПЛООБМЕНА МАКРО-
И МИКРОМАСШТАБОВ
Установки для исследования интенсификации теплоотдачи
к различным средам, включая жидкие металлы
На рис. 3.21—3.24 (см. цветную вкладку) приведены изображения
стендов для исследования интенсификации теплоотдачи к различ-
ным средам, включая жидкие металлы. В работе [3.19] проводились
опыты на стержне диаметром 13,5 мм, длиной 3,5 и 7 м, который встав-
лялся в трубу с внутренним диаметром 17,8 мм. Турбулизация потока
осуществлялась с помощью поперечных ребер прямоугольного сече-
ния, которые представляли собой стальные кольца наружным диа-
метром 15 мм и шириной 2,0 мм, расположенные по высоте с шага-
ми 375, 187 и 94 мм. Опыты проводились при давлении 6,0—13,0 МПа,
массовых скоростях 1000—2500 кг/(м2-с). Результаты исследований
показали, что в канале с интенсификаторами кризис сопровождал-
ся плавным изменением температуры стенок. Оптимальным из ис-
следованных оказался шаг расположения интенсификаторов 187 мм,
при этом получено увеличение мощности на 35—40% относительно
канала без оребрения.
318
Глава 3
Автоматизированный стенд для исследования локальных
и интегральных характеристик интенсификации теплосъема
в широком диапазоне паросодержаний
Автоматизированный экспериментальный стенд [3.19] позволя-
ет исследовать локальные и интегральные характеристики тепло-
обмена при интенсификации теплосъема в вертикальной трубе с
внутренним диаметром 8 мм в широком диапазоне паросодержаний
(рис. 3.25). На стенде исследована интенсификация теплосъема с по-
мощью пористых покрытий и закрутки потока. Стенд обеспечивает
проведение измерений в диапазонах давлений 0,1—7 МПа, массовых
скоростей 10—650 кг/(м2-с), тепловых нагрузок до 1,5 МВт/м2. Обог-
рев рабочего участка осуществляется путем непосредственного про-
пускания переменного тока. Располагаемая электрическая мощность
стенда составляет 300 кВт. На входе и выходе из рабочего участка из-
меряется давление (ИПДЦ-89010) и температура потока (хромель-
алюмелевые термопары).
В качестве рабочих участков исследованы вертикально располо-
женные трубы диаметром 8 мм с толщиной стенки 0,5 и 1 мм из не-
ржавеющей стали длиной 1775 мм и змеевики. Тонкостенный рабо-
чий участок для разгрузки от давления помещен в защитный кожух.
Благодаря тому, что рабочий участок и кожух связаны между собой
через разгрузочную и демпфирующую емкости, в них поддержива-
ется одинаковое давление.
Рис. 3.25. Общий вид экспериментальной установки «Испаритель»
Глава 3
319
Для измерения температуры стенки на наружной поверхности
канала установлены 42 хромель-алюмелевые термопары с диамет-
ром электродов 0,3 мм (рис. 3.26). Регистрация данных измерений и
управление экспериментом осуществляются с помощью ИВК на базе
аппаратуры фирмы HEWLETT-PACKARD с максимальной скоростью
опроса 22 измерения в секунду и разрешающей способностью 1 мкВ
(рис. 3.27). На рис. 3.28 представлены типичные профили осреднен-
ных значений температуры и интенсивности пульсаций температу-
ры стенки по длине трубы. Наличие только распределения темпера-
туры по длине трубы не дает возможности точно определить длину
переходной зоны, Х**—Х*, а значит, и начало участка ухудшенной теп-
лоотдачи, что необходимо для построения надежной методики расче-
Выход
О'
1
2
3'
4
б:
6.
7.
8.
9
10.
11.
12.
13.
14.
15.
16.
17.
18
19’
20
2Г
22
23
24
25
26
27
28'
29'
30'
зС
32.
33
34'
35'
36'
37’
38'
... , ,^-гг . а т? ... «иГГТМ
~	- т	j-A Л !•. ....	11692
1 I г.	.	------* .,81	168'2
, ..- Т- т	_ 	х_. 167'2
" 1 ' _	.’.-/Г ' "..JJ1662
дададдав'	—и 642
 	.......а--	--------------- --.... >1612
ZZ=ZZ-ZZZZZZZ=ZZZZ^==ZZZZZZZ11582
==..=1=...=....:.......-..П552
==================11522
======;=.-.. .z-. —.	......-....==»1492
...-.-............-'-Д	.а.и.и.=1461
--..7 	-..............=3 1431
-----------------------..=11402
=======1373
--   .. 1341
===-"-=-7- —.7"'|— z...„ ;.11312
======T'Z7 ST-S.7.........  1280
—-”--'7 7' ' "........... . .11252
Т-..	—.-az... ,, -И 221
„	„11191
Л-Ь- 7*  '	^11150
Ь	 	>*-	=31111
-...... ...— -т..—;1072
г-	Ц 030
г-..ляг-., л л: ! 1 . 8991
<!»._	ir.iq^n
  I- 1		>910
=====872
— ----------1831
793
==7=„.т:.====з756
........=3714
==633
==554
7'.='=' 2:1474
=393
=313
233
Вход
41
5
0	200	400 600 800 1000 1200 1400 1600 1800
Координата по длине рабочего участка, мм
Рис. 3.26. Схема расположения термопар на рабочем участке
320
Глава 3
-и.
-G
-Р
Рис. 3.27. Схема автоматизации теплофизического эксперимента
та теплообмена в закризисной
области. За начало переходной
области принимается сечение,
предшествующее, началу необ-
ратимого роста осредненной
температуры стенки и интен-
сивности ее пульсаций. Знание
распределения интенсивности
пульсаций температуры стен-
ки позволяет определить длину
переходной области и начало
участка ухудшенной теплоот-
дачи (X**). Как видно из рисун-
ка, интенсивность пульсаций
температуры стенки возраста-
ет по длине переходной облас-
ти, проходит через максимум
Рис. 3.28. Зависимость темпера-
туры стенки (а) и интенсивность
ее пульсаций (б) от паросодержа-
ния: Р = 1,6 МПа; рсо = 17 кг/(м2-с);
q — 54 кВт/м2
Глава 3
321
и уменьшается до значения, характерного для участка ухудшенной
теплоотдачи.
Автоматизированный стенд с электронным нагревом
горизонтально расположенного канала
На стенде исследована интенсификация теплоотдачи в горизон-
тальной трубе, нагреваемой снаружи пучком электронов и охлаж-
даемой изнутри потоком воды в диапазонах массовых скоростей
100—10000 кг/(м2-с), давлений 0,1 — 1 МПа при кипении недогретой
жидкости [3.20]. Стенд имеет замкнутый циркуляционный контур
теплоносителя (рис. 3.29). Рабочий участок представляет собой гори-
зонтально расположенную толстостенную медную трубу с внутрен-
ним диаметром 8 мм и плоской приемной поверхностью 50x15 мм2.
Она устанавливается в вакуумной камере и нагревается пучком
электронов (рис. 3.30, 3.31). В пазах рабочего участка установлены
термопары.
Исследованы следующие рабочие участки:
— труба с технически гладкой поверхностью,
—	труба со спеченным покрытием,
—	труба с закрученной лентой.
1
Рис. 3.29. Схема экспериментальной установки с электронным нагревом гори-
зонтально расположенного канала: 1 — ресивер; 2 — насос; 3 — регулирующий
вентиль; 4 — расходомерное устройство; 5 — датчик давления; 6 — вакуумная
камера; 7 — опытный участок; 8 — катод; 9 — диффузионный насос; 10 — форва-
куумный насос; И — высоковольтный источник питания; 12 — источник питания
катода; 13 — регулятор напряжения катода; 14 — холодильник; 15 — баллон с азо-
том; 16 — термопара для измерения температуры теплоносителя на входе в рабо-
чий участок; 17 — термопары рабочего участка; 18 — термопара для измерения
температуры теплоносителя на выходе из рабочего участка; 19 — ИВК
322
Глава 3
3.30. Рабочий участок экс-
периментальной установки
с электронным нагревом
Рис. 3.31. Вакуумная камера
экспериментальной уста-
новки с электронным на-
гревом горизонтально рас-
положенного канала: 1 —
опытный участок; 2 — осно-
вание вакуумной камеры;
3 — крышка вакуумной ка-
меры; 4 — окно для наблю-
дения; 5 — растяжка катода;
6 — электрод; 7 — основа-
ние узла для ввода электро-
дов; 8 — защитный экран
Методика исследования основана на измерении распределения
температуры стенки и ее пульсаций по периметру трубы. Получен-
ная информация является исходной для восстановления условий
теплосъема на поверхности охлаждения путем решения обратной
задачи теплопроводности.
Управление стендом, сбор и хранение информации, ее обработ-
ка и представление результатов в виде таблиц и графиков автомати-
зированы при помощи ИВК, созданного на базе аппаратуры фирмы
«Hewlett Paccard» (рис. 3.32).
Глава 3
323
Датчики	go измерительных каналов
Рис. 3.32. Схема автоматизации измерений экспериментальной установки
с электронным нагревом горизонтально расположенного канала
Методы исследования интенсификации теплообмена в каналах
сложной формы
При разработке мишеней, облучаемых интенсивными пучками
электронов, ионов или фотонов с плотностью теплового потока свы-
ше 10 МВт/м2, возникает комплексная задача рационального выбора
материала и толщины тепловоспринимающей стенки (для снижения
термических деформаций и напряжений) и обеспечения ее охлаж-
дения подходящим теплоносителем. Из-за быстрого подогрева теп-
лоносителя приходится выполнять систему охлаждения с широкой
сетью коллекторных устройств, расположенных на разных «этажах»
конструкции, со сложными по форме многоканальными (пористы-
ми) системами охлаждения, в которых теплоноситель многократно
меняет направление движения, образуя струйные и отрывные вих-
ревые течения. Такие задачи характерны для мишеней нейтронных
генераторов, лазерных зеркал и других элементов ускорителей и т.п.
Для определения термических деформаций и напряжений и, в ко-
нечном итоге, оптимизации конструкций, а также повышения поро-
гов их разрушения необходимо найти поля температуры и гидравли-
ческие сопротивления в охлаждаемых элементах [3.21, 3.22].
Ниже, после определения необходимых для измерения коэффи-
циентов переноса, кратко приведены экспериментальные методы ис-
следования некоторых систем интенсификации теплообмена.
324
Глава 3
Двухтемпературные уравнения конвективного теплообмена в по-
ристых средах. Охлаждаемый пористый слой мишени с той или иной
структурой микроканалов обычно характеризуется гидравлическим
диаметром менее 1—2 мм. Твердый каркас пористого слоя имеет хо-
рошие тепловой и механический контакты с тонкой тепловоспри-
нимающей стенкой, вдоль которой движется (фильтруется) тепло-
носитель. То есть направления теплового потока (ось z) и скорости
жидкости в пористом слое (осьх) взаимно перпендикулярны. В приб-
лижении пористого тела твердый каркас и движущаяся жидкость об-
мениваются теплом и характеризуются собственными значениями
теплофизических свойств: теплопроводностями Лк и Хж (вдоль оси z),
теплоемкостями Ск и Сж, плотностью. Нестационарные распреде-
ления температуры'каркаса Тк (x,z) и жидкости Тж (x,z) в пористом
слое описываются дифференциальными уравнениями теплообмена
[3.21, 3.22]:
(3.1)
(3.2)
Эти уравнения учитывают продольный конвективный перенос
тепла жидкостью, движущейся относительно каркаса с эффектив-
ной скоростью v вдоль оси х; поперечный кондуктивный перенос теп-
ла от стенки вдоль оси z за счет теплопроводности каркаса и жидко-
сти (с учетом ее перемешивания в пористой среде); теплообмен меж-
ду каркасом и жидкостью, интенсивность которого характеризует-
ся коэффициентом объемной теплоотдачи ау=а£Д(Вт/(м3-К)]. В пос-
леднем выражении а — средний коэффициент теплоотдачи каркаса
в расчете на единицу смоченной поверхности пор, Вт/(м2-К), Sv —
удельная смоченная поверхность пор в расчете на единицу объема
пористой среды, м2/м3.
Перемешивание жидкости в сообщающихся порах определяет
эффективную (турбулентную) диффузию £>ж и теплопроводность
Хж = рСр£>ж . В случае низкотеплопроводного каркаса единственный
механизм переноса тепла в глубь охлаждаемого слоя мишени по нор-
мали к нагреваемой стенке — это турбулентная теплопроводность
жидкости, движущейся вдоль стенки со скоростью фильтрации
гф = Пуэ (уэ — скорость в не занятом каркасом сечении, П — порис-
тость). Обычно величины Рж и Хж прямо пропорциональны скорости
фильтрации жидкости в пористой среде. Для пористых сред с пери-
одической структурой, характеризуемой продольным «ц и попереч-
Глава 3
325
ным s± шагами расположения пор (относительно направления тече-
ния жидкости), получен «предельный закон перемешивания», огра-
ничивающий сверху турбулентную диффузию и теплопроводность
[3.21, 3.22]:
D <Уж—.	(3-3)
ж *8s„
На границе охлаждаемого пористого слоя со стенкой, нагревае-
мой внешним источником, необходимо учитывать перераспределе-
ние теплового потока, исходящего из стенки, между каркасом и жид-
костью в пристенных порах [3.22—3.27]:
д = -Лк^- + аж(Гк-Тж) приг = 0.	(3.4)
Первое слагаемое характеризует долю тепла, отводимого от стен-
ки каркасом, а второе — непосредственно жидкостью. Величина
аж = аП — коэффициент теплоотдачи от стенки пористого слоя при
нулевой теплопроводности каркаса.
Потери давления. Течение (фильтрация) жидкости сквозь порис-
тый слой сопровождается потерями давления, вызванными дисси-
пацией энергии потока в тепло за счет вязкости жидкости. Градиент
давления в жидкости обычно связывают со скоростью ее течения вы-
ражениями
-	Аруф + Bpvl,	(3.5)
dx 2d3 ф *
в которых d3 = 4П/5у — эквивалентный (гидравлический) диаметр
пор (микроканалов); А и В — вязкостный и инерциальный коэффици-
енты гидравлического сопротивления (размерные); — безразмер-
ный коэффициент гидравлического сопротивления; ц-молекулярная
(динамическая) вязкость жидкости, Па-с.
Для практического использования приведенной математической
модели конвективного теплообмена в пористых средах необходимо
располагать данными о зависимости коэффициентов переноса, вхо-
дящих в уравнения (3.1) —(3.5), от расхода и свойств теплоносителя,
структуры и материала пористого каркаса. В работах [3.21, 3.22, 3.26,
3.27] приведены обзор и обобщение экспериментальных данных об
интенсификации теплообмена в разнообразных структурах порис-
тых систем охлаждения (щелевой, вафельной, щеточной, компланар-
ной, из спеченных порошков, сеток, пенометаллов и др.). Ниже приве-
дены некоторые результаты, полученные авторами данной работы.
Типичная экспериментальная установка для исследования интен-
сификации теплообмена в системах пористого охлаждения состоит из
326
Глава 3
контура охлаждения, включающего насос, расходомер, фильтр тон-
кой очистки; сменного рабочего участка с пористым слоем; системы
сбора температурных и манометрических данных; системы нагрева
в виде ионного, электронного или лазерного пучков; металлическо-
го теплопровода («теплового клина») с электрическим нагревателем
и др. [3.21, 3.23, 3.25]. В некоторых опытах обогрев осуществлялся
пропусканием электрического тока через стенку рабочего участка
(обычно стальной трубки). Ребра на образцах получены путем фре-
зерования дисковыми фрезами (алмазными в случае кремния) либо
электроэрозионным методом (сталь, молибден). Образцы из спечен-
ных порошков и порометаллов припаивали к медным теплопроводам
оловянным припоем либо приклеивали интерметаллическим клеем
на основе меди и галлия. Для моделирования низкотеплопроводного
каркаса применяли пакеты сеток из стальной и латунной проволо-
ки (не спеченные). Гидравлический диаметр пор изменялся от 0,1 до
1,5 мм, толщина пористого слоя от 3 до 9 мм, длина (в направлении те-
чения теплоносителя) от 6 до 80 мм.
Составляющие теплообмена в щеточной структуре. Эксперимен-
тальное исследование составляющих теплового потока в «щеточ-
ных структурах» проводилось в каналах прямоугольного сечения
размером 26x30, 19x21 мм2 и длиной 250 мм, изготовленных из орг-
стекла [3.24]. Щеточная структура моделировалась набором медных
или фарфоровых стержней диаметром 2—4 мм, расположенных с
шагом 3—6 мм (пористость 0,65—0,91) в коридорной или шахматной
упаковке. Число рядов стержней вдоль потока воды составляло 16 —
28, а в каждом ряду находилось по 4—8 стержней. Для определения
теплоты, отводимой непосредственно стержнями (шипами щеточ-
ной структуры), проводился нагрев единичных медных стержней,
расположенных в зоне стабилизированного теплообмена (рис. 3.33).
Выступающий за пределы стеклянной стенки конец этих стержней
обогревался электрическим нагревателем. Теплота через стеклян-
ную стенку в канал не поступала. При диаметре стержней 2 мм, тем-
пературном напоре То — Твх = 80°С скорость воды в узком сечении
сборки стержней составляла 1 м/с, удельный тепловой поток вдоль
стержней равен 9—10 МВт/м2 в отсутствие кипения на боковой по-
верхности стержней, что на порядок превышает удельные тепловые
потоки (при таких скоростях воды), отводимые от гладкой стенки ки-
пящей водой (Т — температура основания стержня). Коэффициен-
ты теплоотдачи а на боковой поверхности шипов, необходимые для
определения объемной теплоотдачи щеточной структуры, равны 5—
13 кВт/(м2-К) и весьма близки к расчетным величинам по формуле
А.А. Жукаускаса.
Глава 3
327
Рис. 3.33. Схемы рабочих участков для измерения составляющих теплоотдачи
в пористом теплообменнике со щеточной структурой:
а — для измерения теплоотдачи на боковой поверхности медных шипов; б —для
измерения теплотдачи в межстержневом пространстве; в — для измерения ре-
зультирующей теплоотдачи; 1 — стеклянные стенки; 2 — поток воды; 3 — элект-
рические нагреватели; 4 — нагреваемый медный стержень; 5 — термопары; 6 —
медные стержни щеточной структуры; 7 — медная пластина (теплопровод); 8 —
фарфоровые стержни щеточной структуры; 9 — медные стержни, впаянные в
медный теплопровод
Для определения теплоотдачи аж = аП от ошипованной стенки
в межстержневом пространстве и для исключения теплопроводно-
сти по стержням использовались каналы с фарфоровыми стержнями,
которые одним из своих концов вставлены в нагреваемую внешним
электрическим нагревателем медную пластину (стенку) толщиной
18 мм (см. рис. 3.33). Величина а оказалась близкой к коэффициенту
теплоотдачи на боковой поверхности шипов. То есть трехмерная тур-
булентность в «щеточных структурах» как бы выравнивает теплоот-
дачу на разных поверхностях структуры.
Коэффициент теплоотдачи аэф оребренной стенки определялся
на таком же участке, но фарфоровые стержни заменены медными,
впаянными в медную стенку. Результирующая теплоотдача хорошо
описывается «формулой аддитивности»:
азф=(1-П)74<Аш/й+аП.	(3.6)
Здесь — теплопроводность материала шипа. Согласно получен-
ным данным, доля тепла, переносимого по каркасу [первое слагае-
мое в (3.6)], уменьшается с ростом скорости течения теплоносителя
и увеличением пористости. При числах Рейнольдса Re = vm d/v <500
(vm — скорость в узком сечении), d < 2 мм, П < 80% и высокой тепло-
проводности материала шипов непосредственно от стенки к жидко-
сти передается не более 18% теплоты. Остальные 82% теплоты вое-
328
Глава 3
принимаются от стенки теплопроводными шипами и передаются че-
рез их боковую поверхность в глубинные слои жидкости.
Пределы интенсификации теплообмена в пористых средах. Вы-
сокая теплопроводность пористого каркаса позволяет теплоте про-
никать на относительно большую глубину внутрь пористой среды,
уменьшая тем самым перегрев жидкости вблизи стенки и развивая
поверхность теплообмена. Эксперименты и расчеты показывают, что
рост теплопроводности каркаса в 30 раз (медь вместо инвара) ведет к
повышению коэффициента теплоотдачи в 4—5 раз, то есть приблизи-
тельно как • Для повышения теплопроводности каркаса выгодно
уменьшать его пористость. При этом, однако, увеличивается гидрав-
лическое сопротивление и падает расход жидкости при заданном на-
поре. Поэтому существует оптимальная пористость, которая для раз-
ных структур составляет 40—60%. Если зафиксировать пористость
каркаса и длину пористого слоя, а также перепад давления на этой
длине, то можно обнаружить, что при изменении гидравлического
диаметра пор (дисперсности слоя) величина эффективной теплоот-
дачи стенки проходит через максимум, которому соответствует опти-
мальный гидравлический диаметр. При меньших диаметрах пор вели-
ко гидравлическое сопротивление и мала скорость фильтрации, что
ведет к перегреву жидкости и снижению теплоотдачи. При увеличе-
нии же гидравлического диаметра сверх оптимального увеличивается
скорость жидкости, но снижается удельная поверхность теплообмена.
Эффективная теплоотдача стенки оптимизированного пористого слоя
из меди с межколлекторным расстоянием 10 — 20 мм может достигать
высоких значений (3 — 5) 105 Вт/(м2-К). Столь высокая теплоотдача при
температурных напорах до 100°С может обеспечить отвод тепловых
потоков плотностью 30 — 50 МВт/м2 некипящей водой.
Теплообмен при локальном нагреве. Распределение плотности теп-
лового потока по поперечному сечению греющего пучка в реальных
конструкциях часто бывает неравномерным. Оно может иметь коль-
цевую форму, форму гауссовой кривой либо состоять из большого
числа острых пиков, интенсивность которых значительно превыша-
ет среднюю. Вследствие этого неоднократно наблюдались повреж-
дения мишеней с тонкой стенкой, а данные по мишеням со сравни-
тельно толстой стенкой интерпретировались необъяснимо высокой
теплоотдачей стенки со стороны пористого слоя. Объяснение наблю-
даемым эффектам дано в работах [3.21, 3.22, 3.25]. Известно, что при
нагреве полупространства тепловым потоком плотностью qo в преде-
лах круга радиусом го температура в центре пятна обогрева То превы-
шает температуру вдали Тж согласно формуле
То^Тх + дого/Х.	(3.7)
Глава 3
329
Как видно, несмотря на постоянный приток тепла в неохлажда-
емое полупространство, температура на его поверхности принимает
конечное стационарное значение благодаря радиальным растечкам
тепла от зоны нагрева. При локальном нагреве стенки толщиной 5,
охлаждаемой с противоположной стороны теплоносителем с эффек-
тивной теплоотдачей аэф, температура в центре нагреваемой облас-
ти может превышать температуру, согласно уравнению (3.7), в цент-
ре полупространства, если осэфго/Х<1 [3.21, 3.22, 3.25]. В этом случае
уменьшение толщины стенки ведет не к снижению ее температу-
ры, а, наоборот, к ее росту вследствие большого термического со-
противления радиальным (вдоль тонкой стенки) растечкам тепла.
Увеличение толщины стенки облегчает радиальные растечки теп-
ла и способствует уменьшению плотности теплового потока, отво-
димого теплоносителем под пятном нагрева по сравнению с тепло-
вой нагрузкой qo, что воспринимается как увеличение эффективной
теплоотдачи. Для проверки этих выводов проведены эксперименты
с медной мишенью, имеющей «вафельное оребрение» в виде шипов
квадратного сечения со стороной 1,2—1,4 мм, высотой 3 мм и шагом
2,0—2,2 мм на площади 40x40 мм2 [3.25]. Мишень с толщиной стенки
1—2 мм нагревалась электронным пучком диаметром -10 мм и теп-
ловой нагрузке до 70 МВт/м2. На охлаждаемой поверхности стенки
у основания шипов зачеканивались 10 — 15 медьконстантановых тер-
мопар для определения радиального профиля температуры и измере-
ния теплоотдачи. Результаты измерений удовлетворительно согласу-
ются с расчетом по предложенной методике в области однофазного
теплообмена, реализуемого при до<15—20 МВт/м2. При больших теп-
ловых потоках под пятном контакта температура стенки достигала
100—115 °C и начиналось кипение воды. Высокие тепловые нагрузки
начала кипения обусловлены следующими причинами: 1) высокой
теплоотдачей оребренной стенки — более 100 кВт/(м2-К); 2) радиаль-
ными растечками теплоты в медной стенке, благодаря чему тепловой
поток под пятном нагрева составлял менее половины от тепловой на-
грузки до; 3) большими недогревами воды на входе до температуры
насыщения (80—95 °C). Температура стенки под центром пучка почти
линейно увеличивалась с ростом тепловой нагрузки до 300 °C без
возникновения кризиса теплообмена.
Проведенные эксперименты и математическая модель показали,
что оребренная стенка из высокотеплопроводного материала при ра-
циональном выборе структуры ребер и толщины стенки сохраняет
работоспособность при весьма высоких тепловых нагрузках.
Измерение турбулентной теплопроводности жидкости в порис-
тых средах. Для измерения £>ж и Хж в работах [3.21—3.23] предложены
330
Глава 3
два новых (интегральных) способа, отличающихся от ранее известных
следующими особенностями: 1) размещением датчиков температуры
снаружи (а не внутри) исследуемой среды; 2) быстротой измерений;
3) пригодностью как для мелкодисперсных сред, так и для крупнога-
баритных трубных пучков, решеток, засыпок. Идея метода измерения
турбулентной диффузии заключается в следующем: два плоскопарал-
лельных потока изотермической жидкости движутся с одинаковой
скоростью фильтрации через пористую среду вдоль оси х (рис. 3.34).
Поперечное сечение потоков одинаково (ширина b и высота /1/2).
На участке длиной I (х = 0 — 1) образован участок смешения (переме-
шивания, взаимодействия) потоков. За пределами этого участка пото-
ки разделены непроницаемой перегородкой (металлической фольгой,
тефлоновыми или текстолитовыми тонкими пластинами). В один из
потоков вводится примесь (чернила, краска и т.п.) массой Мо, не влия-
ющей на физические параметры жидкости. Вследствие взаимодейст-
вия часть примеси массой ДМ переходит из одного потока в другой.
Вся примесь, содержащаяся в обоих потоках, собирается в сборные
коллекторы (отдельно для каждого потока). После этого определяет-
ся масса примеси в каждом коллекторе (по мутности и т.п.). Отноше-
ние ДМ/Мо зависит от длины зоны перемешивания и служит мерой
его интенсивности, то есть турбулентной диффузии. Длина зоны вза-
имодействия выбирается из условия минимума погрешности изме-
рения параметров перемешивания. Расчеты показали, что погрешно-
сти минимальны, когда из одного потока в другой переносится около
20 — 30% введенного вещества. Для исключения погрешности, связан-
ной с неодинаковостью расхода потоков, примесь вводится сначала в
один поток, затем в другой.
Для измерения коэффициента турбулентной теплопроводности
жидкости в пористой среде достаточно измерить среднемассовую
температуру жидкости в четырех точках: двух на входе (входят потоки
с разной температурой и одинаковой скоростью) и двух на выходе из
установки. Независимые измерения £>ж и Лж в разных пористых струк-
турах показали, что практически выполняется равенство
Рис. 3.34. Схема установки для
измерения поперечной диффу-
зии в пористой среде, сквозь
которую фильтруется вода:
К — регулировочные вентили;
Р — расходомеры; С — смеси-
тельные камеры; РУ — рабо-
чий участок с пористой средой;
G — расход воды
Глава 3
331
то есть подтверждено, что число Льюиса Lu = pCpD/X для турбулен-
тного потока практически равно 1. Это обстоятельство позволяет оп-
ределить турбулентную теплопроводность по данным более простых
измерений турбулентной диффузии. Этими способами измерены Рж
и Хж в воде, движущейся в сетчатых и щеточных структурах, пеноме-
таллах и спеченных порошках. Величины Рж и 1 практически прямо
пропорциональны скорости фильтрации жидкости. При скоростях
фильтрации около 1 м/с и выше эффективная теплопроводность воды
может превышать 100 Вт/(м-К). Экспериментальные данные для сетча-
тых вставок пористостью 65 — 70% с диаметром проволоки 0,25 и 0,4 мм
в области чисел Рейнольдса Re = 10 — 1000 обобщены формулой
= Do +	(3.8)
где Do — диффузия в пористой среде в случае покоящейся жидкости;
к = 0,075±0,010 — безразмерный коэффициент. Анализ этих резуль-
татов и известных данных позволил установить ранее неизвестную
закономерность, заключающуюся в том, что между турбулентной
теплопроводностью и гидравлическим сопротивлением пористой
структуры существует достаточно общая взаимосвязь. Так, если
данные по гидравлическому сопротивлению (перепаду давления Др
на длине 1) обобщать двучленной формулой (3.5), то коэффициенты
турбулентной теплопроводности удовлетворительно обобщаются
формулой
К = Ч + kpv^CpB/A.	(3.9)
в которой безразмерный коэффициент к = 9 ±2 одинаков для многих
сетчатых и зернистых пористых сред. Здесь 7() — теплопроводность
покоящейся жидкости в пористой среде, А(мг2), В(м-1) — вязкостные и
инерционные коэффициенты сопротивления пористого материала,
Уф — скорость фильтрации. Выражение (3.9) удобно для оценки теп-
лопроводности жидкости в пористой среде по результатам измере-
нйя гидравлического сопротивления этой среды, что можно осущест-
вить с высокой точностью.
Интенсификация теплообмена в струйных системах охлаждения.
Одним из эффективных способов интенсификации теплообмена
является организация струйного течения в изолированных цилин-
дрических ячейках с высокотеплопроводными стенками (рис. 3.35).
Для расчета термических напряжений и деформаций в мишенях со
струйным охлаждением требуется детальная информация о величи-
нах теплоотдачи со дна ячеек и с их боковых поверхностей. При этом
основное внимание уделено «эффекту оребрения», то есть определе-
нию долей тепловой нагрузки, снимаемой отдельно через дно ячеек
и через их боковые стенки. Экспериментальная установка включа-
332
Глава 3
Рис. 3.35. Схемы зеркала со струйной системой охлаждения (а) и рабочих участ-
ков для измерения результирующей теплоотдачи (б) от дна ячейки (в) и поверх-
ности (г)
ет электрический нагреватель с медным теплопроводом цилиндри-
ческой формы; сменные рабочие участки, находящиеся в тепловом
контакте с торцом теплопровода; микрометрическое устройство для
перемещения сопла относительно дна ячейки; системы подвода и от-
вода теплоносителя (водопроводной воды) [3.23]. Внутренний диа-
метр ячейки изменялся от 3 до 15 мм, толщина стенки ячейки — от
0,4 до 1,0 мм, внутренний диаметр сопла (истекающей струи) — от
1,5 до 6,5 мм. Для измерения теплоотдачи от дна ячейки использова-
ли фарфоровые боковые стенки. Для измерения теплоотдачи от бо-
ковой поверхности медных ячеек использовали тефлоновые встав-
ки. Интегральную теплоотдачу измеряли как на единичной ячейке,
так и на модели мишени с девятью ячейками (диаметр мишени 24 мм,
диаметр ячеек струйного охлаждения 3,2 мм). Установлены зависи-
мости коэффициентов теплоотдачи от размеров ячеек, расстояния
между срезом сопла и дном ячеек, скорости истечения воды. Показа-
но, что результирующая теплоотдача в медной мишени имеет экстре-
мум (максимум) при относительной площади дна ячеек 70—80%. На-
Глава 3
333
личие максимума объясняется большим вкладом в результирующую
теплоотдачу «эффекта оребрения», то есть теплоотдачи с боковой
поверхности ячеек. Коэффициент теплоотдачи при этом превышает
100 кВт/(м2-К) при числах Рейнольдса в соплах более 2-Ю4 (скорость
истечения более 6 м/с). Если мишень изготовить из материала с мень-
шей теплопроводностью, чем у меди, то оптимальная пористость (от-
носительная площадь дна ячеек) уменьшится.
3.3. КОЛЕБАНИЯ ПОВЕРХНОСТИ РАЗДЕЛА ФАЗ
Колебания границы раздела фаз при кипении интенсифицируют
перенос теплоты. Методика для исследования колебаний границы
раздела фаз при кипении разработана в [3.28—3.32]. Она основана на
зондировании пучком маломощно-
го излучения пристенного слоя жид-
кости над поверхностью, на которой
происходит кипение (рис. 3.36). Ис-
точником излучения служит гелий-
неоновый лазер (1). В качестве повер-
хности нагрева выбрана трубка (3)
диаметром 3 мм, расположенная гори-
зонтально и выполненная из нержаве-
ющей стали. Пучок излучения прохо-
дит через коллиматор и диафрагму (2)
с характерным размером D и попада-
ет на фотодатчик (4). Сигналы фото-
Рис. 3.36. Схема эксперименталь-
ной установки для исследования
колебаний границы раздела фаз
с помощью оптической и акусти-
ческой диагностики
датчика (4) и пьезоэлектрического датчика (6) регистрируются с по-
мощью цифрового запоминающего осциллографа (5) (рис. 3.37,3.38)и
свидетельствуют о колебанияхпарового пузыря, растущего настенке.
датчика
Рис. 3.38. Сигнал акустического
датчика при различных тепловых
нагрузках
334
Глава 3
Рис. 3.39. Спектры сигналов оптического (а)
и акустического (б) датчиков
Для анализа спектральных
характеристик колебаний
границы раздела фаз при
пузырьковом кипении при-
менен анализатор фирмы
«Брюлль и Къерр». С его
помощью получены спект-
ры сигналов оптического
и акустического датчиков
(рис. 3.39, а, б). Выделенные
частоты на спектрах соот-
носятся как целые числа,
что свидетельствует о вза-
имосвязи колебаний паро-
вого пузыря и давления в
жидкости. Таким образом
было установлено, что при
росте парового пузыря на
стенке в объеме жидкости происходит одновременно как изменение
его формы, так и объема.
В работах [3.32,3.33] предложена модель кинетики роста парового
пузыря и получены аттракторы описывающей его системы уравне-
ний. На рис. 3.40 представлен фазовый портрет колебаний парового
пузыря при его росте на стенке при атмосферном давлении, недогре-
ве воды 5К, тепловой нагрузке 40 кВт/м2.
Рис. 3.40. Фазовый портрет колебаний парового пузыря при его росте на стенке:
а — зависимость первой производной радиуса пузыря во времени от радиуса; б —
зависимость давления пара в пузыре от радиуса
Фазовый портрет (рис. 3.40, а) показан в относительных коорди-
натах: первая производная радиуса пузыря во времени — радиус пу-
зыря. В фазовом портрете обнаруживаются колебания небольших
пузырей (высокая частота и большая амплитуда) и больших (неболь-
шие частота и амплитуда).
Глава 3
335
Список литературы
3.1.	Данилов Ю.И., Дзюбенко Б.В., Дрейцер Г.А., Ашмантас Л.-В.А. Теп-
лообмен и гидродинамика в каналах сложной формы. М.: Машинострое-
ние, 1986.
3.2.	Дзюбенко Б.В., Дрейцер Г.А., Ашмантас Л.-В.А. Нестационарный теп-
ломассообмен в пучках витых труб. М.: Машиностроение, 1988.
3.3.	Дзюбенко Б.В., Сакалаускас А.В., Ашмантас Л.-В.А., Сегаль М.Д.
Турбулентное течение и теплообмен в каналах энергетических установок.
Вильнюс: Исток, 1995.
3.4.	Дзюбенко Б.В. Исследование полей скорости и температуры в межтруб-
ном пространстве теплообменного аппарата с закруткой потока//Совре-
менные проблемы гидродинамики и теплообмена в элементах энергети-
ческих установок и криогенной технике: Межвузовский сб. научн. тр.: М.:
ВЗМИ, 1979. Вып. 8. С. 93-104.
3.5.	Дзюбенко Б.В., Сакалаускас А.В., Вилемас Ю.В. Энергетические
спектры турбулентности в теплообменнике с закруткой потока//Изв. АН
СССР. Энергетика и транспорт. 1983, № 4. С. 125-133.
3.6.	Дзюбенко Б.В. и др. Исследование структуры потока в теплообменнике с
винтообразно закрученными трубами//Там же. 1980. № 4. С. 135-144.
3.7.	Дзюбенко Б.В. и др. Вихревая структура потока в теплообменнике с ви-
тыми трубами/Дам же. 1986. №3. С. 151-157.
3.8.	Дзюбенко Б.В., Вилемас Ю.В., Ашмантас Л.-В.А. Перемешивание
теплоносителя в теплообменнике с закруткой потока//ИФЖ. 1981. Т. 40,
№ 5. С. 773-779.
3.9.	Дзюбенко Б.В., Урбанас П.А., Ашмантас Л.-В.А. Межканальное пере-
мешивание теплоносителя в пучке витых труб/Дам же. 1983. Т. 45, № 1.
С.26-31.
3.10.	Дзюбенко Б.В., Ашмантас Л.-В.А. Тепломассоперенос в закручен-
ном пучке витых труб//Изв. АН СССР. Энергетика и транспорт. 1985. № 6.
С. 135-144.
3.11.	Дзюбенко Б.В. Особенности тепломассопереноса в пучках витых труб//
ИФЖ. 1986. Т. 50, № 4. С. 535-542.
3.12.	Дзюбенко Б.В., Стецюк В.Н. Влияние интенсивности закрутки потока
на перемешивание теплоносителя в пучках витых труб//ИФЖ. 1988. Т. 55,
№ 5. С. 709-715.
3.13.	Дзюбенко Б.В. К вопросу о межканальном перемешивании теплоносите-
ля в пучках оребренных стержней/Дам же. 1979. Т. 37, № 5. С. 777-783.
3.14.	Дзюбенко Б.В. Исследование переносных свойств потока в теплообмен-
нике с винтообразно закрученными трубами/Дам же. 1980. Т. 38, № 6.
С.965-971.
3.15.	Дзюбенко Б.В., Ивлев В.М. Теплообмен и гидравлическое сопротив-
ление в межтрубном пространстве теплообменника с закруткой потока//
Изв. АН СССР. Энергетика и транспорт. 1980. № 5. С. 117-125.
3.16.	Дзюбенко Б.В. Теплообмен на начальном участке в теплообменнике с
закруткой потока//ИФЖ. 1982. Т. 42, № 2. С. 230-235.
336
Глава 3
3.17.	Дзюбенко Б.В. Ашмантас Л.-В.А., Вилемас Ю.В. Интенсификация
теплообмена в поперечно обтекаемых пучках витых труб//Изв. АН СССР.
Энергетика и транспорт. 1982. № 6. С. 120-127.
3.18.	Дзюбенко Б.В., Стецюк В.Н. Закономерности теплообмена и гидравли-
ческого сопротивления в пучках витых труб/Дам же. 1989. № 4. С. 137-145.
3.19.	Кузма-Кичта Ю. А. и др. Исследование интенсификации теплосъема в
парогенерирующих каналах с пористым покрытием/Деплоэнергетика.
1991. №5. С. 42-47.
3.20.	Кузма-Кичта Ю. А. и др. Влияние закрутки потока и пористого покрытия
на кризис теплообмена в горизонтальной трубе с неоднородным нагре-
вом/Депломассообмен. Минск, 1992. Т. 4. Ч. 1. С. 35-38.
3.21.	Харитонов В.В. Теплофизика лазерных зеркал. М.: МИФИ, 1993.
3.22.	Субботин В.И., Харитонов В.В. Теплофизика охлаждаемых лазерных
зеркал/ДВТ. 1991. Т. 29, № 2. С. 365-375.
3.23.	Кошелев С.Б., Субботин В.И., Харитонов В.В. Составляющие теп-
лопередачи при струйном течении воды в ограниченном пространст-
ве/ДВТ. 1985. Т. 23, № 3. С. 542-548.
3.24.	Плаксеев А.А., Субботин В.И., Харитонов В.В. Теплоотдача при вы-
нужденной конвекции в пористом слое со щеточной структурой/Депло-
энергетика. 1983. № 8. С. 63-65.
3.25.	Кузьмин Ю.А., Теряев В.В., Харитонов В.В. Теплоотдача оребренной
стенки при локальном нагревании мощным электронным пучком//Изв. АН
СССР. Энергетика и транспорт. 1991. № 4. С. 144-151.
3.26.	Субботин В.И., Харитонов В.В., Плаксеев А.А., Алексеев С.В. Об ин-
тенсификации теплообмена в капиллярно-пористых теплообменниках//
Там же. 1984. № 6. С. 94-101.
3.27.	Харитонов В.В., Федосеев В.Н. Интегральный метод измерения попе-
речной теплопроводности и диффузии в турбулентном потоке жидкости//
Измерительная техника. 1994. № 7. С. 51-53.
3.28.	Petukhov B.S., Kovalev S.A., Zhukov V.M., Kuzma-Kichta Yu.A.//Proc.
5th Int. Heat Transfer Conf. Tokyo, 1974. N 4. P. 96-99.
3.29.	Кузма-Кичта Ю.А., Зудин Ю.Б., Бакунин В.Г., Устинов А.А., Салтыко-
ва Е.В. Исследование колебаний границы раздела фаз при пузырьковом
кипении методами лазерной диагностики//! 2-я школа-семинар молодых
ученых и специалистов под патронажем акад. Леонтьева А.И. М., 1999.
3.30.	Kuzma-Kichta Yu.A., Ustinov А.К., Ustinov А.А. Investigation by laser
and acoustic method of interface oscillations during boiling//Boiling 2000
Phenomena & Emerging applications Conf., Anchorage, Alaska, Apr. 30-May
5. V. 1. P. 100-115.
3.31.	Kuzma-Kichta Yu.A., Ustinov A.K., Ustinov A.A. Boiling investigation by
laser and acoustic diagnostic method//3rd European Heat Transfer Conf.,
Heildenberg, Germany, 2000.
3.32.	Кузма-Кичта Ю.А., Устинов A.K., Устинов A.A., Холпанов Л.П. Иссле-
дование колебаний границы раздела фаз при пузырьковом кипении/Де-
оретич. основы хим. технол. 2002. № 6. С. 577-583.
3.33.	Устинов А.А. Исследование колебаний границы раздела при кипении.
Дисс. канд. техн. наук. М.: МЭИ. 2005.
Глава 4
РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ
ИНТЕНСИФИКАЦИИ ТЕПЛО- И МАССОВЫЕ НА
4.1. ПУЧКИ ВИТЫХ ТВЭЛОВ И ТРУБ, ВИТЫЕ ТРУБЫ
И КОЛЬЦЕВЫЕ КАНАЛЫ С ВИТОЙ ТРУБОЙ
Продольно обтекаемые пучки твэлов и труб
Структура турбулентного потока при его закрутке
в продольно обтекаемых пучках
Структура трехмерного турбулентного потока в пучках витых
труб (твэлов) исследована с помощью термоанемометра постоянной
температуры и аналоговой аппаратуры при использовании разрабо-
танных оригинальных датчиков и новой техники анализа термоане-
мометрического сигнала. Измеренные при этом поля осредненных и
пульсационных составляющих вектора скорости, а также корреля-
ции пульсационных скоростей представлены на рис. 4.1—4.7 [4.1.1 —
4.1.5].
Рис. 4.1. Обобщение опытных данных по полям скорости (а) и температуры (б)
при использовании в качестве характерного размера толщины пристенного слоя
при Re = 104:®, О, ®, Д — эксперимент при Frm = 318,1530,1560,924 соответствен-
но: 1, 2 — зависимость (4.1.1) прип = 7
338
Глава 4
В ортогональной системе координат продольная составляющая
скорости и направлена параллельно оси пучка, а поперечные состав-
ляющие v и w в соответствии с рис. 4.2. Безразмерные поля полно-
го вектора скорости V/VM, его продольной составляющей п/пм и тем-
пературы газа в пределах тонкого пристенного слоя по нормалям к
стенкам труб описываются степенными законами (рис. 4.1):
_v__fzY/n
и
«м
Т -Т
1W л
Т -Т
1W л
ы1/п
(4.1.1)
где V^, пм — максимальные значения величин Уин (на внешней гра-
нице пристенного слоя); 5 — толщина пристенного слоя; Tw — тем-
пература стенки. Вне пристенного слоя в ядре потока скорости V и
и изменяются незначительно. Поперечные составляющие скорости
в характерной ячейке пучка представлены на рис. 4.2, где сплошны-
ми линиями условно обозначены границы винтовых каналов сосед-
них витых труб. Направление скорости и определяется направлени-
Подветренная
сторона
Наветренная
сторона
Рис. 4.2. Распределение поперечных составляющих скорости в ячейке пучка с
Frm = 296 для v(a) и w(6): Л, •, О — экспериментальные данные для чисел Re = 104,
1,5-104 и 6,7104 соответственно; 1 — условная граница витого канала трубы
Глава 4
339
ем закрутки витои трубы, поэтому на границе соседних труб V = О
из-за противоположного направления вихревых потоков. В цилин-
дрической системе координат (рис. 4.3) во внешней части пристен-
ного слоя изменение тангенциальной скорости пт по радиусу витой
трубы можно в первом приближении описать законом квазитвердого
вращения: ихг'1 = const, а в ядре потока — либо законом постоянства
циркуляции птг = const (для периферийных ячеек пучка), либо более
сложной зависимостью (см. рис. 4.3). Скорость и и радиальная со-
ставляющая скорости иг достигают максимального значения на вне-
шней границе пристенного слоя. С уменьшением чисел Frm и Re ин-
тенсивность вихревого движения в пучке возрастает и поперечные
составляющие скорости увеличиваются.
Составляющая вектора скорости w (см. рис. 4.2) направлена пер-
пендикулярно либо к стенке трубы, либо от нее в подветренной и
наветренной частях профиля трубы, что приводит к непрерывному
конвективному обмену порциями жидкости между пристенным сло-
ем и ядром потока и интенсифика-
ции процессов переноса в пучках ви-
тых труб. Изменение скоростей и, v,
w от нуля до максимального значения
сосредоточено в тонком пристенном
слое, толщина которого на порядок
меньше эквивалентного диаметра ка-
нала. Это свидетельствует о том, что
закрутка потока приводит к допол-
нительному порождению турбулен-
тности, прежде всего, в пристенной
области течения. Поэтому интен-
сивность турбулентности в пристен-
ной области течения в пучке витых
труб возрастает в большей степени,
чем интенсивность турбулентности
в ядре потока, и значительно превы-
шает уровень турбулентности при те-
чении в круглой трубе (рис. 4.6, 4.7а).
При оценке эффектов, обнаружен-
ных в пучках витых труб и твэлов, в
качестве объекта сравнения прини-
мается течение в круглой трубе, по-
скольку структура потока и процес-
сы тепломассообмена в ней наиболее
изучены.
Рис. 4.3. Профили тангенциаль-
ной (ut) и радиальной (ur) состав-
ляющих скорости в центральных
ячейках пучка с Frm = 296: •, А,
О — опытные данные для ut/uw
при Re = 104; 1,5104; 6,7-104 соответ-
ственно: <, х, О — то же для и/и^,
1 — зависимость uxrl = const; 2 —
распределение скорости их, гене-
рируемой разнонаправленными
вихревыми шнурами; 3 — про-
филь радиальной скорости ur; 4 —
овальный профиль витой трубы;
5 — условные границы винтовых
каналов; 6 — направления закрут-
ки витых труб
340
Глава 4
Исследование энергетического спектра турбулентности проводи-
лось с помощью аналоговой аппаратуры и позволило определить, что
по сравнению с течением в круглой трубе течение в пучке витых труб
характеризуется смещением энергетических спектров турбулент-
ности в область высоких частот [4.1.5—4.1.8]. С уменьшением числа
Frm и ростом числа Re вклад высокочастотных составляющих спект-
ра в величину и2 возрастает. При числах Re < 104 энергия в пучке ви-
тых труб в основном переносится низкочастотными крупномасштаб-
ными вихрями и максимальная частота энергосодержащих вихрей
составляет примерно 500 Гц. При Re > 104 интервал частот энерго-
содержащих вихрей расширяется до 2—3 кГц и наблюдается автомо-
дельность в распределении относительной энергии турбулентности
по частотам в диапазоне 20—1000 Гц (см. рис. 4.7,6).
Результаты экспериментального исследования величины
__ ©о
и2 = J E(f)df показали, что с уменьшением чисел Frm и Re интенсив-
0 _
ность турбулентности-----в условиях закрутки потока возрастает
(см. рис. 4.4).
Измеренные величи-
ны интенсивности тур-
булентности и ее масш-
таба позволили оценить
вклад турбулентной
диффузии в межканаль-
ное перемешивание в
пучке витых труб, кото-
рый составляет 8—12%
для s/d = 25—12,5.
Результаты исследо-
вания пульсационных
составляющих векто-
ра скорости и их корре-
Рис. 4.4. Зависимость величины /им от чисел
Re, Frm и положения точки измерения в потоке:
1 — зависимость (4.1.2); 2 — зависимость /им
от числа Re при Frm = 198; ▲, +, х — опытные
данные для максимальных значений величины
/им при Frm = 178, 296 и 1187; •, О, > — то же
для минимальных значений величины /им',
□ — опытные данные для Frm = 198 величины
ляций в зависимости от
числа Re для характер-
ных точек ядра пото-
ка при числе Frm = 198
(s/d = 10,8) представ-
лены на рис. 4.4 и 4.5.
Видно, что в ядре пото-
ка наблюдается сущест-
венная анизотропия его
Глава 4
341
а	б
Рис. 4.5. Зависимость поперечных пульсационных составляющих скорости в ядре
потока, обтекающего пучок стержней, и их корреляций от числа Re и положе-
ния точки измерения: а — за точкой касания соседних стержней; б — в сквоз-
ном канале; V — v2/u2; □ — w2/u2; 0 — u'v'/u2; 0 — u'w'/u2; О — v'w'/u2;
— q2/и2; q2 — удвоенная кинетическая энергия турбулентности; сплошные ли-
нии проведены по опытным точкам
свойств, но с ростом числа Re структура потока стремится к более
изотропной структуре. В диапазоне чисел Re=(6-103)-(1,1-Ю5) экспери-
ментальные данные по Лр / пм описаны формулой:
Tip /uM=ARem,	(4.1.2)
где Аиш зависят от числа Frm (табл. 4.1.1).
Рис. 4.6. Профиль величины
л/172 /им поперек ячейки, образо-
ванной соседними стержнями
двухлопастной формы: • — опыт-
ные данные для пучка с Frm =178
при Re = 3,64 О4; 1, 2 — распреде-
ления	для пучка витых
стержней и круглой трубы соот-
ветственно
342
Глава 4
Влияние числа Fr на А и m
m
Таблица 4.1.1
Число Fr т	Значение А			Значение т		
	Макси- мальное	Мини- мальное	Среднее	Макси- мальное	Мини- мальное	Среднее
178	12,85	2,96	7,5	0,46	0,393	0,437
296	3,26	0,403	1,62	0,347	0,227	0,311
1187	0,61	0,104	0,313	0,230	0,115	0,189
Рис. 47а. Изменение величины
\и 2 /им в ядре потока пучка ви-
тых стержней с Fr^ = 178, свя-
занное с влиянием точек каса-
ния витых стержней и сквозных
каналов при Re = 3,6-104 [4.2]:
• — экспериментальные дан-
ные; х0 = 8 — начало отсчета ко-
жуха; xi—xQ=d — период коле-
баний
Рис. 4.76. Спектральное распределение продольной пульсационной составля-
ющей скорости для точки ядра потока с максимальным значением величины
/итя, 1 — опытные данные для оси труб (d0 = 90 и 28 мм), при Re = 5,6-103 —
1,3-105; 2 —12 — данные для пучков при разных Frm и Re
		Re
2	178	1.2-104
3	-	3,4-104
4	-	7.5-104
5	296	6,7-104
6	-	1.4-104
7	-	4,0-104
8	-	(6,7-1 Ч-Ю4
9	1187	8,1-10*
10	-	1,4-104
11	-	4.1-104
12	-	6,1-104
Глава 4
343
Анизотропия свойств турбулентного потока в пучке витых стерж-
ней объясняется порождением турбулентности в рассмотренных об-
ластях течения в ядре потока. Для течения вблизи оси круглой трубы
турбулентность близка к изотропной.
Относительная удвоенная кинетическая энергия турбулентного
„ ylti^2	y)w'2
движения в пучке витых стержней:	— + ———, опреде-
и и и и
ленная экспериментально, не очень сильно отличается от уровня тур-
булентности, определенного по продольной пульсационной скорости
yfj2 /й (см. рис. 4.4), а турбулентное напряжение трения в ядре пото-
ка в пучке витых труб (см. рис. 4.5) превышает величину q2. Эти за-
кономерности свидетельствуют о существенном отличии структуры
потока в пучке по сравнению со структурой потока вблизи оси круг-
лой трубы. С ростом числа Re поперечные пульсационные состав-
,2
ляющие скорости, отнесенные к и возрастают, т.е. пульсационное
движение в поперечных сечениях потока, обтекающего пучок витых
труб, с увеличением числа Re интенсифицируется, что приводит при
числах Re > 2-104 к автомодельности величины удвоенной кинетиче-
ской энергии турбулентного движения yjq2 /им по числам Рейнольд-
са (см. рис. 4.4). Выявленный характер зависимости y[q^/им =f(Re)
позволяет объяснить наличие излома в зависимостях коэффициента
гидравлического сопротивления £, — S,(Re) и безразмерного эффек-
тивного коэффициента турбулентной диффузии Kqs = Kqs(Re).
Для оценки продольного интегрального пространственного
масштаба турбулентности L изучены автокорреляционная функ-
ция u’(f)u'(t + T) и коэффициент временной корреляции. [4.1.6]:
u'(t)u'(t + T)
Rx =---=?----, а также определен интегральный временной масш-
и
таб Г = J RTdT, где т — задержка времени. Оказалось, что распределе-
о
ния Rx от т для сквозного канала и области течения за точкой касания
стержней при Re = 8300 отличаются существенно друг от друга, а
при Re = 61400 практически описываются одной зависимостью. Сле-
довательно, с ростом числа Re турбулентность в ядре потока в пуч-
ке витых твэлов или труб стремится к более изотропной структуре.
Кроме того, при больших числах Re в ядре потока имеет место ши-
рокий диапазон размеров турбулентных вихрей, о чем говорит рез-
кое снижение коэффициента RT в окрестности точек т = 0. С умень-
344
Глава 4
шением числа Frm эти эффекты проявляются в большей степени.
Пространственные интегральные макромасштабы турбулентности в
пучке витых твэлов или труб, определенные по формуле L = (им) Г,
можно рассматривать как масштабы крупных вихрей в направлении
среднего потока. Таким образом, в пучке витых стержней или труб,
наряду с вкладом турбулентной диффузии в процессе тепломассо-
переноса, наблюдается существенный вклад конвективного перено-
са теплоносителя по винтовым каналам стержней или труб, а также
между пристенным слоем и ядром потока за счет интенсивного вих-
ревого обмена в ячейках пучка.
Анализ результатов исследования структуры закрученного пото-
ка показал, что увеличение интенсивности закрутки приводит к вы-
равниванию параметров и переносных свойств потока по сечению
пучка и позволяет использовать в пучках витых твэлов или труб мо-
дель гомогенизированной среды. Эти исследования позволили уста-
новить механизмы искусственной турбулизации потока при его за-
крутке и интенсификации процессов переноса в пучке витых труб и
пути управления этими процессами путем выбора геометрических
(s/d) и режимных (Re) параметров.
Экспериментальное исследование теплообмена и гидравлического
сопротивления в пучках витых труб проводилось в широком диапазо-
не изменения режимных параметров. Полученные зависимости срав-
нивались с соответствующими выражениями для круглых труб. Было
обнаружено, что закрутка потока приводит к росту коэффициентов
теплоотдачи и гидравлического сопротивления благодаря его допол-
нительной турбулизации и вихревому обмену между пристенным сло-
ем и ядром потока, причем наиболее сильное возрастание теплоотда-
чи наблюдается в переходной области чисел Re [4.1.1, 4.1.9 — 4.1.16].
В области больших шагов закрутки (s/d > 10) удалось обобщить
опытные данные по теплоотдаче и гидравлическому сопротивлению
для геометрически неподобных пучков, введя в качестве характер-
ного параметра число Frm = s2/ddeq, полученное на основании пред-
ложенной модели вихревого течения в пучке, согласно которой поток
закручивается витыми трубами (твэлами) по закону квазитвердого
вращения. При этом были установлены законы теплоотдачи и сопро-
тивления.
На рис. 4.8—4.14 опытные данные обобщены с использованием
различных методов обработки опытных данных, основанных на по-
луэмпирических теориях турбулентности и чисто эмпирическом
подходе с применением методов математической статистики. Так,
для стабилизированного течения (x/deq> 14) и чисел Frm = 232... 2440
получены зависимости:
Глава 4
345
Nud/
Рис. 4.8. Зависимость коэффици-
ента теплоотдачи от числа Рей-
нольдса для Frm = 232: •, х, □, Д —
экспериментальные данные при
x/deq = 19,9; 67; 83,2; 90 соответст-
венно; 1—3 — зависимости (4.1.9;
4.1.3; 4.1.5) соответственно
т \-0,55
Nud/=0,023Rejf
Prf’4(l+3,6Fr~0'357
и для Fr^ = 64 зависимость
Nudf =O,O521Re^sPr,0'4
Г Л-0.55
w
В переходной области чисел Redf
Nudf=83,5Fr-‘'2
Re^Pr,0'4(l+3,6R^357
T x-0,55
£tv
Tfj
(4.1.3)
(4.1.4)
(4.1.5)
где n = 0,212Fr^'194 при Frm < 924 и n = 0,8 при Frm > 924.
Рис. 4.9. Зависимость коэффициен-
та теплоотдачи в пучках витых труб
от чисел Frm и Рейнольдса: х, о, Д —
экспериментальные данные для
Frm = 63,6 при x/deq = 19,6; 66,2 и 82,1
соответственно; •, С5, -I-то же для
Frm = 1052 при x/deq = 20; 83,6; 90,5
соответственно; 1 — 5 зависимости
(4.1.8; 4.1.10; 4.1.4; 4.1.5; 4.1.3) соот-
ветственно
346
Глава 4
Рис. 4.10. Влияние интен-
сивности закрутки потока
на коэффициенты теплоот-
дачи и гидравлического со-
противления при Re = 104:
1 — зависимость (4.1.11);
2 — связи (4.1.12); 3 — зави-
симость (4.1.14); 4 — зависи-
мость £>/^тР;	— расчет
по (4.1.13); •, О — опытные
данные для пучков оваль-
ных и трехлопастных витых
труб соответственно
Если использовать в качестве определяющего размера эффектив-
ную толщину пристенного слоя, то, соответственно, получим формулы:
Nu6m=0,02Re°*Pr°'4;	(4.1.6)
NuSm=6,47Fr^845Re6nmPr“'4
(4.1.7)
при определении физических свойств теплоносителя при средней
температуре поперек пристенного слоя Тт = (Tw + Tf)/2. Представ-
ление опытных данных в таком виде расширяет возможности мо-
делирования и позволяет проводить расчет по локальным характе-
ристикам потока и тепловыделения (см. рис. 4.11). В ряде случаев при
численном расчете более удобно использовать эмпирические форму-
лы для всей области изменения числа Re в форме многочлена второго
порядка в логарифмических координатах:
для Fr = 63,6:
Nud,
= 1115Re
Рг,0'4
Ct V'55
(4.1.8)
—1.214+0,234 lgRedr
df
Рис. 4.11. Зависимостьчисла Нус-
сельта от числа Рейнольдса при
использовании средней толщи-
ны пристеночного слоя в качест-
ве характерного размера: О, •,
Д — опытные данные для чисел
Frm = 232 и x/deq — 20 — 90;
Frm = 924 и x/deq — 20 — 59;
Frm =1050 и x/deq = 20 — 90;
Ff/n =2440 и x/deq =35—103 со-
ответственно: 1 — зависимость
(4.1.6); 2 — зависимость (4.1.7)
Глава 4
347
Рис. 4.12. Изменение мест-
ной теплоотдачи на начальном
участке пучков витых труб:
▲ - Frm = 232; О - Frm = 924;
• - Frm = 1050; Д - Frm = 2440;
1 - Cz= 0,0426(x/deg)-0.287; 2 -
зависимость (4. 1.6);
C,=Nu8m/Re“Pr»'4
-0,55
для Frm = 232:
Nudf = 157Re^’9796+0,2171gRedf pp9-4
для Frm = 1052:
Nud/ = 24,6Re^'7035+0'195IgRedf Prf0,4
Tf
(4.1.9)
(4.1.10)
Если отнести число Nudf к числу NuTp для круглой трубы при
Redf = 104, то получим выражения, отражающие влияние закрутки
потока в пучке витых труб на теплоотдачу и гидравлическое сопро-
тивление (см. рис. 4.10):
для Frm = 63,6—1052:
Nud/ = 2 62 IO8 Ren+OlgRe^’8 рг-2.494+0,2351gFrm
NuTp	df	m
где n = _ir572Fr9'01661-°-043731gFr-;
a = 0,269Frm0'0149"°'1041gFrm ;
для Frm — 232—2440:
NuTp
для Frm = 63,6:
NuTp
дляРгт = 63,6—1052:
gpj.~t6181+0,2631gFrm
^тр
В зависимости (4.1.14) учтена поправка на трение о стенку кожуха
пучка.
Критериальные зависимости для расчета теплоотдачи и гидрав-
лического сопротивления приведены к виду, основанному на исполь-
= l+3,6Fr^
>тр
= 2,27, -2- = 3,46;
^этр
(4.1.11)
(4.1.12)
(4.1.13)
w
(4.1.14)
348
Глава 4
зовании гидродинамической теории теплообмена и позволяющему
проводить расчеты по локальным параметрам потока и тепловыде-
ления:
а* = [30,4 (Re*)0,174 Рг°'6+14,65(Re*)°'09 -11,2 J”1;	(4.1.15)
£* = 0,045 (Re*)-0,221 + (4 • 10-4),	(4.1.16)
где в качестве определяющих скорости и температуры приняты ско-
рость и температура на внешней границе пристенного слоя. Эти за-
висимости хорошо согласуются с опытными данными при использо-
вании величины Re* — специальным образом построенного числа Re.
Для пучков витых труб число Re* выражается зависимостью:
Re* = l,035Regm
I 0,39 J
/(0,39^).
(4.1.17)
Эти зависимости хорошо согласуются с опытными данными
(см. рис. 4.13 и 4.14). В условиях закрутки потока в пучках витых труб
неизотермичность течения по-разному влияет на коэффициенты
теплоотдачи и гидравлического сопротивления. Если на теплоотдачу
влияние температурного фактора значительное, то на коэффициент
гидравлического сопротивления его влияние практически отсутст-
вует. Влияние длины участка гидродинамической стабилизации по-
тока на коэффициент 4 также практически обнаружить не удалось,
что может быть связано с выравнивающим действием закрутки по-
тока, приводящим к расширению области ядра потока и тонкому
пристенному слою на витых трубах, а локальная теплоотдача на на-
чальном участке прих/с/ед = 3,75 — 14 возрастает (см. рис. 4.12). В опре-
а*103
Рис. 4.13. Обобщающая зависимость для безразмерного коэффициента теп-
лоотдачи: 1 — 4 — опытные данные: Frm = 232; 924; 1050; 2440; 5 — по зависимо-
сти (4.1.15)
Глава 4
349
Рис. 4.14. Обобщающая зависимость для коэффициента гидравлического сопро-
тивления: А — Fr = 232, • — Fr = 924, □ — Fr = 1050, О — Fr = 2440; линия
т	т	т	'	т	'
1 — по зависимости (4.1.16)
деленном диапазоне чисел Frm, или s/d, в переходной области течения
теплоотдача возрастает в большей степени, чем гидравлическое соп-
ротивление, а при развитом турбулентном течении в той же степени,
что и гидравлическое сопротивление. Результаты исследования теп-
лоотдачи и гидравлического сопротивления свидетельствуют о том,
что закрутка потока в пучках витых труб существенно интенсифи-
цирует теплообмен в определенном диапазоне изменения геометри-
ческих и режимных параметров.
Эффективность интенсификации тепло- и массообмена путем за-
крутки потока в пучках витых стержневых твэлов с неравномерным
полем тепловыделения в поперечном сечении пучка оценивалась рас-
четным и экспериментальным путем. Эффективность интенсифика-
ции теплообмена путем закрутки потока в теплообменных аппаратах
с продольным обтеканием витых труб определялась путем сравне-
ния объемов теплообменников с интенсификацией и гладкотрубча-
того при одинаковых тепловых мощностях и мощностях на прокач-
ку теплоносителей (одинаковых расходах теплоносителей и потерях
давления). При сравнении предполагалось, что сравниваемые кана-
лы имеют одинаковые периметры, т.е. я = ягл, где индекс «гл» отно-
сится к гладкому каналу, а сравниваемые трубы размещены в пучке
с одинаковым шагом.
Хотя теплообмен интенсифицируется как при течении теплоно-
сителя в межтрубном пространстве, так и внутри труб, наибольший
эффект от применения витых труб получается в том случае, когда ли-
митирующим является термическое сопротивление в межтрубном
пространстве. На рис. 4.10 представлены зависимости Nud/NuT и
£/£гр при Re = 104. При s/d > 12 (Frm« 220) значения Nud/NuTp «
При меньших s/d рост ^/^.р опережает рост Nud/NuTp. При s/d = 6
(Fr^ = 57) значение Nud/NuTp = 2,4 и ^/^,р = 2,8. Отношение объемов
350
Глава 4
аппаратов V/VrA от относительного шага закрутки витых труб s/d из-
меняется при этом в пределах 0,52—0,74. При меньших числах Рей-
нольдса (в переходной области течения) эффективность теплообмен-
ника с витыми трубами будет еще выше. Так, при Re = 3-103 и s/d =12
Nudf/NuTp = 1,75 и ~ 1,5, т.е. наблюдается опережающий рост
Nudf /NurA над ростом S,Для s/d = 6 и Re = З-Ю3 Nudf/NuTp= 3,5 и
^/^,р= 3,0. Использование теплообменных аппаратов с витыми тру-
бами при Re = З-Ю3 позволяет уменьшить объем теплообменника в
2—2,5 раза и более по сравнению с объемом гладкотрубчатых аппа-
ратов.
Интенсификация межканального перемешивания
теплоносителя в пучках витых твэлов и труб
Для пучков витых твэлов и труб характерна высокая интенсив-
ность процесса межканального перемешивания [4.1.1,4.1.2,4.1.6,4.1.9,
4.1.17—4.1.23]. Значения эффективного коэффициента турбулентной
диффузии более чем на порядок превышают значения коэффициен-
та турбулентной диффузии на оси круглой трубы. Это особенно важ-
но для теплообменных устройств с существенной неравномерно-
стью тепловыделения в поперечном сечении пучков труб и с высокой
теплонапряженностью конструкций, когда требуется выровнять не-
равномерные поля температур теплоносителя. Эффективный коэф-
фициент диффузии Deff определялся двумя методами: методом диф-
фузии от точечного источника теплоты и методом диффузии теплоты
от системы линейных источников. При использовании метода диф-
фузии от системы линейных источников теплоты в пучке выделяет-
ся группа труб, которая нагревается путем пропускания по их стен-
кам электрического тока. При этом обеспечивается электроизоляция
нагреваемой группы витых труб от остальных труб пучка. При наг-
реве выделенной группы труб формируется неравномерность поля
температуры теплоносителя в пучке, которая выравнивается по дли-
не пучка за счет поперечного перемешивания.
Эффективный коэффициент диффузии, характеризующий про-
цесс переноса тепла в пучке витых труб, определяется путем сопо-
ставления экспериментально измеренных в выходном сечении пучка
полей температуры теплоносителя с теоретически рассчитанными
полями температуры с использованием метода математической ста-
тистики. Этим методом были определены эффективные коэффи-
циенты диффузии для случаев осесимметричной и асимметричной
неравномерностей поля тепловыделения в поперечном сечении пуч-
ка при Frm = 55—1080, Re = 3,4103 —3,8-104, е = 0,46—0,5 и входной
Глава 4
351
турбулентности потока (1—6)% для стационарной задачи. Типичное
распределение экспериментально измеренных полей температур
теплоносителя при Re — (1,2—1,7) 104 представлено на рис. 4.15. Нерав-
номерность поля температур, сформированная неравномерным по-
лем тепловыделения по радиусу пучка, приводит также к неравно-
мерности продольной скорости потока (см. рис. 4.15).
Изменения рассчитанных температур аналогичны изменениям
экспериментальных распределений этих параметров, но совпадение
опытных и теоретических полей происходит при различных значе-
ниях коэффициента К в зависимости от чисел Fr , Re и пористости
4	п
гу ^eff
в. Чем меньше число Frm, тем больше коэффициент	= —-—, при ко-
тором они совпадают.
Опытные данные по межканальному перемешиванию теплоно-
сителя при стационарных режимах в пучках витых труб (стержне-
вых твэлов), полученные при Re > 104 методом диффузии теплоты от
линейных источников, обобщены зависимостью (рис. 4.16)
Kqs =0,136 Fr'°-256+10Fr’°'66(E-0,46),	(4.1.18)
с которой хорошо согласуется формула, полученная для пучков
стержней со спиральным оребрением:
Kqs = 1,902 Frm'W3e1086	(4.1.19)
Рис. 4.15. Сравнение измеренных полей температуры и скорости потока с полями,
рассчитанными при разных значениях коэффициента К для пучков с Frm = 64 (а)
и 232 (б) : 1—5 — расчет температуры; 6 —8 — расчет скорости; 9, 10 — опытные
данные для температуры (9) и скорости (10)
352
Глава 4
Более точной, обобщающей опытные данные при диффузии теп-
лоты от линейных источников, является зависимость, полученная в
форме многочлена второго порядка в логарифмических координатах
Kqs = 10,35 Fr^1'4232+0’18571gFr-	(4.1.20)
Зависимость, установленная в последнее время,
Kqs =
0,078484 (	8,1
р 0,254	1+с 0,278
(4.1.21)
Рис. 4.16. Влияние критерия Frm на ко-
эффициент Kqs: 1—4 — зависимости
(4.1.20; 4.1.19; 4.1.18; 4.1.21) соответст-
венно: О — опытные данные, получен-
ные методом диффузии тепла от точеч-
ного источника; ▲ — опытные данные,
полученные методом диффузии тепла
от группы линейных источников при
/ = 0,75 м; О — то же самое при I = 1 м
хорошо обобщает опытные данные, полученные различными мето-
дами в интервале Re > 7-103, Frm = 55 —1560, е = 0,46—0,56. Из этих за-
висимостей следует, что чем больше закручен поток, т.е. чем меньше
критерий Frm и шаг закрутки профиля трубы (твэла) s, тем больше
коэффициент Kqs и тем больше интенсифицируются процессы теп-
ломассообмена (возрастают коэффициенты Хе/Г vefft и, Deff).
Таким образом, пучки витых труб характеризуются интенсивным
межканальным перемешиванием, что достигается за счет спираль-
ной закрутки теплоносителя, приводящей к появлению поперечных
составляющих скорости, дополнительной турбулизации и вторич-
ной циркуляции потока, а также к организованному переносу потока
в масштабе диаметра пучка.
Исследования влияния эффектов нестационарности на процессы
тепломассообмена показали, что использование квазистационарно-
го приближения при решении
нестационарных теплогидрав-
лических задач может привес-
ти к значительным ошибкам в
расчете из-за влияния нестаци-
онарных граничных условий на
турбулентную структуру пото-
ка, а следовательно, и коэффи-
циенты турбулентного перено-
са xefr Vefr и Deff [4.1.2, 4.1.6, 4.1.9,
4.1.18, 4.1.24—4.1.39]. Так, при ус-
корении потока теплоносите-
ля во времени при постоянной
мощности тепловой нагрузки
(N = const) на коэффициент
Кип влияют критерий подобия
Фурье Fofc (безразмерное время)
и параметр С2/С{:
Глава 4
353
Кип = Kgs[l-(l,364-103Fob)],
(4.1.22)
npnFob = 0—4,5-Ю'4 и
Кип =Kgs|4,04Fo2+[o,99-4,12(G2/G1-l)3'S]j,	(4.1.23)
при Fob = 4,5-10’4—10‘2; G2/G, = 1,1-1,77; Re > 7103; Frm = 56-220.
В уравнении (4.1.23) п = 1,852—0,927 G2/Gv Зависимости (4.1.22)
и (4.1.23) представлены на рис. 4.17,а, из которого следует, что в пер-
вые моменты времени нестационарного процесса происходит резкое
К
уменьшение коэффициента Кип (коэффициента х= —— ) с последу-
Kqs
ющим плавным его ростом и приближением к квазистационарно-
му значению Kqs (k = 1). Это связано с уменьшением интенсивности
турбулентности в ускоряющемся потоке из-за нарушения равнове-
сия между подведенной к потоку энергией, ее диссипацией, турбу-
лентной диффузией и конвекцией турбулентных молей. Остывание
пучка на режиме G2 = const вызывает перестройку температурных
полей теплоносителя и связанную с этим переменность средней ве-
личины плотности газа во времени. При этом действие сил инерции,
связанных с закруткой потока витыми трубами, вызывает объемную
деформацию турбулентных молей и воздействует на характеристи-
ки турбулентности и коэффициенты переноса, компенсируя перво-
начальное возмущение турбулентности. В случае замедления потока
во времени критериальные зависимости для расчета коэффициента
Кип имеют ВИД (рис. 4.17, б):
Кип
= Kgs(2,57Foi°’0437
(2,95-10"*)
Л
-11,94
+0,993
(4.1.24)
при Frm = 57; G2/G{ = 0,605-0,9; Fob = (0,51440'3Н1,440'2);
к = к
IYun 1Yqs
(0,398Fo^'165 +0,13) 0,645
G2
G,
x—0,818
+ 0,04 ,
(4.1.25)
npnFrm = 220; G2/G{ = 0,579-0,9; Fob = (0,51440'3H0,940-2);
-11,94
Kun
+0,993
(4.1.26)
при Fob = (0—0,51440‘3); Frm = 57-220; G2/G{ = 0,579-0,9.
Влияние нестационарных граничных условий на структуру тур-
булентного потока в пучках витых стержней при изменении во вре-
354
Глава 4
X
1,6.
Рис .4.17. Влияние ускорения потока во времени на коэффициент Кип (а): 1 — зави-
симость (4.1.22); 2-6 — зависимость (4.1.23) при G2/Gj = 1,62; 1,68; 1,71; 1,73 и 1,77
соответственно; 7 — 11 — зависимость k = AFo£ +с при тех же значениях G2/Gt, и
замедления потока на Кип (б): 1 — 3 — зависимость (4.1.24) при G2/Gx = 0,605; 0,665
и 0,765 соответственно; 4 —6 — зависимость (4.1.25) при G2/G{ = 0,579; 0,594 и
0,611; 7 — зависимость (4.1.26)
мени мощности тепловой нагрузки при постоянном расходе теплоно-
сителя (G = const) объясняется действием тех же механизмов, что и в
случае с G = var и N = const. При увеличении во времени мощности
тепловой нагрузки N (рис. 4.18,а)
Рис. 4.18. Влияние роста мощности тепловой нагрузки во времени на коэффици-
ент Кип (а): 1 —3 — зависимости (4.1.27), (4.1.28), (4.1.30), соответственно, иумень-
шения мощности тепловой нагрузки на Кип (б): 1 — зависимость (4.1.31); 2 —
= М -3,73(Fo„-102| 1,669]; 3 - Кт =	3.68(Fom10*)2,07]; х = K„„/K,s
Глава 4
355
Кип = Kqs [(1,1410-5)Fo“2-(1,05310-3)Fo;’ +1,024],	(4.1.27)
при Frm = 57,
Кип = Kgs [(3,07-10"5)Fo-2 -(2,2&10-3)Fo-* +0,91],	(4.1.28)
при Frm = 220,
FOm=Mp+	.	. |ЭЛ7/Эт| (0,043 + 0,957),.	- 'тах	(4.1.29)
CpPh^-bundle	7 BN/Эт ।	imax0	
При Fom = (0,94-10'3) — (1.55-10'3) коэффициент Kun определяется
зависимостью:
кт = Kgs [(4.754-103)Fom -3,369].	(4.1.30)
В случае уменьшения мощности тепловой нагрузки (рис.4.18, б)
Kun =K?s[(4,54-10-6)Fo^-(3,86-10-3)Fo->1,28].	(4.1.31)
Зависимость (4.1.31) справедлива при Frm = 57—220 и Fom = (1,25—
—14)10-3.
Коэффициенты Кип могут существенно отличаться от их квази-
стационарных значений и зависеть от типа тепловой и гидродина-
мической нестационарности. Поэтому учет этих эффектов неста-
ционарное™ при теплогидравлическом расчете теплонапряженных
теплообменных аппаратов и реакторов позволяет обеспечить их на-
дежную и безопасную работу.
Влияние коэффициента К на процесс выравнивания неравно-
мерностей поля скоростей пошлине и радиусу пучка показано на
рис. 4.16. Результаты расчета хорошо согласуются с опытными дан-
ными для сечений пучка стержней на расстояниях х = 0, х = 7,7d и
х = 79,5d при Kqs = 0,09. Процесс выравнивания неравномерностей
поля скоростей, сформированных узлами, расположенными на вхо-
де в пучок твэлов, исследовался расчетно-экспериментальным ме-
тодом на полноразмерной модели пучка витых стержней овального
профиля с Frm = 470 (s/d = 16). При этом профиль скорости по ради-
усу пучка на расстоянии 1 Id от входа в пучок (х = 0) оказалось воз-
можным описать функцией Бесселя нулевого порядка первого рода:
uBX/ucp = 0,8+0,35 Jo (2,405r = r/rk). Из рис. 4.16 видно, что чем больше
безразмерный эффективный коэффициент турбулентной диффузии
Kqs, тем меньше длина пучка, на которой происходит полное вырав-
нивание неравномерностей поля скоростей, сформированных вход-
ными узлами ТВС, расположенными перед пучком витых стержней.
356
Глава 4
Обнаруженные в результате проведенного исследования новые
закономерности интенсификации тепломассообмена при стационар-
ных и нестационарных тепловых режимах объясняются перестрой-
кой турбулентной структуры потока под действием его закрутки и
влиянием нестационарных граничных условий. Учет эффектов пе-
ремешивания теплоносителя при расчете стационарных и неста-
ционарных режимов работы транспортных ядерных реакторов и
установленные пути управления процессами интенсификации теп-
ломассообмена в них позволили выбрать оптимальные безопасные
режимы работы ядерного реактора ЯЭДУ при переходе с двигатель-
ного на энергетический режим работы и обратно (рис. 4.19,а, 4.19,6).
Рис. 4.19 а. Переходные процессы в реакторе ЯЭДУ с увеличение^ (а, б) и
уменьшением (в) мощности: 1, 5 — мощность энерговыделения N = N/N0;
2,6 — температура твэлов Тт вых =7’Г вых/ТГ выХо; 3,7 — температура теплоносите-
ля ТЪых =Т’ВЫХ/ТВЫХО; 4, 8 — расход водорода G = G/GQ (индекс «О» — параметры
для номинального режима работы)
Рис. 4.19 б. Изменение реактивности реактора ЯЭДУ для процессов с увеличени-
ем (а) и уменьшением (б) его мощности: 1 — суммарная реактивность Рх; 2 — ре-
активность, вносимая органами регулирования ррег; 3, 4 — температурный Рг и
плотностный ру эффекты реактивности соответственно
Глава 4
357
Разработанные модели турбулентного течения в каналах, образо-
ванных пучками витых труб и стержней, для стационарных и неста-
ционарных тепловых режимов, предложенный метод замыкания ис-
ходных систем дифференциальных уравнений, описывающих эти
модели, который основан на формально-математическом подходе к
решению задачи и гипотезе о локальном подобии процессов перено-
са, и предложенные обобщающие критериальные зависимости, по-
лученные путем обобщения многочисленных опытных данных по
конвективному теплообмену и межканальному перемешиванию,
позволяют проводить надежные теплогидравлические расчеты ТВС
с витыми стержневыми твэлами и ТА с витыми трубами с учетом
межканального перемешивания теплоносителя и эффектов неста-
ционарности.
Моделирование процессов тепло- и массообмена
при натурных испытаниях тепловыделяющих сборок
с витыми твэлами в составе исследовательских реакторов
Надежность рекомендаций, полученных при исследовании про-
цессов тепло- и массообмена, подтверждена при моделировании теп-
логидравлических процессов в ТВС ЯРД при испытаниях в исследова-
тельских реакторах. При этом в натурных условиях была проверена
работоспособность твэлов и других элементов ТВС и оценена пра-
вильность принятых конструктивных решений и используемых ме-
тодов расчета и установленных на крупномасштабных моделях ТВС
закономерностей по теплообмену и гидродинамике. Возможность
создания надежных твэлов и ТВС ЯРД подтверждена еще в начале
60-х гг. при успешных испытаниях модельных ТВС в импульсном
графитовом реакторе (ИГР). При этом были исследованы различные
конструкции ТВС и твэлов из разных высокотемпературных мате-
риалов с ураном-235, стойких в среде рабочего тела и обладающих
хорошими нейтронно-физическими свойствами, их теплогидравли-
ческие характеристики при нагреве водорода с ингибирующей угле-
родсодержащей присадкой, а также особенности запуска и влияние
переходных режимов на работоспособность твэлов [4.1.9]. Результа-
ты этих исследований использованы при разработке стендового про-
тотипа реактора ЯРД ИРГИТ (исследовательского реактора для груп-
повых испытаний твэлов) и исследовательского реактора с водяным
замедлителем для групповых и петлевых испытаний ТВС (ИВГ-1),
разработанных и созданных в СССР в 60—70-х гг.
Основная идея, нашедшая отражение в реакторе ИРГИТ, состо-
яла в том, что этот реактор, являющийся прототипом реактора ЯРД,
358
Глава 4
преимущества которого перед ЖРД реализованы только при высо-
ких удельных тягах (> 9,5 км/с), должен быть возможно меньших раз-
меров и позволять поузловую отработку элементов его конструк-
ции для снижения затрат на их изготовление, испытания и создание
экспериментальной базы для проведения этих испытаний. Реактор
ИРГИТ [4.1.9] — это тепловой, гетерогенный реактор, размеры актив-
ной зоны которого [диаметр — 430 мм и высота (длина) — 600 мм] оп-
ределены в соответствии с условиями теплообмена и совокупностью
теплофизических, нейтронно-физических, прочностных и весовых
соображений. Активная зона реактора содержит 37 ТВС с витыми
твэлами стержневого типа, изготовленных из карбидов тугоплавких
металлов, позволяющих нагреть водород до -3000 К, обеспечив тре-
буемое значение удельной тяги.
Замедлитель из гидрида циркония — цилиндр, секционирован-
ный по высоте, радиусу и азимуту. Отражатель из бериллия — тор-
цевой и боковой, азимутально секционирован для повышения тер-
мопрочности. Органы регулирования в виде поворотных барабанов
с поглощающими элементами размещены в отражателе. Развиваемая
тяга воспринимается днищами, соединенными цилиндрическим кор-
пусом. Реактор ИРГИТ отличается от реактора ЯРД узлами крепле-
ния ТВС, охлаждением корпуса, замедлителя, отражателя и приво-
дов барабанов (в ЯРД — жидкий водород, в ИРГИТ — газообразный),
а также тем, что каждая ТВС оснащена критическим соплом. Кроме
того, управление, регулирование и аварийная защита реактора осу-
ществляются стендовой системой.
Исследовательский высокотемпературный газоохлаждаемый реак-
тор ИВГ. 1, разработка которого началась примерно в то же время, что и
реактора ИРГИТ, сооружен в начале 70-х гг. На ИВГ.1 в течение 1975 —
1988 гг. проводились испытания по программе отработки ТВС [4.1.24 —
4.1.27]. В этом гетерогенном реакторе использовались ТВС с пучками
витых твэлов, имеющими такие же геометрические характеристики,
как и характеристики твэлов реакторов ИРГИТ и ЯРД. Эти твэлы изго-
товлены из карбидов тугоплавких металлов по одинаковой технологии.
В ИВГ-1 30 ТВС с индивидуальным подводом газообразного водорода
к каждой сборке размещались в водяном замедлителе. Максимальная
тепловая мощность реактора ИВГ. 1 составляла 720 МВт.
Испытания ТВС и активных зон реакторов ЯРД проводились в
ИВГ.1 и ИРГИТ по методике, обеспечивающей реализацию заданных
параметров и их измерение в условиях безопасной работы [4.1.24—
4.1.25]. Наибольший интерес для оценки работоспособности твэлов
представляют энергетические пуски с реализацией заданных значе-
ний мощности реактора и температуры водорода на выходе из ТВС и
Глава 4
359
исследовательские пуски реакторных установок с реализацией за-
данных параметров испытаний ТВС. В 1975—1988 гг. испытаны четы-
ре опытные активные зоны реактора ИВГ (всего 29 пусков) и две — ре-
актора ИРГИТ (всего 4 пуска). При испытаниях ТВС в реакторах ИГР,
ИРГИТ, ИВГ.1 для определения температуры теплоносителя на выхо-
де из ТВС Твых и тепловой мощности использованы различные мето-
ды. Так, для измерения температуры Твых при испытаниях до темпера-
тур 2500—2800 К использовались термоэлектрические термометры.
В случаях, когда температура Твых достигала более высоких значений
(2800—3100 К), использовались косвенные методы определения тем-
пературы Твыхпри испытаниях ТВС [4.1.9,4.1.26,4.1.27]. Следует отме-
тить, что с помощью термопар, расположенных в средней части ТВС
(где максимум тепловыделения) при различных угловых положениях
ср и радиусе г/гк = 0,745, удалось при испытании реактора ИВГ.1 уста-
новить и характер азимутально-радиальной неравномерности в ТВС,
расположенных на различных расстояниях по радиусу от центра ре-
актора (рис. 4.20). На рис. 4.20 с измеренными температурами тепло-
носителя сравниваются теоретически рассчитанные распределения
температуры по углу <р на радиусе ТВС г/гк = 0,745. Расчет проводился
путем решения исходной системы уравнений с соответствующими
граничными условиями при использовании для замыкания этой си-
стемы уравнений эффективного коэффициента турбулентной диф-
Рис. 4.20. Влияние неравномерности поля энерговыделения в реакторе ИВГ.1 на
радиально-азимутальное распределение температуры теплоносителя а, б, в — для
ТВС 1,2 и 3-го ряда соответственно; • — измеренные температуры при г/гк = 0,745;
— — расчет при Kqs = 0,045 и г/гк — 0,745 (Ттах,р — максимальная температура в
центральном сечении ТВС)
360
Глава 4
фузии Kqs = 0,045. Видно, что экспериментальные распределения
температур, полученные при натурных испытаниях реактора ИВГ.1,
хорошо согласуются с результатами теоретических расчетов.
Закрученные пучки витых твэлов и труб
В теплообменном аппарате поток теплоносителя закручен не
только относительно оси каждой трубы (твэла), но и относитель-
но оси пучка. Поэтому в таком пучке действует дополнительный по
сравнению с прямым пучком витых труб механизм искусственной
турбулизации потока, связанный с его закруткой относительно оси
пучка, что приводит к дополнительной интенсификации теплообме-
на и межканального перемешивания теплоносителя. При этом обес-
печивается наиболее эффективное выравнивание полей температур
в условиях значительной азимутальной неравномерности тепловы-
деления или теплоподвода, которая может наблюдаться при боковом
входе теплоносителя в теплообменный аппарат. Более интенсивное
выравнивание неравномерностей поля температур в поперечном
сечении пучка повышает надежность работы теплообменного уст-
ройства, а интенсификация теплообмена улучшает его массогабарит-
ные характеристики.
При расчете полей температур теплоносителя в закрученном пуч-
ке решается система дифференциальных уравнений, учитывающая
кроме продольной и вращательную компоненту скорости относи-
тельно оси пучка. Азимутальный перенос в таком пучке учитыва-
ется эффективным коэффициентом диффузии, характеризующим
перемешивание теплоносителя в пучке и определяемым из экспери-
мента в безразмерном виде К3 = Deff/udeq. Для определения коэффи-
циента К использовался метод диффузии теплоты от точечного ис-
точника. Опыты проводились на моделях теплообменных аппаратов
с различными законами закрутки труб по радиусу пучка: с постоян-
ным углом закрутки у = п/6 (vT = const) и постоянным шагом закрут-
ки s3 = 0,65м (vx/r = const), в диапазоне чисел Re = 8,5-Ю3— 3,4-104 при
трех положениях источника диффузии по радиусу ги/гк = 0; 0,325;
0,638, где гк — радиус пучка труб [4.1.6, 4.1.38].
Опытные данные по коэффициентам К3 для пучка с закруткой по
закону vt = const [у = const (г)] описываются выражением:
К3 =0,0573 = const (Re, ru/rk).	(4.1.32)
Полученные результаты аналогичны данным по влиянию числа
Re и ru/rk на коэффициент К в пучках прямых труб в том же диапазо-
не чисел Re.
Глава 4
361
Опытные данные для коэффициента К3 при законе закрутки
s3 = const (г) в том же интервале чисел Re и гц/гк описываются зави-
симостью:
К3 = O,6Re'0,243 - 0,0161 ru/rk.
(4.1.33)
Результаты выполненного исследования представлены на рис. 4.21.
Видно, что в пучках с закруткой по законам у = const(r) и s3 = const(r)
наблюдается существенное отличие в обнаруженных зависимостях
коэффициента К3, что связано с различием структуры потока в этих
пучках. Если в пучке с закруткой по закону у = const продольная со-
ставляющая скорости равномерно распределена по радиусу пучка, то
в пучке с закруткой по закону s3 = const продольная составляющая
скорости и изменяется по кривой с максимумом в периферийной
части пучка (см. рис. 4.21). Такое распределение скоростей аналогич-
но распределению скоростей за аксиально-лопаточным завихрите-
лем. При этом интенсивность пульсаций скорости в периферийной
области канала составляет -4—7%, а в приосевой области течения до
30—35%. Таким образом, причиной увеличения коэффициента К3 в
центральной области пучка является турбулизация потока за счет
его закрутки.
Экспериментальное исследование теплообмена и гидравличес-
кого сопротивления в закрученном пучке витых труб проводилось в
диапазоне чисел Re = 1,4-Ю3—7-104 на пучках длиной 1,5 м с постоян-
ным шагом закрутки s3 = 0,650 м
и углом закрутки у = я/6 по
радиусу пучка [4.1.1]. Витые
трубы с d = 12,2 мм, 5 = 0,5 мм
имели овальный профиль, за-
крученный относительно оси
трубы с шагом s = 171 мм. Тру-
бы в пучке располагались по
концентрическим окружнос-
тям в количестве 1, 6, 12, 17, 23
труб в ряду. При s3 = const от-
носительный шаг закрутки
труб каждого ряда s3/D = ос;
12,3; 11,6; 8,1; 6,2 соответст-
венно, где D — диаметр окруж-
ности данного ряда.
При исследовании теплоот-
дачи использовался метод ло-
кального моделирования. При
Рис. 4.21. Влияние различных факто-
ров на безразмерный эффективный ко-
эффициент турбулентной диффузии:
1—3 — опытные данные для пучка с
s3 = const(r) при ru/rk = 0, 0,325 и 0,638
соответственно; 4 — 6 — зависимость
(4.1.33) для положений источника диф-
фузии ru/rk ~ 0,325 и 0,638; 7 — зависи-
мость (4.1.32) для пучка с у — const(r);
8 — изменение избыточной скорости по
радиусу пучка с s3 = const (г)
362
Глава 4
Рис. 4.22. Зависимость числа Нус-
сельта от относительного шага за-
крутки пучка и числа Рейнольдса:
1—4 — опытные данные для чисел
Re = 1,4-103; 5-103; 104; 5-104 соответст-
венно
этом электрическая мощность
подводилась к отдельным трубкам
каждого ряда. Длина нагреваемой
выходной части труб составляла
0,4 м. Теплообмен исследовался в
условиях гидродинамической ста-
билизации потока, поскольку дли-
на ненагреваемой части труб рав-
нялась I = 90de<r Опытные данные,
обобщенные в виде зависимости
Nu3/Nunp = f(Ref, s3/D), где Nunp -
число Nu прямого пучка витых
труб, определяемое по (4.1.8) —
(4.1.10), представлены на рис. 4.22.
Видно, что закрутка витых труб
пучка дополнительно интенсифи-
цирует теплообмен и тем больше,
чем меньше относительный шаг
закрутки рядов труб пучка — s3/D, причем чем меньше число Рей-
нольдса, тем выше коэффициент теплоотдачи. Результаты исследова-
ния коэффициента гидравлического сопротивления представлены
4	6 8104	2	4 Ren
Рис. 4.23. Зависимость коэффициен-
та гидравлического сопротивления
от числа Рейнольдса для закрученных
пучков витых труб с s3 = 650 мм;
Е,.кр = °'63иГ = 20"' Е,«Р = 0,62:1 - 2 -
опытные данные, описываемые за-
висимостью е = CRen при С = 5,4;
п = -0,5; С = 0,37, п = -0,22 соот-
ветственно; 3,4 — незакрученный пу-
чок витых труб с s/d =14 при С = 3,5;
п = -0,5; С = 0,29; п = -0,22 соот-
ветственно; 5 — данные для пучка ви-
тых труб с s/d = 14; 6 — зависимость
$ = (0,934-10’2) + (0,316Re7°'25) закру-
ченной трубы при D3aKp/d =9,45; 7 —
гладкая труба; £ — пористость
на рис. 4.23. Видно, что при числе
Ref = 1,4-104 имеет место излом в
зависимости £, = £,(Ref), т.е. харак-
тер изменения коэффициента £
от числа Re аналогичен характе-
ру изменения коэффициента £ в
обычном пучке витых труб. Коэф-
фициент £, закрученного пучка не-
сколько выше коэффициента гид-
равлического сопротивления для
обычного пучка витых труб.
Оценка эффективности тепло-
обменного аппарата с закручен-
ным пучком витых труб показала,
что данный аппарат при Re < 2-Ю4
имеет объем примерно на 30%
меньший, чем объем теплообмен-
ника с прямыми витыми трубами
при одинаковых расходах тепло-
носителя, тепловых мощностях
и мощностях на прокачку тепло-
Глава 4
363
носителей в предположении, что коэффициент теплоотдачи в меж-
трубном пространстве существенно меньше коэффициента теплоот-
дачи внутри труб.
Поперечно обтекаемые пучки витых твэлов
Экспериментальное исследование теплообмена и гидравличе-
ского сопротивления в поперечно обтекаемых пучках витых труб
(рис. 4.24) проводилось в интервале чисел Re = 103—3-104 и темпе-
ратурного фактора Tw/Tf = 1,1—1,5 при s/d = 6,1 и 12,2 [4.1.29]. При
обобщении опытных данных в качестве определяющей скорости
использовалась скорость и = и0/Т, где uQ — скорость перед пучком,
Т — пористость пучка витых труб по теплоносителю. В качестве оп-
ределяющего размера использовался размер dp = 2
(f А
хтр
к >
, где
l-v,
— продольный шаг размещения труб в пучке; f — площадь попе-
речного сечения трубы. Опытные данные по средней теплоотдаче с
постоянной шириной канала между трубами при s/d — 12,2 и 6,1 хо-
рошо описываются зависимостями
Nu = O,74Re0,58;
Nu = 0,51Re°'62.
(4.1.34)
(4.1.35)
Влияние шага закрутки s/d на теплоотдачу слабое, а влияния тем-
пературного фактора не наблюдается. Опытные данные по гидрав-
лическому сопротивлению описываются зависимостями:
Рис. 4.24. Средняя теплоотдача (а) и гид-
равлическое сопротивление (б) при по-
перечном обтекании пучков витых труб:
1 — 3,4 — 6 — опытные данные по теплоот-
даче; 7, 8 — зависимости (4.1.34) и (4.1.35);
9, 10 — опытные данные по гидравли-
ческому сопротивлению; 11 — 14 зави-
симости (4.1.36), (4.1.37), (4.1.38), (4.1.39)
для гидравлического сопротивления;
15—17 — зависимости (4.1.40), (4.1.41),
(4.1.42) для теплоотдачи; 18 — теплоотда-
ча в пучке с круглыми трубами; 19 — 21 —
зависимости (4.1.45), (4.1.44), (4.1.48) для
гидравлического сопротивления; 22 —
для пучка с круглыми трубами
364
Глава 4
для s/d = 12,2:
при Re = 103—4,7-103
Eu = 1,9;	(4.1.36)
при Re = 4,7-103—ЗЮ4
Eu = 8Re'0,17;	(4.1.37)
для s/d = 6,1:
при Re = 103—3,7-103
Eu = 2,0;	(4.1.38)
при Re = 3,7103 —3404
Eu = 5,78Re'0-В * * * * 13.	(4.1.39)
Влияние закрутки труб на число Эйлера слабое. На рис. 4.24 на-
несены также опытные данные по средней теплоотдаче и гидравли-
ческому сопротивлению для пучков витых труб, когда между ними
образуются каналы переменной ширины.
Для s/d = 6,1:		
при Re = 103—104	Nu = 0,538 Re0-59;	(4.1.40)
при Re = 104-3104	Nu = 0,232 Re0-68;	(4.1.41)
для s/d = 12,2: при Re = 103—3-104	Nu = 0,367 Re0-64.	(4.1.42)
В этом случае средняя теплоотдача на 25—33% меньше, чем для
пучков витых труб с постоянной шириной канала между ними. В
гладкотрубном пучке средняя теплоотдача еще меньше:
Nu = 0,498 Re0-6.	(4.1.43)
Полученные результаты свидетельствуют о заметной интенсифи-
кации теплоотдачи при поперечном обтекании пучков витых труб с
каналами постоянной ширины между ними.
Гидравлическое сопротивление пучков витых труб с переменной
шириной канала между ними описывается формулами:
для s/d = 12,2:
при Re = 103—104
Ей = 3,86 Re’0-156;	(4.1.44)
при Re = 104—3104
Eu = 1,84 Re’0-076.
(4.1.45)
Глава 4
365
Для пучка с s/d = 6,1:
при Re = (103—104)
Ей = 1,665 Re’0,06;	(4.1.46)
при Re = 104—З-Ю4
Ей = 1,18 Re’0,021.	(4.1.47)
Для пучка с s/d = 14,2 и шагами размещения труб ab = 1,04,0:
при Re = 2-103—3-104
Ей = 4,65 Re’0,154.	(4.1.48)
Для гладкотрубного пучка при Re = 103—4103:
Ей = 3,84 Re’0,15;	(4.1.49)
при Re = 4403 —3404
Ей = 11,2 Re’0-29.	(4.1.50)
Неравномерность коэффициента теплоотдачи по периметру ви-
той трубы уменьшается с уменьшением шага закрутки s/d и в 2—3
раза меньше, чем неравномерность коэффициента теплоотдачи для
гладкотрубного пучка с шахматным расположением труб, где нерав-
номерность теплоотдачи по периметру круглой трубы составляет
примерно 45%.
Эффективность интенсификации теплообмена путем закрутки
потока в теплообменных аппаратах с поперечным обтеканием ви-
тых труб оценивается путем сравнения объемов теплообменников с
интенсификацией и с круглыми трубами при одинаковых тепловых
мощностях на прокачку теплоносителей (одинаковых расходах теп-
лоносителей и потерях давления). При сравнении предполагается,
что коэффициент теплоотдачи внутри труб существенно выше, чем
снаружи, а сравниваемые пучки труб имеют одинаковые продоль-
ные и поперечные шаги размещения труб в пучке и состоят из труб
с одинаковым периметром — я = л0. Тогда можно получить форму-
лу для отношения объемов сравниваемых аппаратов, используя уста-
новленные критериальные зависимости:
v pEu/Euo)^/^)3*"-2”^	(
V» [	(Nu/Nu0)”+3 j
Результаты расчета V/Vo приведены на рис. 4.25. Индекс «0» —
для аппарата с круглыми трубами. Здесь же приведены зависимости
Nu/Nu0 и при различных числах Re для исследованных пучков.
Видно, что замена круглых труб витыми при числах Re ~ 103 приводит
366
Глава 4
Рис. 4.25. Зависимость £/£,0 (1, 2),
Nu/Nu0 (3, 4), V/Vo (5, 6) от числа Re
для теплообменников с поперечным
обтеканием пучка витых труб: 1, 3,
5 - s/d = 6,1; 2, 4, 6 - s/d = 12,2
к росту теплоотдачи в 1,45 раза при росте гидравлического сопротив-
ления в 1,5 раза, что позволяет уменьшить объем теплообменника на
25%. Эффективность таких аппаратов падает с ростом числа Re.
Течение в витых трубах и кольцевых каналах
Структура турбулентного течения внутри витых труб и в кольце-
вом канале с витой трубой. Исследование осредненного и пульсаци-
онного движения теплоносителя в витой трубе и кольцевом канале
проводилось с использованием термоанемометрической измеритель-
ной техники и конструкций термоанемометрических зондов, разра-
ботанных для изучения трехмерного потока, в витых трубах с мак-
симальным размером овала d = 50 мм в диапазоне изменения чисел
Re = 7,8-103—105 и для относительных шагов закрутки витых труб
s/d = 10,8; 12,8; 25,6 [4.1.2]. Результаты исследования представлены
для течения внутри витых труб в виде распределений продольной и
тангенциальной составляющих вектора скорости (рис. 4.26) и про-
дольной пульсационной составляющей (рис. 4.27) по направлениям
перемещения зонда 1, 2 и 3, представленным на схеме поперечного
сечения витой трубы, где показаны принятые положительные на-
правления составляющих вектора скорости (и, пт, иг) (рис. 4.28). Об-
наружено, что при закрутке потока происходит деформация продоль-
ной скорости в сечениях 1 и 3 на границе витого и сквозного каналов,
причем максимум величины u/ucp смещен по направлению закрутки
от сечения 2. Во всех сечениях профили продольной скорости более
заполненные, чем в случае течения в круглой трубе, а распределение
тангенциальной скорости пт свидетельствует о вихревом движении
теплоносителя. Величина скорости пт является переменной по пери-
метру трубы. Радиальная составляющая скорости иг в 2—3 раза мень-
Глава 4
367
Рис. 4.26. Профили состав-
ляющих вектора скорости
внутри витой трубы для се-
чений 1, 2 и 3: а — профили
продольной составляющей;
б — профили тангенциаль-
ной скорости; V, □, О — для
шага закрутки s/d = 10,8 и
для чисел Re = 7800,49000 и
83000 соответственно; • —
для шага закрутки s/d = 12,8
и числа Re = 78000; ▼ — для
шага закрутки s/d = 25,6 и
Re = 78000
б
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 у/Ь
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 у/Ь
а
б
Рис. 4.27. Распределение относительной продольной пульсационной скорости
Vu*
внутри витои трубы для сечений 2 (а) и 3 (б): 1 —3 — для шага закрутки 10,8
и чисел Re = 24000, 41000 и 100000 соответственно; 4 — для шага закрутки 12,8 и
Re = 8900; 5 — для шага закрутки 25,6 и Re = 9300
368
Глава 4
Рис. 4.28. Схема поперечного се-
чения витой трубы и условно при-
нятые направления составляющих
вектора скорости: 1 — 3 — направ-
ления, по которым проводились
измерения; П и Н — подветренная
и наветренная части профиля тру-
бы соответственно
ше тангенциальной скорости иг. Чем
больше закручен поток (чем меньше
шаг s/d), тем больше тангенциаль-
ная скорость.
Таким образом, течение внутри
витой трубы является трехмерным.
Оно формирует в поперечном сече-
нии трубы вихрь с осью симметрии,
сдвинутой по направлению закрут-
ки потока на некоторый угол от гео-
метрической оси овального профи-
ля трубы. Закрутка потока приводит
к расширению области ядра пото-
ка и более заполненному профилю
скорости при турбулентном режиме
течения по сравнению с течением в
круглой трубе. Поэтому при течении
в витой трубе наблюдается увеличе-
ние коэффициентов теплоотдачи по
сравнению с течением в круглой трубе. В то же время малые значе-
ния радиальной составляющей скорости иг/и в витой трубе по срав-
нению с пучком витых труб уменьшают обменные процессы между
пристенным слоем и ядром потока, что объясняет меньшую интен-
сивность теплообмена в витой трубе, чем в пучке витых труб при од-
ном и том же шаге s/d.
Исследование продольной пульсационной скорости в витой тру-
бе (см. рис. 4.27) позволило установить, что уровень турбулентности
уменьшается с ростом числа Re и увеличением s/d, т.е. уменьшением
закрутки потока. При этом на распределении величины /й по-
являются локальные максимумы в сечении (3—3). Для интенсифика-
ции теплообмена при течении внутри витых труб необходимо допол-
нительно турбулизировать поток путем использования витых труб с
малыми шагами закрутки s/d.
Структура потока при течении в кольцевом канале с внутренней
витой трубой с шагом закрутки s/d =9,7и 12,5 исследовалась на экспе-
риментальном участке, представленном в главе 3. Результаты исследо-
вания распределений составляющих скорости и, иг и иг и продольной
пульсационной скорости в кольцевом канале с s/d = 9,7 представлены
на рис. 4.29 и 4.30. Особенностью течения в таком кольцевом канале
является снижение продольной скорости п/пср в ядре потока винто-
вого канала (справа от пунктирной линии на рис. 4.29) по сравнению
Глава 4
369
с ее значением в ядре потока сквозного канала (слева от пунктирной
линии). При этом скорость п/пср возле внутренней трубы примерно
на 20% выше, чем у стенки наружной круглой трубы, что объясняется
сильным воздействием поперечных составляющих вектора скорости
на пристенный слои витои тру-
бы, приводящим к расширению
ядра потока. Составляющие ско-
рости их и иг принимают макси-
мальные значения вблизи стенки
витой трубы, в 1,5—2 раза превы-
шающие средние значения этих
составляющих скорости в коль-
цевом канале. Причем танген-
циальная скорость их в большей
части канала имеет положитель-
ное направление, совпадающее с
направлением закрутки профи-
ля витой трубы, и лишь для уг-
лов (р » — (60—110°) для s/d = 9,7 и
(р~ —(60—90°) для шага s/d = 12,5
направление их противополож-
но направлению закрутки витой
трубы. Размеры области с отри-
цательной их увеличиваются с
ростом числа Re (см. рис. 4.30)
и шага s/d. Абсолютная вели-
чина радиальной составля-
ющей скорости иг несколько
меньше скорости их практиче-
ски во всей области течения. Век-
тор скорости иг направлен в сто-
рону стенки наружной трубы на
периферийной части канала, а в
середине канала меняет направ-
ление на противоположное — к
стенке витой трубы.
Таким образом, витая труба
индуцирует поперечные со-
ставляющие скорости во всей
области течения кольцевого ка-
нала с внутренней витой трубой.
Это влияние закрутки потока
Рис. 4.29. Профили составляющих век-
тора осредненной скорости в кольце-
вом канале с относительным шагом за-
крутки витой трубы 9,7: (а) — профили
радиальной составляющей, (б) — про-
фили тангенциальной скорости, (в) —
профили продольной скорости; 1, 3,
5,7 — длячислаКе = 7,8-103,uCj, = 1,9м/с;
2, 4, 6, 8 — то же для Re = 1,5-Ю5; иср =
= 34,1 м/с; 1, 2 — длжр = 0°; 3, 4 — для
Ф = 60°; 5, 6 — для ф = -30°; 7, 8 — для
Ф = -60°
370
Глава 4
наблюдается во всем исследованном интервале чисел Re и шагов за-
крутки s/d. Так, для канала с шагом s/d = 9,7 среднее значение попе-
речной скорости составляет около 10% от продольной скорости (см.
рис. 4.29), а для канала с шагом s/d = 12,5 — менее 3%.
Исследования осредненной скорости в кольцевом канале с внут-
ренней витой трубой показали, что интенсивность закрутки при том
же шаге s/d в этом случае меньше, чем при течении в пучке витых
труб. Этим можно объяснить меньшую интенсификацию теплооб-
мена в кольцевом канале, чем в пучке витых труб.
Неравномерные поля осредненных составляющих скорости в
кольцевом канале с витой трубой позволяют судить о многих фак-
торах, влияющих на уровень турбулентности в таком канале. Это —
возросший из-за действия закрутки потока градиент скорости у стен-
ки, тангенциальный разрыв скоростей при взаимодействии потоков
в винтовых и сквозном каналах, отрыв потока при обтекании мень-
ших сторон овального профиля, действие центробежных сил, взаи-
модействие встречных потоков в поперечном сечении канала, гради-
Рис. 4.30. Распределение относитель-
ной продольной пульсационной скорости
/й: а — в кольцевом канале с шагом за-
крутки витой трубы s/d = 9,7: 1 —4 — для
числа Re = 7,8-103, пСр = 1.9 м/с и 5 — 8 —
для Re = 1,5-105, пСр = 34,1 м/с; б — в коль-
цевом канале с шагом закрутки витой тру-
бы s/d = 12,5: 9-12 - для Re = 1.48-105,
цСр = 33,1 м/с; 13 — прямая круглая труба
(0 90 мм); 1, 5, 9 - ср = 0°; 2, 6, 10 - ф = 60°;
3, 7, 11 - ф = -30°; 4, 8, 12 - ф = -60°
ент давления по периметру
витой трубы. Поэтому рас-
пределения относительной
продольной пульсационной
скорости /й для раз-
личных углов <р являются
очень сложными и свиде-
тельствуют о значительной
анизотропии свойств потока
(см. рис. 4.30). При увеличе-
нии числа Re с 8103 до 1,5-105
степень турбулентности в
кольцевом канале с шагом
s/d = 9,7 уменьшается при-
мерно в 2 раза, а при увели-
чении шага s/d при Re «1,5-105
с s/d = 9,7 до 12,5 степень
турбулентности уменьшает-
ся на -10%.
Характер распределения
интенсивности турбулен-
тности по сечению канала
свидетельствует о том, что
генерация турбулентности
Глава 4
371
происходит в основном у стенок канала и вблизи условной границы
винтового и сквозного каналов и что средний уровень турбулентнос-
ти в винтовом канале выше, чем в сквозном (см. рис. 4.30). Выполнен-
ные исследования структуры потока позволили выявить механизмы
переноса, приводящие к интенсификации теплообмена при течении
в кольцевом канале с внутренней витой трубой и при течении внутри
витой трубы, и пути управления этим процессом.
Теплообмен и гидравлическое сопротивление внутри витых труб
и кольцевых каналов
Спиральная закрутка потока интенсифицирует теплообмен внут-
ри витых труб и в кольцевых каналах с такими трубами. Результаты
исследования теплообмена при течении воды в этих каналах и ка-
налах с использованием других методов интенсификации перено-
са получены методом теплообменника (ТА) типа «труба в трубе» при
ReTp = 2,4403—1.05-104 и Rekk = 2—7-Ю3 для теплопередающих труб с
интенсификаторами различной формы [4.1.2, 4.1.14, 4.1.16]. Трубы из
стали марки 12Х18Н10Т имели наружный диаметр до их деформации
(в исходном состоянии) d = 12 мм, толщину стенки 0,6 мм и длину
I = 1,495 м и размещались в круглой гладкой трубе с dH = 18 мм и тол-
щиной стенки 0,7 мм. Греющий теплоноситель протекал в кольце-
вом канале, а нагреваемый — внутри труб с интенсификаторами по
противоточной схеме движения. Тепловая мощность ТА составляла
1,8—5,6 кВт.
Обнаружено, что все рассмотренные трубы с интенсификатора-
ми имеют коэффициент теплопередачи К, в 1,3 —1,8 раза превышаю-
щий коэффициент К для ТА с внутренней круглой гладкой трубой.
При этом для расчета теплоотдачи при течении в кольцевом кана-
ле с витой трубой овального профиля получена зависимость при
d/d2 = 0,725
Nutt/Nu0 = 87,82(s/d)"148 ке^»«фК>.«>5«/<0	(4.1.52)
а для кольцевого канала с внутренней круглой трубой с кольцевой и
винтовой накаткой — формула:
Nukk/Nuo=l+O,64[l-exp(-35,8h/deg)](l-O,274f/deg).	(4.1.53)
В уравнениях (4.52) и (4.53) Nu0 — число Нуссельта для кольце-
вого канала с внутренней круглой гладкой трубой при d1/d2 = 0,725;
Nu0=0,02082Re£f Рг0,4 .Тогда для витой трубы с шагом s/d — 6,2 и для
витых круглых труб с винтовой накаткой с h/deq = 0,1196, t/deq — 1,141,
s/d = 1,31 и кольцевой накаткой с h/dp„ = 0,07065, t/dM = 1,174 опыт-
372
Глава 4
ные данные по теплоотдаче и коэффициенту гидравлического сопро-
тивления хорошо обобщаются степенными зависимостями:
Nu0 = ARenPr0-4,	(4.1.54)
£ = BRe"m.	(4.1.55)
Эмпирические константы А, п, В, т в зависимостях (4.1.54) и
(4.1.55) для исследованных теплопередающих поверхностей при те-
чении воды внутри труб определились путем решения задачи о ми-
нимизации среднеквадратического отклонения экспериментальных
и расчетных значений коэффициента К. При этом использовались
формулы (4.1.52), (4.1.53), а также зависимости коэффициентов тепло-
передачи от термических сопротивлений для цилиндрической стен-
ки (круглой трубы) и для плоской стенки (витые трубы). Опытные
данные по теплоотдаче и гидравлическому сопротивлению представ-
лены на рис. 4.31, 4.32, а величины А, п, В, т приведены в табл. 4.2.
Рис. 4.31. Экспериментальные дан-
ные по гидравлическому сопротивле-
нию и теплообмену при течении воды
внутри витых труб: 1 — закон Блазиу-
са; 2 — закон Гагена-Пуазейля; 3 —6 —
теплообмен для круглой гладкой тру-
бы, витой гладкой трубы, витой трубы
с винтовой накаткой и витой трубы с
кольцевой накаткой соответственно;
7 — 9 — коэффициент гидравлического
сопротивления для витой гладкой тру-
бы, витой трубы с винтовой накаткой и
витой трубы с кольцевой накаткой со-
ответственно
Рис. 4.32. Экспериментальные дан-
ные по гидравлическому сопротивле-
нию и теплообмену при течении воды
внутри круглых труб: 1 — закон Бла-
зиуса; 2 — 4 — теплообмен для круг-
лой гладкой трубы, круглой трубы с
винтовой накаткой и круглой трубы с
кольцевой накаткой соответственно;
5, 6 — коэффициент гидравлическо-
го сопротивления для круглых труб с
винтовой накаткой и круглых труб с
кольцевой накаткой соответственно
Глава 4
373
Таблица 4.1.2
Эмпирические константы в формулах (4.1.54) и (4.1.55)
для различных каналов
Форма канала	А	п	В	т
Гладкая витая труба	0,0737	0,698	7,291	0,632
Витая труба со спиральной накаткой	0,00981	0,985	1,339	0,355
Витая труба с кольцевой накаткой	0,00412	1,096	22,801	0,661
Круглая гладкая труба	0,023	0,8	0,3164	0,25
Круглая труба со спиральной накаткой	0,01261	0,941	0,06	0
Круглая труба с кольцевой накаткой	0,0004746	1,35	0,08	0
Обнаружено, что опытные данные по теплоотдаче к воде в витой
гладкой трубе совпадают с зависимостью для течения воздуха при
Re > 7403. При Re < 7403 закрутка потока в витой трубе в большей
мере интенсифицирует теплообмен, чем при Re > 7403. При течении
воды в кольцевом канале закрутка потока в большей мере интенси-
фицирует теплообмен, чем кольцевая и винтовая накатка в круглых
трубах. В то же время теплоотдача при течении воды в круглых и ви-
тых трубах с кольцевой и винтовой накаткой в 2—3 раза больше, чем
в круглых гладких трубах. Однако в этом случае значительно возрас-
тает и коэффициент гидравлического сопротивления.
При течении внутри витых труб жидких теплоносителей с шага-
ми закрутки профиля труб s/d = 6—12 опытные данные по теплооб-
мену хорошо обобщаются зависимостью
= 0,0235 1+
3,0384
(s/d)0'989
(Re^8-230)(l,8Prf°'3-0,8)x
Nudf
0,14
(d V/3
eg
(4.1.56)

а для течения, близкого к изотермическому, при Re < 7403 может ис-
пользоваться зависимость
Nud/
= 0,0486 1+
3,0384
(s/d)0’97
Re2>698Prf0'4
(4.1.57)
374
Глава 4
Экспериментальные данные по коэффициенту гидравлическго
сопротивления для течения внутри витых труб при s/d = 6—12 и чис-
лах Re < 7-103 хорошо обобщаются зависимостью
4,86 ( 3.0384А
^"Re°’623l s/d У
(4.1.58)
За счет интенсификации тепло- и массообмена методом закрутки
потока созданы компактные теплообменные аппараты с витыми тру-
бами для термической обработки различных пищевых продуктов.
Разработанный и испытанный в составе технологической линии
производства шампанского теплообменный аппарат с витыми труба-
ми обеспечил охлаждение потока шампанского с расходом 2000 л/ч
до температуры -4°С при уменьшении массы (металлоемкости) аппа-
рата в 4,3 раза по сравнению с массой ТА с круглыми трубами [4.1.14,
4.1.16].
Использование витых труб в теплообменном аппарате, предна-
значенном для нагревания растительного масла в технологической
линии его рафинации, позволяет уменьшить массу в 3,35—3,67 раза
по сравнению с ТА, в котором используются круглые трубы.
Список литературы
4.1.1.	Данилов Ю.И., Дзюбенко Б.В., Дрейцер Г.А., Ашмантас Л.-В.А. Теп-
лообмен и гидродинамика в каналах сложной формы. М.: Машиностро-
ение, 1986.
4.1.2.	Дзюбенко Б.В., Сакалаускас А.В., Ашмантас Л.-В.А, Сегаль М.Д.
Турбулентное течение и теплообмен в каналах энергетических установок.
Вильнюс: Исток, 1995.
4.1.3.	Дзюбенко Б.В. Исследование полей скорости и температуры в межтруб-
ном пространстве теплообменного аппарата с закруткой потока//Межву-
зовский сб. науч, трудов «Современные проблемы гидродинамики и теп-
лообмена в элементах энергетических установок и криогенной технике».
М.: ВЗМИ, 1979. Вып. 8. С. 93-104.
4.1.4.	Дзюбенко Б.В., Вилемас Ю.В., Сакалаускас А.В. Исследование струк-
туры потока в теплообменнике с винтообразно закрученными трубами//
Изв. АН СССР. Энергетика и транспорт. 1980. № 4. С. 135-144.
4.1.5.	Дзюбенко Б.В., Сакалаускас А.В. Вихревая структура потока в теплооб-
меннике с витыми трубами//Изв. АН СССР. Энергетика и транспорт. 1986.
№З.С. 151-157.
4.1.6.	Дзюбенко Б.В., Дрейцер Г.А., Ашмантас Л.-В.А. Нестационарный теп-
ломассообмен в пучках витых труб. М.: Машиностроение, 1988.
Глава 4
375
4.1.7.	Дзюбенко Б.В. Гидравлическое сопротивление и теплообмен при вы-
нужденном течении теплоносителя в каналах ядерной энергодвигатель-
ной установки/Друды Российской нац. конф, по теплообмену-3. 2002.
Т. 2. С. 131-134.
4.1.8.	Дзюбенко Б.В., Сакалаускас А.В., Вилемас Ю.В. Энергетические
спектры турбулентности в теплообменнике с закруткой потока//Изв. АН
СССР. Энергетика и транспорт. 1983. № 4. С. 125-133.
4.1.9.	Ашмантас Л.-В., Дзюбенко Б.В. Проблемы теплообмена и гидродина-
мики в ядерных энергодвигательных установках космических аппаратов.
Вильнюс: Исток, 1997.
4.1.10.	Дзюбенко Б.В., Ивлев В.М. Теплообмен и гидравлическое сопротив-
ление в межтрубном пространстве теплообменника с закруткой пото-
ка//Изв. АН СССР. Энергетика и транспорт. 1980. № 5. С. 117-125.
4.1.11.	Дзюбенко Б.В. Теплообмен на начальном участке в теплообменнике с
закруткой потока//ИФЖ. 1982. Т. 42, № 2. С. 230-235.
4.1.12.	Дзюбенко Б.В. Гидравлическое сопротивление в теплообменнике с за-
круткой потока/Дам же. 1983. Т. 44, № 3. С. 357-362.
4.1.13.	Дзюбенко Б.В., Стецюк В.Н. Закономерности теплообмена и гидрав-
лического сопротивления в пучках витых труб//Изв. АН СССР. Энергети-
ка и транспорт. 1989. №4. С. 137-145.
4.1.14.	Дзюбенко Б.В. и др. Интенсификация теплообмена в каналах с искусст-
венной турбулизацией потока/Друды 1-й Российской нац. конф, по теп-
лообмену. 1994. Т. 8. С. 64-69.
4.1.15.	Дзюбенко Б.В. Теплообмен при турбулентном течении в пучках витых
стержней и проблема замыкания системы уравнений/Друды 2-й Рос-
сийской нац. конф, по теплообмену. М.: МЭИ, 1998. Т. 6. С. 83-86.
4.1.16.	Дрейцер Г.А., Дзюбенко Б.В., Якименко Р.И. Интенсификация теп-
лообмена и анализ методов сравнения теплогидравлической эффектив-
ности теплопередающих поверхностей/Дам же. С. 99-102.
4.1.17.	Вилемас Ю.В., Воронин Г.И., Дзюбенко Б.В. и др. Успехи теплопере-
дачи. Интенсификация теплообмена. Ч. 2. Вильнюс: Мокслас, 1988.
4.1.18.	Дзюбенко Б.В., Ашмантас Л.-В.А, Сегаль М.Д. Моделирование ста-
ционарных и переходных теплогидравлических процессов в каналах
сложной формы. Вильнюс: Исток, 1994.
4.1.19.	Дзюбенко Б.В. К вопросу о межканальном перемешивании теплоноси-
теля в пучках оребренных стержней//ИФЖ. 1979. Т. 37, № 5. С. 777-783.
4.1.20.	Дзюбенко Б.В. Исследование переносных свойств потока в теплооб-
меннике с винтообразно закрученными трубами//ИФЖ. 1980. Т. 38, № 6.
С.965-971.
4.1.21.	Дзюбенко Б.В., Вилемас Ю.В., Ашмантас Л.-В.А. Перемешивание
теплоносителя в теплообменнике с закруткой потока/Дам же. 1981.
Т. 40, № 5. С. 773-779.
4.1.22.	Дзюбенко Б.В., Урбанас П.А., Ашмантас Л.-В.А. Межканальное пе-
ремешивание теплоносителя в пучке витых труб/Дам же. 1983. Т. 45,
№ 1.С. 26-31.
4.1.23.	Дзюбенко Б.В., Стецюк В.Н. Влияние интенсивности закрутки пото-
ка на перемешивание теплоносителя в пучках витых труб/Дам же. 1988.
Т. 55, №. С. 709-715.
376
Глава 4
4.1.24.	Dzyubenko B.V., Dreitser G.A. Heat and Mass Transfer in Longitudinal Flow
Helical Tube Heat Exchangers, Int. J. of Heat Exchangers, 2002. V.lll, N 1.
P. 89-104.
4.1.25.	Дзюбенко Б.В., Сегаль М.Д., Ашмантас Л.-В.А. Нестационарное пе-
ремешивание теплоносителя в теплообменнике с витыми трубами//Изв.
АН СССР. Энергетика и транспорт. 1983. № 3. С. 125-133.
4.1.26.	Дзюбенко Б.В., Ашмантас Л.-В.А, Сегаль М.Д., Урбанас П.А. Неста-
ционарный тепломассообмен в теплообменнике с витыми трубами//
Изв. АН СССР. Энергетика и транспорт. 1985. № 4. С. 110-118.
4.1.27.	Дзюбенко Б.В., Ашмантас Л.-В.А., Сегаль М.Д., Багдонавичюс А.Б.
Влияние шага закрутки на нестационарный тепломассообмен в пучках ви-
тых труб//Изв. АН СССР. Энергетика и транспорт. 1987. № 3. С. 131-138.
4.1.28.	Дзюбенко Б.В., Ашмантас Л.-В.А., Багдонавичюс А. Б. Нестаци-
онарный тепломассообмен при уменьшении тепловой нагрузки в тепло-
обменнике с витыми трубами//ИФЖ. 1988. Т. 54, № 4. С. 533-539.
4.1.29.	Дзюбенко Б.В., Ашмантас Л.-В.А., Багдонавичюс А.Б. Нестацио-
нарное перемешивание при увеличении расхода теплоносителя в пучке
витых труб/Дам же. 1988. Т. 55, № 3. С. 357-363.
4.1.30.	Дзюбенко Б.В., Ашмантас Л.-В.А., Багдонавичюс А.Б. Закономер-
ности нестационарного перемешивания при уменьшении расхода теп-
лоносителя в пучке витых труб/Дам же. 1989. Т. 56, № 1. С. 5-11.
4.1.31.	Дзюбенко Б.В., Ашмантас Л.-В.А., Багдонавичюс А.Б. Нестационар-
ное перемешивание при уменьшении расхода теплоносителя в пучке ви-
тых труб//Изв. АН СССР. Энергетика и транспорт. 1989. № 2. С. 108-114.
4.1.32.	Дзюбенко Б.В., Ашмантас Л.-В.А., Багдонавичюс А.Б. Межканальное
перемешивание теплоносителя при периодическом измёнении расхода
во времени в пучках витых труб//ИФЖ. 1991. Т. 60, № 5. С. 724-729.
4.1.33.	Дзюбенко Б. В., Ашмантас Л.-В.А., Багдонавичюс А. Б., Калятна А. В.
Нестационарный тепломассообмен при одновременном изменении
мощности тепловой нагрузки и расхода теплоносителя/Дам же. 1992.
Т. 62, № 3. С. 349-355.
4.1.34.	Захаркин И.И., Коновалов В.И., Овечкин А.Д., Федик И.И. и др. Раз-
работка ЯРД минимальных размеров ИРГИТ. Энергетические испытания
опытного образца ядерного реактора/Друды 3-й межд. конф. «Ядерная
энергетика в космосе. Ядерные ракетные двигатели». Подольск, 1993.
С. 271-278.
4.1.35.	Федик И.И. и др. Ядерно-космическая энергетика//Сб. докладов юби-
лейной науч.-практич. конф., посвященной 50-летию создания атомной
отрасли. М., 1996. С. 256-268.
4.1.36.	Приймак С.П., Федик И.И. Особенности метрологического обеспече-
ния измерений температуры термоэлектрическими преобразователя-
ми в условиях интенсивного реакторного облучения/Друды 3-й межд.
конф. «Ядерная энергетика в космосе. Ядерные ракетные двигатели».
Подольск, 1993. Т 3. С. 327-334.
4.1.37.	Денискин В.П., Наливаев В.И., Паршин Н.Я., Федик И.И. Проблема
высокотемпературных измерений в ТВС ЯРД//С6. докл. 5-й отраслевой
конф. «Температура- 2001». Подольск, 2001.
Глава 4
377
4.1.38.	Дзюбенко Б.В., Ашмантас Л.-В.А. Тепломассоперенос в закрученном
пучке витых труб//Изв. АН СССР. Энергетика и транспорт. 1985. № 6.
С. 135-144.
4.1.39.	Дзюбенко Б.В., Ашмантас Л.-В.А., Вилемас Ю.В. и др. Интенсифи-
кация теплообмена в поперечно обтекаемых пучках витых труб/Дам же.
1982. №6. С. 120-127.
4.2. ИНТЕНСИФИКАТОРЫ ТЕПЛООБМЕНА МАКРО-
И МИКРОМАСШТАБОВ
Течение в каналах со вставками
Расчетно-экспериментальные исследования теплообмена в кана-
лах, заполненных капиллярно-пористыми структурами, проводились
на макетах элементов малогабаритного ионного источника ускори-
теля. Такой способ охлаждения из-за высокого гидравлического со-
противления применим лишь при небольшой протяженности канала.
Поэтому в канале была установлена «щеточная» структура, представ-
ляющая собой коридорный пучок стержней высотой 5 мм с квадрат-
ным сечением 1x1 мм и относительным шагом S = 2,0. Такая структура
выполнена из одной медной заготовки путем фрезерования продоль-
ных и поперечных пазов на теплоотдающей поверхности [4.2.1].
В опытах определялась зависимость коэффициента внутреннего
теплообмена ау от Re‘; в качестве определяющего размера в нем ис-
пользовался размер шипа (1 мм), а в качестве скорости — ее значение
в узком сечении между шипами. В результате решения уравнений,
описывающих температурные поля в рассматриваемых системах
при заданных граничных условиях, получено выражение для темпе-
ратурного перепада между стенкой по длине канала и теплоносителя
на входе (Тст- Тжвх):
= 1 z h2-3y2 । 1
Рж^рж^ бАш ССу

1
^exp
i+M-
ocvn
V2
^Ржсрж^
i+M,
ocvhz
2qh^( lV+i 1
+—X(-l) —exp -
An i-l	M
АШМ2>
avh2?
(4.2.1)
^щМ2
^Ржсрж-^
где ц = Tti.
378
Глава 4
Анализ этого выражения показывает, что при постоянных av и q
коэффициент теплоотдачи от стенки канала имеет различные значе-
ния в начальном участке, переходной области и области стабилизиро-
ванного теплообмена. Следует отличать, однако, начальный участок
стабилизированного теплообмена в самой структуре от начального
участка затесненного канала в целом. Получены большие значения
а к пористой структуре на входном участке (-20 мм). Это объясняет-
ся нестабилизированным теплообменом в пограничном слое. Что ка-
сается начального участка канала в целом, то по расчетам он может
распространяться на длину до 0,5 м. Полагая, что х = 0 и у = h, при-
веденное выше выражение для температурного поля упрощено:
гст (о, л)-тжвх
avh avhi-i
1
1+Хшм2
(4.2.2)
Проверка расчетных зависимостей проводилась в эксперимен-
те на канале, затесненном описанной щеточной структурой. Канал
представлял собой щель шириной 30 мм, высотой 5 мм, длиной 50 мм.
Числа Re изменялись от 6000 до 4300. Полученные в экспериментах
значения ау аппроксимируются формулой Nuv = O,385Re0,563 и удов-
летворительно согласуются с полученными из расчета.
В экспериментах, кроме того, получены профили температуры
охлаждаемой стенки, которые позволили определить коэффициен-
ты теплоотдачи от нее. Полученные значения а приблизительно на
порядок превышают коэффициент теплоотдачи в плоском не затес-
ненном канале, при этом замечена резкая зависимость а = /(Re*) при
Re* до 3000, далее увеличение а от Re* незначительно.
Кроме того, проводился ряд экспериментов с другим затеснени-
ем каналов: металловолокном, гофрированными структурами и др.
Результаты этих экспериментов позволили разработать и создать мо-
дули охлаждения кристаллов и линеек мощных полупроводниковых
лазеров, работающих при температурах до 30°С и обеспечивающих
теплосъем при тепловых нагрузках 1 кВт/см2 и более. Это стало воз-
можным благодаря повышению коэффициентов теплоотдачи в за-
тесненных каналах до (2—5)405 Вт/(м2град) [4.2.1—4.2.3].
Термостатирование энергонапряженных узлов установок с не-
равномерным распределением тепловой нагрузки по поверхнос-
ти осуществлялось с помощью испарения и кипения жидкостей
на капиллярно-пористых структурах в условиях вынужденного
движения теплоносителя и встроенного термоаккумулятора плав-
ления.
Глава 4
379
Каждый из названных методов термостатирования требовал ин-
тенсификации теплообмена, так как использовался в условиях высо-
ких тепловых нагрузок. При этом термостабилизация поверхности
должна была практически исключить термомеханические деформа-
ции (их величина не должна превышать 30 мкм).
Теплообмен в пористых структурах реализовывался в испари-
тельном режиме и режиме кипения, причем первый возможен лишь
в ограниченном диапазоне тепловых нагрузок (0,5—1,0 Вт/см2). Да-
лее происходит пузырьковое кипение, которое сохраняется вплоть
до предельных значений тепловой нагрузки. Максимальный тепло-
вой поток, передаваемый через пористую структуру, определяется
ее транспортными возможностями и кризисом кипения в ней.
Эксперименты по термостатированию проведены на макете резо-
натора специального ускорителя с использованием в качестве тепло-
носителя воды и жидкого азота, а в качестве капиллярной структуры
канавчатых поверхностей с различной шириной канавок (Ь = 0,2—
0,4 мм), глубиной 0,5—1,0 мм и шагом нарезки 0,5—1,5 мм. Канавчатые
поверхности выбраны из-за несложной технологии изготовления и
расчетного анализа гидродинамики и теплообмена, в частности, в ус-
ловиях горизонтального расположения исследуемых поверхностей
(рис. 4.33-4.35).
При термостатировании неравномерно нагреваемых поверхнос-
тей с помощью вынужденного движения теплоносителя его поток
организуется так, что теплоно-
ситель движется вдоль стенки
в направлении убывания тепло-
вой нагрузки. При этом растет
температура жидкости, но убы-
Рис. 4.33. Конструкции узла с эле-
ментами для уменьшения дефор-
маций: а — с жестким каркасом и
тонкими тепловыделяющими обо-
лочками: 1 — жесткий каркас; 2 —
тонкие тепловыделяющие оболочки;
3 — теплоизолирующие вкладыши;
4 — каналы охлаждения; 5 — вход-
ной и выходной коллекторы; б — с
компенсацией термических напря-
жений: 1 — каркас; 2 — тепловыде-
ляющие оболочки с взаимнокомпен-
сирующим и термомеханическими
напряжениями; 3 — каналы охлаж-
дения; 4 — входной и выходной кол-
лекторы
380
Глава 4
Рис. 4.34. Сравнение измеренных и рас-
четных температурных полей по длине мо-
дельного элемента узла (см. рис. 4.33) при
мощности тепловыделения до — 25 Вт/см2
и расходе воды G3k= 8-10‘2кг/с: 1 — непро-
филированный канал; 2 — профилирован-
ный (трапециидальная форма) канал;----
эксперимент;-----расчет
вают перепады температуры в
стенке и на границе «стенка-
жидкость». Можно подобрать
такой расход теплоносите-
ля, при котором, с учетом его
теплоемкости, сумма членов в
уравнении сохранится посто-
янной вдоль поверхности:
t =t I	I	•
1СТХ 1ЖХ '	' n '
^ст
'жх = (жвх + —----•	(4.2.3)
'“’жсрж
Расчет и эксперименты проводились на макете резонатора спе-
циального ускорителя. Результаты проведенных экспериментов на
воде подтвердили высокие возможности рассматриваемого способа
термостатирования, при этом практически идеальное термостати-
рование довольно протяженной поверхности реализовывалось при
треугольной и трапециидальной форме пристенного канала по всей
длине. С помощью такого профилирования температурная неравно-
мерность стенки снижалась в 6 раз.
В случае периодического действия установок термостатирование
наиболее ответственных энергонапряженных узлов может быть ре-
ализовано с помощью встроенных термоаккумуляторов плавления.
В рабочем режиме мощность, передаваемая через стенку узла, пог-
лощается расположенным непосредственно у внутренней ее поверх-
ности термоаккумулирующим веществом (TAB), которое при этом
Рис. 4.35. Неравномерность температуры
вдоль стенки профилированных каналов:
1 — q0 = 5 Вт/см2; 2 — q0 = 10 Вт/см2; 3 —
q0 = 25 Вт/см2
плавится. В нерабочем режи-
ме (период ожидания) тепло,
накопленное за счет теплоты
фазового перехода, отдает-
ся внешнему холодильнику
[4.2.4].
Передача тепла от стен-
ки к замерзающему TAB зат-
руднена из-за большого тер-
мического контактного соп-
ротивления на границе «стен-
ка—ТАВ», поэтому выполне-
ны исследования, имеющие
Глава 4
381
целью снижение этого термического сопротивления путем оребре-
ния термостатируемой поверхности (ТСП) и размещения плавяще-
гося вещества в межреберном пространстве, в металловолокнистой
структуре, соединенной с ТСП, и пристенного плавления за счет
поджатия TAB к ТСП.
При математической формулировке задачи учитывалось вынуж-
денное движение жидкости вдоль теплоотдающей поверхности,
обусловленное плавлением TAB и его поджатием к ТСП, непрерыв-
ное перемещение массы плавящегося вещества перпендикулярно
поверхности фазового перехода (ПФП), так называемый «вдув», пе-
редача теплоты от ТСП к ПФП теплопроводностью.
В результате решения сформулированной задачи получены рас-
четные зависимости, определяющие температурное поле во встро-
енном термоаккумуляторе, скорость «вдува» TAB, коэффициент теп-
лоотдачи к расплаву (см. рис. 4.35).
Для практики рекомендована зависимость, определяющая пере-
грев теплоотдающей стенки относительно температуры плавления
TAB, которая имеет вид:
/	\1/3
,	(4.2.4)
где г — характерный размер поверхности; F — сила поджатия. Таким
образом, при разработке термоаккумулятора с пристенным плавле-
нием и поджатием TAB в первую очередь необходимо стремиться к
сокращению размеров поджимаемого блока TAB и увеличению теп-
лопроводности расплава.
При экспериментальной отработке метода термостатирования
поверхностей результаты расчета подтверждены на ряде TAB (гал-
лии, воде, парафине). При тепловых нагрузках до 175 Вт/см2 перепа-
ды температуры Тст—Тпл составляют градусы для галлия и десятки
градусов (до 40°С) для воды и парафина.
Использование жидкометаллических теплоносителей
для интенсификации теплообмена
В результате проведенных исследований теплоотдачи к жидким
металлам в узких кольцевых каналах и пучках с малыми относитель-
ными шагами получены данные, которые свидетельствуют об интен-
сификации теплообмена при «двустороннем» обогреве каналов до
двух раз. Полученные результаты использованы при разработке и
создании термоэмиссионной энергоустановки космического назна-
382
Глава 4
чения «Топаз», а также быстрых реакторов, охлаждаемых натрием
[4.2.5, 4.2.6].
Еще больший эффект при использовании жидких металлов был
достигнут при так называемом транспирационном охлаждении твэ-
ла газофазного реактора, на основе которого разрабатывались ядер-
ный ракетный двигатель и энергоустановка [4.2.7—4.2.10]. Наличие
в конструкции двигателя и энергоустановки полости с плазменным
шнуром, образованным делящимся топливом, делает условия рабо-
ты защищаемых стенок этой полости близкими к условиям в термо-
ядерном реакторе.
Наряду с тепловой защитой стенок газофазного твэла (при тепло-
вых нагрузках до 10 кВт/см2) необходимо было обеспечить их защи-
ту от агрессивного воздействия паров делящегося вещества, а также
предотвратить их конденсацию, при которой тепловой поток в стен-
ку из жидкой пленки конденсата мог достичь также 10 кВт/см2.
Для достижения работоспособности все поверхности полости и
расположенных за ней узлов, омываемые высокотемпературным ра-
бочим телом (водородом) и плазмой делящегося вещества, выполня-
лись проницаемыми (пористыми) и через них продавливался жидкий
металл, обеспечивая транспирационное охлаждение (рис. 4.36).
Гидравлические исследования пористых материалов (никеля,
молибдена, вольфрама и др.) проводились на натрий-калиевой эв-
тектике, а также воде, спирте и аргоне (для сравнения) как в изо-
Рис. 4.36. Коэффициенты теплоот-
дачи к плавящемуся TAB при раз-
ных тепловых нагрузках и давлени-
ях поджатая:  — галлий; • — вода;
О — парафин
термических условиях, так и в не-
изотермических при наличии по
толщине образцов температурных
перепадов. В последнем случае гид-
равлические исследования были
совмещены с изучением теплооб-
мена от аргоновой плазмы.
Для определения эффективно-
сти пористого охлаждения сравни-
вались тепловые потоки от плазмы
в стенки охлаждаемых сплошного
и пористого образцов, одинаковых
по геометрии и находящихся в рав-
ных условиях обтекания плазмой.
Для увеличения потока на образец
принято, что происходит его ло-
бовое обтекание плазмой. Для ис-
следования температуры натека-
ющей струи использован ориги-
Глава 4
383
нальный калориметрический зонд, позволивший измерить темпера-
туры в струе до 9000 К. Для измерения тепловых потоков в стенке
образцов (сплошного и пористого) использован метод, основанный
на регистрации скорости роста температуры в адиабатном образ-
це с помощью двух термопар, расстояние между которыми извест-
но. Сравнение результатов гидравлических исследований на натрий-
калии, воде, спирте и аргоне показало, что расходные характерис-
тики пористых образцов существенно отличаются друг от друга из-
за зависимости коэффициента проницаемости в формуле Дарси не
только от характеристик пористого материала, но и свойств теплоно-
сителей.
В процессе горячих испытаний пористых образцов с транспира-
ционным охлаждением натрий-калиевой эвтектикой, водой и арго-
ном (до 9000 К) обнаружены значительные, до двух раз, колебания
расхода охлаждающих жидкостей через образец, связанные с дейст-
вием ультразвукового капиллярного эффекта. Исследования пока-
зали, что источником ультразвуковых колебаний в потоке аргоновой
плазмы является истечение ее из сопла и взаимодействие с пористым
образцом.
Наибольшее уменьшение гидравли-
ческого сопротивления пористых ма-
териалов происходит при резонансных
частотах колебаний конструкции и по-
тока (600—900 Гц).
В результате исследования жидко-
металлического транспирационного ох-
лаждения в аргоновой плазме получены
данные, свидетельствующие о большой
эффективности этого метода, особенно
при плотностях теплового потока, начи-
ная с 2 МВт/м2. При тепловой нагрузке
7 МВт/м2 тепловой поток, идущий в ох-
лаждаемую стенку, снижается в 7 раз
(рис. 4.37).
Пленочное охлаждение стенок энер-
гонапряженных конструкций является
предельным случаем пористого охлаж-
дения: зона испарения жидкости выхо-
дит на поверхность защищаемой стенки,
подвергающейся действию высоких теп-
ловых нагрузок. Этот вид теплозащиты
является более простым по сравнению с
Рис. 4.37. Значение плотно-
сти теплового потока в цент-
ре исследуемых образцов на
разных расстояниях от среза
сопла (Z): О — конвективное
охлаждение; • — пористое
охлаждение Na-K; Л — порис-
тое охлаждение дистиллатом;
□ — пористое охлаждение ар-
гоном
384
Глава 4
транспирационным охлаждением, при котором зона испарения ин-
жектируемого теплоносителя находится в пределах толщины по-
ристой стенки. Это связано с некоторыми трудностями, обусловлен-
ными апериодической неустойчивостью пористого испарительного
охлаждения.
Основной проблемой при организации пленочной защиты явля-
ется создание на поверхности тонкой движущейся или стоячей плен-
ки, которая особенно эффективна в случае высоких радиационных
(лучистых) потоков, когда воздействие конвективных потоков, сры-
вающих пленку, сведено к минимуму.
Опыты показали, что образование пленки натрий-калиевой эв-
тектики возможно лишь после полного смачивания поверхности, до-
стигаемого при нагреве ее до 350—400°С в среде эвтектики.
В качестве пленкообразующего распределительного устройст-
ва рекомендуется использовать струйно-щелевое с шириной щели
0,7 мм, к которой жидкий металл подается по вертикальным каналам.
Желательно также предварительное тангенциональное закручива-
ние потока в пленкообразующем устройстве (рис. 4.38).
N
^ = §пл (g/v2)‘/3Re
Re	715	588	496	464
Измеренное 5ПЛ	0,18	0,18	0,20	0,19
Рассчитанное 5ПЛ	0,16	0,17	0,18	0,18
Рис. 4.38. Конструкция пленкообразующего устройства и толщина пленки Na — К:
-----по теории; • — опытные значения; 1 — пленкообразователь; 2 — вкладыш с
каналами; 3 — исследуемая поверхность; 4 — подводящая Na —К трубка; 5 — элект-
ронагреватель; 6 — пленка
Глава 4
385
В экспериментах на вертикальной цилиндрической поверхности
диаметром 80 мм получены ползущие ламинарные пленки толщиной
около 0,2 мм, что удовлетворительно согласуется с расчетным значе-
нием, определенным на основе существующей теории ламинарного
двумерного пленочного течения
^пл
/	о\1/3
Зу2
Re1/3
(4.2.5)
Конденсация паров щелочных металлов является одним из интен-
сивных процессов. Достаточно сказать, что при атмосферном давле-
нии паров натрия и калия коэффициент теплоотдачи находится на
уровне -1406 Вт/(м2°С). Но это справедливо лишь для однокомпонен-
тных щелочных металлов. Так как в космической технике чаще ис-
пользуется эвтектический сплав Na—К (22%Na + 78%К), в основном
из-за его низкой температуры плавления, то предпринята попытка
исследовать процесс конденсации этого сплава. Было показано, что
при поверхностной конденсации пар низкокипящего компонента ка-
лия играет роль неконденсирующегося газа для пара натрия и коэф-
фициент теплоотдачи снижается на 3 порядка по сравнению с а при
конденсации отдельно натрия и калия. Но так как в разрабатываемой
установке на основе газофазного реактора космического назначения
конденсатор должен был работать на сплаве Na—К, то необходимо
было интенсифицировать процесс конденсации пара в целях умень-
шения его массогабаритных характеристик. Это было сделано с по-
мощью организации процесса конденсации в конденсаторе смеше-
ния впрыскивающего типа, на вход которого поступает перегретый
пар эвтектики Na—К. Этот пар затем конденсируется на относитель-
но холодных каплях той же эвтектики, подаваемой в конденсатор
через форсунки. При таком захолаживании значительно улучшены
массогабаритные характеристики системы.
В результате проведенных расчетно-экспериментальных иссле-
дований процесса объемной конденсации пара натрий-калиевой эв-
тектики на собственных каплях получено, что наиболее эффективно
на интенсивность прогрева захолаживающих паровой поток капель
влияют их размер (качество распыла) и температура поступающе-
го пара (при увеличении диаметра капель с 10'5 до 10'4 см длитель-
ность их пробега до приобретения температуры пара увеличилась
в -200 раз: при увеличении температуры пара с 800 до 1100 К длина
пробега уменьшилась в 4,4 раза). Показано, что в условиях экспери-
мента капли получают -80% тепла на длинах пробега 0,5—1,0 см, что
свидетельствует о высокой эффективности процесса: коэффициен-
ты теплоотдачи возросли на порядок. По сравнению с а при поверх-
386
Глава 4
ностной конденсации Na—К передаваемые тепловые нагрузки име-
ли значения до 10 МВт/м2 (рис. 4.39, 4.40).
Рис. 4.39. Экспериментальные и
расчетные данные по прогреву
Na —К в паре Na —К-эвтектики:
-----эксперимент;----расчет
Рис. 4.40. Сравнение экспериментальных и расчетных значений плотности тепло-
вого потока и коэффициента теплоотдачи на разных расстояниях от среза сопла
форсунки (Н):------эксперимент; -----— расчет
Глава 4
387
Влияние пористых покрытий на теплоотдачу при кипении
Влияние пористого покрытия на
теплоотдачу при кипении воды в
прямоугольном канале при низких
массовых скоростях и давлениях
исследовано в Техническом универ-
ситете Берлина в рамках совмест-
ной работы ТУБ-МЭИ [4.2.22]. На
рис. 4.41 представлены кривые кипе-
ния для каналов с технически глад-
кой поверхностью и никелевым
пористым покрытием толщиной
0,15 мм, пористостью 60%, диамет-
ром частиц 40 мкм при течении
воды с недогревом ЗК, массовой
скоростью 28 кг/(м2-с) и давлении
0,11 МПа.
Как установлено, положитель-
ный эффект применения пористого
Q, МВт/м2
0	50	100	150
Г. - Г, К
С S’
Рис. 4.41. Кривые кипения для од-
ностороннего нагреваемого канала
со спеченным никелевым покрыти-
ем толщиной 0,15 мм (1) и без пок-
рытия (2)
покрытия обнаружен во всех режимах кипения: пористое покрытие
приводит к снижению ДТн к, повышению теплоотдачи при кипении,
росту критической тепловой нагрузки в 1,7 раза и коэффициента
теплоотдачи при переходном режиме кипения до 2,4 раза.
Влияние покрытий на теплообмен при пленочном кипении
Рассмотрим влияние пористого покрытия из А12О3, нанесенного
газопламенным напылением на горизонтальном медном диске, на
теплоотдачу при кипении фреона-113 в большом объеме при атмос-
ферном давлении [4.2.13—4.2.15]. На рис. 4.42 показаны зависимо-
сти коэффициента теплоотдачи от
температурного напора для поверх-
ностей без покрытия и с пористыми
Рис. 4.42. Кривые кипения фреона-113 при
атмосферном давлении для горизонталь-
ной медной поверхности без покрытия и
с напыленным покрытием из оксида алю-
миния: • — поверхность без покрытия;
 — поверхность с покрытием толщиной
0,29 — 0,37 мм; □ — поверхность с покры-
тием толщиной 0,85 мм; О — поверхность с
покрытием толщиной 1,65 мм
388
Глава 4
покрытиями. Как установлено, с ростом толщины покрытия коэффи-
циент теплоотдачи растет и его превышение по сравнению с поверх-
ностью без покрытия достигает двух раз.
Отмеченные эффекты интенсификации теплообмена при пленоч-
ном кипении зависят от теплофизических свойств, толщины, шеро-
ховатости поверхности покрытия. Покрытие может иметь большую
по сравнению с поверхностью без покрытия шероховатость. Рост ше-
роховатости поверхности покрытия дестабилизирует паровую плен-
ку, повышает коэффициент теплоотдачи и вызывает более раннее
прекращение пленочного кипения.
С целью выяснения механизма влияния покрытия на теплоотдачу
при пленочном кипении в работах [4.2.16—4.2.19] исследованы коле-
бания границы раздела фаз на горизонтальном цилиндре с помощью
оптического квантового генератора.
Установлено, что малотеплопроводное покрытие приводит к ослаб-
лению крупномасштабных колебаний границы раздела фаз (рис. 4.43)
и уменьшению средней толщины паровой пленки (рис. 4.44).
Это обусловлено следующим. При колебании толщины паровой
пленки происходят изменения во времени температуры поверхно-
сти нагрева. В случае поверхности нагрева с высоким коэффициентом
теплопроводности температура поверхности примерно постоянная.
Рис. 4.43. Спектры колебаний
толщины паровой пленки при
пленочном кипении хладо-
на-1 13 на горизонтальном ци-
линдре при атмосферном дав-
лении: О — поверхность без
покрытия; • — поверхность с
пленкой из клея ВС-ЮТ тол-
щиной 15 мкм
Рис. 4.44. Плотности вероятности толщины
паровой пленки при пленочном кипении
хладона-ИЗ на горизонтальном цилинд-
ре при атмосферном давлении: 1 — повер-
хность без покрытия; 2 — поверхность с
пленкой из клея ВС-ЮТ толщиной 15 мкм;
штриховые линии — распределения по
нормальному закону
Глава 4
389
Если на поверхность нагрева нанесено малотеплопроводное покры-
тие, температура стенки не успевает восстановиться за период коле-
баний толщины паровой пленки, в результате чего жидкость подходит
ближе к поверхности и коэффициент теплоотдачи повышается.
Влияние пористого покрытия ни теплогидравлические
характеристики при кипении в трубе
На поверхности с пористым покрытием имеются готовые цен-
тры парообразования в диапазоне размеров £>min < D п < Dmax, где
Ртах, ^тт “ максимальный и минимальный диаметры пор покрытия
создаются более благоприятные условия для зародышеобразования,
чем на технически гладкой поверхности, что приводит к низким пе-
регревам стенки, соответствующим началу кипения.
Паровой зародыш начинает расти, когда локальный перегрев
жидкости в наиболее удаленной от поверхности нагрева точке пузы-
ря равен необходимому ДТ в соответствии с уравнением
ДТ =------
ф'Ар
Тепловая нагрузка, при которой начинается кипение,
Л.,фр"г(ЛГ„к)2
|П '
(4.2.6)
(4-2.7)
Qhk =
4aTs[l+f(Re)]1
где эффективная теплопроводность определяется по формуле
,	,	,, / 1-е е' e”Y*
^эф=М+(1-У) -j—+v+rz 	(4.2.8)
где X — коэффициент теплопроводности каркаса; в — пористость; в',
в" — объемная доля пара и жидкости в покрытии; X', X" — коэффи-
циенты теплопроводности воды и пара при температуре насыщения
у= 1-еЗ
В первом приближении температурный напор начала кипения
ДТНК можно определить из соотношения (4.2.6), приняв критический
диаметр равным максимальному размеру поры.
Из сравнения с опытными данными определены значения показа-
теля п и вид функции f(Re)
[l+f/(Re)]n =Г1+(Не40"5)]5,1;
.	J	(4-2.9)
0<Re<4,5-104
в диапазоне 0 < Re < 4,5-104.
390
Глава 4
Рис. 4.45. Кривая кипения воды в тру-
бе: 1 — со спеченным покрытием из
нержавеющей стали; 2 — без покры-
тия
Как установлено, значение
ДТНК растет со скоростью потока,
с тепловой нагрузкой и уменьше-
нием давления и Л.Эф.
На рис. 4.45 представлены кри-
вые кипения для поверхности с
пористым покрытием (линия 1) и
без покрытия (линия 2) при давле-
нии 4 МПа и различных массовых
скоростях пароводяного пото-
ка [plV = 200 — 600 кг/(м2-с)] при
фиксированном паросодержа-
нии. Пористое покрытие улучша-
ет теплоотдачу (сдвигает кривую
кипения влево). Скорость пото-
ка в рассмотренных условиях не
оказывает заметного влияния на
теплоотдачу при кипении, так как акип » акон.
Расчет теплоотдачи в докризисной области канала со спеченным
пористым покрытием проводится по интерполяционной формуле
пп
^кип / ^кон )пп •
(4.2.10)
Конвективную составляющую (акон)пп рассчитываем по уравне-
нию Яглома и Кадера для труб с искусственной однородной шерохо-
ватостью, элементы которой имеют различную форму и расположе-
ны настолько близко друг к другу, что течение между ними полностью
определяется их размерами и формой. Эта формула справедлива для
режима с полным проявлением шероховатости. При этом значение
4 не зависит от числа Re и, например, для канала с пористым покры-
тием толщиной 0,22 мм составляет 0,07. Уравнение обосновано экс-
периментально при K/Ro = 0,005—0,18 в диапазоне чисел Рг = 0,7—9
(К — высота шероховатости, Ro — радиус трубы).
При кипении на поверхности с пористым покрытием увеличива-
ется плотность центров парообразования, которая определяется сле-
дующей величиной:
Дпах
Дф у
< 4°Ts '
(4.2.11)
т — коэффициент, который определяется углом наклона кривой ки-
пения.
Уравнение для коэффициента теплоотдачи имеет следующий вид:
Глава 4
391
1
т
(апп)кип
(М2 1
^р"М
2+т( Рпиягр’,У^
< 4a7i ,
1+т
q2+m,
(4.2.12)
где К — коэффициент, учитывающий влияние давления, равный
К = 0,203+1,8Р/Ркр; Ркр — критическое давление. Максимальный
диаметр поры Dmax равен приближенно диаметру частицы. На осно-
ве опытных данных получена зависимость для коэффициента т.
На рис. 4.46 нанесены точки, определяемые тангенсом угла накло-
на кривых кипения, полученных для различных сочетаний стенка —
пористое покрытие: покрытие из меди толщиной 0,4 мм (1), нержаве-
ющей стали толщиной 0,15 мм (2), 0,22 мм (3) и 0,5 мм (4).
Все покрытия получены спеканием сферических частиц диамет-
ром 60—100 мкм. Линия на рис. 4.46 описывается уравнением
т = абпп/\ф + Ь,	(4.2.13)
где b — 4; a = -16,3403 Вт/(м2-К).
Теплоотдача при кипении на поверхности с пористым покрытием
в условиях свободной и вынужденной конвекции описывается урав-
нением
^пп)кип =С(апп)кип'
С = 2,4-Ю-4 (§пп /Хэф)”°'96	(4.2.14)
при 0,2-104 < (6пп/Хэф) < 0,2-103.
На рис. 4.47 опытные данные со-
поставлены с результатами расчета
теплоотдачи по уравнению (4.2.14)
при кипении воды в условиях сво-
бодной и вынужденной конвенции
на поверхностях со спеченными
покрытиями.
Повышение теплоотдачи для по-
верхности с пористым покрытием
более значительно, если использо-
вать спеченные покрытия с мень-
шим термическим сопротивлением.
Из-за соображений коррозионной
стойкости иногда на практике при-
ходится выбирать покрытие с боль-
шим термическим сопротивлением.
В результате в меньшей мере про-
Рис. 4.46. Тангенс угла наклона кри-
вой кипения: 1 — с медным покры-
тием толщиной 0,4 мм; 2 — со сталь-
ным покрытием толщиной 0,15 мм;
3 — со стальным покрытием толщи-
ной 0,22 мм; 4 — со стальным пок-
рытием толщиной 0,5 мм
392
Глава 4
Рис. 4.47. Сопоставление опытных и рас-
четных данных по теплоотдаче: 1 — без
покрытия; 2 — со стальным покрытием
толщиной 0,22 мм; 3 — со стальным пок-
рытием толщиной 0,15 мм; 4 — с медным
покрытием толщиной 0,4 мм
является эффект увеличения
плотности активных центров
парообразования и повыше-
ние теплоотдачи менее сущес-
твенно.
Пористое покрытие ока-
зывает влияние на структуру
потока, механизм и развитие
кризиса теплообмена и может
приводить как к повышению,
так и снижению g [4.2.20—
4.2.23].
Снижение дкр при нане-
сении пористого покрытия
возможно в том случае, если
данные располагаются пра-
вее точки инверсии зависимости дкр
от рИЛ Когда влияние pW на
qK положительное, пористое покрытие приводит к росту дкр [4.2.21,
43.23].
Смена механизма кризиса теплообмена происходит не внезап-
но. Область инверсии может занимать некоторый диапазон паро-
содержаний, и влияние пористого покрытия в ней будет весьма
сложным.
Влияние пористого покрытия на паросодержание х*,
при котором начинается переход в область ухудшенного
теплообмена
В диапазоне pW = 100—600 кг/(м2-с) значение х* для трубы без
покрытия и с пористым покрытием совпадает и его можно рассчи-
тать при Р = (0,1—7) МПа для пароводяного потока по уравнению,
предложенному в работе [4.2.24]:
\0,28
х‘ = 1-64,3
I
лрЖ)" /р^
< G VP",
(4.2.15)
Q
В области pW < 100 кг/(м2-с) для трубы без покрытия обнаружено
снижение граничного паросодержания [4.2.25].
Для трубы с пористым покрытием снижения х* в области
pW < 100 кг/(м2-с) не происходит, что объясняется действием капил-
лярных сил пористой структуры, повышающих устойчивость жид-
Глава 4
393
Рис. 4.48. Зависимости средней темпе-
ратуры стенки (Тс), интенсивности ее
пульсаций (S) и среднемассовой тем-
пературы пароводяного потока от рас-
ходного паросодержания: (р = 1 МПа,
pW = 25 кг/(м2с), q = 70 кВт/м2): 1 — ка-
нал без покрытия; 2 — канал со спечен-
ным покрытием из нержавеющей стали
толщиной 0,2 мм
Рис. 4.49. Зависимость паросодержа-
ния, при котором начинается ухуд-
шение теплообмена, от массовой ско-
рости для трубы без покрытия (1) и с
пористым покрытием (2) (р = 1 МПа,
pW = 25 кг/(м*с), q = 70 кВт/м2)
кой пленки против высыхания (рис. 4.48,4.49). Этот эффект представ-
ляет большой интерес с практической точки зрения [4.2.26, 4.2.27].
Пористое покрытие приводит к уменьшению максимальной ин-
тенсивности пульсаций температуры стенки Smax в переходной об-
ласти до 5 раз (рис. 4.48), что способствует повышению надежности
парогенерирующего канала, его ресурса на 2—3 порядка и является
важным для практики результатом [4.2.26].
Влияние пористого покрытия на термическую
неравновесность потока
Для трубы с пористым пок-
рытием термическое равнове-
сие потока достигается при мень-
шем значении хр на выходе трубы
[4.2.26, 4.2.27] (рис. 4.50).
Зависимости для расчета эн-
тальпии перегретого пара в об-
ласти ухудшенного теплообмена,
полученные на основе опытных
данных и известных представле-
ний, имеют следующий вид для
трубы без покрытия при числе
Fr > (Fr)‘:
Рис. 4.50. Изменения действитель-
ного паросодержания от расходно-
го при Р = 6 МПа, pW = 200 кг/(м2-с)
для трубы: 1 — без покрытия; 2 — с
пористым покрытием
394
Глава 4
(4.2.16)
при числе Fr < (Fr)*
(4.2.17)
и для трубы с пористым покрытием при числе Fr > Fr*
(24.2.18)
где к = (х*)-0,8.
Эффективность применения пористых покрытий
и закрутки потока
Исследование температурных режимов каналов в области ухуд-
шенного теплообмена показало, что пористое покрытие приводит к
существенному понижению температуры стенки и более высоким
выходным паросодержаниям [4.2.26]. Коэффициент теплоотдачи
увеличивается в 2—2,5 раза.
Для расчета теплоотдачи в трубе с пористым покрытием использо-
вана зависимость Яглома—Кадера, которая с учетом высоты шерохо-
ватости поверхности исследованного покрытия (S, = 0,069, К = 0,22)
принимает вид
RePr
140+0,31(Рг2/3-0,2)л/Ёё'
(4.2.19)
На рис. 4.51 показаны изменения коэффициента теплоотдачи и
интенсивности пульсаций температуры стенки по длине трубы без
покрытия (линия 3) и со спеченным покрытием из нержавеющей
стали толщиной 0,2 мм (линия 5) для воды при Р = 4 МПа [4.2.27].
Влияние пористого покрытия проявляется в большей мере при раз-
витом кипении (повышении теплоотдачи в 3 раза) и в меньшей мере
при кипении с недогревом и в области теплоотдачи к парокапель-
ному потоку. Максимальная интенсивность пульсаций температуры
стенки для трубы с пористым покрытием уменьшается в 5 раз, что
чрезвычайно важно для практики. Таким образом, пористое покры-
тие приводит к существенному повышению теплоотдачи и уменьше-
Глава 4
395
а	б
Рис. 4.51. Изменения коэффициента теплоотдачи (а) и интенсивности пульсаций
температуры стенки (б) в зависимости от паросодержания X: без покрытия (1) и
со спеченным покрытием из нержавеющей стали толщиной 0,2 мм (2) для парово-
дяного потока при Р = 4 МПа, р W = 600 кг/(м2-с)
нию интенсивности пульсаций температуры стенки на каждом учас-
тке парогенерирующего канала в диапазоне X = (-0,6—1,4).
Рассмотренное пористое покрытие (линия 2 на рис. 4.51) вызывает
повышение коэффициента гидравлического сопротивления при тур-
булентном течении пара в три раза по сравнению с трубой без покры-
тия (линия 1).
Обнаруженные эффекты влияния пористого покрытия на теп-
лоотдачу и гидравлическое сопротивление для пароводяного пото-
ка воспроизводились в опытах в течение экспериментов общей дли-
тельностью 1000 ч.
Интенсификация теплоотдачи в горизонтальной трубе
с односторонним нагревом
Интенсификация теплоотдачи в горизонтальной трубе исследо-
вана при ее нагреве снаружи пучком электронов и охлаждении из-
нутри потоком воды. Теплосъем осуществляется в горизонтальном
канале без покрытия, с закрученной лентой и пористым покрытием
в диапазонах массовых скоростей 100—10000 кг/(м2-с), давлений 0,4—
1,1 МПа, паросодержаний — 0,33—0,04, коэффициентов неоднород-
ности нагрева 2,5—5,5 [4.2.28—4.2.29]. Коэффициент неоднородно-
сти нагрева — отношение максимальной тепловой нагрузки к сред-
ней по периметру трубы.
При низких pW [<800 кг/(м2-с)] применение закрутки потока не
приводит к увеличению коэффициента теплоотдачи. При больших
396
Глава 4
pW влияние закрутки потока усиливается, и при pW = 3000 кг/(м2-с)
тепловая нагрузка повышается в 1,5 раза [4.2.34].
Пористое покрытие существенно интенсифицирует теплообмен
как в случае конвекции однофазной среды, так и при пузырьковом
кипении. В трубе с пористым покрытием при АТ = 0 тепловая нагруз-
ка в 1,5 раза, а при АТ = 25°С — в 2,5 раза выше, чем в трубе без пок-
рытия. Температурный напор начала кипения в трубе с пористым
покрытием существенно ниже.
Данные по теплоотдаче при кипении в трубе с технически глад-
кой поверхностью и интенсификаторами теплосъема описаны с раз-
бросом ±25% уравнением [4.2.28]
Nu/Nuok = АКп,	(4.2.20)
К = ( q YTP"Y Г ТсК •
гдеК (p-WrJ [р-ДсрДг] к₽'
теплоотдача при течении однофазной среды рассчитывается по урав-
нениям:
Nuok = 0,021 Re0,8 Рг0,43 — для прямолинейного потока;
Nuak=0,021Re°'8Pr0'43(Pr)c/(Pr)c[l + (6-104Re"°'5)] - для за-
крученного потока;
Nuok = 0,023Re0,65 Рг0,4 — для трубы с пористым покрытием.
При достижении параметра К значения Ккр отклонение результа-
тов расчета теплоотдачи по уравнению (4.2.20) от опытных данных
превышает 25% и значения Ккр можно рассматривать как границу
области, в которой реализуются докризисные режимы теплосъема.
Значения для трубы с прямолинейным и закрученным потоком мож-
но найти по формуле
Ккр = B(Fr)c.
Значения постоянных величин, входящих в уравнение (4.2.20),
даны в табл. 4.2.3.
Как установлено, в диапазоне значений параметра, характеризу-
ющего неоднородность нагрева поверхности, Кс = Чтах /д = 2,5- 5,5,
влияние неоднородности распределения тепловой нагрузки по пери-
метру находится в пределах погрешности определения qKp.
Анализ данных по ^кр при различной ориентации источни-
ка нагрева относительно рабочего участка показал, что в области
pW < 1500 кг/(м2-с) значение <?кр при нагреве горизонтальной трубы
Глава 4
397
Таблица 4.2.3
Постоянная величина	Горизонтальная труба		
	С технической поверхностью		С пористым покрытием
	прямолинейный поток	закрученный поток	
А п А В Ккр В С	550 0,71 0,07 0,12 610’3 -0,41	650 0,71 0,07 0,12 5,6-Ю'3 -0,29	105 0,66 0,08 0,063 4-10’2
снизу вследствие влияния свободной конвекции выше. С понижени-
ем pW отмеченный эффект становится более значительным, и при
pW = 200 кг/(м2-с) величина дкр повышается примерно в 2 раза [4.2.20,
4.2.28, 4.2.35].
Закрутка потока начинает влиять на критическую тепловую наг-
рузку при pW> 800 кг /(м2-с). При pW — 3000 кг/(м2-с) закрутка потока
приводит к увеличению qKp в 1,5 раза. Влияние пористого покрытия на
дкр зависит от массовой скорости. При низких pW [< 200 кг/(м2-с)] по-
ристое покрытие приводит к повышению qKp в три раза. С увеличени-
ем массовой скорости влияние
пористого покрытия ослабе-
вает, хотя остается значитель-
ным. При pW = 10000 кг/(м2-с)
значение
^кр
в два раза выше,
чем в трубе с технически глад-
кой поверхностью (рис. 4.52).
Таким образом, в рассмот-
ренном диапазоне параметров
влияние пористого покрытия
на дкр более существенно, чем
закрученной ленты.
Эффект пористого покры-
тия объясняется увеличением
плотности активных центров
парообразования с оптималь-
ными распределением и раз-
Чкр. МВт/М2
35
30
25
20
15
10
5
0	_	. . .__________.
102	1 03	1 04
pW, кг/(м2с)
Рис. 4.52. Зависимость критической теп-
ловой нагрузки от массовой скорости. Па-
роводяной поток Р — 0,5 МПа, X = —0,2:
О — труба с технически гладкой повер-
хностью; Д — труба с пористым покры-
тием; + — труба с закрученной лентой;
— — расчет по предложенному урав-
нению
398
Глава 4
мерами для поверхности с пористым покрытием, что проявляется в
большей мере при низких массовых скоростях.
Выражение для расчета дкр, полученное на основе обработки
опытных данных, имеет вид
I---/	\0,25
q = 9,110-3 г	Re0'26 vHvOHV3nVnn- (4-2.21)
N dr VPnJ
где
1-нагрев снизу
Voh
0,65
нагрев сверху
(4.2.22)

при pW = 100-10000 кг/(м2-с), АТН = (2-150)°С; Р = (0,1-1) МПа.
Влияние закрутки потока описано выражением
(d '|°'34
э
Узп
/	\0,12
£l+i
I д J
(4.2.23)
где d3 =[dr(ndr -4h)]/[dr (n + 2)-2h]; h — толщина скрученной лен-
ты; g — гравитационное ускорение; дс — центробежное ускорение,
определяемое из соотношения
где Н — шаг закрутки ленты на 360°. В опытах установлено, что влия-
qr
ние закрутки потока начинает проявляться при — > 10.
д
Интенсификация теплообмена в змеевике
Интенсификации теплообмена в змеевиках представляет инте-
рес еще и потому, что в этом случае мы имеем дело с комбинирован-
ным методом повышения теплосъема. С этой целью оказалось выгод-
но использовать покрытия, нанесенные спеканием на внутренней
поверхности спиральной трубы [4.2.31, 4.2.37, 4.2.38].
Исследованы характеристики теплоотдачи в переходной и закри-
зисной областях двух спиральных труб: с технически гладкой по-
верхностью и пористым покрытием, которое нанесено спеканием на
ее внутреннюю поверхность. Материал покрытия — сталь Х18Н10Т.
Толщина покрытия 0,22 мм, пористость 60%, диаметр частиц 60 мкм.
Внутренний диаметр спиральных труб равен 8 мм, толщина стен-
ки 1 мм. Ось змеевиков расположена вертикально. Количество вит-
Глава 4
399
ков — 5. Диаметр навивки по осевой линии спиральной трубы равен
120 мм. Шаг навивки 14 мм.
Опытные данные получены в диапазонах массовых скоростей
(100—600) кг/(м2-с), давлений (0,2—4,5) МПа, тепловых нагрузок (0,3—
1,1) МВт/м2 при подъемном течении пароводяной среды. Обнаружено,
что разность температур стенки в окрестности внутренней (<р = 180°)
и наружной (<р = 0) образующих змеевика может составлять 200—
300°С. Это означает, что в змеевике возможно стационарное устойчи-
вое сосуществование в одном сечении канала пузырькового и пере-
ходного кипения и режима теплосъема дисперсным потоком. Такая
же особенность отмечена при неоднородном нагреве горизонталь-
ной трубы, подвергнутой внешнему одностороннему нагреву.
При обработке данных по граничному паросодержанию установ-
лено, что в змеевиковом канале влияние массовой скорости менее су-
щественно, чем в прямых трубах:
Хгр =1-0,45 |qr“1(p',)_0'5^og(p,-p")0'25]| х
x^pWo/o(p/p")°'5] ’ .	(4.2.24)
Неоднородность гидродинамических условий в змеевике и тепло-
отдачи по его периметру тесно связаны. Параметром, отражающим
неоднородность теплосъема по периметру канала, может служить
отношение коэффициентов теплоотдачи для наружной и внутрен-
ней образующих змеевика ан/ав.
Различие между ан и ав наблюдается при пузырьковом кипении, в
переходной и закризисной областях. Наиболее существенно неодно-
родность теплосъема по периметру проявляется в переходной зоне.
Установлена новая закономерность — изменение зависимости
отношения ан/ав от разности х — хгр для змеевика без покрытия и
с пористым покрытием при Р = 4,5 МПа, pW = 120—600 кг/(м2-с). В
обоих случаях отношение проходит через максимум, а затем неодно-
родность теплосъема по периметру плавно уменьшается и величина
указанного отношения достигает 2. Максимальное значение отноше-
ния ан/ав для трубы с пористым покрытием выше примерно в четыре
раза и достигается на длине двух—трех диаметров канала от места
зарождения кризиса теплообмена.
Рассмотрим данные по теплоотдаче в закризисной области змее-
виков с пористым покрытием и без покрытия.
Как установлено, в змеевике с пористым покрытием (рис. 4.53) ко-
эффициент теплоотдачи в закризисной области в два раза выше, чем
в спиральной трубе без покрытия.
400
Глава 4
Рис. 4.53. Коэффициент теплоотдачи для на-
ружной (1, 3) и внутренней (2, 4) образую-
щих змеевика по длине переходной и за-
кризисной областей: 1, 2 — змеевик без
покрытия; 3, 4 — змеевик с пористым пок-
рытием
Таким образом, повышение теплоотдачи в спиральной трубе с по-
ристым покрытием происходит как за счет закрутки потока, так и
влияния покрытия. Рассмотренный комбинированный метод интен-
сификации теплосъема приводит к аддитивному действию двух его
составляющих методов интенсификации теплоотдачи.
Исследование интенсификации теплообмена в трубах
с двухходовой винтовой накаткой
В работе [4.2.39] проведено исследование интенсификации тепло-
обмена в трубах с двухходовой винтовой накаткой. Высота накатки
составляла 3,2 мм. Опытные данные получены для воды в диапазоне
параметров: 7000 < Re < 30000, 2,5 < t < 12, где t = S/D (S — шаг накат-
ки, D — диаметр трубы.
Исследованная труба представлена на рис 4.54.
Рис. 4.54. Труба с двухходовой винтовой накаткой
Глава 4
401
В качестве целевой функции для оптимизации параметров накат-
ки использовалось соотношение
Nu/Nur>
и определялись
'Re-const
условия, при которых оно принимает наибольшие значения. При
этом, если значение целевой функции больше 1, то имеет место опе-
режающий рост теплоотдачи.
В качестве критерия оптимизации использовано отношение теп-
ловой мощности теплообменника NrenA к энергии, затрачиваемой
на прокачку теплоносителя Л/эл (электрическая мощность, потреб-
ляемая насосом): Кэ = -/Утепл /1УЭЛ — коэффициент энергетической
эффективности (числитель определяется теплоотдачей, а знамена-
тель — гидравлическим сопротивлением). Если коэффициент Кэ
возрастает, снижается потребление электрической энергии. Таким
образом, интенсификация теплообмена будет рациональной, если
выполняется условие:
(4.2.25)
где Кэ гл и Кэ — коэффициенты энергетической эффективности, со-
ответственно, для гладкой трубы и трубы с интенсификаторами теп-
лообмена. Поскольку гладкие трубы и трубы с интенсификаторами
теплообмена необходимо сопоставлять при одинаковых условиях,
т.е. при одинаковых Re, то условие (4.2.25) можно представить в виде
'Nu/Nu,/
\ ^э/^эгл 'Re=const
(4.2.26)
где NurA и ^,л, соответственно, число Нуссельта и коэффициент гид-
равлического сопротивления для гладкой трубы, рассчитываемые по
соотношениям
NurA = 0,021 Re0,8 Рг0,4 ,
= (l,821g(Re)-l,64)~2,
(4.2.27)
(4.2.28)
Nu и £,, соответственно, число Нуссельта и коэффициент гидравли-
ческого сопротивления для трубы с интенсификаторами, рассчиты-
ваемые по соотношениям [4.2.40]
Nu = 10“°'83-°'09u ^0,63+0,02 U pj.0,43
(4.2.29)
^+21g-	ос	/л QCl	\ —2-^+		0,022 [1-0,21g(Re)H = 0.	(4.2.30) Rey^ kt	J
Соотношения (4.2.27) —(4.2.30) справедливы при 7000 < Re < 30000,
2,5 < t < 12, t = S/D. На рис. 4.55 и 4.56 [4.2.39, 4.2.40] представлены
402
Глава 4
Рис. 4.55. Коэффициенты гидравличе-
ского сопротивления для гладкой трубы и
трубы с накаткой в зависимости от числа
Re и шага накатки
Рис. 4.56. Число Нуссельта для глад-
кой трубы и трубы с накаткой в за-
висимости от числа Re и шага на-
катки
коэффициенты гидравлического сопротивления и числа Нуссельта
для гладких труб и труб с накаткой в зависимости от числа Re и шага
накатки.
Данные по интенсификации теплообмена представлены на
рис. 4.57 [4.2.39]. Согласно ему, опережающий рост теплоотдачи про-
исходит при И < t < 12, 7000 < Re < 30000. Зависимости, приведен-
ные на рисунке, качественно согласуются с известными представле-
ниями.
После определения оптимальных шага накатки канала и рас-
хода жидкости рассчитаны сопротивление и теплоотдача и ре-
зультаты представлены в координатах £/£гл, Nu/NurA на рис. 4.58
[4.2.39].
Конкретное сочетание параметров для теплообменника в этих
координатах отображено на рисунке точкой, проведенные изолинии
Рис. 4.57. Показатели эффективности (2) при
различных числах Re и относительных шагах
накатки
соответствуют t — const и
Re = const. Поэтому по из-
вестным t и Re можно оп-
ределить £/^.л, Nu/NurA.
Далее, для гладкой трубы
по уравнениям (4.2.27) и
(4.2.28) определяем NurA
и ^,А . Имея эти данные,
находим Nu и £ для кана-
ла с интенсификаторами
теплообмена. На рис. 4.58
кривая 1 соответствует
Глава 4
403
Рис. 4.58. Влияние числа Re и шага вин-
товой накатки на теплоотдачу и гид-
равлическое сопротивление в трубе:
1 — интенсификация теплообмена в
гладкой трубе за счет увеличения рас-
хода жидкости; 2 — граница области
опережающего ростатеплоотдачи, изо-
линии Re = const; 3 — Re = 7000; 4 —
Re = 15000; 5 — Re = 30000, t = const;
6 - t = 12; 7 - t = 7; 8 - t = 4
эквивалентной интенсификации теплообмена для гладкой трубы за
счет увеличения расхода жидкости, кривая 2 отделяет область (выше
кривой), в которой интенсификация рациональная.
Сравнение кожухотрубных теплообменных аппаратов
с различными интенсификаторами теплосъема
Ниже приведено сравнение характеристик теплопередачи, гидро-
динамики и отложений в кожухотрубных теплообменных аппаратах
с различными интенсификаторами теплосъема. Для интенсифика-
ции теплообмена в теплообменниках для систем тепло- и водоснаб-
жения на основе существующих представлений [4.2.40, 4.2.42, 4.2.43]
сравниваются четыре наиболее разработанных и перспективных ва-
рианта на основе использования труб с кольцевой и винтовой накат-
кой, витых и облуненных труб.
Расчет коэффициентов теплопередачи и гидравлического сопро-
тивления, а также влияние солеотложений на теплопередачу прово-
дились на основе известных рекомендаций, обоснованных экспе-
риментальными данными. Расчетные данные получены для условий
в системах теплоснабжения. Для примера рассмотрен теплообмен-
ник, состоящий из 37 труб длиной L = 1340 мм, d = 10 мм, в качестве
материала использовалась сталь с толщиной стенки 1 мм. Парамет-
ры по горячему теплоносителю: расход G = 6,0—7,5 т/ч, температура
на входе Т « 70 °C; параметры по холодному теплоносителю: расход
G = 5,0—7,0 т/ч, температура на входе И °C.
При выборе характеристик интенсификаторов теплосъема в теп-
лообменнике для систем тепло- и водоснабжения использованы ре-
зультаты ряда исследований.
404
Глава 4
Рис. 4.59. Винтообразно
профилированная труба
В работе [4.2.40] исследованы теплопе-
редача и гидродинамика в трубе с винто-
вой накаткой и различным числом заходов
при t/d = 3, где t — шаг накатки, d — диа-
метр трубы при течении воды в диапазо-
не чисел Re = (5—50)-103 (рис. 4.59). Число
Re = Vd/v — безразмерная величина, яв-
ляющаяся числом подобия, характеризую-
щая режим течения (ламинарное течение
при числе Re < 2300 и турбулентное — при
числе Re > 2300) и равная произведению
скорости на диаметр трубы, деленному на
кинематический коэффициент вязкости.
На рис. 4.60 [4.2.42] показаны зависимости
отношения чисел Nu для винтообразно профилированных и гладких
труб, полученные при расчете по формулам, найденным по опытным
данным [4.2.40]. На рис. 4.60 данные для труб с различным радиусом
закругления накатки обозначены 2.1 и 2.2. Как установлено, трубы с
одноходовой накаткой более эффективные, чем двухходовые и трех-
ходовые. С уменьшением числа Re возрастает отношение чисел Nu.
Особенно это заметно для трубы с двухходовой накаткой и радиусом
закругления 3,5 мм.
Рис. 4.60. Зависимость отноше-
ния Nu/NurA отчисла Рейнольд-
са Re: 1 — труба с одноходовой
винтовой накаткой; 2.1 — тру-
ба с двухходовой винтовой на-
каткой г = 3,2; 2.2 — труба с
двухходовой винтовой накат-
кой г = 3,5; 3 — труба с треххо-
довой винтовой накаткой
На основании результатов, пред-
ставленных в работе [4.2.40], выбрана
труба с одноходовой винтовой накат-
кой, при отношении шага накатки к
диаметру трубы t/d = 3.
Выбор характеристик кольцевой на-
катки на трубе (рис. 4.61) проведен на
основе рекомендаций, изложенных в ра-
боте [4.2.43]. Согласно проведенным рас -
Рис. 4.61. Профилированные
трубы (кольцевая накатка)
Глава 4
405
четам выбраны шаг 6 мм и глубина накатки 0,5 мм. В этом случае получе-
на достаточно высокая теплоотдача при допустимых потерях давления.
Выбор характеристик витой тру бы (см. рис. 4.62) проведен на ос-
нове результатов исследования, проведенного в работе [4.2.44]. По-
казано, что при s/d = 8 (s — шаг закрутки витой трубы) витая труба
обеспечивает существенное повышение теплоотдачи при относи-
тельно небольшом росте гидравлического сопротивления (рис. 4.62).
Рис. 4.62. Витая труба
Рис. 4.63. Труба с облунением
Выбор характеристик облуненной трубы (рис. 4.63) сделан на осно-
ве результатов исследования, проведенного в работе [4.2.45]. Соглас-
но указанным рекомендациям, выбираем продольный шаг лунок —
6 мм, диаметр лунки — 3 мм, глубину лунки h « 1 мм.
Результаты расчета
Результаты расчета теплопередачи, потерь давления и отложений
в теплообменниках с интенсификаторами теплосъема и без них для
рассмотренных условий представлены на рис. 4.64—4.66 [4.2.42]. На
рис. 4.64 показана зависимость отношения коэффициентов теплопе-
редачи для теплообменников с интенсификаторами теплообмена и
без них от числа Рейнольдса и расхода по холодному теплоносителю
в межтрубном пространстве для рассмотренных четырех вариантов
интенсификации теплоотдачи.
406
Глава 4
Рис. 4.64. Зависимость коэффициента теплопе-
редачи от числа Рейнольдса и расхода холодно-
го теплоносителя: 1 — труба с кольцевой накат-
кой t/d = 3; 2 — труба со спиральной накаткой
d/D = 0,9, t/d = 0,6; 3 — труба с облунением
h/d = 0,3; 4 — витая труба s/d = 8
Обнаружено, что на-
ибольший рост коэффи-
циента теплопередачи
(до 80% по отношению
к теплообменнику без
интенсификаторов теп-
лообмена) получен в
случае использования
витых труб. В случае
применения облунен-
ных труб при низких
числах Re наблюдает-
ся такой же эффект, од-
нако с ростом числа Re
этот эффект ослабля-
ется в большей степе-
ни, чем для витых труб.
Трубы со спиральной
и кольцевой накаткой
обеспечивают рост теп-
лопередачи до 60%. Су-
щественный рост теп-
лопередачи в теплообменниках с интенсификаторами теплосъема
объясняется тем, что в рассмотренных условиях передача тепла про-
исходит при скоростях, соответствующих переходной области от ла-
минарного к турбулентному течению.
На рис. 4.65 показана зависимость отношения перепадов давле-
ния для теплообменников с интенсификаторами теплообмена (Др*) и
без них (Др) от числа Рейнольдса и расхода холодного теплоносителя
для рассмотренных четырех вариантов интенсификации теплоотда-
чи [4.2.42].
Обнаружено, что наибольший рост отношения Др*/Др (45%) полу-
чен при использовании в теплообменнике труб с кольцевой накаткой.
Спиральная накатка приводит к повышению отношения Др*/Др на
35%. В случае использования в теплообменнике витых труб получен
рост отношения Др*/Др на 25%, в случае облуненных труб — на 20%.
На рис. 4.66 представлены зависимости коэффициента теплопе-
редачи от времени для гладкой трубы, витой трубы и трубы с кольце-
вой накаткой при карбонатной жесткости воды С = 10 мг-экв/л при
числе Re = 3000. При расчете изменения коэффициента теплопере-
дачи во времени использованы зависимости, предложенные в работе
[4.2.46].
Глава 4
407
Рис. 4.65 Зависимость коэффициен-
та гидравлического сопротивления от
числа Рейнольдса и расхода: 1 — труба
с кольцевой накаткой t/d = 3; 2 — тру-
ба со спиральной накаткой d/D = 0,9;
t/d = 0,6; 3 — труба с облунением
h/d = 0,3; 4 — витая труба s/d = 8
Рис. 4.66. Влияние солеотложений
на коэффициент теплопередачи:! —
труба с кольцевой накаткой t/d = 3;
2 — витая труба s/d = 8; 3 — гладкая
труба
Как обнаружено, коэффициент теплопередачи для гладкой трубы
с течением времени уменьшился в результате отложений и за 250 ч
понизился в 2,5 раза. Коэффициент теплопередачи в случае приме-
нения витых труб и труб с кольцевой накаткой вначале уменьшается,
затем его значение стабилизируется. Таким образом, эффективность
использования турбулизаторов с течением времени возрастает.
Влияние луночного рельефа на теплообмен при кипении
на сфере
В работе [4.2.47] исследовано влияние луночного рельефа на теп-
лообмен при кипении на сфере. Исследование теплообмена при пу-
зырьковом, переходном и пленочном режимах кипения проводилось
нестационарным методом путем погружения нагретой выше темпе-
ратуры Лейденфроста медной сферы с луночным рельефом в жид-
кость при атмосферном давлении. Для измерения температуры по-
верхности сфер использовалась хромель-алюмелиевая термопара,
которая с помощью теплостойкого клея ВС-ЮТ заделывалась в глу-
хое отверстие диаметром 1 мм и глубиной 19 мм. Кроме того, проводи-
лись измерения температуры рабочей жидкости и нагревательного
устройства. Сигналы термопар подавались на АЦП, подключенный к
персональному компьютеру с установленной специальной програм-
мой. Сферы с помощью тонкостенного трубчатого зонда поднима-
408
Глава 4
лись в зону нагрева, где выдерживались при заданной температуре, а
затем погружались в жидкость при синхронном включении системы
сбора и обработки данных. Опыты проводились на эксперименталь-
ной установке, снабженной смотровыми окнами для проведения ви-
зуальных наблюдений и видеофотосъемки. В качестве исследуемой
жидкости использовался фреон-113.
Для сравнения данных, полученных при кипении на сфере с лу-
ночным рельефом, проводились также опыты со сферическими мед-
ными образцами с пористым покрытием толщиной 0,4 мм, размером
частиц 0,063 мм и пористостью около 50% и без покрытия.
Для нахождения кривых кипения при охлаждении сферы исполь-
зовалась методика, основанная на регистрации изменения темпера-
туры от времени и его преобразовании в зависимость плотности теп-
лового потока q от температурного напора ДТ. Мгновенное значение
Рис. 4.67. Схема экспериментальной установки
Глава 4
409
плотности теплового потока q на поверхности
сферы рассчитывалось из уравнения теплового
баланса. Методика исследования и описание эк-
спериментальной установки изложены в работе
[4.2.48].
Луночный рельеф на поверхность сферы на-
носился с помощью специального устройства
путем выдавливания лунок пуансоном, на кон-
це которого заделывался шарик диаметром 5 мм.
Способ нанесения лунок позволял изменять рас-
Рис. 4.68. Медная
сфера с лунками
положение лунок и их размеры. В качестве исходной конфигурации
на поверхность сферы были нанесены 31 лунка глубиной h — 0,41 мм
и диаметром d = 2,5 мм (h/d = 0,164), расстояние между лунками по
долготе сферы равно 5,2 мм (рис. 4.68).
Результаты исследования и их анализ
Опыты по теплообмену при кипении фреона-113 на поверхностях
с луночным рельефом проводились в широком диапазоне темпера-
турных напоров от 0 до 250 К, охватывающих все режимы кипения,
при температуре насыщения и в условиях недогрева жидкости. На
рис. 4.69 приведены видеокадры различных режимов кипения насы-
щенного фреона-113 на сфере с луночным рельефом. Вблизи грани-
цы прекращения пленочного кипения на нижней части облуненной
сферы в отличие от гладкой сферы наблюдалось увеличение ампли-
туды колебаний толщины паровой пленки. Снизу и сбоку от сферы
просматривались вторичные конвективные потоки жидкости вбли-
зи границы раздела фаз. В переходной области кипения на облунен-
ной сфере можно было наблюдать образования паровых струй и вих-
рей. В области пузырькового режима кипения при малых плотностях
теплового потока наблюдалось образование пузырьков пара, выходя-
щих из лунок.
а	б	в
Рис. 4.69. Пленочный, переходный и пузырьковый режимы кипения фреона-ИЗ:
а — Ts = 321 К; б — Р = 0,1 МПа; в — сфера с лунками
410
Глава 4
Рис. 4.70. Изменение температуры во вре-
мени при охлаждении сферы во фреоне-
113. Ts= 321 К
На рис. 4.70 [4.2.47] пред-
ставлены типичные кривые
изменения температур глад-
кой сферы и сферы с лунками
во времени при их охлажде-
нии в кипящем фреоне. Вид-
но, что в области высоких и
низких перегревов, соответс-
твующих пленочному и пу-
зырьковому кипению, кривые
совпадают между собой. В об-
ласти резкого изменения тем-
пературы, соответствующе-
го прекращению пленочного и пузырькового кипения, наблюдается
расхождение температурных кривых, причем изменение темпера-
туры сферы с лунками свидетельствует о более интенсивном отводе
тепла по сравнению с гладкой сферой.
Представленные на рис. 4.71 [4.2.47, 2.4.28] кривые кипения фре-
она-113 на гладкой сфере и сфере с луночным рельефом демонстри-
руют влияние луночного рельефа на прекращение пленочного кипе-
ния и теплоотдачу в переходном режиме. Так, температурный напор
ДТ 2, соответствующий прекращению пленочного кипения для сфе-
ры с лунками, увеличился до 105К по сравнению с его значением, рав-
ным для гладкой сферы 95К.
С увеличением недогрева жидкости толщина пленки пара умень-
шается, что приводит к увеличению значений ДГкр2 и дкр2. На рис. 4.72
приведены зависимости критической плотности теплового потока
дкр2 от недогрева жидкости ДТнед для
Рис. 4.71. Кривые кипения фреона-ИЗ на
гладкой сфере и сфере с луночным релье-
фом. Ts = 321К
сфер с различной обработкой
поверхности. Сравнение дан-
ных, представленных на ри-
сунке для сферы без покрытия
и с медным пористым покры-
тием, показывает, что для за-
данной геометрии луночного
рельефа величина дкр2 боль-
ше, чем для гладкой сферы, и
меньше, чем для сферы с мед-
ным пористым покрытием.
Из рис. 4.73 видно, что на-
несение луночного релье-
фа приводит к повышению
коэффициента теплоотдачи
Глава 4
411
при пленочном режиме до
75% вследствие турбули-
зации паровой пленки и
возмущений границы раз-
дела пар—жидкость. Для
выбранной геометрии лу-
ночного рельефа его вли-
яние на теплоотдачу в
пленочном режиме кипе-
ния проявляется в мень-
шей степени, чем в случае
пористого покрытия, что
можно объяснить малой и
неравномерной плотнос-
тью лунок (~12%) по поверх-
ности сферы. Кроме того,
исследованы мелкие лун-
ки (h/d = 0,164 мм), для ко-
торых эффект интенсифи-
кации теплообмена менее
значителен, чем для глубо-
ких лунок.
На рис. 4.74 представ-
лены данные о влиянии
недогрева жидкости на
первую критическую
плотность теплового пото-
ка g . для различных ре-
льефов и состояния повер-
хности нагрева. Для всех
поверхностей с увеличе-
нием недогрева жидкости
значения qкр1 возрастают.
Более сильное влияние на
qKpl оказывает нанесение
на сферу пористого покры-
Рис. 4.74. Влияние недогре-
ва жидкости на прекращение
пузырькового кипения фре-
она-113 для сфер с различным
рельефом и состоянием по-
верхности
qKp2, кВт/м2
-2 0 2 4 6 8 10 1214 1618 2022 242628303234
Рис. 4.72. Влияние недогрева жидкости на пре-
кращение пленочного кипения фреона-113
а, Вт/м2К
85 90 95 100105110115120125130135140145150
Л Г,/С
Рис. 4.73. Теплоотдача при пленочном кипении
фреона-113. Ts = 321К
412
Глава 4
тия, в котором имеется большое количество центров парообразова-
ния. Для сферы с луночным рельефом и гладкой сферы данные прак-
тически совпадают. Это объясняется тем, что нанесение небольшого
числа мелких лунок на поверхность сферы практически не влияет на
количество активных центров парообразования и, соответственно,
интенсивность теплообмена вблизи кризиса кипения.
Обобщение данных по влиянию закрутки потока
на критическую тепловую нагрузку
В работах по управляемому термоядерному синтезу, в частнос-
ти в системах инжекционного нагрева плазмы, плотность тепловых
потоков достигает -100 МВт/м2, и реализовать теплосъем в таких ус-
ловиях возможно с применением закрутки теплоносителя. В рабо-
тах [4.2.49—4.2.63] (табл. 4.2.4) исследовано влияние закрученной
ленты на кризис теплообмена в трубах. В ряде работ получено повы-
шение критической тепловой нагрузки до 1,5—2 раз, однако сущест-
вующие экспериментальные данные и расчетные зависимости для
критических тепловых нагрузок противоречивы и расхождение в
значениях критической тепловой нагрузки может достигать несколь-
ких раз. К тому же отсутствуют массивы согласованных опытных
данных для критических тепловых нагрузок при закрутке потока с
помощью ленты.
На рис. 4.75 показано сопоставление уравнений, предложенных
разными авторами для расчета критической тепловой нагрузки при
закрутке потока в области
отрицательных паросодер-
жаний. Как видно, наблю-
даются сильные количест-
венные и качественные
различия, что обуславлива-
ет необходимость анализа и
поиска методов обобщения
опытных данных.
В работе [4.2.64] обобще-
ны опытные данные работ
[4.2.49—4.2.63] по критиче-
ским тепловым нагрузкам
для закрученных с помощью
ленты потоков теплоноси-
теля в трубах для отрица-
тельных и положительных
Рис. 4.75. Сравнение результатов расчета дкр
по различным зависимостям при р = 1 МПа,
pW = 3000 кг/м2-с, d = 8 мм, LH = 100 мм,
у = 2:1 — Оводков, 2 — Schlosser, 3 — Дедов,
4 — Kinoshita, 5 — гладкая труба
Таблица 4.2.4.
Список исследований влияния закрученной ленты на критическую тепловую нагрузку
Источник	Кол-во точек	Р, МПа	pW, кг/(м2-с)	X	у(18.0°)	LH, м	d, мм	qrKp, МВт/м2
				х< 0				
Gambill, 1961 г.	28	0,1-3,8	4260-26960	-0,35-0	2,3-12,3	0,051-0,441	3-10	8,7-59,3
Viskanta, 1961 г.	10	13,8	680-2710	-0,06-0	2,5-5	0,46	8	1,7-5,0
Feinstein, 1963 г.	27	0,3	6570-33000	-0,27	2-6	0,102	6	15,8-87,4
Koski, 1988 г.	3	1,1	2900-9500	-0,27	2	0,04	8	37,2-60
Ободков, 1990 г.	32	0,1-0,8	200-3000	-0,14-0	3,5	0,035	8	2,4-14,2
Cattadori, 1993 г.	6	2,6-3,6	5000-14500	-0,29--0,09	1-2	0,15-0,30	8-15	26,5-49,6
Kinoshita, 1994 г.	110	0,1-1,5	4600-9000	-0,24--0,04	2,67-3,47	0,1	6	8,5-33,8
Araki, 1996 г.	15	1,0-1,5	4000-20000	-0,29--0,18	3	0,16	7	19,8-45,9
Euratom, 1997 г.	47	1,0-3,7	3000-16000	-0,46--0,13	2	0,085-0,115	10-18	16,8-68,6
Дедов, 2000 г.	63	0,7-1,5	540-8800	-0,38--0,19	1,75	0,07	8	20,0-78,3
Итого...	338	0,1-13,8	200-33000	-0,48-0	1-12,3	0,07-0,46	3-18	1,7-78,3
Viskanta, 1961 г.	44	13,8	680-2710	0-0,37	2,5-5	0,46	8	1,7-5,0
Mayinger, 1964 г.	71	7,0-10,0	2300-3700	0-0,23	2,32-5,71	0,28	7	3,5-6,2
Moeck, 1964 г.	29	7,0	400-1150	0,74-0,95	5,5-34,5	1,02	И	0,3-1,2
Matzner, 1965 г.	27	6,9	1260-4600	0,33-0,88	15	4,87	10	1,0-3,1
ВТИ, 1966 г., 1988 г.	99	4,9-20,1	490-2800	0,22-0,98	10-20	2,0	8-20	0,4- 1,8
Итого...	270	4,9-20,1	400-4600	0-0,98	2,5-34,5	0,28-4,87	8-20	0,3-6,2
Глава 4	413
414
Глава 4
паросодержаний. На основании анализа собранного массива дан-
ных получено уравнение для расчета критической тепловой нагруз-
ки при закрутке потока с помощью ленты. Данные по критическим
тепловым нагрузкам при закрутке потока в вертикальных и гори-
зонтальных трубах охватывают следующие диапазоны параметров:
0,1 < р < 20,1 МПа; 0,95 < LH/d < 480; 1 < у < 34,5; 200 < р!¥<39000 кг/(м2-с),
-0,45 < х < 0,95. Результаты расчета представлены на рис. 4.76.
При обобщении данных получено уравнение (4.2.31).
qKp=0,4(pW)nkxklkyk,	(4.2.31)
где дкр — расчетная критическая тепловая нагрузка, МВт/м2; pW —
массовая скорость потока, кг/(м2-с); к^ кх, klt к — коэффициенты, учи-
тывающие влияние закрутки, недогрева жидкости до температуры
насыщения, начального термического участка и давления, соответст-
венно, и уравнение (4.2.32)
n = 7o,O3(l-x)O125lg(pW), ку=ч/1+3/у, кх = [о,37+0,63(1-х)3]1'15,
к = 1-
Ру
<р£у
4	25000
1 +--------
^еж
(Ргж)^е-°'031^2,
(4.2.32)
, !'3
, ki = 1 ч——  
s^7d
где х — массовое паросодержание на выходе из трубы; у — коэффи-
циент закрутки потока, равный отношению шага закрутки ленты на
180° к диаметру трубы; руи р£ — плотность пара и жидкости на линии
насыщения, кг/м3; LH — длина участка нагрева трубы, мм; d — ди-
аметр трубы, мм; Кеж и Ргж — числа Рейнольдса и Прандтля, рассчи-
танные по температуре жидкости на выходе из трубы. Влияние к, на
дкр сказывается при LH/d <10.
^кр.рас/^кр.экс.
• Viskanta [4.2.50]
- ВТИ [4.2.59]
a Matzner [4.2.62]
« Moeck [4.2.61]
ж MAN [4.2.60]
•	Gambill [4.2.49]
♦	Araki [4.2.56]
•	Euratom [4.2.57]
•	Оводков [4.2.53]
x Дедов [4.2.58]
	Cattadori [4.2.54]
a Koski [4.2.52]
♦	Kinoshita [4.2.55]
•	Feinstein [4.2.51]
0	5000 10000 15000 20000 25000 30000 pW, кг/(м2 с)
Рис. 4.76. Отношение критической тепловой нагрузки, рассчитанной по уравне-
нию (4.2.31), к полученной в опытах, в зависимости от массовой скорости
Глава 4
415
^кр.рас /^кр.экс.
2-1-------------
0,5
+40% —
1,5
• Kinoshita [4.2.55]
 Оводков [4.2.53]
‘Gambill [4.2.49]
• Araki [4.2.56]
«Feinstein [4.2.51]
-40%
0	10000 20000 30000 40000 50000 60000 70000 pW, кг/(м2 с)
Рис. 4.77. Отношение критической тепловой нагрузки, рассчитанной по уравне-
нию (4.2.31), к полученной в опытах для прямолинейных потоков в зависимости
от массовой скорости
В итоге уравнение (4.2.31) описывает 551 точку из 608 (91 %) точек
полученного массива данных по критическим тепловым нагрузкам с
разбросом ±40%. Если из этого уравнения исключить коэффициент
влияния закрутки ку то его можно использовать для расчета крити-
ческих тепловым нагрузок и для прямолинейных потоков. Результа-
ты расчета для прямолинейных потоков представлены на рис. 4.77.
Список литературы
4.2.1.	Свириденко И.П. и др. Особенности теплообмена в каналах с пористым
теплопроводным заполнителем: Препринт ФЭИ, №3.1985.
4.2.2.	Свириденко И.П. и др. Разработка конструкции интегральной линей-
ки лазерных диодов с использованием для жидкостного охлаждения ка-
пиллярно-пористой структуры/Докл. на Минском международном семи-
наре «Полупроводниковые лазеры и системы на их основе», 22-24 июня
1999 г.
4.2.3.	Свириденко И.П. и др. Вопросы интенсификации теплообмена в системе
мощного полупроводникового лазера/Др. 2-й Российской нац. конф, по
теплообмену. М.: МЭИ, 1998.
4.2.4.	Свириденко И.П. и др. Способы затягивания кризиса теплообмена в
большом объеме и при вынужденном движении/Др. 1-й Российской нац.
конф, по теплообмену. 1994. Т. 4. С. 214.
4.2.5.	Свириденко И.П. и др. Теплофизические и физико-химические исследо-
вания в обоснование получения крупноразмерных монокристаллов полу-
проводниковых материалов/Др. II Российского симпозиума с междуна-
родным участием по процессам тепломассопереноса и роста кристаллов.
Обнинск, 1997. С. 334-346.
416
Глава 4
4.2.6.	Свириденко И.П. и др. Исследование теплообмена при турбулентном
течении ртути в кольцевом зазоре//Атомная энергия. 1960. Т. 9, вып. 4.
4.2.7.	Свириденко И.П. и др. Теплоотдача и гидравлическое сопротивление в
плотно упакованных пучках стержней//Там же. 1962. Т. 13, вып. 2.
4.2.8.	Свириденко И.П. и др. Тепло- и гидравлические исследования жидко-
металлической пористой тепловой защиты энергонапряженных конст-
рукций//Тр. VI Всероссийской конф. «Инженерные проблемы термоядер-
ных реакторов», С.-Петербург, 1997. С. 163.
4.2.9.	Свириденко И.П. и др. Теплофизические исследования в обоснова-
ние разработок энергонапряженных систем ЯЭУ космического назначе-
ния: Труды ГНЦ РФ «ФЭИ»//Сб. «ГНЦ РФ «ФЭИ» - 50 лет», 1996. С. 221-
229.
4.2.10.	Свириденко И.П. и др. Теплофизические проблемы энергодвигатель-
ных установок космического назначения/Др. международного семинара
«Космическая энергетика XXI века». Обнинск, 1998.
4.2.11.	Свириденко И.П. и др. Исследование теплообмена при конденсации па-
ра жидкого металла (сплава натрий-калий) двухкомпонентного состава//
Тр. Ill Минского междунар. форума, 20-24 мая 1996 г. Т. IV. С. 121-130.
4.2.12.	Алешин А.А., Кузма-Кичта Ю.А., Москвин В.Н., Сорокин Д.Н. Иссле-
дование теплообмена при парообразовании на поверхности с пористым
покрытием/ДВТ. 1980. Т. 18, № 5. С. 1098-1101.
4.2.13.	Кузма-Кичта Ю.А., Леньков В.А., Москвин В.Н., Сорокин Д.Н. Ис-
следование теплообмена при кипении жидкости на поверхности с порис-
тым покрытием в широком диапазоне давлений/Деплоэнергетика. 1982.
№ 3. С. 55-56.
4.2.14.	Ковалев С.А., Жуков В.М., Кузма-Кичта Ю.А., Казаков Г.М. Тепло-
обмен при кипении жидкости на поверхностях с малотеплопроводными
покрытиями/Деплообмен и физич. газодинамика. 1974. С. 116-119.
4.2.15.	Петухов Б.С., Ковалев С.А., Жуков В.М., Кузма-Кичта Ю.А. Меха-
низм пленочного кипения на поверхности без покрытия и с малотепло-
проводными покрытиями/Деплообмен. Советские исследования. 1974.
С.224-234.
4.2.16.	Кузма-Кичта Ю.А., Леньков В.А., Сорокин Д.Н. Определение тер-
мического сопротивления пористых покрытий//Химич. и нефт. машино-
строение. 1979. №5. С. 10-12.
4.2.17.	Кузма-Кичта Ю.А., Леньков В.А., Сорокин Д.Н. Влияние пористых
покрытий на теплообмен при пленочном кипении//ИФЖ. 1981. Т. 40,
№4. С. 190-196.
4.2.18.	Петухов Б.С., Ковалев С.А., Жуков В.М., Кузма-Кичта Ю.А. Иссле-
дование механизма пленочного кипения с помощью ОКГ//Вопросы теп-
лообмена. М.: Наука, 1987. С. 185-191.
4.2.19.	Кузма-Кичта Ю.А. Устинов А.К., Молошников А.С. и др. Исследова-
ние колебаний границы раздела фаз и механизма переноса тепла при
пленочном кипении/ДВТ. 1994. № 2. С. 53-59.
4.2.20.	Кузма-Кичта Ю.А, Комендантов А.С., Сухов Б.Ю. и др. Исследование
кризиса теплообмена в канале с пористым покрытием. ММФ-96/Депло-
массообмен, 1996. Т. 7. С. 84-88.
Глава 4
417
4.2.21.	Кузма-Кичта Ю.А, Ковалев А.С. Влияние пористого покрытия на харак-
теристики кризиса теплообмена в трубах//Теплоэнергетика. 1997. № 6.
С. 53-57.
4.2.22.	Кузма-Кичта Ю.А, Комендантов А. С., Барч Г. и др. Влияние пористого
покрытия на теплоотдачу при различных режимах кипения в вертикаль-
ном канале/Др. 2-й Российской нац. конф, по теплообмену. М.: МЭИ,
1998. Т. 6. С. 147-150.
4.2.23.	Кузма-Кичта Ю.А. Методы интенсификации теплообмена. М.: МЭИ,
2001.
4.2.24.	Кузма-Кичта Ю.А, Комендантов А.С., Бурдунин М.Н. и др. Исследо-
вание интенсификации теплосъема в парогенерирующих каналах с по-
ристым покрытием/Деплоэнергетика. 1991. № 5, С. 42-47.
4.2.25.	Kuzma-Kichta Yu.A, Sedlov A.S., Abramov A.I., Shkondin Yu.A,
Buyakov D.V., Serbin B.K. Experimental investigation of heat transfer crisis
at low mass velocities and pressures. Intern. Symp. on Physics of Heat transfer
in Boiling and Condensation. 21-24 May 1997. Moscow. Russia.
4.2.26.	Комендантов A.C., Кузма-Кичта Ю.А, Бурдунин М.Н. и др. Иссле-
дование кризиса теплообмена в каналах различной геометрии//ИФЖ.
1988. Т. 55, № 6. С. 885-889.
4.2.27.	Кузма-Кичта Ю.А, Комендантов АС, Бурдунин М.Н. и др. Исследо-
вание интенсификации теплоотдачи в переходной и закризисной об-
ластях при низких массовых скоростях/Деплоэнергетика. 1992. № 5.
С. 44-47.
4.2.28.	Кузма-Кичта Ю.А. , Комендантов А.С., Оводков А.А. и др. Интенси-
фикация теплоотдачи в горизонтальных парогенерирующих каналах//
Химич, и нефт. машиностроение. 1993. № 10. С. 17-19.
4.2.29.	Кузма-Кичта Ю.А, Комендантов АС, Оводков А.А. и др. Исследо-
вание интенсификации теплосъема при кризисе теплообмена в гори-
зонтальном канале в условиях пониженных давлений и массовых ско-
ростей/Друды 1-й Российской нац. конф, по теплообмену.1994. Т. 8.
С. 129-134.
4.2.30.	Петухов Б.С, Ковалев С.А., Жуков В.М., Кузма-Кичта Ю.А. Иссле-
дование местной теплоотдачи при кипении жидкости на неизотермиче-
ской поверхности/Друды конф, по тепло- и массообмену. Минск, 1972.
С. 212-218.
4.2.31.	Комендантов А.С., Кузма-Кичта Ю.А, Панин В.В. и др. Исследование
теплоотдачи в закризисной области змеевика/Деплоэнергетика.1990.
№10. С. 25-28.
4.2.32.	Комендантов А.С., Кузма-Кичта Ю.А, Васильева Л.Т. и др. Исследо-
вание интенсификации теплосъема при неоднородных по периметру ме-
гаваттных тепловых нагрузках//Вопросы атомной науки и техники. Сер.
Термоядерный синтез. 1987. № 4. С. 55-60.
4.2.33.	Комендантов А.С., Кузма-Кичта Ю.А., Бурдунин М.Н. и др. Исследо-
вание температурных режимов канала и термической неравновесности
парокапельного потока/Деплоэнергетика. 1988. № 5. С. 43-45.
4.2.34.	Кузма-Кичта Ю.А., Комендантов А.С., Оводков А.А. и др. Экспери-
ментальное исследование интенсификации теплоотдачи при существен-
но неоднородном нагреве/ДВТ. 1990. № 4. С. 754-758.
418
Глава 4
4.2.35.	Кузма-Кичта Ю.А., Комендантов А.С., Сухов Б.Ю. и др. Влияние за-
крутки потока и пористого покрытия на характеристики теплосъема при
кризисе теплообмена в канале с неоднородным нагревом//Там же. 1992.
№ 4. С. 772-777.
4.2.36.	Кузма-Кичта Ю.А., Комендантов А.С., Сухов Б.Ю. и др. Влияние за-
крутки потока и пористого покрытия на кризис теплообмена в горизон-
тальной трубе с неоднородным нагревом/Др. конф, по тепло- и массо-
обмену. Минск, 1992. Т. 4, ч. 1. С. 35-38.
4.2.37.	Комендантов А.С., Кузма-Кичта Ю.А., Панин В.В. и др. Гидродина-
мика однофазного потока в змеевиковых трубах/Др. МЭИ, 1988. № 153.
С. 87-96.
4.2.38.	Комендантов А.С., Кузма-Кичта Ю.А., Панин В.В. и др. Исследова-
ние гидродинамики и теплообмена в змеевиках//Энергомашиностро-
ение. 1988. №9. С. 12-15.
4.2.39.	Кузма-Кичта Ю.А., Савельев П.А., Корякин С.А., Доброволь-
ский А.К. Исследование интенсификации теплообмена в трубах с винто-
вой накаткой/Деплоэнергетика. 2007. № 5. С. 56-57.
4.2.40.	Темкин А.Г., Савельев П.А. Гидродинамика и теплообмен при течениях
в каналах сложной конфигурации. Рига: Рижский политехнический инс-
титут, 1976. С. 116.
4.2.41.	Дзюбенко Б.В., Кузма-Кичта Ю.А., Кутепов А.М., Свириденко И.П.,
Федик И.И., Харитонов В.В., Холпанов Л.П. Интенсификация тепло-
и массообмена в энергетике. М.: ФГУП «ЦНИИАТОМИНФОРМ», 2003.
240 с.
4.2.42.	Кузма-Кичта Ю.А., Савельев П., Лодвиков К.М. .Кожухотрубные или
пластинчатые теплообменники//Инновации Подмосковья. 2007.09.
4.2.43.	Калинин Э.К., Дрейцер Г.А., Копп И.З., Мякочин А.С. Эффективные
поверхности теплообмена. М.: Энергоатомиздат, 1998.
4.2.44.	Ашмантас Л.-В.А., Дзюбенко Б.В. Проблемы теплообмена и гидроди-
намики в ядерных энергодвигательных установках космических аппара-
тов. Вильнюс: Pradai, 1997.
4.2.45.	Гачечиладзе И.А., Кикнадзе Г.И., Краснов ЮЖ. и др. Теплообмен при
самоорганизации смерчеобразных структур//Сб. «Тепломассообмен
ММФ. Проблемные доклады». Секция 1-2. Минск, 1988. С.83.
4.2.46	Дзюбенко Б.В. Влияние закрутки потока на тепломассообмен в услови-
ях солеотложений в витых трубах/Др. РНКТ-4, 2006, 23-26 нояб.
4.2.47.	Кузма-Кичта Ю.А., Жуков В.М., Агальцов А.М. Особенности нестаци-
онарного теплообмена при кипении фреона-113 на поверхности сферы
с луночным рельефом/Др. конф, по вихревым и закрученным потокам.
Окт. 2007.
4.2.48.	Жуков В.М., Кузма-Кичта Ю.А., Леньков В.А., Рахманов А.А. Неста-
ционарный теплообмен при кипении фреона-113 на поверхности сферы
с пористым покрытием/Др. РНКТ-4. М.: МЭИ, 2006. Т.4. С. 96-99.
4.2.49.	Gambill W.R., Bundy R.D., Wansbrough R.W. Heat transfer, burnout
and pressure drop for water in swirl flow through the tubes with internal twis-
ted tapes//Chem. Engng Progr. Sympos. Ser. 1961. V. 57, N 32. P. 127-137.
Глава 4
419
4.2.50.	Viskanta R. Critical Heat Flux for water in swirling flow // Nucl. Sci. Engng.
1961. V. 10. P. 202-203.
4.2.51.	Feinstein L., Lundberg R.E. Fluid Friction and Boiling Heat Transfer in Water
in Tubes Containing Internally Twisted Tapes. Stanford Res. Inst RAE-TRR.
63.451. Defense documentation Centre A.D. 430889.1963.
4.2.52.	Koski J.A., Groessman C.D. Critical heat flux Investigations for fusion-
relevant conditions with water the use of a rastered electron beam appara-
tus//ASME Paper 88-WA/NE-3. 1988.
4.2.53.	Оводков А.А. Экспериментальное исследование влияния закрутки пото-
ка на кризис теплообмена при неоднородном нагреве и разработка рас-
четных рекомендаций: Автореф. дис.... канд. техн. наук. М.: МЭИ, 1990.
4.2.54.	Gaspari G.P., Cattadori G. Subcooled flow boiling in tubes with and without
turbulence promoters//3World Conf, on Experimental Heat Transfer, Honolulu,
Oct.31. Nov. 5, 1993.
4.2.55.	Kinoshita H., Nariai H., Inasaka F., Yoshida T. Study on the Mechanism
of Critical Heat Flux Enhancement for the Subcooled Flow Boiling in Tube with
Internal Twisted Tape under Non-Uniform Heat Condition//Jap. Soc. Mec.
Eng. B. 1996. V. 62, N. 596. P. 1459-1466.
4.2.56.	Araki M. et al. Critical-heat-flux experiment on the screw tube under one-
sided-heating conditions//Fusion Techn. 1996. V. 29. P. 519-528.
4.2.57.	Boscary J., Fabre J. and Schlosser J. Critical heat flux of water subcooled
flow in one-side heated swirl tubes//lnt. J.Heat Mass Transfer. 42 287.1999.
4.2.58.	Дедов A.B. Экспериментальное исследование теплообмена и крити-
ческих тепловых нагрузок при кипении в закрученном потоке недогретой
воды при одностороннем нагреве: Автореф. дис.... канд. техн. наук. М.:
МЭИ, 2000.
4.2.59.	Кисина В.И., Леонтьев А.И. Кризис теплообмена с винтовыми вставка-
ми/Деплоэнергетика. 2005.
4.2.60.	Henkel D., Mayinger F., Schad О., Weiss E. Untersuchung der Kritischen
Heizflacchenblastung bei Seidendem Wasser. M.A.N.: Report No. 09.02.07.
Maschienfabrik Augsburg-Nuremberg, Nuremberg, Germany, 1964.
4.2.61.	Moeck E.O., Wikhammer G.A., MacDonald I.P. and Collier J.G. Two
methods of improving the dryout heat flux for high pressure steam-water flow.
AECL2109. 1964.
4.2.62.	Matzner B., Moeck E.O., Casterline J.E. and Wikhammer G.A. Critical
Heat Flux in long tubes at 1000 psi with and without swirl promoters, ASME
Paper No. 65 WA/HT-30.1965.
4.2.63.	Петухов Б.С., Генин Л.Г., Ковалев С.А., Соловьев С.Л. Теплообмен в
ЯЭУ. М.: Изд-во МЭИ, 2003.
4.2.64.	Кузма-Кичта Ю.А., Комендантов А.С., КругА.Ф. Повышение надеж-
ности и эффективности элементов ядерных и термоядерных установок
при закрутке потока с помощью ленты//Энергосбережение. 2007. № 1.
420
Глава 4
4.3. КОЛЕБАНИЯ ПОВЕРХНОСТИ РАЗДЕЛА ФАЗ
Согласно модели работы [4.3.1] при пленочном кипении на гори-
зонтальном цилиндре толщина паровой пленки принимается посто-
янной во времени. В работах [4.3.2, 4.3.4] исследованы колебания по-
верхности раздела фаз при пленочном кипении в большом объеме,
показавшие, что толщина паровой пленки переменная во времени.
В работе [4.3.5] колебания толщины паровой пленки учтены при
моделировании пленочного кипения. Согласно модели предполага-
ется, что толщина паровой пленки меняется во времени по синусои-
дальному закону, и рассчитаны локальная плотность теплового пото-
ка, средняя толщина паровой пленки, а также амплитуда колебаний
границы раздела фаз.
На рис. 4.78 представлен фазовый портрет, полученный для фраг-
мента колебаний толщины паровой пленки в трехмерной проекции
фазового пространства. Как видно, фазовая траектория системы
принадлежит некоторой замкнутой области, при этом в процессе
эволюции фазовая точка через некоторый промежуток времени про-
ходит вблизи наиболее вероятного состояния, отмеченного на рисун-
ке точкой.
Таким образом, наиболее вероятным состоянием системы явля-
ется точка ее неустойчивого равновесия. Возмущения, возникаю-
щие в результате отрыва паровых пузырей в окрестности верхней
образующей цилиндра, приводят к тому, что система теряет устой-
чивость, но при этом релак-
сирует в равновесное состо-
яние через некоторое время,
т.е. энергия возмущений дис-
сипирует в системе, в резуль-
тате чего они затухают. Такой
процесс воспроизводится в
виде сложных колебаний и
отвечает режиму детермини-
рованного хаоса. Строго ут-
верждать о возникновении
детерминированного хаоса
при колебании толщины па-
ровой пленки можно, если
окажутся положительными
старшие показатели Ляпу-
нова, рассчитанные согласно
работе [4.3.6].
u(t+ 2тОк mV
u(t), mV
Рис. 4.78. 3-D фазовый портрет:
АТ = ЮК; АТ = 380 К
Глава 4
421
Пузырьковое кипение. Колебания парового пузыря
при его росте на стенке
Впервые колебания паровых пузырей при их росте на стенке за-
фиксированы в работе [4.3.7] (рис. 4.79). С помощью спектрального
анализа сигналов оптического и акустического датчиков исследована
взаимосвязь колебаний границы раздела фаз и давления в жидкости.
Установлено, что происходят изменения как формы, так и объема па-
рового пузыря. При анализе сигнала оптического датчика построена
функция коэффициента корреляции и рассчитаны временные мак-
ро- и микромасштабы Тейлора (рис. 4.80). Найдены аппроксимации
размеров парового пузыря во время его роста (корреляционная раз-
мерность) в виде N(r) - rfv. Здесь N — число точек, a rf — расстояние
между ними в фазовом пространстве; v — корреляционная размер-
ность. Используя значение временной задержки т, равной среднему
арифметическому между временными масштабами Тейлора, постро-
ен фазовый портрет по экспериментальным данным (рис. 4.81) (вре-
менная задержка т = 5,7 мс, корреляционная размерность v = 0,49).
Для анализа колебаний парового пузыря при его росте на стенке ис-
пользована методика, основанная на расчете коэффициентов Ляпу-
нова (4.3.8, 4.3.9]. Максимальный показатель Ляпунова находится
как
1 N
Ai=-£log2
т i=i
ДМ
(4.3.1)
где £(tf) — расстояние между двумя точками на фазовом портрете в
z-й момент времени; N — число измерений; т — значение временной
задержки.
Рис. 4.79. Зависимость диаметра рас-
тущего на стенке парового пузыря
от времени
Рис. 4.80. Коэффициент корреляции и
временные макро- и микромасштабы
Тейлора
422
Глава 4
Для данной временной задержки найден показатель Ляпунова
Xj = 0,0515. Положительное значение показателя Ляпунова свиде-
тельствует о хаотических колебаниях границы раздела фаз.
В работах [4.3.10—4.3.12] предложена модель, описывающая коле-
бания парового пузыря при его росте на стенке. Система модельных
уравнений, описанная в этих работах, включает в себя уравнение
баланса массы в паровом пузыре (4.3.2), уравнение движения (4.3.3)
и уравнение эволюции толщины теплового слоя жидкости, окружа-
ющего пузырь, во времени (4.3.4):
л . ДТЖ 4тс7?2 -2nRh
2TtRhj-X—^-------------
о г
4 з
о
k J
••	•	6
RR+3RR = —
Рп
2о А
Рп-—"Рж
jfv /
X 8(27?+8)
грп ж (7?+8)2 ’
(4.3.2)
(4.3.3)
(4.3.4)
Получено численное решение системы уравнений, описыва-
ющей колебания парового пузыря при его росте на стенке, кото-
рые при определенных условиях становятся хаотическими. Об
этом свидетельствуют показатели Ляпунова, два из которых поло-
жительные (рис. 4.82). Получено согласование расчетных и экспе-
Рис. 4.81. Фазовый портрет коле-
баний парового пузыря, постро-
енный по экспериментальным
данным
Рис. 4.82. Эволюция коэффициентов
Ляпунова на фазовом портрете
Глава 4
423
Рис. 4.83. Проекция че-
тырехмерного фазово-
го портрета исследо-
ванной системы урав-
нений
О 5 10 1520 25 30 354045 50 55 60 65 70 75 80 85 90 95
Безразмерный радиус парового пузыря
риментальных характеристик колебаний границы раздела фаз (рис.
4.81 и 4.83).
Представлены результаты исследования колебаний границы раз-
дела фаз при пленочном и пузырьковом кипении. Эксперименты
проведены при кипении воды и фреона-113 в большом объеме при ат-
мосферном давлении. С помощью лазерной диагностики зафиксиро-
ваны колебания толщины паровой пленки и парового пузыря, расту-
щего на стенке.
Статистические характеристики колебаний парового пузыря ана-
лизируются с помощью фазовых портретов.
ОБОЗНАЧЕНИЯ:
Р — давление, Па;
Т — температура, К;
q — тепловой поток, Вт/м2;
h — толщина пристенного перегретого слоя жидкости, м;
5 — толщина теплового пограничного слоя, м;
R — радиус парового пузыря, м;
X — коэффициент теплопроводности, Вт/(м2-К);
р — плотность, кг/м3;
М — масса, кг;
424
Глава 4
Список литературы
4.3.1.	Bromley L.A. Heat transfer in stable film boiling//Chem. Eng. Progr. 1950.
V. 46. P. 221.
4.3.2.	Ковалев C.A., Жуков B.M., Кузма-Кичта Ю.А. Методика исследова-
ния колебаний границы раздела фаз при пленочном кипении жидкости с
помощью оптического квантового генератора//ИФЖ. 1973. Июль. Т. 25,
№1.
4.3.3.	Petukhov B.S., Kovalev S.A., Zhukov V.M., Kuzma-Kichta Yu.A.
Investigation of the mechanism of heat transfer upon film boiling of liquid//
Proc. 5th Int. Heat Transfer Conf. Tokyo, 1974. N 4. P. 96.
4.3.4.	Кузма-Кичта Ю.А., Молошников A.C., Нигматулин Б. И., Устинов А. К.
Исследования колебаний границы раздела фаз при пленочном кипении.
Ч. 1.//ТВТ. 1994. Т. 33, № 2. С. 273-278.
4.3.5.	Кузма-Кичта Ю.А., Молошников А.С., Нигматулин Б.И., Устинов А.К.
Исследования колебаний границы раздела фаз при пленочном кипении.
Ч. 2.//Там же. 1995. Т. 33, № 2. С. 273-278.
4.3.6.	Шустер Г. Детерминированный хаос. Введение. М.: Изд-во «Мир», 1988.
240 с.
4.3.7.	Кузма-Кичта Ю.А., Зудин Ю.Б., Бакунин В.Г., Устинов А.А., Салты-
кова Е.В. Исследование колебания раздела фаз с помощью лазерной
диагностики//Материалы XII школы-семинара молодых ученых и спе-
циалистов под рук. акад. РАН А.И. Леонтьева «Проблемы газодинамики
и тепломассообмена в энергетических установках». Москва, 25-28 мая
1999 г.
4.3.8.	Анищенко В.С. Введение в нелинейную динамику: Учеб, пособ. М.-
Ижевск: Институт компьютерных исследований, 2002.144 с.
4.3.9.	Данилов Ю.А. Лекции по нелинейной динамике. Элементарное веде-
ние. М.: Постмаркет, 2001. 184 с.
4.3.10.	Kuzma-Kichta Yu.A., Ustinov А.К., Ustinov А.А. Analysis of interface
oscillations during boiling//12th Intern. Heat Transfer Conf. Grenoble, France,
2002.
4.3.11.	Kuzma-Kichta Yu.A., Ustinov A.K., Ustinov A.A., Kholpanov L.P.
Investigation of interface oscillations during boiling//The Third Intern.
Conf. Transport Phenomena in Multifase Systems. Heat-2002. Baranow
Sandomierski, Poland, June 24-27, 2002. P. 45-52.
4.3.12.	Устинов А.А. Исследование колебаний границы раздела фаз при кипе-
нии: Автореф. дис.... канд. техн. наук. М.: МЭИ, 1988. 20 с.
Глава 5
ИНТЕНСИФИКАЦИЯ РАЗЛЕЛЕНИЯ
ГЕТЕРОГЕННЫХ СИСТЕМ В ТЕПЛО- И МАССООБМЕННЫХ
АППАРАТАХ
Процессы разделения гетерогенных систем составляют основу
многих производств химической, нефтехимической, микробиоло-
гической, горнорудной, газовой, металлургической и других отрас-
лей промышленности, тепловой и атомной энергетики, ракетной
техники, опреснения морской воды, МГД-генераторов. Однако при
разработке и осуществлении этих процессов возникают сложные
проблемы, связанные с необходимостью учета полидисперсности
дискретной фазы, ее концентрации, вращения частиц и взаимодейст-
вия их между собой и со стенками канала, турбулентных пульсаций
несущей среды, а также процессов дробления, слияния, конденса-
ции и испарения, характерных для парогазожидкостных сред. Про-
текание процессов во многих аппаратах (например, на тарелках аб-
сорберов и ректификационных колонн, в барботажных реакторах,
аппаратах с псевдоожиженным слоем и др.) усложняется еще тем,
что здесь имеют место крупномасштабные флуктуации движения
взаимодействующих фаз.
Вместе с тем экономичность и эффективность процессов разде-
ления гетерогенных систем во многих тепло- и массообменных ап-
паратах (испарителях, ректификационных и абсорбционных колон-
нах, выпарных аппаратах, распылительных сушилках, ферментерах,
кристаллизаторах, барботажных реакторах и т.п.), сепарационных
устройствах систем совместного сбора и транспортировки нефти
и газа, установках гидравлической и пневматической классифика-
ции, гидроочистки и осветления суспензий определяются величи-
ной уноса диспергированного компонента. Так, наличие конденсата
в природном газе приводит к снижению до 30% производительно-
сти промысловых и магистральных газопроводов и увеличению до
2% энергозатрат на перекачку газа. Межтарельчатый унос жидкости
в ректификационных и абсорбционных колоннах приводит к умень-
шению движущей силы и ухудшению эффективности разделения,
лимитирует нагрузку колонны по пару (газу).
426
Глава 5
Помимо снижения производительности технологического обору-
дования, унос диспергированного компонента вызывает прямые по-
тери целевого продукта и является нередко причиной загрязнения
биосферы. В связи с этим совершенствование технологических про-
цессов в целях уменьшения уноса этого компонента, создание новых
и совершенствование существующих сепарационных устройств, а
также разработка более точных и надежных расчетных методов яв-
ляется важнейшей задачей, непосредственно связанной с интенси-
фикацией разделения гетерогенных систем в тепло- и массообмен-
ных аппаратах.
5.1. ПАРОГАЗОЖИДКОСТНЫЕ СИСТЕМЫ
5.1.1. Сепарация в циклонах
Центробежная сепарация парогазожидкостных систем отличает-
ся высокой эффективностью и широко применяется в тепло- и мас-
сообменной аппаратуре.
Механизм разделения парогазожидкостных систем в поле цен-
тробежных сил инерции представляет собой весьма сложный про-
цесс, зависящий от ряда физических, конструктивных и эксплуата-
Рис. 5.1. Схема циклонного
сепаратора: 1 — штуцер для
тангенциального ввода па-
рожидкостной смеси; 2 —
перфорированный лист; 3 —
циклон; 4 — штуцер для вы-
вода вторичного пара; 5 —
штуцер для вывода отсепа-
рированной жидкости
ционных факторов.
При тангенциальном вводе парогазо-
жидкостной смеси в циклонный сепаратор
(рис. 5.1) капли жидкости частично отбра-
сываются центробежной силой инерции к
стенкам сепаратора, частично под воздейс-
твием радиального течения смеси, обуслов-
ленного вязкостью закрученного потока, пе-
ремещаются к его оси, попадают в осевую
зону разрежения и выносятся из аппарата.
Теоретическими и экспериментальны-
ми исследованиями [5.1] установлено, что
основным критерием, определяющим ус-
ловия центробежной сепарации двухфаз-
ных систем, является критерий циклонно-
го процесса
dV(p'-p")
У V2 р" ’
где w — окружная скорость пара в цик-
лоне.
Глава 5
427
Критерий циклонного процесса характеризует взаимодействие
равнодействующей центробежной и архимедовой сил и сил молеку-
лярного трения и является аналогом числа Архимеда применительно
к процессам, идущим в поле центробежных сил.
Исследования центро-
бежной сепарации вторич-
ных паров при упаривании
растворов показали, что
унос капель жидкости паром
из циклонного сепаратора
характеризуется тремя гид-
родинамическими режима-
ми (рис. 5.2) [5.1]. Первый ре-
жим соответствует условиям
ламинарного осаждения ка-
пель (применим закон Сток-
са), второй режим — переход-
ный, третий режим соответ-
ствует условиям устойчиво-
го турбулентного движения.
В первом гидродинами-
ческом режиме высота сепа-
20 40 60 100 200 400 600 1000
Рис. 5.2. Зависимость солевого уноса от кри-
терия С (р = 0,05 МПа; 41,3%-ный раствор
NaNO3): 1 - Н = 900 мм; 2 - Н = 600 мм;
3 — Н = 300 мм
ратора в исследованных пре-
делах (300—900 мм) не оказывает влияния на качество пара, так как
процесс осаждения в этих условиях осуществляется главным обра-
зом под воздействием центробежных сил инерции. В этом режиме
при Су < 1,81014 унос определяется по уравнению
S = 0,23 40_8Cy87K^°'63,
(5.1.1)
где Кр = р/л/ор(р'-р").
Критерий Кр характеризует отношение абсолютного давления в
системе к скачку давления на границе раздела фаз.
Обобщенная зависимость для уноса при Су< 1,8-1014 приведена на
рис. 5.3. При Су > 1,81014 сепарация в циклоне осуществляется в две
ступени: в первой ступени — под действием центробежных сил инер-
ции, во второй ступени — под влиянием турбулентных пульсаций в
радиальном направлении.
В переходном режиме, ограниченном областью 1,8-1014< Су< 2,75-1014,
солевой унос зависит от критерия Количественная зависимость,
определяющая интенсивность уноса в этой области, может быть вы-
ражена критериальным уравнением
428
Глава 5
СУ1О’2
Рис. 5.3. Обобщение данных по
уносу в циклоне при Су< 1,8-1014;
1 — 4 — 22%-ный раствор NaNO3;
5, 6, 14, 15 — 31,6%-ный раствор
NaNO3; 7 — 13 — 41,3%-ный раст-
вор NaNO3; 16—18 — раство-
ры NaCl с концентрацией 2000,
1600, 1000 мг/кг соответственно;
1,5, 7, 10, 14 -	0,1 МПа; 3, 8, 6,
11 - Р « 0,075 МПа; 2, 4, 12, 15 -
Р«0,05 МПа; 9,13-Р = 1,7 МПа;
16 - Р= 3,ЗМПа; 17 - Р»0,25МПа;
18 — Р«0,9 МПа
(5.1.2)
где В коэффициент.
В области устойчивого турбулентного движения (Су > 2,75Ю14,
третий режим) уравнение для определения уноса имеет вид
S = 0,52540-7Cy87K^°'27
\0,91
/Н
(5.1.3)
Обобщенная зависимость для уноса при Су> 1,8-1014 приведена на
рис. 5.4.
При работе в области вакуума, как это обычно имеет место при
эксплуатации выпарных установок, плотностью вторичного пара р"
в разности (р* — р"), входящей в критерий С , можно пренебречь, так
как при этих условиях р » р".
Одним из основных параметров циклонного сепаратора являет-
ся отношение т площадей поперечного сечения циклона А и штуце-
ра а, тангенциально подводящего парожидкостную смесь. Так как
т = А/a, то а = А/т — 7iD2/(4ni).
Из уравнения расхода G = аюШ1р"= [71Г2/(4п?)]туштр" найдем
^шт “ 4mG/(W2p").
Приняв w)Kp = wiutи подставив найденное значение окружной ско-
рости вторичного пара в критерий циклонного процесса Су, получим
Су = [16m2GVfitWlHfp' - р")/р"].	(5.1.4)
Глава 5
429
Рис. 5.4. Обобщенная зависимость
солевого уноса при Су> 2,75-Ю14:
растворы NaNO3 весовой концен-
трации 22% (точки 3, 5, 6, 9 и 10),
31,6% (точка 4) и 41,3% (точки 1, 2,
7 и 8); 1-4 - Н=900 мм; 5-7 -
Н = 600 мм; 8—10 — Н = 300 мм;
давление от 0,025 до 0,075 МПа
Подставив значение Су из уравнения (5.1.4) в уравнение (5.1.1) и
(5.1.3) и произведя соответствующие преобразования, получим урав-
нение для определения диаметра циклона D в зависимости от его
производительности G и допустимого значения солевого уноса. При
Су< 1,81014 диаметр циклона определяется из равенства
D = (1,4-IO’5 )[mG/(цд$°'58К°'36 )]>/(₽' Р") /р"	(5.1.5)
Высота циклона Н здесь может приниматься из конструктивных
соображений в пределах 300 — 1000 мм.
При Су > 2,75-1014 диаметр циклона определяется из равенства
0,52
.	(5.1.6)
В расчетах обычно //принимают в пределах 1500—1800 мм.
Вопрос о допустимом значении уноса S должен решаться для каж-
дого конкретного продукта с учетом его индивидуальных особеннос-
тей (стоимости, токсичности, способности к отложениям, коррозион-
ной активности) и назначением пара.
При заданном диаметре производительность одного циклона по
р-р'
р"
D 0'91’10 ngS0'58^016
pgd лр
д(р'-р")/Н
вторичному пару определяется по следующим уравнениям:
Су < 1,81014;
G = (о,71405 )(PpgS°'58/Cp 36 / W)7p" /(р' -р");
Су >2,75-Ю14;
G = (l,1404)—------— H	-7-^—?
v 7 w \P'-P"l / V9(P'-PJ
(5.1.7)
(5.1.8)
430
Глава 5
Увеличение окружной скорости допустимо лишь до определен-
ного значения, так как это приводит к росту степени дисперсности
жидкой фазы и уноса.
Для обеспечения более эффективного разделения парогазожид-
костных систем целесообразно идти по пути уменьшения диаметра
циклонов и использовать сепарирующие устройства типа батарей-
ных циклонов или гидроциклонов диаметром 40—250 мм.
Необходимое число циклонных элементов определяется отноше-
нием п = Gz/Gp где Gz — требуемая общая производительность ап-
парата.
Динамический уровень раствора во избежание затопления шту-
цера для ввода парожидкостной смеси должен находиться на 300 —
500 мм ниже его оси.
Отношение т следует принимать в расчетах в пределах 4—10.
Для равномерного распределения осевых скоростей пара по сече-
нию циклона перед пароотводящим штуцером на расстоянии от него,
равном диаметру циклона, устанавливается перфорированный лист
со свободным сечением, составляющим примерно 10% от сечения
циклона. Перфорированный лист может быть заменен жалюзийным
сепаратором.
Приведенные зависимости получены для условий, когда в посту-
пающем в циклонный сепаратор парожидкостном потоке массовый
расход жидкости значительно выше массового расхода пара, т.е. ког-
да речь идет о выделении пара из парожидкостного потока, в котором
он образовался. Для условий, когда в циклонный сепаратор поступа-
ет парожидкостный или газожидкостный поток, в котором жидкости
относительно немного и она распределена в паровой (газовой) фазе
в виде отдельных капель, унос определяется другими закономерно-
стями. Одним из основных факторов, влияющих на эффективность
отделения капельной жидкости в этих условиях, является скорость
ввода парогазожидкостной смеси в тангенциальный патрубок w''B.
На рис. 5.5 представлены зависимости уноса со от w"B при различ-
ных отношениях площадей поперечного сечения циклона и входного
патрубка т. Данные получены на циклоне диаметром 200 мм с пря-
моугольным входным патрубком, в который поступал поток воздуха,
содержащий двухпроцентный водный раствор Na2HPO412H2O*. Со-
держание капельной влаги в воздухе составляло 0,05 кг/кг. Как видно
из рисунка, при всех значениях т влияние w"B на со не однозначно.
* Здесь (о представляет собой отношение содержания Na2HPO4 в 1 кг отводимого из циклона
воздуха к концентрации этой соли в водном растворе и равна количеству влаги, содержащей-
ся в единице воздуха (кг/кг). Унос, выраженный в таком виде, как и обычно, обозначается to, а
унос в абсолютном выражении (мг/кг, г/кг) — S.
Глава 5
431
Рис. 5.5. Зависимость уноса
со от скорости ввода газа w"B
(дн = 0,05 кг/кг, D = 200мм): 1 —
т = 3,14; 2 - т = 6; 3 - т = 10;
4 — т = 15; 5 — т = 20
Сначала с увеличением wBB наблюдается снижение уноса со, затем, по
достижении определенных значений wBB, наблюдается его рост. Воз-
растание со здесь связано с тем, что при больших значениях wBB про-
исходит срыв пленки жидкости со стенок циклона и вторичный унос
образующихся при этом капель.
Визуальные наблюдения показали также, что основная масса от-
сепарированной жидкости при всех рассмотренных режимах стека-
ет в нижнюю часть циклона и выводится через сливной патрубок.
Часть капель, захваченных восходящим закрученным потоком
газа, оседает на стенках циклона выше верхней кромки входного пат-
рубка и также стекает в виде пленки. Однако при увеличении скоро-
сти газа пленка сначала зависает, а затем поднимается вверх и вы-
водится из циклона вместе с газом. Анализ данных ряда авторов и
визуальные наблюдения показали, что вторичный унос зависит от
толщины пленки жидкости и скорости газа, при котором начинает-
ся срыв жидкости со стенок. С увеличением начального содержания
жидкости в потоке дн толщина пленки возрастает. При этом увеличи-
вается также унос со (рис. 5.6).
Сравнивая данные, полученные при различных значениях отно-
шения площади циклона к площади входного патрубка т (см. рис. 5.5
и 5.6), можно также заметить, что существует т, при котором унос
имеет наименьшие значения. В приведенных экспериментальных
данных (см. рис. 5.5 и 5.6) это наблюдалось при т = 15.
В работе [5.2] приводится критериальная обработка эксперимен-
тальных данных, полученных при сепарации жидкости из потоков
432
Глава 5
Рис. 5.6. Зависимость си от начального со-
держания жидкости в газе д : 1 — т = 3,14;
w"B =11,1 м/с; 2 — т = 6; w"B = 21,1 м/с; 3 —
т = 10; vr"B = 35,4м/с; 4 — т = 15;wBB = 53м/с;
5 — т = 20; wBB = 71 м/с
воздуха, содержащих капли раствора Na2HPO442H2O, в циклонах
диаметром 150 и 200 мм (рис. 5.7). Для области, в которой с ростом
влажность уменьшается, экспериментальные данные обобщены зави-
симостью
со = 10-2
w" d3/2
vv ввк.ср.
,_____х-0,8
'Р'-Р"
^рР" J
„0,7-0,53
9н т
(5.1.9)
V
в которой dK ср — диаметр капли средней массы на входе в циклон;
Я = R — Ь/2, где R — диаметр циклона; b — ширина входного (пря-
моугольного) патрубка.
О-4
▼ -5
• -6
Д-7
 -8
4-9
$-10
а- 11
б- 12
и-13
©-14
Э-15
-е—16
ф-17
т
3,14
со
51
4-
3-
2-
ю-5-
8:
6-
4-
6,0
10,0
15,0
3,0
6,0
10,0
15,0
3,14<
2	4	6 810'3	2 3
Рис. 5.7. Обобщение экспериментальных данных: (а) — для области, в которой
унос уменьшается с ростом wBB; (б) — для области, в которой со увеличивается с
ростом w"B; 1 — 4, 9—17 — циклон 0 200 мм; 5 —8 — циклон 0 150 мм. Содержа-
ние жидкости в потоке д'. (а) — 1 — 8 — 0,05; 9 — 0,02; 10, 14 — 0,03; И, 16 — 0,05;
13-17 - 0,06 кг/кг; (б) - 1 -8 - 0,05; 9, 13 - 0,03; 10, 14 - 0,04; И, 15 - 0,05; 12,
16 — 0,06 кг/кг
Глава 5
433
Зависимость (5.1.9) обобщает экспериментальные данные, полу-
ченные, когда d rn изменялся от 70 до 220 мкм, ст — от 0,02 до 0,07,
^3/2 г~;
ш — от 3 до 15, а комплекс - -в кср' -—— — от 20 до 190.
v" у КРР"
При образовании капель в аппарате барботажного типа диаметр
капли средней массы dKcp может быть определен из зависимости
[5.3]:
кср =0,48 Р 0
___5___	UC?(P'-P")J
g(p'-p")
(5.1.10)
Формула действительна при значениях критерия Су< С , где
Супр = 2,04-1О6ш0,73.	(5.1.11)
Для области, в которой с увеличением w"B влажность растет, полу-
чена зависимость
/	w"D„
со = (7,2-10—22)  вв ц
\	/ у"
„0,7-2,75
т
(5.1.12)
где D — диаметр циклона. Экспериментальные данные, использо-
ванные при построении обобщенной формулы, получены при тех же
1р'~р"
диапазонах изменения т и дк, когда комплекс - — — -—— нахо-
V" \ р"
дился в пределах от 4,6106 до 16-106 .
Диапазон значений wBB, котором с увеличением скорости газа во
входном патрубке влажность уменьшается, может быть расширен,
если применить циклон, имеющий специальные щели для отвода
жидкостной пленки. В циклоне такой конструкции (рис. 5.8) большая
часть осадившейся жидкости отводится через вертикальную щель в
корпусе, расположенную вблизи зоны формирования пленки; плен-
ка, образовавшаяся из осадившихся капель выше входного патрубка
циклона, отводится через две кольцевые щели. Значения уноса, по-
лученные при двух т в зависимости от скорости газа, wBB приведены
на рис. 5.9. Из рисунка видно, что в циклоне такой конструкции ско-
рости газа <в могут быть заметно повышены. Полученные при этом
экспериментальные данные обобщаются зависимостью (5.1.9).
Следует иметь в виду, что приведенные зависимости установлены по данным, полученным
в опытах с одной воздухожидкостной средой, и, конечно, не могут применяться для расчета
циклонных сепараторов, в которых протекают другие парогазожидкостные потоки.
434
Глава 5
Рис. 5.8. Схема циклона с
отводами жидкостной плен-
ки: 1 — циклон; 2 — шту-
цер ввода газожидкостно-
го потока; 3 — вывод газа;
4 — камера с кольцевыми
щелями; 5 — камера с вер-
тикальной щелью; 6 — слив
жидкости из камер; 7 — вы-
вод из циклона
810	2	4	6	8 102 <в, м/с
Рис. 5.9. Зависимость со от w"B (1)ц = 150 мм,
дн = 0,05 кг/кг): 1 — ш = 3;2 — ш = 6 — цик-
лон с отводами жидкой пленки; 3 — т = 3; 4 —
т = 6 — циклон без отводов жидкостной плен-
ки
5.1.2 Эффективность циклонных элементов в тарельчатых
аппаратах
На рис. 5.10 показана схема циклонного сепаратора, установленно-
го в тарельчатом тепло- или массообменном аппарате [5.4]. Сепаратор
Рис. 5.10. Циклонный
сепаратор
состоит из внутреннего 1 и наружного (внеш-
него) 2 патрубков, завихрителя 3 и конуса 4. За-
вихритель выполнен в виде радиально распо-
ложенных пластин, установленных под опреде-
ленном углом к горизонту
Пар (газ), содержащий капли жидкости, пос-
тупает в нижнюю часть внутреннего патрубка
и, проходя через зазоры направляющих плас-
тин завихрителя, приобретает вращательное
движение.
Под действием возникающей при этом цент-
робежной силы инерции капли жидкости отбра-
сываются к внутренней стенке патрубка, оседа-
Глава 5
435
ют на ней и движутся в прямотоке с
паром (газом) вверх в виде закручен-
ной пленки. При достижении верхнего
края внутреннего патрубка жидкость
отбрасывается на стенку внешнего
патрубка и под действием силы тяжес-
ти стекает через гидравлический за-
твор на нижележащую тарелку. Отсе-
парированный пар (газ) выходит через
расширительный конус в межтарель-
чатое пространство.
Основные конструктивные харак-
теристики элементов циклонного се-
паратора приведены на рис. 5.11. Ус-
тановлено, что процесс сепарации
протекает наиболее эффективно в се-
Рис. 5.11. Конструктивная схема
циклонного сепаратора:
dl = 85 мм; D— 130 мм; Н=50 мм;
h = 60 мм; d = 105 мм
параторе с диаметром патрубка 100 мм, когда угол атаки завихрителя
составляет а = 30°.
Гидравлическое сопротивление Др сухого завихрителя можно оп-
ределить по зависимости
Др = 3,6p"w2Kp/2,	(5.1.13)
а сухого циклонного сепаратора — по зависимости
Др = 18,Зр"и^кр/2.	(5.1.14)
На рис. 5.12 приведена зависимость уноса жидкости от критерия
циклонного процесса
С =(w2
У \ окр
/R
\ / I----------\3 "I
) (^^(р'-р")) /у2 [(р'-р'О/р"}
Из рисунка видно, что унос жидкости из циклонного сепаратора
в зависимости от критерия циклонного процесса характеризуется
двумя режимами. В первом режиме (Су<2-107для системы вода—воз-
дух и Су< 1-Ю5 для системы веретенное масло—воздух) унос опреде-
ляется по уравнению
S = 0,340"21С* (v'/v")5,5;	(5.1.15)
во втором режиме (Су > 2-Ю7 для системы вода—воздух и Су > Г105 для
системы веретенное масло—воздух) — по уравнению
S = 6C“J(v'-v")0J2.	(5.1.16)
В формулах (5.1.15) и (5.1.16) унос имеет размерность г/кг.
436
Глава 5
Рис. 5.12. Зависимость уноса жид-
кости от критерия циклонного
процесса (система веретенное
масло — воздух): 1 — £>ж = 5м3/(м2-ч);
2 — £>ж = 10м3/(м2-ч), колонна пря-
моугольного сечения 270x150 мм;
3 — колонна диаметром 250 мм;
4 — колонна диаметром 410 мм
Эффективность центробежной сепарации в тарельчатых аппа-
ратах весьма велика. Так, при работе на колонне диаметром 800 мм,
снабженной 13 сепарирующими элементами, унос жидкости при
средней скорости газа по сечению колонны до 1,5 м/с практиче-
ски не наблюдался и достигал 10% только при средней скорости газа
2,2 м/с. Такой унос считается обычно предельным для нормальной
работы тарельчатых аппаратов. На насадочной колонне диаметром
600 мм, снабженной шестью сепариру-
ющими элементами, унос при скорости
газа 1,17 м/с и различных нагрузках по
жидкости также практически отсутст-
вовал (рис. 5.13).
Унос капель зависит от физико-хи-
мической природы жидкости и газа.
Так, при скорости газа по сечению ко-
лонны 2 м/с эффективность улавли-
вания капель на системе вода—воздух
составляет 99,3%, а на системе вере-
тенное масло—воздух — 88,2%.
Рис. 5.13. Унос в зависимости от нагрузки ап-
парата по жидкости 1>ж при постоянной ско-
рости газа: 1 — без сепаратора; 2 — с сепара-
тором
Глава 5
437
5.1.3. Разделение газожидкостных смесей в циклонах-
классификаторах
Циклонные сепараторы используют в основном для более полного
выделения капель жидкости из газового потока. Однако в ряде слу-
чаев возникает необходимость предварительного частичного выде-
ления (классификации) определенной доли капель из газожидкост-
ного потока. Такая классификация возможна в случае конденсации
смеси паров веществ, имеющих различные температуры кипения, и
фракционном выделении конечных ценных продуктов. Кроме того,
классификация может осуществляться в целях уменьшения началь-
ного содержания жидкости в газе qK, поступающем на сепарацию.
Эффективность работы циклонных сепараторов в числе прочих
показателей может оцениваться по наибольшему диаметру капель
dH, не уловленных в циклоне. Нами было установлено [5.9], что на эф-
фективность работы циклонных сепараторов существенное влияние
оказывает дисперсный состав газожидкостных смесей.
В ряде работ [5.10, 5.11] приводятся результаты исследования дис-
персного состава капель на выходе из выпарных аппаратов. Было
установлено, что распределение капель по размерам на выходе из
аппаратов барботажного и безбарботажного типов подчиняется ло-
гарифмически нормальному закону.
Принимая, что распределение капель на входе в циклон логариф-
мически — нормальное, а также зная заданную величину уноса ка-
пельной влаги из циклона GyH, можно определить наибольший диа-
метр капель dH, не уловленных в циклоне.
Доля унесенной жидкости может быть определена по формуле
igd„ M.-W
GyH=—b=fe 2‘9° dlgd,	(5.1.17)
1дсг>/2л
где GyH = w/gH — доля унесенной жидкости.
По заданной доле уноса GyH можно определить dH. Сравним фор-
мулу (5.1.17) с функцией ошибок для нормального распределения слу-
чайной величины
ф-(х) = -Д=/e-'2/2dt,	(5.1.18)
х/2п
где Ф‘(х) — стандартное нормальное распределение — частный слу-
чай общего нормального распределения,
F(x) = ^/2^1e 2°2 dt’	(5119)
т — математическое ожидание; о — среднее квадратичное отклонение.
438
Глава 5
В нашем случае т соответствует Igd, а о — Igo. В соответствующих
формуле (5.1.17) обозначениях будем иметь
G =Ф-р9ан-1д^=ф>(х)
ун I igy J
откуда
,..Jg<4-igd
igy
где х определяется по известным таблицам [5.12].
Потенцируя выражение (5.1.21), получаем
(5.1.20)
(5.1.21)
dH = do*.	(5.1.22)
Так как
или
1	(d
1ду=д(1дйМакс-1дйМин)=1д	(5.1.23)
°	к амин 7
^макс
< ^мин у
(5.1.24)
то выражение для определения dH будет иметь вид:
Qмакс
^мин >
<4
(5.1.25)
Зависимость (5.1.25) получена в предположении, что в циклоне не
происходит перераспределения капель по размерам.
Среднее квадратичное отклонение о можно также определить по
углу наклона а прямой к оси абсцисс графика распределения капель
по размерам в вероятностно-логарифмических координатах [5.13].
Однако для практических расчетов значения dH можно использовать
формулу (5.1.25).
В целях изучения возможности фракционного разделения га-
зожидкостного потока и получения расчетных зависимостей были
проведены исследования [5.9]. Опыты проводились на циклонах диа-
метром 0,15 и 0,2 м. В ходе экспериментов проводились замеры дис-
персного состава капель во входном и выходном патрубках цикло-
нов. Отбор проб капель осуществлялся посредством двухкаскадного
импактора. Максимальный и минимальный размеры капель во вход-
ном и выходном патрубках циклонов составляли 180 и 2; 21 и 2 мкм.
На основе статистической обработки проб капель было установлено,
что распределение капель логарифмически — нормальное. Это сов-
падает с данными ряда авторов [5.10, 5.11] по распределению капель
на выходе из выпарных аппаратов.
Глава 5
439
При оценке влияния дисперсности газожидкостного потока на
величину dH был использован полученный нами модифицированный
критерий циклонного процесса С :
С
УМ)
r^5v V р"
(5.1.26)
где w"B — скорость ввода газожидкостной смеси в циклон, м/с; d —
среднемассовый диаметр капель, м; гср — средний радиус входного
патрубка циклона, м; v — кинематическая вязкость газа, м2/с; р', р" —
плотность жидкой и газовой фаз соответственно, кг/м3.
Необходимо отметить, что начальное содержание жидкости в га-
зожидкостной смеси не оказывает влияния на значение dH при изме-
нении величины qH от 0,02 до 0,07.
Обработка опытных данных позволила получить расчетную зави-
симость (5.1.27) для определения величины dH:
dH=75,6C^5.
и	yMj
(5.1.27)
На рис. 5.14 представлена зависимость dH от критерия циклонного
процесса CyMf
Как видно из графика, экспериментальные точки удовлетворитель-
но группируются около линии, описываемой уравнением (5.1.27), кото-
рое было использовано в методике расчета циклона-классификатора.
Методика расчета основывается на статистическом подходе к оп-
ределению наибольшего диаметра dH капель на выходе из циклона-
классификатора и экспериментальных данных по dH на выходе из цик-
лона в зависимости от величины критерия СуМ1 на входе в циклон.
Для расчета геометрических размеров и режимных параметров
циклона-классификатора задается доля уноса GyH = Ф‘(х), по кото-
рой определяется величина аргумента х [5.12]. Затем по уравнению
(5.1.25) рассчитывается зна-
чение dH, а величина крите-
рия С — по уравнению
(5.1.27).
Для определения геомет-
рических размеров цикло-
на-классификатора задает-
ся величина т [5.9] и рас-
считывается осевая ско-
рость газа w"c по сечению
сепаратора
w” =0,55С^т41,6. (5.1.28)
Рис. 5.14. Зависимость dH, мкм, от критерия
м: 1> 2 — 0; 3, 4 — 0,15. Данные 1, 3 —
опытные; 2, 4 — расчетные [по уравнению
(5.1.27)]
440
Глава 5
Далее определяется диаметр циклона £>ц, площадь	его поперечно-
го сечения Гц и площадь входного патрубка Гп:	
Dji = /	,	(5.1.29)
4 V°'785lC	
Гц=0,785Рц;	(5.1.30)
4 =	(5.1.31)
где V" — объемный расход газа, м3/с, а также величина скорости вво-
да газожидкостной смеси w"B в циклон
<в=ш<с.	(5.1.32)
Для определения геометрических размеров входного патрубка:
ширины b и высоты h рассчитывается величина среднего радиуса
входного патрубка циклона гср, определяемая как	
гср — г (^ц /2^,	(5.1.33)
где г — безразмерный радиус ввода;	
г =	(5.1.34)
Тогда	
b = 2(Рц/2-гср)	(5.1.35)
и h = fu/b	(5.1.36)
Гидравлическое сопротивление циклона Др рассчитывается по
уравнению
Др = 1,472^^22-.	(5.1.37)
Высота парового пространства циклона Нпп над осью входного
патрубка определяется из соотношения Нпп/£>ц = (44-9) [5.1,5.14].
5.1.4. Сепарация струями жидкости
Сепарация парогазожидкостных систем струями жидкости яв-
ляется принципиально новым методом, широко реализованным в
настоящее время в конструкциях тарелок с двумя зонами контакта
фаз [5.5—5.7]. Пленки жидкости, перекрывающие сечение аппарата
и взаимодействующие с паровым (газовым) потоком, оказывают воз-
действие, соизмеримое с сепарирующим эффектом лучших сепари-
рующих устройств.
При подаче парожидкостной смеси под пленку происходит захват
поверхностью пленки капель жидкости и вынос их на стенки сепара-
Глава 5
441
тора. При этом имеет место диспергирование конца пленки проска-
кивающим потоком пара (газа). Визуально установлено, что проскок
пара происходит по кольцу у стенок сепаратора. По мере увеличения
скорости пара неразрушенная часть пленки сокращается, а диспер-
гированная часть увеличивается.
Распад пленки жидкости и вторичный унос образовавшихся при
этом капель является сложным процессом, зависящим от ряда фи-
зических, конструктивных и технологических факторов. В резуль-
тате анализа взаимодействия сплошной пленки жидкости с потоком
пара, содержащим капельную жидкость, установлено, что унос ка-
пельной влаги, в общем виде, может быть выражен зависимостью
т = /(We, Re, Кр) [5.7]. Здесь число Вебера We = р"Лп2/о является ме-
рой отношения инерционных сил потока к силам поверхностного на-
тяжения, т.е. учитывает взаимодейст-
вие деформирующейся пленки с паро-
вой (газовой) средой.
Пленки жидкости, перекрывающие
сечение тарелки, создаются распре-
делительными устройствами, по кото-
рым жидкость перетекает с верхней
тарелки на нижнюю. Распределитель-
ное устройство (рис. 5.15) представляет
собой цилиндрический насадок, в тор-
це которого устанавливается распре-
делительный конус. Плоскость осно-
вания конуса располагается в паровом
Рис. 5.15. Схема распредели-
тельного устройства
пространстве на 150—250 мм над уровнем раствора. Пропускная спо-
собность распределительного устройства определяется из выра-
жения
•^ж	,
где |Л — коэффициент расхода; ащ — площадь сечения цели, м2; Но —
высота столба жидкости в распределительном устройстве, м.
Для устройства, приведенного на рис. 5.15, при турбулентном ре-
жиме истечения коэффициент расхода ц может быть определен по
следующим зависимостям:
для насадка с острой кромкой
ц = О.467(а„/81Ц)о“;	(5.1.38)
для насадка со скругленной кромкой
ц = О,541(с1в/8Щ)0'11;	(5.1.39)
где 5щ — высота щели.
442
Глава 5
Формулы действительны, когда
Re = ^2gH°d3 > (i, 4 -1,б)104.
v
Здесь d3 — эквивалентный диаметр щели.
При меньших значениях числа Re коэффициент ц можно опреде-
лить по формулам:
для насадка с острой кромкой
p = 10,5Re"°'35
2gH0
о/с?эр'
(5.1.40)
для насадка со скругленной кромкой
ti = 3,36Re-«2 в-
(У/фэР
(5.1.41)
Формулы получены на насадках размером 0 45x2,5; 0 65x2,5;
0 106x3 мм в опытах с водой и водными растворами смеси оксиэти-
лированных алкифенов (ОП-7) и натриевой соли карбоксиметилцел-
люлозы (КМЦ-500). Отношение 6щ/с?н находилось в пределах от 0,025
до 0,25 [5.8]. Угол наклона поверхности распределительного конуса
а = 15°.
Схема взаимодействия пленки жидкости с паровым потоком
показана на рис. 5.16. В отсутствие парового потока в сепарацион-
ном пространстве жидкость стекает с конуса (диска) в виде свобод-
но движущейся в радиальном направлении пленки, имеющей форму
параболоида и полностью перекрывающей сечение сепаратора. Уве-
личение напора жидкости Но от 0 до 100—130 мм вод.ст. приводит к
резкому изменению координат пленки, в то время как дальнейшее
увеличение до 700 мм вод. ст. сказывается незначительно.
При поступлении пара под пленку наблюдается некоторый подъем
ее, увеличивающийся с повышением скорости парового потока. Заме-
ры координат конца струи жидкости показали, что основной подъем
происходит при изменении скорости пара w'q от 0 до 0,37 м/с. Даль-
нейшее увеличение
Рис. 5.16. Схема взаимодействия пленки
жидкости с паровым потоком
скорости пара не при-
водит к значительным
изменениям коорди-
нат конца струи. Об-
работка данных пока-
зала (рис. 5.17), что в
пределах изменения
скорости пара в сво-
бодном сечении сепа-
Глава 5
443
Рис. 5.17. Зависимость относи-
тельной высоты подъема кон-
ца струи Ду/у0 от скорости пара
Wq по сечению сепаратора при
различных расходах жидкости
(а = 15°; 8Щ = 6 мм; Р = 0,1 МПа,
5%-ный водный раствор NaNO3):
1 — £> = UmVh; 2-D= 1,4м3/ч;
3 — D = 1,6 м3/ч; 4 — D_= 1,8 мУч
ж r ' ж r
ратора от 0,51 до 2,54 м/с (р = 0,1 МПа) зависимость относительной
высоты подъема струи Ду/у0 от скорости wQ является линейной (при
= const). Установлено, что при высотах кольцевой щели 2—6-мм
пленка жидкости устойчива и имеет разрывы только у стенок сепа-
ратора в местах прорыва пара. С дальнейшим увеличением высоты
кольцевой щели до 5Щ = 7—8 мм истечение жидкости из распреде-
лительного насадка становится неустойчивым, появляются разрывы
по всей поверхности пленки и при взаимодействии ее с перекрест-
ным потоком пара (в интервале скоростей пара по сечению сепарато-
ра w'q от 0,35 до 2,51 м/с) наблюдается пульсационный режим истече-
ния пленки.
Для устойчивого истечения пленки жидкости из распределитель-
ного устройства необходимо, чтобы площадь внутреннего сечения
цилиндрического насадка Ан > ащ. При расходе жидкости в насадке
DH = 0,8—1,8 м3/ч наилучшей сепарационной способностью обла-
дает пленка жидкости, образующаяся при высоте кольцевой щели
5Щ = 6 мм. При этом разделение парожидкостной системы в сепара-
торе является более полным при угле атаки струи а = 15°.
На рис. 5.18 приведены кривые, устанавливающие зависимость
уноса жидкости от приведенной скорости в сепараторе, снабженном
распределительными устройствами, создающими сепарирующие
струи жидкости, и без них. Кривые построены при высоте парового
пространства Н = 1200 мм, т.е. когда унос определяется количеством
транспортируемых капель. Как видно из рисунка, сепарирующие
струи заметно снижают влажность пара. При аппроксимации кри-
вых (построенных при сепарации парожидкостной среды струями
жидкости) степенной функцией со = Cw"n общая кривая может быть
разбита на две области. В первой области со незначительно зависит от
444
Глава 5
Рис. 5.18. Зависимость уноса жидко-
сти из раствора NaNO3 от приведен-
ной скорости пара: 1, 5 — Р = 0,1 МПа;
2 - Р = 0,075 МПа; 3 - Р = 0,05 МПа;
4, 6 — Р = 0,02 МПа; 1 — 4 — сепарация
струями жидкости (а = 15°; 5Щ = 6 мм;
£>ж =1,0 м3/ч; 5%-ный раствор NaNO3);
5, 6 — сепарация в свободном паровом
объеме
Wq , во второй зависимость более резкая, и показатель п принимает
значение, равное 4 [5.7].
При малых скоростях пара образование капель происходит в ос-
новном за счет поверхностной энергии, освобождающейся при раз-
рыве вздутой пленки. По мере увеличения Wp' все большее значение
приобретает кинетическая энергия парового потока, что приводит к
увеличению количества образующихся капель. Таким образом, при
повышенных нагрузках унос состоит из более крупных капель, обра-
зующихся главным образом вследствие дробления пленки жидкости
потоком пара.
Независимо от нагрузки по пару в работе струйного сепаратора
можно наблюдать два режима: устойчивый и неустойчивый. Устой-
чивый режим истечения для приведенной конструкции распредели-
тельного устройства наблюдается при £>ж >0,8 м3/ч. В этих услови-
ях пленка полностью перекрывает сечение аппарата и проскок пара
происходит на периферии струи у стенок сепаратора. Амплитуда от-
клонения конца струи от среднего положения в этих режимах незна-
чительна. Неустойчивый (пульсационный) режим истечения имеет
место при D = 0,4—0,8 м3/ч. В таких режимах вследствие нарушения
сплошности пленки и скачкообразного изменения ее сопротивления
наблюдается пульсация, прорыв пара происходит по всей поверхно-
сти струи и амплитуда отклонения конца струи от среднего положе-
ния заметно возрастает.
С увеличением £>ж от 0,4 до 0,8 м3/ч наблюдается уменьшение уно-
са. При £>ж свыше -1,2 м3/ч унос возрастает с увеличением расхода
жидкости (рис. 5.19).
Глава 5
445
Рис. 5.19. Зависимость уноса (о от
расхода жидкости при различ-
ных приведенных скоростях пара
(а = 15°; 8Щ = 6 мм; Р — 0,1 МПа;
5%-ный раствор NaNO3): 1	—
Wo = 0,51 м/с; 2	= 1,02 м/с; 3 -
w'o = 1,53м/с; 4 - w" = 2,02 м/с; 5 -
Wq — 2,54 м/с
На рис. 5.20 приведены значения 0) в зависимости от скорости газа
при трех значениях высоты парового пространства. Как видно из ри-
сунка, при сепарации капель струями жидкости влияние высоты па-
рового пространства качественно остается таким же, что и при сепа-
рации влаги в свободном паровом объеме.
Все полученные экспериментальные данные обобщаются дву-
мя зависимостями (рис. 5.21 и 5.22). Одна из них (рис. 5.21) обоб-
щает результаты, полученные при режимах, в которых (D^v/q1,6,
а другая (рис. 5.22) — данные, относящиеся к условиям, когда
WooWo'3'6. Первая зависимость построена по данным, полученным
на экспериментальной установке с колоннами диаметром dc, рав-
ными 300 и 500 мм при уносе воды воздухом, и колонне диамет-
ром 260 мм при уносе раствора NaNO3 различных концентраций
[Р = 0,1 МПа). Высота сепари-
рующего объема Нс при этом
изменялась от 650 до 1400 мм,
диаметры насадков имели зна-
чения 35, 40 и 80 мм, а шири-
на щели 6Щ составляла 4—6 мм;
угол а изменялся от 0 до 15° (см.
рис. 5.15). Эта зависимость име-
ет вид
(0 = 0,3-10’9Re1,6Weo,5(HcZdc)'1,6k,
Рис. 5.20. Зависимость со от скорости
воздуха при трех значениях высот
сепарирующего объема Н (5 = 6мм;
£>ж=1,0м3/ч)
446
Глава 5
Рис. 5.21. Обобщение дан-
ных для режимов, в кото-
рых coTCWo : 1 —3 — dc = 300M,
Н = 850, 1400 и 850 мм;
£>ж = 1,0, 1,0 и 1,8 м3/ч; 4-
6 — dc — 500 м, Нс = 850 мм;
D = 1,8; 2,6 и 3,4 м3/ч;
7 _ 8 - dc = 260м, Нс = 1200мм;
£>ж= 1,0и 1,2м3/ч; 1—6 — сис-
тема воздух-вода а = 0°;7,8 —
система пар — 5%-ный раст-
вор NaNO3, а = 15°
где	Re = (Oodc/v; We = 2gH0[i2 cos2 ар"5щ/о, (5.1.42)
k = dc/dc (здесь = 0,3 м); Но - высота столба жидкости в распреде-
лительном устройстве; |л — коэффициент расхода.
Рис. 5.22. Обобщение данных
для режимов, в которых
0)те^о • 1-4 _ dc = 30° мм»
Н = 850, 1480, 650 и 850 мм,
Г>ж = 1,0, 1,0, 1,0 и 1,8 м3/ч,
система вода—воздух; 5 —
9 - dc = 260 мм, Н = 850 (5)
и 1200 (6 -9), Рж = 2,6 м3/ч (5)
и 1,2 м3/ч (6-9), Р = 0,1 МПа
(5,6), 0,75 МПа (7), 0,5 МПа (8),
0,25 МПа (9), система пар —
5%-ный рас твор NaNO3; 10—
12 - d = 400 мм, Нс = 600,
450 и 330 мм, £>ж = 1,5 м3/ч,
система воздух — вода
Глава 5
447
Зависимость (5.42) справедлива в следующих диапазонах пере-
менных: 8,0403<Re<2,7404; 7,940’3<We< 10,040‘2и 1,7<Hc/dc<4,7.
Вторая зависимость (для режимов, когда cdtotvq3,6) построенапо экс-
периментальным данным, полученным при изучении уноса паром
капель жидкости из растворов NaNO3 различных концентраций в
аппарате диаметром dc = 260 мм при давлениях 0,025, 0,050, 0,075 и
0,1 МПа, а также при изучении уноса воды воздухом в колонне диа-
метром 300 мм и на тарелках аппарата диаметром 400 мм. Эта зависи-
мость обобщается формулой
w = 10'4Re3’6 We°'2K“4(Hc/dc)	(5.1.43)
где Kp = P/7ffa(p'-p").
Формула действительна в следующих пределах изменения пере-
менных:
10,9403 < Re < 5.87404; 0,310'2< We< И.О-Ю'2;
0,88 < Hc/dc < 4,7 и 9,5402 < Кр < 4,24 О3.
В числе Вебера We [см. формулы (5.1.22) и (5.1.23)] в качестве ха-
рактерного линейного размера I принята толщина пленки жидкости
на краю распределительного диска, равная толщине щели 5 , а в ка-
честве скорости — скорость жидкости в этом сечении, определяемая
из зависимости = уСу/2дН0 cosa.
При определении числа Рейнольдса Re в качестве характерного ли-
нейного размера Z принят диаметр сепаратора dc, а в качестве скоро-
сти — приведенная скорость пара (газа) w$ в сепарационном объеме.
Приведенные зависимости могут быть использованы при проекти-
ровании струйных сепараторов с раз-
мером ячеек от 260 до 500 мм. Схема
разбивки сечения аппарата на ячей-
ки, в каждой из которых устанавлива-
ется распределительное устройство,
показананарис. 5.23. В каждом распре-
делительном устройстве при 6Щ = 4 —
6 мм удельный расход жидкости ре-
комендуется принимать в пределах
7,7-13,0 м3/ч.
Рис. 5.23. Пример разбивки сечения аппа-
рата на ячейки с распределительными уст-
ройствами струйных сепараторов: 1 — диск
распределительного устройства; 2 — кол-
лектор; 3 — насадок; 4 — перегородка
448
Глава 5
5.2. СТОХАСТИЧЕСКИЙ АНАЛИЗ ГИДРОМЕХАНИЧЕСКИХ
ПРОЦЕССОВ РАЗДЕЛЕНИЯ ГЕТЕРОГЕННЫХ СИСТЕМ
Гидромеханические процессы, как и все другие процессы хи-
мической технологии, имеют стохастическую природу. В их осно-
ве лежат как детерминированные, так и вероятностные (случайные)
физические явления. Адекватный физической сущности гидромеха-
нических процессов разделения подход к их исследованию аналоги-
чен классическим методам исследования броуновского движения и
седиментации частиц диспергированной фазы (ДФ) [5.15—5.17]. Так
же, как и в теории броуновского движения, при гидромеханическом
разделении гетерогенных систем величина случайного силового воз-
действия на «частицу» системы изменяется во времени гораздо быст-
рее, чем вызываемые ими (случайными воздействиями) изменения в
«положении» (обобщенные координаты и скорости) «частиц». Дейст-
вительно, если случайные воздействия на частицу ДФ, взвешенную
в турбулизованной вязкой среде, обусловлены разрушением турбу-
лентных пульсаций (ТП) в окрестности частицы, то в силу вязкост-
ных свойств среды время разрушения ТП много меньше времени
релаксации возникающего при этом в системе среда+частица воз-
мущения (так называемое высокочастное приближение).
Таким образом, временные (лагранжевы) корреляции ординат
случайных силовых воздействий исчезающе малы на характеристи-
ческих для гидромеханических процессов временных интервалах, а
сами случайные воздействия можно рассматривать в качестве стаци-
онарного случайного процесса типа «белого шума» [5.18, 5.19].
В связи с тем, что стохастический анализ систем с «белым шумом»
все шире используется в практике исследований конкретных гидро-
механических процессов в гетерогенных системах (см., например,
[5.20]), возникает необходимость (для корректного его использова-
ния) в единой и однозначной трактовке всех деталей его (достаточно
громоздкого) математического аппарата, включая и терминологию.
5.2.1. Описание эволюции динамических систем
с «белым шумом»
Траектория изображающей точки в обобщенном фазовом про-
странстве для «частиц» динамической системы с «белым шумом»
удовлетворяет системе стохастических дифференциальных уравне-
ний движения (уравнения Ланжевена) [5.16—5.18, 5.21]
dx	л
— = f(t,x)+m(t,x£(t),	(5.2.1)
dt
Глава 5
449
где х = (хр ..., х2п) — совокупность координат 2п-мерного фазового
пространства; f = (fr...,f2n) — совокупность детерминированных, а
£ = (£р...,£2п) — взаимонезависимых случайных воздействий на «час-
тицу» системы; т = (п*у)2п— матрица [5.19] нормирующих случай-
ные воздействия коэффициентов.
В данном случае решение, при соответствующих начальных усло-
вияхх(О)=хо, системы (1) уравнений Ланжевенах=х({) — марковский
случайный процесс, который однозначным образом задается услов-
ной (двумерной) плотностью вероятности
со = w(t,x; t0,x0), t = tQ + т	(5.2.2)
перехода за время т «частицы» из точки (t0, х0) в точку (t, х) обобщен-
ного фазового пространства и одномерной плотностью вероятности
начального состояния w0 = w(t0, х0).
Если начальное состояние детерминировано, то марковский слу-
чайный процесс однозначно характеризуется одномерной плотнос-
тью вероятности конечного состояния
W(T,x) = Jdt0 J w(t0+T,x;t0,x0)5(x0-x0s)8(t0-t0i)dV
0 %
Здесь VXq и — пространство начальных состояний и его эле-
ментарный объем; tQ , х0 — фиксированная точка начального состоя-
ния системы; 5(х0 — х0 ), 5(t0 — t0 ) — функции Дирака.
В свою очередь, условная (переходная) плотность вероятности
(5.2.2) как функция параметров конечного состояния (t, х) удовлетво-
ряет [5.19, 5.22] второму уравнению Колмогорова
(,2.з)
которое аналогично по форме используемому в физической кинетике
уравнению Фоккера-Планка (уравнение диффузии в пространстве
энергий (скоростей) [5.23]. В стохастической теории центробежной се-
парации частиц ДФ [5.24] уравнение (5.2.3) именуется уравнением Кол-
могорова—Фоккера—Планка (КФП). Коэффициенты a = (ар ..., а2л)
и b = (Ду)2п в уравнении (5.2.3) определяются [5.25, 5.26] как «скоро-
сти» изменения во времени 1-го и 2-го условных моментов марковско-
го процессах = x(t):
ц- ('^i x2n) =	(‘+д0- (Ota (ФЛО x2n (0J;
Zit—->и ZAt
t>ij (t.Xi.X2„) = tonI 7-M{[x, ((+ Af)-x, (t)]x
x[x,(t + Aj)-x,•(«)]...,x2n(t)},	i,J = l 2n.	(5.2.4)
450
Глава 5
При использовании формальной стохастической «конструкции»
для описания реальных гидромеханических процессов в гетерогенных
системах необходимо иметь информацию о динамических уравнени-
ях (5.2.1) стохастического движения и корреляционных связях (5.2.4)
между компонентами векторов скорости и ускорения частиц ДФ.
Учет того обстоятельства, что в силу вязкостных свойств реаль-
ной гетерогенной системы время tQ начального состояния — вели-
чина детерминированная, а марковский процесс х = x(t) — стацио-
нарный случайный процесс, позволяет использовать (при решении
проблемы информационного обеспечения реального стохастичес-
кого описания) мощный математический аппарат спектральной те-
ории стационарных случайных процессов [5.19, 5. 27, 5.28] и свести
в конечном счете [5.29] задачу о нахождении коэффициентов (Ь^2п,
в уравнении (5.2.4) к задаче нахождения корреляционных функций
компонент полей скоростей и ускорений несущего потока при задан-
ном аналитическом виде всех детерминированных членов, входящих
в уравнение (5.2.1) движения частицы ДФ.
Итак, наличие адекватной информации об уравнении движения
частицы ДФ — принципиальное обстоятельство при реализации
формальной стохастической «конструкции» в рамках конкретного
гидромеханического процесса.
Подавляющее большинство современных исследований, относя-
щихся к механике гетерогенных систем, базируется на уравнении
Чена [5.30] для одномерного движения малой твердой сферической
частицы, взвешенной в вязком и несжимаемом турбулентном потоке.
Уравнение Чена — обобщение [5.31] результатов, полученных Бассе,
Буссинеском и Озееном в рамках задачи Стокса о «ползущем» дви-
жении частицы ДФ. Аналогичные результаты получены Страхови-
чем [5.32] и Лурье [5.33].
Уравнение Чена неоднократно подвергалось критическому ана-
лизу [5.34, 5.35]. Это связано с тем, что практика [5.36—5.38] исполь-
зования уравнения Чена заставляет сомневаться в корректности вы-
полненного им обобщения. Неясным, в частности, остается вопрос о
границах применимости отдельных членов этого уравнения, что при-
водит иногда к необходимости экспериментального нахождения ко-
эффициентов данного уравнения (см. анализ работ Одара, Торбина
и Бовина в [5.39]). Сомнения вызывают такие члены уравнения дви-
жения стоксовой частицы в вязкой среде, как сила присоединенной
массы [5.40] и введенная Ченом, Коренным и Ламли [5.30, 5.34] сила,
обусловленная градиентом давления жидкости
nd3
fp=—т-gradP.	(5.2.5)
6
Глава 5
451
Анализ [5.41] «ползущего» движения стоксовой частицы при кра-
евых условиях, соответствующих высокочастотному приближению,
привел к выражению для силы сопротивления жидкости движению
частицы
fa (t) = -Зтгф [v(t) - щ, (£)]+
6v?iv dt Q yft-T
(5.2.6)
которая состоит только из двух составляющих — силы мгновенно-
го («лобового») сопротивления (силы Стокса) и силы сопротивле-
ния сферически-симметричного следа вторичного индуцированых
частицей низкочастотных пульсаций несущего потока (сила Бассе).
Причем на нестационарной (начальной) стадии движения сила Бассе
много больше силы стоксового сопротивления движению частицы.
Сравнение результатов [5.33, 5.41] позволяет сделать вывод о том, что
сила (5.2.5) — ошибочный результат — прямое следствие пренебре-
жения вязкостными членами в уравнении Навье-Стокса при беско-
нечном удалении от поверхности частицы.
В приложениях к механике турбулизованных гетерогенных си-
стем сложился традиционный подход к описанию произвольного (в
общем случае не одномерного) детерминированного движения взве-
шенной частицы ДФ в рамках квазистационарного уравнения дви-
жения
dv
dt"
= ——+am
m
Шр
+ QX,
(5.2.7)
включающего простым аддитивным образом как ускорение ат, вы-
зываемое внешними массовыми силами, так и ускорение ах за счет
всех остальных физических эффектов, которые не рассматривают-
ся в модели Стокса и не учитываются в f (5.2.6). Такой подход вряд
ли можно признать корректным. В произвольной по физико-химиче-
ским свойствам и дисперсности гетерогенной системе влияние вне-
шних массовых сил, неоднородностей поля скоростей несущего по-
тока и сил инерции на поле вторичных (индуцированных частицей
ДФ) пульсаций не является уже исчезающе малым по сравнению с
эффектами изотропной и однородной вязкости, как это имеет место
при безинерционном движении стоксовой частицы.
То обстоятельство, что к настоящему времени значительная часть
исследований по гидромеханике гетерогенных систем по-прежне-
му базируется на уравнении типа (5.2.7), обусловлено, прежде всего,
чрезвычайной сложностью краевой задачи (нелинейной, нестаци-
онарной и трехмерной) нахождения поля вторичных пульсаций в об-
щем случае.
452
Глава 5
Отсутствие адекватного (в общем случае) уравнения движения
частицы ДФ и надежной (квазианалитической) информации о лаг-
ранжевых временных корреляциях компонент полей скоростей и ус-
корений несущего потока — основной фактор, тормозящий создание
реальных стохастических «конструкций» для описания гидромеха-
нических процессов в конкретных гетерогенных системах; кроме
того, многомерность стохастического рассмотрения и вытекающая
из этого громоздкость математического аппарата ограничивает про-
ведение стохастического анализа и получение данных о полях кон-
центраций и локальных потоков частиц ДФ.
5.2.2. Описание гидромеханического разделения
гетерогенных систем
В [5.24,5.32] предложена принципиально новая физическая модель
сепарации мелкодиспергированных гетерогенных систем [жидкость —
твердое тело, жидкость — жидкость, (пар) газ—жидкость)], которая
позволяет при реализации формальной стохастической «конструк-
ции» отчасти избежать указанных выше затруднений.
Дело в том, что в случае мелкодиспергированной и слабо «запы-
ленной» системы основной вклад в силу сопротивления потока дви-
жению частицы ДФ (5.2.6) дает сила стационарного стоксового со-
противления. Траектория частицы ДФ практически (в среднем)
совпадает [5.50] с осредненной линией тока элементарного объема
несущего потока
—\ = 0,	(5.2.8)
dt/
а взаимодействие частиц ДФ с ТП потока — дельта-коррелирован-
ный стационарный марковский процесс с нулевым математическим
ожиданием:
M[U(tr.’')] = 0, ^(г)=(2с^/<оо)8(т), 1 = 1,2,3,	(5.2.9)
где = (а^,а^.о„з) - дисперсии; К& = (К^, К^, К^) - автокор-
реляционные функции координат вектора случайных ускорений
частицы ДФ.
Специфика ситуации (5.2.8) состоите том, что система (5.2.1) урав-
нений Ланжевена, описывающих стохастическое блуждание изоб-
ражающей точки в фазовом пространстве, вырождается и движение
частицы ДФ в пространстве скоростей (5.2.1), (5.2.6)
~^(v-u)+am + ijQ(O
at тр
Глава 5
453
описывает одновременно и специфическое стохастическое движе-
ние в координатном пространстве:
(5.2.10)
— = 0=» —= ^2.+u+-^£-^(t).
dt dt Злсф Злф
Что же касается коэффициентов в уравнении КФП (5.2.3), соот-
ветствующем уравнению Ланжевена (5.2.10), то они довольно просто
[5.19] могут быть получены из уравнения (5.2.4) в рассматриваемом
случае (5.2.9):
3rcdu,am+U' bv(t,r) (a J Aj-1-2-3'
•эяац	(Зясф)
(5.2.11)
где Ь- = 2п1р(У^ /й)0 — интенсивность случайных воздействий по z-й
координате частицы; ог^. — символ Кронекера.
Данная модель сепарации позволяет уменьшить в два раза размер-
ность стохастического представления, т.е. перейти к задаче нахожде-
ния w(t, г; t0, г0) условной плотности вероятности как функции компо-
нент только координатного (а не фазового) пространства состояний.
При центробежной сепарации гетерогенных систем* с осевой
симметрией стохастическое уравнение (5.2.10) радиального движе-
ния частиц (капель) может быть записано в следующем виде:
dr_d2(pz/p"-l)<o2f у , mp
dt 18v	г Зяфх
(5.2.12)
где иг = у/г — радиальная компонента скорости несущего потока.
Стохастическому уравнению (5.2.10) может быть поставлено в соот-
ветствие следующее уравнение КФП (5.2.3) для w(t, г) = w(t, г, v; t0, r0):
dw д
dt dr
b d2w
2
(5.2.13)
коэффициенты которого в соответствии с уравнением (5.2.11)
d2(p'/p"-l)(o2 b'	о о
« = 1 !8V ’  b = 77—^' Ь' = 2т2рс1/Шв,
1°v	(Злсф)
причем а характеризует интенсивность инерционных, а Ь’ — случай-
ных силовых воздействий на радиальное движение частиц ДФ.
Решение уравнения (5.2.13) должно быть согласно с краевыми усло-
виями, которые, например, при разделении суспензии в гидроцикло-
нах могут быть записаны в следующем виде:
Центробежная сепарация широко применяется, в частности, для разделения парожидкост-
ных систем в тепло- и массообменных аппаратах [5.42 — 5.45], обогащения полезных ископа-
емых [5.46], отделения целевого продукта [5.47 — 5.49] и очистки газов [5.50] в химической и не-
фтеперерабатывающей [5.51] промышленности, при обработке пищевых продуктов [5.52] и т.п.
454
Глава 5
wjO, г) = v^0(r) — начальное условие;
w(t, Fj) = w(t, Ro) — граничные условия,
где R, г. — радиусы гидроциклона и зоны противотока; и^0(г) — норми-
рованный на единицу начальный радиальный профиль концентрации
частиц. Условия уравнения (5.2.14) соответствуют тому, что все части-
цы ДФ, достигшие стенок аппарата и границы зоны противотока, уно-
сятся из гидроциклона через разгрузочный и сливной патрубки.
Условная плотность вероятности однозначным образом связана с
относительной концентрацией частиц ДФ и имеет туже размерность.
Решение краевой задачи (5.2.13), (5.2.14) предоставляет данные для
получения информации о распределении частиц ДФ в гидроциклоне
в зависимости от трех безразмерных параметров, характеризующих
относительное время пребывания в аппарате t =at/R, относитель-
ные интенсивности центробежной сепарации а = а/ЬР2и радиально-
го сноса у = у/(аР2).
Решение уравнения (5.2.13) с условиями (5.2.14) позволяет также
получить [5.53] необходимые данные для расчета эффективности
разделительного процесса в гидроциклоне. Унос SJf) частиц ДФ че-
рез сливной патрубок за время t определяется с помощью плотности
потока условной вероятности G(t, г):
G(t,r) = (ar-y/r>-	.
or )
Унос частиц Sp(t) через разгрузочное отверстие за время t:
Sp(t) = 1-S/f).
При численном анализе эффективности разделительного процес-
са в гидроциклоне целесообразно [5.53] перейти к непосредственно-
му решению краевой задачи для поля G(t, г):
3G
dt
dG
dr
2 дг2
= 0;
(5.2.15)
начальное условие:
2 dr
(5.2.16)
граничные условия:
dG dG =0
дг г=, дг r=rR
Результаты численного интегрирования краевой задачи (5.2.15),
(5.2.16) методом сеток в рамках симметричной схемы Кранка-Ни-
Глава 5
455
кольсона и расчетные зависимости Sj - Sj (t) для широких интер-
валов изменения параметров а и у приведены в [5.53]. Анализ этих
зависимостей позволил сделать экспериментально подтвержденный
[5.54] вывод о существовании предельного уноса при t -»<». Кроме
того, обнаружено, что для любых фиксированных значений rj.a и у
существует интервал недостижимых предельных уносов, т.е. в гид-
роциклоне предельный унос S- мелкодиспергированных частиц ог-
раничен снизу и (при данных и у) не может быть меньше вполне
определенной величины.
С полной ясностью следует отметить следующее обстоятельст-
во. Практическая реализация изложенного выше стохастическо-
го описания и связанное с этим решение принципиальных проблем
формального стохастического «конструирования» были достигнуты
путем переноса информационного базиса в иную область. Для на-
дежного прогнозирования в рамках краевых задач (5.2.13), (5.2.14) и
(5.2.15), (5.2.16) гидромеханических процессов разделения гетероген-
ных систем необходима адекватная информация о полях скоростей
и = u(t, г) несущего потока и случайных воздействий	(t,r). Оче-
видность этого факта проявилась при первых же апробациях разра-
ботанного стохастического описания. Затем последовали попытки
создания необходимого информационного обеспечения как чисто
теоретическими, так и экспериментальными методами.
В работе [5.55] аналитически решена задача интегрирования
уравнений Навье—Стокса для стационарного закрученного вязкого
и несжимаемого потока. В качестве дополнительных условий исполь-
зовали предположения о постоянстве потока и момента импульса и о
постоянстве давления в окружном направлении. Получены аналити-
ческие выражения для компонент поля скоростей потока и для ради-
ального профиля давления.
В работе [5.56] на основе ламинарного аналога закрученного
осредненного турбулентного течения и в рамках гипотезы Прандт-
ля о конечной диффузионной длине пути перемешивания получено
аналитическое выражение для коэффициента кинематической тур-
булентной вязкости и показано, что |ur/u |е(0,0004; 0,016). При этом
принимали допущение о превалирующем значении компонента
ри'и^р в тензоре турбулентных напряжений сдвига.
Результаты работ [5.55, 5.56] использовали в качестве информаци-
онного базиса при стохастическом анализе [5.53, 5.57] разделитель-
ной эффективности гидроциклонов.
Применительно к стохастическому описанию процессов разде-
ления в конических и цилиндрических гидроциклонах проведены
[5.54] экспериментальные исследования зависимости коэффициен-
456
Глава 5
тов b' интенсивности случайных силовых воздействий от таких па-
раметров, как скорость потока во входном патрубке пвх, отношение
диаметров входного патрубка и циклона Овх/Оц и угол конусности
конической части гидроциклона р. Установлено, что при прочих рав-
ных условиях значения Ь' в цилиндрических циклонах больше, чем
в конических, что свидетельствует о дополнительной турбулизации
потока в цилиндрическом гидроциклоне.
Дальнейшие экспериментальные исследования применительно к
цилиндрическим гидроциклонам [5.58] позволили выявить зависи-
мость Ь' от крупности частиц ДФ, их концентрации и плотности и от
величины тангенциальной скорости несущего потока.
В работах [5.59—5.64] электродиффузионным методом проведены
экспериментальные исследования тангенциальных компонент ско-
рости пф интенсивности Еф =	/ Цр турбулентных пульсаций в
цилиндрических и конических гидроциклонах, а также в турбоцик-
лоне [5.65]. Полученные экспериментальные данные существенным
образом дополняют имеющуюся в настоящее время (см., например,
[5.66]) информацию о характере радиального профиля тангенциаль-
ной скорости в закрученном турбулентном потоке. Показано, что в
гидроциклонах существует пристенная область квазипостоянного
значения тангенциальной скорости и, причем значения и и вели-
чины граничного радиуса пристенной зоны rw зависят, прежде всего,
от конструктивных параметров и могут быть вычислены в каждом
сечении аппарата по эмпирическим аппроксимациям
rw = 1,25(Оц—£)BX)(DBX/DIl)0,58(tgP)0'20;
= 3,1ивх(Рвх/Оц)(£ц/РцГ^2.
Что же касается интенсивности турбулентных пульсаций £ф, то
она остается квазипостоянной величиной в промежуточной области
между газовым столбом и пристенной зоной и линейно возрастает
при дальнейшем приближении к стенке гидроциклона.
На базе единого стохастического подхода [5.67] и результатов эк-
спериментального исследования гидродинамических особенностей
движения гетерогенных систем в аппаратах центробежного принци-
па действия в широком диапазоне изменения физико-химических
свойств, конструктивных и технологических параметров разрабо-
таны универсальные методы расчета прогнозируемых показателей
разделения и других важных эксплуатационных характеристик гид-
роциклонов [5.44, 5.53, 5.57, 5.58, 5.68—5.73], турбоциклонов [5.74—
5.76] и центрифуг [5.48, 5.49].
Эти методы, включающие в себя наиболее реальные предпосыл-
ки и допущения, довольно полно отражают физическую сущность
Глава 5
457
разделительных процессов, происходящих в аппаратах центробеж-
ного типа, и позволяют расчетным путем без проведения модельных
экспериментов определять практически все показатели процессов
разделения.
Стохастический анализ гидромеханических процессов разделе-
ния гетерогенных систем использовался также и в расчетах цилинд-
рических [5.77] и полочных [5.78] отстойников, при описании процес-
сов просеивания частиц произвольной формы [5.79], фильтрования
полидисперсных суспензий с закупоркой пор [5.80], влияния дроб-
ления капель в потоках на сепарацию эмульсий [5.81], установлении
правил оценок уноса и проскока при неизвестной функции распре-
деления дисперсной фазы по размерам [5.82].
Проанализирована также взаимосвязь между статическими ха-
рактеристиками случайной величины — продолжительности пребы-
вания частиц в аппарате — в самом общем случае, при неизвестной
функции ее распределения [5.83].
Полученные расчетные зависимости используются при решении
технологических задач прогнозирования заданного уноса дисперги-
рованной фазы, регулирования работы различных сепарирующих
устройств, а также при подборе параметров, обеспечивающих задан-
ную эффективность процесса.
Созданы и внедрены в различных отраслях народного хозяйства
новые оригинальные конструкции аппаратов центробежного типа,
позволяющие осуществлять надежную регулировку параметров
процессов осветления, сгущения и классификации разнообразных
суспензий и эмульсий, а также повышать эффективность разделе-
ния гетерогенных систем.
Применение, например, гидроциклонов в качестве самостоятель-
ных единиц оборудования вместо отстойников, механических клас-
сификаторов, а также совместно с центрифугами дает существенный
экономический эффект за счет интенсификации процессов, умень-
шения энерго- и материалоемкости оборудования, сокращения про-
изводственных площадей, снижения потерь полезных компонентов,
расходных коэффициентов по сырью и промежуточным продуктам
и перевода процессов химической технологии на непрерывный ре-
жим работы.
Расширение рамок применимости стохастической теории к опи-
санию гидромеханических процессов связано с расширением гра-
ниц его информационного базиса. Это, прежде всего, исследование
эффектов, влияющих на нестационарное движение частиц ДФ в тур-
булентных потоках применительно к получению адекватного урав-
нения их движения [уравнение Ланжевена (5.2.1)].
458
Глава 5
К первоочередным задачам следует отнести задачу о выявлении
связи между характерным размером частиц ДФ и режимом их дви-
жения в турбулентных потоках. Имеющиеся к настоящему времени
данные свидетельствуют о существовании некоторого граничного
значения радиуса частицы, при котором происходит довольно резкое
изменение характера их движения [5.84] и эффективности разделе-
ния [5.85, 5.86] гетерогенной системы.
Остается открытым вопрос об учете (на уровне уравнения дви-
жения частицы ДФ и корреляционных функций несущего потока)
взаимосвязанного влияния как частиц на структуру турбулентности
несущего потока [5.87,5.88], так и структуры (в частности, пространст-
венной [5.89]) турбулентного потока на движение частиц. Например,
в работе [5.79] экспериментально показано, что при отрицательном
градиенте давления крупнодиспергированная (d — 0,2, ..., 0,4 мм)
твердая (полистирол) фаза уменьшает размер вязкого подслоя (за
счет его турбулизации) и увеличивает коэффициент поверхности
трения.
Применение уже разработанной стохастической «конструкции» к
описанию процессов гидромеханического разделения гетерогенных
систем в конкретных аппаратах сдерживается также отсутствием
информации об адекватных краевых условиях, необходимых для ин-
тегрирования уравнения КФП (5.2.3). Несомненно, дальнейшее раз-
витие получат экспериментальные [5.90, 5.91] и теоретические [5.92]
работы, способствующие прогрессу в данной области.
В заключение следует отметить две характерные тенденции, ко-
торые стимулируют дальнейшее развитие стохастической теории
гидромеханических процессов. Во-первых, основные идеи и «конс-
труктивные» элементы стохастического описания выходят за рам-
ки гидромеханических процессов и находят практическое примене-
ние при исследовании тепло- и массообменных процессов [5.93, 5.94]
в гетерогенных системах; во-вторых, это усиливающийся интерес к
использованию общих методов статистической физики [5.95] и фи-
зической кинетики [5.96] в прикладных химико-технологических ис-
следованиях [5.97—5.99].
Список литературы
5.1.	Кутепов А.М. Расчет сепараторов циклонного типа//Хим. пром-сть 1964.
№ 4. С. 55-62.
5.2.	Соловьев В.В., Жихарев А.С., Кутепов А.М. Исследование работы цик-
лонного сепаратора//ЖПХ. 1981. Т. 54, № 1. С. 195-198.
Глава 5
459
5.3.	Кончуков В.А., Жихарев А.С., Кутепов А.М., Соловьев В.В. Статисти-
ческий подход к исследованию уноса при работе струйных сепараторов
в аппаратах барботажного типа//Изв. вузов. Химия и хим. технол. 1979.
Т. XXII, вып. 11. С. 1403-1407.
5.4.	Николаенко А.Д., Кутепов А.М., Тютюнников А.Б. Исследование эф-
фективности циклонного сепаратора/Деор. основы хим. технол. 1970.
Т. IV, № 2. С. 296-300.
5.5.	Жихарев А.С., Кутепов А.М. Экспериментальное исследование сепара-
ции парожидкостных смесей струями жидкости//Хим. и нефтяное маши-
ностр. 1972. № 2. С. 10-15.
5.6.	Жихарев А.С., Кутепов А.М. Исследование гидродинамики распреде-
лительного устройства струйного сепаратора//Хим. пром-сть. 1972. № 6.
С. 62-72.
5.7.	Кутепов А.М., Жихарев А.С. Исследование сепарации парожидкост-
ных систем струями жидкости/Деор. основы хим. технол. 1972. Т. IV, № 2.
С. 208-215.
5.8.	Кончуков В.А. Исследование работы струйных сепараторов для разделе-
ния газопарожидкостных систем: Автореф. дис.... канд. техн. наук. МИХМ,
1979. С. 16.
5.9.	Соловьев В.В. Влияние режимных и геометрических параметров на эф-
фективность разделения газожидкостных смесей в циклонном сепарато-
ре: Автореф. канд. дис. М., 1962. С. 16.
5.10.	Голуб С.И. Исследование уноса сепарации влаги в выпарных аппаратах-
испарителях: Автореф. канд. дис. Свердловск, 1969. С. 30.
5.11.	Garner F.H., Ellis S.R.M., Lasey J.A.//Trans. Inst. Chem. Ing. 1954. V. 32,
N441.P. 222-235.
5.12.	Абезгауз Г.Г., Тронь А.П., Копенкин Ю.Н., Коровина И.А. Справочник
по вероятностным расчетам. М.: Воениздат, 1970. С. 369-375.
5.13.	Коузов П.А. Основы анализа дисперсионного состава пылей и порошков.
Л.: Химия, 1971. С. 279.
5.14.	Акопьянц Б.Е. Повышение эффективности выносных сепараторов пара
и надежности контуров низкого давления: Автореф. канд. дис. Л., 1972.
С. 26.
5.15.	Эйнштейн А, Смолуховский М. Броуновское движение. Л.: ОНТИ, 1936.
5.16.	Чандрасекар С. Стохастические проблемы в физике и астрономии. М.:
Изд-во иностр, лит., 1947.
5.17.	Леви П. Стохастические методы в естественных науках. М.: Наука, 1972.
5.18.	Гардинер К.В. Стохастические методы в естественных науках. М.: Мир,
1986.
5.19.	Свешников А.А. Прикладные методы теории случайных функций. М.: На-
ука, 1968.
5.20.	Крошилин А.Е., Кухаренко В.Н., Нигматулин Б.И.//Изв. АН СССР. Ме-
ханика жидкости и газа. 1985. № 4. С. 57-60.
5.21.	Astrom K.J.//lntert. J. Contr. 1965. V. 1, № 4. P. 301-305.
5.22.	Тихонов A.H., Самарский А.А. Уравнения математической физики. М.:
Наука, 1977.
460
Глава 5
5.23.	Черчиньяни К. Теория и приложения уравнения Больцмана. М.: Мир,
1978.
5.24.	Кутепов А.М., Непомнящий Е.А./Деор. основы хим. технол. 1973. Т. 7,
№ 6. С. 892-896.
5.25.	Андронов А.А., ВиттА.А., Понтрягин Л.С.//Журн. эксперим. итеор. фи-
зики. 1933. Т. 3, № 3. С. 165-169.
5.26.	Колмогоров А.Н.//Успехи мат. наук. 1938. Т. 5. С.5-10.
5.27.	Яглом А.М./Дамже. 1952.Т. 7, №5(51). С. 3-8.
5.28.	Зельдович Я.Б., Мышкис А.Д. Элементы прикладной математики. М.:
Наука, 1972.
5.29.	Левич В.Г., Кучанов С.И./Докл. АН СССР. 1967. Т. 174, № 4. С. 763-767.
5.30.	Tchen С.М. Dis Delf. The Haque. Holland, 1947.
5.31.	Coy С. Гидродинамика многофазных систем. M.: Мир, 1971.
5.32.	Сграхович К.И.//Прикл. мат. и мех. 1935. Т. 2, № 2. С. 297-300.
5.33.	Лурье А.И. Операционное исчисление в приложениях к задачам механи-
ки. Л.; М.:ОНТИ, 1938.
5.34.	Corssin S., Lumley J.//Appl. Sci. Res. 1956. V. 6A, № 2-3. P. 114-118.
5.35.	Буевич Ю.А.//Изв. АН СССР. Механика жидкости и газа. 1966. № 6.
С. 182-186.
5.36.	Шрайбер А.А. Гидродинамика и теплообмен в двухфазных средах. Ново-
сибирск, 1981. С. 63.
5.37.	Gitterman М., Steinberg V.W. Phys. Fluids. 1980. V. 23, № 11. Р. 2154-
2158.
5.38.	Медников Е.П. Турбулентный перенос и осаждение аэрозолей. М.: На-
ука, 1981.
5.39.	Бусройд Р. Течение газа со взвешенными частицами. М.: Мир, 1975.
5.40.	Нигматулин Р.И. Основы механики гетерогенных сред. М.: Наука, 1978.
5.41.	Губанов А.М., Жихарев А.С., Кутепов А.М.//Теор. основы хим. технол.
1985. Т. 19, № 5. С. 637-643.
5.42.	Кутепов А.М., Непомнящий Е.А.//Изв. вузов. Химия и хим. технол. 1973.
Т. 16, № 11. С. 1749-1753.
5.43.	Кутепов А.М., Стерман Л.С, Стюшин Н.Г. Гидродинамика и теплооб-
мен при парообразовании. М.: Высш, школа, 1986.
5.44.	Кутепов А.М.//Хим. пром-сть. 1962. № 1. С. 60-64.
5.45.	Кутепов А.М./Дам же. 1964. № 4. С. 55-58.
5.46.	Поваров А.И. Гидроциклоны на обогатительных фабриках. М.: Недра,
1978.
5.47.	Соколов В.И. Центрифугирование. М.: Химия, 1976.
5.48.	Кутепов А.М., Борисенко А.А.//Журн. прикл. химии. 1977. Т. 50, № 1.
С. 110-113.
5.49.	Соколов В.И., Кутепов А.М., Борисенко А.А./Деор. основы хим. тех-
нол. 1979. Т. 13, № 4. С. 617-620.
5.50.	Коузов П.А., Малыгин А.Д., Скрыбин Г. М. Очистка от пыли газов и воз-
духа в химической промышленности. Л.: Химия, 1982.
5.51.	Мустафьев А.М., Гутман Б.М. Гидроциклоны в нефтеперерабатываю-
щей промышленности. М.: Недра, 1981.
Глава 5
461
5.52.	Карпычев В.А., Семенов Е.В. Гидрохимические процессы технологи-
ческой обработки молочных продуктов. М.: Пищевая пром-сть, 1982.
5.53.	Непомнящий Е.А., Кутепов А.М., Павловский В.В. и др.//Теор. основы
хим. технол. 1979. Т. 13, № 1. С. 86-90.
5.54.	Кутепов А.М., Непомнящий Е.А., Терновский И.Г. и др.//Журн. прикл.
химии. 1978. Т. 51, № 1. С. 614-619.
5.55.	Непомнящий Е.А., Павловский В.В.//Теор. основы хим. технол. 1977.
Т. 11, №1.С. 101-104.
5.56.	Непомнящий Е.А., Павловский В.В.//Там же. 1979. Т. 13, №5. С. 787-
791.
5.57.	Кутепов А.М., Непомнящий Е.А.//Там же. 1980. Т. 14, № 6. С. 890-893.
5.58.	Кутепов А.М., Непомнящий Е.А., Терновский И.Г. и др.//Журн. прикл.
химии. 1983. Т. 56, № 2. С. 438-441.
5.59.	Терновский И.Г., Кутепов А.М., Кузнецов А.А. и др.//Изв. вузов. Химия
и хим. технол. 1979. Т. 22, № 5. С. 630-634.
5.60.	Терновский И.Г., Кутепов А.М., Кузнецов А.А. и др.//Журн. прикл. хи-
мии. 1980. Т. 53, №11. С. 2568-2681.
5.61.	Кутепов А.М., Терновский И.Г., Кузнецов А.А.//Там же. 1980. Т. 53,
№12. С. 2676-2681.
5.62.	Кузнецов А.А, Кутепов А.М., Терновский И.Г.//Изв. вузов. Химия и хим.
технол. 1980. Т. 23, № 11. С. 1442-1445.
5.63.	Терновский И.Г., Кутепов А.М., Лагуткин М.Г.//Журн. прикл. химии.
1981. Т. 54, № 9. С. 2066-2070.
5.64.	Кутепов А.М., Лагуткин М.Г. и др.//Там же. 1983. Т. 56, № 4. С. 926-929.
5.65.	Цыганов Л.Г., Кутепов А.М., Терновский И.Г.//Там же. № 2. С. 311-
315.
5.66.	Ogawa A.//J. Coll. Eng. Ninon Univ. 1983. V. A-24. P. 93-97.
5.67.	Кутепов A.M., Непомнящий Е.А.//Изв. вузов. Химия и хим. технол. 1976.
Т. 19, № 1.С. 151-155.
5.68.	Кутепов А.М., Непомнящий Е.А.//Теор. основы хим. технол. 1976. Т. 10,
№ 3. С. 433-437.
5.69.	Кузнецов А.А., Кутепов A.ML, Терновский И.Г.//Журн. прикл. химии.
1982. Т. 55, № 5. С. 1086-1090.
5.70.	Непомнящий Е.А., Кутепов А.М.//Теор. основы хим. технол. 1982. Т. 16,
№ 1.С. 78-82.
5.71.	Баранов А.Д., Кутепов А.М., Терновский И.Г.//Журн. прикл. химии.
1984. Т. 57, № 5. С. 1181-1184.
5.72.	Лагуткин М.Г., Кутепов А.М., Терновский И.Г.//Изв. вузов. Химия и
хим. технол. 1982. Т. 25, № 10. С. 1276-1281.
5.73.	Кузнецов А.А, Кутепов A.ML, Терновский И.Г. и др.//Там же. 1983. Т. 26,
№ 3. С. 373-377.
5.74.	Терновский И.Г., Кутепов А.М., Цыганов Л.Г.//Там же. 1981. Т. 24, № 1.
С. 119-124.
5.75.	Кутепов А.М., Непомнящий Е.А., Терновский И.Г. и др.//Теор. основы
хим. технол. 1986. Т. 20, № 1. С. 62-68.
5.76.	Баранов А.Д., Кутепов A.Ml., Терновский И.Г.//Химия и технология топ-
лив и масел. 1986. № 3. С. 16.
462
Глава 5
5.77.	Кутепов А.М., Соколов Н.В.//Теор. основы хим. технол. 1981. Т. 15, №3.
С. 405-409.
5.78.	Кутепов А.М., Соколов Н.В.//Там же. № 1. С. 135-139.
5.79.	Кутепов А.М., Соколов Н.В.//Там же. 1983. Т. 17, №4. С. 510-515.
5.80.	Кутепов А.М., Соколов Н.В.//Тамже. 1985. Т. 19, № 1. С. 123-127.
5.81.	Кутепов А.М., Соколов Н.В.//Изв. СО АН СССР. Сер. техн. наук. 1984.
№10, вып. 2. С. 99-103.
5.82.	Кутепов А.М., Соколов Н.В.//Теор. основы хим. технол. 1984. Т. 18, № 1.
С. 125-127.
5.83.	Кутепов А.М., Соколов Н.В.//Изв. вузов. Химия и хим. технол. 1984.
Т. 27, № 10. С. 1246-1249.
5.84.	Процкий А.Е.//Изв. вузов. Энергетика. 1965. № 11. С. 54-58.
5.85.	Ушаков С.Г., Зверев Н.И. Инерционная сепарация пыли. М.: Энергия,
1974.
5.86.	Liu B.Y.H., Agarwall J.K.//J. Aeros. Sci. 1974. V. 5, № 2. P. 145-150.
5.87.	Буевич Ю.А., Гупало Ю.П.//Прикл. механика и техн, физика. 1965. № 4.
С. 89; №5. С. 135-139.
5.88.	Калмыков В.Г./Дам же. 1976. № 2. С. 111-116.
5.89.	Шапиро В.Е.//Там же. С. 98-102.
5.90.	Lodes A., Mierka O.//Chem. Engng. Sci. 1986. V. 14, № 1. P. 195-206.
5.91.	Баранов Д.А., Терновский И.Г.//Межвуз. сб. науч. тр. МИХМ, 1985.
С. 6-10.
5.92.	Семенов Е.В., Жуков В.Г., Карамзин В.А.//Журн. прикл. химии. 1985.
Т. 58, № 9. С. 2055-2060.
5.93.	Nassar R., Too J.R., Fan L.T.//AIChE Journal. 1984. V. 30, № 6. P. 1014-
1020.
5.94.	Непомнящий E.A., Попов Ю.П., Чистовалов C.M.//Teop. основы хим.
технол. 1985. Т. 19, № 6. С. 787-792.
5.95.	Леонтович М.А. Статистическая физика. М.: Гостехиздат, 1944.
5.96.	Туницкий Н.Н., Каминский В.А., Тимашев С.Ф. Методы физико-хими-
ческой кинетики. М.: Химия, 1972.
5.97.	Туницкий Н.Н. Диффузия и случайные процессы. Новосибирск: Наука,
1970.
5.98.	Протодьяконов И.О., Богданов С.Д. Статистические явления переноса
в процессах химической технологии. Л.: Химия, 1983.
5.99.	Мясников В.П.//Механика многокомпонентных сред в технологических
процессах. М.: Наука, 1978. С. 70.
Глава 6
ВНЕЛРЕНИЕ МЕТОДОВ ИНТЕНСИФИКАЦИИ
ТЕПЛО- И МАССООБМЕНА В ТЕХНИКЕ
6.1.	ЭНЕРГОДВИГАТЕЛЬНЫЕ УСТАНОВКИ АППАРАТОВ
ДЛЯ ПИЛОТИРУЕМОЙ ЭКСПЕДИЦИИ НА МАРС
К энергодвигательным установкам космических аппаратов (КА)
и к отдельным их элементам предъявляются жесткие требования по
массе и габаритам, что связано с высокой стоимостью выведения гру-
за на орбиту искусственного спутника Земли, где должна осущест-
вляться сборка КА для решения новых глобальных задач — пило-
тируемых полетов к планетам Солнечной системы и прежде всего к
Марсу и Луне. Для решения этих новых задач в 1991 г. были начаты
разработки ядерных ракетных двигателей (ЯРД) и ядерных энерго-
двигательных установок (ЯЭДУ) для полетов на Марс и Луну в рамках
Инициативы по исследованию космоса (Space Exploration Initiative,
USA) и концепции «Энергоснабжение Земли из космоса» (СССР)
[6.1.1, 6.1.2].
Для выполнения этих задач требуется соответствующее энерге-
тическое обеспечение (табл. 6.1.1). Как видно из табл. 6.1.1, в связи с
высоким потребным уровнем электрической мощности для решения
перспективных задач традиционные источники энергии на базе сол-
нечных фотопреобразователей или солнечных концентраторов не
могут конкурировать с ядерными источниками энергии.
Так, если ядерная энергоустановка SP-1OO электрической мощнос-
тью 100 кВт, разработанная в США, имеет массу -3 т и размещает-
ся свободно в грузовом отсеке космического корабля «Спейс Шаттл»
диаметром 4 м и длиной 18 м, то масса аналогичной по мощности сол-
нечной энергоустановки равняется примерно 6—10 т. При этом пло-
щадь поверхности солнечных фотопреобразователей составляет
около приблизительно 1400 м2 при уровне генерируемой мощности
-70 Вт/м2. Кроме того, ресурс ядерных энергоустановок выше, чем
солнечных, имеющих тенденцию к значительному уменьшению вы-
ходных параметров со временем эксплуатации. При уровнях энер-
464
Глава б
Таблица 6.1.1
Требования к двигательно-энергетическому обеспечению
экспедиций на Марс и Луну*
Параметр	США	Россия
Надежность двигательно-энергетического комплекса экспедиции	—	>0,990
Надежность двигательно-энергетической установки	>0,995	>0,995
Двигательный режим: — тяга, кН — удельный импульс, км/с — ресурс в полете, ч — число включений	333 8,5...9,25 >4,5 >10	200 9,2...9,5 >5,3 >11
Энергетический режим: — электрическая мощность, кВт — ресурс, лет	20 1.3	50—150 1.0
Отношение тяги к массе	>4	>3
* Вероятность выполнения штатной программы экспедиции >0,96 [6.1.2].
гопотребления порядка 5—7 кВт хорошо себя зарекомендовала тер-
моэмиссионная ядерная энергетическая установка «Топаз» [6.1.3],
разработанная в СССР и испытанная в составе космических аппара-
тов серии «Космос», причем мощность, достигнутая в настоящее вре-
мя этим реактором, не является предельной.
При больших уровнях энергопотребления, указанных в табл. 6.1.1,
могут применяться ядерные газотурбинные энергетические уста-
новки (ЯЭУ), работающие по циклу Брайтона [6.1.4] и использующие
в качестве рабочего тела второго контура гелий или гелий-ксеноно-
вую смесь. Тепло, выделяемое в ядерном реакторе, снимается пото-
ком теплоносителя первого контура и передается в теплообменном
аппарате рабочему телу второго контура, подаваемому на турбину
4 (рис. 6.1). Сброс отработанной теплоты производится в холодиль-
нике-излучателе-8. Теплообменник—регенератор-11 позволяет повы-
сить КПД газотурбинной ЯЭУ.
Для уменьшения массы и габаритов ЯЭУ большой интерес пред-
ставляет использование одного ядерного реактора (ЯР) как для выра-
ботки электроэнергии, так и для получения тяги. Такого рода энерге-
тические комплексы могут входить в состав космических аппаратов
для пилотируемых экспедиций к планетам Солнечной системы, в пер-
вую очередь к Марсу. Существует и ряд других концепций энергоус-
тановок: сочетание жидкостного ракетного двигателя для получения
Глава 6
465
Рис. 6.1. Принципиальная схема ядерной энергетической установки с газотур-
бинным циклом преобразования: 1 — ядерный реактор; 2 — первый контур: 3 —
теплообменный аппарат первого контура; 4 — турбина; 5 — электрогенератор;
6 — компрессор; 7 — теплообменный аппарат для отвода тепла от ЯЭУ; 8 — холо-
дильник-излучатель; 9 — контур отвода тепла от ЯЭУ; 10 — насос; 11 — теплооб-
менник-регенератор; 12 — контур газотурбинного преобразования теплоты
тяги и небольшого ядерного реактора для выработки электроэнергии,
а также ядерный энергодвигательный комплекс (ЯЭДК), создающий
с помощью электрореактивного двигателя (ЭРД) тягу и обеспечиваю-
щий электроснабжение других бортовых потребителей.
При выборе двигательной установки, которая должна разгонять
космический аппарат с околоземной орбиты для полета к Марсу, пе-
реводить его на орбиту спутника Марса и возвращать аппарат к Зем-
ле, использование химической энергии ракетного топлива, состо-
ящего из двух компонентов — водорода и кислорода, исключается
из-за больших потребных запасов топлива, что приводит к началь-
ной массе космического корабля (КК), в три раза превышающей на-
чальную массу КК с ядерной энергодвигательной установкой. Таким
образом, для полетов по межпланетным траекториям целесообразно
применять более эффективные источники энергии — ядерные.
В работе [6.1.5] были получены сравнительные характеристики
космического корабля с различными ЯЭДУ (старт в 2018 г.), приведен-
ные в табл. 6.1.2. Из сопоставления этих характеристик следует, что
ЭДК на основе ЯРД (рис. 6.2), имеющий достаточно глубокое теорети-
ческое и экспериментальное обоснование, является наиболее пред-
почтительным, поскольку варианты ЭДК с ЯЭРД (рис. 6.3) в пред-
положении, что удельная масса установки составляет -2 кг/кВт(эл).
[6.1.5], в настоящее время практически нереальны, т.к. эта удельная
масса может быть достигнута только при использовании капельных
холодильников-излучателей. В то же время применение в космосе та-
ких холодильников-излучателей также является проблематичным, а
сброс с ЯЭУ в космос 25—50 МВт с помощью существующих в насто-
ящее время систем теплоотвода оказывается неэффективным.
466
Глава 6
Характеристики КК с различными ЯЭДК
Таблица 6.1.2.
Параметр	Варианты ЯЭДУ			
	На основе ЯРД	ЖРД+ЯЭУсТЭП		ЯЭУ с газотур- бинным пре- образованием тепла
		N = 5МВт ЭЛ	мэл = 7,5МВт	
Длительность экспеди- ции, сут	460	530	615	320
Длительность прохож- дения радиационных поясов Земли, сут	5	1	1	6
Стартовая масса КК при Нсо = 800км, т	800	770	700	550
Затраты рабочего тела, т	490 (Н2)	85(Li) 450(Н2 + О2)	144(Li) ЗЮ(Н2 + О2)	300 (Хе)
Суммарное время работы двигателей, сут	0,25	340	345	129
Суммарная характерис- тическая скорость*, км/с	10	15 (ЭРД) 3,4 (ЖРД)	25(ЭРД) 2,5 (ЖРД)	44
Двигательный режим:				
суммарная тяга, кН	200	2000(ЖРД) 0,17 ...0,26(ЭРД)		0,78-3,5
суммарное время рабо- ты, сут (ч)	5ч	0,2 ч (ЖРД) 345 сут (ЭРД)		129
удельный импульс тяги, км/с	9	4,7 (ЖРД) 4О...6О(ЭРД)		20-90
суммарная тепловая мощность, МВт	1200			—
Энергетический режим:		ЯЭУ	ЯЭУ	ЯЭУ
суммарная электричес- кая мощность, кВт	200	5000	7500	50000
суммарная тепловая мощность, кВт	до 1000		50000	94000
суммарное время рабо- ты, сут	660	700	700	320 (N3a = 50kBt) 129 (ЛГэл = 50 МВт)
суммарная масса, включая радиационную защиту, т	50...70	—	—	Удельная масса 2 кг/кВт(эл.)
Характеристическая скорость КК — скорость, которую приобрел бы КК под действием
тяги ЯРД (ЭРД или ЖРД) при отсутствии других сил (тяготения, сопротивления атмосфе-
ре и др.), ориентации вектора тяги двигателя в одном и том же направлении и движении
по прямой. Действительная скорость КК отличается от характеристической скорости на
величину потерь, связанных с влиянием указанных факторов, и составляет 85% от харак-
теристической скорости.
Глава 6
467
Рис. 6.2. Схема энергодвигательного комплекса на основе ЯРД: 1 — ядерная энер-
годвигательная установка; 2 — баки с рабочим телом ЯРД; 3- секции холодильни-
ка-излучателя; 4 — кабина, возвращаемая на Землю; 5 — жилой блок; 6 — марси-
анский посадочный аппарат
Рис. 6.3. Схема энергодвигательного комплекса на основе ЯЭУ и ЭРД: 1 — ядер-
ная энергоустановка с газотурбинным преобразованием теплоты; 2 — электро-
реактивные двигатели; 3 — капельный холодильник-излучатель; 4 — кабина, воз-
вращаемая на Землю; 5 — жилой блок; 6 — марсианский посадочный аппарат
Результаты оценки характеристик ЭДК, представленные в
табл. 6.1.2, были получены при однокорабельной схеме экспедиции
с массой полезного груза 150 т, длительности пребывания КК на ор-
бите спутника Марса 30 суток и модульной схеме построения ЭДК.
При этом число модулей выбиралось из условия выполнения задач
экспедиции при одном отказавшем модуле за время, увеличенное по
сравнению со штатной ситуацией. Кроме того, при выборе даты стар-
та — май 2018 г. — обеспечиваются минимальные потребности экс-
педиции в суммарном импульсе скорости [6.1.5].
ЭДК на основе ЯРД из трех—четырех одинаковых ЯЭДУ при одно-
временной работе обеспечивают реактивную тягу для разгона КК от
Земли, торможение у Марса, разгон от Марса, торможение у Земли
и коррекцию траектории, а также получение электрической и тепло-
вой энергии для бортовых потребителей и системы длительного хра-
нения жидкого водорода. Если увеличить мощность энергетического
режима до N3A = 800... 1000 кВт, то, используя ЭРД малой тяги, можно
уменьшить либо стартовую массу КК, либо длительность перелета
между Землей и Марсом.
Комбинация ЖРД и ЯЭРД малой тяги (см. табл. 6.1.2) позволяет со-
кратить время пребывания КК в радиационных поясах в сфере гра-
витационного действия Земли.
468
Глава 6
Из существующих многочисленных вариантов энергодвигатель-
ного обеспечения пилотируемой марсианской экспедиции рассмот-
рим более подробно ЯЭДК при использовании ЯРД с высокими выход-
ными параметрами (см. рис. 6.2). Так, чтобы реализовать указанный
в табл. 6.1.1 и 6.1.2 удельный импульс тяги 8,5—9,5 км/с, необходимо
в ядерном реакторе нагреть рабочее тело—водород с ингибирующей
добавкой до температуры, равной 2500—3100К. Как известно, при-
нцип работы ядерного ракетного двигателя состоит в следующем. Ра-
бочее тело—водород с ингибирующей углеродосодержащей добавкой
подается турбонасосным агрегатом в ядерный реактор, являющийся
источником тепла, где нагревается до высокой температуры. Нагре-
тый газ истекает из сопла в космическое пространство, создавая ре-
активную тягу.
Об интенсивности работы реактора как теплообменного устройст-
ва дают представление некоторые значения основных параметров
ЯРД на тягу 333 кН, разработанного по программе «Nerva» в США в
период с 1955 по 1973 г. [6.1.6] применительно к полетам на Марс пило-
тируемого КК. Так, максимальная температура водорода на выходе
из реактора составляла -2500К, а максимальное значение плотности
энерговыделения в активной зоне ЯР достигало до 4500 МВт/м3. При
этом максимальные значения плотности теплового потока с поверх-
ности тепловыделяющего элемента достигали до 5 МВт/м2 и более.
Достаточно высокими параметрами обладают и ядерные реакторы,
предназначенные для космических энергетических установок. Так,
установки, которые работают с использованием турбомашинного
цикла преобразования тепловой энергии в электрическую, предъяв-
ляют повышенные требования к надежности, поскольку их ресурс
должен составлять несколько лет в отличие от ядерного двигателя,
ресурс которого всего несколько часов (см. табл. 6.1.1 и 6.1.2). Необ-
ходимо учесть, что для уменьшения массы этих установок обычно
стремятся увеличить температуру рабочего тела перед турбиной до
1200—1500К. Поэтому такие энергоустановки также принадлежат к
весьма теплонапряженным объектам. Космическая энергоустанов-
ка, сочетающая получение реактивной тяги и выработку электри-
ческой энергии для бортовых нужд летательного аппарата при ис-
пользовании одного ядерного реактора [6.1.1], включает два контура:
открытый, с выхлопом рабочего тела в космическое пространство
для создания тяги, и замкнутый, для выработки электроэнергии в
турбомашинном цикле преобразования теплоты.
При этом предполагается, что тяга создается в форме кратковре-
менных (продолжительностью не более нескольких десятков минут)
импульсов, а электроэнергия вырабатывается в течение всего пери-
Глава 6
469
ода существования установки, т.е. нескольких лет. Рабочим телом
первого контура может служить водород, а второго — либо пары ще-
лочных металлов, либо инертные газы и их смеси. В настоящее вре-
мя считается, что с точки зрения оптимизации термодинамического
цикла желательно использовать смесь гелия и ксенона.
Рассмотрим некоторые особенности конструкций ЯЭДУ на>при-
мере американской энергоустановки (рис. 6.4), предназначенной для
получения импульса тяги на уровне 70 кН и выработки электроэнер-
гии на уровне мощности 10—25 кВт [6.1.6] и разработанной на основе
технологий программы создания ядерного ракетного двигателя. Ак-
тивная зона реактора имеет диаметр около полуметра и состоит из
набора плотноупакованных тепловыделяющих элементов, имеющих
в сечении форму шестигранника с 19 отверстиями для прохода теп-
лоносителя диаметром примерно 1 мм. Топливо — уран-235, обога-
щенный до 93,15%, размещен в матрице из твердого раствора UC-ZrC
и углерода.
Когда установка работает в режиме ядерного ракетного двигате-
ля, через активную зону прокачивается водород, который нагрева-
ется до температуры 2500—2600К и поступает затем в реактивное
сопло. Тепловая мощность реактора на этом режиме составляет не-
многим более 300 МВт.
Для реализации энергетического режима тепловая мощность ус-
тановки снижается до 0,2 МВт. Водород не прокачивается через ак-
тивную зону, а выделяющаяся тепловая энергия отводится из ре-
актора с помощью теплообменников типа трубки Фильда, которые
равномерно размещены по объему активной зоны. Рабочим телом в
этих теплообменниках служит ор-
ганическая жидкость, которая за-
тем направляется в парогенератор,
а образовавшийся пар приводит в
Рис. 6.4. Принципиальная схема ядер-
ной энергодвигательной установки:
1 — бак с жидким водородом; 2 — тур-
бонасосный агрегат; 3 — активная зона
ядерного реактора; 4 — отражатель ней-
тронов; 5 — теплообменник для отвода
тепла в замкнутый энергетический кон-
тур (контур газотурбинного преобразо-
вания теплоты); 6 — реактивное сопло;
7 — компрессор (насос); 8 — турбогене-
ратор; 9 — теплообменный аппарат для
отвода тепла; 10 — холодильник-излуча-
тель; И — клапан
470
Глава б
движение турбогенератор [6.1.6]. Термодинамический цикл — цикл
Ренкина. Ресурс ЯЭДУ — до 10 лет.
Более предпочтительной является концепция перспективной
ядерной энергетической установки для пилотируемого марсианско-
го комплекса, которая базируется на принципе использования отде-
льных модулей, что повышает надежность установки, так как в слу-
чае возникновения аварии либо неисправности модуль может быть
отделен от космического корабля. При этом сохраняется возмож-
ность выполнения программы экспедиции.
Каждый модуль представляет собой самостоятельную энерго-
двигательную установку, в состав которой входит ядерный реактор и
замкнутый контур с турбомашинным циклом преобразования энер-
гии. Максимальная температура водорода на выходе из реактора при
работе на двигательном режиме должна составлять 2900 —3100К, а
максимальная температура газа (смесь гелия и ксенона) перед турби-
ной при работе на энергетическом режиме — 1200К. Электрическая
мощность каждого модуля 50 кВт, а масса (без запаса рабочего тела) —
12,5—17 т. Концепция модульного построения ЯЭДУ, когда вместо ЯРД
большой тяги создаются связки из нескольких ЯРД небольшого раз-
мера, позволяет упростить наземную отработку ЯРД и уменьшить
стоимость стендовой базы и проводимых на ней испытаний.
Параметры единичного ЯРД в связке двигателей для маршрута
Земля—Марс—Земля были определены в работе [6.1.2] с учетом опыта
разработки экспериментального ЯРД на 20 кН, необходимых энерго-
массовых характеристик и надежности связки ЯРД в целом. Результа-
ты этих расчетов приведены в табл. 6.1.3. Видно, что при уменьшении
тяги единичного ЯРД и увеличении числа ЯРД в связке при заданной
суммарной тяге -200 кН масса связки и КК остаются практически не-
изменными, а надежность ЯЭДУ при этом возрастает. В работе [6.1.2]
был сделан вывод, что связка из 3—4 ЯРД является оптимальной, а
тяга единичного ЯРД должна быть равной 70 кН.
В то же время предположения, сделанные в работе [6.1.2] о том, что
высокую экономичность и ресурс ЯРД можно обеспечить только пу-
тем применения твэлов на основе карбидов тугоплавких металлов и
добавки ингибирующей присадки в рабочее тело, являются недоста-
точными. К этим двум требованиям нужно, прежде всего, присово-
купить требования к конструктивному выполнению твэлов, которые
должны обеспечить интенсификацию процессов тепломассообме-
на при течении водорода в каналах активной зоны ЯР и тем самым
уменьшить отрицательное влияние на поля температур допусков на
геометрические размеры карбидных твэлов и величину объемного
энерговыделения. Только в этом случае можно повысить выходные
Глава б
471
Таблица 6.1.3
Результаты предварительных расчетов характеристик ЯРД в связке,
= 8,5 км/с. Маршрут Земля-Марс-Земля, 2011 г.‘
Характеристики	Значения характеристик							
Тяга единичного ЯРД, кН		51		68,6		98	196	392
Количество ЯРД в связке, шт.	2	3	4	2	3	2	2	2
Суммарная тяга, кН	102	153	204	137	206	196	392	784
Длительность работы ЯРД, ч	12,4	7,7	5,3	8,6	5,3	5,4	2,7	1.4
Масса связки ЯРД, т	38	45	54	39	46	46	55	60
Гравитационные потери при уходе от Земли, м/с	1540	910	550	1100	550	560	180	160
Стартовая масса КК, т	815	760	750	770	715	715	715	730
* 2011 г. — период максимального потребного суммарного импульса скорости.
параметры ЯРД, нагреть газ до 2900—3100К и обеспечить заданную
величину удельного импульса тяги 9,2—9,5 км/с (табл. 6.1.1).
Выбор типа реактора и тепловыделяющих сборок (ТВС) связан
также с решением проблем динамики реактора и ЯЭДУ в целом. Ско-
рость протекания переходных процессов в реакторе может оказать
большое влияние на уменьшение массы и габаритов ЯЭДУ и работо-
способность элементов активной зоны.
Так, при переходе с энергетического режима на двигательный
для реактора ЯРД «Нерва» допустимый темп повышения температу-
ры твэлов при нагреве не должен превышать величину 60—100 К/с.
Поэтому время этого перехода составляет 20—30 с. В то же время
для реактора с микротопливом и радиальным течением рабочего
тела при размере частиц топлива -500 мк темпы нагрева составля-
ют 5000—10000 К/с, и такой переход при реальном быстродействии
процесса составит 1—3 с, что позволит уменьшить потребный запас
жидкого водорода на борту ЭДК. При переходе ЯЭДУ с двигательно-
го на энергетический режим путем выбора оптимального режима
расхолаживания реактора с учетом цикличности работы установки
также можно сэкономить расход жидкого водорода. При этом необ-
ходимо учитывать, что для выполнения экспедиции при полете на
Марс необходимо многократное включение ЯЭДУ в режиме ЯРД с
суммарным временем работы на номинальных параметрах, равным
4,5—5,3 ч (табл. 6.1.1), и что остаточное тепловыделение от р,у-распада
накопившихся осколков деления может достигать 3—4% номиналь-

Глава б
ной мощности для реактора, проработавшего -1000 с в импульсном
режиме.
Необходимость многократных быстрых переходов реактора с од-
ного уровня мощности на другой, отличающийся на несколько по-
рядков, предъявляет повышенные требования к эффективности си-
стемы регулирования для обеспечения безопасности работы ЯЭДУ
при переходных режимах. К аварийной ситуации на двигательном
режиме может привести заполнение водородом активной зоны реак-
тора, обладающего положительным эффектом реактивности.
Рассмотренные особенности энергетических установок косми-
ческих аппаратов, которые работают при высоких значениях темпе-
ратур и тепловых потоков, а также других абсолютных и удельных
теплотехнических параметров, показали, что в конструкциях таких
теплонапряженных узлов установки, как тепловыделяющие элемен-
ты ядерного реактора и теплообменные аппараты ЯЭДУ, необходи-
мо использовать наиболее рациональные методы интенсификации
теплообмена. К таким методам относится описанный в ряде работ
[6.1.7—6.1.10] наиболее эффективный метод интенсификации теп-
лообмена и межканального перемешивания теплоносителя путем
закрутки потока витыми твэлами или трубами овального профиля.
В пучках витых твэлов можно обеспечить интенсивное выравнива-
ние температурных неравномерностей в поперечном сечении пучка,
сформированных неравномерным полем энерговыделения в реак-
торе, и тем самым повысить выходные параметры энергоустановки.
Выполненные исследования турбулентного течения и теплообмена
при стационарных и нестационарных условиях работы [6.1.7—6.1.10],
результаты которых представлены в главе 4, позволяют выдать прак-
тические рекомендации для численного анализа теплогидравличес-
ких процессов в ядерном реакторе с витыми твэлами и в теплообмен-
ных аппаратах с витыми трубами ЯЭДУ (глава 2).
Список литературы
6.1.1.	Ашмантас Л.-В.А., Дзюбенко Б.В. Проблемы теплообмена и гидроди-
намики в ядерных энергодвигательных установках космических аппара-
тов. Вильнюс: Pradai, 1997. 370 с.
6.1.2.	Горин А.И., Конюхов Г.В., Коротеев А.С. и др. Концепция ЯРД 1992
го да/Д руды 3-й отраслевой конф. «Ядерная энергетика в космосе. Ядер-
ные ракетные двигатели». Семипалатинск, 1992. С. 91-93.
6.1.3.	Кузнецов В.А., Грязнов Г.М., Артюхов Г.Я. и др. Разработка и создание
ядерно-энергетической установки «Топаз»//Атомная энергия. 1974. Т. 36,
вып. 6. С. 450-457.
Глава 6
473
6.1.4.	Квасников Л.А., Латышев Л.А., Севрук Д.Д. и др. Теория и расчет
энергосиловых установок космических летательных аппаратов М.: Ма-
шиностроение, 1984.331 с.
6.1.5.	Коротеев А.С., Семенов В.Ф., Пульхрова И.Г. и др. Возможные ва-
рианты энергодвигательного обеспечения пилотируемой экспедиции на
М ар с/Д руды отраслевой юбилейной конф. «Ядерная энергетика в кос-
мосе». Ч. I: Доклады советских специалистов. Обнинск, 1990. С. 27-37.
6.1.6.	Angelo J.A., Buden D. Space Nuclear Power. Florida: Orbit Book Company
Inc, 1985. P. 286.
6.1.7.	Дзюбенко Б.В., Сакалаускас A.B., Ашмантас Л.-В.А., Сегаль М.Д.
Турбулентное течение и теплообмен в каналах энергетических устано-
вок/Под ред. Б.В. Дзюбенко. Вильнюс: Pradai, 1995. 300 с.
6.1.8.	Дзюбенко Б.В., Ашмантас Л.-В.А., Сегаль М.Д. Моделирование ста-
ционарных и переходных теплогидравлических процессов в каналах
сложной формы. Вильнюс: Pradai, 1994. 232 с.
6.1.9.	Данилов Ю.И., Дзюбенко Б.В., Дрейцер Г.А., АшмантасЛ.-В.А. Теп-
лообмен и гидродинамика в каналах сложной формы/Под ред. В.М. Иев-
лева. М.: Машиностроение, 1986. 200 с.
6.1.10.	Дзюбенко Б. В., Дрейцер Г. А., Ашмантас Л. -В. А. Нестационарный теп-
ломассообмен в пучках витых труб. М.: Машиностроение, 1988. 240 с.
6.2.	ОПРЕДЕЛЕНИЕ ХАРАКТЕРНЫХ ПАРАМЕТРОВ ЯЭДУ
Для полета на Марс гетерогенный ядерный реактор ЯЭДУ (рис. 6.5)
должен обеспечивать нагрев водорода в ТВС с твердыми поверхнос-
тями теплообмена до температуры перед соплом Тк = 2900...3100К,
что позволяет получить удельный импульс тяги до 9,2—9,5 км/с при
использовании ингибирующей углеродосодержащей добавки в рабо-
чем теле. При таких параметрах обеспечивается потребная суммар-
ная тяга связки из 3—4 ЯРД, равная 200 кН (см. табл. 6.1.1, 6.1.3), а тяга
единичного ЯРД составляет 50—70 кН.
Для ЯЭДУ заданной тяги размеры реактора определяются, пре-
жде всего, размерами поверхности теплообмена, которую требует-
ся разместить в нем. Характерные размеры ядерного реактора и ТВС
определяются из совокупности теплофизических, нейтронно-фи-
зических, весовых и прочностных соображений. Зная удельный им-
пульс тяги и расход рабочего тела, можно определить скорость ра-
бочего тела на выходе из реактора — Увых, перепад давления — Ар,
длину реактора — £р, его массу — Gp, площадь поверхности теплооб-
мена — nS, где п — число каналов охлаждения, и среднюю плотность
474
Глава б
Рис. 6.5. Схема ядерно-
го реактора: 1 — тепло-
выделяющие сборки; 2 —
замедлитель нейтронов;
3 — отражатель нейтронов;
4 — органы управления и
регулирования ядерным
реактором (поворотные
барабаны с поглощающи-
ми элементами на части их
поверхности); 5 — боросо-
держащие накладки; <р —
угловое азимутальное по-
ложение по периметру
периферийных ТВС; у —
угол поворота барабана
теплового потока — qcp. Заданными также являются пористость ре-
актора по рабочему телу — £, температура водорода — Твых и число
Маха Мвых = VBbix/aBblx на выходе из каналов реактора. Число Мвыхне
должно превышать 0,2—0,5. Пористость е имеет большое влияние на
размеры и массу реактора. Чем больше £, тем больше размеры и мас-
са реактора. При определении площади поверхности теплообмена,
потребной для нагрева рабочего тела до нужной температуры — Твых,
предполагается, что во всех каналах течет газообразный водород, а
теплоотдача в каналах реактора описывается формулой
Nu„ = 0,023ARe^8 Рг®'4,	(6.2.1)
где величина множителя А зависит от типа и формы каналов охлаж-
дения с интенсификаторами теплообмена. При турбулентном движе-
нии и равновесной диссоциации водорода критерии подобия в урав-
нении (6.2.1) имеют вид
qdeo Ртт
Num= 
где Д/ = Iw - If, Iw = срГв,, I, = cpTf;
Re = VdeqPm .
m Pm
В формуле (6.2.1) в качестве определяющей температуры принята
средняя температура в пристенном слое
(6.2.2)
(6.2.3)
(6.2.4)
Глава 6
475
Тт =	+ Tf)‘	(6-2.5)
При наличии диссоциации водорода значения температур Tw, Tf
определяются по графику для энтальпии Tf = f(Irp) nTw = f(I^p)- Ко-
эффициент гидравлического сопротивления определяется зависи-
мостью
£ = 0,3164-ARe'0,25,	(6.2.6)
где А > 1 для каналов с дополнительной искусственной турбулизаци-
ей потока, приводящей к интенсификации процессов теплообмена
по сравнению с течением в круглых гладких каналах. Можно также
при оценке характерных размеров ЯР предположить, что в первом
приближении и в каналах с интенсификаторами справедлива гидро-
динамическая теория теплообмена. Тогда можно принять, что
Е, = 8Nu/(RePr0,4).	(6.2.7)
При этом гидравлические потери определяются выражением
Для ориентировочного выбора размеров и типа реактора можно
использовать систему исходных уравнений, определяющих:
—	расход рабочего тела:
G = P/PyA.=nFnpV,	(6.2.9)
где Р — тяга ЯРД; Руд — удельный импульс тяги; Fnn — площадь про-
ходного сечения всех каналов ЯР; Fn — площадь проходного сечения
одного канала;
—	тепловую мощность реактора:
dQ = qcpnTIdl = 4qcpnFndl/deq,	(6.2.10)
где П = 4Fn/deg — периметр одного канала; дср — средняя плотность
теплового потока;
—	объем материала ЯР
dVM=dV„-dVK=^^-nFndl = nFn(l-e)—,	(6.2.11)
£ £
где dVp — объем элемента реактора, dVK — объем элемента канала,
£ = nFn /TtRp, Rp — радиус реактора;
—	массу элемента реактора:
dGp =nFn(l-E)pMd//£,	(6.2.12)
где рм — средняя плотность материала.
476
Глава б
Тогда, используя уравнения (6.2.1) —(6.2.12) и учитывая, что
qcpLp = ^рс?едД1под /4- после ряда преобразований можно получить
выражения для определения:
— массы реактора
Яр
Р
Рг8'84 Рм (1-е)Г Д4одГ
4-0,023 Руд е ДГ •,
— его длины
Рг°-54 ГАД
\0,9
ПОД
4-0,023^ М ,
(1
ср у
>1,2
&eq
ср_____
^2|Др|0'4
( х А0,8
dw
X. Рл7 ) ср
— средней плотности теплового потока
Qcp
Гп А0,8
Д^под|Ар|°’4ЙеР
023	k Р 7 ср
г0'84 (М
1т ,0,2 шпод 1
еЧ а/ J Ыср
(6.2.13)
(6.2.14)
(6.2.15)
— и максимальной скорости потока на выходе из каналов ЯР
V
вых _
^вых
(6.2.16)
Рг0'3
Г1т
"*под j 0,5  Р
А Т	Рвых л
Д-f 7 1Рви
№
гт
Р
где % — показатель адиабаты.
Задаваясь пористостью ЯР и загрузкой урана-235 (GJ, а также ре-
шая систему уравнений (6.2.13) —(6.2.16), можно определить массу
реактора — Gp и его радиус Rp при условии, что делящееся вещест-
во равномерно распределено в объеме замедлителя. Так, при е = 0
и Gu = 3 кг величина Gp — 1000 кг и Rp = 400 мм, а при е = 0,4 и
Gu = 30 кг величина Gp — 1200 кг и Rp = 600 мм. В то же время при
уменьшении массы урана-235 до 20 кг при е = 0,4 масса и размеры ре-
актора значительно увеличиваются (до Gp = 5000 кг и Rp = 850 мм).
Таким образом, при небольшом увеличении загрузки делящегося ве-
щества Gv при е = const можно заметно уменьшить размеры и мас-
су ЯР. Если по условиям теплообмена требуются реакторы большого
размера, такие реакторы будут работать на тепловых нейтронах. В
Глава б
477
случае, если определенные из условий теплообмена реакторы будут
небольших размеров, то они будут работать на быстрых или проме-
жуточных нейтронах.
К массе гомогенного реактора, определенной при решении систе-
мы уравнений (6.2.13) —(6.2.16) с заданной пористостью е, необходимо
присовокупить массу отражателя и массу силового корпуса.
Рассмотренный метод оценки размеров и массы ЯР для ЯЭДУ но-
сит приближенный характер. Действительно, для нагрева рабоче-
го тела до 2900—3100К необходимо использовать твэлы из карбидов
тугоплавких металлов, в которых и помещено делящееся вещество.
Поэтому для ЯЭДУ на основе ЯРД необходимо использовать гете-
рогенный тип реактора, когда тепловыделяющие сборки с высоко-
температурными твэлами распределены в объеме замедлителя, вы-
полненного из материала с более низкой температурой плавления.
Использование гетерогенного типа активной зоны ЯР имеет также
то преимущество, что позволяет обеспечить автономность экспери-
ментальной отработки узлов и элементов ЯРД.
Рассмотрим принципиальную схему ЯРД с гетерогенным реакто-
ром на тепловых нейтронах, описанную в работе [6.2.1]. Размеры это-
го реактора и его загрузка по урану-235 были определены условия-
ми теплообмена между тепловыделяющими элементами (твэлами) и
рабочим телом — водородом, а также необходимыми запасами реак-
тивности. При этом диаметр активной зоны составил Dp = 430 мм и
длина (высота) — Lp = 600 мм [6.2.1]. Твэлы из однородного раствора
карбида урана с карбидами тугоплавких металлов (Nb, Zr и Та) соби-
рались в ТВС. Эти ТВС, представляющие собой автономные конст-
руктивные узлы ЯР, в количестве 37 сборок [6.2.2] размещались в за-
медлителе из гидрида циркония, который секционировался по вы-
соте, радиусу и азимуту. Активная зона ЯР окружалась боковым и
входным торцевым отражателем из бериллия, азимутально-секци-
онированного для повышения термопрочности. В боковом отража-
теле располагались органы управления и регулирования — пово-
ротные цилиндры (барабаны) с поглощающими элементами на части
боковой поверхности этих барабанов с угловым размером 120° [6.2.1,
6.2.2]. Схематически поперечное сечение реактора этого ЯРД пред-
ставлено на рис. 6.5.
Результаты исследования нейтронно-физических характерис-
тик рассмотренного реактора ЯРД минимальных размеров (рис. 6.5)
и вопросов ядерной безопасности представлены в работе [6.2.2]. Эти
результаты были получены экспериментально на критических сбор-
ках и расчетным путем — решением кинетических уравнений пере-
носа в различных приближениях. При этом были рассмотрены следу-
478
Глава 6
Рис. 6.6. Характерные поля энерговы-
деления при трехзонном профилирова-
нии концентрации урана-235 по радиусу
ТВС со стержневыми твэлами: 1 — 3 —
экспериментальные распределения для
входных, средних и выходных секций
ТВС соответственно; 4 — расчетное рас-
пределение по всей длине ТВС
ющие основные характеристи-
ки [6.2.2]: статистические веса
компонентов активной зоны, эф-
фективность органов системы
управления запуском и защиты
(СУЗ), энергораспределение в
ТВС, профилирование, радиаци-
онное энерговыделение в узлах
конструкции, температурные
коэффициенты реактивности,
эффекты реактивности рабоче-
го тела и отравление реактора
продуктами деления.
На рис. 6.6 приведены по-
лученные в работе [6.2.2] поля
энерговыделения в ТВС при
трехзонном профилировании
концентрации урана-235 по ра-
диусу сборки со стержневыми
твэлами (рис. 6.7). Видно, что в этом случае наблюдается симметрич-
ная неравномерность распределения энерговыделения по-радиусу
ТВС. На поле энерговыделения в реакторе оказывают заметное вли-
яние работа органов СУЗ — барабанной системы регулирования (см.
рис. 6.5). При этом поле энерговыделения в реакторе заметно искажа-
Рис. 6.7. Схема возможного размеще-
ния твэлов стержневого типа в ТВС:
1 — 3 — номера зон с различной кон-
центрацией урана-235; 4 — вытесни-
тели
ется в зависимости от положения
органов СУЗ как в радиальном
(рис. 6.8), так и в азимутальном
направлениях (рис. 6.9), а в ТВС
появляется асимметричная не-
равномерность распределения
энерговыделения (рис. 6.10). Эти
распределения энерговыделения
в реакторе и ТВС необходимы
для расчета полей температур в
элементах реактора и рабоче-
го тела, поскольку они влияют
на работоспособность реактора
и ТВС и на выходные парамет-
ры ЯРД (удельный импульс тяги
и тягу двигателя). Следует от-
метить, что трехзонное профи-
лирование концентрации ура-
Глава 6
479
на-235 по радиусу ТВС
позволило снизить не-
равномерность темпе-
ратуры в сечении ТВС
по сравнению с вари-
антом ТВС, имеющим
постоянную концент-
рацию урана-235 по ее
радиусу, в несколько
раз — до -100 °C [6.2.3].
Тепловыделяющая
сборка состоит из шес-
ти нагревных секций
высотой 100 мм каж-
дая. Каждая нагревная
секция содержит пакет
из 151 твэла стержнево-
Рис. 6.8. Распределение среднего энерговыделе-
ния в ТВС по радиусу реактора в зависимости от
положения органов СУЗ: • — при у = 0; ▲ — при
V = 1800
го типа, заключенный в обойму из карбидов тугоплавких металлов,
окруженную теплоизоляцией. Нагревные секции заключены в сек-
ционированный корпус из стали и бериллия (рис. 6.11). Секциониро-
вание ТВС по ее длине позволяет осуществить и продольное профи-
лирование урана-235. Распределение энерговыделения по длине ТВС
представлено в главе 2.
Следует заметить, что описанная конструкция реактора ЯРД во
многом близка к конструкции реактора ЯЭУ «Топаз» [6.1.3], в кото-
ром ТВС также размещены в гидридциркониевом замедлителе, ок-
руженном боковым и торцевым бериллиевым отражателем, а в боко-
вом отражателе размещены шесть компенсационных вращающихся
цилиндров и шесть цилиндров аварийной защиты (см. рис. 6.5). Гру-
бое регулирование осу-
ществляется компенса-
ционными цилиндра-
ми, а тонкое — одним
из цилиндров аварий-
ной защиты. ТВС в за-
медлителе размещены
Рис. 6.9. Влияние азиму-
тального положения ТВС,
согласно рис. 6.5 на отно-
сительное распределение
среднего энерговыделения
в ТВС
480
Глава б
Рис. 6.10. Характерные относительные распре-
деления энерговыделения по азимуту ТВС для
ТВС № 23 (О) и № 24 (•) (см. рис. 6.5)
с неравномерным шагом
с ростом объемной доли
замедлителя от центра к
периферии относитель-
но средней величины,
что снижает неравномер-
ность энерговыделения.
Регулирующие цилинд-
ры также выполнены из
бериллия и снабжены
боросодержащими на-
кладками. Активная зона
описанных реакторов с отражателем размещается внутри цилинд-
рического металлического корпуса.
Протекание теплогидравлических процессов в элементах ядер-
ных энергодвигательных установок и, прежде всего, в ядерном реак-
торе и ТВС, характеризу-
ется рядом особенностей.
Так, течение и теплооб-
мен в них происходят в
условиях чрезвычайно
высоких (близких к до-
пустимым для конструк-
ционных материалов)
температур и тепловых
потоков при значитель-
ной неравномерности по-
лей энерговыделения в
охлаждаемых элементах
ядерного реактора, а те-
чение носит пространст-
венный характер. Кроме
Рис. 6.11. Одна из возможных схем ТВС с витыми
твэлами: 1 — элементы радиационной защиты; 2 —
торцевой отражатель нейтронов; 3 — система вход-
ных решеток; 4, И, 13 — элементы металлического
корпуса из различных материалов; 5 — тепловы-
деляющие элементы; 6, 9 — пружины, фиксирую-
щие подвижные элементы ТВС (твэлы, отражатель
и др.) и компенсирующие удлинение этих элемен-
тов при их нагреве; 7, 10 — стержни, передающие
усилия с пружин на элементы ТВС; 8 — тепловая
изоляция ТВС; 12 — выходная решетка
Глава 6
481
того, рассматриваемые реакторы и ТВС с каналами сложной формы,
а также теплообменные аппараты, входящие в состав космических
энергоустановок, периодически работают в нестационарном режи-
ме, когда быстро изменяется во времени не только тепловая мощ-
ность, но и расход теплоносителя.
Высокие температуры рабочего процесса и наличие неравномер-
ности полей энерговыделения в поперечном сечении реактора и ТВС
требуют повышенной точности математического описания процес-
сов и обязательного учета таких факторов, как зависимость тепло-
физических свойств рабочего тела от температуры и давления, ко-
эффициента теплоотдачи от локальных значений чисел Рейнольдса и
Прандтля, а также температурного фактора.
Весьма важным и специфическим обстоятельством является не-
обходимость учета влияния процессов межканального перемешива-
ния теплоносителя и перераспределения расхода в поперечном сече-
нии ТВС в условиях неравномерного поля энерговыделения. Поясним
это на примере. Пусть поле энерговыделения по объему ТВС отлича-
ется значительной неравномерностью, обусловленной как физичес-
кими особенностями реактора, так и расположением ТВС в активной
зоне. Если ТВС находится вблизи органов регулирования, то возмож-
но появление азимутальной неравномерности поля энерговыделения
(см. рис. 6.10). Кроме того, возможен технологический разброс таких
параметров, как размеры и форма тепловыделяющих элементов и за-
грузка делящегося вещества в каждом элементе.
Все вышеперечисленные неравномерности приводят к возник-
новению неравномерности поля температур в ТВС реактора и к
возможному значительному превышению локальных максимумов
температуры теплоносителя и тепловыделяющих элементов над
средними значениями, полученными из балансных соотношений.
При этом поле температур формируется под влиянием трех факто-
ров: поля энерговыделения, процессов межканального перемешива-
ния теплоносителя и перераспределения расходов в ячейках пучка
твэлов. Возникающие таким образом неравномерности температуры
теплоносителя можно частично выравнить путем интенсификации
процесса межканального перемешивания в ТВС ЯР, который необхо-
димо учитывать при теплогидравлическом расчете ТВС (глава 2).
Как уже отмечалось, важной отличительной особенностью ре-
актора и теплообменников, входящих в состав космических энерго-
установок, является эксплуатация их в нестационарных условиях. В
качестве примера можно рассмотреть рабочий цикл ядерной энерго-
двигательной установки, основные особенности которой изложены
в разделе 6.1. Установка работает в энергетическом режиме, обеспе-
482
Глава б
чивая электроэнергией бортовые потребности космического аппара-
та, и периодически создает кратковременные импульсы реактивной
тяги, работая как ядерный ракетный двигатель. Тепловая мощность
реактора на двигательном режиме составляет 300 МВт, а на энергети-
ческом -1 МВт соответственно. Переходный процесс от энергетичес-
кого режима к двигательному необходимо реализовать достаточно
быстро — за несколько секунд, что необходимо для экономии запаса
рабочего тела на борту. При этом с достаточно высокой скоростью из-
меняется не только тепловая мощность реактора, но и расход тепло-
носителя, что приводит к соответствующим изменениям коэффици-
ентов теплоотдачи и перемешивания теплоносителя во времени по
сравнению с их квазистационарными значениями. Знание количест-
венных характеристик эффектов нестационарности необходимо для
уточненного анализа процессов формирования полей температур
теплоносителя в тепловыделяющих сборках, а также в элементах
конструкции активной зоны реактора и теплообменников энергети-
ческого контура. На основании анализа полей температур определя-
ются основные параметры переходного процесса и допустимые ско-
рости их изменения. В случае переходного процесса с уменьшением
мощности реактора процесс необходимо провести достаточно быст-
ро, чтобы уменьшить до минимума массу рабочего тела (водорода),
требующуюся для расхолаживания реактора до уровня мощности
энергетического режима.
Особенностью таких энергонапряженных объектов, как ядерные
реакторы для ЯЭДУ, является то обстоятельство, что изменение теп-
логидравлических параметров активной зоны реактора во времени
влияет на его мощность. Поэтому при теплогидравлических расчетах
необходимо рассматривать также уравнения нейтронной кинетики,
описывающие изменение мощности реактора во времени [6.1.7,6.2.4],
а также учитывать влияние изменения теплогидравлических пара-
метров на свойства размножающейся среды. Дело в том, что поток
нейтронов, однозначно связанный с мощностью реактора, изменяет-
ся во времени при нарушении условия равновесия цепной реакции.
Если плотность нейтронов в реакторе составляет при зарождении
каждого поколения п см’3, то все эти нейтроны будут либо захваче-
ны в результате поглощения ядрами конструкционных элементов и
ядерного горючего, либо потеряны в результате утечки из объема ак-
тивной зоны. В конце жизненного цикла этого поколения образуется
пКэф новых нейтронов (Кэф — эффективный коэффициент размно-
жения в размножающей среде конечных размеров). Таким образом,
избыток новых нейтронов, полученный в течение среднего времени
жизни, равен п(Кэф — 1).Еслит7 — среднее время жизни одного поко-
Глава б
483
ления нейтронов, то изменение их плотности во времени можно за-
писать уравнением
dn п(КА — 1)
— = _L22—1.	(6.2.17)
dx т7
После интегрирования (6.2.17) с учетом условия: прит — 0, п = п0,
получим
п = пое(Кэф"1)т/т\	(6.2.18)
Величина (Кэф — 1) часто обозначается как Кизб или &К. Очень важ-
ным параметром в теории реакторов является реактивность р, опре-
деляемая как
р = ^цзб=_5£	(6.2.19)
^эф ^эф
Если реактор находится в околокритическом состоянии, то чис-
ленные значения 8К и р очень близки и их часто отождествляют.
Из уравнения (6.2.17), описывающего зависимость мощности ре-
актора от времени, видно, что если величина К. = 1, то плотность
нейтронов и, следовательно, мощность остаются постоянными. Лю-
бое отклонение системы от состояния, при котором Кэф = 1, немед-
ленно вызовет либо уменьшение, либо увеличение мощности.
Оценим на конкретном примере скорость изменения мощности
реактора при внесении возмущений. Предположим, что в реакторе с
тепловым спектром нейтронов (время жизни ® 10’3 с) эффективный
коэффициент размножения увеличивается скачком на 0,01. Исполь-
зуя формулу (6.2.18), получим, что мощность реактора через 1 с воз-
растет в е10 раз, т.е. приблизительно в 2,2-104. Если ядерный реактор
имеет спектр нейтронов, близкий к быстрому (время жизни « 10’5 с),
то аналогичное возмущение коэффициента размножения приведет к
росту мощности в е1000 раз. Столь быстрое возрастание мощности при
наличии определенных изменений реактивности делает ядерный ре-
актор практически неуправляемым объектом. Однако на практике
ядерные реакторы, в том числе космические, успешно поддаются
процессам управления и легко переводятся с одного режима мощ-
ности на другой. Это связано с тем, что процесс деления ядер урана
сопровождается появлением очень небольшого (менее одного про-
цента) количества так называемых «запаздывающих» нейтронов, по-
являющихся через значительный интервал времени после деления.
Эти нейтроны обладают средним временем жизни, превышающим
среднее время жизни нейтронов деления, на несколько порядков. Это
видно из таблицы 6.2.1, иллюстрирующей свойства запаздывающих
нейтронов при делении урана-235 тепловыми нейтронами. Среднее
484
Глава 6
время жизни одного поколения нейтронов с учетом наличия запаз-
дывающих нейтронов можно получить из выражения
i=6
=	(6.2.20)
1=1
Используя данные табл. 6.2.1, можно получить величину т, ~ 0,1 с для
реактора на тепловых нейтронах. Тогда в предыдущем примере мощ-
ность реактора возрастает через 1 с не в е10 раз, а только в е0,1 раз.
В действительности мощность реактора изменяется по более
сложному закону, поскольку необходимо учитывать динамику изме-
нения концентрации запаздывающих нейтронов. Поэтому кинетика
реактора в точечном приближении описывается системой уравне-
ний, приведенной в главе 2.
Величину реЯ легко получить из приведенной выше таблицы как
сумму значений 0.. Для реактора на тепловых нейтронах с исполь-
зованием в качестве делящегося вещества уран-235 величина ре// со-
ставляет -0,0075. Соотношение между реактивностью и периодом
реактора устанавливается уравнением Нордхейма
Р =
^р-^эф 1=1
(6.2.21)
где тр — период реактора, который по физическому смыслу равен
времени, за которое плотность нейтронов (или мощность) увеличи-
лась в е раз. Из уравнения Нордхейма, графически изображенного на
рис. 6.12, хорошо видно, что для реактора со спектром быстрых ней-
тронов введение положительной реактивности по величине, близкой
к доле запаздывающих нейтронов (-0,0075), приводит к очень быст-
рому уменьшению периода реактора и к практически неконтролиру-
емому возрастанию мощности.
Таблица 6.2.1.
Некоторые параметры запаздывающих нейтронов
Номер группы запаздывающих нейтронов	Среднее время ЖИЗНИ, Tf, с	Доля запаздывающих нейтронов по отношению к общему числу нейтронов деления %
1	80,2	0,026
2	31,7	0,17
3	6,5	0,21
4	2,2	0,24
5	0,62	0,084
6	0,071	0,025
Глава 6
485
Рис. 6.12. Зависимость периода ре-
актора от реактивности для раз-
личных времен жизни нейтронов:
1 — 3 — время жизни нейтронов
10 3, 10'4, 10'5 соответственно
Для решения системы уравне-
ний нейтронной кинетики исполь-
зуется алгоритм, предложенный
Я.В. Шевелевым в работе [6.2.5].
Следует также отметить, что си-
стема обыкновенных дифферен-
циальных уравнений в форме
(2.1.104) —(2.1.106) была предложена
в этой работе применительно к го-
могенному реактору. Поэтому при
исследовании динамики и вопро-
сов управления ЯЭДУ реальный
гетерогенный реактор ЯРД заме-
нялся эквивалентным гомогенным
реактором, к которому применя-
лась диффузионная теория [6.1.7].
Размеры реактора, рассмотрен-
ного в данном разделе и определен-
ного по теплогидравлическим характеристикам при загрузке ура-
на-235 с 90%-ным обогащением, позволят иметь реактор на тепловых
нейтронах.
Для учета влияния изменения теплогидравлических параметров
на свойства размножающейся среды, а следовательно, и мощность
ядерного реактора используются соотношения для расчетов эффек-
тов реактивности. При этом значения температурного эффекта ре-
активности pT=f(?T) и плотностного эффекта реактивности PY,
обусловленного использованием в качестве теплоносителя водорода,
определяются из нейтронно-физических расчетов ЯР. Заполнение
реактора водородом приводит к увеличению эффективного коэффи-
циента размножения нейтронов. Реактивность системы изменяется
и за счет перемещения органов регулирования.
Особенностью ЯР для ЯЭДУ является также выделение в нем энер-
гии за счет распада накопившихся осколков деления ядер урана-235.
В первые минуты после останова уровень мощности этого «остаточ-
ного тепловыделения» составляет несколько процентов от мощности
в рабочем режиме. Этот эффект также необходимо учитывать при
расчетах теплогидравлических параметров ЯР и ТВС.
Чтобы достичь выходных параметров ЯРД, соответствующих па-
раметрам, которые заданы в таблице, необходимо нагреть рабочее
тело — водород в ТВС до 2900—3100К. Однако, как показано в работе
[6.2.2], эту среднемассовую температуру перед реактивным соплом
ЯРД требуется достичь в условиях значительной неравномерности
486
Глава 6
энерговыделения, обусловленной работой органов регулирования
реактором (органов СУЗ).
Как видно из рис. 6.8, в зависимости от положения регулирую-
щих барабанов искажается поле энерговыделения по радиусу и ази-
муту ЯР. При этом, если сравнить уровни энерговыделения в ТВС
четвертого ряда ЯР при положениях барабанов, когда они повер-
нуты поглощающей пластиной от реактора (у = 0°) и когда они по-
вернуты поглощающей стороной к реактору (у = 180°), то при но-
минальном расходе водорода при втором положении барабанов в
ТВС четвертого ряда будет недогрев рабочего тела приблизитель-
но на 300 К. В то же время в ТВС, расположенных ближе к центру
ЯР (в ТВС второго и третьего ряда от центра ЯР), энерговыделение
будет превышать номинальное значение, что при заданном расхо-
де водорода может привести к расплавлению твэлов. Поэтому для
наиболее эффективной работы реактора требуется осуществлять
индивидуальное регулирование расхода рабочего тела через каж-
дую ТВС для поддержания постоянной температуры газа на выхо-
де из сборки и заданных выходных параметров ЯРД при условии,
что температура стенки Tw и плотность теплового потока qw не будут
превышать максимально допустимых значений для карбидных твэ-
лов. Однако такое регулирование может оказаться технически не
осуществимым. В этом случае обычно прибегают к использованию
сменных шайб, устанавливаемых на входе в каждую ТВС. При этом
настройка ТВС с помощью шайб должна осуществляться в зависи-
мости от положения сборки в ЯР на такой расход водорода, при ко-
тором ни при каком положении барабанов регулирования не будут
превышаться максимально допустимые для карбидных твэлов тем-
пература и плотность теплового потока. При такой настройке ТВС
ЯР на некоторых режимах работы ЯРД может наблюдаться некото-
рая потеря в удельном импульсе тяги в зависимости от положения
органов регулирования.
Рассмотрим характеристики ЯРД с ТВС, расход рабочего тела че-
рез которые настраивается с помощью сменных шайб. При этом це-
лесообразно рассмотреть схему ЯРД с индивидуальными соплами
для каждой ТВС с давлением на срезе -40 кПа и дорасширительным
насадком с общей степенью расширения такого комбинированного
сопла Ер = рк/ра « 2900.
В процессе работы ЯР при изменении положения регулирующих
барабанов изменяется распределение энерговыделения по радиусу
реактора, а следовательно, и расход рабочего тела G, температура на
входе в реактивное сопло Тк и давление перед соплом рк каждой ТВС
в соответствии с расходной характеристикой сопла, количеством вы-
Глава 6
487
деляемого в ТВС тепла и потерями давления на длине ТВС при задан-
ном давлении на входе рвх и расходе водорода G в ЯРД.
Расчет расхода рабочего тела G и его параметров Тк и рк перед соп-
лом для ТВС каждого ряда целесообразно провести при крайних по-
ложениях регулирующих барабанов (\|/ = 0 и = я), что позволит оце-
нить величины максимальных отклонений этих параметров. Расчет
проводится методом последовательных приближений. При этом ис-
пользуются уравнения расхода через сопло
Х+1
2 U-i
(6.2.22)
и связи между параметрами в адиабатном процессе
р
л кр
(6.2.23)
где х — показатель адиабаты при параметрах и составе рабочего тела
в критическом сечении реактивного сопла (ркр, Ткр); FKp — площадь
критического сечения индивидуального сопла, Гкр = 7rd^p /4; R — га-
зовая постоянная теплоносителя (водорода с ингибирующей угле-
родосодержащей присадкой). В расчетах использовались значения
газовой постоянной R и показателя адиабаты х в зависимости от тем-
пературы и давления, определенные из графиков, представленных
на рис. 6.13 и 6.14, а теплоемкости ср и cv определялись по формулам
ср=Э//ЭТ; cv=cp-R; X = cp/cv.	(6.2.24)
Рис. 6.13. Зависимость газовой постоянной водорода с ингибирующей
углеводородной присадкой от температуры и давления
488
Глава 6
Cp/Cv
							
					75 бар	40 бар	
							20 бар
				1 бар	2 бар		
						5 бар	10 бар
							
							
1 =
1,4
1,2
1,0
0,8
0,6
0,4
0	500	1000	1500 2000	2500	3000	3500 Т, К
Рис. 6.14. Зависимость показателя адиабаты для водорода
с ингибирующей присадкой от температуры и давления
Расходная характеристика индивидуальных сопел ТВС, рассчи-
танная по формуле (6.2.22) и представленная на рис. 6.15, определе-
на в предположении, что параметры торможения р* и Т* равны пара-
Рис. 6.15. Принятая расходная характеристика индивидуального
реактивного сопла ТВС
Глава б
489
метрам потока перед соплом р* = рк и Т* = Т. Погрешность расчета
при таком допущении незначительна, поскольку число Маха перед
соплом было менее 0,1. Используя уравнение баланса тепла для ТВС
4 =^+-7?-.	(6.2.25)
(л
где Оср — среднее энерговыделение в ТВС по радиусу реактора и
К — отношение энерговыделения в ТВС рассматриваемого ряда к ее
средней величине Оср, можно определить температуру перед соплом
Тк = Т(/к, рк). При этом энтальпии 1К и /вх определяются по графику на
рис. 2.3, а рк рассчитывается по формуле
Рк Рвх
R Тк Ркср
^ср ^кср Рк
(6.2.26)
где Gcp, Яср, Ткср, Рксри ApZcp - средние по радиусу реактора парамет-
ры потока, а те же параметры без индекса «ср» относятся к ТВС рас-
сматриваемого ряда. Значения средних по радиусу ЯР параметров
потока определяются путем теплогидравлического расчета ТВС по
средним параметрам. Результаты такого расчета для режима работы
ЯР пониженной мощности по сравнению с номинальным режимом
работы ЯРД представлены на рис. 2.9. Зная значения средних пара-
метров и решая методом последовательных приближений систему
уравнений (6.2.22) —(6.2.26) до получения совпадающих результатов,
можно определить значения параметров G, Т, и рк для ТВС каждого
ряда ЯР на различных режимах работы ЯРД и при различных поло-
жениях регулирующих барабанов.
На рис. 6.16 представлены результаты расчета параметров ТВС в
безразмерном виде для ТВС каждого ряда ЯР при крайних положени-
ях органов регулирования (\|/ = 0 и \|/ = 180°) на номинальном и пони-
женном режимах работы ЯРД. Было обнаружено, что при одинаковом
подогреве рабочего тела во всех ТВС ЯР, достигаемым соответству-
ющим изменением расхода теплоносителя, изменение мощности ЯР
практически не приводит к изменению относительных параметров
ТВС G/Gcp, Тк/Ткср, рк/ркср в рассматриваемой ТВС. Использование
схемы ЯРД с общим соплом для всех ТВС также незначительно вли-
яет на параметры (G/Gcp)0 и (Тк/Ткср)0 по сравнению с параметрами
при рассмотренной схеме комбинированного сопла (индивидуально-
G
го для ТВС и общего дорасширительного насадка):
и
Т
лк
\ кср7и
(см. рис. 6.16). Для схемы ЯРД с общим соплом перепад давлений АрЕ и
давление перед соплом рк одинаково для всех ТВС ЯР, поэтому расчет
490
Глава 6
параметров G и Тк проводился методом итераций путем решения сис-
темы из уравнения (6.2.25) связи Гк = Т(1к, рк) и выражения
G = Gcp
Д:р *кср
R Тк
(6.2.27)
Таким образом, на распределение безразмерных параметров
G/Gcp, Рк^Ркср в ТВС по РАДИУСУ ЯР оказывает существенное
влияние только положение органов регулирования (см. рис. 6.16). От-
сюда следует, что для обеспечения работоспособности ТВС при раз-
личном положении органов регулирования необходимо с помощью
сменных шайб обеспечить такой расход теплоносителя, чтобы при
любом положении барабанов регулирования температура Тк не пре-
вышала номинального значения (3100 К).
Из рис. 6.16 видно, что при заданной величине перепада давления
на ТВС и одинаковой для всех ТВС ЯР [ДрЕ = const(P)] расход G через
ТВС четвертого ряда превышает Gcp при ц/ = п и равен номинальному
значению расхода теплоносителя Gcp при у = 0. Это говорит о том,
что регулирование расхода сменными шайбами по радиусу ЯР не
позволяет удовлетворить все режимы работы ЯРД (при у = 0...1800).
Следовательно, необходимо или увеличить расход G на -15% по срав-
^ср
G
;5-
;3-
;4 -
;2 -
т
т
\ кср7
т
JK
т
Рис. 6.16. Влияние положения органов СУЗ на параметры в ТВС по радиусу ЯР для
вариантов ЯРД с индивидуальными соплами и с общим реактивным соплом: 1 —
f G
р
VrKcP;

Глава 6
491
нению с Gcp при заданной мощности ЯРД, либо снизить мощность ре-
актора на 15% от номинального значения, что, в конечном счете, при-
водит к снижению температуры Тк при заданном расходе Gcp.
Тогда при условии, что ограничение по температуре Тк < 3100К,
при 0 < \|/ < тс, достигается путем снижения мощности реактора на 15%
от номинального значения (см. рис. 6.16), можно получить распреде-
ление параметров ТВС: G, Тк и Рк по радиусу реактора при у = 0 и
= я, представленное на рис. 6.17. В этом случае Тк = Тктах = 3100К
достигается в ТВС третьего ряда при \|/ = п (см. рис. 6.17). Задание
расхода теплоносителя через ТВС в этом случае сводится к подбо-
ру сменных шайб для обеспечения постоянного перепада давлений
на ТВС по радиусу реактора для всех ТВС [ЛрЕ = const(P)]. Тогда тягу
ЯРД можно рассчитать по формуле
2т
—— RT
Х-1
(6.2.28)
+ ^а(Ра Рн)'
где Fa — площадь выходного сечения сопла; ра — давление на срезе
сопла; % и R — показатель адиабаты и газовая постоянная при средних
Рис. 6.17. Результаты расчета ТВС при различном положении органов СУЗ и пони-
жении температуры во всех ТВС до уровня или ниже ее номинального значения
путем снижения мощности ЯР: 1 —
-4 2-
ССр J
;3 -
V кср>
р
<гксР;
492
Глава 6
параметрах по длине сопла. Тяга, рассчитанная по уравнению (6.2.28),
будет меньше номинального значения тяги примерно на 3,7%.
Величина удельного импульса тяги в этом случае составит
-9,05 км/с вместо 9,5 км/с при отсутствии влияния органов регулиро-
вания на энерговыделение в ядерном реакторе. Таким образом, поте-
ря удельного импульса тяги, связанная с работой системы регулиро-
вания при изменении режима работы ЯРД, может составить порядка
-450 м/с при условии, что перед индивидуальным соплом любой ТВС
температура Тк< 3100К при 0 < ц/ < п достигается настройкой расхо-
да водорода через ТВС с помощью сменных шайб, чтобы обеспечить
= const(7?).
Следует отметить, что выполненные оценки носят приближен-
ный характер и позволяют в основном сформулировать проблемы,
подлежащие решению при разработке и расчетно-эксперименталь-
ном обосновании работоспособного ядерного реактора ЯРД, отвеча-
ющего параметрам, представленным в таблице. В то же время рас-
смотренные особенности работы ядерного реактора ЯРД приводят, в
конечном счете, к проблемам теплообмена (теплосъема с элементов
ЯР) и гидродинамики (организации течения рабочего тела).
Список литературы
6.2.1.	Субботин В.И., Коротеев А.С., Конопатов А.Д. идр. Разработка ЯРД на
основе реактора минимальных размеров ИРГИТ. Энергетические испыта-
ния опытного образца ядерного реактора//Труды 3-й отраслевой конфе-
ренции «Ядерная энергетика в космосе. Ядерные ракетные двигатели».
Семипалатинск, 1992. С. 85-87.
6.2.2.	Коновалов В.А., Конюхов Г.В., Мамаев Ю.В. идр. Проблемы нейтрон-
ной физики и ядерной безопасности реактора ЯРД минимальных разме-
ров/Дам же. С. 45-46.
6.2.3.	Кривко-Красько С.В., Попов Е.Б., Паршин Н.Я. и др. Расчетно-теоре-
тическое обоснование работоспособности ТВС реактора ЯРД/Дам же.
С. 29-30.
6.2.4.	Сегаль М.Д., Смирнов Л.П., Зарудин А.В. Численное моделирование
теплогидравлических и переходных процессов в реакторе ядерной энер-
годвигательной установки/Друды отраслевой юбилейной конференции:
«Ядерная энергетика в космосе». Ч. I: Докл. советских специалистов. Об-
нинск, 1990. С. 320-323.
6.2.5.	Крамеров А.Я., Шевелев Я.В. Инженерные расчеты ядерных реакторов.
М.: Энергоатомиздат, 1984. 736 с.
6.2.6.	Yasui G. Reactor Heat Removal Limitations of Nuclear Rockets//ARS J. 1961.
V. 31, N 9. P. 1195-1204.
Глава 6
493
6.3.	ВЫБОР КОНСТРУКЦИИ И МАТЕРИАЛОВ
ТЕПЛОВЫДЕЛЯЮЩЕЙ СБОРКИ
ЯДЕРНОГО ГЕТЕРОГЕННОГО РЕАКТОРА
В США и в России за период с конца 50-х гг. выполнен большой
объем материаловедческих, технологических и исследовательских
работ по созданию ЯРД, разработаны и испытаны высокотемпера-
турные реакторы ЯРД с канальными, стержневыми и шариковыми
твэлами, что позволяет выбрать наиболее рациональную конструк-
цию ТВС реактора ЯЭДУ. ТВС и твэлы являются наиболее теплона-
пряженными элементами и представляют наиболее уязвимое звено
при разработке ЯЭДУ для полетов на Марс, поскольку они должны об-
ладать высокой надежностью и способностью работать длительное
время при высоких температурах в водородной среде (см. табл. 6.2.1),
а также при многократных сменах режима работы. При этом воз-
никает необходимость проведения многочисленных реакторных и
внереакторных испытаний при натурных значениях температуры,
плотности энерговыделения и его распределения, расхода рабочего
тела, давления и ресурса для определения пределов работоспособ-
ности и безопасного использования ТВС с твэлами различной конст-
рукции.
Такие испытания необходимо сочетать с предварительным выбо-
ром наиболее эффективных теплообменных поверхностей, позволя-
ющих интенсифицировать процессы перемешивания теплоносителя
для выравнивания неравномерностей температур по сечению ТВС и
реактора, а также с численным моделированием как стационарных,
так и нестационарных теплогидравлических процессов, позволя-
ющим в определенной мере оценить пределы работоспособности
ТВС. Такой подход позволяет ограничить объем дорогостоящих ре-
акторных испытаний также путем расширения возможностей моде-
лирования натурных процессов теплосъема на крупномасштабных
моделях ТВС и твэлов и детального исследования теплогидравличе-
ских процессов на электронагреваемых моделях с последующим чис-
ленным моделированием при натурных условиях работы [6.3.1].
Как уже отмечалось, теплообменные поверхности реактора, раз-
работанного в США по программе «Nerva», позволяли нагреть водо-
род только до -2500К, т.е. обеспечивали удельный импульс тяги на
уровне 8,5 км/с, в то время как для обеспечения удельного импуль-
са тяги порядка 9,25 км/с (табл. 6.2.1), водород в реакторе должен на-
греваться до 2960К на выходе из ТВС. Таким образом, активная зона
реактора ЯРД «Nerva», состоящая из набора плотноупакованных
494
Глава 6
тепловыделяющих элементов, имеющих форму шестигранника с 19
круглыми отверстиями диаметром 1—2 мм для прохода теплоносите-
ля, представляла собой систему параллельных изолированных кана-
лов, по которым течет рабочее тело. При этом из-за влияния допусков
на геометрические размеры изолированных каналов малого диамет-
ра (1—2 мм) появляются значительные неравномерности температу-
ры газа по радиусу ТВС и реактора и происходит перегрев газа в от-
дельных каналах, что приводит к необходимости снижать среднюю
температуру газа перед соплом и к снижению удельного импульса
тяги ЯРД.
При создании высокотемпературных твэлов и ТВС большое значе-
ние для обеспечения заданных параметров имеет выбор материалов
твэлов, стойких в среде водорода при больших плотностях объем-
ного энерговыделения, а также технологические особенности их из-
готовления, предотвращающие вынос урана-235 из твэлов и их разру-
шение. Так, в случае графитовых твэлов с защитным покрытием при
размещении урана-235 -93%-ного обогащения, заключенного в мат-
рицу из твердого раствора UC-ZrC и углерода [6.1.6], а также при со-
ответствующей углеродосодержащей присадке в рабочее тело мож-
но, по всей вероятности, реализовать параметры, достигнутые при
испытании ЯРД «Nerva», — 2500К. Стремление повысить выходные
параметры этого реактора путем использования в качестве основы
вместо графита карбидов тугоплавких металлов (Nb, Zr, Та), видимо,
не позволит получить желаемый эффект из-за больших допусков на
геометрические размеры карбидных твэлов с изолированными па-
раллельными круглыми каналами, чем на размеры графитовых твэ-
лов. Это связано с различием технологий их изготовления. Кроме
того, такая замена неизбежно приведет к смене и типа реактора, и его
размерности. Изготовление таких твэлов разрезными по длине реак-
тора с размещением между отдельными секциями коллекторов сме-
шения, представляющих собой камеры длиной порядка 10 диаметров
охлаждающих каналов, позволяет только частично выравнить тем-
пературные неравномерности, которые формируются из-за влияния
отклонений геометрических, теплофизических и других параметров
от расчетных значений. Это выравнивание происходит только в мас-
штабе расстояния между соседними каналами, поэтому использова-
ние твэлов такого типа и в случае использования коллекторов смеше-
ния не позволяет заметно снизить неравномерность температур на
выходе из ЯР. Кроме того, организация нескольких коллекторов сме-
шения (4—7) по длине реактора для каждой ТВС существенно увели-
чивает пористость реактора по рабочему телу в, что приводит к ухуд-
шению нейтронно-физических характеристик ЯР, росту потребной
Глава 6
495
загрузки урана-235 и увеличению массы и габаритов ядерного реак-
тора и ЯЭДУ [6.3.2].
Таким образом, реактор ЯРД с канальными твэлами даже с кол-
лекторами смешения не сможет обеспечить нагрев водорода до сред-
несмешанной температуры на выходе из реактора, равной 2960К,
которая обеспечивает удельный импульс тяги 9,25 км/с (табл. 6.1.1).
Поэтому для реализации требований к ЯРД, представленных в
табл. 6.1.1, видимо, необходимо отдать предпочтение ТВС со стерж-
невыми витыми твэлами двухлопостного профиля, которые сущест-
венно интенсифицируют процессы межканального перемешивания
и теплообмена в них [6.1.7—6.1.10, 6.3.1, 6.3.3]. Помимо стержневых
твэлов овального профиля могут использоваться также твэлы трех-
и четырехлопастного профиля. В ТВС с витыми стержневыми твэла-
ми (см. рис. 6.11) можно, выбирая шаг закрутки профиля твэла, обес-
печить интенсивное перемешивание рабочего тела по всей длине
ТВС без организации коллекторов смешения. При этом улучшаются
нейтронно-физические характеристики реактора ЯРД и снижается
потребная загрузка урана-235, что повышает температуру плавле-
ния твэлов, изготовленных из однородного раствора карбидов туго-
плавких металлов (UC-NbC, ZrC-NbC-UC). Спиральная закрутка
профиля твэла позволяет создать плотноупакованный пакет стерж-
ней, который размещается в обойме, изготовленной из карбидов ту-
гоплавких металлов и покрытой слоем эффективной высокотемпера-
турной изоляции. Преимущество такой ТВС по сравнению с ТВС с
твэлами канального типа состоит в отсутствии изолированных кана-
лов, что позволяет избегать накопления неравномерности поля тем-
пературы по длине ТВС и управлять процессом поперечного переме-
шивания теплоносителя, выбирая шаг закрутки твэлов. Чем меньше
шаг закрутки, тем больше интенсивность межканального перемеши-
вания теплоносителя. При этом за счет интенсификации теплообме-
на снижается также температура стенки твэлов, что особенно важно
для выходных нагревных секций ТВС, работающих при температу-
рах, близких к температуре плавления карбидных материалов.
ТВС со стержневыми твэлами обладает по сравнению с каналь-
ными ТВС также рядом преимуществ технологического характера.
Так, в ТВС с витыми твэлами легко осуществлять концентрацион-
ное профилирование загрузки урана-235 по радиусу, азимуту и дли-
не ТВС, повышать термостойкость твэлов путем уменьшения их ди-
аметра, проводить индивидуальный контроль качества изготовле-
ния каждого твэла, а также использовать в качестве основы карбиды
тугоплавких металлов, поскольку увеличение допусков на геометри-
ческие размеры твэлов при замене графита на карбиды не приводит
496
Глава 6
к заметным локальным перегревам благодаря интенсивному межка-
нальному перемешиванию по длине ТВС.
Рассмотрим особенности конструкции ТВС с витыми стержневы-
ми твэлами, которые оказывают существенное влияние на характер
течения, теплообмен и переносные свойства потока в этой ТВС. Пре-
жде всего, благодаря спиральной закрутке овального профиля твэ-
лов, плотноупакованный пучок твэлов обладает радиальной порис-
тостью ег = s4/ss, где 5Ц — площадь цилиндрической поверхности,
через которую теплоноситель рассматриваемых ячеек может обме-
ниваться с теплоносителем в соседних ячейках по длине ТВС, sz —
суммарная площадь цилиндрической поверхности. Поэтому в ТВС с
витыми твэлами действует механизм переноса в масштабе попереч-
ного сечения ТВС, обусловленный организованным конвективным
движением теплоносителя по винтовым каналам твэлов и обменом
массой и теплом на границах между соседними ячейками из-за ради-
альной проницаемости пучка (благодаря пористости £г).
Эффективность организованного конвективного переноса и дру-
гих механизмов обмена массой и теплом в ТВС определяется шагом
закрутки витых твэлов s, отнесенных к максимальному размеру твэ-
ла d. В работах [6.1.7—6.1.10, 6.3.1] показано, что вместо относительно-
го шага закрутки s/d можно рассматривать критерий Fr n = s2/ddeql
который определяет особенности течения и теплообмена в пучках
с витыми трубами или твэлами. На межканальное перемешивание
теплоносителя влияет также и пористость пучка твэлов [6.1.9—6.1.10;
6.2.1; 6.2.2] ег~е, где £ = F^/F^ — пористость ТВС по рабочему телу.
Обычно пористость £ выбирают в пределах £ = 0,3...0,5.
При размещении пучка твэлов в обойме необходимо предусмот-
реть зазоры для компенсации температурных расширений при ра-
боте реактора, а на периферии пучка — фасонные вставки для обес-
печения равномерного поля скоростей в пучке и благоприятного теп-
лосъема со всех твэлов.
При выборе шага закрутки твэлов для обеспечения максималь-
но возможной интенсификации теплообмена и поперечного переме-
шивания в пучке одновременно учитывается необходимость обеспе-
чения заданного перепада давлений на ТВС и числа точек касания
твэлов между собой по длине пучка. При этом шаг между точками
касания t = s/(6nd), где п — число лопастей твэла (п = 2...4), должен
позволить избежать смещения элементов твэла в случае его растрес-
кивания от возможных термических напряжений.
При обеспечении продольного профилирования загрузки ура-
на-235 витые твэлы выполняются разрезными по длине. При этом со-
седние пучки твэлов с различной концентрацией упираются друг в
Глава б
497
друга своими торцами при их размещении в обойме (см. рис. 6.11). Как
уже отмечалось, обойма должна быть многослойной, т.е. состоять из
слоя, воспринимающего нагрузку, и из теплоизолирующих слоев.
При выборе характерных геометрических параметров твэлов ис-
пользуют заданные размеры: относительную длину ТВС lp/deq, внут-
ренний диаметр обоймы d0, эквивалентный диаметр deq и порис-
тость е. Тогда можно определить диаметр твэлов, толщину лопастей
h и их число п по следующей методике. Задавая число рядов твэлов z
(z = 7,9, И, 13...) определяется максимальный размер профиля твэлов
d = d0/z, а также число твэлов N, которые можно разместить в обойме
диаметром d0. Из заданных значений z и d необходимо определить те
значения диаметра d, которые удовлетворяют заданным величинам 8
и = 4Fn/(MITB + По), где Птв — периметр твэла, По — периметр
обоймы. Тогда для каждого определенного значения d вычисляется
площадь поперечного сечения твэла FTB (при 8 = 0,4FTB = l,5Fn/N),
толщина лопасти h = h(d, п), периметр Птв = П(с?, h) и эквивалентный
диаметр deq. Затем по точкам пересечения зависимости d = f(d, п) с
прямой deq = const определяются возможные варианты по диаметру
твэлов d и числу лопастей п (п = 2, 3, 4). Так, при заданных величинах
d0 = 30 мм, deq~ 1 мм и 8 ~ 0,4 расчет по изложенной методике позво-
ляет определить твэлы двухлопастного профиля (и = 2) с диаметром
d ~ 2,2 мм и с толщиной лопасти h = 1,2...1,3 мм.
Конструктивной особенностью ТВС со стержневыми твэлами
является наличие опорной (выходной) и входных перфорирован-
ных решеток, между которыми размещены пучки твэлов (например,
шесть секций длиной 0,1м каждая с различной концентрацией ура-
на-235). Этот пакет твэлов с входными решетками поджимается пру-
жиной, чтобы исключить ударное воздействие на карбидные твэлы
при транспортировке и работе реактора в различных режимах. На-
личие входных решеток, а также торцевого отражателя и элементов
радиационной защиты перед активной зоной (см. рис. 6.11) создают
некоторые проблемы теплосъема с твэлов первой нагревной секции
(7 = 100 мм). Это связано с тем, что решетки и торцевой отражатель
располагаются непосредственно перед первой нагревной секцией
с минимально возможным осевым зазором для обеспечения задан-
ного распределения энерговыделения по длине реактора, причем
пористость отражателя по рабочему телу должна быть минималь-
но возможной для обеспечения достаточной эффективности его ра-
боты. Поэтому рабочее тело натекает на входную решетку и на пер-
вую нагревную секцию в виде системы струй малого диаметра. При
этом возникает необходимость в изучении процесса выравнивания
неравномерностей полей скорости на элементах, расположенных
498
Глава 6
перед первой нагревной секцией, на самой секции и по ее длине. К
элементам радиационной защиты (см. рис. 6.11) предъявляются та-
кие же требования по пористости, как и для торцевого отражателя.
Для уменьшения массы и габаритов реактора ЯРД радиационная за-
щита должна быть расположена как можно ближе к торцевому отра-
жателю [6.3.1 —6.3.3].
Малая пористость по теплоносителю торцевого отражателя и ра-
диационной защиты увеличивает перепады давления на ТВС. По-
этому поиск наиболее благоприятных форм каналов, их числа и расп-
ределения по поперечному сечению элементов, обеспечивающих
приемлемые значения гидравлических потерь и достаточно равно-
мерное поле скоростей по сечению ТВС, проводится эксперимен-
тально при гидравлических испытаниях проточного тракта ТВС. Эти
испытания являются одним из основных этапов в общей программе
экспериментальной отработки ТВС ЯРД.
Таким образом, перечисленные особенности конструкции высо-
котемпературной ТВС с витыми стержневыми твэлами определяют
особенности гидродинамики и теплообмена и должны учитывать-
ся при проведении экспериментальных исследований, математи-
ческом моделировании теплогидравлических процессов с учетом
ядерной безопасности и на всех стадиях реакторных и внереактор-
ных испытаний при определении пределов работоспособности это-
го типа ТВС ЯЭДУ. Размеры активной зоны и мощность реактора оп-
ределяются условиями отвода тепла от твэлов при стационарных
условиях. Расчет полей температур ТВС как в одномерном прибли-
жении, так и для двух- и трехмерных распределений энерговыделе-
ния, проводится путем решения систем уравнений, рассмотренных
в разделе 2.1.
Рассмотрим результаты численных теплогидравлических расче-
тов различных режимов работы ТВС с витыми стержневыми твэла-
ми овального профиля в целях выявления влияния различных фак-
торов на поля температур и, в конечном счете, на мощность реактора,
удельную тягу и тягу ЯРД. Анализ результатов расчета теплогидрав-
лических параметров будем проводить применительно к твердофаз-
ному реактору, для которого известны поля энерговыделения во всех
трех измерениях. Материал твэлов — твердый раствор карбидов ту-
гоплавких металлов. Охладитель — газообразный водород с инги-
бирующей присадкой, предотвращающей вымывание углерода из
основы при высоких температурах. Поэтому проблемы химическо-
го взаимодействия рабочего тела с материалом твэлов не рассматри-
ваются. Охлаждаемые каналы — пучки витых твэлов с deq «1,2 мм,
которые распределены в замедлителе таким образом, чтобы обеспе-
Глава 6
499
чить большую равномерность энерговыделения в поперечном сече-
нии ЯР (см. рис. 6.5).
Сначала рассмотрим одномерную задачу при турбулентном тече-
нии водорода, принимая, что в каждом поперечном сечении ЯР име-
ются равномерные поля энерговыделения и что плотность энерго-
выделения изменяется только в продольном направлении х (вдоль
каналов охлаждения).
Рассмотрим, как влияет продольный профиль плотности энерго-
выделения по длине ТВС (раздел 2.1) на распределение среднемас-
совой температуры теплоносителя (рис. 2.7) при заданных темпера-
турах на входе и выходе из ТВС. Видно, что при наличии торцевого
отражателя нейтронов с холодной стороны ЯР (на входе в ТВС) рас-
пределение температуры Тср (рис. 2.7) становится более равномер-
ным по длине реактора по сравнению с распределением Тср при про-
филе плотности энерговыделения для реактора без отражателя по
закону синуса
gvcp =sin7tx/I.	(6.3.1)
Расчет изменения среднемассовой температуры Тср по длине ТВС
при qvcp по равенству (6.3.1)
тср =TBX+-y(l-C0S7tx/L)	(6.3.2)
без учета изменения теплоемкости ср по длине ТВС дает еще более
заниженные температуры Тср (на -400°) по сравнению с расчетом Тср
для реактора с торцевым отражателем и с учетом зависимости эн-
тальпии газа от температуры и давления для рассматриваемого рабо-
чего тела. Таким образом, изменение среднемассовой температуры
по длине ТВС при одномерном описании течения необходимо прово-
дить по методике раздела 2.1, используя выражения (2.1.17) —(2.1.38) в
соответствии с блок-схемой программы расчета на ЭВМ.
Результаты расчета распределения температур рабочего тела Тср,
стенки твэлов Tw и теплоизолирующей обоймы Т, плотностей тепло-
вого потока с твэлов див стенку обоймы q0 по длине ТВС представ-
лены на рис. 2.9 для режима пониженной мощности реактора. При
расчете на этом режиме так же, как и на режиме номинальных пара-
метров (рис. 2.7) принималось, что температура на выходе из реак-
тора равна Твых = 3050К. На рис. 2.9 представлены также результаты
расчета распределений давления по длине ТВС для режима пони-
женной мощности, а на рис. 2.6 — для номинального режима рабо-
ты реактора. Расчет распределения давлений проводился по методи-
ке раздела 2.1 путем решения уравнений (2.1.41) —(2.1.50). Результаты
500
Глава 6
расчета распределений давлений представлены также в табл. 2.1.1
для различных вариантов конструктивного выполнения ТВС с виты-
ми твэлами как для номинального режима (ри)ср = 370 кг/(м2-с), так
и для режима пониженной мощности — (рп)ср = 148 кг/(м2-с). Числа
Рейнольдса для этих режимов работы реактора соответствуют тур-
булентному режиму течения на всей длине активной зоны реактора
(рис. 2.8), что позволяет использовать для расчета теплоотдачи зави-
симости, полученные при числах Re > 2-Ю3 (глава 4).
Результаты численного моделирования теплогидравлических
процессов при стационарных условиях для среднемассовых ско-
ростей (ри)ср 370кг/(м2 с) представлены на рис. 6.18 при темпера-
турах рабочего тела на входе Тъх = 550К и на выходе из реактора
Гвых = 3050К и при продольном профиле плотности энерговыделе-
ния qvcp, который формируется торцевым отражателем (рис. 2.1).
Как видно из рис. 6.18, с ростом (ри)ср температура стенки твэлов
заметно возрастает только на первых нагревных секциях в облас-
ти сравнительно низких температур, причем возрастание массовой
скорости с 370 до 1200 кг/(м2-с) приводит к максимальному возраста-
нию Tw всего на -200К при х/1 = 0,33. На последних нагревных сек-
циях (на выходе из реактора) это увеличение не превышает -50К.
Таким образом, температурный режим работы ТВС с витыми твэла-
ми практически не ограничивает форсирование мощности реакто-
ра по сравнению с номинальной мощностью при значении массовой
скорости, равной -370 кг/(м2-с).
Рис. 6.18. Распределение темпера-
туры газа и стенки твэлов (а), сред-
ней плотности теплового потока (б)
и перепадов давления на активной
зоне ТВС .(в) по ее длине при одно-
мерном описании течения: 1 — 4 —
для значений среднемассовой ско-
Па роста теплоносителя ри = 370,430,
800 и 1200 кг/(м2-с) соответственно
Глава 6
501
Основными ограничениями для увеличения мощности реактора,
как это видно из рис. 6.18, являются ограничения по средней плотнос-
ти теплового потока и скорости теплоносителя в НС. Так, величина
Qcp max возрастает в -2,15 и в -3,22 раза для (рп)ср = 800 и 1200 кг/(м2-с)
по сравнению с номинальным режимом, что может существенно
превысить максимально допустимый тепловой поток для твэлов рас-
сматриваемого типа и размеров, изготовленных из карбидных мате-
риалов.
Приведем некоторые результаты исследования термической про-
чности твэлов, полученные на электромоделирующих установках,
принимая за критерий термопрочности твэлов плотность теплово-
го потока <7тах, при которой происходит разрыв электрической цепи.
Тогда для твэлов из раствора карбидов ZrC-NbC-UC тепловые пото-
ки gmax в зависимости от температуры стенки твэла Tw имеют следу-
ющие значения: при Tw = 1500К — qmax « 8 МВт/м2; при Tw = 1900К —
Qmax «8,8 МВт/м2 и при Tw = 2400К — gmax «12 МВт/м2. Как видно из
рис. 6.18, этим ограничениям отвечают только два рассмотренных ва-
рианта: при (рп)ср » 370 и 430 кг/(м2 с). Более предпочтительным мо-
жет оказаться использование на первых нагревных секциях (х < 2/3/)
твэлов из карбографита — [(UC+ZrC) + С] с защитным покрытием из
ZrC, которые обладают большей термопрочностью (при Tw = 1500К —
<7max« 13...16 МВт/м2, при Tw = 2000К — gmax = 14,5 МВт/м2). Как видно
из рис. 6.18, при применении таких твэлов запасы по термопрочности
несколько возрастают, но ограничения по (рп)ср в основном сохраня-
ются [(pu)cpmax < 430 кг/(м2-с)].
Выполненные оценки являются приблизительными, поскольку
метод испытаний на термопрочность путем электрического нагре-
вания образцов твэлов дает значительный разброс опытных по gmax
и не моделирует в полной мере условия работы твэлов в реакторе
[6.2.6, 6.3.3]. Поэтому использование твэлов меньших размеров и но-
вых более термостойких материалов для твэлов, а также совершенст-
вование методов определения максимально допустимых тепловых
потоков позволит в дальнейшем увеличить мощность реактора и теп-
ловыделяющих сборок.
Как было показано в работе [6.2.6], в многоканальных реакторах
для обеспечения расчетного теплосъема необходимо избегать усло-
вий, при которых возможно достижение местной скорости звука акр
в каком-либо канале и его запирание. Поэтому, учитывая возмож-
ные неконтролируемые неравномерности скоростей в изолирован-
ных каналах (в случае пучков стержневых твэлов такими канала-
ми является ТВС) реактора, необходимо иметь запас по скорости в
его выходном сечении. Обычно считается, что достаточным огра-
502
Глава 6
ничением для скорости потока на выходе из каналов является ско-
рость пвых, соответствующая числу Маха Мвых = 0,5(пвых = 0,5акр).
Тогда при заданном давлении рабочего тела в камере перед соплом
рк, равном давлению газа на выходе из реактора (рк = рвых), можно
определить суммарные перепады давлений на ТВС Apz при рассмат-
риваемых среднемассовых скоростях потока (рп)ср и построить гра-
фик зависимости Apz = f(pK), как это показано на рис. 6.18, в котором
нанесены также ограничивающие линии umax = акр (при Мвых = 1) и
максимально допустимая средняя скорость в каналах пвых = 0,5акр
(при Мвых = 0,5). Видно, что при заданном давлении в камере перед
соплом рк ~ 5 МПа можно реализовать мощности ядерного реактора,
соответствующие величинам (рп)ср < 800 кг/(м2-с).
Таким образом, при заданных величинах рк, Твх и Твых и степе-
ни расширения газа мощность реактора заданных размеров может
быть увеличена примерно в два раза по сравнению с принятым но-
минальным режимом работы. При этом соответственно в два раза
увеличивается и тяга ЯРД (при неизменной удельной тяги) благодаря
увеличению расхода рабочего тела (среднемассовой скорости пото-
ка). Однако при этом увеличивается давление на входе в реактор, что
может потребовать дополнительных мероприятий по увеличению
прочности корпуса реактора и привести к росту его массы, а наблю-
даемое увеличение плотности теплового потока g (см. рис. 6.18, б)
потребует увеличения термопрочности твэлов.
Из рассмотрения результатов теплогидравлических расчетов при
одномерном описании течения следует, что при х = 2/37, где 7 — дли-
на активной зоны реактора, основным ограничением при повышении
мощности реактора является плотность теплового потока из-за огра-
ниченной термопрочности твэлов. При х > 2/37, т.е. на последних на-
гревных секциях, основным ограничением для роста мощности ре-
актора является температура стенки (Tw = const) (см. рис. 6.18,а). На
этом рисунке пунктирной линией обозначен нижний предел темпера-
туры ТСолтш> при превышении которой твердая фаза начинает пере-
ход в жидкое состояние для секций с максимальной концентрацией
урана. При этом, поскольку в ТВС используется продольное профи-
лирование концентрации урана-235 по длине и концентрация первой
нагревной секции максимальна, то ТСолппп = 3590К относится к твэлам
этой секции. На выходных секциях ТВС концентрация урана в твэлах
меньше, чем на первой секции и ТСолтт = 3680К, поэтому запас по тем-
пературе для этих секций будет выше, чем показано на рис. 6.18,а.
Надо отметить, что для обеспечения работоспособности твэлов
необходимо иметь достаточный запас между температурой в цент-
ре твэлов и температурой солидус карбидных материалов твэлов. Ре-
Глава 6
503
зультаты теплогидравлического расчета в одномерном приближе-
нии для ТВС с витыми твэлами, где кроме изменения температур Тср
и Tw было рассчитано и продольное распределение температуры в
центре твэлов, представлено на рис. 6.19. Этот расчет был выполнен
для продольного профиля плотности энерговыделения, представ-
ленного на рис. 2.1, кривая 3. Из рис. 6.19 видно, что для этого профи-
ля характерно повышение плотности энерговыделения на входной
нагревной секции из-за более эффективной работы торцевого отра-
жателя, что приводит в этой области течения к относительному рос-
ту температур стенки и в центре твэлов. В то же время на выходных
секциях температура в центре твэлов практически не различима с Tw
(Т больше Tw на величину <10°) при работе на режиме пониженной
мощности. При работе на режиме номинальной мощности разность
температур между Тц и Tw не превышает -50°. Сравнение результа-
тов расчета температур Tw и Тц при использовании формулы для рас-
чета теплообмена в многостержневых пучках и формулы для пучков
с числом стержней <19 свидетельствует о том, что использование
формулы с числом стержней <19, на -20% занижающей коэффици-
ент теплоотдачи, заметно завышает температуру стенки Tw и в цент-
ре твэла Тц (см. рис. 6.19).
Это свидетельствует о необ-
ходимости правильного вы-
бора критериальных фор-
мул для расчета локального
теплообмена, учитывающих
все особенности процесса в
диапазоне изменения опре-
деляющих критериев подо-
бия, характерных для реак-
тора ЯРД.
Одной из наиболее важ-
ных проблем, связанных с
отводом тепла от твэлов ре-
актора при стационарных
условиях, является пробле-
ма выравнивания неравно-
мерностей полей температур
теплоносителя, сформиро-
ванных неравномерностями
полей плотности энерговы-
деления в поперечном сече-
нии реактора [6.3.1].
Рис. 6.19. Результаты теплогидравлическо-
го расчета ТВС по средним параметрам при
работе реактора на номинальной мощнос-
ти и продольном распределении плотности
энерговыделения для ЯР с торцевым отра-
жателем: Тср — распределение среднемас-
совой температуры водорода; Тц — рас-
пределение температуры стенки и в центре
твэлов при расчете Tw по формуле для пуч-
ков с большим числом твэлов; Tw, Тц — то
же при расчете Tw по формуле для пучков с
числом твэлов <19
504
Глава 6
Вначале рассмотрим процесс выравнивания неравномерностей
полей температур при осесимметричной неравномерности энерго-
выделения. Этот тип неравномерности наблюдается для центральной
ТВС реактора (см. рис. 6.5,6.6) и других ТВС при таком положении ба-
рабанов регулирования, когда поглощающие пластины барабанов уп-
равления реактором повернуты от активной зоны реактора (\|/ = 0).
Для выравнивания неравномерности энерговыделения по ради-
усу ТВС с витыми твэлами можно было бы использовать семизонное
(по числу рядов твэлов) профилирование концентрации урана-235 по
радиусу ТВС (см. рис. 6.7). Однако в этом случае возникают техно-
логические трудности обеспечения такого точного профилирования
концентрации урана, поэтому целесообразно ограничиться ее трех-
зонным профилированием. При этом создается неравномерное поле
энерговыделения по радиусу ТВС, симметричное относительно ее
оси (см. рис. 6.6), которое формирует неравномерное поле темпера-
тур теплоносителя и твэлов и приводит к необходимости проводить
теплогидравлический расчет по локальным параметрам потока и теп-
ловыделения. Этот расчет проводится путем решения системы урав-
нений (2.1.1) —(2.1.4), (2.1.64) с граничными условиями (2.1.5) —(2.1.7) и
использования для замыкания этой системы эмпирических зависи-
мостей для определения коэффициентов а, £,, Kqs.
Результаты расчета полей температур теплоносителя Т = Т(х, г)
с учетом процесса межканального перемешивания в ТВС с витыми
твэлами представлены на рис. 6.20, а на рис. 6.21 — поля темпера-
тур теплоносителя, стенки и в центре твэлов, используя радиальные
и продольные профили плотностей энерговыделения, представлен-
Рис. 6.20. Изменение температу-
ры теплоносителя, отнесенной к
среднемассовой температуре на
выходе (ГСрвых), по длине ТВС при
осесимметричной неравномер-
ности тепловыделения для ради-
усов с максимальной (2, 4, 6, 8, 10,
12) и минимальной (3, 5, 7, 9, 11,
13) температурой в поперечном
сечении ТВС для различных зна-
чений эффективного коэффи-
циента турбулентной диффузии
Kgs: 1 — Гср; 2, 3 — профили тем-
ператур Гтах и rmin для KgS = 0,015;
4, 5 — то же для Kqs = 0,03; 6, 7 —
то же для KqS = 0,045; 8, 9 — то
же для Kqs = 0,06; 10, И — то же
для Kqs = 0,09; 12, 13 — то же для
Kqs = 0,12
Глава б
505
ные на рис. 6.6 и 2.1 (кривая
1). Как видно из рис. 6.20, для
уменьшения неравномерно-
сти поля температур в выход-
ном сечении ТВС необходимо
выбрать такой шаг закрутки
витых твэлов s, чтобы мож-
но было обеспечить возмож-
но большую интенсивность
поперечного перемешива-
ния теплоносителя. Так, для
s/d = 12, или Frm = 230, ко-
эффициент Kqs = 0,045...0,050
(гл. 4 раздел 2.1). Однако та-
кая интенсивность пере-
мешивания приводит к не-
Рис. 6.21. Изменение температур теплоно-
сителя — Т, стенки — Tw и в центре твэ-
лов — Гц по длине ТВС при Kqs = 0,045, отне-
сенных к ГСРвых для радиусов пучка твэлов
с Гтах и Tmin при осесимметричной нерав-
номерности тепловыделения: 1 — 3 — Гтах,
Fornax и Тц max Соответственно; 4 — 6 — rmin,
и Тц min соответственно
равномерности температур
АГща/Гср = 18'5% (см- ₽ис-
6.20), т.е. при такой неравно-
мерности газ можно нагреть
только до Т__	~ 2900К. В то
сРвых
же время, если использовать
твэлы с s/d = 5,6 (или Frm » 60),
то Kqs = 0,12 (глава 4) и Л7’тах/7’Срвых® 5,6%, что позволяет нагреть газ
в реакторе до -3000 К. Для уменьшения гидравлических потерь на
длине активной зоны ТВС можно выбрать шаг s/d >5,6, чтобы обес-
печить К = 0,09 , ЛТ /Г » 8,8% и Т ® 2960К. При этом твэ-
4s	mdX сРвых	сРвых
лы должны иметь относительный шаг закрутки s/d = 6,8 и обеспечи-
вать число Frm = 85 (глава 4).
Расчет температуры стенки Tw и температуры в центре твэлов Тц
при максимальных и минимальных значениях температуры теплоно-
сителя для пучка твэлов с Frm« 230 (Kqs = 0,045) показывает, что макси-
мальные значения температур в выходном сечении ТВС составляют
Г»тах = 1’072ГсРвых И ГЧ гмх = 1'085Гсрвь1х. Т.е. При Тсрвых = 2900К ПОЛу-
чим Т^тах« 3100К и ТЦтах = 3150К. Это свидетельствует о том, что и
при шагах закрутки (s/d = 6. ..12) можно обеспечить достаточно высо-
кую температуру в камере перед соплом ЯРД Тк = 2900...2960К, кото-
рая лежит ближе к нижнему пределу параметров, необходимых для
осуществления пилотируемой экспедиции КК на Марс в программе
России и к максимальному — для программы США (см. табл. 6.1.1).
Полученные оценки справедливы при заданном запасе по темпера-
турев выходном сечении реактора, равном ДТ= Тсол — ТЦп1ах = 530К, где
506
Глава 6
Тсол — температура солидус твердого раствора карбидов ZrC-NbC-UC,
из которых изготовлены твэлы. В случае уменьшения этого запаса на
100—150 градусов можно обеспечить заданный средний уровень на-
грева водорода в реакторе до -3000К и заданную величину удельного
импульса тяги — до 9,2—9,5 км/с при Kqs = 0,045.
Влияние азимутальной неравномерности тепловыделения на поля
температур теплоносителя можно изучить при численном моделиро-
вании теплогидравлических процессов в ТВС, расположенных в чет-
вертом ряду реактора (см. рис. 6.5), где влияние барабанной системы
регулирования мощностью реактора является наиболее сильным.
Барабанная система регулирования для решения задач хранения ре-
актора в подкритическом состоянии, запуска, перевода реактора с
двигательного режима работы на энергетический и обратно, а также
для останова ЯР приводит к асимметричным неравномерностям по-
лей тепловыделения, при которых распределения энерговыделения
в реакторе искажаются как в радиальном, так и азимутальном на-
правлениях (см. рис. 6.6—6.10). Эти поля энерговыделения были ис-
пользованы при решении системы уравнений (2.1.1) —(2.1.4), (2.1.64) с
граничными условиями (2.1.5) —(2.1.7). Результаты расчета полей тем-
ператур теплоносителя Т и «твердой фазы» 7^в ТВС с витыми твэла-
ми с Kqs = 0,09 представлены на
рис. 6.22. При этом среднемассо-
вая температура теплоносите-
ля на выходе из ТВС составляла
ТсРвых = 2760К. Расчет прово-
дился для положения барабанов
СУЗ, при котором поглощающая
пластина повернута к активной
зоне реактора (\|/ = п) и нерав-
номерность энерговыделения в
ТВС четвертого ряда максималь-
на, а расход теплоносителя че-
Рис. 6.22. Теоретически рассчитан-
ные поля температуры теплоносите-
ля — Г (а) и стенки (твердой фазы) —
Tw (б) в ТВС с витыми твэлами при
азимутальной неравномерности теп-
ловыделения и KqS = 0,09: 1 — 3 — при
<р=0 и г/гк = 1,0, 0,694 и 0,385 соот-
ветственно; 4 — при г/гк = 0; 5, 6 —
при <р = я и г/гк = 0,385 и 1,0 соответ-
ственно
Глава 6
507
рез эту ТВС равен номинальному значению. При этом мощность ТВС
снижается на 15%. Как видно из рис. 6.22, максимальная температура
стенки твэлов в этом случае не превышает температуру Tw на номи-
нальном режиме работы (TVVmax « 3100К), a TWmin = 2400К, т.е. на 700
градусов ниже. При этом неравномерность скорости в выходном се-
чении ТВС составляет в ядре потока -13%.
Результаты расчета полей температур, представленные на
рис. 6.22, описывают процессы тепломассообмена в ТВС четвертого
ряда реактора без учета циркуляционного течения в периферийной
зоне пучка витых твэлов. Учет вихревого течения в этой зоне, вы-
полненный в работе [6.1.1], показал, что максимальная температура
теплоносителя в поперечном сечении ТВС у стенки обоймы снижа-
ется при Kqs = 0,09 на 15% по сравнению с расчетным значением (см.
рис. 6.22) за счет азимутального переноса массы и тепла. При этом
локальный эффективный коэффициент перемешивания в этой зоне
в 1,5—2,0 раза превышает величину Kqs для центральной области те-
чения в пучке витых твэлов [6.1.1].
Список литературы
6.3.1.	Дзюбенко Б.В., Федик И.И., Ашмантас Л.-В.А. Проблемы создания
ядерного ракетного двигателя. Становление и развитие. Вильнюс: Trys
zvaigzdutes, 2008. С. 176.
6.3.2.	Демянко Ю.Г., Коротеев А.С., Повельев А.А. и др. Ядерные ракет-
ные двигатели/Под ред. А.С. Коротеева. М.: ООО «Нормаинформ», 2001.
С. 414.
6.3.3.	НПО «Луч». Дела и люди. История и судьбы/Под ред. И.И. Федика. По-
дольск: НИИ НПО «Луч», 2004. С. 456.
6.4.	РЕАКТОРЫ И ЛАЗЕРЫ
Витые твэлы для газоохлаждаемых ядерных реакторов. Для ре-
шения ряда задач требовались ЯРД с высоким удельным импуль-
сом тяги (около 10000 м/с), что возможно при нагреве рабочего
газа — водорода свыше 3000 К. Кроме того, необходимо было обес-
печить безопасную работу ЯРД при многоразовых запусках реак-
тора. Эти задачи решены с помощью витых твэлов овальной формы
(в сечении), плотноупакованных в тепловыделяющую сборку (ТВС)
(рис. 6.23, 6.24. См. цвет. вкл.). При соответствующем выборе шага
закрутки профиля твэла достигалась существенная интенсификация
процессов межканального перемешивания газа и, как результат, —
508
Глава 6
выравнивание температуры и скорости газа в условиях неравномер-
ного тепловыделения в активной зоне (в радиальном и продольном
направлениях) [6.4.1—6.4.5]. Гарантированное взаимное касание ви-
тых твэлов в плотном пучке ТВС резко снижает вероятность возник-
новения вибраций и снимает проблему дистанционирования твэлов.
Достигнутый при испытаниях отечественного ЯРД удельный им-
пульс тяги почти на 1000 м/с превысил удельный импульс американ-
ского ЯРД «Нерва».
Интенсификация охлаждения и термостатирования
лазерных зеркал, мишеней и резонаторов ускорителей
В процессе создания мощных лазерных технологических и спе-
циальных комплексов одной из критических оказалась проблема ох-
лаждения и термостатирования зеркал, необходимых для усиления,
формирования и фокусировки излучения. Для термостатирования
зеркал и отвода поглощенного тепла авторами разработаны сложные
системы охлаждения на основе микрокапиллярных и пористых, а
также струйных интенсификаторов теплообмена, ограничивающих
термические деформации до 1 мкм. С участием авторов создано новое
направление — охлаждаемая лазерная оптика на стыке нескольких
дисциплин: квантовой электроники, оптики, теплофизики, прочно-
сти, материаловедения и др. Разработка методов интенсификации
теплообмена в лазерных зеркалах позволила оптимизировать их
конструкцию, повысить пороги разрушения зеркал, упростить и уде-
шевить технологию их изготовления.
Результаты теоретических и экспериментальных исследований
интенсификации тепло- и массообмена в каналах с пористыми тепло-
проводными вставками (интенсификаторами), полученные в [6.4.6 —
6.4.11], использованы в ведущих организациях, занимавшихся созда-
нием головных образцов изделий силовой металлооптики. На рис. 6.25
и 6.26 (см. цвет, вкл.) показаны некоторые из исследованных зеркал.
Проблема ограничения термических деформаций существует
также в резонаторах мощных линейных ускорителей. Расположен-
ные с определенным пространственным периодом пластины резо-
натора не должны деформироваться более чем на 2,0—3,0 мкм при
высоком уровне тепловыделения. Авторами предложен оригиналь-
ный метод термостатирования резонаторов в случае периодического
действия электрофизической установки с помощью встроенных тер-
моаккумуляторов плавления.
Результаты измерения интенсивности перемешивания теп-
лоносителя в поперечно обтекаемых щеточных структурах и пуч-
Глава 6
509
ках стержней, полученные в процессе исследования теплообмена в
лазерных зеркалах [6.4.12—6.4.16], использованы для усовершенст-
вования методов расчета теплообменного оборудования ЯЭУ. Резуль-
таты исследований особенностей локального нагрева и термическо-
го деформирования охлаждаемых оребренных стенок лазерных
зеркал использованы для определения погрешностей термодефек-
тоскопии изделий. Эти же данные использованы для усовершен-
ствования конструкции и продления срока службы охлаждаемых
мишеней нейтронных генераторов и ускорительных комплексов
[6.4.17-6.4.22].
Теплофизические обоснования конструкции
термоядерных реакторов (ТЯР) со струйным
жидкометаллическим бланкетом
В работах [6.4.23—6.4.32] разработаны концептуальные проекты
лазерных термоядерных реакторов (ТЯР). Выполнен комплекс иссле-
дований теплогидравлических, нейтронно-физических и термоме-
ханических процессов в бланкете, первой стенке и в фокусирующих
зеркалах ТЯР [6.4.11, 6.4.23, 6.4.33—6.4.40]. Совместно с сотрудника-
ми ФИАН установлены физические ограничения на параметры фо-
кусирующей оптики с учетом мощного импульсно-периодического
нагрева ее материалов лазерным, рентгеновским и нейтронным из-
лучениями.
ТЯР любого типа, в особенности лазерные, нуждаются в высоком
КПД преобразования тепла в электричество из-за больших расходов
энергии на питание лазеров и создание (нагрев) и удержание плаз-
мы [6.4.11, 6.4.33, 6.4.41, 6.4.42]. В целях повышения КПД реактора, а
также тепловой и радиационной защиты корпуса взрывной камеры
реактора (диаметром около 10 м) и фокусирующих зеркал (суммар-
ной площадью в несколько десятков квадратных метров) предло-
жен двухтемпературный струйный бланкет, состоящий из системы
200 струй жидкого лития (в литий могут добавляться крупицы обед-
ненного урана для «размножения» нейтронов и воспроизводства
плутония). Исследования неравновесных процессов теплообмена в
струйном жидкометаллическом бланкете лазерных ТЯР показали
возможность подавления объемного вскипания лития при его нагре-
вании интенсивными потоками нейтронов и рентгеновского излуче-
ния из взрывающейся мишени, а также недопущения разрушения
струй лития и туманообразования при прохождении ударной волны,
что необходимо для обеспечения приемлемой частоты повторения
взрывов.
510
Глава 6
Теплофизические обоснования конструкции
реакторов-лазеров
В [6.4.43—6.4.49] разработаны концептуальные проекты мощ-
ных импульсных реакторов-лазеров (лазеров с ядерной накачкой).
В импульсном реакторе-лазере осуществляется прямое преобра-
зование ядерной энергии в когерентное лазерное излучение. На-
качка лазерно-активной среды реактора-лазера осуществляет-
ся осколками деления урана, нанесенного в виде тонкой пленки
(<10 мкм) на внутренней поверхности более 1000 лазерных трубок
(диаметром около 3 см), окруженных замедлителем нейтронов. Вы-
полненные расчеты тепловыделения и распределения температуры
в лазерных трубках в импульсном режиме работы реактора показа-
ли, что температура газа может значительно превышать температуру
ядерного топлива (что никогда не наблюдается в штатных режимах
обычных ядерных реакторов) [6.4.46, 6.4.48, 6.4.49]. Нагрев лазерно-
активного газа вызывает ряд интересных теплофизических эффек-
тов: тепловые линзы, искривляющие лазерный луч и способные вы-
звать даже срыв генерации; самопрокачку газа, как в ракетном сопле,
и др. Учет этих и других теплофизических эффектов позволил сфор-
мулировать ограничения по температуре и давлению рабочего газа,,
тепловой мощности лазерных каналов и обоснованно проектировать
экспериментальные установки с ядерной накачкой лазеров. Было по-
казано также, что предложенный ранее проект газофазного реакто-
ра-лазера с большой апертурой пучка (около 4 м, что важно для пере-
дачи излучения на большие расстояния) несостоятелен, так как в нем
невозможно совместить условия ядерной критичности гексафторида
урана (используемого в качестве топлива), пороговой мощности теп-
ловыделения и лазерной прозрачности газофазной ядерно- и лазер-
но-активной среды [6.4.44].
Применение жидких металлов для интенсификации
теплообмена в физико-энергетических установках
Создание высокотемпературных физико-энергетических устано-
вок оказалось возможным благодаря развитию в России, и прежде
всего в ГНЦ РФ «ФЭИ», высокой культуры обращения с жидкометал-
лическими теплоносителями. При движении жидких металлов в уз-
ких кольцевых зазорах и сложных каналах, образованных плотно-
упакованными пучками твэлов, происходит двусторонний обогрев
жидкого металла, что увеличивает коэффициент теплоотдачи при-
близительно в 2 раза. Этот эффект использован при проектирова-
Глава 6
511
нии и создании термоэмиссионных энергоустановок космического
назначения [6.4.50—6.4.52].
Большой эффект при использовании жидких металлов был
достигнут при транспирационном охлаждении стенок газофаз-
ного ядерного реактора для ядерного ракетного двигателя. Стенки
газофазного реактора выполнялись из проницаемого (пористого) ма-
териала, через который продавливался жидкий металл, который, ис-
паряясь, не только осуществлял тепловую защиту стенки при тепло-
вых нагрузках свыше 10 кВт/см2, но и предотвращал конденсацию на
стенках агрессивных и радиоактивных паров делящегося вещест-
ва. Эти результаты использованы при проектировании энергодвига-
тельных установок космического назначения [6.4.53].
При разработке конденсаторов космической энергоустановки, ра-
ботающей на эвтектике натрий-калий, выяснилось, что пар низкоки-
пящего компонента калия играет роль неконденсирующегося газа для
пара натрия, что ведет к снижению коэффициента теплоотдачи при
поверхностной конденсации примерно на порядок по сравнению с
теплоотдачей при конденсации отдельно калия и натрия. Эту проблему
решили с помощью «капельного холодильника-конденсатора», в кото-
ром пар эвтектики конденсируется на относительно холодных каплях
той же эвтектики, подаваемой в конденсатор через специальные рас-
пыляющие металл форсунки. В итоге теплоотдача возросла на поря-
док, а габариты конденсатора соответственно уменьшились [6.4.54].
Список литературы
6.4.1.	Захаркин И.И., Коновалов В.И., Овечкин А.Д., Федик И.И. и др.
Разработка ЯРД минимальных размеров ИРГИТ. Энергетические испы-
тания опытного образца ядерного реактора//Тр. 3-й межд. конф. «Ядер-
ная энергетика в космосе. Ядерные ракетные двигатели». Подольск,
1993. С. 271-278.
6.4.2.	Федик И.И. и др. Ядерно-космическая энергетика//Сб. докл. юбилей-
ной науч.-практич. конф., посвященной 50-летию создания атомной от-
расли. М., 1996. С. 256-268.
6.4.3.	Приймак С.П., Федик И.И. и др. Особенности метрологического обес-
печения измерений температуры термоэлектрическими преобразова-
телями в условиях интенсивного реакторного облучения//Тр. 3-й межд.
конф. «Ядерная энергетика в космосе. Ядерные ракетные двигатели».
Подольск, 1993. Т. 3. С. 327-334.
6.4.4.	Денискин В.П., Наливаев В.И., Паршин Н.Я., Федик И.И. Проблема
высокотемпературных измерений в ТВС ЯРД//С6. докл. 5-й отраслевой
конф. «Температура-2001». Подольск, 2001.
6.4.5.	Ашмантас Л.-В.А., Дзюбенко Б.В. Проблемы теплообмена и гидроди-
намики в ядерных энергодвигательных установках космических аппара-
тов. Вильнюс: Исток, 1995.
512
Глава 6
6.4.6.	Харитонов В.В. Теплофизический расчет лазерных зеркал. М.: МИФИ,
1985.
6.4.7.	Харитонов В.В. Теплофизика лазерных зеркал. М.: МИФИ, 1993.
6.4.8.	Холпанов Л.П., Шкадов В.Я. Гидродинамика и тепломассообмен с по-
верхностью раздела. М.: Наука, 1990.
6.4.9.	Холпанов Л.П. Гидродинамика и массообмен в активных гидродина-
мических режимах//Химич. и нефтяное машиностроение. М.: Машино-
строение. 1997. Т. 2. С. 1-7.
6.4.10.	Холпанов Л.П., Малюсов В. А., Жаворонков Н.М. Исследование гид-
родинамики и массообмена при турбулентном течении пленки жидкости
с учетом входного участка//Теоретич. основы хим. технол. 1998. Т. 12,
№ 3. С. 438-450.
6.4.11.	Витков Г.А., Холпанов Л.П., Шерстнев С.Н. Гидравлическое сопро-
тивление и тепломассообмен. М: Наука, 1994.
6.4.12.	Субботин В. И., Харитонове. В., ПлаксеевВ. В., Алексеев С. В. Меж-
канальный теплообмен при поперечном обтекании водой пучка труб//
Теплоэнергетика. 1985. № 1. С. 42-44.
6.4.13.	Харитонов В.В., Федосеев В.Н. Обобщение экспериментальных дан-
ных о теплоотдаче в поперечно-обтекаемых пучках витых труб//ТВТ.
1990. Т. 28, №2. С. 180-182.
6.4.14.	Харитонов В.В., Федосеев В.Н. Интегральный метод измерения попе-
речной теплопроводности и диффузии в турбулентном потоке жидко-
сти//Измерительная техника. 1994. № 7. С. 51-53.
6.4.15.	А.с. № 1122103 от 21.06.1983. Харитонов В.В. и др. Способ определе-
ния эффективной поперечной теплопроводности теплоносителя в по-
ристой среде.
6.4.16.	А.с. № 1303921 от 24.04.1986. Харитонов В.В. и др. Способ определе-
ния коэффициента эффективной поперечной теплопроводности жид-
кости в пористой среде.
6.4.17.	Плаксеев А.А., Теряев В.В., Харитонов В.В. Деформация поверхно-
сти охлаждаемого зеркала при неоднородном нагреве лазерным излу-
чением//Вопросы теплофизики ядерных реакторов. М.: Энергоиздат,
1981. Вып. 10. С. 48-57.
6.4.18.	Харитонов В.В., Плаксеев А.А. Предельные тепловые нагрузки в ла-
зерных зеркалах с охлаждаемой пористой подложкой//ТВТ. 1982. Т. 20,
вып. 4. С. 712-717.
6.4.19.	Кузьмин Ю.А., Харитонов В.В. Предельная мощность локального ис-
точника тепла на поверхности многослойной стенки с внутренним ох-
лаждением//Там же. 1986. Т. 24, № 5. С. 948-956.
6.4.20.	Кузьмин Ю.А., Теряев В.В., Харитонов В.В. Теплоотдача оребрен-
ной мишени при локальном нагревании мощным электронным пучком//
Изв. АН СССР. Энергетика и транспорт. 1991. № 4. С. 144-151.
6.4.21.	Харитонов В.В., Плаксеев А.А, Воскобойников В.В., Тарутин Д.Ю.
Тепловые режимы охлаждаемых медных мишеней при интенсивном ло-
кальном нагреве//ТВТ. 1991. Т. 29, № 5. С. 941-948.
Глава б
513
6.4.22.	Харитонов В.В., Икрянников Н.П., Якутии Н.В. Термические дефор-
мации охлаждаемых дисковых зеркал технологических лазеров: изме-
рение и расчет//Там же. 1996. Т. 34, № 3. С. 419-422.
6.4.23.	Басов Н.Г., Вергунова Г.А., Гришунин П.А., Данилов А. Е., Лебо И.Г.,
Розанов В.Б., Склизков Г.В., Субботин В.И., Федотов С.И., Хари-
тонов В.В. О концентрации лазерного излучения на мишень в условиях
термоядерного реактора: Препринт ФИАН, № 216. М., 1983.
6.4.24.	Басов Н.Г., Белоусов Н.И., Гришунин П.А., Калмыков Ю.К.,
Лебо И.Г., Розанов В.Б., Склизков Г.В., Субботин В.И., Финкель-
штейн К., Харитонов В.В. Гибридный реактор на основе лазерно-
го термоядерного синтеза//Квантовая электроника. 1987. Т. 14. № 6.
С.2068-2081.
6.4.25.	Басов Н.Г., Белоусов Н.И., Гришунин П. А, Розанов В.Б., Суб-
ботин В.И., Харитонов В.В. Гибридный лазерный термоядерный ре-
актор со струйным бланкетом/Дезисы докл. 4-й Всесоюзной конф, по
инж.проблемам ТЯР, Ленинград, 1988. М.: ЦНИИатоминформ, 1988,
С. 14-15.
6.4.26.	Белоусов Н.И., Белоусов Ю.В., Губин С.А., Любимов А.В., Харито-
нов В.В., Гельфанд Б.Е. Экспериментальное моделирование струйной
защиты стенок термоядерного реактора/Дам же. С. 313-314.
6.4.27.	Басов Н.Г., Белоусов Н.И., Гришунин П.А., Розанов В.Б., Суббо-
тин В.И., Харитонов В.В. Лазерный термоядерный реактор-размно-
житель со струйным бланкетом ТИГРИС//Изв. АН СССР. Энергетика и
транспорт. 1988. № 4. С. 3-15.
6.4.28.	Басов Н.Г., Белоусов Н.И., Гришунин П.А., Розанов В.Б., Суббо-
тин В.И., Харитонов В.В. Требования к энергетическим и ядерно-фи-
зическим параметрам ядерных энергетических систем с трансмутато-
ром: Препринт МИФИ, №011-92.1992.
6.4.29.	А.с. № 1443634 от08.08.1988. Басов Н.Г., Белоусов Н.И., Розанов В.В.,
Субботин В.И., Харитонов В.В. Способ получения энергии и нуклидов в
термоядерном реакторе с инерциальным удержанием плазмы.
6.4.30.	А. с. № 1529475 от 29.04.1988. Басов Н.Г., Белоусов И. И., Розанов
В.Б., Субботин В.И., Харитонов В.В. Способ проведения реакций в
инерциальном термоядерном реакторе с жидкой защитой.
6.4.31.	А.с. № 1530068 от 29.04.1988. Басов Н.Г., Белоусов Я. И., Роза-
нов В.Б., Субботин В.И., Харитонов В.В. Способ трансмутации акти-
нидов в инерциальном термоядерном реакторе.
6.4.32.	А.с. № 1538793 От 15.09.1989. Басов Н.Г., Белоусов Н.И., Роза-
нов В.Б., Субботин В.И., Харитонов В.В. Камера инерциального тер-
моядерного реактора со струйной защитой стенок.
6.4.33.	Кокорев Л.С., Харитонов В.В. Прямое преобразование энергии и тер-
моядерные энергетические установки. М.: Атомиздат, 1980.
6.4.34.	Харитонов В.В., Троянский В.Б., Якутии Н.В., Атаманов В.В. Нейт-
ронно-физические расчеты бланкетов термоядерных реакторов. М.:
МИФИ, 1994.
6.4.35.	Кокорев Л.С., Игнатьев В.В., Харитонов В.В. Поглощение высоко-
температурного излучения в веществе//Вопросы теплофизики ядерных
реакторов. М.: Атомиздат, 1977. Вып. 6. С. 15-17.
514
Глава 6
6.4.36.	Теряев В.В., Харитонов В.В. О предельном тепловом потоке через
первую стенку термоядерного реактора//Вопросы теплофизики ядер-
ных реакторов. М.: Атомиздат, 1980. Вып. 9. С. 49-58.
6.4.37.	Субботин В.И., Харитонов В.В., Гришунин П.А. О теплофизике фоку-
сирующих зеркал лазерных термоядерных реакторов//Атомная энергия.
1983. Т. 55, вып. 1. С. 37-42.
6.4.38.	Белоусов Н.И., Гришунин П.А., Субботин В.И., Харитонов В.В.
О нагреве фокусирующей оптики лазерных термоядерных реакто-
ров рентгеновским излучением мишени//Там же. 1984. Т. 56, вып. 4.
С. 225-226.
6.4.39.	Харитонов В.В., Субботин В.И., Гришунин П.А., Тимонин А.С. Ди-
намические эффекты при импульсном нагреве лазерных зеркал/ДВТ.
1983. Т. 21, №6. С. 1127-1133.
6.4.40.	Басов Н.Г., Белоусов Н.И., Вергунова Т.А., Гришунин П.А., Дани-
лов А.Е., Лебо И.Г., Розанов В.Б., Склизков Г.В., Субботин В.И.,
Федотов С.И., Харитонов В.В. О параметрах фокусирующей опти-
ки лазерного термоядерного реактора//Квантовая электроника. 1985.
Т. 12, №3. С. 584-593.
6.4.41.	Кокорев Л.С., Харитонов В.В. Теплофизический расчет термоядерно-
го реактора. М.: МИФИ, 1980.
6.4.42.	Кокорев Л.С., Харитонов В.В. Теплогидравлические расчеты и оп-
тимизация ядерных энергетических установок. М.: Энергоатомиздат,
1986.
6.4.43.	Карелин А.В., Харитонов В.В., Чикин К.Р. О прямом преобразовании
ядерной энергии в световое излучение//Вопросы теплофизики в ЯЭУ.
М.: Энергоатомиздат, 1986.
6.4.44.	Бункин Ф.В., Держиев В.И., Субботин В.И., Троянский В.В., Хари-
тонов В.В., Чикин К.Р., Яковленко С.И. Проблемы газофазного реак-
тора-лазера: Препринт ФИАН, № 199.1985.
6.4.45.	Бункин Ф.В., Держиев В.И., Карелин А.В., Нефедов А.Л., Суббо-
тин В.И., Харитонов В.В., Чикин К.Р., Яковенко С.И. Стационарный
реактор-лазер с поверхностной накачкой: Препринт ИОФАН, № 321.
1985.
6.4.46.	Карелин А.В., Середа О.В., Харитонов В.В., Чикин К.Р., Наумкин
Ф.Ю. Нагрев газа осколками деления//Атомная энергия. 1986. Т. 61,
вып. 1. С. 44-46.
6.4.47.	Миськевич А.И., Середа О.В., Харитонов В.В., Чикин К.Р. Влияние
градиента температуры в резонаторе газового лазера на его выходную
мощность/Деплофизика ЯЭУ. М.: Энергоатомиздат, 1986. С. 95-97.
6.4.48.	Чикин К.Р., Харитонов В.В. Импульсный газоохлаждаемый реактор с
пленочным топливом/Деплофизические проблемы ядерной техники.
М.: Энергоатомиздат, 1987. С. 11-16.
6.4.49.	Кузма-Кичта Ю.А. и др. Проблемы безопасности АЭС//Вестник МЭИ.
1994. №. 3. С. 109-111.
6.4.50.	Чикин К.Р., Харитонов В.В. Расчет нагрева газа осколками деления
в канале импульсного реактора//Атомная энергия. 1988. Т. 65, вып. 6.
С. 435-437.
Глава 6
515
6.4.51.	Свириденко И.П. и др. Исследование теплообмена при турбулентном
течении ртути в кольцевом зазоре//Атомная энергия. 1960. Т. 9, вып. 4.
6.4.52.	Свириденко И.П. и др. Теплофизические исследования в обоснование
разработок энергонапряженных систем ЯЭУ космического назначения:
Труды ГНЦ РФ «ФЭИ»//Сб. «ГНЦ РФ “ФЭИ” - 50 лет». 1996. С. 221-229.
6.4.53.	Свириденко И.П. и др. Теплофизические проблемы энергодвигатель-
ных установок космического назначения/Др. межд. семинара «Косми-
ческая энергетика XXI века». Обнинск, 1998.
6.4.54.	Свириденко И.П. и др. Тепло- и гидравлические исследования жидко-
металлической пористой тепловой защиты энергонапряженных конст-
рукций/Др. VI Всероссийской конф. «Инженерные проблемы термо-
ядерных реакторов». С.-Петербург, 1997. С. 163.
6.5.	ИСПАРИТЕЛИ И ТЕПЛООБМЕННИКИ
ДЛЯ ТЕПЛОСНАБЖЕНИЯ
Для переработки сточных вод и создания безотходных экологи-
чески чистых технологий водоподготовки используются установки
термического обессоливания. Рабочей средой в испарителях являют-
ся водные растворы с высокой концентрацией солей (до 100 г/кг). Дви-
жение водных растворов происходит в трубах с низкими массовыми
скоростями [до 10 кг/(м2-с)] при давлении до 1,6 МПа. Исследования
условий работы таких установок показали, что их производитель-
ность ограничивается низкой величиной критического паросодер-
жания в гладких трубах испарителей. Для интенсификации тепло-
обмена в испарителях внутри труб нанесены спеченные пористые
покрытия. Ресурсные испытания на испарителе ТЭЦ-8 МОСЭНЕРГО
показали, что пористые покрытия увеличивают коэффициент тепло-
передачи на 30%, уменьшают слой отложений на парогенерирующих
поверхностях, ослабляют стояночную коррозию и пульсации темпе-
ратуры стенки. Эти положительные эффекты сохраняются в течение
5 лет эксплуатации (рис. 6.27, 6.28) [6.5.1 —6.5.4].
Пористые покрытия нашли успешное применение в испарителях
холодильников абсорбционного типа «Иней». Благодаря интенсифи-
кации тепло- и массообмена в испарителях температура в морозильной
камере холодильника понижается с -6°С до -15°С [6.5.1]. Полученные
результаты использованы при производстве усовершенствованных
холодильников «Иней-М» на Московском заводе холодильников. Бо-
лее 10 лет усовершенствованные холодильники «Иней-М», имеющие
испарители с пористым покрытием, работают надежно. Их количест-
во, реализованное в торговой сети, превышает 100 тысяч единиц.
516
Глава 6
Устройство
очистки
пара
Вход
промы-
вочной
воды
Выход пара
I Жалюзийный
сепаратор
Рис. 6.27. Двухзонный
испаритель
Рис. 6.28. Коэффициент теплоотдачи:
1 — испаритель типа «И»; 2 — двухзон-
ный испаритель с технически гладки-
ми трубами; 3 — двухзонный испари-
тель, имеющий в первой зоне трубы с
пористым покрытием. Рвт = 1,6 МПа
Использование пористых покрытий в холодильных установках с
компрессионным циклом также приводит к улучшению их характерис-
тик. Испарители охладителей напитков представляют собой спирально
изогнутые медные трубы, на внутренней поверхности которых спека-
нием нанесено покрытие. Как установлено, медное спеченное покры-
тие позволяет существенно улучшить основную характеристику аппа-
ратов — получить уменьшение вдвое времени охлаждения напитков.
Усовершенствование теплообменников для теплоснабжения
За последнее десятилетие благодаря массированной, причем за-
частую не объективной рекламе пластинчатых аппаратов, сформиро-
валось ложное мнение об абсолютном превосходстве пластинчатых
теплообменников над кожухотрубными, вследствие чего последним
грозит полное вытеснение с рынка. Одной из основных причин явля-
ется то обстоятельство, что современные пластинчатые теплообмен-
ники сравнивают с кожухотрубными аппаратами, разработанными в
середине прошлого столетия, в то время как следует проводить срав-
нение с современными аппаратами.
Производители пластинчатых теплообменников утверждают, что
их аппараты занимают приблизительно в 6 — 8 раз меньше места, чем
Глава 6
517
аналогичные им по мощности кожухотрубные и, рекламируя преиму-
щества пластинчатых теплообменников, почти всегда подчеркивают
их небольшой габаритный объем. Но всегда ли это так?
К существенным преимуществам пластинчатых теплообменников
относят их повышенный срок службы. В качестве аргументов отмеча-
ют, что, во-первых, пластины изготавливают из специальной нержа-
веющей стали, благодаря чему они не корродируют, во-вторых, плас-
тины имеют профиль, турбулизирующий поток, что предотвращает
образование отложений, и, в-третьих, аппараты снабжаются резино-
выми уплотнительными прокладками из резины EPDM, способной
выдерживать достаточно высокие температуры.
Заметим, что небольшие размеры каналов, по которым течет жид-
кость (3 — 4,5 мм), свидетельствуют, напротив, об опасности загрязне-
ния теплообменника, которую, конечно, можно устранить, установив
фильтры на входе в пластинчатый теплообменник. Однако если устано-
вить фильтры на входе в кожухотрубный теплообменник с профилиро-
ванными трубами, то проблема отложений для аппаратов будет также
решена. В пластинчатых теплообменниках большое число прокладок,
которые должны не только оставаться невредимыми под давлением, но
и не разрушаться при разборке аппарата. Это требует более мощных
стягивающих устройств. Помимо этого гребни пластин, разделяющие
каналы, не снабжены уплотнениями, вследствие чего жидкость не про-
ходит последовательно из одного параллельного канала в другой, а уст-
ремляется через гребень в смежный канал. При увеличении давления
поперечное движение жидкости усиливается.
К одному из преимуществ пластинчатых теплообменников отно-
сят легкость технического обслуживания. Однако для того, чтобы
можно было чистить пластинчатый теплообменник, он должен быть
разборным, а не паяным. Разборные аппараты и дороже, и по габа-
ритам больше. Наращивание поверхности нагрева и чистка аппарата
ставят под сомнение гарантию его надежной эксплуатации.
Неправильная эксплуатация может привести к повреждению уп-
лотнительных прокладок, которые очень дороги и составляют до 50%
стоимости всего теплообменника. К тому же пластинчатый тепло-
обменник очень чувствителен к изменению расчётного количества
теплоносителя в ту или иную сторону и выдерживает не более пяти
процентов его изменения, в противном случае его характеристики
кардинально нарушаются и он представляет из себя не более чем гру-
ду железа. Кроме того, в переходный и летний периоды, когда тепло-
обменник простаивает, прокладки между пластинами ссыхаются, и
потом при запуске их приходится подтягивать. Таким образом, в од-
них случаях выгоднее использовать пластинчатые аппараты, в дру-
518
Глава 6
гих — кожухотрубные, и для того, чтобы обосновать выбор, нужно
провести предварительно анализ и расчеты.
Описанная в работе [6.5.5] интенсификация теплообмена осу-
ществлялась витой трубой и трубой с кольцевой накаткой. Там же
рассмотрен теплообменник с поперечными перегородками в пучке.
Трубная система аппарата имеет длину 4000 мм, расстояние между
перегородками для всех типоразмеров составляет 350 мм, высота пе-
регородки равняется половине внутреннего диаметра корпуса теп-
лообменника, количество перегородок — 10, диаметры подводящих
патрубков и их расположение выбирались в соответствии с ГОСТом
27590-88. Теплообменные трубы диаметром 16x1 мм изготовляются
из Л75 МК. Безразмерный шаг расположения труб в пучке s/dH « 1,3.
Для аппарата с кольцевой накаткой выбраны три варианта парамет-
ров накатки d/dBH = 0,94,0,92, 0,91 и t/dBii = 0,50,0,52, 1,00. Безразмер-
ный шаг расположения труб в пучке также s/dH «1,3, обтекание труб
в пучке продольное, длина трубы 4000 мм.
На рис. 6.29 представлен чертеж секции экспериментального тепло-
обменника с пучком витых труб. Наружный диаметр корпуса аппара-
та — 219 мм, длина корпуса — 1994 мм, количество труб — 73, длина
трубы — 2000 мм, длина витой части трубы — 1716 мм. Витые трубы
изготовляются из трубы Л75 МК диаметром 16x1 мм, при этом наруж-
ный диаметр витой трубы D = 19,5 мм, ширина — 9,8 мм, шаг закрутки
S = 156 мм, т.е. S/D = 8,0, модифицированное число Фруда Fr»63,5. Шаг
расположения труб в пучке составляет 20 мм, таким образом, s/D « 1,03;
для витой части труб (плотный пучок) s/D « 1,25 в трубной доске.
Расчет теплогидравлических характеристик аппарата с витыми
трубами проводился с помощью соотношений для числа Nu и коэф-
1994(-1,5)
Рис. 6.29. Секция теплообменника с пучком витых труб
Глава 6
519
фициента гидравлического сопротивления £,, приведенных в работе
[6.5.6]. Для расчета характеристик теплообменника с накатанными
трубами использовались экспериментальные данные для Nu и £,, по-
лученные в работе [6.5.7].
При расчете аппарата с перегородками был предложен метод рас-
чета поперечной w12 и продольной составляющих скоростей, ко-
торые в дальнейшем используются для определения числа Nu и
Согласно этому методу, сделаны следующие преобразования: так
как, с одной стороны, Gl — piw^F — p(w12F12 + а с другой —
G} = pWjF, то, учитывая, что w12 = vv^sinfp), = wcosfp), получим:
F = F12 sin(P) + Fn cos(P). Последнее соотношение выполняется, в
частности, если F12 = Fsin(p), Fn = Fcos(P), но тогда F = (F122 + Fn2)0<5.
Представим Gt в виде: Gj = p[w12/sin(P)]F = p(F 2/F12)w12, отсюда
w12 = GjF^/fpF2), аналогично для wn: = G1F11/(pF2). Значения F12 и
Fn можно вычислить по формулам: F12 = 7i(DK2 — NdH2)/4, FnpoA = LLm,
где
dr = DKn/4.
(6.5.1)
Коэффициент теплоотдачи при поперечном обтекании рассчи-
тывался по формулам Жукаускаса, а при продольном обтекании —
по формуле Дрейцера Nu = [0,032(s/dH)2 — O,O144]Reo,8Pr1/3 [6.5.8]. В
итоге коэффициент теплоотдачи определяется по соотношению
а = ап + а12. Предложенный метод протестирован по эксперимен-
тальным данным [6.5.9], при этом среднеквадратичное отклонение
составило 16%.
В витой трубе за счет возникновения вторичного течения увели-
чивается область, занимаемая ядром потока, и уменьшается толщи-
на пограничного слоя, в результате чего повышается коэффициент
теплоотдачи. В результате анализа экспериментальных данных ус-
тановлено, что отношение Nu/NuKp слабо зависит от числа Re при
2300 < Re < 105 и безразмерного шага закрутки при S/D = 6,2—12,2, т.е.
Nu/NuKp « idem — у. Для оценки этой величины в данной работе про-
ведена обработка экспериментальных данных методом наименьших
квадратов по зависимости: Nu = yRe°'8Pr0,4. В результате расчета полу-
чено у = 0,0276. Среднеквадратичное отклонение результатов расче-
та по зависимости Nu = O,O276Re°,8Pr0,4 от экспериментальных данных
составило 9%.
Тогда Nu/NuKP = 0,0276/0,023 «1,2, т.е. витая труба приводит к рос-
ту коэффициента теплоотдачи приблизительно на 20% при течении
внутри трубы. На рис. 6.30 эта зависимость представлена наряду с со-
отношением Б.В. Дзюбенко Nu = O,O72Reo'76Pгo’4(dэ/d)o'16для S/D = 8,0.
520
Глава 6
Рис. 6.30. Зависимость Nu/NuKP от Re
при течении внутри трубы для: 1 — нака-
танной трубы с d/dBH = 0,94, t/dBH = 0,50;
2 — накатанной трубы с d/dBH — 0,92,
t/dBH = 0,52; 3 — накатанной трубы с
d/dBH = 0,91, f/dBH = 1,00; 4 - витой трубы
с 57£>=8,0 (формула Б.В. Дзюбенко); 5 —
Nur/Nukp = = 0,0276/0,023- 1,2
Jo	IX.K
Рис. 6.31. Зависимость Nu/NuKP от Re
при течении в пучке труб для: 1 — нака-
танной трубы с h/d^ = 0,06, t/d3oa = 0,49;
2 — накатанной трубы с h/d3oa = 0,08,
t/d3oa = 0,51; 3 — накатанной трубы с
h/do = 0,09, f/do = 0,97; 4 — пучка ви-
тых труб с Fr = 63,5
Увеличение коэффициента
теплоотдачи в пучке витых труб
более существенное и проис-
ходит за счет дополнитель-
ной турбулизации и закрут-
ки потока, а также обменных
процессов между пристенной
областью и ядром потока за
счет наличия радиальной со-
ставляющей скорости. В част-
ности, при Re = 104 и Fr = 63,5
отношение Nu/NuKP в пуч-
ке труб составляет 2,11, а при
Re = 105 — 2,60. Зависимость
Nu/NuKp от Re для Fr = 63,5
представлена на рис. 6.31. Уве-
личение коэффициента теп-
лоотдачи внутри трубы с коль-
цевой накаткой происходит за
счет турбулизации потока в
пристенной области. Зависи-
мости Nu от Re для d/dBH = 0,94;
0,92; 0,91 и f/dBH = 0,50; 0,52;
1,00 представлены на рис. 6.30.
При продольном обтекании
пучка труб с кольцевой накат-
кой зависимость теплоотдачи
от числа Рейнольдса такая же,
как при течении внутри трубы.
С ростом числа Re сначала ста-
новится выше сопротивление
пучков накатанных труб по
сравнению с гладкотрубными,
а затем теплоотдача. При
Re = Rej отношение Nu/NuKP
начинает возрастать. Зависи-
мости Nu от Re для h/d3oo = 0,06;
0,08; 0,09 и t/d3oo = 0,49; 0,51; 0,97
представлены на рис. 6.32. Как
видно из рис. 6.30 и 6.31 [6.5.6,
6.5.7], витая труба значительно
интенсифицирует теплоотда-
Глава 6
521
чу в межтрубном пространстве,
но слабо влияет на теплообмен
при течении внутри трубы. Для
кольцевой накатки все наоборот.
Следовательно, разумно комби-
нировать эти два метода интен-
сификации теплообмена и иссле-
довать витую трубу с накаткой.
На рис. 6.32, 6.33 представле-
ны результаты расчета коэффи-
циента теплопередачи, потерь
давления в трубном и межтруб-
ном пространствах для рассмот-
ренных теплообменников в виде
зависимости отношения к/к0,
Л.р/Ар0 от расхода теплоносите-
ля, где к0, &р0 — характеристики
аппарата с гладкими круглыми
трубами без перегородок. В рас-
чете предполагалось, что расходы
в трубном и межтрубном про-
странствах каждого из аппаратов
равны.
Как видно, наиболее теплогид-
равлически эффективным явля-
ется аппарат с витыми трубами,
т.к. он имеет самый большой ко-
эффициент теплопередачи во
всем рассматриваемом диапа-
зоне чисел Re, потери давле-
ния в межтрубном пространс-
тве для него в среднем в два
раза меньше, чем для аппарата
с перегородками, и на 10% боль-
ше, чем ДрОм, как и для аппа-
рата с накатанными трубами, од-
нако потери давления в витых
трубах в 3—4 раза меньше, чем
в накатанных. Изготовление и
эксплуатация аппарата с витыми
трубами более трудоемкая, чем
двух других аппаратов.
Gv кг/с
Рис. 6.32. Зависимость отношения к/к0
для: 1 — пучка витых труб; 2 — аппара-
та с перегородками; 3 — пучка накатан-
ных труб с d/dBH = 0,94, t/dBH = 0,50; 4 —
пучка накатанных труб с d/dBH — 0,92,
t/dBH ~ 0,52; 5 — пучка накатанных труб
с d/dBH =0,91, t/dBH = 1,00
Рис. 6.33. Зависимость отношения
Др/Др0 для: 1 — пучка витых труб;
2 — аппарата с перегородками; 3 —
пучка накатанных труб с d/dBH = 0,94,
t/dBH = 0,50; 4 — пучка накатанных
труб с d/dBH = 0,92, t/dBH = 0,52
522
Глава 6
ОБОЗНАЧЕНИЯ:
аи — коэффициент теплоотдачи при продольном обтекании
пучка, Вт/(м2-К);
а12 — коэффициент теплоотдачи при поперечном обтекании
пучка, Вт/(м2-К);
Дрм — потери давления в межтрубном пространстве, Па;
Дрт — потери давления в трубе, Па;
s — шаг расположения труб в пучке, м;
dH — наружный диаметр трубы, м;
dBH — внутренний диаметр трубы, м;
D — наружный диаметр витой трубы, м;
d — внутренний диаметр впадин накатанной трубы, м;
t	—	шаг накатки, м;
h	—	высота выступов, м;
d3oo = [1,102 (s/dH)2 - l]dH, м;
d3	—	эквивалентный диаметр, м;
d = d3{0,5+2[s/(7td3)]2}, м;
DK	—	внутренний диаметр корпуса теплообменника, м;
L	—	длина трубы, м;
Lm	—	средняя ширина пучка труб, м;
S	—	шаг закрутки, м;
г	—	текущий радиус, м;
Р — угол между направлением движения потока и продоль-
ной осью теплообменника, рад;
F — площадь поперечного сечения канала, перпендикуляр-
ная направлению движения потока, м2;
иг — скорость жидкости в межтрубном пространстве, м/с;
Gx — расход жидкости в межтрубном пространстве, кг/с;
Fr — модифицированное число Фруда;
N — число труб в пучке, шт.;
М — число экспериментальных точек.
Список литературы
6.5.1.	Кузма-Кичта Ю.А. Методы интенсификации теплообмена. М.: МЭИ,
2001.
6.5.2.	Седлов А.С., Абрамов А.И., Кузма-Кичта Ю.А., Комендантов А.С.,
Васин В.А., Шкондин Ю.А., Хазиахметов Р.А. Защита окружающей
среды от сброса сточных вод мощных промышленных и промышленно-
Глава 6
523
отопительных ТЭЦ с применением паропреобразователей//Тепло-энер-
гетика. 1996. № 12. С. 46-51.
6.5.3.	Kuzma-KichtaYu.A.,SedlovA.S.,AbramovA.I.,ShkondinYu.A., Buyakov
D.V., Presnov G.V., Borisov A.A. Improvement of evaporation installations by
means of heat transfer enhancement in vapor generating tubes. Desalination.
1999. №126. P. 171-177.
6.5.4.	Кузма-Кичта Ю.А., Седлов A.C., Абрамов A.M., Жидких В.Ф., Шкон-
дин Ю.А., Борисов А.А., Буяков Д.В. Ресурсные испытания пароге-
нерирующих труб с пористым покрытием на испарителе И-1000 ТЭЦ-8
АО «МОСЭНЕРГО»//Энергосбережение и водоподготовка. 1998. № 2.
С. 18-21.
6.5.5.	Кузма-Кичта Ю.А., Лисовый А.Ф., Кавкаев Д.Д. Усовершенствование
теплообменников для теплоснабжения//4-я Российская нац. конф, по теп-
лообмену. Москва, МЭИ, 2006, 23-27 окт.
6.5.6.	Дзюбенко Б.В., Кузма-Кичта Ю.А. и др. Интенсификация тепло- и мас-
сообмена в энергетике. М.: ФГУП «ЦНИИАТОМИНФОРМ», 2003.
6.5.7.	Дзюбенко Б.В. и др. Турбулентное течение и теплообмен в каналах энер-
гетических установок. Вильнус: Pradai, 1995.
6.6.	КОНДЕНСАТОРЫ ВОДЯНЫХ ПАРОВ КОТЛОВ ТЭС
Интенсификация тепло- и массообмена при конденсации
водяных паров из уходящих дымовых газов котлов
В работе [6.6.1] исследована интенсификация тепло- и массооб-
мена при конденсации водяных паров из уходящих дымовых газов
котлов, сжигающих природный газ. Ограничением в случае получе-
ния конденсата при охлаждении уходящих дымовых газов является
недостаточная эффективность процесса тепломассообмена в тепло-
обменнике со стороны газа [6.6.2]. Поэтому актуальным является ис-
пользование интесификаторов тепломассообмена.
В 2003 г. на ГРЭС-24 АО «Мосэнерго» запущен в эксплуатацию
контактно-поверхностный теплообменник, в котором уходящие ды-
мовые газы охлаждаются ниже температуры точки росы и присутст-
вующие в них водяные пары конденсируются на поверхности труб
со спиральным оребрением (рис. 6.34). На рисунке в средней части
виден теплообменник, справа и слева от него — газоходы и над ним
байпас.
524
Глава Б
Рис. 6.34. Установка для получения
конденсата
Рис. 6.35. Оребренная трубка теплооб-
менника из нержавеющей стали установ-
ки для получения конденсата
Рис. 6.36. Пучок оребренных
трубок во время монтажа
Трубки теплообменника
имеют следующие характерис-
тики: материал — 08Х18Н10Т,
диаметр — 25x2,5 мм, высо-
та ребер — 8 мм, расстояние
между ребрами — 8 мм, дли-
на труб — 210 мм, шаг закрут-
ки — 8 мм (рис. 6.35). Пучок
оребренных труб показан на
рис. 6.36.
Для интенсификации кон-
тактной конденсации, создан-
ной впрыском конденсата
до теплообменника, и конден-
сации на поверхности ореб-
ренных труб на участке газо-
хода до теплообменника в мес-
те врезки байпаса установле-
на пластина-турбулизатор
размером 4000x400x3 мм под
углом 60 градусов к встреч-
ному потоку дымовых газов
(рис. 6.37).
На рисунке показан учас-
ток газохода, в который встро-
ены теплообменник, пласти-
на-турбулизатор, контактная
зона, созданная впрыском че-
рез форсунки, расположенные
на расстоянии 1500 мм.
Исследование интенсифи-
кации тепломассообмена при
конденсации водяных паров из
уходящих дымовых газов про-
водилось на установке, рабо-
тающей на ГРЭС-24 АО «Мос-
энерго» (рис. 6.38).
Основными элементами ус-
тановки получения конденсата
являются:
— теплообменник со встро-
енным сепаратором;
Глава 6
525
—	узел приемки конденса-
та (баки приема конденсата и
декарбонизированной воды,
декарбонизатор);
—	узел химической очистки
получаемого конденсата.
Установка оборудована си-
стемой шариковой очистки ана-
логично конденсатору паровой
турбины. В ней осуществляет-
ся конденсация парогазовой
смеси с большим содержани-
ем неконденсирующихся газов.
Рис. 6.37. Схема расположения пласти-
ны-турбулизатора и форсунок в установ-
ке получения конденсата
Для создания контактной зоны пе-
ред теплообменником организован впрыск получаемого конденса-
та через форсунки. Интенсификация теплообмена происходит за
счет вихреобразования парогазового потока при помощи пластины-
турбулизатора, создания контактной зоны перед теплообменником
Рис. 6.38. Схема установки получения конденсата ГРЭС-24
526
Глава 6
и использования спирального оребрения в теплообменнике [6.6.3].
Получаемое при конденсации водяных паров тепло непрерывно от-
водится с охлаждающей водой и получаемым конденсатом.
Уходящие дымовые газы после дымососа поступают в установку
получения конденсата. Часть газов (около 40%) отводится по байпа-
су что исключает низкотемпературную коррозию дымовой трубы
и газового тракта после установки получения конденсата. Основной
поток газов проходит контактную зону и конденсируется на поверх-
ности оребренных трубок пучка. Получаемый таким образом кон-
денсат собирается в бак, из которого часть его идет на форсунки (око-
ло 1 т/ч), а основная часть (около 5 т/ч) поступает на двухступенчатую
химическую очистку. Схема измерений представлена на рис. 6.39.
Опыты проведены в диапазоне чисел Re дымовых газов
10бн-2,34107.
В опытах обнаружено, что пластина-турбулизатор, форсунки и
оребрение труб увеличивают теплоотдачу дымовых газов к поверх-
ности труб теплообменника, вследствие чего количество конденсата
увеличилось от 2,2 т/ч (до модернизации) до 5,76 т/ч (рис. 6.40) [6.6.4].
В дымовую трубу На форсунки
В деаэратор
подпитки теплосети
Рис. 6.39. Схема измерений установки получения конденсата
Глава 6
527
На рис. 6.40 показана зависимость расхода получаемого конденса-
та от удельной паровой нагрузки конденсатора для различных вари-
антов выполнения трубного пучка и интенсификации теплообмена.
Для сравнения приведены данные работы.
В трех сечениях газохода измерялась скорость дымовых газов за
пластиной-турбулизатором. Согласно измерениям обнаружены ха-
отичные потоки дымовых газов и неравномерное распределение
скорости по сечению газохода. За счет повышения коэффициента
теплоотдачи со стороны, омываемой газами, уменьшилась их темпе-
ратура за теплообменником, увеличился нагрев охлаждающей тех-
нической воды. Размеры и угол установки пластины определены по
данным опытов, в которых количество получаемого конденсата, при
прочих равных условиях, было максимальным. Пластина-турбули-
затор обеспечивает срыв газового потока с передней кромки с обра-
зованием в кормовой части вихревых течений. Форсунки создают
контактную зону перед трубным пучком теплообменника, понижая
температуру дымовых газов до температуры точки росы. Оребрение
увеличивает поверхность теплообмена со стороны дымовых газов,
значительно повышая коэффициент теплопередачи. По результатам
проведенных исследований разработана инженерная методика рас-
чета коэффициента теплопередачи от дымовых газов к охлаждаю-
щей воде, основанная на следующем выражении для коэффициента
теплопередачи:
1 d	d	d i А 1
к = _L5ffi+1,i5^1g^ + -L ,	(6.6.1)
< £*ВН	^ст	^вн ®см >
где ав — коэффициент теплоотдачи от стенки трубы к воде, Вт/(м2-К);
асм — коэффициент теплоотдачи от паровоздушной смеси к стенке
трубки, Вт/(м2-К); dHap, dBH — диаметры трубы наружный и внутрен-
Удельная паровая нагрузка конденсатора, кг/(м2-ч)
Рис. 6.40. Влияние ин-
тенсификаторов на теп-
лообмен при конденса-
ции уходящих дымовых
газов: 1 — гладкая труба;
2 — трубный пучок с
оребренными трубами,
без форсунок и плас-
тины-турбулизатора;
3 — трубный пучок с
оребренными трубами,
форсунками и пласти-
ной-турбулизатором
528
Глава 6
ний соответственно; Хст — коэффициент теплопроводности материа-
ла стенки трубки, Вт/(м2-К),
ав = 0,023Re^ ,в. Рг^.в.	(6.6.2)
“вн.
ас„ =0,56a^e0'0032d«'0'40<’7,	(6.6.3)
где £— относительное содержание воздуха (неконденсирующихся га-
зов) в паре; аЛ — среднее значение коэффициента теплоотдачи при
конденсации чистого водяного пара в горизонтальном трубном пучке
определяется по формуле:
—	/	\0,33
—= 19П0Д1Ч1Г0'51 1 + -I (s)0,15,	(6.6.4)
«Nu	V 27
где П = (рпРГп2о)/(ркрс/нар); Wno - скорость пара на входе в трубный
пучок (по площади горловины конденсатора); aNu — коэффициент
теплоотдачи, рассчитанный по формуле Нусельта; z — число ходов
воды; значение s =f/F изменялось в диапазоне от 0,004 до 0,020.
В целях дальнейшей модернизации установки предложено уве-
личить контактную зону до теплообменника.
Внедрение в энергетике подобных установок позволит снизить
себестоимость производства электроэнергии и воздействие электро-
станции на окружающую среду, повысить коэффициент использова-
ния топлива.
Список литературы
6.6.1.	Кузма-Кичта Ю.А., Бухонов Д.Ю., Борисов Ю.В. Интенсификация теп-
ломассообмена при конденсации водяных паров из уходящих дымовых
газов/ДЭ. 2005. № 3. С. 30-31.
6.6.2.	Андреев Е.И. Расчет тепломассообмена в контактных аппаратах. М.:
Энергоатомиздат, 1985. С. 9-15.
6.6.3.	Дзюбенко Б.В., Дрейцер Г.А. и др. Интенсификация теплообме-
на в каналах с искусственной турбулизацией потока/Др. 1-й Россий-
ской нац. конф, по теплообмену. М.: Изд. МЭИ, 1994. Т. 8. С. 64-69.
Глава 6
529
6.7. АППАРАТЫ ДЛЯ РАЗДЕЛЕНИЯ ГЕТЕРОГЕННЫХ СИСТЕМ
Процессы разделения гетерогенных систем составляют основу
многих производств химической, нефтехимической, микробиологи-
ческой, горнорудной, газовой, металлургической и других отраслей
промышленности, тепловой и атомной энергетики, ракетной техники,
опреснения морской воды, МГД-генераторов.
В [6.7.1—6.7.5] разработаны универсальные методы расчета про-
гнозируемых показателей разделения и других важных технологиче-
ских характеристик циклонов, гидроциклонов, турбоциклонов и цен-
трифуг.
Созданы эффективные сепарирующие устройства для разделения
пенящихся парогазожидкостных систем и принципиально новый спо-
соб сепарации парогазожидкостных систем струями жидкости (струй-
ный сепаратор) [6.7.6 —6.7.8].
Разработаны и реализованы на ряде промышленных объектов но-
вые высокоэффективные конструкции гидроциклонных аппаратов,
например в Усолье-Сибирском ПО «Химпром», на Воскресенском
химкомбинате, Череповецком ПО «Аммофос», Крымском заводе дву-
окиси титана, Ферганском заводе азотных удобрений, Целиноград-
ском горно-химическом комбинате, Степногорском биохимическом
заводе, на фабрике «Марат» комбината «Рот Фронт» и ряде других
предприятий.
Применение гидроциклонов на локальных сооружениях очистки
производственных сточных вод обеспечивает возможность создания
компактных и высокоэффективных установок. Так, площадь, занима-
емая гидроциклонами, при равной эффективности в 20 — 50 раз мень-
ше площади, занимаемой отстойниками, при этом капитальные затра-
ты на строительство отстойников в 5 —10 раз превышают суммарные
затраты на монтаж гидроциклонов.
Список литературы
6.7.1.	Кутепов А.М. Расчет сепараторов циклонного типа//Хим. пром-сть. 1964.
№ 4. С. 55-62.
6.7.2.	Соловьев В.В., Жихарев А.С., Кутепов А.М. Исследование работы цик-
лонного сепаратора//ЖПХ. 1981. Т. 51, № 1.
6.7.3.	Кончуков В.А., Жихарев А.С., Кутепов А.М., Соловьев В.В. Статисти-
ческий подход к исследованию уноса при работе струйных сепараторов
в аппаратах барботажного типа//Изв. вузов. Химия и хим. технол. 1979.
Т. XXII, вып. 11. С. 1403-1407.
530
Глава 6
6.7.4.	Николаенко А.Д., Кутепов А.М., Тютюнников А.Б. Исследование эф-
фективности циклонного сепаратора/Деор. основы хим. технол. 1970.
Т. IV, № 2. С. 296-300.
6.7.5.	Терновский И.Г., Кутепов А.М. Гидроциклонирование. М.: Наука, 1994.
С. 350.
6.7.6.	Жихарев А.С., Кутепов А.М. Экспериментальное исследование сепара-
ции парожидкостных смесей струями жидкости//Хим. и нефтехим. маши-
ностр. 1972. № 2. С. 10-15.
6.7.7.	Жихарев А.С., Кутепов А.М. Исследование гидродинамики распреде-
лительного устройства струйного сепаратора//Хим. пром-сть. 1972. № 6.
С. 62-72.
6.7.8.	Кутепов А.М., Жихарев А.С. Исследование сепарации парожидкост-
ных систем струями жидкости/Деор. основы хим. технол. 1972. Т. IV, № 2.
С. 208-215.
531
Оглавление
Введение......................................................3
Глава 1. Выбор и обоснование методов интенсификации
теплообмена...................................................9
1.1.	Интенсификаторы теплообмена макро-, микро-
и наномасштабов...........................................9
1.2.	Закрутка потока в трубах и пучках твэлов и труб....87
1.3.	Колебания поверхности раздела фаз.................101
Глава 2. Теоретические методы исследования интенсификации
тепло- и массообмена........................................108
2.1.	Пучки витых твэлов и труб.........................108
2.2.	Гидродинамика многофазных гетерогенных сред
при действии центробежных сил...........................178
2.3.	Волнообразование в тонкой пленке жидкости.........190
2.4.	Интенсификаторы теплообмена макро-
и микромасштабов .......................................302
Глава 3. Экспериментальные методы исследований
интенсификации тепло- и массообмена.........................308
3.1.	Пучки витых труб..................................308
3.2.	Интенсификаторы теплообмена макро-
и микромасштабов .......................................317
3.3.	Колебания поверхности раздела фаз.................333
Глава 4. Результаты экспериментальных исследований
интенсификации тепло- и массообмена ........................337
4.1.	Пучки витых твэлов и труб, витые трубы и
кольцевые каналы с витой трубой ........................337
4.2.	Интенсификаторы теплообмена макро-
и микромасштабов .......................................377
4.3.	Колебания поверхности раздела фаз.................420
Глава 5. Интенсификация разделения гетерогенных систем
в тепло- и массообменных аппаратах..........................425
5.1.	Парогазожидкостные системы........................426
5.2. Стохастический анализ гидромеханических
процессов разделения гетерогенных систем............448
Глава 6. Внедрение методов интенсификации
тепло- и массообмена в технике .............................463
6.1.	Энергодвигательные установки аппаратов для
пилотируемой экспедиции на Марс.........................463
6.2.	Определение характерных параметров для ЯЭДУ.......473
532
6.3.	Выбор конструкции и материалов тепловыделяющей
сборки ядерного гетерогенного реактора.................493
6.4.	Реакторы и лазеры .................................507
6.5.	Испарители и теплообменники для теплоснабжения .....515
6.6.	Конденсаторы водяных паров котлов ТЭС..............523
6.7.	Аппараты для разделения гетерогенных систем........529
Борис Владимирович Дзюбенко
Юрий Альфредович Кузма-Кичта
Александр Иванович Леонтьев
Иван Иванович Федик
Леонид Петрович Холпанов
ИНТЕНСИФИКАЦИЯ ТЕПЛО- И МАССООБМЕНА
НА МАКРО-, МИКРО- И НАНОМАСШТАБАХ
Монография
Редакторы Г.П. Елисеева, Н.П. Чижова
Компьютерная верстка Е.Н. Кисельникова
Дизайн обложки Е.В. Васильев
Подписано в печать 19.12.2008 Формат 70x100/16. Печать офсетная.
Гарнитура «Балтика».
Усл.-печ. л. 42,7. Уч.-изд. л. 33,4. Тираж 400 экз. Заказ № 128.
Издательско-полиграфическое отделение
ФГУП «ЦНИИАТОМИНФОРМ»
Москва, а/я 971