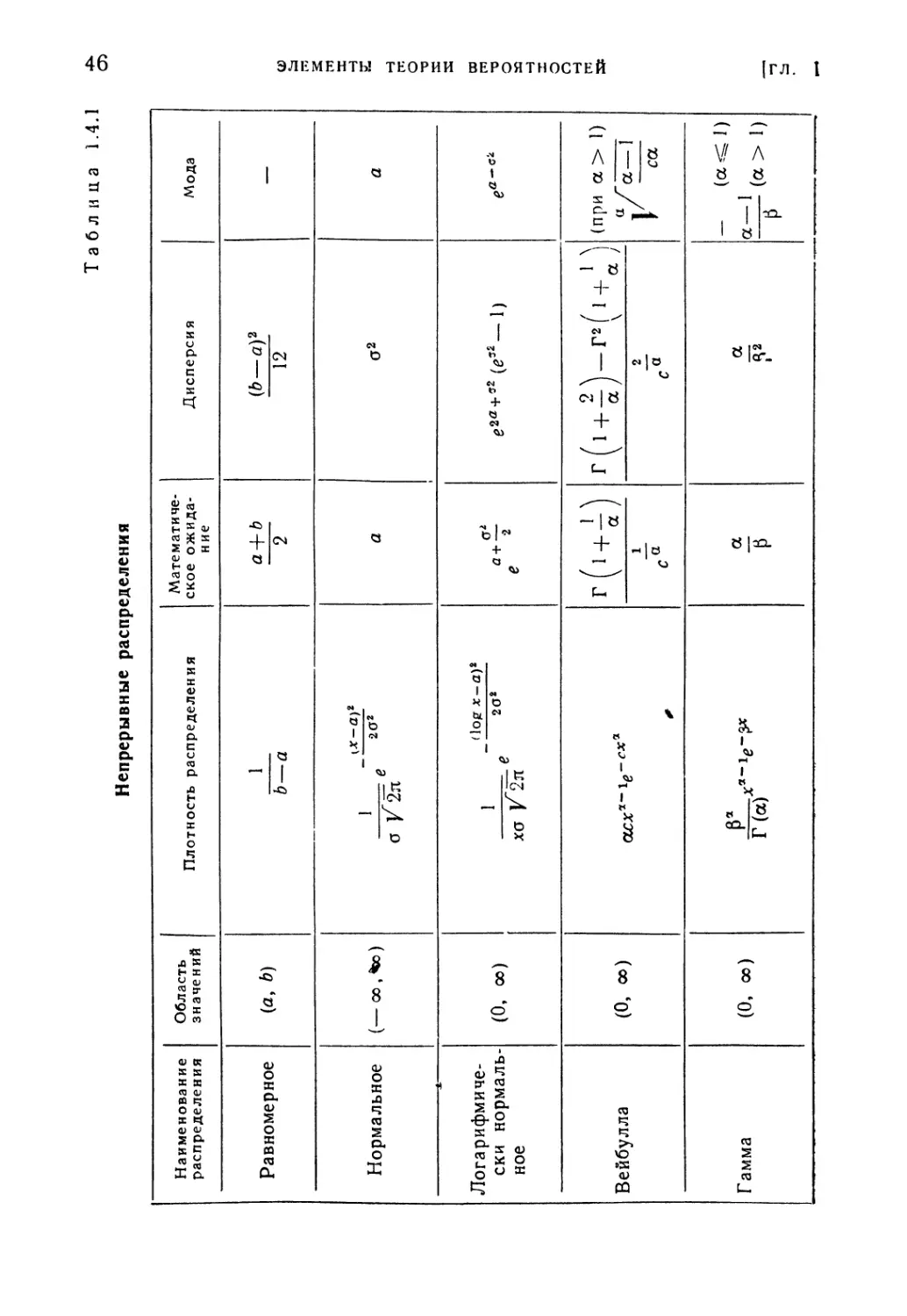
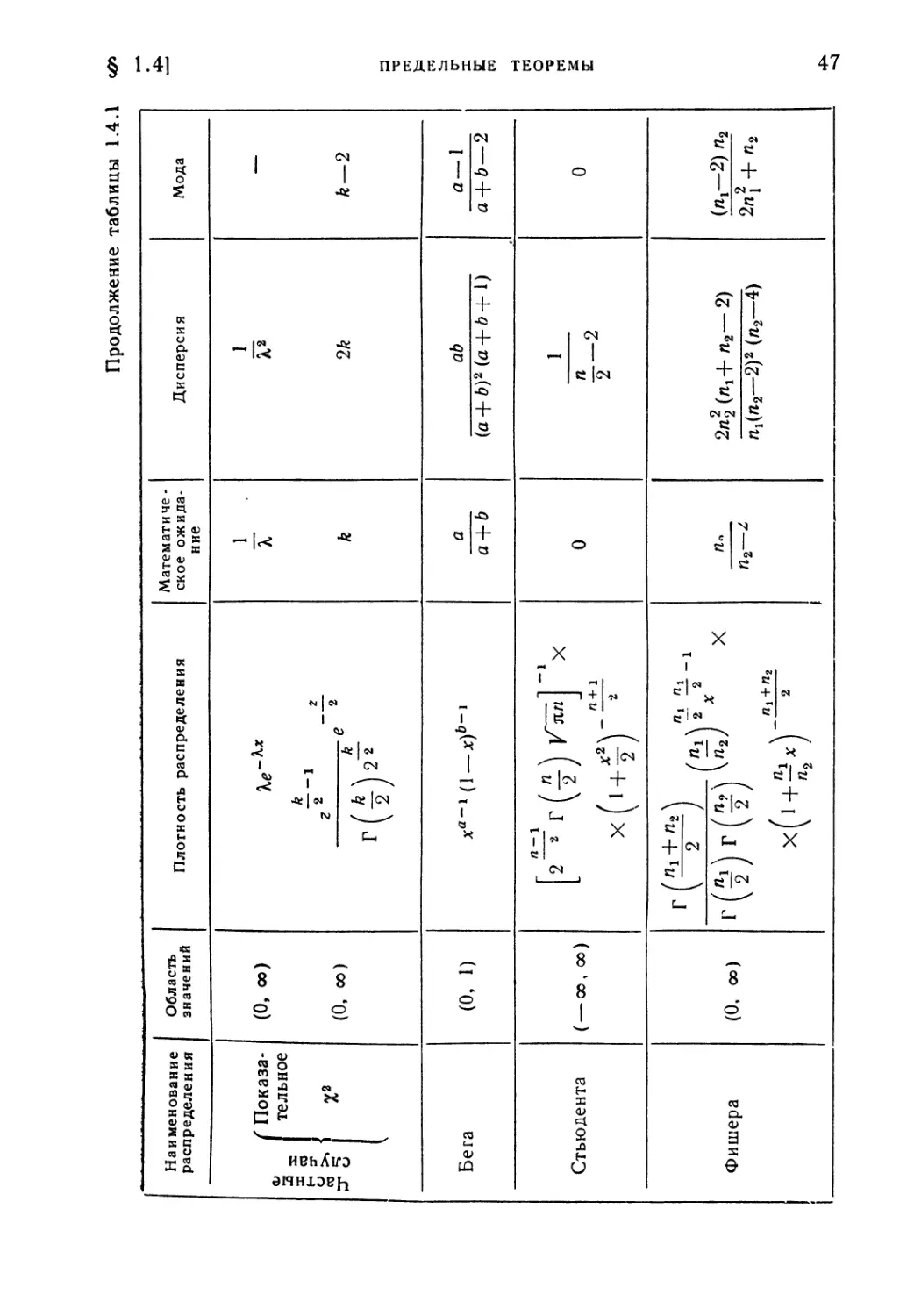
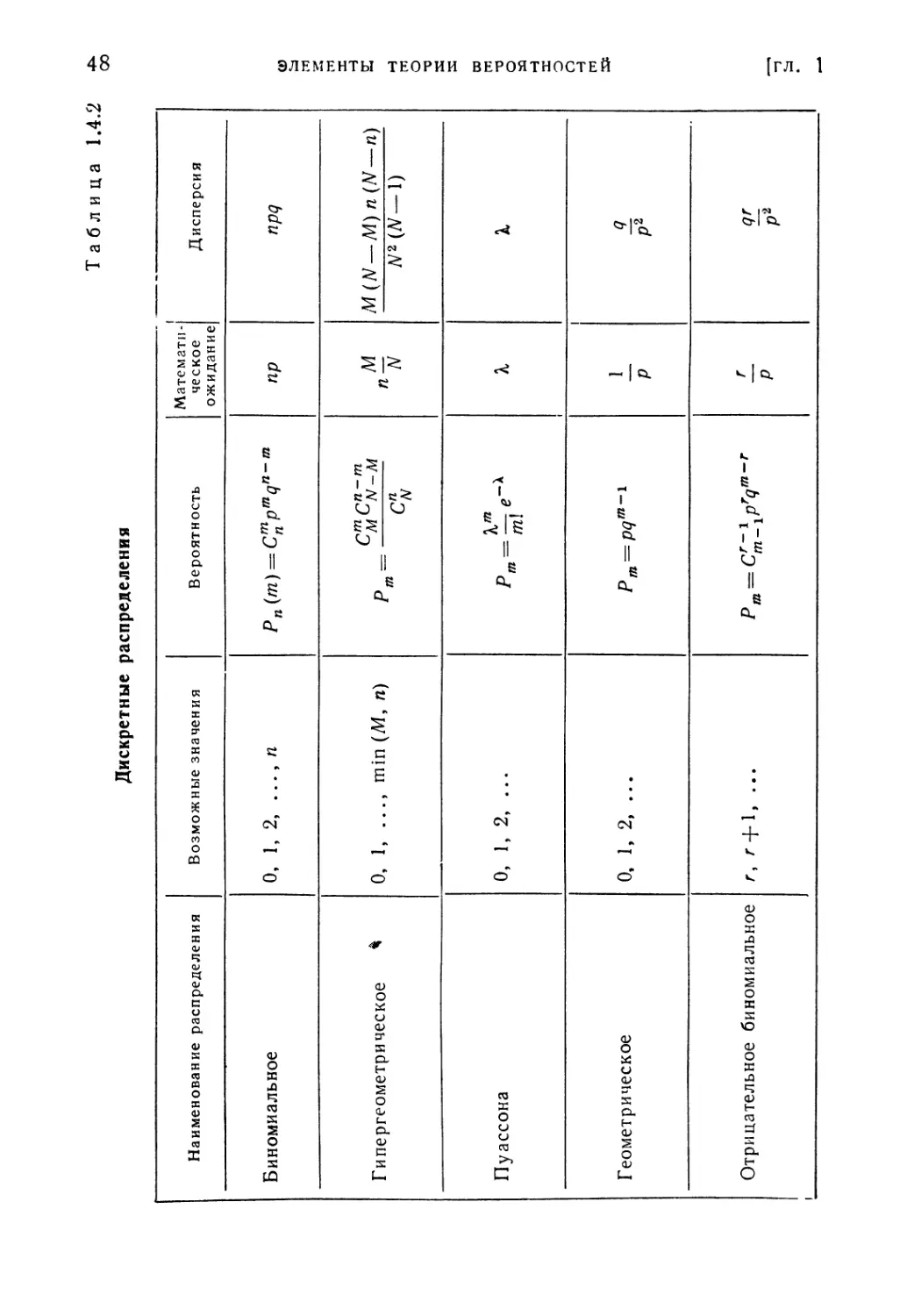
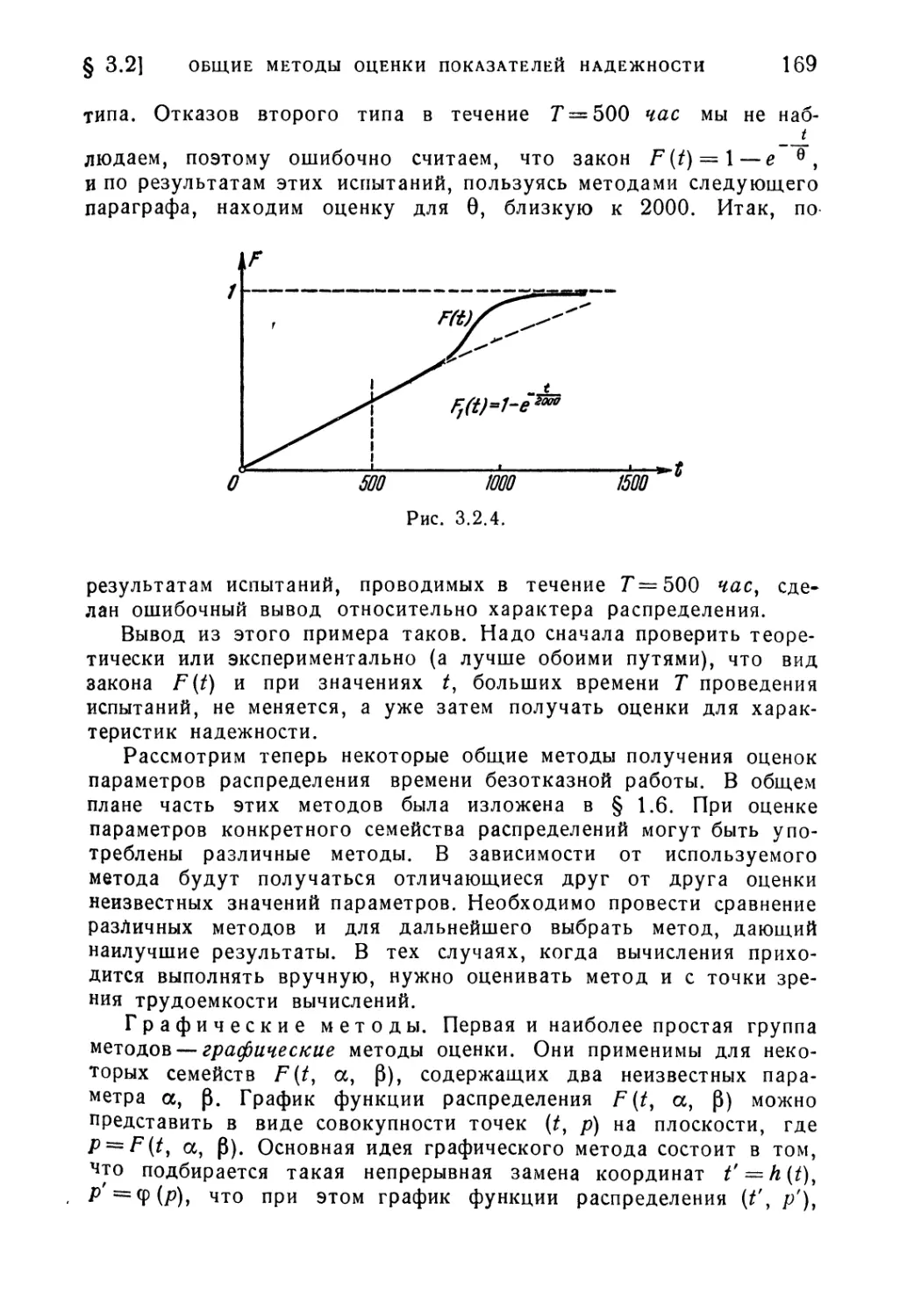
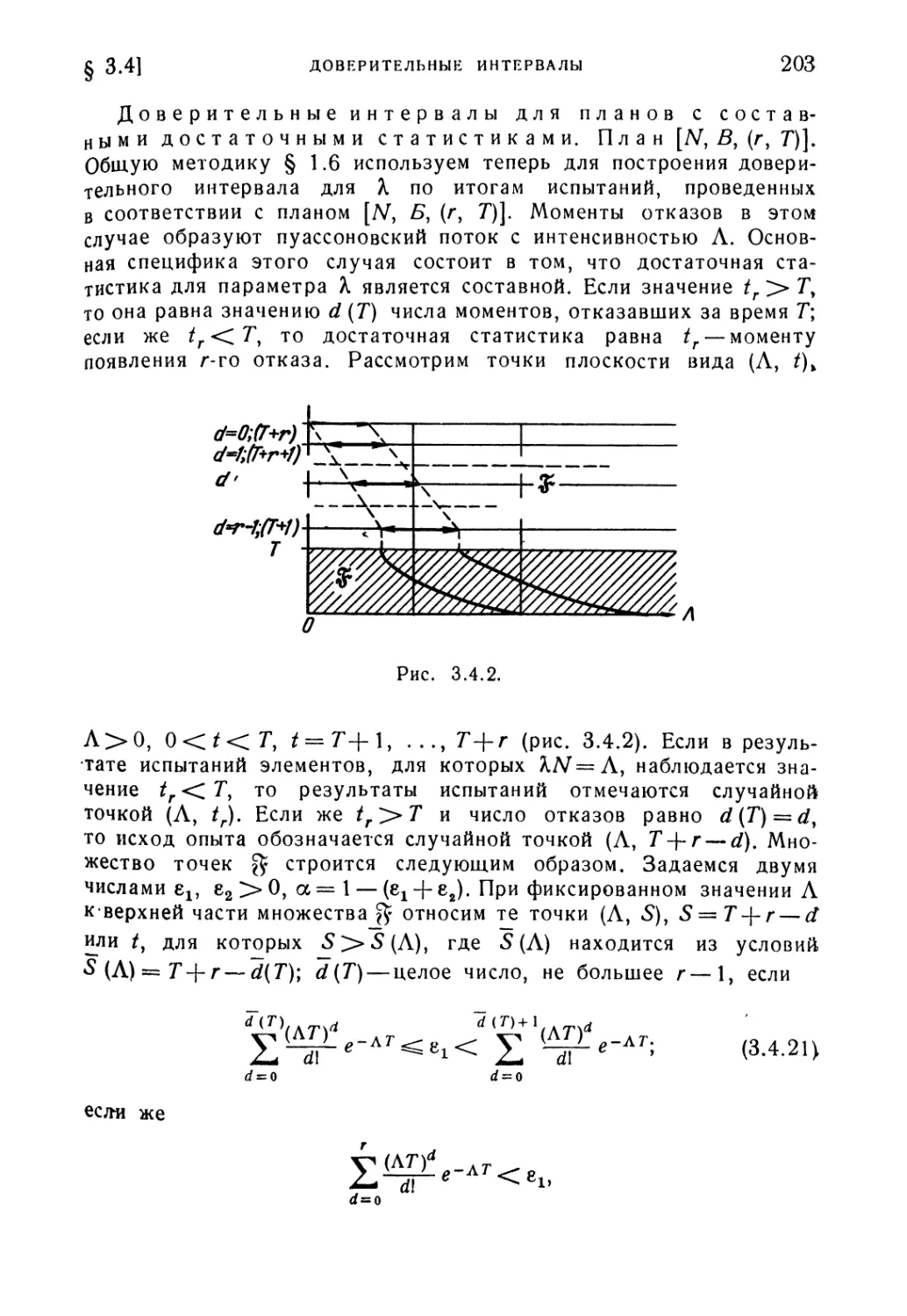
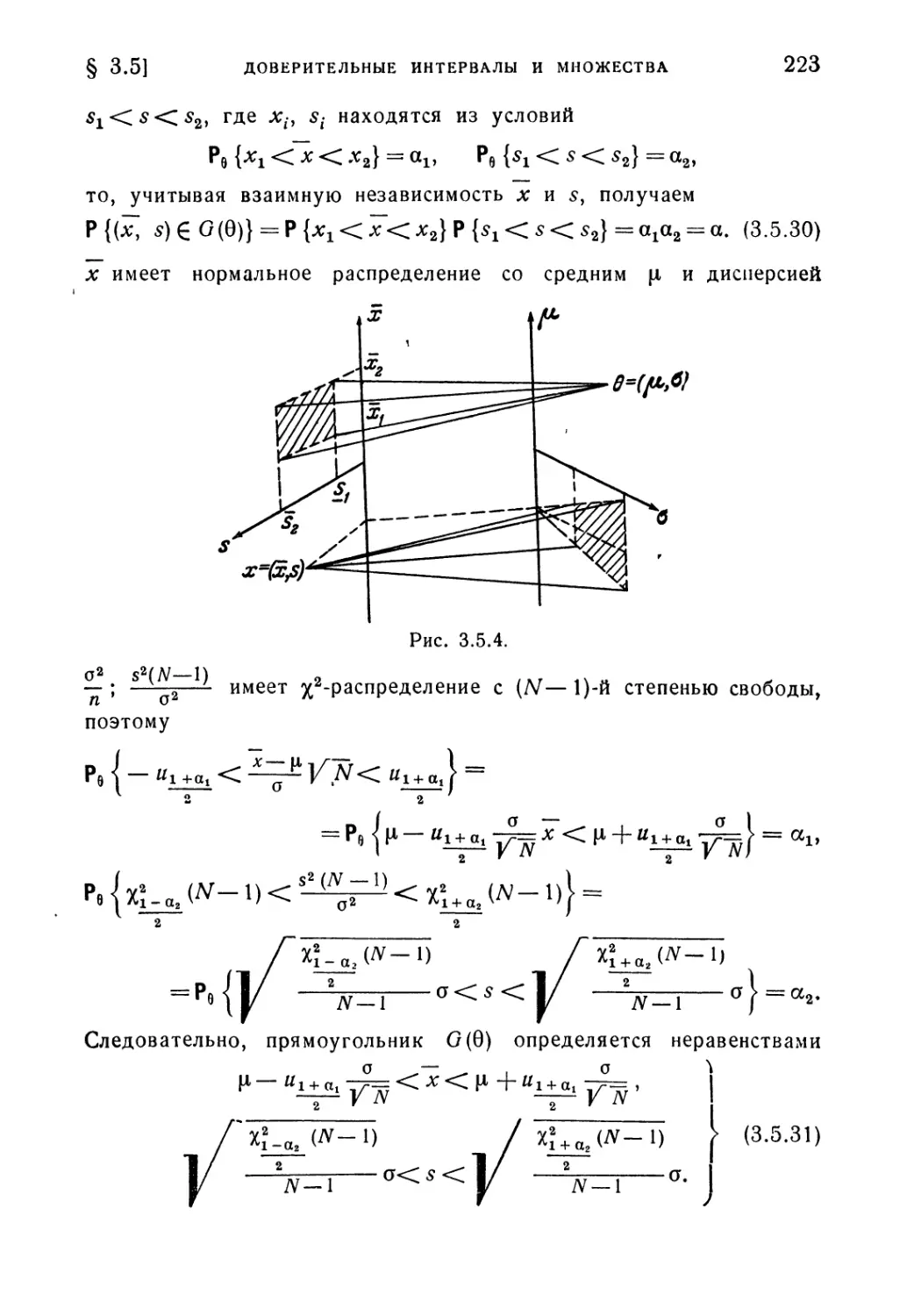
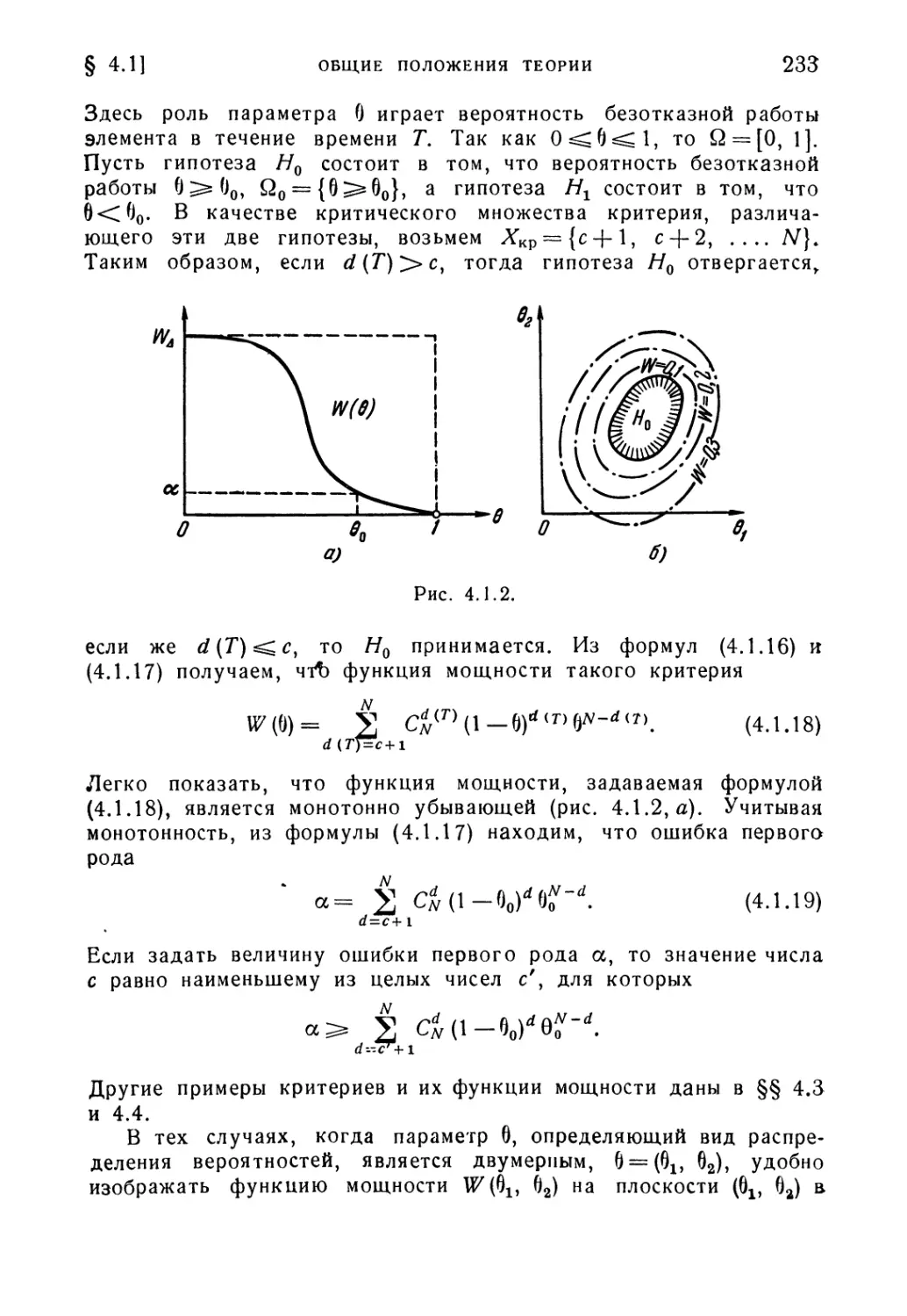
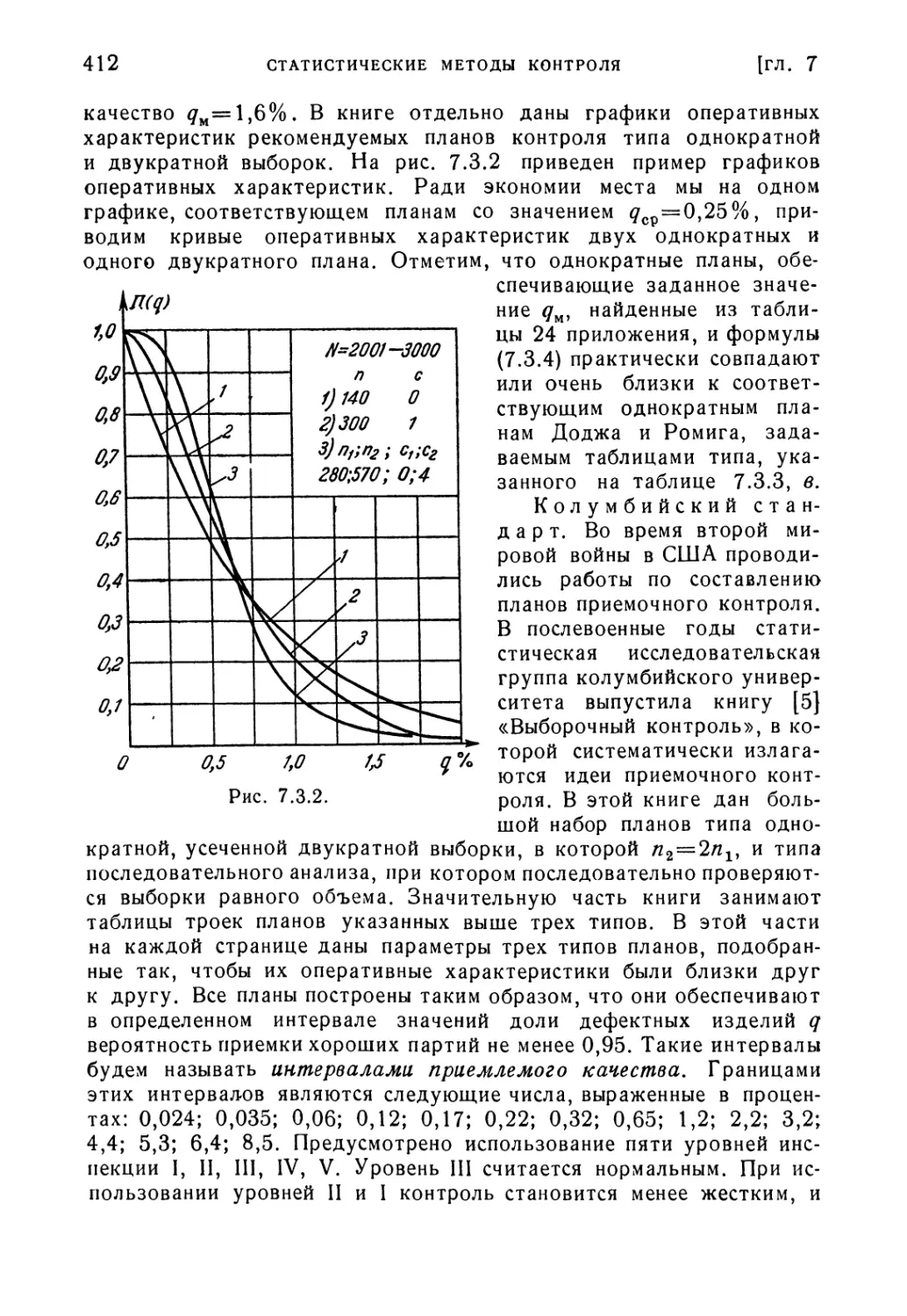
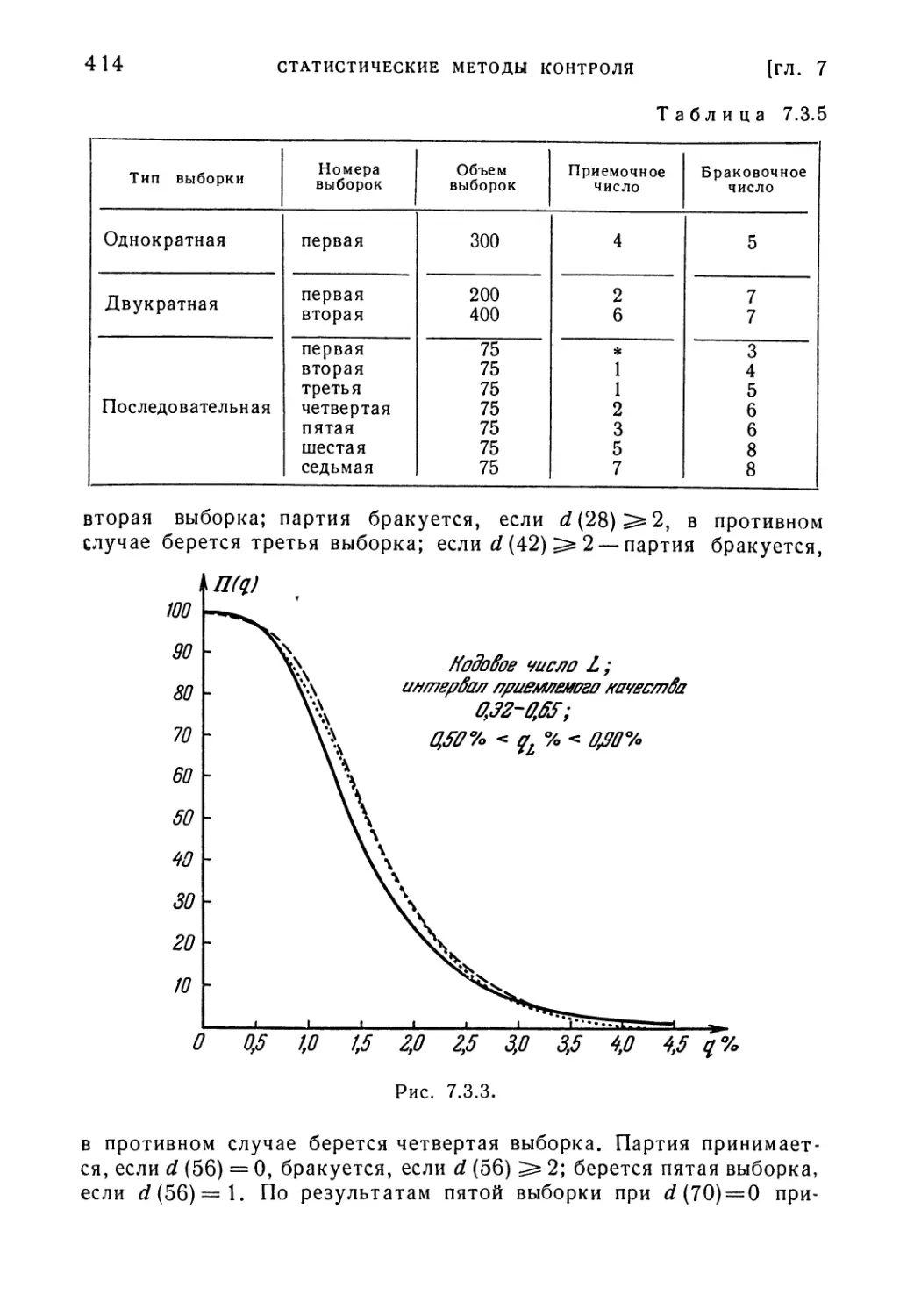
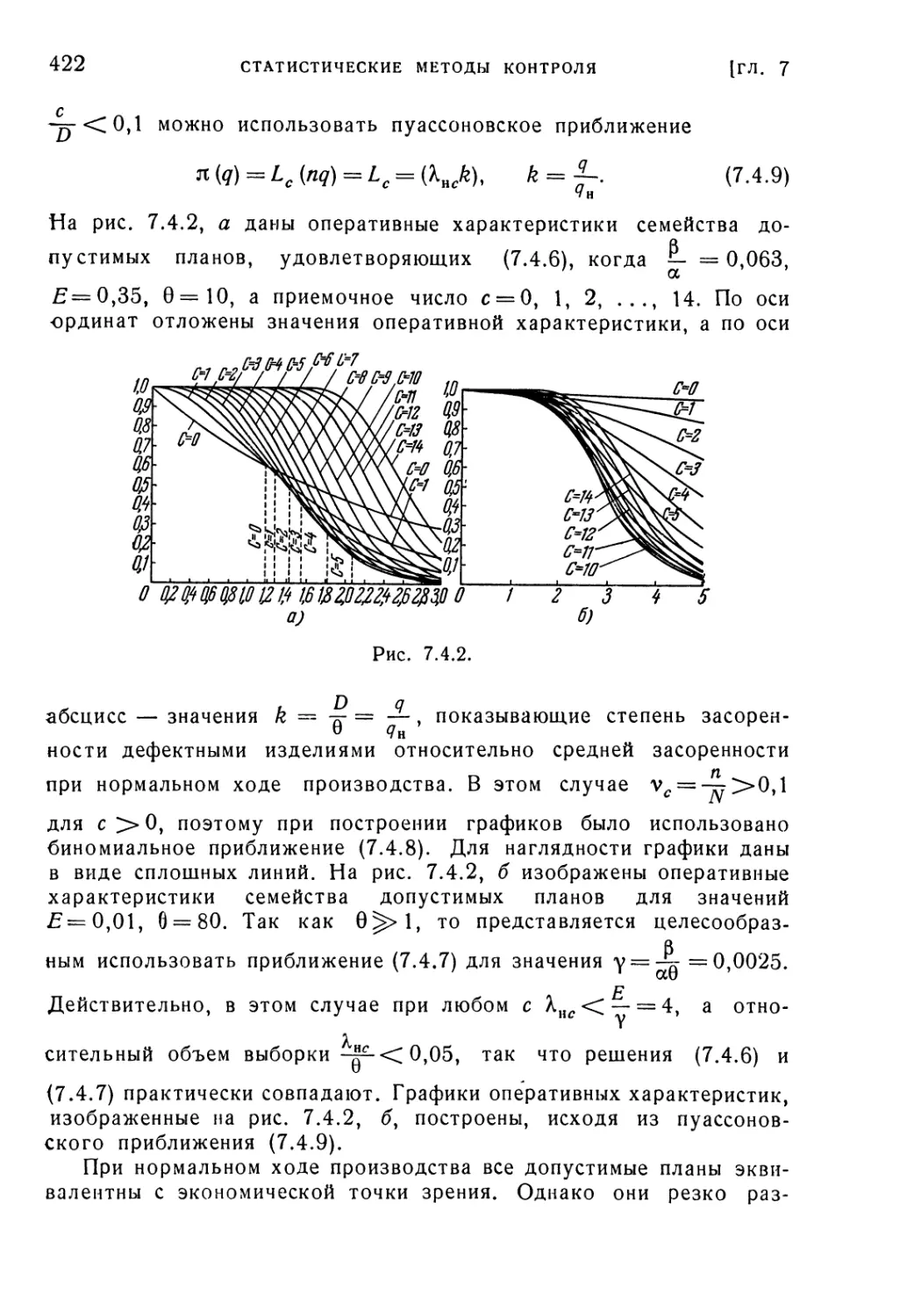
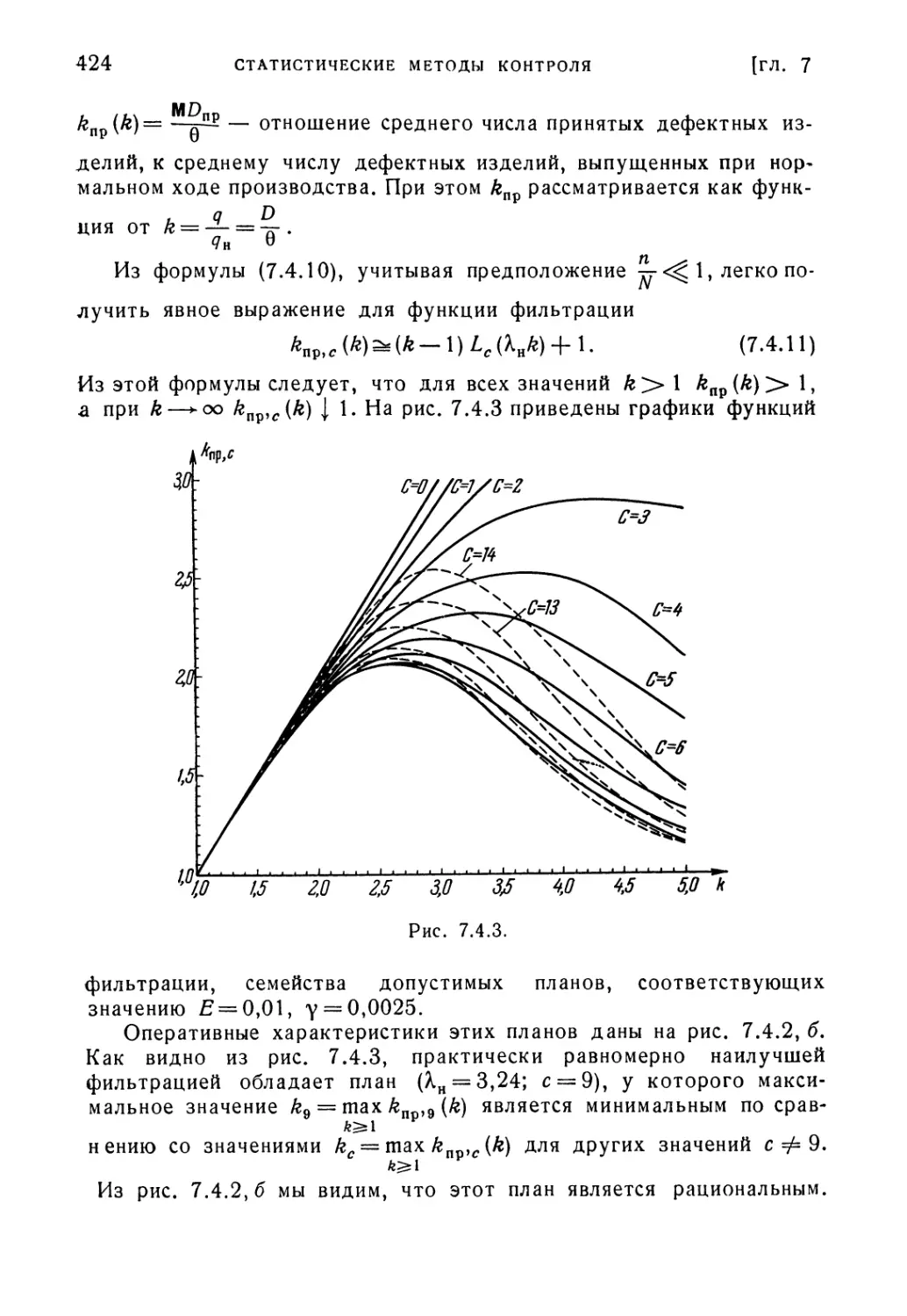
Текст
ФИЗИКО-МАТЕМАТИЧЕСКАЯ БИБЛИОТЕКА ИНЖЕНЕРА
Б. В. ГНЕДЕНКО, Ю. К. БЕЛЯЕВ, А. Д. СОЛОВЬЕВ
МАТЕМАТИЧЕСКИЕ
МЕТОДЫ
В ТЕОРИИ
НАДЕЖНОСТИ
ОСНОВНЫЕ
ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ
И ИХ СТАТИСТИЧЕСКИЙ АНАЛИЗ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1965
Б17.8
Г 56
УДК 519.95
АННОТАЦИЯ
В существующей уже достаточно обширной
монографической литературе по теории надежности
до сих пор нет книги, в которой было бы дано
систематическое изложение основ этой теории. На-
Настоящая книга написана с целью восполнить этот
пробел.
Авторы излагают формализованный подход к
определению основных понятий теории надежности,
различные планы оценки характеристик надежности
по результатам испытаний, методы проверки гипо-
гипотез, теорию резервирования без восстановления
и с восстановлением, методы приемочного контроля.
Книга снабжена большим числом таблиц, многие
из которых были специально подсчитаны для
настоящей книги. Книге предпослана вводная глава,
в которой излагаются необходимые сведения из те-
теории вероятностей, математической статистики и
преобразований Лапласа.
Книга рассчитана на математиков, инженеров
и студентов, интересующихся вопросами теории
надежности. Глава, посвященная контролю качества
продукции, полезна для работников отделов техни-
технического контроля.
Борис Владимирович Гнеденко, Юрий Константинович Беляев,
Александр Дмитриевич Соловьев
Математические методы в теории надежности
(Серия: «Физико-математическая библиотека инженера»)
М., 1965 г., 524 стр. с илл.
Редактор В. Г. Кисунько
Техн. редактор И. Ш. Аксельрод Корректор С. Н. Емельянова
Сдано в набор 18/IV 1965 г. Подписано к печати 20/VIII 1965 г. Бумага 60x90/16.
Физ. печ. л. 32,75. Условн. печ. л. 32,75. Уч.-изц. л. 32,70. Тираж 27 000 экз. Т-10282.
Цена книги 1 р. 79 к. Заказ № 2522.
Издательство «Наука»
Главная редакция физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Первая Образцовая типография имени А. А. Жданова Главполиграфпрома
Государственного комитета Совета Министров СССР по печати.
Москва, Ж-54, Валовая, 28.
ОГЛАВЛЕНИЕ
Предисловие 6
Введение 9
Глава 1. Элементы теории вероятностей и математической стати-
статистики 14
§ 1.1. Понятие случайного события. Основные формулы теории веро-
вероятностей 14
.2. Случайные величины и их функции распределения 22
.3. Числовые характеристики случайных величин 33
.4. Некоторые предельные теоремы теории вероятностей 39
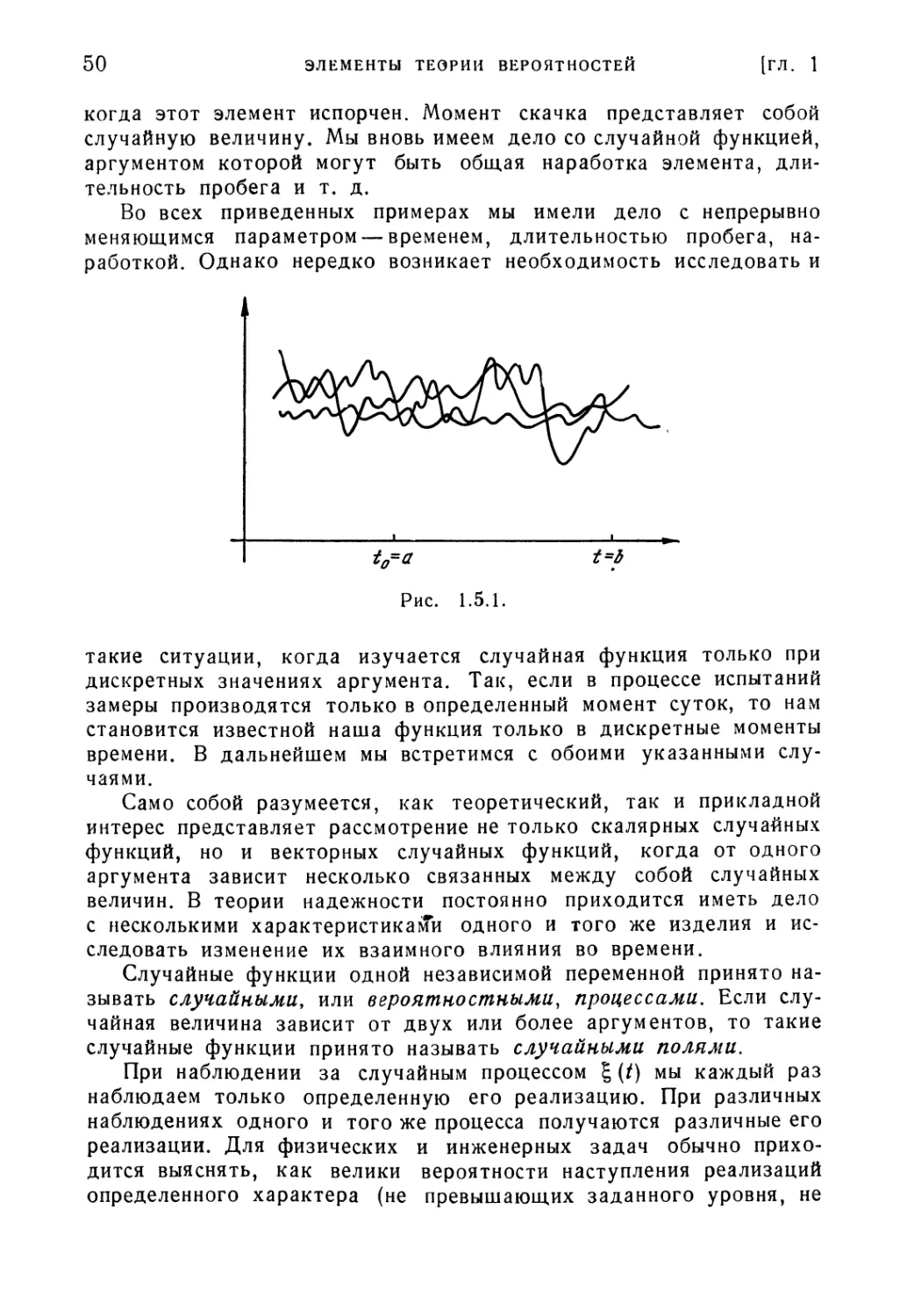
.5. Общие сведения о теории случайных процессов 49
.6. Элементы математической статистики 57
.7. Преобразование Лапласа 71
Глава 2. Характеристики надежности 79
§ 2.1. Основные понятия теории надежности 79
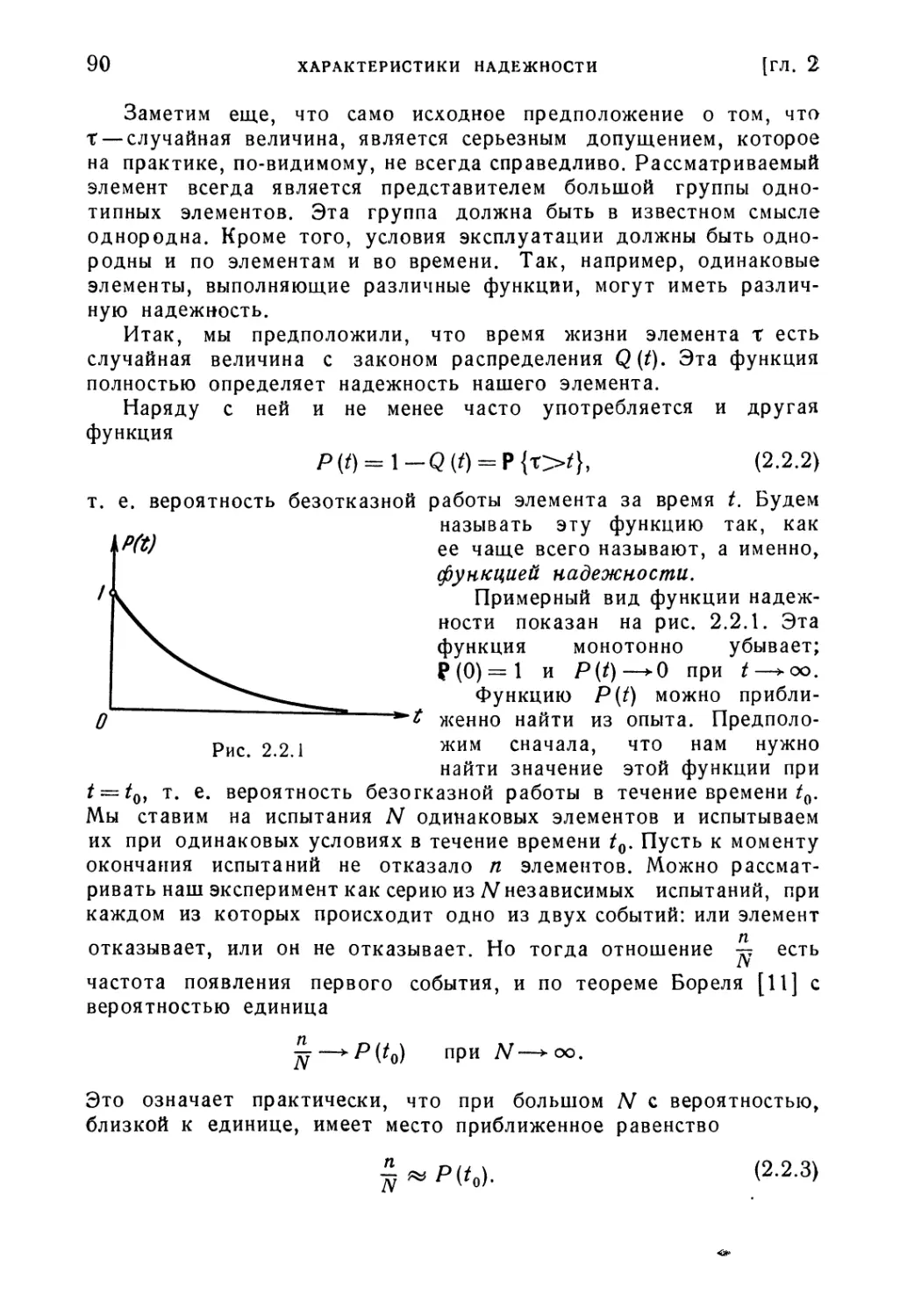
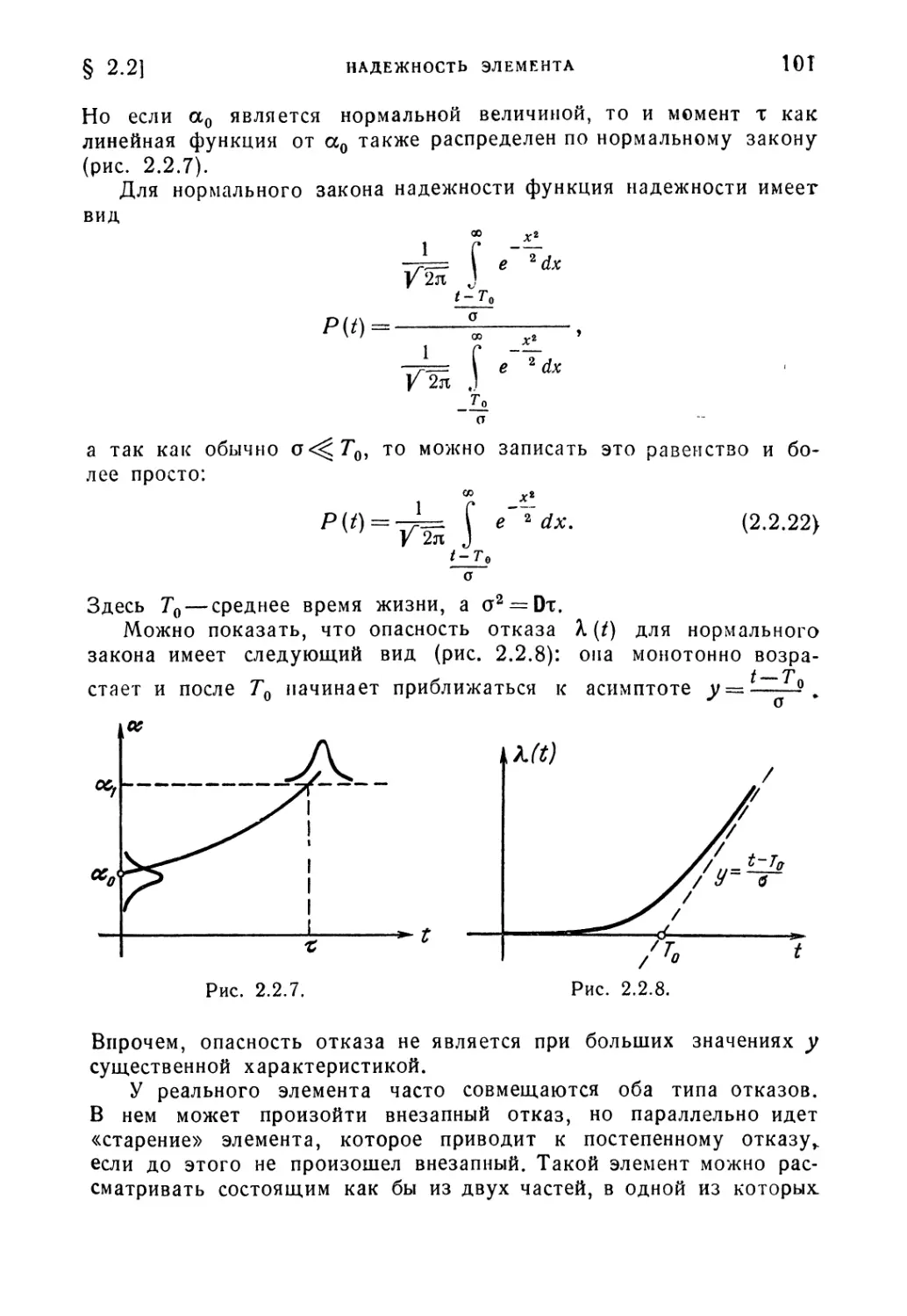
§ 2.2. Надежность элемента, работающего до первого отказа .... 89
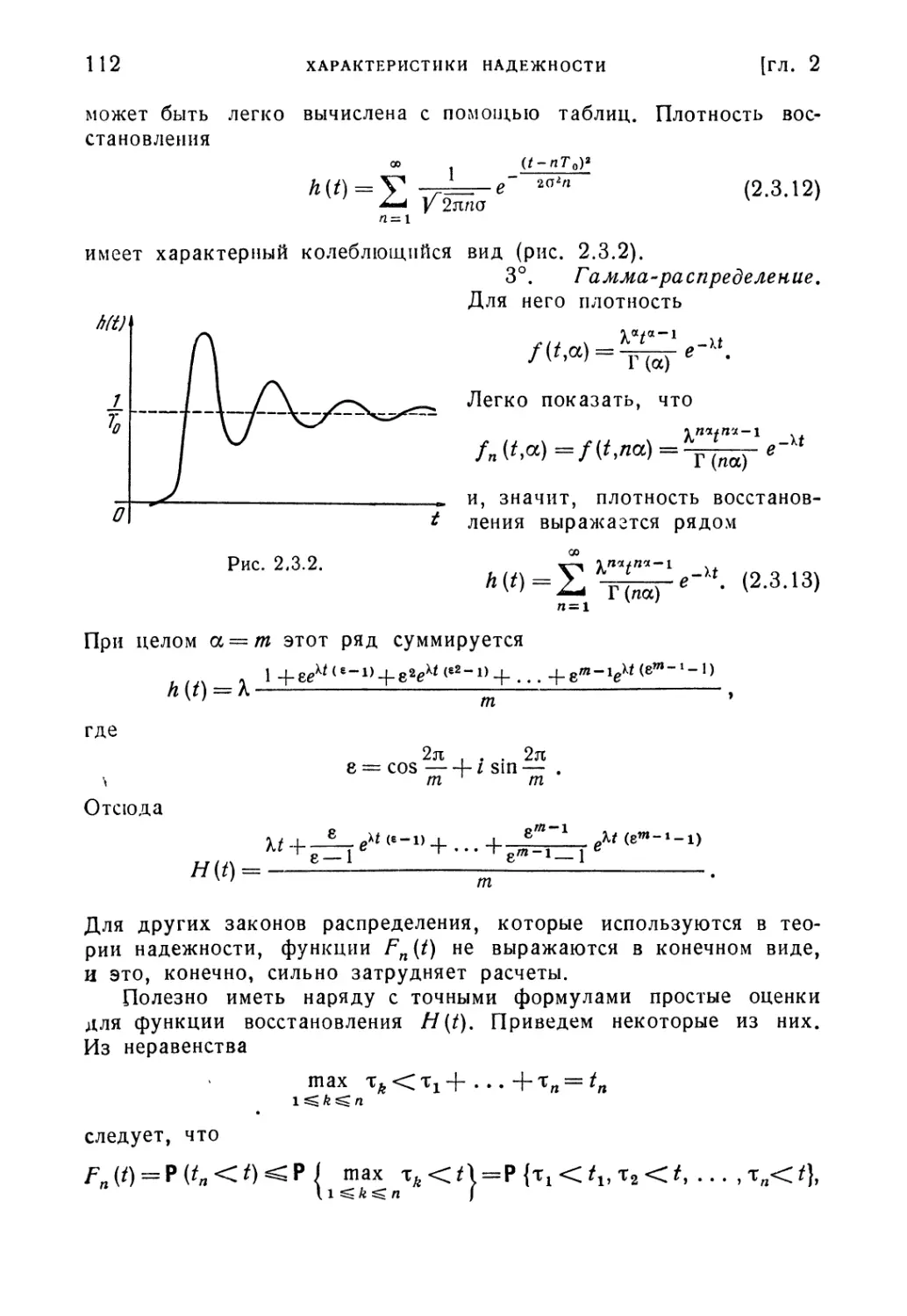
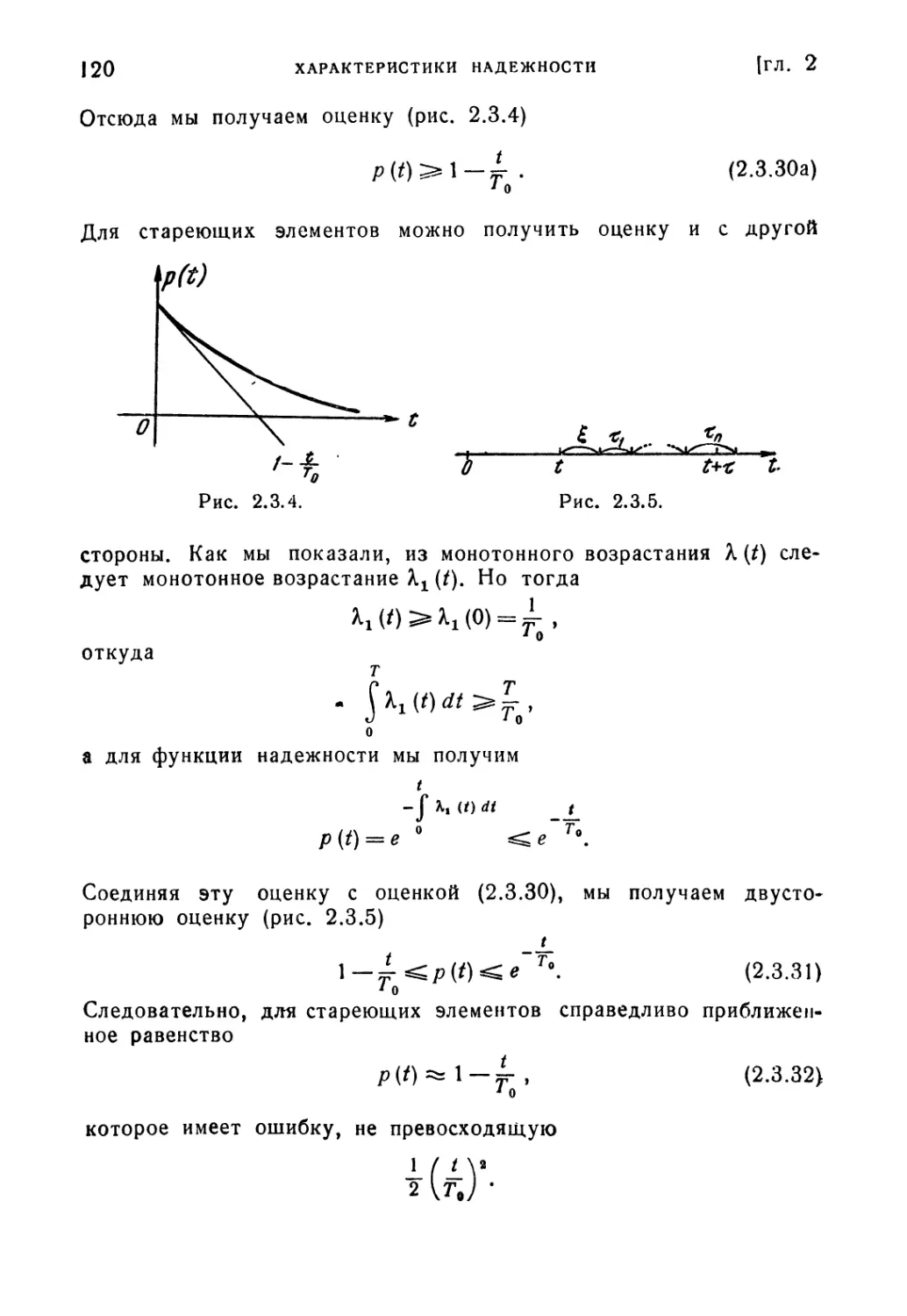
§ 2.3. Надежность восстанавливаемого элемента 108
§ 2.4. Надежность системы 133
Глава 3. Оценка показателей надежности по результатам испытаний 156
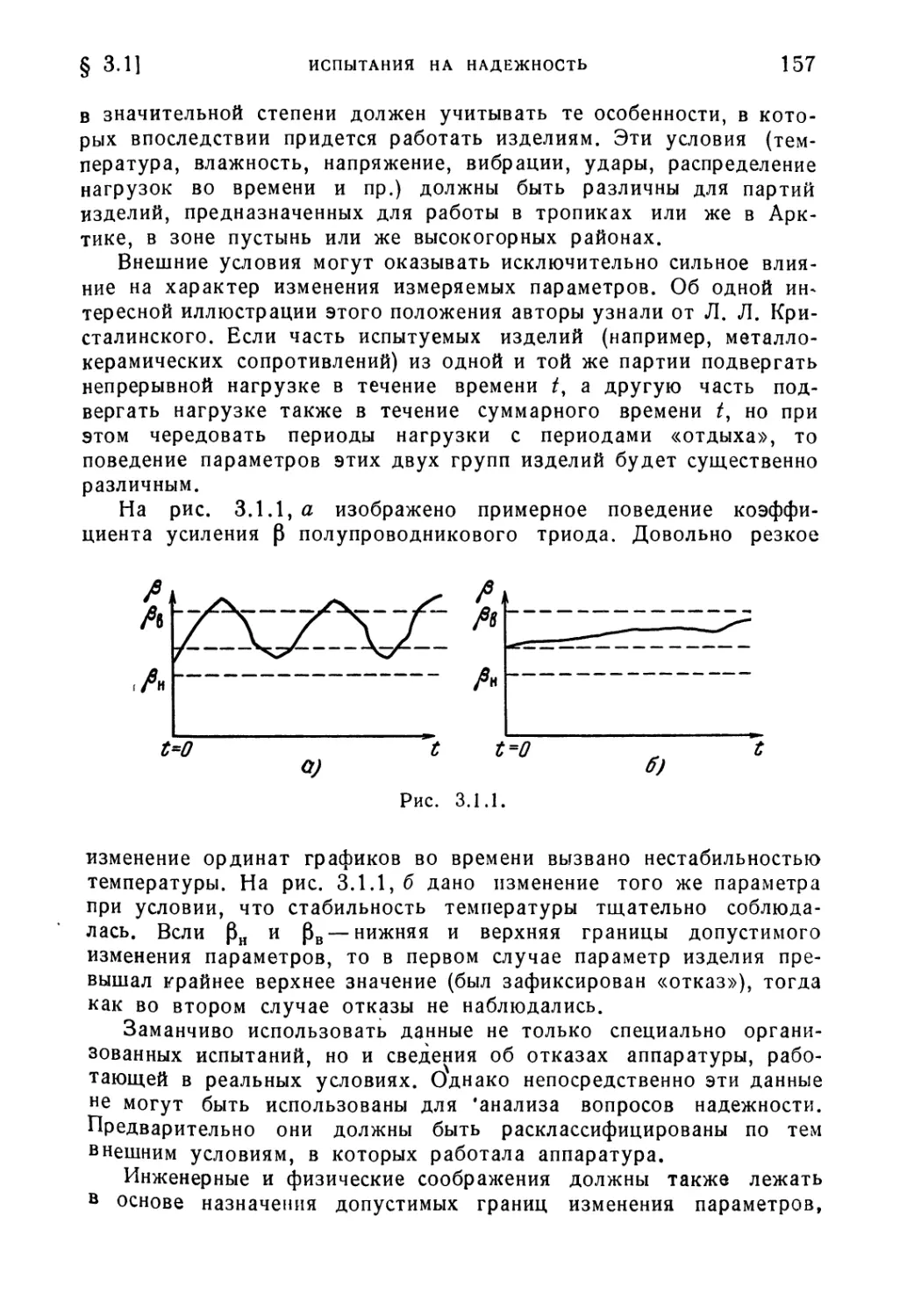
§3.1. Испытания на надежность 156
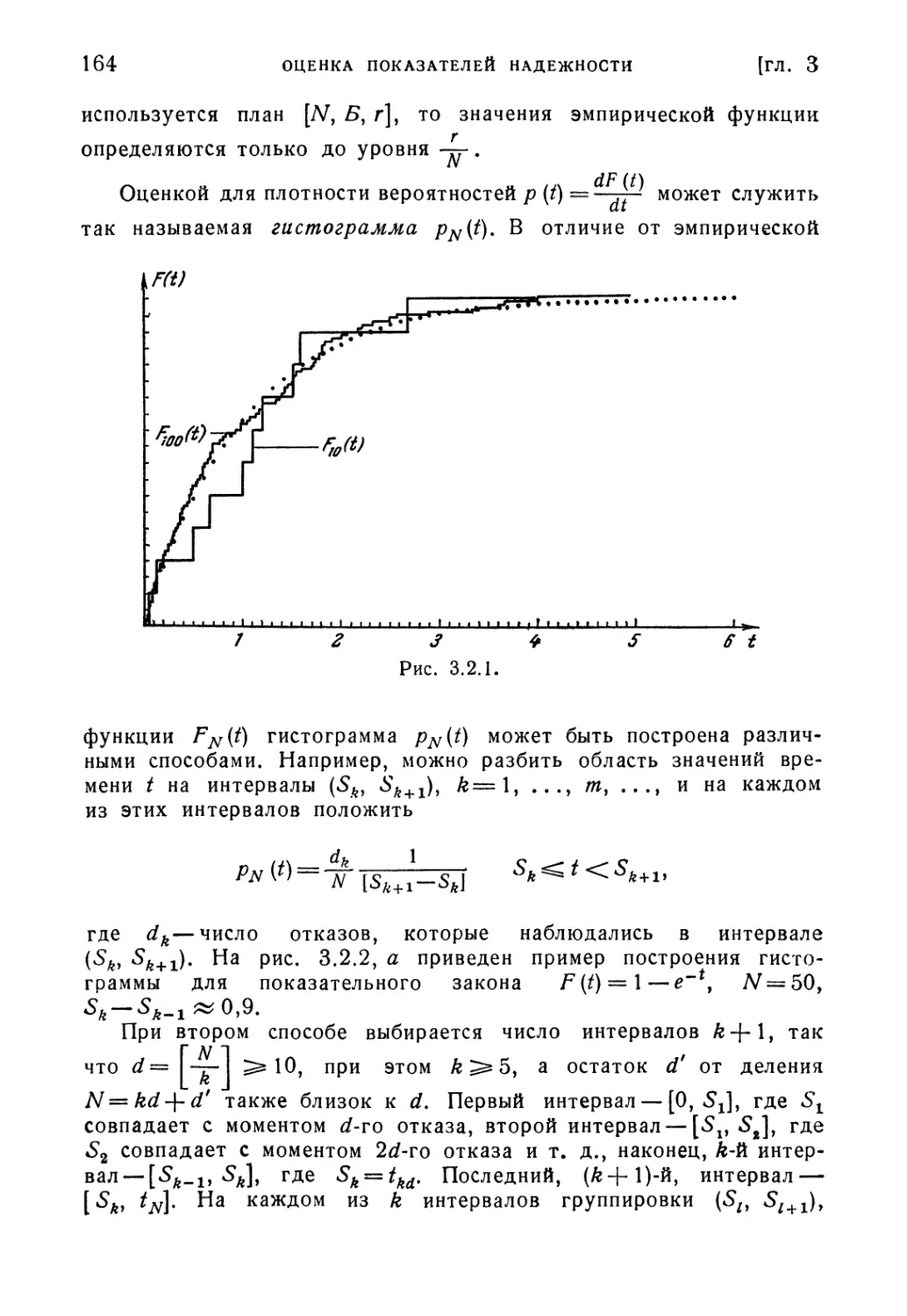
§ 3.2. Общие методы оценки показателей надежности по результатам
испытаний 162
§ 3.3. Оценка параметра экспоненциального закона 181
§ 3.4. Доверительные интервалы для параметра экспоненциального
закона 195
§ 3.5. Доверительные интервалы и множества. Случай многих пара-
параметров 208
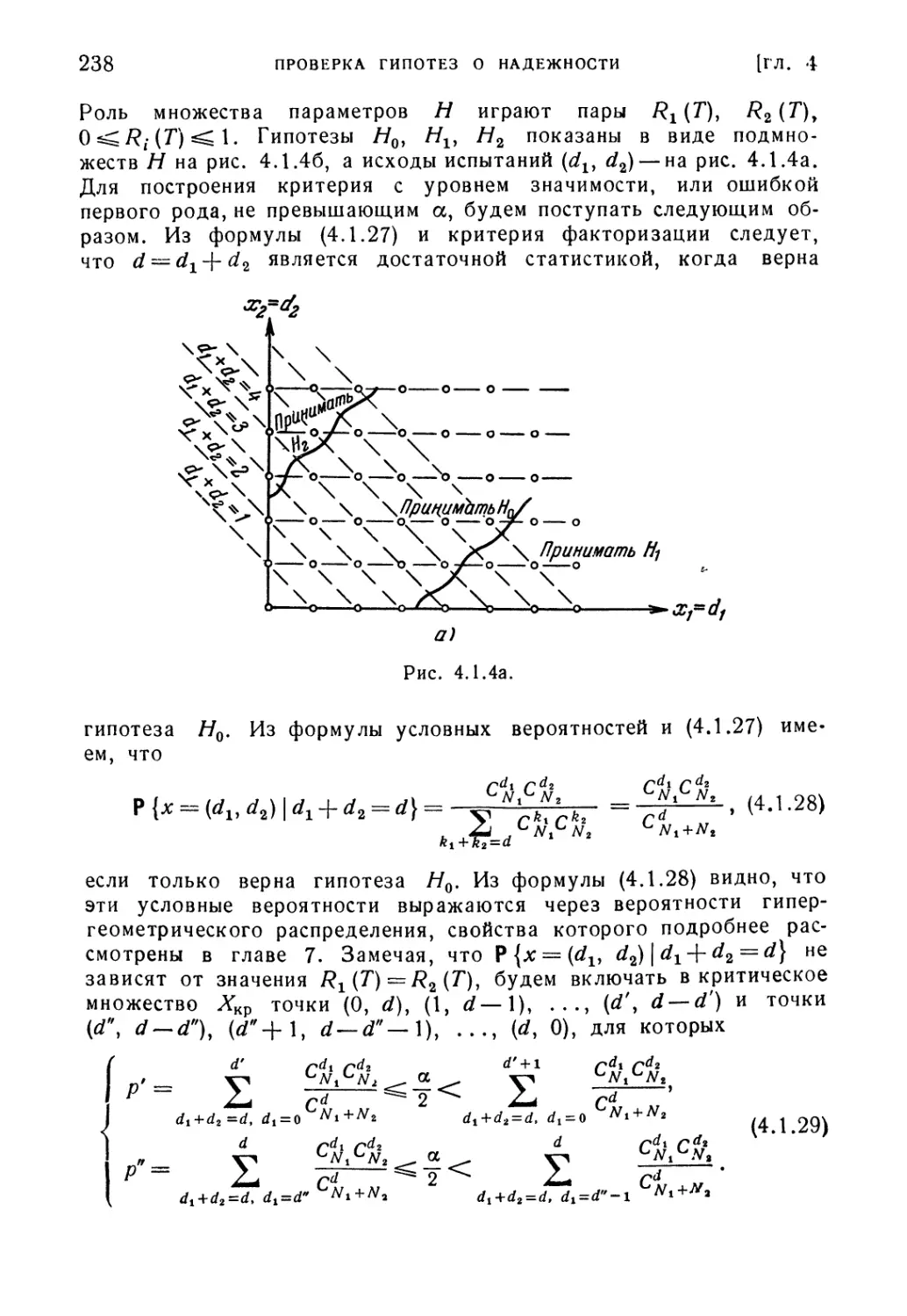
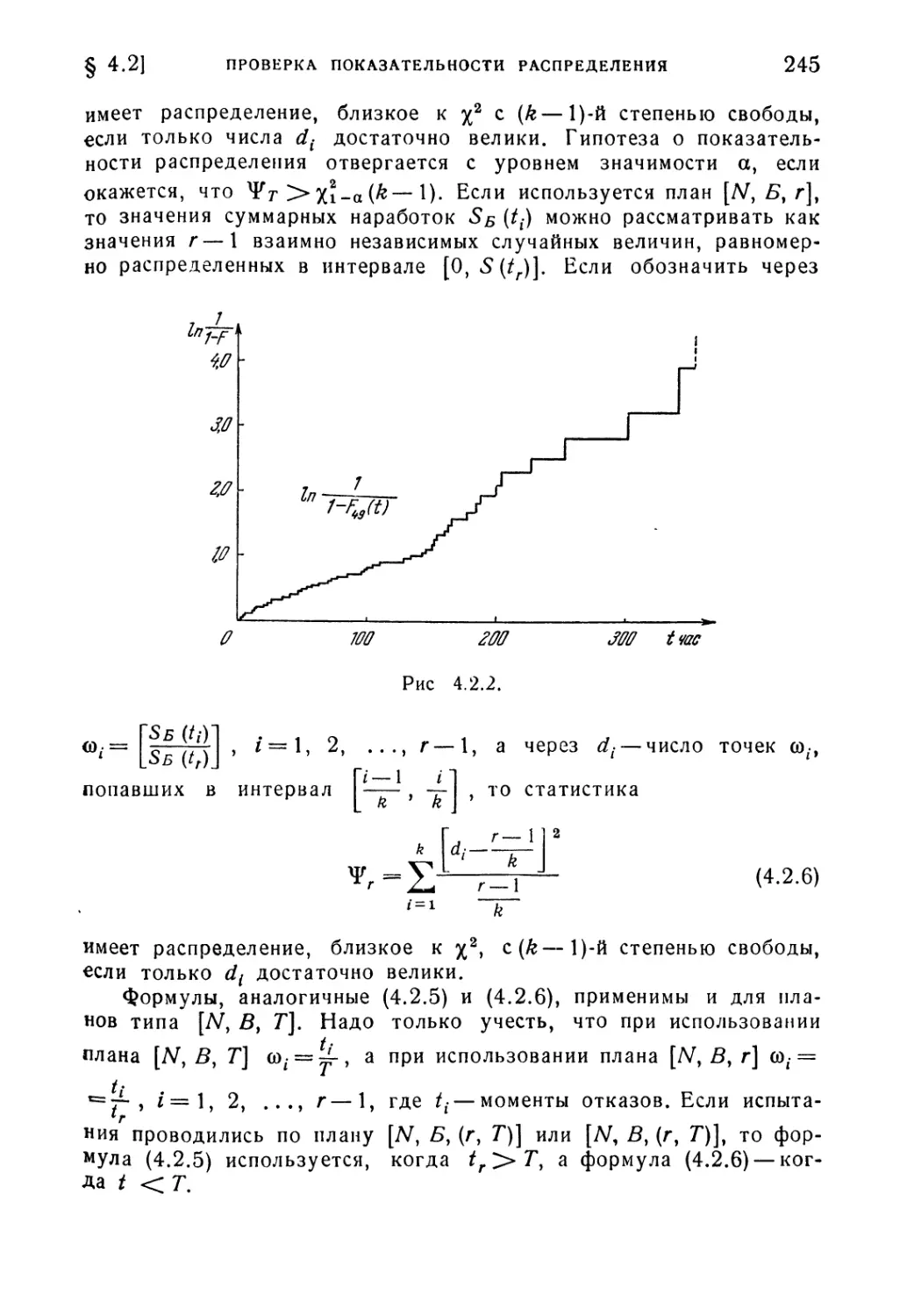
Глава 4. Проверка гипотез о надежности 225
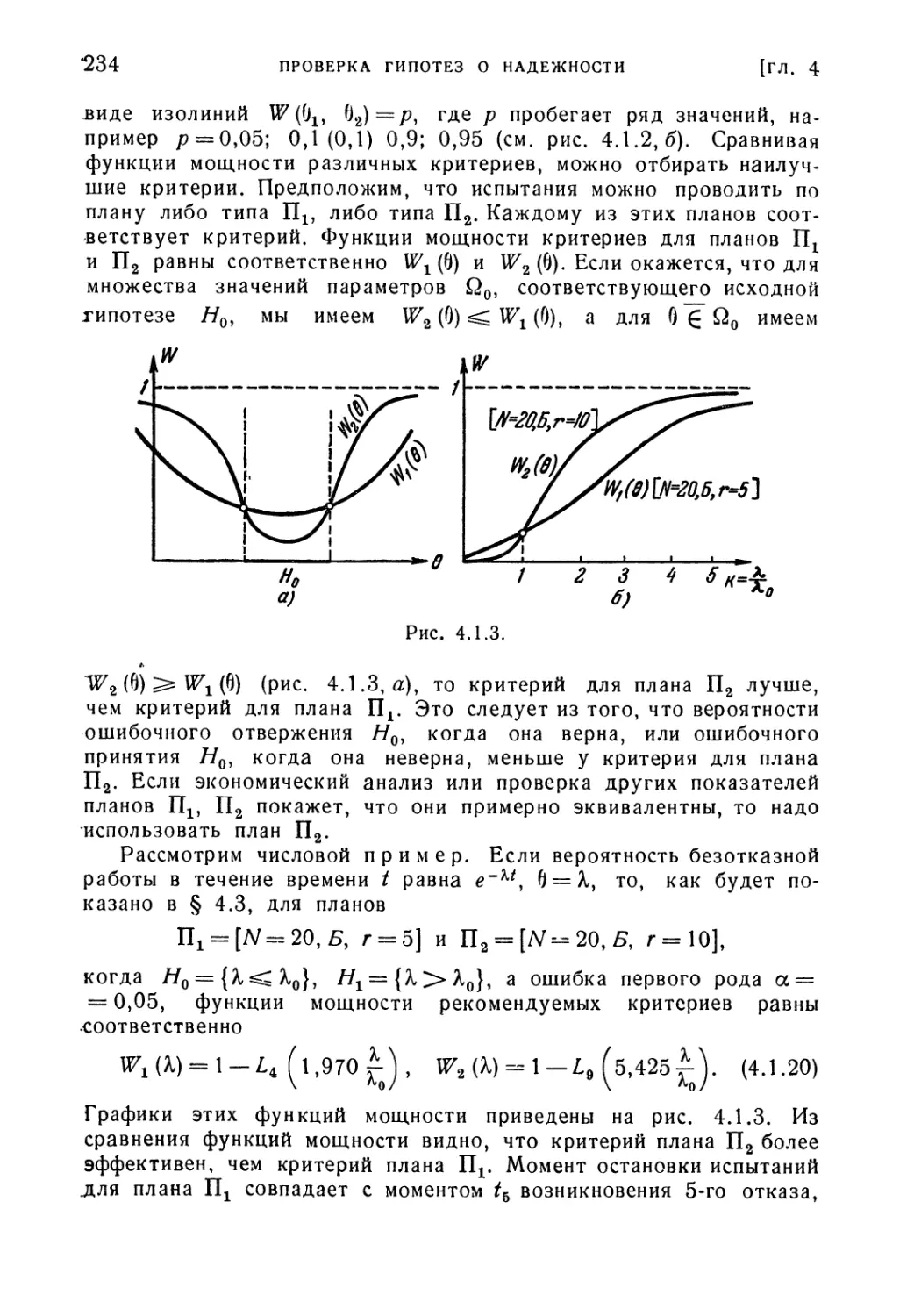
§ 4.1. Общие положения теории проверки статистических гипотез 225
§ 4.2. Проверка гипотезы о показательности распределения времени
безотказной работы 241
§ 4.3. Критерии проверки гипотез о значениях параметра показатель-
показательного распределения 253
§ 4.4. Критерии типа последовательного анализа для проверки гипо-
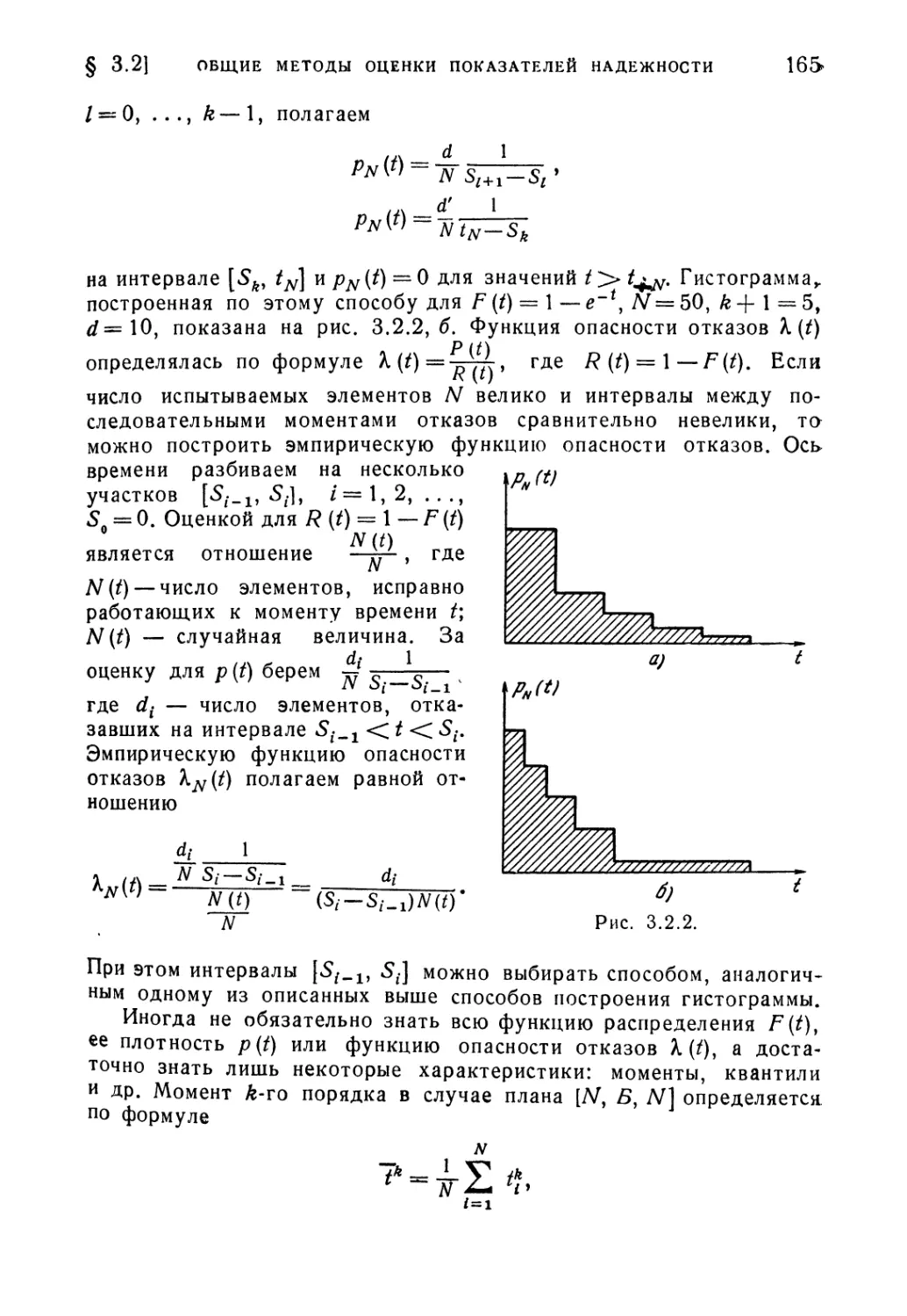
гипотез о значении параметра X экспоненциального распределения 264
§ 4.5. Непараметрические методы оценки однородности статистиче-
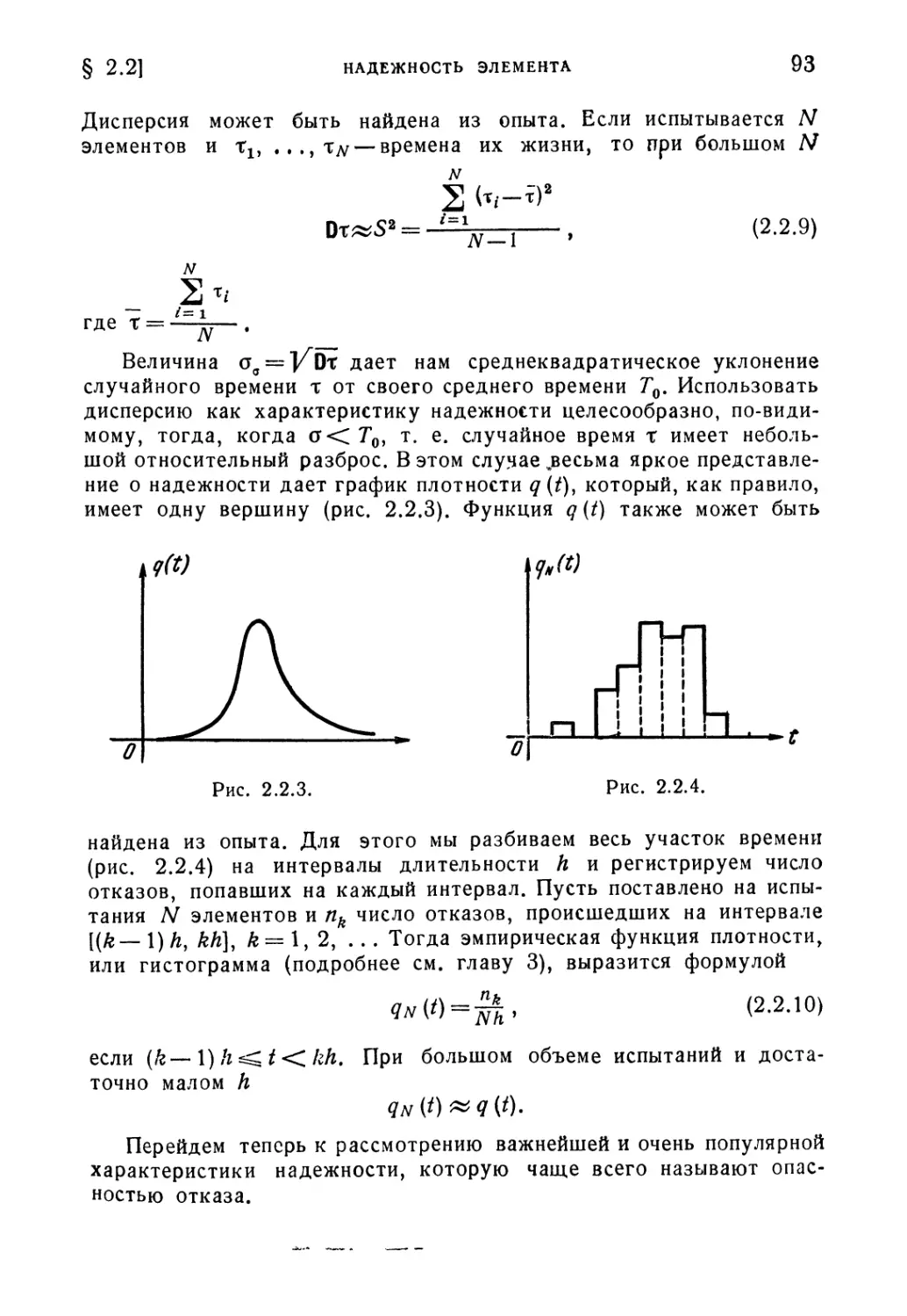
статистического материала 277
1*
4 ОГЛАВЛЕНИЕ
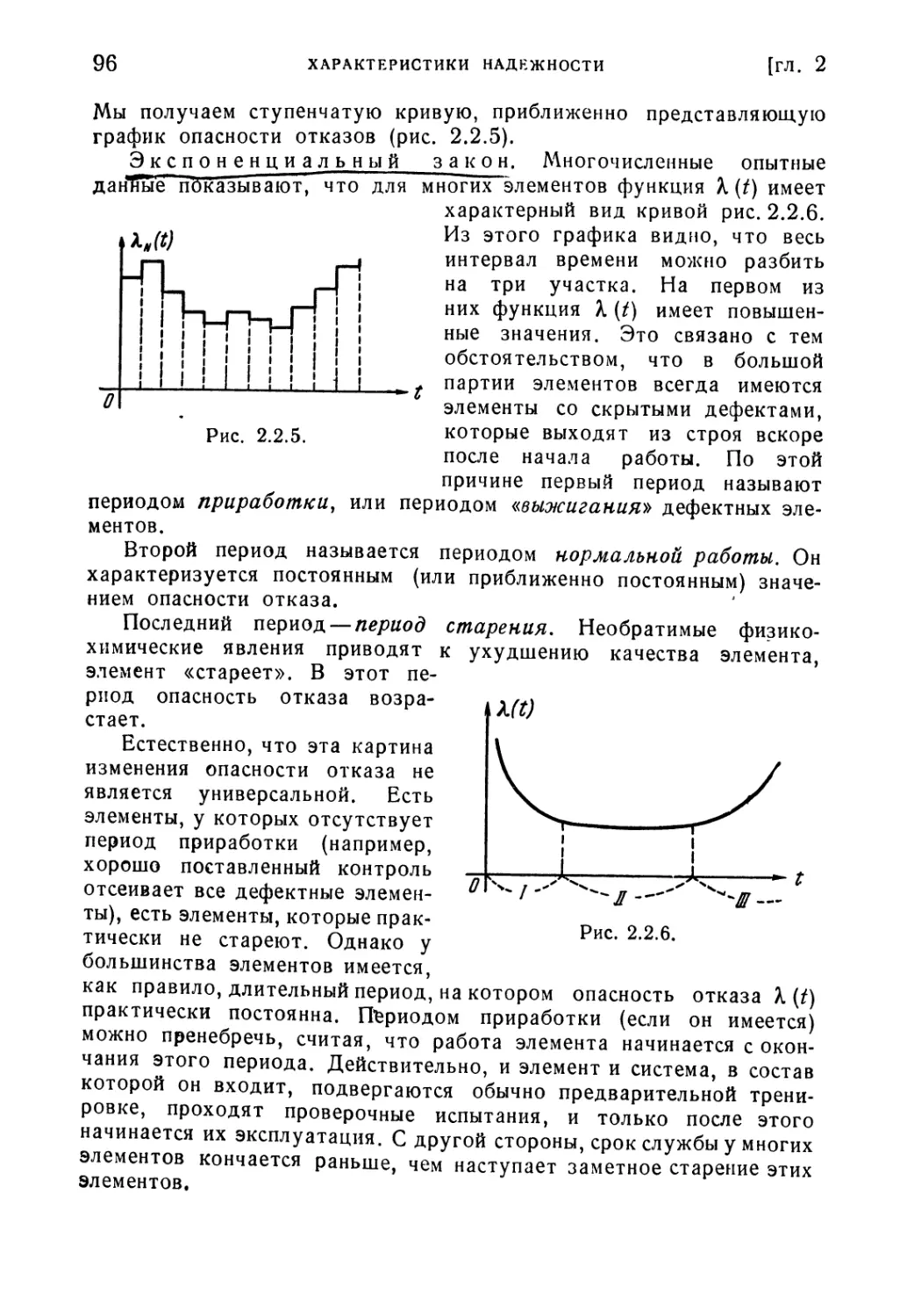
Глава 5. Резервирование без восстановления 288
§ 5.1. Введение 288
§ 6.2. Нагруженный резерв 289
§ 5.3. Схема гибели 297
§ 5.4. Ненагруженный резерв 306
§ 5.5. Облегченный резерв 313
§ 5.6. Учет ненадежности переключателей 322
§ 5.7. Некоторые принципиальные вопросы резервирования системы 329
Глава 6. Резервирование с восстановлением 335
§ 6.1. Введение 335
§ 6.2. Дублирование с восстановлением 336
§ 6.3. Процесс гибели и размножения 346
§ 6.4. Изучение нестационарного периода 352
§ 6.5. Применение процесса гибели и размножения к резервированию
с восстановлением 368
Глава 7. Статистические методы контроля качества и надежности
массовой продукции 376
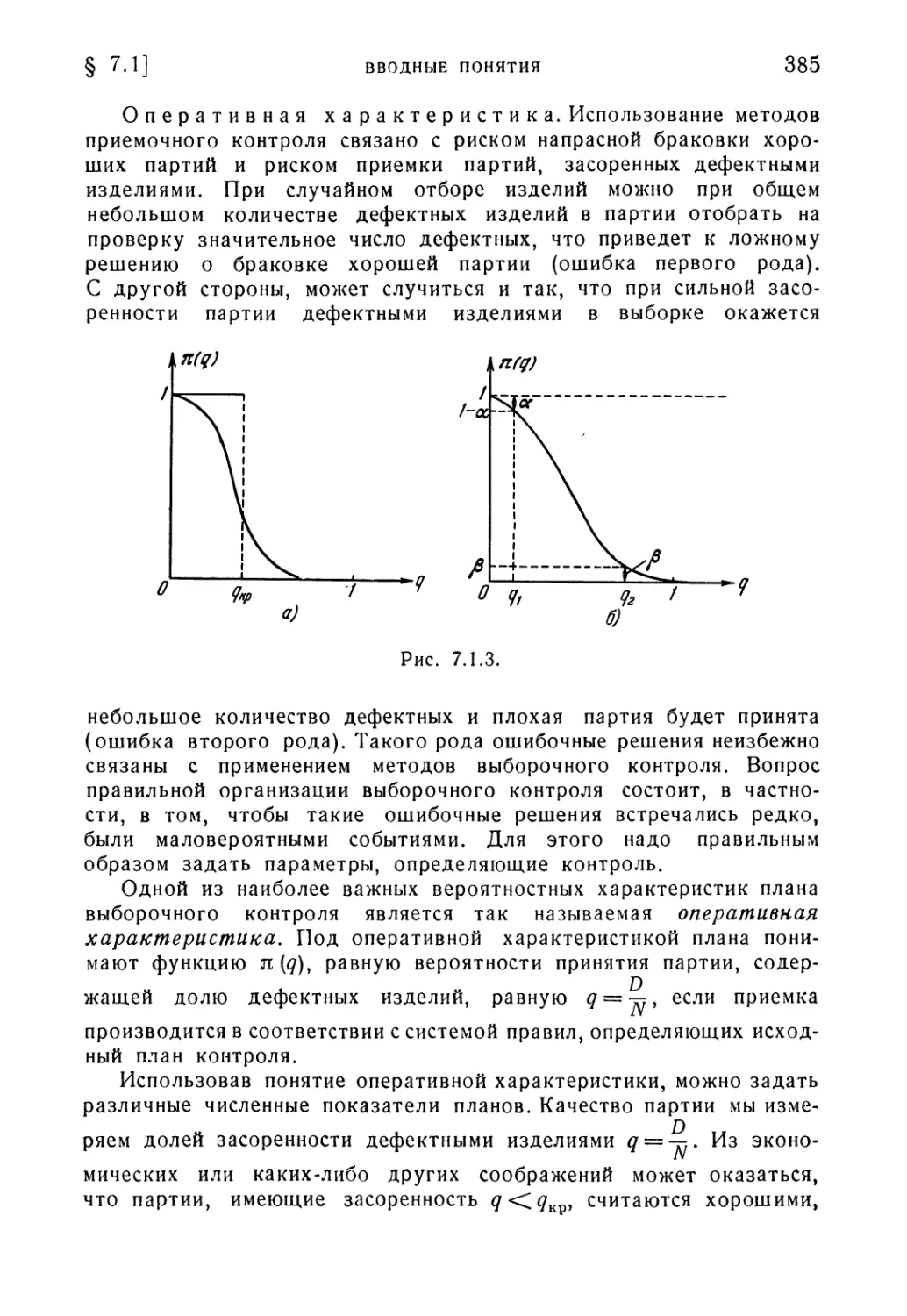
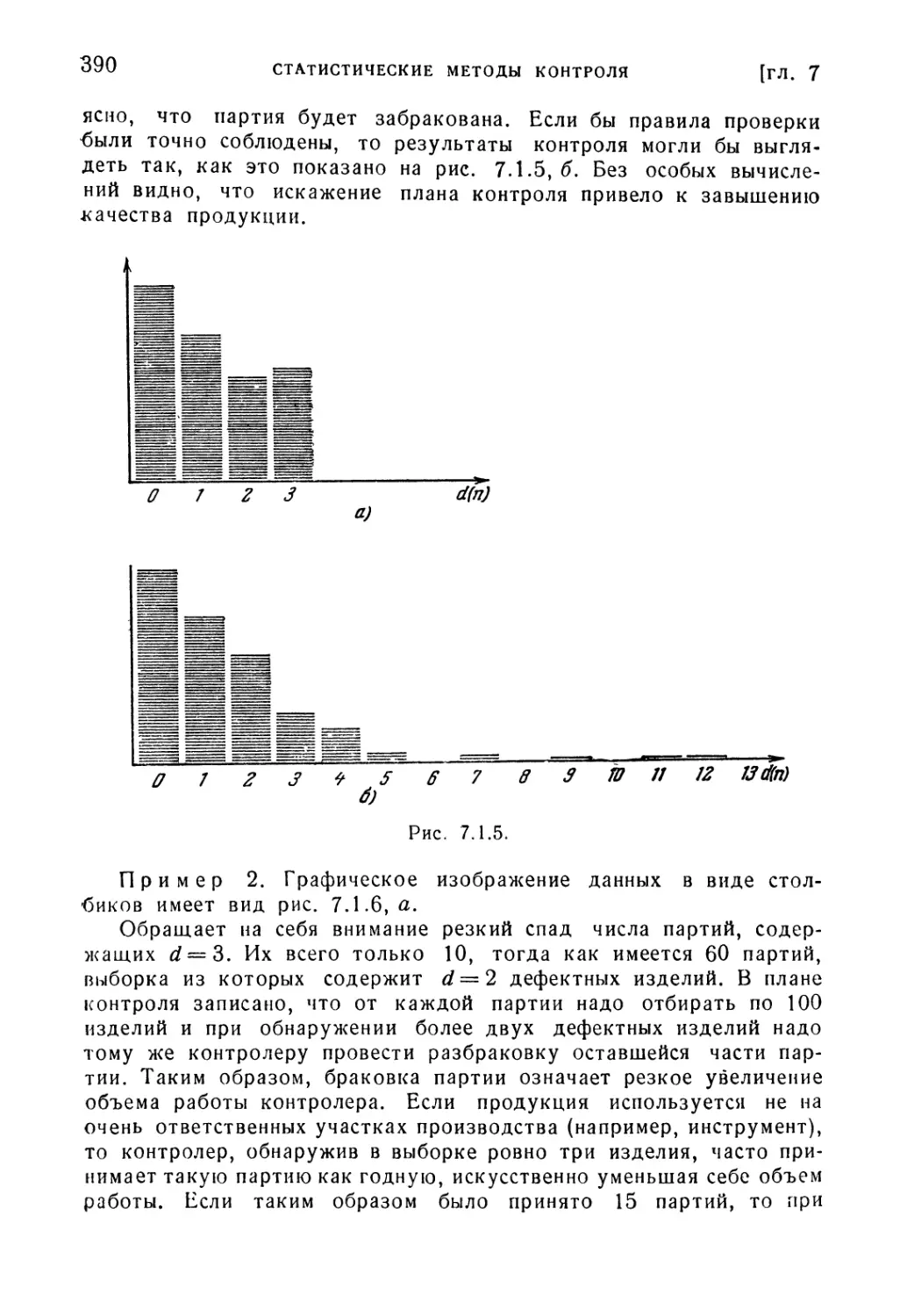
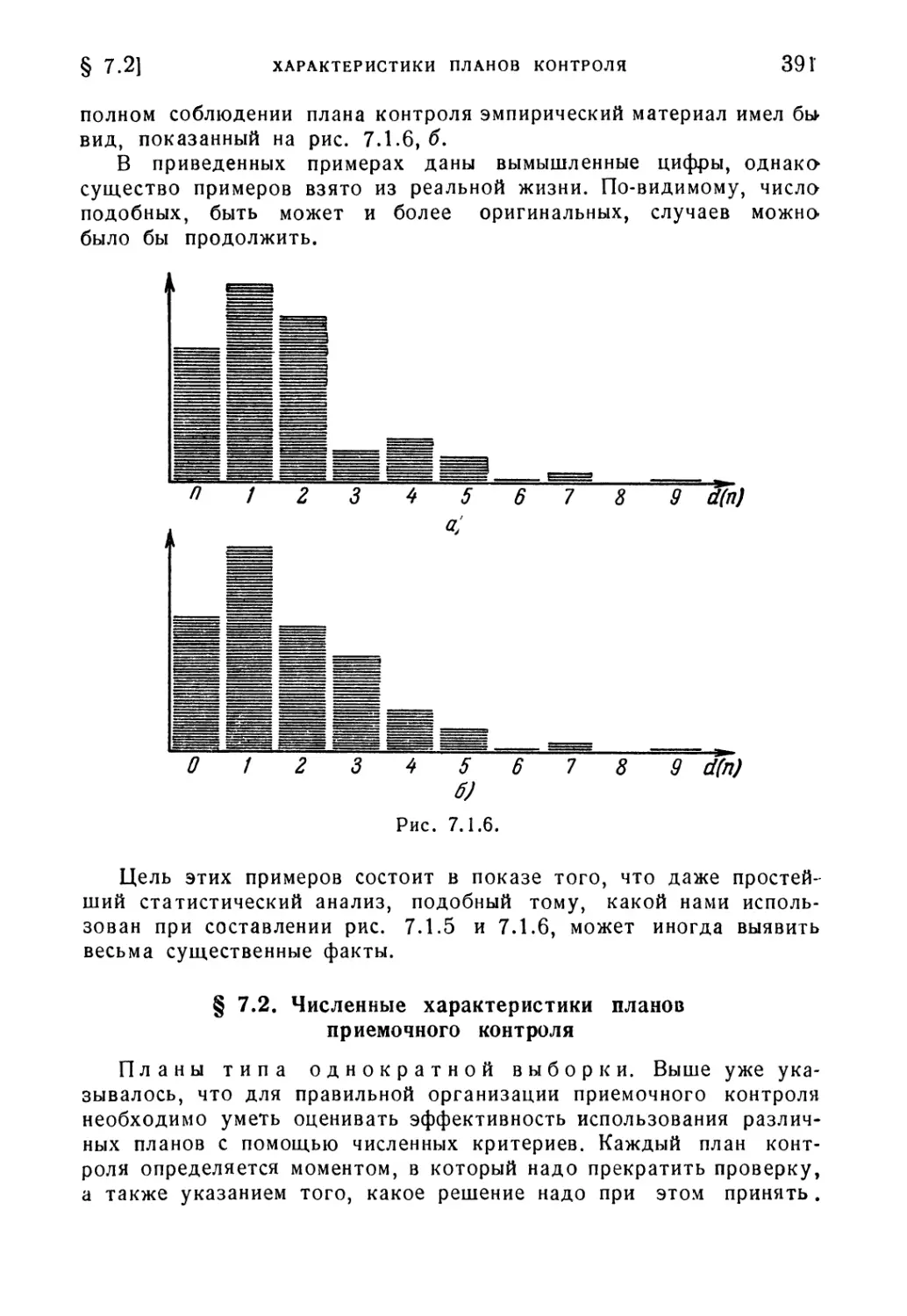
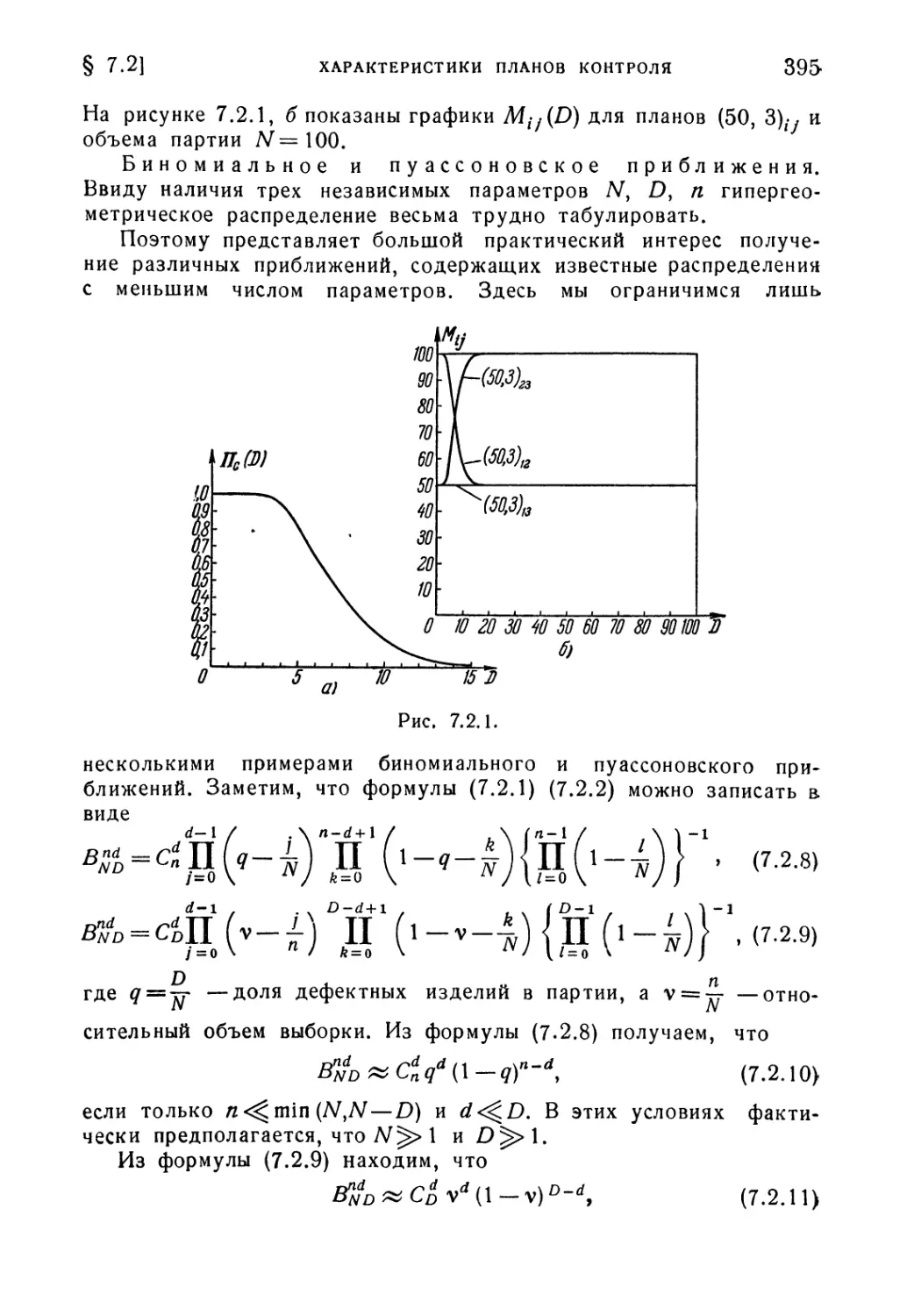
§ 7.1. Вводные понятия 376
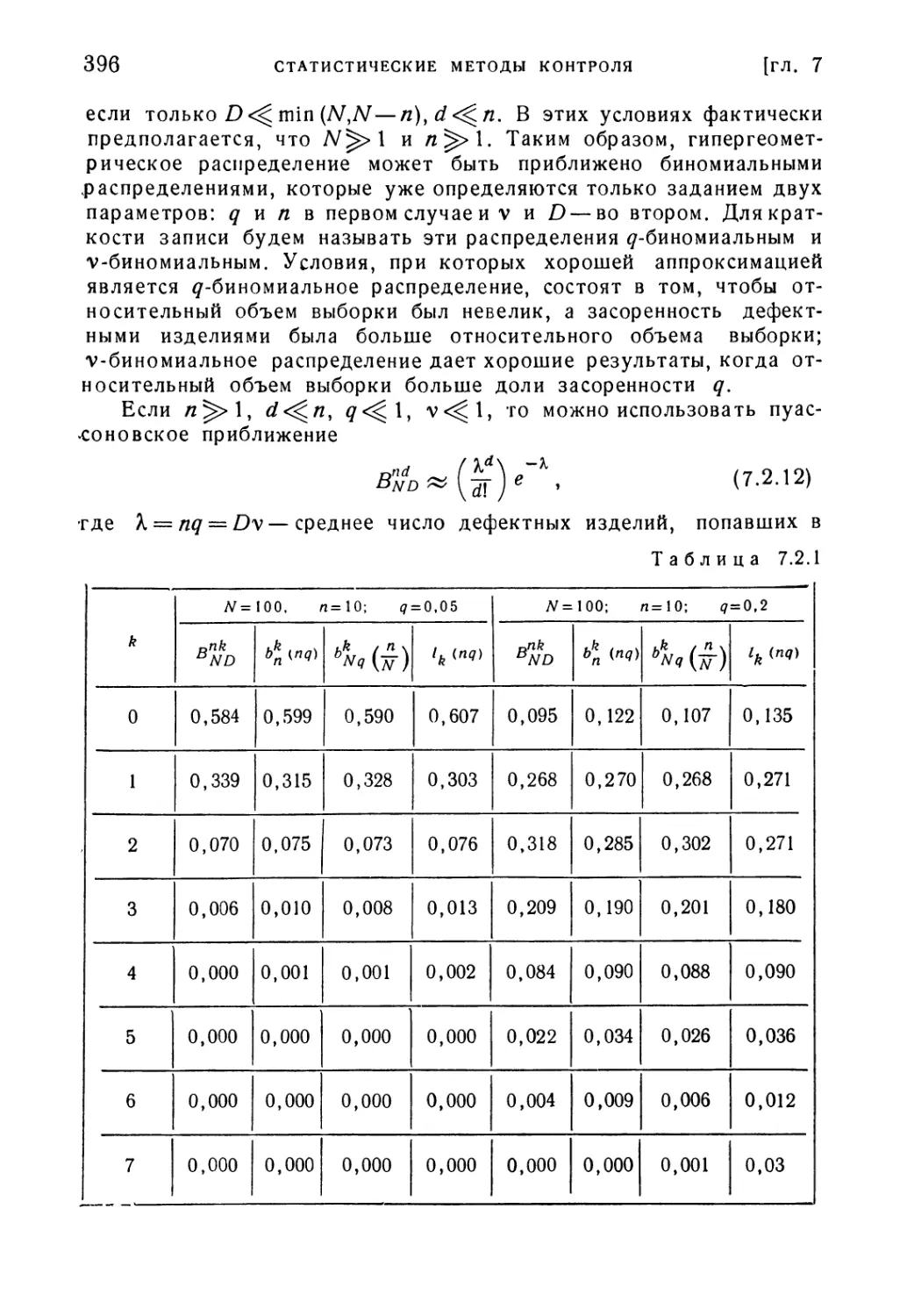
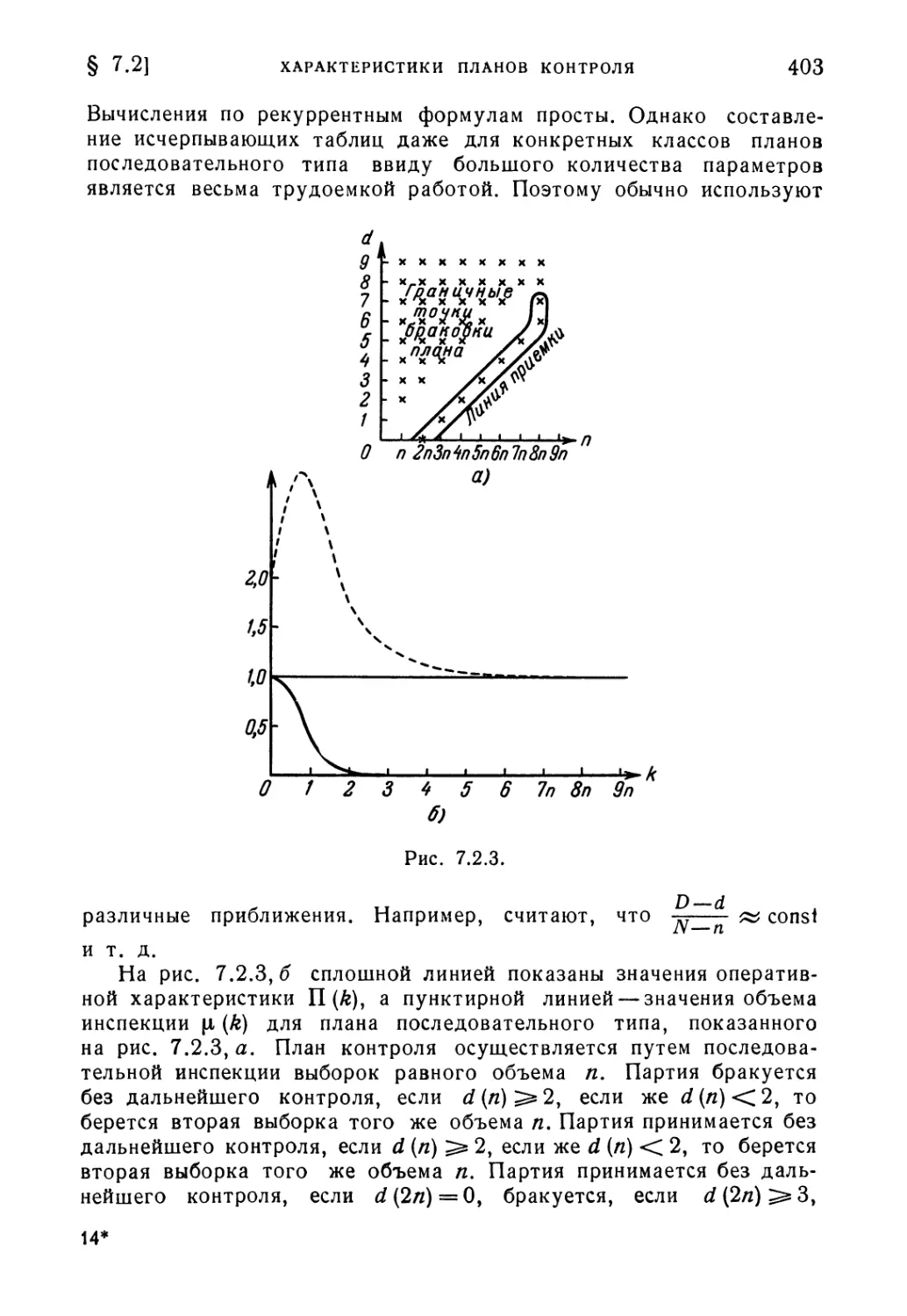
§ 7.2. Численные характеристики планов приемочного контроля . . 391
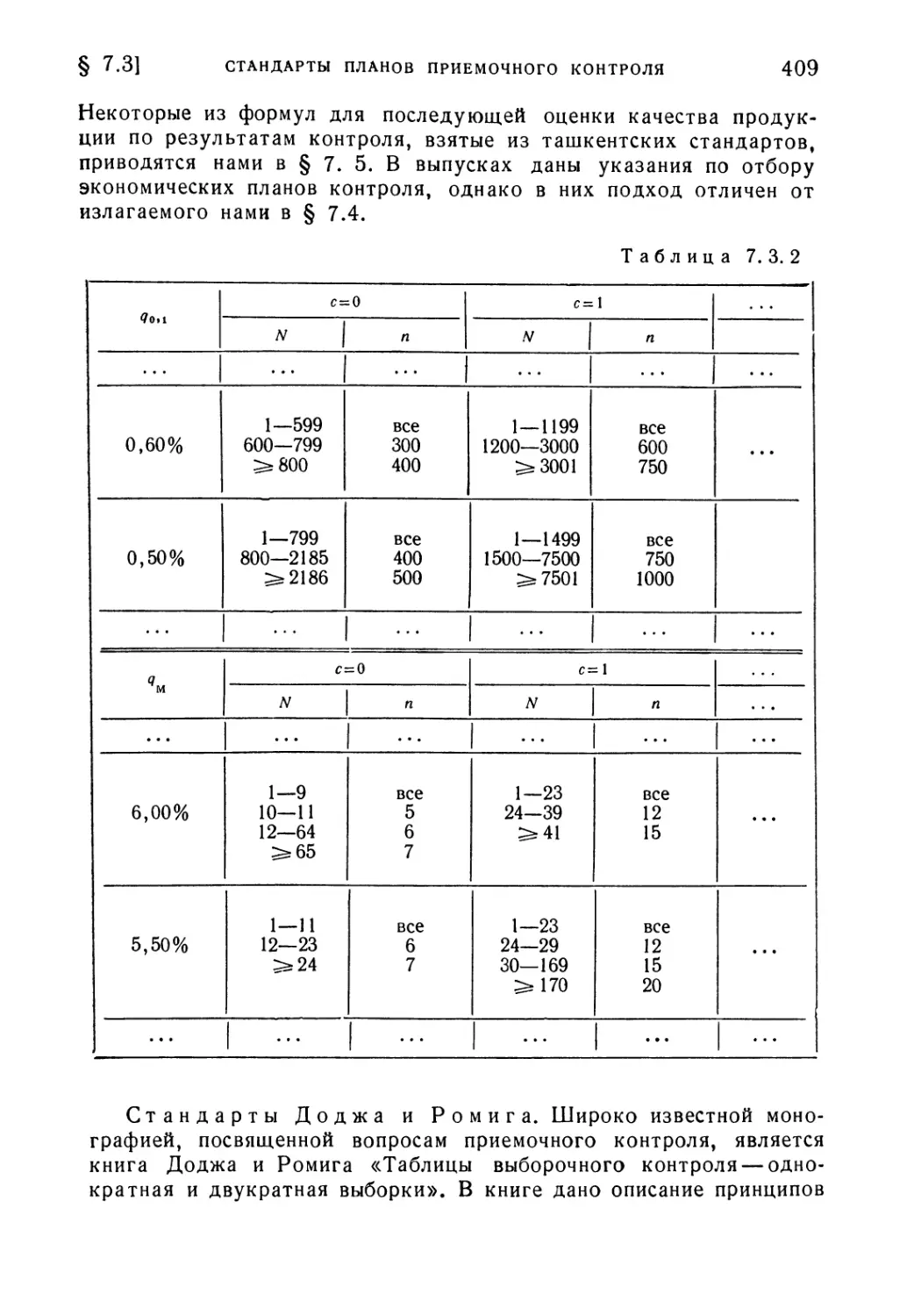
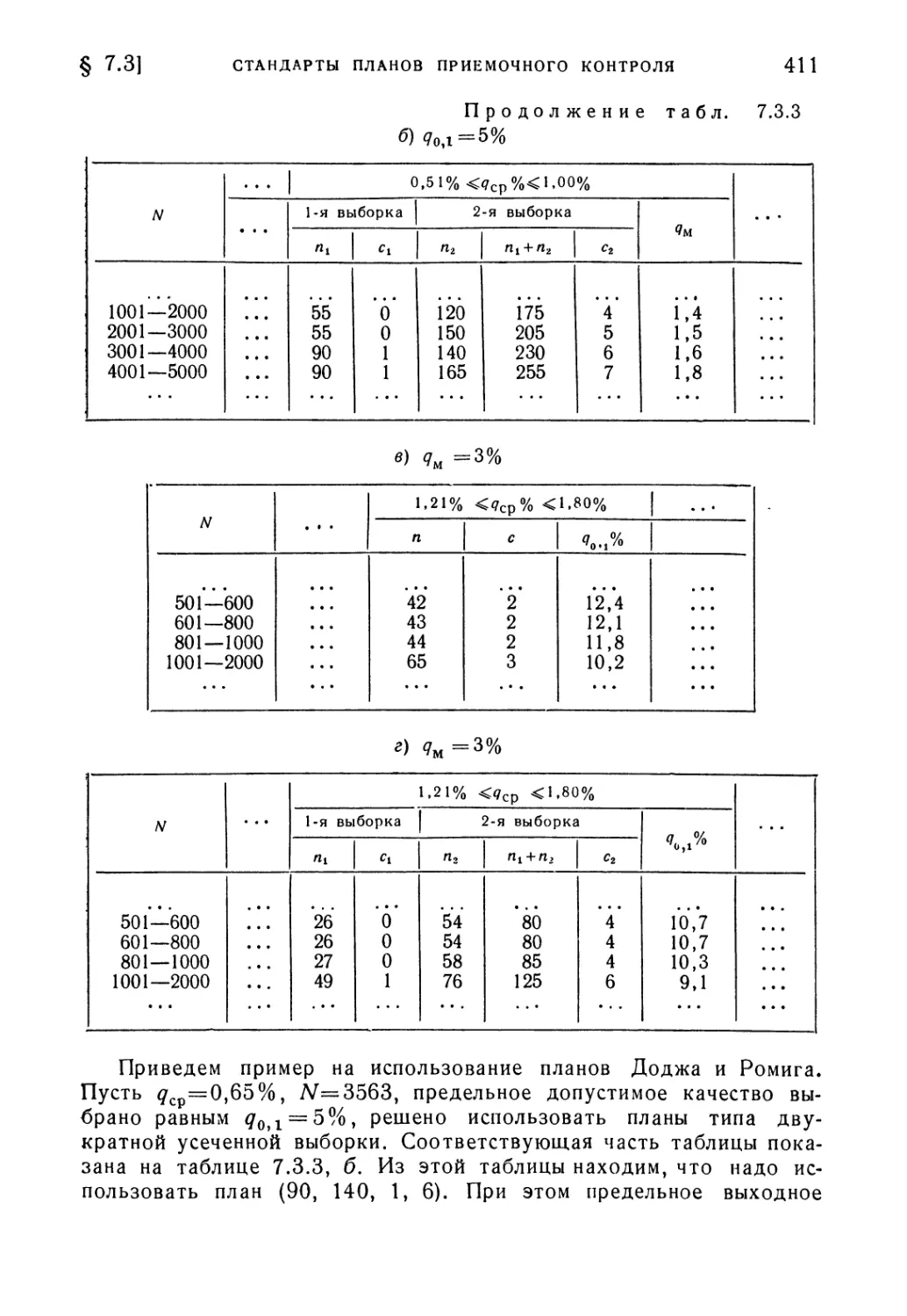
§ 7.3. Стандарты планов приемочного контроля 404
§ 7.4. Экономичные планы контроля 415
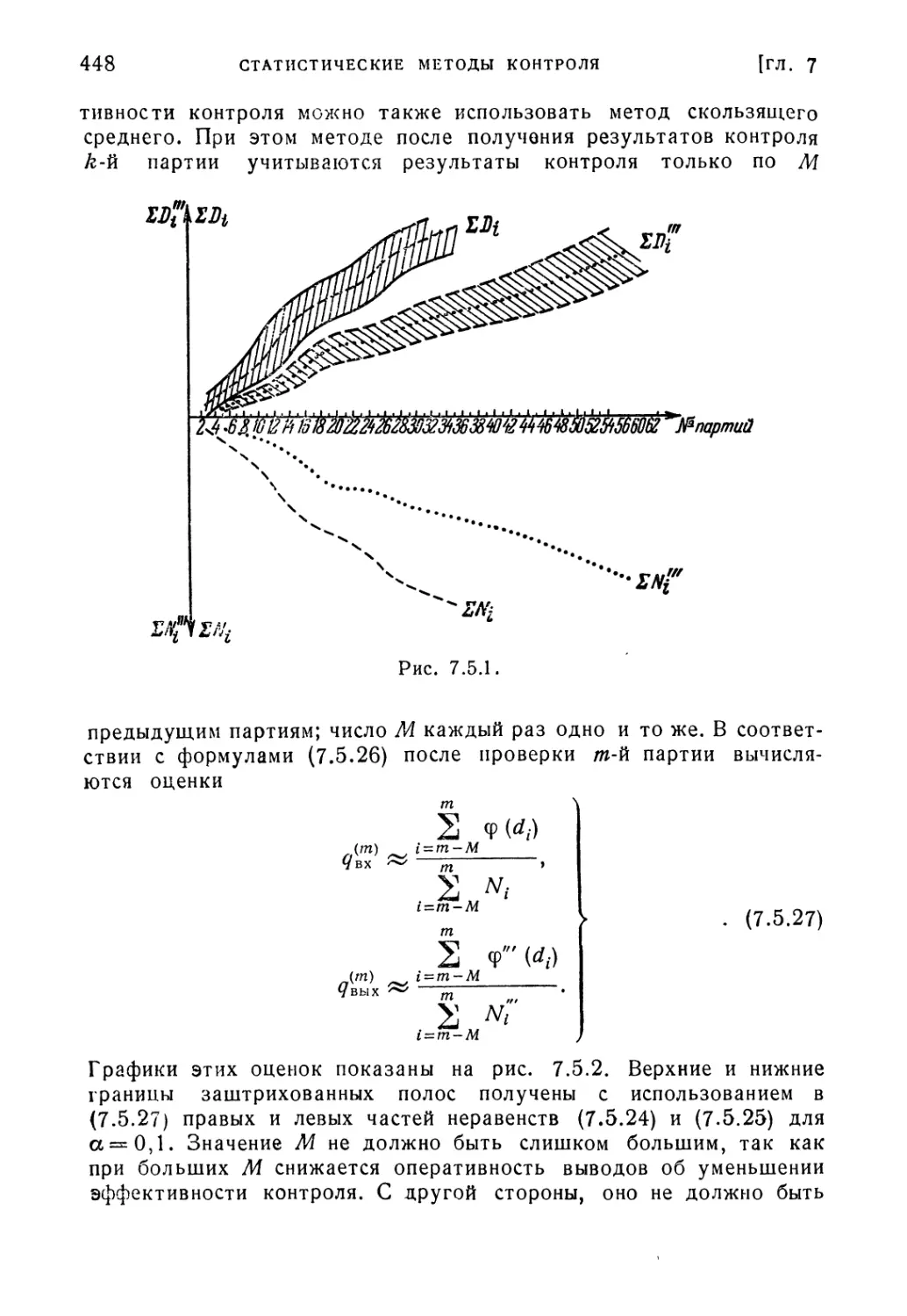
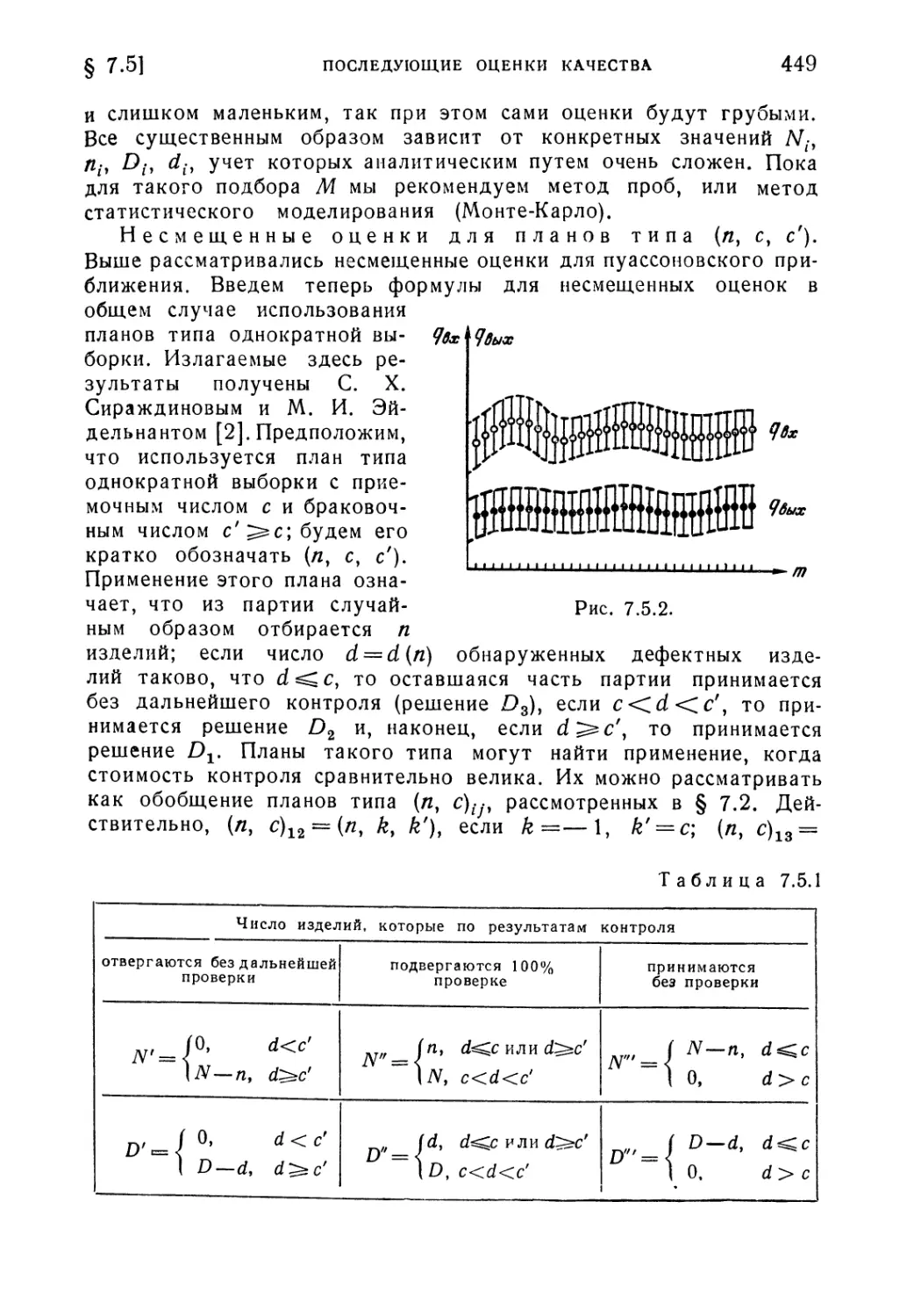
§ 7.5. Последующие оценки качества по результатам контроля . . . 436
§ 7.6. Введение в задачи текущего контроля 459
Приложения
Таблица 1. Значения функции у = е~~х 470
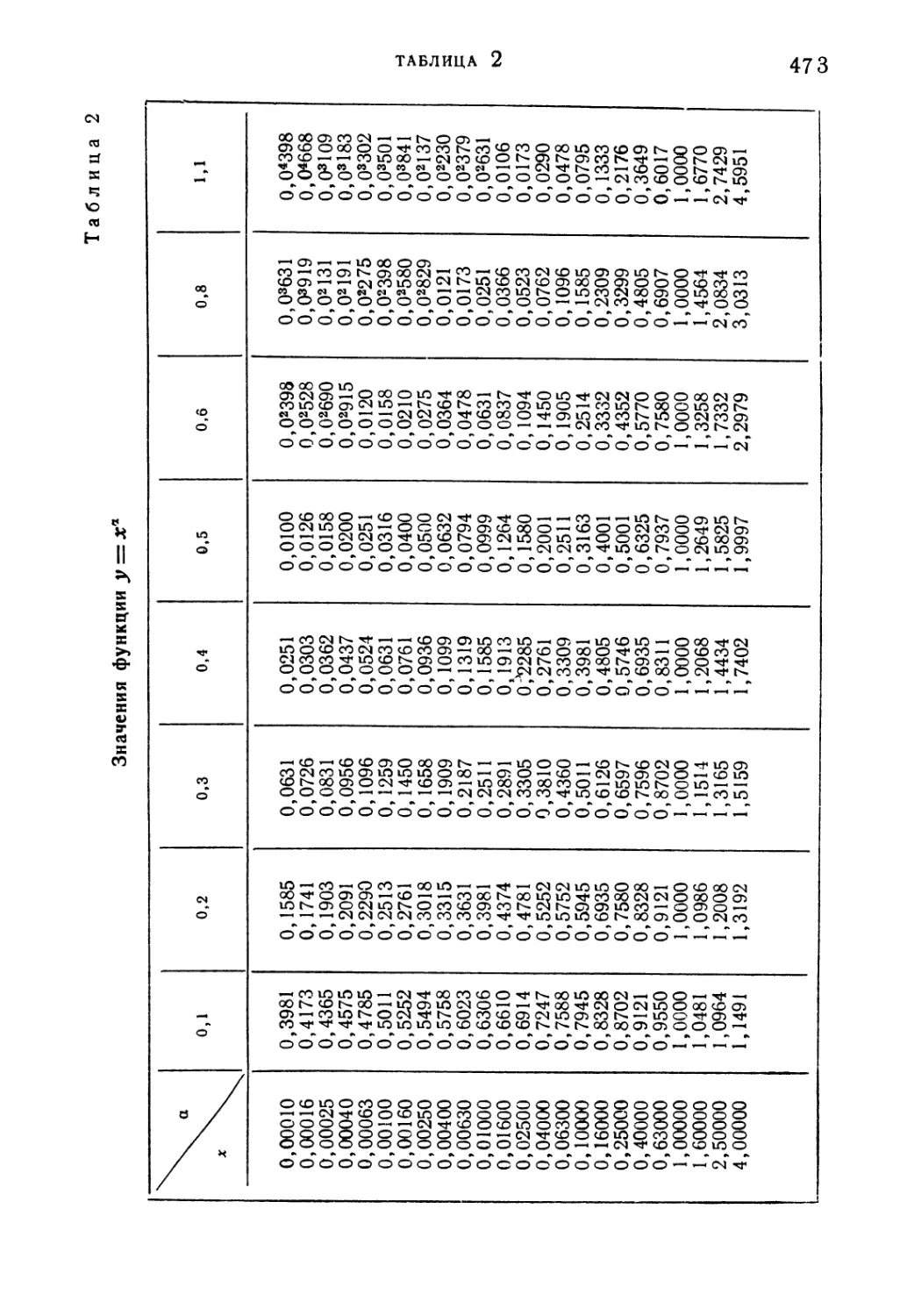
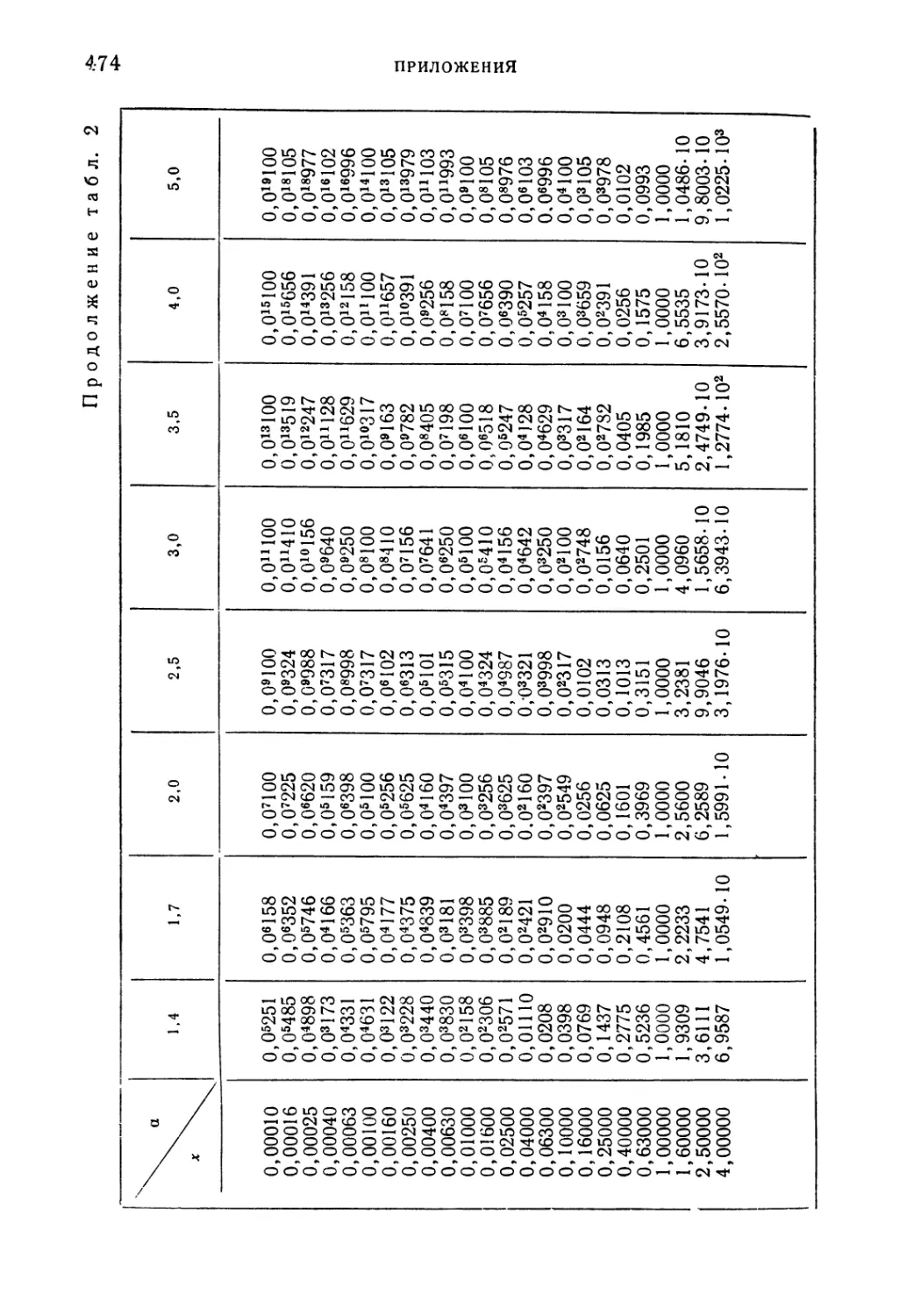
Таблица 2. Значения функции у=*=ха 473
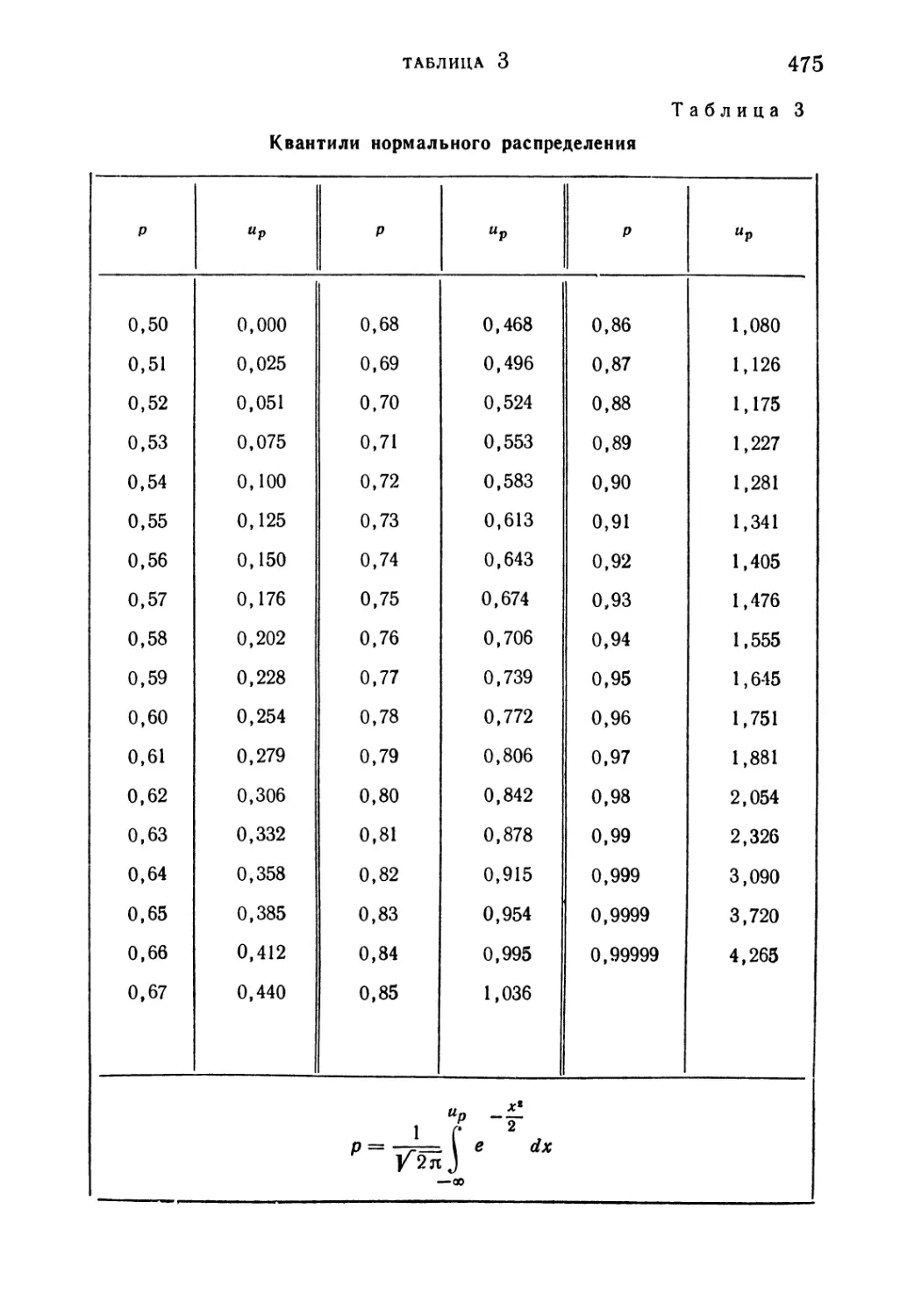
Таблица 3. Квантили нормального распределения 475
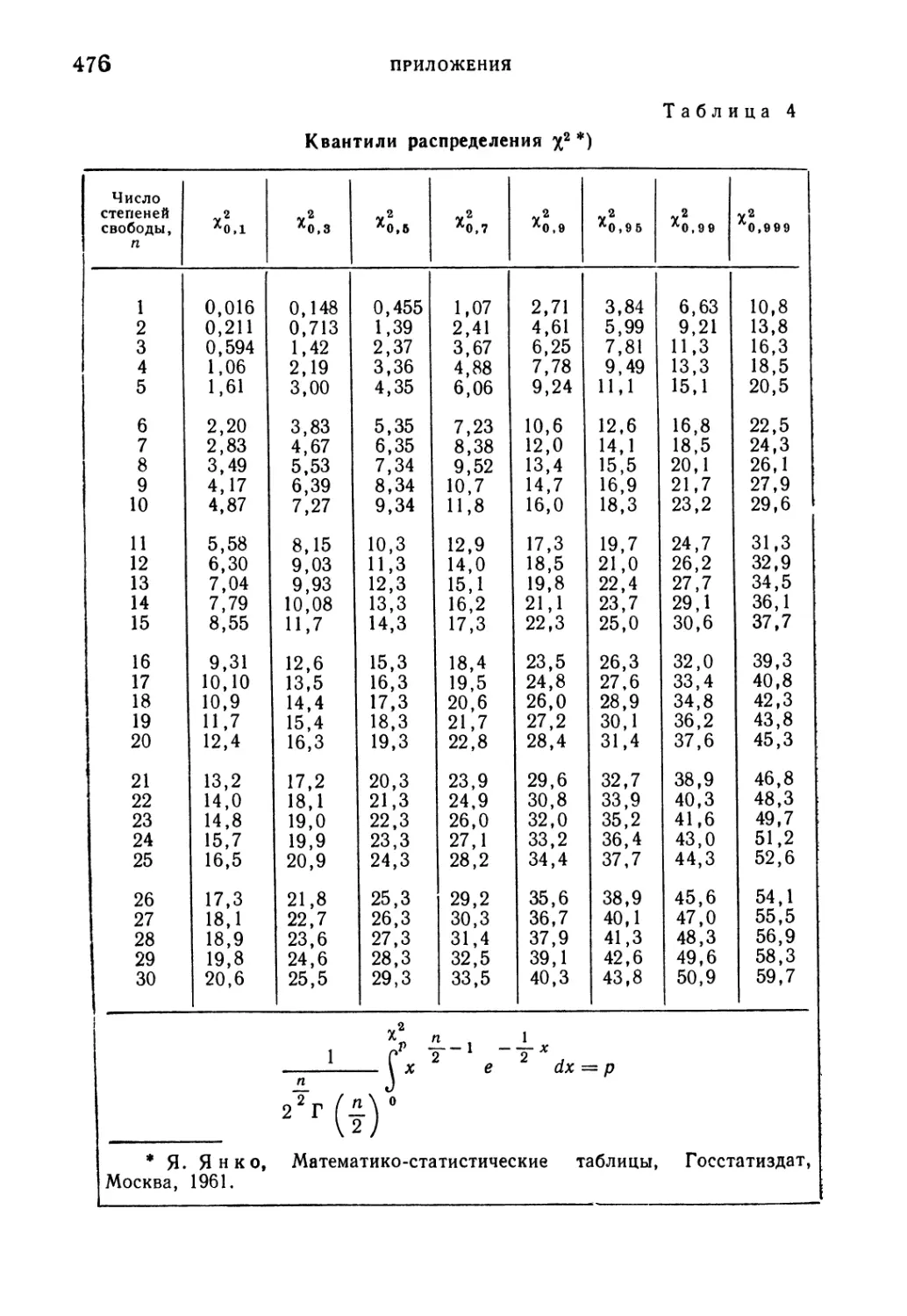
Таблица 4. Квантили распределения %2 476
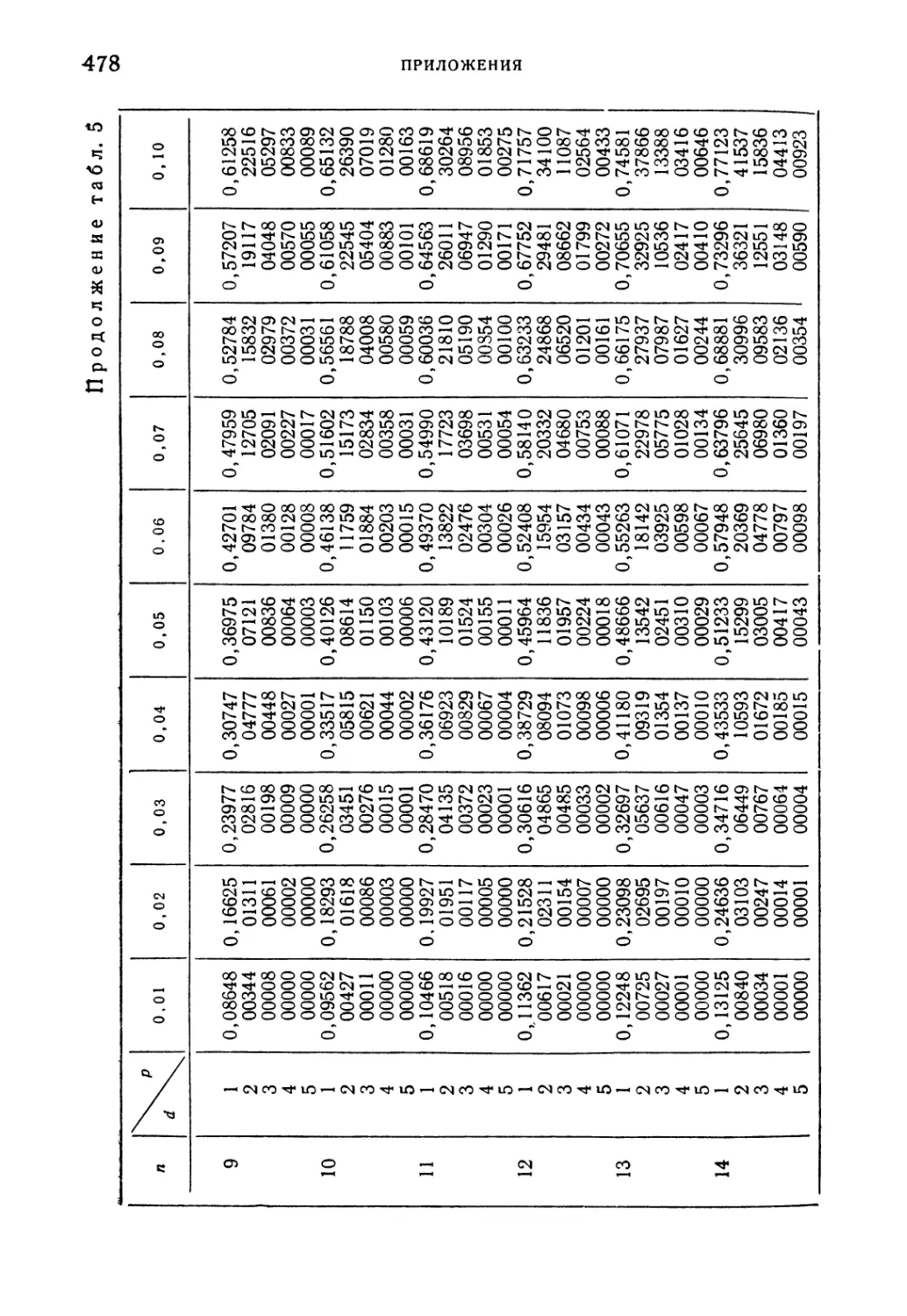
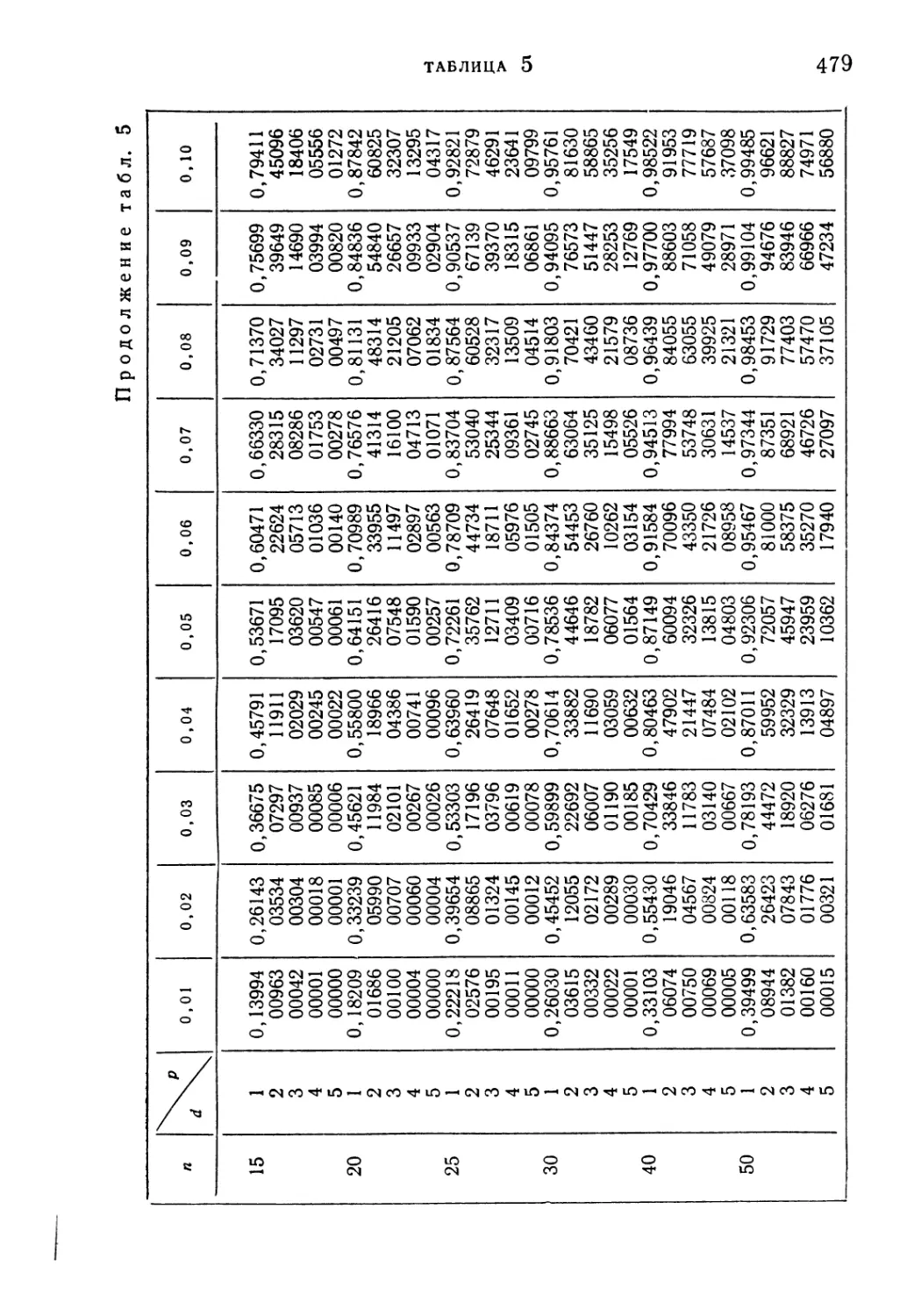
Таблица 5. Сокращенная таблица биномиального распределения . . 477
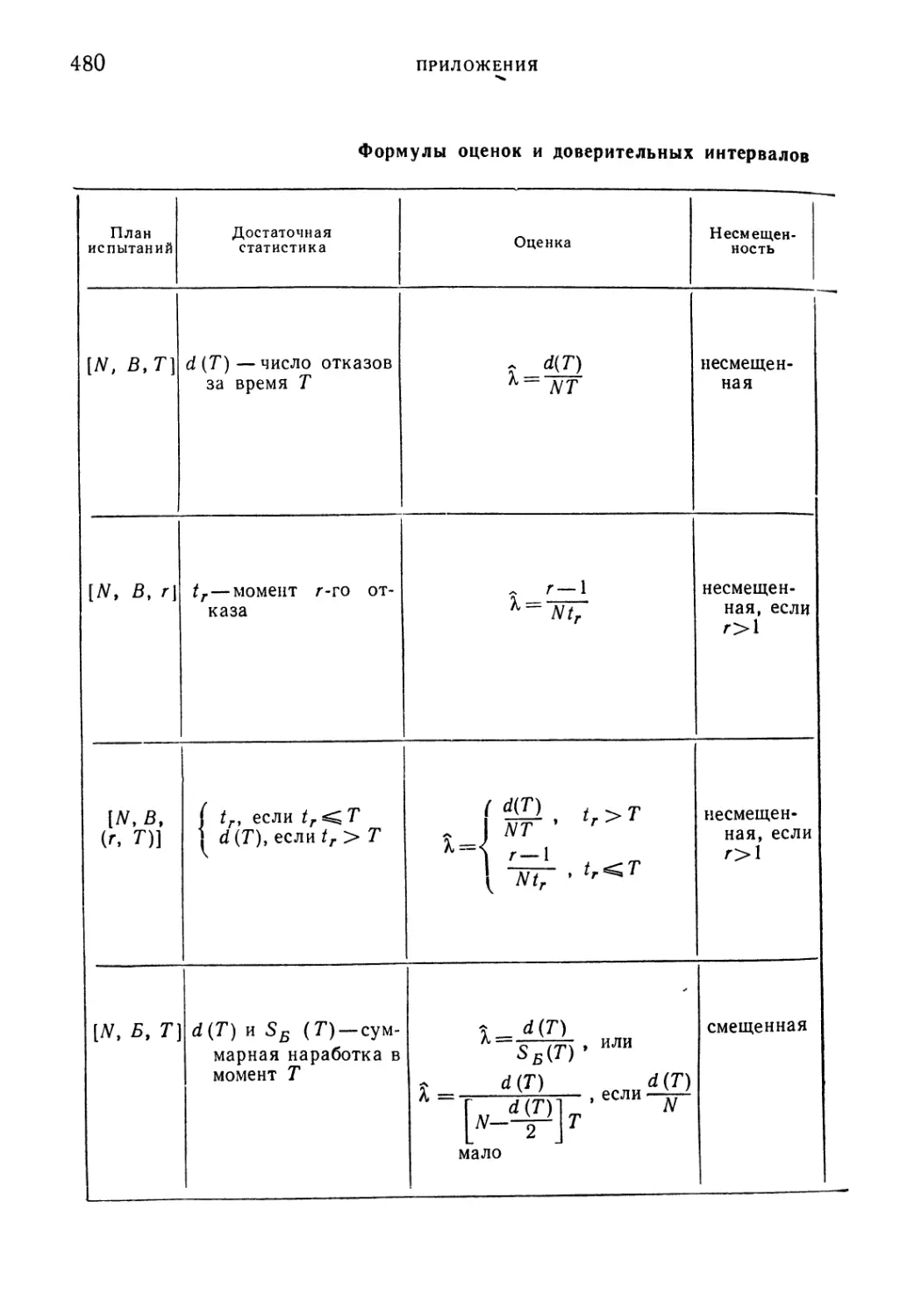
Таблица 6. Формулы оценок и доверительных интервалов для пара-
параметра к экспоненциального закона 480
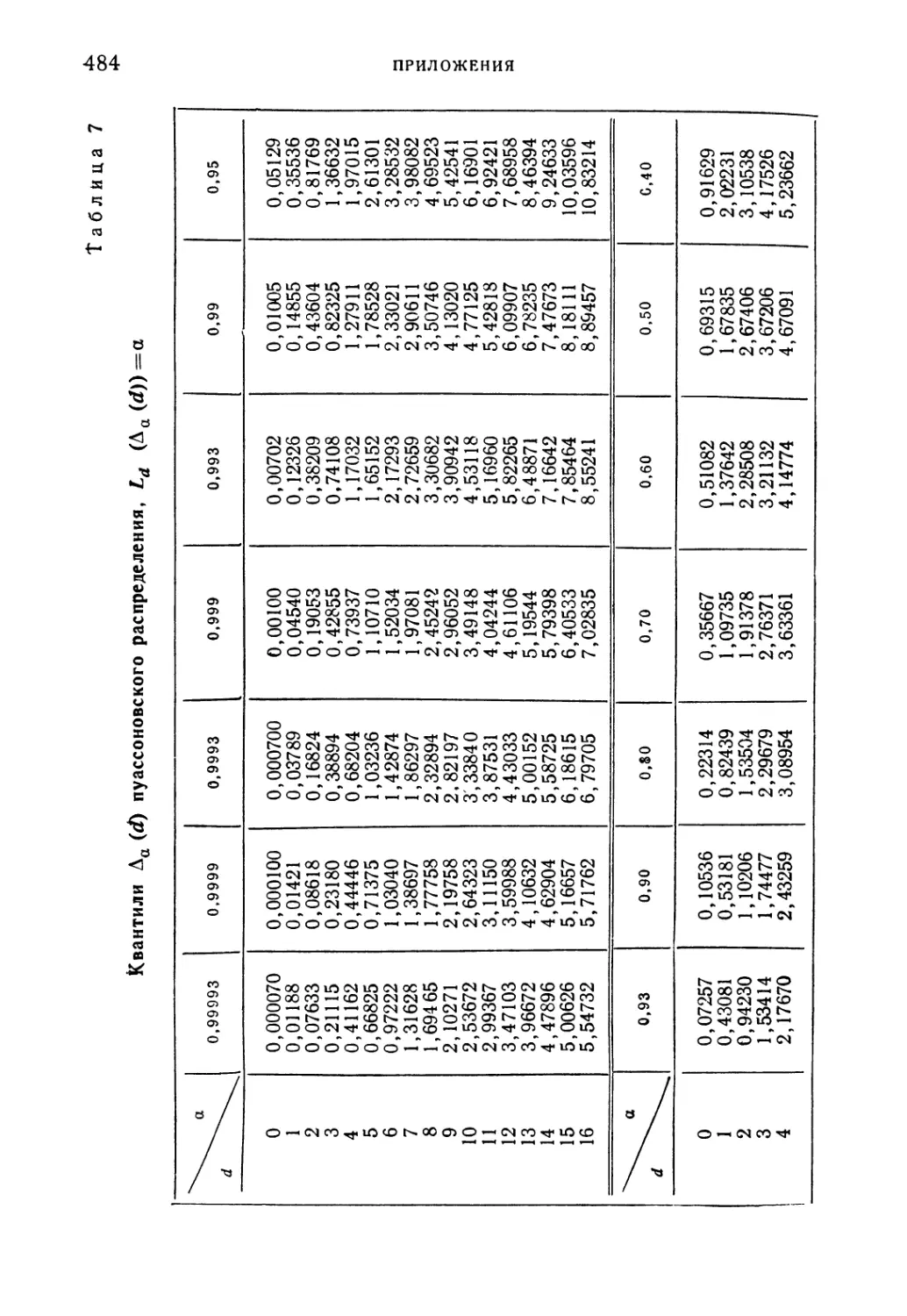
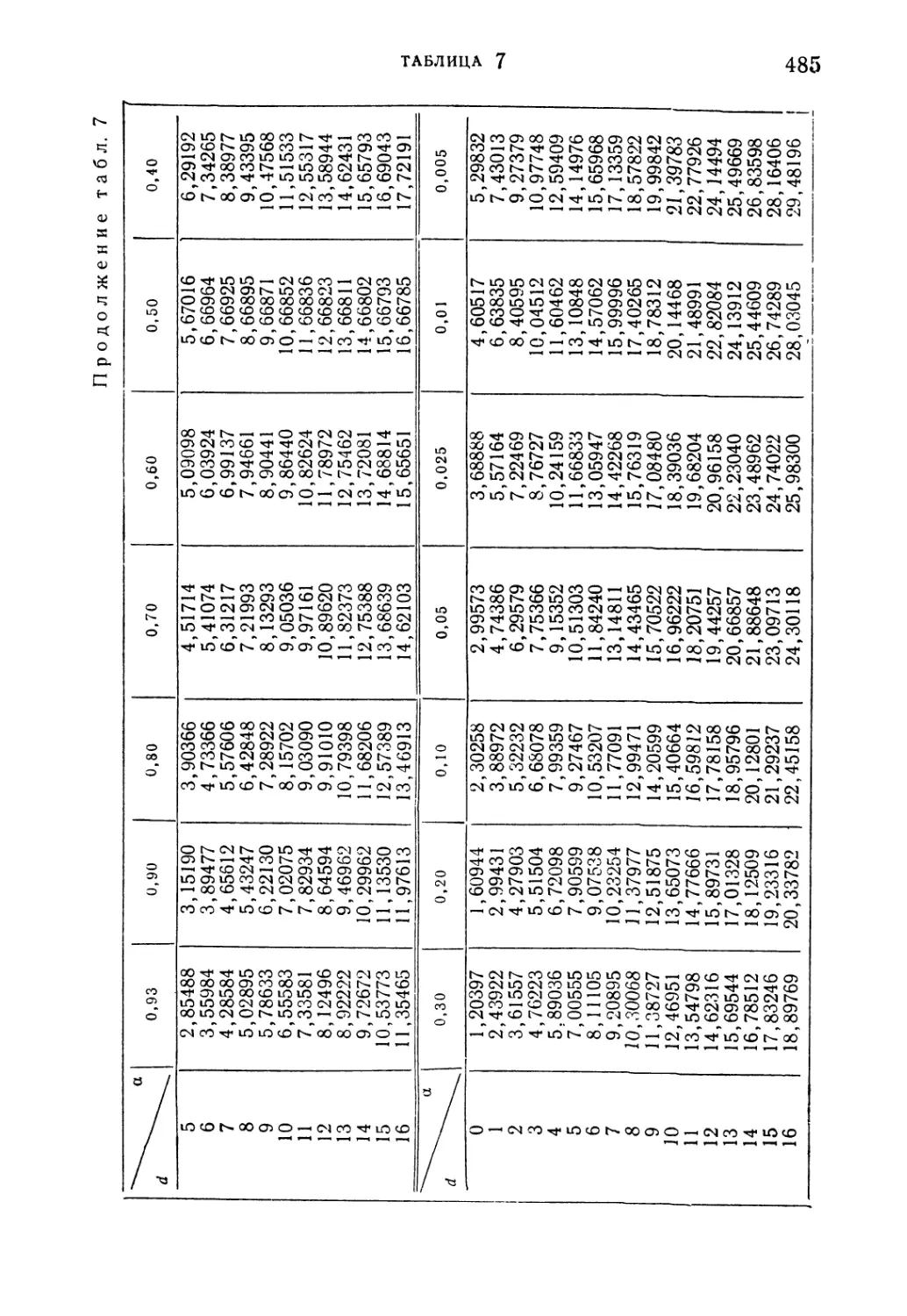
Таблица 7. Квантили Аа (d) пуассоновского распределения,
L<l(Aei(d)) = a/ . . . 484
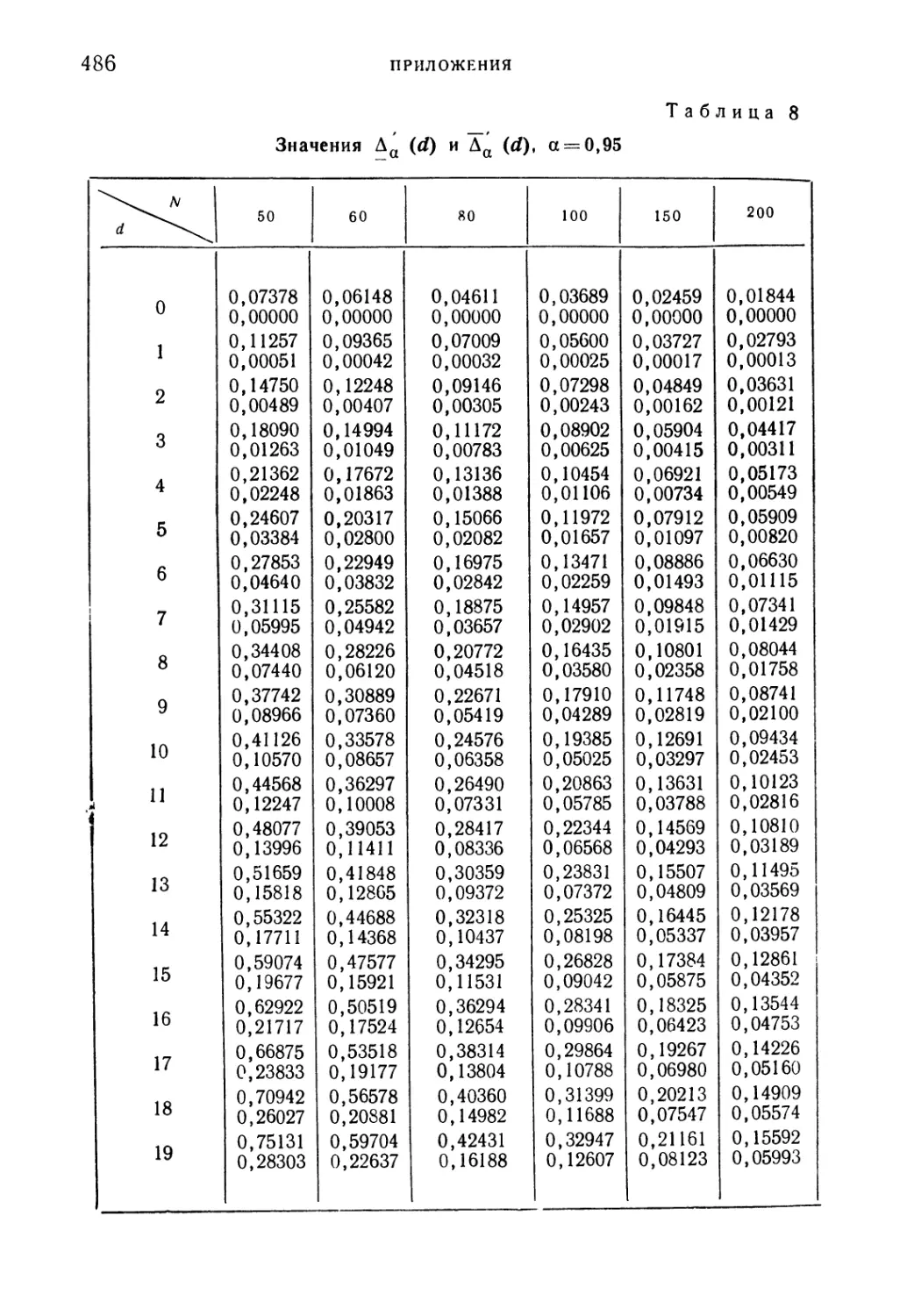
Таблица 8. Значения А^ (d) и &a(d), a = 0,95 486
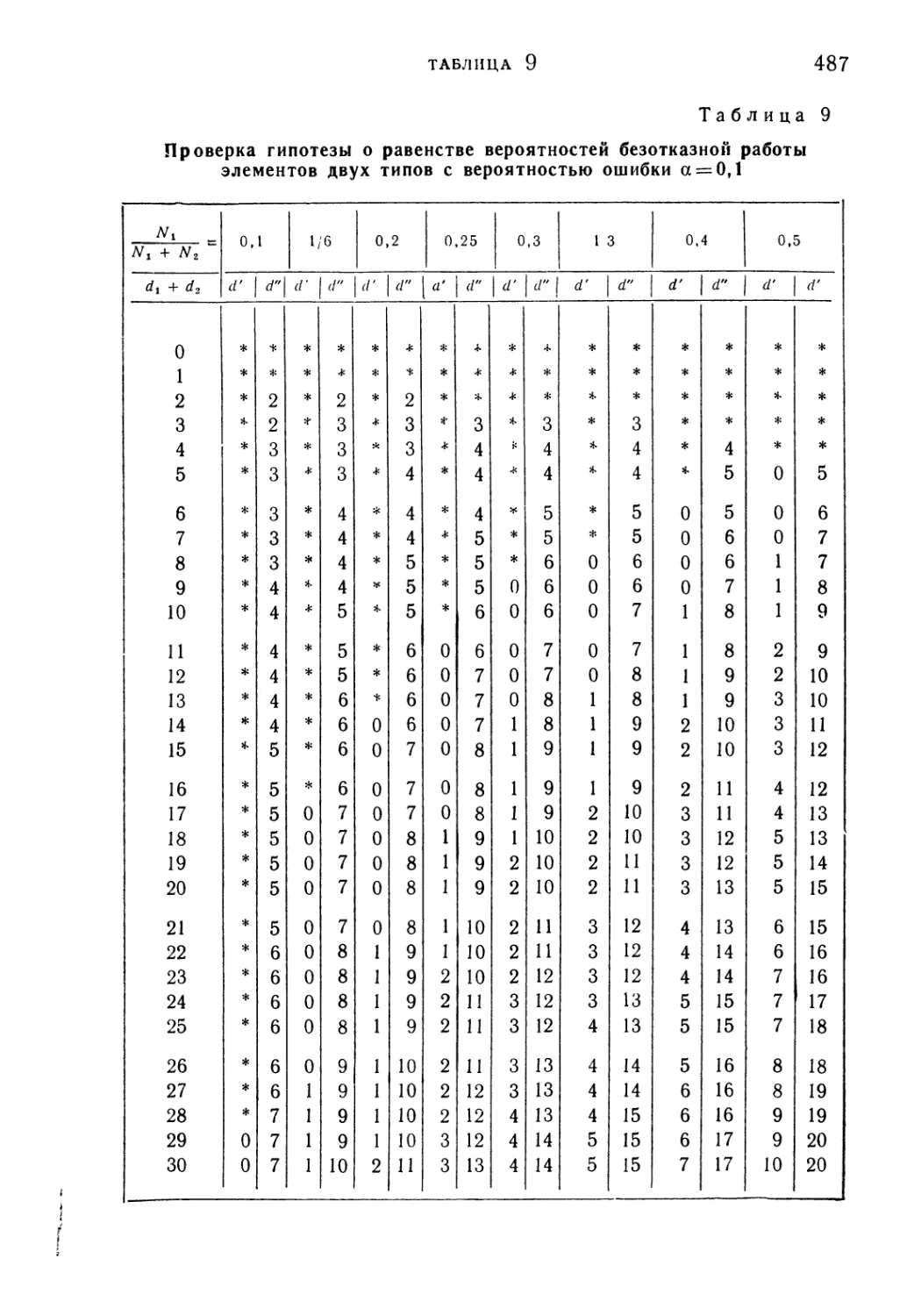
Таблица 9. Проверка гипотезы о равенстве вероятностей безотказной
работы элементов двух типов с вероятностью ошибки а —0,1 487
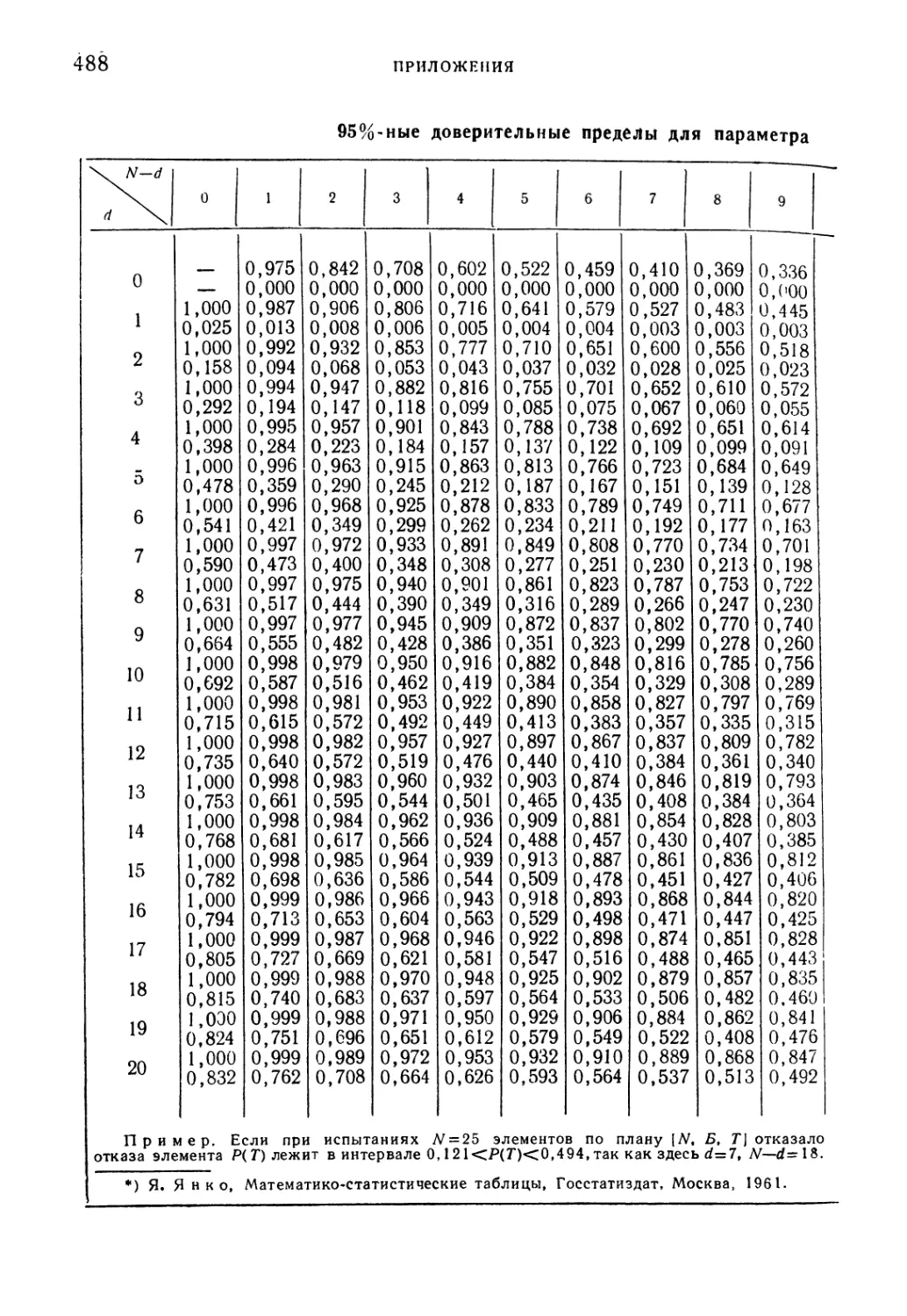
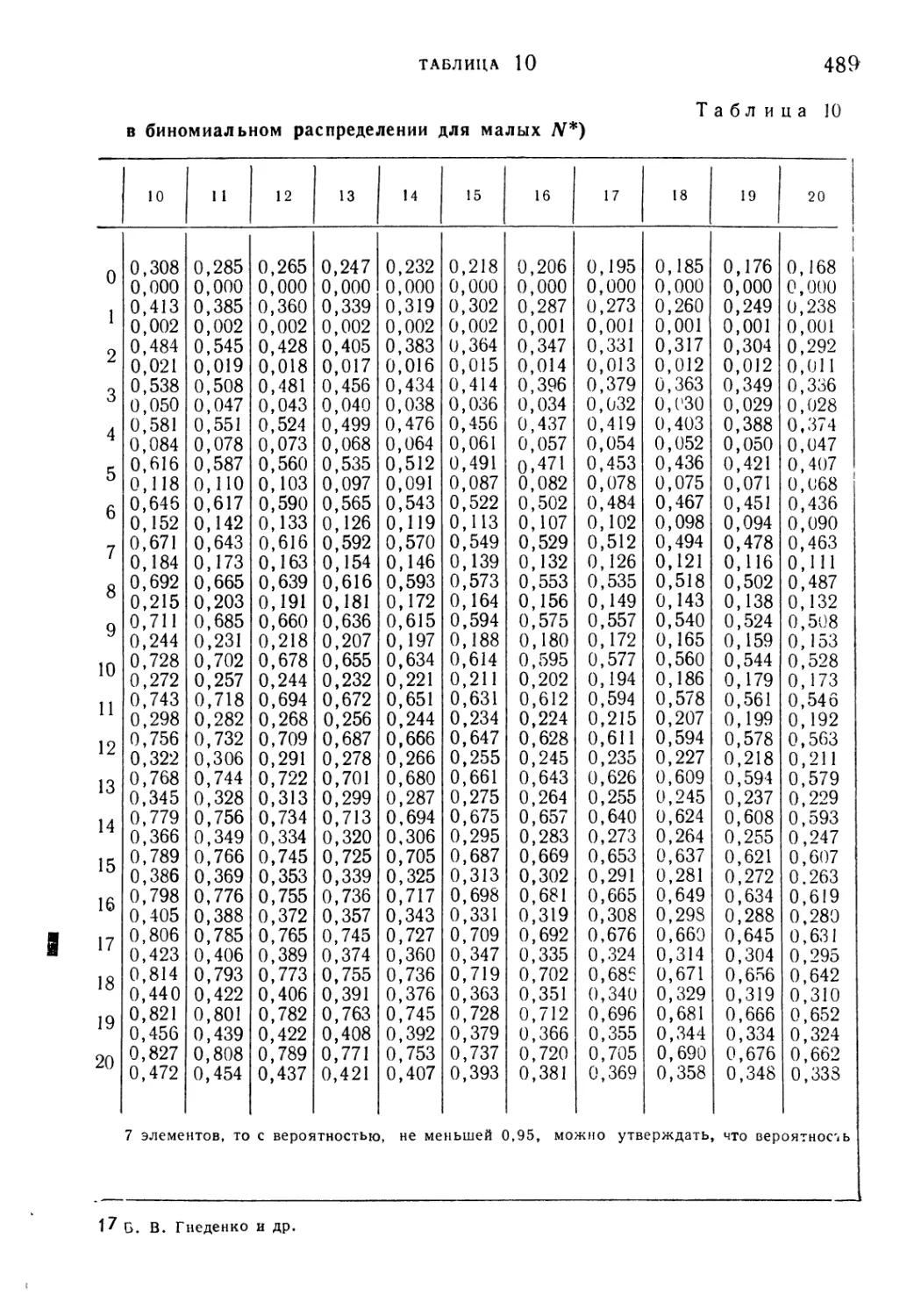
Таблица 10. 95%-ные доверительные пределы для параметра в бино-
биномиальном распределении для малых N 488
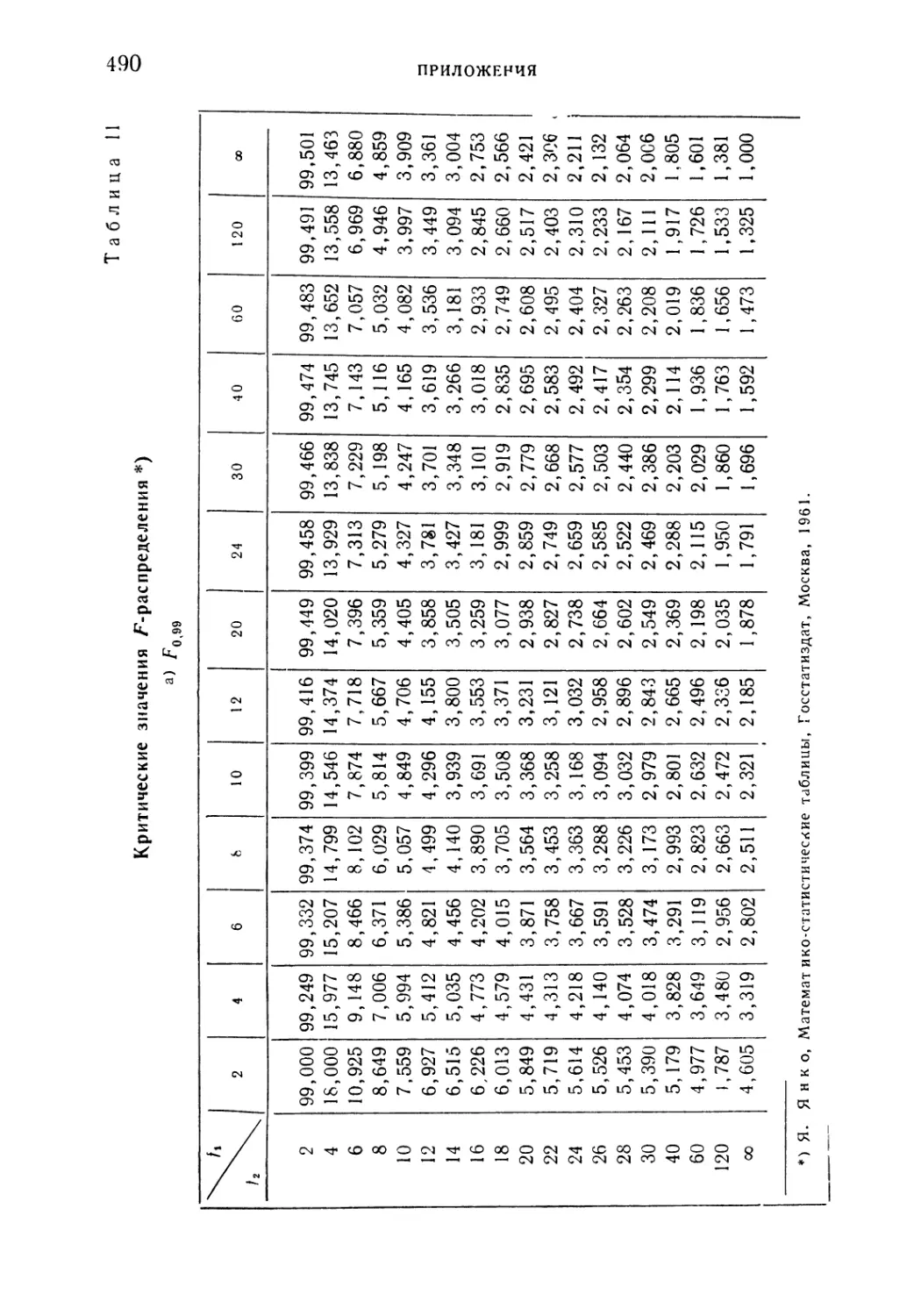
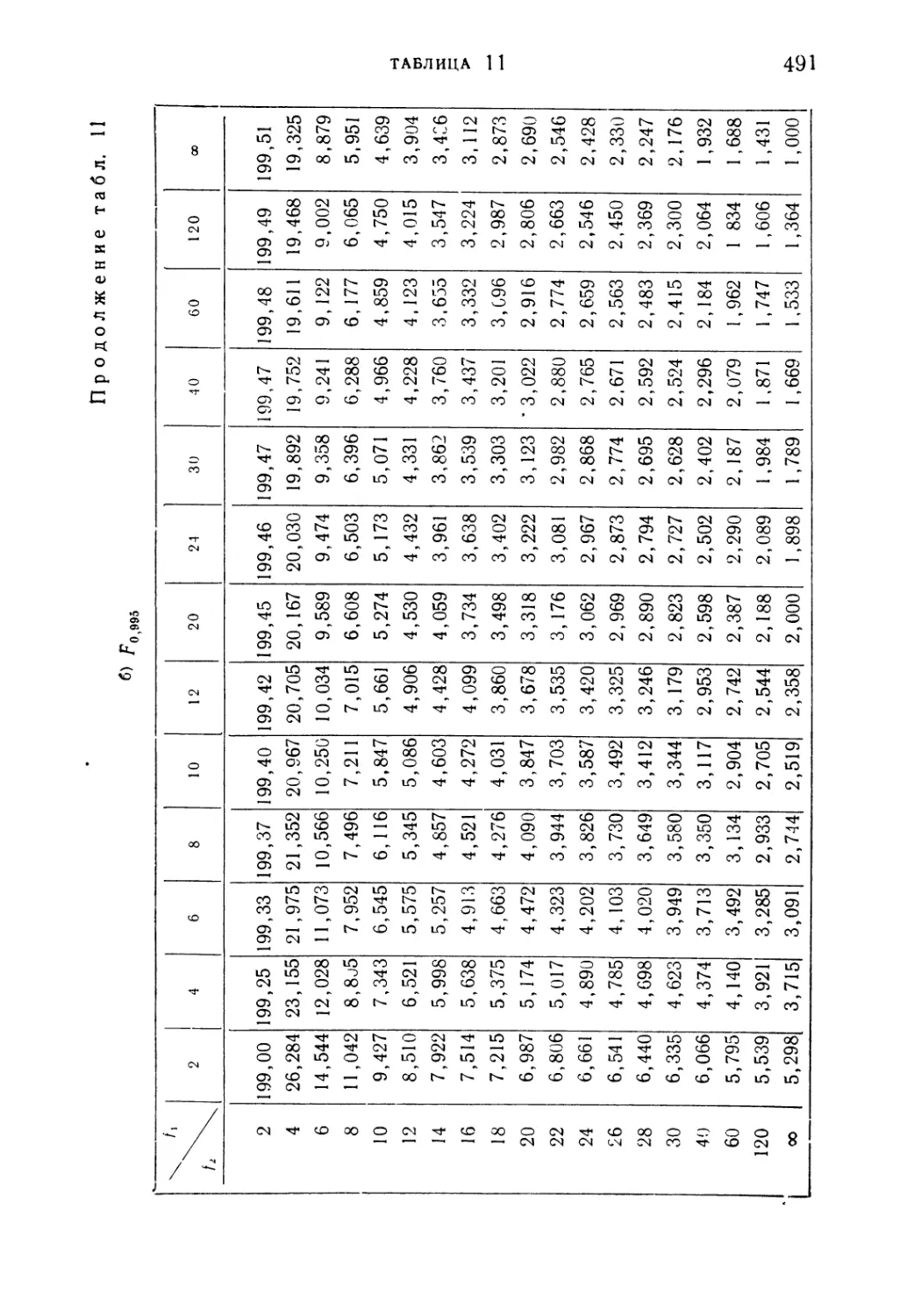
Таблица 11. Критические значения F-распределения a) FOi99% б) F0j995 490
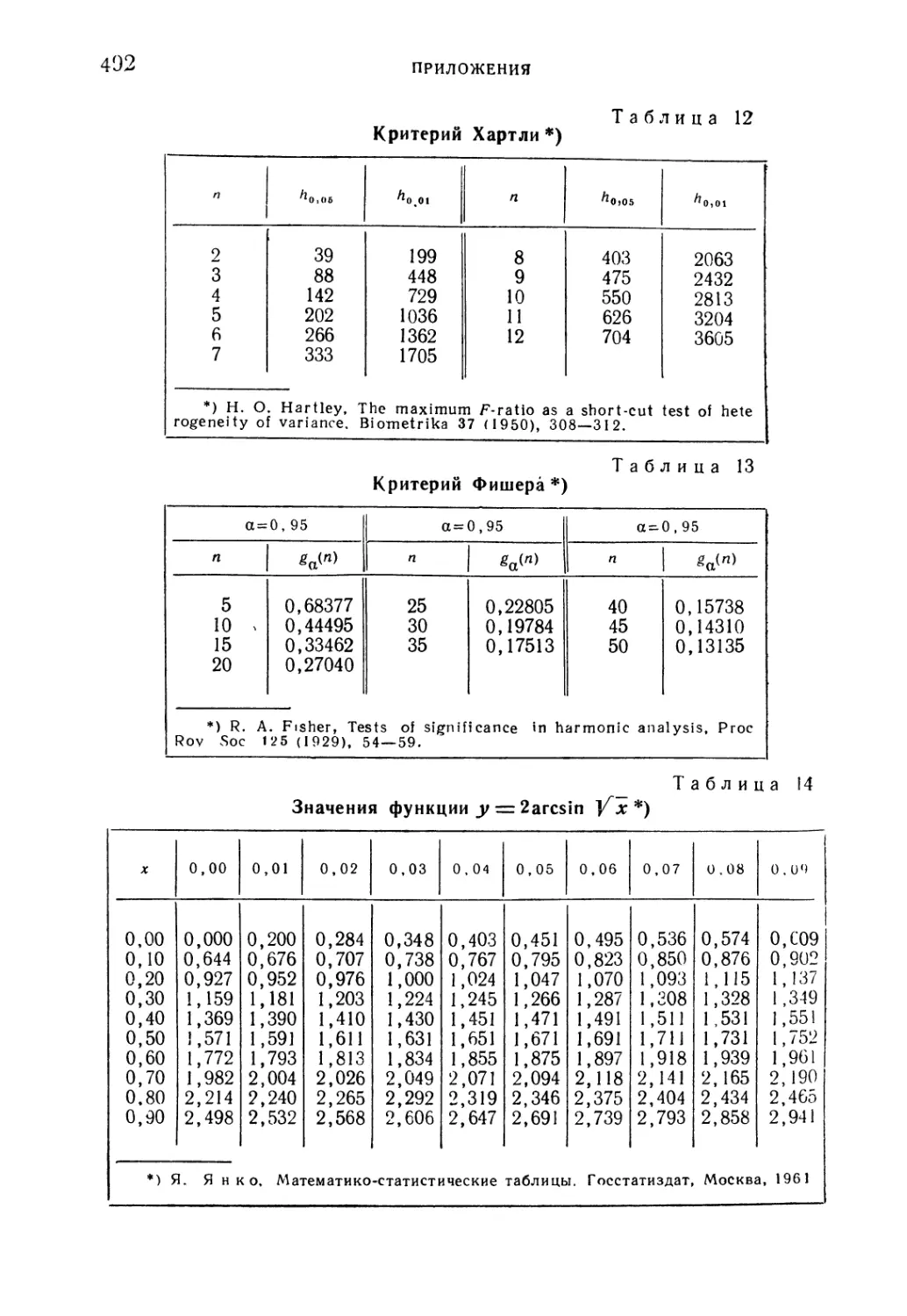
Таблица 12. Критерий Хартли '....'.. 492
Таблица 13. Критерий Фишера 492
Таблица 14. Значения функции r/ = 2arcsin V~x 492
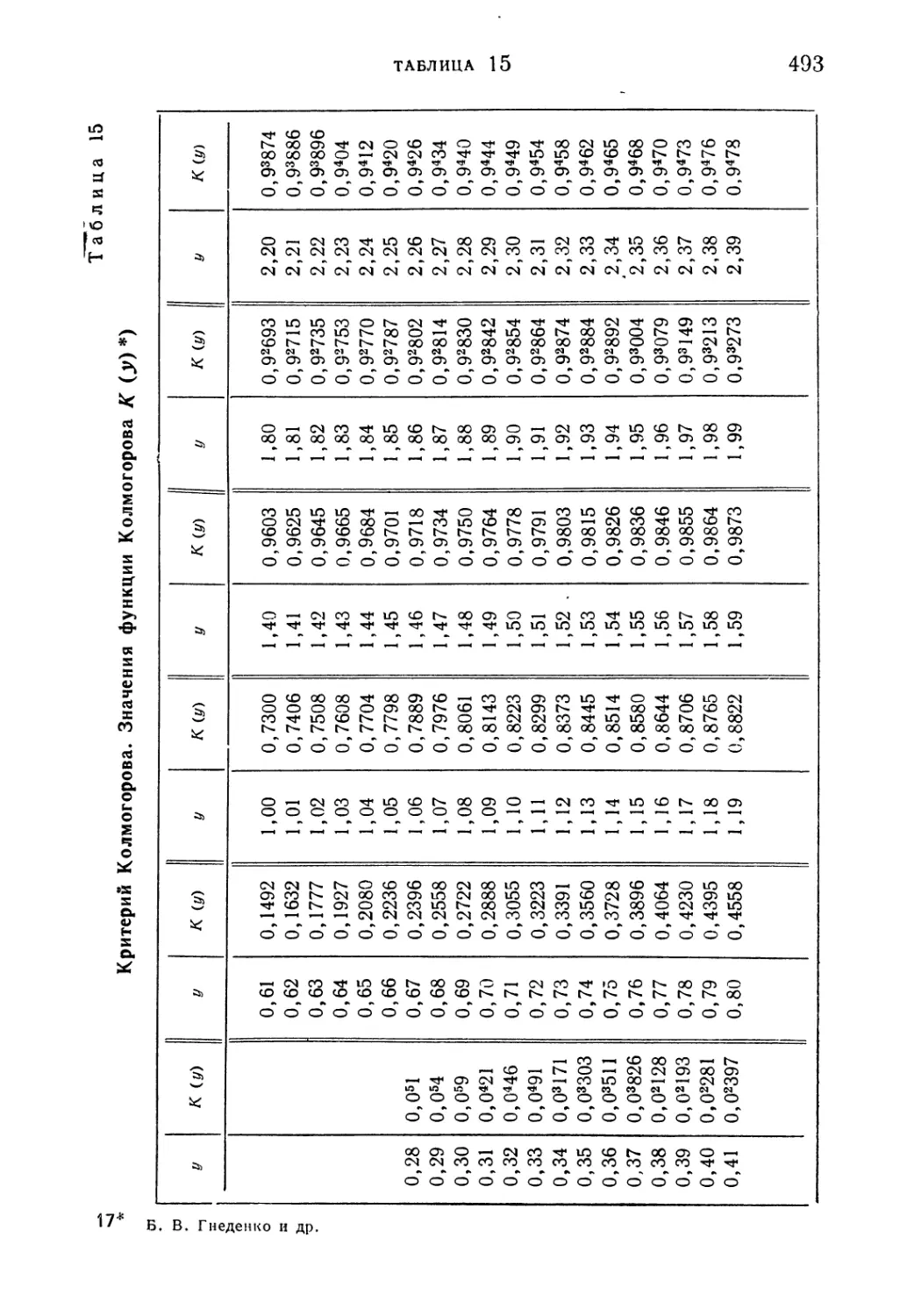
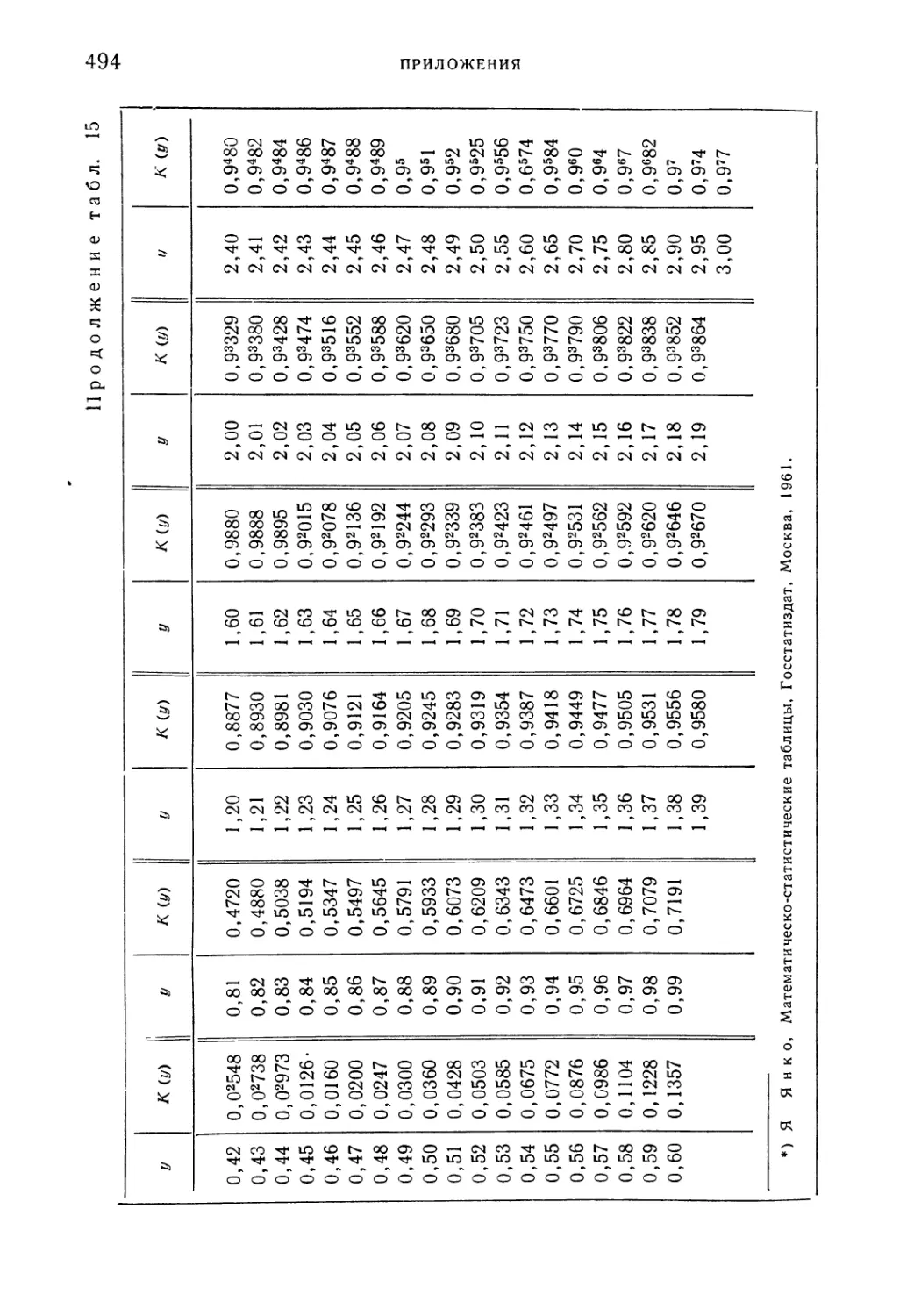
Таблица 15. Критерий Колмогорова. Значения функции Колмого-
Колмогорова К (у) 493
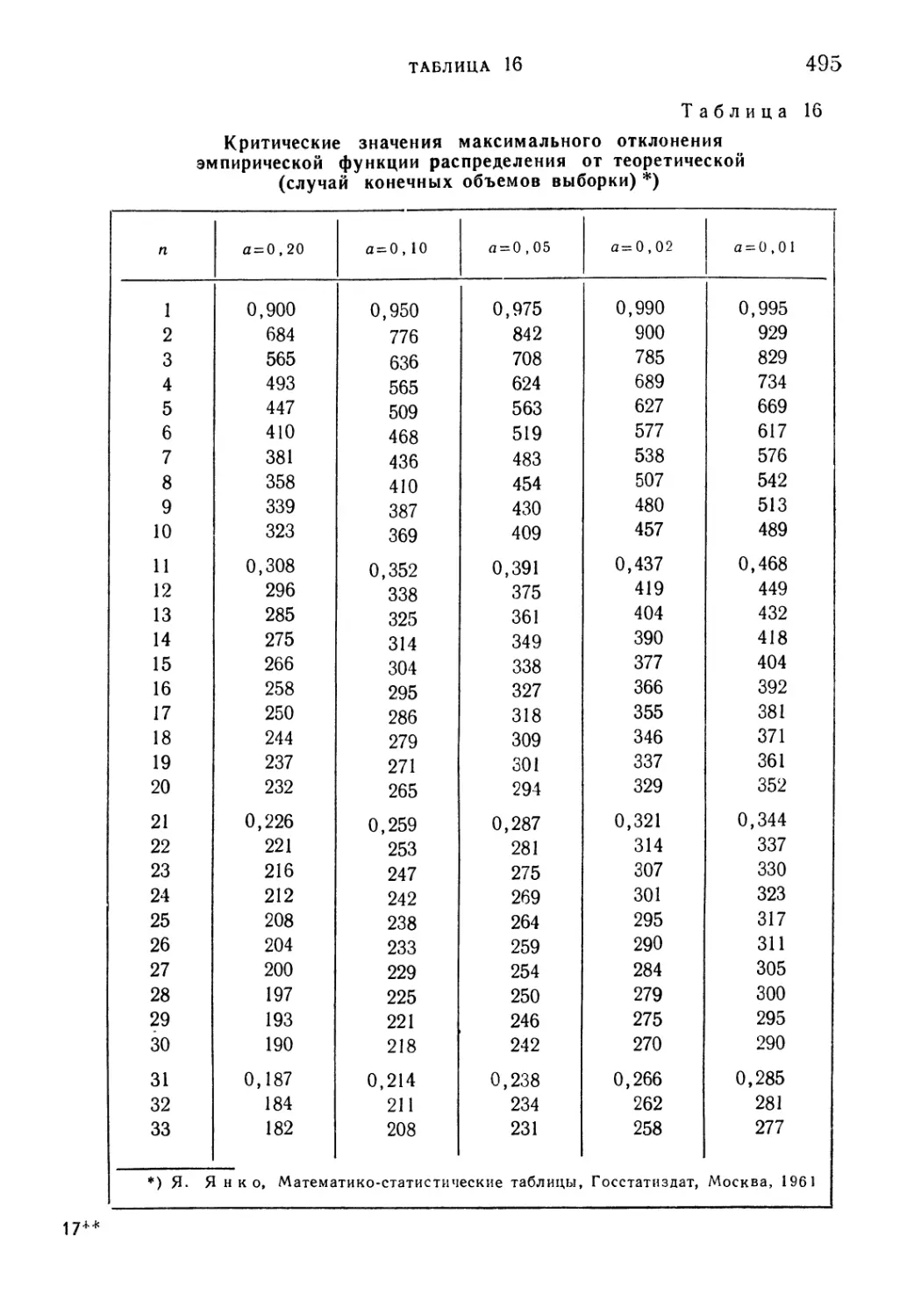
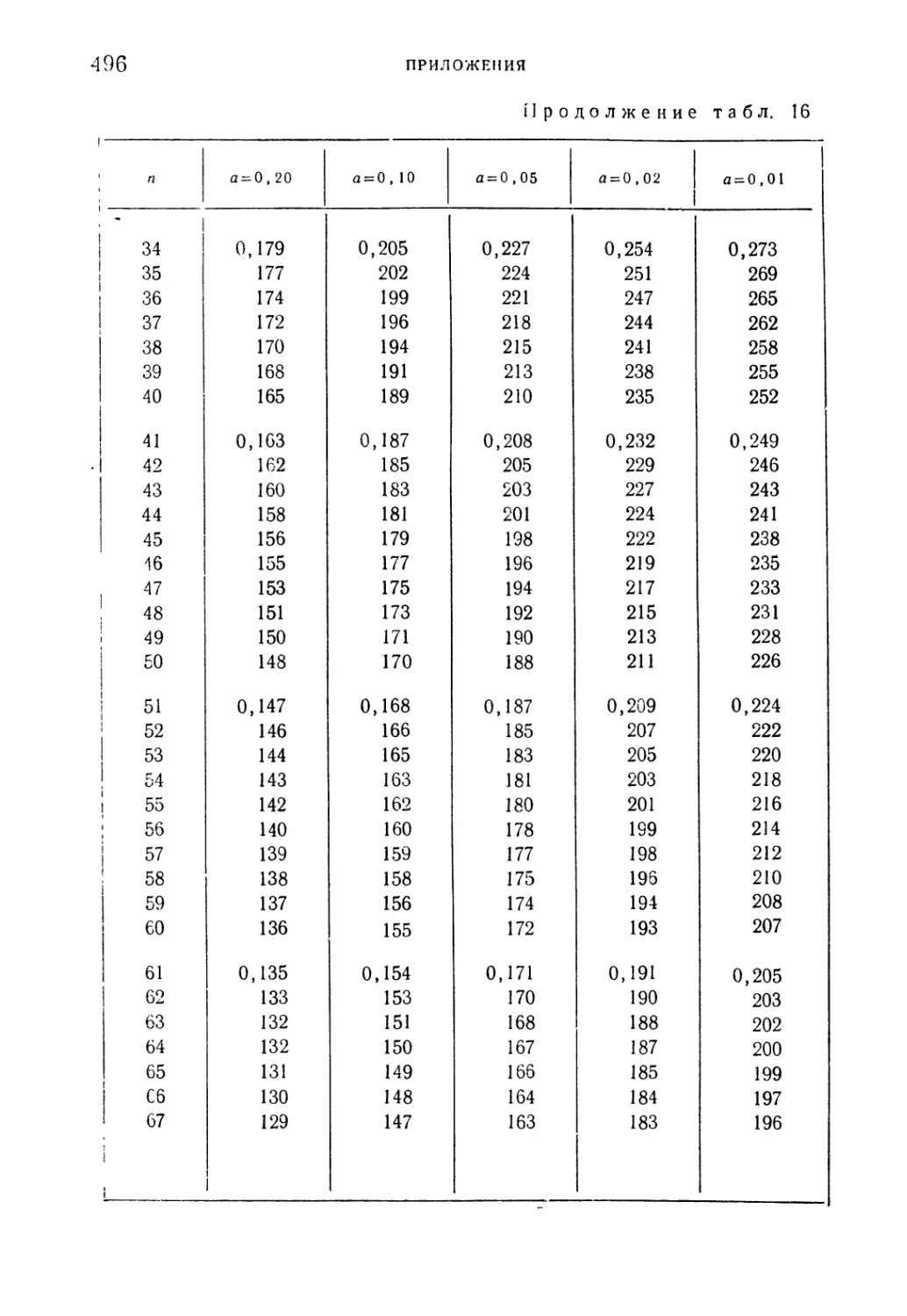
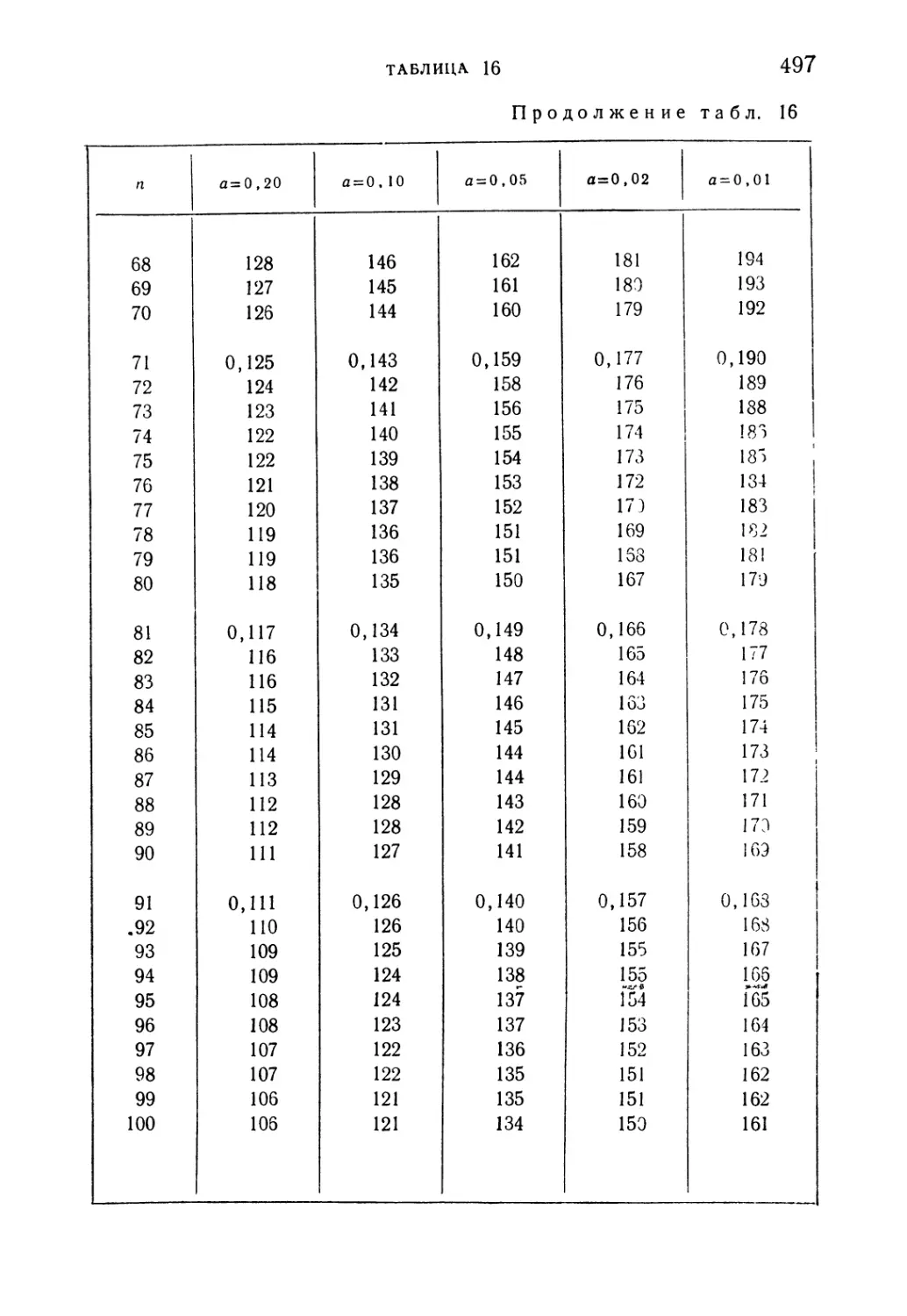
Таблица 16. Критические значения максимального отклонения эмпи-
эмпирической функции распределения от теоретической (случай
конечных объемов выборки) 495
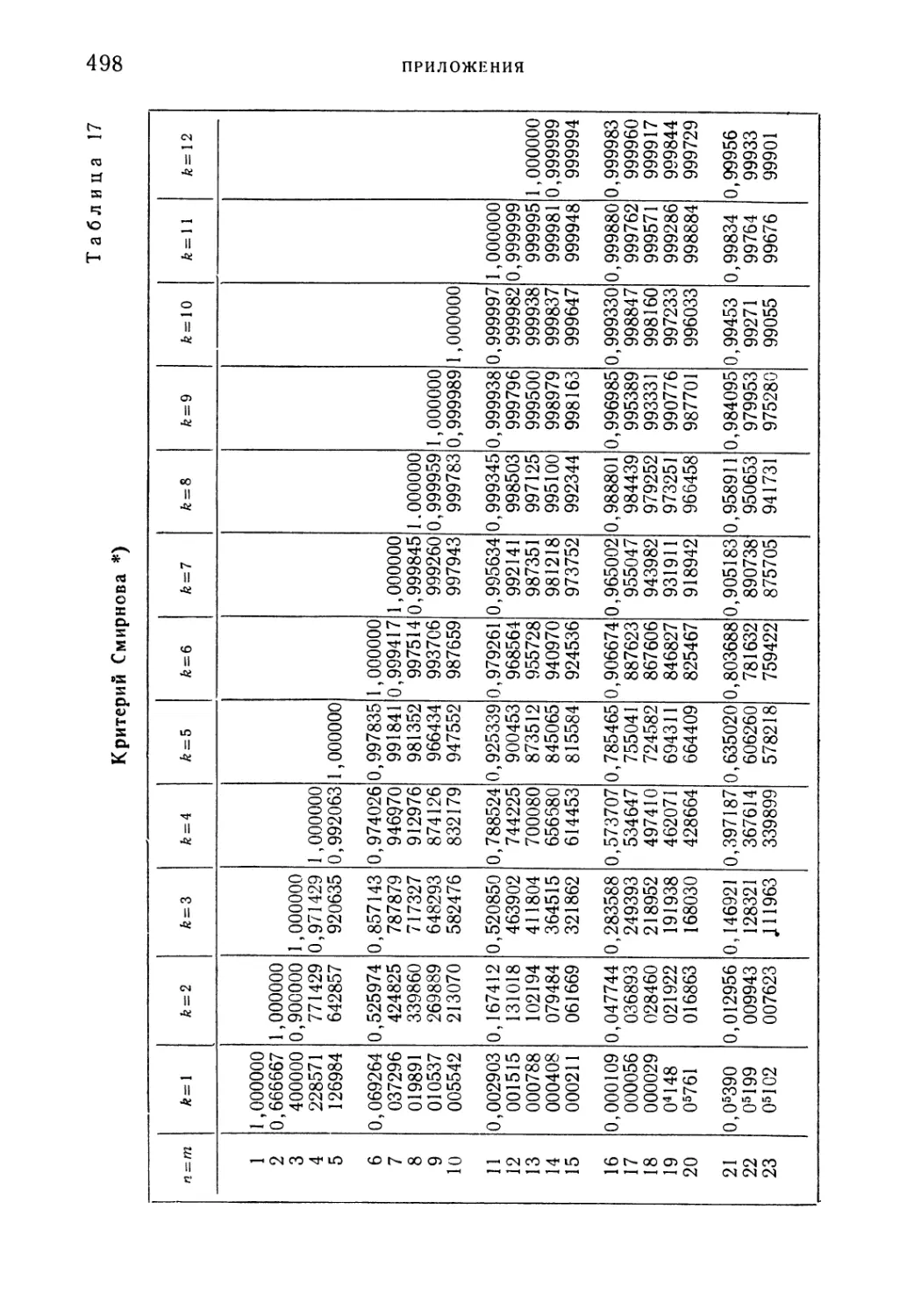
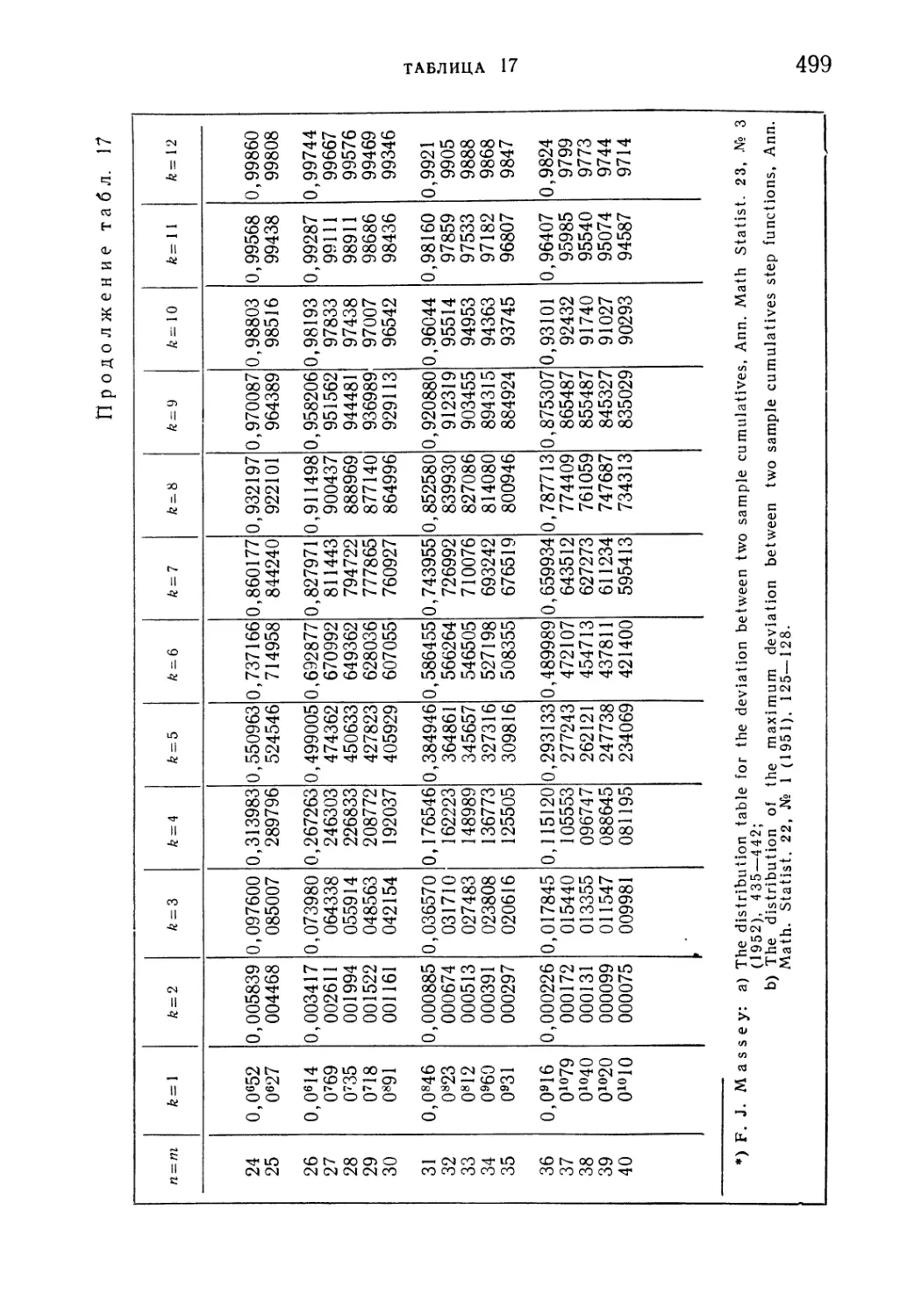
Таблица 17. Критерий Смирнова 498
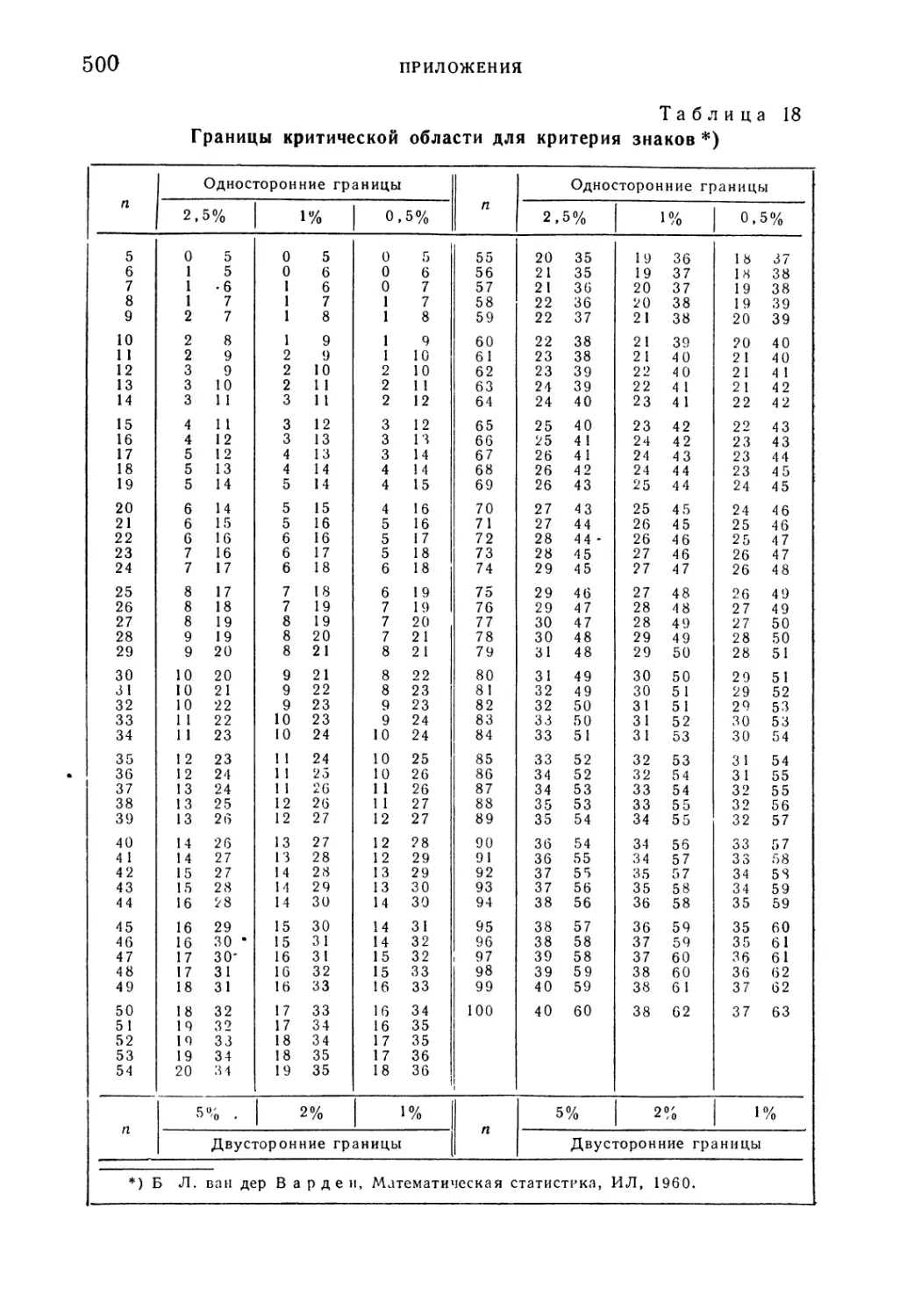
¦ Таблица 18. Границы критической области для критерия знаков . . 500
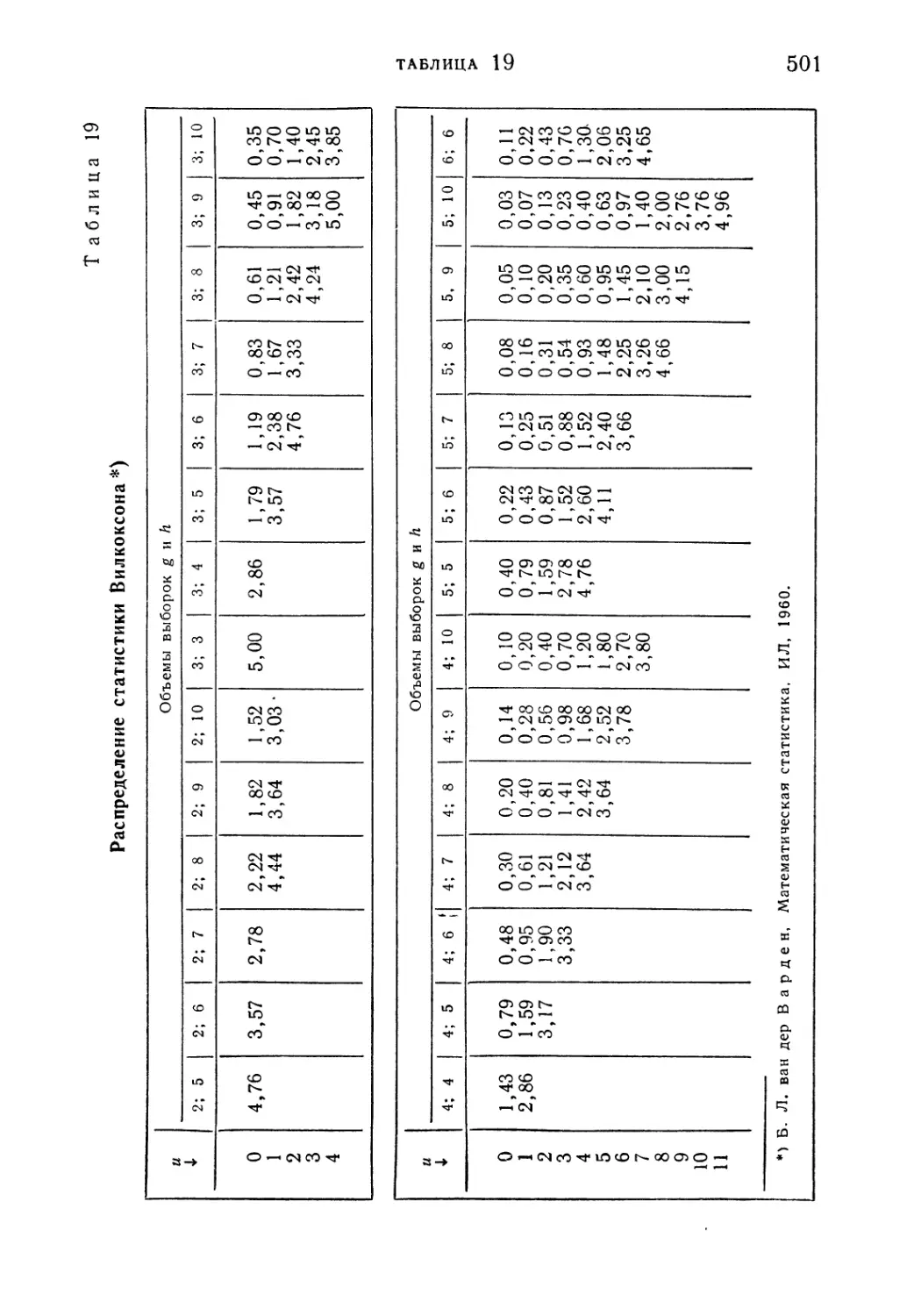
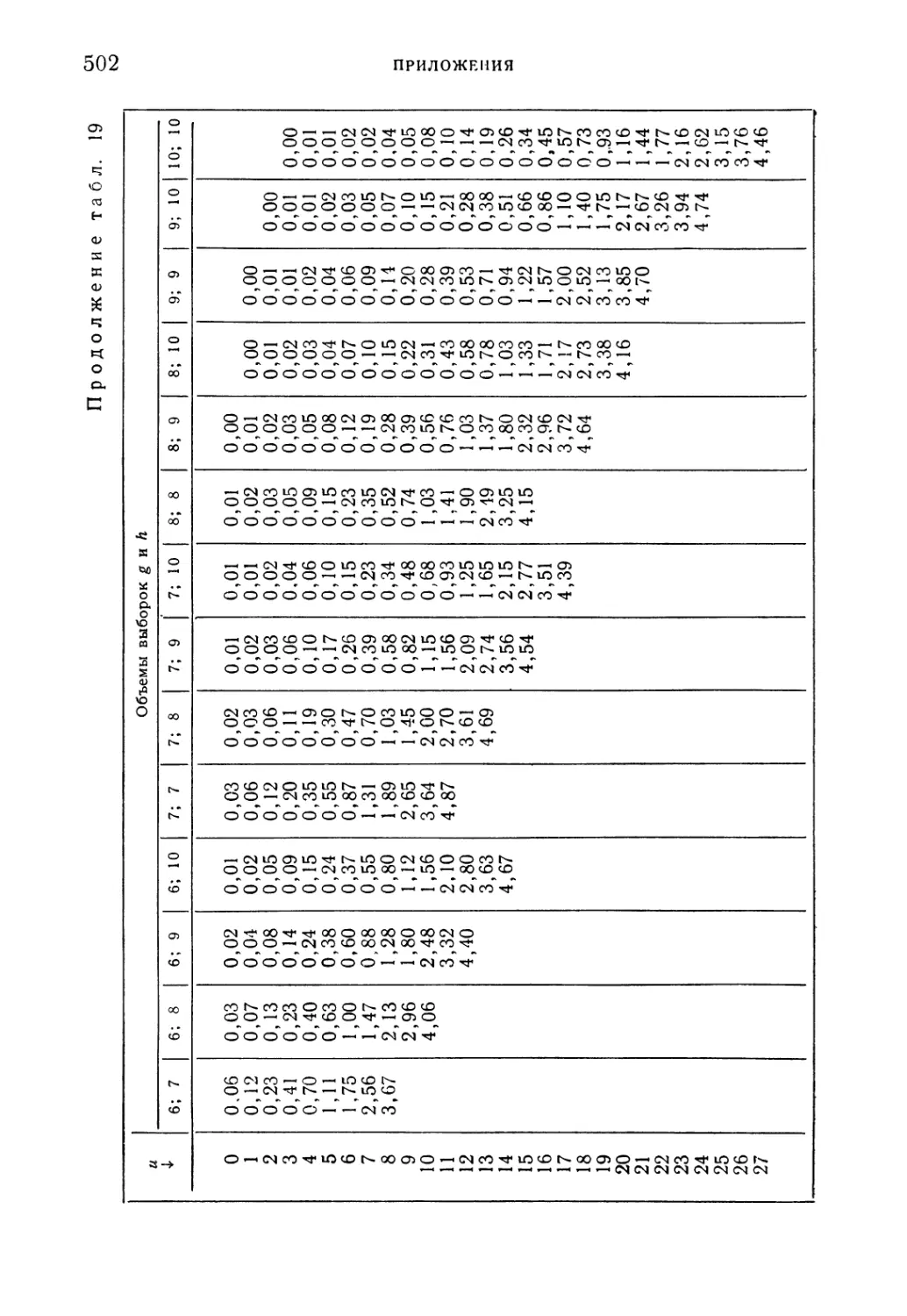
Таблица 19. Распределение статистики Вилкоксона 501
ОГЛАВЛЕНИЕ О
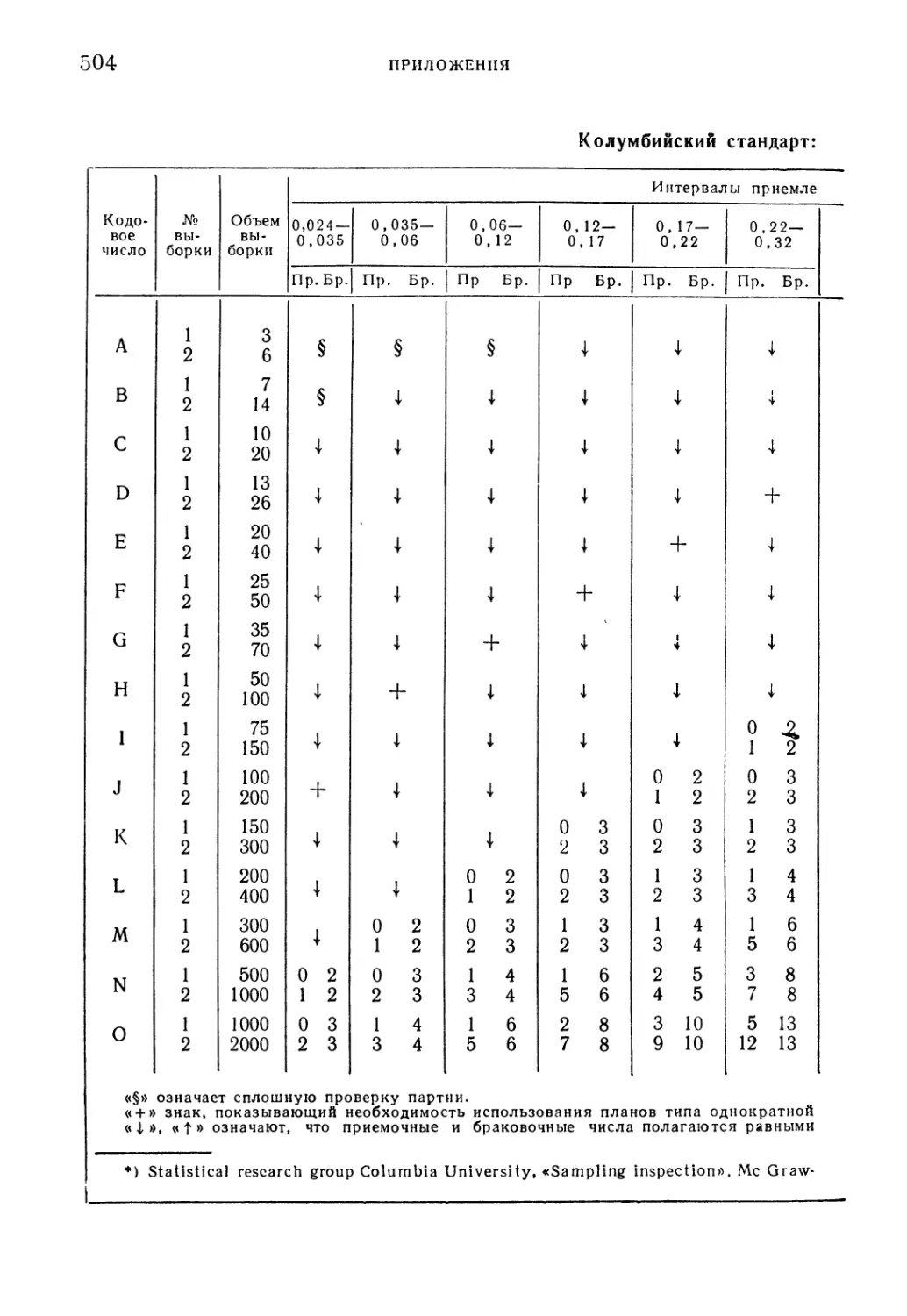
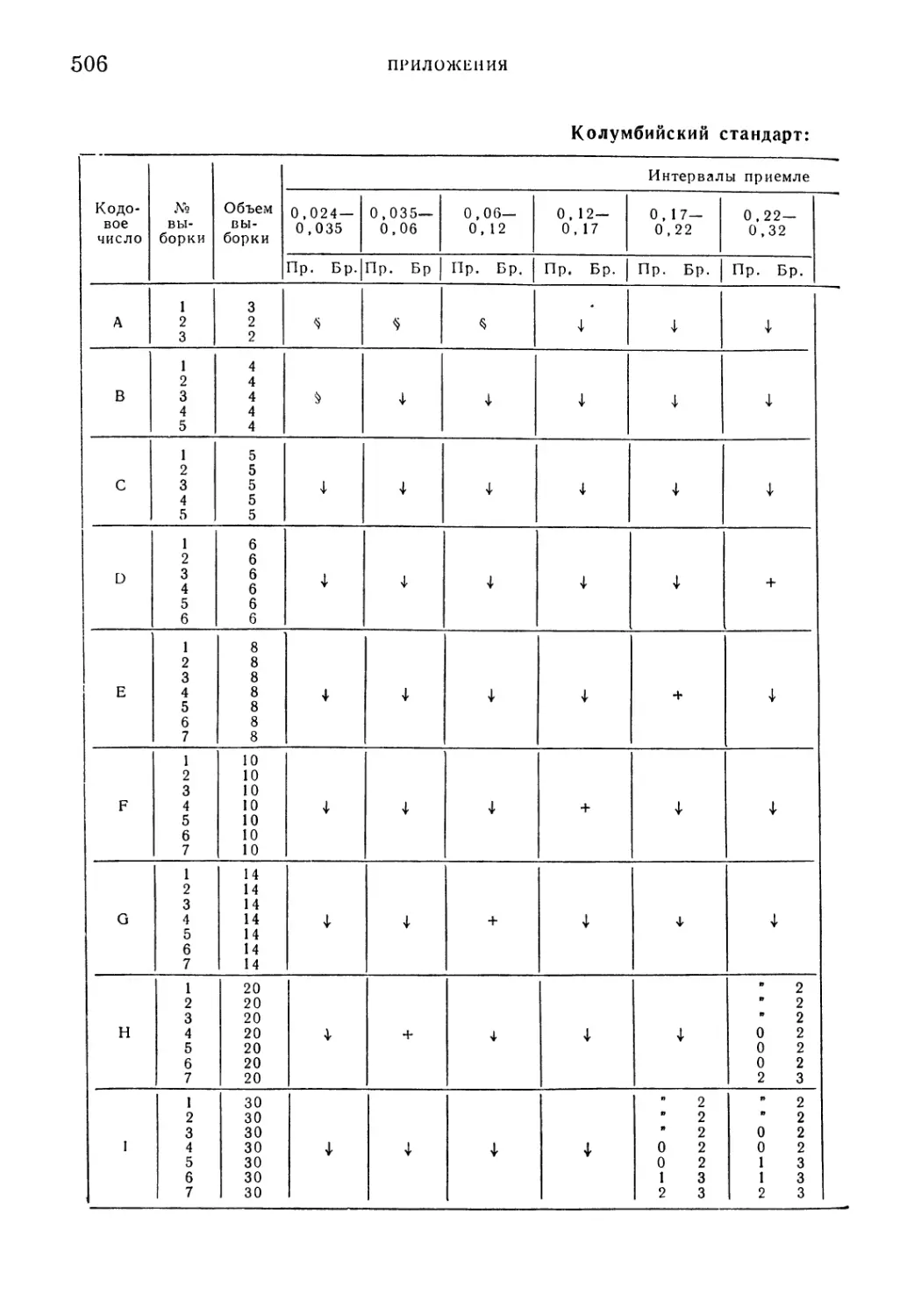
Таблица 20. Колумбийский стандарт: однократная выборка 503
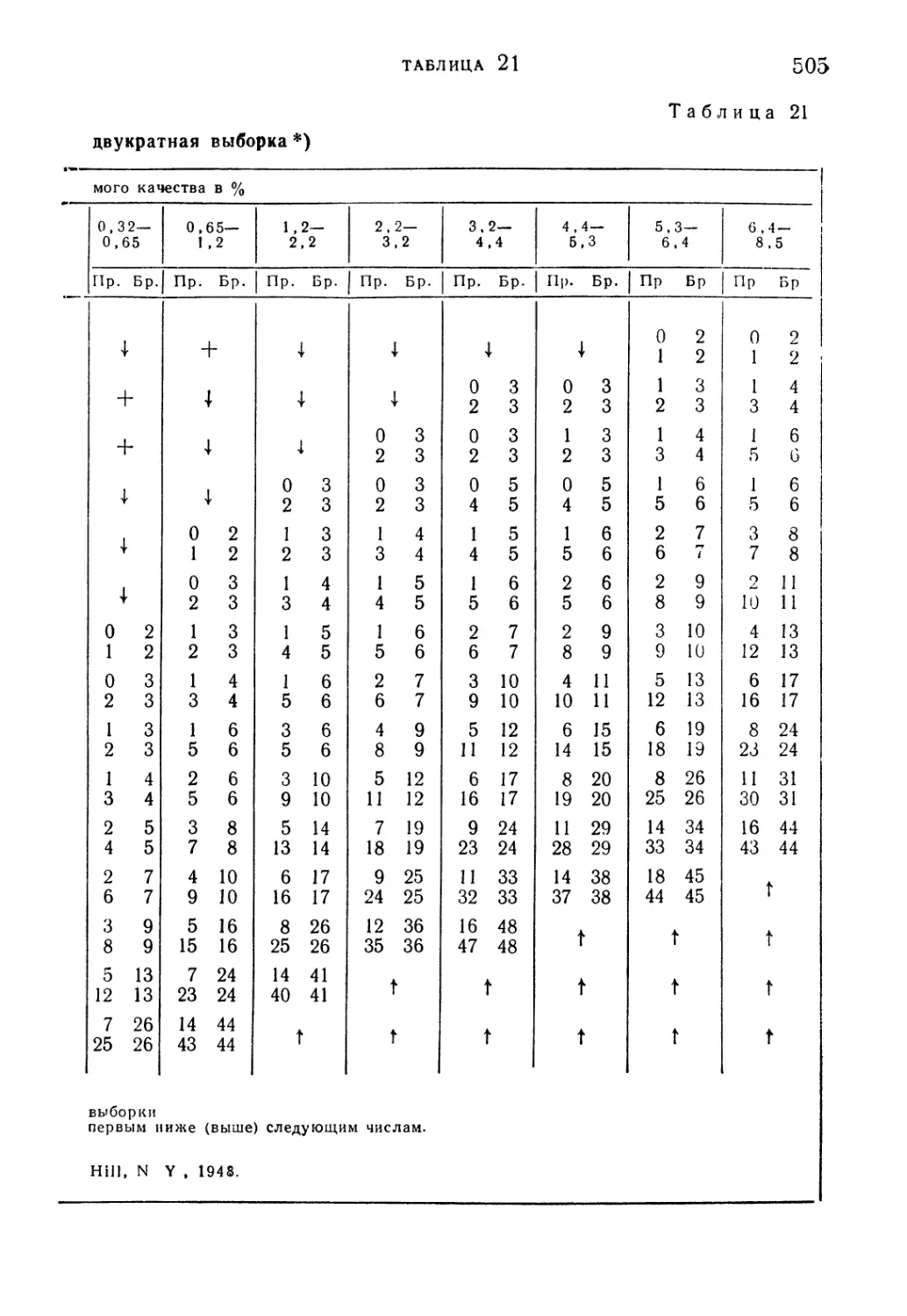
Таблица 21. Колумбийский стандарт: двухкратная выборка 504
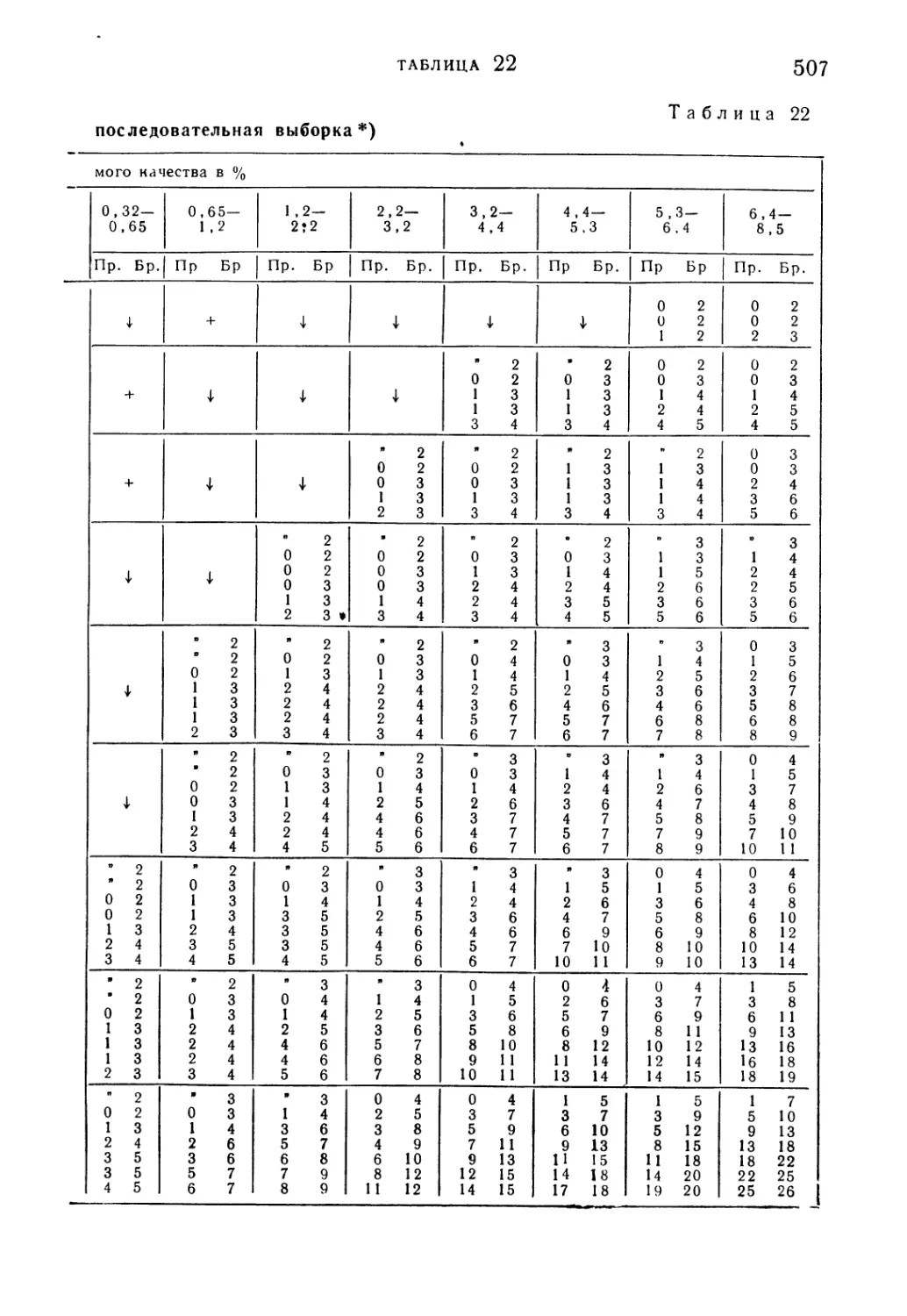
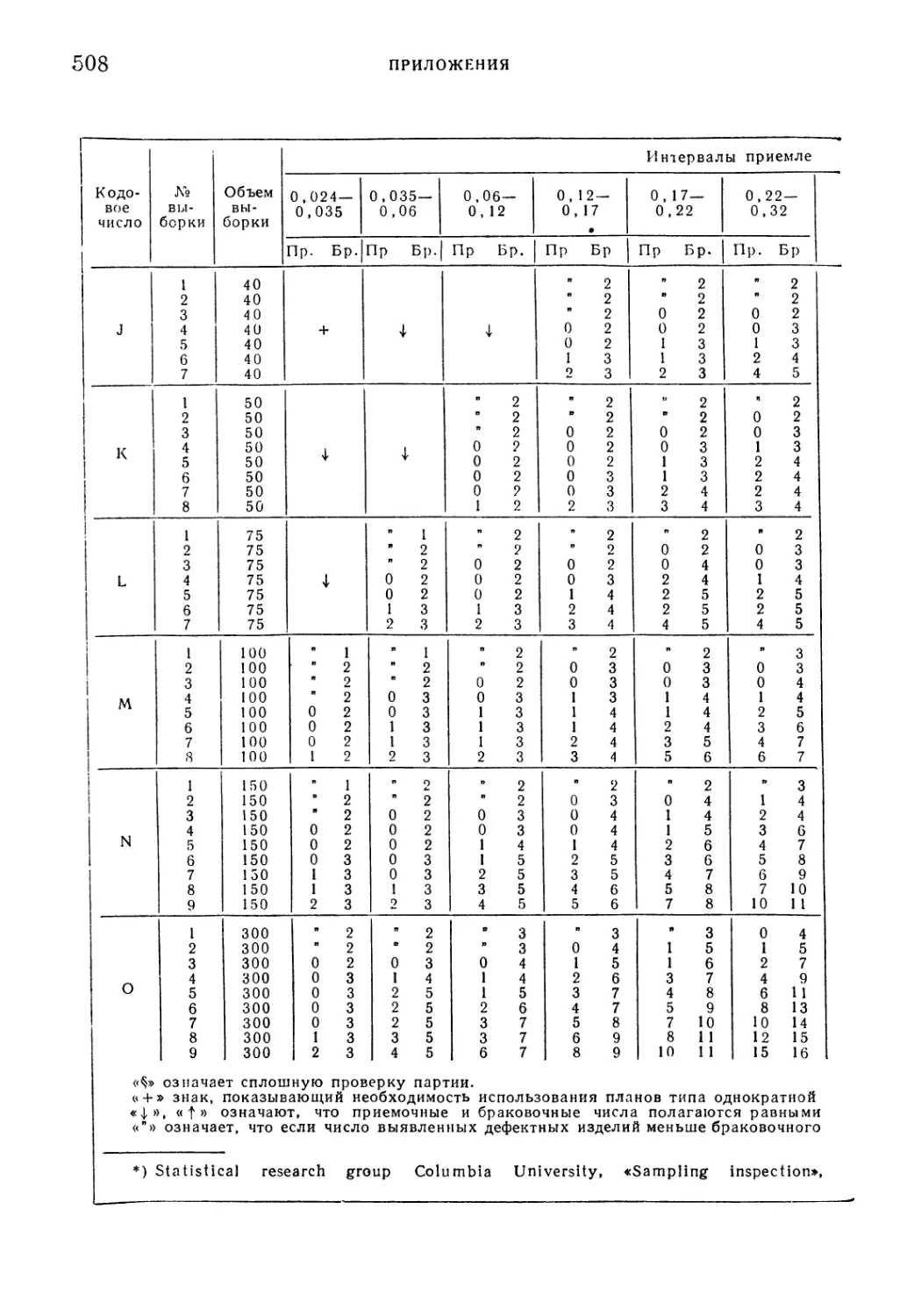
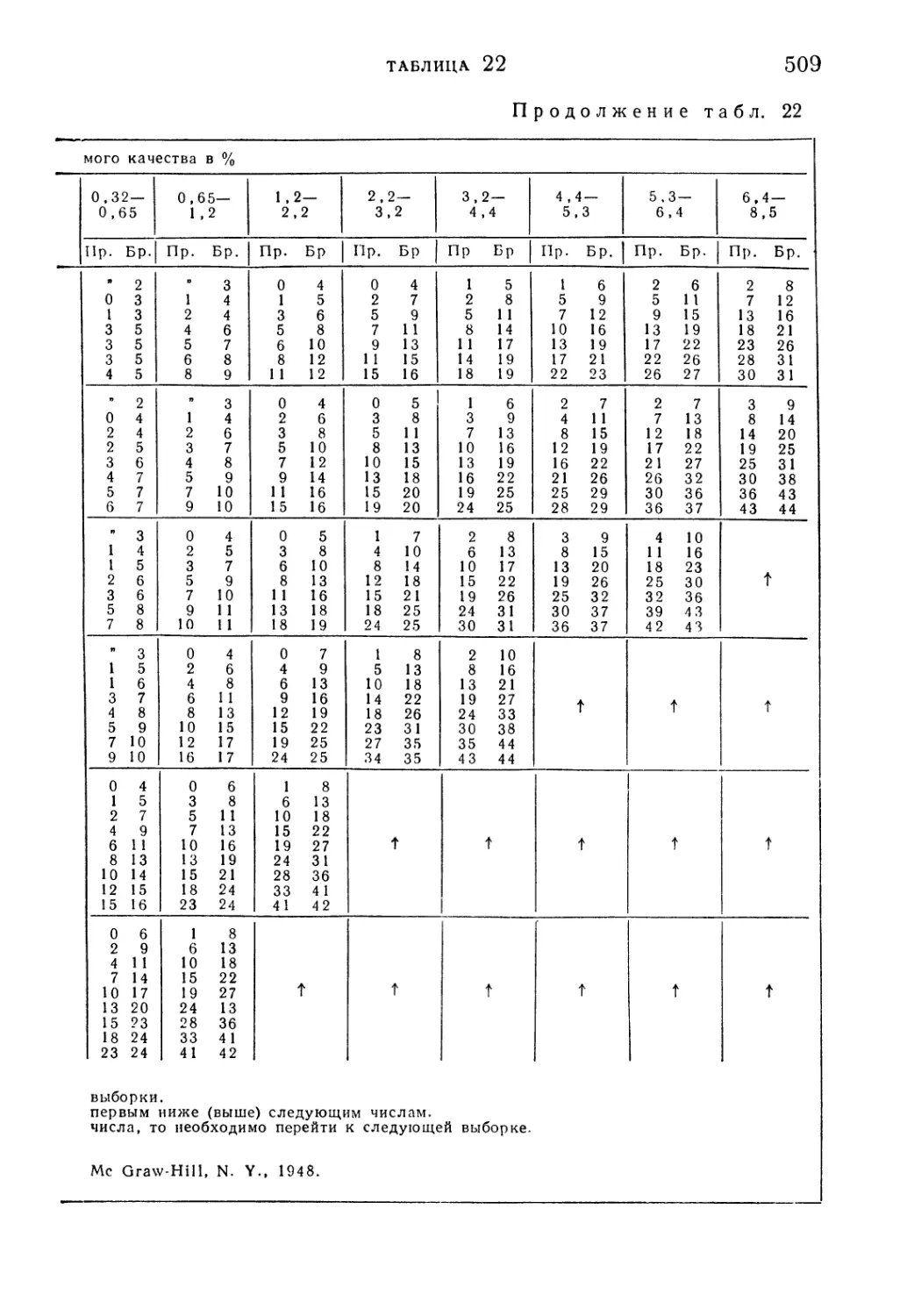
Таблица 22. Колумбийский стандарт: последовательная выборка . . 506
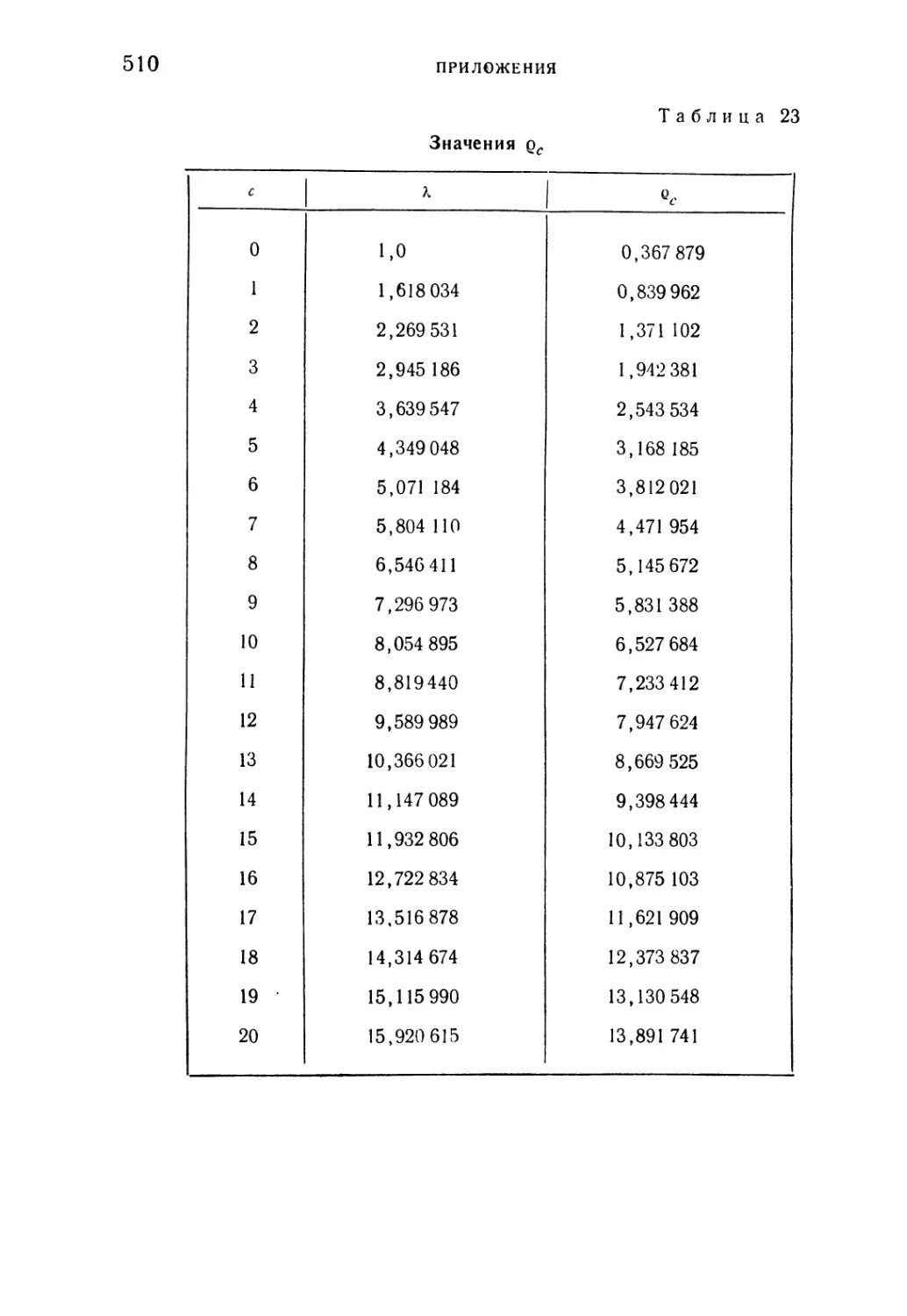
Таблица 23. Значения рс 510
Таблица 24. Значения Qc. Однократные планы типа (п, сJз, обеспе-
обеспечивающие минимум инспекции при заданном предельном
выходном качестве 511
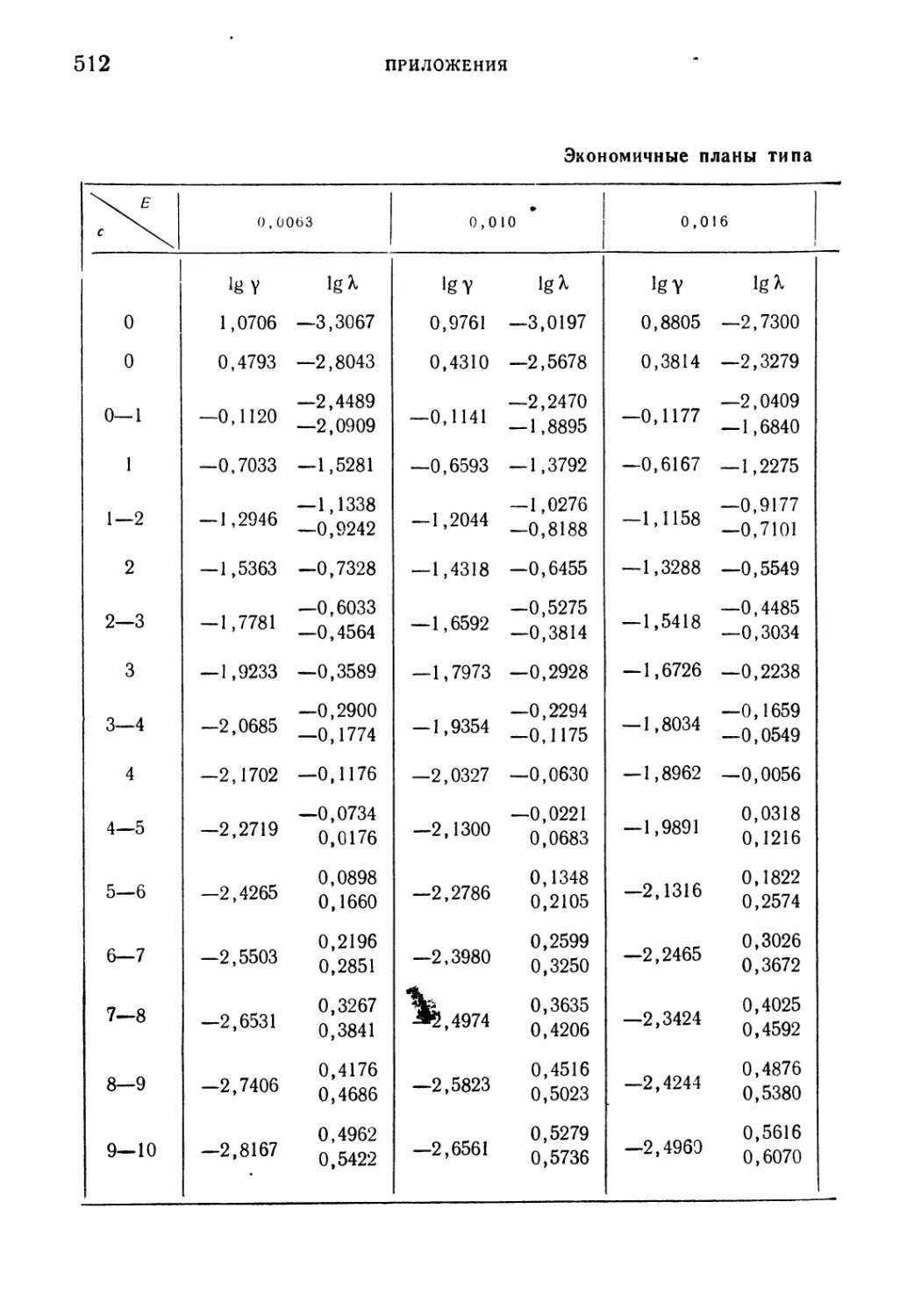
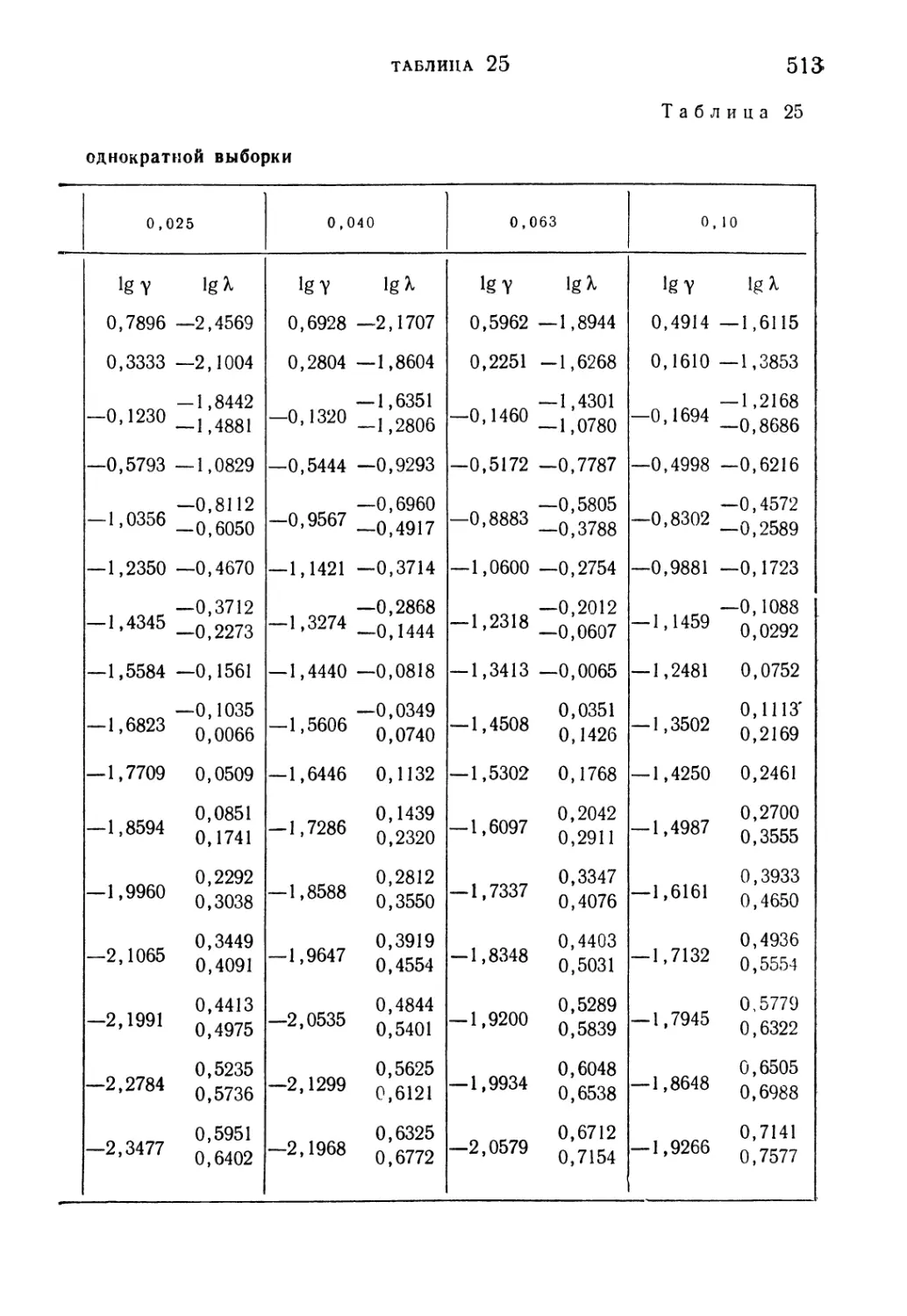
Таблица 25. Экономичные планы типа однократной выборки .... 512
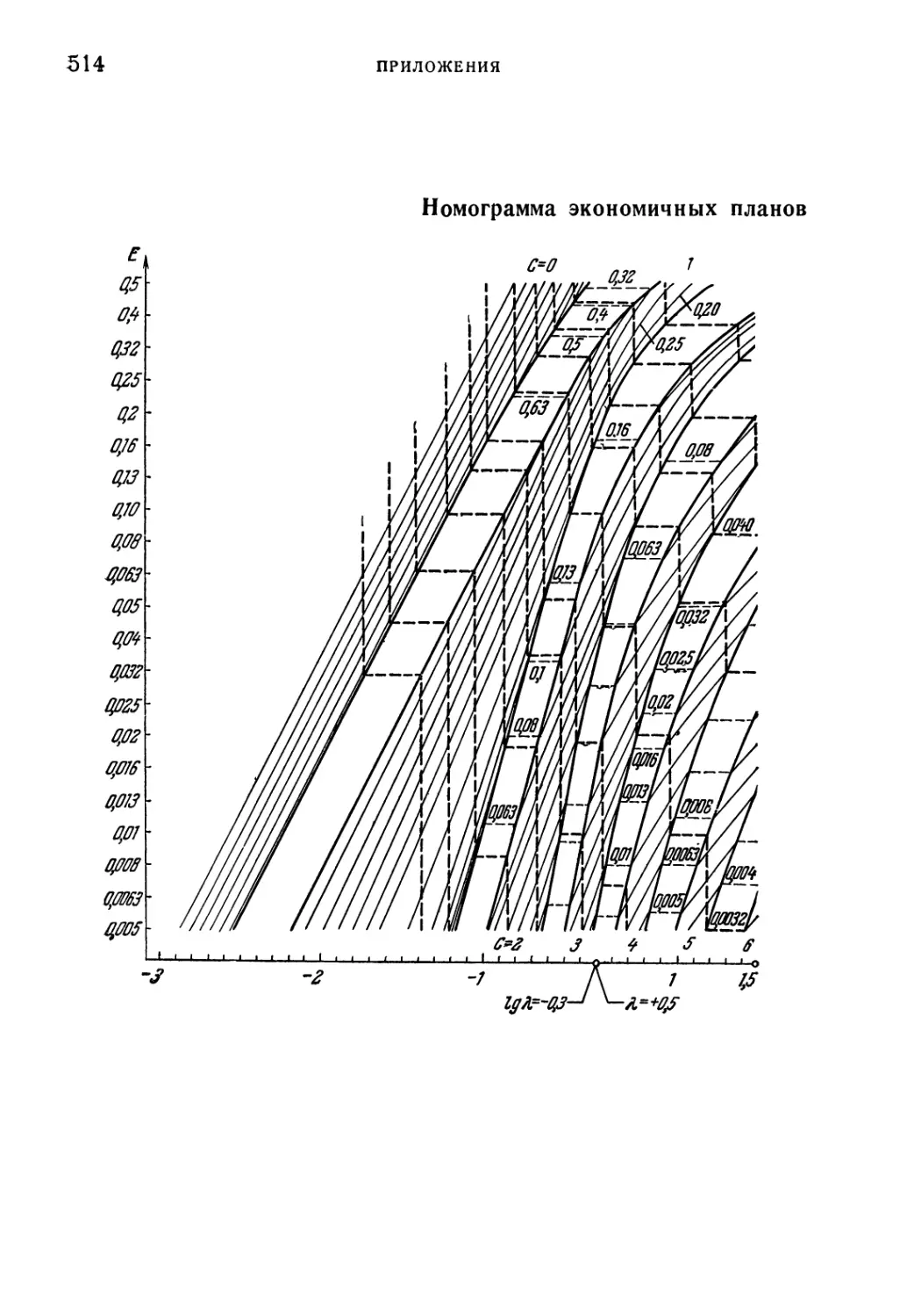
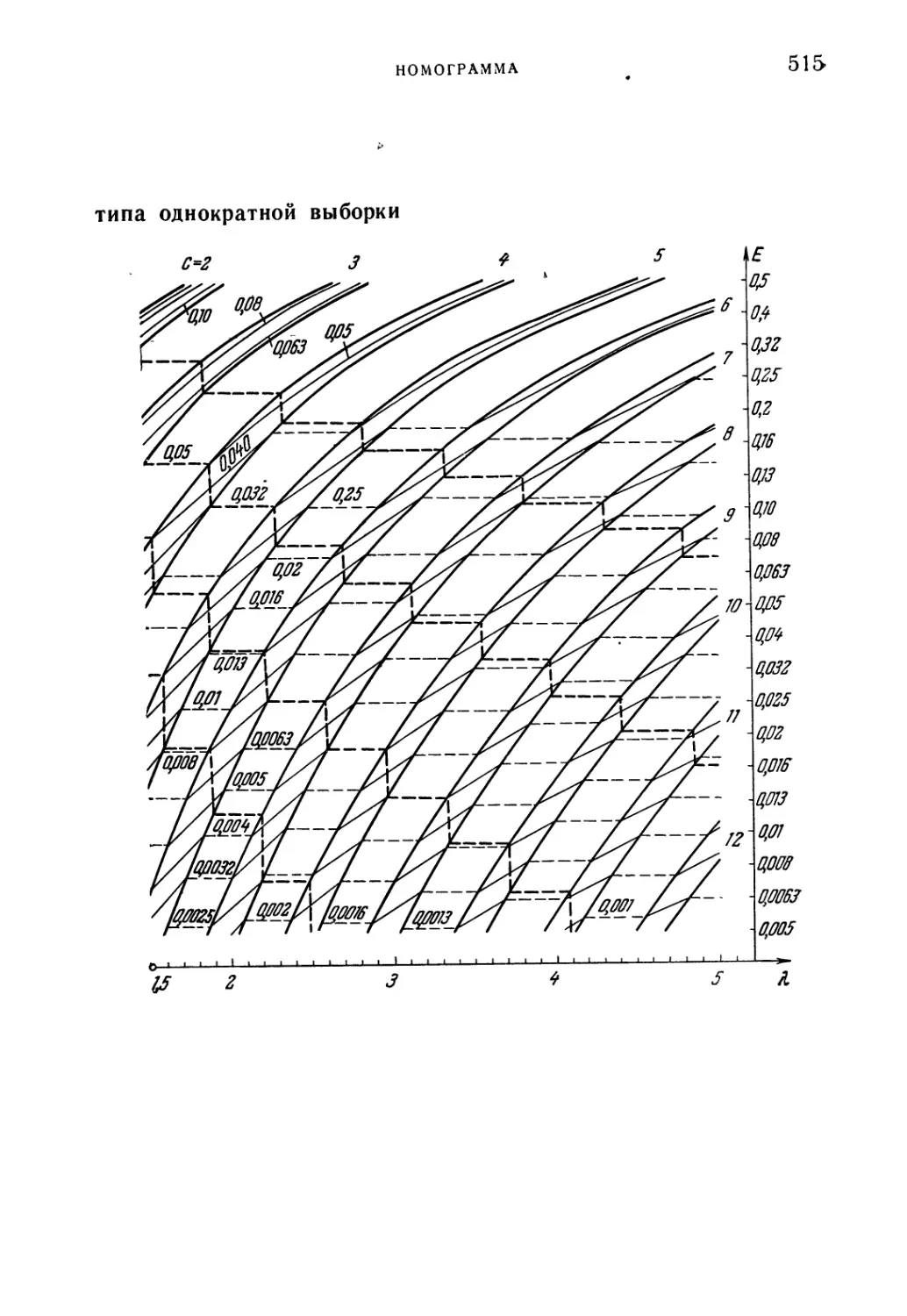
Номограмма 514
Литература 516
Указатель терминов 522
ПРЕДИСЛОВИЕ
Интерес к теории надежности, который сейчас проявляют инже-
инженеры, экономисты, математики, а также организаторы производ-
производства, привел к появлению значительного числа книг, посвященных
общим и специальным ее вопросам (см. литературу к главе 1
[1] — [4]).
Проблемы теории надежности весьма многогранны. В них за-
затрагиваются технологические, экономические, конструктивные, физи-
физико-химические и организационные аспекты и выявляется необходи-
необходимость разработки развитого математического аппарата, приспособ-
приспособленного к специфике выдвигаемых вопросов. В связи с этим есте-
естественно появление книг по теории надежности, освещающих—ее
задачи с разных сторон.
В нашей книге рассмотрены математические методы лишь не-
некоторых разделов теории надежности. Это можно усмотреть уже
из краткого описания содержания книги.
Первая глава носит вводный характер. В ней мы приводим ос-
основные понятия теории вероятностей и математической статисти-
статистики, а также даем формулировки основных теорем, на которые опи-
опираемся впоследствии. В этой же главе дана сводка основных
свойств преобразования Лапласа, необходимых в главах 5 и 6.
Вторая глава посвящена принципиальным вопросам — основ-
основным понятиям теории надежности и выяснению связей между
основными ее числовыми характеристиками. Здесь мы несколько
отступаем от традиционного толкования термина «надежность» и
даем, как нам кажется, достаточно широкий подход, способный
объединить различные определения, предлагавшиеся в научной
литературе. Мы считаем, что теоретико-множественный подход к
теории надежности и ее центральным понятиям в наибольшей сте-
степени способен передать картину изучаемых ею явлений и поэтому
заслуживает достаточно ясного и четкого изложения.
Главы третья и четвертая носят статистический характер.
В них предложены пути оценки параметров надежности на основе
результатов испытаний, а также пути проверки разного типа гипо-
гипотез о надежности. Попутно формулируются и некоторые положе-
ПРЕДИСЛОВИЕ 7
ния математической статистики, на которые мы при этом опира-
опираемся. Значительная часть этих глав посвящена случаю показатель-
показательного распределения, которое пока играет доминирующую роль в
теории надежности.
Главы пятая и шестая изучают важный прием повышения на-
надежности изделий — резервирование. В первой из названных глав
рассмотрены различные задачи резервирования без восстановления,
во второй — резервирование с восстановлением.
Глава седьмая имеет дело с задачами контроля качества про-
продукции. В вопросах текущего контроля мы ограничиваемся при
этом почти исключительно лишь постановками задач. Основное
внимание уделено нами задачам приемочного контроля. Здесь нами
даны некоторые общие схемы, в том числе и такие, которые еще
находятся в состоянии научной разработки. Эта глава стоит
несколько особняком. Ее содержание и изложенные в ней методы
могут быть полезны в первую очередь работникам ОТК, а также
инженерно-техническим работникам, занимающимся вопросами конт-
контроля качества и надежности.
В тексте имеется большое число графиков, многие из них приве-
приведены лишь с целью иллюстрации.
В конце книги помещено большое число таблиц. Если эти
таблицы уже имеются в широко распространенной литературе, то
мы ограничиваемся в них лишь двумя-тремя значащими цифрами.
Если же таблицы труднодоступны или совсем не были опубликованы
на русском языке, то мы приводим их с тем числом знаков, с
каким они приведены в оригинальных работах. Ряд таблиц подсчитан
специально для настоящей книги. Источники, откуда заимствованы
таблицы, указаны в подстрочных примечаниях.
Работа по книге была распределена следующим образом: главы
3, 4 и 7, а также § 2.1 написаны Ю. К. Беляевым; главы 2, 5
и 6~А. Д. Соловьевым; глава 1 и § 4.5 — Б. В. Гнеденко, кото-
которому принадлежит также и согласование всех глав книги. Обсуж-
Обсуждение содержания книги, ее композиции, стиля изложения прово-
проводилось всеми тремя авторами совместно.
В процессе работы над книгой мы получили многое от бесед с
товарищами. Мы пользуемся случаем поблагодарить всех, кто помог
нам своими предложениями, советами, наблюдениями над своеоб-
своеобразием поведения аппаратуры при испытаниях. Особенно мы благо-
благодарны нашему общему учителю А. Н. Колмогорову, прочитавшему
главу 7 и давшему по ней ряд советов. Мы благодарны Я. Б. Шору,
прочитавшему всю рукопись целиком; к сожалению, по независящим
от нас причинам мы не имели возможности воспользоваться всеми
его советами, касающимися расположения материала книги. Ав-
Авторы рады отметить большой труд Т. Н. Топорищевой по вычислению
таблиц; И. А. Ушаков, А. А. Ступаченко и Л. Л. Кристаллинский
8 ПРЕДИСЛОВИЕ
своими беседами существенно дополнили наши сведения об
особенностях тех физических процессов, с которыми приходится
встречаться при проведении испытаний радиоэлектронной аппа-
аппаратуры.
Первоначально мы предполагали в одной книге уместить все
основные результаты, относящиеся к статистическим методам в те-
теории надежности. В процессе работы выяснилось, что эта задача
невыполнима. После того как настоящая часть работы завершена,
авторы предполагают продолжить ее. В новой книге, о которой мы
начали думать, будут затронуты вопросы расчета надежности слож-
сложных систем, оптимального резервирования, оптимального поиска
неисправностей, оптимальной профилактики, прогноза неисправно-
неисправностей, методов ускоренных испытаний, синтеза надежных устройств,
выполняющих логические операции. В предполагаемой книге найдут
отражение новые статистические методы исследования — планирова-
планирование эксперимента, теория управляемых случайных процессов и др.
Настоящая книга предназначена не для беглого просмотра,
а требует от читателя значительного внимания, а также системати-
систематического проведения необходимых вспомогательных выкладок. Осо-
Особенно это относится к главам 3 — 6. Главы 2 и 7 можно читать
независимо от других. Быть может, при изучении глав 3 и 4
полезно иметь под руками хорошую книгу по математической
статистике (например, [7] — [10] по списку литературы к гл. 1).
Впрочем, книга может быть использована и для справок, поскольку
мы стремились основные формулы сводить в специальные справоч-
справочные таблицы, а также достаточно выпукло выделять их в тексте.
Авторы отдают себе ясный отчет в том, что книга не свободна
от недостатков. Поэтому мы обращаемся с просьбой ко всем чи-
читателям сообщать нам пожелания по улучшению книги и инфор-
информацию о замеченных недочетах любому из авторов по адресу:
Москва, В-234, МГУ, Механико-математический факультет, Ка-
Кафедра теории вероятностей.
ВВЕДЕНИЕ
В связи с развитием современной техники особую важность-
приобрели многочисленные вопросы повышения эффективности
различного рода устройств. Комплексная автоматизация произ-
производственных процессов ставит перед управляющими устройствами
исключительно ответственные задачи, которые должны выполняться
безупречно на протяжении всего периода работы автоматической
линии, автоматизированного цеха или предприятия. Перерыв в
работе управляющего устройства может привести не только к
ухудшению качества производимой продукции или к полному
прекращению производственного процесса, но и к весьма серьез-
серьезным авариям, выходящим за локальные рамки предприятия. Тре-
Требования к безотказности механизмов и разного рода устройств
приходится, конечно, предъявлять не только к тем из них, кото-
которым поручено управление теми или иными процессами. К любому
техническому устройству и изделию мы вынуждены предъявлять
эти условия. Какой смысл в самолете, который не может безот-
безотказно совершать перелеты? Какой смысл в тракторе, который не
в состоянии выполнять поручаемые ему работы, или в автомобиле,
который не в состоянии перевозить грузы или пассажиров? Совре-
Современная медицина широко использует разного рода технические
средства как для диагностических и исследовательских целей, так
и для выполнения ответственных функций во время и после опера-
операции. К их работе приходится предъявлять особо высокие требо-
требования, так как перебои в работе, скажем, искусственного сердца
во время операции на сердце могут привести к летальному исходу.
С многочисленными примерами, в которых качество продукции
играет основную роль, каждый из нас встречается в повседневной
жизни.
Общая научная дисциплина, изучающая общие методы и при-
приемы, которых следует придерживаться при проектировании, изго-
изготовлении, приемке, транспортировке и эксплуатации изделий для
обеспечения максимальной их эффективности в процессе исполь-
использования, а также разрабатывающая общие методы расчета ка-
качества устройств по известным качествам составляющих их частей»
10 ВВЕДЕНИЕ
получила название теории надежности. Теория надежности устанав-
устанавливает закономерности возникновения отказов устройств и методы
их прогнозирования; изыскивает способы повышения надежности
изделий при конструировании и последующем изготовлении, а
также приемы поддержания надежности во время их хранения и
эксплуатации; разрабатывает методы проверки надежности изде-
изделий и способы контроля надежности при приемке больших партий
продукции. Теория надежности вводит в рассмотрение количест-
количественные показатели качества продукции.
Несомненно, что теория надежности является наукой комплекс-
комплексной, относящейся в первую очередь к компетенции инженера,
физика, химика и экономиста. Однако большое число вопросов
теории надежности по своему существу носит математический
характер и требует для своего разрешения как уже известных
математических средств, так и разработки новых. Более того,
если желать науку о надежности сделать способной к точным
заключениям и выводам, если стремиться вывести ее из состояния
чисто качественных, а порой и сугубо субъективных заключений,
мы обязательно должны обратиться к языку математики. Утверж-
Утверждения типа: «я уверен, что такая конструкция будет надежнее,
чем иная», «мы убеждены, что наша продукция лучше, чем изго-
изготовляемая соседним предприятием», которые не имеют иных под-
подтверждений, кроме личной уверенности, не могут служить осно-
основой для надежных выводов.
Для исследования и решения значительной части вопросов, воз-
возникающих в теории надежности, оказываются необходимыми ме-
методы теории вероятностей и математической статистики. Это вы-
вызвано существом дела, а не специфическими интересами тех, кто
работает теперь в теории надежности. Как бы мы ни стремились
к сохранению условий постоянства в процессе производства, од-
однородности исходных материалов и неизменности технологии из-
изготовления, неизбежные колебания всех этих компонент приводят
к существенному разбросу свойств готовых изделий. Молекулярные
свойства веществ, играющие исключительную роль при изготовлении
полупроводниковых и электронных приборов, не теряют своего
значения и для механических устройств. Процессы износа и упроч-
упрочнения материалов неизбежно приводят к необходимости изучения
их молекулярной структуры. Вместе с молекулярной структурой
вещества в теорию надежности вносятся и математические методы,
свойственные этой части физики, — методы теории вероятностей и
математической статистики. Далее, в процессе эксплуатации изде-
изделия попадают в разные условия: автомобилю приходится передви-
передвигаться как по совершенным дорогам, так и по проселку. В резуль-
результате он подвергается не только переменным, но и случайным
воздействиям. В процессе изложения мы будем неоднократно ветре-
ВВЕДЕНИЕ И
чаться с реальными примерами, которые проиллюстрируют это общее
положение. Если мы изготовили в определенных условиях из одной
и той же партии сырья большое число определенного типа изделий
и затем собрали статистические данные о длительности их беспе-
бесперебойной работы, то выясняется весьма специфическая картина:
длительность безотказной работы изделия имеет значительный разброс
и в отношении каждого определенного изделия нет возможности
точно предсказать длительность его службы. В то же время отно-
относительно больших партий этих изделий можно делать достаточно
определенные предсказания о доле их, способной проработать то
или иное время, о причинах поломок изделий и пр. В результате
мы оказываемся в типичной обстановке, с которой имеет дело ма-
математическая статистика.
Обратим внимание на то, что перед теорией надежности зачастую
возникают взаимно противоречивые задачи. В связи с усложнением
функций, которые поручаются различного типа устройствам, эти
устройства включают в себя все большее число элементов. Увели-
Увеличение числа элементов приводит к уменьшению надежности их
совокупного действия. Но в то же время ответственность выпол-
выполняемых устройствами заданий требует от них все большей надеж-
надежности. Разрешение возникающего противоречия требует самого
тщательного и всестороннего исследования проблем повышения на-
надежности элементов и устройств: возможность и целесообразность
повышения надежности отдельных элементов, выбор режимов работы,
отыскание целесообразных схем и конструктивных решений, расчет
резервирования и оптимальных режимов профилактики и пр. Сле-
Следует подчеркнуть такую, казалось бы, самоочевидную истину, что
повышение надежности не дается даром и ее получение требует
как определенных материальных затрат, так и систематических
научных поисков.
Отметим, что одной из весьма заманчивых задач теории надеж-
надежности должна явиться разработка таких принципов конструиро-
конструирования сложной аппаратуры, которые позволяли бы получать уст-
устройства, способные сохранять рабочее состояние даже при выходе
из рабочего состояния некоторой части составляющих их элементов.
Биологические системы в высокой степени обладают этим ценнейшим
свойством. Изучение биологических систем с точки зрения принципов
их устройства и обеспечения надежности может дать в руки техники
исключительно богатый набор средств и приемов, полезных для
технического осуществления. Мы убеждены, что природа шла не
только по линии расточительного резервирования, но в первую
очередь по пути выбора оптимальных схемных решений, тщатель-
тщательного отбора элементов, способных сохранять исключительную
устойчивость в работе. Несомненно, что изучение особенностей
биологических систем с позиций теории надежности позволит
12 ВВЕДЕНИЕ
открыть и новые принципы, которые не приходят в голову, когда
к техническим задачам подходят исключительно с позиций тради-
традиционной техники.
О повышении надежности изделий сейчас говорят не тольк о
инженеры и ученые, но и государственные деятели. Нередко повы-
повышение надежности изделий называют проблемой номер один. И это
не дань моде, а настоятельное требование времени и эпохи. Во
вводной главе недавно вышедшей книги двух американских авторов,
Дэвида Ллойда и Мирона Липова, сказано несколько фраз, которые
мы хотели бы здесь воспроизвести. «Ненадежность сказывается на
стоимости, на временных затратах, психологически— в виде неудобств,
а в определенных случаях грозит также безопасности людей и на-
нации. Обычно потери за счет ненадежности представляют собой не
только стоимость выходящего из строя агрегата, но также и стои-
стоимость связанного с ним оборудования, которое портится или раз-
разрушается в результате отказа... Классическим примером психологи-
психологического эффекта ненадежности являются печальной памяти спутники
«Авангард». Соединенные Штаты, остро переживая успехи России,
запустившей Спутник-1, попытались вступить в соревнование,
использовав для этого почти не испытанную ракету, которой при-
пришлось работать почти на пределе своих возможностей. Неудачи и
последовавшие за этим уныние и потеря престижа были очень
серьезны».
В соответствии с теми задачами теории надежности, которые
были нами обрисованы, естественно возникает несколько групп
вопросов, относящихся к обеспечению надежности. На первой стадии
создания изделия, когда его еще нет и появилась только мысль
о нем, уже необходимо думать об его надежности: какие материалы
наилучшим образом способны выдерживать те нагрузки, которые
предстоят во время работы изделию; какие схемы особенно благо-
благоприятны для того, чтобы сохранять устойчивость к внешним воз-
воздействиям; какие режимы следует выбирать дяя работы изделия;
как обеспечить сохранность работоспособности при перегрузках
и т. д. Конструирование изделия завершено, перед запуском в серию
оно должно быть испытано. Испытания на этой стадии создания
обязательно должны предусматривать и проверку надежности изде-
изделия. Здесь очень важно отметить, что испытания должны быть
достаточно представительными, чтобы по ним можно было судить
не только об этих изделиях, изготовленных в тепличных условиях,
но и об изделиях, которые будут изготовляться серийно. На этой
стадии следует также разработать систему правил, которых следует
придерживаться при изготовлении изделий на заводе, приемке,
транспортировке и эксплуатации для наилучшего сохранения надеж-
надежности в работе. Третья стадия обеспечения надежности наступает
после сдачи принятого к производству изделия на предприятие.
ВВЕДЕНИЕ 13
После тщательной проверки схемы необходимо убедиться в качестве
исходных материалов, производственного оборудования, точности
обработки, соответствия технологического процесса техническому
заданию. Никакие временные отступления от задания не допустимы
ни на одной операции.
Проверка качества исполнения может осуществляться многими
путями. Для массового и крупносерийного производства, в част-
частности,— методами текущего статистического контроля. Изготовлена
партия, для проверки надежности изделий должны быть разрабо-
разработаны методы испытаний, а также планы проверки качества, вклю-
включающие в себя количество испытываемых изделий, длительность и
характер проверки. Для периода эксплуатации необходимо разра-
разработать меры обеспечения надежности, включающие в себя перио-
периодичность профилактических осмотров, замену элементов, правила
поиска неисправностей и пр. Расчет надежности, естественно, должен
производиться на стадии проектирования. Подавляющая часть
отмеченных здесь требований носит не математический, а чисто
инженерный характер.
Физико-химические процессы, приводящие к отказам элементов
и изделий, очень сложны. Их природа исследована до сих пор в
очень малой степени. Как правило, число параметров, которые
необходимо учитывать при построении математических моделей
явлений старения, постепенного изменения свойств изделий и др.,
очень велико. Уже одно это обстоятельство должно приводить к
необходимости разработки новых математических методов исследо-
исследования. Мы убеждены, что в самые ближайшие годы теория надеж-
надежности явится источником многих новых математических задач, а
также новых математических теорий. Уже сейчас ясно, что методы
математической статистики, теории вероятностей, демографии, тео-
теории эксперимента нуждаются в серьезном развитии, чтобы они
могли в достаточно полной мере способствовать развитию теории
надежности.
ГЛАВА 1
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
§ 1.1. Понятие случайного события. Основные формулы
теории вероятностей
Представление о случайном событии как о событии, относительно
наступления которого нельзя высказать суждений с полной опре-
определенностью, интуитивно ясно. Однако чтобы стать объектом
математического исследования и получить серьезное прикладное
значение, представление это требует серьезного уточнения. Дейст-
Действительно, одного утверждения, что пробой конденсатора в период
испытания представляет собой случайное событие, для практики
недостаточно. Нам всегда необходимо знать также, как часто
может наступить это событие при испытании большого числа конден-
конденсаторов. Точно так же для практики недостаточно только одного
знания, что автомобиль может пройти без капитального ремонта
двести тысяч километров. Для оценки качества автомобилей важно
выяснение того, как часто может произойти такого рода событие.
Поскольку в теории надежности приходится использовать понятие
случайного события во всей общности и общепринятая система
изложения полезна не только для введения понятий теории вероят-
вероятностей и математической статистики, но и для отчетливого выясне-
выяснения понятий самой теории надежности, мы предпочтем сразу
ввести читателя в общие идеи аксиоматического определения
случайного события и его вероятности, предложенные А. Н. Кол-
Колмогоровым.
Понятие случайного события в концепции, предложенной
Колмогоровым и получившей всеобщее признание, не является пер-
первичным, а строится на базе понятия элементарного события.
Предполагается, что имеется некоторое множество U элементов,
тесно связанное с изучаемой задачей. Природа этого множества,
важная для понимания физической сути задачи, не играет роли
при логическом построении теории вероятностей. Далее рассмат-
§ 1.1] СЛУЧАЙНЫЕ СОБЫТИЯ. ФОРМУЛЫ IS
ривается система $f подмножеств множества U, которая обладает
следующими свойствами:
1°. Система gf в качестве элемента содержит все мно-
множество U.
2°. Если 31 и 23 cj;/»& подмножества множества И и входят-
в % в качестве элементов, то $ содержит также множества
Яи», $ПЗЗ, ^и S).
Как принято в теории множеств, через 91U S3 мы обозначаем
сумму 31 и 23, т. е. множество, каждый элемент которого принад-
принадлежит по меньшей мере одному из множеств 31 и 23; через 3Ifl23
обозначаем пересечение 31 и 23, т. е. множество всех тех и только
тех элементов II, которые принадлежат сразу и 31 и 23; 31 означает
множество тех элементов Ц, которые не входят в 31, т. е. допол-
дополнение 31 до множества Ц.
Поскольку ^ содержит в качестве элемента U, то по требова-
требованию 2°$ обязано содержать также U, т. е. множество без
элементов — пустое множество.
Легко понять, что второе требование влечет за собой принад-
принадлежность к $ сумм и пересечений любого конечного числа мно-
множеств, принадлежащих ?у.
Каждый элемент множества $ называется случайным событием.
Проиллюстрируем сказанное простым примером. Обозначим через
т длительность жизни некоторого изделия в определенных условиях
эксплуатации или испытаний. Примем за исходное множество IX.
все неотрицательные числа, т. е. все мыслимые сроки жизни изделия.
Элементарное событие x = t означает, что изделие проработало в
^точности время t, а затем испортилось. В частности, t = 0 означает,
что изделие испортилось немедленно при включении его в работу.
Предположим теперь, что всякое множество типа т ^ t входит в
систему ?у. Случайное событие т^ t означает, очевидно, что изде-
изделие проработает время не меньшее, чем i. При / = 0 мы получаем
все множество U. Таким образом, первое требование, которое мы,
высказали относительно системы ??, выполнено. Однако система ?у
гораздо богаче элементами, чем те, которые только что были
указаны. Действительно, в силу второго требования наряду с мно-
множествами т^аит^^(с<&) система % содержит также множества
т < а, т <ib и а^% <ib. Мы не станем входить в более подробное
изучение структуры системы.
Может случиться, что для тех или иных целей нам важно
следить за несколькими параметрами, например за диаметром вала,
его конусностью и сопротивлением на изгиб. Пусть возможные
значения диаметра лежат в пределах a^d^b, конусности р —
^Нередко употребляются также обозначения 5*1193 =
9Ш. SI—множество тех элементов 31, которые не входят в
16 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
в пределах а^р^р и сопротивления на изгиб R — в пределах
r1^R^r2i тогда множество элементарных состояний характери-
характеризуется точками трехмерного пространства (d, р, /?), лежащими в
параллелепипеде, определенном ранее написанными неравенствами.
Во многих задачах система ^, подчиненная только ранее указан-
указанным двум требованиям, оказывается слишком бедной и должна быть
пополнена случайными событиями более тонкой природы. В частности,
такое расширение требуется обычно для разного рода предельных пе-
переходов. Мы потребуем от множества $ дополнительно следующего:
3°. Если подмножества Шх, 3B> Sf3> • • • множества U явля-
являются элементами множества gs то их сумма (J Щ и пересече-
пересечение Г) Щ также являются элементами ?у.
Множество $, удовлетворяющее требованиям 1°—3°, называется
полем событий или же G-алгеброй. Последний термин вошел теперь
в теоретико-вероятностной литературе во всеобщее употребление.
В теории вероятностей принята специфическая терминология,
мы считаем нужным ввести ее теперь же.
Если два случайных события А и В не имеют в своем составе
одних и тех же элементов, то они называются несовместимыми
событиями. События 11 и 11 называются соответственно достовер-
достоверным и невозможным событиями. События А и А называются про-
противоположными.
Для приведенного нами примера достоверно, что длительность
жизни изделия будет заключена в пределах от 0 до оо; события
а^х^Ь и c^x^d, если Ь<Сс, несовместимы; события т ^ а
и х > а при любом а > 0 противоположны.
Понятие вероятности случайного события вводится аксиомати-
аксиоматически с помощью следующих аксиом.
1. Каждому случайному событию А из поля ^ поставлено
в соответствие неотрицательное число Р {Л}, называемое его
вероятностью.
2. P{U} = 1.
3. Если события А и В несовместны, то
Последняя аксиома называется аксиомой сложения веро-
вероятностей.
Приведенные аксиомы позволяют получить ряд важных выводов
относительно вероятностей случайных событий.
Вероятность невозможного события равна нулю: Р{Щ = 0; для
любого случайного события А 0^Р{Л}<;1; вероятности противо-
противоположных событий А и А связаны равенством
Р{Л} = 1-Р{Л}. A.1.1)
§ 1.1] СЛУЧАЙНЫЕ СОБЫТИЯ. ФОРМУЛЫ 17
Говорят, что случайное событие А влечет за собой событие В,
если множество В содержит в себе все элементы, составляющие
множество Л. В нашем примере событие А = {т ^ а} влечет за
собой событие В={х^Ь}, если а<.Ь.
Если событие А влечет за собой событие В, то Р{Л}^Р{/?}.
Для произвольных событий А и В имеет место теорема сло-
сложения
Р{АиВ} = Р{А} + ?{В}-Р{АПВ}. A.1.2)
Отсюда вытекают очевидное неравенство
также его обобщение: для любого конечного числа событий
ц ^2> • • • » А* имеет место неравенство
Л/1}. A.1.3)
Построение теории вероятностей во всей полноте требует допол-
дополнительной аксиомы.
Расширенная аксиома сложения. Если событие А
равносильно наступлению хотя бы одного из попарно несовме-
несовместимых событии Ах, Л2, . .. , Ап1 ... , то
В реальных задачах постоянно приходится иметь дело с таким*
положением вещей, когда требуется найти вероятность некоторого
события А при дополнительном условии, что некоторое другое
событие В наступило. Вообще говоря, это дополнительное зна-
знание меняет вероятности событий. Для примера, если мы знаем, что
некоторое изделие уже проработало время Г, то вероятность ему
проработать еще время /, как правило, больше вероятности того,
что начавшее работать изделие проработает срок T-\-t.
Если нужно найти вероятность некоторого события А при усло-
условии, что событие В, имеющее положительную вероятность, уже
наступило, то эту искомую вероятность называют условной веро-
вероятностью и обозначают символом Р {А\В} или же символом Рв {А}.
Строго говоря, всякая вероятность (и безусловная, и условная)
является условной, поскольку о случайном событии и его вероят-
вероятности имеет смысл говорить лишь тогда, когда могут происходить
лишь события, входящие в семейство ?у. Кроме того, сами вероят-
вероятности событий существенно зависят от тех внешних условий, в
которых находится наша система. Для примера рассмотрим дли-
длительность т жизни некоторого изделия при двух различных комп-
комплексах условий. Первый комплекс условий состоит в том,
что изделие работает при постоянной температуре t0 в отсутствие
вибраций. Если эти условия изменяются, температура повысится
2 В. В. Гнеденко и др.
18 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
до tx или же появятся вибрации —в т о р о й комплекс усло-
условий, то вместе с ними, вообще говоря, изменится и вероятность
события т<а. Таким образом, когда говорят о вероятности слу-
случайного события, то всегда предполагают, что имеется некоторый
комплекс условий, при выполнении которого и рассматривается это
случайное событие.
В теории надежности мы тоже не можем говорить о надежности
изделия безотносительно к тем условиям, в которых ему придется
работать. Надежность автомобиля существенно зависит от того,
придется ли ему работать в условиях крайнего севера, Москвы или
песчаной пустыни. При этом может случиться, что исходное мно-
множество U элементарных событий не изменится, но изменятся веро-
вероятности интересующих нас случайных событий.
В силу ряда причин условная вероятность события Л при усло-
условии, что В произошло, определяется посредством равенства
Отсюда, в частности, получаем, что Р{?|?} = 1; это равенство
естественно было ожидать, поскольку нам уже достоверно известно,
что событие В произошло.
Из только что данного определения условной вероятности мы
получаем важное равенство
которое носит название теоремы умножения вероятно-
вероятностей. Так как
A.1.5)
то из последних двух равенств мы делаем заключение
Р {А} Р {В\А}=Р{В} Р {А\В}. A.1.6)
Говорят, что событие А не зависит от В, если Р [А\В] = Р {А}.
Как показывает предыдущее равенство, независимость является
свойством взаимным, т. е. если А не зависит от В, то и В не
зависит от А.
Предположим теперь, что событие В может осуществляться с
одним из п несовместимых событий Av Л2, .. . , Ап. При этих усло-
условиях имеет место важная формула полной вероятности:
Р{Я}=2Р{Л,.}Р{ЯИ,}. A.1.7)
Проиллюстрируем эту формулу простым примером. Пусть не-
некоторые детали (например, конденсаторы) поставляются тремя заво-
§ 1.11
СЛУЧАЙНЫЕ СОБЫТИЯ. ФОРМУЛЫ 19
дами причем вероятность того, что данное изделие изготовлено
1 3 1
на первом заводе, равна -^ , на втором — -^ и на третьем —-^ .
Вероятности того, что при определенных условиях работы конден-
конденсатор сохранит работоспособность в течение времени Г, для пер-
первого, второго и третьего заводов соответственно равны 0,9; 0,92;
0,808. Чему равна вероятность того, что наудачу взятый конденсатор
из имеющегося запаса сохранит работоспособность в течение
времени Г? Этот конденсатор может оказаться с первого (событие Аг)у
второго (событие А2) или третьего завода (событие Л3). Согласно
формуле, интересующее нас событие (событие В) имеет вероятность
р {В} =-0,2.0,9 + 0,3.0,92 + 0,5-0,808 = 0,86.
Мы остановимся теперь еще на одной формуле, которая носит
название теоремы Бейеса. Пусть по-прежнему событие В мо-
может произо?гти~ттгБк"ог вместе с одним из несовместимых событий
у4(/==1, 2, ... , п). В результате испытания оказалось, что собы-
событие В наступило. Какова вероятность того, что оно наступило
вместе с событием Ар Нам нужно найти вероятность Р {Д^Я}.
Согласно равенству A.1.6) находим, что
Вероятность Р {В} может быть вычислена по формуле A.1.7).
Пусть в только что приведенном примере конденсатор не выдер-
выдержал установленного срока работы и отказал. Каковы вероятности
того, что он был с первого, второго или третьего заводов? Вычис-
Вычисления по формуле A.1.8) приводят нас к таким результатам:
Р{Л1|Б} = 0,143; Р{Ла|Д} = 0,171; Р {А3\В} =0,686.
Мы видим, что, после того как становятся известными результаты
испытаний, априорная (доопытная) оценка неизвестных вероятностей
существенно изменяется.
В дальнейшем нам потребуется обобщение понятия независи-
независимости на случай нескольких событий. Мы скажем, что события
Аг, А2, ... , As независимы в совокупности, если для любой группы
Av Av • • • » A* (k*^s) из них выполнены равенства
г г = 1 г
Для независимости в совокупности недостаточно, чтобы были
независимы каждые два события.
Рассмотрим теперь задачу на применение общих правил.
уНайти вероятность того, что некоторое изделие проработает
не меньше, чем время /, если вероятность отказа изделия за
2
i*
20 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
промежуток (t, t-\-h), когда оно проработало уже время ty равна
a(t)h + o(h).
Обозначим через р (t) вероятность того, что изделие прорабо-
проработает по меньшей мере срок t\ тогда в силу условия
p(t + h)=p(t)(\-a(t)h-o(h)).
Отсюда находим, что
p'(t) = — a(t)p{t)
и, значит,
Так как при / = 0 изделие работало, то р @) = 1 и, следовательно,
С=1. Итак,
Если a{t) = a, т. е. вероятность изделию проработать еще не-
некоторое время не зависит от того, сколько оно уже проработало, то
В демографии при составлении таблиц смертности для взрослого
населения нередко пользуются формулой Макетам а, соглас-
согласно которой
Предположение Макегама означает, что смертность происходит
под влиянием двух составляющих: одной, не зависящей от возра-
возраста, и другой, увеличивающейся (при Y>0) или уменьшающейся
(при у<0) в геометрической прогрессии с возрастом. При сделан-
сделанном дополнительном предположении находим, что
p(/) = e-at"-P(eT'-1). A.1.9)
В теории надежности большую роль играет так называемая
схема Бернулли. Предположим, что производится последова-
последовательность п независимых испытаний, в каждом из которых собы-
событие А может произойти с одной и той же вероятностью р. Спра-
Спрашивается, чему равна вероятность того, что событие Л произой-
произойдет при т каких-то испытаниях, а при остальных п—т не про-
произойдет. Если обозначить эту вероятность через Рп{т) и ввести
обозначение q=l—ру то имеет место формула Бернулли
А 1#1] СЛУЧАЙНЫЕ СОБЫТИЯ. ФОРМУЛЫ 21
здесь С% означает число сочетаний из п элементов по т, равное,
как известно, mi(/|lm)| .
Если, для примера, на стенде поставлены на испытания 20 ламп
и вероятность выхода лампы из строя за период испытания рав-
равна 0,1, то вероятности Р20@), Р2о0)> Р2оB) бУДУт соответственно
равны
0,920, 2-0,919, 1,90,918;
вероятность же того, что за время испытаний откажет не более
четырех ламп, равна
S с2тоо,го,э2°-от.
В теории надежности нередко рассматривают так называемое
отрицательное биномиальное распределение, появляющееся из
•следующей модели. Представим себе, что производятся незави-
независимые наблюдения, в каждом из которых некоторое событие
Л (например, проббй конденсатора) может произойти с вероят-
вероятностью р. Испытания повторяются до тех пор, пока не появится
k раз событие Л. Спрашивается, чему равна вероятность того,
что потребуется ровно п наблюдений?
Из самой постановки задачи ясно, что последнее испытание
должно принести наступление события Л, а в предыдущих
п—1 как-то расположатся k—1 ранее наступивших событий.
Вероятность того, что в последнем испытании наступит событие Л,
равн# /?, а вероятность того, что в п — 1 предшествующих испы-
испытаниях как-то разместятся k—1 появлений Л, согласно схеме
Бернулли равна CknZ\Pk~x4n~k- Таким образом, искомая вероят-
вероятность равна
Здесь \х может принимать значения &, ?+1, ? + 2, ...
Обозначим через у величину (х — к, т. е. число испытаний,
которое нужно провести сверх k для завершения требуемой про-
процедуры. Тогда
Cr^1-iPV. A.1.10)
Величина v может принимать значения 0, 1, 2, ...
Легко убедиться, что общий член разложения произведения
по степеням q равен как раз вероятности P{v = r}. В силу это-
этого говорят, что величина v имеет отрицательное биномиальное
22 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ |ГЛ. 1
распределение вероятностей, тогда как обычное биномиальное рас-
распределение получается аналогичным образом, но с заменой —k на к.
Наряду с формулами Бернулли в теории надежности значи-
значительную роль играет одна схема, которая зачастую носит назва-
название схемы невозвращенного шара. Представим себе, что имеется
N предметов, среди которых М обладают определенным свойством
/4, а остальные этим свойством не обладают. Из совокупности N
имеющихся предметов наудачу выбираются п. Спрашивается, чему
равна вероятность того, что среди вынутых предметов т обладают
свойством А, а остальные п — т им не обладают?
Очевидно, что т может принимать лишь значения
/0 = max@, n — N + M), /0+1, /0 + 2, ,. .., min (Ж, п).
Вели же п меньше, чем М и N—M, то т может принимать любые
значения от 0 до л.
Несложные рассуждения приводят нас к равенству
рТП /~* П — tit
р М N-М
Г т рп
U N
Для практических целей особенно интересен случай, когда М зна-
значительно меньше, чем N, и п мало по сравнению с N. В этом
важном для теории надежности случае, очевидно, т может при-
принимать значения 0, 1, 2, .. ., min (/И, п).
Одна из задач, для которых используется приведенная формула,
состоит в следующем: известно, что в партии из N штук изделий
содержится М бракованных. Производится случайная выборка из
этой партии в п штук. Чему равна вероятность того, что в выборке
окажется т дефектных изделий?
§ 1.2. Случайные величины и их функции
распределения
Хорошо известно, что основные характеристики надежности
изделий (длительность безотказной работы, время восстановления,
величина износа за определенный срок и др.), изготовленных,
казалось бы, в одних и тех же условиях и из одних и тех же
исходных материалов, имеют значительный разброс. Для примера
в таблице 1.2.1 приведены данные испытаний на усталость при
консольном изгибе образцов из сплава В 95. Длительность работы
образца измеряется числом N циклов до разрушения. Всего испы-
испытано 463 образца. Результаты испытаний разбиты на группы
в зависимости от величины логарифма числа N.
Таким образом, если взять какое-нибудь из большого числа
изделий, то заранее нельзя предсказать, как долго оно будет
§ 1.21
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 23
Таблица 1.2.1
log jV
4,60—4,65
4,65—4,70
4,70—4,75
4,75—4,80
4,80—4,85
4,85—4,90
4,90—4,95
4,95—5,00
5,00—5,05
Численность
группы
2
3
3
12
12
20
18
27
41
log N
5,05—5,10
5,10—5,15
5,15—5,20
5,20—5,25
5,25—5,30
5,30—5,35
5,35-5,40
5,40—5,45
5,45—5,50
Численнос1Ь
группы
43
41
45
42
38
22
24
14
18
log N
5,50—5,55
5,55—5,60
5,60—5,65
5,65—5,70
5,70-5,75
5,75—5,80
5,80—5,85
5,85—5,90
Численность
группы
12
8
10
5
1
1
1
0
работать. Однако на основании соответствующим образом постав-
поставленных испытаний можно указать, в каком проценте случаев это
изделие способно проработать тот или иной срок. Иными словами,
для любых заданных а и b(a<C.b) можно оценить вероятность
того, что изделие проработает срок, не меньший а и не больший Ь.
Таким образом, для теории и практики надежности необходимо
научиться оперировать со случайными величинами, т. е. с вели-
величинами, которые в зависимости от случая могут принимать те или
иные значения.
(Чтобы охарактеризовать случайную-величину, необходимо ука-
указать, во-первых, какие значения она может принимать, т. е. мно-
множество возможных ее значений, и, во-вторых, вероятности этих
значений. Если случайная величина может принимать только конеч-
конечное или счетное множество значений, то охарактеризовать эту
величину просто: достаточно перечислить ее возможные значения
и указать те вероятности, с какими она их принимает. Для иллюст-
иллюстрации рассмотрим два примера, с которыми мы познакомились
в предыдущем параграфе.
Пример 1. Число^ появлений события А при п независимых
испытаниях, в каждом из которых А может произойти с одной
и той же вероятностью р, представляет собой случайную величину,
способную принять только значения 0, 1, 2, . .., п. Как мы знаем,
вероятность того, что событие А наступит ровно при т испытаниях,
равна Рп(т) = С%рт(\—р)п~т. Рассматриваемая случайная вели-
величина называется биномиально распределенной, а совокуп-
совокупность соответствующих вероятностей — биномиальным распреде-
распределением.
Пример 2. Гипергеометрическое распределение. Случайную
величину (рассмотренную в § 1.1, стр. 22), принимающую цело-
24 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
численные значения /я = 0, 1, 2, ..., min(M, n) с вероятностями
называют распределенной по гипергеометрическому закону.
Только что рассмотренный метод задания случайной величины,
однако, нельзя использовать для всех случайных величин. Дейст-
Действительно, если множество возможных значений несчетно, то при-
приписать каждому возможному значению определенную вероятность
уже нельзя. Возникает задача разыскания такого приема, который
был бы применим во всех случаях. Одним из самых распростра-
распространенных приемов такого рода является использование понятия
функции распределения. Функцией распределения случайной вели-
величины ? называется вероятность того, что | примет значение мень-
меньшее, чем х,
Здесь аргумент х может принимать любое действительное значение.
Любая функция распределения обладает следующими свойст-
свойствами: при увеличении х функция /^ (х) не убывает, т. е. если
*2>*1> Т0
Для нее существуют пределы
/^(-foo)= lim p^(x)=z\y /^(_oo)= Hm /^(*)=0.
X -> +со х -> -ос
Вероятность того, что ? примет значение, меньшее b и не мень-
меньшее а, т. е. вероятность неравенства
вычисляется по формуле
P{e<S<ft} = f6(*)-Fe(a).
Для любого с имеет место равенство
Таким образом, если функция /^ (х) в точке с непрерывна, то
вероятность того, что | примет в точности значение с, равна 0.
Если же в точке с функция F^(x) имеет скачок, то величина
этого скачка равна вероятности того, что ? примет значение с.
На каждую неубывающую функцию F(x), для которой
lim F(x) = \, lim
§ 1.2]
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
25
и при произвольном х
lim
можно смотреть как на некоторую функцию распределения. Для
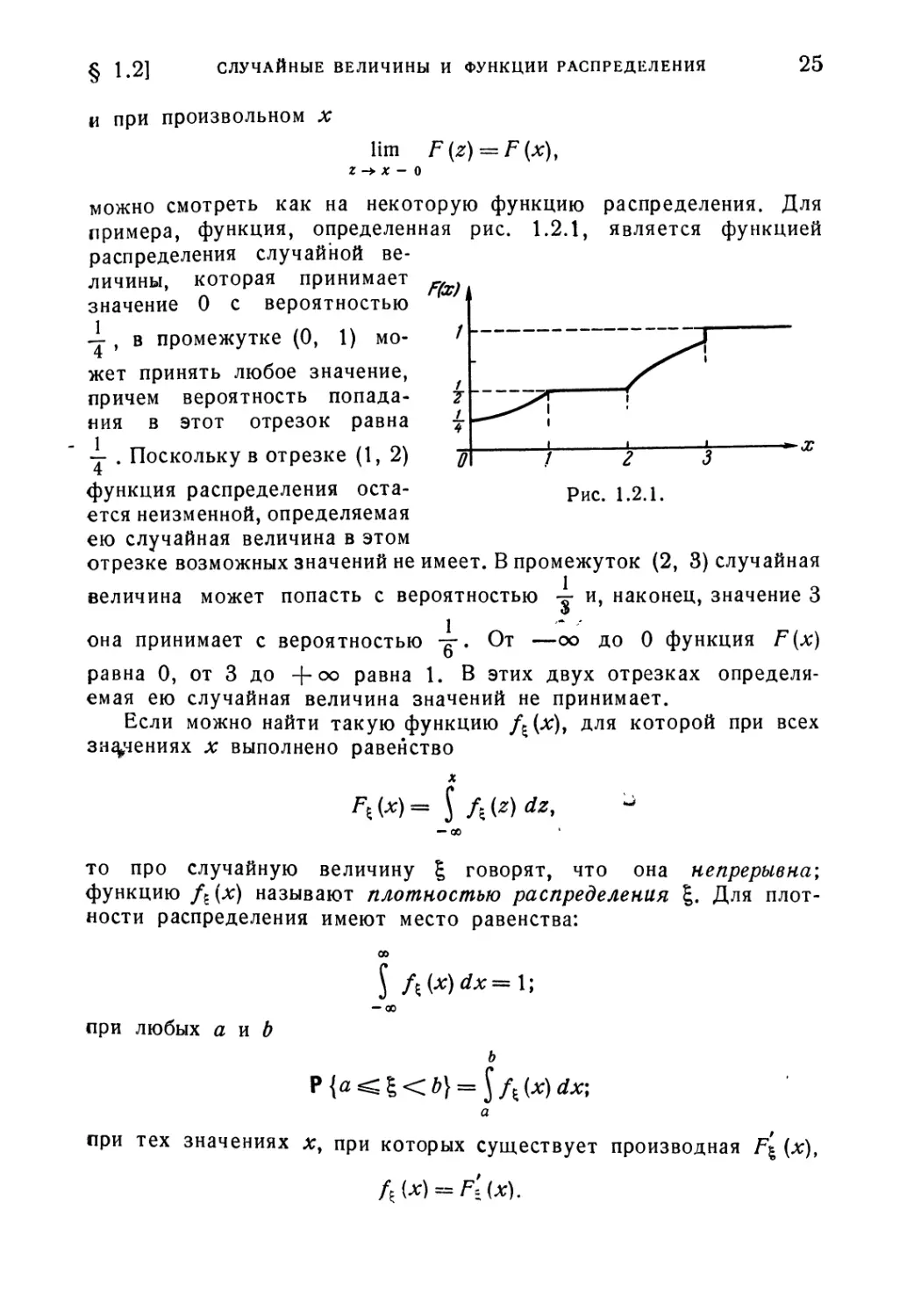
примера, функция, определенная рис. 1.2.1, является функцией
распределения случайной ве-
величины, которая принимает ^
значение 0 с вероятностью
~ , в промежутке @, 1) мо-
может принять любое значение,
причем вероятность попада-
попадания в этот отрезок равна
— . Поскольку в отрезке A, 2)
функция распределения оста- рис> 12.1.
ется неизменной, определяемая
ею случайная величина в этом
отрезке возможных значений не имеет. В промежуток B, 3) случайная
величина может попасть с вероятностью -^ и, наконец, значение 3
1
0
— \
3
она принимает с вероятностью -тт. От —оо до 0 функция F(x)
равна 0, от 3 до +оо равна 1. В этих двух отрезках определя-
определяемая ею случайная величина значений не принимает.
Если можно найти такую функцию Д(#), для которой при всех
зн^ениях х выполнено равенство
= J
то про случайную величину | говорят, что она непрерывна;
функцию fi(x) называют плотностью распределения |. Для плот-
плотности распределения имеют место равенства:
при любых а и b
при тех значениях ху при которых существует производная f'i (x),
26
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
[ГЛ. 1
Теперь мы перейдем к рассмотрению ряда функций распреде-
распределения, представляющих особый интерес для теории надежности.
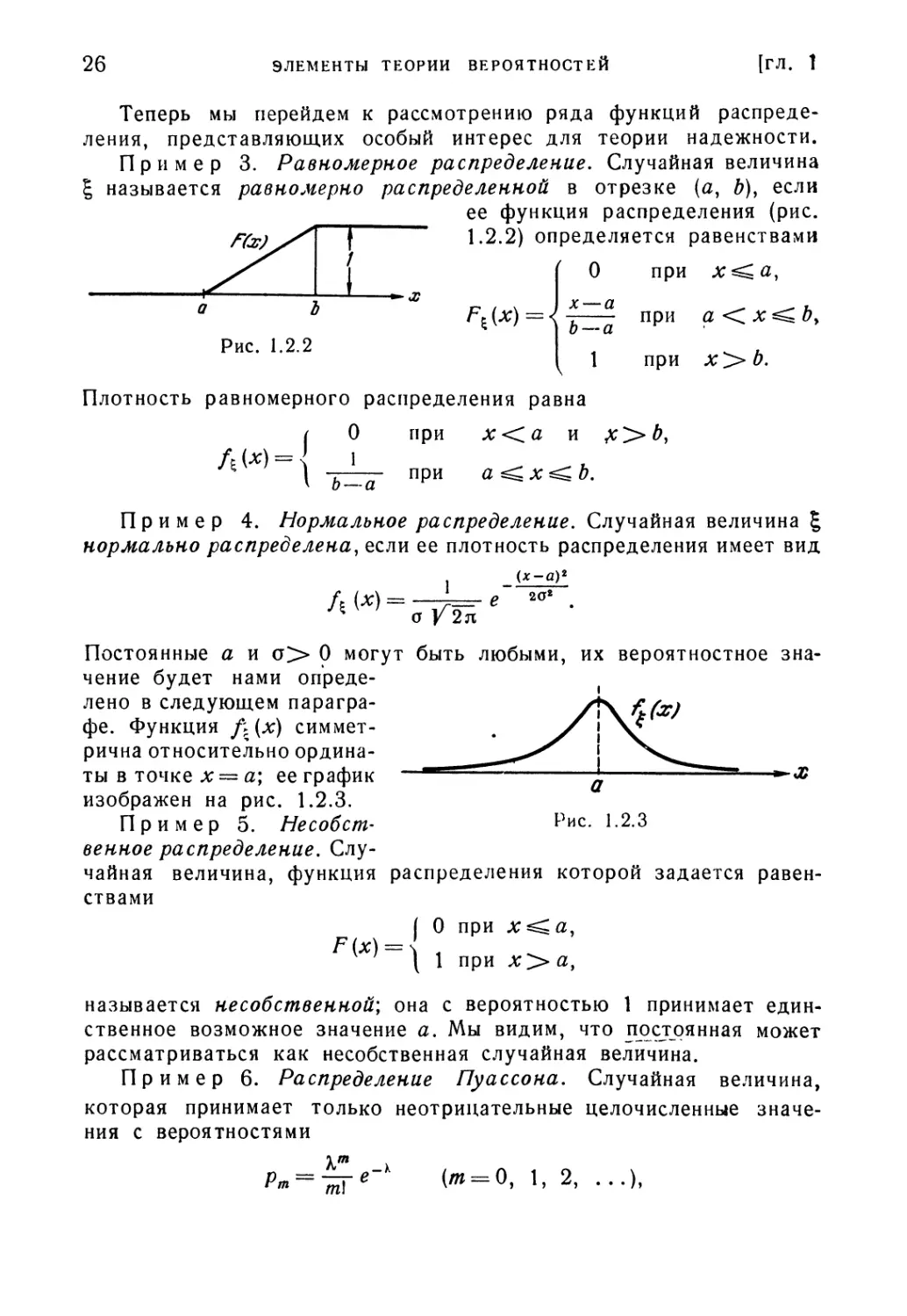
Пример 3. Равномерное распределение. Случайная величина
I называется равномерно распределенной в отрезке (а, ?), если
ее функция распределения (рис.
1.2.2) определяется равенствами
О
Рис. 1.2.2
1
при
при а
при
Плотность равномерного распределения равна
( О при х << а и
Ь — а
при
а
Пример 4. Нормальное распределение. Случайная величина \
нормально распределена, если ее плотность распределения имеет вид
Постоянные а и а> 0 могут быть любыми, их вероятностное зна-
значение будет нами опреде-
определено в следующем парагра-
параграфе. Функция f\(x) симмет-
симметрична относительно ордина-
ординаты в точке х = а; ее график
изображен на рис. 1.2.3.
Пример 5. Несобст- Рис- 12-3
венное распределение. Слу-
Случайная величина, функция распределения которой задается равен-
равенствами
| 0 при
\ 1 при
называется несобственной; она с вероятностью 1 принимает един-
единственное возможное значение а. Мы видим, что постоянная может
рассматриваться как несобственная случайная величина.
Пример 6. Распределение Пуассона. Случайная величина,
которая принимает только неотрицательные целочисленные значе-
значения с вероятностями
2,
| 2]
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
27
называется распределенной по закону Пуассона. Ее функция рас-
распределения представляет собой лестницу с бесконечным множест-
множеством ступенек, начинающихся в неотрицательных целочисленных
абсциссах.
Распределение Пуассона играет особую роль в теории надеж-
надежности, поскольку при широких условиях оно описывает законо-
закономерности появления внезапных отказов в сложных системах.
Смысл параметра X будет выяснен в следующем параграфе.
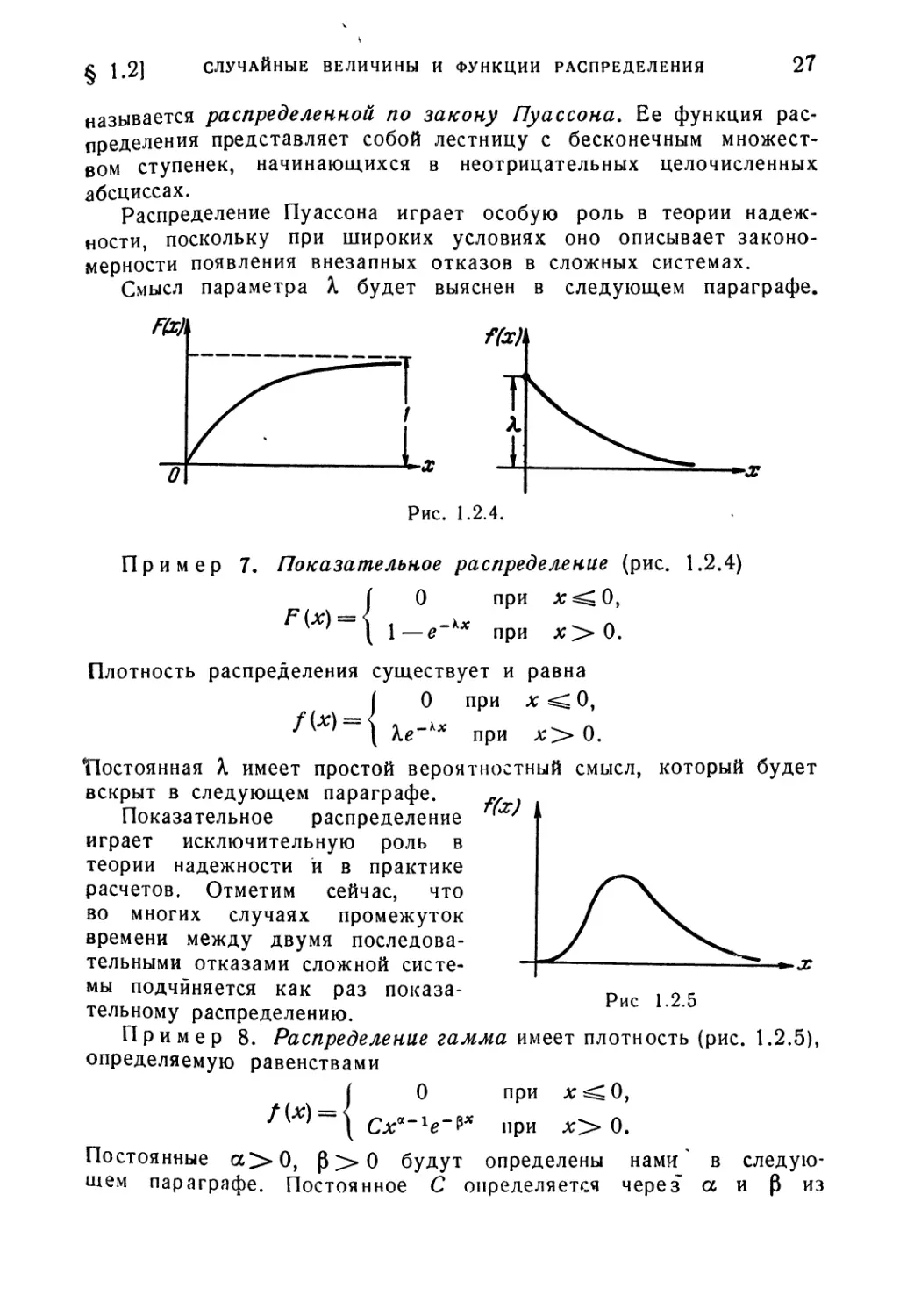
71
Рис. 1.2.4.
Пример 7- Показательное распределение (рис. 1.2.4)
О при х^О}
— е~Кх при х> О.
Плотность распределения существует и равна
О при лг^О,
\.е~Кх при х> 0.
Постоянная X имеет простой вероятностный смысл, который будет
вскрыт в следующем параграфе. „ .
Показательное распределение ' *
играет исключительную роль в
теории надежности и в практике
расчетов. Отметим сейчас, что
во многих случаях промежуток
времени между двумя последова-
последовательными отказами сложной систе-
системы подчиняется как раз показа-
показательному распределению.
Рис 1.2.5
Пример 8. Распределение гамма имеет плотность (рис. 1.2.5),
определяемую равенствами
( 0 при л;^0,
/(ЛГ)==\ С*-1*"** при *>0.
Постоянные а>0, Р>0 будут определены нами' в следую-
следующем параграфе. Постоянное С определяется через а и Р из
28
равенства
откуда
где
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1ГЛ. 1
С =
Г (а) '
В качестве частных случаев распределение гамма содержит
показательное распределение (а=*1) и так называемые
распределения Эрлан-
f(x) га (в случае целочислен-
ныха).РаспределениеЭрланга с
a = k может быть интерпре-
интерпретировано как распределение
длительности промежутка ме-
между первым и (/г -|- 1 )-м отка-
отказом сложной системы (или же
между последовательными вы-
вызовами, поступившими на те-
телефонную станцию, разделен-
разделенными во времени k другими
вызовами).
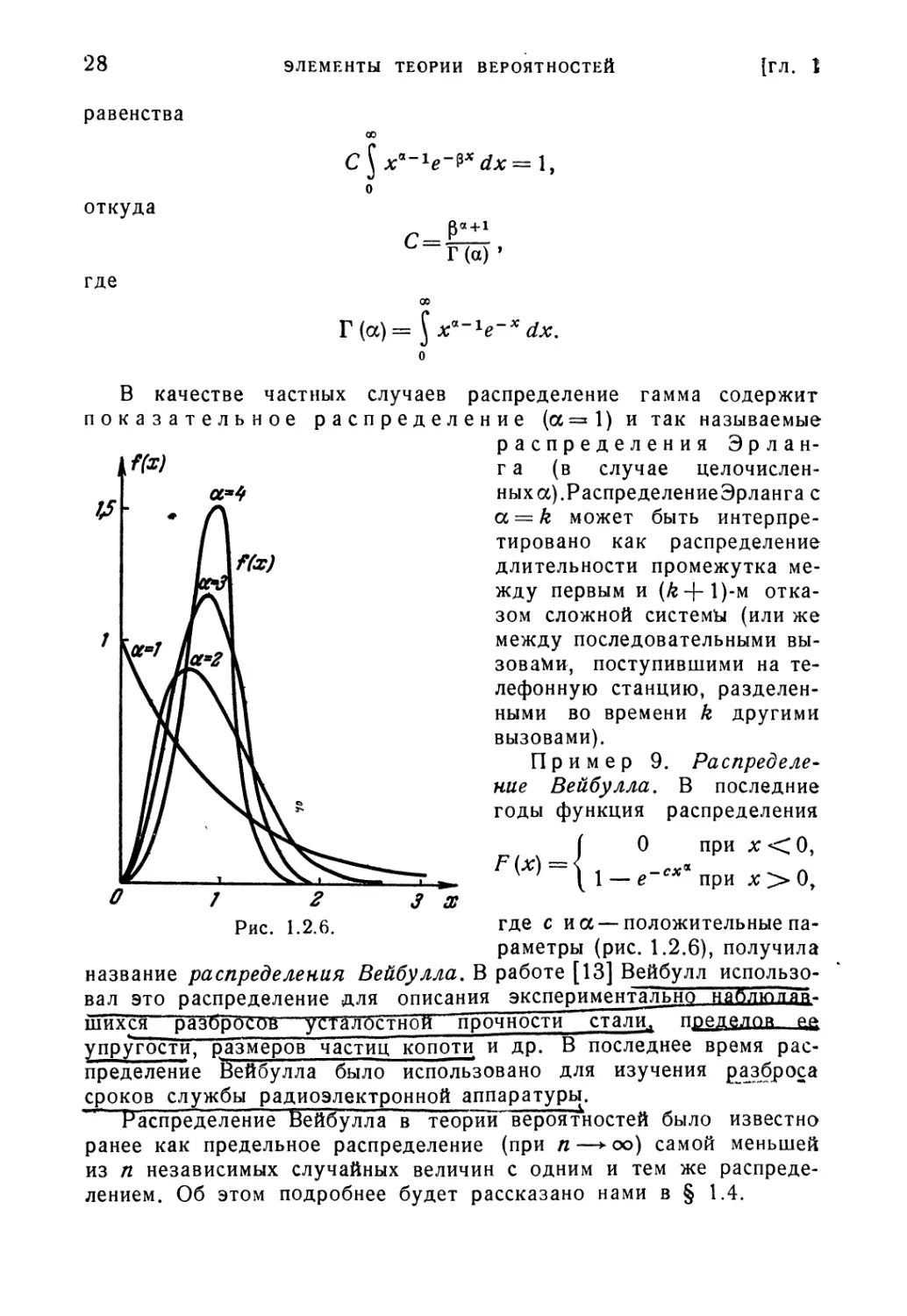
Пример 9. Распределе-
Распределение Вейбулла. В последние
годы функция распределения
О при лг<0,
-*"'*'при х>Оу
О 7 2 3 X
Рис. 1.2.6. где с иа —положительные па-
параметры (рис. 1.2.6), получила
название распределения Вейбулла. В работе [13] Вейбулл использо-
вал это распределение для описания экспериментальнс? наплюггяй-
шйхся разбросов уггаТОстной прочности стали!прелелor eft
упругости, размеров частиц копоти и др. В последнее время рас-
распределение Вейбулла было использовано для изучения разброса
сроков службы радиоэлектронной аппаратуры
Распределение Вейбулла в теории вероятностей было известно
ранее как предельное распределение (при п—*оо) самой меньшей
из п независимых случайных величин с одним и тем же распреде-
распределением. Об этом подробнее будет рассказано нами в § 1.4.
§
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
29
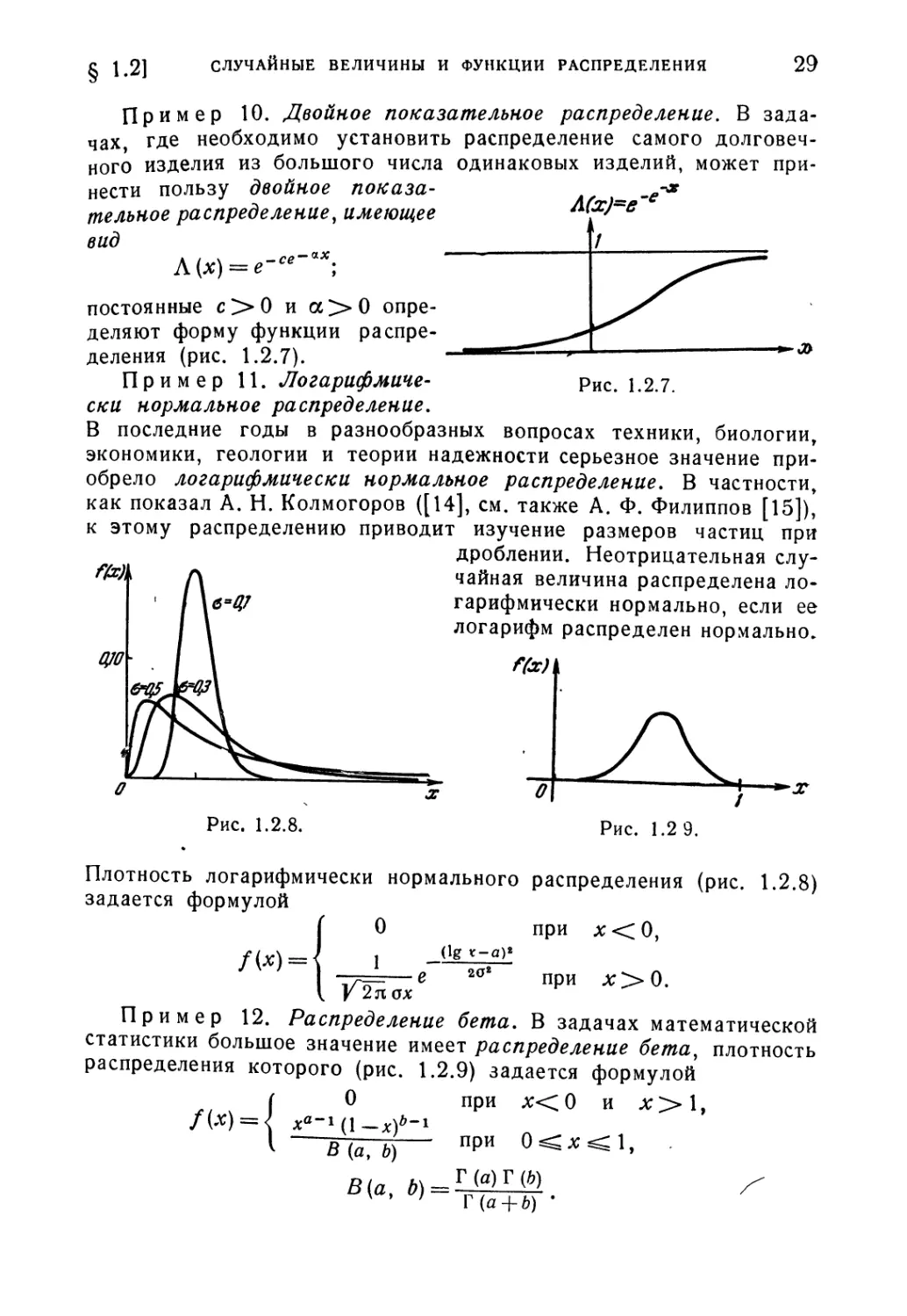
Пример 10. Двойное показательное распределение. В зада-
задачах, где необходимо установить распределение самого долговеч-
долговечного изделия из большого числа одинаковых изделий, может при-
принести пользу двойное показа-
показательное распределение, имеющее
вид
постоянные с>0 и а>0 опре-
определяют форму функции распре-
распределения (рис. 1.2.7).
Пример 11. Логарифмиче- Рис. 1.2.7.
ски нормальное распределение.
В последние годы в разнообразных вопросах техники, биологии,
экономики, геологии и теории надежности серьезное значение при-
приобрело логарифмически нормальное распределение. В частности,
как показал А. Н. Колмогоров ([14], см. также А. Ф. Филиппов [15]),
к этому распределению приводит изучение размеров частиц при
дроблении. Неотрицательная слу-
случайная величина распределена ло-
логарифмически нормально, если ее
логарифм распределен нормально.
ffx)
Рис. 1.2.8.
Рис. 1.2 9.
Плотность логарифмически нормального распределения (рис. 1.2.8)
задается формулой
0 при х<0,
Qg r-qJ
2°2 при *>0.
1
Пример 12. Распределение бета. В задачах математической
статистики большое значение имеет распределение бета, плотность
распределения которого (рис. 1.2.9) задается формулой
0 при лг<0 и л:>1,
В (а, Ь)
при
Г(а+Ь) *
30 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
Пример 13. Распределение смеси. Часто в практических
ситуациях приходится иметь дело с таким положением дел, когда
случайная величина является смесью двух или более случайных
величин с различными распределениями. Для примера, распределе-
распределение деталей на складе по долговечности удовлетворяет как раз
этому условию, если детали поступают с разных заводов или, как
это бываетчна ремонтных заводах, с новыми деталями смешиваются
годные детали, снятые с ремонтируемых машин (обезличенный ре-
ремонт). Пусть смешиваются случайные величины ?х, ?2, . .., ?„,
функции распределения которых соответственно равны Fx (x)y
F2ix), • • .» Fn(x)> причем величина \k берется с вероятностью рк>
2/^=1. Тогда функция распределения и плотность вероятности
смеси имеют вид
x). A.2.1)
Если распределение F(xy X), с которым приходится иметь дело,
зависит от параметра А., который сам является случайным с рас-
распределением Л (X), то функция распределения наблюдаемой слу-
случайной величины равна
F(jc)= J F (х, X)dA(X). A.2.2)
Формула A.2.1) является частным случаем только что напи-
написанной, если за параметр К принять индекс &, а за функцию А (X) —
ступенчатое распределение со скачками pk в точках X = k (k = 1, ..., п).
Если ^(д:, Я)=1—е~)х и X случайно с плотностью распределе-
распределения гамма:
при
то согласно формуле A.2.2)
Пусть, в частности, на склад поступили определенные изделия
с трех заводов; распределения долговечности этих изделий нор-
нормальны, но с разными пара-метрами а{ и а{ (/ = 1, 2, 3). Доля
изделий, поступивших с каждого из заводов, соответственно рав-
равна рЛ, р2 и р3. Спрашивается, если взять наудачу из партии из-
изделий одно, то какова будет плотность вероятности для его
§ 1.2] СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 31
долговечности? Согласно формуле A.2.1)
[{х-ах)% _(*-а2J _(*-о»)'"|
Ряд других важных примеров распределений будет дан в сле-
следующем параграфе.
В практических задачах зачастую приходится рассматривать
не одну-единственную случайную величину, а совокупность случай-
случайных величин, как правило,^ связанных между собой. Для полного
описания совокупности п случайных величин \ХУ ?2, . . . , \п или,
как говорят, /z-мерного вектора, а также л-мерной случайной вели-
величины, употребляют л-мерные функции распределения, т. е. вероят-
вероятности совместного выполнения неравенств \х<^хъ ?2^*2» •••»
F(xl9x2, ... , хп) = Р{Ъ1<х1, 12<х2, ...,1п<хп}-
Случайные величины gx, ?2, .. . , %п называются независимыми,
если при любых х1у х2, .. . , хп выполнены равенства
В терминах функций распределения это равенство записывается так:
п
F(xlt x2, ... , xn) = Y[Fk(xk).
В теории надежности постоянно приходится по данным случай-
случайным величинам образовывать новые случайные величины. Так, на-
например, при расчете влияния введения резервных элементов или
устройств важно бывает рассчитать по функции (или функциям)
распределения длительностей безотказной работы элементов распре-
распределение безотказного периода работы зарезервированной группы.
Если резервирование нагруженное (горячий резерв) и устройство
работает, пока работает хотя бы один элемент (основной или ре-
резервный), то длительность работы резервной группы равна
г)„ =-• max (?x, g2, ... , у,
где Si> ?2» •••> ?„ — длительности работы резервных элементов.
Пусть F(xx, аг2, ... ? хп) — функция распределения |lf ga> ... , ?я>
тогда
= /7(л:, х, .. . , х).
32 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
В случае независимых ?х, ?2, ... , 1п эта формула переписыва-
переписывается в виде
An (*) = Р К < *] = ^1 (*) ^2 (*)... ^ (*) >
где Fk (х) обозначает функцию распределения случайной величины 1-k.
Если все случайные величины, о которых идет речь, вдобавок оди-
одинаково распределены (.например, резервные элементы взяты из той
же партии продукции, из которой взят и основной элемент), то
Плотность распределения величины г\п в случае одинаково распре-
распределенных независимых случайных величин ?х, ?2, ...,?„
Обозначим теперь
Чтобы ?„>.*;, очевидно, необходимо одновременное выполнение
неравенств 51>лг, ?2> ху ..., Ъп>х. Таким образом,
В случае, когда величины \k независимы и одинаково распределены,
Обратим внимание на то, что при любом п для распределения
А(х) = е-е~~х распределение величины т\п получается из исходного
путем сдвига начала координат, как это видно из равенства
^п \х) — е —" е
Точно так же для распределения Вейбулла F (х) = 1—е-** при
любом п распределение ?п получается из исходного путем измене-
изменения масштаба, как это вытекает из равенства
Яя(*)=1--*-''*в=1--?
Изложение в настоящем параграфе носило чисто интуитивный
характер. Теперь мы сделаем набросок понятия случайной величины
с позиций аксиоматики случайного события, о которой речь была
в § 1.1. В соответствии с общими представлениями мы исходим из
множества элементарных событий U. Каждому элементарному со-
событию е поставим в соответствие некоторое число (или группу чисел)
§ 1.3] ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН 33
функция g называется случайной величиной, если она измерима от-
относительно введенной в рассматриваемом множестве U вероятности.
Иными словами, если при каждом действительном х для множе-
множества $* тех еу для которых /(е)<#, определена вероятность. Функ-
Функция распределения случайной величины при этом вводится совершенно
естественно:
§ 1.3. Числовые характеристики случайных величин
Наиболее полная характеристика случайной величины дается ее
функцией распределения, которая указывает, какие значения и с ка-
какими вероятностями принимает данная величина. Однако нередко
требуются некоторые более суммарные представления о случайной
величине. Так, для подсчета примерного числа машин, которые не-
необходимы для выполнения определенной работы, нужно только зна-
знание того, какую работу «в среднем» способна выполнить каждая
из машин. Для теории вероятностей и ее применений, в том числе
для теории надежности, большую роль играют некоторые посто-
постоянные числа, получаемые по определенным правилам из функций
распределения. Среди этих постоянных, служащих для общей ко-
количественной оценки случайных величин, для характеристики их
«в целом», особое значение имеют среднее значение (или, иначе,
математическое ожидание), дисперсия, медиана, мода и мо-
моменты различных порядков.
Если случайная величина ? принимает значения л^, лг2, ...
2
соответственно с вероятностями pv р2, ..., 2л>==1 и
i
то сумма (сумма произведений возможных значений случайной ве-
величины на их вероятности)
M5=S*/Pf A.3.1)
называется математическим ожиданием величины ? или средним
значением \ и обозначается символом Щ (часто также— Е?).
Для примера, математическое ожидание случайной величины,
распределенной по закону Пуассона, равно
k=l
34 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
Отправляясь от формулы A.3.1), можно прийти к определению
математического ожидания в случае, когда задана функция распре-
распределения величины ?. Для этой цели только требуется понятие ин-
интеграла Стильтьеса
М? = ^ xdF(x). A.3.2)
- со
В случае существования плотности распределения
x. A.3.3)
Если случайная величина ? распределена равномерно в отрезке
(я, *), то
ь
xdx a-\-b
т. е. математическое ожидание равно среднему арифметическому
крайних абсцисс отрезка (а, Ь).
Для нормального распределения с параметрами а и о
00 СО
1 с - {х~аJ 1 Г - —
М? = —7= хе ™г dx = ^=. (a-\-zo)e 2 dz.
Так как
00 Z 2 00 Z2
2
TO
e 2 dz = V2n и \ ze
— 00
Мы получили результат: параметр а нормального распределения
равен математическому ожиданию.
Далеко не каждое распределение вероятностей обладает мате-
математическим ожиданием. Так, например, распределение Кеши, для
которого плотность распределения равна р (х) = . 2 2. , не имеет
во
математического ожидания, поскольку для него интеграл J
— во
расходится.
Для практических и теоретических целей важны общие свой-
свойства математического ожидания, которые мы сейчас перечислим.
§ 1.3] ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН 35
1°. Математическое ожидание постоянной С равно этой же
постоянной: МС = С.
2°. Постоянный множитель выносится за знак математи-
математического ожидания: М С%~С М?.
3°. Математическое ожидание суммы любых случайных вели-
чин (как угодно связанных) равно сумме их математических
ожиданий: М(^ + т|) = М ? + М Л-
4°. Математическое ожидание произведения независимых
случайных величин равно произведению их математических
ожиданий: М?т) = М|.Мт).
Для оценки разброса значений случайной величины около ее
среднего значения используется несколько числовых характеристик,
важнейшей из них является дисперсия. Дисперсия определяется
как математическое ожидание квадрата уклонения случайной вели-
величины от ее математического ожидания:
D^ = M(| —Mg)a. A.3.4)
Несложные алгебраические преобразования и использование только
что сформулированных свойств математического ожидания при-
приводят к равенству
A.3.5)
Если случайная величина ? имеет плотность распределения, то для
вычисления дисперсии можно пользоваться следующими формулами:
со Jt\ с© , , /оо \ 2
« Dg= J (* —Mg)VWAe= J x*p(x) dx — (l xp(x) dx) .A-3.6)
Приведем примеры вычисления дисперсии для некоторых
важных распределений.
Дисперсия нормального распределения с параметрами а и о:
00 ^
z2e a dz = o2.
— оо
Мы видим, что для нормального распределения и второй пара-
параметр а имеет простой вероятностный смысл — его квадрат равен
дисперсии.
Дисперсия случайной величины, распределенной по закону
Пуассона с параметром X:
l=—~ \ (х — аJе 2<у2 dx=-^=
36
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
[ГЛ. 1
Мы получили интересный результат, который находит применение
при проверке гипотезы о том, что наблюдаемое распределение
является пуассоновским: математическое ожидание и дисперсия
распределения Пуассона равны по величине.
Дисперсия равномерно распределенной в отрезке (а, Ь) вели-
величины \ равна D?= ~ и, следовательно, является возрастаю-
возрастающей функцией длины отрезка (а, Ь). Дисперсию можно поэтому
рассматривать как меру рассеяния
(разбросанности) значений случай-
случайной величины от ее среднего
значения. Для нормального рас-
распределения (как, впрочем, и для
многих других) соответствующая
случайная величина при любом
положительном значении дисперсии
может принимать любые дейст-
действительные значения. Однако, чем
меньше величина дисперсии, тем
большая доля значений случай-
случайной величины принимается из области, непосредственно примыка-
примыкающей к математическому ожиданию. Для иллюстрации этого заме-
замечания мы приводим на рис. 1.3.1 графики плотности нормального
распределения для а = 0,5; 1; 2.
Дисперсия обладает следующими свойствами:
1°. Дисперсия постоянного равна нулю: DC^O.
2°. Постоянный множитель выходит за знак дисперсии
в квадрате: DC? = C2D|.
3°. Дисперсия суммы попарно независимых случайных веду,~
п п
чин равна сумме дисперсий слагаемых: D2 ?*= 2 ^*-
A: = l fc = l
Моментом k-то порядка величины ? называется математиче-
математическое ожидание k-Pi степени разности (? — а):
Если а = 0, то момент иногда называется начальным, а если
а = М?, то центральным. Дисперсия, таким образом, есть второй
центральный момент. Впоследствии станем обозначать центральные
моменты буквой \ik, а начальные — буквой v^; индекс k означает
порядок момента. Легко проверить, что между центральными и
начальными моментами имеет место равенство (к^\)
§ 1.3] ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН 3?
Для первых четырех моментов, играющих особо важную роль
в теории вероятностей и математической статистике, это равенство*
принимает такую форму:
Ш = v4 — 4v3vx + 6v2v* — 3vJ.
Модой_непрерывного распределения, имеющего плотность р(х),.
называется абсцисса Хм> при которой р (х) достигает максимума.
Нормальное распределение одномодально, для него мода и мате-
математическое ожидание совпадают. Распределение Вейбулла при
а>1 имеет моду, а при а^1 моды не имеет. А. Я. Хинчин [16]
выяснил условия, при которых распределение будет одномодаль-
ным (или, как он назвал, унимодальным).
Пусть F(x) — некоторое распределение. Корень уравнения
называют а-квантилью распределения F(x). Если функция F (х)>
разрывна, то а-квантили существуют не для каждого а, поскольку,
как правило, при заданном а найдется лишь такое л*а, что
Если же F(x) непрерывна и имеет промежутки, в которых она
сохраняет постоянное значение, то для некоторых а имеется целый
континуум а-квантилей — все те значения х, при которых F(x) = a.
Легко проверить по таблицам, что для нормального распреде-
распределения квантили при а = 0,25; а = 0,5 и а = 0,75 равны соответст-
соответственно л:0>25 = а — 0,6745а; хО}5 = а; л:0O5= а + 0,6745а.
Квантиль для а = 0,5 называется медианой распределения.
У нормального распределения медиана совпадает с математическим
ожиданием.
Если случайные величины ? и х\ связаны зависимостью т] = ф(?),
причем функция ф (х) является неубывающей функцией от я, то-
квантили величины г) (обозначим их уа) связаны с квантилями
величины | (л:а) простым соотношением
Пусть F(x) непрерывна. Рассмотрим функцию W (х), обратную-
x), т. е. такую, что при любом х
= *.
•38 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
Ясне, что имеет место равенство хл = у?(а). Это последнее
«равенство используется для изготовления различных «вероятност-
«вероятностных бумаг».
Рассмотрим еще несколько примеров распределений, широко
использующихся в теории надежности.
Пример 14. Распределение %2. Пусть случайные величины
Sn ?г> •••! In независимы и нормально распределены, Щ,. = а,
,0^. = о2. Функция распределения величины
4
носит название распределения %2. Плотность распределения
;равна 0 при jc<0 и при х>0
2Тг(-|
'Число п носит название числа степеней свободы.
Пример 15. Распределение Стьюдента. Если случайные
величины % и т] независимы, ? распределено нормально, М? = 0,
D?=l, а г|а имеет распределение %2» то отношение — распреде-
распределено по закону Стьюдента (Госсета):
Если g нормально распределено, М? = б, D?=l, at] имеет
-^-распределение с п степенями свободы, то отношение — имеет
нецентральное распределение Стьюдента со смещением б. Плотность
нецентрального распределения Стьюдента имеет вид
Г «-JL , v 1-1 1 Пб8
р(х\ б, п) = [2 2
х
хб
dz.
Пример 16. Распределение Фишера — Снедекора. Пусть слу-
случайные величины х2 и %1 независимы и имеют х2"РаспРеДеления
§ 1.4] ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ 39й
с пх и п2 степенями свободы. Отношение г =—- имеет распре-
п\Хъ
деление F. Плотность распределения F дается формулой
§ 1.4. Некоторые предельные теоремы теории вероятностей
Предельные теоремы играют огромную роль в теории вероят-
вероятностей и в ее применениях, поскольку в значительной мере они
позволяют учесть реальные особенности строения изучаемых,
объектов (влияние большого числа воздействий, каждое из кото-
которых незначительно по величине, молекулярное строение и пр.).
Мы здесь укажем несколько теорем такого типа, где общие зако-
закономерности определяются не характером каждого отдельного воз-
воздействия, а большим числом их. С такого рода явлениями в тео-
теории надежности приходится встречаться постоянно по разным-
причинам. С одной стороны, когда переходят к глубокому изуче-
изучению явлений износа трущихся поверхностей или же процессов,
происходящих в современных полупроводниковых приборах, то>
самим ходом событий мы принуждены изучать явления на моле-
молекулярном уровне и даже принимать во внимание атомистическое
строение вещества. Сведения же о природе частиц и их взаимо-
взаимодействии весьма скудны; достоверно лишь то, что их очень много.
Естественно, что в таких условиях особенно удачен и хорошо
приспособлен к объекту исследования аппарат теории вероятностей
и ее предельных теорем: имеется большое число в основном рав-
равноправных ингредиентов и главная цель состоит в разыскании тех
общих закономерностей, которые обусловлены в первую очередь,
именно этим массовым характером явления и лишь в незначитель-
незначительной степени зависят от индивидуального характера составляющих.
Далее, составление математических моделей явлений зачастую
становится более прозрачным, когда откидывается то, что затем-
затемняет картину явления, но не оказывает решающего влияния на него.
^ Теорема Пуассона. Если в п независимых испытаниях
событие A JiMeem малую вероятность р} то при больших зна~
чеГ~~
Рп(т)ж^е-Х A11 = 0, 1, 2, ...),
где к = рп.
В частности, если вероятность изготовления бракованного
изделия мала, то вероятность того, что в партии из п штук.
40 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
встретится то или иное число бракованных изделий, с хорошим
приближением можно считать распределенной по закону Пуассона.
к Интегральная теорема Муавра — Лапласа. Если
-в последовательности независимых испытаний вероятность собы-
события А равна ру причем 0<р<1, то вероятность того, что
число \л появлений события Л в п последовательных испытаниях,
удовлетворяет неравенствам (а и Ь — произвольные числа) '
У npq
при больших п близка к
dz.
Интегральная теорема Муавра — Лапласа находит широкое при-
применение как при теоретических исследованиях, так и при прове-
проведении непосредственно прикладных расчетов. Пусть, для примера,
известно, что в течение сезона какая-нибудь деталь может про-
прослужить без замены лишь в 2/3 случаев, а в */3 случаев такая
замена необходима. В некоторой области имеется 16 200 агрегатов,
в которых имеется по одной такой детали. Сколько необходимо
завезти этих деталей, чтобы обеспечить бесперебойное снабжение
действующих агрегатов?
Обозначим через jli число поломавшихся за сезон деталей.
Тогда согласно теореме Муавра — Лапласа вероятность того,
что будет достаточно запасти 5400 деталей (именно так подсчи-
подсчитывают обычно потребность в запасных частях), равна вероятно-
вероятности того, что число поломок окажется меньшим этого числа,
и z%
— \ р 2 /1у П ^
1/^2я J
Таким образом, при подобном расчете запасов мы сумеем покрыть
потребность лишь с вероятностью 1/2, т. е. лишь в половине слу-
случаев наших запасов будет достаточно.
Естественно спросить себя о таких запасах, которые удовле-
удовлетворили бы потребность с подавляющей вероятностью, например
•с вероятностью 0,95. Итак, каково должно быть Ь, чтобы
Имеем
§
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
41
По теореме Лапласа
b-np
Vnpq
Из таблиц находим, что интеграл Лапласа равен 0,95 при значе-
значении аргумента, равном 1,65; таким образом,
1 on b — np b—5400
165==
Из этого уравнения находим, что для удовлетворения потребности
в подавляющем большинстве случаев достаточно запасти только
5499 деталей.
\i Закон больших чисел в форме Бернулли. Пусть
в последовательности независимых испытаний событие А имеет
неизменную вероятность появления р\ пусть, далее, \х означает
число появлений события А в п последовательных испытаниях.
Тогда, каково бы ни было положительное число е>>0, при
п—их>
В начале нашего века французским математиком Э. Борелем
было обнаружено более сильное предложение, согласно которому
lim t = pl = l.
Теоремы Бернулли и Бореля служат основанием оценки неиз-
неизвестной вероятности события А посредством частоты его появле-
появления,
—
величины —.
п
т. е.
Закон больших чисел в форме Чебышева. Если
последовательность попарно независимых случайных величины
?i, ?2> ••• такова, что их математические ожидания Щ,п — ап
конечны и дисперсии ограничены одной и той же постоянной
C(D^ то при п—иэо и любой положительной постоянной г
Отсюда следует, что при п
42 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
В частности, если все случайные величины имеют одно и то же
•математическое ожидание (ап = а)у то при п—*оо
Центральная предельная теорема (теорема Ляпу-
Ляпунова и ее обобщения). Теоремы типа закона больших чисел уста-
устанавливают сближение сумм независимых случайных величин с неко-
некоторой последовательностью постоянных. Для практических целей,
<как правило, требуется несравненно большее—указание на то,
как часто, т. е с какой вероятностью, может наступать то
или иное отклонение от этих постоянных рассматриваемой
суммы. При весьма общих условиях ответ на этот вопрос дает
центральная предельная теорема. Мы приведем формулировку
этой теоремы в условиях Линдеберга.
Пусть дана последовательность взаимно независимых случай-
случайных величин ?1э ?2> • • •» ?л» •••» ° которых мы предположим,
что они имеют конечные математические ожидания и дисперсии,
f (x-akJdFk(x) = 0, A.4.1)
Если при любом т > О
п
lim — 7
О 2 штшт
И —> оо D „ t,
Т А? = 1 | v
где Fk(x)—функция распределения ?,k, то при любом х
«-г }Хг,-,х«.^[.-ч, A.4.„
«->со I " л а «, I Г ^ '
к — 1 „оо
Условие A.4.1) называется условием Линдеберга; можно дока-
доказать, что если условие Линдеберга выполнено, то обязательно:
лри любом т>> О
i max
ll < k < n
Иными словами, если условие Линдеберга выполнено, то все сла-
•гаемые равномерно малы в том смысле, что вероятность хотя бы
¦одному слагаемому 7"а* превзойти величину т стремится к нулю
при возрастании числа слагаемых до бесконечности.
Теореме Линдеберга предшествовала важная в принципиальном
и прикладном отношении теорема А. М. Ляпунова. Мы
§ 1.4] ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ 43>
сформулируем эту теорему ^ частном предположении наличия
конечных третьих "^мёнтрэГ"Впоследствии именно" в этой форме-
ЙьГ используем ее при изучении вопросов резервирования.
Предположим, что последовательность взаимно независимых
случайных величин ?1э ?2, ..., ?я, ... имеет конечные третьи,
моменты. Введем обозначения
в дополнение к тем, которые были введены при формулировке-
теоремы Линдеберга.
Если при п —*оо отношение Ляпунова
то
г.2
Соотношение A.4.3) носит название условия Ляпунова.
Если все слагаемые одинаково распределены и имеют конечную*
дисперсию, то условие Линдеберга обязательно выполнено и, зна-
значит, для суммы таких слагаемых имеет место равенство A.4.2).
Требование одинаковой распределенное™ слагаемых слишком
сильное7~но оно™ может""быть "ослаблено. Именно, можно требовать-
лишь конечности дисперсий слагаемых, а также того, что среди
функций распределения членов последовательности \х, ?2, ... имеется
лишь конечное число различных.
Точно так же, если все величины \k ограничены сверху и снизу
одними и теми же величинами а и Ь {a^\k^h) и Вп—> оо при
п—юо, то условие Линдеберга выполнено и предельное равенство^
A.4.2) имеет место.
Мы привели два частных случая центральной предельной тео-
теоремы, чтобы составить себе представление о том разнообразии воз-
возможностей, при которых может появляться нормальное распределение.
Предельные теоремы типа центральной предельной теоремы иг-
играют в применениях очень большую роль, поскольку нередко при-
приходится иметь дело с ситуацией, в которой интересующий нас
результат протекает под влиянием большого числа независимо-
действующих факторов, каждый из которых производит лишь не-
незначительное действие по сравнению с суммарным действием всех
остальных. Именно такая картина наблюдается в теории ошибок
наблюдений, в явлениях износа, случайном рассеянии значений
параметров, определяющих качество продукции изделий массового
производства. Условия центральной предельной теоремы нередко-
44 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
можно считать выполненными, и потому распределения, близкие
к нормальному, встречаются в реальных задачах очень часто.
Впоследствии у нас будет много случаев, когда мы станем поль-
пользоваться этим выводом.
Предельные распределения для максимального
и минимального значения. Рассмотрим группу п одина-
одинаково распределенных независимых случайных величин ?х, ?2» • • •» Ел-
Образуем теперь новые величины T)rt = max(?lf ?а, ...,?„) и ?и =
= min(^1, ?2, ...,?„), понимая под этим следующее: пусть вели-
величины 11У ?2, ...,?„ приняли значения Art, лг2, ..., а:л, тогда при-
припишем величине г\п значение, равное max (х1у х2, ...,лгп), а вели-
величине ?„ — значение min (х1у х2} ...,хп). Функции распределения
.величин х\п и ?п определяются равенствами
= \-(\-F(x))n.
Спросим себя, к каким распределениям могут сходиться рас-
распределения величин Т1о~ " и -я~~ " при надлежащем подборе по-
<:тоянных Ьп и ап>0, когда /г—^оо? Оказывается, что предель-
предельные распределения для величин — исчерпываются следующими
типами:
2) Фа(лг) = О при х^О и е~х * при лг>0,
3) Чга (х) = е~{~Х) при а;<0 и 1 при л:>>0.
Предельные распределения для — исчерпываются следующими
ап
типами:
1) Л#(*) = 1—*-*",
2) Ф*(лг) = 1 — е~{-Х)~* при л;<0 и 1 при л;>0,
3) Та(лг) = 0 при х<0 и 1—е~х* при л;>0.
Постоянная а может принимать любое положительное значение.
Существенно заметить, что среди перечисленных распределений
содержится распределение Вейбулла. Быть может, обширные при-
применения распределения Вейбулла на практике могут быть объясне-
объяснены тем, что наблюдаемая величина является минимумом большого
числа независимо действующих величин.
§ 1.4] ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ 45
Условия сходимости к каждому из возможных предельных рас-
распределений хорошо изучены [17], [18].
Об одной модели появления логарифмически
нормального распределения. Из центральной предельной
теоремы можно получить многочисленные следствия, подобные тому,
о котором сейчас пойдет речь.
Если ?i» ?2l ...—последовательность независимых одинаково
распределенных случайных величин, для которых Mlog^ = a и
п
О log ?л = а2, то произведение Ц lk асимптотически распределено
по логарифмически нормальному закону с параметрами па и па2.
По сути дела, эта идея многократно использовалась для созда-
создания моделей явлений, при которых приходится рассматривать ло-
логарифмически нормальное распределение. В частности, А. Н. Кол-
Колмогоров в 1941 г. исходил из близкого принципа при объяснении
распределения размеров частиц при дроблении [14].
В 1903 г. Кэптейном [19] была предложена следующая модель.
Предположим, что состояние некоторого процесса характеризуется
величиной X(t). Изменение X(t) за время от ti до ti+1 пропорцио-
пропорционально достигнутому состоянию
A.4.4)
коэффициент пропорциональности е,- является случайной величиной,
независимой от остальных бу и от величин X(tj). Теперь
п
V р -
к
Л X{ti+1)-X(tt) V'dX
2+ x(t() "* J x •
t
если только значения t. взяты близко одно от другого. Положив
^ ^ мы находим, что
При п большом и надлежащих предположениях относительно ?.t
логарифм X(t) имеет почти нормальное распределение и, значит,
само X(t) распределено асимптотически логарифмически нормально.
Если предположение A.4.4) заменить на
где ф (z) некоторая заданная функция, то схема Кзптейна дает
возможность получить широкое разнообразие возможных предельных
Таблица 1.4.1
Непрерывные распределения
о
Наименование
распределения
Равномерное
Нормальное
Логарифмиче-
Логарифмически нормаль-
нормальное
Вейбулла
Гамма
Область
значений
(а, Ь)
(—00,1»)
@, оо)
@, оо)
@, оо)
Плотность распределения
1
b — a
кх-af
е 2°2
о У2п
(\ogx-a)*
г-е 2°2
Математиче-
Математическое ожида-
ожидание
а + Ь
2
а
ог
а + —
е *
1
са
а
Дисперсия
(Ь — а)*
12
о2
¦•(¦4)--('+i)
2
а
У
Мода
а
(при а> 1)
г са
- (а<1)
Продолжение таблицы 1.4.1 «^
Наименование
распределения
Частные
случаи
' Показа-
Показательное
5С2
Бега
Стьюдента
пера
Область
значений
@, оо)
@, оо)
@, 1)
(— оо, оо)
@, 00)
Плотность распределения
k
2 * 2
г(|Jт"
п + \
\ 2 ) /пЛг 2 г
/пЛ г (пЛ \п2) X
Математиче-
Математическое ожида-
ожидание
1
Я,
/г
а
0
По
Дисперсия
1
26
1
2/i2 (^1~Ь "г— 2)
"i(^2—2J (#2—4)
Мода
/г 2
а—1
а_[_Ь — 2
0
2 /i
2«J + п2
Таблица 1.4.2
Дискретные распределения
Наименование распределения
Биномиальное
Гипергеометрическое *
Пуассона
Геометрическое
Отрицательное биномиальное
Возможные значения
0, 1, 2, ..., п
0, 1, ..., min (M, п)
0, 1, 2, ...
0, 1, 2, ...
а, г + 1, ...
Вероятность
сп
Математи-
Математическое
ожидание
м
X
1
р^
г
Р
Дисперсия
q
Рг
§ 1.5] ОБЩИЕ СВЕДЕНИЯ О ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ 49
распределений: при y(z) = C—обычное нормальное распределе-
распределение; при ф (z) — z — логарифмически нормальное и др.
Модель.Эрланг а. Представим себе, что промежуток вре-
времени между наступлениями двух последовательных событий распре-
распределен по показательному закону с плотностью |$e~fl* при лг>0.
Если нас интересует распределение длительности промежутка не
между соседними событиями, а через к событий, то оно, как легко
подсчитать, имеет плотность распределения Cxfce~&x при л:>0.
Чтобы проиллюстрировать это распределение реальной задачей,
связанной с теорией надежности, поставим вопрос о распределении
промежутка времени между последовательными заменами блоков
при следующих условиях. Каждый блок состоит из основного эле-
элемента и k— 1 резервных; резервные блоки включаются по одному
немедленно после выхода из рабочего состояния того, который ра-
работал перед этим моментом; в резерве элементы не стареют; дли-
длительность жизни каждого элемента имеет показательное распреде-
распределение.
Модель Эрланга имеет характер непредельной закономерности;
мы хотели этой моделью проиллюстрировать возможность появле-
появления в реальной обстановке Г-распределений.
Вид распределений и их основные характеристики даны в таб-
таблицах 1.4.1 и 1.4.2.
§ 1.5. Общие сведения о теории случайных процессов
Вводные замечания. В применениях теории вероятностей
постоянно приходится иметь дело со случайными величинами, ко-
которые являются функциями одного или нескольких параметров. Эти
параметры могут изменяться непрерывно, но могут принимать и
только дискретные значения.
Напряжение тока на аноде электронной лампы в каждый мо-
момент времени, даже при самом строгом поддержании величины
температуры окружающей среды и других управляемых параметров,
подвержено случайным колебаниям. Напряжение является случайной
функцией времени. Если для нескольких ламп с одинаковыми исход-
исходными характеристиками нанести на график фактическое напряжение
тока анода за определенный промежуток времени, то получится
пучок реализаций, различно ведущих себя во времени и отражаю-
отражающих случайные особенности каждой из испытываемых ламп (рис, 1.5.1).
Если исследовать, скажем, зависимость скорости изнашивания
поверхности поршневого пальца от длины пробега автомобиля, та
вновь обнаружится тот же характерный случайный ход износа.
Рассмотрим в качестве третьего примера функцию, равную нулю,
пока определенный элемент сложного устройства (конденсатор,
втулка и т. д.) находится в работоспособном состоянии, и единице,
3 Б. В. Гнеденко и др.
50
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
[ГЛ. 1
когда этот элемент испорчен. Момент скачка представляет собой
случайную величину. Мы вновь имеем дело со случайной функцией,
аргументом которой могут быть общая наработка элемента, дли-
длительность пробега и т. д.
Во всех приведенных примерах мы имели дело с непрерывно
меняющимся параметром — временем, длительностью пробега, на-
наработкой. Однако нередко возникает необходимость исследовать и
Рис. 1.5.1.
такие ситуации, когда изучается случайная функция только при
дискретных значениях аргумента. Так, если в процессе испытаний
замеры производятся только в определенный момент суток, то нам
становится известной наша функция только в дискретные моменты
времени. В дальнейшем мы встретимся с обоими указанными слу-
случаями.
Само собой разумеется, как теоретический, так и прикладной
интерес представляет рассмотрение не только скалярных случайных
функций, но и векторных случайных функций, когда от одного
аргумента зависит несколько связанных между собой случайных
величин. В теории надежности постоянно приходится иметь дело
с несколькими характеристиками одного и того же изделия и ис-
исследовать изменение их взаимного влияния во времени.
Случайные функции одной независимой переменной принято на-
называть случайными, или вероятностными, процессами. Если слу-
случайная величина зависит от двух или более аргументов, то такие
случайные функции принято называть случайными полями.
При наблюдении за случайным процессом ? (t) мы каждый раз
наблюдаем только определенную его реализацию. При различных
наблюдениях одного и того же процесса получаются различные его
реализации. Для физических и инженерных задач обычно прихо-
приходится выяснять, как велики вероятности наступления реализаций
определенного характера (не превышающих заданного уровня, не
§ 1.5] ОБЩИЕ СВЕДЕНИЯ О ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ 51
попадающих в течение заданного периода времени в определенную
область и т. д.).
Рассмотрение первых задач теории случайных процессов отно-
относится к началу нашего века. В первую очередь здесь следует от-
отметить работы А. А. Маркова, касающиеся процессов с дискрет-
дискретным временем, и Л. Башелье по диффузионным процессам. Оба эти
исследователя строили математические модели очень важных в наше
время процессов— марковских цепей и диффузионных процессов.
Позднее Фоккер и Планк при построении теории диффузии полу-
получили дифференциальное уравнение, управляющее такими процессами.
В основу этих результатов была положена простейшая математи-
математическая модель движения частицы. Исследования А. Н. Колмогорова,
А. Я. Хинчина, Е. Е. Слуцкого, П. Леви и ряда других ученых
заложили основы математической теории двух важнейших типов
случайных процессов —марковских и стационарных. В настоящее
~время в теории надежности особую роль играют процессы марков-
марковского типа. Мы должны теперь дать этому классу процессов четкое
определение и выяснить относящиеся сюда понятия.
В классической механике состояние системы может быть опре-
определено различными путями. Для примера, если системой является
материальная точка, то под ее состоянием в момент t0 мы можем
понимать координаты той точки пространства, которую она зани-
занимает в этот момент. Такое понимание состояния не очень удачно,
поскольку для описания развития системы позднее момента t0 нам
недостаточно знания того состояния, в котором она находится
в момент t0. Хорошо известно, что все влияние прошлого на дви-
движение точки по законам классической механики сосредоточено в ее
скорости в данный момент. Таким образом, если под состоянием
точки в момент t0 мы станем понимать координаты ее положения
в пространстве и компоненты скорости, то так понимаемое состоя-
состояние позволяет однозначно определять будущее развитие системы
по ее состоянию в момент t0. Этот простой пример позволит нам
лучше оценить значение последующих определений.
В современной физике, технике, экономике приходится иметь
дело с более сложным положением, когда знание состояния системы
не только в данный момент времени, но даже за всю предыдущую
историю ее развития не определяет однозначно ее будущее, а лишь
меняет вероятность пребывания в том или ином множестве состояний.
Определение случайного процесса. Обозначим че-
через х состояние системы в какой-нибудь момент времени t\ как мы
говорили, х не обязательно представляет собой скалярную вели-
величину, а может быть вектором, функцией или чем-либо еще. Во
многих случаях, однако, приходится рассматривать случай, когда х
является числом или вектором. Пусть для определенности х—ска-
х—скалярная величина. Чтобы задать случайный процесс ? (/), обычно
52 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
идут по следующему пути. Для каждого натурального значения п
и любых возможных значений гъ t2, ..., tn параметра / задают
/7-мерную функцию распределения вектора \ (/х), \ (*2), ..., ?,(tn)
Г (Х^ Х2, . . . , Хп\ Г1? J2, • • • » ^п) ==
При этом на функции F (х1у ..., л:п; ^lf ...,^n) накладывают два
условия:
а) условие симметрии: для любой перестановки iv /2, ...,/„
чисел 1, 2, ..., /г выполняется равенство
б) условие согласованности: при т<Сп и любых
...,^w имеет место равенство
Р (*!, л;2, ...,^, + со, ..., + оо; ^, ^2, ...,tmJ tm+1,
Мы не станем здесь развивать общую теорию случайных про-
процессов, а ограничимся лишь определением марковских случайных
процессов. Обозначим через Р {s, x\ t, Щ вероятность того, что
система, находясь в момент s в состоянии х, в момент t>s ока-
окажется в одном из состояний множества ©. Если дополнительное
знание состояний системы в моменты т<^ не изменяет этой ве-
вероятности при любых $у х, t, @, то такой класс процессов есте-
естественно назвать процессами без последействия. В связи с тем, что
важный частный класс процессов без последействия был введен
в рассмотрение А. А. Марковым, процессы без последействия на-
называются также процессами Маркова.
Марковость процесса в значительной степени зависит от того,
какой смысл вкладывается в понятие состояния системы. Поло-
Положение здесь совершенно аналогично тому, что мы уже видели на
примере классической механики^ если под состоянием движущейся
точки понимать только ее положение в пространстве, то ее буду-
будущие состояния зависят и от прошлого; добавление к положению
в пространстве скорости в данный момент делает наш процесс
процессом без последействия. Таким образом, если угодно, марков-
марковскими являются все процессы, с которыми встречаются в класси-
классической механике.
При соответствующем понимании состояния системы любой слу-
случайный процесс может быть превращен в марковский: для этого
достаточно в понятие состояния включить всю предысторию раз-
развития системы.
Цепи Маркова. Если аргумент t принимает только дискрет-
дискретные значения ts, $=..., —1, о, 1, 2, ..., и процесс l(t) при
§ 1.5] ОБЩИЕ СВЕДЕНИЯ О ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ 53
этом является марковским, то обычно его называют цепью Марко-
Маркова. Часто приходится на практике сталкиваться с необходимостью
изучения цепей Маркова, для которых множество состояний конеч-
конечно или счетно. В этом случае цепи Маркова принято описывать
посредством так называемых переходных вероятностей. Пусть в
момент ts система находится в состоянии (?,-; вероятность pi.{s) =
= P{@t., ts\ @y, ts+i} носит название переходной вероятности. Если
эта вероятность не зависит от момента ts, то цепь Маркова на-
называется однородной. Марковская цепь, для которой существуют
пределы
limPI©,, ts\ ®/э ts+1}=Pj,
называется эргодической. Свойство эргодичности можно трактовать
таким образом: за длительный промежуток времени или, точнее,
за большое число моментов tr, когда система может изменять
свои состояния, вероятность того, что система находится в задан-
заданном состоянии, почти перестает зависеть от исходного состояния.
Одна из простейших и самых ранних эргодических теорем была
доказана еще создателем теории цепей А. А. Марковым: если
марковская цепь однородна, имеет лишь конечное число состоя-
состояний и при любых i и j вероятности Рц положительны, то цепь
эргодична.
В приложениях, в том числе и в теории надежности, нередко
приходится иметь дело со случаем, когда необходимо рассматри-
рассматривать случайный процесс ?(/), вообще говоря немарковский, для
которого удается обнаружить такую последовательность моментов,
что величины \ (t^ образуют последовательность случайных вели-
величин, связанных в цепь Маркова. Такие марковские цепи называ-
называются вложенными цепями.
Простейший поток. Большое значение имеют процессы,
для которых состояние изменяется в слу чайные моменты вре-
времени. Для примера, пусть в случайные моменты времени насту-
наступает некоторое событие (телефонный вызов, поломка устройства,
распад атома). Нас интересует число появлений этого события за про-
промежуток времени от 0 до t. Обозначим это число через b>(t). Ясно,
что %(t) в моменты, когда изменяется его величина, может толь-
только возрастать, и притом лишь на целочисленные значения.
Особую роль играют такого рода процессы, для которых вы-
выполнены следующие три условия: стационарность, отсутст-
отсутствие последействия, ординарность. Процессы ?(*), удов-
удовлетворяющие трем перечисленным условиям, по предложению
А. Я. Хинчина называются простейшими потоками. Они носят
также наименование однородных процессов Пуассона.
В перечисленные условия вкладывается следующий смысл.
54 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
Стационарность означает, что для любой группы из конеч-
конечного числа непересекающихся промежутков времени вероятность
наступления определенного числа событий на протяжении каждого
из них зависит от этих чисел и от длительности промежутков
времени, но не изменяется от сдвига всех временных отрезков на
одну и ту же величину. В частности, вероятность появления k
событий в течение промежутка времени от Т до Т-\-1 не зависит
от Г и является функцией только к и t.
Отсутствие последействия означает, что вероятность наступ-
наступления к событий в течение промежутка времени (Г, T-\-t) не за-
зависит от того, сколько раз и как появлялись события ранее. Это
предположение означает, что условная вероятность появления к со-
событий за промежуток (Г, T-\-t) при любом предположении о наступ-
наступлении событий до момента Т совпадает с безусловной вероятностью.
Отсутствие последействия означает взаимную независимость появ-
появления того или иного числа событий в непересекающиеся проме-
промежутки времени.
Ординарность выражает собой требование практической невоз-
невозможности появления двух или нескольких событий за малый про-
промежуток времени h. Точнее, это означает следующее: обозначим
через P>i (Л) вероятность появления более чем одного события за
промежуток времени к. Тогда условие ординарности состоит в
следующем:
P>i (*) = *(*).
Доказано, что если события в простейшем потоке могут по-
появиться с положительной вероятностью в отрезке времени длитель-
длительности единица и вероятность появления бесконечного числа со-
событий за этот промежуток времени равна нулю, то существует
такая положительная постоянная А, что имеют место формулы
где через ?k (t) обозначена вероятность появления ровно к собы-
событий потока за время t.
Вероятность Ро (t) можно интерпретировать как вероятность
того, что длительность промежутка времени между двумя по-
последовательными появлениями событий окажется большей t. Эта
трактовка нам очень важна для будущего.
Требования, которым удовлетворяет простейший поток, с боль-
большой точностью выполняются в многочисленных естественнонаучных
и технических процессах. Для примера, укажем на число спонтан-
спонтанно распавшихся атомов радиоактивного вещества, на число косми-
космических частиц, попавших на определенную площадку за промежу-
§ 1.5] ОБЩИЕ СВЕДЕНИЯ О ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ 55
ток времени /. Если речь идет о сложной радиотехнической систе-
системе, состоящей из большого числа элементов, каждый из которых
с малой вероятностью может отказать в работе независимо от со-
состояний других элементов, то число элементов, отказавших за
рабочий промежуток времени длительности t} представляет собой
случайный процесс. Во многих случаях этот процесс оказывается
близким к пуассоновскому.
Простейший поток обладает рядом замечательных свойств. Мы
укажем два из «их.
Если известно, что в промежутке времени данной длительности
наступили п событий потока, то оказывается, что при этом усло-
условии моменты появлений всех этих событий независимы между со-
собой и равномерно распределены в этом промежутке.
Пусть имеются два независимых между собой простейших пото-
потока %i(t) и |2 (t) с интенсивностями кг и Я2. Поток ? (tf) =: ?i @+
+ ?2@ является также простейшим потоком с интенсивностью
Я1 + А2.
Проверка условий стационарности, отсутствия последействия
и ординарности для установления пуассоновости интересующего
нас случайного процесса зачастую бывает очень сложна. В то же
время у интересующего нас процесса могут быть некоторые осо-
особенности, которые значительно облегчат эту проверку. Среди ряда
общих предложений, которые в настоящее время известны в этом
направлении, для нас особое значение имеет предложение, форму-
формулировка и доказательство которого в первую очередь является
заслугой А. Я. Хинчина. Мы сформулируем несколько более общий
результат, полученный позднее Б. И. Григелионисом. Для его фор-
формулировки нам необходимо ввести некоторые понятия и обоз-
обозначения.
Назовем случайный процесс %(t) ступенчатым, если прираще-
приращения ?(*)— ?E) ПРИ t>s могут принимать только неотрицатель-
неотрицательные целочисленные значения. Всякий однородный пуассоновский
процесс является ступенчатым. Однако пуассоновскими процессами,
стационарно ведущими себя во времени, класс ступенчатых
процессов не исчерпывается. Мы отметим сейчас только два
типа процессов такого типа, с которыми мы будем иметь дело
позднее.
Процессы восстановления. Предположим, что промежут-
промежутки между последовательными появлениями событий потока пред-
представляют собой независимые одинаково распределенные случайные
величины zlt z2, ... с функцией распределения F(x). Процесс
5@, равный числу появлений событий за промежуток времени от
О до t, представляет собой процесс восстановления. В частности,
если F(x)=\—e~'kx, где Я>0 — постоянная, то процесс восста-
восстановления является однородным пуассоновским процессом.
56 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
Если обозначить через Nt наибольшее целое число такое, что
y^izi<ity то имеет место так называемое тождество Вальда
Неоднородный пуассоновский процесс. Мы скажем,
что процесс ?(*) является неоднородным пуассоновским процес-
процессом с ведущей функцией Л (/), если при произвольных t>s и
неотрицательных целых k имеют место равенства
Р {I @ -1 (s) = k] = tA(O-A(s)]* е. (Л (/)_л E)] ^
где Л (t)— неубывающая непрерывная слева функция, Л(/) = 0 при
/<0 и приращения ? (t) — g (s) независимы для непересекающихся
интервалов (s, f).
При A(t) = Xt мы получаем в качестве частного случая одно-
однородный пуассоновский процесс (простейший поток).
Предельная теорема. Пусть ?„(*)= 231«л @, где ?„Л(*) —
независимые ступенчатые процессы. С такого типа процессами %n(t)
приходится на практике встречаться очень часто. Для примера,
поток судов, прибывающих в данный порт, представляет собой
сумму потоков судов, отправляющихся из портов Л1У А2у ..., Ап
в данный порт. Обозначим через \n(t) поток поломок некоторой
детали. Если в механизме имеется kn деталей и они выходят из
строя независимо одна от другой, то |и (t) = 2j%>nk(t) представля-
k=i
ет собой поток поломок этого механизма. Для простоты мы счита-
считали, что замена поломанной детали на новую не требует времени
и совершается мгновенно.
Введем обозначения: *
pnr{k\t,s) = P{lnr(t)-lnr(s) = kl s<t, ^ = 0,1,2, ...,
A; tts),
kn
Вп{*> s)= 2[1-/>яг@; t, s)-pnr(\\ t, s)].
r = i
Мы скажем, что процессы %пг (t) бесконечно малы, если при лю-
любом фиксированном t
lira max A -pnr @; *, 0)) = 0.
л-»» l<rKkn
§ 1.6] ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 57
Про последовательность процессов %n(t) говорят, что она при
п —"оо сходится к процессу ? (/), если любые конечномерные распре-
распределения процессов %n(t) сходятся к соответствующим распределениям
процесса ?(/).
Теорема Б. И. Григелиониса. Для сходимости сумм
независимых бесконечно малых ступенчатых процессов \п (t) =
k
@ к процессу Пуассона с ведущей функцией A(t) необ-
ходимо и достаточно, чтобы при любых фиксированных s и t
limBn(t, 0) = 0.
При A(t) = kt мы получаем условия сходимости сумм незави-
независимых бесконечно малых ступенчатых процессов к однородному
пуассоновскому процессу (простейшему потоку).
Если мы хотим уяснить качественный смысл только что сфор-
сформулированной теоремы, то он очень прост. Условие бесконечной
малости слагаемых процессов означает, что для каждого из них
вероятность наступления хотя бы одного события (скачка) за про-
промежуток времени длительности t мала, сумма вероятностей в точ-
точности одного скачка является конечной величиной Л(/); сумма же
вероятностей более чем одного скачка бесконечно мала.
Таким образом, если механизм состоит из большого числа де-
деталей, каждая из которых может поломаться лишь с малой веро-
вероятностью и эти поломки для разных деталей независимы между
собой, то суммарный поток поломок может считаться близким к
пуассоновскому.
§ 1.6. Элементы математической статистики
О задачах статистики. До сих пор мы говорили об ос-
основных характеристиках случайных явлений как о чем-то данном
заранее, что нам известно с самого начала. На самом деле с та-
таким положением дел встречаются крайне редко, и все необходи-
необходимые характеристики случайного события, случайной величины или
случайного процесса нужно оценивать из специально поставленно-
поставленного эксперимента или же из систематически проводимых наблюде-
наблюдений за течением явления. Как оценить неизвестную вероятность
случайного события на основании наблюдений? Как оценить не-
неизвестную функцию распределения случайной величины по наблюден-
наблюденным из опыта ее значениям? Как оценить параметры нормального
распределения а и а2, если мы наблюдаем нормально распределенную
58 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
случайную величину, параметры которой неизвестны? Как опреде-
определить характеристики случайного процесса, который мы наблюдаем?
Перечисленные задачи очень важны для практики, в частности
для теории надежности, они составляют значительный объект ис-
исследования математической статистики. Однако к ним не сводятся
все ее вопросы. Наряду с поставленными, на практике постоянно
возникают вопросы другого рода: из тех или иных общих сообра-
соображений выдвинуты некоторые общие гипотезы — случайное событие
обладает в данных условиях определенной вероятностью; две слу-
случайные величины имеют одинаковые распределения; данный слу-
случайный процесс является нуассоновским с неизменной интенсивно-
интенсивностью и т. д. Как проверить правильность выдвинутых гипотез?
Отметим еще одну постановку задачи, в полную силу проявив-
проявившуюся лишь в последние годы. Наблюдается некоторый случайный
процесс, на который в случайный момент может подействовать неко-
некоторая причина, изменяющая его течение (например, его параметры).
Требуется по наблюдениям за течением процесса уловить возможно
точнее момент воздействия этой причины. С такой постановкой
задачи встречаются при контроле наладки станка и во многих
иных практически важных ситуациях.
Возникающие в статистике задачи можно грубо подразделить
на несколько типов, важнейшие из которых таковы:
а) оценка неизвестных параметров,
б) проверка статистических гипотез,
в) принятие решений.
Последняя из сформулированных задач относится к третьему типу;
подавляющее большинство задач, указанных в первом абзаце, при-
принадлежит к типу а), а задачи второго абзаца относятся к типу б).
Мы коснемся в настоящем параграфе только задач типов а)
и б).
Исходным пунктом статистического исследования какой-либо
случайной величины ? является совокупность п наблюдений над
ней, в которых она принимает значения хг, х2, ..., хп. Впослед-
Впоследствии мы будем предполагать испытания взаимно независимыми и
проведенными в неизменных условиях. Эти предположения, конечно,
идеализируют обстановку, поскольку со временем условия несколь-
несколько изменяются. Для примера, если мы исследуем размеры одним и
тем же измерительным инструментом, то в силу износа он не дает
для всех измерений одной и той же точности. Однако этот износ
настолько незначителен, что его можно не принимать в расчет.
Вариационный ряд, эмпирическая функция рас-
распределения, теорема Гливенко. Если последовательность
результатов независимых наблюдений хъ лг2, . .., хп над случай-
случайной величиной | с функцией распределения F(x) расположить
в порядке возрастания х[ ^ х\ ^. . . ^ х*п, то получается так
§ 1.6] ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 59
называемый вариационный ряд, В некоторых случаях в результате
наблюдений мы сразу получаем вариационный ряд. Для примера,
пусть мы на испытательном стенде испытываем образцы на дли-
длительность их жизни при определенной нагрузке. Будем отмечать
буквами tv t2f ..., tn последовательные моменты гибели образ-
образцов. Образец, погибший в момент tlf имел самую короткую жизнь;
больше всех жил образец, погибший в момент tn. Очевидно, что
последовательность чисел tlt t2i ..., tn является вариационным
рядом для наблюдений над случайной величиной — длительностью
жизни образца.
Эмпирической функцией распределения Fn (x) назовем функцию,
определенную равенствами
0 при
k
7Г при ;
1 при х>х*п.
Таким образом, эмпирическая функция при каждом значении х
равна числу значений случайной величины, меньших х, деленному
на общее число наблюдений.
В 1933 г. была доказана важная теорема математической ста-
статистики о соответствии между эмпирической и истинной функциями
распределения случайной величины.
Теорема В. И. Гливенко. При п—>оо имеет место соот-
соотношение
Р {lim sup | F (x) — Fn (x) \ = 0} — 1.
Точечные оценки параметров. Зачастую приходится
иметь дело с такой ситуацией, когда нам необходимо на основа-
основании испытаний оценить значение одного или нескольких неизвест-
неизвестных параметров. С этой задачей сталкиваются как при нахожде-
нахождении функции распределения, когда известен ее аналитический вид,
так и при оценке числовых характеристик случайной величины.
Одним из наиболее распространенных подходов к оценке парамет-
параметра является следующий подход. Пусть F(x, 0) является функцией
распределения случайной величины ?, 0 —неизвестный параметр
@ может быть векторной величиной). Обозначим через х1У х2} ..., хп
результаты независимых испытаний величины ?. Точечной оцен-
оценкой параметра 0 мы будем называть некоторую функцию
ф(*1> *2> •••> хп)> зависящую только от результатов испытаний и
известных величин, но не от неизвестного параметра. Понятно, что
оценка сама является некоторой случайной величиной и поэтому
может изменяться от одной серии испытаний к другой.
60 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
В качестве оценки параметра 9 можно предложить большое
число функций ф, поэтому, чтобы избежать полного произвола,
необходимо наложить на них некоторые естественные условии.
Обычно стремятся, чтобы оценки обладали свойствами несме-
несмещенности, состоятельности и эффективности.
Оценка ф (х1у х2, . . ., хп) параметра 0 называется несмещенной,
если для нее выполнено равенство
Мф-9,
т. е. математическое ожидание оценки совпадает с оцениваемым
параметром.
Если нам нужно оценить математическое ожидание случайной
величины ?(а = М?), то в качестве оценки можно выбрать функцию
ф-ЛГ
Легко подсчитать, что эта оценка является несмещенной. Если
функция распределения F(x) симметрична, т. е. если при любых х
выполнено равенство F(x)'=\—FBa — х)у то величина а может
быть оценена и функцией т — эмпирической медианой, т. е. вели-
величиной, левее и правее которой находится одинаковое число на-
наблюдений. Легко доказать, что эта оценка также является несме-
несмещенной.
При оценке параметра G2 = D| посредством эмпирической дис-
дисперсии
S2 = —
получается смещение Ms2— а2 = —а2.
Если мы хотим получить несмещенную оценку а2, то следует
брать функцию
Оценка ф = ф(л:1, х2, ...,хп) параметра 9 называется состоя-
состоятельной, если при увеличении числа наблюдений до бесконечности
оценка сходится к оцениваемому параметру по вероятности, т. е.
если при любом е>0 имеет место соотношение
Р {| Ф — 9|>е}— 0 (л—оо).
Легко проверить, что все приведенные нами выше примеры
оценок параметров а и а2 являются состоятельными. Для парамет-
§ 1.6] ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 61
ра а2, например, состоятельными являются как оценка б2, так и
оценка s\.
Предположим, что для параметра 0 предложены две оценки:
срх и ф2. Мы скажем, что оценка фх эффективнее, чем оценка ф2,
если
—6J<М(ф2-0J.
При некоторых общих ограничениях, наложенных на аналити-
аналитические свойства оценок ф, можно указать нижнюю грань для всех
оценок рассматриваемого класса:
infM(q> — бJ.
ф
Если оценка ф = ф(#1, х2, ...>хп) такова, что
М(ф — 6J = ЫМ(ф — бJ,
ф
то оценка ф называется эффективной.
Оценка
для параметра а распределения
X
Г(х,а)=\—е а (х^О)
эффективна.
Метод наибольшего правдоподобия. Очевидно, что
одной из основных задач теории оценок параметров следует считать
построение общих методов нахождения хороших оценок. Один из
наиболее распространенных и сильных методов был предложен
английским статистиком Р. Фишером в 1912 г. В частных случаях
этод метод использовался еще Гауссом. Мы рассмотрим этод метод
в предположении, что случайная величина ? имеет плотность рас-
распределения f(x, a).
Функция
п
L (х1ух2, ... , хп; а) = П f(xk, а)
в только что указанном случае называется функцией правдоподобия,
Если случайная величина дискретна и принимает значения zx, z2,. ..
соответственно с вероятностями р± (а), р2 (а), ..., У^Р^ (а) =« 1, то
функция правдоподобия берется в ином виде, а именнЪ;
п
L (*!, хъ ..., хп\ а) = П pki (a),
62 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
где индексы у вероятностей показывают, что наблюдались значения
zkxi zkz, . . ., zkn.
Метод максимума правдоподобия состоит в том, что в качестве
оценок параметра а принимается то значение а, при котором функция
L достигает своего максимума. Поскольку L и \п L достигают
экстремума при одном и том же значении а, то эти критические
значения а определяются из уравнения правдоподобия
d\x\L
да
¦ = 0.
Каждое решение уравнения правдоподобия носит название оценки
максимального правдоподобия.
Легко проверить, что для распределений биномиального pk(a) =
= Спа A —а)' @ ^ k ^ я), Пуассона pk (а) = , , нормального
f(x; a, G2)=—-^=е 2G* , показательного /(х, а) =ае~ах (д:>0)
оценки максимального правдоподобия оказываются единственными
и даются формулами
а = — (т — число появлений события),
1
а = х, o2 = s2, а = =г.
х
Значение метода наибольшего правдоподобия выясняется следую-
следующими двумя предложениями:
Если для параметра а существует эффективная оценка а, то
уравнение правдоподобия имеет единственное решение а.
При некоторых общих условиях аналитического характера
{см. [9]), наложенных на функции f(x; а), решение уравнения
правдоподобия сходится пр& п -> оо к истинному значению пара-
параметра а. Это решение распределено асимптотически нормально
и асимптотически эффективно.
Введем еще понятие достаточной оценки, играющее важную
роль в статистике. Функция правдоподобия является не чем иным,
как совместной плотностью распределения вектора х1у х2, . . ., хп.
Предположим, что имеется такая оценка 8 параметра 0, что условное
распределение вектора хъ х2,...ухп при известном значении 0
не зависит от параметра 0. Такое свойство оценки означает, что
она как бы содержит всю информацию о параметре 0, которая
содержится в результатах наблюдений. Оценки, обладающие этим
свойством, называются достаточными.
§ 1.6] ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 63
Оценка 6 является достаточной тогда и только тогда, когда
функция правдоподобия представима в виде двух множителей, один
из которых зависит лишь от 0 и 6, а второй — только от результатов
наблюдений хъ х2, . . . , хп. Иногда это свойство достаточных оценок
называют критерием факторизации.
Если статистика 0 является достаточной, то для любой
функции f(x), задающей взаимно однозначное отображение, ста-
статистика f (в) также является достаточной.
Заметим, что каждая эффективная оценка является одновремен-
одновременно и достаточной.
Если для параметра 0 существует достаточная оценка 0, то
каждое решение уравнения правдоподобия является функцией от 0.
Для параметров нормального распределения а и о достаточными
статистиками будут
х в случае, когда параметр а известен, а параметр а неизвестен;
п _
2 (xk — аJ в случае, когда параметр а известен, а параметр а
k = i
неизвестен и
_ п __
пара х, 2 (xk — •х;J' когДа °ба параметра неизвестны.
k = i
Метод моментов. Самым первым общим методом точечной
оценки неизвестных параметров следует считать так называемый
метод моментов, который был предложен К. Пирсоном. Этот метод
до сих пор широко используется в практической статистике, посколь-
поскольку нередко он приводит к сравнительно несложной вычислительной
процедуре, тогда как метод наибольшего правдоподобия упирается
как раз в вычислительные трудности.
Идея этого метода состоит в том, что моменты распределения,
зависящие от неизвестных нам параметров, приравниваются эмпири-
эмпирическим моментам. Взяв число моментов, равное числу неизвестных
параметров, и составив соответствующие уравнения, мы получим
необходимое число уравнений.
Эмпирическим моментом k-vo порядка при этом мы называем
величину
vk = — 2*7= x*dFa(x);
центральным эмпирическим (или выборочным) моментом того же
порядка — величину
Н* = т 2j (^у — -v) •
64 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
Приведем для примера оценку параметров а и E так называемого
Г-распределения Пирсона
/(*; а, $) = Сха-1е-*х(х^*0).
Легко подсчитать, что
а а(а+ 1)
vi — у • V2 — рг •
Отсюда уравнениями для определения аир будут
откуда
_ 1 А
- V2 ~ — Z
Оценки, получаемые с помощью метода моментов, не являются
наилучшими с точки зрения их эффективности. Однако очень часто
они используются в качестве первых приближений, отправляясь от
которых удается находить последующие приближения с большей
эффективностью.
Можно доказать (см., например, [9], стр. 384), что совместное
распределение двух центральных эмпирических моментов \it и \ij
асимптотически нормально (при условии существования у исходного
распределения конечных моментов достаточно высоких порядков)
с математическими ожиданиями \xi и (iy и матрицей ковариации,
определяемой равенством
¦¦ (И-/ — !*/) (Ду — I*/) =
Нередко нужно получать хотя бы приближенные значения мате-
математического ожидания, дисперсии и других моментов для некоторой
функции от выборочных моментов. Мы ограничимся простейшим
примером функции от одного аргумента р.: /=/((!.). Если эта
функция непрерывна и имеет непрерывные первые производные, то
=/ (I*,) +
В частности, если /= У \х2 , то
§ 1.6] ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 65
Если случайная величина ?„ нормально распределена и для нее
Щп = ау 0?„ = а„->0 при я->оо, то для достаточно гладкой
функции f(x) можно написать равенство
/(У =/(*)+/' (*) Aп-") + °(Ъп-а)'
Величина |и асимптотически нормально распределена с математиче-
математическим ожиданием f(a) и дисперсией [/' (a)]2 On-
Метод квантилей. Таким же чисто эмпирическим приемом,
как и метод моментов, является метод квантилей. Он состоит в
том, что квантиль теоретического распределения приравнивается к
эмпирической квантили. Если же оценке подлежат несколько пара-
параметров, то соответствующие равенства пишутся для нескольких
квантилей.
Мы отметим одно свойство эмпирических квантилей.
Рассмотрим одномерное распределение ^(д:) с плотностью вероят-
вероятности f(x) = F'(x). Пусть ? = ?р обозначает квантиль порядка р.
т. е. единственный корень уравнения F(t) =р, где О <Р< 1. Пред-
Предположим, что в некоторой окрестности точки x = t,p функция f(x)
непрерывна, имеет непрерывную производную и отлична от 0. Тогда
выборочная квантиль порядка р, т. е. величина zpy для которой
Fn(zp)=py асимптотически нормальна с математическим ожиданием
1р и дисперсией я^ у
В частности, медиана выборки асимптотически нормальна с
математическим ожиданием, равным теоретической медиане, и дис-
Персией 5^ .
Для нормального распределения с параметрами а и а медианой
является параметр а. Выборочная медиана из нормального распре-
распределения асимптотически нормально распределена с математическим
JTCF2
ожиданием а и дисперсией -^— .
Отсюда мы выводим полезное следствие. Если параметра
нормального распределения оценивается посредством двух функ-
функций аг = х и а2 = т, то дисперсия первой оценки равна — , а
дисперсия второй асимптотически будет -^L # Таким образом,
2
асимптотически М (a1 — aJ/M (я2— аJ = —, вторая оценка хуже
первой примерно в 1,6 раза, если сравнивать их по величине дис-
дисперсии.
Предположим, что распределение F (х) имеет дифференцируемую
плотность /(*), 0</?1</?2<. ..<pft< 1 числа ^определены
равенствами f(xi)=pl nfi=f(xi)=^0 при / = 1, 2, ..., k. Совместное
66
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
[ГЛ. 1
распределение эмпирических квантилейzPl,zPii. . ., zPk асимптотически
нормально со средними ?Pl, tPi, . . ., ?Рк и ковариационной матрицей
Ы/
Pi
Pi
Pi
A —Pi)
/;
(i- p2)
/л
(*—Pfe)
P\
p.,
pi
(i
«I
(i
~r2)
-Ps)
— pft)
./ft
Pi A—Pft)
Pa- (\— Pk)
Метод доверительных интервалов. Точечные оценки,
которыми мы до сих пор занимались, являются случайными величи-
величинами. Мы нигде не давали оценки вероятности уклонения получен-
полученной оценки параметра от его истинного значения, поскольку это
требует дополнительных рассмотрений. С других позиций к той же
проблеме оценок предложил подходить Р. Фишер. А именно, вместо
поиска функции 0 (х19 дг2, .. . , хп) от результатов испытаний, кото-
которые принимаются за приближенное значение неизвестного параметра,
он предложил указывать две функции 0Х и 92 от результатов
испытаний (но не от оцениваемого параметра),для которых вероятность
покрытия неизвестного параметра отрезком (Qlt 02) равна заданной
величине. Функции 0Х и 02 называются доверительными границами,
а @Х, 02) — доверительным интервалом для параметра 0.
Если оценивается параметр а нормального распределения при
известном значении параметра а, то вероятность оценки
у п
у п.
равна
dt.
Для распределения
X
F(x)=--\ — e'T (x>0)
в качестве доверительных границ можно выбрать функции
'— и
§ 1.6] ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 67
Для этих границ имеет место равенство
Zl )
Величина р = 1 — со называется доверительным уровнем пред-
предлагаемой оценки, она указывает вероятность выхода параметра за
доверительные границы, а со — коэффициентом доверия.
Доверительные интервалы для неизвестной
вероятности. Простейшая задача, с которой сталкиваются на
практике, состоит в оценке неизвестной вероятности р события по
наблюденной частоте h = — его появления. Наша задача состоит
в том, чтобы найти такие функции p = p(h) и p = p(h), чтобы
вероятность попадания неизвестной вероятности р в интервал
{р,р) была бы не меньше, чем 1 — 2р. Иными словами, мы хотим
указать такое правило, которое при большом числе его применений
может привести к ошибочным заключениям не более чем в 2|3 части
всех случаев.
Английские статистики Клоппер и Э. Пирсон указали такое пра-
правило [22], которое дает гарантию того, что вероятность выхода
из доверительного интервала за каждую из границ не превосходит р.
Предложенное ими правило состоит в следующем: пусть в п не-
независимых испытаниях с постоянной вероятностью р наступления
некоторого события А оно было наблюдено т раз. Тогда в качестве
верхней границы доверительного интервала следует взять единствен-
единственное решение уравнения
а в качестве нижней доверительной границы р — единственное
решение уравнения ~~
2Ур
В таблице 9 приложения даны величины р и р для достаточно
широкого диапазона значений п и р = 0,025. ~
Рассмотрим числовой пример. Пусть п = 20, т = 4. По таблице
9 приложения находим доверительные пределы для р при |3 = 0,025:
р = 0,057, р = 0,437.
О проверке статистических гипотез. Для того чтобы
принять или отвергнуть ту илииную статистическую гипотезу, прибега-
прибегают к наблюдениям.Пусть число наблюдений равно п и их результаты да-
даны последовательностью чисел xlt х2, . .., хп. Мы нуждаемся в правиле,
68 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
которое позволяло бы по результатам наблюдений принять или
отвергнуть исследуемую гипотезу. Идея образования таких правил
состоит в том, что пространство выборок, т. е. множество всех
возможных результатов наблюдений (хх, х2, . . . , хп), разделяется на
два непересекающихся подмножества Rnl и /?„2. Проверяемая гипо-
гипотеза принимается, если результат наблюдений, т. е. если выбороч-
выборочная точка (хг, х21 . . . , хп) попадает в область Rnl1 и отвергается
при попадании в множество Rn2. Область Rn2 носит название кри-
критической. Очевидно, что выбор критической области Rn2 однозначно
определяет и область Rnl.
Если мы принимаем партию продукции, которая разделяется на
годную и бракованную, то мы заинтересованы в том, чтобы в при-
принимаемой партии количество бракованных изделий было очень малым.
Обозначим через р0 величину, лежащую между 0 и 1 и такую,
что считается возможным принимать партии, в которых доля брако-
бракованных изделий не превосходит р0, и браковать их, если доля
бракованных изделий превосходит рг. При испытании каждого
отдельного изделия станем приписывать результатам испытания
число 0 или 1 в зависимости от того, оказалось изделие годным или
бракованным. Выборочное пространство состоит из всех групп
(*i» #2» • • • > хп) п0 п чисел X;, каждое из которых может принимать
лишь значения 0 и 1. Критическая область, которая обычно
используется в описанной задаче, определяется неравенством
Предположим, что мы принимаем некоторые изделия, относитель-
относительно которых известно, что определяющий их качество параметр
распределен нормально с известной дисперсией а2. Относительно
другого параметра требуется, чтобы он был равен а. Гипотеза,
предполагающая, что математическое ожидание определяющего пара-
параметра равно я, должна проверяться на основании выборки хх, х2,... ,хп
из п предметов. Критическая область, которая обычно используется
при решении этой задачи, строится по следующему правилу: гипо-
гипотеза отвергается тогда и только тогда, когда
\х — а | ^ со,
где с — соответствующим образом выбранная постоянная.
Приняв или отвергнув интересующую нас гипотезу //, мы можем
совершить ошибки двух типов: отклонить гипотезу Н, когда она
правильна; принять гипотезу И, когда она ложна. Первый тип
ошибок называется ошибкой первого рода; второй тип ошибок —
ошибкой второго рода. Вероятности ошибок первого и второго рода
однозначно определяются выбором критической области. Для любой
критической области Rn2 мы станем обозначать через а вероятность
ошибки первого рода, т. е. вероятность отклонить гипотезу Я при
§ 1.6] ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 69'
условии, что она правильна; через Р станем обозначать вероятность
ошибки второго рода, т. е. вероятность принять гипотезу Я, если
она ложна. Символически принятые обозначения мы можем записать
в виде равенств
Само собой разумеется, что наша задача состоит в том, чтобы
найти самую выгодную критическую область, т. е. такую область
Rn2, для которой величины аир принимают наименьшие значения.
Оказывается, что при заданном объеме выборки невозможно
одновременно сделать и а и р сколь угодно малыми. Задачу при-
приходится ставить иначе: выбрав по тем или иным соображениям а,
найти ту область Rn2, для которой Р принимает наименьшее воз-
возможное значение.
Каждый раз, когда приходится проверять гипотезу Я, имеют
дело не с одной, а по меньшей мере с двумя гипотезами: Я и
не Я. В зависимости от того, сколько возможностей имеется в самой
гипотезе Я и ей противоположной, рассматривают простые и слож-
сложные гипотезы. Так, если гипотеза Я состоит в том, что параметр а
нормального распределения равен а0, а ей противоположная — в
том, что он равен ах (при известном параметре а), то мы проверяем
простую гипотезу. Точно так же, если проверяется гипотеза Я,
состоящая в том, что исследуемое распределение F(x) равномерно
в отрезке @, 1), а ей противоположная — в том, что оно нормально
с параметрами @,5; 2) то мы имеем дело с простой гипотезой.
Если же гипотеза Я состоит в том, что распределение F(x) рав-
равномерно в @, 1), а ей противоположная — в том, что F(x) состоит из-
всех возможных распределений, за исключением названного равномер-
равномерного, то мы имеем дело с гипотезой сложной. Точно так же, если
гипотеза Я состоит в том,что изучаемая нами случайная величина
распределена по закону Пуассона с каким-нибудь параметром Xf
то это — гипотеза сложная.
Относительно простых гипотез доказана важная теорема, назы-
называемая по имени ее авторов теоремой Неймана —Э. Пирсона.
Теорема Неймана — Пирсона. Пусть проверяется про-
простая гипотеза Я, состоящая в том, что имеет место распределе-
распределение Ро с плотностью вероятностей р0 (х) против конкурирующей
гипотезы «имеет место распределение Рх с плотностью вероят-
вероятностей Рх(д;)».Критическая область Rn2 с заданной ошибкой первого
рода а имеет наименьшую ошибку второго рода, если она определена
по правилу: x = {xlt х2>... ,хп) принадлежит Rn2 тогда и только
тогда, когда
Pi (х) > ср0 (х).
70 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
Константа с определяется из того условия, что ошибка первого
рода равна а.
Верно и обратное: если имеется критическая область с задан-
заданной ошибкой первого рода а и с минимальной ошибкой второго
рода, то эта критическая область определяется по только что
указанному правилу. Обратное предложение неверно только в том
случае, когда имеется критическая область с ошибкой первого рода,
меньшей а, и Р = 0.
Заметим, что ошибку первого рода называют также уровнем
значимости критерия проверки гипотезы. Величину 1—Р, т. е.
вероятность отвергнуть гипотезу Н, когда она ошибочна, называют
мощностью критерия.
Мы не касаемся здесь некоторых тонкостей, связанных с тем,
как добиться данного уровня значимости, — об этом можно прочесть
в книге [7] (стр. 95) или в книге [5] (стр. 365).
Критерий согласия %2. Для проверки статистических ги-
гипотез часто используется удобный для применений критерий согла-
согласия %2. Предположим, что нам нужно проверить гипотезу /У, состоя-
состоящую в том, что наши наблюдения образуют выборку из п значений
х{ случайной величины с данным распределением Р (S) (вероятность
попадания значения случайной величины в множество 5 равна P(S).
Это обозначение удобно, в частности, мы можем вести рассуждения
над распределениями любого числа измерений). Разобьем все про-
пространство значений наблюдаемой величины на непересекающиеся
области 5г, S2, . . . , Sr. Обозначим через pi вероятности попада-
попадания в области S( (p. = P (S()), а через vi — числа попавших в них
наблюдений. Рассмотрим
Легко подсчитать, что
Величина г—1 называется числом степеней свободы.
Доказано, что при п—> оо плотность распределения величины %2
сходится к распределений
1 r^l ±
*(*) Х'е 2
§ 1.7] ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 71
Пусть п достаточно велико. При применении критерия %2 на
практике поступают следующим образом: пространство выборок
разбивают на непересекающиеся области так, чтобы число наблюде-
наблюдений, попавших в каждую из этих областей, оказалось не меньше 10.
Далее, вычисляется величина %2. Пусть ее значение равно %* .
Для распределения kr_x (х) вычислены таблицы вероятностей
/? = Р {5B <с Хо}• Если р близко к 1, то вероятность неравенства
%2>%1 мала, и поэтому считают, что если на практике оно обна-
обнаружено, то гипотезу И следует отбросить.
Если распределение Р (S) зависит от 5 неизвестных параметров.
а1У а2, . . . , Оу, которые определяются по результатам наблюдений,
то для одного класса оценок имеет место простое правило
Р. Фишера: распределение %2 в этом случае при п—*оо схо-
сходится к распределению kr_s_1{x). Число степеней свободы умень-
уменьшается на число оцениваемых параметров. Параметры ai оценива-
оцениваются из уравнений
g = 0 (/=1,2,...,,)
и дают, следовательно, минимум %2.
Подробности, касающиеся теории критерия %2, и примеры их
применений можно найти в книгах [8] и [9].
§ 1.7. Преобразование Лапласа
В теории надежности мы имеем дело почти исключительно с
положительными случайными величинами. Для таких величин
вместо преобразования Фурье, рассматриваемого обычно в курсах тео-
теории вероятностей, удобнее пользоваться преобразованием Лапласа.
Пусть функция f(t) определена при / ^ 0, кусочно непрерывна
и растет не быстрее некоторой показательной функции, т. е. суще-
существуют С>0 и а>0, для которых
\f(t)\<Ceat
при всех t ^ 0.
Преобразованием Лапласа для этой функции называют интеграл
ti). A.7. и
Этот интеграл сходится при Rez^>a. Поэтому функция /(г) опре-
определена в комплексной полуплоскости Re^>a и является в этой
полуплоскости аналитической функцией.
х) В этом параграфе ради удобства мы будем обозначать преобразование
Лапласа той же буквой, что и саму функцию, но только с волной наверху.
Это обозначение не является общепринятым.
72 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
По известному преобразованию Лапласа можно восстановить
л саму функцию. Справедлива следующая формула обращения:
c + i оо
= J-. f f(z)eztdz, A.7.2)
c-i со
где интеграл берется по вертикальной прямой Rez = c, c>a.
Рассмотрим некоторые свойства преобразования Лапласа.
1°. Преобразование Лапласа является линейной операцией, т. е.
преобразование для суммы равно сумме преобразований, и если
функция умножается на число, то и ее преобразование Лапласа
умножается на это число
5 [cj(t) + cig(t)\e-zidt = cx\f (t)e~ztdt + c2 $ g{t) e~ztdt.
2°. Рассмотрим преобразование Лапласа для производной и ин-
интеграла от функции f(t):
ОС СО 00
\ /' (t) e-ztdt = \ e-zt d/(t) =f(t) e'zt °° + z $ /@ e~et dt =
•0 0 0
= zf(z)-f(O), A.7.3)
ec / t \
' f(x)dx)e-ztdt =
t CO
-*'<tt = ± /B?). A.7.4)
Таким образом, при дифференцировании функции /(/) ее преобра-
преобразование Лапласа умножается на аргумент z. Из произведения вы-
вычитается начальное значение функции /@). При интегрировании
•функции f(t) от нуля до t преобразование Лапласа делится на z.
Применяя формулу A.7.3) несколько раз, можно получить преобра-
преобразование Лапласа для /z-й производной
(n) (t) e'zX dt = znf(z) — zn-lf(O)— . . . — /(n-X) @).
Это свойство преобразования Лапласа часто используется при ре-
решении линейных дифференциальных уравнений, так как, переходя
от неизвестных функций к их преобразованиям Лапласа, мы полу-
получаем для последних линейные алгебраические уравнения.
§ 1.7] ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 73-
3°. Теорема запаздывания. Пусть
О, t<x,
Л О-'» f(t-x),
тогда
l/1(t)e-tdt=
. A.7.5)
Мы получили, что при сдвиге графика функции f(t) вправо на
величину х ее преобразование Лапласа умножается на е~гх.
4°. Теорема смещения. Пусть функция f(t) умножается
на e~Kt. Тогда
A.7.6)
т. е. при умножении функции е~хх на экспоненту аргумент ее
преобразования Лапласа увеличивается на К.
5°. Преобразование Лапласа для свертки. Интеграл
называется сверткой функций f(t) и g(t). Найдем преобразование
Лапласа для свертки:
00 t
\e-ztdt\f{t-%)g{x)dx =
О О
ОС 00
= S gM e~*X S Я'-т) е-г('-т> dt =
e-"d%=f~g. A.7.7)
о
Таким образом, если две функции свертываются, то их преобра-
преобразования Лапласа перемножаются. Это свойство полезно использо-
использовать, например, при решении интегральных уравнений, содержащих
74 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ.. 1
/интегралы типа свертки. Рассмотрим в качестве примера уравнение
t
где f(t) — заданная функция.
Умножим обе части уравнения на e"zt и проинтегрируем по
t от нуля до бесконечности. Получим
гу (z)-y @) = Ху (z) - ку (z) /(г),
откуда
Так как f(z)—>0 при Rez—юо, то знаменатель не обращается
в нуль в некоторой полуплоскости Re2>a и, применяя формулу
«обращения, мы получим
= 1 Г *(<»
2ш J г-к
с —I со
эта формула позволяет изучать асимптотическое поведение реше-
решения y(t) при t—> + <».
6°. Часто бывают полезны предельные соотношения для функции
и ее преобразования Лапласа:
а)
lim zf(z)=f@). A.7.8)
г -*¦ оо
б) Если существует lim /@=/(°°)> т0
/(оо)= [imzf(z). (U.9)
2 -*> О
Можно сказать, таким образом, что поведение функции f(t) в
окрестности нуля определяется поведением преобразования Лапласа
в бесконечности и, наоборот, поведение функции /(/) в бесконеч-
бесконечности определяется поведением функции f(z) в окрестности нуля.
7°. Очень часто, например при решении линейных дифферен-
дифференциальных уравнений, преобразование Лапласа для искомой функции
оказывается рациональной функцией. В этом случае сама функция
может быть выражена в конечном виде.
Найдем предварительно преобразование Лапласа для функ-
функции tne"u
^- A-7Л0)
§ 1.7] ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 75
Можно показать, что это равенство верно и для комплексных зна-
значений X. Пусть теперь преобразование Лапласа для функции /(/)
имеет вид
P{z) и Q (z) — многочлены, причем степень числителя меньше сте-
степени знаменателя, так как f(z) обязаны стремиться к нулю с ро-
ростом z. Как известно, всякая правильная рациональная дробь может
быть разложена в сумму простейших дробей:
где zk — корни знаменателя, а $Л — кратности этих корней. В частном
случае, когда все корни просты,
п А
R(z)=:^-?k-y A.7.12)
причем
Подставив в формулу обращения A.7.2) сумму A.7.11) и исполь-
использовав A.7.10), находим
S5 1
c-ico
. . М^_?__
где pk (t) — многочлены степени, на единицу меньшей кратности
корня zk.
В частности, когда все корни простые,
Ч0»? $$-•*. A-7.14)
Заметим еще, что если некоторые корни — комплексные,
76 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
то по формуле Эйлера соответствующие слагаемые в сумме A.7.13)
выразятся через тригонометрические функции
ezkt ^ eakt (cos pft/ _f_ / sin fikty
Пусть теперь ?¦—положительная случайная величина с законом
распределения
и плотностью f{t) = F'(t).
Преобразованием Лапласа для этой величины называется пре-
преобразование Лапласа для плотности f(t)
Заметим, что этот интеграл есть математическое ожидание е~г^,
т. е. ф*(z) = flle~z*-. Функция ф*(?) обладает следующими свой-
свойствами:
вообще
Ф<Я>(О) = (-1)ПМГ; A.7.15)
значит, по известному преобразованию Лапласа мы можем найти
все моменты случайной величины, в том числе среднее значение
и дисперсию.
2. Если величины ? и г] независимы, то преобразование Лапласа
для их суммы ? = ? + т) выражается так:
Фс B?) = Ш~* = Ш-г*е-гц = Ме-гте~гУ] = ^ (z)^ (г). A.7.16)
Следовательно, если независимые случайные величины склады-
складываются, то их преобразования Лапласа перемножаются. Заметим,
что это свойство эквивалентно свойству A.7.7).
8°. Преобразование Лапласа для линейной функции т) = а?
равно
Ф^ (z) = Ме-{Ч+Ь)г = е-ОгМе-аг1 = е~ь\ (az).
§ !.7] ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 77
Обычная схема применения преобразования Лапласа в теории ве-
вероятностей такова: искомые вероятности часто удовлетворяют
некоторым линейным уравнениям (дифференциальным, интегральным
или смешанным). Применяя к обеим частям уравнений преобразо-
преобразование Лапласа, мы получаем новые уравнения, из которых находятся
преобразования Лапласа для наших вероятностей. Зная эти пре-
преобразования, мы можем в некоторых случаях найти явное выражение
для вероятностей. Но даже если эти вероятности не выражаются
через известные функции, мы можем, зная преобразования Лапласа,
получить существенную информацию об искомых вероятностях.
Можно найти моменты, исследовать асимптотическое поведение
вероятностей, найти для них приближенные формулы и т. п.
Вычислим в заключение преобразование Лапласа для некоторых
законов распределения, которые используются в теории
надежности.
1°. Экспоненциальный закон. Плотность f(t) = Хе~иу
2°. Нормальный закон
(f-7-p)»
2л о
Пусть а<^Г0, тогда вероятность того, что случайная величина
примет отрицательное значение, мала, и мы можем считать, что
наша величина положительная
Так как в наших предположениях плотность f(t) очень мала для
отрицательных значений /, то мы можем распространить интегри-
интегрирование на всю бесконечную прямую. Сделаем, кроме того, замену
-""" °==х. Получим
roZ+?l?l i л
¦f2n J
е ъ dx =
— GO
78 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. 1
3°. Гамма-распределение
Преобразование Лапласа равно
ГЛАВА 2
ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ
§ 2.1. Основные понятия теории надежности
Систематическое изложение ряда задач теории надежности мы
начинаем с определения основных понятий, таких как надежность,
отказ, долговечность и т. п. Терминологические вопросы не явля-
являются ведущими в надежности. Однако чтобы избежать путаницы
в использовании ряда терминов, надо дать им четкое определение.
Еще совсем недавно эти терминологические вопросы волновали мно-
многих исследователей как в нашей стране ([1], [2]), так и за рубе-
рубежом ([3]). В итоге работы специальной комиссии была издана бро-
брошюра [4], посвященная терминологии надежности в области радио-
радиоэлектроники. Определения основных понятий даны также в статье
«Надежность» [5].
Как и в других областях науки, основные понятия теории на-
надежности воспринимаются путем описания соотношений между ними.
Под изделием мы будем понимать элемент, систему или ее часть
и т. д. Эксплуатация изделия понимается как совокупность всех
фаз его существования: транспортировка, хранение, подготовка
к использованию по назначению, обслуживание и ремонт. Понятие
о надежности изделия существенным образом связано с понятием
о его качестве. Качеством изделия называется совокупность свойств,
определяющих* степень пригодности изделия для использования по
назначению. Таким образом, понятие о качестве изделия сущест-
существенным образом зависит от способа его использования. Например,
если изделия радиоэлектроники используются в стационарных усло-
условиях при поддержании определенной температуры и влажности, то
свойство влагостойкости не играет определяющей роли в понятии
качества изделий. Совсем другое положение возникает в тех слу-
случаях, когда аппаратура используется в полевых условиях без гер-
герметизации. Здесь свойство влагостойкости является неотъемлемой
частью других свойств, определяющих качество. Качество сложных
изделий, особенно систем управления, как правило, определяется
80 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
весьма большим набором свойств. С течением времени свойства, со-
составляющие качество изделия, видоизменяются и чаще всего в не-
нежелательную сторону. В зависимости от их изменения меняется
и само качество. Под надежностью изделия мы будем понимать
способность изделия сохранять качество при определенных условиях
эксплуатации. Другими словами, надежность — это качество, раз-
развернутое во времени. Надежность определяется качеством и усло-
условиями эксплуатации. Мы подчеркиваем, что понятие надежности
связано с теми свойствами, которые либо были у изделия в момент
его изготовления или проверки перед эксплуатацией, либо должны
были быть. Например, не имеет смысла говорить о ненадежности
радиоприемного устройства по отношению к определенному виду
помех, если свойство помехозащищенности не было учтено при раз-
разработке этого устройства. Другое дело, если есть определенные
участки схемы, которые выполняют функции, обеспечивающие по-
помехозащищенность. Для таких систем в комплексе свойств, опре-
определяющих качество и надежность, нужно включить помехозащи-
помехозащищенность.
Проблема повышения надежности изделий становится все более
важной и актуальной в связи с комплексной механизацией и авто-
автоматизацией производственных процессов во многих областях про-
промышленности, на транспорте, в технике связи и т. п. Важность этой
проблемы определяется тем, что недостаточная надежность изде-
изделий вызывает большие затраты на их обслуживание, возникают
частые простои оборудования, могут быть аварии, связанные с боль-
большим ущербом и даже человеческими жертвами. В некоторых случаях
автоматические устройства оказываются менее рентабельными по
сравнению с неавтоматическими в основном по причине их ненадеж-
ненадежности. Недооценка факторов, связанных с надежностью, приводит
к тому, что расходы в течение первых лет эксплуатации существенно
превосходят начальную стоимость изделий. В настоящее время ма-
машины проникают во все сферы деятельности человека, в том числе
и в сферу управления производством и других процес-
процессов управления. Задачи, которые решают машины, и особенно
управляющие машины, становятся все сложнее. Возрастающая слож-
сложность решаемых задач приводит к тому, что сложнее становятся
машины, предназначенные для решения этих задач. Налицо одно из
основных противоречий в развитии современной техники: с одной
стороны, все увеличивающаяся сложность систем приводит к сни-
снижению их надежностих_^ с другой стороны, ставятся все более
жесткие требования к надежной работе этих систем. Поиском путей
разрешения этого противоречия и служит теория надежности. Воз-
Возможны два принципиально различных пути. Первый путь состоит
в повышении качества и надежности отдельных элементов, из ко-
которых составляется сложная система* Второй путь заключается
§ 2.1] ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НАДЕЖНОСТИ 81
в разработке специальных методов конструирования сложных на-
надежных систем из ненадежных элементов, а также в разработке ме-
методов обслуживания таких систем в процессе эксплуатации. В статье
«Надежность» [5] дается следующее определение задач теории на-
надежности: «Теория надежности —это новая научная дисциплина*/
изучающая общие закономерности, которых следует придерживаться
при проектировании, испытаниях, изготовлении, приемке и эксплу-
эксплуатации изделий для получения максимальной эффективности от их
использования».
Одним из основных понятий теории надежности является поня-
понятие об отказе и безотказности. Под безотказностью понимается
способность изделия сохранять работоспособность (т. е. не иметь
отказов) в течение определенного интервала времени в определен-
определенных условиях эксплуатации. Отказ — это частичная или полная
утрата или видоизменение таких свойств изделий, которая суще-
существенным образом снижает или приводит к полной потере работо-
работоспособности. В отдельных случаях понятие отказа является четко
определимым. Типичным примером изделий такого сорта могут слу-
служить электрические осветительные лампочки. Для их работы, как
правило, характерны два состояния: либо нормальное свечение, либо
потеря свечения. Однако применительно к изделиям радиоэлектро-
радиоэлектроники понятие отказа является весьма относительным, так как оно
существенным образом зазисит от конкретных условий использова-
использования изделий. Как пример рассмотрим сопротивления, для которых
основным параметром, определяющим качество, является величина
сопротивления, выраженная в омах. Обычно под отказом сопротив-
сопротивления понимают уход величины сопротивления от номинального
значения Ro за предельно допустимые границы Ro ± Д/?о. Таким
образом, к моменту t будут считаться отказавшими те сопротив-
сопротивления, величины которых лежат вне (Ro — Д/?о, /?0 + Д/?0). Вели-
Величина Д/?о никак не связывается, да и не может быть связана с кон-
конкретными условиями использования этих сопротивлений, так как
в различных схемах величины допусков Д/?о будут существенным,
образом отличаться друг от друга. Если схема сконструирована
оптимальным образом, то выход за пределы Д/?о может не привести
к отказу. Наоборот, могут встретиться и такие случаи неустойчиво
работающих схем, когда даже незначительные изменения величины
сопротивления, меньшие Д/?о, приведут к отказам в работе схем.
Несмотря на всю относительность, понятие отказа является полез-
полезной и содержательной характеристикой надежности, так как оно
позволяет вводить различные численные характеристики надежно-
надежности. По этим численным показателям можно сравнивать надежность
различных типов изделий или изделий одного типа, но выпущенных
в разное время и т. п.
4 Б. В. Гнеденко и др.
82 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
По своему характеру в первом приближении отказы могут быть
разделены на внезапные и постепенные. Постепенные отказы воз-
возникают при постепенном изменении параметров, определяющих ка-
качество изделия (в основном в результате старения или износа),
когда эти параметры выходят за пределы установленных допусков.
Одной из важных задач теории надежности является исследование
возможности прогноза постепенных отказов. Внезапные отказы
определяются резким изменением параметров, определяющих ка-
качество изделия. Целесообразно рассматривать и другие типы отка-
отказов. Для вычислительных машин, например, характерны сбои, т. е.
самоустраняющиеся отказы. Более полную классификацию отка-
отказов можно найти в уже упоминавшейся ранее брошюре по терми-
терминологии [4].
Другим важнейшим понятием теории надежности является дол-
долговечность. Под долговечностью изделия понимают его способность
к длительной эксплуатации при необходимом техническом обслу-
обслуживании, в которое могут входить и различные виды ремонтов.
В конце срока, определяющего долговечность, в изделии появля-
появляются такие процессы, связанные с износом или старением, устра-
устранение которых либо невозможно, либо экономически нецелесообразно.
Долговечность характеризуется либо временем, либо числом циклов,
либо объемом произведенной работы. Для некоторых изделий по-
понятия долговечности и безотказности могут совпадать, но в общем
случае это — самостоятельные характеристики надежности.
Для тех изделий, в которых работоспособность поддерживается
с помощью специальных восстановительных воздействий, называе-
называемых ремонтом, важным показателем надежности является ремон-
ремонтопригодность. Ремонтопригодностью изделия называется его
приспособленность к предупреждению, обнаружению и устранению
отказов. Она характеризуется затратами труда, времени и средств
на ремонтные работы.
Итак, понятие надежности более подробно раскрывается
совокупностью трех понятий: безотказности, долговечности
а ремонтопригодности.
Характеристики качества и надежности изделий существенным
образом связаны с экономическими показателями (себестоимостью)
изделий. Повышение надежности изделий, как правило, сопровож-
сопровождается увеличением себестоимости изделий к моменту окончания
их изготовления и приемки потребителем. В этом смысле более
дорогие надежные изделия невыгодно отличаются от менее надеж-^
ных, но зато более дешевых изделий. Однако заключение — какие
изделия лучше, должно учитывать не только величину себестои-
себестоимости изготовления. Экономическая эффективность использования,
окупаемость у более надежных изделий может перекрыть повышение
ifх себестоимости. Разработка методов учета факторов надежности
§ 2.1] ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НАДЕЖНОСТИ 83
и себестоимости, по нашему мнению, является одной из актуальных
и важных проблем экономической науки.
Более конкретно задачу теории надежности можно сформулиро-
сформулировать следующим образом. Теория надежности устанавливает
и изучает количественные характеристики [критерии) надежно-
надежности, исследует связь между показателями экономичности^
эффективности и показателями надежности-,
—разрабатывает методы проведения испытании на надежность
и методы обработки и оценки результатов этих испытаний;
— разрабатывает методы контроля надежности, методы опти-
оптимальных режимов профилактических (регламентных) работ при
эксплуатации изделий, методы обоснования норм запасных частей
(элементов, деталей).
В теории надежности разрабатываются методы установления
режимов и выбора характеристик, обеспечивающих оптимальную
надежность, методы выбора оптимальных конструкций и схем,
обеспечивающих заданную надежность, оптимальные методы оты-
отыскания неисправностей в сложной аппаратуре и т. п.
При решении задач теория надежности использует резуль-
результаты исследований физических и химических процессов, лежащих
в основе явлений, связанных с потерей качества,
В ряде разделов теории надежности широкое применение нахо-
находят математические методы, такие как методы теории вероятно-
вероятностей и математической статистики, теории информации, теории
массового обслуживания, линейного и нелинейного программирова-
программирования, математической логики, методы статистического моделирова-
моделирования на электронных вычислительных машинах и др.
Теория надежности ввиду актуальности решаемых ею задач становится
в настоящее время модной наукой. Количество статей, так или иначе свя-
связанных с проблемами обеспечения надежности, растет. По нашему мнению,
наблюдается необоснованный разрыв экспериментальных и теоретических
исследований. Есть работы чисто экспериментальные, без попыток обобще-
обобщения и построения теории, описывающей явления, и есть много работ, ко-
которые можно рассматривать как математическое жонглирование индексами,
примитивное с точки зрения специалиста, хорошо знающего математику.
В этой связи мы обращаем внимание читателя на статью «Бандвагон», опу-
опубликованную недавно на русском языке в сборнике работ К- Шеннона [6],
посвященную аналогичному вопросу о «модности» теории информации.
Рассмотрим соотношение между понятиями надежности и
эффективности. Среди части инженеров, занимающихся проектиро-
проектированием сложных систем, распространено мнение, что понятия
теории надежности неприменимы для сложных систем. Утверждается,
что понятие надежности сложной системы лишено смысла и надо
говорить только об эффективности таких систем. При этом,
однако, неявно критикуется понятие отказа сложной системы.
Действительно, понятие качества сложной системы, созданной для
84 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
работы в меняющейся внешней обстановке, включает в себя сово-
совокупность многих десятков, а иногда и сотен свойств, определяющих
качество. Многие из этих свойств играют существенную роль
только при определенной внешней обстановке. Поэтому понятие
отказа, связанное с полной или существенной потерей работоспо-
работоспособности системы, выглядит весьма искусственным. Более приемле-
приемлемым является введение сводного показателя качества — эффек-
эффективности, являющейся мерой производительности системы с учетом
внешней обстановки и способа применения. Понятие эффективности,
вообще говоря, является независимым от понятия надежности.
Можно говорить об эффективности абсолютно надежных систем и
сравнивать системы по количественным показателям эффективности.
Однако если составные части системы не являются абсолютно на-
надежными, то их качество существенным образом сказывается на
эффективности. В таких случаях под надежностью системы следует
понимать стабильность эффективности с учетом надежности частей,
составляющих систему.
До сих пор мы говорили о понятиях надежности в самом общем
плане. Однако если мы попытаемся ввести количественные пока-
показатели введенных выше понятий, то неизбежно приходим к необ-
необходимости введения вероятностной трактовки таких показателей.
В большинстве статей под надежностью понимается вероятность
безотказной работы в течение заданного промежутка времени.
Наряду с этим встречаются и другие толкования этого термина.
В этом нет ничего удивительного, так как разнообразие практи-
практических задач приводит к необходимости прибегать то к одной, то
к другой характеристике надежности устройств в работе. Так, в
одних случаях важно, чтобы средняя длительность безотказной
работы была максимальна, в других нужно, чтобы максимальной
была вероятность безотказной работы в течение заданного про-
промежутка времени длины 7; может возникнуть необходимость в
других количественных показателях. Более того, в ряде случаев
может оказаться нужным достижение максимального уровня на-
надежности сразу по нескольким показателям. Иногда эти требова-
требования могут оказаться противоречивыми. В таком случае, речь может
идти об определении оптимального решения относительно предъ-
предъявляемых требований. Здесь следует подчеркнуть, что оптимальность
не может быть определена вне конкретной системы и ее назначения.
Так, для примера, очень важно добиться такого положения,
чтобы сельскохозяйственные машины были приспособлены для вос-
восстановления их функций путем ремонтных работ и чтобы их
долговечность была возможно большей. Однако с точки зрения
интересов отдельных хозяйств и государства в целом особенное
значение имеет надежность этих машин в смысле высокой вероят-
вероятности безотказной работы в течение периода полевых работ.
§ 2.1] ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НАДЕЖНОСТИ 85
Ущерб хозяйству будет велик, если тракторы и комбайны, имея
-большую долговечность, будут часто останавливаться в период
посевных или уборочных работ и если на их ремонт потребуется
время в самый ответственньй период. Точно так же для самолета
необходимо добиться максимальной вероятности безотказной
работы на период всего рейса. Долговечность, т. е. общая дли-
длительность эксплуатации самолета (за вычетом времени, потрачен-
потраченного на ремонты) до полного его износа, являясь важной
характеристикой его качества, отступает здесь на второй план.
Таким образом, количественных характеристик надежности
много, в каждом конкретном случае решающую роль могут играть
различные показатели надежности.
В настоящей части книги мы ограничиваемся только матема-
математическими моделями, связанными с использованием методов теории
вероятностей и математической статистики. Общий подход к по-
построению таких моделей может быть изложен следующим образом.
Из всех состояний, в которых может находиться система, мы
выделяем множество 0? = {х} таких состояний х, которые разли-
различаются между собой с точки зрения надежности. Множество (?
назовем фазовым пространством системы. Например, если система
состоит из п блоков различных типов, каждый из которых может
находиться либо в рабочем, либо в неисправном состоянии, то
фазовое пространство системы образует точки вида х = (г1У . .., еп),
где 8^ = 0, если 1-й блок исправен, и et-=l, если 1-й блок неис-
неисправен. Если неисправные блоки могут ремонтироваться, а время
ремонта является случайной величиной с некоторой функцией
распределения FpeM (x), вообще говоря, отличной от показатель-
показательного закона, то естественно считать, что состояния системы раз-
различаются, если различны времена, уже затраченные на ремонт
неисправных блоков. При этом мы приходим к необходимости
рассмотрения более сложного фазового пространства (?, состоящего
из наборов точек x = (ev tx, 82, /а, ... , еи, tn), где е? = 0;1 в
зависимости от того, исправен 1-й блок или нет, a ti = 0 для
€t. = 0. Для 8; = 1 ti равно времени, уже затраченному на ремонт
i-ro блока. Могут встретиться случаи, когда значения х имеют
физический смысл. Предположим, что наиболее важными показа-
показателями качества полупроводникового триода являются коэффициент
усиления р и уровень шумов F. В этом случае фазовое прост-
пространство (? состоит из совокупности точек плоскости х — (х1У х2)у
где #! = Р, x2 = F. В множество (? включаются точки х первого
квадрата плоскости л^^О, л:2^0. Можно было бы привести
примеры систем и с более сложными фазовыми пространствами.
Итак, в качестве первого шага построения математической
модели необходимо выбрать соответствующее фазовое простран-
пространство <? = {*}.
86
ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ
[гл. 2
С течением времени в составных частях системы происходят
различные изменения, например связанные со старением элементов,
составляющих систему. Поэтому, если в момент t состояние системы
описывалось точкой хх, то в момент времени t2>tx состоянию
системы соответствует точка х2. При этом может оказаться, что
х2фхг. Если обозначить через х (t) ? (S состояние системы в момент
времени /, то последовательность состояний x(t), t^O, можно
рассматривать как процесс, протекающий во времени. Так как
изменение состояний носит случайный характер, то значения х (t)
можно рассматривать как траекторию случайного процесса, про-
протекающего в фазовом пространстве состояний системы (?.
Вторым шагом построения математической модели является
определение этого случайного процесса в зависимости от кон-
конкретных условий постановки задачи. Рассмотрим пример. Пусть
система состоит из п одинаковых блоков, один из которых
является основным, а остальные находятся в резерве. Каждый из
блоков может быть либо исправным, либо отказавшим. Отказы
наступают независимо друг от друга. Восстановление отказавших
блоков не производится, а надежность каждого из блоков харак-
характеризуется вероятностью безотказной работы в течение времени t,
равной p(t) — е~м. При отказе основного блока он заменяется
резервным. В качестве фазового пространства можем выбрать
(? = {0, 1, ...,#}. Считаем, что x(t) = k, если в момент времени/
исправны к блоков. Случаям «холодного» резерва, когда резервные
блоки не отказывают, и «горячего» резерва, когда вероятность
отказа блока, находящегося в резерве, также равна p(t) = e~u,
соответствуют различные случайные процессы лгхол (t) и xrop(t).
При сделанных выше допущениях эти процессы являются одно-
однородными по времени марковскими процессами с конечным числом
состояний. В первом случае матрица интенсивностей переходов
равна А1У во втором — А2
А -
1
\—пХ
0
0
0
1
1
— к
0 1
0
0
пХ
0
0
X
-X
0
0
-\)Х
0
X
0
0
0
0
0
0
п-
• • •
0
-1Ь
0
0
0
0
1 —А
0
0
0
X
0
•
. 1
у
0
0
-X
0
0
0
X
0
К однородным по времени марковским процессам с конечным числом
состояний приводит постановка задач на системы с резервиродаа-
§ 2.1] ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НАДЕЖНОСТИ 87
нием, рассматриваемые в настоящей книге (см. главы 5 и 6).
Существует, однако, большое количество задач, решение которых
представляет непосредственный практический интерес и которые
приводят к необходимости изучения марковских процессов более
сложной природы. Важным частным случаем являются марковские
процессы с дискретным вмешательством случая. Систематическое
изложение методов решения задач теории надежности с исполь-
использованием марковских процессов с дискретным вмешательством
случая будет дано в задуманной нами книге. Из вышедших в свет
работ мы отметим [8], [9], [10].
Небесполезно заметить, что многие задачи теории массового
обслуживания приводят к моделям, тождественным моделям теории
надежности. В связи с тем, что теория массового обслуживания
начала развиваться значительно раньше, представляет практический
интерес использование приемов и методов, а иногда и самих
моделей для решения задач теории надежности. Иногда для ис-
использования результатов теории массового обслуживания в теории
надежности достаточно слово «вызов» или «покупатель»
заменить словом «отказ», а длительность «разговора» или «об-
«обслуживания» — временем «ремонта».
Когда определено фазовое пространство ($, = {х) и в нем задан
случайный процесс #(/), описывающий эволюцию системы во вре-
времени, то следующим этапом является выбор различных числовых
характеристик надежности системы. Как мы уже отмечали, такой
выбор зависит от конкретных условий и назначения системы.
Более того, иногда представляется целесообразным вычислить
одновременно несколько числовых показателей надежности. В са-
самом общем плане характеристики надежности можно рассматривать
как математическое ожидание от некоторого функционала Ф,
определенного на траекториях процесса x(t). Говорят, что функ-
функционал Ф определен на процессе x(t), если каждой траектории
x(t) ставится в соответствие некоторое число <P[x(t)\. Показатель
надежности ф определяется как математическое ожидание от этого
функционала, т. е.
ф = МФ[х@1. B.1.1)
Такой подход фактически состоит в том, что каждой траектории
процесса х (t) мы приписываем некоторый вес, а затем за показа-
показатель надежности принимаем среднее значение этого веса. Напри-
Например, вероятность безотказной работы P(t) можно получить сле-
следующим образом. Вначале в фазовом пространстве (S определяется
такое подмножество (?отксE (рис. 2.1.1, а), что система считается
неработоспособной, когда ее состояние х (t) ? EОтк. Для полупро-
полупроводникового триода в случае учета только параметров коэффи-
коэффициента усиления и уровня шумов при испытаниях на надежность
88
ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ
[ГЛ. 2
вид области (?отк показан на рис. 2.1.1,6. Функционал Фх опреде-
определяем следующим образом. Мы полагаем Ф1 [х (t)] = 0, если хотя
бы при одном значении s^t траектория х (s) проходит через
точки подмножества (?Ог<» в противном случае полагаем Ф1[лг(^)]1 =
= 1. Очевидно, что ШФ1 [х (t)] =p (/), т. е. равно вероятности
безотказной работы в интервале [0, if]. Функционал Ф2 [a: (t)] равен
гкр
'нкр /»Кр
б)
Рис. 2.1.1.
длительности интервала времени от начала работы системы до
первого попадания траектории в множество (?Отк. Константа
7=МФ2 [x(t)] представляет собой важную числовую характери-
характеристику надежности системы — среднее время безотказной работы
системы.
Возможны и другие подходы к определению оптимальной на-
надежности системы с точки зрения ее эффективности. .При этом
мы приходим к необходимости сравнения показателей надежности
различных систем с различными фазовыми пространствами состоя-
состояний и отбора наилучшей из них. Типичными постановками задач
такого рода являются задачи оптимального резервирования при
одном или нескольких ограничениях [7].
Одна из возможных экономических трактовок задач теории
надежности такова: пусть надежность системы характеризуется
функционалом Ф[лг(?), Г], где Т—назначенное время ее использо-
использования, a w{<P[x(t),T]} — ущерб за время Г. Если устранение
каждого отказа стоит с, а число отказов за время Т равно Л/"(Г),
то общие расходы, связанные с эксплуатацией системы за время Ту
равны в среднем
М^{Ф[лг@, Т]} + сШ(Т). B.1.2)
При проектировании и эксплуатации можно в некоторых случаях
исходить из требования, чтобы сумма расходов в B.1.2) принимала
минимальное значение.
§ 2.2] НАДЕЖНОСТЬ ЭЛЕМЕНТА 89
Возможны и другие постановки задач по определению опти-
оптимальной экономической эффективности. Не может быть сомнения,
что обоснованное сочетание высокой надежности и экономической
эффективности представляет большой хозяйственный интерес и
относящиеся сюда вопросы заслуживают всесторонней разработки.
§ 2.2. Надежность длемента, работающего
- до первого отказа
Основные характеристики надежности. В этом
параграфе мы будем рассматривать работу элемента до первого
отказа и изучать различные характеристики надежности таких
элементов.
Под словом «элемент» мы будем понимать не только нераз-
неразложимую часть системы, но и любое устройство, надежность
которого изучается независимо от надежности составляющих
его частей.
Пусть в момент t = 0 элемент начинает работу, а в момент
t = x происходит отказ. Будем говорить, что Хгг- время жизни
элемента1). Предположим, что т—случайная величина с законом
распределения
{} B.2.1)
Функция Q (t) есть вероятность отказа элемента до момента t. Мы
будем предполагать, что функция Q (t) непрерывна и существует
непрерывная плотность вероятности отказа
Эти условия удобны для дальнейшего, кроме того, в теории на-
надежности они естественны.
Так, например, разрыв функции Q (t) означает, что в какой-то
наперед заданный момент элемент может отказать с конечной
вероятностью, что вряд ли может быть на практике. Исключение
составляет лишь начальный момент / = 0, так как некоторые
элементы отказывают в момент включения. К таким отказам при-
приводят скрытые, но серьезные дефекты в элементе или небрежное
хранение и транспортировка этого элемента. Однако, как правило,
отказ в момент включения сразу же обнаруживается и элемент
заменяется новым. Поэтому мы можем не принимать во внимание
такие отказы, и тогда функция Q (t) будет непрерывна и при
* 0
*) Если элемент работает с перерывом и если во время простоев его
параметры не меняются и он не может отказать, то все написанное ниже
будет справедливо и для таких элементов, если под т понимать не кален-
календарное время, а чистое время работы.
90 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
Заметим еще, что само исходное предположение о том, что
т —случайная величина, является серьезным допущением, которое
на практике, по-видимому, не всегда справедливо. Рассматриваемый
элемент всегда является представителем большой группы одно-
однотипных элементов. Эта группа должна быть в известном смысле
однородна. Кроме того, условия эксплуатации должны быть одно-
однородны и по элементам и во времени. Так, например, одинаковые
элементы, выполняющие различные функции, могут иметь различ-
различную надежность.
Итак, мы предположили, что время жизни элемента т есть
случайная величина с законом распределения Q(t). Эта функция
полностью определяет надежность нашего элемента.
Наряду с ней и не менее часто употребляется и другая
функция
B.2.2)
т. е. вероятность безотказной работы элемента за время t. Будем
называть эту функцию так, как
ее чаще всего называют, а именно,
функцией надежности.
Примерный вид функции надеж-
надежности показан на рис. 2.2.1. Эта
функция монотонно убывает;
Р@) = 1 и P{t)-+O при *-*оо.
Функцию P(t) можно прибли-
приближенно найти из опыта. Предполо-
Рис. 2.2 1 жим сначала, что нам нужно
найти значение этой функции при
t = tOi т. е. вероятность безотказной работы в течение времени t0.
Мы ставим на испытания N одинаковых элементов и испытываем
их при одинаковых условиях в течение времени t0. Пусть к моменту
окончания испытаний не отказало п элементов. Можно рассмат-
рассматривать наш эксперимент как серию из N независимых испытаний, при
каждом из которых происходит одно из двух событий: или элемент
отказывает, или он не отказывает. Но тогда отношение -^ есть
частота появления первого события, и по теореме Бореля [11] с
вероятностью единица
jj-+P(t0) при N—>oo.
Это означает практически, что при большом N с вероятностью,
близкой к единице, имеет место приближенное равенство
B.2.3)
§2.2]
НАДЕЖНОСТЬ ЭЛЕМЕНТА
91
Если мы хотим найти функцию P(t) для всех значений t^t0} то
мы должны проводить испытания в течение времени t0 и отмечать
моменты возникновения отказов. Зная эти моменты, легко опре-
определить функцию n(t), которая равна числу элементов, не отка-
отказавших к моменту t. В начальный момент эта функция равна
n@) = Ny а в момент каждого отказа она уменьшается на еди-
единицу. Отношение PN(t)=^-^- называется эмпирической функцией
надежности (рис. 2.2.2). С ростом
N эта функция равномерно при-
приближается к функции P(t)y и для /
больших N имеет место прибли-
приближенное равенство
B.2.4)
О
Рис. 2.2.2.
Следует заметить, что если ис-
испытания проводились на каком-то
участке времени, то за пределами этого участка мы ничего
о функции сказать не можем. Иными словами, функцию Р(t) в
общем случае нельзя экстраполировать. Правда, очень часто из
физических соображений или из предшествующего опыта мы знаем
аналитический вид функции P(t), она выражается некоторой фор-
формулой, содержащей один или несколько неизвестных параметров.
Тогда, проводя испытания, мы можем определить эти парамет-
параметры, а по ним и саму функцию на всем бесконечном участке
времени. .
Как это делается, будет сказано ниже. Заметим еще, что при
одной и той же точности для оценки функции P(t) требуется
гораздо больший объем испытаний, чем для оценки вероятности
P(t0). По этой причине во многих случаях надежность характе-
характеризуют не функцией P(t), а некоторыми числовыми величинами.
Важнейшей из них является среднее время безотказной работы,
которое определяется как математическое ожидание случайной
величины т,
То = Mr = J tq (t) dt
Полезно преобразовать этот интеграл к другому виду, взяв его
по частям
00
T0=\tq{t)dt=-tP(t)
92 характеристики надежности [гл. 2
или
00
70= $/>«)<«. B.2.5)
о
(Мы предполагаем, что написанные интегралы сходятся, и в даль-
дальнейшем это оговаривать не станем.) Из последней формулы видно,
что среднее время То геометрически выражается площадью, огра-
ограниченной осями координат и кривой P(t).
Среднее время может быть найдено по результатам испытаний.
Для этого нужно испытывать элементы до отказа последнего из
них. Пусть тх> ..., xN—времена жизни этих элементов. Рассмот-
Рассмотрим эмпирическое среднее время
Т~~ N '
Согласно усиленному закону больших чисел [11], с вероятностью
единица
t—> То при N—юо.
Поэтому при большом N имеет место приближенное равенство
т^70. B.2.6)
К сожалению, последние испытания часто практически неосущест-
неосуществимы, так как время испытаний ограничено и мы не можем ждать,
пока откажут все элементы. Пусть, например, за время t при ис-
испытании N элементов произошло п отказов в моменты тх, т2, . . ., хп.
Единственное, что можно сделать в этом случае, это дать оценку
снизу для среднего времени. Действительно,
Т N >
N > N
и, значит, при большом N
7-о>Т1+-+;" + (*-П)/. B-2.7)
Естественно, что пользоваться этой оценкой имеет смысл только
тогда, когда п близко к N.
Другой характеристикой надежности является дисперсия времени
жизни
От = М (т - 7-0J = Мт2 - (МтJ = J t2q (t) dt - f0 =
—71. B.2.8)
§ 2.21
НАДЕЖНОСТЬ ЭЛЕМЕНТА
93
Дисперсия может быть найдена из опыта. Если испытывается N
элементов и тх, ...,Tjv — времена их жизни, то при большом N
2 to-*>
/=1
N— 1
B.2.9)
N
гдет = ^г-.
Величина ae=|/Dt дает нам среднеквадратическое уклонение
случайного времени т от своего среднего времени Го. Использовать
дисперсию как характеристику надежности целесообразно, по-види-
по-видимому, тогда, когда а<С То> т. е. случайное время т имеет неболь-
небольшой относительный разброс. В этом случае ^весьма яркое представле-
представление о надежности дает график плотности q(t), который, как правило,
имеет одну вершину (рис. 2.2.3). Функция q{t) также может быть
q(t)
Рис. 2.2.3.
Рис. 2.2.4.
найдена из опыта. Для этого мы разбиваем весь участок времени
(рис. 2.2.4) на интервалы длительности h и регистрируем число
отказов, попавших на каждый интервал. Пусть поставлено на испы-
испытания N элементов и nk число отказов, происшедших на интервале
[(&—1)/г, Щ, /5 = 1,2, ... Тогда эмпирическая функция плотности,
или гистограмма (подробнее см. главу 3), выразится формулой
если (ft— l)ft«
точно малом h
qN{t)=J&9 B.2.10)
; t < kh. При большом объеме испытаний и доста-
Перейдем теперь к рассмотрению важнейшей и очень популярной
характеристики надежности, которую чаще всего называют опас-
опасностью отказа.
94 характеристики надежности [гл. 2
— Рассмотрим сначала такую задачу. Пусть элемент проработал
безотказно до момента t. Какова вероятность того, что он не
откажет на участке (t, ttO Обозначим эту вероятность через
P(t, t^. Пусть Л — событие, означающее безотказную работу эле-
элемента на @, t), а В— событие, означающее безотказную работу на
(t, tx). Тогда наша вероятность есть условная вероятность
?{АВ\ . 1:
7i ¦ ^ "
Но событие АВ означает безотказную работу элемента на @, tt).
Поэтому
Вероятность отказа на (/, tx) выразится, очевидно, так:
Q (*, tx) - 1 -Р(/, ^i) = P(V(f)(/l) ' B-2Л2)
Положим теперь tx = t-\-At и устремим А^ к нулю. Тогда
Q{t, t + Af> =
Введем обозначение
Р'
При малом Д^
Q(t9 t + M)&K(t)M. B.2.14)
Из этой формулы видно, что величина X (t) является локальной
характеристикой надежности, определяюш^инадежность элемента
в каждый данный момент времени. Говоря «по-инженерному», X (t)
есть вероятность того, что элемент, проработавший безотказно до
момента t, откажет в последующую единицу времени (если, ко-
конечно, эта единица мала). В терминах теории вероятностей X (t)
есть плотность условной вероятности отказа в момент t, при условии,
что до этого момента элемент работал безотказно.
Функция X(t), определяемая из формулы B.2.13), и называется
опасностью отказа.
Уравнение B.2.13) может быть легко разрешено относительно
функции надежности P(t). Сделав это, мы получим
B.2.15)
§ 2.2] НАДЕЖНОСТЬ ЭЛЕМЕНТА 95
Из этой важной формулы следует, что вероятность безотказной
работы на интервале (tlt t2) выражается так:
-/мол
P(tvt2) = e U . B.2.16)
Функция к (t) может быть определена по результатам испытаний.
Мы, как и выше, испытываем N элементов и наблюдаем их отказы.
Пусть п (t) — число элементов, не отказавших к моменту t.
Тогда при достаточно малом Д^ и достаточно большом N
n(t)-n
. Р' (t) ^ P(Q —P(f+AQ ^ jV __ Arc
h('~~~PW^ M P (t) ^ AtliD. ~~&tnA)y
N
где An— число отказов на участке (/, t-\-At).
Итак, если At достаточно мало, a An при этом велико, то
к^^ШТГ)' B.2.17)
Значит, статистически опасность отказа равна числу отказов, про-
происшедших за единицу времени, отнесенному к числу не отказавших
к данному моменту элементов. Пользуясь этой статистической трак-
трактовкой, попытаемся показать на примере, что к (t) действительно
является локальной характеристической надежностью. Пусть испы-
тывается 1000 одинаковых элементов и за первый час выходит из
строя 50 элементов, через 30 часов работы остается в живых
60 элементов, а в последующий час выходит из строя 20 элементов.
Спрашивается, когда элемент более надежен, вначале или после
30 часов работы? Ясно, что абсолютные цифры, 50 и 20, не могут
служить для сравнения надежности. Ведь за первый час выходит
из строя 50 элементов из тысячи, т. е. каждый двадцатый элемент,
а после 30 часов работы за час выходит 20 элементов из 60, т. е.
каждый третий. Таким образом, мы видим, что надежность элемента
в каждый момент времени характеризуется отношением числа отказов
за единицу времени к общему числу уцелевших к данному моменту
элементов. Но это и есть опасность отказа. Практически при опре-
определении опасности отказа удобно поступать так же, как и при
построении гистограммы g(t). Мы разбиваем весь участок времени
на интервалы длительности h и находим число отказов, попавших
в каждый интервал. Пусть nk — число отказов на интервале
[(/5 — 1)/г, kh], A=l,2, ... Тогда эмпирическая опасность отказа
(*-!)*</<**.
96
ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ
[ГЛ. 2
Рис. 2.2.5.
Мы получаем ступенчатую кривую, приближенно представляющую
график опасности отказов (рис. 2.2.5).
Э к с п о н енциальный закон. Многочисленные опытные
данй'ые показывают, что для многих элементов функция К (t) имеет
характерный вид кривой рис. 2.2.6.
Из этого графика видно, что весь
интервал времени можно разбить
на три участка. На первом из
них функция К (t) имеет повышен-
повышенные значения. Это связано с тем
обстоятельством, что в большой
^ партии элементов всегда имеются
элементы со скрытыми дефектами,
которые выходят из строя вскоре
после начала работы. По этой
причине первый период называют
периодом приработки, или периодом «выжигания» дефектных эле-
элементов.
Второй период называется периодом нормальной работы. Он
характеризуется постоянным (или приближенно постоянным) значе-
значением опасности отказа.
Последний период — период старения. Необратимые физико-
химические явления приводят к ухудшению качества элемента,
элемент «стареет». В этот пе-
период опасность отказа возра-
возрастает.
Естественно, что эта картина
изменения опасности отказа не
является универсальной. Есть
элементы, у которых отсутствует
период приработки (например,
хорошо поставленный контроль
отсеивает все дефектные элемен-
элементы), есть элементы, которые прак-
практически не стареют. Однако у
большинства элементов имеется,
как правило, длительный период, на котором опасность отказа X (t)
практически постоянна. Периодом приработки (если он имеется)
можно пренебречь, считая, что работа элемента начинается с окон-
окончания этого периода. Действительно, и элемент и система, в состав
которой он входит, подвергаются обычно предварительной трени-
тренировке, проходят проверочные испытания, и только после этого
начинается их эксплуатация. С другой стороны, срок службы у многих
элементов кончается раньше, чем наступает заметное старение этих
элементов.
О
Рис. 2.2.6.
§ 2.2] НАДЕЖНОСТЬ ЭЛЕМЕНТА 97
Вышеприведенные соображения показывают, что для широкого
класса элементов мы можем принять, что
X(t) = X = const.
Остановимся на этом важном случае. Из формулы B.2.15) следует,
что для постоянной опасности отказов функция надежности имеет вид
P{t) = e~u. B.2.18)
Такой закон надежности называется экспоненциальным. Для него
вероятность отказа за время t равна
а плотность вероятности отказов
Среднее время жизни элемента для этого случая
l. B.2.19)
О
Таким образом, для экспоненциального закона опасность отказа
обратна среднему времени. Поэтому функцию надежности можно
записать и так:
Существенно отметить, что То может в действительности и не быть
средним временем. Ведь опасность отказа, постоянная на рассмат-
рассматриваемом участке времени, может вне этого участка и не быть
постоянной, так как, в конце концов, любой элемент начинает
«стареть». Поэтому более правильно сказать, что То — это среднее
время такого элемента, опасность отказа которого постоянна на
всем бесконечном интервале времени, а на рассматриваемом участке
времени совпадает с опасностью отказа нашего элемента.
Часто интересующее нас время t во много раз меньше среднего
времени,
/<^Г0, или jt-<^\.
1 о
Тогда можно пользоваться простыми приближенными формулами
Plt\s**s\ __ D(i\^^—-. (О 9 9fW
Л It- 1/^/ 1 rj-, , \a? It- Iz-V/^T" , \&,6.L\j\
1 0 ^0
Ошибка в них не превосходит -^ ( =-) . Заметим еще, что эти при-
z \ ' о/
олиженные формулы дают и оценку для наших вероятностей с нужной
98 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
стороны, ибо для любого t справедливы неравенста Р(/)^1—-~-и
t °
Q(t)^7p~. Они следуют из выпуклости функции е~х — касательная
' о
ух=\—х лежит ниже самого графика у2 — е~х, т. е. Ух^у2,
1—Ж*-*.
Экспоненциальный закон очень популярен в теории надежности.
Эта популярность объясняется тем, что экспоненциальный закон,
физически очень естественный, прост и удобен для использования.
Почти все задачи, возникающие в теории надежности для экспо-
экспоненциальных законов распределения, оказываются на порядок проще,
чем для произвольных законов. Почти все формулы в теории надеж-
надежности в случае экспоненциального закона резко упрощаются.
Основная причина этого состоит в том, что экспоненциальный
закон надежности обладает следующим важным свойством: для
экспоненциального закона вероятность безотказной работы на
данном интервале (/, t + x) не зависит от времени предшествую-
предшествующей работы t, а зависит только от длины интервала т. Иными
I словами, если нам известно, что в данный момент элемент испра-
вен, то будущее его поведение не зависит от прошлого.
Действительно, вероятность безотказной работы на (/, t + i) по
формуле B.2.11) равна
—е
Покажем, что это свойство является характеристическим, т. е.
если оно выполняется для какого-то закона P(t), то этот закон
обязательно будет экспоненциальным.
Пусть отношение ^ ^ т^ не зависит от t. Тогда Lt =фМ»
но Р@) = 1 при / = 0, поэтому
P{t + %) = P(t)P(x) B.2.21)
для любых /^0 ит^О.
Отсюда по индукции получим
... p(ta).
Пусть
Полагая t1 = t2= . •. —tn=;— , мы получим
или
§ 2.2] НАДЕЖНОСТЬ ЭЛЕМЕНТА 99
Подставив теперь t1 — t2=...tn=-~ —, мы придем к формуле
Пусть t^O — любое число. Тогда при любом целом т>0 найдется
единственное #>0 такое, что п~~ ^ t ^— . Так как функция
P(t) монотонно не возрастает, то
Р Dr
или
п
При т—>оо дроби — и — >t и, переходя к пределу, мы по-
получим
Если # = О, то P(t) = O при любом ^>0, т. е. элемент отказывает
в момент включения в работу; если же <7=1, то P(t)=\, т. е.
элемент абсолютно надежен. Отбросив эти несущественные крайние
случаи, мы можем записать постоянную q в форме
? = *~\ где
и тогда окончательно
В некоторых случаях, зная природу отказов и характер работы
элемента, мы можем непосредственно показать, что рассмотренное
выше свойство для него имеет место, откуда уже будет следовать
экспоненциальный закон надежности.
Приведем два приме р~а7~ "' " '~~~
A. Пусть отказ в космическом корабле может возникнуть только
из-за попадания в него достаточно крупного метеорита. Если пред-
предположить, что метеориты распределены равномерно в пространстве
и во времени, то ясно, что вероятность попадания метеорита
в корабль на данном участке времени не зависит от того, попадали
или нет метеориты в корабль в прошлом. Следовательно, закон
надежности в этом случае экспоненциальный.
2. Пусть элемент, входящий в состав некоторой системы, может
отказать только по одной причине —из-за отрыва пайки. Предпо-
Предположим также, что во время работы система вибрирует и возника-
возникающие при этом индукционные силы являются единственной причиной
100 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
возможного отрыва пайки. Пусть Fo— наименьшая сила, при кото-
которой наступает отрыв.
Изменение во времени сил инерции, действующих на пайку,
представляет собой быстро меняющийся стационарный случайный
процесс. Зависимость между соседними амплитудами этого процесса
очень быстро исчезает с увеличением расстояния. Поэтому вероят-
вероятность того, что на данном участке (t, t-\-x) амплитуда процесса F
будет меньше критического значения Fo> практически не зависит
от того, как вел себя этот процесс до момента t. Значит, и в этом
^примере закон надежности экспоненциальный.
Другие законы надежности. В последнее время все чаще
раздается критика в адрес экспоненциального закона. Следует согла-
согласиться с тем, что часто этот закон применяют некритически, что
единственным оправданием для его использования служит то, что
с этим законом проще решать задачу, что без него вообще задача
«не решается». По-видимому, применимость экспоненциального закона
зависит в основном от характера отказов элемента. Внезапные
отказы^ носящие_ случайный характер, обычно довольно хорошо
описываются экспоненциальным законом; наоборот, отказы, возни-
возникающие в результате износа, в результате необратимых физико-
химических изменений физических параметров элемента уже не
подчиняются экспоненциальному закону. Эти отказы, носящие_назва-
ЛИ?_/Е0степеиных, во многих случах довольно" хорошо описываются
нормальным законом/
Рассмотрим одну общую модель, которая приводит к нормаль-
нормальному закону надежности.
Пусть надежность элемента определяется одним физическим
параметром а. Предположим, что начальное значение параметра а0
есть нормальная случайная величина с небольшой дисперсией — это
производственный разброс, то, что было заложено в элементе при
его изготовлении. Предположим также, что во время работы пара-
параметр меняется детерминированным образом, а = /(/, а0), и пусть
для простоты функция f(t, а0) монотонна по t. По условию отказ
наступает тогда, когда значение параметра превысит некоторый
критический уровень av Значит, момент отказа t = x определяется
из уравнения
/(т, ао) = а1э
или
т = ф(а0, ах);
ф-— обратная к /по первому аргументу функция. Так как се0 имеет
малую дисперсию, то, раскладывая функцию ф по формуле Тейлора
в точке а = Ма0 и пренебрегая членами второго порядка, мы получим
т«ф (а, аг) + ф'а (а, а±) (а0 — а).
§ 2.2]
НАДЕЖНОСТЬ ЭЛЕМЕНТА
ЮТ
Но если а0 является нормальной величиной, то и момент т как
линейная функция от а0 также распределен по нормальному закону
(рис. 2.2.7).
Для нормального закона надежности функция надежности имеет
вид
— Г
dx
t-r0
G
2я J
V~2n
e 2dx
I*
a
а так как обычно
лее просто:
Го, то можно записать это равенство и бо-
бо-VT 1 '
"*'
B.2.22)
Здесь То — среднее время жизни, а о2 = 0т.
Можно показать, что опасность отказа k(t) для нормального
закона имеет следующий вид (рис. 2.2.8): она монотонно возра-
возрастает и после То начинает приближаться к асимптоте у = ¦"""" Р »
к aft)
Рис. 2.2.7.
Рис. 2.2.8.
Впрочем, опасность отказа не является при больших значениях у
существенной характеристикой.
У реального элемента часто совмещаются оба типа отказов.
В нем может произойти внезапный отказ, но параллельно идет
«старение» элемента, которое приводит к постепенному отказу^
если до этого не произошел внезапный. Такой элемент можно рас-
рассматривать состоящим как бы из двух частей, в одной из которых.
102 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
может произойти только внезапный отказ, а в другой — только
постепенный. Элемент работает до первого из этих отказов. Если
РгУ) — вероятность того, что за время t не произойдет внезапный
отказ, а Р3 @ — вероятность того, что за это время не произой-
произойдет постепенного отказа, то, предполагая, что отказы возникают
независимо друг от друга, мы получим, что функция надежности
элемента P(t) равна
P(t) = P1(t)P2(t) = e-u^ J e'^dx. B.2.23)
t-T0
Вычислим для этого случая среднее время жизни элемента, пред-
предполагая, что а<^70, а То и -у одного порядка. Имеем
|Н7 I
о о t-T0
G
Сделаем замену ? =z и проинтегрируем по частям. Получим
1 е~КТ(> 1
Т
%
2я J e
GO
— f
Г2Й J
б * dz= — I 1—
окончательно
7- ' i p~ 0+ 2 ) /о о 94.\
Можно, конечно, найти и точное значение Гср, используя таблицы
нормального закона.
Рассмотрим кратко некоторые другие законы распределения,
используемые в теории надежности.
Закон Вейбулла. Функция надежности для него имеет вид
P(t)==e-Kt\ B.2.25)
Среднее время жизни элемента
00 Г ( ¦ -}-1 )
Т° = I e~M*dt = ^^— # B.2.26)
О 1 а
§ 2.21
НАДЕЖНОСТЬ ЭЛЕМЕНТА
юа
Дисперсия времени жизни
Опасность отказа
При а>1 опасность отказа монотонно возрастает от нуля, при-
а<С 1 опасность отказа монотонно убывает и не ограничена при.
t =z 0. Экспоненциальный закон являет-
являетос>2
ся частным случаем закона Вейбулла
при а= 1 (рис. 2.2.9).
Если Xta<^.\, то можно пользо-
пользоваться приближенной формулой
Р@« \ — Xt\ B.2.27)
По-видимому, основной причиной ши-
широкого использования закона Вейбулла
в надежности является то, что он, обоб-
обобщая экспоненциальный закон, содержит Рис. 2.2.9.
дополнительный параметр а. Подбирая
нужным образом параметры Я и а, мы можем получить лучшее
соответствие опытным данным по сравнению с экспоненциальным
законом, который зависит только от одного параметра X. Так,
у элемента, у которого часто встречаются скрытые дефекты, но
который в течение долгого времени не «стареет», опасность отказа
резко повышена вначале, а потом быстро падает. Функция надеж-
надежности такого элемента должна хорошо приближаться законом
Вейбулла при а<1. Наоборот, если у элемента почти не бывает
скрытых дефектов, но зато он быстро «стареет», то опасность
отказа монотонно растет, и функция надежности должна хорошо
приближаться законом Вейбулла с параметром а> 1 (см. рис. 1.2.6).
Впрочем, в некоторых случаях закон Вейбулла возникает есте-
естественным образом. Рассмотрим один характерный пример. Устрой-
Устройство, надежность которого мы ищем, состоит из п последовательно
соединенных дублированных элементов. В каждой паре работают
оба элемента, а отказ пары наступает тогда, когда откажут оба
элемента. Отказ всего устройства наступает при отказе хотя бы
одной пары. Надежность каждого элемента подчинена экспонен-
экспоненциальному закону, опасность отказа у элементов &-й пары равна Xk.
Тогда можно показать, что если величина
! = X фиксиро-
104 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
аана (этого всегда можно добиться выбором единицы времени), а
п
lim 2 ^ = 0,
то функция надежности системы имеет предел
lim p{t) = e~M*.
П-> GO
Мы получим распределение Вейбулла с показателем а =2.
Гамма-распределение. Функция надежности имеет вид
РD\— I'f р"х Ну A 9 9R\
J 1 ((I)
Плотность распределения отказов
. D' /А ^ * _ Л-М
а
Среднее время жизни
дисперсия
DT = a2 = J.
При а = " и ^ = *9- мы получаем ^-распределение, при а=1 —
экспоненциальный закон.
Гамма-распределением удобно приближать те законы надеж-
надежности, у которых плотность q (t) имеет одновершинный несиммет-
несимметричный вид.
Логарифмически нормальное распределение. Для
«его функция надежности
У 2я J
B.2.29)
inf
среднее время
Степенное распределение. Функция надежности
Р(*) = 7 Wt. B-2-3°)
§ 2.2] НАДЕЖНОСТЬ ЭЛЕМЕНТА 10S
Среднее время конечно при
Эти два распределения дают в некоторых случаях неплохое при-
приближение для закона надежности.
В заключение мы рассмотрим два общих подхода к изучению
надежности элемента, которые позволят получить оценки надеж-
надежности и сделать некоторые качественные выводы о надежности.
Стареющие элементы. Назовем элемент стареющим, если его
опасность отказа монотонно не убывает, т. е. для любых 0 <C.tx<Ct2
Это означает, что с течением времени надежность элемента можег
только уменьшаться.
Введем обозначение
t
Из наших предположений следует, что А(/) выпукла вниз. Функ-
Функция надежности выразится так:
Я (*)
= *-а
Рассмотрим среднее время жизни То и попытаемся оценить era
сверху
То = ] е~А (О dt = } ^-* ^ф (дг),
о о
где ф(д:) — функция, обратная к h(t). Взяв последний интеграл па
частям, мы получим
Функция ср(х) выпукла вверх, поэтому ее график лежит ниже
касательной. В частности, при любом х
Отсюда для среднего времени мы получаем оценку
Г0<фA)
106 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
ИЛИ
что равносильно неравенству
МГ0)<1.
Функция К (t) выпукла вниз, и поэтому зе график на
<0, То) лежит ниже хорды, т. е.
Из этого неравенства следует, что функция надежности
P(t)>e~r° для t<T0. B.2.31)
Отсюда можно сделать такой вывод: если мы для оценки надеж-
надежности стареющего элемента пользуемся экспоненциальным за-
законом, подставляя в него истинное среднее время, то мы тем
самым занижаем функцию надежности для всех моментов t,
не превосходящих среднего времени. Заметим, что оценка вероят-
вероятности безотказной работы снизу более приемлема, чем оценка этой
вероятности сверху, так как прогнозы надежности, сделанные по
заниженным вероятностям, в действительности будут оправдываться
•с большой достоверностью. Как мы увидим ниже, для стареющих
элементов можно написать целый ряд неравенств, подобных нера-
неравенству B.2.31). Отметим еще, что для стареющих элементов
атогда как для экспоненциального закона дисперсия равна квад-
/ рату среднего времени.
Надежность элементов неоднородной партии. Вначале пред-
представим себе, что два завода изготовляют элементы одного типа,
причем первый завод поставляет 100/^% всей продукции, а вто-
второй завод—100р2% всей продукции (р1-\~р2=\). Предположим,
что любой элемент имеет надежность, подчиненную экспоненциаль-
экспоненциальному закону, причем опасность отказа равна Хх для элементов,
сделанных на первом заводе, и равна к2 для элементов, сделанных
«а втором заводе. Допустим, наконец, что продукция обоих заво-
заводов хаотически перемешивается. Легко видеть, что надежность
наугад взятого элемента выражается формулой
§ 2.2] НАДЕЖНОСТЬ ЭЛЕМЕНТА 107
Если вместо двух заводов взять произвольное число п, оставив,
неизменными прочие условия, то получим функцию надежности
Мы можем, наконец, предположить, что опасность отказа Я яв-
является случайной величиной, заданной на множестве элементов.
Пусть F (Я) — закон распределения величины X. Тогда, как и выше,,
функция надежности
00
^~udF(X). B.2.32)
Чтобы понять, когда такая модель реализуется, вернемся к при-
примеру на стр. 99, в котором мы говорили о разрыве пайки. Опас-
Опасность отказа к в этом примере зависит от критической силы Fo>
X = 'k(F0). Но ясно, что эта сила определяется качеством пайки
и меняется от элемента к элементу, являясь случайной величиной.
Докажем теперь, что элементы, функция надежности которых
определяется формулой B.2.32), обладают следующим свой-
свойством: опасность отказа у таких элементов монотонно
убывает. Опасность отказа из B.2.32) равна
Xe-ktdF (X)
Для монотонного убывания функции X (t) достаточно, чтобы
2 со со
Г
I
$»•¦
Так как знаменатель положителен, то достаточно доказать, что
числитель отрицателен. Для этого рассмотрим интеграл
оэ
О < J (z — КJ е~и dF (X) = Az2 - 2Bz + С,
108 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
где
А = J <rxt rfF(X), S = J"ke~xt dF(k),
о
Квадратный трехчлен неотрицателен при любом z, поэтому его ди-
дискриминант
?2--ЛС<0,
но это и есть числитель. нашей дроби. Утверждение доказано.
Можно показать еще, что
lim k(t) = kOi
t -> со
тде к0 есть наименьшая точка роста функции F(k). (Точкой роста
функции F (к) называется такая точка к, для которой F(k-\-e) —
— F (к — е)>0 при любом е>0.) Рассмотренная нами модель
хорошо объясняет тот известный из практики факт, что многие
элементы с течением времени становятся все более и более надеж-
надежными. Действительно, если элемент проработал безотказно до мо-
момента tOy то его функция надежности равна
to+t
- J к tx) dx
Г('оГ = *
Но тогда из монотонного убывания к (т) следует, что при любом t
с ростом t0 эта функция возрастает, т. е. надежность элемента
¦с течением времени растет.
§ 2.3. Надежность восстанавливаемого элемента
Определение процесса восстановления. В преды-
предыдущем параграфе мы изучали работу элемента до первого отказа.
Теперь мы будем предполагать, что после отказа элемент восста-
восстанавливается. Это восстановление может носить различный характер:
элемент может либо заменяться новым, идентичным ему элементом,
либо подвергается такому ремонту, который полностью восстанав-
восстанавливает все его исходные свойства. Для нас несущественно, каким
образом происходит восстановление, и в дальнейшем ради удоб-
удобства мы будем считать, что в момент отказа элемент заменяется
новым. Предположим также, что время восстановления пренебре-
§ 2.3] НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА 109
жимо мало по сравнению с временем жизни элемента, и поэтому
можно считать, что восстановление происходит мгновенно. Пусть
элемент начинает свою работу в момент ^ = 0 и, проработав слу-
случайное время тх, выходит из строя. В этот момент он заменяется
новым элементом, который, проработав время т2, выходит из строя
и заменяется третьим элементом. Этот процесс продолжается не-
неограниченно. Естественно предположить, что времена жизни эле-
элементов тх, т2, ... независимы. Случайные времена хъ т2, ...
имеют один и тот же закон распределения, который мы обозначим
через F(t):
^гт? Vf
U Zt l2 Ъ3 Ъп о
Моменты отказов (рис. 2. 3. 1) рис 2.3.1
или восстановлений t1=T1,t2=
=тх+ т2, ..., *п = т1+. . .+тл, ... образуют случайный поток,
который мы будем называть процессом восстановления [12].
Предположим также, что среднее время жизни элемента и его
дисперсия конечны:
= Мт„=$ [\-F(t)]dt,
О
= От„ = 2$ t[\-F(t)]dt-Tl B.3.1)
Пусть, наконец, существует непрерывная плотность распределения
Основные характеристики процесса восстанов-
восстановления. При изучении процесса восстановления основную роль
играет случайная величина v (/), равная числу отказов, происшед-
происшедших за время t.
Величина v (t) определяется из условия
Величина v (t) может принимать только целые неотрицательные
значения. Найдем распределение v (t). Для этого заметим, что
</} = /=;(/), B.3.3)
где функции Fn(t) — законы распределения tn — определяются так:
t
ПО ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
Из этого очевидного, но важного равенства B.3.3) следует, что
Pn(t) = P{v(t)=n} = Fn(t)-Fn+1(t). B.3.4)
В частности,
Эти формулы и дают искомое распределение v(^). Фундаменталь-
Фундаментальное значение при изучении процесса восстановления играет так
называемая функция восстановления H(t)] которая равна среднему
числу отказов, происшедших до момента_Х Используя формулы
B.3.4), мы можем легко найти эту функцию:
H(t)= №v(t) = 2лЯя@=2л[/?я@-/7„+1@] =
= 2 «ад-2 (n-\)Fn(t)= s Fn(t),
П = 1 П = 2 /2 = 1
ИЛИ
"@=2 ад- B-3-5>
П = 1
Можно показать, что функция И (t) всегда конечна. Функция Н (t)
удовлетворяет интегральному уравнению [12]
B.3.6)
которое удобно использовать при изучении некоторых свойств H{t).
Важная роль функции /. (t) объясняется тем, что через нее выра-
выражаются все основные характеристики нашего процесса. Так, дис-
дисперсия числа отказов v (t) равна
2(t). B.3.7)
Среднее число отказов на участке (tv t2), очевидно, равно
//()
i
Вместо функции Hit) часто рассматривают дифференциальную
характеристику
Функция h(t) называется плотностью восстановления1). Она равна
среднему числу отказов, происшедших в момент t за единицу вре-
1) В теории надежности функцию h It) называют также интенсивностью
отказов.
§ 2.3] НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА 111
мени, начиная с момента t (если эта единица мала). Из B.3.5)
следует, что плотность восстановления выражается рядом
* С) =23/»('>• где fn{*)=Fn(t). B.3.8.)
Рассмотренные нами величины Pn(t), H(t) и h(t) можно использо-
использовать при решении некоторых задач теории надежности. Пусть, на-
например, нам нужно найти наименьшее число запасных элементов /г,
которых с вероятностью, не меньшей 1—а (а—малое число), хва-
хватит на время t. Чтобы п запасных элементов хватило на время t,
число отказов за это время не должно превосходить п. Отсюда
для определения п мы получаем условие
P{v(/)</z}^l— а или ?{v(t)>n}<a.
Из формулы B.3.3) получаем
Fn+I(t)<a. B.3.9)
Наименьшее я, при котором выполняется это неравенство, и дает
нам искомое число запасных элементов. Надо заметить, что /z-крат-
ная свертка функции F(t)Fn(t) лишь в редких случаях вычис-
вычисляется в конечном виде. Перечислим эти случаи для тех распреде-
распределений, которые встречаются в теории надежности.
1°. Экспоненциальный закон
В этом случае процесс восстановления будет образовывать пу-
ассоновский поток и наши характеристики имеют простой вид
Р„(<) = Р^Й = л} = тгЛ B.3.10)
Заметим, что среди всех процессов восстановления только пуассонов-
ский процесс является стационарным процессом без последействия.
2°. Нормальный закон. Как и выше, мы предполагаем, что
о<70. Тогда
Функция восстановления
(°?0??) B-ЗЛ1)
112
ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ
[ГЛ. 2
1
может быть легко вычислена с помощью таблиц. Плотность вос-
восстановления
Jt-nT0)*
" 2О'п B.3.12)
у znnu
имеет характерный колеблющийся вид (рис. 2.3.2).
3°. Гамма-распределение.
Для него плотность
) ¦
Легко показать, что
и, значит, плотность восстанов-
ления выражается рядом
Рис. 2,3.2.
При целом а = т этот ряд суммируется
где
2я . . . 2я
8 = COS И Sin —
Отсюда
Для других законов распределения, которые используются в тео-
теории надежности, функции Fn(t) не выражаются в конечном виде,
и это, конечно, сильно затрудняет расчеты.
Полезно иметь наряду с точными формулами простые оценки
для функции восстановления H(t). Приведем некоторые из них.
Из неравенства
max
следует, что
max
о о Ql НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА 1 1 3
ИЛИ
Fn(t)<*Fn(i). B.3.14)
Отсюда
яэ 00
,пы,_ F{t)
Принимая во внимание очевидное неравенство И (t)^F(t), мы по-
получаем желаемую оценку
Д. B.3.15)
Из нее следует, что на начальном участке времени, где
справедливо приближенное равенство
H(t)&F(t). B.3.16)
Далее, беря математическое ожидание от обеих частей неравенства
и используя тождество Вальда [12], мы получим
*<Г0 [//(*)+ 1],
откуда
С другой стороны, для стареющих элементов, у которых опасность
отказа к (t) = i__Fm монотонно возрастает, можно получить оценку
Таким образом, функция восстановления стареющих элементов для
любого момента t удовлетворяет неравенству
i 1<Я@<^-- B.3.17)
¦'о ^о
Асимптотическое поведение процесса восста-
восстановления. На практике основной интерес представляет изучение
процесса восстановления для большого времени t, нас интересует
поведение процесса на тех участках, которым предшествует боль-
большое число отказов. Поэтому, говоря математически, мы должны
изучить асимптотическое поведение нашего процесса и его харак-
характеристик при t—>оо. *
5 Б. В. Гнеденко и др.
114 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
Приведем теперь основные факты из теории восстановления,
которая в основном и занимается изучением асимптотических свойств
процесса восстановления [12].
1°. Для любого закона распределения F(t)
lim^iO^ * B.3.18)
t -> оо t To
Интерпретация этого утверждения очень проста: для большого
участка времени среднее число отказов, приходящихся на еди-
единицу времени, близко к величине, обратной среднему времени
жизни элемента.
2°. Теорема Блекуэлла. Если случайное время т,. рас-
распределено непрерывно, то для любого а
3°. Во многих вопросах очень удобно использовать теорему
Смита, которую сам автор назвал узловой теоремой восстанов-
восстановления. Если время жизни элемента х( распределено непрерывно,
a Q(t)— монотонно невозрастающая, интегрируемая на @, оо)
функция, то
t 00
lim [Q(t — t)dH(%) = ±-{Q(x)dx. B.3.19)
t -* оо J I 0 J
0
0
Это равенство удобно тем, что, беря различные функции Q(t), мы
можем получать различные предельные предложения для процесса
восстановления.
4°. если %t имеют конечную дисперсию а2, то
Отсюда следует, что для большого времени t верна приближенная
формула
5°. Если непрерывная плотность распределения f(t)—> () при
t —> оо, то
lim h (t) = 4-- B.3.21)
<-+оо 'О
Это важное утверждение отражает тот факт, что с течением вре-
времени процесс восстановления становится стационарным и его ло-
локальные характеристики перестают зависеть от времени.
§2 3] НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА 115
Исследуем теперь более подробно вопрос об асимптотическом
поведении величины v (t) — числа отказов за время t — с ростом
времени.
Вернемся к равенству B.3.3)
Так как величины т/ одинаково распределены и имеют конечную
дисперсию о2, то дробь
с. __тг+ ...+тя — пТ0
о у п
сходится при п—* оо к нормальной случайной величине ? с нуле-
нулевым средним и дисперсией, равной единице. Пусть теперь t—>оо, а
n = ±- + znVl
1 о
где zn выбирается так, чтобы zn—>z (z — произвольно выбранное
число), а п было бы целым.
Перепишем равенство B.3.3) в форме
При t—*оо мы получаем
t
Т 2 2
Сделаем замену х — —-—. Топа
Отсюда следует, что случайная величина v(t) асимптотически нор-
норB.3.24)
мальна со средним Mv (t) -v. -L и дисперсией
1 о
116 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
Доказанный факт позволяет просто и достаточно точно оценить
возможное число отказов на большом интервале времени. Дейст-
Действительно, из равенства B.3.23) мы получаем, что с вероятностью
A—а) число отказов на большом интервале времени @, t) будет
заключено в пределах
^-Ua°-^<v(t)<^r + ua°-lQ-i B.3.25)
А *р 2 А т 2
i-o о
где и а находится по таблицам для нормального закона из условия
tb
Приведем пример. Пусть среднее время жизни элемента
70=100 час, дисперсия времени жизни а2 = 3600 час2. Требуется
с достоверностью 0,95 оценить число запасных элементов, необхо-
необходимое для бесперебойной работы в течение времени ? = 8000 час.
Учитывая, что в данном примере нам нужна лишь односторонняя
оценка, мы при заданном a = 0,05 находим по таблицам иа из
условия
и
УТп)
е 2d/=l—а;
лга=1,65 (см. таблицу 3 приложения).
Тогда с вероятностью 0,95 выполняется неравенство
v(t)<jr + xa^T- = 80+1,65.0,6 /80 «89;
отсюда следует, что для непрерывной работы в течение 8000 час
нужно взять 89 запасных элементов.
" Надежность элемента на заданном участке вре-
мени. Рассмотрим теперь другую интересную и не менее важную
задачу: какова вероятность того, что элемент проработает безот-
безотказно на участке (t, t-\-x). Эта задача возникает для таких уст-
устройств, которые постоянно находятся в рабочем состоянии, но
выполняют свои функции лишь на отдельных участках времени.
$ 2 3] НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА 117
Обозначим искомую вероятность pt(r) и будем ее искать. Рас-
Рассмотрим систему несовместных событий
Событие Ап означает, что до момента t произошло ровно п
отказов и на участке (f, t + r) отказов не было. Очевидно, что
интересующее нас событие Д заключающееся в безотказной работе
элемента на интервале (t, f + т), есть сумма всех событий
00
В= UAn.
Отсюда в силу несовместимости событий Ап мы получим
Найдем теперь вероятность события Ап. По формуле полных ве-
вероятностей
Отсюда
t
\ x)]h(x)dx. B.3.26)
Из этой формулы при т = Д?—>0 нетрудно получить, что
1 —pt (M) = h{t)M + o (A/). B.3.27)
Отсюда вытекает, что плотность восстановления h(t) равна ве-
вероятности отказа за единицу времени (если эта единица мала).
Этот факт является, по-видимому, причиной того, что многие сме-
смешивают две различные характеристики—опасность отказа Х(/) =
= 1-_р (t) и плотность восстановления h(t). Эта путаница усугуб-
усугубляется еще и тем, что во многих работах обе величины, X(t)
и h(t)y имеют одно и то же название—интенсивность отказов.
Между тем эти величины совершенно различны: плотность восста-
восстановления h(t) приближенно равна безусловной вероятности отказа
118 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
за единицу времени (которая достаточно мала), а X (t) — условной
вероятности отказа за единицу времени при условии, что до мо-
момента t отказов не было.
Формула B.3.26) почти никогда не используется на практике,
так как нас обычно интересуют далекие моменты времени, для ко-
которых процесс восстановления становится стационарным и вероят-
вероятность pt (т) перестает зависеть от времени t. Поэтому в равенстве
B.3.26) мы перейдем к пределу, устремив t—>-оо. Первое слагаемое
в правой части 1—F(t-\-x) с ростом t стремится к нулю, а для
нахождения предела интеграла
t
мы воспользуемся узловой теоремой восстановления, взяв в равен-
равенстве B.3.19)
Тогда мы получим
= lim
00
= ~ f [1 — F(x + x)]dx,
или
B.3.28)
Интерпретировать полученный результат можно следующим обра-
образом. Время, протекшее от момента t до очередного отказа, мы
tf t2 ?v
Рис. 2.З.З.
назовем остаточным временем жизни элемента и обозначим через
\t (рис. 2.3.3). Очевидно, что функция распределения для %t
С ростом t величина gt сходится к некоторой стационарной вели-
величине |, функция распределения которой выражается формулой
=p(x) = i-J[l — F(t)]dt.
§2 3] НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА 119
Найдем некоторые характеристики этого закона. Среднее время
да оо оо
Т = \ р(т) dx — jr- \ d% \ [1 — /^ (^)j dt =
о о х
= Y [t[\—F(t)]dt = y- V^f(t)dt = ° 2T °, B.3.29)
о о
или
Интересно заметить, что на первый взгляд среднее время 7\ должно
Т
равняться ¦—, так как момент t должен делить время жизни эле-
элемента tv+t в среднем пополам. На самом деле, как видно из
B.3.29), среднее время больше. Это объясняется тем, что момент
t с большей вероятностью попадет на больший интервал т,., поэтому
средняя длина того интервала xiy на который попал момент ty бу-
будет больше, чем То.
Опасность отказа Х1 (t) для величины ? выражается формулой
t (t) = 1""f@ . B.3.30)
J
t
Интересно заметить, что если элемент стареющий, т. е. X(t) моно-
монотонно возрастает, то и Хх (/) монотонно возрастает. Действительно,
из B.3.30) мы получаем
С другой стороны,
оо
-F (t) = J/(at) dx^ J X (х) [1 -F(x)] dx^X (t) J [1-F(jc)] dx,
t t t
J
t
откуда
и, следовательно, k[(t)^Oy т. е. Xt (t) монотонно возрастает.
Полезно иметь для функции p(t) простые оценки. Так как
Р"(*)=^О,
то функция p(t) выпукла вниз и ее график лежит выше касательной.
120
ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ
[ГЛ. 2
Отсюда мы получаем оценку (рис. 2.3.4)
p(t)^\—L . B.3.30а)
Для стареющих элементов можно получить оценку и с другой
Рис. 2.3.5.
стороны. Как мы показали, из монотонного возрастания X(t) сле-
следует монотонное возрастание Хг (t). Но тогда
откуда
\dt
а для функции надежности мы получим
t
- J к и) dt j^
JL
Соединяя эту оценку с оценкой B.3.30), мы получаем двусто-
двустороннюю оценку (рис. 2.3.5)
1— Jr^p(t)^e T\ B.3.31)
1 о
Следовательно, для стареющих элементов справедливо приближен-
приближенное равенство
p(f)=s- I—I B.3.32)
которое имеет ошибку, не превосходящую
\_( t\*
2
§ 2.3]
НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА 121
Вычислим теперь для стационарного случая вероятность по-
появления на (/, t-\-x) ровно п отказов. Обозначим случайное число
отказов на (/, t + x) через vT. Тогда
и, так как величины ? и %{ независимы, то
X
Р {vT ^п) = 1 j [1 - F(i-x)} Fn_x (x) dxt
1 о
о
откуда
X
T = п} = J-J [1 - /=• (т - ж)] [Fn_, (ж) - Fn
О
a+l(x))dx. B.3.33)
о
Заметим еще, что согласно теореме Блекуэлла среднее число от-
отказов на (t, t-\-x) при большом t равно
MvT = ^-. B.3.34)
Из формулы B.3.33) можно вычислить и дисперсию vT. Она равна
Заметим еще, что при т —>оо справедлива предельная теорема
B.3.23), т. е. vx распределена асимптотически нормально со сред-
средним ^ и дисперсией ^
о г
Процесс восстановления с конечным временем
восстановления. До сих пор мы предполагали, что восста-
восстановление отказавшего элемента происходит мгновенно. В действи-
действительности это восстановление требует часто времени, которым
нельзя пренебречь, которое сравнимо со временем жизни элемента.
Время восстановления складывается обычно из времени, которое
нужно, чтобы найти неисправный элемент или обнаружить,
что он неисправен, и времени, которое требуется, чтобы заме-
заменить отказавший элемент новым или произвести ремонт отказав-
отказавшего элемента. Ниже мы будем рассматривать время восстанов-
восстановления в целом, не интересуясь, из каких частей оно складывается.
Итак, будем рассматривать следующий процесс (рис. 2.3.6).
Элемент, проработав случайное время т'1э выходит из строя и
122 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
восстанавливается в течение случайного времени х\; восстановленный
элемент работает время т2 и восстанавливается время т2; и т. д.
Моменты
1+Чп, /1 = 1, 2, ...,
будем называть от/сазами элемента, а моменты
*п = т1 + Т1+Та + *а+...+Тя + Тл, 'о = О, Л=1, 2, ...,
будем называть восстановлениями.
Рис. 2.З.6.
Мы будем предполагать, что все величины т/ и х] независимы.
Предположим также, что все периоды работы хп распределены оди-
одинаково по закону
со средним 7\ = Мтп и дисперсией о\ = Dxn и все периоды восста-
восстановления также распределены одинаково по закону
со средним Г2 = Мтл и дисперсией ol = 0xn. Будем ради удобства
предполагать, что эти законы имеют непрерывную плотность
f(t) = F'(t) и g(t) = G1(t). Кроме того, чтобы не отвлекаться на
вырожденный случай, будем считать, что о\ -{-о\ =?0. Определен-
Определенный таким образом процесс будем называть процессом восстанов-
восстановления с конечным временем восстановления.
Рассмотрим основные характеристики этого процесса.
Коэффициент готовности. Основной характеристикой надеж-
надежности нашего элемента является так называемый коэффициент готов-
готовности kr(t)y который равен вероятности того, что в момент t
наш элемент находится в исправном состоянии.
Для определения коэффициента готовности рассмотрим события
Л» = {'» <*<?+!}, л = 0, 1, 2, ...
Событие Ап означает, что до момента t произошло ровно п вос-
восстановлений и в момент t элемент исправен. Очевидно, что собы-
§ 2.3] НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА 123
тие By заключающееся в исправной работе элемента в момент t,
равно сумме всех событий Ап
00
В= UAn.
/г=о
Отсюда в силу несовместимости событий Ап мы получим
kr(t) = P{B} = 2?{Ап}. B.3.36)
Чтобы определить вероятности Р{Ап}} введем некоторые обозна-
обозначения.
Пусть
in\ = Ti + Т2 + • • • + х'п и tn2 = т\ + Та + . • . + т„.
Заметим, что ^„i + ^n2==^/i. Законы распределения ?rtl, ^й2 и ^
обозначим так:
= О» (О
а их плотности—fn(t)=Fn(t) и gn{t) — Gn(t). Эти законы опре-
определяются через исходные законы F(/) и G(t) следующим образом:
Рп @ = J ^-х « - Jt) rf/7 (x), Fx (t) = F(t),
0
t
Gn(t) = J Onmml (t-x) dG(x)y Ox (t) = 0(/)
0
Вернемся теперь к вычислению вероятностей
По формуле полных вероятностей
+dx}P{xn+l> t-x}
t
124 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
Подставляя найденные вероятности в формулу B.3.36), получим
-F(t-x))h2(x)dx, B.3.37)
где h2 (х) = 2 Ф* (*)•
Моменты восстановлений tn образуют процесс восстановления.
Функция h2(t) является, очевидно, плотностью восстановления для
этого процесса. Среднее расстояние между соседними точками
этого процесса равно
Формула B.3.37) почти никогда не используется, так как на прак-
практике под коэффициентом готовности понимают обычно то ста-
стационарное значение, к которому стремится функция kr(t) с рос-
ростом времени. В равенстве B.3.37) устремим t к бесконечности.
Воспользуемся опять узловой теоремой восстановления, взяв в ра-
равенстве B.3.19)
Тогда
kt = Urn ftr (t) =
t->OD
00
f И —
откуда окончательно
<2-3-38>
Можно привести еще один эвристический вывод коэффициента
готовности.
Возьмем большой участок времени, на котором умещается
ровно п периодов работы и п периодов восстановления, и рас-
рассмотрим отношение
t
«1
равное доле времени, которое элемент пребывает в исправном со-
состоянии. При п -* оо дроби
§ 2.3] НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА 125
согласно закону больших чисел с вероятностью единица сходятся
по вероятности к соответствующим средним Тг и Т2. Поэтому
наша дробь сходится по вероятности
Отсюда видно, что коэффициент готовности есть средняя доля
времени, которое система пребывает в исправном состоянии.
Для процесса восстановления с конечным временем восстанов-
восстановления мы можем рассмотреть две случайные величины
vt(t) — число отказов на @, /),
v2(t) — число восстановлений на @, t)
и соответствующие средние
Vlv1(t)=H1(t) — среднее число отказов на @, t)
и
Mv2 (t) = H2 (t) — среднее число восстановлений на @, t).
Так как нас в основном интересует поведение этих величин
для больших значений tly а асимптотически vx (t) и v2 (t) ведут
себя одинаково, ибо они могут отличаться друг от друга самое
большее на единицу, то мы рассмотрим только моменты восста-
восстановлений. Расстояния между соседними моментами суть случайные
величины
распределенные по закону
t
Поэтому функция восстановления
а плотность восстановления
С ростом времени h2(t) приближается к пределу Т ;
среднее число восстановлений за единицу времени, величина v2
* это —
126 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
при t -> оо асимптотически нормальна со средним - 7=г и диспер-
7 + Г
сиеи , что дает возможность, как и выше, оценивать
число восстановлений за время /. Заметим, что число отказов vx (t)
за время / имеет точно такую же асимптотику.
Совершенно аналогично ищется в нашем случае вероятность
безотказной работы на (t, ^ + т). Она равна
t
pt (х) = 1 -F(t + x) + J [1 - F(t + х- x)} h2 (x) dx.
о
Воспользовавшись, как и выше, узловой теоремой восстановления,
мы получим, что
00
р(х)= lim Л(Т) = _L_ Г [\ — F(x)]dx. B.3.39)
*->оо L 1 "Г I 2 J
Т
Эту формулу можно записать также в виде
откуда следует, что вероятность безотказной работы в течение
времени т равна произведению вероятности того, что в начальный
момент мы застанем систему исправной, на вероятность исправной
работы элемента в течение времени т для обычного процесса
с мгновенным восстановлением (см. B.3.28)).
Случай экспоненциальных законов. На практике
часто рассматривают специальный случай процесса восстановления
с конечным временем восстановления, когда длительность жизни
и длительность восстановления элемента подчинены экспоненци-
экспоненциальному закону
F(t)=l—e-Kt% 0№=*1—е-**.
Все характеристики для этого случая можно было бы вывести из
общих формул, но удобнее и поучительнее рассмотреть этот слу-
случай отдельно. Если обозначить через я (t) вероятность исправного
состояния, а через г (t) = 1—п (t) — вероятность неисправного со-
состояния в момент ty то, сравнивая наш процесс в два бесконечно
близких момента времени t и t + At, мы по формуле полных ве-
вероятностей получим
n(t + Д^ = [1-(Н/ + о (Д/))] я (t) + I11M + о (М)] г (t).
§ 2.3] НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА 127
Переходя к пределу, мы получим дифференциальное уравнение
или
Решая это уравнение, мы найдем искомую вероятность, которая,
как легко видеть, есть коэффициент готовности
B.3.40)
Стационарное значение этого коэффициента равно
Вероятность исправной работы на (/, * + т) при большом t выра-
выражается так:
*(т) = ГнПИ"Хт- B-3-41>
Из формулы B.3.40) видно, с какой скоростью приближается ко-
коэффициент готовности к своему предельному значению х_Г . Ско-
рость оказывается экспоненциальной
В общем случае для произвольных законов F(t) и G(t) найти,
с какой скоростью наш процесс устанавливается, очень трудно.
Можно высказать только одно качественное соображение — при
фиксированных средних временах процесс устанавливается тем мед-
медленнее, чем меньше суммарная дисперсия aj+cja- Заметим еще,
что если плотности /(/) и g(t) стремятся к нулю с экспоненци-
экспоненциальной скоростью, т. е.
то и наш процесс устанавливается с экспоненциальной скоростью
Распределение суммарной наработки. Рассмотрим
теперь такую задачу. Назовем суммарной наработкой за время t
сумму всех периодов работы т/ до момента t, включая, может
быть, и неполный период работы, примыкающий к моменту t
128 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
(рис. 2.3.7). Обозначим суммарную наработку через ht. Наша задача
заключается в том, чтобы найти закон распределения случайной
величины ht и исследовать ее асимптотическое поведение при t -> оо.
Введем в рассмотрение еще одну случайную величину т5, рав-
равную тому случайному моменту, когда суммарная наработка дос-
достигнет величины s. На практике часто задают суммарную нара-
наработку изделия s, по достижении которой изделие заменяется
Рис. 2.3.7.
новым. Тогда xs будет календарным временем жизни изделия, и для
нас важно уметь заранее оценить это время. Легко заметить, что
между величинами ht и xs существует простая связь
Р{*,<*} = Р{т,>/}. B.3.42)
Чтобы найти точный закон распределения ht (а значит, и т5), рас-
рассмотрим отдельно два потока: поток, образованный последова-
последовательными, рабочими периодами, и поток, образованный периодами
восстановления. Пусть vx (t) — число отказов до момента t в пер-
первом потоке, a v2 (t) — число восстановлений до момента t во вто-
втором потоке. Докажем, что следующие два события эквивалентны,
а значит, их вероятности равны
К (s)>v, (/-*)} = {т,Х}.
Заметим прежде всего, что с вероятностью единица момент Ту
попадет внутрь рабочего периода. Поэтому
так как число отказов, происшедших до момента Ту, равно числу
восстановлений до этого момента. Тогда из события xs^> t сле-
следует, что v1E) = v2(t^ — s)^v2(t — s). Наоборот, если произошло
событие v2(t — s)^ vx (s) == v2 (xs — s), то t^xr в силу монотон-
монотонности функции v2(#), что эквивалентно неравенству t<Cxs.
Итак, вероятность
®(sit) = P{ht<s} = P{xs>t} = P{v1(s)^v2(t-s)}. B.3.43)
Но последнюю вероятность можно легко вычислить, зная распре-
распределение Уг(х) и v2(x). По формуле B.3.4) мы легко получим, что
(t-s)]Fn(s), B.3.44)
/1=0
§ 2.3] НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА 129
где, как обычно,
Полученную формулу можно использовать, если время t неве-
невелико по сравнению со средним временем жизни и восстановления
элемента, хотя и в этом случае выкладки велики. Заметим еще,
что ряд B.3.44) существенно не упрощается даже для экспоненци-
экспоненциального закона, когда
/=•(*) = 1 — е~иу G (х) = 1 — в'**.
Для этого случая мы получаем
ф (в, ,) в ? ^^ .-»<«-« 2 ^ •-* • B-3.45)
Если же время t велико, то для вычисления рядов B.3.44) и B.3.45)
потребуется брать много членов ряда, что делает эти формулы
практически малопригодными. По этой причине мы исследуем асимп-
асимптотическое поведение вероятности <D(s,tf) при 5 и t—*оо. Как уже
было доказано (см. стр. 115), число восстановлений v (t) при t—> оо
распределено асимптотически нормально со средним •=- и диспер-
•* о
оЧ
сией —. Отсюда следует, что при s—»-оо величина v1(s) асимп-
' о
s °\s
тотически нормальна со средним -— и дисперсией —— э а величина
1 ^i
v2 (t — s) при t — s—> ex» асимптотически нормальна со средним
*-s н cjJ(/-s)
Y~- и дисперсией —-—-— .
Так как величины v±(s) и v2(t — s) независимы, то их разность
v2 (t — s) — vx(s) при s и (t — s)—>-oo также асимптотически нор-
t—-s s a?s °\(t —s)
мальна со средним -= ^ и дисперсией -V + -f—=—•
1 2 l 1 T\ T\
Преобразуем вероятность Ф($, t)
Пусть <—voo и eej^y.^ + ^V* . Тогда s, (t—s)—*оо и левая
часть неравенства под знаком вероятности асимптотически
130 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
нормальна со средним нуль и дисперсией единица. Правая часть
этого неравенства имеет конечный предел, равный
«- \ Г * 1 I * 2'
Отсюда при t—> oo и
(л; — фиксированная величина)
,t) = nmP{ht<s}=y=\j e *dx,
V
или
lim P
B-3-46>
Иными словами, величина ht асимптотически нормальна со сред-
т
ним Ш+ ~„ * t и дисперсией
Совершенно аналогично показывается, что при s—> оо вели-
•I \ к>
чина т^ асимптотически нормальна со средним Мт^ ~ 11"—-s и
дисперсией 0т„
J Т\
Приведем один пример. Пусть Г, = 5 час, Т2 = 3час, о1 — 3часу
2 = 2час. Требуется оценить суммарную наработку ht за время
= 800 час. Из общих формул получаем, что
500 час, УЩ ~ 13 час.
§ 2.3] НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА 131
Значит, например, с вероятностью 0,95 суммарная наработка будет
заключена в пределах
474 < Л, < 526.
Найденное выше распределение суммарной наработки позволяет
легко решить еще одну задачу.
Надежность устройства с переменным режимом
р а б о т ы. Придадим случайным величинам ть ть т/2, т2, ... дру-
другой физический смысл. Предположим, что рассматриваемый элемент
может находиться в двух состояниях, которые периодически сме-
сменяют друг друга и тг, т2, т3, ...—времена пребывания элемента
в первом состоянии, а т1у т2, т3, ...—времена пребывания эле-
элемента во втором состоянии. Пусть, находясь в первом состоянии,
элемент может отказать за время At с вероятностью X±At -}-o (At)
независимо от прошлого поведения элемента, а находясь во втором
состоянии, элемент за время Д^ может отказать с вероятностью
K2At + o(At). Требуется найти вероятность безотказной работы
элемента на участке @, t).
Легко видеть, что эта вероятность равна
р= М [е~^ *<-** <*-*<>]. B.3.47)
Пусть теперь время t велико. Тогда ht асимптотически нормальна.
Обозначим через h0 ее среднее, а через а*-—ее дисперсию. Из
B.3.47) получим1)
]
1 С 2(J2
Р« r • \ е ° dx.
V 2яап J
— 00
После замены -=z имеем
со
Г
J
Вычисляя последний интеграл, приходим к формуле
-М.-х,(/-лв) + г—°
г) Интеграл берется в полных пределах, а не от нуля до tt потому что
на промежутках (—оо, 0) и (t, oo) он практически равен нулю.
132 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
Т
Величины h0 и а0 были найдены выше; в частности, ho = т * tf
1 IT •* 2
и мы приходим к окончательной формуле
\ Я^е » ^ .1 B.3.48)
Вероятность Я часто считают по очень грубой формуле
)
е г* + г* .у B.3.49)
Наша формула является более точной, а второе слагаемое в
показателе определяет, какова погрешность этой грубой формулы.
На практике периоды т1у т2, ... часто рассматривают как пери-
периоды простоя элемента, и в этом случае Я2 = 0, а формула B.3.48)
получает вид f . ._
1 2 2 I
Лт А, О. /
1' 1 1 О /
Г г.+7-, +~^~.) B.3.50)
Рассмотренная нами задача является частным случаем более общей
задачи, которая ставится так: Устройство может находиться в п
состояниях. Находясь в k-м состоянии, оно может отказать за
время Д? с вероятностью
Время пребывания в k-м состоянии есть 'случайная величина, рас-
распределенная по закону Fk(x). Смена состояний образует марковскую
цепь, т. е. вероятность перехода из &-го состояния в /-е состояние
не зависит от прошлого и от длительности &-го состояния и рав-
равна Pkr
Пусть xk(t) — суммарное время пребывания устройства в состоя-
состоянии k на участке @, t). Тогда вероятность безотказной работы
устройства на @, t) равна
п
- 2 hTk (t)
Если время t очень велико, то нетрудно показать, что
B.3.51)
где pk — финальные вероятности в нашей марковской цепи, или,
говоря другими словами, pk — вероятность того, что в наугад взя-
взятый момент времени устройство находится в состоянии к.
§ 2.41 надежность системы 133
п
Если доказать, что сумма т (t) = 2^- &тл (О ПРИ *—^оо асимптоти-
асимптотически нормальна, и вычислить ее дисперсию Dt(?)=o2, to, как и.
выше, нетрудно показать, что
-2^<+т
* * = 1 . B.3.52)
§ 2.4. Надежность системы
Надежность системы с независимыми элемен-
элементами, работающей до первого отказа. Под системой
мы будем понимать любое устройство, состоящее из частей, на-
надежность которых задана. Эти части мы будем называть элемен-
элементами. Структура системы и характер ее работы должны быть
известны нем настолько, чтобы для любой группы элементов си-
системы мы знали, вызывает ли отказ всех элементов этой группы
отказ системы или нет. Мы предположим также, что элементы
отказывают независимо друг от друга, т. е. отказ любой группы
элементов не изменяет надежности других элементов.
Рассмотрим вначале работу системы до ее первого отказа.
В этом случае надежность системы полностью определяется функ-
функцией надежности P(t), которая равна вероятности безотказной
работы системы в течение времени /. Пусть система состоит из п
элементов, функцию надежности которых мы обозначим через.
Pi@, л@, ..., Рп(*)-
Наша задача заключается в том, чтобы выразить функцию
надежности системы P(t) через функции надежности элементов.
Разберем сначала самый простой и самый важный случай. Мы
скажем, что п элементов в системе соединены последовательно &
смысле надежности, если отказ любого элемента вызывает отказ
всей системы.^
Тогда для безотказной работы системы в течение времени t
нужно, чтобы каждый элемент работал безотказно в течение этого
времени. Так как элементы независимы в смысле надежности, та
Итак, при последовательном соединении функции надежности пе-
перемножаются. Выразим функции надежности через опасности от-
отказа
t t t
- J * (s) ds - J Kt (s) ds - . . . - J* Xn is) ds
e ° =<> о о
откуда
134 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
т. е. при последовательном соединении опасности отказа склады-
складываются. В частности, для экспоненциального закона, когда кк (t) =
= Xk — const,
*-<**+ ..+*»>*, B.4.3)
значит, надежность системы также будет подчиняться экспо-
экспоненциальному закону. Если обозначить в этом случае через То
среднее время жизни системы, а через Tk — среднее время жизни
•&-го элемента, то
Г» =т —Г- BА4>
T- + ...+f-
В сложной системе всегда имеются группы одинаковых элементов.
Если эти одинаковые элементы находятся в примерно одинаковых
условиях или различие условий не влияет существенно на их на-
надежность, то надежности этих элементов равны. Пусть, например,
в первой группе находится пх элементов с функцией надежности
р1 (t), во второй группе — п2 элементов с функцией надежности
р2 (t) и т.д. Тогда формулы B.4.1)—B.4.4) записываются так:
а в случае экспоненциальных законов — в виде
Т
0
г, + • • •+ г,
В частности, когда все элементы системы имеют одинаковую на-
надежность pk(t)=p(t)> то
я для экспоненциального закона
Введем теперь в рассмотрение вероятности отказа
Q(t) = l-P(t) и ?*Ю=1-Р*(О.
Тогда для последовательного соединения
Q (/) = 1 _[1 _^ @] [1 _?, @1 • • .[1 -<7„ (t)]. B.4.5)
§ 2.4] НАДЕЖНОСТЬ СИСТЕМЫ 135-
Можно доказать по индукции неравенство
< О -Л). • -О -Яп) <
- (дг + . . . +дп)
откуда следует, что если
?i W+ ?aW+ ..
то справедлива приближенная формула
Q it) да ^ @ + ...+</„ (О, B.4.6>
погрешность которой не превосходит
Рассмотрим теперь второй простейший случай соединения эле-
элементов в системе. Мы скажем, что элементы в системе соединены
параллельно, если отказ системы наступает только тогда, когда
отказывают все входящие в систему элементы.
Примером системы с таким соединением элементов является
устройство, состоящее из нескольких частей, выполняющих одну
и ту же фУнкиию. Эта функция будет нарушена только тогда,
когда откажут все эти части. Так как элементы независимы в
смысле надежности, то мы получаем
Q (t) = qx (t) q2 (t) ... qn (t), B.4.7)
т. е. при параллельном соединении вероятности отказа перемно-
перемножаются. В частности, когда все элементы равнонадежны, а этот
случай здесь наиболее интересен, мы получаем
Q(t) = qn(t). B.4.8)
Если надежность каждого элемента подчиняется экспоненциальному
закону, то надежность системы уже не будет подчиняться этому
закону. Например, для случая равных элементов
В этом случае можно найти среднее время жизни системы
оо
О
Сделаем замену 1—е~м = х,
' = 11пП^> dts=K(\*-xj>
136 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
откуда
или
При большом п
1 ], где С=0,577...
Рассмотрим теперь общий случай надежности системы с неза-
независимыми элементами [14]. Пусть система состоит из п элементов
и pk(t)—функции надежности, a qk(t) = \—Р*@> &в1, • • • > л.
Если нам известна структура системы, то для каждого множества
элементов системы (а таких множеств 2п—1) нам должно быть
известно, вызывает отказ всех элементов этого множества отказ
системы или нет. Назовем группой отказа множество элементов,
отказ которого вызывает отказ системы, а отказ любой собствен-
собственной части этого множества еще не вызывает отказа системы.
Пусть
Г Г Г
— все группы отказа.
Пусть Ak — событие, заключающееся в том, что группа Гк не
отказала за время ty т.е. не отказал хотя бы один ее элемент.
Тогда надежность системы
P(t) = P {At. .^.} = 1 -PJAtU .. .UAm } =
= 1-2рШ+2р{/^}- 2 P{AkAlAs}+..., B.4.10)
к k<l k<l<s
где Ak — событие, противоположное событию Ak. Любая вероят-
вероятность вида
Р{*/Л, . .. Ai} = gst V) QsAt) . • • q*{t),
где $1} s2i ..., st—номера всех элементов, входящих в группы
1\, Г/а, ..., Г/л. (Некоторые элементы могут входить сразу в
несколько групп.) Таким образом, формула B.4.10) дает возмож-
возможность вычислить надежность системы в общем случае, но когда
число т велико, то пользоваться ею неудобно, так как в правой
части этой формулы содержится 2т слагаемых.
§ 2.4] НАДЕЖНОСТЬ СИСТЕМЫ 137
. Для упрощения вычислений можно поступить так:
Назовем две группы отказа связанными, если их можно со-
соединить цепочкой пересекающихся групп. Тогда все группы отказа
разбиваются на классы связанных групп. Пусть группы Гх, Г2, ..., 1\
образуют первый класс, группы rSl + i> Г51+2, •••, FSl—второй
класс и т. д. События Ак из> разных классов независимы и надеж-
надежность системы выражается так:
P(t) = р {АгА% ...Ап}^?{А1...АШх\? {ASi + 1 ... Л2} ... B.4.11>
Каждый сомножитель в правой части равенства может быть под-
подсчитан по формуле B.4.10). Если классы связанных групп состоят
из небольшого числа элементов, то вычисления существенно со-
сокращаются. Следует заметить, что в большинстве случаев связи
элементов в системе приводятся к комбинациям последовательного
и параллельного соединений, и в этих случаях расчет надежности
системы может быть произведен проще. Формула B.4.10) показы-
показывает, что в самом общем случае функция надежности системы с
независимыми элементами P(t) есть многочлен от функций надеж-
надежности элементов pk (/), — в этом и заключается основной смысл
доказанного выше предложения.
О надежности системы с зависимыми элемен-
элементами. Вёз&е выше мы предполагали, что элементы системы не-
независимы в смысле надежности. Это очень сильное допущение, в
в реальных системах оно часто не выполняется. Отказы одних.
элементов могут существенно влиять на надежность других эле-
элементов, изменяя параметры, определяющие надежность элементов.
В случае параллельного соединенид^щхааы^о^них элементов при-
^Ъдд^Т^1Г^х^й^^~ 1^ЮО^^[щимоиплъной нагрузки~~~н!Г оставшиеся в
живых элементы, и _лх надежность падаетТТРас^люГриТи такой ха-
характерный пример. Система» состоит из п одинаковых элементов,
соединенных параллельно.ДПредположим, что опасность отказа
каждого элемента не зависит от времени, но зависит от числа
неотказавших элементов. Если в данный момент работает k эле-
элементов, то опасность отказа каждого из них равна А.^1). Обозначим
через fih(t) вероятность того, что в момент t работает ровно k
элементов. В этом случае мы скажем, что система находится в
состоянии k. Из этого состояния за бесконечно малое время At
она может с вероятностью
перейти в состояние (?—1) и с вероятностью \—kXkAt + o (At)
*) Во избежание недоразумений заметим, что под опасностью отказа
вдесь понимается вероятность отказа за малую единицу времени, более
точно, вероятность отказа на интервале (/, t + Ы) равна KkM+o(At).
138 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
остаться в состоянии к. Сравнивая состояние системы в два беско-
бесконечно близких момента t и t-\-kty по формуле полных вероятно-
вероятностей получим
pk (t + M) = [(А+ 1) K+i Ы + о(Щрк+1 (t)
Разделив обе части равенства на А* и переходя к пределу при
At—> (), мы получим
Pk (t) = (к + 1) lk+1Pk+1 (t) - kXkPk @, B.4.12)
k = 0y 1, 2, ..., л-1.
При k — n аналогично получается
Так как в начальный момент t = 0 все элементы работают, то
рп @) — 1 и Рл@)=0 при k<Cn. Для решения этой системы ис-
используем преобразование Лапласа. Пусть
Умножив каждое уравнение на e"zt и проинтегрировав по t, мы
лолучим
—1 + zan (г) = — /Д„а„ (z),
2?ал Bг) = (к + 1) А,л+1 ал+1 (г) — klkak (г),
к=0, 1,2, ... , (л-1).
Решив эту алгебраическую систему, находим
/ v \k -f- 1) Afc+i Ctfc + i \Z) (k -f- 1) Afc + i . . . flhn
В частности,
откуда по формуле обращения
2jxt J
§ 2.4] НАДЕЖНОСТЬ СИСТЕМЫ 139
Очевидно, что р0 (t) есть вероятность того, что к моменту t все
элементы отказали, т. е. произошел отказ системы. Поэтому
P0(t) = Q(t) = ^-P(t).
Таким образом, вероятность отказа системы выражается интегра-
интегралом B.4.13). Этот интеграл может быть выражен в виде суммы
кХ?к^ B.4.14)
где
со (х) = (х + Кг) (х + 2Х2)
Чтобы найти среднее время жизни системы, рассмотрим интеграл
СО 00
A (z) = j P(t) e-zX dt = j [1 -p0 @1 «"" dt = j-a0 (z).
0 0
Устремив z к нулю, мы получим
+ (-^Tbz-+---+i- B-4Л5>
Мы рассмотрели один из простейших примеров системы с зависи-
зависимыми элементами. В общем случае задача об определении надеж-
надежности таких систем не решена. И дело здесь не в формулах. Фор-
Формулу для надежности системы с зависимыми элементами всегда
можно написать, если известны условные вероятности отказа одних
элементов при условии отказа других. Эти формулы очень гро-
громоздки и содержат интегралы типа сверток. Но основная трудность
состоит не в вычислении по этим формулам, а в том, что нам
неизвестны условные вероятности, а их опытное определение требует
необозримого объема испытаний. По-видимому, к оценке надежности
сложных систем, состоящих из большого числа элементов, надо
подходить совсем по-другому. Можно, например, разбить систему
на такие части, которые из физических соображений независимы,
и каждую такую часть считать одним элементом. Если надежность
этих частей определена из опыта, то надежность всей системы
может быть уже просто рассчитана. Возможны и другие подходы к
оценке надежности системы.
Нам кажется весьма перспективным следующий подход, который
в настоящее время очень популярен. Пусть работа каждого А.-го
элемента характеризуется параметром ад, который меняется случай-
случайным образом во времени. Работу системы характеризует выходной
140 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
параметр иу который функционально связан с параметрами akt
tt=/(alf a2, ...,an).
Мы считаем работу системы нормальной, если этот параметр нахо-
находится в некоторых пределах
U1<tt<Utl
и говорим, что наступил отказ, если параметр U выходит за эти
пределы. Неравенству
^1 </(«!, ...,«„)<?/, B.4.16)
соответствует некоторая область в /г-мерном пространстве
a = (alf a2, . .., ап).
Вели мы знаем из опыта или из физических соображений природу
случайных процессов ak = ak(t) и если нам известны параметры этих
процессов, то можно в принципе рассчитать вероятность того, что
за указанное время t многомерный случайный процесс a (t) не выйдет
за пределы области, определяемой неравенством B.4.16). Практи-
Практически приемлемое решение этой общей задачи найдено только для
некоторых конкретных случаев. Так, если предположить, что пара-
параметр u = u(t) меняется монотонно, то в этом случае для безотказ-
безотказной работы системы в течение времени t достаточно, чтобы неравен-
неравенство B.4.16) выполнялось лишь в конечный момент времени t. Но
тогда вероятность неравенства B.4.16) можно найти, если известно
одномерное распределение случайных функций ak(t) в момент t.
Часто предполагают [15], что случайные функции ak(t) линейны
ah(t)=lkt + x\k. B.4.17)
Распределение пары (?л, т]л), которое по условию не зависит от
времени, может быть найдено следующим образом. Если на
участке @, Т) нам даны реализации случайного процесса cx,k(t) —
— 9i(*)> Фг(*)» •••» Фт@» Т0 Для каждой из этих реализаций мы
ищем линейную функцию xst-\-ys, приближающую функцию <р,(/)
наилучшим образом в среднем. Для этого мы находим минимум
интеграла
т
no xs и ys. Таким образом, мы получаем пары чисел (х^ уг)у . . .
• • •> (хт> Ут)> которые можно рассматривать как серию независимых
наблюдений случайной величины (|л> r\k). Если число наблюдений т
§ 2.4] НАДЕЖНОСТЬ СИСТЕМЫ 141
достаточно велико, то по ним можно с соответствующей точностью
определить закон распределения пары (§Л, r\k). Если предположить
еще, что /z-мерная область, определяемая неравенством B.4.16),
выпуклая, то для безотказной работы системы в течение времени t
нужно, чтобы в конечный момент t выполнялось неравенство B.4.16).
Если распределение всех пар (?*, r\k) нам известно, то можно найти
и распределение выходного параметра u(t) в момент t. Тогда
вероятность безотказной работы системы до момента t равна вероят-
вероятности неравенства
\ в этот момент t.
Г~~~"Рассмотрим еще одну модель, где зависимость элементов в сис-
системе возникает из-за того, что на надежность этих элементов влияют
меняющиеся внешние условия.
Пусть внешние условия, в которых находится система, задаются
числовой или векторной величиной а(/), меняющейся с течением
времени, и пусть опасность отказа каждого &-го элемента зависит
только от величины <x(t)}
Тогда и опасность отказа системы зависит только от
Вероятность безотказной работы системы выразится, очевидно,
так:
j dx
P(t) = e ° . B.4.18)
Если внешние условия меняются случайно, то функция надежности
равна
We о f B.4.19)
где усреднение производится по всем реализациям a (t). Если пред-
предположить, что процесс изменения внешних условий стационарный,
а время t велико по сравнению с временем корреляции процесса, то
t
\fk[a{i)]d% ^ ДО Ma),
о
и тогда
P(t) ^=e-/MMa), B.4.20)
142 характеристики надежности [гл. 2
т. е. в этом случае можно брать средние опасности отказа Кк=Шк(а)
и считать элементы независимыми.
Мы рассмотрели несколько подходов к оценке надежности си-
системы с зависимыми элементами. Естественно, что они далеко не
исчерпывают всех идей и подходов, которые возникают в этой
трудной и важной проблеме. До сих пор мы предполагали, что все
элементы в системе работают непрерывно, без простоев. На самом
деле во многих реальных системах, таких, например, как вычисли-
вычислительные машины, работает только часть элементов, а остальные
элементы или выключены, или включены, но не выполняют никаких
функций. С течением времени работающая часть системы меняется,
одни элементы переходят в нерабочее состояние, другие, наоборот,
включаются в работу. Предположим, что опасность отказа каждого
элемента постоянна, но зависит от состояния элемента — работает
он или нет. Тогда опасность отказа всей системы постоянна на тех
участках, где работает одна и та же группа элементов, и меняется
скачком в те моменты, когда какие-то элементы переходят из рабо-
рабочего состояния в нерабочее или наоборот. Групла работающих эле-
элементов определяет состояние системы. Пусть N—число всех воз-
возможных состояний системы. Каждому состоянию соответствует своя
опасность отказа системы
Предположим также, что процесс смены состояний стационарный
и эргодический. Это означает следующее: пусть т^(^) — случайное
время, которое система пребывает в состоянии k до момента t.
Тогда с вероятностью единица
Ц^-^Р* k=\,2,...,N,
где pk—вероятность того, что в наугад взятый момент система
находится в состоянии k.
Если времена тх (t) ... iN(t) известны, то условная вероятность
безотказной работы системы равна
Поэтому для случайных времен Tk(t) функция надежности системы
равна
Предположим теперь, что время t—> оо, а произведения Kkt остаются
ограниченными. Тогда с вероятностью единица
§ 2.4]
НАДЕЖНОСТЬ СИСТЕМЫ
143
Это предельное соотношение означает, что в тех случаях, когда
смена состояний происходит относительно быстро, так что до отказа
система успевает много раз сменить свое состояние, справедлива
приближенная формула
P(t) же
B.4.21)
N
Сумму 2 ^Л можно рассматривать как среднюю опасность отказа
системы.
Надежность восстанавливаемой системы. До сих
пор мы рассматривали работу системы до первого отказа. Теперь
мы предположим, что каждый элемент системы после отказа вос-
восстанавливается.
Рассмотрим сначала тот случай, когда восстановление происхо-
происходит мгновенно. Как и выше, мы будем считать, что исходные свой-
свойства элемента восстанавливаются полностью. Предположим также,
что работа, отказы и восстановление одного элемента никак не
влияют на надежность других элементов. Моменты отказов каждого
элемента образуют процесс восстановления, причем в силу наших
предположений эти процессы независимы. Обозначим через Fk(t)
(&= 1, 2, ... , п) закон распределения времени жизни &-го элемента.
3*-
j_ I _ I ^ i j \ _
I
-1-Й-
Рис. 2.4.1.
Мы предполагаем, как обычно, что эти законы имеют непрерывную
плотность fk(t) и существуют среднее время жизни элемента Tk и
его дисперсия о\. Ниже мы будем рассматривать только тот слу-
случай, когда элементы в системе соединены (в смысле надежности)
последовательно и отказ любого элемента вызывает отказ системы,
пели моменты отказов всех элементов отложить на общей оси
времени, то мы получим поток отказов системы. Этот поток есть
сумма п процессов восстановления (рис 2 4 1)
Наша задача заключается в том, чтобы изучить поток отказов
системы и найти его основные характеристики; Пусть vk(t)-слу-
vk(t)-случайное число отказов *-го элемента до момента *, 4=1,2, ...Д
144 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
a v (/) — случайное число отказов системы до момента t. Очевидно,
что
v@=v1@+...+vll(/). B.4.22)
Отсюда совсем просто находится среднее число отказов системы до
момента t, которое мы обозначим через
И (t) = Mv (t) = Mvx (t) + . .. + MvB (t) =
= Нг (t) + H2{t)+ ...+Hn (t), B.4.23)
где Hk(t) — функция восстановления для &-го элемента.
Производную
назовем интенсивностью отказов. Она равна среднему числу отка-
отказов за единицу времени (если эта единица мала). Интенсивность
отказов h(t), являющаяся основной характеристикой потока отказов
системы, может быть определена из опыта.
Для этого мы регистрируем моменты отказов системы и разби-
разбиваем все время наблюдений на интервалы длины h так, чтобы в каж-
каждый интервал попало достаточное число отказов (не менее десяти).
Пусть пх,пг,пъ, ..., nk — число отказов, попавших соответственно
на первый, второй, третий и т. д. интервалы. На каждом k-м интер-
интервале мы строим столбик высотой ^. Полученная ступенчатая кри-
кривая и дает нам оценку функции h(t). К сожалению, погрешность
этой оценки трудно определить, так как в общем случае вероят-
вероятностная природа потока отказов системы очень сложна.
Из равенства B.4.22) можно найти и распределение числа отка-
отказов системы v(f). Мы знаем из B.3.4) распределение числа отказоз
для процесса восстановления
(Здесь Fks(t) — ^-кратная свертка закона распределения Fk(t).)
Чтобы найти распределение v (/), введем производящие функции
для числа отказов элемента
Так как величины v^(/) независимы, то производящая функция от-
отказов системы
s=o
*' «> Иг*' <« ... M*v««> = P1 (t, z) Рг (t, z) ... Р„ (t, s), B.4.24)
где
§ 2.4] НАДЕЖНОСТЬ СИСТЕМЫ 145
Зная производящую функцию P(t, z), мы можем найти и иско-
искомые вероятности ps(t)>
Ps @ = 2 Pi*i С) P2s2 (t) ... Pnsn (t). B.4.25)
st+ ... +sn=s
На практике часто важно знать, проработает ли система безотказно
на интервале (t, t-\-x). Это событие наступит тогда и только тогда,
когда каждый элемент не откажет на этом интервале. Обозна-
Обозначим через pt (т) вероятность безотказной на (t, t-\-%) работы системы,
а через р\ )(т) вероятность безотказной работы k-io элемента на
(^, / + т). Так как элементы независимы, то
), B.4.26)
где каждая вероятность p\k) (т) определяется по формуле B.3.26).
Можно было бы найти и целый ряд других характеристик, напри-
например: вероятность появления на (t,t-{-%) ровно s отказов, распреде-
распределение 5-го отказа системы, распределение промежутка между сосед-
соседними отказами системы и т. п. Мы не будем заниматься выводом
всех этих формул, так как они подобно формулам B.4.25) и B.4.26)
очень сложны и вряд ли представляют интерес для практики.
Вместо этого мы рассмотрим асимптотические свойства потока
отказов системы, из которых и выведем простые и практически прием-
приемлемые приближенные формулы для различных характеристик потока
отказов системы. Система, как правило, состоит из большого числа
элементов, доходящего до тысяч и даже десятков тысяч. Вместе
с тем каждый в отдельности взятый элемент имеет относительно
большой срок службы, отказывает редко. Таким образом, поток
отказов системы есть сумма большого числа редких потоков вос-
восстановления. Согласно нашим предположениям эти потоки незави-
независимы. Доля каждого элемента в общем потоке отказов системы
очень мала, так как обычно в системе нет элемента, поток отказов
которого был бы сравним по интенсивности с потоком отказов всей
системы. В потоке отказов системы зависимы только те отказы,
которые принадлежат одному элементу, но они с вероятностью,
близкой к единице, разделены большим числом отказов других эле-
элементов. Отсюда следует, что появление отказов на одном участке
времени не меняет (точнее, почти не меняет) вероятности появления
какого-либо числа отказов на другом участке, не пересекающемся
с первым. Из этих физических соображений следует, что при сде-
сделанных выше предположениях в потоке отказов системы должно
отсутствовать последействие. Кроме того, мы предположили выше,
что законы распределения Fk\t) имеют непрерывные плотности.
Отсюда следует, что функция И(*) — среднее число отказов —не-
прерывна и, как нетрудно показать, поток отказов системы является
В. В. Гнеденко и
др.
146 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
ординарным, т. е. вероятность одновременного появления двух
отказов равна нулю. В теории массового обслуживания доказы-
доказывается, что ординарный поток с непрерывной функцией #(/), в кото-
котором отсутствует последействие, является простейшим нестационарным
потоком. Это значит, что вероятность появления 5 отказов на любом
участке (tly t2) выражается формулой
Ps Vi> к) = [Н (t2)~}H {tl)] e~lHЫ-Н«М , B.4.27)
и для любой системы неперекрывающихся интервалов события, заклю-
заключающиеся в появлении заданного числа отказов на каждом интер-
интервале, независимы. Итак, мы показали, что при достаточно общих
условиях поток отказов системы будет, по крайней мере прибли-
приближенно, простейшим нестационарным потоком. Проведенные выше
рассуждения, хотя они являются достаточно убедительными, не дают
все же строгого доказательства этого факта. Такое доказательство
имеется [16], однако мы ограничимся сказанным выше и не будем
его приводить. Из формулы B.4.27) видно, что число отказов на
каждом интервале распределено по закону Пуассона. По этой при-
причине такой поток отказов называют часто пуассоновским потоком
с переменным параметром. Этим переменным параметром является
интенсивность отказов h(t). Формулу B.4.27) можно записать и так:
г'2 Y *
h(t)dt
Если на участке (ty t-{-%) функция h(t) приближенно линейна, то
хорошее приближение для этих вероятностей дает равенство
B.4.28)
Если же функция h(t) на этом участке приближенно постоянна,
h (t) « К то
^^. B.4.29)
Этой последней формулой чаще всего и пользуются.
В частности, вероятность безотказной работы на интер-
интервале (/,
PoV, t + T)&e-tH«+v-HW. B.4.30)
§ 2.4] НАДЕЖНОСТЬ СИСТЕМЫ 147
Если, как и выше, h(t) приближенно постоянна на этом интер-
интервале, то
po(t, t + T)ate-hW\ B.4.31)
Из формулы B.4.30) следует, что среднее время до первого отказа
после момента t равно
оо оо
7ср = J e-W «+х)-н </)] dx = ен it) J е-н (x) dXt B.4.32)
о t
Если же на участках между соседними отказами h (t) почти не
меняется, то, как следует из B.4.31), это среднее время выра-
выражается приближенной формулой
Г«р«Щ. B-4-33)
Рассмотрим еще несколько характеристик нашего потока.
Пусть tlt t2i . . ., t3— моменты последовательных отказов системы.
Найдем закон распределения момента s-vo отказа ts
B.4.34)
fe=S
отсюда среднее время до s-то отказа
Нетрудно найти закон распределения времени между 5-м и (s-f 1)-м
отказами
§s^)<tx, B.4.35)
О
а его среднее значение
00
"('.+i-',) = JI-^V"@<«. B.4.36)
О
Очень часто нас интересует надежность системы на начальном
участке времени, на котором среднее число ожидаемых отказов
системы ничтожно мало по сравнению с числом элементов в системе,
ото значит, что
148 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
Если надежность всех элементов примерно одного порядка, то
отсюда следует, что Hk{t)<^\ и тем более Fk(f)<^\. Но при этих
условиях было показано, что
Hk(t)&Fk(t).
Значит,
23^@, B.4.37)
причем относительная погрешность этого равенства не превосходит
Использование этого приближенного равенства сильно упрощает
все расчеты.
С другой стороны, работа системы нередко продолжается столь
долго, что почти все элементы системы успевают отказать по
нескольку раз. При этих условиях процессы восстановления ста-
становятся стационарными и, значит, поток отказов системы также
устанавливается. Так как плотности восстановления для каждого
элемента стремятся к пределам
\lm hk(i) = ±
t-wo l k
то интенсивность отказов системы имеет предел
I. B.4.38)
к
При этом поток системы становится пуассоновским потоком
с постоянным параметром, т. е. простейшим потоком. Для этого
потока вероятность появления 5 отказов на участке времени дли-
длительности х не зависит от положения этого участка и выражается
формулой
ps (Т) = (^El! е-Лот. B.4.39)
В частности, вероятность безотказной работы системы в течение
времени х равна р0 (х) =e~h<>x и, значит, среднее безотказной работы
равно
Тс=±. B.4.40)
Заметим еще, что если надежность каждого элемента в системе
подчиняется экспоненциальному закону
§ 2.4] надежность системы 149
то процесс восстановления для каждого элемента будет образо-
образовывать простейший поток и, значит, поток отказов системы как
сумма простейших потоков также будет простейшим с интенсив-
интенсивностью
п
k
B.4.41)
Надежность системы с конечным временем вос-
восстановления. Перейдем теперь к изучению надежности системы
в том случае, когда восстановление каждого элемента требует
некоторого времени, которым уже нельзя пренебречь. Пусть
Fk(t) — закон распределения жизни &-го элемента, a Gk(t) — закон
распределения времени его восстановления. Мы, как всегда, пред-
предположим, что эти законы имеют непрерывные плотности Д (t)
и gk(t) и существуют конечные средние Tkl и Tk2 и дисперсии
Во время восстановления элемента система может вести себя
по-разному. Мы рассмотрим только два случая.
1) Во время восстановления любого элемента система
выключена, не работает. За это время во всех других элемен-
элементах не происходит никаких существенных изменений, и поэтому
<: момента восстановления они начинают работать так, как если
<5ы восстановление произошло мгновенно.
2) Во время восстановления одного элемента все другие эле-
элементы продолжают работать. Отказы и восстановления
элемента не влияют на надежность других элементов. Время вос-
восстановления элемента не зависит от того, происходят в это время
отказы других элементов или нет. Иными словами, каждый элемент
отказывает и восстанавливается независимо от других.
Разберем сначала первый случай. Мы предположим, как и выше,
что число элементов в системе велико, а интенсивность отказов
каждого составляет бесконечно малую долю от общей интенсив-
интенсивности отказов системы. При этих условиях поведение системы легко
описать. Участки работы системы чередуются с участками, где
происходит восстановление.
Отдельно взятые участки работы т?, т'2, .. . образуют пуассо-
новский поток с переменным параметром. Распределение x's нахо-
находится^ по формуле B.4.32). Длина каждого участка восстановле-
восстановления xs практически не зависит от длин соседних участков работы
и восстановления, так как отказы, принадлежащие одному эле-
элементу, разделены большими интервалами. Поэтому нетрудно найти
Распределение интервалов восстановления %s. Вероятность того,
Что на бесконечно малом участке (f, t + M) произошел отказ k-vo
150 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ
элемента, равна
[ГЛ. 2
а вероятность отказа системы на этом участке равна
где
Отсюда следует, что условная вероятность отказа &-го элемента
на этом участке при условии, что на нем произошел отказ системы,
равна
МО А'+о (АО = МО , пПу
h{t) ~ru\i>-
Значит, вероятность того, что отказ системы, происшедший
в момент /, принадлежит &-му элементу, равняется
МО
h(t) '
Поэтому распределение длительности периода восстановления,
начавшегося в момент t, может быть найдено по формуле полных
вероятностей
B-4-42)
k — 1
Распределение начала 5-го периода восстановления может быть
найдено, если известно распределение предыдущих периодов работы
и восстановления. Отсюда, применяя опять формулу полных вероят-
вероятностей, мы можем найти безусловное распределение периода т^. Такой
путь приведет к очень сложным формулам. Поэтому мы исследуем
поток отказов и восстановлений системы несколько иным путем.
При наших предположениях интенсивности отказов hk [t) и h (t)
меняются очень медленно. Мы предположим, что на рассматри-
рассматриваемом участке времени они постоянны,
hk(t)=hk, h(t)~h.
Тогда периоды работы будут распределены по экспоненциальному
закону
t) =\—e-htf
B.4.43)
§ 2.4] НАДЕЖНОСТЬ СИСТЕМЫ 151
а периоды восстановления будут иметь, как следует из B.4.42),
распределение
P{t;</}=Xf Ok(t) = О (*), B.4.44)
причем все эти периоды будут независимы. Таким образом, поток
отказов и восстановлений системы образует уже рассмотренный
выше процесс восстановления с конечным временем восстановления.
Поэтому для изучения надежности системы мы можем исполь-
использовать найденные выше характеристики такого процесса.
Среднее время работы системы из B.4.43) равно
00
-h'dt = -j, B.4.45)
О
а среднее время восстановления
=Хт-т*- <2-4-46)
k =1
Следовательно, коэффициент готовности на данном участке выра-
выражается формулой
Вероятность безотказной работы в течение времени t равна
t__
р (t) = kve-ht = kre тк B.4.48)
рт достаточно долг
и h (t) приближаются к своим пределам
lim
Если система работает достаточно долго, то интенсивности hk (t)
h (t
*-*00 / kl ^00 ~j l kl
Для этого случая формулы B.4.45)—B.4.48) получают вид
п
ri = -Fi—: r.= riZS?: ftr= 2 . B.4.49)
ke~
152 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
Заметим, что если время работы и время восстановления каждого
элемента подчиняются экспоненциальному закону, то формулы
B.4.49) являются точными на любом участке времени и при любом
числе элементов.
Перейдем теперь к рассмотрению второго случая [17], когда
каждый элемент работает и восстанавливается независимо от дру-
других. В этом случае поток отказов и восстановлений системы есть
сумма п независимых процессов восстановления с конечным време-
временем восстановления. Для такой системы очень просто находится
коэффициент готовности kr(t), равный вероятности того, что
в момент t система окажется исправной. Рассмотрим единичные
случайные функции v^(^) E=1,2, ...,/z), которые определяют-
определяются так:
если в момент t 5-й элемент исправен,
если в момент t 5-й элемент неисправен.
"•<"={ о!
Тогда функция
равна единице, если в момент t система исправна, и равна нулю,
если она неисправна. Функции vs(t) по условию независимы,
и поэтому
Ar(<) = P{vW = l} = "v(/) =
- Mvx (t) Mv2 (t)..Mvn (t) = k™ (t) k(r2) (t)...k(rn) (*), B.4.50)
где k^ (t) — коэффициент готовности 5-го элемента, вычисляемый
по формуле B.3.37). С течением времени поток отказов и восста-
восстановлений системы становится стационарным и для этого случая
h 1П
1 11 "Г * 12 1 21-Т1 22 ' nl"T J П9
Определяя другие характеристики надежности системы, мы огра-
ограничимся стационарным случаем, предполагая, что система работала
достаточно долго. Пусть в момент t произошло восстановление
системы. Найдем вероятность того, что система проработает без-
безотказно в течение времени т. Для вывода этой вероятности рас-
рассмотрим следующие события:
Л (А/, т) — на участке (t — At,t) произошло восстановление
системы и на участке (/, t-\-x) система работала безотказно,
A (At) — на участке (t — Д/, t) произошло восстановление системы.
Очевидно, что искомая вероятность равна
р (т) = lim Р {А (М, т) | А (Щ = lim ?^^*^
Ato м
§ 2.4] НАДЕЖНОСТЬ СИСТЕМЫ 153
Если пренебречь событиями, вероятность которых бесконечно мала
ло сравнению с Д/, то событие А (Д/, т) представляется суммой
непересекающихся событий
Л (А*, т) = Ах (А/, т) + А2 (А/, х)+...+Ап (А/, т),
где событие Лт(Д?, т) состоит в том, что т-& элемент восстанав-
восстанавливается на интервале (t — Д^, t) и на (/, t-\-%) работает безотказно,
а остальные элементы работают безотказно на (ty t-\-x). Вероят-
Вероятность этого события равна
со
J [l-Ft(x)]dx
l^{x)U % о (At).
Отсюда
Так как событие А (Д/) = A (At, 0), то
Теперь мы можем найти искомую вероятность
Р{А(М,%)}
= lim
Р {Л (ДО}
Чтобы привести эту формулу к компактному виду, обозначим закон
распределения остаточного времени жизни 5-го элемента через
1 si
о
и пусть ф5 (т) = ф'8 (т) = "~ s ^ — его плотность. Введем еще одно
обозначение 5l
п
о —это среднее время между соседними отказами системы при
154 ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ [ГЛ. 2
мгновенном восстановлении. Тогда наша вероятность может быть
записана так:
Р (т) = Т0Уёсрт (х) П П ~ Ф, (т)] =-Г0)П[1-Ф, (т)] } . B.4.52)
т—\ s 9е т Vs—1 /
s 9е т
Отсюда очень легко найти среднюю длительность рабочего периода
системы
со
Тг = $ р (т) d% = - То П 11 -Ф, (г)] |" = Го. B.4.53)
О & = 1
Итак,
Мы видим, что среднее время работы системы оказывается таким же,
как и при мгновенном восстановлении.
Пусть теперь Т2 — среднее время восстановления системы. Тогда,
с одной стороны, коэффициент готовности системы kT равен
к -
С другой стороны, этот коэффициент выражается формулами
B.4.51). Приравнивая эти выражения
7\i -\-Tl2 T21 -fT22 "' Тп1 + Тп2 r'
мы получаем уравнение, из которого определяется среднее время Г2:
ГЯ = ЛЦ^- B.4.54)
Если предположить, как мы это делали выше, что число элемен-
элементов велико, а доля каждого элемента в потоке отказов и восста-
восстановлений системы бесконечно мала, то можно найти для вероят-
вероятности р (т) более простое приближенное выражение:
__L
р(х)же тк B.4.55)
§ 2.4] НАДЕЖНОСТЬ СИСТЕМЫ 155
Отсюда вероятность безотказной работы системы на (t, t-\-x) равна
т
Ь п (т\ су, Ь р Т^ (9 4- Ъ(\\
В заключение заметим, что в случае, когда время жизни элемен-
элементов распределено по показательному закону Fk(t) = \—e~^kty
а время восстановления распределено произвольно, можно не только
определить средние времена работы и восстановления системы, но
и найти точные законы их распределения. Не приводя подробного
вывода, укажем лишь на его идею.
Для этого заметим, что периоды работы и восстановления си-
системы для нашего случая независимы, причем период работы рас-
распределен по закону
где
а период восстановления системы распределен по неизвестному
закону, который мы обозначим Ф@«
Коэффициент готовности системы
и, таким образом, нам известен. С другой стороны, этот коэффи-
коэффициент kT (t) может быть выражен через функцию Ф(/).
Пусть
t
<р (t) = Ф' (t) и г|> (t) = J Хе-*> <*-*> ф (л:) dx.
о
Тогда по формуле B.3.37)
t
kT (t) = е~и -f J е-* <'-*> /г (*) Ja:, B.4.57)
о
где h(x)— 2 ^ (х) — плотность моментов восстановлений системы.
k-i
Из уравнения B.4.57) можно найти функцию h (/), а по ней
определить и искомый закон Ф(/). Преобразование Лапласа для
закона O(t) легко выражается через преобразование Лапласа от
Функции h(t).
ГЛАВА 3
ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
ПО РЕЗУЛЬТАТАМ ИСПЫТАНИЙ
§ 3.1. Испытания на надежность
Организация и проведение испытаний изделий на надежность
выходит далеко за пределы использования лишь математических
методов.
Центральным моментом организации испытаний является выбор
тех параметров, оценка значений которых должна считаться основ-
основной целью испытаний. Этот выбор определяется прежде всего
физической значимостью предложенных характеристик, а также
теми узкими местами, которые выявились в работе опытных изделий
или же при эксплуатации изделий прежних выпусков. Несомненно,
что этот этап работы ложится основной своей тяжестью на плечи
физиков, химиков и инженеров. Роль математика выявляется позд-
позднее, когда возникнет необходимость оценки взаимной зависимости
избранных параметров и обработки результатов испытаний.
Даже для относительно простых элементов — конденсаторов,
сопротивлений, диодов и пр.— достаточно полная характеристика
надежности редко может быть получена посредством измерения
значения одного-единственного параметра. Как правило, требуется
знание нескольких величин, чтобы можно было составить отчетли-
отчетливое представление об изделиях. Так, для примера, если речь идет
о поршневом пальце, то важны не только его геометрические раз-
размеры (включая «конусность»), но и равномерность цементации.
Точно так же сопротивление недостаточно характеризуется только
величиной его сопротивления в омах. Для оценки надежности
большую роль играет устойчивость сопротивления к тепловым
и электрическим воздействиям, длительности хранения, влиянию
влажности.
Вторым по важности моментом организации испытаний следует
считать выбор внешних условий, включая сюда и рабочий режим
проведения испытаний. Само собой разумеется, выбор условий
§ 3.1]
ИСПЫТАНИЯ НА НАДЕЖНОСТЬ
157
в значительной степени должен учитывать те особенности, в кото-
которых впоследствии придется работать изделиям. Эти условия (тем-
(температура, влажность, напряжение, вибрации, удары, распределение
нагрузок во времени и пр.) должны быть различны для партий
изделий, предназначенных для работы в тропиках или же в Арк-
Арктике, в зоне пустынь или же высокогорных районах.
Внешние условия могут оказывать исключительно сильное влия-
влияние на характер изменения измеряемых параметров. Об одной ин-
интересной иллюстрации этого положения авторы узнали от Л. Л. Кри-
сталинского. Если часть испытуемых изделий (например, металло-
керамических сопротивлений) из одной и той же партии подвергать
непрерывной нагрузке в течение времени t, а другую часть под-
подвергать нагрузке также в течение суммарного времени /, но при
этом чередовать периоды нагрузки с периодами «отдыха», то
поведение параметров этих двух групп изделий будет существенно
различным.
На рис. 3.1.1, а изображено примерное поведение коэффи-
коэффициента усиления р полупроводникового триода. Довольно резкое
А
¦ А
л
А
t tmo
Рис. 3.1.1.
б)
изменение ординат графиков во времени вызвано нестабильностью
температуры. На рис. 3.1.1, б дано изменение того же параметра
при условии, что стабильность температуры тщательно соблюда-
соблюдалась. Вели Рн и рв — нижняя и верхняя границы допустимого
изменения параметров, то в первом случае параметр изделия пре-
превышал крайнее верхнее значение (был зафиксирован «отказ»), тогда
как во втором случае отказы не наблюдались.
Заманчиво использовать данные не только специально органи-
организованных испытаний, но и сведения об отказах аппаратуры, рабо-
работающей в реальных условиях. Однако непосредственно эти данные
не могут быть использованы для 'анализа вопросов надежности.
Предварительно они должны быть расклассифицированы по тем
внешним условиям, в которых работала аппаратура.
Инженерные и физические соображения должны также лежать
в основе назначения допустимых границ изменения параметров,
158 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
выход за пределы которых должен считаться отказом. В значи-
значительной мере эти границы определяются назначением элементов,
так как в одной аппаратуре допустимы столь большие колебания
его параметров, какие для другой аппаратуры должны неизбежно
считаться «отказом». Понятие отказа было подробно освещено
нами в § 2.1.
Момент наступления отказа заранее не может быть указан, он
случаен. Собственно, вероятностный характер носят все параметры,
определяющие надежность изделий, поскольку их значения меня-
меняются от одного изделия к другому и это изменение не упорядо-
упорядочено, случайно. Это обстоятельство приводит к необходимости
оценивать на основании испытаний распределения интересующих
нас числовых характеристик надежности, а также существующие
между ними связи. Мы приходим, таким образом, к постановке
основных задач математической статистики: а) оценке значений
неизвестных параметров распределений, а также б) проверке
различного рода статистических гипотез.
Проведение испытаний может быть организовано многими пу-
путями. В зависимости от тех правил, в соответствии с которыми
будут проводиться испытания, говорят о том или ином плане их
проведения. План испытаний должен включать в себя ряд указа-
указаний, в частности количество изделий элементов или комплексов
аппаратуры, которые необходимо поставить на испытания; когда
производить проверку изделий (непрерывно или в заранее задан-
заданные моменты времени); заменять или не заменять отказавшие изде-
изделия; когда прекращать испытания или же добавлять новые изде-
изделия для продолжения испытаний.
Для удобства записи будем использовать следующие обозначе-
обозначения: обозначим буквой «?» планы, в которых отказавшие элементы
не заменяются новыми, буквой «Б» — те, в которых каждый отка-
отказавший элемент заменяется новым, идентичным ему элементом.
Предполагаем, что наблюдения за отказами производятся непре-
непрерывно, в результате чего отказы обнаруживаются в моменты их
возникновения. Через г обозначим планы, в которых наблюдения
ведутся до момента появления r-го отказа, через Т—планы, при
которых наблюдения ведутся в течение времени Т. Т обычно изме-
измеряется в часах. Иногда используются смешанные планы, когда
наблюдения ведутся до момента tr появления г-го отказа, если
ir<C.T, или до момента Г, если tr^T. Такие планы будем обо-
обозначать через (г, Т). Ради сокращения и уточнения записи введем
обозначения для различных планов: станем указывать вначале
число N испытываемых элементов, затем наличие или отсутствие
замены отказавших элементов и, наконец, длительность испытания.
План, при котором испытывается N элементов, каждый отказавший
элемент не заменяется новым, а наблюдения ведутся до момента Г,
§ 3.1]
ИСПЫТАНИЯ НА НАДЕЖНОСТЬ
159
обозначается через [N, Б, Т]. Обозначение [N=100, ?(г = 15,
Т== 1500)] соответствует плану, при котором испытывается 100 эле-
элементов, каждый отказавший элемент заменяется новым, а наблю-
наблюдения ведутся либо до момента tlb появления 15-го отказа, либо
в течение 1500 час, если ^15^1500. Легко видеть, что в указан-
указанных условиях возможны лишь шесть различных планов:
[N, Б, Т}; [N, Б, г}; [N, Б, (г, Т)];
[N, В, Т]; [N, В, г]; [N, В, (г, Т)].
Обозначим через d(t) число отказов, возникших к моменту t.
Функция d(t), как это следует из определения, не может убывать
и принимает последовательно значения 0, 1, 2, ... Точки роста
d{t) отвечают случайным моментам времени t(. Реально наблюден-
наблюденную во время испытаний функцию d(t) называют реализацией
процесса d(t) или траекторией процесса d(t).
Обозначим через G ту область плоскости (/, d(t)), попадания
в которую траектории процесса d(t) приводит к окончанию испы-
испытаний. Для планов [N, Б, Т] и [N, В, Т] в качестве области G мы
idft)
6)
должны взять полуплоскость t>T. Испытания при этих планах
прекращаются в момент 7, как бы ни шла траектория d(t)
(рис. 3.1.2, а).
В случаз планов (рис. 3.1.2,6) [Л/, Б, г], [N, В, г] испытания
прекращаются в момент tr первого попадания траектории d(t)
в множество G={(d, t):d^r}. Наконец, для планов [N, Б, (г, 7)],
[N, В, (г, Т)] испытания прекращаются в момент первого попада-
попадания в множество G={(flf, t)}: или d^r, или t^T} (рис. 3.1.2, в).
В ряде случаев испытания могут планироваться на основе по-
полученных значений суммарной наработки. Если через N (t) обозна-
обозначить число элементов, безотказно работающих до момента t,
N(t)=N—d(t), то значение суммарной наработки S (t) в момент^
определяется как сумма времен, в течение которых безотказно
160
ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
[гл. 3
работали испытываемые элементы. Таким образом, имеем
* d (О
C.1.1)
где t{ — моменты отказов элементов. Так как для планов типа В
значение S(t) = Nty то нетривиальным дополнением к указанным
выше шести планам являются следующие два плана типа Б. Для
первого плана, обозначаемого [N, Б} HS0]y момент остановки
испытаний /* определяется как момент, когда впервые SH(t*) = S0;
если же окажется, что S (tN)<i So, то t* = tN. Для второго плана
момент остановки t* определяется как момент, когда впервые
наступает одно из следующих событий: либо S (t*) *=S0 и d (/*) < г,
либо t***tr, но S (t*) <.S0. Здесь tr — момент появления г-го от-
отказа. Такой план будем обозначать [Л/, Б, (г, HS0)]. Полезно иметь
в виду, что [ЛГ, Б, HS0] = [N, Б, (N, HS0)]. Аналогичным образом
имеем [N, Б, (TV, T)] = [N, Б, Г], однако [N, Б, (N, Т)] ф [N, В, Т].
Из рис. 3.1.2, а, бу в легко понять, что в принципе можно
рассматривать планы типов Б, В, у которых момент прекращения
испытаний совпадает с моментом первого попадания в множе-
множество О, граница которого, вообще говоря, может быть произ-
произвольной формы (рис. 3.1.3, а). На рис. 3.1.3, б показан вальдовский
rft)k
V/G///////
W
}' 1
/
///ж
/к
Ш
ш
б)
Рис. 3.1.3.
план типа последовательного анализа, о котором будет подробнее
сказано в § 4.4 следующей главы. Для вальдовских планов гра-
границы множества G точек остановки испытаний задаются в виде
двух параллельных прямых Lx и L2, показанных пунктиром на
рис. 3.1.3,6. Момент остановки t* полагается равным первому
моменту достижения траекторией d (t) одной из прямых: Lx или L2.
Часть из описанных выше планов типов Б и В рассматривалась
ранее в литературе по надежности см., например, [1], [2], [3], [4].
В ряде случаев могут понадобиться планы, отличные от описанных
выше. Так, при установочных испытаниях вновь разрабатываемых
§ 3.1] ИСПЫТАНИЯ НА НАДЕЖНОСТЬ 161
изделий в определенные моменты часть из них может сниматься
с испытаний. В результате этого число испытываемых изделий ме-
меняется не только за счет отказавших, но и в результате отбора
части изделий для исследования; на планы такого типа дано ука-
указание в книге [7], стр. 355.
Если выбраны внешние условия проведения испытаний, согласо-
согласована с'заказчиком вероятностная характеристика и выбран план
проведения испытаний, то по результатам испытаний, вся инфор-
информация о которых содержится в отрезке траектории процесса d(t)
до момента первого попадания в множество G, требуется дать
методику оценки выбранной характеристики надежности или мето-
методику построения доверительного интервала. Этим мы и займемся
в следующих параграфах настоящей главы.
В заключение параграфа сделаем несколько замечаний, которые
носят скорее характер пожеланий и не содержат решения или даже
указания путей решения поднимаемых вопросов.
В § 2.1 подчеркивалась относительность понятия отказа, выте-
вытекающая из произвольности понятия границ допуска. Позднее мы
увидим, что определение вероятностных характеристик по момен-
моментам отказов даже со сравнительно умеренной степенью достовер-
достоверности приводит к необходимости постановки на испытания огром-
огромного количества образцов. Количество испытываемых образцов
можно резко сократить, если эти же вероятностные характери-
характеристики оценивать, учитывая весь ход изменения параметров во вре-
времени, а не единственный момент наступления отказа. Фиксируя
лишь моменты отказов, мы, как правило, теряем большое количе-
количество ценной информации и эту потерю вынуждены восполнять тем,
что проводим испытания на большем числе образцов. На пути
решения этой задачи возникают немалые трудности. Во-первых,
необходимо наличие специальной аппаратуры, с помощью которой
можно было бы следить за изменением параметров испытываемых
образцов. Во-вторых, необходимо построить теоретические модели,
которые можно использовать для описания процессов изменения
параметров во времени и на основе которых производились бы
оценки требуемых вероятностных характеристик. Следует отметить,
что часто изменения параметров, приводящих к отказу, не могут
быть измерены непосредственно, но могут быть измерены другие
величины, в которых содержится информация о возможном отказе.
Например, известно, что отказ определяется значениями пара-
параметра ах(/); однако этих значений мы не знаем, но зато знаем
значения параметра а2 (t). Известно, что ах (t) и а2 (^ — взаимосвя-
взаимосвязанные между собой процессы (характер взаимосвязанности опре-
определяется в каждом конкретном случае по-своему). Требуется по
значениям процесса а2 (t) оценить требуемые вероятностные харак-
характеристики процесса ax(t).
162 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
Помимо сокращения числа испытываемых образцов весьма акту-
актуальной является также и проблема уменьшения длительности испы-
испытаний. Дело в том, что в ряде случаев необходимы данные об
отказах за длительный интервал непрерывной работы, порядка
нескольких лет, а требуется эти данные получить по результатам
испытаний за весьма небольшой промежуток времени. Возникает
необходимость проведения ускоренных испытаний, когда испыты-
испытываемые элементы (образцы аппаратуры) находятся в утяжеленных
условиях работы (повышена температура окружающей среды,
увеличена амплитуда или частота колебаний платформы с образ-
образцами, повышено напряжение и т. д.). Процессы «старения» при
утяжеленных режимах работы протекают быстрее, отказы насту-
наступают раньше. Требуется построить модели подобия, которые
позволяли бы по результатам ускоренных испытаний оценивать
вероятностные характеристики, соответствующие нормальным усло-
условиям работы. Первоначально планировалось, что ускоренным испы-
испытаниям в нашей книге будет посвящен отдельный параграф. Однако
внимательное изучение литературы и разговоры с инженерами при-
привели нас к выводу, что это направление исследований находится
на самом начальном этапе своего развития.
Мы считаем, что основные задачи развития метода ускоренных
испытаний связаны с изучением физики процессов старения в зави-
зависимости от внешних условий и рабочего режима. Обычно используе-
используемый подход, основанный на установлении подобия для двух эмпи-
эмпирических функций распределения отказов — одной для нормальных
внешних условий и второй, полученной в результате проведения
ускоренных испытаний,— нам кажется недостаточным, так как при
этом полностью игнорируются те физические процессы старения,
которые происходят в испытываемых элементах. Исключение состав-
составляют лишь некоторые работы по ускоренным испытаниям конден-
конденсаторов. Интересные экспериментальные данные о результатах
ускоренных испытаний конденсаторов приведены в работе [6].
§ 3.2. Общие методы оценки показателей надежности
по результатам испытаний
Эмпирическая функция распределения и гисто-
гистограмма результатов испытаний. В настоящем параграфе
рассматриваются общие методы получения оценок параметров,
определяющих надежность изделий. Эти методы могут быть
использованы при обработке результатов наблюдений над изде-
изделиями, срок безотказной работы которых подчинен тому или иному
распределению — показательному, Вейбулла, логарифмически нор-
нормальному и др. Однако чисто технические трудности заставляют
нас ограничиться при этом только планами [N, ?, г] и [jV, Б, Г].
§ 3.2] ОБЩИЕ МЕТОДЫ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ 163
Естественно, что последующие результаты применимы при обра-
обработке результатов испытаний не только элементов, но и сложных
систем.
Напомним, что план [N, Z>, N] означает испытание N элементов
до отказа последнего элемента; отказавшие элементы не заме-
заменяются новыми. План [7V, Б, N] можно использовать или в случае,
когда элементы сравнительно ненадежны, или же при проведении
ускоренных испытаний. Предположим, что испытываемые элементы
занумерованы числами 1, . . ., N и /-й элемент отказывает в момент xi%
Первый отказ наступает в момент /1 = т1п(л:1, . . ., xN); t1 = xii, где
ix — номер элемента, оказавшегося первым; it — случайное
число. Второй отказ наступает в момент /2 = min(A:1, ..., лг^-i,
Xit + i, ..., xN) и т. д. Наконец, в момент tN=max(xly ...,xN)
отказывает последний элемент.
В статистике так упорядоченную последовательность чисел
tx <[ t2 <; .. . ^ tN называют вариационным рядом для результатов
наблюдений лгх, .. ., xN.
При использовании [N, Бу Т] наблюдаются только те отказы,
которые происходят до момента времени Т. Если ^^/2^...—
последовательные моменты отказов, то в результате испытаний мы
наблюдаем случайное число d(T) = Oy 1, . ..,Л/" отказов, происхо-
происходящих в моменты tx ^ /2 ^ .. . ^ tdi т) ^ Т. (Отказ с номером
d(TL-\y если он возможен, наступает после момента Т.) Таким
образом, d (T) означает номер последнего отказа, который проис-
происходит до момента Т окончания испытаний. Если элементы доста-
достаточно надежно работают в интервале времени (О, Г), то нередко
случается, что отказы не наблюдаются и d(T) = 0. Заметим теперь
же, что отсутствие отказов во время испытаний, т. е. условие
d(T) — 0, не дает нам права заключить, что надежность изделий
равна 1. Впоследствии мы укажем правило оценки надежности
в подобных случаях, основанное на понятии доверительного ин-
интервала.
Как уже указывалось выше (§ 2.2), наиболее полной характе-
характеристикой для надежности элементов является функция распределе-
распределения F(t) для времени безотказной работы. О виде функции рас-
распределения можно судить по так называемой эмпирической функции
распределения, определяемой посредством равенства FN(x) •¦= -тт-
Для значений х, tk^x < tk+1. Согласно теореме Гливенко (см. § 1.6)
с вероятностью 1 sup | FN (х) — F (х) \ —-* 0 при N—>оо. На
Рис. 3.2.1 показаны эмпирические функции распределения F10(t)
^ ^юо @> когда теоретическая функция распределения F (t) = 1 —е~*.
Если используется план [А/', Б, Т], то значения эмпирической функ-
Ции ^jv(O могут быть определены только для t^T. Если же
164 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
используется план [TV, Z>, г], то значения эмпирической функции
определяются только до уровня -тт-.
Оценкой для плотности вероятностей р (t) =—^ может служить
так называемая гистограмма pN(t). В отличие от эмпирической
rm
S * S 6 t
Рис. 3.2.1.
функции FN(t) гистограмма pN(t) может быть построена различ-
различными способами. Например, можно разбить область значений вре-
времени t на интервалы (Ski Sk+1)9 &=1, ..., т, ..., и на каждом
из этих интервалов положить
где dk—число отказов, которые наблюдались в интервале
(Sky S^+i). На рис. 3.2.2, а приведен пример построения гисто-
гистограммы для показательного закона F(t) = \—е~г, N=50,
При втором способе выбирается число интервалов &+1, так
что d= -г- ^Ю, при этом k ^5, а остаток d' от деления
N=kd-\-d' также близок к d. Первый интервал — [0,5^], где St
совпадает с моментом d-го отказа, второй интервал — [Sv St], где
6 совпадает с моментом 2d-ro отказа и т. д., наконец, /f-й интер-
интервал— [5л-1, 5А], где Sk = tkd. Последний, (й+1)-й, интервал —
[Sk, tN]. На каждом из k интервалов группировки (Sly Sl+1)9
§ 3.2] ОБЩИЕ МЕТОДЫ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
/ = 0, ..., & — 1, полагаем
d'
на интервале [Sk, tN] и pN(t) = O для значений t^t^. Гистограмма^
построенная по этому способу для F (t) = 1 —е~\ N = 50, k-\- 1 =5,
^=10, показана на рис. 3.2.2,6. Функция опасности отказов X (t)
Р it)
определялась по формуле X(t)=-^jp-1 где R(t) = I —F(t). Если
число испытываемых элементов N велико и интервалы между по-
последовательными моментами отказов сравнительно невелики, та
можно построить эмпирическую функцию опасности отказов. Ось
времени разбиваем на несколько
участков [?,-_!, S{], /=1,2,...,
So = 0. Оценкой для R (t) = 1 — F (t)
N(t)
является отношение
N
где
N (t) — число элементов, исправно
работающих к моменту времени t;
N(t) — случайная величина. За
оценку для р (t) берем —' ^—«—
где d{ — число элементов, отка-
отказавших на интервале Si_1 <C t < Sim
Эмпирическую функцию опасности
отказов KN(t) полагаем равной от-
отношению
d,
1
dt
N
При этом интервалы \S{mml9 S{] можно выбирать способом, аналогич-
аналогичным одному из описанных выше способов построения гистограммы.
Иногда не обязательно знать всю функцию распределения F(t),
ее плотность p(t) или функцию опасности отказов к (*), а доста-
достаточно знать лишь некоторые характеристики: моменты, квантили
и др. Момент &-го порядка в случае плана [jV, 5, ЛЛ определяется
по формуле
N
1*.
¦?<!.
166
ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
[ГЛ. 3
центральный момент &-го порядка—по формуле
N
1 = 1
Число tp такое, что F(t^~py называется квантилъю уровня р.
Эмпирической квантилъю i уровня р называется одно из реше-
решений уравнения FN(tp)=p. Мы всюду предполагаем, что F(t) яв-
является непрерывной.
Три типа статистической устойчивости. В случае
плана [jV, Б, N] нам известна вся эмпирическая функция распре-
распределения FN(t), а в случае плана [Ny Бу Т] — лишь часть ее опре-
определенная для значений t*^T. Для оценки неизвестной функции
распределения F(t) и различных числовых ее характеристик воз-
возможны три принципиально различных подхода, соответствующих
различным реальным условиям, в которых решается задача.
В первом, наиболее простом случае заранее известен тип
закона распределения F(t). Например, в результате теоретических
исследований и последующей экс-
экспериментальной проверки показа-
показано, что для определенного типа
элементов и аппаратуры закон
распределения времени безотказ-
безотказной работы является показатель-
показательным, т. е. F(t) = 1 — е"}\ t^O.
Неизвестно лишь значение пара-
параметра Я, которое надо оценить
по результатам проведенных испы-
испытаний.
Во втором случае нет тео-
теоретических соображений, из кото-
которых следовало бы, что тип за-
закона распределения F(t) должен
быть вполне определенным, на-
например показательным, логариф-
логарифмически нормальным или каким-то
другим. Однако результаты испы-
испытаний показывают, что эмпириче-
эмпирические функции распределения мо-
могут быть приближены плавно меняющимися функциями распре-
распределений. Из предварительной обработки экспериментальных данных
видно, что качественный характер поведения эмпирических функ-
функций распределения или гистограмм не меняется от партии к пар-
партии На рис. 3.2.3 показан вид двух гистограмм, соответствующих
двум различным партиям продукции. Анализируя вид гистограмм,
§ 3.2] ОБЩИЕ МЕТОДЫ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ 167
мы замечаем, что обе они имеют существенную асимметрию и обе
одновершинны. В таких случаях подбирают одно из возможных
семейств функций распределения, для которого качественное пове-
поведение функций распределения, или плотностей, соответствует
полученным экспериментальным данным. Наиболее часто исполь-
используемые в практике надежности семейства были списаны в § 1.2.
Если семейство распределений выбрано, то задача определения
функции F(t) и ее характеристик сводится к оценке по резуль-
результатам испытания неизвестных значений параметров или функций
от них. Например, если мы пытаемся приближенно описать дан-
данные с помощью логарифмически нормального закона (см. § 1.2Г
пример 11), то неизвестными значениями параметров являются
|i и а. При этом в самом начале работ полезно сравнить резуль-
результаты, получаемые при использовании двух-трех типов семейств
распределений. Если два семейства дают одинаково хорошие
результаты, то для дальнейшего использования выбирается то из
них, для которого можно предложить теоретические обоснования.
В том же случае, когда теоретических предпосылок для выбора
распределения нет, нужно предпочесть то, для которого трудоем-
трудоемкость числовых расчетов меньше.
Возможен, однако, и третий случай условий производства,
когда качественный характер эмпирической функции FN(t) меняется
от- партии к партии или же когда для приближений нужны семей-
семейства со многими неизвестными параметрами и соответственно
требуются громоздкие вычисления необходимых характеристик.
В этих случаях можно использовать некоторые методы непарамет-
непараметрической статистики (см. § 4.5), т. е. методы, не связанные с ана-
аналитическим видом функции распределения F(t).
Для весьма надежных элементов реализация плана [jV, Z>, N]
или [N, В, N] приводит к необходимости проведения испытаний
в течение многих тысяч часов. Именно по этой причине часто
используются различные планы с фиксированной длительностью
испытаний ([N, ?, Г], [N, В, Г], [W, Б, (г, Г)], [N, В, (г, Т)]
и др.). При этом по наблюдениям, полученным за ограниченный
промежуток времени, нужно оценить различные показатели надеж-
надежности, связанные с отказами, которые могут произойти после
момента Г, среднее время безотказной работы в течение времени
Т3>Т и др. Использование результатов за ограниченное время
наблюдения для получения оценок всевозможных характеристик
надежности законно в первом случае, когда вид функции рас-
распределения F (t) нам известен до опыта и только неизвестны зна-
значения параметров, определяющих этот закон. Весь следующий
параграф относится к этому случаю лишь с тем ограничением, что
рассматривается функция распределения F(t) = 1 — е~и. Во вто-
втором случае надо иметь достаточный статистический материал,.
168 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
который хотя бы косвенно подтверждал правильность выводимых
числовых оценок. Таким косвенным подтверждением могут слу-
служить результаты испытаний отдельных партий элементов, прово-
проводившихся в течение длительного времени, или сведения об отка-
отказах эксплуатируемого оборудования. Наконец, в третьем
случае, когда нет устойчивости даже качественного поведения
эмпирической функции распределения, получение оценок любых
характеристик надежности, которые определяются по значениям
F(t) для />Г, где Т—время испытаний, не является законным.
В этом случае прежде всего необходимо отладить технологиче-
технологический процесс.
В подтверждение этих соображений рассмотрим следующий
пример. В нем мы намеренно «сгустили краски». Предположим,
что проводятся ист тания N=1000 элементов. Каждый элемент
состоит из двух частей, отказ каждой из которых приводит к от-
отказу элемента (например, проводящий слой сопротивления и кон-
контакты). Отказы обеих частей происходят независимо друг от друга.
Таким образом, если tx — момент, когда произойдет отказ первой
части (обрыв), a t2 — момент отказа второй части (уход параметра
за пределы допуска), то считается, что отказ элемента произой-
произойдет в момент t = min(tly t2). Предположим далее, что
о у г тс J
где 9 = 2000 час, ji=1000 час, а =100 час. Однако эксперимен-
экспериментатору неизвестно, что закон распределения времени безотказной
работы
(*иJ
F (t) = 1 -Р {min (tv /2) > t} = 1 -e~ e _*
о у 2я./
dx.
.
Вид функции F(t) показан на рис. 3.2.4. Было решено проводить
испытания в течение Г=500 час. Вероятность отказа первого
элемента равна
г^
F(T)& \—e e =1—е-о.**.
Таким образом, мы в среднем наблюдаем NF(T) ж 100 отказов,
причем практически все наблюдаемые отказы будут только пер-
первого типа (обрыв), так как отказы второго типа (уход
пара метров) при сделанных выше предположениях начнут на-
наступать после 800 час работы, но зато уже к 1200 час работы
почти все элементы выйдут из строя вследствие отказов второго
§ 3.2] ОБЩИЕ МЕТОДЫ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ 169
типа. Отказов второго типа в течение 7 = 500 час мы не наб-
наблюдаем, поэтому ошибочно считаем, что закон F(t) = \—е е,
и по результатам этих испытаний, пользуясь методами следующего
параграфа, находим оценку для 0, близкую к 2000. Итак, по
500
1500
Рис. 3.2.4.
результатам испытаний, проводимых в течение Г=500 час, сде-
сделан ошибочный вывод относительно характера распределения.
Вывод из этого примера таков. Надо сначала проверить теоре-
теоретически или экспериментально (а лучше обоими путями), что вид
закона F(t) и при значениях t, больших времени Т проведения
испытаний, не меняется, а уже затем получать оценки для харак-
характеристик надежности.
Рассмотрим теперь некоторые общие методы получения оценок
параметров распределения времени безотказной работы. В общем
плане часть этих методов была изложена в § 1.6. При оценке
параметров конкретного семейства распределений могут быть упо-
употреблены различные методы. В зависимости от используемого
метода будут получаться отличающиеся друг от друга оценки
неизвестных значений параметров. Необходимо провести сравнение
различных методов и для дальнейшего выбрать метод, дающий
наилучшие результаты. В тех случаях, когда вычисления прихо-
приходится выполнять вручную, нужно оценивать метод и с точки зре-
зрения трудоемкости вычислений.
Графические методы. Первая и наиболее простая группа
методов —-графические методы оценки. Они применимы для неко-
некоторых семейств F(ty a, C), содержащих два неизвестных пара-
параметра а, р. График функции распределения F(t, a, C) можно
представить в виде совокупности точек (t, p) на плоскости, где
P = F(t, a, P). Основная идея графического метода состоит в том,
что подбирается такая непрерывная замена координат t' = h(t)y
Р' = Ф(р), что при этом график функции распределения (f, р),
170 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
где p'z=y(F(ty а, [$)), становится прямой линией // = г|)(ос, P)tf' +
+ %(а> Р)- Если такую замену переменных удалось отыскать, то
на плоскости (/', р') любая функция распределения этого семей-
семейства будет предстазима в виде прямой р' = г|) (а, РМ' + %(а> Р) или,
что то же, в виде прямой
<V(F(t, а ,Р)) = г|)(а, Р)А(/) + Х(«. Р)- C.2.1)
Используем этот факт для оценки параметров а, р. Предпо-
Предположим, что в результате испытаний получены N значений неко-
некоторой случайной величины (например, времени безотказной работы
элемента или интервалов между отказами в аппаратуре). По этим
значениям мы можем построить эмпирическую функцию распреде-
распределения FN(t). Так как эмпирическая функция FN(t) при больших N
лежит вблизи от теоретической функции распределения F(t, a, Р),
то после замены переменных график (t\ р^), где f = h(t)f a
p'N = q>[FN(t)], будет лежать в непосредственной близости от гра-
графика (/', р'), являющегося прямой вида C.2.1). Оценив с помощью
линейки тангенс наклона k и свободный член b и приравняв их
теоретическим значениям, получаем уравнения
ft = !>(a, р), Ь = %(ау р), C.2.2)
из которых находим оценки неизвестных значений параметров аир.
Уместно заметить, что графический метод применим для лю-
любого из планов [N, Б, г], [N, В, г], [N, Б, Г], [N, В, Т],
[/V, Б, (г, Г)], [N, В, (г, Т)]. Например, в случае плана [N, Я, (г, Т)]
ло результатам испытаний можем построить только часть FN(t)
для значений t<,mm{tr, T) и FN(f)^-^~t где d(T)^r—число
элементов, отказавших за время проведения испытаний. Если к
полученному куску эмпирической функции распределения приме-
применить преобразования t' = h(t)9 p' = <p (FN(t)), то на плоскости
(t\ p') получим кусок ломаной, близкой к одной из прямых вида
C.2.1). По этому куску оцениваем ft и b и снова приходим
к уравнениям C.2.2).
Для примера, рассмотрим три семейства распределений. В слу-
случае нормального семейства распределений
F(t, (х, а) = ф(^) , где ф(/)^ ^
в качестве преобразования ф (р) рассмотрим функцию Ф~Чр),
обратную к функции р = ф(/). При этом получаем
^ • C-2.3)
§ 3.2] ОБЩИЕ МЕТОДЫ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
Таким образом, C.2.3) соответствует C.2.2), когда
171
<'= А (/) =
f
Для удобства пользования выпускается специальная нормальная
вероятностная бумага. По оси абсцисс отложены значения t слу-
случайной величины, а по оси ординат — значения функции Ф~1(р).
При этом ось t проводится через точку 0, соответствующую
ф^^). Около каждого значения ф (р) отмечается соответ-
соответствующее ему значение р (рис. 3.2.5). Функция распределения
Рис. 3.2.5,
записывается в виде прямой у = х. Прямой у — -—- соответ-
соответствует функция распределения нормальной случайной величины со
средним [д, и дисперсией а2. Таким образом, с помощью вероят-
вероятностной бумаги можно легко проверять «на глаз» нормальность
закона распределения, а заодно и оценивать его параметры. Если
ломаная имеет заметную искривленность, то это говорит о том,
что истинный закон распределения не является нормальным. Если
же искривленности нет, то, проводя «на глаз» прямую, наиболее
плотно прилегающую к ломаной, легко находим оценки для и иа.
¦^j- равно абсциссе точки Л, где Л — точка пересечения прямой
с осью /; а равно расстоянию от А до В> где В—точка на оси ty
в которой величина перпендикуляра, опущенного из точки прямой
на ось t, равна 1 (в единицах масштаба оси абсцисс).
172 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
В случае логарифмически нормального закона F(t, fi, a) =
^L^f поэтому р' = ф(р) = Ф"МЛ), h(t) = lnt, i|?(fx, о) =
1 , ч LI
-5-' Х(^^) = ~-'
Если задано семейство показательных распределений со сдвигом
где t^\i. Поэтому в качестве р' = <р(/?) выбираем функцию
ф(р) = 1п г^~. Сравнивал C.2.4.) с C.2.1), видим, что tf =h(t) = ty
Наконец, если нам задано семейство распределений Вейбулла
F(t, p, в)=1-Гв,
то
Сравнивая C.2.5) с C.2.1), находим, что
Р' = Ф (Р) = lg lg i^ э <' = А (*) = In /,
Вид бумаги для закона Вейбулла показан на рис. 3.2.6. Таким
образом, тангенс угла наклона равен р, а логарифм 0 равен вели-
величине отрезка ОЛУ отсекаемого прямой на оси ординат.
Методы квантилей и моментов. Для получения оце-
оценок неизвестных значений параметров, определяющих вид закона
распределения времени безотказной работы, могут быть использо-
использованы методы моментов и квантилей. Применительно к случаю
выборки объема N эти методы были описаны в § 1.6. Здесь мы
рассматриваем эти методы с точки зрения обработки результатов
испытаний, полученных при использовании некоторых планов
типа Б, Для определенности мы ограничимся случаем двух неиз-
неизвестных параметров а, р.
Пусть закон распределения времени безотказной работы
F(t, a, P) имеет непрерывно дифференцируемую плотность, прини-
принимающую положительные значения для любых возможных значений
§ 3.2]
ОБЩИЕ МЕТОДЫ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
173
параметров а, р. Если испытания проводились по плану [Л/", Z>, г],
/^>1, то момент tti появления /гго отказа можно рассматривать
как эмпирическую квантиль, соответствующую уровню 97 = ^-,
i=l, 2, ... Если lt и N достаточно велики, то можно считать
0
X
Дд1д
-0,999
•0,99
•0,9
У
1
2 3
Рис. 3.2.6.
(см. § 1.6), что 6//.=^. — tQi (/ = 1, 2) имеют нормальное распре-
распределение с нулевыми средними и матрицей дисперсий
Ntdt
где
f ~
A-
J
Jt
Если бы значения квантилей tqi, tQ2 были нам известны точно, то
значения параметров a, P можно было бы найти из уравнений
a, P)=<
C.2.6)
Нам известны лишь приближенные значения этих квантилей — мо-
моментыft и tr появления /-го и r-го отказов. Заменяя в уравне-
уравнениях C.1.6) значения квантилей их оценками, получаем уравнения
C.2.7)
174 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
решения которых а, р являются состоятельными оценками для па-
параметров а, Р, при N—*оо, — = const, -тт- = const, что непосред-
непосредственно следует из непрерывности функции F(t, а, р). Можно
показать, что эти оценки при весьма общих предположениях типа
гладкости функции F(t, a, P) являются асимптотически несмещен-
несмещенными и асимптотически нормально распределенными. Поэтому наи-
наиболее существенными показателями качества таких оценок являются
их дисперсии.
Проиллюстрируем метод квантилей на примере закона Вейбулла
F(t, р, 0) = 1—е е, t>0. Испытания проводятся по плану
[N, Бу г]. Выбирается значение /(можно выбрать ^~у). В ре-
результате испытаний фиксируются значения tt и tr моментов /-го
и r-го отказов. Уравнения C.2.7) переписываются в виде
1"~~е ="лГ' Х~~е """AT*
Разрешая их относительно неизвестных значений параметров /?, 9,
получаем оценки
In In rrz In In г; r 1
Если предположить, что у F(t, a, P) существуют вторые непре-
непрерывные частные производные по t и параметрам а, Р, то, исполь-
используя обычный прием (см. § 1.6) разложения в ряд Тейлора, можно
получить приближенное выражение для дисперсии оценок пара-
параметров а, р.
Введем обозначения q.= -±; F(tq., а, Р) = ^-; bti = tii — tq ,
1=1,2; 6а = а — а; бр = р — р. Из уравнений C.2.7) находим
F(tUi a, to = F(tgi, а, ^
+ ^ ба+ ц бр + о(б^, ба, 6Р) = ^.
Заметив, что F(tqxi a, P)==ylf получаем с точностью до беско-
бесконечно малых высших порядков
dF(tq a, P) dF(tq, а, Р) dF (tg , а, Р)
32 *''+ Та ба+ k бР = °- C-2-8)
§ 3.2] ОБЩИЕ МЕТОДЫ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ 175
Аналогично находим, что
,«, Р) №«„. а, Р)
Й35 ба "¦ Щ бР = °- C'2-8 )
разрешая эти линейные уравнения C.2.8) и C.2.8') относительно
ошибок ба и бр, получаем их в виде линейных комбинаций от
Ыи и Ыи:
Отсюда, используя матрицу вторых моментов для квантилей
U > '/,> М(>жно найти дисперсии ошибок
D (a) г* eS,,M F*,,)" + 2aaltaaUW6tl6tu + в«,М (б/2J, j
D (p) ai аэ1"« (б^J + 2аР1гар,2АШ,,б^ + e^M (б^зJ, > C.2.9)
cov(a, Р) = 2оа,
В частности, в случае закона Вейбулла получаем
'и
'-g.)c о _
i
Метод квантилей в несколько видоизмененной форме можно исполь-
использовать и в случае планов [TV, Б, Г]. В этом случае вместо урав-
уравнений C.2.6) можем записать
F(T19 a, p)=<7i, /Ч^, ^ р)=^а> C.2.10)
f<zieTi<^2^^ Однако значения F(t, a, Р) при t=T1 и /=Г2
«ам неизвестны. Нам известны лишь числа d (Тх) и d (Г2) отказов,
происшедших к моментам 7\ и Г2. При больших значениях N
отношения ¦ ^,- и ^2- близки к теоретическим значениям qx и q2.
Поэтому, заменяя в C.2.10) значения дг, q2 их оценками, полу-
получаем уравнения
f a, P)=^-\ F(Tt, a, P)=^ C.2.11)
Для нахождения оценок аир. Используя разложение функции
**(*! a, P) в ряд Тейлора по параметрам аир, можно найти
приближенные выражения для дисперсий оценок.
176 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
В книге [7], посвященной непараметрическим методам в ста-
статистике, дано решение задачи о наиболее рациональном выборе
уровней квантилей для случаев испытаний [N, ?, N] и законов
нормального и экспоненциального типов. Если объем выборки N
велик, то можно для получения оценки параметров использовать
не все данные, а только значения к определенным образом вы-
выбранных эмпирических квантилей, ^(лм,... t(Nk)> где Nk = [Npk]-{-
+ 1, 0</?!< . . . <рл< 1 . .. При этом числа р1э .. ., pk подби-
подбираются таким образом, чтобы дисперсии ошибок неизвестных пара-
параметров были бы минимальными. Например, для случая закона
_t_
экспоненциального типа F(t) = \—е 0 оценка ищется в виде ли-
линейной комбинации
2 C.2.12)
где коэффициенты Ь{ и числа ЛЛ подобраны таким образом, чтобы
дисперсия оценки была наименьшей. Как известно, наилучшей
оценкой для параметра G при использовании всех данных является
N
0 = (-JT ] 2ш**1- Подсчет отношения дисперсий xA = -p[J этих оце-
\ / z=1 I J
нок в зависимости от выбранного числа квантилей k показал, что
х1=:0,65, х2 = 0,82, х3 = 0,89, и10 = 0,98.
В книге [7] приведены таблицы оптимальных значений р{ и bt\ так,
Pl = 0,64, ^ = 0,52, /?2 = 0,93, ^2 = 0,18 для & = 2.
Так же как и метод квантилей, метод моментов может быть
использован только при обработке результатов испытаний, в ко-
которых наблюдаемое число отказов достаточно велико. Если испы-
испытания проводятся в соответствии с планом [Af, Б, Г], то условная
плотность вероятности распределения момента отказа при условии,
что такой отказ произошел за время испытаний Г, равна ;;, ' а> [,; .
Таким образом, для момента &-го порядка, относящегося к наблю-
наблюдаемым отказам, имеем
ЯНН8]=ф*{а'Р)- C-2лз)
Если d (Т) — число зарегистрированных за время Т отказов, а мо-
моменты отказов 0^ tx^ . . . <; td(T) ^ T, то эмпирические моменты
d(T) d(T)
первого и второго порядков равны соответственно ¦'. х^. • и - 1_ - .
§ 3.2] ОБЩИЕ МЕТОДЫ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ 177
Если d (T) достаточно велико, то в силу закона больших чисел
значения эмпирических моментов близки к теоретическим. Прирав-
Приравнивая значения теоретических моментов в C.2.13) значениям
эмпирических моментов, получаем уравнения для нахождения
оценок a, J3:
d(T)
Фу (а, Р) = ^(Ь"> У=1. 2- C.2.14)
Если испытания проводились в соответствии с планом типа
[N, ?, г], г^>1, то соответствующие уравнения для оценок можно
получить, исходя из средних значений для членов вариационного
ряда. Здесь имеем
' a- P) FV> a- P)'!! -^C. a- Р)]^"'<«. C-2.15)
Выбирая два порядковых номера /<С&<^г, получаем уравнения
для нахождения оценок
Y/(«. Р) = '<*>. Y*(«> Р) = '<*» C.2.16)
где Y/(a» Р) определяется по формуле C.2.15).
В заключение заметим, что можно также использовать и сме-
смешанные методы, когда одно из уравнений для нахождения оценок
описывается в соответствии с методом квантилей, а другое — в соот-
соответствии с методом моментов. Сравнение эффективности различных
методов можно проводить путем сравнения дисперсии полученных
оценок. При этом могут быть применены асимптотические методы,
аналогичные методу разложения в ряд Тейлора и последующего
использования асимптотической нормальности отклонений. Этим ме-
методом были получены выражения C.2.9) для дисперсий оценок
в методе квантилей. Выражение для матрицы ковариаций моментов
дано в § 1.6.
В качестве примера, иллюстрирующего метод моментов, рассмот-
рассмотрим оценку параметров a, P в случае, когда плотность вероятности
отказов принадлежит семейству гамма-распределений f(t, a, |3) =
№, а испытания проводились в соответствии с планом
[N, Б, N]. Так как
<Pi(a.P)=f, Ф2(а,Р)=^^, C.2.17)
7 Б. В. Гнеденко и др.
178 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
N N
а оценками для фх и ф2 являются i= jj- У d tiy t2=^— 2I t], то, за-
меняя в C.2.17) моменты оценками, получаем уравнения
7—А р_^ g(g+l)
~ Р ' Р2
Решения этих уравнений имеют вид
Введем обозначения 6/ = ^ — -^ , 6t2==t2—а rZ и используем
метод разложения в ряд Тейлора
J"n бГ2,
I
C.2.19)
мн. (/ fail .— i
Гая, (Г, 7*I бр
L л1 J '
гая,] гая,]
Символы —— , —=т означают, что рассматриваются значения
изводных при 1 = j,
Заметим теперь, что
производных при 1 = j, ^2 =oc(aj'1)
C.2.20)
Из C.2.19) и C.2.20) находим выражения для дисперсий и кова-
риации оценок, полученных методом моментов:
cov
(a, p) = M(a-a
Метод максимального правдоподобия. Для оценки
параметров наиболее часто используется метод максимального
правдоподобия. Описание этого метода было дано в § 1.6. Там же
было сказано, что при ограничениях типа регулярности с помощью
§ 3.2] ОБЩИЕ МЕТОДЫ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ 179
метода максимального правдоподобия можно получать асимптоти-
асимптотически эффективные оценки. Однако планы типа [N, Z>, N] очень
редко могут быть использованы при испытаниях весьма надежных
элементов, так как их проведение связано с большой длительностью
испытаний. В этом случае можно использовать другие планы [N, Б, г],
Ш, Б, (г, Т)] и т. д. (r<^/V). Встает вопрос о том, насколько
хороши будут оценки, полученные в результате использования
метода максимального правдоподобия для планов, отличных от
плана [Ny Б, N]. К настоящему времени авторам неизвестны какие-
либо существенные результаты, полученные в этом направлении.
Однако основная идея получения оценок максимального правдопо-
правдоподобия остается той же. В случае плана [N, Б, N] множество данных,
полученных после проведения испытаний, имело однородную струк-
структуру. В результате каждого испытания получаем N чисел tx ^ t2 ^. ..
... ^Jni соответствующих моментам отказов. В случае других планов
структура множества полученных данных может изменяться от опыта
к опыту. Например, может случиться, что при использовании плана
[N, Б, (г, Т)] за время испытаний Т не произошло ни одного отказа
(событие Ао) или произошло d отказов (событие Ad), d^r. В случае
события Ао множество данных — пустое множество, данных нет;
в случае события Ad, d^r, множество данных является наборами d
чисел 0 ^ tx ^ ... ^ td ^ Г. Итак, в общем случае мы получаем дан-
данные, принадлежащие подмножествам определенного вида, на которых
заданы семейства распределений, зависящие от неизвестных значений
параметров. Для плана [N, Б, (г, Т)] это распределение вероятностей *
имеет вид: вероятность события AQ—p(AQi а, р) = [1—F(Ty а, Р)]^э
плотность вероятности того, что произошло событие Ad, d<C,ry
и отказы наблюдались в моменты tly ..., td, равна
= N(N- 1). ..(N-d+ 1) f[p(th а, р) [1 -F(T, а, Р)]"-*,
плотность вероятности того, что произошло событие Аг и отказы
наблюдались в моменты tXi . ..,/r, равна
гДе P(t,a, P) = —' ' а* Р'. Если результаты испытаний рассматри-
рассматривать как набор случайных чисел, то вероятность или плотность
вероятностей исходов испытаний (в нашем примере р(А0, а, р),
Р Ид> t, . .., tdi а, Р), d^r) также являются случайными величинами.
Как и в случае плана [N, Б, N] эти случайные величины называют
7*
180 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
функциями правдоподобия. Для оценки параметров а, р мы подби-
подбираем такую пару чисел a, j$, что значение функции правдоподобия
при фиксированных значениях исходов опыта обращается в максимум.
Полученные таким образом оценки называются оценками лакеи-
малъного правдоподобия. Необходимым условием обращения функции
двух переменных в максимум является равенство нулю ее частных
производных по а и р. Если функция не обращается в нуль, то для
отыскания точки, где функция обращается в максимум, можно при-
приравнять к нулю частные производные от логарифма этой функции.
Для плана [N, Б, (г, Т)] и события Ad, d^ry уравнения максималь-
максимального правдоподобия имеют вид
dL(Ad,tl,...,tdta,to_() dl(Ad%tx **,<», Р)_о /о о 91\
Ш -U 5р -° FZZI)
где L (Ad, tly .. ., td, a, P) = In р (Ad, /1? . .., td, а, р). Как правило,
уравнения C.2.21) являются трансцендентными и решение их вручную
занимает много времени. Однако если испытания с использованием
одного и того же плана проводятся систематически, то становится
целесообразным использование для вычислений электронных машин.
При этом предварительно следует убедиться в существовании ре-
решений C.2.21). Если решение этих уравнений не единственно, то
необходимо привлечь дополнительные соображения для выбора
одного из них. Для показательного закона распределения F(ty 0) =
t_
= 1—е е уравнение правдоподобия (в случае одного параметра
будет одно уравнение), как правило, решается в явном виде. Этот
случай будет подробно изучен в следующем параграфе.
В заключение параграфа заметим, что из явного выражения
функции правдоподобия можно сразу выписывать совокупность
достаточных статистик (см. § 1.6), содержащих в себе всю инфор-
информацию об оцениваемых параметрах. Для этого нужно только вос-
воспользоваться критерием факторизации (см. § 1.6). Применительно
к плану [N, Z>, (г, Т)] из критерия факторизации получаем, что если
функция правдоподобия представима в виде
Р (A* h, • • •, U) = Ф Elf . . ., Sk, a, p) h (*lf .. ., td), C.2.22)
где Sly . . ., Sk — функции от tly . . ., td, a h(tx, . . ., td) не зависит
от а, р, то статистики 51э . . ., Sk являются достаточными для пары
параметров а, р. Например, если
§ 3.3] ОЦЕНКА ПАРАМЕТРА ЭКСПОНЕНЦИАЛЬНОГО ЗАКОНА 181
ТО
C.2.23)
поэтому, полагая h(tly ..., td) = \ и сравнивая C.2.23) с C.2.22),
а
получаем, что статистики 5Х = d; S2 = JJ thS3 = tx+ . . . + ^явля-
ются достаточными для параметров а, |3. В случае d = r доста-
г
точными будут статистики 52 = ТТ t[y S3 = t1-\-...-{-tr. К сожале-
i = l
нию, достаточные статистики, отличные от полного набора tly . . ., td
существуют не всегда. В частности, они не существуют для семейства
распределений Вейбулла (см. [8]).
§ 3.3. Оценка параметра экспоненциального закона
Оценке параметра X экспоненциального закона F(t, Х) — \—е~и,
tf>>0, мы посвящаем специальный параграф по двум причинам.
Во-первых, экспоненциальный закон находит серьезные применения
в задачах теории надежности, к настоящему времени имеется боль-
большое число работ, посвященных этому вопросу. Во-вторых, для
случая показательного закона многие задачи удается разрешить
в явной форме, выписав ответ в виде простых формул. Таким обра-
образом, на примере показательного закона можно изложить основные
идеи методов получения оценок, не затемняя их сложными расчетами.
Уместно также будет заметить, что обычно в литературе по на-
надежности [5], предполагают при оценке параметров закона Вейбулла
F(t) = \—ехр (— Х^), что значение параметра р нам известно.
Однако при таком предположении закон Вейбулла заменой времени
? = tp может быть сведен к показательному закону. Так называемый
логарифмически показательный закон, для которого F(t) = \ —
— (*+1)-\ ^>0, Х>0, также заменой переменных t' = ln t может
быть сведен к показательному. Таким образом, приводимые ниже
оценки с учетом замены времени могут быть использованы и в этих
случаях.
В качестве основного параметра, для которого в настоящем
параграфе строятся оценки, выбрано значение X. Однако можно
было бы строить оценки для параметра О^Я, равного среднему
значению времени безотказной работы. В ряде случаев может
возникнуть необходимость получения оценок для вероятности
182 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
безотказной работы в течение заданного времени Г3, R (Т3) =е~Хт*.
В конце параграфа даны формулы для несмещенных оценок R(Ts)y
соответствующие планам [/V, ?, г], [Л/, В, г].
Планы типа В. Вначале рассмотрим планы испытаний с вос-
восстановлением отказавших элементов [Л/, Б, Г], [/V, В, г], [7V, ?(/*, Г)].
Для этих планов моменты наблюдаемых отказов образуют пуассо-
новский поток с интенсивностью (см. § 1.5) | Л = А.Л/Д Действительно,
так как времена безотказной работы каждого элемента взаимно
независимы, то последовательность моментов {tik}, &=1,...,N,
/=1,2, . . ., замен элементов в &-й ячейке стенда образует процесс
восстановления (см. §2.2), у которого интервалы Sik = ti+lk — tiik
являются взаимно независимыми показательно распределенными
случайными величинами, Р {Sik^> t} = e~xt. Но такой процесс вос-
восстановления является пуассоновским потоком (см. § 1.5) с интен-
интенсивностью, равной Я. Моменты замен элементов (отказов) взаимно
независимы, поэтому взаимно независимы пуассоновские потоки
моментов замен, соответствующие N различным ячейкам стенда.
Так как поток всех отказов, которые происходят при испытаниях,
является суперпозицией N взаимно независимых пуассоновских
потоков с интенсивностями X, то он также будет пуассоновским
потоком с интенсивностью А = ХМ. Это утверждение является прямым
следствием результатов главы 2.
План [Л/, В, Т]. В случае плана [Л/, В, Т] мы наблюдаем пуас-
соновский поток отказов с интенсивностью A = XN в течение вре-
времени Г. Пусть d(T) — число наблюдаемых отказов, которые прои-
произошли в моменты ^, ..., td(T)- Плотность вероятности этого собы-
события можно получить следующим образом. Вероятность того, что
первый отказ произойдет в интервале (tx, t1-]-dt1)i равна Ae~Aidtly
условная вероятность того, что второй отказ произойдет в интервале
(/2, t2-\-dt2) при условии, что первый отказ произошел в интервале
(*i» ^i + ^i)> Равна Ае~А (**-**) dt2 и т. д. Наконец, условная вероят-
вероятность того, что d (Т)-1\ отказ произошел в интервале (td(T), ^(л +
-\~dtd(T)), а в интервале (^(Г) + ^^(г>, 7*) других отказов не было
при условии, что отказы произошли в интервалах (tly t1-\-dtj), . . .
. .., (*</<п-1> ^(r)-i + ^rfG-)-i), равна Ae-A{'dm-td(T)-i) dtd{T)X
Хе~А(т"^(Т)). Вероятность события, что отказы произошли в ин-
интервалах (tl9 t1 + dt1), .... (td(T)y td(T) + dtd{T))j равна произведению
этих условных вероятностей,
Таким образом, плотность вероятностей наступления отказов в мо-
моменты tly . . ., td(T) равна
-Лг. C.3.1)
§ 3.3] ОЦЕНКА ПАРАМЕТРА ЭКСПОНЕНЦИАЛЬНОГО ЗАКОНА 183
Вероятность того, что за время испытаний Г не произойдет ни одного
отказа, равна
=е-*т. C.3.2)
Рассматривая C.3.1) и C.3.2) как функции правдоподобия, получаем
уравнение максимального правдоподобия
d\np(Ad,t tdlT)) _d(d(T) In A-\T)_d(T) T ,, „ ~
Ж ал —л—т' C-6-6)
решение которого имеет вид
л=
d(T)
C.3.4)
Так как Л = ХМ, то оценкой параметра X является
C.3.5)
t_d(T)
/V . тгг,
NT
Так как Р {d (T) = d} = ^p е~АТу то
d=o d=i
т. е. оценка C.3.5) является несмещенной.
d=o
-4М-Л2=^-, C.3.7)
D X 1 = 1
Можно показать, что эта оценка является эффективной. Заметим
также, что из вида плотности C.3.1) следует, что в случае плана
[N, В, Т] достаточной статистикой является только число d (T) отка-
отказов, происшедших за время испытаний, а сами моменты отказов
'l» •••»^rf(D никакой дополнительной информации о параметре X
we содержат.
Пример. Испытания проводились по плану [ЛГ= 100, Ву Г = 200].
Отказы произошли в моменты ^ = 51, *а = 78, t3=\\0y *4=135,
^5= 180. Общее число отказов dB00) = 5. По формуле C.3.5) на-
наводим, что
1 5
100.200
184 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
План [А/", В, г]. Для плана [N, В, г], рассуждая аналогичным
образом, полумаем, что вероятность того, что отказы произойдут
в интервалах (/х, tx -f^i),.. ., (tn tr -\-dtr), равна
Ле~л/» dtxAe~A <'*-'»> dt2. . .Лб"Л(/*-~/»--») fi^r = Are~Atrdt1.. .*//r.
Отсюда следует, что плотность вероятностей наступления отказов
в моменты tl9 ...,^r равна
р (/1э . .., *г, К) = Аге~А'г. C.3.8)
Из C.3.8) следует, что достаточной статистикой для оценки пара-
параметра X является момент tr наступления г-го отказа. Уравнение
максимального правдоподобия имеет вид
ainpfo, ..., trk) = d(r\nA—Atr) = Q C39)
откуда получаем оценку
C.3.10)
Заметим теперь, что tr — t1-\-(t2 — *i)+...+(fr — ^r-i)> т- е- ^г
является суммой г интервалов между последовательными отказами.
Выше (§ 2.2) было показано, что эти интервалы являются взаимно
независимыми случайными с плотностями вероятностей, равными
Ae~At. Поэтому плотность вероятностей tr, равная свертке г плот-
плотностей p(t) = Ae~At, имеет вид
Artr"x
= G1ГТ)| *"Л'Г- C'ЗЛ1)
Из C.3.11) и C.3.10) получаем
Artr~l
e
а Г
= \ Ar~1tr-*c-
(г—l)! J A lr e
r г > г>1. C.3.12)
Следовательно, оценка Л1? полученная методом максимального
правдоподобия, является смещенной, а при г=1 ее математическое
ожидание равно бесконечности. Смещение легко устранить, если
рассмотреть оценку
= -^, 1 г>1. C.3 13)
§ 3.3]
ОЦЕНКА ПАРАМЕТРА ЭКСПОНЕНЦИАЛЬНОГО ЗАКОНА
185
Из C.3.13) и C.3.12) следует, что МЛ1 = Л. Вспомнив, что A = Nk,
получаем несмещенную оценку для X
V л
Ntr '
C.3.14)
Для дисперсий оценок C.3.13), C.3.14) имеют место формулы
X» е
Дисперсии оценок существуют только для значений г>2.
Пример. Испытания проводились в соответствии с планом
{/V=200, В, г = 10]. Момент регистрации десятого отказа f10 =
= 551 час. Из формулы C.3.14) находим оценку
План [N, Ву (г, Т)]. При исследовании более общего плана
[А/, Б, (г, Т)] испытания прекращаются либо в момент Г, и при
этом наблюдается d(T)<ir отказов, или в момент tr появления
г-го отказа, если tr<C Tt В первом случае плотность вероятности
. наступления отказов в моменты /1?..., td (T) записывается по формуле
C.3.1), а во втором случае плотность вероятности наступления
отказов в моменты tly...,tr — по формуле C.3.8). Используя метод
максимального правдоподобия в виде, изложенном в конце преды-
предыдущего параграфа мы получаем оценку для Л
если tr>Ti
По аналогии с только что разобранным случаем плана [N, В, г]
мы можем улучшить эту оценку, устранив смещение. Вводим оценку
tr>T,
C.3.17)
186
ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
[ГЛ.
которая является несмещенной. Действительно, использовав фор-
формулу для условных математических ожиданий, получаем
= М(Л \tr
{tr < Т} =
d=o
r(r-l)Ars'-' л„rf лу (АГ)"
,) s (г —1)Г as-7V2- d! e
АГ_
о d = o d — т— l
Аналогичным способом можно найти дисперсию этой оценки Л
Г-2
-лг. C.3.18)
d\
—2 ^ d!
d=r-2
Для несмещенной оценки параметров (Х=-дт, MX —Я) имеем
*, если tr > Г,
, если tr ^ Г,
Л —
C.3.19)
(XNT)d n^x
е
A,2 ^
7=2 2-
C.3.20)
В заключение части параграфа, посвященной планам типа В, отме-
отметим изящный результат, полученный Л. Н. Большевым [9]. В конце
§ 3.1 указывался общий класс
планов проведения испытаний, в
которых момент остановки испы-
испытаний t* определялся как момент
первого достижения траекторией
(/, d (t)) границы множества G.
Здесь d (i) — число элементов, от-
отказавших к моменту t. Предполо-
жим, что граница Г множества G
является невозрастающей функ-
функцией от t (рис. 3.3.1).
Рис. 3.3.1. Точки границы Г разбиваются
на два класса. Назовем точку
(/, d) точкой класса Ау если правее ее на уровне d все точки не
принадлежат множеству О. Точки класса А обведены на рис. 3.3.1
§ 3.3] ОЦЕНКА ПАРАМЕТРА ЭКСПОНЕНЦИАЛЬНОГО ЗАКОНА 187
кружками. Точки границы Г, не являющиеся точками класса Л,
назовем точками класса Б. Эти точки на рис 3.3.1 показаны тонкими
сплошными линиями. Л. Н. Большее показал, что несмещенная
оценка для параметра X строится следующим образом. Если в мо-
момент первого достижения траекторией (t, d (t)) границы Г точка
(/*, d (t*)) ? Г есть точка класса А, то оценка определяется по
формуле
Если же точка (/*, d (/*)) есть точка класса ?, то оценка для X
находится по формуле
Л- Nt* '
Заметим, что с вероятностью единица момент достижения точек
класса Б совпадает с моментом наступления отказа.
Планы типа Б. Рассмотрим теперь планы [Л/, Б, Г], [Л/*, Б, г],
[N, Б, (г, Т)]у в которых отказавшие элементы не заменятся
новыми.
План [Af, Бу Т]. Выражение для плотности вероятностей того,
что при испытаниях по плану [N, Б} Т] отказы произойдут в мо-
моменты tly . . . , td(T), можно получить следующим образом. Плот-
Плотность вероятностей того, что в эти моменты откажут элементы
с номерами /1э ... yid(T), равна, в силу взаимной независимости
моментов отказов, произведению плотностей вероятностей для мо-
моментов отказов каждого из этих элементов, умноженных на веро-
вероятность того, что в интервале (О, Т) отказов у остальных N—d (T)
элементов не произойдет, т. е. равна
\e-Hi Хе-н* . . . Xe-Hd{T) е-им-а{т)\ т, C.3.21)
Событие, состоящее в том, что моменты отказов равны tx, . .. , td{T),
может осуществиться А%^Т) ~N(N— 1) ... [N— d (T) + 1 ] спосо-
способами, так как из N чисел можно сделать N . . . [М—d(T)-\-\]
различных выборок номеров /х, . . . , id{Ty Умножая C.3.21) на А^т\
получаем выражение для искомой плотности вероятностей
P{tly ... ,^(Г), Х) =
/d(T) \
>и+[Ы-с1(Т)]Т )
[ ] i /. C.3.22)
Таким образом, в случае плана [Ny Б, Т] достаточными статисти-
статистиками будут: число d (T) элементов, отказавших за время 7, и
188 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
еИТ)
сумма SE (T) = 2jti-\-[N—d(T)]T времен, в течение которых про-
проработал каждый элемент, т. е. суммарная наработка элементов
за время проведения испытаний. Из C.3.22) получаем, что
In/>(*!, . . . ,tdm, h) =
= \nN(N—\) ... [N—d(T)+l] + d(T)\nk — kSB(T). C.3.23)
Отсюда имеем
Таким образом, оценка максимального правдоподобия равна
C.3.25)
Эта оценка является смещенной. Точный подсчет смещения при-
приводит к очень громоздким формулам, которые мы опускаем. По
этой же причине мы опускаем формулу для дисперсии оценки А.
Заметим, что для сравнительно надежных элементов при
плотность условного распределения момента отказа, происшедшего
в интервале (О, Т) равна — _яг « A^jL, а среднее значение
1 -~~ В А1 J
Т
каждого t{ приближенно можно считать равным у. Отсюда для
10 и .у <С0, 1, исходя из закона больших чисел, можно
Ш) Г 1 ^ 1 а(Т)т
считать, что р? t,< = d (Т) \Л <т\ 2^ t, \~ 2 • Подставив это
'=1 L /=1 J
выражение в знаменатель формулы C.3.25), получаем
5 _ d(T) d(T)
C-3.26)
Формулой C.3.26) часто пользуются на практике. Следует, однако,
иметь в виду, что она применима при —^^0,1,
Если считать, что формула C.3.25) слишком сложна, то для оценки
X также можно исходить из формулы оценки вероятности по час-
частоте (см. § 1.6). Оценкой для вероятности R (Т) = е~кт безотказной
работы элемента является отношение числа элементов Af—d(T),
безотказно проработавших в течение времени Г, к общему числу N
§ 3.3] ОЦЕНКА ПАРАМЕТРА ЭКСПОНЕНЦИАЛЬНОГО ЗАКОНА 189
элементов. Приравняв оценку к теоретическому значению вероят-
вероятности, получаем для нахождения оценки Я уравнение
-=-е
N
откуда
C.3.27)
Этой формулой можно пользоваться для значений 0,2 < ^-^ < 0,8.
Заметим, что смещение оценки C.3.27) является бесконечным, так
как с положительной вероятностью может получиться, что d (T)=N.
Пример. Испытания проводились в соответствии с планом.
[N = 100,5, Г=500]. Отказы произошли в моменты fA) = 3U
f(8) = 353, *(9) = 383, fA0) = 436, ^(И) = 477. Общее число отказав-
отказавших элементов d E00) = 11, суммарная наработка 5$ E00) = 31 -f-
4- 49 + 90 + 135 + 161 + 249 + 323 + 353 + 383 + 436 + 477 + 89 х
X 500 = 47147. По формуле C.3.25) находим оценку для пара-
параметра к
И(Т} 11
л __ и К* ) х 1 9 4^.10""^
Если исходить из упрощенной формулы C.3.26), то Я =
-Ц-ггг = 2,328 • Ю-4.
План [N, Б, г]. Для плана [N, Б, г] плотность вероятностей
появления отказов в моменты tly . .. , tr получаем из рассуждений,
аналогичных тем, которые были использованы для плана [N, Б, Т].
Плотность вероятностей того, что в моменты tly .. . , tr откажут
элементы с номерами /15 . . . , /r, I ^ik^N, 1кф11у кф1, а осталь-
остальные N—г элементов в интервале @, tr) не дадут отказов, равна
Учитывая, что число возможных наборов по г различных цифр из
N равно N(N— 1) ... (N—г+ 1), получаем, что плотность вероят-
вероятностей наступления г отказов в моменты tlt ... , tr
P(tv ...,*„*) =
/г \
= /VGV_i) ... (ЛА — г + 1) Уе t = 1 . C.3.28)
190 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
Из этой формулы следует, что достаточной статистикой является
суммарная наработка всех испытываемых элементов
(tr — tr_l). C.3.29)
Заметим, что, введя новые переменные s1 = t1, sk = tk—tk_ly
& —2, ... , г, плотность C.3.28) можно, учитывая C.3.29), перепи-
переписать в виде
рг (sl9 . .. , sr) =
ov-'-iUsr. C.3.30)
При этом мы учитываем, что якобиан перехода от координат
*!, . .. , tr к координатам sx, . . . , sr равен 1. Из C.3.30) следует,
что случайные величины s1 = tly..., sr = tr — tr_x являются
взаимно независимыми, при этом плотность sk равна (N —
— k-\-1) \e~(N-k + 1)ks, соответственно плотность случайной вели-
величины (N—k-\-\)sk равна Xe~Xs. Таким образом, из C.3.30) следует,
что s является суммой г взаимно независимых показательно рас-
распределенных случайных величин. Отсюда получаем, что плотность
распределения суммарной наработки SB (tr) равна
Прологарифмировав плотность C.3.28), находим
1пр(/1э ... ,tn X) = \n[N ... (N — r+l
откуда получаем уравнение максимального правдоподобия
Оценка максимального правдоподобия имеет вид
1* = 8ЖГ \
Использовав выражение C.3.31) для плотности вероятностей сум-
суммарной наработки, находим, что
Таким образом, оценка к является смещенной. Это смещение можно
§ 3.3] ОЦЕНКА ПАРАМЕТРА ЭКСПОНЕНЦИАЛЬНОГО ЗАКОНА 191
устранить, если использовать оценку
Дисперсия этой оценки равна
nt _} fr-l\r УяГ~* X
DA~J [ *' ) (Титр
г>2. C.3.34)
Пример. Испытания проводились в соответствии с планом
Ш=50, Б, (г = 8)]. Моменты отказов равны /A) = 91, /B)=145,
221 * 285 * 317 * 328 * 411 * 496
(8) , D> F) (б) , G) (8)
Значение суммарной наработки S5 (tiS)) = 91 + 145 J,- 221 + 285 +
+ 317 + 328 + 411+496E0 —7) = 21 965. По формуле C.3.33) на-
находим оценку для параметра К
* 3210-4
План [N, Б, (г, Т)]. Если используется план [jV, Б, (г, Т)]г
то испытания прекращаются либо в момент 7\ если tr > Г, либо
в момент tr, если tr<^T. Соответственно в первом случае плот-
плотность вероятностей наступления d (Т) отказов в моменты tlt . . ., td{T)
записывается по формуле C.3.22), а во втором, для моментов от-
отказов t1,...ytr, — по формуле C.3.28). Как и в случае плана
[N, В, (г, Г)], находим, что оценка максимального правдоподобия
имеет вид
d(T)
если tr>T, где SB(T) =? tt + [N-d (T)] Г,
, если tr^T, где 5Б (*г) = ?',• +(^-')'г-
По аналогии с предыдущим случаем мы можем использовать улуч-
улучшенную оценку для случая tr^T. Окончательно получаем
, если tr>T, где SB (Т)=
C.3.33)
192 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
Эта оценка является смещенной; ввиду громоздкости формул,
выражающих смещение и дисперсию, мы вынуждены пропустить их.
План GV, ?, (г, HS0)]. В заключение этого параграфа рассмот-
рассмотрим еще один план проведения стендовых испытаний, который
также находит практическое применение. Проводятся испытания N
элементов без восстановления отказавших. Испытания прекращаются
в тот момент, когда либо суммарная наработка испытываемых
элементов станет равной заданному до начала испытаний числу *S0,
либо в момент отказа г-го элемента, если при этом суммарная
наработка оказывается меньше So. Такой план сокращенно будем
обозначать через [Ny Б, (г, HS0)]. Если обозначить через N (t) число
элементов, оставшихся исправными к моменту /, то суммарная
наработка S (t) испытываемых элементов к моменту t равна
t
SB (t)—\ N(s) ds. Допустим, что отказы элементов произошли в
о
моменты tx, . . . , tdit)y тогда суммарная наработка к моменту вре-
времени t задается формулой
to — O, если d(t)~O. Испытания прекращаются в тот момент s,
когда либо суммарная наработка
SB (s) =
=Nt1 + (N- 1) (f,-^) + ... + (N-d(s)) (s-td^) = S0 C.3.36)
(при этом d(s)<Cr), либо в момент tr отказа г-го элемента
+ ...+(N-r+\)(tr-tr_1)<S0. C.3.37)
Выше было показано, что при испытаниях N элементов без восста-
восстановления отказавших случайные величины Ntlt (N — \) (t2 — tx),
(N — r-{-\)(tr—/г-1) являются взаимно независимыми, одинаково
распределенными с плотностью Хе~)Л. Таким образом, условия C.3.36)
и C.3.37) фактически означают, что мы наблюдаем пуассоновский
поток отказов с интенсивностью А, и прекращаем наблюдения либо
в «момент» SOi либо в «момент» S (tr) наступления г-го отказа.
Но задачу оценки параметра Л пуассоновского потока мы уже
решили, разбирая случай плана [N, В, (г, Т)]. Чтобы воспользоваться
оценкой C.3.17), в ней надо считать tr = S (tr), T= So и в формуле
§ 3.3] ОЦЕНКА ПАРАМЕТРА ЭКСПОНЕНЦИАЛЬНОГО ЗАКОНА 193
для дисперсии оценки C.3.18) считать Л = А,. Окончательно,
——-, где t0 находится из условия
° SB (g = 50> если S (tr) > SQy C.3.38)
?±у если SB(t,)<S0.
Sb (t) находится по формуле C.3.35). Как уже было доказано, эта
оценка несмещенная, ее дисперсия в соответствии с формулой
C.3.18) равна
d\
d-r-%
C.3.20)
Как это следует из рассмотрения плана [Му В, (г, Г)], достаточными
статистиками будут d (/0), если 5 (tr) > 50, и 5 (/г), если S (tfr) < So.
Пример. Испытания проводятся в соответствии с планом
[N=100, Б, (г = 5, HS= 10 000)]. Первый отказ наступил в момент
t{1) = 34, значение суммарной наработки Sb (/A)) = 3400 < 10 000.
Второй отказ был зарегистрирован в момент ?B) = 75, значение
суммарной наработки стало равным *S^ (^B)) = 7459 <С Ю 000. В ин-
интервале от ^B) = 75 до ?0= 100,71 отказы не наблюдались. В мо-
момент to= 100,71 значение суммарной наработки достигло заданного
уровня 10 000. В соответствии с верхней частью формулы C.3.38)
находим
Несмещенные оценки для вероятности безот-
безотказной работы. Одним из наиболее важных показателей на-
надежности является вероятность безотказной работы в течение
заданного времени Г3. В случае показательного закона эта веро-
вероятность /?G3) = ехр(—АТд). Используя полученные выше формулы
.для оценок К параметра \, можно в качестве оценки для R (Т3)
рассматривать
C.3.39)
Можно показать, что эта оценка при увеличении числа /V испыты-
ваемых элементов является состоятельной и асимптотически эффек-
эффективной, если только А,—асимптотически эффективная оценка для
К Однако при конечных значениях N оценка, задаваемая форму-
формулой C.3.39), является смещенной. Это смещение может быть весьма
существенным в практически важном случае, когда R (Т3) близка
к единице. Величина смещения зависит также от типа плана, в
соответствии с которым проводятся испытания. Так же как и для
194 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
оценок параметра X, можно поставить задачу отыскания несмещен-
несмещенных оценок для R (Т3) = ехр (— ХГ3). Мы ограничиваемся здесь
разбором только двух типов планов [/У, /?, Т] и [N, Б^ г]. Основная
идея построения несмещенных оценок с минимальными дисперсиями
заключается в следующем. Сначала отыскивают несмещенную оценку
для заданной функции от неизвестного параметра. Если эта не-
несмещенная оценка — функция от достаточной статистики (и притом
единственная), то она имеет (см. § 7.5) наименьшую дисперсию.
Если же эта несмещенная оценка не является функцией от доста-
достаточной статистики, то в качестве новой несмещенной оценки
рассматривается условное математическое ожидание от исходной
оценки при условии, что фиксировано значение достаточной
статистики.
Пусть испытания проводились по плану [N, Б, Т]. Достаточной
статистикой является число d (T) элементов, отказавших за время
проведения испытаний, d (T) имеет пуассоновское распределение с
параметром NhT. Основное уравнение для несмещенной оценки
ф (d) для R (Т3) имеет вид
^ е-^з. C.3.40)
d(T) = o
Поделив обе части на e—KNT и разложив еМ^г-Гз) по степеням X,
получаем, что тождество C.3.40) справедливо тогда и только
тогда, когда
^~= y"'dl '*' ¦ C.3.41)
Таким образом, из C.3.41) получаем выражение для несмещенной
оценки R (Т3): —,
\R (TJ = <р Id (Т)) = ( \ —^РгУт. C.3.42)
1 . ^ ^ 1
Дисперсия оценки задается формулой
—тт 1
C.3.43)
Заметим, что несмещенная оценка для значений T3^>NT дает
отрицательные значения при нечетном числе отказов и значения,
большие единицы, при четном числе отказов. Оценку C.3.42) можно
рекомендовать только для значений T3<iNT.
Пусть испытания проводились в соответствии с планом [Af, Бу г].
Если t(/'} — моменты отказов, /=1, •••, г, то случайные величины
x( = (N—i + 1) (t{[) — /(/_!,), *'= 1, • • • , г, t{Q) = O взаимно независимы
и имеют показательное распределение с параметром X, Р{т|->7'3} =
= ехр (—kT3)=R(T3). Следовательно, в качестве несмещенной
оценки для R(T3) можно взять отношение числа d(r) случай-
§ 3.4] ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛА 195
ных величин х{ таких, что xi >> Г3, к общему числу г. Оценка
R1(T3) = —— является несмещенной. Однако она не есть функция
от достаточной статистики SB (tr). Взяв условное математическое
ожидание Ri(T3) относительно Ss (tr), получаем выражение для
улучшенной несмещенной оценки
( f1"^)' sB(tr)>T,
i = < V *BVr)J C.3.44)
0, SB (tr) < Т.
Учитывая, что плотность вероятности суммарной наработки SB (tr)
задается формулой C.3.11), легко проверяем несмещенность оценки
C.3.44). Действительно, имеем
т
v = o
г -1
r-i
• е
1 3
/=o
Оценка C.3.44) была получена в 1962 г.Е.М. Одноробовой. Анало-
Аналогичная оценка опубликована в работе [10].
§ 3.4. Доверительные интервалы
для параметра экспоненциального закона
Недостаточность точечных оценок. В предыдущем
параграфе были рассмотрены различные оценки для параметра X
экспоненциального закона. Однако, какими бы хорошими свойствами
эти оценки ни обладали, например несмещенностью и эффектив-
эффективностью, все же в ряде случаев, представляющих большой практи-
практический интерес, оказывается недостаточным характеризовать каче-
качество и надежность изделий только с помощью оценок. Если отказ
элемента приводит к большому ущербу, то используются только
очень надежные элементы. В случае показательного закона отказов
это означает, что величина X должна быть крайне мала. Поскольку
время Т проведения испытаний ограничено, то малость к приводит
196 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
к тому, что среднее число отказов, наблюдаемых при проведении
испытаний, также мало. Может оказаться, что при проведении
испытаний отказы вообще не наблюдаются. Если обратиться к оцен-
оценкам, которые были рекомендованы в предыдущем параграфе, то
мы увидим, что в этих случаях качество оценивается как отличное,
т. е. считается, что Я = 0. При этом никак не учитывается объем N
партии испытываемых элементов. В тех случаях, когда наблюдаемое
число отказов отлично от нуля, но невелико, естественная мера
разброса значений случайной оценки — отношение корня из диспер-
дисперсии к математическому ожиданию — велика (> 1), поэтому величина
оценки резко меняется от испытания к испытанию и не может
служить устойчивой характеристикой надежности элементов. Эти
критические значения подводят нас к целесообразности использова-
использования для оценки параметра X экспоненциального закона метода
доверительных интервалов. Двусторонним доверительным интер-
интервалом для параметра~~Х"~с коэффициентом доверия, не меньшим уу
называется случайный интервал (Я (л:), К (#)), концы которого
Я (х) < X (х) зависят только от исходов испытаний х и для лю-
любого Х> О
Верхним (О, к(х)) и нижним (к(х), +оо) односторонними ин-
интервалами называются такие случайные интервалы, для которых
при любом Х>0 соответственно
l)}^y, Р { М
При построении доверительных интервалов мы будем использовать
общий метод, изложенный в § 1.6. При этом в качестве случайных
величин, распределение которых зависит от неизвестного пара-
параметра X, мы будем брать значения достаточных статистик, которые
получаются в результате проведения испытаний. Заметим, что
поскольку оценки для параметра X являются монотонными функ-
функциями от рассматриваемых ниже достаточных статистик, то, как
это было показано в § 1.6, доверительные интервалы, полученные
исходя из оценок, с одной стороны, и достаточных статистик,
с другой, — совпадают. Мы несколько изменим порядок изложения,
рассмотрев вначале более простые планы [/V, В, 7], [N, В, г],
[/V, Б, г], [N, Б, 7], а затем более сложные планы [ДГ, В, (г, 7)],
[N, Б, (HS)], [N, Б, (г, Г)].
Доверительные интервалы для планов с про-
простыми достаточными статистиками. Для плана [Л/, Б, Т]
достаточной статистикой является число d (T) наблюденных отказов.
d (T) — случайная величина, имеющая пуассоновское распределе-
распределение с параметром Д=ХД^Г. На плоскости (Д, d) исходы опыта
§3.4]
ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ
197
представляются в виде случайных точек <2 = (Д, d), где Д — значе-
значение параметра пуассоновской величины, a d — число наблюденных
отказов. Исходя из методики, изложенной в § 1.6, для построения
верхней границы доверительного интервала с коэффициентом до-
доверия, не меньшим а, мы должны для каждого значения Д указать
такое целое число d (Д), что вероятность того, что достаточная-
статистика примет значение, не большее <2(Д), не превышает 1—ау
а вероятность принять не большее [й?(Д) + 1] — уже больше, чем
d(u),d(A)
s 6
уууууух/х/х. -
///////У.
ж
* ///////////////////
Рис. 3.4.1.
1—а. Так как величина d (T) распределена по закону Пуассона,
то d (Д) определяется из соотношения
(Д)< 1 -а < Р { d (T) ^ d_ (Д) + 1 } =
(Д), C.4.1)
Р { d (T) ^ rf (д)} =
где Ld(A) = 2~к~ь\е~^' Заметив, чт0 Ld(&) является монотонно
убывающей функцией параметра Д, мы получаем, что d (Д) — не-
неубывающая функция от Д. Так как d (Д) принимает только цело-
целочисленные значения, то d (T) является ступенчатой неубывающей
функцией (рис. 3.4.1). При этом из C.4.1) следует, что d (Д) впер-
впервые достигает уровня d при таком значении Д1_а(^/), для которого
Z.rf(A1»a(flf)) = l—а. C.4.2)
Определим множество FB как совокупность точек (Д, d) Д > О,
d = 0, 1, 2, ..., для которых d(A)<Cd (Д). Из определения сле-
следует, что вероятность того, что случайная точка (Д, d(T)),
где A=XNT, а d (T) — число отказавших элементов, попадет
в множество FB, ни при каком значении Д не превышает
1—Qt. Событие C=(Д, d (T)) ? /^ эквивалентно тому, что зна-
значение Д лежит левее случайной точки Д1^а(^(Г)), определяемой
198 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
из C.4.2). Вероятности эквивалентных событий равны поэтому
Р { А < A (d)} = Р{ Q Т%в }^P{d>d(T)} =
= \-P{d^d(T)}^a. C.4.3)
Таким образом, A1_ct((i) является верхней доверительной границей
с коэффициентом доверия, не меньшим а. Так как A = A,/V7\
то Я = А~" является верхней доверительной границей для па-
параметра X с тем же коэффициентом доверия а.
При построении двустороннего доверительного интервала для па-
параметра А пуассоновской случайной величины d (T) с коэффициен-
коэффициентом доверия а выбираем два числа ех и е2>>0, 1—a = e1-f-e2
{обычно &1 = &2) и строим множество $ точек (A, d), для которых
или
^(АХб!, или 1— ^М(Д)<82. C.4.4)
Из условий C.4.4) следует, что вероятность Р (Q g g) попадания
случайной точки Q=(A, d) в множество $ не превышает 1—а =
= е1 + е2. Учитывая, что функция Ld (A) — монотонно убывающая
из C.4.4), получаем, что точка (A, d) ? $ тогда и только тогда,
когда значение А лежит левее точки A (d) и правее точки A (d),
для которых
Ld (K(d)) = elf 1 - Ld-t (A (d)) = e2, C.4.5)
так как только при этом не выполняется хотя бы одно из не-
неравенств C.4.4). Итак, событие { A (d) < А < A (d)} эквивалентно
событию {(A, d) g ^}. Отсюда получаем
= 1—Р{(Л, d) € ^}^l-(e1 + e2)=a. C.4.6)
Учитывая, что значения Aa(d), определяемые формулой
Ld(\(d))=a, C.4.7)
даны в таблице 7 приложения, и исходя из C.4.5), можно записать
~K(d) = Aei(rf), A (d) = Д^е, (rf- 1). C.4.8)
Таким образом, интервал (А1_р2(й?—1), A8l (d)) является довери-
доверительным с коэффициентом доверия, равным а. Учитывая снова,
что Х = -—у получаем доверительный интервал для оцениваемого
значения к,
§ 3.4] ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ 199*
где значения кг-г2{с1—1) и A?l (d) находятся как решения уравне-
уравнений C.4.5). Если d = 0, то значение Да@—1) считаем равным нулю.
Пример. Предположим, что проводились испытания по плану
[ДГ= 500, В, Г=100] и при этом было зарегистрировано 5 от-
отказов: й(Т) — Ь. Требуется найти верхний доверительный предел
с коэффициентом доверия а = 0,9. Из таблицы 7 приложения на-
находим, что Дод E) — 9,275 для а = 0,9. Отсюда
истинное значение А с вероятностью 0,9 не превосходит найденного
значения X. Построим теперь двусторонний доверительный предел,
соответствующий значению а = 0,9; 81 = е2 = 0,05; пользуемся
той же таблицей 7, из которой находим Д0,9б D) = 1,970;
До Об E) = 10,513. Отсюда по формуле C.4.9) находим
0 ^ = =
При использовании плана [Л/", В, г] достаточной статистикой
является момент tr появления r-го отказа. Плотность вероятностей
этой статистики задается формулой C.3.11). Заметим теперь, что
плотность случайной величины Atr имеет вид
''' C410>
т. е. не зависит от неизвестного значения параметра Л. Если за-
задаться значением коэффициента доверия а=1—(Cx + eg), ех, е2!>0,
и значениями ДЕ1 (г—1) и Ах-е2(г—1) такими, что
А, „ (г-1)
(/I! ^'ldt^E2, C.4.11)
AgV-i)
то из вида плотности C.4.10) следует, что
Ле {г~г)
Р { Дх_82 (г- 1)< Atr < Дв1 (г- 1)} = J (^ij e-^/ =
А1-г2(^1)
со
Д (г-1)
=а. C.4.12)
'200 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
Неравенства в C.4.12) эквивалентны неравенствам — <^
<;Л< -. , поэтому имеем
Р \ j <Л< j j>=a. C.4.13)
Так как соотношение C.4.13) выполнено для любого Л>0, то
случайный интервал ( , I является доверитель-
доверительным интервалом для параметра Л с коэффициентом доверия а.
Соответственно для параметра ^ = tt доверительный интервал
имеет вид
Ai-e2(r-l) Ae,(r—1
C*4Л4)
Односторонний интервал с коэффициентом доверия а получаем
из C.4.14), полагая е2 = 0, ех = 1—а. При этом Ах(г—1)^0,
^ Д81 (г—1) = Д1-а(г—1). Значения Аа (г) для различных г и а
приведены в таблице 7 приложения.
Пример. В результате испытаний в соответствии с планом
j/V=500, В, г =15] получено, что /15=1211 час. Найти верхний
доверительный интервал с коэффициентом доверия а = 0,99. Из таб-
таблицы 7 приложения находим, что значение Д0H1 A4) = 25,446.
Из формулы C.4.14) получаем значение верхней границы довери-
доверительного интервала для К
25,446
500-1211
5
Аналогичным способом можно построить доверительный интер-
интервал для плана [N, Б, г]. Здесъ достаточной статистикой яв-
является суммарная наработка испытываемых элементов Sg (tr) =
г
= 2*i~MN—r)tr, где flf ..., ^моменты отказов элементов. Как
было показано в § 3.3, плотность этой статистики имеет вид C.3.31),
поэтому случайная величина X имеет плотность C.4.10). Повто-
Повторяя рассуждения, использованные при выводе формулы C.4.13),
получаем, что
С 3.4] ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ 201
Итак, двусторонний доверительный интервал для Я, соответствую-
соответствующий коэффициенту доверия а — г1-\-г21 будет иметь границы
д 8.(/-—1) _ де (Г—1)
где SB(tr) — суммарная наработка элементов за время проведения
испытаний. Соответственно верхняя граница одностороннего интер-
интервала с коэффициентом доверия а равна
Значения коэффициентов Aa(f), повторяем, даны в таблице 7
приложения.
План [N, Б, Т]. В случае плана [N, Б, Т] достаточными ста-
статистиками являются число d (t) отказавших элементов и суммарная.
d(T)
наработка SB (T) = 2 t(-{-[M— d (T)] Т. Для высоконадежных эле-
ментов значение ЯГ<^1, поэтому условная плотность распределе-
распределения момен-юв отказов практически совпадает с плотностью равно-
мерного распределения, так как она равна =—«-^г , А7<^ К
Поэтому при фиксированном значении достаточной статистики S (Т}
распределение статистики d(T) практически не зависит от значе-
значения параметра Я, если только ЛГ<^1. Следовательно, в наиболее
важной области малых значений параметра Я практически вся ин-
информация об этом параметре сосредоточена в достаточной стати-
статистике d(T). Исходя из этого, мы ограничиваемся только стати-
статистикой d(T). Можно было бы рассмотреть значения самой оценки
А IT1 \
для параметра Л, равной с , однако этот путь приводит к гро-
моздким, мало пригодным для использования формулам. Так как
каждый элемент может отказать независимо от отказов других
элементов, а вероятность отказа р=\ —е~кт, то распределение
отказов d (T) является биномиальным
Случай построения доверительного интервала (p(d(T))y p(d(T))
Для параметра р биномиального распределения был уже рассмот-
рассмотрен в § 1.6. Функция Я = у In у— является монотонной по р,
поэтому неравенство p(d)<Cp<P(d) эквивалентно неравенству
202 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
тр- In << А, <-тр- In —=-— . Следовательно,
±ln^ <Я<4-1п—4-Л =
Г 1 _ р (d) ^ 1 — р (dj |
+сс. C.4.17)
Так как при eL = 0 p(d) = 0 для d = 0, 1, ..., /V, то из C.4.17),
полагая г1=^0, е2 = 1—ос, получаем односторонний доверительный
интервал @, -=г In—=—) с коэффициентом доверия, не мень-
V 1 \—p(d)J
шим а. В целях удобства построения доверительных интервалов
для значений а = 0,95, е1 = е2 = 0,025 и N=50, 60, 80, 100, 150, 200
в приложении приведена таблица 8 коэффициентов
Д'(</Iп1A'(flf) ln LC.4.18)
Д(</Iп, A(flf) ln L.
- 1-РМ \-p(d)
Из C.4.17) находим, что двусторонний доверительный интервал
имеет вид
^ = =7"^. Х==-Т"' C-4Л9)
где A' (d), A' (d) находятся из C.4.18), а р (d) и p{d) — по форму-
1 гч
лам § 1.6 для значений &l = e2=—~. Односторонний интервал
равен
'О, ^) , C.4.20)
где соответствующее значение р (d) находится по формулам § 1.6
для е2 = 1 — а.
Пример. Испытания проводятся по плану [Л/= 150, Б,
7=100 час]. За время испытаний отказало 5 элементов. Требуется
найти двусторонний доверительный интервал с коэффициентом
доверия а = 0,95.
Из таблицы 8 приложения находим, что А'A0) = 0,079;
.Д' = 0,011. Таким образом, из формулы C.4.19)
1
-~ 100
1 0,079
100
§3.4]
ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ
203
Доверительные интервалы для планов с состав-
составными достаточными статистиками. План [N, В, (г, Г)].
Общую методику § 1.6 используем теперь для построения довери-
доверительного интервала для X по итогам испытаний, проведенных
в соответствии с планом [N, Б, (/*, Т)]. Моменты отказов в этом
случае образуют пуассоновский поток с интенсивностью Л. Основ-
Основная специфика этого случая состоит в том, что достаточная ста-
статистика для параметра X является составной. Если значение tr>Ty
то она равна значению d (Т) числа моментов, отказавших за время Т;
если же tr<^T, то достаточная статистика равна tr — моменту
появления г-го отказа. Рассмотрим точки плоскости вида (Л, t)%
Рис. З.4.2.
Л>0, 0<^<Г, t = T+\, ...,7-fr (рис. 3.4.2). Если в резуль-
результате испытаний элементов, для которых KN=A, наблюдается зна-
значение tr < 7, то результаты испытаний отмечаются случайной
точкой (Л, tr). Если же tr>T и число отказов равно d(T) = dy
то исход опыта обозначается случайной точкой (Л, T-\~r — d). Мно-
Множество точек ^ строится следующим образом. Задаемся двумя
числами е1? е2>0, а=1 — (?i + e2). При фиксированном значении Л
кверхней части множества ^ относим те точки (Л, 5), S=T-\-r — d
или /, для которых 5>vS(A), где S (А) находится из условий
«S (Л) = T-\-r — d(T); d(T) — целое число, не большее г—1, если
C.4.21)
если же
d\
лг
204 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
то S(A) = t(A), где t (А) находится из условий
*(\т\<* f* As Г* Л. s
X ^ У1 * i р — AT ! \ g — Asrfg —~ V g —AS tf§ =:g C422\
d = 0 Г (А) Г(А)
Аналогичным образом к нижней части множества ^ относим
точки (A, S), для которых S <C S (Л), где 5 (Л) находится из условий
S_(A)
С У^.^. g"Astfg ^e2; C.4.23)
о
г
«если же \ s • e~As ds< e2, то в качестве 5 (Л) выбирается
о
число vS (Л) = T-\-r — d (Г), где d (T) — целое число, не большее г— 1,
«аходится из условий
Вероятность того, что исход испытаний будет отмечен случайной
точкой (Л, S) ? $ не превышает 1—a = el + e2 по построению
множества §\ Соответственно вероятность противоположного со-
события (Л, 5) ? ^ не меньше а. Если в результате проведения
испытаний наблюдалось d(T) — d^r—1 отказов, то событие
{Л, S) ? $ эквивалентно событию
A(d)<A<A(d), C.4.25)
где A(d) и A(d) — функции, обратные к S (Л), S (А) для тех зна-
значений Л, при которых S(A) или^(Л) равны T+r — d, d = 0y . . .,
/•— 1. Из уравнений C.4.21) и C.4.24) находим, что A{d) и A(d)
§ 3.4] ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ 205
определяются уравнениями
^<rXs ds=ev C.4.26)
e~-S^ = e2- C-4.27)
Но эти уравнения эквивалентны уравнениям C.4.11). Отсюда
находим, что
^ ^-^', C.4.28)
где
Л (d) = X (d) Ny Л (</) = _Я (rf) ЛГ.
Напоминаем, что значения коэффициентов Да (d) даны в таблице 7
приложения. Если же момент г-го отказа tr<ZT> то событие
(Л, ^г) С $ эквивалентно событию
Л(О<Л<Л(д, C.4.29)
где Л(?), A(S)—функции, обратные к 5 (Л), S (Л) для тех зна-
значений Л, при которых значения 5 (Л) и S (Л) не превышают Г.
Из C.4.22) и C.4.23) находим, что Л (*г) и Л (tr) определяются
уравнениями
J^j*"*-"!. C-4.30)
^s'-4-±^°ds = e2. C.4.31)
О
Эти уравнения эквивалентны уравнениям C.4.11), в которых
д (г) = л (о tr = X (О м„ д (г) = л (д ^г = л (О мг,
Таким образом, построение доверительного интервала для
оценки параметра А. при использовании плана [Л/", Ву (г, 7)] нужно
производить так же, как при использовании планов [Af, В, Т) и
IN, 5, г], в зависимости от того, имеем мы tr>T или tr<iT.
206 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
План [N, Б, (г, HS0)\. В § 3.3 было показано, что план
[/V, ?, (г,/У?о)] эквивалентен плану [N=\, В,(г, So)]. Поэтому
двусторонний доверительный интервал имеет вид
X = A'-e'(d-1), Я = -^, если SB(tr)>S0, C.4.32)
А1е!:Г')^^ , если SB «,) < 50, C.4.33)
d(t)
где 5 (/) = 2^ tj + [N—d (t)} t, d (t) — число элементов, отказавших
к моменту t. Значения коэффициентов Да(д0 находятся из таблицы 7
приложения. Односторонний доверительный интервал получаем из
формул C.4.32), C.4.33), полагая в них X = 0, что соответствует
значению ех = 1 — а, е2 = 0.
Пример. Испытания проводились в соответствии с планом
[Л/=500, Б, (г = 20, HSQ=: 20000)]. К моменту окончания испыта-
испытаний, когда суммарная наработка стала равной 20 000, отказало
16 элементов. Требуется найти верхний доверительный предел,
соответствующий коэффициенту доверия а = 0,99. Так как значе-
значение S(^2o)^^o> т. е. суммарная наработка элементов достигла
уровня 50, заданного до начала испытаний, раньше, чем наступил
отказ 20-го элемента, то верхняя доверительная граница нахо-
находится по формуле C.4.32). Из таблицы 7 приложения находим,
что До.01 A6) = 28,030, откуда
Т„ 28.030 з
План [Му Б, (г, Т)]. Вполне аналогичным способом можно по-
получить доверительные интервалы для случая плана [/V, Б, (г, Т)].
Здесь достаточная статистика равна либо наработке S (tr) к мо-
моменту tn если /Г^Г, либо является двумерной (d(T), SB (T))>
если tr>Ty где d (Т) — число отказавших элементов, a SB (T) =
d(T)
N'—d(T)]T—суммарная наработка. Однако по тем же
соображениям, которые приводились для случая плана [Л/, Б, Т\у
статистику S5(T) мы исключаем из рассмотрения. Итак, значение
случайной величины, исходя из которой мы строим доверительный
г
интервал, равно d(T), если /Г>Г, и равно SE (tr) = s [ t,- +
i = l
-f (N—r) tn если tr<ZT. На плоскости (Л, t) мы рассматриваем
§ 3.4] доверительные интервалы 207
множество точек Л > 0, 0 < t < NT, t = NT+\, . . . , NT + ry
XSB (tr) = NXtx + (N- 1) X(t2-tl)+... +(N-r + 1) X {tr-tr_x),
где (N—*') (^- + i — ti)(i = 0,..., r—1, tQ = 0)—взаимно независи-
независимые (см. § 3.3) неотрицательные случайные величины с плотностью,
равной е~и. Поэтому
?{kSB(tr)<xy Ktr< Г}-
е Х ^i ... dsr = Fr{x} T). C.4.34)
Соответственно
Р{5(/г)<5, *г< Г} = /=¦,. (ta, ХГ). C.4.35)
Далее, в точности повторяя все рассуждения, использованные при
построении множества $ и затем доверительных интервалов для
плана [N, В, (г, 7)], и учитывая, что распределение d (T) является
биномиальным, получаем доверительные интервалы для параметра X
с коэффициентом доверия не меньшим а=\ — (e1-f-e2). Если к мо-
моменту 7 окончания испытаний общее число отказов d(T) = d<^r,
то верхняя граница X доверительного интервала находится из
уравнения
?b(l-e-Xr)*«-('V-*)X7'=ei2*0, C.4.36)
а нижняя—из уравнения
? CkN(\-e-±T)ke-{"-k)±T = e2^0. C.4.37)
k=d
Если же момент появления г-го отказа ^г<7, то верхняя граница
находится из уравнения
X Скы(\-е-кт)ке~(М-к)КТ +F(XS(tr), ХГ) = е1, C.4.38)
/5 = 0
а нижняя — из уравнения
/?(Я.5(/г)ДГ)=е2, C.4.39)
^де 5 (^ — суммарная наработка элементов к моменту tr.
208 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
Сравнивая C.4.36), C.4.37) с формулами § 1.6 для довери-
доверительных границ параметра биномиального распределения р и за-
замечая, что X —-f In , , получаем, что для случая tr>T
i A#(d) T A' (rf)
Значения A' (*/) и Д' (d) приведены в таблице 8 приложения. Дли
случая tr^T необходимо иметь таблицы решений уравнений
C.4.38), C.4.39).
Если для выбранного значения г плана [N, ?, (г, Т)] отношение
-^-<0, 1, то планы [N, ?, (г, Т)] и [N, Б, (г, Т)] практически
эквивалентны; соответственно эквивалентны планы [N, Б, г] и
[Л/, Б, г], так как число заменяемых элементов составляет не-
незначительную часть от их общего числа. Поэтому в первом при-
приближении для построения доверительных интервалов можно считать,
что испытания проводились не по плану [Л/, Бу (г, Г)], а но плану
[ЛГ, В, (г, Г)]. По той же причине оказываются практически экви-
эквивалентными доверительные интервалы, построенные исходя из плана
[N, Б, Т] и плана [Л/, В, Г], если только наблюдаемое число
d (T) отказавших элементов значительно меньше общего числа Л/
испытываемых одновременно элементов,
Основные формулы настоящего параграфа даны в таблице 6
приложения.
§ 3.5. Доверительные интервалы и множества.
Случай многих параметров г)
В начале предыдущего параграфа указывалось, что иногда
недостаточно характеризовать различные показатели надежности
только посредством точечных оценок. Эти соображения остаются
в силе и для многих неизвестных параметров. Если моменты отка-
отказов являются случайными величинами, функции распределения
которых известным образом зависят от нескольких параметров, то
числовые показатели надежности (вероятность безотказной работы
в течение времени Г, среднее время до первого отказа и т. д.)
являются вполне определенными функциями от значений этих
параметров. При этом возникает большое количество задач. Чтобы
показать, насколько разнообразными могут быть возможные по-
1) Часть материалов, изложенных в этом параграфе, требует специаль-
специальной математической подготовки.
§ 3.5] ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И МНОЖЕСТВА 209
становки задач, мы отметим три различных пути, приводящих
к необходимости решения многопараметрических задач. Во-первых,
для целого ряда элементов функция распределения момента появ-
появления отказа зависит от двух или более параметров. В § 1.4
приводились различные семейства функций распределения, завися-
зависящих от нескольких параметров: закон Вейбулла, нормальный и
логарифмически нормальный законы и др. При этом структура
статистических данных, исходя из которых надо построить дове-
доверительный интервал для заданной функции от неизвестных значе-
значений параметров, может соответствовать одному из планов, опи-
описанных в § 3.1. Более сложная ситуация возникает на втором
пути, когда производятся испытания элементов (или систем), со-
состоящих из нескольких частей, отказы каждой из которых при-
приводят к отказу работы всего элемента.
Если, например, отказы частей происходят взаимно независимо
друг от друга, а функция распределения момента отказа для /-й
части равна F((t, a{i Pf), т. е. зависит от двух параметров, то
вероятность безотказной работы такого элемента в течение вре-
времени Т равна R{T) = Y[[\—Fi(T, с^Д)]. Здесь Л^—число частей,
составляющих элемент. Таким образом, мы видим, что важная
числовая характеристика надежности R(T) является функцией 2/V
неизвестных значений параметров. Заметим, что в этой ситуации
число возможных планов проведения испытаний может быть зна-
значительно увеличено по сравнению с планами, описанными в § 3.1.
Действительно, момент прекращения испытаний может зависеть от
того, в каких составных частях элемента наблюдаются отказы.
Наконец, многопараметрические задачи возникают при «прогнози-
«прогнозировании» показателей надежности системы, состоящей из многих
отличающихся друг от друга блоков. При этом надо исходить из
статистических данных, полученных в отдельности для каждого
типа составляющих систему блоков. Например, представляет инте-
интерес построение доверительного интервала для вероятности без-
безотказной работы R(T) в течение времени Г, когда блоки отказы-
отказывают независимо и вероятность безотказной работы /-го блока
равна Pj^RtiT). Если /и — число различных типов блоков, а
ki—1—число резервных блоков одного типа (резерв нагружен-
нагруженный), входящих в систему, то
m
Предполагается, что испытания блоков /-го типа проводились
в соответствии с одним из возможных планов, например [Nh Б, Т].
Если считать, что роль параметров играют m неизвестных значе-
° Б. В. Гнеденко и др.
210 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
ний Pi = Ri(T)y то мы снова приходим к задаче построения дове-
доверительного интервала для функции от многих неизвестных значе-
значений параметров. На первый взгляд может показаться, что эту
задачу можно легко свести к случаю одного неизвестного пара-
параметра Pi = Ri(T). Для этого надо только найти доверительные
интервалы (Ph P.) отдельно для каждого из N параметров Р( =
= /?,(Г), а затем взять за доверительный интервал (/?, R) для
R(T), где ~
— t=l — i=l
Заметим, что если коэффициент доверия для интервала (Р,-, Р()
т
равен ah то коэффициент доверия для R не хуже а=Ц at. Од-
/=i
нако а оказывается слишком малым даже для небольших значе-
значений т. Например, если m=10, at==0,9, то а — @,9I0 ^ 0,35.
Следовательно, мы можем ручаться, что в среднем из 100 по-
построенных доверительных интервалов лишь не менее 35 будут
содержать истинное значение вероятности R(T). Редукция к мень-
меньшему числу параметров, осуществленная таким образом, оказалась
неудачной.
Доверительные интервалы для случая последо-
последовательной цепи элементов. Рассмотрим простейшие слу-
случаи построения доверительного интервала для вероятности без-
безотказной работы системы, состоящей из т последовательно
соединенных элементов / типов. Число элементов /-го типа, вхо-
дящих
в систему, равно mh /=1, ... , /, 2Lmi==m- Предпола-
гается, что элементы отказывают независимо друг от друга и что
отказ любого из них приводит к отказу всей системы. Обозначим
через R( (T) вероятность безотказной работы элементов /-го типа
в течение времени Г. Вероятность безотказной работы системы
R(T) задается формулой
e^1 . C.5.2)
Так как обычно Ri (Г)«1, то, используя соотношение ln/?t- (Г) ^
«1—R((T), можно также вместо C.5.2) исходить в расчетах из
приближенной формулы
R (Т) = ехр { — X Щ [1 - Я, (Г)] } . C.5.2')
§ 3.5] ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И МНОЖЕСТВА 211
Учитывая монотонную зависимость R (Т) от ^ mi 'n &i (Л» можно
i=i
задачу отыскания нижнего доверительного интервала для R (Т)
свести к эквивалентной задаче отыскания верхнего доверительного
интервала для суммы ^т;\п R;(T) выпуклых функций.
Построение доверительного интервала существенным образом
зависит от того, какие статистические данные о неизвестных па-
параметрах R{(T) имеются в нашем распоряжении. Предположим,
что элементы /-го типа испытываются в соответствии с планом
[Niy />, G1)], / = 1, ... , /, и что при этом было зарегистрировано
d; отказов. Если элементы достаточно надежные и N; велико
(/Vt->20), то можно считать, что di имеют пуассоновское распре-
распределение с параметром Ki = Ni[\—Ri(T)]. Соответственно вместо
формулы C.5.2) используем формулу C.5.2'). .
Рассмотрим два пространства: пространство исходов испытаний
(dly . . . , dt) и пространство параметров (к1У . . . , Kt). Так как
dly . . . , dt имеют пуассоновское распределение, то сумма их
d — dx-\-...A-dl также имеет пуассоновское распределение с па-
параметром Я = Ях+. . .+Х/. Если Аа (d) — квантиль пуассоновского
распределения (таблица 7 Да(^) дана в приложении), то утвержде-
утверждение { Х1-\- . . . -{-Х1 ^ Да(^)} эквивалентно утверждению {dl+...
a ^ • • +^i)}, гДе da(k) находится из условия
По построению &a(d) имеем
P { Кг + ... + \t < A,_a (d)} ^ a. C.5.3)
Исходя из C.5.3), рассмотрим множества в пространстве парамет-
параметров,, задаваемые условиями
/<Д1-аИ. </-<*!+...+<*,. C.5.4)
Если на множестве, определяемом неравенствами C.5.4), рассмот-
реть максимум функции ф— /^mf In R: (T)
= max ^ mt In Rt (Г), C.5.5)
t=i
8*
212 ОПЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
то для событий имеем
I
\ ф=тах? at, In Я,- (Г)><р = ? т,1п/?,(Г) \ ^
pl^+...+^^Д^а^)}. C.5.6)
Так как вероятность события { Хх+ . . . -\-Уч ^ Лх-а (d)} не мень-
меньше а, то, учитывая C.5.6), и подавно имеем Р{ф>ф}^а.
В качестве нижней доверительной границы для R (Т) можно
взять /?(Г) = ехр{— ф }. Таким образом, задача отыскания нижней
доверительной границы сведена к задаче отыскания максимума
функции C.5.5) при ограничениях C.5.4). Если воспользоваться
приближением C.5.2'), то C.5.5) заменяется условием
mt A-Я, (Г)). C.5.7)
Максимум C.5.7) при ограничениях C.5.4) легко найти в явном
виде. Здесь имеем
Ф = Д1_а(^) max —¦ . C.5.8)
Исходя из формулы C.5.8), получаем, что нижний доверительный
предел для вероятности R (Т) безотказной работы с коэффициен-
коэффициентом доверия, не меньшим а, равен
_Г max ^1 Ai_a (d±-\- . . . + dL) \ . C.5.9)
Построенный по формуле C.5.9) нижний доверительный предел
не для всех значений параметров 'Ki = Ni{\—Ri(T)] будет давать
хорошее приближение к R (ГL В тех случаях, когда Xt и соответ-
соответственно d{ велики, можно использовать нормальное приближение,
предложенное в работе Р. А. Мирного и А. Д. Соловьева [11].
Заменяя Xi оценками d{ и учитывая нормальность распределения
г- dh можно утверждать, что с вероятностью, близкой к а,
/
l/ Y4i*L(x-*L\
f ~ Ni N( V NiJ*
]^di + ua
где иа — квантиль нормального распределения (см. таблицу 3
приложения).
§ 3.5] ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И МНОЖЕСТВА 213
Таким образом, нижний доверительный предел для вероятности
R (Т) имеет вид
t<3;*—У ?$%(*-%
В качестве второго примера рассмотрим случай построения ниж-
нижней доверительной границы для вероятности безотказной работы, за-
задаваемой формулой C.5.2), когда Ri (T) = е~^т. Таким образом, здесь
R(T) = e i=1
Будем предполагать, что данные о неизвестных значениях пара-
параметров X; получены в соответствии с планами испытаний [Nh Z>, г{].
Пусть значения суммарных наработок SB(tr.)=Sh / = l,...t /.
S; являются достаточными статистиками. Замечая, что 2XiSi имеет
Х2-распределение с 2г( степенями свободы и что при сложении
случайных величин, имеющих Х2-распределение, степени свободы
складываются, получаем
1=1
гдеХа(л) — квантиль Х2-распределения с п степенями свободы
(см. таблицу 4 приложения). Событие
мы можем рассматривать как неравенства, наложенные на пара-
параметры Xh вероятность выполнения которых равна а. Если рас-
рассмотреть максимум функции
i
? {ki C.5.12)
на множестве, заданном неравенствами C.5.11), то, очевидно,
имеем
t=i
214 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
Отсюда находим
«=1
i
2Z
Таким образом, задача отыскания нижнего доверительного интер-
интервала для R (Т) сведена к задаче отыскания максимума функции
C.5.12) при ограничениях типа неравенств C.5.11). Ответ нахо-
находится в явном виде:
Таким образом, нижний доверительный предел с коэффициентом
доверия, не меньшим а,
=exp - max f V 1=1 )j V
R(D
При больших значениях rt можно использовать нормальное при-
приближение для оценок %i=J—— . Здесь, заменяя к( оценками Я-,
имеем, что с вероятностью, близкой к а,
Таким образом, приближенная формула для нижнего доверитель-
доверительного предела с коэффициентом доверия а имеет вид
C-5.12').
Общий метод построения доверительных интер-
интервалов. Сформулируем теперь в самом общем плане постановку
задачи о построении доверительных интервалов в случае многих
неизвестных параметров.
Задано пространство статистических данных Х= {х}. Резуль-
Результаты испытаний являются точками х из этого пространства. На
этом пространстве задано семейство вероятностных мер P.j {*}„
§ 3.5] ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И МНОЖЕСТВА 215
зависящих от значений многомерного параметра 0 = (Э1, . . ., 0#) ? Q,
где Q — множество возможных значений параметра 0; задана также
известная числовая функция ф @). Требуется по известным резуль-
результатам х построить доверительный интервал (ф(#), ф(х)) такой,
что для любого 0 ? Q
Р« {ф (*)< Ф F) <Ф (*)}>«•
Если а—наибольшее из чисел, удовлетворяющих этому неравен-
неравенству, то а называется коэффициентом доверия для доверительного
интервала (Ф(л:), фМ)- В противном случае говорят, что построен
доверительный интервал с коэффициентом доверия, не мень-
меньшим а.
Постановку этой общей задачи, метод решения которой мы
дадим ниже, проиллюстрируем на двух примерах.
Пример 1 (постановка задачи). Испытания элементов прово-
проводились по плану [Л/, Б, N]. Функция распределения моментов отка-
отказов F(t, [А, а)=ф( -1, где Ф (t) — функция распределения для
нормального закона. Неизвестные значения параметров
Вг = \1, 02 = сг, Q = {—оо<01< + сю, 0<а<оо}.
Достаточными статистиками для параметров [i, а являются
N N
{си. § 1.6), поэтому пространство X состоит из точек х = (х> S)>
Семейство мер Ро {л:} является совместным распределением
статистик х и S. Требуется построить доверительный интервал
(ф(х, S), 1) для функции ф @) =-ф г ((Л, а) = 1 — ф (-~J > т. е.
вероятности безотказной работы элемента в интервале времени
@, Т).
Пример 2. Система содержит k{ блоков /-го типа, / = 1, ... ,ЛЛ
Вероятность безотказной работы системы R(T) задается формулой
C.5.1), где вероятности безотказной работы /-го блока Р|. = /?/(Г).
Испытания блоков 1-го типа проводятся по плану [Л/"., Б, Т\. Так
как достаточной статистикой для Р. является число d;(T) эле-
элементов, отказавших за время Т проведения испытаний, то в каче-
качестве пространства X выбираем совокупность ЛЛмерных векторов
X=(dly ..., им), где d,- = 0, I, ...,^V?- равно числу элементов /-го
типа, отказавших за время проведения испытаний. Неизвестный
216
ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
[ГЛ. 3
параметр 9 = (Рь . . ., Р*), Q = {0</>.< 1, / = 1, ..., Л/}. Так
как предполагается, что моменты отказов различных элементов
взаимно не зависят друг от друга, то d((T) имеет биномиальное
распределение и семейство вероятностных мер в пространстве X
задается формулой
Рб {Х} =п^Рв {d. (T) = di}=nC}jl (\-PyiPN-*.
Требуется построить нижний доверительный интервал для ф (9) =
= /?G), т. е. для вероятности безотказной работы системы.
Общая методика построения доверительного интервала является
естественным обобщением методики для случая одного неизвестного
параметра, которая была изложена
в § 1.6. В качестве случайной
величины, распределение которой
зависит от неизвестного значения
параметра 9=;(81, ..., 9дг), мы
выбираем оценку ф (х) для значе-
значения заданной функции ф (9). Далее
рассматривается пространство @
точек (9Х, ..., 9#, Ф (х)). Каж-
Каждой точке 6 = Fг, ..., 9дг) на оси
значений ф сопоставляется такое
множество 0(9), что
Рис. 3.5.1.
a. C.5.13)
При этом система множеств 0(9) строится таким образом,
чтобы неравенство C.5.13) нельзя было улучшить для всех значе-
значений 9, а само значение вероятности Р{ф6О(9)} было бы по воз-
возможности ближе к а. Если функция распределения оценки F% (х) =
= Р{ф F)<#} непрерывная, а параметр 9 одномерный, то в качестве
множества 0(9) выбираем интервал @F), 6(9)), где
Fb @F)) = l—б!, Fe@F)) = ea, а=\-(Е1 + г2).
Если теперь рассмотреть подмножество ^с@ точек (91? . ..,6^,ф),
для которых (p?G(9), то из C.5.13) следует, что
Р{(в, ф)б^}^ос. C.5.14)
Фиксируем теперь значение ф = х, и в множестве Q возможных
значений параметра 9 выделим подмножество #(ф), или H(x)aQ
(рис. 3.5.1), состоящее только из таких точек (9, х), для которых
§ 3.5] ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И МНОЖЕСТВА 217
x?G(Q). По построению событие {ф ? G(9)} эквивалентно событию
@, ф) ?$. Так как вероятности эквивалентных событий совпадают,
то, учитывая C.5.14), получаем
а. C.5.15)
Каждому значению оценки ф мы сопоставляем случайные величины
= ш? ф F), ф =
Вообще говоря, утверждение о том, что Ф (ф), ф (ф) являются
случайными величинами, требует специального доказательства,
однако во всех практически интересных случаях это будет так.
Событие 0?#(ф) влечет за собой событие {ф (ф) <Ф @)< Ф (ф)Ь
поэтому из C.5.15) получаем
Р {ф (ф) < Ф (9)< Ф (ф)} > Р {е € И (ф)} > «.
Доверительный интервал с коэффициентом доверия, не меньшим а,
построен.
Примеры. Воспользуемся этой общей методикой для реше-
решения задач, постановки которых были даны в примерах 1 и 2.
Для случая примера 1 в качестве несмещенной оценки для
фг(И<, а) возьмем найденную А. Н. Колмогоровым [12] несмещен-
несмещенную оценку
ф(л- 5) = 1— /М ^т^ ) , C.5.16)
\ у NS )
где
г /лг-1
ЛМ-^TJb' ' Л "
если \t\^YN—\; /л/@ = 0, если \t\>VN— 1. Так как F(y) —
монотонная функция от у, то из C.5.16) следует, что оценка
ф(лг, 6") является также монотонной функцией от значений стати-
статистики х У~N. Поэтому доверительные интервалы, построенные
л rp ~
исходя из оценки ф (х, S)y или статистики —^— у N совпадают,
и мы можем вместо статистики ф взять —-—у N. Действительно,
218
ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
[ГЛ. 3
если использовать метод уровней с числами ех, е2, а= 1 — (
то соответствующие множества #(ф (ху S)) и И'
совпадают. Числитель и знаменатель статистики ф = —^—у N
являются взаимно независимыми случайными величинами. При этом
~х j/iV имеет нормальное распределение со средним б =
Рис. 5.3.2.
и единичной дисперсией, а —2 имеет распределение %2 с (N—1)-й
степенью свободы. Таким образом, статистика ф имеет нецентраль-
нецентральное распределение Стьюдента (см. § 1.6) с параметром 6 = -]/л/
и (N—1)-м числом степеней свободы. Обозначим через р вероят-
вероятность отсутствия отказов в интервале (О, Т); р=\ — Ф ( ——~\ , по-
поэтому, используя обычные обозначения и формулу для квантилей
нормального распределения, получаем, что на всех точках полу-
полупрямой (а>0)
^—-=ир C.5.17)
и
значения искомой вероятности равны р. Для разных значений
O^p^l полупрямые образуют пучок, исходящий из точки (О, Т).
В частности, полупрямой T=\i, а^ 0 соответствует значение р =
= 0,5. Полупрямым с углом наклона О^0<^, ctgQ = up (рис.
3.5.2) соответствуют значения /?>0,5. Множества GF), 0 = (fx, a)
§ 3.5] ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И МНОЖЕСТВА 219
полагаются равными интервалам (у, у), где FN.1(yy б) = 1 — е1%
FN-i(y> 6) = е2> ее = 1 — (ег + е2)» а ^w-i (У> б)—функция распре-
распределения смещенного закона Стьюдента с (Л/—1)-й степенью сво-
свободы и смещением, равным б. При эгом значения у, у одинаковы
вдоль полупрямых \/~N = б = const, поэтому множество ^явля-
^является совокупностью точек, лежащих между двумя линейчатыми
поверхностями О и О (см. рис. 3.5.2). Пусть известно значение
статистики ф = —=—]/N\ тогда множество H((p)dQ состоит из
таких точек 9 = (fx, а), для которых б (ф) < б = -]/N<i
< б (ф), где б (ф) и б (ф) находятся как решения уравнений
Для решения этих уравнений можно составить соответствующие
таблицы. Таким образом, границами множества #(ф) являются
два луча
и—Т б(ф) и— Т 6"(ф)
=—4^-, = т^. C.5.19)
о V N & v N
б$ б"(ф)
Заметим, что ^=<С 7r=-t Поэтому из C.5.17) получаем, что
значения р (ф) и р (ф) находятся из уравнений
tfp (ф) = —
В нашем случае события {р (ф) <Cp<ip (ф)} и {0 6^(ф)} эквива-
эквивалентны, поэтому
а. C.5.21)
Итак, доверительный интервал (ру р) строится в два этапа. Сначала
из уравнений C.5.18) подсчитываются значения границ доверитель-
доверительного интервала для смещения б, а затем, исходя из C.5.20), по
таблице квантилей нормального закона (см. таблицу 3 приложе-
приложения) находятся искомые значения р и р.
Для задачи, сформулированной во втором примере, мы сможем
получить точный ответ в явном виде только для одного частного
220
ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
[гл.
случая, когда в результате испытаний по планам [Nh Z>, Т] отказы
не наблюдались, т. е. di (Г) —0. Решение задачи в этом частном
случае было впервые найдено Р. А. Мирным. Первоначально ответ
показался авторам книги настолько неожиданным, что они сочли
его, вообще неверным.
Так как несмещенными оценками для вероятностей безотказной
работы R((T) являются отношения —-— ' , то состоятельной оцен-
оценкой для R (Г), задаваемой форму-
формулой C.5.1), является
N
(Pf*(f)
C.5.22)
ф принимает конечное число зна-
значений. Перенумеруем эти значе-
значения в порядке их убывания гх =
= 1 > г2 > г3 > . . . . Пространст-
во © состоит из точек (9, х), где
Рис 353
' ' ' *
(р1э ,p) /
Пусть г (а, 0) — наименьшее из
чисел riy удовлетворяющих условию
Р{ф<г(а, 0)}>сс; C.5.23)
тогда в качестве множества G@) возьмем набор всех значений
г/^г(а, 6). Функция г (а, 6) имеет вид ступенчатой функции,
примерный вид которой показан на рис. 3.5.3. Расписывая C.5.23),
имеем
Р{ф<г(а, в)} = 1-
2
rt> r (а, В)
где сумма 2' берется по всем векторам (/х, ..., 1^) таким, что
значения оценки ф в формуле C.5.22) равны числам г(>г(ау 0).
Множество Я(ф) состоит из точек Q = (Plt ..., PN), удовлетво-
удовлетворяющих условиям 0^Р,-^1 и условию
C.5.24)
где 2" берется по всем векторам (/1т ..., lN) таким, что значе-
значения оценки в формуле C.5.22), где надо положить d( (T) —lh равны
числам г{. При этом г{ не меньше полученного значения ф по фор-
§ 3.5] ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И МНОЖЕСТВА 221
муле C.5.22), исходя из данных испытаний. Так как функция ф (8) =
= R(T)y определяемая по формуле C.5.1), является монотонно воз-
возрастающей функцией аргументов Ph то ф (ф) = inf ф (9) достигает-
достигается на границе области #(ф), которая задается, исходя из C.5.24),
уравнением
2"П CJJO-/>,)" ^"-'«=1-0, C.5.25)
1 = 1
где 0<Pf<l.
Итак, задача построения нижнего доверительного интервала
(ф(ф)> 1) с коэффициентом доверия, не меньшим а, сведена к зада-
задаче отыскания минимума функции ф F) = /? (Т) на гиперповерхности,
задаваемой уравнением C.5.25). В том частном случае, когда
система состоит из N различных блоков (все &;=1), а отказы
при испытаниях не наблюдаются (все dt G)=0), ф=1 и 2" со-
содержит только один член. Уравнение C.5.25) переписывается в виде
= 1—а. C.5.26)
Можно показать, что нижняя граница ф функции
Ф(в)=/?(Г) = П^ C.5.27)
*=i
при условии C.5.26) равна A—а)*, эе = max -^ . Учитывая, что
U<i<N /Vi
при отсутствии отказов у N испытываемых элементов нижний до-
доверительный интервал (ф, 1) с коэффициентом доверия а опреде-
ляется из соотношения ф = A—а) N , мы можем полученный ре-
результат сформулировать в следующем виде.
. Если известно, что в результате испытаний элементов различ-
различных типов, проводимых по планам [Л^., Б, Г], отказы не наблю-
наблюдались, то нижняя доверительная граница для вероятности без-
безотказной работы системы в течение времени Г, определяемой по
формуле C.5.27), с коэффициентом доверия а равна нижней дове-
доверительной границе с тем же коэффициентом доверия, подсчитанной
для элементов /-го типа, у которых число N( = min (Nly . ..,Л/Я).
Доверительные множества. В заключение параграфа
сделаем несколько кратких замечаний, относящихся к методике
построения так называемых доверительных множеств, которые
можно использовать для одномерной оценки нескольких неизвест-
неизвестных параметров. Общая постановка задачи аналогична только что
222 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
рассмотренной задаче построения доверительного интервала для
Ф @Х, ..., 0дг). Мы предполагаем, что имеется пространство Х^={х},
точки которого соответствуют результатам испытаний. На этом
пространстве задано семейство вероятностных мер Ре, зависящих
от значений векторного параметра 9 = @Х, . .., 0;v)gQ, где Q —
множество всех возможных значений параметра 0. Если каждому
значению х?Х поставлено в соответствие подмножество И(х)
такое, что
C.5.28)
то подмножества Н (х) называются доверительными множествами.
Если неравенства C.5.23) нельзя усилить, увеличив а, то а назы-
называется коэффициентом доверия доверительного множества Н (х);
в противном случае говорят, что коэффициент доверия не хуже а.
Сопоставим теперь каждому значению 0?Q такое множество
8 что
а- C.5.29)
Фиксируем значение х и определим множество Н (х) как совокуп-
совокупность всех точек 0, для которых x?G(Q). События {x?G(Q)} и
{д?Н(х)} являются эквивалентными, так как каждое из них вле-
влечет за собой другое, поэтому вероятности этих событий совпа-
совпадают. Учитывая C.5.29), получаем, что для построенных множеств
И (х) выполнены неравенства C.5.28). При этом, если хотя бы для
одного значения 0 неравенство C.5.29) обращается в равенство,
то при этом же значении 0 обращается в равенство и C.5.28);
поэтому в данном случае а является коэффициентом доверия для
множеств Н(х).
Проиллюстрируем изложенный общий метод построения дове-
доверительных множеств на простом примере. Предположим, что функ-
функция распределения F (t) для момента отказа имеет нормальное рас-
распределение с неизвестным значением среднего fx и дисперсии а2.
Испытания проводятся по плану [Л/, Б, Л/]. Достаточными стати-
статистиками являются
N N
где tt — моменты отказов. В качестве пространства X выбираем
множество точек плоскости (a:, s), — оо<; л; < + оо, s ^ 0; Q
является множеством точек 0 = (|Л, а), —сх><|ьК[ + 00» cf>0.
Пусть ах, а2 — такие положительные числа, что заданный коэффи-
коэффициент доверия а= а^.
Если теперь каждой точке 0 — (fx, а) (см. рис. 3.5.4) мы сопо-
сопоставим множества G@), являющиеся прямоугольниками хг <.
ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И МНОЖЕСТВА
223
§ 3.5]
sx < 5 < s2, где лг,-, Sj находятся из условий
Р» {хх<х<х2} = а1( Ре {*i< s<52} = а2.
то, учитывая взаимную независимость х и s, получаем
P{(je; *)€GF)} = P{*i<r<^2}P{51<s<s2}=a1a2 = a. C.5.30)
л; имеет нормальное распределение со средним [i и дисперсией
Рис. 3.5.4.
— ; 2—- имеет ^-распределение с (N—1)-й степенью свободы,
поэтому
x
Следовательно, прямоугольник С@) определяется неравенствами
TV—1
-a.
C.5.31)
224 ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ [ГЛ. 3
Разрешая неравенства C.5.31) относительно pi и а, мы получаем
искомые доверительные множества И (х) с коэффициентом доверия
а, имеющие вид трапеций, принадлежность точек (jn, а) к кото-
которым определяется неравенствами
С помощью изложенных выше общих методов можно строить
различные системы доверительных интервалов и множеств. Так,
например, каждой оценке ф будет соответствовать своя система
доверительных интервалов. Мы скажем, что система доверитель-
доверительных интервалов Сг = {ф (фх (х)), ф (фх (х))} (доверительных мно-
множеств [Нх (х)}) предпочтительней системы С2 = {ф (ф2 (х)), Ф (ф2
({Н2(х)})} если для каждого значения х?Н
Ф (ф2 (*)) < ф_(фх (а:)), <р (ф"х (а:)) < <р (ф2 (л;)),
где для хотя бы одного значения х имеют место строгие неравен-
неравенства (И1 (х) сИ2 (х) и И2(х) и Иг(х) не пустые), а коэффициенты
доверия а у обеих систем совпадают. Систему доверительных
интервалов С= {ф (ф (*)), ф (ф (л:))} (доверительных множеств И(х))
назовем допустимой, если нет более предпочтительной системы
интервалов. Встает задача построения критериев определения допу-
допустимости для заданной системы доверительных интервалов (мно-
(множеств). Если имеются две допустимые системы доверительных
интервалов (множеств) Сх и С2, коэффициенты доверия которых
одинаковы, то их можно сравнивать с помощью различных вероят-
вероятностных характеристик, например с помощью средней длины дове-
доверительного интервала (в случае доверительных множеств — с по-
помощью средней длины диаметра доверительного множества и т. д.).
Если вероятностный показатель качества систем доверительных
интервалов (множеств) выбран, то встает задача отыскания такой
допустимой системы, у которой этот показатель является наилуч-
наилучшим. Таким образом, открывается обширное поле деятельности,
результаты которой могут найти широкое применение, в частности
в области теории надежности. Желание привлечь внимание к этим
вопросам главным образом математиков и является основной целью
настоящего параграфа, в котором лишь намечены некоторые воз-
возможные направления исследований.
ГЛАВА 4
ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ
§ 4.1. Общие положения теории проверки
статистических гипотез
Основные понятия. В главе, посвященной проверке гипо-
гипотез о надежности испытываемых элементов, настоящий параграф
играет вспомогательную роль. В нем без доказательств, но со
ссылками на доступные источники даны формулировки ряда теорем,
которые будут нами использованы в последующих параграфах.
Исходными понятиями теории проверки статистических гипотез
являются понятия основной и конкурирующей гипотез. Для про-
простоты изложения мы предположим, что пространство Х={х)
исходов испытаний не зависит от того, какие будут приниматься
решения. Допущение, что исход испытаний является случайным,
эквивалентно предположению, что в пространстве X существует
распределение вероятностей Я, в соответствии с которым возникает
тот или иной исход испытаний. В большинстве случаев вид Р
неизвестен, известно лишь, что Р принадлежит некоторому классу
распределений вероятностей. Обозначим этот класс через f, вхо-
входящие в него распределения вероятностей — через Р9, где 0 —
параметр1), с помощью которого различаются распределения,
и через Q множество возможных значений параметра 0.
Таким образом, утвержделие Pe?f эквивалентно утверждению
0?Q. Например, если испытания проводятся по плану [N, Z>, N],
то пространство исходов испытаний Х={х} состоит из точек
N-мерного пространства х = (х1} ..., лг#), где х{— момент отказа
/-го элемента. Допустим, что отказы взаимно независимы и имеют
логарифмически нормальное распределение с неизвестными парамет-
параметрами [хиа2 (см. гл. 1). Тогда семейство f вероятностей распределения
Вообще говоря, Э является вектором. Так, для нормального распре-
я 9== (ix, a2).
деления 0 = ([х, а2).
226 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
задается плотностями вида
N 1 (In Xj-цJ
Роль параметра играют пары 8 = (|х, а2), —оо<[|ы< + оо,
а2>0.
Таким образом, множество значений параметров, или простран-
пространство параметров й, состоит в рассматриваемом примере из точек
полуплоскости ([X, а2): —оо<|ы<;оо, а2^0. Пространство пара-
параметров Q может иметь весьма сложное строение. Так будет в тех
случаях, когда класс t может включать распределения вероятно-
вероятностей многих типов.
Гипотезой И называется любое утверждение о виде распределе-
распределения вероятностей Ре. Если сформулирована гипотеза, то класс всех
возможных распределений вероятностей разбивается на два подкласса.
В один подкласс входят распределения Ре, обладающие свойством,
сформулированным в гипотезе, а в другой — не обладающие этим
свойством. Таким образом, пространство значений параметров Q
разбивается на два непересекающихся подмножества Qo и Qly
Q = Q0(jQi. Гипотезу Ио условимся называть исходной или основ-
основной, а дополнительную к ней гипотезу Нг — конкурирующей.
Могут, конечно, встретиться и задачи, в которых формулируются
несколько взаимно исключающих друг друга гипотез. Мы в основ-
основном ограничимся только случаем проверки двух гипотез Но и Нг.
В приведенном выше примере испытаний N элементов с логариф-
логарифмически нормальным распределением времени безотказной работы
можно сформулировать ряд гипотез. Например, исходная гипотеза
Но может состоять в том, что |А1<Ц0, а2 — любое. В этом случае
конкурирующая гипотеза Нх соответствует значениям параметров
И<^^о> <т2>0 (рис. 4.1.1, б).
После того как описаны пространство возможных исходов
испытаний Х={х}у класс i распределений вероятностей и сформу-
сформулированы гипотезы, ставится задача построения критерия, прове-
проверяющего согласованность исходов опыта с одной из гипотез.
Под критерием понимают систему правил обработки исхода
испытаний, на основании которой принимается (лучше даже гово-
говорить проверяется) одна из гипотез, а остальные отвергаются. Если
значение х известно, то для большинства критериев принимается
определенная гипотеза Н(, i — i(x). Такие критерии называются
нерандомизированными. Нерандомизированный критерий опреде-
определяется заданием критического множества Хкр, являющегося частью
пространства X исходов испытаний. Если исход испытаний х?Хкр,
то гипотеза Но отвергается, если же лг?ЛГкр (?—«не принадле-
принадлежит»), то гипотеза Но принимается. В некоторых случаях оказы-
оказывается полезным рассматривать критерии, в которых i(x) является
§ 4.1]
ОБЩИЕ ПОЛОЖЕНИЯ ТЕОРИИ
227
случайной величиной при фиксированном х. Такие критерии назы-
называются рандомизированными.
Примеры критериев. Вид используемых критериев суще-
существенным образом зависит от класса f и гипотез Н(. Довольно
четко выделяются две большие группы задач. В первую группу
входят задачи, связанные с проверкой вида семейства распределе-
распределений, которыми описываются вероятности безотказной работы.
Типичными здесь являются задачи такого содержания: «проверить
гипотезу #0, состоящую в том, что вероятность безотказной
работы соответствует логарифмически нормальному распределе-
распределению» и т. д. Таким образом, здесь нулевую гипотезу составляет
б)
Рис. 4.1.1.
целый класс распределений. Роль конкурирующих гипотез также
выполняют классы распределений. Во вторую группу входят задачи,
связанные с проверкой конкретных значений параметров, опреде-
определяющих распределения. Здесь предполагается, что вид распреде-
распределения, принадлежность его к некоторому семейству уже заданы и
требуется только проверить значения параметров. Задача, соот-
соответствующая рис. 4.1.16, относится ко второй группе. Тому част-
частному случаю, когда проверяется гипотеза об экспоненциальности
вероятности безотказной работы, посвящается целиком § 4.2. Рас-
Рассмотренные в нем задачи относятся к первой группе. В §§ 4.3 и
4.4 рассмотрены критерии проверки гипотез о значениях парамет-
параметров экспоненциального распределения. Это типичные примеры
задач второго типа.
В большинстве задач первой группы поступают следующим
образом. Стараются найти такую статистику S(x), т. е. функцию
от исхода испытания, распределение которой оставалось бы неиз-
неизменным для любого значения параметра 0 ? Qo, входящего в исход-
исходную гипотезу. В критическое множество Хкр включают те точки
228 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
х, для которых | S (х) | > Se. Значение 5а находится из условия
Ре(|5(х)|>5а)<а, D.1.2)
где 6 ? Qo. Поскольку распределение S(x), если гипотеза верна,
не зависит от параметра 6, индекс G в левой части неравенства
можно было бы не писать. Число а можно трактовать как вероят-
вероятность ложного отвержения гипотезы //0, когда она верна. При-
Приведем несколько примеров критериев первого типа.
Критерий %2.
а) Непараметрический случай. Допустим, что исходами опыта
могут быть только события Аъ . . ., Лп вероятности которых равны
г
Pi, •••> Pf> 2 А<==1' Pi^Q- Если в результате N независимых
1 = 1
опытов событие А{ осуществлялось N( раз, то статистика
NPi
D.1.3)
при больших N имеет распределение %2 с (г—1)-й степенью сво-
свободы. Это означает, что
г-\)}жр, D.1.4)
где %1(п) находится из условия
Х2р(п)
2ТГ
(т)
I
D.1.5)
В таблице 4 приложения даны значения %1{п), когда 1—р = 0,001;
0,01; 0,05; 0,1@,1) 0,9; /г -= 1 A) 30. Таким образом, исходная
гипотеза //0, состоящая в том, что вероятности событий Ai равны
заданным числам р., принимается, когда Т (Nl9 ..., N2X
<Xi-a(r—^)i и отвергается в противном случае. Вероятность
ошибки первого рода приближенно равна а.
б) Параметрический случай. Постановка задачи та же, что и
в непараметрическом случае, только предполагается, что вероят-
вероятности pi=Pi(Q1, ..., 05), ?</— 1, где 61, ..., 05 — неизвестные
значения параметров. Пусть 6?. — оценки, которые получаются в
результате решения уравнений
§ 4.1] ОБЩИЕ ПОЛОЖЕНИЯ ТЕОРИИ 229*
где Т (Л^, ..., Nr) находится по формуле D.1.3). Введем обозна-
обозначения pi=pi(Qli ..., Qs). Тогда статистика
? <»'-?*' D.1.7)
имеет ^-распределение с (г — 5—1)-й степенью свободы. Таким
образом, исходная гипотеза /Уо, состоящая в том, что р{ =
= р,-(в1, ..., 6Г), принимается тогда и только тогда, когда
Т (N(J ..., NrX%l_a(r — s—\), где а — вероятность ошибки
первого рода.
Критерий %2 подробно описан во многих учебниках по математи-
математической статистике (см. [6]). Некоторые случаи испытаний на на-
надежность могут быть сведены к полиномиальной схеме, лежащей
в основе критерия %2. Предположим, что испытываются N элементов,
замена отказавших элементов не производится, испытания про-
проводятся до момента Т; в наших обозначениях этот случай
соответствует использованию плана типа [N, Z>, Т]. Разобьем
интервал (О, Л на г-1 интервалов Д1== [0, Тг], А2 = [7\ Г2], ...,
А/--1 [^V-2> ^r-iL где ?,._!= Т, а г-й интервал положим равным
Аг — [Тг_1у + оо). Если обозначить через А( событие, состоящее
в том, что отказ элемента произошел в интервале Д., а через
N( — число элементов, отказавших в интервале А,-, /=1, . .., г,
то мы приходим к описанной выше полиномиальной схеме.
F-к ритерий Фишера.
Если ?х, ?2 — две взаимно независимые случайные величины,
плотности которых имеют вид
О, Ж О,
. л о D.1.8)
1 2
то функция распределения случайной величины ^ = 4^ легко выра-
жается через неполную В-функцию [4]
Можно показать, что
4 (^) D.1.9)
Функция вида D.1.9) называется функцией распределения Фишера
'230 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
с п1} п2 степенями свободы, если a1 = pi = ^> a2 — Рг^^г-
В приложении даны значения квантилей распределения Фишера
с четным числом степеней свободы /0,995 (#i> n2) и /0,99 {ni, #2)
= 0,995. D.1.10)
F-критерий применяют в тех случаях, когда найдется такая
статистика S(x)y распределение которой для всех значений 9,
составляющих исходную гипотезу #0, совпадает с распределением
Фишера с Пц п2 степенями свободы. Из формулы D.1.9) легко
вывести, что /р(пг, n2)=/ilp(n2y nx). Таким образом, событие,
•состоящее в том, что
{/а К, n2)<S(x)<f ±(пг, п2)} D.1.11)
2 2
эквивалентно событию
а_(пъ п2)у
Таким образом, вероятности событий D.1.11) и D.1.12) совпадают
и равны 1—а, когда справедлива гипотеза Ио. Формула D.1.12)
позволяет использовать таблицы только со значениями fp(nv /z2),
где р близко к единице.
Использование критерия Фишера проводится по следующей
схеме. Вычисляется статистика 5(л;), имеющая /^-распределение с
п1У п2 степенями свободы, когда верна гипотеза Но. Но прини-
принимается тогда и только тогда, когда S(x)<,f a (пъ п2) и
2
S~l (х) </ а (/z2, пх). При этом ошибка первого рода равна а.
а
2
Пример на использование /^критерия приведен в § 4.2.
Для критериев, аналогичных критериям %2 и F, характерно
отсутствие описания конкурирующих гипотез. Эти критерии обес-
обеспечивают заданную величину вероятности ошибки первого рода,
но надо быть уверенным, что малы вероятности ложного решения
о справедливости гипотезы Яо, когда она неверна. Всегда суще-
существуют такие конкурирующие гипотезы, на которые используемый
критерий не реагирует в том смысле, что с большой вероятностью
принимается исходная гипотеза И0У тогда как она неверна. За
примером подобного рода для случая использования критерия
Вилкоксона мы отсылаем читателя к материалу, изложенному в
§4,5.
§ 4.1] ОБЩИЕ ПОЛОЖЕНИЯ ТЕОРИИ 231
Критерий А. Н. Колмогорова проверки типа
распределения по малым выборкам.
Для получения достаточно достоверных результатов о виде
закона распределения времени безотказной работы требуется, как
правило, испытывать большое количество однотипных элементов.
На практике могут встретиться такие случаи, когда испытания
проводятся только небольшими группами. Такие испытания часта
р-азделены большими интервалами времени, вследствие чего трудна
ожидать, что вероятности безотказной работы у различных групп
элементов будут совпадать. Сделать достоверный вывод о при-
принадлежности распределений вероятностей безотказной работы одной
группы элементов к определенному типу семейств законов распре-
распределения нельзя, так как4 объем группы невелик. Тем не менее,,
используя излагаемый ниже прием, предложенный А. Н. Колмого-
Колмогоровым, можно с большой степенью достоверности проверить при-
принадлежность групп элементов к одному типу семейств законов,
распределения. В основе критерия лежит элементарная
Лемма 4.1.1. Если случайная величина ? имеет непрерыв-
непрерывную функцию распределения F (t) = P{|<C t}, то случайная вели-
чина У) = F(|) имеет равномерное распределение в интервале [0,1].
Доказательство следует из соотношений
где F (х)— обратная функция для F(t), O^jc^I.
Критерий Колмогорова проверки по малым выборкам можно
использовать только в том случае, когда существует такая ста-
статистика S(X;), где х{— исход испытания z-й группы, распределение
Fs,i (t) которой ,не зависит от конкретных значений параметровг
определяющих функцию распределения вероятностей безотказной
работы. Предполагается при этом, что верна исходная гипотеза //0,
состоящая в том, что функция распределения времени безотказной
работы элементов входит в заданное семейство. Используя лемму
4.1.1, получаем, что случайные величины
Fs>1 (?(*!)), ..., FSik(S(xk)) D.1.13)
являются взаимно независимыми, равномерно распределенными в
интервале [0,1], если только верна гипотеза Но. Здесь k — числа
групп испытываемых элементов. Задача проверки гипотезы Но све-
свелась к совсем простой стандартной задаче проверки гипотезы о том,
что k случайных точек равномерно распределены в интервале [0, 1].
Этот прием можно использовать, например, для проверки гипо-
гипотезы о показательном виде вероятности безотказной работы
по результатам периодических испытаний на надежность неболь-
небольших групп элементов. Предположим, что испытания /-й группы
'232 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
проводятся по плану [Nh Б, г(]у г{^ 2, /=-. 1, ...,&. Пусть
rt = r\ -f г*, r/rt->0, Sfi,,-, 5^,/, величины суммарной наработ-
наработки в интервалах @, tr>) и (t/, tr.). Используем тот факт, что
случайные величины (TV—k-\-\)(tk — t^-i) взаимно независимы и
имеют плотности вида Ке~м, легко показать, что статистики
D.1.14)
имзют /^распределение с числом степеней свободы, равным 2г\,
2г] и не зависят от величины параметра к. Все эти утверждения
справедливы только в том случае, когда верна гипотеза Яо, т. е.
когда вероятности безотказной работы в /-й группе равны
д. (t) = ?-M. Если обозначить через Fnxt n2(x) функцию распреде-
распределения Фишера с Пц п2 степенями свободы, то для проверки исход-
исходной гипотезы Но нужно проверить, что случайные величины
li к k
взаимно независимы и равномерно распределены в интервале
[О, 1].
Функция мощности критерия. Важнейшей числовой
характеристикой критерия является функция мощности W(ty).
Функция мощности равна вероятности отвергнуть исходную гипо-
гипотезу НОу когда значение параметра, определяющего вид распре-
распределения вероятностей в пространстве исходов испытаний Ху
равно 0. В том случае, когда критерий нерандомизированный,
P{*€*KP|6}. D.1.15)
Если гипотезе Но соответствует множество значений параметров
Но и 0gQo, то W(b) равна вероятности ложного отвержения
гипотезы Ио. В том случае, когда гипотеза Но сложная, т. е. Ио
содержит более одной точки 0, ошибка первого рода а опре-
определяется по формуле
а= sup\F@). D.1.16)
QeH0
Рассмотрим пример. Предположим, что испытания на надеж-
надежность проводятся по плану [А/, Б, Т]. В результате испытаний
регистрируется только число d (T) элементов, отказавших к мо-
моменту Т. Таким образом, пространство исходов испытаний Х =
= {0, 1, ..., N}. Если предположить, что элементы отказывают
взаимно независимо друг от друга, то d (T) — случайная величина,
имеющая биномиальное распределение
c?[l-0]^~rf. D.1.17)
§ 4.1]
ОБЩИЕ ПОЛОЖЕНИЯ ТЕОРИИ
233
Здесь роль параметра 0 играет вероятность безотказной работы
элемента в течение времени Г. Так как 0 ^6^1, то Q = [0, 1].
Пусть гипотеза Ио состоит в том, что вероятность безотказной
работы 0^0о, Q0 = {6^60}, а гипотеза Иг состоит в том, что
6<0о. В качестве критического множества критерия, различа-
различающего эти две гипотезы, возьмем ^YKp = {c + l, с+ 2, .... N).
Таким образом, если d(T)^>c} тогда гипотеза Но отвергается.
б)
Рис. 4.1.2.
если же d(T)^:c, то Ио принимается. Из формул D.1.16) и
D.1.17) получаем, чтЪ функция мощности такого критерия
N
D.1.18)
Легко показать, что функция мощности, задаваемая формулой
D.1.18), является монотонно убывающей (рис. 4.1.2, а). Учитывая
монотонность, из формулы D.1.17) находим, что ошибка первого
рода
п— V СйкЛ\ u)dbN~d /I 1 1 Q\
Если задать величину ошибки первого рода а, то значение числа
с равно наименьшему из целых чисел с', для которых
Другие примеры критериев и их функции мощности даны в §§ 4.3
и 4.4.
В тех случаях, когда параметр 6, определяющий вид распре-
распределения вероятностей, является двумерным, 6 = FХ, 62), удобно
изображать функцию мощности W FX, fJ) на плоскости (бх, 6а) в
-234
ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ
[ГЛ. 4
Биде изолиний W ф1у Ь2)=р, где р пробегает ряд значений, на-
например /> = 0,05; 0,1@,1) 0,9; 0,95 (см. рис. 4.1.2,6). Сравнивая
функции мощности различных критериев, можно отбирать наилуч-
наилучшие критерии. Предположим, что испытания можно проводить по
плану либо типа Пх, либо типа П2. Каждому из этих планов соот-
соответствует критерий. Функции мощности критериев для планов Пх
и П2 равны соответственно W1(b) и W2 F). Если окажется, что для
множества значений параметров Qo, соответствующего исходной
гипотезе #0, мы имеем W2 @) <; W± @), а для 0 ? Qo имеем
а)
Рис. 4.1.3.
W2 F) ^ Wx F) (рис. 4.1.3, а), то критерий для плана П2 лучше,
чем критерий для плана П1. Это следует из того, что вероятности
ошибочного отвержения Яо, когда она верна, или ошибочного
принятия Яо, когда она неверна, меньше у критерия для плана
П2. Если экономический анализ или проверка других показателей
планов Иъ П2 покажет, что они примерно эквивалентны, то надо
использовать план П2.
Рассмотрим числовой пример. Если вероятность безотказной
работы в течение времени t равна е~и, Ь = Х, то, как будет по-
показано в § 4.3, для планов
11! = ^= 20, 5, г = 5] и n2 = [yV-20,?, r =10],
когда Но = {А,^Я0}, Я1 = {Х>Л0}, а ошибка первого рода а —
= 0,05, функции мощности рекомендуемых критериев равны
соответственно
(fy l^a (X) = 1 — /:9 E,425^). D.1.20)
Графики этих функций мощности приведены на рис. 4.1.3. Из
сравнения функций мощности видно, что критерий плана П2 более
эффективен, чем критерий плана Ylv Момент остановки испытаний
для плана Hi совпадает с моментом tb возникновения 5-го отказа,
§ 4.1] ОБЩИЕ ПОЛОЖЕНИЯ ТЕОРИИ 235
тогда как для плана П2 с моментом t10 — возникновения 10-го отказа.
4
Средняя продолжительность испытаний для Пх равна V B0 —
d=o
_яГ)-и-1 = 0,2795 V1, а для П2 равна 2 B0—d)-lK'l=
Таким образом, для более эффективного плана П2 среднее
время испытаний в 2,4. раза больше, чем для плана П^. Если
время испытаний не является ограничивающим фактором, то нужно*
использовать план П2.
Может оказаться, что у различных критериев, соответствующих
разным планам, функции мощности совпадают. В таких случаях
нужно использовать те критерии, у которых лучше другие пока-
показатели, например такие, как среднее время испытания.
Критерий отношения правдоподобия. Для кри-
критериев второй группы, когда вид распределения вероятностей
Pq известен, но неизвестно лишь значение параметра 6, наибо-
наиболее простым является случай простой исходной и простой ко?-
курирующей гипотез. Гипотезы НОУ Нг называются простымиг
когда соответствующие им множества параметров Qo и Qx содер-
содержат только по одной точке 0о, 0х. При этом наиболее важными
показателями критерия являются ошибка первого рода W(b0) и
ошибка второго рода 1 — Wtf^). Ошибка второго рода равна
вероятности ложного отвержения конкурирующей гипотезы Н1У
когда эта гипотеза верна. Одним из возможных подходов к оты-
отысканию оптимальных критериев является следующий. Из всех кри-
критериев с ошибкой первого рода W(Q0) ^ а отыскивается критерий,,
имеющий наибольшую мощность W @^ или наименьшую ошибку
второго рода 1 — ^(Qi). Наиболее фундаментальным в этом от-
отношении результатом является теорема Неймана — Пирсона. Каж-
Каждый критерий можно характеризовать заданием вероятности р (х\
отвержения гипотезы Яо, где х — исход испытаний.
Теорема 4.1 Л (Неймана —Пирсона). Пусть обе гипотезы —
исходная Но и конкурирующая Их являются простыми, а соот-
соответствующие им вероятностные меры имеют плотности р0 (х)
и рг(хI). Тогда имеют место следующие утверждения.
I. Существует критерий для проверки гипотезы Но протиа
гипотезы Нг, задаваемый функцией вероятности отвержения
исходной гипотезы р(х), такой, что ошибка первого рода равна
1) В общем случае это плотности относительно некоторой меры
формулы верны с заменой dx на \i (dx).
236 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
где
, ч j 1, Pi(*)>APo(*). , 1 ft
»<Н о, *(*)<*,.<*>, *>o. DЛ-22)
II. ?с/ш критерий удовлетворяет условиям D.1.21) и D.1.22)
для некоторого k>0, то он является наиболее мощным кри-
критерием для проверки гипотез #0, И1у и ошибка первого рода
равна ос.
III. Если $(х)— наиболее мощный критерий с ошибкой первого
рода, не превышающей а, то для некоторого &>0 выполняется
условие D.1.21). Условие D.1.22) выполнено, если только не сущест-
существует нерандомизированный критерий с ошибкой первого рода,
менъщей а, и нулевой ошибкой второго рода.
Доказательство теоремы Неймана —Пирсона читатель
может найти в книге Лемана [1].
Из формулы D.1.22) следует, что в тех случаях, когда
Р {р1(х) = kpo(x)} = 0, / = 0, 1, наиболее мощный критерий явля-
является нерандомизированным. Критическая область такого критерия
находится из уравнения
{Ш} DЛ-23)
где С подбирается таким, чтобы ошибка первого рода была
равна а. В том случае, когда плотности р0 (х) —р (л:|0о), рх (х) =
= Р (#|9i)» гДе Р (х\®) — параметрическое свойство с достаточной
статистикой S(x), в соответствии с критерием факторизации (см.
§ 1.6), имеем
p(x\Q) = g(S(x), Q)h(x). D.1.24)
Из D.1.23) и D.1.24) получаем, что
}Xc{Q<>>0i)- D-L25)
Таким образом, критическая область для .наиболее мощного кри-
критерия выражается через достаточные статистики.
Мы скажем, что из двух критериев Кх и К2 с функциями
мощности №^(9), W2 @), имеющих одинаковые ошибки первого
рода, критерий Кг равномерно более мощный, чем критерий /С2,
если
Wr1(9)>Wra(9), 9 g Qlf
причем Wx (9) >> W2 (9), хотя бы для одного значения 9. Если
критерий К.г равномерно более мощный, чем любой другой кри-
критерий с той же ошибкой первого рода, то он называется равно-
равномерно наиболее мощным. Как правило, равномерно наиболее мощ-
мощные критерии не существуют. Однако для того частного случая,
когда вероятность безотказной работы R(t)=e~li и используются
§ 4.1] ОБЩИЕ ПОЛОЖЕНИЯ ТЕОРИИ 237
планы типа В или планы [Л/, ?, г], равномерно наиболее мощные
критерии существуют. Подробное изложение этих критериев дается
в § 4. 3. Достаточные условия существования равномерно наиболее
мощного критерия дает
Теорема 4. 1. 2. Если критическая область Хс (90> ^i)» за~
даваемая формулой D.1.25), не зависит от значений пара-
параметра 0lf то равномерно наиболее мощный критерий существует.
Так будет в том случае, когда
? Dл-26)
где f (у) —неубывающая или невозрастающая функция от у.
В ряде случаев оказывается полезным использовать б ей ее о в-
с к и е критерии, основанные на понятиях функции риска и апри-
априорных вероятностях. За подробным изложением теории мы отсы-
отсылаем читателя к литературе, посвященной решающим функциям
[2], [3], [12], [13], [14]. Два частных примера бейесовских крите-
критериев, построенных для задач проверки гипотез о значениях пара-
параметра X экспоненциального распределения рассмотрены в § 4. 4.
Там же даются определения функции риска и априорных вероят-
вероятностей.
Сравнениевероятностей безотказной работы эле-
элементов двух типов. В заключение параграфа рассмотрим
задачу сравнения вероятностей безотказной работы двух типов
элементов или систем. Предположим, что были выпущены две опыт-
опытные партии элементов. Объем первой партии Nv объем второй —
N2. Элементы испытывались в одинаковых условиях в течение
времени Т. Предположим также, что отказы происходят независимо
друг от друга и в первой партии отказало dx элементов, а во вто-
второй d2. Допустим, что основным показателем надежности яв-
является R( (T) — вероятность безотказной работы элемента /-й партии в
течение всего времени испытаний. Требуется построить критерий,
в соответствии с которым можно было бы проверять или отвергать
гипотезу Но о том, что Rl(T)=R1(T). Если гипотеза Но отвер-
отвергается, то принимается одна из двух конкурирующих гипотез
^i = {Ri(T)<R2(T)} иди hT2 = {Rl(T)>R2(T)}. Ошибка первого
рода аяне должна превышать заданного значения. Пространст-
Пространство исходов опыта Х={х} состоит из точек x==(dx, d2),
^• = 0,1, ..., N{. Для определенности мы будем считать, что
Nx ^ N2. В противном случае вторую партию будем называть первой.
Случайные величины йъ d2 взаимно независимы и имеют бино-
биномиальное распределение. Вероятность появления исхода (d^ d2)
задается формулой
Р {* = (<*!, rf,)}- П С#Л1-#/(Г)]"'?1.(Г)м. D.1.27)
1 = 1, 2
238
ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ
[ГЛ. 4
Роль множества параметров И играют пары R\{T), R2(T)y
О s^R; (Г)«^1. Гипотезы /Уо, Hv Н2 показаны в виде подмно-
подмножеств Н на рис. 4.1.46, а исходы испытаний (dly d2)— на рис. 4.1.4а.
Для построения критерия с уровнем значимости, или ошибкой
первого рода, не превышающим а, будем поступать следующим об-
образом. Из формулы D.1.27) и критерия факторизации следует,
что d = d1-{- d2 является достаточной статистикой, когда верна
\s
NS*
\
\
\
о о о о о
ч v N
о_о_о—\_o_o_
\ \ \ПрицимЬтьНп/
х_о_о_0_0_5^
\о_\о_\ _\ >С \ Принимать п7
о о —о о о—о
а)
Рис. 4.1.4а.
гипотеза Но. Из формулы условных вероятностей и D.1.27) име-
имеем, что
Р{*-
' DЛ-28)
если только верна гипотеза Ио. Из формулы D.1.28) видно, что
эти условные вероятности выражаются через вероятности гипер-
гипергеометрического распределения, свойства которого подробнее рас-
рассмотрены в главе 7. Замечая, что Р{д: = (^1, d2)\d1 + d2 = d} не
зависят от значения R1(T)=R2(T), будем включать в критическое
множество Хкр точки @, </), A, d—1), ..., (d\ d — d') и точки
(d\ d — d"), (d"+l, d — d"— 1), ..., (d, 0), для которых
d'
d, dt=d
D.1.29)
§ 4.11
ОБЩИЕ ПОЛОЖЕНИЯ ТЕОРИИ
239
Если верна гипотеза #0, то вероятность Ро попадания в крити-
критическое множество с учетом D.1.27) — D.1.30) не превышает а.
Действительно, при любом значении
Ро=
rfo
?x (Г) =
D.1.30)
Критерий с уровнем значимости, не превышающим а, для проверки
гипотезы #() = {/?! (Т) =/?2 (Л) против конкурирующих гипотез
#! = {#! (Г) < #2 (Л} и Я2 = {/?! (Т) >/?2 (Т)} описывается следую-
следующей системой правил. Если результаты испытаний задаются парой
/
(йъ d2), то из формул D.1.29), D.1.30) находятся значения d' и
,*Г. Если окажется, что d' <.d1<.df\ то гипотеза Но принимается.
В том случае, 'если dx^d', то гипотеза Но отвергается и при-
принимается гипотеза Нг; если же dx ^ d", то Но отвергается и при-
принимается гипотеза Я2. При испытаниях высоконадежных элементов
вероятность отказа к?(Т) невелика. В таких случаях оказывается,
что д/<^1, если только Ni велико. Получение значений d' и d"
по формулам D.1.29), D.1.30) связано с большим количеством
вычислений. Замечая, что в том случае, когда
240 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
из D.1.28) получаем приближенную формулу
• D.1.31)
Таким образом, гипергеометрическое распределение заменяется
биномиальным. Если ввести обозначения bdl (р) ==- Cddxpdx A—p)d~d\
то согласно D.1.31) можно вместо D.1.29), D.1.30) использовать
для нахождения d\ d" уравнения
d'
р'= S
bd/(p)y D Л .33)
dt+d2=d, dt=d"
где /? = д. г^ , TVj^yVg. В таблице 9 приложения приведены
числа дГ, d", найденные исходя из биномиального приближения для
случая, когда а = 0,1, a d1-\-d2 = 0 A) 30.
В том случае, когда dx, d2 велики и отношения тг >0,1, мож-
но воспользоваться тем фактом, что частоты ^ имеют распреде-
распределение, близкое к нормальному. Здесь удобно использовать пре-
преобразование у = 2 arcsin ]/~x, таблицы которого имеются в книге
у г^, /=1, 2,
Я. Янко [4]. Можно показать, что ??. =2 arcsin у г^, /=1, 2, име-
имеют распределение, близкое к нормальному, со средними, равными
2 arcsin ]/[1—R((T)], и дисперсиями, равными^. Так как эти
случайные величины взаимно независимы, то их разность в том случае,
когда верна гипотеза Но, будет иметь нормальное распределение со
средним, равным нулю, дисперсией, равной дт~+^7 ^
iV х IV 2
Отсюда следует, что случайная величина
Q(dlt rf,)= (
2 arcsin }/^-2 arcsin |/^
имеет распределение, близкое к нормальному, с нулевым средним
и единичной дисперсией. Таким образом, если Rx (Г) =#2(Г), то
§ 4. 2] ПРОВЕРКА ПОКАЗАТЕЛЬНОСТИ РАСПРЕДЕЛЕНИЯ 241
где и а — квантиль нормального распределения. Полученный при-
приближенный критерий состоит в том, что гипотеза Ио — [Rx (T) =-R2(T)}
отвергается всякий раз, когда \Q(dly d2) \ > и а.
2
Проиллюстрируем использование таблицы 10 приложения на конк-
конкретном примере. Испытывались две партии элементов. В первой
было 500 элементов, из которых отказало 5, во второй —250, от-
отказало 10. В наших обозначениях /^ = 250, iV2 = 500, dl = \0i
^2 = 5, -д. * = -^ . Из таблицы 10 приложения для значения
^ = ^4-^2=15 находим, что rf' = l, d" = 9. Так как dx = 10 >
;>d" = 9, то гипотеза о равенстве вероятностей R; (Т) безотказной
работы отвергается и принимается гипотеза Я2 = {R1 (T)< R2 (Г)}.
§ 4.2. Проверка гипотезы о показательности распределения
времени безотказной работы
В § 4.3 описаны критерии, которые позволяют эффективно раз-
различить гипотезы о значениях интенсивности X испытываемых эле-
элементов или системы. Эги критерии существенным образом основы-
основываются на гипотезе, состоящей в том, что вероятность безотказной
работы в течение времени / равна е~п. При этом же допущении
верны формулы точечных и интервальных оценок, приведенные
в §§ 3.3 и 3.4. Возникает задача проверки гипотезы, что вероят-
вероятность безотказной работы R (t) = e~lt.
Ниже приводится набор критериев для проверки этой гипотезы.
Многообразие приводимых ниже критериев необходимо по существу
дела. Действительно, в качестве конкурирующих гипотез к исход-
исходной гипотезе R (t) = e~lt могут встретиться различные распределения
(например, распределения Вейбулла, логарифмически показательное
и др.; см. главу 1. Каждый конкретный критерий может с большой
достоверностью, при ограниченном количестве данных об испытаниях
.на надежность, различать показательное распределение только от не-
некоторого числа других распределений. Таким образом, могут встре-
встретиться такие конкурирующие распределения времени безотказной
работы, которые существенно отличаются от показательного распре-
распределения. Тем не менее результаты обработки данных в соответствии
с использованным критерием будут ложным образом согласовываться
с гипотезой о показательном характере вероятности R (t) безот-
безотказной работы. Чтобы избежать таких ошибок, рекомендуется
проверку гипотез о показательности проводить по нескольким
критериям. Ниже приводится набор ряда критериев для проверки
гипотезы R (t) = e~}t. Авторы существенно использовали обзорную
работу Эпштейна [5].
9 Б. В. Гнеденко и др.
242 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
Показательная бумага. Используя общий подход для
построения вероятностных бумаг, изложенный в § 4.2, можно постро-
построить показательную вероятностную бумагу. На этой бумаге семей-
семейство функций распределения
1 _*-><«-«> при <>Д|
О при t<a D'2Л)
представляется в виде полупрямых у = К (х — а), х^а. Для по-
построения бумаги используется тот факт, что при отображении
x = t, у~ —In A—F) точек полу полосы (t, F), t^a, O^F^l,
в точки плоскости (х, у) линии вида (/, F(t))} где F (t) задается
по формуле D.2.1), переходят в полупрямые у ~ X (х — а), х^а.
Показательное распределение получается в частном случае, когда
# = 0. По теореме Гливенко эмпирическая функция распределе-
распределения должна проходить вблизи теоретической функции распределе-
распределения. Строя изображение эмпирической функции распределения,
нужно в случаях существенного отклонения ее графика от луча
прямой у = Хху х^О, проходящей через начало координат, от-
отвергать гипотезу о показательности распределения. При этом по-
полезно иметь в виду, что трехпараметрическое семейство распре-
распределений Вейбулла, для которого
?~д)р при t^a} D 2 2)
при t < а,
дает на показательной вероятностной бумаге линии вида у =
= k(t—а)р. На рис. 4.2.1. показаны графики этих линий; случай
/ соответствует р>1, слу-
случай П—р=\ и случай
/// —р < 1. Следуя качествен-
качественной картине, изображенной
на рис. 4.2.1, нужно отвергать
гипотезу, состоящую в том,
что функция распределения
имеет вид D.2.1), в пользу
гипотезы о виде, задаваемом
формулой D.2.2), когда эм-
эмпирическая функция распре-
распределения, нанесенная на вероят-
вероятностную бумагу, имеет выпуклость вверх (р<1) или вниз (р>1).
Построение эмпирической функции распределения производится
различными способами в зависимости от типа используемого пла-
плана испытания.
Если испытания N элементов проводились по плану типа Б, а
наблюдаемые моменты отказов оказались равными t1} t2} ..., tdy
§ 4.2] ПРОВЕРКА ПОКАЗАТЕЛЬНОСТИ РАСПРЕДЕЛЕНИЯ 243
то первый способ построения состоит в том, что эмпирическая
функция задается формулой
Fil(t)=d-P, D.2.3)
где d (t) — число отказов, происшедших до момента t. При таком по-
построении нам известна лишь часть эмпирической функции распре-
распределения, если d<ZN. В случае использования второго способа вычи-
вычисляются значения Si суммарных наработок в интервалах между отка-
зами, S^Nt» S2 = (W-1) №,-*!), ...,^ = (W-tf+D(^-^-i).
Выше было показано, что ^. — взаимно независимые величины,
имеющие функции распределения вида D.2.1), где а = 0. Эмпири-
Эмпирическая функция строится по формуле
f D.2.4)
где d(s) — число St <s, a d — общее число наблюденных отказов.
При испытаниях типа В также можно использовать эги способы.
В первом способе учитываются только моменты t1, t2, ..., td
первых отказов, т. е. если в /-й стендовой ячейке в начале испы-
испытаний стоял элемент, который отказал в момент tiiy то моменты
отказов последующих элементов, поставленных в эту ячейку, не
учитываются. С учетом моментов tly ..., td эмпирическая функ-
функция строится по формуле D.2.3) При втором способе учитываются
все моменты отказов t1} ..., td. Так как в случае планов типа
В поток моментов отказов — пуассоновский с итенсивностью NX,
то случайные величины S1 = Nt1, S2 = N {t2 — t1I ...,
Sd = N(td—td_^) имеют функции распределения вида D.2.2),
где а = 0. Эмпирическая функция распределения строится по фор-
формуле D.2.4).
Мы привели эти способы построения потому, что каждый из
них в разной мере чувствителен к различным конкурирующим ги-
гипотезам. Графики, показанные на рис. 4.2.1 для гипотезы вида
D.2.2) относятся только к первому способу построения.-
Пример. Пусть испытания проводились в соответствии с пла-
планом [N=49,3, 7V=49]. Моменты отказов испытываемых элементов
приведены в таблице 4.2.1; см. также [5].
• Для построения эмпирической функции можно воспользоваться
формулой D.2.3). Заметим, однако, что планов типа [А/', Б, г]
J если /<r, f(/) = l—<?-4 У нас план [N, Б, N],
поэтому вместо формулы C) можно использовать несколько видо-
видоизмененную формулу
№«)=?$, td<t<td+1. D.2.3')
9*
244
ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
Таблица 4. 2. 1
...
! 2,2
4,9
5,0
6,8
7,0
1 12,1
13,7
15,1
15,2
23,9
24,3
25,1
35,8
38,9
47,9
48,4
49,3
53,2
55,6
62,7
72,4
73,6
76,8
83,8
95,1
97,9
99,6
102,8
108,5
128,7
133,6
144,1
147,6
150,6
151,6
152,6
164,2
166,8
178,6
185,2
187,1
203,0
204,3
229,5
253,1
304,1
341,7
354,4
Вычисляя значения /.-= —In 1 — N_. A , строим на показательной
вероятностной бумаге график эмпирической функции. Вид полу-
полученного при этом графика показан на рис. 4.2.2. Согласие с гипо-
гипотезой о показательном характере распределения очень хорошее.
Критерий %2 для проверки показательности. Огра-
Ограничимся двумя примерами использования критерия %2 для провер-
проверки показательности. Пусть испытания проводились в соответствии
с планом [Ny Б, Т]. Наблюдаемое число отказов велико (d(t)^20).
Пусть tly ..., td(t) суть моменты отказов. Как уже указывалось
в главе 2, случайные величины со.= J5 ,Д , где SB(t) — значение
суммарной наработки к моменту /, образуют вариационный ряд
d (t) взаимно независимых равномерно распределенных в интервале
[0, 1] случайных величин. Разобьем интервал [0, 1] на k равных
частей; тогда из d (T) точек со. в среднем в каждый из k интер-
интервалов попадает по -~-^ точек. Пусть di — фактическое число то-
точек со,-, попавших в 1-й интервал. Как известно (см. § 1.6), статис-
статистика
k di—7-
D.2.5)
§4.2]
ПРОВЕРКА ПОКАЗАТЕЛЬНОСТИ РАСПРЕДЕЛЕНИЯ
245
имеет распределение, близкое к f с (k—1)-й степенью свободы,
если только числа di достаточно велики. Гипотеза о показатель-
показательности распределения отвергается с уровнем значимости а, если
окажется, что YT >Xi-a (*— !)• Если используется план [N, Б> г],
то значения суммарных наработок Sb (^) можно рассматривать как
значения /•—1 взаимно независимых случайных величин, равномер-
равномерно распределенных в интервале [0, 5(/г)]. Если обозначить через
, /
3,0
2,0
In
1-F.Jt)
700 200
Рис 4.2.2.
JOO t vac
Ц- , /=1, 2, ..., г—1, а через dt — число точек со,,
1Ш
попавших в интервал , -г-1 , то статистика
D.2.6)
имеет распределение, близкое к %2У c(k—1)-й степенью свободы,
«ели только dt достаточно велики.
формулы, аналогичные D.2.5) и D.2.6), применимы и для пла-
планов типа [7V, В} Т]. Надо только учесть, что при использовании
плана [TV, В, Т] 0),. = —-, а при использовании плана [N, В, г] a>i =
t=-i. э /=1, 2, ..., г—1, где t{ — моменты отказов. Если испыта-
ния проводились по плану [Ny Б, (г, Т)] или [N, В, (г, Г)], то фор-
формула D.2.5) используется, когда tr>T, а формула D.2.6) — ког-
Да t < Т.
246 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
Подробный обзор общих вопросов, связанных с использованием
критерия %2, излагается в работе Кохрана [6]. Таблица значений
квантилей у?р (k) дана в приложении 4.
Критерий Колмогорова. Как и обычно, SB(t) и SB(t)
равны значениям времени суммарной наработки при использовании
планов типа Б и В. Если t* — момент остановки испытаний,
d = d(t*) — общее число наблюдаемых отказов, то при использо-
использовании планов [TV, Z>, Т], [N, Б, г] точки
"'-SiW < = *. 2, ...,*(Г); «, = !§$, :/ = 1, ..,К
D.2.7)
образуют вариационный ряд, соответствующий независимой выбор-
выборке объема d(t*)} равного ^(Т)или г—1, из равномерно распре-
распределенных в интервале [0, 1] случайных величин. При использовании
плана [N, Б, (г, Т)] аналогичными свойствами обладают точки со,.,
которые вычисляются по левой формуле D.2.7), когда tr > Г, и
по правой, когда tr<C Т. Аналогичные вариационные ряды образуют
точки
Ю/ = ^, /=1, 2, ..., d(T); ©, = ?, /=1, 2, ..., г~1, D.2.8)
которые вычисляются при использовании планов типа [N, Ву Г],
[N, В, г], [ЛГ, Б, (г, Г)]. Таким образом, теоретическая функция
распределения /7(со) = со, O^co^l, а эмпирическая функция
^эмп(со) = ~, ©^ <©<©,.+!, D.2.9)
где rf* либо равно d(T), если ^*=Г, либо d* = r—1, если ^* = г.
А. Н. Колмогоров исследовал асимптотическое поведение
Dd*= sup | Пмп (со) — со | = max ijtli —a). , ~ — ©. II.
0<@<l l</<rf* U в d \)
D.2.10)
Он показал, что
при ;;<0,
/е=- со
D.2.11)
Значения функции К(у) даны в таблице 15 приложения.
Впоследствии были вычислены некоторые квантили случайных
величин Dn, задаваемых формулой D.2.10). В таблице 16 прило-
приложения даны значения Dna, a = 0,2; 0,1; 0,05; 0,02; 0,01 и
п—\ AI00. Числа Dn(X удовлетворяют условию
}=<х. D.2.12)
§ 4.2] ПРОВЕРКА ПОКАЗАТЕЛЬНОСТИ РАСПРЕДЕЛЕНИЯ 247
Критерий Колмогорова для проверки экспоненциальности времени
распределения состоит в следующем. В зависимости от типа ис-
используемого плана по формулам D.2.7) и D.2.8) вычисляются зна-
значения точек со-. Затем по формуле D.2.10) находится значение
Д/*. Если yV*>100, то производится нормировка умножением на
У d*'. Гипотеза о показательном характере вероятности безотказ-
безотказной работы отвергается с уровнем значимости а, если ]/"d* Dd* >
>/С1_а; здесь K(kp)=py т. е. kp—квантиль уровня р для распре-
распределения Колмогорова. Если d*^ 100, то производим сравнение с
числами Dn(X таблицы 16е приложения. Гипотеза о показательном
характере распределения отвергается с уровнем значимости 1—а,
если Dd*>Dd*,a\ в противном случае эта гипотеза принимается.
Критерии, основанные на однородных статисти-
статистика х со и v. Пусть tv t2, ..., td—моменты отказов, зарегистри-
зарегистрированные при испытаниях. Мы назовем статистику f = f(tly ..., td)
однородной, если ее значение при любом Х>0
f(Xtv ..., Md)=f(tl9 ...,*,)• D.2.13)
Из условия D.2.13) следует, что в том случае, когда вероятность
безотказной работы имеет показательное распределение, распреде-
распределение статистики /(/1} ..., td) не зависит от А.. Если заранее рас-
рассчитать таблицу квантилей fdp таких, что
то можно строить критерии для проверки показательности. Кри-
Критерий, соответствующий уровню значимости а, состоит в том, что
гипотеза о показательном характере отвергается, когда />/^, i-aj
и принимается, когда f^fd, i-a- В сущности, все критерии на-
настоящего параграфа построены по этому принципу. Однако здесь
мы ограничимся только указанием на две статистики: со и г;. Эти
статистики задаются формулами
2 К— 7| _
©=^~—, « = f, D.2.14)
2пх s
п п
где jF== —^#,., s2 = \4^(Х1—хJ- Статистику со называют
статистикой Шермана [7], [8]. Если вместо xt подставить зна-
значение суммарной наработки в интервале между (/ — 1)-м и 1-м
отказами, то легко убедиться, что обе статистики удовлетворяют
условию однородности, и их можно использовать для проверки
гипотезы об экспоненциальности. Авторам неизвестны таблицы
248 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
квантилей или функций распределения этих статистик. Можно
показать, что в том случае, когда значения — х{ суть взаимно не-
независимые случайные величины с функцией распределения F(t)
= 1—e~fy то при п—*оо двумерный случайный вектор
имеет нормальное распределение со средними, равными нулю, и
матрицей ковариаций Цс-уЦ, сп = 1, с22 = 8, с12 = с21 ~2. Исполь-
х
зуя асимптотическую лемму из § 1.6, где И(хуу)= -т^-, полу-
У у
чаем, что
НтРК<1+^}«174= \e~dz. D.2.15)
— 00
Таким образом, если окажется, что п^>\ и | \fn (vn—\)\>иау
2
где иа—квантиль нормального распределения, то гипотезу о
2
показательном виде вероятности безотказной работы надо отвер-
отвергнуть. Барфоломью [8] исследовал сравнительную асимптотическую
эффективность критериев, основанных на статистиках о) и vy
когда роль конкурирующих гипотез играли Г-распределения и
распределение Вейбулла. Однако эффективность понималась в бо-
более узком, локальном смысле, когда значения параметров Г-рас-
Г-распределения и распределения Вейбулла изменялись таким образом,
что эти распределения в пределе давали также показательное
распределение.
F-к ритерий для проверки постоянства функции
опасности отказов. Как известно (см. главу 2), утверждение,
состоящее в том, что вероятность безотказной работы R (t) = e~Kty
эквивалентно условию, что функция опасности отказов X (t) =
= — D /./ = X. В качестве конкурирующих гипотез можно рас-
яг {I)
сматривать такие, для которых X(t) является либо монотонно
убывающей, либо монотонно возрастающей функцией от t. Пусть
испытания проводятся в соответствии либо с планом [N, Бу г], ли-
либо с планом [N, В, г]. В первом случае подсчитаем значения
$. (/ = 1,2, ...,г) суммарной наработки между отказами по фор-
формулам si = (N — i + 1) (tfj—-*,-_!), ^о^ 0» i = Ь ...,>% во втором слу-
случае— по формулам si = N(ti — ^-_i). В обоих случаях sc — взаимно
независимые случайные величины с функциями распределения, рав-
равными 1—e~Kt. Отсюда следует, что 2\s{ имеет ^-распределение
с двумя степенями свободы. Пусть г~г1-^-г2, где г1>0, г2>0;
§ 4.2] ПРОВЕРКА ПОКАЗАТЕЛЬНОСТИ РАСПРЕДЕЛЕНИЯ 249
тогда из формулы 4.1.9 следует, что случайная величина
'.2«/
<?(rvr,) = ^— D.2.16)
'1/и2+1-<
имеет /^-распределение с числом степеней свободы v1 = 2r1, v2 =
= 2г2. Пусть fp(vlt v2) — квантиль /^-распределения, соответствую-
соответствующий уровню р.
/^критерий, соответствующий уровню значимости 1—а, с ну-
нулевой гипотезой H0 = {h(t) = K} против конкурирующей гипотезы
Нг = {h(t) ^= const, h(t) либо возрастает, либо убывает} описыва-
описывается следующей системой правил.
Гипотеза Ио принимается, если
V (/"!, га) = max {ф (г1э г2), [ф 1
Г1> г2)</ _а (rlf Г3),
1 2" D.2.17)
в противном случае эта гипотеза отвергается. Если окажется, что
^(ri» гг) ^Ф (ri> Г2) >/ а (гх, г2), то принимается конкурирующая
гипотеза, состоящая в том, что Я (/) убывает, если же я|? (гх, г2) =
= [ф(г1? Га)] >/ а (/*2» ri)> T0 принимается конкурирующая ги-
гипотеза, что Я (/) возрастает.
Рассмотрим численный пример. Пусть испытания проводились
в соответствии с планом [N=100, Б, г = 6]. Моменты отказов ока-
оказались равными t1 = 3y ^2=10, ^g^^O, ^4 = 34, tb = 48, te — 70.
Значения суммарных наработок соответственно равны ?х = 300,
тогда
П оч_ 300 + 693 + 980 ^ngv-x
(P^' 6)~ 1358+ 1344 + 2090 ^ ^>D) *
Так как ф<1, то г|) C, 3) = [ф C, З)]» 3,5. Из таблицы, анало-
аналогичной таблице 11 приложения, находим, что /0>в F,6) = 3,055 <С
<[ф C,3) = 3,5; таким образом, гипотеза Но должна быть отверг-
отвергнута, если уровень значимости 1—а = 0,9. Заметим, однако, что
/о,95 F,6) =4,284. Таким образом, если бы был выбран уровень
1 — а = 0,95, то гипотезу Но следовало бы принять. Как же по-
поступить, если очевидно, что выбор а = 0,1 весьма условен?
Можно рассуждать следующим образом. Налицо имеется тен-
тенденция к уменьшению функции опасности отказов h(t). Однако
250 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
количество данных, полученных в результате испытаний, явно не-
недостаточно. Образно говоря, испытания были прекращены «в са-
самом интересном месте». Решаем продолжить испытания до г = 10.
В результате продолжения испытаний имеем ^7=Ю8, ^8 = 147,
/9 = 204, /10 = 264. Значения соответствующих суммарных нара-
наработок равны s7 = 3572, s8 = 3627, s9 = 5244, slo = 6OOO. Пусть те-
теперь гх = 5, г2 = 5. Здесь ф E,5) = D,4)"; таким образом, ф E,5)^^
«4,5. /о,975 A0,10) = 3,717 < 4,5, поэтому гипотезу H0 = {k(t) =
= X} следует отвергнуть в пользу гипотезы, что X(t) является
монотонно убывающей функцией. Степень уверенности в отверже-
отвержении гипотезы Ио резко возросла.
Критерий х2 для проверки постоянства функции
опасности отказов. При описании критерия Колмогорова
отмечалось, что в том случае, когда верна гипотеза Ио = {X (t) =
= Х>0}, точки (о,-, / = 1, ..., d*, рассчитанные по формулам
D.2.7) или D.2.8), можно рассматривать как вариационный ряд
из */* взаимно независимых случайных величин ?1? ..., 2^*, каж-
каждая из которых имеет равномерное распределение в интервале
[0, 1]. Так как — 2\n^>i имеет %2-распределение с 2 степенями сво-
свободы, то
d* d*
yd*= — 2 2 111©,. = —2 2 Ing, D.2.18)
имеет Х2-распределение с 2d* степенями свободы. Если используется
план одного из типов [А/, Б, г], [N, Б, Т\, [N, В, г] и т. п., то по
соответствующей формуле D.2.7) или D.2.8) мы можем найти зна-
значения точек со,., а затем по формуле D.2.18) подсчитать значение
статистики уа*. Если окажется, что (a) yd* > X2 а Bа?*) или (б)
yd* <%2а B*/*), где ll Bd*) — квантили уровня р для Х2-распреде-
ления с 2d* степенями свободы, то гипотеза Ио= {X (t) —-X} отвер-
отвергается и в случае (б) принимается гипотеза, что X (t) монотонно
возрастает, а в случае (я) —что X(t) монотонно убывает. Эпштейн
в своей статье [5] рекомендует также использовать известный кри-
критерий Бартлетта для проверки постоянства дисперсий D??-.
Критерий Фишера для проверки совместимости
гипотезы о показательности с наличием большого
интервала между отказами. Иногда может оказаться, что
один из испытываемых элементов работает безотказно в течение
очень большого интервала времени испытания. Может также слу-
случиться, что при испытаниях системы встретится один очень боль-
большой интервал безотказной работы. Излагаемый ниже критерий
Фишера [9] может быть использован для проверки совместимости
§ 4.2] ПРОВЕРКА ПОКАЗАТЕЛЬНОСТИ РАСПРЕДЕЛЕНИЯ 251
наличия такого интервала с гипотезой о показательном характере
распределения времени безотказной работы.
Статистика
max
^<?2 D.2.19)
2*/
является однородной. Следовательно, если х{ взаимно независимы
и имеют показательное распределение F(t) = \ — e~Kt, то распреде-
распределение г\п не зависит от К. Фишер [9], показал, что
Р{П„>?}= 2(-1)*-1С*A-й§У1-1. D.2.20)
В таблице 13 приложения даны значения ga(n), a = 0,05, такие, что
Р{Л»>?(л)}=а, л = 5EM0.
Как уже неоднократно указывалось выше, при использовании
планов, в которых момент остановки t* = tr или t* = Г, значения
времени Si суммарной наработки в интервалах (//-i, t^ между двумя
последовательными отказами — взаимно независимые случайные вели-
величины с функциями распределения, равными 1—е~^. Из этого сле-
следует, что при выполнении гипотезы Ио = {к (t) = X > 0}
max 5/
1 < i < d*
>ga(d*)
d(t*) = d* V=a, D.2.21)
где 5* — значение суммарной наработки к моменту t* остановки
испытаний и flf* = r, если t* = tr; если t* = T, то S* = 5 (ta (т)) и
d* — d(T). Значения ?,. вычисляются по формулам
(Af—/+1)(^—J^) для планов типа Б,
N (ti — ti_1) для планов типа В.
Критерий Фишера, соответствующий уровню значимости а,
состоит в том, что гипотеза Ио == {X (t) = Я> 0} отвергается, когда
max -^г> ga{d*)\ в противном случае гипотеза Но принимается .
Рассмотрим числовой пример на использование этого крите-
критерия. Предположим, что производится регистрация отказов, возни-
возникающих в цифровой вычислительной машине. Результаты регистра-
регистрации оказались следующими: ^=16, t2:=39y t3 = 45, t4^55t
*5 = 305, ^в = 319, ^7 = 325, /8 = 345, *9 = 376, tlo = 420. Поскольку
испытывается один образец и возникающие отказы устраняются, то
в соответствии с полученными данными можно считать, что испыта-
испытания проводятся по плану типа [N= 1, В, г = 10]. По формуле D.2.22)
252 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4-
находим, что ^=16, 52=13, 53 = 6, S4=10, 5б = 250, 5в=14,
S7 = 6, S8 = 20, S9 = 31, Slo = 44. Вычисляя статистику, входящую
под знаком вероятности в формулу D.2.21), получаем, что
max 5/
1 < i < 1 о 250 п - п /1 л\
S(tu) =^0 = 0'59>g<M>"(l0>;
таким образом, гипотеза о показательном характере распределения
интервалов должна быть отвергнута.
Появление большого интервала между отказами может быть
связано с тем, что гипотеза //0 = {X (t) = X >0} не имеет места.
Но ведь могут быть и другие неожиданные причины. В данном
случае оказалось, что работник, регистрировавший отказы, ушел
в отпуск, в течение которого отказы не регистрировались. Этот
пример поучителен тем, что привлекает внимание исследователей
к необходимости более тщательного предварительного анализа
достоверности полученных данных.
Критерий Хартли для проверки совместимости
гипотезы о показательности с наличием большо-
большого и малого интервалов между отказами. Для проверки
совместимости наличия малого и большого интервалов между
отказами можно использовать критерий, предложенный Хартли [10].
Хартли изучил распределение однородной статистики
max X{
1 < / < а
где хъ .. ., хп — взаимно независимые случайные величины, имеющие
^-распределение с г степенями свободы. Для различных значе-
значений г, п им были подсчитаны таблицы квантилей hi-a(r, л), для
которых
Р{А(г, /i)>A1-a(r, п)} =а,
где а = 0,05, а = 0,01. Таблица 12 значений этих квантилей дана
в приложении. Если обозначить через 5?- значения суммарных нара-
наработок, вычисленные по формулам D.2.22), а через */* —число отка-
отказов, происшедших за время испытаний, то статистика
max S[
h B, d*) = i<i<d\ D.2.24)
x ' ; mm S( \ • f
Ki<d*
имеет распределение, совпадающее с распределением статистики,
задаваемой формулой D.2.23), когда г = 2, n = d*. Это непосред-
непосредственно вытекает из того факта, что 2X5,- взаимно независимы и
имеют Х2-распределение с двумя степенями свободы. Таким образом,
§ 4.3] КРИТЕРИИ ПРОВЕРКИ ГИПОТЕЗ 253
применительно к задаче проверки гипотезы об экспоненциаль-
экспоненциальном характере вероятности безотказной работы критерий Хартли,
соответствующий уровню значимости а, описывается следующей
системой правил. Если значение статистики, вычисляемой по фор-
формуле D.2.23), таково, что h B, d*) >Лх_а B, a(*), то гипотезу
Ио = {К (t) = К >0} следует отвергнуть. В противном случае эта
гипотеза проверяется. Заметим, что было бы полезно иметь значе-
значения квантилей ha B, п) для малых значений а = 0,05 @,01), так как
тогда можно было бы проверять гипотезу Но, когда роль конкури-
конкурирующей гипотезы играют распределения, близкие к регулярным.
§ 4.3. Критерии проверки гипотез о значениях параметра
показательного распределения
Предположим, что вероятность безотказной работы мож.чо счи-
считать равной е~и, где Х^О — неизвестное нам значение пара-
параметра X. В задачах теории надежности наибольший интерес пред-
представляет проверка сложных гипотез вида Ио = {X ^Хо}, Нх = {Х>Я0},
где XQ — фиксированное значение параметра. Значение Ко
задают таким образом, что при Я ^ Ло продукцию (элементы, сис-
системы и т. п.) можно считать надежной, а при значениях Х^>Х0—
ненадежной или недостаточно надежной. Можно предстазить и более
общую постановку вопроса, когда имеется несколько гипотез, напри-
например //о = {А<^о}, Н'1 = {к0<1<\1}, и'2 = {1^Хг}. Здесь н'о
соответствует высоконадежным элементам, и[ — элементам средней
надежности, а /72 — элементам с низкой надежностью. Мы ограни-
ограничимся только случаем построения критериев для проверки двух
гипотез Но~ {%^Х0}, Я1 = {Х>Я0}. При этом критерии будут
строиться на основе теоремы 4.1.1 (Неймана — Пирсона). Вид кри-
критерия существенным образом зависит от плана, в соответствии
с которым производятся испытания на надежность. Будем считать,
что в начальный момент испытываются N элементов. Одна из весьма
общих схем планирования испытаний состоит в том, что заранее
задается система правил, определяющих момент t* окончания испы-
испытаний. При этом предполагается, что момент окончания испытаний
зависит от моментов отказов элементов ti ^ /*, т. е. t* — величина, не
зависящая от будущего. В этом случае достаточными статистиками
будут d (t*) — число отказавших к моменту остановки t* элемен-
элементов и 5 (t*) — суммарная наработка. Для планов типа В (см. главу 3)
SB(t*) = Nt*, D.3.1)
а для планов типа Б
$б (П - tx + . . . + /</«*) + [ЛГ- d (t*)} t\ D.3.2)
254 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
Пространство Х={х) исходов опыта состоит из последовательно-
последовательностей моментов отказов ti^:t*i происшедших ранее момента оста-
остановки, т. е. x = (tly .. ., td(t*)y t*). Соответственно функция правдо-
правдоподобия при использовании планов типа В задается соотношением
Р (*i, . • •, idwb ** | М = №)««*> е-^в(Пf D.3.3)
где SB(t*) находится по формуле D.3.1). В случае применения пла-
планов типа Б
p{h, ...,tcnn, **\Ц =
= Х"«*>ЛГ(ЛГ—1) _ [N_d{t*) + \]e-^Bint D.3.4)
где SB (t*) находится по формуле D.3.2).
Из D.3.3) и D.3.4) получаем, что отношение правдоподобия
|
$ = exp [d (t*) fin ЬЛ _ (X — A, ) 5 (**)], D.3.5)
* p (* I К
где Я,1>Л0. Таким образом, из D.3.5) следует, что критическое
множество отбирается среди семейства множеств вида
4 . D.3.6)
Как следует из теоремы Неймана — Пирсона, критерий с критичес-
критическим множеством, входящим в семейство множеств, определяемых
формулой D.3.6) при заданной ошибке первого рода, соответствую-
соответствующей значению А = Я0, имеет наименьшую ошибку второго рода при
Л = Л1 (всюду ниже А,Х>>А,О). Рассмотрим теперь конкретные планы
стендовых испытаний, введенные в главе 3.
План типа [N, В, Т\. При использовании плана [TV, В, Т\ мо-
момент остановки испытаний t*=T, т. е. не зависит от хода испыта-
испытаний. Статистика s(t*)=*NT не содержит в себе никакой информа-
информации о параметре Я, так как ее значение может быть вычислено до
начала испытаний. Поэтому из D.3.6) находим, что семейство мно-
множеств, содержащих критическое, имеет вид
c}. D.3.7)
Напомним обозначения, использовавшиеся в главе 3,
е~Х L(Д
Напоминаем также, что значения At(d) даны в таблице 7 прило-
приложения. Для построения критерия, имеющего уровень значимости,
не большим а при значении А, = Х0, мы отбираем такое
§ 4.3] КРИТЕРИИ ПРОВЕРКИ ГИПОТЕЗ 255
наименьшее целое с>0, что
d=c+l
Замечая, что Ld (x) является убывающей функцией от х, получаем,
что в качестве с надо взять наименьшее целое с, для которого
М0Г<Дх_а(С). D.3.9)
Итак, критерий состоит в том, что приемочное число с, найденное
из D.3.9) сравнивают с фактическим числом отказов d(T). Если
d (Т) ^ с, то гипотеза Х = Х0 или Ио =? {X ^ Хо} проверяется, а гипо-
гипотеза Нх = {Х^>Х0} отвергается. При этом величина ошибки первого
рода равна 1 — Lc (X0NT) ^ а. Замечая далее, что выполнено второе
условие теоремы 4.1.2, получаем, что найденный критерий является
равномерно наиболее мощным. При этом функция мощности равна
вероятности отвержения гипотезы. Когда значение параметра
равно Х>0, функция мощности задается формулой
W(K) = \—Lc(NkT). D.3.10)
W (X) является неубывающей функцией от X.
Если параметры, определяющие критерий, заданы и найдено зна-
значение с = с(а, 7), то можно проводить испытания по сокращенной
программе, прекращая испытания в момент tc+1 наступления (c-f 1)-го
отказа, если только tc+1<T. При этом гипотеза Но отвергается.
При таком перепланировании мы фактически переходим от использо-
использования плана [NyB, T] к плану [N,B,(c+\yT)]> что должно быть
учтено при построении точечных и интервальных оценок параметра
X. При этом, однако, функция мощности остается неизменной и за-
задается формулой D.3.10).
План типа [N, В, г]. Испытания прекращаются в момент tr
наступления г-го отказа. Так как t* = try то d(tr)=r и стати-
статистика d (/*) становится тривиальной. Вся информация о параметре X
содержится в суммарной наработке 5В(^Г), которая имеет распре-
распределение (см. § 3.3), задаваемое формулой
х
D.3.11)
Семейство множеств Хс в формуле D.3.6) эквивалентно семейству
{SB(tr)<S}.
Учитывая D.3.11), находим такое Sa, для которого
Р {SB (tr) < Sa\K0} = !-?,_! (k0Sa) =a. D.3.12)
256 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
Из уравнения D.3.12), используя обозначения D.3.8), имеем
Sa -Al"\(/'~~1). D.3.13)
Условия теоремы D.1.2) снова выполнены, поэтому критерий, соот-
соответствующий плану [А/, В, г] с уровнем значимости а, является
равномерно наиболее мощным. Функция мощности критерия
kl_a(r—I) ~\. D.3.14)
План тина [N, В, (гу 7)]. Если при использовании плана
[iV, В, (г, 7)] окажется, что tr>Ty то t* = 7 и статистика
S (t*) = NT является тривиальной, если же ir ^ 7, то t* = tr и три-
тривиальной является статистика d(t*)=r. Семейство критических
множеств имеет вид D.3.6).
Рассмотрим на плоскости (х, у) точки (d(t), SB(t)). В момент
остановки испытаний t* = min (tr, T) значения (d(/*), SB (**)) на-
находятся на прямой d ~ r, SB (t) = Mr << 7V7, если tr<C.T или в одной
из вертикально расположенных точек d (Т) = 0,1,..., г—1 и
SB (t*) = А/7, если /г ^ 7. Возможные состояния показаны на рис. 4.3.1
жирной линией и точками. На плоскости (х,у) семейство критических
множеств представляется совокупностью точек (d (t*),SB (/*)),лежащих
выше прямой (In (-г*) ) у — (кг — %Q) x = k, где Я, > Хо. При уменьше-
нии k вероятность попадания финального состояния (d(t*), SB(t*))s
это критическое множество яв-
является неубывающей функцией.
Возможны два случая. В первом
k = kx велико и критическое мно-
множество состоит только из точек
отрезка, являющегося частью от-
отрезка d (/*) = г, 0 < SB (/*)< NT.
Во втором случае h = k2 мало
(k2 < &х) и критическое множест-
г
р-1
во состоит из точек всего отрезка
Рис 43 1 d{t*)=r9 0^S(t*)*ZNT, и
точек (rf(D; ^7), где d{T)>c.
Оба эти случая показаны на рис. 4.3.1; k=kx соответствует
прямая /lt а k = k2 — прямая /2. При выборе критического множества,
задающего критерий с уровнем значимости, не большим а, надо
поступать следующим образом. Если
Р {/, < Г| Хо} = 1 - Lr_L (Ла0Г) S* a,
то находим число Sa, для которого
Р (SB (tr) < Sa | к0) = 1 -Lr_x (Я05„) = a. D,3.15)
§ 4. 3] КРИТЕРИИ ПРОВЕРКИ ГИПОТЕЗ 257
D.3.15) эквивалентно соотношению Sa = 1~*/ -. Если же ока-
жется, что Р {tr < Т\ Хо} <а, то в критическое множество вклю-
включаем часть точек d(T)>c, SR{T)~NT, где с<г—1. Как легко
заметить, событие, состоящее в том, что либо tr<C Т, либо d (Т) > с,
эквивалентно событию d (T) > с. Следовательно, приемочное число с
находится из условия
?{ИГ< Л и [*г>7\ </(Г)>с]} =
^D.3.16)
причем в качестве с берется наименьшее целое число, удовлетво-
удовлетворяющее D.3.16). Итак, критерий для проверки гипотезы Но = {А, ^ XQ}
с уровнем значимости, не большим а, состоит в следующем.
Если Sa = *~a. ^r~~ ' <C NT, то испытания проводим до момента
о
^r, T). Если при этом окажется, что SB (tr)<C Sa, то гипо-
гипотезу Но = {K^Xq} отвергаем и принимаем гипотезу Hl = [k^'kQ\.
Если же либо tr<T и SB(tr)^ Say либо tr>T, то гипотезу
H0 = {K^:Xq} принимаем. Если же Sa > /VT, то из условия D.3.16)
находим наименьшее целое с такое, что NK0T^ Ах_а (с). Испытания
проводим до момента f* = min(fr, Г). При этом, если либо tr<^Ty
либо tr>T и d(T)>cy то гипотеза #0--{А,^А,0} отвергается и
принимается конкурирующая гипотеза H1=z {X^X0}. Если же
ir^> Т и d (Т) «^ с, то принимается гипотеза Но = {X ^ А,о}. Замечая,
что при этом нигде не было использовано значение X = XV входя-
входящее в конкурирующую гипотезу, мы убеждаемся в справедливости
первой части теоремы 4.1.2. Таким образом, построенный критерий
является равномерно наиболее мощным среди нерандомизированных
критериев с уровнем значимости, не большим а. Функция мощ-
мощности этого критерия определяется по формуле
f l-LM(A,-.(r-l)}), если A[rl)
\ V KJ *• D.3.17)
\-Lc(NlT), если NT<Al-\{r-l).
He меняя функции мощности, испытания можно провести по
сокращенной программе. Действительно, если NT>Sa = 1~а '
то испытания прекращаются либо в тот момент f < /* = min (tn Г),
когда значение суммарной наработки равно Sa, если при этом
^ (О < г, либо в момент /г, если 5В (tr) < 5а . В этом случае вместо
плана [TV, Л, (г, Г)] используется план [Ny Б, (г, #<SJ], т. е. план, при
котором наблюдения ведутся либо до момента tn либо до момента
258 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
t'<itn если суммарная наработка SB(tf) = SaL. В том случае, когда
NT<iSaJ вместо плана [N, В, (г, Т)] используем план [N, В, (с, 7)],
где с — наименьшее из целых чисел с, таких, что NX0T^ Ai_a(c).
План типа [N, В, (г, HS^)]. Как уже указывалось, в некоторых
случаях план типа [N, В, (г, Т)] сводится к такому плану. Следует,
однако, заметить, что в свою очередь план [N, В, (г, HS0)] эквива-
эквивалентен плану UV, В, [г> jt) i так как момент достижения ? < tr
суммарной наработки SR (tf) =Ntf — S'o задает момент окончания
испытаний f = Т = SJN.
Планы типа 5. План [N, Б, Т\. Как следует из D.3.4), до-
достаточные статистики d(T) и SE(T) обе являются нетривиальными.
d(T) имеет биномиальное распределение
Р {d (t) = d | Ц = CdN A - e~lT)d е-ьт <*-<0. D.3.18)
d d
При условии, что d (T) = d >0,5Б(Г)= 2 tk+(N—d) Г, где ?d= 2 ^
есть сумма J значений взаимно независимых случайных величин с
функциями распределения, имеющими плотности p(t)=—-—г для
значений 0 < / < Т и р (t) = О,
когда t>T или ^<0.
Плотность p(t\X, d) распреде-
распределения Ss (t) при условии
d(T)—r можно легко найти,
используя обратное преобра-
преобразование Фурье характеристи-
N
N
ческой функции
А,)Aв))в
Рис 4 3 2
Если по оси Ол: отложить
значения SB(T), а по оси
Оу — d(T), то в момент Т значения достаточных статистик попадут в
интервалы точек (ху у), лс = О,. . ., N; (N—л:) T<Cy<C.NT. Критическое
множество состоит из точек, удовлетворяющих неравенству D.3.6),
т. е. лежащих выше прямой / (рис. 4.3.2), задаваемой уравнением
h^j d (T)-^-^) SB (T) = k. D.3.19)
Пусть p(s\\,d) — условная плотность вероятностей наработки
Sb (T), когда d(T) = d; тогда константа k находится из условия
ЛГ fR(d,k) п
I P{$\d> K)ds 'CdN[\—eloTYe'^T(N-d)==ai D.320)
AN-d)T J
§ 4.3] КРИТЕРИИ ПРОВЕРКИ ГИПОТЕЗ 259
где R(d,k), как это следует из D.3.19), определяются соотно-
соотношением
{ [(j?)] } . D.3,21)
Построенный критерий, имеющий уровень значимости 1—а, состоит
в том, что в момент t = T испытания прекращаются. Если
[ln(jj)] d(T)-(\1-K0)SB(T)>ka, D.3.22)
то гипотеза Ио = {}i^X0} отвергается и принимается конкуриру-
конкурирующая гипотеза. В противном случае гипотеза Но = {Х^Х0} про-
проверяется. Этот критерий имеет наибольшую мощность в точке X —Хх,
однако он не является равномерно наиболее мощным. Функция
мощности для этого критерия определяется по формуле
N R (d, ka)
W(X) =]? J p(s\d, X) dsCdN[\ -е-><туе ~*<тW~d\ D.3.23)
d = l (N -d) T
Из формул D.3.20)—D.3.23) видно, что для использования этого
критерия нужны специальные таблицы, которых в настоящее время
нет1). Может быть предложен упрощенный критерий (и заведомо
худший сравнительно с описанным выше) принятия решения только
по значениям статистики d(T). Здесь рекомендуется подобрать
наименьшее целое с такое, что
N
о >< а.
d=c + i
Гипотезу Ио =¦= {X ^ Хо} отвергают в пользу конкурирующей, если
d(T)"^>c. Если же d(T)^c, то гипотеза Ио принимается.
Заметим, что без изменения функции мощности W(X)t задава-
задаваемой формулой D.3.23), испытания можно проводить по сокращен-
сокращенной программе. Момент остановки t* соответствует тому моменту,
когда уже очевидно, что при t=T для d (Т) и S Б (Т) будет
выполняться неравенство D.3.22) или противоположное ему нера-
неравенство. В общем случае t* зависит от положения прямой /, и для
краткости изложения мы опускаем описание правил сокращения
времени испытаний без изменения функции мощности, заданной
уравнением D.3.23).
1) Как показали численные расчеты, проведенные Ю. К. Беляевым
совместно с Е. В. Чепуриным и Т. Н. Топорищевой, для малых отно-
отношений d(T)/N выигрыш от использования пары статистик {^(Г), Sб(Т)}
невелик. Здесь хорошие результаты дают рандомизированные критерии,
аналогичные D.3.7), но со случайным выбором с.
260 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
План типа [N, ?, г]. Здесь'!*» = tr, d{t*)=r, т. е. тривиаль-
пая статистка, a Ss(/r)= 2 U +(N—d)tr имесг функцию рас-
d = 0
пределепия, для которой
P{SB{t,)<S\\}= ^J^e-'dt. D.3.24)
0
Критическое множество имеет вид
где в соответствии с D.3.24) и D.3.8) Sa находится как решение
уравнения
V* ir~l
\ T-zru}e~tdt==li[—Lr-i(KoSo) = a, D.3.25)
о
т. е. Sa= 1~аУ -. Итак, если SБ (tr) < ~1~*?'~~~ > т° гипотеза
^^{a^Aq} отвергается, если же 5а^ % > то гипотеза
^о= {^ ^ ^о} принимается. Этот критерий является равномерно
наиболее мощным критерием с уровнем значимости а. Функция
мощности равна
D.3.26)
При испытаниях по сокращенной программе t* определяется как
момент, когда либо суммарная наработка достигла уровня Sa
и *г>**, либо t* = tr и
vt/=dft*) 7 sb (tr) < 5tt. В первом случае от-
/ вергается гипотеза Их = {Я>Я0},
во втором случае отвергается
У о гипотеза /Уо = {X =^ Хо}. Заметим,
что при таком сокращении испы-
испытания проводятся по плану
, В, (г,
2
7
О 7 ^ ^ " План типа [N, Б} (г, Т)].
Построение критерия проводится
Рис. 4.3.3. аналогично построению для пла-
плана [TV, Б, Т]. Момент остановки
/* =min (tn Г), поэтому возможные значения d(t*), S (t*) совпа-
совпадают с интервалами, содержащими точки вида (d, у), где
rf = 0, ..., г, (N-d)T^y^NT. Заметим, что Р {d (/*) = k \ Ц =
1-Р)^-Л> где l-p = e-^, a
§ 4.3) КРИТЕРИИ ПРОВЕРКИ ГИПОТЕЗ 261
N
= 2 С*кРк О—p)N~k. Пусть рБ (s\ d, Я) —условная плотность
k-r
распределения SБ (Т*) при условии d(t*) = d. Критическое мно-
множество состоит из точек, лежащих выше прямой / (рис. 4.3.3).
Константа k = ka подбирается таким образом, чтобы при 'к==1к(>
вероятность того, что значения d(t*), SБ (t*) попадут выше пря-
прямой, была бы равна а. Выражая эту вероятность через условные
плотности Рв(^\ГуК) и приравнивая а, получаем трансцендентное
уравнение
г R (k9, a)
X J Рб (s\X0, d)ds?{d(t*) = d} = a, D.3.27)
d=i (N-d) T
где /?(fte, a) = max [(Л/-а) 7, (ln^-)
Итак, если ka найдено, то гипотеза ^"}
когда имеет место неравенство
In Ь) d (Р) - (Хх - Ло) SB (t*) > ft. D.3.28)
Если выполняется неравенство, противоположное D.3.28), то гипо-
гипотеза Я0 = {Х^Х0} принимается. Так же как и критерий для плана
[N, Б, Г], построенный критерий не является равномерно наиболее
мощным. Он обеспечивает наименьшую ошибку второго рода только
в точке Х = ХХ. Функция мощности для такого критерия задается
формулой
г R (а, &а)
1П*)=]? S Ps(s\d, X)dr.P{d(**) = d|X}. D.3.29)
.Как и для случая плана типа [N, Б, Г], не изменяя функции
мощности, можно было бы проводить испытания по сокращенной
программе, прекращая их в тот момент, после которого при любом
дальнейшем ходе испытаний знак неравенства D.3.28) или проти-
противоположного ему неравенства уже не может измениться.
План типа [N, Б, (г,Я50)]. Для планов типа [N, Бу (г, HS0)}
момент остановки t* совпадает либо с моментом tn либо с момен-
моментом, когда впервые значение суммарной наработки станет равным
заданному числу So. Частным случаем планов такого типа является
план {N, Б, (N,HS0)], соответствующий значению г = ЛЛ При поль-
пользовании планом [7V, Б, (NyH So)] момент /* остановки испытаний
совпадает либо с моментом /# отказа последнего элемента из N
62 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
поставленных на испытание элементов, либо с моментом, когда
впервые значение суммарной наработки достигает заданного
уровня 50. В § 3.3 предыдущей главы было показано, что если
в качестве временного параметра взять значения суммарной нара-
наработки, то «моменты» отказов, записанные в таком «времени»,
равные S( = Ss (t(), образуют пуассоновский поток отказов с интен-
интенсивностью, равной X. Как и всюду в § 4.3, мы предполагаем, что
вероятность безотказной работы каждого испытываемого элемента
равна e~Kt, Таким образом, план [/V, Б, (г, HS0]) эквивалентен
плану [N, В, (г, Г)], где в качестве временного параметра надо
рассматривать значения суммарной наработки и соответственно
Т=-?. Таким образом, переформулируя критерий, соответствую-
соответствующий плану [N, В, (г, Г)], получаем критерий в классе нерандо-
нерандомизированных критериев с уровнем значимости, не большим а, для
проверки гипотез Ио = {Х^Х0} и Н1 = {Х>Х0}. Этот критерий
задается следующей системой правил.
Если Sa= x~*/~~ • <?о» то испытания проводим до момента
/* = min (tn t0) где t0 находится из условия, то значение суммарной
наработки Ss (t0) = So. При этом в случае, когда t* = tr и
*$б (**,.)< Sa, гипотеза //0 = {Х^Я0} отвергается. В тех случаях,
когда t* = t0 гипотезу Но = {X ^Хо} принимаем. Может случиться,
что S — 1-<\ ~ >?0. В таком случае надо найти наименьшее це-
лое с (с<г) такое, что X0S0 = Ai_a(c). Гипотеза Но = {Х^Х0}
принимается, когда to<C.tr и d (tQ) ^ с. Если же окажется, что
to<tr и d(to)>c или tr<CtQi то гипотеза Н= {Х^Х0} отвер-
отвергается.
Функция мощности для такого критерия задается соотноше-
соотношениями
So^ Al"*i(r"~ }>
\-Lc(NXT)t So< Al-^~1}.
В заключение рассмотрим правила объединения результатов
испытаний на надежность, полученных при разнотипном
планировании. Может случиться, что в нашем распоряжении
окажутся данные об испытаниях на надежность, проведенных
в различных организациях с использованием различных планов
испытани-й. Типичными в этом отношении являются испытания
дорогостоящих образцов оборудования или систем. Ставится
задача построения критерия с заданным уровнем значимости для
различия гипотез Ио = [X ^ Хо} и Нх = {Х>Х0} о значениях пара-
§ 4.3] КРИТЕРИИ ПРОВЕРКИ ГИПОТЕЗ 263
метра, определяющего надежность элемента. Пусть Xi = {xi}—¦
пространство исходов испытаний, соответствующее использованию
плана типа ГГ (например, одного из рассмотренных выше),
1=1, ..., т\ Pi(x\\) — плотность вероятностей получения исхода
Xi^X}. Естественно предположить, что исходы опытов (xv .,., хт)
являются взаимно независимыми случайными величинами. При
таком предположении всю совокупность опытов x = (xlt ..., хт)
можно рассматривать как случайную величину, принимающую зна-
значения из пространства Х=ХХХ . . . XХт, плотность вероятностей
т
которой равна р (х | X) = YI.Pi (xi I ^)- Теперь можно использовать-
t-i
стандартную технику выделения достаточных статистик и исполь-
использования критерия отношения правдоподобия. Для иллюстрации мы
ограничимся разбором двух примеров.
Пусть в /-й организации на испытание было поставлено N;
элементов, /=1, ..., т. Испытания проводились по плану
[N, В, Г,]. Требуется построить критерий с уровнем значимости,
не большим а, различающий гипотезы Но = {к^\0},
Я1 = {Я>Х0}. Из формулы D.3.3) получаем, что плотность вероят-
вероятностей p(x\i) объединения всех исходов испытаний имеет вид.
т т
f X^idi( К 1 1\ D.3.31>
Из формулы D.3.31) следует, что ?>= 2^И^') является доста-
/=i
точной статистикой. Так как с1;(Т() являются, но предположению^
взаимно независимыми случайными величинами, имеющими пуассо-
новское распределение с параметрами XNjT;, то D также имеет
m
пуассоновское распределение с параметром Л= 2^/^r ^ соот-
i = i
ветствии с D.3.6) набор критических множеств имеет вид (D>&),
/5 = 0, 1, 2, ... В качестве k отбирается наименьшее целое число
с, для которого
?{D> c\lo} = \-Lc(?koNiTi)^a. D.3.32>
i
Используя обозначения D.3.8), можно переписать D.3.32) в виде
неравенства
m
^Ji < Ai-.(c- 1). D.3.33)
Таким образом, критерий описывается следующей системой правил.
Гипотеза Я0 = {Х^Я0} отвергается, когда общее число отказов Dr
*264 проверка гипотез о надежности [гл. 4
-наблюдавшихся во всех т организациях, больше числа с, найден-
найденного из условия D.3.33). Если же D = с, то гипотеза Я0 = {Х^Х0}
принимается. Этот критерий является равномерно наиболее мощ-
мощным в классе нерандомизированных критериев с уровнем значимо-
значимости, не большим а.
В качестве последнего примера рассмотрим случай двух серий
испытаний. В первой серии использовался план [Nx, Б, гх], во вто-
второй— план [М2у Б} Т2]. Совместная плотность вероятностей обоих
исходов испытаний имеет вид
р (х | X) = (Nx)ri (N2)di {Тш) к гг+*лтш),-ь ^цГ1) + з^\тг)] ^ D 3 34)
где (N)n
Из формулы D.3.34) следует, что при Я = Хо достаточной
статистикой будет пара (d(T2)y S^(trt) -{- S^ (Т2))у где d2 (T2) — число
отказов во второй серии испытаний, а ?^(Г2) — значение суммарной
наработки в момент t в /-й серии испытаний. Взяв логарифм
отношения правдоподобия р « -, где Хх;>?10, получаем, что
критическое множество имеет вид
In ^М йB (Т2) — (Я.! — Хо) [?(Л (/г) + 5^) (Г2)] > ka. D.3.35)
Значение ka находится из условия, что при Х = Х0 вероятность
выполнения неравенства D.3.35) должна быть равна а. Построен-
Построенный критерий состоит в том, что гипотеза Ио = {X^Kq} отвер-
отвергается тогда, когда выполнено неравенство D.3.35), и принимается
тогда, когда выполнено неравенство, противоположное D.3.35).
Этот критерий дает наименьшую ошибку второго рода при Х = к1.
Однако он не является равномерно наиболее мощным.
§ 4.4. Критерии типа последовательного анализа
для проверки гипотез о значении параметра X
экспоненциального распределения1)
В предыдущих параграфах рассматривались критерии, соответ-
соответствующие тем случаям, когда испытания проводились по конкрет-
конкретным планам типов Б и В. Возможен другой подход к построению
критериев, основанный на понятии функции риска. К сожалению,
1) Материал, излагаемый в этом параграфе, несколько выходит за
рамки этой книги. Мы опускаем детали доказательств, в связи с чем изло-
изложение носит эвристический характер. В задуманном продолжении книги
будет дано систематическое изложение применений теории управляемых
случайных процессов к задачам теории надежности.
§ 4.4] КРИТКРИИ ТИПА ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА 265
в большинстве случаев построенные критерии имеют пока весьма
относительную практическую ценность. Причина этого заключается
в том, что для построения функции риска требуется задавать
определенные численные значения априорных вероятностей и зна-
значение ущерба от принятия ложного решения. Вид критерия суще-
существенным образом зависит от этих параметров, значения которых
могут быть оценены лишь с большой степенью неопределенности.
Хотя субъективность выбора параметров существенным образом
влияет на вид полученного критерия и снижает его практическую
ценность, все же описание класса оптимальных критериев полезно
во многих отношениях. В ряде случаев полученные таким образом
критерии обладают весьма ценными свойствами. Одной из жемчужин
этой теории является последовательный критерий отношения прав-
правдоподобия Вальда [2], [3]. В настоящем параграфе мы ознакомимся
с этим критерием на примере проверки гипотез о значении интен-
интенсивности пуассоновского потока.
Рассмотрим задачу построения критерия для проверки двух
простых гипотез о значении параметра X потока отказов. Пусть
испытываются N элементов, вероятность безотказной работы каж-
каждого элемента в течение времени t равна R (t) = e-kt. Исходная
гипотеза Ио состоит в том, что Х = К0, а конкурирующая
Н1= {'к — 'к1}у А,1>Л0. Если испытания проводятся с заменой
отказавших элементов (планы типа В), то возникающий случай-
случайный поток моментов отказов является пуассоновским с интенсив-
интенсивностью, равной NX( (см. § 3.2), когда верна гипотеза И{. Если
замена отказавших элементов не производится (планы типа />), то
интенсивность отказов изменяется (см. § 3.2). Пусть до испытаний
нам заданы два числа: Эо — вероятность того, что верна гипотеза
/Уо, и 6Х—вероятность того, что верна гипотеза Нг\ 0о-}-91=1.
Эти вероятности 6,. носят название априорных. Под критерием
будем понимать правило, по которому определяется момент
прекращения испытаний и принимается одна из гипотез И{. Пусть
вероятность ошибочно принять гипотезу Н(, когда верна гипотеза
Яу, равна а;.. Обозначим через Wj величину ущерба от того,
что будет принята Hh в то время как верна H1_i. Условимся
обозначать через т)* реализацию случайного потока отказов в
интервале от 0 до t. Если /1? ..., t<t(t)—моменты отказов, та
Ti* = (^1, ..., td(t)j О- ДЛЯ удобства обозначений будем каждый
критерий и соответствующие ему характеристики отмечать одной
и той же буквой б. Например, момент t* остановки испытаний,
соответствующий критерию б, обозначаем через tb. Как уже было
показано ранее, плотность вероятностей появления реализации ц*
задается формулами
pt (цг | X) -
266 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
для планов типа В и
pt (л* I ty = (N)r№ <'> е-™б (О D.4.2)
для планов типа Б. Здесь SB (t) и Ss(t) — значения суммарных
наработок,
SB(t)=M, SB{t)=:[N-d(t)}t+2tiy D.4.3)
1 = 1
где ti<Ct—моменты отказов.
Проведение испытаний связано с определенными расходами.
Предположим поэтому, что за интервал времени (/, t-\~At) рас-
расходы равны с(т)*)А/. Таким образом, расходы за время испыта-
г"
ний до момента остановки равны j с (r\s) ds. Очень часто оказы-
о
вается целесообразным считать с(гу) = су Аг>0. Однако при
использовании планов типа Б могут встретиться и такие случаи,
когда с {rf) — с [N— d (t)]. Средние расходы г @О, б), связанные с
использованием критерия б, состоят из среднего ущерба от
ложных решений и расходов от проведения испытаний. Расписывая
подробно, получаем
rF0, 6) = 0oaoro + 01a1\F1 + 0oMo[5 с (r\s) ds] +
О
с (rf) ds] . D.4.4)
Щ; означает, что математическое ожидание соответствует гипо-
гипотезе И{. Нашей задачей является теперь построение такого кри-
критерия б, для которого при заданных значениях априорных вероят-
вероятностей 6;, величин ущерба Wt и стоимости с (vf) значение функ-
функции риска минимально. Критерии, минимизирующие функцию риска,
называются бейесовскими.
План типа В. Предполагаем, что с(г)*) = с>0. Из D.4.4)
получаем
г (в0, 6) = eo[aol^o + cMo/sl + [l-eo][a1W1 + clVl1^]. D.4.5)
Используя D.4.5), легко получить, что для значения Эо = о
+ (\ — ЯH(о2\ где 0<А.<1, О<0(О<1) имеет место соотно-
соотношение
в , б). D.4.6)
Равенством D.4.6) мы воспользуемся позднее. Пусть 0^ — апосте*
§ 4.4] КРИТЕРИИ ТИПА ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА 267
риорная вероятность того, что справедлива гипотеза Hh если
наблюдается реализация потока отказов гг*. По формуле Бейеса
имеем
9*=* в/Р* (Л* I *>/) D47ч
Будем рассматривать только такие критерии, которые являются
предельными для критериев дискретного типа. В. С. Михалевич
[121 называет такие критерии регулярными. Критерии дискретного
типа характеризуются тем, что для них решение об остановке
или о продолжении испытаний принимается лишь в моменты, крат-
кратные Atf. Случай непрерывного времени получается в результате
предельного перехода, когда Д/jO. Случайный поток отказов г\г
является пуассоновским, поэтому число отказов, возникающих
в интервале (t, t-\-kt), не зависит от того, в какие моменты и
в каком количестве наблюдались отказы в интервале @, /). Отсюда
следует, что число отказов d(s), происшедших за время s>
O^s^t, является реализацией марковского процесса с независи-
независимыми приращениями. Из общей теории управляемых процессов
(см. [3], [13]) следует, что оптимальное решающее правило-кри-
правило-критерий, минимизирующий функцию риска D.4.5), зависит лишь
от значения апостериорной вероятности 6?. Значения 8?, зада-
задаваемые формулой D.4.7), образуют марковский процесс. Это сле-
следует из того, что Q*o может быть взаимно однозначным образом
выражено через отношение правдоподобия pt (rr* | X1)/pt (r\f | Яо).
Ниже мы увидим, что отношение правдоподобия, или, что экви-
эквивалентно, его логарифм, является марковским процессом.
Так как в каждый момент времени t принимается одно из двух
возможных решений об остановке испытаний и принятии
одной из гипотез Hi или же о дальнейшем продолжении испы-
испытаний, то полезно рассмотреть две функции риска, связанные с
этими решениями. Пусть р0Ст (во)— минимальный риск от
принятия решения об остановке испытаний в момент
/, когда значение апостериорной вероятности равно 60, 0! = 1 — 0О .
Если при этом принимается верной гипотеза Н^ то с вероятностью
6/ это решение ложно и среднее значение ущерба равно 6/IF,-.
Уа рис. 4.4.1 по оси абсцисс отложены значения во, а по оси
ординат — значения ущерба. Минимальный ущерб в условиях оста-
остановки процесса в момент t задается, как это видно из рис, 4.4.1,
формулой
D.4.8)
268
ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ
[гл. 4
Таким образом, чтобы ущерб в момент остановки / был минима-
лен, надо при значениях "о < ^ , «
при значениях 80 >> ш Л1Ш принимать гипотезу Ио.
принимать гипотезу И1} а
Пусть G—класс критериев, для которых с вероятностью единица
по достижении момента t принимается решение о дальнейшем про-
продолжении испытаний. Введем понятие минимального риска
от оптимального продолжения испытаний рпр Fq),
задав его формулой (ср. [1])
= inf r(Q'0,6). D.4.9)
б € G
Для оптимального критерия, мини-
минимизирующего риск D.4.5), воз-
возможно принятие как решения об
остановке, так и решения о про-
продолжении испытаний. Поэтому зна-
значение минимального риска
Рис. 4.4.1. D 4 10)
Если бы нам было известно значение рпр(9о), то с учетом D.4.10)
оптимальный критерий б описывался бы следующей системой правил.
Пусть к моменту времени t значение апостериорной вероятности
стало равно 9q. Нужно вычислить значение рост (9о) и рпр(9о). Если
окажется, что рост(9о) ^ рпр (9о)> т0 нужно принимать решения об
остановке испытаний, если же росг(^о)> Рпр(9о), то испытания надо
продолжить. Если в момент ^§ остановки 0о < w/ ,1 ш , то прини-
мается гипотеза Нг; в противном случае принимается гипотеза //0.
Заметим, что уравнение D.4.10) является типичным уравнением
динамического программирования [14].
Значение рпр (9q) нам неизвестно, и найти его не так просто.
Постараемся обойти эту трудность. Из уравнения D.4.6) следует,
что
+ A— X)infr@J4 б) D.4.11)
Используя обозначение D.4.9), можно переписать D.4.11) в виде
-пр'
+ О - X) 9^B))
FSA)) + A - Л) pnp (8S(г)). D.4.12)
§ 4.4] КРИТЕРИИ ТИПА ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА 269
Из D.4.12) следует, что рпр (G) является выпуклой функцией по 9.
Так как каждая ограниченная сверху выпуклая функция является
непрерывной, то из очевидного неравенства рпр @)^=0 вытекает
непрерывность рпр(8).
Примерный вид графика рпр @) показан на рис. 4.4.1. Пусть
существует интервал @', 0") такой, что из 0 ? @', 0") следует
Рпр F) < Рост (в); тогда до тех пор, пока значение Q[ ? @', 0"), надо
продолжать испытания. Испытания прекращаются в момент ^8, когда
впервые значение 0*0 выйдет из интервала @', 0"). Если 0О6 ^ 0', то при-
принимается гипотеза Hlt если же 0об ^ 0", то принимается гипотеза Нх.
Вычисление значений 0{ по формуле D.4.7) неудобно. Поэтому
сделаем некоторые преобразования. Из формулы D.4.7) получаем, что
ж @- [inbl-Mn \ЩЩ = ГшЫМп \^=ф-\ • D.4.13)
L М Lpf (л* i^o)-l L X°J L e'oe, J
Формула D.4.13) задает взаимно однозначное отображение точек
боб (°Л) в точки x(t) ? (—оо, -}¦ оо). При этом неравенство 0t <62,
6(.?@,1), переходит в пераБенство хг < хг, где х1 — образ точки G,-.
Используя формулы D.4.1) и D.4.3), получаем, что левая часть
D.4.13) имеет вид
x(t) = d(i) — ct, D.4.14)
Принимать Hf
где c =
Пусть х0 — образ 0', а хг — образ 0" при использовании преобразо-
преобразования D.4.13), когда 0о€@',9")-
Тогда оптимальный критерий,
минимизирующий риск D.4.5), со-
состоит в том, что надо регистриро-
регистрировать число отказов d(t)t проис-
шедших до момента t включи-
включительно, а затем по формуле
D.4.14) находить значение х (t).
Испытания прекращаются в мо-
\г
Принимать h0
мент tb, когда впервые значе- Рис 4.4.2.
ние x(t) окажется вне интерва-
интервала (хо,хх). Если х(/5)<а:0, то надо принимать гипотезу Яо,
если же x(tb)^x1} то надо принимать гипотезу Hv
Такая интерпретация оптимального критерия является следствием
монотонности отображения, задаваемого формулой D.4.13). В силу
монотонности события 0' <0о <0'\ Оо <0',0о ^9" эквивалентны
270 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
событиям х0 <С х (t) <С х1У х (/) ^ хъ х (t) ^ х0. Примерный вид траек-
траектории x(t) показан на рис. 4.4.2. Значения граничных точек х0 и
хх находятся из требований, чтобы значения ошибок первого и
второго рода были соответственно равны а0 и ах. Ошибка первого
рода равна вероятности пересечения уровня хх раньше уровня хОу
когда значение Х = Я0. Ошибка второго рода равна вероятности
пересечения уровня х0 раньше уровня хх, когда х^К1. Из этого
мы замечаем, что на оптимальность критерия не влияют как значе-
значения ущербов Wh так и значения априорных вероятностей 8^. Сле-
Следовательно, если б* — критерий, отличный от оптимального, а,* — его
ошибки первого и второго рода, такие же, как и у оптимального
критерия, то
г@о, 6)<г(90, 6*). D.4.15)
Пусть Wo*=\ — W, W1^W; тогда для любого 0og(O,l) из D.4.5)
и D.4.15) получаем
еом<Л+A - е0) мл < еомо*б + (i - е0) м^*. D.4. ie>
Из неравенства D.4.16) получаем, что
М0*8<Лул., М^^М^б*. D.4.17)
Этот результат можно интерпретировать следующим образом.
Свойство оптимального критерия. Оптимальный
критерий, различающий две простые гипотезы Н0 = [Х = Хо] и
Нх = [Я *= Хх] с заданными ошибками первого рода а0 и второго
рода аг, требует в среднем меньше времени на проведение
испытаний, чем любой другой критерий с теми же ошибками
первого и второго рода.
Не следует забывать, что минимальное среднее время соответ-
соответствует только значениям X = Яо или Х^Х^ Существуют другие
критерии, которые требуют меньшего времени проведения испыта-
испытаний для некоторых значений ХфХь / = 0,1.
Рассмотрим теперь вопросы, связанные с вычислением значений
х0 и хх таких, что ошибки первого и второго рода равны а0 и ах.
Пусть \ij—условное математическое ожидание отношения правдо-
правдоподобия в момент достижения уровня xh / = 0,1, когда верна
гипотеза Hj. По формуле условных математических ожиданий
где %i — случайные величины, задаваемые формулами
\,x(tt)=--x0, j 0, х(*,) = х0
§ 4.4] КРИТЕРИИ ТИПА ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА 271
Замечая, что Мо Pt (л / ' h) %, = MlXl- = Р {х« =» 1 I * = М, и У™-
Lpt (л д I ^о) J
тывая очевидные отношения
P{Xl = l|X = X1} = l-o1, P{xi = l|* = M = «o. D-4.20)
из D.4.18), D.4.19) и D.4.20) находим, что
В условиях принятия решения о справедливости гипотезы Hi в
момент окончания испытаний
ei <-5 } = eL K* 6 ^el ,D.4.22)
Pt (Л 6l^i)
о
где .у (rfs) = ln^ a: (M, sup и inf берутся по всем значениям х (t*) в
L AoJ / i
такие моменты окончания испытаний, которым соответствует при-
принятие гипотезы #•. Величины, стоящие в левой и правой частях
неравенств D.4.22), уже не являются случайными. Используя эти
неравенства в формуле D.4.18) и учитывая D.4.21), получаем
неравенства
„ supy(t д)
e'=i в «ji^^e'-i 6 . D.4.24)
а0
Если в момент tb принимается гипотеза Яо, то л:(^) = д:0, поэтому
неравенства D.4.23) эквивалентны равенству
T-^- = eV Xo . D.4.25)
1-а0
Из уравнения D.4.25) находим значение уровня принятия гипотезы Но
A:0 = lnr^i—:1пЬ . D.4.26)
В момент t<Ctb x(t)<Cxlt следовательно, в момент t=tb x (t0) <3
^^i+^j так как с вероятностью 1 отказы в предположении о
показательности вероятности безотказной работы не могут наступить
одновременно. Учитывая это, из D.4.24) имеем
272 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
Разрешая неравенства D.4.24) относительно хх, получаем верхнюю
и нижнюю оценки для уровня хг принятия гипотезы Hi~[X = Х1\;
Если 1 ^> гр , то в качестве хг можно взять значение
а0 Ао
/1 ГУ \
In ( ~~ 1 ) . Заметим, что при этом получается критерий, имеющий
\ ао У
меньшие, чем а0 и ах, ошибки первого и второго рода. При этом,
однако, время проведения испытаний в среднем несколько увели-
увеличится. В явном виде значение уровня хг получить нельзя. Однако,
используя технику дифференциально-разностных уравнений, можно
получить трансцендентные уравнения, решением которых является д:х.
Ниже излагаются результаты работы [11]; см. также [15].
Случайный процесс x(t), задаваемый формулой D.4.14), является
марковским. Это является простым следствием того, что отказы,
которые могут возникнуть в будущем, не зависят от течения
процесса х (t) в прошлом. В момент / = 0 х @) = 0, однако мы рас-
смотрим сначала более общий случай, когда х@)=х. Пусть
Р% (х) — вероятность принятия гипотезы Н1 = {X = Ях}, когда значе-
значение параметра равно Л, х@)=х. Другими словами, Рк(х) равна
вероятности того, что процесс пересечет уровень хх раньше, чем
уровень х0. Вероятность ошибки первого рода а0 = РХо @), а веро-
вероятность ошибки второго рода — ах — 1— /\ @).
Граничные условия имеют вид
0,
Учитывая возможные изменения значений процесса х (t) за время
@, ДЛ, для значений х, х0 < х < хъ по формуле полных веро-
вероятностей имеем
рх (х) = (\—МКМ) Рх (* — сМ) + NKMPX (х+\— сМ) + о (М).
D.4.30)
Из уравнения D.4.30), где | о (At) \ < X2 (AtJ, 0 < M<Nk'1, полу-
получаем, что Рх (х) — непрерывная функция от х в интервале (х0, л^).
В точке х = хг эта функция имеет разрыв, так как из D.4.29)
§ 4.4] КРИТЕРИИ ТИПА ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА 273
Учитывая это и переписывая уравнение D.4.30) в виде
Jx(x)-Px(x-cM) ==_NKp^ (X-cAt)+NkPx (x+ 1 - сМ) + о (Д*),
D.4.31)
получаем, что Ях (х) дифференцируема в интервале (х0, хг), за
исключением одной точки х = хг — 1 в том случае, когда х0 < хг — 1.
Из D.4.31), переходя к пределу A^jO, получаем дифференциально-
разностное уравнение
d^p y D.4.32)
где xQ<x<Zx^ х Ф хх — 1. Решение D.4.32) определяется инте-
интегрированием по кускам. Единственность обеспечивается выполнением
условий:
(I) Рх(х) непрерывна для значений x<xlt
(II) Рх(*0) = 0,
A11) Рх(х) = 1, x>xv
Пусть п(х) — целое число, такое, что
хг — х — 1 ^ п (*) < хх — х.
Непосредственной проверкой можно убедиться, что решением урав-
уравнения D.4.32), удовлетворяющим указанному выше условию D.4.1),
является функция
Использовав условие (II), получаем выражение для константы с:
D.4.34)
Таким образом, с учетом D.4.33) и D.4.34) P)i(x)==g(xOyx1^,x\ f
где
\ „m
k=o I J
k = 0
D.4.35)
Значениех0 нам известно; вспомнив связь /\@) с ошибками первого
^0 Б. В. Гнеденко и др.
274 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
и второго рода, получаем два трансцендентных уравнения, любое
из которых можно использовать для нахождения хг:
х Мо (Л=а0> )
лп \ \ D.4.36)
у * П 1 — 1 (У
°' Х^ с ' UJ -l-ai- )
Полезно заметить, что —- = N[ ln~ ) ( ~—1) , —^ = А/1пг^-х
с \ л0 j \к0 ) с л0
хA—т^)» откуда следует, что решение хх уравнений D.4.36)
зависит от Яо, 'к1 только через их отношение -й.
Если значение параметра X Ф Х{1 / = 0, 1, то вероятность L (к)
принятия гипотезы Яо, называемая оперативной характеристикой,
задается формулой
?(Л) = 1_/\@) = 1-/- Nk
Другой полезной характеристикой оптимального критерия является
среднее время 7\ проведения испытаний, когда значение параметра
равно Л. Мы уже показали, что для оптимального критерия при
одинаковых ошибках первого и второго рода среднее время 7\
проведения испытаний не больше, чем у любого другого критерия
для значений Я = Х0 и к = 'к1. Если обозначить через 7\ (л;) сред-
среднее время проведения испытаний при условии, что х@)—ху то
аналогичным образом можно вывести дифференциально разностное
уравнение, которому удовлетворяет ^(х). Это уравнение имеет вид
х (х) = 1 + NX7\ (х). D.4.38)
Решение уравнения D.4.38) задается формулой
Л=о /=о
Постоянная с' находится из условия 7\(лго) = О. Введенная выше
характеристика 7\, равная среднему времени продолжения испы-
испытаний, легко выражается через Тх(х):
Гх=Тх@). D.4.40)
§ 4.4] КРИТЕРИИ ТИПА ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА 275
В работе [15] даны таблицы функции g(x0, х1У —, 0) для
различных значений ~. Там же приведены значения функции
h (xQi xly «-М . Средняя продолжительность испытаний
D.4.41)
Планы типа Б. Для случая планов типа Б достаточными
статистиками являются число отказов d(t), происшедших до мо-
момента t, и значение суммарной наработки SB (t)y задаваемой фор-
формулой D.4.3). Апостериорная вероятность Qf0 того, что верна
гипотеза //0 = [Х = Я0], как и для случая планов типа В, вычис-
вычисляется по формуле D.4.7), где pt (г)'| А) задается формулой
D.4.2). Таким образом, 6q зависит от значений SB(t) и d(t).
Заметим, что 6q уже не является марковским процессом, как это
было для планов типа В. Если предположить, что стоимостный
коэффициент расходов с (г)') = с (N—d(t)), то в соответствии
с формулой D.4.4) среднее значение риска для критерия б равно
(в0, 6)= 2 eja^ + cM.Ss^)]. D.4.42)
0
Здесь мы воспользовались соотношением Ss(t) — \[N — d(s)]ds.
о
Центральной задачей является отыскание оптимального критерия,
для которого значение функции риска обращается в минимум.
В настоящее время мы не можем дать полного решения этой за-
задачи и только наметим пути ее решения. Как и раньше, в каждый
из моментов времени t надо принимать одно из двух решений:
либо прекращать испытания, либо продолжать их дальше. Для при-
принятия оптимального решения надо из всех полученных данных
знать только значение Sg (t) и d(t). Введем две функции риска:
Рост(^> ^) — минимальный риск от остановки испытаний и
рпр E, d) — минимальный риск от продолжения испытаний, где
^=^б@> d = d(t). Фазовое пространство значений марковского
процесса SB(t); d (t) состоит из точек (х, у) лучей плоскости.
:^0, у — О, 1, ..., N. Если значение d фиксировано, а
пробегает значения от 0 до +оо, то значение апостериор-
апостериорной вероятности 6q возрастает от числа, равного 7T~w> до *•
Ч?)
Минимальный риск от остановки испытаний
ростE, rf) = min[0'orO) в!^]. D.4.43)
10*
276
ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ
[ГЛ. 4
Пусть G—класс критериев б, для которых по достижении значе-
значений SB(t)=S и d(t) = d принимается решение о продолжении
испытаний; тогда
РпР (S, d) = jirf г (9о (St d)} d). D.4.44)
Если значения этих рисков известны, то минимальный риск р (S} d)
в общем случае удовлетворяет уравнению
рE, </) =
, d)y pnp(S,
D.4.45)
Структура оптимального критерия описывается следующей систе-
системой правил. Если до момента td появления d отказов принималось
Рис. 4.4.3.
решение о продолжении испытаний, то в моменты t^td прини-
принимается решение о продолжении испытаний только в том случае,
когда Рпр(^б@» d) <Рост №б (t)> d). Решение об остановке испы-
испытаний принимается в момент tdi как только Рпр(^б(^)» d)^
^ P0CT(Sb (t)y d), или в момент t, td<t<td+1, если впервые
в этот момент pnpEs(/), d) ^ рОСт (Sb @» d). Таким образом, все
точки луча (S, d), 5^0, разбиваются на три зоны (рис. 4.4.3).
Для значений S<C.S' испытания прекращаются и принимается
гипотеза Иъ для значений 5, Sd><C.S<iSd'' испытания продол-
продолжаются и, наконец, для значений S*>S" испытания также прекра-
диются и принимается гипотеза Но. Рассчитав по значениям а(-,
Wh с, 9,. функции рисков рост (S, d) и рпр (S, d), можно найти для
значений d = 0, ..., N—1 пары критических точек Sdi Sj. Заме-
Заметим, что в момент t^ отказа последнего элемента испытания надо
прекращать; таким образом, SN =S^ = SN} т.е. критическая точка
* 4.5] непараметрические методы 277
одна. SN находится из уравнения
00 (SB (tN), N)W0-=Q1 (SB (tN), M) Wv D.4.46)
являющегося следствием правил, определяющих критерий и урав-
уравнения D.4.43). f m
На рис. 4.4.4 интервалы (Sdi Sd) выделены жирными откры-
открытыми отрезками. Пока траектория (SB(t)9 d(t)) проходит через
точки интервалов (Sd, Sd), ис-
испытания нужно продолжить. Если
траектория пересекает правую
границу, то принимается реше-
решение об остановке и принятии
гипотезы #0, если же происхо-
происходит пересечение левой границы,
то испытания прекращаются с
принятием гипотезы Hv Значе- О
ния pnp(S, d) можно получить рис 44^
как решения системы дифферен-
дифференциальных уравнений. Например,
рассматривая изменения S, d за время {t, t + M), когда d = До-
Дополучаем
?
j
/JS*
от o(M). D.4.47)
Из D.4.47) получаем дифференциальное уравнение
Аналогичным образом можно вывести и другие уравнения.
§ 4.5. Непараметрические методы оценки однородности
статистического материала
Одной из существенных статистических задач теории надеж-
надежности следует считать проверку однородности имеющегося в рас-
распоряжении исследователя материала (изготовленной продукции по
качеству, отсутствия влияния испытательных установок на резуль-
результаты испытаний, изменения технологического процесса на качество
изделий и т. д.). При этом зачастую нас совсем не интересует,
каково будет распределение вероятностей изучаемого показателя
однородности; задача состоит лишь в проверке гипотезы, что
распределение остается неизменным. Мы ограничимся здесь
рассмотрением лишь простейших постановок задач, для которых
278 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4-
предложены достаточно простые и во многих случаях удачные
способы решения.
Мы начнем с рассмотрения следующей классической задачи
математической статистики: имеются две серии результатов неза-
независимых наблюдений
Уъ У*, •, Уп-
Первая серия наблюдений произведена над случайной величиной
с непрерывным распределением Fx (х), а вторая —над случайной вели-
величиной с непрерывным распределением F2(x). Требуется выяснить:
можно ли считать, что F1(x) = F2(x); не противоречат ли этой гипо-
гипотезе результаты наблюдений? В точности так же ставится вопрос,
когда желают выяснить, можно ли продукцию двух заводов счи-
считать одинаковой по качеству? Близкая постановка вопроса нередко
возникает при выяснении влияния смены на качество продукции
и во многих других случаях.
Для решения этой задачи предложено большое число методов,
основанных на различных принципах; с некоторыми из них мы
ознакомимся в настоящем параграфе.
Критерий знаков. Этот критерий очень прост в примене-
применении, но использует информацию, содержащуюся в результатах
наблюдений, очень неэкономно. Тем не менее во многих случаях
он может оказаться весьма полезным для предварительной при-
прикидки, поскольку он совсем не требует сколько-нибудь сложных
вычислений. При использовании критерия знаков предполагается,
что F1(x) = F2(x). Строим разности
z1 = x1—yly z2 = x2 — y2, ..., zn = xn—yn.
В силу независимости величин xt и у( каждая из разностей с ве-
вероятностью половина может принимать положительное и с вероят-
вероятностью половина —отрицательное значение (значение 0 для не-
непрерывной функции • распределения может быть принято лишь
с вероятностью, равной 0), если гипотеза Fx(x) = F2{x) верна.
Таким образом, мы находимся в условиях схемы Бернулли. Если
наша гипотеза верна, то число положительных разностей будет
сравнительно немного уклоняться от -у Таким образом, как боль-
большое число отрицательных, так и большое число положительных
разностей должно наводить на мысль об ошибочности сделанной
гипотезы.
Поскольку, согласно формуле Бернулли, вероятность того, что
число положительных разностей окажется в наших наблюдениях
§ 4.5] НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ 279
равным &, есть Рп(к) — СпкпУ т0 мы можем построить такое пра-
правило: зададимся уровнем значимости а (т. е. вероятность отбросить
правильную гипотезу меньше или равна а). Станем отбрасывать
гипотезу Fx (х) = F2 (х) всякий раз, как только число положитель-
положительных разностей окажется большим числа га, где га —минимальное
из чисел, для которых
Сформулированное правило представляет собой односторонний
критерий знаков. Уровень значимости при нашем выборе га не
превышает а.
С не меньшим правом, чем в случае излишне большого числа
положительных разностей, можно отвергать проверяемую гипотезу
и в том случае, когда велико число отрицательных разностей
-(т. е. число положительных разностей мало). Если для числа отри-
отрицательных разностей мы примем ту же границу га, что и для
положительных разностей, то двусторонний критерий знаков
должен быть сформулирован так: гипотезу Fl(x) = F2(x) мы отбра-
отбрасываем каждый раз, как только число положительных разностей
окажется большим га или меньшим п — га. Вероятность ошибочного
отбрасывания гипотезы F1(x)=F2(x) при этом не превышает 2а,
поскольку она равна
Для п от 5 до 100 составлены границы критической области
в случае 1%, 2%, 5%-ных уровней значимости для двустороннего
критерия знаков. Те же таблицы применимы и для одностороннего
критерия знаков, но соответственно с 0,5°/0, 1% и 2,5%-м
уровнями значимости. При п ^100 с успехом может быть исполь-
использована интегральная предельная теорема Муавра — Лапласа и за-
записано приближенное равенство
чг -п
из которого с помощью таблиц нормального распределения легко
Для каждого п найти га. Для примера, если /z==225, то для одно-
одностороннего критерия знаков при a = 0,005; 0,01; 0,025 следует
соответственно выбрать ra=131; 129; 127.
280
ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ
[гл. 4
Для иллюстрации пользования критерием знаков приведем при-
пример, заимствованный нами из книги И. В. Дунина-Барковского и
Н. В. Смирнова [28]. На стр. 268 и 183 указанной книги приве-
приведены выборки по 20 штук изделий горизонтально-ковочной машины
Таблица 4.5.1
№№ колец в порядке
обработки
За 6 марта
За 12 марта
Знак разности
№№ колец в порядке об-
обработки
За 6 марта
За 12 марта
Знак разности
№№ колец в порядке об-
обработки
За 6 марта
За 12 марта
Знак разности
_____
1
31,44
32,17
—
8
31,28
31,74
—
15
31,62
31,60
+
2
32,22
32,61
—
9
31,72
32,46
—
16
31,73
32,47
—
3
31,98
32,68
—
10
31,58
32,48
—
17
31,48
32,74
—
4
31,88
32,29
—
11
31,87
31,70
—
18
31,88
32,26
—
5
31,44
32,36
—
12
32,12
32,30
—
19
31,96
32,92
—
6
31,17
32,25
—
13
31,04
31,73
—
20
31,49
32,63
—
7
31,68
32,28
—
14
31,87
32,28
—
и указаны размеры высоты последовательно отштампованных внут-
внутренних колец шарикоподшипников соответственно 6 и 12 мар-
марта 1951 г. Результаты приведены в таблице 4.5.1. Спрашивается:
можно ли считать, что наладка штампа не изменилась с 6 по
12 марта?
Из таблицы 18 приложения видно, что гипотеза неизменности
распределения высоты колец должна быть отброшена. Вероятность
§ 4.5] НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ 281
того, что при этом мы отбросим правильную гипотезу, меньше
0,0003.
Заметим, что при применении критерия знаков никак нельзя
забывать, что при подсчете числа знаков берутся неупорядоченные
по величине результаты наблюдений. Поэтому, если мы наблюдаем,
например, длительность жизни определенных изделий двух заво-
заводов и регистрируем последовательно длительности жизни изделий
в порядке выхода их из строя для первой партии tx, t2, ..., tn
и для второй партии т1? т2, ..., т„, то мы не можем к этим
двум последовательностям применять критерий знаков. Однако
небольшая «хитрость» позволяет критерий знаков использовать
в случае плана [N, Z>, N]. Для этого мы заранее нумеруем
изделия в произвольном порядке до постановки их на испытания
и затем сравниваем результаты испытаний, записав обе последова-
последовательности испытаний в порядке этих номеров.
Критерий Вилкоксона. Простой в употреблении и одно-
одновременно весьма мощный критерий для проверки гипотезы, что
одна случайная величина в среднем будет больше, чем другая,
был предложен около двадцати лет назад Вилкоксоном и известен
под его именем.
Пусть случайные величины ^ и т] имеют соответственно непре-
непрерывные функции распределения Fx (х) и F2(x). Мы скажем, что
случайная величина ? меньше, чем г), если при всех х выполняется
неравенство Fx(x)>F2(x). Так как F2 (x) возрастает медленнее,
чем F1(x)i то это означает, что при каждом х у величины г\
остается ббльшая вероятность превзойти х, чем у ?. Эта задача
представляет значительный интерес как для теории надежности,
так и для других областей практики.
Имеются две последовательности взаимно независимых резуль-
результатов наблюдений
х1у х2у .. ., хт
и
Уъ У2, ..-, Уп-
Спрашивается, можно ли считать, что Fx (х) = F2 (xO
Перемешаем обе последовательности наблюдений и расположим
их в порядке возрастания величины. В результате получим после-
последовательность неубывающих чисел (всего их т-\-п). Если гипотеза
F1(x)=zF2(x) верна, то можно ждать, что числа обеих последова-
последовательностей хорошо перемешаются. Для оценки степени перемеши-
перемешивания в критерии Вилкоксона подсчитывается число инверсий
членов первой последовательности относительно второй. Если
fi упорядоченной общей последовательности некоторому х пред-
предшествует у, то мы скажем, что имеет место одна инверсия.
Если некоторому х предшествует k значений у, то это значение х
282 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
имеет к инверсий. Общее число инверсий равно сумме числа
инверсий всех х.
Согласно одностороннему критерию Вилкоксона гипотеза Fx [х)=^
= F2 [х) отбрасывается, если наблюденное число инверсий О пре-
превосходит некоторую границу Ua.
В двустороннем критерии Вилкоксона гипотеза Fx {х) = /72 (х)
отбрасывается как в том случае, когда число инверсии превосхо-
превосходит границу ?/а, так и в том случае, когда число инверсий ока-
оказывается меньшим границы Ua.
Наша задача теперь состоит в определении этих границ.
Оценим сначала математическое ожидание и дисперсию числа
инверсий. Для каждой пары наблюдений xt и yj определим слу-
случайную величину ztj следующим путем:
г<>={ о,
если
если
Ясно, что Р{*,->.у1\} = Р{х|'<.У/}1) и что ?/=2*//» где сумми-
суммирование производится по всем значениям / и у. Отсюда, поскольку
IVUj-y =-о" и число всех слагаемых в сумме равно тп, находим,
что
Несколько усложнив подсчеты, можно найти все центральные
моменты величины U. В частности,
Доказано, что при min (m, п)—*оо имеет место предельное
равенство
При этом выяснено, что эта теорема дает хорошее приближение
уже при т + п^20 и min (w, /г)^3.
х) Если величины ? и ц независимы и имеют непрерывную функцию
распределения F (х), то
со X
— 00 — 00
§ 4.5] НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ 283
Если провести подсчеты для данных, приведенных в табли-
таблице 4.5.1, то окажется, что число инверсий U равно 40. В силу
приведенного предельного соотношения можно написать цепочку
равенств
Отсюда мы заключаем, что и критерий Вилкоксона, как и крите-
критерий знаков, отвергает гипотезу о неизменности настройки штампа
6 и 12 марта.
При малых значениях тип для критерия Вилкоксона состав-
составлены таблицы критических значений Ua и Ua с заданным уровнем
значимости а. Эти таблицы приведены нами в настоящей книге
(см. таблицу 19 приложения).
Обратим внимание на то, что критерий Вилкоксона не учиты-
учитывает значений, принимаемых случайной величиной при испытаниях
№ 1, № 2 и т. д. Для его применения нужно только знание
упорядоченной по величине последовательности результатов наблю-
наблюдений. Отсюда вытекает, что метод Вилкоксона хорошо приспо-
приспособлен, в частности, для использования при сравнении однород-
однородности качества материалов двух серий на срок жизни при стен-
стендовых испытаниях типа [JSfy Z>, N]. При этом в каждой серии
испытаний может быть различное число изделий.
По поводу критериев Вилкоксона и знаков мы сделаем одно
замечание, которое покажет, что оба эти критерия, вообще
говоря, не могут служить для сравнения гипотезы Fx (х) = F2 (x)
с иной произвольной гипотезой. Простой пример покажет нам,
что можно найти такой случай, в котором заведомо оба рас-
распределения Fx (x) и F2 (x) существенно различны, но как кри-
критерий знаков, так и критерий Вилкоксона приводят к хорошему
согласию с гипотезой F1(x) — F2(x). Вдобавок оказывается, что
при увеличении числа наблюдений до оо вероятность решения
принять эту гипотезу будет стремиться к 1.
Пусть распределение Fx (x) таково:
ф (л:) при х ^ а,
/^(л:)^ у при а<лг<?,
i]) (х) при х ^ Ь\
функции ф (л:) и г|? (х) — неубывающие, непрерывные, первая из них
возрастает от 0 до -тг> вторая —от -^ до 1.
284 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4-
Распределение F2 (х) определяется равенствами
0 при
X(*) ПРИ
1 при х ^ Ь;
% (х)—непрерывная функция, возрастающая от 0 до 1.
Легко понять, что для нашего примера число знаков в крите-
критерии знаков всегда будет вблизи от — и число инверсий вблизи от
-тр . Таким образом, оба критерия почти всегда будут приводить
нас к ошибочному заключению. Конечно, наш пример специально
придуман, и в реальной обстановке трудно предположить, чтобы
встретились такие искусственные распределения. При беглом прос-
просмотре статистического материала разделение знаков на две груп-
группы, так же как и инверсий на две резко различные группы, бро-
бросается в глаза, и даже малоопытный исследователь не может оши-
ошибиться.
Критерий Н. В. Смирнова. Интересный (и притом состоя-
состоятельный х)) критерий для проверки однородности статистического
материала был предложен и разработан Н. В. Смирновым. Пусть
по-прежнему имеются две последовательности взаимно независимых
наблюдений, результаты которых
Л> >'2> •-м Уп-
Построим две эмпирические функции распределения
где кг(х) и k2 (#)— соответственно числа *,. и ур оказавшиеся мень-
меньше, чем х. Построим величины
D+n = sMSm(x)-Tn(x)] и DMn = sup\Sm(x)-Tn(x)\.
Как доказал Н. В. Смирнов, при min (my n)—>оо имеют место
предельные соотношения
ф (г) = Р т/ тп р
*) Т. е. такой, для которого вероятность принять ложную гипотезу
стремится к нулю с ростом числа испытаний до бесконечности.
§ 4.5]
НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ
285
Ф.™(*) = р{
При /я = л, как было выяснено Б. В. Гнеденко и В. С. Королюком,
можно найти не только простые предельные закономерности, но и
точные распределения для каждого п. Для каждого значения z
определим целое число с по формуле
Тогда если гипотеза Fx (х) = F2 (x) верна и функция Fx (x) не-
непрерывна, то
при ;
при О
VI-
Г-1
Lc-J
(-1)*
-ck
и
L2n
при
при
<z
Y\-
Мы не приводим доказательства этой теоремы, чтобы не отвле-
отвлекать внимание читателя от основной цели книги техническими
деталями вывода.
Как и всякий статистический прием, предлагаемый метод дей-
действует тем лучше, чем больше произведено наблюдений. С веро-
вероятностью, не меньшей 0,95, следует говорить об изменении рас-
распределения, если при числе наблюдений п величина nDn достигла
или превзошла значения, указанные в таблице 4.5.2.
Таблица 4.5.2
п
nDn
9
6
10
6
12
7
15
8
20
9
25
10
30
11
35
12
50
14
75
17
100
19
286 ПРОВЕРКА ГИПОТЕЗ О НАДЕЖНОСТИ [ГЛ. 4
Приведенные данные показывают, что при малых п критерий
Н. В. Смирнова малочувствителен. Заметим дополнительно, что
для критерия Смирнова нельзя построить примеров, подобных
построенному в связи с критериями знаков и Вилкоксона; этот
критерий состоятелен. В таблице 21 приложения приведены зна-
значения вероятности
P{n\Sn(x)-Tn(x)\^k }
для целочисленных значений k.
Приведенные теоремы могут быть распространены на более
сложную задачу, когда проверяется совпадение функций распре-
распределения Fx (х) и F2 (x) не во всей области их изменения, а толь-
только в отрезке от—оо до того значения х, при котором Fx (х) =
= F2 (x) = 6. Именно с таким положением дел приходится встре-
встречаться в испытаниях, проводящихся по плану [N, />, г]. Пред-
Представим себе, что поставлены две серии испытаний указанного типа.
В первой серии взято т изделий, во второй — п. В первом слу-
случае испытания проводятся до г-го отказа, во втором — до s-ro от-
отказа. Предположим далее, что т и п выбраны так, что — = — = 0.
В предположении, что F1 (x) = F2 (x) и представляет собой непре-
непрерывную функцию, И. Д. Квит [21] доказал ряд предельных теорем
относительно максимального уклонения двух эмпирических распре-
распределений на определенном интервале. Мы ограничимся частными
случаями его результатов.
Обозначим
^„@)= S"P [Sm(x)-Tn{x)]
Dmn(Q)= sup \Sm(x)-Tn(x)\.
x, Ft(x) sS 9
Тогда при min (m, n)—»-oo
+ i>O+(z, 6)
Dmn '.в)< 2} — Ф (z, 9),
где
Ф+ B, 6) = y== Г J e du-e~2z' "j e du\
L — 00 —» J
§ 4.5]
НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ
287
Здесь
-и2
—2k2z2
ah —til
l + ft(l_6)
а-к
z.
J • '*]•
—в)' н V 6A—9)
Для случая т~п Е. Л. Рвачева [25] нашла точные распределения
для статистик D^n(Q) и DA77n(9). Г. М. Мания были рассчитаны raj*
лицы распределений Ф+ (zfi) и <b(zfi) [22], [23].
ГЛАВА 5
РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ
§ 6.1. Введение
Резервирование является одним из основных методов повыше-
повышения надежности, который позволяет, по крайней мере в принципе,
безгранично повышать надежность систем.
Резервирование состоит в том, что к элементу (или блоку)
системы мы присоединяем один или несколько резервных элементов
(или блоков), которые по мере возникновения отказов последова-
последовательно подключаются на место основного элемента (или блока) и
выполняют его функции.
В дальнейшем ради удобства мы будем говорить о резервиро-
резервировании элемента, понимая под словом «элемент» и элемент, как
неразложимую часть системы, и блок, и даже всю систему в целом.
Совокупность основного и его резервных элементов мы будем
в дальнейшем называть резервной группой.
В зависимости от того, в каком состоянии находятся резерв-
резервные элементы до момента их включения в работу, резервирование
элемента делится на несколько типов.
/°. Нагруженный резерв. Резервные элементы находятся в том
же режиме, что и основной элемент, их надежность не зависит
от того, в какой момент они включились на место основного.
Здесь и в дальнейшем в этой главе под надежностью мы бу-
будем понимать вероятность безотказной работы в течение заданно-
заданного времени, а под ненадежностью—вероятность возникновения
отказа за это же время.
2°. Ненагруженный резерв. Резервные элементы находятся в
выключенном состоянии и по условию до момента их включения
на место основного не могут отказать.
3°. Облегченный резерв. Резервные элементы находятся в об-
облегченном режиме до момента их включения на место основного.
Во время ожидания в резерве они могут отказать, но с вероят-
вероятностью меньшей, чем вероятность отказа основного элемента.
Очевидно, что облегченный резерв является наиболее общим типом
§ 5.2] нагруженный резерв 289
резервирования, тогда как первые два типа будут его крайними
частными случаями.
В настоящей главе мы подробно рассмотрим эти три типа
резерва, выведем точные и приближенные формулы, оценивающие
надежность резервной группы, а также рассмотрим некоторые об-
общие свойства зарезервированных систем. Задача об оптимальном
резервировании системы в этой главе не рассматривается. Ниже
мы будем предполагать, что замена отказавшего элемента резерв-
резервным совершается мгновенно. Будем также считать, что отказав-
отказавшие элементы не восстанавливаются (отсюда и название главы).
Резервирование с восстановлением будет рассмотрено в главе 6.
§ 5.2. Нагруженный резерв
В случае нагруженного резерва элемент находится в одном и
том же режиме и до и после включения в работу. Поэтому на-
надежность каждого элемента не зависит от того, в какой момент
он перешел в рабочее состояние, т. е. не зависит от моментов
отказа других элементов. Мы считаем, что время, в течение которого
отказавший элемент заменяется резервным, практически равно
нулю, а переключающее устройство (если оно есть)
абсолютно надежно.
Пусть у нас имеется один основной и п—1
резервных элементов (рис. 5.2.1).
Обозначим через
Pi (О, А (О,-., Рп(*)
надежности соответствующих элементов, а их не-
ненадежности — через
Рис. 5.2.1.
fi('), ft(fl, »., ?„@ (9k=l~Pk)-
Пусть Pn(t) — надежность резервированной группы, a Qn(t) —
ее ненадежность.
По условию отказ наступает в тот момент, когда выходит из
строя последний из работающих элементов. Поэтому для того,
чтобы в течение времени t отказала резервированная группа,
нужно, чтобы в течение этого времени отказал каждый из п эле-
элементов. Так как все отказы независимы, то по теореме умноже-
умножения вероятностей мы получаем
<?„(')=ft С) ft. (О - ?„(')• E-2.1)
Если переписать это равенство для надежностей, то мы получим
р,@] - П-Р»(О]. E-2.2)
290 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
Из этих формул, между прочим, следует, что надежность ре-
резервной группы не зависит от порядка включения резервных эле-
элементов. Из них также следует, что надежность резервной группы
определяется величинами надежности элементов в этот момент и
совершенно не зависит от того, как менялись функции надежности
элементов до данного момента.
Если все элементы имеют одинаковую надежность, т. е.
Pi (') =Ра (*) = ... =Pn (t) = р @, ?(') = ! -Р О,
то формулы упрощаются:
(т. е. ненадежность резервной группы равна ненадежности элемента,
возведенной в степень, равную кратности резерва) и соответст-
соответственно
Pn(t) = \-[\-p(t)]n. E.2.4)
Формула E.2.3) очень проста и удобна. Она легко разрешается
относительно каждой входящей в нее величины. Если, например,
нам задана ненадежность элемента q (t) и требуется найти такое
число резервных элементов, при котором ненадежность Qn(t) не
будет превосходить заданной величины Q, то из неравенства
получим
d
Если же, наоборот, задавшись числом резервных элементов,
определять, какой должна быть надежность каждого из них, то
мы получим
Для случая экспоненциального закона
полезно заметить, что если надежности элементов близки к
единице, то
?*(*) = 1-е"**'« V.
и тогда
д„«яЛ..л/\ E.2. Г)
а для равнонадежных элементов
Qn « №)". E.2.3')
§ 5.2] нагруженный резерв 291
Относительная ошибка в формуле E.2.1)' не превосходит величины
Кроме того, правые части равенств E.2.Г) и E.2.3') не только
являются приближением, но и дают для ненадежности оценку
сверху.
Из неравенства 1—е~х^х следует, что gk(t) ^Xkt\ откуда
Формулы E.2.Г) и E.2.3') удобны в том случае, когда нам
заданы не надежности элементов, а соответствующие опасности
отказа Xk.
Среднее время работы резервной группы определяется из фор-
формулы
со
Tn = \pn{t)dt. E.2.5)
О
Если надежности элементов заданы аналитически, то среднее
время во многих случаях вычисляется в конечном виде.
1) Экспоненциальный закон
/i ь • " • —. . . 1 dt =
fe"< s k < s < /
k k <s k<s<l
Для случая равных надежностей
среднее время получается еще проще
О
Введем новую переменную
292 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
Тогда
Так как среднее время работы одного элемента 7\ = -г-, то
E.2.6)
Если п велико, то среднее время можно вычислить приближенно
по
,
формуле Тп « 7\ (\пп + С -\- х- ) , где С =9,57712. . . — постоян-
постоянная Эйлера.
2) Закон Вейбулла. Ограничимся здесь и в следующем
пункте случаем равных надежностей
00 П
о
п
ИЛИ
п
3) Степенной закон p(t) = — —- (а>1, иначе сред-
среднее время не существует),
_
С—=)—С1—=¦
Если функция надежности р (t) задана графически или в ряде
точек, то среднее время можно определить по формуле E.2.5) чи-
численным интегрированием.
§ 5.2] нагруженный резерв 293
Пусть мы провели испытания N одинаковых элементов, доведя
их до отказа последнего элемента, и в результате испытаний по-
получили величины
О < хх < т2 < . .
— случайные времена работы элементов, расположенные в порядке
возрастания. Эмпирическая функция надежности Р(^) = 1 —--, где
k — число отказов, происшедших до момента t. Подставив эту
функцию в формулу E.2.5), получим
Таким образом, среднее время работы резервной группы па
результатам испытаний можно определить непосредственно.
Написанное может вселить уверенность, что среднее время ГЛ
можно легко вычислить либо по точным формулам, либо с доста-
достаточной точностью по результатам испытаний. Однако это не так,
во всяком случае не совсем так. Дело в том, что величина сред-
среднего времени Тп определяется в основном поведением функции
надежности p(t) при больших значениях времени, значительна
превосходящих среднее время работы элемента. Чем быстрее убы-
убывает функция р (t) при t—*оо, тем меньше величина Тю и на-
наоборот, причем теоретически Тп может меняться в довольно ши-
широких пределах, а именно,
В то же время функция надежности p\t) чаще всего известна нам
лишь на ограниченном интервале времени, который или меньше,
или, по крайней мере, соизмерим со средним временем работы одного
элемента, ибо это среднее время часто измеряется десятками и
сотнями тысяч часов, и мы физически не можем испытывать эле-
элементы такое время.
В том случае, когда надежность задается аналитически, эти
соображения также сохраняют свою силу.
Действительно, говоря, например, что надежность подчиняется
экспоненциальному закону, мы обычно понимаем под этим следую-
следующее: на интересующем нас участке времени опасность отказа
ХУ) = к постоянна. Что будет дальше, нам неизвестно, а эта
дальнейшее поведение X(t) и определяет величину Тп.
Поэтому вышеприведенные формулы пригодны, вероятно, для
Довольно узкого класса элементов, а именно, для элементов, у ко*
торых хорошо изучен период «старости».
294 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
Для большинства элементов достаточно иметь простую, хотя и
грубую оценку для среднего времени Тп. Выведем такую оценку.
Предположим, что функция q (t) выпукла вверх
Tn=][\-g"(t)]dt.
О
Сделаем замену z — q(t)y t — г|)(г). Функция -ф (z) выпукла вниз.
После замены интегрируем по частям
1 1
Тп= J (I -z") rfo|> (z) = п J z"-lty (z) dz.
0 0
Далее,
y{z)^y(a) + y'(a)(z — a),
так как выпуклая вниз кривая лежит выше любой касательной
к этой кривой.
Отсюда
(а) + г|/ (a) (z - a)] dz = г|) (а) + г|/ (а) (^ - а) .
Так как число а произвольно, положим а = ,-. Получим
»^0ттт) или
окончательно
/'^«Х^Л- E-2-7)
Чтобы понять, насколько точно это неравенство, выведем ана-
аналогичную оценку снизу. Для этого предположим, что наш элемент
стареющий, т. е. опасность отказа X(t) монотонно возрастает.
Тогда
\{t)dt
p(t)=e =e
причем функция Л(^) выпукла вниз
о
Сделаем замену z = Л (t)y t = q>(z) и проинтегрируем по частям
со оа
о о
§ 5.2] нагруженный резерв 29S
Действуя как и в предыдущем случае, получим
L
Положим
а= +у+ ••• + "й" •
Тогда
или
Отсюда для надежности получается оценка
р(Тп) =
Легко показать, что разность
монотонно убывая, стремится к пределу, равному — С. Поэтому
*-с = 0,56... E.2.8)
Условия, при которых справедливы неравенства E.2.7) и E.2.8),.
можно ослабить. Достаточно, чтобы, начиная с некоторого t = to>
касательные к графикам p(t) и 1п[р(/)]-1 лежали ниже этих кри-
кривых. Тогда, если Tn>t0, справедливо неравенство
0,56 « е~с< (п + \)р(Тп) < 1. E.2.9>
Это неравенство показывает, что для определения среднего времени
работы резервной группы можно пользоваться приближенной фор-
формулой
P(Tn) = ^r E.2.10)
При этом мы немного занижаем среднее время, т. е. истинная ве-
величина Тп будет несколько больше расчетной.
При выводе этой приближенной формулы мы предполагали, что
функции q (t) и K(t) = \n—rrc выпуклы вниз. Если эта выпуклость
имеет место, начиная с некоторого /, то неравенство E.2.9) будет
иметь место, начиная с некоторого номера л.
96 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
Из формулы E.2.10) видно, как растет среднее время с ростом
кратности резервирования. Например, для закона Вейбулла
среднее время растет медленно.
Для степенного закона
1
среднее время растет значительно быстрее.
При рассмотрении горячего резерва мы предполагали, что ра-
работает всегда один элемент, а остальные находятся в резерве.
В некоторых случаях характер системы таков, что все п элементов
одновременно выполняют некоторую функцию, причем для удов-
удовлетворительного выполнения этой функции необходимо, чтобы по
меньшей мере m элементов из п было исправно. Значит, отказ
резервной группы наступает в тот момент, когда происходит
{п — т+ 1)-й отказ.
Если предположить, что отказы элементов независимы, то на-
надежность резервной группы может быть легко найдена. В общем
случае, когда надежности элементов различны, рассмотрим много-
многочлен
Р (х) = (ргх + qx) (р2х + q%)... (рпх + qn) =
= Рппхп+ Рпп_гхя-1 + ... + Рякх*+ ... + Рпо.
Очевидно, что коэффициент Pnk есть вероятность того, что к дан-
данному моменту из п элементов останется в живых ровно k.
Отсюда
Р„=2Л,*. E.2.11)
Если все элементы равнонадежны, то
Рп= 2 Cknpkqn~k. E.2.12)
В заключение этого параграфа укажем на одну теоретико-вероят-
теоретико-вероятностную интерпретацию горячего резерва.
§ 5.3] схема гибели 297
Пусть тх, т2, ..., хп—случайные времена работы основного и
резервных элементов, которые мы считаем равнонадежными, а
%{п) — случайное время работы резервной группы. Тогда очевидно,,
что
) = max(t1, т2, ..., хп).
Мы можем рассматривать величины xk как независимые наблюде-
наблюдения случайной величины с законом распределения q(t). Пусть
t'i < г'2 < ... т'п
— величины тл, расположенные в порядке возрастания. Последова-
Последовательность Xk называется вариационным рядом. Легко заметить, что
Таким образом, момент отказа резервной группы является крайним
членом вариационного ряда. Для последнего случая, описываемого
формулой E.2.12), момент отказа
г(«) _ г
Значит, при изучении горячего резерва мы можем применять хо-
хорошо развитую теорию распределения членов вариационного ряда [2],
§ 5.3. Схема гибели
Рассмотрим одну теоретико-вероятностную схему, которая мо-
может быть широко использована при изучении различных типов ре-
резервирования [3]. Для удобства мы будем описывать эту схему
в терминах теории надежности, хотя она применима и в целом
ряде других случаев (например, в биологии, медицине и т. д.).
Пусть дана система, состоящая из некоторого числа элементов, и
в этой системе происходят отказы элементов. Возникающий поток
отказов подчиняется следующим условиям:
1. Если к моменту t произошел k—1 отказ, то независимо от
моментов возникновения этих отказов вероятность того, что на
бесконечно малом участке (tyt-^-At) произойдет один отказ, равна
а вероятность того, что на этом участке не произойдет отказа,
равна
2. В момент, когда происходит я-й отказ, работа системы пре-
прекращается и никаких изменений в системе в дальнейшем не про-
происходит. Поэтому Xrt+1 = 0.
98 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [гл. 5
Эти два условия, как мы покажем, полностью определяют ко-
конечный поток отказов, и если они выполняются, то несущественно,
какие элементы составляют систему, как они соединены в системе,
какие из элементов отказывают и как влияют одни отказы на
другие.
Заметим еще, что второе условие не очень существенно и свя-
связано со спецификой задач в теории резервирования — ведь резерв
всегда конечен и, следовательно, до отказа резервной группы мо-
может произойти лишь конечное число отказов.
Если к моменту t произошел к—1 отказ, то мы говорим, что
наша система находится в состоянии k. Обозначим через nk(t) ве-
вероятность того, что в момент / система находится в состоянии к.
Тогда яп+1 (t) =Qn (t) есть вероятность того, что система откажет
к моменту t, т. е. ненадежность системы. Сравнив состояния си-
системы в два бесконечно близких момента t и t + ktt по формуле
полных вероятностей получим
Отсюда при Д^—> 0 получаем систему дифференциальных уравнений
E.3.1)
Величины zik(t) удовлетворяют начальным условиям л1@)=1>
jstk@) = 0 при k>\.
Чтобы получить решение этой системы в замкнутом виде, удобно
использовать преобразование Лапласа.
Введем обозначение
00
в» (/>) = $ я» (*)«"" Л.
$ »
О
Величины ak (t) удовлетворяют соответствующей системе алгебраи-
алгебраических уравнений:
pak (р) = Xk_x ak_x (р) - V* (Р) (* = 2, 3, ..., /2), E.3.2)
Pan+i(P) = han(P)-
Разрешив эту систему, получим
§ 5.3] СХЕМА ГИБЕЛИ 299
откуда
t>- (в.з.з>
Применив формулу обращения преобразования Лапласа, мы
находим искомую вероятность
c+ico
Пп+Л^Ь^К J __?__dp (c>0). E.3.4>
с -i со
Вертикальный контур интегрирования мы можем заменить замкну-
замкнутым контуром, обходящим в положительном направлении нули
знаменателя. Тогда по основной теореме о вычетах
... к F.3.5)
где (д(х)
Зта формула годится только для случая, когда все числа Xk
различны. В противном случае формула несколько усложняется, и
мы не будем ее выписывать. Отметим только частный случай
%k = X, Тогда
С
Продифференцируем обе части равенства по /, тогда
Отсюда
Вычислять вероятность яп+1(/) по формуле E.3.5) не очень
удобно. Дело в том, что эта вероятность обычно мала (напомним,
что в наших задачах яп+1 (t) — ненадежность резервной группы), в то
время как слагаемые в правой части E.3.5) велики. Поэтому каж-
каждое слагаемое должно вычисляться с большим числом значащих
цифр. Кроме того, из формулы E.3.5) трудно усмотреть, какой
качественный характер имеет зависимость ял+1(/) от времени и
параметров Xk.
Поэтому целесообразно найти простые приближенные формулы
для пп+1 (/), каждая из которых годилась бы для определенного
диапазона изменения времени и параметров Kk.
300 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
Первая приближенная формула. Разложим функцию
яп+1 (t) в ряд по степеням t.
Для этого подынтегральную функцию в формуле E.3.4) раз-
разложим в ряд
ept ept
где
Возьмем в качестве контура интегрирования круг радиуса
Я > max Яд и проинтегрируем этот ряд почленно. Получим
к = О
Докажем, что этот ряд обладает следующим замечательным
свойством, характерным для многих правильных знакопеременных
рядов: при любых значениях />0, п и Лл>0 ошибка, возникаю-
возникающая при отбрасывании всех членов ряда, начиная с некоторого,
имеет тот же знак, что и первый отброшенный член, а по абсо-
абсолютной величине всегда меньше этого члена.
Рассмотрим для удобства функцию
@ _ JL Г в—
К 2) ( + Х)
= *»+l@ _ JL Г в— Ип
К 2т) р (р + Хх) ... [р + Ю Р'
Возьмем производную
f"(t) ~ 55 J ?"
с
J
с
Отсюда в силу того, что /„@^0, получаем /n@^A-i@ или
1МЛ; /oW = l, следовательно,
/2 /Я
§ 5.3] СХЕМА ГИБЕЛИ 301
Теперь будем искать оценку снизу
или
t
tn+1
t_i\w -v — „я (/l + 1)! •
0
Отсюда
Продолжая таким образом, мы получим искомую оценку
^^S^!-!)*. E.3.8)
При /=0, в частности, получим
или
11 i I 1 Л1
откуда следует, что для вероятностей пп+1(t) справедлива при-
приближенная формула
nn+1(t)tt%ll*n;-Ktn, E.3.Ю)
причем относительная ошибка этой формулы не превосходит
величины
ЯТ1 L
Как показывает неравенство E.3.9), формулой E.3.10) можно
пользоваться даже тогда, когда относительная ошибка велика,
ибо она дает для нашей вероятности оценку сверху. В случае
необходимости можно взять и еще несколько членов ряда E.3.7),
так как этот ряд быстро сходится.
Как будет выяснено ниже, величины %k в задачах теории резер-
резервирования равны сумме опасностей отказа некоторых элементов*
302 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
составляющих систему. Формула E.3.10) будет точна в том случае
когда величины Xkt в среднем малы. Но если Xkt малы, то
Поэтому \kt будут приближенно равны суммам ненадежностей соот-
соответствующих элементов.
Следовательно, приближенная формула E.3.10) применима в
задачах резервирования в тех случаях, когда надежности элемен-
элементов, составляющих резервную группу, сравнительно близки к
единице. В этом случае кратность резервирования бессмысленно
делать большой.
Вторая приближенная формула. Можно добиться
высокой надежности и другим путем — составлять резервную группу
из большого числа ненадежных элементов. В этом случае формула
E.3.5) заведомо малопригодна. Не годится также приближенное
равенство E.3.10). Поэтому мы без вывода приведем вторую
приближенную формулу, которая пригодна для случая,
когда величины \kt конечны, а п велико.
Если -г^(^J—^ ПРИ п—'°°>то для больших п имеет
/г = 1
место приближенная формула
- s Ч'
nn+1(t)ttXlX*n;-X"tnek^n , E.3.11)
причем главный член относительной ошибки равен
Выше мы изучали поведение вероятности nn+1(t) главным образом
для тех случаев, когда она мала. Рассмотрим теперь другой
п-1
Рис. 5.3.1.
подход к схеме гибели, который даст нам возможность изучить пове-
поведение функции я„+1(/) для больших значений времени. Обозначим
через %k случайное время, протекшее между (k—1)-м и k-u отка-
отказом (рис. 5.3.1).
§ 5.3] схема гибели 303
Тогда
есть случайное время жизни нашей системы. В силу определения
вероятность
является законом распределения случайной величины Тп. Далее,
из условий, сформулированных в начале этого параграфа следует,
что величины xk взаимно независимы и каждая из них распределена
по экспоненциальному закону
Отсюда среднее время жизни системы равно
п
ПТп= ?~, E.3.12)
а дисперсия
Распределение величины Тп как суммы независимых случайных
величин с ростом номера п при определенных общих условиях
должно стремиться к нормальному. Удобнее всего воспользоваться
условиями Ляпунова: если
з_
_ _ =0, E.3.13)
то
Отсюда для вероятностей яя+1(^) мы получаем третью при-
приближенную формулу.
Если выполняется условие E.3.13), то при большом п для
всех ^, для которых отношение
\Гътп
ограничено, имеет место приближенное равенство
304 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
Проиллюстрируем применение схемы гибели на примере на-
нагруженного резерва.
Пусть надежности наших элементов одинаковы и подчиняются
экспоненциальному закону
На участке времени до первого отказа работают все п элементов.
Рассмотрим на этом участке бесконечно малый отрезок времени
(/, t + h). Вероятность того, что на этом участке данный элемент
не откажет, равна e~lhy а вероятность того, что не откажет ни
один из п элементов, равна
e-nhl=\—nXh+o(h).
Так как вероятность появления двух или более отказов на этом
участке имеет порядок /*2, то вероятность появления ровно одного
отказа равна
nkh + o(h).
Таким образом,
На участке между первым и вторым отказами работает (п—1)-й
элемент, поэтому
Яа = (л— 1) X.
Вообще
k)X (*=1, 2 л),
Далее, так как отказы элементов независимы и подчиняются экспо-
экспоненциальному закону, появление отказа элемента на данном участке
не зависит от того, сколько времени проработает данный элемент
и когда произошли отказы других элементов. Следовательно, наш
поток отказов есть процесс типа гибели.
Применяя формулы E.3.5), мы получаем, что ненадежность нашей
резервной группы равна
Если надежности элементов для данного отрезка времени близки
к единице, а п невелико, то согласно первой приближенной
формуле
)
§ 5.3] СХЕМА ГИБЕЛИ 305
Вторая и третья приближенные формулы в этом случае несправед-
несправедливы. Среднее время жизни резервной группы согласно E.3.12)
равно
Мы получили формулы, которые выше были получены непосред-
непосредственно.
Рассмотрим теперь более сложный случай нагруженного резерва,
когда отказы одних элементов изменяют надежность других. Физи-
Физически мы можем представить себе этот случай так: работают
одновременно п элементов, выполняя одну и ту же функцию. Если
один из элементов отказывает, то на долю остальных ложится
большая нагрузка, меняются параметры их работы и поэтому
изменяется надежность работающих элементов.
Предположим, что на каждом участке между соседними отка-
отказами опасность отказа элемента постоянна и зависит только от
числа работающих элементов. Если к данному моменту не отка-
отказало k элементов, то опасность отказа каждого из них равна [ik.
В обозначениях схемы гибели получаем
Отсюда ненадежность нашей резервной группы можно вычислить по
формуле E.3.5). Если надежности всех элементов близки к еди-
единице, то первая приближенная формула дает
Среднее время жизни резервной группы
МГ«==^+(п-1)^_1+ •••+?•
Рассмотрим частный случай
И»=1*,1-1= •••=»** = *> »*«-! ==...= 1*1 = 0,
т.. е. отказы одних элементов не изменяют надежности других,
но резервная группа справляется со своими функциями, пока
число работающих элементов не меньше т. В тот момент, когда
число работающих элементов становится равным т—\, наступает
отказ резервной группы. В этом случае
Х1-=пХ, Я2 = (/г — 1) А, .. . >к
Б. В. Гнеденко и др.
306 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
и ненадежность нашей резервной группы равна
(m-_
(ml)! k\(n — k)l (* — т)\ '
Преобразовав эту сумму, мы получим окончательно
что можно вывести и непосредственно.
Для случая высоких надежностей первая приближенная формула
дает
Среднее время жизни резервной группы
МГ = * 1 1 1 4
Если тип велики, то
причем ошибка имеет порядок «тл-(—* г)
§ 5.4. Недогруженный резерв
В случае ненагруженного резерва будем предполагать, что
резервный элемент не может отказать, находясь в нерабочем
состоянии, и что пребывание резервного элемента в нерабочем
состоянии не изменяет его надежности в рабочем состоянии. Кроме
того, как и выше, мы считаем, что время, в течение которого
отказавший элемент заменяется резервным, практически равно
нулю и переключающее устройство абсолютно надежно.
Пусть у нас имеется один основной и п—1 резервных элемен-
элементов. Обозначим через pk(t) надежность &-го по порядку элемента,
а через qk(t) — его ненадежность.
Основной элемент, проработав некоторое случайное время tlt
выходит из строя и на его место становится первый резервный
элемент, который работает случайное время т2, и т. д. Последний
резервный элемент, проработав случайное время хп, выйдет из
строя, а с ним выйдет из строя и вся резервная группа. Таким
§ 5.4] НЕНАГРУЖЕННЫЙ РЕЗЕРВ 307
образом, случайное время жизни резервной группы Тп равно
7>=т1 + т2+...+т„. E.4.1)
Величины xk независимы и
?{lk<t}=qk(i).
Обозначим через Qn (t) ненадежность резервной группы. Функция
Qn(t), как закон распределения суммы п независимых слагаемых,
определяется из формул
ln(t-*)Qn-x(f)dx, E.4.2)
Последовательно применяя эту формулу для л = 2, 3, ..., мы
можем вычислить точно или приближенно величину Qn(t).
Очень просто определяется среднее время жизни резервной
группы
Т# = МТп = S Мт, = 2 *<*>. E.4.3)
В частности, если все элементы равнонадежны, то
7^ = л-'сР. E.4.4)
Пусть теперь надежности наших элементов подчинены экспонен-
экспоненциальному закону
Р* № = *-**'.
Согласно предыдущему параграфу
Следовательно, для вычисления ненадежности Qn (t) можно использо-
использовать формулы E.3.4), E.3.5), E.3.7) и приближенные формулы
E.3.10), E.3.11) и E.3.14).
Отметим особо приближенную формулу E.3.10)
Q
n
Величины ЯЛ*«1—в"х*/ = ^д (/), так как эта формула справедлива,
когда Xkt малы. Следовательно, мы можем записать ее в виде
Q.W
AtLt(t)'--4«it)
n!
E.4.5)
Эта формула дает ясное представление о выигрыше, которого
мы добиваемся, применяя ненагруженный резерв (ср. с E.2.1)).
308 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
Если ненадежности всех элементов равны
то по формуле E.3.6)
Подставив в это равенство единицу в форме
е~'\
мы получим формулу
00
Qw (t) = / л , t e~ , E.4.6)
более удобную для вычислений. Исходя из этого ряда, можно вы-
вывести простую и очень точную приближенную формулу
k = n
или
E.4.7)
При этом относительная ошибка имеет порядок
Если А/<^1, то можно пользоваться и совсем простой приближен-
приближенной формулой
q и\ ~QD1 E.4.8)
которая является частным случаем E.3.10).
Величина Qn(t) вычисляется и в случае, когда надежности эле-
элементов подчиняются нормальному закону
1 Г 20t
е k dx (ob<?ab).
§ 5.4] НЕНАГРУЖЕННЫЙ РЕЗЕРВ 309
Случайное время жизни резервной группы Тп будет суммой
независимых нормальных величин xk и поэтому само будет рас-
распределено по нормальному закону со средним значением
a = ai + a2-\- ... -\-ап
и дисперсией
Следовательно,
(Так как а<^а, то можно пренебречь частью интеграла от — оо
до нуля.)
Наконец, функцию Qn(t) легко вычислить для случая, когда
надежности всех элементов равны и частота отказов выражается
формулой "~ " """ ~~" " ——
Тогда
*п\ч- Т(па) - •
В большинстве случаев величина Qn (t) не вычисляется в конечном
виде. Поэтому особый интерес приобретают различные приближен-
приближенные формулы и оценки надежности в этом случае. Докажем пред-
предварительно простое утверждение, позволяющее находить такие
оценки.
Пусть q1(tI q2(t), ..., qn{t) — ненадежности основного и ре-
резервных элементов и пусть существуют монотонно неубывающие
функции qj(t)y q^(t)y ...,q_n(t) и ^ (/), q2(t), ..., qn(t) такие,
что на рассматриваемом участке времени
Пусть, далее, функции Qn(t) и Qn(t) определяются соответст-
соответственно через функции qk(t) и qk(t) так же, как функция Qn(t)
определяется через функции qk{t) [см. E.4.2)).
Тогда на данном участке времени
Qn(t)^Qn(t)^Qn(t). E.4.9)
Докажем эти неравенства по индукции. При # = 1 они оче-
очевидны. Предположим, что E.4.9) справедливо для немера n = k.
310 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
Тогда
о
t t
-т) Q'k (х) dx = J Qk (т) q'k + 1 (t-x) dx <
(t) dt = Qk+1 (t),
k
О О
t t
или
Аналогично доказывается и левое неравенство. Используем теперь
полученные неравенства.
1) Пусть ненадежности элементов удовлетворяют на данном
участке времени неравенствам
Легко показать, что
откуда
2) Пусть опасности отказов наших элементов удовлетворяют
на данном интервале времени неравенствам
h^hW^h- E.4.11)
Тогда
1—е"^<?л@ = 1—в ° <1—e-W E.4.12)
и мы в качестве оценок можем использовать формулы E.3.5),
E.3.6) и E.3.7), подставляя в них соответственно Kk и Яд. Кроме
того, из E.4.12) следует, что
откуда вытекает неравенство
§ 5.4] НЕНАГРУЖЕННЫЙ РЕЗЕРВ 311
3) Обобщая случай 1), мы можем предположить, что наши
ненадежности удовлетворяют неравенствам
Такой случай имеет место, например, когда надежности элементов
подчиняются закону Вейбулла " """"*
Тогда q(t)~\—?-*•'*<№". Нетрудно показать, последовательно
интегрируя по формуле E.4.2), что
< *"" Г (а/+.1.+af+"?+ ° ^а< + -^- E-4.13)
Между прочим, в этом случае можно показать, что если
^1 М, то
4) Предположим теперь, что наши элементы стареющие, т. е.
опасности отказа
монотонно не возрастают. Обозначим через Ak (t) = j Xk (r) dr.
о
Функции Ak(t) выпуклы вниз, поэтому на участке @, t) имеют
место неравенства
Следовательно,
Як (*) = 1 —е-Аь (т) < 1 — е~Х ~т~',
так что для оценки сверху функции Qn (t) можно использовать
формулу E.3.7), подставив в нее вместо Xk величины ^ '. Уси-
Усилив неравенство, мы можем написать, что
E.4.14)
х) Это естественно, так как если бы а^ были меньше единицы, тэ
опасность отказа была бы в нуле неограниченной.
312 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [гл. 5
В частности, если надежности всех элементов одинаковы, Ak(t)=-
= A(t), то
^-^. E.4.15)
В результате проведенных выше оценок мы приходим к очень
важному выводу: почти во всех случаях величина
п\
D
либо.является хорошим приближением для функции Qn(t), либо
дает для нее оценку сверху. Заметим, что, завышая ненадеж-
ненадежность Qn(t), мы завышаем тем самым и ненадежность всей системы.
Поэтому наши прогнозы будут несколько хуже действительности.
Все эти соображения дают нам право пользоваться приближенной
формулой E.4.5), во всяком случае тогда, когда ненадежности
flfr(n доста^чнс^малы'! Удобство этой приближенной формулы
состоит, между прочим, еще и в том, что для определения по ней
надежности резервной группы нам достаточно знать значения
надежностей элементов только в конечный момент времени /, в то
время как при использовании точной формулы E.4.2) мы должны
знать поведение функций надежности на всем интервале @, t).
В заключение сравним между собой нагруженный и ненагру-
женный резервы. Пусть
— случайные времена работы основного и резервных элементов.
Тогда случайное время работы резервной группы для нагруженного
резерва равно
ъ т2, ...,т„)
а для ненагруженного резерва равно
Но ясно, что
Отсюда мы делаем вывод: ненагруженный резерв в любом случае
выгоднее нагруженного *).
J) Напомним, что мы считаем пока переключатели абсолютно надеж-
надежными.
§ 5.5] ОБЛЕГЧЕННЫЙ РЕЗЕРВ 313
Чтобы сравнить количественно эти два типа резерва, выпишем
для случая нагруженного резерва точную формулу
и приближенную формулу для случая иенагруженного резерва
qB) /^ ^ Я\ @ Яг @ • • • Яп (О
Последняя, как мы показали, верна, если на интересующем нас
участке времени функции qk(t) приблизительно линейны.
Отсюда
Q{1n (О
т. е. при переходе к ненагруженному резерву ненадежность
уменьшается в п\ раз. Посмотрим, наконец, как увеличивается
среднее время. Предположим, что все элементы имеют одинаковую
надежность, подчиненную экспоненциальному закону.
Тогда для нагруженного резерва
СР \ 2 п )
а для ненагруженного резерва T^p=ntcp. Отсюда
« . 1 . .1
ср
Чем больше кратность резервирования, тем больше выигрыш
в среднем времени. Например, при п — 2
ср
а при п = 10
т А
r(i) 3 ~ 1>о>
ср
§ 5.5. Облегченный резерв
Во многих случаях нам невыгодно применять нагруженный
резерв, так как из-за отказов резервных элементов он не дает
желаемого выигрыша в надежности. Вместе с тем мы не можем
использовать и ненагруженный резерв, ибо от момента включе-
включения элемента до момента, когда он становится работоспособным,
314 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
проходит некоторое время — элемент «разогревается», а условия
эксплуатации не допускают перерыва в работе нашей системы.
В подобных случаях часто применяют так называемый облег-
облегченный резерв, суть которого в том, что резервный элемент до
момента включения в работу, находится в облегченном режиме,
а после включения начинает работать в нормальном рабочем:
режиме. При этом элемент может отказать, находясь в нерабочем
состоянии, однако, вообще говоря, с меньшей вероятностью.
Пусть резервная группа состоит из одного основного и п—1
резервных элементов. Обозначим через pty (t) надежность А»-го
элемента в нерабочем состоянии и через piPk (x, t) — условную ве-
вероятность того, что k-ft резервный элемент не откажет, находясь
в рабочем состоянии на участке времени (т, t) при условии, что
он не отказал на участке @, т), находясь в нерабочем состоянии
(т — момент включения элемента). Каждый резервный элемент вклю-
включается в тот момент, когда откажет последний (по времени, а не
по номеру) из предыдущих элементов.
Обозначим через
Т1> Т2> Т3> • • • » Тп
случайные времена работы основного и резервных элементов; пусть
Tk= max г,..
1 ^ / ^ k
Очевидно, что в момент Tk происходит включение в рабочее
состояние очередного (&-|-1)-го элемента.
Рассмотрим функции
Ясно, что Qx (t) — это ненадежность основного элемента, a Qk (t) —
ненадежность резервной группы из основного и (k—1)-го резерв-
резервного элемента. Qn(t) — искомая ненадежность нашей резервной
группы. Заметим еще, что случайные времена %к зависят друг ог
друга, так как время жизни резервного элемента зависит от того,
в какой момент он перешел в рабочее состояние, т. е. зависит
от предыдущих времен т/#
Выведем формулу, связывающую две последовательные фупк-
иии Qk(t) и Qk+1(t),
Q*+iW = P {Тк^<*} = ? {Tk<t, xk+1<t} =
t
§ 5.5] ОБЛЕГЧЕННЫЙ РЕЗЕРВ 315
Вероятность
откуда
t
S П -^+i W KPii <T> 0] <*Q* (*)¦ E.5.1
Так как Qx(t) — ненадежность основного элемента — нам известна,
то по этой формуле мы можем последовательно определить все
функции Qk{t). Однако использование этой формулы затрудняет
то обстоятельство, что нам обычно неизвестна функция pty (т, ().
Ее опытное определение требует огромной статистики, так как
эта функция зависит от двух аргументов. Поэтому в качестве
первого приближения мы можем предположить, что пребывание
элемента в облегченном режиме не изменяет его надежности
в рабочем состоянии. Тогда
Л'(т, О=Р(Р(<—с).
Заметим еще, что нагруженный и ненагруженный резервы являются
частными случаями облегченного резерва.
Для нагруженного резерва в обозначениях, принятых выше,
^)(t)=pft(t), ЛР)(т, O-jf$-.
а для ненагруженного резерва
Чтобы получить эффективные формулы для надежности резерв-
резервной группы в случае облегченного резерва, предположим, что
надежности элементов и в рабочем и в нерабочем состоянии под-
подчиняются экспоненциальному закону и надежность элемента в ра-
рабочем состоянии не зависит от времени пребывания в нерабочем
состоянии. Сначала разберем тотчхлучай, когда надежности всех
элементов одинаковы. Пусть (?)— опасность отказа элемента
в облегченном режиме, (^jh-опасность отказа элемента в рабочем
режиме. Если к данному моменту времени отказал (k—1) эле-
элемент, то один из неотказавших элементов находится в рабочем
режиме, а (п — k) в облегченном режиме. Поэтому суммарная опас-
опасность отказа
— к) К.
Ясно, что наш процесс является частным случаем процесса гибели
и мы можем применить все выведенные ранее формулы.
316 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
Подставляя величины Kk в формулу E.3.4), получим
2я/ л
ePfdp
Возьмем от обеих частей равенства производную по t и в по-
получившемся интеграле сделаем замену
] Г
J i
. . . (n— \)X С estds
С
2ш J s(s + X) ... [s + (n — \)X] *
Легко видеть, что второй сомножитель есть ненадежность резерв-
резервной группы из п — 1 элементов для случая нагруженного резерва.
Поэтому
Отсюда
S^W
При небольших п и надежностях элементов не слишком близ-
близких к единице этой формулой пользоваться удобно. В случае
высоких надежностей можно использовать формулу E.3.10), кото-
которая будет иметь вид
А<А + У^ + <п^\ E.5.3)
причем относительная ошибка не превосходит величины
Наконец, можно использовать для вычисления Qn(t) ряд E.3.7).
Рассмотрим теперь более общий случай, когда элементы имеют
различные опасности отказа.
Пусть Xk — опасность отказа k-то элемента в нерабочем состоя-
состоянии, a Ak — опасность отказа &-го элемента в рабочем состоянии.
§ 5.5] ОБЛЕГЧЕННЫЙ РЕЗЕРВ 317
При рассмотрении этого случая мы не можем уже воспользо-
воспользоваться схемой гибели, ибо суммарная опасность отказа зависит не
только от числа происшедших к данному моменту отказов, но и
от того, какие элементы отказали. Для определения надежности
резервной группы воспользуемся общей формулой для облегчен-
облегченного резерва.
В нашем случае
Подставляя эти величины в формулу E.5.1), получим
с* (о = $ [1 -«-**
E 5 4)
Отсюда можно было бы вычислить функции Qk(t), так как
все интегралы легко берутся. Однако еще удобнее использовать
преобразование Лапласа. Пусть
о
Продифференцировав равенство E.5.4), получим
t
0
Умножив это равенство на e~ft и проинтегрировав по t> получаем
ak(p) = "k-i(p)-irZT:ak-i(P + :
/ \_ Л1
E.5.5)
Отсюда мы определяем ап(р), которая, как легко заметить, будет
рациональной дробью с известными нулями знаменателя
А(р)
Обратное преобразование Лапласа дает формулу
(Можно было бы получить и явную формулу для Qn(t), однако
она очень громоздка.) Из формулы E.5.5) легко определяется
среднее время работы резервной группы.
318 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
Пусть Tckp— среднее время работы резервной группы, состав-
составленной из k первых элементов нашей большой резервной группы.
Очевидно, что
[ ср —
о
Дифференцируя E.5.6) и подставляя р = О, получим
С* Л* *"' E.5.7)
откуда мы можем определить величину Т^\ Выведем теперь при-
приближенную формулу для Qn(t), предполагая, что надежности резерв-
резервных элементов близки к единице. Это означает, что малы опасности
отказа ЛЛ и Ak. Мы можем выбрать большую единицу времени,
чтобы величины Xk и Ак не были малы. Тогда, очевидно, будет
мал тот интервал времени, на котором мы рассматриваем нашу
резервную группу.
Поэтому, выводя нашу приближенную формулу, мы можем при-
принять такую схему: величины Xk, Ak и п фиксированы, а время t—>О.
Разложим функции Qk(t) в ряд по степеням t
(Разложение начинается с tk, так как для того, чтобы за малое
время t отказали первые k элементов в нашей резервной группе,
должно произойти, по крайней мере, k отказов, вероятность каж-
каждого отказа имеет порядок /, а вероятность k отказов имеет по-
порядок tk.)
Тогда величины ak(p) будут иметь разложение
Подставляя его в формулу E.5.5) и сравнивая коэффициенты
при старших степенях, получим
откуда
§ 5.5] ОБЛЕГЧЕННЫЙ РЕЗЕРВ 319
Так как время t—> (), то, беря в разложении по степеням t первый
член, мы получим искомую приближенную формулу
р9 E#5>8)
(Сравните ее с E.5.3).)
Используя эту формулу, поставим и решим такую задачу:
В каком порядке нужно расположить данные резервные элементы,
чтобы надежность резервной группы была наибольшей? Интересно
заметить, что в случае нагруженного и ненагруженного резервов
надежность резервной группы не зависит от порядка элементов.
Предположим, что порядок является оптимальным. Тогда переста-
перестановка любых двух соседних элементов может только увеличить
функцию Qn{t).
Поэтому
~ {t)_Al{A2 + \2).
где Qn (^ — ненадежность резервной группы, в которой поменялись
местами &-й и (&+1)-й элементы.
Сокращая на общие множители, получим
[А„ + (к - 1) Хк) (ЛА+1 + кХк+1) < (Л* + к\к) [Ак+1
или, после преобразований,
откуда следует, что в случае наивыгоднейшего расположения
элементов должны выполняться неравенства
Нетрудно дать и физическое истолкование этих условий: если у двух
элементов надежности в рабочем состоянии равны, то сначала нужно
использовать тот из них, который в облегченном режиме менее
надежен, ибо тогда с большей вероятностью успевают поработать
оба элемента; наоборот, если два элемента равнонадежны в облег-
облегченном режиме, то на первое место нужно поставить тот элемент,
который более надежен в рабочем состоянии, так как у первого
элемента больше шансов быть использованным, чем у последую-
последующего, который к моменту, когда до него дойдет очередь, может
отказать с большей вероятностью. Неравенства E.5.9) количественно
уточняют эти соображения.
320
РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ
[ГЛ. 5
Хотя облегченный резерв включает в себя как крайние частные
случаи и нагруженный и ненагруженный резервы, не следует ду-
думать, что он является наиболее общей схемой резервирования
элемента.
Можно было бы попытаться чисто умозрительным путем построить
такую общую схему, однако вряд ли в этом имеется потребность.
Рассмотрим лучше две конкретные схемы, которые покажут неко-
некоторые пути для такого рода обобщений.
1) Предположим, что имеется один основной и п—1 резервных
элементов (рис. 5.5.1). На промежутке между двумя соседними отка-
отказами опасность отказа каждого элемента постоянна и зависит
только от того места, которое занимает данный
элемент в ряду неотказавших элементов.
v / Пусть \хх — опасность отказа работающего
\ \5^/ / в данны^ момент элемента, ji2 — опасность отка-
* ' за следующего из неотказавших элементов и
т. д. Грубо говоря, каждый элемент по мере при-
приближения своей очереди в ряду не отказавших
элементов разогревается все сильнее и сильнее.
На рис. 5.5.1 из пяти элементов не отказали два.
Если к моменту t произошел (k—1)-й отказ,
то суммарная опасность отказа равна
Рис. 5.5.1. k~
и мы снова приходим к схеме гибели.
2) Иной характер носит вторая схема [4]. В некоторых радио-
радиоэлектронных системах различают два типа отказов — обрыв и замы-
замыкание. Если в последовательной цепи произошло замыкание, то
данный элемент не работает., но ток через него идет и поэтому
работа остальных элементов не нарушается. Наоборот, если проис-
происходит обрыв, то вся цепь перестает работать.
В случае параллельного соединения элементов замыкание приво-
приводит к отказу всех элементов, так как сопротивление элемента, в
котором произошло замыкание, становится практически равным
нулю и через остальные элементы ток не идет. В то же время
обрыв о^.см о элемента не приводит к отказу других.
Такип образом, замыкание резервируется последовательным
соединением, а обрыв — параллельным, и для того, чтобы застра-
застраховаться от этих двух типов отказов, мы применяем последова-
последовательно параллельное соединение. В каждой последовательной
цепочке п элементов, а таких цепочек т штук (рис. 5.5.2). Для
решения задачи предположим, что обрывы и замыкания не изменяют
надежности тех элементов, которые продолжают работать. Будем
также считать, что если произошел обрыв данного элемента, то
не может произойти его замыкание, и наоборот.
§ 5.5]
ОБЛЕГЧЕННЫЙ РЕЗЕРВ
321
Чтобы определить надежность всей резервной группы, введем
следующие события. A{j — исправная работа на данном участке
времени /-го элемента у-й цепочки, B(j—обрыв этого элемента,
Cij — его замыкание. Aj — исправная работа у-й цепочки; это событие
наступит в том случае, если не будет ни одного обрыва и если
по крайней мере в одном элементе не произойдет замыкания.
Bj — обрыв у-й цепочки, который происходит в том случае, когда
наступает обрыв хотя бы одного из элементов цепочки. Cj—замы-
Cj—замыкание у-й цепочки, которое наступает, когда происходит замыкание
всех элементов цепочки.
Рис. 5.5.2.
Наконец, А — исправная работа всей резервной группы. Эти
события связаны между собой так:
гЛ
1=1 /=1
Отсюда можно найти искомую надежность. Пусть
Тогда
а ненадежность резервной группы
E.5.10)
322 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [гл. 5
Исходя из этой формулы можно, например, рассчитать при заданном
числе резервных элементов N=mn оптимальную длину цепочек,
для которой надежность Ртп будет наибольшей.
Совершенно аналогично изучается схема, в которой параллельно
соединенные группы элементов образуют последовательную цепочку.
Конечно, мы рассмотрели простейший и поэтому не очень реальный
вариант нашей задачи. Здесь возможны различного рода усложнения;
разумно, например, считать, что после обрыва не может быть замы-
замыкания, а после замыкания может быть обрыв и притом с другой
вероятностью; естественно также предположить, что замыкания
в цепочке меняют надежность элементов в цепочке, а обрыв
всей цепочки меняет надежность элементов других цепочек.
§ 5.6. Учет ненадежности переключателей
Чтобы отключить отказавший элемент и включить на его место
в системе очередной резервный элемент, необходимо некоторое
устройство, которое мы будем в дальнейшем называть переключа-
переключателем. Конечно, иногда роль такого «переключателя» может играть
человек, однако в этом случае, как правило, требуется значительное
время, чтобы найти неисправность и заменить отказавший элемент.
Там, где такие перерывы в работе системы недопустимы или неже-
нежелательны, ставят автоматические переключатели, которые в момент
отказа очередного элемента мгновенно включают следующий элемент.
До сих пор при расчете надежности резервной группы мы считали,
что переключатели абсолютно надежны, и поэтому не принимали
их во внимание. Однако в действительности могут отказывать и сами
переключатели. Сейчас мы займемся вычислением надежности резерв-
резервной группы с учетом этого фактора.
Сначала будем решать задачу в простейших предположениях.
Будем считать, что переключатель может отказать только в момент
включения и вероятность этого отказа не зависит ни от номера
включаемого резервного элемента, ни от времени работы преды-
предыдущих резервных элементов. Наконец, предположим, что переклю-
переключатель срабатывает и в том случае, когда к моменту своего вклю-
включения резервный элемент вышел из строя. Далее можно рассмотреть
два случая.
В первом случае резервная группу выхолит из строя, как
только отказывает переключатель(этобудет,например, тогда,
когда на все резервные элементы ставится один переключатель, или
же ВТОМ случае, когда отказ одного переключателя не дает воз-
возможности сработать другим переключателям).
Во втором случае у каждого резервного элемента есть свой
переключатель. Если какой-то переключатель не сработал, то всту-
вступает в действие следующий переключатель.
§ 5.6] УЧЕТ НЕНАДЕЖНОСТИ ПЕРЕКЛЮЧАТЕЛЕЙ 323
Рассмотрим эти случаи отдельно для нагруженного и ненагру-
женного резервов. Будем ради простоты принимать, что все элементы
равнонадежны, и обозначим через р (t) их надежность, а через
q (t) — ненадежность.
а) Нагруженный резерв, первый случай. Резервная
группа состоит из одного основного элемента, п—1 резервных
и п-—\ переключателей.
Пусть Ak — событие, заключающееся в том, что первым откажет
k-fi переключатель, а Ап — событие, заключающееся в том, что
сработают все переключатели. Если а — вероятность отказа пере-
переключателя, то
Р {Ak} « а A - a)k-\ Р {Ап} = A - а)"-1.
Если произошло событие Ak> то в нашей резервной группе будут
работать основной и (к—1)-й резервный.
Поэтому согласно формуле полных вероятностей ненадежность
резервной группы
g 7+a<? E-6.1)
к — 1
С ростом числа п наша ненадежность стремится к пределу, отлич-
отличному от нуля,
О щ
Это и есть та минимальная ненадежность, которой мы можем
достигнуть в данном случае.
Если p(t)=e~Ktt то из формулы E.6.1) можно вычислить сред-
среднее время
Г{п)_ 1 *
б) Нагруженный резерв, второй случай. Пусть Ak —
событие, заключающееся в том, что за время работы резервной
группы из п—\ переключателей сработало к переключателей,
Тогда ненадежность резервной группы
/S*V*V 1. E.6.2)
В этом случае Qn(t) стремится к нулю с ростом номера п и, значит,
увеличивая число резервных элементов, мы можем добиться сколь
угодно высокой надежности резервной группы.
324 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [гл. 5
Если/? (t) = e'Kt9 то среднее время работы резервной группы равно
т(п) _ 1 V< I—a* , а
в) Ненагруженный резерв, первый случай. Пусть
события Ak имеют тот же смысл, что и в пункте а). Обозначим
через Qk (t) ненадежность группы из к элементов с абсолютно на-
надежными переключателями. Тогда по формуле полных вероятностей
-a)ll-1QII@- E.6.3)
Исходя из этой формулы, нетрудно вычислить среднее время работы
резервной группы Т^р. Если tcp — среднее время работы элемента, то
p. E.6.4)
Наибольшее среднее время, которого мы можем добиться, увели-
увеличивая неограниченно число резервных элементов, равно
7с°°р =i^2Гср" = ~*~я
Если надежности элементов подчинены экспоненциальному закону
. _ -_—
то ненадежность Qn (t) вычисляется в конечном виде. Для этого
случая
и . k-i
Подставляя эти величины в формулу E.6.3) и преобразуя полу-
полученную сумму, мы приходим к окончательному выражению
E.6.5)
С ростом числа п надежность стремится к пределу
. 1pX^Mt^^JJ
§ 5.6] УЧЕТ НЕНАДЕЖНОСТИ ПЕРЕКЛЮЧАТЕЛЕЙ 325
Это равенство показывает, что в случае ненадежных переключа-
переключателей первого типа надежность не может быть сделана сколь
угодно высокой.
Если Я/<^1, то можно пользоваться приближенной формулой
[H(L«>!:. E.6.6>
Из нее, между прочим, следует, что число резервных элемен-
элементов нецелесообразно брать слишком большим. Если
то присоединение дополнительных резервных элементов уже несу-
несущественно увеличивает надежность. Например, если Л.^ = 0,1;
а = 0,01, то нецелесообразно иметь более двух резервных элемен-
элементов, так как
@,1 )з
3!
-<0,001.
г)Ненагруженный резерв, второй случай. Пусть
события Ak те же, что и в пункте б), a Qk(t)y как и выше, — не-
ненадежность группы из k элементов с абсолютно надежными пере-
переключателями. Тогда
Qn W =1 C*-i 0 -a)kan-k-*Qk+1 (/). E.6.7)
k = o
Можно показать, что в отличие от предыдущего случая
Значит, увеличивая число резервных элементов, можно добиться
сколь угодно высокой надежности резервной группы. Из формулы
E.6.7) легко определяется среднее время работы резервной группы
Я? - 'ср "S Cn-i A -а)V-*-1 (ft + 1) - 'ср И + (п- 1) A -а)].
E.6.8)
Для случая экспоненциального закона p(t) = e~lt формула E.6.7)
принимает вид
и
^^e-xdx E.6.9)
0
и далее не упрощается.
326 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [гл. 5
Однако из нее можно получать простые приближенные форму-
формулы. Например, если М<^1, то интегралы можно заменить прибли-
приближенно так:
и
о
а если вероятность а мала, то можно в сумме E.6.9) оставить
только последние одно-два слагаемых.
Рассмотренные выше задачи, конечно, не описывают всех слу-
случаев, которые могут встретиться при резервировании с ненадежными
переключателями.
Во-первых, переключатели могут отказывать не только в момент
переключения, но и в другие моменты. Во-вторых, иногда пере-
переключатель может сработать в случайный момент времени и пере-
переключить работу с одного резервного элемента на следующий
тогда, когда в этом нет еще необходимости. Такое событие мы
назовем ложным переключением.
Оказывается, что можно решить задачу, т. е. найти надежность
резервной группы, и с учетом этих двух факторов.
Будем рассматривать ненагруженный резерв. Мы предположим,
что резервная группа состоит из основного элемента и п резерв-
резервных, надежности которых подчиняются экспоненциальному закону
Р (') = *-".
Далее мы предположим, что отказ переключателя не восста-
восстанавливаемый, т.е. после его отказа работа резервной группы
заканчивается тогда, когда выходит из строя тот резервный, во
время работы которого отказал переключатель.
Как уже было сказано выше, отказ переключателя может быть
двух типов. Это, во-первых, отказ «постепенный», происхо-
происходящий во время работы одного из элементов. Мы будем считать,
что время до этого отказа распределено по экспоненциальному
закону с параметром (л. Во-вторых, переключатель может отказать
и в момент переключения. Вероятность этого события
обозначим через а.
Мы считаем, что отказы этих двух типов независимы. Кроме
того, предположим независимость появления отказов в моменты
переключений. Предположим далее, что поток ложных переключе-
переключений пуассоновский с параметром у и ложные переключения могут
возникать до тех пор, пока раоотает переключатель. Будем, на-
наконец, считать, что отказы элементов, отказ переключателя и
ложные переключения независимы.
Построим марковский процесс, описывающий работу нашей
резервной группы, составим соответствующую ему систему диффе-
§ 5.6] УЧЕТ НЕНАДЕЖНОСТИ ПЕРЕКЛЮЧАТЕЛЕЙ 327
ренциальиых уравнений и, решив ее, найдем искомую надежность
резервной группы.
Занумеруем элементы: основной обозначим номером 0, а резерв-
резервные— номерами 1, 2, 3, ..., п.
Введем следующие состояния, характеризующие работу резерв-
резервной группы:
(ft, 1), ft = 0, 1, ..., л,
— работает ft-й элемент и переключатель исправсм;
(ft, 0), * = 0, 1, ..., л,
— работает ft-й элемент и переключатель неисправен; @) — резерв-
резервная группа не работает. Вероятность этих состояний в момент t
обозначим соответственно
Очевидно, что po(t) есть искомая ненадежность резервной группы.
За бесконечно малый промежуток времени At возможны следующие
переходы из одного состояния в другое:
1) (ft, l)->(ft + l, 1), k<n,
— произошел или отказ ft-ro элемента или ложное переключение
и при этом переключатель сработал. Вероятность этого события,
равна (X + v)(l—а) Д/ + 0(Д*).
2) (ft, l)->(ft, 0)
— отказал переключатель. Вероятность этого события равна.
3) (ft, !)-> @)
— произошел отказ элемента или ложное переключение и пере-
переключатель не сработал. Вероятность этого события равна
4) (ft, 1) — (ft, 1)
— состояние системы не изменилось. Вероятность этого события
равна 1—(A.
5) (л, 1)->(/*, 0)
— отказал переключатель. Вероятность равна
6) (я, 1) —@)
28
РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ
[гл. 5
— последний элемент отказал или произошло ложное переключение.
Вероятность составляет (k-\- v) Д/ + 0 (А/).
7) (л, 1)—(л, 1)
— состояние системы не изменилось.
8) (ft, 0)—@), А = 0, 1, 2, ..., /if
— произошел отказ элемента. Вероятность события равна
+ 0(Д*).
9) (ft, 0)—@)
— изменений не произошло. Вероятность этого равна 1—
@)—@)
Ю)
имеет вероятность, равную единице.
Отсюда мы легко составляем систему дифференциальных урав-
уравнений
Po
= l, 2, ..., л,
=W*i-^Ao, ft = 0, 1, ....л, [ E.6.10)
n
(A- + v) a +pnl (X + v)+ 2
fe0
t n-\
o = 2
k-0
Начальные условия
= l. P«@)=0,
Используем для решения этой системы преобразование Лапласа и
введем функции
о
оо
«О (*) =
§ 5.7] принципиальные вопросы резервирования 329
Тогда с учетом начальных условий наша система для этих,
функций запишется в виде
zakl = (X + v) A — а) ал_!, х — (X + |x + v) akv
za^Q— l^a^ — Xfl^Q,
n-i n
za0 = a (X + v) 2 aki + ani (X + v) + X 2 ako-
Решение этой системы упрощается из-за того, что она разбивается:
на три подсистемы. Решая первую, мы находим akl, подставляя
их во вторую группу уравнений, находим ak0, а подставляя все
эти величины в последнее уравнение, находим ao(z). В результате
вычислений получается
, v [(X + v)(l—a)]* ^
а - И-
где X1 = X + |A + v и Х2 = (Х + v) A — а). Отсюда
Делая обратное преобразование Лапласа, можно получить явное
выражение для po(t) в виде громоздкой суммы слагаемых пуассо-
новского вида. Впрочем, для небольших п эта сумма может быть
вычислена без труда. Исходя из E.6.11), можно определить сред-
среднее время работы резервной группы
Та=.(\ 1 *
\ 1^
E.6.12).
Из этой формулы при необходимости нетрудно усмотреть, как вли-
влияют на надежность резервной группы параметры X, (я, v, a.
§ 5.7. Некоторые принципиальные вопросы
резервирования системы
Масштаб резервирования. При резервировании системы
мы можем резервировать либо отдельные элементы системы, либо
блоки, входящие в систему, либо всю систему в целом. Уровень,
на котором производится резервирование системы, мы будем назы-
называть масштабом резервирования. Чем большая часть системы
330
РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ
[гл. 5
резервируется как единое целое, тем крупнее масштаб резервиро-
резервирования.
Докажем, что как для нагруженного, так и для ненагруженного
резерва любое укрупнение масштаба резервирования уменьшает
надежность системы. Всякое укрупнение масштаба резервирова-
резервирования можно представить себе так:
Имеется т частей системы и каждая часть имеет п подоб-
подобных себе резервных частей (рис. 5.7.1). Эти части образуют в
системе некоторый блок. Объ-
[/УтгBУт- -г(/77)т— единяя все первые резервные час-
части и т. д., мы получим п резерв-
ных блоков, подобных нашему.
Рис. 5.7.1 .
Рис. 5.7.2.
Мы хотим доказать, что надежность системы при таком
объединении резерва уменьшается.
Всякое объединение резерва частей системы можно предста-
представить как последовательное объединение резерва пар частей; напри-
например, мы объединяем резерв первой и второй частей, получаем
новую часть системы, ее резерв объединяем с резервом третьей
части системы и т. д. Поэтому при доказательстве нашего утверж-
утверждения мы можем ограничиться рассмотрением случая, когда объеди-
объединяются резервы двух частей системы. Далее, объединение резерва
этих двух частей можно рассматривать последовательно как объеди-
объединение всех первых резервных элементов, потом всех вторых и т. д.
Отсюда следует, что при доказательстве нашего утверждения
можно ограничиться случаем, когда каждая из двух частей системы
имеет по одной резервной части (рис. 5.7.2). Итак, рассмотрим
две задублированные части системы. Каждую из этих четырех
частей будем называть ниже привычным словом элемент.
Пусть т1? т/, т2, т/ —случайные времена работы этих элементов
и их резервных элементов. Мы сравниваем два способа резервиро-
резервирования и хотим показать, что во втором случае надежность этой
группы из четырех элементов будет не больше, чем в первом.
§ 5.7] ПРИНЦИПИАЛЬНЫЕ ВОПРОСЫ РЕЗЕРВИРОВАНИЯ 331
Рассмотрим отдельно случай нагруженного и ненагруженного-
резерва.
Нагруженный резерв. Время работы группы для первой
схемы выражается в виде
r1 = min[max(x1, т^), max (т2, т^)],
для второй схемы —
Т2 = max Imin (т^ т2), min (т^, т'2)].
Но очевидно, что
Т2 < max (т1э т[)
и
Г2<тах(т2, Та).
Следовательно,
Т2 < min [max (xlf %[), max (r2, т2)] = Tv
Но неравенство
означает, что вторая схема имеет не большую надежность, чем
первая.
НенагруженныЙ резерв. Случайные времена работы на-
нашей группы выражаются так:
i, Та).
Но очевидно, что
Следовательно,
и мы вновь приходим к тому же результату. Интересно заме-
заметить, что этот вывод совершенно не зависит от закона надежнос-
надежности элемента. Итак, чем крупнее масштаб резервирования, тем
меньше надежность.
Скользящий резерв. Обычно в системе имеются группы
одинаковых элементов. В этом случае вместо того, чтобы резер-
резервировать каждый элемент в отдельности, можно объединить все
резервные элементы и устроить так называемый скользящий резерв
(рис. 5.7.3).
332 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [гл. 5
I
При таком способе резервирования имеются группа одинаковых
(или взаимозаменяемых) основных элементов и одна группа резерв-
резервных элементов. При отказе одного из основных элементов он заме-
заменяется очередным резервным. Отказ всей резервной группы насту-
наступает в момент первого отказа одного из основных элементов,
после того, как кончились все резервные элементы (т. е. были ис-
использованы или отказали
О>— —("У- в резерве).
Нетрудно рассчитать
надежность резервной груп-
группы при скользящем резерве.
Будем предполагать, что
; надежности всех элемен-
(т\ тов, основных и резерв-
ных, одинаковы и рав-
Рис. 5.7.3. ны p(t), а ненадежности
равлы q(t). Рассмотрим
отдельно случаи нагруженного и ненагруженного резервов.
Нагруженный резерв. Пусть п — число основных элемен-
элементов, а т — число резервных. Очевидно, что наша резервная группа
не откажет за время t тогда и только тогда, когда за это время
произойдет не более т отказов элемента.
Следовательно, надежность резервной группы
т
^kk)p"^-k{t). E.7.1)
Если надежность подчиняется экспоненциальному закону
то легко находится среднее время (см. § 5.3)
+ + ' # ' "+" п' E.7.2)
i-1)
Ненагруженный резерв. Для общего случая надежность
выражается весьма сложно через интегралы типа сверток и даже
среднее время работы имеет сложный вид. Поэтому предположим,
что надежность подчиняется экспоненциальному закону
В этом случае нетрудно подсчитать, что надежность резервной
группы
1
nKt
§ 5.7] ПРИНЦИПИАЛЬНЫЕ ВОПРОСЫ РЕЗЕРВИРОВАНИЯ 333
так как суммарная интенсивность отказа равна пК и работа резерв-
резервной группы заканчивается в момент (т+1)-го отказа. Среднее
время работы
*-=*?¦• <5-7-4>
В заключение этого параграфа рассмотрим такой общий вопрос:
пусть имеются две группы со скользящим резервом, в одной пг
основных и т1 резервных, а в другой п2 основных и т2 резервных.
Мы объединяем эти две группы, и, таким образом, в объединенной
группе у нас будет /zx + #2 основных и т1-}-т2 резервных элемен-
элементов. Увеличивается ли в результате такого объединения надеж-
надежность системы?
Докажем для случая, когда все элементы, входящие в эти
группы, имеют одинаковую надежность, что объединение резервов
этих групп всегда увеличивает надежность системы.
Пусть т1? т2, т3, ...—последовательные моменты отказов эле-
элементов (основных и резервных) первой группы, тх, т'2, ...—после-
...—последовательные моменты отказов элементов второй группы. Тогда
первая группа отказывает в момент f =%mi + 11 а вторая группа —
в момент t" = тт2 + 1. Следовательно, группа, составленная из этих
двух групп, отказывает в момент ^1 = min(^', t"). Будем отклады-
откладывать отказы обеих групп на одной оси и обозначим моменты от-
отказов объединенной группы
Если мы объединяем резервы этих групп, то отказ объединенной
группы наступает в момент t2 = tml + mi + i* Пусть для определенности
<Tm2
+ !•
Тогда к моменту tmi + 1 произошло не более т2 отказов второй
группы и, следовательно,
Значит, отказ объединенной группы с общим резервом наступает
не раньше, чем отказ этой группы с разделенными резервами.
Можно оценить выигрыш при объединении резервов и количест-
количественно сравнивая средние времена работы в том и другом случае.
Если надежность элементов подчиняется экспоненциальному закону
P(t) — e~u, то для раздельных резервов среднее время работы равна
1
334 РЕЗЕРВИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ [ГЛ. 5
а в случае общего резерва —
То = ~
Для конкретных случаев по этим формулам можно оценить тот
выигрыш, который дает объединение резерва. Из них также сле-
следует, что наименьший выигрыш будет тогда, когда
ml m2
пх~ п2
Это нетрудно понять и физически,— ведь в этом случае обе группы*
отказывают в среднем в один и тот же момент и поэтому объеди-
объединение резерва почти ничего не дает.
Скользящий резерв дает большой выигрыш в надежности, однако,
применяя его, следует иметь в виду и другую, чисто техническую
сторону этого вопроса: если замену отказавшего элемента резерв-
резервным осуществляет не человек, а автоматическое устройство, то
в случае скользящего резерва требуется огромное количество соеди-
соединений и переключателей, ведь каждый резервный элемент должен
быть соединен с каждым рабочим элементом. Это обстоятельство
в значительной мере обесценивает идею скользящего резерва.
ГЛАВА 6
РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ
§6.1. Введение
В предыдущей главе, изучая системы с резервом, мы предпола*
гали, что отказавшие элементы не восстанавливаются. На практике,
однако, часто прибегают к восстановлению для повышения надеж-
надежности системы, увеличения срока ее службы. Естественно, что для
количественного описания работы таких систем понадобилось соз-
создать соответствующие математические модели и методы. При этом
оказалось, что системы, в которых происходит восстановление,
хорошо описываются методами теории массового обслуживания.
Обнаружилось, что многие задачи, возникшие в теории надежности,
математически тождественны известным задачам из теории массо-
массового обслуживания. Выяснилось, что многие задачи массового обслу-
обслуживания можно перевести на язык надежности, если, например,
слово «требование» заменить словом «отказ», а слово «обслуживание»
заменить словом «ремонт».
Связь, установленная между теорией надежности и теорией
массового обслуживания, обогатила обе эти науки. В теории надеж-
надежности были использованы методы и готовые решения задач теории
массового обслуживания. С другой стороны, в самой теории мас-
массового обслуживания появились новые идеи, новые постановки задач
из теории надежности.
Изучая резервные системы с восстановлением, обычно предпола-
предполагают, что время жизни распределено по показательному закону.
При этих условиях работа нашей системы всегда описывается одно-
однородным марковским процессом с конечным (а иногда и со счетным)
числом состояний. Чаще всего ограничиваются изучением процесса
только в установившемся режиме, и тогда задача описания работы
системы сводится к решению системы алгебраических уравнений.
Во многих задачах такого рода с успехом используется так
называемый процесс гибели и размножения, который ранее применялся
в теории массового обслуживания, биологии, медицине и т. п.
336 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [гл. Q
В настоящей главе этот процесс будет подробно изучен и при-
применен к ряду задач теории надежности. Выше уже говорилось, что
при описании систем с восстановлением обычно предполагают, что
все законы распределения — показательные. По-видимому, для боль-
большинства систем эти предположения неверны; так, например, время
восстановления почти никогда не распределено, хотя бы прибли-
приближенно, по показательному закону. Тем не менее и сейчас почти все
задачи в теории надежности решаются в предположениях экспонен-
циальности всех законов. Делается это не от хорошей жизни — если
отказаться от экспоненциальности законов, то все задачи резко
усложнятся. В последние годы в теории массового обслуживания
решен целый ряд задач, в которых часть законов распределения
или даже все законы произвольны. Выработаны методы решения
таких задач (метод вложенных цепей Маркова, метод интегро-диф-
ференциальных уравнений, метод, использующий тождество Спицера,
и т. п.).
К сожалению, эти методы слабо используются в теории надеж-
надежности. Причина этого не только в том, что эти методы сложны и
малодоступны для инженеров, но также и в том, что решение таких
задач приводит к громоздким формулам, малопригодным для вычи-
вычислений.
По-видимому, единственный путь, способный устранить этот раз-
разрыв между теорией, давшей решение многих задач, и практикой,
которая не может использовать эти решения, заключается в поисках
приближенных формул, в доказательстве ряда асимптотических
теорем, из которых можно вывести приближенные формулы.
Выводу простых приближенных формул в настоящей главе уде-
уделено большое внимание. Отдельно рассмотрен случай дублирования,
когда резервная группа состоит из двух элементов. Все задачи,
возникающие в этом случае, решаются при весьма общих предпо-
предположениях.
§ 6.2. Дублирование с восстановлением г)
Мы рассмотрим сначала простейший случай резервирования —
дублирование, когда к рабочему элементу присоединен один резерв-
резервный, который в случае отказа рабочего элемента заменяет его.
Резервную группу, состоящую из двух элементов — основного и
резервного, мы будем коротко называть парой.
В теории резервирования без восстановления не имело особого
смысла выделять этот случай. Сейчас, когда мы начали рассматри-
рассматривать резервные системы, в которых происходит восстановление
отказавших элементов, разумно отдельно рассмотреть случай дубли-
1) Результаты этого параграфа принадлежат в основном Б. В. Гнеденко.
§ 6.2] ДУБЛИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ 337
рования, так как это позволит решить нам целый ряд задач в пред-
предположениях максимальной общности [1] — [4].
1°. Предположим сначала, что время жизни элемента подчи-
подчиняется показательному закону, а время восстановления (или ремонта)
распределено произвольно. Рассмотрим общий случай облегченного
резерва. Пусть к — опасность отказа рабочего элемента, Хг — опас-
опасность отказа резервного элемента, a G(t) — закон распределения
времени ремонта. Очевидно, что при Х1 = 0 мы получим случай
холодного резерва, а при Х = Х1 — случай горячего резерва. Мы
считаем, что оба элемента, основной и резервный, одинаковы, но
в резервном состоянии опасность отказа меньше, чем в рабочем.
Когда отказывает основной элемент, на его место мгновенно стано-
становится резервный, а основной начинает восстанавливаться и после
восстановления становится в резерв. В этот момент основной и
резервный элементы меняются ролями. Расстояние между соседними
моментами восстановлений мы назовем циклом. Ясно, что все циклы
независимы и одинаково распределены. Отказ нашей пары наступает
тогда, когда на каком-нибудь цикле во время восстановления одного
элемента отказывает другой.
Обозначим через p(t) вероятность безотказной работы пары до
момента t. Нетрудно составить интегральное уравнение для вероят-
вероятности p(t). Событие, заключающееся в безотказной работе пары
на @, /), распадается на следующие несовместные события:
1) Первый отказ наступает после момента t. Вероятность этого
события равна g-^+^i) *.
2) Первый отказ наступает до момента ^, но первый цикл закан-
заканчивается после момента t. Резервный элемент, включившийся в работу
в момент отказа, работает безотказно до момента t. Вероятность
этого события равна
(X _|_. хг) е-(к+К) х [\ _ Q(t — *)] е-* <'-*> dx
3) Первый цикл заканчивается до момента ty во время первого
восстановления второй элемент работает безотказно и на остав-
оставшемся до момента t участке времени пара работает безотказно»
Вероятность такого события равна
где g(x) = G'(x).
12 Б. В. Гнеденко и др.
338 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [ГЛ. 6
Складывая эти три вероятности, мы получим, очевидно, искомую
вероятность
t
р (t) = e-(^i) t _|_ е-и (X -f Хг) J e-^x [1 — 0(t — х)] dx +
о
t X
+ lp(t — x)e-kx(X + X1)dx \e~^z g{x — z)dz. F.2.1)
о о
Мы получили интегральное уравнение вида
t
где
t
A(t) = *-<*+*!> * + e~u (X + Xx)
0
Отсюда можно получить представление вероятности p(t) в виде ряда
p(t) = B0(t) + B1(t) + Bi(t)+...+Bn(t)+..., F.2.2)
где
t
Если время t мало по сравнению со средней длительностью цикла,
то этот ряд можно использовать для вычисления вероятности p(t),
так как он быстро сходится и первые два-три слагаемых дают
достаточно точно сумму ряда. Если же время велико, то ряд F.2.2)
практически бесполезен. На практике как раз интересен тот случай,
когда вероятность отказа пары на одном цикле, равная
СО
= § A — е~и) dG(t),
о о
мала и, следовательно, среднее время жизни пары во много раз
больше средней длительности цикла. Чтобы исследовать асимптоти-
асимптотическое поведение вероятности p(t) при а—>(), применим преобразо-
преобразование Лапласа. Введем обозначения
a (s) = J e-st A (t) dt, с (s) = $ e~st dG(t),
b(s) = \ e~st B(t)dt, m(s)=\ e'stp(t)dt.
о о
§ 6.2] ДУБЛИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ 339
Нетрудно вычислить функции a (s) и b(s):
Из уравнения F.2.1) получаем
m / c\ - a(s) -
Если т — случайное время жизни пары, то
Р{т >/}=/>(*).
Отсюда среднее время жизни пары
Если бы не было восстановления элементов, то среднее время
жизни пары равнялось бы
т __!_д.±
Отсюда выигрыш в среднем времени, который дает восстановление,
равен
Т
Чем меньше вероятность а отказа пары на одном цикле, тем
больше выигрыш.
Изучим теперь асимптотическое поведение вероятности р (t).
Для этого заметим, что при a—>0
Естественно поэтому ожидать, что распределение нормированной
величины at будет при этом сходиться к некоторому предельному
распределению. Нетрудно найти распределение величины
Преобразование Лапласа для этой функции
e-stp (L)dt = aq> (as) = a
0
12*
340 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [ГЛ. 6
Пусть теперь параметры к и Ях фиксированы, а закон распределе-
распределения G(t) меняется так, что
о
Сделаем вспомогательную оценку
с (А) —
as J fc-w dG (/) < ^ j A - e-H)dO (t) = ^ ,
О О
т. е.
с (A.) — c(as + X)=-^9, где 0<9<1.
Отсюда при a—^0 равномерно на любом конечном отрезке изме-
изменения s
(as) = а
Итак, доказано следующее утверждение:
^ й ^ фиксированы, а
lim P {at > t] = *-<*+*!> *. F.2.6)
a -> о
Отсюда следует, что при малом а вероятность безотказной работы
пары в течение времени t выражается приближенной формулой
F.2.7)
Более детальное исследование показывает, что лучше использовать
другую приближенную формулу
Р«)*Г?. F.2.8)
где То берется из F.2.4).
Если формула F.2.7) имеет относительную погрешность по-
порядка а, то формула F.2.8) имеет относительную погрешность
§ 6.2] ДУБЛИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ 341
порядка а2. Некоторое неудобство этих формул заключается в том,
что для их использования нужно знать величину а. Если при а —>0
закон G(t) меняется так, что
*¦¦ V- 0 F29)
\ U dG (t)
К IW1 Трем
(трем — случайное время ремонта), то, как нетрудно видеть,
о о
где О<0, 0Х< 1, и тогда из F.2.9) следует, что
МЯтр,.
а
Таким образом, если а мало, а
то Штрем « а и имеет место приближенная формула
G4 F.2.10)
где
Это означает, что асимптотически закон распределения времени
жизни пары не зависит от закона распределения времени восста-
восстановления G(t)y а зависит только от среднего времени восстанов-
восстановления 7\. Заметим еще, что условие F.2.9) легко проверяется
статистически.
2°. Выше мы рассмотрели дублирование с восстановлением для
случая, когда времена жизни рабочего и резервного элементов
распределены по показательному закону. В ряде случаев это до-
допущение неверно, и приходится рассматривать общий случай, ког-
когда времена жизни и времена восстановления распределены произ-
произвольно. Рассмотрим сначала случай ненагруженного резерва.
Пусть F(t) — закон распределения времени жизни элемента, а
G(t) — закон распределения времени восстановления элемента. Мы
предполагаем, что элемент, находящийся в резерве, не отказывает
и не стареет, а ремонт полностью восстанавливает исходные свой-
свойства элемента. Работа нашей пары происходит следующим образом:
342 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [ГЛ. 6
основной элемент, проработав случайное время т0 (рис. 6.2.1), от-
отказывает и затем восстанавливается за случайное время ?1# В
момент его отказа резервный элемент мгновенно включается и ра-
работает случайное время тх. После отказа резервный элемент вос-
восстанавливается случайное время ?2, а восстановленный основной
Рис. 6.2.1.
элемент работает случайное время т2, и т. д. В силу наших пред-
предположений величины г,- и ?у независимы м
Отказ пары наступает тогда, когда к моменту отказа одного эле-
элемента второй не успевает восстановиться. Обозначим через т слу-
случайное время работы пары. Очевидно, что т может быть записано
в виде
где v—случайный номер того периода, в конце которого насту-
наступает отказ. Для удобства рассмотрим сначала величину
т/ = т1 + т2+ ... +tv.
Иными словами, мы рассматриваем работу нашей пары с момента
т0, принимая его за начальный. Обозначим закон распределения
т' через Фх (/),
Событие, состоящее в безотказной работе пары до момента /, раз-
разбивается на следующие несовместные события:
1) Первый период хг закончится после момента t. Вероятность
этого события равна
2) Первый период хг закончится до момента t\ в конце этого
периода элемент, стоящий в резерве, успеет восстановиться и на
оставшемся до момента t участке времени наша пара не откажет.
Вероятность этого события равна
t
\[\-(D1(t-x))O(x)dF(x).
§ 6.2] ДУБЛИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ 343
Складывая эти две вероятности, мы получим вероятность безот-
безотказной работы пары 1— Фх (/),
t
\—Ol{t) = l—F(t) + \[\—O1(t^x)]a{x)dF(x). F.2.11)
о
Если обозначить закон распределения % = %0-{-т' через Ф (/), то
ф(/)= $ ОМ* — x)dF(x). F.2.12)
о
Решая интегральное уравнение F.2.11) методом последовательных
приближений, можно получить для функции Фг (t)y а потом и для
Ф(/) представление в виде ряда, подобного ряду F.2.2). Однако
этот ряд по причинам, изложенным выше, практически бесполе-
бесполезен. На практике в первую очередь интересен тот случай, когда
вероятность отказа пары на одном периоде
мала. Это значит, что время восстановления элемента в среднем
значительно меньше времени безотказной работы элемента. Чтобы
изучить асимптотическое поведение вероятности Ф(t) при а—>О,
воспользуемся, как и выше, преобразованием Лапласа. Пусть
00 00
a (s) = f e~st dF (/), b (s) = J e'st G(t) dF (t),
0
Тогда из F.2.11) мы получим
Al{s) - \-b(s) •
а из F.2.12) находим, что
A(s) = a(s)Al{s)=a(s)^=F^l. F.2.13)
Отсюда среднее время безотказной работы пары
Го=-Л'(О) = 7\+г-^д5=Г1 + ^-, F.2.14)
00
где 7\= [ tdF(t) — среднее время жизни элемента. Формула F.2.14)
344 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [ГЛ. 6
дает возможность оценить тот выигрыш, который мы получаем в
результате восстановления элементов. Если бы восстановления не
было, то среднее время жизни пары равнялось бы
Отсюда выигрыш равен
Т 2а "
о
Чем меньше вероятность а отказа на одном периоде, тем больше
выигрыш.
Переходя к изучению асимптотического поведения вероятности
Ф (/), мы предположим, что закон распределения времени жизни
элемента F{t) фиксирован, а закон распределения времени восста-
восстановления Qn (t) меняется по некоторой последовательности таким
образом, что
*n=][\-On(t)]dF(t)-+0.
о
Соответственно этому снабдим индексом законы и преобразования
Лапласа Ф„@> An(s)> bn(s)- Введем обозначение
00
ca(s) = a(s)-ba(s)=^e-t[l-On(t)]dF(t).
О
Очевидно, сп@) = ап. Рассмотрим разность
ans [An J [1 - 0„ @] dF (t) + ]t dF (t)]
А
Если положить Л„=—^=:, то оба слагаемых в квадратной скобке
V а«
будут стремиться к нулю, и мы приходим к следующему утвер-
утверждению:
Нш с»(«яДI=а1 F.2.15)
равномерно на любом конечном отрезке изменения s.
§ 6.2] ДУБЛИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ 345
Рассмотрим нормированную случайную величину апт. Ее закон
распределения
Преобразование Лапласа для этого закона
$ «-•*'ф. (?)=*¦ «v>.
о
Тогда, используя F.2.15), мы получим, что при ап
gns) cn&J)-* 1+зТг
равномерно на любом конечном отрезке изменения s. Отсюда сле-
следует, что
t
} = 1-Гг» . F.2.16)
Это предельное соотношение означает, что, когда вероятность
отказа пары на периоде
*=][\-G(t)]dF(t)
о
мала, вероятность безотказной работы пары в течение времени t
выражается приближенной формулой
Р {т > t) = 1 -Ф (t) « е" . F.2.17)
Эта формула и дает практически приемлемое решение нашей задачи.
3°. Рассмотрим теперь случай нагруженного резерва, предпо-
предполагая, как и в предыдущей задаче, что законы распределения вре-
времени жизни и восстановления элементов F(t) и G(t) произвольны.
Предположим, что каждый элемент работает и восстанавливается
независимо от состояния другого и отказ наступает тогда, когда
отказывают оба элемента. В § 2.4 рассматривалась система, со-
состоящая из п элементов, которые работают и восстанавливаются
независимо от состояния других элементов. Система отказывает,
если отказывает хотя бы один элемент. Были найдены точное
распределение времени работы системы и средние времена работы
и простоя системы в стационарном режиме. При этом оказалось,
346 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [ГЛ. 6
что средние времена выражаются теми же формулами, какие по-
получаются в случае экспоненциальных законов времени жизни и
восстановления элементов. Если в этой задаче мы поменяем роля-
ролями участки работы и участки простоя, то мы получим систему,
которая отказывает, когда отказывают все входящие в нее эле-
элементы, т. е. получим резервную группу для случая нагруженного
резерва. Замеченная двойственность в постановке задач позволяет
сразу написать формулы, дающие решение нашей задачи в общем
случае, когда резервная группа состоит из п элементов.
00
Пусть 7\= С tdF(t) — среднее время жизни элемента, а Г2 =
о
00
= С* dG(t) — среднее время восстановления элемента. Тогда сред-
о
нее время безотказной работы резервной группы из п элементов
(включая и основной) в стационарном режиме выражается так:
Конечно, первый период безотказной работы резервной группы, в
начале которого все элементы исправны, будет иметь другое, не-
1+—-J вели-
велика, то это различие несущественно. Более того, из общих сообра-
1+—J ^>1, закон распределения слу-
случайного времени безотказной работы резервной группы должен
быть достаточно близок к экспоненциальному. Иными словами,
должна иметь место приближенная формула: вероятность безот-
безотказной работы резервной группы в течение времени t
}p(t)&eTo , F.2.19)
где То выражается по формуле F.2.18).
§ 6.3. Процесс гибели и размножения
Если задача о дублировании с восстановлением может быть
решена при весьма общих предположениях о законах распределе-
распределения времени жизни и времени восстановления элементов, то при
переходе к случаю, когда число элементов в системе произвольно,
задача резко усложняется. В этом случае для эффективного ре-
решения задачи мы вынуждены предположить, что времена жизни и
восстановления элементов распределены по показательному закону.
§ 6.3] ПРОЦЕСС ГИБЕЛИ И РАЗМНОЖЕНИЯ 347
При таком предположении описание системы с восстановлением
сводится к изучению некоторого однородного марковского про-
процесса с конечным или счетным числом состояний. Одним из таких
процессов является процесс гибели и размножения [5], который с
успехом применяется не только в теории надежности, но и в тео-
теории массового обслуживания, в биологии, экономике и т. п.
Рассмотрим однородный марковский процесс с конечным или
счетным числом состояний, которые мы будем обозначать числами
О, 1, 2, 3, ... Если в момент t наш процесс находится в состоя-
состоянии &, то за бесконечно малое время Д^ он с вероятностью XkAt-{-
-}-о (At) перейдет в состояние (k+\), с вероятностью \ikAt + o(At)
перейдет в состояние (k—\) и с вероятностью 1—(^4-^*)^ +
+ o(At) останется в состоянии k. Из начального состояния 0 он
может перейти в состояние 1 с вероятностью X0At-\-о (At) и ос-
остаться в состоянии 0 с вероятностью 1—X0At -\-о (At). Если чис-
число состояний конечно и равно я, то из состояния п процесс мо-
может перейти в состояние (п—1) с вероятностью \лп At + о (At) и
остаться в прежнем состоянии с вероятностью 1—\\,nAt-\-o (ДО-
Определенный таким образом процесс и называется процессом ги-
гибели и размножения. Обозначим через pk (t) вероятность того,
что в момент t процесс находится в состоянии k. Сравнивая состоя-
состояние процесса в два бесконечно близких момента времени t и
t-^-Aty мы по формуле полных вероятностей получим
Перенесем член pk(t) в левую часть, разделим обе части равенст-
равенства на Д^ и устремим At к нулю. В пределе мы получим уравнение
Pk U) = h-iPk-i W - (h+Pk)Pk @ + Pk+iPk+i @-
Аналогично выводится уравнение для случая & = 0
Если процесс имеет конечное число состояний, то последнее урав-
уравнение имеет вид
Положим (ло = Х_1 = 0, а в случае конечного числа состояний
Яп=0. Тогда для любого k уравнения будут иметь одинако-
одинаковый вид
348
РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ
[ГЛ. 6
Полученная система дифференциальных уравнений и определяет
поведение нашего процесса. Для того чтобы эта система имела
единственное решение, надо задать начальные условия pk @),
& —0, 1, 2, ... , т. е. задать вероятности начальных состояний
процесса.
Рассмотрим сначала случай конечного числа состояний
F.3.Г)
k=\y 2,
л-1,
Рп (t) = K-lPn-1 @ ~ VnPn (')•
На практике обычно интересуются поведением процесса на тех
участках времени, которые далеки от начального. В теории
вероятностей доказывается, что для любого начального состояния
процесса существуют пределы
lim pk(t)=pk1
= 0, 1, 2,
причем если для любого
F.3.2)
(б.з.з)
то эти финальные вероятности не зависят от начального состоя-
состояния процесса. (Условия F.3.3) означают, что множество состояний
не разбивается на несообщающиеся подмножества.) Финальным
вероятностям pk можно дать еще одну интерпретацию, отличную
от той, которую дает их определение.
Рассмотрим единичную случайную функцию ek(t)y которая
равна единице, если в момент t процесс находится в состоянии k>
и нулю в противоположном случае. Тогда величина
т
есть доля времени, которое процесс пребывает в состоянии k на
участке @, Т). Имеет место следующее утверждение: случайная
величина т:к(Т) при Т—> оо сходится по вероятности к pky т. е.
при любом е >> 0
lim Р{|тл(Г) —pJ>e} = 0. F.3.4)
Это значит, что при большом Т с вероятностью, близкой к единице,
§ 6.3] ПРОЦЕСС ГИБЕЛИ И РАЗМНОЖЕНИЯ 349
Иными словами, финальная вероятность pk есть средняя доля
времени, которое процесс пребывает в состоянии k. Это эргоди-
ческое свойство марковского процесса будет неоднократно исполь-
использовано ниже. Переходя к пределу в системе F.3.1), мы получим
для финальных вероятностей систему алгебраических уравнений
F.3.5)
Кроме того, сумма всех вероятностей равна единице,
п
Система F.3.5) легко решается.
Введем обозначение
V'kPk "к- \Pk -1 == я?»
Тогда наша система запишется в виде
Отсюда
nk = 0, * = 0, 1, 2, . . ., п.
Если \ik Ф 0, то
и отсюда мы получаем
Окончательно из условия F.3.6) находим
Ра = 5^ во=1. F.3.7)
s = 0
(Заметим, что если k0 — наибольший номер, для которого [х^0 = 0,
найденные финальные вероятности легко выражаются все одномерные
характеристики нашего процесса. В частности, среднее состояние
350 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [ГЛ. 6
процесса
Перейдем теперь к изучению процесса гибели и размножения с
бесконечным числом состояний. Такой процесс уже не обязан все-
всегда иметь стационарное распределение. Для этого параметры \k
и \ik должны удовлетворять некоторым условиям. Чтобы найти такие
условия, предположим, что стационарное распределение существу-
существует. Тогда финальные вероятности pk должны удовлетворять системе
?=1,2,...
Предположим для простоты, что \ькфЪ при
Решая, как показано выше, эту систему, мы получим
ЛпЛ>1 ... hi и I r\
Вероятности pk должны в сумме давать единицу, поэтому
2 рк= 2
k=o
oo
Так как/H=т^0 (в противном случае и все/^ = О), то ряд 2 9^<°°'
fe = o
и мы получаем первое условие, необходимое для существования
стационарного распределения. Вывод второго условия потребует
несколько больших усилий. Мы можем мыслить наш процесс как
ступенчатую случайную функцию v(/), которая в каждый момент t
принимает значение к, равное состоянию процесса в этот момент.
Пусть в какой-то момент времени наш процесс находится в состоя-
состоянии к. Случайное время, протекшее до момента первого прихода
процесса в состояние /, обозначим через Tkh а его среднее — че-
через Tkl. Обозначим еще то/ = т/, Т01—Ть. Пусть в начальный мо-
момент процесс находился в состоянии 0. Чтобы найти Тп, заметим
прежде всего, что
\
§ 6.3] ПРОЦЕСС ГИБЕЛИ И РАЗМНОЖЕНИЯ 351
Для определения величины Tkyk+1 рассмотрим процесс гибели и раз-
размножения с конечным числом состояний, равным &+1, у которого
параметры Х?. и \i( при t^k совпадают с параметрами нашего
процесса, a Xk+1 = 0. Случайные периоды, на которых процесс
находится в состоянии (&+1), чередуются с периодами, на кото-
которых процесс находится в состояниях, меньших (k+\). В силу одно-
однородности процесса все первые периоды распределены одинаково по
закону 1 — e~V'k+itt Отсюда средняя длительность этого периода
равна ТA) = . Все периоды, на которых процесс находится в
состояниях, меньших (?-(-1), исключая, конечно, начальный период,
также распределены одинаково, и так как в начале этого периода
процесс находится в состоянии к, а в конце периода приходит в
состояние (k-\-\)y то средняя длительность периода равна Г<2) =
= Tki k+1. Кроме того, в силу марковости процесса и первые и вто-
вторые периоды независимы. Вероятность пребывания процесса в со-
состоянии (&+1) в стационарном режиме равна (см. главу 2, § 3)
7М1ЦГ7Т2) •
С другой стороны, эта вероятность равна Рд+1, где pi — финальные
вероятности вспомогательного процесса. Итак, мы получили ра-
равенство
Pk+i ~
из которого без труда находим Ta) = Tki
'?-• F.3.9)
Отсюда искомое среднее время перехода из нулевого состояния
в /z-e равно
k k
п-\ 2 0< л-1 2
F-зл0)
Вернемся теперь к нашему процессу с бесконечным числом состоя-
состояний. Последовательность Тп монотонно возрастает и, следовательно,
либо стремится к бесконечности, либо имеет конечный предел.
Предположим, что lim Гп= 70< оо. Тогда из неравенства Чебы-
п -> со
шева следует, что
РК<лго}>1-^-^1-1.
352 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [ГЛ. 6
Это неравенство означает, что процесс за конечное время с веро-
вероятностью единица уйдет в бесконечность. В этом случае нет смысла
говорить о стационарном распределении, так как наш процесс
обрывается. Поэтому вторым необходимым условием существова-
существования стационарного распределения будет условие
lim Tn= оо.
Итак, для существования стационарного распределения необ-
необходимо выполнение условий
и) 2еА<°°.
fe = o
F.3.11)
где
Можно доказать, что эти условия являются также и достаточными
[6] для существования стационарного распределения. Заметим, что
наиболее существенным из этих двух условий является первое
и при выполнении этого условия второе практически почти всегда
выполняется. Если стационарное распределение существует, то ста-
стационарные вероятности выражаются формулами
рк=-?-. F.3.12)
§ 6.4. Изучение нестационарного периода
1°. В предыдущем параграфе мы рассмотрели процесс гибели
и размножения в стационарном режиме. Интересно, однако, ис-
исследовать наш процесс на начальном периоде времени, когда
вероятности состояний существенно зависят от времени. Такое ис-
исследование позволит, во-первых, установить, насколько быстро
вероятности pk(t) стремятся к своим финальным значениям, и тем
самым определить, начиная с какого момента процесс можно
с достаточной точностью считать стационарным. Во-вторых, в при-
приложениях к теории надежности нас часто интересует поведение
процесса гибели и размножения только на начальном участке времени,
на котором процесс заведомо не успевает войти в стационарный
режим.
§ 6.4]
ИЗУЧЕНИЕ НЕСТАЦИОНАРНОГО ПЕРИОДА
353
Рассмотрим сначала случай конечного числа состояний. Он
описывается системой F.3.Г). Чтобы найти решение этой системы
в замкнутом виде, удобно использовать преобразование Лапласа.
Введем функции
ak(s)= \e-stpk{t)dt.
Умножив каждое уравнение F.3.Г) на e~st и проинтегрировав
его по t, получим алгебраическую систему
F.4.1)
ak (s) — \ik+1ak+1 (s) = 0,
/e=l, 2, ..., /2—1,
-!<**-! (*) + №„ + *) an(s)=0.
Мы, как и выше, предполагаем, что в начальный момент процесс
находится в состоянии 0. Решая эту систему по правилу Крамера,
найдем явное выражение для функций ak(s):
F.4.2)
где
=A(s> К> ^1» •••>
0
0
0
о
о
. F.4.3)
ДиЛИ = Л0Х1..Дл.1ДE, Хл+1> ..., Яя, цл+1, ..., ця). F.4.4)
Если, пользуясь известными правилами, разложить определитель
Дп+1 (^) по последнему столбцу и последней строке, то мы полу-
получим рекуррентное соотношение
или, короче,
причем
»-а. 1^о> •-., !*„-«). F.4.5)
-VnK-lbn-l(s), F-4.6)
Ао (*) =
354 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [гл. §
(Во избежание недоразумений заметим, что формулы F.4.2) — F.4.6)
справедливы для любых Хп и \лп, но в нашем случае A0 = 0и Лп = 0.)
Из рекуррентных соотношений F.4.5) и F.4.6) можно опреде-
определить многочлены Д„+1 (s) и Ank($) и, подставив их в равенство
F.4.2), получить представление ak (s) в виде некоторой правиль-
правильной рациональной дроби.
По известной формуле обращения вероятности pk (t) выразятся
контурным интегралом
где контур 5 охватывает все нули знаменателя. Для вычисления
этого интеграла необходимо знать корни многочлена An+1(s).
Используя уравнение F.4.6), можно показать, что корни этих
многочленов обладают следующими свойства-ми [9]:
1. Если \k положительны, то все корни Ak(s) различны
и отрицательны.
2. Корни соседних многочленов Дл-1E) и Ak(s) чередуются,
т. е. между каждой парой корней многочлена Ak_1(s) (в том
числе и между нулем и наименьшим по модулю корнем), лежит
один корень многочлена Ak[s).
3. Сумма корней Ak (s) равна
откуда следует, что наибольший по модулю корень лежит пра-
правее —Ak.
4. Если kk>§ при k<in и Хп = 0, то все предыдущие свой-
свойства сохраняются, но один из корней равен нулю. (Свойства 1
и 2 доказываются в теории ортогональных многочленов.)
Перечисленные выше свойства позволяют вычислять корни много-
многочлена Ak(s), если известны корни предыдущего многочлена.
Действительно, пусть —рх, —Р2, ..., —$ъ-\ суть корни Ak_x (s).
Тогда в каждом из интервалов
(-Ак, — Р*_ж), (-P*_i, -Р*-,), .-., (-Р1( 0)
лежит по одному корню многочлена Д^ (s). В этом случае корни
легко вычисляются, например, методом «вилки», что особенно
удобно делать с применением вычислительной техники.
Итак, пусть 0, —аг, ..., —ап—известные корни многочлена
An+i(s). Тогда A,,+1(s) = s(s + ai) ... (s+an) и мы можем разло-
разложить рациональную дробь nk у на простейшие дроби
§ 6.4] ИЗУЧЕНИЕ НЕСТАЦИОНАРНОГО ПЕРИОДА 355
где
Подставляя это выражение в интеграл F.4.7) и пользуясь изве-
известными формулами обращения, мы получим
Эта формула и дает решение системы F.4.2).
Так как l\mpk(t) =pk —AkOi то равенство можно записать и так:
^kle~4. F.4.9)
Оценивая сумму, стоящую в правой части этого равенства, мы
можем оценить, насколько быстро стремятся вероятности к своим
финальным значениям.
Отметим еще один чисто вычислительный момент. При малых
t и k>0 pk(t) мала, а слагаемые в правой части F.4.9) велики.
Поэтому при вычислении вероятности pk (t) с заданной относитель-
относительной погрешностью слагаемые в правой части приходится вычислять
с большим числом значащих цифр.
2°. В случае бе с к о н е ч н о г о числа состояний процесс описы-
описывается бесконечной системой дифференциальных уравнений F.3.1).
Решение этой системы в замкнутом виде получено лишь для не-
нескольких частных случаев. Мы рассмотрим здесь два примера,
которые интересны для теории надежности, и на них продемон-
продемонстрируем наиболее эффективные методы решения бесконечных систем
вида F.3.1).
ч а) Хп = Ху firt = jx, X<(x. Предположим, что в начальный момент
процесс находится в нулевом состоянии, т. е.
Ро(°) = 1> Р„@) = 0 при л>0.
Для решения системы F.3.1) используем преобразование Лапласа.
Пусть
о
Тогда из F.3.1) мы получим
— 1 = — (А + s) a0 (s) + \iax (s),
F.4.10)
при л>0.
356
РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ
[ГЛ. 6
Как мы видим, последовательность ап (s) удовлетворяет линейному
однородному рекуррентному уравнению с постоянными коэффи-
коэффициентами. Решение этого уравнения имеет вид
где zx и гг—корни квадратного уравнения
Определим постоянные Сх и С2.
Во-первых, из того, что pn(t)—> () при п—*оо, следует, что
an(s)—>0 при п—^оо, если s>0. Но нетрудно проверить, что
при 5>0 ^<1, a z2>\.
Отсюда С2 —0.
со
Далее, ^ Pn{t) — \ (так как соблюдается второе из условий
п = о
F.3.11)). Значит,
откуда
Итак,
* —
По формуле обращения преобразования Лапласа искомые вероят-
вероятности pn(t) выразятся интегралом
i
а -г сю
Исходя из интеграла F.4.11), можно выразить вероятности pn(t)
через бесселевы функции, но мы не будем этого делать. Вместо
вывода громоздких и бесполезных формул для рп (t) сделаем более
полезную работу — оценим, насколько быстро приближаются вероят-
вероятности pn(t) к своим финальным значениям, которые, как нетрудно
подсчитать, равны
(Ш4)
§ 6.4] ИЗУЧЕНИЕ НЕСТАЦИОНАРНОГО ПЕРИОДА 357
Для этого в интеграле F.4.11) переместим вертикальный контур
(а — /оо, а + /оо) в левую полуплоскость. При этом выделится
вычет в точке s = 0, равный финальной вероятности рп^
e^-lhlhds, a<0.
a — i<x>
Функция z1 = z1(s) регулярна и однолистна вне отрезка [ —
+ VVJ, —(V\i—V^J]» а в бесконечности стремится к нулю»
Поэтому мы можем преобразовать вертикальный контур в замкну-
замкнутый контур, идущий по верхней и нижней сторонам этого отрезка.
Легко подсчитать, что на таком контуре
Тогда обычная оценка интеграла по максимуму модуля дает
Это неравенство позволяет довольно точно оценить скорость
вхождения процесса в стационарный режим.
б) В качестве второго примера рассмотрим процесс, для.
которого
^n = ^» Pn = *V-
Пусть, как и выше, в начальный момент процесс находился в со-
состоянии 0, т. е. Ро(О) = \, р„@) = 0 при /z>0. Система F.4.1)
будет иметь вид
л = 1, 2, ...
Для решения этой системы удобнее всего использовать метод про-
производящих функций, который в применении к таким системам при-
приводит обычно к некоторому линейному уравнению в частных про-
производных. Пусть
оо
Р (t, z)=r. 2 Рп (О *п-
/1 = 0
Умножим п-е уравнение на zn и просуммируем по всем п. Мы по-
получим
г). F.4.14)
358 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [ГЛ. §
Из теории известен способ решения этого уравнения. Составляем
•сопряженную с нашим уравнением систему обыкновенных диффе-
дифференциальных уравнений
dt dz dP
решение которой дает нам два интеграла
-—г
(z 1U-^ — Г* Dp & Г
Тогда общее решение уравнения F.4.14) имеет вид С2=/(С1), или
А
ре~ \х — flllz 1 \ ^•~**М (fi 4 1 ^\
где f(x) — произвольная функция. Для определения этой функции
используем начальные условия
Подставляя в F.4.15) * = 0, получим
е »* =/^_1), т. е.
Окончательно
Разложив эту функцию по степеням z, мы найдем искомые вероят-
вероятности
где a(t) = — A — е'т). При t—> оо a (t)—>— и, следовательно,
Из этих формул легко усматривается скорость вхождения процесса
в стационарный режим.
3°. Задача о первом пересечении высокого
уровня. В приложениях важное значение имеет следующая за-
задача: для процесса гибели и размножения с конечным или счет-
счетным числом состояний требуется найти вероятность того, что
в течение заданного времени t наш процесс ни разу не достиг-
достигнет заданного уровня т, т. е. в любой момент t' <it v (t') <C &•
§ 6.4] ИЗУЧЕНИЕ НЕСТАЦИОНАРНОГО ПЕРИОДА 359"
Дадим сначала точное решение этой задачи. Предположим
ради простоты, что в начальный момент процесс находится в со-
состоянии 0. Рассмотрим вспомогательный процесс гибели и размно-
размножения, который отличается от данного процесса только тем, что-
состояние т является для него поглощающим. Это значит, что, если
первоначальный процесс характеризовался параметрами (Xk1 \хк), то
параметры вспомогательного процесса (Kki [ik) определяются так;
Xk = Xk, \*> = y<k при k<Cm,
До момента первого прихода в состояние т оба процесса ведут
себя одинаково; но вспомогательный процесс, попав в состояние т,
навсегда останется в нем. Поэтому вероятность того, что исходный
процесс хотя бы раз до момента t побывает в состоянии т, равна
вероятности того, что в момент t вспомогательный процесс нахо-
находится в состоянии т. Но эта вероятность рт (t) может быть най-
найдена из системы уравнений
P*(') = **-iP*-i(O-<
^=1,2, ..., m— 1,
Используем, как и выше, преобразование Лапласа. Пусть
ak{s) = )e-slpk{t)dty
о
ft = 0, 1, . . ., m.
Тогда из формулы F.4.2) легко получаем
а- (S> ~ sAm (s) •
где многочлены Ak(s) удовлетворяют рекуррентному уравнению
F.4.6). Отсюда искомая вероятность
В § 6.3 мы рассматривали величины тл —случайное время, в те-
течение которого процесс переходит из состояния 0 в состояние п.
Применительно к нашей задаче хт—-тот случайный момент, когда
процесс первый раз приходит в состояние т. Отсюда следует, что
360 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [гл. g
вероятность рт (t) = Р [хт < t) есть закон распределения величины
хт. Формула F.4.18) дает точное решение нашей задачи, и при
малых т ее можно использовать для вычисления вероятности рт (л
так, как это делалось в начале параграфа. При больших т эта
формула малоэффективна и поэтому желательно иметь простое,
хотя и приближенное, выражение для нашей вероятности. Такое
решение задачи разумно еще и потому, что процесс гибели и
размножения в большинстве приложений сам является лишь гру-
грубой, приближенной, моделью реальных процессов. Задача о первом
пересечении данного уровня ставится обычно либо для стационар-
стационарных процессов, либо для процессов, которые быстро входят в ста-
стационарный режим. Пересечение данного уровня в реальных процес-
процессах означает некоторое нежелательное событие, катастрофу, и по-
поэтому сам уровень выбирается достаточно «высоким». Это значит,
что вероятность достичь или превзойти этот уровень в данный
момент очень мала. Отсюда ясно, что приближенное решение нашей
задачи должно заключаться в определении асимптотического пове-
поведения случайной величины хт при т—юо. Грубые вероятностные
соображения позволяют понять, каким должно быть асимптотиче-
асимптотическое распределение величины хт. Если уровень т велик, то и ве-
величина хт в среднем велика и можно считать, что наш процесс
на рассматриваемом участке времени стационарный (предпо-
(предполагается, что стационарное распределение существует). Обозначим
через P(t) вероятность того, что на участке длины t процесс ни
разу не достигнет уровня т. В силу стационарности эта вероят-
вероятность не зависит от положения участка. Рассмотрим два соседних
участка времени длины t± и t2. Пусть Аг— событие, состоящее
в том, что уровень т не будет достигнут на первом участке, а
А2 — соответствующее событие для второго участка. Если уровень т
очень высок, то, как подсказывает интуиция, события Ах и Л2
практически независимы. Отсюда следует, что
Р (*i + *,) = Р {AtA2} « Р {Аг} Р {А2) = Р (tx) P (*,),
или
Из этого функционального уравнения следует (см. § 2.2), что
Но по определению вероятности P(t)
поэтому
т — 1 j?j в/
§ 6.4] ИЗУЧЕНИЕ НЕСТАЦИОНАРНОГО ПЕРИОДА 361
Следовательно,
Итак, из наших грубых вероятностных соображений следует, что
величина тт при некоторых естественных условиях должна быть
асимптотически распределена по показательному закону.
Для строгого доказательства этого факта [10] рас-
рассмотрим нормированную случайную величину
% -Is.
fe/я т
1 m
Ее закон распределения равен
С \'mJ С \Тт)
где Дт (s) = г-л-—^р—. Из этого равенства следует, что для тогог
чтобы величина хт с ростом т асимптотически была распределена
по показательному закону, т. е.
необходимо и достаточно, чтобы
lim дГ JL j = l+s F.4.20)
m-> оо V ' т,
равномерно по s в любой конечной области. Как следует из F.4.6)г
нормированные многочлены Дт (s) удовлетворяют рекуррентному
соотношению
&n+i (s) == A -f- у^ -[-«— J Дп (s) — ip Дп_х (^), F.4.21)
л"«=1,В2, ....
Запишем это соотношение в виде
и разрешим его относительно разности An+1(s) — Ап (s). После ряда
выкладок мы получим
F22>
362 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [гл. §
Нетрудно показать из F.4.21), что Дя @) = I. Пусть
An(s) = \+cnls + cn2s* + . . . +cnns\
Из неравенства F.4.22) мы легко получаем рекуррентные соотно-
соотношения для коэффициентов сп1
F.4.23)
Из него, в частности, следует, что первый коэффициент
k
—Г
равен среднему времени до первого прихода процесса в состояние п.
¦Обозначим еще cn+lil — cnl = bnl. Из F.4.23) мы видим, что все
коэффициенты сп1 положительны и монотонно возрастают по но-
номеру /г. Следовательно,
сл + 1,/— сп1 ^= cn,l-l Vc« + l,l cnl) ^= ся+1,/-1сп + 1Д сп,1-1 сп1' VO.4r.Z4:)
Суммируя эти неравенства по номеру /г, мы получим
Cnl ^ Cnj-1 CnV
KD другой стороны, используя неравенство .F.4.24), докажем по
индукции, что *
ci
Cni<*-f. F.4.25)
При /= 1 это неравенство тривиально. Пусть оно доказано для
некоторого /. Тогда
J J+i J+i
Последнее неравенство следует из того, что при
ь
Суммируя неравенство
§ 6.4] ИЗУЧЕНИЕ НЕСТАЦИОНАРНОГО ПЕРИОДА 36$
по номеру п, получим
Итак, неравенство F.4.25) доказано.
Рассмотрим теперь многочлены
_ Cml
Очевидно, что ат1 = -—-, и поэтому из неравенств F.4.24) к
F.4.25) следуют неравенства
Теперь мы в состоянии доказать теорему:
Для того чтобы выполнялось условие F.4.20), необходимо и;
достаточно, чтобы
lim am2= lim -ifl = 0. F.4.27>
m -> oo m -> oo "
Доказательство. Необходимость условия F.4.27) очевидна.
Пусть это условие выполнено. Рассмотрим произвольную конечную»
область D в комплексной плоскости s, и пусть
/? = sup| s\.
D
Возьмем произвольное е>0 и выберем /0 так, чтобы
^ /! ^ 2 #
/
Зафиксировав номер /0, выберем число т0 так, чтобы при т^>
а < 8
Тогда, используя неравенства F.4.26), мы получим, что при т >
и 5gD
/о /л
)|
/ + 1 "
364 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [гл. 6
равномерно по s?D, т. е.
lim Дш (-?-) =
ш
Теорема доказана. Тем самым мы доказали, что условие F.4.27)
необходимо и достаточно для того, чтобы случайная величина
?да = — = ;=?*- асимптотически была распределена по экспоненциаль-
ст\ l m
ному закону. Докажем еще одно полезное предложение:
Если процесс гибели и размножения с течением времени
устанавливается, т. е. выполняются условия F.3.11), то вы-
палняется и условие F.4.27), т. е. величина хт асимптотически
распределена по экспоненциальному закону.
Доказательство. Пусть выполнены условия F.3.11)
k
00 00 2 Q?
Из соотношений F.4.23) следует, что
m-i
= ?'-
k
-l 2 С/гЭ/ т-\ т-\
_ =о ^ V* . л V* 1
т2
откуда
2% в
00
Возьмем произвольное 8>0и выберем /0 так, чтобы 2* ^i^T*
Затем при фиксированном /0 выберем т0 так, чтобы
00
^-<?, где 5=X9ft-
Тогда при т>т0
10 т — \ оо
Следовательно,
lim am2 =
m->> oo
и утверждение доказано.
§ 6.4] ИЗУЧЕНИЕ НЕСТАЦИОНАРНОГО ПЕРИОДА 365
Итак, если процесс гибели и размножения с течением времени
становится стационарным, то момент первого достижения высокого
уровня распределен асимптотически по показательному закону
В заключение этого пункта сделаем несколько существенных з а-
м е ч а н и й.
1. При решении задачи о первом пересечении высокого уровня
мы предполагали, что в начальный момент процесс находился в
нулевом состоянии. Нетрудно показать, что асимптотическое по-
поведение величины хт при т—> оо не зависит от начального состоя-
состояния процесса. Действительно, пусть в начальный момент процесс
находился в состоянии k. Случайное время, через которое процесс
первый раз придет в состояние т, мы обозначили (§ 6.3) через
хктУ а его среднее-через Tkm. Но тЛя| = тЛ —тА и Tkm=Tm-Tk.
Нормированная величина
1 km I m i Tk '
1 m
Первая дробь, как мы показали, имеет в пределе показательное
распределение, а вторая дробь сходится по вероятности к единице.
Следовательно, величина \km имеет то же асимптотическое рас-
распределение, что и величина \т.
2. Рассматривая асимптотическое поведение величины %т, мы
считали, что параметры Xk и \ik фиксированы, а уровень т—*оо.
В приложениях этой задачи к теории надежности мы часто имеем
дело с тем случаем, когда параметры Xk и \лк меняются вместе
с уровнем т. Чтобы охватить более широкий класс случаев, встре-
встречающихся в теории надежности, расширим постановку задачи о
пересечении высокого уровня. Пусть дан процесс гибели и размно-
размножения с конечным или счетным числом состояний. Предположим,
что и параметры процесса Xk и jli^,, и число состояний п, и задан-
заданный уровень т зависят от некоторого направленного параметра а:
Не ограничивая общности, можно считать, что а—>-0. Требуется
найти условия, при которых момент первого достижения уровня хт
распределен асимптотически по показательному закону, т. е.
lim P {is- > *1 = е-*. F.4.29)
а_* о I * да )
366 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [ГЛ. (>
Если внимательно просмотреть проведенный выше вывод усло-
условия F.4.27), то можно заметить, что этот вывод остается справед-
справедливым и для такой расширенной постановки. Иными словами, для
справедливости предельного равенства F.4.29) необходимо и
достаточно, чтобы
lim i^2. = o, F.4.30)
где
с -Т
В каждой конкретной задаче условие F.4.30) нетрудно проверить.
Можно еще показать, что при этом условии относительная по-
погрешность равенства F.4.28) будет иметь порядок
а = -^2L
т2 '2тг '
Рассмотрим один важный пример.
В применениях процесса гибели и размножения к теории надеж-
надежности параметры Xk равны интенсивностям отказов, а параметры
\xk— интенсивностям восстановлений. Среднее время восстановления,
как правило, во много раз меньше среднего времени безотказной
работы. Это означает, что параметры kk во много раз меньше
параметров \ik. В этих условиях разумно рассмотреть такую схему:
фиксирован уровень т и параметры \ik, а параметры Kk(a) = Kkay
где а—>0. Несложные подсчеты и оценки дают нам, что при а—> О
0@) а*Л-1 э
^«0 ат1
т-1
§ 6.4] ИЗУЧЕНИЕ НЕСТАЦИОНАРНОГО ПЕРИОДА 367
откуда видно, что условие F.4.30) выполняется и, следовательно»
величина %т распределена асимптотически по показательному за-
закону. Заметим еще, что в этой постановке можно уточнить при-
приближенную формулу F.4.28). Оказывается, что при ос —>0 на
порядок более точной формулой будет такая:
,-V-L
m-i
?{%m<t}&\-e . F.4.32)
Это в свою очередь дает возможность оценить погрешность фор-
формулы F.4.28). Как следует из F.4.28) и F.4.32), главный член
относительной погрешности в формуле F.4.28) равен
F-4-331
3. Выше мы рассмотрели распределение времени до первого
прихода в состояние т. Дальнейшее поведение процесса нас не
интересовало. В теории надежности, где используется процесс
гибели и размножения, часто возникает такая задача: найти сред-
среднюю длительность тех участков, на которых процесс находится
в состоянии, не меньшем т. При этом, естественно, предпола-
предполагается, что процесс имеет стационарное распределение. Обозначим
через ГA> среднюю длину каждого участка, начиная со второго, на
котором v(t)<my а через ГB) —среднюю длину каждого участка,
на котором v(t)^m. Последовательность длин этих участков,
начиная со второго, образует то, что мы (см. § 2.3) назвали про-
процессом восстановления с конечным временем восстановления. Тогда,
как было показано,
lim P{v(t)<m} = ?/>* = foS?W>- F.4.34)
С другой стороны,
-. J
Отсюда и из F.4.34) мы находим искомое среднее время
F.4.35)
00
368 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [ГЛ. 6
§ 6.5. Применение процесса гибели и размножения
к резервированию с восстановлением
1°. Процесс гибели и размножения может быть применен для
изучения резервных систем, в которых происходит восстановление
отказавших элементов.
Пусть имеется система, в которой время безотказной ра-
работы каждого элемента распределено по показательному закону
(рис. 6.5.1). Каждый элемент после отказа идет в ремонтное уст-
устройство, где восстанавливается, а
после восстановления снова возвра-
возвращается в систему. Предположим, что
время восстановления также распреде-
распреде6 5 . лено по показательному закону. В
силу экспоненциальности всех законов
работа такой системы всегда описы-
описывается марковским процессом с конечным числом состояний. Число сос-
состояний в общем случае равно 2N, где N — число элементов системы,
так как для описания работы системы мы должны в каждый момент
знать множество неисправных элементов, а таких множеств 2N.
Решение системы дифференциальных уравнений, а в стационарном
случае системы алгебраических уравнений, сопряжено с большими
трудностями вычислительного и алгебраического характера. Однако
для ряда реальных систем число состояний может быть существенно
сокращено. Если для каждого состояния системы суммарная интен-
интенсивность отказов и суммарная интенсивность восстановлений зависят
не от множества неисправных в данный момент элементов, а только
от их числа, то такая система описывается марковским процессом
с числом состояний, равным (N+1).
Пусть ^-суммарная интенсивность отказов, а
|л,? — суммарная интенсивность восстановления при
условии, что в системе к неисправных элементов. Тогда за время
Д^ с вероятностью ХлД*+о(Д*) произойдет один отказ, т. е.
система перейдет в состояние (?+1), и с вероятностью \ik&t-\-o (At)
произойдет одно восстановление, т. е. система перейдет в состояние
(k—1). Но это означает, что наша система описывается процессом
гибели и размножения.
Рассмотрим теперь конкретную систему такого рода (рис. 6.5.2).
В системе имеется N=n + m + l+s одинаковых элементов (заметим,
что под словом элемент мы можем понимать и элемент как
неразложимую часть системы и часть системы, и
вообще любое устройство). Время безотказной работы каж-
каждого элемента распределено по показательному закону, п элементов
находятся в рабочем состоянии и имеют опасность отказа, равную
Jl, m элементов находятся в нагруженном резерве с той же опас-
§ 6.5]
ПРИМЕНЕНИЕ К РЕЗЕРВИРОВАНИЮ С ВОССТАНОВЛЕНИЕМ
369
ностью отказа Я, I элементов составляют облегченный резерв и
имеют опасность отказа v и, наконец, s элементов находятся в не-
нагруженном резерве и в этом состоянии не отказывают. Каждый
отказавший элемент мгновенно поступает в ремонтное устройство,
которое состоит из г ремонтных единиц. Каждая ремонтная единица
может одновременно ремонтировать (или восстанавливать) один
элемент. Случайное время ремонта элемента распределено по по-
показательному закону с параметром \л. Если все ремонтные единицы
ЯагруМеш/й
резерб
резерд
резерв
*
Рабочие
элементь/
Рис. 6.5.2.
г
Ремом
устро
77//ое
йс/пбо
заняты, то отказавший элемент ставится в очередь. Каждый отка-
отказавший рабочий элемент мгновенно замещается элементом из на-
нагруженного резерва, каждый отказавший или перешедший в рабочее
состояние элемент из нагруженного резерва мгновенно заменяется
элементом из облегченного резерва и, наконец, каждый отказавший
или перешедший в нагруженный резерв элемент из облегченного
резерва мгновенно заменяется элементом из ненагруженного резерва.
Каждый восстановленный элемент поступает в ненагруженный резерв.
Система работает исправно, если число исправных элементов не
меньше п. Под состоянием системы мы будем понимать число
неисправных в данный момент элементов. Ясно, что работа такой
системы описывается процессом гибели и размножения, причем
параметры процесса (kk, \ik) выражаются формулами
Хк = { (п + т)
(п + т) К -f- v/, если
v(l-\-s — &), если
+ l+s — k) X, если l
k\iy если &<;/*,
ф, если k>r.
0
; s,
F5Л)
Отметим еще один случай, который не укладывается в нашу схему.
Число элементов в ненагруженном резерве может быть практически
13 Б. В. Гнеденко и др.
370 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [ГЛ. 6
неограниченно, s = oo. Очевидно, что в этом случае не имеет
смысла вводить нагруженный и облегченный резервы. Такая система
описывается процессом гибели и размножения с бесконечным числом
состояний, причем параметры этого процесса выражаются так:
Аи, если k^.r.
F.5.2)
г(л, если и ^ -
Наша схема включает в себя большое число частных случаев.
Отметим те случаи, которые часто встречаются в практике на-
надежности, и вычислим для них финальные вероятности.
а) Система состоит из п элементов. Из них (п — т) находятся
в рабочем состоянии и т в нагруженном резерве. Число ремонт-
ремонтных единиц г^п.
Xk= (л-А) А, |хл = *|*,
_rk ^У-* F.5.3)
б) Система та же, но ремонтная единица одна, г=1. Для
этого случая
1 = 0
в) В системе п рабочих элементов и неограниченный ненагру-
женный резерв. Число ремонтных единиц также неограниченно.
Здесь
к
е~Т. F.5.5)
г) Система та же, но ремонтная единица одна, г=1. Для та-
такой системы
Здесь стационарное распределение существует при условии
лЯ<|я, и в этом случае финальные вероятности выражаются фор-
формулами
§ 6.5] ПРИМЕНЕНИЕ К РЕЗЕРВИРОВАНИЮ С ВОССТАНОВЛЕНИЕМ 371
2°. Параметры надежности резервных систем с
восстановлением. Надежность резервной системы с восстанов-
восстановлением в зависимости от ее структуры и характера выполняемых ею
функций может оцениваться разными параметрами. Рассмотрим
основные параметры надежности такой системы. Ради конкретности
мы будем все делать для рассмотренной выше системы с параметрами
(л, т, /, s, г, X, v, (а).
Вероятность безотказной работы в течение
времени t. Система будет работать безотказно до момента ty
если ни разу до этого момента число отказавших элементов не
превысит N — п, т. е. v(t')^N—п при /'<Ж Мы предполагаем,
что в начальный момент все элементы системы исправны, т. е.
v @) = 0.
Следовательно, вероятность безотказной работы системы равна
где Ptf-n+1(t) выражается точной формулой F.4.18). Если уровень
N—/г+1 «высок», т. е. выполняется условие ciN_n+ly2<^:\ (см.
F.4.27)), то вероятность безотказной работы выражается прибли-
приближенной формулой F.4.28)
e T"-n+i. F.5.7)
Рассмотрим конкретные примеры,
a) Xk=(n — &) Я, \ik = k\x.
Для этого случая отказ системы наступает, когда число от-
отказавших элементов становится равным (т+1). Среднее время
безотказной работы системы равно
где
Можно преобразовать эту сумму к более простому виду
(j'" ' i —
13*
372 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [ГЛ. 6
В частности, если т = п—1, т. е. имеется один рабочий эле-
элемент, то
Можно показать, что приближенная формула F.5.7) справедли-
справедлива, если
б) Xk = (n — k)Ky |хл = |х.
Отказ системы, как и в первом примере, наступает, когда система
приходит в состояние (т-\-\). Среднее время безотказной работы
выражается формулой
k — n—m l — k
Приближенная формула F.5.7) имеет место, например, если к и [х
фиксированы, а т велико.
Коэффициент готовности системы. Пусть p(t) —
вероятность того, что в момент t система исправна. Назовем
коэффициентом готовности системы предельное значение этой
вероятности
kr = \im p(t).
t->co
Легко видеть, что для нашей системы
ftr = limP{v(*)<N—лв+1}« jffft- F.5.11)
Как уже отмечалось выше, коэффициент готовности равен средней
доле времени, в течение которого система находится в исправном
состоянии. В некоторых случаях знания коэффициента готов-
готовности недостаточно для оценки надежности системы — нужно знать
еще и среднюю длительность участков исправного и неисправного
состояний. Средняя длительность исправного состояния системы
(исключая начальный период) равна
N-n
fcS Pk
TN-n> „_„+1= *^L F.5.12)
"N-n PN-n
§ 6.5] ПРИМЕНЕНИЕ К РЕЗЕРВИРОВАНИЮ С ВОССТАНОВЛЕНИЕМ 873
в среднее время неисправного состояния системы по формуле
F.4.35) равно
N
F.5.13)
Основные характеристики ремонтоспособности
системы. Как мы уже говорили, каждый отказавший элемент
идет в ремонтное устройство, состоящее из г единиц. Если все
ремонтные единицы заняты восстановлением, то элемент становится
в очередь. Качество ремонтного устройства может быть охарак-
охарактеризовано двумя параметрами:
k' — среднее число элементов, стоящих в очереди,
k" — среднее число занятых ремонтных единиц.
Естественно, что эти характеристики определяются для стаци-
стационарного режима и не зависят от времени. Нетрудно выразить
эти числа через финальные вероятности. Пусть, как и выше,
v (t) — число неисправных элементов в момент t. Тогда длина
очереди в этот момент равна нулю, если v (?)<;/*, и равна
у (t) — г, если v(^)>r. Средняя длина очереди в момент t выра-
выразится так:
S (k-r)pk(t).
k = r+l
Тогда в стационарном режиме
Совершенно аналогично находится второй параметр
Можно подойти к оценке ремонтоспособности и вообще к
оценке качества нашей системы по-другому. Каждый элемент в
процессе работы системы многократно проходит цикл
работа — ожидание ремонта — ремонт — резерв.
Пусть tx — среднее время пребывания элемента в рабочем со-
состоянии, t2 — среднее время ожидания ремонта, t3 — среднее время
ремонта и ^4 — среднее время пребывания в резерве.
Обозначим to = t1 + t2-\-t3-\-tt. Тогда отношения
ъ —h ь —i<L k — *3 и k — *Л
го *о го *о
дадут нам соответственно среднюю долю времени, которое элемент
пребывает в том или ином состоянии. Ясно, что в силу равноправия
374 РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ [ГЛ. б
всех элементов эти коэффициенты не зависят от номера рас-
рассматриваемого элемента.
Введенные так коэффициенты достаточно хорошо и полно
определяют качество нашей резервной системы с восстановлением.
Например, большое значение коэффициента kz указывает на то,
что ремонт идет медленно, большое значение k2 говорит о том,
что мало число ремонтных единиц, а большое число коэффи-
коэффициента ?4 свидетельствует о том, что в системе неоправданно
большой резерв.
Выразим наши коэффициенты через финальные вероятности.
Соответственно четырем состояниям элемента —работа, ожидание
ремонта, ремонт, резерв — введем четыре единичные функции
?а#)(/), /=1, 2, 3, 4. е[1) (t) равна единице, если &-й элемент в
момент t находится в /-м состоянии, и равна нулю в противопо-
противоположном случае. В силу эргодичности нашей системы (см. § 6.2)
Л, = lira i-
Г-*оо '
О
Пусть
— число элементов, находящихся в момент t в l-м состоянии. Так
как все элементы равноправны, мы можем написать
т , т
± [е[° (bdt = l\m -^[viV) dt^+flimttVtV). F.5.16)
1 О r->ooyvyJ yv f-»<»
Но легко видеть, что Mvx (t) — среднее число элементов, находя-
находящихся в рабочем состоянии, Mv2 (t) — среднее число элементов,
находящихся в ожидании ремонта, Mv3 (t)—среднее число элемен-
элементов, находящихся в ремонте, a Mv4 (t) —среднее число элементов,
находящихся в резерве.
Далее
л, если v(t)^N—л,
^— v(t), если v(t)>N — n9
О, если v (t) <;r,
v It) = <!
2 w i V(/) — r, если v(t)>r,
v (t)y если v (t) ^г,
г, если v (t) > r,
N—n — v(t)y если v(t)<:N—nf
О , если v(/) ^N—n.
§ 6.5] ПРИМЕНЕНИЕ К РЕЗЕРВИРОВАНИЮ С ВОССТАНОВЛЕНИЕМ 375
Отсюда легко получаются окончательные формулы для наших
коэффициентов:
n-п N
0Ь
N
2 (*-*•)р*. F-5Л8>
N
lT 2 Р*. F-5-19)
o fe=r+i
N-n
Заметим в заключение, что введенные нами характеристики не
дают, конечно, полного описания нашей системы—для разных
систем и в разных условиях возможны и другие характеристики.
Нам важно было показать, с одной стороны, что все такие ха-
характеристики всегда можно выразить через финальные вероятности,
и, с другой стороны, мы хотели продемонстрировать те методы,
которыми наиболее удобно вычислять эти характеристики.
ГЛАВА 7
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ КАЧЕСТВА
И НАДЕЖНОСТИ МАССОВОЙ ПРОДУКЦИИ
§ 7.1. Вводные понятия
Контрольная операция — основа статистиче-
статистического контроля. Настоящая глава посвящена систематическому
изложению вопросов, связанных с планированием приемочного конт-
контроля главным образом по качественному признаку (годен — него-
негоден). Задачи статистического контроля теснейшим образом связаны
с задачами обеспечения надежности. Все зависит от конкретного
вида контрольной операции. Если при контрольной операции вы-
выявляется возможность появления отказа, то статистический контроль
является в то же время и контролем надежности. Но, вообще го-
говоря, задачи статистического контроля шире. Например, контроль
по внешнему виду прямо не связан с контролем надежности. По-
Появление в книге по надежности специальной главы, посвященной
вопросам статистического контроля, объясняется тем, что пра-
правильно организованный статистический контроль является дейст-
действенным средством повышения надежности изделий.
В настоящем параграфе рассматриваются вопросы, связанные с
задачами статистического контроля на производстве. Вводится по-
понятие о нормальном ходе производства и об априорном распределе-
распределении числа дефектных изделий. Даны определения типоз планов прие-
приемочного контроля и их оперативной характеристики. Приведены
примеры возможных нарушений при практическом использовании
планов приемочного контроля. В § 7.2 исследуются различные пока-
показатели планов приемочного контроля, а в § 7.3 приводится при-
пример стандарта, основанного на предельном выходном качестве, и дан
обзор широко используемых стандартов планов приемочного конт-
контроля. Экономический подход, основы которого были предложены
А. Н. Колмогоровым, излагается в § 7.4. Работа по вычислению
таблиц к этому стандарту еще не закончена, поэтому в книге
приведены таблицы планов только типа однократной выборки.
Формулы для последующей оценки показателей эффективности
§ 7.1] вводные понятия 377
применяемых планов контроля даны в § 7.5. Случай планов типа
однократной выборки исследовался в работах Колмогорова [1],
Сираждинова и Эйдельнанта [2]. Несколько в стороне стоит мате-
материал § 7.6, посвященного вопросам текущего контроля по ко-
количественному признаку. Здесь мы ограничиваемся главным образом
постановкой задач, которые необходимо исследовать для правиль-
правильной организации текущего контроля по количественному признаку.
Организация текущего контроля является важной частью общей
программы организации статистического контроля на предприятии.
Производство элементов (особенно радиоэлектроники) в на-
настоящее время обеспечивается сложными технологическими про-
процессами, включающими в себя десятки, а иногда и до сотни раз-
различных операций. На качество и надежность выпускаемых элементов
влияют многие факторы. Поставить все факторы под контроль
не представляется возможным. В итоге даже два выпущенных
друг за другом элемента могут резко различаться по своим свой-
свойствам, хотя при этом все основные условия технологических ре-
режимов будут соблюдены. Если же вдобавок произошли серьез-
серьезные отклонения от нормального хода производства, то засоренность
продукции негодными, недоброкачественными элементами может
резко возрастать. Выпуск недоброкачественных элементов связан
с ущербом двоякого рода. Во-первых, зря тратятся труд и мате-
материалы на выпуск негодной продукции, во-вторых, использование
негодной продукции может явиться причиной ущерба в результате
аварий и остановок оборудования для восстановления.
Как же может произойти, что некачественная и ненадежная
продукция будет выпущена предприятием и затем использована
потребителем? Дело в том, что, во-первых, многие свойства эле-
элементов, составляющие его качество, либо очень трудно проверить
в заводских условиях, либо просто невозможно проверить в ре-
результате разрушительного характера испытаний (классическим при-
примером может служить проверка взрывателей). Во-вторых, недобро-
недоброкачественность элементов может заключаться в том, что параметры,
характеризующие их работу, нестабильны. Во время проверки их зна-
значения вполне приемлемы для потребителя, но затем, в результате хра-
хранения и небольшого времени эксплуатации, недопустимо изменяются.
Проведение контрольной операции (КО) по определению степени
пригодности сырья, полуфабриката или готового элемента часто
является весьма сложным делом, требующим предварительных спе-
специальных исследований по методике испытаний и разработки спе-
специальной испытательной аппаратуры. Представим себе технологи-
технологический процесс как цепочку элементарных технологических опера-
операций, которые последовательно проходят полуфабрикаты до прев-
превращения в готовое изделие-элемент (рис. 7.1.1). Отдел техническо-
технического контроля (ОТК) в результате предварительных исследований
378
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
должен решить, где целесообразно поставить контрольные посты
(КП), на которых будет проверяться качество продукции, и ка-
какие параметры при этом необходимо замерять. Как правило, та-
такие КП ставятся в самом начале технологического процесса для про-
проверки качества исходного сырья (входной контроль), а также
в самом конце для проверки качества и надежности готовых изде-
изделий (приемочный контроль). КП ставятся также после наиболее
ответственных и наиболее тяжело поддающихся регулировке техно-
технологических операций для проверки нормального хода производства
на этих операциях. Такой контроль называется текущим.
фабрикаты с
других пред-
предприятий
Снлад гото-
6ойпродупции[
Рис. 7.1.1.
Степень жесткости контроля на КП в конечном итоге пресле-
преследует одну цель: готовая продукция должна состоять из пригодных
для потребителя элементов. Введение контроля, с одной стороны,
приводит к повышению себестоимости продукции, с другой —
к снижению себестоимости, так как уменьшаются затраты на про-
производство некачественных изделий. Влияние введения контроля
на повышение себестоимости учесть сравнительно просто. Значи-
Значительно сложнее произвести учет выигрыша от введения контроля.
При этом выигрыш перекроет расходы на контроль только при
условии научной обоснованности такого контроля.
Требования к контролю со стороны производителя и потреби-
потребителя противоречивы. Для предприятия контроль представляется
лишней обузой, связанной с непроизводительными расходами, из
чего следует, что контрольных постов должно быть меньше,
объем работы на них также должен быть минимальным; потре-
потребителя, наоборот, интересует самое высокое качество используе-
используемых элементов, и он заинтересован в жестком контроле (при
этом, конечно, прежде всего в самом жестком выходном — при-
приемочном контроле). Иногда потребитель даже, не довольствуясь дан-
§ 7.1] .вводные понятия 379
ными ОТК, еще раз проверяет готовую продукцию. Таким образом,
степень жесткости и объем контроля в конечном итоге являются
результатом спора о допустимом качестве выпускаемых изделий.
На КП определено, какие параметры изделий (элементов или по-
полуфабрикатов) надо измерять. Степень пригодности изделий
к дальнейшему использованию можно определять различными спо-
способами. Можно регистрировать точные численные значения пара-
параметров (контроль по количественному признаку), можно
отмечать лишь категории, классы, которым принадлежит проверя-
проверяемое изделие. Наконец, можно принимать одно из двух решений:
пригодно изделие для дальнейшего использования или нет. Если
изделие непригодно, то оно объявляется дефектным. Такой конт-
контроль называется качественным. В настоящей главе мы огра-
ограничимся в основном случаем качественного контроля.
Само понятие дефектности изделия самым существенным об-
образом зависит от вида изделия и условий его использования. Очень
часто дефектность определяется как выход за пределы допусков
хотя бы одного из замеряемых параметров. Например, если со-
сопротивление промаркировано на 10Ш±2%, то если фактическое
значение омического сопротивления выйдет за указанные пределы
и будет равным, например, 10,ЗШ, то это сопротивление счи-
считается дефектным. Однако если допуск был определен в ±5%,
то это же сопротивление считалось бы годным. В практике могут
встречаться такие случаи, когда одно и то же изделие при пос-
последовательных измерениях оказывается то годным, то дефектным.
Примером могут служить измерения обратного тока сетки после
испытания ламп на вибрационных стендах. Проводя такие испы-
испытания последовательно одно за другим и регистрируя обратный
ток, одну и ту же лампу приходится то считать годной, то бра-
браковать как дефектную по причине недопустимо большого обрат-
обратного тока. Контроль по качественному признаку обладает рядом
преимуществ по сравнению с контролем по количественным приз-
признакам. Во-первых, он проще как по объему вычислений, так и
по методам проверки. Можно заготовить простые шаблоны, или
автоматические измерительные устройства, которые будут разбра-
разбраковывать изделия на годные и дефектные. Во-вторых, методика,
основанная на качественном контроле, не зависит от вида распре-
распределений измеряемых параметров и поэтому является более уни-
универсальной, тогда как в большинстве случаев при контроле по
количественному признаку предполагается, что измеряемые пара-
параметры имеют нормальное распределение (см. W. Allen Wallis,
Techniques of Statistical Analysis, 1947). Однако следует отме-
отметить, что при контроле по качественному признаку используется
лишь малая часть информации, содержащейся в наблюдениях,
что приводит к необходимости проведения большого количества
380 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
измерений. Сама операция контроля может носить двоякий харак-
характер. В одних случаях она не наносит никакого вреда изделиям,
т. е. изделие, признанное в результате контроля годным, остается
годным и после контроля. В других случаях операция проверки
связана с изменением качества, а иногда даже и разрушением
проверяемых изделий. Испытания на прочность и надежность, как
правило, носят разрушительный характер. Итак, в первом при-
приближении контроль может быть разрушительным или неразруши-
неразрушительным.
Поскольку в теории надежности особое значение имеет про-
проверка стабильности параметров в зависимости от различных внеш-
внешних условий, контроль обычно является разрушительным или, во
всяком случае, изменяющим качество изделий. Поэтому представ-
представляет первостепенный интерес разработка таких методов контроля
по косвенным признакам без разрушения изделий, чтобы по их
результатам можно было судить о качестве изделий по пара-
параметрам, требующим для своей оценки разрушительного контроля.
Испытания по количеству проверяемых параметров могут резко
отличаться друг от друга. Время от времени проводятся также
испытания по расширенной программе, включая различные клима-
климатические условия, вибрацию, удары и т. п. Испытания такого рода
носят название периодических.
В итоге проведения операции контроля мы должны выяснить,
пригодно или же дефектно проверяемое изделие. Иногда встреча-
встречаются такие случаи (примером могут служить замеры обратного
тока сетки, о которых говорилось выше), когда мы лишь с опре-
определенной вероятностью можем определить дефектность проверяемого
изделия. Ниже будут рассматриваться только случаи, когда раз-
разделение изделий на годные и дефектные производится без ошибок.
Если контрольная операция неразрушительная и стоимость ее не-
невелика, то в этих условиях очень часто применяется сплошной
контроль. При сплошном контроле проверяются все изделия. Зна-
Значительно чаще встречается такое положение, когда либо велики
общие расходы, связанные с контролем, либо контроль носит раз-
разрушительный характер. В этих случаях контрольную операцию
проходят только некоторые изделия, отбираемые специальным об-
образом. Такой контроль носит название выборочного. При расста-
расстановке КП (см. рис. 7.1.1) часть из них проводит сплошной контроль,
а часть — выборочный. Если общей целью введения контроля яв-
является снижение доли дефектных изделий в готовой продукции,
то на каждом из контрольных постов для этого принимаются
различные решения. На внутренних КП проводится текущий конт-
контроль, по результатам которого принимаются решения о подна-
ладке оборудования. На входном и выходном КП организуется
приемочный контроль. Здесь необходимо принимать решения о ка-
§ 7.1] вводные понятия 381
честве массивов продукции — партий. Если среди изделий, состав-
составляющих партию, много дефектных, то такая партия должна подвер-
подвергаться либо сплошной разбраковке, либо отвергаться как негодная.
Последнее решение принимается в тех случаях, когда сплошная
проверка либо слишком дорога, либо контроль носит разрушитель-
разрушительный характер. Чтобы выяснить степень засоренности партии де-
дефектными изделиями, нет необходимости проводить сплошную
проверку всех изделий. Достаточно проверить только часть пар-
партии, а уже затем по результатам этой частичной проверки решить,
что сделать с остальными изделиями.
По своим целям контроль может быть дочищающим» или «пре-
«предупредительным». Это деление несколько условно. Очищаю щи й
контроль применяется тогда, когда он является неразрушительным
и когда сравнительно часто на контроль поступают партии, сильно
засоренные дефектными изделиями. Браковка партии по результа-
результатам выборочного контроля означает проверку оставшейся части
партии с устранением всех дефектных изделий и их последующей
заменой на годные из числа имеющихся на предприятии. При очи-
очищающем контроле проверяется значительная доля всех предъявлен-
предъявленных изделий. Если же производство хорошо отлажено и почти
все партии содержат низкий процент дефектных изделий, вполне
удовлетворяющих потребителя, то приемочный контроль должен
носить предупредительный характер. Это означает, что по резуль-
результатам контроля решение о браковке будет приниматься для пар-
партий, содержащих намного больше дефектных изделий, чем это
бывает обычно. Если приемочный контроль является разрушитель-
разрушительным, то он может носить только предупредительный ха-
характер. Действительно, в случае разрушительного контроля мы
не можем уменьшить (в среднем) долю засоренности партии де-
дефектными изделиями, так как, определив, годно или дефектно
изделие, мы разрушаем его. Однако по результатам правильно
организованного выборочного контроля, проверив только часть
партии, мы можем с большой степенью достоверности предугадать,
содержит данная партия небольшое количество дефектных изделий
или доля дефектных изделий велика.
Нормальность хода производства. Одним из важных
понятий, которое может быть существенным образом использовано
для правильной организации приемочного контроля, является по-
понятие засоренности дефектными изделиями при нормальном ходе
производства. Под нормальным ходом производства понимается
такое его состояние, когда основные требования технологии соб-
соблюдены. Засоренность дефектными изделиями при нормальном ходе
производства невелика, но она резко возрастает, если имеют место
существенные нарушения технологии. На рис. 7.1.2 показаны ре-
результаты сплошной разбраковки 108 партий, каждая из которых
382 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
содержала по 1000 элементов. По горизонтали каждый столбец
черточек соответствует числу d (N) дефектных изделий, обнару-
обнаруженных в партии. Проверив партию и обнаружив в партии d(N)
дефектных изделий, мы в столбце со значением d (N) ставим чер-
черточку. Таким образом, наличие четырех черточек в столбце с d (N) = 0
означает, что из 108 проверенных партий только в четырех не
было обнаружено дефектных изделий. Предположим, что для каж-
каждой из этих 108 партий известно, выпущена она при нормальном
ходе или где-то имели место разладки. Пусть при этом оказалось,
что партии, содержащие до 8 дефектных изделий, выпущены при
20
10
0 1 2 3 4 5 6 7 8 9 10 11 1213 ft 15 . ..29.. .Л1 80 89d(N)
Рис. 7.1.2.
нормальном ходе производства, партии, содержащие 10, 12, 13,
14, — при наличии незначительных отклонений технологических ре-
режимов, а партии с d(/V) = 29, 41, 80, 89 выпущены при серьезных
нарушениях технологического режима. Из рис. 7.1.2 видно, что
при условии нормального хода производства число d (N) дефект-
дефектных изделий в партии, состоящей из N элементов, можно считать
случайной величиной, имеющей вполне определенное распределе-
распределение. Вид этого распределения Fn (D) = Р {d(Л/)<D} можно най-
найти только в результате специальных исследований. В ряде случаев
в качестве первого приближения можно использовать биномиаль-
биномиальное или пуассоновское распределение. Точно биномиальное распре-
распределение d(N) будет в том случае, когда каждый элемент м©жет
оказаться дефектным с одной и той же вероятностью. Распреде-
Распределение FH (D) называется априорным распределением для числа де-
дефектных изделий в партии, выпущенной при нормальном ходе
производства. Представляется весьма сомнительным, что можно
§ 7.1] вводные понятия 383
определить какое-то фиксированное распределение FV(D) для числа
дефектных изделий в партии в том случае, когда имеются разладки.
Предположим на время, что такое распределение FV(D) суще-
существует и что с вероятностью р, близкой к единице, сохраняются
все основные условия, определяющие нормальность хода произ-
производства, а с вероятностью q=\—р наступает разладка. В этом
случае априорное распределение F(D) для числа D дефектных
изделий в партии определяется по формуле
т. е. является суперпозицией двух распределений. Если распреде-
распределения FH(D) и FV(D) таковы, что FH(D) уже близко к 1, тогда
как FV(D) еще мало, то задача организации приемочного конт-
контроля заключается в следующем. Надо так организовать контроль,
чтобы большинство партий, выпущенных при нормальном ходе
производства, принималось, тогда как большинство партий, выпу-
выпущенных при разлаженном ходе производства, браковалось.
Для краткости назовем это свойством разделимости. При орга-
организации контроля, обладающего свойством разделимости, можно
исходить из конкретного вида распределения FH (D), однако это
свойство разделимости должно сохраняться по отношению к раз-
различным распределениям FV(D). Требование нечувствительности
к виду Fv (D) объясняется сильной зависимостью Fv (D) от сущест-
существа причины, вызвавшей разладку.
Задание априорного распределения F(D) часто является наи-
наиболее слабым местом планов, основанных на экономических сооб-
соображениях. Вид априорного распределения существенным образом
влияет на эффективность использования плана контроля. А. Н. Кол-
Колмогоров предложил авторам следующий пример. Пусть проводится
выборочный контроль, при котором от каждой партии отбирается
некоторое количество изделий для проверки. Если в выборке будет
обнаружено хотя бы одно дефектное изделие, то партия бракуется.
Если дефектные изделия в выборке не содержатся, то партия
принимается. На первый взгляд кажется естественным, что такой
контроль никогда не может ухудшить качества принимаемой про-
продукции. Однако предположим, что априорное распределение F(D)
таково, что в каждой из партий, предъявляемых на контроль,
либо все изделия годные, либо дефектно только одно изделие.
При таком априорном распределении будут браковаться партии,
в выборках из которых выявлено одно возможное дефектное изде-
изделие. Ясно, что качество продукции, принятой при использовании
плана статистического контроля, будет хуже, чем без контроля.
Однако при других априорных распределениях тот же самый
план контроля может оказаться вполне эффективным.
384 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
Для организации приемочного выборочного контроля надо
задать систему правил — план контроля, в котором указы-
указывается, как надо отбирать изделия для проверки, после какого
количества проверенных изделий принимать решение о браковке,
приемке партий в целом или о дальнейшем продолжении контроля.
Наибольшее распространение получили три типа планов выбороч-
выборочного контроля по качественному принципу.
I. Планы типа однократной выборки. Из партии
объема N отбираются случайным образом п (п^М) элементов,
которые подвергаются проверке. Если число обнаруженных дефект-
дефектных изделий среди п элементов равно d(n)<ic} где с — целое
число, называемое приемочным числом, то партия принимается.
Если же df(/z)>c, то партия бракуется.
II. Планы типа двукратной выборки. Из партии
объема N случайным образом отбирается пг элементов (первая
выборка), если число обнаруженных дефектных изделий d (/г1) ^ с,
то партия принимается, а если d (пх) > с2 > с1у то бракуется,
если же сх < d (п^ ^ с2, то берется вторая выборка из п2
элементов. Если общее число обнаруженных в двух выборках
дефектных элементов d (n1-\-n2) ^ с3, то партия принимается, а если
же d (п1-\-п2) > с3, то партия бракуется. Часто используются усе-
усеченные планы типа двукратной выборки, в которых с2 = с3.
III. Планы типа последовательного анализа. При
использовании этих планов задаются объемы последовательных
выборок nh i=\, 2, . . ., п1 <N, n1 + n2 <.N и т. д., а также
пары целых чисел сь с'.. Пусть di = d(n1+ . . . +#,) — число дефект-
дефектных изделий, обнаруженных в первых / выборках. В начале конт-
контроля берется выборка объема пг. Если dx ^ с1у то партия прини-
принимается, если d±^> c'v—бракуется, если же сг <С dx ^ c'v то берется
выборка объема п2 и т. д. На /-м шаге, если dt^ch то партия
принимается, если^->с'., — бракуется, если с,< dt ^ с'.у то берется
выборка объема ni+1 изделий и т. д.
Каждый из указанных выше типов обладает рядом преиму-
преимуществ и недостатков. Более подробный анализ будет дан в сле-
следующем параграфе. Мы только отметим, что планы типа одно-
однократной выборки значительно проще с организационной точки
зрения. Здесь к тому же заранее известен объем выборки. В пла-
планах типа двукратной выборки и последовательного анализа можно
при том же среднем объеме выборки получить большую достовер-
достоверность соответствия принимаемых решений с истинным положением
дела. Однако здесь могут встретиться случаи, когда объем
инспекции будет чрезмерно велик. Оценка качества продукции
для планов типов II и III значительно сложнее, чем для планов
типа I.
§ 7.1]
ВВОДНЫЕ ПОНЯТИЯ
385
Оперативная характеристика. Использование методов
приемочного контроля связано с риском напрасной браковки хоро-
хороших партий и риском приемки партий, засоренных дефектными
изделиями. При случайном отборе изделий можно при общем
небольшом количестве дефектных изделий в партии отобрать на
проверку значительное число дефектных, что приведет к ложному
решению о браковке хорошей партии (ошибка первого рода).
С другой стороны, может случиться и так, что при сильной засо-
засоренности партии дефектными изделиями в выборке окажется
n(q)
а)
небольшое количество дефектных и плохая партия будет принята
(ошибка второго рода). Такого рода ошибочные решения неизбежно
связаны с применением методов выборочного контроля. Вопрос
правильной организации выборочного контроля состоит, в частно-
частности, в том, чтобы такие ошибочные решения встречались редко,
были маловероятными событиями. Для этого надо правильным
образом задать параметры, определяющие контроль.
Одной из наиболее важных вероятностных характеристик плана
выборочного контроля является так называемая оперативная
характеристика. Под оперативной характеристикой плана пони-
понимают функцию n(q)y равную вероятности принятия партии, содер-
содержащей долю дефектных изделий, равную tf=yy> если приемка
производится в соответствии с системой правил, определяющих исход-
исходный план контроля.
Использовав понятие оперативной характеристики, можно задать
различные численные показатели планов. Качество партии мы изме-
измеряем долей засоренности дефектными изделиями q = jj- Из эконо-
экономических или каких-либо других соображений может оказаться,
что партии, имеющие засоренность q<qKV> считаются хорошими,
386 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
их следует принимать, а партии с q>qKV—плохими и их надо
браковать. В этих случаях было бы желательно использовать план
с идеальной оперативной характеристикой (рис. 7.1.3, а), которая
равна 1 для значений q<qKV и равна нулю при q>qKV. Однако
таких планов выборочного контроля с относительным объемом
выборки v = -^<l нет среди планов типа однократной выборки.
Нет их и среди других типов планов. Оперативная характеристика
каждого плана контроля является монотонно убывающей функ-
функцией. Примерный вид оперативной характеристики показан на
том же рис. 7.1.3, а. Для наглядности оперативные характери-
характеристики всюду ниже показаны в виде сплошных линий, хотя на
D
самом деле имеют смысл только их значения в точках q = jr.
Не всегда можно так категорично с помощью только одного
числа <7кр делить партии на плохие и хорошие. Часто возникает
зона неопределенности, когда мы не можем точно сказать, плохи
эти партии или нет. В таких случаях партии считаются заведомо
хорошими при q<qx и заведомо плохими при q>q2> </2>tfi*
Поскольку оперативная характеристика плана выборочного конт-
контроля является монотонно убывающей функцией и поскольку неиз-
неизбежны ошибочные решения о приемке и браковке, желательно,
чтобы вероятности ложных решений были невелики. Пусть я (q) —
оперативная характеристика плана. К плану предъявляются требо-
требования, состоящие в том, чтобы я (q) ^ 1—а при q<Cqi и
я {q2) <1 Р при q>q2. Вероятность 1—л;^), т. е. вероятность
браковки заведомо хорошей партии, носит название ошибки пер-
первого рода или риска поставщика, доля qx называется приемле-
приемлемым качеством. Вероятность ложной приемки плохой партии,
равная я (q2), называется риском потребителя, а доля q2 назы-
называется предельным допустимым качеством в том смысле, что
при <71<#<<?2 партии считаются еще допустимыми. Итак, требо-
требования к плану могут состоять в том, чтобы вероятности ошибок—
риски производителя и поставщика — были соответственно не
больше аир (рис. 7.1.3, б).
Обычно в таблицах используются только некоторые наборы значе-
значений а, р, например 0,1; 0,05; 0,01. Если используется план выбороч-
выборочного контроля, у которого риски а = 0,01; Р = 0,05 при значениях
^ — 0,01 и #2 = 0,05, то это означает, что в среднем из каждых
100 партий, имеющих засоренность не выше 1%, будет забрако-
забраковано не более одной партии, а из 100 партий, содержащих более
5% дефектных изделий, будет принято в среднем не более пяти
партий. Выбор пары чисел q2y P осуществляется с учетом требо-
требований потребителя. Выбор qx и а производится таким образом,
чтобы гарантировать от напрасного бракования хорошие партии.
§ 7.11
ВВОДНЫЕ ПОНЯТИЯ
387
Очень часто значение qx берут немного больше среднего значения
доли засоренности при нормальном ходе производства, чем и
гарантируют, что почти все партии, выпущенные при соблюдении
основных требований к технологии, будут приняты. Будем обо-
обозначать через qa такую долю засоренности партии дефектными
изделиями, при которой вероятность ее приемки равна а, т. е.
О 1
7-8
'd(n)
Рис. 7.1.4.
n(qa) = a. qt называется безразличным качеством при исполь-
зовании плана с оперативной характеристикой я(q). Если план
контроля уже выбран и доля засоренности совпадает с безразлич-
безразличным качеством, то в среднем половина таких партий будет забра-
забракована, а другая половина будет принята.
Например, для планов типа однократной выборки надо задать
объем выборки п и значение приемочного числа с. Для примера,
рассмотрим случай выбора значения приемочного числа с на
основе данных, приведенных на рис. 7.1.2, когда уже решено
отбирать на контроль по п =100 изделий от каждой партии
объема N=1000. Предположим, что результаты сплошной про-
проверки были скрыты от контролеров и все дефектные изделия были
оставлены во всех 108 партиях. Результаты выборочного контроля
оказались следующими: в выборках из 75 партий дефектных эле-
элементов не оказалось, в 24 было найдено по 1 дефектному изде-
изделию, в 4—по 2, в 2 выборках —по 4, встретилась одна выборка,
388
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
содержащая 6 дефектных элементов и две — по 8 дефектных эле-
элементов (рис. 7.1.4). При сопоставлении результатов сплошной
выборочной проверки оказалось, что все 75 партий, в которых
число обнаруженных дефектных изделий d(n) = 0, выпущены при
нормальном ходе производства, из 24 партий с d (п) = 1 23 выпу-
выпущены при нормальном ходе производства, из 4 с d(n) = 2 только
две выпущены при нормальном ходе производства.
Из этого видно, что полагать с = 0 невыгодно, так как 23
партии, выпущенные при нормальном ходе производства и содер-
содержащие сравнительно небольшое число дефектных изделий, будут
забракованы. На сравнительной таблице 7.1.1 показана вероят-
вероятность бракования партии объема N=1000, содержащей D негод-
негодных изделий по выборке объема /2= 100, когда с = 0, 1, 2, 3. Расчет
был проведен с использованием гипергеометрического распределе-
распределения по формулам § 7.2. Из расчетов видно, что прис = 0 вероят-
вероятности ошибок первого и второго рода соответственно равны 0,41 и
0,04; при с =1—0,08 и 0,18; с = 2 —0,01 и 0,42; с = 3 — 0,002 и 0,66.
Таблица 7.1.1
ю
20
30
50
100
0,271244 0,410168 0,653072 0,880975 0,959003 0,995516 0,999974
0,027788 0,082284
0,263705 0,610773 0,817792 0,969173 0,999648
0,000978 0,009702 0,069238 0,322752 0,585332 0,894179 0,997651
0,00000
0,001773 0,011980 0,130887 0,341777
0,471999 0,989713
Здесь считается хорошей партией та, в которой D ^ 5, а плохой
D^30. Наиболее подходящим значением приемочного числа с
является с=1. Проводить такие вычисления каждый раз заново,
учитывая изменение N и /z, является весьма трудоемким делом.
Поэтому разрабатываются определенные системы отбора планов
приемочного контроля из большого набора таких планов.
В настоящее время издан ряд книг, содержащих таблицы планов,
пользуясь которыми можно организовать приемочный контроль
(см. [4] — [7]). Обзор ряда стандартов планов выборочного конт-
контроля дан в § 7.3. Однако проблема не является исчерпанной
и в настоящее время. Трудность разработки методики выбора
§ 7.1] вводные понятия 389
наиболее приемлемых планов контроля заключается главным обра-
образом не в математической стороне дела, а в удачном учете всех
факторов производства, предопределяющих этот выбор. Сущест-
Существуют различные численные показатели эффективности использова-
использования каждого плана. Примерами могут служить ошибки первого и
второго рода. Систематически различные показатели будут опре-
определены в следующем параграфе. Для правильного выбора плана
приемочного контроля в ряде случаев решающую роль могут
играть экономические соображения. Один из возможных вариантов
организации приемочного контроля исходя из стоимостных пока-
показателей рассмотрен в § 7.4.
Возможные нарушения правил контроля. В § 7.5
даны методы оценки качества продукции исходя из результатов
контроля. Приводятся несмещенные, т. е. в среднем точные, оценки
качества предъявленной и принятой продукции. Основная задача
состоит в следующем. Пусть на контроль поступают партии
объема Л/;, содержащие D; дефектных изделий. После проведения
контроля принимается Л//пр изделий из каждой партии, из кото-
которых Dinv оказываются дефектными. Зная результаты контроля,
требуется оценить, какова была доля дефектных изделий в предъ-
предъявленной продукции (входное качество) и какова доля,
дефектных изделий в принятой продукции (выходное каче-
качество). При использовании методик вычисления несмещенных оце-
оценок для входного и выходного качеств продукции особое внима-
внимание следует обратить на точное соблюдение правил проведения
приемочного контроля, исходя из которых выведены формулы для
оценок. Однако иногда имеют место разного рода нарушения.
Приведем два примера возможных нарушений.
Пример 1. Для проверки от каждой партии отбирается по
100 элементов вне зависимости от объема партии. Все отобранные
изделия проверяют; если число обнаруженных дефектных изделий
й?>2, то партия бракуется, если же d^2y то принимается. Общее
число обнаруженных дефектных изделий отмечается в журнале. На
основе зарегистрированных данных составляем столбики числа пар-
партий, имеющих одинаковое число d (n) обнаруженных дефектных
изделий. Полученные данные приведены на рис. 7.1.5, а. По заре-
зарегистрированным данным оказывается, что совсем не было партий,
выборки из которых содержат более трех дефектных изделий. Из
рис. 7.1.5, а мы видим, что число партий, содержащих ^ = 3
дефектных изделий, равно 35, a d = 0, d—\ и d = 2 — соответст-
соответственно 60, 45 и 33. Наиболее правдоподобное объяснение состоит
в том, что контроль проводился только до обнаружения первых
трех дефектных изделий. Контролеру, который не знает, как
влияет искажение плана контроля на оценку качества, казалось
напрасным проверять оставшуюся часть выборки, когда и так
390
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
ясно, что партия будет забракована. Если бы правила проверки
<5ыли точно соблюдены, то результаты контроля могли бы выгля-
выглядеть так, как это показано на рис. 7.1.5,6. Без особых вычисле-
вычислений видно, что искажение плана контроля привело к завышению
качества продукции.
3*567 д S ГО // J2 13d(n)
Рис. 7.1.5.
Пример 2. Графическое изображение данных в виде стол-
столбиков имеет вид рис. 7.1.6, а.
Обращает на себя внимание резкий спад числа партий, содер-
содержащих d = 3. Их всего только 10, тогда как имеется 60 партий,
выборка из которых содержит d = 2 дефектных изделий. В плане
контроля записано, что от каждой партии надо отбирать по 100
изделий и при обнаружении более двух дефектных изделий надо
тому же контролеру провести разбраковку оставшейся части пар-
партии. Таким образом, браковка партии означает резкое увеличение
объема работы контролера. Если продукция используется не на
очень ответственных участках производства (например, инструмент),
то контролер, обнаружив в выборке ровно три изделия, часто при-
принимает такую партию как годную, искусственно уменьшая себе объем
работы. Если таким образом было принято 15 партий, то при
§ 7.2]
ХАРАКТЕРИСТИКИ ПЛАНОВ КОНТРОЛЯ
391
полном соблюдении плана контроля эмпирический материал имел бы*
вид, показанный на рис. 7.1.6,6.
В приведенных примерах даны вымышленные цифры, однако*
существо примеров взято из реальной жизни. По-видимому, числа
подобных, быть может и более оригинальных, случаев можно
было бы продолжить.
9 dfn)
Цель этих примеров состоит в показе того, что даже простей-
простейший статистический анализ, подобный тому, какой нами исполь-
использован при составлении рис. 7.1.5 и 7.1.6, может иногда выявить
весьма существенные факты.
§ 7.2. Численные характеристики планов
приемочного контроля
Планы типа однократной выборки. Выше уже ука-
указывалось, что для правильной организации приемочного контроля
необходимо уметь оценивать эффективность использования различ-
различных планов с помощью численных критериев. Каждый план конт-
контроля определяется моментом, в который надо прекратить проверку,
а также указанием того, какое решение надо при этом принять .
392 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
Как правило (см. [7]), принимается одно из следующих трех
решений:
Dx — отвергнуть оставшуюся непроверенной часть партии без
контроля;
D2 —провести 100%-ную разбраковку оставшейся части партии;
D3 — принять оставшуюся часть партии без дальнейшего конт-
контроля.
В некоторых случаях возможны и другие решения, такие, как
снижение сортности, изъятие отдельных частей продукции для
последующей переработки и использования и т. д.
Планы типа однократной выборки характеризуются двумя
параметрами — объемом выборки п и приемочным числом с. Если
через d(n) обозначить число дефектных изделий в выборке, то
при d(n)^>c партия бракуется (т. е. принимается одно из двух
решений: Dx или D2), а при d(n)<C.c партия принимается (т. е.
принимается решение D3 или D2). Условимся планы типа одно-
однократной выборки обозначать через их параметры (л, с). При этом,
если браковка означает принятие решения Diy а приемка — Dp
такой план будем обозначать (п> с) {j.
Возможны следующие типы планов (я, сI2, (я, сI3, (#, сJ3.
Например, план A20; 1J3 означает, что из партии надо отобрать
случайным образом и затем проверить 120 элементов. Если
dA20) >1, то необходимо произвести сплошную разбраковку
оставшейся части партии. Если же я? A20)^ 1, то оставшуюся часть
партии следует принять без дальнейшего контроля. Планы типа
(я, сI2 используются в тех случаях, когда контроль н е р а з р у-
шительный, стоимость его велика и требования к качеству
высокие. Планы типа (я, сI3 применяются главным образом при
разрушительном контроле или в тех случаях, когда стоимость
контроля велика. Наконец, планы (л, сJ3 находят применение как
при разрушительном, так и при неразрушительном контроле,
когда представляет интерес получение дополнительной информа-
информации о качестве продукции. Без всяких расчетов видно, что сред-
среднее количество проверяемых изделий различно для каждого из
этих планов. Различными будут как засоренность дефектными
изделиями продукции, принятой по результатам контроля, так и
методы ее оценки, рассматриваемые в § 7.5. Если контроль не
является разрушительным, то выявленные дефектные изделия могут
заменяться годными. В этом случае объем принимаемой партии
остается неизменным. Факт замены дефектных изделий годными
будем отличать штрихом (п, с)', отсутствие замены — крестиком
(я, с)х. Разрушительность контроля — звездочкой (я, с)*.
Иногда могут оказаться полезными планы типа однократной
выборки с двойным уровнем контроля. Здесь задаются объем
выборки п и два критических числа: приемочное число с и бра-
§ 7.2] характеристики планов контроля 393"
ковочное число с'. Если число обнаруженных дефектных изделий
d(n)^c, то принимается решение D3> если c<^d(n)<,c\ прини-
принимается решение ?J, наконец, если d(n)^c\ принимается реше-
решение Dx. Такие планы могут оказываться экономически целесообраз-
целесообразными, если контроль неразрушительный, но дорогой, и сравни-
сравнительно часто встречаются партии, сильно засоренные дефектными
изделиями. Такие планы обозначаются тройкой чисел (л, с, с').
Изучим влияние засоренности партии дефектными 'изделиями
на вероятность принятия возможных решений и на общий объем
инспекции. Партию, предъявленную на контроль, можно характе-
характеризовать парой чисел: объемом партии N и числом содержащихся
в ней дефектных изделий Z), которое нам неизвестно. Пусть
используется план (я, c)tj. Число обнаруженных дефектных изде-
изделий d (n) является случайной величиной. Вероятности nd = P {d (n) =
= d}y d = 0(\)n можно подсчитать двумя способами.
В первом способе рассматриваем всевозможные размещения D
элементов по N местам, среди которых п мест означают выборку.
Общее число размещений элементов, различных только по призна-
признаку годности или дефектности, равно С,у. При этом d дефектных
изделий можно разместить С* различными способами среди п мест,
зафиксированных для выборки, a D — d не попавших в выборку
дефектных изделий можно разместить C^Zdn способами по N—n
местам. Общее число благоприятных для события {d(n) = d} исхо-
исходов равно CnC^Zn. Таким образом, мы получаем
Во втором способе мы рассматриваем всевозможные различные
выборки по п элементов из N элементов. Общее число их равна
С%. При этом число выборок из D дефектных элементов по d
элементов равно Со, а число выборок по n — d годных элементов
из N—D годных элементов C^ZdD. Общее число благоприятных
случаев равно Со C^IJd, откуда имеем
Cd
п
. n — d
Говорят, что случайная величина d(n), принимающая целочислен-
целочисленные значения 0A) п с вероятностями ndi задаваемыми формулами
G.2.1), G.2.2), имеет гипергеометрическое распределение. Можна
показать, что среднее значение доли дефектных элементов в
выборке и дисперсия вычисляются по формулам
^ Dy_\ N-nDJN-D)
394 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
Действительно, число всех возможных выборок по п элементов
из N элементов с учетом их порядка равно A = M(N—1) ...
... (N — n-{~\). Число случаев, в которых фиксированное изделие
•будет проверено /-м, равно A = (N—1)(A/"—2) ... (N—/z+1),
число же случаев, в которых оно окажется дефектным, равно
B — D(N—\)(N—2) . .. (N—я+1). Таким образом, вероятность
того, что /-е извлечение для проверки изделия окажется дефект-
В D
лым, равна-д=дт» Так как d (n) = ?>1+ ... +?„, где ?,. = 1, когда
i-e изделие дефектной P(^.= l)==— j, и ?/ = () в противном случае,
fd(ri\\ n D
то М f ——¦ )=п~1 МB i,) = P (S|-= 1) = -тг. Следовательно, доля
V п J ffI **
дефектных изделий, обнаруженных в выборке, является несме-
несмещенной оценкой для доли дефектных изделий в партии. Аналогич-
Аналогичным образом можно доказать и вторую формулу G.2.3). Для того
чтобы подчеркнуть зависимость этого распределения от трех
параметров Д^, D, /г, будем вероятности nd гипергеометрического
распределения всюду обозначать символом Bj}o. Для плана (nt c){j
вероятность IItf принятия решения j равна
G.2.4)
Соответственно вероятность браковки партии с решением / равна
l-Uc(D).
UC(D) как функция от засоренности D дефектными изделиями
называется оперативной характеристикой. Это один из наиболее
полных функциональных показателей действия плана. Вид опера-
оперативной характеристики для плана E0,3) и N= 100 показан на рис.
7.2.1, а. Из рисунка видно, что вероятность принятия партии
резко убывает с ростом засоренности. Уже при D=10 П3 = 0,18,
г при D=15 П3<0,02. Второй важной характеристикой контроля
является зависимость математического ожидания общего объема
проверки от величины D. При использовании плана (/г, сI2
оставшиеся непроверенными N—n изделий проверяются, если
d(n)^c. Таким образом, средний общий объем инспекции M12(D)
задается по формуле
= n+(N-n)Ile(D). G.2.5)
Аналогичным образом для плана (л, сI8
M13(D) = n, G.2.6)
а для плана (я, сJ3—
G.2.7)
§ 7.2]
ХАРАКТЕРИСТИКИ ПЛАНОВ КОНТРОЛЯ
395
На рисунке 7.2.1, б показаны графики M^iD) для планов E0, 3),-, и
объема партии Л/=Ю0.
Биномиальное и п у а ее о н о вс к о е приближения.
Ввиду наличия трех независимых параметров Л/', D, п гипергео-
гипергеометрическое распределение весьма трудно табулировать.
Поэтому представляет большой практический интерес получе-
получение различных приближений, содержащих известные распределения
с меньшим числом параметров. Здесь мы ограничимся лишь
0 Ю 20 30 40 50 60 70 SO
несколькими примерами биномиального и пуассоновского при-
приближений. Заметим, что формулы G.2.1) G.2.2) можно записать в.
виде
n-d+l
где <7 = тг —доля дефектных изделий в партии, a v = ^- —отно-
—относительный объем выборки. Из формулы G.2.8) получаем, что
BnNdDttCdnqd{\-q)n-d, G.2.10)
если только n<^m\n(N}N—D) и d<^D. В этих условиях факти-
фактически предполагается, что N^> 1 и ?)^>1.
Из формулы G.2.9) находим, что
BnNdDttC?vd(\-v)D~d, G.2.11)
396
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
если только D<^min (NyN — h),d<^n. В этих условиях фактически
предполагается, что iV^>l ил^>1, Таким образом, гипергеомет-
гипергеометрическое распределение может быть приближено биномиальными
распределениями, которые уже определяются только заданием двух
параметров: q и п в первом случае и v и D — во втором. Длякрат-
кости записи будем называть эти распределения ^-биномиальным и
v-биномиальным. Условия, при которых хорошей аппроксимацией
является ^-биномиальное распределение, состоят в том, чтобы от-
относительный объем выборки был невелик, а засоренность дефект-
дефектными изделиями была больше относительного объема выборки;
v-биномиальное распределение дает хорошие результаты, когда от-
относительный объем выборки больше доли засоренности q.
Если #^>>1, d<^n, q<^\, v<^l, то можно использовать пуас-
^оновское приближение
где К = nq = Dv— среднее число дефектных изделий, попавших в
Таблица 7.2.1
•ft:
0
1
2
3
4
5
6
7
# =
Б#о
0,584
0,339
0,070
0,006
0,000
0,000
0,000
0,000
100. /
bkn inq)
0,599
0,315
0,075
0,010
0,001
0,000
0,000
0,000
1=10; q
Nq \~n~ )
0,590
0,328
0,073
0,008
0,001
0,000
0,000
0,000
= 0,
'
0
0
0
0
0
0
0
0
05
,607
,303
,076
,013
,002
,000
,000
,000
E
o,
0,
o,
o,
o,
0,
o,
0,
#=
Jlk
;ND
095
268
318
209
084
022
004
000
100;
b\ (nq)
0,122
0,270
0,285
0,190
0,090
0,034
0,009
0,000
n=10; q
0,107
0,268
0,302
0,201
0,088
0,026
0,006
0,001
= 0,
lk
0,
0,
o,
0,
o,
0,
0,
o,
2
(nq)
135
271
271
180
090
036
012
03
§ 7.2] ХАРАКТЕРИСТИКИ ПЛАНОВ КОНТРОЛЯ 397
выборку. Таблица 7.2.1 содержит сравнительные данные для точ-
точных значений вероятностей В*}?о и рассмотренных выше различных
приближений (ср. [6], стр. 445).
Условимся использовать обозначения
G.2.13)
=2 bi(a), М*) = 2
d 0 d
Из формул G.2.10), G.2.11), G.2.12) получаем, что оперативная
характеристика приближенно может вычисляться по формулам
Пс {D)^Bcn{q)> П, (D)^flb(v), Пс (D)*zLe (X). G.2.14)
В тех случаях, когда могут быть использованы указанные
выше распределения и объем выборки #>30, целесообразно вместо
дискретного параметра п ввести непрерывный параметр t = —,
п0
где п0 — число изделий, в которых при нормальном ходе произ-
производства встречается в среднем одно дефектное изделие. Зная ty
мы можем найти значение п из равенства n = tn0. Полученные
дробные числа будем округлять до ближайшего целого числа.
Например, если /го = 5О, а ^ = 2,331, то п =116,55, или, округляя,
считаем окончательно п = 117. Ошибки от такого округления будут
невелики и ими можно пренебречь, учитывая, что уже имеются не-
некоторые ошибки от использования биномиального или пуассонов-
ского приближений. Пусть случайным образом отобранные изделия
проверяются последовательно одно за другим, п{ — номер испыта-
испытания, при котором проверяемое изделие оказалось дефектным. По-
ложим ^o = M ~п Ь */= t тогда имеет место
Теорема 7.2.1. Если -^—>(), N—юо, D—>оо, то после-
последовательность «моментов времени» th /=1, 2, 3,..., образует
пуассоновский поток с интенсивностью X.
Доказательство этой теоремы можно получить, показав,
исходя из точной комбинаторной формулы, что в пределе конеч-
конечномерные распределения моментов t{ совпадают с распределения-
распределениями пуассоновского потока. Однако ввиду громоздкости записи фор-
формул мы опускаем это доказательство.
Таким образом, объем выборки можно рассматривать как вре-
временной параметр, а выявление дефектных изделий — как появление
событий случайного потока. С этой точки зрения появление
пуассоновского распределения G.2.12) объясняется тем, что мы
398 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
наблюдаем события пуассоновского потока (выявление дефектных из-
изделий) в течение фиксированного «времени» X = — ==nqy no = q~r.
Полезно также отметить, что пуассоновское приближение ос-
остается справедливым и при сколь угодно больших относительных
объемах выборки v, если априорное распределение числа дефект-
дефектных изделий является биномиальным и при этом значение пара-
параметра qQ достаточно мало (до<О,\).
Как уже отмечалось выше (см. § 7.1), при нормальном ходе
производства число D дефектных изделий в партии объема N
можно считать случайной величиной с функцией распределения
FR(D). Если при этом каждое изделие независимо от других и с
одной и той же вероятностью qQ может оказаться дефектным, то
Fn(D) = B%(qQ).
Теорема 7.2.2. Если априорное распределение для числа
дефектных изделий D является биномиальным с функцией рас-
распределения Fe(D) = Bn (qo)j то распределение числа дефектных
изделий d(n), обнаруженных в выборке объема п, также являет-
является биномиальным с функцией распределения B^(q0).
Доказательство основано на тождестве
Batd bDN (q0) = hi (q0) b%Zdn (q0), G.2.15)
в справедливости которого можно легко убедиться непосредствен-
непосредственной проверкой. В силу этого тождества имеем
N
D = 0
5 bN (°o) =
ud
(?o)
N
D = o
o).
что и завершает доказательство.
В ряде случаев априорное распределение не является биноми-
биномиальным, однако его можно приблизить суперпозицией биномиаль-
биномиальных распределений. Иначе говоря, приближение осуществляется с
1
помощью распределения FE (D) = Jfi^(^0)rfOH (#0), где GH (#0)—функ-
0
ция распределения Он (— 0) = 0, GHA)=1. Таким образом, апри-
априорное распределение приближается биномиальным распределением
со случайным значением параметра q0. Мы ограничимся при рас-
расчетах в следующем параграфе только случаем чисто биномиаль-
биномиального распределения, при котором Gn(q) = 0, если q<iqOy Ga (q) = 1,
если q>q0, 0<^0<^ Можно ожидать, что Gn(q) будет иметь
два скачка, если на контроль поступают в случайном порядке
§ 7.2]
ХАРАКТЕРИСТИКИ ПЛАНОВ КОНТРОЛЯ
399
партии, изготовленные различными бригадами, и если при этом
для каждой бригады характерно свое значение доли q дефектных
изделий.
Планы типа двукратной выборки. В тех случаях,
когда особенно остро стоит вопрос о сокращении объема испыта-
испытаний, могут быть использованы планы типа двукратной выборки
или последовательного анализа (см. § 7.1*). Рассмотрим сначала
усеченные планы типа дву-
двукратной выборки. При ис-
использовании этих планов у
сначала отбирают пг изде- 6
лий, если d{n^) <: с1? то 5,
принимается решение Dnpl 3
(обычно DnPl — D3 или D2)y j
если d(nx) >c2 >cx, то
партия бракуется с приня- °
тием решения D6pt (?>6Pl =
= ?>! или D2); если же
ci < d(n±) ^ с2, то берется
дополнительная выборка
объема п2. Если d (#х +
+п2)^с2, то партия при-
принимается с решением DnPt
(DnPt = D2 или D3), а если
d (#i + п2) > сгч т0 партия
бракуется с решением Dcp2
фбр2 = О1 или D2). На
рис. 7.2.2, а дано схе-
схематическое изображение усеченного плана типа двукратной
выборки. Здесь / = — пропорционально объему проверенной про-
п0
дукции, например i* + t2 = l n*'« Крестиками обозначены точки,
п0
в которых принимаются те или иные решения, а ломаной линией
d(t) — число обнаруженных дефектных изделий к «моменту» ? = — •
п0
Каждой из граничных точек обязательно приписано одно решение,
которое и принимается, если траектория d(t) достигает этой гра-
граничной точки. Итак, усеченный план типа двукратной выборки
характеризуется набором четырех параметров п1у я2, сх, с2 и рас-
расстановкой решений по четырем граничным участкам. Будем такие
планы обозначать набором (пг; п2; сг; с2) ,6pi, /npi, ^бра, /пра, где
inpx = i, если Dnpt = D/, и т. д. Например, план B0, 20, 0,1I312
означает, что при dB0) = 0 оставшаяся непроверенной часть
400 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
партии принимается без контроля, при dB0)^2 оставшаяся часть
партии бракуется без проверки. В том случае, когда в первой
выборке обнаружено только одно дефектное изделие, берется по-
повторная выборка в 20 изделий. Если теперь не обнаружено новых
дефектных изделий, то партия принимается с последующей раз-
разбраковкой, если же я?D0)>1, то партия бракуется без дальней-
дальнейшей проверки. Аналогичным указанному выше образом могут быть
использованы знаки ( )' и ( )*.
Используя формулу полных вероятностей, легко выписать
формулы для вероятностей принятия тех или иных решений. Здесь
мы имеем
,.d d I ]~) \ ^t^ r\ti*d 11 о 1 а\
г?>> ' X^Gpi} — 2j Bm?>) \l .ZAO)
d=c2+l
BnNi^nBnddJni,D.dl, G.2.17)
..-..-1 + i^-»-D-"«- G>2Л8)
Очень часто Dnpi = Dnp2 = Dh DePl = D6p2 = Dj, т. е. партия при-
принимается и бракуется только с одним решением. В таких случаях
важным показателем плана является оперативная характеристика
П (D), показывающая зависимость вероятности приемки партии от
числа дефектных изделий. Из G.2.16), G.2.17) находим, что
ri t B№B%dJnuD.d, G.2.19)
d1=cl+\ «2 = 0 х l
Аналогичным образом получаем, что средний объем инспекции
для плана (nlt с1э /22, с2I313 равен
М1313 {D) = n1 + nJl- J]o BnN^\ G.2.20)
Для плана {пъ сх, п2, с2I212 получаем
D
dx=cx + \
В№+ 2 В№*21 BUdJnuD-d\ G.2.21)
Аналогичные формулы можно выписать и для других усеченных
планов типа двукратной выборки.
§ 7.2] ХАРАКТЕРИСТИКИ ПЛАНОВ КОНТРОЛЯ 401
Если выполнены условия теоремы 7.2.1, то можно воспользо-
воспользоваться пуассоновским приближением. При этом формула G.2.19)
для оперативной характеристики принимает вид
G-2.22)
где Lc(x) определяется из G.2.13).
Планы последовательного анализа. Более общий
класс планов приемочного контроля последовательного типа можно
получить, если после каждого проверенного изделия либо при-
принимается решение о продолжении проверки еще одного изделия,
либо контроль прекращается и принимается одно из возможных
решений, например Dz-, *=1, 2, 3. Если предположить, что любое
решение принимается только с учетом данных о количестве про-
проверенных изделий п и количестве обнаруженных дефектных изде-
изделий d(n)y то такой класс правил можно представлять в виде
блуждания по точкам целочисленной решетки (л, d). Пребывание
в точке (/г, d) означает, что проверено п изделий, из которых
d было дефектных. Точки (л, d)y в которых принимаются реше-
решения, назовем граничными. На рис. 7.2.2, б, в показаны примеры
таких планов. Граничные точки обозначены крестиками. Легко
заметить, что все рассмотренные ранее планы контроля типа
однократной и двукратной выборки являются частными случаями
планов последовательного типа. Как правило, для планов последо-
последовательного типа не существует простых явных формул для веро-
вероятности принятия в итоге проведения контроля того или иного
решения, а также формул для среднего объема инспекции. Однако
можно дать очень простую методику, по которой с помощью
приводимых ниже простых рекуррентных соотношений можно найти
численные значения указанных характеристик. Пусть Г,- — множе-
множество граничных точек (я, d), в которых принимается одно и то
же решение Д-. Тогда вероятность принятия решения Di означает,
что в процессе проведения контроля первой граничной точкой
окажется (я, fl?)?l\-. Обозначим через Рг. (я, d) вероятность то-
того, что впервые достигнутая граничная точка принадлежит мно-
множеству Г,. В тех случаях, когда (я, d) является граничной и
(я, d) ? Г,-, мы имеем
Рг, (л, d) = l. G.2.23)
Если же (я, d) граничная, но (л, d)^Th то
Рг<(л, d) = 0. G.2.24)
Эти граничные условия являются отражением того факта, что
после достижения граничной точки контроль прекращается.
14 Б. В. Гнеденко и др.
402 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
В частности, условие G.2.24) означает, что если в итоге проведения
контроля мы достигли граничной точки (п, d) ? Г,-, то испытания
прекращаются, и мы уже не можем попасть в точку (п, d) ? Г,-. За-
Заметим теперь, что если проверяется партия объема N, содержа-
содержащая D дефектных изделий, то пребывание в точке (л, d) означа-
означает, что еще не проверены N—п изделий, среди которых D— d
дефектных. Из этого следует, что при случайном выборе (/г+1)-го
7V— л—D + d
изделия с вероятностью ^ !— оно окажется годным, а с
вероятностью -^ дефектным. В первом случае из точки (п, d)
переходим в точку (п-\-\, d), во втором — в точку (/z+1, d+\).
Пусть вероятности Pri(/z+^> d) подсчитаны для всех возможных
значений (я+1, d)\ тогда для каждой возможной точки (я, d)
имеем
G.2.25)
Последовательно уменьшая значения /z, мы придем к точке @, 0).
Ргч @, 0) и является интересующей нас вероятностью Р (Д) при-
принятия решения D;. Итак, доказана
Теорема 7.2.3. Вероятность Р (Д) = РГгпринятия решения Dt
определяется граничными условиями, условиями G.2.23), G.2.24)
и рекуррентными соотношениями G.2.25).
Если при окончании контроля принимается только два реше-
решения: Dt при браковке (/=1, 2) и Dy- при приемке партии (у = 2, 3),
то оперативная характеристика является функциональным выраже-
выражением зависимости вероятности приемки партии Р (Dy) от числа D
содержащихся в ней дефектных изделий.
Аналогичным образом может быть доказана
Теорема 7.2.4. Средний объем инспекции т = т@, 0) при
использовании последовательного плана контроля партии объема Ny
содержащей D дефектных изделий, определяется из граничных
условий
m(nyd) = 0 G.2.26)
{когда (л, d) — граничная) и рекуррентных соотношений
m (л, d) = 1 + ^Е~т (п+ 1, rf+ 1) + N~nNZDn^dm (n + *. <*). G.2.27)
Примечание. Если необходимо подсчитать общий объем ин-
инспекции, то условие G.2.26) заменяется условием
,у\_/^—я, если принимается решение D2,
туп, ) — | q если Принимается ОдНо из решений Dx или D3.
§ 7.2]
ХАРАКТЕРИСТИКИ ПЛАНОВ КОНТРОЛЯ
403
Вычисления по рекуррентным формулам просты. Однако составле-
составление исчерпывающих таблиц даже для конкретных классов планов
последовательного типа ввиду большого количества параметров
является весьма трудоемкой работой. Поэтому обычно используют
2,0
1,5
1,0
0,5
d
9
8
7
6
5
3
2
1
0 n 2пЗп4п5п6п 7п8п9п
а)
О / 2 3 4 5 6 7п 8п 9п
б)
Рис. 7.2.3.
D —d
различные приближения. Например, считают, что д^Г~~ ^cons*
и т. д.
На рис. 7.2.3,6 сплошной линией показаны значения оператив-
оперативной характеристики П (&), а пунктирной линией — значения объема
инспекции |ы (k) для плана последовательного типа, показанного
на рис. 7.2.3, а. План контроля осуществляется путем последова-
последовательной инспекции выборок равного объема п. Партия бракуется
без дальнейшего контроля, если d (п) ^ 2, если же d (n) < 2, то
берется вторая выборка того же объема п. Партия принимается без
дальнейшего контроля, если d (п) ^ 2, если же d (n) < 2, то берется
вторая выборка того же объема п. Партия принимается без даль-
дальнейшего контроля, если dB/z) = 0, бракуется, если dBK
14*
404 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
берется случайная выборка объема п, если dBn) = \ или 2 и т. д.
в соответствии с рис. 7.2.3, а. При расчетах было использовано
пуассоновское приближение; k = nqy т. е. равно среднему числу
дефектных изделий, обнаруживаемых в выборке. Объем инспекции
[I (k) на рис. 7.2.3,6 дан в относительных единицах, кратных п.
Так, при п = 20 и k=\ (i(l) = 2,91, что эквивалентно среднему
объему инспекции 2,91x20^58 изделий.
§ 7.3. Стандарты планов приемочного контроля
Общие положения. Пример. Рассмотрим требования,
предъявляемые к стандартам, определяющим способ использования
выборочного контроля на практике. Прежде всего стандарт планов
выборочного контроля должен быть достаточно простым, чтобы
им мог пользоваться персонал предприятий, не имеющий специаль-
специальной математической подготовки. Стандарт должен содержать сра-
сравнительно большое количество планов, имеющих различные опера-
оперативные характеристики. Это позволит гибко изменять планы кон-
контроля в соответствии с изменениями качества продукции и требо-
требований потребителя. Помимо указания конкретного плана стандарта,
должны быть приведены различные характеристики используемого
плана. Например, желательно иметь графики оперативных характе-
характеристик и объемы инспекции, как функции от доли засоренности
партии. Наконец, желательно, чтобы в стандарте были указаны
планы различных типов: планы типа однократной, двукратной вы-
выборок и планы последовательного типа. Использование стандарта
должно предусматривать те или иные гарантии производи-
производителю от ложного бракования хороших партий и потребителю от
пропуска плохих партий. Таким образом, использование стандарта
должно, как минимум, оказывать давление на производителя в
сторону улучшения качества. Подобное давление может быть уч-
учтено с помощью введения более жесткого контроля в тех
случаях, когда проведенные оценки качества показали с боль-
большой степенью достоверности недопустимое его ухудшение. На-
Наоборот, в тех случаях, когда качество весьма высокое, можно
использовать планы облегченного контроля.
В настоящее время имеется ряд публикаций, посвященных из-
изложению различных стандартов (см. [4] — [8]). Кроме того, в ряде
учебников и монографий по математической статистике также
имеются главы и таблицы планов приемочного контроля. Здесь мы
отметим книги Коудена [6] и Шора [9]. Ниже дается краткий
обзор ряда широко используемых стандартов приемочного контроля.
В частности, изложение Колумбийского стандарта дополнено
соответствующими таблицами. Такие таблицы были включены в
книгу в связи с тем, что материалы, относящиеся к Колумбийскому
§ 7.3]
СТАНДАРТЫ ПЛАНОВ ПРИЕМОЧНОГО КОНТРОЛЯ
405
0,05
0,03
0,02
0,01
стандарту, ранее в отечественной литературе не публиковались.
В последнее время в США широкое применение нашел так на-
называемый Mil St 105 (А,В). Мы опускаем описание этого стандарта,
так как такое описание читатель может найти в книге Коудена [6].
В Англии был принят к использованию стандарт DEF-131. Его опи-
описание, а также полезные критические замечания к другим стан-
стандартам приведены в английском статистическом журнале (см. [8]).
Рассмотрим один из простейших примеров построения стандар-
стандартов планов приемочного контроля. Будем предполагать, что КО
не является разрушительной и что все выявленные дефектные из-
изделия заменяются полными годными изделиями. Для простоты
ограничимся случаем планов типа однократной выборки (/z, с]чъ*
Предполагаем также, что в
вычислениях гипергеометри-
гипергеометрическое распределение может
быть заменено пуассоновским.
Допустим теперь, что потре-
потребитель готовой продукции
настаивает на введении такого
контроля, при котором значе-
значение доли дефектных изделий
в принятой продукции в сред-
среднем не превышает некоторой
заданной величины. В этом
случае числовой характерис-
характеристикой, показывающей, на-
насколько эффективным является приемочный контроль, будет так
называемое предельное выходное качество #м. Эта характеристика
определяется следующим образом. Если на КП поступила партия
объема А/", содержащая D дефектных изделий, то DBUX — число
дефектных изделий в принятой потребителем продукции — опреде-
определяется соотношениями Ьвых = 0, если партия забракована с реше-
решением D2, DBUX~D — d, если партия принята с решением D3. Здесь
d — число дефектных изделий, обнаруженных в выборке. Среднее
значение для доли засоренности qBUX (Я) — М ( хг™ ) в принятой про-
продукции является функцией от засоренности q продукции, посту-
поступающей на контроль. Для планов типа однократной выборки (/г, с)
-^)<О- G-3.1)
Вид графика qBhlx для плана A00,1J3 и N=10000 показан
на рис. 7.3.1. Из рисунка видно, что qBblx<Cq и достигает в не-
некоторой точке <7п своего максимального значения qhr В общем
О 0,010,02 №0,04 0,050,06 0,07 0,08 0,09 0,10 q
Рис. 7.3.1.
406 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
случае qu = max #вых (q) называется предельным выходным ка-
чеством для используемого плана. Для случая пуассоновского
приближения при использовании плана типа (/z, сJ3 из G.3.1)
и G.2.4) получаем
±pc1 G.3.2)
п
где pc = maxLc(x). Таблица значений р^ для с = 0 A) 20 дана в
>о
приложении. Если, например, используется план выборочного кон-
контроля, для которого предельное выходное качество равно #м —3%,
то это означает, что в среднем засоренность принятой продукции
будет не более 3%. Итак, независимо от доли брака в предъяв-
предъявляемых партиях показатель qu может быть использован потреби-
потребителем в качестве требования, накладываемого на используемые
планы. Напоминаем, что эта характеристика пригодна только для
планов, в которых единственными возможными решениями являют-
являются D2 и D3. Для гарантии .требований потребителя выберем пре-
предельное выходное качество #м равным предельно допустимой доле
брака в принятой продукции. Пусть qYl — средняя доля засоренности
дефектными изделиями при нормальном ходе производства. Если
N—объем партии, то Q = NqH — среднее число дефектных изделий
в партии при нормальном ходе производства. В таблицах будем
задавать относительное значение k= — . Так как контроль не
м Ян
является разрушительным, а браковка партии означает ее сплош-
сплошную проверку, то целесообразно отбирать такие планы (/г, сJ3,
для которых среднее значение объема полной инспекции, задава-
задаваемое формулой G.2.7), будет минимальным. Таким образом, при-
приоритет отдается потребителю, который, зная quy выбирает значение
<7М. Обычно &м> 1,5—2, так как в противном случае процент
проверяемой продукции становится соизмеримым с общим количе-
количеством продукции, предъявляемой на контроль. Если использовать
пуассоновское приближение G.2.12), то
[1 с
-Q^iiNq — d)
i
1 —
9 7 G.3.3)
Ян L e J пЯн
где 0 = NqB.
Таким образом, если значение приемочного числа с известно,
то объем выборки п, исходя из G.3.3), можно найти по формуле
G.3.4)
§ 7.3] СТАНДАРТЫ ПЛАНОВ ПРИЕМОЧНОГО КОНТРОЛЯ 407
Чтобы отобрать план, обеспечивающий заданное значение &м
и имеющий минимальное значение для среднего объема инспекции,
надо среди всех планов типа (п, сJ3, где п находится из G.3.4),
отобрать тот, для которого является минимальным
В таблице 24 приложения для значений &м = 1,25 @,25) 3,0 @,5)
6AI0, 12, 15 приведены критические значения параметра вс.
Если 9^60 при заданном значении &м, то приемочное число на-
надо полагать равным нулю, если же fy-i^O^Gj, то надо пола-
полагать с = /.
Рассмотрим пример. Пусть потребитель, зная, что qu = 0,01,
выбрал значение ^м = 0,02. На контроль подается партия объема
ДГ=750. Из колонки k = 2 таблицы 24 приложения находим, что
6Х = 6,723, 02=17,854. В нашем примере 6 = AtyH = 750.0,01 =7,5,
0Х<<6<С92> следовательно, с = 2. Из таблицы 23 приложения нахо-
находим р2=1,37, откуда по формуле G.3.4) находим объем выборки
п = 62,77, или, округлив до ближайшего целого числа, окончатель-
окончательно находим, что наиболее экономным является использование
плана B35,2)'23 •
Ташкентский проект стандарта. В заключение это-
этого параграфа мы дадим краткий обзор существующих стандартов.
Обзор начинаем с выпущенного недавно в г. Ташкенте проекта
стандарта планов контроля по качественному признаку. В пред-
предварительном издании стандарт состоит из пяти выпусков, в кото-
которых даны общие положения о статистическом контроле, приведе-
приведены формулы для вычисления различных показателей планов типа
(/г, с)/у., (/=1,2,3, а также формулы для оценки качества про-
продукции, принятой по результатам контроля. Планы приводятся
лишь для небольших значений приемочных чисел с — 0AL и срав-
сравнительно большого набора возможных объемов выборок /гг- = 12,
15 E) 30 A0) 60, 75 B5) 200 E0) 300 A00) 600, 750 B50) 1000. Кроме
того, для с = 0 даны значения п- = 5 (\) \0. Для каждого плана
{/г, с) возможные значения относительного объема выборки v = -^ =
= 0,5 @,1) 0,1; 0,05; 0. Значение v = 0 используется в тех случаях,
когда объем выборки п^ пренебрежимо мал по сравнению с объе-
объемом партии. В обширной таблице 2, помещенной в выпуске 2Б[7],
для каждого плана (nh с) приведены различные характеристики
(см. таблицу 7.3.1, на которой приведена часть таблицы 2). Здесь
L — вероятность приемки партии, содержащей долю q3 дефектных
изделий, д± — средняя доля дефектных изделий в принятой по-
потребителем партии при использовании плана (я, сJ3, q2 — средняя
доля дефектных изделий в принятой продукции при использовании
408
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
плана (/г, сI8. В таблице значения qt для удобства исполь-
использования умножены на 104. \лх равно отношению среднего объема
инспекции для планов (/г, сJ3 к среднему числу принятых изде-
изделий. Значения \1г даны умноженными на 103. Значения L являют-
являются входным параметром.
Таблица 7. 3. 1
L
0,999
0,998
0,995
0,950
0,925
0,900
...
...
17
17
19
35
41
47
13
14
15
28
32
36
17
17
19
37
44
51
Hi-103
201
202
204
240
260
280
...
...
В таблицах даны значения 1 = 0,999; 0,998; 0,995; 0,990; 0,975
@,025) 0,875; 0,95 @,05) 0,50; 0,125 @,025) 0,025, 0,010; 0,005;
0,002; 0,001. Значения предельного выходного качества дн можно
найти из столбца значений q3, полагая его равным max q3. Зада-
Задаваясь долями засоренности, соответствующими хорошему качеству и
предельно допустимому качеству, мы можем найти значения оши-
ошибок первого и второго рода. Например, если хорошее качество
соответствует засоренности ^3 = 0,35%, то из таблицы 7.3.1
находим, что вероятность приемки партии L = 0,95, соответственно
ошибка первого рода, равна 0,05. Ташкентский стандарт содержит
также таблицы планов типа (я, с), обеспечивающих заданную веро-
вероятность а приемки партий для определенного набора значений q0L
доли дефектных изделий. Таблицы даны для значений а = 0,95;
0,90; 0,50; 0,10; 0,05. При этом ?а = 0,125; 0,1; 0,09; 0,08 @,005)
0,04 @,0025) 0,01 @,001) 0,002. Для значения а = 0,1 даны также
уровни ^0}1 = 0,35 @,05) 0,15; 0,008, для ?о,о5 = о>4° @,05) 0,15,
для ?0M = 0,20; 0,15; 0,0015; 0,001 @,0002) 0,0002, для q0y9b и
^090='0,0015; 0,001 @,0002) 0,0002; 0,0001. Приводятся также
таблицы планов, обеспечивающих заданное значение предель-
предельного выходного качества qM. Набор уровней qH совпадает с набо-
набором #0,90* В таблице 7.3.2. даны части таблиц такого сорта.
Приведены также таблицы, в которых для каждого плана (/г,-, с)
дана сводка его показателей qa, qM для ~=0,5 @,1) 0,1, 0,05, 0.
§ 7.3]
СТАНДАРТЫ ПЛАНОВ ПРИЕМОЧНОГО КОНТРОЛЯ
409
Некоторые из формул для последующей оценки качества продук-
продукции по результатам контроля, взятые из ташкентских стандартов,
приводятся нами в § 7. 5. В выпусках даны указания по отбору
экономических планов контроля, однако в них подход отличен от
излагаемого нами в § 7.4.
Таблица 7. 3. 2
0,60%
0,50%
6,00%
5,50%
...
с = 0
N
1—599
600—799
^800
1—799
800—2185
^2186
п
...
все
300
400
все
400
500
с = 0
...
1—9
10—11
12—64
^65
1—11
12—23
^24
...
п
...
все
5
6
7
все
6
7
...
с—\
N
1 — 1199
1200—3000
^3001
1—1499
1500—7500
^7501
п
все
600
750
все
750
1000
N
...
1-23
24-39
^41
1—23
24—29
30—169
^170
...
п
все
12
15
все
12
15
20
...
...
...
...
...
...
Стандарты Доджа и Ромига. Широко известной моно-
монографией, посвященной вопросам приемочного контроля, является
книга Доджа и Ромига «Таблицы выборочного контроля — одно-
однократная и двукратная выборки». В книге дано описание принципов
410
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
выборочного контроля по качественному признаку. Дано описа-
описание методики, на основе которой были составлены таблицы.
Планы, представленные в книге Доджа и Ромига, разбиваются на
две группы. Одни обеспечивают заданные значения вероятности 0,1
для приемки партий, содержащих долю qOil дефектных изделий,
другие — заданное значение qu для предельного выходного качест-
качества. При этом в таблицах приведены планы, дающие минимум
среднего значения инспекции в условиях принятия решений D2, D3
для заданной средней засоренности продукции #ср дефектными
изделиями. Значительную часть книги занимают графики опера-
оперативных характеристик планов, указанных в таблицах. Приведем
последовательность действий, которые надо произвести при ис-
использовании планов Доджа и Ромига. A) Надо уяснить, какие
параметры изделий надо проверять и какие из проверенных изде-
изделий считать дефектными. B) Уточнить понятие партии и подсчи-
подсчитать ее объем N. C) Выбрать вид защиты от принятия партий,
содержащих большое количество дефектных изделий. В данном
случае делается выбор между двумя показателями q0>l или qM.
D) Решается вопрос о выборе между планами типа однократной
и двукратной выборок, при этом во внимание могут быть при-
приняты результаты пункта G). E) Проводится оценка qcp — средней
засоренности продукции дефектными изделиями. F) По таблицам
(примеры которых мы приводим ниже) находится соответствующий
план выборочного контроля. При этом план отыскивается с учетом
выбора значения qOil или qM и значений qzv и N. G) Отыскивается
чертеж со значением оперативной характеристики, в зависимости
от вида которой могут быть внесены изменения в выбор плана.
(8) Проводится контроль партии в соответствии с выбранным пла-
планом. (9) Результаты контроля регистрируются для последующего
пользования при оценке качества продукции.
В таблицах приведены только усеченные планы типа двукрат-
двукратной выборки (п1у п21 сг, с2J323. В таблице 7.3.3 приведены при-
примеры таблиц из книги Доджа и Ромига.
Таблица 7.3.3
N
201—300
301—400
401—500
501—600
...
0.41% «7ср% <0,80%
п
'85
90
90
125
с
т
1
1
2
4м %
0,71
0,72
0,77
0,87
...
§ 7.3]
СТАНДАРТЫ ПЛАНОВ ПРИЕМОЧНОГО КОНТРОЛЯ
Продолжение табл.
411
7.3.3
N
Ю01—2000
2001—3000
3001—4000
4001—5000
. . .
...
0
1-я выборка
пх
55
55
90
90
0
0
1
1
.51% <
2
п2
120
150
140
165
7ср%<1.00
-я выборка
ni + n2
205
230
255
Сг
"а
5
6
7
Ям
l',5
1,6
1,8
...
=3%
501—600
601—800
801—1000
1001—2000
...
1,21% <<7Ср% <1.80%
п
42
43
44
65
с
2
2
2
3
1*2,4
12,1
11,8
10,2
...
г) <7М ='
501—600
601—800
801—1000
1001—2000
...
...
1-я выборка
пх
26
26
27
49
0
0
0
1
1,21% <
По
54
54
58
76
Cqcp <1.80%
2-я выборка
п1 + п2
80
80
85
125
Сг
*4*
4
4
6
10,7
10,7
10,3
9,1
...
Приведем пример на использование планов Доджа и Ромига.
Пусть <7ср=0,65%, Л/=3563, предельное допустимое качество вы-
выбрано равным <7о,г = 5%, решено использовать планы типа дву-
двукратной усеченной выборки. Соответствующая часть таблицы пока-
показана на таблице 7.3.3, б. Из этой таблицы находим, что надо ис-
использовать план (90, 140, 1, 6). При этом предельное выходное
412
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
качество #м=1,6%. В книге отдельно даны графики оперативных
характеристик рекомендуемых планов контроля типа однократной
и двукратной выборок. На рис. 7.3.2 приведен пример графиков
оперативных характеристик. Ради экономии места мы на одном
графике, соответствующем планам со значением ^ср = 0,25%, при-
приводим кривые оперативных характеристик двух однократных и
одного двукратного плана. Отметим, что однократные планы, обе-
обеспечивающие заданное значе-
значение q4, найденные из табли-
таблицы 24 приложения, и формулы
G.3.4) практически совпадают
или очень близки к соответ-
соответствующим однократным пла-
планам Доджа и Ромига, зада-
задаваемым таблицами типа, ука-
указанного на таблице 7.3.3, в.
Колумбийский стан-
стандарт. Во время второй ми-
мировой войны в США проводи-
проводились работы по составлению
планов приемочного контроля.
В послевоенные годы стати-
статистическая исследовательская
группа колумбийского универ-
университета выпустила книгу [5]
«Выборочный контроль», в ко-
которой систематически излага-
излагаются идеи приемочного конт-
контроля. В этой книге дан боль-
1,0
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
№001-3000
п с
f)UO О
2K00 1
3)л,;п2; сг;сг
280;570; О;4
0,5 1,0
Рис. 7.3.2.
шой набор планов типа одно-
однократной, усеченной двукратной выборки, в которой п2=2п1, и типа
последовательного анализа, при котором последовательно проверяют-
проверяются выборки равного объема. Значительную часть книги занимают
таблицы троек планов указанных выше трех типов. В этой части
на каждой странице даны параметры трех типов планов, подобран-
подобранные так, чтобы их оперативные характеристики были близки друг
к другу. Все планы построены таким образом, что они обеспечивают
в определенном интервале значений доли дефектных изделий q
вероятность приемки хороших партий не менее 0,95. Такие интервалы
будем называть интервалами приемлемого качества. Границами
этих интервалов являются следующие числа, выраженные в процен-
процентах: 0,024; 0,035; 0,06; 0,12; 0,17; 0,22; 0,32; 0,65; 1,2; 2,2; 3,2;
4,4; 5,3; 6,4; 8,5. Предусмотрено использование пяти уровней инс-
инспекции I, И, III, IV, V. Уровень III считается нормальным. При ис-
использовании уровней II и I контроль становится менее жестким, и
§ 7.3]
СТАНДАРТЫ ПЛАНОВ ПРИЕМОЧНОГО КОНТРОЛЯ
413
объем инспекции составляет соответственно 3/4 и */2 от объема
по уровню III. При использовании уровней IV и V контроль оже-
ожесточается, объем инспекции возрастает соответственно в 1,5 и 2
раза. В приводимой таблице 7.3.4 даны значения кодовых чисел.
Каждому кодовому числу и интервалу приемлемого качества соот-
соответствуют три плана: однократной, двукратной выборки и последо-
последовательного анализа. Параметры этих планов находятся из таблиц
20 — 22 приложения.
Приведем примеры. Пусть на контроль поступает партия объема
N=350. Решено использовать нормальный уровень контроля. При-
Приемлемое качество <70)95 = 0,015. Из таблицы 7.3.4 находим, что
кодовое число равно G. Из таблицы 20 приложения получаем, что
букве G соответствует выборка объема 55.
Таблица 7.3.4
Таблица кодовых чисел
Объем партии
<25
25— 50
60- 100
100— 200
200— 300
300— 500
800— 1 300
1300— 3 200
3 200— а ооо
8 000— 22 00J
22 000—110 000
110 000 — 500 000
> 550 000
Кодовое число для уровней инспекции
I
А
А
В
С
D
Г.
G
И
I
Y
К
L
N
и
А
В
С
D
Е
F
Н
I
Y
К
L
М
N
ш
В
с
D
Е
F
G
I
Y
К
L
М
N
О
IV
С
D
Е
F
G
Н
Y
К
L
М
N
N
О
V
D
Е
F
G
Н
I
К
L
М
N
N
О
О
Так как 0,12 <^0)9б = 0,15 < 0,17, то в столбце, соответствующем
интервалу приемлемого качества @,15; 0,17), находим, что с=1.
Если мы хотим использовать план типа усеченной двукратной
выборки, то из таблицы 21 приложения находим, что числу G и
интервалу @,12; 0,17) соответствует план C5, 70, 0,2). Заметим,
что при объеме N=250 в таблице 21 приложения дано указание
использовать только планы типа однократной выборки. Если решено
использовать планы типа последовательных равных выборок, то из
таблицы 22 приложения находим, что нужно использовать план
из семи последовательных выборок по /7 = 14 изделий в каждой.
Партия бракуется, если д?A4)^2, в противном случае берется
414
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
Таблица 7.3.5
Тип выборки
Однократная
Двукратная
Последовательная
Номера
выборок
первая
первая
вторая
первая
вторая
третья
четвертая
пятая
шестая
седьмая
Объем
выборок
300
200
400
75
75
75
75
75
75
75
Приемочное
число
4
2
6
*
1
1
2
3
5
7
Браковочное
число
5
7
7
3
4
5
6
6
8
8
вторая выборка; партия бракуется, если d B8)^2, в противном
случае берется третья выборка; если d D2) ^ 2 — партия бракуется,
100
so
80
70
60
50
40
30
20
10
nfq)
Кодовое число L ;
ин/лврбал приемлемого хаме/яда
U,32-0,SS;
О 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 q%
Рис. 7.3.3.
в противном случае берется четвертая выборка. Партия принимает-
принимается, если d E6) = 0, бракуется, если d E6) ^ 2; берется пятая выборка,
если dE6)=l. По результатам пятой выборки при dG0) = 0 при-
§ 7.4] ЭКОНОМИЧНЫЕ ПЛАНЫ КОНТРОЛЯ 415
нимается, d G0) ^ 2 бракуется, при dG0) = \ берется шестая вы-
выборка. По результатам шестой выборки при d (84) = 1 принимается,
при d (84) ^ 3 бракуется и при d (84) = 2 берется последняя, седьмая,
выборка. Если d(98) = 2, партия принимается, если же d (98)^3,
партия бракуется. Таким образом, в таблицах 21, 22 приложения,
в колонках, озаглавленных «Пр», даны значения приемочных чисел,
знак «#» означает, что решение о приемке еще не принимается,
а в колонках, озаглавленных «Бр», даны значения браковочных
чисел. На таблице 7.3.5 приведен пример набора трех типов пла-
планов, соответствующих кодовому числу L и интервалу 0,32 — 0,65?^
приемлемого качества, 0,50%<CqL%<.0,90%. Значения оператив-
оперативных характеристик этих планов показаны на рис. 7.3.3.
В книге [5] для наглядности кривые оперативных характеристик
различных типов планов были напечатаны разным цветом. Одна-
Однако это привело к большим относительным смещениям линий,
что весьма снижает ценность информации ввиду необходимости в
большей точности при малых значениях доли q. Этот недостаток
был бы не так сильно выражен, если бы авторы использовали не-
неравномерный масштаб изображения по оси ординат, растянув его
при вероятностях, близких к единице.
§ 7.4. Экономичные планы контроля
Экономическая оценка эффективности при-
приемочного контроля. В предыдущем параграфе был дан крат-
краткий обзор существующих стандартов выборочного контроля. Инте-
Интересы производителя учитывались либо заданием величины риска
производителя, либо использованием планов, дающих в среднем
минимальное количество инспекции при заданном #м, что возможно
только в случае принятия решений ZJ, D3. Более гибкая система пла-
планов, включающая случаи разрушительного и неразрушительного
контроля, может быть построена при учете стоимостных факторов,
связанных с введением контроля. Разработке наиболее экономич-
экономичных, рациональных методов выборочного контроля в последнее
время уделяется значительное внимание (см. [10] — [И]). Трудность
решения этой проблемы состоит главным образом в правильном
учете внешних условий, факторов, предопределяющих выбор мето-
методов контроля. По-видимому, универсальной методики выбора рацио-
рациональных планов контроля, пригодной на все случаи жизни, не су-
существует. Об этом говорят многочисленные критические замечания
к уже существующим методам выборочного контроля (см., на-
например, [8]). В настоящем параграфе дается один из возможных
подходов к построению стандартов экономичных планов контроля.
Идея такого подхода была предложена одному из авторов книги
416
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
академиком А. Н. Колмогоровым (см. [13]). Основные расчеты были
выполнены в лаборатории статистических методов МГУ.
Решение о приемке или браковке партии, содержащей долю q
дефектных изделий, связано с ущербом двоякого рода. С одной
стороны, не все изделия в партии являются дефектными, поэтому,
решив забраковать партию, мы несем ущерб Ебг (q) от браковки
годных изделий. С другой стороны, приняв решение о приемке
партии, мы принимаем содержащиеся в ней дефектные изделия,
использование которых на последующих этапах производства или
потребления приведет к ущербу
?пд (q). Примерный вид Е6г (q),
Епл (q)y как функций от q = -77- ,
показан на рис. 7.4.1. Введем
понятие <7кр посредством равенства
рис 7 4 j
пд кР бг кР р
решения о приемке или браковке
партий эквивалентны с экономиче-
экономической точки зрения.
Если q <С?кр, то выгоднее при-
принять данную партию. Если же
q>qKV, то, наоборот, выгоднее
9 забраковать ее. Так просто обстоит
дело только в том случае, когда
нам известны значения q и qKr
На практике значение q неизвест-
неизвестно, и его можно найти, только
проверив все изделия, входящие в партию. Значение qKV можно
задать лишь приближенно, так как получение явного выражения
для ?пд (q) является трудной экономической задачей. Наша основ-
основная гипотеза заключается в том, что при нормальном ходе произ-
производства, когда соблюдаются все основные условия технологии, доля
засоренности дефектными изделиями q является меньше qKV и вполне
удовлетворяет потребителя. Предполагается, что при нормальном
ходе производства значения q группируются в непосредственной
близости от среднего значения qH. Если же предъявленная партия
выпущена при наличии существенных нарушений технологии, то
доля засоренности q много больше qH и часто больше значения qKV.
Итак, если партия выпущена при нормальном ходе производства,
то она содержит небольшое число дефектных изделий, ущерб от
приемки которых много меньше ущерба от браковки этой партии.
Если же партия выпущена при наличии нарушений технологии, то
она содержит много дефектных изделий, ущерб от приемки которых
часто превышает ущерб от браковки всей партии. Однако еще раз
подчеркнем, что нам неизвестно, выпущена данная партия при
§ 7.4] экономичные планы контроля 417
нормальном ходе производства или нет. Чтобы определить это, мы
должны выделить дополнительные средства Ек (q), обеспечивающие
проведение контроля. Эти расходы представляются в виде суммы
двух слагаемых: среднего ущерба принятия решения о браковке и
стоимости контроля части изделий.
Таким образом, Ек (q) равно среднему ущербу только произ-
производителя, ущерб потребителя от приемки дефектных изделий сюда
не включается. С экономической точки зрения введение контроля
является целесообразным только в том случае, когда Ек (q) <С.Е6г (q)
при <7<<7кр. Конечно, контроль будет тем экономичнее, чем меньше
будет отношение g к -- , однако при этом следует учитывать и
^бг Wh)
интересы потребителя, что накладывает определенные ограничения
на выбор плана контроля. При условии задания всех экономиче-
экономических параметров можно было бы подсчитать и суммарный ущерб
^2 (?), который складывается из расходов на контроль, ущерба от
браковки годных изделий, если партия бракуется, и ущерба от при-
приемки дефектных изделий, если партия принимается. В этих усло-
условиях при разумном выборе плана контроля Е% (q) оказывается зна-
значительно меньше max [?пд (</), Е6г (q)] для большинства значений q.
Однако вычисление Ena(q) затруднительно, поэтому мы ограничимся
только характеристикой EK(q).
Средние расходы на контроль при нормальном
ходе производства. Пусть контролируемая партия состоит
из N изделий, среди которых D дефектных. До принятия решения
было проверено п изделий, среди которых оказалось d дефектных,
в общем случае D, как и d, может быть случайной величиной.
Если партия выпущена при нормальном ходе производства, то
q =-тг <^ 1 , поэтому число годных изделий, оставшихся непро-
непроверенными, N— п — {D—d)&N — п. Рассмотрим следующие
стоимостные показатели: а — ущерб от браковки одного годного
изделия, р — стоимость проверки одного изделия. В этом случае
средние расходы EK(q), связанные с проведением контроля, равны
Ек (q)^a(N-n')[l-n(q)] + fn, G.4.1)
где п — среднее число проверенных изделий (средний объем инс-
инспекции), п' — среднее число проверенных изделий при условии,
что партия забракована, 1—я (q) — вероятность браковки партии,
содержащей D = qN дефектных изделий. В условиях нормального
хода производства, как это отмечалось в § 7.1, можно считать,
что q является случайной величиной с функцией распределения
FH(q), среднее значение \qdFH(q) —qH. С учетом этого априорного
418 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
распределения средние расходы на контроль при нормальном ходе
производства
lH(q)dF,(q), G.4.2)
где FH (q) растет только в точках, кратных TV".
Напоминаем основные допущения, связанные с понятием нор-
нормального хода производства. Мы предполагаем, что производство
является «отлаженным» и основная часть партий выпускается при
нормальном ходе производства. При наличии нарушений техноло-
технологии q резко возрастает. Однако задавать при этом какое-то фик-
фиксированное распределение для q нам представляется нецелесооб-
нецелесообразным, так как трудно ожидать стационарного (в статистическом
смысле) возникновения разладок определенного вида. Исходя из
этого, предлагается планировать расходы на контроль только при
нормальном ходе производства. При заданном уровне средних рас-
расходов Ек на проведение контроля при условиях нормального хода
производства будут отыскиваться планы контроля, в данном па-
параграфе в основном только планы типа однократной выборки, ко-
которые обеспечат практически наибольшую вероятность браковки
партий, сильно засоренных дефектными изделиями.
Мы сохраняем обозначение (л, с) для планов типа однократной
выборки» Однако индексы ijy (я, с)^ опускаются, так как при эко-
экономическом подходе влияние вида решений, принимаемых по ре-
результатам проверки, учитывается в значениях стоимостных парамет-
параметров. Для определенности мы будем предполагать, что априорное
распределение для числа D дефектных изделий является биноми-
биномиальным со значением параметра q = qYi<^\. Для плана типа од-
однократной выборки (я, с) при /zS^>c, л>20-т-30 можно использовать,
учитывая теорему 7.2.2, пуассоновское приближение. При этом ве-
вероятность я (qH) приемки партии, выпущенной при нормальном ходе
М-ъ Lc (nqH)f G.4.3)
где Lc(x) определяется формулой G.2.14). Из G.4.1), G.4.2) и
G.4.3) получаем, что средние расходы, связанные с использованием
плана типа (я,с) при нормальном ходе производства, равны
Ек = a (N-n) [1 - Lc (nqH)] + §п. G.4.4)
Разделив обе части G.4.4) на aN, получаем
v)[1-^(^)]+4v) G.4.5)
§ 7.4] экономичные планы контроля 419
где ^н = /г<7н~ среднее число дефектных изделий, попадающих
в выборку объема п при нормальном ходе производства. Замечая,
X
что v = -^-, где 6 = iV^H —среднее число дефектных изделий, со-
содержащихся в партии, выпущенной при нормальном ходе произ-
производства, можем переписать G.4.5) в следующем виде:
Заметим, что в условиях биномиальное™ априорного распреде-
распределения для числа дефектных изделий в партии среди предположе-
предположений, приводящих к формулам G.4.5), G.4.6), нет ограничения на
величину относительного объема выборки v=-rr. Так как дн<^\у
соответственно N&N—D, то величину Е можно рассматривать
как долю средств, связанных с проведением контроля, от ущерба,
вызванного решением о браковке без всякого контроля партии,
выпущенной при нормальном ходе производства.
При планировании расходов, связанных с проведением контро-
контроля при нормальном ходе производства, можно исходить из прин-
принципа пропорциональности этих расходов общему объему изделий
в контролируемых партиях. Поясним этот принцип подробнее.
Пусть объем месячной продукции по определенному типу изделий
известен заранее, т. е. известно число AfcyM, изделий, которые бу-
будут выпущены в течение месяца. Эти NCyM изделий предъявляются
на контроль в виде т партий, объемы которых равны Nh 1 = \ут,
т
Ncум = 2 Ni- Если на обеспечение контроля в течение месяца выде-
1
Сум 7=Ti
лены средства ?сум, то, исходя из принципа пропорциональности,
на обеспечение расходов, связанных с контролем партии объема
Nh выделяются в среднем средства Ei = Ecyu (jr*—) • Поэтому стои-
стоимостный коэффициент Е{ в левой части G.4.6) надо полагать рав-
Е- /^сум\
ным ——¦ = а ( ^— 1 = Е. Таким образом, из принципа пропорцио-
пропорциональности следует, что стоимостный коэффициент Е в G.4.6) не
зависит от объема инспектируемой партии. Это уменьшает объем
таблиц и облегчает пользование ими. Однако надо иметь в виду,
что при использовании принципа пропорциональности резко воз-
возрастает вероятность пропуска партий небольшого объема /V, силь-
сильно засоренных дефектными изделиями. Вследствие этого на прак-
практике обычно либо объединяют несколько небольших партий в
одну, либо проводят сплошную разбраковку партий, объем ко-
которых меньше заданного Мкр. Таким образом принцип пропорци-
420 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
ональности без всяких дополнений применим лишь в тех случаях,
когда объем партий, поступающих на контроль, меняется незна-
незначительно.
Понятие о рациональности плана приемочного
контроля. Для простоты вычислений будем предполагать, что
объем выборки п может быть равен любому положительному числу.
Поэтому, найдя соответствующее значение /z, для практического
использования за объем выборки надо принимать [л] + 1, если
только п не целое. Здесь [п] означает целую часть числа. Так
как в большинстве случаев #>30, то погрешность от такого до-
допущения незначительна. Для краткости записи будем обозначать
парой чисел (Хнс, с) план типа однократной выборки, у которого
объем выборки п = -П?-у соответственно ^н<г = л<7н, а с — приемоч-
ное число. Как и ранее, дн означает среднюю долю засоренности
при нормальном ходе производства. Если на проведение контроля
выделены определенные средства, исходя из которых подсчитан
стоимостный коэффициент Еу то надо использовать планы (^нс, с),
которые удовлетворяют уравнению G.4.6). Так как ¦б-=лг!"==
= дт ^ 1, то при любом целом значении с = 0,1,2,.. . имеет смысл ис-
искать корни Хнс только в интервале 0 ^ХНС^.Ь. Непосредственной
проверкой легко убедиться, что вторая производная правой части
G.4.6) лишь один раз меняет свой знак в интервале 0^А,^9.
Учитывая далее, что при Х = в значение правой части равно — ,
можем заключить, что либо
является монотонно возрастающей функцией в интервале @, 6),
либо /(Я) имеет в этом интервале одну экстремальную точку
(максимум), в которой значение /(X) больше —.
Если Ек—средние расходы, выделенные на обеспечение контроля
партии, содержащей N изделий, то, замечая, что стоимость сплош-
сплошной проверки равна fW, а ущерб от браковки партии равен
a(N—DH)»a7V, заключаем, что выборочный контроль с экономи-
экономической точки зрения целесообразен только в том случае, когда
плошной контро
равно доле средств, выделенных на организацию выборочного конт
—^т <-^д7 = —. В противном случае выгоднее производить
сплошной контроль. Таким образом, отношение Е:— =EK:$N, т. е.
§ 7.4] экономичные планы контроля 42!
роля, по отношению к средствам, необходимым на проведение
сплошного контроля. Всюду ниже мы будем предполагать, что
?<— . Учитывая сделанные выше замечания относительно харак-
характера поведения функции /(Я), получаем, что при E<d — для.
каждого целого значения с уравнение G.4.6) имеет в интер-
интервале @, 6) единственное решение Кнс.
Планы (Хнс, с), удовлетворяющие G.4.6), являются эквивалент-
эквивалентными с экономической точки зрения, так как при использовании
любого из них средние расходы равны Ек = EaN. Будем такие
планы называть допустимыми. Заметим, что при малых отноше-
отношениях л-<^1 (<0,1) уравнение G.4.6) можно заметить приближен-
приближенным уравнением
, G.4.7)
=-&г — стоимостный коэффициент. Уравнение G.4.7) значи-
значительно проще, так как его решения являются функциями только
двух параметров Е и y» тогда как решения G.4.6) зависят от
трех параметров: -!-, ?,6. Легко показать, что корни G.4.7)
меньше, чем корни уравнения G.4.6), что затрудняет выяснение
границ применимости G.4.7) вместо G.4.6). Заметим, однако, что
решения G.4.7) обладают свойством Хс <С Хс+1 <?: -^ . Поэтому при
Е: — <0,1 можно пользоваться решениями G.4.7) вместо G.4.6).
Проверки показывают, что если решение Хнс G.4.7) удовлетворяют
условию -тг-<0,1, то оно с достаточной степенью точности сов-
совпадает с соответствующим решением G.4.6). Из семейства допу-
допустимых планов (Хнс, с) мы должны выбрать рациональные планы.
Как указывалось выше, основные показатели планов можно найти,
исходя из оперативных характеристик, которые в общем случае
можно считать по формуле G.4.3). Если же учесть, что при нор-
нормальном ходе производства #н<^1, то можно воспользоваться би-
биномиальным приближением. В этом случае оперативная харак-
характеристика вычисляется по формуле
S
= -~ = ^. Наконец, в случае -!^-< 0,1, /z=^-
422
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
-д-<0,1 можно использовать пуассоновское приближение
Le = {Xuek), 6 = f. G.4.9)
На рис. 7.4.2, а даны оперативные характеристики семейства до-
допустимых планов, удовлетворяющих G.4.6), когда — =0,063,
?=0,35, 6=10, а приемочное число с = 0, 1, 2, ..., 14. По оси
ординат отложены значения оперативной характеристики, а по оси
(И) 0=7
/ /
м
Рис. 7.4.2.
D
1 D а
абсцисс — значения k = -к = -1-, показывающие степень засорен-
ности дефектными изделиями относительно средней засоренности
при нормальном ходе производства. В этом случае vc = -^
для с>0, поэтому при построении графиков было использовано
биномиальное приближение G.4.8). Для наглядности графики даны
в виде сплошных линий. На рис. 7.4.2, б изображены оперативные
характеристики семейства допустимых планов для значений
?=0,01, 6 = 80. Так как 6^>1, то представляется целесообраз-
ным использовать приближение G.4.7) для значения Y^"^ =0,0025.
Действительно, в этом случае при любом с A.lur< — = 4, а отно-
относительный объем выборки
; 0,05, так что решения G.4.6) и
G.4.7) практически совпадают. Графики оперативных характеристик,
изображенные на рис. 7.4.2, б, построены, исходя из пуассонов-
ского приближения G.4.9).
При нормальном ходе производства все допустимые планы экви-
эквивалентны с экономической точки зрения. Однако они резко раз-
§ 7.4] экономичные планы контроля 423
личаются, когда на контроль поступают партии, сильно засорен-
засоренные дефектными изделиями. Естественно из допустимых планов
отбирать такие, при использовании которых с большей вероят-
вероятностью бракуются партии, сильно засоренные дефектными изде-
изделиями. Из рис. 7.4.2, я, б видно, что при различных значениях
k = — наилучшими в этом смысле являются различные планы. На-
Например, для параметров рис. 7.4.2, а в интервале A,550-5-1,815)
значений k наилучшим планом является (Янс = 3,20; с = 4), а
в интервале A,815-^-2,075) — план (Хнс = 3,77; с = 5). В реальных
условиях производства неизвестно, в каком интервале находится
значение k для инспектируемой партии. Поэтому целесообразно
использовать тот план, оперативная характеристика которого лежит
по возможности ближе к нижней огибающей семейства оперативных
характеристик допустимых планов. Из рис. 7.4.2, а, б видно, что
такие планы существуют, например, для параметров рис. 7. 4.2, 6*t
такими планами являются (Ян9 = 3,24; с = 9), (Хн10 = 3,55; с=10)»
Многочисленные проверки показали, что планы, у которых опера-
оперативные характеристики практически равномерно близки к ниж-
нижней огибающей всего семейства допустимых планов, существу-
существуют в весьма широкой области значений параметров — , ?, Э, (Е,у).
Условимся такие планы называть рациональными.
Рассмотрим теперь несколько возможных подходов к отбору
рациональных планов контроля.
Модель 1. Предположим, что относительный объем выборки
дт-<^1, так что можно воспользоваться уравнением G.4.7). Пусть
каждая забракованная партия, содержащая D дефектных изделий,
заменяется партией, выпущенной при нормальном ходе производ-
производства, и, следовательно, содержит в среднем Q = NqH дефектных
изделий. Так будет, в частности, тогда, когда операция контроля
является разрушительной. Если ограничиться случаем пуассонов-
ского распределения для числа d дефектных изделий, обнаружен-
обнаруженных в выборке объема #, то число Dnp принятых дефектных
изделий
[yd \ «
> — d, d = 0, ...,с с вероятностью (-тт-) е , G.4.10)
где X^nq, Я„ = л?„, Pc(Kh) = [l—Lc(b)][Lc(h)]~1- Показа-
Показателем «фильтрующей» способности плана (Анс,с) может служить
424
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
, ,,ч MDnp
#npW = " q — отношение среднего числа принятых дефектных из-
изделий, к среднему числу дефектных изделий, выпущенных при нор-
нормальном ходе производства. При этом &пр рассматривается как функ-
q D
ЦИЯ ОТ k = — = -rr.
Из формулы G.4.10), учитывая предположение -гг <^ 1, легко по-
получить явное выражение для функции фильтрации
kn^c(k)^(k — \)Lc(XHk) + \. G.4.11)
Из этой формулы следует, что для всех значений &> 1 &пр(&)> 1,
а при k—*оо kuv,c (k) | 1. На рис. 7.4.3 приведены графики функций
1,5
2,0 2,5 3,0 3J5 4,0 4,5 5,0 к
Рис. 7.4.3.
фильтрации, семейства допустимых планов, соответствующих
значению ? = 0,01, у = 0,0025.
Оперативные характеристики этих планов даны на рис. 7.4.2, б.
Как видно из рис. 7.4.3, практически равномерно наилучшей
фильтрацией обладает план (Хн = 3,24; с = 9), у которого макси-
максимальное значение k9 = max kn ,9 (k) является минимальным по срав-
нению со значениями kc = max knv>c(k) для других значений сф9.
Из рис. 7.4.2,6 мы видим, что этот план является рациональным.
§ 7.4] экономичные планы контроля 425
Как показали численные расчеты, рациональность допустимого
плана (А,,с) в широкой области значений параметров Е,у совпадает
со свойством минимальности значения kc. Исходя из этого, для
различных значений параметров Е и у был проведен отбор планов,
обладающих минимальными значениями kc по сравнению с другими
допустимыми планами. Основные вычисления были произведены в
вычислительном центре МГУ.
Результаты вычислений представлены в таблице 25 и соот-
ретствующей этой таблице номограмме (см. приложение). Зна-
Значения стоимостного коэффициента Ei {E{> Ei+1) выбирались таким
образом, чтобы In (у, l ) 2= 0,1. В первом левом вертикальном столб-
\ti+lJ
це указаны значения приемочных чисел с или с~с-)-1. В осталь-
остальных столбцах, соответствующих различным значениям Е(, даны
соответственно величины lg Y^ и '§ ^с или lg^ с , lg^ с и lg Л. с *
с+1 с+1 с+\
Если выбрано значение Е; и для инспектируемой партии
lgy'c-i ^lgY^'gY'c > т° Для рационального плана приемочное
Т" с+\
число равно с, при этом значение lg Янс находится линейной ин-
интерполяцией по lg^*_j и lg X' с . Для повышения точности ли-
с с+ 1
нейной интерполяции для небольших значений с = 0, ..., 4 были
даны промежуточные значения \gyc и соответствующие им значе-
значения lg Яс. В номограмме приложения по оси абсцисс отложены
значения Я = /гс^, где пс — объем выборки. При этом значения
Х>0,5 наносились в обычном масштабе, а значения А,<0,5 —
— в логарифмическом масштабе. По оси ординат в логарифмиче-
логарифмическом масштабе отложены значения стоимостного коэффициента
расходов Е. Каждой паре значений Е и у соответствует рацио-
рациональный план (X, с). Если зафиксировать значение у = Y/='const
и менять Е, то для рационального плана К = g (?, у?-)• Функция
K = g(E, у-) — кусочно-гладкая и при некоторых значениях Е имеет
скачки. В номограмме изображена сетка Х-линий, соответствующих
различным значениям у.. При этом оказалось удобным выбирать
значения Yi>Y/+i так> чтобы \glo[ -^- )^0,1. При скачкообраз-
\ Y/ +1 /
ном изменении X значение приемочного числа с изменяется на 1.
Для значений у < 0,16 при увеличении Е X увеличивается, а с
скачками возрастает на 1. Непрерывные куски линий X = g(E, у/К
соответствующие одному значению с, объединены в зоны, соеди-
соединенные горизонтальными пунктирными линиями. Значения при-
приемочных чисел с, которым соответствуют эти зоны, крупным
шрифтом даны на полях номограммы. Пунктирные линии соединяют
426 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
значения функции k = g(E, y{) в точках разрыва. Над этими
пунктирными линиями указаны значения стоимостного парамет-
параметра Y/- Итак, при фиксированном значении Е каждому с соот-
соответствует интервал возможных значений К, при которых существуют
рациональные планы. В промежутках между этими интервалами
рациональных планов нет. Ниже под осью абсцисс для различных
приемочных чисел с можно вычертить шкалы значений точек к,
показывающих, при каком относительном увеличении засорен-
засоренности к = — = -*- значение оперативной характеристики плана
равно 0,1.
Равная степень жесткости контроля отражена в номограмме
сеткой жирных пунктирных линий. Каждому рациональному плану
(к, с) соответствует предельная фильтрация кс (Х)^та\(к—1) X
xLc(kk)-\-\, равная максимальному значению функции фильтрации.
Линии были проведены через те точки плоскости (Е, Х{)у для ко-
которых значения предельной фильтрации постоянны, kc(kci) = к{ =
const. Значения kc(kci) при фиксированном с не зависят от ?,
поэтому линии проходят через зону рациональных планов, соот-
соответствующих одному значению с, параллельно оси ординат. При
переходе из одной зоны с в другую зону с + 1 значение Xc + 1)/,
для которого kc+1 (кс+1,() =k( = const, изменяется скачками. Точ-
Точки разрыва соединены пунктирной линией.
Таблицей 25 и номограммой приложения можно пользоваться
как в случаях разрушительного, так и не разрушительного контро-
контроля, если только относительный объем выборки-д- = тт-<ф «0,1).
Для этого надо найти а, Р, q вычислить значение стоимостного
D
параметра у =-^r-,Q = NqH и выбрать величину Е стоимостного
коэффициента. Примеры на отыскание планов контроля с по-
помощью таблицы или номограммы будут даны ниже.
Модель 2. Для того случая, когда — >0,1, при расчете
таблиц рациональных планов можно поступать следующим обра-
образом. Как показали многочисленные проверки, рациональными пла-
планами в широкой области значений параметров Е, «-, 9 являются
такие планы, у которых площадь под оперативной характеристи-
характеристикой является минимальной. Будем исходить из того, что Л/^>1,
-тт-<0,1. В этих предположениях можно воспользоваться биноми-
биномиальным приближением G.4.8.) для выражения оперативной ха-
характеристики n(q). Так как q может принимать только зна-
значения q— -гт , D = 0, 1, 2, ..., /V, то аналогом площади под
§ 7.4] экономичные планы контроля 42?
оперативной характеристикой плана (Янс, с) может служить
D=0
I) 2 tr 2# (?>- \)...(D-d+ 1) A— v)D-d =
d 0al D 0
гдеЛнс = я^н является решением уравнения G.4.6), а v = -^-. При
заданных значениях — и Е среди семейства допустимых планов,.
удовлетворяющих G.4.6) и соответственно эквивалентных с эконо-
экономической точки зрения, отбирается тот, у которого значение Sz
с-\- 1
или (см. G.4.12))-у-—является минимальным. С вероятностной точки
зрения планы с минимальным значением Sc являются оптимальны-
оптимальными, когда априорное распределение для числа дефектных изде-
изделий при наличии разладок является равномерным, т. е. P{D = k} =
= (N-{- l)~1,&=0, ... ,iV, таккак-вероятность приемки таких партий
равна Sc. Для фиксированных значений — и Е можно найти зна-
значения 6 с такие, что если для инспектируемой партии 0 c_i ^
с+1 с
<;0<;0 с , то приемочное число надо полагать равным с. Часть таб-
лицы такого сорта показана ниже (таблица 7.4.1.)
Соответствующее значение Хнс находится путем интерполяции
значений Х'с, Я'^. Например, если ? = 0,02, ~ = 0,1, <7н = О,О9, объем.
инспектируемой партии N=1000, то 0 = 9. Из таблицы 7.4.1 имеем*
04_=:7,97О1<9<0? = 11,0627, откуда следует, что с = 5. Линейная
5 6
интерполяция значений Яб, Я5 дает значение Ян5» 1,46. Относитель-
Относительный объем выборки -^ =-~- = 0,16. Если заранее считать, что-
~<^1, то из таблицы 25 приложения для ?=0,02, y = -it =
= 0,0111... lg y= 1,9542 находим, что с = 5, а Янс=1,45. Таким:
образом, иногда даже при сравнительно большом относительном,
объеме выборки с помощью таблицы 25 приложения можно полу-
чить достаточно хорошее приближение.
Примеры. Сравнение с планами Доджа и Ромига.
Рассмотрим примеры на использование таблицы 25 и номограм-
номограммы приложения. Выбор стоимостного коэффициента Е определяется,.
428
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
Таблица 7.4.1
а ~~ '
\Е
С >v
4 5
5-6
...
...
...
? = 0,02
94 =7,9701
5~
95 =11,0627
6~
А,4 = 1,14973
Хд = 1,37967
А,'5 = 1,61555
Ь'б = 1,88481
...
...
...
...
исходя из возможностей предприятия и требований потребителя.
Если на предприятии уже используется статистический выборочный
контроль по качественному признаку, то можно по формуле G.4.5)
подсчитать значение стоимостного коэффициента Е. Это значение
используется затем для отыскания рационального плана. Напоми-
Напоминаем, что значение стоимостного параметра у — —^—, необходи-
необходимого для отыскания плана контроля, определяется конкретными
условиями производства. При такой замене контроль при той же
стоимости становится более чувствительным к партиям с большой
засоренностью дефектными изделиями.
Пример 1. Пусть отношение р-стоимости проверки одного
изделия к ущербу а от браковки годного изделия равно— =0,5.
Доля засоренности продукции дефектными изделиями при нормаль-
нормальном ходе производства равна #„ = 0,01. Решено на обеспечение
контроля выделить 10% от средств, необходимых для покрытия
ущерба при сплошной проверке продукции, т. е. == 0,10. Из
этого условия находим, что ? = 0,05. Пусть объем контролируемой
лартии N = 1500. При указанных выше данных 0 = NqH= 1500-0,01 =
§7.41
ЭКОНОМИЧНЫЕ ПЛАНЫ КОНТРОЛЯ 429
О -I
'=15, Y~ ~^ = Ж ' '&Y = —1,4771. Из таблицы 25 приложения
для ?=0,05 находим, что lgYL = —l,2793>lgY = —l,4771>
3
^>lgY3 =—1,5055. Поэтому у рационального плана приемочное
число с=3. Значение объема выборки п находим линейной интер-
интерполяцией значений lg к3 = — 0,0453 и lg А3 = — 0,0010 относительно
4~
соответствующих значений lgY- lg (#<7H) ^ lg^s + 0S^3 — lg ^з) X
X &3ft - -0.0453 + 0,0443 X ???\%{— 0.0,2,.
4
Используя таблицы антилогарифмов, имеем nqH = 0,9725, соответ-
соответственно п «97. Итак, рациональным является план (97,3).
П р и м е р 2. Известно, что — = 3, дн = 0,015, значение стоимост-
стоимостного коэффициента решено положить ?" = 0,10. Объем инспекти-
инспектируемой партии N = 1000. Требуется найти рациональный план типа
однократной выборки. Будем исходить из номограммы приложения.
Значение стоимостного параметра у = -тг = 0,2. Пересечение пря-
прямой, проходящей параллельно оси абсцисс через значение ?=0,1,
на оси ординат происходит с линией, соответствующей значению
Y = 0,2 в зоне приемочного числа с=1. При этом на оси абсцисс
находим значение lg Хн = lg (nqH) =—0,54 (напоминаем, что правее
Я = 0,5 значения Я по оси абсцисс даны в обычном масштабе,
тогда как левее — в логарифмическом). Используя таблицы анти-
антилогарифмов, находим nqH = 0,2885, п « 19. Итак, рациональным
является план A9,1). Можно показать, что XOjl=13,5. Таким
образом, если доля засоренности продукции дефектными изделиями
X
будет в ? = -^'- = 46,8 раз больше, чем при нормальном ходе про-
изводства, то такие партии будут приниматься с вероятностью,
меньшей 0,1. Если такой контроль будет потребителем признан не-
неоправданно слабым, то в этом случае производителю придется
увеличить плановые расходы на контроль, что будет соответство-
соответствовать выбору большего значения для стоимостного коэффициента Е.
Эту серию примеров мы заканчиваем иллюстрацией сравнения
оперативных характеристик, рекомендуемых в книге Доджа и Ро-
мига [4], с оперативными характеристиками рациональных планов,
найденных исходя из таблицы 25 приложения.
На рис. 7.4.4, а сплошной линией проведена оперативная характе-
характеристика L плана C7,3), рекомендуемого Доджем и Ромигом
в случае контроля партии N = 900 изделий, qH = 0,025. Этот план
430
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
обеспечивает значение ^м = 0,05. План C7,3) практически совпадает
с рекомендуемым нами планом для случая —=1. Если же-?-=^=1,
то использование рациональных планов дает лучшие результаты.
Пунктиром показаны оперативные характеристики Lly L2, L3, I4
Q
рациональных планов, соответствующие значениям — = 5; 0,5; 0,2;
0,1. При фиксированном значении—ущерб от использования ра-
рационального плана при нормальном ходе производства полагался
равным ущербу, связанному с использованием плана C7,3).
а)
Рис. 7.4.4.
На рис. 7.4.5, б за основу был взят план A60,4), рекомендуемый
в книге Доджа и Ромига для контроля партии объема N = 3500 и
<7н = 0,01. Из рис. 7.4.4, а, б можно видеть, что рациональные
планы, «стоящие» производителю столько же, сколько и план
Доджа и Ромига, более чувствительны к ухудшению качества
продукции.
Рациональные планы типа двукратной выборки.
В заключение параграфа рассмотрим вопросы, связанные с отыска-
отысканием рациональных планов контроля типа усеченной двукратной
выборки (л1э я2, съ с2). Для простоты вычислений будем пред-
предполагать выполненными условия, приводящие к пуассоновскому
распределению (см. § 7.2). Введем «временной» параметр t, полагая,
что t=\ соответствует числу проверенных изделий по==д,т. е.
среднему числу изделии, при котором в условиях нормального
хода производства встречается ровно одно дефектное изделие.
Таким образом, объему пг первой выборки соответствует значе-
значение /i = /21^H, объему п2 второй выборки t2z=n2gH- Обнаруженные
числа дефектных изделий d{ в i-й выборке имеют пуассоновское
распределение с параметрами th i=l,2. В этих условиях средние
расходы, связанные с проведением контроля по плану (/zlJ /z2, cx, c2)
§ 7.4] экономичные планы контроля 431
при нормальном ходе производства равны
^
Коэффициентом при а является среднее число забракованных год-
годных изделий в предположении, что <7Н<^ 1, а коэффициентом при р —
средний объем выборки до принятия решения о браковке или
приемке. Если разделить обе части на aiV, то имеем
Сг
s
G.4.14)
где v(. =/2z/yV. Всюду ниже мы ограничимся случаем выборок с отно-
относительно малым объемом, когда vx +v2<^ 1 (< 0,1). В этом слу-
случае, полагая vz = 0, переписываем G.4.14) в виде
G.4.15)
где y=$/o<NqHy а [г — средний объем выборки, выраженной во «вре-
«временных» единицах, т. е.
5 = 1—я(^) равна вероятности браковки партии, выпущенной при
нормальном ходе производства, — это риск производителя.
Уравнение G.4.15) является аналогом уравнения G.4.7) для пла-
планов типа однократной выборки. Уравнению G.4.15) удовлетворяет
бесконечное множество усеченных планов типа двукратной выбор-
выборки. Однако при фиксированных значениях \i и б имеется лишь ко-
конечное число таких планов. Действительно, если задать значения
|г, б и пару приемочных чисел сх и с2 > съ то из уравнения G.4.16)
можно выразить t2 как функцию от tx
J^Y1. G.4.17)
432 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
Значение t1 находится как решение трансцендентного уравнения
l-6 = ICl(^)+ 2 Jf e-''?c2_dl('2('i)). G.4.18)
которое получается из условия равенства риска поставщика выб-
выбранному значению б. Можно показать, что это трансцендентное
уравнение либо имеет только одно решение tly либо два решения
t\ и tf\>t'ly либо совсем не имеет решений (при выбранных зна-
значениях |ях б, сь с2). Отыскав значение tly значение t2 находим из
G.4.17). Таким образом, окончательно получаем, что планом,
удовлетворяющим условиям равенства риска производителя 6^
имеющим средний объем инспекции [X^J1, является (t1qu1it2qa1i
с1у с2). Установлено, что при наличии двух корней t' 1<t t'\ наилуч-
наилучшие результаты дают планы с использованием большего корня
t'\7>t\. Оперативные характеристики таких планов имеют мень
шие значения в области больших значений засоренностей партий
дефектными изделиями. Обозначим правую часть G.4.18) через
f(tl9 съ с2). Легко непосредственным сравнением слагаемых убедить-
убедиться в справедливости неравенств
LCx U1X/U1, съ c2)<f(tly съ с2+1), 0<^^[Х. G.4.19)
Таким образом, если LCl (t^) > 1—б, то уравнение G.4.18) не
имеет корней. Так как для любого б найдется такое с, что
??! Ui) > 1 — б для всех 0^:t1^\i, то число планов, имеющих
заданные значения [А и 8, конечно, и если нет планов для с1У с2,
то их нет и для значений съ c2-\-k, k=\, 2, ... Простой про-
проверкой можно убедиться также в справедливости неравенства
l9 c±; q+lX/tfi, q+1, Ci + 2), 0<^<ji. G.4.20)
Из этого неравенства следует, что если нет планов для значений
ci> ci+l> то их нет и для всех значений с\, с'2, с'1>с]|
c'2>ci+^- ^се эти результаты суммирует
Теорема 7.4.1. Существует конечное число планов типа
усеченной двукратной выборки, имеющих заданные значения рис-
ка производителя б и среднего объема инспекции до принятия
решения \л (\л <^ 9 = NqB). Пары приемочных чисел съ с2 (с2 > сх),
для которых существуют такие планы, образуют множество,
содержащее точки вида съ с2, где с1 = 0,1,..., с± (pi, б), а
с2 = сг+\,..., c2(|i, б, сг).
На рис. 7.4.5, а для значений 6 = 0,1 и A=1 показаны зна-
значения с1у с2у при которых существуют планы. При этом цифрой 1
отмечено наличие одного корня /, цифрой 2 — двух корней. На
рис. 7.4.5, б показаны оперативные характеристики этих планов
для некоторых значений (съ с2). В качестве признака, показываю-
§7.4]
ЭКОНОМИЧНЫЕ ПЛАНЫ КОНТРОЛЯ
433
щего степень рациональности плана, можно использовать площадь
5 под .оперативной характеристикой. Формула для пло-
площади 5 под оперативной характеристикой плана (ti<]~x,i qul,c
с2) в условиях применимости пуассоновского приближения имеет вид
(dt+d2)i
G.4.21)
Однако отбор планов только по этому показателю оказывается
недостаточным. Численные расчеты показали, например, что при
6 = 0,0025, ц = 2,0 наименьшее значение S имеет план, у которо-
которого t± = 0,948, t2 = 4,297, сх = 1, с2 = 9; при этом значение Sx = 2,512.
W
0,9
0,8
0,7
0,6
0,3
02
пт
в
6
7
В
5
3
2
1
—
а
2
2
&
2
t
1
1
О
mm
—
2
2
2
1 2
2
¦ 1
У
—.
7
—
—
—
—
в
1
—.
—
2
—
—
—
—
—
—
—
—
—
3
б к
б)
Рис. 7.4.5.
Однако существует план со значением S2*= 2,546, лишь незначи-
незначительно большим Sly который характеризуется параметрами tx = 0,849,
^2 = 2,013, Сх — О, с3 = 6. Несмотря на несколько большую пло-
площадь, второй план в некоторых случаях может оказаться более
привлекательным.
Дело в том, что у второго плана максимальный объем выборки
равен (t1-\-t2)q~1=*2,S№ q'1, тогда как у первого плана он ра-
равен 5,058 q-1, т. е. почти в 2 раза больше, хотя напоминаем, что
при нормальном ходе производства в среднем объем инспекции
15 б. В. Гнеденко и др.
434
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
одинаков для обоих планов и равен ^q~x. Использование планов
с большим отношением t2:t1 — n2:n1 может быть затруднительным
в связи с ограниченной пропускной способностью контрольной ап-
аппаратуры. Кроме того, использование таких планов может привес-
привести к неравномерной загрузке в работе контрольных постов. Итак,
при заданных значениях Е и у, меняя значения 6 и [л в соответствии
с уравнением G.4.15), мы можем отобрать несколько планов,
имеющих относительно небольшие площади S и умеренные значе-
значения t1 + t2. Использование двукратных планов хотя и сопряжено
с некоторыми неудобствами, однако дает выигрыш в большей
\П(Н)
3 Н
Рис. 7.4.6.
чувствительности к партиям, сильно засоренным дефектными
изделиями. На рис. 7.4.6 приведены оперативные характерис-
характеристики рационального плана типа F,526^^,11) и плана типа
(\fiq~1, 6,9#~х, 2,15), соответствующих значениям ?=0,1
и у = 0,01.
Из рис. 7.4.6 видно, что чувствительность плана типа двукрат-
двукратной выборки значительно выше чувствительности рационального
плана типа однократной выборки при засоренности q большей, чем
2<7Н. Оперативная характеристика плана типа двукратной выборки
дана в виде пунктирной линии. При сочетании высоких требова-
требований к стабильности качества принятой продукции с высокой стои-
стоимостью контрольной операции этот выигрыш приводит к целесооб-
целесообразности использования рациональных планов типа двукратной
выборки. Поэтому представляется целесообразным составление
стандартов экономичных планов типа двукратной выборки.
§ 7.4] экономичные планы контроля 435
Общая задача отыскания рациональных пла-
планов. В заключение рассмотрим общую задачу отыскания рацио-
рациональных планов типа последовательного анализа. При этом тре-
требуется, чтобы расходы на проведение контроля были равны
заданному значению. Если предположить, что априорное распределе-
распределение задается значениями вероятностей/H(D) = P {DH = D},D — 0,1,...
..., /V, а план последовательного типа характеризуется пара-
параметрами: n = n(N, D) — средний объем инспекции до принятия
окончательного решения, после которого контроль прекращается,
7гбр = n6v (A/, D) —средний объем инспекции при условии отверже-
отвержения партии, d6v = d6v(N, D) — среднее значение числа обнаружен-
обнаруженных дефектных изделий при условии отвержения партии. В этих
обозначениях средние расходы на проведение контроля на нор-
нормальном ходе производства равны
?«= 2,fuiD)[N-ntv-(D-d6v)]9tv(N, D) + fn. G.4.22)
Здесь Рбр (/V, D) — вероятность браковки (отвержения) партии объ-
объема Л/, содержащей D дефектных изделий. Каждому плану, удов-
удовлетворяющему условию G.4.22), при заданном значении Ек можно
сопоставить функционал, по значениям которого можно было бы
судить о степени рациональности этого плана. Например, можно
рассматривать функционалы вида
Ф= 2<p(D)II(?>), G.4.23)
где П (D) —значение оперативной характеристики плана, а ф (D)—¦
набор чисел D = 0, 1,...,ЛЛ В случае, когда ф (D) — <р0, значение
Ф пропорционально «площади» под оперативной характеристикой.
Общая задача может быть сформулирована следующим образом.
Требуется среди всех планов, удовлетворяющих условию G.4.22),
при заданном значении расходов Ек найти такой, для которого
значение функционала Ф является минимальным. Пока эта задача
в таком общем виде не решена.
Рассмотренные выше случаи планов типа однократной и двукрат-
двукратной выборок являются частными случаями общей задачи, соответ-
соответствующими оптимальным планам, минимизирующим G.4.23) в за-
заданных классах однократных и двукратных планов. В качестве еще
одного примера рассмотрим планы вальдовского типа (рис. 7.4.7).
Вальдовские планы имеют границы браковки и прием-
приемки партии, представляющие прямые линии пересекающие ось,
п — числа проверенных изделий и ось d (n) — числа обнаруженных
дефектных изделий на расстояниях /1? /2 соответственно, ф —угол
наклона этих прямых (см. рис. 7.4.7). Таким образом, семейство
15*
436 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
вальдовских планов является трехиараметрическим. Предположив,
что решение о приемке или браковке партии принимается по
относительно малой выборке и что априорное распределение для
D — биномиальное, мы можем воспользоваться формулами для сред-
среднего объема испытаний и оперативной характеристики из книги
Вальда ([14], глава 5). Обозначим средний объем инспекции через М
и выразим его в единицах [х, кратных qZ \ где qE — среднее значе-
значение доли засоренности продукции дефектными изделиями при
нормальном ходе производства. Ошибку первого рода обозначим
через 6. Стоимостный план, например E = EJaNy задается соотноше-
соотношением Е= 6 + YM^ r#e Y = cx/P^h- Соотношению G.4.2) удовлетворяет
двухпараметрическое семейство
„^ вальдовских планов, являющихся
нг fiOa*^X s подсемейством общего трехпара-
W .nOtx ^*a метрического семейства вальдов-
вальдовских планов. Фиксируя значения
Еу у и меняя значения 6V 6п = р
(ошибок первого и второго ро-
рода), отбираем план, у которого
1 * " *~п значения оперативной характерис-
характеристики лежат вблизи нижней огиба-
Рис. 7.4.7. ющей оперативных характеристик
всего двухпараметрического семей-
семейства планов, удовлетворяющих G.4.2). На рис. 7.4.8, а, б по-
показаны оперативные характеристики трех типов планов: однократ-
однократной, двукратной выборок и вальдовского плана; рис. 7.4.8,a
соответствует значениям ? = 0,01, у — 0,1, а рис. 7.4.8,6 — значе-
значениям ?"=0,063, у — 0,25. Из этих примеров видно, что планы
вальдовского типа могут иметь некоторое преимущество перед
эквивалентными им по расходам планами типа однократной и дву-
двукратной выборок. Таким образом, в стандарт планов приемочного
контроля должны быть включены планы различных типов, включая
планы типа последовательного анализа. В настоящей книге мы
приводим таблицы планов типа однократной выборки только по-
потому, что соответствующие таблицы для планов других типов
пока не подсчитаны; эта работа близка к завершению.
§ 7.6. Последующие оценки качества
по результатам контроля
Введение. Если план контроля выбран, то возникает задача
оценки эффективности действия этого плана. Эта эффективность
может измеряться по-разному. Например, ее можно понимать как
отношение числа принятых дефектных изделий к общему числу
предъявленных дефектных изделий. Возникает обширный класс
§ 7.5]
ПОСЛЕДУЮЩИЕ ОЦЕНКИ КАЧЕСТВА
437
\ПМ
1,0
€.5
70.
однократный (к;с)=@,0693;1)
дбукратный (г,;гг;с^
последовательный
g0=O,Of q,=0,/86
0=0,00025
fi-0,2
Е=О,0/
10 20 30 40 50 60
*\ \> ДЗукратный
•х Однократный
\ Последовательный
Однократный (k,c) @,2962;f)
Дбукратный @,/78;0,781 i 0; 4)
Последовательный
—*^>'
1 2 3 4 5 6 7 8 9 10 // /2 13 /4/5 16 17 18 19 20 k
Рис. 7.4.8.
438 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
задач, связанных с получением оценок различных характеристик
по имеющейся информации о приемке и браковке партий изделий.
Особый интерес представляет получение несмещенных оценок [1],
т. е. таких оценок, которые в среднем дают точные значения.
Нужно отметить, что точность этих оценок зависит от количества
данных, по которым они вычисляются. Иногда несмещенные оценки
могут давать отрицательные значения. Так будет при использова-
использовании несмещенной оценки для числа принятых дефектных изделий
в случае двукратной выборки. Эти отдельные случаи выглядят
абсурдными, так как число принятых дефектных изделий не мо-
может быть меньше нуля. Однако при оценке суммарного числа при-
принятых дефектных изделий по результатам разбраковки большого
числа партий включение отрицательных значений необходимо, что-
чтобы избежать завышения суммарного числа принятых дефектных
изделий. Несмещенные оценки существуют не для всех характери-
характеристик и не для всех планов контроля. Однако можно, применяя
специальные методы, так изменить тип используемого плана, что
желаемая несмещенная оценка начинает существовать. Примером
такого рода методов может служить описанное ниже правило про-
проверки (/г+1)-го изделия, предложенное С. X. Сираждиновым и
М. И. Эйдельнантом [2]. В практике приемочного контроля широко
используются планы типа двукратной выборки и последовательного
анализа. К сожалению, теория несмещенных оценок разрабатыва-
разрабатывалась до настоящего времени главным образом применительно к
планам типа однократной выборки. Как известно (см. теорему 7.5.2),
несмещенные оценки точнее, если они являются функциями от
достаточных статистик. Следовательно, в случае двукратной
выборки нужно учитывать суммарное число дефектных изделий,
обнаруженных как в первой, так и во второй выборках. Однако
в большинстве работ с использованием планов типа двукратной
выборки либо вообще не ставится вопрос о нахождении таких
оценок, либо, в лучшем случае, дается рекомендация получения
оценок только по результатам первой выборки. Теория несмещен-
несмещенных оценок применительно к задачам приемочного контроля раз-
развивалась пока главным образом усилиями наших ученых-вероятно-
стников (см. [1], [2], [16], [17], [18]). В объемистой книге Коудена
[6], где описанию методов приемочного контроля выделено 11 глав,
не нашлось места для задач получения несмещенных оценок.
Несмещенные оценки. Основные теоремы. Учиты-
Учитывая интересы инженеров-производственников, мы переформулируем
теоремы о несмещенных оценках в случае дискретного про-
пространства исходов опыта. Теоремы 7.5.1 и 7.5.2 приведе-
приведены в статье Колмогорова [1].
Пусть Х={х} — пространство исходов опыта. Точками этого про*
странства являются цепочки из нулей и единиц, вообще говоря,
§ 7.5] ПОСЛЕДУЮЩИЕ ОЦЕНКИ КАЧЕСТВА 439
разной длины я*, х = гъ ..., е„, где 8, = О или 1, если соответ-
соответственно 1-е проверенное изделие оказалось годным или дефектным.
Таким образом, п* можно трактовать как число проверенных из-
п*
делий, а 2 €>i = d* — как число обнаруженных при такой проверке
х=1
дефектных изделий. Как и раньше, через N обозначим объем кон-
контролируемой партии, а через D — число содержащихся в ней дефект-
дефектных изделий. Оценкой называется любая функция h(x)y значения
которой не зависят явно от величины D, когда D неизвестно. Общее
число исходов х конечно. Обозначим через kh число решений уравне-
уравнения h(x) = h. Перенумеруем все точки х парами индексов /г, &,
обозначая x=Xh,ky если h(x) = h, /5=1,..., kh. Так как каждое х
дает какое-то значение h (x)y то все точки х будут перенумерованы.
Обозначим также через phk = phk (D) вероятность того, что исходом
опыта явится значение хн,к- В силу критерия факторизации (см.
главу 1) статистика S (х) является достаточной тогда и только
тогда, когда имеет место факторизация, т. е.
ph,k{D)=p(S(xh9k),D)qh9kf G.5.1)
*л
где qh,k^0 не зависят от D, 2?л»*=1- Оценка ф (xhyk) = yhyk
k = \
называется несмещенной для функции /(D), если для любого
?) = 0, 1, ...,7V Мф (х) =/(D), или, подробнее, если выполняется
*л
2 Фл,*Рд,* =
Это понятие можно обобщить. Если задана случайная величина gt
т. е. функция g(xhyk) = ghk от исходов опыта, то оценка ф (xhyk) =
= <ph,k называется несмещенной для ghiki если их математические
ожидания совпадают, т. е. если для D = 0, 1,...,jV
kh kh
Следующая теорема утверждает, что с помощью достаточной ста-
статистики из одной несмещенной оценки можно построить другую
несмещенную оценку, которую будем называть улучшенной.
Теорема 7.5.1. Если (phyk является несмещенной оценкой
для gfy^ cl h(xh}k) = h — достаточная статистика, то оценка
€нова является несмещенной.
440 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
Доказательство. Используя G.5.3) и G.5.1), имеем
р* = Ъ*нРк V>) = 2 Щ 2 Pk,n {D) -
h к-\
= 22 Ф*,»7А,*Р (А, Я) = 2 Ф
что и требовалось доказать.
Теорема 7. 5. 2. ?"с^« ф а ф* — соответственно несмещен-
несмещенная и улучшенная оценки, то их дисперсии D[<p] и Р[ф*] свя-
связана соотношением
G.5.5.)
из которого следует, что
Доказательство.
М (Ф -Ф*) (Ф* - Щ) = 2(ФА>*- Фл) (Фл - Щ) Phtk(D) =
hk
2(
h,k
= 2(фл — Mg-)pA(A, D) 2 (Фа,* —фл) ?л,л =
так как
2ФЛ,Л ФЛ,А 2Ф
/г= 1 ^ = 1
Таким образом, оценка ф* является более точной в том смыс-
смысле, что ее дисперсия может быть только меньше или равна дисперсии
исходной несмещенной оценки. Если существует единственная
оценка, являющаяся функцией от достаточной статистики, то она
имеет наименьшую дисперсию в классе несмещенных оценок.
Теорема 7.5.2 привлекает наше внимание к достаточным ста-
статистикам, возникающим при проведении контроля партий. Наибо-
Наиболее полный ответ о структуре достаточных статистик дает
Теорема 7.5.3. Пусть п* — номер изделия, проверяемого
последним, a d* — общее число дефектных изделий, обнаружен-
обнаруженных при проверке*, тогда случайный вектор (п*, d*) является
достаточной статистикой.
§ 7.5] ПОСЛЕДУЮЩИЕ ОЦЕНКИ КАЧЕСТВА 44 1
Доказательство *). Мы ограничиваемся только случаем
нерандомизированного правила остановки контроля, т.е. предпо-
предполагаем, что условная вероятность остановки контроля по резуль-
результатам контроля всех предыдущих изделий равна либо нулю,
либо единице, В аналитической форме записи это означает, что
P{/z*= k\ ^...e^} = 0 или 1. Будем также предполагать, что мо-
момент остановки не зависит от будущего, т. е. если Р {п* =
— ^1 8i--e/J — 1» то Для любых значений eft+1, ... п* = п* (sv..eky
ek+v-) — k c вероятностью единица. Пространством исходов опы-
опыта являются цепочки 815...,е^, где Р {#* = k [ ех...е^} = 1. Вероятность
появления цепочки ev..en* равна
G.5.6)
т.е. равна отношению числа всех возможных продолжений этой
цепочки до полной проверки всех N изделий к числу всех воз-
возможных размещений D дефектных изделий по N номерам, соответ-
соответствующим порядку проверки. Сравнивая G.5.6) с G.5.1), находим,
что P(e1...en*)=p(n*,d*,D)q(cv..en*), где
a f(n*,d*) — число цепочек, имеющих длину, равную п* и28/ =
/ = i
Значение q (е1,...,е/г*) выбирается из условия нормировки
Таким образом, из критерия факторизации находим, что (n*yd*)
является достаточной статистикой.
Из доказанной теоремы следует, что вся информация о ходе
контроля содержится в паре чисел: числе п* проверенных изде-
изделий и числе J* обнаруженных дефектных изделий. Эти две ха-
характеристики надо регистрировать в журналах или, что более
удобно для последующей обработки, на перфокартах. Таким об-
образом, пространство исходов опыта сужается до Х= {х}, где
x = (n*9d*).
Примеры. При использовании планов типа однократной вы-
выборки (я, сI3 здесь /z*^/z, d* = d(n). Первая компонента п* — п
не несет информации, так как уже до проведения контроля известно,
*) Доказательство проводится для частного случая, когда точки оста-
остановки образуют монотонно убывающую границу. Однако, используя ту же
идею, его можно провести и в общем случае.
442 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
что ri* = n. Здесь /(/г*, d*) —Cdn. Таким образом, достаточной
статистикой является число d* обнаруженных дефектных изделий.
При использовании плана типа двукратной выборки (^1)C1>/z2)C2I313
достаточной статистикой является d* = d(n1)y если либо c2<id(n1)i
либо din^^c^ где din^ — число дефектных изделий, обнаружен-
обнаруженных в первой выборке, если же с1<С d (n^ ^с2, то достаточной
статистикой является пара {n1-\-n2^d{n1-\-n2)). При использовании
плана (/21,c1,/z2,c2J323 достаточная статистика имеет вид n* = N9
d* = D, если либо d (ях) > с2, либо с1 < d (п^) < с2, но d (nx -\- п2) >
>с2; п* = п1у d* = d(n1), если rf^Xq; n* = n1 + n2i d* =
= */(/*! +л2), если сх< ^(/гх) <с2, но ^(л1 + л2Хс2.
Примеры на построение несмещенных оценок.
Рассмотрим теперь методы построения несмещенных оценок для
различных характеристик в случае использования различных пла-
планов типа однократной выборки. При этом мы используем некото-
некоторые результаты работ А. Н. Колмогорова [1], [16], С. X. Сираж-
динова и М. И. Эйдельнанта [2], [17], а также [7]. Как и в § 7.2,
мы ограничимся рассмотрением планов, в которых по результа-
результатам контроля, принимается одно из трех решений:
Dx — отвергать без дальнейшего контроля оставшуюся непрове-
непроверенной часть продукции,
D2 — провести 100% проверку,
D3 — принять оставшуюся часть партии без дальнейшего
контроля.
В соответствии с этими решениями весь объем партии N и
общее число дефектных изделий D разбиваются на три части,
N=N' + N" + N"\ D=D'+D"+D"\ G.5.8)
где N' — число изделий, отвергнутых без проверки, среди них
содержится D' дефектных, ЛГ' — число проверенных изделий, D" —
— число дефектных изделий, обнаруженных при такой проверке.
ЛГ'' — число изделий, принятых без проверки, D'" — число приня-
принятых дефектных изделий. В случае планов типа однократной выбор-
выборки известны значения ЛГ, N", ЛГ", D", неизвестны D, D', D"'. Цель
настоящего параграфа состоит в выводе формул несмещенных оце-
оценок для D, D' D'". Иногда представляет интерес получение несме-
несмещенных оценок и для более сложных характеристик, например для
априорных вероятностей. По этому вопросу мы отсылаем читателя к
работе М. И. Эйдельнанта и И. Инамова [17]. Полезно заметить,
что при учете результатов сплошной разбраковки, при использо-
использовании решения Ь2, нужно быть уверенным, что разбраковка про-
проводится по тем же правилам, что и разбраковка изделий в выбор-
выборке. Чтобы убедиться в этом, полезно сравнить оценки как с
учетом результатов разбраковки, так и без такого учета.
§ 7.5] ПОСЛЕДУЮЩИЕ ОЦЕНКИ КАЧЕСТВА 443
Для краткости записи будем использовать следующие
обозначения:
с п
пс 'V П nd ттпс
d=0 d=c ^ G.5.9)
с n
Mnc SJ jr>nd nc ^1 , r>nd
nd = 2j dBND, Wwd = 2j dB
d=0 d=c
где В*м?) определяются по формулам G.2.8) или G.2.9).
Изложение начнем с рассмотрения плана типа (#,сJ3. Достаточ-
Достаточная статистика, как это следует из теоремы 7.5.3, имеет вид
TV, rf>c, \ D,
При использовании таких планов существует несмещенная оценка
ф (d*) для любой функции f(D). В соответствии с G.5.2) уравне-
уравнение для несмещенной оценки имеет вид
Ъ ^(d)Nc + p()UNDf(D)J D = 0,l, ...,N. G.5.10)
Подставляя в G.5.10) значения D = 0,l, ..., с и учитывая, что
П^?> = 1, когда D = 0,l, ..., с, получаем с+1 уравнений для
нахождения ф @), ..., ф (с). Эти уравнения имеют вид
(а?) ?&!=/(?), /г = 0, 1, .... с. G.5.11)
Используя эти значения ф (d) из G.5.10), получаем значение
для ф (D):
П(О)-2 9(<0Bj5d1
11 G'5Л2)
Таким образом, несмещенная оценка существует и задается фор-
формулами G.5.11), G.5.12).
В качестве второго примера получим несмещенные оценки, соот-
соответствующие использованию планов типа (я, сI3. Здесь N" = n,
D" = d, D' и D" являются случайными величинами. Представляет
интерес получение несмещенных оценок для D' и D"'. Действи-
Действительно, несмещенная оценка для ТУ" позволяла бы оценить число
принятых дефектных изделий, а оценка для D' — число отвер-
отвергнутых годных изделий, равное N' — D'. Так как D'"=D — d,
для d^c и D"' = 0, если d>c, то MD'" =yi{D — d) b"Jd.
444 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
В соответствии с G.5.3) уравнение для несмещенной оценки
Ф"' Мф"' = IWD"' имеет вид
У Ф'" (d) BnNdD = 2 (D -d) BnNdD. G.5.13)
Однако это уравнение противоречиво, так как не существует та-
такой функции ф (d), которая бы удовлетворяла G.5.13). Это сле-
следует из того факта, что В%о является многочленом /2-й степени
относительно D (см. G.2.8)). Действительно, в правой части G.5.13)
стоит многочлен (л+1)-й степени, тогда как в левой — только
/z-й степени по D.
Несмещенную оценку для D"' можно получить в предельном слу-
случае, когда число d обнаруженных дефектных изделий имеет пуас-
соновское распределение. Условия этого, сформулированные в § 7.2,
состояли в том, что d<^n<<^N, d<^.D<^M. В этих предположе-
предположениях можно считать, что B%d =Pd (^) = зт ?~\ где Х = п(-тт-
Используя очевидное соотношение Kpd (X) = (d-\- \)Pd+1 (X), мы
можем переписать G.5.13) в виде
2 Ф"' (d)/>#) = D^4W=t <я) 2
d=0 k=0 k=0
4s
d— 1
При этом мы использовали условие, что -^-<^1, и опустили чле-
члены вида -jj , полагая их равными нулю. Рассматривая G.5.14)
как тождество по X, находим, приравнивая коэффициенты при
pd(k), стоящие в левой и правой частях G.5.14), что несмещенная
оценка ф'" (d) имеет вид
' 0, d>c+\,
Совсем просто убедиться, используя аналогичные рассуждения,
что несмещенная оценка ф (d) для D имеет вид
?(rf) = ^rf. G.5.16)
Для получения доверительных границ при оценке эффективности
контроля по результатам контроля большого числа партий нам
§ 7.5]
ПОСЛЕДУЮЩИЕ ОЦЕНКИ КАЧЕСТВА
445
будет полезно иметь несмещенные оценки для дисперсии самих
несмещенных оценок ф (d) и ф"' (d). Для дисперсии оценки числа
предъявленных дефектных изделий имеем
Чф]-иф<<0«-<|ц> «/»¦=
Так как несмещенная оценка для К равна d, то несмещенная
оценка (рх (d) для дисперсии D [<р] имеет вид
- G.5.17)
Ф1 W = f ?"
Так как ф'" (й) является несмещенной оценкой для случайной ве-
величины D"', то здесь представляет интерес получение несмещен-
несмещенной оценки для дисперсии D"' — ср"' (d). Предварительно заметим, что
fl?<c,
Г.5.18)
Учитывая G.5.18), находим, что
2
d=0
/N\2 f r c
= (r) U S (d+\)Pd(K)-2k 2
G.5.19)
Уравнение G.5.3) в нашем случае имеет вид
G.5.20)
Подставляя явное выражение G.4.19) правой части в G.5.20) и
приравнивая затем коэффициенты при одинаковых функциях pd (к)у
446 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
находим, что
ф2(d)= _
О,
является несмещенной оценкой для дисперсии D [D"' —ф"' (d)].
Оценка эффективности приемочного контроля.
Воспользуемся полученными несмещенными оценками для выясне-
выяснения эффективности приемочного контроля. Пусть на контроль по-
поступили партии, объемы которых равны Nh i=\, ..., rn\ m^>\.
Для контроля 1-й партии был использован план (п(, с(I3, число
обнаруженных дефектных изделий при этом оказалось равным dt.
Обозначим через D( неизвестное нам число дефектных изделий,
содержащихся в 1-й партии, а через D"',- — число дефектных из-
изделий в принятой части партии. Несмещенными оценками для об-
т
щего числа предъявленных дефектных изделий, равного 2 ^ь и
т
общего числа принятых дефектных изделий, равного У] D"/, бу-
будут в соответствии с G.5.15) и G.5.16) служить
т т
2 ФК) и 2 ф"Ю- G.5.22)
т
Так как 2 Ф №) имеет при больших т распределение, близкое
к нормальному со средним и дисперсией, равными соответственно
™ "L /уу \ 2 f Di\
2) В/ и Jj \~7ГГ) ^/» где ^"/== \ "аГ. / пь т0 с вероятностью, близ-
КОЙ К 1 — С?,
G.5.23)
т / т / дг Го
/ 1 \ °° J1.
где wa —квантиль нормального распределения ( -ш/-<г—' if e 2 dt =
2" \^ ZJI J и а
2
= -о-. Точные значения дисперсии ( —) ^/ нам неизвестны, поэ-
§ 7.5] последующие оценки качества 447
тому, заменяя их оценками G.5.17), получаем, что при больших
т с вероятностью, близкой к 1—а,
т
/
: 2 Ф Щ + и± у Jj Ф1 (</,). G.5.24)
Аналогичные рассуждения можно использовать и при оценке
суммарного числа принятых дефектных изделий. Здесь дисперсия
т т
отклонения 2 ф"' (d() от V D"',- равна сумме членов вида G.5.21).
Заменяя дисперсии D [ф"' (d() — D["\ оценками ф2 (d(), найденными
по формуле G.5.21), получаем, что с вероятностью, близкой к
^ Ю- G.5.25)
Эффективность контроля можно выявить, сравнивая долю qBX
дефектных изделий в предъявленной на контроль продукции с
долей дефектных изделий #ВЬ1Х в принятой продукции. В соответ-
соответствии с оценками G.5.22) имеем
mm mm
S d, 2фК) Sa" 2ф'"Ю
?в> = ^~^ . </вь,х = ^ * '^_ G.5.26)
Ход контроля можно отображать на графике. Примерный вид
графика показан на рис. 7.5.1. По оси ординат отложены номера
партий. По положительной части оси абсцисс отложены значения
к к
оценок 2 Ф №)> а ниже — оценок 2 ф"' №)• Заштрихованные об-
ласти построены с использованием формул G.5.24), G.5.25) для
значений а = 0,1. Вдоль отрицательной части оси пунктиром по-
показаны значения суммарного числа предъявляемых на контроль
k
изделий, равного 2 Nh а точками — значения числа принятых
k
изделий, равного 2 М • Для графического отображения эффек-
448
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
тивности контроля можно также использовать метод скользящего
среднего. При этом методе после получения результатов контроля
k-ft партии учитываются результаты контроля только по М
EDi
Рис. 7.5.1.
предыдущим партиям; число М каждый раз одно и то же. В соответ-
соответствии с формулами G.5.26) после проверки т-й партии вычисля-
вычисляются оценки
т
Am)
Ыт-М 1
т
. G.5.27)
Графики этих оценок показаны на рис. 7.5.2. Верхние и нижние
границы заштрихованных полос получены с использованием в
G.5.27) правых и левых частей неравенств G.5.24) и G.5.25) для
а = 0,1. Значение М не должно быть слишком большим, так как
при больших М снижается оперативность выводов об уменьшении
эффективности контроля. С другой стороны, оно не должно быть
ПОСЛЕДУЮЩИЕ ОЦЕНКИ КАЧЕСТВА
449
§7.5]
и слишком маленьким, так при этом сами оценки будут грубыми.
Все существенным образом зависит от конкретных значений Nh
//., Dh dh учет которых аналитическим путем очень сложен. Пока
для такого подбора М мы рекомендуем метод проб, или метод
статистического моделирования (Монте-Карло).
Несмещенные оценки для планов типа (я, с, с').
Выше рассматривались несмещенные оценки для пуассоновского при-
приближения. Введем теперь формулы для несмещенных оценок в
общем случае использования
планов типа однократной вы- Чеховых
борки. Излагаемые здесь ре-
результаты получены С. X.
Сираждиновым и М. И. Эй-
дельнантом [2]. Предположим,
что используется план типа
однократной выборки с прие-
приемочным числом с и браковоч-
браковочным числом с'^с; будем его
кратко обозначать (я, с, с').
Применение этого плана озна-
означает, что из партии случай- Рис. 7.5.2.
ным образом отбирается п
изделий; если число d = d(n) обнаруженных дефектных изде-
изделий таково, что d^cy то оставшаяся часть партии принимается
без дальнейшего контроля (решение D3), если c<d<c', то при-
принимается решение D2 и, наконец, если d^c\ то принимается
решение Dv Планы такого типа могут найти применение, когда
стоимость контроля сравнительно велика. Их можно рассматривать
как обобщение планов типа (п, с)/;-, рассмотренных в § 7.2. Дей-
Действительно, (п, сI2 = (л, k, k'), если k——1, k' = c; (n, c)ls =
Таблица 7.5.1
Чвых
• т
Число изделий, которые по результатам контроля
отвергаются без дальнейшей
проверки
iV'=|°' d<c>
\N—п, d^zc'
подвергаются 100%
проверке
(n> d<c или fee'
|iV, c<d<c'
(df d^c или flfec'
D = <
(D, c<d<c'
принимаются
без проверки
N" = <
1 0, d>c
( D—d, d<c
D = <
| 0, d > с
•
450 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
= (я, &, &')> если k = c,k' = c+\; (л, сJ3 = (я, k, k'), если & = с, &' =
= л+1. В таблице 7.5.1 приведены сводные данные о значениях
N\ N\ AT, D\ D", D'".
Как следует из теоремы 7.5.3, достаточной статистикой является
выявленное число дефектных изделий D". Наша задача состоит в
выводе формул для несмещенных оценок ф' (D") и ф"' (D") случай-
случайных величин D' и D'". Несмещенную оценку ф (D') для D можно
получить из соотношения
y(D") = y'(D") + D" + y'"(D"). G.5.28)
Несмещенные оценки для D, D', D'", удовлетворяющие G.5.28),
называют согласованными. Так как вывод формул для несмещенных
оценок несложен, то мы проведем его только для ф' (D"). D'—•
случайная величина, математическое ожидание которой равно
ИЮ'= S (D-d)BnNdD.
d=c
Поэтому уравнение G.5.3) имеет вид
Ф' (D") BnNdD = Д (D - d) BnNdD. G.5.29)
Учитывая значение U (по таблице 7.5.1), можно уравнение
G.5.29) записать в виде
(d) BnD + 2 Ф' (D) bnd + 21 ф' M S5& = 2 (? — <*) Д
G.5.30)
ф' (б?) должны удовлетворять этому уравнению при Z) = 0, 1, . . ., TV.
Как следует из формулы G.2.8), правая часть является многочле-
многочленом (/г+1)-й степени по D. Левая часть также будет многочленом
(/г+1)-й степени, если считать, что ф {D) = aD -\-b. Таким образом,
мы можем решить это уравнение, приравнивая коэффициенты при
одинаковых степенях D. Еще проще получить решение, полагая
последовательно D = 0, 1, ..., N. ЕслиС = 0, ...,с, тоВ^о — О,
с, поэтому из G.5.30) получаем, что ф' (d) = 0, d ^ с. Полагая
затем D = N, находим, что ф' (N) = ( -)п; при D = N—1 име-
имеем ф' (ЛГ— 1) = ^=^(Л— 1) и т. д.; при D = N— 2, ..., N — n —
— с'-\-\ ф'(^) = dy если только d^c . Подставляя полученные
§ 7.5] ПОСЛЕДУЮЩИЕ ОЦЕНКИ КАЧЕСТВА
результаты в G.5.30), получаем уравнение
451
) 2
c<d<cr
Из этого уравнения находим, что
W
— Und
Точно так же находятся несмещенная оценка ср'" (D"), а затем,
с использованием формулы G.5.28), и несмещенная оценка ф (D"). По-
Полученные формулы сведены в таблицу 7.5.2.
Таблица 7.5.2
d
d^c
с <d <
d^c'
D"
d
D
d
ф' (D")
0
li/VD ~LiND
N — n.
d
n
ф"'Ф")
d
n
DUnc I 1 Mnc
UnND~- y-^-J MND
LlND ~~liND
0
D
n
Nd
n
Правило проверки (/z + 1 )-г о изделия. Пользоваться
полученными оценками неудобно, так как вычисление функций
Пмо» M!nd представляет значительные трудности. Можно, однако,
используя правило проверки (/z + 1 )-го изделия, предложенное в
работе С. X. Сираждинова и М. И. Эйдельнанта [2], получить весь-
весьма простые формулы для несмещенных оценок. Правило проверки
(#+1)-го изделия при использовании плана типа (п, с, с') состоит
в следующем. По результатам разбраковки п изделий принимают
решение в соответствии с планом (/z, с, с'). Однако если окажется,
что d^ с или d^c\ то производят проверку еще одного (/z+1)-го
изделия. Результаты проверки (/г+1)-го изделия не влияют на при-
принятое ранее решение, но они существенным образом используются
при построении несмещенных оценок. Пусть d' — общее число де-
дефектных изделий с учетом результатов проверки (п -f 1)-го изделия.
Таким образом, d' = d-j- ew+1, где е„+1 = 1, если (п-\- 1)-е изделие
452 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
дефектное, и ел+1 = 0, если оно годное. При использовании прави-
правила проверки (/z-j-l)-ro изделия
0, d<c\ п (п+1, d^c или d^c\
N
N ===\N\ d^\ N I N, c<d<c\
(N-n-\, d^c,
N"f = <
\ 0, d>c.
В соответствии с теоремой 7.5.3 достаточная статистика имеет вид
(D", ЛГ), где
fd\ если c'^d
D" = < или d^c,
[D, если c<C.d<C.cf.
Заметим, что D" = d' = с + 1 только тогда, когда d (п) = с, ew+1 == 1;
соответственно D" = d' = с' только тогда, когда d(n) = c' еп+1 —0.
При выводе формул для несмещенных оценок полезно использо-
использовать тождества
d=0 "^
«+i G.5.31)
Тождества G.5.31) являются следствием простого, легко проверя-
проверяемого тождества
(D-d)B%dD = ^(d+\)BnN+Dud+l. G.5.32)
Числа D', D", D"' при использовании правила проверки (п-\-\)-го
изделия уже отличаются от указанных в таблице 7.5.2. Допуская,
что результаты проверки (я+1)-го изделия не учитываются
(в частности, если ?„+1= 1, то все равно это дефектное изделие вхо-
входит в число принятой продукции), можно найти несмещенные
оценки ф' и ф". Заметим, однако, что фактическое число D"
принятых или D' отвергнутых дефектных изделий будет выра-
выражаться соотношением
/Г = тах@, ?Г—ея + 1), со = ', ;". G.5.33)
Если несмещенная оценка для ?)ш найдена и равна фш, то в соот-
соответствии с G.5.33) в качестве оценки для ?)ш можно использовать
фю = тах[0э Фю-е11+1], ю = ', ". G.5.34)
§ 7.5]
последующие оценки качества
453
Такая оценка, вообще говоря, будет смещенной*), однако сме-
смещение относительно Ш5Ш невелико. Ограничимся выводом формулы
для оценки ф"\ Уравнение Мф'" = MD"' имеет вид
S 2 4>'''(d+zn + 1)BnNdDB^n,D-d+<p'f'(D) 2 BnNdD_
d<c en+1 c<d<C —
dC
с
= ^{D-d)BnNdD. G.5.35)
n Db0 TV—n — (D — d)
Замечая, что ?;v-/z, D-rf = д^г^ :,
D —
]^ = Bnd
и учитывая G.5.31), мы можем переписать G.5.35) в виде
"йТТ^^'ВГо1-"'. G.5.36)
Существует много решений уравнения G.5.36). Естественно пред-
предположить, что q/"(D) = O. При таком допущении решение G.5.36)
легко получить, приравнивая коэффициенты при Вщз"а в левой и
правой частях G.5.36). Окончательный результат задается фор-
формулами
>= ) N—n , d'=d+l=c+l,
0 , d'>c+l.
Из G.5.34) и G.5.37) получаем
G.5.37)
Ф
^d'-l, d'=d+\<c+\y
N—n—\ , d' = d+l = c+l,
0 , d'>c+\.
G.5.38)
Аналогичным образом можно найти выражения для оценок ф', <р'.
) ср10 останется несмещенной при условии D>n.
454
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
Здесь имеем
rf'
N — n
/V —/г
/г + 1
d'— 1, d' = d+\
0 , d'^c'.
G.5.39)
G.5.40)
Несмещенные оценки для планов (/г,с)/у-. Исходя из по-
полученных результатов, дадим набор формул для несмещенных
оценок D, D', D'" при использовании планов типов (/г, c)iJ%
План (л, сI2. Так как (/г, сIа = (/г, k, k'), k =—1, k'=c+ 1,
то из таблицы 7.5.2 находим, что
G.5.41)
(DUnt+Dl-[T)ViND
\N —
d>c.
Вопрос о вычислении оценки ф'" (D") отпадает, так как D'" = 0.
При использовании правила проверки (п + 1)-го изделия из G.5.40)
находим, что оценка для D' имеет вид
О , с
G.5.42)
Можно также, не прибегая к правилу проверки (#+1)-го изде-
изделия, использовать и упрощенную несмещенную оценку
Ф' (d,D) =
N — n
п
d,
G.5.43)
В работе [2] указывается, что эта оценка имеет меньшую точ-
точность, чем оценки G.5.41), G.5.42).
План (/г, сJ3. Для планов этого типа D' = 0, поэтому пред-
представляет интерес только получение несмещенной оценки для D'".
Замечая, что (пу cJS = {ny k, k')} k = c, A;=/z + l, из формул
§ 7.5] ПОСЛЕДУЮЩИЕ ОЦЕНКИ КАЧЕСТВА
таблицы 7.5.2 находим, что
N — n,
n
ni ND-
.—M
ND
., d>c.
45Г>
G.5.44)
При использовании правила проверки (я+1)-го изделия из G.5.38)
находим, что оценка для D'" имеет вид
'N—nJt
G.5.45>
d'— 1, d'=d+\<c+l,
n+l
N — n
n+l
N — n — 1 , d'=d+l =c+lf
0 , d'>c+l.
Здесь также существует менее точная несмещенная оценка
G.5.46)
id~D .
План (/z, cI3. При использовании планов типа (я, сI3 100%
разбраковка не производится. Это резко уменьшает информацию-
о засоренности партий дефектными изделиями. Вообще можно по-
показать, что при использовании плана (п, сI3 несмещенных оценок
для ?)' и D'" не существует. Однако здесь с успехом можно
использовать правило проверки (/z+l)-ro изделия. Выражения для
оценок Z)', ?>"', полученные аналогично выводу формул G.5.38)>
G.5.40), приводятся ниже:
о,
N—n
п+1
N—n
я+1
d'—
d'
I, d'
G.5.47>
N — n
N—n
n+l
N—n—1, d' = i
0, d'>c+\.
d'— 1,
G.5.48)
456 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
Построение несмещенных оценок для планов
типа двукратной выборки. В заключение параграфа рас-
рассмотрим некоторые соображения, связанные с построением несме-
несмещенных оценок для случая использования планов типа двукратной
выборки. В американской литературе по вопросам надежности [19]
неоднократно встречаются указания, что несмещенные оценки
для D надо строить по первой выборке. Такие рекомендации,
по-видимому, связаны с простотой формулы G.5.16), по которой
вычисляется эта оценка. Однако достаточная статистика не совпа-
совпадает с числом d дефектных изделий, обнаруженных в первой вы-
выборке. В том случае, когда объем проверяемой продукции невелик,
желательно для получения более точных оценок учитывать ре-
результаты проверки второй выборки. К сожалению, до настоящего
времени вопросы построения несмещенных оценок для случаев
использования планов типа двукратной выборки еще не иссле-
исследованы. Соответственно нет и оценок величин выигрыша в точ-
точности при более полном использовании информации о результатах
разбраковки. По-видимому, одной из причин такого застоя явля-
является сложность получения соответствующих формул. С точки зре-
зрения методов никаких трудностей принципиального характера не
возникает. Вывод соответствующих формул можно проводить
вполне аналогично тому, как это делалось выше. Для примера
мы ограничимся только случаем использования плана типа дву-
двукратной выборки (#i#2cic2)i3i3- Достаточная статистика (jV", D")
имеет вид
/ 1> ^1>С2 ИЛИ <*1<<Ч,
или d1
где d{—число дефектных изделий, обнаруженных в / = Й выборке.
Аналогичные соотношения можно выписать для N'y AT", D', D"'.
В соответствии с G.5.2) и G.5.3) формулы для несмещенных оце-
оценок имеют вид
Mcp=D, M<p' = MD', M(p'" = MD"\ G.5.49)
Если искать несмещенные оценки в классе функций, зависящих
только от N" и D", т.е. от числа проверенных и числа обнару-
обнаруженных дефектных изделий, то для несмещенной оценки ф, рас-
расписывая более подробно левую формулу G.5.49), имеем
2 Ф№> !)??# +
+ 2 2ф(^ + ^2, 2)В&&В&1"пио-ь=*О. G.5.50)
d1=ct + 1 </2 = 0
§ 7.5] ПОСЛЕДУЮЩИЕ ОЦЕНКИ КАЧЕСТВА 457
Здесь ф(d, 1) соответствует случаю, когда проверялась только
первая выборка, а ф (d, 2) — когда проверялись две выборки. Это
соотношение должно быть справедливым при любом D = 0, 1 ,..., N.
Левая часть является многочленом (п1-\-п2)-& степени по D, а пра-
правая часть равна D, поэтому можно, приравнивая коэффициенты
при одинаковых степенях D в левой и правой частях G.5.3), сос-
составить п1-\-п2-{-\ уравнений для нахождения такого же количест-
количества неизвестных ф (d, 1) и ф (d, 2). Число значений ф (d, 1) равна
#i — (С2 — ci)+l> a число ф(я?, 2) равно п2-\-(с2 — сг). Заметим,
что для решения G.4.50) проще использовать прием подбора
частных значений D. Полагая сначала D — 0> ..., с, а затем D = Nr
N—\9 ..., А/^— (/гх — с2) + 1, мы найдем все значения ф (d, 1):
или dL = d>c2. G.5.51)
Значения ф (d, 2) можно после этого найти, подставляя в G.5.50)
значения D = c1+1, ct + 2, ... Полученная система уравнений име-
имеет треугольную матрицу коэффицентов при неизвестных ф (d, 2)y
d=cx-\-\, ... , л2 + (с2 — сх). Это позволяет алгоритмизировать
процесс вычислений, последовательно находя значения ф (d, 2).
Если пойти тем же путем для построения несмещенных оце-
оценок ф'(</, i) и (p'"(dy i), то левую часть Alkp'^MD', Щ'" =:tAD'"
надо записать аналогично G.5.50), а в правой части вместо D
поставить
G.5.52)
fHDf и MD"\ как это следует из G.2.8) и формул G.5.52), G.5.53),
являются многочленами (пг-\-п2-\- \)~й степени по D, тогда как
Мф7 и Мф"' суть многочлены степени пх-\-п2 по D. Таким обра-
образом, второе и третье уравнения G.5.49) не имеют решений, не-
независимых от D и удовлетворяющих им при любых значениях
?)=з0,1,...,ЛЛ Противоречивость уравнений приводит к необходимо-
необходимости повысить на единицу степень многочленов, выражающих Мф'
и Мф'". Этого можно достичь разными способами. Одним из эконо-
экономичных способов является правило проверки (п1 + п2+ 1)-го из-
изделия. Применительно к плану («1/22с1с2I313 эт0 правило означает>
458
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
что решение принимается так, как если бы испытания проводились
в соответствии с планом (/21/г2с1с2I313. Однако, когда c1<C.d^c2y
после проверки второй выборки и принятия соответствующего
решения проверяется еще одно изделие, (/г1-(-/22+1)-е. Под-
Подчеркиваем, что результаты проверки (п1 + п2+1)-го изделия не
влияют на принятое ранее решение.
Будем записывать е = 0, если (пг-\- п2 + \)-е изделие годное, и
е=1, если оно дефектное. Из теоремы 7.5.3 следует, что доста-
достаd d
точной статистикой является (dlt
(d+d +
если
у
1, или d1^tc1
l Д 1
+ п2+ 1), если сг <d1<c2. Поскольку величины п1
и п2 нам известны до начала проверки, то эквивалентным выраже-
выражением будет пара (d1 + d2+e, 2), если c^dj^Cg, и пара (dly 1)
в противоположном случае. Значения величин D' и D"', соответ-
соответствующие случаю использования правила проверки (п1 + п2-\- 1)-го
изделия, приведены в таблице 7.5.3.
Таблица 7.5.3
dx
dl<icl
сх < dx < с2
d!+d2<:C2
cL < dj ^ c2
d1-}-d2> c2
dL>c2
D'
0
0
^-(di + di + e)
D — dx
Ь"
D—di
D-(d1 + d2 + z)
0
0
В соответствии со значениями таблицы 7.5.3 правые части урав-
уравнений |?!ф/ = МО/ и Мф'" = М?>'" имеют вид
'= 23 {D-dx)B№
rf1
S 2 [0—(d!
2=c—rft+1 8=0,1
X BX/d1 B^i2», o-rf, В (s), G.5.54)
2 S
6 = 0,1
nNt2
X B^d1 BnNt2nxt D-dx В (е),
где В (е) = В^_(„1 + ^2) ^_^1+^2). Левые части уравнений
и Мф//; = MD'" в соответствии с правилом проверки (я1 +
G.5.55)
/ = М/^/
2+ 1)-го
§ 7.6] введение в задачи текущего контроля 459
изделия записываются в виде
мфш= 2 фЖ, 1)в## +
dtKCi, dx>c2
+ 2 2 2 Фш Wi + 4 + е, 2) В## Д#Д. D_rfl Б (е), G.5.56)
dt^Ct+X d2 = 0 8 = 0,1
где со = ' или со = '" в зависимости от того, какая несмещенная
оценка отыскивается. Теперь уже левая и правая части уравнений,
полученных приравниванием G.5.54) и G.5.55) к G.5.56), являются
многочленами степени пг + п2 + 1. Эти уравнения можно разрешать
относительно неизвестных точно так же, как это делалось для случая
использования однократной выборки. Рекомендуем, как и при ре-
решении G.5.50), сначала найти значения фш (d, 1); если значения
фш найдены, то, используя соотношения G.5.53) и G.5.34), можно
построить оценки фш, имеющие небольшие смещения относи-
относительно Z)w.
Из приведенных примеров видно, что возникающие трудности
получения различных оценок в случаях планов типа двукратной вы-
выборки носят вычислительный характер. Можно составить программы
для получения несмещенных оценок на электронных вычислитель-
вычислительных машинах. Следует иметь в виду, что уже в ближайшее деся-
десятилетие вычислительные машины будут помогать управлять произ-
производством на многих крупных предприятиях. Как частный пример
такой помощи можно рассматривать вычисление эффективности
приемочного контроля. Один раз составив (или получив от дру-
другой организации) программу обработки результатов контроля пар-
партий, можно будет получать сводки о ходе контроля, оперативно
перестраивая его в зависимости от ухудшения или улучшения ка-
качества и изменения требований заказчика.
§ 7.6. Введение в задачи текущего контроля
Общие положения. Все предыдущие параграфы этой гла-
главы были посвящены вопросам приемочного контроля с альтернатив-
альтернативным делением изделий на годные и дефектные. Это, конечно, не
означает, что приемочный контроль играет ведущую роль в стати-
статистических методах контроля качества, а объясняется большей ос-
осведомленностью авторов в вопросах приемочного контроля. К на-
настоящему времени вышло несколько книг, в которых подробно раз-
разбираются вопросы текущего контроля (см. [3], [20]). Очень полно,
с изложением деталей и числовыми примерами, вопросы текуще-
текущего контроля рассматриваются в 17 главах книги Коудена [6].
Уделив в настоящем издании этим вопросам только один параграф,
460
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
мы излагаем их в более широком плане, чем это делается в кни-
книге Коудена.
В отличие от приемочного контроля, где определяется степень
пригодности для использования уже готовых партий продук-
продукции, текущий контроль должен обеспечить нормальный отла-
отлаженный ход технологического процесса. Таким образом, теку-
текущий контроль надо рассматривать как систему правил, обес-
обеспечивающих быстрое выявление недопустимых отклонений качест-
качества производимой продукции. Текущий контроль проводится на
I
no
700
S0\
:
140 W 160 ПО 780 ISO 200 270 220 а:
Рис. 7.6.1.
контрольных постах (КП), либо с помощью автоматизирован-
автоматизированных устройств, либо путем непосредственного измерении. Таких
КП * организуется несколько. Они ставятся после наиболее от-
ответственных операций, результаты которых играют решающую роль
-в обеспечении качества. Поскольку нужно своевременно выявить
возникшие отклонения от нормального хода процесса, то желатель-
желательно использовать всю информацию, полученную в результате из-
измерений. В силу этого контроль по количественному признаку иг-
играет доминирующую роль в методах текущего контроля. Объемы
выборок здесь, как правило, значительно меньше, чем при проведе-
проведении приемочного контроля. Ниже будут даны другие причины, при-
приводящие к целесообразности использования количественных резуль-
результатов измерений. Важной фазой разработки правил текущего контро-
контроля является выбор измеряемых параметров. Объем измеряемых па-
параметров ограничивается экономической целесообразностью. Сле-
§ 7.6]
ВВЕДЕНИЕ В ЗАДАЧИ ТЕКУЩЕГО КОНТРОЛЯ
461
дует также учитывать и возможную взаимную зависимость изме-
измеряемых параметров, что также может привести к уменьшению не-
необходимого объема измерений. На рис. 7.6.1 показаны результаты
измерений 118 образцов отожженной стали. По оси х отложены
значения твердости, выраженные в кг/см2, а по оси у — сопро-
сопротивление на разрыв. Этот рисунок взят из книги Коудена (стр. 375).
Измерения на твердость проще и не разрушают изделий. Ввиду
большой корреляции можно уменьшить объем испытаний на разрыв,
О 5 10 15 20 25 SO S5
Рис. 7.6.2.
4S SO 55
заменив их испытаниями на твердость. Выявление таких зависи-
зависимостей представляет особую ценность в тех случаях, когда измере-
измерения одного из параметров стоят значительно дороже, чем измерения
другого коррелированного с ним параметра.
Если уже решено, какие параметры надо измерять, то ча-
чаще всего текущий контроль проводится по следующей схеме.
Из каждых TV выпущенных изделий отбирают /zD~-20) изделий. Пусть
xkii • • • ">xkn — численные значения измеряемого параметра в ?-й вы-
выборке. По этим результатам вычисляют среднее xk = (xkl-\- . . . -j-
+ xkn)/n и размах Rk = xk(o—xkJO, где хш - max xki, xkJ0 = minxki.
Значения xk и Rk наносятся на соответствующие контрольные кар-
карты средних и размахов. На рис. 7.6.2, взятом также из книги
Коудена, показаны результаты измерений 35 выборок на сопротив-
сопротивление разрыву хлопчатобумажной ткани. Пунктирные линии ВКП и
НКП соответствуют так называемым верхним и нижним контрольным
пределам. Выход хотя бы одного из значений xk и Rk за контроль-
контрольные пределы является сигналом к проверке нормальности хода
технологического процесса. Отчетливо видна тенденция уменьше-
уменьшения средних значений в выборках с номерами 30 — 35. Исследо-
Исследование показало, что причиной уменьшения сопротивления на раз-
разрыв явилось ухудшение качества начальной смеси. О других мето-
методах использования контрольных карт см. [21], [22].
Необходимость исследования разладок нор-
нормального производства. Исследование статистических
свойств параметров может оказать существенное влияние на выбор
462
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
методов проведения текущего контроля. Оно может оказаться по-
полезным и при уже выбранной методике, подобной только что опи-
описанной схеме двух контрольных карт. Особое внимание при этом
надо обратить на выделение наиболее характерных видов нежела-
нежелательных изменений статистических свойств параметров — разладок.
Как правило, при нормальном ходе производства результаты изме-
измерений параметров большого количества изделий имеют гистограммы,
аналогичные приведенной на рис. 7.6.3. На этом рисунке постро-
построена гистограмма значений величины сопротивлений в омах. Для
г-ГЪ
а\
\Ъ
Рис. 7.6.3.
*-Rom
гистограммы характерно наличие большой группы элементов, имею-
имеющих значения, лежащие в пределах интервала (а, Ь). Эта группа
элементов характеризуется таким разбросом значений параметров,
для которого можно предположить наличие плотности вероятностей,
задаваемой определенной статистической зависимостью вида f(x, 0),
где 6 — параметр, характеризующий плотность. Число изделий, имею-
имеющих значения параметров вне интервала (а, Ь), невелико по
сравнению со всем количеством проверенных изделий. А. А. Ступа-
ченко группу изделий, имеющих распределение f(x, 0), называет
«здоровой» частью продукции. Большие отклонения значений
параметров связаны, как правило, с наличием дефектов или, что
бывает реже, вызваны неудачной комбинацией многих исходных па-
параметров, определяющих в итоге значение измеряемого парамет-
параметра. При стабильном ходе технологического процесса вид и значе-
значения параметров 0, определяющих плотность вероятностей /(х, 6)
«здоровой» части продукции', меняются несущественно. Такое до-
допущение об устойчивости f(x, 6) выполняется уже значительно
реже для элементов, имеющих большие отклонения этих параметров.
Таким образом, нельзя считать, что большие отклонения парамет-
параметров происходят в соответствии с определенным распределением
§ 7.61
ВВЕДЕНИЕ В ЗАДАЧИ ТЕКУЩЕГО КОНТРОЛЯ
463
вероятностей, не меняющим своего вида с течением времени. Трудно
ожидать статистической устойчивости больших отклонений пара-
параметров, так как причины, вызывающие эти отклонения, могут быть
весьма специфичны.
Очень часто, но, конечно, не всегда, «здоровая» часть продукции
имеет распределение, близкое к нормальному или логарифмически
нормальному распределению. Однако могут встретиться случаи,
когда распределение «здоровой» части продукции многовершинное.
Многовершинность может получиться в результате смешивания
ff* a
в)
ъ дь
Рис 7.6.4.
исходной продукции от двух технологических цепочек, имеющих
различные режимы работы. Исходя из вида гистограммы, показан-
показанной на рис. 7.6.3, разладки можно разбить в первом приближе-
приближении на три группы. На рис. 7.6.4, а показан идеализированный
случай, когда технологический процесс отлажен и значения пара-
параметров «здоровой» части продукции, характеризующих качество,
лежат в пределах интервала допусков (g*H, g-B). Изделий, имеющих
большие отклонения параметров, нет. Разладка типа I состоит
в том, что распределение «здоровой» части продукции настолько
сильно смещается в сторону одной из границ поля допуска, что
значительная часть изделий имеет значения параметров, лежащие
вблизи границы допуска или даже превышающие ее (рис. 7.6.4, б).
При наличии разладки типа I плотность вероятностей распре-
распределения значений параметров имеет тот же аналитический вид
(, Э'), но 0'=^9. Разладка типа II характеризуется резким воз-
464 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
растанием разброса значений измеряемых параметров, когда зна-
значительная часть элементов имеет значения, либо выходящие за
пределы интервала допусков (g*H, gB)y либо лежащие вблизи его
границ. График плотности вероятностей f(x, 6") в случае разладки
типа II показан на рис. 7.6.4, в.
Наконец, на рис. 7.6.4, г показан график плотности/(х) для рас-
распределения вероятностей в случае разладок типа III. Здесь вид плот-
плотности распределения здоровой части продукции примерно тот же,
что и в идеализированном случае, показанном на рис. 7.6.4, а.
Однако здесь резко возрастает число изделий, имеющих большие
отклонения значений параметров. Если обозначить через pt число
таких элементов, а через gf(x) — плотность вероятностей их распреде-
распределения, соответствующую времени выпуска /, то общая плотность веро-
вероятностей представится в виде суперпозиции /(jt) = (l —pt) f(xfi)-\-
+ ptgt(x). На практике эти разладки могут встретиться в раз-
различных комбинациях. Например, возможно, что нарушения нормаль-
нормального хода технологического процесса приведут к одновременному
появлению разладок типа II и типа III и т.п. Возможны и другие
принципиально отличные типы разладок. Выяснение типов разладок
необходимо для построения математической теории, дающей рацио-
рациональные решающие правила остановки технологического процесса
на подналадку. На языке терминов проверки статистических гипотез
такое выяснение эквивалентно описанию конкурирующих гипотез
для исходной гипотезы, соответствующей нормальному ходу про-
производства.
Проведенный выше анализ типов разладок позволяет заключить,
что в общем случае необходим текущий контроль как по коли-
количественным, так и по качественным признакам. Учитывая числен-
численные значения замеряемых параметров, можно более оперативно
измерять отклонения в «здоровой» части продукции, тогда как
для учета числа изделий, имеющих большие отклонения, надо
использовать непараметрические методы. Например, целесообразно
учитывать только число изделий, имеющих большие отклонения
от параметров изделий, входящих в группу «здоровой» про-
продукции. Трудность использования параметрических методов для
оценки числа изделий, имеющих большие отклонения, обусловлена
тем, что вид плотности gt{x) может очень сильно и самым непред-
непредвиденным образом меняться с течением времени t. Если это не так,
то и здесь можно использовать более полную информацию о чис-
численных значениях параметров изделий, когда эти параметры имеют
большие отклонения.
Характеристики планов текущего контроля.
Связь с теорией управляемых процессов. После выяс-
выяснения статистической структуры параметров, характеризующих ка-
качество при нормальном ходе производства и наличии разладок
§7.6]
ВВЕДЕНИЕ В ЗАДАЧИ ТЕКУЩЕГО КОНТРОЛЯ
465
на участке А технологического процесса, разрабатывается алго-
алгоритм обработки данных об измерениях. В результате обработки
либо принимается решение об определенном виде подрегулировки
процесса, либо подается сигнал об остановке работ на участке А.
После этого выясняются и устраняются причины, вызвавшие ухуд-
ухудшение качества. Вычисления в соответствии с алгоритмом либо
проводятся вручную, либо строится оптимизатор Б, в который
поступает информация о качестве продукции на выходе участка А.
Оптимизатор либо воздействует на параметры технологического
процесса, либо подает сигнал для аварийной остановки (рис. 7.6.5),
Вход* А
_ Сигнал Г
подрегулиробпи Т
Выход
Разладка
\Информация
\окачестве
J--1
| Сигнал аварийной
остановки
Рис. 7.6.5.
Рис. 7.6.6.
Если остановка технологического процесса стоит больших средств,
то в алгоритм целесообразно включить переход с облегченного
контроля на более жесткий для получения более достоверного ре-
решения об остановке. Переход на более жесткий контроль, напри-
например, может означать увеличение объема выборки п.
Если исходить из типов разладок, показанных на рис. 7.6.4,
то в каждый момент времени t качество выпускаемых изделий ха-
характеризуется значениями параметров 6t и pt. Эти параметры меня-
меняются со временем. Из экономических или иных соображений выби-
выбирается область С допустимых значений параметров 0, р (рис. 7.6.6).
С этой точки зрения разладка наступает тогда, когда значения
параметров 0t, pt выходят за границу области G. О значениях па-
параметров 0j, pt мы можем судить лишь по результатам измерений
параметров изделий. Таким образом, информация о значениях 0^ и
pt является неполной. При таком подходе явственно выступает
связь задач текущего контроля с рождающейся сейчас теорией
управления случайными процессами по неполным данным. Мы обра-
обращаем внимание на вышедшие недавно работы Чернова [22] и Ши-
Ширяева [23].
О степени пригодности решающих правил, в соответствии с ко-
которыми принимается решение об остановке процесса на подналадку,
16 Б. В. Гнеденко и др.
466
СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
[гл. 7
можно судить по значениям оперативных характеристик и функций
оперативности. Оперативной характеристикой плана текущего
контроля называют функцию P(t)=.P(t, О, р), равную вероят-
вероятности принять до момента t решение об остановке процесса на
подналадку, если 0^=0, р^ = 0 для 0 <s < t. Функцией опе-
оперативности назовем среднее время 7=7@, р), необходимое
для принятия решения об остановке процесса на подналадку, ког-
когда 05 = 0, ps = p, O^s^t. Функция P(t) зависит от трех пере-
переменных t, 0, р, поэтому встает вопрос о наиболее целесообразном
численном или графическом ее задании. Наибольший интерес
Р 4
Рис. 7.6.7.
представляют значения tg = t(Q, p, q), для которых P(tq,Q, p)=^q.
Задавшись значением #( = 0,9 или 0,1), можно на плоскости
значений параметров 0, р для определенного набора времен
<1<*2<*8<-" нанести линии t(p, 0, q) = th Для значений пара-
параметров 0, р, лежащих на линии, соответствующей tk, вероятность
остановки процесса на подналадку за время t^tk равна q. Ана-
Аналогичным образом можно на плоскости значений @, р) нанести
линии 7@, p) = Th 71<72<...<7Л<... Примерный вид полу-
полученных графиков показан на рис. 7.6.7, а, б. Если взять точку
Qo^fio* A))€ О, то из рис. 7.6.7, а видно, что для обнаружения
такой разладки с вероятностью 0,9 требуется время, большее t±J
но меньшее /2. Если же процесс имеет параметры Q1 = @1> рг) ? О,
т.е. разладки нет, то из рис. 7.5.7, б находим, что среднее вре-
время до остановки процесса на подналадку 72 < 7@Х, рх)< 73.
В данном случае Т(ръ 0Х) является средним временем до ложной
тревоги. Если же значения параметров 0, р лежат вне области G,
то T(Q,p) — среднее время запаздывания в обнаружении разладки.
Пример на вычисление характеристик плана те-
текущего контроля. В заключение параграфа рассмотрим част-
частный пример на вычисление оперативной характеристики и функции
оперативности. Предположим, что из каждых N изделий отбира-
отбираются п изделий, для которых производятся измерения параметра
х, характеризующего качество. Пусть статистическое исследование
§ 7.6] ВВЕДЕНИЕ В ЗАДАЧИ ТЕКУЩЕГО КОНТРОЛЯ 467
показало, что могут иметь место только разладки типов I и II
(pt = 0) и что плотность вероятностей/^, 0)= —~г= е 2а* , где
Э = (A?а2). Область G допустимых значений параметра 8 описыва-
описывается неравенствами \ia<i\x<Cl^B, 0<сг2<а2. Пусть в результате
проверки k-Pi выборки получены значения параметров xkl ,...,xkn.
Несмещенными оценками для (i и а2 являются xk и s\:
Хь = ~Г
G.6.1)
Решение об остановке процесса на подналадку производится сле-
следующим образом. Задаем контрольные пределы ую уъ для х и z\
9J011
3 4 5 6 7 8910111213
Рис. 7.6.8.
для s2. Процесс останавливается на подналадку, когда нарушает-
нарушается хотя бы одно из неравенств
Уп<~*к<Ую 0<s2<Zb. G.6.2)
Для наглядности результаты измерений наносятся на контрольные
карты среднего и эмпирической дисперсии. Вид контрольных карт
показан на рис. 7.6.8. При таком узком подходе задача состоит
в обоснованном выборе значений контрольных пределов уя, ую z*
и объема выборки п. Для этого необходимо знать оперативную
характеристику и функцию оперативности.
Так как xk имеет нормальное распределение со средним \х и
дисперсией —, когда 0 = (|ы,о2), то
Pi
dt.
G.6.3)
где Лн =
^п , Ав =
Ув~~^]/"п
]/"п . Из леммы Фишера получаем,
16*
468 СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ [ГЛ. 7
что s п~ имеет распределение %2 с {п— 1)-й степенью свободы.
Поэтому
П—\ ^ /2-3 t
2 е VG.6.4)
Учитывая взаимную независимость статистик х и s2, находим, что
вероятность р ([л, а2) одновременного выполнения неравенств G.5.2)
Р (Ц, о) = Pl (\i} о2)р2 (fx, a2), G.6.5)
где р1э р2 определяются по формулам G.6.3), G.6.4). Результа-
Результаты измерений оценок xky s* взаимно независимы от выборки к
выборке, так что номер v выборки, по результатам измерений
которой принимается решение об остановке на подналадку, есть
случайная величина, имеющая геометрическое распределение:
Р {v = к] = [1-р (Ц,а2)]р Ох.а8)*, А=1, 2,... G.6.6)
Здесь, конечно, предполагается, что во всех выборках |х и а2 одина-
одинаковы. Если измерения производятся через одинаковое время Sy то
функция оперативности
7(|i, o) = SMv = S[\-p([iyo2)]-1. G.6.7)
Соответственно для оперативной характеристики
Р С, Р, о) = Р {vS<*} = I -pk (|х,ая), G.6.8)
где k= \-q\, [a] — целая часть числа а. Значения контрольных пре-
пределов ую ув и величины объема выборки выбираются из условий
min Г(ц, а) > 7\, max Г(|г, а2) < Г2, G.6.9)
где Gt S G, т. е. часть допустимой области, a G2 zd G. Можно вы-
выписать аналогичные требования, наложенные на оперативные ха-
характеристики и задающие для точек (fi,a2) g G вероятности лож-
ложных тревог, а для точек (fx,a2) ? G—вероятности пропуска разла-
разладок за выбранное время t. Значения Т^ t и Gx, G2 можно выбирать
с учетом экономических соображений.
ПРИЛОЖЕНИЯ
\енко к АР-
Таблица 1
Значения функции у = е"
X
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1.1
1,2
1,3
1.4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
0
1,0000
0,9048
8187
7408
6703
6065
5488
4966
4493
4066
0,3679
3329
3012
2725
2466
2231
2019
1827
1653
1496
0,1353
1225
1108
1
0,9900
8958
8106
7334
6636
6005
5433
4916
4449
4025
0,3642
3296
2982
2698
2441
2209
1999
1809
1636
1481
0,1340
1212
1097
2
0,9802
8869
8025
7261
6570
5945
5379
4867
4404
3985
0,3606
3263
2952
2671
2417
2187
1979
1791
1620
1466
0,1327
1200
1086
3
0,9704
8781
7945
7189
6505
5886
5326
4819
4360
3945
0,3570
3230
2923
2645
2393
2165
1959
1773
1604
1451
0,1313
1188
1075
4
0,9608
8694
7866
7118
6440
5827
5273
4771
4317
3906
0,3534
3198
2894
2618
2369
2144
1940
1755
1588
1437
0,1200
1177
1065
5
0,9512
8607
7788
7047
6376
5769
5220
4724
4274
3867
0,3499
3166
2865
2592
2346
2123
1920
1738
1572
1423
0,1287
1165
1054
б
0,9418
8521
7710
6977
6313
5712
5168
4677
4232
3829
0,3465
3135
2836
2567
2322
2101
1901
1720
1557
1409
0,1275
1153
1043
7
0,9324
8437
7634
6907
6250
5655
5117
4630
4189
3791
0,3430
3104
2808
2541
2299
2080
1882
1703
1541
1395
0,1262
1142
1033
8
0,9231
8353
7558
6839
6188
5599
5066
4584
4148
3753
0,3396
3073
2780
2516
2276
2060
1864
1686
1526
1381
0,1249
ИЗО
1023
9
0,9139
8270
7483
6771
6126
5543
5016
4538
4107
3716
0,3362
3042
2753
2491
2254
2039
1845
1670
1511
1С67
0,1237
1119
1013
¦о
о
X
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
0
0,1003
0907
0821
0743
0672
0608
0550
0,0498
0450
0408
0369
0334
0302
0273
0247
0224
0202
0,0183
0166
0150
0136
0123
0111
0101
l
0,0993
0898
0813
0735
0665
0602
0545
0,0493
0446
0404
0365
0330
0299
0271
0245
0221
0200
0,0181
0164
0148
0134
0122
ОНО
0100
2
0,0983
0889
0805
0728
0659
0596
0539
0,0488
0442
0400
0362
0327
0296
0268
0242
0219
0198
0,0180
0162
0147
0133
0120
0109
0099
3
0,0973
0880
0797
0721
0652
0590
0534
0,0483
0437
0396
0358
0324
0293
0265
0240
0217
0196
0,0178
0161
0146
С132
0119
0108
0098
4
0,0963
0872
0789
0714
0646
0584
0529
0,0478
0433
0392
0354
0321
0290
0263
0238
0215
0194
0,0176
0159
0144
0130
0118
0107
0097
5
0,0954
0863
0781
0707
0639
0578
0523
0,0474
0429
0388
0351
0317
0287
0260
0235
0213
0193
0,0174
0158
0143
0129
0117
0106
0096
6
0,0944
0854
0773
0700
0633
0573
0518
0,0469
0424
0384
0347
0314
0284
0257
0233
0211
0191
0,0172
0156
0141
0128
0116
0105
0095
П р о д о j
7
0,0935
0846
0765
0693
0627
0567
0513
0,0464
0420
0380
0344
0311
0282
0255
0231
0209
0189
0,0171
0155
0140
0127
0114
0104
0094
i же н и е
8
0,0926
0837
0758
0686
0620
0561
0508
0,0460
0416
0376
0340
0308
0279
0252
0228
0207
0187
0,0169
0153
0138
0125
0113
0103
0093
табл. 1
9
0,0916
0829
0750
0679
0614
0556
0503
0,0455
0412
0373
0337
0305
0276
0250
0226
0204
0185
0,0167
0151
0137
0124
0112
0102
0092
К
X
4,7
4,8
4,9
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6,0
6,2
6,4
6,6
6,8
0
0,0091
0082
0074
0,0067
0061
0055
0050
0045
0041
0037
0033
0030
0027
0,0025
0020
0017
0014
ООП
0,0090
0081
0074
0,0Э67
0060
0055
0049
0045
0041
0037
0033
0030
0027
0,0025
0020
0016
0013
ООН
2
0,0089
0081
0073
0,0066
0060
0054
0049
0044
0040
0036
0033
0030
0027
0,0024
0020
0016
0013
ООН
3
0,0088
0080
0072
0,0065
0059
0054
0048
0044
0040
0036
0032
0029
0027
0,0024
0020
0016
0013
ООП
4
0,0087
0079
0072
0,0065
0059
0053
0048
0043
0039
0036
0032
0029
0026
0,0024
0019
0016
0013
ООН
5
0,0086
0078
0071
0,0064
0058
0052
0047
0043
0039
0035
0032
0029
0026
0,0024
0019
0016
0013
0010
6
0,0085
0078
0070
0,0063
0057
0052
0047
0043
0038
0034
0031
0029
0026
0,С023
0019
0016
0013
0010
Продолжение
7
0,0085
0077
0069
0,0063
0057
0051
0046
0042
0038
0034
0031
0028
0026
0,0023
0019
0015
0013
0010
8
0,0084
0076
0069
0,0062
0056
0051
0046
0042
0038
0034
0031
0028
0025
0,0023
0019
0015
0013
0010
табл. 1
9
0,0083
0075
0068
0,0062
0056
0050
0046
0041
0037
0034
0031
0028
0025
0,0023
0019
0015
0012
0010
а
-о
к
О
Таблица 2
Значения функции у =:
X ^v
0,00010
0,00016
0,00025
0,00040
0,00063
0,00100
0,00160
0,00250
0,00400
0,00630
0,01000
0,01600
0,02500
0,04000
0,06300
0,10000
0,16000
0,25000
0,40000
0,63000
1,00000
1,60000
2,50000
4,00000
0,1
0,3981
0,4173
0,4365
0,4575
0,4785
0,5011
0,5252
0,5494
0,5758
0,6023
0,6306
0,6610
0,6914
0,7247
0,7588
0,7945
0,8328
0,8702
0,9121
0,9550
1,0000
1,0481
1,0964
1,1491
0.2
0,1585
0,1741
0,1903
0,2091
0,2290
0,2513
0,2761
0,3018
0,3315
0,3631
0,3981
0,4374
0,4781
0,5252
0,5752
0,5945
0,6935
0,7580
0,8328
0,9121
1,0000
1,0986
1,2008
1,3192
0,3
0,0631
0,0726
0,0831
0,0956
0,1096
0,1259
0,1450
0,1658
0,1909
0,2187
0,2511
0,2891
0,3305
0,3810
0,4360
0,5011
0,6126
0,6597
0,7596
0,8702
1,0000
1,1514
1,3165
1,5159
0.4
0,0251
0,0303
0,0362
0,0437
0,0524
0,0631
0,0761
0,0936
0,1099
0,1319
0,1585
0,1913
0 ,^2285
0^2761
0,3309
0,3981
0,4805
0,5746
0,6935
0,8311
1,0000
1,2068
1,4434
1,7402
0.5
0,0100
0,0126
0,0158
0,0200
0,0251
0,0316
0,0400
0,0500
0,0632
0,0794
0,0999
0,1264
0,1580
0,2001
0,2511
0,3163
0,4001
0,5001
0,6325
0,7937
1,0000
1,2649
1,5825
1,9997
0.6
0,02398
0,02528
0,02690
0,02915
0,0120
0,0158
0,0210
0,0275
0,0364
0,0478
0,0631
0,0837
0,1094
0,1450
0,1905
0,2514
0,3332
0,4352
0,5770
0,7580
1,0000
1,3258
1,7332
2,2979
0,8
0,03631
0,03919
0,02131
0,02191
0,02275
0,02398
0,02580
0,02829
0,0121
0,0173
0,0251
0,0366
0,0523
0,0762
0,1096
0,1585
0,2309
0,3299
0,4805
0,6907
1,0000
1,4564
2,0834
3,0313
1,1
0,04398
0,04668
0,03109
0,03183
0,03302
0,03501
0,03841
0,02137
0,02230
0,02379
0,02631
0,0106
0,0173
0,0290
0,0478
0,0795
0,1333
0,2176
0,3649
0,6017
1,0000
1,6770
2,7429
4,5951
>
S
>
to
00
Продолжение табл. 2
\^ а
X ^ч.
0,00010
0,00016
0,00025
0,00040
0,00063
0,00100
0,00160
0,00250
0,00400
0,00630
0,01000
0,01600
0,02500
0,04000
0,06300
0,10000
0,16000
0,25000
0,40000
0,63000
1,00000
1,60000
2,50000
4,00000
1,4
0,05251
0,05485
0,04898
0,03173
0,04331
0,04631
0,03122
0,03228
0,03440
0,03830
0,02158
0,02306
0,02571
0,01110
0,0208
0,0398
0,0769
0,1437
0,2775
0,5236
1,0000
1,9309
3,6111
6,9587
1.7
0,06158
0,06352
0,05746
0,04166
0,05363
0,05795
0,04177
0,04375
0,04839
0,03181
0,03398
0,03885
0,02189
0,02421
0,02910
0,0200
0,0444
0,0948
0,2108
0,4561
1,0000
2,2233
4,7541
1,0549-10
2,0
0,07Ю0
0,07225
0,06620
0,05159
0,06398
0,05Ю0
0,05256
0,05625
0,04160
0,04397
0,03100
0,03256
0,03625
0,02160
0,02397
0,02549
0,0256
0,0625
0,1601
0,3969
1,0000
2,5600
6,2589
1,5991-10
2,5
0,09100
0,09324
0,09988
0,07317
0,08998
0,07317
0,0402
0,0^313
0,05101
0,05315
0,04100
0,04324
0,04987
0,03321
0,03998
0,02317
0,0102
0,0313
0,1013
0,3151
1,0000
3,2381
9,9046
3,1976-10
3,0
0,000
0,0п410
0,010156
0,09640
0,09250
0,08100
0,08410
0,07156
0,07641
0,06250
0,0бЮ0
0,05410
0,04156
0,04642
0,03250
0,02100
0,02748
0,0156
0,0640
0,2501
1,0000
4,0960
1,5658-10
6,3943-10
3,5
0,013Ю0
0,013519
0,012247
0,0п128
0,0п629
0,010317
0,09163
0,09782
0,08405
0,07198
0,06Ю0
0,06518
0,0б247
0,04J28
0,04629
0,03317
0,02164
0,02732
0,0405
0,1985
1,0000
5,1810
2,4749-10
1,2774.102
4,0
0,015Ю0
0,015656
0,014391
0,013256
0,012158
0,0п100
0,0и657
0,010391
0,09256
0,08158
0,07100
0,07656
0,06390
0,05257
0.04158
0,03Ю0
0,03659
0,02391
0,0256
0,1575
1,0000
6,5535
3,9173-10
2,5570-102
5,0
0,019100
0,018105
0,018977
0,016Ю2
0,016996
0,014100
0,013Ю5
0,013979
0,0п103
0,0п993
0,09100
0,08105
0,08976
0,0403
0,06996
0,04100
0,03105
0,03978
0,0102
0,0993
1,0000
1,0486-10
9,8003-10
1,0225-103
ТАБЛИЦА 3
Квантили нормального распределения
475
Таблица 3
р
0,50
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,60
0,61
0,62
0,63
0,64
0,65
0,66
0,67
ир
0,000
0,025
0,051
0,075
0,100
0,125
0,150
0,176
0,202
0,228
0,254
0,279
0,306
0,332
0,358
0,385
0,412
0,440
Р
0,68
0,69
0,70
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,78
0,79
0,80
0,81
0,82
0,83
0,84
0,85
л —
р vr*
ир
0,468
0,496
0,524
0,553
0,583
0,613
0,643
0,674
0,706
0,739
0,772
0,806
0,842
0,878
0,915
0,954
0,995
1,036
Г dx
— 00
р
0,86
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,94
0,95
0,96
0,97
0,98
0,99
0,999
0,9999
0,99999
Up
1,080
1,126
1,175
1,227
1,281
1,341
1,405
1,476
1,555
1,645
1,751
1,881
2,054
2,326
3,090
3,720
4,265
476
ПРИЛОЖЕНИЯ
Таблица 4
Квантили распределения %2 *)
Число
степеней
свободы,
п
2
*0,1
..2
*0,3
V2
*0,5
2
Л0,7
2
Л0,9
2
Л0,95
2
^0,99
0,999
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
0,
о,
о,
1,
1,
2,
2,
з,
4,
4,
5,
6,
7
7
8
9
10
10
11
12
13
14
14
15
16
17
18
18
19
20
016
211
594
06
61
20
83
49
17
87
58
30
04
79
55
31
10
9
7
4
,2
,0
,8
,7
,5
,3
,1
,9
,8
,6
0,
0,
1,
2,
3,
з,
4,
5,
6,
7,
8,
9,
9
10
11
12
13
14
15
16
17
18
19
19
20
21
22
23
24
25
148
713
42
19
00
83
67
53
39
27
15
03
93
08
7
6
5
4
4
,3
,2
,1
,0
,9
,9
,8
,7
,6
,6
,5
0,
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
И,
12,
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
455
39
37
36
35
35
35
34
34
34
3
3
3
3
3
3
3
3
3
,3
,3
,3
,3
,3
,3
,3
,3
,3
,3
,3
1,
2,
з,
4,
6,
7,
8,
9,
ю,
и,
12,
14
15
16
17
18
19
20
21
22
23
24
26
27
28
29
30
31
32
33
07
41
67
88
06
23
38
52
7
8
9
0
1
2
3
4
5
,6
,7
,8
,9
,9
,0
,1
,2
,2
,3
,4
,5
,5
2,
4,
6,
7,
9,
ю,
12,
13,
14
16,
17
18
19
21
22
23
24
26
27
28
29
30
32
33
34
35
36
37
39
40
71
61
25
78
24
6
0
4
7
0
3
5
8
1
3
5
,8
,0
,2
,4
,6
,8
,0
,2
,4
,6
,7
,9
,1
,3
3,
5,
7,
9,
И,
12,
14,
15
16
18
19
21
22
23
25
26
27
28
30
31
32
33
35
36
37
38
40
41
42
43
84
99
81
49
1
6
1
5
9
3
7
0
4
7
,0
,3
,6
,9
,1
,4
,7
,9
,2
,4
,7
,9
,1
,3
,6
,8
6,63
9,21
11,3
13,3
15,1
16,8
18,5
20,1
21,7
23,2
24,7
26,2
27,7
29,1
30,6
32,0
33,4
34,8
36,2
37,6
38,9
40,3
41,6
43,0
44,3
45,6
47,0
48,3
49,6
50,9
10,8
13,8
16,3
18,5
20,5
22,5
24,3
26,1
27,9
29,6
31,3
32,9
34,5
36,1
37,7
39,3
40,8
42,3
43,8
45,3
46,8
48,3
49,7
51,2
52,6
54,1
55,5
56,9
58,3
59,7
22Г
* Я. Ян ко,
Москва, 1961.
Математико-статистические таблицы, Госстатиздат,
Сокращенная таблица биномиального распределения
T a ii л i д а 5
В таблице даны значения ;У С рк A— р)п~к. Например, если испытываются 15 элементов по плану [N, Б, Т], вероятность
& "
отказа элемента р = 0,06, то вероятность того, что будет зарегистрировано три или более отказов, равна 0,05713, а вероятность того,
что число отказов равно трем, есть 0,05713 — 0,01036 = 0,04677
п
5
6
7
8
\. р
d \.
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
0
0
0
0
0,01
,04901
00098
00001
00000
00000
,05852
00146
00002
00000
00000
,06793
00203
00003
00000
00000
,07726
00269
00005
00000
00000
0
0
0
0
0,02
,09608
00384
00008
00000
00000
,11416
00569
00015
00000
00000
,13187
00786
00026
00001
00000
,14924
01034
00042
00001
00000
0
0
0
0
0,03
,14127
00847
00026
00000
00000
,16703
01246
00050
00001
00000
,19202
01709
00086
00003
00000
,21626
02234
00135
00005
00000
0,04
0,18463
01476
00060
00001
00000
0,21724
02155
00117
00004
00000
0,24855
02938
00198
00008
00000
0,27861
03815
00308
00016
00001
0
0
0
0
0,05
,22622
02259
00116
00003
00000
,26491
03277
00223
00009
00000
,30166
04438
00376
00019
00001
,33658
05724
00579
00037
00002
0,06
0,26610
03187
00197
00006
00000
0,31013
04592
00376
00018
00000
0,35152
06178
00629
00039
00001
0,39043
07916
00962
00075
00004
0,07
0,30431
04249
00308
00011
00000
0,35301
06082
00584
00032
00001
0,39830
08127
00969
00071
00003
0,44042
10347
01470
00134
00008
0,08
0,34092
05436
00453
00019
00000
0,39364
07729
00851
00054
00002
0,44215
10259
01401
00118
00006
0,48678
12976
02110
00220
00015
0,09
0,37597
06738
00634
00030
00001
0,43213
09515
01183
00085
00003
0,48324
12548
01933
00184
00011
0,52975
15768
02889
00341
00026
0
0
0
0
0, 10
,40951
08146
00856
00046
00001
,46856
11427
01585
00127
00006
,52170
14969
02569
00273
00018
,56953
18690
03809
00502
00043
01
СЛ
п
9
10
11
12
13
14
X
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
0,01
0,08648
00344
00008
00000
00000
0,09562
00427
00011
00000
00000
0,10466
00518
00016
00000
00000
0,11362
00617
00021
00000
00000
0,12248
00725
00027
00001
00000
0,13125
00840
00034
00001
00000
0,02
0,16625
01311
00061
00002
00000
0,18293
01618
00086
00003
00000
0,19927
01951
00117
00005
00000
0,21528
02311
00154
00007
00000
0,23098
02695
00197
00010
00000
0,24636
03103
00247
00014
00001
0,03
0,23977
02816
00198
00009
00000
0,26258
03451
00276
00015
00001
0,28470
04135
00372
00023
00001
0,30616
04865
00485
00033
00002
0,32697
05637
00616
00047
00003
0,34716
06449
00767
00064
00004
0,04
0,30747
04777
00448
00027
00001
0,33517
05815
00621
00044
00002
0,36176
06923
00829
00067
00004
0,38729
08094
01073
00098
00006
0,41180
09319
01354
00137
00010
0,43533
10593
01672
00185
00015
0,05
0,36975
07121
00836
00064
00003
0,40126
08614
01150
00103
00006
0,43120
10189
01524
00155
00011
0,45964
11836
01957
00224
00018
0,48666
13542
02451
00310
00029
0,51233
15299
03005
00417
00043
0,06
0,42701
09784
01380
00128
00008
0,46138
11759
01884
00203
00015
0,49370
13822
02476
00304
00026
0,52408
15954
03157
00434
00043
0,55263
18142
03925
00598
00067
0,57948
20369
04778
00797
00098
0,07
0,47959
12705
02091
00227
00017
0,51602
15173
02834
00358
00031
0,54990
17723
03698
00531
00054
0,58140
20332
04680
00753
00088
0,61071
22978
05775
01028
00134
0,63796
25645
06980
01360
00197
Продолжение
0,08
0,52784
15832
02979
00372
00031
0,56561
18788
04008
00580
00059
0,60036
21810
05190
00S54
00100
0,63233
24868
06520
01201
00161
0,66175
27937
07987
01627
00244
0,68881
30996
09583
02136
0,09
0,57207
19117
04048
00570
00055
0,61058
22545
05404
00883
00101
0,64563
26011
06947
01290
00171
0,67752
29481
08662
01799
00272
0,70655
32925
10536
02417
00410
0,73296
36321
12551
03148
00354 00590
табл. 5
о,ю
0,61258
22516
05297
00833
00089
0,65132
26390
07019
01280
00163
0,68619
30264
08956
01853
00275
0,71757
34100
11087
02564
00433
0,74581
37866
13388
03416
00646
0,77123
41537
15836
04413
00923
п
15
20
25
30
40
50
\v Р
d Ns^
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
0,01
0,13994
00963
00042
00001
00000
0,18209
01686
00100
00004
00000
0,22218
02576
00195
00011
00000
0,26030
03615
00332
00022
00001
0,33103
06074
00750
00069
00005
0,39499
08944
01382
00160
00015
0,02
0,26143
03534
00304
00018
00001
0,33239
05990
00707
00060
00004
0,39654
08865
01324
00145
00012
0,45452
12055
02172
00289
00030
0,55430
19046
04567
00824
00118
0,63583
26423
07843
01776
00321
0,03
0,36675
07297
00937
00085
00006
0,45621
11984
02101
00267
00026
0,53303
17196
03796
00619
00078
0,59899
22692
06007
01190
00185
0,70429
33846
11783
03140
00667
0,78193
44472
18920
06276
01681
0,04
0,45791
11911
02029
00245
00022
0,55800
18966
04386
00741
00096
0,63960
26419
07648
01652
00278
0,70614
33882
11690
03059
00632
0,80463
47902
21447
07484
02102
0,87011
59952
32329
13913
04897
0,05
0,53671
17095
03620
00547
00061
0,64151
26416
07548
01590
00257
0,72261
35762
12711
03409
00716
0,78536
44646
18782
06077
01564
0,87149
60094
32326
13815
04803
0,92306
72057
45947
23959
10362
0,06
0,60471
22624
05713
01036
00140
0,70989
33955
11497
02897
00563
0,78709
44734
18711
05976
01505
0,84374
54453
26760
10262
03154
0,91584
70096
43350
21726
08958
0,95467
81000
58375
35270
17940
1
0,07
0,66330
28315
08286
01753
00278
0,76576
41314
16100
04713
01071
0,83704
53040
25344
09361
02745
0,88663
63064
35125
15498
05526
0,94513
77994
53748
30631
14537
0,97344
87351
68921
46726
27097
1p одо л же н ие
0,08
0,71370
34027
11297
02731
00497
0,81131
48314
21205
07062
01834
0,87564
60528
32317
13509
04514
0,91803
70421
43460
21579
08736
0,96439
84055
63055
39925
21321
0,98453
91729
77403
57470
37105
0,09
0,75699
39649
14690
03994
00820
0,84836
54840
26657
09933
02904
0,90537
67139
39370
18315
06861
0,94095
76573
51447
28253
12769
0,97700
88603
71058
49079
28971
0,99104
94676
83946
66966
47234
га б л. 5
0,10
0,79411
45096
18406
05556
01272
0,87842
60825
32307
13295
04317
0,92821
72879
46291
23641
09799
0,95761
81630
58865
35256
17549
0,98522
91953
77719
57687
37098
0,99485
96621
88827
74971
56880
480
ПРИЛОЖЕНИЯ
Формулы оценок и доверительных интервалов
План
испытаний
Достаточная
статистика
Оценка
Несмещен-
Несмещенность
В,Т]
d{T)—число отказов
за время Т
d(T)
'- NT
несмещен-
несмещенная
IN, В, г\
tr—момент г-го от-
отказа
r — 1
-ж
несмещен-
несмещенная, если
[К, В,
(г, Т)]
если tr<T
Ntr
, tr<,T
несмещен-
несмещенная, если
[N, Б, Т)
d(T) и SB (Г)-сум-
марная наработка в
момент Т
SB(T)>
d(T)
или
смещенная
, если
d(T)
N
мало
ТАБЛИЦА 6
для параметра X экспоненциального закона
481
Таблица 6
Дисперсия
оценки
Доверительный интервал с
коэффициентом доверия,
не меньшим а = 1—(8i + е2)
Таблицы
*. = _!:
NT
ia (d) даны в
таблице 7
D М=
7^2'r>2
Aa(d) даны в
таблице 7
(/--о
Если tr<*T, для X, и X
используются формулы
плана [JV, В, г]; если же
?г > Т, то используются
формулы плана [N, В, Т]
сложная формула в виде
ряда
А'» Л' даны в
таблице 8
для а = 0,95
482
ПРИЛОЖЕНИЯ
План
испытаний
Достаточная
статистика
Оценка
Несмещен-
Несмещенность
Б. г
SB (tr)—суммарная
наработка в мо-
момент tr
несмещен-
несмещенная
IN, Б,
(г, Т))
d (T), SB(T), если
tr>T;
SB (<,), если tr<T
%=<
d(T)
SB IT)
г—1
SB(tr)
, tr>T
смещенная
[V, Б,
(r, HS0)\
(SB (tr), если
tr < T;
|с((/0),если
SS(<)
несмещен-
несмещенная
ТАБЛИЦА 6 483
Продолжение табл. 6
Дисперсия
оценки
ИМ — ^* . r>2
г—2
сложная формула в виде
ряда
Доверительный интервал с
коэффициентом доверия, не
меньшим а = 1— (гх + е2)
Если tr > Г, используется
формула для X, X плана
[N, Б, Т], "если же
tr*^T, то X и А, нахо-
находятся как решения
уравнений C.4.38), C.4.39)
А.-•.<*-»
если So < SB (tr)\
It 6| • если
Таблицы
Aa (d) даны в
таблице 7
Aa (d) даны в
таблице 7
Квантили Аа (d) пуассоновского распределения, Ld (Aa(*f))=a
Таблица 7
s\^ a
d ^"^\^
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
^\^^ а
d ^^\^
0
1
2
3
4
0,99993
0,000070
0,01188
0,07633
0,21115
0,41162
0,66825
0,97222
1,31628
1,69465
2,10271
2,53672
2,99367
3,47103
3,96672
4,47896
5,00626
5,54732
0,93
0,07257
0,43081
0,94230
1,53414
2,17670
0,9999
0,000100
0,01421
0,08618
0,23180
0,44446
0,71375
1,03040
1,38697
1,77758
2,19758
2,64323
3,Ш50
3,59988
4,10632
4,62904
5,16657
5,71762
0,90
0,10536
0,53181
1,10206
1,74477
2,43259
0,9993
0,000700
0,03789
0,16824
0,38894
0,68204
1,03236
1,42874
1,86297
2,32894
2.82197
3,33840
3,87531
4,43033
5,00152
5,58725
6,18615
6,79705
0,80
0,22314
0,82439
1,53504
2,29679
3,08954
0,999
0,00100
0,04540
0,19053
0,42855
0,73937
1,10710
1,52034
1,97081
2,45242
2,96052
3,49148
4,04244
4,61106
5,19544
5,79398
6,40533
7,02835
0,70
0,35667
1,09735
1,91378
2,76371
3,63361
0,993
0,00702
0,12326
0,38209
0,74108
1,17032
1,65152
2,17293
2,72659
3,30682
3,90942
4,53118
5,16960
5,82265
6,48871
7,16642
7,85464
8,55241
0,60
0,51082
1,37642
2,28508
3,21132
4,14774
0,99
0,01005
0,14855
0,43604
0,82325
1,27911
1,78528
2,33021
2,90611
3,50746
4,13020
4,77125
5,42818
6,09907
6,78235
7,47673
8,18111
8,89457
0,50
0,69315
1,67835
2,67406
3,67206
4,67091
0,95
0,05129
0,35536
0,81769
1,36632
1,97015
2,61301
3,28532
3,98082
4,69523
5,42541
6,16901
6,92421
7,68958
8,46394
9,24633
10,03596
10,83214
С,40
0,91629
2,02231
3,10538
4,17526
5,23662
^~"^\ а
d ^^"^\
5
6
7
8
9
10
11
12
13
14
15
16
~~----^^^ а
d ^""^\^
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
0,93
2,85488
3,55984
4,28584
5,02895
5,78633
6,55583
7,33581
8,12496
8,92222
9,72672
10,53773
11,35465
0,30
1,20397
2,43922
3,61557
4,76223
5.89036
7,00555
8,1П05
9,20895
10,30068
11,38727
12,46951
13,54798
14,62316
15,69544
16,78512
17,83246
18,89769
0,90
3,15190
3,89477
4,65612
5,43247
6,22130
7,02075
7,82934
8,64594
9,46962
10,29962
11,13530
11,97613
0,20
1,60944
2,99431
4,27903
5,51504
6,72098
7,90599
9,07538
10,23254
Л, 37977
12,51875
13,65073
14,77666
15,89731
17,01328
18,12509
19,23316
20,33782
0,80
3,90366
4,73366
5,57606
6,42848
7,28922
8,15702
9,03090
9,91010
10,79398
11,68206
12,57389
13,46913
0,10
2,30258
3,88972
5,32232
6,68078
7,99359
9,27467
10,53207
11,77091
12,99471
14,20599
15,40664
16,59812
17,78158
18,95796
20,12801
21,29237
22,45158
0,70
4,51714
5,41074
6,31217
7,21993
8,13293
9,05036
9,97161
10,89620
11,82373
12,75388
13,68639
14,62103
0,05
2,99573
4,74386
6,29579
7,75366
9,15352
10,51303
11,84240
13,14811
14,43465
15,70522
16,96222
18,20751
19,44257
20,66857
21,88648
23,09713
24,30118
0,60
5,09098
6,03924
6,99137
7,94661
8,90441
9,86440
10,82624
11,78972
12,75462
13,72081
14,68814
15,65651
0,025
3,68888
5,57164
7,22469
8,76727
10,24159
11,66833
13,05947
14,42268
15,76319
17,08480
18,39036
19,68204
20,96158
22,23040
23,48962
24,74022
25,98300
Продолжен
0,50
5,67016
6,66964
7,66925
8,66895
9,66871
10,66852
11,66836
12,66823
13,66811
14,66802
15,66793
16,66785
0,01
4,60517
6,63835
8,40595
10,04512
11,60462
13,10848
14,57062
15,99996
17,40265
18,78312
20,14468
21,48991
22,82084
24,13912
25,44609
26,74289
28,03045
и е т а б л. 7
0,40
6,29192
7,34265
8,38977
9,43395
10,47568
11,51533
12,55317
13,58944
14,62431
15,65793
16,69043
17,72191
0,005
5,29832
7,43013
9,27379
10,97748
12,59409
14,14976
15,65968
17,13359
18,57822
19,99842
21,39783
22,77926
24,14494
25,49669
26,83598
28,16406
29,48196
ОО
486
ПРИЛОЖЕНИЯ
Таблица 8
Значения Аа (d) и Аа (d), а = 0,95
50
60
80
100
150
200
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
0,07378
0,00000
0,11257
0,00051
0,14750
0,00489
0,18090
0,01263
0,21362
0,02248
0,24607
0,03384
0,27853
0,04640
0,31115
0,05995
0,34408
0,07440
0,37742
0,08966
0,41126
0,10570
0,44568
0,12247
0,48077
0,13996
0,51659
0,15818
0,55322
0,17711
0,59074
0,19677
0,62922
0,21717
0,66875
0,23833
0,70942
0,26027
0,75131
0,28303
0,06148
0,00000
0,09365
0,00042
0,12248
0,00407
0,14994
0,01049
0,17672
0,01863
0,20317
0,02800
0,22949
0,03832
0,25582
0,04942
0,28226
0,06120
0,30889
0,07360
0,33578
0,08657
0,36297
0,10008
0,39053
0,11411
0,41848
0,12865
0,44688
0,14368
0,47577
0,15921
0,50519
0,17524
0,53518
0,19177
0,56578
0,20881
0,59704
0,22637
0,04611
0,00000
0,07009
0,00032
0,09146
0,00305
0,11172
0,00783
0,13136
0,01388
0,15066
0,02082
0,16975
0,02842
0,18875
0,03657
0,20772
0,04518
0,22671
0,05419
0,24576
0,06358
0,26490
0,07331
0,28417
0,08336
0,30359
0,09372
0,32318
0,10437
0,34295
0,11531
0,36294
0,12654
0,38314
0,13804
0,40360
0,14982
0,42431
0,16188
0,03689
0,00000
0,05600
0,00025
0,07298
0,00243
0,08902
0,00625
0,10454
0,01106
0,11972
0,01657
0,13471
0,02259
0,14957
0,02902
0,16435
0,03580
0,17910
0,04289
0,19385
0,05025
0,20863
0,05785
0,22344
0,06568
0,23831
0,07372
0,25325
0,08198
0,26828
0,09042
0,28341
0,09906
0,29864
0,10788
0,31399
0,11688
0,32947
0,12607
0,02459
0,00000
0,03727
0,00017
0,04849
0,00162
0,05904
0,00415
0,06921
0,00734
0,07912
0,01097
0,08886
0,01493
0,09848
0,01915
0,10801
0,02358
0,11748
0,02819
0,12691
0,03297
0,13631
0,03788
0,14569
0,04293
0,15507
0,04809
0,16445
0,05337
0,17384
0,05875
0,18325
0,06423
0,19267
0,06980
0,20213
0,07547
0,21161
0,08123
0,01844
0,00000
0,02793
0,00013
0,03631
0,00121
0,04417
0,00311
0,05173
0,00549
0,05909
0,00820
0,06630
0,01115
0,07341
0,01429
0,08044
0,01758
0,08741
0,02100
0,09434
0,02453
0,10123
0,02816
0,10810
0,03189
0,11495
0,03569
0,12178
0,03957
0,12861
0,04352
0,13544
0,04753
0,14226
0,05160
0,14909
0,05574
0,15592
0,05993
ТАБЛИЦА 9
487
Таблица 9
Проверка гипотезы о равенстве вероятностей безотказной работы
элементов двух типов с вероятностью ошибки а = 0,1
dt + do_
0
l
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
o,
d'
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
0
0
1
a
*
2
2
3
3
3
3
3
4
4
4
4
4
4
5
5
5
5
5
5
5
6
6
6
6
6
6
7
7
7
i
d'
*
*
*
*
*
*
*
*
*
*
*
*
0
0
0
0
0
0
0
0
0
0
1
1
1
1
6
d"
2
3
3
3
4
4
4
4
5
5
5
6
6
6
6
7
7
7
7
7
8
8
8
8
9
9
9
9
10
0
d'
*
*
*
*
*
*
*
*
*
*
*
*
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
2
2
d"
2
3
3
4
4
4
5
5
5
6
6
6
6
7
7
7
8
8
8
8
9
9
9
9
10
10
10
10
11
0
a'
*
*
*
*
*
*
*
*
#
0
0
0
0
0
0
0
1
1
1
1
1
2
2
2
2
2
2
3
3
25
d"
*
3
4
4
4
5
5
5
6
6
7
7
7
8
8
8
9
9
9
10
10
10
11
11
11
12
12
12
13
0
d'
*
*
*
*
0
0
0
0
0
2
2
2
2
2
3
3
3
3
4
4
4
,3
*
3
4
4
5
5
6
6
6
7
7
8
8
9
9
9
10
10
10
11
11
12
12
12
13
13
13
14
14
l
d'
*
*
*
*
*
*
*
0
0
0
0
0
1
1
1
1
2
2
2
2
3
3
3
3
4
4
4
4
5
5
3
d-
*
*
*
3
4
4
5
5
6
6
7
7
8
8
9
9
9
10
10
11
11
12
12
12
13
13
14
14
15
15
15
0,
*
*
*
*
*
*
0
0
0
0
1
1
1
1
2
2
2
3
3
3
3
4
4
4
5
5
5
6
6
6
7
4
d"
*
*
*
4c
4
5
5
6
6
7
8
8
9
9
10
10
11
11
12
12
13
13
14
14
15
15
16
16
16
17
17
o,
d'
*
*
*
*
0
0
0
1
1
1
2
2
3
3
3
4
4
5
5
5
6
6
7
7
7
8
8
9
9
10
5
d'
*
*
*
*
5
6
7
7
8
9
9
10
10
11
12
12
13
13
14
15
15
16
16
17
18
18
19
19
20
20
488
ПРИЛОЖЕНИЯ
\W—d
d >\
0
1
2
Q
О
*
4
0
/»
6
8
9
10
* i
11
i л
12
13
1 Л
14
1 Г
10
1 С
16
1 7
1/
1 Q
lo
1У
20
П р и i
0
1,000
0,025
1,000
0,158
1,000
0,292
1,000
0,398
1,000
0,478
1,000
0,541
1,000
0,590
1,000
0,631
1,000
0,664
1,000
0,692
1,000
0,715
1,000
0,735
1,000
0,753
1,000
0,768
1,000
0,782
1,000
0,794
1,000
0,805
1,000
0,815
1,030
0,824
1,000
0,832
л ер. Е
о,
о,
о,
о,
о,
о,
о,
о,
о,
о,
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
975
000
987
013
992
094
994
194
995
284
996
359
996
421
997
473
997
517
997
555
998
587
,998
,615
,998
,640
,998
,661
,998
,681
,998
,698
,999
,713
,999
,727
,999
,740
,999
,751
,999
,762
ели npi
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0
0
0
0
о
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
А
отказа элемента P( Г) лежит
*) Я. >
Знко,
95 9
2
842
000
906
008
932
068
947
147
957
223
963
290
968
349
972
400
975
444
977
482
979
,516
981
572
,982
,572
,983
,595
,984
,617
,985
,636
,986
,653
,987
,669
,988
,683
,988
,696
,989
,708
j-ные
0,
0,
о,
о,
о,
о,
0,
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
3
708
000
806
006
853
053
882
118
901
184
915
245
925
299
933
348
940
390
,945
,428
,950
,462
,953
,492
,957
,519
,960
,544
,962
,566
,964
,586
,966
,604
,968
,621
,970
,637
,971
,651
,972
,664
испытаниях
в интервале 0
доверительные i
0,
о',
0,
0,
0,
о,
о,
о,
о,
о,
0
0
0
о
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
N=
,1-
4
602
000
716
005
777
043
816
099
843
157
863
212
878
262
891
308
901
349
,909
,386
,916
,419
,922
,449
,927
,476
,932
,501
,936
,524
,939
,544
,943
,563
,946
,581
,948
,597
,950
,612
,953
,626
= 25 s
21<Р
0,
0,
0,
о,
0,
о,
0,
0,
0,
0,
о,
0,
0
о
0
0
0
о
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
5
522
000
641
004
710
037
755
085
788
137
813
187
833
234
849
277
861
316
872
,351
,882
,384
,890
,413
,897
,440
,903
,465
,909
,488
,913
,509
,918
,529
,922
,547
,925
,564
,929
,579
,932
,593
0,
0,
0,
0,
о,
о,
0,
0,
0,
о,
о,
0,
о,
о,
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
элементов
(Т
Математико-статистические таблицы, I
194
пределы для
6
459
000
579
004
651
032
701
075
738
122
766
167
789
211
808
251
823
289
837
,323
,848
,354
,858
,383
,867
,410
,874
,435
,881
,457
,887
,478
,893
,498
,898
,516
,902
,533
,906
,549
,910
,564
о,
0,
о,
о,
0,
о,
о,
0,
о,
о,
о,
о,
о,
о,
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
7
410
000
527
003
600
028
652
067
692
109
723
151
749
192
770
230
787
266
802
,299
,816
,329
,827
,357
,837
,384
,846
,408
,854
,430
,861
,451
,868
,471
,874
,488
,879
,506
,884
,522
,889
,537
по плану \N
,так
0,
0,
о,
о,
о,
о,
о,
0,
о,
о,
о',
о,
о,
о,
0,
о,
о,
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
. Б
как здесь d
параметра
8
369
000
483
003
556
025
610
060
651
099
684
139
711
177
734
213
753
247
770
278
785
308
797
335
,809
,361
,819
,384
,828
,407
,836
,427
,844
,447
,851
,465
,857
,482
,862
,408
,868
,513
. Т]
•
0,
о,
0,
о,
0,
о,
0,
0,
о,
о,
о,
о,
о,
0,
о,
о,
о,
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
э
336
(Ю0
445
003
518
023
572
055
614
091
649
128
677
163
701
198
722
230
740
260
756
289
769
315
,782
,340
,793
,364
,803
,385
,812
,406
,820
,425
,828
,443
,835
,460
,841
,476
,847
,492
отказало
= 7, N—d=l&.
"осстатиздат, Москва, 1961
ТАБЛИЦА 10
в биномиальном распределении для малых JV*)
489
Таблица 10
ю
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
0,308
0,000
0,413
0,002
0,484
0,021
0,538
0,050
0,581
0,084
0,616
0,118
0,646
0,152
0,671
0,184
0,692
0,215
0,711
0,244
0,728
0,272
0,743
0,298
0,756
0,322
0,768
0,345
0,779
0,366
0,789
0,386
0,798
0,405
0,806
0,423
0,814
0,440
0,821
0,456
0,827
0,472
0,285
0,000
0,385
0,002
0,545
0,019
0,508
0,047
0,551
0,078
0,587
0,110
0,617
0,142
0,643
0,173
0,665
0,203
0,685
0,231
0,702
0,257
0,718
0,282
0,732
0,306
0,744
0,328
0,756
0,349
0,766
0,369
0,776
0,388
0,785
0,406
0,793
0,422
0,801
0,439
0,808
0,454
0,265
0,000
0,360
0,002
0,428
0,018
0,481
0,043
0,524
0,073
0,560
0,103
0,590
0,133
0,616
0,163
0,639
0,191
0,660
0,218
0,678
0,244
0,694
0,268
0,709
0,291
0,722
0,313
0,734
0,334
0,745
0,353
0,755
0,372
0,765
0,389
0,773
0,406
0,782
0,422
0,789
0,437
0,247
0,000
0,339
0,002
0,405
0,017
0,456
0,040
0,499
0,068
0,535
0,097
0,565
0,126
0,592
0,154
0,616
0,181
0,636
0,207
0,655
0,232
0,672
0,256
0,687
0,278
0,701
0,299
0,713
0,320
0,725
0,339
0,736
0,357
0,745
0,374
0,755
0,391
0,763
0,408
0,771
0,421
0,232
0,000
0,319
0,002
0,383
0,016
0,434
0,038
0,476
0,064
0,512
0,091
0,543
0,119
0,570
0,146
0,593
0,172
0,615
0,197
0,634
0,221
0,651
0,244
0,666
0,266
0,680
0,287
0,694
0,306
0,705
0,325
0,717
0,343
0,727
0,360
0,736
0,376
0,745
0,392
0,753
0,407
0,218
0,000
0,302
0,002
0,364
0,015
0,414
0,036
0,456
0,061
0,491
0,087
0,522
0,113
0,549
0,139
0,573
0,164
0,594
0,188
0,614
0,211
0,631
0,234
0,647
0,255
0,661
0,275
0,675
0,295
0,687
0,313
0,698
0,331
0,709
0,347
0,719
0,363
0,728
0,379
0,737
0,393
0,206
0,000
0,287
0,001
0,347
0,014
0,396
0,034
0,437
0,057
0,471
0,082
0,502
0,107
0,529
0,132
0,553
0,156
0,575
0,180
0,595
0,202
0,612
0,224
0,628
0,245
0,643
0,264
0,657
0,283
0,669
0,302
0,681
0,319
0,692
0,335
0,702
0,351
0,712
0,366
0,720
0,381
0,195
0,000
0,273
0,001
0,331
0,013
0,379
0,032
0,419
0,054
0,453
0,078
0,484
0,102
0,512
0,126
0,535
0,149
0,557
0,172
0,577
0,194
0,594
0,215
0,611
0,235
0,626
0,255
0,640
0,273
0,653
0,291
0,665
0,308
0,676
0,324
0,686
0,340
0,696
0,355
0,705
0,369
0,185
0,000
0,260
0,001
0,317
0,012
0,363
0, ('30
0,403
0,052
0,436
0,075
0,467
0,098
0,494
0,121
0,518
0,143
0,540
0,165
0,560
0,186
0,578
0,207
0,594
0,227
0,609
0,245
0,624
0,264
0,637
0,281
0,649
0,298
0,660
0,314
0,671
0,329
0,681
0,344
0,690
0,358
0,176
0,000
0,249
0,001
0,304
0,012
0,349
0,029
0,388
0,050
0,421
0,071
0,451
0,094
0,478
0,116
0,502
0,138
0,524
0,159
0,544
0,179
0,561
0,199
0,578
0,218
0,594
0,237
0,608
0,255
0,621
0,272
0,634
0,288
0,645
0,304
0,656
0,319
0,666
0,334
0,676
0,348
0,168
0,000
0,238
0,001
0,292
0,011
0,336
0,028
0,374
0,047
0,407
0,(J68
0,436
0,090
0,463
0,111
0,487
0,132
0,508
0,153
0,528
0,173
0,546
0,192
0,563
0,211
0,579
0,229
0,593
0,247
0,607
0,263
0,619
0,280
0,631
0,295
0,642
0,310
0,652
0,324
0,662
0,333
7 элементов, то с вероятностью, не меньшей 0,95, можно утверждать, что вероятность
17 G. В. Гнеденко и др.
Таблица 11
Критические значения /^распределения *)
4
СО
О
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
40
60
120
00
¦) Я.
2
99,000
18,000
10,925
8,649
7,559
6,927
6,515
6,226
6,013
5,849
5,719
5,614
5,526
5,453
5,390
5,179
4,977
1,787
4,605
Я н к о,
4
99,249
15,977
9,148
7,006
5,994
5,412
5,035
4,773
4,579
4,431
4,313
4,218
4,140
4,074
4,018
3,828
3,649
3,480
3,319
6
99,332
15,207
8,466
6,371
5,386
4,821
4,456
4,202
4,015
3,871
3,758
3,667
3,591
3,528
3,474
3,291
3,119
2,956
2,802
ь
99,374
14,799
8,102
6,029
5,057
4,499
4,140
3,890
3,705
3,564
3,453
3,363
3,288
3,226
3,173
2,993
2,823
2,663
2,511
Математ ико-статистически
10
99,399
14,546
7,874
5,814
4,849
4,296
3,939
3,691
3,508
3,368
3,258
3,168
3,094
3,032
2,979
2,801
2,632
2,472
2,321
? таблиць
12
99,416
14,374
7,718
5,667
4,706
4,155
3,800
3,553
3,371
3,231
3,121
3,032
2,958
2,896
2,843
2,665
2,496
2,326
2,185
20
99,449
14,020
7,396
5,359
4,405
3,858
3,505
3,259
3,077
2,938
2,827
2,738
2,664
2,602
2,549
2,369
2,198
2,035
1,878
24
99,458
13,929
7,313
5,279
4,327
3,781
3,427
3,181
2,999
2,859
2,749
2,659
2,585
2,522
2,469
2,288
2,115
1,950
1,791
30
99,466
13,838
7,229
5,198
4,247
3,701
3,348
3,101
2,919
2,779
2,668
2,577
2,503
2,440
2,386
2,203
2,029
1,860
1,696
I, Госстатиздат, Москва, 1961.
40
99,474
13,745
7,143
5,116
4,165
3,619
3,266
3,018
2,835
2,695
2,583
2,492
2,417
2,354
2,299
2,114
1,936
1,763
1,592
60
99,483
13,652
7,057
5,032
4,082
3,536
3,181
2,933
2,749
2,608
2,495
2,404
2,327
2,263
2,208
2,019
1,836
1,656
1,473
120
99,491
13,558
6,969
4,946
3,997
3,449
3,094
2,845
2,660
2,517
2,403
2,310
2,233
2,167
2,111
1,917
1,726
1,533
1,325
сю
99,501
13,463
6,880
4,859
3,909
3,361
3,004
2,753
2,566
2,421
2,306 ,
2,211
2,132
2,064
2,0С6
1,805
1,601
1,381
1,000
Продолжение табл. 11
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
40
60
120
2
199,00
26,284
14,544
11,042
9,427
8,510
7,922
7,514
7,215
6,987
6,806
6,661
6,541
6,440
6,335
6,066
5,795
5,539
5,298
4
199,25
23,155
12,028
8,8j5
7,343
6,521
5,998
5,638
5,375
5,174
5,017
4,890
4,785
4,698
4,623
4,374
4,140
3,921
3,715
6
199,33
21,975
11,073
7,952
6,545
5,575
5,257
4,913
4,663
4,472
4,323
4,202
4,103
4,020
3,949
3,713
3,492
3,285
3,091
8
199,37
21,352
10,566
7,496
6,116
5,345
4,857
4,521
4,276
4,090
3,944
3,826
3,730
3,649
3,580
3,350
3,134
2,933
2,744
10
199,40
20,967
10,250
7,211
5,847
5,086
4,603
4,272
4,031
3,847
3,703
3,587
3,492
3,412
3,344
3,117
2,904
2,705
2,519
б)
12
199,42
20,705
10,034
7,015
5,661
4,906
4,428
4,099
3,860
3,678
3,535
3,420
3,325
3,246
3,179
2,953
2,742
2,544
2,358
^0,995
20
199,45
20,167
9,589
6,608
5,274
4,530
4,059
3,734
3,498
3,318
3,176
3,062
2,969
2,890
2,823
2,598
2,387
2,188
2,000
199,46
20,030
9,474
6,503
5,173
4,432
3,961
3,638
3,402
3,222
3,081
2,967
2,873
2,794
2,727
2,502
2,290
2,089
1,898
30
199,47
19,892
9,358
6,396
5,071
4,331
3,862
3,539
3,303
3,123
2,982
2,868
2,774
2,695
2,628
2,402
2,187
1,984
1,789
40
199,47
19,752
9,241
6,288
4,966
4,228
3,760
3,437
3,201
* 3,022
2,880
2,765
2,671
2,592
2,524
2,296
2,079
1 ,871
1,669
60
199,48
19,611
9,122
6,177
4,859
4,123
3,655
3,332
3,096
2,916
2,774
2,659
2,563
2,483
2,415
2,184
1,962
1,747
1,533
120
199,49
19,468
9,002
6,065
4,750
4,015
3,547
3,224
2,987
2,806
2,663
2,546
2,450
2,369
2,300
2,064
1 834
1,606
1,364
GO
199,51
19,325
8,879
5,951
4,639
3,904
3,4С6
3,112
2,873
2,690
2,546
2,428
2,330
2,247
2,176
1,932
1,688
1,431
1,000
402
ПРИЛОЖЕНИЯ
Таблица 12
п
2
3
4
5
6
7
*) Н. О
rogeneity о
Vo.
39
88
142
202
266
333
Критерий
Voi
199
448
729
1036
1362
1705
Хартли *)
n
8
9
10
11
12
^0,05
403
475
550
626
704
. Hartley, The maximum F-ratio as a short-cut
f variance. Biotnetrika 37 A950), 308—312.
2063
2432
2813
3204
3605
test of hete
Таблица 13
п
5
10 *
15
20
*) R. А
0, 95
0
0
0
0
. F
Rov Soc t25
,68377
,44495
,33462
,27040
Критерии
Фишера *]
a = 0,95
n
25
30
35
ga(n)
0,22805
0,19784
0,17513
sher, Tests of significance in
A929),
54—59.
n
40
45
50
harmonic
a = 0,9E
0,
0,
0,
>
15738
14310
13135
analysis, Proc
Таблица 14
X
0,00
0,10
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
*) 9
0,00
0,000
0,644
0,927
1,159
1,369
1,571
1,772
1,982
2,214
2,498
Значения функции у-
0,01
0,200
0,676
0,952
1,181
1,390
1,59]
1,793
2,004
2,240
2,532
0,02
0,284
0,707
0,976
1,203
1,410
1,611
1,813
2,026
2,265
2,568
< о, Математико
0,03
0,348
0,738
1,000
1,224
1,430
1,631
1,834
2,049
2,292
2,606
0,04
0,403
0,767
1,024
1,245
1,451
1,651
1,855
2,071
2,319
2,647
-статистические
= 2arcsin Ух
0,05
0,451
0,795
1,047
1,266
1,471
1,671
1,875
2,094
2,346
2,691
0,06
0,495
0,823
1,070
1,287
1,491
1,691
1,897
2,118
2,375
2,739
*)
0,07
0,536
0,850
1,093
1,308
1,511
1,711
1,918
2,141
2,404
2,793
таблицы. Госстатиздат
0,08
0,574
0,876
1,115
1,328
1,531
1,731
1,939
2,165
2,434
2,858
Москв.
о.оч
0,С09
0,902
1,137
1,349
1,551
1,752
1,961
2,190
2,465
2,941
а, 1961
Критерий Колмогорова. Значения функции Колмогорова К (у) *)
Таблица 15
У
0,28
0,29
0,30
0,31
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,40
0,41
К (у)
0,051
0,054
0,059
0,0421
0,0446
0,0491
0,03171
0,03303
0,03511
0,03826
0,0428
0,02193
0,02281
0,02397
у
0,61
0,62
0,63
0,64
0,65
0,66
0,67
0,68
0,69
0,70
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,78
0,79
0,80
К {у)
0,1492
0,1632
0,1777
0,1927
0,2080
0,2236
0,2396
0,2558
0,2722
0,2888
0,3055
0,3223
0,3391
0,3560
0,3728
0,3896
0,4064
0,4230
0,4395
0,4558
у
1,00
1,01
1,02
1,03
1,04
1,05
1,06
1,07
1,08
1,09
1,10
1,11
1,12
1,13
1,14
1,15
1,16
1,17
1,18
1,19
К (у)
0,7300
0,7406
0,7508
0,7608
0,7704
0,7798
0,7889
0,7976
0,8061
0,8143
0,8223
0,8299
0,8373
0,8445
0,8514
0,8580
0,8644
0,8706
0,8765
0,8822
у
1
1
1
]
1
1
1
1
]
,40
,41
,42
,43
,44
,45
,46
,47
,48
,49
,50
,51
,52 .
1,53
1,54
1,55
,56
1,57
1,58
1,59
К (у)
0,9603
0,9625
0,9645
0,9665
0,9684
0,9701
0,9718
0,9734
0,9750
0,9764
0,9778
0,9791
0,9803
0,9815
0,9826
0,9836
0,9846
0,9855
0,9864
0,9873
у
,80
,81
,82
,83
,84
,85
,86
,87
,88
,89
,90
,91
1,92
1,93
1,94
[,95
1,96
1,97
1,98
1,99
К (у)
0,92693
0,92715
0,92735
0,92753
0,92770
0,92787
0,92802
0,92814
0,92830
0,92842
0,92854
0,92864
0,92874
0,92884
0,92892
0,93004
0,93079
0,93149
0,93213
0,93273
У
2,20
2,21
2,22
2,23
2,24
2,25
2,26
2,27
2,28
2,29
2,30
2,31
2,32
2,33
2,34
2,35
2,36
2,37
2,38
2,39
К (у)
0,93874
0,93886
0,93896
0,9404
0,9412
0,9420
0,9426
0,9434
0,9440
0,9444
0,9449
0,9454
0,9458
0,9462
0,9465
0,9468
0,9470
0,9473
0,9476
0,9478
Продолжение табл. 15
со
4
У
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,50
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,60
*)
К {у)
0,02548
0,02738
0,02973
0,0126-
0,0160
0,0200
0,0247
0,0300
0,0360
0,0428
0,0503
0,0585
0,0675
0,0772
0,0876
0,0986
0,1104
0,1228
0,1357
Я Я н к о,
У
0,81
0,82
0,83
0,84
0,85
0,86
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,94
0,95
0,96
0,97
0,98
0,99
К (у)
0,4720
0,4880
0,5038
0,5194
0,5347
0,5497
0,5645
0,5791
0,5933
0,6073
0,6209
0,6343
0,6473
0,6601
0,6725
0,6846
0,6964
0,7079
0,7191
У
1,20
1,21
1,22
1,23
1,24
1,25
1,26
1,27
1,28
1,29
1,30
1,31
1,32
1,33
1,34
1,35
1,36
1,37
1,38
1,39
Математическо-статистические i
К (у)
0,8877
0,8930
0,8981
0,9030
0,9076
0,9121
0,9164
0,9205
0,9245
0,9283
0,9319
0,9354
0,9387
0,9418
0,9449
0,9477
0,9505
0,9531
0,9556
0,9580
У
1,60
1,61
1,62
,63
1,64
1,65
,66
,67
,68
1,69
1,70
1,71
1,72
,73
1,74
[,75
1,76
,77
1,78
1,79
габлицы, Госстатиздат,
К (у)
0,9880
0,9888
0,9895
0,92015
0,92078
0,92136
0,92192
0,92244
0,92293
0,92339
0,92383
0,92423
0,92461
0,92497
0,92531
0,92562
0,92592
0,92620
0,92646
0,92670
У
2,00
2,01
2,02
2,03
2,04
2,05
2,06
2,07
2,08
2,09
2,10
2,11
2,12
2,13
2,14
2,15
2,16
2,17
2,18
2,19
Москва, 1961.
К (у)
0,93329
0,93380
0,93428
0,93474
0,93516
0,93552
0,93588
0,93620
0,93650
0,93680
0,93705
0,93723
0,93750
0,93770
0,93790
0,93806
0,93822
0,93838
0,93852
0,93864
2,40
2,41
2,42
2,43
2,44
2,45
2,46
2,47
2,48
2,49
2,50
2,55
2,60
2,65
2,70
2,75
2,80
2,85
2,90
2,95
3,00
Д' (у)
0,9480
0,9482
0,9484
0,9486
0,9487
0,9488
0,9489
0,95
0,94
0,952
0,9525
0,9556
0,6574
0,9584
0,960
0,964
0,967
0,9б82
0,97
0,974
0,977
ТАБЛИЦА 16
495
Таблица 16
Критические значения максимального отклонения
эмпирической функции распределения от теоретической
(случай конечных объемов выборки) *)
п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
а = 0,20
0,900
684
565
493
447
410
381
358
339
323
0,308
296
285
275
266
258
250
244
237
232
0,226
221
216
212
208
204
200
197
193
190
0,187
184
182
а = 0, 10
0,950
776
636
565
509
468
436
410
387
369
0,352
338
325
314
304
295
286
279
271
265
0,259
253
247
242
238
233
229
225
221
218
0,214
211
208
а = 0,05
0,975
842
708
624
563
519
483
454
430
409
0,391
375
361
349
338
327
318
309
301
294
0,287
281
275
269
264
259
254
250
246
242
0,238
234
231
*) Я. Я н к о, Математико-статистические таблицы,
а=0,02
0,990
900
785
689
627
577
538
507
480
457
0,437
419
404
390
377
366
355
346
337
329
0,321
314
307
301
295
290
284
279
275
270
0,266
262
258
Госстатиздат,
а = 0,01
0,995
929
829
734
669
617
576
542
513
489
0,468
449
432
418
404
392
381
371
361
352
0,344
337
330
323
317
311
305
300
295
290
0,285
281
277
Москва, 1961
17*
496
ПРИЛОЖЕНИЯ
Продолжение табл. 16
п
34
35
36
37
38
39
40
41
42
43
44
45
16
47
48
49
I 50
51
| 52
53
54
I 55
| 56
57
58
59
60
61
62
63
64
65
C6
67
0,
o,
o,
0
i
0,20
179
177
174
172
170
168
165
163
162
160
158
156
155
153
151
150
148
147
146
144
143
142
140
139
138
137
136
135
133
132
132
131
130
129
a-
0,
o,
о
0
0, 10
205
202
199
196
194
191
189
187
185
183
181
179
177
175
173
171
170
168
166
165
163
162
160
159
158
156
155
,154
153
151
150
149
148
147
a = 0,05
0,227
224
221
218
215
213
210
0,208
205
203
201
198
196
194
192
190
188
0,187
185
183
181
180
178
177
175
174
172
0,171
170
168
167
166
164
163
-
0,
o,
0
0
0,02
254
251
247
244
241
238
235
232
229
227
224
222
219
217
215
213
211
209
207
205
203
201
199
198
196
194
193
,191
190
188
187
185
184
183
a = 0,01
0,273
269
265
262
258
255
252
0,249
246
243
241
238
235
233
231
228
226
0,224
222
220
218
216
214
212
210
208
207
0,205
203
202
200
199
197
196
ТАБЛИЦА 16 497
Продолжение табл. 16
п
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
•92
93
94
95
96
97
98
99
100
а=0,20
128
127
126
0,125
124
123
122
122
121
120
119
119
118
0,117
116
116
115
114
114
113
112
112
111
0,111
ПО
109
109
108
108
107
107
106
106
а = 0, 10
146
145
144
0,143
142
141
140
139
138
137
136
136
135
0,134
133
132
131
131
130
129
128
128
127
0,126
126
125
124
124
123
122
122
121
121
а = 0,05
162
161
160
0,159
158
156
155
154
153
152
151
151
150
0,149
148
147
146
145
144
144
143
142
141
0,140
140
139
138
137
137
136
135
135
134
а=0,02
181
180
179
0,177
176
175
174
173
172
173
169
158
167
0,166
165
164
163
162
1G1
161
160
159
158
0,157
156
155
155
1*54
153
152
151
151
150
а = 0,01
194
193
192
0,190
189
188
183
185
134
183
182
18!
179
0,178
177
176
175
174
173
172
171
170
169
0,103
168
167
166
Гб5
164
163
162
162
161
Таблица 17
Критерий Смирнова *)
со
00
k-4
k-1
k=\0
?=11
?=12
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
1,000000
0,666667
400000
228571
126984
0,069264
037296
019891
010537
005542
0,002903
001515
000788
000408
000211
0,000109
000056
000029
04148
05761
0,05390
05199
05102
1,000000
0,900000
771429
642857
0,525974
424825
339860
269889
213070
0,167412
131018
102194
079484
061669
0,047744
036893
028460
021922
016863
0,012956
009943
007623
1,000000
0,971429
920635
0,857143
787879
717327
648293
582476
0,520850
463902
411804
364515
321862
0,283588
249393
218952
191938
168030
0,146921
128321
J11963
,000000
0,992063
1,000000
0,974026 0
946970
912976
874126
832179
,997835
991841
981352
966434
947552
0,788524
744225
700080
656580
614453
0,573707
534647
497410
462071
428664
0,397187
367614
339899
0,925339
900453
873512
845065
815584
0,785465
755041
724582
694311
664409
0,635020
606260
578218
,000000
0,999417
997514
993706
987659
0,979261
968564
955728
940970
924536
0,906674
887623
867606
846827
825467
0,803688
781632
759422
,000000
0,999845
999260
997943
0,995634
992141
987351
981218
973752
0,965002
955047
943982
931911
918942
0,905183
890738
875705
1.000000
0,999959
999783 0
,000000
,999989
0,999345
998503
997125
995100
992344
0,988801
984439
979252
973251
966458
0,958911
950653
941731
0,999938
999796
999500
998979
998163
0,996985
995389
993331
990776
987701
0,984095
979953
975280
1,000000
,999997
999982 0
999938
999837
999647
1,000000
,999999
999995
999981
999948
,000000
0,999999
999994
О
а:
s
S3
0,999330
998847
998160
997233
996033
0,99453
99271
99055
0,999880 0
999762
999571
999286
998884
,999983
999960
999917
999844
999729
0,99834
99764
99676
0,99956
99933
99901
Продолжение табл. 17
п — т
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
*) F
0,0652
0627
0,0614
0769
0735
0718
0*91
0,0846
0823
0812
0960
0931
0,0916
01079
01040
01020
О1010
fe = 2
0,005839
004468
0,003417
002611
001994
001522
001161
0,000885
000674
000513
000391
000297
0,000226
000172
000131
000099
000075
o,
o,
o,
o,
. J. M a s s e у: a) The
/Inc
097600
085007
073980
064338
055914
048563
042154
036570
031710
027483
023808
020616
017845
015440
013355
011547
009981
/2 = 4
0,313983
289796
0,267263
246303
226833
208772
192037
0,176546
162223
148989
136773
125505
0,115120
105553
096747
088645
081195
k = 5
0,550963
524546
0,499005
474362
450633
427823
405929
0,384946
364861
345657
327316
309816
0,293133
277243
262121
247738
234069
0,737166
714958
0,692877
670992
649362
628036
607055
0,586455
566264
546505
527198
508355
0,489989
472107
454713
437811
421400
k = 7
0,860177
844240
0,827971
811443
794722
777865
760927
0,743955
726992
710076
693242
676519
0,659934
643512
627273
611234
595413
0,
0,
0,
0,
distribution table for the deviation between two s
O\ Л О С АЛО.
/2 = 8
932197
922101
911498
900437
888969
877140
864996
852580
839930
827086
814080
800946
787713
774409
761059
747687
734313
0
0
0
0
970087
964389
958206
951562
944481
936989
929113
920880
912319
903455
894315
884924
,875307
865487
855487
845327
835029
fc=10
0,98803
98516
0,98193
97833
97438
97007
96542
0,96044
95514
94953
94363
93745
0,93101
92432
91740
91027
90293
0
0
0
0
ample cumulatives, Ann. Math
\ I W ^. ) , t О <J 11 *. ,
b) The distribution of the maximum deviation between two
Math. Statist. 22, № 1 A951), 125—128.
sample cumulatives
k= 1 1
99568
99438
99287
99111
98911
98686
98436
98160
97859
97533
97182
96807
,96407
95985
95540
95074
94587
Statist
0
0
0
0
k=\2
99860
99808
99744
99667
99576
99469
99346
,9921
9905
9888
9868
9847
,9824
9799
9773
9744
9714
23, № 3
step functions, Ann.
>
en
>
^3
CO
500
ПРИЛОЖЕНИЯ
Таблица 18
Границы критической области для критерия знаков *)
п
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
*) I
2
0
1
1
1
2
2
2
3
3
3
4
4
5
5
5
6
6
6
7
7
8
8
8
9
9
10
10
10
1 1
1 1
12
12
13
13
13
14
14
15
15
16
16
16
17
17
18
18
19
19
19
20
3 Л
Односторонние
5%
5
5
•6
7
7
8
9
9
10
1 1
1 1
12
12
13
14
14
15
16
16
17
17
18
19
19
20
20
21
22
22
23
23
24
24
25
26
26
27
27
28
28
29
30 •
зо-
31
31
32
32
33
34
:и
5% .
0
0
1
1
1
1
2
2
2
3
3
3
4
4
5
5
5
6
6
6
7
7
8
8
8
9
9
9
10
10
1 1
1 1
1 1
12
12
13
13
14
14
14
15
15
16
16
16
17
17
18
18
19
1%
5
6
6
7
8
9
9
10
1 1
1 1
12
13
13
14
14
15
16
16
17
18
18
19
19
20
21
21
22
23
23
24
24
25
26
26
27
27
28
2 8
29
30
30
3 1
31
32
33
33
34
34
35
35
2%
Двусторонние
ван д€
Ф
В
а Р д
границы
0,
0
0
0
1
1
1
2
2
2
3
3
3
4
4
4
5
5
5
6
6
7
7
7
8
8
8
9
9
10
10
10
1 1
1 1
12
12
12
13
13
14
14
14
15
15
16
16
16
17
17
18
границы
5%
5
6
7
7
8
9
10
10
11
12
12
П
14
14
15
16
16
17
18
18
19
19
20
21
21
22
23
23
24
24
25
26
26
27
27
28
29
29
30
30
31
32
32
33
33
34
35
35
36
36
%
е и, Млтемати
п
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
2
20
21
21
22
22
22
23
23
24
24
25
25
26
26
26
27
27
28
28
29
29
29
30
30
31
31
32
32
33
33
33
34
34
35
35
36
36
37
37
38
38
38
39
39
40
40
Односторонние
5%
35
35
36
36
37
38
38
39
39
40
40
41
41
42
43
43
44
44 -
45
45
46
47
47
48
48
49
49
50
5 0
51
52
52
53
53
54
54
55
55
56
56
57
58
58
59
59
60
5%
19
19
20
20
21
21
21
22
22
23
23
24
24
24
25
25
26
26
27
27
27
28
28
29
29
30
30
31
31
31
32
32
33
33
34
34
34
35
35
36
36
37
37
38
38
38
1%
36
37
37
38
38
39
40
40
4 1
41
42
42
43
44
44
4 5
45
46
46
47
48
48
4 9
49
50
50
51
51
52
53
53
5 4
54
55
55
56
57
57
58
58
59
59
60
60
61
62
2%
Двусторонние
ческа я статистика,
ИЛ,
1960
границы
0,
18
18
19
19
20
20
21
21
21
22
22
23
23
23
24
24
25
25
26
26
26
27
27
28
28
29
29
29
30
30
31
31
32
32
32
33
3 3
34
34
35
35
3 5
36
36
37
37
5%
37
38
38
39
39
40
40
41
42
42
43
43
44
45
45
46
46
47
47
48
4 9
49
50
50
51
51
52
53
53
54
54
55
55
56
57
57
58
5S
59
59
60
61
61
62
62
63
1%
границы
Таблица 19
Распределение статистики Вилкоксона*)
и
i
0
1
2
3
4
Объемы выборок g и h
2; 5
4,76
2; 6
3,57
2; 7
2,78
2; 8
2,22
4,44
2; 9
1,82
3,64
2; 10
1,52
3,03>
3; 3
5,00
3; 4
2,86
3; 5
1,79
3,57
3; 6
1,19
2,38
4,76
3; 7
0,83
1,67
3,33
3; 8
0,61
1,21
2,42
4,24
3; 9 | 3; 10
0,45
0,91
1,82
3,18
5,00
0,35
0,70
1,40
2,45
3,85
и
0
1
2
3
4
5
6
7
8
9
10
11
4; 4
1,43
2,86
4; 5 |
0,79
1,59
3,17
4; 6 !
0,48
0,95
1,90
3,33
4; 7
0,30
0,61
1,21
2,12
3,64
4; 8
0,20
0,40
0,81
1,41
2,42
3,64
Объемы выборок g и
4; 9
0,14
0,28
0,56
0,98
1,68
2,52
3,78
4; 10
0,10
0,20
0,40
0,70
1,20
1,80
2,70
3,80
5; 5
0,40
0,79
1,59
2,78
4,76
h
5; 6
0,22
0,43
0,87
1,52
2,60
4,11
5; 7
0,13
0,25
0,51
0,88
1,52
2,40
3,66
5; 8
0,08
0,16
0,31
0,54
0,93
1,48
2,25
3,26
4,66
5, 9
0,05
0,10
0,20
0,35
0,60
0,95
1,45
2,10
3,00
4,15
5; 10
0,03
0,07
0,13
0,23
0,40
0,63
0,97
1,40
2,00
2,76
3,76
4,96
6; 6
0,11
0,22
0,43
0,76
1,30.
2,06
3,25
4,65
*) Б. Л. ван дер В а р д е н, Математическая статистика, ИЛ, 1960.
Продолжение табл. 19
ел
о
to
и
4-
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
6; 7
0.06
0,12
0,23
0,41
0,70
1,11
1,75
2,56
3,67
б; 8
0,03
0,07
0,13
0,23
0,40
0,63
1,00
1,47
2,13
2,96
4,06
6; 9
0,02
0,04
0,08
0,14
0,24
0,38
0,60
0,88
1,28
1,80
2,48
3,32
4,40
6; 10
0,01
0,02
0,05
0,09
0,15
0,24
0,37
0,55
0,80
1,12
1,56
2,10
2,80
3,63
4,67
7; 7
0,03
0,06
0,12
0,20
0,35
0,55
0,87
1,31
1,89
2,65
3,64
4,87
Объемы выборок g и
7; 8
0,02
0,03
0,06
0,11
0,19
0,30
0,47
0,70
1,03
1,45
2,00
2,70
3,61
4,69
7; 9
0,01
0,02
0,03
0,06
0,10
0,17
0,26
0,39
0,58
0,82
1,15
1,56
2,09
2,74
3,56
4,54
7; 10
0,01
0,01
0,02
0,04
0,06
0,10
0,15
0,23
0,34
0,48
0,68
0,93
1,25
1,65
2,15
2,77
3,51
4,39
h
8; 8
0,01
0,02
0,03
0,05
0,09
0,15
0,23
0,35
0,52
0,74
1,03
1.41
1,90
2,19
3,25
4,15
8; 9
0,00
0,01
0,02
0,03
0,05
0,08
0,12
0,19
0,28
0,39
0,56
0,76
1,03
1,37
1,80
2,32
2,96
3,72
4,64
8; 10
0,00
0,01
0,02
0,03
0,04
0,07
0,10
0,15
0,22
0,31
0,43
0,58
0,78
1,03
1,33
1,71
2,17
2,73
3,38
4,16
9; 9
0,00
0,01
0,01
0,02
0,04
0,06
0,09
0,14
0,20
0,28
0,39
0,53
0,71
0,94
1,22
1,57
2,00
2,52
3,13
3,85
4,70
9; 10
0,00
0,01
0,01
0,02
0,03
0,05
0,07
0,10
0,15
0,21
0,28
0,38
0,51
0,66
0,86
1,10
1,40
1,75
2,17
2,67
3,26
3,94
4,74
10; 10
0,00
0,01
0,01
0,02
0,02
0,04
0,05
0,08
0,10
0,14
0,19
0,26
0,34
0,45
0,57
0,73
0,93
1,16
1,44
1,77
2,16
2,62
3,15
3,76
4,46
Таблица 20
Колумбийский стандарт: однократная выборка*)
Кодо-
Кодовое
число
А
В
С
D
Е
F
G
Н
I
J
К
L
М
N
О
«§» с
«4.»
Объем
вы-
выборки
5
10
15
20
30
40
55
75
115
150
225
300
450
750
1500
означает
0,024—
0,035
§
§
4
4
4
4
4
4
4
0
4
4
4
4
1
0,035—
0,06
§
4
4
4
4
4
4
0
4
4
4
4
4
1
2
Интервалы i
0,06—
0, 12
§
4
4
4
4
4
0
4
4
4
4
4
1
2
3
0, 12—
0,17
4
4
4
4
0
4
4
4
4
4
1
2
3
4
0, 17—
0.22
4
4
4
4
0
4
4
4
4
4
1
2
2
3
6
0,22—
0,32
4
4
4
0
4
4
4
4
4
1
2
2
3
5
8
- сплошную проверку партии.
, «t» означают,
что за 1
*) Statistical research group
триемочное берется первое число
Columbia University, «Sampling
триемлемого качества в %
0,32—
0,65
4
0
0
4
1
4
1
1
2
2
3
4
5
8
13
0,65—
1,2
0
4
4
4
1
1
2
2
3
4
5
7
9
13
24
стоящее ниже
inspection», Me
1 ,2—
2,2
4
4
4
1
2
2
3
3
5
6
8
10
14
23
t
2,2—
3,2
4
4
1
1
2
3
3
4
6
8
11
14
20
t
t
3,2 —
4 ,4
4
1
1
2
3
3
4
6
8
10
14
18
26
t
t
выше) этой стрелки
Graw-Hill, N. Y., 1948.
4 ,4—
5,3
4
1
2
2
3
4
5
7
10
12
17
22
1
t
t
5.3—
6,4
1
2
2
3
4
5
6
8
11
14
21
27
1
t
t
6,4 —
8,5
1
2
3
3
5
6
8
10
14
18
25
1
1
t
t
504
ПРИЛОЖЕНИЯ
Колумбийский стандарт:
Кодо-
Кодовое
№
вы-
выборки
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
Объем
вы-
выборки
3
6
7
14
10
20
13
26
20
40
ел to
о ел
35
70
50
100
75
150
100
200
150
300
200
400
300
600
500
1000
1000
2000
Интервалы приемле
0,024-
0,035
0,035—
0,06
0,06—
0, 12
0,12—
0, 17
0,17-
0,22
0,22—
0,32
Пр.Бр.| Пр. Бр. | Пр Бр. | Пр Бр. | Пр. Бр. | Пр. Бр.
А
В
С
D
Е
F
G
Н
1
J
К
L
М
N
О
0 2
1 2
0 3
2 3
§
§
4
4
4
4
4
4
4
§
4
4
4
4
4
4
-t
4
0 2
1 2
0 3
2 3
1 4
3 4
2
2
3
3
4
4
6
6
0 3
2 3
1
2
1
5
2
7
0 3
2 3
1 3
2 3
2 5
4 5
3 10
9 10
о ?
1 2
0 3
2 3
1 3
2 3
1 4
3 4
1 6
5 б
3 8
7 8
5 13
12 13
«§» означает сплошную проверку партии.
« + » знак, показывающий необходимость использования планов типа однократной
«i», «t» означают, что приемочные и браковочные числа полагаются равными
*) Statistical research group Columbia University, «Sampling inspection», Me Graw-
ТАБЛИЦА 21
505
Таблица 21
двукратная выборка *)
мого качеств*
0,
0,
Пр
0
1
0
2
1
2
1
3
2
4
2
6
3
8
5
12
7
25
3 2—
65
Бр.
+
i
см см
со со
СО СО
4
4
слсл
7
7
9
9
00 СО
26
26
0,
1
Пр.
0
1
0
2
1
2
1
3
1
5
2
5
3
7
4
9
слсл
7
23
14
43
выборки
первым ниже
ни
1, N
Y , 1
в %
65—
,2
Бр.
4
4
см см
СО 00
СО СО
4
4
6
6
CD CD
8
8
10
10
16
16
24
24
44
44
(выше
948.
1,
2
Пр.
0
2
1
2
1
3
1
4
1
5
3
5
CD CO
5
13
6
16
8
25
14
40
1
2—
,2
Бр.
[
^
3
3
со со
4
4
5
5
CD СО
6
6
10
10
14
14
17
17
CD CD
CM CM
41
41
t
) следующим
2,
3
Пр.
0
2
0
2
1
3
1
4
1
5
2
6
4
8
5
11
7
18
9
24
12
35
2—
,2
Бр.
4
4
3
3
3
3
4
4
слсл
6
6
7
7
CD CD
CM CM
19
19
25
25
CD CD
CO CO
t
t
числам.
3,
4
Пр.
to о
too
0
4
1
4
1
5
CM CD
CD CO
5
11
6
16
9
23
11
32
16
47
2—
,4
Бр.
4
coco
coco
СЛСЛ
СЛСЛ
CD CD
7
7
10
10
CM CM
17
17
24
24
33
33
48
48
t
t
4
6
Пр.
0
2
1
2
0
4
1
5
CM 1С
CM 00
4
10
6
14
8
19
11
28
14
37
4
,3
Бр.
4
coco
3
3
5
5
6
6
6
6
CD CD
11
11
15
15
20
20
29
29
CO CO
00 00
t
t
t
5,
6
Пр
0
1
1
2
1
3
1
5
CM CD
CM 00
3
9
5
12
6
18
8
25
14
33
18
44
3—
,4
Бр
to to
CO CO
4
4
6
6
7
CD CD
10
10
CO CO
19
19
26
26
34
34
45
45
t
t
G,
8
Пр
0
1
1
3
1
5
1
5
3
7
2
10
4
12
CD CD
8
23
11
30
16
43
4—
,5
Бр
CM CM
4
4
6
G
6
6
8
8
11
11
CO 00
17
17
24
24
31
31
44
44
t
f
t
t
506
ПРИЛОЖЕНИЯ
Колумбийский стандарт:
Кодо-
Кодовое
число
А
В
С
D
Е
F
G
Н
1
Кя
вы-
выборки
1
2
3
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
6
!
2
3
4
5
6
7
1
2
3
4
5
6
7
1
2
3
4
5
6
7
1
2
3
4
5
6
7
1
2
3
4
5
6
7
Объем
вы-
выборки
3
2
2
4
4
4
4
4
5
5
5
5
5
6
6
6
6
6
6
8
8
8
8
8
8
8
10
10
10
10
10
10
10
14
14
14
14
14
14
14
20
20
20
20
20
20
20
30
30
30
30
30
30
30
Интервалы приемле
0,024 —
0,035
0,035—
0,06
Пр. Бр.|Пр. Бр
4-
i
4-
1
1
+
4'
0,06-
0, 12
Пр. Бр.
4-
1
1
4-
4-
1
0, 12—
0,17
Пр. Бр.
Ф
1
4-
1
1
+
0,17—
0,22
Пр. Бр.
4-
4-
1
+
4-
Ф
4'
2
2
2
0 2
0 2
1 3
2 3
0,22—
0,32
Пр. Бр.
1
1
1
+
1
Ф
4-
2
2
2
0 2
0 2
0 2
2 3
2
2
0 2
0 2
1 3
1 3
2 3
последовательная выборка
мого качества
0,
0
Пр.
•
*
0
0
1
2
3
»
"
0
1
1
1
2
•
0
1
2
3
3
4
32—
,65
Бр.
1
¦V
i
I
2
2
2
2
3
4
4
2
2
2
3
3
3
3
2
2
3
4
5
5
5
0,
1
Пр
-
¦
0
1
1
1
2
в
"
0
0
1
2
3
-
0
1
1
2
3
4
¦
0
1
2
2
2
3
•
0
1
2
3
5
6
в %
65-
, 2
Бр
_^_
1
1
2
2
2
3
3
3
3
2
2
2
3
3
4
4
2
3
3
3
4
5
5
2
3
3
4
4
4
4
3
3
4
6
6
7
7
1
2
Пр.
-
0
0
0
1
2
-
0
1
2
2
2
3
»
0
1
1
2
2
4
»
0
1
3
3
3
4
»
0
1
2
4
4
5
•
1
3
5
6
7
8
2—
?2
Бр
1
1
2
2
2
3
3
3 ¦
2
2
3
4
4
4
4
2
3
3
4
4
4
5
2
3
4
5
5
5
5
3
4
4
5
6
6
6
3
4
6
7
8
9
9
2,
3
Пр.
»
0
0
1
2
-
0
0
0
1
3
.
0
1
2
2
2
3
•
0
1
2
4
4
5
»
0
1
2
4
4
5
»
1
2
3
5
6
7
0
2
3
4
6
8
11
ТАБЛИЦА
2—
,2
Бр.
2
2
3
3
3
2
2
3
3
4
4
2
3
3
4
4
4
4
2
3
4
5
6
6
6
3
3
4
5
6
6
6
3
4
5
6
7
8
8
4
5
8
9
10
12
12
3,
4
Пр.
»
0
1
1
3
-
0
0
1
3
-
0
1
2
2
3
»
0
1
2
3
5
6
•
0
2
3
4
6
»
1
2
3
4
5
6
0
1
3
5
8
9
10
0
3
5
7
9
12
14
22
2-
,4
Бр.
1
2
2
3
3
4
2
2
3
3
4
2
3
3
4
4
4
2
4
4
5
6
7
7
3
3
4
6
7
7
7
3
4
4
6
6
7
7
4
5
6
8
10
1 1
11
4
7
9
И
13
15
15
4 ,
5
Пр
•
0
1
1
3
.
1
1
1
3
-
0
1
2
3
4
п
0
1
2
4
5
6
-
2
3
4
5
6
»
1
2
4
6
7
10
0
2
5
6
8
11
13
1
3
6
9
И
14
17
4
,3
Бр.
1
2
3
3
3
4
2
3
3
3
4
2
3
4
4
5
5
3
3
4
5
6
7
7
3
4
4
6
7
7
7
3
5
6
7
9
10
1 1
4
6
7
9
12
14
14
5
7
10
13
15
18
18
1
5,
6
Пр
0
0
1
0
0
1
2
4
-
1
1
1
3
-
1
1
2
3
5
»
2
3
4
6
7
•
1
2
4
5
7
8
0
1
3
5
6
8
9
0
3
6
8
10
12
14
1
3
5
8
11
14
19
' а б л
3-
4
Бр
2
2
2
2
3
4
4
5
2
3
4
4
4
3
3
5
6
6
6
3
4
5
6
6
8
8
3
4
6
7
8
9
9
4
5
6
8
9
10
10
4
7
9
11
12
14
15
5
9
12
15
18
20
20
И Ц
6
1
Пр.
0
0
2
0
0
1
2
4
0
0
2
3
5
•
1
2
2
3
5
0
1
2
3
5
6
8
0
1
3
4
5
7
10
0
3
4
6
8
10
13
1
3
6
9
13
16
18
5
9
13
18
22
25
507
а 22
4
1,5
Бр.
2
2
3
2
3
4
5
5
3
3
4
6
6
3
4
4
5
6
6
3
5
6
7
8
8
9
4
5
7
8
9
10
11
4
6
8
10
12
14
14
5
8
И
13
16
18
19
7
10
13
18
22
25
26 |
508
ПРИЛОЖЕНИЯ
Кодо-
Кодовое
число
ЛЬ
вы-
выборки
Объем
вы-
выборки
Пр. Бр.|Пр Бр.| Пр Бр. | Пр Бр | Пр Бр. I Пр. Бр
Интервалы приемле
0,024—
0,035
0,035—
0,06
0,06—
0, 12
0, 12 —
0, 17
0,17—
0,22
0,22-
0,32
40
40
40
40
40
40
40
50
50
50
50
50
50
50
50
75
75
75
75
75
75
75
I M
100
100
100
100
100
100
100
100
150
150
150
150
150
150
150
150
150
1
2
3
4
5
6
7
10
300
300
300
300
300
300
300
300
300
3
4
5
7
8
10
3
5
6
7
8
9
10
11
0
1
2
4
6
8
10
12
15
«$» означает сплошную проверку партии.
« + » знак, показывающий необходимость использования планов типа однократной
«4-», «t» означают, что приемочные и браковочные числа полагаются равными
«"» означает, что если число выявленных дефектных изделий меньше браковочного
*) Statistical research group Columbia University, «Sampling inspection»,
таблица 22 509
Продолжение табл. 22
мого
качества
0,32-
0,65
Пр.
»
0
1
3
3
3
4
»
0
2
2
3
4
5
6
-
1
1
2
3
5
7
»
1
1
3
4
5
7
9
0
1
2
4
6
8
10
12
15
0
2
4
7
10
13
15
18
23
Бр.
2
3
3
5
5
5
5
2
4
4
5
6
7
7
7
3
4
5
6
6
8
8
3
5
6
7
8
9
10
10
4
5
7
9
1 1
13
14
15
16
6
9
11
14
17
20
?3
24
24
выборки
первым
в %
0,65-
1
Пр.
»
1
2
4
5
6
8
„
1
2
3
4
5
7
9
0
2
3
5
7
9
10
0
2
4
6
8
10
12
16
0
3
5
7
10
13
15
18
23
1
6
10
15
19
24
28
33
41
ниже
2
Бр.
3
4
4
6
7
8
9
3
4
6
7
8
9
10
10
4
5
7
9
10
1 1
11
4
6
8
11
13
15
17
17
6
8
11
13
16
19
21
24
24
8
13
18
22
27
13
36
41
42
1,
2
Пр.
0
1
3
5
6
8
1 1
0
2
3
5
7
9
11
15
0
3
6
8
11
13
18
0
4
6
9
12
15
19
24
6
10
15
19
24
28
33
41
2-
2
Бр
4
5
6
8
10
12
12
4
6
8
10
12
14
16
16
5
8
10
13
16
18
19
7
9
13
16
19
22
25
25
8
13
18
22
27
31
36
41
42
t
2,
3
Пр.
0
2
5
7
9
1 1
15
0
3
5
8
10
13
15
19
1
4
8
12
15
18
24
1
5
10
14
18
23
27
34
2—
2
Бр
4
7
9
11
13
15
16
5
8
11
13
15
18
20
20
7
10
14
18
21
25
25
8
13
18
22
26
31
35
35
t
t
(выше) следующим числам.
числа, то необходимо перейти
Мс
Graw-Hill
, N. Y., 1948.
3,
4
Пр
1
2
5
8
11
14
18
1
3
7
10
13
16
19
24
2
6
10
15
19
24
30
2
8
13
19
24
30
35
43
2—
,4
Бр
5
8
1 1
14
17
19
19
6
9
13
16
19
22
25
25
8
13
17
22
26
31
31
10
16
21
27
33
38
44
44
t
t
к следующей выборке.
4,
5
Пр.
1
5
7
10
13
17
22
2
4
8
12
16
21
25
28
3
8
13
19
25
30
36
4—
.3
Бр.
6
9
12
16
19
21
23
7
11
15
19
22
26
29
29
9
15
20
26
32
37
37
t
t
t
5,
6
Пр.
2
5
9
13
17
22
26
2
7
12
17
21
26
30
36
4
\ \
18
25
32
39
42
3_
,4
Бр.
6
11
15
19
22
26
27
7
13
18
22
27
32
36
37
10
16
23
30
36
4 3
4 3
!
t
t
6,
8
Пр.
2
7
13
18
23
28
30
3
8
14
19
25
30
36
43
4
,5
Бр.
8
12
16
21
26
31
31
9
14
20
25
31
38
43
44
t
t
i
t
t
510
ПРИЛОЖЕНИЯ
Таблица 23
Значения qc
с
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 •
20
к
1,0
1,618 034
2,269 531
2,945 186
3,639 547
4,349 048
5,071 184
5,804 ПО
6,546411
7,296 973
8,054 895
8,819440
9,589 989
10,366 021
11,147 089
11,932 806
12,722 834
13,516878
14,314 674
15,115 990
15,920 615
0,367 879
0,839 962
1,371 102
1,942 381
2,543 534
3,168 185
3,812021
4,471 954
5,145 672
5,831 388
6,527 684
7,233 412
7,947 624
8,669 525
9,398 444
10,133 803
10,875 103
11,621909
12,373 837
13,130 548
13,891 741
Таблица 24
Значения G^. Однократные планы типа (п, сJ3> обеспечивающие минимум инспекции при заданном предельном
выходном качестве
с
0
1
2
3
4
5
6
7
8
9
с
0
1
2
3
4
с
0
2
3
4
*Л=1.25
1,8577
5,9938
12,8489
22,8056
36,2546
53,6074
75,3021
101,8075
133,6275
171,3037
1 ,5
1,7801
6,2035
14,3061
27,2709
46,5288
73,8210
111,2667
161,4402
227,4595
313,0920
ЛЖЛ.Б
1,5269
8,6207
32,9793
106,5346
312,7753
*л* = 7'0
1,4136
13,5897
92,4665
540,6050
2885,6530
1.75
1,7218
6,4506
15,9794
32,7432
60,1200
102,7752
167,1075
261,8326
398,7442
593,7016
4.0
1,4998
9,3039
39,4335
141,7821
464,1827
8,0
1,3984
15,0531
115,5311
763,0557
4601,0190
2,0
1,6761
6,7231
17,8538
39,3031
77,6940
143,2597
251,6220
426,3712
702,7834
1133,1702
4,5
1,4782
10,0002
46,5761
184,6943
667,6728
9,0
1,3864
16,5250
141,2726
1040,3821
6994,2623
2.25
1,6393
7,0138
19,9201
47,0379
99,9893
198,6348
376,3707
688,5724
1225,9578
2135,5421
5,0
1,4606
10,7061
54,4014
236,0230
934,1697
10,0
1,3767
18,0032
169,6862
1378,6538
10223,1926
2.5
1,6090
7,3181
22,1727
56,0381
127,8114
272,8749
556,2021
1095,1553
2098,7605
3934,8835
2.75
1,5836
7,6328
24,6074
66,3953
162,0318
370,6220
809,8459
1709,7170
3512,8680
7059,7682
5,5
1,4459
11,4195
62,9057
296,5222
1275,6565
12,0
1,3619
20,9723
234,5184
2262,3052
19916,9796
3.0
1,5619
7,9559
27,2215
78,2018
203,5869
497,2384
1160,5589
2617,1010
5742,6847
12321,9866
6,0
1,4335
12,1386
72,0860
366,9476
1705,1578
15,0
1,3468
25,4460
351,7536
4196,8272
45696,8272
512
ПРИЛОЖЕНИЯ
Экономичные планы типа
0,0063
0,010
0,016
0
0
0—1
1
1—2
2
2—3
3
3—4
4
4—5
5—6
6—7
7-8
8—9
9—10
1,0706
0,4793
—0,1120
-0,7033
— 1,2946
-1,5363
— 1,7781
— 1,9233
-2,0685
-2,1702
-2,2719
—2,4265
-2,5503
—2,6531
—2,7406
—2,8167
—3,3067
—2,8043
—2,4489
—2,0909
—1,5281
— 1,1338
—0,9242
-0,7328
—0,6033
—0,4564
—0,3589
—0,2900
—0,1774
—0,1176
—0,0734
0,0176
0,0898
0,1660
0,2196
0,2851
0,3267
0,3841
0,4176
0,4686
0,4962
0,5422
0,9761
0,4310
-0,1141
-0,6593
-1,2044
-1,4318
-1,6592
-1,7973
-1,9354
-2,0327
-2,1300
-2,2786
-2,3980
,4974
•2,5823
2,6561
—3,0197
—2,5678
—2,2470
— 1,8895
— 1,3792
—1,0276
—0,8188
—0,6455
-0,5275
—0,3814
—0,2928
—0,2294
—0,1175
—0,0630
—0,0221
0,0683
0,1348
0,2105
0,2599
0,3250
0,3635
0,4206
0,4516
0,5023
0,5279
0,5736
0,8805
0,3814
-0,1177
-0,6167
-1,1158
-1,3288
-1,5418
-1,6726
-1,8034
-1,8962
-1,9891
-2,1316
-2,2465
-2,3424
-2,4244
-2,4960
—2,7300
—2,3279
—2,0409
— 1,6840
— 1,2275
—0,9177
—0,7101
—0,5549
—0,4485
—0,3034
—0,2238
—0,1659
—0,0549
—0,0056
0,0318
0,1216
0,1822
0,2574
0,3026
0,3672
0,4025
0,4592
0,4876
0,5380
0,5616
0,6070
ТАБЛИЦА 25
513
Таблица 25
однократной выборки
0,025
0,040
0,063
0, 10
0,7896
0,3333
-0,1230
-0,5793
-1,0356
-1,2350
-1,4345
-1,5584
-1,6823
-1,7709
-1,8594
-1,9960
-2,1065
-2,1991
-2,2784
-2,3477
—2,4569
—2,1004
— 1,8442
— 1,4881
— 1,0829
—0,8112
—0,6050
—0,4670
—0,3712
—0,2273
—0,1561
—0,1035
0,0066
0,0509
0,0851
0,1741
0,2292
0,3038
0,3449
0,4091
0,4413
0,4975
0,5235
0,5736
0,5951
0,6402
0,6928
0,2804
-0,1320
-0,5444
-0,9567
-1,1421
-1,3274
-1,4440
-1,5606
-1,6446
-1,7286
-1,8588
-1,9647
-2,0535
-2,1299
-2,1968
—2,1707
— 1,8604
— 1,6351
— 1,2806
-0,9293
—0,6960
—0,4917
—0,3714
—0,2868
—0,1444
—0,0818
—0,0349
0,0740
0,1132
0,1439
0,2320
0,2812
0,3550
0,3919
0,4554
0,4844
0,5401
0,5625
0,6121
0,6325
0,6772
0,5962
0,2251
-0,1460
-0,5172
-0,8883
-1,0600
-1,2318
-1,3413
-1,4508
-1,5302
-1,6097
-1,7337
-1,8348
-1,9200
-1,9934
-2,0579
—1,8944
-1,6268
— 1,4301
— 1,0780
—0,7787
—0,5805
—0,3788
—0,2754
—0,2012
—0,0607
—0,0065
0,0351
0,1426
0,1768
0,2042
0,2911
0,3347
0,4076
0,4403
0,5031
0,5289
0,5839
0,6048
0,6538
0,6712
0,7154
0,4914
0,1610
-0,1694
-0,4998
-0,8302
-0,9881
-1,1459
-1,2481
-1,3502
-1,4250
-1,4987
-1,6161
-1,7132
-1,7945
-1,8648
-1,9266
-1,6115
-1,3853
— 1,2168
—0,8686
—0,6216
—0,4572
—0,2589
—0,1723
—0,1088
0,0292
0,0752
0,1113'
0,2169
0,2461
0,2700
0,3555
0,3933
0,4650
0,4936
0,5554
0,5779
0,6322
0,6505
0,6988
0,7141
0,7577
514
ПРИЛОЖЕНИЯ
Номограмма экономичных планов
Oft
$32
Ц25
Ц2
0,16
QJ3
OJO
щ
щз
0,032
QP2S
0,02
0,0/6
0,0/3
0,0/
¦ ¦¦¦... I
-,
НОМОГРАММА
515
типа однократной выборки
С=2 3
S
ЛИТЕРАТУРА
К главе 1
I. Маликов И. М., Половко А. М., Романов Н. А., Ч у к-
реев П. А., Основы теории и расчета надежности, Судпромгиз, 1960.
2. Шор Я. Б., Статистические методы анализа и контроля качества и
надежности, «Советское радио», 1962.
3. Ллойд Д., Л ипов М., Надежность. Организация исследования, ме-
методы, математический аппарат, «Советское радио», 1964.
4. Bazovsky I., Reliability theory and practice, Prentice-Holl, Engle-
wood Cliffs, New Jersey, 1962.
5. Гнеденко Б. В., Курс теории вероятностей, Физматгиз, 1961.
6. Вентцель Е. С, Теория вероятностей, Физматгиз, 1962.
7. Леман Э., Проверка статистических гипотез, «Наука», 1964.
8. Дунин-Барковский И. В. и Смирнов Н. В., Теория вероят-
вероятностей и математическая статистика в технике (общая часть), ГТТИ,
1955.
9. Крамер Г., Математические методы статистики, ИЛ, 1948.
10. Ван дер Варден Б. Л., Математическая статистика, ИЛ, 1960.
II. Колмогоров А. Н., Основные понятия теории вероятностей, ОНТИ,
1936.
12. Серенсен С. В., Когаев В. П., Степнов М. Н., Гиацин-
Гиацинтов Е. В., О законе распределения долговечности при усталостных
испытаниях, Заводская лаборатория 24, 3 A958), 324 — 329.
13. Wei bull W., A statistical distribution function of wide applicability,
J. Appl. Mech. 18, 3 A951), 293 — 297.
14. Колмогоров А. Н., О логарифмически нормальном законе распре-
распределения размеров частиц при дроблении, ДАН СССР 31, 2 A941),
99—101.
15. Филиппов А. Ф., О распределении размеров частиц при дроблении,
Теория вероятностей и ее применения 6 A961), 209 — 318.
16. X и н ч и н А. Я., Об унимодальных распределениях, Томск, Изв. НИИ
матем. и механ. ун-та 2, 2 A938), 1—7.
17. Gnedenko В., Sur la distribution limite du terme maximum d'une
serie aleatoire, Ann. Math. 44, 3 A943).
18. Gumbel E., Statistics of extremes, Columbia University press, N. Y.,
1958.
19. Kapteyn J. C, Skew Frequency Curves, 1903.
20. Хинчин А. Я., Математические методы теории массового обслужи-
обслуживания, Изд-во АН СССР, 1955.
21. Григелионис Б., О сходимости сумм ступенчатых процессов к пуас-
соновскому, Теория вероятности и ее применения 8, 2 A963).
22. С 1 о р р е г J., Pearson E., The use of confidence or fiducial limits
illustrated in the case of the binomial, Biometrica 26, 404—413 A934).
ЛИТЕРАТУРА 51?
К главе 2
1. Маликов И. М., Половко А. М., Романов Н. А., Ч у к р е-
ев П. А., Основы теории и расчета надежности, Судпромгиз, 1960.
2. Проблемы надежности радиоэлектронной аппаратуры (Сборник докладов
пятого национального симпозиума США), Оборонгиз, 1960.
3. Knight G. R., Gervis E. R., Herd E. R., The definition of terms
of Interest in the study of reliability, Trans. IRE, PGRQC, April 1955,
p. 34.
4. Теория надежности в области радиоэлектроники, Терминология, Изд-во
АН СССР, 1962.
5. Гнеденко Б. В., Шор Я. Б., Надежность, Энциклопедический спра-
справочник «Автоматизация производства и промышленная электроника»,
т. 2, Советская энциклопедия, 1963, 348—353.
6. Шеннон К., Бандвагон, Сб. «Работы по теории информации и ки-
кибернетики», ИЛ, 1963.
7. Bellman R., Dreyfus S., Dynamic Programming and the Reliability
of Multicomponent Devices, Operation Research 6, 2 A958), 200 — 206.
8. Беляев Ю. К-, Линейчатые марковские процессы и их приложение к
задачам теории надежности, Труды VI Всесоюзного совещания по тео-
теории вероятностей и математической статистики, Вильнюс, 1962, 309 — 323.
9. Севастьянов Б. А., Эргодическая теорема для марковских процес-
процессов и ее приложение к телефонным системам с отказами, Теория веро-
вероятностей и ее применения 2, 1 A957), 106 —116.
10. Марьянович Т. П., Надшшсть системи 3i зм1шаним резервом, ДАН
УРСР 8 A961), 944 — 947.
11. Гнеденко Б. В., Курс теории вероятностей, Физматгиз, 1961.
12. Смит В., Теория восстановления, Сб. переводов, ИЛ. «Математика» 5,
3 A961), 95—150.
13. X и н ч и н А. Я., Работы по теории массового обслуживания. Физмат-
Физматгиз, 1963.
14. Соловьев А. Д., Математические вопросы теории надежности, Радио-
Радиоэлектронная промышленность 4 A958).
15. Дружинин Г. В., Предсказание сохранности элементов и систем ав-
автоматики при векторных определяющих параметрах, Изв. АН СССР,
Энергетика и автоматика 2 A961), 165—170.
16. Григелионис Б. И., Предельные теоремы для сумм процессов вос-
восстановления, Сб. «Кибернетику на службу коммунизму», Изд-во «Энер*
гия», т. 2 A964), 246 — 265.
17. Соловьев А. Д., Надежность систем с восстановлением, Сб. «Кибер-
«Кибернетику на службу коммунизму», т. 2, Изд-во «Энергия», 1964, 189—193.
К главе 3
1. Epstein В., Testing for the validity of the assumption that the un-
underlying distribution of life is exponential, Technometrics 1—2 A960),
83 — 101, 167—183.
2. Epstein В., Sobel M., Life Testing, J. Amer. Stat. Assoc. 48 A953),
486 — 502.
3. Epstein В., Sobel M. Sequential Life Tests in the Exponential
Case, Ann. Math. Statist. 26, 1 A955), 82 — 93.
4. Buck land W. R., Statistical assesement of the life characteristic,
Griffin's statistical monographs & courses, London, 1964 (a bibliographic
guide).
518 ЛИТЕРАТУРА
5. Као J. Н. К., Computer Methods for Estimating Weibull Parameters
in Reliability Study, Trans. IRE, PGRQC, July 1958, 15 — 22
6. E n d i с о t t H. S., Zoellner J. A., A preliminary investigation
of the steady and progressive stress testing of mica capacitors, Proc.
7-th Nat. Symp, on reliability and quality control, 1961, 229 — 240.
7. S a r h a n A., G r e e n b e r g В., Contributions to Order Statistics, N. Y.,
1962.
8. Дынкин Е. Б., Необходимые и достаточные статистики для семейст-
семейства распределений вероятностей, Успехи матем. наук 6, 1 A951), 68 — 90.
9. БольшевЛ. Н., О сравнении параметров распределения Пуассона,
Теория вероятностей и ее применения 7, 1 A962), 119—120.
10. Pugh E. L., The best estimate of reliability in the exponential case,
Oper. Res. 11, 1 A963), 57 — 61.
11. Мирный Р. А., Соловьев А. Д., Оценка надежности системы по
результатам испытаний ее компонент, Сб. «Кибернетику на службу ком-
коммунизму», т. 2, Изд-во «Энергия», 1964, 213 — 218.
12 Колмогоров А. Н., Несмещенные оценки, Известия АН СССР, сер.
матем. 14 A950), 303 — 326.
К главе 4
1. Л е м а-н Э., Проверка статистических гипотез, «Наука», 1964
2 В а л ь д А., Последовательный анализ, Физматгиз, 1960.
3. Wald A., Statistical decision functions, N. Y., 1950.
4. Я н к о Я., Математико-статистические таблицы, Госстатиздат, 1961.
5. Epstein В., Testing for the validity of the assumption that the
underlying distribution of life is exponential, Technometrics 2, 1 — 2
A960), 83—101, 167—183.
6. Cochran W. G., The X2 test of goodness of fit, Ann. Math. Statist. 23,
3 A952), 315 — 345.
7. Sherman В., A random variable related to the spacing of sample
values, Ann Math. Statist. 21 A950), 339 — 361
8. Bartholomew D. J, Testing for departure from the exponential
distribution, Biometrika 44 A957), 253 — 256.
9. Fisher R. A., Tests of significance in harmonic analysis, Proc. Roy.
Soc. A 125 A929), 54 — 59.
10 Hartley H. O., The maximum F-ratio as a short-cut test of hetero-
heterogeneity of variance, Biometrika 37 A950), 308 — 312.
11 Dvoretzky A., Kiefer J., W о 1 f о w i t z I., Sequential decision
problems for processes with continuous time parameter, testing hypot-
hypotheses, Ann. Math. Statist. 24 A953), 254 — 264.
12 M и x а л е в и ч В. С, Последовательные бейесовские решения и опти-
оптимальные методы приемочного статистического контроля, Теория вероят-
вероятностей и ее применения 1, 4 A956).
13. Ширяев А. Н., К теории решающих функций и управлению процес-
процессом наблюдения по неполным данным, Trans, of the 3 Prague conference
on information theory, Prague, 1964, 657—681.
14. Беллман Р., Динамическое программирование, ИЛ, 1960.
15. Kiefer J., Wolfowitz I., Sequential tests of hypotheses about the
mean occurence time of a continuous parameter Poisson process, Naval
research logistics quarterly 3, 3 A956), 205—219.
16. В а н дер Варден Б. Л., Математическая статистика, ИЛ, 1960,
321—357.
17. Г не де и ко Б В., Курс теории вероятностей, Физматгиз, 1961, 354—
360.
ЛИТЕРАТУРА
18. Гнеденко Б. В., О критерии Вилкоксона сравнения двух выборок*
Бюлл. Польск. АН, сер. матем., астр, и физ. наук VI, 10 A958), 611 —
614.
19. Гнеденко Б. В., Проверка неизменности распределения вероятнос-
вероятностей в двух независимых выборках, Matheni. Nachr. 12, 1—2 A954),.
29-66.
20. Б ер л ян д X. Л., Кв1т I. Д., Про одну задачу пор1вняння двох ви-
борок, ДАН УРСР 1 A952), 13—15.
21. Квит И. Д., О теореме Н. В. Смирнова относительно сравнения двух
выборок, ДАН СССР 71, 2 A950), 229—231.
22. Мания Г. М., Практическое применение оценки максимума двухсто-
двухсторонних уклонений эмпирической кривой распределения в заданном ин-
интервале роста теоретического закона, Сообщ. АН Груз. ССР 14, 9 A953),
521—524.
23. Мания Г. М., Практическое применение оценки максимума односто-
односторонних уклонений эмпирической кривой распределения в заданном ин-
интервале роста теоретического закона, Тр. Груз, политехи, ин-та 30A954),.
89—94.
24. Mann Н. В. and W h i t n e у D. R., On a Test of Whether One of Two
Random variables is Stochastically Larger than the Other, Ann. Math.
Statist. 18, 1 A947), 50—60.
25. P в а ч е в а Е. Л., О максимальном расхождении между двумя эмпириче-
эмпирическими распределениями, Укр. матем. ж. 4, 4 A952), 373—392.
26. Masse у F. J., The distribution table for the deviation between two
sample cumulatives, Ann. Math. Statist. 23, 3 A952), 435—442.
27. Massey F. J., The distribution of the maximum deviation between
two sample cumulative step functions, Ann Math Statist. 22, 1 A951),
125—128.
28. Дунин-Барковский И. В. и Смирнов Н. В., Теория вероят-
вероятностей и математическая статистика в технике (общая часть), Гостехиз-
дат, 1955.
К главе 5
1. Гнеденко Б. В., Курс теории вероятностей, Физматгиз, 1961.
2. Смирнов Н. В., Предельные законы распределения для членов вари-
вариационного ряда, Тр. Матем. ин-та АН СССР 25 A949).
3. Ф ел л ер В., Введение в теорию вероятностей и ее приложения, Изд-во
«Мир» 1964.
4. Ллойд Д, ЛиповМ., Надежность, «Советское радио», 1964, стр. 323.
5. Синица М. А., Методы резервирования радиоаппара^ры, Электро-
Электросвязь 4 A959).
К главе 6
1. Гнеденко Б. В., О ненагруженном дублировании, Изв. АН СССР,
Техническая кибернетика 4 A964).
2. Гнеденко Б. В., О дублировании с восстановлением, Изв. АН СССР,
Техническая кибернетика 5 A964).
3. Соловьев А. Д., Асимптотическое распределение времени жизни
дублированного элемента, Изв. АН СССР, Техническая кибернетика
5 A964).
4. С о л о в ь е в А. Д., Об определении резервов для систем многократ-
многократного действия, Изв. АН СССР, Энергетика и автоматика 2 A962),.
124—129.
520 ЛИТЕРАТУРА
5. Karlin S., Me Gregor J., The differential equations of Birth and
Death processes and the Stieltjes moment problem, Trans. Amer. Math.
Soc 85, 2 A957), 489—546.
6 Феллер В., Введение в теорию вероятностей и ее приложения, «Мир»,
1964.
7. X и н ч и н А Я., Работы по математической теории массового обслужи-
обслуживания, Физматгиз, 1963.
8. Гнеденко Б. В,, Коваленко И. Н., Лекции по теории массово-
массового обслуживания, Киев, 1964.
9. Натансон И. П., Конструктивная теория функций, ГТТИ, 1949.
10 Соловьев А. Д., Надежность систем с восстановлением, Сб. «Кибер-
«Кибернетику на службу коммунизму», т. 2, Изд-во «Энергия», 1964.
П. Беляев Ю. К., Линейчатые марковские процессы и их приложение к
теории надежности, Труды VI Всесоюзного совещания по теории вероят-
вероятностей и математической статистике, Вильнюс, 1962, 309—323.
12. Epstein В., Н о s f о г d Т., Reliability of some two units redundant
systems, Proc. 6-th Nat Symp. on reliability and quality control,
1960, 466—476.
13. Gaver D. P, Time to failure and availability of paralleled systems
with repair, Trans. IRE, PGRQC, June 1963, 30—38.
К главе 7
1. Колмогоров А. Н., Несмещенные оценки, Изв. АН СССР, сер. ма-
тем 14, 4 A950), 303—326.
2. С и р а ж д и н о в С. X., ЭйдельнантМ. И., К вопросу об оценках
качества продукции по результатам выборочного контроля, Тр. Ин-та
магем. АН УзССР, Ташкент, 22 A961).
3. Alen Wall is W., Techniques of Statistical Analysis, 1947.
4. Dodge H. F., Romig H. G., Sampling inspection, N. Y., 1959.
5 Statistical Research Group Columbia University, Sampling inspection,
N. Y., 1948
6 Коуден Д., Статистические методы контроля качества, Физматгиз,
1961.
7. Стандарты статистического контроля (проект), Ин-т матем. АН. УзССР,
Ташкент, 1961.
8. Hill J. D., Sampling inspection and defence specification, DEF-131
(with discussion), J. Roy. Statist. Soc. A125, 1 A962), 31—87.
9. Шор. Я. Б., Статистические методы анализа и контроля качества и
надежности, «Советское радио», 1962.
10 Horsnell G, Economical acceptance sampling schemes, J. Roy.
Statist. Soc. A120 A957), 148—201.
11 Van der WaerdenB. L., Sampling inspection as a minimum loss
problem, Ann Math. Statist. 31, 2 (I960), 369—384.
12. Hald A., The compound hypergeometric distribution and a system of
single sampling inspection plans based on prior distributions and costs,
Technometrics 2, 3 A960), 275—340, discussion 361—372.
13. Беляев Ю. К., Колмогоров А. Н., Экономичные планы прие-
приемочного контроля, Доклад на IV Всесоюзном математическом съезде,
Ленинград, 1960.
14. Вальд А., Последовательный анализ, Физматгиз, 1960.
15. С и р а ж д и н о в С. X., Несмещенные оценки доли пропущенного брака
при методе однократной выборки, Тр. Ин-та матем. и механ. АН
УзССР, Ташкент, 20 A955), 89—100.
16. Колмогоров А. Н., Статистический приемочный контроль при до-
допустимом числе дефектных изделий, равном нулю, Ленинград, 1951.
ЛИТЕРАТУРА 521
17. Эйдельнант М. И., Инамов И., О практическом применении
оценочных функций для анализа результатов статистического контроля
качества продукции, Теория вероятностей и математическая статистика
1 A954), Изд-во «Наука» АН УзССР, 48—57.
18. Ргос. Nat. Symp. on Reliability and Control in Electronics, USA, № 1—9,
1954 — 1963.
19. Bowker A. H., Good H. P., Sampling inspection by variables, N. Y.,
1952.
20. Barnard G. A., Control charts and stochastic processes (with discussion),
J. Roy. Statist. Soc. A 21, 2 A959), 239—271.
21. Goldsmith P. L., W h i t f i e 1 d H., Average run lengths in cumula-
cumulative chart quality control schemes, Technometrics 3, 1 A961). 11—20.
22. Chernoff H., Sequential tests for the mean of a normal distribution,
Proc. 4-th Berkeley Symp. on math. stat. and probability 1, A961),
79—91.
23. Ширяев А. Н., К обнаружению разладок производственного процес-
процесса, Теория вероятностей и ее применения 8, 3 A9ВЗ), 264—281, 4 A963),
431—443.
УКАЗАТЕЛЬ ТЕРМИНОВ1)
Абсолютная непрерывность 25
Аксиомы вероятностей 16
Априорные вероятности 265
Априорное распределение числа де-
дефектных изделий 382
Безотказность 81
Безразличное качество 387
Бейесовские критерии 266
Больших чисел закон 41
Вариационный ряд 59, 297
Вероятностная бумага |нор*мальная
171
~ показательная 242
Входное качество 389
Выходное качество 389
Гипотеза простая 69
— сложная 69
— основная 226
— конкурирующая 226
Гистограмма 164
Графические оценки параметров 169
Группа отказа 136
Двукратная выборка 384, 399
Дисперсия 35
Доверительный интервал 66, 196
Доверительный интервал для Я, план!
[N, Я, Т] 197
~ [N, В, г] 199
— [N, Б, г] 200
— N, Бу Т] 201
~ N, В, (г, Т)\ 203
— N, Б, (г, HSQ)] 206
~ Ny Б, (г, Т)] 207
Доверительные множества 222
Доверительный уровень 67
Долговечность 82
Достаточная статистика 63, 440
Изделие 79
Инверсия 281
Интенсивность отказов 144
Качество 79
Квантиль 37
Коэффициент готовности 122, 125
Коэффициент доверия 67, 196, 215
Контроль входной 378
— выходной 378
— качественный 379
— по количественному признаку 379
— неразрушительный 380
— очистительный 381
— предупредительный 381
— приемочный 378
— разрушительный 380
— текущий 378, 460
Критерий 226
— Вилкоксона 281
— для проверки гипотез о значении
параметра к, план | [/V, В, Т] 254
~ [N, В, г] 255
~ N, В, (г, 7I 256
~ N, Б, Т] 258
— N, Б, г] 260
— N, Б, (г, Т)\ 260
— N, Б, (г, HS0)] 261
~ для разнотипных данных 268
~ типа В последовательного ана-
анализа 266
~ типа Б последовательного анали-
анализа 275
Критерий знаков 278
— Колмогорова проверки показа-
показательности 246
— Колмогорова проверки типа рас-
распределения 230
— нерандомизированный 226
— основанный на однородных ста-
статистиках 247
— отношения правдоподобия 235
— равномерно наиболее мощный
237
— рандомизированный 227
— регулярный 267
— Смирнова 284
— согласия X2 70, 228, 229
— Фишера для большого интервала
250
— F Фишера 229, 248
— Хартли 252
х) В указателе терминов ~ (тильда) заменяет группу слов, отделенную
вертикальной чертой в предыдущем термине,— (тире) заменяет слово.
УКАЗАТЕЛЬ ТЕРМИНОВ
523
Критерий X2 Для проверки показа-
показательности 244, 250
Критическая область (множество) 68,
226
Математическое ожидание 33
Масштаб резервирования 329
Медиана 37
Метод доверительных интервалов 66
— квантилей 65, 172
— моментов 63, 172
— наибольшего (максимального)
правдоподобия 61, 178
Множества 14
Множество пустое 15
Мода 37
Момент /г-го порядка 36, 176
~ начальный 36
~ центральный 36
Надежность восстанавливаемой си-
системы 143
— изделия 80
— системы с конечным временем
восстановления 149
Несмещенная оценка для | вероят-
вероятности безотказной работы 193
~ дисперсии 445
~ случайной величины 439
Несмещенные оценки для планов
контроля | (п, с, с') 451
~ (я, сI2 454
~ (/г, сJ3 455
~ (л, сI3 455
Несмещенные оценки для функции
от D 439
Нормальность хода производства 381
Однократная выборка 391, 384
Опасность отказа 94, 117
Оперативная характеристика плана
контроля 394, 385
Ординарность 55
Отсутствие последействия 54
Оценка 60
— достаточная 63
— максимального правдоподобия 62
— несмещенная 60
— состоятельная 60
— эффективная 61
— эффективности контроля 446
Оценка параметров экспоненциаль-
экспоненциального закона, план | [N, В, Т] 182
~ [N, Я, г] 184
~ [N, Я, (г, T)] 185
~ [N, Б, Т] 187
Оценка параметров экспоненциаль-
экспоненциального закона, план | [Л*, Б, г] 189
— [N, Б, (г, Т)] 191
— [N, Б, (г, HS0)] 192
Ошибка 1-го рода 68, 232
Ошибка 2-го рода 68
Переключатель 322
Пересечение высокого уровня 358
— множеств 15
План испытаний 158
~ типа Б 158
~ типа В 158
~ типа [Л7, Б, Г], [Л/, В, г] и др.
159, 160
~ типа последовательного анализа
384, 401
Плотность распределения 25
— восстановления ПО
Поле событий (а—алгебра) 16
Поток простейший 148
Правило приемкигс + 1-го изделия 451
— Фишера 71
Предельное выходное качество 405
— допустимое качество 386
Преобразование Лапласа 71
~ нормального закона 77
~ экспоненциального закона 77
— гамма-распределения 78
Переходные вероятности 53
Период выжигания 96
— нормальной работы 96
— приработки 96
— старения 96
Приемлемое качество 386
Производящая функция 144
Процесс восстановления 55, 109
~ с конечным временем восстанов-
восстановления 122
Процесс Маркова 52
— неоднородный пуассоновский 56
— Пуассона 53
— случайный 50
Процесс типа гибели 304
~ и размножения 335, 347
Пуассоновский поток с переменным
параметром 146
Распределение биономиальное 23
— бэта 29
— Вейбулла 28, 102, 242
— гипергеометрическое 23, 239, 393
— гамма 27, 104
— двойное показательное 29, 104
— логарифмически нормальное 29,
104
524
УКАЗАТЕЛЬ ТЕРМИНОВ
Распределение несобственное 26
— нормальное 26
— нецентральное Стьюдента 38, 218
— отрицательное биномиальное 21
— показательное (экспоненциальное)
27, 96, 97
— Пуассона 26
— равномерное 26
— смеси 30
— степенное (логарифмически пока-
показательное) 104
— Стьюдента 38
— Фишера — Снедекора 38, 229
— Эрланга 28
— X2 38
Резерв нагруженный 288
— ненагруженный 288, 306
— облегченный 288, 313
Решения Dlt D2, D3 392, 442
Риск поставщика 386
— заказчика 386
Сбой 82
Свертка функций 73
Свойство оптимального критерия
270
Система 133
Случайная величина 33
Случайное событие 15
Случайные величины независимые 31
Событие достоверное 16
— противоположное 16
События независимые 18
— несовместимые 16
Соединение последовательное 133
— параллельное 135
Состоятельность критерия 284
Средний объем инспекции 402
Стандарт Доджа и Ромига 409
— Колумбийский 412
— Ташкентский 407
— экономичных планов 436
Статистика Шермана 247
Статистическая гипотеза 67
Стационарность 54
Степени свободы распределения | %2
38
~ Стьюдента 38
Стоимостной коэффициент 421
Сумма (объединение) множеств 15
Суммарная наработка 127, 159
Схема Бернулли 20
— невозвращенного шара 22
Теорема Бейеса 19
— Блекуэлла 114
— Гливенко 59
— Григелиониса 57
— запаздывания 73
— Ляпунова 42
— Муавра — Лапласа 40
— Неймана — Пирсона 69, 235
— Пуассона 39
— Смита (узловая) 114
— умножения вероятностей 18
— центральная предельная 42
Тождество Вальда 57
Улучшенная несмещенная оценка 439
Ускоренные испытания 162
Условия Линдеберга 42
— Ляпунова 43
Условная вероятность 17
Уравнение правдоподобия 62
Уровень значимости критерия 70
Фазовое пространство состояний си-
системы 85
Формула Бернулли 20
— Макегама 20
— полной вероятности 18
Функция восстановления ПО, 125
— мощности критерия 232
— надежности 90
— правдоподобия 61
— распределения случайной вели-
величины 24
— риска 264
Цепь вложенная 53
— Маркова 52
— однородная 53
— эргодическая 53
Экономичные планы контроля | до-
допустимые 421
~ рациональные однократные 423
~ рациональные двукратные 430
Элемент 89
— стареющий 104
Эмпирическая квантиль 166
Эмпирические моменты 63
~ центральные 63
Эмпирическая функция | распреде-
распределения 59, 162
~ надежности 91
~ опасности отказов 165
ОПЕЧАТКИ
Стр
115
128
165
264
Строка
6 СН.
1 СН
4 ев
10 ев
Напечатано
3
Т 2
02
Gn + 1 = (
t>l-N
3
t>tN
Xrx+d>uv> е-к{ ]