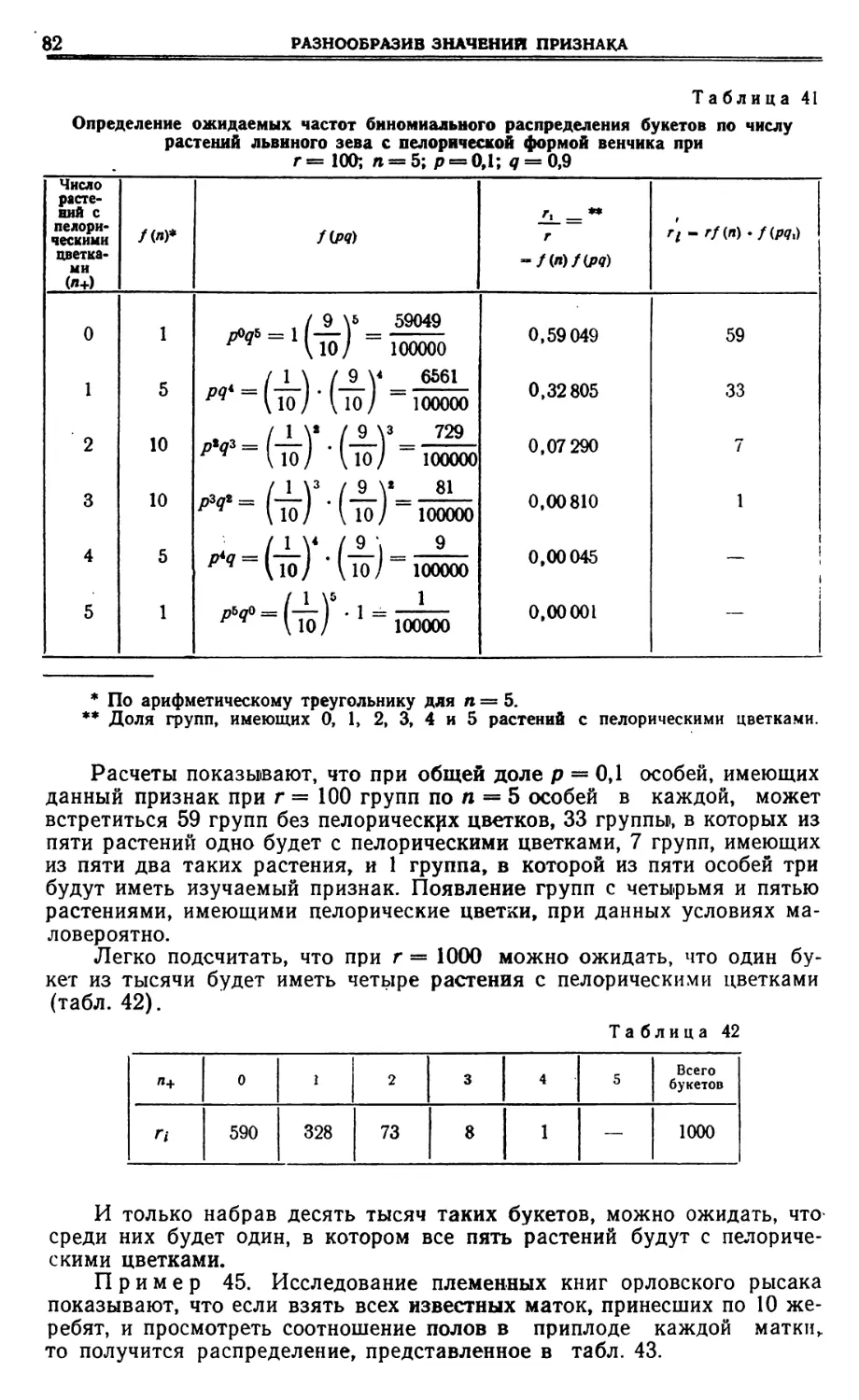
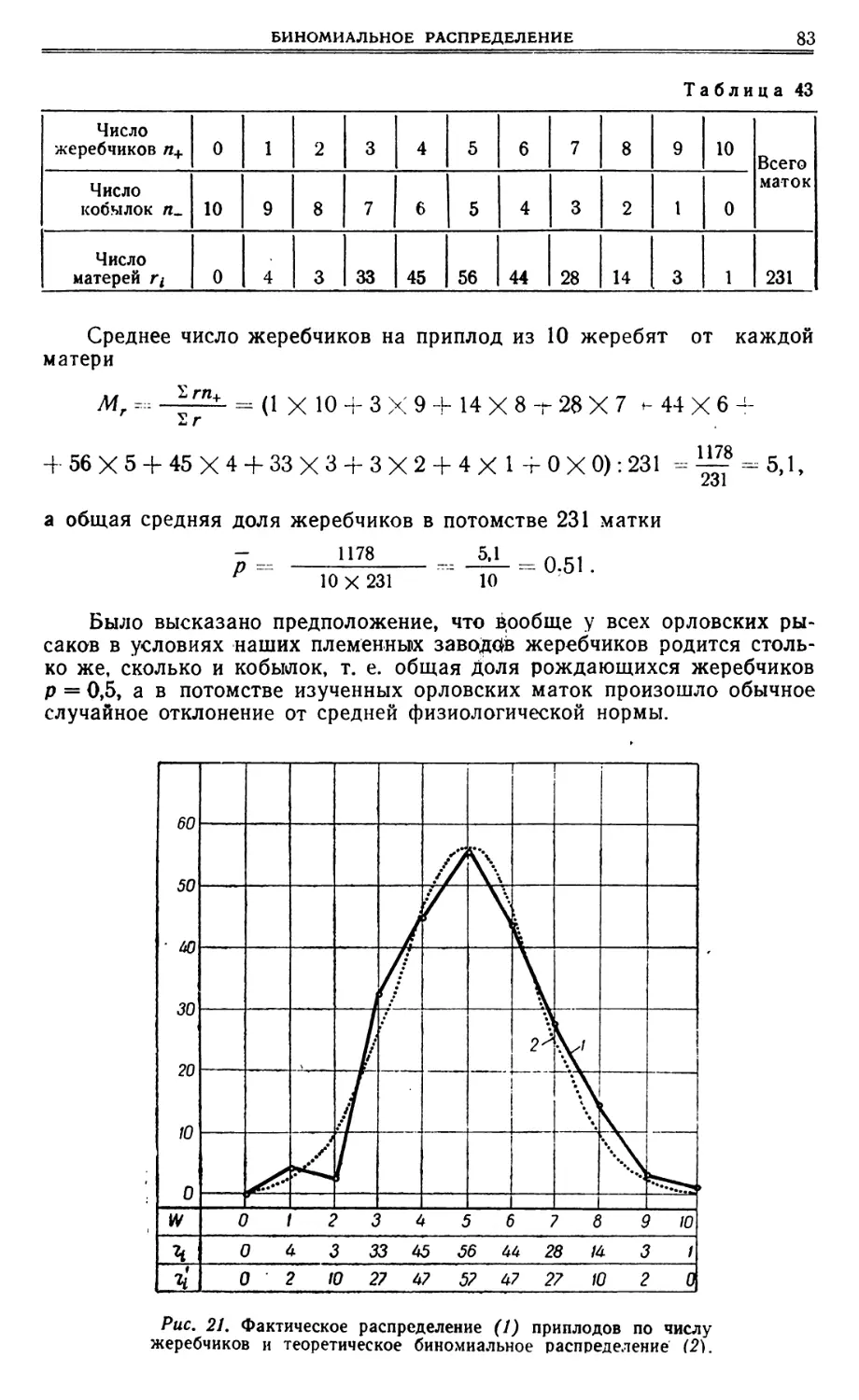
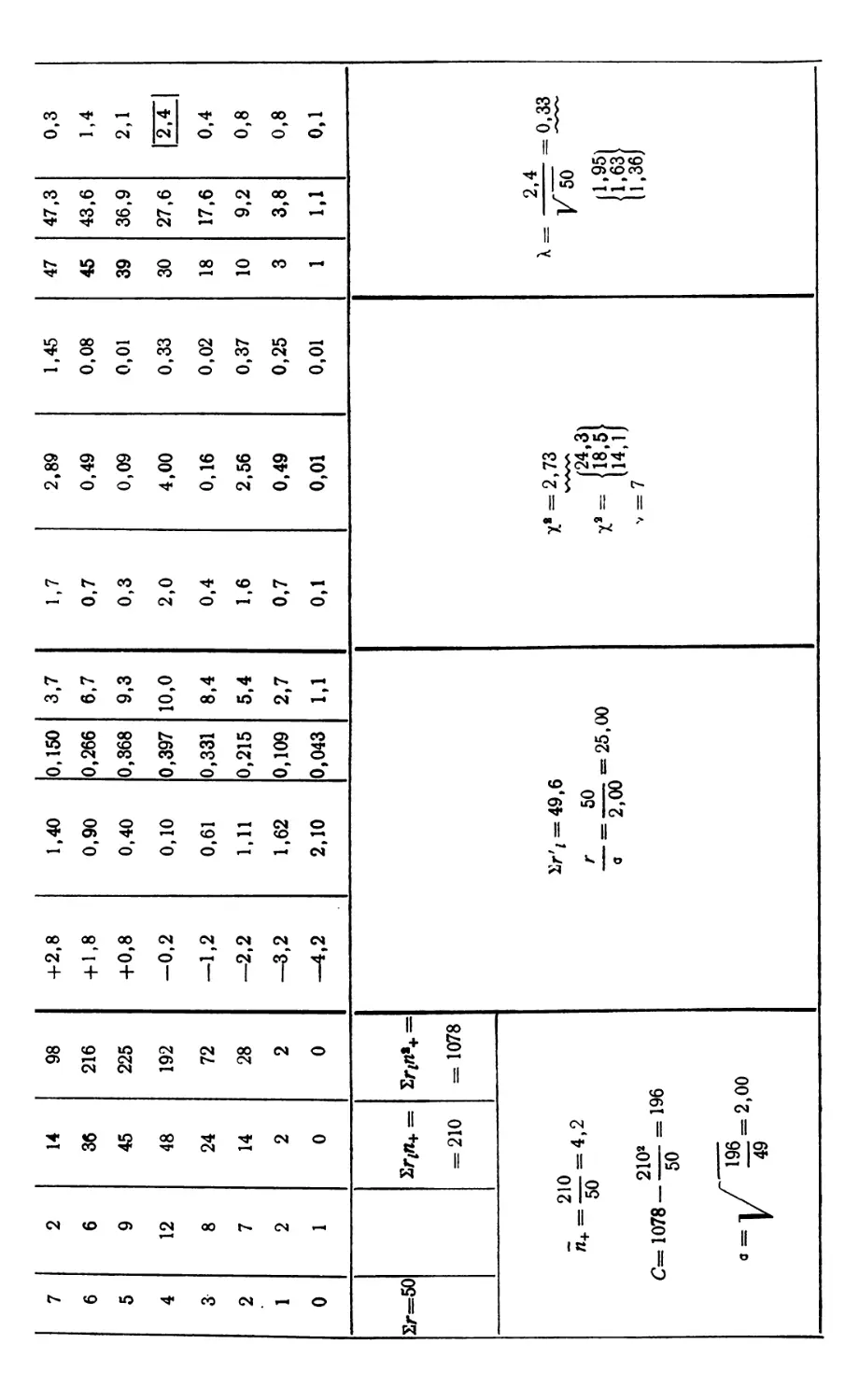
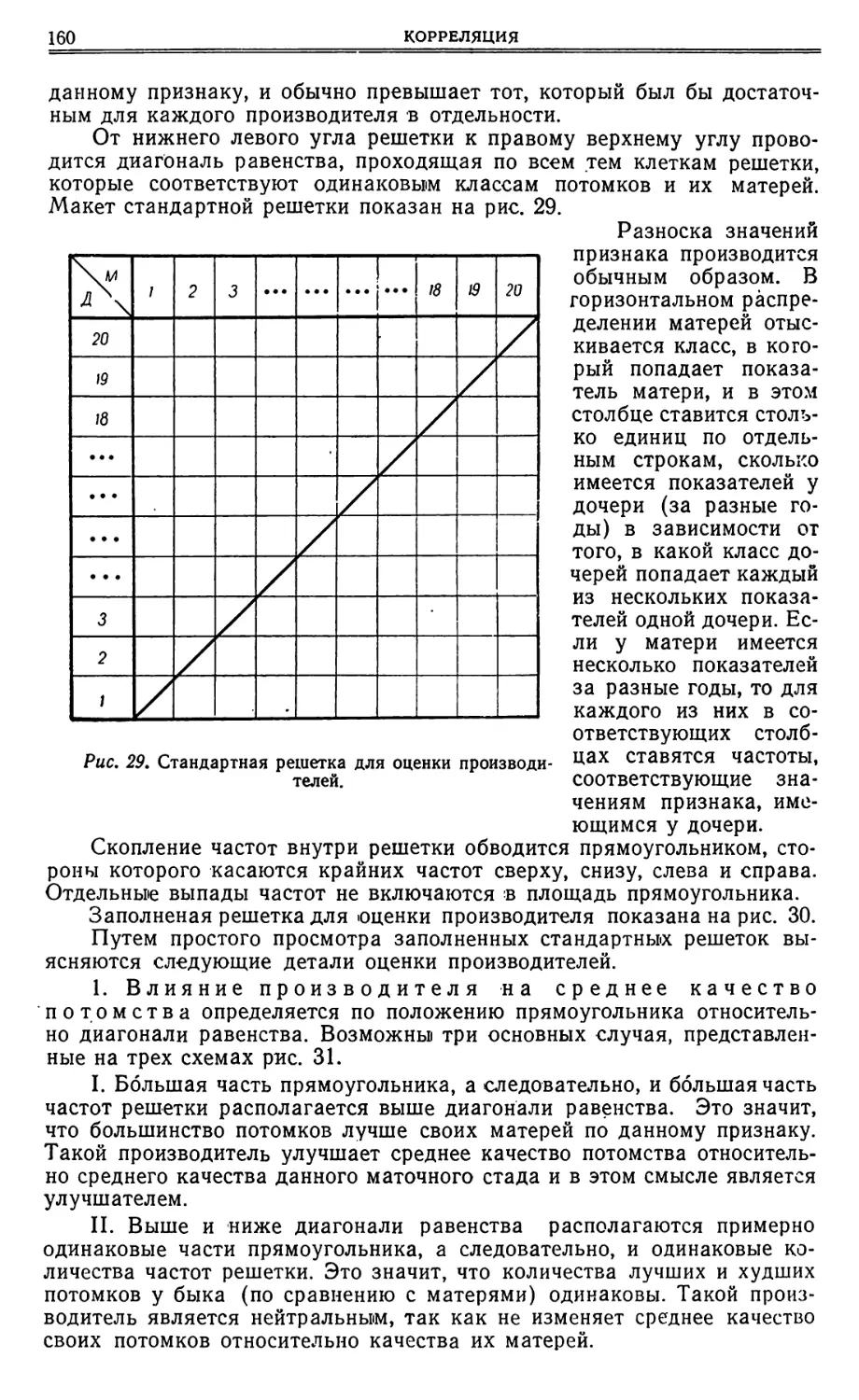
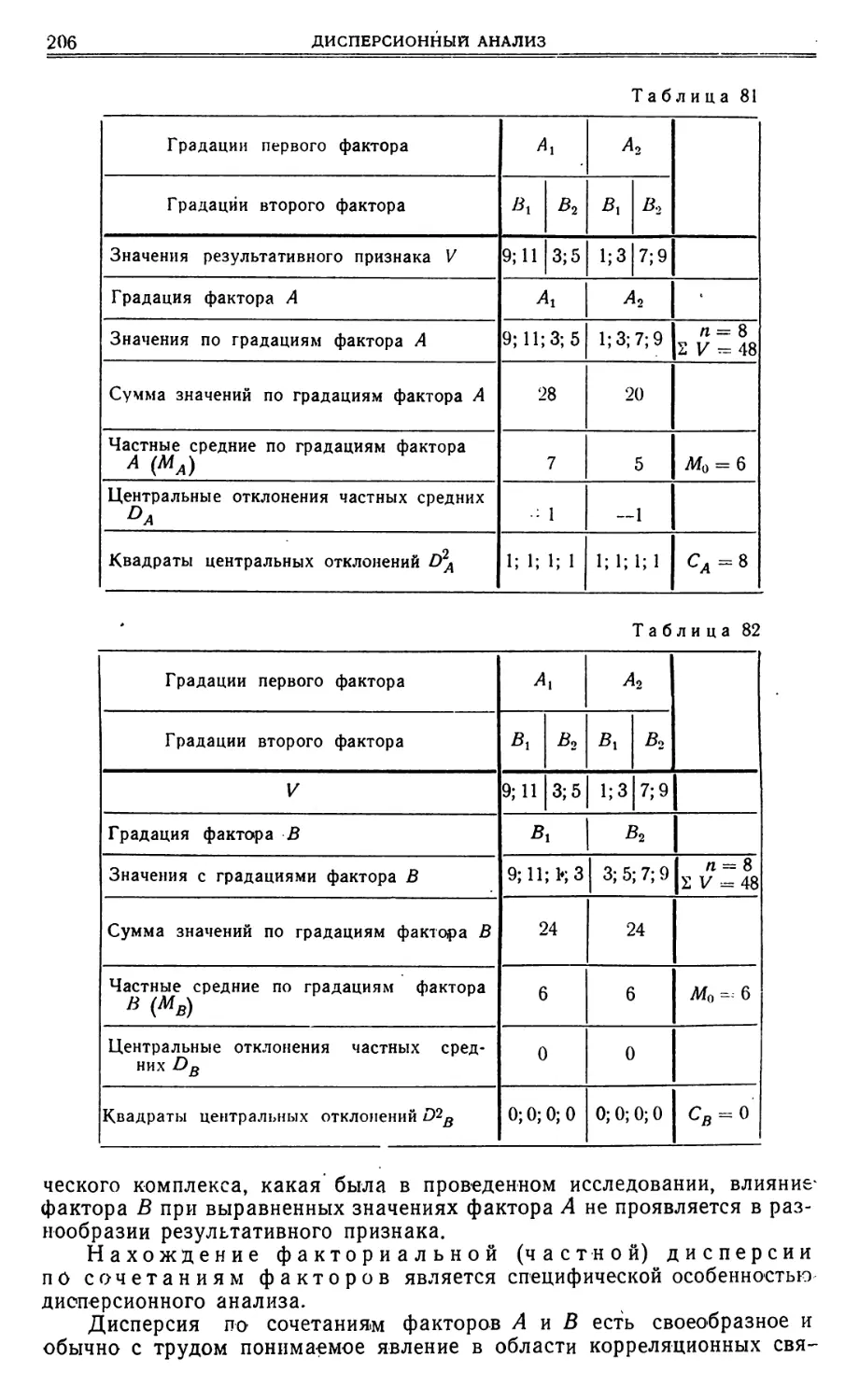
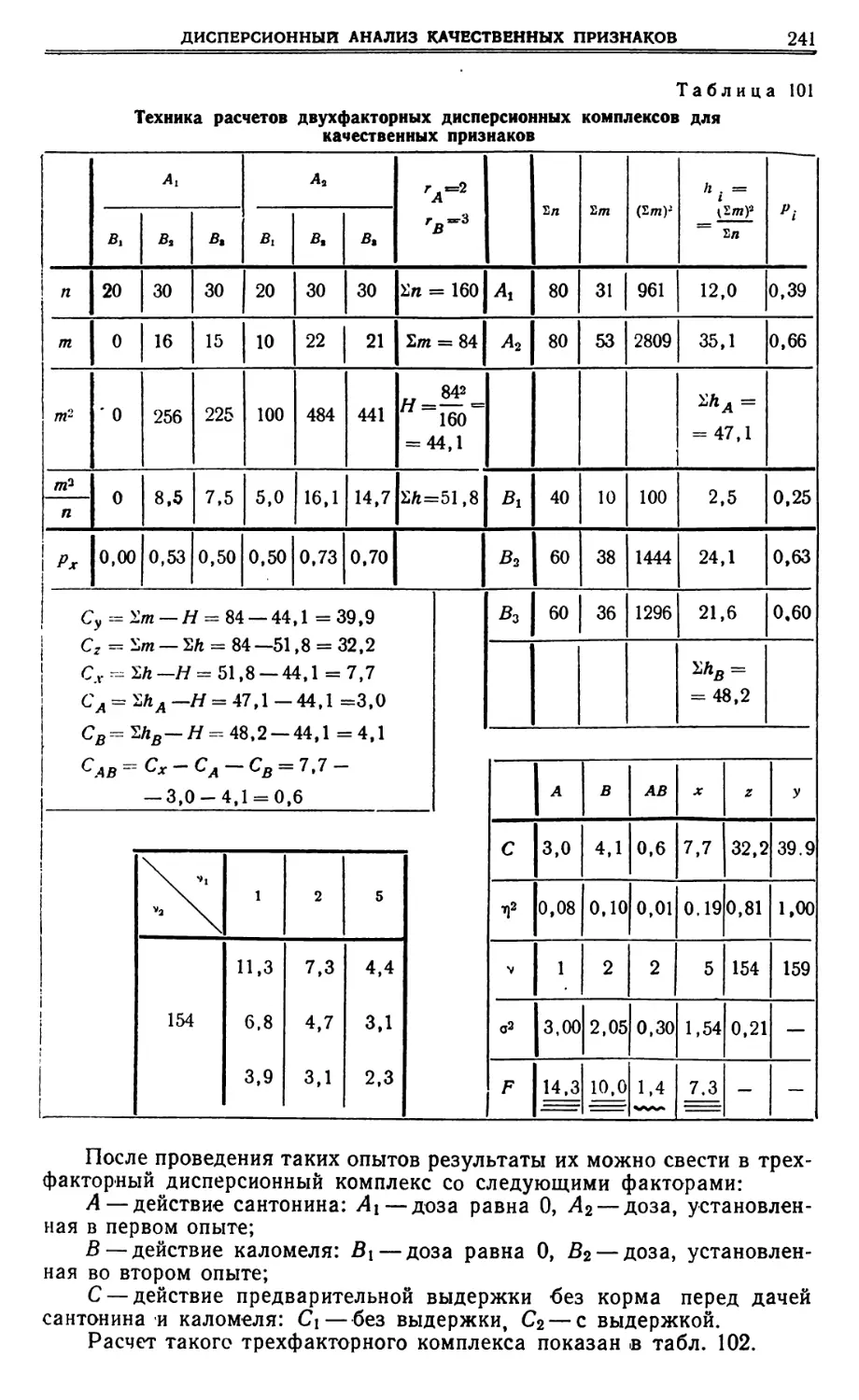
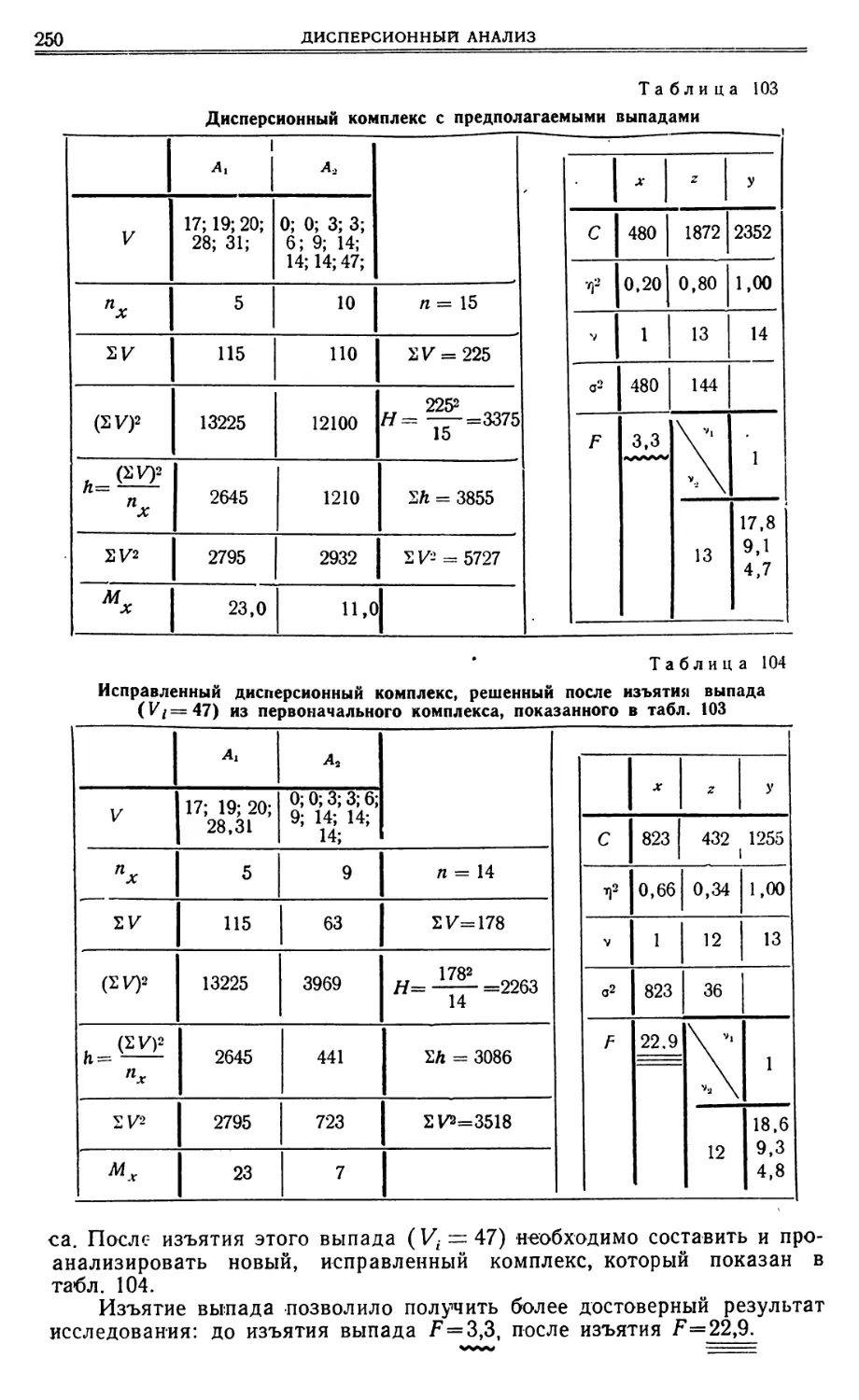
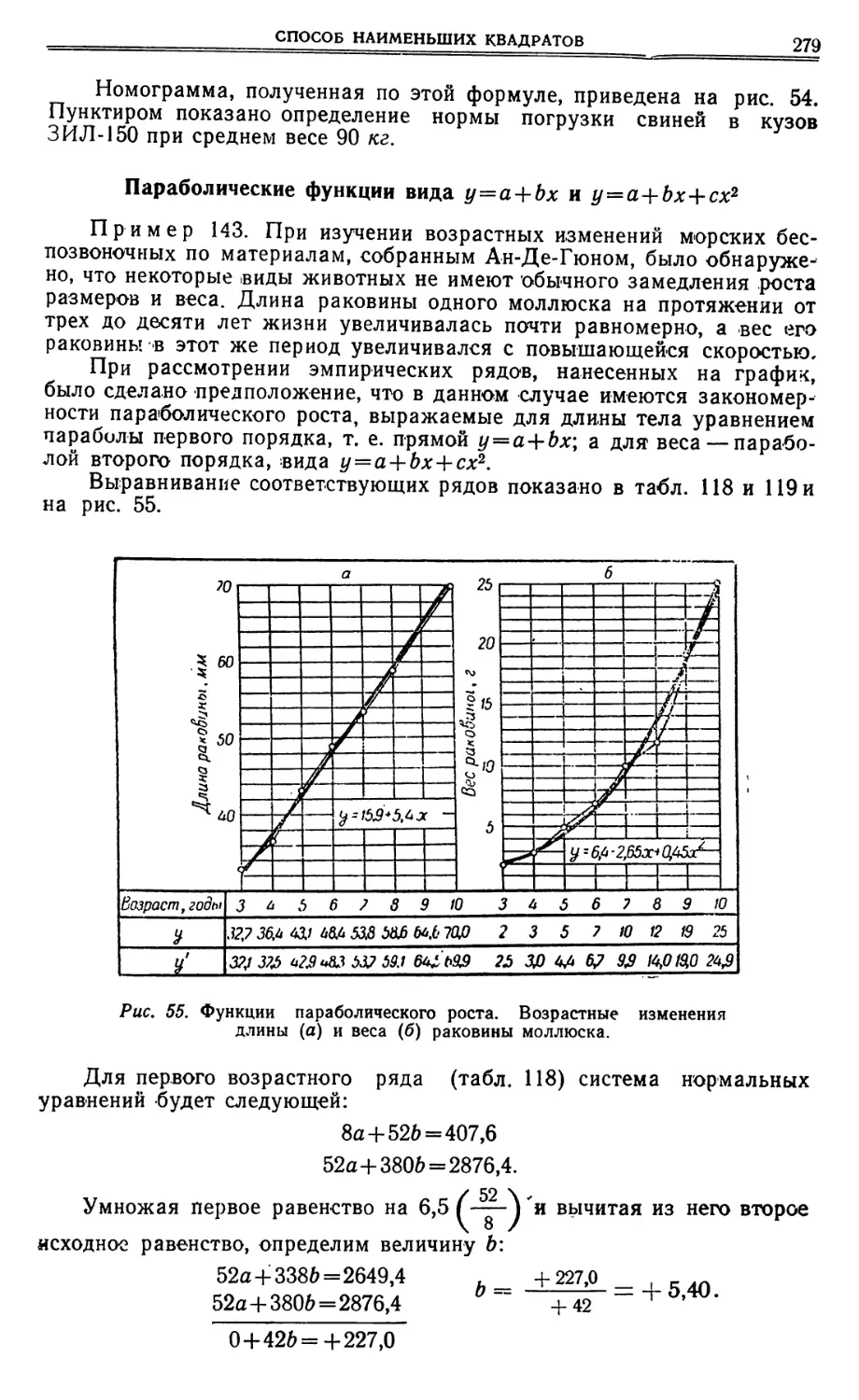
Текст
АКАДЕМИЯ НАУК ССС РСИЬИРСКОЕ ОТДЕЛЕНИЕ н плохински( ИзаЛТ СЛ ЬСТВОCNGNPCNOI ОТДаюеНИЯ ЛН CCCPНОВОСИ ЬИ РСК — 1961
Николай А лександрови,ч ПлохинскийВИОМеТРИД Редактор Р. Л. Дудник.Художсственный редактор В. И. Желнин.Обложка худ. В. И. Коядрвшкинв,Техн. редакторы А. Ф. Мвэуровв, А. М. Вялых.Корректоры: Л. Я Кормтика, М. А. Бвшковв. Сдано в набор 2 апреля 1961 г. Подписано в печать 21 сентября !961 г. МН 03360, Бумага70Х108/«. 22,75 леч. л,- 3I,2 усл. печ. л., 30,2 уч.-изд. л. Тираж 5000. Издательство Снбирского отделения Академии наук СССР. Новосибирск, Советская. 20. Зак. 306.Типография % l Полнграфнздата Новосибирск, Кра~ный проспект, 20. Цена 2 р. 26 к.
ВВЕДЕНИЕ Методы математической статистики широко используются и в тео- ретических исследованиях, и в практической биологии — агрономии, зоотехнии, медицине. При проведении любого эксперимента или наблюдения биолог об- ращается к математвке для решения трех основных вопросов: 1. Как отобрать объекты длязапланированного исследования, в ка- ком количестве и каким способом их выбирать из общей массы? 2. Как на основе индивидуальных измерений или описаний получить сводные показатели по всей изученной группе особей? 3. Как на основе. исследования выбранной группы, представляющей только часть изучаемой категории растений или~ животных, получить ха- рактеристику всей совокупности особей данной категории; как по части охарактеризовать целое с достаточной точкостью? Общее теоретическое решение этих вопросов дается в теории веро- ятностей и математическои статистике. Приложение методов теории вероятностей и математической ста- тистикы к изучению биологических объектов излагается обычно в само- стоятельных курсах, носящих разные названия: вариационная статисти- ка, биаметрия, статистические методы в биологии, методика анализа экспериментальных данных и др. К таким курсам относится и предлагаемая читателю книга «Био- метрия», предназначаемая для научных и практических работников в различных отраслях биологии и, в частности, для агрономов и зоо- техников. Цель книги — показать применение методов математической статис- ти~ки при обработке и анализе числовых результатов экспериментов, наблюдений и производственной отчетности, а также при планировании опытных работ. Все элементы изложения — общая структура пособия, описание математических лри~емов, символика, подбор иллюстративного материала — рассчитаны на те потребкости и ту математическую подго- товку, которая имеется у работников названных специальностей. Приводимые в книге примеры имеют единственной целью иллюстри- ровать применение того или иного математического приема при разре- шении большого круга задач, обычно возникающих при проведении биологических наблюдений и опытов. бранные измерений для примеров подобраны с таким расчетом, чтобы не затрудн ть процесса ознаком- ления с новым методом излишней для данных це ей сложностью число- вых взаимоотношений. Сделано это путем более или менее сильнойсхе- матизации результатов многочисленных исследований, относящихся к различным разделам биологических наук. В книге шесть глав.
ВВЕДЕНИЕ В главе «Средние величины» излагаются общие и частные свойст- ва различных средних показателей, описываются способы их расчета и приводятся примеры их правильного применения. В главе «Разнообразие значений признака» описываются показате- ли и закономерности разнообразия — основного свойства всякой сово- купности. В работах по биометрии приводятся другие названия этого свойства — изменчивость, колеблемость, рассеяние. Эти термины менее приемлемы в данном случае, так как обозначают совершенно другие яв- ления: измеыение признаков во времени, колебательные движения, раз- брасывание. В главе «Репрезентативность выборочных показателей» излагаются некоторые элементы теории вероятностей в применении к определению достоверности выборочных характеристик. В этом же разделе приводят- ся способы планирования достаточной численности выборок при изу- чении средних и долей, а также при изучении разности средних и разно- сти долеи. В главе «1~орреляция» даются способы измерения корреляционных связей — прямолинейных и криволинейных. Практическое применение показателей связи иллюстрируется численными примерами. «Основы дисперсионного анализа» излагаются в объеме, достаточ- ном для перваначального ознакомления с этим методом. В главе «Регрессия» излагаются методы выравнивания эмпириче- ских рядов для функций, встречающихся в биологических исследовани- ях: параболических (первых трех степеней), яепараболических, асимп- тотических, логистических, периодических. Рассмотрены также графи- ческий способ выравнивания и метод скользящей средней.
ГЛАВА IСРЕДНИЕ ВЕЛИЧИНЫ сновной показатель биометрии — средняя величина широко используется и в науке, и в практике. При изучении растений, животных, микроорганизмов и человека расчет средних показателей составляет основу обработки первичных ма- териалов. Средние размеры особей служат для харктеристики видов, разно- видностей, сортов, пород и других биологических групп; средние показа- тели физиологических процессов характеризуют интенсивность различ- ных сторон обмена организмов или силу действия биологических аген- тов и медицинских препаратов. В производстве средние показатели используются для оценки рабо- ты отдельных специалистов, хозяйств, областей. Среднее количество молока, мяса на 100 га сельскохозяйственной площади, средний удой на фуражную корову, средний процентжира в молоке, средний привес телят или откормочников, средний настриг шер- сти, средняя яйценоскость, средняя плодовитость, средний урожай зер- новых, кормовых, технических культур — все эти показатели стали обыч- ными характеристиками работы совхозов и колхозов. Средняя, величина какого-нибудь признака определяется для того, чтобы получить характеристику этого признака для всей изучаемой груп- пы в целом. Средняя величина признака определяется различными способами в зависимости от объекта наблюдения и от поставленных целей. Поэтому имеется не один, а несколько видов средних. Для биологов наибольшее значение имеют четыре средних: средняя арифметическая, средняя гео- метрическая, средняя квадратическая и средняя гармоническая. Кроме того, для характеристики биологических совокупностей иногда употреб- ляются мода и медиана. ОБЩАЯ ФОРМУЛА СРЕДНИХ ВЕЛИЧИН Четыре основные вида средних величин можно выразить единой формулой:
СРЕДНИЕ ВЕЛИЧИНЫ где Ср — средняя величина, V — дата (вариант), отдельное значение изучаемого признака, ре- зультат измерения признака у каждого объекта исследования, Х — знак суммирования (греческая буква сигма), т — показатель, определяющи~й вид средней, и — число усредняемых дат (вариантов). Придавая показателю т разные значения: 1, 2,— 1, 0, можно полу-чить формулы для отдельных видов средних. Это показано на следую-щих примерах вычисления разных средних для одной и той же группы, которая в целях большей наглядности взята предельно простой (состоя-щей всего ив 5 дат — 1; 4; 5; 5; 5). При т=1 получается формула средней арифметической: 1 у 1+4+5+5+5 20 — -- 4,00; при т= 2 — формула средней квадратической: 1 V~ '1 г E V-" и, п 5 1~ + 4- -+ 52 -+- - + 5 р ~з4 — 4,29: при т= — 1 — формула средней гармонической: 1 gi y — 1 1 1 1 1 1 + + — — ' 1 4 5 ' " 5 V 1 V 8,) при т=О после специальных преобразований — формула средней гее- метрической: ~ = ~/ П У = ~б 1 4 ° 5 ° 5 ° 5 = )/ 500 = 3,47 (П — знак произведения). Если в общую формулу средней подставить m= — оо и и=+ оо, то после преобразований получим два крайних значения в труппе: min — наименьшее значение и тах — наибольшее значение. ОБЩИЕ СВОЙСТВА СРЕДНИХ ВЕЛИЧИН Для правильного использования средних величин необходимо знать свойства этих показателей: срединное расположение, абстрактность и единство суммарного действия. По своему численному значению все средние величины занимают промежуточные положения между минимальным и максимальным зна- чениями признака. При этом наименьшую величину имеет средняя гар- моническая, а наибольшую — средняя квадратическая, что можно пред- ставить следующей схемой: min (Н(6(М (S (тах. Учет указанных взаимоотношений между средними величинами по- могает при проверке произведенных вычислений. Например, если сред- няя арифметическая оказалась выше максимального значения признака или если средняя геометрическая больше средней арифметической, то очевидно, что в расчетах имеются ошибки. Средняя признака показывает, какую величину имел бы каждый из
ОБЩИЕ СВОЙСТВА СРЕДНИХ ВЕЛИЧИЯ представителей изучаемой группы, если бы все они были одинаковыми и суммарное их действие было такое же, как и фактических неусреднен- ««ых значений этой группы. При использовании средних величин пред- полагается, что пока они применяются, разнородная группа заменена однородной группой, в которой все значения признака одинаковы и рав- ны средней величине. Например, если имеется лять значений признака: 1; 4; 5; 5; 5 со сред- ««ей величинои М=4, то при использовании этой средней предполагается, что разнородная группа заменена на однородную с одинаковыми зна- чениями: 4; 4; 4; 4; 4. Эта особенность средних:величин лежит в основе таких обычных производственных выражений как «ат каждой коровы получено по 3000 л молока», «с каждого гектара получено по 500 ц свеклы», «с каж- дого улья получено по 80 кг меда», «при откорме получено по 100 кг при- веса на каждую голову» и т. п. 1~оравы дают, конечно, различные удои, на разных участках получен разный урожай и т. д. И все же для производственной характеристики хозяйства и особенно для плановых расчетов оказалось удобным услов- но принять, что все коровы дали или будут давать одинаковый удой, равнь«й средней величине этого признака для данного стада и года («от каждой коровы»), или, что с каждого гектара получен один и тот же урожай, равный среднему урожаю с общей площади («c каждого гек- тара»). Заменить разнородную группу однородной можно только путем от- влечения от тех различий, которые существуют в действительности. Только абстрагируясь от имеющихся индивидуальных разнообразных значений, можно дать требуемую характеристику группы одним чис- лом — - средней величиной признака. В этом смысле всякая средняя величина есть преждевсего абстракт- ная величина, которая часто в действительности не существует, а иног. да и не может существовать. Если средний вес особей какого-нибудь вида в определенных услови- ях равен 40,57 кг, то существование такого экземпляра возможно, но крайне мала вероятность того, что какая-нибудь определенная особь будет весить точно 40,57 кг. Если в совхозе среднее количество деловых ягнят, полученных на одну овцематку, равнялось 1,7 ягненка, то такое число живых ягнят во- обще не может существовать в действительности, тем не менее эта средняя имеет вполне определенное производственное значение, напри- мер, при сравнении этого совхоза с другим, где аналогичная средняя равна 1,2. Абстрактность средних величин вызывает необходимость при вы- числении их определять, от какого разнообразия необходимо отвлечься в данном случае. Самая полная абстракция получается в тех случаях, когда средняя рассчитывается для всех особей изучаемой совокупности. Если требуется учитывать какое-нибудь одно или несколько усло- вий, например пол, возраст особей, сезон года, ареал распространения, физиологическое состояние, принадлежность к опытным и контрольным группам, происхождение от определенных родителей и т. д., то необхо- димо в той или иной степени освобождаться от полной абстракции и определять среднюю величину для отдельных частных групп. Чем боль ше таких частных групп и чем они мельче, тем менее абстрактной ста- новится средняя величина. Не всякое выравнивание различий в группе может привести к пра- вильной средней величине. Вычисление средних величин необходимо вес.
CPERHHB ВЕЛИЧИНЫ В данном случае применение этой средней не будет правильным, так как два усредненных значения в своем суммарном действии не да-дут того же результата, какой дали два фактических неусредненных значения. Фактический общий суммарный прирост популяции за два года определяется следующим образом; К концу первого года популяция составляет 100- 100 == 120~, 100 к концу второго года— 120 60100 . 120 =- 192%. Прирост за два года равен 100 92 У 100 Если же принять за средний прирост 407о, то к концу первого года по-пуляция составит 100 + 100 ° 100 =- 140%, к концу второго года— 40 100 ° 140 =- 196 М, 140 + а прирост за два года— 196 — 100 ° 100 = 969о. 100 Ошибка в данном случае заключалась в неправильном выборесред- ней величины — взята средняя арифметическая, а для вычисления сред- него прироста надо пользоваться средней геометрической. Если использовать среднюю геометрическую, то средний прирост ог(ределится следующим образом: х == ~ 120 16(( - — 100 = 38,5( " ти таким образом, чтобы суммарное действие выравненных значений признака было бы равно суммарному действию первоначальных не- усредненных значений. Например, если четыре взрослых особи какой- нибудь промысловой птицы весили 2; 3; 3; 4 кг, то средний вес этих 2+3+3+4 й ПТИЦ =3 кг. Суммарный вес четырех усредненных значе- 4 ний 3+3+3+3=12 кг. Такой же суммарный вес имелся и вдействитель- ности: 2+3+3+4=12 кг. В данном случае выбор средней величины —- средней арифметической — сделан правильно. Но так бывает не всегда Например, требуется рассчитать среднегодовой прирост популяции какого-нибудь вида за два года, если известно, что за первый год при- рост составил 20о/о, а за второй — 60% (от начала второго года). Ис- пользуя способ средней арифметической, получаем: =- 40оЯ„ 2
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ При этом суммарный результат будет равен фактическому: 100-~ ' 100 = 138,57%, 100 138,57 + 100 Прирост за два года составляет 192 — 100=92ф~. Единство суммарного действия служит проверкой правильности вы- бора той или иной средней. Если суммарный результат усредненных значений не равен результату, полученному по первоначальным факти- ческим значениям, значит или средняя выбрана неправильно, или вычис- ления проведены с ошибками. ° 138,57 = 192>0%. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ Самым распространенным показателем среднего качества является средняя арифметическая. Вычисляется она, как указывалось, по формуле где M — средняя арифметическая, Z — знак суммирования, V — дата, отдельное значение изучаемого признака, и — число использованных значений признака. В развернутом виде эта формула имеет следующий вид: Я ~> + ~~ + .. + ~п tt Например, для пяти значений 1; 4; 5; 5; 5 средняя арифметическая 1+4+5-~-5+5 20 5 5 МАТЕМАТИЧЕСКИЕ СВОИСТВА СРЕДНЕИ АРИФМЕТИЧЕСКОЙ Средняя арифметическая, обладая в полной мере общими свойст- вами средних:величин, имеет свои особенности, которые можно выра- зить следующими формулами: 1. Z(V — М) =0; т. е. сумма центральных отклонений равна нулю. Например, для значений 1; 4; 5; 5; 5 средняя арифметическая M=4. Центральные отклонения будут следующие: 1 — 4= — 3, 4 — 4=0, 5 — 4=+1, 5 — 4=+1, 5 — 4=+1, а сумма центральных отклонений — 3+0+1+1+1=0. Это свойство средней арифметической используется для проверки нравильности ее расчета: если Z(V — М) оказалась неравной нулю, значит допущена ошибка в вычислениях. 2. E ( V — А) ~ь 0; М = А + т. е. сумма условных отклонений (отклонеиий дат от любого значения ие равного средней) не есть нуль. Если же эту сумму распределить
10 СРЕДНИЕ ВЕЛИЧИНЫ Х V — А покажет равнамерно по всем датам, то полученная величина ll как далеко средняя арифметическая отстоит от принятой в данном слу- чае условной средней. Например, для пяти значений: 1; 4; 5; 5; 5 отклонения от условной средней, например от А=5, следующие: 1 — 5= — 4; 4 — 5= — 1; 5 — 5=0; 5 — 5=0; 5 — 5=0. Сумма условных отклонений Z (V — А) = — 4 — 1+0+0+О= — 5. На каждую дату приходится отклонение Х(V — А) Это означает, что средняя арифметическая меньше данной условной средней на единицу и чтобы получить значениу средней арифметической, V — А надо по приведенной формуле М --=- А < к условной средней ll прибавить полученную (в данном случае отрицательную) поправку: М= =5+ ( — 1) =4. Полученная величина в точности равна значени~ю сред- ней арифметической. Если для этого примера взять другую условную среднюю, напри- мер, А =2, то сумма условных отклонений Х (V — А) = (1 — 2) + (4 — 2) + (5 — 2) + (5 — 2) + (5 — 2) = + 10, а средняя 11 2, + 10 5 =2~2 =-4, казано ниже. 3. Х(V — М)'-» min; Х(V — М)2(Х(V — А)' т. е. сумма квадратов центральных отклонений меньше суммы квадратов отклонений от любой другой величины (табл. 1). Таблица 1 т. е. такая же, как при непосредственном расчете. Описываемое свойство средней арифметической используется для облегчения вычислительной работы при многочисленных группах. Ког- да усредняется большое количество значений, гораздо легче рассчиты- вать среднюю арифметическую не непосредственно, а через условную X(V — А) среднюю по формуле М = А -' Как это делается, будет по- й
МАТЕМАТИЧЕСКИЕ СВОЙСТВА СРЕДНЕЙ АРИФМЕТИЧЕСКОИ Сумма квадратов центральных отклонений для приведенного при- мера оказалась равной 12, в то время как сумма квадратов условных от- клонений при любой условной средней больше 12. Описанная особенность средней арифметической положена в ос- нову способа наи~меныших квадратов, который применяется при изуче- нии степени и формы зависимости какого-либо признака от одного или нескольких влияний. 1~' (V — А))-' 4. Ш~ =-. Е ( V - - М)-' -= Е ( V --- -А)'-' т. е. сумму квадратов центральных отклонений можно получить через условные отклонения. Для разбираемого примера при A=5 Z(V — А) = — 5, ХЮ=Е(У — А)~=!7, откуда ( — 5)' 12 5 М =- 17 что совпадает с величиной, определенной прямым расчетом. При другом значении, например А=2, получаем то же значение цля суммы квадратов центральных отклонений: Z(V — А) =-)-10, Z(V — А)~=32, откуда Ш' -= > ( V — М)'-' = 32 — = 32 - 20 ---- 12. 5 Эта особенность средней арифметической используется для облег- чения вычислительной работы при анализе многочисленных групп. В та- ких случаях гораздо легче получить сумму квадратов центральных отклонений не непосредственно, а через условные отклонения по ука- занной формуле. Как это делается, будет показано в главе о показате- лях разнообразия. 5. М„,,> --- М„+а. Если к каждому значению признака прибавить постоянную величи- ну а (или ее вычесть), то средняя арифметическая из измененных дат будет равна средней арифметической из первоначальных дат увеличен- ной (или уменьшенной) на величину а. Так, если в разбираемом примере к каждой из первоначальных дат 1; 4; 5; 5; 5 прибавить 3, то для полученных величин 4; 7; 8; 8; 8 средняя М=7 ровно на 3 больше первоначальной средней M=4. Если в этой группе из каждого значения вычесть, например, 1, то для уменьшенных значений 0; 3; 4; 4; 4, средняя М=З будет на 1 меньше первоначальной средней М=4. Это свойство средней широко используется при вычислении сред- ней арифметической для больших групп при многозначных датах, что значительно упрощает и облегчает счетную работу. 6. М =аМ„ т. е., если каждое значение умножить на постоянное число а, тб средняя арифметическая из измененных дат будет точно в а раз больше перво- начальной средней арифметической. Так, если в разбираемом примере.все значения 1; 4; 5; 5; 5 умно- жить на 10, то для полученных увеличенных дат (10; 40; 50; 50; 50) средняя арифметическая М=40 ровно в 10 раз больше той, которая по- лучена для неувеличенных дат (M=4).
СРЕДНИЕ ВЕЛИЧИНЫ Если а равно дробному числу, то каждая дата, а также и каждая средняя будут уменьшены в столько же раз. Если в разбираемом при- мере все даты умножить на '/5, то средняя арифметическая из умень- шенных дат (0,2; 0,8; 1; 1; 1) М=,0,8 точно в 5 раз меньше средней арифметической, .полученной для неизменных дат (M=4). Это свойство средней арифметической также широко используется при преобразовании дат и при работе с многочисленными группами для облегчения счетной работы. ВЫЧИСЛЕНИЕ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙДЛЯ МАЛОЧИСЛЕННЫХ ГРУПП Чтобы 'рассчитать среднюю арифметическую по обычной формуле Е Р М:=- —, нужно все имеющиеся значения признака сложить и полу- й ченную сумму разделить на число дат. Этим способом можно пользо- ваться во всех случаях, когда имеется возможность без особых трудно- стей сложить все даты, что бывает при обработке малочисленных групп. П р и м е р 1. Три параллельных определения содержания гемогло- бина в крови у одного и того же животного в одно и то же время, про- веденные тремя разными лаборантами, дали такие результаты: 75; 80; 70. Наиболее вероятное содержание будет равно средней арифметиче- ской из параллельных проб: — 75+ 80+ 70 =-- 75,0. П ример 2. На восьми парных опытных делянках получены сле- дующие отклонения урожая нового сорта кукурузы от стандарта (в пе- ресчете на гектар): +6; +3; — 2; — 3; +5; 0; — 3; +2 ц. Среднее от- клонение урожая нового сорта, полученное в проведенном сортоиспы- тании, будет равно средней арифметической. из отдельных разностей: -б-6+3 — 2 — 3+5+Î — 3+2 +88 ==+1,0 ц. В некоторых случаях при вычислении средней арифметической общая сумма значений признака делится не на число дат, а на другие величины. Так бывает, например, при расчете среднего удоя на одну фуражную корову. Пример 3. Предположим, что 16 коров, закрепленных за одной дояркой, дали в сумме за год 86387 кг молока. При этом одна перво- телка вступила в группу 1 октября и за год была в ней всего 92 дня, другая первотелка переведена в группу коров 1 августа и была в груп- пе 163 дня, две старых коровы были выбракованы — одна из них была в группе 35. а другая 107 дней. Средний удой на фуражную корову в данном случае рассчитывается следующим образом: 86387 13,09 86387 86387 4777: 365 (365 - 12 + 92 -~- 163 +- 35 -',- 107): 365 В подобных случаях при вычислении средней общую сумму дат- весь удой от групы коров за год — делят не на число коров, давших это молоко, а на пересчетную величину — на число фуражных коров. для разобранного примера число корсво-дней будет 365 ° 14+92+163-1- +35+107=4777, а число фуражных коров — 4777: 365=13,09. Среднюю относительных величин (индексы, выходы) можно рас-
ВЫЧИСЛЕНИЕ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ ДЛЯ МАЛОЧИСЛЕННЫХ ГРУПП считывать двумя способами: как среднее отношение и как отношение сумм (или как отношение средних). П р и м е р 4. Четыре повторных посева одного сорта сахарной свеклы при анализах на сахаристость дали следующее содержание са- хара (в %) 16; 14; 13; 17. Средняя сахаристость сорта, полученная в данном испытании. 16+ 14+ 13+ 17 = — = — 15% . 60 4 В данном случае получено среднее отношение. Пример 5. На мясокомбинате за сутки переработано 300 голов крупного рогатого скота. Требуется определить фактический средний выход мяса. Яля этой цели суммарный вес всех туш (в кг) относят к сумме при- емных живых весов переработанной группы скота. Оказалось, что пер- вая <умма XV~=45862 кг, вторая сумма ZV>=102791 кг. Средний вы- ход в данном случае рассчитывается как отношение сумм: М= ' 100= Е V, . 45862 Е V, 102791 ° 100 = 44,62% ° Пример 6. При переработке десяти подопытных свиней получе- ны следующие данные (табл. 2): Таблица 2 8 9 19 М животного Приемный живой вес Vg 1)5 127 130 123 129 124 121 135 128 1274 Вес отделяемого жира- сырца V~ (после стан- дартной переработки) 14,9 13,6 11,9 10,7 8,2 12,2 8,3 12,4 8,2 9,0 11.4 108,0 9,8 9,9 64 102 6~1 7 (1 9,2 6,3 7,4 Выход сала, Е — 100 ~1 V2 10,2 + 6,1 + 7,0 + 11,9 + 10,7 + 7,4 -}- 10 6,3+ 9,9+ 6,4+ 9,2 = — = 8,51%. 85,1 10 10 Если же требуется выхода, полученные в эксперименте, сравнитьс выходами, получаемыми в производстве или с плановыми, то в такихслучаях средний выход должен быть рассчитан так, как это делаетсяв производстве, т. е. как отношение сумм:М, = ' . 100= ' ° 100 =8,48%. 1274 При проведении экспериментов индивидуальные выхода могут рас- сматриваться как показатели качества отдельных подопытных живот- ных. Чтобы выявить среднее качество группы, надо сумму всех таких индивидуальных показателей разделить на их число, т. е. получить среднюю арифметическую обычным способом — как среднее отношение:
СРЕДНИ Е ВЕЛИЧИНЫ П ример 7. В зверосовхозе, разводящем голубых норок, получе- но от двух самцов и одной и той же группы самок 20 щенков, с раз- личной окраской меха в потомстве каждого самца'. от почти белого до темно-голубого. Требовалось выяснить, какой из производителей дает в потомстве более темную окраску меха. Затруднением IIpH этом слу- жит то обстоятельство, что нет способа измерения интенсивности окрас- ки волоса у норок. В таких случаях можно применить метод ранжирования. Всех по- томков оцениваемых производителей надо распределить в ранжиро- ванный ряд в порядке усиления серого цвета, причем при каждом по- рядковом номере (ранге) такого ряда поставить номер отца: Ранг . . 1 2 3 4 5 б 7 8 9 10 ll 12 13 14 15 16 17 18 19 20 Мотца I I[ [ II I I II I 1 1 [I I И II II ft I Ц [[ Ц На основе такого ряда можно рассчитать средние ранги окраски в потомстве каждого производителя и по этим показателям сравнить Hx: 1 + 3 + 5 +- 6 -1- 8 —; — 9; — 10 + 12 —,' 17 71 --= — ==- 7,9, 9 9 139 2 -~ 4 - 7 + ll -I- 13 + 14 -i- 15 -',- 16 -- 18 -1- 19 — 20 ВЗВЕШЕННАЯ СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ Обычно, как уже указывалось, чтобы рассчитать среднюю арифме-тическую, складывают все значения признака и полученную сумму де-лят на число дат. В этом случае каждое значение входит в сумму оди-наковым образом, увеличивая ее на полную свою величину. Но не всегда это возможно. Иногда значения признака должны входить в сумму с неодинаковой поправкой. Эта поправка, выраженная опре-деленным множителем, называется иа'гемагичесхии весом значения. Средняя, рассчитанная для значений признака с неодинаковыми весами, называется взвешенной средней. Взвешенная средняя арифме-тическая рассчитывается по следующей формуле: И ~ 1 Ð К1 Р~ ~ ~гРг < ° +1~и Рп 83В ~ P Pi -1- Р + . ° ° + Рп где V — значение признака, дата, р — математический вес усредняемого значения. Чтобы рассчитать взвешенную среднюю арифметическую, необхо-димо каждое значение признака помножить на его вес, все эти произ-ведения сложить и полученную сумму разделить на сумму весов. П р и и е р 8. Имеются результаты двух исследований длины хо-ботка пчел: в одном случае получена средняя длина хоботка 6,6 мм, в другом — 6,0 мм. Требуется получить общую среднюю, причем из-вестно, что в первом исследовании были измерены хоботки у 100 пчел, а во втором — у 20. В данном случае значениями признака являются средние М~ —— 6,6 и М2 —— 6,0; их весами — численности групп р~=100 и р> 20. Взвешен-ная средняя арифметическая рассчитывается следующим образом: М, Р, + М„Р. (6,6 X 100) + (6,0 >( 20) 780 Pi + P". 100+ 20 120 Пример 9. В 100 кг кормовой смеси содержатся следующие ко-личества отдельных кормов: ВЗВ
ВЗВЕШЕННАЯ СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ 50 кг, с содержанием в ннх лереварнмого белка 3%, сена молотой овсяной соломы..... 10 кг, » » » 1%, жмыха подсолнечного дробленого » » » » 33% ° отрубей пшеничных грубых...... 20 кг, >> » »» % Требуется определить содержание белка в данной смеси. Яля решения этой задачи необходимо рассчитать взвешенную среднюю арифметическую. В данном случае значениями признака яв-ляются содержания белка в отдельных кормах: 3; 1; 33 и 11%, а их ма-тематическими весами — физические веса кормов, входящих в смесь.. 50; 10; 20 и 20 кг. Содержание в смеси переваримого белка 20 кг, ° Юе 11 3 Xl50 + 1 х 10 + 33 х 2+ 11 >( 20 '"�' = 10 40 У 100 50 --'- 10+ 20 - 20 т. е. в каждом килограмме смеси содержится 104 г переваримого белка. Таким же способом рассчитываются средние выхода продукта по нескольким партиям сырья. П р и м е р 10. Проведено три независимых наблюдения числа со- кращений пульсирующей вакуоли у амебы в определенной среде. В пер- вом наблюдении зарегистрировано 24 сокращения в час, во втором— 16 к в третьем — 23, причем первое наблюдение длилось 4, второе — 2 и третье — 3 часа. Для определения среднего числа сокращений в час в данном случае необходимо найти взвешенную среднюю арифметиче- скую. Значениями признака будут наблюдавшиеся количества сокра- щений в час (24, 16 и 23), их весами — продолжительность отдельных наблюдений (4, 2 и 3 часа). Следовательно, 24 Х 4+ 16 Х 2+23 Х 34--,' 2+3 197 3 П р и м е р 11. В качестве индивидуальной характеристики жирно- молочности каждой отдельной коровы у нас принята взвешенная сред- няя арифметическая из измерений процента жиздра в молоке в пробах зн 2 смежных дня в каждом месяце лактации. Определение этой характе- ристики можно показать на следующем примере. Лактация коровы началась 20 марта 1957 г. и закончилась 17 фе- враля 1958 г. Продолжительность лактацик — 334 дня..Удой за всю лактацию — 4160 кг, за последние 34 дня надоено 190 кг, поэтому удой за 300 дней лактации равен 4160 — 190=3970 кг. Удои по месяцам и процент жира в молоке даны в табл. 3. Ta6лица 3 VI I I IX Х VII Ч Vl Месяцы года I I I I V Х I I Число дойных дней 31 30 31 30 31 30 11 30 31 31 14 Процент жирав молоке V 3,8 3,9 180 570 4,0 4,1 4,1 4,2 420 390 330 300 3,9 3,9 510 480 4,0 4,4 4,5 240 450 3970 Удой р в кг 100 Однопроцент- ное молоко Vp 1680 1599 1353 1260 1056 15966 450 1989 1872 1800 684 2223
16 CPEQHHE BEJIHRHHbl В данном случае значениями признака является жирность моло- ка (в %) по месяцам, математическими весами — их месячные удои. Средний процент жира в молоке за 300 дней лактации вычисляется пу-. тем деления количества однопроцентного молока (сумма произведений месячных процентов жира на месячные удои) на удой за 300 дней: 1 1".966 =-= 4,02% . 3970 Е~р Хр ВЫЧИСЛЕНИЕ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ ДЛЯИНОГОЧИСЛЕННЫХ ГРУПП При изучении многочисленных групп при немеханизированном сче- те очень сильно возрастает трудоемкость работы. Чтобы получить искомый показатель с меньшей затратой труда и с большей гарантией безошибочности, применяются особые приемы нахождения средней арифметической для многочисленных групп. Отнесение групп в разряд многочисленных зависит только от степени технической оснащенности работы по суммированию вариантов. Применение конторских счет позволяет группы из нескольких де- сятков дат еще не считать многочисленными. При наличии же одно- фазных комптометров, на которых установка числа автоматически при- бавляет его к ранее установленным, группы любой численности можно считать «малочисленными» и вести расчет средней арифметической обычным способом по формуле Расчет средних арифметических способами, разработанными для многочисленных групп, вызывается, во-первых, необходимостью рабо-тать и без счетных машин и, во-вторых, тем обстоятельством, что про-межуточные величины, которые получаются при вычислении средней арифметической, могут быть использованы для получения других по-казателей, например, среднего квадратического отклонения, что значи-тельно сокращает общую работу. При расчете средних арифметических для многочисленных групп применяются следующие способы: 1. Способ распределения дат. 2. Способ взвешенных вариаций. 3. Способ условных отклонений: а) способ произведений, б) способ сумм. Способ ра сп редел е н и я дат. Если изучаются признаки, выражаемые только целыми числами, то при небольшом размахе зна-чений от минимума до максимума вычисление средней арифметической для многочисленных групп производится по формуле м= '~' Л где М — средняя арифметическая, V — дата, значение признака, f — частота, показывающая, сколько раз встретилось данное зна- чение признака в изученной группе, и' — общее число измеренных значений, сумма всех частот (л=Е~). Л ~i+f2 ~ + "° +fn КЛ +/2 ~ +fn
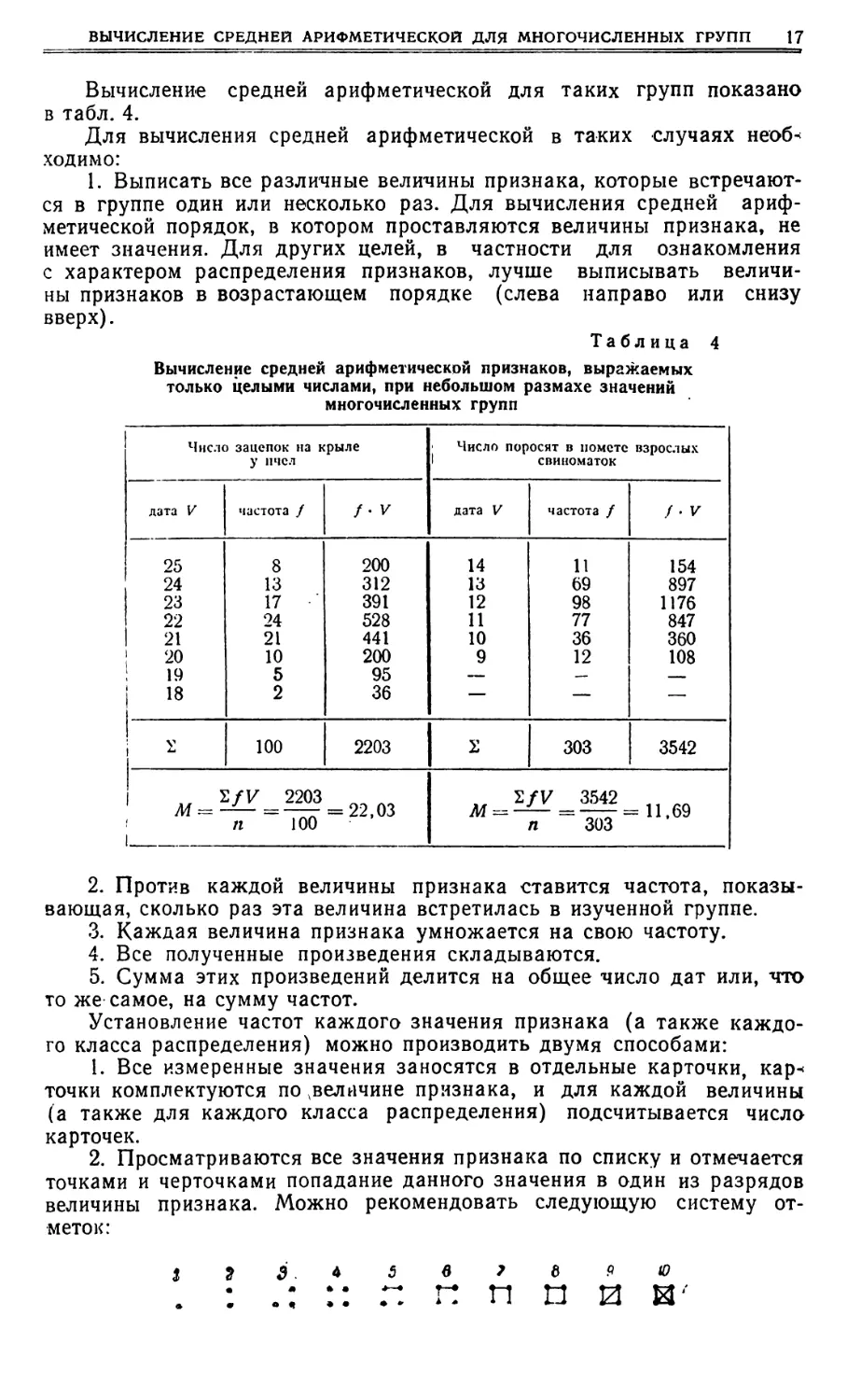
ВЫЧИСЛЕНИЕ СРЕДНЕИ АРИФМЕТИЧЕСКОЙ ДЛЯ МНОГОЧИСЛЕННЫХ ГРУПП 17 Вычисление средней арифметической для таких групп показано в табл. 4. Для вычисления средней арифметической в таких случаях необ ходиыо: 1. Выписать все различные величины признака, которые встречают- ся в группе один или несколько раз. Для вычисления средней ариф- метической порядок, в котором проставляются величины признака, не имеет значения. Для других целей, в частности для ознакомления с характером распределения признаков, лучше выписывать величи- ны признаков в возрастающем порядке (слева направо или снизу вверх). Таблица 4Вычисление средней арифметической нризнаков, выражаемыхтолько целыми числами, при небольшом размахе значениймногочисленных групп Число поросят в помете взрослык 1 свиноматок Число зацепок на крылеу пчсл )' ° У частота ( частота f дата V лата V f-v 200 312 391 528 441 200 95 36 14 И 12 11 10 9 11 69 98 77 36 12 8 13 17 24 21 10 5 2 154 897 1176 847 360 108 24 23 22 21 20 19 18 100 2203 303 3542 М — — — 22,03 ЕfV 2203 и l00 ЕfV 3542 М =- = — = 11,69 и 303 4 Л 6 > д 1.1 О g И И' 2. Против каждой величины признака ставится частота, показы- вающая, сколько раз эта величина встретилась в изученной групне. 3. Каждая величина признака умножается на свою частоту. 4. Все полученные произведения складываются. 5. Сумма этих произведений делится на общее число дат или, что то же самое, на сумму частот. Установление частот каждого значения признака (а также каждо- го класса распределения) можно производить двумя способами: !. Все измеренные значения заносятся в отдельные карточки, кар» точки комплектуются по, величине признака, и для каждой величины (а также для каждого класса распределения) подсчитывается число карточек. 2. Просматриваются все значения признака по списку и отмечается точками и черточками попадание данного значения в один из разрядов величины признака. Можно рекомендовать следующую систему от- меток:
срЕдниЕ вЕличины Таблица 5 Разноска дат для примеров, при|веденных в табл. 4, имеет следую- щий вид (табл. 5): Составление вариационного ряда. Если признак может быть выражен любым числом — и целым и дробным или если при выражении призна- ка только целыми числами размах величин его велик, то для расчета средней арифметической и других показателей нужно предварительно составить распределение или вариационный ряд признака. Яля этого все величины признака разбиваются на разные интер- валы — классы. Предварительно необходимо установить число классов, их величину, границы, средины и частоты. Число классов. Весь размах значений признака от минимума до максимума разделяется обычно на 8 — 12 равных интервалов. При бо- лее точных исследованиях устанавливается большее число классов (15 — 20 — 30), а при менее точных — меньшее число (6 — 8). Чем больше число классов, тем точнее получаются искомые сводные показатели, но при этом более трудоемким становится процесс вычисления, и, наобо- рот, чем меньше число классов, тем менее точный результат вычисле- ний, но проще процесс вычисления. Величина классов или величина классового промежутка равна размаху значений от минимума до максимума, деленному на принятое
ВЫЧ ИСЛЕНИ Е-. СРЕДНЕ1Ч Л РИФМ ЕТИЧ ЕСКОЯ ДЛЯ МНОГОЧИСЛЕННЫХ ГРУП П числз классов. Обычно величина классов устанавливается по прибли-женной, легко запоминающейся формуле: 1п ах — Ш1п /г = — ~- от 8 до 12 где k — величина класса, 1113x — - максимальное значение, min — минимальное значение. Если при делении размаха между максимальным и минимальным значениями на число классов получается число с дробью, то за величи-ну классового промежутка можно принять ближайшее целое число. П1аХ — 1П1П Например, если =- 43,4, то за величину классового 12 промежутка k можно взять 45 или 40. Величяну классового промежутка можно рассчитывать более точно по формуле 1113 Х — 1111 fl 1 - 331gn Если при исследовании 100 объектов оказалось, что тах=90, а иип=40, то лучше всего за величину классового промежутка выбрать 50 50 90 — 40S -- З,з 1~ 10О — - 6,6=7 или 6. "",6 1+ 3,3;~ 2,000 ~ раницы классов можно выбирать любые, при этом разница между границами соседних классов должна быть равна величине классового промежутка. Совершенно не обязательно за начало минимального клас- са брать фактический минимум. Лучше за начало классов принимат„ легко запоминающиеся цифры. Например, если при размахе признака в пределах 39 — 93 установлена величина класса 1=5, то начала классон можно установить следующие: 35 — 40 — 45 — 50... 85 — 90. 1(онец каждого класса должен быть меньше начала следующего на величину, равную принятой точности измерения. Например, если изме- ряется длина животных с точностью до 1 см и установлена величина классового промежутка k=5 см, то границы классов, начиная с ниж- него минимального, будут такими: 100 — 104, 105 — 109, 110 — ! 14, 115 — 119 и т. д. В тех случаях, когда обыирный материал для первоначальной счет- ной работы раздробляется и отдельные его части обрабатываются раз- ными сотрудниками с тем, чтобы впоследствии эти части соединить, обязательно требуется установление единых как велинины, так и нача- ла классов. В противном случае такое соединение будет невозможно. Средины классов устанавливаются двумя способами. Если признак может быть выражен любым числом — и целым и дробным, то для установления средины класса нужно к началу клас- са прибавить половину классового промежутка. Так, в предыдущем примере срединами классов будут ° Ю 110 —,'- — ' -- 112,5 и т. д. 105 -~- — == 107,5; 100 + =- 102,5; Иногда удобней сначала установить средины классов, а после этого определить их границы. В таких случаях начало каждого класса будет меньше его средины на половину классового промежутка. Например,
20 СРЕДНИЕ ВЕЛИЧИНЫ если установлены средины классов — 100; 105; 110; 115 и т. д., то нача- лами этих классов будут 5 5 5 100 — — = 97,5; 105 — — = 102,5; =-. 107,5 и т. д., 2 2 2 110-- а .концами классов в данном случае будут: 102,4; 107,4; 112,4 и т. д. В тех случаях, когда признак выражается только целыми числами (яйценоскость, плодовитость, число поврежденных клеток на каждую сотню, число ульев на пасеке, число плодов на 1 куст помидоров и т. д.), средина классов равна полусумме начала и конца класса. Например, если составлен вариационный ряд 1 — 3, 4 — 6, 7 — 9 и т. д., то срединамй 1+3 4+ б 7)9 этих классов будут целые числа — = — 2, — = 5; =- 8 и т, д.; 2 2 ' 2 для ряда 1 — 4, 5 — 8, 9 — 12 и т. д. срединами классов будут дробные числа: — =25; = 65; ' =105 ит д. 1+4 5+8 9+12 2 ' 2 ' 2 Средины классов называются еще вариациями и будут обозначать- ся символом W. Частоты классов устанавливаются путем разноски дат по классам любым из двух описанных выше способов. Обозначаются частоты клас- сов символом f. 1(аждая дата, попав в соответствующий класс прирав- нивается по величине ко всем другим датам, попавшим в этот класс. Например, если в класс веса животных от 200 до 249 кг (1=50 кг) по- пали 2 варианта — 230 и 240, то при дальнейшей обработке вариацион- ного ряда будет считаться, что обе эти даты имеют одинаковую величи- 50 ну, равную средине этого класса 225 200+ — . После разноски две эти даты дадут в сумме 450 кг, тогда как в действительности их сумма равна 230+240=470 кг. На этом примере видно, что метод расчета средней арифметиче- ской (и других показателей) путем составления вариационного ряда не является абсолютно точным. Но погрешности этого метода незначи- тельны, и с ними можно не считаться. Погрешности эти становятся практически заметными только при распределении малочисленных групп на крупные классы. Составление вариационного ряда для 400 значений веса овцематок показано в табл. 6. Таблица 6 Средины классов или вариаций Q7 Границы классовW„= ~Р;„ Частоты классов f 97,4 92,4 87,4 82,4 77.4 72,4 67,4 62,4 57,4 52.4 47,4 42,4 2 12 28 46 71 79 72 45 30 9 5 1 95 90 85 80 75 70 65 60 55 50 45 40 92,5 87,5 82,5 77 5 72,5 67,5 62.5 57,5 52,5 47,5 42,5 37,5 Еf =и=400
ВЫЧИСЛЕНИЕ СРЕДНЕЯ АРИФМЕТИЧЕСКОЯ ДЛЯ МНОГОЧИСЛЕННЫХ ГРУПП Минимальный вес был равен 39 кг, максимальный — 96 кг. Вели- 96 — 39 чина классового промежутка, при 10 классах k =- =- 5,4, а по 10 точной формуле k =- = 5,6. Для удобства разноски дат бы- 54 1+ ЗД1g 400 ла принята величина классового промежутка k=5. При условии, что средины классов должны делиться без остатка на величину класса, необходимо установить средину минимального клас- са, равную 40 кг, а началом — это значение, уменьшенное на полкласса, т. е. 40 — — =37,5. Началом следующего класса будет 37,5+5=42,5, 5 2 срединой — 40+ 5 = 45. Срединой максимального класса будет 95, а его началом 95 — - — =- 92,5. 2 Максимальная граница каждого класса должна быть в данном слу- чае на 0,1 меньше начала следующего. Для минимального класса это будет 37,4, для следующего 37,4+5=42,4 и т. д., а для максимально. ro — 97,4. Расчет средней арифметической по вариационному ряду можно вес- ти двумя способами: по взвешенным вариациям и по условным от- ХЛОНСНИЯМ. Способ взвешенных вариаций употребляется в тех слу- чаях, когда вариации, или, что то же самое, средины классов, выраже- ны однозначными или двузначными числами, умножение которых на частоты не представляет большого труда. При наличии счетных ма- шин, дающих возможность легко получить сумму произведений трех- значных и четырехзначных вариаций на их частоты, можно и при мно- гозначных вариациях вести вычисление способом взвешенных ва- риаций. При этом способе каждая вариация (средина класса) умножается на свою частоту («взвешивается» частотой), все произведения склады- ваются и полученная сумма произведений делится на число вариантов. Вся работа ведется по формуле ГД(' М — средняя арифметическая, W — вариация (средина класса), f — частота класса, u = Zf — число дат. Вычисление средней арифметической по способу взвешенных вари- аций показано в табл. 7. Способ условных отклонений употребляется в тех слу- чаях, когда вариации выражены многозначными числами и перемноже- ние их на частоты с последующим суммированием полученных произ- ведений при имеющейся вычислительной технике становится затрудни- тельным. В таких случаях в предварительно составленном вариационном ряду средины классов заменяются отклонениями их от условной сред- ней, выраженными в классовых промежутках. Вместо ряда многозначных чисел получается ряд простых на- туральных чисел обычно в пределах первого десятка: О, 1, 2, 3 И7. Д,.
22 СРЕДНИЕ ВЕЛИЧИНЫ Таблица Расчет средней арифметической по способу взвешенных вариаций средина класса 1Г (начало класса плюс половина классового проме- жутка) срединакласса Я~(полусумманачала нконцакласса) частота граница класса частота граница классаУ,„. %'„, Я~ . Я~ 23 О 85 140 99 24 )О 2 23 20 17 14 11 8 5 ig 1 0 5 10 9 3 2 1 22 —:24 19-:-21 16-';-18 13-:-15 10 —:12 7-: — 9 4-: — 6 1 — :- 3 10 27 48 70 66 35 16 6 1 3 6 10 11 7 4 10 9 8 7 6 5 4 3 9,5-:-10,4 8,5-: — 9,4 7,5-: — 8,4 6,5-: — 7,4 5,5 —: 6,4 4,5-: — 5,4 3,5-: — 4,4 2,5-: — 3,4 383 27S Е/W 383 М == == =12 35 и 31 ЕfW 78М =- — = == 6,32и 44 Счетная работа с такими числами значительно облегчается. Расчеты ведутся по формуле М-=А -, 'Й П М — средняя арифметическая, А — условная средняя — средина одного из центральных классов. Удобней в качестве условной средней брать или средину класса с наибольшей частотой (модаль- ный класс), или средину класса, который находится между центром всего распределения и модальным классом, k — величина классового промежутка, f — частоты классов, Ф' — А условное отклонение каждого класса, выраженное в классовых промежутках. Это отклонение показывает, на сколько классов отстоит данный от того, средина которого принята за условную среднюю. Яля классов, средина которых меньше условной средней, а являет- ся отрицательной величиной; для классов, средина которых больше условной средней, а — положитель- ная величина, n=Zf — общее число дат в группе, Zfa — сумма произведений частот на отклонения — основ- ная величина при вычислении средней арифметиче- ской для больших групп; она может быть и положи- тельной и отрицательной. Рассчитывать ее можно или способом произведений или способом сумм. где Для признаков, выражаемых любым числом- целык и дробным (вес, объем, высота и т. д.) Яля признаков, выражаемых только целыкнчислами (число ульев на пасеке, яйценоскость,плодовнтость и т. д.)
ВЫЧИСЛЕНИЕ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ ДЛЯ МНОГОЧИСЛЕННЫХ ГРУПП Расчет по способу произведений показан в табл. 8 для вариацион- ного ряда, из которого взяты только средины классов. Таблица 8 Вычисление средней арифметической для больших групп по способу произведений А = 210; Е fu = — 462 й =20; и =1000 Еfa М =- А + Й — = Ш = 210+ 20 ( — 462) 1000 = 200,76 В первом столбце табл. 8 даны средины классов (W). За условную среднюю принята средина ~шестого класса А=210. Во втором столбце даны частоты классов /, а в третьем — отклонения а вариаций от услов- ной средней. выраженные в классовых промежутках. д~ля шестого класса, средина которого принята за условную сред- нюю, a=0. 230 — 210 При W=230 отклонение и = =, 1, т. е. этот класс от- 20 к.1оняется от условной средней на один классовый промежуток. При W=170 и 170 — 210 — 2, т. е. отклонение составляет два 20 классовых промежутка с отрицательным знаком. На основе этих примеров можно установить простое правило со- ставления ряда значений а. Для этого нужно против того класса, сре- дина которого принята за условную среднюю, поставить нуль, а затем по обе стороны от него написать ряд натуральных чисел: 1, 2, 3, 4 и т. д. ,Яля классов, средины которых меньше условной средней (вниз), перед числами поставить знак минус, а для тех классов, средина которых больше условной средней (вверх), IIocTBBHTb знак плюс. В столбце fa для каждого класса дано произведение отклонения на частоту. Сложение этих произведений лучше производить раздельно для положительной и отрицательной частей. Сумма положительных отклонений в нашем случае равна 378, а от- рицательных — 840. Таким образом общая сумма отклонений Zfa= = + 378 — 840 = — 462. Если разделить полученную сумму отклонений на число дат, то частное покажет, на сколько классовых промежутков средняя арифме- тическая больше или меньше условной средней: 0,462. 1000 В данном случае для облегчения счетной работы используется одно из описанных выше свойств средней арифметической.
24 СРЕДНИЕ ВЕЛИЧИНЫ В разбираемом примере среднее условное отклонение оказалось равным — 0,462. Это значит, что средняя арифметическая М меньше принятой условной средней А на 0,462 классового промежутка или на 20 - (0,462) =9,24 единицы измерения. Поэтому, чтобы получить среднюю арифметическую, надо из услов- ной средней вычесть полученную поправку: 210 — 9,24=200,76. В других случаях, когда сумма условных отклонений получается Еfa положительной, надо к условной средней прибавить величину Й = П Все эти действия выражаются общей формулой М =А+А Яля рассматриваемого примера.~И 210 20—1000 200,76. Способ сумм еще больше облегчает счетную работу при вычисле- нии средней арифметической для больших групп при многозначных ва- риантах. Этим способом получают точное значение суммы произведе- ний частот на отклонения (Zfa), при этом не производится ни одного перемножения и вся работа сводится только к суммированию неболь- ших чисел. Преимущества способа сумм особенно сильно проявляются при вычислении других показателей — среднего квадратического откло- нения, показателя асимметрии, показателя эксцесса, т. е. когда нужно получить сумму отклонений во второй, третьей и четвертой степени. Для получения этих показателей требуются все начальные действия, произ- водимые по способу сумм для расчета средней арифметической. Вычисление средней арифметической по способу сумм производит- ся по формуле М : А -+- Й )! где М — средняя арифметическая, А — условная средняя, устанавливаемая так же, как и при спосо- бе произведений, k — величина классового промежутка, S> — первая сумма, получаемая путем вычитания суммы отрица- тельных накопленных частот (r>) из су»а- копленных частот (q~): 5~ —— q~ — r~, и — общее число дат. Порядок вычисления средней арифметической по способу сумм по-казан в табл. 9 для того же распределения, которое служило приме-ром для способа произведений. Для вычисления средней арифметической по способу сумм требует-ся составить два ряда значений — для вариаций W и частот f — и уста-новить условную среднюю А так же, как и для способа произведений. Затем к этим двум столбцам нужно прибавить еще один столбец— первый ряд накопленных частот, который составляется следующим образом. Противев класса, средина которого принята за условную среднюю, ставится черточка ( — ). С обоих концов распределения по направле-нию к середине (условной средней) составляется ряд накопленных час-тот. Каждая из двух частей этого ряда (положительная и отрицател»-ная) доводится до центральной черточки.
ВЫЧИСЛЕНИЕ СРЕДНЕИ АРИФМЕТИЧЕСКОЯ ДЛЯ МНОГОЧИСЛЕННЫХ ГРУПП Составление положительной части первого ряда накопленных час- тот для распределения, представленного в табл. 9, производилось сле- дующим образом„ Таблица 9 Вычисление средней арифметической по способу сумм Первый ряд накопленных частот Частота ВариацияИ~ А =210 и = 1000 1=20 310 290 270 250 230 210 190 170 150 130 110 1 3 18 88 268 492 242 82 22 2 1 2 15 70 180 240 250 160 60 20 2 S> — — q> — rs — — 378 — 840 = — 462 Si М=А+Й — = и =- 210 + 20 — 200,76( — 462)1000 ~1 —— 378 r~ =840 n — 1000 Первое число (сверху) этого ряда равно 1 — частоте максималь- ного класса. для получения второго числа нужно к первому числу ряда приба- вить частоту второго класса: 1+2=3. Третье число ряда получается путем сложения второго числа ряда с частотой третьего класса: 3+15=18 и т. д. до встречи с черточкой. B разбираемом примере положительная часть первого ряда накоп- ленных частот составляется следующим образом: 1; 1+2=3; 3+15=18; 18+70=88; 88+180=268. Аналогичным образом получена и отрицательная часть ряда накал. ленных частот: 2; 2~-20=22; 22-+-60=82; 82+160=242; 242+250=492. Закончив эти действия, возможно проверить их результаты по сле- дующему правилу. Три числа, окружающие центральную черточку: 268 — конец положительной части ряда накопленных частот, 492 — ко- нец отрицательной части этого ряда и 240 — частота класса, средина ко- торого принята за условную среднюю, в сумме должны давать общее число дат. Сумма этих чисел 268+492+240=1000. Это показывает, что все предыдущие действия произведены без арифметических ошибок. После того, как получены все числа первого ряда накопленных час- тот, необходимо сложить отдельно все числа положительной части ря- да (расположенные выше черточки) и все числа отрицательной части ряда по другую сторону (ниже черточки). В разбираемом примере сумма чисел положительной части ряда 1+3+18+88+268=378. Это число, обозначаемое символом ~у~, в точно- сти равно сумме положительных отклонений, умноженных на частоты, получаемой по способу произведений: q~=Zf(+a). Для отрицательной части ряда сумма его чисел (2+22+82+242+ +492=840) равна сумме произведений частот на отрицательные откло- нения r~.
СРЕДНИЕ ВЕЛИЧИНЫ Для того, чтобы получить общую сумму произведений частот на от- клонения нужно из суммы положительных частот вычесть сумму отри- цательных частот: S> = q~ — r> — — Zfa. В разбираемом примере общая сумма первого ряда накопленных частот S, = q, — r ~ — — 378 — 840 = — 462, т. е. в точности такой же величине, какая была получена по способу произведений. Дальнейшие действия способа сумм аналогичны действиям способа произведений. Сумму первого ряда накопленных частот S> нужно раз- делить на число дат и частное помножить на величину классового про- межутка. Сумма условной средней и полученной поправки и есть сред- няя арифметическая. Для разбираемого примера: М = А -',— /г ' = 210+ 20 =- 200,76. $1 ( — 462) и 1000 В табл. 10 дано сопоставление трех основных способов расчета сред- ней арифметической для многочисленных групп. Таблица 10 Сопоставление трех способов вычисления средней арифметической для больших групп Вычисление средней арифметической Составление вариационного ряда способы условных отклонений 1 способ взвешен-ных вариаций вариа-ции границы классов частоты Ш способ сумм П способ произведений Ч1 — 378 q, =- 378 ri =- 840 S, =- q,— r> —— ° =378 — 840= — 462 2f =1000 Е/g~ =- 200760 > fa =- — 462 $~ М= — А+ й — = и ~ fWи ХfaМ===А-'-Й—и и =- 1000 й =--20 =-- 210 —;- 20 X — 462 y, — = 200,76 1000 =-- 210 -; — 20 у, 200760 А =-- 210 lu00=-. 200,76 — 462 >< — == 200,76 1000 300 —:319 280 —:299 260 —:279 240 —:259 220 —:239 200 —:219 180 —:199 160-:-179 140 —:159 120 —:139 100 —:119 310 290 270 250 230 210 190 170 150 l30 110 1 2 15 70 180 240 250 160 60 20 2 31О 580 4050 17500 41400 50400 47500 27200 9000 2600 220 +5 +4 +3 +2 +1 0 — 1 — 2 — 3 — 4 — 5 5 + 8 + 45 +140 + 0 — 250 — 320 — 180 — 80 — 10 1 3 18 88 268 492 242 82 22 2
СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ Чтобы получить среднюю геометрическую для группы с и датами. нужно все даты перемножить и из полученного произведения извлечь корень и-ой стелени: G y'ï~ (G — средняя геометрическая, п — число дат, ПГ — произведение дат). Например, средняя геометрическая из 12 и 3 будет равна 0 = p 12. з ==- ~зб =- 6. Если число дат больше трех, то извлечение корня п-ой степени за- труднительно, поэтому обычно значение средней геометрической нахо- дят путем логарифмирования величин, входящих в основную формулу: ( ~~К~ 1g V, '1g V.+ . ' 10 Vn и Например, для вариантов 1; 4; 5; 5; 5 среднюю геометрическую можно получить следующим образом: 0,000 0,602 0,699 0,699 д,699 Z Ig U=2,699, 1g V 2,699 и 5 0,5398, G = 3,466. х — средний попериодный прирост за ряд периодов равнойпродолжительности,а — фактический прирост за тот или иной период, выражен-НЫИ В ДОЛЯХ,n — число периодов,П(1+а) — произведение величин (1+а). ' Доля — процент, деленный на 100. Для проверки правильности вычисления средней геометрической можно использовать принцип единства суммарного действия: произведе- ние всех пяти вариантов (1 4 5 ° 5 ° 5=500) практически равно произведению пяти выравненных вариантов,:равных средней геометри- ческой (3,466Х 3,466 Х 3,466 Х 3,466 Х 3,466 = 500,2) . Это означает, что средняя в данном случае рассчитана правильно. Применяется средняя геометрическая во всех случаях, когда необ- ходимо узнать или спланировать средние приросты за определенный пе- риод. При расчетах среднего попериодного прироста возможны два ос- новных способа применения средней геометрической. Первый способ применяется, когда имеются сведения о приростах за каждый период, выраженных в процентах или долях* от начала каж- дого периода. В таких случаях расчет среднего прироста ведется по формуле:
СРЕДНИЕ ВЕЛИЧИНЫ Из этой формулы следует, что для нахождения среднего прироста по первому способу нужно долю фактического прироста за каждый пе- риод прибавить к единице, полученные величины ( +а) перемножить и из их произведения извлечь корень и-й степени и вычесть единицу. Если периодов много (и)2), то операцию извлечения корня целе- сообразно заменить логарифмированием: Х Ig (1 + а) lg (1 + а,) + lg (1 + а ) + ... -+ lg (l + а„) 1g ~~(1+а) = П й По этой формуле находят логарифмы средней геометрической из величин (1+а), затем находится сама величина <1) +,) и вычитанием из нее единицы получается искомая средняя доля прироста. П р и м е р 12. Поголовье кроликов в совхозе увеличилось за первый год на 5%, за второй — на 20%, за третий — на 50% и за четвертый- на 50%, считая каждый раз от начала истекшего года. Потребуется оп- ределить среднегодовой прирост за эти 4 года в совхозе. Необходимые расчеты приведены в табл. 11. Таблица 1] Расчет среднегодового прироста Фактический приростза каждый год > 1g(1 —,' а) = 0,4520,452tgO„ ' =-0,11З4 Годы 1+ а 1g(1+ а) ДОЛЯа G,+„ = 1,286х = 0,296 = 29, б ~ I.,05 1,2Q 1,50 1,50 0,05 0,20 0,50 0,50 5 20 50 50 0,021 0,079 0,176 0,176 1954 1955 1956 1-й колхоз . . . . 50 30 20 2-й колхоз . . . . . 20 30 50 g Требуется выяснить, в каком колхозе темп прироста был выше. 3 В данном случае используем формулух = ~11(1- a) 1 Величины 50 30 20 а будут соответственно = 0,5; — == 0,3; = ==- 0,2. Величины (1+а) 100 100 100 получат значения 1,5; 1,3; 1,2, а их произведение 1,5>< 1,3>< 1,2=2,34. Дальнейшие действия будут состоять в логарифмировании формулы 3 (Х+1) = 1~П(1 —,а) ° Зная 1д(х-<-1), можно определить и саму величину (х+1), а вычи- тая из нее 1, получить искомый среднегодовой прирост. Все эти расче- ты.приведены в табл. 12. Среднегодовые приросты оказались в обоих колхозах одинаковыми (32,8% ) . Это общее заключение может показаться неправильным: первый колхоз из года в год снижал прирост (50, 30, 20%), в то время как вто- рой регулярно наращивал темпы развития свиноводства (20, 30, 50%) ° Однако тут необходимо иметь в виду, что выводы о снижении и наращи- П р и м е р 13. В двух соревнующихся колхозах увеличение пого- ловья свиней выразилось в следующих процентах (считая от численно- сти на начало каждого года):
29 СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ- ванин темпов не могли быть получены путем сопоставления средних приростов. В данном случае среднегодовые приросты получены, как и всякие средние, путем отвлечения от тех различий по отдельным годам, на основании которых можно сделать заключение о снижении или нара- щивании прироста. Т а блица 12 Таким образом, .средние в данном примере получены правильные: они правильно характеризуют средний уровень прироста поголовья сви- ней в обоих колхозах, но этих средних еще недостаточно, чтобы дать полную характеристику развития свиноводства в двух колхозах Это обстоятельство всегда необходимо иметь в виду при интерпретации сред- них попериодных приростов, как и вообще всех средних величин. Бторой способ расчета средних приростов применяется в тех слу- чаях, когда имеются данные об абсолютных количествах особей на на- чало и конец общего большого периода и требуется рассчитать средний прирост за более мелкие периоды. В таких случаях средний прирост рассчитывается по формуле и A Х: л А, При логарифмировании получаем: Ал 1g А, 1д(х+ 1) = где х — средний прирост за более мелкие периоды: среднегодовой за пятилетку, среднемесячный за год, среднесуточный за ме-: СЯЦ И Т. Д. А„— количество особей на конец общего периода, или, что то же самое, на конец последнего и-ro мелкого периода. А~ — количество особей на начало исследуемого общего периода, или, что то же самое, на начало первого мелкого периода. П р и м е р 14. В колхозе на начало пятилетки было 100 ульев, а к концу стало 140. Определить среднегодовой процент увеличения пасеки за этр пятилетку. Применяя указанную формулу, получим: х= — -- 1; Ig(x+1) = 140 1g 1,4 0,146 100 5 5 = 0,0292. х+1=1,0697; а=0,0697, или 6,97%. Пример 15. Запланировано за пять лет увеличить производство мяса на 60%. Требуется распределить это задание равномерно по годам.
30 СРЕДНИЕ ВЕЛИЧИНЫ В данном случае не даны абсолютные количества в начале и кон-це общего периода, но дан общий процент прироста за весь период— А„ 60'/о, что дает возможность легко получить требуемое отношение А, Объем продукции должен увеличиться на 60О/о. Это значит, что на каж-дые 100 единиц, бывших в начале общего периода, должно быть 160 А„ » 160 единиц в конце. Тут А„== 160, А, 100, — "- = — - 1,6. A 1ОО ~1ля выполнения такого задания среднегодовой прирост производ-ства мяса можно запланировать следующим образом: — 1Я - 1. и1,6 о,2О4 0,0408, Д 5 1g (x+ 1) х -+- 1 = 1,0985; х = 0,0985, ил и 9,85 о/о . А lg — ):л =. = lg (х + 1) Aïlg—А> Aï AI в ло qflX в 41,4 44,2 41,4 38,0 О, 1505 0,1590 0,1505 0,1398 1,414, 0,414 1,442 0,442 1,414 0,414 1,380 0,380 0,301 0,477 0,602 0,699 Первый Второй Третий Четвертый Выяснилось, что наивысший темп прироста был во втором пруду, в котором среднегодовой прирост оказался равныи 44,2О/о и. за 3 года репродукция увеличилась в 3 раза. Наименьший темп — 38,0О/о — был в четвертом пруду, в котором за 5 лет репродукция увеличилась в 5 раз. П р и м е р 17. После проведения оздоровительных мероприятий чис- ло серебристо-черных лисиц, пораженных глистными заболеваниями, со- кратилось: в первом зверосовхозе в 2 раза за 2 года, во втором — в 3 ра- за за 3 года, в третьем — в 4 раза за 4 года и в четвертом — в 5 раз за Оказалось, что для увеличения производства за пятилетку на 60О/о 6О достаточно обеспечить среднегодовой прирост на 9,85 , а не — -- ]2" как это могло показаться без учета того, что средний прирост образует- ся по принципу средней геометрической, а не средней арифметической. П р и ме р 16. Вылов зеркального карпа увеличился в первом пру- ду в 2 раза за 2 года, во втором — в 3 раза за 3 года, в третьем — в 4 раза за 4 года и в четвертом — в 5 раз за 5 лет. В каком пруду репро- дукция зеркального карпа увеличилась наиболее бьгстро? Kaz в предыдущем примере, тут даны отношения — ", на основе 1 которых рассчитьгвается средний прирост. Если репродукция увеличи- лась в 2 раза, то это значит, что отношение конечного количества к на- чальному — ==- 2, при увеличении в 3 раза А и т. д. Искомые А„ А„ А, А1 среднегодовые приросты могут быть рассчитаны следугощим образом: 3,— для 1-го пруда х- 1 ==-1' 2, для 2-го прудах+1-- y;~ и т. д Элементы расчета для этого примера даны в табл. 13. Та блица 13
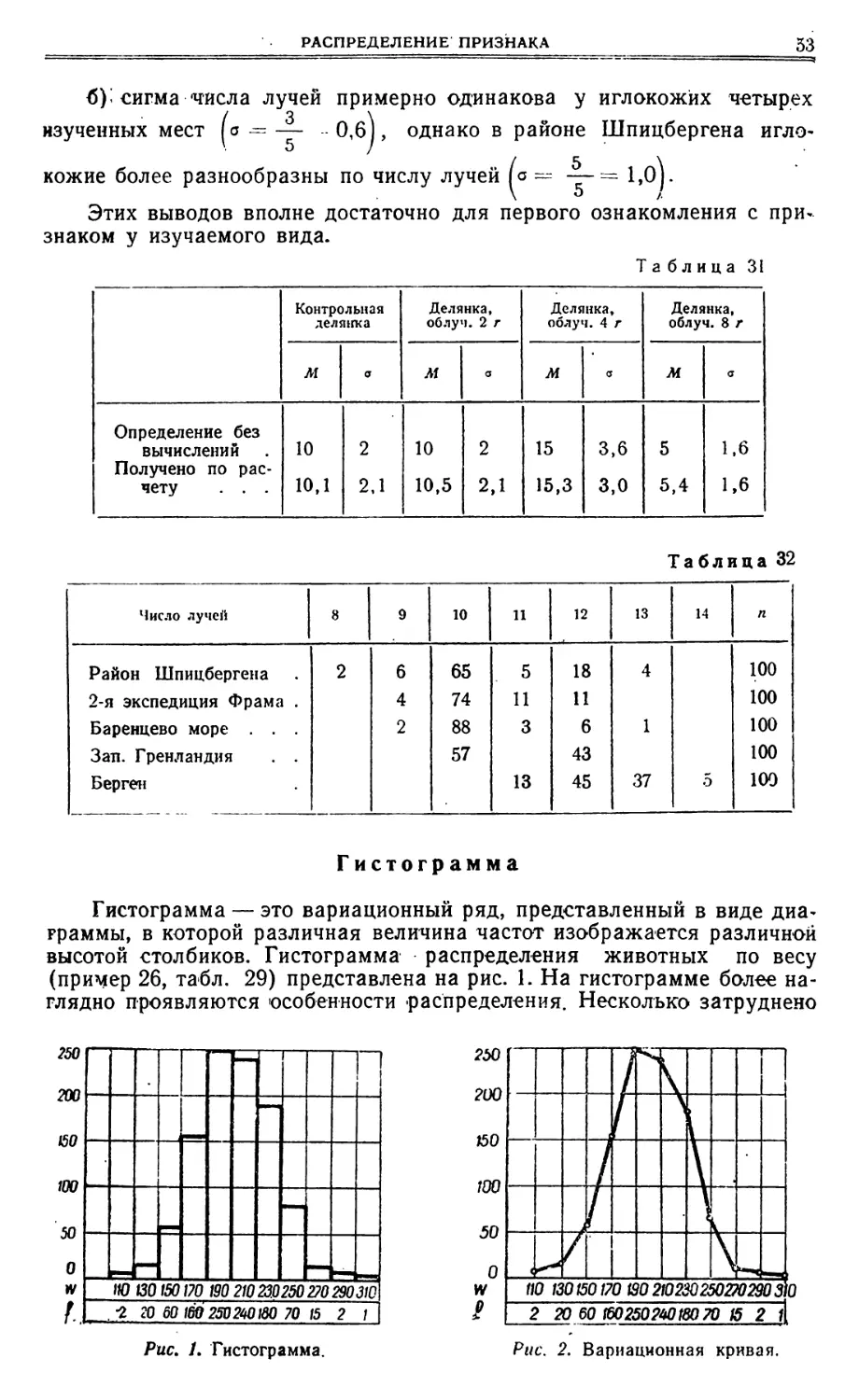
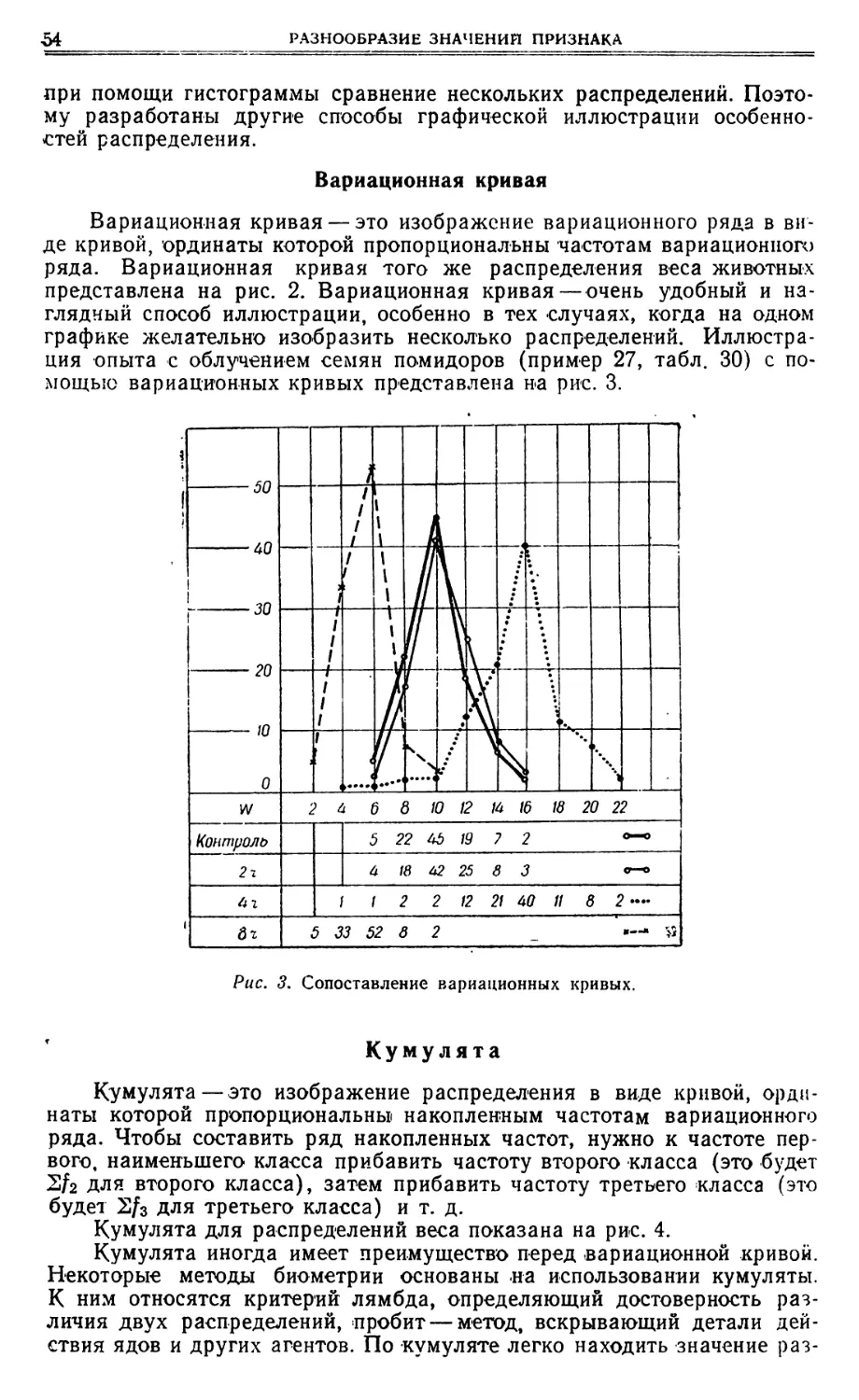
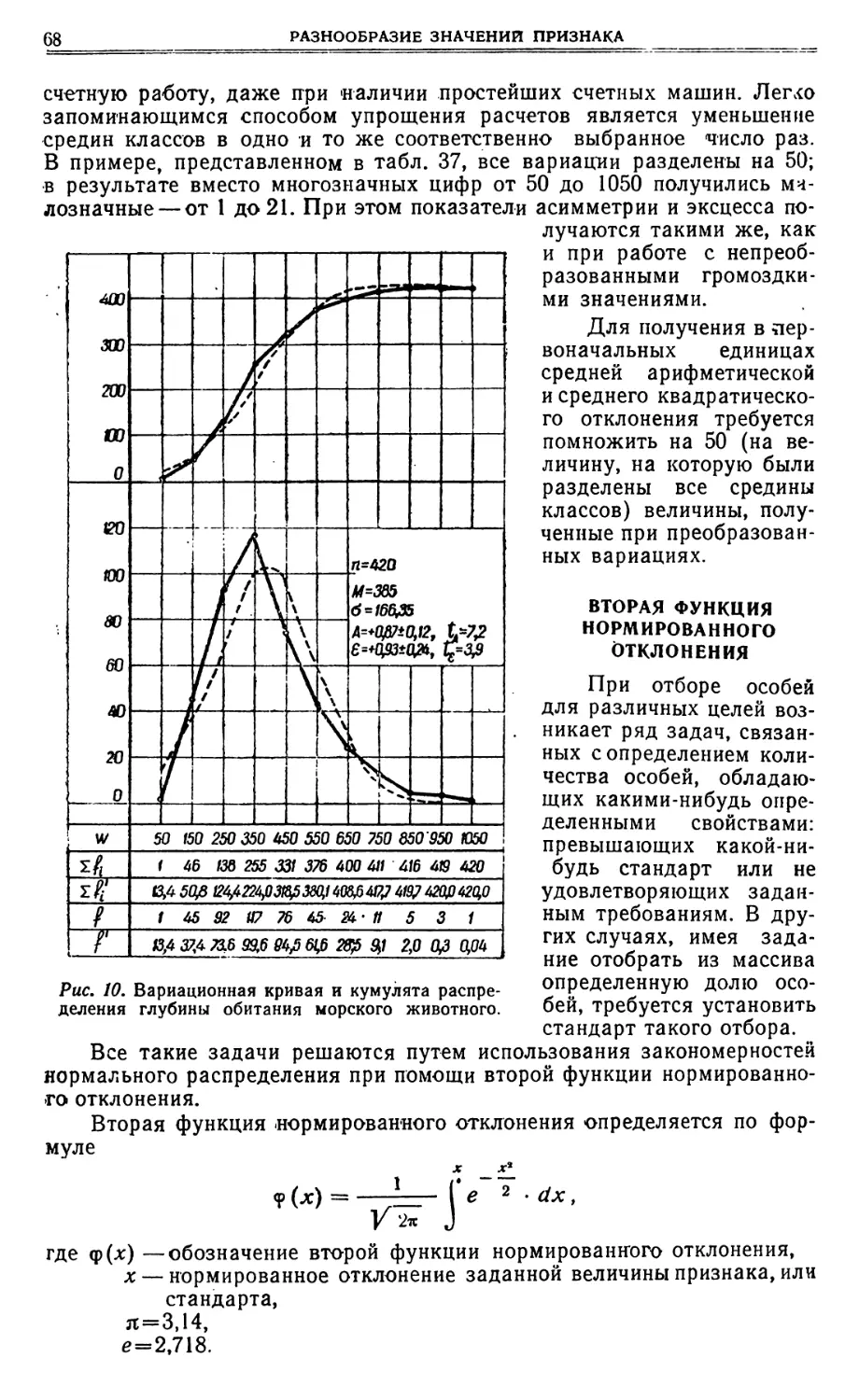
СРЕДНЯЯ КВАДРАТИЧЕСКАЯ 5 лет. Требуется определить, в каком совхозе темп дегельминтизации оыл наивысшим? В данком случае требуется определить среднегодовое уменьшение, П а не прирост. Это можно сделать по общей формуле х -';-1 = А, Ап в которой отношение А, нуля, т. е. отрицательной величиной. будет меньше единицы, а х будет меньше 1 Длв первого зверосовхоза л -Г- 1:-- 1 — , Ллв второго — х -, '1 = 2 1 — для четвертого зверосои- 4 1 — для гретьего — х -'; — 1 = 3 э 1 5 Решение здесь аналогичное предыдущему примеру, несколько усложненное из-за отрицательных значений логарифмов (табл. 14). хоза — х-1-1= Таблица 14 Ап 1g— 1а(х ... 1) х -т- 1 Ал)g—А, Ап А, СОВХ~С В ДОЛЯХ — 29,2 — 30,6 — 29,2 — 27,5 Оказалось. что наивысший темп дегельминтизации был во втором совхозе, в котором среднегодовое уменьшение гельминтозных лисиц со- ставляло 30,6% и за 3 года число больных лисиц сократилось в 3 раза. СРЕДНЯЯ КВАДРАТИЧЕСКАЯ Средняя квадратическая вычисляется по формуле /~ ~/з(г т. е. она равна корню квадратному из суммы квадратов дат, деленной на их число. Например, если имеется пять дат: 1, 4, 5, 5, 5, то средняя «вадратическая — — 18,4 =- 4,' . +4>%5г--'Р 5~ Употребляется средняя квадратическая при расчете средних ради- усов. окружностей. П р и м е р 18. Измерение диаметров колоний, полученных от посе- ва микробов определенного вида, дали следующие результаты (в мл~): 15; 20; 10; 25; 30. Первый Второй Третий Четвертый 0,5 0,333 0,25 0,2 1,699 1,522 1,398 1,301 — 0,301 — 0,478 — 0,602 — 0,699 — 0,1505 — 0,159 — 0,1505 — 0,1398 1,8495 1,8410 1,8495 1,8602 0,708 0,694 0,708 0,725 — 0,292 — 0,306 — 0,292 — 0,275
СРЕДНИЕ ВЕЛИЧИНЫ Яля сравнения этого посева с другими требуется определить сред- ний диаметр колоний. Применив формулу средней квадратической, имеем: 2250 = 21,22 мм. 5 152 + 202 .+ 102 .+ 25с .+ 30~ Средняя арифметическая диаметров15+ 20+ 10+ 25+ 805 1005 -=- 20,0 СРЕДНЯЯ ГАРМОНИЧЕСКАЯ Средняя гармоническая рассчитывается по формуле:й йН=1Е—V 1 1 1+ + ° +1~л ,Яля пяти дат: 1, 4, 5, 5, 5, средняя:гармоническая — — 2,70. 1,85 1 1 1 1 1— + — + — + — -"—1 4 5 5 5 Применяется средняя гармоническая при усреднении меняющихся скоростей. Пример 19. Почтовые голуби одной станции к месту кормежки летят со скоростью 50 км/час, а в обратном направлении — со скоро стью 40 км/час. Если кроме этих данных, ничего больше неизвестно и требуется выяснить среднюю скорость полета для обоих направлений (расстояния, очевидно, равны), то сделать это можно, рассчитав про- стую среднюю гармоническую для двух дат — 50 и 40: 2 2 2 ==. 44,4 км/час. 0,020 + 0,025 0,045 1 1+50 40 П р имер 20. Рысак на тренировках пробегал одну за другой три дистанции, различные по состоянию дороги. Скорость на первой дис- танции составляла 13 км/час, на второй — 20 км/час и на третьей— 10 км/час.,Ялика дистанций не сообщается, указывается только, что пер- вая дистанция была в 2 раза, а вторая в 4 раза длиннее третьей. По этим дает неправильную характеристику группы. Это можно проверить по правилу единства суммарного действия. Общая площадь всех пяти колоний была 3,14 (7,52+10'+5'+12,5'+ +15') =1766,25 мм2. Если взять пять одинаковых кругов с диаметром, равным средней арифметическои М=20, то общая площадь составит 5>(3,14X10'=1570 мм2, что гораздо меньше общей фактической пло- щади. Если же взять пять кругов с одинаковым диаметром, равным средней квадратической S=21,22 мм, то общая площадь будет: 5X3,14(10,61)'=1767,4 млд, т. е. практически той же суммарной пло- щади, которую имели пять измеренных колоний.
МОДА данным можно определить показанную рысаком среднюю скоростьпо всем трем дистанциям, рассчитав не простую, а взвешенную среднюю гармоническую из значений 13, 20, 10 соответственно с весами 2, 4, 1 по формуле + ~г + ° ° ° ~ k„ 1~1 '112, ~ 2П + 1 ~2 1ï V Взвешивание скоростей производится обычно по расстояниям. По- скольку в данном примере расстояния неизвестны, то весами могут служить отношения первой и второй дистанции к третьей. Такая замена математических весов не повлияет на точность результата, так как для правильного расчета взвешенной средней гармонической имеют зна- чение не абсолютные величины расстояний, а их отношения. Средняя скорость рысака за весь пробег 2+ 4+ 1 7 7 2 4 1 0,154+ 0,2 + 0,1 0,454 13 20 10 = 15,4 ки)час. П р и м е р 21. При решении неравномерных дисперсионных комплек- сов требуется заменить имеющийся неравномерный комплекс равномер- ным с одинаковыми частотами, равными средней гармонической фак. тических частот. Если в неравномерном двухфакторном комплексе численность элементарныхградацийбыла3,4,5,4,5,5, то в новом рав- номерном комплексе все частоты градаций должны быть одинаковыми и равными по величине: = 4,187. 1 1 i 1 1 — + — + + -'- — +— 3 4 5 4 ' б 5 1,433 подд Модой, или модусом, называется такая дата или класс распределе- ния дат, который в исследуемой группе особей встречается наиболее часто. В качестве примера рассмотрим распределение, представленное в табл. 15. Та бли ца 15 280 — 299 300 — 319 240 — 259 260 — 279 220 — 239 180 — 199 200 — 219 140 — 159 160 — 179 100 — 119 120 — 139 Классы 2 2 70 15 180 250 240 2 20 60 100 Частоты B этом распределении наиболее многочисленным является пятый класс (180 — 99) с частотой 250. Это модальный класс. В качестве первого приближения можно принять за моду сре- дину модального класса, т. е. 190. Более точное значение моды можно получить по формуле hfD= W.+Й 2f 2 — Л — /2 где Мо — мода, Г~. — начало модального класса,
СРЕДНИЕ ВЕЛИЧИНЫ k — величина классового промежутка, f( — частота класса, предшествующего модальному, f2 — частота модального класса, fs — частота класса, следующего за модальным. Для приведенного распределения W =180, k=20, f) — — 160, /2=250 и /з —— 240. Следовательно, мода этого распределения М„ — = 180 + 20 = 198. 500 — 160 — 240 Обычно, если классы взяты не слишком мелкие (10 — 12 на всю группу), имеется всего один модальный класс. В некоторых распределениях встречается два или три модальных класса. Иногда это может быть следствием того, что в изучаемую груп- пу попал разнородный материал, относящийся к разным категориям (более крупной и менее крупной) по изучаемому признаку. МЕДИАНА Медианой называют такое значение признака, которое разделяет всю группу на две равные части: одна часть имеет значение признака меньшее, чем медиана, а другая половина — большее. Например, если имеется группа из 9 значений признака: 1, 2, 3, 4, 5, 6, 7, 8, 9, то медианой этой группы будет 5. Для многочисленных групп- медиану можно рассчитать по формуле И Яе= W,.4-Й ' ), где Ме — медиана, W.— начало того класса, в котором находится медиана, k — величина классового промежутка, п — общее число дат в группе, Z — сумма частот классов (начиная с меньшего), предшествующих классу, в котором находится медиана, f — частота класса, в котором находится медиана. Нахождение медианы можно показать для распределения, пред-ставленного в табл. 16. Та блица 16 10 11 Номера классов Начало клас- сов 240 260 70 15 3001 120 20 280 220 180 180 250 200 240 100 140 60 160 160 и = 109' Частоты Накопленныечастоты 492 732 82 242 22 Судя по ряду накопленных частот, медиана находится в шестом классе, так как в первых пяти классах имеется 492 варианта, а меньше медианы должна быть половина всей группы, т. е. 500 вариантов. Не- достающие до 500 восемь вариантов находятся в шестом классе.
35 Медиана Для данного распределения W. 200, k=.20, —" = 500, "- — — 492, 2 ~ =240, а медиана равна ~Не --= 200,— 20 240 = 200,Ê. Медиана, обладая в полной мере всеми общими свойствами сред- них величин, дает начало целой серии показателей разнообразия, кото- рые носят общее название квантиль. 1~вантиль — это такое значение признака, которое отсекает в распределении определенную часть дат больше себя и определенную часть дат меньше себя. K таким показа- телям относятся, кроме медианы (средней величины), показатели раз- нообразия: квартили, децили и перцентили. Три квартиля разделяют группу на четыре равночисленные части. Второй квартиль равен медиане, а расстояние между третьим и первым квартилем является одним из показателей степени разнообразия зна- чений признака в группе. Девять децилей разделяют группу на десять равночисленных час- тей. Пятый дециль равен медиане, а расстояние между девятым и пер- вым децилем служит одним из показателей разнообразия. Девяносто девять перцентилей делят группу на сто равночисленных частей. Пятидесятый перцентиль равен медиане; девяносто девятый и первый перцентиль используются иногда в качестве максимума и мини- мума группы; расстояние между девяносто девятым и первым перценти- лем служит показателем размаха признака и разнообразия дат в этой группе.
ГЛА ВА 11РАЗНООБРАЗИЕ ЗНАЧЕНИЙ ПРИЗНАКА сякая группа состоит из особей, отличающихся друг от друга по каждому из признаков. Различия эти иногда очень велики, иногда 'они почти незаметны. но они всегда имеются, так как невозмож- но найти даже двух особей абсолютно одинаковых. Поэтому одним из основных свойств совокупности является объ- единение неодинаковых особей с разнообразными значениями любого признака. ПОКАЗАТ Е Л И РАЗ Н ООБРАЗ ИЯ При изучении общих свойств совокупностей невозможно ограни- читься одними средними величинами; требуется еще привлечь и такие показатели, которые характеризовали бы степень разнообразия особей в группе. Такими показателями являются: лимиты lim, среднее квадра- тическое отклонение а и коэффициент вариации CV. I(poMe того, иногда употребляется квартильное отклонение или децильное отклонение. Общим свойством показателей разнообразия является их способ- ность отмечать различную степень и различные особенности разнооб- разия. Л ИМИТЫ Простейшим показателем разнообразия группы являются лимиты признака, т. е. имеющиеся максимум и минимум. Иногда вместе с ли- митами указывается и размах признака — разность между максималь- ным и минимальным значениями. Размах приписывается к лимитам в скобках: 2 — 7 (5}. П р и м е р 22. При изучении веса быков в двух совхозах получены следующие данные (табл. 17}. Средние живые веса бы- Средний живой вес, кг М быка второй совхоз первый совхоз !!т~ = 640 — 660 (20), 11тг —— 600 — 700 (100) . 1 2 3 4 5 n=5 640 645 650 655 660 М, =650 кг 600 630 6"0 680 700 М~ — — 650 кг ков в обоих совхозах одинако- вы — 650 кг, при этом разнооб- разие быков по весу во вто- ром совхозе больше, чем в первом. Наиболее просто это мож. но показать при помощи ли митов и размаха:
37 СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ Оказалось, что во втором совхозе размах веса быков в пять раз больше, чем в первом. Иногда характеристика разнообразия группы в виде лимитов и раз- маха имеет столь большое производственное значение. что кладется в основу денежной 'оценки продукта. П р и м е р 23. Если средний вес тушек бекона в одной партии Aft=90 кг и lim~ — — 88 — 92 (4) кг, а в другой М2=90 кг и Итз —— 80 — 100 (20) кг, то ясно, что первая партия как стандартная получит более вы- сокую оценку по сравнению со второй. При проведении параллельных анализов лимиты результатов и их размах служат показателями качества проведенной работы. Кроме показаний степени разнообразия, лимиты дают характери- cTHK„" как достижений, так и недостатков, имеющихся в группе по изу- чаемому признаку. В некоторых случаях лимиты могут служить единственной харак- теристикой признака. Например, при описании простейших приводятся только лимиты их размеров: кишечная амеба lim..... 20 — 30 мк, трипонозома lim 20 — 70 л~к, инфузории толстых кишок lim . 30 — 150 мк. Эти данные являются вполне достаточными для первого ознаком- ления с этими объектами. Поэтому лимиты представляют большой ин- терес даже при наличии более точных показателей разнообразия. Одна- ко лимиты не могут служить осковным показателем разнообразия, так как они не отражают очень важных его особенностей. Предположим, что сравниваются две группы каких-либо особей по длине (табл. 18). Т а блица 18 Средние и лимиты в обеих группах одинаковы, и в то же время сте- пень разнообразия этих групп явно различна. В первой группе все осо- би различны, а во второй семь особей из девяти имеют один и тот же размер. Изменчивость первой группы явно больше, чем второй, но отме- тить это при помощи лимитов в данном случае невозможно. Наиболее точно охарактеризовать степень разнообразия можно при помощи особого показателя — среднего квадратического отклонения. СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ Среднее квадратическое отклонение имеет совершенно исключи- тельное значение в математической статистике. Этот показатель исполь- зуется в качестве абсолютной меры разнообразия и, кроме того, поло он в основу почти всех характеристик изменчивости, распределения, корреляции, регрессии, дисперсионного анализа.
РАЗНООБРАЗИЕ ЗНАЧЕНИЯ ПРИЗНАКА 38 Основная формула, среднего квадратического отклонения- =- l' ~ хп f х(y — м)* где а (сигма) — среднее квадратическое отклонение; название этого символа перешло и на сам показатель, так что сред- нее квадратическое отклонение называют часто просто сигмой; D= V — М — централъное отклонение, разность между датой и сред- ней арифметической, v — число степеней свободы; при расчете сигмы число степеней свободы равно числу дат без одной: т=п — 1. Чтобы рассчитать сигму для группы, состоящей из п дат, нужно: 1) найти среднюю арифметическую, 2) получить для каждой даты центральное отклонение (D= V — М), 3) каждое центральное отклонение возвести в квадрат (D~), 4) все квадраты центральных отклонений сложить (ZD2), 5) сумму квадратов центральных отклонений разделить на число степеней свободы, которая в данном случае равна числу дат без одной. оя Полученная величина имеет особое название — девиата (или ва- и — 1 ри акса), 6) извлечь квадратный корень из девиаты: Вь~числение сигмы для двух групп (см. табл. 18), лимиты которых не могли отразить различий, приведено в табл. 19. Та блнца 19 Вычисление среднего квадратического отклонения непосредственным способом г у~ оо формуле с~ Вторая группа Первая группа D"- D"- п=9 п=9 л 4 0 0 О О +4 +3 +2 126М = — =149 125М =- — =149 60 8 32 8 = 1' 4,0 = 2,00 V7,5= 2,74 Е V=126 ~D"- =-- 32 ~Q =0 ZD-" = 60 ~~ = l26 xD =0 18 17 16 15 14 13 12 11 10 16 9 4 1 0 1 4 9 16 18 14 14 l4 14 14 14 14 10 16 0 0 0 0 О О 0 16
СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ 39 Ч исло ст е п е н ей свободы. Число степеней свободы равно числу элементов свободного разнообразия. Оно равно числу всех имею- щихся элементов изучения без числа ограничений разнообразия. Пусть, например, для исследования требуется взять три объекта с любым развитием изучаемого признака. В данном случае величина признака не имеет никаких ограничений, поэтому число степеней сво- боды равно v=3 — 0=3. Если для исследования берется три объекта, но с условием, что сумма значений изучаемого признака должна быть равна определенной величине, например, 100, то первый объект может иметь признак лю- бой величины, например, 20 (одна степень свободы), второй объект может также иметь любое значение признака, например, 30 (вторая сте- пень свободы), третий же объект может иметь только одно определенное значение 50 (100 — 20 — 30) и поэтому не имеет свободы разнообразия. Таким образом, для трех дат при одном ограничении разнообразия имеются две степени свободы (v=3 — 1=2). Для п дат при k ограничениях имеется v =n — k степеней свободы. При вычислении средней арифметической вся сумма значений приз- нака относится к одному элементу из числа образующих эту сумму, причем никаких ограничений величины значений признака не имеется. Поэтому число элементов, образующих среднюю арифметическую, рав- но числу дат. При вычислении среднего квадратического отклонения имеется одно ограничение величины признака у изучаемых объектов. Сигма вычисляется для определенной группы, имеющей определенную сред- нюю арифметическую. Поэтому разнообразие элементов, образующих среднее квадратическое отклонение, ограничено этим одним условием и в данном случае число степеней свободы равно числу дат без одной: ч=п — 1. Последняя дата при образовании определенной суммы не имеет свободы разнообразия. При определении степени соответствия эмпирических распределе- ний теоретическим — нормальному или биноминальному, числу элемен тов свободного разнообразия равно числу классов распределения без двух: v=r — 2, так как особенности этих распределений ограничивают- ся и целиком определяются двумя условиями: определенной средней арифмегической и определенным средним квадратическим отклонением. Расхождения распределений в тех случаях, когда в качестве тео- ретического распределения берется распределение редких событий (распределение Пуассона), оцениваются при числе степеней свободы, равном числу классов распределения без одного (v=r — 1), потому что особенности распределения редких событий ограничены и целиком оп- ределены только одним условием — определенной средней арифмети- ческой. Определение критерия достоверности разности ~ = — двух сред- md них величин производится при числе степеней свободы v=n~+n2 — 2. Это связано с тем, что ошибка разности определяется на основе ошибок а — обеих средних, каждая из которых имеет число степеней И свободы (для соответствующей сигмы) n — 1. В сумме число степеней свободы v = n~ — 1+ n2 — 1 = n~+ nq — 2. Вычисление среднего квадр атического отклоне. н ия. Вычисление сигмы по основной формуле почти никогда не произ-
РАЗНООБРАЗИЕ ЗНАЧЕНИЯ ПРИЗНАКА водится, так как при этом возникают технические неудобства. Средняя арифметическая обычно получается в виде числа с дробью, поэтому центральные отклонения получаются многозначными, а квадраты их ~ еше большим количеством десятичных знаков. При этом возникают значительные трудности, связанные с суммированием большого коли- чества многозначных чисел. Поэтому разработано несколько способов вычисления сигмы для малочисленных и многочисленных групп и для малозначных и много- значных вариантов. Все эти способы дают требуемое значение сигмы, и при этом значительно упрощают сам процесс вь|числения. Они основаны на том, что для получения суммы квадратов цент- ральных отклонений достаточно взять отклонения от любого числа (условной средней) и произвести с ними действия по формуле : Р (1 Д)г l'- (1~ А)1'-' Л Использование этого свойства средней арифметической позволило значительно облегчить получение суммы центральных отклонений как для больших, так и для малых групп. Если за условную среднюю принять нуль, то указанная формула имеет следующий вид: (т v)2 [z (v — о)р Е,0' = — Е ( V -- 0)-' V 4»» Эта формула сильно облегчает работу по вычислению сигмы для малочисленных групп при малозначных вариантах, что показано в табл. 20. Таблица 20 Вычисление среднего квадратического отклонения для малочисленныхгрупп и малозначных вариантов по формулеX D-' и — 1 ',), 'D2 g P2(~ ~)-"В 81 � =- — -=- 11,57 7 п= 7 ~' V= 81 (> V) 2 = 6561 (Z V)2 в п = 937,3 ~ ~-2=989 41,7б ' = г' 6,95 =- 2,64 ~.0-" = — 41,7 При многозначных вариациях сумму квадратов центральных откло- нений легче получить через условные отклонения, взяв за условную сред- нюю какое-нибудь удобное число, близкое к предполагаемой средней. Все вычисления удобней расположить так, как показано в табл.2].
СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ 41 Табли ца 21 Вычнсление среднего квадратического отклонения для многочисленных групп и многозначных вариантов по формуле хп- г ~Э У и — 1 (~~)"- . ь=v — л и А = 125 — 18 М = 125+ — =- 9 п=9 = 123,0 ~Ь = — 18 (ХЬ)"- = 324 (Ш)-': п = 36 ~Ь-' = 234 1988 = )' 24,75 = 4,97 '-".0'- == ]98 Проверка:1107М — — 1239 Для многочисленных групп способы вычисления среднего квадрати-ческого отклонения классифицируются так же, как и способы расчета средней арифметической: 1) способ распределения дат, 2) способ взвешенных вариаций, 3) способ условных отклонений: а) способ произведений, б) способ сумм. Вычислительные действия, необходимые для нахождения сигмы, яв-ляются продолжением действий, требующихся для расчета средней арифметической. Поэтому способы расчета сигмы будут показаны на тех же группах, на которых были показаны способы вычисления средней арифметической. Способ распределения дат употребляется, когда многочисленная группа состоит из малозначных вариантов при не очень большом раз-махе от минимума до максимума. В этом случае распределение со-стоит из ряда дат, не объединенных в классы, и частот, показывающих, сколько раз встретился каждый из вариантов. Составление такого рас-пределения и расчет средней арифметической были показаны в табл. 4. Сигма в таких случаях рассчитывается по формуле 7 л — 1 где гм с с' iг~ (-У V)'- У И При получении ZfV2 не требуется возводить каждое значение вари- антов в квадрат и потом умножать его на частоту, -а достаточно полу-
~',3 РАЗНООБРАЗИЕ ЗНАЧЕНИЯ ПРИЗНАКА I I r I J Ф 1 I) й O ° ° ° ° ° в ° 1 J ° r ° ° sâ ° ° 1 ° у g ° ю а ю ю 1 й ° й ° ° ° s e» ° Э ° ° ° ° I J ° ° ° I r ю ° ю Э а ° ° ° I I I I в ° ° I I ° а 1 I а ° ° ° ° ° ° ° ° ° ° ° ° 1 ° ° в ° в й в ° ) 1 ° lI ° I ° ° ° 1 Ф в ° ) I ° ° ° ° ° ° 1 ° ° ° ° ° J ° Ф I ° J ° ° ° ° ° Э ° 1 ° в ° ° й ° В ) ° ° ° ° 1 ° ) Ф ° 1 ° ) ° й j й ° ° ° ° ° У ° Ф ° в ° ° ° ° 1 ° ° ° r ° 1 1 ° й ) 1 ° Ф ф ° ф ф ф й й Ю ° й ) й ) ° ° Э ° 1 ° ° ° ° 1' J r ° 1 66 а r 6 в ° ° ° ° ° 1 й 1 ° ! ° й й ° й ф ° I ю ° е~ ' ° ))ЭЭ ° r ) I r ° й ° °: ° ° I ° I r ° ° ° ° в ° I ° ° ° В ° ф й ° ° в ° В ° й 1 й 1 ° ю ° ° 1 ) ° ° ° r 1 ) ° ° 16 )
СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ 43 5' — А условное отклонение вариаций (средин классов),выражен- ное в классовых промежутках составленного распределе- ния, f — частота классов, n = Z f — число дат, вошедш их в р а сп редел ение. Та 6.чица 23 Вычисление среднего квадратического отклонения для больших групп по способувзвешенинх вариаций по формуле (~УР f fW ~а -- ~о~ 100 243 384 490 396 175 64 18 10 27 48 70 66 35 16 6 9,5-:-10,4 8,5-:- 9,4 7,5-: — 8,4 6,5 —: 7,4 5,5-: — 6,4 4,5 —: 5,4 3,5-: — 4,4 2,5-:- 3,4 10 g 8 7 6 5 4 3 1 3 6 10 11 7 4 2 278М= — =6,344 ~ f W = 278(>)'W)-" = 77284= 1756,5п 113,543 = 1' 2,64 = 1,625 ~ f W2 = 1870 Е D~ = 113,5 44 278 1870 Основную величину для вычисления сигмы — Z6' — так же, как и основную величину для вычисления средней арифметической— Zfa, можно находить двумя способами: способом произведений и спо- собом сумм. Способ произведений состоит в том, что величина Хо'рассчитыва- ется непосредственно путем перемножения на частоты условных откло- нений в первой и во второй степени (отсюда и название способа) и про- ведения с этими величинами действий, указанных формулой. Яля получения ряда fa' не обязательно каждое отклонение возво- дить в квадрат, а потом умножать на частоту. Проще этот ряд получа- ется путем перемножения уже полученных .произведений fa на а. Расчет сигмы по способу произведений показан в табл. 24 для груп- пы, которая была использована при расчете средней арифметической способом произведений (табл. 8). Способ сумм наиболее простой способ расчета среднего квадратиче- ского отклонения для больших групп при многозначных датах. Осо- оенность его заключается в том, что основные величины — суммы произведений условных отклонений в первой и второй степени на часто- ты — получаются без перемножения чисел, путем одного только сложе- ния небольших величин.
РАЗНООБРАЗИЕ ЗНАЧЕНИЯ ПРИЗНАКА Т аблица 24 Вычисление среднего квадратического отклонения для больших групп по способупроизведений по формуле (E fa)~ ~~2 ~" 3 ~0 = . Д — 462iW = 210 -; — — . 20-.=200,761000 и = 1000 А = 210 й =-20 а=20 =- 20 ~ 2,2408 == 29,94 vD2 ksZ02== 400 . 2238,6 = 895 440 11ри обработке материалов экспериментов применение метода сумм значительно сокращает счетную работу и дает большую экономию времени. Расчет сигмы по способу сумм показан в табл. Q5 Та блица 25 Вычисление среднего квадратического отклонения для больших групп по способусумм: l и — 1 Si == ~у, — г,, S„= rl, — r, + 2 (q —, r.) 202 =- $.,— q == 137 q,=За n =- 1000 А =210 1=20 М =210- ° 20— 4621000 1 4 с)2 110 = 200,76 S = — 462 $'~~ — — 213 444 348106242 $1 .' и = 213,4 $ =2452 Я~ = 2238,6 I ~ — — 840 1000 ri = 480 310 290 270 250 230 210 190 170 150 130 110 1 2 15 70 180 240 250 160 60 20 2 1 't3 18 88 268 492 242 82 22 2 E f n =- — 462(E fn)~ = 213444(E fa)~: n..==- -213,4Efa' = 2452дг 2238, 6 = 20 ' = 29,94 2238, 6 999 S,=Efa ! 2 (S =E fa
СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ Для расчета среднего квадратического отклонения по способу сумм необходимо произвести следующие действия: 1. Составить вариационный ряд способом, показанным в табл. 9. 2. Составить первый ряд накопленных частот способом, показанным в табл. 9. В разбирае.лом примере первый ряд накопленных частот дал сумму положительных отклонений q> — — 378 и сумму отрицательных отклонений r> — — 840, откуда сумма условных отклонений, выраженных в классовых промежутках, S> =q> — r> — — 378 — 840= — 462. 3. Составить второй ряд накопленных частот. Для этого в столбце второго суммирования ставят три черточки (см. табл. 25). После этого с обоих концов распределения составляют ряд накопленных частот вто- рого порядка, так же, как и для первого столбца суммирования. Для разбираемого примера (см. табл. 25) числа второго ряда суммирования, относящиеся к положительным отклонениям (сверху вниз), следующие: 1: 1+3=4, 4+18=22, 22+88=110, а для отрицательных отклонений (снизу вверх) 2; 2+22=24, 24+82=106, 106+242=348. 4. Произвести суммирование чисел, полученных во втором ряду на- копленных частот: qua=137 и rq=480. 5. Найти сумму квадратов условных отклонений, выраженных в классовых промежутках: S>=q>+r1+2 (q>yr;) =378+-840+2 (137+480) =2452. 6. Найти сумму центральных отклонений, выраженных в классовых промежутках: $21 = 2452 — — = 2238,6. 462"- 1000 ЕУ=S, 7. Рассчитать среднее квадратическое отклонениеа.=- Й~~ = 20 ' = 29,94.я — 1 999 8. Рассчитать среднюю арифметическую по формуле М = А -,'-/г ' =-210+ 20 =200,76. $1 — 462 и 1000 9. Проверить правильность произведенных действий по способу сумм: a) сумма трех чисел, окружающих центральную черточку (частота центрального класса, конечное число первого суммирования сверху и конечное число первого суммирования снизу), должна быть равна числу дат в группе. Для примера, показанного в табл. 25, 240+ 268+ 492 = 1000 = n; б) сумма верхних конечных чисел первого и второго рядов сумми- рования должна быть равна величине q, а нижних — величине r~. Для примера, показанного в табл. 25, 268+ 110=378, 492+ 348 = 840. Яля сравнения описанных способов расчета среднего квадратическо- го отклонения в табл. 26 дано сопоставление этих способов для одной к той же группы.
РАЗНООБРАЗИЕ ЗНАЧЕНИЙ ПРИЗНАКА Таблица 26 Сопоставление трех способов вычисления среднего квадратического отклонения Вычисление М и e' Вариацион-ный ряд по условным отклонениям по вариациям способ сумм способ 11роизведений Л == А -}- й— $, л Я=А-,'-k—> fa/1 ЯЕ f%~л ( f ~~)' ". и-' - z уг —— и ~21o'-' S, ——и$,-q,— r,~,=~7э+rз+2(qÿ т ~'~) (> fu)'-'и q, 34 ~ q,=21 fa 15 15 () 3 1 155 425 r =21 48 2705 - З44 — 211 123 13 —;13 М =-55+5 48 2705М =- = = 56,3548 ~13 М = 55 + 5 ° — = 56,35 48 и=48 А =55 4=5 = 56,35 ~ fa = -1- 13(Е fa)' = 169(E fa)~: n =3,52Е fa~ = 123~'У = 119,48 Е (W = = 2705(Z f W)~ =- 7 317 025(> f И~)': п = 152 438Е/И7~ = 155425'- D~ = 2987 Si = -,'- 13 Я = 169 8,: и =3,52 $» = 123~о~ =- 119,48 298747 119,48 119.4847= 7,97 =- 7,97 = 7,97 a=5 СРЕДНЯЯ И СИГМА СУММАРНОЙ ГРУППЫ Иногда бывает необходимо определить среднюю и сигму для сум- марного .распределения, составленного из нескольких распределений. При этом известны не сами распределения, а только их средние и сигмы. Средняя и сигма в таких случаях находятся по следующим фор- 1~~Лам: 75 70 65 60 55 50 45 35 1 3 6 9 17 б 4 1 E 75 210 390 540 935 300 180 40 35 5625 14700 25350 32400 51425 15000 8100 1600 1225 - — 4 —,3 +2 +1 0 — 1 — 2 — 3 — 4 — 49 ! -- 12 ь Ч 0— 6— 8— 3— 4 16 27 24 9 0 6 '16 9 16 1 4 10 19 12 6 2 1
КОЭФФИЦИЕНТ ВАРИАЦИИ где и, — численность отдельных объединяемых групп; М, — среднее арифметическое каждой объединяемой группы; ~,— сигма каждой объединяемой группы. Пример 24. Четыре независимых наблюдения величины одного и того же вида амеб в сходных условиях дали следующие результаты (в микронах): М 29 31 ll15050 30 31 100 100 По этим данным средний размер амеб и сигма могут быть вычисле- ны, как показано в табл. 27. Табл и ца 27 Вычисление М и б по четырем независимым наблюдениям '-' п; == 400 100312 100 30 3 150 29 50 Лю ~с 31 1200и — =- зо,о400 2324 — 300 2 a„„— 4350 3000 3100 9 4 891 396 0 +1 0 1 0 100 1550 пЙМИ02l Е п~М; =- 12000 Е (и — 1) а,". = 2324 х~,(~, =- 300 = 5,073 ~,. =2,25 441 (hfl — М )-' ng (Mg — М~ ) 150 50 КОЭФФИЦИЕНТ ВАРИАЦИИ живой вес при рождении . 3 <а процент жира в молокс . живой вес взрослык коров . 48» высота в колкс . удой за лактацию.... б1)0» 0,2 кг 7,2 С.1с Среднее квадратическое отклонение является основным показате- лем разнообразия дат, объединяемых в изучаемые группы. При этом сигма служит непосредственным показателем разнообразия только при соблюдении следующих условий: 1. сравниваются только одинаковые признаки; 2. средние сравниваемых групп не очень отличаются друг от друга. Например, если для длины зеркального карпа в одном садке М~ — — 28 см и a> — — 2 см, а во втором садке М~ — — 27 см, и о> 5 см, то ясно, что во втором садке разнообразие больше и рыбы менее стандартны. Если указанные условия не выполняются и необходимо сравнивать разнообразие разных признаков или одинаковых признаков при резком различии средних, сигма непосредственно не может быть использована для сравнения разнообразия. П р и м е р 25. Имеются данные о величине среднего квадратичс- ского отклонения следующих признаков:
РАЗНООБРАЗИЕ ЗНАЧЕНИЯ ПРИЗНАКА По этим данным невозможно установить, какой из указанных при- знаков более разнообразен. Нельзя сравнить 600 кг удоя с 7,2 см высоты в холке или с 0,2% жира и т. д. Поэтому для сравнения разнообразия различных признаков употреб- ляется особый показатель — коэффициент вариации CV. Этот показатель является функцией обоих основных показателей — среднего квадрати- ческого отклонения и средней арифметической, выражается отвлеченным числом и поэтому очень удобен для сравнения разнообразия любых приз~ аков. Вычисляется коэффициент вариации по следующей формуле: CV =- M Например, если а=30, а М=150, то30.100150 — 20% . 4 Определение коэффициента вариации для приведенного примера 25 вносит достаточную ясность в вопрос о том, какой из признаков более разнообразен: Мс СУ30 кг 3 кг 10%400 » 48» 12»3000 » 600 » 20 »4,0 » 0,2 5 »120 сл~ 7,2 сл~ 6» живой вес при рождении живой вес взрослых коров . удой за лактацию процент жира в молоке высота в холке Оказалось, что у исследованной группы животных наиболее раз- нообразным, изменчивым признаком является удой за лактацию, а наи- менее изменчивым — жирномолочность. Высота в холке менее изменчи- ва, чем живой вес, а живой вес при рождении немного менее измен- чив, чем живой вес взрослых коров. НОРМИ РОВА ННОЕ ОТКЛОНЕН И Е Обычно степень развития признака определяется путем его измере- ния и выражается определенным именованным числом: 3 кг веса, 15 см длины, 20 зацепок на крыле у пчел, 4% жира в молоке, 15 кг настрига шерсти, 700 г привеса в сутки и др. Этот основной способ характеристи- ки признаков оказывается недостаточным, когда требуется еще и оце- нить полученное значение, т. е. определить, можно ли его считать зна- чительным или, наоборот, недостаточным, или находящимся в норме. Задачи подобного рода возникают очень часто как в научных ра- ботах, так и в производственных условиях. Предположим, что из двух коров надо выбрать одну, лучшую по удою. Первая дала за 300 дней лактации 3500 кг молока, вторая в том же хозяйстве за тот же год дала 4500 кг за 300 дней лактации. Можно ли на основании только этих данных заключить, что вторая корова лучше первой по обильномолочности? Нет, еще нельзя. При всех прочих равных условиях (оптимальные условия кормления и содержа- ния, примерно равные периоды сухостоя, даты отела, продолжительности лактаиии и т. д.} коровы меняют свой удой в зависимости от возраста. Первая корова дала 3500 кг молока за свою первую лактацию, а вторая дала 4500 кг после шестого отела. Первая только начинала раз- даиваться, а вторая была в периоде полного развития организма.
НОРМИРОВАННОЕ ОТКЛОНЕНИЕ Ясно, что простое сравнение удоев этих двух коров не даст пра- вильного ответа на вопрос о том, какая из них лучше по обильномо- ЛОЧН ОСТИ. ! Предположим, что все первотелки данного стада в данном году дал.~ за 300 дней лактации в среднем по 2500 кг молока, а коровы после ше- стого отела — в среднем по 3500 кг. Из этих данных следует, что удой первой коровы на 1000 кг (3500 — 2500) больше среднего по группе пер- вотелок, а второй — на 1000 кг больше (4500 — 3500) среднего по группе коров по шестому отелу. Такая характеристика — отклонение от средней для соответствую- щей группы — дает уже более правильное основание для выбора лучших или для выбраковки худших. Центральные отклонения (V — М), фигурирующие при таком спо- собе, не позволяют сравнивать развитие разных признаков, так как это числа именованные. Кроме чого, характеристика по центральному от- клонению не учитывает степени разнообразия, свойственной группе, к которой относится изучаемая особь. В зависимости от того, мала или велика степень разнообразия в группе сверстниц, 1000 кг удоя могут считаться и большим превышени- ем средней величины и малым. Предположим, что для группы первотелок степень разнообразия, выражаемая средним квадратическим отклонением, равна o> — — 400 кг, а для группы коров по шестому отелу а~ — — 500 кг. Тогда первая корова -~ F00,i будет отличаться от своих сверстниц на ' =+25~, а вторая на 400 1001> . =- + 2,0~. Теперь, с учетом качества соответствующих групп по 500 обоим основным показателям (М и а), мы получили полные характе- ристики обеих коров, причем оказалось, что вторая корова все же хуже по обильномолочности, несмотря на более высокий удой и одинаковое центральное отклонение от группы сверстниц. Для получения таких полных оценок измеренных значений призна- ков лринят особый показатель — нормированное отклонение, который рассчитывается по формуле где х — нормированное отклонение, V — дата, результат непосредственного измерения признака, М — средняя арифметическая соответствующей группы, из которой взята изучаемая особь, а — среднее квадратическое отклонение этого признака в группе. Нормированное отклонение показывает, на сколько сигм отклоняет- .я значение признака от средней для соответствующей группы. Нормированное отклонение — величина неименованная, что пред- .тавляет большое удобство при сравнении развития различных призна- <ов. Н-ïðèìåð, ,если корова имеет следующие показатели: :удой — 4000 кг, ~кивой вес — 450 кг, процент жира в молоке — 3,5, высота в холке— 120 i;ht, то на основе только этих данных невозможно решить, какие из ~тих признаков у данной коровы развиты хорошо, а какие плохо. Такую комплексную характеристику особи по нескольким призна- кам можно легко сделать при помощи нормированных отклонений, учи- тывая при этом качество группы сверстниц этой коровы {табл. 28). Оказалось, что бонитируемая корова достаточно хороша по обильно- ~юла;ности, но имеет недостаточную жирномолочность; живой вес у нее
РАЗНООБРАЗИЕ ЗНАЧЕНИЙ ПРИЗНЛКА 50 незначительно отличается от нормы, но мясные формы выражены слабо, общие же размеры. тела удовлетворительны. Таким образом, нормированное отклонение есть такая мера разви- тия признаков, при помощи которой можно вести сравнительную оценку особей, принадлежащих к разным видам, разным породам, возрастам, по разным признакам. Табл ица 28 Оцениваемое животное Группа сверстниц Признак V — М < 500 0„= � 50100,05 35ОЭ 3,62 455 118 0,57 4000 3,50 4ГО 120 0,52 —;-1,0 — 0,6 — 0,1 ',-0,2 — 1,0 Удой за лактацию, кг Процент жира )Кивой вес, кг Высота в холке, см Индекс мясности При помощи нормированного отклонения можно унифицировать шкалы бонитировки животных разных видов и пород. ЗАКОНОМЕРНОСТИ РАЗНООБРАЗИЯ РАСПРЕДЕЛЕНИЕ ПРИЗНАКА Гсли имеется многочисленная группа особей, изучаемых по какому- нибудь признаку, то различные значения этого признака встречаются неодинаковое число раз: одни значения встречаются чаще, другие реже. Это явление называется распределением признака. Закономерности рас- пределения заключаются в том, что для определенных признаков у осо- бей, развивающихся в оггределенных условиях, всегда наблюдается преимущественное появление определенных значений признака — сред- них, или несколько меньших, чем средние, или несколько больших, чем средние. Обычно на .протяжении всего распределения от максимума дс минимума бьгвает одна группа близких значений, которая появляется заметно чаще других значений. Но в некоторых распределениях наблю- даются две или три таких группы. Основным свойством всякой совокупности является разнообра:ше входящих в нее особей. Знание закономерностей, по которым форми- руется разнообразие признака в групнс, имеет большое практическое н иаучное значение. В малочисленных группах трудно подметить какую-либо закономер- ность в разнообразии дат. Обычно все значения признака бывают раз- личны. иногда встречаются большие значения, иногда — малые, иног- да — средние, а чаще — разные значения повторяются без всякой видн- мой закономерности. По мере увеличения численности изучаемых групп все более и бо.1ес выступает закономерность в разнообразии признаков, та закономер- ность. которая в малочисленных группах была скрыта случайной фон- мой своего проявления. В достаточно больших группах эта закономерность проявляется уже достаточно ясно в самой форме распределения значений признака груп t.e.
РАСПРЕДЕЛЕНИЕ ПРИЗНАКА 5I В процессе изучения многих совокупностей по различным призна- кам наметилось несколько типов распределения признака в группе, по- лучивших математическое оформление. При исследовании биологических объектов наибольшее значение имеют часто встречающиеся нормальное распределение, биномиальное распределение и расп~ределение редких событий. Изобразить распределение признака можно различными способами: вариационным рядом, гистограммой, вариационной кривой, кумулятой, огHBGH. Вариационный ряд Вариационный ряд — это двойной ряд чисел, состоящий из обозна- чения классов и соответствующих частот. П р и м е р 26. Вес изученных животных дал распределение 1000 дат по !1 классам (через 20, начиная со 110 до 310), представленное в. табл. 29. Таблица 29 Средины К.1ЭССОВ 23О 250 270 190 21(> МО 290 130 150 170 W 110 n — = 1000 250 240 180 70 15 20 60 160 Частоты Вариационный ряд включает в себя весь первичный материал по измерению одного признака у всех представителей изучаемой группы Этот материал в вариационно~~ ряду приведен в определенный порядок, таким образом, что становится возможным даже для очень многочислен- ных групп достаточно легко рассчитать все показатели, характеризую- щие признак как по среднему уровню развития, так и по различным де- талям разнообразия. Рассмотрение вариационного ряда без всяких вычислений позволяет определить величину основных показателей среднего качества и разно- образия с таким приближением, которое вполне достаточно для перво- го ознакомления с признаком. В некоторых случаях внимательное рассмотрение вариационного ряда избавляет от необходимости расчета точных показателей. Но даже и при наличии рассчитанных средней арифметической и сигмы вариа- ционный ряд не теряет своего значения, так как более наглядно пока- зывает все детали распределения признака в данной группе. Если взять вариационный ряд, приведенный в примере 26, то без вычислений можно сказать следующее: а) средняя арифметическая признака находится между 190 и 210, вероятно, недалеко от 200, б) мода признака равна 190, в) лимиты и размах признака 110 — 310 (200), г) среднее квадратическое отклонение признака 200 : 6=33, так как в большинстве распределений в размахе признака от минимума до максимума укладывается обычно шесть сигм. Если желательно несколько уточнить определение сигмы, то для групп с числом объектов меньше 200 (но не менее 30) нужно размах признака делить не на 6, а на 5, а для групп с числом объектов более 1000 — на 7. Точный расчет показателей для приведенного примера (см. табл. 25)
РАЗНООБРАЗИЕ ЗНАЧЕНИЯ ПРИЗНАКА 52 дал очень близкие результаты: средняя арифметическая равна 200,7б, сигма — 29,94, мода — 198. Пример 27. В опыте семена помидоров подвергались облучению различными дозами рентгеновских лучей: 2; 4 и 8 г. На контрольной и трех опытных делянках на случайно выбранных 100 кустах подсчитыва- лось число завязавшихся плодов. Результаты представлены в виде сле- дующих четырех вариационных рядов (табл. 30). Таблица 30 20 22 14 И 18 10 12 2 4 G 8 7 2 Контрольная делянка 45 19 100 100 100 I дел. (облуч. 2 r П» (» 4г Цi » (» 8I) 422 25 12 3 3 21 40 11 4 18 1 2 52 8 8 2 Без вычислений можно установить: а) облучение дозой в 2 r не дало заметного эффекта: сводные пока- затели числа плодов на контрольной делянке g первой опытной пример- но одинаковы: М„10, М~, = 10, а„= а~,16 — б 1б — б5 5 б) облучение дозой в 4r дало положительный результат. Число плодов заметно увеличилось: М, = 10, М„= 15, кроме того, при этом наблюдалось явное увеличение разнообразия: 22— l э а„ ~g, о в) облучение дозой в 8 r неблагоприятно сказалось на величине за- вязавшихся плодов: М„= 10, М„=5, размах признака уменьшен и сжат в сторону минимума: l0 — 2 =16. 5 а„2, Таким образом, из даннного эксперимента можно сделать вывод, что наиболее благоприятной дозой облучения является доза в 4 г. Для подтверждения этого вывода необходимо выяснить достовер- ность результатов выборочного исследования. Как это сделать, будет показано в главе об ошибках репрезентативности. Такие значения М и а для разобранного примера можно получигь по способу взвешенных вариаций, определив для каждого ряда две ис- ходные величины — XfW и Х/W~ — и проведя необходимые расчета (табл. 31). Пример 28. По данным литературы, для числа лучей у иглоко- жих Soluster papposus L. из различных мест обитания составлены сле- дующие пять вариационных рядов (табл. 32). По этим вариационным рядам без вычислений легко дать харак- теристику иглокожих по числу лучей в зависимости от места оби- тания: а) в зоне Бергена иглокожие данного вида имеют заметно боль- ше лучей (M = 12,4) по сравнению с иглокожими других мест (M=-10 —.' 11),
РАСПРЕДЕЛЕНИЕ' ПРИЗНАКА б) сигма числа лучей примерно одинакова у иглокожих четырех 3 изученных мест а = — — 0,6, однако в районе Шпицбергена игло- 5 5 кожие более разнообразны по числу лучей ~ =- — = 1,0 . 5 Этих выводов вполне достаточно для первого ознакомления с при- знаком у изучаемого вида. Та блица 31 Делянка, облуч. 2 r Делянка, облуч. 8 r Делянка, облуч. 4 r Контрольнаяделянка Определение безвычисленийПолучено по рас-чету 2 15 1,6 10 10 2 10,1 2,1 5,4 1,6 2,1 15,3 3,0 10,5 Таблица 32 12 10 Число лучей 5113 37 13 Гистограмма Гистограмма — это вариационный ряд, представленный в виде диа- граммы, в которой различная величина частот изображается различной высотой столбиков. Гистограмма распределения животных по весу (пример 26, табл. 29) представлена на рис. 1. На гистограмме более на- глядно проявляются особенности распределения. Несколько затруднено 60 Рис. 2. Вариационная кривая. Рис. I. Гистограмма. Район Шпицбергена 2-я экспедиция Фрама Баренцево море Зап. Гренландия Берген 65 74 88 57 18 11 6 43 45 100 100 100 100 109
РАЗНООБРАЗИЕ ЗНАЧЕНИЙ ПРИЗНАКА при помощи гистограммы сравнение нескольких распределений. Поэто- му разработаны другие способы графической иллюстрации особенно- стей распределения. Вариационная кривая Вариационная кривая — это изображсние вариационного ряда в ви- де кривой, 'ординаты которой пропорциональны частотам вариационной ряда. Вариационная кривая того же распределения веса животных представлена на рис. 2. Вариационная кривая — очень удобный и на- глядчый способ иллюстрации, особенно в тех случаях, когда на одном графике желательно изобразить несколько распределений. Иллюстра- ция опыта с облучением семян помидоров (пример 27, табл. 30) с по- мощью вариационных кривых представлена на рис. 3. Рис. 8. Сопоставление вариационных кривых. 3(у муля та Кумулята — это изображение распределения в виде кривой, орди- наты которой пропорциональны накопленным частотам вариационного ряда. Чтобы составить ряд накопленных частот, нужно к частоте пер- вого. наименьшего класса прибавить частоту второго класса (это будет Zf> для второго класса), затем прибавить частоту третьего класса (это будет Zf3 для третьего класса) и т. д. Кумулята для распределений веса показана на рис. 4. Кумулята иногда имеет преимущество перед вариационной кривой. Некоторые методы биометрии основаны на использовании кумуляты. К ним относятся критерий лямбда, определяющий достоверность раз- личия двух распределений, пробит — метод, вскрывающий детали дей- ствия ядов и других агентов. По кумуляте легко находить значение раз-
Медиана Tpemuu кбартиль J° е °° ° 9 9 ° в Ф j ° Э ° . ° Я i e )вЭФTi j j в ° ° j 3 Э ° j( В °j ° ° В „, ИИИИИИГИИ ИГИ ,„ИИЮИИИЮИй ИГ Ю' /ю ° '„ЙБИЙИЮ ИИИ ГИ „ШИШШИИЙИИШ Г „ИИИИИИИИИИИИИ „И ИИИаПИИГаГГ gin <It в ИВИЙЙИИИИГИ ИГАФИЙЙИИИИГИ ю~~ДУЩУИИИИГИ ( г ) ( ° ) ( ) ) I ° I ) I е) ю( I I il ° в (() ° ю 6 ° ° ° ю 9 Э в ° Ф в в° у ° ° М ° J ° ° 6 6 ° 1111111111!11111!1!111 IIIIIINI 11116!!! П11!1Н И ИИ!11 , IIIIIII 11 И11П ., ПИП!! ! 1 Hll . IIIIIIIII 1 1 IIII " IIIIIIII II IIIIIIN ю ( ( ( ю ю ~ю ( (у РАСПРЕДЕЛЕНИЕ ПРИЗНАКА 55
РАЗНООБРАЗИЕ ЗНАЧЕНИЙ ПРИЗНАКА 5Q H0PMAJI ЬНОЕ РАС П Р ЕДЕЛЕН И Е В большинстве распределений, с которыми приходится встречаться биологу, растениеводу, зоотехнику, медицинскому работнику, проявляет- ся определенная закономерность: крайние значения — наименьшее и наибольшее — появляются редко; чем ближе значение признака к сред- ней арифметической, тем оно чаще встречается; в центре распределения имеются такие значения, которые встречаются наиболее часто и обра- зуют в вариационном ряду модальный класс. Такое распределение значений признака так часто встречается в самых различных областях науки и практики, что первоначально при- нималось за норму всякого массового случайного проявления признаков и в соответствии с этим получило особое название: нормальное рас- пределениее. В настоящее время нормальным называется такое распределение, которое следует закону, выраженному определенной математической формулой, предложенной Гауссом и независимо от него Лапласом: и А о 2;с 1 Принимая во внимание, что' — = 0,39894, получим: и Й ° 0,39894 е /' — теоретическая частота классов вариационного ряда, полностью соответствующего закону нормального распределения, и — общая численность группы, k — величина классового промежутка, а — среднее квадратическое отклонение, я — 3,1416, е — 2,71828 (основание натуральных логарифмов), W — М х = — -нормированное отклонение средины класса. где Этой формулой выражаются следующие основные отличия нор- мального распределения от остальных распределений: 1. Аргумент формулы (х) берется в квадрате. Поэтому при отрч- иательных значениях х — для классов меньших средней — формула дает точно такую частоту, как и при положительных значениях аргумента. Это значит, что описываемое распределение симметрично относитель- но центральной модальной частоты. Из этого следует, что в нормаль- ных распределениях средняя арифметическая, мода и медиана совпа- дают по сноеи величине. Симметричность нормальных распределений. значительно облег- чает практическое использование особенностей этого тигга распреде- лений. 2. Частота каждого класса определяется его удаленностью от цен- тра: чем больше нормированное отклонение класса, тем меньше его частота. Например, для модального класса, при х=О частота приобре- тает свое максимальное значение: 0 39894 e0 '0 39894 6 о
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ При х=З частота приобретает очень малое значение: 9 '. 0,398948 = 0,004 При х=4 частота становится совсем незначительной: 16 0,39894 е ' = 0,0001 Это значит, что максимальное и минимальное значения признака в нор- мальном распределении практически не удаляются от среднего значе- ния больше, чем на три сигмы: т1П'=М — За, тах = М-~-За, и только в очень многочисленных группах имеется практическая воз- уожность встретить особей, у которых изучаемый признак отличается от среднего значения больше, чем на три сигмы. Это свойство нормального распределения дат в не очень малочис- ленных группах имеет очень большое значение при нахождении гене- ральных величин по выборочным и при определении достоверности вы- борочных показателей, что будет подробно изложено в главе об ошибках репрезентативности. 3. Если крайние значения распределения отстоят от средней при- мерно на три сигмы, то весь размах признака включает в себя около шести сигм. Этим обстоятельством пользуются для быстрого ориентировочного определения величины среднего квадратического отклонения: П1аХ — min 0 ~~ б В большинстве работ при характеристике фактических распределе- ний и определении достоверности выборочных величин предполагается, что имеется нормальное распределение значений признака. Поэтому необходимо бывает проверить это допущение, т. е. установить, доста- точно ли изучаемое распределение соответствует нормальному, можно ли считать, что отступления фактических частот от таких, которые точ- но следуют закону нормального распределения, произошли от случай- ных причин. Для этой цели необходимо: 1. Рассчитать теоретический нормальный ряд на основе показате- лей изучаемого эмпирического ряда, использовав свойства первой функ- ции нормированного отклонения. 2. установить достоверность расхождения между эмпирическим теоретическим рядами, применив один из критериев расхождения рас- пределений. ПЕРВАЯ ФУНКЦИЯ НОРМИРОВАННОГО ОТКЛОНЕНИЯ Формула частоты нормального распределения состоит из двух со- м ножителей: и 0,39894 е
РАЗНООБРАЗИЕ ЗНАЧЕНИЙ ПРИЗНАКА и й Первый множитель целиком зависит от показателей изучас- мой группы. Рассчитать его легко, разделив численность группы на сиг- му, выраженную в классовых промежутках. Второй множитель изменяется от класса к классу. в зависимости величины х — нормированного отклонения классов. В этом выражении аргументом является нормированное отклоне- ние, а функцией, т. е. величиной, зависящей от аргумента,—,величи~на, которая получится, если по данному значению х вычислить множитель l- 0-39894 е Эта,величина будет называться первой функцией нормированного отклонения и обозначаться символом ((х). Следовательно, значение пер- вой функции нормированного отклонения выражается формулой: f (х) = 0,39894 e Рассчитать значение f(x) для каждого отдельного значения х легко если предварительно прологарифмировать функцию: 1О f (х) = 1g 0,39894 — — 1g е = — 0,39909 — х'-' 2 ' 2 = 0,39909 — 0,217145 х-'. Например, для класса, средина которого отстаит от средней на +-1а, х= и расчет первой функции нормированного отклонения лает следующий результат: 1'(x) =0,39909 — 0,217145 . 1 = — 0,61624= 1,38376, . f(х), где f' — теоретическая частота, показывающая, какую частоту имел бы каждый класс изучаемого эмпирического распределения при показателях и, k, М и а, если бьг это распределение в точ- ности соответствовало нормальному, и — численность изучаемой группы, k — величина классового промежутка, б — среднее квадратическое отклонение изучаемой группы, f(x) — первая функция нормированного отклонения. Вычисление частот нормального распределения показано в табл. 33. Для нахождения теоретических частот ряда нужно сделать сле-дующее: ' Римскими цифрами указаны номера таблиц, данных в прило>кении. откуда f(x)~,242. Можно облегчить работу по вычислению теоретических частот рас- пределения, рассчитав заранее значение f(x) для всех возможных зна- чений нормированного отклонения. Таблица ординат нормальной кривой с рассчитанными заранее значениями первой функции нормированного отклонения приведена в табл. VI*. Имея таблицу значений первой функции нормированного отклоне- ния, легко рассчитать теоретические частоты ряда по формуле гг. fg
ПЕРВАЯ ФУНКЦИЯ НОРМИРОВАННОГО ОТКЛОНЕНИЯ и ° й 1. Рассчитать М, а и найти величину . В разбираемом при- G 256 Х 1о мере эта ве.пичина равна = 180,3. 14,') Табли ца 33 Вычисление частот нормального распределения 50 ЗО 2. Рассчитать нормированные отклонения каждого класса. Для это- го сначала составить ряд величин W — М, а потом, разделив кажду~о из этих величин на а, получить ряд нормированных отклонений. О � Ю 3040 50 бО ~О Bg ggigg 2 7 2~ бО 68 50 27 9 ! (t) Р ( 8 27 5б ю 5б 27 8 t (2) Рис. 6. Сопоставление фактическо- го (1) и нормального (2) распре- делений по взриационным кривым. рис. 7. сопоставление фактического (1) и нормального (2) распределений по кумулятам.
РАЗНООБРАЗИЕ ЗНАЧЕНИЯ ПРИЗНАКА 3. Для каждого класса по его нормированному отклонению найти в таблице первую функцию нормированного отклонения. 4. Для каждого класса помножить постоянную для данного рас- и -)г пределения величину на первую функцию нормированного откло- о кения. Округлив полученные цифры, получить теоретический ряд час- тот изучаемого ряда с точностью до единицы. Сопоставление фактиче- ского и нормального распределений можно представить не только в ви- де двух вариационных рядов, но и графически в виде вариационной кривой (рис. 6) или кумуляты (рис. 7). ДОСТОВЕРНОСТЬ РАЗЛ ИЧ ИЯ РАСПРЕДЕЛ ЕН И И Не всегда эмпирическое распределение так хорошо соответствует нормальному, как это имеется в примере, показанном в табл. 33 и на рис. 6 и 7. Для практических и научных работ бывает необходимо установить, сильно или слабо расходятся эмпирический и теоретический ряды. Не- обходимо установить такой предел, недостижение которого означает, что расхождение между эмпирическим и нормальным распределением еще не настолько велико, чтобы с ним считаться, и что данный эмпи- рический ряд еще можно практически принять за нормальный. Для этой цели применяются особые показатели, из которых в био- логических исследованиях используются критерий ~' и критерий Х. 3(ритерий Х2 (хи квадрат) Критерий т' предложен Пирсонам и применяется вообще во всех случаях, когда необходимо определить степень отличия фактического распределения частот от теоретического. Определяется величина у2 по следующей формуле: > т (~ Ю где j — эмпирическая частота, j' — теоретическая частота. Нахождение критерия у2 табл. ЗЗ, показано в табл. 34, для распределения, приведенного в Та бл ица 34 Вычисление критерия ~2 256,8 256 Предельные значения ~2 при v =-9 — 2= 7 равны: 3 14,1 100 90 80 70 60 50 40 30 20 1 9 27 58 68 60 24 7 2 1,4 7,9 27,0 56,3 71,6 56,3 27,0 7,9 1,4 0,4 1,1 0.0 J,7 3,6 3,7 3,0 0,9 0,6 0,16 1,21 0,00 2,89 12,96 13,69 9,00 0,81 0,36 О,ll 0,15 0,00 0,05 0,18 0,24 0,33 0,10 0,26
ДОСТОВЕРНОСТЬ РАЗЛИЧИЯ РАСПРЕДЕЛЕНИЙ Если крайние классы распределения имеют теоретические частоты меньше единицы, то при вычислении г2 их необходимо объединить в один класс вместе с ближайшим классом, имеющим частоты f' > 1. Вместе с теоретическими надо объединить и соответствующие фак- тические частоты. При подсчете числа классов объединенные классы на каждом кон- це распределения надо считать за один класс. Например, если в рас- пределении было 12 классов и потребовалось объединить два макси- мальных и три минимальных класса, то после объединения стало 12 — 5+ 2 = 9 кл ассов. После объединения классов (если оно требуется) для нахождения величины x' необходимо: 1) рассчитать разности между фактическими и теоретическими частотами, 2) все разности (f — f') возвести в квадрат, 3) квадраты разностей разделить на соответствующие теоретиче- ские частоты, (f Р о 4) полученные величины сложить. После нахождения величины у2 требуется определить, велика или мала она для данного распределения. Для этого пользуются таблицей предельных значений х2 (табл. IX). Для того, чтобы пользоваться этой таблицей, необходимо предвари- тельно установить число степеней свободы для изучаемого распреде- ления. Если в качестве теоретичеекого распределения берется нормаль- we, все детали которого определяютед двумя постоянными величинами М и а, то число степеней свободы в таких случаях равно числу классов без двух. Например, если число- классов равно 9, то число степеней свободы для этого распределения будет равно 9 — 2=7. За число клас- сов берется то, которое получилось после объединения классов с дроб- ными теоретическими частотами. ,Яля каждого числа степеней свободы в табл. XI указаны три циф- ры. Это три предельных значения X', соответствующие трем стандартным степеням вероятности (Ра=0,999, Р2 — — 0,99 и Р~=0,95) того, что распре- деления, показавшие такие значения г2 или большие, различаются до- стоверно*. Под достоверным различием понимается такое расхождение распределений, которое не может произойти в порядке обычных случай- ных отклонений фактических частот от теоретических или выборочных частот от генеральных. ~ля обычных биологических исследований можно допускать боль- шую вероятность различия частот распределений, определяемую треть- им порогом вероятности Ра=0,999 и наибольшим предельным значе- нием ~'. Это Означает, что в обычных исследованиях даже при больших рас- хождениях между фактическим и теоретическим распределениями, при которых у2. приближается к своему третьему большему предельному значению, все еще можно принимать фактическое распределение за нормальное. При более ответственных исследованиях необходимо уже при меньш=м значении у' считать, что фактическое распределение не соот- ' Если полученное значение величины у2 (или другого ноказателя) равно или пре- вышает третье предельное значение, соответствующее Р~ —— .0,999, то оно подчеркивает- с» тремя чертами; есги оно превышает второе значение — его подчеркивают двумя чертами, если первое — то одной чертой, если оно мсньше первого значения — волнис- той линией.
РАЗгЮОБРАЗИЕ ЗНАЧЕНИЯ ПРИЗНАКА 62 ветствует законам нормального распределения. Если фактическое зна- чение у,' меньше первого значения, соответствующего Р=0,95, то в~ всех случаях можно считать различие между распределениями недо- стоверным. Если фактическое значение у' больше третьего значения, соответ- ствующего Р=0,999, то во всех случаях можно считать различие между распределениями достоверным. Для разбираемого примера фактическая величина x-' оказалась рав- ной 1,42, число степеней свободы равно 9 — 2=7, три предельные зна- чения у' при v=7 равны 14,1; 18,5; 24,3 (см. табл. XI). Фактическая ве- личина y' далеко не достигает предельных значений, и поэтому это распределение должно считаться вполне соответствующим закономерно- стям нормального распределения. Критерий Х (ламбда) Критерий Х предложен советскими учеными А. Н. Колмогоровым и Н. В. Смирновым и может применяться для определения достовер- ности расхождения между фактическими и теоретическими распреде- лениями, а также различий между любыми двумя распределениями частот одного и того же признака даже в том случае, когда число клас- сов и число дат у этих распределений неодинаково.,Яля применения критерия лямбда не требуется определять число степеней свободы и не нужны таблицы для определения трех предельных значений критерия, так как для любого числа классов эти предельные значения одинаковы: 1,36; 1,63; 1,95 и соответствуют обычным трем степеням вероятности достоверного различия — P> — — 0,95; Р~ —— 0,99; Рз — — 0,999. Единственным. условием применения критерия лямбда является достаточная численность сравниваемых распределений — не менее не- скольких десятков дат. Для сравнения эмпирического распределенич с теоретическим при одинаковом числе классов и при одинаковой общей численности групп критерий ламбда определяется по формуле '-f — '-'f с так ). = id[ где ф — максимальная разность (без учета ее знака) между накоплен- ными частотами в эмпирическом и теоретическом распределе- ниях для одного и того же класса, и — общее число дат, образовавших эмпирическое распределени . ~ля определения критерия ламбда требуется составить ряды на. коплепных частот для обоих сравниваемых распределений Е f; и Е f; взять наибольшую разность (без учета ее знака) между этими величи- нами~dI = Е,'Г, — ~,~;,„и полученную разность разделить на gn. Пример 29. При опытных посевах нового сорта пшеницы поле было разбито на 840 делянок. Из поделяночных урожаев было состав- лено распределение с классами через 7 г на квадратный метр. Потребо- валось проверить, можно ли считать полученное распределение нор- мальным. Яля этой цели было составлено нормальное распределение по по- лученным значениям М и а и применен критерий лямбда для выяснения достоверности расхождения полученных распределений. Применение метода лямбда в этом исследовании показано в табл. 35. В ряде разностей между накопленными частотами по обоим рас-
63 ДОСТОВЕРНОСТЬ РАЗЛИЧИЯ РАСПРЕДЕЛЕНИЙ Таблица 3о Вычисление крктерня лямбда при сопоставлении эмпирического и теоретического распределений ~~1/ '\1 (Ю Б LV 9,899,О== 0,34 1,95 1,63 1,36 840 88,5 пределениям (последний столбец табл. 35) наибольшей величиной яв- ляется 9,8 в восьмом классе (сверху). Это значение и берется в качестве числителя дроби, в которой знаменатель равен 1 840. Таким образом, для разбираемого примера критерий лямбда =- 0,339. /84О 29,98 Такая величина критерия лямбда — меньшая первого предельного значения (1,36) — указывает на то, что расхождение между фактиче- cKHM H теоретическим распределениями недостоверно и распрелелрние поделяночных урожаев пшеницы можно считать нормальным. 3» выяснения достоверности различия между двумя лгобыми рас- пределениями частот одного и того же признака при неодинаковом чис- ле дат и классов критерий лямбда вычисляется по формуле / Г гг, л ] — - = ~ / ю 'L У П -;11)ДО; 1l) П2 где — -суммы накопленшы~ частот по каждому классу пео- вого распределения (начиная с меньшего), деленные на общее число дат, — то же по второму распределешио, максимальное абсолготное значение (без учета зны- и., ка) разности частных от деления накопленных частот на численности групп по каждо~~~ классу, начиная с наимсньшего, ll), гг2 — общее число дат по первому и второму распреде- лениям. Пример 30. В одном антропологическом обследовании получены материалы по обхвату груди трех групп взрослых мужчин: туркменов 161 154 147 140 133 126 1 1с} 112 105 98 91 84 77 70 I 1 ср 9 54 125 203 201 141 72 19 7 4 1 0,1 Q 5 3,4 16,4 53,7 121,2 189,4 201,9 147.1 73,6 25,2 6,0 0,9 0,1 840 839 838 836 827 773 648 445 244 103 3~ 12 5 1 839,5 839,4 838,9 835,5 8i9,1 765,4 644,2 454,8 252.9 105,8 32.2 7,0 1,0 0,1 0,5 0,4 0,9 0,5 8,9 7,6 3.8 9,8 8,9 2,8 1 <~ 5,0 4,0 0,9
РАЗНООБРАЗИЕ ЗНАЧЕНИЯ ПРИЗНАКА Мерва, узбеков Ташкента и узбеков Хорезма. Первичные данные были разнесены по трем распределениям, а затем при помощи критерия лямб- да было выяснено, какие из них различаются между собой достоверно. Расчеты приведены в табл. 36. Таблица Зб Вычисление критерия Х при сравнении эмпирических распределений ~1--3(о,ооц А1 — 2(о,ооц ~2 — 3(0,001) из и 59 100 118 Г 6962 0,246 — = 0 246 ° 177 59()0 = 0,375 159 59 18 Л,„.= 0,246 6,27 =- 1,64 1,95 59+ 118 1,63 59 100 г0,375 59 + 100 1'8 100 Лгз = 0 194 — 0,194 118 + 100 Л,,з — — 0,375 6,09 = 2,28 1,36 11800 — = 0,194 ° 7,36 = 1,43 218 Применение критерия лямбда показало, что три изученных распре- деления достоверно отличаются друг от друга, но с различной вероят- КОСТЬЮ. Первая группа от второй (туркмены Мерва от узбеков Ташкента) отличается при вероятности различия, превышающей только первый IIO- рог: (195 ~ Pd < 0,99. Псрвая группа от третьей (туркмены Мерва от узбеков Хорезма) отличается при наибольшей вероятности различия: Рд) 0,9~9 Вторая группа от первой (узбеки Ташкента от узбеков Xope3Ma) отличается при вероятности различия, превосходящей первый пора 0,95 < / „< 0,99. Аg MMETPИЯ И ЭКСЦЕСС HeKoTopbIe признаки растений и животных при объединении осо- бей в группы дают Распределения, значительно отлича!ощиеся от нор мал ьного. В тех случаях, когда какие-нибудь причины благоприятствуют по- явлению значений признака, отличающихся от средней величины в сто- 60 59 58 57 '6 55 54 53 52 51 50 49 48 47 46 1 2 1 1 7 14 10 7 6 6 3 1 1 1 3 2 9 11 10 16 15 21 10 9 7 1 2 1 2 7 2 13 10 11 11 20 4 8 4 3 3 1 59 58 Ьб 55 54 47 33 23 16 10 4 1 118 1)7 1l6 113 111 102 91 31 65 50 29 19 10 3 2 100 99 97 90 88 75 65 54 43 23 19 11 7 4 1 1,0()0 О,983 0,9~9 0,932 0,915 0,797 0.559 0,389 О,')71 О,!69 0,068 0,017 l,000 0.992 0.983 0,958 0.941 0,865 0,771 0,687 0,55) 0,424 0,246 О,!61 0,085 0,025 0,017 1,000 0,990 0,970 0,900 0,880 0,750 0,650 0,540 0,43 0,23 0,190 0,1!О 0,070 0,040 0,010 42 42 84 161 228 ~46 135 143 110 84 43 0 100 103 !99 282 375 367 329 199 161 99 28 7 02135861115121137121194 i6ь5115157
АСИММЕТРИЯ И ЭКСЦЕСС рону уменьшения или в сторону увеличения, образуются асимметричные распределения. При асимметрии эмпирическое распределение имеет увеличенные (против симметричного расположения) частоты или. в левой части, или в правой части. В соответствии с этим различают или левую, или правую асимметрии, которые показаны на рис. 8. Рис. 8. Асимметрия. 1 — левая, положительная и 2 — правая, отрицательная (схема). В тех случаях, когда какие-нибудь причины благоприятствуют пре- имущ=ственному появлению и средних и крайних значений признака, образуются положительные эксцессивные распределения, имеющие вид острой пирамиды с расширенным основанием (рис. 9). При отрицательном эксцессе в центре распределения имеется не вершина, а впадина,,причем распределение становится двумодальным, а вариационная кривая — двувершинной. В некоторых исследованиях требуется выяснить, действительно ли распределение изучаемого признака имеет асимметрию или эксцесс. Например, при изучении ареалов распространения морских живот- ных можно предположить, что распределение особей этого вида по глубине обитания должно быть асимметричным, так как свободному распространению его в одном из направлений — вверх — препятствует естественная граница: поверхность моря. Это предположение можно проверить, исследовав степень асимметричности распределений. Нали- чие эксцессивного распределения одного из жизненно важных призна- ков изучаемого вида животных или растений может указать на тенден- цию этого вида образовывать не только обычные, типичные формы, но такх<е давать в повышенном количестве новые для него вариации, от- клоняющиеся от нормы и стремящиеся стать родоначальниками новых разновидкостей.
РАЗНООБРАЗИЕ ЗНАЧЕНИЯ ПРИЗНАКА Рис. 9. Эксцесс положительный (схема). Показатели асимметрии и эксцесса с их ошибками репрезентатив-ности определяются по следующим формулам:.ХШ 6 АА =' — тll ~АllА- 3. тл ZD~ 6 с 3: т =-2 —; t,=. 3, й О4 й А — показатель асимметрии, ХЮ =Х ( й' — М)' — сумма кубов отклонений средин классов от средней арифметической (центральных откло- нений), аа — среднее квадратическое отклонение, возведен- ное в третьцз степень, е — показатель эксцесса, ZD4=Z(W — M)' — сумма четвертых степеней центральных откло- нений средин классов, о4 — четвертая степень среднего квадратического о г- клонения, п — общее число датв эмпирическом распределении, m„, m, ошибки репрезентативности (см. главу о репре- зентативности выборочных показателей) асим- метрии и эксцесса, гА, f — критерии достоверности выборочных показате- лей асимметрии и эксцесса. Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают свою ошибку репрезентативности в три и более раз. где Для выяснения достоверности того, что изучаемое распределение отличается от нормального именно в сторону асимметрии или эксцесса, применяют обычный в биометрии метод сравнения показателей с их ошибками репрезентативности.
ф б а а а ° ° а ° б ° ° ° ° ° ° ° ° ° ° ° ° ° в ° ° Э ° ° ° ! ° ° s l ° ° ° в ° в Ф ° б ° ° в ° 1 r ° ° l б ° ° ° ° -- I ° ° r r l ° ! б ° ° ° ° в l б ° ° ° ° Э ° ° в ° ° ° ° I ° ° ° ° 11 ° I 1 ° ° ° ° ° в 1 ° .' в ° ° ° ° ° ° °в° ° ° ° ° ° ° ° ° ° ° ' ° ° ° 1е '! Ф1! ° ° в 1 ° ° 1 б 1 ° ° ° ° б ° ° в 1 °,' ° ° ° е ° в ° ° ! ° ° ф б ° ° ф с ° ° ф б ° в в 9 ° ф ) ° ° в 11 ° в ) '11 '' 111 ° ° ° 9 ° в @б I r Э Ф ° с ° ° Ф ф б ф а j ° в Э l ° S ° б ° Ф Ф Э в ° r ° ° 9 l ° ° Э ! ° ° ° ° ) ° а ° ° ю ° > ° ° ° ° ф ' ° ° ° ф а а ° б ° ° ° ° ° в ° ° ° ° ° б б ° ° а ° ° 9 ° ° 9 ) ° ° ° ° ° l r ф ° ° ° ° ф ° ° ° ° r ° Ф Ф Э ! I в ° I ) ° ° а ° ° ° I r в ° I ' ) ° r а ф ° ° Ф s ° Ф в ° ° ° б ° в ! ° ° а ю ° ! б в ° ° Я ! ° ° ). ° ° ° ° а ° r r Э ° ° 9° l° 9 l а а а ° а ф ° й° ° ° r °; ° I l ° ° ° ° ! ) 9 ф ° ° ° ) а ° ° ° а ° ! И У ° Ill° ° ° ° ° ° r r ° ° ° ! 1 1 1 1 1 е 1 1 1 1 I ° r 9 ° ° э I l ° ° в ° Э ° ° с I ее li ее ° ° ° в ° ' 1 I I
РАЗНООБРАЗИЕ ЗНАЧЕНИИ ПРИЗНАКА счетную работу, даже при наличии простейших счетных машин. Лег<о запоминающимся способом упрощения расчетов является уменьшение средин классов в одно и то же соответственно выбранное число раз. В примере, представленном в табл. 37, все вариации разделены на 50; в результате вместо многозначных цифр от 50 до 1050 получились ма- лозначные — от 1 до 21. При этом показатели асимметрии и эксцесса по- лучаются такими же, как и при работе с непреоб- разованными громоздки- ми значениями. Для получения в пер- воначальных единицах средней арифметической и среднего квадратическо- го отклонения требуется помножить на 50 (на ве- личину, на которую были разделены все средины классов) величины, полу- ченные при преобразован- ных вариациях. ВТОРАЯ ФУНКЦНЯ НОРМИРОВАН НОГО ОТКЛОНЕНИЯ При отборе особей для различных целей воз- никает ряд задач, связан- ных с определением коли- чества особей, обладаю- щих какими-нибудь опре- деленными свойствами: превышающих какой-ни- будь стандарт или не удовлетворяющих задан- ным требованиям. В дру- гих случаях, имея зада- ние отобрать из массива ис. 10. цариационная кривая и кумулята распре- определенную долю осо- деления глубины обитания морского животного. бей, требуется установить стандарт такого отбора. Все такие задачи решаются путем использования закономерностей нормального распределения при помощи второй функции нормированно- го отклонения. Вторая функция нормированного отклонения определяется по фор- муле Х Х е 2 dx, где ~р(х) — обозначение второй функции нормированного отклонения, х — нормированное отклонение заданной величины признака, или стандарта, и=3,14, е = 2,718.
6S ВТОРАЯ ФУНКЦИЯ НОРМИРОВАННОГО ОТКЛОНЕНИЯ Вторая функция есть определенный интеграл первой функции в границах от 0 (от средней) до х, т. е. до заданного значения признака, выраженного, в нормированных отклонениях. Вторая функция нормированного отклонения указывает ту долю особей, которые находятся между средней арифметической и заданной величиной признака. Взаимоотношения между второй и первой функциями нормирован- ного отклонения показаны на рис. И. ж= ~,'0 4фв~МД -Ж-Зб -Ж 0 +6 +2б+Зб44 ~МЬ-"Яб- 36 д +Ю-�~3М Рис. 11. Первая и вторая функции нормированного откло-нения. На первом графике этого рисунка нормированное отклонение х= =+1,0, т. е. стандарт больше средней на одну сигму, на втором графике х= — 1,0. Тут стандарт меньше средней на ту же величину. Первая функция или отсекающая ордината пропорциональна частоте распределения в точке заданной величины признака, или в точке стан- дарта. Вторая функция равна доле особей, у которых значение призна- ка больше средней, но не больше стандарта. Это относится к таким рас- пределениям, которые в точности соответствуют нормальному распреде- лениюю. Так же как и для первой функции можно заранее рассчитать зна- чения второй функции для любой величины нормированного отклонения. Такой расчет ведется по специальным рабочим формулам (интеграла нормальной кривой или интеграла вероятностей): !. Для малых значений х х7 «9 24 4! 9 ) 2.3! 3 2* . 2! 5 2З- 3) ° 7 2. Для больших значений х 1-3 5 7 1 3 1 3-5 ° ° Э O х8 х2 Значения второй функции нормированного отклонения приведены в табл. VII. Применение свойств второй функции нормированного отклонения можно показать на следующих примерах. П р и м е р 31. Для данной породы пчел длина хоботка имеет М=6,0 мм и а=0,3 мм, а для того, чтобы легко опылять клевер, тре- буется хоботок длиной 6,6 мм. 1~акое количество пчел этой породы бу- дет легко опылять клеверные поля?
70 РАЗНООБРАЗИЕ ЗНАЧЕНИИ ПРИЗНАКА В данном случае имеется стандарт признака — 6,6 мм, который +0,6 больше срелнсй для породы на 6,6 — 6 0=0 6 мм, или на ' == - 2,0 0,3 сигмы. Это и есть нормированное отклонение стандарта. При х=+2,0 вторая функция ~р(х) =0,477 (см. табл. VII). Это до- ля пчел, у которых хоботок длиннее среднего хоботка для породы, но не превосходит стандарта. Всего в породе имеется 0,5 (50о/о) пчел с хоботком длиннее сред- него, из них 0,477 (47,7о/о) пчел не удовлетворяют стандарту, следова- тельно, опылять клевер будут 0,5 — 0,477=0,023, или 2,3 /о пчел. Решение таких задач ведется по общей формуле: q=0,5 — ~р(х). Решение этого примера иллюстрируется рис. )2. Х=+2,0 х= ф7 -Зб -Гб -1б О + +' +Рб +Зб ~б -2б -tg О ~ t g +gd' +ЯЦРис. 18. Величина q = 0,5 — <р(х)при х =+ 0,7. МРис. 12. Величина q =0,5 — (р(х) при х == +2,0. П р и м е р 32. Селекцией выведена новая порода пчел. Длина хо- ботка для этой породы имеет М=6,4 мм и а=0,3 мм. Какое количествз пчел новой породы будет опылять клевер? 6,6 — 6,4 Нормированное отклонение стандарта х =- ' '; 0,7, вто- 0,3 рая функция этого отклонения равна 0,258 (см. табл. VII). Следовательно, в новой породе имеется 25,8о/о пчел с длиной хобот- ка больше средней, но не удовлетворяющих стандарту. Опылять клевер будут 50 — 25,8=24,2'/о. Решение этого примера показано на рис. 13. Пример 33. Пчел, у которых М=6,4 мм и а=0,3 мм, перевели на другой сорт клевера. ~ля его опыления им достаточно иметь хобо- ток длиной 6,1 мм. Какое количество пчел будет опылять этот сорт клевера? Теперь стандарт оказался меньше средней, значит опылять клевер будет вся лучшая половина пчел плюс та часть, которая имеет хоботок короче среднего для породы, но длиннее требуемого стандарта. Задача может быть решена по формуле q=0,5+~р(х) следующим образом: 6,1 — 6,4 х == 0,3
71 ВТОРАЯ ФУНКЦИЯ НОРМИРОВАННОГО ОТКЛОНЕНИЯ р(х) =0,341, q=P,5-}-0,341=0,841, или 84,1%. Решение этого примера показано на рис. 14. х, - 0,6) rр=+ О,б1 Х =-1,0 -Зб -Гб -16 О +1~) +gg Я -Зб -2б - ~б 0 '<6' +25 ~Дб'М Рис. 14. Величина q = 0.5 -1- (р(х}при х ==- — 1,0. Рис. 15. Величина р + q = 2~р(х) ==0,5; х=0,67. II р и м е р 34. Из популяции решено было брать для коллекции ти.—.и шые экземпляры.,Яля этого были отобраны особи из той централь- ной части распределения, которая составляет половину всей популяции. Определить верхний и нижний стандарты отбора, если известно, что в популяции величина признака, по которому ведется отбор особей для коллекции, имеет М=100 мм и а=10 мм. Из центральной половины одна часть — 0,25 превышает средню:о дпину, а другая, равная ей часть, имеет длину меньше средней Следовательно, центральная часть состоит из суммы двух вторыi функций нормированного отклонения, из которых каждая равна q>(x) =0,25. Такой величине второй функции соответствует x=0,67 (см. табл. VII). Поэтому стандарты отбора будут следующие: нижний стандарт 100 — (0,67 X 10) =93,3 мм; верхний стандарт 100+ (0,67Х10) =106,7 мм. Решение этого примера показано на рис. 15. П р и м ~ р 35. В молочных совхозах области, по данным бонити- ровки, средняя жирность молока всех имеющихся коров М=3,8% и а=0,15%. 1(акой процент составит племенная группа, предназначаемая для производства быков, если выделять коров, имеющих процент жи- ра в молоке не менее 4,0? Нормированное отклонение стандарта 4,0 — ~~,8 -~- 1,33. 0,15 Вторая функция (см. табл. VII) q)(x) =0,408, поэтому q= (0,500 — 0,408) 100=9,2% (рис. 16, а).
РАЗНООБРАЗИЕ ЗНАЧЕНИЯ ПРИЗНАКА 72 П р и м е р 36. Из того же массива было решено выранжировать из воспроизводящей части стада коров с процентом жира меньше 3,7. Ка- кая часть всего массива останется в воспроизводящей части стада? Нормированное отклонение стандарта 3,7 — 3,8 (),15 7. Вторая функция ~р(х) =0,249 после выранжировки останется q= (0,500+0,249) 10074,9'ф (рис. 16, б). х~= ф Я в ° ]Я М Рб -б О +б +Гб Зб -Зб -?б -б О ~d 36 'Зб Зб М -d О 'Рб'Зб 'И Рис. 17. (Р+ ч) = ф(«) +<р(х) г = 0,433 + 0,341 = 0,774. Рис. 16.а — величина p = 0,5 — (р(х) при х 1,33; б — величинаp = 0,5+ (р(х) при х — 0,67. П р и м е р 37. Для определенных целей заготовляются куриные яйца не легче 50 г и не тяжелее 65 г. Имеется массовая партия яиц, для которой М=59 г и @=6 г. Какой процент яиц из этой партии соответст- вует указанным требованиям? Найдем нормированные отклонения стандартов: 50 — 59 для нижнего стандарта х, =- — — - — 1,5, 65 — 59 для верхнего стандарта х., =- ~- 1,0. 6 Соответственно этому для нижнего стандарта ~р(х1) =0,433, для верхнего стандарта я)(х~) =0,341. Искомый процент будет равен сумме этих функций, на 100: ум ножен ной (p+q) = (0,433+0,341) 100=77,4% (рис. 17).ТРЕТЬЯ ФУНКЦИЯ НОРМИРОВАННОГО ОТКЛОНЕНИЯ Вторая функция нормированного отклонения позволяет определить долю особей, у которых значение изучаемого признака превышает или не достигает какое-нибудь заданное значение. В некоторых исследованиях встречается необходимость предусмотреть среднее качество особей, удовлетворяющих или не удовлетворяющих заданному стандарту, или среднюю признака для отсеченной части. Это можно сделать при по- мощи третьей функции нормированного отклонения, которая в дальней- шем будет обозначаться символом F(x).
73 тРБТЪЯ ФУНКЦИЯ НОРМИРОВАННОГО ОТКЛОНЕНИЯ Третья функция нормированного отклонения показывает, насколь-ко сигм отстоит от общей средней средняя отсеченной части: М, М„,- F(x) а, где М, -- средняя для отсеченной части, например средняя для особей, превышающих по какому-нибудь признаку заданный стандарт, Мо — средняя для всего массива особей, F(x) — третья функция нормированного отклонения, а — среднее квадратическое отклонение всего массива особей. Определить третью функцию нормированного отклонения можно по следующему правилу: третья функция равна отсекающей ординате (первой функции), деленной на отсеченную долю. Это выражается фор-МУл ОЙ р( ) f() 0,5 + <р (х) где t(x) — первая функция нормированного отклонения. или отсекаю- щая ордината, гр (x) — вторая функция нормированного отклонения, показывающая долю особей в пределах от средней до заданного значения признака (или между центральной и отсекающей ордина- тами). Если стандарт больше средней, то доля особей, превышающих зна- чение стандарта, равна 0,5 — ~р (х), если стандарт меньше средней, то доля особей, превышающих значение стандарта, равна 0,5+ q>(x) . Взаимоотношение между тремя функциями нормированного откло- нения показано на рис. 18. 1(ак видно из графиков, каждое значение стандарта отсекает по обе стороны от себя две части распределения: справа — особей, превы- шающих заданное значение, слева — особей, у которых величина приз- нака меньше стандарта. Поэтому и средних для отсеченных частей мо- жет быть две — одна для правой части, где признак больше стандарта,, и другая — для левой, где величина признака меньше заданной вели- чины. Поэтому каждому зна- чению нормированного от- .'Ж= 1,0 клонения соответствует два значения третьей функции: Рр (х) — для левой части и Р,(х) — для правой части 02 X=- 1,0 распределения. В зависимости от того, для какой части определя- ется средняя (для левой или для правой), а также и от 1б/ ) РF~(xf ' F< (~У=- О,Лб + 1,585I того, какое значение имеет нормированное отклонение (х=0, х(0, х)0), вычисле- Мр МО ние идет по разным схемам, рис. я. Первая — f(x), вторая — (р(х) к третья— показанным в табл. 38. р(х) функции нормированного отклонения.
74 РАЗНООБРАЗИЕ ЗНАЧЕНИЙ ПРИЗНАКА Пр,р мер 38. Из большой партии яиц необходимо отобрать луч- шую часть с весом яйца 70 г и более и предусмотреть, какие средние веса будут в отобранной части и в оставшейся, худшей части. Известно, что эта партия получена от породы кур, которая в условиях данной птице- фабрики дает обычно яйца с средним весом M=70 г и а=10 г. Таблица 38 хО Ю<0 Части Обо- раслределения зиаченил f (х) /(х) Р, (х) 0,79788 = 0,8 0,,5+ р(х) 0,5 — <р (х) f() f (х) F» (х) 0,79 788 = 0,8 0,5 — <p (х) 0,5 + y (х) Мо — F> (х) ~ М(,- — Fp (x) а Мо 0,8(~ м М„~- F«(х) а М„-.- F«(x) М +О,8 В данном случае стандарт отбора равен средней для всего массива; вычисление третьей функции необходимо вести по схеме первого столб- ца табл. 38. Яля лучшей части средняя М„=М,+08~- 704 8=78 г, для худшей М,=М, 08а=70- 8=- 62 г. П р и м е р 39. Из большого стада овец со средним настригом шер- сти N=4,0 кг и а=1,0 кг решено отобрать элитную часть овец, дающих 5,0 кг и более шерсти за год. Требуется предусмотреть, какой при этом можно ожидать средний настриг у отобранной элитной части и у остав- шейся части. Стандарт больше общей средней, следовательно, расчет средних для обеих частей (лучшей и худшей) надо вести по третьему столбцу табл. 38. 5,0 — 4,0 Нормированное отклонение стандарта х =- 1,0 первая функция f(x) =0,242, вторая функция <р(х) =0,341. Для лучшей, элитной части третья функция 0,242 0,242 f (х) 1,522, 0,159 0,5 — 0,341 0,5 — + (х) р~1~ ~о М м g=fe u Ю () М С Схема вычисления третьей функции нормированного отклонения Левая(меньшестандарта)Правая(большестандарта) Левая(меньшестандарта)Правая(болыиестандарта)
7,' ТРАНСГРЕССИЯ для худшей, оставшейся частиf (х)0,5 + ~(х) 0,242 0,242 0.288. 0,841 0,5 + 0,341 Искомые средние: для лучшей части Fq (x) 4,0 + 1,522 . 1,0 = 5,52 кг, для худшей части М„- = М„-~- Р„(х) = 4,0 — 0,288 1,0 =- 3,71 кг. St=Mp — ха=4,0 — 1,0 . 1,0=3,0 кг и овец, дающих настриг менее 3,0 кг, можно выбраковать. Стандарт в данном случае меньше средней, значит расчет третьей функции надо вести по второму столбцу табл. 38. При х=1 первая функция f(x) =0,242, при х=1 вторая функция rp(x) =0,341. Для лучшей части, оставляемой в хозяйстве, третья функция /(х) 0,242 0,242 0,5+ ~(х) 0,5+ 0,341 0,841 для худшей, выбраковываемой части 0,242 f (х) 0,242 1,525. 0,5 — ~ (х) 0,5 — 0,341 0,159 Для оставляемой части искомая средняя М, =. М, -',— F, 4,0+ 0,288 1,0 -=- 4,29 кг, для выбракованных овец М =- М, — I-„а = 4,0 — 1,525 1,0 -= 2,48 кг. Эти взаимоотношения иллюстрируются правым графиком рис. 18. ТРАНСГРЕСС ИЯ При выяснении различий между группами объектов — разновидно- стями одного вида, сортами, породами, штаммами — почти всегда иссле- дователь наблюдает захождение одного распределения в пределы друго- го. Очень часто две разновидности, сравниваемые по развитию какого-ни- будь одного признака, дают такие распределения его, при котором мак- симум меньшего признака заходит за минимум большего. Такое явле- Количе."тво овец, которые попадут в элитную группу, составляе1 [0,5 — ср(х)] ° 100= 15,9%. Разобранный пример иллюстрируется левым графиком рис. 18. П р имер 40. Из стада, описанного в предыдущем примере (М= =4,0 кг; а=1,0 кг), решено было выбраковать 15,9% худших по настри- гу овец. Потребовалось определить, с каким настригом овцы еще могут быть оставлены в стаде и какой средний настриг можно ожидать ) оставшейся части стада. Если выбраковывается 15,9%, то в худшей половине остается 0,5 — 0,159=0,341, или 34,1% овец. Вторая функция ~р(х) =0,341 соот- ветствует нормированному отклонению х = 1,О. Следовательно, стандарт отбора
РАЗНООБРАЗИЕ ЗНАЧЕНИЙ ПРИЗНАКА 76 ние называется трансгрессией. На рис. 19 показаны примеры малой и большой трансгрессии нормальных распределений. Степень трансгрессии двух распределений можно охарактеризовать показателем трансгрессии, который рассчитывается по формуле у- н~р1 + угря П1+пъ м пип mom, ц) $0 9,5 6,0 М, т~л~ NO ЩО Рис. 19. Трансгрессия (трансгрессирующие части распреде-лений заштрихованы}. где где Т — показатель трансгрессии; п1 и n~ — общее число дат в первом и втором распределении; Р1 и р~ — доля трансгрессирующих дат в первом и во втором рас- пределении. Таким образом показатель трансгрессии есть средняя доля транс- грессирующих дат, взвешенная численностью сравниваемых групп, т. е. доля трансгрессирующих дат в сумме обоих распределений. Яоли трансгрессирующих дат определяются по формулам р~ — — 0,5» ч(х~), mi>g — Я1 x, =- min =М с
77 ТРАНСГР ЕССИЯ Р2=0~5~'р (~2) з аах, — М~ тах, М, +3~,. Х где Яля понимания этих формул достаточно внимательно просмотреть схему определения трансгрессирующих долей, представленную на рис. 20. PQc. 20. Схема определения тр ансгрессир ующий долей. П р и м е р 41. Две разновидности одного вида, обитающие в резкоразличающихся экологических условиях, изучались по высоте растений. В результате получены два распределения, заходящие одно за другое,со следующими сводными показателями:М= 8; а1 — — 10: и=100;М2=14; а2=1,5; п~=200. Этих данных вполне достаточно, чтобы определить показатель трансгрессии между этими разновидностями по высоте растений.
РАЗНООБРАЗИЕ ЗНАЧЕНИЙ ПРИЗНАКА 78 Расчеты лучше провести в следующем порядке, рассмотрев предва- рительно верхний график рис. 19, на котором изображены эти два рас- пределения в нормализованном виде. пип2 — — М2 — За2 —— 14 — 3 ° 1,5 = 9,5; т ах, = М, + За1 — — 8+ 3 ° 1,0 = 11,0; 9,5 — 8 min2 — М, — 1,5; ° (х,) =- 0,433; х, ==- 1,0 11 — 14 max, — М» р, = 0,5 - — 0,433 == 0,067; х, = р ° 1,5 ср(хД = 0,477; p> — — 0,5 — 0,477 = 0,023; 100;к, '0,067 -+- 200 >( 0,023 -- 0,038, или 3,8%. 11,3 зоо 100 + 200 Малый показатель трансгрессии свидетельствует о том, что изучен- ные разновидности, обитая в разных условиях, очень сильно различают- ся по высоте растений. Это расхождение оказалось столь значительным, что стало возможным с очень малой вероятностью ошибиться, относить отдельные экземпляры к той или иной разновидности только по одному пр изнаку — высоте. П р и м е р 42. При определении плодовитости по среднему числу поросят на один опорос, племенные свиноматки были разделены на две группы — лучшую, более плодовитую, и худшую, менее плодовитую. От обеих групп свиноматок было получено достаточное количество дочерей,. у которых была зарегистрирована плодовитость за три года. Результа- ты были сведены в два распределения по средней плодовитости дочерей, которые имели следующие сводные показатели: М1 — — 11; а1 — — 1,2; n~ — — 200; M2 — — 13; ар —— 1,0; n2 — — 100. Для решения вопроса о том, можно ли по плодовитости дочери определить, к какой категории принадлежала ее мать (к худшей или лучшей половине}, был рассчитан показатель трансгрессии между рас- пределениями обеих групп дочерей. Нормализованные вариационные ряды этих распределений показаны на нижнем графике рис. 19. При ознакомлении с порядком расчета показателя трансгрессии для данного случая лучше иметь этот рисунок (а также схему рис. !8) перед глазами.. ш1» = M> — 3 а~ = 13 — 3 Х 1,0 = 10,0; max~ — — М~+Заi — — 11+ЗХ1,2 = 14,6; min2 М1 10 — 11 0,83; (х,) = 0,297; 1 2 Р, --0,5-1- 0,297 == 0,797; шах, — М» 14,6 — 13,0 + 1,60; J(х ) - 0445: 1,0 р =- 0,5 — 0,445 -- 0,945; 200 )~; 0,797 + 100;х, '0,945200 --' 100 253,9 300 = 0,846, или 84,6Ж.
БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 7с) Оказалось, что распределения дочерей (от худших и лучших мате- рей) настолько сильно трансгрессируют, что совершенно безнадежно по плодовитости дочери судить о том, к какой группе принадлежала ее мать. Можно предположить, что причиной этому, вероятно, служит сла- бая наследуемость плодовитости в данном стаде свиней при данных природно-хозяйственных условиях. П р им ер 43. Если в исследованиях, описанных в примерах 41 и 42, потребуется определить возможные средние для лучшей и худшей нетрансгрессирующих частей, то сделать это можно при помощи треть- ей функции нормированного отклонения следующим образом: а) для примера 41 М2=14, а,=!,5; х~ -— — — 2,0; /(х,) =- 0,054 ~ (х) == 0,477 0,054 0,054 0,5 -+- 0,477 0,977 М", = 14,0 + 0,055 Х 1,5 = 14,082М> 8; а1=1; х1 — — +-1,5; (см. рис. 19); f (х,) — — 0,130 р(х,) = — 0,433 0,130 0,130 Р(х) =: =- 0,139; 0,5 + 0,433 0,933 М' = 8,0 -- 0,139 X 1,0 =- 7,861 (см. рис. 191; б) для примера 42 М2=13; a~=1,0; хр=+-1,60; /(х,) = 0,111 ~ (х2) =- 0,445 0,111 0,111 =-- 2,02; 0,055 0,5 — 0,445 М" == 13,0 + 2)02 Х 1,0 = 15,02; д 1 М~ — — 11; а1 — — 1,2; х1 — — — 0,83; f (х,) =- 0,283 ~ (х,) =- 0,297 0,283 0,283 -= 1,394; 0,203 0,5 — 0,297 1,394 Х 1,2 — 9,33. М,', = 11,0— БИ НОМ ИАЛЬНОЕ РАС ПРЕДЕЛ ЕН И Е Группа особей может изучаться не только по количсственным признакам, которые могут иметь различную степень своего проявления и измеряются именованными величинами — в килограммах, литрах, сантиметрах и других единицах измерения. Есть признаки, которые обычно не имеют градаций (мужской пол, красная масть и др.). У каждой отдельной особи такой признак может или быть, или не быть. Такие признаки называются качественными или аль тернативныии. Принципиальной разницы между количественными и качественны- ми признаками нет. У. большинства признаков, которые считаются ка- чественными, при более тщательном изучении может быть найдена и измерена степень его проявления, и тогда качественный признак станет кол ичественным.
80 РАЗНООБРАЗИЕ ЗНАЧЕНИЯ ПРИЗНАКА Если изучается несколько (r) групп, одинаковых по числу входящих в них особей (n), то можно составить распределение таких групп по числу особей, имеющих изучаемый признак. Например, в каждом десятке выловленных рыб могут встретиться О, 1, 2, 3, 4, 5, 6; 7; 8; 9 и все 10 особей, пораженных какой-нибудь глист- ной инвазией. Несколько десятков не будут иметь в своем составе по- раженных рыб, несколько десятков будут иметь только по одной боль- ной рыбе, несколько десятков — по 2 рыбы и т. д. В результате составится распределение, в котором вариациями бу- дут величины и„— число особей, имеющих изучаемый признак в отдель- ных равночисленных частных группах, а частотами г; — количество соответствующих групп. Пример распределения 20 десятков выловленных карпов по числу рыб, пораженных глистной инвазией, представлен в табл. 39. Та бли ца 39 Число больных рыб в каждом десятке (и+) Всего десят- ков 1 2 8 9 10 Число десят- ков (г~) 5 3 2 1 3 4 0 0 0 20 Такие распределения частных равночисленных групп по значени1о и+ (по числу особей в каждой группе, имеющих изучаемый признак) называются биномиальными. Такое название объясняется, во-первых, тем, что признак может иметь всегда только два варианта: он есть или его нет; во-вторых, закономерности таких распределений имеют «оличе- ственное выражение, связанное с коэффициентами разложения бинома Ньютона, который в применении к этому типу распределений может быть выражен следующим образом: ~в ~п — з + +n,7о n(n — 1) (и+ 2) 1 1 2 ° 3 1 где р — средняя или ожидаемая доля особей, имеющих изучаемый признак, среди всех особей данной категории (в генеральной совокупности); q= l — р; и — одинаковая численность каждой изучаемой группы. Характеристика группы по качественному признаку заключается в указании, сколько в этой группе имеется особей с наличием данного признака и у скольких особей его нет. Для такой характеристики употребляются следующие обозначения: и — общее количество особей в группе (например, 200), и, — количество особей, имеющих изучаемый признак (120), и — количество особей, не имеющих данного признака (80), и+ 120 р = — ' — шаля особей, имеющих признак —:= 0,60, 200 П 80 р =- — — доля особей, не имеющих признака „„=' 0,40 Ш Очевидны следующие равенства: и+ + и = и (120 + 80 ==-. 200); P+q=1; q=1 — р(0,60+-0,40=1,00; 0,40=1 — 0,60).
BHHOMHAJIbHOE РАСПРЕДЕЛЕНИЕ 81' каждый член бинома может быть представлен в виде произведе- ния, из которых первый множитель целиком зависит от величины и: п n(и — 1} f(n) = — —; и т. д., а второй — от соотношения р и q: f(p., q)— 1 ' 1 2 =q"; pq" ' и т. д. Первые множители каждого члена бинома — коэффициенты бино- ма — определяются в зависимости от величины и {число особей в каж- дой частной группе) по арифметическому треугольнику, в котором каждое число равно сумме двух чисел, стоящих над ним (табл. 40). Таблица 40 Арифметический треугольник 0,5 1 11 2 11 3 3 11 4 6 4 1 0,25 0,125 0,0625 0,03125 0,015625 0.0078125 0.00390625 0,00i953125 1 0,0009765625 и=- 2 и= и= — 4 и=- 5 и= 6 и= 7 и= 8 1п= 9 и=10 1 10 10 5 1 1 б 15 20 ~5 6 1 7 21 35 35 21 7 1 28 8 70 56 836 84 126 126 84 3645 120 210 252 210 120 45 28 9 1 10 10 Чтобы определить ожидаемые доли частных групп такого распределе- ния, надо взять числа f(n)1, f(n)g и т. д. из соответствующей (п) стро- ки арифметического треугольника и каждую из ннх помножить на одно и то же число,5", стоящее в той же строке табл. 40. П р и м e p 44. Среди одной популяции львиного зева пелорическая форма цветка встречается у 10'/о растений. Если взять 100 групп (букетов) по 5 растений в каждом, из .разных мест без выбора, то сколько можно ожидать букетов без пелорических цветков и букетов с 1, 2, 3, 4 и 5 растениями, имеющими такие цветки. В данном случае имеется r = 100 групп, по п = 5 особей в каждой, причем общая доля особей, имеющих изучаемый признак, равна р = О.l. Определение ожидаемых частот <; такого распределения представ- лено на табл. 41. Подставляя в формулу бинома величины f(n) и f (p, д) и решая ее относительно величины р, можно получить следующие значения: q" — нулевой член бинома (содержащий р в нулевой степени), дает ожидаемую долю таких равиочисленных групп, в ко- торых из и особей ни одна не имеет изучаемого признака; npq" ' — первый член бинома (с р'), дает долю групп, в которых только одна особь имеет ожидаемый признак; л (и — 1 р'д" '-' — второй член бинома (с р'), дает долю групп, в которых изучаемый признак имеет по две особи; Й-ый член бинома соответствует доле групп, в которых име- ется Й особей с изучаемым признаком; р" — последний член бинома, дает долю равночисленных групп, в которых все и особей имеют изучаемый признак. В тех случаях, когда ожидаемые доли р и q равны, что может быть только при р = q = 0,5, формула бинома значительно упрощается: 'Л П 0 И П 1 . 1 ° 2
82 РАЗЯООБРАЗИВ ЗНАЧЕНИИ ПРИЗНАКА Таблица 41Олределение ожидаемых частот бнномиальыого раслределения букетов ло числурастений львиного зева с пелорической формой венчика приr= 100; и=5; р О,1; у=0,9 Чнсло расте- RHO c пелори- ЧВСКИХИ цветка- ХИ (/3-+) r �~ т ! r jt - rf (л) - f (я1) Ф f (л)* У0 ~) - f (~) f (~ч) 1 ~ 9 з 729 рВ~З 10 10 100000 р3дЗ- =(4)' — =,-'- 0,59 049 59 0,32 805 33 10 0,07 290 0,00 810 0,00 045 1 1 pbq0= — -1 = 10 100000 0,00001 * По арифметическому треугольнику для а= 5. ** дроля групп, имеющих О, 1, 2, 3, 4 и 5 растений с пелорнческнмн цветками. Расчеты показывают, что при общей доле р = 0,1 особей, имеющих данный признак при r = 100 групп по и = 5 особей в каждой, может встретиться 59 групп без пелорических цветков, 33 группы, в которых из пяти растений одно будет с пелорическими цветками, 7 групп, имеющих из пяти два таких растения, и 1 группа, в которой из пяти особей три будут иметь изучаемый признак. Появление групп с четырьмя и пятью растениями, имеющими пелорические цветки, при данных условиях ма- ловероятно. Легко подсчитать, что при r = 1000 можно ожидать, что один бу- кет из тысячи будет иметь четыре растения с пелорическими цветками (табл. 42}. Та блица 42 Всегобукетов 328 73 590 И только набрав десять тысяч таких букетов, можно ожидать, что среди них будет один, в котором все пять растений будут с пелориче- скими цветками. Пример 45. Исследование племенных книг орловского рысака показывают, что если взять всех известных маток, принесших по 10 же- ребят, и просмотреть соотношение полов в приплоде каждой матки, то получится распределение, представленное в табл. 43.
83 БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ Таблица 43 Числожеребчиков и+ 6 0 1 4 5 10 Всего маток Число кооылок и» 4 3 6 5 10 9 8 7 Числоматерей r~ 0 4 45 56 14 231 44 28 Среднее число жеребчиков на приплод из 10 жеребят от каждой матери ' =- (1 Х 10 + 3 ~ 9 + 14 Х 8 -- 28 X 7 " 44 X 6 -'.— vr + 56 Х 5 + 45 Х 4 + ЗЗ Х 3 + 3 X 2 + 4 Х 1 + 0 Х О): 231 = =- 5,1, 231 а общая средняя доля жеребчиков в потомстве 231 матки 5,1 10 1178 ,51 . 10 Х 231 Ьыло высказано предположение, что вообще у всех орловских ры- саков в условиях наших племенных заводов жеребчиков родится столь- ко же, сколько и кобылок, т. е. общая доля рождающихся жеребчиков р = 0,5, а в потомстве изученных орловских маток произошло обычное случайное отклонение от средней физиологической нормы. Рис. 21. Фактическое распределение (1) приплодов по числу жеребчиков и теоретическое биномиальное даспдеделение' (>).
РАЗНООБРАЗИЕ ЗНАЧЕНИЯ ПРИЗНАКА Табли ца 44 Расчет ожидаемых частот биномиального распределения приплодов от орловских1Окобыл по числу родившихся жеребчинов при r = 231; и = 10; р = q = 0,5; р2 по формуле (0,5+ 0,5) « = 0,5~о+ f(n), 0,5~о+ f(и)2 0,5~о+... 1 1024 Нахождение теоретических частотраспределения 1(ритерий k 1<ритерий х' (г i' )~ r'.«г/'(n) )<+0,51О (г. i')~ r.— г'< f (и) f (и) ° 0,5" 231 231,() О 10 9 0,2 2,5 1 0,00097 1,5 2,25 0,90 230,8 228,5 г18,3 191,2 143,9 87,1 39,8 12.7 «9,5 230 227 213 185 141 85 40 7 4 0.8 1.5 5,3 б.2 2,9 2,1 0,2 5,7 1,5 3 14 28 44 56 45 33 3 4 2,3 10,2 27,1 47,3 56,8 47,3 27,1 10 ° 2 2,3 2,5 0,2 10 45 120 210 252 210 120 45 10 0,00977 0,04395 0,11719 0,20508 0,24608 0,20508 0,11719 0,04395 0,00977 14.44 0,81 10,89 0,64 5,29 34.8l 51,84 2,25 3,8 0,9 3,3 0,8 2.3 5,9 7,2 1,42 0,03 0,23 0,01 0,11 1,28 5,08 0,90 1 0,00097 0,2 0,2 yI = 9.3124,3~с — 18,,~14,1ч =9 — 2=7 231,0 6,2 6,2 It = /231 15,2 = — 0,4 1,95 1,Я 1,36 1 Для проверки этого предположения было рассчитано биномиальное распределение по данным описанного исследования: r = 231, и = 10 и р = 0,5. Расчеты показаны в табл. 44. Расчеты, а также рис. 21 показали, что если принять гипотезу о том, что жеребчиков родится столько же, сколько и кобылок, то выте- кающее из этого биномиальное теоретическое распределение очень близко к фактическому и незначительное расхождение теоретического и фактического распределений недостоверно (и по критерию y„', и по кри- терию Х). Таким образом, описанные факты из истории коннозаводства не опровергли гипотезы о том, что вообще у лошадей орловской породы жеребчиков родится столько же, сколько и кобылок, по крайней мере, у матерей, принесших по 10 жеребят каждая. Если исследуется распределение многочисленных групп, то значи- тельно усложняются расчеты членов бинома при большом значении и. В таких случаях с достаточным приближением можно получить теоретическое распределение групп, применив формулу нормального распределения в следующем виде:
БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ У "; — теоретическая частота i-го класса частных групп, в кото- рый отнесены группы, имеющие определенное число {~ = О, 1, 2, 3 и т. д.) особей с изучаемым признаком. r — общее число исследованных равночисленных групп по п особей в каждой; ~ — среднее квадратическое отклонение числа особей, обладаю- щих изучаемым признаком; j(x) — первая функция нормированного отклонения, значения которой приведены в табл. VI; где Ш — Л, + ф нормированное отклонение числа особей, имеющих изучаемый признак (т. е. нормированное отклонение чи- сел О, 1, 2, 3 и т. д.). и„--число особей в группе, имеющих изучаемы"; по этому числу изучаемые равночисленные группы разносят- ся по классам распределения; и, — среднее число особей, имеющих изучаемый признак, по от- дельным равночисленным группам. Средняя арифметическая и, и сигма а числа особей, имеющих изучаемый признак, рассчитываются различно, в зависимости от исход- ных данных. Если имеется только эмпирическое распределение равночисленны1х частных групп по числу особей, имеющих изучаемый признак, и нет никаких предположекий или сведений о доле, имеющих изучаемый признак среди всех особей данной категории, то в таких случаях и+ и п определяются по формулам: 0 С C=Er,.à+- r — 1 У - rln (E rq n+)'-' IE — численность изучаемых частных групп (одинаковая для всех групп); Р — доля особей, имеющих изучаемый признак среди всех особей данной категории; Q=1 — Р — доля особей, не имеющих данного признака среди всех особей изученной категории. П р и м е р 46. В пятидесяти контрольных уловах одного вида рыбы по 20 особей в каждом определялось число самцов. Распределение уло- ва представлено в табл. 45. Чему равна средняя доля самцов и возмож- но ли считать распределение уловов по числу самцов биномиальным? где и — среднее число особей, имеющих изучаемый признак; r, — число равночисленных групп, имеющих одно определенное число особей с изучаемым признаком; это частоты биноми- ального эмпирического распределения; и, — число особей с изучаемым признаком (О, 1, 2, 3 и т. д.); это величина классов биномиального распределения; Е г,. =- r — общее число изученных равночисленных групп, каждая из ко- торых имеет всего и особей, из которых и+ особей имеют изучаемый признак. Если же имеются сведения или высказывается гипотеза о доле осо-бей, имеющих изучаемый признак среди всех особей данной категории, то е, и ~ рассчитываются по формулам и — — пР, g npQ,
° й Ю ° ° ° ° Ю Ф Ю Ю Ю Ю Ю ~ ° ° ° ° ° ° ° ° ° ° ° ~ф е е е ° ~ .1 ~ е ° ~ Ю ° °
СО Ф ~ '~' Ф ОО ОО Ю Ф Ф Ю Ю Ш ° в О СЧ СЧ О О О О ф О в Ц ) СЧ еО CD Cb CD CQ СЧ ОО еб Ю t t О> сО ~Э' Ф сО СЧ С5 О QO О Сб Щ ~<;) ~ фе ОО CQ СЧ ~~ ~О О О СО О еб СЧ О О C' О О О О О Сф Мф- ° в ю е СО 'Ф ОО M СЯ ~е ~ ° СЧ О~ Ch Ф О сО cD СЬ Ф Ф О О ~ ~О 'Ф О СЧ О О Ф О СЧ О О Ц И И 46 Ю Л Щ O ~ф ф ~ м C5 CD ОО 'A СЧ ~~ ф сО CD о 8 О> ир О О О ° СЧ (7) чф~ е ° Ц.) уе ~7 Ю Ю Ю ° в Ю Ю Ю Ю О О О О ~ ° СЧ 1! 11 ь Н 00 О0 О0 СЧ СЧ СЧ СЧ СЧ СЧ ° О О ° СЧ Сб (О ~О ~ СЧ ОО СЧ О СЬ ° СЧ (:Ь с СЧ СЧ СЧ и'> и 'е' 'е' сч о t Ю Щ 4' 6Р СЧ О CO Ю Ю О О сО оО сО сО СЧ еО О О О О Ф Ю Ю Ю Ю Ю ° в СЧ О ° О О и.) Q) Щ Ol 03 ~ C> Я О О О О О CDtI Щ ll
сО Э'Ch'Фt t Ю ООО ~Я�~О сО cO Cb M Ch C)СЧ N СЧО ° ч« о Ь о М и OJ «) «-«ю CJ С4 о Ю Е CO о + Я il Ъ~ Ъ И~ СЬ CO 'Ф СЧ l! еф Ю II л ° ч L rr1 Сс С) г Ю й~ СЭ G4 ««« С'3 С4 L :1 о C о М и Ю МФ г 6) 00 ~л~ Ф~ ч ° ч cOCC ~ СЧ ОО О ~О — ОФ О О( (' «» Ю «» Ю л Ю «» Ю - -3'~О O сО~О Ch С~3 ОО М> O L» сь Сф Ф СЧ 11 сь ~Э' О О Щ а СЧ 11 СЯ М'.) е-~ ю ю л Фоо Ф СЯ е» 11 Х СМ ЮФ щ Щ11 Х eOаЭ О Ооъ СМОЛОЮ «ОО ппсОсо С) сс~~~ СЧ Ф' с'Эb3 й'» о Х Ое Ю (-«~ Ое М ь (.Ь ~Р O СЧ )I сООЮ~ '~~ О~ Ф СЧ ~О сО сО О сО Ф ( ф~ ° у < о<>воа � cOYD~OO L г4 СЧ ОО ч~ОФЯОЮ~ > O % е в О О О О ~.~ФЮ ООФ «ч л о Сю о М CJ ФЭ М (-«~ ФЭ С4 о OJ &~ сО ср~1 о~в СЧ + IIЪ~ 11ь ° л IIС)O11Q„11~й ~ Cl ~4 .о« и ~ ap C ° ° Q ~î. (.-. И ~ и Я о. 2 Ю йф CJ М oо йй ~( ~с щ О О О4 1l ~ Юс. Ф о~ 'e о 1I О CO О gg О ~ф ~î й( Ю В О i йй Ф Вй Ф В ц) й( ~ «о р( М С4 v Я о~ Ж о < 63 Я ~- Ы д CJ В ~й Ф В М В Ю В в3 Э В И g щ Ф р.о (р ФЭ РАЗНООБРАЗИЕ ЗНАЧЕНЯЯ ПРИЗНАКА ~со соаресt O Э'~ Ф О @@~~~ООВ О ЩС„-ОО" э''Ф э' Ф Ф' со с~ сб ° ф ОООРООC ~ Ф О�ОСО ° ~О~~'Э ~О ~Ф ~Ф ~Ф '~' с'Э с'Э ! ООООООООО О ООООО О СЧ СО 'Ф ~О Ю ОО О~ О С~ ~0 Ю ~О 'Ф Я СЬ'ФО>'Ф О> Э'О> ФO ~Э' О~ Ф'Cb'ФCh СОСОСЧС~~~OOO О C — СЧСЧ �~ ~' с~-~ ~О '~~' ~~:~ СЧ О С~ сО M ~О Ю ++'+++++ ~ !!! ~ ~ ~ C× Ж ~0 ~ ÎÎ ~ ~ ~ ф ' ° 3с, ~l О Ф ОО ~ сО Щ M еб СЧ ~ч О Р СО C Ф Л с3' с'Э СЧ О СЯ у ° еа ° е-м ~ еч у ° у ° ~ ° ее
РАСПРЕДЕЛЕНИЕ РЕДКИХ СОБЫТИЙ При составлении распределения выяснилось, что самое большое число самцов в группе из 20 особей было равно 10. Наиболее часто повторялись группы с четырьмя самцами. Таких групп было 12 из 50. ~óMìà произведений вариаций а, на частоты г; в эмпирическом — 210 распределении E r, и „— 210, откуда средняя частота и. =-- = — =4,2 салща. 50 Если в каждой группе в среднем по 4,2 самца, а всего в группе особей и = 20, то средняя доля самцов в исследованных уловах равна = () 2] или 21%. Исходя из средней частоты (4,2) и сиг- мы частот (2,00), можно составить теоретическое распределение, также как и для обычных вариационных рядов (см. табл. 33). Как видно из табл. 45 теоретическое распределение очень мало от- личается от эмпирического, что подтверждается обоими критериями различия распределений (y' и Х). Этот пример показан на рис. 22. Рис. 22. Сопоставление эмпирического (1) и теоретических биномиальпых распределсиий: по и и а; эмпирического (2), а исходя из гипотезы, что Р = 0,3 (8). Пример 47. При анализе материалов примера 46 было высказа- но предположение, что в среднем у рыб данного вида в том сезоне, в котором были взяты контрольные уловы, доля самцов должна быть равна не 0,21, а Р = 0,3, фактически же распределение представляет случайное отклонение от нормы, возможное при том сильном разнообра- зии отношения полов, которое свойственно рыбам данного вида. Про- верка этой гипотезы показана в табл. 46 и на рис. 22. Оказалось, что фактическое распределение настолько сильно и до- стоверно отличается от теоретического, что гипотезу о доле самцов Р=0,3 ни в какой степени нельзя считать подтвержденной. РАСПРЕДЕЛЕНИЕ РЕДКИХ СОБЫТИЙ События, происходящие редко, один или небольшое число раз па 1000, 10000 и больше. обычных явлений, могут быть сведены в особое распределение, в котором вариациями является различное число редких случаев, а частотами — количество больших групп, среди которых ред- кос событие произошло опредсленнос число раз.
90 PA3HOOGPA3HE ЗНАЧЕНИЙ ПРИЗНАКА I r= — г.е"' Х! илн Ха~— =е-аГ х! I ~, — — теоретическая частота распределения, ожидаемое число больших групп, среди которых редкое событие произошло х раз; r =- Е г» — общее количество исследованных больших групп; е = 2,21828; х — число редких событий, происшедших в каждой боль- шой группе; обычно х равно небольшому целому чис- лу: 0. 1, 2, 3 и т. д.; х! — произведение натуральных чисел от 1 до х (факто- риал}. Считается, что факториал нуля равен едини- це: О!=1; ~ ХГ " --среднее число редких случаев на каждую большую группу. Теоретическое распределение редких событий имеет одну особен- ность: в нем значение средней величины примерно равно квадрату сиг- мы (девиате). Поэтому, если в других распределениях основных вели- чин две — М.,и а, то в распределении редких событий обе основные ве- личины сведены к одной — к среднему числу таких событий на каждую большую группу. Из этой особенности распределения редких событий вытекают два следствия. Во-первых, все теоретическое распределение может быть построено на основании только одной средней, полученной для изучаемого эмпи- рического распределения. Это обстоятельство дает возможность рассчи- тать заранее относительные частоты ~х -а =е Г Х! для всех возможных значений а, что значительно упрощает процесс составления теоретического распределения по данному эмпирическому. Величины относительных частот распределения редких событий для разных значений а = ~хг, приведены в приложении, табл. VIII. Г Во-вторых, при определении достоверности отличия теоретическогс распределения от эмпирического при помощи критерия y„' число степе. ней свободы для этих распределений равно числу классов без одного так как все распределение редких событий ограничивается одним усло. вием — величиной средней встречаемости. П р и м е р 48. При проверке засоренности семян клевера оказалось, что в каждой навеске семян имелось разное количество семян повили. ки — от О до 3. Для выяснения причин наличия семян повилики в семе. нах клевера потребовалось определить, нет ли отклонений в выявлении семян повилики от обычной засоренности, вызываемой случайными об-стоятельствами. Для этой цели было произведено сопоставление факти. ческого распределения признака с теоретически ожидаемым. Распределения таких редких, случайных событий обычно подчиня- ются определенному закону, который выражается Формулой, предло- женной Пуассоном:
РАСПРЕДЕЛЕНИЕ РЕДКИХ СОБЫТИЙ Таблица 47 Сопоставление эмпирического и теоретического распределений числа семян повидики среди клеверных семян (редкое событие) ! Эмииричсскос расиределснис Теоретичсскос расирсдслснис !<ритерни отличия эмниричсского распрсдслсния от теоретического х Рх — 'х 3 r'х х х т х ~х бх Ер' х Еr~ = 1000 8 8 = — = О,25 у О 31,62 >r'х = 1000 ~mr 499 а= 1000 1000 = 0,499 =0,5 семян повилики '=5 — 1 =-4 Расчеты приведены в табл. 47, сопоставление распределений показа- но на рис. 23. Оказалось, что появление в семенах клевера семян повилики (что бывает редко) вполне соответствует закономерности редких явлений. Рис. 24. Эмпирическое распределение (Ц числа смертей от удара лошади (очень ред- кий случай) и теоретическое распределение (2), составленное по закону появления редких событий. Рис. 28. Эмпирическое распределение (1) числа семян повилики в пробах сеь|ян клевера (редкий случай) и теоретиче- ское распределение (2), составленное по закону ц,оявления редких событий. П р и м е р 49. Смерть человека вследствие того, что его лягнула лошадь — явление чрезвычайно редкое. Были изучены отчеты десяти армейских корпусов за 20 лет. Всего исследовано 200 больших групп, причем в 109 группах не было зарегистрировано ни одной смерти от число семян ПОВИЛИ- ки х ЧИСЛОнавесоксемянклевераr~~ 0 12 74 315 599 г(потабл. ЧШ) 0,0016 0,013 0,076 0,303 0,607 1 13 76 303 607 1 1 2 12 8 1 1 4 144 64 1,00 0,08 0,05 0,46 О,ll 1000 1000 988 914 599 1000 999 986 910 607 1 2 4 8
92 РАЗНООБРАЗИЕ ЗНАЧЕНИИ ПРИЗНАКА удара лошадью, в 65 группах было по одному такому случаю, в 22 груп- пах — по 2 случая, в трех группах — по 3 и в одном корпусе за один год зарегистрировано 4 смерти от удара лошади. Анализ показал, что рас- пределение таких редких случаев вполне соответствует закономерно- сти Пуассона. Это показано в табл. 48 и на рис. 24. Таблица 48 Сопоставление эмпирического и 1еоретического распределений числа смертей отудара лошади (очень редкий случай) Критерии отличия распределений Теоретическое распределение Х Р (по табл. Ч111) Х (I Г' )~1r йг .ФР т г' р у" 2 2('.0 200 '),01 0,08 200,09 200 Ug 0,00004 0,0004 0,09 0,08 4,69 0,69 0,10 0,48 ),6 4,0 0,25 0,01 0,01 2,2 0,8 0,8 4,84 0,64 0,64 19,8 65,8 109,8 ~r'x = 200 09 122 — = 0,61 = 0,6 200 0,6 0,6 Л -= ' — 0,04 200 14,15 1,95 1,~3 1,36 лучаев ~=4 — 1=3 Таблица 49 Сопоставление эмпирического и теоретического распределений числа рожденийчетверней (очень редкое событие} в Пруссии за каждый год Эмпирическое распределение Теоретическое распределение Критерии разлириш распределений я rx rx гд — ~' ) rx 'х Е г — Ег х х 'х 0,1 0.3 1,60 1.2 3.8 1,23 1,96 1,4 1,000 69,0 Л = ' — ' — 0,21,5 1,569 8,3!'1,361,63~1,95 .« =2,23 ~8,5) 13,3' 9,5/ ~ xrx 109 r 69 = — 1,58 = 1,6 четверни ~=5 — 1 4 7 6 5 4 3 2 1 О 9 17 24 14 0,003 0,020 0,099 0,329 0,549 trxr(по табл.ЧП1) О,С01 0,005 0,01Ь 0,055 0,138 0,258 0,323 0,202 9,4 17,7 22,7 13,8 1,8 0,4 0,7 1,3 0,2 3,24 0,16 0,49 1,69 0,04 О,85. 0,020,030,070,�3 20» 199 196 174 109 69 69 68 66 64 55 38 14 200 199,4 195,4 175,6 109,8 69,0 68,9 68,6 67,4 63,6 54,2 36,5 13,8 Ц 0,4 0,6 1,6 0,8 О О,l О,б 1,4 0,4 0,8 [1,5) 0,2
РАСПРЕДЕЛЕНИЕ РВДКИХ СОБЫТИИ Рис. 25. Эмпирическое распределение (наклонная штрихов- ка) числа рождений четверик (очень редкое событие) и теоретическое распределение (вертикальная штриховка), составленпос по закону появлсния редких событий. П р и м е р 50 По материалам регистрации рождений в Пруссии за 69 лет рождение четверней наблюдалось в количествах (за год по всем рождениям), указанных в табл. 49. Анализ эмпирического и теоретиче- ского распределения (табл. 49, рис. 25) показывает, что и это очень редкое событие появляется в соответствии с законом распределения редких событий.
Г JTA ВА IIIРЕПРЕЗЕНТАТИВНОСТЬВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ ривлечение объектов для исследования можно проводить дву- мя основными методами. Можно подвергнуть изучению всех особей определенного массива или только их часть, определенным об- разом выбранную. В первом случае проводится сплошное обследование всей генераль- ной совокупности, во втором случае производится выборочное иссле- дование. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА Весь массив особей определенной категории называется генеральной совокупностью. Объем генеральной совокупности определяется задачами исследования. Если изучается какой-нибудь вид диких животных или растений, то генеральной совокупностью будут все особи этого вида. В данном случае объем генеральной совокупности будет очень большим и при расчетах он принимается за бесконечно большую величину. Если изучается сорт культурных растений или порода домашних животных, то генеральная совокупность будет по объему меньше, чем при изучении всего вида. Если изучается действие какого-нибудь агента на растения и живот- ных определенной категории, например, новое удобрение или новый прием обработки почвы, новый прием выращивания или кормления жи- вотных, то генеральной совокупностью будут все растения и животные той категории (вида, пола, возраста, хозяйственного назначения), к ко- торой относились подопытные объекты. Это уже не очень большое коли- чество особей, но еще недоступное для сплошного изучения. Не всегда объем генеральной совокупности недоступен для сплош- ного исследования. Иногда изучаются небольшие совокупности, напри- мер, определяется средний удой или средний настриг шерсти у группы животных, закрепленных за определенным работником. В таких случаях генеральнои совокупностью будет совсем небольшое количество особей, которые все исследуются. Небольшая генеральная совокупность бывает также при исследовании растений или животных, имеющихся в какой- нибудь коллекции, с целью характеристики определенной группы в дан- ной коллекции. Сплошное обследование генеральных совокупностей производится редко, например, при общегосударственных переписях и др. В большинст- ве случаев проводятся выборочные исследования частей генеральных со- вокупностей.
I ЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА Часть генеральной совокупности, определенным образом отобранная и исследуемая с целью характеристики всей генеральной совокупности, называется выборкой. Для того, чтобы по выборке можно было получить правильную ха- рактеристику всей генеральной совокупности, необходимо организовать правильный отбор объектов из генеральной совокупности. Теорией и практикой разработано несколько систем отбора особей в выборку. Общим для всех этих систем является стремление обеспечить максимальную возможность выбора любого объекта из генеральной сово- купности. Тенденциозность, предвзятость при отборе объектов для вы- борочного исследования препятствуют получению правильных общих вы- водов, делают результаты выборочного исследования непоказательными для всей генеральной совокупности, т. е. нерепрезентативными. Например, если изучаются свойства вида, сорта, породы с целью вы- явить характерные особенности этих массивов, то нельзя выбирать толь- ко лучших представителей из лучших условий обитания, из лучших хо- зяйств; также неправильно для указанной цели изучать только средних или треть лучших, треть средних и треть худших. При такой порочной ор- ганизации наблюдения получается не объективная, а искаженная харак- теристика генеральной совокупности. Эта характеристика будет с таким распределением особей по их качеству, которое совершенно не соответст- вует действительному составу генеральной совокупности и только отра- жает то, что исследователю казалось лучшим или худшим еще до про- ведения самого исследования этого вопроса. Для получения правильной, неискаженной характеристики всей ге- неральной совокупности необходимо стремиться обеспечить возможность отбора в выборку любого объекта из любой части генеральной сово- купности. Это основное требование должно выполняться тем строже, чем бо- лее изменчив изучаемый признак. Вполне понятно, что при разнообразии, приближающемся к нулю, например, в случае изучения цвета волос или перьев некоторых видов любой способ отбора выборки даст репрезента- тивные результаты. В различных исследованиях применяются следующие способы от- бора объектов в выборку: 1. Сл уча й ны й повтор ный отбор, при котором объекты изучения отбираются из генеральной совокупности без предварительно- го учета развития у них изучаемого признака, т. е. в случайном (для дан- ного признака) порядке; после отбора каждый объект изучается и затем возв~ращается в свою генеральную совокупность, так что любой объект может попасть повторно в выборку. Такой способ отбора равносилен отбору из бесконечно большой генеральной совокупности, для которого разработаны основные пока- затели взаимоотношений между выборочными и генеральными вели- чинами. 2. Сл уч айны й бес повтор ны й от бо~р, при котором объек- ты, отобранные как и при предыдущем способе — случайно, не возвра- щаются в генеральную совокупность и не могут повторно попасть в выборку. Зто наиболее распространенный способ организации выборки; он равносилен отбору из большой, но ограниченной генеральной совокупно- сти. Это учитывается п~ри определении генеральных показателей по вы- борочным. 3. М е х а н и ч е с к и й о т б о.р, при котором производится отбор объектов из отдельных частей генеральной совокупности, причем эти части предварительно намечаются механически по квадратам опытного
96 РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЯ поля, по случайным группам животных, взятых из разных ареалов попу- ляции и т. д. Обычно намечается столько таких частей, сколько предполагается взять объектов для изучения, поэтому число частей. бывает равно числен- ности выборки. Механический отбор иногда осуществляется выбором для изучения особей через определенное число, например, при пропускании животных через раскол и отборе каждого десятого, сотого и т. д., или при взятии укоса через каждые 100 или 200 метров, или отборе одного объек- та через каждые встретившиеся 10, 100 и т. д. экземпляров при исследо- вании всей популяцИи. 4. Типический прапор цион ал ьн ы й отбо р, предпола- гающий необходимость предварительного изучения генеральной сово- купности по общебиологическим или хозяйственным особенностям. На основе такого изучения вся генеральная совокупность ~разбивается на части по типу растительных сообществ, в которых обитает вид, по релье- фу местности, по виду хозяина паразита и т. д. Из каждой такой части для изучения выбирается в случайном порядке число экземпляров, про- порциональное населенности отдельных частей. Например, при изучении определенной породы рыб берутся уловы из разных водоемов и из каж- дого улова берется число экземпляров, пропорциональное степени засе- ленности или объему водоема. При определении среднего процента жира за лактацию коровы про- бы молока для исследования берутся за контрольные дни каждого ме- сяца пропорционально удою за эти дни. На основе такой выборки дается характеристика жирномолочности удоя за всю лактацию, который в данном случае является генеральной совокупностью, разбитой на типи- ческие части — месячные удои. Типический пропорциональный отбор производится также при опре- делении качества шерсти у группы овец по пробам, взятым из каждого руна пропорционально весу рун. 5. Сер и й н ы й отбор, при котором генеральная совокупность разбивается на части — серии. Некоторые из них исследуются целиком. Этот способ отбора называется также гнездовым. Применяется этот спо- соб с успехом в тех случаях, когда исследуемые объекты достаточно равномерно распределены в определенном объеме или на опреде.чснной территории. Например, при исследовании зараженности воздуха или во- ды микроорганизмами берут для исследования пробы, которые затем подвергаются сплошному исследованию. В некоторых случаях гнездовым способом могут быть обследованы также сельскохозяйственные объекты. Так при изучении выходов мяса и других продуктов переработки мясной породы скота в выборку можно взять всех животных этой породы, поступивших на два-три мясокомби- ната. При изучении величины яйца в колхозном птицеводстве можно в нескольких колхозах провести изучение этого признака у всего пого- ловья кур. Часть никогда не может полностью охарактеризовать все целое, поэ- тому характеристика генеральной совокупности на основе выборочного исследования всегда будет не точной, всегда будет иметь некоторую большую или меньшую ошибку. Такие ошибки являются ошибками обобщения, ошибками. связанны- ми с перенесением результатов, полученных при изучении выборки, на всю генеральную совокупность и называются ошибками репрезента- тивности. Для более глубокого понимания сущности ошибок репрезентатив- ности необходимо рассмотреть классификацию ошибок, встречающихся в научных и производственных исследованиях.
97 ОШИБКИ ИССЛЕДОВАНИИ ОШИБКИ ИССЛЕДОВАНИЙ При всяком исследовании имеется опасность допустить целый ряд ошибок самого разнообразного характера. Все эти ошибки могут быть сведены в следующис группы. А. Общие ошибки, свойственные как сплошному, так и выборочному исследованиям. К ним относятся: 1. Методические ошибки: а) применение порочной методики проведения опыта (нарушеиие стандартных правил фиксации препаратов и химического анализа, выбоп неправильного направления исследования, несоответствующего постав- ленным задачам, и др.); б) невыравпснность условий жизни для контрольных и опытных особей. 2. Ошиоки точности: а) использование непроверенных и неправильно градуированных из- мерительных приборов; б) расчеты с недостаточной точностью. Нецелесообразными являюг- ся расчеты с избыточной точностью, так как отнимают без пользы много времени. 3. Случайные ошиоки: а) описки, просчеты; б) перепутывание опытных образцов. Б. Ошибки выборочного исследования, свойственные только выбо- рочным исследованиям. К ним относятся: 4. Ошибки типичности: а) отбор в выборку таких объектов, которые неправильно, односто- ронне отражают свойства генеральной совокупности, например, исследо- вание только выдающихся особей или только средних или треть лучших, треть средних и треть худших; б) отбор в выборку особей, развивавшихся в условиях, резко отлич- пых от тех, которые характерны для всей генеральной совокупности; в) при типическом пропорциональном отборе — отбор не из всех частей популяции и без учета объема типических частей; г) при серийном (гнездовом) отборе — отбор нехарактерной серии или изучение тенденциозно выбранных особей в серии. Все указанные категории ошибок вызываются или неправильной ме- тодикой исследования или неумелым и небрежным выполнением рабо- ты. Избежать их или свести к минимуму возможно при продуманной и тщательной организации эксперимента или обследования. 5. Ошибки репрезентативности. При выборочном исследовании существует еще особый тип ошибок, вытекающих из самой сущности выборочного исследования и имеющих причиной то обстоятельство, что вся генеральная совокупность характе- ризуется на основании изучения лишь ее части — выборки. Таких ошибок — ошибок репрезентативности — невозможно избе- жать ~в выборочном исследовании даже при идеальной организации ис- следовательской работы. Тем не менее выборочное обследование может дать точную характеристику генеральной совокупности вследствие на- личия двух благоприятных обстоятельств: а) величину ошибок репрезентативности можно свестн к минимуму определенной организацией выборочного исследования; б) ~разработаны мстоды, позволяющие по выборочным данным опре- делить возможную величину ошибок репрезентативности с тем, чтобы учитывать их при переходе от выборочных показателей к генеральным.
РЕПРЕЗЕНТАТИВЯОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ Математическая статистика дает способы определения ошибок ре- презентативности (ошибок выборочных показателей) — ошибки средней арифметической т, ошибки доли т, ошибки разности двух выборочных показателей ггг,г, ошибки коэффицйента корреляции m, и др. Рассчитывать величину ошибок репрезентативности требуется толь- ко для выборочных показателей. Предположим, две отары овец иссле- дуются в порядке серийного отбора как выборки из двух, различных ге- неральных совокупностей, например из двух пород, для характеристики этих пород. В этом случае, расчет ошибок репрезентативности средних показателей совершенно необходим для получения правильных выводов и для правильного сравнения обеих генеральных совокупностей — - пород по изучаемому признаку. Если же исследуются не выборки, а генеральные совокупности, опре- делять ошибки репрезентативности не нужно. Например, определяется, в отаре какого чабана получен больший настриг шерсти за год. Для этой цели исследуются две отары и по каждой определяется требуемая сред- няя годовая величина настрига. В данном случае расчет ошибок репрезентативности не будет иметь ни теоретического, ни практического применения. Обе отары в этом слу- чае являются генеральными совокупностями, сравниваемыми, на основе сплошного исследования. Поэтому любой статистический показатель по этим стадам определяется без ошибок репрезентативности. Такие невы- борочные показатели могут иметь все другие категории ошибок, не учи- тываемых математической статистикой, но ошибок репрезентативности они не имеют. Определять величину ошибок репрезентативности следует только в тех случаях, когда организация исследования исключает все другие виды ошибок или когда все они сведены к минимуму. Пусть, напр1имер, изу- чается вес рыб, идущих косяком, в котором обычно впереди — самки, за ними — молодь и сзади — самцы. Если в выборку попали рыбы главным образом из головной части косяка, то при определении среднего веса для всего косяка будет допущена ошибка типичности: в выборку попали особи только из одной части генеральной совокупности, отличающейся от остальных частей. Очевидно, что в данном случае расчет ошибок репрезентативности уже не поможет, так как отбор особей в вьгборку произведен непра- ВИЛЬНО. ОШИБКА ВЫБОРОЧНОЙ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ Ошибка репрезентативности средней арифметической зависит от двух величин: от степени разнообразия признака в генеральной совокупности и от численности:выборки. Предположим, что разнообразие признака в генеральной совокупности равно нулю. Это значит, что все особи данной совокупности совершенно одинаковы. Примером мо>кет слу>кить цвет пера у одноцветных вахидов птиц. В таких случаях любая выборка, даже в один экземпля~р дает точную характеристику всей генеральной совокуп- ности без какой бы то ни было ошибки репрезентативности. Чем больше разнообразие признака, тем он более изменчив, тем больше возможность попасть на такую выборку, средняя которой сильно отличается от гене- ральной средней. Таким образом, чем больше разнообразие, тем больше ошибка ~репрезентативности. Легко также понять зависимость ошибки выборочной средней от численности выборки. Чем больше эта численность, тем большая часть
ОШИБКА ВЫБОРОЧНОЙ СРЕДНЕЙ АРИФМЕТИ~1ЕСКОЙ генеральной совокупности исследуется, тем с меньшей ошибкой может быть дано заключение о средней для всей генеральной совокупности. При увеличении численности выборки ошибка средней уменьшается, и, когда численность выборки достигает численности генеральной сово- купности, ошибка выборочной средней становится равной нулю. При этом обследуется вся генеральная совокупность и полученная средняя уже не выборочная, а генеральная средняя. Величина ошибки средней арифметической определяется в основ- ном исходя из данных, полученных в выборочном исследовании. Предложено несколько формул для расчета ошибки средней — для каждого способа отбора объектов изучения. В большинстве биологических исследований, при любом способе отбора особей в выборку можно применять единую формулу ошибки средней, формулу для случайного бесповторного отбора: 11 1 —— Я Получаемая по этой формуле величина ошибки сказывается слегка завышенной для механического, типического и серийного методов отбора. Это не представляет опасности, так как при этом получается немного более строгий подход к перенесению вьгборочных данных на всю гене- ральную совокупность. Формула ошибки репрезентативности выборочной средней арифме- тической имеет следующие особенности. В точной формуле ошибки средней арифметической в числителе должна стоять сигма генеральной совокупности (0), так как в данном случае требуется мера того разнообразия, которое свойственно признаку по всей массе особей, а не в отдельных ее частях. Точную формулу ошибки средней можно применять в тех редких случаях, когда средняя и сигма генеральной совокупности ~или известны, или в отношении этих величин предлагаются гипотезы, которые нужно проверить путем изучения нескольких выборок. В большинстве исследований генеральная сигма неизвестна, так как вся генеральная совокупность биологических объектов или бесконечно велика, или для не очень больших генеральных совокупностей полностью недоступна для исследователя. Поэтому в указанной формуле пользуют- ся значением ошибки уп = где п илп просто o — выборочное среднее квадратическое откло- нение, полученное для изученной выборки. В формуле ошибки средней.показатель разнообразия o' стоит в чис- лителе, а показатель величины выборок п — в знаменателе. Это соответ- ствует указанным выше зависимостям: чем больше разнообразия призна- ка, тем больше ошибка средней; чем больше численность выборки, тем меньше ошибка средней. / / 1l Множитель ~ 1 — — или превращает о мулу ошибки срсд- 1V ней в формулу для случайного повторного отбора, или обращает ве- личину ошибки в нуль, что видно из следующих простых преобразо- ва ний.
РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗЛТЕЛЕЯ При бесконечно большой генеральной совокупности, т. е. при 1~ =оо Г т — i — o Это и есть формула ошибки средней для случайного повторного отбора. Когда численность выборки приближается к численности всей геке-ральной совокупности, т. е. при n=N, ошибка средней стремится к нулю: В таких случаях исследуется вся генеральная совокупность и полученные показатели не имеют ошибок репрезентативности. В подкоренном выражении частное — равно доле выборки, а все N подкоренное выражение 1 — — равно доле особей, оставшихся в reH".- N ральной совокупности после изъятия выборки. В зависимости от этих 1 — — для общей величины N долоЙ меняется значение множитол~1 ошибки средней, что показано в табл. 50. Табли ца 50 0,05 0,1 0,001 0,5 0,005 0,01 0,7 0,8 0,9 0,95 N N1 ——N 0,9975 0,9950 0,9747 О, 9487 0,83б7 0,7071 0,9995 0,5477 0,4472 0,3162 Э,223б Очевидно, что множитель в формуле ошибки сред- N ней оказывает влияние только в тех случаях, когда в выборку попадает значительная часть генеральной совокупности, не менее 30 — 50%. Обыч- но же, когда в выборке исследуется не более 5 — 10% особей генераль- ной совокупности и более 90 — 95% из них остаются неизученными, мно- / и житель 1 — настолько лизок к единице, что практически не N меняет значения ошибки средней. В таких случаях и для расчета ошиб- ки средней можно применить более простую формулу: а РАСПРЕДЕЛЕНИЕ ВЫБОРОЧНЫХ СРЕДНИХ Представим, что из генеральной совокупности взято большое число отдельных выборок так, что все они исчерпали всю генеральную совокуп- ность: Zn = N. Каждая из этих выборок имеет свою среднюю арифмети-
РАСПРЕДЕЛЕНИЕ ВЫБОРОЧНЫХ СРЕДНИХ )01 ческую. Все эти средние, величины не одинаковы и из них можно соста- вить распределение, в которое 'в качестве дат войдут выборочные сред- ние (рис. 26). Как доказывается в математической статистике, средняя величина этого распределения будет равна генеральной средней, а среднее квадра- тическое отклонение этого распределения выборочных средних будет равно ошибке выборочной средней, приближенную величину которой рассчитывают по приведенным выше формулам. с й < ~ < ~л <~ < ~ < й < M < tv> < M < ~ < Й < м < м < м < м(и (и V< V~ V~ V< Ч< V< V< V с V< V< V< V< Vс Ч< V~ V~ Ч< Ч ° Чс y< VЗб Рб -д М i g ~~ ° ~я -4ш -Зт -Гт - т,д - т +pm 3т +4щ- гг(>]=$652N! ~-~~(~!=ОбдГбд-~— г~р у=оди3 f'(ç) =0,9973 — 2~(г]=ЩЬМ — — zy ~л=оа9гз Рис. 2Г>. Нормальное раслределение дат (а) и выборочных средних (6). Таким образом, рассчитывая величину ошибки выборочной средней, мы тем самым узнаем с достаточной для практики точностью сигму ряда, составленного из выборочных средних для всех выборок из общей изу- чаемой генеральной совокупности. Очень важным свойством распределения таких выборочных средних ,является то, что распределение имеет достаточную близость к нормаль- ному даже в тех случаях, когда распределение индивидуальных дат в генеральной совокупности отличается от нормального. Во всяком нормальном распределении в определенных границах значений признака имеется определенная доля дат. Эту долю можно найти при помощи таблиц интеграла вероятностей или по второй функ- ции нормированного отклонения (табл. VII). Например, если в границах от М до М + а имеется 0,341, или 34,1 ", всего числа особей в группе, т. е. <р (1) =0,34134, то в границах от М до М — o количество будет тем же (34,1%) вследствие симметричности нормального распрсделения. Таким образом, в границах от М+ а до М — o имеется 34,1 + 34,1 = 68,2% дат, что равно удвоенной второй функции нормированного.отклонения при х = 1: 2ср(1) = 2 )< 0,341 = 0,682, или 68,2%. Это означает, что 68,2% дат по своему значению не отличаются от средней величины более чем на ~ 1а. Если за границы взять М ~- 2а, то окажется, что процент дат, отли- чающихся от средней не более чем на ~ 2а, равен 2~р(1) = 2 Х 0,477 = 0,954, или 95,4"!o, т. е. 954% всех дат укладываются в границы от М — 2а до М + 2а. За эти пределы выходит только 4,6% дат.
РЕПРЕЗЕНТАТИВНОСТЬ BblBOPQ×ÍÛÕ ПОКАЗАТЕЛЕЙ 102 Если в качестве границ значений признака взять М+ +Зп, то окажет- ся, что внутри этих границ имеется в нормальном распределении 2q) (3) =2)(0,49865=0,997, или 99,7%, дат, а вне этих пределов— 0,370 дат. В~ границах М+ 4а имеется 2ср(4) = 2 )< 0,49997 = 0,99994, или 99,994%, дат, а вне этих границ 0,006% дат. ВЕРОЯТНОСТЬ ОТЛИЧИЯ ВЫБОРОЧНОЙ СРЕДНЕЙОТ ГЕНЕРАЛЬНОЙ Та б лица 51Вероятность нахождения любой даты в пределах М Я и вне этихпределов Вероятность нахождения Возможность ошибочного суждения, если считать, что любая дата находится внутри пределов М g t e: в пределах М:~ t e:Р~ --t(t)(х= t) вне пределов М + ta:1 — Р~ = — 1 — ~~(1) 1:P — Р,) 0,999936 0,99900 0,99730 0,99000 0,98758 0,95450 0,95000 0,68268 0,50000 0,000064 0,00100 0,00270 0,01000 0,01242 0,04550 0,05000 0,31732 0,50000 4 3,30 'Э ~Э 2,58 25 2 1,96 1 0,6745 1: 15625 1: 1000 1: 370 1 - 100 1:81 1:22 1:20 1:3 1:2 Из всего множества значений , равных значениямнор- в табл. 51 приведены только те, мированных отклонений х ==- а которые применяются или применялись в биологических исследованиях. ,Яоли особей, находящихся в пределах М» 1а (t=1, 2, 3, 4), указы- вают на ту вероятность, с которой взятая наугад особь будет иметь зна- чение признака, отличающееся от средней не более чем на ta, или любая выборочная средняя будет больше или меньше генеральной средней не более чем на tm. Определение вероятности наибольшего возможного от- клонения от средней означает определение вероятности условного пред- положения, что все особи распределения вмещаются в заданные грани- цы, например, в пределы М+2а или М+2т. Это поедположение допускается во всех случаях при определении достоверности выборочных показателей и имеет характер основной гипо- тезы всякого биометрического исследования. Определение критериев хи квадрат и лямбда, ожидаемого отклонения выборочных средних от гене- ральной средней, достоверности разности двух выборочных величин, до- стоверности различий девиат, достоверности коэффициента корреляции и корреляционного отношения совершенно невозможно без предваритель- ного установления условных границ, включающих все распределение или вероятности того, что наугад взятая дата окажется в определенных за- данных границах. Вероятности нахождения любой взятой наугад даты в пределах +to (от средней) для некоторых 1, имеющих практическое значение, приведены в табл. 51 и на рис. 26.
ТР!! СТЕПЕНИ ВЕРОЯТНОСТИ БЕЗОШИБОЧНОГО СУ;ЖДЕНИЯ 103 ТРИ СТЕПЕНИ ВЕРОЯТНОСТИ БЕЗОШИБОЧНОГО СУЖДЕНИЯПРИ ОПРЕДЕЛЕНИИ ГЕНЕРАЛЬНЫХ ВЕЛИЧИНПО ВЫБОРОЧНЫМ Многолетняя и обширная практика применения методов математи- ческой статистики в биологических исследованиях у нас и в зарубежных странах показала, что пределы допустимых границ И+ За или М+3m слишком велики и исходят из требований излишней осторожности. Критерий l = 0,6745, при котором все распределение разбивается на две равные части: Р, =0,5 и 1 — Р, =0,5, применялся как множитель в формулах ошибок репрезентативности для получения величин «вероят- ной ошибки». Например, вероятная ошибка средней арифметической выражалась формулой Е,, = 0,6745 Q . В настоящее время эта ве- личина как обязательный множитель в формулах ошибок не применяется. / = 1, 2, 3, 4 — «круглые» легко запоминающиеся значения показа- телей границ. Условно считается, что вся совокупность дат или выбороч- ных сводных величин включена в пределы этих границ. При этом, ко- нечно, допускается ошибка, возможность которой показана в правом столбце табл. 51. Например, если принять, что все распределение целиком включается в границы М+ 4а или М+ +4т, то Р, = — 0,999936 есть вероятность того, что это предположение правильно, вероятность ошибиться составляет 1 — Р, = 0,000064, т. е. один случай на 15625. Это значит, что если будет проведено 15625 исследований и в каждом будет условно принято, что вся совокупность находится в границах М+4п, то ошибка в этом отно- шении будет допущена только в одном исследовании. Вероятность в дан- ном случае настолько ничтожна, что возможностью такой ошибки вполне можно пренебречь в любом биологическом исследовании и считать, что любая дата не может отличаться от средней более чем на 4а и любая выборочная средняя не может отличаться от генеральной средней боле» чем на 4т. Такой осторожный подход к вопросу об условных границах, вмещающих все распределение, требуется не всегда. Очевидно, что ве- роятность ошибочного суждения может быть принята и большей чем 0,000 064, а возможность ошибиться может быть допущена и чаще чем 1 раз на 15625. В исследованиях можно пренебречь ошибкой, вероятность которой для данного исследования может считаться малой, так как по известно- му постулату теории вероятностей маловероятные события считаются невозможными. В различных научных работах по общей и прикладной биологии и в практике условно принимались различные показатели границ, в кото- рых вмещаются все даты распределения. Первоначально считалось, что такими границами является М+ Зо или М+ 3 т. Возможность ошибки при таком допущении — 1: 370. Она считалась малой и, следовательно, такой, которой можно пренебречь в большинстве исследований. На основе этих соображений и было введено в практику исследова- ний «правило трех сигм» (М + За), считавшееся единым критерием гра- ниц, условно включающих в себя все распределение. Обладая простотой и легкостью запоминания, такой критерий во многих случаях приводил к отказу от определенных выводов и к резкому обеднению результатов работы.
РЕПРЕЗЕНТАТИ В НОСТЬ ВЫ БОРОЧН ЫХ ПОКАЗАТЕЛ ЕИ В большинстве работ можно сузить границы, условно вмещающие все распределение, приняв за такие границы М+2а. В настоящее время применяются три степени вероятности того, что заключение о границах, вмещающих все распределение, не будет оши- бочным: М»-2а; М»-2,5а и М» За или М»=2т; М»=2,5т и М»-Зт. В соответствии с этим устанавливаются три стандартных фиксиро- V — М М — М ванных значения х = или t .= . При t = 2 условно счи- 3 ОЕ тается, что все распределение включается в пределы М»- 2т, т. е., «T;> выборочная средняя не может отличаться от своей генеральной более чем на 2т. Вероятность безошибочного суждения при этом равна 0,9545, возможность ошибиться 1: 22. Такая вероятность безошибочного пред- положения вполне допустима для большинства исследований в общей биологии, цитологии, физиологии, генетике, ботанике, зоологии, расте- ниеводстве, зоотехнии, медицине. При t = 2,5 условно считается, что все распределение ие выходит за пределы М»- 2,5т, т. е. выборочная средняя не может отличаться от своей генеральной более чем на 2,5т. При этом вероятность безошибоч- ного суждения Р2,5=0,98758, возможность ошибиться 1: 81. Такая ве- роятность безошибочного суждения требуется в экономич 'cl<Hx исследо- ваниях, связанных с рекомендациями проведения затрат денежных средств и труда, а также при обоснованиях реорганизации произ- водства. Повторные исследования биологических обьектов, уточняющие пре- дыдущие наблюдения, также требуют второй степени вероятности сужде- ния о границах, включающих все распределение. При t = 3 вероятность безошибочного суждения, как уже указыва- лось, Р~ — — 0,9973, возможность ошибиться — 1: 370. Такая вероятность безошибочного суждения требуется в особо от- ветственных работах: в исследованиях, проверяющих спорные теоретиче- ские выводы, в экспериментах, выясняющих вредное действие веществ, и др. Первоначально при установлении границ, условно включающих все распределение при «круглых» значениях t или х : 2; 2,5; 3, считалось, что величины соответствующих вероятностей соответственно равны 0,95; 0,99 и 0,997, в то время как точные значения этих вероятностей 0,9545; 0,98758 и 0,9973. При разработке методов дисперсионного анализа за показатели границ, условно включающих все распределение, стали приниматься не величины 1 или х, а «круглые» значения вероятностеи: для первой степе- ни 0,95000, для второй — 0,99000 и для третьей — нес1<олы<о повышенное значение 0,99900. Af — A~I В соответствии с этим были уточнены и значения 1= — — —: длч т 11ервой степени вероятности t~ — — 1,96 (а не 2), для второй t~ —— 2,58 (а не 2,5) и для третьей t3 —— 3,30 (а не 3) . В настоящее время биологические исследования переходят на эту систему границ и при расчете таблиц, и при определении достоверности всех выборочных показателей. В некоторых работах предельные границы, включающие условно вс<. распределение, называются «доверительными границами». V — М М — hf Взаимоотношения показателей х .=. или t — и соот- 0 )й ветствующих степеней вероятностей, показанные в табл. 51, справед..1ивы
. 105 ВОЗМО)КНАЯ ВЕЛИЧИНА ГЕНЕРАЛЬНЫХ СРЕДНИХ ~+ 3 — 1,5t где t, -- показатель вероятности для выборок с числом степеней сво- 4 боды ъ, t — показатель вероятности для больших выборок. В зависимости от типа исследований он равен или ti —— 1,96 (Pi — — 0,95), или ~,=2,58 (Р2=0,99), или t3 —— 3,30 (Рз — — 0,999); ъ — число степеней свободы. При определении генеральной средней по выборочной v = и — 1, при определении достоверности раз- ности средних для некоррелированных выборок v =- n~+ nz — 2 и т. д. Установление условных границ, включающих все распределение, при lloh1oLllè одного из трех фиксированных предельных з~'.ачений— V — М 1 М1 — М необходимо при решении многих задач, возникающих при биологиче-ских исследованиях. BO3MO)K НАЯ ВЕЛ ИЧ И НА ГЕНЕРАЛ ЬНОЙ СРЕДНЕИ При определении по выборочным данным соответствующих гене- ральных показателей, считается, что генеральная величина показателя (или средней, или разности средних, или коэффициента корреляции, или сигмы и т. д.) может отстоять от своих выборочных значений не более чем на 1 ошибок репрезентативности. При этом величина t устанавливается по указанным правилам. Из трех возможных значений выбирается тем большее значение, чем ответственнее выводы исследования только для таких исследований, которые имеют дело с достаточно мно- гочисленными выборками. При малочисленных выборках распределение выборочных средних, а также всех выборочных величин уже достаточно сильно отличается от нормального и следует закону распределения малых выборок, установ- ленному английским ученым Гассетом, писавшим под псевдонимом Stu- dent (Стьюдент) . Распределение Стьюдента отличается от нормального тем больше, чем меньше численность выборки, причем для каждой численности ма- лой выборки имеется свое частное распределение. Для каждого значения численности малых выборок можно заранее рассчитать величины t для трех принятых степеней вероятности. Например, при первой степени вероятности (Р1 — — 0,95) и при чис- ленности выборки и = 10 показатель вероятности t> — — 2,3, а при числен- ности и = 3 t~ —— 4,3. Значение величины l для любой численности выборок и для трех степеней вероятности безошибочного суждения приведены в табл. Х. При использовании этой таблицы для нахождения возможной вели- чины генеральной средней арифметической число степеней свободы равно числу дат в выборке без однои: v = и — 1. Поэтому надо брать ту строку табл. Х, которая соответствует числу n — 1, если n — численность вы- борки. Если нет таблиц, подобных указанной, то величину t можно опре- делить приближенно по формуле
l OCi РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ Гечеральная средняя определяется по формуле М- Мl tm. Это значит, что величина средней в генеральной совокупности мо- жет иметь значение не менее М — tmи не более М -~- tm. Наименьшая возможная величина, генеральной средней =М — tm в некоторых случаях приобретает большое практическое зна- чение в качестве гарантированного минимума. П р и м е р 51. При изучении веса животных получены следующие выборочные показатели: n=1000; M=200,76; а=29,92. Предположим, что массив, из которого взята выборка, очень велик и численность ге- неральной совокупности может быть принята равной бесконечности. Тогда ошибку этой выборочной средней надо рассчитывать по формул т = - —, что дает следующий результат: l и / П / у Она будет равна / 1 — =- 0,947 V 0,75 = 0,819. 4000 2 9,92 Теперь пределы генеральной средней М =- 200,76 + 2 )( 0,819 не более 202,4=202 / П р и м е р 53. Предположим, что выборка предыдущих примеров получена из генеральной совокупности, насчитывающей всего 1500 особей. В этом случае ошибка выборочной средней — = 0,946 Р о,ззз = 0,546, 15ОО 29,92 lr, 1 ' 29,92 0 946 Ошибка выборочной средней приписывается к этой средней через знак ~-: М=200,76~-0,946. В разбираемом примере при t=2,0 генеральная средняя М --= 200,76++2 Х 0,947 не менее 1 , = 19 не более 202,7=203 Это, конечно, еще не есть точная величина средней в генеральной совокупности, но вполне достаточное практически приближение к нему. П р и м е р 52. Предположим, что выборка предыдущего примера взята как проба из гурта в 4000 особей. Ошибка выборочной средней в данном случае должна рассчиты- ваться по формуле
107 ВОЗМО)К!ИЯ ВЕЛИЧИНА ! ЕНЕРАЛЬНЫХ СРЕДНИХ а пределы генеральной средней М =- 200,76 2 Х 0,546 не менее 199,7 200не более 201,9= 202 Приведенные примеры подтверждают, что применение полной фор- мулы ошибки выборочной средней оправдывает себя только в тех случаях, когда в выборку попала значи- тельная часть генеральной совокупности, например больше трети. П р им ер 54. Предположим, что в предыдущих примерах выбороч- ные показатели М» т=200,76~-0,946 получены в выборке из бескон»ч- ной генеральной совокупности на основе изучения всего 10 экземпляров, причем по условиям задачи требуется высшая третья степень вероятно- сти безошибочного суждения: Р, > 0,999. Для малой выборки, численностью в 10 экземпляров, показатель третьей степени вероятности безошибочных суждений t3 — — 4,8. Эта вели- чина взята из табл. Х для числа степеней свободы v =n — 1 =10 — 1 =9. При этих условиях возможная величина генеральной средней М — 200,76 4,8 Х 0,946 ««» MeHee 196,2 196 не более 205,3=205 J Определение генеральной средней в таких широких пределах может иметь значение только при самых грубых первоначальных исследова- ниях. Для исследования, при котором необходима третья степень веро- ятности безошибочного суждения, такие результаты, конечно, не дают ответа с требуемой точностью. В таких случаях необходимо исследовать значительно более многочисленную выборку. П р им е р 55. Для 100 пробных делянок, взятых в случайном по- рядке из разных мест большого массива пшеницы, был рассчитан сред- ний выборочный урожай: n=100; М=15,6 ц/га, а=2,5 ц/га. На основе этих данных ожидаемый средний урожаи по всему массиву при v=100— 2,5 — 1=99, t« — — 2(Р« — — 0,95) и и . ' 0,25 может быть определен в «оо следующих размерах: М = 15.,6+2,0 у,' 0,25 н» более 16,1 ц/га Если требуется особенно осторожно подойти к прогнозу урожая длявсего массива посевов, то гарантированный минимум определяется при/в=3 3 (Рз=О 999): Мяа 15,6 — 3,3 Х 0,25 = — 14,775 = 14,8 ц,,'га. При мер 56. При испытании нового сорта кормовой свеклы уро- жаи каждого из 20-ти опытных участков сравнивался с урожаем каж- дого из 20-ти соседних контрольных участков. В результате получено 20 разностей для каждой пары опытного и контрольного участков. Неко- торые разности были положительными — новый сорт дал больший уро- жай, некоторые разности были отрицательными — новый сорт дал мень- шии урожай. Для таких выборочных разностей были рассчитаны сред-
РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕП няя арифметическая М=+1 ц/га, а=2,5, ошибка средней = 0,56, и=20 и М~-т=+1,0~-О,56 ц/га. Возможное превышение нового сорта над стандартным при засеве 6oJIbIIIHx площадей, исходя из первой стадии вероятности безошибочно- го суждения Р» — — 0,95, для v=19 при 3» — — 2,1 (см. табл. Х) равно не менее 0,18 ц/га 1 не более + 2,18„ц/га М ==- + 1 + 2,1 )( 0,56 Оказалось, что на больших массивах новый сорт может быть и бо- лее урожайным (d=+2,18) и менее урожайным (d= — 0,18), по сравне- нию со стандартным сортом. Такие результаты указывают на то, что новый сорт при испытании не показал преимущества перед стандартным. П р и и е р 57. При испытании другого сорта на 40 парных участках (опытиых и соседних контрольных) были получены такие данные: 3,0 и - 40; М- » 40 ц/га; == 30; т 0,47. При вероятности безошибочного суждения P»=0,95; v=39; 1=2,0 при посеве на больших площадях ожидаемое общее преимущество ново- го сорта — не менее + 3,06 ц/га ~не более»-4,94 ц/га ~ В данном случае можно с уверенностью ожидать, что новый сор~ будет более урожайный, «ем старый. Превышение урожайности будет ие менее чем на 3 ц/га. П р и~» ер 58. Стимулятор ожирения испытывался на 30 подсви»»- ках, получавших препарат, которые сравнивались с 30 аналогами, не получавшими препарата. При полной выравненности условий кормления и содержания в конце опытного периода было получено 30 разностей для средних суточных привесов опытных подсвинков и их аналогов. В<с раз- ности оказались положительными: и- 30; М 1,82 г 'cyzzza.zz. О»»ределение возможного эффекта действия препарата при массовом откорме подсвинков, исходя из первой степени вероятности безошибоч- ного суждения P» — — 0,95 при v=29 и t» —— 2,0, дало следующий результат: — не менее»- 46,4 г'сушкине более —,' 53,6 г,'сутки Очевидно, можно ожидать благоприятные действия препарата, та»; как он повышает привесы не менее чем на 46 г/сутки. П ример 59. Так как цена препарата описанного в примере 58, велика, потребовалось с большой осторожностью подойти к прогнозу целесообразности его применения. Поэтому на основе первичных мате- риалов, приведенных в примере 58, было подсчитано возможное превы-
ВОЗМОЖ,НАЯ ВЕЛИЧИНА ГЕНЕРАЛЬНЫХ СРЕДНИХ 109 шение привесов исходя из высшей, третьей степени вероятности без- ошибочного суждения Рз — — 0,999, при v=0,29 и t3 — — 3,7: М = + 50+3 7 Х 1,82 ( не менее + 43,3 г,сутки 1 не более +56,7 г/сутки J Оказалось, что с большой уверенностью можно ожидать повышения привесов по крайней мере на 43 г(сутки. Расчеты показали, что при такам гарантированном минимуме повы- шения привесов применение этого препарата все еще будет рента- бел ьнь~ м. Пример 60. При оценке производителей по потомству за показа- тель наследственной ценности иногда берется индекс производителя, равный разности между удвоенной средей признака по дочерям и сред- ней по матерям: B=2D — М. Ошибка репрезентативности индекса может быть рассчитана по формуле 2a„+ 2'о 'м2 2 2 где в числителе стоят квадраты сигм по ряду .разностей (d=D — М) по ряду дочерей и по ряду матерей, а в знаменателе — число сравниваемых пар дочь — мать. Например, при оценке быка Богатыря-60 по 59 его дочерям полу- чены следующие средние по проценту жира в молоке: по дочерям и =59, М„=5,16, ~„==-0.34; по матерями =59, М„= 3,57, ~,„=0,39; по распределению разностей (дочь — мать) n=59, М~ = +1,59, ~„=0,40. По этим выборочным показателям индекс Богатыря-60 по жирно- м олоч и ости В =2X5,16 — 3,57=6,750/о, л ошибка индекса / 2 0,402 + 2 0,343 — 0,39'-' m„:=- =-- 0,08Ц . Наибольшее практическое значение в данном случае имеет гаранти- рованный минимум генеральной оценки. Если его определить с макси- мальной третьей степенью вероятности безошибочного суждения (Р, =- 0,999) при — -- 58 и t=3,4, будем иметь BKIB — 6,75 — 3,4 X 0,08 = 6,48N . Это свидетельствует об очень высоком вероятном уровне наследствен- ных задатков производителя по жирномолочности. При массовой оценке производителей гарантированный минимум индекса может быть приравнен величине В;„=- В -- 2ш . На основе полученных выборочных показателей (n=59, B=6,75, m> =0,08'~~), приняв первую степень вероятности безошибочного сужде- ния Р1 — — 0,95, v=58, t~ — — 2,0, можно дать прогноз генеральной оценки производителя: 75, 2 0 8 не менее 6,59N не более 6,91N
110 РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕИ Пример 61. Для выяснения возможного ввса раковины устрицы было взвешено последовательно 16 экземпляров. Получены следующие данные: =- 2,0 г. n=16, М=150 г, а=8, т =- 16 Таблицы значений t не было, поэтому величину показателя вероят- ности первой степени определили по приближенной формуле: 2~20 20 15 — 3 — 1,5;к,' 2,0 18 — 3 <,5 =-- 2,0+ Бо всей генеральной совокупности возможный средний вес раковин — не менее 145,4= 145 г ~ не более 154,6=155 г П р и м е р 62. Для уточнения веса раковины устрицы было взвеше- но последовательно 400 экземпляров. Получены следующие данные: 10 п=400, М=-152 г, 10, т= =0,5 г. Приняв t =2,6 (как для исследования проверяющего результаты предыдущих работ), можно найти более точно генеральное значение среднего веса раковины: — не менее 150,7=151 гне более 153,3 = 153 г ДОСТАТОЧЙАЯ ЧИСЛЕННОСТЬ ВЫБОРКИПРИ ИЗУЧЕНИИ СРЕДНИХ ВЕЛИЧИН Исходя из формулы ошибки репрезентативности для средней ариф- метической, можно заранее рассчитать тот объем выборки, при которои выборочная средняя будет характеризовать генеральную среднюю с за- данной точностью. Если установить, что допустимая неточность в величине генеральной средней при определении ее по выборочной средней и выразить ее в сигмах: Л -Й~, то приравняв эту максимально допустимую неточность t-кратной ошиб-ке репрезентативности, получим следующее равенство: А==Фа- -tm =t Il Определив из этого равенства и, получим: N й" -1 о N
ДОСТАТОЧНАЯ ЧИСЛЕННОСТЬ ВЫБОРКИ ПРИ И3УЧЕНИИ СРЕДНИХ ВЕЛИЧИН 1] ) При N= ~ это выражение значительно упрощается: 1 ~2 0 = ф2 J~ëÿ установления необходимой численности выборки ири изучении средней арифметической признака требуется предварительно наметить значения величин, характеризующих генеральную совокупность, и ве- личин, определяемых в соответствии с задачами исследования. Для характеристики генеральной совокупности требуется предвари- тельно наметить следующие две величины: 1. Объем генеральной совокупности N. Обычно в биологических ис- следованиях число объектов в генеральной совокупности (в пределах вида, разновидностей сорта, породы и т. д.} столь велико, что вполне до- пустимо принять его равным бесконечности и определение необходимой ~2 численности вести по формуле и -- —. фе~ 2. Сигму признака в генеральной совокупности: N — 1 Примерная наметка этой величины можст быть сделана следующими способа ми. а) На основе предыдущих исследований, если в каждом из них можно определить выборочные значения сигм. За генеральное значение сигмы можно принять среднюю из имеющихся выборочных сигм, рас- считав или простую среднюю 1+ ~2+ ~З ' ' ° ~п или взвешенную среднюю (когда даются более ответственные заклю- чения}: '-'(ni — 1) а,". + v nl (А4; — NE)" "(и; — 1) где , — отдельная выборочная сигма, М,. — - отделыная средняя, Ч -- общая средняя для всех имеющихся выборок, и, — численность отдельных выборок. б} По предполагаемому значению генеральной средней и примерно- му значению коэффициента вариации: — М CV При этом можно считать для признаков со слабым разнообразием CV(10, со средним разнообразием CV= 16--:20, с сильным разнообра- зием C V) 20. Например, если средняя арифметическая признака равна около200, а разнообразие средней степени (CV = 15}, то — 200 15 5 100 в} По примерным значениям минимальной и максимальной величин признака, которые могут встретиться в генеральной совокупности. При этом размах делится на 6 (или на 5, или на 7 в зависимости от числа особей, по которым установлены примерные крайние значения}.
РЕПРЕЗЕНТАТИВНОСЧ'Ь ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ 80 — 405 N = 10 000, Ь= 2 кг, k = = — 0,25; t=-1,96,=, 8 Исходя из задач проводимого исследования требуется предвари- тельно наметить следующие величины: 1. Допустимую неточность искомой величины генеральной среднеи в единицах изучаемого признака: b. — = (И -- M. При весе какого-нибудь зверя .примерно 100 — 150 кг допустимая иеточ~ ость может быть принята, например, равной 3 кг. Если при этом генеральное значение в действительности составляет 120 кг, допускает- ся, что по данным выборкам эта величина будет определена равной не менес I 17 и не более 123. Б первых ориентировочных исследованиях можно допускать ~~оль- шую неточность в определении возможного значения генеральной сред- ней. В тех случаях, когда уже имеется опыт в изучении данного призна- ка у данных особей и требуется внести уточнения к уже имеющимся сведениям, необходимо планировать меньшую неточность в определении возможного значения генеральной средней (для предыдущего примерз, например, Л=1 кг). 2. Показатель точности, т. с. допустимая неточность, выраженная в сигмах: ~ == —. ° ю ч Если M=120 и а=10 примерные генеральные величины, то при 5 1 Л=З кг показатель точности k= — =0,5, а при Л=1 кг k=- — =-О,i. lu 10 Иногда показатель точности приходится устанавливать без нред- вари-ельного определения Л и а. Это бывает в тех случаях, когда нч одним из описанных способов невозможно определить значение гене- ральной сигмы: исследуется совершенно неизвестная популяция. Для таких случаев можно условно принять для первого ориентировочною ознакомления с популяцией Й = 0,3+0,5, для исследований средней точности Й = О,1-'-,-О,3 и для исследований повышенной точности >~ = 0,1. 3. Показатель вероятности (t) того, что заданная степень неточно- сти действительно не будет превышена. Установление показателя вероятности в данном случае вполне воз- можно HpoBQQIITb по уже описанным правилам: а} для большинства биологических исследований 3~ =1,96; P,=0,95, б) для исследований, проверяющих биологические гипотезы, з так>ке относящихся к вопросам экономики производства, t2 — — 2,58: P~ — — 0,99; в) для исследований, дающих особо ответственныс выводы, при изучении действия ядов и других вредных влияний /~ — — 3,30: P> — — 0,999. П р и м е р 63. Планируется исследование, в котором предполагает- ся выяснить средний вес кабарги в определенной зоне обитания. Чис- ленность генеральной совокупности в данной зоне не более 10 000. Из отдельных убитых экземпляров можно видеть, что встречаются взрослые животные с наименьшим весом 40 кг и наибольшим 80 кг. Исследований, подобных предполагаемому, еще не проводилось. Исходя из этих данных, показатели, необходимые для определения численности выборки, будут следующими:
ДОСТАТОЧНАЯ ЧИСЛЕННОСТЬ ВЫБОРКИ ПРИ ИЗУЧЕНИИ СРЕДНИХ ВЕЛИЧИН 113 Численность выборки и должна быть не менее10 0000,25~10 ооо. — '2~ =- 63,5=64 особей ° 10 000 = 231 особь. 0,132 10000. — ' 2~ Если при этом повысить показатель вероятности до tg — — 2,58 (Р~ ——=0,99), достаточная численность выборкиП =10000=- 385 особей.0,1 1210000 ' + Ъ2,6~ П р и м е р 65. Если численность всей популяции кабарги принять равной бесконечности (N= со), то достаточная численность выборки была бы равна 2~ при k =-0,25 t= 1,96, и = — =64 особей, 0,253 = 236,7=237 особей, при /г =-0,13 t = 1,96, и = 0,0169 п'ри k =0,13 t =- 2,58, и = = 400 особей. 0,169 П р и м е р 66. Устанавливается длина пищевода взрослого мужчи- ны, для разработки конструкции гастроскопа. Возможная длина пише- вода М=30 см, что при среднем разнообразии CV=10 —.' 15 дает а= =4 см. Допустимая неточность, по требованиям конструкции гастро скопа, нс должна превышать Л=0,5 см. Следовательно, показатель точ- 0,5 ности Й = — ' = 0,125. 4 Показатель вероятности был задан второй степени tq 2,58 (Рр= =0,99). Достаточная численность выборки 2,58~ 6,6564 0,125' 0,015625 П1,и возможности допустить большую неточность Л =- 1,0 см, Й = 1 — == 0,25 необходимая численность выборки может быть снижена: 4 6,6564 0,0625 2,58'- = 106,5=107. П р и м е р 64. Первая наметка в предыдущем примере показала, что возможно задаться меньшим показателем точности при определении генеральной средней веса кабарги. Поэтому Л была принята равной 1 кг. Это значит, что если генеральная средняя в действительности рав- на, например, 60 кг, то допускается, чтобы выборочная средняя была не 1 менее 59 и не более 61 кг. При этом показатель точности k = — = 0,13, 8 и при неизменных остальных исходных данных достаточная численность выборки определится следующим образом:
РЕПРЕЗЕНТАТИВНОСТЬ ВЪ|БОРОЧНЫХ ПОКАЗАТЕЛЕЙ 114 ОШИБ1~А РАЗНОСТИ ВЫБОРОЧНЫХ СРЕДНИХ Если сравниваются генеральные совокупности, то разность между соответствующими средними определяется без какой бы то ни было ошибки репрезентативности: всякая генеральная разность полностью достоверна. Все другие категории ошибок такая разность может иметь. Например, если в одном совхозе средний суточный привес каждо- го из откормочников за год был 810 г, а в другом 800 г, то не может быть никакого сомнения в том, что в первом совхозе привес за данныи год действительно больше, чем во втором, и при том на полную вели- чину полученной разности: 810 — 800= + 10 г. Совершенно по-другому оценивается разность между двумя выбо- рочными средними. При анализе такой разности всегда возникает воп- рос о ее достоверности, т. е. о том, правильно ли разность между дву- мя выборочными средними характеризует ту генеральную разность средних, которая имеется. между двумя соответствующими генеральны- ми совокупностями. Например, в совхозе, разводящем одну породу свиней, при опти- мальных условиях средний суточный привес за год составляет 820 г. В соседнем совхозе, разводящем другую породу, при таких оптимальных условиях средний суточный привес за год составляет 800 г. Можно ли на основании полученной разности (820 — 800=+20 г) заключить, что все откормочники первой породы при данных условиях будут давать привесы, большие на 20 г в сутки по сравнению с откор- мочниками второй породы? Такого заключения сделать пока нельзя. В данном случае каждая из сравниваемых групп является серийной выборкой: первая — из первой породы, вторая — из второй породы. 1~аждая из полученных средних (М,=820 г и M> —— 800 г} является выборочной средней и имеет свою ошибку репрезентативности. Поэтому и разность между ними также имеет ошибку репрезентативности. Следо- вательно, выборочная разность характеризует различие между обеими генеральными совокупностями по изучаемому признаку всегда с ошиб- кой репрезентативности. Ошибки при определении генеральной разности по выборочной мп- гут привести к следующим результатам. Может оказаться, что, несмотря на то, что по выборкам первая по- рода оказалась лучше второй, на самом деле генеральная средняя боль- ше у второй, а не у первой породы. Может случиться также, что при наличии разности между выборками генеральные совокупности по изу- чаемому признаку одинаковы или, наоборот, при отсутствии разницы между выборками между соответствующими генеральными совокупно- стями имеется достаточное различие. Поэтому для каждой выборочной разности необходимо определить ее достоверность, т. е. выяснить, правильно или искаженно она харак- теризует искомую разность между соответствующими генеральными средними. На практике это сводится к вопросу о возможности обобще- ния результатов научного или производственного эксперимента и наблюдения. Решаются эти вопросы при помощи особого показателя — ошибки выборочной разности т„. Ошибку выборочной разности можно определить, зная ошибки обе-
ОШИБКА РАЗНОСТИ ВЫБОРОЧНЫХ СРЕДНИХ их средних и коэффициент корреляции между сравниваемыми особями по изучаемому признаку: 2 2 Щ = y m)+ Щ — 2rm,т2 д — К / где щ„- ошибка репрезентативности разности двух выборочных сред- них арифметических, т, — ошибка репрезентативности первой средней, щ~ — ошибка репрезентативности второй средней, r — коэффициент корреляции между сравниваемыми группами особей по изучаемому признаку (показывает степень стати- стической связи между изменениями двух признаков или од» ного признака у двух групп особей). При полной прямой свя- зи r=+1,0 (максимально возможное значение) при отсутствии связи r=0 и при полной обратной связи r= — 1,0 (минимально возможное значение). В зависимости от величины коэффициента корреляции общая фор-мула ошибки разности может иметь следующие частные значения: 1. При r=0 с 2 2 m" - rn. В этом случае или нельзя ставить вопрос о статистической связи (напри- мер, при сравнении разных групп, пород, видов и т. д.), или связь вооб- ще может быть, но в данном случае она отсутствует. По 'этой формуле ошибка разности равна корню квадратному из суммы квадратов ошибок сравниваемых средних. При графическом оп- ределении ошибки разности она равна гипотенузе прямоугольно- го треугольника, катетами которого являются ошибки сравниваемых средних. 2. При r-, О, гФ +1, r Ф — 1 (коэффицнент корреляции не равен нулю и не равен предельным значениям) формула ошибки разности имеет общий вид: 2 2 с m д т + т~ — -2rm т 1 3. При к=+1 2 2 щ~ -- т, -t- m> — 2m,m.. — P(m, щ р In, — m, m„== т,; m2-~ т,т., = ~ (щ, . щ„)в — щ, -щ,, 2, 2 / где m> — большая из двух ошибок. В этом случае существует прямая полная связь между сравнивае- мыми группами особей по изучаемому признаку: с увеличением приз- нака у особи первой группы происходит также увеличение признака у соответствующей особи второй группы. Это может быть при тщатель- ном подборе аналогов в опытную и контрольную группы и при равно- мерном изменении признака у обоих представителей каждой пары ана- логов, а также при проведении опытов по методу периодов и при со- хранении особями своего ранга и в контрольном, и в опытном периодах.. Та!< как практически коэффициент корреляции бывает равен точно r=+1,0 очень редко, то к этой формуле прибегают в тех случаях, ког- да между сравниваемыми группами особей по изучаемому признаку должна быть заведомо значительная прямая связь. 4. При r= — 1
РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ В этом случае между группами особей по изучаемому признаку су- ществует полная обратная связь или же предполагается значительная обратная зависимость. Это может случиться при неодинаковом дейст- вии какого-нибудь агента на разные подопытные объекты, например, если испытываемый фактор понижает вес крупных подопытных лабо- раторных животных и повышает вес мелких животных. Тогда в конце опыта более крупным аналогам в контроле будут соответствовать более мелкие аналоги в опыте. BO3MO)КНАЯ ВЕЛИЧИНА ГЕНЕРАЛЬНОЯ РАЗНОСТИ Для нахождения генеральной разности по выборочной имеются предпосылки, аналогичные тем, которые имеются и для генеральной средней. Если составить вариационный ряд из всех возможных разностей между всеми парами выборок, которые можно получить из двух срав- чиваемых генеральных совокупностей, то сигма этого ряда будет равна ошибке выборочной разности, которая рассчитывается по приведенным выше формулам. Это распределение выборочных разностей можно также принять за нормальное, поэтому весь размах ряда умещается обычно в пределах М ~- 1а или в данном случае в пределах d + tmd. Исходя из этих общих предпосылок, можно принять, что генераль- ная разность отличается от выборочной не более чем на величину 3-кратной ошибки разности: d = — — d+ tmd. Величина t определяется также, как и при изучении количественных признаков по табл. Х. Число степеней свободы при определении воз- можных границ, включающих все распределение выборочных разностей, равно суммарной численности обеих выборок без двух: v=n>+nq — 2. Следовательно, при использовании табл. л надо брать строку, со- ответствующую этому числу степеней свободы. Яля многочисленных выборок можно принять одно из трех значе- ний критерия: t~ —— 2,0 (или 1,96) при (n~+n2 — 2) не менее 30, t2 — — 2,6 (или 2,58) при (n~+nq — 2) не менее 70, t3 —— 3,3 при (n~+n2 — 2) не ме- нее 200. Для малочисленных групп, при отсутствии табл. Х можно примерно определить величину t по той же формуле, что и при изучении количе- ственны~ признаков: ч+ 3 — 1,51~ при этом v =п1+п2 — 2. П р и м ~ р 67. Сравнивались по весу две разновидности зеркально- го карпа одного и того же возраста, разводившиеся в количестве не- скольких сотен. При вылове в один и тот же срок все рыбы были взве» шены, а затем получены следующие сводные .показатели по весу: для первой разновидности n,=100, М,=-610 г, ~,=15, т,= = 1,5 г; 1О
КРИТЕРИЯ ДОСТОВЕРНОСТИ ВЫБОРОЧНОЯ РАЗНОСТИ 117 для второй разновидности 20 =2,0 г. n — -100; М,==600 г: ~,= 20; т== g 1CO Разность средних Becoadt 2 =- 610 — 600 т,~ = g 1,5' -~- 2,0' == 2,5 г.. Генеральная разность на основе таких выборочных данных, при обычной для больших, выборок степени вероятности Р1 — — О,95 (tI —— 2) можег иметь следующее значение: + 10г, ошибка разности не менее -y 5 z не более + 15 > d. =- Ш+2т,~ = КРИТЕРИЙ ДОСТОВЕРНОСТИ ВЫБОРОЧНОЙ РАЗНОСТИ Не всегда t-кратная ошибка выборочной разности меньше самон разности. Иногда t-кратная ошибка разности превышает саму разность, и тогда нижний предел генеральной разности оказывается отрица- тельным. П р имер 67. Для двух сравниваемых сортов арахиса среднее со- держание жира в семенах М~ — — (30» 3) '/о и М2 — — (38» 4) '/0. Ошибка средней арифметической приписана к средней через двой- ной знак»-. На основе этих данных разность средних и ошибка раз- ности будут равны: з,-4 =5ОО. Если по этим данным определить возможное значение генеральной разности, то при 1=2 получим не менее — 2/о не более + 18N Эти результаты исследования позволяют сделать следующие вы- воды: 1. Оба возмох<ные пределы генеральной разности имеют положи- тельный знак. В данном случае t-кратная ошибка разности не оказа- лась больше самой разности. Это очень важное обстоятельство указы- вает на то, что полученная разность достоверна, что разновидность, которая в выборке оказалась лучшей, будет лучшей и во всей генераль- ной совокупности, что вывод, полученный в опыте, можно перенести на всю первую разновидность: она в данных условиях будет давать в сред- нем больший вес по сравнению с второй разновидностью. 2. Возможное преимущество первой разновидности определяется достаточно широким размахом пределов генеральной разности: первая разновидность может давать прибавку в весе на 5 — 15 г больше второй, или на 0,8 до 2,5О/о от среднего веса второй разновидности (600 г). Улучшение это незначительно по сравнению с средним весом рыб. 3. Полученные пределы генеральной разности указывают на то, что повторные выборочные исследования, подобные проведенному, могут дать различные разности между весами сравниваемых разновидностей, причем эти выборочные разности будут находиться примерно в найден- ных пределах: не менее +5 и не более +15 г.
118 РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЯ т. е. наименьшее значение генеральной разности может быть и отрица- тельным. Это значит, что лучшим сортом по содержанию жира может быть и второй сорт (d> 1 = — -~- 18),и первый сорт (dz .1 == — 2). Выборочная разность с большой ошибкой, дающая такие неопреде- ленные результаты, называется недостоверной выборочной разностью. Как ясно из приведенного примера, достоверность выборочной раз-. ности определяется ее отношением к собственной ошибке. На основе этого положения введен особый показатель — критерий достоверности разности: Ш 7 md где 1~ критерий достоверности разности, d — выборочная разность, т„— ошибка выборочной разности. Разность считается достоверной, если критерий достоверности раз-ности равен или превышает принятый в исследовании показатель веро-ятности безошибочного суждения: t~ » или ИЛИ где значения t~, t2, t3 определяются по табл. Х или по указанным выше формулам. При определении критерия достоверности разности могут быть по- лучены две основные категории результатов. Если td > t,, разность достоверна. Это значит, что выводы, полу- ченные на основании выборочной разности в общем виде можно пере- нести и на генеральную разность При этом, если средняя первой груп- пы больше средней второй группы, m и средвяя всей первой генераль- ной совокупности будет больше средней всей второй генеральнои совокупности. В этом случае будет вполне правильным, репрезентатив- ным и тот общий вывод, который сделает исследователь по материалам своего эксперимента или наблюдения. Если td < t,, разность недостоверна. Это значит, что выводы, ко- торые получаются при сравнении выборочных средних, не могут быть распространены на соответствующие генеральные совокупности, что эти выводы правильны только для изученных групп — выборок — и что нельзя придавать этим выводам общего значения. При этом надо помнить, что недостоверная разность только не под- твержлает разности генеральных средних, но не утверждает отсутствия различия между ними. Не менее важным является вопрос о причинах недостоверности раз- ности. Разность может оказаться недостоверной вследствие недостаточ- ной численности сравниваемых выборок. Тогда, при повторении иссле- дования на более многочисленном материале, получается достоверная разность, дающая репрезентативный и вполне определенный ответ о том, какая из сравниваемых групп имеет большую генеральную среднюю. Выборочная разность может оказаться недостоверной и по другой причине, потому, что сравниваются такие генеральные совокупности,
119 Е РИ1'ЕРИ й ДОСТОВЕРНОСТИ ВЫБОРОЧНОЙ РАЗНОСТИ которые по данному признаку имеют практически одинаковые гене- ральные средние. Поэтому в одних исследованиях выборки показывают преимущество одной группы, а в других — другой. В таких случая~ IIoBTopc'Hèå выборочных исследований на более обширном материале дает тоже неопределенный ответ: разность опять оказывается недост.>- верной. При увеличении численности выборок уменьшается ошибка pa ~- ности их средних, но в то же время и сама разность становится меньшс и опять не превышает своей ошибки в установленное число раз. Применение критерия достоверности выборочной разности можно показать на ряде примеров. Во всех этих примерах предполагается, что организация исследования исключает все виды ошибок, кроме неустра- нимых — ошибок репрезентативности. П р и м е р 68. При изучении действия ионизации воздуха на pas- витие кроликов были исследованы две группы: 1 — кролики, содержав- шиеся в обычных условиях, П — кролики той же породы, пола, воз- раста, содержавшиеся в таких же условиях, но при ионизации воз- духа. В качестве результативного признака были взяты средние суточ- ные привесы ках<дого кролика за весь период опыта. Обработка мате- риалов и полученные результаты показаны в табл. 52. Пример 69. В опыте, выяснявшем влияние стимулятора ожирс- ния на откормочников, были рассчитаны среднесуточные привесы жи- вотных в станках, где применялся стимулятор, и в контрольных станках, где стимулятор не применялся. Все остальные условия откорма были одинаковыми. Получено для опытной группы М> — — 750+ 60 г, для контрольной группы М2 —— 600~ 80 г. Дальнейшие расчеты дали следующие результаты: И=750 — 600=150 г, m„+GO -~во =- 100 г, 2,6 150 — 1,5, 1(ритерий достоверности оказался меньше t< — — 2,0. В данном случае опыт не дал репрезентативного результата: повышение привеса в опыт- ной группе оказалось недостаточным по сравнению со своей ошибкой и поэтому не может быть перенесено на всех откормочников в данным условиях. П р и м е р 70. После опыта, описанного в предыдущем примере, был поста~влен другой опыт с тем же количеством откормочников, но при строгом подборе аналогов в опытную и контрольную группы. Пред- варителыно было отобрано около 150 пар животных предельно одина- ковых между собою по породе, полу, возрасту, дате опороса, весу и те- лосложению. Число исследованных пар было таким же, как и число животных в опытных станках при проведении первого опыта. Одного из каждой пары переводили в опытную группу, другого — в контрольную. По окончании опыта получены такие же средние привесы, как и в первом опыте: М>=750~-60 г; M2 — — 600+. 80 г. I 1 При данной постановке опыта между откормочниками опытной > контрольной групп существует достаточно большая корреляционная
РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ О ъО 'Ф О CO ОО (.Ь ОО ОО ~О ~ф ОО Cb О Щ ('~ 'Ф О ОФс~сч;) тю м;) Сч ~О~ О ~О СЧ СЧ «~~ «Ф~ь С~l t ~О Cb CD С'Э Е ! II ~2 CO СО tD ( »О t ~»' eu СЧ сб СЬ 00 с~:) С~1 ~О О ~О О ~О О ~О О LO О Cb Оъ 00 ОО ~ t сО (Ю ~ ~О ~-е ~ ~-е ~е ~ ~ е ~» е~ 1 I I I ~ I I I ( i! йО И~ 1.О И~ И~ ~О И~ И~ и ~ аО И~ С~4 ( СЧ ~ СЧ ~ СЧ ( С~ ( Ф Ф ОО ОО t C Ф Ф ~О ~О 4' ° ° т~ ~ ~ у ° у~ »~ т ° ~ г~ у~ ~О Cb сО сО 'Ф С5 СЧ СЧ ~О СЧ 00 сО 'Ф Ф W W ('» ~О ~О Ф О ОО ОО ( - ОЪ ОО т4»~э ~4 ую е4 ~ ~ С~~ ~ ° »4 еФ »6 Я Ф Ю ОО ('» ~ Ф О Ф ~ аО Ю ° Ф ~О ОО W Ф ОО ОО ~ ОО ОО Ф Ф ОО Ю ОО Ф ( ~6 ~ ~ уЮ ~а ~ ~ ~ ° ~ ~ »4 ~ ~а»» ~О»~~ ~О с~~ Ф Ю 'Ф Я О Ю ( ° СЧ Ф О Cb W ~ ~ ~И ~ сО ~' сО Оъ сЮ ( ~'~4 Ф'~»~ ~"'Ю ° '~Ф ~ 4»~~'4 ~ ~ ~Й ~'»» ° ~ ~ »4 у < 1' Оъ СЧ Ь» СЬ с~ СЧ оо ор с~ цр е ир m ир оо е с Ф е c m е ж т4 ~ »6 ~ ° ~ ф4 у~ е4 ~4 ~е ~ ~е ~Ф еа аО СЧ Фь Cb II И~ Щ О сО 1) ОО СЧ + ФГ~ ф СЧ И О М~ II + ~О и~ СЬ СЧ ( С5 СЧ И
121 критЕрий ДостовЕрности выБорочной рАзности связь. Расчет показал, что коэффициент корреляции r=+0,875. Ошибку разности надо в данном случае рассчитывать по общей формуле т~= m> --, т2 — 2Гт~т~ 2 2 дальнейшие расчеты дали следующие результаты: d=750 — 600=150 г, т~ =- p 6am + 802 — 2 ~ о,875 )< Бо )< во == 40 г, =-38, f, = 262,0 150 40 В этом опыте критерий достоверности разности превышает третью, высшую, степень вероятности безошибочного суждения: 1„.~ (t, = 3,3). Теперь с полной уверенностью можно заключить, что стимулятор может повысить привесы всех откормочников данной городы в данных условиях. П р и,м е р 71. После получения репрезентативных результатов (ом. пример 70) было проведено производственное испытание способа от- корма с применением изученного стимулятора на большом поголовье жкормочников. В результате по откормочникам, получавшим стимулятор, привес М,=750+ 30 г, по откормочникам, не получавшим стимулятор, M2 —— =600+ 40 г. ,цальнейшие расчеты дали: d=750 — 600=150 г, т~ = — 1/зо +- 4о~ ==- 50 г, =-3,0, 1,. = 2,62,0 150 50 Разность получилась достоверной со второй степенью вероятнос1л безошибочных суждений; производственные испытания подтвердили эф- фективпость введения стимулятора в рационы откормочников. Из анализа проведенных опытов следует, что в первом опыте не по- лучалось достоверных, репрезентативных выводов из-за малочисленно- сти подопытного материала. В двух других опытах получены достовер- ные выводы при том же абсолютном значении разности: 750 — 600= =150 г. Во втором опыте та же по величине разность оказалась достоверной вследствие применения метода аналогов, при котором получаются более достоверные разности, разности с меньшими ошибками репрезентатив- ности. В третьем опыте та же по величине разность оказалась достовер- ной вследствие значительного увеличения численности подопытного материала, что уменьшает ошибки средних, а значит ошибку разности этих средних. Такое увеличение достоверности разности при увеличении числен- ности выборок бывает не всегда. В описанных опытах увеличение до-
РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ 122 стоверности разности происходило потому, что ошибки разности умень- шались, а сама разность оставалась неизменной. Может случиться и так, что после опыта, давшего недостоверную разность, при увеличении численности подопытного материала, разность опять окажется недостоверной, так как вместе с уменыпением ошибки разности и сама разность уменьшится. В таких случаях, как уже указывалось, недостоверная разность, по- лучавшаяся в нескольких опытах, означает не только то, что опыт и дал репрезентативного результата В этих случаях недостоверный ре- зультат говорит и о том, что между соответствующими генеральными средними нет достаточной разницы. В описанных выше трех опытах такой результат означал бы, что испытываемый стимулятор не повы- шает привесо1в у откормочников данной 1породы в данных условиях П~р и м е р 72. )~ля изучения действия радиационного излучения на развитие помидоров было исследовано 20 кустов, выращенных из облу- ченных семян, и 20 контрольных кустов, выращенных на соседней де- лянке. Получены следующие сводные показатели по числу завязавшихся плодов: )im 5,8 4,5 2 — 28 1 — 20 13,0 10,0 Опытные кусты .. 20 Контрольные кусты . 20 Оказалось, что выборочная разность d=3,0, ее ошибка m„: P/'1,8з.3 1Р -= 1,64. Показатель вероятности 1 в данном случае должен уста|навливать- ся, исходя из v=ï~+п~ — 2=20~-20 — 2=38. Критерий достоверности разности 3,0 1,64 ill m, ккил кг Груши g 30'-'+40-' =50 200 1850~30 1б50~40 Опытная Контрольная Разность оказалась недостоверной: критерий ее достоверности ни- же наименьшего показателя первой степени вероятности безошибочного суждения. Первый ориентировочныи опыт не дал репрезентативных результа- тов; на основе полученных данных нельзя считать, что у всех помидо- ров при данном типе облучения семян будет увеличиваться число завя- завшихся плод'ов. П р и м е р 73. В опыте по откорму бройлеров эффективность про- веряемого нового рациона оценивалась также и по калорийности мяса. Этот показатель удалось определить, в группе, получавшей новый ра- цион, по трем пробам и в контрольной группе — по двум. Получены следующие результаты:
ДОСТОВЕРНОСТЬ РАЗНОСТИ СРЕДНИХ ПРИ КОРРЕЛИРОВАННЫХ ВЫБОРКАХ 1(ритерий достоверности разности 1 5,8 200 =40, 50 v =3+2 — 2=3 Несмотря на крайне незначительную численность выборок, опыт дал ре;трезентативные результаты. С первой степенью вероятности Р1= =0,95 можно ожидать что новый рацион будет способствовать получе- нию более калорийного мяса при его массовом применении. П р и м е р 74. На мясокомбинате для уточнения условий приемки двух отар овец нужно было выяснить, какая из них состоит из более упитанных животных. Определение упитанности решено было провести австралийским способом — по толщине накостного слоя (мускулы, жи- ровая и соединительные ткани) на поперечных отростках поясничных позвонков у контрольных животных, выбранных из каждой отары и пе- реработанных стандартным способом. Из первой отары взято 5 овец, у которых после переработки зарегистрированы минимальная и'макси- мальная толщины накостного слоя на пояснице: llm~ — — 1,1 — 2,1 см. Из второй отары взято 6 овец. У них после переработки Ит~ — — 0,7 — 1,7 си. Больше данных не было, таблицы значений t тоже не было. Выяснение достоверности преимущества первой отары при таких первичных материалах можно провести следующим образом: 1,1 -+- 2,1 2 1 — 1,1 М — ' ' — 16см а,= 2 5 и, =-5; 0,7 + 1,7 0,2~5 2m~ =- =1,2 см; =-0,008; n2 ==- 6, М., = 1,7 — 0,7, 0,2 =-0,2; тр = -= 0,007; 1,6 — 1,2 = 0,4 с.и; т„=. Qg,opg + ю,о1>у = 0,12 v=5+6 — 2=9; =- 3,3; t„ =- 2,0 + 9+3 — 1,Q 2 0,4 4' У 0,12 2 X 2,69+ 3 — 1,5 )( 3,6 Та ки м обр азом, с достаточной вероятностью можно сч итать, ч го первая отара состоит из более упитанных овец (в массе). ДОСТОВЕРНОСТЬ РАЗНОСТИ СРЕДНИХ ПРИ КОРРЕЛИРОВАННЫХ ВЫБОРКАХ Иногда по средней величине признака сравниваются такие выборки, в которых каждой особи в одной выборке соответствует определенная особь в другой выборке. В таких случаях выборки всегда равночислен- ны, и все исследуемые особи могут быть соединены в пары, число кото- рых (и) и есть численность каждой коррелированной выборки. Так бывает при проведении опытов по методу аналогов или по методу перио- дов, а гак>ке при сравнении дочерей (или вообще потомков) с их мате- рями или отцами.
124 РЕП РЕЗЕНТАТИ ВНОС'ГЬ ВЫБОРОЧН ЫХ ПОКЛЗАТЕЛ ЕИ ФКак уже указывалось, в таких случаях должна быть примененаформула ошибки разности в 'общем виде:2 2щ = т1 -+- т2 — 2rm,т»d где r — коэффициент корреляции между сравниваемыми группами по изучаемому признаку. Можно значительно упростить вычисления и определить точное значение ошибки разности средних при коррелированных выборках, не вычисляя коэффициента корреляции. Для этого необходимо определить разности между значениями признаков для каждой пары. Какую вы- борку считать для всех имеющихся пар первой — безразлично. При этом если в выборке, которая для всех пар считается второй, значение при- знака у представителя пары больше, чем у его аналога, то разность по- лучается отрицательная. Для группы полученных разностей А г нужно рассчитать основ- ные показатели: К~11 г среднюю арифметическую М,, - = D 3 среднее квадратическое отклонение п — 1 'ш ошибку репрезентативности средней арифметической т = Критерием достоверности в таких случаях будет отношение средней разности к ее ошибке: td =- Шд Показателями трех степеней вероятности безошибочного сугкде»я (t,.) определяются при сравнении коррелированных BbI6op0K обычныM способом, исходя из числа сравниваемых пар без одной: к=п — 1. П р и ме р 75. При изучении значения прогулок для высокомолоч- ных коров был проведен опыт по методу периодов. Из стада выбирались коровы на третьем .месяце лактации, дающие свыше 20 л молока в сут- ки; таких коров удалось отобрать 8 голов. В течение первого периода — предварительного — коровы содержа- лись, как и все стадо, без прогулок; в течение второго периода — опыт- ного — коровам регулярно каждый день предоставляли прогулку и в третьем — заключительном — периоде коровы опять содержались без прогулок. Каждый период длился 15 дней. По окончании опыта были рассчитаны среднесуточные удои для каждой коровы за каждый из трех пер иодов. данные первичной обработки материалов оказались следующими: Л~ кОрон 27 31 28 21 25 23 1IIIll 25 27 2б 22 25 21 30 31 2g 27 30 27 29 31 29 31 30 30 Среднесуточные удои по периодам, кг Обработка этих материалов приведена в табл. 53. Оказалось, что разность между удоями за опытный и предваритель- -ный периоды достоверна, так как критерий достоверности td = 3,8 пре-
ДОСТОВЕРНОСТЬ РАЗНОСТИ СРЕДНИХ ПРИ КОРРЕЛИРОВАННЫХ ВbIБОРКАХ 1~5 4 ° s ° ° J ° 3 ° ° ° ° ° ° ° ° ! ° ! ° ° Ф l ° ° ° в 1 el r Ф !3 ° ° ° ° ° ° 3 ° ! ! а ° э в ! ° ° 3 ° ° в ° ° б ° 3 ° ! ° Ю ° в ° j ° ° ° а ° ! ° 11~'1! 1 I е!j!а ° I ! ° ! ) С ° J ° ° ! ° ! 3 ° ! ° ° ° ° ! ° 3 ° ° ! ° ° ° ев !r ° ! ° ll а j в 1 в ° а ! ° ° ° в ! ! ° ° в 3 ° ° ! ° й ° С в 4 ° ° ° ° ° ° ° С ° ° r r ° а° !'3 4 ° С ° ° а ° ° ° ° ° ° С ! ° ! ! ! а ° 3 ° ° 4 ° ° ! ! ° ° ° ° ° ° ° С ° ! ° l. ° С ° ° ° 1 ° ' ° ° ° ° ° s ° 4 ° ° ! а ° C ' -; ' ' Э ° II 1) С ! ° 1 ° ° ° б ф Удои ио псриодам, кг Рэсности улосв Il — ! И — Il
126 РЕПРЕЗЕНТАТИ ВНОСТЬ ВЪ|БОРОЧНЫХ ПОКАЗАТЕЛЕЙ Пример 77. В опыте, описанном в предыдущем примере, прове-. рялось также и число клубней, полученных с одного куста. Получены следующие сводные показатели по соответствующим разностям: и = 100; И~=+3 клубня;о=-30; и=3,0. Критерий достоверности разности ра~вен: + 3,0 3,0 ~ =99 По этому признаку получены нерепрезентативные результаты. Опыт не подтвердил свойства нового удобрения повышать также и количество клубней в кусте. П р и м е р 78. При оценке быка Богатыря-60 по жирномолочности 59 его дочерей из каждого показателя дочери вычитался показатель его матери. Эти 59 разностей можно разнести в вариационный ряд и про- извести необходимые расчеты (табл. 54). Таблица 54Распределение разностей (дочь — мать) по проценту жирав молоке и =59 Мд — — +- 1,58 + 0,0571,58= — =30,60,057 3,5 2,7 2,0 = 59 — 1 = 58 Оказалось что средняя разность по проценту жира в молоке между дочерьми быка Богатыря-60 и матерями имеет положительное и для данного признака очень большое значение: +1,59%, и превышает свою, ошибку репрезентативности в 31 раз. Бо атырь-60 является сильным и достоверным улучшателем жирно- М ОЛОЧ'Н ОСТИ. П р и м е р 79. При проверке действия стимулятора ожирения, опи- санного в примере 58, получены следующие сводные показатели ряда разностей привесов между подсвинками, получавшими препарат, и ко'- трольными аналогами: и =30; .М,,— +50г; о,, —:10:, т,,-1,82г В данном случае по двум коррелированным выборкам критерий до- стоверности разности ,72,8 1- 50 1,82 ~~г1 t d т~ — — 27 5; Опыт подтвердил достоверное благоприятное действие препарата. П р и м е р 80. При испытании нового сорта кормовой свеклы, onн. +2,85 —: -+3,14 +2,55 —: -+-2,84 +2,25 —: +2,54 +1,95 =: .-+-2,24 +1,б5 —: -+-1,94 +1,35 —: +1,64 +1,05 —: +1,34 +0,75 —: +1,04 +-0,45 —: -[-0,74 -з,о +2,7 +2,4 +2,1 +1,8 +1,5 +1,2 +0,9 +О,б 1 1 1 8 11 19 14 3 1
127 ДОСТЛТОЧНАЯ ЧИСЛЕННОСТЪ BblBOPKH ПРИ ИЗУЧЕНИИ РАЗНОСТИ СРЕДНИХ санном в примере 56, получены следующие сводные показатели по ра.. ностям урожаев на каждом опытном и контрольном участках: и ==- 20; М„-',- 1 ц,'га, -.,„2,5 и т,, -: (1,56 цуга.. 1(ритерий достоверности разности средних по двум коррелирован- ным признакам ,92,92,1«=1 +1,0 М~ md — 1,8, 0,56 Разность оказалась недостоверной, испытание не подтвердило пр- имущество нового сорта. П р и м ер 81. В другом испыта~нии, описанном в примере 57, ра;- пределение разностей урожаев на опытных и соседних контрольны~ участках имело следующие сводные показатели: и — 40; М,, "- 4,0 ц,га; -„3,0; и„0,47 ц га. критерий достоверности разности средних по двум коррелировац- ным выборкам У2,7 4,0 0,47 8,51, md Разность оказалась в вь|сшей степени достоверной. Можно с боль- шой уверен1ностью ожидать, что новый сорт в аналогичных услови ) к будет болес урожайным. ДОСТАТОЧНАЯ ЧИСЛЕННОСТЬ ВЫБОРКИПРИ ИЗУЧЕНИИ РАЗНОСТИ СРЕДНИХ При планировании эксперимента или обследования можно заранее установить допустимое расхождение между выборочной разностью (d =- М, — М.,) и соответствующей генеральной разностью (d=M,--hf ). Это будет такая неточность в 'определении разности между двумя гене- ральными средними, которой можно пренебречь, исходя из задач ис- следованияия. Эта неточность Л, выраженная в единицах измерения признака, мо- жет быть приравнена t-кратной ошибке разности: Г 2 2 621 4) 2 1т,, = 1 m>+m2 и П2 Это значит, что при численности выборок п1 и п> выборочная разность с вероятностью, ссютветствующей принятой величине t, не будет отли- чаться от своего генерального значения более чем на величину 1т„ или менее чем на заданную величину неточности Л. Приравняв п~ — — ап~ и определив из приведенного равенства п,, по лучим: 1 2 — — — а1 -~-— 2 ~ 2 1 2 2 ) ) и1 а и, . а 02+ 62 1 2 n,+ап, Л..t
РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ 128 откуда: ") Зто и есть общая формула планирования численностей выборок и| и и2, достаточных для изучения разностей с допустимой неточностью определения генеральной разности Л и с заданной вероятность;о безошибочных суждений [~=3(P)]. Если нет 'оснований считать, что средние квадратические отклоне- ния а1 и а~ различны для сравниваемых групп, то можно прин~.ть их одинаковыми: а~=а~=а. Tora формула определения достаточной чи"- леннос=и выборок будет иметь более простую структуру: а (n2 —— аи,). Если при этом выразить допустимую неточность Л через сигму, оди- наковую для обеих групп, то получим, что при Ь И, наконец, если не обязательно планировать разную численность срав-ниваемых выборок и есть возможность отобрать для исследования оди-наковые по объему группы, то а=1, n~ —— n2 и формула приобретает со-всем простое строение: 1 и,= — 1+— И 1 2Р (nq — — n~). Пять величин, которые необходимы для планирования достаточной численности выборок при изучении разностей средних, определяются по тем же правилам, как и при изучении средних: N — численность генеральных совокупностей. Проще принять за бесконечность, что мало изменит результаты, а если изменит, то только в сторону более осторожного подхода к вопросу о не- обходимом количестве экспериментального материала; о — среднее квадратическое отклонение. В обеих группах может быть одинаковое или различное; устанавливается или на осно- max — min ве предыдущих исследований, или по размаху ~= или по предполагаемой средней и примерному коэффициенту вариации; — допустимая абсолютная неточность в определении генеральной разности. Устанавливается, исходя из степени изученности во- проса и ответственности выводов; Й=Л: а, t,. — показатель вероятности безошибочных суждений. Устанавли- вается по общим правилам. t~ — — 1,96; t~ — — 2,58; t3 — — 3,30, что со- ответствует вероятностям P> — — 0,95; Р2 —— 0,99; P3 — — 0,999.
ДОСТАТОЧНАЯ ЧИСЛЕННОСТЬ ВЫБОРКИ ПРИ ИЗУЧЕНИИ РАЗНОСТИ СРЕДНИХ П р и м е р 82. Планируется испытание стимулятора роста жемчу- жин при следующих исходных данных: 1) N= co, 2} А=10 мг. Это значит, что если действительное действие стиму- лятора при его массовом применении будет равно, например, Ш = М»— —.Мг=+100 мг, то в выборках эта разность не должна выходить за пределы d = М, — М» = ()- 90 —: + 110) мг, 3) а=20 мг. Определено, исходя из примерного среднего веса жем. чужин Af=500 мг и коэффициента вариации 4 — 5%, 4) Й=Л: а=10: 20=0,5, 5) t=2 (обычный биологический эксперимент). Достаточная численность выборок: 2Р 2,2' = — = 32, и =32. »г 05г Необходимо исследовать не менее чем 32 раковины, получившие стимулятор, и 32 раковины контрольного садка. П р и м е р 83. Планируется изучение эффективности дегельмин- тизации по увеличению среднесуточного прироста телят, освобож- денных от инвазии печеночной двуусткой при следующих исходных данных: 1} N= со, 2) Л=20 г. Это значит, что если действительный эффект дегельмин- тизации в массе выражается в генеральной прибавке привеса, например, d =: М, — М„=100 г, то при выборочной проверке дегельминтизирован- ные телята могут дать прибавку привеса в пределах d = М, — М» = (+ 80 г —: + 120 г), 3) а — сигма среднесуточных приростов равна 60 г (исходя из пред варительного анализа хозяйственных записей), 4) '=20: 60=0,33, 5) t=2,6 (эксперимент имеет большое экономическое значение). Достаточная численность выборок должна быть: 0,33~ = 124, n.» ,= 124. Необходимо исследовать не менее 124 телят дегельминтизированных и 124'телят с неликвидированной инвазией. При мер 84. В следующем эксперименте телята отбирались про- порционально числу обработанных (20%) и числу необработанных (80%). Следовательно, в этом случае n>=4n<, a=4. За сигму привесов взято для обработанных телят 60 г, а для необработанных — 40 г. При Л=20 г достаточная численность выборок в этом случае определяется следующим образом: 2 ~Р 2 '2 2,б2 40~ — г1 + — = — ' 60'+ — = 68, ~2 а 20~ 4 n» — — 68 ° 4=272, т. е. необходимо взять из дегельминтизированных 68, а из необработан- ных — 272 телят.
РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ ОШИБКА ВЫБОРОЧНОЙ ДОЛИ Ошибка репрезентативности выборочной доли определяется по та- 'ким же формулам, как и ошибка средней арифметической: т ~Р Р 7L и 1 ——Ф При Л'= с~ т Р Р и Необходимая при этом величина среднего квадратического отклоне- ния доли ,=Уж где Р — доля особей в генеральной совокупности, обладающих изучаемым признаком, Q=1 — Р — доля особей в генеральной совокупности, не имеющих данного признака. Определение генеральных показателей в большинстве случаев не- возможно. Поэтому на практике пользуются приближенными значения- МИ СИГМЫ ДОЛИ: а =Ур.,у, где р и q=1 — р — выборочные доли. Среднее квадратическое отклонение доли обладает однои особен- ностью, которой нет у сигмы количественных признаков: сигма доли не может быть более~, = 0,5, что видно из табл. 55. Таблица 55 Урд ' =Ур РЧ 0,24 0,21 0,16 0;09 0,0099 0,09 0,1б 0,21 0,24 0,25 0,3 0,4 0,46 0,4б 0,50 0,4 0,3 0,2 0,1 0,01 0,9 0,8 0,7 0,6 0,5 О,б 0,7 0,8 0,9 0,99 0,1 0,2 0,3 0,4 0,5 0,49 0,4б 0,4 0,3 0,0995 Этой особенностью пользуются в тех случаях, когда требуется знать долю признака в генеральной совокупности, а никаких данных для это- го нет. Тогда принимается максимально возможное значение: ~ = — 0,5. Если подставить значение сигмы доли в основную формулу, то по- лучится рабочая формула для определения ошибки репрезентативности доли: r ) и и m~ = при N + ~ РЧ и ll 1 ——Ф m~=
ВОЗМО)КНАЯ ВЕЛИЧИНА ГЕНЕРАЛЬНОЙ ДОЛИ ВОЗМО)КНАЯ ВЕЛИЧИНА ГЕНЕРАЛЬНОЙ ДОЛИ Возможная величина генеральной доли определяется на основе вы- борочных показателей по таким же правилам, как и возможная величи- на генеральной средней: 0,04 )с 0.96 рочной доли при У= ~ т = ' ' =0,009. SC0 Если принять вероятность безошибочного суждения P> — — 0,95, то при v=500 — 1=499 t=2,0 (см. табл. Х). Следовательно, возможная гене- ральная доля р= 0,04 ]-2,0)(0,009 не менее 0,022, или,2N не более 0,058, или 5,8Уо Пример 86. При исследовании 200 особей одного вида у 60 из них оказалась повышенная способность выдерживать сильное пониже- ние температуры. Как часто такие особи могут встречаться среди всей популяции? В данном случае выборочная доля Р= 60 200 = 0,30, ошибка выбороч- 0,3 )( 0,7 ной доли m 200 Принимая P( — — 0,95 и t=2,0 (см. табл. Х для v = 199), можно опре- делить генеральную долю: не менее 0,236, или 23,6М не более 0,364,. или 36,4Я П р и м е р 87. Проверялась гипотеза опыляемости клевера пчела- ми. Были прослежены 10 полетов пчел, причем оказалось, что 6 из них- о~ылякпцие. Требовалось выяснить возможный процент опыляющих по- летов у всей изучаемой породы пчел с вероятностью третьей степени (P =0,999). Проведены следующие расчеты: = — =06, т„= 6 / 0,6 х 0,4 10 10 = 0,155. При v=10 — 1=9 t3=4,8, поэтому возможная величина генераль ной доли не менее — 0,17 ( — 17N) не более 1,37 (137N) Р= ptm . При заданной вероятности безошибочного суждения (P> — — 0,95, или Р~ —— 0,99, или Рз — — 0,999) считается, что генеральная доля может отли- чаться от выборочной не более чем на величину своей t-кратной ошибки Величину t в данном случае можно определить по общим правилам (по табл. Х) для v=n — 1 или по приближенной формуле, как и при определении генеральной средней. П р и м е р 85. При исследовании нового сорта кукурузы оказалось, что среди 500 осмотренных початков у 20 из них цвет зерен был значи- тельно темнее, по сравнению с обычным цветом зерен этого сорта. Како- ва возможная доля этой аномалии в масштабах всех сортовых посевов? 20 В данном случае выборочная доля р == — — ==- 0,04, ошибка выбо- 500
132 РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕИ Так как по условиям задачи процент пчел не может быть ни отри- цательным, ни большим 100, то полученные результаты нужно пони- мать так, что генеральная доля может быть в пределах от 0 до 100%. Такой ответ равносилен отсутствию всякого ответа, что является след- ствием малочисленности изученной выборки. Полезным выводом опи- сываемого исследования является вывод, что данный признак в ответ- ственных исследованиях нельзя изучать по выборке в 10 особей. Это бы- ло учтено в последующей работе. П р и м е р 88. Для изучения опыляемости клевера пчелами той же породы было проверено значительно большее число полетов. Из 209 изученных посещений цветков разными пчелами 140 оказались опыляю- щими. Расчеты дали следующие результаты: 0,7 х 0,3200 140 р= — =-07: ш 200 При v=199 Ка — — 3,3, поэтому возможная величина генеральной доли не менее 0,6, или 60Ж +. не более 0,8, или 80% В данном случае получен достаточно определенный результат: во всей породе количество пчел, опыляющих клевер, не менее 60'/о и не более 80'/о. П р и м е р 89. При просмотре 80 клеток роговицы кролика, подверг- шегося радиационному облучению определенной интенсивности, в четы- рех из них были обнаружены нарушения хромосомного аппарата. 1~ак определить возможную долю таких клеток среди всех клеток роговицы исследованного кролика, если под руками нет таблицы крите- риев достоверности (табл. Х)? 4 В этом исследовании выборочная доля р= — =0,05; ошибка вы- 80 0,05 )< 0,35 0 024 Р 80 Величину t (второй степени) при отсутствии таблицы критериев достоверности можно определить по приближенной формуле: 179 =2,6+ (v = 80 — 1 = 79) . 79+ 3 — 1,5;~ 2,6 Генеральная доля определится следующим образом: Р = 0,05 2,61;< 0,024 не более + 0,112 барочной доли = 2,67 Отрицательная граница генеральной доли означает, во-первых, что и генеральной совокупности может и совсем не быть особей с изучаемым признаком и, во-вторых, что данное исследование проведено на недо- статочно многочисленной выборке. П ример 90.,Яля уточнения выводов, полученных в предыдущем примере, было просмотрено 500 клеток, среди которых обнаружено 30 с ыарушениями хромосомного комплекса. Табл. Х не было. В этом случае выборочная доля = 0,06. 30 500 0,06 х 0,94 = 0,011. Ошибка выборочной доли т, = 500
ДОСТАТОЧНАЯ ЧИСЛЕННОСТЬ ВЪ|БОРКИ ПРИ ИЗУЧЕНИИ ДОЛЕЙ Величина t была принята второй степени вероятности, как для ис- следований, уточняющих выводы предыдущих работ (12 — — 2,6; Р2=0,99). Поэтому возможная величина генеральной доли не менее 0,031, или 3,1% не более 0,089, или 8,9% ДОСТАТОЧНАЯ ЧИСЛЕННОСТЬ ВЫБОРКИ ПРИ ИЗУЧЕНИИ ДОЛЕЙ достаточная численность выборки, необходимая для определения генеральной доли с заданной точностью, определяется по таким же формулам, как и при определении генеральной средней: при У ,— Й ~ ,ф2N — +1/2 а при N = ~ /2 и= /~г В этих формулах N — численность генеральной совокупности. Она принимается рав- ной или бесконечности, или конечной величине (порядка нескольких ты- сяч и менее). В зависимости от этого применяется одна из двух формул Ь k = — — показатель точности. Так же, как и при определении доста- а точной численности выборки, при изучении количественных признаков иногда можно не устана~вливать значений Л и а, В этих случаях при обычных исследованиях принимают k = 0,3 —:0,5, при исследованиях средней ответственности k =0,1 —:0,3 и при особо ответственных рабо- тах k(0,1. Л — допустимая неточность в определении генеральной доли, т. е. допустимое расхождение между выборочной и генеральной долями (Л=р — Р). Предварительно устанавливается в долях: 0,001; 0,01; 0,02 и т. д. Яля первых ориентировочных исследований можно допускать несколько большие неточности, чем для последующих. а — сигма генеральной совокупности при изучении качественных признаков. Определяется она или по примерному значению генеральной доли, которое можно предположить на основе имеющихся данных: а —.= g pg или другими уже описанными способами. При отсутствии каких-либо сведений о генеральной совокупности принимается максимально воз- можное значение генеральной сигмы: а=0,5. t — показатель вероятности, устанавливаемый по тем же правилам, что и при определении достаточной численности выборки для определе- ния величины генеральной средней. I Ь Если а=0,5, то k = = 2Ли формула достаточной численности 0,5 приобретает следующий вид: р /2 N и= ~2 или e= 4Ь2N 1~г
РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕИ 134 Последние две величины взяты второй степени точности, так как вы- воды исследования могут иметь большое экономическое значение. Исходя из этих данных, достаточная численность выборки 2 б~ 676 и = ' = ' =- 169 животных, взятых в случайном порядке. 0,2- 0,04 П р и м е р 92. Исследуется распространение многососковости сре- ди коров одной породы, причем известно, что процент таких коров нс может быть более 10, а всего коров данной породы — 10000. Сколько надо просмотреть коров, чтобы определить генеральный процент много- сосковых коров с допустимой неточностью не более 2%? В данном случае N=10000; Р=0,1; 0,02 = ~01><09 =03; Ь =002; k= =-0)07; P(=0,95; t=2,0. Достаточная численность выборки 10000 fL =- 0,07~ 10000 = 769 коров. При бесконечной генералыной совокупности 22Il = — =0,072 =- 816 коров. 0,0049 Иногда требуется предусмотреть такую численность выборки, при которой гарантировано наличие хотя бы одной особи, обладающей изу- чаемым признаком, если известна или предполагается доля Р таких особей в генеральной совокупности. Определить такую численность выборки можно по формуле и= 1g (~ — Р~) Ig (1 — P) Р — доля особей в генеральной совокупности, обладающих изу- чаемым признаком, 1 — Р — доля особей в генеральной совокупности, не имеющих изу- чаемого признака, P, — вероятность безошибочного суждения (P) — — 0,95, Р~ — — 0,99, Рз=0 999) 1 — P, — вероятность ошибки при определении достаточной числен- ности выборки. П р и м е р 93. Если среди архаров рождение двоен бывает в од-ном случае на 100 рождений, то чтобы найти хотя бы одну двойню с ве-роятностью 0,95, нужно исследовать 1g (1 — 0.95) 1g 0,05 2,6990 — 1,3010 О = 1g (1 — 0,01) Ig 0,99 1,9956 — 0,0044 где = 296 рождений. П р им ер 91. Выясняется возможный процент самцов у одного ви- да животных в определенном сезоне года. Предполагается, что пример- ный процент самцов в это время равен 20 — 40, допустимая неточность может быть принята равной 10%. В данном случае%= со; p=0,3; ~„=-- p'о,ау 0,7 = 0,46; А=0,1; Й = ' =0,2; P =-0,99; t =-2,6. Э
135 МАКСИМАЛЬНАЯ ГЕНЕРАЛЬНАЯ ДОЛЯ ПРИ НУЛЕВОЙ ВЫБОРОЧНОЙ Для предварительных наметок подобного рода служит табл. 56, в которой заранее рассчитаны необходимые'величины. П р имер 94. В популяции имеется 60% особей, обладающих изу- чаемым признаком. Сколько таких особей может быть в выборках с 30 экземплярами? Столбцу «0,6» и строке «30» в табл. 56 соответствуют два числа (10 и 26). Это значит, что в таких выборках особей с наличием изучае- мого признака может быть не менее 10 и не более 26. Таблица 56 Число особей, имеющих изучаемый признак, которые могут встретиться в выборке из иособей минимальное (левые цифры) и максимальное (правые цифры) число раз,в зависимости от доли признака в генеральной совокупности Доля признака в генеральной совокупности Численностьвыборки 0,6 0,4 О," 0,3 0,5 0,9 0,2 0,8 0,1 П р и м е р 95. В популяции имеется 20% особей с изучаемым приз- наком. Какова должна быть численность выборки, чтобы в нее попала хотя.бы одна такая особь? В табл. 56 в столбце «0,2» есть строка, в которой левая цифра рав- на единице. Эта строка соответствует численности выборки в 50 экземп- ляров. Значит, чтобы гарантировать наличие хотя бы одной особи с изучаемым признаком, требуется взять выборку в 50 экземпляров, хо- тя такое количество может появиться и в выборках из 5 экземпляров (см. правую цифру для строки «5» и столбца «0,2»). МАКСИМАЛЬНАЯ ГЕНЕРАЛЬНАЯ ДОЛЯ,ПРИ КОТОРОЯ BO3MO)KHA НУЛЕВАЯ ВЫБОРОЧНАЯ Предположим, что в выборке не оказалось ни одной особи с нали- чием изучаемого признака. Эт;, может быть или погому, что и в генеральной совокупности нет таких особей, или при наличии их в генеральной совокупности, гене- ральная доля очень мала, и вследствие малочисленности выборки ни од- на из таких редких особей в выборку не попала. Решить этот вопрос можно при .помощи определения величи1ны той максимальной генеральной доли, при которой возможна нулевая вы- борочная доля. Найти такое значение можно, установив допустимую вероятность того, что все распределение выборок из данной генеральной совокупно- сти вместится в границы Р~- 1т„. Очевидно, что генеральная доля не может быть уменьшена в вы- борке больше чем на величину t-кратной ошибки репрезентативности. Если при таком уменьшении она окажется равной нулю, значит искомая 5 10 15 20 25 30 40 50 75 100 0 3 0 4 0 5 0 6 0 7 0 8 0 10 О 12 0 )б 1 19 0 4 0 6 0 8 0 9 0 11 0 13 0 16 1 19 4 26 8 32 0 5 0 8 0 10 О 12 0 15 1 18 3 21 5 25 10 35 16 44 0 5 0 9 0 12 l 15 3 18 4 20 б 25 9 31 17 43 25 55 0 5 0 10 1 14 3 17 5 20 6 23 10 30 14 36 24 51 35 65 0 5 ) 10 3 15 5 19 7 23 1О 2b 14 34 19 41 32 58 45 75 0 5 2 10 5 15 8 20 10 25 13 29 19 37 25 45 40 65 5б 84 1 5 4 10 7 15 10 20 14 25 17 30 24 40 31 49 49 71 68 92 2 5 б10 10 15 14 20 18 25 22 30 30 40 38 50 б0 75 81 99
13б РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ иаксималыная величина генеральной доли равна t-кратной ошибке ре- презентативности. Это можно выразить следующей формулой при Р=О: P тах У Я иЛИ $2 Ртах и+И где P,„— максимально возможная генеральная доля при нулевой вы- борочной, и — численность выборки, в которой не оказалось ни одной осо- би с наличием изучаемого признака, t — показатель вероятности безошибочных суждений. П р и м е р 96. Предпольжено, что процент крипторхов у курдючных овец в определенных природно-хозяйственных условиях равен 15'/о; Сре-ди первых 10 баранов не оказалось ни одного крипторха Возможно ли это объяснить случайностью, а не тем, что ожидания были основаны по неподходящей гипотезе? Приняв t=2,6, получим: P ' = = 0,403. 10 + 2,62 16,76 6,76 max Отсутствие крипторхов среди первых 10 баранов можно объяснить слу- чайностью, так как даже при гораздо большей генеральной доле (0,40) возможна нулевая выборочная. П р и м е р 97. Для уточнения результатов, описанных в предыдущем примере, было исследовано 100 баранов, взятых из разных мест разве- дения этих овец. Среди 100 баранов также не оказалось ни одного крип- торха (ожидалось 15). Максимально возможная доля в породе при t3=3,3 (как при про- верке биологической гипотезы) р 3,3' 10,89 100 -+ 3,3 = 0,0982. 110,89 В данном случае при такой численности выборки уже нельзя объяс- нить отсутствие ожидаемых особей случайностью. При и=100 могла по- лучиться нулевая выборочная доля только при генеральной доле, равной максимум 0,0982, т. е. гораздо меньшей, по сравнению с ожидаемой— 0,15. Отсутствие особей с ожидаемым признаком возможно объяснить или тем, что была высказана неподходящая гипотеза, неподтверждаемая фактами, или при правильной гипотезе — действием какого-нибудь не- учтенного фактора, или,,наконец, — ошибками регистрации (крипторхи не были замечены). Если такие методические ошибки исследования были исключены, то необходимо сделать вывод: в проведенном обследовании гипотеза не подтверждена. ОШИБКА РАЗНОСТИ МЕЖДУ ВЫБОРОЧНЫМИ-ДОЛЯМИ Ошибка разности двух выборочных долей имеет такое же значение, как и ошибка разности средних и рассчитывается по общей формуле. При r=0 md — Ш1 + Ш22 2
137 ОШИВКА РАЗНОСТИ МЕЩДУ ВЫВОРОЧНЫМИ ДОЛЯМИ Критерий достоверности разности долейШ Р1 — Р21„= — =md PHi P_#_s ni Я2 Три фиксированных значения показателя достоверности выбороч- ной разности (tr, t>, ts), соответствующие трем степеням вероятности безошибочных суждений (Pr — — 0,95, Р~=0,99, РЗ=0,999), определяются, как и для количественных признаков, по табл. Х или, при отсутствии таблиц, по описанным выше правилам. Число степеней свободы, необходимое для нахождения в таблице нужной строки, определяется так же, как и для разности средних: ч=п~+п~ — 2. Практическое использование всех этих показателей можно иллюстрировать следующими примерами П р и м е р 98. При изучении планктона оказалось, что из 6 особей одного вида 5 были самцами, а из 7 экземпляров другого родственного вида только 2 были самцами. Можно ли на основании этих данных сделать заключение, что у первого вида процент самцов в данном сезоне выше, чем у второго? Произведены следующие расчеты: 0,83 )( 0,17 р, = — =0,83;5 = 0,153; 2 = 0,29; = 0,171; т~ = т, = g o,1 53 -1- o,1ï = 0,23. Ш = 0,83 — 0,29 = 0,54; 3,1 = 2,3; 0,23 ч= 6+7 — 2= 11 Оказалось, что разница между видами по проценту самцов даже ври сравнении долей в таких малых выборках превышает нижний по- рог достоверности. Поэтому с достаточной для первой ориентировки уве- ренностью можно заключить, что процент самцов в данном сезоне у пер- вого вида больше, чем у второго. Пример 99. Из 1000 цыплят, получавших 'облученные дрожжи, болело рахитом 10, а из 2000, не получавших облученных дрожжей, болело 80. Требуется определить эффективность прибавки в. корм цьп;- лятам облученных дрожжей. Расчеты показали следующее: р, = — =0,01; 10 1000 р, = =004; 20 000 2m~ = = 0,0000099; Ш = 0,01 — 0,04 = — 0,03; т,, = p о,ооооо99-+ о,оооон2 = Q,QQ5; 0,005 2,6
РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ Опыт подтвердил с большой достоверностью, что прибавка облу- ченных дрожжей снижает заболевание цыплят рахитом не только в изученной выборке, но и во всей их массе при данных условиях содер- жания.. П р имер 100. Ста кобылам был впрыснут пролан А. Из них при- шло в охоту 80 кобыл и ожеребилось 6 кобыл. Из 400 непроланирован- ных кобыл пришло в охоту в тот же период времени 80 кобыл и оже- ребилось 20 кобыл. Определить эффективность действия пролана А на вызывание охоты и на оплодотворение кобыл. Ява поставленных вопроса решаются следующим образом: 1. В ызыв а ние охоты: 0,8 )< 0,2 80 100 80 400 2m) = — 0,0016; == 0,.8; Р1 = 1000,2 Х 0,8 2m» = = 0,0004; 400 d =- 0,8 — 0,2 ==- + 0,6; = 0,045; md= td= 06 — 133 ° 0,045 = 100 + 400 — 2 = 498 II. Оплодотворение: 6 0,06 Х 0,94m~ ——1000,05 )~ 0,95m2 =400 = 0,06; = 0,000564; = 0,000120; Pi = 100 Р2 Ю5~ 20 400 d = 0,06 — 0,05 = + 0,01; т,= y/o,000564+- о,ооо120 0 026. э 2,6 2,0 0,026, v =498 На основании проведенного анализа можно сделать следующие Bht- ВОДЫ: а) исследование с большой достоверностью td = 13,3 подтвердило, что пролан,А может вызвать охоту не только в изученном поголовье, но и у всей массы кобыл в сходных условиях; б) проланированные кобылы ожеребились в ббльшем проценте (6% — 5% =+1%). 1-1о превышение это оказалось столь мало достовер- ным (td — — 0,4), что на основании проведенного опыта нельзя сделать заключения о возбуждении проланом А плодотворной охоты у всех ко- был в сходных условиях. П ример 101. При выборочном обследовании городы из 1148 ко- ров 623 были комолыми, а остальные 525 — рогатыми. Требуется опре- делить, действительно ли в породе преобладают комолые животные? Расчеты дают следующие результаты: 0,54 >(0,46 = 0,015; 1148 623 1148 = 0,54;
139 ОШИБКА РАЗНОСТИ МЕЖДУ ВЫБОРОЧНЫМИ ДОЛЯМИ Ю,4б Х 0,541148 525 q = — = О 46; 1148 т, = g о,о18 -+ о,о1р = 0,021; d = 0,54 — 0,46 = + 0,08; 2,6 =3,8;0,080,021 Разность получилась вполне достоверной, комолые коровы преоб- ладают не только в выборке, но и во всей соответствующей генеральной СОВОК~'ПНОСТИ. Пример 102. При исследовании влияния радиационного облуче- ния животных на качество их спермы было найдено, что у самцов, по- лучивших определенную дозу рентгеновского облучения из 3000 сперми- ев, взятых на ранних стадиях сперматогенеза, обнаружено 150 уродли- вых спермиев, а из 2800 спермиев, взятых на поздних стадиях спермато- генеза, уродливых сперматозоидов оказалось 196. Требуется определить достоверна ли разница в доле уродливых спермиев на ранних (Р1) и на поздних (P2) стадиях сперматогенеза у рентгенизированных лабораторных животных. Произведены следующие расчеты: о,о5 х о,95 0 0000158 3000 = 0,05 3ООО = 0,07; 2800 2 о,о7х о'93 = О 0000233. 2800 md = g 0,0000158 + 0,0000233 = 0,006; d = 0,5 — 0,7 = — 0,2; 72,6 — 0,2 О,ООб Разность оказалась достоверной с третьей степенью вероятности. С большой уверенностью можно ожидать, что при данной дозе облуче- ния у исследованных животных доля уродливых спермиев,на раннкх стадиях сперматогенеза будет меньше, чем на более поздних. Пример 103. При изучении хромосомных перестроек в клетках роговицы глаза крыс необходимо было выяснить, насколько сильно по этому признаку различаются отдельные животные. Яля этой цели были взяты подряд две крысы и в роговице их глаз просмотрено по несколь- ку сотен клеток. У первой крысы было просмотрено 302 клетки, и в них обнаружено 36 хромосомных перестроек; у второй крысы просмотрено 392 клетки, и, в ннх обнаружено 33 хромосомные перестройки. Определение достоверности различия дало следующие результаты: я 0,119 х 0,881 0,000347; 302 р, =- — = 0,119; 36 302 2 0,084 х 0,91б 0 000196 392 33 392 = 0,084; Р2 d=0,119 — 0,084= — 0,035; ш =~ 0,000347 — 0,00019б =0,0233;
140 РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ — 0,035 =- 1,5; 1„= 0,0233 2,0 ~ =692 Разность оказалась недостоверной. Наблюдение не подтвердило предположения о различии данных крыс по доле хромосомных пере- строек во всех клетках их роговиц. П р и м е р 103 а. Из 6 проб колбасы, взятых из партии, изготовлен- ной первой бригадой, было при дегустации забраковано 2 пробы (33%), а из 1 проб колбасы того же сорта, взятых из партии, изготовленной второй бригадой, запрещено к выпуску в торговую сеть 4 пробы (57%). Можно ли на основании этих данных считать, что и вся партия колба- сы, изготовленная второй бригадой, будет иметь больший процент бра- ка, по сравнению с партией первой бригады? Из расчета следует: р, = =0,333; 0,333 )( 0,667m~ =б0,571 >( 0,429 = 0,037; б 4 7 2~~2 = 0,035; = 0,571; d = 0,571 — 0,333 = 0,238; m, = ~о,оз7 — о,озь = 0,268; 3,1 0,238 0,268 =6+7 — 2=11 1(ритерий достоверности разности оказался значительно меньше ми- нимального порога. На основе имеющихся данных нельзя заключить о большом проценте брака во всей партии второй бригады, несмотря на то. что выборочная доля брака в продукции второй бригады оказалась гораздо больше, чем в продукции первой бритады. ДОСТАТОЧНАЯ ЧИСЛЕННОСТЬ ВЫБОРКИПРИ ИЗУЧЕНИИ РАЗНОСТИ ДОЛЕЙ достаточную численность выборок можно определить по общей формуле, и при изучении разности средних: при изучении разности дол еи которая выводится так же, как (1 ) + Р2 (! Р'-') (пг — — ап1), n> — численность первой выборки с долей р1, пг=ап1 — численность второй выборки с долей р,; t — показатель вероятности безошибочных суждений; A=d — Т — допустимая неточность в определении генеральной раз- ности выборочпой. Здесь d = р, — р„d = Р, — Рг; гр(1 — u) П р и м е р 104. При планировании испытаний новой предохрани-тельной прививки установлены следующие исходные данные: N= о~, Где
ОШИБКА РАЗНОСТИ МЕ)КДУ ВЫБОРОЧНОЯ И ГЕНЕРАЛЬНОЯ ДОЛЯМИ 141 0'=0,5 (так как не было никаких сведений о возможной доле за- болевших особей, получивших прививку); Л=0,10. Это значит, что если в действительности, в массе прививка снижает заболеваемость, например, на 50 (p+=0,2, р =0,7), то по выборкам допустимо получить d не менее 0,4 и не более 0,6 (например, po — — 0,3; р,=0,7 или po=0,20; p„=0,80 и т. д.); t=2,0 (первое исследование); й 1. Достаточная численность привитых и контрольных особей опреде- ляется следующим образом: Р, 0,5Р. 0 5 2' и, = {0,25 + 0,25) = — ' Ь"- = 200; 0,01 no — — 200. П р имер 105. В испытании, описанном в предыдущем примере, были получены доли заболевших: среди привитых особей — 0,15 (150/О), среди непривитых — 0,62 (620/О). Исходя из этих данных, было заплани- ровано второе, проверочное, испытание со следующими исходными дан- НЫМИ: N= ~; р,„=02; p„=06; А=005; t=26; и, = и,. Определим численности: и, = ' (0,2 X0,8+ 0,6X0,4) =- 0,05> X0,4= 1082; 0,0025 и~= 1082. OO 1 р> =0,10; p> — — 0,02; Л=0,03; t=2,6; ив=2 и. 0,032 а, = ' 0 1Х09~- ' ' ) 2 и2 1500. X 0,0998 = 750, 0,0009 ОШИБКА РАЗНОСТИ МЕЖДУ ВЫБОРОЧНОЙИ ГЕНЕРАЛЬНОЙ ДОЛЯМИ В большинстве исследований все усилия ~направлены на то, чтобы определить неизвестную характеристику генеральной совокупности с возможно большим приближением. Но имеется особая категория исследований, когда в основу работы кладутся генеральные показатели, или известные, или предполагаемые. Пример 106. Планируется исследование по выяснению влияния радиационных излучений на хромосомный аппарат крыс по доле пере- строек, обнаружвнных в клетках костного мозга у облученных живот- ных. Контрольных животных (а значит и их клеток) исследовать мож- но в два раза больше, чем облученных. Относительно генеральных долей нет никаких точных сведений. Предполагается, что среди необ- лученных крыс доля перестроенных клеток может быть примерно p„=0,02, а среди облученных р,„=0,10. Намечены исходные данные:
РЕП РЕЗЕНТАТИ В НОСТЬ BbI BOP O×ÍÛÕ ПОКАЗАТЕЛ F H В некоторых исследованиях требуется выяснить различия между изучаемой группой и какой-нибудь более обширной группой особей, от- носящейся к изучаемой, как генеральная совокупность к выборке. Такая необходимость может возникнуть, когда требуется отнестл впервые исследуемую группу к тому или иному виду, породе, сорту и т. д. При этом генеральные показатели для более обширной группы уже известны и требуется установить, возможно ли считать изучаемую новую группу принадлежащей именно к данной генеральной совокуп- НОСТИ. В таких исследованиях (первого типа) выборочные показатели про- веряются по уже известным генеральным путем определения достовер- ности разности между выборочной и генеральной долями. Имеются также и такие исследования, в которых, наоборот, гене- ральные величины проверяются по выборочным (исследования вто- рого типа}. Такая необходимость возникает, когда по генеральной совокупно- сти с неизвестными генеральными показателями строятся предположе- ния, выдвигаются гипотезы о возможной величине генеральных долей. В таких случаях правильность выдвинутой гипотезы проверяется на практике по одной или нескольким выборкам путем сопоставления гипо- тетической генеральной доли с фактически полученными выборочными долями и определения достоверности разности между выборочной и ге- неральной долями. В исследованиях подобного рода определение и интерпретация ошибки разности и критерия достоверности разности имеют свои спе- цифические особенности. Ошибка разности между выборочной и генеральной долями по общим правилам должна быть равна корню квадратному из суммы квадратов ошибок сравниваемых величин: 2 2 щ~, — т +т„ 4 P Р m> — ошибка выборочной доли в тех случаях, когда извест. ны или предполагаются генеральные доли, ~р — — P pQ — генеральная сигма качественного признака, где Тут под корнем стоят квадраты двух величин: ошибки выборочной доли и ошибки генеральной доли. Однако генеральная доля, как и всякая генеральная величина, не имеет ошибок репрезентативности и поэтому второе слагаемое под кор- 2 нем равно нулю: т„= О. Исходя из этого, формула ошибки разности между выборочной и генеральной приобретает совсем простой вид: 2 2 щ~ ~> — т +О= т =щ, т. е. ошибка разности между выборочной и генеральной долями равна ошибке выборочной доли. Ошибка выборочной доли в описываемых исследованиях имеет так-же свои особенности. В этих работах генеральные доли или известны, или предполагаются. Поэтому имеется возможность рассчитать точное значение ошибки выборочной доли, используя генеральные доли, а не выборочные:
ОШИЕКА РАЗНОСТИ МЕЖДУ ВЫБОРОЧНОЙ И ГЕНЕРАЛЪНОЙ ДОЛЯМИ 143 Р, Q — доли особей, имеющих и не имеющих признак в гене- ральной совокупности, n — численность изучаемой выборки. Достоверность разности в описываемых исследованиях имеет также свои особенности. В обычных работах, если разность достоверная и критерий досто- верности разности превышает установленный порог, это означает, что между двумя соответствующими генеральными совокупностями имеется такая же разница (по направлению), какая найдена между выборками. В обычных работах достоверная разность служит показателем благо- приятных, репрезентативных результатов опыта. А что означает достоверная или недостоверная разность между вы- борочной и генеральной долями? Если эта разница оказалась достоверной в работах первого типа, т это значит, что различие между изучаемой группой и той генеральной группой, принадлежность выборки к которой проверяется. столь велика, что первоначальные предположения не оправдались. Если эта разность оказалась достоверной в работах второго типа, то это означает, что при предположенных генеральных показателях не могло быть такого резкого отличия их от выборочных показателей. Ги- потеза оказалась неверной, не подтвержденной практикой. Поэтому в таких ра|ботах достоверная разность является показате- лем не положительного, а отрицательного результата проведенного ис- следоьо ния. И, наоборот, недостоверная разность, которая обычно является не- благоприятным результатом исследования, в работах, где сравниваются выборочные и генеральные доли, указывает на положительные выводы. В работах первого типа недостоверная разность говорит о том, что различия между изучаемой группой и ее предполагаемой генеральной совокупностью оказались невелики и предположение о принадлежно- сти выборки именно к данной генеральной совокупности не опро- вергнуто. В работах второго типа недостоверная разность указывает на то, что различия между выборочными и гипотетическими показателями оказались столь незначительными, что не могут опровергнуть выдви- нутую гипотезу. В данном случае этого достаточно, так как каждая гипотеза до тех пор считается правильной, пока не опровергнута практикой. 1(ритерий достоверности разности в описываемых работах приобре- тает свое особое значение, обратное тому, которое он имеет в обычных работах. Причем, чем больше критерий достоверности разности, тем более благоприятные выводы можно сделать, чем ответственней работа, тем больший критерий требуется. В описываемых работах, наоборот, чем меньше полученный крите- рий достоверности разности, тем более положительные выводы можно сделать и о принадлежности изученной выборки к определенной гене- ральной совокупности, н о правильности выдвинутой гипотезы. Большой критерий достоверности разности в этих ра~ботах указывает на непра- вильность высказанных предположений и гипотез. Поэтому в работах, где оценивается близость выборочной доли к ге- неральной, наиболее благоприятным порогом достоверности будет не верхний, а нижний, определяемый значениями1„= 2,0 и Р~ = 0,95. Для более ответственных работ такого типа требуемая вероятность разности не повышается, а понижается, так что порог критерия досто-
РЕПРЕЗЕНТАТИВНОСТЬ ВЪ|БОРОЧНЫХ ПОКАЗАТЕЛЕЯ 144 верности разности снижается до 1,5, что соответствует вероятности раз- ностиР'~ =- 0,866 и даже до td = 1 при Pd = 0,682. Практическое использование ошибки разности между выборочной и генеральной долями можно показать на следующих примерах. П р и мер 107. В изучаемой партии коконов шелкопряда из 50 ко- конов 40 были темноокрашенными. Требуется проверить предположение о том, что эта.партия принадлежит определенной расе, в которой доля темноокрашенных коконов довольно постоянная и равна половине. В данном случае известны генеральные доли Р=0,5 и Q=0,5, по- этому можно получить точное значение ошибки выборочной доли: Р=0,5; о.5 х о,5 0,071; 50 40 = 0 8. У 1 50 т„= т = 0,071; d = — 0,8 — 0,5 = 0,30; У 2,6 2,0 =42; озо О,О71 Достоверность разности оказалась очень велика, и поэтому общий вывод должен быть отрицательным: предположение о принадлежности изученной партии к данной расе по этому признаку не подтвердилось. Если бы был получен критерий достоверности, разности td (1,96, тогда можно было бы заключить, что разница между изученной и пред- полагаемой расой столь мало достоверна, что эту партию можно счи- тать представительницей данной расы. П р и мер 108. При изучении физиологии размножения вида была высказана гипотеза о том, что в нем к половозрелому состоянию на каждые 7 самок должно быть 9 самцов. Для проверки этой гипотезы было выделено 100 половозрелых особей данного вида, из которых 60 оказались самцами, а 40 — самками. Подтверждена ли гипотеза? Расчеты показывают следующее: P= =0,5625; Я= 19 16 = 0,4375; 0,5625 )( О,È75 60р = — =0,6;100 = 0,0496; m Р 100 d = 0,6 — 0,5625 = 0,0375; md = т, = 0,0496; 2,6 0,0375 0,0496 =0,8; ,Ностоверность разности оказалась столь мала, что бесспорен поло- жительный вывод: пробный вылов не опроверг гипотезы. МЕТОД (р (ФИ) А. P. Фишер показал, что определить достоверность выборочной разносги долей можно точнее и проще, если вместо каждой доли взять угол q;, синус которого равен корню квадратному из этой доли: q агсв1п]/ р.
l45 М ЕТОД (р (ФИ) Определенный таким образом угол q обладает следующими свой- ствами. 1. Ошибка репрезентативности угла g) не зависит от величины этого угла и определяется в зависимости только от численности группы по следующему равенству: 820,7 2m~= 2. Для малых долей (меньше 0,25) и больших долей (больше 0,75) определение достоверности разности по соответствующим углам у дает более правильные результаты. 3. Для долей в пределах 0,25(р(0,75 замена их углами q дает практически такие же результаты, какие получаются без этой замены, но техника вычислений при этом упрощается. Определить величину <р по данной доле р можно по обычным таб- лицам синусов, приняв за синус искомого угла величину р, или по специальной таблице (табл. ХШ). Если ошибки углов имеют самостоятельное значение, например, для определения возможных пределов генерального значения угла, то эти ошибки находятся по формуле 28,648 4. Если требуется определить только достоверность разности срав- ниваемых долей, то это можно сделать по. формуле (91 92)820,7 vi— = 1, при ч,=а,+а,— 2. n>+ и» ni=5440; pi=0,00055; ~р~=1,34; а2=551; р~=0,00540; ~р~=4,21; 6,6 5440 551 (4,21 — 1,34)2820,7 = 5,0; 5440 + 551 Определение достоверности различия этих долей, проведенное обыч ным способом, приводит к выводу о недостоверной разности: р, = 0,00055; т~ = ' ' = 0,000000101; 5440 0,1"10540 . 0,99460 ~~2 = 551 = 0,000009747; р; = 0,00540; Предельные значения показателя достоверности F, соответствую- щие трем принятым степеням вероятности безошибочного прогноза, определяются по обычной таблице стандартных отношений девиат дан- ной табл. XI. Например, если сравнивается доля 0,00055, полученная в группе из 5540 особей, с долей 0,00540, полученной в группе из 551 особи, то до- стоверность разности этих долей при помощи метода q можно опреде- лить следующим образом:
РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЪ|Х ПОКАЗАТЕЛЕН 146 т~ = 0,0000101 + 0,0009747 =- 0,000009848md = — 0,00314;d = 0,00540 — 0,00055 = 0,00485; 2,6 0,00485 0,00314 Для приведенного примера более правильное решение дает метод у. Огределение достоверности разности долей при помощи метода ч~ можно значительно упростить, если заранее рассчитать величину 820,7 — для различных значений численности группы. Тогда пока- )l затель достоверности разности углов rp можно определить по формул (~ — ч )-' F,( 2 > 101, - )П., ° ) ° ) причем величины )N> H ~п~ определяются без вычислений из заранее 820,7 составленной таблицы значений т' — — ' (табл. XIV). 17 Для приближенного, быстрого определения достоверности разности углов g) можно значительно сократить вычисления, составив таблицу минимальных достоверных разностей (табл. XV). Для этого исполь- зуется формула h--k где d;„- Минимальная достоверная разность углов у при первом пороге вероятности безошибочного прогноза Р=0,95; n< — численность меньшей группы; k=n;: nt — число, показывающее, во сколько раз численность боль- шей группы превышает численность меньшей группы; при k=1 численности сравниваемых групп равны; t — показатель достоверности при Р=0,95 и при числе степе- ней свободы v=ni(k+ I) — 2 находится по табл. Х. Если для первой группы п> =551 и ~р1 —— 4,21, а для второй n2 — — 5440 и ~р2 — — 1,34, то разность углов d=4,21 — 1,34=2,87. При n~=551 =600 и k=10 минимальная достоверная разность d;„=2,4 (см. табл. XV). По- лученная в эксперименте разность 2,87 оказалась больше минимально достоверной, т. е. в исследовании получена достоверная разность углов (p и соответствующих долей.
ГЛА ВА IVКОРРЕЛЯЦИЯ о многих исследованиях требуется изучить несколько призна- ков в их взаимной связи. Если вести такое исследование по отношению к двум признакам, то можно заметить, что изменчивость одного, признака находится в неко- тором соответствии с изменчивостью другого. В ~некоторых случаях такая зависимость проявляется ~настолько сильно, что при изменении первого признака на определенную величину всегда изменяется и второй .признак на олределенную величи~ну, поэтому каждому з~начению первого признака всегда соответствует совершенно определен~кое, еди~нствен~ное значение второго признака. Такие связи на- зываютсяся ф у н к ц и о Б а л ь.н ы м и. Встречаются функциональные связи в физических и математических обобщениях. Площадь треугольника точно определяется его высотой и основанием, длина оиружности — радиусом, скорость падения является функцией времени падения и ускорения силы тяжести, скорость проте- ка~ния определенной химической реакции находится в зависимости от температуры. Необходимо учесть, что в чистом виде функциональные связи встре- чаются только в идеальных условиях, когда предполагается, что никаких посторонних влияний нет. На практике это недостижимо. Никогда нельзя точно измерить фак- тически имеющийся радиус круга, причем .вычисленная площадь никогда неравна в точности фактической, вследствие практической невозможнос- ти начертить точную окружность. Скорость падения реального тела в реальных условиях будет всегда различна при одних и тех же времени и ускорении силы тяжести. На практике всегда действуют посторонние для данной функциональной зависимости факторы, которые нарушают точность этой зависимости в разных случаях по-разному. Пока такие ~нарушения остаются настолько незначительными, что их практически мажино ~не учитывать, связь считается функциональной. При изучении живых объектов — диких видов, культурных расте- ний, домашних животных — приходится иметь дело со связями другого рода. Яивой организм развивается в связи с условиями его жизни, под действием бесконечно большого числа факторов, которые по-разному определяют развитие разных признаков. У живых объектов связь между любыми двумя признаками ~настоль- ко часто и сильно нарушается и модифицируется, что не всегда даже может быть достаточно просто обнаружена. У раствний и животных связь между признаками обычно проявляет- ся оообьгм образом. Тут каждому определенному з~начению перьвого при- знака соответствует не одно э~качение второго признака, а целое распре- деление этих значений при вполне определенных основных показателях
148 КОРРЕЛЯЦИЯ этого частного распределения — средней величины и степени разнооб- разия. Такая связь называется ко р р е л я ц и о ~н.н о й с в я з ь ю или просто к о р р е л я ц iH е й. Корреляционная связь, ~например, между весом животных и их дли- ной выражается в том, что каждому значению длины соответствует оп- ределенное распределение веса (а не од~но значение веса), такое, что с увеличением длинны увеличивается и средний вес?KHBQTHblx. Подоб~ных примеров .из области биологии, растениеводства и жи- вотноводства можно привес~и очень много. Корреляционная связь не является точной зависимостью одного признака от другого, поэтому эта связь может иметь различную сте- Рис. 27. Схема прямолинейных корреляционных связей. пень — от полной независимости до очень сильной связи. Кроме того, характер связи между разными ~признаками может быть различен. По- этому возникла необходимость определять форму, направление и сте- пень корреляционных связей. По форме корреляция может быть прямолвнейной и,криволиней- IHoH, по направлению — прямой ~и обратной. Степень корреляции изме- ряется различ~ными показателями связи, введенными для уста~новления силы связи между количественными и качественными признаками.
149 КоэФФициЕнт КоррЕляции Такими локазателями являются коэффициент корреляции r, корре- ляционное отношение q, тетрахорический и полихорический показатели связи, частный и множественный коэффициенты корреляции. Изобразить корреляцио|нную связь двух признаков можно тремя способами: 1. При помощи корреляцио~нного ряда, состоящего из ряда пар зна- чений, из которых одно относится к первому признаку, а другое в этой паре относится ко второму признаку, связа~нному с первым. На рис. 27 показаны схемы корреляционных рядов при пяти степе~них корреляцион- ной связи. 2. При .помощи корреляционной решетки, в которой каждой особи соответствует определенная клетка. На рис. 27 показана (слева) схема корреляцион~ных решеток для пяти степеней корреляционной связи меж- ду двумя признаками. Значения, первого признака на~несены по оси абс- цисс, значения второго — по оси ординат. 3. При помощи ликии .регрессии, абсциссы которой пропорциональ- ны значениям первого признака, а ординаты — значениям второго при- знака, корреляционно связанного с первым. На рис. 27 (справа) показа. ны схемы лишний регрессиями для пяти степеней корреляционной связи между двумя .приз~каками. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ Коэффициент корреляции измеряет степень и определяет направле- ние пря:мол.инейных связей. Прямолинейная связь между признаками, это такая связь, при ко- торой равномерным изменениям первого признака соответствуют рав- номерные (в сред~нем) изменения второго признака при незначительных и беспорядочных отклонениях от этой равномерности. Налример, при увеличении длины тела на каждый са~нтиметр, ши- рина также увепичивается в среднем на 0,7 см. При графическом изображении прямолинейных связей (рис. 27), если по оси абсцисс отложить значения .первого признака, по оси орди- нат — второго и полученные точки соединить, получается прямая или такая кривая, среднее течение которой проходит по прямой. - При изображении,прямоляней~ных корреляцион~ных связей в форме корреляционных решеток (рис. 27) частоты анутри располагаются в форме эллипса. Большая ось этого э.плипса проходит или ~по диагонали от угла наименьших э~качений (при положительной,корреляцион~ной связи), или ло диагонали от угла, где сходятся наименьшие значения одного признака и наибольшие э~качения другого, к противоположному углу (при отрицательной корреляцио~нной связи). При измерении степени связи между разными признаками прихо- дится сравнивать величи~ны, выраженные в разных единицах измере- ния. Например, лри измерении связи между весом животного и его дли- ной надо сопоставить килограммы веса с сантиметрами длины. В других случаях изменения объема сопоставляются с изменениями возраста, изменения веса ру~на в килограммах с изменениями содержания в нем жиропота:в процентах, длина ног в са~нтиметрах со скоростью бега в минутах и др. Проводить такие срав~нения оказалось возможным путем использо- вания нормированного отклонения вычисляемого по формуле. V — М х=
150 КОРРЕЛЯЦИЯ Как уже было указано, ~нормированное отклонение является уни- версальной и ~неименова~нной мерой развития признаков. Эти свойства нормированного отклонения и позволили ввести основной показатель корреляционной связи — коэффициент корреляции. Основная формула, из которой следует сущность этого показателя, имеет совсем простую структуру: Е Х1Х2 r — коэффициент корреляции, ~1 ~1 +1 X = — — нормированное отклонение первого при- ~1 а, знака и этой же особи. V< — дата, М1 — средняя арифметическая. Е (V — M)э где v=n — 1, D 1 1 ° ~max для отрицательных, или обратных связей, — — = — 1,0. Гтах 3. При полном отсутствии корреляционной связи между признаками сумма произведений нормированных отклонений равна нулю, и поэтому коэффициент корреляции в этих случаях тоже равен нулю: О Предельные значения коэффициента корреляции (r=+1,0; r=o,o; т= —,0) яа практике встречаются край~не редко; обычно значения это- х — — нормированное отклонение второго при- ~2 О.р знака у этои же особи. Сумма произведений нормированных отклонений, входящая в фо~р- мулу для коэффициента корреляции, обладает следующими тремя осо- быми свойствами: 1. Если оба признака изменяются параллельно, то сумма произве- дений их нормированных отклонений дает положительную величину. Если при увеличении одного признака другой уменьшается, то прихо- дится умножать положительные числа на отрицательные и вся сум- ма произведений нормированных отклонений дает отрицательную вели- чину. Поэтому коэффициент корреляции может определять ~направление связи: при прямых связях он положителен, а при обратных связях— отрицателен. 2. При полных связях, когда изменения обоих признаков строго соответствуют друг другу и корреляционная связь превращается в функ- ционалыную, сумма произведений нормированных отклонений становит- ся равной числу степеней свободы: Zx<x> — — v=n — 1. Поэтому максимальное значение коэффициента корреляции равно (: для положительных, или, прямых связей,
КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ Vi Afi V2 — Я2~2 Ч~~ ~ Х1Х2 Если теперь вынести произведение сигм за знак суммирования и выразить сигмы в развернутом виде, то после сокращения получим ра- бочую формулу для коэффициента корреляции: X (~1 ~2) ХDl D2 Далынейшие упрощения заключаются в том, что сумма произведе- ний центральных отклонений (ZD! Щопределяется не непосредственно, а косвенным, более легким и простым способом, например, по формуле: 2 1+ 2 d >D,D,. = где Е ф, Е D2 -- суммы квадратов центральных отклонений по ряду первого и по ~ряду второго признака, Е д~! — сумма квадратов центральных отклонений по ряду попарных разностей между значениями первого и вто- рого признаков. го показателя находятся между нулем и положительной или отрица тельной единицеи. Пять основных видов .прямолиней~ной корреляционной связи, соот- ветствующие коэффициентам корреляции +1,0; +0,8; 0,0; — 0,8 и — !,О, локлза1ны на рис. 27. ~~ ! Х1Х2 Основная формула коэффициента корреляции ! = — хорошо вскрывает сущность этого показателя, но для работы крайне, неудобна, особенно при многочисленных группах. Поэтому разработаны раз~нооб- разные рабочие формулы для практических расчетов в разных услови- ях — для малых и больших групп при малозначных и многозначных вариантах. Все эти формулы дают оди~наковый результат и применение той или другой формулы обусловливается только удобством и простотой ~необ- ходимых вычислений. Если требуется рассчитать один, два или вообще немного коэффи- циентов корреляции, то можно брать любую формулу. Если нужен расчет целых серий.коэффициентов корреляции, то луч- ше сначала подобрать, наиболее подходящую формулу. Это сильно сократит работу и значительно уменьшит возможность ошибок в вы- численияхях. Все формулы для практических расчетов коэффициента корреляции являются модификацией приведенной основной формулы. Если в ней выразить нормированные отклонения в развернутом виде, TQ получим:
КОРРЕЛЯЦИЯ 152 Если для сокращения ZD обозначить через С, то формула коэффи- циента корреляции примет вид: где С,. — сумма квадратов центральных отклонений: для ряда первого лриз~нака С~, для ряда второго признака С~, для ряда раз~кос- тей между значениями первого и второго признаков С~. Величина С вычисляется по следующим формулам: 1. Для малых групп, при малозначных датах С=Е V2— П где V — дата, значение признака или разности значений, признаков. 2. gIJIH малых групп, но при многозначных датах С=КА'— П где Л — условное отклонение, отклонение значения признака или разнос- ти от условной средней. 3. Для больших групп g2 С = ~г П где S>, 82 — первая и вторая суммы, получаемые в процессе работы по способу сумм. ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ДЛЯ МАЛЫХ ГРУПП Вычисление коэффициента корреляции для малых групп можно вести двумя основными способами: способом дат и способом условных отклонений. Рроме того, имеется особый способ, названный способом произведений. Способ дат употребляется при малозначных датах; всевычисле- ния по этому способу показаны в табл. 57. Действия эти настолько просты, что ые нуждаются в дополнительных пояснениях. Способ условных отклонений употребляется при много- значных датах, причем опнесение дат в категорию многозначных опреде- ляется только имеющейся вычислительной техникой. Ввиду того, что способ услов~ных отклонений значитель~но сложнее, лучше переходить к условным отклонениям, оачииая с четырехзначных дат. При двухзнач- ных и треха~кажных датах и при наличии арифмометра не труд~но вычис- лить коэффициент корреляции для малых групп по способу дат. Способ условных отклонений требует лредварительного преобразо- вания дат. Это вызвано тем обстоятельством, что обычная замена их на условные отклонения уменьшает знач~ность чисел недостаточно. Ве- личины Л= (V — А) все еще имеют иного знаков, так что возведение кх в квадрат приводит к шести и более значным цифрам. При пребразованни дат используется особенность структуры коэф- фициента корреляции, которая позволяет безизменениярезультата мно- жить и делить все имеющиеся значения на любое число, оди~наковое для всех дат каждого признака в отдельности. Например, значения связа~нных признаков можно разделить на 10 и с лолученными частными производить все действия, требуемые соответ-
153 ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ДЛЯ МАЛЫХ ГРУПП ствующей формулой. В результате получится точное значение коэффи- циента корреляции. В тех случаях, когда, не все даты делятся без остатка на выбранное число, вполне возмож~но дробную часть получевного частного округлить по простому правилу: если дроб~ная часть меньше 0,5 — она просто от- брасывается, если же дроб~ная часть равна или более 0,5, то при ее от- брасывании последняя целая цифра числа увеличивается .на единицу. Таблица 57 1й13'2 (X V)2 1/10 И 9оснесенных 10 курами в феврале;снесенных в феврале их полными5 6321 Вычисление коэффициента корреляции для малочисленныхгрупп при малозначных датах по формулам: г C1+С» — Cd gg~г 2~ С,С, 1-ый признак — число яиц, 2-ой признак — число яиц, сестрами. /2345б7Д910V, V) V1 V1 п=10 4 Зб 25 64 16 55 23 78 (> ~)2 3025 б084 529 (Е V)2И 302,5 б08,4 10 64 100 9 49 100 81 49 1б9 740 A/2 385 1б 10 131,б 5б,1 82,5 13 36 16 1619б25 82,5 + 131,6 — 5б,1 14 81 36 25 + 158,0 — + 0,7б 208,4 55 385 740 78 +23 109 Еvi 55 82,5 = 3,03 9 С 1и — 1 — 5,5; 10 131,6 3 82 9 78 С2и — 1 — 7,8; 10 В табл. 58 показаны все действия, необходимые для расчета коэф- фициента корреляции по способу условных отклонений. В разбираемом примере даты первого признака разделены ~на 10 и округлены; вместо трехзначных чисел получены двухзначные (V> ). ga-
КОРРЕЛЯЦИЯ ты второго признака раделены на 100 и округлены, вместо четырехзнач- У ных чисел получены двухзначные( V>). С полученными преобразован~ными датами деитвия выполняются так же, как и с обычными датами. Условные средние по обоим призна- кам устанавливаются уже для преобразованных дат, и для них рассчи- тываются три ооновные величины: С„С.„С„. Таблица 58 Вычисление коэффициента корреляции для малочисленных групп при многозначных датах по формулам: с,+с,— с ( ~ /~2 С,С., и г к ~/V V = — -'1 й 2 ф1-ый признак — живой вес первотелок;2-ой признак — удой за 300 дней их первой лактации. 2000 I 2(йа == 100) IV(ga,=10) л = 10ЕЬ d О 1 2 2 <2 1 2 hq (А= 45) (A=25 gf = Ь,— Ь) Vg — 5 -5 (ЕЬ)-" 25 25 2,5 2,5 и 86 85 59 86,0 С 82,5 56,5 82,5 + 5б,5 — 86 f' 2 ~82,5 )< 56,5= + 0,39 4453 24565 445 85 59 0 86 245 ( =445,3 > ~ 5~ 5 = 10 45 — — = 445,0 и 10 м =-u, A» = 24%,5245б510 ч~~ Д 5 М. = й. А,, -1- — = 10 25 — — = 2450 0 10 с — 10 n — 1 = 30,3, 9 = 100 ' = 250,5 и — 1 9 = й с Вычисленный коэффициент корреляции не'требует никаких попра- вок, которые восстанавливали бы изменения первичных дат, допущен- ные при их преобразовании. Эти искажения автоматически погашаются в процессе вычисления коэффициента корреляции. При определении сред~ней арифметической и среднего квадратиче- ского отклонения поправка нужна. Она заключается в том, что М' и а', полученные по датам, разделенным на величину k, нужно умножить на эту величину (см. табл. 58). С п о с о б п р о и з в е д е н и й употребляется для малых групп, ког- да имеется возможность легко перем~ножить даты. При наличии ариф- 493 479 471 460 452 438 427 421 412 400 2395 2817 2286 2734 2640 2б99 2131 2082 2278 2503 49 48 47 46 45 43- 42 41 40 24 28 23 27 26 27 21 21 23 25 +4 +3 +2 -{-1 — 0 — 1 — 2 — 3 — 4 — 5 — 1 +3 — 2 +2 +1 +2 — 4 — 4 — 2 0 16 9 4 1 0 1 4 9 1б 25 1 9 4 4 1 4 1б 16 4 0 — 5 0 — 4 -}-1 +1 +3 — 2 — 1 +2 +5 25 0 16 1 1 9 4 1 4 25
ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ДЛЯ МАЛЫХ ГРУПП мометра этим способом можно работать при двухзначных вариа~нтах, а если имеются электрические счетные машины, то и при трехзначных, и четырехзначных. При этом способе вычисления ведутся .по формуле v V1Е V= Х ViV2— ~с,с, которая позволяет просто и быстро вычислять коэффициент корреляции. Применение способа произведений показано в табл. 59; оно настолько просто, что не требует дополнительных пояснений. Таблица 59 Вычисление коаффициента корреляции лля малочисленныхгрупп по формуле - ~1~~г ~ V1V- —- ф' с,с i-ый признак — число яиц, снесенных в феврале 10 курами; 2-ой признак — число яиц, снесенных в феврале их полны- ми сестрами. 23455789)0 2 2 V21 V, n=1О V) V, 78 55 (Х V}2 3025 б084 4290 z V1z V2 ~~', ~)2и Z V„ZV„ (>) 302,5 608,4 429 ХV2 740 508 131,6 +79 С 82,5 а — b + 79 + 79 — + 0,76 104,2 78 385 740 508 55 10 — 5,5, 82 ° 5 3 ()8 9 С1и — 1 131,6 — 3,82 9 78 с2п — 1 М2 = а =- 7,8, 10 5 1 8 3 10 7 4 9 б 6 8 2 10 7 9 13 4 14 5 4251649 100 491б81Зб 36 64 4 100 49 81 169 1б . 196 25 12 40 2 80 21 90 91 1б 126 30 ф 1,3 !2 л !О 9 8 7 б 5 4 3 2 1
156 КОРРЕЛЯЦИЯ ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИДЛЯ БОЛЬШИХ ГРУПП Таблица 60 Форыа корреляционной решетки 125 — И4 135 — 144 145-154 155 — 164 165 — 174 175 — 184 ] 85 — 194 Для многочислевных групп, когда вычисление коэффициента кор- реляции способами, предназначенными для малых групп, становится затруднительным, применяют другие способы. Общим для них являются д~ва основных этапа работы: составление корреляционной решетки и расчеты вспомогательных величин и коэффициента корреляции. Составл ение корр ел я цио~н ной р ешет ки. Корреляци- он~ная решетка составляется путем разноски пар значений в соответ- ствии со значениями обеих дат у каждой особи по классам. Составление корреляцио~нной решетки мажино показать на следую- щем примере. Яля разработки методов определения веса животных на основе ли- .нейных измерений были получены коэффициенты корреляции между каждым измерением и живым весом. Наивысшая кор~реляцион~ная связь с живым весом в одной из опытных групп оказалась у обхвата груди. Для того, чтобы это выяснить, нужно было провести следующую работу. 1. Каждое животное измерить и взвесить, чтобы для каждой особи имелось по па~ре значений: две даты от двух изучаемых признаков. 2. По каждому,пр|изнаку составить распределения, для чего предва- рительно ~наметить число, величину, границы и среди~ны классов спосо- бами, уже описанными выше. В данном исследовании по обхвату груди величина классов k~= =10 см, по живому весу kq — — 50 кг. Срвдины классов по обхвату груди: 130, 140, 150 и т. д., по живому весу: 200, 250, 300 и т. д. Соответственно этим э~качениям были намечены и граняцы классов: по обхвату груди — 125 — 134, 135 — 144, 145 — 154 и т д., по живому ве- су — 175 — 224, 225 — 274, 275 — 324 и т. д. 3. Обозначить классы первого признака по верхней грани корреля- ционной решетки слева направо, а классы второго признака — по левой грани снизу вверх так, как это показано в табл. 60. 4. Линии, разделяющие классы первого приз~кака, продолжить вниз, а линии, разделяющие жлассы второго признака, продолжить вправо.
157 ВЪ|ЧИСЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ДЛЯ БОЛЬШИХ ГРУПП Рис. 28. Заполнение корреляционной решетки. 6. При очень многочисленных группах для дальнейших работ лучше корреляционную решетку перечертить, поставив вместо границ, классов их средины, а вместо точек и черточек — частоты. При не очень больших группах все это можно сделать на той же ре- шетке, на которой производилась разноска особей. 7. Подсчитать суммы частот по столбцам (n>) и по строкам (n>) и общую сумму частот: и = Zn~ — — Zn2. После этого .корреляционная решетка (табл. 61) готова для даль- нейших расчетов корреляции. Уже самый вид корреляцио~нной решетки позволяет приблизительно уста~новить направление и степень прямолинейных связей, а также ха- рактер криволинейных связей. При известном опыте по виду корреляционной решетки можно всегда получить первое представление об особенностях и силе связи между изучаемыми признаками. Облегчает решение этой задачи схема степеней прямолинейной корреляции, показанная в табл. 62. В этой схеме приведены стандартные корреляционные распределения 50 особей при различных степенях прямолинейной связи по девяти градациям от r=+1,0äîr= — 1,0. Горизонтальные, и, вертикальные линии пересекут друг друга и образуют клетки или ячейки корреляционной решетки. 5. Ячейки корреляционной решетки ~надо заполнить частотами, что можно сделать двумя способами. Первый способ состоит в том, что индивидуальные карточки, со- ставленные при измерении и взвешивании на каждое отдельное живот- ное, раскладывают по ячейкам корреляционной решетки в соответствии с величи~нами дат по обоим признакам. Когда карточки разложены, их подсчитывают и число их ставят в соответствующие ячейки. Второй способ состоит в том, что первичные списки по измерению и взвешива~нию просматриваются подряд для каждого животного, причем точками и черточками отмечается попадание каждой особи в определен- ,ную ячейку в зависимости от значений первого и 1второго признаков. Например, в левую нижнюю ячейку решетки заносятся такие особи, у которых первый признак имеет величину от 125 до 134 см, а живой вес от 175 — до 224 кг. В правую верхнюю ячейку надо заносить особей, имеющих обхват груди в пределах 85 — 194 см, а живой вес в пределах 525 — 574 кг. Г1ервич~ная разноска особей по ячейкам корреляционной ре- шетки показа~на на рис. 28.
158 КОРРЕЛЯЦИЯ Схемой степеней прямолинейной корреляции можно пользоваться как эталоном для первоначального ориентировочного отнесения изуча- емой связи к одной из условных степеней («сильная», «средняя», «сла- бая») только по одному виду корреляционной решетки. В некоторых случаях такая грубая оценка бывает достаточна для вы|яснения предва- рительных вопросов исследования. Та бли ца 61 Заполненная корреляционная решетка 190 1бО ь40 i 50 П2 2 20 32 51 Щ 59 41 3 55Р 500 450 400 350 300 250 200 116141 41625241 1244132 1 27 25 () 1 1311 2 33 63 98 70 32 и, Например, при исследовании корреляции нескольких признаков с каким-нибудь основным в целях выборки наиболее с ним связанных достаточно просмотреть корреляционные решетки. Такой просмотр, а также и сопоставление полученных решеток со стандартными по схеме степенеи прямолинейной корреляции позволят отбросить признаки явно слабо связанные с основным и оставить для последующих расчетов только признаки, показавшие наибольшую кор- реляцию с основным признаком. Выбор из них самого лучшего (для поставленной задачи) возможен, конечно, только уже на основе вычис- ления коэффициента корреляции. В некоторых случаях простое рассмотрение корреляционной решет- ки, составленной определенным образом, дает результаты, имеющие большое производственное значение. Это может иметь место, например, при оценке производителей по потомству с при менением станда ртной кор реляционной решетки. Стандартная корреляционная решетка составляется следующим образом. Для каждого признака, по которому производится оценка, устанав- ливается единое распределение для потомков и их матерей. Размах этого распределения должен включать все возможные значения призна- ка, которые могут встретиться в большом массиве скота, например, во всех совхозах и колхозах области или края. Минимум и максимум обоих распределений устанавливаются с некоторым запасом: немного меньше известного фактического минимума и немного больше встречавшегося максимума. Классы обоих распределений устанавливаются не крупные, чтобы не снизить точность оценки производителей. Классы признака по матерям располагаются слева направо в верх- ней заглавной строке корреляционной решетки (это первый признак), классы признака по дочерям располагаются снизу вверх в левом за- главном столбце (это второй признак). Решетка получается всегда точно квадратная. Размер сторон (число градаций) единый для всех производителей, оцениваемых по
° ° ° ° ° <в gs ° Э Э ° ° полная отсутствие корреляции полная
160 КоррЕляция данному признаку, и обычно превышает тот, который был бы достаточ- ным для каждого производителя в отдельности. От нижнего левого угла решетки к правому верхнему углу прово- дится диагональ равенства, проходящая по всем тем клеткам решетки, которые соответствуют одинаковым классам потомков и их матерей. Макет стандартной решетки показан на рис. 29. Разноска значений признака производится м . обычным образом. В Л горизонтальном распре- делении матерей отыс- кивается класс, в кого- рый попадает показа- тель матери, и в этом Я столбце ставится столь- ко единиц по отдель- ным строкам, сколы'.о имеется показателей у дочери (за разные го- ды) в зависимости от того, в какой класс до- ° ° ° черей попадает каждыи из нескольких показа- 3 телей одной дочери. Ес- ли у матери имеется несколько показателей 1 за разные годы, то для каждого из них в со- ответствующих столб- рис. 29. Стандартная решетка для оценки производи- цах ставятся частоты, телей. соответствующие зна- чениям признака, име- ющимся у дочери. Скопление частот внутри решетки обводится прямоугольником, сто- роны которого касаются крайних частот сверху, снизу, слева и справа. Отдельны|е выпады частот не включаются в площадь прямоугольника. Заполненая решетка для оценки производителя показана на рис. 30. Путем простого просмотра заполненных стандартных решеток вы- ясняются следующие детали оценки производителей. 1. Влияние производителя на среднее качество п о то м ст в а определяется по положению прямоугольника относитель- но диагонали равенства. Возможны три основных случая, представлен- ные на трех схемах рис. 31. 1. Большая часть прямоугольника, а следовательно, и большая часть частот решетки располагается выше диагонали равенства. Это значит, что большинство потомков лучше своих матерей по данному признаку. Такой производитель улучшает среднее качество потомства относитель- но среднего качества данного маточного стада и в этом смысле является улучшателем. П. Выше и ниже диагонали равенства располагаются примерно одинаковые части прямоугольника, а следовательно, и одинаковые ко- личества частот решетки. Это значит, что количества лучших и худших потомков у быка (по сравнению с матерями} одинаковы. Такой произ- водитель является нейтральным, так как не изменяет среднее качество своих потомков относительно качества их матерей.
ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ДЛЯ БОЛЬШИХ ГРУПП 161 Рис. И. Возможные положения прямоугольника отно-сительно диагонали равенства. IV. Прямоугольник имеет примерно одинаковые стороны и по фор- ме приближается к квадрату. Это значит, что размах признака от ми- нимума до максимума одинаков у потомков и у их матерей. Такой производитель дает потомков столь же разнообразных по данному при- знаку, как и то маточное поголовье, на котором получено его потомство. Ч. Прямоугольник имеет вертикальные стороны (по потомкам} ко- роче горизонтальных (по матерям}. Это значит, что потомство произ- водителя имеет меньшее разнообразие по данному признаку по сравне- нию с разнообразием матерей. В таких случаях производитель дает III. Большая часть прямоугольника, а следовательно, и ббльшая часть решетки располагается ниже диагонали равенства. Это значит, что большинство потомков производителя хуже своих матерей. Такой производитель ухудшает среднее качество потомства и в этом смысле является ухудшателем. Сочетаемость производителя с от- матеря ! 2 3 " " 8 9 !о м и определяется по час- тотам, расположенным 1, ! 1 или выше, или киже диз- ) гонали. 1~аждая единица I 9 частот, расположенных г ° ° ~~ ~ф tÔ ° выше диагонали равенст- ва соответствует матери, ! ~Л с которой производитель дает хорошее потомство даже тогда, когда среднее качество его потомства плохое. 1~аждая единица частот, расположенных ниже диагонали равенст- ва, соответствует матери, с которой производитель дает плохое потомство да- же тогда, когда среднее качество его потомков лучше, чем у матерей. рио. щ Заполненная ращетка для осення нфонаао- 3. Влияние про- ди телей. итводителя на р а з- нообразие потомства определяется по форме прямоугольника Возможны три основных случая, представленные на трех схемах р«32.
162 КОРРЕЛЯЦИЯ более однообразное, выравненное, стандартное потомство. Это обстоя- тельство благоприятно, если производитель при этом является улучша- телем (схема V") и неблагоприятно, если производитель — ухудшатель (схема V'). VI. Прямоугольник имеет вертикальные стороны (по потомкам) длиннее горизонтальных (по матерям). Это значит, что потомство про- изводителя разнообразнее матерей по данному. признаку. Такой произ- водитель дает разнообразное, невыравненное, нестандартное потомство. Рис. 82. Возможные формы прямоугольника. Это обстоятельство всегда неблагоприятно, так как от таких произво- дителей невозможно ожидать чего-нибудь определенного и поэтому трудно определить его дальнейшее назначение. 4. К а ч е с т в о м а т е р е й определяется по положению прямо- угольника в горизонтальном направлении (слева направо) на различ- ных уровнях распределения матерей. Возможны три основных случая, представленные на трех схемах рис. 33. Рис. 33. Возможные положения прямоугольника в го-ризонтальном направлении. VII. Прямоугольник располагается в левой части решетки, что со- ответствует матерям со слабым развитием признака. Если при этом производитель оказывается улучшателем, то необходимо принять во внимание, что улучшает он потомство от худших матерей. VIII. Прямоугольник расположен в средней части (по горизонтали) решетки, что соответствует матерям со средним развитием признака. В таких случаях производитель оценивается на среднем маточном пого- ловье, что является благоприятным условием оценки. IX. Прямоугольник расположен в правой части решетки, что соот- ветствует лучшей части матерей по данному признаку. Если при этом производитель оказался ухудшателем, следует принять во внимание, что ухудшает он потомство, полученное от лучших матерей. 6. Наследуемость признака по матерям в потом- с т в е п р о и з в о д и т е л я определяется по форме корреляционного эллипса аналогично составлению и рассмотрению обычных корреляци-
ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ДЛЯ БОЛЬШИХ ГРУПП онных решеток. Возможны три основных случая, показанные на трех схемах рис. 34. Х. Частоты внутри прямоугольника располагаются так, что стано- вится очевидным, что корреляция между дочерьми и матерями близка к нулю. Это значит, что наследуемость признака по матерям при дан- ном составе матерей и при данных общих условиях крайне незначитель- на и отбор по матерям в потомстве данного производите.пя по данному признаку будет неэффективен. Рис. 34. Различные формы корреляционного эллипса. Х1. Расположение частот внутри прямоугольника указывает на не- значительную корреляционную связь между дочерьми и матерями по данному признаку в потомстве оцениваемого производителя. -)то значит, что при данном составе матерей и в данных хозяйственных условиях проявляется незначительная наследуемость этого признака по матерям и что отбор по матерям в потомстве оцениваемого производителя при данных общих условиях может дать некоторый, хотя и небольшой, эффект. Х11. Расположение частот внутри прямоугольника указывает на сильную корреляцию между дочерьми и матерями, а следовательно, и на хорошо выраженную наследуемость признака по матерям в потомстве оцениваемого производителя. Это значит, что при данном составе мате- рей и при данных хозяйственных условиях отбор дочерей по качеству матерей в потомстве данного производителя может быть эффективным: от лучших матерей можно ожидать и лучших дочерей. Т е х н и к а р а с ч е т о в. Существует несколько способов вычисления коэффициента корреляции для больших групп по корреляционной ре- шетке. Как показала практика, самым простым и удобным способом яв- ляется с п особ сумм, при котором все вычисления наиболее удобны, просты, экономны и промежуточные результаты счета могут проверять- , ся в процессе работы. Вычисление коэффициента корреляции способом сумм ведется по следующим уже знакомым формулам: ~~2 C=S.,— — '. C,+ C~ — С~ 2 )~'С, С,, При работе по этим формулам требуется предварительно получить следующие величины: 2 С, = Е 5> — сумму квадратов центральных отклонений, выраженных Q в классовых промежутках о = — по ряду первого k признака, распределение которого находится на верх- ней грани корреляционной решетки.
КОРРЕЛЯЦИЯ Находится величина С~ точно так же, как и при вычислении сигмы по способу сумм, на основе двух вспомогательных величин: $~ — — q< — r< и За —— q~+ r> — 2 (да+ га}. При этом С = F о~ ~— сумму квадратов центральных отклонений по ряду вто- рого признака, распределение которого находится на левой грани корреляционной решетки. Определяется С~ по формуле Та бли~а 63 Вычисление коэффициента корреляции для больших групп по способу суыы: С1+ C» — Сд ~1 = Ч1 — ~'1 ' ~' = А + ~'1 + 2 (й + ~'з). 2 ~ CC> 1-ый признак — обхват груди, 2-ой признак — живой вес у) 183 gI — — 104 130 140 150 160 170 l 80 190 q> — — 140 q.==38 104 34 2 36 2 35 98 37 г1 — — 135 2 гг —— 39 2 S) 428,9 + 627,4 — 187,4 = + 0,84 2 V 428,8 Х 637,4 81(1) ~, = А+~1 и = 160+ 10 +5 1-ый признак 428,9299 А1 — — 160, 1=10 а,=k = 10 1(2) +33 2-ой признак М~ —— А, + Й,— =350+ 50 Х ll 300 Аг — — 350, k = 250 637,4300 =50 и — 1 ог= Рг ~~21. С= S» ——и +5 25 2 --~-33 1089 +28 784
165 ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ДЛЯ БОЛЬШИХ ГРУПП С = ЕР'(о — о,) — сумму квадратов центральных отклонений по ряду разностей между центральными отклонениями, выра- женными в классовых промежутках второго и первого признаков. Этот ряд разностей составляется путем сум- мирования частот решетки по диагоналям, проходящим вдоль всего распределения частот. При прямых связях суммирование производится по диагоналям, ко- торые проходят от угла с наименьшими классами к углу с наибольшими классами по обоим признакам. В решетке, показанной в табл. 63, сум- мирование должно вестись по тем диагоналям, которые начинаются у левого нижнего угла и кончаются у правого верхнего. Величина С~ определяется так же, как С1 и С2. ~-2 1 С =S — —. 1Z 1 Здесь вспомогательные суммы S~ и Sg находятся для распределения указанных разностей. Составление ряда разностей показано на рис. 35. б е»» (~~е ~ / Рис. 85. Составление ряда разнос- тей в корреляционной решетке. Для получения вспомогательных сумм S~ и Sg для трех рядов (пер- вого признака, второго признака и ряда разностей) необходимо пред- варительно установить для этих рядов условные средние, т. е. те классы, средины которых будут использованы в качестве условных средних Как для первого признака, так и для второго условную среднюю можно установить вполне произвольно, руководствуясь теми немногими указаниями, которые уже были высказаны. Но если установлены услов- ные средние для обоих признаков, то условную среднюю для ряда раз- ностей необходимо установить уже в строгом соответствии с ними. Условной средней для ряда разностей должна быть нулевая раз- ность, т. е. такая разность, которая соответствует одинаковым условным отклонениям (выраженным в классовых промежутках) по обоим при- знакам.
166 КОРРЕЛЯЦИЯ Частота нулевык разностей получается при суммировании той диа- гонали, которая проходит через центральную ячейку. Центральной ячейкой называется ячейка. находящаяся на пересечении того столбца и той строки, средины классов которых приняты за условные средние первого и второго признаков. Установление условных средних лучше производить следующим образом. Внутри корреляционной решетки устанавливается центральная ячейка. Для последующих вычислений удобней установить центральную ячеику в месте наибольшего скопления частот, но не очень далеко от гео- метрического центра решетки. Центральная ячейка обводится четырех- угольником. В табл. 63 центральной ячейкой можно считать ячейку с частотой 41, что соответствует для первого признака классу с срединой 160, а для второго — 350. Это и будут условные средние. Рласс, срединой которого является условная средняя для ряда раз- ностей, устанавливается по сумме частот диагонали, проходящей через центральную ячейку. При обработке ряда разностей по способу сумм четыре центральные черточки надо ставить против частоты того класса разностей, который соответствует условной средней. В разбираемом примере это будет частота 137, что видно из рис. 35. Вычисление коэффициента корреляции по способу сумм показано в табл. 63. Оно проводится по следующим этапам. 1. В готовой корреляционной решетке устанавливается центральная ячейка. Против нее находятся условные средние по первому и по вто- рому признакам. В разбираемом примере, как указывалось, А~ — — 160 и А~ — — 350. 2. Составляется ряд разностей, и для него устанавливается класс условной средней. В разбираемом примере это класс ряда разностей с частотой 137. При суммировании диагоналей надо помнить, что цент- ральная диагональ, проходящая через центральную ячейку, соответст- вует нулевым разностям. В разбираемом примере это диагональ с час- тотами 1, 3.1, 25, 41, 25, 14. Диагонали, находящиеся справа (и вниз) от центральной диаго- нали, соответствуют отрицательным разностям, а диагонали, находя- щиеся влево (и вверх) от центральной диагонали, соответствуют поло- жительным разностям, если из условного отклонения второго признака вычитается условное отклонение первого признака (d = а~ — a~). Поэтому, если распределение разностей записывается где-нибудь столбцом, то сверху лучше записать частоты диагоналей, начиная с край- ней левой и кончать внизу крайней правой. Если же ряд разностей запи- сывается строкой, то лучше частоты записывать слева направо, начиная с крайней правой диагонали и кончая крайней левой. Такой порядок суммирования частот по диагоналям корреляционной решетки очень упрощает и уточняет проверку последующих вычислений. В разбираемом примере, в табл. 63, ряд разностей написан столб- цом в правом верхнем углу таблицы. Диагонали суммировались начиная с крайней левой (1 + 1 + 4 + + 1 = 7), переходя через нулевую диагональ (1 + 31 + 25 + 41 + 25 + + 14 = 137) и кончая крайней правой (1 + 0 + 1 = 2). 3. Производится расчет трех полученных распределений по методу сумм так, как это делается при вычислении среднего квадратического отклонения.
167 ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ДЛЯ БОЛЬШИХ ГРУПП После проведения этих расчетов в разбираемом примере (см. табл. 63) получены следующие величины, нужные для дальнейших расчетов: для первого признака Я( = 140 — 135 = + 5; Sg = 140 + 135 + 2 (39 + 38) = 429, для второго признака$) = 183 — 150 = + 33;Sg = 183 + 150 + 2 (104 + 50) = 641, для ряда разностей Si = 100 — 72 = + 28;S~ = 72 + 100 + 2 (2 + 7) = 190. 4. Производится проверка проведенных вычислений, возможная только при вычислении коэффициента корреляции по способу сумм. Если все вычисления сделаны без арифметических ошибок, то долж- но быть выполнено следующее условие: S1 (2) S1 (1) = S1 (Ш) у т. е., если из первой вспомогательной суммы второго ряда вычесть соот- ветствующую сумму первого ряда, то должна получиться первая вспо- могательная сумма ряда разностей. В разбираемом примере такое условие выполнено: (+33) — (t5) = = + 28. Если это не выполняется, то значит в предыдущих вычислениях имеются арифметические ошибки. Проверка правильности расчета вторых вспомогательных сумм S2 производится путем повторного сложения величин второго ряда сумми- рования в обратном порядке. 5 Составляется вспомогательная табличка, куда записываются по- лученные вспомогательные суммы S) и Sg, и результаты вычисления 2 1 1 2 2 S),, S — . По этим данным получают суммы квадратов Л Л центральных отклонений, выраженных в классовых промежутках. Для разбираемого примера С, = 428,9; C = 637,4; С~ = 187,4. 6. Зная C„C н C„, по формуле г = вычисляют коэф- С1+ СЯ — Cd фициент корреляции. Расчет средних арифметических и средних квадратических откло- нений для обоих признаков производится по обычным формулам спосо- ба сумм, путем использования величин, уже полученных при вычисле- нии коэффициента корреляции. При описанной системе вычислений величина С получается не в единицах изучаемого признака, а в классовых промежутках. Это нужно учитывать при вычислении М и а: Си — 1
КОРРЕЛЯЦИЯ Применение описанного способа, при котором используются разно- сти отклонений, наиболее удобно при обычно встречающихся прямых корреляционных связях между признаками. Если встречается обратная корреляция, что можно заметить по виду заполненной корреляционной решетки (ряд разностей получается очень растянутым), то в таких случаях проще использовать не разности, а суммы отклонений и вычисление коэффициента корреляции вести по формуле С~ — С1 — С, 2~С,С,~212=S ——й где Для получения ряда сумм отклонений надо суммировать частоты по диагоналям, перпендикулярным тем, которые дают разности. Все остальные действия проводятся точно так. же, как и при ис- пользовании разностей отклонений. П р и м е р 109. При изучении видового состава пищи осетров путем исследования содержимого их пищеварительного тракта было высказа- но предположение, что процент гаммаридов в пище меняется с возрастом осетров. Для проверки этого предположения была составлена корреля- ционная решетка и рассчитан коэффициент корреляции между разме- ром осетра в сантиметрах (ч1) и процентом гаммаридов в их пищи (v2). Расчет показан в табл. 64. Таблица 64 Вычисление отрицательного коэффициента корреляции для большик груни.. С~ — С1 — С2 ~2 c=s— C= Ха~ 2~ С1С~ п с, = KD2 (ь, + о,); I.-ый признак — размер осетров в сантиметрах, 2-ой признак — процент гаммаридовв их пище
ОШИБКА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ОШИБКА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ 1(ак и всякая выборочная.величина, коэффициент корреляции имеет свою ошибку репрезентативности, вычисляемую для больших выборок по формуле 1 — r' ) и — 1 Здесь r — коэффициент корреляции в генеральной совокупности, из ко- торой взята выборка; и — численность выборки, т. е. число пар значений, по которым вычислялся выборочный коэффициент корреляции. Поскольку в числителе формулы ошибки выборочного коэффициен- та корреляции стоит квадрат генерального коэффициента корреляции, то эта формула может применяться лишь в исключительных случаях, когда заранее известна или предполагается степень корреляции в гене- ральной совокупности. П р и м е р 110. Яля проверки гипотезы о том, что коэффициент корреляции между детьми и родителями r=+0,5, была сопоставлена плодовитость 226 свиноматок и их дочерей в соответствующем возрасте и в сходных условиях. коэффициент корреляции оказался равным + 0,41. Подтверждает или опровергает этот результат гипотезу? В данном случае разность между выборочным и генеральным коэф- фициентами d = + 0,41 — (+ 0,50) = — 0,09, а ее ошибка равна ошиб- ке выборочного коэффициента, так как генеральные величины не имеют ошибок репрезентативности. Яля вычисления ошибки коэффициента корреляции имеется возможность применить точную формулу с гене- ральным коэффициентом в числителе: =005. ~/ ~~~ 15 т =Т 0.09 Оказалось, что критерий достоверности разности~~, —,> —— ' —— — 1.8 0,05 не превышает даже первого порога достоверности (( = 2, Р = 0,95). Гипотеза в данном исследовании не опровергнута, так как эмпири- ческий коэффициент корреляции недостоверно отличается от гипоте- тического. В большинстве исследований значение коэффициента корреляции в генеральной совокупности неизвестно, поэтому вместо точного значе- ния ошибки коэффициента корреляции берут приближенное значение 1 — г" 10 г г ll — 1 где r — выборочный коэффициент корреляции, полученный при изуче- нии выборки; и — численность выборки (число пар дат). Это вполне допустимо при больших выборках. П р и м е р 111. При исследовании 400 зерен кукурузы найдено, что коэффициент корреляции между длиной и высотой зерна r = + 0,85. Определить, какова возможная величина коэффициента корреляции в генеральной совокупности. Ошибка найденной величины 1 — 0,85~ 0,2775 gggg 19,97 = 0,014 °
170 КОРРЕЛЯЦИЯ Отсюда при t> = 2,0 генеральный коэффициент корреляции,85+2,0. 0,014 не менее +0,822не более + 0,878 П риме р 112. При разработке методов определения высоты дере- ва по его обхвату для двух пород деревьев получены коэффициенты корреляции между обхватом ствола на высоте груди измеряющего и высотой дерева от земли до верхушки: и, =200; r, = +0,57; т~ = = 0,0034; 1990,4375 n — 1 1 — r2 и, = 150; r., =+0,75; т~ = = 0,0029. 149 и — 1 Для выяснения возможности применения единой формулы пере- счета требовалось выяснить, достоверно ли отличается связь указан- ных двух измерений для первой и второй породы. достоверность разности полученных коэффициентов корреляции определялась следующим образом: d =0,75 — 0,57 = 0,18; m„= ~ о,ooa4+ -о,оо29 = 0,079; з 2,6 2,0 0,079 ч = 200 + 150 — 2 = 348 критерий достоверности коэффициента корреляции, определяемый по формуле и — 2 1 — r~ mr Оказалось, что изученные две породы деревьев достоверно отлича- ются по степени связи между обхватом и;высотой ствола, поэтому нель- зя для них разрабатывать единую формулу пересчета высоты по об- хвату. По отношению к величине критерия достоверности коэффициента корреляции целиком применимы все положения о вероятности выбороч- ной величины, о которых указывалось при разборе ошибок разности между средними и между долями. Описанные методы определения достоверности коэффициента кор- реляции применимы только для больших выборок — не менее 100 пар значений. Для малых выборок (и ( 100) эти методы дают менее точ- ные, а иногда и совсем неправильные результаты, что объясняется сле- дующими причинами: 1) при и ( 1ОО сильно снижается возможность замены генерально- го коэффициента корреляции выборочными; 2) при и ( 100 распределение выборочных коэффициентов сильноот- личается от нормального и от распределения Стьюдента, поэтому нару- шается обычное соотношение между степенью вероятности безошибоч- ных суждений (Р,) и показателем этой вероятности (г;). При малых выборках, в которых имеется менее чем по 100 значе- ний каждого из коррелируемых признаков, необходимо пользоваться другой формулой ошибки выборочного коэффициента корреляции: 1 — г2 m= и — 2
171 ОШИБКА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ оценивается так же, как и критерий достоверности разности средних или .долей, путем сравнения фактически полученного значения t, с фиксиро- ванными значениями ~„соответствующими трем степеням вероятности безошибочных суждений. Число степеней свободы при определении принимается равным v =и — 2. П р и м е р 113. Для выяснения силы действия модифицирующих факторов при сравнении двух сортов кукурузы взяты 20 соседних участ- ков, на которых попарно были высеяны один и другой сравниваемые сорта, а затем рассчитан коэффициент корреляции между урожаями сравниваемых сортов. Большой коэффициент должен указывать на слабое действие моди- фицирующих агентов, малый коэффициент при этом исследовании бу- дет указывать на то, что различия между парными участками по уро- жаю сравниваемых сортов подверглись в течение опыта каким-то силь- ным и разнообразным (для разных пар) влияниям. Получены следующие результаты: 1 — 068 0 18 18 и = 20; r =+0,63; т, = 2,9 =35; r 063т, 018 ~ = 20 — 2 = 18 Получен вполне достоверный коэффициент корреляции между уро- жаями соседних участков. Это означает в данном случае, что различия опытных участков по плодородию почвы и другим факторам, определя- ющим урожай, были не настолько сильны, чтобы не дать проявиться различию испытуемых сортов. В тех случаях, когда сама ошибка коэффициента корреляции несу- щественна для исследования, а требуется определить только достовер- ность или коэффициентов корреляции, или их разности, лучше исполь- зовать особый показатель, предложенный Фишером — показатель z. Показатель z есть функция коэффициента корреляции, определяе- мая по формуле 1 3 1 5 z = — ( Iп (1 + r) — Iп (1 — r) } = r + — r3 + — гз + — г' +... 2 3 5 7 Заранее рассчитанные значения z, в зависимости от величины r, приведены в табл. 65. Таблица 65Значения z в зависимости от величины коэффициента корреляции (цнфры доz = 0,9962 приведены без нуля целых) 07 ов 05 04 03 02 00 01 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 0000 1003 2027 3095 4236 5493 6932 8673 1,0986 1,4722 0101 1105 2132 3206 4356 5627 7089 8872 1,1270 1,5275 0200 1206 2237 3317 4477 5764 7250 9077 1,1568 1,5890 0300 1308 2342 3428 4599 5901 7414 9287 1,1881 1,6584 0400 1409 2448 3541 472~ 6042 7582 9505 1,2212 1,7381 0501 1511 2554 3654 4847 6184 7758 9730 1,2562 1,8318 0601 1614 2661 3767 4975 6328 7928 9962 1,2933 1,9459 0701 1717 2769 3884 5101 6475 8107 1,0203 l,3331 2,0923 0802 1820 2877 4001 5230 6625 8291 1,0454 1,3758 2,2976 0902 1923 2986 4118 5361 6777 8484 1,0714 1,4219 2,6467
]72 КОРРЕЛЯЦИЯ Использование показателя г при определении достоверности коэф- фициента корреляции имеет следующие преимущества: 1. Ошибка выборочной величины z не зависит от значения z в гене- ральной совокупности и определяется по формуле 1 и — 3 Поэтому критерий достоверности величины определяется по простой формуле = zion — 3. 2. Распределение выборочных 2 для выборок, взятых из генераль- ной совокупности, достаточно приближается к нормальному при любых значениях z в генеральной совокупности даже при очень малой числен- ности выборок. Поэтому показатели достоверности t> = 2,0; <2 = 2,6; t~=3,3 могут применяться как при больших, так и при малых выбор- ках, если вместо коэффициента корреляции берется соответствующая ему величина z. Прим ер 114.. Исследовалась связь длины передних ног рысака и скорости его бега, определяемой временем, затрачиваемым на пре- одоление определенной стандартной дистанции. Для 28 лошадей меж- ду указанными признаками получен коэффициент корреляции, равный r= — 0,50. То обстоятельство, что коэффициент отрицательный, означае~, что при увеличении одного признака — длины ног, другой признак— время пробега — уменьшается. Можно ли ожидать таких соотношений в генеральной совокупности и вести отбор рысаков по длине ног? Для решения этого вопроса была определена достоверность полученного коэффициента корреляции при помощи величины z. По табл. 65 для r= — 0,5 определяем z= — 0,5493, 25 и — 3 s 0,5493 т, 0,2 12,6 z1' и — 3=-05493. 5=27, Коэффициент корреляции оказался достоверным с вероятностью Р, =0,99. Следовательно, можно ожидать, что и соответствующий ге- неральный показатель будет также иметь отрицательную величину (с увеличением длины ног время пробега уменьшается). Если желательно предусмотреть также и примерную величину коэффициента корреляции в генеральной совокупности, то сделать это можно при помощи величины z следующим образом: 2 0 = Q 5493 2,Q . Q 2 не менее 0 9493 1 не более — 0,1493 J По той же табл. 65 можно предельные величины z перевести в ве- личины 7' не менее — 0,75 не более — 0,15
173 ДОСТАТОЧНАЯ ЧИСЛЕННОСТЬ ВЫБОРКИ Такой большой размах возможных значений генерального коэффи- циента корреляции объясняется малой численностью выборки: и = 28. ЧИСЛЕННОСТЬ ВЫБОРКИ, ДОСТАТОЧНАЯ ДЛЯ ДОСТОВЕРНОСТИПОЛУЧЕННОГО КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ 1~аждая выборочная величина z при данных требованиях вероятно- сти достоверна лишь при вполне определенной численности выборки. Эту численность выборки легко рассчитать заранее. Если учесть, что в конечном итоге требуется получить одну из трех степеней достоверности величины z (или1, = 2,0, или t, = >,6, или t, = 3,3), то можно зара- нее рассчитать, при какой численности выборки данная величина z, а значит соответствующая ей величина коэффициента корреляции будет достоверна с заданной степенью вероятности. Сделать это можно, при- равняв величину критерия достоверности z(t,) заданной величине t;: з=~,, откуда r,, = +0,414; и =43; (23; 38; 60), r, =-+0,423; и=34; (22; 36; 57), r„= +0,260; и = 33; (57; 97; 157). Справа от фактических численностей выборок выписаны из табл. XII предельные численности, достаточны~е для достоверности коэффици- ентов корреляции с фиксированными тремя степенями вероятности. Определение достоверности коэффициентов корреляции проведено без вычислений, путем простого сопоставления фактических численностей с предельными. Коэффициенты корреляции подчеркнуты при третьей степени достоверности тремя прямыми, при второй — двумя, при пер- вой — одной и недостоверное значение подчеркнуто волнистой линией. Величина z очень облегчает, а для малых, выборок значительно уточняет решение вопроса о достоверности разности между двумя коэф- фициентами корреляции. 11остоверность разности между коэффициента- ми корреляции равна достоверности разности между соответствующими величинами z. По этой формуле можно заранее рассчитать требуемую численность вы~борки (число пар значений} для достоверности той величины z, кото- рая соответствует определенному значению коэффициента корреляции. Эти численности выборок приведены в табл. XI I.. Удобство работы с указанной таблицей заключается в том, что она применима для выборок любой численности — и для больших, и для малых; кроме того, определение достоверности коэффициента корреля- .ции при наличии табл. XII не требует никаких вычислений. П р и м е р 115. Изучалась корреляция удоя за первые 180 дней первой лактации и за первые 180 дней последующих лактаций. Получе- ны следующие коэффициенты корреляции: r„=+0,765; n=50; (7; 9; 14), r„=+0,654; и =52; (9; 14; 21),
КОРРЕлЯЦиЯ 174 Ошибка разности величин z 1 1 m„= — J и — з'и» — З' Критерий достоверности разности величин z Ш gf ~2 td = — = md 1' 1+и,— 3 и» — 3 П р и м е р 116. Для разработки методов отбора шерстных овец получены коэффициенты корреляции между тониной ости у маток и ве- личиной завитка у приплода: весенняя шерсть r = + 0,187; и = 201; осенняя шерсть r = +0,046; и = 1012. Требовалось выяснить, достоверно ли различие в степени корреля- ции весенней и осенней шерсти. Для этого был рассчитан критерий до- стоверности разности: z, =0,1923 (по табл. XII для r = 0,19); = 0,071; 201 — 3 z, = 0,0501 (по табл. XII для г = 0,05); m2 = —— 0,031;1012 — 3Рm„= g о,от~* ~- о,оз1 = 0,078; сК, = 0,1923 — 0,0501 = 0,1422; 2,6 2,0 0,1422 0,072 Шtd = — =my = 1,8, Оказалось, что различие по корреляции весенней и осенней шерсти между указанными признаками недостоверно. ЧАСТНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ В некоторых исследованиях требуется выяснить, не является ли связь между двумя признаками обусловленной влиянием какого-нибудь третьего признака. Например, при изучении статистических связей между урожаем и средней температурой воздуха имеет смысл учесть влияние третьего признака — количества осадков, который влияет на оба признака —, и на урожай, и на среднюю температуру воздуха. Точно также при изучении корреляционной связи развития тела животных и какого-нибудь показателя нх интерьера, например диамет- ра мускульных волокон, требуется выяснить, не является ли наблюдае- мая при этом связь результатом влияния такого мощного фактора, как калорийность пищи, изменение которой, конечно, вызывает одинаково направленные изменения веса животного и диаметра мышечных волокон и поэтому, несомненно, в какой-то мере и обусловливает связь между этими признаками. Для того, чтобы выяснить в таких исследованиях, влияет или не влияет третий признак на корреляционную связь между первым и вто- рым признаком, необходимо исследовать эту связь при постоянных зна- чениях третьего признака.
175 чАстныя КоэФФициЕнт коррЕляции 112 ° 3— 1 — Г12 1 — Г23 Здесь г,» °, — частный коэффициент корреляции между первым и вторым признаком при исключенном влиянии третьего; г», г» и r~3 — обычные коэффициенты корреляции между при- знаками, номера которых указаны в индексе. П р и м е р 117. При исследовании корреляционной связи между весом животных (1) и диаметром мускульных волокон (2), при исклю- ченном влиянии на эту связь калорийности пищи (3), т. е. при постоян- ном значении калорийности пищи, были получены следующие коэффи- циенты корреляции: между весом и диаметром r» — — + 0,6; между весом и калорийностью г» = + 0,8; между диаметром и калорийностью г~з = + 0,7. Частный коэффициент корреляции + 0,6 — (-~- 0,8) . (+ 0,7) -]- 0,04 д д о,82) . (i — о,7-) 112 ° 3— Выявилась очень малая частная корреляция. Исследование пока- зало, что если исключить статистическое влияние калорийности пищи, т. е. выравнять калорийность рационов, то между весом животных и диаметром их мускульных волокон не будет почти никакой корреляции, Например, при изучении корреляционной связи между весом живот- ных и диаметром их мышечных волокон можно третий признак — кало- рийность пищи — разбить на разные классы, организовав в каждом классе кормление при одном определенном уровне калорийности пищи. В каждом из этих классов третий признак имеет практически оди- наковое значение для всех животных, попавших в этот класс, но первый и второй признаки имеют у этих животных, конечно, вполне выражен- ное, хотя несколько ограниченное разнообразие. Пользуясь этим обстоятельством, можно определить степень связи между первым и вторым признаком в каждом из организованных клас- сов. Из всех полученных коэффициентов корреляции можно вывес1и средний коэффициент, который и будет мерой связи между первым и вторым признаком при постоянном значении третьего. Постоянное значение признака означает, что с чисто внешней сто- роны (а не с внутренней, что изучает физиология) невозможно подме- тить статистического влияния этого признака на все остальные. При постоянном значении признака возможно только констатировать, что в изменчивости других признаков нет его влияния: он постоянен, а дру- гие признаки изменяются. Поэтому коэффициент корреляции между первым и вторым призна- ками при постоянном значении третьего признака считают коэффициен- том корреляции между двумя признаками при исключительном влиянии третьего. Такой показатель носит название ч а с т н о г о к о э ф ф и ц и- е н т а к о р р е л я ц и и и обозначается символом r» 3. Для получения частного коэффициента корреляции не всегда нуж- но проводить такой сложный эксперимент, какой был описан выше для выяснения сущности частного коэффициента корреляции. Если связь между парой признаков прямолинейна или отличается от прямолиней- ной незначительно, то величину частного коэффициента корреляции можно определить по обычным коэффициентам корреляции: Г1~ — Г33 ' Г23
376 КОРРЕЛЯЦИЯ хотя обычно, без выравнивания калорийности пищи, эта связь внешне выражается довольно значительным коэффициентом: + 0,6. При совместном изучении трех признаков можно исключить влия- .ние не только третьего, но также и первого или второго признака: Г13 Г12 ' Г23 113 ° 2 = 1 Г12 1 Г23 Г23 Г1ъ ' ГИ 123 ° 1 = П р и м е р 118. Яля стандартизации разруба свиных туш была ,изучена взаимосвязь осаливания трех основных частей туши: окорока (1), корейки (2) и грудинки (3). Получены следующие коэффициенты корреляции между каждой парой этих частей по содержанию жира: между окороком и корейкой г з=+0,70; между окороком и грудинкой гд = + 0,10; между корейкой и грудинкой гзз — — + 0,14. Потребовалось выяснить, влияет ли на связь между каждой парой частей степень осаливания третьей части. Для этой цели были рассчи- fGHbl три частных коэффициента корреляции: 1 + 0,70 — (+ 0,10) (+ 0,14) ~ 12 ° 3— (1 — 0,10~) (1 — 0,14~) + 0,10 — (+ 0,10) (+ 0,14) ~ 13 ° 2'= V (1 — 0,70~) (1 — 0,142) + 0,14 — 1~- 0,70) (+ 0,10) ~23 ° 1 = g (1 — 0,70I) (1 — 0,10 ) Оказалось, что на значительную связь между окороком и корейкой (по степени осаливания) не влияет степень осаливания грудинки и, вообще, взаимосвязь по осаливанию между каждой парой частей свиной туши почти не зависит от осаливания третьей части. Можно исключить влияние двух признаков и получить частный коэффициент корреляции второго порядка по следующей формуле: Г12 ° 4 Г13 - 4 Г23 ° 4 Г12.34 ——— ° ° f (1 — ~1з.4) (1 'ъз ~) где г12.3$ — частный коэффициент корреляции второго порядка между первым и вторым признаками при исключен- ном влиянии третьего и четвертого признаков, т. е. при постоянном их значении; 1JQ4, г1з4, гзз.4 — частные коэффициенты корреляции первого порядка. П р и м е р 119. Для выяснения селекционного значения индекса мясности (отношение полуобхвата зада к высоте в холке) необходимо было выяснить, как влияют на его связь z убойным весом прямые пока- затели развития мясности — живои вес и возраст. Яля этого надо было подобрать достаточно многочисленную груп- пу скота, выравненную по полу, породе, характеру откорма и упитан- ности, и на каждом животном группы измерить указанные четыре при- знака (одни до переработки, другие после переработки), и по этим
ЧАСТНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ '.77 113 ° 4 = Оказалось, что индекс мясности при указанных выше условиях имеет очень большую частную связь с убойным весом и что разнообра-зие живого веса и возраста значительно снижают эту связь до г~р = 0 5. Иногда вычисление частного коэффициента корреляции дает ре-зультаты, кажущиеся на первый взгляд невероятными. При более же внимательном анализе явления, уже не с математической, а со специ-альной точки зрения эти результаты становятся вполне понятными и легко объяснимыми. Пример 120. При изучении зависимости:веса древесины от раз-меров дерева — обхвата на уровне груди измеряющего и высоты ство-ла — были получены следующие коэффициенты корреляции: между обхватом (1) и высотой (2) гд = +0,5, между обхватом (1) и весом (3) ~r~3 — — + 0,9, между высотой (2) и;весом (3) гд = + 0,8. Частные коэффициенты корреляции каждого размера с весом при исключенном влиянии другого размера не вызывают никаких недо- умений и указывают на большую частную корреляцию обхвата и высо- ты с весом древесины: 0,90 — 0,50 0,80 =+096. 113 ° 2 = (1 — 0,25) (1 — 0,64) 0,80 — 0,50 0,90 = + 0,92. 123 ° 1— g (1 — 0,25) (1 — 0,81) Частная корреляция между обоими размерами при исключенном влиянии веса, т. е. при его постоянном значении 0,50 — 0,90 0,80 = — 0,84. 112 ° 3— (1 — 0,81) (1 — 0,64) Оказалось, что между обхватом и высотой дерева получилась зна- чительная отрицательная частная зависимость: при увеличении высоты данным рассчитать частный коэффициент корреляции между индексом мясности (1) и убойным весом (2) при исключенном статистическом влиянии живого веса (3) и возраста (4). Предварительно необходимо было рассчитать по четырем призна- кам шесть обычных коэффициентов корреляции и три частных первого порядка (пример схематизирован): г12=+0,5, гд=+0,1, г~4= — 0,2, гааз=+0,9; гр4=+0,5; гз4=+0,6; ~- 0,5 — ( — 0,2) (~- 0,5) + «1 ' ( i — 0,2 ) (1 — 0,5 ) + 0,1 — ( — 0,2) (+ 0,6) Г ) (1 — 0 2г) (1 — 0 6â) + 0,9 — (+ 0,5) (+ 0,6) + 0,866 (1 — 0 2г) (1 — 0 6в) По этим коэффициентам можно уже получить и искомую величину частного коэффициента корреляции второго порядка: + 0,707 — (+ 0,281) . (+ 0,866) 112 34 = g (1 — 0,2812) (1 — 0,866')
178 КОРРЕЛЯЦИЯ обхват дерева уменьшается. Это, казалось бы, явно противоречит обыч- ным процессам развития деревьев: если увеличивается высота, то, конеч- но, увеличивается и обхват. Объяснение этого мнимого противоречия заключается в основном условии частной корреляции — постоянстве исключаемого признака. Если взять деревья одного и того же веса, то среди таких деревьев увеличение высоты может происходить только за счет уменьшения об- хвата. Если бы увеличивались оба размера, не мог бы оставаться посто- янным вес древесины. ОШИБКА ЧАСТНОГО КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ 4 Ошибка репрезентативности выборочного частного коэффициента корреляции рассчитывается по такой же формуле, как и обычный коэф- фициент корреляции при малочисленньпх группах: При оценке критерия достоверности частного коэффициента корре- ляции, предельные значения показателя вероятности 1; берутся из той строки табл. Х, которая соответствует числу степеней свободы v = и — 2 — k, где k —. число элиминированных признаков. Объем выборки в данном случае равен числу пар значений (и), одинаковому для всех обычных коэффициентов корреляции, которые не- обходимы для расчета частного коэффициента корреляции. КОЭФФИЦИЕНТ ПРЯМОЛИНЕЙНОЙ РЕГРЕССИИ Как уже упоминалось, прямолинейная корреляция отличается тем, что при этой форме связи каждому из одинаковых изменений первого признака соответствует вполне определенное и тоже одинаковое в сред- нем изменение другого признака, связанного с первым или зависящего от первого. Та величина, на которую в среднем изменяется второй признак, при изменении первого на единицу измерения, называется к о э ф ф и ц и- е н т о м р е г р е с с и и. Рассчитывается он по формуле ~2R = г]2,~1 ~г ф~ т == Р ~1 где R — коэффициент регрессии; о2 — среднее квадратическое отклонение второго признака, который изменяется в связи с изменением первого; 0) — среднее квадратическое отклонение первого признака, в связи с изменением которого изменяется второй признак; r~ — коэффициент корреляции между первым и вторым приз- наками. Ошибка коэффициента регрессии равна ошибке коэффициента кор- реляции, умноженной на отношение сигм:
179 УРАВНЕНИЕ ПРЯМОЛИНЕЙНОЙ РЕГРЕССИИ Критерий достоверности коэффициента регрессии равен критерию достоверности коэффициента корреляции: 1 . 0,8292575 685 685 3,9 ' ' ~ 3,9 (+ 0,829) -= + 145 6 кг; т 137,2 кг -+ 153,8 кг R = Я+-2тр —— + 145,6 !!-2 . 4,2 не менее не более Вычисления показали, что в данном случае коэффициент регрессии Ягп = + 145,644,2 кг. Это значит, что при увеличении высшего суточ- ного удоя на каждый 1 кг удой за 300 дней лактации увеличивается на + 145,6 кг с возможными отклонениями этой величины в пределах 138-: — 154 кг. Таким образом, ссли, например, у группы коров высший суточный удой в среднем на 5 кг больше среднего по сверстницам, то можно ожи- дать, что удой за 300 дней лактации этих коров будет на 5 145,6 = = 728 кг больше среднего по их сверстницам. УРДВНЕНИЕ ПРЯМОЛИНЕЙНОЙ РЕГРЕССИИ Как видно из приведенного примера, коэффициент прямолинейной регрессии показывает также, на сколько от своей средней отклоняется второй признак, если первый признак от своей средней отклонился на единицу измерения. Это можно выразить следующей формулой: (p2 Ш) = — ~2/1 (~] М1) ° Обозначая V) через х, V> через y, R>~> через b и произведя необходи-мые преобразования этого выражения, можно получить рабочую фор-мулу прямолинейной регрессии: y — М = b(x — М,), у — М = Ьх — ЬМ„ у = М — ЬМ,.+Ьх, y=a+bx, а =М,— ЬМ» b = Л,(., По этой формуле, зная значение х(аргумент), можно определить значение у (функция) без непосредственного его измерения: нужно ар- П р и м е р 121. При разработке методов селекции молочного ско- та выяснялась связь высшего суточного удоя с удоем за 300 дней той же лактации. Всего изучено 577 лактаций, проходивших в оптимальных условиях. Получены следующие данные: высший суточный удой (1): n~ — — 577; М1 — — 17,2 кг; п1 = 3,9 кг; удой за 300 дней лактации (2): n2 — — 577; М2 = 3250 кг; а~ = 685 кг; коэффициент корреляции: гд = + 0,829. Можно рассчитать коэффициент регрессии удоя за 300 дней по высшему суточному удою:
180 КОРРЕЛЯЦИЯ гумент х помножить на коэффициент регрессии Ь и к полученному про- изведению прибавить (или отнять) свободный член а. П р и м е р 122. Яля разработки способа определения веса по про- мерам, было взвешено 16 8 лошадей и у каждой из них измерен обхват груди. Обработка полученного материала дала следующие результаты: х — обхват груди: и, = 1618; M» = 174; а, .= 7,9 ся; у — вес лошади: и = 1618; Му = 424; ~у = 56,8 кг. Коэффициент корреляции r~~ = + 0,89. На основе этих данных сначала рассчитаем коэффициент регрессии: (+ 0,89) = + 6,4. 1 (/ — К у!» Й у м о Определив a=M~ — bM„., можно составить уравнение прямолиней- ной регрессии: а = 424 — 6,4 174 = — 690;у= — 690+6,4 х=6,4 х — 690. Следовательно, чтобы определить живой вес лошади без взвешива- ния по этому способу, надо обхват груди лошади умножить на постоян- ный коэффициент 6,4 и из полученного произведения вычесть постоян- ное число — 690. На основе уравнения прямолинейной регрессии можно заранее рас- считать значение функции для каждого значения аргумента. Например, таблица для определения живого веса лошадей по об- хвату груди может иметь простую форму, представленную в табл. 66. Таблица 66 200 590 140 206 220 718 240 846 180 462 160 334 Обхват груди, см )Кивой вес, кг у = 6,4х — 690 ТЕТРАХОРИЧЕСКИЙ ПОКАЗАТЕЛЬ СВЯЗИ (а + b) (с + d) (а + с) (b + d) Пример 123. При проверке действия прививки против сыпного тифа получены первичные материалы о числе заболевших ( — ) и неза- При альтернативном разнообразии, когда оба качественных при-знака выражаются только наличием или отсутствием их у особей, корре-ляционная связь между двумя признаками измеряется тетрахорическим показателем связи. Если изучаются у каждой особи два признака, то вся группа раз-бивается на следующие четыре части: а — особи, имеющие оба признака (++), b — особи, имеющие первый признак, но не имеющие второго (+ — ), с — особи, не имеющие первого признака, но имеющие второй ( — +), Ш — особи, не имеющие обоих признаков ( — — ). Если обозначить численность этих четырех групп этими же буква-ми (а, b, с, d), то степень связи наличия первого признака с наличием второго признака будет определяться тетрахорическим показателем связи, который вычисляется по формуле ad — bc
181 ПОЛИХОРИЧЕСКИЙ ПОКАЗАТЕЛЬ СВЯЗИ болевших (+) из числа получавших (+) и не получавших ( — } при- вивку, представленные в табл. 67. Г 54 44 — 6 106 + 1740 0,2 5. [/60 150 . 160 50 8485,3 Табли ца 67 Не получившиепрививку Получившиепри вивыу {а+с) =160 {byd) =50 — +c=106 — — d=44 ++а=54 + — b=6 Не заболели + Заболели— n=210 (c+d) =150 {а+Ь) =60Ф Определить достоверность тетрахорического показателя связи мож- но по величине Х2, которая в данном случае равна X2 = nI-2 ++ При числе степеней свободы v=1 (что имеет всегда место для тет- рахорической связи) предельные значения у2, соответствующие трем степеням вероятности отличия от нуля (Р1 — — 0,95; Р> 0,99; Рз — — 0,999), равны соответственно 3,8; 6,6 и 10,8 (см. табл. XI). Для приведенного примера достоверность связи прививки с пре- дохранением от заболевания определится так: 1 6,6 у' = 210 0,205'- = 8,8, ){' = 1 V Исследование подтвердило вполне достоверную связь (Р) 0,99) между прививкой и незаболеванием сыпным тифом. Если представляет интерес только достоверность тетрахорического показателя связи, то величину у' можно рассчитать, минуя вычисле- ° -r++ ноя показателя связи: (ad — be)' n/(а —, Ь) (с —' ,d) (а + с) (Ь --, d)Для приведенного примера по этой формуле получим имевшеесчранее значение: {54 44 — 6 106)' 21060 150 160 50 635 796 000 72 ООО 000 ПОЛИХОРИЧЕСКИЙ ПОКАЗАТЕЛЬ СВЯЗИ Есть такие количественные признаки, степень развития которых характеризуется не результатом точного измерения, не числом, а каче- ственными градациями, которые определяются субъективно, путем осмотра, ощупывания и вкусовой пробы. Цвет пера птицы может оцениваться как светло-серый, серый и тем- но-серый; развитие статей экстерьера — сильное, среднее, слабое; вкус
l82 КОРРЕЛЯЦИЯ ъ сливочного масла — слабо-, средне- и сильносоленый; упитанность жи- вотных — жирная, вышесредняя, средняя, нижесредняя, тощая и т. д. Определение степени корреляционной связи Между такими призна- ками можно производить при помощи полихорического показателя свя- зи, обозначаемого греческой буквой р и вычисляемого по следующей формуле: а — 1 1 (r, — 1) (г — 1) где о — полихорический показатель связи, и, f — частоты ячеек корреляционной решетки по первому и второ- му. п ризн а кам, гг, — частоты ряда первого признака по столбцам в нижней сум- марной строке, а2 — частоты ряда второго признака по строкам в правом сум- марном столбце, f~,1g — число градаций на которые разбиты первый и второй при- знаки, и — общая численность группы. Полихорический показатель связи всегда выражается положитель-ным числом, поэтому определение характера связи производится по виду корреляционной решетки. П р имер 124. При исследовании связи между крепостью телосло-жения производителей (1) и густотой их спермы (2) получены данные, представленные в табл. 68. Та блица 68 1(репость телосложения и„ слабая сильная средняя Сперма: 40 30 30 125 3052 921 густая средняя жидкая 30 33 37 П1 Сведение материалов в корреляционную решетку выявило вполне заметную связь между изучаемыми признаками: при сильной крепости телосложения большинство производителей имело густую сперму, а при слабом телосложении большинство из них (конечно, в сравнимых усло- виях) имело сперму жидкую. С1епень связи между этими признаками можно определить, рассчи- тав полихорический показатель связи, что показано в табл. 69. Выя ни- лось, что между изученными признаками имеется корреляционная связь достаточной степени: р =0,43.
ПОЛИХОРИЧЕСКИЙ ПОКАЗАТЕЛЬ СВЯЗИ Таблица 69 Вычисление полихорического показателя связи по формулам: уг а — 1 a=E n~ Р= э и, (r> 1) (r — 1) Крепость телосложения n=100; r~=3; r~ слабая средняя сильная Сперма: 1(1) 0,02 4(16) 0,53 25(625) 2о,83 9(81) 2,02 21(441) 14,70 3(9) 0,30 30(900) 22,50 5(25) 0,83 2(4~ 1,86 — 1 Р= 2,2 = 0,43 40 густая средняя жидкая 30 30 30 37 33 П1 21,38 > (f'-' и.) 17,02 23,46 a=1,86 > (f-': n,) 0,71 0,52 0,63 ni Расчет полихорического показателя связи нужно производить пэ следующим этапам: 1. Составить корреляционную решетку. 2. Подсчитать частоты и> по первому признаку суммы по столбцам (37, 33, 30) и общую численность группы n=Zn~=kn~ n = 37+ 33+ 30 = 40+ 30+ 30 = 100. 3. В каждой ячейке возвести в квадрат частоту и полученный ре-зультат (f2) записать в той же ячейке в скобках. Затем квадрат частоты ячейки разделить на частоту второго признака по той же строке, в ко-торой находится ячейка, и полученный результат (f~: пз) записать в той же ячейке под двумя ранее записанными цифрами. Например, в крайней верхней левой ячейке (табл. 69) частота f =30 квадрат этой частоты f2=900, а квадрат частоты, деленный на частоту второго приз-нака соотвегствующей строки — f: n2 — — 900: 40=22,5. 4. Последние числа ячеек (f2: пз) сложить по столбцам т. е. по градациям первого признака. и суммы записать в строке под частотамя первого признака. Например, по первому столбцу эта сумма равна 22,50+0,83+0,13= =23,46; по второму столбцу Z(f2: n2) =2,02+14,70+0,30=17,02, а по третьему столбцу Z(f': пз) =0,02+0,53+20,83=21,38. 5. Полученные значения Z(f~: па) разделить на частоты ряда пер-вого признака и результаты записать в следующей строке. Для перво-го столбца ' ' = ' =0,63, для второго столбца ' = 0,52, Х (f-': n,) 23,46 17,02 п1 37 .'3 21,38 для третьего ' = 0,71'. 30 6. Найти сумму значений цифр последней строки. Это будет вели. чина а= < ' - '=0,63+0,52+0,71 =, 1,86. и,
184 КОРРЕЛЯЦИЯ 7. Значения а, r~, г~, и подставить в формулу для полихорического показателя связи. Достоверность полихорического показателя связи можно определить при помощи критерия у~~, который для данного показателя равен и{а — 1) при числе степеней свободы v= (r> — 1) (r> — 1). Для разбираемого примера 18,5у."- = 13,3 у' = 100 (1,86 — 1) = 86,0; ~=2.2=4 КОРР ЕЛЯ ЦИОЫ ЫОЕ ОТЫОШ ЕЫ И Е Корреляционное отношение измеряет степень криволинейных связей. Криволинейная связь между признаками — это такая связь, при которой равномерным изменениям .первого признака соответствуют не- равномерные изменения второго, причем эта неравномерность имеет оп- ределенный закономерный характер. При графическом изображении криволинейных связей, когда по оси абсцисс откпадывают значения первого признака, а по оси ординат— значения второго признака и полученные точки соединяют, получают изогнутые линии. Характер изогнутости зависит от природы коррели- руемых признаков. При изображении криволинейных связей в форме корреляционной решетки частоты внутри решетки не располагаются в форме прямого эллипса. Ареал их расположения имеет форму изогнутых неправильных фигур. По виду корреляционной решетки очень часто можно выяснить характер связи (прямолинейная или криволинейная), что показано ь табл. 70. Та бли ца 70Корреляционные решетки при прямолинейной и криволинейной связях 21 10 8 1 35 56 28 7 1 7 8 1 35 70 35 18 1 21 28 7 56 211 351 21 56 35 35 1 28 21 35 16 3 156 21 7 28 21 3 1 1 8 7 В тех случаях, когда первый признак принимает разные значенич, а второй признакостается неизменным, можно заключить, что разнооб- разие второго признака никак не зависит 'от разнообразия первого ц связь между ними равна нулю. Если при значительном разнообразии первого признака второй име- ет незначительное разнообразие, можно заключить, что статистическая связь между разнообразием обоих признаков имеется, но она не- большая.
185 КОРРЕЛЯЦИОННОЕ ОТНОШЕНИЕ В тех случаях, когда при изменениях первого признака, второй признак изменяется часто и значительно, можно сделать вывод о боль- шой связи изменений обоих признаков. Таким образом, для получения показателя криволинейной связи не- обходимо определить численно степень разнообразия второго признака при определенном разнообразии первого. Делается это при помощи ря- да частных средних, рассчитанных для второго признака при разных значениях первого. Обозначаются частные средние второго признака по первому символом М2.1. Получение таких средних можно показать на следующем простом примере. Имеется группа из 6 особей, у каждой особи измерено два призна- ка (первый и второй). В результате получены следующие два ряда зна- чений: 4 6 6 4 14 18 8 8 4 12 Как видно, особи по первому признаку могут быть разбиты на группы с одинаковым значением этого первого признака (4, 6 и 8). В каждой такой группе будет по 2 особи. У первых двух особей первый признак имеет одинаковое значение, второй признак у них неодинаков! у одной особи он равен 8, у другой — 4. Если взять среднюю из этих значений, то это и будет частная средняя второго признака при определенном значении первого: 8+4 ~И 2 ° 1 =6. 2 Вторые две особи с одинаковым значением первого признака (6) имеют неодинаковый второй признак (14 и 18). В этом случае частная средняя И 14+ 18 — 16. 2 И, наконец, две особи третьей группы имеют одинаковое значение первого признака (8), а второй признак у одной особи равен 4, а у другой — 12. В данном случае частная средняя второго признака по первому 2 ° 1 4+ 12 2 двум рядам можно приписать третий ряд — ряд признака по первому: 4 4 6 6 8 8 8 4 14 18 4 12 6 6 16 16 8 8 ~И 2 ° 1 Теперь к имеющимся частных средних второго V1 ~г Ж1 Простое сопоставление полученного ряда частных средних второго признака с рядом первого признака показывает, что второй признак не остается неизмененным при изменениях первого. При изменении первого признака на одну и ту же величину (2) второй признак сначала резко увеличивается с 6 до 16, а потом столь же резко уменьшается с 16 до 8. При не очень большом разнообразии первого признака (от 4 до 8) разнообразие второго, судя по разнообра- зию частных средних, получилось довольно значительным — от 6 до 16,. что, конечно, указывает на большую связь второго признака с первым. Степень разнообразия частных средних можно выразить не только лимитами, но и более точным показателем — суммой квадратов цент- ральных отклонений, или дисперсией. Для получения дисперсии надо
К0РРЕлЯЦиЯ рассчитать общую среднюю для всех частных средних второго признака М2, затем для каждой из них определить центральное отклонение. D2.1 — — М2. > — М., полученные величины возвести в квадрат и резуль- таты сложить: Q Q2 — Q (Д~ Я )'-' В разбираемом примере этот расчет дан в последних нескольких строках. Сумма центральных отклонений для ряда частных средних второго признака по первому С2.1 = D',, = 112. Это величина именованная имеет значение только для небольшой группы, которая анализируется с целью выявления сущности корреляционного отношения. 6 6 8 8 4 4 14 18 4 12 ~ V .=60 V-» М» — — 10 60 6 6 16 16 8 8 D2 1 — — (М2 1 — М) — 4 +6 +6 — 2 — 2 Р2 1 — — (М2 1 ™г) 2 ~В2 1 — — 112= С2 36 36 4 4 16 16 D2 ( V2 М2! — -2 — 6 +4 +8 — 6 +2 2 (~2 М2) 2 ХО',=- 160= С, 4 36 16 64 36 4 Чтобы выяснить, насколько велика эта величина, необходимо отне- сти ее к сумме центральных отклонений по всему второму признаку {С2), которая рассчитывается обычным путем по разностям между каж- дой датой и общей средней изучаемого признака. Оказалось, что Корреляционное отношение второго признака по первому для рас- сматриваемого гримера 112 = 0,84, 160 С2.,С» ~2 ° 1— C = >D,'= 160. Это значит, что степень разнообразия второго признака, связанная с изменчивостью всех факторов, влияющих на его развитие, выражается для разбираемого примера числом 160. Разнообразие этого же признака, происшедшее в связи с тем, что первый признак принимал различные постепенно увеличивающиеся зна- чения, выражается меньшим числом С2 1 =112. Отношение этих двух по- казателей — частного и общего разнообразия — есть квадрат корреля- ционного отношения второго признака по первому: С2 ° 1 212 ° 1 — ° С2
КОРРЕЛЯЦИОННАЯ ОТНОШЕНИЕ 187 0 что свидетельствует о сильной корреляционной связи второго признака ° с первым. Может возникнуть вопрос — зачем понадобился новый показатель. нельзя ли и:в этом случае измерить степень связи при помощи основ- ного показателя — коэффициента корреляции? Для разрешения этого вопроса достаточно рассчитать коэффициент корреляции для случая явно криволинейной связи, например, для толь- ко что изученной группы из 6 особей. Получился очень малый коэффициент корреляции (r=+0,16), что находится в явном противоречии и с видом корреляционных рядов, и с величиной корреляционного отношения. Объясняется это тем обстоя- тельством, что коэффициент корреляции не может характеризовать сте- пень криволинейной связи. 36' ~' V1 — -- 36 С, =- 232— = 16 4 4 60~ = 160 6 С~ — — — 760— "-' V» = 60 12 18 ~ V> =- 232 121 36 16 16 36 36 60 ZD( Dg —— 368 — — =+8 6 Х ~',=- 760 12 324 16 196 144 84 . +8 — + 0,16 ~ V,V =368 108 32 32 16 96 16 . 160 Если связь между двумя признаками прямолинейна или достаточ- но приближается к прямолинейной, то коэффициент корреляции пра- вильно измеряет .связь между двумя признаками. При всех формах кри- волинейной связи коэффициент корреляции дает или приуменьшенные, или совсем неверные результаты. Поэтому и потребовалось ввести новый показатель — корреляционное отношение,— который правильно измеряет степень любой криволинейной связи. ВЫЧ ИСЛ ЕН И Е КОРРЕЛЯЦИОН НОГО ОТНОШЕН ИЯ Определение суммы квадратов центральных отклонений ряда част- HbIx средних С2 1 =. др 1 — (hf~, — M.,)'можно значительно упростить. Это облегчит и уточнит всю работу по вычислению корреляционных от- ношений. В разобранном примере для получения этой величины для каж- дого класса первого признака вычисляли частную среднюю второго при- знака, затем получали центральные отклонения ряда и возводили их в квадрат. Это сделано в учебных целях, чтобы вскрыть структуру кор- реляционного отношения. Применяя специальные рабочие формулы, можно получить точную величину С~. q гораздо проще. Способ расчета корреляционного отношения для малых групп по- казан в табл. 71.
К0РРЕляция }88 Таблица 71 Вычисление корреляционного отношения для малых групп по формулам: (> Vg.1)'- — с,, =>a — a„> = ~ 2 и, д y,,)ã 2 — — ~ Г2 Vi 4 4 12 4 6 6 8 Х V' 60 V2 18 14 8 Х К2 — 760 2 144 16 16 196 64 324 и=-6 Х Г2.1=60 12 2 ° 1 16 (> V,.,)~ 144 1024 256 ( 2 ° 1) й- и, Zh = 712 72 512 128 60гH = — = 6006 и=6 >h = 712 Z 022 = 760 С2 1 —— 712 — 600 = 112 С2 — — 760 — 600 = 160 112 =М 0,7 = 0,84 2 ~2 ° 1 — 0,7 160 При этом требуется произвести следующие действия: 1. Изучаемую группу разбить на классы с одинаковым значением первого признака, так чтобы в каждом таком классе было бы не менее двух особей. Если по первому призна~ку все особи различны, то в классы можно объединить особей с близкими значениями первого признака. Если этого сделать не удается, то для такой малой группы нельзя рас- считать корреляционное отношение. Требуется добавить несколько осо- бей, чтобы после этого выполнялось указанное условие. 2. Расположить особи по возрастающему или по убывающему зна- чению первого признака и для каждой особи записать три начальных столбца или строки: V1 — даты первого признака, V~ — даты, второго 2 признака и V~ — квадраты дат второго признака. Числа второго и треть- его столбцов или строки сложить. Получим > V, и ~ V~. В табл. 71 ~ Г, = 60, 'Е Г~ = 760. 3. Дальнейшие действия требуется вести уже не по каждой особи, а по ыассам первого признака. Таких кла ов оказалось 3: первый для особей со значением первого вризнака, равным 4, второй для особе|'. у которых первый признак равен 6 и третий — 8. 4. В каждом классе первого признака поставить частные частоты данного класса nl. В табл. 71 частные частоты по классам равны 2, 2, 2- Сумма частнь|х частот равняется сумме всех особей: 2и =и.
ВЫЧИСЛЕНИЕ КОРРЕЛЯЦИОННОГО ОТНОШЕНИЯ 189 5. По каждому классу подсчитать частные суммы дат второго при- знака (Е V2.1). В пашем примере эти частные суммы равны 16; 32; 12. Сумма этих чисел должна ~быть равна сумме всех дат второго признака: EF V2 . 1 — — F V == 16 + 32 + 12 = 60. 6. Все частные суммы вариантов:возвести в квадрат и затем (~2 )' разделить на частные частоты. Полученные величины h= П1 сложить, что даст величину Zh. В табл. 71 Zh=712. 7. Получить вспомогательную величину Н, для чего сумму ~всех дат второго признака возвести в квадрат и разделить на общую численность группы: (g ~',)2 602 = 600. и 6 8. Вычитанием из Zh величины Н получить С2.1= 712 — 600=112, вычитанием из Е V,' той же величины. Н получить С2=760 — 600=160. Обе эти величины получились в точности равные тем величинам, кото- рые рг)ee были найдены непосредственным способом: ~2 ° 1 = ~' ~2 ° 1 = ~ (~И2 ° 1 ~2) — 112р C = D2 = > ( V, — М2)2 = 160. С~ 1 112 9. Отношение полученных величин 1)2- = ' = — = 0,7 имеет с, мс самосгоятельное значение. Оно показывает ту долю разнообразия вто- рого признака, которая отражает действие организованного разнообра- зия первого признака. ~2.1 10. Путем извлечения квадратного корня из отношения мож- С2 но найти величину корреляционного отношения второго признака по первому: q2.1 — — p о,7 = 0,84. Вычисление корреляционного отношения для больших групп пока- зано в табл. 72. Расчеты надо вести в следующем порядке: 1. Составить корреляционную решетку, подсчитать частоты второго признака n: (суммы частот по строкам), частоты первого признака п( (суммь. частот по столбцам) и общую численность группы: п=Хп2=2п1. 2. Для второго признака установить условную среднюю А и на- лисать ряд ffcJIOBrIbIx отклонений, выраженных 'B классовых промежут- ках а. В табл. 72 А=450 и ряд условных отклонений начинается с +'3, кончается — 5 и имеет 0 против класса, средина которого равна 450. 3. Справа, рядом с частотами второго признака, расположить два столбца — два ряда накопленных частот по второму признаку (так же, как это делается при вычислении среднего квадратического отклоне- ния) — и получить величины д1 и г1 для первого ряда и д2 и г2 для вто- рого ряда.. В табл. 72 q) — — 533, r1 — — 123, q2 — — 247, r2=87. 4. Получить две вспомогательные суммы: SI(2) и $2(2) по второму рому признаку. В табл. 72 эти суммы оказались следующими: Ь'1 (2) = 533 — 123 = + 410; S2 (2) —— — 533 —' ,123 + 2 (247 + 87) = 1324 5. Под,рядом частот первого признака написать сумму условных отклонений, обозначаемую символом Zfa2. Для этого в каждом столбце
КОРРЕЛЯЦИЯ надо перемножить частоты на соответствующие отклонения и все про- изведсния сложить. Для 4-го столбца (возраст 5 лет) Zfa равна 35Х (+1) +56 Х (0) + +21Х ( — 1) =+14. Для 9-го столбца (возраст 10 лет) Zfa> равна 1Х (+3)+1X (+2) = =+5. 6. Все значения Zfag возвести в квадрат и записать в следующей строке. Та бли ца 72 Вычисление корреляционного отношения второго признака по первому: С~., ~12 ° ! (~; fu )г -'h = С~ — ~Ь — H и, 2 1 (2) Cg Sg (g) 1-ый признак — возраст, годы; 2-ой признак — вес животных, кг. ф = 533 6 7 9 10 10 28 18 21 56 35 40 207 35 70 35 35 56 21 21 28 3 49 25 10 3 r,==512 123 6 16 52 1'12 140 112 16 2 56 87 4-14 -+-140 +210 ° -27 — 41 — 34 +39 +5 8~ (g) —— + 410 S2 (2) ---- 1324 085,1 Еfu, +104 729 1681 1156 196 19 600 10 816 (Y. fu„)~ (g fu~)г 1521 25 95,1 12,5 44 100 121,5 105,1 1,8 140,0 393,8 22 2 193,1 4102 = 328,3 512 756,8 — 0,76 995,7 S (~) — — 533 — 123 = + 410 5' = 533 -+- 123 +- 2 (247 -1- 87) = 1324 С~ — — Х й — Н =- 1085,1 — 328,3 = 756,8 С. = S~ (~) — Н = 1324 — 328,3 = 995,7 '1о. ~ = ~0.76 = 0,87 7. Получить по каждому классу h = и записать их в последнюю и, столбца Ь = — = 121,5; 729 6 196 h= — = 1,8; для последнего столбца 112 первого признака величины строку. Например, для первого: для четвертого столбца (возраст 5 лет) Ь = =12,5. 2 600 550 500 4;0 400 350 300 250 200 +3 +2 -+1 0 — 1 — 2 — 3 4 — 5 40 127 1'59 112 50 9 8 4 3 40 167 326 74 24 15 7 3
191 свойствА коррЕляционного отношЕния 8. Все цифры последней строки сложить: Zh=1085,1. 2 1 (2) 9. Рассчитать общую поправку Н = — . В табл. 72 Н = П 41G2 5!2 = 328,3. 10, Проделать остальные действия для нахождения величины С>.1, С„щ.1, q>.1 по формулам, указанным в табл. 72. 2 СВОЙСТВА КОРРЕЛЯЦИОННОГО ОТНОШЕНИЯ Основным свойством корреляционного отношения является способ- ность измерять корреляцию при любой ее форме. Кроме того, корреляционное отношение обладает рядом других свойств, представляющих большой интерес в статистическом анализе корреляционных связей. В отличие от коэффициента корреляции, который дает одинакову~о меру связи признаков первого со вторым и второго с первым, корреля- ционное отношение второго признака по первому обычно не бывает рав- но корреляционному отношен;ио первого признака по второму: ~~2 ° 1 1~1 ° 2 ° На первый взгляд это кажется невозможным. Казалось бы, между двумя признаками может быть только одна связь, которая в данный момент всегда равна самой себе, независимо от того, с какого признака мы начинаем ее измерять: от второго к первому или наоборот. 1-1» самом деле это положение не всегда подтверждается практикой измерения обратных связей в биологии и сельском хозяйстве. Конечно, если изучается связь между такими парами признаков, как длина и ширина тела, цвет волос и цвет глаз, вес и объем продукта, уро- жай на соседних делянках, равенство обратных связей не подлежит со- мнению. Однако существуют такие пары коррелируемых признаков, для ко- торых очевидно, что обратные связи не могут быть равны. Например, связь с возрастом различных признаков животных и растений всегда имеет характер односторонней зависимости. Вес, размеры, объем, про- дуктивность, плодовитость, жизненность имеют явную зависимость от возраста, при, этом сам возраст изменяется совершенно независимо от этих признаков: он регулярно и неотвратимо увеличивается с каждым днем, месяцем, годом. Связь урожая с количеством осадков или с тем- пературой также имеет характер явно односторонней зависимости: уро- жай связан с температурой воздуха, но температура воздуха никак не зависит от урожая. Это неравенство обратных связей между условиями жизни и жнз- ченными функциями и отражается в неравенстве двух обратных корре- ляционных отношений: ~~2.1 Ф ~1. 2 ° Яля иллюстрации неравенства обратных корреляционных отношс- ний в табл. 73 показан расчет корреляционного отношения первого при- знака по второму для примера, рассмотренного в табл. 72, где корреля- ционное отношение второго признака по первому >z.1 — 0,87 Вычисления обратного корреляционного отношения проводятся по той же системе, только меняются местами дополнительные строки и столбцы. Расчет величин Е fa„(> fà~), ~ = приводится справа оч 2 и. корреляционной решетки, а первый и второй ряды накопленных частот
192 КОРРЕЛЯЦИЯ . Та оли ца 73 Вычисление корреляционного отношения первого признака по второму для большихгрупп по формулам: С1 2 С1.2= Ха — Н; а— 1 (Х fa,)' и .2 ~1 ° 2 11 ° 2~ C1 — — S2 (~) — H; 1-й признак — возраст, годы; 2-й признак — живой вес, Ц. 10 й =(Е /а,)"-и, fa1 +3 +4 О +1 40 119,0 10 600 8 1 21 147,8 127 28 7 1 550 35 56 70 35 9,6 18 159 500 35 35 85,8 112 21 56 450 1 28 21 50 128,0 400 6 3 350 64,0 72,0 250 200 56,3 48,0 140 112 112 16 2 18 2 Zh = 730,5 512 16 52 56 186 74 280 186 288 136 74 28 102 20 2 116 82 512 S (ц — — 280 — 288 = — 8 $,11 — — 280 + 288 ~- 2 (116 + 136) = 1072 С1 2 —— 730,5 — 0,1 = 730,4 C1 — — 1072 — 0,1 =- 1071,9 =0,1 730,4 — 0,68 1071,9 ''1~ . 2 = ~0,68 = 0,825 помещаются внизу корреляционной решетки. Все остальные действия при вычислении q>.~производятся так же, как и при вычислении~1д.1 В результате расчетов, показанных в табл. 73, получено второе кор- реляционное отношение, которое меньше первого: г~,., — 0,83 {~~,. =0,87). Такое неравенство обычно для этого показателя, оно является отраж»- кием неравенства некоторых зависимостей, проявляющихся в области развития живых организмов. Неравенство обратных связей можно иллюстрировать и графически. Например, для группы из 6 особей (см. табл. 7 ) зависимость между признаками можно изобразить в виде двух графиков. На одном по оси
193 СВОЙСТВА КОРРЕЛЯЦИОННОГО ОТНОШЕНИЯ абсцисс отложены значения первого признака, а по оси ординат — вто. рого; на втором — наоборот: го оси абсцисс отложены значения второго признака, а по оси ординат — первого. Результаты показаны на рис.36. При одинаковых масштабах первого и второго признаков на графи- ках явно выявилось неравенство обратных связей. При относительлэ незначительном изменении первого признака (I график) второй пока зываст увеличение, а потом уменьшение, что обычно для зависимости многих жизненных функций от возраста или от регулярно нарастающих доз к~кого-нибудь фактора. И, наоборот, при относительно значитель- ных изменениях второго признака (П график), первый признак изме» няется незначительно, давая, небольшие отклонения от среднего зна- чения. f2 1Î 10 4 б д 8e ие ~ф б д 0 2 f4 16 Щ, a, е д 6 б рис. gg. г рафическое изображение обратных связей: 1 — изменения второго признака по градациям первого; II — из- менения первого признака по градациям второго. 2 ° 1— Яля обратной связи частные средние получены путем умножения сре-дин классов первого признака (градаций возраста) на частоты ячеек каждой строки и деления суммы таких произведений на сумму частот каждой строки: 1 ° 2— П2 Неравенство обратных связей может быть столь велико, что одно из корреляционных отношений, например, второго признака по первому может иметь достаточную величину, а другое — первого признака по второму — равно нулю. Такой случай показан в табл. 74 и на рис. 37. В табл. 74 приведено схематизированное распределение двух при- знаков: 1) возраста (число отелов) и 2) удоя за лактацию (центнеров). Кроме корреляционной решетки, сбоку и внизу даны ряды частных сред- них:hf>.1 — удоя по возрасту и М1.~ возраста по удою. Частные средние рассчитаны по способу взвешенных вариаций, пу- тем умножения средин классов второго признака на частоты ячеек каж- дого столбца и деления суммы таких произведений на сумму частот каждого столбца:
194 КоРРЕлЯЦиЯ Таблица 74Корреляционная решетка и два ряда частных средних: удоя по возрасту и возрастапо удою (схема). 1-й признак — возраст в отелах, 2-й признак — удой за лактацию, и. ля М1 r 0,00;. = 0,00 ~2.1 = 0,51; Оба ряда частных средних изображены. на графиках рис. 37. По виду корреляционной решетки, представленной в табл. 74, труд- но выяснить, какой характер, направление и степень связи имеется меж- ду коррелируемыми признаками. P] ]1 Р 3 4 5 б 7 д У 10 f1 Юр 6 20ЛЗОЛ4045.505560 kf~..( Ж30.'@3~54041 41 У,ЮЗАМ 3025 М, ~ б 6 б б б б б б б б Р«. 37. Графическое изображение зависимости удоя от возраста(1) и возраста от удоя (Ц). Данные табл. 40. Коэффициент корреляции, рассчитанный для этого распределения, оказался в точности равным нулю, корреляционные отношения для это- го распределения оказались следующими: для удоя по возрасту ~~ 2.1- —-- =0,51, для возраста по удою >J). ~ — — 0,00. Очень большое неравенство об- ратных связей показали и два ряда частных средних. В данном случае корреляционные отношения в статистической фор- ме полностью отразили физиологическое неравенство обратных связей между парой признаков: удой — возраст. Так бывает не всегда. В большинстве случаев коррсляционцые от- чошення отражают лишь частично, неполно физиологическое неравенст. во обратных связей. Например, в показанном в табл. 72 и 73 распределении пары при- знаков вес — возраст меньшее корреляционное отношение возраста по 60 55 50 45 40 35 30 25 20 15 ni 2 ° 1 1 1 1 3 4 4 4 18 25,0 42 40 М 36 32 30 28 2б 24 1 1 2 3 6 5 3 1 22 30,0 1 2 1 6 5 3 2 1 25 34,0 1 1 3 4 6 8 5 2 1 1 32 37,6 11510875214040,0 12510975114140,7 11510875214040,0 1 1 3 4 6 8 5 2 1 1 32 37,5 1 2 1 4 6 5 3 2 1 25 34,0 1 1 2 3 6 5 3 1 22 30,0 1 1 1 3 4 4 4 18 25,0 5 8 27 44 51 57 53 53 23 14 314 6,0 6,0 6,0 6,0 6,0 6,0 6,0 6,0 6,0 6,0 6,0
195 ДОСТОВЕРНОСТЬ КОРРЕЛЯЦИОННОГО ОТНОШЕНИЯ ДОСТОВЕРНОСТЪ КОРРЕЛЯ ЦИО ННОГО ОТНОШ ЕН ИЯ Ошибка репрезентативности и критерий достоверности корреляци- онного отношения рассчитываются так же и имеют такое же применение, как и для коэффициента корреляции: и — 2 весу все же оказалось значительной вели ~иной: '<~i . > —— 0,83. 1(оэф- фициент корреляции для этого распределения также оказался большим: r = -+-0,82. Тут может возникнуть вопрос: если возраст совершенно не зависит от любого показателя развития животных, в том числе и от их веса, гэ почему оба пок 1зателя связи — и коэффициент корреляции r = + 0,82 и корреляционное отношение возраста по весу ~~> . ~ =0,83 — указывают на сильную корреляционную связь именно возраста с весом. Объяснение такого противоречия заключается в том, что статисти- ческие показат~ели связи характеризуют лишь внешнее проявление фи-: зиологических зависимостей Внешнее же разнообразие явлений, осо- бенно биологических, бывает столь велико, что часто скрывает те внут- ренние физиологические закономерности, которые лежат в основе внеш- него разнообразия. Поэтому и неравенство обратных статистических связей обычно очень неполно отражает неравенство соответствующих обратных физи- ологических зависимостей. Возраст изменяется вне всякой внутренней физиологической зависи- мости от веса, который сам сильно зависит от возраста. Это неравенство обратных физиологических связей нашло свое да- леко неполное отражение в том, что корреляционное отношение возраста по весу (qi .2 —— О,ьЗ) все же меньше корреляционного отношения веса по возрасту(~р. 1 — — 0,87). Точно также изменения метеорологических факторов никакие за- висят от урожая, получен~ного на каких-нибудь участках, а урожай на этом участке сильно зависит от погоды. Составив корреляционную ре- шетку для пары .признаков, например, урожай — сумма температур, мы получили бы два неравных корреляционных отношения. Из них меньшее все еще будет достаточно велико и. не будет равно нулю, хотя сумма температур не имеет никакой внутренней зависимости от урожаев. Тем не менее эту статистическую неточность в характеристике об- ратных внутренних связей можно использовать на практике. Можно, измерив или взвесив животное, примерно определить его возраст. Например, если кролик весит 2 кг, то значит это взрослое жи- вотное, а если 100 г — значит молодое. Если бык весит 500 кг — это взрослое животное, если 200 кг — это молодняк 1,5 — 2,0 лет, если 100кг- это теленок 6 — 8 месяцев, если 30 кг — это новорожденное животное.. Тут используется достаточная статистическая обратная связь воз- раста весом при полной физиологической независимости увеличения возрасза от изменений веса. Если в засушливой местности получен большой урожай, значит осадков выпало много, если же урожай не велик, значит осадки были не- значительны. При таких обычных в практике заключениях также ис- пользуется обратная статистическая связь количества осадков с урожа- ем при полной внутренней метеорологической независимости осадков от урожая.
196 КОРРЕЛЯЦИЯ Предельные значения показателя вероятности безошибочных суж- дений t, для P> — — 0,95. P2 — — 0,99 и Р=0,999 при определении достоверно- сти выборочного корреляционного отношения можно находить по таб- лице критериев достоверности (табл. Х), в строке, соответствующей ч=п — 2. КРИТЕРИЯ КРИВОД ИНЕЯНОСТИ где I( — мера криволинейности, равная разности квадратов корреляци- онного отношения и коэффициента корреляции: К=т)' — r', т,< — ошибка меры криволинейности, рассчитываемая по формулс т,, = — („=21 l( — K~(2 — т — r') ). Л Например, при т)=0,7; т)2=0,49; К=0,24; 9=0,0576; n=100; r=+0,5; r2=0,25 „ = 21 0,24 — 0,0578 ð — o,49 — o,л) = 0,818;т„= ' = 0,0818;0,818 26 3,3 0,4 29 0,082 tl,— Все обычно наблюдаемые связи в той или иной степени криволиней- ны. Точно прямолинейная связь является редчайшим исключением. Од- нако некоторые связи имеют такую незначительную степень KpHBQJI?I- нейности, что практически их можно принять за прямолинейные и эти:t значительно облегчить все дальнейшие работы по определению частной корреляции и по исследованию простой и множественной регрессии. Яля практических целей необходимо установить порог криволи- нейности, перейдя который связь уже не может считаться прямоли- нейной. Установление такой границы производится при помощи крите- рия криволинейности t, Если он равен трем или большему числу, то значит связь настолько криволинейна, что принять ее за прямолинейную уже нельзя. При t„(3 связь практически может быть принята за пря- молинейную. При более точных работах можно принимать связь за прямолиней- ную только при ti; (2,5 и даже при ti;(2,0. Вычисляется критерий кри- волинейности по формуле
ГЛАВА VДИСПЕРСИОННЫЙ АНАЛИЗ OCHOBbl МЕТОДА ущность дисперсионного анализа состоит в изучении стати- стического влияния одного или нескольких факторов на ре- зультативный признак. Результативный признак (у) — это признак, который изучается как результат статистического влияния факторов: организованных в иссле- дованиях (х) и неорганизованных (г). Факторы — это любые воздействия или состояния, разнообразие ко- торых может так или иначе отражаться на разнообразии результатив- ного признака. Под статистическим влиянием факторов в дисперсионном анализе понимается отражение в разнообразии результативного при- знака того разнообразия изучаемых факторов, которое организовано в исследовании. Под разнообразием мы будем понимать наличие неодинаковых зна- чений каждого признака у разных особей, объединенных в группу. Раз- нообразие группы особей по изучаемому признаку может иметь разную степень, которая обьгчно измеряется показателями разнообразия (или «изменчивости»): лимитами, средним квадратическим отклонением, коэффициентом вариации. В дисперсионном анализе степень разнооб- разия индивидуальных и средних значений признака измеряется и срав- нивается особыми способами, составляющими специфику этого общего метода. Организацчя факторов заключается в том, что каждому изучаемо- му фактору придается несколько значений. В соответствии с этими зна- чениями каждый фактор разбивается на несколько градаций; для каж- дой традации подбирается по принципу случайной выборки несколько особей, у которых впоследствии и измеряется величина результативного признака. Организация факторов может осуществляться путем подбора опыт- ных и контрольных групп для последующего проведения эксперимента или путем привлечения первичных материалов ранее проведенных на- блюдений. Для того, чтобы выяснить степень и достоверность влияния изучае- мых факторов, надо измерить и оценить ту часть общего разнообразия, которая вызывается этими факторами. Делается это при помощи двух величин: дисперсии и девиаты. Дисперс и ей мы будем называть и само наличие разнообразия в группе и первичную меру, которая определяет степень этого разнооб- разия. Дисперсия как первичная мера разнообразия равна сумме квад- ратов центральных отклонений: C=ZD'
198 ДИСПЕРСИОННЫЙ АНАЛИЗ Общая дисперсия признака С = Е (V — М„)-' = Е И, Здесь V — дата. отдельное значение результативного признака, Мо — общая средняя по всему комплексу. Общее разнообразие, результативного признака всегда больше того разнообразия, которое связано со статистическим влиянием организо- ванных факторов. Происходит это потому, что ни в одном исследова)нии нельзя освободиться от действия всего множества остальных факторов, так или иначе влияющих на изменение результативного признака; во многих исследованиях этого и, не требуется. Поэтому при проведении дисперсионного анализа общая дис- п е р с и я п р и з н а к а С, в изучаемой группе расчленяется на дис- персию, вызванную организованными факторами или ф а к т о р и- ал ьную дисперсию (части а я ди с перси я) C„, и дисперсию, вызванную остальными.,неорганизованными в данном опыте факторами, или с л у ч а й н у ю д и с п е р с и ю (о с т а т о ч н а я д и с п е р с и я) С,, причем сумма факториальной и случайной дисперсий всегда равна общей дисперсии: С„ -) С» = С, Факториальная дисперсия: С,.= Е {М» — М,}' = ED», а случайная дисперсия: С» = Е (V — М,)'-' = ED,', ~ ~1 + ~ ~~2 + ° ° ° —) ,~ ~~п — ~ ОО. Если взять отношения частных дисперсий к общей, то сумма всех таких отношений (долей или процентов) будет равна единице, или 1рр 0/ Каждое отношение будет показывать долю участия отдельного фактора в формировании общего разнообразия результативного при-знака. Эти отношения частных дисперсий к общей и принимаются в дисперсионном анализе за показатели степени статистического влияния на результативный признак факторов, организованных в опыте — .л» =- С, С» — и неорганизованных — т~, = . При этом =с, С,, * С учетом числа вариантов, для которых рассчитана каждая формула примет следующий вид: С» = n,.(М, — Mz)-" = '-' гг»В~., средняя М~, эта где М» — частная средняя результативного признака по каждой отдель- ной градации организованных факторов. В дисперсионном анализе используется свойство суммы квадратов центральных отклонений, заключающееся .в том, что если несколько полностью независимых источников разнообразия действуют одновре- Memo и создают общее разнообразие признака, то сумма частных дис- персий, измеряющих частные влияния, всегда равна общей дисперсии, характеризующей общее разнообразие признака, возникшее под дей- ствием .всех источников разнообразия:
ОСНОВЫ МЕТОДА есть корреляционное отношение — обычный показатель криволкнейной связи двух признаков. Дисперсия как показатель разнообразия зависит от числа особей в группе. Для определения степени влияния факторов это обстоятель- ство не имеет значения. Для других же целей, в частности для установ- ления достоверности влияния факторов, обнаруженного при выбороч- ном исследовании, необходим показатель, свободный от указанной за- висимости, допускающий сравнение групп, различных по числу входя- щих в них элементов. Таким показателем является девиата. Д е в и а т о й мы будем называть дисперсию, приходящуюся на один элемент свободного разнообразия или на одну степень свободы. Девиата равна сумме центральных отклонений, деленной на число сте- пеней свободы: гд» а ИЛИ ~ (~ — ~ио) 2а ° 2 ~ (~» — ~о) Х Х 2 ~ (~ — +») 'г— 2 х 2 о Если это отношение равно или больше определенной стандартной величины, влияние считается достоверным с определенной степенью вероятности. Стандартные отношения девиат определяются по специаль- ным таблицам, приведенным в приложении. Значение отдельных приемов дисперсионного анализа можно пока- зать на следующем упрощенном примере. Изучается действие на результативный признак у (например, рост, продуктивность, плодовитость, размеры, выживаемость и т. д.) двух факторов А и В. Каждый фактор берется в двух градациях: А1 и А2, 2 'Здесь а„— общая девиата по всему комплексу; 2, — частная девиата по организованным факторам, или факто- 2 риальная девиата; ',— частная девиата по неорганизованным факторам, или слу- 2 чайная девиата; v — число степеней свободы; D — центральное отклонение; М,, М,— частная и общая средние. / 'Р Д2 Корень квадратный из девиаты ~ = есть обычный пока- 1ф загель математической статистики — среднее квадратическое откло- нение. Девиаты используются в дисперсионном анализе для определения достоверности влияния, обнаруженного в выборочном исследовании. Достоверность влияния фактора определяется отношением факториаль- ной девиаты к случайной:
ДИСПЕРСИОННЫИ АНАЛИЗ В~ и В2. Для обоих факторов первая градация — это слабая степень, вторая — сильная (например, низкая и высокая температура, слабая и сильная влажность, малая и большая доза химического или биологи- ческого препарата, различные условия кормления, двухкратная и трех- кратная дойка и т. д.). Для каждой из четырех градаций двух факторов — А1В~, А1В,', А2В1, А2В~ — по способу случайной выборки выбрано по две особи; у всех восьми особей измерен .в определенное время результативный признак; результаты записаны в виде статистического комплекса, по- казанного в табл. 75. Т а блица 75 А, Градации первого фактора в, В Градации второго фактора Значения результативного признака 7;9 3;5 9; 11 При анализе подобных комплексов обычно решаются два основных вопроса: 1). Имеют ли значение для результативного признака изучаемые факторы в их общем суммарном действии? 2) Какова роль каждого фактора в отдельности и в их сочетаниях? Знакомство с приемами дисперсионного анализа лучше начинать с разрешения первого, более простого, вопроса. Для этой цели можно принять, что действует один фактор х, имеющий все указанные гра- дации, которые организованы в исследовании для всех изучающихся факторов. Такой обобщенный статистический комплекс показан в табл. 76. Табли ца 76 Градации факторов Х2 Варианты результативного признака 3;5 1;3 9; 11 7; 9 Анализ полученного комплекса проводится по следующим этапам. Нахождение общей дисперсии С, Как ужеуказывалось, С„= (Е V — Мо)2. В приведенном примере сумма всех дат ZV = 9+11+3+5+1-+- +3+7+9=48; число дат п=2Х4=8. Следовательно, общая средняя ЕV 48 М = — = — =6. и 8 Сумма .квадратов отклонений каждой даты от общей средней Z(V — M0)' = (9 — 6)~+ (11 — 6)'+ (3 — 6)2+ (5 — 6)'+ (1 — 6)'+ + (3 — 6)2+-- (7 — 6)2+ (9 — 6)-"=9+--25+9+--1+25+--9+--1+--9=88. Это и есть общая дисперсия всего комплекса .вариантов: С,, =88. Нахождение фактор и а л ь ной дис п ер сии С». Для вы- яснения величины факториальной дисперсии надо рассчитать средние результативного признака для каждой градации, затем из каждой та-
201 ОСНОВЫ МЕТОДА кой частной средней вычесть общую среднюю комплекса. получен- ные центральные отклонения возвести в квадрат, помножить на соот- ветствующую частоту градации и произведения сложить: С» =- Е n „D» = Е и» (М — М )'. Для приведенного примера эти действия показаны в табл. 77. Таблица 77 Градации факторов х x$ х Значения результативного признака 1; 3 3; 5 9; 11 7; 9 n=8 20 16 Z V=48 С~л~л1ы значений Мо=б 10 Частные средние М„ Центральные отклонения ря-да средних (М» — Mp) Квадраты центральных от- клонений D„. =(М» — Mp)2 Cx = 80 4; 4 16; 16 4; 4 16; 16 Полученные квадраты центральных отклонений нужно для сравни- мости дисперсий подставить вместо каждой даты, поэтому централь- ных отклонений взято столько, сколько дат результативного признака имеется в каждой градации. Сумма всех этих значений и есть фактори- альная дисперсия С» =- ) D»2 = 80. Н а х о ж д е н не степ е н и в л и я н и я ф а к т о р а производится путем деления факториальной дисперсии на общую: 7 80 09 С, 88 Это значит, что 91 % всего разнообразия результативного признака определяется разнообразием организованных факторов. Эта величина является показателем степени статистического влияния данного факто- ра на результативный признак. Н зхожден ие случайно й дисперсии С. Нахождение слу- чайной дисперсии С, = > (V — ~„)' = > D» для приведенного примера показано в табл. 78. Таблица 78 Градации факторов х х., Х9 Значения результативного признака 7; 9 9; 11 3; 5 1; 3 10 Частные средние М~ Частные центральные откло- нения — 1; +1 — 1; +1 Квадраты частных централь- ных отклонений и', =- (v — м,) C„- =8
202 ДИСПЕРСИОННЫЯ АНАЛИЗ Значения первой градации 9 и 11 имеют центральные отклонения от своей частной средней (М,. = 10), равные — 1 и + l. квадраты цен- тральных отклонений равны +1 и +1, а ) D~ = 1+ 1 = 2. Для второй градации > D, = 1 + 1 = 2, для третьей градации Е D, = = 1+1=2 и для четвертой градации E D, = 1 + 1 = 2. Сумма квадратов центральных отклонений дат от частных средних для всех четырех градаций равна 8. Это и есть случайная дисперсия. Случайная дисперсия в сумме с факториальной дисперсией состав- ляет общую дисперсию: С + С, =- 80+ 8 =-. 88 = С, Степень .влияния неорганизованных факторов = 0,09. С 88 Это значит, что влияние неорганизовавных факторов в приведенном примере составляет всего 9% от общего влияния ~всех факторов Таким образом, в приведенном примере выявилась степень влия- ния факторов на разнообразие результативного признака в следующих размерах: влияние организованного фактора (объединенноедействие двух факторов — А и В).... 91%влияние факторов, неорганизованных в данномопыте.......... 9%влияние всех факторов.... 100% М 10х, Такие результаты указывают на большую силу влияния изучаемо- го фактора. Графическое изображение влияния фактора при однофакторном комплексе можной выполнить следующим образом: по оси абсцисс нано- сят на равных расстояниях столько точек, сколько имеется градаций Ю фактора. Из каждой такой точки по 0 оси ординат отмеряется расстояние, 8 пропорциональное значению частной 7 средней для данной градации факто- б ра. Полученные точки соединяются прямыми линиями. 5 3 Для разбираемого примера гра- 2 фическое изображение влияния на 1 результативный признак фактора .~ представлено на рис. 38. График показывает, что при из- 2 ~3 4 [,в] [a,â,] [л,в] [л,.в] Me"eHH" ôaKToð' от ~1 z~ ~4 резуль тативный признак сначала уменьша- Рис. 88. График влияния фактора (объе- ется, потом возрастает. Такое влия- диненного) на результативный признак ние одного необъединенного факто- ра встречается редко. Но в данном случае градациями фактора х являются четыре комбинации градаций двух факторов. Поэтому раскрытие причин такого сложного влияния необходимо производить, восстановив двухфакторный статистический комплекс, что и будет показано в соответствующем разделе. А теперь продолжим изучение однофакторного комплекса. Определение достоверности влияния организо- в а н н о г о ф а кто р а. Для определения достоверности влияния организованного фактора необходимо рассчитать факториальную и слу- чайную девиаты, взять отношение их и по специальной таблице опреде- лить достоверность полученного отношения. Для получения девиаты на-
ОСНОВЫ МЕТОДА 203 до дисперсию разделить на число степеней свободы, которые в однофак- торном комплекс~ определяются следующим образом: а) для общей дисперсии число степеней свободы равно числу зна- чений результативного признака без одного: v=n — 1, 8 — 1=7; б) для факториальной дисперсии число степеней свободы равно числу градаций, фактора без одного: v,.=r,. 1, 4 — 1 =3; в) для случайной дисперсии число степеней свободы равно числу значений результативного признака без числа градаций фактора: ~,= и — r», 8 — 4=4; г) суммы степеней свободы частных дисперсий должны быть рав- ны числу степеней свободы общей дисперсии: ч»+ ч= ч,„3+4 = 7; В приведенном примере девиаты имеют следующие значения: 80 факториальная девиата а„= = 26,7, 3 8 случайная девиата а = — = 2,0. 4 Для получения показателя достоверности влияния организованного фактора надо найти отношение факториальной девиаты к случайной: а 2 26,7 F.=- = ' =13,4. ,2 2 cz Чтобы определить, достаточен ли полученный показатель для того, чтобы считать слияние организованного фактора достоверным, необхо- димо сравнить полученный критерий со стандартным отношением де- виат при данных числах степеней свободы. При данных «» и, и при заданной вероятности того, что различие сравниваемых дисперсий не случайно, необходимо, чтобы отношение 2 . 2 было равно или больше определенного, стандартного отношения девиат. Например, если дисперсия по фактору х имеет три степени сво- боды, а по случайным факторам — четыре степени свободы(~» = 3, =4), то стандартными отношениями их девиат будут следующие три числа: 6,6; 16,7; 56,1. Эти числа взяты из таблицы стандартных отно- шений девиат (табл. IX), которая составлена таким образом, что первое число соответствует вероятности Pi — — 0,95, второе — Рр —— .0,99 и третье — Рз = 0,999. В нашем примере критерий Р,. =13,4 превышает первую сте" пень вероятности и приближается ко второй, что для многих исследова- ний считается достаточным (Р)0,95). Это значит, что наблюденное в опыте влияние фактора не может быть объяснено случайными причи- нами, так как факториальная дисперсия оказалась достоверно больше случайной дисперсии. Вследствие этого заключение о сильном влиянии фактора, изучен- ного в .выборке, можно перенести и на всю генеральную совокупность в соответствующих условиях. В таблице стандартных отношений девиат в верхней строке для каждого столбца даны значения v> — числа степеней свободы для пер- вой девиаты, стоящей в числителе отношения и относящейся к факто. риальной дисперсии.
ДИСПЕРСИОННЫЯ АНАЛИЗ В левом столбце таблицы для каждой строки указаны э~качения v2 — числа степеней свободы для каждой второй девиаты, стоящей в знаменателе отношения и относящейся к случайной дисперсии. В каждой клетке таблицы приведено три значения стандартных отношений девиат, соответствующих трем указанным ступеням веро- ятности. Таблица стандартных отношений девиат может быть использована также при сравнении обычных выборочных сигм. Для этого надо сигмы возвести в квадрат, ббльшую девиату разделить на меньшую и полу- ченный показатель сравнить со стандартными отношениями в соответ- ствии с числами степеней свободы, которые в данном случае равны чис- лу значений без одного. В приведенном примере выяснено влияние на результативный при- знак суммарного действия двух факторов А и В, которое в целях упро- щения было принято за действие одного фактора. Установлено, что суммарное действие этих двух факторов на данный результативный признак очень велико и достоверно. Остались невыяс- ненными два вопроса: 1. Каково значение каждого из этих факторов в отдельности при выравненном действии другого? 2. Каково значение различий их совместного действия при разных комбинациях градаций? Для разрешения этих вопросов требуется развернутый статисти- ческий комплекс, показанный в табл. 79. Таблица 79 Градации первого фактора Градации второго фактора Значения результативного признака Такой комплекс называется д в у х ф а к т о р н ы м. Решение двухфакторного статистического комплекса проводится по следующим этапам. Нахождение общей дисперсии (производится так же, как и при однофакт.>рном комплексе): С = — (9 — 6)' + (l l — 6)'+ (3 — 6)-' -'; (5 — 6)' + (1 — 6)' + —:,— (3 — 6)" + (7 — 6)'-'+ (9 — 6)' = 88. Н а х о ж д е н и е с л у ч а й н о й д и с п е р с и и (производится так же, как и для однофакторного комплекса): а) частные средние по четырем градациям: 10;4;2;8; б) отклонение каждого значения от своей частной средней: — 1; + 1; — 1; + 1; — 1; + 1; — 1; + 1; в) квадраты этих отклонений: ~- 1; + 1; + 1; + 1; + 1; + 1; + 1; + 1; г) сумма квадратов этих отклонений:
ОСНОВЫ МЕТОДА 205 Нахожде ни е диспер сии сум ма р ного действия для организованных факторов показано в табл. 80. Таблица 80 Градации первого фактора Градации второго фактора Значения результативного признака Ох D2Х В последней строке величины D» надо взять в каждой градации столько раз,.сколько значений имеется в этой градации. Делается это для того, чтобы можно было сравнивать дисперсии; полученные из раз- ного числа слагаемых. Нахождение частных факториальных дисперсий отдельно по каждому фактору проводится следующим образом. Дисперсия по фактору А измеряется степенью разнообразия част- ных средних по градациям этого фактора: С =Е nA(AIA — М,)'-'. В приведенном примере фактор А имеет две градации: А> и А2. Для каждой такой градации имеется одинаковая комбинация градаций дру- гого фактора: В> и В>. Это обстоятельство дает право считать выравненным действие фак- тора В для разных градаций фактора А. Для каждой градации фактора А имеется по четыре значения. Если сумму всех значений разделить на их число, то по каждой градации мы получим частные средние Мд. Для получения дисперсии таких средних надо взять сумму квадра- тов их отклонений от общей средней (взвешенных численностью гра- дации фактора). Это показано в табл. 81. Для каждой градации рактора А надо взять по четыре квадрата центральных отклонений — по числу значений. Это необходимо для сравнимости частных и общих дисперсий. В нашем примере получилось, что в суммарном действии обоих факторов (C»=80) действие фактора А равно C„=8 или составляет всего 10% от суммарного действия организованных факторов и 9% от общего действия всех факторов. Аналогично вычисляется дисперсия по фактору В. Расчет ее для приведенного примера показан в табл. 82. Оказалось, что дисперсия по фактору В равна С = О. Такой результат есть следствие равенства частных средних по фак- тору В: Ма = 6 и Мв — 6 (средние по градациям не различаются, дис- персия равна нулю). Это значит, что при такой организации статисти.
ДИСПЕРСИОННЫЙ АНАЛИЗ 206 Таблица 81 Градации первого фактора Градации второго фактора Значения результативного признака Градация фактора А Значения по градациям фактора А Сумма значений по градациям фактора А Частные средние по градациям фактора А (MA) Центральные отклонения частных средних ~А Квадраты центральных отклонений DA 2 Таблица 82 Градации первого фактора Градации второго фактора Градация фактора В Значения с градациями фактора В Сумма значений по градациям фактора В Частные средние по градациям фактора B (M~) Центральные отклонения частных сред- них DB Квадраты центральных отклонений ~2~ ческого комплекса, какая была в проведенном исследовании, влияние. фактора В при выравненных значениях фактора А не проявляется в раз- нообразии результативного признака. Нахождение факториальной (частной) дисперсии п О с о ч е т а н и я м ф а к т о р о в является специфической особенностью. дисперсионного анализа. Дисперсия по сочетаниям факторов А и В есть своеобразное и обычно с трудом понимаемое явление в области корреляционных свя-
207 ОСНОВЫ МЕТОДА зей. Эта дисперсия составляет ту часть. общей дисперсии результатив- ного признака, которая вызвана различным действием одного фактора при разных градациях другого. Для выяснения сущности дисперсии по сочетаниям факторов раз- берем более подробно приведенный пример двухфакторного комплек- са. В этом примере действие каждого фактора в отдельности оказалось очень слабым (Я =9% и Я=0%') несмотря на то, что ряд частных средних (табл. 82а), а также рис. 39, на котором дано графическое изо- бражение действия фактора А и фактора В, указывают на то, что эти факторы вносят значительное разнообразие в дисперсию результативно- го признакй и, следовательно, действуют сильно, а не слабо Табли ца 82а Градациифакторов А и В А В, А В А, В., А, В, 10 30 9 д 7 б 5 ф 3 2 f М„~ 10 4 2 8 ) 10 2 д~ В~ ф В~ ~ А, А~ ~д, ~а, ~ ~в,, дА, А Рис. 39. График частных влияний.I — фактора В при разных градациях фактора А. I I — фактора Апри разных градациях фактора В. Достаточно фактору В измениться, как при одной градации перво- го фактора (А,) результативный признак резко уменьшается (с 10 до 4}, а при другой градации этого фактора (А2) — резко увеличивает- ся (с 2 до 8). Точно так >ке действует и фактор А. При одной градации второго фактора (В~) изменение фактора А приводит к резкому падению значения результативного признака (с 10 до 2), а при другом значении (Вр} — к заметному увеличению (с 4 до 8). По поводу полученных результатов может возникнуть еще одно недоумение, если вспомнить, что суммарное влияние обоих этих факто- ров на результативный признак очень велико: 91% от общего влияния всех факторов. Как могли факторы, незначительно ( -„=9%) или совсем не влия- ющие на результативный признак (т,' == О), при совместном действии оказать очень большое влияние (т,'„=-91%) В разбираемом примере соотношение показателей v~'„' = 0,09, =0,00 и vP =(>,91 вполне объяснимо, так как отражает часто встре- чающуюся в жизни обусловленность влияний одних факторов другими.
208 ДИСПЕРСИОННЫЯ АНАЛИЗ Не так уж редко отдельный фактор проявляется только тогда, ког- да другой фактор действует определенным образом. В качестве приме- ра может служить влияние температуры и влажности на рост организ- мов, влияние кормления и поения на вес и продуктивность животных, действие витамииа и его растворителя на крепость молодняка и т. д. Предположим, изучается влияние двух факторов — температуры и влажности — на рост каких-нибудь растительных организмов. Вполне возможны следующие взаимоотношения этих факторов, аналогичные тем, которые обнаружились в разбираемом примере. При нормальной температуре А1 нормальная влажность B( благоприятна для роста, а повышенная влажность В2 уже угнетает рост. В нашем примере так и получилось: при сочетании градаций А1В1 М,. = 10, а при сочетании А~Вр М„= 4. При повышенной температуре А2, наоборот, низкая влажность В1 недостаточна для нормального роста, и поэтому он замедлен, а повы- шенная влажность В2 благоприятна, и рост усиливается. В нашем примере при сочетании градаций А~В1 М,. = 2,, а при А2В2 Л~„= 8. Если рассматривать каждый фактор в отдельности, то окажется, что температура без регулирования влажности и влажность без регули- рования температуры слабо проявляются в разнообразии роста: Я = 0,09; ~~2а —— 0,00. Если же организовать определенное сочетание факторов (их гра- даций), например., при определенной температуре обеспечить опреде- ленную влажность, то различные комбинации градаций этих факторов создадут значительное разнообразие результативного признака, что и покажет их большое суммарное действие: ~P — 0,91. Из этих соображений возникла необходимость вскрывать и изме- рять степень влияния не только каждого фактора в отдельности, но также и их сочетаний, как части общего суммарного влияния. Проявляется влияние различных сочетаний изучаемых факторов заметнььм образом только в тех случаях, когда имеется различие в дей- ствии одного фактора при различных градациях другого. Специфическое действие сочетаний в дисперсионном комплексе вы- является тогда, когда при одной градации первото фактора второй фактор действует очень слабо или угнетающе, а при другой градации— сильно и стимулирует развитие результативного признака. Например, при низких температурах повышение влажности тормо- зит рост, а при высоких, наоборот, стимулирует. Поскольку всегда имеется .некоторое различие в действии одного фактора при различных градациях другого, то всегда в каждой града- ции дисперсионного комплекса суммарное действие всех организован- ных факторов слагается из действия каждого ф а кто р а в отдельности и специфического действия их соче- таний. Яля расчета факториальной дисперсии по сочетаниям (СА ) необ- ходимо произвести следующие действия. 1. Составить ряды частных средних для каждой градации диспер- сионного комплекса: а) по суммарному действию организованных факторов (М„), б) по фактору А (М ), в) по фактору В (М ) Как составлять ряды частных средних, показано в табл. 83. Они уже ранее были рассчитаны и представлены в табл. 80, 81, 82.
основы мЕтодл Таблица 83 Для расчета дисперсии сочетаний частные средние необходимо рас ставить по градациям комплекса определенным образом. Значения М, — 10; 4; 2 и 8 ставятся в соответствующих четырех градациях. По первой градации фактора А величина М„=7. Она ста- вится в двух первых градациях — AIBI и А1В2, так как эти града- ции комплекса вместе и представляют одну первую градацию фак- тора А. По второй градации фактора А величина 1lfA —— -5. Ставится она в двух последних градациях комплекса — А2В1 и А2В2, так как они вместе составляют вторую градацию фактора А. По первой градации фактора В величина М = 6. Ставится она в первой и третьей градациях комплекса — А~В1 и А2В1, так Таблица 84 А, как они вместе составляют од- ну первую градацию фактора В. По тем же соображениям, величина Мв =6 по второй гра- дации фактора В ставится во второй и четвертой градации комплекса. 2. gIJIH трех рядов частных средних рассчитать централь- ные отклонения. Для этого нужно вычесть из каждой част- ной средней общую среднюю М=б. Эти действия показаны в табл. 84. 3. Рассчитать ряд цент- ральных отклонений по ряду 48М= — =68 в, в, в, 7;9 3;5 Мх 10 Мв Dx -+1 -+1 Ов ( АВ) сочетаний Для этого из каждого значения D,. нужно вычесть с соблюдением правила знаков DA и Вв. АВ ~ А В Полученные значения для ВА надо возвести в квадрат и взять столько раз, сколько имеется дат в соответствующей градации. Сумма
210 ДИСПЕРСИОННЫЙ АНАЛИЗ Та бли ца 85 А1 в., в, в, 3;5 7;9 1;3 Dx DB +2+1 — 0=+3 — 2 — 1 — 0= — 3 — 4-+-1 — 0= — 3 АВ 2~АВ САВ —— 72 9;9 9;9 9;9 Дисперсия по сочетаниям факторов получилась в масштабах разби-раемого примера значительной: СА — — Еп2 = 72. Это указывает на то, что. в изучаемом комплексе действие одного фак-тора сильно зависит от градаций другого. Тут необходимо отметить следующие очень важные обстоятельства. Полученные в анализе три частные дисперсии — СА, С и Сд — в сумме дают дисперсию суммарного действия организованных факторов: C,=C„+C +C„~ 80 = 8+0+72. Так бывает только при определенной организации дисперсионных комплексов — при равномерных и пропорциональных комплексах, кото-.рые будут 'описаны ниже. Возможны три вида взаимоотношений между суммой указанных трех частных дисперсий и дисперсией суммарного действия: С„+С +С„=С», С„+С +С„~)с„, С„-С +-С„,<C„. Первый случай дает возможность более просто находить дисперсию сочетаний без предварительного определения величины ОАв. При анализе равномерных и пропорциональных комплексов диспер- СИЯ СОЧеТЯ Н И Й Н Я ХОДИТСЯ ОЧЕНЬ ЛРГКО: С„ = С» — CA — С . Для нашего примера С =80 — 8 — 0= 72. Второй и третий вид соотношений между суммой частных дисперсий и дисперсией суммарного действия имеет место в неравномерных дис- персионных комплексах. Поэтому при описании этих комплексов и бу- дут указаны способы расчета дисперсии сочетаний. всех значений Е)~а и будет дисперсией по сочетаниям факторов (C„„)' Эти действия показаны в табл. 85.
ОСНОВЫ МЕТОДА Нахождение степ ен и влияния факторов и их со- ч е т а н и й производится так же, как и при однофакторном комплексе, путем деления частных дисперсии на общую. Показатели влияния для приведенного примера имеют следующие значения: 8 88 лля фактора А ~~А — — 0,09; О для фактора В Я = — =0,00; 88 для сочетаний факторов А и В Я = = 0,82; 72 8Ы 80 для суммарного действия организованных факторов у,' = 48 г) для дисперсии сочетания факторов число степеней свободы рав- но произведению этих чисел для обоих факторов: "АВ — 'А ' 'a д) для суммарной дисперсии по организованным факторам число степеней свободы равно произведению числа градаций по обоим факто- оам без единицы: ч =г гв — 1, 2)(2 — 1 =3; , 1. Проверка: ф = q'„+ ~~' + у~2А = 0,09 + 0,00 + 0,82 = 0,91. Для случайных факторов q, = — = 0,09; 88 88 для всех факторов $y —: 1,00. 88 Проверка: q~ = ~j» + т~, = 0,91 + 0,09 = 1,00. Оказалось, что действие каждого из изученных .факторов настолько сильно зависит от градаций другого, что при очень слабом .влиянии каждого из них порознь различие их совместного влияния достаточно велико — 82% от общей суммы влияний всех признаков. Приведенный выше ряд значений ~~2 и рис. 39 представляют об- щую характеристику результатов двухфакторного комплекса. Нахождение достоверности влияний факторов и и х с о ч е т а н и Й производится путем определения отношений между а2 факториальными дееиатами и случайной дееиатой (F,. = и солс- а ставления полученных показателей достоверности со стандартными от- ношениями девиат, находимыми по таблице. Необходимые для получения девиат числа степеней свободы при двухфакторном комплексе 'определяются следующим образом: а) для общей дисперсии число степеней свободы равно числу зна- чений результативного признака без одного: v =и — 1 8 — 1=7; У Ф б) для дисперсии по первому фактору число степеней свободы рав- но числу градаций этого фактора без одного: ч =г — 2, 2 — 1=1; в) для дисперсии по второму фактору число степеней свободы рав- но числу градаций этого фактора без одного: =г — 1, 2 — 1=1;
212 ДИСПЕРСИОННЫЯ АНАЛИЗ е) для случайной дисперсии число степеней свободы равно числу значений результативного признака без произведения числа градаций по обоим факторам: ч. = — и — r„гв, 8 — (2 )(2) = — 4; ж) сумма степеней свободы для всех частных дисперсий должна быть равна числу степеней свободы для общей дисперсии: ч — 'ч -~-ч = — ч,, 1-~-1+1 =3, А ' В ~ АВ ч, =- v~„3 + 4 =- 7 . Чтобы получить девиаты. надо каждую дисперсию разделить на число степеней свободы, что для приведенного примера даст следующие результаты: для фактора А ~A —— — =- 8,0; 8 1 — = — 0,0; () 1 9 G" В— для фактора В 72 АВ 1 для сочетаний факторов А и В = 72,0; 80для суммарного действия организованных факторов ~',. = — =26,7;У8 <для случайных факторов ~' = — = 2,0.4Показатель достоверности получается путем деления каждой фак-ториальной дисперсии на случайную:е,одля фактора А F„= ' =4,0;2,0ля акта а В F = =00.О в 72,0 для сочетания факторов А и В FA~ — — ' — — 36,0; 2,0 26,7 для суммарного действия организованных факторов F»= — '= 13,3. 2 Для окончательного суждения о достоверности влияний необходимо сравнить полученные показатели до- стоверности со стандартными отноше- ниями девиат. Для этого нужно выпи- сать из табл. XI числа тех клеток, ко- торые соответствуют имеющимся в комплексе числам степеней свободы. Достоверность влияния факторов 56,1 16,7 6,6 74,1 21,2 7,7 и их сочетаний в приведенном примере определяется следующим образом: 1. Для фактора А F„= 4,0, т. е. меньше первого стандартного от- ношения (7,7). Влияние изолированного фактора А при выравненных значениях фактора В недостоверно. Нельзя считать, что и в соответст- вующей генеральной совокупности фактор А при выравненном действии фактора В будет оказывать влияние на изменения результативного признака. 2. Для фактора В ~ = 0,0. 3. Для сочетаний факторов А и В FA~ = 36,0.В этом случае показа- тель достоверности превысил второе стандартное отношение (21,2).
21Э ТЕХНИКА ДИСПЕРСИОННОГО АНАЛИЗА ТЕХНИКА ДИСПЕРСИОННОГО АНАЛИЗА Для того, чтобы, пользуясь дисперсионным анализом, получить правильные результаты, необходимо выполнять определенные правила организации дисперсионных комплексов. Кроме того, для облегчения счетной работы необходимо усвоить способы расчета дисперсий по спе- циальным рабочим формулам. ЛОДБОР ФАКТОРОВ При организации однофакторных комплексов фактором считается любой признак, влияние которого на результативный признак требуется изучить. Это могут быть другие признаки того же животного или рас- тения, различные условия жизни, химические или биологические атенты и другие влияния. При организации двух- и многофакторных комплексов свободный выбор факторов для исследования ограничен требованием полной неза- висимости их между собою. Для таких комплексов нельзя в качестве двух факторов брать, например, вес и размер животных, так как эти признаки нельзя подбирать независимо друг от друга: при малом весе невозможно подобрать такие же значения размера, как и при большом весе. Независимыми факторами могут быть, например, температура и влажность, пол и уровень кормления, химическое и биологическое воз- действие. РАЗДЕЛЕНИЕ ФАКТОРОВ НА ГРАДАЦИИ При проведении дисперсионного анализа не требуется, чтобы фак. торы были разделены обязательно на количественные градации в фор- ме вариационного ряда. Как для однофакторных, так и для двух- и мно- гофакторных комплексов факторы могут иметь и качественные града- ции, например, пол — мужской, женский; цвет волоса или пера — свет. ло-серый, серый, темно-серый; упитанность — жирная, выше средней„ средняя, ниже средней; крепость телосложения — слабая, нормальная. сильная. При установлении градации факторов нужно помнить, что резуль- таты дисперсионного анализа в большой степени зависят от того уров- ня, на котором установлены градации факторов. Если, например, изучается действие температуры, то при градаци- ях 15', 20', 25"С может быть найдено достоверное влияйие этого факто- ра на результативный признак, но это совсем не значит, что такое же сильное влияние будет при другом уровне градаций, например, 5' 10' 15'С. Влияние различий в сочетании факторов достаточно достоверно: Р„а)0,99. Это значит, что результаты данного выборочного исследова. ния можно перенести и на всю соответствующую генеральную совокуп ность. И в ней различие сочетаний факторов оказывает большое влия. ние на результативный признак. 4. Для суммарного действия организованных факторов F» = 13,3— показатель достоверности превысил первое стандартное отношение де- виат (при v> —— 3, v> — — 4) и приближается ко второму. Это указывает на то, что суммарное действие изученных факторов также может считать- ся достоверным.
214 диспЕрсионный АнАлиз Точно так же совместное различное действие пола и упитанности ка привесы может проявиться в определенной степени при определенных градациях упитанности, но это не значит, что в той же степени про- явится это влияние при других градациях упитанности. Большое значение также имеет уровень группы неорганизованных факторов, которые составляют фон дисперсионного анализа. Например, комбинированное действие возраста и какого-нибудь стимулятора ожи- рения дают при одном уровне общего кормления и содержания опре- деленный эффект, а при другом, например скудном кормлении и плохом содержании, может и совсем не проявиться. ПОДБОР ОСОБЕЙ � По-английски random — выбранный наугад. Результаты дисперсионного анализа в основном зависят от того, насколько правильно подобраны особи как по качеству, так и по ко- личествуу. По своему качеству особи для дисперсионного анализа должныот- ражать ту генеральную совокупность, для изучения которой и проводит- ся исследование. По величине результативного признака особи должны быть подо- браны по принципу случайной выборки. Лучше всего при отборе объек-, тов для дисперсионного анализа поступать следующим образом. Пусть для данной .градации требуется, например, 20 особей, а име- ется всего таких.особей 30. Тогда номер каждой особи нужно записать на карточку. Все 30 карточек хорошо перетасовать и взять подряд без выбора первые 20 карточек или, наоборот, взять подряд только первые 10 карточек. В первом случае отберутся особи для исследования, во вто- ром откинутся особи, лишние для данной градации. Нарушение принципа случайности при отборе особей для диспер- cHoHHoI'о анализа всегда приводит к неправильным, нерепрезентативным результатам. Организация дисперсиокного комплекса с выполнением принципа случайности отбора вариантов называется р э н до м и з а ц и е й*, а комплексы, организованные таким образом, называются р э н дом из и- р о в а н н ы м и. По количеству особи могут распределяться по градациям факторов различными способами: поровну, пропорционально, неравномерно. В со- ответствии с этим и организованные комплексы бйвают равномерными, пропорциональными и неравномерными. При равномерных и пропорциональных комплексах, как уже ука- зывалось, сумма частных дисперсий равна общей (CA+ С + СА = С ) если все этк дисперсии рассчитывать по указанным основным формулам независимо друг от друга. Наличие такого соотношения между дисперсиями очень облегчает проведение всего дисперсионного анализа. При практическом проведении исследований методом дисперсион- ного анализа не всегда возможно организовать равномерный или про- порциональный комплекс. Иногда в процессе проведения опыта одна или несколько особей выбывают из опыта вследствие болезни, гибели или по другим причинам; иногда бывает очень трудно или невозможно найти требуемое количество особей для какой-нибудь одной или двух градаций. В таких случаях приходится работать с неравномерным ком- плексом, что очень усложняет расчеты.
ПОДБОР ОСОБЕЙ 215 В дальнейшем описание приемов дисперсионного анализа будетда- но в основном для пропорциональных комплексов и для частного слу- чая их — для равномерных комплексов. В заключение будут даны методы работы и для случая неравномерного дисперсионного комплекса. Пропорциональным комплекс будет в тех случаях, когда для раз- ных градаций одного фактора частоты другого находятся в одинаковой пропорции, напркмер: А> An В в, в, 12 пх 1:2 Отношения частот Неравномерным комплекс будет 'в тех случаях, когда для разных градаций одного фактора частоты другого нахс~дятся в неодинаковых пропорциях: 1:1, ббб Отношения частот равномерный комплекс есть частный случай пропорционального, когда отношение частот равно 1: 1; 1: 1: 1 и т. д. В некоторых случаях бывает легко организовать пропорциональ- ный комплекс на базе имеющегося неравномерного. Как это сделать, можно показать на следующем примере. Предположим, имеется некоторое количество особей, которые по своему качеству отвечают требованиям градаций двухфакторного ком- плекса, но по количеству не отвечают требованиям пропорциональности, что показано в табл. 86. Тут отношение частот фактора В по разным градациям фактора А неодинаково. Для А1 отношение частот равно 1: 3,3: 4,3; для А2 — 1: : 2,7 : 3,6. Но в этом неравномерном комплексе отношения частот по градаци- ям каждого фактора в отдельности (что показано в правой части таб- лицы) близки к определенным целым числам: А~.А2=1:3;В~.Вр. Вз -— 1:3:4. Эти числа пропорциональности можно использовать для построения пропорциональното комплекса. Для этого в каждой градации по обоим факторам надо перемно- жить соответствующие числа пропорциональности, затем фактические частоты разделить на эти произведения и взять наименьшее из получен.
ДИСПЕРСИОННЫИ АНАЛИЗ 216 Таблица 86 Пропор.ЧИСЛО Сумма частот по градациям ных частных (a;„). Эту величину надо умножить на произведения чи- сел пропорциональности. Таким образом, мы получим частоты пропорци- онального комплекса, который образован из имеющегося непропорцио- нального с наименыпей выбраковкой особей. Эти действия показаны в табл. 87. Та блица 87Организация пропорционального дисперсионного комплекса на базе имеющегосянепропорционального Равномерные и пропорциональные комплексы называются ортого- нальными. ПРЕОБРАЗОВАНИЕ ЗНАЧЕНИИ РЕЗУЛЬТАТИВНОГО ПРИЗНАКА Для облегчения счетной работы можно значения результативного признака, неудобные для счета — многозначные, дробные, преобразо- вать в удобные — малозначные .и выражаемые целыми числами. После проведения всей счетной работы с преобразованными датами 2 2 С~ Qg показатели ~~ = и Р = получаются точными и не требуют ни- с 02 z каких поправок. Другие показатели — C =ED', ~' = и М = С Е~ V и требуют восстановления, что легко сделать путем применения действий обратных тем, при помощи которых были преобразованы варианты ре- зультативного признака. Возможны следующие преобразования: 3 +- 10 -+- 13 26 (А1) 11 + 30 + 39 = 80 (Ар) 3+ 11 = 14 (В,) 10+ 30 = 40 (Вр) 13 + 39 = 52 (Вд) Примеч а ние. В скобках даны числа пропорциональности. 1,0 3,1 1,0 2,9 3,7
ПРЕОБРАЗОВАНИЕ ЗНАЧЕНИЯ РЕЗУЛЬТАТИВНОГО ПРИЗНАКА 217 Табли ца 88 Способы преобразования дат и поправки для восстановления конечныхрезультатов при дисперсионнои анализе ать, чтобы исправить конечные результаты анализа, проведен- ного на преобразованных датах с, ,~2— Су поправка не нужна умножитьна И умножитьнаk поправка не нух<на разделитьна И разделитьна k прибавитьА поправка не нужна умножитьна И умножить на A и при-бавить А 1. Все даты можно разделить на одно и то же число к. Это делает- ся не только тогда, когда все значения делятся на это число без остат- ка, Hp и в случае перехода к новым единицам измерения. Если, напри- мер, признак выражен, в миллиметрах болыпими числами с большим размахом крайних значений, то простая перемена единицы измерения на сантиметры будет равносильна делению всех чисел на 10. Точно так же перемена единицы измерения годового удоя с килограммов на цент- неры равносильна делению всех чисел на 100, что можно сделать при большом размахе значений удоя .в пределах изучаемого комплекса. При перемене единицы измерения не требуется никаких поправок в новых единицах, результаты получаются точными. Если деление происходит без изменения единицы измерения, то в конечные результаты надо внести соответствующие поправки: С= ПР Е V и а2= С/v, нужно умножить на к2, а М = — умножить на к. 7L 2. Все значения можно умножить на одно и то же число к. Это де- лается тогда, когда даты выражены дробными числами, например,0,25, 0,37 и т. д. Умножая все даты на 100, можно получить целые двухзнач- ные числа, удобные для счета. Поправки в конечные результаты при таком преобразовании надо вносить обратные тем, которые вносятся .в предыдущем случае. 3. От всех значений можно отнять одно и то же число А. Это лучше делать тогда, когда даты образуют небольшой размах и деление их на число к или умножение с последующим округлением может заметно снизить имеющиеся разнообразия результативного признака. Поправку в окончательный результат при этом способе преобразования требуется вносить только для средней арифметической М: нужно прибавить чис- ло А. Значения С, ч~, а2 и F никаких поправок не требуют: они получа- ются точными в первоначальных единицах. Вычитать лучше наименьшие значения. 4. Можно сделать двойное преобразование, аналогичное тому, ко- торое проводят при расчете М и а для больших групп на основе услов- ных отклонений, выраженных в классовых промежутках. Из каждого значения можно вычесть одно и то же число А, а полученный результат
218 ДИСПЕРСИОННЫЯ АНАЛИЗ разделить на другое число к. Полученные после такого преобразования С и а2 для восстановления нужно умножить на к2, а М — умножить на к и прибавить .к произведению А. Величины т12 и F в этом случае не тре- буют никаких поправок. Основные способы преобразования дат с указанием требуемых по- правок для конечных результатов приведены в табл. 88. ТЕХНИКА РАСЧЕТОВ ОДНОФАКТОРНЫЙ КОМПЛЕКС Когда изучается действие на результативный признак одного фак- T0ð~ то имеется только одна пропорция частот по градациям этого фактора. Так как другого фактора нет, то эту пропорцию и не с чем сравнивать. Поэтому для однофакторных комплексов отпадает требова- ние пропорциональности или равномерности: однофакторные комплек- сы ортогональны при любом соотношении частот по градациям фактора. К однофакторным комплексам в полной мере относится требование рэндомизации, т. е. освобождения от тенденциозности в вьгборе объек- тов эксперимента и наблюдения. И, наконец, при однофакторных ком- плексах вполне применимы все описанные выше приемы преобразова- ния дат. Техника расчетов однофакторного комплекса для малых групп мо- жет быть показана на следующем примере. П р и м е р '.25. При изучении действия одного из стимуляторов ожирения были установлены три градации этого фактора: первая до- за — 0 (контрольная группа), вторая доза — 10 г и третья доза — 20 г в суточном рационе. В качестве результативного признака был принят привес животных за опытный период. Для каждой градации фактора было выбра~но с сохранением прин- ципа рэндомизации по 2 особи, которые за опытный период показали разный привес, выражающийся в следующих числах: при первой дозе— 12 и 4 г, при второй дозе — 18 и 14 г, при третьей дозе — 8 и 4 г. Оказалось возможным эти числа легко преобразовать путем вычи- тания из всех чисел минимального привеса (4 г), в результате чего по- лучены даты более удобные для счета: для первой градации — 8 и О, Расчет дисперсионных комплексов удобнее проводить по специаль- ным рабочим формулам, отличающимся от тех формул, которые приво- дились в главе об основах метода в целях вскрытия сущности приемов дисперсионного анализа. Рабочие формулы дают те же результаты, но значительно упроща- ют вычислительную работу. Техника расчетов неодинакова для малых и больших групп: для болыших групп невозможно технически провести работу так же просто, как и в случае малых групп. Отнесение имеющегося материала к большой или малой группе обусловливается имеющейся вьгчислительной техникой. При наличии только простейших вычислительных приборов — конторских счет, ариф- мометра, логарифмической линейки — группу в 40 — 50 многозначны.с дат приходится считать уже большой группой. При наличии более совершенных счетных машин, типа Кел, Архи- мед, Сар, Мерседес, группа из 100 двузначных дат' может считаться еще малой группой.
ОДНОФАКТОРНЫЙ КОМПЛЕКС 219 для второй градации — 14 и 10 и для третьей — 4 и О. Такое преобра- зование не требует никаких поправок к окончательным результатам дисперсионного анализа (см. табл. 88). Таблица 89Техника расчетов при дисперсионном анализе однофакторногокомплекса для малых групп 20 Зо 4;0 14; 10 ~ V=36 80 196; 100 16;0 64;0 Е V' = 376 n=-6 (~ ~х) 576 16 (~ ~х)~Х Хй =328 288 32 М — 6 МХ=Е V„:n 12 (> VP ЗУН = — — = 216В 6 160 112 48 Су —— Е V~ — Н = 376 — 216 = 160 0,70 0.30 1,00 С~ — Х V~ — Х й = 376 — 328 = 48 С~ = Z й — Н = 328.— 216 = 112 16 56 Проверка: 112 —,' 48 =- 160 3,5 148,530,89,6 Порядок вычислений показан в табл. 89. В первой строке записаны значения градаций (х) фактора,: О; 10; 20 и число градаций r= 3. Во второй строке записаны значения результативного признака (даты V) для соответствующих градаций в преобразованном виде (8 и О, 14 и 10, 4 и О) и сумма всех дат XV=36. В третьей строке записаны квадраты дат (64 и О, 196 и 100, 16 и О) и сумма квадратов дат ZV2= 376. В чет- вертой строке записаны частоты по градациям (2; 2; 2) и сумма всех частот и = ~а,.=6. В пятой строке записаны суммы дат(~ V,) покаж-
220 ДИСПЕРСИОННЫЙ АНАЛИЗ дой градации (8; 24; 4). В ~пестой строке записаны квадраты сумм дат по каждой градации (64; 576; 16). В седьмой строке записаны частные от деления этих значений на соответствующие частоты (32; 288; 8) и сумма полученных величин Ш = 328. В восьмой строке записываются частные средние результативного признака по, градациям фактора М». Эти средние используются толь- ко для иллюстрации действия фактора, а не для расчета дисперсий. 'В приводимом примере частные средние получены в преобразован- ном виде: на 4 единицы меньше действительных. Чтобы восстановить их действительное значение, нужно к каждой средней прибавить ту ве- личину, которая была вычтена из каждой даты (4). После этого полу- чим ряд средних привесов: 8; 16; 6. В данном исследовании выяснено, что малая доза стимулятора (10 г) благоприятно действует на привесы; увеличение дозы до 20 г уже угнетающе действует на привесы — они становятся меньшими, чем в контрольной группе. Ряд средних результативного признака по градациям изучаемого фактора дает только первое представление о том, что получилось в дан- ном исследовании. Для окончательных выводов требуется определить, как уже указывалось, степень или силу воздействия фактора:на резуль- тативный признак и достоверность результатов, полученных в прове- денном .выборочном исследовании. Для определения степени влияния фактора,:необходимо найти от- ношение факториальных дисперсий к общей, а для определения досто-, верности .влияния необходимо нанти, отношение девиат (факториальной к случайной). Расчеты, показанные в табл. 89, дают возможность полу- чить наиболее простым способом требуемые дисперсии и девиаты. После описанного выше заполнения клеток расчетной таблицы дальнейшие действия лучше провести в следующем порядке: 1. Определить вспомогательную величину Н путем возведения в квадрат общей суммы дат и деления полученной величины на общее- число дат: (Е V)~ 36' 1296 и б б 2. Определить величину общей дисперсии результативного призна- ка. Делается это не непосредственно, как было показано в главе об ос- новах метода, а по рабочей формуле: С = Е V' — Н= 376 — 216=- 160. 3. Определить величину случайной дисперсии: С, = > V-' — Е h = 376 — 328 = 48. 4. Определить величину факториальной дисперсии: С, = Е Ь — Н = 328 — 216 = 112. Дальнейшие действия лучше расположить в форме сводки, приве- денной в правом нижнем углу табл. 89. Все расчеты, необходимые для сводки, объяснены .в главе об основах метода. Соответствующие форму- лы сгруппированы в табл. 90. Общий итог данного анализа можно выразить следующим 'образом. влияние организованного фактора ... 70% влияние неорганизованных факторов .. 30» влияние всех факторов . '. 100»
221 ОДНОФАКТОРНЫЙ КОМПЛЕКС Таблица 90 Сводка результатов дисперсионного анализа однофакторного комплекса для малых групп х Z V-' — Н ~p yy g ys ~p Дисперсии Сх с, с, с, 1,00. Степень влияния факторов и — 1 r — 1 Число степеней свободы и — r С, сх Девиаты 2 6 2 а Показатель достоверности влияния Стандартные отношениядеви ат Изучаемый фактор в выборке показал сильное влияние на резуль- тативный признак, но влияние это оказалось недостоверным, так что вывод о сильном влиянии еще нельзя перенести на генеральную сово- купность. Для решения этого вопроса необходимы повторные исследо- вания на более многочисленном материале. Лля многочисленных групп техника расчетов однофакторного дис- персионного комплекса показана на примере, представленном в табл.91. При изучении возрастных .изменений веса животных была составле- на обычным способом корреляционная решетка, в которой было девять градаций фактора .возраста (от 2 до 10 лет, с интервалом 1 год) и де- вять классов результативного признака — веса (от 200 до 600 кг, с ин- тервалом 50 кг). Градации фактора (х) обозначены в заголовках девяти столбцов решетки, а классы результативного признака (средины классов) про- ставлены при обозначении строк (у). Рядом с обозначением классов распределения результативного признака проставлены условные отклонения, выраженные в классовых промежутках (а). Установление классов и условных отклонений при- знаков производится по обычным правилам обработки вариационных рядов по способу произведений. В клетках решетки ставятся частоты, указывающие сколько осо- бей данного возраста имеют вес в пределах границ данного класса. Со- ставление корреляционной решетки производится по обычным прави- лам, применяющимся при расчетах коэффициента корреляции или кор- реляционного отношения. В дисперсионном анализе однофакторного комплекса обработка корреляционной решетки начинается так, как это делается при вычис- лении корреляционного отношения, но заканчивается она особым спо- собом, являющимся специфическим отличием дисперсионного анализа. Требует~я вначале приписать к корреляционной решетке внизу че- тыре строки, а справа — три столбца.
222 ДИСПЕРСИОННЫЯ АНАЛИЗ Та бли ца 91 Техника расчетов при дисперсионном анализе однофакторного комплексадля больших группх — фактор (возраст),у — результативный признак (вес) 550 500 450 350 300 250 200 995,7 756,8 238,9 410~ $ = 533 — 123 = + 410; Н = — = 328,3 512 0,76 0,24 Яз —— 533 -+- 123+ 2 (247+ 87) = 1324 Су — — Sg — Н = 1324 — 328,3 = 995,7 <g = ~ьг — ~ й = 1324 — 1085,1 = 238,9 Сх — ~ h — Н = 1085,1 — 328,3 = 756,8 511 503 94,6 0,47 ц2 201,3 3,4 '~,5 2,0 503(400) В первой строке — и„— ставятся суммы частот по столбцам. Это есть вариационный ряд фактора (возраста) в разбираемом примере. Во второй строке нужно проставить суммы произведений частот на отклонения (Zfa). В разбираемом примере эти суммы составились сле- дующим образом: для первого столбца (возраст 2 года) Х(а=3 ° ° ( — 5) +3 . ( — 4) =.— 15 — 12 = — 27; для четвертого столбца (воз- раст 5 лет) Zfa=35 (+1) +56 (0) +21 ° ( — 1) =+35 — 21=+14 и т. ч.
223 ОДНОФАКТОРНЫЙ КОМПЛЕКС В третьей строке надо проставить (Zfa)2: ( — 27)а=.729, ( — 41)' = = — 1681 и т. д. Величины третьей строки нужно разделить на соответствующую д > частоту, и все полученныечастные сложить. Этобудет величина h = их (четвертая строка). В разбираемом примере h для первого столбца равно 729: 6= 121,5, а для всего комплекса Xh= 1085,1. Составление ряда квадратов дат для больших групп в целях облег- чения вычислительной работы заменено расчетами вариационного ряда результативного признака, проводимыми щ трех столбцах справа от корреляционной решетки. В первом столбце записываются суммы частот и, по строкам, что и дает вариационный ряд результативного признака. Сумма чисел этого столбца (> и ) должна быть равна > и» и составлять общую численность комплекса и. В разбираемом примере и = Е и = > и» = 512. Во втором и третьем столбцах производится расчет вариационного ряда по способу сумм, в результате чего получаются две суммы — S> и S2. Делается это по обычным правилам обработки распределений по способу сумм. В разбираемом примере суммы накопленных частот в первом столб- це будут q> —— .533 и r~ — — 123, а во втором — q~ — — 247 и r2=87. Исполь- зуя эти величины, определяются две суммы, требующие для дальней- шего анализа: а) первая сумма: S~ — — q~ — r~ — —,533 — 123 =+410. Эта сумма должна быть равна сумме чисел второй добавочной строки: S~ — — Zfa =+410. Если S~ возвести в квадрат и полученное значение разделить наобщую численность комплекса, то получится вспомогательная величина. и 5]2 б) вторая сумма рассчитывается следующим образом: S2 — — q> yr1+2 (д2+г2) = 533+123+2(247+87) = 1324. Расчет дисперсий проводится при помощи уже полученных величин: C~ = S, — Н = 1324 — 328,3 = 995)7, C, = S2 — E Ь = 1324 — 1085,1 = 238,9, CÄ = > h — И = 1085,1 — 328,3 = 756,8. Все эти действия приведены в нижней части табл. 17. Полученные результаты анализа — т12, а2 и F — лучше оформить в сводку (см. правый нижний угол табл. 91). Формулы, по которым рас- считываются величины, проставляемые в сводке, приведены в табл. 92. В приведенном примере получены следующие окончательные ре- зулы аты: 76~/о влияние. возраста на вес влияние неорганизованных факторов... 24» в.пияние всех факторов . . . 100 »
ДИСПЕРСИОННЫЙ АНАЛИЗ 224 Таблица 92 Сводка результатов дисперсионного анализа при обработке одкофакторного комплекса для больших групп Неорганизованные Все факторы факторы (я) (r) ~2 = ™ Дисперсии Степень влияния факторов (квадрат корреляционного отношения) С, с 1,00 Число степеней свободы и — 1 и — r Деви аты Стандарт-ные отно-шения де-виат Отношение девиат — критерийдостоверности влияния Влияние изученного фактора оказалось сильным и настолько досто- верным, что это заключение может быть с уверенностью перенесено на всю генеральную совокупность. ДВУХФАКТОРНЫЙ КОМПЛЕКС При изучении действия двух факторов в одном комплексе появ- ляются новые требования, которых не было при анализе однофактор- ного комплекса. В двухфакторных комплексах обязательно требуется независимость изучаемых факторов и, кроме того, желательно иметь пропорциональ- ность частот, так как в этом случае расчеты значительно облегчаются. Как и все другие комплексы, двухфакторные должны быть рэндо- мизированы; датью также могут быть преобразованы любым из спосо- бов, указанных ранее. Изучая действия более одного фактора, необходимо учитывать не только влияние каждого фактора в отдельности, но и их сочетаний. В разделе об основах дисперсионного анализа был показан на примере непосредственный способ определения этих показателей (см. табл. 80 — 85}. Там были рассчитаны частные средние по фактору А, по фак- тору В, по сочетаниям факторов АВ и по их общему суммарному дей- ствию — по фактору х. По каждому ряду средних мы рассчитывали центральные отклонения, сумма квадрат в которых и давала диспеосию по каждому фактору: C„=8, С ==О, А — 72; С„= 80. В табл. 93 и 94 на том же примере, который приводился в разделе об основах дисперсионного анализа, показана техника расчетов двух- факторного комплекса для малых групп с применением рабочих фор- мул. Результаты получились те же: С =88, С =8, С,.=80, С„=8, C„=O, С „=72.
ДВУХФАКТОРНЫИ КОМПЛЕКС Расчет основного корреляционного, ряда H оформление конечных ре- зультатов производится в основном, как и .в случае однофакторного комплекса. рассмотрим более подробно получение новых показателей: C„CB, и Ав. 11о каждой градации фактора А и фактора B подсчитывается сум- ма частот и сумма дат (см. правую верхнюю часть табл. 93). Получен- Таблица 93 Техника расчетов при дисперсионном анализе двухфакторного комплексадля малых групп л, тд 2 g~2 (Е V)'-' в,. в, в, 7;9 Х V=48 А, 28 784 1 400 ' 100 Е V'=376 81; 121 9;25 1;9 49;81 20 2 n=8 48~Н= — =8=- 288 16 4 24 576 256 16 144 (Е V)~ h 128 Хй =368 ~ Ьв == 288 8 48 32 8 200 и- АВ О 72 80 8 88 0,00 0,82 0,91 0,09 1,� 0,09 i376 — 288 == 88 376 — 368 =- 8 .368 — 288 = 80 296 — 288 === 8 288 — 288 == О 80 — 8 — 0 =- 72 Р1Р 1 3 4 С; 2,0 0. 72 26,7 36 74,1 И,1 21,2 16,7 7,7 6,6
Н,исперсии C»A < '-~д — H Степень 8/IHRBsl' 1P '-А '-у С'д ~„'-АБ Су С С С,./Cy 1~00 ЪИЦ!а l L CllD3CA lOU is t 1 r 1 „„r r 1 ss r r es 1 60gb) " 'A ' 'в ' 'А в 'A'â — '" 'A'â Девины ~з ~ А ~А ~'в vi) САд 'Ад С„, C=/vz ° Э ° I ° ° ° l в в ° l 1 r ° ° ° l ! ° ° ' I 3 r ° ° ° ' ' IIr ° Эа ° ° Э в ° ° ° ° в ° в ° ° ° П r ° Э Ю й ° ° Э а ° ° r ° l ° ° ° ° в ° ° ° в в б J ° ° Ю 1 ° Э! ~ ° ° ° ° 1а ° l ° ° в ° ° а ° ° ° ~ ° ° ° ° в ° II ° 1 ° 9 в 3 ° ° Ю 1 111 ° 11 I ! s 1 1 1 ° 1 1 ° ° 1 ! ° 1 в ° ° ° ° ° ° в ° б J б ° ! ° а ° Э ° ° ° ° 3 ° II а ° ° ° 9 r ° ° й ° ° 1' l ° ° в а ° ° ! а l I II r ° 1 ° ° ° ° ° в а 9 ° ° ° 9 ° 9 ° в ° g ° ] в ° ! ° 1 ° ° l ° в l ° ° ° ° а ° ° ~ ° 1 Э ° ° ° а ° ° ° В В ° 1 ° ° ° ° 9 Э Э ! ° е J ! ° ° ° ° ~ ° 1 ° ° ° ° Э ° 1 J а J ° ° а Э в Э 9 ° а ° Э й ° ° а ° 1 ° ° Э °, ° 3 а ° в A Э а Э ° ° ° ° ° ° ! ° ° в 9 Э ° Э ° ° ° ° ° J ° в а ° а в ° 4 4 ~ ° ° ° ° 9 9r I Ф ° ° 1 ° ° 1 ° ° ° J ° 1 1 ° 1 ° ° l ° ° I ° 9 ° ° ° ° ! ° ° ° ° ! 1 ! ° ° ! ° ~° J ° ° ° а ° ° ° Э а ° ° а в
ДВУХФАКТОРНЫЙ КОМПЛЕКС Таблица % Техника расчетов при дисперсионном анализе двухфакторного комплексадля больших групп I'A =- 2 fB --3 Сбор медэ И hc ( fn)'и,. Еф'а (Еф'а)-' В, В, Вз В, Вг 61 5 (~(а)'Й=-пх С . = '-'Ь — Н = 188,2 — 1,9 == 186,3 Ы = 188,2 30,1 0 48,3 68,1 34,7 7,0 CA ihA — Н = 8,2 — 1,9»6,3 CB =EhB — ~= 181 7—— 1.9 = 179,8 CAB = Сх CA — СВ 186,3—— Г),3 — 179,8 = 0,2 6,3 179,8 0,2 67,8 254,1 186,3 Р-С,:С У 0,02 0,71 0,00 0,73 1,00 0,27 11,5 7,4 4,5 =С;. Cl 6,3 89,9 37,3 0,68 0,1 69 48 32 132,2 0,01 55,0 9,3 3 9 3,1 2,3 Результаты дисперсионного анализа показаны в табл. 95 В данном случае приходится оперировать с трехзначными цифрами (72,5 — 638 и т. д.), поэтому первичная обработка корреляционной ре- шетки проведена с применением условных отклонений. Для получения дисперсий по отдельным факторам была составле- на дополнительная табличка, помещенная в верхней правой части табл. 95. Эта табличка составляется так же, как и для малых групп. Здесь получены две необходимые всличины: Е h„=8,2 и Е Ьа= 181,7. Расчет дисперсий С,„С., С,, C„, С~, С дан в правой части табл. 95. Окончательные результаты приведены в нижней части табл. 95 по той же форме, что и для малых групп. Тут же выписаны стандартные
228 ДИСПЕРСИОННЫЙ AHA.JIИЗ отношения девиат, взятые из табл. IX, в соответствии с имевшимися сте- пенями свободы. Итог исследования можно кратко представить в следующем виде: 271 ~р влияние породы «л и 51 ние сткмулиру1ощей !1Одкорм ки влияние сочетания пород с разными доза- ми подкормки суммарное влияние породы и подкормки 0~ 7З» 27» влияние неорганизованных факторов влияние всех факторов... 100 ~ Влияние породы в данном случае оказалось незначительным, но до- статочно достоверным: Р„ - 0,99. При одинаковом разнообразии и сред- нем уровне весенней подкормки первая порода дала в среднем 62,5+5 ° ° 0,17=63,35 кг меда с улья, а вторая 62,5 — 5 0,33=60,85 кг, причем разность между этими величинами должна считаться достоверной в та- кой же степени, как и влияние породы в проведенном исследовании (Р, = S„> 0,99 ~ Влияние весенней подкормки в данных условиях оказалось очень значительным — 71о~о от влияния всех факторов и в высшей степени до- стоверным — Р >0,999. Влияние сочетаний изученных факторов оказа- лось равным нулю. Это значит, что по градациям первого фактора (т. е. как на первую, так и на вторую породы) второй фактор (подкормка) действовал одинаково. Организованные в наблюдении факторы — порода и подкормка— составили вместе большую часть общего влияния — 73%, а остальные, неорганизованные — 27%. Исследование дало четкие, достоверные, реп- резентативные результаты. П р и м е р 127. В описываемом исследовании изучались различия указанных пород пчел еще и по их агрессивности (злобности, злобливо- сти), кторая оценивалась в баллах — от 1 до 5. Исследования проводи- лись после дифференцированной весенней стимулирующей подкормки (фактор В в предыдущем примере, с градациями В1, В2, Вз) и для тех же двух пород пчел (А ~ и Ав) . Полученные материалы также были обработаны методом дисперси- онного анализа. Техника обработки в данном случае представляет ин- терес в том отношении, что результативный признак выражается целы- ми малыми числами (от 1 до 5). Это позволяет еще более упростить рас- четы, что и показано в табл. 96. Сравнение тех же двух пород, в тех же условиях, но по степени аг- рессивности дало результаты, выражаемые следующим общим итогом: 57~ влияние породы влияние подкормки . . . . . . . . . . . 19 » влияние сочетаний пород с различными дозами подкормки ............ ° З » суммарное действие организованных факторов . 79» влияние неорганизованных факторов .... 2l » влияние всех факторов . . . '00 >
ДВУХФАКТОРНЫЙ КОМПЛЕКС 229 Таблица 96 3'ехника расчетов двухфакторных дисперсионных комплексовдля количественных признаков й( —— РЮ' r,1 — -= 2 и °! V-' V ъ1 V (3 V) ° res =--= 3 В, В, В,. А, 42 93 8G49 I 20э,<) 63 246 6%1G 960,6 3,9 4 16 16 6 105 339 "(~А = 1166 5 3.2 6241 208,0 2,6 30 79 15876 396,9 3,1 В, 40 1'26 17956 513.0 3,8 Вз 35 134 b 3,2 "~В = 1117" 105 339 Н= — = 1094.4 (> V)' 339' и 105 С = Е Р-' — Н = 1221-- V — 1094 4 = 1266 = ~ V-' — Иг = 1221— 2 — 1193,9 = 27.1 = М — Н = 1193.9 х — 1094,4 = 99,5 CA = 3hA — Н = 1166.5—— 1094,4 = 72,1 СВ = ЕЬВ — Н = 1117,9 —.— 1094,4 = 23,5 СЛВ= C„С.< -C~ = 99.5 — 7'2,1 — 23,5.= 3,9 11,5 6,9 3.9 7,4 4,8 3,1 4,5 3,2 2,3 По агрессивности пчел породные различия оказались очень значи- тельными: эти различия обусловили 57% обшего разнообразия резуль- тативного признака; вторая порода имела средний балл за агрессив- ность — 3,9, а первая всего 2,2, причем разность между этими средин ми — 1.7 балла — должна считаться столь же достоверной, как и выяв ленное в опыте влияние поролы: F, =- '267, Р,.-. П.999.
„Ц1СПГРСИОННЫЯ АНАЛИЗ Влияние подкормки на последующую агрессивность пчел оказалось достаточным (p-'=0,19) и в сильной степени достоверным (Р =43 >»0,999). Также вполне достоверным оказалось и различие совмест- ного действия обоих изучавшихся факторов: породы и подкормки— F4~ =7, Рла>0,999. Это говорит о том, что эти две породы по-разному 132 ] 2 4 63 В 8, ~Р . А-Ч y. ~ ~<A.— л.S У ~2 б2,5 5Э.д в в, 4,— Wб А2 в, 24 в, Г,5 ~~.5 ) «. 4О. Изменения сбора меда (1) и агрессивности пчел (1I) в зависимости от величины весенней подкормки (В) и породы (А) пчел. 1 радайв1 В; - подкормка отсутствует, l3~ — слабая иодкормка. % — по-111аx подкормка. Градация Л1 -- первая пород». Л втор» я 11орода. ~ис. 47. Степень влияния породнчс различий (~~) p��- ср личий в подкормке (~~>), различий совместного действия у «Э породы и подкормки ("~Ав) н неорганизованных фак- СР торов (т,„) на сбор меда (1) и агрессивность пчел (11). увеличивают агрессивность при одинаковом увеличении подкормки. Это ясно видно из изменения средних баллов: первая порода увеличивает агрессивность в среднем на 0,8 балла (с 1,7 до 2,5), а вторая — на 1,4 балла (с 3,3 до 4,7) при том же увеличении подкормки с В1 до Ва. Результаты. дисперсионного анализа хорошо могут быть показаны графическим способом. Для двух последних примеров графики даны на рис. 40 и 41 ТРЕХФАКТОРНЫЙ КОМПЛЕКС Дисперсионный анализ трехфакторного комплекса не имеет прин- ципиальных отличий от анализа двухфакторного комплекса. С каждым новым фактором-сильно возрастает сложность расчетов. Расчеты и ана- Х 72 70 бд бб ~ ба б2 бО с.~ 58 5б 54 Э~ 3 Ж съ 2 ::р- 1
ТРЕХФАКТОРНЫИ КОМПЛЕКС 23! 6.и 0» 23» действие первого стимулятора {А) действие второго стимулятора {В) действие полноценности рациона {С) действие сочетаний первого стимулятора со вто- рым {АВ) 53» действие сочетаний первого стимулятора с пол- ноценностью рациона {АС) действие сочетаний второго стимулятора с полно- ценностью рациона {BC) действие сочетаний трех организованных фак- 0> 0» торов (ABC) . . . . . . . . . 6 » суммарное действие организованных факторов {~} 88» действие неорганизованных факторов (z) 12» действие всех факторов {у)... 100» лиз трехфакторного дисперсионного комплекса можно показать на сле- дующем примере. Пр имер 128. Для выяснения действия двух различных стимуля- торов яйценоскости при различной полноценности рациона кур-несушек был проведен опыт по методу трехфакторного дисперсионного комплек- са с организацией следующих факторов: 1. Фактор А — первый стимулятор с двумя градациями: A> —.раци- оны без стимулятора и Аз — рационы. со стимулятором. 2. Фактор В — второй стимулятор с двумя градациями: В~ — раци- оны без стимулятора и Вз — рационы с этим стимулятором. 3. Фактор C — полноценность рациона с двумя градациями: C>— обычные для данного хозяйства рационы без добавления минеральных веществ. и С2 — рационы с добавлением минеральных веществ. Результативным признаком была яйценоскость, выражаемая чис- лом снесенных яиц за опытный период. Даты были преобразованы путем вычитания из них постоянной ве- личины, равной 20. Такое преобразование не требует никаких поправок к основным по- казателям дисперсионного анализа (см. табл. 88), и только для сред- них величин (M), полученных для разных градаций факторов и их со- четаний, требуется очень простая поправка: прибавление 20. Например, если в результате анализа при комбинации градаций A> B> C> получена средняя яйценоскость М =О, то это значит, что за опытный период ку- ры снесли в среднем 0+20=20 яиц. Техника расчетов трехфакторного комплекса показана в табл. 97. Здесь приведен пример для малых групп и равномерных комплексов. Этот пример подобран таким образом, что будет пригоден и для боль- ших групп и для пропорциональных комплексов. При больших группах вместо первого ряда требуется отдельно составить, корреляционную ре- шетку и ее итоги (n», Zfa) выписать в две строки. Это и будут первые две строки расчетного корреляционного ряда, обозначенного в табл. 97 символами и, и > V. Все дальнейшие действия должны производить- гя, как это показано в таблице. Эта таблица может служить кратким справочником по техникерас- четов трехфакторного комплекса для малых и больших групп равномер- ных и пропорциональных комплексов. Итог всего анализа трехфакторного комплекса в приведенном при. мере выразился в следующих показателях:
ДИСПЕРСИОННЫР1 АНАЛИЗ 232 Табл и ца 97 Техника расчетов при дисперсионном анализе трехфакторного комплекса А., й~- ——~~ 1~Ул!у I'A =2 f'â =2 ~~- — — 2 в, в, С, С Ci С, С А, Ая 64 96 4096 9216 512 1152 В ]9 9;15 20;28 3;5 6;10 2;6 5;11 15:25 0;0 16 ]О 1 n= 16 2„' 2 2 2 2 2 пх Я, 8 В, 8 16 ~] ~=160 8 16 40 24 48 8 0 ]6 64 256 1600 576 2304 64 (> V)~ 0 С, я С, В 614 й= (3 V)3 — о л 16 128 Eh 2560 288 1152 32 128 800 l60 ЫС = 1856 10 ]6 784 ]4 ]296 18 144 G А,В~ А, В> А, в, Апвп 8567224 6431365184576 136 Е V-' = 2696 306 1184 >V* 0 8 М 10 12 24 М 0 4 8 20 )и ЬЬАВ = 2240 10 (3 РР 16Уи- — — — — иоол 16 I 256 64 2304 57Ñ 1024 256 4096 ]024 4l2l6 16 48 32 64 A~Ci A,С Аас, Азу 160 ЕУ~BC ~ 1856 10 16 "А =<A =2 — 1=] юВС =- 'tgtC ~ =] !-.t vB= rB ] =2 — ] =] "С =~(2 АВС х! z I А В АВ АС ВС = и — гл~вг~ =16-- 8 8 ' АВ "А "В=l ° l = I 64 0 576 0 g 0 =n — 1= =16 — 1 = 16 У 'А С ="А ~С==] ° ] =1 С, я~~ив ~ с„ 0,06 0,00 1,00 0,06 0,88 0,12 0,23 0,53 0,00 0,00 1 1 1 7 8 16 0 2561 576 0 0 64 137 17 12,5 62 3,5 25,4 11,3 5,3 3,8 0 15,1 33,9 0 0 3,8 8,1 Анализ результатов дисперсионного анализа многофакторных ком- плексов лучше начинать с общих вопросов, касающихся суммарного действия всего комплекса организованных факторов. Бывает лолевно выяснить, насколько сильно влияние организован- ных факторов на повышение или понижение величины результативного. Е РЯ — И ~ 2696 — 19Ю 1096 у С 3Ув — Е h =-2696 — 2560 = 136 М С >h — Н = 2560 — 1600 960 Х СА - ~hZ — И- 1664 — 1600 64 Су ЗЬВ — Н = 1600 — 1600 = О Сс - ЗЬС — И 1856 — 1600 = 256 САУ ~ ЗЬАВ — И — СА — СВ * 2240 — 1600 — 64 — 0 = 576 САС МАС — И — СЛ — СС = 1920 — 1600 — 64 — 256 = 0 СДС МВС .— И — СВ — СС ]856 — 1600 — 0 — 256 0 СЯВС ~ C~ — СА — СВ — СС — САВ — САС — СВС ~ 960 — 64 — 0 — 256 — 576 — 0 — 0 = 64 160 ЗЬА = ]664 80 6400 800 8О 6400 80О ]6'~ ~hB 48 2304 288 ll2 ]2544 ]568 чAgj(' = тямВмс =- ! =1 1 ° 1 ] I л~в с Х — 1=8 — 1 - 7
ТРЕХФАКТОРНЫИ КОМПЛЕКС признака относительно того среднего уровня, который поддерживается всеми факторами (организованными и неорганизованными). В приведенном примере влияние организованных факторов соста- вило 88О~. На остальные, неорганизованные факторы, пришлось всего 12Я>. Это указывает на то, что факторы, взятые для исследования, ока- зались достаточно сильными в их общем влиянии на яйценоскость и что это сильное влияние достоверно: С,. = 88'Ъ, Р,. ) 0,99. После анализа общего действия организованных факторов следует перейти,к изучению влияний каждого фактора сначала в отдельности, а потом в сочетании с другими факторами. В приведенном примере выявилось достаточно сильное и достовер- ное действие фактора С — введение в рацион минеральных веществ С, =- 23%> Р,) 099. 4G 8 Зб б 32 3 28 1+ 24 20 k1ii |'. р~3ОЛ ЬНЙЯ л;.днорм .~ «Q, [; С С Стимуляп/ор и — — -«а ,Г г С~,/...:/ / '-~.А,~ '6~ 8; Р~сс. 42. Влиянис минеральной подкорыки и двух стиму- ляторов на яйценоскость кур: C> — подкорыка отсутствует, C> — подкормка введен» ири раз- личинх градациях двух стимуляторов А и 8: А~ и В~ -- сгиму- лятор отсутствует. А~ и В~ — стимулятор введец. Как именно выразилось это действие, показывает основной ряд. частных средних М,, представленный в форме графика на рис. 42 (см. также табл. 97). Здесь ко всем значениям М,. прибавлено 20: А, 8, С, 20 А, 8 C, — 28 А., В, С, 32 1 А., 8., С, 24 ~ А, В,С, 24 А, В C — 40 АВ, C 44 I А.,В.,С., 28 I Из числового ряда (или из графика) ясно видна особенность действия фактора С: при всех градациях факторов А и В фактор С действовал одинаково: при градации С~ (при отсутствии минеральной подкормки) яйценоскость была низка, при С2 (с минеральной подкормкой) она по- вышалась. Вывод о том, что минеральная подкормка положительно влияет на яйценоскость, оказался настолько достоверным, что стало возможным в. качестве первого практического результата проведенного опыта заклю- чить о недостатке минеральных веществ в обычных рационах птичника и уверенно внести рекомендацию: добавлять в рацион всех несушек те минералыные вещества, которые были испытаны в опыте. Сочетания фактора С с обоими другими оказались равными нулю: Сiq —.— О, C~~ = 0. Это указывает на то, что добавка минеральных веществ повышает яйценоскость одинаково как при наличии, так и пр.и отсутствии каждого из двух испытанных стимуляторов.
234 ДИСПЕРСИОННЫЙ АНАЛИЗ Анализ действия каждого из остальных двух факторов показал, что каждый из испытанных стимуляторов в отдельности имеет слабое дей- ствие на яйценоскость: C„=.6'È>, C~=0%. В то же время очень боль- шое и достоверное влияние показало их сочетание. С:= 53,"~, Р,д ) 0,999. Как уже указывалось при анализе двухфакторного комплекса, та- кие результаты могут быть вследствие нМдинакового или обратного действия одного фактора при разных традациях другого. Это становит- ся ясным, если обратить внимание в табл. 97 на ряд частных средних по комбинациям градаций обоих стимуляторов, помещенных в столбце -Ч (к числам ряда прибавлено 20). Результативный признак при А, В, 2", ~ ', А,В — 26. А й — '4 ~ А., В, — 38 При отсутствии обоих стимуляторов яйценоскость была самая низ- кая: А1В1 — 22. Если введен какой-нибудь один стимулятор, яйцено- скость резко увеличивается: А ~В~ — 34, А2В1 — 38. Если же при одном стимуляторе введен второй, яйценоскость повы- шается слабо: при А~Вр 26 — яиц. Эти соотношения иллюстрируются рис. 43. Я ,3б 34 32 30 38. 36 Р4 Р2 30 2Ц 26 � 28 2б 24 Рис. 48. Влияние на яйценоскость кур стимуляторов А и В при усредненных величинах минеральной под- кормки (Cf CQ); градации: и B~ — стимулятор отсутствует; А2 и B> — сгимулятор введен. Очевидно, что химическая структура стимуляторов такова, что при совместном введении их в рацион несушек благоприятное действие на яйценоскость, в значительной мере взаимно погашается. Таким образом, вторым практическим выводом из проведенного опыта должна быть уверенная рекомендация применять какой-нибудь один из этих двух стимуляторов (лучше А). НЕРАВНОМЕРНЫЕ КОМПЛЕКСЫ Для лучшега усвоения способов анализа неравномерных комплексов необходимо выяснить различия между этим видом комплексов и равно- мерными или пропорциональными комплексами.
НЕРАВНОМЕРНЫЕ КОМПЛЕКСЫ Равномерныс и пропорциональные комплексы имеют особые мате- матические свойства и носят общее название ортогональных комплексов. Различия между ортогональными и неортогональными комплекса- ми в основном сводятся .к следующему: 1. В ортогональных комплексах автоматически нарушены все ста- тистические связи между отдельными факторами. Происходит это вслед- ствие того, что для каждой градации одного фактора все градации дру- гого фактора подбираются с равными или пропорциональными часто- тами. В неравномерных жс комплексах частоты градаций одного факто- ра в пределах градаций другого не равны и не пропорциональны. Поэ- тому в неравномерных комплексах создаются случайные статистические связи между отдельными факторами, что нарушает ортотональность и создает значительные трудности в вычислении интерпретации таких комплексов. 2. ~В ортогональных комплексах вследствие отсутствия связей меж- ду отдельными факторами сумма частных дисперсий, рассчитанных не- зависимо от дисперсии суммарного действия, всегда равна этой суммар- ной дисперсии: С„-< С„1- С„= С, Это обстоятельство значительно облегчает всю работу с ортогональными комплексами. В частности, как уже указывалось, именно эта особенность ортого- нальных комплексов дает возможность вычислять дисперсию сочетаний Слв не непосредственно, а значительно более легким способом, путем вычитания из суммарной дисперсии уже полученных частных дисперсий: С„—. С,. С, -- C„ В неравномерных комплексах такое упрощенное вычисление невоз- можно. В них сумма частных дисперсий С, + С + Сдв, рассчитанных независимо, не равна дисперсии суммарного действия организованных факторов: С, С ",С„--С, 3. Указанное выше различие между ортогональными и неортого- нальными комплексами сказывается только в той части комплекса, ко- торая относится к частным факториальным дисперсиям CA, C~, С„„ и к дисперсии их суммарного действия С„. В другой части комплекса, относящейся .к дисперсии по организо- ванным факторам С,, случайной дисперсии С, и общей дисперсии C„, различия между ортогональными и неортогональными комплексами нет. ~ля обоих видов комплексов всегда справедливо равенство: С,. -,'- С, =- С, Происходит это потому, что расчет основных показателей комплекса —- С„ С. и С,, — ведется всегда по принципу' однофакторного комплекса, в котором действует один фактор х, представляющий объединенное действие всех организованных факторов. Однофакторные же комплексы, как уже указывалось, всегда ортогональны. В неравномерных комплексах получается два различных значения суммарной факториальной дисперсии: одно для общей части комплекса ~С,. + С, = С ) и другое для факториальных дисперсий (CÄ.= С + Св —,— Слв)- Чтобы получить единую структуру комплекса, необходимо заменить эти два разные значения одним значением для всех частей ком- плекса.
236 ДИСПЕРСИОННЫЙ АНАЛИЗ Сделать это можно различными способами, поэтому предложено несколько систем расчета неравномерных дисперсионных комплексов. В болышинстве случаев наиболее точные результаты дает система расчетов неравномерных комплексов, показанная в табл. 98 и 99. ДИСПЕРСИОННЫЙ АНАЛИЗ КАЧЕСТВЕННЫХ ПРИЗНАКОВ где Следовательно, g~=p есть девиата качественного признака в элементарной группе дисперсион- ного комплекса. Исходя из этого, дисперсия качественного признака XD2 = по2 может бь1ь определена следующим образом: ÐÈ I е Л С--. Е/)2 и э2 = npi) = и. ---= ('1 1 откуда in?' . ni Эта формула является основной во всех расчетах дисперсионных комплексов для качественных признаков. Все остальные показатели дисперсионного анализа качественных лризнаков рассчитываются точно так же, как и для количествс~шьл признаков. Техника расчстов при дисперсионном анализе качественных призна- ков может быть показана на следующих примерах. П р и м е р 129. Предположим, что для борьбы с аскаридозом свиней был испробован сантонин в пяти увеличивающихся дозах. Результаты наблюдений можно организовать в форме однофакторного дисперсион- ного комплекса. Пятью градациями фактора являются различные дозы сантонина, а результативным признаком — доля свиней, освобожденных от этой глистной инвазии. Расчет этого комплекса показан в табл. 100. Характеристика группы по качественному признаку выражается в указании количества особей в этой группе, имеющих данный признак (IToJI, окраска, заболевание, наличие реакции на воздействие, достиже- ние определенного порога в развитии и т. д.). Если в группе из п осо- бей у т особей имеется данный качественный признак, то доля этого m признака в группе р= — -имеет то же значение, что и средняя арифме- й тическая для количественных признаков. Поэтому при дисперсионноч анализе качественных признаков за общие и частные средние принима- ются доли. признака в общих и частных группах. Среднее квадратическое отклонение доли р — ! p g)
237 ДИСПЕРСИОННЫЯ АНАЛИЗ КАЧЕСТВЕННЫХ ю1РИЗНАКОВ Таблица 98 Техника расчетов неравномерных двухфакторных дисперсионных комплексов А, А, И О й и2 И С,1 йф с~ ф ° у О» РА =г ЯВ =3 в„ в, В.. в, 2. 3; 4; 5; 5' 5; 6 7; 8: 8; 9; 9 4; 5; 6;";8 3;3 12,3 16,81 4.1 2; 3; 4 3;4 3;4 и=26 16,2 29,16 5,4 и 3V = 130 12 25 13 30 Х V ! 1" ЛФя = 45,97 2 G 28,6 625 144 1681 169 900 81 В 2 6,0 3,0 9,00 (g УРи1хI 125,0 Ш = 746,5 36,0 336.2 42,3 180,0 27,0 11,5 5,8 127 E V'= 766 43 339 190 29 Вч 2 , 11,0 5,5 Э0,25 ЕМ,. - 28,5 8,2 3,0 3,0 6,0 3,3 мх 2 Е МВ= 72,89 28,5 9,00 67,24 25,00 36,00 9,00 10,89! Н =- ур fl 1 ° 1 = 650 М'-' = 22,56 I 1 I CA =и 45,97 — n,M ) = i>.~Я 2 ч 2 мИA — — Я' =- 2G ~Л Сч " > — Н= 766 — 650=116 72,89 =- 26 — 22,56 =. 45,24 3 157,13 = 28 — 22 66 = 94 38 6 С = У' — Е Ь = 766 — 746,5=19,5 С ~. =- " l! — Н = 746,5 — 650 = аа с 4УЪУ4М I I С,. =-и , rArB Сх 96 5 = — = 1,022 94,38 I f I I САВ С. СЛ СВ 04 38 11'18 46 24 = 37 96 V 37.96 94,38 45,24 С' 38,8 96,5 46,3 l 9óý С.~;С 11,4 116.0 С; 0,334 0,398 0,830 0,170 0,098 1,0 С., rA ra — 1= » — 'A a= и — 1=25 rв 1 =2 rA — 1= =1 чд ' чВ =2 С,. 19,4 19,3 0,98 23,2 11,4 а. r=—i2 Oz 19,6 19,8 11,6 23.8
ДИСПЕРСИОННЫЙ АНАЛИЗ Техника расчета - трехфакторных А, Л I в, В в, ~В =2 ~с=-2 с., с, с, с, с, с, с, С1 с, 4; 8; 10; 0' б 5' 8' 11 11;!2 0; 1; 2;3;4 0;4 0;2 5 2 4 3 2 3 1 2 п =36 24 11 XV = 263 576 121 256 507 98 720 128 405 18 192 121 20 8 2 Ей=- 2475 пх 515 100 740 136 445 210 121 36 30 16 4 ~,~~ = 2619 8 11 2 2 1 Мх ХМх — — 84 м2 1 ЕМх=7742 169 49 144 64 81 9 64 121 4 4 Числосредних g 2 Е Afx А~В, 21 10,5 110,25 А~вг 19 9,5 90,25 7 49 28 АгВ, 17 8,5 72.25 16 16 Аз Х М~ — — 165 АгВг 30,25 5 5 А, В, 13 6,5 42,25 51 Bl Азвг 2,25 1,5 33 Вг 2 МАВ — 10200 42,25 6,5 39 С1 56,25 45 7,5 С2 25 12 5 А~Сг М~с — — — 98 5 5,5 27 9 в,с, АгС» 72,25 17 8,5 В,C> 64 42,25 6,5 в.,с, 12 4 16 АзСг 2,25 1,5 В2С2 21 ЕМвс = 210 ХЛ4Ас — — - 359,5 67; 11; . 911 12; 9, 10 13 15 б~ 8 '13 15 ' б~ 10 Z V 32 39 14 60 16 (> V)~ 1024 1521 196 3600 256 13 7 12 8 8,5 72,25 25 5 2 45 б 2025 36 10 4 2100 16 4 Ч :Я by II !~ 156,25 30.25
ДИСГ!ЕРСИОННЫГ1 АНАЛИ3 КАЧЕСТВЕННЫХ ПРИЗНАКОВ 239 .Т а б л и ц а 99 неравномерных дисперсионных комплексов М= — — — 7, М~=49 '. М, 84 А ~В~С = 1921 ZNx 774 — 64 12 ~À ГВГС А А E М~~ 98,5 — 49,25 С С — 52,5 С = С'. ~ 214,5 80,4 8,9 0,12 0,01 0,31 80,4 8,9I 107,3 134 15 ! 17.9 (E V)' 263' Н= и 36 165 3 — 55,0 ЕМ~~ 102,5 ф — = 51,25 1В Х М„'В Ю5 й — '= 57,92 АВ ГА EB Е МАС 359,5 АС А С — 59,92 б ZМвс 210 h 4 ~В ~'С 4 С~ = Е С' = 216 + 81 -[- 9 + 24 + Су — — Е V — Н=2619 — 1921 =6 С,=Х V~ — Ей=2619 — 2475= С„= Х й — Н = 2475 — 1921 = 55 Сх 554 й —, —, — 0,993 558 х С = и (й — М~) = 36 (55,0 — 49) = 216 С - п (й — М') = 36(51,25 — 49) = 81 Сс и (h~ — М') = 36 (49,25 — 49) = 9 С~~ — — и(йА~ — и,4 — p>+ М') =
240 ДИСПЕРСИОННЫИ АНАЛИЗ Ч а б л и ц а 100 Техника расчетов одиофакторных дисперсионных комплексовдля качественных признаков(Всего особей l) группе — и, из них освободилось от иивазии — пг особей) 21 20 20 50 30 ' и 16! 10 'rn = 69 28 69' — — 29,6 161 121 121 784 -'й == 35,3 6.1 15,7 5,0 2,7 5,8 О,=б 0,52 0,30 0,50 0,55 б 1 ° ) ! 155 Результаты анализа показывают вполне достоверное действиесан- тонина: F=5,5, P)0,999. Из анализа видно, что один сантонин не может дать стопроцентную дегельминтизацию: часть свиней (примерно 50%) остается зараженной. Кроме того, анализ показывает, что третья, четвертая и пятая дозы (все увеличивающиеся) уже ничего не прибавляют к результатам вто- рой дозы: доля выздоровевших остается практически той же. Предположим, что после этого испробовали действие сантонина со- вместно с каломелем. Действие сантонина исследовалось в двух града- циях: A! — доза сантонина равна нулю, A> — доза сантонина равна вто- рой дозе в предыдущем исследовании. Действие каломеля исследовалось в трех градациях: В! — доза ка- ломеля равна нулю и в двух увеличивающихся дозах — Вр и Вз. Результаты наблюдений можно свести в двухфакторный комплекс, расчет которого показан в табл. 101. Такой анализ показывает вполне достоверное действие как сантони- на, так и каломеля. Совместное их введение повышает эффект дегельминтизации при- мерно до 70%, но все же стопроцентного выздоровления еще не на- ступает. Предположим, что решили испытать еще одно средство: су- точную выдержку без корма перед дачей сантонина совместно с кало- мелем.
ДИСПЕРСИОННЫИ АНАЛИЗ 3ЮЧЕСТВЕККЫХ ПРИЗНАКОВ 241 Таблица !О!Техника расчетов двухфакторных дисперсионных комплексов длякачественных признаков А1 80 31 961 0,39 30 ~n = 160 30 12,0 30 30 20 и 20 21 Хт = 84 Аг 80 53 2809 22 35,1 0,66 0 16 15 10 84гН=—160= 44,1 А 25б 225 100 484 0 = 47,1 В~ б0 Зб 129б 21,б 0,60 Cу — — 'm — Н = 84 — 44,1 = 39,9 Cz =- m — М = 84 — 51,8 = 32,2 В= 48,2 C,. ==- Ш — Н = 51,8 — 44,1 = 7,7 С ='a„— И=e7,1 — 44,1=3,О Cв —— -h~ — Н =- 48,2 — 44,1 = 4,1 Сдв -- Сх — СА — Св — 7,7— — 3,0 — 4,1= 0,6 7,7 32,2 39.9 4,1 3,0 0,6 0,81 1,00 0,10 0,01 0,08 0,19 2 2 154 159 3,00 2,05 0,30 1,54 0,21 14,3 10 О 1,4 7.3 После проведения таких опытов результаты их можно свести в трех- факторный дисперсионный комплекс со следующими факторами: А — действие сантонина: А~ — доза равна О, А2 — доза, установлен- ная в первом опыте; В — действие каломеля: В~ — доза равна О, В2 — доза, установлен- ная во втором опыте; С — действие предварительной выдержки без корма перед дачей сантонина и каломеля: С~ — без выдержки, Се — с выдержкой. Расчет такого трехфакторного комплекса показан в табл. 102.
242 ДИСПЕРСИОННЫИ АНАЛИЗ Таблица 102 Техника расчетов трехфакторных дисперсионных комплексовдля качественных прнзнаков 0,78 а.' 0 Ва 100 78 16,1 11,3 30,0 Иг = 85,0 5,0 5,0 17,6 Ей = 71,08 В 0,73 0,75 1,00 0,00 0 50 0 77 0 50 0,44 0,63 1225 15,31 5625 46,88 35 75 С, 80 С> 120 С = Ет — Н = 110 — 60,5=49,5 С = m — Ей = 110 — 85,0 = 25,0 С = М — Н = 85 — 60,5 = 24,5 Ей = 62,19 С 0,00 0,66 0,64 0,90 0 21,78 20,48 40,50 0 1089 1024 2025 0 33 32 45 А, В, 50 АВ, 50 АВ, 50 А,В~ 50 С = Иг — Н = 70,18 — 60,5 = 9,7 СВ — — И — Н = 71,08 — 60,5 = 10,6 С = Ий — Н= 62,19 — 60,5 = 1,7 M 82,76 СА'В ~~А — СА С — Н = 82,76 — 9,7 — 10,6 — 60,5 = 2,0 АВ А В С = Ы — С — С — Н = 72,02 — 9,7 — 1,7 — 60 5 = 0,1 АС АС А С СВС ~~ВС СВ — С — Н = 73,02 — 10,6 — 1,7 — 60,5 = 0,2 0,25 0,38 0,63 0,87 2,50 8,82 15,63 45,07 100 529 625 2704 40 10 60 23 40 25 60 52 А,С, А,С> А,С, А,С, ABC = — CA — СВ СС САВ САС С C — — 24 5— — 9,7 — 10,6 — 1,7 — 2,0 — 0,1 — 0,2 = 0,2 Еfg = 72,02 А В АВС х АВ АС ВС 9,7 0,2 24,5 25,0 10,6 2,0 49,5 1,7 0,1 0,2 Eh = 73,02 С. 9 С У 0,20 0,21 0,03 0,01 0,49 1:э 1,00 0,00 0,00 0,04 1 1 1 7 192 1 1 Cl 10,6 1,7 2,0 9,7 О,Я 3 5 0,13 0,1 0,2 :3,7 11,2 6,8 3,9 192 74 6 81,5 13,1 15,4 0,8 1,5 26,9 1,5° сФМЪф 2,0 Оказалось, что каждый из трех факторов (сантонин, каломель и предварительное голодание) оказывают дегельминтизирующее действие при наличии той комбинации других факторов, какая была в проводи- мых опытах. Последние замечания особенно необходимо помнить при анализе действия предварительного голодания (фактор С): само по себе голода- ние в течение 24 часов не может излечить от аскаридоза. В изученном
СРАВНЕНИЕ СРЕДНИХ ВНУТРИ ДИСПЕРСИОННОГО КОМПЛЕКСА 24 же трехфакторном комплексе действие каждого фактора, в том числе и голодания, изучалось при усредненных значениях двух остальных фак- торов. Поэтому указанное действие голодания (~)' — — 3%, Рс —— 13,1, Рс)0,999) выявилось только при условии определенного действия сан- тонина и каломеля в тех комбинациях, которые были организованы в дисперсионном комплексе. Общие же результаты анализа показывают в высшей степени до- стоверное дегельминтизирующее действие изученных трех факторов. Та- кие общие выводы находятся в полном соответствии с методами борь- бы с аскаридозом свиней, применяемыми на практике. При этой инва- зии прописывается дача сантонина совместно с каломелем после 24-ча- сового голодания. СРАВНЕНИЕ СРЕДНИХВНУТРИ ДИСПЕРСИОННОГО КОМПЛЕКСА ,Яисперсионный анализ дает возможность значительно усовершен- ствовать способы сравнения средних величин и получить более точные показатечи достоверности разности между частными средними для групп, составляющих дисперсионный комплекс. Обычно достоверность разности между двумя выборочными сред- ними определяется критерием достоверности разности: d t„=-— md где Ш=М~ — М2 — разность между двумя выборочными средними, т~ — ошибка репрезентативности разности, квадрат кото- рой равен сумме квадратов ош~ибок репрезентативно- 2 2 2 сти сравниваемых средних: т,~ — m> + m>. Правильность суждений о достоверности полученной в опыте раз- ности целиком зависит от того, насколько точно определены ошибки репрезентативности сравниваемых выборочных средних. Математическая статистика дает точную формулу для расчета ошибки репрезентативности выборочной средней арифметической: где о — среднве квадратическое отклонение для всей генеральной со- вокупности (а не для данной выборки!), из которой взяты одна или несколько,вы~борок; п — численность каждой отдельной выборки; N — численность генеральной совокупности. Использование точной формулы для определения ошибки репре- зентативности средней арифметической требует: а) одинакового значения сигмы для всех выборок, относящихся к одной генеральной совокупности; 6) определения величины такого среднего квадратического откло- нения, которое характеризует разнообразие не каждой отдельной вы- борки, а генеральной совокупности; в) поскольку значения критерия достоверности разности (2,0; 2,5; 3,0) и соответствующие вероятности (0,95; 0,99; 0,997) установлены, ис- ходя из закономерностей формирования случайного разнообразия (нор- мальное распределение), генеральная сигма, стоящая в числителе фор-
ДИСПЕРСИОННЫЯ АНАЛИЗ мулы, есть среднее квадратическое отклонение случайной неорганизо- ванной изменчивости признака. В большинстве экспериментов применение точной формулы для на- хождения ошибки средней арифметической невозможно, так как неиз- вестна генеральная сигма. Поэтому на практике применяется приближенная формула: 0т= ——1 где а — среднее квадратическое отклонение признака в данной изучае- мой выборке (а не генеральной совокупности), п — численность вы~борки. Условия использования приближенной формулы отличаются от ус- ловий использования точной формулы: вместо единой генеральной сиг- мы берется выборочная сигма, неодинаковая для разных выборок. Это неправильно характеризует ту степень случайного разнообразия, которое свойственно изучаемому признаку в данной генеральной сово- КУпности. Организовав в исследовании дисперсионный комплекс, можно зна- чительно уменьшить искажения, связанные с использованием лрибли- женной формулы. Яля этого при сравнении частных средних внутри дисперсионного комплекса необходимо для всех средних при вычислении ошибки репре- зентативности за показатель разнообразия взять сигму случайного раз- нообразия — ~,. В этом случае ошибка репрезентативности для любой частнойсред- ней данного дисперсионного комплекса будет определяться по формуле: 2 m,. =— )/ d td = —. т~ Квадрат критерия достоверности разности F~= Pg (Р т~ о 2 а и, 2 где а, = ~ — сигма случайного разнообразия, единая для всехчаст- ных групп данного комплекса, или среднее квадрати- ческое отклонение той части разнообразия результа- тивного признака, которая обусловлена неорганизо- ванными факторами; л; — численность той группы (по градациям факторов), для которой рассчитана данная частная средняя. Эта формула дает результаты, более близкие к тем, которые полу- чились бы, если можно было бы использовать точную формулу для ошибки средней. Используя это общее значение среднего квадратического отклоне- ния, можно упростить и самую формулу для нахождения ошибки раз- ности двух средних из одного комплекса, и технику вычислений досто- верности разности между этими средними. Для этого несколько преобразуем приведенную выше формулу крк- терия достоверности разности:
24:i СРАВНЕНИЕ СРЕДНИХ ВНУТРИ ДИСПЕРСИОННОГО КОМПЛЕКСА где знаменатель 2 6? I Г п1 2 2 Og И1 - - n2 n, . n2 2 =о~. П1 Таким образом, критерием достоверности разности любых двух частных ередних из одного дисперсионного комплекса может быть показатель F d ~Р И1 П при j ч1 — — 11 л, -+ п V .М Здесь d — разность между любыми двумя частными из одного дис- персионного комплекса; ~,— девиата неорганизованных факторов этого комплекса; 2 и> и п3 — численности частных трупп, для которых взяты сравнивае- мые средние; ~, — число степеней свободы для неорганизованных факторов изу- чаемого комплекса; ~1 и ~2 — числа степеней свободы, необходимые для определениястан- дартных отношений девиат, а значит, и достоверности. Стандартные отношения девиат, как уже указывалось, находятся по табл. IX. Требуемые отношения девиат находятся в первом столбце (так как v> — — f — 1=2 — 1=1) и в той строке, которая соответствует числу степеней свободы неорганизованных факторов (~, = ~,). Если сравниваются средние групп одинаковой численности, то по- казатель достоверности разности частных средних упрощается: при A)'- = й~ =?Ъ = tg— при J " 7.) V d б Определение достоверности разности частных средних внутри дис- иерсионного комплекса можно показать на следующих примерах. Пример 130. Обычные ком пл ек сы. В исследовании, ана- лиз которого дан в табл. 96, выявлено влияние породы пчел А1 и А2 и весенней стимулирующей подкормки (В1, В3, В3) на агрессивность пчел. В процессе обработки первичных материалов получены частные средние. Обозначим средний балл для первой породы при отсутствии под- кормки (первая градация фактора В) через М11. В нашем исследова- нии оказалось M» — — 1,7. Для первой породы при слабой подкормке соответственно имеем М» — — 2,4, для первой породы при полной подкорм- ке М» — — 2,5. Для второй породы были получены следующие частные средние: М21 — — 3,3; М22=3,7; Mgg —— 47 Кроме того, получены средние баллы: для всех групп первой породы .4~о=2,2, для второй породы Agp — — 3,9, для обеих пород без подкормки Во1 —— 2,6,. со слабой подкормкой Bpg — — 3,1 и при полной подкормке Bpg=3,8. Кроме результатов дисперсионного анализа, представленных в ре- зультативной табличке (см. табл. 96), могут иметь практическое значе- ние решения некоторых частных вопросов путем выяснения достоверно- сти различия между частными средними. В разбираемом примере потребовалось выяснить, как влияет увели- чение подкормки с В, до В3 на агрессивность пчел для каждой из изу- ченных пород. Для этого надо сравнить частные средние М12 с М» для первой по- роды и М» с M» — для второй. В данном случае оценку достоверности Р и, . n> разности средних надо сделать по формуле Р„=, при- n,+и
ДИСПЕРСИОННЫЯ АНАЛИЗ 246 няв за ~, (как и для любой средней данного комплекса) девиату неор- ганизованных факторов, уже найденную при решении этого дисперси- онного комплекса ~, =, п и Для первой породы расчет дает следующие результаты: и„= 16, М, = 2)4; d==0,1; ~';=0,27; а„= 14; M» — — 2,5, d'-' = — 0,01, ~, = 99; ' 11,5 16 . 14 d Ф 0,01 0,2~7 =- 0,3 16 -',- 14 1(ритерий достоверности различия среднихР~ = 0,3 оказался значи- ° Файф тельно меньше наименьшего из стандартных отношений девиат, най- денных по таблице для v> — — 1, ~, = 99 (соответствующие значения выпи- саны в ~фигурных скобках рядом со значением Fd). Разность между средними оказалась недостоверной. Это значит, что то увеличение агрессивности, которое наблюдалось в опыте для первой породы, не может быть обобщена. На основе проведенного исследования нельзя заключить, что все пчелы, первой породы будут повышать агрес- сивность при повышении весенней стимулирующей подкормки с В> до Вз. В результате аналогичного расчета для второй породы имеем. а =24; M =37 d=10; а,—. 027; Ю = 1,00; М,,=4,7; аз —— 21; v,=99. 11, 6,9 24 21 — 41 4 24 + 21 10,27 и„= 30; М„= 2,6; d=. 1,2; ~,=0,27; d~ = 1,44. ч, = 99; Моз — 3,8; nо, —— 35; 1 1,5 6,9 =859 30+ 35 1,44 0,27 Разность между средними оказалась в высокой степени достоверной (~~ ) 0,999). Это значит, что для второй породы можно с большой уверенностью обобщить результаты выборочного исследования и утверждать, что все пчелы этой породы (а не только та~ их часть, которая была изучена в опыте) будут повышать агрессивность при увеличении весенней стиму- лирующей подкормки с В> до Вз. Таким же способом можно сравнить любую пару средних из это- го дисперсионного комплекса. При всех этих сравнениях надо брать одни и те же величины: ~~ = 0,27, v, = 1, ~ = 99 и соответствующие ста~ндартные отношения девиат: 11,5; 6,9 и 3,9. Например, если требуется оценить достоверность влияния полной весенней подкормки совместно для обеих пород, достаточно сравнить общие средние, приведенные в правом верхнем углу табл. 96 (Ми=2,6 и Моз — — 3,8 при по1 =30 и noз — — 35). Расчеты дают следующий результат:
СРАВНЕНИЕ СРЕДНИХ В НУТРИДИСП ЕРСИОН НО ГО КОМПЛЕКСА 247 Пример 131. Комплексы с преобразованными вари- а нта м и. В исследовании, анализ которого дан в табл. 95, изучалось влияние породы пчел (А~ и А2) и весенней стимулирующей подкормки (В~, В~, Вз) на сбор меда с улья за следующее лето. Получены средние сборы меда по тем же группам внутри диспер- сионного .комплекса, что и в предыдущем примере. Однако в данном случае средние получены не в обычных единицах (килограммах меда), а в условных отклонениях, выраженных в классовых промежутках. Так получилось потому, что для облегчения вычислений первичные вариан- ты были преобразованы. Преобразование заключалось в следующем. Варианты были разнесены по классам, и вследствие этого все ва- рианты, попавшие в один класс, получили общее одинаковое значение, равное средине класса. Затем из средины каждого класса была вычте- на условная средняя (в данном комплексе А=62,5), полученные раз- ности разделены на величину классового промежутка (в данном случае на Й=5). В результате и получился тот ряд условных отклонений, вы- раженных в классовых промежутках (а= — 3; — 2; — 1; 0; +1; +2; +3), который и прошел всю дальнейшую обработку. Как уже 'указывалось, такое преобразование значений результа- V — А тивного признака V' = а = совершенно не сказывается на й величине показателя F. Поэтому сравнение средних внутри таких дис- кfa; персионных комплексов можно сделать по средним и =. и. Е Vi водя их в средние обычного вида М = — '. Например, можно следую- nl щим образом определить, достоверно ли влияние увеличения подкорм- ки с В2 до Вз на сбор меда пчелами первой породы путем сравнения ередних а, = 0,0 и а» = + 1,9: и =16, а =00, И=19, ~,'=069; n,, = 14, а„= -1- 1,9, Ю = 3 61, °, = 99; , не пере- 6,9 =- 39,0 0,69 16 — 14 Если потребуется получить обычные средние по группам диспер- сионного комплекса, обработанного на основе преобразованных значе- ний результативного признака, то это можно сделать, пользуясь указа- ниями табл. 88. Чтобы получить в обычных единицах измерения среднюю арифме- тическую, необходимо величину а помножить на величину классового промежутка и к полученному произведению прибавить условную сред- нюю. Средние рассматриваемого примера получат следующие значе- НИЯ: Мд=62,5+5 0,0=62,5; М» =62,5+ 5 1,9 = 72,0. Чтобы получить девиату в обычных единицах, необходимо девиату, полученную для преобразованных величин, помножить на квадратклас- сового промежутка. Пля разбираемого комплекса (табл. 95) величина девиаты неорганизованных факторов примет следующее значение: 52 = /г'-' (5')„= 25 0,69 = 17,25.
ДИСПЕРСИОННЫИ АНАЛИЗ Сравнение восстановленных средних дает тот же результат, как и сравнение средних, полученных на преобразованных вариантах: и„=16, hf, =625, d=95, а,=1725; и„= 14, М„= 720, ' = 9025, «,=99; 11,5 Р„ 6,9 18. 14 - 39 16 + 14 90,2о 17,25 СРАВНЕНИЕ ОДНОЙ ГРУППЫ С СУММОЙ ДРУГИХ ГРУППВНУТРИ ДИСПЕРСИОННОГО КОМПЛЕКСА В пределах дисперсионкого комплекса можно образовать любые новые средние и сравнить их с уже имеющимися и между собой при по- 2 MOIQH общих BeJIHBHH Пример 132. Сравнение одной группы с двумя дру- гимии.' В исследовании, анализ которого дан в табл. 96; потребовалось выяснить влияние весенней подкормки (любой ее степени} на агрессив- ность пчел первой породы. Для этой цели сравним группу А1В1 с груп- пой, объединяющей две градации: А1В2 и А1ВЗ. Определим достовер- ность разности средних М11 — — 1,7 (n» — — 12) и объединенной среднеи ~12+13. Эту объединенную среднюю можно рассчитать по формуле ~ 1'1" -' ~ ~1з 38-'-25 73 = 2 43 12 + 13— 1 и„-,'- и,, 1б -',- 14 30 При общих величинах комплекса а, = 0,27,, = )9 результат cpas- 2 кения будет следующий: 1 1,5 6,9 3, 30 12 30 + 12 (2,43 — 1,70)'0,27 = 16,9 Пример 133. Сравнение одной группы комплекса со всеми остал ь н ы м и. Когда изучается действие нескольких агентов без контрольной группы, то для более глубокой характеристи- ки одного из этих агентов требуется выделить его группу и исследовать, достоверно ли она отличается от всех других. Иногда это требуется сделать по каждой градации факторов, например при 'оценке произво- дителей по потомству. Такой анализ можно провести по формуле Д2 и; 1и — и1) v =1 при / Е — с — средняя для выделяемой группы; М,. = ГД6 МЕ средняя для всех остальных групп ком- плекса; и,— численность выделяемой группы; и — и, — численность суммы остальных групп ком- плекса; а„«» — девиата и число степеней свободы в общем комплексе для разнообразия, вносимого не- организованными факторами. Пример 134. Проверка вы п адов. Иногда вместо выделяе- мой группы берется одна дата, величина которой сравнивается со сред.
249 срАвнЕниЕ одноЙ группы с суммой других ней для всех остальных дат. Такой анализ необходим в тех случаях,. когда в какой-либо группе имеется дата, резко отличающаяся от дру- гих, причем внешне невозможно установить, является ли эта дата край- ним отклонением в нормальном разнообразии признака или это оши- бочная величина, связанная с ошибками точности, типичности или со случайными, или методическими ошибками, т. е. то, что обычно казы- вается «выпадом». Критерием в данном случае будет степень достоверности отличия этой даты от средней для всех остальных дат, что можно рассчитать по следующей формуле: ( v( — м~}~ n; — 1 F= . ' при (U2) nl где V; — проверяемая дата; М,.— средняя для остальных дат той группы, к которой была при- числена проверяемая дата. Эта средняя получается, если из первоначальной суммы дат в группе вычесть проверяемую и полученную величину разделить на число оставшихся дат; r % ° а ) — — случайная девиата нового, комплекса, в котором одна из прежних групп уменьшена изъятием проверяемой даты. Эту величину можно определить (не составляя нового комплек- са) по формуле: 'г1 -- 1 С (а ) 1 'ю- — 1 У где С и (v,— 1) — случайная дисперсия и число степеней свободы для случайной дисперсии нового комплекса. Величину С, можно рассчитать по формуле: С =С, ( V,. — М,.)'. — 1 Здесь C„n,, М,— случайная дисперсия, численность и средняя группы проверяемой даты в первоначальном комплексе (без изъятия из него проверяемой даты). Рассмотрим исследование, анализ которого проведен в диспер- сионном комплексе, представленном в табл. 103. В этом комплексе сомнительной является дата V, = 47 во второй градации фактора. Проверка его дает следующие результаты: С, = С, — ' ( Г, — М,}' = 1872 — (47 — 11)' = 432; п~ — 1 ' 9 С 432 12 (а,) = v — 1 110 — 47 М~ —— = 7,0; 18,6 9,3 n~ — 1 — = 40. 36 10 =1 Отличие проверяемой даты ог остальных дат группы оказалось в высшей степени достоверным, так что с большой степенью вероятко- сти можно считать эту дату выпадом, подлежащим изъятию из комплек-
° ° ° Y ! l ! ° ° ° ( в в l I 1 I ) ) 1 е) а ° 1 r ° в ° I ° ! ! ! 1 I ° I ° ° I ° ° ° 3 ° в ° ° ° в ю ° е ю ю ° ЭЭв в ° д Л Ш 4 ° ° в ° ° 3 ° ° ° ° 4 в ° в ° ° °! ° ° ' ° ° i 3 ° ° ° ю ° ° ° ° ° в
CPABHEHHE СРЕДНИХ, НЕ ВХОДИВШИХ В ДИСПЕРСИОННЫЙ КОМПЛЕКС 251 Следует отметить, что после изъятия выпада величина С, в новом комплексе получилась равная рассчитанной по приведенной выше фор- муле и без составления нового комплекса. В новом комплексе, показанном в табл. 104, может вызвать подо- зрение максимальная из оставшихся дат — V; = 31 (первая градация фактора). Проверка этой даты дает следующий результат: 31 — 23)г 352 4 С =С,— (V, — М,)- '= 432— пь — 1 С 352 (а ) v — 1 115 — 31 12 — 1 1М~— =21; (31 — 21)"- 4 — =2,5 32 5 ч,=12 — 1 =11 Отличие этой даты (V, = 31) от остальных оказалось недостовер- ным. Поэтому необходимо признать его возможным отклонением в нор- мальном разнообразии признака и оставить его в комплексе. СРАВНЕНИЕ СРЕДНИХ, НЕ ВХОДИВШИХВ ДИСПЕРСИОННЫЙ КОМПЛЕКС Используя принципы дисперсионного анализа. возможно унифици- ровать и упростить методы сравнения любых средних величин. Обычно, если имеются две средние величины, М1 и М2, то для того, чтобы выяснить достоверкость различия между .ними, рассчитывают их ошибки репрезентативности и m = m, =- получают ошибку разности 2 2щ т1 — m, — 2r т,пг» н определяют критерий достоверности разности d / =- —. md Все необходимые при этом расчеты можно значительно сократить, а само определение достоверности уточнить, если составить из двух имеющихся рядов простейший однофакторный комплекс и определить достоверность различия между двумя средними этого комплекса опи-санными выше способами по формуле (М, — М,)' и, . и, 02 п1 + п2 az при v,=п, +и, — 2 ~' где с,n,,+п~ — 2С EV2 — Eh 20
Яgr ° yg i ° еф'4ю Э ° ' ° 9 J е - J ° ° ~ ° ° ° J ° 3 ° ° ! ° в Э r 1- 3 ° е i. ° 9 Г ° .. г ° ° -' 1 J ° ° ~ ° 3 ! 1: ! ! 1 ! l ° r ° 1 ° ° ° ° ° ° ° I ° ° ° ° ° ° ° ° Я2 ДИСПЕРСИОННЫИ АНАЛИЗ
СРЛЬНЕНИЕ СРЕДНИХ, НЕ ВХОДИВШИХ В ДИСПЕРСИОННЫЯ КОМПЛЕКС П р и м е р 136. Имеется два вариационных ряда с многозначными вариациями: 90 99 108 117 126 135 144 3 12 24 45 41 11 2 И~ 99 1~8 117 126 135 144 28 6 15 49 13 Требуется определить достоверность различия средних при наличии в рядах трехзначных:вариаций (средних классов) и достаточной чис- .ленности групп. ()пределение достоверности различия средних в таких случаях про- водится по-разному, в зависимости от имеющихся вычислительных средств. При наличии таких вычислительных машин, как арифмометр >К-1, яК-3, САр, Мерседес, можно приведенные группы считать малыми и вести расчеты так, как это показано в табл. 106. Таблица 106 'Определение достоверности различия средних при многозначных вариантахв многочисленных группах при наличии счетных машин Xh = 1914438,5+— 1703130,7 = 3617569,2>>W'f = )930716++ 1714851 = 3645567С~ — — 3645567—— 3617569,2 =- 27987,8~, = 138 + 115 — 2 = 251Cg 27987,8vz 251 Если же имеются только обычные конторские счеты, то необходи- мо эти группы признать уже ~большими и облегчить технику расчета введением условных отклонений, выраженных в классовых проме- жутках. Если требуется только определить, достоверно ли различие сред- них, то сравнение можно вести по величинам М и а2, выраженным в классовых промежутках, не переводя их в величины, выраженные в еди- ницах измерения изучаемого признака. Расчеты, относящиеся к данно- му случаю, приведены в табл. 107. Если же нужно, кроме того, дать и обычные характеристики сред- ,ней величины и степени разнообразия, то требуется указанные величи-
ДИСПЕРСИОННЫЙ АНАЛИЗ Таблица 107 I II 115 138 Пг = — 1,043+ 31,304 =-= 32,347 2 4 [ 12 ЕЕа-".f = 202 + 17G=378 135 +2 11 13 Cz = 378 — 32,347= = 345,655 - -0,522 —; -0,087 49 ч~ = 138 + 115 — 2 = 251 3600 144 28 С~ 345,655 108 — 1 24 15 (Еа f) h =- u 251 = 1,377 31. 3()4 1,043 99 — '2 12 176 "02 'а'-' f 90 — 3 3 Еа, f — h, 2 202 — 1,043 — 10,90 — 137 и,— 1 251 (200) 1а2. f /~., 176 — 31,304 - 10 26 114 а.,=~2 и» — 1 ны выразить в единицах измерения признака. Расчеты для TBKHX 'лу- чаев показаны в нижней части табл. 107. 11 р и M е р 137. Имеются два вариационных ряда с неодинаковыми классами: 10 4 10 20 18 12 0 3 6 9 V 19 6 3 1 i7 Требуется определить достоверность отличия их средних. В этих рядах неодинаковые классовые промежутки и поэтому. да- ты подобраны в классы с различными представителями. Такие ряды: невозможно объединить в единый вариационный ряд, Определение достоверности различия средних при многозначных датах в многочисленных группах, при отсутствии счетных машин (имеются только конторские счеты) 126 +1 ) 41 117 0 45 F ' ' . ' — 86(0,087 — 0,522)-" 138 1151,377 138 — , '115lgf —— A f + k f а~ — — 117 —, 9.0,087 = 117,8М2 —— А2+ А а~ — — 117+ 9 0,522 = 121,7 11,2 6,8 3,9
СРАВНЕНИЕ СРЕДНИХ, НЕ ВХОДИВШИХ В ДИСПЕРСИОННЫЯ КОМПЛЕКС 255 поэтому определение достоверности различия средних необходимо вес-ти на основе величин, рассчитанных для каждого ряда в отдельности, так, как это показано в табл. 108. Таблица 108 Определение достоверности различия средних для групп, разнесенныхло неодинаковым классам С~ = С~+ Со»== 188,9+ 716,8 = 905,7 и ~ 44 ~,=и1+п2 — 2= = 44+51 — 2 = 93 12 18 332 405 XVf 10 7,54 7,94 905,793— 9,74 2 С8 20 12 110224 164025 (Е Vf)'- 19 10 9 (Е Vf)2 2505,1 3216,2 4 6 13 1 3 7 3933 2694 11,5 6,9 3,9 0 2 716,8 188,9 c=rл у — н 93 (1оо) (7,54 — 7,94)2 F— 9 74 44 51 44+51 =0,4 Для многочисленных групп, когда вычисления ведутся на основе условных отклонений, выраженных в классовых промежутках, необхо- димо в случаях, аналогичных представленному в табл. 108, все искомые величины по каждому ряду перевести в единицы измерения признака, для чего средние рассчитать по уже приводившейся формуле (см. табл. 107) М=А+ка, а дисперсии помножить на квадрат величины классового промежутка по каждому ряду в отдельности. Только после этих действий можно рассчитать разность средних М1 — М2 и сумму дисперсии 1 С, + Й С = С,. Р2 2 B последнем случае получается та случайная дисперсия, которая после разделения на число степеней свободы (~. = и, + n — 2) дает тре- буемую случайную девиату ~2 Остальные действия показаны в табл. 108. П р и м е р 138. Имеются сведения о двух группах по определенно- му признаку: 1 II 132 75 26,34 25.37 4,0 3,0 Вариационных рядов нет. Требуется определить достоверность разли-чия средних между этими группами.
256 ДИСПЕРСИОННЫЯ АНАЛИ3 Яля того, чтобы применить формулу показателя достоверности раз- личия средних п1 п2 и, --'- и» требуетсч знать случайную девиату, которая в данном случае получает- ся делением суммы дисперсий обеих групп на общую численность обеих групп без двух: С1+ Сд 2 G 2 и, +и.» — 2 Обе дисперсии можно легко получить, произведя вычисления от сигмы до дисперсии в обратном порядке (С=ж'). Яля разбираемого примера все необходимые действия показаны в табл. 109. Табл и ца 109 Определение достоверности различия средних по свод- ным показателям и, М, о при отсутствии вариационных рядов 132 75 26,34 25,37 4,0 3,0 16,00 9,М ц2 131 )( 9 = 1179 74 X 16.= 1184 С= чу 1179 + 1184 = 2363 Cg - С, + С2 132 + 75 — 2 = 205 Ч 2363 — = 11,53 205 2 С, 0 2 >z F (25,37 — 26,34)~ 132 75 — 3,9 11,53 132+ 75 СРАВЫЕЫИЕ ДОЛЕИВЫУТРИ ЙИСПЕРСИОЫЫОГО КОМПЛЕКСА При изучении качественных признаков в дисперсионных комплек- т еах вместо средних величин рассчитываются доли объектов —, имею- 2Ъ щих данный признак. (Ni М21в 02 az 11,2 6,8 3,9
СРАВНЕНИЕ ДОЛЕИ ВНУТРИ ДИСПЕРСИОННОГО КОМПЛЕКСА 2~7 Сравнение таких частных долей ведется по такой же формуле, как и при сравнении средних величин: де п1 Йг d при 2GZ и, + пг 2 z d — разность сравниваемых долей (d=p> — р~); 2 о — девиата неорганизованных факторов по всему ком- Ю плексу; и~ и и~ — численности сравниваемых групп; ~, — число степеней свободы разнообразия, вызванного не- организованными факторами. Кроме этой общей формулы, применяется еще и упрощенная фор- мула показателя достоверности различия долей. Эта формула основа- прд на на том, что девиата качественного признака ~~ не может быть п — 1 где 2 и больше величины ~m» 0,25 n — 1 Приняв это максимальное значение за девиату неорганизованных факторов, можно получить частный случай общей формулы: (и, — 1) (n~ — ~) 1 при n1+пг — 2 ,=и, +n — 2 J Эта формула применима при сравнении любой пары долей как внутри дисперсионного комплекса, так и вне его. При этом надо иметь в виду, что по ней получают уменьшенные значения достоверности разности. Поэтому, если требуется провести целую серию сравнений многих пар долей, лучше для сокращения работы сначала провести расчет по второй формуле, а в тех случаях, когда получен недостоверный резуль- тат, проверить его по первой формуле, организовав простейший одно- факторный дисперсионный комплекс из двух градаций. П р и м е р 139. В исследовании, анализ которого приведен в табл. 01, потребовалось определить, достоверно ли увеличение доли выздоровевших животных при добавке каломеля без сантонина и сни- жение этой доли при увеличении дозы каломеля с В~ до Вз при даче его совместно с сантонином (А~). Для решения этих вопросов надо сравнить доли выздоровевших в группе А|В~ с первой, контрольной группой A,B), а затем сравнить группу А~В~ с А~В3. Для первого случая имеем доли p»=0,00 и p~> — — 0,53, n» —— 20, п~~ —— =30 и общие величины ~ =0,21, «,=454. 2 F„„„- = 4d'-' 11) 6,8 (0,00 — 0,53)~0,21 20 30 = 16,1 20+ 30 Для второго случая имеем: p»=0,73, р»=0,70, n» — — 30, n» — — 30 и те же общие величины о = 0,21, ~, = 154. 2 (11,3 ] 6,8 39 2 (0,73 — r,70)10,21 = 0,1 П р и м е р 140. Среди 40 сыновей барана № 1 оказалось 5 крип- торхов, а среди 50 сыновей барана № 2 крипторхов оказалось 10. Опре-
Я ДИСПЕРСИОННЫЙ АНАЛИЗ l ° I ° ° в ° ° ii 3 ° r ° I ° е I ° ~ ° ° Ф e ° r ! ° ° э f ° е ! ° ° ° Irве f4 ° I Ir l ° 1 ° вa I ° 9 ° ! ° ° ° а I ° е ° I r I ° Э а В
ГЛА ВА ИРЕГРЕССИЯ егрессией называется изменение функции при определенных из- менениях одного или нескольких аргументов. Функцией называется признак, зависящий от другого признака— аргумента. Зависимость функции от аргумента может быть или физио- логической или условно принятой в исследовании. Примером физиологической зависимости может служить зависи- мость веса животного (функции) от его возраста (аргумента). Если по длине определяется вес животного, считается, что вес за- висит от длины, если же необходимо предусмотреть размеры животных разного веса, то принимается, что длина зависит от веса. Это пример условн< й зависимости. Взаимоотношение между функцией и аргументом обычно кратко выражается формулой у=/(х),т. е. признак у есть функция признака х,или xi — — f (хр), т. е. первый признак является функцией второго. Термин «функция» употребляется не только для обозначения при-знака, который зависит от аргумента, но и для обозначения формы этой зависимости. Вскрыть функцию — значит найти закономерность, по ко-торой изменяется изучаемый признак в зависимости от изменения одно-го или нескольких других признаков. Если изменения функции исследуются в зависимости от одного ар-гумента, регрессия называется простой: у=((х), если от двух и более аргументов — множественной: g= f (x~, х~,..., Хл) . Если при любом значении (малом, среднем, большом) аргумента одинаковь;е приращения его вызывают (или имеют тенденцию вызы- вать) одинаковые приращения функции, регрессия называется прямо- линейной. Если при одинаковых приращениях аргумента, но при разныхего зна- чениях (малом, среднем, большом) функция имеет неодинаковые при- ращения, причем среднее течение изменений не идет по прямой, регрес- сия называется криволинейной. Для изображения регрессии используются ряд регрессии (эмпириче- ский и теоретический), линия регрессии (эмпирическая и теоретическая), коэффициент регрессии, уравнение регрессии.
PE ГРЕССИЯ 260 Эмпирический ряд регрессии — это двойной ряд цифр, включающий значения аргумента и соответствующие средние значения функции, по- лученные в опыте. Пример эмпирического ряда регрессии дан в табл. 110. Таблица 110 Эмпирический ряд регрессии живого веса сычевских помесей по возрасту 10 Возраст, годы 454 477 43] 433 451 460 462 394 414 )Кывой вес, кг Рис. 44. Эмпирический ряд и линия регрессии живого веса сы-чевских помесей по возрасту. Течение эмпирической линии регрессии почти никогда не бывает плавным: в пределах одних интервалов аргумента функция имеет по- вышенное, других — пониженное, а инотда и отрицательное прираще- ние, что на графике дает ломаную кривую. Ломаный характер эмпирической линии регрессии отражает обыч- ную невь~равненность общих условий развития функции на различных участках течения аргумента. Если изучается регрессия веса по возра- сту, то становится очевидным, что напряжение всех агентов, влияющих на возрастные изменения веса, не остается одинаковым на всем протя- жении периода роста. В одном возрасте вся сумма влияний складывает- ся в комплекс, более благоприятный для роста, в другом возрасте этот комплекс влияний менее способствует приросту веса. По виду эмпирической линии регрессии всегда можно установить, на каких участках течения аргумента функция развивалась в лучших, а на каких в худших условиях. Из эмпирической линии, представленной на рис. 44, следует, что в возрасте 5 лет все условия, определившиедан- ный средний вес, были менее благоприятные, чем в предыдущие годы, а в возрасте 9 лет появились какие-то сильные причины, приведшие к При графическом изображении эмпирического ряда регрессии— аргумент, например возраст, откладывается по оси абсцисс, а функция, например вес, откладывается по оси ординат — получаем эмпирическую линие регрессии (рис. 44). 4
261 ОБЩИЕ СВЕДЕНИЯ — 470 72 10 — о,1 за. ' ~~' — теоретический живой вес, х — возраст в годах, 470 — максимальное значение живого веса, к которому асимпто- тически приближается данная функция по мере увеличе- ния аргумента, где понижению среднего веса. В возрасте 6 и особенно 10 лет весь комплекс факторов, определяющих возрастное увеличение веса, был очень бла- гоприятен, что вызвало повышенные средние значения. Анализ эмпирической линии регрессии, подобный приведенному, всегда дает практически ценную характеристику всех обстоятельств, связанных с зависимостью изучаемой функции от избранного аргумента Но таким разбором индивидуальных особенностей отдельных участ- ков течения аргумента часто невозможно ограничиться. Яля выясне- ния основных форм зависимости функции от аргумента требуется выяс- нить такое течение функции при равномерном увеличении аргумента, которое соответствует усредненному и, следовательно, одинаковому на- пряжению всего комплекса условий, определяющих развитие функции. Нахождение усредненного выравненного течения функции в неко- торой степени подобно определению средней арифметической несколь- ких значений признака. Средняя арифметическая получается путем сглаживания индиви- дуальных различий усредняемого признака. Кроме того, средняя ариф- метическая наи1более близко стоит ко всем индивидуальным значениям, так что сумма квадратов отклонений индивидуальных значений от их средней есть величина наименьшая. Эти же принципы положены и в основу нахождения усредненного течения функции. Однако между ус- реднением течения функции и определением средней арифметической имеются и большие отличия. Средняя арифметическая усредняет инди- видуальные различия в статике, выравненное течение функции усред- няет различия комплекса условий в динамике. Средняя арифметическая всегда имеет дело с одной переменной величиной (от особи к особи), выравненное течение функции всегда имеет дело с двумя или несколь- кими переменными величинами, из которых одна (функция) зависит от других (аргументы). Процесс получения усредненного течения функции при равномер- ном увеличении аргумента называется выравкиванием эмпирических ря- дов В результате выравнивания на основе эмпирической ломаной ли- нии. получается усредненная, плавная теоретическая линия регрессии, отражающая основную закономерность зависимости функции от ар- гумента. Выравнивание эмпирических рядов производится графически или а нал итически. При аналитическом методе выравнивания эмпирических рядов пу- тем составления уравнения регрессии первоначально вскрывается фор- ма зависимости данной функции от избранного аргумента. Уравнение регрессии указывает на действия, которые необходимо выполни1ь над данным значением аргумента, чтобы получить теорети- ческое значение функции. Подставляя в уравнение регрессии последова- тельные значения аргумента, можно определить теоретический ряд значений функции, а нанося эти значения на график — получить теоре- тическую линию регрессии. Яля эмпирического ряда, показанного в табл. 110 и на рис. 44, уравнение регрессии имеет следующий вид:
262 РЕГРЕССИЯ 72 — сумма прироста от первого имеющегося значения возраста до его значения при остановке роста, 0,1312 — показатель темпа роста. Теоретический ряд и теоретическая кривая, построенные по этому уравнению регрессии, приведены на рис. 45. Рис. 45. Эмпирическая (1) и теоретическая (2) линии регрес- сии и соответствующие ряды живого веса сычевских помесей по возрасту. В простейшем случае, при прямолинейной регрессии, зависимость функции от аргумента может быть выражена одним числом — коэффи- циентом регрессии, показывающим, в каком направлении и на сколько изменяется функция при увеличении аргумента на одну единицу из- мерения. В природе существует множество явлений, обусловленных множе- ством причин. Поэтому существует очень много форм зависимости функ- ций от различных аргументов. Исследование этих форм, выраженных математическими уравнени- ями, составляет основное содержание учения о регрессии признаков. Выравнивание эмпирических рядов регрессии имеет большое и раз- ностороннее применение. Вскрывая усредненное течение функции. исследователь выявляет ту закономерность изучаемого явления, которая в эмпирическом ряду была скрыта случайностями своего проявления. Эта вскрытая законо- мерность, выраженная формулой или теоретическим рядом регрессии, помогает более точно, с меньшими ошибками дать описание внешних проявлений закономерности, что, в свою очередь, может помочь вскры- тию и внутренних факторов, управляющих данным явлением. В этом и заключается познавательное значение исследований регрессии различ- ных признаков у биологических объектов. Результаты этих исследований имеют также широкое применение и в нрактике.
°, а ° ° ° ° J ° ° е ° а ° ° ! ° ° ° l ° ° в ° 1 J ° ° ° ай е 1' l ° ! ° ° ° й Ю ° ° ° ° ' е o ° J r o ° ° ° в ! ° й а ° ° ° ! J ! ° в ° й в ° ° ° й ° ° ° ° Э ° ° ° ! r ° ° r I I ° е ° ° Ю ! ° ° ! ° ! ° ! ° ° а ° 1 l а ° й в O ° Ф ° ! а ! й ° ° а ° ° ° ° ° ° ° ° ° в ° ! ° e ° ! ° ° й ю ° в ° ° й Ю В в ° а а ° а ° ° ° а в Ф ° а ° ° O° ° в ° r I а а й ° ° I ° ° Р ! ! ° ° J ° ° r в И ° I ° I й ! а ° ° ! ° ° ° r ° ! ° ° I'J Ф ° ! ° а ° ° ° I ° е ° й ! ! ° J ° ° ° ю 3 ° 1 1 I 1 1 1 ' J е 1 ' I 1 1 1 ° ° 1 J ° ° ° Э ю ° 1 ° ! е ° 1 ~ ! ~ ° ° ! ° ! t ' ° 1 ° ° ° 3 ! ° ° ! ° ф й ° ° б ° Эr;r Ю ° ° ° ~ ° ! J J Ф ° ° ° ° а ' ° I r J ю
PE ГРЕССИЯ значений функции и и — число особей. Средняя получается простым де- лением первого числа на второе: ni При многочисленных группах лучше первичные данные представить в виде корреляционной решетки, в которой значения аргумента находят- ся в верхней заглавной строке, а значение функции — в левом заглав- ном столбце. Эмпирический ряд регрессии получается путем вычисления средней арифметической по каждому столбцу такой решетки: ф1 п~ Здесь f — частота ~-го столбца, W — средины классов функции, и; — сумма частот по ~-му столбцу. Составление эмпирического ряда регрессии показано в табл. 111. ОБЩИЕ СПОСОБЫ ВЫРАВНИВАНИЯ ЭМПИРИЧЕСКИХ РЯДОВ К общим способам выравнивания эмпирических рядов относятся: графический способ, способ скользящей средней и способ наименьших квадратов. ГРАФИЧЕСКИЙ СПОСОБ Графический способ дает возможность с достаточным приближе я- ем получить теоретическую линию, а затем и теоретический ряд регрес- сии без каких-либо вычислений. Наиболее простым оказывается применение графического способа к прямолинейной регрессии. В этих случаях на график наносится сна- чала эмпирическая линия регрессии, затем между крайними выступа- ми ломаной эмпирической линии проводится прямая так1~м обрамил, чтобы сумма расстояний теоретической прямой от точек эмпирической линии была бы наименьшей. При известном навыке это можно сделать от руки; мо>кст пома|ь при этом нагянутая нитка или прозрачная линейка с нанесенной пря- мой чертой. Натянутая нить располагается по среднему течению эмпи- рической линии, и после нахождения наилучшего положения нитки на графике отмечаются две крайние точки: для минимального и максималь- ного значения аргумента. Теоретической линией регрессии буд т прямая, соединяющая эти две точки. По теоретической прямой можно определить числовые значения функции (ординаты), соответствующие определенным значениям аргу- мента (абсциссы). Графическое выравнивание при прямолинейной регрессии показа- но на рис. 46. Если регрессия не может считаться прямолинейной, то графическое выравнивание эмпирической .кривой также может быть проведено но для этого необходимо иметь представление об общих закономерностях изменения функции. При изучении, возрастных изменений живого веса сельскохозяйст- венных животных требуется учитывать, что живой вес, увеличиваясь с возрастом, постепенно приближается к некоторому максимальному зна- чению, после чего прирост прекращается и значение его остается при- мерно на одном максимальном уровне.
ГРАФИЧЕСКИЙ СПОСОБ 265 При графическом выравнивании возрастных изменений лактацион- ных удоев нужно учитывать, что примерно до 6 — 7 лактаций обильно- молочность коров с каждой лактацией увеличивается, затем начинает снижаться в связи с общим старением организма. При выравнивании кривых регрессии веса по линейным размерам тела нужно иметь в виду, что по мере увеличения, например, длины, ши- рины или обхвата тела увеличение веса идет с возрастающей скоростью, вследствие чего кривая регрессии имеет вид линии постепенно загиба- ющейся кверху. Рис. 46. Графическое выравнивание эмпирического ряда прямо.пикей-ной регрессии. На рис. 47 показано графическое выравнивание ряда возрастных изменений живого веса сычевских помесей второго поколения. Для со- поставления на рисунке дана теоретическая кривая, точки которой рас- считаны по формуле асимптотического роста. Совпадение результатов графического метода с результатами аналитического оказалось доста- точно близким. Графический анализ может быть проведен на основе индивидуаль- ных значений без расчета средних значений эмпирического ряда — при помощи точечного графика. Для составления точечного графика устанавливаются две перпен- дикулярные ~шкалы: горизонтальная шкала аргумента, идущая слева направо, и вертикальная шкала функции, идущая снизу вверх. Ни ар- гумент, ни функция не разделяются на градации. ~аждая особь отмечается на графике точкой, положение которой определяется по абсциссе значением аргумента, а по ординате значени- ем функции. Получается вытянутое скопление точек, которое дает воз- можность провести приближенную теоретическую линию регрессии, а по ней графически установить теоретический ряд регрессии. 1(роме то- го, точечный график позволяет легко выделить выдающихся особей, не приводя значение функции к единому значению аргумента.
РЕГРЕССИЯ 266 Преимущество такого графика заключается в том, что он нагляд- но показывает и среднее течение функции, и то разнообразие значений, которое характерно для данной функции при данном аргументе. Рис. 47. Сопоставление графического (1) и аналитического (2) спо- собов выравнивания рядов возрастных изменений живого веса сы- чевских помесей. Рис. 48. Точечный график зависимости живого веса ярослав- остфризских телят от возраста. 1 — 7 — выдающиеся экземпля- ры, принятые на ВСХВ. 'уочечный график был применен, например, при выделении выдаю- щихся ярослав-остфризских телят на основе разновозрастных данных по живому весу (рис. 48). По этому графику легко определить. выдаю- щихся особей по данному признаку (на, графике они занумерованы), средний живой вес в любом возрасте (в возрасте 30 дней средний вес
267 СПОСОБ СКОЛЬЗЯЩЕЙ СРЕДНЕЙ телят — 50 кг, в возрасте 60 дней — 75 кг и т. д.) и крайние отклонения веса в любом возрасте (эти отклонения до 60 дней составляют пример-но~-10 кг, после 60 дней — примерно~ 15 кг). СПОСОБ СКОЛЬЗЯЩЕЙ СРЕДНЕЙ Если форма функции неизвестна, то сгладить изломы эмпирической кривой можно, применив способ простой скользящей средней. Этот спо- соб заключается в том, что для каждого значения аргумента берется средняя арифметическая из нескольких (соседних) значений функции. Если скользящая средняя берется:по трем значениям аргумента, то складываются значения функции для меньшего значения аргумента, для данного и для большего. Частное от деления этой суммы на 3 дает выравненное значение функции для данной .величины аргумента. Выравнивание эмпирического ряда методом простой скользящей средней показано в табл. 112. Выравненная этим методом кривая да- на на рис. 49. Та бл ица 112 Выравнивание эмпирического ряда по способу простой скользящей средней. Аргумент — содержание переваримого белка (~/о) в рационе телят до шести- месячного возраста. функция — вес телят (кг) в возрасте шести месяцев Сумма трех соседних значений живого веса Живой вес в возрастешести месяцев Выравненные значе-ния живого веса Процент белкав рационе 348 = 103+ 120+125 392 = 120-~- 125-', 147 Выравнивание эмпирических рядов способом простой скользящей средней применяется, когда не требуется особой точности и когда име- ется достаточно длинный ряд и можно пренебречь потерей двух значе- ний функции, соответствующих крайним значениям аргумента. Более точные и не связанные с потерей крайних значений резуль- таты получаются при использовании взвешенной скользящей средней. При этом способе с обоих концов ряда добавляется по два значения— по два члена ряда. Определяются они следующим образом. Первое (от конца) значение ряда (у1) умножается на 2, к получен- ному произведению прибавляется второе значение (у2), третье (уз) про- пускается, а из суммы вычитается четвертое (у4). Полученное число де- лится на 2. Частное будет первым добавочным значением: у+ i (для максимального конца ряда) или у — 1 (для минимального конца ряда). 56 53 50 47 44 41 38 35 32 29 26 23 20 17 103 120 125 147 139 153 147 154 154 149 159 140 152 118 348~ 392"" 411 439 439 454 4á5 457 462 448 451 410 116 131 137 1~6 146 151 152 153 154 149 150 137
PEГРЕССИЯ 268 Все эти действия можно выразить следующей формулой: -2У1 + У2 У4 у+ i = s) Второе добавочное значение )y 1' yi — уз Для его расчета нужно использовать первое добавочное значение и первое и третье значения первоначального эмпирического ряда. Рис. 49. Ряд, выравненный способом простой скользящей средней. Чтобы избежать ошибок при расчете, можно на краю листка бума- ги записать коэффициенты +2, +1, О, — 1 для минимального края ряда и — 1, О, +, 1, +2 — для максимального: Приставляя край такого листка к эмпирическому ряду, легко видеть, что надо делать с каждым из че- тырех последних значений ряда, чтобы получить добавочные значения. Для примера в двух верхних и в двух нижних строках третьего столбца табл. 113 показано получение добавочных значений ряда. При короткис рядах добавочные значения можно получать, пользу- ясь формулами: 4yi+ У — 2V 4у+ -', у, — 2у +2— После установления добавочных значений приступают к выравни- ванию эмпирического ряда. Выравненные значения получаются путем вычисления взвешенной средней арифметической из пяти соседних эмпирических значений функ- ции, взятых соответственно с весами 1; 2; 4; 2; 1. Для того, чтобы получить, например, первое выравненное значение функции, нужно сумму второго добавочного, удвоенного первого до- бавочного, учетверенного первого эмпирического, удвоенного второго эмпир~ического и третьего эмпирического значений функции разделить на сумму весов (1+ 2+ 4+ 2+ 1 = 0) .
269 СГ1ОСОБ СКОЛЬЗЯЩЕЙ СРЕДНЕЙ Для рассматриваемого эмпирического ряда первое выравненное значение функции 78,5 + 2 89,5 -~- 4 103 + 2 120 + 125 = 117,25. 10 В табл. 113 приведен расчет всех выравненных значений функции .для рассматриваемого примера. Обычно эти действия не записываются. Пять эмпирических значений, помноженных на коэффициенты взвеши- Banns, складываются на счетах, сумма уменьшается в 10 раз, и полу- ченное значение взвешенной средней функции для данной величины ар- гумента записывается в столбец рядом со столбцом (или строкой) эм- пирических значений. Таблица 113 выравнивание эмпирического ряда способом взвешенной скользящей средней.Аргумент — содержание переваримого белка в рационе телят до шести-месячного возраста, функция — вес телят в возрасте шести месяцев. Функция Лргу-мс нт эмннриисскнй рял с добаво1нымн зна- чсниямн расчет выравнснных н добавочных эначсний у = (2 89,5 -~- !03 — 125): 2 = 78,5 у, = (2 . 103 +- 120 — 147): 2 =- 89,5 у. ~ =-78,5 у+, — — 89,5 у, =1О3 у =- 120 у1 — — 125 у, == 147 у;, =-139 у„, -153 у; == 147 у,, = 154 у, = 154 у,о - 149 y» —— - 159 у1р —— 140 У1з = 152 у14 = — — 118 Ряд живого в~а шестимесячных елят, вырав «енный методом .взвешенной скользящей средней, показан на рис. 50. Чтобы избежать числовых просчетов, нужно на краю листка бума- ги написать коэффициенты взвешивания: 1; 2; 4; 2; . Если этот край 56 53 50 47 44 41 38 35 32 29 26 23 20 17 Это можно выразить следующей формулой: у+2-> 2у+1+4y, +2y2 > y3 )I1 10 89,5 -~ 4 103 + 2 . 120 + 125): 10 = 103,45 ° 103 — ', 4 120 -1- 2 125 -+ 147): 10 = 117,25 120 +- 4 . 125 +- 22 147 --',- 139}: 10 = 127,6 125 + 4 147 +- 2 139 + 153): 10 = 138,9 147 -1- 4 139 +- 2 153 -+- 147): 10 = 142,8 139 + 4 153 + 2 147 + 154): 10 = 148,5 153 -,'- 4 147 +- 2 154 + 154): 10 = !49,5 147 + 4 154 ~- 2 154 — ,'- 149}: 10 = 152,0 154 + 4 154 + 2 149 + 159): 10 = 152,8 154 + 4 149 + 2 159 — 140): 10 = 151,6 149 +- 4 I59 + 2 140 + 152): 10 = 152,0 159 — ,' 4 140 -t- 2 152 +- 118): 10 = 144,9 140 + 4 . 152 (- 2 . 118 + 114,5): 10=--. 139,75 152 '' 4 118 ~2 114,5+-103,5): 10 = 124,85 у, = (78,5+ 2 уг —— (89,5 + 2 у = (103 + 2 . у =(~20+2. у = (125 -~- 2 . у = (147 + 2 . у, = (139+ 2 ° у .= (153+ 2 ° у =(147+2 у1с = 154+ у„= (154+ 2 . 1 У1г — (149+ 2 '. у,з — — (159+ 2 . y,'4, ==(140 i-2 ° у > — — 114,5 у > —— (2 118+ 152 — 159}: 2 = 114,5 У г =103,5 у г — — (2 114,5+-1~8 — 140): 2=103,5
270 РЕГP EGGH Я прикладывать последовательно к каждым пяти соседним ' значениям функции и множить эти значения на соответствующие коэффициенты, то сумма произведений, деленная на 10, и будет искомой средней. За- писывается она против среднего коэффициента (4). Способом скользящей средней можно произвести выравнивание се- мейства .кривых в тех случаях, когда изучается развитие признака под влиянием одного фактора у нескольких категорий особей или под влия- нием двух факторов, из которых каждый разделен на несколько гра- даций. Рис. БО. Ряд живого веса, выравненный способами простой (1) ивзвешенной (2) скользящей средней. Таблица 1ИСреднесуточные удои (кг) пяти опытных групп коров за первыешесть недель пастбища Недели пастбища Группа коров Упитанность коров 16 14 11 12'138 ll 9 6 17 15 16 10 6 7 14 i1 10 Выше средней Средняя Ниже средней Тощая (после заболе- вания) . Истощенная (после длительной болезни) 12 В табл. 114 приведены результаты опыта, в котором выяснялось. действие пастбища на молочных коров в первые недели. При этом упи- танность коров, вышедших на пастбище, была различной. В таблице приведены среднесуточные удои по пяти группам коров за первые шесть недель пастбища; эти же результаты представлены графически на рис. 51. Для выравнивания нескольких связанных рядов регрессии (семей- ства кривых) требуется первоначально получить по одному добавочному значению для каждой строки, для каждого столбца и для каждого угла таблицы, в которой записаны в обычном порядке все эмпирическиезна-
2! СПОСОБ СКОЛЬЗЯЩЕЙ СРЕДНЕЙ чения функции. 1(аждае добавочное значение получается на основе че- тырех крайних, по тому же правилу, что и при выравнивании одной эм- яирической кривой: 2V + уг r4 4r~ + у" 2уз у+ 1 = 2 или у+1— 3 Рис. И. Выравненные семейства кривых способом взвешенноскользящей средней.a — кривые до выравнивания, б — кривые после выравнивания (в кружкак-номера групп). Таблица 115Выравнивание семейства кривых методом взвешеннойскользящей средней 21 18 14 17 15 4 2 6 12 10 10 Добавочные значения для примера, приведенного в табл. 114, по- казаны в крайних строках и столбцах табл. 115. Добавочное число app — — 10, стоящее в левом верхнем углу таблицы, получено по четырем
272 РЕГРЕССИЯ эмпирическим значениям, расположенным по диагонали, идущей от это-го угла: аоо = (2 11+ 6+ 0 — 8): 2 = 10. Добавочное число а47 — 14 для четвертой опытной группы справа получено по четырем крайним значениям этой строки: а47 — — (2 11+9+0 — 3): 2=14. Добавочное число для первой недели пастбища получено по четы- рем нижним эмпирическим значениям: ао1 — — (2 2+5+0 — 9): 2=0. После установления добавочных чисел производится выравнивание эмпирических значений. В данном случае выравнивание каждого эмпирического значения производится путем усреднения девяти значений функций. из которых одно, центральное, есть выравниваемое значение, а остальные восемь— значения, окружающие его со всех сторон. При суммировании центральное значение удваивается, остальные восемь берутся без изменений и полученная сумма делится на 10. Например, выравненное значение удоя для 1-й группы за 1-ю не- делю получено путем усреднения девяти величин, составляющих квад- .рат, в центре которого стоит выравниваемое значение: 10 13 11 8 11 10 5 9 6 а „= ( 10+ 13+ 11+ 8+ 2 . 11+ 10+ 5+ 9+ 6): 10 = 9,4. Выравненное значение удоя для 1-й группы за 2-ю неделю опреде- ,ляется квадратом чисел: 13 ll 17 11 10 12 9 6 13 а„= (13~-11+7+11+2 10+12+9+6+13): 10=11,2. Выравненные значения показаны в табл. 115 и на рис. 51,б. Чтобы избежать счетных ошибок при выравнивании семейства кри- вых по методу взвешенной скользящей средней, можно в листке бумаги вырезать квадрат таких размеров, чтобы он охватывал девять клеток таблицы эмпирических значений. Прикладывая этот листок так, чтобы в центре вырезанного квадрата находилось выравниваемое значение функции, можно каждый раз открывать только те величины, которые нужны для выравнивания данного значения функции. Выравнивание методом скользящей средней, имеющей в некоторых случаях самостоятельное значение, может также применятьсд как спо- соб подготовки сильно невыравненных данных к дальнейшему вырав- ниванию графическим или аналитическим методом.
СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ 273 СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ Наиболее общим аналитическим способом выравнивания эмпири- ческих рядов регрессии является способ наименьших квадратов. Этим способом получаются такие выравненные значения функции, квадраты отклонения которых от эмпирических значений дают наименьшую сумму. Способом наименьших квадратов можно выравнивать функции прямолинейные и криволинейные, простые и множественные. Выравни- вание эмпирических рядов регрессии способом наименьших квадратов осуществляется по следующим этапам: 1. Определение общего вида уравнения регрессии. Производится на основе предварительного биологического анализа процессов, определя- ющих течение функции, или на основе рассмотрения эмпирической кривой. 2. Составление системы нормальных уравнений. Производится по следующим правилам: а) Все члены исходного равенства умножаются на коэффициент при свободном члене а и суммируются. Число слагаемых и равно чис- лу пар значений аргумент — функция. Например, для исходного равен- ства а+Ьх+сх' будем иметь: an+ bZx+ cZx'=~у. 6) Все члены исходного равенства умножаются нах исуммируются: aZx+ bZx~+ cZx' = Zyx. в) Все члены исходного равенства умножаются на х2 и суммируются: а~х2+ bZxÇ+ cZx4 Zyx2 г) Полученные уравнения дают систему нормальных уравнений: an+bZx+cZx~=Zy, aZx+ЬХх'+сХх' =Zyx, aZx~+bZx' +cZx4=Zyx' Zx, Zx' Zx', ~х' Zy, Zyx, Zyx' 4. Определение коэффициентов основного уравнения. Производит- ся путем решения системы нормальных уравнений обычными алгебраи- ческими приемами. В рассматриваемом примере (исходное равенство у=а+Ьх+сх') .коэффициентами будут о, b, с. Выравнивание эмпирических рядов регрессии способом наимень- ших квадратов можно показать на следующих примерах. Прямолинейные функции вида у=а+Ьх П р и м е р № 141. В некоторых случаях имеет смысл определение возраста коров по числу колец на рогах. Связь между числами колецна рогах и возрастом возникает оттого, что каждый отел, происходящий обычно ежегодно, оставляет на рогах коровы кольцо, отражающее за- медление роста рога в периоды глубокой стельности, когда главная мас- са питательных веществ тратится на питание плода. Поэтому если к среднему числу лет, прошедших до первого отела прибавить число ко- лец, умноженное на средний межотельный период, то это и будет при- мерным возрастом коровы. Это можно выразить уравнением у=а+Ьх, 3. Определение числового значения сумм, входящих в нормальные уравнения. Производится путем суммирования предварительно вычис- ленных рядов:
274 РЕГРЕССИЯ где а — число лет до первого отела, х — число колец на рогах, у — вовраст коровы в годах, b — средний межотельный период. Зная исходное уравнение, можно составить систему нормальных уравнений. В данном случае она будет простой: an+ bZx= Zy, aZx+ bZx'=Zyx. Следовательно, нужно определить четыре величины: Zx, Zx', Zy, Zyx. Эти суммы приведены в табл..116. Таблица 116Выравнивание эмпирического ряда регрессии возраста коров (у) по числу колецна рогах (х) способом наименьших квадратов:у'= a+ bx, ап+ ЬХх = Zy@ZAN+ ЬХх2 = Бух П остроеине теоретического ряда Нахождение параметров полинома У — У Ьх ух ~у =92,7 ~yx =665,8 Ех2 =506 Xx=66 11a + 66b = 92,7 66а + 506b = 665,8 у' = 2,45 + 0,996х Яля определения этих сумм были использованы данные по 1509 коровам Племенной книги ярославского скота (часть I, том III). Для каждой коровы был рассчитан средний возраст у по числу отелов или, что то же самое, по числу колец на рогах х. Полученная система нормальных уравнений 11a+ 66b =92,7, 66a+ 506b = 665,8 решается путем постепенного исключения неизвестных. В данном слу- чае это легко сделать, помножив все члены первого равенства на 6 66 и вычитая полученное равенство из второго уравнения: 11 66a —,' 396Ь = 556,2 66a + 506b = 665,8 = + 0,996. 109,6 110 0 + 110Ь = + 109,6 11 10 9 8 7 6 5 4 3 2 1 13,3 12,4 11,5 10,5 9.5 8,3 7,4 6,5 5,5 4,4 3.4 121 100 81 64 49 36 25 16 9 4 1 146,3 124,0 103,5 84,0 66,5 49,8 37,0 26,0 16,5 8,8 3,4 10,955 9,960 8,964 7,968 6,972 5,975 4,980 3,984 2,988 1,992 0,996 13,4 12,4 11,4 10,4 9,4 8,4 7,4 6,4 5,4 4,4 3,4 +0,1 0,0 — 0,1 — 0,1 — 0,1 +0,1 0,0 — 0,1 — 0,1 0,0 0,0
СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ 275 Подставляя полученное значение b= +0,996 в первое нормальное урав- нение и определяя из него а, будем иметь: 92,7 — 66 . (+ ОЯ96) а= 11 Таким образом, теоретические значения возраста по числу колецна рогах можно определить по формулеу'= 2,45+ 0,996х,где у' — теоретическое значение возраста при числе колец на рогах, рав-НОМ Х. Рис. Б2. Прямолинейная функция. Определечие возраста коров(средины лактации) по числу колец на рогах. + При сопоставлении эмпирического и теоретического рядов эмпирические значе- ния аргумента обозначены через у, а теоретические — через у'. Возраст, определяемый этой формулой, относится к средине того межотельного периода, перед началом которого образовалось последнее кольцо. Чтобы получить возраст отела, надо из величины, полученной по формуле, вычесть половину межотельного периода, т. е. 0,996: 2=0,498. Тогда формула примет следующий вид: у" = 1,952+ 0,996х, где y" — возраст отела, номер которого равен х. Эта формула очень близка к тому правилу, по которому на прак- тике определяют возраст по числу колец — корове столько лет, сколько у нее колец на рогах плюс 2: у=2+х. Теоретический ряд возраста по числу колец на рогах показан на рис. 52.
276 РЕ ГР ЕССИЯ Показательные функции вида у = ax' П р имер 142. 11ля разработки норм погрузки животных в автома- шиньг потребовалось установить нормы потребной площади пола на 1 голову в зависимости от среднего веса животных в загружаемой груп- пе. При проведении опытных перевозок были получены данные о весе перевозимых свиней и о их количестве в .кузове, имеющем определен- ную площадь пола. При обработке материалов получены средние пло- щади, приходившиеся на 1 голову при разном среднем весе свиней (от 40 до 220 кг). Потребовалось выравнять полученный эмпириче- ский ряд. Общий вид уравнения был намечен исходя из следующих сообра- жений: 1) в уравнении не должно быть свободного члена, так как при весе, равном нулю, и потребная площадь тоже равна нулю (при х=0, у=0), 2) изменение потребной площади не может быть пропорциональ- но весу, так как крупные животные на единицу веса требуют меньшую площадь пола, чем мелкие животные. Такие функции могут иметь вид: y= axý что после логарифмирования дает уравнения прямой: lgy =lga+ blgx. Система нормальных уравнений в данном случае составляется по обычным правилам: (1ga)n+bZ(lgx) =Z(lgy),(lga) Zlgx+ ЬХ (1 gx) '= Х (Igy) (lgx) . Таблица 117 Выравнивание эмпирического ряда регрессии потребной площади пола (у) иа 1 голову при перевозках на автомашинах по среднему живому весу свиней (х): g = ИХ6. (1йа) и+ bZ (Igx) = Z(Igy) Igy = Iga + blgx, (Iga) Z (1gx) + Ь (Igx)' = Z (Igy) (Igx) Нахождение параметров полинома Построение теоретического рида — 1,797+ 0,666 1gx ~<) '666 1~ . 1gy' (1g.r)' (1gy)(1gx) V у, л-' 1gx 1gy +20,610 — 4,249 + 42 998 — 8,390 10 Iga+ 20,610 Ь = — 4,24920,610 Iga+ 42 998 Ь = — 8,390 1gy' = — 1,797 + 0,666 Ig» = 00160xî,к6 д 220 200 180 160 140 120 100 80 60 41~ 0,60 0,52 0,54 0,45 0,46 0,41 0,35 0,27 0,22 0,19 2,342 2,3)01 2,255 2,204 2,146 2,079 2,000 1,903 1,778 1,602 i,778 l,716 1,732 1,653 1 663 1,613 1,544 1,431 1,342 1,279 — 0,222 — О, 284 — 0,268 — 0,347 — 0,337 — 0,387 — 0,456 — 0,569 — 0,658 — 0,721 5,485 5,295 5,085 4,858 4,605 4,322 4,00 ) 3,621 3,161 2,566 — 0,520 — 0,653 — 0,604 — О, 765 — 0,723 — 0,805 — 0,912 — 1,083 — 1, 170 — 1,155 1,560 1,532 1,502 1,468 1,429 1,385 1,332 1,267 1,184 1,067 — 0,237 — 0,265 — 0,295 — О, 329 — 0,368 — 0,412 — О, 465 — 0,530 — 0,613 — 0,730 1,763 1,735 ! 705 1,671 l,632 Я8 1,535 1,470 1,387 1,270 0,5?9 0,543 Р,507 0,467 0,424 0,387 0,343 0,295 0,244 О,l86
СПОСОБ HAHMEHblllHX КВАДРАТОВ 277 В табл. 117 приведены расчеты всех требуемых сумм: Z(lgx), Z(lgx)', Z(lgy), Z(1gy) (1gx). была получена система нормальных уравнений101g+ 20,6101 gb = — 4,2119,20,6101ga+ 42,9981 gb = — 8,390. Для решения этой системы можно умножить все члены первого ра- 20,(i10 венства на 2,061 ' и вычесть из полученного равенства второе 10 / уравнение: 20,6101 ga+ 42,998b = 8,390 20,6101ga+ 42,447b = 8,757 О+0,551b =0,367, откуда + 036 . 6. -1- 0.,551 Подставляя значение b=+0,66 в первое исходное уравнение, on ределим Iga: — 4,249 — 0,6G6 20,610 — 1,7975 = 2,203, 10 а = 0,0160. Таким образом, искомое уравнение имеет вид: у =. 0,0160 . х ' я'-' или в логарифмической форме: 1gy= — 1,797+0,6661g х м2. Выражая потребную площадь в см' получим: у=160л ' Igy=2,203+0,666 lgx. Теоретический ряд регрессии приведен в табл. 117 и на рис. 53. График, представленный на рис. 53, может служить номограммой для определения потребной площади пола в автомашине по среднему живому весу перевозимой группы свиней. Например, если средний вес составляет 130 кг, то на каждую голову требуется 0,41 м' пола (см. рис. 53). На основе полученной формулы можно получить формулу для определения числа голов, которые можно погрузить в автомашину с пло. щадью пола А при среднем ввсе х: А O ахь Если перевозки проводятся в кузове грузовика ЗИЛ-150, имеющем площадь пола 7,97 м', то приведенная выше формула будет иметь сле- ду~оший sHZ: 7,97 О 0160хо 666
РЕГРЕССИЯ 278 Рис. 53. Показательная функция. Зависимость потребной площадипола в автомашине на 1 голову от среднего веса свиней. Рис. 54. Номограмма для определения числа свиней, которых можно погрузить в кузов автомобиля ЗИЛ-150 (7,97м~), в за- висимости от их среднего веса.
СПОСОБ НАИИЕНЬШИХ КВАДРАТОВ 279 Номограмма, полученная по этой формуле, приведена на рис. 54. Пунктиром показано определение нормы погрузки свиней в кузов ЗИЛ-150 при среднем весе 90 кг. Параболические функции вида у=а+Ьх и у=а+Ьх+сх' П р и м е р 143. При изучении возрастных изменений морских бес- позвоночных по материалам, собранным Ан-Де-Гюном, было обнаруже- но, что некоторые виды животных не имеют 'обычного замедления .роста размеров и веса. Длина раковины одного моллюска на протяжении от трех до десяти лет жизни увеличивалась почти равномерно, а вес его раковины в этот же период увеличивался с повышающейся скоростью. При рассмотрении эмпирических рядов, нанесенных на график, было сделано предположение, что в данном случае имеются закономер- ности параболического роста, выражаемые для длины тела уравнением параболы первого порядка, т. е. прямой у=а+Ьх; а для веса — парабо- лой второго порядка, вида у=а+Ьх+сх'. Выравнивание соответствующих рядов показано в табл. 118 и 119и на рис. 55. Рис. 55. Функции параболического роста. Возрастные изменениядлины (а) и веса (б) раковины моллюска. Для первого возрастного ряда (табл. 118) система нормальных уравнений будет следующей: 8a+ 52Ь = 407,6 52a+ 380b = 2876,4. 52 Умножая первое равенство на 6,5 — и вычитая из него второе 8 исходное равенство, определим величину b: 52a+ 338b = 2649,4 52a+ 380b = 2876,4 ' 540 + 42 0+42b = -(-227,0
280 РЕГРЕССИЯ Таблица 118 Выравнивание эмлирического ряда регрессии длины раковины моллюска (у) по возрасту (х) способом наименьших квадратов: ап+ bZx = Zy aZx + bZx2 = Zyx у'=а+ bx, Определение параметров уравнения Построение теоретического ряда х,годы у'=a+ bx bx У У У, мм ух 70,0 64,6 58,6 53,8 48,4 43,1 36,4 32,7 700,0 581,4 468,8 376,6 290,4 215,5 145,6 98,1 2876,4 52 407,6 380 Яа+ 52b = 407,652a+ 380д = 2876,4 у' = 15,9 — ', 5,40х Таблица 119Выравнивание эмпирического ряда регрессии веса раковины моллюска (у)по возрасту (х) способом наименьших квадратов:an + bZx + cZx~ = Zyy = а + bx + cx'. aZx + bZx2+ cZx3= ZyxaZx'+ bZR + cZx4 = Zyx' Построение теоретического ряда Определение параметров уравнения хгодм Ьх cx' У У — У x' ух 380 3016 25316 83 672 52 5740 8а+ 52b+ 380с = 83 52a -~- 380b + 3016с =- 672 380a + 3016b + 25316с = 5740 у' = + 6,4~ — 2,%х+ 0,45õ-" Подставляя полученное значение Ь=+5,40 в первое исходное ра- венство, определим а: 407,6 — 6,40 52 а= 8 10 9 8 7 6 5 4 3 10 9 8 7 6 5 4 3 100 81 64 49 36 25 16 9 1000 729 512 343 216 125 64 27 100ll0 6561 4096 2401 1296 625 256 81 100 81 64 49 36 25 16 9 25 19 12 10 7 5 3 2 250 171 96 70 42 25 12 2500 15е9 768 490 252 125 48 18 54,0 48,6 43,2 37,8 32,4 27,0 21,6 16,2 — 26,50 — 23,85 — 21,20 — 18,55 — 15,90 — 13,25 — 10,60 — 7,95 69,9 64,5 59,1 53,7 48,3 <2,9 37,5 32,1 --;45,00 -',-36,45 +28,80 - 22,05 + 16,20 +11,25 +7,20 +4,05 — 0,1 — 0,1 +0,5 — 0,1 — О,l — 0,2 --', 1, l — 0,6 24,9 19,0 14,l~ 9,9 6,7 4,4 3,0 2,5 — 0,1 0,0 +2,0 — 0,1 — 0,3 — 0,6 0,0 — 0,5
СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ Таким образом, уравнением прямолинейного, роста будет у=15,8+5,40 х. Полученный теоретический ряд регрессии (табл. 118, рис. 55a) сви-детельствует о достаточно близком совпадении выравненных значений длины раковины с эмпирическими. Для решения системы нормальных уравнений 8а+ 52b+ 380с = 83, 52а+ 380b+ 3016с= 672, 380а+ 3016Ь+ 25 316с = 5740, полученнь1х для второго возрастного ряда (табл. 119), умножим nep-' 3b0 380 вое равенство на 47,5 —, а второе на 7,3077 и после этих 8 д2 преобразований вычтем из второго равенства первое, а из третьего— второе. Получим два новых равенства без свободного члена: О+ 306,9Ь-+-3990,Ос=968,3, О+ 239,lb+ 3276,0с = 829,2. 306,9 Второе из этих равенств умно>ким на 1,2836 ' и вычтем из наго 239,1 первое. Получим: + 306,9Ь+ 4205,1с = 1064,4 +306,9Ь+3990,0c= 968,3 0 + 215,1c= 96,1 откуда с = ' = -~-0,45. + 96,1 + 215,1 Подставив величину с=+0,45 в первое равенство, можно определить b: b= 968,3 — 0,45 3990 306,9 Подставляя значения с и b в первое нормальное уравнение, можно определить а: = — - 2,65. 83 + 2,65 52 — 0.45 3808> Таким образом, уравнение роста веса раковины моллюска имеет вид: у'= + 6,40 — 2,65х+ 0,45х2. Теоретический ряд регрессии (табл. 119, рис. 55б) достаточно хо- рошо соответствует эмпирическим значениям веса по возрастам. Это обстоятельство подтверждает гипотезу о том, что возрастные изменения веса раковины следуют закономерностям параболического роста. Результаты такого описания явлений могут подсказать направление дальнейших биологических исследований. СГиперболические функции вида у = а + bx -',— — 'Х П р и м е р: 144. Изучалась скорость движения морских беспозвоноч- ных в зависимости от их размеров. Эмпирические ряды регрессии ско- рости по длине тела имели значительные изломы, что отражало нерав- номерное напряжение других факторов, влияющих на скорость на от-
282 РЕГРЕССИЯ дельных участка~ пути. Чтобы выделить из всех влияний влияние дли- ны тела, необходимо было найти теоретическое течение скорости по дли- не при усреднения всех остальных факторов. Это было проведено по материалам, собранным М. И. Константино- вой. Выравнивание проведено по уравнению гиперболы вида у = — ~+ + Ьх+ —, принятом на основании рассмотрения эмпирической кривой. Так как по условиям наблюдения чрезвычайно трудно подобрать особей с длиной тела, различающейся на одну и ту же величину, зна- чения функции были получены через различные неодинаковые проме- жутки аргумента. Это обстоятельство не препятствует выравниванию эмпирических рядов, если 'оно проводится при помощи общего способа наименьших квадратов. Зависимость скорости движения от длины тела для некоторых бе- позвоночных показана в табл. 120, теоретический ряд — на рис. 56. Рис. бб. Гиперболическая Функция. Скорость движения бес-позвоночного в зависимости от длины тела. Яля облегчения расчетов аргумент взят в преобразованном виде: х — 80 Х1 —— «)О Это дает возмож.-юсть заменить трехзначные значения фактической дли- ны рядом натуральных чисел: 1, 2, ... 29, 30. Обратный переход от преобразованных значений аргумента к фак- тическим, как легко видеть. можно сделать по формуле х = 80+ 20х~. Яля решения полученной системы нормальных уравнений (табл. 120): l2a +169b +2,1919с=11,9 169a+ 3455b+ 12с = 144,3 2,1919а+ 12b+ 1,2147с = 3,025
СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ Таблица 120 Выравнивание эмпирического ряда регрессии скорости движения беспозвоночного (y)по длине тела (х) способом наименьших квадратов:с 1у=а+Ьх+ — —, ап + bZx+ cZ — =~'yХ Х х — 80 X1 = 20 аХх+ ЬЕх~+ cn= >y~ 1 1aZ — + bn+ cZ — =- ZХ ЛР OnpeaeëñíHå параметров уравнения Построение теоретического ряла 2 ! с — ( +) )'е me/се~ Ух~ х, мк у/х, bx> ( — ) Х1 У — У х, 900 0,0343 0,0011 24,0 0,027 0,8 0,0 729 0,0370 0,0014 0,04! 29,7 — 0,3 576 0,0417 0,0017 0,0455 0,0021 0,025 0,027 14,4 13,2 0,6 +0,2 484, 0,6 +0,2 324 0,0555 0,0031 16,2 0,9 0,050 0,0 0,0769 0,0059 0,0909 0,0083 0,1111 0,0123 169 11,76,610,8 0,9 0,6 1,2 0,069 0,055 0,134 0,0 )21 +--0,3 81 — 0,2 36259 7,8 4,5 3,6 1,8 0,0278 0,0400 0,1111 1,0000 0,1667 О,2000 0,3333 1,0000 0,217 0,180 0,400 1,800 1,3 0,9 1,2 1,8 — 0,3 +0,2 0,0 0,0 169 3455 2,1919 1,2147 11,9 144,3 3,025 12a + 169b + 2,1919с = 11,9 169a + 3455b + 12с = 144,3 2,1919a + 12Ь + 1,2147c = 3,025 0,916 у = 0,903 — O,ОО56х1 + ~1 169 все члены первого равенства умножались на 14,08333 12 а третье- 169 после чего второе уравнение вычиталось 2,1919 77)10205 го — на 680 660 640 620 600 580 560 540 520 500 480 460 440 420 400 380 360 340 320 300 280 260 240 220 2(0 180 160 140 120 100 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 1ig 11 10 9 8 7 б 5 4 3 2 1 0,1680 0,1624 0,1568 0,1512 О,!455 0,1400 0,1344 0,1288 0,1232 0,1176 0,1120 0,1064 0,1008 0,0952 0,0896 0,0840 0,0784 0,0728 0,0672 0,0616 0,0560 0,0504 0,0448 0,0392 0,0336 0,0250 0,0224 0,0168 0,0112 0,0056 0,031 О,! 32 0,033 0,034 0,035 0,037 0,038 0,040 0,042 0,о44 0,046 0,048 0,051 0,054 0,057 0,061 0,%5 0,071 0,076 0,083 0,092 0,102 0,115 0,131 0,153 0,183 0,229 0,306 0,457 0,916 0,766 0,773 0,779 0,786 0,792 0,800 0,807 0,814 0,822 ~i,829 0,337 0,845 0,853 0,862 0,870 0,880 0,890 0,901 0,912 0,924 0,939 0,955 0,973 0,995 1,022 1,058 1,110 1,192 l,349 1,813
284 РЕГРЕССИЯ из первого, а затем — из третьего. Полученные два новых равенства не имеют первого члена: 0 — 1074,91723b+ 18,86925с = 23,29163 0 — 2529,77540b+ 81,65586с = 88,93370. 2529,77540 1074,91723 и полученный результат вычесть из второго равенства, то можно опре- делить величину с: Если первое из этих равенств умножить на 2,35346 — 25'9,775 b + 44,40803 с = 54,81592 — 2529,775 b + 8l,6~586 с =- 88,93370 О + 37,24783 с ==- 34,11778 + 34,11778 + 37,24783 Подставив полученное значение с в первое из преобразованных ра- венств, можно определить b: 54,81592 — 0,916 - 44,40803 — 2529,775 После подстановки b=0,0056 и с=+0,916 в первое исходное равенство получим: 11,9 + 0,0056 169 — 0,916 2,1919 = + 0,903. 12 Таким образом, уравнение регрессии скорости движен|ия у по дли- не тела х имеет вид: у' = + 0,903 — 0,0056 х, + где х — 80 20 Параболические функциис одним максимумом у=а+Ьх+--сх' Пример 145. В работах по селекции молочного скота большое практическое значение имеет выяснение закономерностей возрастных изменений обильномолочности. Для анализа зависимости удоя за 300 дней лактацчи от возраста были использованы, первичные материа- лы по средним удоям, полученным от одной и той же большой группы коров (около 5000 коров из передовых совхозов Центральной части Со- юза) за первую лактацию, вторую и т. д. Ряд эмпирических средних имел, как обычно, изломы, но общая тенденция возрастных изменений обильномолочности наметилась совер- шенно четко: до 5 — 8 лактации удои повышаются, а затем снижаются (в среднем}, если только не проведена интенсивная выбраковка недо- статочно продуктивных животных. Такая закономерность обычно выражается у.равнением парабольг второго порядка: у=a+ bx+ сх2. Выравнивание средних лактационных удоев по этой формуле при- ведено в табл. 121, теоретическая кривая показана на рис. 57.
285 СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ Таблица 12< Выравнивание эмпирического ряда регрессии удоя за 300 дней лактации {у) по лактациям (x) способом наименьших квадратов: ап+ bZx + СХх~ = Ху у = а + bx + сх~, aZx+ bZx'+ coax' = Zyx ~,~~Р+ bZx3+ cZx4 = ~.у~~ Определение параметров уравнения Построение теоретического ряда су' ( — ) Ьх (+) х, лак- 2 тации х У — У ух ух~ У х' 78 ..у 650 6084 60710 332 2193 18041 12a + 7ЬЬ + 650c = 332 78а + 650b + 6084c = 2193 у = + 17,05 + 4,115 х — 0,2977 х~ 650а + 6084Ь + 60710с = 18041 Рис. 57. Параболическая функция с одним максимумом. Возраст-ные изменения лактационных удоев. 12 11 10 9 8 7 6 5 4 3 2 1 144 121 100 81 64 49 36 25 16 9 4 1 1728 1331 1000 729 512 343 216 125 64 27 8 1 20736 14641 30000 6561 4096 2401 1296 625 256 81 16 1 24 26 29 9 3О 32 31 30 30 27 23 21 288 286 290 261 240 224 186 150 120 81 46 21 3456 3146 2900 2349 1920 1568 1~16 750 480 243 92 21 49,38 55,26 41,15 37,03 32,92 28,80 24,69 20,57 16,46 12,31 8,23 4,!1 42,87 36,02 29,77 24,11 19,05 14,59 10,72 7,44 4,76 2,68 l,19 0,30 23,56 26,29 28,43 29,97 0,92 31,26 3l,02 30,18 28,75 26,7! 24,09 20,86 О 0 — 1 +1 +1 — ! 0 0 — 1 0 +1 0
РЕГРЕССИЯ 286 Т а блица 122 Вычисление поправок на возраст Лактации 6 7 9 10 11 12 Теоретич. ряд, удоев (кг) по табл. 121 2409 2671 2875 3018 2086 3102 3126 3092 2997 2843 2629 2356 2671 3018 «0 сg 1~ы1исление пр-11равок (множитс-лсЙ) 2671 2671 3102 3126 0~86 =0,85 2671 2409 =1,11 2671 2876 =0,93 2671 2671 =1,00 '~671 2086 =1,28 2671 2671 2671 3092 2997 2843 =0,86 =0,89 =0,94 2671 2629 =1,02 '671 2356 =1,13 Нахождение возраста максимального раздоя можно сделать по гра- фику или по формуле 2с где Т — возраст (в отелах), в котором вероятно получение максималь- ного удоя от нормальных коров; Ь, с — параметры параболы второго порядка, найденные при вырав- нивании эмпирического ряда регрессии лактационных удоеь по лактациям. В разбираемом примере при уравнении регрессии у=+17,05+ + 4,115õ — 0,298x', b = + 4,1 5 и с = — 0,298, поэтому Т= ' = 6,88=.7 отелов. — 4,115 2 ( — 0,298) Установление стандартов удоя за разные лактации можно произ- водить, установив предварительно три исходные величины: Решение системы нормальных уравнений проведено обычным, опи- санным выше сп'осооом. В результате получено уравнение регрессии у = + 17,05+ 4,115х — 0,298х', в котором второй (положительный) член отражает действие всех фак- торов, благоприятствующих росту, а третий (отрицательный) член от- ражает результаты увеличивающегося с возрастом действия факторов, тормозящих рост. Следует иметь в виду, что полученная формула пра- вильно отражает возрастные изменения удоев только в пределах изу- ченных возрастов: от 1-й до 12-й лактации. Формула теряет значение при х=0 и при х большем 12. Поэтому свободный член уравнения а=+17,05 следует понимать, как отражение подготовки молодого ор- ганизма к тому, чтобы за первую лактацию дать удой, равный и+Ь+с=17,05+4,115 — 0,298=20,87 ц. Оказалось, что теоретический ряд удоев, полученный на основе па- раболического уравнения второго порядка, достаточно близок к эмпи- рическим значениям. Это обстоятельство позволяет использовать тео- ретический ряд для решения некоторых практических задач Установление поправок на возраст при определении лактационных удоев необходимо для сравнения разновозрастных групп коров (напри- мер, дочерей одного производителя и их матерей). Поправки находятся путем приравнивания удоя за какую-нибудь лактацию (например, 3-ю) единице и деления удоя за эту лактацию на удой по каждой из осталь- ных лактаций (табл. 122).
СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ 287 y~ — удой за первую лактацию (например, 3000 кг), 4 — удой за максимальную лактацию (например, 6000 кг), Т — номер максимальной лактации (например, 6-й). По этим данным можно найти параметры уравнения у=а+Ьх+сх'. С:— А — y1 6000 — 3000 20 (Т — 1)' (б — 1)' Ь = — с 2T = 120 ° 12 = + 1440, и = у1 — b — с = 3000 — 1440+ 120 = 1680. По найденным параметрам строится теоретический ряд удоев по лактациям. Значения этого ряда (табл. 123) и являются искомыми стан- дартами удоя. Таблица 123Построение теоретического ряда удоев (у) по лактацням (z) на основе заданных .величин:а = + 1680, Ь =+ 1440, с = — 120 +1440х — 120хг у', кг 7200 8640 10080 — 3000 4320 — 5880 5880 6000 5880 1440 2880 4320 5760 — 120 — 480 — 1080 — 1920 3000 4080 4920 5520 11520 12960 — 7680 — 9720 5520 4920 14000 — 12000 4080 Множественные прямолинейные функции вида y=a,+bx+cz Пример 146. Способ наименьших квадратов применим и в слу- чае нахождения теоретического ряда функции по двум аргументам. Например, при нахождении способов определения живого веса у по двум промерам — по обхвату груди х и по косой длине туловища z— для первой ориентировки были измерены и тотчас же после измерения взвешены 10 коров средней упитанности. Таким образом, для каждого животного было определено три при- знака, из которых один (вес) считался функцией двух остальных. Было сделано допущение, что зависимость веса от каждого промера прямо- линейна и формула регрессии имеет следующее строение: y = a+ bx+ cz. ,. = 3,44х — 90. 3. По косой длине туловища у, = 3,97z — 56. Определение выравненных значений функции, а также теоретиче- ских значений веса по каждому промеру показано в табл. 124 Столбцы х', ~', xz, gx, yz обычно цифрами не заполняются, так как при наличии арифмометра и других счетных машин требуемые значе- ния Zx', Zz' и т. д. получаются путем постепенного накапливания ре- зультатов суммирования произведений или квадратов. Оказалось, что живой вес можно определить по следующим фор- мулам: 1. По двум промерам у —. 2,03х + 1,82z — 102,2. 2. По обхвату груди
288 РЕГРЕССИЯ Таблица 124 Нахождение теоретических значений функции (живого веса у} по двум аргументам— обхвату груди х и косой длине туловища z и по одному из этих аргументов: ап+ bZx+ cZz = Zy д = а+ Ьх+ c'z, aZx+ ЬЕх'+ cZxz = Zyx абая+ bZxz+ сХя2 = Zyz ап+ bZx = Zy aZx+ bZx~ = Zyx ап+ bZz = Zy у =e+bz, а.'~я + bZz> = Zyz у — ~-ó- bx, Функция одного ар-гумента Функция двух аргу-ментов Нахождение параметров уравнения гУ хг g Z У'Х ДХ dZ Д Х2 CZ Ьх 2- Х' уЯ Х2 113400 126000 32400 36000 40000 ° °t° ° °10000 ° ° ° ° ° °2600 23400 81000 Z J 5 (45 Цц=159 ц Я=221 ля «4 5 М =15,9 М =22,1 сй1д1 ( д1 ' 1д1 769000 625800 1600 1300 4600 2656000 176000 215400 10а + 1600в + 1300с = 4600 1600а + 265 600Ь + 215 400c = 769 000 1300a + 215 400Ь + 176 000с = 625 800 У xz = 2,03х+1,82z — 102,2 10а+ 1600Ь = 46000 1600а+ 265 600Ь = 769000 10а + 1300с = 4600 1300a+ 8100с = 625 800 у'х = 3,44х — 90 У'z = 3,97д — 56 Сравнение точности определения одной функции различными спо- собами можно сделать по среднему отклонению теоретически~ значе- ний от эмпирических, которое рассчитывается по формуле — '-'1~! ~л~ = Ю и и где М~ь| — средняя арифметическая из абсолютных значений ошибок ф = ly — 'yl — абсолютное значение ошибки, при определении функции по одному или нескольким аргументам. n — число определении. В табл. 124 показан расчет этих показателей точности (средние ошибки): по двум промерам М~ д ~ = 4,5 кг, по обхвату груди М~ д ~ — — 15,9 кг, по косой длине туловища М~л~ — 22,1 кг. Очевидно, определение веса по двум промерам будет значительно точнее, чем при «аждом промере в отдельности. Уравнение функции по двум аргументам можно получить и другим способом: на ос,>ве вычисления средних арифметических, средних ква- дратических отклонений по функции и по каждому аргументу и коэф- 20~~ 200 18<> 180 160 160 160 140 120 11' 180 160 150 120 140 130 120 110 100 90 630 600 540 480 480 450 440 390 330 260 406,0 406,0 365,4 365,4 324,8 324,8 324,8 284,2 243,6 203,0 327,6 291,2 273,0 218,4 254,8 236,6 218,4 200,2 182,0 163,8 631 595 536 482 477 459 441 382 323 265 +1 — 5 — 4 +2 — 3 +9 +1 — 8 — 7 +5 598 590 529 529 46() 460 460 392 323 254 — 32 — 2 — 11 +49 — 20 +10 +20 +2 — 7 — 6 659 579 5чО 420 500 460 420 381 341 3 1 +29 — 21 — 0 — 60 +20 +-1 — 20 — 9 +11 +41
289 СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ 118000 = 114,6; X (х — х)й — 1 (200 — 160)~ -~- . + (100 — 160)~ 96009 = 32,7; Z (; — g)ll — 1 (180 — 130)~+ ... + (90 — 130)~ = 27,9;70009 ~ (у — у) (х — x) + 0,9805; ryx = ~ ~(у — у)' х(х — х)' + 27800g 118000 . 7000 = + 0,9673; Z (х — х) (~ — g) + 7400g 9600 7000 ' = + 0,9027. Параметры. уравненйя регрессии функции по двум аргументам по- лучаются следующим образом. Коэффициент при первом аргументе г „— r» r». а 0,9805 —,9673 0,9027 114,6 1 г~» а» 1 — 0,9027' 32,7 Эта величина называется частным коэффициентом регрессии функ- ции по пер~вому аргументу при исключенном, влиянии второго аргу- мента Я»„., коэффициент при втором аргументе r». — г „r» а 0,9673 — 0,9805 0,9027 114,6 С = о~ 1 — 0,9027~ 27,9 ХЗ Эта величина называется частным коэффициентом регрессии функ ции по второму аргументу при исключенном влиянии первого аргу- мента R»,. фициентов корреляции между функцией и каждым аргументом и между обоими аргументами.,1~ля 10 животных, данные о которых приведены в табл. 124, исходными, величинами будут следующие: у= У = =460, и 10 — Х х 1600 Х: = — = 160, и 10 и 10
РЕГРЕССИЯ Свободный член уравнения а = у — bx — cz = 460 — 2,03 160 — 1,82 . 130 = — 102,2. Найденное уравнение регрессии в точности такое же, как и полу- ченное непосредственно, способом наименьших квадратов: у = — 102,2+ 2,03х+ 1,82z. Подобным образом можно получить уравнения регрессии функции по каждому аргументу в отдельности. Для определения веса по обхва- ту груди коэффициент при аргументе b=r, ~ =+09805 ' =+344. ~х Э Это коэффициент регрессии живого веса по обхвату груди. Он по- казывает, на сколько единиц изменяется функция при изменении аргу- мента на одну единицу. В разбираемом схематизированном примере при увеличении обхвата груди на 1 см относительно средней величины этого промера живой вес увеличивается на 3,44 кг относительно своей средней. Это можно выразить равенством у — у = R„(x — х) . При просмйших преобразованиях этою равенства получается урав- нение регрессии функции по одному аргументу: у=Я~,х — Я х+у, где R=b, у — R,„õ=à. Подставляя в это общее уравнение конкретные данные у = 460 R7, = + 3,44, х = 160, получим: b= + 3,44, a = 460 — 3,44 ° 160= — 90; у., = + 3,44х — 90, т. е. в точности такое же уравнение, какое было получено способом наи-меньших квадратов. Для определения веса по косой длине туловища параметры урав-нения определяются следующим образом: c= r, ~ =+09673 ' =+397, Og 2 р а =- у — cz = 460 — 3,97 130 = — 56, y = +3,97z — 56. Способ нахождения уравнения множественной регрессии при по-мощи частных коэффициентов регрессии применяется при наличии боль-шого количества исходных данных, когда суммирование первичных дат,. ' их квадратов и их произведений становится затруднительным. В таких случаях для определения функции по двум аргументам составляются три корреляционные решетки — для функции и первого аргумента, для функции и второго аргумента и для первого и второго аргументов. По решеткам рассчитываются три необходимые коэффи-циента корреляции, три средних величины и три сигмы. По этим данным определяются два частных коэффициента регрессии и свободный члеч уравнения;
СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ 291 Пусть, например, при нахождении способа прижизненного опреде- ления убойного веса, т. е. веса парной туши после стандартной раздел- ки (1), по двум промерам — обхвату груди (2) и косой длине тулови. ща (3), получены следующие исходные данные по 2500 животным: Признэки hf Убойный вес, у Обхват груди, х Косая длина туловища, z 43 кг 16 см 15 см г12 =+ 0,85 газ =+ О 75 '23 -- — -+ 0,70 131 кг 156 см 143 см По этим данным можно получить уравнение множественной регрес.- сии следующим образом: е 0,85 — 0,75 0,7~ о2 1 — 0,70~ 43 ° — — + 1,71; 16 Г19 Г13 Г23~ — ~12 ° 3—1 — Г232 а, 0,75 — 0,85 0,70 о„. 1 — 0,70' 43 15 С Ru 13 г12 ' 23 ° —— + 0,87; 1 — Г23 2 а = Мi — ЬМ: — СМ3 —— 131 — 1,71 ° 156 — 0,87 143 = — 260,17; xi — — 260,2+ 1,71х., + 0,87х,; у'= — 260,2+ 1,71x+ 0,87г. Если обхват груди равен 160 см, а косая длина туловища 150 с~4, то количество мяса (на костях) от такого животного у'= 1,71 ° 160+0,87 ° 150 — 260= 144,1 кг. Составив по данным, полученным из этой формулы, таблицу, можно в дальнейшем пользоваться ею для определения убойного веса без вы- числений (табл. 125). Верхняя дополнительная строка и левый допол- нительный столбец првведены только для иллюстрации способа по- строения подобных таблиц. Таблица 125Прижизненное определение убойного веса (у) крупного рогатогоскота по обхвату груди (x) и косой длиней туловища (я};у' = 1,71х + 0,87z — 260 266,6 ~ 266,1 ) 273,6 239,4 I 243,0 282,2 290,7 0,87' 155 140 145 150 165 170 183 179 174 170 166 161 170 166 161 157 ]53 148 157 153 149 144 140 135 144 140 126 131 127 123 131 127 123 >18 114 110 118 1]4 ]10 105 101 97 106 101 97 93 88 84 Для того, чтобы, пользуясь такой таблицей, определить искомый вес, надо в верхней заглавной строке найти значение первого аргумен- та — обхвата груди, например 160, в левом заглавном столбце отыскать 152,3 147,9 143,6 139,2 134,9 130,5 126,2 121,8 117,5 113,1 108,8 104,4 175 170 165 160 155 150 145 140 135 130 125 120
292 РЕГРЕССИЯ значение второго аргумента — косой длины туловища, например 155, и на их пересечении прочитать искомый вес — 149. Нахождение прямолинейной функции по двум аргументам можно производить и по номограмме, состоящей из трех вертикальных шкал. Одна шкала (левая) — для первого аргумента, другая (средняя) — для функции и третья (справа) — для,второго аргумента (рис. 58). Прило- жив концы натянутой нитки к значениям обоих аргументов (на край- них шкалах), можно найти значение функции на пересечении эточ нитки со средней шкалой. у=-2бО+/Р/Х+ОбГ g 190 tg5 ~80 r70 65 (бО A/5 150 r5O ЦО <50 5 5 !f0 ~ III юо Q0 90 80 70 25 масш~па6 (б с)h 2,58мм-/см промера Oafam груй,см Убойный bee,az 115 Хосая флияа тулобища,см Рис. N. Номограмма для определения убойно- го веса у по двум аргументам: обхвату груди х и косой длине туловища z. Примеры: I õ-170. ~160, у=170: II х -160, ,z 145, у 140; III <' = 150, < 130, g 110. Рис. 59. Схема построения номо- граммы для определения функции по двум аргументам по уравнению у = — 260+ 1,71х+0,87а. На рисунке 58 показано три примера нахождения искомого веса. Схема построения подобных номограмм дана на рис. 59. Расстоя- ние между шкапами х и у устанавливается пропорциональным с — ко- эффициенту при z, а расстояние между у и z пропорционально b — ко- эффициенту при х. Номограмма на рис. 58 построена по формуле у= — 260+1,71 х+- +0,87 z. Поэтом~ расстояние между у и х равно 50 0,87=43,5 мм, а между у и z оно составляет 50 ° 1,71=85,5 мм. Затем на шкалах на одной прямой наносятся значения средних по аргументу х, по функции у и по аргументу z. На рис. 58 этим точкам соответствуют на шкале х — 156 см, на шкале у — 131 кг и на шкале z — 143 см. И, наконец, устанавливаются масштабы шкал таким образом, что- бы при делении шкалы у, равном единице, деления шкал обоих аргу ментов были равны одинаковой величине, равной сумме коэффициентов при х и при z. На рис. 58 взяты следующие масштабы: на шкале у 1 мм соответ- ствует 1 кг веса, на шкалах х и z 1,71+0,87=2,58 мм соответству- ют 1 см промера.
293 ЧАСТНЫЕ СПОСОБЫ ВЫРАВНИВАНИЯ ЭМПИРИЧЕСКИХ РЯДОВ При пользовании номограмой значительно ускоряется процесс на- хождения функции по двум аргументам. Вместо натянутой нити лучше пользоваться прозрачной линейкой, у которой на нижней плоскости нанесена тонкая прямая черта. ЧАСТНЫЕ СПОСОБЫ ВЫРАВНИВАНИЯЭМПИРИЧЕСКИХ РЯДОВ K частным способам выравнивания относятся такие, которые раз- работаны для выравнивания функций определенного вида — параболи- ческих (полиномы. Чебышева), асимптотических, логистических, пе- риодических, асимметричных, эсообразных. СПОСОБ ЧЕБЫШЕВА(ВЫРАВНИВАНИЕ ПАРАБОЛИЧЕСКИХ ФУНКЦИЙ) Выравнивание параболических функций при наличии равномерно го ряда регрессия может быть значительно упрощено применением способа Чебышева. По этому способу ряд значений аргумента заменяется рядом чисел Чебышева, которые берутся из специальных таблиц, приведенных в при- ложениях (табл. XVI). В этих таблицах ряды. чисел Чебышева даны для ~ арабол первых трех порядков и для градаций аргумента в пределах от r=5 до r=32. Яля параболы первого порядка берется один ряд чисел Чебыше- ва — р~, для параболы второго порядка берется два ряда чисел Чебы- шева — р~ и р~, а для параболы третьего порядка берется три ряда чисел Чебышева — р|, р~, рз. Каждое число Чебышева умножается на соответствующее значение функции у, все произведения данного ряда складываются, и получен- ная сумма делится на сумму квадратов чисел Чебышева (приведенных в табл. XVI): - VPi у 2 ° p] у = и+ рр1+ 7 ра+ орз. l — свободный член полинома, 3 = Г "VPi2 ° ( 1 — УР р 2 где Ar з -УР у 2 — Рз Частный полинам Чебышева для параболы первого порядка вклю- чает первые два члена общего полинома: б V> = «+ рр1 для параболы второго порядка — три первые члена общего полинома: t у-'=-'+ ~р1 . 'р» а для параболы третьего порядка — все четыре члена полинома: I V3 — а + Зр, — ",р., —, ~р~. Из полученных выражений можно составить общий полином' (мно- гочлен) Чебыш ва:
РЕГРЕССИЯ 294 При использовании способа Чебышева значительно облегчается Вычислительная техника по нахождению теоретического ряда функции и имеется возможность постепенно повышать порядок параболы, что дает возможность результаты всех предыдущих ~вычислений полностью использовать для дальнейших расчетов. Применение способа Чебышева можно показать на следующих примерах. Парабола первого порядка: у=а+~а~ Пр имер 147. Накопление клетчатки в кормовых травах в неко- торых случаях идет пропорционально возрасту растений, следователь- но, ряд регрессии этой функции может быть выражен уравнением пара- болы первого порядка. Анализы зеленой массы озимого рапса через каждые 10 дней за период с 25/V по 5/VIII показали следующую динамику содержания клетчатки в этом растении. Дата укоса 25/VI 5/'1г11 25/V I! 5/Ч111 Содержание клетчатки, %% 1,2 2,1 3,7 4,9 15/VI I3,4 Для вскрытия закономерности накопления клетчатки в данном рас- тении и для получения возможности определить содержание клетчатки на любую дату потребовалось ~выравнять имеющийся эмпирический ряд. Все немногочисленные и простые действия, необходимые для этого, показаны в табл. 126. Та блица 126Выравнивание эмпирического ряда регрессии содержания клетчатки в озимом раисе {у}в зависимости от возраста растения (х):у=а+~р~ м/л~ ж/чп 5/Vl! 5/Ч1П r=5 3,7 3,4 4,9 1,2 у, % ~у = 15,3 Числа Чебышева {по табл. ХЧ!) Zp', =10 0 +1 +2 +3,7 — 2,4 — 2,1 +9,8 yPI =+ 9,0 . ур! +9,0 — — + 0,9 10 -~-1,8 — 0,9 +0,9 — 1,8 15,3 а = — = -~- 3 1 5 4,9 3,1 2,2 4,0 1,3 — 0,3 0,0 +0,1 +0,3 — 0,1 g — g у' = 3,1 + 0,9 р, Оказалось. что накопление клетчатки в озимом рапсе идет по за- кону у'=+3,1+0,9 р~. В пределах сезона с 25/VI по 5/VIII получается увеличение содержания клетчатки в среднем на 0,9% за каждые 10 дней. Чтобы использовать это уравнение регрессии для нахождения зна- чения функции при любом значении аргумента, достаточно теоретиче-
СПОСОБ ЧЕБЫШЕВА (ВЫРАВНИВАНИЕ ПАРАБОЛИЧЕСКИХ ФУНКЦИИ) 295 Рис бО. Парабола первого порядка. Содержание клетчатки взеленой массе озимого рапса по срокам укоса. Выравнивание этого ряда по способу Чебышева показано в табл. 127. В формуле, полученной по способу Чебышева, аргументом являет- ся условное число ð!. Во многих случаях это не имеет значения, так как целью выравнивания считается получение теоретического ряда функции. В случаях, подобных разбираемому примеру, даже и не принято выра- жать аргумент — возраст озимой культуры — в обычных единицах (в месяцах или чнях, прошедших от посева). Переход к формуле, в которой аргумент выражен не условным числом р>, а в обычных единицах измерения, при параболе первого по- рядка можно осуществить следующим образом. Для получения в формуле у=а+Ьх коэффициента при аргументе нужно разность любых двух членов теоретического ряда функции раз- делить на разность соответствующих значений аргумента: I I V«69,9 — 32,1 -]- 37,3 ,!О — 3 7 Для определения свободного члена нужно из первого теоретиче- ского значения функции вычесть произведение первого значения аргу- мента на коэффициент при аргументе: а = y> — bx, = 32,1 — а,4 3 = + 15,9. В результате получаем уравнение у= -]-15,9+5,4х, точно такое же, что и способом наименьших квадратов, но гораздо бо. лее простым путем. ский ряд нанести на график и использовать его в качестве номограм- мь!. График-номограмма накопления клетчатки в растениях озимого рапса показан на рис. 60. Пунктиром показано содержание клетчатки на 31 июля — 4,5%. П р и м е р 148. Сокращение вычислительной работы, достигаемое при использовании способа Чебышева, можно показать на примере вы- равнивания эмпирического ряда возрастных изменений длины ракови. ны моллюска (см. пример 143, табл. 118 и рис. 55).
РЕГРЕССИЯ Таблица 127Выравнивание эмпирического ряда регрессии длины раковины моллюска (у)но возрасту (x) способом Чебышева:у' = а+ рр1 г=8 х, годы 10 ~у = 407,6 70,0 32,7 58,6 у (по табл. 118) 64,6 36,4 43,1 48,4 53,8 2 ~ р1 = 168 р, (по табл. XVI) +1 -+490,0 > ypi = + 454,0 + 323,0 — 484 +538 — 228,9 — 182,0 — 129,3 + 175,8 +454 3= — =~-27 168 — 18,9 — 13,5 +13,5 +2,7 — 2,7 +8,1 +1,89 1р и= ' =519407,68 У 48,3 37,5 64,5 32,1 59,1 42,9 53,7 69,9 у' (по способунаименьших квад-ратов) 64.5 69,9 32,1 59,1 37,5 42,9 48,3 53,7 у' = 51 0 + 2,7 р> 69,9 — 32,110 — 3 37,8 у~о уа х,„— х„ = + 5,4 а = у — bx = 32,1 — 5.4 ° 3=+ 15,9y = + 15,9+ 5,4х Парабола второго порядка у'=а+~р1+~р2. Пример 149. При изучении содержания протеина в зеленой мас- се гороха, используемого в качестве пастбищной культуры, брались пробные укосы в стадии бутонизации (10/VI), в стадии цветения (15/VI и 20/VI), в стадии образования бобов (25/VI, 30/VI и 5/VII) и в стадии молочной спелости ( О/VII). Результаты анализа показали, что содер- жание протеина при переходе от стадии бутонизации к стадии цветения уменьшается, а затем в стадии образования бобов начинает увеличи- ваться. Эмпирические данные необходимо было выравнять. Для данного течения эмпирического ряда это можно сделать по уравнению парабо- лы второго порядка, решение которого по способу Чебышева приведено в табл. 128 и показано на рис. 61, который может служить в .качестве номограммы для определения содержания протеина в горохе. Для при- мера на рисунке определено содержание протеина на 3 июля. Приме.р 150. При анализе массовых производственных записен по кормлению молочного скота и по удоям за 300 дней лактации вы- яснилось то оптчмальное содержание кормовых единиц в различных категориях кормов, при котором были получены максимальные удои. Такие данные имеются во 2-й части III тома Племенной книги яро- славского скота. Они приведены в табл. 129, в которой показано вырав- нивание подобных эмпирических рядов по способу Чебышева. Теорети- ческий ряд показан на рис. 62. По этому графику, как по номограмме, можно установить, что в определенных условиях наивысший удой
297- СПОСОБ ЧЕБЫШЕВА (ВЫРАВНИВАНИЕ ПАРАБОЛИЧЕСКИХ ФУНКЦИЙ) Таблица 128Выравнивание эмпирического ряда регрессии содержания протеина в зеленой массегороха {у) по возрасту, измеряемому сроками укоса (х) способом Чебышева:у' = а+ рр~ + тря 15/Ч1 ю/И 20/И 5/VI! 10/И1 25/V I 30/Ч I у <» 3О 2,7 2,3 2,4 4,9 3,3 4,2 ~у ==22,8 P р2 .Р8 +3 +2 pi ~~р2 = 84 1 5 — 9,0 +8,4 +14,7 1 — 2,3 кур, = — 9,7 +3,3 — 6,9 + 24,5 — 9,6 — 9,9 +9,7 = — = + 0,346 28 — 0,692 -+0,692 +1,038 — 0,346 +0,346 + 13,1 у — ' -- -', 0,156 84 0 +0,780 +0,780 — 0,468 — 0,624 — 0,468 22,8 — + 3,257 3,00 3,95 5,08 2,57 2,44 2,63 3,14 0,0 У Y — 0,2 +0,2 — 0,1 +0,1 +0,2 — 0,2 p' == + 3,26 —,' 0,346 p1 + 0,156 р» А=28,24 ц. Он получен при содержании в годовом рационе 38,5% кор--мовых единиц, скормленных в грубых кормах. Уменьшение или увели-чение содержания грубых кормов против этой оптимальной величины. ведет к сниженио удоя. ур +15,0 рр, — 1,038 Рис. б1. Парабола второго порядка. Содержаниепротеина в зеленой массе кормового гороха посрокам укоса.
298 РЕГРЕССИЯ 28,5 33,5 48,5 53,5 38,5 43,5 х, Ж 235 58,5 63,5 г=9 26,2 28,5 28,3 28,3 27 6 27,3 25,9 25,4 23,2 ~у = 240,7 Ц 2 Е Р1 — 60 +2 +3 pi 2 3 р2 = 2772 +28 — 17 — 8 — 20 +7 +28 — 17 — 104,8 — 28,3 — 85,5 — 56,6 0 +27,3 +51,8 +76,2 +92,8 ~ Ур~ — — — 27,1 ур1 урй +733,6 -481,1 — 552,0 — 464,1 — 207,2 +177,8 +649,6 +199,5 -226,4 ~ ур = — 170,3 — 27,1 — = — 0.453 60 +1,812 — 0,453 — 0,906 — 1,359 — 1,812 +1,359 -+-.0,906 +0,453 0 -170,3 7 = — ' = — 0,0514 2772 +1,044 -+1,228 +1,044 +0,491 — 0,430 -1,719 Т ра — 1,712 — 0,430 240,7 a = —.' = 25,744 9 у 28,24 27,97 27,34 26,33 24,96 23,21 26,84 28,14 27,67 y' — y +06 — 0,6 — 0,4 — 0,2 +04 00 — 0,8 -0,1 у' = 26,74 — 0,453 р5 — 0,0614 2уб — у~ — ув у = + 17,89 + 0,554х — 0,0074x* = — 0,0074 2 2 2 2х5 — х2 — х8 2 21(Ув — УД — с х8 — хЦ b = + 0,554 Т = — — = 37,43 2с Ь = а + — T= 28,26 ц. 2 Хб хв 4') а = у~ —.Ьх, — сх2 = +17,89 А Рис. б2. Парабола второго порядка. Изменение лактационных удоев в за-висимости от содержания в годовом рационе коров грубых кормов. Таблица 129Выравнивание вмпирического ряда регрессии удоя ва 300 дней {у} по содержаниюв годовом рационе грубых кормов (х} способом Чебышева:У = а+ Sue + 7Рг
СПОСОБ ЧЕБЫШЕВА (ВЫРАВНИВАНИЕ ПАРАБОЛИЧЕСКИХ ФУНКЦИИ) Переход от формулы с аргументом, выраженным условными чис- лами р~ и ря, к обычным единицам измерения в случае уравнения па- раболы второго порядка y=a+bx+cxя, производится следующим образом. Для получения коэффициента при квадрате аргумента нужно ис- пользовать три равноотстоящих теоретических значения функции, на- пример 2-е, 5-е, З-е, и три соответствующих значения аргумента: с = " '-' ' = ' ' ' = — 0,0074, 2у., — у» — у~ 2 27,97 — 27,67 — 24,96 2 ° 43,5' — 28,5' — 58,5' 5 2 8 Для получения коэффициента при аргументе в первой степени нуж- но использовать два любых, не слишком близких, теоретических значе- ния функции, например 5-е и 8-е, и два соответствующих им значения аргумента: b= ' = ' ' ' ' ' =+0554. (Ув — Уь) с (~8 — x5j 24,96 — 27,97 + 0,0074 (58,s~ — 43,s~) Х8 — Х„. 58,5 — 43,5 Для получения свободного члена можно использовать любое значе- ние функции и соответствующее ему значение аргумента: а = у, — bx — cx> — 27,67 — 0,554 28,5 + 0,0074 28,5' = + 17,89. Таким образом, зависимость удоев от содержания в .годовом ра- ционе коровы кормовых единиц, выраженных в грубых кормах, опреде- .ляется уравнением у'= + 17,89+ 0,554х — 0,0074х', тде х — процент кормовых единиц в грубых кормах. При наличии уравнения регрессии удоя по содержанию грубых кор- мов можно решить ряд практических задач. 1. Определение удоя для любого содержания грубых кормов в го- .довом рационе. Производится путем подставления значения аргумента в общую формулу и решения ее. Если в тех условиях,.в которых лакти- ровали коровы, давалось, например, в годовом рационе 50% кормовых единиц в грубых кормах, то средний удой этих коров уц=17,89+0,554 ° 50 — 0,0074 ° 50'=27,09 ц. 2. Определение оптимального содержания грубых кормов в годо- вом рационе производится следующим образом: b + 0,554 Т= — — = ' =+3443. 2с 2 ( — 0,0074) Найденная величина показывает. что для изученных молочных ко- ров при определенных условиях наилучшее содержание в годовом ра- ционе грубых кормов (выраженных в кормовых единицах) составляет 37,43%. 3. Определение максимального значения функции: А = а+ Т= 17,89+ ' 37,43= 28,26 ц. 2 2 Парабола третьего порядка у=а+ ~р~+ (ря+брз П р и мер 151. язучался урожай зеленой массы культур зеленого конвейера в зависимости от даты стравливания. Брались пробные уко- сы через каждые 5 дней с 5р до 15/ЧП. Для каждого укоса опреде- ,лялся урожай зеленой массы щ центнерах с гектара.
300 ~ Е г P E C C H 5l Для вскрытия закономерностей изменения урожая, для определе- ния возможного урожая на любую дату и для установления времени максимального урожая эмпирический ряд средних урожаев (у) по пя- тидневкам (х) был выравнен. Так как никаких предположений о форме изменений урожая не было, выравнивание эмпирического ряда .прово- дилось по уравнению параболы первого порядка, затем второго и, на- конец, третьего порядка. При использовании способа Чебышева это можно сделать с минимальными затратами времени Для этой цели проще всего произвести все действия, .необходимые для решения урав- нения параболы третьего порядка, тогда для решения уравнений пара- болы первого и второго порядка никаких дополнительных действий не потребуется. Рис. б8. Параболы повышающихся порядков. Урожай зеленой массы культур зеленого конвейера по срокам стравливания. Сопоставление теоретического ряда, рассчитанного по уравнению параболы первого порядка с эмпирическими данными, выявляет значи- тельные расхождения теоретических и фактических значений. Средняя Такое выравнивание показано в табл. 130 и на рис. 63. Если предположить, что увеличение урожая зеленой массы про- порционально числу дней, прошедших от 15/Ч, то следует использовать установленное уравнение параболы первого порядка: y'= 130,52+ 8,29 р ~.
301 СПОСОБ ЧЕБЫШЕВА М;) чР О су) СЧ О OG СЧ 00 М;) М;) О Щ Н 3 Ю Р' З О 00IIСЧ ° °00lICI IIСЧ ° ° О11CI О + 11 м С~С, 1 II С~С, И 00Й>II~4 ч ~»4 О lI И ~4 II ° ь C) 'Ф СЯ 4 t + 'ФII (~) м О С~4 «» 00 фЧ 00 Я ° ь Ю 00 Щ О (:Ь СЧ 00 М;) 'Ф + М;)00° ьLQ Щ О сь СЧ О О О сч~СЧ»ьО О 00 М;) + Щ е~ ° ь »ь 00 00 00 СЬ кГ~ 00 00 00 сь фМ') + СЬ с.'~ М~ 00 О СЧ О О 00»ь00 CO00СЧ1 О СЧ чР ~. <:Ь СЧ 00 + О с~~О'Ф и~ 00° ь00ф) сь° ь00 сь° ь001 СЧ »ь ° ь О ( с~э сч О е со 1 ~Ф'00° ь00 М;) ° ь ° ь СЧ ~О О М;) О О р~1 О + 00 <:Ь ф) 'Ф° ь ! 'Ф ~фФ° ь ° ьЩ вФ 00 М;) 00 + О 00 фм') ~~ ) »ь ° ь ч цр О со мЧ + 00 М:) eaasl (ьь° ь ° ь00 ф 00 Ю СЧ 00 ° ь Ю Ж СЧ с~ О Щ ° СЧ + CO 00 Щ Ь~ I_#_ 0с В Cg З 63 i й О (ф CL Ю ° ° О о 3 с~ 3 о ~-Ю О ,~ ~.-. O ВВ+ < Я э~~ е~ с~. э Яасо.a В cJ а. + О а aS c~ й(:3' ~ai~ а. '-„о =3~ е с) СЧ р ф:) Ф ф) 3 <~ » 1 Я Е с~ Q) gp «» И» ~»~ с~ ес О � б ~р ~~ о о фф~»~»»~ ~) eg ° ~ д к: О 4~ '-" cg а. ~- с~ '~с~ со В й( ф ci ф,~) Й~~ а. о ф,'» =3~ щ Ы Ф CO а е О М 4) Ф' й а Ф И й Щ й X Og й В С0 63 а 3 Ф (ВЫРАВНИВАНИЕ ПАРАБОЛИЧЕСКИХ ФУНКЦИИ)
РЕГРЕССИЯ нз абсолютных отклонений теоретического ряда от эмпирического ве- лика — М~ д ~ = 11,8 ц/га. Если предположить, что урожай увеличивается с постепенно за- медляющейся скоростью, то следует использовать уравнение параболы второго порядка: у" = 130,52+-8,29p > — 0,234рз, в котором первые два члена соответствуют правой части уравнения па- раболы первого порядка. Расхождение теоретического ряда с фактиче- ским в этом случае несколько уменьшается, но все еще остается значи- тельным. Средняя из абсолютных отклонений теоретического ряда от фактического М~ g i —: 8,2 ц/га, теоретическая линия регрессии во многих пунктах далеко проходит от эмпирической. Если, наконец, предположить, что урожай по мере роста трав сна- чала увеличивается с возрастающей, а затем с уменьшающейся ско- ростью, которая в определенный срок становится равной нулю, после чего он начинает уменьшаться, то необходимо использовать уравнение параболы третьего порядка: у"'= 130,52+ 8,29р~ — 0,234рз — 0,465рз, в котором первые три члена соответствуют правой части уравнения па- раболы второго порядка. В этом случае получено наилучшее соответствие теоретических уро- жаев с фактическими: средняя,из абсолютных отклонений теоретическо- го ряда от эмпирического имеет наименьшую величинуМ~~~ — 3,3 ц/га,, теоретическая линия регрессии очень близка к эмпирической (см. рис. 63). Перевод уравнений регрессии с условными аргументами р~, р> и рз, полученных по способу Чебышева, в уравнения с фактическими аргу- ментами для разбираемого примера производится следующим образом. 1. Для параболы первого порядка надо два любых теоретических значения функции, например y» — -205,1 и уз — — 55,9, и соответствую- щие фактическис значения аргумента (число дней, прошедших с 1 V) х» — — 65 и хз — — 20 подставить в формулы Р Р У" — У' 205.1 — 55,9 + 3 316, X) g — Хо 60 — 20 < = уз — Ь«2 = 55,9 — 3,316 ° 20 = — 10,42. Получим у'= — 10,42+ 3.316 х. 2. Для параболы второго порядка надо три любых равноотстоящих теоретических значения функции, например y3 — 72,3, y7 — 147,0 и y» — — 199,3, и соответствующие фактические значения аргумента хз 25,. «7 45 и х»=65 подставить в формулы и И ' И 2У7 — Уз — У» 2 147,0 — 72,3 — 199,3 С= 2X2 — х2 — х2 2 . 452 — 25' — бз' ~7 3 11 It /1 2 2 b= = ' ' ' =+5695,. У» — Уз ~ «» «з ~ 99,3 — 72,3+ 0,028 (65' — 25') Х11 Х3 65 — 25 ~ = уз — М, — схз = 50,1 — 5,695 20+ 0,028 20' = — 52,60, y" = — 52,6 + 5,695х, — 0,028õ~.
СПОСОБ ЧЕБЫШЕВА (ВЫРАВНИВАНИЕ ПАРАБОЛИЧЕСКИХ ФУНКЦИЯ) Таблица 131 Составление теоретических уравнений и системы разностей для примера 151 1. Теоретические уравненчя:у = a+ Ьх+ сл'+ Ch3 62,5 = а+25Ь+ 625c+ 15625d 127,2 = а -+- 40Ь+ 1600с+ 64000d }87,6 = а + 55b + 3025с -}- 166 375 d 193,5 = а+ 70Ь+ 4900c+ 343000d 2. Разности: А" у 4 "Хз 4 Щ А' х' Ь' ха Ь Х Ь' ч 54 СОО — 50,2 74 200 — 4,3 — 54,5 20 250 48 375 102 375 176 625 450 450 64 7х 60,4 5,9 975 1425 1875 .15 15 15 127,2 — 62,5 = 64,7; 187,6 — 127,2 = 60,4; 193,5 — 187,6 = 5,9 Используя полученные разности, можно рассчитать параметры уравнения y = a+bx+ cx2+dx' по следующим формулам: d = = ' = — 0,00248, д» „з 20250 Ь" у — d Д" хз — 4,З + 0,00248 54000 с= Ь" х' 450 Ь „— C Ь' h' — d Ь' ХЗ 64,7 — 0,288 975 + 0,00248 . 4837515— ю- а =у — bx — cx' — dx'=-62,5+ 6,405 ° 25 — 0,2879 625+ 0,00248 XX 15625=+81,43. Проверка: а = 193,5+ 6,405 70 — 0,2879 ° 4900+ 0,00248 343000 = + 81,44. Таким образом, уравнение регрессии с фактическими аргументами'. для разбираемого примера будет иметь следующий вид: у"' = -+- 81,43 — 6,405х+ 0,288х' — 0,00248хз, 3. Яля параболы третьего порядка надо из четырех теоретических равноотстоящих значений функции, например y:- = 62,5, у6 — 127,2, y9 — 187,6 и уд — 193,5, и соответствующих значений фактического аргу- мента x> —— 25, х6=40, x>=55. х12=70 составить систему теоретических уравнений H таблицу первых, вторых и третьих разностей. Система теоретических уравнений для параболы третьего порядка должна включать четыре уравнения с четырьмя выбранными теоретиче- скими значениями функции и с соответствующими значениями аргумен- та в первой, второй и третьей степени. Первые разности функции и ар- гументов составляются путем вычитания из каждого последующего зна- чения предыдущего. Вторые разности составляются путем такого же вычитания первых разностей, третьи разности составляются по вторым. Составление теоретических уравнений и системы разностей показа- но в табл. 131.
304 РЕ ГРЕССИ Я где;х — число дней, прошедших от 1/V, д"' — урожай (ц/га) зеленой массы кормовых культур зеленого .конвейера. Это уравнение можно использовать для решекия некоторых прак--тических задач. 1. Определение возможного урожая на любую дату. Для этого в 'формулу подставляется значение х, равное числу дней, прошедших до .этой даты от! мая: у„= 81,43 — 6,405 27+-0,2879 ° 729 — 0,00248 19 683=69,5 ц/аа. При нахождении теоретических значений функции для таких зна-чений аргумента, для которых не была измерена функция. необходимо помнить, что уравнения регрессии могут быть использованы главным образом для интерполяции. Экстраполяция по этим уравнениям может быть допущена только для ближайших одного-двух интервалов в ту и другую сторону. 2. Определение значений аргумента, соответствующих максималь-ному или минимальному значениям функции. Для уравнения параболы третьего порядка это можно сделать следующим образом: а) найти первую производную функции и приравнять ее нулю: f (x) = + 81,43 — 6,405х+ 0,2879x' — 0,00248х', f'(х) = — 6,405+ 0,578х — 0,00744х2 = 0; ,б) решить полученное квадратное уравнение: — 0,576 + ~ 0,33154564 — 0,19061280 ==+ 14, — 0,3754 х,= — 0,576 — ~ 0,33154564 — 0,19061280 =+ 64. — 0,3754 В разбираемом примере максимальный урожай зеленой массы был получен на 64-й день после 1 мая, т. е. 4-го июля, а минимальный полу- чился бы на 14-й день, т. е. 14 мая. Такая экстраполяция в данном слу- чае вполне допустима. 3. Определсние максимального значения функции. Для этого нуж- но найденное значение аргумента подставить в общую формулу. Для разбираемого примера > „. = — 81,43 — 6,405 64, 0,288 64' — 0,00248 64' = — 200,6 ц/га. АСИМПТОТИЧЕСКИЕ ФУНКЦИИ Асимптотическими называются функции, стремящиеся к определен- ному пределу, которого они достигают теоретически при бесконечно больтном значении аргумента. Этот предел называется асимптотой функции. Асимптотическое течение функции .наблюдается при возрастных из- менениях веса и размеров тела у многих животных и растений, а так- же при изменениях веса животных 1вследствие непродолжительного го- лодакия. \ АСИМПТОТИЧЕСКИИ РОСТ В качестве биологической основы асимптотического роста можно положить часто наблюдаемое явление: скорость роста пропорциональ-. -на разности между значением функции в данном возрасте и ее асимп-
АСИМПТОТИЧЕСКИИ РОСТ 305 тотои. Такая закономерность у животных наблюдается после рождения: сначала вес животного и размеры его тела растут с большой скоростью, а по мере того, как уменьшается та часть, которую остается дорасти, уменьшается и скорость роста. Это может быть описано дифференциальным уравнением которое выражает наблюдаемую закономерность следующим образом: скорость течения возрастных изменений признака в каждый момент пропорциональна разности между максимальным и текущим значения- ми этого признака. Как указывалось, эта закономерность может быть распространена только на постэмбриональный период (у крупного рогатого скога- начиная с 2 — 3 месяцев жизни), так как в эмбриональном периоде жи- вотные растут с увеличивающейся скоростью. При использовании приведенното дифференциального уравнения для выравнивания возрастных рядов надо иметь в виду, что значение признака при рсждении (yp) .не выравнивается по следующим сообра- жениям. Колебания признака при рождении отчасти уже выравнены тем, что берется средняя величина его; усреднение же различий напряжения внешних факторов, создающих разнообразие признака от возраста к возрасту, тут не имеет смысла. Эти внешние условия не могли сказать- ся на величине признака при рождении. Величина признака при рожде- нии есть сумма прироста за эмбриональный период, а действие внеш- них агентов в этом периоде через организм матери хотя и имеет место, но выражено в значительно более слабой степени, чем в постэмбрио- нальном периоде. Интегрируя дифференциальное уравнение роста, получим: = Й(А — y), = jkdx,— 1n(A — у) =Йх+с. Так как при х=О y=yp, то за константу интегрирования можно взять величину с= — In (А — уо) = — InD, логарифм разности между асимптотой (А) и величиной признака при рождении (уо), т. е. логарифм суммы постэмбрионального прироста. Тогда вывод формулы асимптотического роста легко сделать сле- дуюшим образом: — 1n(A — у) =Йх+ с,— In(A — у) =Йх — InD,1п0 — In(A —. у) =Йх,1n = — /г;А — уD
РЕГРЕССИЯ При переходе к десятичным логарифмам имеем: у А Q IQ /ск где А — максимальное значение, к которому стремится возрастной ряд (а симптота), 0 — сумма прироста от рождения до остановки роста, А: — константа роста, определяющая темп возрастных изменений, л — возраст. Эту общую формулу роста можно вывести и не прибегая к интегри- рованию, если основную закономерность выразить равенством = — const, А — у, где g) и gg — последовательные значения признака, взятые через равные промежутки времени. Ряд величин d=A — у, взятых через равные возрастные интервалы, составляет геометрическую прогрессию, и, следовательно, ряд логариф- мов этих величин (Igd) есть убывающая арифметическая прогрессия с разностью k, соответствующей константе роста. В арифметической прогрессии всякий член равен первому плюс (ми- нус) разность прогрессии, умноженная на число членов между первым и данным. Если первый член прогрессии Ig(A — уц) =IgD, то какой-нибудь по- следующий член, относящийся к возрасту х, будет равен Igd = I gD — kx. Из этого равенства легко вывести формулу асимптотического роста: Igd — 1gD = — kx, Ш D — IP-kx 0 d D. Irk' А — y=D 10 ~", — А Q . IP-kx Здесь А — максимальное значение признака, к которому стремится весь ряд, D=A — уо — сумма прироста за постэмбриональный период, Ь1д А — у константа роста, т. е. приращение логарифма раз- ности между максимальным и текущим значениями признака в единицу времени, х — возраст, выраженный в любых интервалах. Использование этого уравнения регрессии при выравнивании асимп- тотичвских возрастных рядов можно показать на следующих примерах. П р и ме р 152. При изучении возрастных изменений живого веса истобенских быков были установлены средние веса при рождении, в воз- расте 1 года, 2 лет и т. д. (до 11-летнего возраста). Полученный эмпири- ческий возрастной ряд живого веса у приведен в табл. 132. Выравнива- ние таких рядов производится следующими этапами. 1. Нахождение максимального значения А. Это можно сделать гра- фически или аналитически. При графическом способе первоначально на- ходится ряд значений Ig(A — у), причем за величину А условно прини-
307 АСИМПТОТИЧЕСКИЯ РОСТ Та бли ца 132Выравнивание эмпирического ряда живого веса {у) по возрасту (х).Асимптотическая функция у = А — D 10 Эмпири1еские зна1сння Теоретические значения у =37 А =600 D= А — У0= 562 ig D — 1gd lг'= lgd' = 1gD- kx Х dI d=A — у У 1gd Ig D — 1g d 562 324 186 107 62 Я 20 12 6,8 3,9 2,2 1,3 38 276 414 493 538 565 580 588 593,2 596,1 597,8 598,7 38 236 400 521 500 575 575 585 595 598 602 599 2,750 2,510 2,270 2,030 1,790 1,550 1,310 1,070 0,830 0,590 0,350 0,110 0 1 4') 3 4 5 6 7 8 9 10 11 0,000 0,189 0,449 0,852 0,750 1,352 1,352 1,636 2,051 2,449 2,750 2,750 2,561 2,301 1,898 2,000 '.,398 1,398 1,~14 0,699 0,301 0,000 562 364 200 79 100 25 25 13 5 2 1 0,189 0,225 0,284 0,187 0,270 0,226 0,232 0,256 0,282 0,250 Е й' = 2,401 у' = 600 — 562 10 Ей' ih = — = 2,401: 10 = 0,240 r 2 V2 У1 УЗ 2ур — (уt + уз) где у~, уя, уз — эмпирические значения функции, взятые через равные интервалы. Для получения более надежных р~езультатов надо по указанной фор-. муле определить А для всех соседних трех значений функции и взять среднюю величину. мается несколько (не менее трех) значений асимптоты, выбранных на основе рассмотрения эмпирического ряда и эмпирической линии регрес- сии. При рассмотрении ряда регрессии живого веса по возрасту (см. табл. 132) выясняется, что асимптота должна быть близка к 600 кг. По- этому составляется три ряда значений Ig(A — у): с А=600, затем с A=610 и A=590. Составление этих трех рядов показано в нижней~ час- ти рис. 64. Эти ряды, нанесенные на график, показывают разные сред-: ние течения. Первый ряд, соответствующий А =610, явно загибается кверху. Третий ряд, соответствующийА=590, загибается вниз. Средний ряд, соответствующий А =600, дает такое среднее течение,,которое очень близко к прямой линии, что легко установить при помощи натянутой нитки или прозрачной линейки с нанесенной прямой чертой. Это обстоятельство — прямолинейность среднего течения ряда Ig(A — у) — и есть указание на то, что асимптотой данного ряда дол- жна быть соответствующая величина А, т. е. 600. Если среднее течение ряда Ig (А — у) не идет по прямой, то значит величина А выбрана большей или.меньшей, чем нужно. В первом случае среднее течение кривой загибается кверху, во втором — вниз. Аналитически максимальное значение признака А можно опреде- лить по формуле
PEI ÐÅÑÑÈß 308 Определение суммы постэмбрионального прироста. Для этого нуж- но из асимптотического значения вычесть значение признака при рож- дении: D=> — уо. Рис. 64. Нахождение асимптоты А асимптотической функции роста живого веса истобенских быков графическим способом. 3. Определение показателя темпа роста k. Для каждого возраста составляется ряд величин D=A — у, затем ряд логарифмов этих вели- чин (1gD) и ряд разностей (1gD — 1gd). При делении этих разностей на соответствующие возрасты получаются частные значения показателя темпа р'оста: lg0 — lgd Общий (для данного ряда) показатель темпа роста получается пу- тем усреднения частных значений k': Xk" Все эти действия показаны в табл. 132. 4. Нахождение теоретического ряда функции. Производится на ос- нове найденных значений уо, А и Й в следующем порядке. Определяет- ся 1gd'=IgD — Йх, затем находится d' (по 1gd') и, наконец, у'=А — d'.
309 АСИМПТОТИЧЕСКИЯ РОСТ ,Яля разбираемого примера А=600, p=38, D=A — gp — — 600 — 38= =562, 1gD=2,750, Й=0,240. Определение величин d' и у' для каждого возраста показано в табл. 132. Сопоставление теоретического и эмпири- ческого рядов регрессии живого веса истобенских быков по возрасту по- казано на рис. 65. Рис. оо. Асимптотическая функция. Возрастные измененияживого веса истобенских быков. где D — сумма прироста в постэмбриональном периоде, А — асимптота функции, Й =- " константа роста. Slg А — у> 5,х Яля разбираемого примера А=600, D=562, Й=0,240 2 750 — 2,778+ 2 1,972 = 8,2 го ~й 0,240 0,240 Кроме биологической скоропелости признака, можно определить и его условную, или хозяйственную, скороспелость, измеряемую возрастом достижения функции определенной величины, например 500 кг веса для животных определенной категории. Пользуясь этим графиком .как номограммой, можно определить значение функции для любого значения аргумента. Например, в воз- расте 2,5 лет наиболее вероятный вес истобенских быков в сходных ус- ловиях будет равен 450 кг. При помощи выравненного возрастного ряда асимптотической функ- ции можно решить следующие задачи, имеющие практическое значение. Можно определить биологическую скороспелость признака, если ус- ловиться, что среднее значение биологической скороспелости для опре- деленной группы объектов и в определенных условиях соответствует возрасту практической остановки роста при достижении признаком 99% своего максимального значения. Такой показатель биологической скоро- спелости признака определяется по формуле T=- 1g9 — 1g A+ 2 й
310 РЕГРЕССИЯ Показатель условной, или хозяйственной, скороспелости определяет- ся по формуле 1g D — 1g (А — у„,) т- й (y — заданная величина живого веса). Если за показатель условной, или хозяйственной, скороспелости при- нять возраст, при котором быки достигают веса в 500 кг, то для разби- раемого примера 1g 562 — Ig (600 — 500) 2,750 — 2,000 0,24О 0,240 = 3,1 года. П р и м е р 153. Изложенный выше способ выравнивания возраст- ных асимптотических рядов применим в тех случаях, когда имеются дан- ные о значении признака при рождении. При отсутствии таких сведений можно пользоваться формулой А d 10 — к(л — л') где d) =4 — у) — сумма прироста от первого значения возрастного ряда до асимптоты, х) — возраст, с которого начинается данный ряд. Эта формула отличается от основной тем, что вместо величины D=A — gp берется величина d) —— А — у) и вместо аргумента х берется разность между текущим и первым значением возраста: х — х). Кроме того, в этом случае и первое имеющееся значение функции выравнивается так же, как все остальные эмпирические значения, так как оно не имеет всех тех особенностей, которые свойственны признаку при рождении. Если эту формулу после небольшого преобразования прологариф- мировать, то получим: = А — d 10'" 10к (х — х,) n1gd)+kZ(x — x)) =Е Igd,Х (x — х))1д d)+ЙХ (х — х)) 2=2 (х — х)) 1g d. Выравнивание по формуле у = А — d, 10 "" ') показано в табл. 133 на примере расчета теоретических значений живого веса сычевских помесей; графическое преобразование этого ряда дано на рис. 45. Определение асимптоты проведено указанным выше графическим способом. Оказалось, что А =470. В таблице для каждого возраста указаны величины, необходимые для составления нормальных уравнений: х, у, d=A — у, 1gd, (х — х)), (х — х))2, (х — х))1~d. Решение системы, нормальных уравнений путем постепенного ис- ключения неизвестных дало следующие результаты: 1g di =1,856, di — — 72, k= — 0,1312. 1gd =1gd>+ Й (х — х) ), т. е. уравнение параболы первого порядка, которое легко решается спо- собом наименыпих квадратов; два неизвестных 1gd> и k находятся по двум нормальным уравнениям:
311 АСИМПТОТИЧЕСКИЙ РОСТ Таким образом, уравнение регрессии запишется в виде 470 72 . 10 0 1312 (х 21 ИЛИ Ig d( = 1,856 — 0,312 (х — 2) . Подставляя значения х и решая каждый раз второе уравнение, можно получить ряд теоретических значений 1я Ш'=1я (А — у)', а затем и теоретический ряд величин d'=А — у'. Вычитанием d' из А находится теоретический ряд регрессии живого ве са по возрасту. Таблица 133 Выравнивание возрастного ряда живого веса сычевских помесей при отсутствииданных о живом весе при рождении:у =А — Ш,10 Решение уравнения1gd-1gd, ++ й(x — x,) Нахождение теоретических значенийживого веса Эмпирические данные(А — 470 кг) х м~ b0 'с х о Ж 1@d' - d' = 1,856 — а = (А — у') Ч I й~ =0,1312 Х Х (x — x,) У 398 1,881 0 394 76 1,748 3,182 4,704 5,112 5,000 5,418 8,428 11,173 28 140 33,592 8 1g dq + 28k = 11,173 28 1g d + 1401 = 33,592 lg dq — — 1,856 й = — 0,1312 и lg d, + Й Х (х — х,) = Е ig d~ (x — x1,) lg di + k Z (х — х,)' = Z (х — х,) lg d= 470 72 10 о,1з12 („,- 2) Показатели биологической и условной скороспелости при отсутствии сведений о живом весе при рождении можно определить по следующим формулам: 1g Ш,— 1gА+2й t=x, +йследующие (см. табл. 133):1,856 — 2,672 -+- 20,13121,856 — 1,000лет.0,1312 Т=х,+ Для сычевских помесей эти показателиlg 72 — lg.470 + 20,13121g 72 — lg (470 — 460)~во = 2+0,1312 =11,0 лет, 3 4 5 6 7 8 9 10 414 431 433 451 460 462 454 477 56 39 37 19 10 8 16 1,748 1,591 1,568 1,278 1,000 0,903 1,204 1 2 3 4 5 б 7 1 4 9 16 25 36 49 — 0,1312 — 0,2624 — 0,3936 — 0,5248 — 0,6560 — 0,7872 — 0,9184 — 1,0496 1,856 (1gdj) 1,725 1,594 1,462 1,331 1,200 1,069 0,938 0,806 72 ("') 53 39 29 31 16 12 9 6 417 431 441 449 454 458 461 464
РЕГРЕССИЯ АСИМПТОТИЧЕСКИЕ ПОТЕРИ ВЕСА П р и м е р 154. При автоперевозках сельскохозяйственных живот- ных без кормления и поения в пути происходят потери веса этих живот- ных. Как показали опытные перевозки длительностью до 15 часов, эти потери происходят с определенной закономерностью. В начале пути по- тери быстро возрастают, затем при увеличении продолжительности перевозок нарастание потерь замедляется, и спустя некоторое время по- тери веса практически не увеличиваются при дальнейшем увеличении расстояния и времени перевозок. Наблюдается то же, что и при асимптотическом росте: скорость изменения функции пропорциональна разности между ее данным зна- чением и некоторой асимптотой. Наличие асимптоты потерь веса скота при автоперевозках объяс- няется тем, что при этом теряется главным образом содержимое желу- дочно кишечного тракта, после чего увеличение потерь веса прекращает- ся, так как до практически заметного распада тканей тела при макси- мальной длительности перевозок, равной 15 часам, дело не доходит. Поэтому в основу закономерности нарастания потерь веса скота при автоперевозках можно также положить дифференциальное урав- нение — = k (А — у). Шя дх Первые этапы интегрирования этого уравнения в данном случае осуществляются так же, как в случае асимптотического роста: = k(A — у), х — 1Il —: х С. А — у Константа интегрирования устанавливается иначе. Так как в начальный момент перевозок потерь еще не бывает. то при х=О у=О и константа интегрирования с= — Iп А. Дальнейший вывод уравнения регрессии идет так: Iп А — In(A — у) =kx, 1n = — Йх, А — у А =Ае" э у = А(1 — е «")., у =А (1 — 10 «"). Для нахождения параметров этого уравнения необходимо: 1. Прологарифмировать это уравнение: у = А — А1О-»', 1g(A — y) =1gA — kx. 2. Привести полученное равенство к виду, удобному для дальней- ших расчетов: 1д А — 1д (А — у)
АСИМПТОТИЧЕСКИЕ ПОТЕРИ BECA 3. Определить величину А графически или аналитически, как опи- сано выше. 4. Для каждого значения аргумента определить величину Й. 5. Найденные величины А и k подставить в уравнение регрессии. Для построения теоретического ряда регрессии необходимо найден- ную формулу подставить в логарифмированном виде— 1g(A — у) =1g А — Йх и, подставляя последовательные значения аргумента, HBHTH cH3~13JI3 теоретические значения 1~(А — у), по ним определить величины d=A — у' Н, наконец, вычитая d' из А, получить теоретические значения функции. Рис. 66. Асимптотическая функция. Потери веса крупногорогатого скота при автоперевозках. Лля выравнивания таких рядов .не требуется, чтобы эмпирические значения имелись через равные интервалы аргумента. При анализе зависимости потерь веса крупного рогатого скота (у, %) от расстояний при автоперевозках (х, км) получено уравнение ег ессии р р = 4.,2 (1 — 10 ' ). Теоретический ряд, составленный по этому уравнению, показан на рис. 66. На основе этого ряда можно установить допустимые нормы по- терь веса при автоперевозках на различные расстояния, а также раз- работать систему дифференцированных скидок с живого веса на со- держимое желудочно-кишечного тракта.
'314 РЕГРЕССИЯ ЛОГИСТИЧЕСКИЕ ФУНКЦИИ Насыщение замкнутого объема живыми существами (растущими дрожжами, бактериями, водорослями) или проникающим веществом, рост популяции в новой для нее местности — все подобные явления про- Л текают в соответствии с особой У а-8х +С закономерностью, изображен- ной на рис. 67. лрямая Первоначально насыщение объема идет с возрастающей скоростью, затем, в связи с уменьшением свободного про- А странства и с возникновением тормозящих факторов, ско- Д +~ рость замедляется до постоян- ной, после чего наступает пе- риод затухания скорости рос- С та, и, наконец, когда дальней- Д шее увеличение насыщающей в массы в данном объеме стано- вится невозможным, рост оста- Рис. б7. Схемы логистических функций. навливается — наступает пери- од равновесия. Функции, изменяющиеся подобным образом в прямом или обрат- ном направлении, называются лоаистическиии, течение их следует зако- номерности, выраженной уравнением Ферхюльста: А +с, 1+ 1О~+ где у — вес или объем насыщающей массы, х — время, прошедшее с начала роста, А — расстояние между верхней (А+с) и нижней (с) асимптотами, с — нижняя асимптота, предел, с которого начинается рост функ- ции, или при обратном течении функции — минимальный уро- вень равновесия, а, Ь — параметры, определяющие наклон, изгиб и точку перегиба ло- гистической линии регрессии. Для решения логистического уравнения первоначально надо опре-делить верхнюю и нижнюю асимптоты. Это с достаточной точностью можно сделать по эмпирическому ряду путем простого его просмотра. Значение верхней асимптоты можно проверить аналитически по фор-муле 2У~ Ув Уз — У~ (У1 + Уз)2 э2У1 У3 У2 где у1 у2, у~ — три эмпирических значения функции, взятые через рав- ные интервалы аргумента. После нахождения величины А и с надо прологарифмировать логн- стическое уравнение: — 1 =а — ох, 1g у — с 1gz = а+ Ьх.
5 !О бО 200 450 700 850 ббО Ш О 1 2 3 4 5 б 7 б ы tv Э 1 ° ° ° 1 ° Э ° в 1 в Э ф ° Э j а ° 1 ° ° ° ° r j ° ° ° s ° ° ° i j ~ а ° I r ° ° 1 а ) ] ° ° а ° ° ° а ° ° Э r ° а а ° 1 а / ) ! ° ° а r ! ° 3 а ° ° ° а ° ° а ° 1'j ° 1 j ° ° а а ° Э а!а ° ° ° ° 1 ° ° ' ° Э ° в ° j ° ° в ° ° ° ' а ° а а ° ° ° ° ° ° ° в а ° ° ° j ! ° ° в ° ° ° ° в ° 3 а 1 ° ° ° ° ° 1 ° 1 ° 1 а в а а $ а ° в ° ~ ° ° ° ° ° вв а ° ° а ° вФ а ° ° в в а ! а j а ° ° ° 1 ° 1 а ° 1 а ° 1 ° ° ° а Ю а ° Э ° ° ° ИИИИИ 6ggg6g ° ИИИИИ 66666И ИИИИИИ ,гд66666 'ИИИИИИ ° ИИИИИ ° 66666 ° 66666 ° ° ю а °У ° Ф Ф Ф Ф Ф ' ° ° ° ° ф ю ° ° 9 ° ° в ° 3 ° 1 ° ° ° ° ° 3 ° ° 3 ° ° 1 ° в а а ° ° ° ° ° ° 1'3 ° а ° а ° а в а ° ° в ° l в I s ) 9 ° ° в ° ° j ° ° ° ° ' ° ° ° 1 а ° ° ° ° 1 ° В ° .. ° ° ° ° ° 1 ° ° ° в ° ° ° ° ° j ° ° ° ° а а Эа ° ° а j ° в ° в ° ° ° ° ° ф ' ° ° ° ° ! ° ° 1 ЛОГИСТИЧЕСКИЕ ФУНКЦИИ 315
316 00 сь 00 » ° 00 О О СЧ СЧ О О СС) СЧ О [ СЧ О м~ ~У')ОЮМ;) И М М ФЭ :г И & Ю С4 о ФЭ н С~ СЧ О О 00 О О О СЧ СЧ О О О Щ СЬ О Ю О ~Ч~ СС) О СЧО1' Ъ~ + 11 . СЧ ~Ч~ сь 00 ~М~) О 00 [ сь СЧ ИР О~ ~Ч~ ~Ф' Ю СЧ 00 С4 сО О О 00 О М;) СС) См') ~Ф' О СЧ Щ СЧ М;) О CD Ю О ° й( М о И ~а 1~ ь„+~1», ~ О СЧ СЧ О 00 СЧ CD О О СЧ О~ О CD Ю О 00 CD О ° ь СЧ Ф 00 СЧ 1' СО ( Сьь ( СЧ СЧ CD СЬ 'Ф О ° ь Ю ~4 00 СЧ CD О О О =РО° ьЩ О СС) СЬ М:) СС) О CD ° ь 00 00 сь СО О М:)О1 М + 0 О 1° ~'6I О C) 00 СЬ Я О О О О СЧ О СЧ II 11 11 ~Ощ 'Ф 00 4' 00СЧ с~'ФЮ ° ьО СЧ О О О C) О О ° ь СЬ 00 О СР О О 1<:) С4 О СР О См') СЧ О О О О Cl М М ФЭ % С4 X И Ы Ж (е О О О О СЧ сО00СЧЮ Щ СЧ О (Ь Щ О О «1», т сэ ФЯ, %е 'C О О О 00 00 C) О аО 00 00 М Я сэ О О 3й~[ О Ф й3 й3 63 О З й( О Я 63 й( Ф О О О hC Ф1 т Й О й3 И й Щ й' й3 63 й3 Ж 63 С4 З Ж О t~ СО CD СЧ РЕГРЕССИЯ О 00 <Q Я;) 00 С5 CD t~ Ю ОЪ ~ CD 1' ( CD 00 о> co ~ 1 00 О ~О 'Ф' t CD ~а О Ф 00 О СЧ 'Ф Ch СО CD СЧ ( СЧ СЧ 00 00 Се О~ ~О 'Ф' 00 СЧ Ю ° ь ° ь сО еО СЧ сь со ~о 'Ф' Щ сО О> СЧ СЧ О + 8 о о О О О ~О ° О О 'СЬ 00 о о а дъ с~ь ~ 1 ььъ00СЧ Ъ~ 'Ф СЧ ~Ф' М~ О о 1 Il +
317 ЛОГИСТИЧЕСКИЕ ФУНКЦИИ Если потребуется определить момент перехода возрастающей скоро- сти в убывающую, то это можно сделать, определив координаты точки перегиба логистической кривой: х= = ' = 5,12 суток, ! а ( 2,7748 ( Ь ~ 0,5424 900 = 450 яг. 2 А 2 Рис. 69. Логистическая обратная функция. Изменение числа глазных фасеток у плодовой мушки в стадии имаго в зависимости от продолжи- тольности выдержки насекомых при высокой температуре. Если отдельные результаты сопоставления числа фасеток с выдерж- кой мушек при температуре 27'С нанести на точечный график, то ста- нет заметен логистический обратный характер течения функции с верх- ней асимптотой А+с=130 и нижней с=55 фасеток (A=130 — 55=75). В целях более точного описания найденной закономерности эмпи- рические данные были выравнены в соответствии с логистическим урав- нением регрессии, что показано в табл. 135 и на рис. 69. Аргумент имеет значения через неодинаковые интервалы, что не препятствует решению .логистическопо уравнения. Обе асимптоты были найдены по точечному графику. Это значит, что переход возрастающей скорости в убывающую на- ступает спустя 5,12 суток с начала размножения водоросли. В этот мо- мент в каждом кубическом сантиметре среды будет накоплено 450 мг ° органической массы. Пример 156. Гаузе и Алпатов изучали действие высокой темпе- ратуры на организм плодовой мушки. Насекомые выдерживались х ча- сов при температуре 27'С, а затем переносились в термастат с темпера- турой 17'Ñ. В зависимости от длительности выдержки при высокой температуре (х=48 —.100 часов) у насекомых в стадии имаго имелось раз- личное число глазных фасеток (у=126 —.' 56), при этом чем дольше вы- держивались мушки при высокой температуре, тем меньше было глаз- ных фасеток.
318 РЕГРЕССИЯ Таблица 135 Выравнивание ампирических данных зависимости числа глазных фасеток (у) у плодовой мушки в стадии имаго от продолжительности выдержки насекомых при высокой температуре (х). А Логистическое уравнение у = + с — 10 или А 1g — 1 =а+ Ьх у — С Эмпирические данные (А = 75, с = 55) Нахождение теоретических значений х be -~~ 'и И~ х l II Ф Ф II ° °I 27а + 1890b = + 5,9171890a + 136 548b= + 714,500 и = 27~х = 1890 Ех~ = 136548 >z =+5,917 Exz = -+- 714,5 Ь = + 0,0707 а = — 4,73 75 А = 75 У = с=55 + 55 1+ 10 — 4,73 + 0,0707х 1890 136 548 + 5,917 -+-714,5 В основу решения положено общее логистическое уравнение в ло- гарифмической форме: ( у — с 1) = а+ Ьх. Это уравнение параболы первого порядка легко решается способом наименьших квадратов. В табл. 135 указаны все этапы выравнивания данного логистического ряда. Если потребуется определить «точку перегиба», т. е. момент пере- хода возрастающей скорости в убь'вающую, то это можно сделать по следующим формулам:, 4,85 х=- [а[ IbI = 67,0 часов, 0,0724 у = — + с = — + 55 = 92,5 фасеток. А 75 2 2 100 (97) 90 89 88 84 80 80 76 74 72 72 70 70 68 67 66 66 64 64 62 60 59 59 58 54 50 ', 48) 48 10000 '(9409) 8100 7921 7744 7056 6400 6400 5776 5476 5184 5184 4900 4900 4624 4489 4356 4356 4096 4096 3844 3600 3481 3481 3364 2916 2500 (2304) (2304) 56 (54) 58 58 59 60 59 57 71 76 66 79 . 77 82 76 101 108 91 98 113 118 120 118 122 125 127 (130) 126 1 3 3 4 5 4 5 2 16 21 11 24 22 27 21 46 53 36 43 58 63 65 63 67 70 72 (75) 71 75,0 25,0 25,0 18,8 15,0 18,7 15,0 37,5 4,69 3,57 6,82 3,13 3,41 2,78 3,57 1,63 1,42 2,08 1,74 1,29 1,19 1,15 1,19 1,12 1,07 1,04 (1,00) 1,06 74,0 24,0 24,0 17,8 14,0 17,7 14,0 36,5 3,69 2,57 5,82 2,13 2,41 1,78 2,57 0,63 0,42 1,08 0,74 0,29 0,19 0,15 0,19 0,12 0,07 0,04 (0,00) 0,06 +1,869 +1.380 +1,380 +1,250 +1,146 +1,248 +1,146 +1,562 +0,567 + 0,410 +0,765 -+0,328 -+-0,382 -+-0,250 +0,410 — 0,201 — 0,377 +0.033 — 0,131 — 0,538 — 0,721 — 0,824 — 0,721 — 0,921 -1,155 -1,398 — 1,222 + 186,9 + 124,2 +122,8 +110,0 + 96,3 + 99,8 + 91,7 +118,7 + 42,0 -+- 29,5 + 55,1 + 23,0 + 26.7 -+- 17,0 + 27,5 — 13,3 — 24,9 + 2,1 — 8.4 — 33,4 — 43,3 — 48,6 — 42,5 — 53,4 — 62,4 — 69,9 — 58,7 11~ 105 100 95 90 85 80 75 70 65 60 55 50 45 40 35 30 +3,037 +2,394 + 2,340 +1,987 + 1,633 + 1,280 +0,926 +0,573 + 0,219 1,865 1,512 1,159 2,805 z,452 2,098 3,745 3,391 1114,0494,3218,897,142,919,08,433,741,660,730,320,140,060,030,0130,0060,0025 1115,0495,3219,8Я8,143,820,09,434,742,661,731,32. 1,141,061,031,0131,0061,0025 0,1 0,2 0,3 0,8 1,7 3,8 8,0 15,8 28,2 43,2 56,7 65,7 7О,7 72,9 74,0 74,6 74,8 55,1 55,2 55,3 55,8 56,7 58,8 63,0 70,8 83,2 98,1 111,7 120,7 125,7 127,9 129,0 129,6 129,8
319 ПЕРИОДИЧЕСКИЕ ФУНКЦИИ Это значит, что уменьшение числа фасеток с увеличивающейся ско- pocTbä (по мере увеличения х) идет вплоть до 67-часовой выдержки мушек при высокой температуре. При дальнейшем увеличении выдерж- ки скорость уменьшения числа фасеток затухает и стремится к нулю. Число фасеток в «точие перегиба», т. е. при х=67 часам, рав- но 92,5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ Некоторые биологические явления протекают таким образом, что регулярно, через определенные промежутки времени, нарастание явле- ния сменяется затуханием. 1~ таким явлениям относятся цикличные из- менения численности популяции, сезонные изменения физиологических показателей организма (температура тела; пульс и т. д.), метеорологи- ческие показатели по месяцам года, ритмические изменения веса жвач- ных по дням месяца, флуктуации структурных элементов клетки и т. и. Такие функции называются периодическими. Периодические функции подчиняются закономерностям, которые обычно достаточно близко выражаются тригонометрическим уравнением регрессии: 360 360 y = <+ b sin — х + с cos — х, Г Г где у — значение периодической функции, r — число измерений функции, взятых в течение одного полного цик- ла через равные промежутки времени. Например, если полный цикл длится 1 год, а измерялась функция ежемесячно,тог=12, х — порядковый номер измерения, начиная с х~ — — 0. Последний номер измерения в цикле равен х„,. Параметры периодического уравнения регрессии .находятся по сле-дующим формулам: Zy 1 Г у за r/2 360 у . cos x Г r/2 Выравнивание периодических рядов можно показать на следующих примерах. П р и мер 157. После того как популяция достигла предела своей численности в данной местности, начинаются периодические изменений числа особей этой популяции. Уменьшение численности вызывается уве- личением количества хищников и паразитов, а также уменьшением за- пасов пищи, приходящихся на одну особь дикого вида. Если возрастающее сопротивление среды не приведет к полному уничтожению популяции, то для оставшихся особей через определенный период образуются условия, благоприятствующие размножению. К это- му времени жизненное пространство будет расширено, запасы пищи на одну особь дикого вида увеличатся, хищники в значительной части или погибнут, или перекочуют в другие места.
320 РЕГРЕССИЯ По этим причинам численность популяции начинает увеличиваться, а дойдя до некоторого максимума, снова начинает уменьшаться. Примером довольно правильных циклических изменений численно- сти популяции могут служить колебания численности канадского зайца, установленные по данным годовых заготовок пушнины, по числу шку- рок, поступающих ежегодно в заготовительные конторы. За период с 1920 по 1930 гг. (10 лет) прошел полный цикл перио- дического изменения численности зайца в Kavape. В начале цикла чис- ленность равнялась 2 тыс. особей, в средине — 50 тыс. и в конце (перед началом нового цикла) — 15 тыс. особей. Численность (у) популяции по годам приведена в табл. 136; там же показано и выравнивание эмпи- рического ряда периодической функции по указанным формулам. 36о При числе интервалов r=10,— =36, поэтому в табл. 136 исполь- Г зуется преобразованный аргумент х1 — — 36х. Таблица 136Выравнивание эмпирического ряда регрессии численности канадского зайца (у)по годам развития популяции (х).360 360Периодическая функция у = а + Ь sin — х + с cos — хr r умах, bsinx, У х, =36x 8)I1 х, Год у cosx, сов х, сcosx + 17, 118 — 102,082 280 280 у = + 28,0 — ' 3, 4236 sin х, — 20, 4164 cos х, = + 28,00 10 -}- 17,118 — + 3,4236 х, =Збх 5 — 102,082 — — 20,4164 Для облегчения нахождения синусов и косинусов в приложении да- на табл. V, в которой приведены эти две тригонометрические. функции 360 для любого значения преобразованного аргумента х, == ' х в преде- г лах одного полного цикла: от х~ — — 0 до х1о — — 359. Выравненная линия регрессии численности канадского зайца по го- дам показана на рис. 70. Изменения численности канадского зайца происходят примерно на одном среднем уровне — 28 тыс. голов, причем этот средний уровень 1920 1921 1922 1923 1924 1925 1926 1927 1928 1929 0 36 72 108 144 180 216 2Ы 288 324 0,000 +0,588 + 0,951 +0,951 +0,588 0,000 — 0,588 — 0,951 — 0,951 — 0,588 +1,000 +0,809 +0,309 — 0,309 — 0,809 — 1,000 — (),809 — 0,309 +0,309 +0,809 2 10 30 38 45 50 40 30 20 15 0,000 + 5,880 +28,530 +36,138 +26,460 0,000 — 23,520 — 28,530 — 19,020 — 8,820 + 2,000 + 8,090 + 9,270 — 11,742 — 36,405 — 50,t'00 — 32,360 — 9,270 + 6,180 +12,135 0,00 +2,01 +3,26 -+3,26 +2,01 0,00 — 2,01 — 3,26 — 3,26 — 2,01 — 20,42 — 16,52 — 6,31 + 6,31 -+16,52 +20,42 +16,52 + 6,31 — 6,31 — 16,52 7,61 13,5 25,0 37,6 46,5 48,4 42,5 31,1 18,4 9,5
ПЕРИОДИЧЕСКИЕ ФУНКЦИИ остается практически постоянным для трех-четырех соседних циклов. Так бывает не всегда. Есть такие периодические функции, средний уро-' вень которых повышается (понижается) или с постоянной, или с пере- менной скоростью, что можно показать на следующих примерах. П р Имер 158. При изучении изменчивости веса сельскохозяйствен- ных животных проводились ежедневные определения живого веса коров на первых месяцах стельности. За вес принималась средняя величина из трех взвешиваний, проводившихся каждый день утром, в полдень и вечером перед дачей корма и воды. Кормление и содержание коров за весь период опыта — 72 дня — были изо дня в день совершенно оди- наковыми. В результате по каждому животному были обнаружены до- вольно значительные колебания живого веса, имевшие явно периодиче- ский характер. Рис. 70. Периодическая функция. Изменение численности но" пуляции канадского зайца по годам. У большинства коров средний уровень колебаний веса не оставался одинаковым для соседни~х циклов — у некоторых он повышался, у неко- торых понижался, а у отдельных коров средний уровень циклов сам из- менялся па типу периодических функций. для таких сложных периодических функций выравнивание эмпири- ческих рядов ведется по нескольким ступеням. Сначала весь ряд выравнивается по уравнению параболы первого или второго порядка: у'=а+Ьх или у'=a+bx+cx '. Если изменения среднего уровня колебаний функции имеют периоди- ческий характер, то весь имеющийся ряд предварительно выравнивается как периодическая функция с одним общим большим периодом, для- щимся от начала до конца всего исследования. Теоретические значения у', полученные при предварительном вы- равнивании среднего уровня колебаний, подставляются вместо свобод- ного члена в уравнение периодической функции у"=у'+ bsin х1+ cosx>,
322 РЕГРЕССИЯ найденное при выравнивании ряда в пределах каждого цикла. Напри- мер, у жоровы .Брикки за 60-дневный период наблюдались 2 полных цикла изменения живого веса по 30 дней в каждом. )Кивой вес изме- нялся в пределах от 578 до 613 кг, причем средний уровень периодиче- ских колебаний постепенно возрастал с постоянной скоростью. Если эмпирический ряд веса Брикки выравнять по уравнению па- раболы первого порядка, то получится уравнени!е у'= 585-1- 0,233х. Это значит, что средний суточный прирост среднего веса Брикки (среднего уровня колебаний веса} составлял 233 г, а за весь 60-дневный период средний вес Брикки увеличился на 0,233>(60= 14 кг. Анализ показал, что в пределах циклов живой вес Брикки изменял- ся в соответствии с уравнением у" = у' — 7,61sin12õ — 7,61cos! 2х, где у'= 585+ 0,233 х. Эмпирические и теоретические значения среднесуточных живых ве- сов Брикки приведены в табл. 137 и на рис. 71. Таблица 13Т Периодические изменения среднесуточного живого веса коровы Брикки: . ,х — дни наблюдения, у — эмпирические значения (в кг), у'=585+0,233x — нарастание среднего уровня колебаний веса, у" = у' — 7,61sin12x — 7,61cos12x — тридцатидневные циклы изменений веса. 1 HcPBbl)5 цик.!1 Второй цикл У V У Более короткие циклы колебаний веса — двадцатидневные — на- блюдались у коровы Амики, живой вес которой периодически менялся в соответствии с уравнением у" = у' — 0,5sin18õ — 5,5cos18x,у'= 509,4+0,175х. Наиболее сложный характер имели колебания веса коровы Асте- рии — они были трехстепенными, так как происходили путем наложения трех отдельных элементарных изменений. 3 4 5 6 7 8 9 10 11 12 13 14 ~5 16 17 576 570 578 588 590 578 582 590 585 591 597 603 591 602 603 586 586 586 58~ 587 587 587 587 588 588 588 588 589 589 589 575 575 576 577 578 580 582 585 587 590 592 594 596 597 599 18 19 20 21 22 23 24 25 26 27- 28 29 30 31 32 596 605 591 597 603 598 594 602 592 597 595 592 583 583 585 589 589 590 590 590 593 591 591 591 59! 59~ 592 592 592 593 600 600 600 599 598 597 596 594 592 59Э 588 586 584 5ЧЗ 582 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 581 580 586 587 584 592 598 601 601 599 599 597 610 594 607 593 593 593 593 594 59< 594 594 595 595 595 595 59б 595 596 582 582 583 584 585 587 589 592 594 597 599 601 603 604 606 48, 49 50 51 52 53 54 55 55 57 58 59 60 61 62 610 613 609 604 603 610 598 601 600 597 597 601 597 585 592 596 59б 597 597 597 597 598 598 598 598 599 599 599 599 599 607 607 607 607 606 604 603 601 599 597 595 593 591 590 589
ПЕРИОДИЧЕСКИЕ ФУНКЦИИ 323 б10 л ~М ~о боо > 590 Я р) ~å 580 Я З~ Ж 44 . 49 54,~9 фф Я- ни 4 Ряс. 7l. Сложная периодическая функция. Тридцатидневные циклы колебаниясреднесуточного живого веса коровы. Брикки с повышающимся среднимуровнем. Средний уровень циклов у этой коровы сам изменялся как периоди- ческая функция с семндесятидвухдневным периодом, имеющая свой средний уровень, который нарастал прямолинейно. Поэтому общая фор- мула периодической функции имеет в данном случае тройное обозна- чение: у"' = у" — 0,4s i n18x — 3,0cos18x. у" = у' — 2,54sin5x — 3,32cos5x, у' = 598,3+0,023х. Периодические кривые изменений веса коров Амики и Астерии по- казаны на рис. 72. Вскрытые закономерности ритмического изменения веса крупного рогатого скота могут быть использованы теоретически и практически. Ясно выраженная периодичность изменений веса при тех условиях, в которых проводились описанные наблюдения (выравненность кормле- ния и содержания, определение среднесуточного веса из трех взвеши- ваний в день перед дачей корма в воды), указывает на такие физиоло- гические особенности формирования общей массы тела крупного рога- того скота, на которые прежде не обращалось должного внимания. Первое объяснение вскрытой ритмичности может заключаться в, не- совпадении правильного ритма наполнения пищеварительного тракта (регулярное кормление и поение) с довольно беспорядочными сроками его освобождения. В результате такого несовпадения пищеварительный тракт может наполняться некоторое время без компенсирующего осво- бождения. После определенного срока переполненный пищеварительный тракт начинает освобождаться в большей степени, чем это требуется для компенсации его наполнения. В первом периоде прои~сходит повышение живого веса, во втором- его уменьшение. Амплитуда таких колебаний и~когда достигает значи- тельных размеров. Например, среднесуточный вес коровы Брикки за время с 47-го по 50-й день опыта увеличивался с 599 кг до 613 кг, т. е. за 3 суток на 14 кг, или по 4,7 кг в сутки, а в следующие 3 дня среднесу-
ни 4 9 14 ig 24 29 З4 39 44 49 54 Я б4 б9 Рис. 72. Сложные периодические ункции. Двадцатидневные циклы колебания сред- несуточного живого веса коров с равномерно повышающимся средним уровнеы егорова домика и с периодически изменяющимся средним уровнем (корова Астерия, Э ° ° й ° ° I °: б ° б 1 ) ° е! й ° I ° б ° I ° ° ) ° ° ° ° ° в ° б ° ° ° ) Ф ° ! ° ° «j ° ° й ) й ° б ° й б ° Э ° б ° ! ) ° ) ° ° ) б ° ° ° ° ° 1 ° ° ° ) ° ° ° ° Э ° ° ° 1 Ф ) ° ) ° ° ° ° ° ° е ° Ф Ф Э й ° ° й ) ° ° в ° й ° 1 й Ф в ° ° ° ° Ф ° й ° ° ° ) й i ° ° ° ° ° ю ° ° ) й ° ) ° ° Э ° ) й ° ° й ° ° ° й й б ° ! й 1 ! ° ° Э ° ° Э ° Э ° б ° ° ° й ° ° ° ° ° Э s ° Ф ° Э ° ° ° ° ° й° б ° ° ° ° ° ° й ° ° ° б ° ° ) ° б Э') ° s ° ° sâ ) б ° I ° ! ° ° Ф ) ° б Э ° Э б Ф ° ° б ° ° Э б ° Ф ° Ф ° ° ° ° б ° ) ° ° й I б ° ° Э ° й в ° б ° Э ° в ° ° ° ю ° ю й ° ° ° I 4 Ф ° ° ° ° ° Э ° ° й ° ° ° 1 ° ° Э ° в ° ° ° ° ° ° й б ° ° б ° ° ° й ° ° ° Э ° ° ° ° ° ° ° ° ° ° ° ° б ° ° I ° : ° ° ° 1 ° ° ° й ° Э й ) ° й ° й ° ) ° ! ° ° ° ° I ° ) Ф й Ф I ° ° Ф ) r й Э ° ° в ° ° ! ° й й й Ф ) ° Э ° ! й ° ° й ! ° ° й ° Э й й ю ° б й ю й ) ° ° б ° ° ) Ф ° ° I ° й ° ° б ° ° ° ) ° ° ! ° в ° ° ° й ° Э ) ° ° ° б ° ) й ) й ° ° II ю ° ° б ° й е ) ° Э ° ф ° ° ° б й ° 1 ° ° ° ° й ° ° ° ° ° б ° ° Э б й Э й ° Э ° I ° ° ° ° ) ° ° ° ° ° ° ° й ° ° ) ° ° ° аавевааеевааоаоаоюеомоаваоооавююаоаававвовв ЮЮООЮ ааааоваиоаюоаиииаивиббиааабивюиибаювив6066â ф й @ ' ивииииииииивибиббииибибаиибиоииибаир~ю° 566È е ° Ф ° ° а 6 ю о а а о 6 в ю 6 ю в в и 6 и а ю о 6 и а и а 6 и 6 ю 6 ф 6 а у' 1 в и ° ИИИО ° ибибаиибаиаииаииаааибиаиабюавивир Явою ЮЮООЮ l~ 1 ввааи ааиваювиивбибаиииввиабюаииии'.ваваЮЮОИЮ ювоаоюаооаювюов~~~чаббив~аиаааво аааааиаиоюююоюи ивоюоюаюи~й6661%666666656066'4иииаюиюооююоюаоивааоюоаию юоиаииоюоюиюоааююоюооюооа аоюp'.ÞÈÞÂÎÅ'èèssè565566ã +t «ааюаииавббиваааиииааавааииибибаиаюаиавиаииааиааиаюлаббаии"аиаив~глью ioaaOOiаиацрибиививиабааиии ааиюбибар.да~ 1виюиюбааиааиа дивоиааюа .~смавиааю.иааааааиивиаавюаааааюиаиаою овивбаиикаааив100иювааббвюкабелек=ааб~1ввавюаю)6659555ююаа>иююао(оааовоювюоавюовоо лсаовюааюаюооюиое~ Аы<ииоаааооывввюатбооаю>авиваааеаваааю - - еааваеааеаааввкввааааю~ ааю~к=ааююаюоюооввюоооь ааию[абибиюаюю ЮЮЮОООЮЮЮ б5ЮЮE-ОSОЮ6ЮОООЮО ° 6г JбaЮЮОЮю«б ° «аабiбиаil6066665656666,166Ю)aбиааббаф ИИИВГВИИб~бйаааа'ИВИИЮВВОИВИЮOs5~66aaahЧИИИИИВ) Ибабаббваабиабй ./6ИИИВИИВИЮааиа ° àaÞËOIaaaÂËaàaaas×Ñ Яабаавааваи~ Иббибб ЛвбибвбааиаббаавйаабабббИИбааИИИИИИЮ~МИВИ0ИИЮ@ Ч ЛааббИВТ ИИИИЮИ)ИИВИИ,160ИЮ'~ИИВИбабббИЮббббИббИИИббаИИИИИаюоо@аюаае~ъаюа~ вававаав лввааааваававв~ае .ваавааваеаааааааиаваааааваавееg ааааа~-.aseeraeSSS iaaSSSa~,аеаааЮЮаЮЮЮЮОЮВ=ВВЮЮВЮОВОИОаааииирииааааиииюаиаЮйб4оЮ 1 Йююю иаююоооыю оооFМ ииоою0аоааааоавааиваавssа иrrss sssssssааайаааююаааиюи 'йюааа юиаа а юаа,~а иэг46 оюи аав а и ааиюа аааюа юииаа йвюою виюваооюаюоа ЮЮ65ГЙЮИВЮИИЮВООЮЮЮ» ~й'4ЮОЮОВ аюиюовабвиюбаииооиююоибю>биюююиибаиаию ююоулиююююиоюааоюююииооюо~ив j i аиоаоиаоааиаавииииюиибоииввюииииювюбиююбое'лиивюааиоиавбаюаюибвииюббаю>июииюиииииибвиииивибииаи ббвбюбаиииибиаибаюЮЮИИЮИИИИИИИаббИИИЮбббйббббИЮбИЮИИИИИИВИИббИИИИбабббайбббИЮббИИИббиайбИИюйабааииивавиаввииваиииииаибваааавиаииииавбииювибибвввювбиввббиююииааииааююооииоююююоаюооарюиоооюиюооаюююиююаюиюоавибиюбибибюаюивб66066иииииивибиюююввюиаююаюаииаиюиюиииви)ибааи иаююююю)юииииииивиоио(биюавовииоюююэиююювююg у иивбюиыаюиваааииювюиивии ° IOOaa56aaaaèa60566aaoaoaOÞOaaaoOOÈ66aaaèâaoâîaèююоовбоюалиоюоа>аюаю >июаю>оооюооюаюээаобоои° aooè1oaaaþ6a6o60a0aа ° ° ибавиибааиииаиииаиюиаиииви>ибиаиюбииаииии> е е ° ° иабавиибиаабиииббиавбааиибаиибаииииювюиюиии ° ° 60èo660þè6aaaèaþèâaþg юибю>ииюююивюоаиюваю )й° ° àaà6o66èà6aaa66aoèàâèиаиииаиииибиивбииию ° ° 65þ иоаоииоююю ооюаиоюиювававааоаввввоаааю ° ° 65È 6O66È È6a55 1665È 65Èюааои ииаао >юааа юаааиююоюююоааоиоюоюоюююю ° ' g фааюаваеаае ааааа вааавовоаюоиавюиоюаюииаююбюв° ° иаюбоовдивюююииают::5 Ю ааав ~ оббаввивюиюваааишба'ююаюЮаои иоююо иоюоооюююииоооо оооои авиюо ааюаю ааааа аааюаювиаюооооиюоюююоб йо0оююююаавеаюаоававаовююаиаававоаааюаиавваоавюавоююаюою~. еоооюе~-к=. -чрааююаюааоааааоюааоююювоооюоаео аюоввюююаюаююваааююот. ° à60àü -а~ааааа ваввовл Юааарбааг: ~аааиааарбаааауб ° яяиииииаииия~лиииамвь'~ффиир.~~Йииюфбаф ~ ! ~~~~6~iaaaaiiaaaaaaaaaaaaa ! у ~~~~~~~и~~~~Фч~ий~бби~ аааааиааиаaaa09;g=i6a6ah>6aa506o06aa6 ююиююаююою 1 ~~~ 'яюрй%% 1 гп2?л Есной,"би.лйийбймЭ<ау < лил 9яъ~ >th10 700? с)ЛЕиьо JILlLLJüüéбмь~ыюг бюоюаиииибииаюиоюююибаюивюю~вааааюаоиавлавчвювивввввиав~=:ааюаювюаа-~.ююоаюиаюаоаооаваюююаиаааааю 30S36SS56rSS6S0» ° ТИИТЮЮОЮЮИУ ЮЮОЮИь 1ЮИЮ~ФюЮОГФЮООЮВЮОЮВВООВИИИИЮЮИИИИИбай ааао~вааававаооою ñþ~à65âþ.~àà56ààaü.-«56606~ìaao6aaèèaþ66oaèè6aaaþþaoèoaaИ ЮООЮОЮОИЮа%60аайв CF (ЛабЮв. is~~éaaa0600360Â6666éáOéaa46009661° воаоюююь~аюю .4оооиювиююююивииюииююааоваюою0оооюшювююююоюаиоюю° 551)в»ааиибаююо)>юаюиюиаюииююиваюа)ииибвааиии>ии)биаюбюювибавиааюваавааавоавааииаваюииаааабаииаииаабиаввоававваюиоаааивв° 6665îàààé âþàâàààîâàþîàààþþîþèààèîþþþàåþàâîþþоооюваоаююооююввае/
ПЕРИОДИЧЕСКИЕ ФУНКЦИИ 325 К таким указаниям может относиться требование более частого взвешивания подопытных животных — гораздо чаще, чем только в на- чале и конце опытных периодов. Несомненно также, что лучшие результаты дадут более длительныс опытные периоды, при которых возможно избежать попадания только на одну восходящую или на одну нисходящую ветвь периодических из- менерий веса животных. Вскрытие периодичности изменений живого веса, пока полностью необъяснимых, но протекающих внешне с определенной математической закономерностью, освещает также и те спорные случаи продажи-покуп- ки и сдачк-приемки скота, при которых возникают конфликты и судеб- ные дела, связанные с оценкои живого веса сдаваемого и принимаемого. скота. Резкие изменения веса, происходящие за короткое время у скота в период сдачи-приемки, в тех случаях, когда они не могут быть объясне- ны резким изменением наполненности пищеварительного тракта перед самым взвешиванием, обычно объясняются или подменой животных, или искажением регистрации результатов взвешивания, что не всегда пра- вильно отражает действительную причину этих колебаний,
ПРИЛОЖЕН
329 ЙРилоЖЕни Е чис ел 16 196 576 1156 1936 2916 4096 5476 7056 8836 9 169 528 1089 1849 2809 3969 5329 6889 8649 10609 12769 15129 17689 20449 23409 26569 29929 33489 37249 0 100 400 900 1600 2500 3600 4900 6400 8100 10000 12100 14400 16900 19600 22600 25600 28900 32400 36100 4 144 484 1024 1764 2704 3844 5184 6724 8464 36 256 676 1296 2116 3136 4356 5776 7396 9216 1 121 441 961 1681 2601 3721 5041 6561 8281 49 289 729 1369 2209 3249 4489 5929 7569 9409 64 324 784 1444 2304 3364 4624 6084 7744 9604 81 361 841 1521 2401 3481 4761 6241 7921 9801 10 11 12 13 14 15 16 17 18 19 10201 11321 14641 17161 19881 22801 25921 29241 32761 36481 10816 12996 15376 17956 20736 23716 26896 30276 33856 37636 41616 45796 50176 54756 59536 64516 69696 75076 80656 86436 11664 13924 16384 19044 21904 24964 28224 31684 35344 39204 11449 13689 16129 18769 21609 24649 27889 31329 34969 38809 10404 12544 14884 17424 20164 23104 26244 29584 33124 36864 И 881 14161 16641 19321 22201 25281 28561 32041 35721 39601 40401 44521 48841 53361 58081 63001 68121 73441 78961 84681 20 21 22 23 24 25 26 27 28 29 40000 44100 48400 52900 57600 62500 67600 72900 78400 84100 41209 45369 49729 54289 59049 64009 69169 74529 80089 85849 91809 97969 l04329 110889 117649 124609 131769 139129 146689 154449 42849 47089 51529 56169 61009 66049 71289 76729 82369 88209 40804 44944 49284 53824 58564 63504 68644 73984 79524 85264 43681 47961 52441 57121 62001 67081 72361 77841 83521 30 31 32 33 34 35 36 37 38 39 90601 96721 103041 109561 116281 123201 130321 137641 145161 152881 90000 96100 102400 108900 11560о >22500 129600 136900 144400 152100 92416 98596 104976 111556 118336 125316 132496 139876 147456 155236 163216 171396 179776 188356 197136 206116 215296 224676 234256 244036 94249 100489 106929 113569 120409 127449 134689 142129 149769 157609 95481 101761 108241 114921 121801 128881 136161 143641 151321 159301 91204 97344 103684 110224 116964 123904 131014 138384 145924 153664 161604 169744 178084 186624 195364 204304 213444 222784 232324 242064 160000 168100 176400 184900 193600 202500 211600 220900 230400 240100 160801 168921 177241 185761 194481 203401 212521 221841 231361 241081 162409 170569 78929 187489 196249 205209 214369 223729 233289 243049 40 41 42 43 44 45 46 47 48 49 163649 173889 182329 190969 199809 208849 218089 227529 237169 ~247009 167281 175561 !84041 192721 202601 210681 219961 229441 239121 249001 Квадраты 25 225 625 1225 2025 3025 4225 5625 7225 9025 11025 13225 15625 18225 21025 24025 27225 30625 34225 38025 42025 46225 50625 552М 60025 65025 70225 75625 81225 87025 93025 99225 105625 112225 119025 126025 133225 140625 148225 156025. 164025 172225 180625 189225 198025 207025 216225 225625 235225 245025 11236 13456 15876 18496 21316 44336 27556 30976 34596 38416 42436 46656 51076 55696 б0516 65536 70756 76176 81796 87616 93636 99856 106276 112896 119716 126736 133956 141376 148996 156816 164836 173056 181476 190096 198912 207936 217156 226576 236196 246016 Та бл ица 43264 47524 51984 56644 61504 66564 71824 77284 82944 88804 94864 101124 107584 114244 121104 128164 135424 142884 150544 158404 166464 174724 183184 191844 200704 209764 219024 228484 238144 248004
330 ПРИЛО)КЕНИЕ Окончан ие табл. 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 ° 98 99 250000 260100 270400 280900 291600 302500 313600 324900 336400 348100 360000 372100 384400 396900 409600 422500 435600 448900 462400 476100 490000 504100 518400 532900 547600 562500 577600 592900 608400 624100 640000 656100 672400 688900 705600 722500 739600 756900 774400 792100 810000 828100 846400 864900 883600 902500 921600 940900 960400 980100 251001 261121 271441 281961 292681 303601 314721 326041 337561 349281 361201 373321 386641 39М61 410881 423801 436921 450241 463761 477481 491401 505521 519841 534361 549081 564001 579121 594441 609961 625681 641601 657721 674041 690561 707281 724201 741321 758641 776161 793881 811801 829921 848241 866761 885481 904401 923521 942841 962361 982081 252004 262144 272484 283024 293764 304704 315844 327184 338724 350464 362404 374544 382884 399424 412164 425104 438244 451584 465124 478864 494204 506944 521284 535824 550564 565504 580644 595984 611524 627264 643204 659344 675684 692224 708964 725904 743044 760384 777924 795664 813604 831744 850084 868624 887364 906304 925444 944784 964324 984064 253009 263169 273529 284089 294849 305809 316969 328329 339889 351649 363609 375769 388129 400689 413449 426409 439569 452929 466489 480249 494209 508369 522729 537289 552049 567009 582169 597529 613089 628849 644809 660969 677329 693889 710649 727609 744769 762129 779689 797449 815409 833569 851929 870489 889249 908209 927369 946729 966289 986049 254016 264196 274576 28Я56 295936 306916 318096 329476 341056 352836 364816 376996 389376 401956 414736 427716 440896 454276 467856 481636 495616 509796 524176 538756 553536 568516 583696 599076 614656 630436 646416 662596 678976 695556 712336 729316 746496 763876 781456 799236 817216 835396 853776 872356 891136 910116 929296 948676 968256 988036 255025 265225 272625 286225 207025 308025 319225 330625 342225 354025 366025 378225 390625 403225 416025 429025 442225 455625 469225 483025 497025 501225 525625 540225 555025 570025 585225 600625 616225 632025 648025 664225 680625 697225 714025 731025 748225 765625 783225 801025 819025 837225 855625 874225 893025 912025 931225 950625 970225 990025 256036 266256 276676 287296 298116 309136 320356 331776 343396 355216 367236 379456 39]876 404496 417316 430336 443556 456976 470596 484416 498436 512656 527076 541696 556516 571536 586756 602)76 617796 633616 649636 665856 682276 698896 715716 732736 749956 767376 784996 802816 820836 839056 857476 876096 894916 913936 933156 952576 972196 992016 257049 267289 277729 288369 299209 310249 321489 332929 343369 356409 368449 380689 393129 405769 418609 431649 444889 458329 471969 485809 499849 514089 528529 543169 558009 573049 588289 603729 619369 635209 651249 667489 683929 700569 717409 734449 751689 769129 786769 804609 822649 840889 859329 877969 896809 915849 935089 954529 974169 994009 258064 268324 278784 289444 300304 311364 322624 334084 345744 357604 369664 381924 394384 407044 419904 432964 446224 459684 473344 487204 501264 515524 529984 544644 559504 574564 589824 605284 620944 636804 652864 669124 685584 702244 719104 736164 753424 770884 788544 806404 824464 842724 861184 879844 898704 917764 937024 956484 976144 996004 259031 269361 279841 290521 30140! 312481 323761 335241 346921 358801 370881 383161 395641 408321 421201 434281 447561 461041 474721 488601 502681 516961 531441 5461Л 561001 576081 591361 606841 622521 638401 654481 670761 687241 703921 720801 737881 5161 772641 790321 808201 826281 844561 863041 881721 900601 919681 938961 958441 978121 998001
331 BРИЛО~КЕНИЕ Та бл ица Ц К вадратные корни 2,450 4,000 5,099 6,000 6,782 7,483 8,124 8,718 9,274 9,798 2,646 4,123 5,196 6,083 6,856 7,550 8,185 8,775 9,327 9,849 1,414 3,464 4,690 5,657 6,481 7,211 7,874 8,485 9,055 9,592 10,100 10,583 11,045 11,489 11,916 12,329 12,728 13,115 13,491 13,856 10 11 12 13 14 15 16 17 18 19 10,296 10,770 11,225 11,670 12,083 12,490 12,884 13,267 13,638 14,000 14,353 14,697 15,033 15,362 15,684 16,000 16,310 16,613 1о,912 17,205 20 91 22 23 24 25 26 27 28 29 30 31 32 33 34 35 6 37 38 39 17,493 17,776 18,056 18,330 18,601 18,868 19,131 19,391 19,647 19,900 20,149 20,396 20,640 20,880 21,119 21,354 21,587 21,817 22,045 22,271 40 41 42 43 44 45 46 47 48 49 О 3,162 4,472 5,477 6,325 7,071 7,746 8,367 8,944 9,487 10,000 10,488 10,955 11,402 11,832 12,247 12,649 13,038 13,416 18,784 14,142 14,491 14,832 15,166 15,492 15,811 16,125 16,432 16,733 17,029 17,321 17.607 17,886 18,166 18,439 18,708 18,974 19,235 19,494 19,748 20,(ЮО 20,249 20,494 20,736 20,976 21,213 21,448 21,680 21,909 22,136 1,000 3,317 4,587 5,568 6,403 7,141 7,810 8,426 9,000 9,539 10,050 10,538 11,000 11,446 11,874 12,288 12,687 13,077 13,454 13,820 14,177 14,526 14,866 15,199 15,524 15,843 16,156 16,462 16,763 17,059 17,349 17,635 17,917 18,193 18,466 18,735 19,000. 19,261 19,519 19,774 20,025 20,273 20,518 20,761 21,000 21,237 21,471 21,703 21,932 22,159 14,213 14,560 14,900 15,232 15,556 15,875 16,186 16,492 16,793 17,088 17,378 17,664 17,944 18,221 18,493 18,762 19,026 19,287 19,545 19,799 20,050 20,298 20,543 20,785 21,024 21,260 21,494 21,726 21,955 22,181 1,732 3,606 4,796 5,745 6,557 7,280 7,937 8,544 9,110 9,644 10,149 10,630 11,091 11,533 11,958 12,369 12,767 13,153 13,528 13,892 14,248 14,595 14,933 15,264 15,589 15,906 16,217 16,523 16,823 17,117 17,407 17,692 17,972 18,248 18,520 18,788 19,053 19,313 19,570 19,824 20,075 20,322 20,567 20,809 21,048 21.284 21,517 21,749 21,977 22,204 2,000 3,742 4,899 5,831 6,633 7,349 8,000 8,602 9,165 9,695 10,198 10,677 11,136 11,576 12,000 12,410 12,806 13,191 13,565 13,928 14,283 14,629 14,967 15,297 15,621 15,937 16,248 16,553 16,852 17,146 17,436 17,720 18,000 18,276 18,547 18,815 19,079 19,339 19,596 19,849 20,100 20,347 20,591 20,833 21,071 21,307 21,541 21,772 22,000 22,226 2,236 3,873 5,000 5,916 6,708 7,416 8,062 8,660 9,220 9,747 10,247 10,724 11,180 11,619 12,042 12,450 12,845 13,229 13,602 13,964 14,318 14,663 15,000 15,330 15,653 15,969 16,279 16,583 16,882 17,176 17,464 17,748 18,028 18,103 18,574 18,841 19,105 19,365 19,621 19,875 20,125 20,372 20,616 20,857 21,095 21,331 21,564 21,795 22,023 22,249 10,344 10,817 11,269 11,705 12,124 12,530 12,923 13,304 13,675 14,036 14,388 14,731 15,067 15,395 15,716 16,031 16,340 16,643 16,941 17,234 17,521 17,805 18,083 18,358 18,628 18,894 19,157 19,417 19,672 19,925 20,174 20,421 20,664 20,905 21,142 21,378 21,610 21,840 21,068 21 294 2,828 4,243 5,292 6,164 6,928 7,616 8,246 8,832 9,381 9,900 10,392 10,863 11,314 11,747 12,166 12,570 12,962 13,342 13,711 14,071 14,422 14,765 15,100 15,427 15,748 16,062 16,371 16,673 16,971 17,263 17,550 17,833 18,111 18,385 18,655 18,921 19,183 19,442 19,698 19,950 20,199 20,445 20,688 20,928 21,166 21,401 21,633 21,863 22,091 22,316 3,000 4,359 5,387 6,245 7,000 7,681 8,307 8,888 9,434 9,950 10,440 10,909 11,358 11,790 12,207 12,610 13,000 13,379 13,748 14,107 14,457 14,799 15,133 15,460 15,780 16,094 16,401 16,703 17,000 17,292 17 578 17,861 18,138 18,412 18,682 18,947 19,209 19,468 19,723 19,975 20,224 20,470 20,712 20,952 21,190 21,424 21,656 21,886 22,113 22,338
332 П РИЛОЩЕ Н И Е Оконч ан ие табл. И 22,361 22.583 22 804 23,022 23.2З8 23,452 23,('64 23,875 24,083 24,290 22,428 22,650 22,869 33,087 23.302 23,516 23,728 23,937 24,145 24,352 24,556 24,759 24,960 25,160 25,357 25,554 25,749 25,942 26,134 26,325 ~6,514 26,702 26,889 27,074 27,258 27,4~1 27,623 27,803 27,982 28,160 28,337 28,513 28,687 28,862 29,035 9,206 29,377 29,547 29 715 29,883 30 050 30,316 30,381 30,545 30,708 30,871 31,032 31,193 31,353 31,512 22,472 2 ~,б'94 22,913 23,130 23,345 23,558 23,770 23,979 24,187 24,393 22,40.~ 2 ',627 22,847 23,(~65 23,281 23,495 23,707 23,917 24,125 24,331 24,536 24,739 24,940 25,140 25,338 25,534 25,729 25,923 26..115 26,306 22,539 22,760 22,978 23,195 23,409 23,622 23,833 24,042 24,249 24, �4 22,494 22,716 22,935 23,152 23,367 23,580 23,791 24,000 24,207 24,413 50 51 52 53 54 55' 56 57 58 59 24,617 24,819 25,020 25,219 25,417 25,613 25,807 26,.000 26„192 26,38~ 24,658 24,860 25,060 25,259 25,456 25,652 25,846 26,038 26,230 26,420 24,495 24,698 24,90~ 25,10~> 25,298 25,495 25,691 25,884 26,077 26,268 60 61 й2 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 , 89 90 91 92 93 94 95 96 97 98 99 26,458 26,646 2~,833 27,019 27,203 27,386 27 568 27,749 27,929 27,107 28,284 28,461 28,636 28,81о 28,983 29,155 29,326 29,496 29,665 29,833 30.000 30,166 30,332 30.496 30,659 30,82Я 30,984 31,<45 31.3О5 31,464 22,383 22,605 22,825 23,043 23,259 23,473 23.685 23,896 24,104 24,311 24,515 24,718 24,920 25,120 25,318 25,515 25,710 25,904 26.096 26,287 26,476 26,665 26,851 27, ~~37 27,221 27,404 27,586 27,767 27,946 28,125 28,302 28,478 28,653 28,827 29,000 29,172 29,343 29,513 29,682 29,850 30,017 30,18 ~ 30,348 30,512 30,676 30,838 31,000 31,161 31,321 31,480 26,495 26,%3 26,870 27,056 27,240 27,423 27,604 27,785 27,964 28,143 28,320 28,496 28,671 28,844 29,017 29,189 29,360 29,530 29,499 29,866 30,033 3'), 199 30,365 30.529 30,692 30,855 31,016 31 177 31,337 31,496 22,450 22,672 22,89) 23.108 23,324 23,537 231749 23,958 24,166 24,372 24,576 24,779 24,980 ".5,179 25,377 25,573 25,768 25,962 26,153 26,344 26,533 26,721 26,907 27,092 27,276 27,459 27,641 27,821 28,000 28.178 28,355 28,53! 28,705 ~8,879 29,052 29,223 29,394 29,564 29.732 29,90 ~ 30,067 30 232 30,397 30 561 30,725 30,887 31.048 31.209 31,369 31,528 24,597 24,799 25,000 25,199 25,397 25,593 25,788 '25,981 '26,173 26,363 26,552 26.740 26,926 27,111 27,295 27,477 27,659 27,839 28,018 28,196 28,373 28,518 28,723 28,896 29,069 29,240 29,411 29.580 29,749 29,917 30,083 30.249 30,414 30,579 30,741 ЗО,У)3 31,064 31,~25 31,385 31,544 26.57! 26,758 26,944 27,129 27,313 27,496 27,677 27,857 28,036 28,214 28,390 28,566 28,740 28,914 29,086 29,258 29.428 29,597 29,766 29,933 3<>,100 30,266 30,430 30,594 30,757 30,919 31,081 3i,24> 31,401 31,560 22,517 22,738 22,957 23,173 23,388 23,601 23,812 24,021 24,228 24,434 24,637 24.840 25,040 25,239 25,436 25,632 25,826 26.019 26,211 26,401 26,590 26,777 26,963 27,148 27,331 27,514 27,695 27,875 28,056 28,231 28,408 28,583 28,758 28,931 29 103 29,275 29,445 29,614 29,783 29,950 30,116 30,282 30,447 30,611 30,773 30,935 31,097 31,257 31,417 31,575 26,608 26,796 26,982 27,166 27,350 27,532 27,713 27,893 28,071 28,249 28,425 28,601 28,775 28,948 29,120 29,292 29,462 29,Я1 29,799 29,967 30,133 30,299 30,463 30.627 30,790 30,952 31,113 31,273 3l,433 31,591 22,561 22,782 23,000 33,216 23,431 23,643 23,854 24,062 24,269, 24,475 24,678 24,880 25,080 25,278 25,476 25,671 25,865 26,058 '26,249 26,439 26,627 26, Ы4 27,000 27,185 27,368 27,550 27,731 27,9!1 28,089 28,267 28,443 28,618 28,792 28,966 29,138 29,309 29,479 29,648 29,816 29,983 30,150 30,315 30,480 30,643 30,806 30,968 31,129 31,289 31,448 31,607
Та бл ица Ш Логарифмы чисел 0374 0755 1106 1430 1732. 0128 0531 0899 1239 1553 0086 0492 0864 1206 1523 0170 0569 0934 1271 1584 0212 0607 0969 1303 1614 1903 2175 2430 2672 2900 3118 3324 3522 3711 3892 0253 0645 1004 1335 1644 0294 0682 1038 1367 1673 0334 0719 1072 1399 1703 0043 0453 0828 1173 1492 0000 0414 0792 1139 1461 »61 2041 2304 2553 2788 10 11 12 13 14 1847 2122 2380 2625 2856 3075 3284 3483 3674 3856 1818 2095 2355 2601 2833 1959 2227 2480 2718 2945 3160 3365 3560 3747 3927 1931 2201 2455 2695 2923 1875 2148 2405 2648 2878 1790 2068 2330 2577 2810 3032 3243 3444 3636 3820 2014 2279 2529 2765 2989 3201 4304 3598 3784 3962 1987 2253 2504 2742 2967 3181 3385 3579 3766 3945 15 16 17 18 19 3054 3263 3464 3655 3838 4014 4183 4346 4502 4654 3139 3345 3541 3729 3909 3096 3304 3502 3692 3874 3010 3222 3424 3617 3802 20 21 22 23 24 4082 4249 4409 4564 4713 4133 4298 4456 4609 4757 4099 4265 4425 4579 4728 3997 4166 4330 4487 4639 4116 4281 4440 4594 4742 4031 4200 4362 4518 4669 4814 4955 5092, 5224 5353 3979 4150 4314 4472 4624 25 26 27 28 29 480О 4942 5079 5211 5340 4857 4997 5132 5263 5391 4871 5011 5145 5276 5403 5527 5647 5763 5877 5988 4786 4928 5065 5198 5328 30 31 32 33 34 5478 5599 5717 5832 5944 5465 5587 5705 5821 593:3 5453 5575 5694 5809 5922 35 36 37 38 39 6053 6160 6263 6365 6464 6561 6656 6749 6839 6928 7016 7101 7185 7267 7348 6042 6149 6258 6355 6454 6096 6201 6304 6405 6503 6031 6138 6243 6345 6444 40 41 42 43 44 6571 6665 6758 6848 6937 7024 7110 7193 7275 7356 6551 6646 6739 6830 6920 6599 6693 6785 6875 6964 7050 7135 7218 7300 . 7380 6542 6637 6730 6821 6911 45 46 47 48 49 7007 7093 7177 7259 7340 6998 7084 7168 7251 7332 50 51 52 53 54 8 4771 4914 5051 5185 5315 5441 5563 5682 5798 59l1 6021 6128 6232 6335 6435 6532 6628 6721 6812 6902 6990 7076 7160 7243 7324 пРиД0ЖЕHHB 4048 4216 4378 4533 4683 4829 4969 5105 5237 5366 5490 5611 5729 5843 5955 6064 6170 6274 6375 6474 4065 4232 4393 4548 4698 4843 4983 5119 5250 5378 5502 5623 5740 5855 5966 6075 6180 6284 6385 6484 6580 6675 6767 6857 6946 7033 7118 7202 7284 7364 5514 5635 5752 5866 5977 6085 6191 6294 6395 6493 6590 6684 6776 6866 6955 7042 7126 7210 7292 7372 4886 5024 5159 5289 5416 5539 5658 5775 5888 5999 6107 6212 6314 6415 6513 66Э9 6702 6794 6884 6972 7059 7143 7226 7308 7388 4900 5038 5172 5302 5428 5551 5670 5786 5899 6010 6117 6222 6335 6425 6522 6618 6712 6803 6893 6981 7067 7152 7235 7316 7396
334 ЛРИЛОЩВН И Е Окончание табл. 1И 7443 7520 7597 7672 7745 7435 7513 7589 7664 7738 7451 7528 7604 7679 7751 7427 7505 7582 7657 7731 55 56 57 58 Ь9 7419 7497 7574 7649 7723 7459 7536 7612 7686 7760 7474 7551 7627 770) 7774 7466 7543 7619 7694 7767 7407 7482 7559 7634 7709 7412 7490 ° 7566 7642 7716 7810 7882 7952 8021 8089 7796 7868 7938 8007 8075 7839 7910 7980 8048 8116 7803 7875 7945 8014 8082 7818 7889 7959 8028 8096 7832 7903 7973 8041 8109 7789 7860 7931 8000 8069 7825 7896 7966 8035 8102 60 61 62 63 64 7782 7853 7924 7993 8062 7846 7917 7987 8055 8122 8182 8248 8312 8376 8439 8176 8241 8306 8370 8432 8156 8222 8287 8351 8414 8129 8195 8261 8325 8388 8169 8235 8299 8363 8426 8162 8228 8293 8357 8420 8142 8209 8274 8338 8401 8149 8215 8280 8344 8407 8136 8202 8267 8331 8395 65 66 67 68 69 8189 8254 8319 8382 8445 8494 8555 8615 8675 8733 8451 8513 8573 8633 8692 8482 8543 8603 8663 8)22 8463 8525 8585 8645 8704 7.0 71 72 73 74 8457 8519 8579 8639 8698 8500 8561 8621 8681 8739 8470 8531 8591 8651 8710 8506 8567 8627 8686 8745 8797 8854 8910 8965 9020 8751 8808 8865 8921 8976 8756 8814 8871 8927 8982 75 76 77 78 79 8768 8825 8882- 8938 8993 8802 8859 8915 8971 9025 9074 9128 9180 9232 9284 9031 9085 9138 9191 9243 9047 9101 9154 9206 9258 80 81 82 83 84 9079 9133 9186 9238 9289 9325 9375 9425 9474 9523 9335 9385 9435 9484 9533 9294 9345 9395 9445 9494 9330 9380 9430 9479 9528 9309 9360 9410 9460 9509 85 86 87 88 89 9566 9614 9661 9708 9754 9542 9590 9638 9685 9731 9576 9624 9671 9717 9763 9552 9600 9647 9694 9741 9581 9628 9675 9722 9768 9557 9605 9652 9699 9745 9547 9595 9643 9689 9736 90 91 Я 93 94 9777 9823 9868 9И2 9956 9809 9854. 9899 9943 9987 9800 9845 9890 9934 9978 9818 9863 '. 9908 . 9952 9996 9814 9859 9903 9948 9991 95 96 97 98 99 9791 9836 9881 9926 9969 9782 9827 9872 9917 9961 9786 9833 9877 9921 9965 9036 9090 9143 9196 9248 9299 9350 9400 9450 9459 8762 8820 8876 8932 8987 9042 9096 9149 9201 9253 9304 9355 9405 9455 9504 8476 8537 8597 8657 8716 8774 8~31 8887 8943 8998 9053 9106 9159 9212 9263 9315 9365 9415 9465 9513 9562 9609 9657 9703 9750 9795 9841 9886 9930 9974 8779 8837 8893 8949 9004 9058 9112 9165 9217 9269 9320 9370 9420 9469 9518 8488 8549 8609 8669 8727 8785 8842 8899 8954 9009 9063 9117 9170 9222 9274 9571 9619 9666 9713 9759 9805 9850 9894 9939 9983 8791 8848 8904 8960 9015 9069 9122 9175 9227 9279 9340 9390 9440 9489 9538 ~с 9586 9633 9680 9727 ' 9773 .
1007 1030 1054 1079 1104 1130 1156 1183 1211 1239 1009 1038 1057 1081 1167 1132 1159 1186 1213 l242 1021 1045 1069 1094 1119 . 1146 1172 1199 1227 1256 1002 1026 1050 1074 1099 )125 1151 1178 1205 1233 ) 000 1023 1047 1072 1096 1122 1l48 1175 1202 1230 1019 1042 1067 1091 1117 1143 1169 1197 1225 1253 1012 1035 1059 1084 1109 1135 1166 1189 1216 1245 1014 1038 1062 1086 11~2 1138 1164 1191 1219 1247 100> 1028 1052 1076 1)02 1127 i) 53 l 180 1208 1236 1016 1040 1064 1089 1114 1140 1167 1194 1222 1250 00 01 02 о3 04 05 06 07 08 09 1269 1297 1337 1358 1390 1422 . 1455 1489 1524 1560 1259 1288 1318 1349 1380 1413 1445 1479 1514 1549 1271 1300 1330 1361 1393 1426 1459 1493 1528 1563 1285 1315 1346 1377 1409 1442 1476 15l0 1545 1581 1262 1291 132! 1352 1384 1416 1449 1483 1517 1552 10 11 12 13 14 15 )6 17 18 19 1265 1294 1324 1355 1387 1419 1452 1486 1521 1556 1274 1303 1334 136ý 1396 ) 429 1462 1496 153~ 1567 1279 1309 1340 1371 1403 1435 469 1503 1588 157а 1276 1306 1337 1368 1400 1432 1466 1500 1535 1570 1585 1622 1660 1698 1738 1778 1820 1862 1905 1950 20 21 22 23 24 25 26 27 28 29 1589 1626 1663 1702 1742 1782 1824 1866 1910 1954 1600 1637 1675 1714 1754 1795 1837 1879 1923 1968 1618 1656 1694 1734 1774 1816 1858 1901 194б 1991 1603 1641 1679 1718 1758 1799 1841 1884 1928 1972 1592 1629 1667 1706 1746 1786 1828 1871 1914 )959 ) 611 1648 1687 1726 1766 1807 1849 1892 1936 1982 1596 1633 1671 1710 1750 1791 1832 1875 1919 19b3 30 31 32 33 34 35 36 37 38 39 2014 2061 2109 2158 2208 2259 2312 2366 2421 2477 1995 2042 2089 2138 2188 2239 2291 2344 2399 2455 2037 2084 2133 2183 2234 2286 2339 2393 2449 2506 2000 2046 2094 2143 2193 2244 2296 2350 2404 2460 2018 2065 2113 2163 22l3 2265 2317 2371 2427 2483 2004 2051 2099 2148 2198 2249 2301 2355 2410 2466 2028 2075 2123 2173 2223 2275 2328 2382 2438 2495 2009 2056 2104 2153 2203 2254 4307 2360 2415 2472 40 41 42 43 44 45 46 47 48 49 2529 2588 2649 27) 0 2773 2838 2904 2972 3041 3112 2564 2624 2685 2748 2812 2877 2944 3013 3083 3155 2518 2576 2636 2698 2761 2825 2891 2958 3027 3097 2541 2600 2661 2723 2786 2851 2917 2985 3055 3126 2523 2582 2642 2704 2767 2831 2897 2965 3034 3105 2535 2594 2655 2716 2780 2844 2911 2979 3048 3119 2512 2570 2630 2692 2754 2818 2884 2951 3020 3090 2553 2612 2673 2735 2799 2864 2931 2999 3069 3142 2559 2618 2679 2742 2805 2871 2938 3006 3076 3148 ПРИЛОЖЕНИЕ А и т и л о гари ф м ы 1607 )644 1683 1722 1762 1803 1845 1888 1932 1977 2023 2070 2118 2168 2218 2270 2323 2377 2432 2489 2547 2606 2667 2729 2793 2858 2924 2992 3062 3133 Та бл ица 1Ч 1282 1312 1343 1374 1406 1439 1472 1507 1542 1~78 16) 3 1652 1690 1730 1770 1811 1854 1897 1941 1986 2032 2080 2128 2178 2228 2280 2333 2388 2443 2500
ПРИЛОЖЕНИЕ Окон ч ание табл. IV 3228 3304 3381 3459 3540 3622 3707 3793 3882 3972 3170 3243 3319 3396 3475 3556 3639 3724 3811 3899 3162 3236 3311 3388 3467 3548 3631 3715 3802 3890 3221 3296 3373 3451 3532 3614 3698 3784 3873 3963 3214 3289 3365 3443 3524 3606 3690 3776 3864 3954 3192 3266 3342 3420 3499 3581 3664 3750 3837 3926 3206 3281 3357 3436 3516 3597 3681 3767 3855 3945 3177 3251 3327 .3404 3483 3565 3648 3733 3819 3908 3184 3258 3334 3412 3491 4573 3656 3741 3828 3917 3199 3273 3350 3428 3508 3589 3673 3758 3846 3936 50 51 52 53 54 55 56 57 58 59 4046 4140 4236 4335 4436 4539 4645 4753 4864 4977 3990 4083 4178 4276 4375 4477 4581 4688 4797 4909 4064 4159 4256 4355 4457 4560 4667 4775 7887 5000 3999 4093 4188 4285 4385 4487 4592 4699 4808 4920 4027 4121 4217 4315 4416 4519 4624 4732 4842 4955 4009 4102 4198 4295 4395 4498 4603 4710 4819 4932 4055 4150 4246 4345 4446 4550 4656 4764 4875 4989 4036 4130 4227 4225 4426 4529 4634 4742 4853 4966 60 61 62 63 64 65 66 67 68 69 4018 4111 4207 4305 4406 4503 4613 4721 4831 4943 5093 5212 5333 5458 5585 5715 5848 5984 6124 6266 6412 6561 6714 6871 7031 7194 7362 7534 7709 7889 8072 8260 8453 8650 8851 9057 9268 9484 9705 9931 5 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 3981 4074 4169 4266 4365 4467 4571 4677 4786 4898 5012 5129 5248 5370 5495 5623 5754 5888 6026 6166 6310 6457 6607 6761 6918 7079 7244 7413 7586 7762 7943 8128 8318 8511 8710 8913 9120 9333 9550 9772 5023 5140 5260 5383 5508 5636 5768 5902 6039 6180 6324 6 171 6622 6776 6934 7096 7261 7430 7603 7780 7262 8147 8337 8531 8730 8933 9141 9354 9572 9795 5035 5й2 5272 5395 5521 5649 5781 5916 6053 6194 6339 6485 6637 6792 6950 71l2 7278 7447 76 ~1 7798 7980 8166 835э 8551 8750 8954 9l62 9376 9594 9817 5047 5164 5284 5408 5534 5662 5794 5929 6067 6209 8353 6501 6653 68(>8 6966 7123 7295 7454 7638 7816 7998 8188 8375 8570 8770 8974 9183 9397 9616 9840 5058 5176 5297 542д 5546 5675 5808 5943 6081 6223 6368 6516 6668 6823 6982 7i45 7311 7482 7656 7834 8017 8204 8395 8590 8790 8995 9204 9419 9638 9863 5070 5188 5309 5433 5559 5689 5821 5957 6095 6237 6383 6531 6683 6839 6998 716 [ 7328 7499 7674 7852 8035 8222 8414 8610 88~0 9016 9226 9441 9661 9868 5082 52~F0 5321. 5445 5572 5702 5834 597О 6109 6252 6397 6546 6699 6855 7015 7178 7345 7о16 7691 7870 8054 8241 8433 8630 8831 9036 9247 9462 9683 99'~8 5105 5224 5346 5470 5598 5728 5861 5998 6138 6281 6427 6577 6730 6887 7047 7211 7379 7551 7729 7907 8091 8279 8472 8670 8872 9078 9290 9506 9727 995 ~ 5117 5236 5358 5483 5о10 5741 5875 6012 6152 6295 64~2 6592 6745 6902 7063 7228 7396 7568 7745 7925 811~> 8299 8492 8690 8892 9099 9311 9528 9750 9977
337 ПРИЛОЖЕНИЕ Таблица V Синусы (верхние числа) и косинусы (нижние числа)(без нуля целых) I +,1392 +,1564-«-,9903 -{-,9877 0,0000 +,0175 -«- 1,0000 {-,9998 +,0349 +,9994 +,0523 @,0698 -«-,9986 +,9976 +,0872 -{-,1045 -{-,1219 -«-,9962 -«-,9945 {-,9925 -{-,1736 -~-,1908 -{-,9848 -{-,9816 +,2079 +,9781 -{-,2588 +,2756 -{-,2924 -{-,9659 {-,9613 -{-,9563 +,2250 -«-,2419 +,9744 +,9703 -{-,3090 {-,3256 -{-,9511 -[-,9455 +,3746 +,9272 -{-,3420 -«-,3584 -{-,9397 -{-,9336 +,3907 +,4067 +,9205 ~-,9135 +,4226 +,4384 -{-,4540 -«-,9063 -«-,8988 -{-,8910 -{-,4695 +,4848 +,8829 {-,8746 +,5000 -{-,5150 -{-,8660 -{-,8572 -{-,5299 +,8480 +,5446 -{-,5592 +,8387 «-,8290 -«-,5736 +,5878 -«-,6018 +,8192 -{-,8090 +,7986 +,6157 +,6293 +,7880 +,7771 -~,6428 -~-,6561 +,7660 «-,7547 +,6820 -«-,6947 +,7314 +,7193 +,6691 +,7431 +,7071 +,7193 -{-,7314 -{-,7071 -«-,6947 {-,6820 +,7431 {-,7547 +,6691 ~,6561 +,7660 +,7771 +,6428 +,6293 +,8192 -{-,8290 {-,8387 -{-,5736 -«-,5592 +,5446 +,7880 +,6157 +,7986 -«-,8090 +,6018 -{-,5878 +,8480 -«-,8572 +,5299 +,5150 +,8829 +,4695 -{-,8910 -{-,8988 -«-,4540 -«-,4384 +,9063 +,9135 +,9205 +,4226 +,4067 +,3907 -{-,9272 +,9336 +,3746 +,3584 -{-,9397 -«-,9455 -~-,3420 +,3256 +,9511 +,3090 -{-,9563 -{-,9613 -{-,2924 -{-,2756 -«-,9659 -{-,9703 +,9744 -«-,2588 {-,2419 +,2250 +,9781 +,9816 +,2079 +,1908 -{-,9962 -{-,9976 +,9986 +,0872 +,0698 +,0523 +,9994 +,9998 +,0349 +,0175 +,9903 +,1392 -{-,9848 +,9877 +,1736 -{-,1564 +,9925 +,9945 +,1219 -{-,1045 +,9903 -{-,9877 — ,1392 — ,1564 +,9994 —,0349 -«-,9962 +,9945 +,9925 —,0872 —, 1045 —, 1219 +,9986 -{-,9976 — ,0523 — ,0698 +1,0000 «--,9998 0,0000 — ,0!75 +,9781 —,2079 «-,9659 -«-,9613 +,9563 —,2588 —,2756 —,2924 -{-,9511 +,9455 —,3090 —,3256 +,9744 +,9703 —,2250 —,2419 -]-,9848 -«-,9816 — ,1736 — ,1908 +,9272 —,3746 +,8829 -«-,8746 —, 4695 —,4848 -]-,9205 +,9135 —,3907 —,4067 +,9063 -[-,8988 +,8910 —,4226 —,4384 —,4540 -',—,8387 +,8290 — ,5446 — ,5592 +,7880 {-,7771 —,6157 —,6293 -«-,8192 -{-,8090 +,7986 —,5736 —, '878 —,6018 +,8480 —,5299 +,8660 -{-,8572 — ,5000 — ,5150 «--,6691 +,6561 — ,7431 — ,7547 +,7314 +,7193 —,6820 —,6947 +,7071 1-,6947 1-,6820 —,7071 —,7193 —,7314 +,7660 +,]Я7 —,6428 —,6541 +,7431 —,6691 +,5299 -{-,5150 —, 8480 —,8572 -«-,5736 -{-,5592 «-,5446 —,8192 —,8290 —,8387 +,6157 —,7880 -1-, 6428 -~-,6293 — ,7660 — ,7771 -]-,6018 -{-,5878 —,7986 —,8090 -{-,4226 -{-,4067 {-,3907 —, 9063 —,9135 —,9205 —,', 3746 +,3584 —,9272 —,9336 -«-,4695 —,8829 -«-,5000 +,4848 —, t.'660 —,8746 -{-,4540 {-,4384 —,8910 —,8988 +,2079 +, 1908 — ,9781 — ,9816 +,2588 +,2419 +,2250 —,9659 —,9703 —,9744 +,2924 +,2756 —,9563 —,9613 +,3090 —,9511 +,0523 +,0349 —,9986 —,9994 +,~ 872 -«-,0698 —,9962 —,9976 +, 1219 +, 1045 —,9925 —;9945 +,1392 —,9903 +,8660 -«-,8746 +,5000 «-,4848 -{-,9397 +,9336 — ,3420 — ,3584 -{-,3420 « ,3256 — ,9397 — ,9455 -]-,1736 +,1564 — ,9848 — ,9877 +,0175 —,9998
338 ПРИ ЛОЖЕ НИ Е Оконч а н ие табл. Ч —,0349 —,9994 =,0523 —,9986 —,0698 —,9976 —,0872 —,9962 —, 1045 —, 1219 — ,9945 — ,9925 —, 1392 —, 1564 — ,9903 — ,9877 18 — ,1736 — ,1908 — ,9848 — ,9816 —,2079 —,9781 —,2250 —,9744 —,2419 —,9703 — 2588 —,9659 — ,3090 — ,3256 — ,9511 — ,9455 —,2756 —,2924 —,9613 —,9563 19 — ,3420 — ,3584 — ,9397 — ,9336 —,3907 —,9205 —,4067 —,9135 —,4226 —,9063 — ,4695 — ,4848 —,8829 —,8746 — ,4384 — ,4540 —,8988 —,8910 20 —,5592 —,8290 —,5736 —,8192 —,6) 57 —,6293 —,7880 —,7771 —, 5878 —,6018 —,8090 —,7986 21 — ,6428 — ,6561 — ,7660 — ,7547 —,6947 —,7193 —,7071 —,7071 — ,7431 — ,7547 —,6691 —,6561 —,7193 —,7314 — ,6947 — ,6820 22 — ,7660 — ,7771 — ,6428 — ,6293 — ,8480 — ,8572 — ,5299 — ,5150 —,8290 —,5592 —,8387 —,5446 23 — ,8660 — ,8746 — ,5000 — ,4848 —,8988 —,4384 —,9272 —,9336 —,3746 —,3584 —,9135 —,9205 —,4067 —,3907 24 — ,9397 -,9455 — ,3420 — ,3256 —,9563 —.2924 —,9511 —,3090 —,9613 —,9659 —, 2756 —,2588 — ,9781 — ,9816 —,2079 —,1908 —, 9703 —,9744 —,2419 —,2250 25 —,9925 —,1219 —,9848 —,9877 —, 1736 —, 1564 —,9994 —,9998 — ,0349 — ,0175 — 9976 — ,9986 — ,0698 — ,0523 26 —,9998 +,0175 —,9976 +,0698 —,9903 —, 9877 -~,1392 +,1564 —,9962 +,0872 — ,9945 — ,9925 +,1045 -]-,1219 27 —,9703 —,9659 -!- 2419 + 2588 — ,9511 — ,9455 +,3090 -]-,3256 —,9613 —,9563 +,2756 +,2924 28 —,9336 +,3584 — ,8829 — ,8746 -[-,4695 +,4848 —,9272 +,3746 —,9135 —,9063 -]-,4067 +,4226 — ,8988 — ,8910 +,4384 +,4540 29 —,8572 -~-,5150 —, 8290 —,8192 -~-,5592 +,5736 —,8480 +,5299 —,7880 —, 7771 -[-,6157 -]-,6293 —,7986 +,6018 —,8090 +,5878 30 —,7547 +,6561 —,7314 -[-,6820 —,7431 -~-,6691 — ,6691 — ,6561 -~-,7431 -~-,7547 —,7193 —,7071 +,6947 4-,7071 —,6820 +,7314 —,6947 +,7193 31 —,5736 +,8192 —,5150 +,8572 —,5878 +,8090 32 —,4540 +,8910 —,4848 +,8746 —,4226 +,9063 —,3746 +,9272 —,4695 +,8829 —,5907 +,9205 —,4384 +,8988 33 —,2924 +,9563 —,3256 +,9455 —,3090 +,9511 —,2079 +,9781 —,2250 +,9740 —,2756 +,9613 —,24!9 +,9703 34 —,1219 +,9925 —,0349 —,0175 +,9994 +,9998 —, 1564 +,9877 —,1392 +,9903 —,0698 +,9976 —,1045 +,9945 35 0,0000 — 1,0000 —,5000 —,8660 — 1,0000 0,0000 —,9848 +,1736 —,9397 +,3420 — ,8660 +,5000 —,7660 +,6428 —,6428 +,7660 —,5000 +,8660 —,3420 +,9397 —, 1736 +,9848 —,0175 —,9998 —,5150 —,8572 —,9816 +, 1908 —,6293 ~-,7771 —,3746 —,9272 —,5299 —,8480 —,6691 —,7431 —,7880 —,6157 —,8829 —,4695 —,9903 —,1392 —,9994 +,0349 —,9781 +,2079 —,6157 +,7880 —,5446 —,8387 —,6820 —,7314 —,7986 —,6018 —,8910 —,4540 —,9986 +,0523 —,9744 -~,2250 —,9205 +,3907 —,8387 —,5446 —,6018 +,7986 —,8090 —,5878 —,9945 —,1045 —,8192 —,5736 —,9063 —,4226 —,9962 —,0872 —,2588 +,9659 —,0872 -~-,9962 —,5592 +, 8290 —,4067 -', — ,9135 —,5446 +,8387 —,0523 +,9986 —,5299 +,8480 —,3584 +,9336 —,1908 +,9816
ПРИЛОЖЕН И Е Таблица VI Первая функция нормированного отклонения Х 1 2 F(x) = (ординаты нормальной кривой) 39844 39822 39448 39387 38667 38568 37524 37391 36053 35889 39797 39322 38466 37255 35723 39767 39253 38361 37115 35553 39876 39559 38853 37780 36371 39733 39181 38251 36973 35381 39886 39608 38940 37903 36526 39894 39695 39104 38139 36827 39892 39654 39024 38023 36678 0,0 0,1 0,2 0,3 0,4 33912 31874 29659 27324 24923 33521 31443 29200 26848 24439 34294 34105 32297 32086 30114 29887 27798 27562 25406 25164 35207 33322 31225 28969 26609 24197 21785 19419 17137 14973 33718 31659 29430 27086 24681 22265 19886 17585 15395 13344 34667 32713 30563 28269 25888 23471 21069 18724 16474 14350 0,5 0,6 0,7 0,8 0,9 34849 32918 30785 38504 26129 35029 33121 31006 28737 26369 22983 22747 20594 20357 18265 18037 16038 15822 13943 13742 22025 19652 17360 15183 13147 1,0 1,1 1,2 1,3 1,4 12001 11816 10226 10059 08628 08478 07206 07074 05959 05844 11270 09566 08038 06687 05508 11450 09728 08183 06814 05618 04586 03706 02965 02349 01842 12376 10567 08933 07477 06195 05082 04128 03319 02643 02083 12188 10396 08780 07341 06077 04980 04041 03246 02582 02033 1,5 1,6 1,7 1,8 1,9 12952 11092 09405 07895 06562 04491 03626 02898 02294 01797 04879 03955 03174 02522 01984 04780 03871 03103 02463 01936 01506 01160 00885 00668 00499 2,0 2,1 2,2 2,3 2,4 05399 04398 03547 02833 02239 01545 01191 00909 00687 00514 01394 01071 00814 00613 00457 00337 00246 00178 00127 00090 01625 01256 00961 00727 00545 00405 00298 00216 00156 00111 01431 01100 00837 00631 00470 2,5 2,6 2,7 2,8 2,9 01585 01223 00935 00707 00530 00393 00288 00210 00151 00107 01468 01130 00861 00649 00485 00358 00264 00190 00136 00097 01667 01289 00987 00748 00562 00417 00307 00224 00161 00115 01753 01358 01042 00792 00595 00443 00327 00238 00172 00123 00381 00370 00279 00271 00203 00196 00146 00141 00104 00100 3,0 3,1 3,2 3,3 3,4 00348 00254 00184 00132 00094 3,5 3,6 3,7 3,8 3,9 00084 00059 00041 00528 00019 00079 00055 00038 00026 00018 00073 00071 00051 00049 00035 00034 00024 00023 00016 00016 00087 00061 00042 00029 00020 00063 00044 00030 00021 00014 00000 00076 00053 00037 00025 00017 00081 00057 00039 00027 00018 00006 00068 00047 00033 00022 00015 00001 00066 00046 00031 00021 00014 0000о 4,0 00013 00009 00002 00002 00001 23955 21546 19186 16915 14764 12758 10915 09246 07754 06438 05292 04307 03470 02768 02186 01709 01323 01014 00770 00578 00430 00317 00231 00167 00119 23713 21307 18954 16694 14556 12566 10741 09089 07614 06316 05186 04517 03394 02705 02134 39862 39505 38762 37654 36213 34482 32506 30339 28034 25647 23230 20831 18494 16256 14146 22506 20121 17810 15608 13542 11632 09893 08329 06943 05730 04682 03788 03034 02406 01888
ПРИЛОЖВКИ Е Таблица V3E Вторая функция нормированного отклонения Z X~ 1 у (х)— dx О (интегралы вероятностей) 0,0 0,1 0,2 0,3 0,4 00000 03983 07926 11791 15542 19146 22575 25804 28814 31594 00798 04776 08706 12552 16276 01595 05567 09483 13307 17003 02392 06356 10257 14058 17724 03188 07142 11026 14803 18439 21904 25175 28230 31057 33646 03586 07535 11409 15173 18793 22240 25490 28524 31327 33891 0,5 0,6 0,7 0,8 0,9 19847 23237 26424 29389 32121 20540 23891 27035 29955 32639 35083 37286 39251 40988 42507 43822 44950 45907 46712 47381 21226 24537 27637 30511 33147 1,0 1,1 1,2 1,3 1,4 34614 36864 38877 40658 42220 43574 44738 45728 46562 47257 35993 36214 38100 38298 39973 40147 41621 41774 43056 43189 1,5 1,6 1,7 1,8 1,9 44408 45449 46327 47062 47670 48169 48574 48899 49158 49361 2,0 2,1 2,2 2,3 2,4 47932 48382 48745 49036 49266 49446 49585 49693 49774 49836 49882 49916 49940 49958 4997) 47831 48300 48679 48983 49224 49413 49560 49674 49760 49825 49874 49910 49936 49955 49969 48077 48500 48840 49111 49324 49492 49621 49720 49795 49851 49893 49924 49946 59962 49974 2,5 2,6 2,7 2,8 2,9 49430 49573 49683 49767 49831 49878 49913 49938 49957 49970 49520 49643 49736 49807 49861 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 49900 49929 49950 49965 49976 49977 49984 49989 49993 49995 49978 49985 49990 49993 49995 49998 49978 49985 49990 49993 49996 49999 49979 49986 49990 49994 49996 49999 49980 49986 49991 49994 49996 49999 49981 49987 49991 49994 49996 49981 49982 49987 49988 49992 49992 49994 49995 49996 40996 49983 49983 49988 49989 49992 49992 49995 49995 49997 49997 4,0 49998 34134 36433 38493 40320 41924 43319 44520 45543 46407 47128 47725 48214 48610 48928 49180 49379 49534 49653 49744 49813 49865 49903 49931 49952 49966 00399 04380 08317 12172 15910 19497 22907 26115 29103 31859 34375 36650 38686 40490 42073 43448 44630 45637 46485 47193 47778 48257 48645 48956 49202 49396 49547 49664 49752 49819 49869 49906 49934 49953 49968 01197 05172 09095 12930 16640 20194 23565 26730 29673 32381 34850 37076 39065 40824 42364 43699 44845 45818 46638 47320 47882 . 48341 48713 49010 49245 01994 05962 09871 13683 17364 20884 24215 27337 30234 32894 35314 37403 39435 41149 42647 43943 45053 45994 46784 47441 47982 48422 48778 49061 49286 49461 49598 49702 49781 49841 49886 49918 49942 49960 49972 35543 37698 39617 41308 42786 <4062 45154 46080 46856 47500 48030 48461 48809 49086 49305 49477 49609 49711 49788 49846 49889 49921 49944 49961 49973 02790 06749 10642 14431 18082 21566 24857 27935 30785 33398 35769 37900 39796 41466 42922 44179 45254 46164 46926 47558 44295 45352 46246 46995 47615 48124 48537 48870 49134 49343 49506 49632 49728 49801 49856 49896 49926 49948 49964 49975
ПРИЛОЖЕНИЕ 341' Табл ица ЧИ3Относительные частоты распределения редких событийr axе- Эr х! 0,1 0,3 0,5 0,8 0,4 0,6 0,7 0,9 1,0 0,2 67032 26813 05363 007!5 00072 00006 60653 30327 07582 01264 00158 00016 00001 74082 22224 03334 ООЗЗЗ 00025 00002 81873 16375 01637 00109 00006 54881 32929 09879 01976 00296 00036 00004 90484 09048 00452 00015 1,5 1,7 1,6 1,4 1,3 1,8 1,9 1,2 2,0 2,4 2,6 2,3 :3,О 2,9 2,5 2,1 2,2 0 1 2 3 4 5 6 7 8 9 10 11 0 1 2 3 4 5 6 7 8 9 10 11 12 13 33287 36616 20!39 07384 02031 00447 00082 00013 00002 12246 25716 27002 18901 09923 04168 01459 00438 00115 00027 00006 00001 30119 36143 21686 08674 02602 00625 00125 00021 00003 11080 24377 26814 19644 10865 04759 01745 00548 00151 00037 00008 00002 27253 35429 23029 09979 03243 00843 00183 00034 00006 00001 10026 23060 26518 20831 11690 05378 02061 00677 00195 00050 00011 00002 24660 34524 24166 11278 03947 01105 00258 00052 00009 00001 09072 21772 26127 20901 12541 0602о 02408 008'26 00248 00066 00<'16 00004 00001 22313 33470 25102 12551 04707 01412 00353 ОС076 00014 00002 08208 20521 25652 21376 13360 06680 02783 00994 00311 00086 00022 00005 00001 20190 32303 25842 13783 055)3 01764 00470 00108 00022 00004 00001 07427 19311 25101 21757 '14142 07354 03187 0)184 00385 00111 00029 000о7 00002 49658 34761 12166 02839 00497 00070 00008 00001 18268 31056 26398 14959 06358 02162 00612 00149 00032 00006 00001 06721 18146 24496 22047 14882 08036 03616 01395 00471 00141 00038 00008 О0СО2 44933 35946 14378 03834 00767 00123 00016 00002 16530 29754 2б778 16067 07230 02603 00781 00201 00045 00009 00002 06081 17027 23838 22248 15574 08721 04070 01628 00570 00177 00050 00013 00003 00001 40657 3659 ~ 16466 04940 01112 00200 00030 00004 14957 28418 26997 17098 08122 03086 00977 00265 00063 00013 00002 05502 15957 23137 22366 16215 09405 04546 01883 00683 О 220 00064 00017 С0004 00001 36788 36788 19394 06131 01533 00307 0005~ 00007 00001 13534 27067 27067 18045 09022 03609 01203 00344 00086 00019 00004 00001 04979 14936 22404 22404 16803 10082 05041 02160 00810 00270 00081 00022 00006 00001 О 1 2 3 4 5 6 7 8 9 10 11 0 1 2 3 4 5 6 7 8 9 10 11 /PAP ° 12 13
ПРИЛОЖЕНИЕ 342 VIII Продолжение табл. 3,4 3,5 3,6 З,З 3,2 3,1 3,7 3,8 3,9 4,0 03020 02732 10569 О9836 18496 17706 21578 21247 18881 19122 02472 02237 02024 01832 09148 08501 07894 07326 16923 16!52 15394 14652 20872 20459 20012 19537 19307 19436 19512 19537 04505 04076 13965 13044 21966 20870 22368 22262 17335 17809 12029 12636 13217 13768 06616 07160 07710 08261 03119 03478 03855 04248 01286 01478 01686 01912 00472 00588 00656 00765 14287 14771 15219 15629 08810 09355 09892 10420 04657 05078 05512 05954 02154 02412 02687 02977 00885 01018 01164 01323 10748 11398 05553 06079 02459 02779 00953 01112 00328 00395 00156 00190 00230 ОР275 00047 00059 00073 00090 00013 00017 00021 00027 00003 00004 OJ006 00008 00001 00001 00001 00002 00328 00387 00454 00529 00110 00134 00161 00192 00034 00042 00052 00064 00010 00012 00016 00020 00003 00003 00004 00006 15 15 00001 00001 00001 00002 4,5 4,1 4,6 4,7 4,2 4,8 4,9 5,0 4,4 4,3 00910 00823 00745 04275 03950 03649 10046 09481 08940 15738 15169 14601 18492 182ОЗ 17887 01357 01228 01111 05834 05402 04999 12544 11884 11248 17980 17430 16872 19328 19174 18981 01657 01500 06795 06298 13929 13226 19037 18516 19513 19442 01005 04624 10635 16307 18753 00674 03369 08422 14037 17547 16000 16332 10934 11432 06404 06859 03282 03601 01495 01680 16622 16873 17083 11913 12373 12812 07318 07778 08236 03933 04278 04633 01879 02091 02316 00613 00706 00228 00270 00078 00094 00025 00030 РРРР7 00009 01318 01472 01637 00563 00642 00(29 03221 00257 00298 00080 00095 00112 00027 00032 00039 00808 00920 01042 00316 00368 00426 00113 00135 00160 00037 00046 00055 00012 00014 00018 15 16 17 00003 00001 00003 00004 00005 00001 00001 00002 00007 00002 00002 10 11 12 13 14 10 11 12 13 14 15 16 17 00102 00029 00007 00002 00126 00037 00010 00002 00001 03688 12171 20083 22091 18225 03337 11347 19290 21862 18582 17252 13227 08692 04998 02555 01175 00491 00188 00067 00022 17383 17475 17529 13617 13980 14315 09143 09586 10021 05371 05752 06138 02805 03068 03342 00008 00010 00013 00002 00003 00004 00001 00001 00001 17547 14622 10444 06528 03627 01813 00824 00343 00132 00047 03016 00005 00001 10 !1 12 13 14 10 11 12 13 14
ПРИЛОЖЕНИЕ Окончание табл. 11,0 12,0 14,0 8,0 10,0 6,0 13,0 15,0 9,0 7,0 00004 00002 00001 00034 00012 00248 00091 00268 00111 01074 00500 02863 01499 05725 03374 09160 06073 00045 00018 00007 00227 00101 00044 00757 00370 00177 01892 01019 00531 03783 02242 01274 12214 09109 13959 11712 13959 13176 12408 13176 09926 11858 р411р 02548 06458 04368 08879 01552 10853 08731 11938 10484 11937 11437 10943 11437 09260 10557 07275 09049 05335 07239 07219 09702 04813 07276 02962 05038 01692 03238 00903 01943 03668 05429 02373 03832 01450 02555 00840 01614 00462 00968 00451 01093 00212 00579 00094 00289 00040 00137 00016 ОС062 00089 00242 00553 00040 00121 00302 00018 00058 00158 00007 00026 00079 00003 00012 00038 00001 00001 00001 8 9 10 11 12 13 14 15 16 17 18 19 20 2) 22 23 24 25 26 27 28 29 30 31 32 33 34 01487 04462 08924 13385 16062 ]6062 13768 10326 06884 04130 02253 01126 С0520 00223 00089 00033 00012 00004 00001 00638 02234 05213 09123 12772 14900 14900 13038 10140 07098 04517 02635 01419 00709 00331 00145 00060 00023 00008 00003 00006 00002 00001 00026 00011 00004 00002 00001 06306 09008 11260 12511 12511 11374 09478 07291 05208 03472 02170 01276 00709 00373 00187 00005 0()002 00001 00017 00008 00003 00001 00003 00001 00019 00008 00083 00038 00269 00)33 00699 00373 01515 00870 02814 01739 04573 03044 06605 04734 08587 06628 10148 08436 10994 09842 10994 10599 10209 10599 08848 09892 07189 08656 05497 07128 03970 05544 02716 04085 01766 02860 01093 01906 00646 01213 00365 00738 00198 00431 00103 00241 00051 00130 00025 00067 00012 00034 00005 00016 00002 00008 00003 00002 00001 00003 00017 00064 00194 00484 01037 01944 03241 04861 06629 08285 0956) 10244 10244 09603 08474 07061 05575 04181 02986 02036 01328 00830 00498 00287 00160 00OS6 00044 00022 00011 00005 00002 00001 6 7 8 9 10 11 12 13 14 15 16 1i 18 19 20 21 22 23 24 25 26 27 28 29 30 3) 32 33 34
ПРИЛОЖЕНИЕ Стандартные отношения,степеням вероятности достоверногопри степенях свободы соответствующие трем 7 8 9 10 11 12 2 3 4 5 4 5 G 7 8 9 10 11 12 1 2 167,534,110,174,121,27,747,016,36,635,5 13,4 6,029,212,35,625,411,35,322.910,65,121,0 10,0 5,019,79,74,818,69,34,8 17,8 9,14,717,18,94,61G,68.74,5 16,1 8,54,5 15,7 8,44,515,48,34,4 148,530,89,6 61,2 18,86,936,6 !3,3 5,827,0]0,95,1 21,7 9.64,718,58.74,616,48,04,314,97,94,113,87,24,012,36,93,9 12,3 6,73,811,86,53,711,36,43,711,06,23,610,76,13,610,46,03,5 141,1 29,5 9,356,1 16,7 Ь,б33,212,15,423,79,84,818,88,54,415,87,64,113,97,03,612,36,63,711,66,23,610,86,03,510,25,73,49,75.63,39,35,43,39,05,33,28,75,23,28,55,13,2 137,128,79,153,416,06,431,11l,45,221,99,24,517,27,94,114,47,03,812,66,43,611,36,03,510,45,73,49,65,43,39,15,23,28,65,03,18,34,93,17,94,83,07,74,73,07,54,62,9 134,628,29,051,715,56,329,811,05,120,88,84,416,27,54,013,56,63,711,76,13,5 10,5 5,63,39,65,33,28,95,13,18,44,93,07,94,73,07,64,62,97,34,42,97,04,32,86,84,22,8 132,927,98,950,515,26,228,810,75,020,08,54,3 15,5 7,23,912,96,43,6 11,1 5,83,49,95,43,29,15,13,18,44,83,07,94,62,97,44,52,97,14,32,86,84,22,76,64,12,76,44,02,7 131,827,78,949,815,06,128,210,54,919,58,34,215,17,03,8.12,56,23,510,85,63,39,65,23,18.84.93,08,14,72,97,64,42,87,14,32,86,84,12,76,54,0 2,7 6,33,92,66,13,82,6 130,627,58,849,014,86,0 27.6 10,34,819,08,14,l14,66,83,712,06,03,410,45,53,29,25,13,18,44,73,07,74,52,97,24,32,86,8 '4,12,76,54,02,66,23,92,66,03,82,65,83,72,5 130,027,48,848,614,76,027,310,24,818,88,04,114,46,73,711,85,93,410,25,43,29,05,03,08,24,62,97,54,42,87,04,2'2,,7б,64,02,76,33,92,66,13,82,55,83,72,55,63,62,7 129,527,28,848,214,76,027,010,14,718,57,94,114,26,63,611,65,83,310,05,33,18,94,93,08,04,52,97,44,3. 2,8>,94,'1 2,7 6,53,92,66,23,82,65,93,72,55,73,62,55,53,52,4 128,9 ~7,1 8,8 47,8 14,5 59 26,7 10,0 4,7 18, ~ 7,8 4,0 13,9 6,5 3,6 11,4 5,7 3,1 9,8 5,2 3,1 8,7 4,8 2,9 7,8 4,5 2,8 7,2 4,2 2,7 6,7 4,0 2,6 6,3 3,9 2,6 6,0 3,7 2,5 5,8 3,6 2,5 5,5 3,5 2,4 5,3 3,4 2,4 128,3 27 1 8,7 47,4 14,4 5,9 26 4 9,9 4,7 18,0 7,7 4,0 13,7 6,5 3,6 11,2 5,7 3,3 9,6 5,1 3,1 8,5 4,7 2,9 7,6 4,4 2,8 7,0 4,2 2,7 6,5 4,0 2,6 6,1 3,8 2,5 5,8 3,7 2,5 5,6 3,5 2,4 5,3 3,5 2,4 5,1 3.4 2,3
пРило)КЕниЕ Таблица !Х аевиат (квадратов сигм), различия разнообразия: Р1= 0,95, Р~= 0,99, ДЛЯ 01 И Чр ДЛЯ 2 2 Рз= 0,999 20 100 200 500 30 40 50 75 14 16 12,9 10 12 14 15 3,0 2,1 4,0 2,9 2,1 4,0 2,9 2,1 16 17 3,9 18 2,9 2,1 14 16 20 24 30 40 75 200 500 127,726,98,747,014,25,926,19,84,617,77,64,013,56,43,511.05,63,29,45,03,08,34,62,97,44,32,76,84,12,66Д3,92,65.93,72,55,63.62,45,43,52,45,13.42,35,03,$2,3 127,1 26,8 8,7 46,6 14,1 5,8 25,8 9,7 4,6 17,5 7,5 3,9 13,2 9,3 3,5 10,8 5,5 3,2 9,2 4,9 3,0 8,1 4,5 .2,8 7,3 4,2 2,7 6,7 4,0 2,6 6,2 3,8 2,5 5,8 3,6 2,4 5,5 3,5 2,4 5,3 3,4 . 2,3 5,0 3,3 2,3 4,8 3,2 2,2 126,5 26,7 8,7 46,2 l4,0 5,8 25,4 9.6 4,6 17,2 7,4 3,9 13,0 6,2 3,4 10,5 5,4 3,2 8,9 4,8 2,9 7,8 4,4 2,8 7,1 4,1 2,7 6,5 3,9 2,5 6,0 3,7 2,5 5.6 3,5 2,4 5,3 3,4 2,3 5,1 3.3 2,3 4.8 3,2 2,2 4,7 3,1 2,2 l25.9 26,6 8,6 45,8 13,9 5,8 25,1 9,5 4,5 16,9 7,3 3,8 12,7 6,1 3,4 10,3 '5,3 3,1 8,7 4,7 2,9 7,6 4,3 2,7 6,9 4,0 2,6 6,3 3.8 2,5 5,8 3,6 2,4 5,4 3,4 2,4 5,1 3,3 2,3 4,9 32 2,2 4,6 3,1 2,Z 4,5 3,0 2.1 125,626,58,645,613,85,724,99,44,516,87,23,812,66,03,410,25,23,18,64.62,97,54,32,76,83,92,66,23,72,55,73,52,45,33.32,35.03,22,34,83,12,24,53,02,24,42,9а,1 125,3 26,4 8,6 45,4 !3,7 5,7 24,8 9,3 4,5 16,b 7,1 3,8 12,5 5,9 3,3 l0,1 5,1 3,1 8,5 4.6 2,8 7,4 4,2 2,7 6,7 3,9 2.5 6,1 3,6 2,4 5,6 3,4 2,3 5,2 3,3 2,3 4.9 3,~ 2,2 4,7 3,0 2,2 4,4 2,9 2,1 4,3 2,8 2,1 125,026,48,645,213,75,724,69,24,416,57,13.812,35,93,310,05,13,08,44,52,87,34,12,66.63,82,56.03,62,45,53,42,35.13 'Р2,24.83.12,24,63,02,14,32,92,14,22,82,0 124,7 26,3 8,6 45,0 13,6 5,7 24,5 9,1 4,4 16,4 7,0 3,7 12,2 5,~ 3,3 9,9 5,0 3,0 8,3 4,5 2,8 7,2 4,1 2,6 6,5 37 2,5 5,9 3,5 2,4 5,4 3,3 2,3 5,0 3,1 2,2 4,7 3,0 2,2 4,5 2,9 2,1 4,3 2,8 2,0 4,1 2,7 2,0 124,4 26,2 8,6 44,7 13,5 5,7 24,3 9,1 4,4 16,2 7,0 3,7 12 1 5,8 3,3 9,7 5,0 3,0 8,1 4,4 2,8 7,1 4,0 2,6 6,3 3,7 2,5 5,7 3,5 2,4 5,3 3,3 2,3 4,9 3,1 2,2 4,6 3,0 2,1 4,4 2,9 2,1 4,2 2,8 2,0 4,0 2,7 2,0 124, 1'Р6,28,544,513,55,724,19,14,416,16,93,712,05,73,39,64,93,08,04,42,77,04,02,66,23,2,45,63,42,35,23,22,24,83,12,24,52,92,14,32,82,04,12,72,03,92,61,9 123,8 26,1 8,5 44,3 13,5 5,6 24,0 9,0 4,4 15,9 6,9 3,7 11,8 5,7 3,2 9,5 4,9 2,9 7,9 4,3 2,7 6,9 3,9 2,6 6,1 ~,6 2,4 5,Ь 3,4 2,3 5,1 3,2 2,2 4,7 3,0 2,1 4,4 2,9 2,1 4,2 2,8 2,0 4,0 2,7 2,0 3,8 2,6 1,9 !23,5 26,1 8,5 44,1 13,5 5,6 23,8 9,0 4,4 15,8 6,Ч 3,7 11,7 5,7 3,2 9,4 4,9 2,9 7,8 4,3 2,7 6,8 3,9 2,5 6,0 3,6 2,4 5,4 3,4 2,3 5,0 3,2 2,2 4,6 2,1 4,3 2,9 2,1 ' 4,1 2,8 2,0 3,9 2,7 2,0 3,7 2,~ 1,9 5,8 3,2 8,6 4,6 2,8 6,9 4,0 2,6 6,0 3,7 2,4 5,3 3,5 2,4 5,0 3,4 2,3 4,8 3,3 2,3 4,6 3,2 2,2 4,4 3,1 2,2 4,3 3,1 22 4.~ 3,0 2,2 4,1 3,0 2,1 4,1
ПРИЛО)КЕНИЕ 6 7 8 9 1 2 3 4 5 10 11 12 20 21 23 24 25 26 27 '3,0 7,2 4,6 28 2,9 7,1 4,5 2,9 7,1 29 4,5 ° 2,9 7,0 4,5 2,9 7,0 4,4 2,9 6,9 4,4 2,9 6,8 4,3 2,8 6,7 4,3 2,8 30 32 36 38 40 10 11 12 4 5 6 7 8 9 15,1 8,2 4,4 14,8 8,1 4,3 14,6 8,0 4,3 14,4 4,3 14,2 7,9 4,3 14,0 7,8 4,3 13,9 7,8 4,2 13,7 7,7 4,2 13,6 7,7 4 2 13,5 7,6 4,2 13,4 7,6 4,2 13,3 7,6 4,2 13,2 7,5 4,1 13,1 7,4 4,1 ]3,0 7,4 4,1 12,9 7,3 4,1 12,8 7,3 4,1 10,2 5,9 3,5 10,0 5,8 3,5 9,8 5,8 3,5 9,6 5,7 3,4 9,5 5,7 3,4 9,3 5,6 3,4 9,2 5,6 3,4 9,1 5,5 3,4 9,0 5,5 3,3 8,9 5,4 3,3 8;9 5,4 3,3 8,8 5,4 3,3 8,7 5,3 3,3 8,6 5,3 3,3 8,6 5,2 3,3 8,5 5,2 3,2 8,4 5,2 3,2 8,3 5,0 3,1 8,1 4,9 3,1 7,9 4,9 3,1 7,8 4,8 3,0 7,7 4,8 3,0 7,6 4,7 3,0 7,5 4,7 3,0 7,4 4,6 3,0 7,3 4,6 7,3 4,5 2,9 7,1 4,4 2,9 7,0 4,4 2,8 6,8 4,3 2,8 6,7 4,3 2,8 6,6 4,2 2,8 6,5 4,2 2,8 6,4 4,1 2,7 6,3 4,1 2,7 6,3 4,1 2,7 6,2 4,0 2,7 6,1 4,0 2,7 6,0 4,0 2,7 6,0 3,9 2,6 5,9 3,9 2,6 5,8 3,9 2,6 5,8 3,8 2,6 6,6 4,2 2,7 6,5 4,1 2,7 6,3 4,0 2,7 6,2 4,0 2,7 6,1 4,0 2,6 6,0 3,9 2,6 5,9 3,9 2,6 5,8 3,8 2,6 5,7 3,8 2,6 5,7 3,8 2,6 5,6 3,7 2,5 5,5 3,7 2,5 5,4 3,7 2,5 5,4 3,6 2,5 5,3 3,6 2,5 5,3 3,5 2,5 5,2 3,5 2,4 6,2 3,9 2,6 6,0 3,9 2,6 5,9 3,8 2,6 5,8 3,8 2,6 5,6 3,7 2,5 5,6 3,7 2,5 5,5 3,6 2,5 5,4 3,6 2,5 5,3 3,6 2,5 5,2 3,5 2,4 5,2 3,5 2,4 5,1 3,5 2,4 5,0 3,4 2,4 5,0 3,4 2,4 4,9 3,3 2,4 4,9 3,3 2,3 4,8 3,3 2,3 5,9 3,8 2,5 5,7 3,7 2,5 5,6 3,6 2,5 5,5 3,6 2,5 5,4 3,5 2,4 5,3 3,5 2~4 5,2 3',5 2,4 5,1 3,4 2,4 5,1 3,4 2,4 5,0 3,4 2,4 5,0 3,3 2,3 4,9 3,3 2,3 4,8 3,2 2,3 4,8 3,2 2,3 4,7 3,2 2,3 4,7 3,1 2,3 4,6 3,1 2,2 5,6 3,6 2,5 5,4 3,6 2,4 5,3 3,5 2,4 5,2 3,4 2,4 5,1 3,4 2,4 5,0 3,4 2,4 4,9 3,3 2,3 4,8 3,3 2,3 4,8 3,3 2,3 4,7 3,2 2,3 4,7 3,2 2,3 4,6 3,2 2,3 4,5 3,1 2 2 4,5 3,1 2,2 4,4 3,0 2,2 4,4 3,0 2,2 4,3 3,0 2,2. 5,5 3,5 2,4 5,3 3,4 2,4 5,2 3,4 2,4 5,1 3,3 2,4 5,0 3,3 2,3 4,9 3,2 2,3 4,8 3,2 2,3 4,7 3,2 2,3 4,7 3,1 2,2 4,6 3;1 2,2 4,6 3,1 2,2 4,5 3,1 2,2 4,4 3,0 2,2 4,4 3,0 2,1 4,3 2,9 2,1 4,3 2,9 2,1 4,2 2,9 2,1 5,3 3,4 2,4 5,1 3,4 2,3 5,0 3,3 2,3 4,9 3,3 2,3 4,8 3,2 2,3 4,7 3,2 2,3 4,6 3,1 2,2 4,5 3,1 2,2 4,5 3,1 2,2 4,4 3,0 2,2 4,4 3,0 2,2 4,3 3,0 2,2 4,2 2,9 2,1 4,2 2,9 2,1 4,1 2,9 2,1 4,1 2,8 2,1 4,0 2,8 2,1 5,2 3,4 2,3 5,0 3,3 2,3 4,9 3,2 2,3 4,8 3,2 2,3 4,7 3,1 2,2 4,6 3,1 2,2 4,5 3,0 2,2 4,4 3,0 2,2 4,4 3,0 2,2 4,3 2,9 2,1 4,3 2,9 2,1 4,2 2,9 2,1 4,1 2,9 2,1 4,1 2,8 2,1 4,0 2,8 2,1 4,0 2,7 2,1 3,9 2,7 2,0 5,0 3,3 2,3 4,8 3,2 2,3 4,7 3,2 2,2 4,6 3,1 2,2 4,5 3,1 2,2 4,4 3,0 2,2 4,3 3,0 2,2 4,2 3,0 2,1 4,2 2,9 2,1 4,1 2,9 2,1 4,1 2,9 2,1 4,0 2,8 2,1 3,9 2,8 2,1 3,9 2,8 2,0 3,8 2,7 2,0 3,8 2,7 2,0 3,7 2,7 2,0
ПРИЛОЖЕНИЕ Продолжение 20 16 24 30 40 50 100 75 200 4,1 2,8 2,0 4,0 2,7 19 2,0 3,8 2,6 2,0 3,7 2,6 1,9 3,6 2,5 1,9 3,5 21 22 23' 2,5 1,9 3,5 24 2,4 1,9 3,4 2,4 1,8 3,3 25 26 2,4 27 1,8 3,3 2,3 1,8 3,2 2,3 1,8 3,2 2,3 1,8 3,2 2,2 1,8 3,1 2,2 1,7 3,1 2,2 1,7 3,0 2,1 1,7 3,0 2,1 1,7 28 30 32 34 36 38 14 16 20 50 40 30 24 75 200 500 4,8 3,2 2,3 4,7 3,1 2,2 4,5 3,1 2,2 4,4 3,0 2,2 4,3 3,0 2,1 4,2 2,9 2,1 4,2 2,9 2,1 4,1 2,9 2,1 4,0 2,8 2,1 4,0 2,8 2,1 3,0 2,8 2,0 3,9 2,7 2,0 3,8 2,7 2,0 3,8 2,7 2,0 3,7 2,6 2,0 3,7 2,6 2,0 3,6 2,6 1,9 4,7 3,1 2,2 4,5 3,0 2,2 4,4 3,0 2,1 4,3 2,9 2,1 4,2 2,9 2,1 4,1 2,8 2,1 4,0 2,8 2,1 3,9 2,8 2,0 3,9 2,7 2,0 3,8 2,7 2,0 3,8 2,7 2,0 3,7 2,7 2,0 3,7 2,6 2,0 3,6 2,6 1,9 3,6 2,5 1,9 3,5 2,5 1,9 3,5 2,5 1,9 4,5 3,0 2,1 4,4 2,9 2,1 4,2 2,9 2,1 4,1 2,8 2,1 4,0 2,8 2,0 3,9 2,7 2,0 3,9 2,7 2,0 3,8 2,7 2,0 3,7 2,6 2,0 3,7 2,6 2,0 3,6 2,6 1,9 3,6 2,5 1,9 3,5 2,4 1,9 3,5 2,5 1,9 3,4 2,4 1,9 3,4 2,4 1,9 3,3 2,4 1,8 4,4 2,9 2,1 4,2 2,9 2,1 4,0 2,8 2,0 3,9 2,7 2,0 3,8 2,7 2,0 3,7 2,7 2,5 3,7 2,6 2,0 3,6 2,6 1,9 3,5 2,5 1,9 3,5 2,5 1,9 3,4 2,5 1,9 3,4 2,5 1,9 3,4 2,4 1,9 3,3 2,4 1,8 3,3 2,3 1,8 3,2 2,3 1,8 3,2 2,3 1,8 2,9 2,1 4,1 2,8 2,0 3,9 2.7 2,0 3,8 2,7 2,0 3,7 2,6 2,0 3,6 2,6 1,9 3,6 2,5 1,9 3,5 2,5 1,9 3,4 2,5 ' 1,9 3,4 2,4 1,9 3,3 Р,4 1,8 3,3 2,4 1,8 3,2 2,3 1,8 3,2 2,3 1,8 3,1 2,3 1,8 3,1 2,2 1,8 3,0 2,2 1,7 4,0 2,7 2,0 3,9 2,6 2,0 3,7 2,6 ),9 3,6 2,5 1,9 3,5 2,5 1,9 3,4 2,4 1,9 3,4 2,4 1,8 3,3 2,4 1,8 3,2 2,3 1,8 3,2 2,3 1,8 3,1 2,3 1,8 3,1 2,2 1,8 3,1 2,2 1,7 3,0 2,1 1,7 3,0 2,1 1,7 2,9 2,1 1 2,9 2,0 1,7 3,9 2,6 2,0 3,8 2,6 1,9 3,6 2,5 1,9 3,6 2,5 1,8 3,5 2,4 1,8 3,4 2,4 1,8 3,3 2,3 1,8 3,2 2,3 1,8 3,2 2,2 1,8 3,1 2,2 1,7 3,0 2,2 1,7 3,0 2,2 1,7 3,0 2,1 1,7 2,9 2,1 1,6 2,9 2,0 1,6 2,8 2,0 1,6 2,8 2,0 1,6 3,8 2,6 1,9 3,7 2,5 1,9 3,6 2,5 1,9 3,5 2,4 1,8 3,4 2,4 1,8 3,3 2,3 1 8 3,2 2,3 1,8 3,1 2,2 1,8 3,1 2,2 1,7 3,0 2,2 1,7 2,9 1,7 2,9 2,1 1,7 2,8 2,1 1,7 2,8 2,0 ),6 2,7 2,0 1,6 2,7 2,0 1,6 2,6 1,9 1,6 3,7 2,5 1,9 3,6 2,5 1,9 3,5 2,4 1,8 3,4 2,4 1,8 3,3 2,3 1,8 3,2 2,3 1,8 3,1 2,2 1,7 3,0 2,2 1,7 3,0 2,2 1,7 2,9 2,1 1,7 2,8 2,1 1,7 2,8 2,1 ],7 2,7 2,0 1,6 2,6 2,0 1,6 2,6 l,9 1,6 2,6 1,9 1,6 2,5 1,9 1,5 3,6 2,5 ),9 3,5 2,4 1,8 3,4 2,4 1,8 3,3 2,3 1,8 3,2 2,3 1,8 3,1 2,2 1,7 3,0 2,2 1,7 2,9 2,1 1,7 2,9 2,1 1,7 2,8 2,1 1,7 2,7 2,1 1,6 2,7 2,0 1,6 2,6 '2,0 1,6 2,6 1,9 1,6 2,5 1,9 1,6 2,5 1,9 1,5 2,4 1,8 1,5 3,5 2,5 1,9 3,4 2,4 1,8 3,3 2,4 1,8 3,2 2,3 1,8 3,1 2,3 1,8 3,0 2,2 1,7 2,9 2,2 1,7 2,8 2,1 1,7 2,8 2,~ 1,7 2,7 2,1 1,6 2,6 2,0 1,6 2,6 2,0 1,6 2,5 2,0 1,6 2,5 1,9 1,5 2,4 1,9 1,5 2,4 1,8 l,5 2,3 1,8 1,5 т абл. IX 3,9 2,9 2,1 3,9 2,8 2,1 3,8 2,8 2,1 3,8 2,8 2,1 3,8 2,8 2,1 3,8 3,8 2,1 3,6 2,8 2,1 3,6 2,8 2,1 3,7 2,8 2,1 3,7 2,8 2,1 3,7 2,8 2,0 3,6 2,8 2,0 3,6 2,7 2,0 3,6 2,7 2,0 3,6 2,7 2,0 3,6 2,7 2,0 3,6 2,7 2,0
П РИЛОЩЕН И Е 10 11 12 4 5 6 1 2 12,7 7,3 4,1 42 12,5 7,2 4,1 12,4 7,2 4,0 12,3 7,2 4,0 48 12,2 7,2 4,0 50 12,1 7,1 4,0 55 12,0 7,1 4,0 11,9 7,0 4,0 65 11,6 7,0 4,0 11,6 7,0 4,0 11,5 6,9 3,9 70 80 100 11,4 6,8 3,9 11,3 6,8 3,9 11,2 6,8 3,9 11,0 6,7 3,9 10,9 6,7 3,8 10,8 6,6 3,8 1000 1 2 3 4 5 6 7 8 9 10 11 12 8,3 5,1 3,2 8,2 5,1 3,2 8,1 5,1 3,2 8,1 5,1 3,2 8,0 5,1 3,2 7,9 5,0 3,2 7,8 5,0 3,1 7,7 5,0 3,1 7,6 4,9 3,1 7,5 4,9 3,1 7,4 4,8 3,1 7,4 4,8 3,1 7,3 4,7 3,1 7,2 4,7 3,0 7,1 4,7 3,0 7,0 4,6 3,0 6,9 4,6 3,0 6,7 4,3 2,8 6,6 4,3 2,8 6,5 4,2 2,8 6,4 4,2 2,8 6,4 4,2 2,8 6,3 4,1 2,8 6,2 4,1 2,8 6,1 4,1 2,7 6,0 4,1 2,7 6,0 4,0 2,7 5,9 4,0 2,7 5,8 3,9 2,7 5,7 3,9 2,7 5,6 3,9 2,6 5,6 3,8 2,6 5,5 3,8 2,6 5,4 3,8 2,6 5,7 3,8 2,6 5,6 3,8 2,6 5,6 3,8 2,6 5,5 3,7 2,6 .5,4 3,7 2,6 5,4 3,7 2,5 5,3 3,6 2,5 5,2 3,6 2,5 5,2 3,6 2,5 5,1 3,6 2,5 5,0 3,5 2,5, 5,0 3,5 2,4 4,9 3,4 2,4 4,8 3,4 2,4 4,7 , 3,4 2,4 4,7 3,4 2,4 4,6 3,3 2,4 5,2 3,5 2,4 5,1 3,5 2,4 5,0 3,4 2,4 5,0 3,4 2,4 4,9 3,4 2,4 4,9 3,4 2,4 4,8 3,3 2,4 4,7 3,3 2,4 4,7 3,3 2,3 4,6 3,2 2,3 4,5 3,2 2,3 4,5 3,2 2,3 4,4 3,1 2,3 4,3 3,2 2,3 4,2 3,1 2,2 4,2 3,3 2,2 4,1 3,0 2,2 4,8 3,3 2,3 4,7 3,2 2,3 4,6 3,2 2,3 4,6 3,2 2,3 4,5 3,2 2,3 4,5 3,1 2,3 4,4 3,1 2,2 4,3 3,1 2,2 4,3 3,1 2,2 4,2 3,0 2,2 4,1 3,0 2,2 4,1 2,9 2,2 4,0 2,9 2,2 3,9 2,9 2,1 3,8 2,8 2,1 3,8 3,0 2,1 3,7 2,8 2,1 4,6 3,1 2,2 4,5 3,1 2,2 4,4 3,0 2,2 4,4 3,0 2,2 4,3 3,0 2,2 4,3 3,0 2,2 4,2 2,9 2,2 4,1 2,9 2,1 4,1 2,9 2,1 4,0 2,9 2,1 3,9 2,8 2,1 3,9 2,8 2,1 3,8 2,8 2,1 3,7 2,7 2,0 3,6 2,7 2,0 3,6 2,8 2,0 3,5 2,6 2,0 4,3 3,0 2,2 4,2 2,9 2,2 4,1 2,9 2,1 4,1 2,9 2,1 4,0. 2,9 2,1 4,0 2,8 2,1 3,9 2,8 2,1 3,8 2,8 2,1 3,8 2,8 2,1 3,7 2,7 2,0 3,7 2,7 2,0 3,6 2,6 2,0 3,5 2,6 2,0 3,5 2,6 2,0 3,4 2,5 2,0 3,4 2,7 1,9 3,3 2,5 1,9 4,2 2,9 2,1 4,1 2,8 2,1 4,0 2;8 2,1 4,0 2,8 2,1 3,9 2,8 2,1 3,9 2,7 2,0 3,8 2,7 2,0 3,7 2,7 2,0 3,7 2,7 2,0 3,6 2,6 2,0 3,6 2,6 2,0 3,5 2,6 1,9 3,4 2,5 1,9 3,4 2,5 1,9 3,3 2,5 1,9 3,3 2,5 1,9 3,2 2,4 1,9 4,0 2,8 2,1 3,9 2,7 2,0 3,8 2,7 2,0 3,8 2,7 2,0 3,7 2,7 2,0 3,7 2,7 2,0 3,6 2,6 2,0 3,5 2,6 2,0 3,5 2,6 2,0 3,4 2,5 1,9 3,4 2,5 1,9 3,3 2,5 1,9 3,2 2,4 1,9 3,2 2,4 1,9 3,1 2,4 1,8 3,1 2,4 1,8 3,0 2,3 1,8 3,9 2,7 2,0 3,8 2,7 2,0 3,7 2,7 2,0 3,7 2,6 2,0 3,6 2,6 2,0 3,6 2,6 2,0 3,5 2,6 1,9 3,4 2,5 1,9 3,4 2,5 1,9 3,3 2,5 1,9 3,3 2,4 1,9 3,2 2,4 1,9 3,1 2,4 1,8 3,1 2,3 1,8 3,0 2,3 1,8 3,0 2,3 1,8 2,9 2,2 1,8 3,7 2,6 2,0 3,6 2,6 2,0 3,5 2,6 2,0 3,5 2,6 2,0 3,4 2,6 1,9 3,4 2,5 1,9 3,3 2,5 1,9 3,2 2,5 1,9 3,2 2,4 1,9 3,1 2,4 1,9 3,1 2,4 1,8 3,0 2,3 1,8 2,9 2,3 1,8 2,9 2,3 1,8 2,8 2,2 1,8 2,8 2,3 1,8 2,7 2,2 1,7
ПРИЛОЖВКИE Продолжение т абл. ЦС 20 24 30 40 50 75 100 200 500 16 3,6 2,7 2,0 42 3,5 70 80 125 1000 30 20 14 16 24 75 50 200 100 500 со 3,6 2,5 1,9 3,5 2,5 1,9 3,4 2,5 1,9 3,4 2,5 1,9 3,3 2,5 1,9 3,3 2,4 1,9 3,2 2,4 1,9 3,1 2,4 1,8 3,1 2,3 1,8 3,0 2,3 1;8 3,0 2,3 1,8 2,9 2,2 1,8 2,8 2,2 1,8 2,8 2,2 1,7 2,7 2,1 1,7 2,7 2,2 1,7 2,6 2,1 1,7 3,4 2,5 1,9 3,4 2,4 1,9 3,3 2,4 1,9 3,3 2,4 1,9 3,2 2,4 1,8 3,2 2,3 1,8 3,1 2,3 1,8 3,0 2,3 1,8 3,0 2,3 1,8 2,9 2,2 1,8 2,8 2,2 1,7 2,8 2,1 1,7 2,7 2,1 1,7 2,6 2,1 1,7 2,5 2,0 1,7 2,5 2,1 1,6 2,4 2,0 1,6 3,3 2,3 1,8 3,2 2,3 1,8 3,1 2,3 1,8 3,1 2,3 1,8 3,0 2,3 1,8 3,0 2,2 1,8 2,9 2,2 1,7 2,8 2,2 1,7 2,8 2,1 1,7 2,7 2,1 1,7 2,7 2,1 1,7 2,6 2,0 1,6 2,5 2,0 1,6 2,5 2,0 1,6 2,4 1,9 1,6 2,4 2,0 1,6 2,3 1,9 1,6 3,1 2,3 1,8 3,1 2,2 1,8 3,0 2,2 1,7 3,0 2,2 1,7 2,9 2,2 1,7 2,9 2,1 1,7 2,8 2,1 1,7 2,7 2,1 1,7 2,7 2,1 l,7 2,6 2,0 1,6 2,5 2,0 1,6 2,5 1,9 1,6 2,4 1,9 1,6 2,3 1,9 1,6 2,2 1,8 1,5 2,2 1,9 1,5 2,1 1,8 1,5 3,0 2,2 1,7 2,9 2,1 1,7 2,8 2,1 1,7 2,8 2,1 1,7 2,7 2,1 1,7 2,7 2,1 1,7 2,6 2,0 1,6 2,5 2,0 1,6 2,5 2,0 1,6 2,4 1,9 1,6 2,4 1,9 1,6 2,3 1,8 1,5 2,2 1,8 1,5 2,2 1,8 1,5 2,1 1,7 1,5 2,1 1,8 1,5 2,0 1,7 1,5 2,9 2,1 1,7 2,9 2,1 1,7 2,8 2,0 1,5 2,8 2,0 1,6 2,7 2,0 1,6 2,7 2,0 1,6 2,6 1,9 1,6 2,5 1,9 1,6 2,5 1,9 1,6 2,4 1,8 1,5 2,3 1,8 1,5 2,3 1,7 1,5 2,2 1,7 1,5 2,1 1,7 1,4 2,0 1,6 1,4 2,0 1,7 1,4 1,9 1,6 1,4 2,8 2,0 1,6 2,8 2,0 1,6 2,7 2,0 1,6 2,7 2,0 1,6 2,6 1,9 1,6 2,6 1,9 1,6 2,5 1,9 1,6 2,4 1,8 1,5 2,3 1,8 1,5 2,3 1,8 1,5 2,2 1,7 1,5 2,1 1,7 1,4 2,0 1,7 1,4 1,9 1,6 1,4 1,9 1,6 1,4 1,8 1,6 1,4 1,7 1,5 1,3 2,7 1,9 1,6 2,7 1,9 1,6 2,6 1,9 1,6 2,6 1,9 1,6 2,5 1,9 1,5 2,5 1,8 1,5 2,4 1,8 1,5 2,3 1,8 1,5 2,2 1,7 1,5 2,2 1,7 1,4 2,1 1,6 1,4 2,0 1,6 1,4 1,9 1,6 1,4 1,8 1,5 1,3 1,8 1,5 1,3 1,7 1,5 1,3 1,6 1,4 1,3 2,6 1,9 1,6 2,5 1,9 1,6 2,4 1,9 1,5 2,4 1,8 1,5 2,3 1,8 1,5 2,3 1,8 1,5 2,2 1,7 1,5 2,1 1,7 1,5 2,1 1,7 1,4 2,0 1,6 1,4 1,9 1,6 1,4 1,9 1,5 1,4 1,8 1,5 1,3 1,7 1,5 1,3 1,6 1,4 1,3 1,6 1,4 1,3 1,5 1,4 1,2 2,4 1,8 1,5 2,4 1,8 1,5 2,3 1,8 1,5 2,3 1,8 1,5 2,2 1,8 1,5 2,2 1,7 1,5 2,1 1,7 1,4 2,0 1,6 1,4 2,0 1,6 1,4 1,9 1,6 1,4 1,8 1,5 1,3 1,8 1,5 1,3 1,7 1,4 1,3 1,6 1,4 1,3 1,5 1,3 1,2 1,5 1,4 1,2 1,4 1,2 1,2 2,4 1,8 1,5 2,3 1,8 1,5 2,2 1,8 1,5 2,2 1,7 1,5 2,1 1,7 1,5 2,1 1,7 1,4 2,0 1,6 1,4 1,9 1,6 1,4 1,8 1,6 1,4 1,8 1,5 1,3 1,7 1,5 1,3 1,6 1,4 1,3 1,5 1,4 1,2 1,4 1,3 1,2 1,4 1,2 1,2 1,3 1,2 1,1 ,1,2 1,1 1,1 2,3 1,8 1,5 2,2 1,7 1,5 2,1 1,7 1,5 2,1 1,7 1,4 2,0 1,7 1,4 2.0 1,6 1,4 1,9 1,6 1,4 1,8 1,6 1,4 1,7 1,5 1,3 1,7 1,5 1,3 1,6 1,4 1,3 1,5 1,4 1,2 1,4 1,3 1,2 1,3 1,3 1,2 1,3 1,2 1,1 1,2 1,1 1,1 1,1 1,0 1,0 2,7 2,0 3,5 2,7 2,0 3,5 2,7 2,0 3,5 2,7 2,0 3,5 2,7 2,0 3,4 2,7 2,0 3,4 2,6 2,0 3,4 2,6 2,0 3,4 2,6 2,0 3,4 2,6 2,0 3,4 2,6 2,0 3,4 2,6 2,0 3,3 2,6 2,0 3,3 2,6 2,0 3,3 2,6 2,0 3,3 2,6 2,0
ПРИЛОЩЕИЯЕ 350 Таблица ХЗначения критерия t для трех степеней вероятности(P)= 0,95, Рз= 0,99, Ра= 0,999}~ — число стекленей свободы 4~ ' ~~ ~ ~ Та блица Х1 Значения критерия /~ для трех степеней вероятности(Р~= 0,95, Р2= 0,99, P~ — — 0,999)~ — число степеней свободы 2 И 2ХЗ ° 7/2 2/3 9 /3 2~2 '2/) 2Х1 29 30 32 34 36 38 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 3,9 13,8 7,8 9,5 11,1 12,6 14,1 15,5 16,9 18,3 19,7 21,0 22,4 23,7 25,0 26,3 27,6- 6,6 9,2 11,3 13,3 15,1 16,8 18,5 20,1 21,7 23,2 24,7 26,2 27,7 29,1 30,6 32,0 33,4 10,8 13,8 16,3 18,5 20,5 22,5 24,3 «6,l 27,9 29,6 31,3 32,9 34,5 36,1 37,~ 39,3 40,8 18 19 20 21 22 23 24 25 26 27 28 28,9 30,1 31,4 32,7 33,9 35,2 36,4 37,7 38,9 40,1 41,3 42, ~~ 43,8 46,2 48,6 51,0 53,4 34,8 ЗГ,2 3',6 38,9 40,3 41,6 43,0 44,3 45,6 47,0 48,3 49,6 50,9 53,5 56,0 58,6 61,1 42,3 43,8 45,3 46,8 48,3 49,7 51,2 52,6 54,1 55,5 56,9 58,3 59,7 62,4 65,2 67,9 70,7 40 42 44 46 48 50 55 60 65 /О 75 S0 85 90 95 100 55,8 58,1 60,5 62,8 65,2 67,5 73,3 79,1 S9,8 90,5 96,2 )01,9 107,5 113,1 118,7 124,3 63,7 66,2 68,7 71,2 73,7 76,2 82,3 88,4 94,4 100,4 1Со,4 112,3 118,2 124,1 130,0 135,8 73,4 76,1 78,7 81, 1 84,0 86,7 93,2 99,6 106,0 112,3 118,:> 124,8 131,0 137,1 143,3 149,4
ПРИЛОЖЕНИЕ Табл ица выборочного (л = —, + 3) Х1! Ря 0т е Рз-0~999 Р, 0,95 р.= 0 99 РЗ — 0Ъ999 Р, 0,99 Рэ=0Ж~ Р,=0,95 t =1,96 Р, =0,95 t,=1,96 t,=3,30 1,= 2,58 ta= 2,58 э'з — — 3,30 t =1,96 t,=2,58 эз - — 3,30 108903 27228 40 31 32 66503 16628 7392 68 109 102 61 11 16 38407 9603 4269 О! 38 02 63 60 62 63 16 10 36 12103 33 96 15 03 10 34 6809 56 53 4159 2263 2403 1539 64 65 90 85 109 15 04 05 32 35 14 30 28 36 1850 3028 50 06 1069 07 787 66 80 37 47 2225 1360 1042 67 75 27 38 39 1704 68 71 08 09 26 42 824 1347 661 108> 548 896 462 754 477 69 70 67 24 40 10 383 11 317 12 267 40 64 23 41 71 38 60 22 42 72 07 36 22~8 196 21 43 392 337 295 73 16 15 15 13 640 550 20 44 74 10 14 33 3 7 19 45 15 75 481 31 10 46 259 151 14 76 10 422 30 16 47 17 133 228 373 204 332 77 29 18 14 45 48 78 llg 107 13 43 27 18 17 49 9 13 9 12 79 183 165 297 26 41 16 19 97 50 80 25 39 270 16 20 51 12 87 80 37 15 81 24 21 52 23 15 82 83 22 73 11 10 34 14 22 21 23 54 68 84 33 14 24 85 5 7 10 7 10 62 20 32 13 25 57 56 13 20 86 26 30 29 53 27 12 87 57 58 19 49 28 29 30 28 18 46 89 78 27 59 125 18 73 117 6 8 90 43 26 17 60 Количество пар знайений, достаточное для достоверности коэффициента корреляции (г), при трех степенях вероятности 149 242 136 211 124 202 114 185 105 170 97 157 90 145 83 135 25 24 23 22 21 14 20 13 20 13 19 12 18 12 18 11 17 11 16
352 ПРИЛОЖЕНИЕ Таблкца Х1И Угол y=arcsiri 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 2 3 ф 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 0 1,81 2,56 3,14 3,63 4,05 4,44 4,80 5,13 5,44 5,74 8,13 9,98 11,54 12,92 14,18 15,34 16,43 17,46 18,44 19,37 20,27 21,13 21,97 22,79 23,58 24,35 25,10 25,84 26,56, 27,28 27,97 28,66 29,33 30,00 30,66 31,31 31,95 32,58 0,57 1,90 2,63 3,19 3,67 4,09 4,48 4,83 5,16 5,47 6,02 8,33 10, l4 11,68 13,05 14,30 15,45 16',54 17,56 18,53 19,46 20,36 21,22 22,06 22,87 23,66 24,43 25,18 25,9 2 26,64 27,35 28,04 28,73 29,40 30,07 30,72 31,37 32,01 32,65 0,81 l,99 2,69 3,24 3,72 4,13 4,52 4,87 5,20 5,50 6,29 8,53 10,31 11,83 13,18 14,42 15,56 16,64 17,66 18,63 19,55 20,44 21,30 22,14 22,95 23,73 24,50 25,25 25,99 26,71 27,42 28,11 28,79 29,47 30,13 30,79 31,44 32,08 32,71 0,99 2,07 2,75 3,29 3,76 4,17 4,55 4,90 5,23 5,53 6,55 8,72 10,47 11,97 13,31 14,54 15,68 16,74 17,76 18,72 19,64 20,53 21,39 22,22 23,03 23,81 24,58 25,33 26,06 26,78 27,49 28,18 28,86 29,53 30,20 30,85 31,50 32,14 32,77 1,15 2,14 2,81 3,34 3,80 4,21 4,59 4,93 5,26 5,56 6,80 8,91 10,63 12,11 13,44 14,65 15,79 16,85 17,85 18,81 19,73 20,62 21,47 22,30 23,11 23,89 24,65 25,40 26,13 26,85 27,56 28,25 28,93 29,60 30,26 30,92 31,56 32,20 32,83 1,28 2,23 ~,87 3,39 3,85 4,25 4,62 4,97 5,29 5,59 7;04 9,10 10,78 12,25 13,56 14,77 15,89 16,95 17,95 18,91 19,82 20,70 21,56 22,38 23,19 23,97 24,73 25,48 26,21 26,92 27,63 28,32 29,00 29,67 30,33 30,98 31,63 32,27 32,90 j,<0 2,29 2,92 3,44 3,89 4,29 4,66 5,00 5,32 5,62 7,27 9,28 10,94 12,39 13,69 14,89 16,00 17,05 18,05 19,00 19,91 20,79 21,64 22,46 23,26 24,04 24,80 25,55 26,28 26,99 27,69 28,38 29,06 29,73 30,40 31,05 31,69 32,33 32,96 1,52 2,36 2,98 3,49 3,53 4,33 4,69 5,03 5,35 5,65 7,49 9,46 11,09 12,52 13,81 15,00 16,11 17,16 18,15 19,09 20,00 20,88 21,72 22,55 23,34 24,12 24,88 25,62 26,35 27,06 27,76 28,45 29,13 29,80 30,46 31,11 31,76 32,39 33,02 1,62 2,43 3,03 3,53 3,97 4,37 4,73 5,07 5 39 5,68 7,71 9,63 11,24 12,66 13,94 15,12 16,22 17,26 18,24 19,19 20,09 20,96 21,81 22,63 23,42 24,20 24,~5 25,70 26,42 27,13 27,83 28,52 29,20 29,87 30,53 31,18 31,82 32,46 33,09 1,72 2,50 3,09 3,58 4,01 4,40 4,76 5,10 5,41 5,71 7,92 9,81 11,39 12,79 l4,06 15,23 16,32 17,36 18,34 19,28 20,18 21,05 21,89 22,71 23,50 24,27 25,03 25,77 26,49 27,20 27,90 28,59 29,27 29,93 30,59 31,24 31,88 32,52 33,15
ПРИЛОЖЕНИЕ Продолжение табл. ХШ р, М 33,52 34,14 34,76 35,37 35,97 36,57 37,17 37,76 38,35 38,94 39,52 40,ll 40,69 41,27 41,84 42,42 42,99 43,57 44,14 44,71 45,29 45,86 46,43 47,01 47,58 48,16 48,73 49,31 49,89 50,48 51,06 51,65 52,24 52,83 53,43 54,03 54,63 55,24 55,86 56,48 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 33,21 33,83 34,45 35,06 35,67 36,27 36,87 37,47 38,06 38,65 39,23 39,82 40,40 40,98 41,55 42,13 42,71 43,28 43,85 44,43 45,00 45;57 46,15 46,72 47,29 47,87 48,45 49,02 49,60 50,18 50,77 51,35 51,94 52,53 53,13 53,73 54,33 54,94 55,55 56,17 33,27 33,89 34,51 35,12 35,73 36,33 36,93 37,52 38,12 38,70 39,29 39,87 40,46 41,03 41,61 42,19 42,76 43,34 43,91 44,48 45,06 45,63 46,20 46,78 47,35 47,93 48,50 49,08 49,66 50,24 50,83 51,41 52,00 52,59 53,19 53,79 54,39 55,00 . 55,61 56,23 33,34 33,96 34,57 35,18 35,79 36,39 36,99 37,58 38,17 38,76 39,35 39,93 40,51 41,09 41,67 42,25 42,82 43,39 43,97 44,54 45,11 45,69 46,26 46,83 47,41 47,98 48,56 49,14 49,72 50,30 50,89 51,47 52,06 52,65 53,25 53,85 54,45 55,06 55,67 56,29 30,40 34,02 34,63 35,24 35,85 36,45 37,05 37,64 38,23 38,82 39,41 39,99 40,57 41,15 41,73 42,30 42,88 43,45 44,03 44,60 45,17 45,75 46,32 46,89 47,47 48,04 48,62 49,20 49,78 50,36 50,94 51,53 52,12 52,7l 53,31 53,91 54,51 55,12 55,73 56,% 33,46 34,08 34,70 35,30 35,91 36,51 37,1.1 37,70 38,29 38,88 39,47 40,05 40,63 41,21 41,78 42,36 42,94 43,51 44,08 44,66 45,23 45,80 46,38 46,95 47,52 48,10 48,68 49,26 49,84 50,42 51,00 51,59 52,18 52,77 53,37 53,97 54,57 55,]8 55,80 56,42 33,58 34,20 34,82 35,43 36,03 36,63 37,23 37,82 38,41 39,00 39,58 40,16 40,74 41,32 41,90 42,48 43,05 43,62 44,20 44,77 45,34 45,92 46,49 47,06 47,64 '48,22 48,79 49,37 49,95 50,53 51,12 51,71 52,30 52,89 53,49 54,09 54,70 55,30 55,92 56,54 33,65 34,27 34,88 35,49 36,09 36,69 37,29 37,88 38,47 39,06 39,64 40,22 40,80 41,38 41,96 42,53 43,11 43,68 44,25 44,83 45,40 45,97 46,55 47,12 47,70 48,27 48,85 49,43 50,01 50,59 51,18 51,77 52,36 52,95 53,55 54,15 54,76 55,37 55,98 56,60 33,71 34,33 34,94 35,55 36,15 36,75 37,35 37,99 38,53 39,11 39,70 40,28 40,86 41,44 42,02 42,59 43,17 43,74 44,31 44,89 45,46 46,03 46,61 47,18 47,75 48,33 48,91 49,49 50,07 50,65 51,24 52,83 52,42 53,01 53,61 54,21 54,82 55,43 56,04 56,66 33,77 34,39 35,00 35,61 36,21 36,81 37,41 38,00 38,58 39,17 39,76 40,34 40,92 41,50 42,07 42,65 43,22 43,80 44,37 44,94 45,52 46,09 46,66 47,24 47,81 48,39 48,97 49,54 50,13 50,71 51,30 51,88 52,48 53,07 53,67 54,27 54,88 55,49 56,11 56,73
fIРило3КЕниЕ О конч анке табл. ХШ Р,УФ 56,79 57,42 58,05 70 71 72 56,98 57,04 57,10 57,61 57,67 57,73 58,24 58,31 58,37 56,85 57,48 58,12 57,23 57,86 58,50 56,91 54,54 58,18 57,17 57,80 58,44 57,29 57,92 58,56 57.35 57,99 58,63 59,15 73 58,69 58,76 74 59,34 59,41 75 60,00 60,07 76 60,67 60,73 77 61,34 61,41 78 62,03 62,10 79 62,72 62,80 80 63,44 63,51 81 64,16 64,23 58,82 58,89 58,95 59,02 59,08 59,21 59,28 59,80 60,47 59,54 60,20 59,60 59,67 60,27 60,33 59,47 59,74 60,40 59,87 60,53 59,93 60,13 61,14 60,80 60,87 60,94 61,00 61,48 61,55 61,62 61,68 62,17 61,24 62,31 62,37 62,87 62,94 63,01 63,08 63,58 63,65 63,72 63,79 61,07 61,21 61,27 61,82 61,89 62,58 61,75 61,96 62,51 62,44 62,65 63,22 63,29 63,15 63,36 63,94 64,01 63,87 64,08 64,67 64,38 64,45 64,52 64,75 64,30 65,05 64,60 64,82 65,42 65,20 65,27 65,50 82 65,57 83 84 85 86 87 ° 88 89 90 91 92 93 94 95 96 97 98 99,0 99,1 99,2 99,3 99,4 99,5 99,6 99,7 99,8 99,9 100,0 64,90 65,65 66,42 67,21 68,03 68,87 69,73 70,Я 71,56 72,54 73,57 74,66 75,82 77,08 78,46 80,02 81,87 84,26 84,56 84,87 85,20 85,56 85,95 86,37 86,86 87;44 88,19 90,00 64;,97 65,73 66,50 67,29 68,11 68,95 69,82 70,72 71,66 72,64 73,68 73,77 75,94 77,21 78,61 8О,19 82,08 84,29 84,59 84,90 85,24 85,60 85,99 86,42 86,91 87,50 88,28 65,80 66,58 67,37 68,19 69,04 69,91 70,81 71,76 72,74 73,78 74,88 76,06 77,34 78,76 80,37 82,29 84,32 84,62 84,93 85,27 85,Я 86,03 86,47 86,97 87,57 88,38 65,12 65,88 66,66 67,45 68,28 69,12 70,00 70,91 71,85 72,84 73,89 75,00 76,19 77,48 78,91 80,54 82,51 84,35 84,60 84,97 85,31 85,67 86,07 86,51 87,02 87,64 88,48 65,96 66,74 67,54 68,36 69,21 70,09 71,00 71,95 72,95 74,00 75,11 76,31 77,61 79,06 80,72 82,73 84,38 84,68 85,00 85,34 85,71 86,11 86,56 87,08 87,71 88,60 - 66.03 66,81 67,62 69,44 69,30 70,18 71,09 72,05 73,05 74,11 75,2З 76,44 77,75 79,22 80,90 82,96 84,41 84,71 85,03 85,38 85,75 86,55 86,61 87,13 87,78 88,72 65,35 66,11 66,89 67,70 68,53 69,38 70,27 71,19 72,15 73,15 74,21 75,35 76,56 77,89 89,37 81,09 83,20 84,44 84,74 85,07 85,41 85,79 87,20 86,66 87,19 87,86 88,85 66,19 66,97 67,78 68,61 69.47 70,36 71,28 72,24 73,26 74,32 75,46 76,69 78,03 79,53 81,28 83,45 84,47 84,77 85,10 85,45 85;83 86,24 86,71 87,25 87,93 89,01 66,27 67,05 67,86 68,70 69,56 70,45 71,37 72,34 73,36 74,44 75,58 76,82 78,17 79,69 81,47 83,71 84,50 84,80 85,13 85,48 85,87 86,28 86,76 87,31 88,01 89,19 66,34 67,13 67,94 68,78 69,64 70,54 71,47 72,44 73,46 74,55 75,70 76,95 78,32 79,86 81,67 83,98 84,53 84,84 85,17 85,52 85,91 86,33 86,81 87,37 88,10 89,43
lI Р и л о )К Е н и' Е Таблнц а XIV arcsin Ошибки репрезентативности угла у 820.7 >и и 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 З~ 38 39 40 41 42 43 44 45 46 47 48 49 50 . 51 52 53 54 55 8,207 7,461 6,839 6,313 5,862 5,47! 5,129 4,828 4,559 4,319 4,104 3,908 3,730 3,568 3,420 3,283 3,157 3,040 2,931 2,830 2,736 2,647 2,565 2,487 2,414 2,345 2,280 2,218 2,160 2,104 2,052 2,002 1,954 1,909 1,865 1,824 1,784 1,746 1,710 1,675 1,641 1,609 1,578 1,548 1,520 1,492 8,126 7,394 6,783 G,265 5,821 5,435 5,098 4,799 4,534 4,297 4,083 3,890 3,714 3,553 3,40б 3,270 3,145 3,029 2,921 2,821 2,727 2,639 2,557 2,480 2,407 2,339 2,~74 2,212 2,154 2,099 2,047 1,997 1,950 1,905 1,861 1,820 1,780 1,742 1,707 1,672 1,638 1,606 1,575 1,545 1,517 1,489 8,046 7,328 6,727 6,217 5,750 5,399 5,066 4,772 4,509 4,275 4,063 3,871 3,697 3,538 3,393 3,258 3,134 3,018 2,911 2,811 2,718 2,631 2,549 2,472 2,400 2,332 2,268 2,206 2,149 2,094 2,042 1,992 1,945 1,900 1,857 1,816 1,776 1,739 1,703 1,668 1,635 1,603 1,572 1,542 1,514 1,467 7,968 7,263 6,b72 6,171 5,739 5,364 5,035 4,744 4,485 4,252 4,043 3,853 3,680 3,524 3,379 3,245 3,122 3,007 2,901 2,801 2,709 2,622 2,542 2,465 2,393 2,326 2,261 2,201 2,143 2,088 2,037 1,988 1,94} 1,896 1,853 1,812 1,773 1,735 1,700 1,665 1,631 1,600 1,569 1,540 1,512 1,484 7,891 7,199 6,619 6,125 5,699 5,329 5,004 4,717 4,460 4,230 4,023 3,835 3,664 3,509 3,365 3.233 3,110 2,996 2,891 2,792 2,700 2,614 2,534 2,458 2,386 2,319 2,255 2,195 2,148 2,083 2,032 1,983 1,936 1,891 1,849 1,808 1,769 1,732 1,696 1,661 1,628 1,597 1,566 537 1,509 1,482 7,816 7,137 6,566 6,079 5,660 5,295 4,974 4,690 4,436 4,209 4,003 3,817 3,648 3,494 3,352 3,220 3,099 2,986 2,881 2,783 2,692 2,606 2,526 2,451 2,380 2,313 2,249 2,189 2,132 2,078 ia,027 1,978 1,932 1,887 1,844 1,804 1,765 1,728 1,693 1,658 1,625 1,594 1,563 1,534 1,506 1.479 7,742 7,075 6,513 6,035 5,621 5,261 4,944 4,663 4,41 2 4,187 3,984 3,800 3,631 3,479 3,338 3,207 3,087 2,975 2,870 2,774 2,683 2,598 2,518 2,443 2,373 2,306 2,243 2,183 2,126 2,073 2,022 1,973 1,927 1,883 1,840 1,800 1,761 1,724 1,689 1,655 1,622 1,590 1,560 1,531 1,503 1,476 7,670 7,015 6,462 5,991 5,583 5,227 4.!>14 4,637 4,389 4,166 3,965 3,782 3,615 3,4б4 3,324 З,195 3,075 2,96~ 2,860 2,764 2,674 2,590 2,510 2,436 2,366 2,300 2,237 2,177 2,121 2,068 2,017 1,968 1,922 1,878 1,836 1,796 1,757 1,721 1,686 1,651 1,619 1,587 1,557 1,528 1,500 1,474 7,599 6,955 6,412 5,947 5,545 5,194 4,885 4,6! 1 4,365 4,145 3,946 3,765 3,600 3,450 3,310 3,182 3,063 2,953 2,850 2,775 2,665 2,581 2,503 2,429 2,359 2,293 2,230 2,172 2,115 2,062 2,012 1,964 1,918 1,874 1,832 1,792 1,754 1,7l7 1,682 1,648 1,615 1,584 1,554 1,526 1,498 1,471 7,529 6,897 6,362 5,904 5,508 5,162 4,856 4,585 4,342 4,124 3,927 3,747 3,584 3,435 3,297 3,170 3,052 2,942 2,840 2,745 2,656 2,573 2,495 2,421 2,352 2,287 2,224 2,166 2,110 2,057 2,007 1,959 1,914 1,869 1,828 1,788 1,750 1,714 1,679 1,644 1,612 1,581 1,551 1,523 1,495 1,469
ПPHЛОЩанВE П р одолжен ие табл. XIV 1,453 1,428 1,403 1,380 1,357 ~,335 1,314 1,293 1,273 1,253 1,234 1,216 1,198 1,181 1,1~4 1 148 1,132 1,117 1,102 1,087 1,073 1,059 1,043 1,030 1,020 1,007 0,9949 0,9829 0,9713 0,9599 0,9483 0,9380 0,9274 0,9170 0,9 ~69 0,8970 0,8873 0,8778 O.~685 0,8594 0,8505 0,8418 0.8332 0,8249 0,8167 0,8086 0,8007 0.7930 0,7854 0,7779 0,7706 0,7635 0,7564 0,7495 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 103 109 1,466 1,440 1,415 1,391 1,368 1,345 1,324 1,303 1,282 1,263 1,243 1,225 1,207 1,189 1,172 1,156 1,140 1,124 1,109 1,094 1,080 1,066 1,052 1,034 1,�6 1,013 1,001 0,9888 0,9770 0,9655 0,9543 0,9433 0,9326 0,9221 0,91l9 0,9019 0,8Ч21 0,8825 0,8731 0,8Я9 0,3549 О,М61 0,8374 0,8290 0,8207 0,8126 0,8046 0,7968 0,7891 0,7816 0,7742 0,7670 0,7599 0,7529 1,463 1,438 1,413 1,389 1,366 1,343 1,322 1,301 1,280 1,261 1,241 1,223 1,205 1,187 1,170 1,154 1,I38 1,123 1,108 1,093 1,079 1,065 1,050 1,033 1,025 1,012 0,9998 0,9876 0,9759 0,9644 0,9532 0,9422 0,9316 0,92' l . 0,9109 0,9009 0,8911 0,8816 0.87~2 0,8630 0,3540 0,8452 0,8366 0,8282 0,8199 0,8118 0,8038 0,7960 0,7884 0,7809 0,7735 0,7663 0,7592 0,7522 1,461 1,435 1,410 1,386 1,363 1,341 1,320 1,299 1,278 1,259 1,2 '9 1,221 1,202 1,186 1,169 1,153 1,137 1,121 1,106 1,091 1,077 1,063 1,043 1,032 1,023 1,011 0,9986 0,9864 0,9747 0,9633 0,9521 0,9412 0,930~ 0,9201 0,9099 0,8999 0,8%2 0,8806 0,8713 0,8621 0,8531 0,8444 0,8357 0,8273 0,8igl 0,8110 0,8030 0,7953 0,7876 0,7801 0,7728 0,7656 о.7585 0,7516 1,458 1,433 1,408 1,384 1,361 1,339 1,318 1,297 1,276 1,257 1,238 1,220 1,202 1,184 1,167 1,151 1,135 1,120 1,1(.5 1,690 1,076 1,062 1,047 1,032 1,022 1,009 0,9973 0,9853 0,9736 0,9621 0,9510 0,9401 0,9295 0,9190 0,9089 0,8990 0,8892 0,8797 0,8703 0,8612 0,8Ь23 0,8435 0,3 349 0,8265 0,8183 0,8102 0,80~3 0,7945 0,7869 0,7794 0,7720 0,7649 0,7578 0,7509 1,456 l,430 1,405 1,382 1,359 1,337 1,316 1,295 1,274 1,255 1,236 1,218 1,200 1,182 1,166 1,150 1,13 1,118 l,103 1,088 1,074 1,060 1,045 1,031 1,021 1.008 0,9961 0,9841 0,9724 0,9610 О,Ч499 0,939! 0,9 i84 О,9180 0,9079 0,8980 0,8883 0,8787 0,8694 0,8603 0,8514 0,8426 0,834(> 0,8257 0,8175 0,8094 0,8015 0,7937 0,7861 0,7786 0,7713 0,7642 0,7571 0,7502 1,450 1,425 1,401 1,377 1,354 1,332 1,311 1,290 1,271 1,251 1,232 1,214 1,19б 1,179 1,162 1,146 1,130 1,115 1,100 1,086 1,072 1,058 1,041 l,029 1,018 1,006 0,9937 0,9817 0,9701 0,9588 0,9477 0,9369 0,9263 0,9160 0,9059 0,8960 0,8863 0,8769 0,8676 0,8585 0,8496 0,8409 0,8324 0,8240 0,8158 0,8078 0,7999 О,7922 0,7846 0,7772 0,7699 0,7627 0,7557 0,7488 1,448 1,423 1,398 1,375 1,352 1,330 1,309 1,288 1,269 1,249 1,230 1,212 1,194 1,177 1,161 1,145 1,129 1,114 1,099 1,084 1,070 1,056 1,i 39 1,028 1,017 1,005 0,9925 0,9805 0,9690 0,9577 0,9466 0,9358 0,9253 0,9150 0,9049 0,8950 0,8854 0,8759 0,8667 0,8576 0,8487 0,8400 0,8315 0,8232 0,8150 0,8070 0,7991 0,7914 0,7839 0,7764 0,7692 0,7620 0,7550 0,7481 1,445 1,420 1,396 1,373 1,350 1,328 1,307 1,286 1,267 1,247 1,229 1,211 1,193 1,175 1,159 i,143 l,127 1,112 1,097 1,083 1,069 1,056 1,038 l,028 1,016 1,003 0,9912 0,9794 0,9678 0,9565 0,9455 0,9347 0,9242 0,9139 0,9039 0,8941 0,8844 0,8750 0,8657 0,8567 0,847~ 0,8391 0,8307 0,8224 0.8142 0,8062 0,7984 0,7906 0,7837 0,7751 0,7684 0,7613 0,7543 0,7474 1,443 1,418 1,393 1,370 1,347 1,326 1,305 1,284 1,265 l,245 1,227 1,209 1,191 1,174 1,158 1,142 1,126 1,'111 1,096 1,081 1,067 1,'()53 1,036 1,027 1,014 1,�2 0,9900 0,9782 0,9667 0,9554 0,9444 0,9337 0,9232 0,9l29 О,ь029 0,8931 0,8835 0,8740 0,8648 0,8%8 0,3470 0,8383 0,8298 О,8215 0,8134 0,8054 0,7976 О,i899 0,7824 0,7749 0,7677 0,7606 0,7536 0,74~8
ПРИЛОЖЕНИЕ Таблица XV й =10 и, 19,8 23,3 26,9 19,0 .10 10 18,0 20,9 16,2 15 15,5 15 18,1 15,6 14,0 13,4 20 14,8 12,8 30 11,0 12,8 9,9 9,5 40 10,5 9,0 7,8 8,1 9,1 80 7,8 6,7 80 7,0 8,1 )00 7,0 6,0 6,3 6,6 150 150 5,7 4,9 5,1 5,7 4,9 4,2 4,7 3,5 4,0 3,6 4,0 3,0 3,5 3,1 2,9 3,3 6СО 2,6 2,5 2,1 2,2 2,9 2,5 1,9 2,6 2,0 2,2 1,5 2,1 1500 1,6 1,8 1,3 .1,6 2000 1,8 1,4 1,3 3000 1,5 0,9 4(хЮ 1,3 1,0 0,8 0,8 0,9 1,0 0,7 0,7 8000 0,8 0,9 0,6 0,6 0,8 10000 0,7 Минимальная достоверная разность углов г" ( arcsin ~/ ~в ) при Р =0,95: n< — численность меньшей группы, пр —— Й п~ — численность большей группы, й=n>.ï<
IlPHËÎÙÂÍÊÂ 1+++ 1((+ !+++~1(~- ++11(1++ +IIII+ II(+++ +III+ СЧ 'Ф ~О ~ СЧ СЧ ~О ~Ф' СЧ ~ СО СО ~ ~ ~Э ~О ~ 'Ф ++++IIII+ ++ < l ( l 7 (++ (111(+++++ 00( 00&COC ООC 00 ++IIIII++ 'Ф ~О СЧ ° ( ) ~ СЧ С~.') ~ф' 1111 ++++ t ~ ~ сОа~~ 11 I++++ ~О I++ ((+ ~ООСО МОЛ + ( I + еО СЧ ~ О ~ СЧ СО ((1 +++ Ж ( ~Ф' ( I++ l+ ~ СЧ О СЧ ~ i+ I+ СЧ ~О~СЧ 11 ++ ~О <~t ~ООЪсОсОО~ ~О ~сО ~О С5ФЮ ОЮC ЮЮ~<ООЮФФ~О I(++++++(()(I(++ ~~-~ ~ О~ ~ Cb ~O Cb ~ ~ С~ и~ (Р~ ~ ~Р~ е ц~ СЦ +++1 ! ( 11111 I I+++ 5 ~ОСО~ ОЪ t ~О СО~ ~ СО Ж t Ch~ СО~О С) « IIII++++++++ 5 ~О~ООО~ОЪ ССО CCh~ОО~ОСОII+++++ IIII(++ ~ ~CBOOK ~О<О~О О~ООО~СЧ~ +++II (~IIII+++ 111(111 ++(-+(++ I(+++++(Ill(++ +++1(1((111+++ (111+++++++ ~ Q) (О 00 N Ф О Ф ~ О0 ~ ~:~ ~ 1 ++++ 1111 + СЧ ~ СЧ Л О ~О Ф ~О О Л С~ ~ С~ +++IIIIIIII++ Ю ~О M СО СЧ ~ CO ~ СЧ СО M ~О Ю IIIIII ++++++ (+++++IIIII+ +++IIIIII+++ 111111~ +++++ О CO СОСО Ф О Ф СО СЧ Ю О I++++ Ill(+ ++IIIII(I++ mMceW~CO~~ceM~ l(l(( +++++
ПРИЛОЖЕНИЕ й'° ~{:~Щt О 00 СО СЧ lD й: Cf Ч О й:( С CL !.+++++++ -' I I I 1 I ! 11++ ОЪ еО ОЪ СО СО ~ ~ ~ СО СО ~ ~ ~ СО СО {:Ь СО ОЪ ( СО СЧ СЧ СЧ СО СО СО С' О СЧ СЧ СЧ СО ++++ 1 I 1 I 1 1 I I I I I 1++++ 1 I I I I ! +-'- —.' +++++++ 00 00 Ф О Ю СЧ Я ~Ф О '~' С' О СЧ Ф С Ф 00 00 О Ф СЧ 00 СЧ СЧ ~ 00 'Ф ° Ф 00 СЧ СЧ 00 СЧ CO О 1+++++++ I I I I I I I++ 'Ф Ch . Ф 1-'. 'Ф ~ Ю 0~ О 0~ Ф ~ ~~' Л CO Ch ~О СО ~ СЧ СЧ СЧ СО СЧ СЧ СЧ С' О И~ ++++ I 1 I 1 I 1 1 1 I I I ++++ Ch ~Х) ~ CO ~С 'Ф СО СЧ ~ CO ~ СЧ СО 'Ф Ж СО ~ 00 Ch 1: 1 ~ 1 ~ 1 1 ! +!- ++++++ 00 О С' О СЧ СЧ Ж С' О 00 00> W A СЧ СЧ СО & CO 00 (D СЧ 'Ф 'Ф СО ~~l СЧ СО 'Ф Ф ОЪ ~ СЧ Ц:) 1+++++++ I I I I I 1 ~++ 00 Л О СЧ ~' О О ~' СЧ О Л С' О 'Ф 00 CO СЧ ~ СЧ С' О С",) M Ф СО СО СЧ ~ СЧ ~Ф' (D +++ I I I I I I I I I I ++++ СУ~ ~ ~У~ лО С~~ ~ л ~ {Р~, 1 1 ! 1 1 1 1 1 1+- --.-+++ t~ C < 00 ~- С' О t O t~ С' О C 00 й t~ ~-- СЧ ~4 г4 СЧ ++++++ I 1 I 1 1 >++ ~О СЧ ™ 00 Л О С' О 'Ф С' О О ~С 00 4 СЧ СЧ СЧ СЧ СЧ СЧ СЧ ++++ 1 1 1 1 I I I I I ++++ 00 ~~ Ю ~О 'Ф С' О СЧ О 4 СЧ С' О '4' Л Ю 1 1 1 1 1 1 1 1 ++"' -', ++++
360 ПРИЛОЖЕНИЕ ° е е е е ее е Фе ° е ° е ° е ° ° ° ° ° ° ° ° д е ° ее е ее ее е ю ю е ° ° ° е ° е ° ю э а е ее ч Ю ъ O ч ~ ч ° ° ° е ° е ° ° е ее е ° ° ° ° ю е ее ° ° у ев ° ° е е е Ю Ф ч Ю ° е е ее е ю е е ее е ее g е е
ПРИЛОЖЕНИЕ аЭ arj ir СЬ ~О Ж ~ Оъ - Ж Ж Ж О~ Cb ~О ~О ~ ~ Ch ~О ~О ~О Оъ~О ~О~О 00 СЧ ~ Ф ~ ~О О СЧ ~ О> Ф 0(0 ~ СО СО ~ 00 ~Ф' 0~ ° СЧ CD ~О ('Ф~СЧ0(0 И~ СО ~ СЧ СО СО СО СЧ СЧ ~ СЧ СЧ СО СО СО СЧ ~ ~СОа~ 1 1 I (- + 1 + (- + ~ ( + ++ I 1 I 1 I 1 I I I 1 I +++ t t ~О Ж t ОЪ СО ~О ~О СО Ch СО ~О ~О СО ОЪ СО ~О Ж СО ОЪ t ~О~О t ~ t ~ChСОMСЧ СЧ СО M Ж ~О СО СО ЧР СО ~О Ж M СО СЧ СЧ M СО ОЪ ~ ++++-(-+ I I 111 ( 111111 ( 111++++++ Ж СО ~ Ch C ~О СО ~ ОЪ C ~Î СО ~ ~ СО ~О C ОЪ ~ СО ~О t Ch~~~t СЧ СЧ СЧ СЧ ~ « ~ 1-е СЧ СЧ СЧ СЧ 1 1 1 1 1 ( 1 1 1 1 1 1 ! 1 -(-+ (-+ -(-++ -(- 1 +++-(--(- 00 О СО О О СЧЛ СЧ О О СО О СЧ О Л 00 О 00 К О СЧ О СО О О СЧ ~ОСЧОО СО С СЧ~ Ф CO t t C Ч:) Ж СО~ ~ СО~ОQO t C t ЧР ~Ф'~СЧC СО I I ++++++++++ I I 1 I I I I 1 I I+++ О СЬ ~ОО СО~ОЛ'Фt 'ФЛОФСЧФОЛM t M~ОО ~00~О~ СЧ Л00 ° Ю ~ СО ( О СО Л ( ( 00 C ( Л СО О ( СО ~ Ю ~СО~(СЧ СО СЧ з ° т~ т4 з ° тй т4 е4 т4 ф4 ~ т4 ~~СЧСО ++(-+++ I 1 I 11 I I I 11 ( I ( I t +~+~+ СОСЧ~ОФСО~ОЛФСОСЧО~СЧСОМ~СО~000)ОСЧСО 1 1 1 1 1 1 1 1 1 1 1 1 1 +++++++++++++ CD О С:Ь СО CD 00 О М~ CD О 00 'Ф CD С~1 со СО ЪГ~ О CD СО 00 ° ~ СО О ( ОЪ Ю 00 Л ( Ф Ф ( ~О 00 Ю О~ ( О 00 ~ ° 00Я 0~ С~ ~ С:~ Ю СО'Ф О 0~ ~Ф'0000 Ф 0~ ~ О Ф СО С~(~> ~ ЮО~М ~Э~'Ф ЖСОСОСО~ОСОСЧ СЧ СО~ОСОСО СО~О з' Ж 1((++++++++++11!1111111+++ CD 00 (- (- 00 О (- СО 00 СЧ ~О (- 00 00 ~- ~О СЧ 00 СО ~ О 0O ~- ~.-0ОО СО СЧ ~ ~ СЧ СЧ СЧ СЧ СЧ СЧ СЧ СЧ ~ СЧ СО ~О +++++ IIIIIIIIIIIIII (-++++ И~СО С:Ь( а~СО~С:Ь C U СО~~СОИ~ t С:Ь~СОИЭ t С:Ь~СОЖ СЧ СЧ СЧ ~ ~ ~-~ ~-ю ~,-~ ~ ~ СЧ СЧ СЧ 111111111(III'+(-+++(-++++++ Ю СО~(~ОЮ 0~ ~' ~О00 ~ 0~ ~' О C 0~ '00~-О Л ~б Ф Ф ~О 00 0(0 Л ~ Ф C ~ Ф ~ Л 00 00 ~О Ф Ф ~О ~Î 1 1 1 +++ +++ ++ -(- I 1 1 I I 1 I 1 I -'-++ СЧ О> СО О) СЧ РЭ CD ~ CD с'Э СО СЧ «СО Q CD ~ CD РЭ СЧ О> со О>СЧ ,'-(++;-111( 11111111!I+++++ СЧ 4 О 0(~ 00 (' Ю <Q Ф СО СЧ ~ О ~ СЧ СО Ф ~О CO ~' 00 0~ О ° СЧ 1111(IIIIIII ++-(--(-++++++++ О а~ 00 И~
БРИЛОЩЕНИЕ Ср~ и~ С~ (:ЬО;) О) ОЪ|О~ ~ ~ ~ООЪ~Ъ ~ '~~~Ъ' ~ ~Ъ в щ в в в о в вавлФЩЩФЛВФЩВСаввав QO ~О СЧ ~ Щ СО 'Ф'Ф'Ф'Ф СО СОСЯ ~ СЧСО СО'Ф'Ф'Ф'Ф ~ÑÎ~ СЧ ~QO 1 1( 1 + ~~ +++'+!-+++II!>1111~111++++ ~О t ~ t ~О ~О СООЪСО~О~ОСОСЬСО~О~ОСОСЬСО~О~ОСООЪСО~О~О( t ~Oa~ СЧ ОЪ t 'Ф СЧ СЧ'Ф~ОСОt tCbQOQOQOt t СО~О'ФСЧ~ СЧ'Ф(О)СЧ~О +++++++ I 11 ! 1 ~ I I I I I 111111+++++++ ОЪ t iО СО ОЪ t iОСО~ОЪt iОСО СОЛОt ОЪ СОiОtОЪ- СОiОtОЪ~ СО СЧ СЧ СЧ СЧ СЯ ° ~ ~ ю-в ~ СЧ СЧ СЧ СЧ СЧ СО 1 1 1 ! ! ! ! ~ ! ! «+++++++;++-~-+--++-+- ~О ЯЪ СО СЧ ЯЪ ~О ° СЧСООЪ~ОСОtСООЪООЪ~~CD~ОЪСОСЧ ~~ООЪСЧСООЪ~ОCO t~ CD Ю ~ СО~ОСООЪСЧСОСО~ ~СОСОСЧОЪСО~ОСО~Ю~) ~ОC) Ю СЧ СЧ СО 'Ф ~О~О~О'Ф'ФСОСЧ ~ СОСО'Ф'Ф~О~О~О'ФСОСЧ СЧЮО 1 1 I ++++++ >++ I 1 I I ! I I I I 1 1! I ++++ Ю ОЪ '~~' ~ О ~ Ю ~'Ф~':1' ЮОЪООЪЮ ~':1'~О~- Ю «О~'ФChCD~ QO Ю 'Ф СЧ ~ СО~ф'ЩCD t t t QO t t t СО ~О'сф'СО~ СЧ'сф'CDQO~'Ф +++++++ I I I ! 111111 ! I ( 11 I I++ ', ++++ 'Ф СО СЧ ° О ОЪ 00 ~ CD ~О'Ф СО СЧ О ~ СЧ СО'Ф ~О CD ~ QOОЪ О СЧ.СО ~" ~О О 00 % фФ сО I I 1 I I I IIIIIIII +++++++!-+++++'+ О СО О О Ю ~ СО 'Ф О~(00'ФЛСЧСЧ~~О'4'00(~~О'ФСО(-ОС- ~О Ф СЧ О с~0 00О ~О~О сОсО ~ сОсО ~О~ОО0000ОЯ ~1'~О~ С~ О 'Ф 'Ф ~ QO ОЪ О ОЪ 00 ( ~О СО ~ ~ СО ~О ( ~0 Р О Р Ф ( 'Ф '4' О 00 1++++++!++ I ++ I I ! I I !11 ! 111+++ СЧ CD СО СО 'Ф 00ОЪ (СЧ'Ф ОООЪ СЧСЧОЪОО'Ф СЧ (ОЪ00~1'СО СОЖА СО CD СЧ 00 Л СЧ СЧ'ФСООООЪОО «ОООЪ00Ф'ФСЧ СЧ~О00СЧЭО ++++++ I I 1 I 1 ! I 1 1 1 I ! 1 1 I I ! 1 > I-++++ Cb t ~О СО ~ Cb t ~ОСО СЫ ДАССО ~СО~Оt СЬ ~<OtCb- СО~Оt ОЪ СЧ СЧ СЧ СЧ СЧ 1-~ ° ~ СЧ СЧ СЧ СЧ СЧ ~ ! I I ~ I I IIII!III+++1-+++++++++++ ОЪ QO СЧ 'Ф iО CD СЧ QO ОЪ О CD СЧ СО 'Ф О ~ СО СЧ С~:> О С> QO СЧ Ю iО M ~t QO ОЪCD QO Ф ~ СО Ф ФСЧЮОЪОО ОООЪОСЧ~Ф' Э~СО Ф�>Ю-QO .-3' ~ СЧ СО с3' 'Ф с3'с3' СОСЧ СЧ ~ ~ СЧСЧ СО'Ф M ~Р'Ф СО СЧ ~ 'Ф QO1 I ++ I ++++++++ I I I I > I !111+++ Оъ 'Ф О 4 cD «'ФЛ'Ф «ООъООъО'Ф~О'4' «се~О~'~~'~ъс~:~ Ch C ~О СО ~ СОСО'Ф~ОCDCDCD[- ЖCDCD~О'ФСОСЧ СО~С( ОЪС~3 ++++++ ~ ! ~ I I 1 1 1 1 I ( 1 1 ! 1 11++++++ сО СЧ О ОЪ QO ~ О ~О'Ф сО СЧ ~ О «Я сО':~' ~с~-> ~ с~0 ~ЪО 'С~ сО "1' т« ~ ° е-~ е-~ ° « I I I I I i I 1 1 I I 1 I ++++< +++++++++ О сО С0 СЧ -б' О Ф' СЧ О CD СО СЧ 'Ф CD О О сО 'Ф О О~ ~Г~ 00
ЗАМЕЧЕННЫЕ ОПЕЧАТКИ Стр. Строка Должно быть Напечатано 12 41 52 365 . 12 малочисленных 365 ° И многочисленных 3 58 61 102 отстоит отстаит XI 25 М 103 М — М 104 7 сверху 105 25 сверху ч -+- 3 — 1,5t 10 ~+ 3 — 1,58 30 108 12 снизу 30О, 13г2~ 300,1322г указанной выше формулеУ 3,09 ~- 4,50 = 2,750,2' 118 120 = 0,007 123 6 20 125 7 снизу 100 )00 n=~P Ч 2 0,04х0,% 2 2000 130 17 сверху 3 снизу 137 0,035 =- 1,5 0,0233 — 0,035 140 1 сверху 0,0233 = 2,4 = 2,5 146 149 4 снизу 15 снизу угла наименьших значений ь углу наибольших значен ий не нужно 168 Табл. 64, подзаглавием26 сверху 168 2,3 170 174 174 2,3 по табл. X I I 15 сверху 13 сверху 14 сверху по табл. 65 по табл. 65 по табл. XI I 1 — r' m 12 3 178 14 сверху 15 сверху и — 2 ]86 l1 снизу 15 снизу 212 3 снизу 2 сверху табл. 30, 3 строка, графа 8 18 сверху 21 сверху 8 снизу, 1 графа 5 сверху 11 сверху 22 — 23 сверху 2 снизу 16 снизу указанным выше формулам ~~ 3,09 +- 4,50 = 2.75 0,2 — —. 0,007 6 угла наименьших значений c=zС,=ED@, ~Ь,1 1 — м,)с =(Eч — м1'табл. XI а =-ф' р-q, 0,04 Х <~,9Ь 2 — 2000 с, хо <,. +,,> С, = E(V — М1*табл. IX
Строка Стр. Напсчатано Дол>кно быть 219 14 сверху,5 графа 17 снизу 16 снизу 4 сверху 4 сверху 5 сверху i~ Х . ° . i~'Z 303 343 1 сверху «оиомстрия 276 276 Я77 277 277 277 277 277 277 288 9 сверху 10 сверху 14 сверху 15 снизу табл. 124, графа «функция одного аргумента» 15 снизу М — 6ах6ь(lgx) ~10 lg20,610 lgb42,988 lgb8,3908,757+0,662,203 74200 окончание табл. ЧИ . М-6gg~bZ (lgx) '10 lga20,610 Ь42,988 b— 8,390— 8,757+0,6662,203 74250 окончание табл. Ч1И
О ГЛАВЛ ЕНИЕ Введение Глава I. Средние величины Общая формула средних величин Общие свойства средних величин Средняя арифметическая Математические свойства средней арифметической Вычисление средней арифметической для малочисленных групп Взвешенная средняя арифметическая Вычисление средней арифметической для многочисленных групп . Средняя геометрическая Средняя квадратическая Средняя гармоническая М ода ° ° ° ° Медиана Глава ((. Разнообразие значений признака Показатели разнообразия Лимиты Среднее квадратическое отклонение Средняя и сигма суммарной группы . Коэффициент вариации Нормированное отклонсние Закономерности разнообразия Распределение признака Вариационный ряд Гистограмма Яариационная кривая Кумулята О гива ° ° ° ° ° ° ° Нормальное распределение Первая функция нормированного отклонения Достоверность различия распрсдслений Критерий у~ (хи квадрат) Критерий Х (ламбда) Лсимметрия и эксцесс Вторая функция нормированного отклонения Третья функция нормированного отклонения Трансгрессия Биномиальное распределенис Распределение редких событий . Глава III. Репрезентативность выборочных показателей Генеральная совокупность и выборка . Ошибки исследований Ошибка выборочной средней арифметической . Распределение выборочных средних Вероятность отличия выборочной средней от генеральной Три степени вероятности безошибочного суждения при определе- нии генеральных величин по выборочным Возможная величина генеральной средней . ,достаточная численность выборки при изучении средних величин Ошибка разности выборочных средних ° Возможная величина генеральной разности . Критерий достоверности выборочной разности ° Достоверность разности средних при коррелированных выборках . Достаточная численность выборки при изучении разности средних Ошибка выборочной доли 5 5 6 9 9 12 l4 1б 27 31 32 33 34 Зб :36 36 37 46 47 48 50 50 51 53 54 54 55 56 57 60 60 62 64 68 72 75 79 89 94 94 97 98 100 102 103 105 110 114 116 117 123 127 130
ОГЛАВЛЕНИЕ Возможная величина генеральной доли Достаточная численность выборки при изучении долей . Максимальная генеральная доля, при которой возможна нулевая выборочная Ошибка разности между выборочными долями достаточная численность выборки при изучении разности долей . Ошибка разности между выборочной и генеральной долями . Метод <р (фи) Глава Ш. Корреляция Коэффициент корреляции Вычисление коэффициента корреляции для малых групп . Вычисление коэффициента корреляции для больших групп Ошибка коэффициента корреляции . Численность выборки, достаточная для достоверности полученного коэффициента корреляции Частный коэффициент корреляции Ошибка частного коэффициента корреляции Коэффициент прямолинейной регрессии Уравнение прямолинейной регрессии Тетрахорический показатель связи Полихорический показатель связи Корреляционное отношение Вычисление корреляционного отношения Свойства корреляционного отношения Достоверность корреляционного отношения Критерий криволинейности Глава V. Дисперсионный анализ Основы метода Техника дисперсионного анализа Подбор факторов Разделение факторов на градации . Подбор особей Преобразование значений результативного признака Техника расчетов Однофакторный комплекс Двухфакторный комплекс Трехфакторный комплекс Неравномерные комплексы Дисперсионный анализ качественных признаков Сравнение средних внутри дисперсионного комплекса . Сравнение одной группы с суммой других групп внутри диспер- сионного комплекса Сравнение средних, не входивших в дисперсионный комплекс . Сравнение долей внутри дисперсионного комплекса . Глава VI. Регрессия Составление эмпирического ряда регрессии Общие способы выравнивания эмпирических рядов Графический способ Способ скользящей средней Способ наименьших квадратов Прямолинейные функции вида у = а+ Ьх Показательные функции вида у = ах~ Параболические функции вида у = а+ Ьх и у = а+ Ьх+ сх' с Гиперболические функции вида у = а + Ьх + х Параболические функции с одним максимумом у = а + Ьх + -1- «r.ç2 Множественные прямолинейные функции вида у = а+ Ьх+ cz Частные способы выравнивания эмпирических рядов . Способ Чебышева (выравнивание параболических функций} Парабола первого порядка у = а + РР~ Парабола второго порядка у' = а + РРi т ( P> Парабола третьего порядка у = а + ppi + ( Р~ + оРз . Асимптотическне функции Асимптотический рост Асимптотические потери веса Логнстические функции Периодические функции Приложение 131 133 135 136 140 141 144 147 149 152 156 169 173 174 178 178 179 180 181 184 187 191 195 19б 197 197 213 213 213 214 216 218 218 224 230 234 236 243 248 251 256 259 263 263 263 267 273 273 276 279 281 284 287 293 293 294 296 299 304 304 312 314 319 327