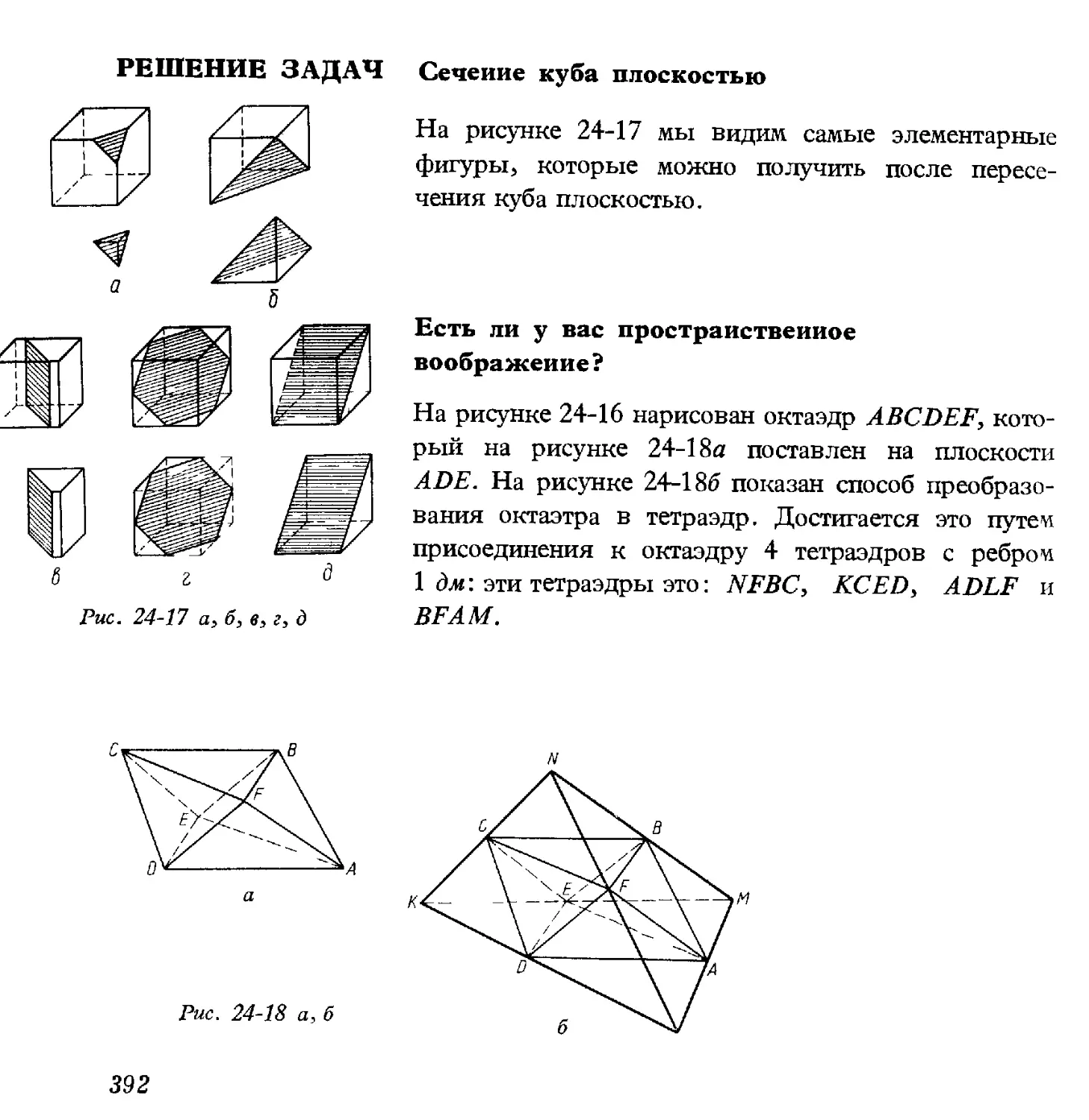
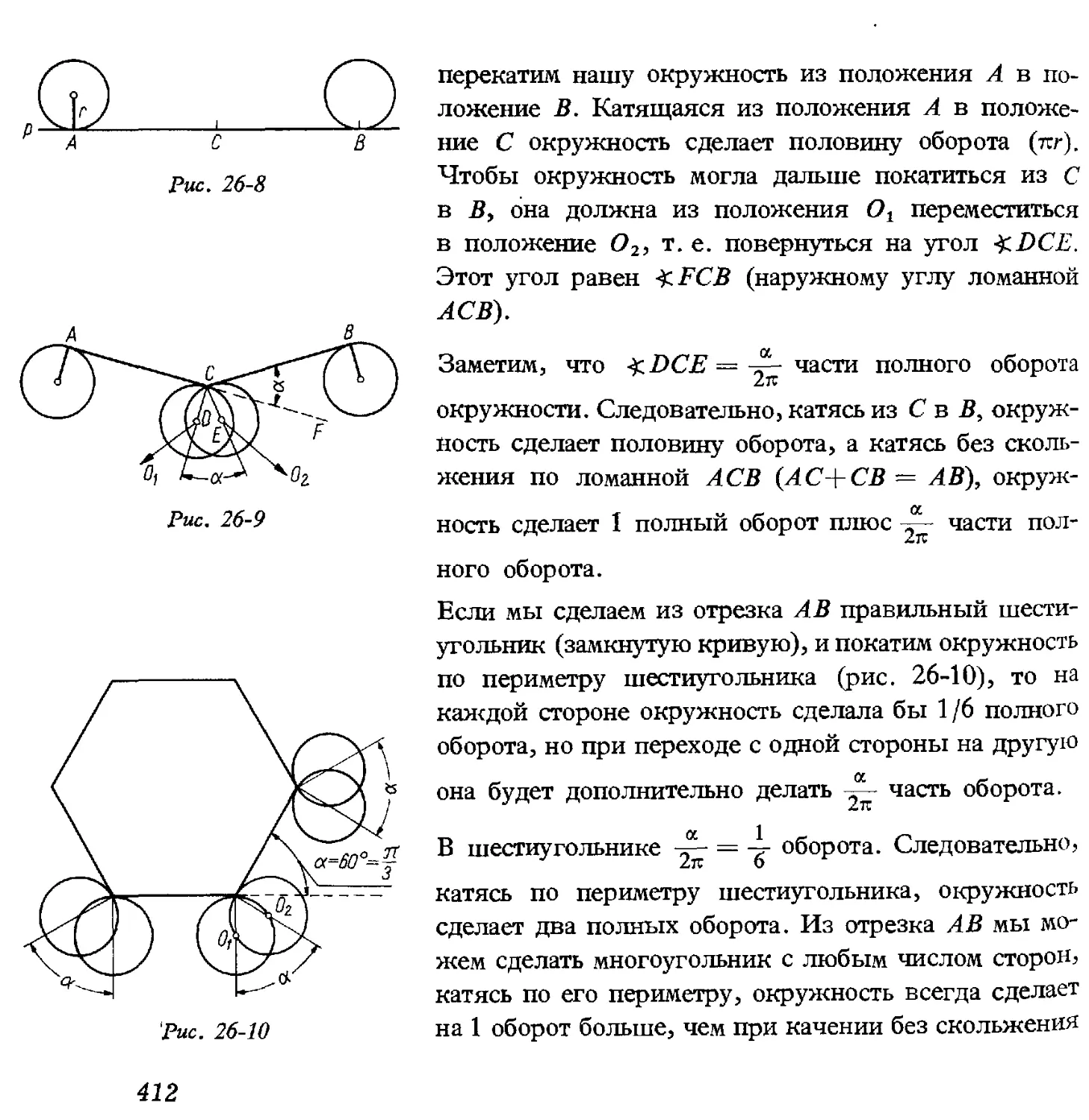
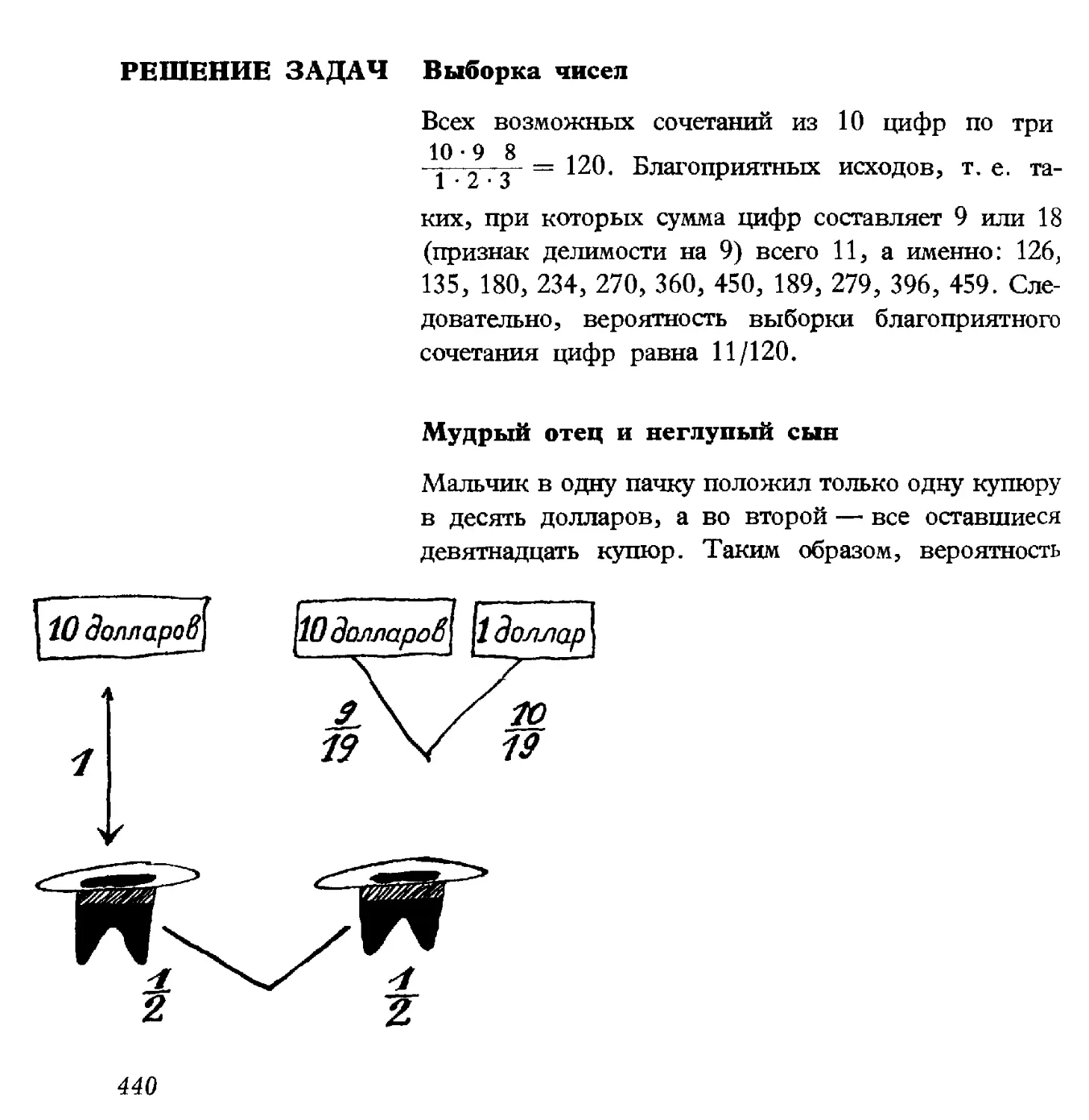
Автор: Коваль С.
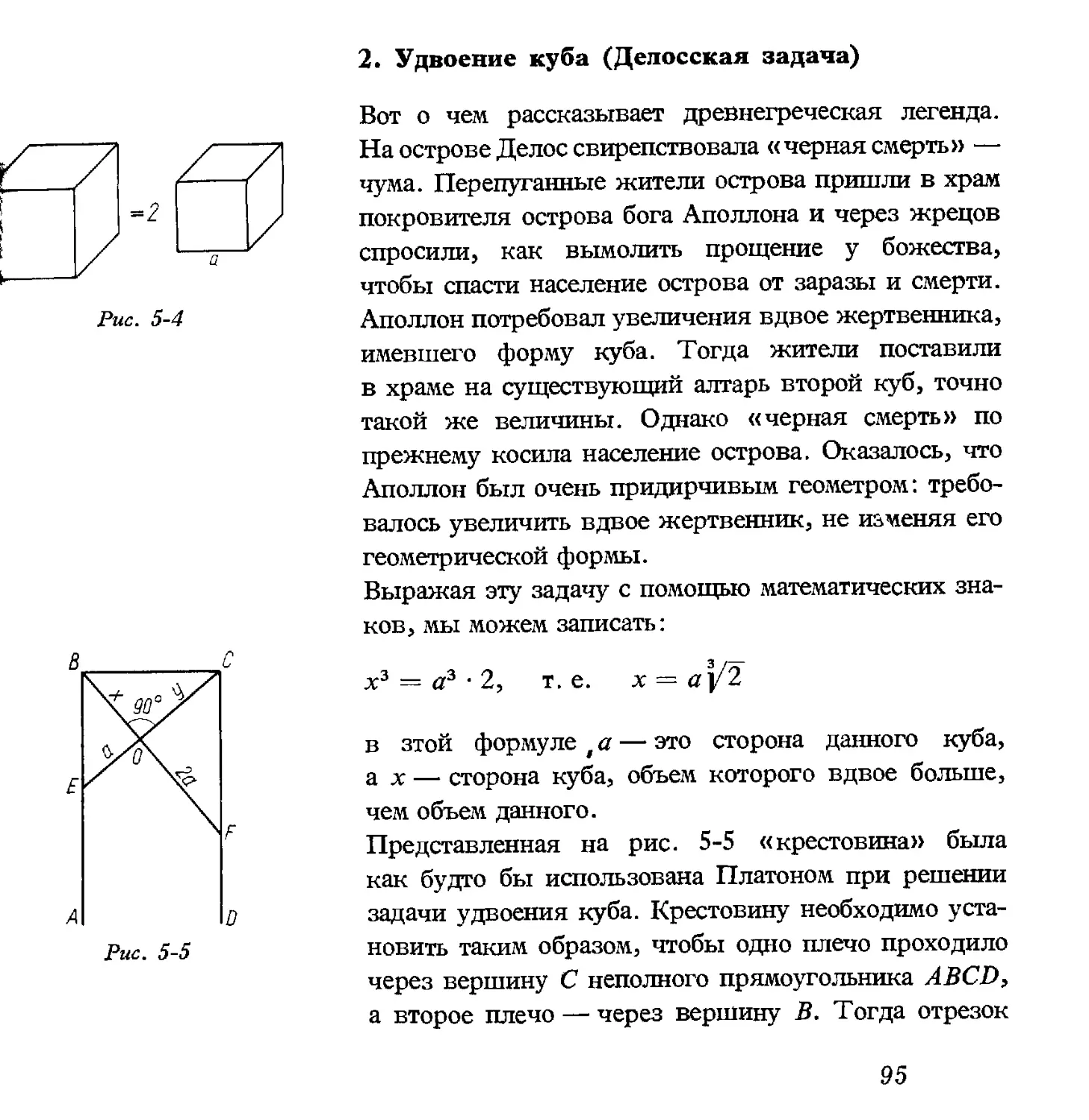
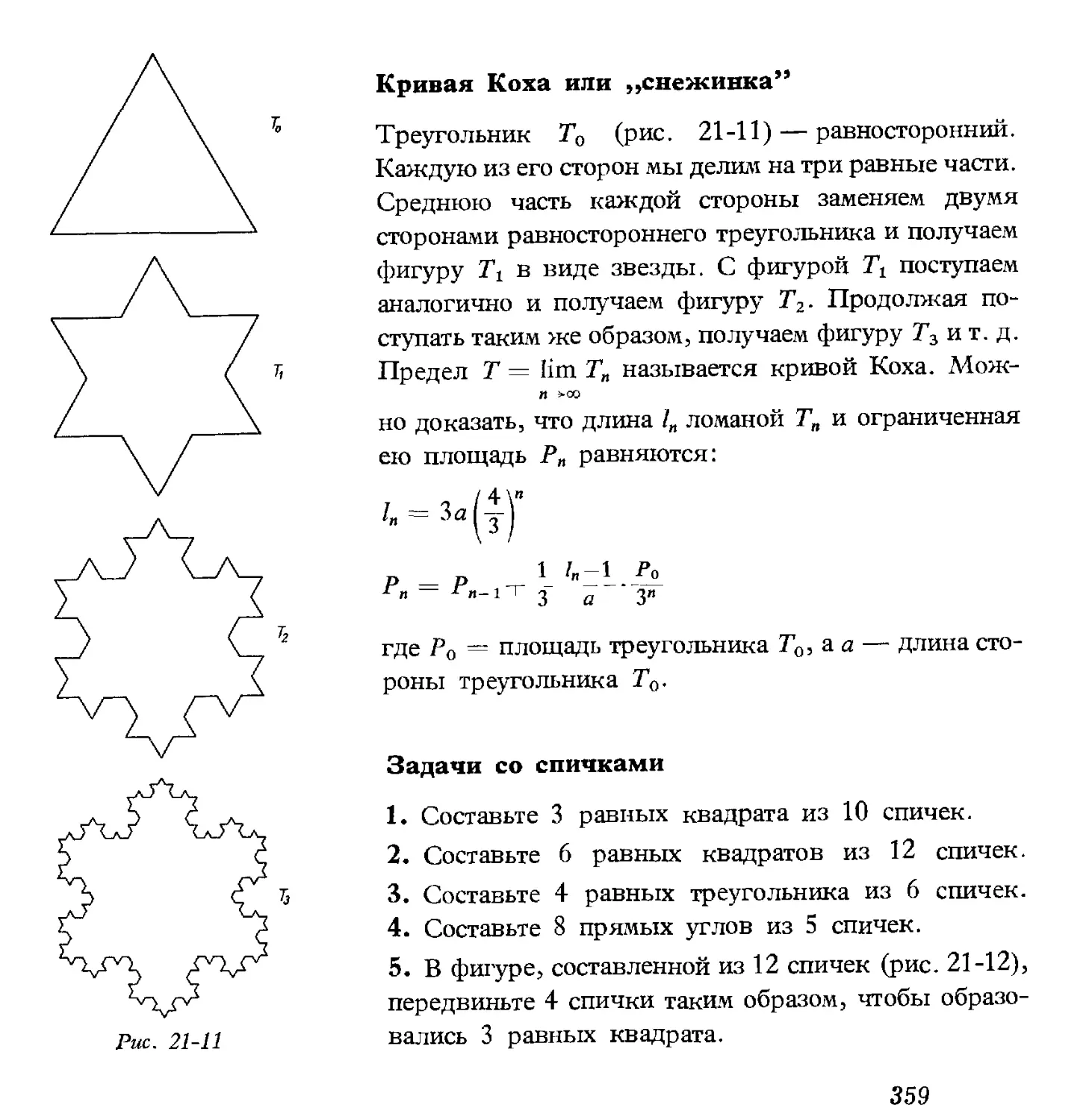
Теги: математика занимательные задачи история математики занимательная математика
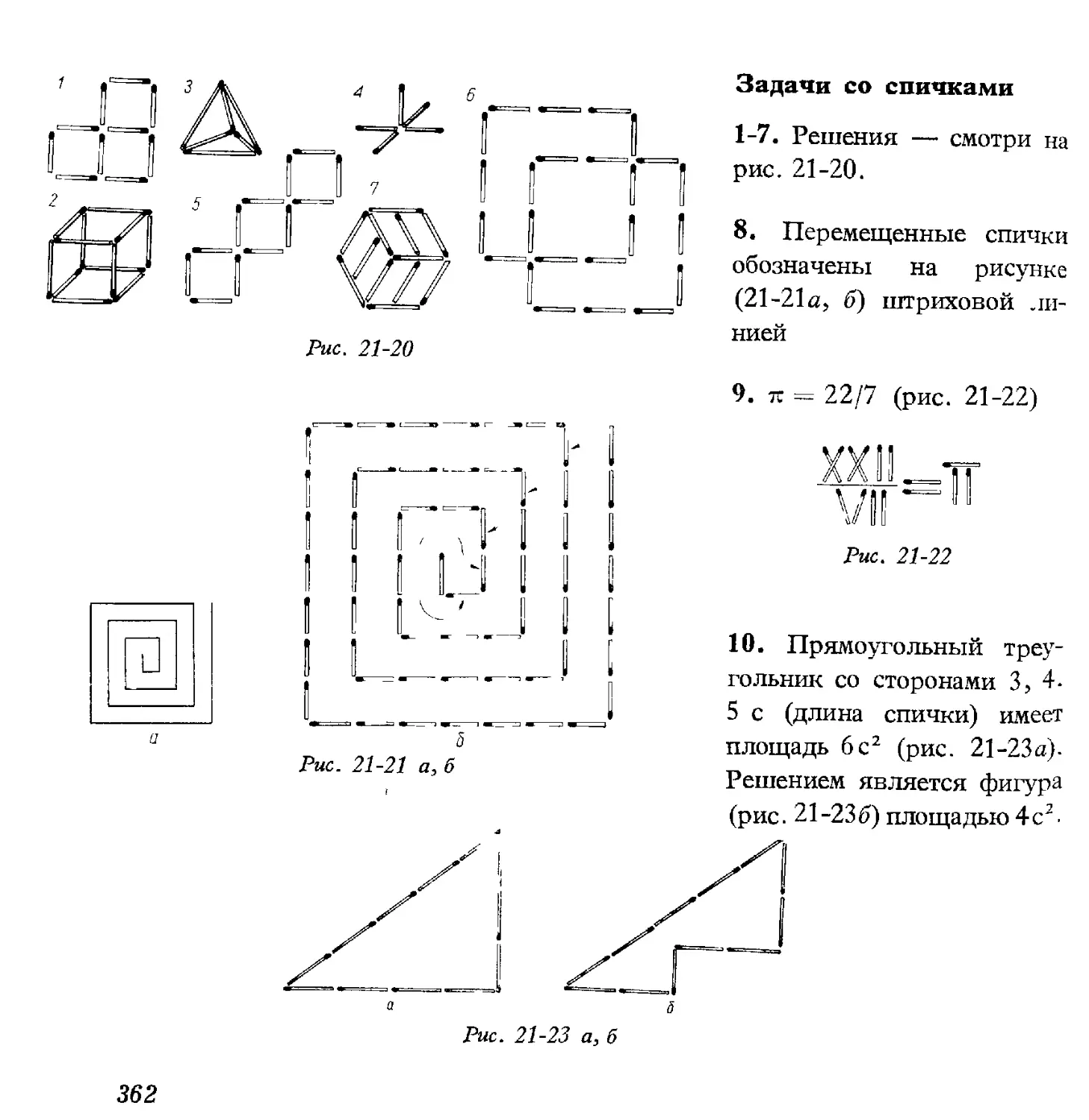
Год: 1972
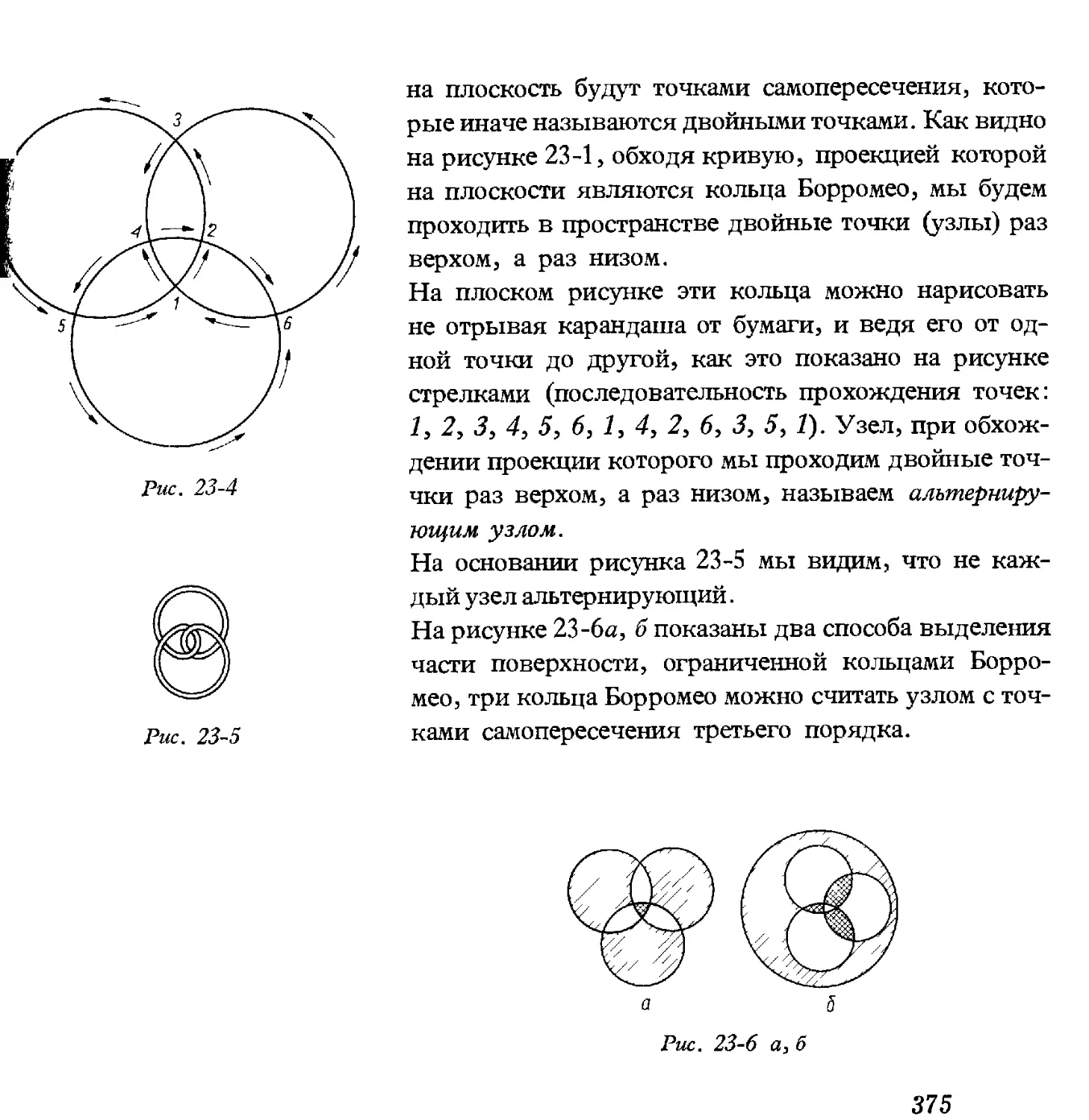
Текст
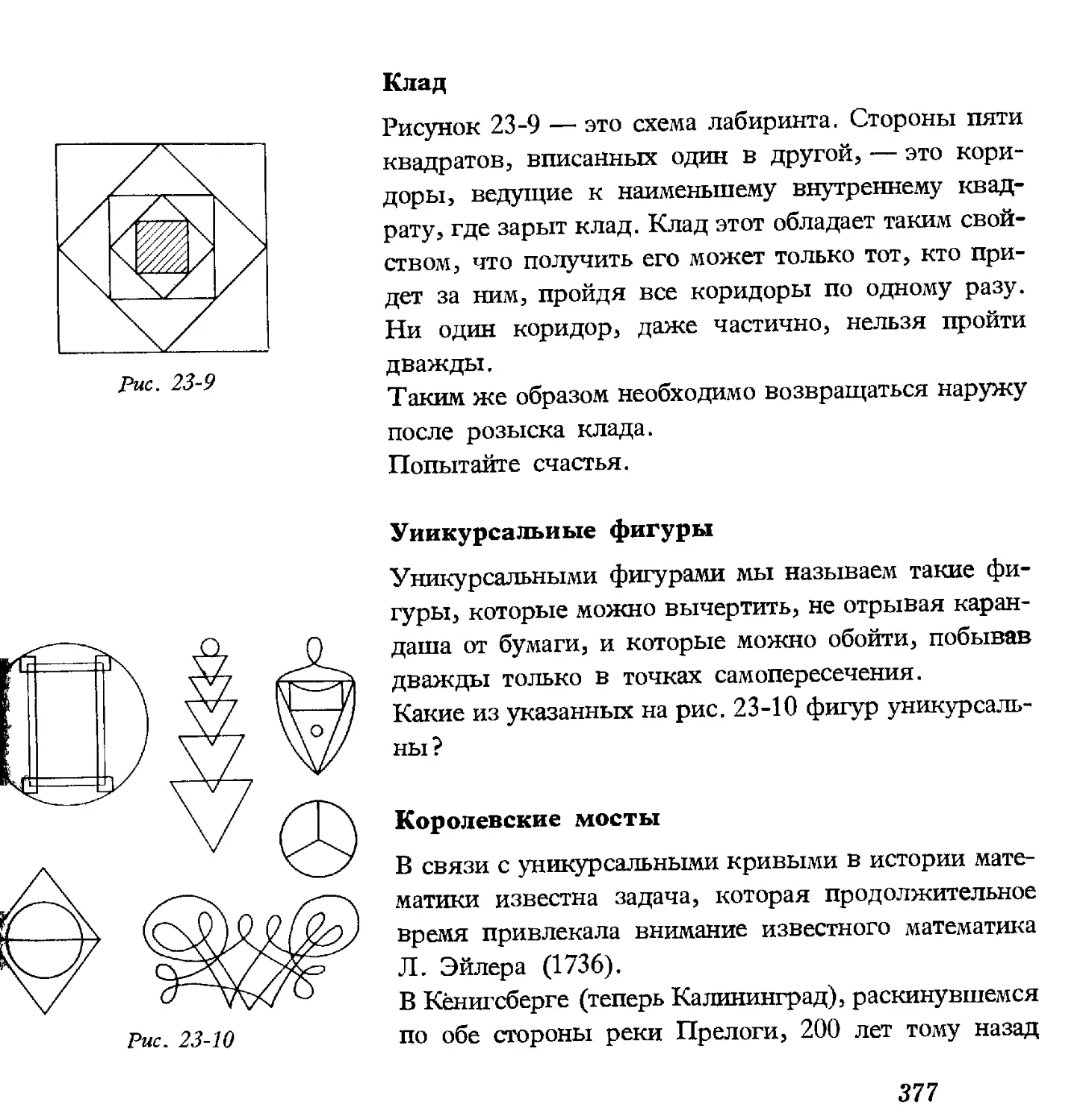
з»*
\ от разйлечоня к знаниям
^--^Ъл \ Cos &=(
Станислав Коваль
ОТ РАЗВЛЕЧЕНИЯ К ЗНАНИЯМ
Математическая смесь
Перевод с польского
Ольгерд Унгурян
WYDAWNICTWA
NAUKOWO-TECHNICZNE
WARSZAWA
WYDAWNICTWA NAUKOWO-TECHNICZNE
WARSZAWA 1972
All rights reserved
Printed in Poland
Drukaraia 1m Rewolucji Paidziernikowej, Warszawa
К ЧИТАТЕЛЮ
Эта книга не является систематическим курсом «за-
«занимательной математики». Ее цель — совершенно
другая.
Читая об интересных и полезных вещах, о которых
повествует книга, читатель сможет увлекательно про-
провести время, сможет хорошо отдохнуть после работы.
Рассказы, из которых она состоит, очень короткие,
но они затрагивают вопросы, несомненно заинтере-
сующие каждого любознательного читателя. Более
трудные темы перемежаются в книге с веселыми
историями, афоризмами и головоломками, а также
короткими рассказами из истории математики и смеж-
смежных наук. Чтобы не принуждать читателя решать
все, иногда довольно трудные задачи, автор привел
в конце каждой главы их решения, но, конечно,
читатель может самостоятельно испытать свои силы
и решить все задачи, не заглядывая в указанные
решения. Материал этой книги подобран не только
из разделов элементарной математики, в книге име-
имеются темы посвященные некоторым разделам выс-
высшей математики (аналитической геометрии, топо-
топологии, вариационному исчислению, теории вероят-
вероятности), которые, по сути дела, вовсе «не так страшны,
как их малюют».
Изобилие иллюстраций должно внести некоторое
разнообразие при чтении книги и сделать более на-
наглядным ход ее повествования.
Кроме оригинального материала, многое в книге за-
заимствовано из различных польских и зарубежных
источников.
Многие читатели поставят, очевидно, автору в упрек
отсутствие последовательности в расположении ма-
материала. Автор сделал это вполне сознательно, счи-
считая, что систематическое расположение материала
может довольно быстро «набить оскомину» читателю
и утомить его, так как у него может возникнуть
ощущение, что он имеет дело с учебником. Развле-
Развлечение и отдых — вот цель этой книги, а им чужды
педантичность и систематика.
ВМЕСТО
ПРЕДИСЛОВИЯ
1. Аристотель:
Мы сладостно вкушаем математику и с нами со-
совершается то, что с Лотофагами, ибо, отведав ее,
мы не хотим от нее отступиться и она овладевает
нами, как цветы лотоса.
2. Евклид:
В математике нет особых путей для королей.
3. Роджер Бэкон:
Кто пренебрегает достижениями математики, тот
приносит вред всей науке, так как тот, кто не
знает математики, не может изучить другие точ-
точные науки и не может познать мир.
4. Иммануил Кант:
В каждом познании столько науки — сколько
есть в нем математики.
5. Ян Снядецкий:
Математика — царица всех наук, ее любимцем
является истина, а простота и бесспорность —
одеянием... Математика, которая оказала столько
услуг обществу, наукам и искусству, станет также
путеводной звездой человеческого разума во всех
областях познания.
МЫ ЖИВЕМ
СРЕДИ ЧИСЕЛ
ГЛАВА 1
Мы живем среди чисел. Мы все время должны
рассчитываться или предъявлять какие-нибудь сче-
счета. В конструкторских бюро, в лабораториях и в ма-
магазинах — везде мы должны что-то измерять, счи-
считать. На любом крупном предприятии отделы пла-
планирования и статистики, бухгалтерия выполняют
важные задачи, а работа их сводится, по-существу,
к расчетам и замерам, причем считают и мерят не
только люди, но и призванные служить человечеству
машины.
Современный уровень нашей цивилизации требует
от людей умения пользоваться не только очень боль-
большими, но и очень маленькими числами. Но 5000 лет
тому назад человек уже не мог обойтись без счета.
Об этом свидетельствуют надписи на надгробных
плитах, глиняные таблички и папирусы. Ученые,
которые исследуют, каким образом человечество осво-
освоило счет, обращаются не только к древним докумен-
документам, но также изучают культуру существующих в на-
настоящее время первобытных племен, а также раз-
развитие понятия числа у маленьких детей.
Американский историк математики Ф. Кэджори
в своей книге «История элементарной математики»,
изданной в 1896 году, указывает, что одно из индей-
индейских племен, проживавшее в лесах в районе среднего
течения Амазонки, число «три» выражает словом
«поэтаррароринкоароак». Путешественник, который
об этом сообщил, принял это слово за название числа
«три», но можно вполне предположить, что это бы-
было не одно слово, а целое предложение. Это предло-
предложение могло, конечно, также обозначать какое-то
«очень большое» (содержавшее более, чем два эле-
элемента) множество предметов, для которого это племя
еще не нашло соответствующего числительного.
Современный человек начинает пользоваться числа-
числами уже с раннего детства. Такие числа, как 1,2,3,....
т. е. натуральные числа, нужны малышу уже в дет-
детском саду. Однако, несмотря на обиходный характер
натуральных чисел, немногие знают о их некоторых
очень интересных свойствах. Существует целый
раздел математики, именующийся «теория чисел»
(смотри главу 6), который занимается изучением
натуральных чисел. Теоремы теории чисел обладают
очень интересным свойством, все они кажутся очень
простыми. Словесное изложение этих теорем понят-
понятно даже среднеобразованному человеку, однако, до-
доказательства этих простых теорем — вещь чрезвы-
чрезвычайно кропотливая и очень часто оно не под силу
даже крупнейшим математическим умам.
Прежде, чем начать считать, необходимо решить две
задачи: выбрать систему счисления и установить наз-
названия числительных. Уже много тысячелетий тому
назад почти все народы, принадлежащие к нашей
цивилизации, избрали одну и ту же систему счисле-
10
ния, основанную на десятичной системе: десяток со-
содержит десять единиц, сотня — 10 десятков, тыся-
тысяча — 10 сотен и т. д. Однако, названия числительных
каждый народ установил в зависимости от своих
потребностей. В русском языке имеются отдельные
названия для первых десяти цифр и первых трех
ступеней числа десять: 101 (десять), 102 (сто) и 103
(тысяча). Древние греки имели также название ми-
мириады для обозначения числа 104, а древние оби-
обитатели Индийского полуострова, которые пользова-
пользовались санскритом, имели наименования числительных
для обозначения и дальнейших ступеней числа десять
вплоть до 1О10. Пока требования, предъявляемые
повседневной жизнью и наукой, были относительно
незначительны, вполне хватало числительных и их
производных: 10 тысяч, 100 тысяч, 1000 тысяч и т. д.
Но уже в позднем средневековье, благодаря про-
прогрессу науки и развитию экономических отношений,
потребовались более крупные числа чем тысяча
тысяч, а тем самым, возникла необходимость дать
им определенные названия. Так возникли такие чи-
числительные, как: миллион, миллиард, биллион,
триллион, квадриллион, квинтиллион и т. д.
Очень любопытно, что на разных языках эти назва-
названия употребляются для обозначения разных чисел.
Итак, например, в Польше, Великобритании, Гер-
Германии миллион обозначает 10б, миллиард 109,
биллион 1012, триллион 1018, квадриллион 1024,
квинтиллион 1О30, в то время как во Франции, Co-
Coветском Союзе и Соединенных Штатах Северной
Америки биллион обозначает 109, триллион 1012,
квадриллион 1015 и т. д.
Происхождение таких названий как биллион, трил-
триллион, квадриллион, квинтиллион становится вполне
понятным, если вспомнить латынь: эти названия со-
состоят из двух несколько видоизмененных латинских
слов: bis (два раза), ter (три раза), quarter (четыре
раза)... и суффикса «Поп». Только числительное
«миллион» происходит от итальянского «milione»,
что означает «жирная тысяча».
С помощью этих терминов можно бьшо назвать боль-
большие числа, встречающиеся в астрономии, физике,
географии, как, например:
Среднее расстояние от Земли до Солнца
150 000 000 км
Площадь земного шара 510 000 000 км2
Объем земного шара 1 083 000 000 000 км3
Масса земного шара
6 000 000 000 000 000 000 000 т
Так как вьшисывать столь большие числа — опера-
операция довольно-таки трудоемкая, да и для этого тре-
требуется много бумаги, ученые решили вместо длин-
длиннющего ряда нулей писать эти числа в виде 10".
Символ п указывает, сколько необходимо дописать
нулей. Итак, например, число 1 083 000 000 000
можно записать в виде 1083 • 109, а число
12
Рис. 1-1
6 000 000 000 000 000 000 000 — соответственно в ви-
виде 6 • 10".
Такой способ записи позволил представить даже
самые большие числа, с которыми мы встречаемся
при астрономических исчислениях, в очень простом
виде. Астрономы утверждают, что наиболее отда-
отдаленные галактики, иначе говоря, громадные скоп-
скопления звездных систем, состоящие из миллиардов
звезд, находятся от нас на таких расстояниях, что
солнечному лучу, бегущему со скоростью 300 000
км/сек, нужно миллиард лет, дабы преодолеть такое
расстояние. Из этого следует, что это расстояние
порядка 1022 км. Но даже такое, столь необъятное
разумом, расстояние, которое отделяет нашу крохот-
крохотную Землю от самых удаленных галактик, можно
представить очень просто в миллиметрах весьма не-
несложным числом 1028, так как
Ю22 км= 1022-106 мм;
1 км= 103ж= 103- Ю3мм.
Человек второй половины XX века умеет хорошо
считать. Правда, может быть, не столь быстро, как
этого от него требуют темпы современного ритма ра-
работы и научного прогресса. Но для этого у него есть
вычислительные машины. Несовершенство зрения
компенсировали очки, микроскоп и телескоп, несо-
несовершенство слуха — микрофоны, а несовершенство
наших вычислительных способностей — электрон-
электронные вычислительные машины, которые считают со
«скоростью света».
ЦИФРЫ РАЗНЫХ
НАРОДОВ И ЭПОХ
Рис. 1-2
Следующий раздел посвящен числовым обозначе-
обозначениям, иначе говоря, цифрам, этим буквам замеча-
замечательного математического алфавита, с помощью ко-
которых мы в состоянии выразить и записать любые
числа.
Вавилон
Знакомясь с числами, мы не можем не заняться зна-
знаками, с помощью которых числа обозначаются на
бумаге. Знаки эти мы называем цифрами.
Самыми древними цифровыми знаками являются
вавилонские знаки. Если мы взглянем на карту (рис.
1-2), то увидим на ней две черные жирные извива-
извивающиеся линии — реки Тигр и Евфрат. Древние
греки назвали эту страну Месопотамией, что по рус-
русски означает междуречье, так как расположена она
была в долине между двумя реками-близнецами.
Часть Месопотамии занимало могучее государство,
столицей которого был город Вавилон.
Уже четыре тысячелетия назад в Вавилоне расцве-
расцветала наука и существовали библиотеки. Правда, в те
времена еще не было печатных книг, но зато суще-
существовали глиняные таблички, на которых вавилон-
вавилонские мудрецы писали свои труды. Современные уче-
ученые нашли 44 таблички, на которых записана вся
математическая наука, известная вавилонцам. Уче-
14
п
В
5
I
А
Рис. 1-3
"И
Рис. 1-4
^=1000 <Y=7/
Рис. 1-5
Y 4 ^у=60+Ю + 4 = 7'
< Ш <« YYY
12-602 + 0-60 +33 = 43233
Рис. 1-6
ные Вавилона пользовались, так называемой, клино-
клинописью. Клинописных букв было очень много, но
цифровых знаков — мало.
На рисунке 1-3 изображена одна из табличек с за-
записью кодекса законов царя Хаммурапи.
Вавилонские числа являются, собственно говоря,
комбинацией трех клинописных знаков: единицы,
десятка и сотни (рис. 1-4).
С помощью этих знаков можно было написать чис-
число тысяча, а также любое другое число, при этом
использовались, как принцип сложения, так и умно-
умножения, а более крупные числа всегда предшество-
предшествовали меньшим (рис. 1-5).
Кроме этого способа записи чисел вавилонцы при-
применяли также позиционную систему и шестидесяти-
шестидесятиричный счет. В этом счете знак единицы может обо-
обозначать соответственно: 1, 60, 602 и т. д. в зависи-
зависимости от места, которое занимает (рис. 1-6).
Также в зависимости от занимаемого места знак де-
десятки может соответственно означать: 10, 10 • 60,
10 • 602, 10 • 603 и т. д.
Вавилонцы имели некое подобие знака нуль. Для
выражения недостающего места они писали наклонно
два знака единицы.
Вавилонцы умели также пользоваться простыми
и шестидесятиричными дробями (со знаменателями
60, 602, 603 и т. д.), которые записывали так, как
мы пишем десятичные дроби. Они умели также вы-
выполнять четыре арифметических действия на нату-
15
СЕЕЮ
Рис. 1-7
10
I
1
г
7
. -
40
кг
II
2
' ю3
III
3
: &
9
'1
50
Рис.
10' 10
а
Т
1 Л
10
'±1
so
5
1-8 а,
' 10
"I
5
л
20
)
70
б
' К
Б
Л
30
'JM
80
в в еяттттяи ооооо
100+100+100+10+Ю+Ю+Ю+Ю+Ю+Ю
Рис. 1-9
^ ^ ральных числах и дробях, подсчитывать проценты,
{ q делить числа на пропорциональные части. Из обла-
области геометрии они знали лишь столько, сколько им
бьшо необходимо для нужд строительства и земле-
землемерного дела: умели подсчитать площадь фигур, огра-
ограниченных отрезками, например,, площадь треуголь-
треугольника, четырехугольника и т. д.
Египет
Почти столь же древними являются и египетские
цифры.
Для выражения своих мыслей и слов на бумаге
египтяне использовали знаки, которые мы в насто-
настоящее время называем иероглифами (рис. 1-7).
Затем иероглифное письмо бьшо заменено более про-
простым иератическим письмом.
В обоих видах письма египтяне имели специальные
знаки для цифр (рис. 1-8й, б).
Египтяне в начале писали числа высшего порядка,
а затем нисшего. При этом использовался принцип
сложения (рис. 1-9) или умножения.
Египтяне умели также пользоваться дробями. Все
египетские дроби имели в числителе единицу, дру-
других дробей они не умели даже выговорить (исклю-
(исключение составляло 2/3). Дроби писались так же, как
и натуральные числа, только над ними ставилась
s=375 Точка, причем для 1/2 и для 2/3 имелись специаль-
специальные знаки (рис. 1-10).
16
Q
w
Рис.
СИ
cp
1-10
1
г
Чтобы записать какую-либо дробь, египтяне пред-
ставляли ее в виде дробей с числителями равными
- 23
единице, итак, например, дробь -^ записывали в сле-
г х х 1,1,1
дующем виде: -г-г-к-, что обозначало -г + -?- + -о- =
= 40" "
Главньш источником наших знаний о египетской ма-
математике является так называемый папирус Ахмеса1 >
(примерно 2000—1700 гг до н. э., сравни стр. 37),
писца фараона, найденный в 1853 году.
Египтяне писали примерно так, если 23 хлеба мы
разделим между 40 людьми, то каждый получит
одну четвертую, одну пятую и одну восьмую часть
одного хлеба.
Греция и Рим
Римские цифры общеизвестны и используются еще
сейчас, между прочим, на циферблатах часов, в над-
надписях на мемориальных досках, при нумерации стра-
страниц книг и т. д.
Известно, например, что L — это 50, С — это 100,
D — это 500, М — это 1000. Знаки С и М — это
') Иначе именуемый папирусом Ринда от фамилии владель-
владельца, приобретшего папирус в 18S8 году. Ныне папирус хра-
хранится частично в лондонском Британском музее, а частично
в Нью-Йорке (прим. переводчика).
17
первые буквы слов «.centum» — 100 и «mille» —
1000. Знаки L и D очевидно также были первыми
буквами каких-то слов, однако слова эти до нас не
дошли. Можно только предполагать, что это были
этрусские слова или же выражения какого-то ла-
латинского наречия. С помощью этих цифр римляне
писали числа, используя правила сложения и вы-
вычитания, например, LX = 60 E0+10);
XL == 40E0-10); СМ = 900 A000-100);
МС = 1100 A000+100) и т. д.
Римские цифры
1 = 1 X = 10 С = 102 М = 103
V = 5 L = 50 D = 500
Римляне пользовались дробями со знаменателем 60
(вавилонские) и со знаменателями 12, 24, 48:
1 1 1
-~д — это половина, a -js это одна четвертая -^-.
Римские ученые осваивали дроби в связи со сче-
счетом денег и использованием мер и весов. Римская
монета Ас, чеканенная первоначально из меди, весила
один фунт и делилась на двенадцать унций. Суще-
Существовало даже специальное название «deunx» для
выражения -гч- {deunx — de uncia), т. е. Ас без одной
унции.
Вычисление «в уме» облегчало пользование так на-
называемого абака (abacus), счетной доски, разделенной
18
Рис. 1-11
1
II
III
Nil
Г
PI
П1
ПИ
П1П
д
Д1
дг
дд
30
40
50
so
70
80
90
100
200
400
500
WOO
Ю 000
ддд
дддд
р
РД
РДД
РДДД
РДДДД
н
нн
нннн
с
X
м
Рис. 1-12
на вертикальные полосы, по которым передвигались
находившиеся там камни или фишки (рис. 1-11).
Греки применяли два способа записи чисел: атти-
аттическую нумерацию и ионическую. При использо-
использовании ионической нумерации числа выражались бук-
буквами алфавита. Чтобы можно было отличить число
от слова, над буквами, представлявшими числа, ста-
ставилась черточка. Этот способ записи чисел приме-
применялся жителями Милета, Александрии и других гре-
греческих областей, находившихся под влиянием куль-
культуры этих городов. По всей вероятности, ионической
нумерацией пользовались Фалес, Евклид, Архимед,
Апполлоний, Герон и другие философы и ученые
Александрии и Малой Азии.
Афинцы для обозначения чисел пользовались на-
начальными буквами слов—числительных (рис. 1-12):
Г — обозначает пять, потому что Гете по-афински
значит пять,
Д — обозначает десять, потому что Леях по-гре-
по-гречески — это десять,
Н — обозначает сто, потому что Hmxw по-гре-
по-гречески — это сто,
X — обозначает тысячу, потому что это первая бук-
буква слова XiXiaC, которое по-гречески обозна-
обозначает тысячу,
М — обозначает десять тысяч, потому что это пер-
первая буква слова Mvqmx.?, которое по-гречески
обозначает десять тысяч.
I, II, III, ПП обозначали соответственно 1, 2, 3 и 4.
19
Рис. 7-
С помощью этих цифр житель Древней Греции мог
выразить каждое нужное ему число.
Греки, которые для выражения чисел использовали
буквы, желая указать на то, что данная буква выра-
выражает не целое число, а дробь с числителем один,
писали знаменатель, а рядом ставился диакритичес-
диакритический знак (два раза — рис. 1-13).
Если в числителе была не единица, а какое-то другое
число, то греки писали один раз числитель (с одним
знаком) и два раза знаменатель (с двумя знаками).
Был также и другой метод записи дробей: числитель
писался над знаменателем, но без черты. Так писал
дроби, например, Диофант, великий математик III—
IV веков нашей эры.
7
?
<* I
^- я
У Ч
(i
1
<0
@
1
«7
б
Z
Я-
Я
2
4
) »
Ъ
Л
9
г
2
3
4
4
б
7
9
0
Рис. 1-14
Индийская нумерация
Цифры, которыми мы пользуемся в настоящее вре-
время, пришли к нам из Индии (рис. 1-14). Европей-
Европейские народы познакомились с ними благодаря ара-
арабам. Известный математик Леонардо Пизанский пер-
первым упоминает о них в своем основном труде «Кни-
«Книга Абака» («.Liber Abaci»), изданном в 1202 году.
Польша была одной из первых стран, которая ввела
у себя индийскую нумерацию; произошло это в XIV
веке. Арифметика, основанная на индийской нуме-
нумерации, преподавалась в Польше в Краковской ака-
академии.
20
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Архимед B87—212 до н э )
Архимед и число
Нормальный стакан емкостью 250 см3 заполнен чи-
чистыми мельчайшими песчинками1*. Сколько песчи-
песчинок находится в этом стакане?
Если вслед за Архимедом мы примем, что в одном
маковом семени помещается 10 000 мельчайших пес-
песчинок, и учтем, что диаметр макового семени со-
составляет примерно 1/2 мм, т. е., что в 1 мм3 можно
поместить 8 маковых семян, то ответ на поставлен-
поставленный вопрос может быть найден легко.
В 1 мм3 помещается 80 000 песчинок, следовательно,
в 250 см3 поместится 80 000 • 1000 • 250, т. е. 20 мил-
миллиардов песчинок.
Совершенно неожиданное число. Желая доказать,
что нет такого множества, которое нельзя было бы
сосчитать, Архимед рассчитал, сколько песчинок по-
поместится в шаре, радиус которого равен расстоянию
от Земли до звезд. Для своих рассчетов Архимед
разработал специальную систему счислений, едини-
единицей которой были мириады, т. е. 10 000. Чтобы хоть
в какой-то мере дать представление о величине чис-
числа, полученного Архимедом в результате его рассче-
та, попытаемся подсчитать, сколько песчинок может
поместиться в сфере приблизительно равной нашей
Земле, которая по сравнению со сферой Архимеда
подобна песчинке.
1i Архимед, собственно говоря, имел ввиду пылинки.
21
Объем Земли, как известно, составляет примерно
10" см3.
Чтобы заполнить песком сферу, равную по вели-
величине Земле, с помощью стакана объемом 250 см3
— нужно наполнять его 1027:250 = 4 • 1024 раза.
Если принять, что с помощью какого-то специального
автомата мы можем высыпать 1000'стаканов песка
в секунду, то для того, чтобы наполнить 4 • 1024
стаканов песка необходимо 4 • 1024 :1000 = 4 • 1021 сек.
В году насчитывается 31 536 000 сек (будем счи-
считать примерно 32 000 000 сек). Тогда автомат дол-
должен работать 4 • 1021 : 32 000 000 « 1 • 1014 лет,
A00 000 000 000 000 лет), т. е. 100 триллионов лет.
Вспомним, что, по подсчетам геологов, возраст на-
нашей планеты — примерно 5—8 миллиардов лет,
т. е. почти в 10 000 раз меньше, чем должен был бы
работать наш автомат.
Дайте мне точку опоры и я ...
Описывая жизнь Архимеда B87—212 г. до н. э.),
Плутарх из Херонеи E0—125) утверждает, что ве-
великий математик был столь убежден в мощности
своих машин, что сказал «Дайте мне точку опоры —
и я сдвину землю». Мы знаем, что точка опоры
Архимеда должна находиться где-то вне Земли, на
какой то другой планете. Давайте попробуем отве-
ответить на вопрос, какой длины должно быть плечо
рычага, чтобы Архимед мог сдвинуть Землю.
22
Масса Земли составляет 6 • 1024 кг. Предположим,
что человек в состоянии поднять в течение одной се-
секунды 60 кг на высоту 1 м. Тогда одно плечо ры-
рычага должно быть во столько раз длиннее второго,
на сколько 6 • 1024 больше 6 • 10, т. е. в 1023 раза.
Пусть конец более короткого плеча рычага поды-
подымается (вместе с Землей) только на 1 см, тогда конец
более длинного плеча должен опуститься на
1 см-1023 = 1 м- 1021 = 10" кж
Это расстояние в 6000 миллионов раз больше рас-
расстояния от Земли до Солнца.
Предположим, что скорость опускания составляет
1 MJceK. Тогда движение более длинного плеча долж-
должно продолжаться 1012 лет. Но если бы мы даже
предположили, что более длинное плечо рычага бу-
будет опускаться со скоростью света C00 000 км/сек),
то и так это движение должно продолжаться 100 ты-
тысяч лет.
Таким образом горделивая фраза Архимеда — всего
лишь поэтическая гипербола.
Энергия голоса
Допустим, что одновременно говорит 100 000 че-
человек. Если можно было бы превратить энергию
возникших звуковых волн в электрическую энергию,
то оказалось бы, что ее хватит лишь на то, чтобы
зажечь лампочку карманного фонарика. Мощность,
образующаяся при одновременном разговоре всех
23
жителей Земли, более менее соответствует мощности
автомобильного двигателя. Ничего удивительного,
что старинная пословица гласит: «Сколько ни го-
говорить, а с разговора сытым не быть».
Исторический анекдот
Ежи Оссолинский, отправляясь в свое посольство
в Рим (в XVII веке) и желая поразить всех роскошью
своего убранства, заказал для своей лошади серебрян-
ные подковы и велел прибить их золотьши ухналя-
ухналями. Когда кузнечных дел мастер назвал свою цену,
Оссолинский заявил, что это слишком дорого и что
он столько платить не намерен. Тогда мастер улыб-
улыбнулся и сказал: — Я сделаю Вам 4 серебрянных под-1
ковы даром, но за 24 золотых ухналя Вы мне запла-
заплатите следующим образом: за первый ухналь 2 гро-
гроша, за второй — 4 гроша, за третий — 8 грошей
и так далее, за каждый следующий ухналь вдвое боль-
больше предыдущего.
Не ожидая какого-либо подвоха, Оссолинский при-
принял это условие, тем более, что про себя он уже под-
подсчитал, во сколько ему обойдется первая подкова
и признал, что 126 грошей — это не так то уж много.
Когда лошадь подковали и кузнечных дел мастер
принес выписанный на пергаменте счет, Оссолин-
Оссолинский ужаснулся и вежливо стал просить старого ма-
мастера, чтобы он согласился принять названную им
раньше сумму. Мастер довольный научкой, какую
24
дал ясновельможному пану, согласился принять пла-
плату, соответствующую первоначально названной це-
цене. Какая сумма была написана на пергаменте? Сколь-
Сколько денег должен был бы заплатить Ежи Оссолин-
ский, если бы мастер не уступил?
25
Вдовья копейка
Известна евангельская притча о вдовьей лепте1*.
Если бы вдова положила свою копейку в тогдашнюю
сберегательную кассу, то учреждение, в пользу ко-
которого вдова завещала бы свой капитал, получило
бы, например, в 1968 году ... Давайте подсчитаем,
сколько действительно получило бы учреждение по
истечении 1968 лет. Пусть сберегательная касса на-
начисляет 4% годовых. По истечении 1 года 1 копейка
/ 4 ^
превратиться в 11 -f- jkq\ коп. = A,04)х коп. По исте-
истечении двух лет — в A,04J, спустя три года —
в A,04K ... и т. д. После 1968 лет 1 копейка пре-
превратиться в A,04I968 коп. Обозначим Х= A,04I968,
тогда
igX = 1968 • lgI,04 = 1968 • 0,0170 = 33,4560
а из этого следует, что
X х, 286 • 1031 коп. « 286-1029 рублей
Предположим, что бюджет Советского Союза уве-
увеличится до 2860 миллиардов рублей B86 ¦ 1О10 руб.)
и сохранится на зтом уровне, тогда из капитала вдо-
вдовы можно было бы покрывать расходы бюджета
в течение /B86 • 1029): B86 • Ю10) = 1019 лет.
Астрономы подсчитали, что возраст солнечной си-
системы составляет примерно 10 миллиардов лет, чи-
число t примерно в 10 миллиардов раз больше.
1) Лепта — мелкая монета {примечание переводчика).
26
Сколько дней?
1. Примерно миллион дней минул со дня первых
Олимпийских игр Древней Греции G76 год до
н. э.).
2. Примерно 3/4 миллиона дней минуло от начала
нашей эры.
3. Дольше всех в Польше царствовал король Вла-
Владислав Ягелло: 17 532 дня.
4. Михаил Ломоносов жил примерно 19 500 дней,
Юлий Словацкий — 15 000 дней, а Фридерик
Шопен еще короче, всего только 14 245 дней.
Эти числа порождают горькие раздумья...
РЕШЕНИЕ ЗАДАЧ
Исторический анекдот
Ухнали для второй подковы стоили бы:
128+256+512+1024+2048+4096 = 6064 грошей
Для третьей подковы:
8192+16 384+32 768+65 536+131 072+262 144 =
= 516 096 грошей
наконец, для четвертой подковы ухнали стоили бы:
524 288+1 048 576+2 097 152+4 194 304+8 388 608+
+16 777 216 = 33 030 144 гроша
Это громадная сумма, которую не каждый польский
магнат мог бы уплатить.
МИФ О ГЛАВА 2
ИРРАЦИОНАЛЬНЫХ
ЧИСЛАХ
Пифагор E70—496 до н.э.)
Великий немецкий математик Леопольд Кронекер
A823—1891) сказал: «целые числа создал добрый
бог, а все остальные — люди». Греческий философ
Пифагор был именно одним из тех, которые спо-
способствовали открытию новых, до того времени не
известных чисел и которые много лет спустя были
названы иррациональными. Пифагор был родом
с острова Самос, но он поселился и учил в греческой
колонии «Великая Греция» (на юге Италии) в го-
городах Кротон и Тарент. Иррациональные числа Пи
фагор открыл при доказательстве теоремы о гипо-
гипотенузе, которую мы сейчас называем обычно теоре-
теоремой Пифагора АС1 = АВ2+ВС2.
Эти странные числа, которые не были ни натураль-
натуральными числами ни дробями (а только такие числа
были тогда известны) Пифагор назвал «алогой» —
«невыразимыми». Это открытие было для него пол-
полной неожиданностью и очень сильно его поразило,
так как оказалось, что существуют геометрические
соотношения, как, например, отношение диагонали
квадрата к его стороне АС.АВ (рис. 2-1), которые
нельзя было выразить никаким известным в те вре-
времена числом. Это разрушало все философское миро-
возрение Пифагора, согласно которому числа управ-
управляют не только мерой и весом, но также и всеми
28
\
\
1
/
/
2
X
/ \
4
/
3
\
\
\
\
Рис. 2-2
явлениями, происходящими в природе, и являются
сущностью гармонии, царствующей в мире, душой
космоса. О своем открытии Пифагор рассказал под
присягой «тетрактис»1* своим наиболее посвящен-
посвященным ученикам. Но открытие Пифагора было столь
ошеломляющее, что один из его учеников не выдер-
выдержал и выдал тайну, которую ему доверил учитель.
Легенда гласит, что в назидание другим — ученик
был строго наказан богами: он погиб во время штор-
шторма в морской пучине.
Если длина стороны квадрата ABCD составляет 1,
то на основании теоремы Пифагора получим (рис.
2-2)
АС2 = 12+12 = 2, из этого: АС = \/2
Отрезок, который можно таким образом построить,
выражается числом \/2. Это не натуральное число,
поскольку оно больше 1: (\/2 > 1, так как (}/2J >
> I2, т. е. 2 > 1) и меньше 2: {\/2 < 2 потому, что
(]/2J < 22, т.е. 2<4). Из зтого следует, что
1 < ^2<2.
Докажем, что между 1 и 2 нет никакой дроби, квад-
квадрат которой составляет (у 2) , т. е. 2.
Доказательство: предположим, что такая
дробь существует и что ее самая простая форма после
1) Тетрактис — мифическое число 36 =A+3+5+7) +
+B+4+6+8), сумма первых четырех нечетных чисел и че-
четырех четных чисел.
29
m
сокращения —, где т и и натуральные или простые
числа, тогда
— = i/2
п
т. е. -J- = 2, т. е. «г2 = 2и2 A)
Мы видим, что правая сторона этого равенства де-
делится на 2. Из этого следует, что и левая сторона
должна делиться на 2, т. е. что т делится на 2.
Пусть т = 2&, где к натуральное число. Тогда из
равенства A) следует:
BкJ = 2я2,
т. е. 4к2 = 2и2, т. е. 2к2 = и2 B)
Из уравнения B) следует, что п должно делится на 2,
т.е., что числа тип имеют общий делитель больше 1.
Это противоречит условию теоремы, что дробь —
несокращается. Ложность вывода вытекает из лож-
ложности предпосылки, что существует такая дробь, ко-
которая равняется у/2. Из этого следует, что j/2 не
является ни натуральным числом, ни рациональным
числом (дробью).
„ Иэ этих наших рассуждений следует, что j/2 нахо-
-1—' ' ' '—- дится в интервале [1,2].
Рис. 2-3 Известно, что точкам числовой оси (рис. 2-3) соот-
соответствуют действительные числа, каждой точке од-
одно и только одно действительное число.
30
Рис. 2-4
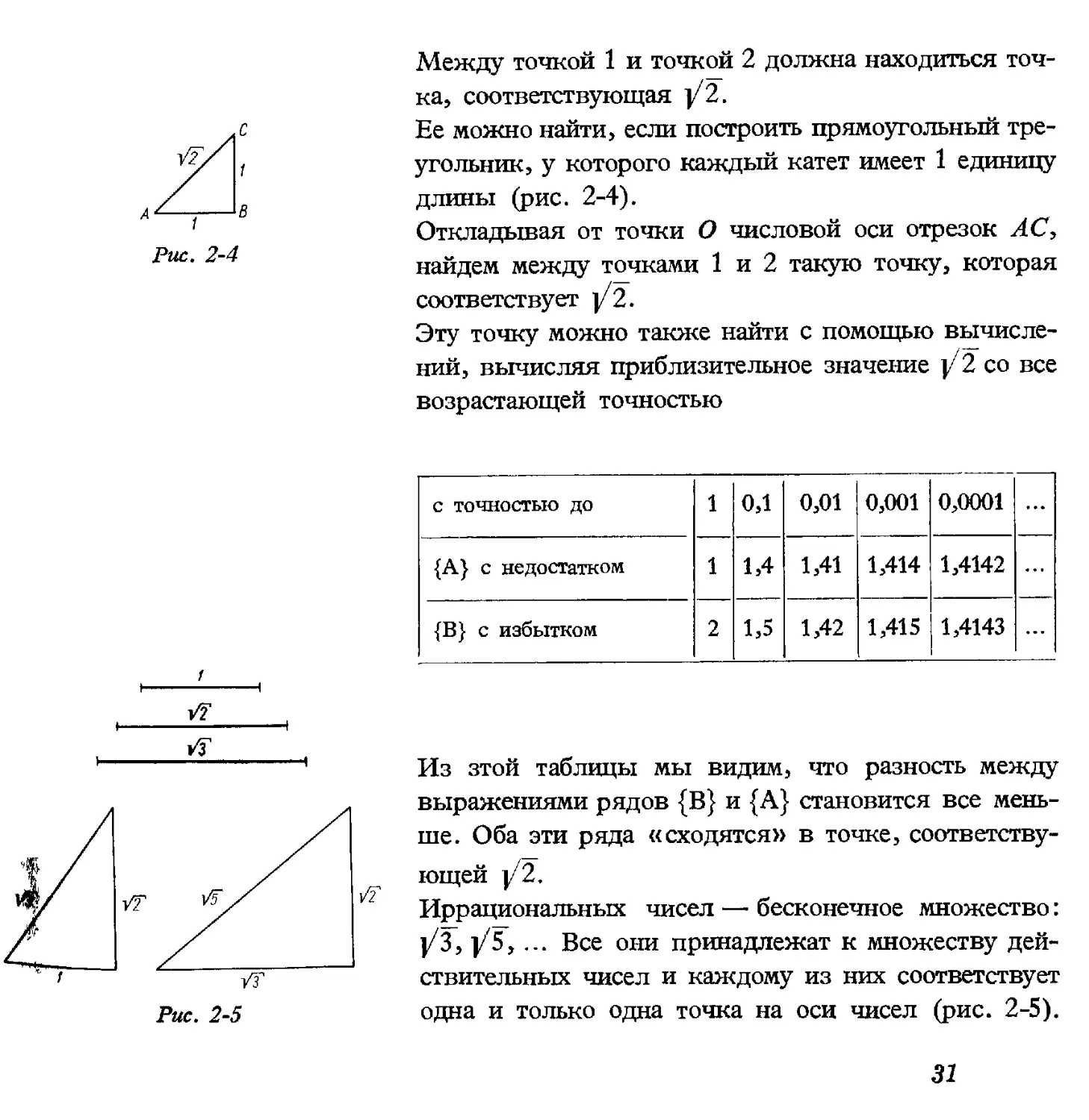
Между точкой 1 и точкой 2 должна находиться точ-
точка, соответствующая ]/2.
Ее можно найти, если построить прямоугольный тре-
треугольник, у которого каждый катет имеет 1 единицу
длины (рис. 2-4).
Откладывая от точки О числовой оси отрезок АС,
найдем между точками 1 и 2 такую точку, которая
соответствует |/2.
Эту точку можно также найти с помощью вычисле-
вычислений, вычисляя приблизительное значение j/2 со все
возрастающей точностью
V?
с точностью до
{А} с недостатком
{В} с избытком
1
1
2
0,1
1,4
1,5
0,01
1,41
1,42
0,001
1,414
1,415
0,0001
1,4142
1,4143
—
Рис. 2-5
Из зтой таблицы мы видим, что разность между
выражениями рядов {В} и {А} становится все мень-
меньше. Оба эти ряда «сходятся» в точке, соответству-
соответствующей |/2.
Иррациональных чисел — бесконечное множество:
j/З, \/'5, ... Все они принадлежат к множеству дей-
действительных чисел и каждому из них соответствует
одна и только одна точка на оси чисел (рис. 2-5).
ДВА ЗНАМЕНИТЫХ
ИРРАЦИОНАЛЬНЫХ
ЧИСЛА
Иррациональных чисел бесконечное множество, но
два из них, относящиеся к так называемым трансцен-
трансцендентным числам, необходимо выделить: число Архи-
Архимеда, которое позднее стало обозначаться символом
тс, и Неперово число, обозначаемое символом е. Оба
символа установил швейцарский математик и физик
Леонард Эйлер A707—1783). Число тс достаточно
хорошо известно читателям. Более подробно оно
описано в V главе. Здесь мы можем только напом-
напомнить, что искал его уже ученик Пифагора Гиппократ
Хиосский (вторая половина V в. до н. э.), который
утверждал, что площадь круга Р прямо пропорцио-
пропорциональна площади квадрата со стороной г (к г2). Сегод-
Сегодня коэффициент этой пропорциональности мы обо-
обозначаем буквой тс:
= тс,
а из этого
Р= кг2
Задачей, которую не смог решить Гиппократ, занял-
занялся Архимед (ок. 287—212 до н. э.). Он решил найти
сторону квадрата, площадь которого равна площади
круга. В главе V описаны важнейшие попытки ре-
решить эту задачу, иначе говоря, найти число тс.
В 1873 году (а тогда, как известно, еще не было
вычислительных машин) английский математик
В. Шенкс вычислил 707 десятичных знаков для числа
тс. Так как практическое значение имеют только два
первых десятичных знака, мы приводим далее в тек-
тексте лишь ради интереса число тс с точностью до 30
32
десятичных знаков:
ти = 3,141 592 653 589 793 238 462 643 383 279...
Число е выражается бесконечной десятичной дробью,
приближенно (с точностью до 0,000 01) равной е =
= 2,718 28 .'Это число является основанием натураль-
натуральных логарифмов1* (символ In) в отличие от деся-
десятичных логарифмов, основанием которых является
число 10 (символ lg). Число е было подсчитано
в 1728 году Д. Бернулли с помощью формулы
Сущность числа е легко понять, если рассмотреть
два способа возрастания какой-либо величины. Для
упрощения наших рассуждений, предположим, что
эта величина — 1 рубль = 100 коп.
I. Простое возрастание. Банк начисляет
простые проценты, например, 4%. По истечении од-
4 1
ного года банк начислит -т^г = -^г рубля на каждый
положенный рубль. Через 25 лет 1 рубль, поло-
положенный в сберегательную кассу, превратиться в
1 + -jc" -25 = 2 рубля, т. е. капитал удвоиться.
') Логарифмом называется показатель степени, в которую
надо возвысить основание логарифма, чтобы получить ло-
логарифмируемое число, например, Iog232 =,5 так как 25 =
= 32. В этом примере число 2 — это основание логарифма,
32 — логарифмируемое число.
33
П. Сложное возрастание. Банк начи-
начисляет сложные проценты, например, 4%. По исте-
чении одного года 1 рубль превратиться в 11 + тла~
V iuu/
рублей, т.е. в A,04)* рублей, через два года —
в A,04J рублей, через три года в A,04K, а через
двадцать пять лет — соответственно в A,04J5 =
= 2,6600 рублей = 2,66 рублей. Если бы процен-
проценты начислялись каждые полгода, т. е. 50 раз в те-
течение 25 лет, то через 50 полугодий 1 рубль пре-
1 + -tqq-I рублей, т. е. в 11 + -^-] РУб~
лей = 2,6912 рублей. Если проценты будут начис-
начисляться еще чаще, например, каждый квартал A00
1 раз в течение 25 лет), то один рубль по истечении
/ 1 \100
100 кварталов превратиться в П + тпгП рублей.
Из этого можно сделать вывод, что если бы банк
начислял проценты не 4 раза в году, а еще чаще,
например, каждый час, то по истечении 25 лет каж-
каждый внесенный рубль превратился бы в относительно
большую сумму. Это однако не так. Общая формула
возрастания рубля имеет вид:
«„ = A+1)" A)
В этой формуле п — зто число, которое показывает,
сколько раз в течение 25 лет начисляются сложные
проценты. Когда п стремится к бесконечности
(и-*оо), то последовательность A) стремится к
2,718 281...Х); это всего примерно на 0,028 рубля «
« 3 копейки больше, чем в том случае, если процен-
проценты начисляются два раза в году. Пределом после-
последовательности A) является число е
е =
(« — натуральное число).
В таблице указаны выражения ряда A) при все
возрастающем п.
и
ш
1
2
2
2,2500
3
2,37037
4
2,44146
5
2,48832
...
...
10
2,59930
...
...
100
2,69100
Независимо от величины процента, который банк
начисляет за время, в течение которого 1 рубль
удваивается при простых процентах, этот же рубль
превращается в е рублей при сложных процентах,
начисляемых непрерьшно в течение всего периода.
Этот способ возрастания — уникален, так как в каж-
каждый момент возрастание пропорционально состоя-
') Мы говорим, что последовательность а„ стремится к пре-
пределу (числу) g, если п стремится к бесконечности, в том
случае если для каждого положительного числа е сущест-
существует такой номер N члена последовательности, что для чле-
членов последовательности с большими номерами, чем Ny
т. е. для п > N выполняется неравенство g—е < а„ < g+e.
35
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
нию нарастающей величины. Таким образом на-
нарастает снежный ком, скатывающийся с вершины
горы, покрытой снегом.
Такое нарастание часто называют органическим, так
как очень много органических процессов протекает
по этому закону. Одним из примеров такого нара-
нарастания является рост населения нашей планеты.
Математические игры и головоломки
Математические игры и головоломки были уже ши-
широко распространены в древние времена.
Их мы находим уже в папирусах Ахмеса. Одна из
них называется «Лестница чисел». В этой задаче
говорится о числах 7, 49, 343, 2401, 16 807. Рядом
с этими степенями числа 7 виднеются иероглифы,
обозначающие слова: дом, кошка, мышь, ячмень,
мера. В папирусе нет никаких указаний относительно
решения этой головоломки, но по предположению
немецкого-историка математики М. Кантора A829—
1920) разъяснение можно найти в задаче, указанной
почти 3000 лет спустя в труде итальянца Леонардо
Пизанского (Фибоначчи), изданном в 1202 году под
названием «Книга абака» («Liber Abaci»). А вот со-
содержание задачи Фибоначчи:
«7 старух идут в Рим, каждая из них ведет 7 мулов,
на каждом из мулов по 7 мешков, в каждом мешке
36
Площадь фиг
ACJD
= площади
окружности JK
Площадь фиг
А08СА =
= площади
окружности DC
н [тесак мясника)
Рис. 2-6
по 7 хлебов, а в каждом хлебе по 7 ножей, каждый
из ножей—в 7 ножнах. Сколько всего предметов?»
На"основании этой задачи можно предположить, что
смысл задачи Ахмеса сводится к следующему: «В 7
домах — по 7 кошек, каждая кошка съела по 7 мы-
мышей, а каждая мышь съела по 7 колосьев ячменя,
из каждого колоса может вырасти по 7 мер. Какую
последовательность чисел можно построить, исходя
из условий этой задачи и какова их сумма?».
Задачи-шутки были распространены в Древней
Греции и Древнем Риме, а в средние века также
и на западе Европы. В древние времена шуточными
задачами занимался даже великий Архимед об этом
свидетельствуют его подсчеты, касавшиеся салино-
на (солонки) и арбелона (тесака мясника).
Известен сборник задач, изданный в VIII веке епи-
епископом Алкуином G35—804). Некоторые из задач
Алкуина, например: «О волке, козе и капусте» или
«О собаке и зайце» по сегодняшний день увлекают
молодежь.
Из папирусов Ахмеса
Примерно 2000 лет до нашей эры при дворе фараона
Аменемхета III состоял в качестве придворного пис-
писца и математика Ахмес. Более подробных данных
о жизни Ахмеса история не сохранила, но в 1853
году в одной из пирамид был найден папирус, пере-
переписанный в свое время Ахмесом.
37
Этот папирус имеет почти 5,25 м длины и 33 см
ширины, содержит описание всего, что в ту эпоху
было известно египтянам в области арифметики
и геометрии.
Папирус содержит, между прочим, следующую за-
задачу: «Сто мер зерна необходимо разделить между
пятью работниками таким образом, чтобы второй по-
получил на столько мер больше, чем первый, на сколь-
сколько третий рабочий получит мер больше, чем второй,
четвертый — чем третий, а пятый — чем четвертый.
Кроме того, двое первых рабочих вместе должны
получить в семь раз меньше зерна, чем трое осталь-
остальных.
Сколько мер зерна получил каждый рабочий?»
Задаче этой — почти четыре тысячи лет, однако ее
решение доставит Вам по всей вероятности не мало
удовольствия.
Задача Диофанта
Последний великий греческий математик Диофант,
который жил в III веке до н. э. в Александрии,
сформулировал и решил такую задачу: «Найти та-
таких три числа, сумма которых, а также сумма каждой
пары этих чисел была бы квадратом другого числа».
Диофант нашел эти три числа.
Это 80, 320 и 41.
Действительно 80+320+41 = 441 = 212.
38
Сумма каждой пары из этих чисел также является
квадратом числа
80+41 = 121 = И2
320+41 = 361 = 192
80+320 = 400 = 202
Каким образом Диофант нашел эти числа?
Используя современную математическую символику
(и то в большом сокращении) ход его рассуждений
должен был бы быть следующий: обозначим иско-
искомые числа а, Ъ, с. Диофант пользовался только од-
одним неизвестным х, и предположил, что
I. a+b+c = x2+2x+l = (х+1J
II. a+b = х2
III. b+c = x2-2x+\ = (x-1J
Из этих уравнений он определил а = 4х и с = 2л:+1,
а из этого уже следует, что а+с = 6х+1.
Учитывая, что а+ с — это квадрат какого-то числа,
Диофант определил, что х может быть только равно
20.
Принимая во внимание все вышеуказанное, попытай-
попытайтесь найти три таких числа а, Ъ и с, чтобы а-\-Ь-\-с
и а+b и Ь+с были квадратами других чисел.
Примечание: а-\-с не является квадратом.
Головоломка Иосифа Флавия
Есть такие легенды и предания, которые передаются
из поколения в поколение, но есть также и такие
математические задачи, которые известны с неза-
39
памятных времен. О них не забывают и они всегда
увлекают тех, кто с ними встретится. К таким за-
задачам принадлежит одна головоломка, относящаяся
к первому веку нашей эры, которая сохранилась,
впрочем, в нескольких вариантах.
Один из этих вариантов связан с именем иудейского
историка Иосифа Флавия.
Иосиф Флавий происходил из рода священнослу-
священнослужителей. Родился он в 37 году в Иерусалиме. На-
Находился в Риме при императоре Веспасиане, затем
вернулся в Иудею и принял участие в восстании
евреев против римского владычества. Был взят в плен,
но два года спустя отпущен на свободу императором
Веспасианом, принял его родовое имя Флавий и по-
получил римское гражданство. С тех пор Иосиф Фла-
Флавий полностью посвятил себя литературной деятель-
деятельности, которую понимал как служение своему народу
(евреям). Иосиф Флавий написал несколько трудов
на иудейскую тематику, из которых самым крупным
было произведение «Иудейская война».
40
Флавий писал свои труды по-гречески, ибо в дре-
древние времена это был международный язык, язык
ученых. Греческий переводчик Хегесиппос перевел
«Иудейскую войну» на латынь (IV в) и к переводу
приобщил жизнеописание Иосифа Флавия, а в нем
такую^легенду.
После подавления иудейского восстания и разруше-
разрушения Иерусалима, римские воины вылавливали вос-
восставших и брали их в рабство. Флавий с горсткой
восставших D1 человек) бежал и спрятался в гроте.
Не видя какого-либо другого выхода, Флавий пред-
предложил уставшим, выбившимся из последних сил
воинам, чтобы они сдались в плен римлянам. Но
воины впали в ярость. Они решили лучше уничто-
уничтожить друг друга, чем сдаться на милость победите-
победителей. Не помогали никакие уговоры. Иудейские вои-
воины пригрозили Флавию, что взаимное уничтожение
начнут именно с него. Но мудрый Флавий придумал
одну уловку, в которую посвятил только своего
единственного друга. В критический день Флавий
выстроил всех воинов (в том числе себя и своего
друга) в один ряд и объявил, что убиению подлежит
каждый третий воин, считая с левой стороны. По-
После первого расчета, произойдет второй, затем тре-
третий, и так до тех пор, пока все они будут убиты.
На котором месте в ряду поставил Флавий своего
друга и на котором стоял сам, чтобы ни при одном
из расчетов жребий не пал на них, хотя были убиты
все остальные 39 воинов.
41
Непроверенная легенда
Одним из крупнейших арабских математиков был
Мухаммед ибн Муса ал-Хорезми (Магомет сын
Мусы из Хорезма). Жил он в IX веке, родился в Хо-
Хорезме (ньше Узбекская ССР). Мухаммед ибн Муса
упоминается в истории математики в связи с деся-
десятичной нумерацией и развитием алгебры в Европе.
Творческий период своей жизни ибн Муса провел
в Багдаде в годы царствования мудрого халифа
ал-Ма'муны. Со своей родины ибн Муса должен
был бежать, так как навлек на себя гнев хана Хо-
Хорезма.
42
Л Единица измерения
Рис. 2-7
Рис. 2-8
В связи с этим событием существует следующая ле-
легенда.
Заключенному в темнице математику хан предложил
свободу и награду, если последний правильно решит
предложенную ему задачу. Если же ибн Муса не
сумеет привести правильное решение, то ему отре-
отрежут правую руку. Математик согласился, задачу
решил правильно, обрел свободу и получил награду,
но затем предусмотрительно покинул свою родину
и прибыл в Багдад.
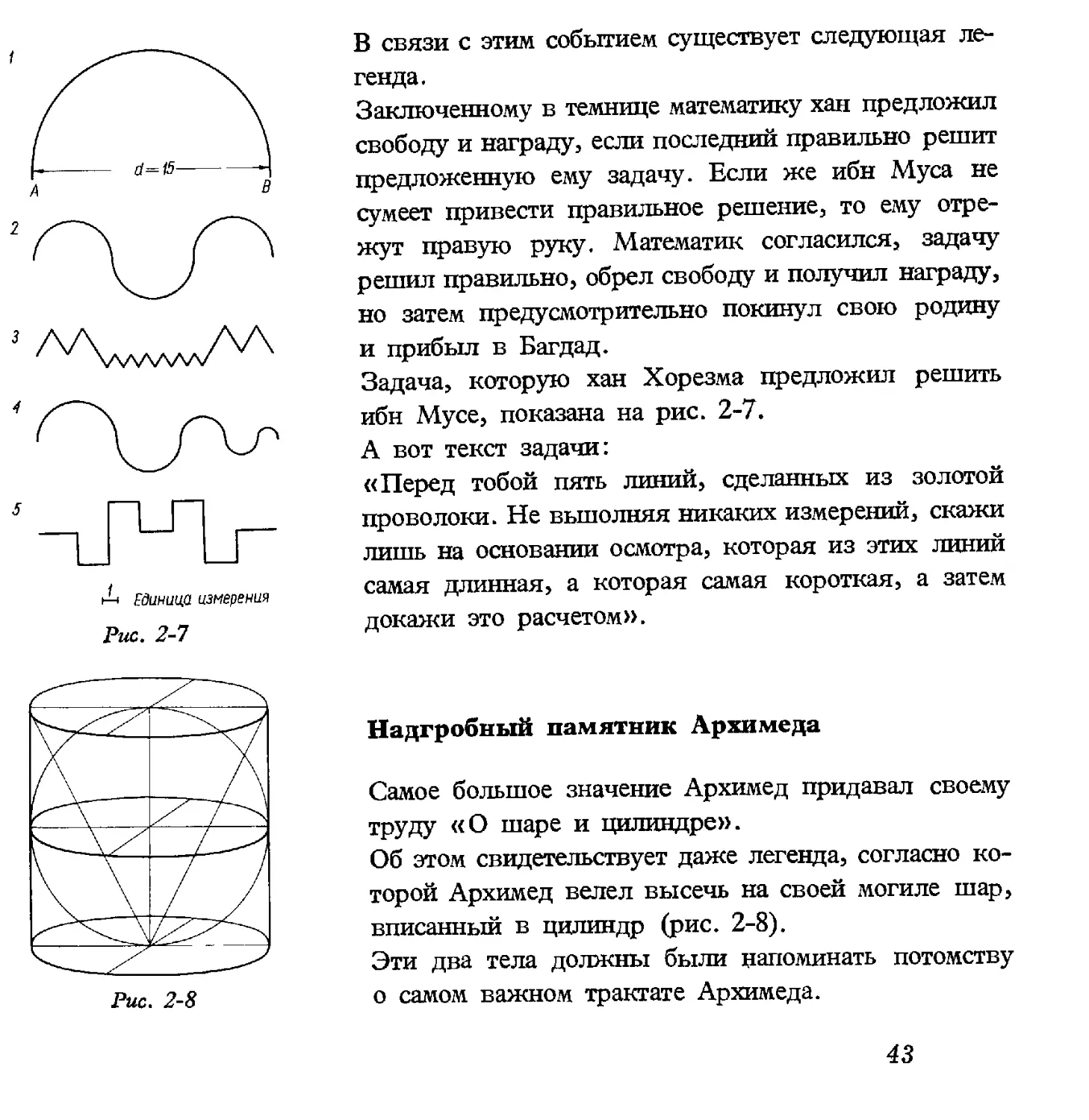
Задача, которую хан Хорезма предложил решить
ибн Мусе, показана на рис. 2-7.
А вот текст задачи:
«Перед тобой пять линий, сделанных из золотой
проволоки. Не выполняя никаких измерений, скажи
лишь на основании осмотра, которая из этих линий
самая длинная, а которая самая короткая, а затем
докажи это расчетом».
Надгробный памятник Архимеда
Самое большое значение Архимед придавал своему
труду «О шаре и цилиндре».
Об этом свидетельствует даже легенда, согласно ко-
которой Архимед велел высечь на своей могиле шар,
вписанный в цилиндр (рис. 2-8).
Эти два тела должны были напоминать потомству
о самом важном трактате Архимеда.
43
Архимед доказал, что
V1:V2:V3 = 1:2:3
где:
V2 = -~-то-3 — объем шара с радиусом г,
V3 = 2га-3 — объем цилиндра, описанного вокруг
этого шара,
2
Fx = у то-3 — объем конуса, вписанного в этот ци-
цилиндр.
РЕШЕНИЕ ЗАДАЧ
Из папирусов Ахмеса
Согласно условию задачи, количество мер зерна, ко-
которое получили отдельные работники, образует ариф-
арифметическую прогрессию. Обозначим первый член
этой прогрессии через а, а ее разность через d.
Тогда на основании формулы суммы первых чле-
членов арифметической прогрессии Sn = (ai+an)y; по-
получим
| = 100
7 (a+a+d) = у (a+2d+a+4d)
то есть
a+2d = 20 Ha+7d = 3a+9d
44
На основании этих уравнений вычисляем a vs. d.
Ответ. Работники получили соответственно:
—; ю|-; 20; 29^-; 38у мер зерна.
Задача Диофанта
Ответ, а = 20; b — 5; с = 11. Соответствующие
суммы составляют 36, 25 и 16. Сумма а+с = 31 не
является квадратом натурального числа.
Гоповопомка Иосифа Фпавия
Ответ. Места, какие заняли в ряду Иосиф Флавий
и его друг, обозначены жирным шрифтом:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31,
32, 33, 34, 35, 36, 37, 38, 39, 40, 41.
Давайте проверим. Убивались согласно договору
воины со следующими номерами:
после первого пересчета: 3, 6, 9, 12, 15, 18, 21, 24,
27, 30, 33, 36, 39;
после второго пересчета: 1, 5, 10, 14, 19, 23, 28, 32,
37,41;
после третьего пересчета: 7, 13, 20, 26, 34, 40;
после четвертого пересчета: 8, 17, 29, 38;
после пятого пересчета: 11, 25, 2, 22;
после шестого пересчета: 4, 35.
45
Остались только воины, находившиеся на 16 и 31
местах, которые, конечно, не имели намерения уби-
убивать друг друга.
Примечание. Существует и другой вариант
этой легенды: о 15 турках и 15 христианах. Согласно
этому варианту, христиане и турки установлены
в круг и каждый девятый, начиная счет от опреде-
определенного человека, выкидывается эа борт. Задача за-
заключается в том, чтобы турков и христиан устано-
установить по кругу в такой последовательности, чтобы за
борт выкидывались только турки.
Решение этого варианта представлено на рис. 2-9,
на котором темными кружками обозначены христиа-
христиане, а светлыми турки. Счет необходимо начать от
кружка, рядом с которым поставлен крестик.
Решение этой задачи в общем виде все еще не най-
найдено.
Непроверенная легенда
Ответ. 1) Линии, обозначенные номерами 1, 2 и 4 —
равны. Длина каждой из них составляет -у^г/.
2) Самая длинная линия обозначена номером 5, са-
самые короткие линии—линии, обозначенные соот-
соответственно как 1, 2, 4.
3) При выбранной нами единице соответствующие
длины линий составляют: № 5 — 31 единица, № 3 —
30 единиц, №4 = №2 = № 1 = у
15 = 23у.
ОБ ГЛАВА 3
Отрицательных
числах
ГРЕЧЕСКАЯ
МАТЕМАТИКА
История отрицательных чисел — это один из инте-
интереснейших разделов последовательного развития ма-
математической мысли, иллюстрирующий процесс ста-
становления математических понятий, свидетельству-
свидетельствующий о взаимозависимости развития общественных
производственных сил и прогресса в области мате-
математики, подтверждающий фундаментальный тезис,
что решающим критерием ценности теории является
практика: ведь человечество не захотело признать
отрицательных чисел до тех пор, пока не возникли
конкретные, обусловленные нуждами общественной
и производственной практики, возможности их при-
применения.
Математики древнего мира вообще не занимались
относительными числами. Греческие математики приз-
признавали только натуральные числа и, хотя они знали
дроби, но не считали их числами, а лишь единицами
нисшего порядка, чем-то вроде более мелких единиц
длины, веса или денежных единиц нисшего порядка.
Первым среди греческих математиков, который стал
рассматривать дроби наравне с другими числами, был
Диофант Александрийский (вторая половина III
и первая половина IV века нашей эры).
47
ИНДИЙСКАЯ
МАТЕМАТИКА
Диофант различал также «слагаемые» и «отнимае-
«отнимаемые» числа и применял для обозначения «отнимае-
«отнимаемых» чисел символ «^н (перевернутая греческая
буква пси), он постиг также правила умножения
«слагаемых» и «отнимаемых» чисел. Однако, Дио-
Диофант ограничился только рассмотрением случаев, при
которых уменьшаемое больше вычитаемого и, что
более существенно, прилагал к рассматриваемым
уравнениям также условия, при соблюдении кото-
которых корни уравнения были всегда положительными
числами. Отрицательные корни, если они встреча-
встречались, Диофант считал недопустимыми и попросту их
отвергал.
В области арифметики относительных чисел несколь-
несколько дальше продвинулись индийские математики. Бра-
магупта (рожд. в 598 г.) использовал в своих вы-
вычислениях числа, подробные современным отрица-
отрицательным числам, которые он обозначал, ставя над
ними точку. Индийские математики по-разному на-
называли положительные и отрицательные числа, ис-
используя с этой целью слова, обозначающие «имуще-
«имущество» и «долг». Индийские математики знали отри-
отрицательные корни уравнений, однако, отвергали их,
объясняя это тем, что «люди не признают отрица-
отрицательных чисел».
48
Шбждевременность
открытия
отрицательных
ЧИСЕЛ
АРАБСКАЯ
МАТЕМАТИКА
Много веков прошло, прежде чем в XIII веке,
а особенно в конце XV века, математики снова заин-
заинтересовались относительными числами, найдя для
них многочисленные возможности применения. Та-
Таким образом, лишь спустя девять веков отрицатель-
отрицательные числа начали проникать в математику.
Мы мало знаем о развитии греческой математики
в III—VI веках. Это была эпоха, в которой рабовла-
рабовладельческий строй, раздираемый внутренними про-
противоречиями, приходил в упадок.
В Византии, в Восточной Римской империи, импера-
император Юстиниан I E27—565) издавал все более суро-
суровые декреты, направленные против последователей
различных ересей, а в 529 году издал закон, запрещав-
запрещавший изучение философии в Афинах.
Изданный в Афинах кодекс Юстиниана содержал
статью, озаглавленную «О злоумышленниках, ма-
математиках и им подобных лицах», в которой имелась
следующая фраза: «Прежде всего, запрещается, до-
достойное порицания, математическое искусство». В зти
времена пришли в упадок все мирские науки, а с ни-
ними и математика.
Народом, который сберег творения ученых древне-
древнего мира, были арабы.
Арабы проявляли исключительную восприимчи-
восприимчивость к культуре и быстро перенимали культурное
49
наследство от покоренных народов. За годы прав-
правления Халифа Харун-ал-Рашида и его сына ал-Ма-
муна почти все научные труды классиков древнего
мира были переведены на арабский язык.
Арабская математика развивалась на базе греческой
и индусской математики. Среди арабских матема-
математиков на первое место выдвинулся математик,
астроном и географ Мухаммед ибн Муса ал-Хо-
резми (Магомет сын Мусы из Хорезма, позднейшей
Хивы, который жил в начале IX века в Багдаде).
Ал-Хорезми был автором первого учебника мате-
математики, изданного под названием «Книга о восста-
восстановлении и противопоставлении» (Китаб алъ-джебр
Ьалъ-мукабала). Это было первое изложение мате-
математики с точки зрения ее практического примене-
применения в исчислениях, дополненное многими приме-
примерами решения уравнений.
Слово «Джебр» обозначает то же, что и «восста-
«восстановление», а в современном толковании — пере-
перенос отрицательных величин уравнения на другую
сторону.
Слово «Мукабала» обозначает «выравнивание»
или «противопоставление», а в современном тол-
толковании, замену подобных выражений по обеим
сторонам уравнения одним выражением.
Например, в уравнении 10х = 8х+8, имеем с правой
стороны «избыток» 8х, который приводим, в ре-
результате чего получаем 2х = 8.
50
Название сочинения ал-Хорезми перекочевало в Ев-
Европу в переводе на латинский язык под названием
«Algebra et Almucubala» и положило начало упот-
употреблению термина алгебра.
В своем учебнике ал-Хорезми подобрал задачи
таким образом, чтобы при решении избежать полу-
получения отрицательных корней.
В тех немногочисленных примерах, где невозможно
было избежать появления отрицательных корней,
ал-Хорезми обходит их молчанием.
Таким образом, хотя арабские математики и поло-
положили начало применению алгебры в качестве совре-
современного инструмента при математических вычисле-
вычислениях, однако в области отрицательных чисел они
явно отставали от достижений индусской матема-
математики.
Математика в европе
эпохи феодализма
До XI века в странах Западной Европы проис-
происходил процесс формирования феодальной системы
производства.
В XI веке феодальный строй вступает в эпоху своего
наивысшего расцвета, и этот период продолжается
до XV века. Происходит углубление общественного
разделения труда, ремесло отделяется от земледель-
чества, возникают города, значение которых увели-
увеличивается все больше и больше, возникают внутренние
рынки.
В XI веке, в результате роста производственных
сил, развития общества, разделения труда и обмена
происходит принципиальное изменение в области
внешней торговли, все более существенное значение
во внешней торговле начинают приобретать евро-
европейские купцы, которые постепенно вытесняют
с рынков арабских и византийских купцов.
В связи с развитием внешней торговли у европей-
европейских купцов все больше увеличивается интерес
к Востоку.
Экономические и коммерческие соображения побуж-
побуждают европейских купцов предпринимать путешес-
путешествия в страны Востока.
В XI веке начинаются крестовые походы, которые
продолжаются до 1270 года и оказывают громадное
влияние на дальнейшее развитие европейских стран.
Крестоносцы знакомятся с достижениями техники
и культуры Востока, что оказывает существенное
влияние на развитие потребностей и запросов пра-
правящих классов общества и становится стимулом для
дальнейшего развития промышленности и торговли.
Крестовые походы способствуют также оживлению
и дальнейшему развитию внешней торговли со стра-
странами Востока и увеличению товаро-денежного об-
обращения. В конце средневековья возникают неко-
некоторые отрасли промышленности, которые благопри-
благоприятствуют дальнейшему экономическому развитию;
строятся первые доменные печи, литейные заводы,
расширяется мореплавание, прежде всего, благодаря
52
изобретению компаса, появляются бумага, порох,
часы.
Быстро развивающееся денежное обращение вы-
вытесняет натуральный обмен.
Открытие Америки A492) и морского пути в Индию
A498) оказывают громадное влияние на развитие
различных отраслей производства. В эпоху расцвета
феодализма, которая продолжается до XI века,
нельзя обнаружить каких-либо следов математи-
математического творчества в Европе. Очень выразительным
примером, характеризующим эту эпоху, является
история Герберта из Овернии, в последствии римс-
римского папы Сильвестра II (945—1003), который
большую часть своей жизни провел в Испании, где
приобретал математические знания, обучаясь в араб-
арабских школах и который был обвинен в колдовстве
именно из-за своих математических знаний.
Однако, еще в эпоху наивысшего расцвета феодализ-
феодализма в Европе начинает пробуждаться математическое
творчество.
В XII веке новый экономический порядок начинает
устанавливаться в Италии, а прежде всего, в ее се-
северной части.
В первом десятилетии XIII века Леонардо Пизанский,
иначе называемый Фибоначчи, что значит сын Бо-
наччия A180—1250), пишет знаменитый, как на те
времена, труд «Книга Абака» (Liber Abaci), в кото-
котором он изложил все важнейшие сведения из области
математики.
53
Фибоначчи не признавал отрицательных корней
уравнений. Однако, в изданном примерно в 1225
году сочинении «Цветок» (Flos) Фибоначчи при-
привел задачу, которую он получил во время математи-
математического турнира, происходящего при дворе импера-
императора Фридриха II, от своего соперника, придворного
математика и нотариуса Джованно из Палермо.
Это была задача, решавшаяся с помощью квадрат-
квадратного уравнения, у которого одним из корней было
отрицательное число. Леонардо Пизанский считал
эту задачу неразрешимой, однако, он добавил, что
задача имела бы смысл, если бы один из компаньо-
компаньонов (задача касалась расчетов акционерного общес-
общества) имел вместо капитала долг. В конце XV века
в математику начинают довольно широко проникать
из купеческой практики знаки «+» и «—»; они
встречаются одновременно во многих рукописях тех
р^ времен. Итак, знак «—» появляется в немецкой
\ алгебре, составленной примерно в 1486 году (рис.
Рис. 3-1 3-1, в современной записи это выражение обозна-
обозначает 15-22л:).
Знак «+» появляется в латинской алгебре, состав-
составленной также примерно в 1486 году (рис. 3-2;
в современной записи это выражение обозначает
В печатном тексте знаки «+» и « —» встречаются
Рис. 3-2 впервые в немецком учебнике арифметики, состав-
составленном примерно в 1489 году Иоганном Видманом.
Из содержания учебника следует, что эти знаки
54
проникли в математику из купеческой практики
и должны были обозначать избыток или недостаток
веса. Видман свободно оперирует знаками «+»
и «—» и считает их уже не только знаками матема-
математических действий, но и символами, предшествую-
предшествующими числам и выражениям.
Итальянец Лука Пачоли, в своем труде «Сумма
знаний по арифметике, геометрии, отношениям и про-
пропорциональности» («Summa de Arithmetica, Geome-
tria, Proportioni et Proportionalita»), изданном в 1494
году, приводит правила арифметических действий
на положительных и отрицательных числах, но еще
не использует знаков «+» и «—». Эти правила
изложены чисто формально, например, для умно-
умножения приведено такое правило:
Плюс, умноженный на плюс, дает всегда плюс,
Минус, умноженный на минус, дает всегда плюс,
Плюс, умноженный на минус, дает всегда минус,
Минус, умноженный на плюс, также дает минус.
Очень любопытно, что в изданном в 1474 году,
т.е. почти одновременно, трактате «Наука о числах,
в трех частях» («Le triparty en la science des nomb-
res») французский автор Николай Шюке, рассматри-
рассматривает отрицательные величины при решении задач
наравне с положительными и добавляет при этом:
«Хотя бы даже другие авторы считали такое реше-
решение невозможным». Однако, как в распадавшемся
феодальном строе прогрессивные силы боролись
55
МАТЕМАТИКА В ЭПОХУ
ЗАРОЖДЕНИЯ
КАПИТАЛИСТИЧЕСКИХ
ОТНОШЕНИЙ
с консервативными, так и в математике передовые
идеи неоднократно встречали отчаянное сопротивле-
сопротивление. Это очень хорошо видно на примере истории
отрицательных чисел. Названия, добавляемые им
«фальшивые числа», «абсурдные числа», «фик-
«фиктивные числа» лучше всего свидетельствует, что
и в области математики старый строй усиленно
сопротивляется проникновению новых идей.
В XVI веке феодализм вступает в эпоху своего рас-
распада, зарождаются капиталистические отношения.
Этот период охватывает XVI—XVIII века и являет-
является, начиная с XVII века, периодом бурного развития
математики на фоне стремительного роста произ-
производственных сил.
Первым математиком, который в известной степени
упорядочил арифметику относительных чисел, был
монах ордера св. Августина Михаэль Штифель
A486—1567). Правда, Штифель не признавал отри-
отрицательных корней в уравнениях, а отрицательные
числа называл «абсурдными» (в противополож-
противоположность истинным, т.е. положительным числам), но
к его заслугам следует отнести то, что он не побоялся
расширить понятие числа путем введения чисел, ко-
56
торые были «меньше, чем ничто» (numeri minores ni-
hile, ut sunt 0—3; 0—8 etc.).
«Ничто, — писал Штифель, — стоит между истин-
истинными числами и «абсурдными» (Id est nihil, quod me-
diat inter numeros veros et absurdos).
Штифель считал, что с абсурдными числами все
происходит наоборот, абсурдно: «Сложение вызы-
вызывает уменьшение, а вычитание — увеличение».
Современник Штифеля, итальянец Джироламо Кар-
дано A501—1576), автор большого труда «Великое
искусство или об алгебраических правилах» (Ars
magna, sive de regulis algebraicis) называл, правда, от-
отрицательные числа фиктивными, в противополож-
противоположность истинным, но он был первым человеком в ис-
истории математики, который не отбросил отрицатель-
отрицательных корней в результатах решений уравнений второй
и третьей степени.
Такая точка зрения не была еще в то время обще-
общепринятой в математике. В конце XVI века великий
французский математик Франсуа Виет A540—1603),
отбрасывал отрицательные корни решений урав-
уравнений, а англичанин Томас Харриот A560—1621)
считал даже, что уравнения не могут иметь отрица-
отрицательных решений.
Решительный перелом в области отрицательных чи-
чисел произошел в математике только в XVII веке.
Немец Петер Роте (автор изданной в 1608 году книги:
«Философская арифметика или прекрасное новое
основательное чрезвычайно искусное исчисление
57
Исаак Ньютон A642—1727)
косе или алгебра») и фламандец Альберт Жирар
A590—1633) явно признают отрицательные корни
уравнений в связи с теоремой о числе корней урав-
уравнений.
Жирар первым использует математическое выраже-
выражение типа 7— —2, или в современном написании
7— (—2). Он рассматривает также положительное
и отрицательное решение определенной задачи как
отрезки, направленные в противоположные сто-
стороны .
Мысли Жирара были затем использованы Декартом
A596—1650), создателем аналитических методов
в геометрии. Декарт называет отрицательные числа
фальшивыми, а буквы в его расчетах, имеют также
как и у Виети только положительные значения
Отрицательные величины Декарт обозначал, про-
проставляя перед буквой знак «—», если же буква
имела и положительное и отрицательное значение,
то Декарт ставил перед буквой точку вместо опре-
определенного знака. Только голландец Йохан Гедде
A628—1704) освободил буквенное исчисление от
этих ограничений.
Третью часть своей «Геометрии» Декарт посвятил
полностью решению уравнения. Он признавал отри-
отрицательные корни уравнений, но считал их «фальши-
«фальшивыми».
Только в XVIII веке вопрос этот выяснился окон-
окончательно. В 1707 году издается труд Исаака Ньюто-
Ньютона: «Общая арифметика, или книга об арифмети-
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
ческом анализе и синтезе» («Arithmetica universalis,
sive de compositione et resolutione libervi). В этой книге
Ньютон пишет совершенно определенно: «Величины
могут быть или положительными, иначе говоря мо-
могут быть больше, чем ничто, или отрицательными,
т. е. меньше, чем ничто». Интересно отметить, что
еще Ньютон считал нуль «ничем». С историей отри-
отрицательных чисел связаны также имена и многих
других видных математиков: XVIII века — Лейбни-
Лейбница A646—1716), Маклорена A698—1746), д'Алам-
бера A717—1783).
Современное толкование арифметики относительных
чисел возникло, однако, только в XX веке.
Как он поделил деньги?
Четверо мальчиков: Костя, Боря, Миша и Витя
возвращались из города в деревню.
— Если бы я нашел кошелек с деньгами, — сказал
Костя, — то поделился бы с вами. Себе взял бы
только одну треть найденных денег, а остальные,
вместе с кошельком, отдал бы вам.
На это возразил Боря:
— Если бы это я нашел кошелек с деньгами, то по-
поделил бы найденные деньги между всеми нами
поровну.
— Что касается меня, — произнес Миша, — то я
59
удовлетворился бы одной пятой частью, а все осталь-
остальное отдал бы вам.
— Ну, а я вам скажу, что меня удовлетворила бы
и одна шестая часть найденных денег, — добавил
Витя.
Так разговаривая, они продолжали свой путь в де-
деревню и вдруг увидели валявшийся в пыли кошелек
с деньгами. Когда они его подняли и пересчитали
находившиеся в нем деньги, то оказалось, что в ко-
кошельке было 10 монет, среди которых одна стои-
стоимостью в 20 копеек, а остальные монеты были стои-
стоимостью в 10, 50 копеек и 1 рубль. Так как Костя
первый заметил кошелек, Боря его поднял, а Миша
находился рядом с Борей и тоже сделал движение,
чтобы поднять кошелек, то все согласно решили,
что Костя получит одну треть найденных денег,
Боря — одну четвертую часть, Миша — одну пя-
пятую, а Витя одну шестую, т. е., что каждый получит
ту часть, которую хотел себе оставить. Однако,
когда мальчики начали делить деньги, то никак не
могли этого сделать, так как не имели мелких мо-
монет.
Когда они ломали голову, как разделить деньги,
мимо проезжал велосипедист. Мальчики решили
попросить его, чтобы он им разменял монету стои-
стоимостью 10 копеек, так как они иначе не могут про-
провести дележ.
— У меня тоже нет мелочи, — сказал велосипе-
велосипедист, — но я могу поделить вам деньги.
60
— Хорошо, — сказали мальчики, — если ты это
сделаешь, то мы отдадим тебе кошелек.
Тогда велосипедист вынул из своего кармана монету
стоимостью в 10 копеек и бросил ее в найденный
кошелек.
Затем он сказал:
— Ты, Костя, должен получить одну треть содер-
содержимого кошелька, возьми ее.
— Ты, Боря, хотел получить четвертую часть —
вот она, получи.
— Ты, Миша, получишь, как и хотел, одну пятук
часть, а ты, Витя, — одну шестую.
— Получил ли каждый из вас свою долю ?
— Да, — ответили мальчики.
— Ну значит до свидания, очень вам благода-
благодарен, — сказал велосипедист и быстро удалился.
Когда велосипедист исчез, Костя спросил свош
товарищей:
— Послушайте, ребята, за что он нас благода-
благодарил?
— Очевидно, что-то здесь не в порядке, — замети!
Боря, — давайте посчитаем, сколько мы получил!
монет от велосипедиста.
— Я получил две монеты, — сказал Костя.
— Я тоже две, — ответили Боря и Витя.
— А я три, — прибавил Миша. — Итого, мы полу-
получили девять монет, а где десятая, ребята, кто полу-
получил двадцатикопеечную монету?
Оказалось, что никто из мальчиков ее не полу-
получил.
— Вот жулик, зашумели мальчики, взял нашг
деньги и удрал. Обманул нас.
—' Подождите, подождите, — проговорил Костя;
который немного знал арифметику и что-то подсчи-
подсчитывал. Затем он заявил, что велосипедист не толькс
его не обманул, но даже дал немного больше, чем
ему причиталось. После того, как Костя посчитал;
62
сколько причиталось каждому и сколько получили
мальчики, то оказалось, что каждый из них получил
от велосипедиста немного больше, чем ему причи-
причиталось.
— Я получил на две с половиной копейки больше, —
заявил Боря.
— А я на 2 копейки, — сказал Миша.
— Я тоже почти на 2 копейки, — произнес Витя.
— Что за чертовщина, — закричали мальчики, —
каждый из нас получил больше, чем ему причита-
причиталось, а велосипедист не только забрал свою монету,
но и прихватил нашу?
Сколько денег было в кошельке ? Обманул ли вело-
велосипедист мальчиков ?
Какие монеты получил каждый из мальчиков?
Как разделить наследство?
Некий римлянин, умирая, составил за-
завещание в пользу своей жены и ребенка,
который должен был родиться. Если на
свет появится мальчик, то он должен был
получить две трети наследства, а жена одну
треть. Если же на свет появиться девочка,
то она должна была получить одну треть,
а две трети — мать. Но на свет пришли
близнецы: мальчик и девочка. Как раз-
разделить наследство ?
63
Сумеете пи вы ответить?
Мы редко задумываемся над окружающими на<
повседневьши предметами.
Можно сомневаться, ответит ли каждый из вас т
поставленные здесь очень несложные вопросы.
1. В музее естествознания вы видите глобус, диа-
диаметр которого составляет 1 м. Какую высоту не
этом глобусе должна иметь гора Эльбрус, истинная
высота которой составляет 5633 м над уровне»
моря.
2. На площади города стоит избирательная урт
в форме куба, ребро которого равно 1 м. Все т
избиратели этого города, число которых равняется
миллиону, смогут проголосовать, бросая в урн>
шарики диаметром 1 см?
3. Какова должна быть величина квадратной пло-
площади, чтобы на ней смогло поместиться все населе-
население Польши C0 миллионов)?
Примечание: Принимаем, что на площади в 1 м"
могут находится 4 человека.
4. Размеры комнаты, в которой вы работаете, состав-
составляют 4x4x3,5 м. Сколько весит находящийся
в ней воздух ? Тяжелее- ли он вас ? Тяжелее ли ок
пробкового шара диаметром 1м?
Примечание: 1 литр воздуха весят 1,293 Г, удель-
удельный вес пробки — 0,24 Г/см3.
64
5. Вы купили слишком тесный воротничок, кото-
который чересчур плотно облегает шею. Вы должны
купить воротничок большего размера, такой, чтобы
зазор между вашей шеей и воротничком составлял
3 мм. На сколько номеров должен быть больше ваш
воротничок, если каждый следующий номер во-
воротничка означает его удлинение на 1 см.
6. Рядом стоят два квадратных стола — большой
и маленький. Периметр большего стола составляет
8 м, периметр меньшего — 4 м. Вокруг каждого
стола стоят скамьи. Длина скамьи, окружающей
большой стол составляет 10 м, а скамьи, окружа-
окружающей маленький стол, — 6 м. За которым из этих
двух столов удобнее сидеть? (У которого стола
расстояние между скамьей и столом больше?).
7. Французский инженер Густав Эйфель построил
в 1889 году в Париже башню, высота которой —
300 м. Железо, из которого сооружена башня, весит
8 000 000 кГ. Сколько будет весить модель зтой
башни, сделанная из того же материала и геометри-
геометрически ей подобная, высотой 30 см}
8. Кусок мыла, который лежит на вашем умываль-
умывальнике, имеет форму параллелепипеда. Вы расходуете
мыло равномерно, каждый день то же количество.
Спустя 7 дней все размеры вашего мыла уменьши-
уменьшились вдвое, так как мыло смылилось. На сколько
дней вам еще хватит этого мыла, если вы будете им
пользоваться так же интенсивно ?
65
9. Вы пускаете мыльные пузыри. Восхищаетесь их
расцветкой и видом и решаете удвоить их радиус.
Что станет с оболочкой пузыря, если Вы удвоите
его радиус? Изменится ли его расцветка? Почему?
10. Баночка емкостью 100 см3 заполнена пилюлями-
шариками радиусом 1 мм. Больной принимает по
5 пилюль в сутки. На сколько дней ему хватит
пилюль?
11. Пробочный спасательный круг весит 2 кГ.
Сколько весит вытесненная им вода ?
12. Тетрадный лист разграфлен таким образом, что
20 горизонтальных параллельных линий пересекает
16 параллельных линий под углом 60°. Сколько
имеется на этом листе параллелограмов ?
РЕШЕНИЕ ЗАДАЧ
Как он поделил деньги?
1. В кошельке было 5 руб. 90 коп., так как велоси-
велосипедист добавил туда 10 коп., то в нем стало 6 руб.,
т. е. число, делимое на 3, 4, 5 и 6.
2. Костя получил 6 руб.: 3 = 2 руб.; 1 руб.+1 руб.
Боря получил 6 руб.: 4 = 1 руб. 50 коп.
1 руб.+50 коп.
66
Миша получил 6 руб.: 5 = 1 руб. 20 коп.
1 руб.+10 коп.+Ю коп.
Витя получил 6 руб.: 6 = 1 руб.; 50 коп.+50 коп.
3. В кошельке было 4 монеты по 1 руб., 3 монеты по
50 коп., 1 монета в 20 коп., 2 монеты по 10 коп.,
т. е. 10 монет.
4. Костя, Боря, Миша и Витя получили вместе
2 руб.+1 руб. 50 коп.+1 руб. 20 коп.+1 руб. =
5 руб. 70 коп.
5. Велосипедист взял кошелек и 30 коп. B0 коп.+
+10 коп.).
6. Если бы мальчики сами делили найденные деньги,
то каждый из них получил бы меньше, чем ему дал
велосипедист, так как:
5 руб. 90 коп.: 3 меньше, чем 2 руб.
5 руб. 90 коп.: 4 меньше, чем 1 руб. 50 коп.
5 руб. 90 коп.: 5 меньше, чем 1 руб. 20 коп.
5 руб. 90 коп.: 6 меньше, чем 1 руб.
Как разделить наследство?
Римский юрист Сальвий так решил эту задачу:
наследство необходимо разделить на 7 частей;
4/7 получит сын, 2/7 — жена и 1/7 — дочь. При
таком дележе будет соблюдена воля отца, чтобы
67
сын получил долю, вдвое большую, чем мать,
а дочь — вдвое меньшую.
Сумеете пи вы ответить?
1. Принимая, что диаметр Земли равен примерно
12 500 км = 12 500 000 м, и обозначая через х вы-
высоту Эльбруса на глобусе, мы получим:
х:5 633 = 1: 12 500 000
а из этого
х = |-2 500 000 К A»00045 м « 0,45 мм
2. Да, так как 1 м3 = 1 000 000 см3.
3. Если сторона квадратной площади составляет х,
то его площадь х2 и на ней может разместиться
4х2 человек.
Из этого: 4х2 = 30 000 000 и х к 2 740 м.
4. Кубатура комнаты, в которой вы находитесь,
составляет:
4x4x3,5 = 56 мэ = 56 000 дм3, т. е. 56 000 литров
воздуха, вес которого равен:
1,293 х 56 000 = 72 408 Г « 72,4 кГ
Пробковый шар диаметром 1 м весит:
4-ти • 1003 • 0,24 Г = ~ ¦ 3,14 • 1 000 000 • 0,24 Г «
о о
« 125,600 л-Г,
т. е. вес шара почти вдвое превышает вес воздуха,
находящегося в комнате размером 4x4x3,5 м.
68
5. Длина воротничка равняется 2-кг. Добавим к это-
этому х см, тогда длина воротничка составит
2-пг+х
При этом радиус удлиненного воротничка будет
равен:
2пг+х
т = ¦
2тг
а из этого:
lizr+х х __ 3
2тг 2к ~ М
х = 3 мм ¦ 2ти = 3 мм • 6,28 = 18,84 мм х 20 мм =
= 2 см
Следовательно, необходимо взять воротничок на
2 номера больше.
6. Периметр скамьи, установленной вокруг большего
стола, составляет: 4а = 8 м; \Ъ = 4 м
(а+2х) ¦ 4 = 4а+8х = 10 м;
ИЗ ЭТОГО
8л: = 10-4а = 10-8 = 2
т. е. х = -?¦ метра (зазор между скамьей и столом).
Периметр скамьи, установленной вокруг маленького
стола, составляет:
(Ь+2у) ¦ 4 = 4Ь+8у
69
из этого следует, что:
4Z>+8j = 6; 8j = 6-ib; 8у = 6—4 = 2
т.е. У = -г метра (заэор между скамьей и столом).
Следовательно, зазоры одинаковы так как х = у.
7, Модель весит х дкГ. Следовательно
х: 80 000 000 = 303: 30 0003
х - ^ооооооозо! _ 0 8
30 0003 ~ ' 1
8. Первоначальный объем мыла равнялся:
х ¦ у • z
Спустя семь дней объем мьша составлял:
1111
z
Разность составляет:
1 7
xyz
(столько мыла смылилось за семь дней).
Мыла хватит только на один день, так как осталась
всего -g- часть первоначального количества мыла.
о
9. Первоначальная площадь оболочки мыльного пу-
пузыря составляла 4w2. Увеличив радиус пузыря
70
вдвое, мы увеличим поверхность ее оболочки до
4тиBгJ = 16га-2
Таким образом, мы уменьшим толщину оболочки
пузыря четырежды, вследствие чего она будет пре-
преломлять другие лучи и ее расцветка изменится.
10. Объем пилюли равняется -у 4тс • A ммK к 4,2 мм3
Объем баночки составляет: 100 см3 = 100 • 1000 мм3
Из этого следует, что в баночке находится
100 000 : 4,2 = 23 809 пилюль.
Это количество пилюль достаточно на 23 809: 5
дней, т. е. примерно на 13 лет и 17 дней.
11. Объем пробкового круга весом 2 кГ составляет:
у= гк' » 8,3 дсм3
0,24 кГ/дсм3
При полном погружении круга в воду, вытесненная
вода весит 8,3 кГ. При свободном плавании на по-
поверхности воды круг вытесняет 2 кГ воды.
12. Если и горизонтальных параллельных линий
пересекает к параллельных линий под углом а ф 0,
то число образовавшихся параллелеграмов составит
12 ' 1-2
В нашей задаче оно равно:
20:19 . Д^ = 190 • 120 = 22 800
КОМПЛЕКСНЫЕ
ЧИСЛА
ГЛАВА 4
Комплексными числами называем выражения вида
a+ib, где а и Ъ — вещественные числа (например,
2, —5, j/3, ...), a i— некоторый символ, мнимая
единица (г2 = —1).
Квадратный корень из числа — 1, т. е. ]/—1> назы-
называется мнимой единицей. Ее символом является
буква i т. е. |/—1 = i. Впервые этот символ введен
был в XVI веке, когда были уже известны иррацио-
иррациональные числа, открытые Пифагором, и отрицатель-
отрицательные числа. Мнимая единица и связанные с ней
комплексные числа являются дальнейшим расши-
расширением понятия число. Сам термин «мнимая еди-
единица» и символ i вошли в употребление после вы-
выхода в свет в 1817 году трактата Гаусса A777—1855)
из области теории чисел и работ Коши A789—-
1857).
Исторически первое действие на комплексных чис-
числах выполнил Кардано, несмотря на то, что он не
признавал их настоящими числами, а называл со-
софистическими. Кардано A501—1576) решил следу-
следующую задачу: «Число 10 разделить на две такие
части, произведение которых равно 40».
Следовательно
х • A0-— х) = 40, из этого
х2-10х+40 = 0
72
Кар дано нашел следующее решение:
первый корень = 5—|/—15
второй корень = 5+\/—15
Действительно
E- |/=15 ) + E+ ]/=11) = Ю
а произведение E—|/—15) • E+]/—15), подсчитан-
подсчитанное по форме (а—Ь)(а+6) = аг—Ъг составляет:
52_ (|/^Т5"J = 25-(-15) = 25+15 = 40
В 1629 году А. Жирар дал решение уравнения:
= 0
при этом он указал четыре возможных решения:
xt = 1, х2 = \, хэ = —1+)/—2; хх= — I]/—2
и заметил, что комплексные решения очень полезны
при общих решениях уравнений.
Долгие годы математики не могли дать мнимой
единице геометрическую интерпретацию. Эту за-
задачу решили только Ж. Арган, который в 1806 году
опубликовал свою работу «Попытка геометрическо-
геометрического представления мнимых чисел», и норвежец
К. Вессель A745—1818). С того времени мнимые
числа откладываются на оси,, перпендикулярной
к оси действительных чисел, принимая в качестве
единицы а = |/—1 •
На рис. 4-1 графически представлены числа
3+2/; 2-3г; -1-2/.
73
-2 -1
| у
1
/
/
-3t
-2t
- (
Ось
\
-t \
-2i
/ i
/ i
^ 1
-^ 1
бещестбенных чисел
/ 2 3
\ |
\
\ I
Puc. 4-1
Действия на комплексных числах мы выполняем
согласно правилам, действительным для веществен-
вещественных чисел, с учетом того, что /
/3 = —/; i* = 1 и т. д., например,
(a+ib)+(c+id)= (a+c)+i(b+d)
умножение
(a+ib) ¦ (c+id) = (ac—bd)+i(ad+bc)
i
i; i
2
-1;
деление
a + ib (a+ib) ¦ (c-id)
ac+bd . be—ad
c+id (c+id) ¦ (c-id) c2+d2 ^ c2+d2
Каждой точке комплексной плоскости соответству-
соответствует одно и только одно комплексное число. Например,
точке М (рис. 4-1) соответствует число 3+2/, точ-
точке N—число 2—3/. Расстояние точки М от точки О
(точки пересечения оси вещественных чисел с осью
мнимых чисел), т. е. отрезок ОМ = г = ]/32+22 =
= j/l3. Выражение ]/ТЗ называется модулем числа
3+2/. В общем говоря: модулем комплексного
числа a+ib является число j/a2-srb2. Модуль ком-
комплексного числа называют также его абсолютной
величиной.
Учитывая, что из точки О можно описать окруж-
окружность радиусом ОМ = г, все комплексные числа,
которые соответствуют точкам, лежащим на этой
окружности, имеют тот же модуль (в нашем слу-
случае \/Щ.
74
!|
S
к
1
\
\
А
/ 1
1
1
\ Ось инимая
Рис. 4-2
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Комплексные числа не делятся, как вещественные
числа, на большие и меньшие.
Комплексное число можно представить в тригоно-
тригонометрической форме. Угол q>, образованный вектором
О А с осью действительных чисел (рис. 4-2), называ-
называется аргументом комплексного числа: <р = аргумент
числа a-\-ib.
Имеем а = rcos<p; b = r s\n<p, из которого
a+ib = r (cos q>+i sirup)
например, если имеем комплексное число 1 +|/3 г,
то а = 1; Ъ = ]/3; г = у'а2 -\-Ь2 = уЧ = 2;
о. 1 b l/З
— = у = cos 60°; — = -^j- — sin 60°;
i = 2(cos60°+zsin60e).
Сколько раз?
а) Сколько раз в течение суток стрелки часов
(минутная и часовая) образуют прямой -угол
(90°)?
б) Часы показывают четыре часа. Сколько раз
в течение суток стрелки часов установятся так,
чтобы угол между ними бьш такой же как в 4 часа
A20°)? Стрелки начинают свой ход ровно в пол-
полночь.
75
в) Сколько раз в течение суток часовая и минутная
стрелки совмещаются?
Испорченные часы
Часы ходят хорошо, но плохо бьют, не пробивают
двенадцать, а после одиннадцати бьют час. Вследствие
этого очень редко на основании боя часов можно
узнать сколько время. Но иногда случается, что
часы пробьют точное время. Так случилось в по-
понедельник в десять часов утра. Часы пробили
десять раз.
Когда снова часы пробьют точное время?
А вот ответы:
1) в понедельник в одиннадцать часов;
2) в субботу в час дня. •
Попытайтесь найти ход решения.
Машины часы
Машины часы опаздывают каждый час на 2 мину-
минуты. Если по радио передают сигнал 12 часов, то
через сколько времени на часах Маши будет две-
двенадцать часов, если мы знаем, что ее часы показы-
показывали точное время ровно 5 часов тому назад.
Кант и часы
Один из крупнейших немецких философов Им-
Иммануил Кант A724—1804), профессор Кенигсберг-
76
скогох) университета, был одиноким, старым холос-
холостяком. Он вел столь регулярный образ жизни, что
граждане Кенигсберга проверяли свои часы, когда
видели его выходящим из своего дома и направля-
направляющимся быстрым шагом на лекции в универси-
университете.
Однажды вечером Кант с ужасом заметил, что его
настенные часы остановились, так как не были
заведены. По всей вероятности, слуга, которого
Кант принял накануне, не знал, что часы необхо-
необходимо завести. Великий философ завел часы, но не
мог их точно поставить, так как свои карманные
часы он накануне отдал часовых дел мастеру в ре-
ремонт. Глянув на часы, Кант пошел к своему другу
Шмидту, который жил примерно на расстоянии
одного километра от дома философа. При входе
в квартиру Шмидта Кант бросил взгляд на часы,
которые висели в коридоре. Кант пробыл в доме
Шмидта некоторое время и, прощаясь с ним, снова
взглянул на часы в коридоре. Домой Кант воз-
возвращался по тому же пути, что и шел к Шмидту,
своим обычным, размеренным шагом. Возвратив-
Возвратившись домой, Кант немедленно и точно поставил
стрелки своих часов. ,
Откуда Кант мог знать точное время ?
Ныне город Калининград.
77
Приказ о вылете
Во время войны польская эскадрилья получила при-
приказ совершить боевой вылет на немецкие позиции.
Подробности приказа находились в конверте, кото-
который командир эскадрильи должен был вскрыть
между часом и двумя, в тот момент, когда минутная
стрелка совместится с часовой. Определите точно
этот момент.
Что больше?
1. Что больше: З23 или 8! (факториал)?
2. Что больше: j/З или |/4 ?
3. Что больше: 109 или 910?
5. j/ГОили ^/г+уТ?
Примечание: не пользоваться приблизитель-
приблизительными исчислениями.
Сколько молодежи было в аудитории?
В аудитории собралась молодежь: студентки и сту-
студенты. Вместе их было больше 70, но меньше 90.
Всего скамеек, на которых сидели студентки и сту-
студенты, было на 1 больше, чем сидело на каждой
из них студентов. Студентки сидели по одной на
каждой скамейке. Сумма числа скамеек и студен-
студентов составляла число молодежи.
78
Сколько человек находилось в аудитории и на сколь-
скольких скамейках они сидели ?
Курьезы, загадки, головоломки
Их роль — это полезное развлечение. Решая их,
можно упражнять свои способности логического
мышления не хуже, чем при решении задач, требу-
требующих составления уравнений.
1. На середине бассейна находится фонтан. Вода
вытекает из него через 16 трубок диаметром 1/2 см
каждая. Вода из бассейна выливается через отвер-
отверстие диаметром 2 см. Однажды садовник открыл
доступ воды в бассейн, но забыл закрыть сливное
отверстие. Через сколько часов вода заполнит бас-
бассейн?
I.- Задумай любое двухзначное число. Первую циф-
цифру этого числа умножь на 2. К полученному числу
добавь единицу, то, что теперь получилось, умножь
на 5 и прибавь вторую цифру. Скажи мне, что
у тебя получилось, а я скажу задуманное тобой
число.
Как это делается?
От названного тобою числа я отниму 5. Попытай-
Попытайтесь объяснить эту головоломку.
3. Задумай любое четырехзначное число. Напиши
его без последней цифры, затем без двух последних
цифр, затем без трех последних цифр и сложи эти три
79
РЕШЕНИЕ ЗАДАЧ
записанных числа. Полученную сумму умножь на 9
и к полученному произведению добавь сумму цифр
задуманного тобой числа. В результате получишь
задуманное тобой число. Объясни почему?
4. Один рабочий может выкопать колодец глубиной
2 метра и диаметром 1 метр в течение 4 часов. В те-
течение скольких часов могут выкопать этот колодец
8 рабочих?
5. Класс шел парами. Один из учеников глянул
вперед и насчитал 9 пар, затем обернулся назад
и насчитал 5 пар. Сколько всего учеников шло
в колонне?
Сколько раз?
Предварительное замечание. Дви-
Движение стрелок часов выполняется в двух циклах.
Малый цикл продолжается несколько больше одно-
одного часа, начинаясь в момент старта и кончаясь)
когда стрелки впервые совместятся.
Большой цикл продолжается ровно 12 часов, начи-
начинаясь в момент старта и заканчиваясь, когда стрелки
снова совместятся в месте старта (в точке, соответ-
соответствующей 12).
а) Давайте рассмотрим взаимное положение стрелок
при малом цикле.
1. В течение 1 мин минутная стрелка опережает
1 °
часовую на 6 "—-у =
2. Минутная стрелка опережает часовую на 90°
в течение:
90
/ с 1 \°1 90-2 180 .,, 4
:|5у| шин = —^— мин = -^-мин = 16-^-
4
В течение \6-rr-мин минутная стрелка передвинется
4 / 2 \°
на угол 16^г • 6° = (98-ту I , а часовая стрелка на
Угол между стрелками будет составлять
3. Так как стрелки передвигаются равномерно, то
о / 4 \
по истечении 32-^г-мин 116-^=- • 21 большая стрелка
/ 4 \°
передвинется на угол 1196^- , а маленькая — на
Угол между ними составит:
A96^-)°-A6-1-)° = 180=.
81
4. По истечении 16-j^- • 3 мин большая стрелка пе-
98у-1 • 3 = [294^-1 , а малая
Угол между ними составит 270°.
4 5
5. По истечении 16^=- • 4 = 65-тт-мин большая стрел-
стрелка опередит маленькую на угол 360°. Тогда про-
произойдет конец первого маленького цикла, часовые
стрелки совместятся первый раз с момента старта.
Часы показывают тогда Ъ-^мин второго. Цикл про-
продолжался 1 ч S^r-мин. В этот момент происходит
второй старт (начинается второй малый цикл).
Третий старт произойдет в момент, когда насы бу-
будут показывать 10-тт-мин третьего.
6. До того момента, когда обе стрелки снова ока-
окажутся в месте первого старта, (т. е. в пункте 12),
т. е. в течение 12 часов, произойдет:
5 60
1 ч : 5^рр мин = 60 мин: -гг- мин =11 малых циклов.
В каждом малом цикле можно выделить как бы
4 фазы:
первая — угол между стрелками 90 °— годится,
вторая — угол между стрелками 180° — не годит-
годится,
третья — угол между стрелками 270° — годится,
четвертая — угол между стрелками 0° — не го-
годится.
Таким образом, в каждом малом цикле дважды
угол между стрелками составит 90°, соответственно
в 11 циклах это произойдет 22 раза, а в течение
суток 44 раза угол Между стрелками часов будет
составлять 90°.
6) Угол между стрелками составляет 120°.
1. Минутная стрелка опережает часовую на 120е
в течение
120° : E±)° = ^мин = 2\~-мин
2. За это время большая стрелка переместиться на
угол:
а малая — на угол
2 11 \ И
Угол между стрелками составит:
3. Второе опережение на следующие 120° произой-
произойдет через *ЭД мин
83
Часы будут показывать тогда 43^т-лдан после 12.
Минуты
Минуты
4. Третье опережение на 120° -3, т. е. на 360°
произойдет спустя -^- мин, т. е. спустя 1 ч Ь^г-мин.
Тогда произойдет конец малого цикла и часы будут
показывать Ь^гт-мин второго.
5. В течение 12 ч произойдет:
12 ч : 1 ч 5—мин = 720 мин: -^г-
= 11 малых цик-
циклов движения стрелки. В течение этих 11 циклов
стрелки 22 раза образуют угол 120° и 11 раз угол
0° (совместятся), возвращаясь в точку старта. Следо-
Следовательно в течение суток стрелки образуют 44 раза
угол 120°.
Очень интересно отметить, что в обоих случаях
(угол 90° и угол 120°) малый цикл продолжается
65-jT- мин, из чего можно сделать вывод, что незави-
независимо от угла между стрелками, малый цикл движе-
движения стрелки часов всегда продолжается 65^рг- мин.
в) Смотри рис. 4-3
На рисунке горизонтальная ось, изображающая час,
поделена на 12 частей, а вертикальная ось, соот-
соответствующая минутам, — на 60 частей. Наклонная
жирная линия изображает движение часовой стрел-
стрелки, более тонкие наклонные линии — движение
минутной стрелки. Точки пересечения соответ-
соответствуют моментам, когда стрелки совмещаются. Вре-
Время совмещения отсчитывается на осях.
Испорченные часы
Два раза в сутки бой часов опережает показания
часов на один час. Чтобы бой снова совпал с пока-
показаниями стрелок, он должен опередить ход на
12 ч.
Так как в понедельник в 10 ч утра часы пробили
10 раз, это означает, что и в 11 ч они пробьют 11 раз,
более того, это значит, что часы бьют правильное
время с часа ночи. Каждые 11 ч бой опережает
показания на 1 ч. На 12 ч бой опередит ход спустя
11 -12 = 132 ч, т. е. через 5-^- суток. Поэтому в по-
понедельник часы еще раз точно пробьют 11, а затем
снова начнут бить правильно время в субботу от
13 до 23.
Машины часы
Когда по радио передавали точно 12 ч, то Машины
часы показывали на 10 мин меньше, т. е. 11 ч 50 мин.
Оставалось еще 10 мин, но в течение этих 10 мин
часы Маши отстанут еще на 20 сек.
Ответ: 12 часов на Машиных часах будет через
10 мин и 20 сек.
85
Кант и часы
Кант определил время следующим образом:
1. Выходя из дому, он точно заметил время и сделал
это вторично сразу же после возвращения домой.
Таким образом он легко мог высчитать сколько
времени он находился вне дома (а ч).
2. Входя к Шмидту в дом Кант также заметил время
и при выходе сделал это вторично. Следовательно,
он мог высчитать сколько времени он оставался
в доме Шмидта (Ь ч).
3. Разница (а—Ъ), разделенная на 2, — это время,
которое Кант затратил на дорогу, чтобы вернуться
домой, а зная точно во сколько он вышел от Шмидта,
он без труда определил время и поставил стрелки
своих часов.
Приказ о вылете
Минутная стрелка (большая) пробегает мимо 60 де-
делений часового циферблата за то же самое' время,
за которое часовая стрелка (маленькая) проходит
пять таких делений. Из этого следует, что маленькая
стрелка двигается 12 раз медленнее, чем большая
F0: 5). Когда большая стрелка переместится на
1 деление, маленькая стрелка пройдет всего на
-ту этого деления. Из этого можно сделать вывод>
86
что за каждую минуту большая стрелка опережает
маленькую на-г=- делений11—ут\- Когда маленькая
стрелка находилась против цифры 1, то большая
показывала 12. Расстояние между ними составляло
5 делений. Большая стрелка, догоняя маленькую
11
каждую минуту на -т=- деления, догонит ее и совмер-
/ 11 \ '^
титься с ней по истечении 15: ^у), т. _е, спустя
60 1 _ пп 3
-гр мин, иначе говоря через 1 ч 5 мин и ^/~уг сек.
Что больше?
1. 8! >323,
так как 8! = 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 = 40 320,
аЗ23 = З8 = 6 561.
2. \/3 > |/4,
так как |/4 = f/Тб", а \/3 = У^П, а |/27"> \'Ш.
3. 910 > 109,
так как lg(910) > lgA09); lgA09) =^= 9 lglO = 9;
lg(910) = 10 Ig9 > 9, так как 10 • 0,9542 = 9,542 > 9.
4. O,320 = (O,32I0 = 0,0910; 0,110 > 0,0910.
5. (\/WJ= 10 = 5+5;
= 2+3+»/24 =
5+5 ^
87
Сколько человек было в аудитории?
Скамеек было z. На каждой скамейке сидело х сту-
студентов и одна студентка. Имеем z — х-\-\; следова-
следовательно было z(x+l) = z2 человек; так как 82 <
70 < z2 < 90 < 102, тем самым z = 9 и х = 8.
В аудитории было 81 студентов и студенток. Моло-
Молодежь сидела на 9 скамейках.
Курьезы, загадки, головоломки
1. Бассейн никогда не заполнится водой, так как
16 трубок диаметром 1/2 см имеет общее сечение,
равное 16 ' 7г(х) см1 = ж см1> а отверстие диаметром
2 см имеет сечение равное тс • A смJ = ти см2.
2. Двухзначное число 10а-\-Ь; Bа+1) • 5 = 10a-f-5;
Юа+5+6-5 = 10а+Ь
3. Четырехзначное число:
A00a+l0b+c)+(l0a+b)+a = llla+116+c;
(llla+m+c) • 9 + (a+b+c+d) = 1000a+1006+
+lOc+d.
4. Задача не имеет смысла — ведь 8 человек ра-
рабочих не могут копать отверстие диметром 1 метр!
5. 5 пар+9 пар+1пара = 15 пар; 2 • 15 = 30 (уче-
(учеников).
1РИ ЗНАМЕНИТЫЕ глава 5
рЕВНЕГРЕЧЕСКИЕ
ЗАДАЧИ
1. Квадратура круга
Задача о квадратуре круга или, иначе говоря, на-
нахождении такого отрезка х, чтобы площадь квадра-
квадрата со стороной х равнялась бы площади круга,
радиус которого равняется г т. е. х2 = -кг2 имеет
очень длинную и поучительную историю, тесно
переплетающуюся с историей числа тс.
Две тысячи лет до нашей зры писец и очевидно ма-
математик фараона Аменемхата III указал, что площадь
круга диаметром 2 равняется площади квадрата
8 /8 \
со стороной равной -^ диаметра круга l-g- • 2г\. Очень
простой расчет показывает ошибочность этого ут-
/8 \2
верждения. В действительности, если (-g--2J = тсг2,
256 , ,
т. е. если -~г- г2- = ш2-, то следовательно тс должно
равняться -„г- = 3,1604... Ошибка имеется уже во
втором знаке после запятой (тс = 3,14159...).
Переняв геометрию от египтян, греки получили от
них также в наследство задачу о квадратуре круга,
которая была одной из трех неразрешимых задач
древнего мира (две другие задачи это: удвоение
куба и трисекция угла).*Квадратурой^круга занима-
лись философы, софисты и математики: в V веке
до н. э. Анаксагор Милетский и Гиппий из Эллиды,
в IV веке до н. э. Гиппократ Киосский и софисты
Антифон и Бризон (создатели метода исчерпывания),
наконец, — величайший математик древнего мира
Архимед B87—212 до н. э ).
Архимед написал трактат «Измерение круга». Пло-
Площадь круга Архимед высчитывает, вписывая в него
шестиугольник, а затем удваивая число его сторон
до девяностошестиугольника. Затем этот многоу-
многоугольник Архимед превратил в квадрат. Получен-
Полученное Архимедом значение числа тс составляет Зу,
а точнее 3-= это одно из наиболее точных прибли-
приближений этого числа.
В более поздние века также неоднократно дела-
делались попытки решить эту задачу, занимались ей
Леонардо Пизанский (Фиббоначчи в XIII веке),
Виет (XVI в), Лейбниц и Валлий (XVII), Эйлер
(XVIII в). Встречаются также и физики, например,
Гюйгенс (XVII в.). Подсчитанные значения числа к
становились все более и более точными, особенно
после создания дифференциального и интегрального
исчислений.
Квадратурой круга занимались не только европейцы
Индусский математик Ариабхата (V век) указал зна-
значение числа тс = ]/Ш, другой — индус Бхаскара
(XII век) рассчитал тс = 754/240.
1 M
г
Г
1
\
^*-
к
А
Яг
>
™ N
0
V
\
АМг=А? LE=7tr г=Лгг
5
Рис. 5-1 а, б
Китаец Чу-Пей-Сван (III век) определил, что тс =
= 3, а его соотечественник Лю-Хуэй (VI век) вы-
высчитал, что тс = 157/50.
Среди «квадратистов» нельзя не упомянуть о поль-
польском ученом Адаме Адаманде Коханьском A631—
1700), библиотекаре и придворном математике польс-
польского короля Яна Собеского. Он выполнил одну из
самых красивых и самых простых из известных
квадратур круга Коханьский сделал ее не изменяя
раствора циркуля, которым вычерчен круг. Мы
приводим метод, которым он это выполнил:
На рис. 5-1а отрезок ОБ = г; СЕ _L AB; хорда
BD = г, ОС ± DB, СЕ = Ъг;
Докажем, что АЕ х пг,
Имеем: AB = 2r ; OB = r; BD = г; СЕ = Ъг.
Из треугольника СОВ, находим
СВ=
??= CE-CB= 3r-r-!y-=rl3—iy
Из треугольника ABE получаем:
АЕ2 = AB2+BE2 = BrJ+i
АЕ=
С другой стороны, мы знаем, что длина полуокруж-
полуокружности лиг = 3,14159/".
Из этого мы видим, что поляк вычислил число тг
с точностью до 0,0001. Коханьский далее рассуждал
следующим образом1*: квадрат перпендикуляра к ди-
диаметру окружности, опущенный из любой точки
этой окружности, равен произведению отрезков, на
которые этот перпендикуляр делит диаметр (рис.
5-1 д) AM2 = AKi ¦ АЕ; EL = AK^ = г.
Площадь квадрата AMNO — площади прямоуголь-
прямоугольника AELK. Площадь прямоугольника AELK =
= АЕ • EL = пг ¦ г = ш2.
Следовательно, площадь квадрата AMNO = пло-
площади прямоугольника AELK — площади круга ра-
радиусом г, т. е. w2.
Другим очень удобньш решением квадратуры круга
является решение инженера Бинга.
Так как сторона искомого квадрата х меньше диамет-
диаметра круга, пусть дуга АВ = х (смотри рис. 5-2), т. е.
(АВJ = -кг2. Из треугольника ADB имеем АВ =
= 2rcosa, из этого BrcosaJ = -кг2; 4cos2cw2 = то'2;
cos2a = -j- далее
1 ./-
получаем: cos a = -=- j/tc да 0,886;
св
а&27°36'. Соотношение —-= равняется тангенсу угла
а, а следовательно tga = tg 27°36' = 0,523 или приб-
23 11,5
Рис. 5-2
лизительно -т-т- =
44
22
1) В прямоугольном треугольнике квадрат высоты, опущен-
опущенной на гипотенузу равен произведению проекции катетов на
гипотенузу.
92
Последний результат, показанный на рисунке, поз-
позволяет легко построить треугольник Бинта. Прикла-
Прикладывая этот треугольник к диаметру круга, сразу же
можно определить сторону квадрата х. Квадратуру
Бинта можно применять, когда для технических
нужд не требуется очень точный результат.
Математики не прекратили поисков квадратуры кру-
круга. Присылаемые в Парижскую Академию Наук
«решения» были столь многочисленны, что в 1775
году Академия отказалась рассматривать поступа-
поступающие в ее адрес решения задачи о квадратуре
круга. Только во второй половине XIX века два
математика: француз Ш. Эрмит A822—1901) и не-
немец Ф. Линдеман A852—1939) доказали, что с по-
помощью циркуля и линейки нельзя точно выполнить
квадратуру круга.
Какова причина неразрешимости задачи о квадра-
квадратуре круга с помощью циркуля и линейки ?
Если х — это сторона искомого квадрата, то
х2 = яг2, т. е. х = г ]/я.
Это значит, что, имея отрезок г (радиус данного
круга), необходимо построить другой отрезок в ]/тс
раза длиннее отрезка г. Мы знаем, что число п
показывает во сколько раз окружность круга длин-
длиннее его диаметра (п = 3,1415...). Ученые древнего
мира утверждали, что это рациональное число и очень
упорно его искали. В действительности, имея отре-
отрезок г можно с помощью циркуля и линейки построить
93
не только отрезок 2г^ -^г, но и отрезки
2nr
Рис. 5-3
г у 10—2 у/5 (стороны вписанных в окружность тре-
треугольника, квадрата и пятиугольника). Однако,
нельзя построить отрезка г]/-и, так как число -к —
это трансцендентное число, т. е. такое, которое не
может быть корнем никакого алгебраического урав-
уравнения с целыми коэффициентами. Это доказал
в 1882 году Линдеман, после того как Эрмит доказал
в 1873 году, что число е также трансцендентное
С тех пор никто этим вопросом больше не занимается,
так как в отношении этой задачи уже совершенно
точно определилось отрицательное решение: с по-
помощью циркуля и линейки (вычерчивая окружности
и прямые линии) решить эту задачу абсолютно не-
невозможно. Однако, существуют методы практи-
практически точного решения этой задачи.
Великий итальянский ученый и художник XV века
Леонардо да Винчи заметил, что боковая поверх-
поверхность цилиндра радиусом г и высотой г/2 (рис. 5-3)
равняется точно площади окружности его основания
Тем самым достаточно этот цилиндр опоясать полос-
полоской бумаги шириной г]2> чтобы получить прямо'
угольник размерами 2ш и г]2, который затем очей11
легко преобразовать в квадрат точно такой *е
площади, что и площадь окружности радиусом г так
как мы имеем
2tw • г/2 = го2
94
2. Удвоение куба (Депосская задача)
Рис. 5-4
Рис 5-5
Вот о чем рассказывает древнегреческая легенда.
На острове Делос свирепствовала «черная смерть» —
чума. Перепуганные жители острова пришли в храм
покровителя острова бога Аполлона и через жрецов
спросили, как вымолить прощение у божества,
чтобы спасти население острова от заразы и смерти.
Аполлон потребовал увеличения вдвое жертвенника,
имевшего форму куба. Тогда жители поставили
в храме на существующий алтарь второй куб, точно
такой же величины. Однако «черная смерть» по
прежнему косила население острова. Оказалось, что
Аполлон был очень придирчивым геометром: требо-
требовалось увеличить вдвое жертвенник, не иаменяя его
геометрической формы.
Выражая эту задачу с помощью математических зна-
знаков, мы можем записать:
х3 = а3-2, т.е. х = а|/2
в зтой формуле t a — это сторона данного куба,
ах — сторона куба, объем которого вдвое больше,
чем объем данного.
Представленная на рис. 5-5 «крестовина» была
как будто бы использована Платоном при решении
задачи удвоения куба. Крестовину необходимо уста-
установить таким образом, чтобы одно плечо проходило
через вершину С неполного прямоугольника ABCD,
а второе плечо — через вершину В. Тогда отрезок
95
Рис. 5-6
OB = х и является ребром куба, объем которого
вдвое больше, объема данного куба.
Доказательство. Из прямоугольных тре-
треугольников ЕВС и BCF (смотри рисунок крестови-
крестовины) следует, что:
A)
х2 = ау
и что
у2 = 2ах
B)
Из уравнения A) следует, что у = х2\а. Подставляя
это значение у в уравнение B), найдем, что х*/а2 =
= 2ах, следовательно х3 = 2а3.
Таким образом крестовина Платона позволила най-
найти два средние пропорциональные отрезки х и у
между а и 2а, это следует из того, что равенство
х2 = ау и у2 = 2ах можно представить в виде
пропорции:
а х
— = — и
х у
х
У
т. е. — = — =
у
1а
это соответствовало утверждению Гиппократа Хиос-
Хиосского, что нахождение стороны куба, объем которого
вдвое больше данного, сводится к определению
двух средних пропорциональных. Афинский мате-
математик Менехм (IV век до н. э.), который так*е
пытался решить дедосскую задачу, использовал для
этого две параболы (рис. 5-6). Используя современ-
современную математическую символику, его решенйе
96
можно представить следующим образом:
уравнение параболы A):
х2 = ау
уравнение параболы B):
у2 = 2ах
(А)
(В)
Чтобы найти координаты точки пересечения М этих
парабол, необходимо решить систему уравнений (А)
и (В). В результате решения найдем х3 = 2а2, из
этого следует, что абсцисса точки М и является
искомой стороной куба, объем которого вдвое больше
заданного.
АВ=ВС=г
Рис. 5-7
3. Трисекция угла
Третьей задачей, которую математики древнего мира
передали своим потомкам нерешенной, была задача
о разделении данного угла на 3 равные части, только
с помощью циркуля и линейки. На первый взгляд
эта задача кажется чрезвычайно простой. Действи-
Действительно некоторые углы, например, прямой угол
(90°) очень просто можно разделить на три равные
части (рис. 5-7).
Пифагорцы, которые занимались правильными мно-
многоугольниками, пытались также разделить угол 120°
на три равные части, так как это позволяло постро-
построить правильный девятиугольник. Часто, однако,
приближенный раздел принимался за точный.
97
Рис. 5-8 а, б
Для приближенного разделения любого угла ци
три равные части было придумано несколько специ-
специальных приборов. Один из них основан на кривой,
названной затем квадратрисой, которую ввел Гиппий
из Элиды (V век до н. э.), другой — на кривой,
названной конхоидой Никомеда.
На рис. 5-8 показана квадратриса, там же показан
метод ее вычерчивания. Квадратриса образуется
в результате двух равномерных движений: сторона
CD квадрата ABCD, сохраняя положение парал-
параллельное первоначальному, перемещается равномер-
равномерным движением в направлении стороны АВ, одно-
одновременно сторона (радиус) АС вращается вокруг
точки А (смотри стрелки). В то время, как сторона
CD переместится до совпадения со стороной АВ,
радиус АС повернется на угол 90° и также совпа-
совпадет со стороной АВ. Геометрическое место точек
пересечения стороны CD и радиуса АС называется
квадратрисой.
Квадратрису можно нарисовать на основании ее
—; где г = АР направляющий
2а
уравнения г =
радиус, т. е. расстояние точек квадратрисы от по-
полюса А; а = CD сторона данного квадрата; а —¦
угол, величина которого изменяется от 0 до тс/2-
Придавая углу а значение от 0 до тс/2, получим
соответствующие длины направляющего радиуса г,
соединяя концы г, получим квадратрису. Необхо-
sina * л
димо при этом помнить, что -*¦ 1, при а -*¦ U.
98
Рис. 5-9
Допустим, что необходимо разделить некий угол а
на 3 равные части. С этой целью одну сторону угла а
прикладываем к стороне АС квадрата, а через точ-
точку F, в которой вторая сторона АЕ угла а пересекает
квадратрису проводим прямую, параллельную к АВ
E-5). Отрезок D—5 делим на три равных части
и через точку деления проводим прямые, парал-
параллельные к АВ (рис.5-8).
Точки, в которых эти параллельные пересекаются
с квадратрисой, соединяем прямыми с полюсом А
(чертим радиусы г). Эти прямые делят угол а на
3 равные части.
Мы не будем здесь более подробно заниматься вы-
выяснением использования описанных выше кривых
для разделения любого угла на 3 равных части,
а опишем лишь один из методов приблизительного
выполнения трисекции угла, который на первый
взгляд приводит к правильному решению рассматри-
рассматриваемой задачи. Этот метод трисекции угла с помощью
кривой, называемой конхоидой, был известен уже
математикам древнего мира. Впервые его применил
Никомед.
Предположим, что необходимо разделить угол ABC
(смотри рис. 5-9) на 3 равные части.
Для этого надо из произвольно выбранной точки А
на стороне АВ опустить перпендикуляр АК на ВС
и провести параллельно стороне ВС отрезок AD.
Затем из точки В мы проводим прямую BE таким
образом, чтобы отрезок SE составлял 2АВ.
99
\\\
N ^ч \ \
if - -v. N \
\
L
4
P ,
—-A
A /
0
/ ,
// /'
//' /
X
Puc. 5-10
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Рис. 5-11
Теперь ZEBC = у
ABC.
Действительно ZBEA = %ОАЕ = *цЕВС = а.
Из этого следует, что ^сАОВ = ^сАВО = 2а (ОА =
= ОЕ; и -KAOS — это внешний угол в треуголь-
треугольнике АОЕ).
Слабым местом этого решения является вычерчи-
вычерчивание отрезка BE так, чтобы его длина составляла
SE = 2АВ. Это можно выполнить только методом
проб.
Никомед сделал это (т. е. нашел точку Е) с помо-
помощью конхоиды (рис. 5-10); выбирая AKkslk ось кон-
конхоиды, В — как ее полюс и отрезок равный 2АВ —
как ее параметр. На рис. 5-10 — точка О — полюс,
KL — ось, В А = АР — параметр.
Геометрическая смесь
1. Квадрат 1 разделить на 5 частей и собрать из них
восьмиугольник (рис. 5-11).
2. Из трех шестиугольников
а построить шестиугольник б
(рис. 5-12).
Рис. 5-12 а, б
100
Рис. 5-13
Задачи на построение
Точки А и В являются вершинами квадрата. Найти
две остальные вершины С и D этого квадрата, поль-
пользуясь только циркулем. После построения доказать,
что точки С и D действительно являются верши-
вершинами квадрата A BCD.
Рассчитать площадь поверхности
Треугольник ABC (рис. 5-13) равнобедренный, его
сторона равняется 6 см. Высчитать площадь заштри-
заштрихованной части этого треугольника.
Рис. 5-14
Площадь шестипепестковой розы
Изображенная на рисунке 5-14 шестилепестковая
роза вычерчена радиусом г.
Если мы очень подробно начнем рассматривать ро-
розу, то убедимся, что она состоит из шести одинако-
одинаковых полумесяцев. Нарисуйте эту розу и высчитайте
ее площадь. Обратите внимание на вспомогатель-
вспомогательный рисунок.
Об одной экскурсии
Двое друзей, Иван и Леонид, отправились на экс-
экскурсию. Они выехали одновременно из того же
самого места и поехали по тому же шоссе. Иван
ехал на велосипеде со скоростью 20 км/ч. Леонид
101
же отправился на мотоцикле и ехал в среднем со
скоростью 60 км 1ч. Друзья договорились, что Лео-
Леонид, который осуществлял надзор за лесозаготов-
лесозаготовками, проедет до лесосеки, расположенной на рас-
расстоянии 70 км от места отправления, и немедленно
оттуда выедет навстречу Ивану, чтобы вместе про-
провести свой досуг на лужайке, перекусить, а затем
сообща вернуться домой.
По истечении какого времени с момента выезда
друзья встретились ?
Неудачная экскурсия
Двое членов велосипедного клуба Александр Алек-
Александрович и Борис Петрович отправились на экс-
экскурсию в местность, находившуюся на расстоянии
672 км от места отправления. Борис Петрович пое-
поехал на экскурсию на обычном велосипеде и проез-
проезжал на нем в день 40 км, а Александр Александрович
поехал на мотовелосипеде и проезжал в день 56 км-
Однажды клуб отправил в тот же день обоим экс-
экскурсантам телеграммы, вызывавшие их немедленно
домой. Оба сразу же повернули обратно. При этом
оказалось, что Борис Петрович находился от цели
путешествия на расстоянии втрое большем, чем
Александр Александрович.
Сколько дней путешествовали Александр Алек-
Александрович и Борис Петрович, на каком расстоянии от
цели путешествия находился каждый из них.
102
Эту задачу можно решить, не составляя уравне-
уравнений.
Странствующий отряд
Странствующий отряд пионеров отправился из го-
города на озеро.
У озера пионеры отдохнули, а затем по той же тро-
тропинке вернулись в город. Тропинка, по которой
пионеры шагали, сначала поднималась в гору, затем
опускалась вниз и наконец шла по равнине. Идя
в гору, отряд шагал со скоростью 3 км/ч, спускаясь
вниз — со скоростью 5 км/ч, а идя по равнине,
пионеры проходили 4 км/ч. Весь путь туда и обратно
занял пионерам 6-г=- ч, расстояние от города до озера
равнялось 12 км.
Спрашивается, сколько километров тропинка бе-
бежит по равнине ?
Математика в кухне
Однажды между поваренком и пионервожатым в ла-
лагере произошел такой разговор:
— Какой сегодня будет суп?
— Вкусный.
— Много ли его будет?
— Больше всего в супе будет чистой родниковой
воды, по весу столько же, сколько крупы, картошки,
луку, и жира вместе взятых.
103
— Этот ответ меня не удовлетворяет.
— В таком случае я еще могу только добавить, что
крупы я взял столько, сколько картошки, лука
и жира вместе взятых.
— А картошки?
— Ровно столько, сколько жира и лука.
— А жира ?
— Вдвое меньше, чем лука.
— А ну-ка поставь суп на весы.
— Сию минуту.
— ... семь килограммов.
— Вместе с кастрюлей, а она, когда хорошо вымыта
и высушена, весит один килограмм.
— Спасибо.
Нам очень любопытно, сколько же по весу поваре-
поваренок взял воды, крупы, картошки, лука и жира.
Попытайтесь это посчитать.
Кто скорее?
Два мальчика, Миша и Гриша, живут в деревне,
а учатся в сельскохозяйственном техникуме, в горо-
городе, на расстоянии 6 км.
Однажды автобус, которым они обычно ездили,
испортился и мальчики решили пойти в техникум
пешком. Миша первую половину пути шел со ско-
скоростью 4 км/ч, а вторую половину со скоростью
2 км/ч, Гриша же поступил иначе, первую половину
времени, которое он шагал из деревни до города,
104
он шел со скоростью 4 км/ч, а во второй половине
делал всего 2 км/ч.
Который из мальчиков пришел раньше в школу
и насколько ?
Два пассажира
Из поезда вышли два пассажира, которые пошли по
тому же пути в гостиницу, находившуюся на рас-
расстоянии а км от станции. Первый пассажир половину
времени, израсходованного на путь до гостиницы,
прошел со скоростью v^ км/ч, а вторую половину
времени — со скоростью v2 км/ч. Второй пассажир
первую половину пути от станции до гостиницы
шел со скоростью vx км/ч, а вторую половину со
скоростью ©2 км/ч.
Который из пассажиров пришел в гостиницу рань-
раньше?
8 5 3
Рис. 5-15
Задача Пуассона
Во время экскурсии один из ее участников купил
бутыль вина емкостью 8 четвертей. Купленное вино
необходимо было разделить пополам. Как можно
было это осуществить, если на постоялом дворе
было только два сосуда — один емкостью 5 четвер-
четвертей и второй емкостью три четверти (рис. 5-15).
Сколько раз необходимо было переливать вино из
сосуда в сосуд ?
105
РЕШЕНИЕ ЗАДАЧ
Как она справилась?
В кастрюлю необходимо налить 4 литра воды.
У хозяйки есть только два сосуда: один емкостью
5 литров, а второй емкостью 3 литра.
Как поступила хозяйка ?
Геометрическая смесь
1. Из квадрата можно сложить восьмиугольник так,
как это показано на рис. 5-16.
2. А вот так можно из трех шестиугольников сло-
сложить один шестиугольник (рис. 5-17).
Рис. 5-16
Рис. 5-17
Задачи на построение. План решений
1) Строим равносторонний треугольник ABE со сто-
стороной равной АВ.
2) Находим точку F, симметричную точке Е отно-
относительно отрезка АВ.
106
Рис. 5-18
3) Из точки В радиусом АВ вычерчиваем окруж-
окружность и на этой окружности намечаем точку Gs
симметричную точке А относительно точки В.
4) Радиусом EF (двойная высота равностороннего
треугольника ABE) вычерчиваем из точек А и G
две небольшие дуги (рис. 5-18). Точка Н пересе-
пересечения этих дуг является вершиной равнобедрен-
равнобедренного треугольника AGH, а его высота НВ равняется
диагонали искомого квадрата.
5) После того как найдена сторона квадрата АВ
и его диагональ НВ без труда можно найти вершины
Си/).
Доказательства: АВ = a; EF = GH =
= д/3"; НВ = a ]/2~.
Рис. 5-19
Рассчитать площадь поверхности
Треугольник ABC состоит (рис. 5-19) из 36 элемен-
элементарных треугольников (таких, например, как у вер-
вершины С). Фигуру, площадь которой мы имеем,
можно получить, если от площади треугольника
ABC мы отнимем площадь 3 элементарных треуголь-
треугольников, 12 равнобочных трапеций и 6 ромбов, обра-
образующих шестиконечную звезду. Площадь элемен-
элементарного треугольника равняется 1/36 площади тре-
треугольника ABC, 12 трапеций = 3/4 элементарного
треугольника х 12 = 9 элементарных треугольни-
треугольников, 6 ромбов = 1/2 элементарного треугольника X
хб = 3 элементарных треугольника. Площадь за-
107
штрихованной фигуры равняется 36—15 = 21 эле-
элементарному треугольнику, т. е. 21/36 площади тре-
треугольника ABC. Обозначив АВ = а имеем РАВС =
а2]/3~
= —т—> а тем самым площадь, заштрихованной
фигуры будет составлять
Рис. 5-20
Площадь шестилепестковой розы
Площадь треугольника ABC =
5-20)
площадь фигуры
3/-V3
(смотри рис.
АтВп =
2-
Площадь одного лепестка розы составляет
Вся площадь розы равняется:
Bтг+3
11,47г2
Об одной экскурсии
1. Для того, чтобы проехать 70 км Леониду потре-
потребовалось 1 ч 10 мин
108
2. До момента, когда Леонид завернул, Иван про-
проехал:
on 1 1 140
о о
3. В этот момент расстояние между ними составляло:
_п 140 ,,2
70 км у— = 46-д- тем
о л
4. Леонид и Иван сближались со скоростью F0+20)
км/ч, т. е. со скоростью 80 км/ч
5. Встреча наступила по истечении
2 7
46^- км : 80 лглс/ч = -ту ч = 35 жмн
6. С момента выезда прошло 1 ч 10 лшн+35 лшн,
т. е. 1 ч 45
Неудачная экскурсия
Александр Александрович надеялся проехать 672 км
в течение 672: 56 = 12 дней. Борис Петрович за то
же время проехал бы 40 км • 12 = 480 км, т. е. на
F72—480) км = 192 км меньше. Если бы, несмотря
на получение телеграммы, Александр Александро-
Александрович продолжал свой путь с той же скоростью, а Бо-
Борис Петрович тоже поехал дальше, настолько уве-
увеличив свою скорость, чтобы доехать до цели путе-
путешествия одновременно с Александр Александрови-
109
чем, то он должен был бы в соответствующем вре-
времени нагнать 192 км. Так как Борису Петровичу
необходимо было преодолеть втрое большее рассто-
расстояние, чем Александру Александровичу, то он дол-
должен был бы проезжать в один день 56 • 3 = 168 км.
Если от этой величины отнять по 40 км в день, то
оставшиеся 168—40 = 128 км в день позволили бы
Борису Петровичу нагнать недостающие 192 км.
Тем самым при увеличенной скорости Борис Петро-
Петрович нуждался бы в 192: 128 = 11/2 днях, чтобы
преодолеть остаток дороги, а из этого следует, что
до момента получения отзывающей их телеграммы
велосипедисты были в пути 12—11/2= 101/2 дня
В течение 101/2 дня Александр Александрович про-
проехал на велосипеде 56 • 10 1/2 = 588 км и до финиша
ему оставалось 672—588 км = 84 км. Борис Петрович
за зто время проехал 40 км • 10 1/2 = 420 км и до
финиша ему оставалось 252 км, т. е. 3 раза больше,
чем Александру Александровичу.
Странствующий отряд
Обозначим:
длину тропинки вверх — х км ;
длину тропинки вниз — у км;
длину тропинки по равнине 12— (х+у) км;
теперь мы имеем:
х у П-(х+у) 12~(х+у) ,У_,±_ (.±_
3 + 5 + 4 + 4 +3i~5 15
ПО
или
х+у . х+у 12-(х+у) _ 94
3 + 5 + 2 ~ 15
Обозначив'*+j; = а, получим:
из этого а = 8. Следовательно, по равнине тропинка
проходит 12—а = 12—8 = 4 км
Математика в кухне
Если взято: воды w кг, круп к кг, картошки z кг,
жира t кг, лука с кг, а всего получилось 7—1 = 6 кг,
то
1) w-\-k-\-z-\-t-\-c = 7 кг—1 кг = 6 лгг;
2) w == fc+z+t+c;
3) /с = z+t+c;
4\ г —
5) ( = ус или с = It
2w = 6 лгг, w = 3 кг
w = 2fc; 2k = 3 лгг;
^z = 1-х- лгг; z = -г- лгг;
3^ = хл:г; f = — лгг;
С Zt з С — *
Задачу можно решить без составления уравнений
в уме, если начать рассуждения с пункта 5 и продви-
продвигаться вверх до пункта 1.
Кто скорее?
Миша шагал в школу:
А +1. -2-1
Гриша шел Ь км t ч. Следовательно:
Т" ТС At * ~~х р'?j TCAI * ~л~ — О ТСЛ*
Из этого: t = 2 ч
Поэтому Гриша пришел в школу раньше на чет-
четверть часа, чем Миша.
Два пассажира
Первый пассажир шел до гостиницы tx ч, а вто-
второй — t2 ч. Поэтому:
Vx Ц-+ь2Ц- = а, из этого tx = —
2. 2. (
а , а а I 1 , 1
ИЗ ЭТОГО
112
>O
2
а
5 0 1
г з 1
5 2
А 3
4 О
Рис. 5-21
следовательно f2 > 'i •
Первый пассажир пришел в гостиницу раньше, чем
второй.
Задача Пуассона
Чтобы разделить вино пополам, необходимо было
7 раз переливать его из сосуда в сосуд (смотри
рис. 5-21).
Как она справилась?
Хозяйка заполнила 5-литровую посуду. Из нее она
перелила 3 литра в 3-литровую посуду и затем эти
3 литра она вылила в раковину. Оставшиеся в 5-ли-
5-литровом сосуде 2 литра воды она вылила в 3-литро-
3-литровый сосуд. Затем она снова заполнила 5-литровый
сосуд водой и из него перелила один литр в 3-литро-
3-литровую посудину. В большой посудине осталось ровно
4 литра.
ВЕЛИКАЯ
ТЕОРЕМА ФЕРМА
ГЛАВА 6
Пьер Ферма A601—1665)
Рис. 6-1
Теория чисел занимается свойствами натуральных
положительных чисел. Теоремы теории чисел, очень
простые на первый взгляд, бывают иногда чрезвы-
чрезвычайно трудно доказуемы. Некоторые теоремы теории
чисел не доказаны до настоящего времени; к тако-
таковым принадлежит и великая теорема известного
французского математика Пьера Ферма A601—1665),
эта теорема касается обобщения теоремы Пифа-
Пифагора.
Обозначая катеты прямоугольного треугольника
х и у, а гиротенузу — z (рис. 6-1), мы можем на
основании теоремы Пифагора записать следующее
равенство:
х2+у2 = z2 (А)
Это неопределенное уравнение с тремя неизвестны-
неизвестными. Одно из решений этого уравнения известно
каждому школьнику, а именно х = 2, у = 4-, z = 5.
Это решение приводит к построению так называе-
называемого Пифагорова треугольника. Но как найти осталь-
остальные решения ?
Общее решение уравнения (А) имеет вид
х = 2аЪ
у = ь2-а2 так как BabJ+(b2~a2J = (Ъ2+а2J
г = Ь2+а2
114
при этом числа а и Ъ — это любые натуральные
числа и а < Ъ.
Например, для
12
16
15
35
63
b
3
5
7
9
а =
X
12
20
28
36
= 2
У
5
21
45
77
Z
13
29
53
85
b
4
8
10
14
а
X
24
48
60
84
= 3
у
7
55
91
187
г
25
73
109
205
То, что эти числа удовлетворяют уравнению (А),
вытекает из тождества
BabJ + (b2-a2J = (a2+b2J
При рассмотрении уравнения х2+у2 = z2 возникает
вопрос, имеют ли решение аналогичные уравнения
вида
= 2Г5
(В)
= z"
115
Математики XVI и XVII веков пытались безрезуль-
безрезультатно решить эти уравнения в натуральных числах.
Пьер Ферма пришел к выводу, что не существует
натуральных чисел х, у, и z для п ^ 3, которые
удовлетворяли бы уравнению (Б). И хотя до насто-
настоящего времени общее доказательство этой теоремы
еще не выведено, имеется ряд доказательств для
некоторых величин п больших, чем 2.
Л. Эйлер A707—1783) доказал, что уравнения
хъ-\-у3 = z3 и x4+j'4 = z*, не имеют решений в виде
натуральных чисел.
А. Лежандр A752—1883) и П. Г. Л. Дирихле A805—
1859) доказали, что также и уравнение х5-\-у5 = г5
неразрешимо в целых числах.
Г. Ламе A795—1870) доказал, что уравнение (Б)
не имеет решения в целых числах при и = 7.
В половине прошлого столения Э. Э. Куммеру уда-
удалось доказать, что теорема Ферма верна лишь для
некоторых особых значений и что она, наверно,
верна для величин п меньше 100. Однако, общего
доказательства теоремы Ферма Куммер не смог
вывести.
Так как теорема Ферма получила большую попу-
популярность в математической литературе и способство-
способствовала открытию новых методов решения задач, ее
стали назьшать великой теоремой Ферма.
116
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Сколько ?
Через железнодорожную станцию прошло три воен-
военных состава. В первом находилось 462 солдата, во
втором — 546 и в третьем — 630.
Можно ли высчитать сколько вагонов было в каж-
каждом составе, если известно, что в каждом вагоне
находилось одинаковое число солдат и что зто число
было максимальное из всех возможных?
Сколько было учеников?
Ввиду болезни преподавателя уроки не состоялись
в двух классах. Тогда директор школы попросил
117
преподавателя физкультуры, чтобы он забрал учени-
учеников этих классов на экскурсию. Преподаватель
физкультуры собрал всех учеников вместе и хотел
их построить парами, однако, оказалось, что при
этом один ученик остается без пары. То же самое
произошло, когда учитель хотел построить учеников
тройками и четверками. Всегда оставался один
ученик. Только, когда учитель построил всех пятер-
пятерками не осталось ни одного ученика вне строя.
Сколько было учеников ?
О пожарных и дежурствах
В пожарную команду были приняты 5 новых по-
пожарников: А (Александр), Б (Борис), В (Виталий),
Г (Геннадий) и Д (Димитрий).
Все они заступили на дежурство в понедельник
первого числа. А имел 24-часовое дежурство каж-
каждые третьи сутки, Б — каждые четвертые сутки,
В — каждые пятые сутки, Г — каждые шестые сут-
сутки, Д— каждые седьмые сутки.
а) Есть ли в неделе такой день, когда на 24-часовом
дежурстве встретятся все пять пожарников?
б) Есть ли такие дни, когда не дежурит ни один из
них?
Сколько недель должно содержать расписание де
журства для пяти новых пожарников ?
118
Напишите
1. Напишите самое крупное число тремя цифрами.
2. Выразите 1000 с помощью:
а) пяти или девяти девяток,
б) шести троек,
в) тринадцати пятерок,
г) всех десяти цифр.
3. Выразите 1 с помошью:
а) цифр 1,2, 3;
б) всех десяти цифр.
4. Выразите 65 536, употребив для этого четыре
двойки.
5. Выразите 100, употребив для этого пять единиц,
пять троек и пять пятерок (двумя способами).
Какие арифметические действия?
Между цифрами поставьте знаки таких арифмети-
арифметических действий, чтобы было удовлетворено ра-
равенство :
а) 1234 = 2
б) 12 345 = 2
в) 123 456 = 2
г) 1 234 567 = 2
д) 12 345 678 = 2
119
Действия необходимо выполнять в такой последо-
последовательности, в какой проставлены знаки действий.
Две или три последовательно стоящие цифры можно
считать одним
12,23 или 34.
числом, например, в строчке а)
Что это за число?
Найти двухзначное число, которое, разделенное на
сумму своих цифр, дает в частном одну треть суммы
своих цифр.
Приключение в сберкассе
Костя, заглянув в свою сберегательную книжку
и убедившись, что на счету у него нет даже 50 зло-
злотых, был очень недоволен. «Ликвидирую сберкниж-
сберкнижку, а после Нового года открою другую, — подумал
он, — может быть сбережения будут на ней быстрее
копиться». Сказано — сделано. Костя вошел в сбер-
сберкассу, предъявил кассиру книжку и получил с нее
деньги полностью. Получая деньги, Костя даже не
глянул, сколько вручил ему кассир, а быстро вышел
из сберкассы, сел в проходящий мимо трамвай
и лишь там, выкупив за 50 грошей билет, пересчи-
пересчитал деньги. С удивлением он обнаружил, что даже
после уплаты за билет у него еще осталось вдвое
больше денег, чем было на книжке.
120
— «Кассир ошибся, — подумал Костя, — очевидно
был чем-то озабочен. Надо ему немедленно вернуть
то, что он переплатил». Так думая, Костя вышел
из трамвая и вернулся в сберкассу.
Кассир сердечно поблагодарил честного мальчика
и объяснил, что по ошибке выплатил ему столько
злотых, сколько на книжке было грошей и столько
грошей, сколько хранилось злотых.
Сколько злотых и сколько грошей было на книжке
у Кости ?
Какое это число?
На месте единиц в трехзначном числе стоит цифра 2.
Если эту цифру мы перенесем на первое место, то
получится число, больше заданного на одну треть.
Какое задано число ?
Четырехзначная головоломка
Подумайте, что это за число:
1) Оно четырехзначное,
2) первая цифра вдвое больше второй,
3) сумма первой и второй цифр равняется третьей,
4) если сложим все четыре цифры, то получим
число, в котором первая цифра равняется разнице
между четвертой и третьей, а ее произведение на
вторую цифру заданного числа, равняется первой
цифре заданного числа.
121
Хариты и музы (древнегреческая задача)
Три хариты, богини изящества, красоты и веселья:
Аглая, Эвфросина и Талия несли в корзинках оди-
одинаковое число прекрасных яблок. Они повстречали
девять муз, покровительниц искусства и наук. Каж-
Каждая харита дала каждой музе то же самое количество
яблок и тогда оказалось, что у каждой хариты и каж-
каждой музы одинаковое количество яблок.
Сколько яблок было в корзинке каждой хариты до
встречи ?
122
Как они рассчитались?
Покупатель приобрел в универмаге товары на сум-
сумму 37 рублей. У него были только пятирублевые
купюры, а у кассира оказались только двухрубле-
двухрублевые.
Как рассчитался покупатель с кассиром?
Определите это число
а) Не используя неизвестной хине составляя урав-
уравнения, определите такое натуральное число, чтобы
квадратный корень из третьей части этого числа,
сложенный с двумя третьими этого числа дал сумму,
которая была бы на 20 меньше искомого числа.
б) Есть много чисел, начинающихся единицей, но
среди них есть такие, которые увеличиваются вдвое,
если цифру, стоящую на конце, перенести на пер-
первое место.
Попробуйте найти одно такое число и указать спо-
способ нахождения этих чисел.
Сколько у меня было денег?
Когда я выходил из дому, то у меня в кармане было
немного денег в рублях и пятирублевых купюрах,
всего у меня было больше 140 рублей, но меньше
150. Я израсходовал одну треть денег, после чего
у меня осталось столько пятирублевых купюр,
123
сколько до этого было рублевок и столько рублевок,
сколько было пятирублевых купюр.
Сколько у меня было рублевок и пятирублевых ку-
купюр, когда я выходил из дому ?
Размен купюры
Группа учеников и учениц, в которой не было де-
десяти человек, получила за собранную макулатуру
одну пятирублевую купюру. Ученики более актив-
активно собирали макулатуру, чем ученицы и поэтому
каждый из них получил на десять копеек больше.
Чтобы поделить полученные деньги ученики раз-
разменяли купюру на двадцати- и пятидесятикопеечные
монеты, что позволило произвести правильный де-
дележ.
1) Сколько каких монет было получено при размене
купюры? Сколько имеется различных способов вы-
выдать пять рублей двадцати- и пятидесятикопеечными
монетами? Сколько было учеников и сколько уче-
учениц?
2) Как происходил бы дележ, если бы учеников
и учениц вместе взятых было больше десяти, на-
например, 11 или 12?
124
РЕШЕНИЕ ЗАДАЧ Сколько?
Да. Искомое число является наибольшим общим
делителем чисел 462, 546 и 630, т. е. — это 42.
В каждом вагоне ехало, следовательно, 42 солдата.
В первом составе было 11 вагонов D62: 42), во вто-
втором — 13 вагонов E46: 42) и в третьем — 15
F30:42).
Сколько было учеников?
Всего учеников было 85. Это число можно опреде-
определить следующим образом: 2-3-2, т.е. 12, делится
на 2, 3, 4; 12 • 5, т. е. 60, делится на 2, 3, 4, 5. Если
к 60 добавим 2-12 + 1, то полученное число 60+
+24+1 = 85 будет делится на 5, но разделенное
на 2, 3, 4 будет давать в остатке 1.
Примечание: Мы не принимаем во внимание
числа 25 так как занятий не было в двух классах.
О пожарных и дежурствах
а) Нет такого дня в неделе.
б) Такими днями являются в первую неделю —
вторник и среда, во вторую — пятница и воскре-
воскресенье; в третью неделю — четверг и суббота; в чет-
четвертую неделю — вторник, четверг и воскресенье;
в шестую неделю — среда, четверг и воскре-
воскресенье.
125
в) Все возможные комбинации дежурств произой-
произойдут в течение 60 недель, т. е. 420 дней; 420 дней —
это самое маленькое число, которое делится на 3, 4,
5, 6 и 7.
Напишите
1. 99 — для выражения этого числа необхо-
необходимо использовать 369 693 100 цифр. Лента бумаги,
необходимая для написания этого числа должна бы
была иметь 2000 км длины.
2. а) 999-|; 999Ц-
б) 333-3+у
в) 5 -5 -5 -5+5 -5 -5+5 -5 -5+5 -5-5
г) 90-5 -4:2+87+16-3
или 90 ¦ 4 • 3-8 • 6-7 • 5+2+1
3. .)!+?-; М. 2_р
б) A23 456 789)-
22
4. 2222=65 536
= 33
= E+5+5+5)-5
5. 111-11 = 33 -3 + у = 5 -5 -5-5 -5 =
126
Какие арифметические действия?
а) 1-2-3-4 = 2
б) A-2-3+4): 5 = 2
в) A+2)-3+4-5-6 = 2
г) 1-2-3+4+5-6-7 = 2
д) A+23): 4+5+6-7-8 = 2
Какое это число?
Если искомые цифры обозначим х и у, то искомое
число выражается следующим образом Юх+у. Из
условий задачи следует, что:
(Юх+у): (х+у)= (х+у)[3
Умножая обе стороны этого уравнения на Ъ(х-\-у),
получим
3A0*+.);)= (х+уJ
Решающего может смутить, что мы имеем только
одно уравнение с двумя неизвестными. Однако,
если мы обратим внимание, что правая сторона на-
нашего уравнения является квадратом натурального
числа, то из этого следует, что и левая сторона —
это квадрат натурального числа, делимый на 3.
Таких двухзначных квадратов имеется только два —
это числа 36 и 81. Давайте проверим каждое из
этих чисел:
1) 3 (Юх+у) = 36; 10дг+^ - 12, т. е. х = 1 и у - 2;
127
12
= 4; 4 Ф A+2)/3. Это решение не годится.
2) 3A0x+jO = 81; Юх+j; = 27, т. е. * = 2, у = 7;
Решение правильное, следовательно, искомым чис-
числом является 27.
Примечание: (х+уJ может быть также трех-
трехзначным числом.
Из трехзначных квадратов годится только 144.
Если мы теперь подставим 144 в наше уравнение, то
получим:
Юх+у = 48, т. е. х = 4 и у = 8; D+8)/3 = 4
Приключение в сберегательной кассе
У Кости на сберегательной книжке было х злотых
и у грошей, т. е. (IOOx+jO грошей. Кассир выплатил
Косте у злотых и х грошей, т. е. (КЮу+Jt) грошей.
Следовательно:
(ЮОу+х-50) = (IOOjc+j;) • 2
После преобразования получим:
98.у-199* = 50
lX+
_
У -
98
Зж+50 о , . . Зл+50
где t = —-^—; у = 2x+t; t = —^~
128
а из этого
л; = 32*-16+2 •-?=! = 32^—16+2*!
^ = 2_L; < = 3<i+l; x = 32t~\6+2t1.
Теперь, выражая х и у через ti, получим:
д: = 16+98^; у = 33+199*1. (А)
В уравнениях (A) *i может равняться нулю или лю-
любому натуральному числу. Принимая tx = 0, полу-
получим х = 16; у = 33. Другие величины х, у, которые
можно получить на основании уравнений (А), не
годятся, так как согласно условию Костя имел на
книжке меньше 50 злотых.
Следовательно, Костя имел на книжке 16 злотых
и 33 гроша, а кассир выплатил ему 33 злотых и 16
грошей.
Какое это число?
WOjc+lO.y+2
2 • 100+IOjc+j; = у A00jc+-10y+2)
Из этого: 370*+37.); = 592; т.е. Ш+у = 16
поэтому: у = 16—Юл:; у = 6, х = 1.
Число 162.
Проверка: 216 = у • 162 = 54 • 4 = 216.
129
Четырехзначная головоломка
Пусть нашими цифрамми будут а, Ъ, с, d.
Тогда а = 2Ь; с = а+b = ЪЬ.
Так как каждая цифра меньше или равна 9, то
цифрой Ъ может быть 1, 2 или 3.
Пусть первой цифрой суммы a+b+c+d будет aL,
Тогда axb = а, т. е. аф = 2Ь, а из этого а± = 2.
Теперь Й! = d— с = d—ЪЬ. Подставляя 2 вместо ах
и последовательно 1, 2 и 3 — вместо Ъ найдем после-
последовательно три значения для d: d = 5, d = &, d = II
(не годится).
После проверки получим а = 4, b = 2, с = 6,
d = 8. Искомое число 4268.
Хариты и музы
Каждая харита имела в корзинке х яблок и дала
каждой музе у яблок.
Следовательно, х—9у — Ъу, т. е. х — \2у.
Ответы могут быть разные, однако, учитывая, что
хариты несли корзинки, а не большие корзины,
можно предположить, что у равняется 1, 2 или 3.
Тогда соответственно х будет равно 12, 24 или 36.
Как они рассчитались?
Предположим, что покупатель дал кассиру х пяти-
пятирублевых купюр, а кассир выдал ему у двухрубле-
130
вых купюр, следовательно:
Sx-2y = 37 A)
Это, так называемое, неопределенное уравнение, та-
такими уравнениями занимался и преуспевал в их
решении, как мы уже упоминали, Диофант.
Из уравнения A) следует:
_ 5л:—37 4-х+х—36—1 _ г. 1Q , х—1
У- 2 = 2 -/*1»+
х~1
где t = —^—> эт0 определенное целое число, следо-
следовательно
х = 2t+l и
у = 2*-18+* = 2 Bf+l)-18+f = —16+5?
поэтому получается:
х = \+2t; у = -16+5*.
Так как х и у — натуральные числа, то
1+2* > 0, из этого (>-|и -16+5* > О,
16 „1
а из этого * > -=-, т.е. * > 3-=-.
Из этого следует, что * = 4, 5, 6, ...
Соответственно:
* = 9,11,13,...
j; = 4,9,14, ...
Проверьте.
131
Определите это число
а) Свойства искомого числа:
1. Делится на 3.
2. Из третьей части числа можно извлечь квадрат-
квадратный корень.
3. Число больше 20.
Эти три свойства имеются у числа 27,48,75,108.
После сравнения этих чисел с условиями задачи,
легко убедиться, что отвечает им только число 75,
так как 27 и 48 слишком маленькие числа, а 108 —
слишком большое число.
б) Свойства искомого числа:
1. Число должно начинаться цифрами 1, 0 ... на его
окончании должны стоять цифры ... 4, 2 (почему?)-
2. После переноса двойки на первое место, искомое
число будет выражаться следующим образом1
210... 4.
3. Цифры, стоящие на месте точек между 4 и О,
будем находить, умножая на 2 цифру 4 и последу
ющие, до тех пор пока не получим произведения ДО-
Например, 4-2 = 8, пишем 8, в уме 105 ... 84,
далее умножаем 8*2= 16, пишем 6, в уме 1, полУ'
чим 105 ... 684, далее 6 • 2+1 = 12+1 = 13, пишем
3, в уме 1 и так далее до получения при очередно*1
умножении произведения 10.
132
Искомое число:
105 263 157 894 736 842 (А)
Если теперь цифру 2 перенесем на первое место,
то получим число 210 526 315 789 473 684, которое
ровно в два раза больше числа (А).
Сколько у меня было денег?
Когда я выходил из дому, то у меня было д: пяти-
пятирублевых купюр и у рублевок.
После возвращения у меня было у пятирублевых
купюр и х рублевок.
По условиям задачи имеем:
2
у • Eх+у) = х+5у
Из этого после преобразований будем иметь 7х = 13у,
а из этого получим у = 7 ¦ ~. Так как у — это
целое число, то правая сторона уравнения должна
быть также целым числом, т. е. делится на 13.
Из этогв следует, что Л/13 = 1, 2, 3, 4 ... и т. д.
Следовательно, л; = 13, 26, 39, ..., а у соответ-
соответственно равняется 7, 14, 21 ...
Так как выходя из дому я имел больше, чем 140
рублей но меньше, чем 150, то этому условию соот-
соответствует только одна пара решений л; = 26
и у = 14.
133
Следовательно, когда я выходил из дому, у меня
было 26 пятирублевых купюр и 14 рублевок,
т. е. 144 рубля.
Размен купюры
Пятирублевую купюру можно разменять на двад-
двадцатикопеечные и пятидесятикопеечные монеты че-
четырьмя способами :
1) 20 раз по 20 и 2 раза по 50;
2) 15 раз по 20 и 4 раза по 50;
3) 10 раз по 20 и 6 раз по 50;
4) 5 раз по 20 и 8 раз по 50.
Вместе учеников и учениц было 9, 11 или 12.
В первом случае 5 учеников получило бы по 60 ко-
копеек и 4 ученицы по 50 копеек (второй размен); во
втором случае 6 учеников получило бы по 50 ко-
копеек и 5 учениц по 40 копеек (третий размен); в тре-
третьем случае — 2 ученика по 50 копеек и 10 учениц
по 40 копеек (первый размен).
СРЕДНЕЕ ГЛАВА 7
ГАРМОНИЧЕСКОЕ
Среднее нескольких чисел — это такое число, кото-
которое не больше самого большого и не меньше самого
меньшего из этих чисел. В элементарной математике
известны три средних: среднее арифметическое, гео-
геометрическое среднее и среднее гармоническое. Если
имеется только два числа а и Ъ (например, 4 и 9),
то:
среднее арифметическое этих чисел будет равно:
аЛ-Ь _ 4+9 _ , -
~Т~ ~ ~~2~~ ~~ '
среднее геометрическое будет равно:
У~аЬ = /4-9 = 6
а среднее гармоническое — соответственно:
2аЬ 2-4-9 _ ^2_ ,_7
~" 13
аЛ-b ~ 4+9 ~" 13 13
Как видно из этих вычислений, самым малым
lab Г7
средним является среднее гармоническое —jx~ 5 т^,
а самым большим — среднее арифметическое
а+Ь _ Л
~^Г -Ь2-
Среднее геометрическое находится между двумя
этими средними и связано с ними пропорциональной
зависимостью.
235
Фактически:
a+b
a+b
: ]/ab = \/aF:
например,
с 7 ,
(А)
Справедливость равенства (А) легко можно прове-
проверить, учтя, что произведение крайных членов про-
пропорции должно равняться произведению средних
членов. В действительности мы имеем:
lab a+b , /-г- ,—r
-^ • —г- = ab и \/ab ¦ ]/ab = ab
Из трех вышеупомянутых средних — среднее гар-
гармоническое менее всего известно, а поэтому мы
займемся именно им.
Из трех чисел а, Ъ, с число с является средним гар-
гармоническим в том случае, если обратная величина
с является средним арифметическим обратных ве-
величин а и Ъ, т. е. в том случае, когда
+
с - 2
Преобразуя это уравнение, находим:
lab
с ~ а+Ь
136
i
a+b
Рис.
, EF\\a,
7-1
EF\\b
a
Рис.
7-2
Если теперь мы изобразим числа а и Ь в виде отрез-
отрезков и построим трапецию с основаниями, равными
избранным отрезкам а и Ь, то отрезок EF (рис. 7-1),
проведенный через точку пересечения О диагоналей
АС и 5D параллельно ЛЯ, является средним гармо-
гармоническим отрезком отрезков а и Ь. Доказать это
можно, рассматривая подобные треугольники.
Доказательство:
Докажем, что EF = . .
Обозначим (рис. 7-2): АС = dx; DB = d2; ?0 = с;
ОС = е. Из рисунка следует, что треугольник ABD
подобен треугольнику EOD; треугольник ABC по-
подобен треугольнику OFC; треугольник АОВ — тре-
треугольнику DOC, так как соответствующие углы
этих треугольников равны между собой. Поэтому
имеем:
из треугольников ABD и EOD;
!)- = ¦
' т
2) -г = —%:— из подобия треугольников АОВ и DOC.
Из уравнения 2) следует:
~> а+6 йг а
а из 3) следует, что: т =
4) — = — из подобия треугольников ABC и OFC;
5) -j- = —— из треугольников ЛОВ и DOC;
из уравнения 5) получаем:
аЪ
137
LP!=KL-LM
Рис. 7-3
6)
a+b
а из 6) следует, что: п =
ab
a+b '
Следовательно:
EF = m+n =
ab ab
lab
a+b a+b a+b '
Соединяя середины непараллельных боковых сто-
сторон G и Н (смотри рис. 7-1), находим среднее ариф-
арифметическое отрезков а и Ъ.
Все эти средние можно представить на одном ри-
рисунке. Для этого на любой полупрямой (рис. 7-3)
откладываем от точки К отрезок KL = EF = —-т ,
а затем отрезок LM = GH =
а+Ь
и вычерчиваем
полуокружность, радиус которой является суммой
отрезков KL и LM.
Из точки L восстанавливаем перпендикуляр к КМ;
перпендикуляр LP является средней геометричес-
геометрической отрезков KL и LM, так как (LPJ = KL • LM-
Среднее гармоническое можно использовать в раз-
разных целях.
Вот практическая задача, решением которой явля-
является среднее гармоническое чисел, встречающихся
в задаче.
Мотоциклист проехал расстояние от Москвы до
Горького со средней скоростью vx = 90 км 1ч; а об-
обратно он ехал со средней скоростью v2 = 60 км/ч.
138
Подсчитать среднюю скорость езды мотоциклиста
на трассе Москва-Горький-Москва.
На первый взгляд кажется, что средняя скорость ра-
равняется среднему арифметическому данных скорос-
Vi+v2 90+60 -г ,
теи, т. е., что v = —^—' т-е-—т— = 75 км/ч.
Однако это не так. А вот рассчеты: Пусть расстоя-
расстояние Москва-Горький составляет а км. Тогда — =
= ^ — зто время, затраченное на путь от Москвы
до Горького, а — = t2 — время езды из Горького
в Москву. Полное время в обе стороны состав-
составляет
а средняя скорость езды в обе стороны
_ 2а_ _ 2а 2
V ~ ~Т ^ — + — ~ —+ —
Vi V2 Vi Vi
Из этого^находим:
1 1
1 «1 1
т. е. v = -
Как видно из этого уравнения, средняя скорость
является не средним арифметическим, а средним
гармоническим заданных скоростей. Подставляя
»! = 90 км/ч и v2 = 60 км/ч, найдем, что
v = 72 км/ч, а не 75 км/ч
139
Таким же образом решается задача с тремя различ-
различными скоростями. Три города А, В и С расположены
на таком расстоянии друг от друга, что расстояния
АВ, ВС и С А равны между собой и образуют равно-
равносторонний треугольник. Автомобиль едет из А в В
со скоростью г>! км/ч, из В в С со скоростью v2 км/ч,
а из С в А — со скоростью v3 км/ч (например,
vx = 60 км/ч, v2 — 45 км/ч, v3 = 36 км/ч). Какова
средняя скорость автомобиля?
Средняя скорость автомобиля на этом пробеге бу-
будет равняться не среднему арифметическому
vt+v2+v3 60+45+36 , лп ,
——- = -у-1-— км/ч = 47 км/ч
а среднему гармоническому:
V2
К такому заключению мы придем, если будем рас-
рассуждать подобным образом, как в предыдущей
задаче:
АВ = а;
~
средняя скорость на всей трассе:
Vi ' V2
140
а из этого v =
J_ - J_+JL
Vi V2 V3
Следовательно, средняя скорость:
•и = =
км/ч —
3-60 45-36
~ 60-45+60 36+45 36
= 45 км/ч
Докажите это самостоятельно.
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Прежде всего пунктуальность
Интернат горного училища находился на довольно
значительном расстоянии от учебного корпуса и уче-
учеников привозили на занятия автобусом к 8 часам
утра. Если бы автобус с учениками ехал со скоростью
30 км/ч, то он приехал бы в школу на 30 мин раньше
времени, если же, отправляясь из интерната в то же
время, он ехал бы со скоростью 20 км/ч, то прибыл
бы с опозданием на 30 мин.
Какое расстояние от интерната до школы и с какой
скоростью должен ехать автобус, чтобы, отправляясь
в путь в назначенный час, он приехал в школу точно
к 8 часам утра ?
141
Разумный бухгалтер
Совхоз, колхоз и МТС расположены на некотором
расстоянии от шоссейной дороги по соседству друг
с другом. Для облегчения связи с сельсоветом эти
три хозяйства решили собственными силами проло-
проложить подъездную дорогу до шоссе. Совхоз доставил
для строительства дороги 20 телег щебня, МТС —
пять грузовиков щебня, что составляло вместе со-
содержимое 25 телег, а колхоз выплатил эквивалент
своей доли в строительстве дороги деньгами, в сумме
450 рублей. Каким образом поделить эти деньги
между совхозом и МТС?
142
Совхоз предложил поделить 450 рублей поровну,
но МТС не согласилась, а предложила разделить
деньги пропорционально поставленному количеству
щебня: совхозу за 20 телег — 200 рублей, а МТС
за 25 телег — 250 рублей.
Бухгалтер колхоза, который присутствовал при этом
дележе улыбнулся и сказал:
— Нет, товарищи, и дележ поровну й дележ про-
пропорционально поставленному числу телег щебня,
неправильны. Я разделю вам 450 рублей таким
образом, что никто не будет обижен.
Какой способ дележа предложил бухгалтер ?
Виноторговец и его помощник
Один виноторговец имел помощника, обязанностью
которого было приносить вино из погреба в лавку.
Однако помощник бьш любителем спиртного и вы-
выпивал тайком каждый день по 4 стакана, т. е. по
1 литру вина из 20-литрового боченка, а чтобы это
не обнаружилось доливал туда столько же воды.
Так продолжалось четыре дня, а на пятый день
этот боченок был куплен одним трактирщиком.
Вскоре однако возмущенный трактирщик прибежал
к виноторговцу и со скандалом потребовал возвраще-
возвращения денег, говоря, что платил до 2,5 рубля за вино,
а не за воду.
— Принесите мне обратно проданный боченок вина
и я верну Вам столько, сколько Вам причитается.
143
Воду я не продаю, но за вино Вам придется запла-
заплатить.
— Но как мы узнаем, сколько воды было долито
до вина?
— А сейчас позовем виновника.
Вызванный помощник честно признался, что долил
4 литра воды.
— А, значит я плачу за 16 литров — воскликнул
трактирщик — отдайте мне мои 10 рублей.
— О нет, любезный, сказал виноторговец, рассчет
более сложен, сейчас я подсчитаю сколько Вам при-
причитается.
Сказав это, виноторговец вынул карандаш и начал
считать.
Давайте, не ожидая расчета виноторговца, и мы
посчитаем, сколько причиталось денег трактир-
трактирщику.
В сельмаге
Покупатель зашел в сельмаг и попросил 2,25 кг
сахара. Продавец отвесил товар, положив сахар на
правую тарелку весов, а гири на левую. Но получив
сахар, покупатель выразил свое сомнение относи-
относительно правильности взвешивания и перевесил са-
сахар, однако положив его на правую тарелку, а ги-
гири — на левую. Оказалось, что весвх показывают
1,44 кг. В магазине возникла суматоха и разразился
скандал.
144
Присутствовавший при этом агроном быстро вынул
свою записную книжку и выполнив какие-то рас-
счеты, обратился к покупателю со словами:
— Заплатите за 1,8 кг сахара, так как именно столько
вы получили.
Обе стороны согласились с расчетом агронома.
Правильно ли агроном подсчитал, сколько сахара
получил покупатель ?
В зоологическом магазине
Владелец зоологического магазина купил некое число
зайцев и сколько-то пар кроликов. Число пар кро-
кроликов составляет половину числа купленных зайцев.
За каждого зайца владелец платил по 2 рубля, а за
каждого кролика по 1 рублю. Розничная цена, за
которую купец продавал каждое животное была
на 10% выше покупной B,2 руб. и 1,1 руб.). Когда
все животные, за исключением 7, были проданы
купец обнаружил, что все деньги, затраченные им
на покупку, уже возвратились. Следовательно, его
чистая прибыль — это как раз продажная цена
оставшихся семи животных.
Какова чистая прибыль купца ?
Кто продает дешевле?
Некий американский фабрикант консервов выпустил
на рынок шпроты в масле в прямоугольных кон-
10
сервных банках с размерами основания а и Ъ и высо-
высотой h. Его конкурент тоже выпустил на рынок по-
подобные шпроты в прямоугольных банках той же
высоты h, но с увеличенной на 20% длиной основа-
основания и уменьшенной на 20% шириной. Цены банок
были одинаковые. Кто из фабрикантов продавал
шпроты дешевле ?
Учет товаров
При проведении учета товаров в одном магазине
контролеры обнаружили счет, в котором многие
цифры были неразборчивы. Если на местах, где
стояли неразборчивые цифры, мы поставим значки
х, то счет будет выглядеть следующим образом:
23х7хх
X ххх5
ххххх2х
х347хх
хх9570
704ххх
7хххххххх
Контролерам, однако, удалось расшифровать счет.
Каким образом ?
На фепме
Два фермера Джон и Билл продали стадо овеЦ;
взяв за каждую овцу столько долларов, сколько
146
овец было в стаде. Желая разделить выручку по-
пополам, скотоводы брали из полученной суммы по
очереди по одной 10-долларовой монете. Джон
взял на 10 долларов больше. Для того, чтобы вы-
равнять счет, Джон отдал Биллу остаток, который
был меньше 10 долларов, и бумажник. Спрашивает-
Спрашивается, сколько стоил бумажник?
РЕШЕНИЕ ЗАДАЧ
Прежде всего пунктуальность
1) Разница во времени между приездом с опозданием
и преждевременным приездом составляет
30 лшн+30 мин = 60 мин
2) При езде со скоростью 30 км/ч для преодоления
расстояния в I км требуется 2 мин, а при скорости
20 км/ч — соответственно 3 мин, т. е. на 1 км потеря
составляет 1 мин.
3) Так как разница во времени между приездом с
опозданием и преждевременным приездом состав-
составляет 60 мин, следовательно, расстояние от интерната
до училища равно 60 км.
4) На весь путь автобус должен затратить
60_
30
а следовательно, он должен ехать со скоростью
60 км:2^ч = 24 км/ч
147
Обратите внимание, что полученный ответ — 24 км/ч
является не средним арифметическим скоростей
30 км/ч и 20 км/ч, а их средним гармоническим:
2.30-20 _ 1200 _Г).
30+20 50
Разумный бухгалтер
Совхоз и МТС вместе доставили 45 телег щебня.
Из этого следует, что на каждого партнера прихо-
приходилось по 15 телег щебня. Стоимость 15 телег щебня
составляет 450 руб. Следовательно, стоимость одной
телеги щебня равна 450 руб.: 15 = 30 руб. Совхоз
доставил 20 телег, а следовательно, он должен полу-
получить за 20—15 = 5 телег по 30 руб., т. е. 150 руб
МТС доставило 25 телег, а следовательно, за 10 те-
телег МТС причитается 10 • 30 руб. = 300 руб.
Виноторговец и его помощник
В первый день помощник выпил 1 литр чистого
вина, в боченке осталось 19 литров вина и 1 литр
воды.
На второй день он выпил 19/20 литров чистого
19
вина, в боченке, следовательно, осталось 19—-жг —
= -^д- литров чистого вина.
20
На третий день история повторилась, следователи»,
148
192
помощник выпил ~2fl2" чистого вина и в боченке
193
осталось -^qj- литров чистого вина.
193'
На четвертый день помощник выпил -^ чистого
вина.
Всего помощник выпил:
+ Ж + F + ~W~) ШГа вина = 3'7098 литров.
Следовательно виноторговец должен был вернуть
трактирщику: 2,50 руб. • 3,7098 « 9,27 руб.
В сельмаге
I Предположим, что сахар весит х кг, а плечи весов
_^ |— -j_ имеют соответственно длину а и Ъ см (смотри рис.
225 кг 1,44 кг х кг 7-4")
Рис. 7-4 В соответствии с законом равновесия рычага мы
получим при первом взвешивании ха = 2,25 Ь,
а при втором xb = 1,44 а.
Умножая сторонами зти уравнения мы получим:
х2 • а ¦ Ъ = 2,25 • 1,44 • а • Ь, из этого
х2 = 2,25 • 1,44,
т.е. х = i/2725 • 1,44 = 1,8.
Следовательно, сахар весит 1,8 кг.
Вывод: правильная масса предмета, взвешенного
на неравноплечных весах, равняется средней гео-
геометрической обоих взвешиваний m и п, т. е.
х = \/пгп
149
В зоологическом магазине
Пусть х — это число купленных зайцев, а у — число
непроданных зайцев; число купленных кроликов
также равно х.
Число непроданных кроликов равняется 7— у, а по-
поэтому число проданных кроликов равно х— G~у);
за проданные зайцы торговец получил 2,2 (х—у)
рублей, а за проданных кроликов он получил
1.1 (л;—7-\-у) рублей, итого получено за проданных
животных
2.2 (х-у)+1,1 (x-7+y) рублей
Эта сумма равняется сумме денег, уплаченной за
всех зайцев Bх рублей) и за всех кроликов (х руб-
рублей). Следовательно, всего было уплачено Зх руб-
рублей.
Из этого можно составить уравнение:
2,2(x-y)+l,l (x-7+y) = Зх
После преобразования получим:
Из этого уравнения можно сделать вывод, что не-
необходимо выбрать такую величину меньше 7 G —¦
это число всех непроданных животных), чтобы
числитель дроби A) делился на 3. Такой величиной
у может быть 2 или 5. Для у = 2, х = 33. Следо-
Следовательно, величина у = 2 не годится, так как 33 не
150
делится на 2, а хозяин магазина покупал кроликов
парами. Величина у = 5 годится, так как для у = 5,
л; = 44.
Следовательно, торговец купил 44 зайца и 22*пары
кроликов и заплатил за них 132 рубля. Он продал
39 зайцев и 21 пары кроликов и получил за них
также 132 рубля. Чистая прибыль составляет стои-
стоимость 5 зайцев и 2 кроликов, т. е. 13,2 рубля.
Кто продает дешевле
Дешевле продает тот, кто за ту же самую цену про-
продает банку консервов большего объема.
Первый фабрикант берет какую-то сумму денег за
банку шпрот объемом abh. Второй за те же деньги
продает банку объемом:
6 4 ,, 24
= Te'Tufc=25
т. е. на 4% меньшую, чем первый.
Учет товаров
Так как во втором частичном произведении цифры
3 и 7 такие же, как и соответствующие цифры мно-
множимого, то цифра тысяч множимого должна быть 4,
цифра сотен тысяч во втором частичном произве-
произведении — 3, а цифра десятков множителя — 1. При
проверке третьего частичного произведения можно
151
обнаружить, что множимое — это 234 785, а множи-
множитель— х215. Четвертое частичное произведение
704ххх позволяет определить цифру тысяч множи-
множителя — зто 3. Таким образом, установлено, что мно-
множимое— 234 785, множитель — это 3215, а следо-
следовательно, произведение — это 754 833 755.
На ферме
Пусть стадо овец насчитывало Юа+Ь штук (а и b —
это цифры). Полученная за проданных овец сумма
денег составляет A0а+&J = A00a2+20ab+b2)
долларов. Часть этой суммы, составляющую 100а2 +
+20а ¦ Ъ фермеры поделили между собой, беря по
очереди по 10 долларов. Остаток, т. е. Ь2 (b < 10),
содержит нечетное число десятидолларовых монет
и монеты меньше 10 долларов. Следовательно,
Ъ2 может составлять только 16 или 36. В обоих слу-
случаях остаток равняется 6 долларам.
ДВОИЧНАЯ ГЛАВА 8
СИСТЕМА
Природа наделила человека пятью пальцами на
одной руке, десятью — на двух, и двадцатью — на
обеих руках и ногах. Используя этот дар природы,
человек считал пятерками, десятками или же двад-
двадцатками. Только один раз человек отступил от этого
правила в Вавилонии. Древние вавилонцы считали
шестидесятками.
Научившись считать, человек должен был также
научиться записывать числа какими-то знаками. Там,
где основанием системы счисления было число де-
десять, человек должен был найти десять числовых
знаков, названных позднее цифрами, там где осно-
основанием системы счисления было число пять — пять'
знаков, а там где в качестве основания принято
было шестьдесят — было найдено другое решение,
но об этом мы здесь писать не будем, ибо предметом
настоящей главы не является история цифровых
знаков.
После продолжительной борьбы разных направле-
направлений, во всем цивилизованном мире была принята
десятичная система счисления и введены в упот-
употребление цифровые знаки, изобретенные в Индии,
затем заимствованные арабами и уже через арабские
страны попавшие в Европу при участии математика
и коммерсанта XIII века Леонардо Пизанского
153
(Фибоначчи). Мы все очень хорошо знаем эти
знаки:
0,1,2,3,4,5,6,7,8,9.
Эти знаки вместе с позиционной системой, которая
заключается в том, что каждая цифра имеет опре-
определенное значение не только в зависимости от своей
графической формы, но и от места (позиции), кото-
которое она занимает в записи числа, вполне удовлетво-
удовлетворяли и простых людей и ученых до момента появле-
появления вычислительных машин.
Сущность десятичной системы счисления заключа-
заключается в том, что в многоцифровых числах только
первая цифра, считая с правой стороны, обозна-
обозначает единицы. Цифра, записанная на втором месте
(на второй позиции) с правой стороны выражает
десятки, на третьем месте — сотни, на четвертом —
тысячи и т. д. Одним словом, каждое последующее
место принадлежит следующей степени числа де-
десять. Например: 20 456 = 2 • 104+0 • 103+4 • 102 г
+5 • 104-6 • 10° (нуль служит для обозначения, что
данная позиция — пустая, что число не имеет ка-
какой-то степени числа десять, в нашем примере —
десяти в третьей степени).
Для вычислительных машин использование десяти
цифровых знаков оказалось очень неудобным из
чисто технических соображений, потребовались бы
чрезвычайно сложные устройства. Поэтому кон-
конструкторы отказались от десятичной системы счис-
154
ления. В электронных вычислительных машинах
числа представлены с помощью элементов, которые
могут принимать два устойчивые состояния. Самой
простой оказалась двоичная позиционная система:
при этой системе требовались только две цифры,
все арифметические действия в этой системе чрезвы-
чрезвычайно простые, а то, что они содержат много знаков
и выглядят как длиннющие ряды, не составляет
для машины каких-либо трудностей, так как машина
осуществляет запись молниеносно.
Поскольку электронные вычислительные машины
и двоичная система часто бывают предметом раз-
различных дискуссий, мы считаем нелишним ознако-
ознакомить наших читателей с этой системой счисления.
Как мы записываем двоичные числа?
Двоичная система использует только две цифры:
О и 1
Система — позиционная. Только первая цифра с пра-
правой стороны обозначает единицу, вторая цифра
с правой стороны обозначает двойку. Пишется она
так 10 (два в первой степени); третье место с правой
стороны занимает четыре: 100; четвертое место —
восемь: 1000; пятое — шестнадцать: 10000 и т.д.
Каждое следующее место занимает следующая сте-
степень двойки.
Каждое число можно записать в двоичной системе.
155
Например, запись: 110101101 следует понимать сле-
следующим образом:
1 • 28+1 • 27+0 ¦ 26+1 • 25+0 • 24+1 • 23+1 • 22 +
+0-21+1 -2° =
= 256+128+0+32+0+8+4+0+1 = 429
как видно из этого, число 429 выраженное в двоич-
двоичной записи состоит из девяти знаков (разрядов).
Запись 100100 обозначает 1 • 25+0 • 24+0 • 23 +
1 • 22+0 • 2*+0 • = 32+4 = 36, число 36 в дво-
двоичной записи оказывается шестизначным числом.
Как перейти от десятичной системы записи
к двоичной?
Дано число 543; необходимо выразить его в дво-
двоичной системе. Для этого нужно разделить 543 на 2
543
271 (остаток 1 подписываем под делимым 543)
Затем делим число 271 на два:
271
1
135 (остаток 1 подписываем под делимым 271)
Затем делим 135 на два
135 2
1 67
156
Выполняя таким образом деления до самого конца,
мы получим следующую картину
543 2
1 271 I 2
135
1
2
67
1
2
33
1
2
16
0
2
8
0
2
4
0
2
2
2
Oil 2
1
О
Выписывая все остатки в обратной последователь-
последовательности, получим: 1000011111. Зто и есть число
54310 (индекс 10 у числа 543 напоминает нам, что это
число записано в десятичной системе счисления).
Таблица сложения и умножения в двоичной
системе
Сложение: 0+0 = 0; 0+1 = 1+0 = 1; 1+1 = 10
Умножение: 0-0 = 0; 1-0 = 0-1=0; 1-1 = 1
Читатель должен признать, что обе таблицы очень
просты и их легко запомнить. Несложны и арифме-
арифметические действия.
157
Сложение
Необходимо только помнить, что две единицы каж-
каждого разряда дают одну единицу следующего раз-
разряда, четыре — две и т. д.
А вот пример:
1011101 = 93
10010 = 18
110011 = 51
+ 1011100 = 92
11111110 = 254
Вычитание
11001011 = 203
- 1010110 = 86
1110101 = 117
Двоичное дополнение
Дополнительной десятичной дробью до 1 (например,
дополнительной дробью дроби 0,2703) будет дробь
@,7297), которая, сложенная с данной, дает в сумме
единицу:
0,2703+0,7297= 1
Десятичным дополнением данного числа до единицы
ближайшего высшего разряда является число, ко-
которое, сложенное с данным, дает нам в сумме эту
единицу высшего разряда, например, десятичным
дополнением числа 3806 до 10000 является 6194,
так как 3806+6194 = 10000.
158
Дополнительную десятичную дробь мы найдем, если
вычтем данную дробь из единицы, десятичное до-
дополнение числа найдем, вычитая данное число из
единицы ближайшего высшего разряда. Мы гово-
говорим о дополнениях, так как вычитание можно заме-
заменить сложением с дополнением.
Например, вычитание:
0,8705—0,6028 можно выполнить следующим обра-
образом:
0,8705
+ 0,3972 (это дополнительная десятичная дробь)
1,2677-1 = 0,2677.
И действительно: 0,8705-0,6028 = 0,2677.
Вычитание 8736—538 = 8198 можно выполнить сле-
следующим образом
8736
+ 462 (это десятичное дополнение до 1000)
9198-1000 = 8198.
Этот же метод можно применить и в двоичной сис-
системе счисления, что значительно облегчает выпол-
выполнение вычитания, так как двоичное дополнение
чрезвычайно просто найти: первую единицу с пра-
правой стороны и все нули (если они есть), которые на-
находятся за ней, пишем без изменений, а в остальной
части вместо нулей пишем единицы и наоборот
число: 1011100100
двоичное дополнение: 0100011100
259
Примечание: Нули в начале (с левой сто-
стороны) двоичного дополнения необходимо пропус-
пропустить.
А вот пример замены вычитания сложением с дво-
двоичным дополнением
11001011-1010110 = 11010101
11001011
+ 0101010 (двоичное дополнение)
11110101-10000000 = 1110101
Умножение
Умножение в двоичной системе счисления — зто
самое простое действие и сводится к умножению
на 1 и сдвигу.
Затем выполняется сложение частичных произведе-
произведений, число которых равно числу единиц во мно-
множителе
1010011 • 1001101 = 1100011110111 (= 63911О)
Сравнение выполнения этого действия в двоичной
системе счисления и в десятичной выглядит так:
1010011
х 1001101
1010011 83
1010011 х 7?
1010011 581
1010011 581
1100011110111 6391
B12+21>-)-27+26+2'+24+22+21+1) -6391
160
Из этого примера видно, что в двоичной системе
счисления запись несколько длинее, но техника
выполнения умножения значительно проще.
Деление
В двоичной системе счисления деление выполняет-
выполняется также механически, однако за счет длинной и не
очень легкой записи. Покажем это на примере.
Запись действия такая же, что и при делении в де-
десятичной системе счисления, но под делимым будем
записывать не произведение делителя на последова-
последовательную цифру частного, а его двоичное дополне-
дополнение (нули в начале можно не вычеркивать).
дополн.
дополн.
дополн.
10101111
+ 00111
110010
100000
100101
00111
101100
100000
0011001
00111
100000
100000
11001
111
То же самой действие в десятичной системе счи-
счисления: 175 : 25 = 7.
161
А вот еще один пример деления с остатком:
11011101
01001
100100
100000
100101
01001
101110
100000
10111
1001
1110
Частное от деления 1001, остаток 1110.
Как видно из всех этих примеров двоичная система
счисления очень мало пригодна в повседневной
практике и довольно-таки громозка. Однако, по
нашему мнению, стоит научиться пользоваться его
и самостоятельно проделать несколько упражне-
упражнений.
Двоичные дроби
Так как вычислительные машины пользуются дво-
двоичными дробями, то стоит и нам познакомиться
с ними.
Известно, что обыкновенная дробь выражается ко-
конечной десятичной дробью, если разложение ее
знаменателя на простые множители не содержит
других множителей, кроме 2 и 5. Другие дроби
при их преобразованиях в десятичные выражаются
бесконечными дробями. Еще более ограничена воз-
162
можность преобразовать дробь в двоичную: в дво-
двоичную дробь можно преобразовать только такую
обыкновенную дробь, у которой знаменатель можно
разложить только на двойки (иначе говоря, знамена-
знаменатель которой — это какая-то степень числа два). Дво-
Двоичные дроби мы записываем так же, как и деся-
десятичные :
0,0111; 10,101, что соответственно обозначает:
0,0111 =4+^+1+^ = 1
10,101= 2 + 1 + ^ + 1 = 2|
Из этого можно сделать следующий вывод: каждую
двоичную дробь можно превратить в десятичную.
Представим в виде бесконечной двоичной дроби
Дробь у.
1. Прежде всего, преобразуем обыкновенную дробь
1
у в десятичную:
у = 0,142857 (с точностью до 0,000001)
2. Затем дробь 0,142857 преобразуем в двоичную.
Поступаем следующим образом
0,142857
0,285714
Из этого следует, что дробь 0,142857 меньше -=-,
163
так как умноженная на 2 она не дала в результате 1,
а поэтому на первом месте после запятой будем
иметь 0, т. е.
0,0.
Затем снова выполняем умножение на 2:
0,285714
0,571428
Таким образом и после второго умножения на 2 мы
не получили 1, а следовательно, наша дробь меньше
-г; т. е. второе место после запятой также ноль.
0,00...
Далее третий раз выполняем умножение на 2:
0,571428
х 2
1,142856
Из этого следует, что первоначальная дробь больше
-о . Поэтому третье место в двоичной дроби занимает
о
единица:
0,001...
Таким же образом мы проверяем четвертое место:
0,142856
0,285712
164
(мы пропустили целую часть дроби 1,142856, так
как в нашем разборе ее можно не учитывать). Чет-
Четвертое место после запятой занимает, следовательно,
ноль. Теперь мы имеем:
0,0010...
таким образом, проверяя пятое, шестое и седьмое
место мы получим:
у = 0,001001001... с точностью до ~^.
Мы обнаружили, что наша дробь 0,001001001... —
это периодическая дробь = 0,@01).
Преобразуем еще одну десятичную дробь, например,
0,359375 в двоичную:
0,359375
х 2
0,718750 -+ 0,0...
х2
1,437500 -> 0,01...
х 2_
0,875000 -+ 0,010.
х 2
1,750000" -+ 0,0101...
х 2_
1,500000 -> 0,01011..
х 2
1,000000 -+ 0,010111
Таким образом, 0,359375 = 0,010111
165
Двоично-десятичная и двоично-восьмиричная
системы счисления
Как мы уже сказали, в вычислительных машинах
числа представлены с помощью двух сигналов: один
сигнал соответствует единице (ток есть), а второй
нулю (тока нет). Поэтому в машинах используется
двоичная система. Однако, входные и выходные
данные являются числами, записанными в десятич-
десятичной системе.
Следовательно, машина должна «перевести» дан-
данные числа из десятичной системы в двоичную си-
систему. Для этого используется двоично-десятичная
система. В этой системе число представляется в обыч-
обычной десятичной форме, а затем каждая десятичная
цифра записывается в двоичной системе. Десятич-
Десятичные цифры требуют для своего двоичного написа-
написания различного числа двоичных разрядов: некоторые
(О и 1) — одного, другие, например, 2 и 3 — двух
A0 и 11); цифры 4, 5, 6 и 7 — трех A00, 101, ПО,
111); наконец, цифры 8 и 9 — четырех знаков A000
и 1001). Поэтому для каждой десятичной цифры
используется в двоичной системе четыре знака:
9
Tool
Каждая такая группа предназначена для выражения
в двоичной системе счисления одной из десяти цифр
и называется тетрадой. Для двоичного написания
0
0000
1
0001
2
0010
3
ООН
4
0100
S
0101
6
оно
7
0111
8
1скхГ
166
любого данного числа в десятичной системе необ-
необходимо столько тетрад, сколько цифр имеет число,
например, число 42678 в двоично-десятичной си-
системе будет иметь следующий вид:
4
0100
2
0010
6
оно
7
0111
1000
В нашем примере эти тетрады записаны с интервала-
интервалами, чтобы их легче можно было прочитать, в дей-
действительности такие интервалы не делаются, необ-
необходимо только помнить, что каждые четыре знака
образуют тетраду.
По некоторым соображениям систему тетрад замени-
заменили системой двоично-восьмиричного счисления (с те-
тетрадами возникают некоторые неудобства при вы-
выполнении арифметических действий, не каждая тет-
тетрада выражает цифру: так, например, 1011 не выра-
выражает никакой цифры, так как выражает число
одиннадцать ит. д.). Этих недостатков лишена двоич-
двоично-восьмиричная система.
Прежде всего, восьмиричная система счисления
использует только восемь цифр A, 2, 3, ..., 7, 0), она
очень похожа на десятичную систему; числа, запи-
записанные в этой системе, требуют почти того же коли-
количества цифр, что и в десятичной системе, например,
389 в восьмиричной системе будет записано следу-
следующим образом
6058 = 6 • 82+0 • 81+5 • 8° = 3891О
6|0
267
J89
S
8
48
0
8
б|8
168
(делим на 8, получаем 48 в остатке 5, снова делим
на 8, получаем 6 и остаток 0. Затем записываем пос-
последнее частное и остатки от конца к началу).
Т. е. 3891О = 6058
Кроме того, для выражения цифр 0, 1, 2, 3, .. 7,
необходимы лишь три знака двоичной системы, ко-
которые записываем в виде триад:
0
000
1
001
010
3
011
4
100
5
101
6
по
J7
Ш
Итак, например, число 2658 в двоично-восьмиричной
системе будет записано следующим образом:
2
010
6
ПО
5
101
И, наконец, что самое существенное, двоично-вось-
двоично-восьмиричная запись числа совпадает с его двоичной за-
записью, а зто следует из того, что число восемь явля-
является степенью числа два (8 = 23). Действительно,
если мы выразим, например, число 3891О в двоичной
системе, то получим
389 2
1
194
97
48
0
24
0
2
12
0
2
6
0
2
3
1
2
1|2
1 0
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Из этого следует, что:
3891О = 110000101
При переводе этого же числа в восьмиричную сис-
систему получим:
3891О = 6058 (А)
Записав это восьмиричное число в двоичной системе
получим:
100
0
000
101
т. е. то же самое число, что в (А). Вследствие та-
такого совпадения записи можно читать двоичные
числа так, как будто это двоично-восьмиричные чи-
числа.
Из вышесказанного следует, что арифметика в двоич-
двоичной системе счисления — вещь несложная. Необхо-
Необходимо только освоиться с числом два и его степенями.
Увеселительная игра
Мы здесь опишем один фокус (веселую игру), исполь-
использующий свойства двоичной системы счисления.
Предложите Вашему другу задумать любое число
от 1 до 31. Затем дайте ему картонную дощечку
с записанными на ней числами.
169
№
1
2
3
4
5
2
4
8
16
3
3
5
9
17
5
6
6
10
18
7
7
7
11
19
9
10
12
12
20
11
11
13
13
21
13
14
14
14
22
цифры
15
15
15
15
23
17
18
20
24
24
19
19
21
25
25
21
22
22
26
26
23
23
23
27
27
25
26
28
28
28
27
27
29
29
29
29
30
30
30
30
31
31
31
31
31
Затем попросите Вашего друга, чтобы он, не воз-
возвращая Вам таблицы, назвал строки, в которых за-
записано задуманное им число. Как только Вы будете
зто знать, то сразу можете назвать задуманное число.
Пусть, например, задуманное Вашим другом число —
29. Оно находится в строчках, обозначенных номе-
номерами 1, 3, 4 и 5.
Если Вы теперь запишете в двоичной системе счи-
счисления число, ставя единицы на первом (с правой
стороны), третьем, четвертом и пятом местах, а ноль
на втором, то получится:
11101 = 24+23+22+1 = 16+8+4+1 = 29
Если задумано число 18, то оно находится в 2 и 5
строчке, следовательно, единицу мы запишем на вто-
втором и пятом месте, считая с правой стороны, а осталь-
170
ные места заполним нулями:
10010 = 2-Ч21 = 16+2 = 18
Если задумано число 5, то оно находится, в 1 и 3
строчке, а следовательно, будем иметь:
°- 4 + 1 = 510
Из дневника любителя математики
«...Я увлекаюсь математикой со 120-летнего воз-
возраста, т. е. с тех времен, когда я учился еще в сред-
средней школе. Когда я родился? Сколько мне лет?
Я очень аккуратно праздновал каждый день своего
рождения, однако, поступая в университет, я отпразд-
отпраздновал его всего 4 раза, хотя мне уже исполнилось
19 лет. По этому Вы очевидно догадаетесь в какой
день я родился.
Сколько мне лет ? Это вопрос как известно несколько
щекотливый и поэтому я открою Вам этот секрет
в сильно зашифрованном виде.
Подумайте над дробью ^-. В ней содержится ответ
на поставленный вопрос.
С 2200011 года я живу в Варшаве, а точнее говоря
в районе этого города, называемом Прагой.
Номер моего дома состоит из двух цифр. Если между
цифрами этого номера поставите запятую, то полу-
получится десятичная дробь, которая является средней
арифметической этих цифр.
171
Моя комната — это прямоугольник, стороны кото-
которого — натуральные числа. Число, выражающее пе-
периметр этого прямоугольника, равняется числу, вы-
выражающему площадь пола.
172
Хобби хроникера
Моя комната способствует размышлениям над чис-
числами, особенно над такими числами, которые выра-
выражают годы седьмой декады текущего века: начиная
с 1960 г. и по 1970 г. Размышления о числах — это
мое хобби. Очень интересное свойство я обнаружил
в номере 1962 года: этот номер — сумма трех трех-
трехзначных чисел с очень интересной особенностью. По-
Подумайте, что это за числа ?
Номер 1960 года не менее интересен. Не изменяя
порядка цифр в этом номере, можно получить число,
которое равняется единице.
Из цифр 1961 года, используя только один знак
арифметического действия, и выполнив только два
действия, можно получить число, которое в сто
миллионов раз больше числа атомов, образующих
нашу планету, число, которое назвал в своей книге
«Образ вселенной» Фриц Кан (Fritz Kahn к Design
of the Universe»).
Номер 1963 — это число, состоящее из 151 злополуч-
злополучных чертовых дюжин, ведь 1963 = 151 ¦ 13, однако,
из цифр 1, 9, 6, 3 можно составить два простых
числа. Что это за числа?
Число 1964 — составное, но прочитанное справа на-
налево: 4691 — образует простое число. Этим свойст-
свойством не обладает число 1965, так как 5691 — это также
сложное число, можно ли, однако, из чисел 1,9, 6, 5
составить простое число?
173
Номер моего телефона 5-47-48 — также необычное
число. Он состоит из пяти цифр, если сложим пятые
степени этих пяти цифр, то получим
55+45+75+45+85 = 54748,
т. е. как раз номер моего телефона. Я подумал, что
очевидно существуют и трехзначные числа с теми
же свойствами, т. е., числа, у которых сумма кубов
цифр равняется данному числу.
Я нашел два таких числа. Если обозначим цифры
первого а, Ь, с, то цифры второго будут соответ-
соответственно обозначены^ dfjt, т. е.
а3+Ь3+с3 = ЮОд+Юй+с
c3+d3+a3 = ЮОс+Ш+я
Может Вы сумеете определить, что это за числа?
Я обнаружил, что номер 1973 года является простым
числом, что до конца второго тысячелетия мы бу-
будем иметь еще шесть таких лет (какие это года) и что
во всем нашем тысячелетии было только 140 лет,
номера которых были простьши числами (какие это
года?). Но давайте закончим с номерами лет. Я
предлагаю Вашему вниманию обычную игру с циф-
цифрами, которая надеюсь займет Вас не один вечер-
А вот и она:
Игра с цифрами
1. Из девяти цифр 1, 2, 3, ..., 9 составить такие
числа, чтобы их сумма равнялась 100. Цифры, обра'
174
зующие каждую составленную Вами сумму, должны
встречаться в ней только раз и располагаться в на-
натуральной последовательности. Между числами мож-
можно ставить знаки плюс и минус. Перед первым чис-
числом знак минус стоять не может.
1) Сколько таких сумм можно составить?
2) Каково максимальное и каково минимальное число
знаков плюс и знаков минус, которые могут быть
поставлены между числами?
Для примера я привел одну такую сумму:
1+2+3-4+5+6+78+9 = 100
G знаков: 6 раз плюс и один раз минус).
2. Выполнить ту же'самую задачу, но при других
условиях: цифры должны быть расположены в об-
обратной последовательности, т. е. от 9 до 1.
Для примера одно решение:
9+8+76+5-4+3+2+1 = 100
G знаков: 6 раз плюс и один раз минус).
Для облегчения поиска решений этой игры с циф-
цифрами я спешу сообщить вам, что по мнению доктора
Эрнеста Дюднейя {Ernest Dudeney), выраженном
в письме, адресованном в журнал «Сайентифик
Америкен» {«Scientific American»), первый вариант
имеет 11 решений, а второй — 15.
175
РЕШЕНИЕ ЗАДАЧ Расшифровка дневника любителя математики
1. Автор дневника увлекается математикой со 120
летнего возраста, а в то время он еще учился в сред-
средней школе. Следовательно, число 120 записано
в троичной системе:
1203 = 1 -32+2 -34-0= 15
и он увлекается математикой с пятнадцатилетнего
возраста.
2. До девятнадцатилетнего возраста он праздновал
всего четыре раза день своего рождения, следова-
следовательно, он родился 29 февраля.
3. Свой возраст он указал в зашифрованном виде,
рекомендуя подумать над дробью ^-; если мы эту
дробь превратим в десятичную, то получим беско-
бесконечную периодическую дробь 0,78787878... Повто-
Повторяющийся период 78 — подсказывает нам возраст
любителя математики.
4. Он живет в Варшаве с 2 200 011 года. Так как
автор дневника записьшает числа в троичной системе
счисления, то, следовательно, он живет в Варшаве с
2200 0113 = 2 -36+2 • 35+0-33+0-32+1 -34-1 =
= 1948 года
5. Обозначая х и у цифры номера дома, получим:
(х +у): 2 = (\0х+у): 10, т. е. 4-у = 5х, а из этого
х = 4 и у = 5; номер дома 45.
176
12
6. Обозначив и и v размеры комнаты, получаем
2(u+v) = uv, т.е. я = ——2" = 2Н——у
Так как и м и г> должны быть натуральньши числами,
то и 4 : (и— 2) должно быть натуральным числом. Это
возможно только при и = 3,4, 6. Следовательно,
комната имеет размеры 3x6 метров или 4x4 метра.
Хобби хроникера
1. 1962 год — это сумма трех чисел 987+654+321 =
= 1962. Эти цифры расположены в последователь-
последовательности 9, 8, 7, 6, 5, 4, 3, 2, 1.
2. Из 1960 можно получить 1, не изменяя порядка
цифр, а лишь записав это число следующим образом
196°, (любое число в нулевой степени равняется 1;
а0 = 1, при а ф 0).
3. Из цифр номера года 1961, используя только один
знак арифметического действия (плюс) и вьшолняя
два действия: сложение и возведение в степень,
можно получить A+9N1 = 1061.
Это число больше числа атомов, из которого состоит
земной шар. Согласно мнению американского уче-
ученого Ф. Кана, земной шар состоит из 10" атомов.
4. С помощью цифр 1, 9, 6, 3 можно написать два
простых числа 3169 и 3691.
177
5. С помощью цифр 1, 9, 6, 5 нельзя написать про-
простого числа, потому что 1+9+6+5 = 21, а 21 де-
делится на 3.
6. Двумя трехзначными числами с таким свойством
являются:
153 = 13+5з+зз и 371 = 33+73+13
7. До конца второго тысячелетия нашей эры будет
еще шесть лет, выраженных простыми числами:
1973, 1979, 1987, 1993, 1997, 1999.
Игра с цифрами
1)
123-45-67+89 = 100
123+4-5+67-89 = 100
123+45-67+8-9 = 100
123-4-S-6-7+8-9 = 100
12-3-4+5-6+7+89 = 100
1+23-4+5+6+78-9 = 100
1+2 + 34 -5+67-8+9 = 100
12+3-4+5+67+8+9 = 100
1+23-4+56+7+8+9 = 100
1+2+3-4 + 5+6+78+9 = 100
Минимальное число знаков 3, ма ^симальное — 7.
178
2)
98-76+54+3+21 = 100
9-8+76+54-32+1 = 100
98-7-6-5-4+3-21 =100
9-8+7+65-4+32-1 = 100
9-8+76-5+4+3+21 = 100
98-7+6 + 5+4-3-2-1 = 100
98+7-6 + 5-4+3-2-1 = 100
98+7+6-5-4-3+2-1 =100
98+7-6+5-4-3+2+1 =100
98-7+6 + 5-4+3-2+1 =100
98-7+6-5+4+3+2-1 = 100
98+7-6-5+4+3-2+1 = 100
98-7-6 + 5+4+3+2+1 =100
9+8+76 + 5+4-3+2-1 = 100
9+8+76 + 5-4+3+2+1 =100
Минимальное число знаков 4, максимальное — 7.
ВИКТОРИНЫ,
ТЕОРИЯ
ИНФОРМАЦИИ
И КИБЕРНЕТИКА
ГЛАВА 9
Хорошо известна игра в ответы на вопросы из раз-
разных областей знания, называемая викториной. Про-
Проводится она иногда следующим образом: один из
участников игры выходит из комнаты; остальные
участники выбирают и прячут какой-либо предмет,
а затем приглашают в комнату водящего, который
должен угадать, какой предмет спрятан. Для того,
чтобы получить дополнительные сведения о спря-
спрятанном предмете, водящий имеет право задавать о-
пределенное число вопросов. Однако, эти вопросы
должны быть сформулированы таким образом, чтобы
на каждый из них можно бьшо ответить только «да»
или «нет». Смысл игры заключается в том, чтобы
водящий назвал спрятанный предмет, задав при этом
минимальное число вопросов. Вот пример:
На столе находится колода из 32 карт.
Играющие сообщают водящему, что спрятана одна
из 32 находившихся на столе карт. Водящий спра-
спрашивает:
— Спрятанная карта — красной масти?
— Да.
Водящий получил первую информацию: карта крас-
красной масти, т. е. зто либо бубны либо черви.
— Это бубны? — спрашивает он дальше.
— Нет.
180
Водящий получил вторую информацию — спрятан-
спрятанная карта не бубны, значит это черви.
— Это фигура?
— Нет (третья информация — это может быт, сле-
следовательно, семерка, восьмерка, девятка или десятка).
— Имеет ли карта четное число очков?
— Да (четвертая информация — следовательно,
спрятанная карта либо восьмерка либо десятка).
— Это десятка?
— Нет (пятая информация — следовательно, это
восьмерка).
На основании полученных пяти информации отга-
отгадывающий угадал, какая карта спрятана — это вось-
восьмерка червей. Процесс получения информации мож-
можно записать символически 10010. В этой записи 1
(один) обозначает «да»; 0 (нуль) — обозначает «нет».
Таким же образом можно понять любую запись, со-
состоящую только из единиц и нулей, т. е. каждое
число, записанное в двоичной системе счисления.
Например, запись 10001 обозначает: да — нет —
нет — нет — да. Напомним здесь нашим читателям,
что в двоичной системе счисления мы используем
только две цифры: нуль и один, и что число 10010
является двоичным сокращением записи. 1 • 24+
+0-23+0-22+1 -гЧ-О-г0 = 18 (в десятичной
системе счисления).
Из вышесказанного мы видим, что информацию
можно записывать в форме математических симво-
символов, и именно так это делается в том разделе матема-
181
Hop6tpm Bm*p A894-1964)
тики, который называется «теорией информации»
и который стал развиваться в связи с возникнове-
возникновением и развитием кибернетики.
Слово кибернетика, греческого происхождения,
обозначало искусство управления. Отцом совре-
современной кибернетики считают недавно скончавшегося
американского математика Норберта Винера, автора
труда «Cybernetics or Control and Communication in
the Animal and the Machine» (Кибернетика, или уп-
управление и связь в животном и машине). Термин
«управление» в кибернетике обозначает придание
соответствующего направления произвольным явле-
явлениям. Управлением является, например, регулиро-
регулирование уличного движения, регулирование давления
в котле, управление автомобилем или руководство
методами обучения в школе, улучшение физиологи-
физиологических процессов в живом организме или рационали-
рационализация производственных процессов на заводе, усо-
усовершенствование способов управления обществом
и т. п.
В связи с таким чрезвычайно общим характером во-
вопросов, затрагиваемых кибернетикой, ее можно свя-
связать с логикой и математикой.
В разговорном языке понятие информация имеет ка-
качественный оттенок: совершенно другое значение
имеет для нас информация о том, что произошла же-
железнодорожная катастрофа с поездом, которым дол-
должен был приехать наш знакомый, чем информация,
что наш сосед потерял пуговицы от жилета.
182
В теории информации каждое сообщение может быть
измерено количественно. Если, например, какое-то
событие может иметь несколько различных исходов,
и мы не знаем, который из этих исходов будет иметь
место, то существует некоторая неопределенность от-
относительно появления того или иного исхода. На-
Например, неопределенность относительно агрегатного
состояния, в котором выступает вода, является нео-
неопределенностью, касающейся ее грех возможных со-
состояний, так как вода может встречаться в газооб-
газообразном, жидком и твердом агрегатном состоянии.
Информация о том, что вода выступает в жидком
состоянии уменьшает неопределенность относительно
трех остальных агрегатных состояний воды и тем
самым является равновесомой трех информации
сразу. По этому принципу можно было бы оценивать
количество (давать количественную оценку) инфор-
информации.
Однако, значительно лучше оказался способ оценки
количества информации с использованием показателя
степени, в которую нужно возвести двойку, чтобы
получить число исходов (состояний), которые могут
встречаться в рассматриваемом явлении. Если, к при-
примеру, некоторое явление может иметь два исхода:
или исход X, или исход Y (например, брошенная вверх
монета может упасть только орлом или решкой), до-
достаточно получить только одну информацию. Эта за-
зависимость между числом исходов и количеством ин-
информации может быть выражена числом 21 (два
283
исхода, одна информация). В случае угадывания
спрятанной карты мы имели 32 возможных исхода
C2 карты) для того, чтобы угадать спрятанную карту
нам потребовалось пять простых информации C2 —
= 25).
Единицей простой информации является так назы-
называемый бит. Этот термин образовался из двух англий-
английских слов binary digit, что по-просту обозначает
«цифра двоичной системы счисления». Таким обра-
образом, для того, чтобы отгадать карту (восьмерку чер-
червей) потребовалось пять битов информации. Оценка
количества информации с помощью показателя сте-
степени числа 2, т. е. с помощью счета в двоичной си-
системе счисления, стала основанием применения вы-
вычислительных машин, которые, как известно, ис-
используют, в основном, двоичную систему счисления
(сигналы: «да» и «нет»), при котором требуются
лишь две цифры: 0 и 1.
Развитие кибернетики выдвинуло вопрос, в какой
степени электронная вычислительная машина может
равняться с разумом человека, может ли она пре-
превзойти его ? И хотя машины считают в десятки, сотни
и тысячи раз быстрее и точнее, чем человек (в те-
течении нескольких часов решая задачи, на которые
многочисленньш коллектив математиков затратил бы
несколько месяцев), мы можем с полной уверенно-
уверенностью сказать, что даже самая точная, самая совер-
совершенная машина не сможет равняться с человеческим
разумом, так как число элементов (нейронов), поз-
184
УПРАВЛЕНИЕ
(ПУТЬ СОБАКИ)
воляющее человеку ассоциировать информацию, рав-
равно, примерно, 10 миллиардам, в то время как число
электронных элементов-нейронов самой совершенной
машины не превышает нескольких сот тысяч.
Образцом, а в то же время недостижимым идеалом
для электронной вычислительной машины является
мозг человека, в котором происходят все процессы,
связанные с принятием решений. Эти процессы —
адаптивные процессы управления. Принцип: «По-
«Поступи как можно правильнее в положении, в котором
находишься», — позволяет нам справляться в наи-
наиболее непредвиденных ситуациях. Этот принцип
можно представить в форме математического алго-
алгоритма или же превратить его в множества правил
для точной формулировки процесса управления.
Биологическая эволюция снабдила органами управ-
управления не только человека, но и животных. Этот ор-
орган управления у животных называется инстинк-
инстинктом. Более организованные животные обладают тем,
что мы обычно называем интеллигенцией, которую
можно определить как способность решать задачи
на основе имеющегося опыта (адаптивное управле-
управление).
Начиная с 1945 года, когда в Соединенных Штатах
бьша построена первая электронная вычислительная
машина, названная ENIAC (сокращение от Elec-
185
tronic Numerical Integrator and Computer) напряжен-
напряженная работа над ее усовершенствованием не прекраща-
прекращается ни на минуту, а число ей подобных увеличивается
из года в год.
В Польше также производятся электронные вычи-
вычислительные машины. Разнообразные проблемы, ко-
которые ставит перед человечеством современная ци-
цивилизация, заставляют ученых и инженеров прово-
проводить исследования в области теории управления и раз-
разрабатывать самые разнообразные системы управле-
управления. Создание этих систем было бы невозможным
без участия вычислительных'машин.
Имеются машины, управляющие процессами, кото-
которые получают из системы необходимые данные, ка-
касающиеся параметров работы системы, процессов
в ней протекающих, анализируют их и представля'от
рекомендации, используемые в дальнейшем челове-
человеком-оператором; есть и такие машины, которые свои
решения передают непосредственно в устройства
управления процессом для автоматического внесения
поправок.
В статье «Control Theory» (Теория управления), о-
публикованной в сентябре 1964 г. в американской
журнале «Сайентифик Америкзн» {Scientific Ameri-
American) Ричард Беллман пишет: «Вычислительная ма-
машина становится необходимостью, когда требуется
принять за короткое время сложное решение (много-
(многократное), например, при старте космической ракеты-
В этом случае мы имеем дело с необходимостью мно-
186
гократно принимать решения, которые следуют одно
за другим в зависимости от получаемой информации
и ее поступления в систему управления по мере раз-
развития процесса. Вычислительная машина на борту
космического корабля или на земле необходима для
принятия ряда решений с очень большой скоростью.
z_^x Мы говорим, что такая машина работает в режиме
100 м обработки данных одновременно с их поступлением,
Рис- 9'1 в «действительном» времени, так как она поспевает
за фактическим развитием событий в процессе, ко-
который она контролирует».
Математик, который управляет процессом, требу-
требующим многократных решений, в зависимости от по-
поступающей к нему информации по ходу развития дан-
данного процесса, должен осуществлять выбор среди
определенного количества переменных, определя-
определяющих состояние процесса на следующем этапе. Это
положение, в свою очередь, можно свести к решению
системы нескольких уравнений, однако, решение этих
уравнений часто связано с большими трудностями.
Примером необходимости многократного принятия
решений по ходу протекания процесса является сле-
следующая задача.
Собака находится в точке Р (смотри рис. 9-1) на
расстоянии 50 метров от охотника, находящегося
в точке М. Собака увидела зайца в точке Z, которая
находится на расстоянии 100 метров от точки М.
Собака пустилась в догонку за зайцем, который бе-
бежит вправо по прямой MZ. Собака все время видит
187
i z, гг i3
Рис. 9-2
зайца и устремляется в его направлении. Какова
траектория движения собаки, если заяц убегает со
скоростью 5 м/сек, а собака его догоняет со скоро-
скоростью 10 м/сек?
Эту задачу можно решить арифметически. При этом
получается довольно-таки сложное уравнение1' этой
кривой, способ решения которого для читателя мо-
может оказаться слишком трудным и мало интересным.
Как поступает, однако, собака, которая ведь не обу-
обучена решению уравнений, а решает зту задачу без
малейших колебаний. Попробуем объяснить этот воп-
вопрос нашим читателям графически. Заяц находится
в точке Z, в точке Р — собака. В первый момент
собака мчится прямо на зайца по линии PZ (рис.
9-2).
В первую секунду заяц пробежит расстояние ZZ^,
а собака РРХ. Во второй секунде заяц покроет рас-
расстояние ZlZ2, а собака, устремляющаяся за ним, —
расстояние РХР2. В третьей секунде заяц пробежит
Z2Z3, а собака Р2Рз и т.д.: заяц Z3Z4. — собака
РъРь, ... По рисунку мы видим, что в первом прибли-
приближении траектория погони представлена в виде ло-
') Уравнение «собачьей» кривой:
У =
2 1--
(а -жI -•>/«> +
где: а — расстояние от точки Z до начала системы координат,
w — скорость собаки; v — скорость зайца.
188
манной линии РР1Р2РзРь.-- Однако, решения со-
собаки относительно направления погони принимаются
не каждую секунду, а в значительно более коротких
промежутках времени, это могут быть промежутки
равные ОД; 0,01; 0,001 секунды или даже еще более
короткие отрезки времени, так как процесс погони
является непрерывным процессом. Если бы мы могли
представить на рисунке траекторию погони в отрезках
времени равных 0,1 секунды, то получили бы ломан-
ломанную линию, состоящую из десятикратно большего
числа десятикратно более коротких отрезков пря-
прямых, при 0,01 секунды мы получили бы ломаную
кривую, которая была бы еще лучшим приближением
фактической траектории погони собаки, которая
является непрерывной кривой.
Математики назвали зту кривую «собачьей кри-
кривой ».
Более сложные варианты этой задачи встречаются
при расчете возможно наилучшей траектории полета
космической ракеты: в этом случае задача заклю-
заключается в определении мест, в которые нужно напра-
направить ракету, чтобы она вышла на заданную орби-
орбиту.
К этой же категории задач относится точное опреде-
определение места, в котором находится запущенный ис-
куственный спутник.
189
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Рис. 9-3
Рис. 9-4
Обман зрения при оценке величины и формы
A. У огородника было двое рабочих. Одному из них
огородник поручил отнести на почту, которая нахо-
находилась в 3 о от огорода, посылку весом 10 кг, вто-
второй рабочий должен был отнести в овин корзины
с яблоками. Каждая корзина весила 10 кг. Корзины
стоят под яблонями, которые растут вдоль прямой
на расстоянии 10 м одна от другой. Всего яблонь —
25, а овин находится на расстоянии 10 м от первой
яблони.
Какое из этих заданий Вы бы выбрали ? Почему ?
Б. Вычерчиваем спиральную линию, как это пока-
показано на рис. 9-3: вычерчиваем полуокружность диа-
диаметром АВ = 1г, к этой полуокружности достраи-
достраиваем полуокружность ОВ, диаметр которой в два
раза меньше, чем диаметр полуокружности АВ, далее
достраиваем полуокружность ОС диаметром два раза
меньшим, чем диаметр О В и т. д. Какова длина та-
такой спирали с бесконечным числом витков ? Является
ли эта величина бесконечно большой? Подсчитайте
длину такой спирали.
B. На рис. 9-4 имеем квадрат ABCD и фигуру
KLMNPO. Прикиньте на глаз, является ли средняя
часть фигуры KLMNPO (KLNP) прямоугольником
или квадратом и каково ее соотношение с квадратом
ABCD?
190
Рис. 9-5
Г. На рис. 9-5 имеем сложенный лист бумаги, ска-*1
жите выдвинута ли вперед или же отведена назад|
сторона АВ~>
Д. Под елочкой лежит шоколадная бомба радиусом
5 см. Бомба внутри пустая, толщина шоколадной скор-
скорлупы составляет 1 см. Рядом с бомбой лежит пакет
с 400 шоколадными драже. Диаметр каждого драже
1 см. Драже сплошные и сделаны из того же сорта
шоколада, что и большая бомба. Что бы Вы выбрали:
большую бомбу или пакет с 400 драже?
12 маленьких вопросов?
1. Каким образом получить 50, вычитая из 40 де-
десять?
2. Как доказать, что половина тринадцати равняется
восьми ?
3. Какие натуральные числа, записанные с помощью
двух цифр, увеличиваются после удаления одной
цифры, стоящей с левой стороны?
4. Что это за дробь, у которой числитель меньше
знаменателя и которая не изменяется, если ее запись
повернуть вверх ногами?
5. Как уменьшить число 989 на 303, ничего из него
не вычитая?
191
Рис. 9-6
6. Молодая хозяйка положила в суп слишком мало
соли из-за чего суп необходимо было досаливать за
столом. На следующий раз, наученная опытом, хозяй-
хозяйка всыпала в такое же количество супа в три раза
больше соли, чем в первый раз, но несмотря на это
и на сей раз необходимо было досаливать суп на
столе, правда, используя для этого в три раза меньше
соли, чем предыдущий раз. Какую долю необходимо-
необходимого количества соли положила в суп хозяйка первый
раз?
7. В одной семье пять братьев. Каждый из них имеет
сестру. Сколько всего детей в этой семье ?
8. Длина металлического стержня—1 метр. Разрезать
стержень пополам стоит 5 копеек. Сколько нужно
заплатить, чтобы разрезать его на 10 равных час-
частей?
9. Французский математик Франсуа Лукас A847—
1891), специалист в области теории чисел, занимаясь
поиском простого объяснения формы арабских цифр»
столкнулся с легендой о перстне царя Соломона.
Легенда гласит, что на драгоценном камне, украшав-
украшавшем перстень, была изображена таинственная фигу-
фигура, квадрат с двумя диагоналями (рис. 9-6), из ко-
которой, по Лукасу, можно получить фигуры всех деся-
десяти цифр. Попробуйте это сделать.
10. Однажды Иванова спросили, кто изображен на
портерете, который висит на стене.
192
Рис. 9-7
Иванов ответил:
— Отец, изображенного на портрете лица, является
единственным сыном того, кто это говорит.
Чей это портрет?
11. Пасека состоит из 16 ульев, расставленных в че-
четыре ряда, по четыре улья в каждом ряду. Расстоя-
Расстояние между ульями, стоящими по соседству, составля-
составляет 5 метров. Может ли пчеловод обойти все улья
таким образом, чтобы его маршрут состоял из шести
отрезков прямой. Какова длина самого короткого
маршрута? Нарисуйте его.
12. В витрине кондитерского магазина выставлен
громадный куб из шоколада. На одном его ребре
сидит муха (рис. 9-7).
Может ли муха обойти все ребра шоколадного куба,
проходя по каждому ребру (или его части) только
один раз?
РЕШЕНИЕ ЗАДАЧ
Обман зрения при оценке величины и формы
А. Рабочий, который относил посылку на почту,
выполнил при этом работу, равную
10 кГ • 3 000 м = 30 000 кГм
Кроме того, он прошел 3 000 м (обратный путь)
без груза.
293
Рабочий, который носил корзины в овин, выполнил
работу:
= 32 500 кГм
Кроме того, он прошел без груза:
A0+250)^
Таким образом, рабочий, который относил посылку
на почту, выполнил меньшую работу, хотя этот ре-
результат трудно было на первый взгляд предви-
предвидеть.
Б. Длина полуокружностей образует геометрическую
прогрессию с первым членом равным а = от и зна-
знаменателем q = 0,5. Это бесконечная убывающая
прогрессия. В соответствии с формулой для суммы
бесконечной убывающей прогрессии:
S= а
получим:
S = TH-f-2-7w+-^r
Длина спирали составляет, следовательно, 2тсг т. е.,
как раз длину окружности с радиусом г.
В. Это квадрат. Квадрат KLNP равняется квад-
квадрату ABCD.
194
Г. Выдвинута вперед, однако, ответ «отведена на-
назад» также правильный.
Д. Объем массы шоколадной бомбы составляет
уиE3-43) = у-3,14A25-64) « 255,4 еж3
Объем массы шоколадного драже составляет:
4 /1
TW 2
у-(у -400 « 210 ел*3
Таким образом, объем массы пустотелой шоколад-
шоколадной бомбы больше объема массы шоколадных шари-
шариков на 45,4 см3. Из этого количества шоколада
можно бы было сделать еще почти 88 штук драже
диаметром 1 см.
12 маленьких вопросов
1. XL = 40, если теперь удалим X от XL, то оста-
останется L = 50.
2. Если римское число XIII разрежем пополам гори-
горизонтальной чертой, то получим VIII, т. е. 8.
3. Числа записанные с помощью римских цифр,
например, IV, IX, CD, ... после удаления цифры,
стоящей с левой стороны, становятся больше: V,
X, D,...
4. Дробь-^-,
6
повернув ее «вверх ногами» получим снова -g-.
195
Рис. 9-8
5. Число 989 следует повернуть на 180°, получим
686; 989-686 = 303.
6. В суп следовало добавить а г соли. Хозяйка всы-
всыпала х г соли, следовательно, недостаток соли соста-
составлял (д—х) г соли.
При вторичной варке супа хозяйка всыпала Ъхг соли,
недостаток соли составлял при этом (а—Зх) г соли.
Теперь:
а—Ъх =
а—х
3(а—Зж) = а-х
За—9х = а—х, т. е. х = ~
Когда хозяйка варила первый раз суп, то она всы-
всыпала 1/4 часть нужного количества соли.
7. Шестеро.
¦х -LJ 8. 45 копеек.
Рис. 9-9
9. Вот фигуры цифр, которые можно получить из
квадрата с двумя диагоналями (рис. 9-8).
10. Это был портрет внука Иванова.
11. Нет. 75 метров (рис. 9-9).
12. Нет. Путь, который должна пройти муха имеет
6 узлов, а следовательно это уникурсальная кривая,
иначе говоря, зту линию нельзя вычертить, не от-
отрывая карандаша от бумаги. Попробуйте.
196
МАГИЧЕСКИЕ
КВАДРАТЫ
ГЛАВА 10
Магическим квадратом мы называем квадратную
(т. е. с одинаковым количеством столбцов и строк)
таблицу, состоящую из п2 элементарных клеток,
в которые списано и2 натуральных чисел, и имею-
имеющую одинаковую сумму чисел по всем строкам,
столбцам и двум диагоналям. Эту сумму, обозна-
обозначаемую Sn, называемым постоянной магического
квадрата, а число п — порядком квадрата. Если
сумма одинакова только по всем столбцам и строкам,
а суммы по диагоналям разные — то мы говорим,
что имеем дело с полумагическим квадратом. Если
же кроме вышеуказанных, квадрат имеет еще другие
свойства, то его называют обычно сверхмагичес-
сверхмагическим.
В глубокой древности составление магических квад-
квадратов было либо развлечением, либо занятием ма-
магов. Но уже много столетий магическими квадратами
занимаются математики, заинтересовавшиеся изу-
изумительной красотой и внутренней гармонией расста-
расстановки чисел. Математики классифицировали маги-
магические квадраты, назвали их, открыли способы их
составления и их свойства. Имеются целые книги,
посвященные магическим квадратам, мы здесь,
однако, ограничимся лишь некоторыми элементар-
элементарными сведениями из этой области:
197
11
s
22
8
19
9
23
20
1
12
2
16
13
24
10
18
7
4
15
21
25
14
6
17
3
а) магические квадраты делятся на четные (с чет-
четным количеством клеток: 4, 16, 36, 64 ...) и нечет-
нечетные (9, 25, 49 ... клеток).
б) Постоянную магического квадрата Sn можно вы-
высчитать на основании формулы
в которой и — зто число клеток в каждом столбце
и в каждой строке.
Например, в квадрате третьего порядка постоянная
равна:
в) Нечетные квадраты имеют так называемое сред-
среднее число. В вышеуказанном квадрате, средним
числом является 5, среднее число подсчитывается
по формуле:
в квадрате пятого порядка среднее число составляет
(Ss = 65)
А вот еще несколько примеров интересных маги-
магических квадратов.
198
Сверхмагический
Ч Ч
N^2
ч
ч
16
10
24
13х
/
/ /
9ч
\
12
/
?.о/
/
/
\ \
"ч
ЧД<| )
/ /
г/
/
/
квадрат
\ ^
18 25.:
21ч ^>Зч
15>417xN
4Ач6^
/ X
/ \
/ N
пятого порядка:
>2 А ,\\
ч V /
\ь гъ f
' 4V/ Ч /
Ч / ч К
10 12^ ^19^
/' ^ч/' ^ /У^
/ ч Чч \
M3/N<20 X22
X Ч \
/ чч хч ч
Д8
7У
/
21
ч
\
N^4
\
ч
/
/
\
ч
гъ'
14
3
17
чб
\
После его дополнения с правой стороны таким же
квадратом образуются одинаковые суммы по диаго-
диагоналям.
Полумагический квадрат восьмого порядка:
50
23
10
61
48
59
6
3
И
62
49
22
7
4
47
58
24
51
64
9
60
45
2
5
63
12
21
52
1
8
57
46
14
25
40
33
20
53
44
31
37
34
13
28
41
32
19
56
26
15
36
39
54
17
30
43
35
38
27
16
29
42
55
18
199
96
88
61
19
И
69
86
98
89
91
18
66
68
16
99
81
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Рис. 10-1
200
который имеет постоянную для столбцов и строк
равную Ss = 260 (суммы по диагоналям другие)
построен ходом шахматного коня. Последователь-
Последовательные ходы коня обозначены последовательными на-
натуральными числами (начиная с 1).
И, наконец, квадрат изображенный рядом составлен
из «обратимых» чисел, т. е. чисел, транскрипция
которых не^теряет смысла после поворота квадрата
на 180° (вверх ногами), причем магический квадрат
не теряет своих свойств.
Найти трехзначное число
Найти такое трехзначное число, которое после пе-
переноса первой цифры вправо за цифру единиц,
превращается в трехзначное число равное 3/4 иско-
искомого числа. Если таких чисел много, то укажите
все.
Магический треугольник
Имеем фигуру в виде треугольника, состоящую из
15 маленьких треугольников с вписанными буква-
буквами А, В, С, ... (рис. 10-1).
Необходимо заменить буквы цифрами, таким обра-
образом, чтобы имелись следующие соотношения:
1) A+B + C+D + E = E+F+G + H+K = K+L + M+N+A
2) N+P + Q+F = D+Q+R+L = H+R+P+B
3) A+E+K = C+G+M = P+Q+R
4) Z>+F = H+L = JV+B
Примечание: Каждая буква обозначает дру-
другое число от 1 до 15.
Эта задача имеет 300 разных решений.
Шахматная доска
С шахматной доской мы встречаемся в бесконечном
количестве задач. Прежде всего, хорошо известна
легенда о «скромном» требовании ее изобретателя,
который попросил шаха, чтобы ему на первую
клетку доски положили одно зерно пшеницы, а на
каждую следующую вдвое больше. Оказалось,
что это, на первый взгляд, скромное требование
приводит к астрономическим числам: оказывается
на 64-ой клетке надо положить 263 ж 918 • 1016
зерен, а сумма зерен на всех клетках шахматной дос-
доски — почти вдвое больше. Хорошо известны также
задачи, связанные с ходами отдельных шахматных
фигур. Ниже приведены несколько очень простых
задач на движение ферзя и коня.
Как известно, ферзь является самой сильной шах-
шахматной фигурой. Он может двигаться в произволь-
произвольном направлении вправо, влево, вверх, вниз и па
диагонали на произвольное количество клеток.
201
пга||||Ш
— --В-
— —о
Рис. 10-2
1. Поставьте ферзя на клетку А (рис. 10-2) и че-
четырьмя последующими ходами обойдите все клетки
с горизонтальной штриховкой.
2. Поставьте ферзя на клетку, обозначенную бук-
буквой D (место белой королевы) и пройдите макси-
максимальное количество клеток за пять ходов. Ферзь
не может ни проходить два раза через ту же самую
клетку, ни пересекать трассы своих ходов, которая
проходит через середину клетки.
3. Поставьте ферзя на клетку В. За 15 ходов прой-
пройдите все клетки по одному и только одному разу,
и закончите последний ход на клетке С.
4. Поставьте ферзя в угловой клетке. За 14 ходов
пройдите все клетки шахматной доски и вернитесь
в исходную клетку. Через каждую клетку можно
проходить более одного раза. Такой ход ферзя про-
продемонстрировал впервые в 1867 году американский
шахматист С. Лойд. Необходимо здесь отметить, что
такой обход всех клеток не может быть выполнен
менее, чем за 14 ходов.
5. Обойдите ходом коня все клетки шахматной доски,
состоящей из 5 X 5 = 25 клеток, не побывав ни на
одной клетке дважды.
Уклончивый ответ
Рабочий копал яму. На вопрос прохожего, какой глу-
глубины будет яма, которую он роет, рабочий ответил:
202
«Мой рост 1 л 80 ел. Когда я вырою яму до конца,'
то моя голова будет на столько ниже уровня земли,
на сколько сейчас, когда я уже вырыл половину,
она находится выше ее уровня».
Какой глубины яму роет рабочий?
Квадратный корень из феодализма
А. Предположим, что каждая из девяти букв слова
феодализм обозначает какую-то цифру (нуль не учи-
учитываем). Тогда из слова феодализм получилось бы
девятизначное число. Предположим также, что
еедди — это пятизначное число, которое является
квадратным корнем числа, зашифрованного словом
феодализм. Иначе говоря:
у феодализм = еедди
Попробуйте узнать эти числа.
Б. После того, как Вы найдете зти два числа, впи-
впишите число феодализм в шахматный квадрат, состо-
состоящий из девяти клеток таким образом, чтобы трех-
трехзначное число, которое будет записано в нижней
строке, было суммой чисел, записанных в двух
верхних строчках.
Существует ли какой-либо способ записи, в виде
натурального ряда, чисел, записанных в клетках
шахматного квадрата?
203
Задача Киркмава A850 г.)
В детском саду было 15 детей. Воспитательница
каждый день организовывала 5 групп, состоящих
из трех детей. Составьте расписание детских групп
таким образом, чтобы каждый ребенок ежедневно
имел других товарищей.
Рис. 10-3
Числовая задача
Перед нами шахматный квадрат, состоящий из
9 клеток, в каждую из которых вписаны цифры.
Этот квадрат имеет следующие свойства:
1) среди цифр нет нуля,
2) число, образованное цифрами третьей строчки
D59) является суммой чисел, образованных цифрами
первых двух строк, 459 = 176+283,
3) каждая из цифр встречается в квадрате только
один раз.
Сколько трехзначных троек чисел с такими же
свойствами можно уложить из девяти цифр?
Лабиринт с 42 помещениями
Какова Ваша способность ориентации? Проверьте
с часами в руке, сколько времени Вам потребуется,
чтобы пройти все 42 помещения, из которых состоит
лабиринт, нарисованный на рис. 10-3, в порядке
204
РЕШЕНИЕ ЗАДАЧ
а
2
3
4
Ь
1
2
3
с
6
4
2
натурального ряда чисел A, 2, 3, ..., 41, 42} первый
раз, затем, после пятиминутного отдыха, второй раз
и, наконец, снова после пяти минут перерыва, тре-
третий раз.
Сколько минут Вам потребовалось, чтобы пройти
лабиринт первый раз, второй и третий?
Пройдите лабиринт в обратном направлении. Сколь-
Сколько времени вам на это^потребовалось ?
Найти трехзначное число
Предположим, что искомое число имеет вид:
100а+ЮЬ+с
Тогда:
^ A00а+10&+с) = ШЬ+Ш+а, т. е.
ЗООа+306+Зс = 400*+40с+4в
Следовательно:
296а = 3706+37с; 8а = 106+с; с = 8а-Ш
Буквы а, Ь, с обозначают цифры меньше или рав-
равные 9. Вот таблица некоторых значений букв.
Искомыми числами являются 216, 324, 432, 648,
756,864,972,...
После переноса первой цифры получаем соответ-
соответственно: 162, 243, 324, 486, 567, 648, 729, ...
205
Магический треугольник
Вот четыре решения:
1
2
3
4
А
15
12
10
13
в
3
2
2
1
С
13
11
11
15
D
1
1
3
3
Е
8
14
14
8
F
6
6
4
4
G
11
9
7
11
Я
5
4
6
г
к
10
7
о
12
L
2
3
1
2
М
9
13
15
7
N
4
5
5
6
Р
7
8
8
9
Q
12
10
12
10
R
14
15
13
14
1
2
3
4
Л
14
11
13
15
В
6
7
12
10
С
13
14
3
3
D
2
5
2
5
?
5
3
10
7
А]
F
8
8
11
11
зот еще 4 решения:
G
7
4
9
8
И
9
12
6
12
К
11
13
4
2
L
1
1
7
4
М
10
9
15
13
N
4
6
1
6
Р
3
2
5
1
Q
15
15
14
14
R
12
10
8
9
Предлагаем читателю поискать дальнейшие реше-
решения.
206
2)
/
s
4
11 1
л
—
\
\
-
s
=
—
-,
Щ
— ^
7
Ш
13
1
z?23
23
свЗ
19
im
17
25
Ш
9
11
15
120:
5
ш
21
Щ
3
Рис. 10-4
Шахматная доска
Решение ходов ферзя и коня показано на рис. 10-4.
На последнем рисунке мы видим, что конь с белой
клетки переходит на черную клетку и наоборот.
Все клетки с нечетными номерами — белые, а с чет-
четными номерами — черные (или наоборот).
Уклончивый ответ
Пусть х — это глубина ямы, которую роет рабочий,
' а у — высота выступания его головы над копаемой
ямой, в момент, когда яма вырыта на половину.
у +у=180; х-у=Ж
из этих уравнений получим:
360-2
~п~ X —
X—
= 2 м 40 см
Квадратный корень из феодализма
А. Из условий задачи следует, что (ееддиJ =
= феодализм. Буква е не может равняться единице,
так как пятизначное число, начинающее с 11 и воз-
возведенное в квадрат, не будет девятизначным числом.
Буква е не может быть цифрой, большей 2, так как
квадрат самого малого числа, начинающегося с 3 уже
девятизначное число. Из этого следует, что е = 2.
207
1
4
5
2
3
6
9
8
1
I 1
Рис. 10-5
208
Последней цифрой квадратного корня не может
быть ни 1, ни 5, ни 6, так как числа, заканчиваю-
заканчивающиеся этими цифрами, возведенные в квадрат,
заканчиваются таким же числом, а в нашем случае
феодализм заканчивается на м, а не на и. Принимая
это во внимание, мы приходим к выводу, что су-
существует тридцать возможных комбинаций цифр для
расшифровки числа еедди, например: 22 334,
22 337, ... Этот очень длительный поиск можно зна-
значительно сократить, введя концепцию «одноцифро-
вого корня». Сумма девяти цифр A+2+3+4+5 \-
+6+7+8+9 = 45) слова феодализм, составляет, как
видно, 45, а сумма цифр числа 45 равна 9. Можно
поэтому предположить, что этим свойством обла-
обладает также число еедди. Сумма его цифр должна
быть числом, сумма цифр-которого также составля-
составляет 9. Следовательно сумма цифр e+e+d+d+и мо-
может равняться 36, 27, ... и т. д. Принимая во вни-
внимание все вышеуказанные ограничения для цифр
числа еедди можно прийти к выводу, что еедди =
= 22 887. Сумма цифр числа 22 887 — 27, а сумма
цифр числа 27 — это 9. Возведя 22 887 в квадрат,
получим 523 814 769. Следовательно, феодализм —
это число 523 814 769. Это число содержит все
цифры кроме нуля.
Б. Эти цифры можно записать в девяти клетках
квадратной шахматной доски, как это показано на
рис. 10-5.
Легко проверить, что трехзначное число, образо-
образованное цифрами последней строки, равно сумме
чисел, образованных цифрами предыдущих строк.
Эти числа можно расположить в натуральный ряд
по ходу туры на шахматной доске (смотри рисунок).
Построение квадрата легко запомнить.
В середине квадрата стоит цифра 3, в его вершинах
остальные нечетные цифры, средние места зани-
занимают четные цифры 2, 4, 6, 8.
Задача Киркмана
Группы
пон.
вторн.
среда
четв.
пята.
субб.
воскр.
1,
1,
1,
1,
1,
1,
1,
I
2,
4,
10,
9,
6,
8,
5,
3
7
13
15
12
11
14
4,
2,
2,
2,
2,
6,
2,
II
5,
5,
11,
14,
7,
2,
9,
6
8
14
10
13
15
12
7,
3,
3,
3,
3,
3,
3,
III
8,
12,
6,
5,
8,
7,
4,
9
15
9
11
14
10
13
ю,
ю,
4,
7,
4,
4,
7,
IV
И,
14,
8,
4,
9,
12,
И,
12
13
15
6
И
14
15
13,
13,
7,
13,
10,
13,
ю,
V
14,
и,
5,
8,
5,
5,
8,
15
6
12
12
15
9
9
Дети пронумерованы соответственно от 1 до 15.
Числовая задача
Указания для решения задачи:
1) Всего трехзначных чисел, которые можно выра-
выразить с помощью всех цифр (от 1 до 9) 729.
а) от 111 до 199 имеем 81 число без нулей
209
б) от 211 до 299 имеем 81 число без нулей
и) от 911 до 999 имеем 81 число без нулей
Итого 81 • 9 = 729
2) Трехзначных чисел, в которых каждая цифра
встречается только один раз, всего 504
(Al = 9 • 8 • 7 = 504, сравните главу 27)
3) Так как сумма цифр самого большого числа, встре-
встречаемого в задаче D59), составляет 18, то ищем все
трехзначные числа с такой суммой цифр. Таких
чисел — 44:
189, 198, 279, 297, 369, 378, 387, 396, 459, 468, 495,
549, 567, 576, 594, 639, 648, 657, 675, 684, 693, 729,
738, 756, 765, 783, 792, 819, ..., 954, 963, 972, 981
4) Из этих чисел только 31 число может быть сум-
суммой двух других трехзначных чисел, вот эти чи-
числа:
459, 468, 495, 549, 567, 576, 594, 639, 648, 657, 675,
693, 729, 738, 792, 819, 837, 846, 864, 873, 891,918,
927, 936, 945, 954, 963, 972, 981
Читатель сам найдет по 2 трехзначных числа, суммы
которых составляет одно иэ приведенных выше
трехзначных чисел.
РЯДЫ ГЛАВА 11
Числовым рядом называем алгебраическую сумму
бесконечного числа элементов:
которую символически обозначаем обычно: У^ и,
Элементы и^игиъ ¦•¦ называются членами ряда.
Числа:
52 = их+и2
53 = «t
называются частичными суммами ряда.
Если последовательность частичных сумм стремит-
стремится к определенному числу S, пределу ряда, т. е. мо-
может приблизиться бесконечно близко к числу S то
ряд называется сходящимся, и мы записываем:
..; +М„) -* S
или иначе Нт5и = 5.
И->00
В этом случае мы называем число S суммой ряда.
211
Например, ряд 1 +у + •§- + ••• + "jr + • • • сходящей-
3 13
ся, а его сумма S = -^, так как S = г- = -^-.
1 3
Каждая бесконечная десятичная дробь является
суммой определенного ряда, например, дробь 0,222...
можно представить в виде ряда
2 2 2
_?_ 4-—— | 4-
10 ^ 100 ^ 1000 ^ •''
/ 2\
Этот ряд имеет сумму I число-g-l, которую можно
высчитать как сумму членов бесконечно убывающей
геометрической прогрессии на основании формулы
S = -. , где а — первый член ряда, а а — знаме-
1—<7
натель ряда, равный отношению двух последующих
членов ряда. Следовательно:
S=-- + _-4—^-+
10 ^ 100 ^ 1000 ^ ¦" 1 9
Если последовательность частичных сумм ряДа
Si, S2, S3, •. • не имеет предела, то мы говорим, что
это расходящийся ряд, например:
1-1 + 1-1 + 1-1+...
i.l.l.l. 1,1,
1 + + + + + +
зто расходящиеся ряды.
212
В высшей математике доказывается, что ряд:
.4__4__4_4__4_ 4_
1 3 + 5 7 + 9 1 + "•
сходящийся, и что его сумма равняется числу тс.
Существуют также ряды, с помощью которых вы-
считываются приблизительные значения тригоно-
тригонометрических функций синуса и косинуса:
_
1-2 з + 1-2-3-4-5 ' 1-2 3 4-5-6.7
cosx = х~-.
1-2 ^ 1-2-3 4 1-2 3 4-5-6 ' -"
(в этих рядах х — это мера угла, выраженная в ра-
радианахI К
Последние три примера рядов позволяют высчи-
высчитать приблизительные значения величин тригоно-
*) Угол можно измерять либо с помощью угловых градусов,
в этом случае в качестве единицы измерения применяется 1 /90
часть прямого угла — 1 °, или же с помощью радианной меры.
Единицей радианной меры является радиан, т. е. центральный
угол, опирающийся на дугу, длина которой равна радиусу г.
Так как длина дуги полного угла C60°) составляет 2пг, то
360° 180°
1 радиан (рад) = ^ = —^Г~ 57°17'44". Существует фор-
формула перехода от угловой меры а к радианной мере а, т. е.
а = . Для а = 30°, 45°, 60°, 90° и 180° получим соот-
360
ГС ГС ГС ГС
ветственно: — ; —; —; —; гс радианов.
213
метрических функций — синуса или косинуса, а так-
также числа тс. Мы находим эти значенния, беря в ука-
указанных рядах большее или меньшее число членов
(например, 3), чем больше членов мы возьмем, тем
точнее будет результат, тем точнее мы высчитаем
величину искомой функции или числа тс.
Систематическая теория рядов является предметом
математического анализа, однако, с самыми просты-
простыми рядами нас знакомит уже арифметика (периоди-
(периодические дроби) и алгебра (геометрическая прогрес-
прогрессия).
С учетом некоторых дополнительных условий, ариф-
арифметические действия на рядах выполняются с соб-
соблюдением тех же простых правил, которые мы ис-
используем, выполняя действия с многочленами. На
этом основании решение многих задач физики и тех-
техники значительно облегчится, если данные и иско-
искомые величины мы будем рассматривать как суммы
рядов, членами которых являются простейшие
функции (например, степенной ряд, тригонометри-
тригонометрический ряд).
С такими рядами, как арифметическая и геометри-
геометрическая прогрессия мы встречаемся уже в греческих
папирусах. Греки расширили использование рядов,
рассматривая бесконечную геометрическую прогрес-
прогрессию.
Архимед использовал бесконечную геометрическую
прогрессию (ее сумму) для рассчета площади участка
параболы.
214
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
В средние века наука о рядах стояла на месте. Боль-
Большой шаг вперед сделал лишь Ньютон в XVII веке.
В 1665—1666 гг. он разложил в степенной ряд
функции ln(l+x), ех, sinx, cosx. Лейбниц и шот-
шотландский математик Грегори также занимались ря-
рядами. Оба они, независимо друг от друга, определили
ряды для числа тт и для тангенса.
В XVIII веке английский математик Тэйлор вывел
общукг формулу разложения функции в степенной
ряд.
В XIX веке были разработаны тэоретические осно-
основу рядов.
Путешествие гусеницы
По стволу дерева вверх по прямой ползет к бли-
ближайшей ветке гусеница. Очевидно у гусеницы по-
поврежден огран движения, так как ползет она с тру-
трудом, причем так, что в первую минуту она продви-
продвигается на 5 дм, во вторую—2-^- дм, в третью —
1-7- дм, в четвертую -=- дм и т. д. До первой ветки
чуть-чуть больше одного метра.
Через сколько минут гусеница доползет до вет-
ветки?
Доползет ли гусеница до ветки перед заходом солн-
солнца B0 часов), если она начала ползти на рассвете
(в 4 часа утра) ?
215
Ахиллес и черепаха
Вопрос, догонит ли Ахиллес черепаху, привлекает
внимание не только философов. Этот парадокс сфор-
сформулировал Зенон Элейский около 500 лет до нашей
эры. Многие утверждения Зенона — это парадоксы.
Среди них наиболее известны парадоксы о быстро-
быстроногом Ахиллесе, который не может догнать чере-
черепаху и о выпущенной из лука стреле, которая в каж-
каждый неделимый момент времени покоится, а следо-
следовательно — она неподвижна.
Давайте рассмотрим парадокс Ахиллеса и черепахи
с точки зрения математики. Пусть черепаха нахо-
находится в пункте Z, а Ахиллес в пункте А (рис. 11-1).
Расстояние между этими точками составляет d м.
Предположим, что черепаха двигается со скоростью
v м[сек, а Ахиллес со скоростью w м/сек; тогда:
1) время, за которые Ахиллес пробежал рас-
расстояние AZ;
2) w путь, пройденный за это время черепа-
черепахой;
216
z
3) —: w = ~ — время, за которое Ахиллес пробе-
пробежит путь, пройденный до этого черепахой;
лч vd v2d
4) v —г = —г путь, пройденный черепахой, за вре-
время, высчитанное в п. 3.
I Рассчитаем подобным образом отрезки времени, за
4| которые Ахиллес пробегал последовательные от-
отрезки пути и отрезки пути, пройденные за это же
Рис. 11-1 время черепахой. Предположим, что Т — это сумма
отрезков времени, когда Ахиллес догонял черепаху.
Тогда
vd ,v2d __ d Л , v
¦••)-
d
w
1
1
1
—
V
w
Сумма отрезков пути, пройденных черепахой, со-
составляет:
vd v2d v3d _ vd
— + -^+-^3"+ •¦¦ —
vd 1 vd ,
(
(V V W—W
~ w
Так как первоначальное расстояние составляло d м,
то путь, который пробежал Ахиллес, равняется:
, . vd wd , ¦.
а-\ = (м)
w—v w—v v
217
Пробежав этот путь, Ахиллес догонит черепаху.
Если первоначальное расстояние AZ = 100 м, ско-
скорость Ахиллеса 10 м/сек, а скорость черепахи
0,1 см/сек, то
wd
1000 ¦ 10 000
см = 10 001 см к 100,01 м
т. е. Ахиллес догонит черепаху примерно через
10 сек после начала погони (точнее примерно через
10,001 секI\
Рис. 11-2
0 ломаных пиниях
На рисунке 11-2 мы видим две ломаные линии.
Линия / не имеет конечной длины, так как можно
доказать, что a+b+c+d+ ... = 1+у+ у+"+•¦¦
стремится к оо.
1У Задача об Ахиллесе и черепахе имеет более широкий ас-
аспект. Таким же образом можно, например, доказать, что боль-
большая стрелка часов, находящаяся против цифры 12, никогда
не догонит малой стрелки, которая находится, скажем, против
цифры 3, или же, что мотоциклист, который едет со скоро-
скоростью 80 км/ч, не догонит велосипедиста, находящегося на
1 километр впереди и едущего со скоростью 20 км/ч.
d vd
Формулы: Т =
w — v
дачи на тему «погони».
и S
w — v
пригодны для любой за-
218
Длина линии II, состоящей из отрезков к+т+
111
+«+ ¦¦• = 1+-^-+-}- + -^-+... является сулшой чле-
L т- О
нов бесконечной геометрической прогрессии и со-
ставляет:
Ряд 1 + 1- + 1+ L+ ... + 1 + ... (и = 1,2, 3...) на-
зываем гармоническим рядом. Это название объясня-
объясняется тем, что каждый член этого ряда (начиная со
второго) является средним гармоническим (см. стр.
135) соседних членов, т.е.
г. 2ас
О =
а + с
(а, Ъ, с — последовательные члены). Например,
с = т
(" = 0' Ь 2...)
называем геометрическим рядом. Это сходящийся
ряд, а его сумма называется 2.
Каждый член этого ряда начиная со второго явля-
является средней геометрической двух соседних членов,
т. е.
1
3
Ряд
2-
1
2
1 +
1
2 '
- +
т
1
т
1
т
+
("
1
~~ 2'
f ... -
*-
1- 2"
1
3
+
Ъ = У ас , например 4" = j/ 2 "s
8
219
Из окна вагона
Пассажир, который едет в скором поезде со средней
скоростью 60 км/ч, видит в окне своего вагона встреч-
встречный пассажирский поезд (федняя скорость которого
равняется 40 км/ч). Какова длина пассажирского
поезда, если пассажир видел поезд в течение 6 сек?
Квадратный корень
Чему равен квадратный корень из числа
12345678987654321 ? Укажите ответ, не извлекая
корня. Ответ найдете, если будете возводить в квад-
квадрат И, 111, 1111,...
Проверка железнодорожных путей
Путейный мастер во время обхода своего участка,
заметил, что пригородные поезда нагоняют его каж-
каждые 15 мин, а встречные проходят около него каж-
каждые 5 мин.
Рассчитайте, какова частота курсирования пригород-
пригородных поездов и какова их средняя скорость. Прини-
Принимаем, что пригородные поезда и путейный мастер
двигаются с постоянной скоростью.
Путешествие господина Смита
В 10 часов утра господин Смит отправился с женой
из своего дома в Коннектикут навестить родителей
220
жены в Пенсильвании. По пути они решили оста-
остановиться только пообедать в ресторане в местности
Вестчестер.
Перспектива встречи с тестем и неприятного разго-
разговора на тему денег испортила господину Смиту на-
настроение. В автомобиле царило тягостное молчание.
Примерно в 11 часов мадам Смит решилась задать
вопрос:
— Как далеко мы уже отъехали от дома?
Господин Смит, глянув на счетчик километров, от-
ответил:
— Мы проехали половину расстояния, которое нам
еще осталось проехать до ресторана в Вестчестер.
В ресторан Смиты приехали ровно в полдень. Они
не спеша пообедали и сразу же поехали дальше.
Примерно около 5 часов вечера они находились на
расстоянии 200 км от того места, в котором мадам
Смит задала свой вопрос. Теперь она снова спросила
мужа:
— Сколько километров нам еще осталось проехать?
— Половина того пути, который мы проехали от
ресторана в Вестчестер до этого места, — ответил муж.
К дому тестя в Пенсильвании Смиты подъехали
в 7 часов вечера. И хотя господин Смит вел машину
с разной скоростью, можно с большой точностью
высчитать длину пути от их дома в Коннектикут до
дома тестя в Пенсильвании.
Попытайтесь бпределить этот путь.
221
РЕШЕНИЕ ЗАДАЧ Путешествие гусеницы
Гусеница переместится на:
Сумма этого ряда составляет т~ = 10 дм
Ответ: гусеница никогда не доползет до ветки.
Из окна вагона
Скорый поезд проезжает в течение 1 сек путь, рав-
равный:
60_ __!_
"б0тбб'*л~ 60"**
Пассажирский поезд проходит за 1 сек путь, равный
40
"*Л~
60-60*Л~ 90 *Л
За 6 сек скорый поезд пройдет расстояние
1-6 1
КМ = -ттг КМ
60 '""- 10
а пассаж:ирский поезд гфойдет за то же время
1-6 1
- км = кл
Для пассажира скорого поезда длина пассажирского
поезда кажется короче фактической длины на столь-
222
Ск8а
ко метров, сколько за это время проехал скорый
поезд. Поэтому к пути, пройденному скорым поез-
поездом, необходимо добавить путь, пройденный за то
же время пассажирским поездом
-Tjj-км+ у? км = -gg-км = ~^км х 166,7 м
Таким образом, длина пассажирского поезда равня-
равняется 166,7 м.
Квадратный корень
И2 = 121; 1 1112 = 1234321
1112 = 12321; 1llll2 = 123454321 и т. д.
у/12345678987654321" = 111111111
Проверка железнодорожных путей
Пусть пригородные поезда выходят из конечных
станций каждые х мин. Среднюю скорость приго-
~ родных поездов мы рассчитываем сначала на осно-
Бабцшкино
вании частоты прохождения поездов, нагонявших
путейного мастера.
Первая встреча произошла в точке А (рис. 11-3).
Ба5цшкино Через 15 мин мастера нагонит следующий поезд.
с
D В этот момент мастер находится в точке В. Следо-
Рис 11-3 вательно, участок АВ мастер пройдет за 15 мин,
а поезд пройдет это же расстояние за A5— х) мин.
Следовательно, тот участок пути, который мастер
223
проходит в течение 1 мин, поезд проезжает в течение
15 — х
—т-=— мин. Рассчитаем теперь скорость поезда на осно-
вании частоты встреч мастера с поездами, идущими
ему на встречу. Пусть первая встреча произойдет
в точке С, вторая встреча в точке D. Участок пути
CD поезд проедет в течение (х—5) мин. Путь, прой-
пройденный мастером в течение 1 минуты, поезд проедет
в течение —?— мин. Участки пути, пройденные в те-
15-х х-5 - „
чение —т~с— и —г— мин равны между собой по длине,
15-х х-5
поэтому мы можем записать: —т^— = —=—, а из этого
находим: х = 7-=- мин. Частота курсирования приго-
пригородных поездов—7у мин. Средняя скорость при-
пригородных поездов 30 км/ч.
^_"__ _ ПеншпьЪашя Путешествие господина Смита
1 Расстояние Коннектикут-Пенсильвания составляет
—L— i ^ 1
\-х — гх—4—ОТ-&-4- 100-х- (рис 11-4):
Рис. 11-4 (х+200+100-х) = 300 км
ОБ ОТНОШЕНИЯХ ГЛАВА 12
Кроме хорошо известного всем числа тт имеется зна-
значительно менее известное число q> (фи), которое
обозначает, однако, не менее существенное отноше-
отношение, выступающее всегда там, где его меньше всего
ожидают. Объясним на примере, что обозначает (р
(Фи).
Предположим, что отрезок а (рис. 12-1) необходимо
разделить на две неравные части таким образом, что-
чтобы большая из них была средней пропорциональной
меньшей части и всего отрезка, иначе говоря, при
этом делении должно быть соблюдено равенство:
а: х = х:(а—х); т. е. х2+ах—а2 = О (I)
в котором а — это отрезок в целом, ах — это его
большая часть.
Отрезок х находим путем решения уравнения (I).
Получим х = a ' .——.
Рис 12-1 Определив х, найдем (а—х), а также отношение
l + i/iT
a: x = —у—; этой же величине равняется и отно-
отношение х: (а—х).
Это отношение американский математик Марк Барр
обозначил буквой <р (фи), а такое деление отрезка
называется «золотым сечением». Тем самым мы
225
15
видим, что (р выражает отношение двух частей от-
отрезка, разделенного «золотым сечением». Золотое
отношение: <р = —~-— = 1,61803398...; довольно
интересно отметить, что обратная величина, т.е.—
равняется 0,61803398...
1
- можно получить из числа ср вычитая
Мы видим, что
<Р
единицу, (цифры после запятой не меняются). Это
единственное положительное число, обладающее та-
таким свойством. Древние греки знали «золотое сече-
сечение» и сознательно его использовали в искусстве
и архитектуре; особенно часто ими пользовались ар-
архитекторы Иткинос и Калликратес при строитель-
строительстве храма Афины-Парфенос на Акрополе в Афинах.
Крупнейший скульптор древности Фидий также
очень часто использовал золотое сечение в своих
скульптурах. Можно предположить, что пифагорцы
избрали пятиконечную звезду (рис. 12-2) в качестве
эмблемы своего тайного братства, потому что в этой
фигуре каждый отрезок разделен золотым сечением
по отношению к соседнему меньшему.
АВ _ AD
~A~D ~ ~AB^~AD
A)
Дуга С В = 72°; треугольник АС В подобен треуголь-
А О CR
нику CDB, следовательно, -?,„-— п^;яо СВ— CD~
— AD и DB — AB—AD. После подстановки полу-
получаем отношение A).
Рис. 12-3
$ЭЛОТОЙ ТРЕУГОЛЬНИК
и золотой
ПРЯМОУГОЛЬНИК
Название «золотое сечение» начало применяться
только в XIX веке. В средние века и в эпоху Возрож-
Возрождения математики были столь заворожены числом у,
что пропорцию, которую оно обозначает, называли
«божественной пропорцией» (divina proportio). Один
из крупных математиков эпохи Возрождения Лука
Пачоли издал в 1509 году трактат «О божественной
пропорции» с иллюстрациями Леонардо да Винчи.
Этот трактат бьш переиздан в 1956 году. Он содержит
чрезвычайно интересные примеры, в которых встре-
встречается отношение q> в плоских и пространственных
фигурах (например, в десятиугольнике вписанном
в окружность).
Рж. 12-4
Будем называть прямоугольник, у которого отноше-
отношение сторон равно ср, золотым прямоугольником. Так
вот, если в икосаэдр (двадцатигранник) (рис. 12-3)
мы впишем три взаимно перпендикулярных золо-
золотых прямоугольника, то их вершины окажутся в 12
вершинах икосаэдра. Если эти 3 золотых прямоуголь-
прямоугольника (взаимно перпендикулярных) мы впишем в
правильный додекаэдр (двенадцатигранник), то их
вершины окажутся в центрах граней додекаэдра
(рис. 12-4).
227
6
F С
Рис. 12-5
A t
L
с
В .
II
1
г
1
7
М
F К С
Золотые прямоугольники
ABCD, EBCF, GHCF, G3KF, G3ML
Рис. 12-6
Золотые прямоугольники имеют очень много инте-
интересных свойств. Если от золотого прямоугольника
ABCD отнять квадрат AEFD, то оставшаяся часть
EBCF будет также золотым прямоугольником (рис.
12-5). Если от прямоугольника EBCF отрезать квад-
квадрат EBHG, то оставшаяся часть по-прежнему являет-
является золотым прямоугольником и т. д. Мы видим,
что положение золотых прямоугольников изме-
изменяется, прямоугольники как бы «поворачиваются»
(рис. 12-6).
Архимедова спираль (рис. 12-7) — хорошо известная
кривая с неограниченным количеством витков. Ме-
Менее известна спиральная кривая, называемая лога-
логарифмической (по ее уравнению г = a ekv). Ее вы-
вычерчивание (рис. 12-8) связано с вращающимся
3*."
Золотые прямоугольники
ABCD, EBCF, GHCF, S3KF, S3ML
Рис. 12-8
Рис. 12-9
«золотым прямоугольником», а также с вращающи-
вращающимся «золотымтреугольником» (т.е. равнобедренным
треугольником, в котором отношение основания к бо-
боковой стороне равно (р, в таком треугольнике углы
основания равны 72°, а угол вершины равен 36°).
Из чертежа видно, что последовательные точки,
определяющие «золотое сечение» расположены на
спирали. Заметим, что «золотые прямоугольники»
вращаются не только в сторону их уменьшения, но
и в сторону увеличения, из прямоугольника GJML
можно получить прямоугольник ABCD, а из него
дальнейшие, все более крупные, «золотые прямо-
прямоугольники». Полюс логарифмической спирали на-
находится в точке пересечения диагоналей А С и BF.
В спирали, вычерченной с помощью вращающихся
«золотых треугольников» (рис. 12-9), все вершины
этих треугольников лежат на спирали, а ее полюс
находится в точке пересечения медиан AM и DN
сторон ВС и АВ. Отметим, что витки логарифмичес-
логарифмической спирали могут увеличиваться неограниченно.
Увеличенная до размеров галактики или же умень-
уменьшенная до микроскопических размеров логарифми-
логарифмическая спираль имеет всегда одну и ту же форму.
Форму логарифмической спирали мы обнаруживаем
у многих творений природы. Например, раковина,
в которой живет моллюск, увеличивается вместе
с ростом его тела, но всегда сохраняет неизменную
форму, благодаря чему внутренняя форма домика
моллюска имеет всегда тот же самый вид.
229
РЯД ФИБОНАЧЧИ
Отношение <р тесно связано с так, называемым, рядом
Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
Ряд Фибоначчи — это, так называемый, аддитивный
ряд. Это значит, что каждый последующий его член
(кроме первых двух) равен сумме двух предыдущих:
12-10
Так вот, соотношение двух последовательных членов
ряда Фибоначчи, по мере возрастания этого ряда,
все более приближается к значению величины <р,
например:
у = 1,666...;
21
= 1,619...;
f =1,618...
Рис. 12-11
Иллюстрацией ряда Фибоначчи может служить до-
довольно-таки много явлений природы, например, из
области биологии, ботаники.
В качестве любопытного примера ряда Фибоначчи
приведем здесь известный геометрический парадокс.
На рис. 12-10 мы видим квадрат, состоящий из 64
квадратных элементарных единиц. Квадрат этот был
разделен на 4 части, из которых затем был построен
прямоугольник, площадь которого составляет 65 эле-
элементарных квадратных единиц (рис. 12-11). Обратите
внимание, что отрезки, которые образуют стороны
частей квадрата и прямоугольника, имеют длину: 3,
5, 8, 13. Это члены ряда Фибоначчи.
Этот парадокс объясняется тем, что отрезок АС не
является прямой линией и что у этого отрезка обра-
230
СТАНДАРТНЫЕ
ПРЯМОУГОЛЬНИКИ
И ТРЕУГОЛЬНИКИ
•с_ i
Цб
5
4
3
г
1
зуется фигура, площадь которой равна 1 элементар-
элементарной квадратной единице. Парадокс вызван тем, что
аддитивный ряд можно создать из произвольно выб-
выбранных двух первых чисел, например: 2, 7, 9, 16,
25,...
Несмотря на это, соотношение двух последующих
членов этого ряда постепенно все более и более
приближается к числу q>. В нашем примере ряд
3, 5, 8, 13 не образует фигур, из которых можно бы
было составить прямоугольник с соотношением сто-
сторон равным числу ср.
Рис. 12-12
Кроме «золотого прямоугольника» мы можем также
рассмотреть другой прямоугольник, который скром-
скромно назовем «стандартным». Форма стандартного
прямоугольника — это форма хорошо известного нам
листа бумаги для пишущей машинки. Возник он из
квадрата. Более короткой стороной стандартного пря-
прямоугольника является сторона выбранного квадрата,
а большая сторона равна гипотенузе этого квадрата
(рис. 12-12а).
Соотношение сторон стандартного прямоугольника
AD:AB = \/2 x 1,4142. Интересным и очень по-
полезным свойством стандартного прямоугольника
является то, что его половина KLMN образует также
стандартный прямоугольник, с таким же соотноше-
231
ал/1
а В
Рис. 12-13
нием сторон (KL: KN = |/2). Прямоугольники 1,2,
3, ... стандартны и себе подобны. Таких прямоуголь-
прямоугольников из данного прямоугольника A BCD можно по-
получить неограниченное число.
Если мы назовем треугольник ABC, у которого ос-
основание АВ = а, а стороны АС — СВ — а\/2 —
стандартным треугольником (рис. 12-13), то в таком
треугольнике соотношение АС: АВ = ]/2 = 1,4142.
Если радиусом а мы вычертим дугу из точки В, то
получим точку D. Треугольник ABD подобен тре-
треугольнику ABC и также стандартен {АВ: AD = ]/2 ) .
Таким же образом мы получим треугольник ADE
{АЕ = AD), в котором АЕ: DE = ]/2. То же самое
мы можем сказать о треугольниках DEF и EFG. Все
зти треугольники стандартны. В этих треугольниках
отношение стороны к основанию всегда равно у 2.
Таких треугольников можно построить неограничен-
неограниченное количество.
f
- в
УА
ш
т.
к
с
А
\
А
м
щ
щ
1
а
1
в
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Рис. 12-14
Крест Лотарингии
Крест Лотарингии, представленный на рис. 12-14,
состоит из 15 элементарных квадратов. Через точку
А проведена прямая BG, которая делит площадь крес-
креста на две половины, т. е. BGKF = BGDL. В каком
отношении точка В делит отрезок FC?
232
Катание на санях
Лошадь тянула ряд саней. Двое друзей Павел и Гри-
Гриша шли, споря о длине ряда саней.
Павел сказал:
— Вместо того, чтобы спорить, нужно измерить этот
ряд.
— Но как? У нас ничего нет под рукой, —• ответил
Гриша.
— У меня есть свой способ, — возразил на это Па-
Павел.
Затем он прошел равномерным шагом вдоль саней,
сначала в направлении их движения, а затем в про-
противоположном направлении.
Какой длины был ряд саней если шагая от его кон-
конца к началу, Павел сделал 120 шагов, а в противо-
противоположном направлении ему потребовалось для этого
40 шагов? Каждый шаг Павла равен 1 метру.
233
Сколько раз?
Сколько раз необходимо сложить число а с самим
собой (например 3), чтобы получить о" (например
Зб)? (и—натуральное число).
Кубический метр
Кубический метр разрезали на кубические милли-
миллиметры и из полученных кубиков уложили тонкий
пруток сечением 1 мм2. Сколько времени потребуется,
чтобы проехать вдоль этого прутка на мопеде со ско-
скоростью 50 км/ч.
У самовара
На столе стоит самовар. Вода в самоваре кипит не-
непрерывно. Пять человек может выпить кипяток из
самовара в течение 1,5 часа, а восемь человек — в те-
течение 1 часа. Сколько времени одшшадцать человек
будут опорожнять самовар? (принять, что порции
чая одинаковые и что вода выкипает равномер-
равномерно).
Головоломка
У Вани есть младшая сестренка Маша и старший
братишка Вася. Когда Ване исполнилось 6 лет, т°
Маше и Васе вместе было в 2 раза больше лет, чеМ
234
самому Васе. Подсчитай, сколько лет было Маше,
когда возраст Васи увеличился вдвое и сколько было
лет всем троим, учитывая, что как раз столько лет
было отцу, когда он умер.
Примечание: Возраст отца, Маши, Вани и Ва-
Васи выражен натуральными числами.
Сколько страниц?
Для того, чтобы пронумеровать страницы одного
крупного научного труда потребовалось 3389 цифр.
Сколько страниц в этой книге?
Птицы и рыба
В дно озера вбиты две сваи. Одна свая выстает над
уровнем воды на 2 метра, а вторая — на 1 метр.
Расстояние между сваями 10 метров. На каждой свае
сидит птица, подстерегающая рыбу. Скорость полета
птицы, сидящей на более высокой свае, в два раза
больше скорости полета птицы, сидящей на более
низкой свае. Когда на прямой между сваями появи-
появилась рыба обе птицы одновременно бросились на
добычу. В котором месте выплыла рыба, если обе
птицы настигли ее одновременно?
235
РЕШЕНИЕ ЗАДАЧ Крест Лотарингии
1) Площадь треугольника BDG = 2-^- (рис. 12-15),
вс=
X
г Л
\
х
г
А
\
\
0
Г
у
Рис. 12-15
а следовательно:
BD- DG (х+1) • 0+1)
2 ~ 2
= 5
A)
2) Площадь треугольника ВСА+площадь треуголь-
треугольника AEG = 3/2 едг, следовательно:
\
1-
B)
3) Решая уравнения A) и B) найдем, что:
х- вс-
1 f»_ уТ-1
X Л -fc i/ * л
Из этого следует, что точка В делит отрезок FC зо-
золотым сечением.
Катание на санях
Длина ряда саней составляет х м. Когда Павел де-
делает один шаг, ряд саней перемещается на у метров-
При таком условии мы получим систему уравнений:
= 120; х = 40+40у
Решая эти уравнения, найдем, что х = 60 м.
236
Сколько раз?
а"-1. Если а = 3, то чтобы получить Зб =729, не-
необходимо сложить число три 243 раза (З5 = 243).
Кубический метр
go^_ = 1000 км
1000 км: 50 км/ч = 20 ч
У самовара
Восемь человек выпьет кипяток из самовара в те-
течение 1 часа, следовательно, в самоваре находится 8
порций чая и какое-то количество воды, которое
испарилось в течение 1 часа. Однако, из первого усло-
условия следует, что количество воды в самоваре со-
составляет 5-1,5 порций чая плюс количество воды,
которое испарится в течение 1,5 часа, т. е. 7,5 порций
чая и вода, испарившаяся в течение 1,5 часа.
Из этого следует, что в течение 0,5 часа испаряется
0,5 порции чая, а в течении одного часа — 1 порция.
Следовательно, в самоваре находится 9 порций чая
(8+1).
11 человек в течении 0,5 часа выпьют 11 • 0,5 = 5,5
порций чая, а при этом испарится 0,5 порции, сле-
следовательно, через полчаса из самовара убудет 5,5 +
+0,5 = 6 порций чая. Остальные 3 порции (9—6)
исчезнут в течении 0,25 часа. Следовательно, 11 че-
человек опорожнят самовар в течение 45 минут.
237
Головоломка
Головоломка имеет пять возможных решений. Если
Ване было 6 лет, то Маша (младшая сестра) могла
иметь: 5, 4, 3, 2, 1 год, а Вася соответственно — 7,
8, 9, 10, 11 лет. В момент смерти отца Маше было
12 лет. Соответственно Васе было 22, 20, 18, 16 или
14 лет, Ване — 17, 16, 15, 14 или 13 лет. Отцу было-
51, 48, 45, 42 или 39 лет (смотри таблицу).
Ваня
Маша
" Вася
Отец
Возраст
6
5, 4, 3,
7, 8, 9,
2, 1
10, И
В момент
13
12
14
39
14
12
16
42
смерти отц<
15
12
18
45
16
12
20
48
1
17
12
22
51
Сколько страниц
Для того, чтобы пронумеровать страницы от 1 до
9, необходимо 1-9 = 9 цифр.
Для того, чтобы пронумеровать страницы от 10 до
99, необходимо 2 • 90 = 180 цифр.
Для того, чтобы пронумеровать страницы от 100 до
999, необходимо 3 ¦ 900 = 2700 цифр,
следовательно, для того, чтобы пронумеровать
страницы от 1 до 999 необходимо 9+180+2700 —
2889 цифр. Остаток 3389-2889 = 500 цифр исполь-
использовались для нумерации следующих страниц, начи-
238
ная со страницы 1000. Этщ страниц было 500 : 4 =
= 125.
Следовательно, всего в книге 999+125 = 1124 стра-
страницы.
Птицы и рыба
скорость полета птицы, сидящей на более
высокой свае.
2 о
скорость полета птицы, сидящей на
более низкой свае.
—I 1Л i_ (смотри рис. 12-16); из
х ' 10-х t t
Рис. 12-16 этого:3х2-80х+400 = 0. Следовательно, х = 6уЛ.
,ОРИГАМИ" ГЛАВА 13
Кроме китайской игры, для которой используется
квадрат, разделенный на 7 частей, (рис. 13-1), су-
существует не менее интересная и древняя японская
игра «оригами». Для этой игры (в ее классической
форме) необходимо иметь лишь квадратный лист бу-
бумаги, который при смекалке и ловкости, может пре-
преобразиться в рыб, птиц, животных и разные пред-
предметы, причем лист бумаги можно только сгибать, но
его нельзя разрезать, склеивать, к нему нельзя что-
либо добавлять или что-либо на нем рисовать. Од-
Однако, современные правила «оригами» разрешают
использовать не только квадратный лист бумаги, но
и прямоугольный, а также дополнять сконструиро-
сконструированную фигуру рисунком.
Начала игры «оригами» уходят далеко в глубь ис-
истории японской культуры. Раньше «оригами» рас-
рассматривалось в Японии как прикладное искусство
В течение какого-то времени эта игра была распро-
распространена среди девушек в высших слоях общества
Теперь она стала предметом занятий в японских шко-
школах. Влиянием «оригами» можно, очевидно, объяс-
объяснить и наши школьные игрушки, сделанные из листа
бумаги. Кто из нас не помнит птиц, стрел, воздушных
змеев, корабликов, которые мы делали из бумаги
к огорчению наших учителей. Любопытно, что из-
Рис. 13-2
Рис. 13-3
вестный испанский филосов и писатель Мигель де
Унамуно A864—1937) был большим любителем
«оригами».
Японская игра имеет также свою любопытную мате-
математическую сторону. Из квадратного листа бумаги
без особого труда можно получить правильный тре-
треугольник, квадрат, шестиугольник, восьмиугольник
и т. д., но уже конструкция правильного пятиуголь-
пятиугольника вызывает большие затруднения. Самый прос-
простой способ получения из полосы бумаги правильного
пятиугольника следующий: из полоски бумаги раз-
размером, например, 20 см • 2 см необходимо сделать
узел, который затем следует сплюснуть, а его пра-
правый конец перебросить налево (смотри рис. 13-2а).
Кроме отчетливо видимого пятиугольника ABCDE,
в полученной фигуре таится еще один сюрприз. Пе-
Переложив правый конец ленты CEFD налево, взгля-
взгляните под свет и Вы увидите слегка проступающий
контур известной пифагоровой звезды (рис. 13-26).
Если Вы возьмете лист бумаги (необязательно квад-
квадратный), выберете на нем недалеко от стороны АЕ
точку F (рис. 13-3) и согнете его 15—20 раз таким
образом, чтобы всякий раз основание листа прехо-
преходило через точку F (на рисунке участок АВ), то сле-
следы сгибов расположатся таким образом, что обозна-
обозначится парабола, которую следы сгибов как бы «пе-
«пеленают».
Кривая, которая при этом образуется, — это дей-
действительно парабола, так как все точки касания оди-
241
наково удалены от точки F (фокуса) и основания
листа АЕ (директрисы).
Касательные к параболе были получены путем сгиба
основания листа бумаги в направлении фокуса F, на-
например, линия сгиба ВС является касательной к па-
параболе. Имеется одна любопытная задача на вычис-
вычисление, непосредственно связанная с этим вопро-
вопросом.
Предположим, что у нас имеется лист бумаги раз-
размером 8x11 см. Этот лист бумаги необходимо со-
согнуть таким образом, чтобы след сгиба ВС (смотри
рис. 13^) имел минимальную длину, причем правый
нижний угол листа А должен находиться на его ле-
левой стороне (в точке А'), по которой он может пере-
перемещаться вверх и вниз. Иначе говоря, задачу можно
сформулировать следующим образом: на каком рас-
расстоянии х = АВ след сгиба должен пересечь осно-
основание АЕ, чтобы длина ВС была минимальной.
Это задача на вычисление. Рассчеты, хотя и неслож-
несложные, занимают довольно много места. Оставляя в сто-
стороне подробности вычислений, мы здесь приводим
результаты отдельных этапов расчета:
1) АВ = х
2) ЕВ (8-х)
3) ЕА'2 = х2—(8—хJ; из этого ЕА' = 4\/х—4
4) BАОJ = 82+ЕА'2 = 16х,
а из этого АО = 2 \/х ВО2 = х2—АО2 = х2-4х,
т. е. ВО = \/х2—4-х
242
5) АО2 = ВО- ОС
АО2 4-х
а следовательно, ОС —
во
6) АС2 = ОС2Л-АО2 =
из этого А С =
х-\
2х
7) ВС2 = ЛС2+х2 = —
а из этого 5С =
18*
/х-4
Задача сводится к нахождению минимума функции
у = ; С помощью дифференциального исчисле-
\х—4
ния найдем ответ: при х = 6 функция j/ достигает
минимум. Как видно из этого, определение точки С
вопрос довольно-таки трудоемкий, в то же время
нахождение этой точки путем сгиба—вещь чрезвы-
чрезвычайно простая:
АВ = 4- • АЕ = \- ¦ 8 = 6 см
4 4
Сгиб должен пересечь основание АЕ в точке, уда-
удаленной от точки А на расстояние 3/4 АЕ.
Все другие величины, обозначенные нами в пунктах
от 3) до 7), найдем очень легко, подставляя число 6
вместо буквы х. Тогда:
BE =2
ЕА' = 4 i/2
243
ВО = 2 у/Т
ОС = 4 |/Т
ЯС = 6 j/З"« 10,38 ел
После этого математического экскурса можно за-
заняться непосредственно искусством «оригами». Са-
Самым эффектным из всех конструкций «оригами»
является птица, которая может махать крыльями.
Для этого необходимо взять квадратный лист бумаги
со стороной 20 см. Последовательные сгибы показа-
показаны на рис. 13-5. Сперва мы сгибаем лист бумаги по
диагоналям A). Затем поворачивает бумагу на дру-
другую сторону, таким образом, чтобы все углубления
стали выпуклостями, и сгибаем его через середины
сторон B). На рисунке все вогнутые следы сгибов
обозначены штрихпунктирными линиями, а выпук-
выпуклые следы сгиба — сплошными. Следующий шаг
C) — это сгиб двух сторон с общей вершиной таким
образом, чтобы эти стороны после сгиба соприка-
соприкасались. Если такие же сгибы мы сделаем у каждой
вершины, то получим 8 вогнутых следов D). Итого,
будем иметь 2 выпуклых следа (сплошные линии)
и 10 вогнутых следов (штрихпунктирные линии)-
Последующие сгибы показаны на очередных рисун-
рисунках от 5 до 14. Среди «оригами» есть двигающиеся
игрушки или пригодные для запуска: например, ры-
рыба открывает рот, птица машет крыльями, лягушка
прыгает и т. п.
ТРЕУГОЛЬНИК
ПАСКАЛЯ И ПОКЕР
Переводчик сочинений Мигеля Унамуно рассказы-
рассказывает, что великий писатель любил придумывать та-
такие «живые» игрушки выпив свой послеобеденный
кофе в кафе в Саламанке. Эти маленькие бумажные
игрушки привлекали внимание детворы, которая,
прижавшись носами к стеклу витрины, рассматривала
пожилого симпатичного господина и его странные
бумажные диковинки.
Великий французский философ, моралист и матема-
математик Влез Паскаль A623—1662) вынужден был заин-
заинтересоваться азартными играми, в результате чего
он стал одним из создателей теории вероятности.
Треугольник, который назван его именем и которым
мы пользуемся в вероятностных задачах, имеет та-
такую форму:
1 О
1 1 I
12 1 II
13 3 1 III
14 6 4 1 IV
1 S 10 10 5 1 V
1 6 15 20 15 6 1 VI
1 7 21 35 35 21 7 1 VII
1 8 28 56 70 56 28 8 1 VIII
1 9 36 84 126 126 84 36 9 1 IX
1 10 45 120 210 252 210 120 45 10 1 X
XI
245
Числа, стоящие в строчках, являются биномальны-
ми коэффициентами. Например, числа, записанные
в строчке, обозначенной цифрой X, являются коэф-
коэффициентами развернутого бинома (а+ЬI0:
(а+ЬI0 = 1 • alo+10a9b+i5a8b2+120a1b3 +
+2Wa5b*+252a5b5+2Wa4b5+\20a3b1+
+45a2b8+10ab9+l ¦ b10
Числа, записанные в IX строчке, являются коэффи-
коэффициентами развернутого бинома (а+Ь)9; в строчке
VIII — бинома (а+Ь)8 и так далее до бинома (а+&I=
= 1 • а+\ • Ъ, коэффициенты которого записаны
в I строчке. Каждый коэффициент в этом треуголь-
треугольнике является суммой двух коэффициентов, сто-
стоящих налево и направо в строчке над ним, например,
в строчке IV: коэффициент 4 является суммой коэф-
коэффициентов 1 и 3 из строчки III; 6 — это сумма коэф-
коэффициентов 3 и 3 и т. д.
В разделе математики, называемом комбинаторикой,
доказывается, что сумма коэффициентов в каждой
строчке треугольника равняется 2", где п — это но-
номер строчки, например, сумма коэффициентов строч-
строчки X (и = 10) составляет:
1+10+45+120+210+252+210+120+45+10+1 =
= 210 = 1024
сумма коэффициентов строчки IX (п — 9), равняется
соответственно:
1+9+36+84+126+126+84+36+9+1 = 29 = 512
и так далее до строчки I, сумма которого: 1+1 =
= 21 = 2.
246
Там же доказывается, что последовательные числа
каждой строчки равняются числу возможных соче-
сочетаний, которые можно получить из п элементов (и —
это номер строчки). Если индексом 1,1 обозначим
число сочетаний, которые можно получить из п эле-
элементов по к, то
("
"Н20
Ч)-1* (l°o) = >
Таким образом из 10 элементов можно образовать
1024 (т. е. 210) разных сочетаний.
Теперь, после этих замечаний, касающихся треуголь-
треугольника Паскаля, можно перейти к вопросам покера.
Какова вероятность, что из пятидесяти двух карт
одной колоды можно получить пять карт одной ма-
сй-и?
х) Символ ("I — это обозначение коэффициента бинома Нью-
Vе!
тона, его высчитываем следующим образом:
и\ п\ 1 • 2 • 3 • ... и
к] ~ к\{п-к)\ ~~ 1 • 2 ¦ 3 ¦ ... ¦ к[\ ¦ 2 ¦ 3 • ... • (и-*)]
я! (и — факториал) обозначает произведение всех натураль-
натуральных чисел от 1 до п включительно, при этом считается, что
О! =1.
247
В колоде находится 4 раза по 13 карт той же масти,
/13\
следовательно, необходимо подсчитать .1. Коли-
Количество раздач, в которых можно получить 5 карт
одной масти, составит соответственно во всех четырех
мастях 4 • I ).
С другой стороны, число возможных сочетаний из
52 карт по 5 составляет I I.
Соотношение этих двух величин и будет как раз ме-
мерой вероятности получения «масти»:
, 9-10-11-12-13 48-49-50 5152
1-2-3-4-S
1-2-3-4-5
33
~~ 16 600
таким образом существует меньше, чем 0,2% вероят-
вероятности (иначе гйворя, меньше двух шансов на тыся-
тысячу)-
А вот еще одно применение треугольника Паскаля.
Подбрасываем монету 10 раз. Какая вероятность
больше: того что монета упадет орлом вверх пять раз
или четыре раза.
Интуиция нам подсказывает ошибочно в первый мо-
момент, что имеется большая вероятность выпадания
орла четыре раза. Однако, расчеты убеждают в об-
обратном. Десятая строка треугольника Паскаля гово-
говорит, что общее число всех сочетаний для 10 элемен-
элементов равно 1024. Среди 1024 сочетаний имеется 210
248
сочетаний, содержащих четыре элемента, и 252 со-
сочетаний, содержащих 5 элементов. Следовательно,
вероятность выпадания орла 4 раза эа 10 бросков
210
составляет ^-^j, т.е. примерно 21%, а выпадания
1024
252
орла 5 раз — соответственно . , т. е. примерно
25%. Таким образом, вероятность выпадания орла
5 раз при 10 бросках больше.
Из этой же десятой строки мы узнаем, что вероят-
вероятность выпадания орла 1 раз при 10 бросках такая
п / Ю \
же, как и выпадание орла У раз I ... 1, то же можно
о о / 45 \
сказать и о выпадании орла Z и о раз 1П„. I или же
3 и 7 раз.
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Колдовство хитреца
Один хитрец услышал, что существует волшебное за-
заклинание, с помощью кЪторого можно разбогатеть
без труда. Он распрашивал об этом заклинании всех
встречных и поперечных и наконец какой-то стран-
странствующий кудесник открыл хитрецу волшебство.
Необходимо, мог, взять с собой строго определенную
сумму денег, выйти в полночь к реке, бросить в воду
5 рублей, вымолвить волшебное заклинание «ego
sum stultus» что по русски обозначает по просту «я
249
дурак», и деньги немедленно утроятся. Хитрец ре-
решил поступить строго в соответствии с указаниями
чародея. Он взял с собой указанную сумму денег,
пришел в полночь к реке и бросил в воду 5 рублей,
затем подсчитал сколько у него осталось денег, вы-
вымолвил торжественно заклинание и на его глазах
деньги утроились. Обрадованный хитрец снова бро-
бросил в воду 5 рублей и снова повторил заклинание.
Таким образом он поступил 3 раза. Затем вынул свои
деньги и с удивлением обнаружил, что у него как
раз столько денег, сколько он имел вначале.
Сколько денег было у хитреца, когда он пришел
к реке?
Задача Льва Толстого о косарях
Лев Толстой A838—1910) был не только великим
писателем, но и педагогом. В своем имении в Ясной
Поляне он создал школу и обучал в ней крестьян-
крестьянских детей, он же составлял для них учебники.
Здесь нам хочется рассказать об одной интересной
задаче, составленной Львом Толстым.
Группе косарей поручили скосить сено на двух лу-
лугах : при этом площадь одного из них была в два раза
больше площади второго луга. Полдня вся группа
косарей косила сено на большом лугу, во второй по-
половине дня группа разделилась на две. Часть про-
продолжала косить большой луг и до конца дня закон-
250
чила полностью косьбу. Вторая группа пошла косить
меньший луг, который она косила до конца дня, но
не закончила работу. Остаток травы на маленьком
лугу скосил один косарь на следующий день, прора-
проработав там весь день.
Сколько косарей было в группе?
Валька и Иоська — логическая головоломка
Летом во время каникул Валя помогал родителям
по хозяйству в деревне, где пас коз.
Иоська, его школьный друг, жил в соседней деревне
и, идя как-то полевой тропой, увидел Валю.
— Привет! Это все козы твоего отца? — спросил он
у Вальки,
— Нет, эти козы принадлежат четырем хозяевам,
моему деду, моему дяде, моей тете и моему отцу,
у каждого из них разное число коз, у моего отца их
больше всего.
— А у кого меньше всего?
— У моего деда.
— А сколько коз у твоего деда? Одна или больше?
— У деда ... коз (Валя сказал, сколько коз у деда).
—¦ А сколько коз всего? Они разбежались по лугу
и, их трудно счесть.
— Сколько всего коз? Меньше восемнадцати. Но
самое любопытное, что произведение всех чисел коз
отдельных хозяев составляет как раз столько же
251
гривенников, сколько я получу в награду за то, что
пасу коз во время каникул.
— А сколько ты получишь?
Валя сказал Иоське, сколько он получит за работу.
— После всего этого, что я узнал от тебя, — сказал
Иоська, — я могу тебе сказать сколько коз имеет
каждый из хозяев.
— А это интересно, скажи.
— У деда ... коз, у дяди ... коз, у тети ... коз,
а у отца ... коз.
Решите эту головоломку.
252
РЕШЕНИЕ ЗАДАЧ Колдовство хитреца
Отправляясь на реку, хитрец имел х рублей.
После первого утроения капитала у хитреца стало:
3(*-5) = 3*-15 (руб.)
Капитал хитреца увеличился на
(Зх-15)-х = 2х-1Б (руб.)
После второго утроения капитала у хитреца стало:
3(Зх-15-5) = 9х-60 (руб.)
После третьего утроения капитала у хитреца стало:
3(9х-60-5) = 27х-195 (руб.)
Из условий задачи следует, что х = 27л:—195, из
чего получим х = 7,50.
Когда хитрец отправлялся к реке у него было 7,50
рублей.
Задача Льва Толстого
(без составления уравнений)
После минутного раздумья легко убедиться, что по-
половина группы косарей за полдня может скосить 1 /3
большого луга.
Так как производительность косарей на меньшем
лугу была такая же, что и на большем, то скошенная
половиной группы косарей площадь меньшего луга
равняется 1/3 площади большого луга.
253
Теперь можем подсчитать, сколько осталось неско-
шенной площади на меньшем лугу:
1 /2 площади большего луга — 1/3 площади большего
луга =1/6 площади большего луга.
Для того, чтобы скосить 1 /6 площади большего луга,
потребовалось, чтобы один косарь косил траву це-
целый день. Следовательно, для того, чтобы скосить
целиком весь больший луг F/6 частей) и часть мень-
меньшего луга B/6 частей большего), скошенную в пер-
первый день, потребовалось
6^6 6
В группе было 8 косарей.
Валя и Иоська — (решение головоломки)
В качестве исходных данных мы должны принять
информацию Вали о том, что коз меньше 18, что
у деда меньше всего коз, у отца — больше всего,
что владельцев четверо и что каждый из них имеет
разное число коз.
Может ли дед иметь три козы?
Если бы у деда было три козы, то минимальная сумма
коз при соблюдении всех условий задачи, равнялась
бы 18 = 3+4+5+6. Следовательно дед не может
иметь три козы, а может иметь одну или две.
Давайте рассмотрим обе возможности.
254
1) У деда две козы. Тогда возможны следующие
последовательности чисел, соответствующих числу
коз
Последовательность
чисел
2, 3, 4, 5
2, 3, 4, 6
2, 3, 4, 7
2, 3, 4, 8
2, 3, 5, 6
2, 3, 5, 7
Сумма
чисел
14
15
16
17
16
17
Произве-
Произведение
120
144
168
192
180
210
Другие последовательности дают суммы больше 17.
Какую из рассмотренных возможных последователь-
последовательностей необходимо выбрать, можно будет решить
только после рассмотрения второй возможности.
2) Дед имел одну козу. Тогда возможны следующие
последовательности
Последовательность Сумма Произве-
чисел чисел дение
1,
1,
1,
1,
2,3,
2, 3,
2,3,
2, 3,
4
5
6
7
10
И
12
13
24
30
36
42
255
Последовательность
чисел
1, г, 4, ю
1, 3, 4, 5
1, 3, 4, 9
1» 3, 5, 6
1, 2, 3, 10
1, 2, 3, 11
Сумма
чисел
17
13
17
15
16
17
Произве-
Произведение
80
60
108
90
60
66
1, 3, 5, 7
1, 3, 5, 8
1, 3, 6, 7
1, 4, 5, 6
1, 4, 5, 7
16
17
17
16
17
105
120
126
120
140
Другие последовательности дают сумму больше 17.
Так как Валя получает возйаграждение независимо
от последовательности рассматриваемых чисел, то
можно принять во внимание только 3 последователь-
последовательности:
2,3,4,5; 1,3,5,8; 1,4,5,6.
А так как решение должно быть однозначно, то мы
должны принять 2, 3, 4, 5 и отбросить два преды-
предыдущих.
Следовательно, дед имел 2 козы, дядя — 3, тетка —
4 и отец — 5, а Валька заработает за лето 120 гривен-
гривенников, т. е. 12 рублей.
КАК
УКЛАДЫВАЕТСЯ
ПАРКЕТ
Рис. 14-1
А, С
Рис. 14-2
ГЛАВА 14
Можно доказать, что существуют только три пра-
правильных многоугольника, которыми можно покрыть
плоскость вокруг точки таким образом, что покры-
покрывающий ее многоугольник повторяется неограничен-
неограниченное число раз. Такими многоугольниками являются:
равносторонний треугольник, квадрат и правильный
шестиугольник (рис. 14-1).
Однако, существует бесконечное множество непра-
неправильных многоугольников, которыми можно таким
образом покрыть плоскость.
К примеру, любой тупоугольный треугольник ABC
(рис. 14-2) можно разделить на четыре равных и по-
подобных треугольнику ABC треугольника А1В1С1;
каждый из четырех треугольников J4151C1 можно
в свою очередь разделить на четыре равных и подоб-
подобных треугольнику Л151С1 треугольника А2В2С2,
каждый из шестнадцати треугольников А2В2С2 мож-
можно в свою очередь поделить на четыре равных и по-
подобных треугольнику А2ВгС2 треугольника А3В3С3
и т. д.
Треугольник ABC можно таким же образом увели-
увеличивать, получая подобные треугольники, площадь
которых в четыре раза больше площади'треуголь-
площади'треугольника ABC.
257
Рис. 14-3
II
Рис. 14-4
А
У
А
V
V2
>
*
*
Vk
77
Рис. 14-5
Рис. 14-6
Плоскость можно покрыть и другими фигурами,
например, трапециями.
На рис. 14-3 показаны три формы трапеций {А, В,
С). Каждую из них можно разделить на 4 равные
и подобные первоначальной трапеции, которые в
свою очередь можно делить или уменьшать до,бес-
до,бесконечности.
Произвольный параллелограмм ABCD (рис. 14-4)
можно разделить на 4 параллелограмма равных и по-
подобных параллелограмму ABCD или же увеличи-
увеличивать в четыре раза до бесконечности.
Параллелограмм или прямоугольник со сторонами
1 и j/2 (рис. 14-5) можно до бесконечности делить
пополам или удваивать, получая все новые и новые
прямоугольники, подобные заданному. На этом
свойстве прямоугольника со стороной 1 и \/2 основан
принцип ряда для форматов бумаги и игральных
карт.
Параллелограмм со сторонами 1 и ]/3 можно разде-
разделить на 3 равных параллелограмма подобных за-
заданному. Итак, параллелограмм со сторонами 1 и |/А:
можно делить на к равных и подобных заданному
параллелограммов (смотри рис. 14-5).
Представленный на рисунке 14-6 пятиугольник, ко-
который можно бы было назвать «сфинксоидальньиг
пятиугольником», является единственной формой
пятиугольника, который можно поделить на 4 рав-
равных, сфинксоидальных пятиугольника подобных за-
заданному. Известны также три формы шестиуголь-
258
\
-1 1 1 1
1 I
•—г
1—
._.! i r ---!
i—
i
i
i—
i
Рис. 14-7
Рис. 14-9
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Рис. 14-8
ников, которые можно поделить на четыре равных,
подобных заданному, шестиугольника (рис. 14-7).
Каждую трапецию можно поделить на девять рав-
равных и подобных заданной трапеций (рис. 14-8).
Так как все описанные многоугольники можно не
только уменьшать до бесконечности, но и увеличи-
увеличивать, то этот вопрос можно рассматривать как за-
задачу на укладывание паркета (рис. 14-9).
Геометрия ножниц
1. На рис. 14-10 представлены 4 фигуры. Одним
разрезом поделите каждую из них на две части
и сделайте из них квадрат.
2. На рис. 14-11 представлены 3 фигуры. Сделайте
из них квадрат.
Рис. 14-10 а, б, в, г
Рис. 14-11
17*
259
Рис. 14-12
Рис. 14-13
Рис. 14-14
а)
3. Из трех таких шестиугольников, как показано на
рис. 14-12, уложите равносторонний треугольник.
Как разделить торт?
Торт имеет форму равнобочной трапеции (рис. 14-13),
у которой верхнее основание, а также непараллель-
непараллельные стороны в два раза короче, чем нижнее осно-
основание.
Как разделить торт на четыре равных части ?
Деление треугольника
А теперь проверим вашу геометрическую смекалку.
Для решения этой задачи нет нужды знать какие-
либо теоремы или аксиомы. Произвольный тре-
треугольник ABC (рис. 14-14) разрезать в два приема
на 3 такие части, чтобы из них можно было соста-
составить прямоугольник.
Деление квадрата на шестиугольники
Разделите квадрат на 4 равных шестиугольника.
Как разрезать?
Равносторонний треугольник, который вы видите
на рис. 14-15а, разрежьте на 3 части, чтобы из них
можно было уложить фигуру, представленную на
рис. 14-155 (щит).
Рис. 14-16
Как разделить квадрат на половины
Квадрат состоит из 16 элементарных квадратных
клеток (рис. 14-16). Разделите его пополам, не по-
повредив элементарных клеток. Сколько существует
методов деления ?
Квадратный лист бумаги
Разделите квадратный лист бумаги пересекающи-
пересекающимися прямыми линиями на 56 неравных частей, при-
причем через одну и ту же точку могут проходить
только 2 прямые.
Сколько потребуется для этого прямых? Сколько
различных цветов необходимо использовать, чтобы
полученный клетчатый рисунок правильно закра-
закрасить, т. е. чтобы две соседние клетки были во всех
случаях покрашены в разные цвета?
Как разделить без спора?
Когда двое детей хотят что — либо разделить, очень
часто возникает по этому поводу спор. Существует,
однако, простой метод, который позволяет избе-
избежать спора. Метод заключается в том, что один
делит, а второй выбирает. Ни один из делящих не
может чувствовать при этом обиды, так как каждый
принимает активное участие в дележе: один делит,
а второй добровольно выбирает ту часть, которая
кажется ему более выгодной.
261
Бокал сока
Рис. 14-17
Бокал, который вы видите на рис. 14-17, наполнен
до краев соком. Петр и Ян хотят поделится этим
соком. Петр предложил, чтобы Ян разделил сок, а он
будет выбирать. Ян согласился и перелил в другой
сосуд такое количество сока, что остаток в бокале
достигал 3/4 прежней высоты. После раздумья
Петр выбрал то, что осталось в бокале. Правильно
ли выбрал Петр ?
Шоколадный торт
Если деление на две части вещь относительно лег-
легкая, то уже деление на три части значительно труд-
труднее.
Трое мальчиков: Гриша, Саша и Яша хотели раз-
разделить между собой шоколадный торт, но не знали,
как это сделать, чтобы никто не чувствовал себя
обиженным. Когда они раздумывали над способом
дележа, пришел отец Гриши и посоветовал посту-
поступить согласно правилу: один делит, а второй вы-
выбирает; таким образом: сначала разделить торт по-
пополам, а затем каждую половину разделить на три
части.
— Поняли? — спросил отец.
— Поняли — ответили мальчики.
Как мальчики разделили торт ?
262
Рамка из квадрата
Из картонного квадрата ABCD (рис. 14-18) сделай
рамку MNOPRSTU. Необходимо использовать на
рамку весь квадрат.
Рис. 14-18
РЕШЕНИЕ ЗАДАЧ Геометрия ножниц
Смотри рис. 14-19, 14-20 и 14-21.
а 5
Рис. 14-19 а, б, в, г
Как разделить торт?
Как разделить торт на 4 равных части, показано на
рис. 14-22.
Рис. 14-20
Рис. 14-21
Рис. 14-22
263
Рис. 14-23
ill
1
1
m
Рис. 14-24
OD=jCD йЕЦАС
Рис. 14-25
Деление треугольника
Решение показано на рис. 14-23.
Деление квадрата на шестиугольники
Самое простое решение, хотя и не единственное,
показано на рис. 14-24.
Как разрезать?
Смотри рис. 14-25.
Как разделить квадрат на половины
Квадрат можно разрезать на две половины пятью
разными способами (рис. 14-26).
Квадратный лист бумаги
Одна прямая делит лист бумаги на 2 части, две
прямые — на 4 части, 3 — на 7 частей, 4 — на
11 частей и т. д.
число прямых и
число частей у
0
1
1
2
2
4
3
7
4
11
Из таблицы мы видим, что число частей у зависит
от числа проведенных пересекающих прямых и.
264
i
i
m
щ
ш
w,
Ш
if
i
i
d
m:
1
Ш
Ш
if
Ш
if
Ш
Ш
Ш
Ш
Ш
ж
p
ii
Puc. 14-26
Число у не является, однако, линейной функцией
числа п, так как число у увеличивается неравно-
неравномерно. Давайте проверим, не является ли у квад-
квадратной функцией числа п ?
Если это так, то должно выполняться равенство
у = аи2_|_?и_|_с (общИй вид квадратных функций).
Коэффициенты а, Ь, с мы найдем, зная, что для
« = 1, у = 2, для п = 2, у = 4, для л = 3, у = 7.
Следовательно:
2 = а+Ь+с
4 = 4а+2?+с
7 = 9а+ЗЬ+с
Решая эту систему уравнений, найдем:
1
а = у,
т- е-
Теперь подставляя в нашу формулу и = 4, получим
у = 11, т. е. величину, равную значению у при л = 4
по таблице.
Теперь мы можем уже легко высчитать, сколько
нужно линий, чтобы разделить квадрат на 56 частей
56 = 1«+1«+1
из этого 112 = и
265
1
i
I
li
a
\f 2
5
4 /L
TTIW^f
1 / 1
mil/ N
1
Puc, 14-27 а, б, в, г, g
решая это уравнение, получим:
-1±|/44Г _ -1±21 .
'к 2 =
«=10
2 2
Следовательно, с помощью 10 линий мы можем по-
поделить квадрат на 56 неравных частей. Из рис.
14-27 видно, что сетка, образованная одной линией,
может быть покрашена двумя цветами (рис. 14-276),
например, черным и белым. Сетка, образованная
двумя прямыми, может быть также окращена дву-
двумя цветами. Части 1 и 3 и 2 и 4 не имеют общей
границы (общая точка не образует общей границы).
Такое же положение мы видим на рис. 14-27г. Про-
Проводя доказательство методом математической ин-
индукции, которое мы здесь не указываем, можно
убедиться, что сетка, образованная любым коли-
количеством прямых линий, может быть правильно
окрашена с помощью двух красок1 \
Как разделить без спора?
Бокал сока. Если мы обозначим объем сока в пол-
полном бокале, Vp, а объем сока в бокале после того,
') Этот вопрос можно рассматривать в значительно более ши-
широком аспекте, рассматривая деление пространства с помощыо
плоскостей, проходящих через одну общую точку таким об-
образом, что никакие три плоскости не проходят через одну
и ту же самую прямую. Если у обозначает число пространств,
на которое и плоскостей делит пространство, то:
у = и(и—1)+2 или у = и2—п+2
266
%
%
ж
ж
как часть сока была отлита Vq, то соотношение Vp
к Vq равняется соотношению кубов высоты сока
в бокале:
I3
it
27
Из этого найдем:
27
37
27
Рис. 14-28
Разность Vp—Vq — это та часть сока, которая была
отлита в другой сосуд. Из этого мы видим, что от-
отлитое количество сока, которое досталось Яну, на
10 единиц больше того объема, который выбрал
Петр.
Шоколадный торт. Гриша разделил торт на две,
по его мнению равные части. Из них Саша выбрал
одну. Затем Гриша и Саша разделили каждый свою
половину на 3 части. После чего Яша выбрал по
одной из трех от Саши и Гриши, оставляя им осталь-
остальные.
Нетрудно сделать иэ этого вывод, что такое деление
исключает возможность споров.
Рамка из квадрата
Смотри рис. 14-28.
САМОЛЕТ И ВЕТЕР ГЛАВА 15
Летчик-испытатель должен провести испытание но-
нового типа самолета на максимальную скорость по-
полета. Пробный рейс должен быть выполнен на
замкнутой трассе Варшава-Краков-Варшава. По-
Повлияет ли на результаты полета дующий на трассе
ветер?
Интуитивно нам кажется, что ветер практически
никакого влияния не окажет так как, если ветер
дует равномерно, например, в соответствии с на-
направлением полета из Варшавы в Краков, то на
этом участке он увеличивает скорость полета, а при
обратном перелете из Кракова в Варшаву ветер
уменьшит в такой же степени скорость самолета.
Однако, более тщательный анализ этого явления
убедит нас в ошибочности такого вывода. Полет
самолета с попутным ветром на трассе Варшава—
Краков продолжается короче, чем против ветра
(рис. 15-1) на трассе Краков—Варшава. Иначе го-
Рис. 15-1 воря, положительное влияние ветра на скорость
самолета продолжается короче, чем отрицательное-
Вследствие этого время полета по замкнутой трассе
при ветренной погоде будет дольше, чем при без-
безветренной погоде. При безветренной погоде продол-
продолжительность полета Варшава—Краков такая же как
и полета Краков—Варшава. От этих чисто качест-
268
венных рассуждений, давайте перейдем к вычисле-
вычислениям.
Пусть / — это длина воздушного пути Варшава—
Краков (или Краков—Варшава). Скорость ветра
пусть равняется w, a v — это скорость самолета
в безветренную погоду.
При безветренной погоде время, необходимое на
преодоление расстояния Варшава—Краков—Варша-
Варшава—Краков—Варшава:
Когда дует ветер, тогда скорость самолета с по-
попутным ветром составляет v-\-w, а против ветра —
соответсвенно v—w. Следовательно, время fl5 необ-
необходимое для пролета самолета при наличии ветра,
составит:
l
1 v+w v—w v2—w2 v2—w2
Разделив числитель и знаменатель дроби (II) на
v получим:
h = -^г- (Ш)
Знаменатель дроби (III) меньше знаменателя дроби
(I)» так как w2/v > 0.
Вследствие этого ^ > t.
269
Пример: Пусть I = 500 км, v = 400 м\сек, w = 25 м/сек
Тогда:
2 ¦ 500 000 м
25 • 25 \
400- 400 \м\сек
= 250938 сек
1000000-400
4-100-4-100-25 -25
сек —
Напраблёние бепра
Варшаёа
Рис. 15-2
2 • 500 000 м
t — —грт\—-, = 2500 сек
400 м/сек
Следовательно ft > /, при этом ft — t — 9,8 сек.
А теперь давайте предположим, что ветер дует пер-
перпендикулярно трассе полета Варшава—Краков—Вар-
Варшава—Краков—Варшава. Помогает ли он при этом или'мешает? Дуя
поперек дороги, ветер сносит самолет с трассы,
а тем самым мешает полету.
Давайте рассмотрим этот случай более подробно.
Рис. '15-2 иллюстрирует решение этой задачи.
На этом рисунке отрезок Варшава—Краков пред-
представляет трассу полета. Вектор v = АВ обозначает
скорость самолета при безветренной погоде, а век-
вектор w = ВС обозначает скорость ветра.
Результирующим вектором векторов v и w является
вектор АС = vw. Вследствие влияния ветра, само-
самолет не будет лететь по прямой в Краков, его будет
сносить вправо на определенный угол /?. Абсолют-
Абсолютная величина его скорости vw будет, правда, больше,
чем v, но самолет будет сходить с правильного курса.
Чтобы лететь на Краков летчик вынужден будет
270
взять курс влево, под определенным углом а. Угол
этот должен быть выбран таким образом, чтобы ре-
результирующий вектор векторов АЕ и DE {АЕ = АВ;
ED — ВС) был направлен на Краков. Из чертежа
мы видим, что этим вектором, является вектор
vp = AD, этот вектор меньше вектора АВ (AD <
< АВ).
Вывод: Боковой ветер уменьшает скорость са-
самолета. Из треугольника AED имеем sin а = —,
а из треугольника ABC получим tg/? = —, а из этого
sina = tg/?, значит a < /?.
Это означает, что самолет должен лететь под углом
большим, чем угол, на какой его сносит ветер.
Давайте рассчитаем еще дополнительно «вредное
влияние» ветра.
При безветренной погоде время полета самолета на
трассе Варшава—Краков—Варшава составляет t =
11
= —. При дующем боковом ветре время полета
составит:
2/ 2/ t
*
1 АЕ acosoc cosa
Следовательно:
ti—t = t — t\ 1 = A— cosa) =
cosa \cosa / cosa v '
a
It sin2 ~Y I \
= >0 1—cosa = 2sin2^-
cosa \ 2/
271
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
так как из неравенства 0 < а. < -у, следует, что
cos a > 0.
Примечание: Можно сказать, что при ветре,
дующем равномерно с постоянной скоростью, само-
самолет ведет себя так, как моторная лодка, пересека-
пересекающая прямолинейное русло реки nog прямым углом.
Двукратное эхо
На расстоянии 1 км от каменного карьера нахо-
находится пляж. Ежедневно, примерно в полдень, слы-
слышен взрыв, производимый в каменеломне для полу-
получения строительного камня. Когда я нахожусь во
время взрыва в городе, то слышу его один раз.
Однако, когда я в это время нахожусь на пляже
и купаюсь, то звук взрыва я могу услышать дважды.
Момент взрыва я могу всегда определить точно,
так1 как с пляжа видно облако пыли, образующееся
в момент взрыва.
Почему когда я нахожусь в городе, то слышу взрыв
один раз, а на пляже — дважды ?
272
Вода и лед
В цилиндрический стакан с площадью основания
равной 18 см2 налита вода, а туда опущен кубик
льда с гранью 3 см. Лед плавает на поверхности
ч
воды, а уровень воды устанавливается на высоте
7 см над дном стакана. Какова будет высота уровня
воды, когда лед полностью растопится?
Примечание: Не следует принимать во вни-
внимание очень незначительных изменений уровня,
вызванных изменением температуры воды и льда.
Тем, кто предполагает, что это им потребуется, мы
напоминаем, что удельный вес льда равен примерно
0,9 г/см3.
Какова емкость бутыли?
Бутыль наполнена серной кислотой (H2SO4) и весит
б = 19,34 кг. Эта же бутыль, наполненная керо-
керосином, весит q — 9,1 кг. Какова емкость бутыли
и сколько она весит пустая, если удельный вес
серной кислоты D = 1,834 г 1см3, а керосина d =
= 0,81 г/см3.
Какая была температура?
Один из учеников ежедневно обязан был перед на-
началом занятий измерять температуру в классе и запи-
записывать ее в специальный журнал. Случайно так
оказалось, что температура с 15 до 25 мая возрастала
ежедневно на 0,5 °С. Средняя температура за этот
период составила 18,25°С. Какая была температура
17 мая?
273
Рис. 15-3
Приводной ремень
Механизм приводится в движение с помощью двух
пар ременных шкивов (рис. 15-3).
Шкив К1 делает 50 оборотов за то же время, за
которое шкив КА делает 450 оборотов.
Каково соотношение радиусов этих шкивов ?
Скорость езды
Сколько секунд я должен вращать педали велоси-
велосипеда, чтобы провернуть их столько раз, сколько
составляет моя скорость, подсчитанная в км/ч?
Четыре снаряда
Из четырех углов квадратного поля со стороной
20 км одновременно выстрелено 4 снаряда, самона-
самонаводящихся на цель, как это показано на рис. 15-4.
Во время полета каждый из них поворачивает
вправо, постоянно стремясь попасть в снаряд, на-
находящийся перед ним, до того момента, когда все
четыре снаряда встретятся в центре квадрата. Если
скорость всех четырех снарядов одинакова и состав-
составляет 1 км[сек, то как долго они будут лететь до ко-
конечной точки взаимного попадания?
274
Два пловца
Были ли вы когда-нибудь на соревнованиях по
плаванию? Видели ли вы когда-либо плавательный
бассейн ?
Так вот послушайте.
Два пловца А к В тренируются на соседних дорож-
дорожках. Пловцы стартуют одновременно и плывут с не-
неодинаковой, но постоянной скоростью, А обгоняет
В и, доплыв до конца бассейна, возвращается. На
обратном пути он встречает В на расстоянии 5 м
от конца бассейна, плывет дальше, доплывает до
места старта, поворачивает и снова плывет. Плывя,
он снова встречает В (не обгоняет, а встречает) на
расстоянии одной пятой длины бассейна от места
старта.
Какова длина бассейна ?
is*
275
РЕШЕНИЕ ЗАДАЧ Двукратное эхо
Когда я купаюсь, то могу слышать взрыв дважды,
раз, когда, например, плывя кролем, нахожусь
под водой, а второй раз — когда выныриваю, так
как скорость распространения звука в воде и воз-
воздухе разная.
Вода и лед
Уровень воды не изменится. Архимед доказал бы
это без расчетов. Действительно, лед плавает по-
потому, что его вес уравновешен силой выталкивания,
которая равняется весу вытесненной воды. Это
значит, что вес кубика льда равен весу воды, объем
которой равен части льда, погруженной в воду.
Когда лед растает, то вода, образовавшаяся изо
льда, займет объем, который занимала до этого
часть льда, погруженная в воду. Следовательно,
уровень воды в стакане не изменится.
Какова емкость бутыли?
1) Объем бутыли
Q-q A9,34-9,10) кг _ t з _ ц
У - D~d ~ A,834-0,81) кг/дм* ~ ш ом ~шл
2) Масса бутыли
М = Q-DV= 19,34 «гг—1,834 кг/л • 10 л = 1 кг
276
Какая была температура?
Ученик записывал температуру в течение 10 дней.
Если температуру в первый день обозначим через а,
то в следующих днях температура будет соответ-
соответственно равняться:
д+0,5; а+1; а+1,5; а+2; ... а+4,5
г
Сложив эти температуры (т. е. рассчитав сумму
10 первых членов арифметической прогрессии) с раз-
разностью прогрессии 0,5 и первым членом а, полу-
получим число 10а+22,5 . Следовательно, —— ' =
= 18,25, из этого следует, что а = 16.
Значит 17 мая термометр показывал 17°С.
Приводной ремень
Пусть диаметры шкивов К1 и К2 будут равны 2R
и 2г, а их соотношение 2R:2r = х. Тогда R = гх,
а из этого следует, что число оборотов шкива Кг
х раз больше числа оборотов шкива К^. За время,
когда шкив Ki сделает 50 оборотов, шкив К2 сде-
сделает 50х оборотов. Столько же E0х) оборотов сде-
сделает шкив К3. Соотношение радиусов шкивов К3
и К4 также равняется х, следовательно шкив КА
делает х раз больше оборотов, чем шкив К3, т. е.
Б0х-х = 50х2. Следовательно 50х2 = 450, т. е.х = 3.
Радиусы шкивов Kt и К3 в 3 раза больше, чем шки-
шкивов К2 и КА.
277
Скорость езды
Пусть к обозначает число полных оборотов педалью,
это одновременно и скорость в км/ч
р — величина соотношения числа зубьев переднего
и заднего зубчатых колес (передачи),
а — окружность заднего колеса в м,
t — искомое время в сек.
Если я поверну педаль к раз, то заднее колесо по-
повернется кр раз, а путь, пройденный за это время,
составит а кр метров.
Средняя скорость на этом участке будет составлять:
кра ,
v = —— м/сек
при этом она должна равняться числу оборотов
педалью, т. е. скорости, высчитанной в км/час, т. е.
кра. , , ,
—^м/сек =^кг км/ч
Переписав это уравнение в одинаковых единицах
измерения A км = 1000 м, 1 ч = 60 • 60 сек),
получим:
кра -60-60 _ ,
ПбОО '
а из этого t = 3,6 pa.
Пример: Переднее зубчатое колесо имеет 46 зу-
зубьев, заднее — 18, следовательно:
278
Окружность накачанного колеса составляет
а = 2,18 м
Из этого t = 3,6 • 2,55 • 2,18 = 20,01
Следовательно, когда я еду на велосипеде, то дол-
должен считать число оборотов педалью в течение
20 сек. Это число оборотов как раз и будет равняться
скорости езды в данный момент в км/ч.
Четыре снаряда
Математическое решение требует составления диф-
дифференциального уравнения, но можно эту задачу ре-
решить также и путем рассуждения. Следует вообра-
вообразить себе, что 4 снаряда во время полета находятся
постоянно в четырех углах квадратного поля, кото-
которое, однако, уменьшается и вращается по ходу ча-
часовой стрелки. Затем необходимо забыть о вращении
и рассматривать только уменьшение квадрата. Так
как снаряды нацеплены один на другой, их путь про-
проходит постоянно вдоль стороны уменьшающегося
квадрата в направлении снаряда, находящегося в со-
соседнем углу. Таким образом, скорость уменьшения
стороны квадрата равняется скорости снаряда, т. е.
составляет 1 км/сек. Начальное расстояние составляет
20 км, следовательно, до столкновения снаряды бу-
будут лететь 20 сек.
279
Два пловца
Пусть бассейн имеет х м длины. С момента старта
до первой встречи пловец А проплыл (х+5) м, а В
проплыл (х—5) м. Разность между этими расстоя-
расстояниями составляет (х+5)—(х—5) = 10 м. Момент
первой встречи можно рассматривать, как момент
вторичного старта. Следовательно, при следующей
встрече пловец А снова проплывет на 10 м больше.
Следовательно, пятая часть длины бассейна состав-
составляет 10 л, а длина всего бассейна равна 50 м.
СКОЛЬКО ВЕСИТ
СТАНИСЛАВ
ГЛАВА 16
Прежде, чем ответить на этот вопрос, необходимо
сказать несколько слов на тему метрологии. Ее
основная задача — установление единиц измерения,
воспроизведение их в виде эталонов и разработка
методов точных измерений.
До конца XIX века метрология занималась описа-
описанием различного вида мер. Описывались меры дли-
длины, площади, объема, массы, времени, стоимости
и т. п.
Благодаря введению единой системы мер, современ-
современная метрология уже не занимается ни описанием
различных, сегодня уже устаревших национальных
единиц измерений, ни установлением их соотношений.
Этими вопросами занимается ныне историческая мет-
метрология.
Современная метрология — зто отрасль физики,
науки, в которой на первый план выдвинулись иссле-
исследования, базирующиеся на экспериментах, нужда-
нуждающихся в измерениях очень высокой точности. Поэ-
Поэтому пределы метрологии значительно расширились.
Кроме классических единиц длины, площади, объема
и т. п. метрология устанавливает теперь также ме-
механические, тепловые, электрические, магнитные,
световые и многие другие виды единиц изме-
измерений.
281
Взвешивание является очень существенным разде-
разделом метрологии. Так как мы должны ответить на
поставленный вопрос: «Сколько весит Станис-
Станислав ?» — то, прежде всего, нам необходимо позна-
познакомиться с краткой историей основного прибора,
используемого для взвешивания, с историей весов
Весы являются одним из наиболее древних измери-
измерительных приборов. Рисунки весов в виде равнопле-
чевого рычага мы находим уже на памятниках еги-
египетской и вавилонской культур (свыше 3000 до н. э.)
Также и в Древней Греции использовались весы,
основанные на принципе равноплечьего рычага
Первыми, кто использовал в конструкции вест;
принцип неравноплечьего рычага, были арабы. На
этом принципе были сконструированы так называе-
называемые безмены, которые имеют на одном плече ры-
рычага нанесенную шкалу, по которой перемещается
гиря. Безмены были широко распространены в Рим-
Римском государстве.
В 1670 году были сконструированы стальные весы
с чашками, расположенными над плечами рычага.
Знаменитый математик Л. Эйлер разработал науч-
научную теорию весов A738). В 1818 году были скон-
сконструированы первые десятичные весы, а в 1831 го-
году— первые сотенные весы A:100).
Во второй половине XIX века было начато произ-
производство очень чувствительных весов для целей нау-
науки, а также автоматических и пружинных весов
282
Одновременно были разработаны методы точного
взвешивания.
Взвешивание может базироваться на различных за-
законах физики, например, на законе Архимеда об
уменьшении веса тела, погруженного в воду, на ве-
величину, равную весу вытесненной телом воды (гид-
(гидростатические весы, ареометр); на законе Гука об
удлинении пружины, пропорциональном действу-
действующей на нее силе (пружинные весы); на законе
равновесия рычага и на многих других.
Очень чувствительные и точные метрологические
весы, за показаниями которых наблюдают из спе-
специального отдельного помещения (чтобы избежать
влияния на показания весов со стороны лица, вы-
выполняющего взвешивание), предназначены для про-
проверки точности гирь, используемых в технике, науч-
научных лабораториях и некоторых отраслях торговли.
На этих весах можно взвешивать массу до 1 кг, при-
причем их верность достигает 0,002 мг.
Для взвешивания драгоценных камней и субстан-
субстанций для точного химического анализа используются
специальные аналитические весы. На этих весах
можно взвешивать массу, не превышающую 200 г.
Когда требуется чрезвычайно точное взвешивание
небольших масс, используются микроаналитические
весы. Максимальная допустимая для взвешивания
на этих весах масса — 20 г.
А теперь мы можем возвратиться к нашему вопросу
и попытаться ответить, сколько же весит «Станис-
283
КОРЕЦ, ЛОКОТЬ И ФУТ
лав». На очень чувствительных и точных аналити-
аналитических весах был взвешен лист чистой бумаги, затеч
на этом листочке написали обычными чернилами имя
«Станислав» и снова взвесили. Оказалось, что бу-
бумажка с именем Станислав весит больше на 0,3 мг,
чем та же бумажка без надписи. Следовательно,
«Станислав» весит 0,3 мг. Принимая, что первая
строчная буква С весит вдвое больше прописной
буквы, можем сказать, что десять прописных букв
весят приблизительно 0,3 мг, а следовательно, одна
буква весит 0,03 мг.
Точка — знак препинания — весит примерно 0,0015
мг, а геометрическая точка ничего не весит, так как
она не имеет размеров.
Корец, локоть, фут и пядь — это старые единицы
измерения. Как следует из этих названий, они заим-
заимствованы частично из названий частей человеческого
тела.
Не только наш язык, но и другие языки мира сви-
свидетельствуют, что первоначально в качестве мер ис-
использовались натуральные размеры человеческого
тела: польское слово «stopa», английское «foot»>
немецкое «fuss» и французское «pied», которые все
обозначают ступню, лучшее этого доказательство.
То же самое можно сказать и о названии «локоть»?
его эквиваленты на старофранцузском языке «aul-
284
пе», датском «я/и», немецком «е//е», итальянском
«braccio» обозначают локоть и всегда использова-
использовались в качестве единиц измерений.
«Не отдадим ни пяди родной земли» — этот призыв
хорошо известен всем нам. Однако, такие единицы
измерений вызывали немало трудностей, ибо и лок-
локти бывают разные и пядь пяди не равна. Согласно
преданию праэталоном французской «ступни» была
ступня императора Карла Великого, а эталоном анг-
английского ярда, на древнеанглийском — «gyrd», уста-
установленного английским королем Генрихом I в 1101
году, была длина его руки, измеренная до конца
среднего пальца.
Предание гласит, что в Польше длину «ступни» уста-
устанавливали таким образом: в праздничный день, ког-
когда крестьяне выходили после богослужения из ко-
костела, устанавливали гуськом 30 человек, таким об-
образом, чтобы ступня касалась ступни, измеряли это
расстояние, а затем делили его на 30. Так получа-
получалась «средняя ступня».
Что касается локтя, то не только почти каждый го-
город имел свою меру, но даже разные материалы ме-
мерились разными, специально для этого предназна-
предназначенными мерами, локтем одной длины мерили, на-
например, полотно, другим локтем сукно, а еще иным —
парчу. Недаром ведь говорили «Покажи, каким лок-
локтем меришь?».
Корец был мерой сыпучих тел (объема). Прежде, чем
он стал названием меры, это было просто название
285
обычного сосуда. Хотя корец был хорошо известен
во всей Польше, его объем не был точно определен.
Делили его на 4 четверти, как гарнец делили на
4 кварты.
В законах, установленных польским королем Влади-
Владиславом Ягелло в 1420 году, имеется указ для воевод,
чтобы они ежегодно в определенный день устана-
устанавливали меры ржи, сукна и других товаров «со-
«согласно издавна принятым обычаям».
В конституции Петрковского Сейма (при Сигизмун-
де II Августе) от 1565 года имеется «Указ о мерах
и весах», являющийся попыткой провести унифи-
унификацию мер. В этом документе записано: «... Мы по-
повелели уже по всему нашему краю установить еди-
единый вес.
Локоть единый для измерения всяческих товаров по
всей Короне устанавливается и коронным именуется,
а быть ему в согласии с краковской нынешней мерой.
Корец же по справедливости быть по всей Короне
должен единым, каковым он есть в главнейшем го-
городе одного воеводства либо земли».
Попытки унифицировать единицы меры и веса про-
продолжались почти два века. В 1764 году при Стани-
Станиславе Августе коронная Скарбовая комиссия по по-
поручению конвокационного Сейма составила «Уста-
«Установление генеральной меры», ссылаясь на «Указ
о мерах и весах» от 1565 года, а Сейм в том же год}'
утвердил это постановление. На основании его были
ликвидированы все локти, гарнцы, полугарнцы.
286
кварты и т. д. и установлена единая генеральная ра-
тушная варшавская мера, обязательная для всей Поль-
Польши. Кроме того, в Указе был также описан метод
измерения с помощью корца.
Великая французская революция опрокинула тра-
традиционный порядок и полностью реформировала
систему мер и весов. Вместо семидневной недели
была введена декада A0 дней), летоисчисление ве-
велось от первого года революции, а не от рождения
Христова, изменены были названия месяцев; вместо
футов, локтей и корцев был введен метр — одна
десятимиллионная часть четверти парижского ге-
географического меридиана, т. е. «мера» (метрон — по
гречески обозначает меру), базирующаяся на посто-
постоянной величине, на длине меридиана. Мерой объема
стала производная десятой части метра — кубический
дециметр (литр), а тысяча литров воды образовала
тонну — единицу веса.
В годы всех этих преобразований Польша пережила
катастрофу — потеряла свою независимость. Пора-
Поработители поделили ее на части и по своему усмотре-
усмотрению хозяйничали на отторгнутых землях, устанавли-
устанавливая там свои меры и веса.
На землях, находившихся под властью России, а точ-
точнее говоря, в Королевстве Польском, Королевское
общество друзей науки под предводительством Ста-
Станислава Сташица разработало новую систему мер
и весов. Традиции было воздано должное, сохра-
сохранены вековые названия мер и весов, а также их
287
ФАЛЬШИВАЯ МОНЕТА
взаимные отношения: корец и его деление, локоть
и его деление на 24 дюйма. Но Сташиц базировал
новопольские меры на метрических мерах. Итак, но
инициативе Сташица, было установлено, что ново-
новопольский дюйм будет равняться точно 24 мм, а ново-
новопольская кварта будет содержать точно один литр.
Эта реформа Сташица защитила Королевство Поль-
Польское от аршинов, саженей и четвериков.
Господин X получил некоторое число золотых ду-
дукатов. Однако, он узнал, что среди этих дукатов
имеется один фальшивый и что этот фальшивый
дукат чуть легче настоящих. У господина X есть
весы, с помощью которых он надеется обнаружить
фальшивую монету, но у него нет гирь. Каким обра-
образом он может обнаружить фальшивую монету, про-
произведя минимальное число взвешиваний?
Всякий раз при взвешивании необходимо на каждую
тарелку весов класть одинаковое число монет. Мо-
Монеты мы делим на три части: А, В а С. Группы Аи В
должны содержать одинаковое число монет.
При взвешивании следует положить на одну тарелку
группу А, а на другую тарелку группу В монет.
Это взвешивание может иметь два исхода:
1. Группы А и В имеют разный вес. Тогда в той из
групп, которая легче, находится фальшивая монета.
2. Обе группы весят одинаково. Следовательно,
фальшивая монета находится в группе С.
288
Если общее число монет, скажем, два или три, то
для обнаружения фальшивой монеты будет достаточ-
достаточно одного взвешивания. При 4 монетах может ока-
оказаться необходимым выполнить уже два взвешива-
взвешивания. Действительно, ведь независимо от того, какова
численность групп А и В (по одной монете или по
две), после нахождения группы с фальшивой мо-
монетой (если эта группа состоит из двух монет) она
обнаружится при втором взвешивании. Теперь уже
можно сформулировать вопрос, сколько самое боль-
большое может быть монет, чтобы было достаточно вы-
выполнить два взвепишания для обнаружения фальши-
фальшивого дуката?
Так как исход первого взвешивания неизвестен, то
необходимо чтобы после первого его выполнения
возникло положение, при котором во втором взве-
взвешивании может быть найден результат. Следователь
но, должны быть соблюдены два условия:
1. Группа С может содержать максимум 3 монеты,
так как, если окажется после первого взвешивания,
что фальшивая монета в группе С, то при втором
взвешивании можно обнаружить фальшивую мо-
монету максимум при наличии трех монет в группе.
2. Группы А и В должны по той же причине такж**
содержать максимум по 3 монеты.
Итак, доказано, что 9 монет это максимальное число,
при котором можно обнаружить фальшивую монету
в два взвешивания.
289
АНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Любителям такого рода размышлений предоставляем
возможность доказать, что трех взвешиваний доста-
достаточно, чтобы обнаружить фальшивую монету из числа
максимум 27 штук. Обобщая можно доказать, что
п взвешиваний достаточно для того, чтобы обнару-
обнаружить фальшивую монету (более легкую или более
тяжелую) из максимум числа 3 л монет.
Задачу нахождения фальшивой монеты можно зна-
значительно усложнить, если принять, что неизвестно
какая это монета — более легкая или же более тя-
тяжелая, или же, что число фальшивых монет неиз-
неизвестно; можно также усложнить задачу введением
дополнительной оговорки, что неизвестно, исправны
ли весы, на которых взвешиваются монеты.
Девять шариков
У вас девять шариков для пинг-понга. Один из них
тяжелее остальных. Необходимо с помощью двух
взвешиваний на рычажных весах без гирь найти,
который из шариков тяжелее.
290
Задача о 12 дукатах
Используя рычажные весы, но без гирь, с помощью
трехкратного взвешивания найти из 12 дукатов один
фальшивый, который очень незначительно отли-
чается весом от настоящих. Мы не знаем, тяжелее
фальшивый дукат или же легче настоящих.
Эта задача не столь проста. Нам бы, однако, хоте-
хотелось, чтобы каждый из вас решил ее самостоятельно,
а поэтому мы даем вам лишь некоторые предваритель-
предварительные указания:
1. обозначим отдельные настоящие дукаты буква-
буквами Д, а буквой Ф — фальшивый,
2. прежде всего, разделим все дукаты на три группы
по 4 дуката в каждой,
3. берем две произвольные группы и кладем их на
тарелку весов. Третья группа остается на столе. При
взвешивании возможны три случая:
а) ДДДД = ДДДД обе тарелки в равновесии, сле-
следовательно, фальшивый дукат находится в третьей
группе, на столе,
б) ДДДД > ДДДД левая тарелка тяжелее,
в) ДДДД < ДДДД правая тарелка тяжелее,
в обоих (б и в) этих случаях фальшивый дукат на-
находится на тарелках весов, а на столе лежат насто-
настоящие дукаты.
Все три случая необходимо тщательно проанализи-
проанализировать. Это проделаете вы, уважаемый читатель,
в вашем распоряжении остались два взвешивания.
Существует облегченный вариант этой задачи: мы
знаем, что фальшивый дукат тяжелее настоящих.
Попробуйте сначала решить облегченный вариант
задачи, а потом займитесь более сложным.
291
Десять вопросов
Если на заданные здесь десять вопросов вы ответи-
ответите правильно в течение 8 минут, то у вас очень хоро-
хорошая арифметическая смекалка, если вы ответите
в течение 10 минут — то можете считать^ что ваши
арифметические способности хорошие. Если же вам
потребуется 10 минут для того, чтобы ответить лишь
на шесть вопросов — то ваши арифметические спо-
способности можно признать лишь удовлетворительны-
удовлетворительными. Итак, берите часы и отвечайте. Отвечать можете
в любой последовательности. А вот вопросы:
1. Сколько разных четырехзначных чисел вы мо-
можете написать, используя для этого цифры 1,2,3,4?
В каждом написанном числе должны выступать все
четыре цифры.
2. Число 12 можно разделить на 2, 3, 4, 6 частей.
На сколько долей необходимо разделить 12, чтобы
произведение этих долей было самым большим чис-
числом?
3. 1 кг яблок, 1 кг слив и 1 кг помидоров стоят вме-
вместе 4 руб.; 2 кг яблок, 1 кг слив и 1 кг помидоров
стоят 4 руб. 80 коп.; 1 кг яблок, 2 кг слив и 1 кг по-
помидоров стоят 5 руб. 20 коп. Сколько стоит 1 кг яб-
яблок, сколько 1 кг слив, а сколько 1 кг помидоров?
4. Напишите число, которое содержит 22 тысячи,
22 сотни и 22 единицы.
292
РЕШЕНИЕ ЗАДАЧ
5. В одной школе имеется шесть классов. В I, II
и III классе вместе взятых 120 учеников. ВIV классе
на 8 учеников меньше, чем в III, в V классе на 10
учеников больше, чем в I, а в VI классе на 2 ученика
больше, чем во И. Сколько всего учеников в школе?
6. Сумма каких чисел больше: от 1 до 11 включитель-
включительно или от 11 до 15 включительно?
7. Разность двух положительных чисел составляет 1,
а их сумма равняется 6. Назовите эти числа.
8. Используя цифры 2 и 3 и математические знаки,
напишите 10 положительных чисел, в которых встре-
встречаются только эти две цифры.
9. В какой системе исчислений 100 обозначает 25?
10. Произведение трех последовательных натураль-
натуральных чисел равняется 120, произведение крайних
чисел — равняется 24. Укажите эти числа.
Девять шариков
9 шариков делим на три группы по 3 шарика в каж-
каждой. На левую тарелку кладем первую группу, а на
правую вторую. Может быть два исхода:
1. Обе группы весят одинаково. Значит более тяже-
тяжелый шарик находится в третьей группе, на столе.
Снимаем первые две группы с весов, а на каждую
293
тарелку весов кладем по одному шарику из третьей
группы. Третий шарик третьей группы остается на
столе. Если теперь одна из тарелок опускается вниз,
то значит, на ней находится более тяжелый шарик.
Если обе тарелки уравновешиваются, то искомый
более тяжелый шарик остался на столе.
2. Группы не уравновешиваются. Тогда, конечно,
не подлежит сомнению, что более тяжелый шарик
находится на тарелке, которая перевешивает. Берем
из этой группы два шарика и кладем их по одному
на тарелки весов. Если тарелки уравновешены, то
более тяжелый шарик остался на столе.
Задача о 12 дукатах
Как уже упоминалось в условиях задачи возможны
3 случая:
I ДДДД=ДДДД
II ДДДД > ДДДД
III ДДДД < ДДДД
Начинаем с исследования первого возможного слу-
случая, когда, как мы установили, фальшивый дукат
остался в третьей группе, и лежит на столе. В этом
случае поступаем следующим образом:
1. На левую тарелку кладем любых три настоящих
дуката, на правую тарелку любых три дуката из
третьей группы (это второе взвешивание);
294
2. Если теперь снова ДДД = ДДД, то фальшивый
дукат остался на столе (это четвертый дукат
из третьей группы);
3. Обнаруженный фальшивый дукат кладем на пра-
правую тарелку, а на левую любой настоящий (третье
взвешивание). Если левая тарелка идет вверх, зна-
значит Ф тяжелее Д, если вниз — значит Ф легче Д.
Если после второго взвешивания окажется, что
ДДД ф ДДД, то на правой тарелке находится фаль-
фальшивый дукат, при этом возможны два случая:
а) ДДД > ДДД и
б) ДДД < ДДД
Если ДДД > ДДД, т. е. в случае а), то это значит,
что Ф легче, чем Д. Чтобы обнаружить этот более
легкий фальшивый дукат, берем любые два дуката
из группы, содержащей Ф, и кладем их по одному
на тарелки весов. При этом возможны два исхода:
обе тарелки уравновешиваются — следовательно
фальшивая монета осталась на столе, одна иэ монет
весит меньше — это и есть фальшивый дукат.
В случае б), т. е. если ДДД < ДДД, фальшивый
дукат тяжелее настоящего. Метод проверки тот же,
что и в случае а) с тем, конечно, что при третьем
взвешивании фальшивый дукат лежит на тарелке,
которая перетягивает.
Таким образом мы проверили все возможные ком-
комбинации первого случая.
Теперь перейдем к исследованию второго возмож-
возможного случая (согласно условиям):
295
II) ДДДД > ДДДД
Следовательно, фальшивый дукат находится на та-
тарелках весов, а на столе в третьей группе остались
хорошие дукаты.
Так как дальнейший ход рассуждений довольно-таки
запутанный, введем следующие обозначения:
дукаты, которые находились при первом взвешива-
взвешивании на левой тарелке, обозначим соответственно:
Ди Да. Дз, Да
дукаты, которые находились при первом взвешива-
взвешивании на правой тарелке, соответственно:
Д5, Дб> Дп, Дг
дукаты (настоящие), которые остались на столе при
первом взвешивании, будем по-прежнему обозна-
обозначать просто буквой Д.
Затем проводим второе взвешивание: кладем на ле-
левую тарелку дукаты Д1У Д2, Дз> Дьу а на правую
Дь и ДДД, (т. е. три настоящих дуката из группы,
которая до этого лежала на столе).
При этом взвешивании возможны три исхода:
а) Д^ДгДъДь = ДаДДД
б) Д,Д2ДзД5 > Д*ДДД
в) ДгДгДъД* < Д*ДДД
При первом а) исходе Ф находится на столе в группе
Д6Д7Да и следовательно Ф легче Д. При третьем
296
взвешивании исследуем группу ДвДпДъ следующим
образом: кладем на тарелки Д6 и Д7, при этом, если
Д6 = Д7, то Ф = Д8, если Д6 > Д7, то Ф = Д7,
если Д6 < Д7, то Ф = Д6.
При исходе б) рассуждаем следующим образом: так
как ДгД2Д3Дя > Д*ДДД, то дукаты Д6Д7Да насто-
настоящие; Д* также настоящая монета, так как в против-
противном случае Д*ДДД было бы тяжелее, чем Д^ДгДъДь
вспомним, что при первом взвешивании Д4 был
в более тяжелой группе. Так как Д5 при первом
взвешивании был в более легкой группе, то он так-
также не оказывает влияния на неравенство Д\ДгДгДъ>
> Д*ДДД. Следовательно, Д5 также настоящая мо-
монета, а Ф находится в, группе ДуДгДы тем самым
мы установили, что Ф тяжелее Д. При третьем взве-
взвешивании мы сравниваем Д1 с Д2, если при этом
Дх = Д2, то Ф = Д3, если Дх > Д2, то Ф = Д1У
а если Д1 < Д2, то Ф = Д2.
Исход в). Так как ДхДгДгДъ < Д*ДДД> то дукаты
Д6Д1Дъ — настоящие. Дукаты Д1Д2Д3 должны так-
также быть настоящими, так как при первом взвешива-
взвешивании они были в более тяжелой группе вместе с Д*,
а теперь оказались в более легкой группе, следова-
следовательно, сами по себе они не оказывают никакого вли-
влияния на неравенство веса. Следовательно, Ф это
либо более легкий дукат Д5, либо более тяжелый
Д*, что несложно обнаружить путем третьего взве-
взвешивания с любым хорошим дукатом.
297
Таким образом, исчерпаны полностью все возмож-
возможные исходы второго случая. Остается выполнить
анализ третьего случая, при котором ДДДД <
< ДДДД, однако, этот анализ, как сами читатели
догадались, аналогичен только что проделанному
и поэтому мы оставляем его выполнение читателям,
как увлекательное логическое упражнение.
Десять вопросов
1. Столько, сколько составляет произведение
1-2-3 • 4 = 24.
2. На четыре части, так как самым большим произ-
произведением будет 3 ¦ 3 • 3 • 3 = 81.
3. 1 кг яблок стоит 80 коп., слив — 1 руб. 20 коп.,
помидоров — 2 руб.
4. 24 222.
5. 244, так как в IV, V и VI классах на 4 ученика
A0+2—8) больше, чем в I, II и III классах.
6. Сумма от 1 до 11, т. е. 66, больше суммы от 11 до
15, равной 65.
7. Вот пара таких чисел: 3,5 и 2,5.
8. 23; 32; 2,3; 3,2; 2/3; 3/2; 23; З2; |/2; \/Т.
9. В пятиричной системе счислений:
100E)= 1 .Б^О-БЧО -5° = 25.
10. 4; 5; 6.
О СРАВНЕНИИ глава 17
Целые числа, дающие одинаковые остатки при их
делении на тот же делитель, называемый модулем,
принято называть сравнимыми по модулю. Из выше-
вышесказанного следует, что разность двух сравнимых по
модулю чисел делится без остатка на модуль.
Итак, например, числа 9 и 17 сравнимы по модулю
4, так как и 9 и 17 при делении на 4 дают в остатке 1.
Это записывается с помощью математических знаков
следующим образом:
9 = 17 (mod 4)
Аналогично числа 7 и 2 сравнимы по модулю 5:
7 s 2 (mod 5)
так как 7—2 делится без остатка на 5.
Такие числа называются иногда также равнооста-
точными. В качестве модулей могут использоваться
только натуральные числа, да и вообще о сравнимо-
сравнимости по модулю можно говорить только в отношении
целых чисел.
Числа а и Ъ, сравнимые по модулю т, записываем
в общем виде следующим образом:
а = Ъ (mod m)
Сейчас мы займемся выяснением некоторых свойств
сравнений:
299
1) Каждое число а сравнимо с самим собой по произ-
произвольному модулю, т. е. а = a (mod /я).
2) Если а = с (mod т), и Ъ = с (mod /и), то а = Ъ
(mod /я), например: 9 = 5 (mod 4)
и 13 = 5 (mod 4), то 9 = 13 (mod 4).
3) Сравнивая с общим модулем можно почленно
складывать (или вычитать): 23 = 3 (mod 5);
9 s 24 (mod 5), следовательно 32 = 27 (mod 5).
4) К каждой части фавнения можно прибавить (или
отнять от нее) любое число, кратное модуля, напри-
например: 19 = 7 (mod 4), если теперь добавим к обеим
частям по 4 • 3 = 12, то получим: 31 = 19 (mod 4).
5) Сравнение можно почленно перемножать и воз-
возводить в степень, например: 9 = 5 (mod 4),следова-
4),следовательно:
а) 90 = 50 (mod 4) — обе стороны умножены на 10.
6) 81 г 25 (mod 4) — обе стороны возведены в квад-
квадрат.
На основе всех вышеперечисленных свойств срав-
сравнений можно доказать, что число 2256—I при де-
делении на 7 дает в остатке 1.
Мы имеем:
23 (т. е. 8) s I (mod 7)
B3)8S в 18S (mod 7), т. е. 225S = 1 (mod 7)
теперь, умножая обе части этого сравнения на 2, по-
получим:
2256 = 2 (mod 7)
300
затем из обоих частей сравнения вычитаем единицу:
ДЕЛИМОСТЬ* ЧИСЕЛ
из этого сравнения следует, что число 22S6—\ при
делении на 7 дает в остатке единицу.
Признаки делимости чисел всем нам хорошо извест-
известны из начальной школы. Это верно, однако, мы ни-
никогда не ассоциировали этих знакомых нам правил
с какими-либо интересными явлениями нашей жиз-
жизни. А таких явлений не мало.
Чтобы поговорить об этом давайте прежде вспом-
вспомним, каковы признаки делимости чисел на числа от
2 до 15. Вот они:
на 2 делятся все четные числа, например, 272,380,...;
на 3 делятся все числа, сумма цифр которых делится
на 3, например: 2817, так как сумма 2+8+1+7 = 18
делится на 3;
на 4 делятся числа, двухциферное окончание кото-
которых делится на 4, например: 268, так как 68 делится
на 4;
на 5 делятся числа, оканчивающиеся на 0 или 5;
на 6 делятся числа, которые делятся на 3 и на 2;
на 8 делятся числа, трехциферное окончание которых
делится на 8, например: 8720 делится на 8 так как
число 720 делится на 8; вообще говоря на число 2"
делятся такие числа, у которых и последних цифр
образуют число, делимое на 2";
301
на 9 делятся числа, сумма цифр которых делится
на 9, например: 2817 делится на 9, так как 2+8 +1 ~
+7 = 18 делится на 9;
на 10 делятся числа, оканчивающиеся на 0;
на 12 делятся числа, которые обладают одновременно
признаками делимости на 4 и 3;
на 14 делятся числа, которые обладают одновременно
признаками делимости на 7 и на 2;
на 15 делятся числа, которые одновременно обладают
признаками делимости на 3 и на 5.
Как вы заметили, мы пропустили — вполне созна-
сознательно — признаки делимости на 7, 11 и 13, которые
далеко не столь просты, как все здесь перечислен-
перечисленные и, практически говоря, значительно проще про-
проверить вычислением делимость заданного числа на 7,
11 или 13, чем воспользоваться этими признаками.
Однако, знание этих признаков делимости позволит
нам решить не одну задачу, которую без этого не-
нелегко было бы решить.
Признак делимости на 7 связан с понятием сравни-
сравнимости чисел.
Если два числа а и Ъ имеют одинаковые остатки
приделении на т, то говорят, что а и Ъ срав-
сравнимы по модулю т или, иначе говоря, сравнение
а = Ъ (mod m) имеет место в том и только в том
случае, если разность а—Ъ делится на т.
Например: 26 и 12 сравнимы по модулю 7 так как
26—12 = 14, а 14 делится на 7, иначе говоря, 26: 7
и 12: 7 имеют одинаковый остаток.
302
Каждое многозначное число может быть представ-
представлено в виде многочлена, упорядоченного по степе-
степеням числа 10, например
426 738 = 4 • 105+2 • 104+6 • 103+7 ¦ 102+3 • 101 +
+8 • 10°
Давайте теперь рассмотрим сравнимость отдельных
степеней числа 10 по модулю 7.
10° = 1 (mod 7), так как 1-1 = 0,
а 0 делится на 7;
101 = 3 (mod 7), так как 10-3 = 7,
а 7 делится на 7;
102 = 2 (mod 7), так как 100-2 = 98,
а 98 делится на 7;
103 з 6 (mod 7), так как 1000-6 = 994,
а 994 делится на 7.
Аналогично можно доказать, что
10* з 4 (mod 7);
10s = 5 (mod 7).
Исследуя дальнейшие степени числа 10, мы убедимся,
что дальше будет постоянно повторятся этот же ряд
чисел: 1, 3,2, 6, 4, 5, например:
106 з 1 (mod 7);
107 = 3 (mod 7);
108 = 2 (mod 7) и т. д.
Этот ряд называется характерным рядом модуля 7.
303
Иначе этот ряд можно представить следующим об-
образом
108 107 10б 10s 10* 103 102 101 10° = 1
2 3 15 4 6 2 3 1
Теперь используя свойства сравнения, мы можем
приступить к определению признака делимости чи-
чисел на 7. Проделаем это на примере числа 426 738.
Запишем это число в вышеуказанной форме много-
многочлена, упорядоченного согласно степеней числа де-
десять, а под каждым членом запишем число, сравни-
сравнимое с ним по модулю 10:
4 • 105+2 • 10*+6 • 103+7 ¦ 102+3 • 10^8 • 10° =
= 426 738
4 • 5+2 • 4+6 • 6+7 • 2+3 • 3+8 • 1 = 20+8+36+
+14+9+8 = 95
Следовательно, 426 738 = 95 (mod 7), а так как 95 не
делится на 7, то и наше число не делится на 7 (оста-
(остаток от деления числа 426 738 на 7 равен остатку от
деления 95 на 7, т. е. 4).
Возьмем следующий пример, необходимо проверить
делится ли число 1 620 941 на 7.
1 • 106+6 • 105+2 • 10*+0 • 103+9 • 102+4 • 10* +
1 • 10° = 1 620 941
1 . 1+б • 5+2 • 4+0 • 6+9 • 2+4 • 3+1 • 1 = 70
Так как 70 делится на 7 без остатка, то и число
1 620 941 делится на 7.
304
го
Таким образом, чтобы узнать, делится ли натураль-
натуральное число на 7, нужно справа налево подписать под
цифрами этого числа коэффициенты характерного
ряда модуля 7.
...2, 3, 1, 5,4, 6,2, 3, 1
Затем умножить каждую цифру на стоящий под ней
коэффициент и полученные произведения сложить,
если найденная сумма делится на 7, то и данное число
также делится на 7.
Признаки делимости чисел на II и 13 аналогичны.
Чтобы их узнать, необходимо высчитать характер-
характерные ряды. Для 11 этот ряд имеет вид
...,-15+1, -1, +1, -1, +1, -1
а для 13 соответственно:
..., 5, 1, 4, 5, 1, 4, —-J, 1
Давайте проверим, например, делится ли число
80 828 на 11 и 13 (для упрощения запись ведем
в столбиках).
Получим:
8-(-D = -8 8-(+1) = +8
2.(+1) = +2 2-(-3) = -6
8 • (-1) = -8 8 • (-4) = -32
О • (+1) =0 0 • (-1) = ' 0
8 • (-1) = -8 8 ¦ (+3) ^ +24
-22 -6
305
ЧИСЛО ШЕХЕРЕЗАДЫ
Так как —22 делится на 11, а —6 не делится на 13,
мы можем сказать, что взятое нами число делится
на 11, но не делится на 13.
Из характерного ряда модуля 11 выводится более
простой признак делимости на 11, о котором мы рас-
расскажем далее.
Существуюг числа, носящие имена великих матема-
математиков: число Архимеда, или иначе число п = 22/7,
Неперово число, т. е. основание натуральных лога-
логарифмов е = 2,718281. Не умаляя ни в чем достоин-
достоинство этих знаменитых чисел, мы попытаемся здесь
рассказать вам еще об одном числе, правда не так
полезном как те, но — по крайней мере, нам так ка-
кажется — не менее популярном. Это число Шехере-
зады 1001, которое виднеется в заглавии бессмерт-
бессмертных сказок «Тысяча и одна ночь». С точки зрения
математики число 1001 обладает целым рядом инте-
интереснейших свойств:
1) это самое малое натуральное четырехзначное чи-
число, которое можно представить в виде суммы кубов
двух натуральных чисел: 1001 = 103 + 13;
2) число 1001 состоит из 77 злополучных чертовых
дюжин A001 = 77 ¦ 13), из 91 одиннадцаток или из
143 семерок (вспомним, что число 7 считалось маги-
магическим числом); далее, если будем считать, что год
306
20*
равняется 52 неделям, то 1001 ночь состоит
1+1+1/2+1/4 года E2 • 7+52 • 7+26 • 7+13 • 7)
частичная сумма S= 1+1/2+1/4 является частью
довольно часто встречаемого в арифметике беско-
бесконечного ряда 1+1/2+1/4+ ... +1/2"; таким об-
образом мы видим, как в числе Шехерезады литерату-
литература переплетается с математикой;
3) на свойствах числа 1001 базируется метод опреде-
определения делимости числа на 7, на 11 и на 13. Этот ме-
метод мы объясним на примерах.
Пример 1:
Делится ли на 7 число 348 285 ?
Число 348 285 можно представить в следующем ви-
виде:
348 285 = 348 • 1000+285 =
= 348 • 1000+348-348+285 =
= 348 ¦ 1001-C48-285)
Чтобы число 348 285 делилось на 7, достаточно,
чтобы на 7 делилась разность 348—285 (почему?).
Так как 348—285 = 63, а 63 делится на 7 то и 348 625
также делится на 7.
Пример 2:
Делится ли на 7 число 946 988 875 ?
Запишем данное число в виде:
946 988 • 1000+946 988-946 988+875 =
= 946 988 • 1001-(946 988-875)
307
ЛЮБОПЫТНЫЕ ЧИСЛА
Согласно нашему правилу, 946 988 875 делится на 7,
если на 7 делится разность 946 988—875 = 946 113.
946 113 = 946 • 1000+946-946+113 =
= 946-1001-(946-ИЗ)
а так как 946—113 = 833 делится без остатка на 7,
то на 7 делится число 946 113; следовательно, и за-
заданное нам число 946 988 875 делится на 7.
Из этого вытекает правило: для того, чтобы узнать,
делится ли на 7 (на 11 и на 13) заданное число, не-
необходимо от этого числа без последних трех цифр
вычесть число, образованное последними тремя чи-
числами, если эта разность делится на 7 A1 или 13), то
заданное число также делится на 7 A1 или 13).
Обратите внимание на числа 11 и 12 A1 = 10+1;
12 = 10+2)
102-l2
103+l3
10*—1*
105+l5
106-16
107+Г
10a-ls
делится на
» зз
» 33
ЗУ 33
3} 33
33 33
33 ЭЭ
и
и
и
11
и
и
и
ю2
103
10*
10*
106
ю7
и т
-22
+23
-2*
+2*
—26
+27
¦ д.
делится на
» S3
33 З.Л
33 33
33 33
УЗ 33
12
12
12
12
12
12
и т.д.
Объясните, почему?
Обратите внимание на остаток, который получается
при делении степеней числа 10 на эти числа. Особен-
308
ПРИЗНАК ДЕЛИМОСТИ
НА 11
но при делении на 11, так как это позволит вам по-
понять еще одну головоломку: почему, если мы к ка-
какому-либо числу припишем с правой стороны число,
содержащее те же цифры, но в обратном порядке,
то мы всегда получим число, которое делится на 11.
Например, к числу 68 дописываем 86, получаем 6886,
которое делится на 11, к числу 136 дописываем 631,
получаем 136631, которое делится на 11.
Указание: для того, чтобы доказать, что числа
6886 и 136 631 делятся на 11, их необходимо разде-
разделить справа налево на группы по 2 цифры в каждой,
затем необходимо принять во внимание остатки от
деления каждой группы на 11.
Делятся ли на 11 числа: 61 974, 38 148, 30 316, 3025?
Ответ: для того, чтобы число делилось на 11, необ-
необходимо и достаточно, чтобы разность между суммой
его цифр, стоящих на нечетных местах (считая спра-
справа налево), и суммой цифр, стоящих на четных ме-
местах, делилась на 11.
Например: 61 974; D+9+6)-G+1) = 19-8 = И.
Следовательно, 61 974 делится на 11.
Возьмем другое число: 30 316; F+3+3)—@+1) =
= 11, следовательно, 30 316 делится на 11. Испро-
Испробуем число 3025; @+5)— B+3) = 0. Следователь-
Следовательно, 3025 делится на 11.
309
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Этот признак делимости был уже известен арабскому
математику ал-Кархи (XI век), но в современной фор-
форме он был сформулирован впервые французским ма-
математиком Ж. Л. Лагранжем A736—1813).
Под которым деревом находится клад?
Некий миллионер-чудак оставил после своей смерти
такое завещание:
«В моем саду растет 6 фруктовых деревьев: 1 — че-
черешня, 2 — груша, 3 — яблоня, 4 —¦ орех, 5 — сли-
слива, 6 — вишня. Под одним из этих деревьев я зарыл
клад. Чтобы его найти необходимо считать от 1 до
10 004 последовательно называя: черешня — 1, гру-
груша — 2, яблоня — 3, орех — 4, слива — 5, вишня —
6, слива — 7, орех — 8, яблоня — 9, груша — 10,
черешня — 11, груша—12, яблоня — 13, орех —
14, слива — 15, вишня — 16, слива — 17 и т. д. Клад
зарыт под деревом, при котором будет названо число
10 004».
Конечно, только очень наивный человек стал бы
ходить от дерева к дереву и последовательно назы-
называть числа. Умный человек быстро выполнил бы
необходимый расчет, а затем фазу же направился бы
к нужному дереву, под которым находится клад.
310
Четыре загадки
Решение этих загадок основано на вышеупомянутых
признаках делимости.
1. Напишите произвольное шестизначное число, ко-
которое не делится на 7, например, 431 576 (остаток 5);
это число можно также записать следующим образом:
431 576 = 5 (mod 7). Напишите шесть других шести-
шестизначных чисел, которые делятся на 7, и которые
состоят только из цифр данного числа (числа могут
повторяться).
2. Один ваш знакомый имеет больше 9 лет, но меньше
100 (например, 58 лет). Напишите его возрост три раза
рядом друг с другом и у Вас получится шестизначное
число (например, 585 858). Докажите, что это число
делится на 7.
3. Напишите самое меньшее число, которое, разде-
разделенное на 2, 3, 4, 5, 6, 7, 8, 9 и 10 дает соответ-
соответственно в остатке 1, 2, 3, 4, 5, 6, 7, 8, 9.
4. Какой остаток получится, если мы возведем чи-
число 3 в 12 345 678 степень, а затем разделим на 7?
РЕШЕНИЕ ЗАДАЧ
Под которым деревом находится клад?
Клад зарыт под орехом.
Каждый расчетный цикл: 1, 2, 3, 4, 5, 6, 5, 4, 3, 2,
1,2, ... содержит 10 чисел. 10 004: 10 = 1000 ци-
кла+4. Четвертое дерево — это орех.
311
Четыре загадки
1. Так как 431 576 = 5 (mod 7), то
431 576-5 = 431 571 делится на 7.
После этого вступления напишем следующую таб-
таблицу:
4 3 1 5 7 Л
4 3 1 5 В 6
4 3 1 С 7 6
4 3 D 5 7 6
4 ? 1 5 7 6
F 3 1 5 7 6
Вместо букв А, В, С, D, E, F необходимо поставить
такие цифры, чтобы полученное число делилось на 7.
Мы уже знаем, что вместо буквы А необходимо по-
поставить единицу. Теперь необходимо сравнить число
71 со стоящим под ним числом 2?6. Разделив 71 на 7
получаем остаток 1. Чтобы получить такой же оста-
остаток при делении числа ВЬ на 7, вместо В необходимо
поставить цифру 3. Теперь мы уже знаем, что второе
искомое число —¦ это 431 536. Записываем это число
под числом 431 571. Ищем третье число. Над Cl
стоит число 53. Число 53, разделенное на 7, дает
в остатке 5. Чтобы С1 при делении на 7 дало тоже
в остатке 4, вместо С необходимо поставить 6. Полу-
Получаем третье искомое число: 431 676.
Поступая аналогично мы найдем, что D = 6; Е = 7
и F= 3.
312
Таким образом искомые цифры:
4 3 15 7 1
4 3 15 3 6
4 3 16 7 6
4 3 6 5 7 6
4 7 15 7 6
3 3 15 7 6
2. Каждое шестизначное число N можно предста-
представить в виде N = 1000а+6, где а и Ъ — это трех-
трехзначные числа, обозначающие тысячи и единицы.
Это равенство можно записать еще иначе, а именно:
ЮООа+Ь = lWla-a+b = 1001а- (а-Ь)
Пусть теперь возраст вашего друга будет представлен
числом ху, тогда а = хух, Ъ = уху. Использовав для
чисел хух, уху коэффициенты характерного ряда
для модуля, 7 получим:
х 1 ¦ х у 1 • у
у 3 • у х 3 ¦ х
х 2•х у 2 -у
Зх+Зу Зх+Зу
а—Ъ — (Зх+Зу)— (Зу+Зх) = 0, следовательно раз-
разность а—Ъ делится на 7, а как мы помним, если
в числе 1001а— (а—Ь), второй член, т. е. (а—Ь) де-
делится на 7 то делится на 7 и все число, что и требо-
требовалось доказать.
3. Заметим, что в соответствии с условиями задачи
искомое число при делении на 2, 3, 4, 5, 6, 7, 8, 9,10
313
должно давать в остатке делитель уменьшенный на
единицу. Следовательно, искомое число равняется
самому меньшему общему кратному чисел 2, 3, 4, 5,
6, 7, 8, 9, 10 уменьшенному на единицу, т. е.
23-32-5 -7-1 =2519
4. Остаток 1. Доказательство:
36 = 729, 729:7= 104+1.
Запишите это следующим образом: З6 s I (mod 7).
Обе части сравнения возводим в степень:
12 345 678:6 = 2 057 613
Получим: (З6J057613 = 12057613 (mod 7);
или З12345678 = 1 (mod 7);
следовательно, 312 345 678 при делении на 7 дает оста-
остаток 1.
ОБ АЛГЕБРЕ глава 18
Алгебра — очень важный и крупный раздел матема-
математики, который выделился из арифметики.
Есть несколько уровней алгебры: самый низкий, это
так называемая элементарная алгебра, являющаяся
предметом обучения в средней школе. Разработка
алгебры в этом объеме полностью закончилась в XVII
веке. Алгебра на более высоком уровне стала пред-
предметом изучения в XVIII и XIX веках. Она препо-
преподается в высших учебных заведениях. Наконец, су-
существует еще, так называемая, абстрактная алгебра.
Нас, однако, интересует алгебра на первом уровне.
Ее предметом являются, кроме четырех основных
арифметических действий (сложения, вычитания,
умножения и деления), также и такие действия, ко-
которые можно считать дополнением арифметических
действий: возведение в степень, извлечение корня,
логарифмирование.
Кроме хорошо известных из арифметики (натураль-
(натуральных и дробных) чисел, алгебра рассматривает и та-
такие числа, которые не используются в арифметике,
например, относительные, иррациональные и ком-
комплексные числа типа т-\-\ — п (т и я это действи-
действительные числа, п 5? 0), которые должны были быть
созданы, ибо элементарная алгебра занимается, в ос-
315
яовном, решением уравнений, которые не всегда
можно бы было решить, без этих чисел.
Характерной чертой алгебры является также и то,
что для обозначения чисел она применяет буквы:
а, Ь, с, d, ...,x, yt z, ..., А, В, С, ..., X, Y, Z, и
пользуется значительно более богатой символикой,
чем арифметика, которая использует только четыре
знака действий, знак равенства и скобки.
Символизация алгебры продолжалась несколько сто-
столетий. В основном, этому способствовали Виет
A540—1603), Декарт A596—1650) и Ньютон A643—
1727). Первоначально алгебра была полностью рито-
риторической, все писалось словами, не использовались
никакие символы, даже для обозначений четырех
арифметических действий. Затем наступил период
так называемой синкопированной алгебры, когда
некоторые, наиболее часто встречаемые понятия, вы-
выражались в виде сокращений соответствующих слов,
например, вместо слова «сложить» писали букву/?,
а вместо «вычесть» — букву т (это начальные бу-
буквы соответствующих латинских слов plus — сло-
сложить и minus •— вычесть). Символическая алгебра
приобрела современную форму лишь в начале XVIII
века.
После того, как математики упорядочили символи-
символику, они занялись решением уравнений третьей, чет-
четвертой, пятой степеней и т. д. (поэтому очень долго
считали, что предметом алгебры является состав-
составление и решение уравнений). Вскоре были, однако,
316
МЕТАМОРФОЗА
СИМВОЛИКИ
УРАВНЕНИЙ
|к. ПРОТЯЖЕНИИ ВЕКОВ
найдены общие решения третьей и четвертой сте-
степеней и доказано, что для уравнений пятой и выс-
высших степеней, такие общие решения не существуют.
Несмотря на это, поиски универсальной формулы,
позволяющей решать уравнения произвольной сте-
степени, продолжались. Такую формулу «вывел», на-
например, польский математик Гене-Вронский A778—
1853), однако,, она оказалась неправильной.
Так выглядели первые уравнения, составленные че-
человеком. На рис. 18-1 мы видим фрагмент папируса
Ахмеса (по Ф. Кайори), а на рис. 18-2 мы видим
уравнение Диофанта, относящееся к IV веку нашей
эры.
А вот примеры эволюции алгебраической символики
на протяжении XV—Х\11 веков:
1. Уравнение 16л:2+2000 = 680х в транскрипции
Региомонтана A436—1476) известного математика,
астронома и астролога, было записано таким образом:
16 census et 2000 aequales 680 rebus
nnn
A
Рис. 18-1
317
26х3 + 6х - 26х2 = 7х - х
2
Рис. 18-2
х2 - 4х - 4
Census — обозначает квадрат неизвестного. Это еще
полностью реторическая запись, без символов.
2. Уравнение х3+6х = 20 в транскрипции извест-
известного итальянского математика и философа Джиро-
ламо Кар дано A501—1576) имеет вид:
cubus p 6 rebus aequantur 20
cubus — обозначает куб неизвестного, р — знак +j
6 rebus — шесть неизвестных, aequantur — равня-
равняется.
3. Уравнение х3—8х2+16х = 40 в транскрипций
Виета A540—1603) имеет следующий вид:
lC'-8Q+16Naequ. 40
при этом: С" = cubus = x3; Q = х2; N— это не-
неизвестное, т. е. х.
4. Уравнение x3jrpx+q — 0 Декарт записывает
в следующем виде:
x3+px+q ~ 0
318
в этой записи знак ~ соответствует нашему знаку
равенства.
Алгебраическая запись Ньютона уже тождественна
нашей.
К этому нам еще остается добавить, что английские
математики XVII века Рекорд, Гарриот и Отред
ввели в математику знаки =, < и >, а также х —
в качестве знака умножения. Вот сколь длительным
и кропотливым был путь, пройденный алгеброй,
прежде, чем она приобрела свою современную, столь
стройную, символику.
Но достижения математики XVII века не ограничи-
ограничиваются только алгеброй. В этом столетии математику
обогатили два крупнейших открытия: Декарт раз-
разработал аналитическую геометрию, а Лейбниц одно-
одновременно с Ньютоном создал дифференциальное
исчисление. Об этих крупных открытиях мы вам
расскажем более подробно в одной из дальнейших
глав. Здесь мы лишь ограничимся утверждением,
что, как разработка аналитической геометрии, так
и создание дифференциального исчисления являют-
являются для математики целой эпохой; Декарт своей ана-
аналитической геометрией направил геометрические ис-
исследования на совершенно новые пути, отличные
от методов Евклида, а дифференциальное исчис-
исчисление ликвидировало установленный еще Аристо-
Аристотелем раздел величин на дискретные и непрерыв-
непрерывные, а тем самым сделало возможным использование
математики для исследований явлений природы,
319
ОБ АЛГОРИТМЕ
чем в громадной степени расширило область ее
практического применения.
Алгоритм — это схема формальных действий, с по-
помощью которых обычными механическими вычисле-
вычислениями можно найти решение всех задач определен-
определенного типа.
Примером алгоритма является, например, схема
действий, которые необходимо выполнить для нахо-
нахождения наибольшего общего делителя для двух
натуральных чисел а и b (так называемый алгоритм
Евклида) или алгоритм, с помощью которого опре-
определяем корни уравнения типа
ах2+Ьх+с = 0; а ф 0, т. е.
_ -Ь± \/b2-4ac
4.2
A)
Вполне понятно, что уравнений типа ах2-\-Ьх+с = 0
имеется неограниченное количество, однако, реше-
решение каждого из этих уравнений можно найти, вы-
выполняя соответствующие действия согласно предпи-
предписаниям алгоритма A) в следующей последователь-
последовательности:
1. Возвести в квадрат число Ъ.
2. Из квадрата числа Ъ вычесть четыре произве-
произведения числа а на число с.
320
3. Из разности b2— 4ac извлечь квадратный ко-
корень.
4. Полученный результат сложить с числом, противо-
противоположным числу Ъ (или, что то же самое, из полу-
полученного результата вычесть число Ь).
5. Результат последнего действия разделить на удво-
удвоенное число а.
Алгоритм должен быть представлен в такой форме,
чтобы его предписания можно было передать для
выполнения любому лицу, чтобы этих предписаний
(операций) было конечное число и чтобы выполне-
выполнение отдельных операций, предписанных алгоритмом,
не зависело от воли выполняющего эти операции
и являлось определенным процессом, который в лю-
любую минуту может быть повторен и выполнен
кем-либо другим.
Алгоритм решает все задачи того же типа. Неко-
Некоторые вопросы считаются в математике решен-
решенными, если разработан алгоритм, на основании ко-
которого можно их решить. Разработка таких алго-
алгоритмов — это задача математики. Разделы матема-
математики (да и не только математики), в которых поль-
пользуемся алгоритмами, довольно многочисленны.
Доказано, что алгоритмы могут быть составлены
так, что для их выполнения достаточно четырех
действий арифметики. Особенно существенным свой-
свойством алгоритма является то, что его предписания
может выполнять автоматически даже лицо, которое
не понимает существа решаемой задачи. От исполни-
321
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
теля предписаний алгоритма требуется лишь, чтобы
он выполнял эти элементарные, самые простые,
операции, на которые распадается весь вычисли-
вычислительный процесс. Следовательно, предписания алго-
алгоритма может выполнять и машина. Так и бывает
в действительности.
Здесь необходимо заметить, что все процессы, ко-
которые реализуются в электронно-вычислительных
машинах, в принципе аналогичны тем, которые вы-
выполняет без машины счетовод.
Для своих расчетов счетовод использует цифры,
буквы и другие символы, которые он записывает на
листе бумаги. Машины таких символов не исполь-
используют, но заменяют их разными, отличающимися
друг от друга физическими состояниями, например,
электрическими напряжениями.
Торопящийся господин
Один всегда торопящийся господин подымался по
двигающемуся вверх экскалатору со скоростью
1 ступенька в секунду. При таком «ускорении»
движения вверх, этот господин, проделав 20 ша-
шагов, был уже наверху. Однажды он особенно спе-
спешил и входил по ступенькам двигающегося вверх
экскалатора, шагая по две ступеньки в секунду.
Пройдя 32 ступеньки, он оказался наверху экскала-
экскалатора. Сколько ступенек было в экскалаторе.
322
Два брата и Джек
Два брата, жившие на берегу моря, Андрей и Борис,
имели верного друга — собаку Джека, за которой
заботливо ухаживали. Как-то в праздничный день,
братья забрали с собой собаку и пришли к морскому
берегу. На этом участке побережья было три места
| | для купания (назовем их А, В и С), расположенные
м В м С друг от друга на расстоянии АВ = ВС = 50 м (смо-
Рис 18-3 три рис. 18-3).
Мальчики решили испытать верность Джека таким
образом: Андрей вместе с Джеком стали в точке А,
а Борис — в точке В. В тот же самый момент Андрей
и Борис прыгнули в воду и поплыли: Андрей к точ-
точке В, а Борис к точке С. Джек немедленно прыгнул
также в воду и поплыл за Андреем, не теряя, однако,
из виду Бориса. Обогнав Андрея, Джек догнал Бо-
Бориса, дружески его лизнул и немедленно повернул
обратно к Андрею. Так случилось, что на берег
вышли все одновременно: Андрей с Джеком в точ-
точке В, а Борис в точке С.
Какое расстояние (сколько метров) и за какое время
(сколько минут) проплыл Джек от Андрея до Бориса
и обратно до Андрея, желая им доказать, что он
в равной степени им верен и одинаково их любит.
Примечание: Принимаем, что Андрей и Бо-
Борис плыли с одинаковой скоростью и что Джек
плыл быстрее их, но равномерно.
21*
323
РЕШЕНИЕ ЗАДАЧ
Среди автомобилистов
Два автомобилиста отправились одновременно из
местности А в местность В. Оба ехали той же дорогой,
но с разными, хотя и постоянными средними ско-
скоростями, которые выражаются натуральными чис-
числами. Разность скоростей автомобилей — это прос-
простое число. Расстояние от А до В составляет 100 км.
После двух часов езды расстояние от автомобиля,
передвигающегося с меньшей скоростью, до мест-
местности А, было в пять раз больше, чем расстояние,
разделяющее автомобиль, передвигающийся с боль-
большей скоростью, с местностью В.
С какой средней скоростью ехали автомобили?
Четыре четверки
С помощью четырех четверок и знаков алгебраи-
алгебраических действий (+, —, X, :, знака дроби, корня
и т. д.) можно написать очень много натуральных чи-
чисел. Между прочим, можно написать по очереди все
числа от 0 до 100. Предлагаем написать с помощью
четырех четверок числа 13, 43, 50.
Торопящийся господин
Принимаем, что эскалатор состоит из л ступенек
и что v — это скорость ступенек, т. е. число сту-
324
пенек, передвигающихся в течение 1 секунды. Те-
Теперь:
и = 20+20© и и = 32+C2: 2) о
Решая систему этих уравнений первой степени, най-
найдем, что v = 3 ступеньки в секунду и п = 80 сту-
ступенек.
Два брата и Джек
Два упрощения записи обозначим: АВ = ВС = а
(расстояние между местами для купания) и самое
далекое расстояние (от А до Е — в месте, где Джек
догнал Бориса) АЕ = d.
Предположим, что расстояние а Андрей проплыл
за единицу времени. Пусть v — это скорость, с ко-
которой плывет Джек и t —• это время, в течение
которого Джек плыл от точки А до точки Е. Тогда
d = vt, а его обратный путь (как это видно из ри-
рисунка 18-4) ЕВ = d— а. Путь ЕВ можно высчитать
следующим образом: полный путь АЕ+ЕВ Джек
проплыл за единицу времени, следовательно, путь
ЕВ он проплыл за время A—f)> а так как он плыл
со скоростью v mjmuh, то v0.—t) = d—a или
v—vt = vt—a A)
так как: d = vt. За это же время, когда Джек
Рис. 18-4 проплыл до места В, Борис проплыл расстояние at,
следовательно, весь путь Джека, который он про-
проплыл вперед, равен a-\-at.
325
Подставляя в уравнение A) a+at вместо vt, полу-
получим:
v~{a+at) = a+at—а, из этого v = a+2at
Умножая последнее уравнение на t и подставляя
a+at вместо vt, получим:
a+at = at+2at2 т. е. t2 = у; t = j/y
Следовательно, Джек проплыл <^л вперед и (d—d) м
в обратном направлении, итого
2d~a = 2 (a+aO-fl = я+2а' = 50+2 • 50 l/y =
= E0+50 -j/2) = 121 м
в течении стольких минут, сколько потребовалось
Андрею для того, чтобы проплыть от А до В, а Бо-
Борису от В до С.
Среди автомобилистов
Обозначим буквой d расстояние, которое более
быстрый автомобиль проехал в направлении В в те-
течение двух часов. В этом случае его расстояние от
В составляет A00—f/) км, а расстояние от А более
медленного автомобиля составляет A00—d) ¦ 5 =
== 500—5d. Принимая, что скорость более быстрого
автомобиля составляет v км/ч, а менее быстрого
w км/ч, мы можем записать два уравнения:
— = 2 и = 2
V W
326
Из этих уравнений следует, что:
3) 2v = 100-у w
4) w = 250-5»
Теперь разность скоростей автомобилей:
c-w = w-250+5w = 6w-250 = 2Cw-125)
Чтобы число v~w было простьш, разность Cw—125)
должна равняться 1.
Из уравнения 3^—125 = 1 находим v = 42, т. е.
w = 40.
Четыре четверки
43 = -4Д
± т/4
.D) V^
50 = -4-+41- l/4
j/4
Примечание: Символ 4!, который читается
четыре факториал, обозначает произведение
1 -2-3 -4; символ .D) обозначает 0,4444..., т. е. -д-.
О ГЕОМЕТРИИ ГЛАВА 19
Геометрия рассматривает пространственные соот-
соотношения и фигуры (формы) тел; при этом она вы-
выводит свои теоремы, абстрагируя их от конкрет-
конкретных предметов, т. е. она определяет соотношения
между фигурами не в виде соотношений конкрет-
конкретных предметов, а как соотношения абстактных
тел.
Теоремы геометрии Евклида относятся к фигурам
на плоскости и не применимы к телам, например,
они не верны для фигур на сферической поверхности.
В геометрии на поверхности шара «линиями» явля-
являются большие окружности. Они образуют (как пря-
прямые на плоскости) углы, фигуры, площади. Теоре-
Теоремы геометрии на шаре другие, чем теоремы геометрии
на плоскости. Например, длина окружности на шаре
непропорциональна ее радиусу, сумма углов тре-
треугольника — величина непостоянная и больше двух
прямых углов и т. п.
Это наводит на мысль, что Евклидова геометрия
только приблизительно описывает свойства реаль-
реального пространства, например, можно предположить,
что сумма углов очень большого треугольника не
равняется 180°. Подтверждение этой гипотезы мы
находим в общей теории относительности, которая
доказывает, что в космических масштабах простран-
328
ственные соотношения не подчиняются законам Ев-
Евклидовой геометрии.
Евклидово пространство — это такое пространство,
в котором удовлетворяются аксиомы Евклида. С по-
помощью методов аналитической геометрии Евкли-
Евклидово пространство мы обобщаем в такое пространс-
пространство, которое имеет более, чем три размерности, на-
например, четыре, пять, ... л.
Понятие о том, как образуются другие простран-
пространства, можно получить на следующих примерах.
I. Пространство цветов. Каждое восприятие цвета
является суммой трех основных цветов: красного (К),
желтого (Ж) и синего (С). Если концентрацию этих
цветов обозначим соответственно х, у, z, то
цвет = хК+уЖ+zC
Каждая система величин х, у, z, дает нам соответ-
соответствующий цвет, «точку». Из этих «точек» полу-
получаем цветную «линию», а из «линии» — фигуру, по-
поверхность и т. д.
П. Состояние газа в цилиндре под поршнем опре-
определяют : температура Т и давление р газа. Придавая
температуре Т и давлению р разные значения, полу-
получим двухразмерное «пространство состояния газа».
В этом пространстве указьшаются определения «то-
«точек», «линии», «фигур», например, постоянное
изменение состояния газа может быть представлено
«линией», нарисованной в этом пространстве.
329
МЕДОНОСНЫЕ
АРХИТЕКТОРЫ
Современная геометрия исследует также «абстракт-
«абстрактные пространства». Точками абстрактного простран-
пространства могут быть фигуры. Соответствующим образом
определяются пространство прямых, окружностей,
сфер и т. п.
В механике и теории относительности рассматрива-
рассматривается абстрактное четырехмерное пространство, в ко-
котором кроме трех координат введена четвертая —
время.
Базой каждой геометрии является система опреде-
определений, аксиом, начальных понятий. Евклидова гео-
геометрия основывается на немногочисленных опреде-
определениях, аксиомах и начальных понятиях, принятых
Евклидом.
Евклидовы принципы были окончательно упоря-
упорядочены в XIX веке Д. Гильбертом.
Геометрия находит широкое применение в естест-
естественных науках. Картография, кристаллография, гео-
геодезия, астрономия не могли бы существовать без
геометрии.
Строение пчелиных сотов очень давно интересова-
интересовало не только математиков. Занимался им философ'
физик Аристотель (IV век до н. э.), естествовед
Плиний Старший (I век н. э.), физик Реомюр
(XVIII век) и многие математики: Папп (III век);
330
Ян Брожек (XVII век), Кениг, Маклорен, Люйллер
(XVIII век), Лаланд, Браугхам (XIX век) и другие.
Они исследовали архитектуру сотовой ячейки и вос-
восхищались удивительным инстинктом пчел, которые
своим восковым жилищам придали такую форму,
чтобы при минимальном расходе материала (воска)
и затрате труда построить наиболее емкое помещение
и максимально рационально использовать небольшое
пространство улья.
Уже Пифагор заметил, что существует только три
правильных многоугольника, с помощью которых
можно покрыть без пустых мест всю плоскость
вокруг какой-либо точки: равносторонний треуголь-
треугольник, квадрат и правильный шестиугольник (мы
уже об этом упоминали в главе 14). Следовательно,
только одна из этих фигур может быть основой
ячейки, а именно та, которая имеет минимальный
периметр и одновременно максимальную площадь
поверхности. Оказывается, что такими свойствами
обладает правильный шестиугольник. Правда, ок-
окружность с площадью Р имеет еще меньший пери-
периметр, однако, если бы сотовые ячейки имели форму
цилиндров, то осталось бы много неиспользованной
площади, что значительно уменьшило бы общий
полезный объем улья. Поэтому ячейки должны
иметь форму правильной призмы с шестиугольным
основанием.
Второй вопрос — это вопрос, какой формы должна
быть крышка (верхнее основание) этих призм —
331
плоская или какой-либо другой формы. Довольно
сложные вычисления доказывают, что плоская
крышка медовой ячейки не была бы наиболее эко-
экономичной, что более экономичной является крышка,
образованная тремя ромбами с общей вершиной
К (рис. 19-1), расположенной на продолжении оси
00 у rvpw3mbiABCDEFF1A1B1C1D1E1F1 (рис. 19-2).
Следует заметить, что точки, расположенные на про-
продолжении оси ООх, имеют следующее интересное
свойство: 3 плоскости, проложенные через любую
точку К, выбранную на продолжении оси ОО1} и че-
через стороны правильного треугольника B^tFi впи-
вписанного в шестиугольник А^В^С^^Е^^ образуют
новый многогранник с таким же объемом, что и приз-
призма ABCDEFF^iB^CiDtE^. На рисунке 19-2 мы
видим, что одна из таких плоскостей (B^KxDiK) от-
отсекает угловую часть K^BrCxDu но добавляет тре-
треугольную пирамиду KBxDxOi, с равным объемом,
так как оба тела имеют одинаковые основания и оди-
одинаковую высоту. То же самое происходит и с двумя
другими плоскостями, проходящими через точку К
и стороны .Fjt-Di и FtBt правильного треугольника
B1D1F1. Описанные здесь преобразования не изме-
изменяют объема призмы, но изменяют ее поверхность.
Поверхность ячейки будет зависеть от того, где бу-
будет выбрана точка К. Позтому необходимо высчи-
высчитать, на каком расстоянии от точки Ох следует вы-
выбрать точку К, чтобы поверхность сотовой ячейки
была минимальной, и чтобы на ее построение нужно
332
ус
А В
а
к к
было затратить минимальное количество материала
и труда. Обозначив расстояние ОХК через х и вы-
высчитывая площадь трех ромбов, подобных КВ^К^^
и шести граней, подобных K1CDD1 можно составить
формулу для расчета поверхности р ячейки без ниж-
нижнего основания
р = y
• 3 +у а B6-х) • 6
где а — CD — это сторона основания призмы,
Ъ = DD± — это боковая грань.
Разделив обе стороны этого равенства на За и обозна-
обозначив р\Ъа = h, решаем это равенство относительно х.
Исследуя дискриминат зтого уравнения, найдем, что
минимальное значение h, при котором х является
действительным числом, составляет
При этой величине имеем О^К — х = а|/2/4.
А< Поверхность сотовой ячейки (без нижнего основания)
при этом оказывается самой меньшей и равняется
6ab + -
(I)
Рис. 19-3
Модель сотовой ячейки с минимальной поверхно-
поверхностью и развертка этой модели показаны на рис.
19-За и б.
Если бы сотовая ячейка имела сверху плоскую крыш-
крышку, то ее площадь без нижнего основания составляла
бы:
333
6ab + -
(П)
ЛИСТ МЁБИУСА
Рис. 19-4
разница между величиной (II) и (I) составляет:
-|a2(j/J-j/2) « \аг • 0,3 = 0,45а2
т. е. экономия материала (воска) составляет пример-
примерно 2%. Из сэкономленного таким образом на 54 ячей-
ячейках воска пчелы могут соорудить одну дополнитель-
дополнительную пятдесят пятую ячейку.
Математики XVIII и XIX веков, о которых мы упо-
упоминали в начале этой главы, установили, что пчелы,
руководимые удивительным инстинктом, строят кры-
крышки своих ячеек таким образом, что в каждом из
трех ромбов углы имеют всегда по 109°28' и по
70°32' и что именно при таких углах ромбов поверх-
поверхность ячеек минимальная.
Если из стандартного листа бумаги мы вырежем
вдоль его длины полоску шириной 3—4 см и концы
ее склеим, то получим^бумажный обруч. Божья ко-
коровка, ползущая по этому обручу прямо вперед, мо-
может обойти весь обруч и вернуться в место, из кото-
которого вышла (рис. 19-4). При этом божья коровка
обойдет только одну сторону обруча. Если бы она
хотела пройти также и по другой стороне, то она
должна бы была свернуть со своего прямого пути
или ее нужно бы было перенести на другую сторону-
334
Рис. 19-5
ТРИ РАЗА „ИН":
ИНТЕРПОЛЯЦИЯ,
ИНВЕРСИЯ,
ИНВОЛЮЦИЯ
Если мы разрежем такой обруч вдоль пути божьей
коровки, то получим два обруча.
Если бы мы, однако, прежде, чем склеить бумажную
полоску, один из ее концов повернули на 180°
и лишь затем их склеили, как это показано на рис.
19-5, то путь божьей коровки выглядел бы совер-
совершенно иначе. Предлагаем читателю склеить таким
образом полоску бумажки и ответить на следующие
вопросы:
1) вернется ли божья коровка в место, из которого
она вышла, если она будет все время двигаться пря-
прямо вперед;
2) какой путь (сколько сантиметров) должна про-
проползти божья коровка, чтобы вернуться в точку
отправления (длина бумажной полоски 30 см);
3) обойдет ли божья коровка одну или обе стороны
полоски ?
Полоска, склеенная, как это показано на рис. 19-5,
называется листом Мёбиуса; Август Мёбиус A790—
1868), немецкий математик и астроном, считается од-
одним из создателей современной геометрии.
Интерполяция определение промежуточного (при-
(приблизительного) значения определенной функции на
основании двух ее известных значений. Предполо-
335
Рис. 19-6
жим, что мы ищем значение функции sin 20°35', а в
таблицах имеем только
sin 20° = 0,3420 и sin 21 ° = 0,3584
Разность между углами составляет 1° = 60', а раз-
разность между значениями синусов этих углов
0,3584-0,3420 = 0,0164
Из этого следует, что для 35' разность будет соста-
составлять
@,0164: 60) • 35 « 0,0096
Теперь можем высчитать значение
sin 20°35' « 0,3420+0,0096 = 0,3516
Интерполяция базируется на предпосылке, что на
ограниченном участке возрастание функции (в нашем
примере синуса) прямо пропорционально увеличению
независимой переменной (угла).
Инверсия в геометрии обозначает некоторое преоб-
преобразование точек плоскости. Например, инверсия от-
относительно данной окружности с радиусом г и цент-
центром в точке О обозначает такое преобразование точ-
точки, при котором произвольно выбранной точке ЛЛ
отличной от точки О, соответствует такая точка Mi
на прямой ОМ, что ОМ • OMt = г2 (рис. 19-6).
Точку О называем при зтом центром (полюсом) ин-
инверсии, а число г — коэффициентом или степенью иН'
версии.
336
Инверсией мы называем также такое вычисление,
при котором мы выполняем в обратной последова-
последовательности действия, обратные чем это указано в за-
задаче. Поясним это примером:
Нам необходимо решить задачу:
Какое число после удвоения, возведения полученно-
полученного результата в квадрат, и деления этого квадрата на
3 даст в результате число 300?
Если теперь искомое число мы обозначим буквой X,
а число, полученное в результате выполнения всех
действий, указанных в условиях задачи буквой А3
то выполняя действия, обратные указанным в усло-
условиях задачи, и в обратной последовательности мы
придем от числа Х1 к числу X:
300 • 3 = 900
j/900 = 30
30:2 = 15
следовательно, искомое число X равняется 15.
Инволюция — преобразование, повторное применение
которого приводит к исходному положению.
Например, инволюцией является симметрия отно-
относительно любой точки. Если точка М после симмет-
симметричного преобразования преобразуется в М15 то
точка Мх после такого же преобразования преобра-
преобразуется снова в точку М.
То же можно сказать и об инверсии; повторно при-
примененная относительно того же полюса и окружности,
она приводит к исходной точке.
337
ЗАНИМАТЕЛЬНЫЕ Квадрат и прямая
ЗАДАЧИ
Через середину квадрата со стороной равной 1 про-
провести произвольную прямую PR. Рассчитать сумму
квадратов расстояния этой прямой от четырех углоп
квадрата.
Проверьте свою геометрическую смекалку
Нарисуйте правильный шестиугольник, приведите
все возможные диагонали (9) и высчитайте, сколько
при этом образовалось треугольников.
Еще о листе Мёбиуса
Давайте проделаем следующий опыт: разрежем мыс-
мысленно лист Мёбиуса вдоль пути, пройденного божьей
коровкой, и подумаем, что у нас получится:
1) два листа Мёбиуса,
2) один лист Мёбиуса,
3) один лист, но не Мёбиуса, т. е. лист, который не
обладает свойствами листа Мёбиуса?
Затем разрежем мысленно лист, полученный после
первого разреза, еще один раз, в результате у нас
получится... ?
А что получится, если лист Мёбиуса разрезать не
по середине, а в двух местах на расстоянии 1/3 или
1/4 от края?
338
Сколько лет дяде?
— Дядя, сколько тебе лет?
— Два раза столько, сколько лет тете Вале.
— А сколько лет тете Вале?
— В три раза меньше, чем тете Гале.
— А сколько лет тете Гале?
— Тетя Галя на 20 лет старше Нюры.
— Дядя, а сколько лет Нюре?
— Нюра в пять раз старше Ани.
— А сколько лет Ане?
— Не надоедай. Через год ей исполнится шесть лет.
— Дядя, а дядя, я сейчас тебе скажу, сколько тебе
лет.
А и вправду, сколько лет дяде?
Справедливый отец
К Новому году один фермер подарил каждому из
своих детей по столько долларов, сколько каждому
из них исполнилось лет. Всего он подарил 24 доллара,
но при этом он выразил следующее желание:
«Пусть самый младший из вас половину получен-
полученных от меня денег оставит себе, а остальные поровну
разделит между своими братьями. Затем пусть сред-
средний сын половину денег, которые будет иметь оста-
оставит себе, а остальные разделит поровну своим брать-
братьям. Наконец, пусть также поступит самый старший
из вас».
339
В результате такого дележа каждый из братьев по-
получил одинаковое количество долларов.
В каком возрасте были братья?
Кройка в геометрия
На новогодний маскарадный бал одна мама решила
сшить своему маленькому сыну костюм клоуна. Для
этого она купила материал, который сверху был крас-
красного цвета, а снизу — синего.
Чтобы костюм стал пестрым, мама решила вырезать
из материала несколько треугольников и вывернув
их наизнанку, синим цветом вверх, снова вшить
в вырезанные места. Однако, оказалось, что это не
столь просто. Треугольники точно вшивались в ста-
старое место только в том случае, когда они были равно-
равносторонними или равнобедренными. В других случаях
возникали непредвиденные осложнения. После не-
некоторого раздумья мама нашла способ вывернуть
наизнанку все треугольники независимо от того, ка-
какие они имели углы и бока. Можете ли вы объяснить,
как она это сделала?
Модница и поясок
Одна модница попросила свою портниху, чтобы та
переделала ей шелковый поясок, который перестал
быть модным, так как имел наискось срезанные (под
углом 45°) концы и был чересчур широкий.
340
л
2
'Ш.
щ
3
Щ
ш
Рис. 19-7
При этом произошел, примерно, такой разговор:
— Будьте любезны, переделайте мне поясок таким
образом, чтобы его концы были прямые, но чтобы
ничего не обрезать и чтобы немного его сузить.
— Может быть, мы завернем концы пояска таким
образом (смотри рис. 19-7).
— О, нет, при такой закладке поясок будет иметь
разную толщину, в А будет двойная толщина, в В —
тройная, да и затем, я не знаю, как бы вы его сузили
не разрезая.
— Хорошо, я подумаю и сделаю так, как вы хотите,
поясок будет иметь прямоугольные концы, будет
сужен и будет одинаковой толщины по всей своей
длине.
Как портниха переделала поясок?
Рис. 19-8
Недружные соседи
Три хозяина имели три дома на одном огороженном
участке (рис. 19-8). Однако, они жили недружно
и владелец большего дома жаловался, что ему ме-
мешают дети соседей. Чтобы от этого избавиться он
построил для себя огороженную дорожку от своего
дома до средней (в нижнем углу) калитки (А). За-
Затем владелец правого домика также решил отгоро-
отгородиться и построил огороженную дорожку.от своего
дома до левой калитки (В). Вскоре после этого и вла-
владелец домика с левой стороны построил себе ого-
огороженную дорожку до правой калитки (С). Так как
341
все дорожки были огорожены, то они, конечно, не
могли пересекаться. Как были эти дорожки проло-
проложены ?
Не в лоб, так по лбу
Гриша и Миша начали работать одновременно на
двух разных предприятиях, при этом им была наз-
назначена одинаковая заработная плата. Год тому назад
Гриша получил десятипроцентную прибавку, а Ми-
Мише на 10% снизили заработную плату. В этом году
положение изменилось. Грише снизили зарплату на
10%, а Мише повысили на столько же процентов
жалование. Сколько теперь получает каждый из них?
РЕШЕНИЕ ЗАДАЧ
Квадрат и прямая
Мы должны рассчитать AAl+DDf + СС\-+-ВВ\ (смо-
(смотри рис. 19-9). Прямоугольные треугольники ON К
и О ML равны, а из этого следует, что: NK = ML;
DK= BL; AK= CL; AAt = CCX; BBt = DDt; да-
далее проводим диагонали АС и BD и получаел!
Ь.ААХО = ADDiO, а из этого АА} = DtO и
= А}0
Следовательно, искомая сумма равняется:
Рис. 19-9
2 (AAi+DDf) = 2АО2 = 2
= 1
342
Рис. 19-10
Рис. 19-11
Рис. 19-12
Рис. 19-13
Проверь Свою геометрическую смекалку
60 треугольников (смотри рис. 19-10).
Еще о листе Мёбиуса
После того, как лист Мёбиуса будет разрезан по
средней линии (рис. 19-11), по которой ползет божья
коровка, он приобретает вид, как это показано на
рис. 19-12; т.е. он не распадается на два листа,
а образовавшийся лист имеет все свойства листа Мё-
Мёбиуса.
Если мы вторично разрежем лист еще на две поло-
половины вдоль средней линии, то мы получим цепь, об-
образованную двумя звеньями, как это показано, на
рис. 19-13.
Если же мы лист Мёбиуса разрежем не вдоль сред-
средней линии, а на расстоянии 1/3 или 1/4 от края (рис.
19-14), то образуются две переплетенные ленты (рис.
19-15); одна такая, как на рисунке 19-11, а вторая
такая, как на рисунке 19-12.
Сколько лет дяде?
Ане 5 лет.
Нюре 52 = 25 лет.
Тете Гале 25+20 = 45 лет.
Тете Вале 45 : 3 = 15 лет.
Дяде 15 • 2 = 30 лет.
Справедливый отец
В результате раздела каждый из братьев получил
по 8 = B4: 3) долларов.
Прежде чем старший брат разделил половину своих
денег между остальными братьями у него было, сле-
следовательно, 16 долларов. Из них 4 получил средний
брат, а 4 — младший. Следовательно, и у среднего
брата и у младшего было до этого также по 4 доллара
Прежде чем средний брат поделил половину своих
денег, у него было 8 долларов, из которых он затем
два отдал старшему брату и два — младшему. Сле-
Следовательно, до этого у старшего брата было 14 дол-
долларов, а у младшего — 2 доллара. Прежде чем млад-
младший брат разделил половину своих долларов, он
имел 4 доллара, из которых затем один он отдал
старшему, и один среднему брату. Следовательно,
перед этим старший брат имел 13 долларов (получен-
(полученных от отца), средний — 7 долларов, а младший — 4.
Из этого следует, что старшему сыну фермера — 13
лет, среднему — 7, а младшему — 4 года.
344
Рис. 19-16
Рис. 19-17
У
/
к
\
Поя ieped переделкой
Пояс па is переделки
Рис. 19-18
\
L
/
1
\
С
1
0
Кройка и геометрия
Равнобедренный треугольник можно повернуть на
180° и приложить в его первоначальное место так,
что все его стороны будут прилегать к вырезу.
Если ABC — это остроугольный треугольник, то его
можно разделить всегда на три равнобедренных
треугольника с общей вершиной О (рис. 19-16)
в центре описывающей окружности. Каждый из этих
равнобедренных треугольников можно после выво-
выворачивания наизнанку вставить на место, таким об-
образом, что все стороны будут прилегать к краям
выреза.
Так АОАВ будет прилегать к t\OBA, a AOAC
к АОСЛ а т. д., т. е в целом красный треугольник
ABC будет прилегать к вырезу ВАС с синей стороны
материала.
Если же ABC — это треугольник с тупым углом Ь
(рис. 19-17), то его можно разделить на 4 равнобед-
равнобедренных треугольника. Для этого из вершины В опу-
опускаем высоту ВН и определяем точку О (середина
стороны ВС) и точку Oj — середина стороны В А.
Получим 4 треугольника, которые можно вывернуть
наизнанку ОВН, ОСН, О^ВЕ, ОХАН; все эти тре-
треугольники — равнобедренные.
Модница и поясок
После переделки длина пояска составляла KL, а ши-
ширина CD (рис. 19-18).
345
Рис. 19-19
Недружные соседи
На рисунке 19-19 показано, как соседи провели свои
дорожки.
Не в лоб, так по лбу
1. В прошлом году Гриша получил: 1 + ^тг^
первоначальной зарплаты.
2. Миша получил 1 т-у — -^- первоначального жа-
10
лования.
3. В этом году Гриша получил .-^- прошлогодней зар-
9 И 99
платы, т. е. -tq- • ^г = ^.т^ первоначального жаловд-
ния,
11
99
Из этого следует, что и Миша и Гриша получили
в этом году на 1% меньше своего первоначального
оклада.
346
ГЕОМЕТРИЧЕСКИЕ глава 20
СОФИЗМЫ
Рис. 20-1
Рис. 20-2
Очевидно не найдется среди наших читателей того,
кто не знает теоремы Пифагора. Гласит она, что,
если стороны прямоугольного треугольника измере-
измерены одной и той же единицей длины, то квадрат ги-
гипотенузы равен сумме квадратов длин катетов. Име-
Имеется много способов доказать эту теорему — как гео-
геометрических (с помощью рисунка), так и алгебраи-
алгебраических — вычислениями. Один из них, самый про-
простой, приписывают самому Пифагору. Он до того
прост, что достаточно иметь рисунок и сказать:
«смотри» (рис. 20-1).
Но наверное немногие читатели пробовали доказать
обратную теорему: если в треугольнике квадрат од-
одной стороны равен сумме квадратов двух других
сторон, то такой треугольник — прямоугольный.
Доказательств этой теоремы также несколько. А вот
одно из них.
Условие теоремы: в треугольнике ABC со
сторонами а, Ь, с (рис. 20-2) справедливо уравнение
с2 = а2+Ь2.
Утверждение теоремы: угол С — пря-
прямой.
Доказательство. Из условия следует, что
с2-Ь2 =- а2
347
а из этого:
0.
Л
N
Т.
А-
i
Л-
A L Н ?
Рис. 20-3
(c+b) (c-b) = a1;
с+Ъ
0)
На стороне с = АВ откладываем отрезок AD =
= АС = Ъ. Теперь DB = с—Ъ.
Из пропорции A) следует, что треугольники ВВС
и ЕВС (-?2? — общий), подобны, а следовательно:
= A80°-*dD): 2 '= 90°-1/2* CAD =
следовательно:
= 90°
= 90°
Таким образом, верны и прямая и обратная теоремы.
Но вот, однако, доказательство того, что гипотенуза
равна сумме катетов ... (?)
Пусть ДABC (рис. 20-3) будет прямоугольным тре-
треугольником. Для упрощения будем рассматривать
равнобедренный треугольник (АС = СВ = а)
Докажем, что АВ = АС+СВ — 2а
Из рисунка следует, что
АС+СВ = AE+ED+DF+FB = ^ • 4 = 2а или
AH+HI+IK+KD+DS+ST+TR+RB = ~ • 8 или
¦¦¦ = 4- • 16
о
и т. д.
348
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Рис-20-4
Когда число отрезков ломанной, заключенной между
концами An В составит и, то наша формула приобре-
приобретет вид: — • 2и = 2а
п
Но когда и-юо, то ломанная ALMNI... становится
прямой АВ. Следовательно, АВ = 2а. Теперь, воз-
возводя обе стороны последнего равенства в квадрат,
находим, что АВ2 = 4а2, что явно противоречит тео-
теореме Пифагора, на основании которой мы вправе
утверждать, что АВ2 = 2а2.
Где ошибка в наших рассуждениях?
Кансдая окрунсность имеет два центра
Выбираем произвольный угол PRS (рис. 20-4) и две
произвольные точки С и D на сторонах этого угла.
Восстанавливаем перпендикуляр СМ к PR и перпен-
перпендикуляр DM к SR. Эти два перпендикуляра пере-
пересекаются в точке М. Через точки С, М и D описы-
описываем окружность. Эта окружность пересекает сто-
стороны угла в двух точках, которые обозначим А и В.
Точки А и В соединяем с точкой М. Угол ВСМ —
прямой и вписан в окружность, т. е. он должен опи-
опираться на диаметр, этим диаметром является отрезок
ВМ. Но то же самое можно сказать и об угле ADM:
это прямой угол, он вписан в окружность и опирается
на диаметре AM. Из этого следует, что окружность,
проведенная через точки С, М и D, имеет два центра
О и Ох. Найдите ошибку в наших рассуждениях.
349
Каждый треугольник — равнобедренный
Сейчас мы вам докажем, что каждый треугольник —
это равнобедренный треугольник. Найдите ошибку
в нашем доказательстве.
Рисуем треугольник ABC, у которого все стороны
разные (рис. 20-5). В этом треугольнике проводив
биссектрису %.ВАС; а из середины стороны ВС
(точка D) восстанавливаем перпендикуляр (ось сим-
симметрии стороны ВС). Биссектриса %.ВАС и ось chvi-
метрии стороны ВС пересекаются в точке О. Следо-
Следовательно, точка О расположена на равном рассто-
расстоянии от сторон -? ВАС (OF = ОЕ) и от вершин В и С
(ВО = ОС). Из этого следует, что треугольники AFO
и АОЕ равны, так же как и треугольники OBD
и OCD. Из равенства первой пары треугольников
следует, что AF = АЕ, из равенства второй пары
следует равенство треугольников BFO и СОЕ, а ш
этого FB = ЕС. Складывая сторонами эти два ра-
равенства, находим: AF+FB = АЕ-гЕС, т.е. АВ -
АС. Таким образом, мы доказали, что любой тре-
треугольник равнобедренный.
Кредитор и должник
Кредитор, который ехал трамваем, заметил своею
должника, шедшего вдоль трамвайной линии, в на-
направлении противоположном движению трамвая.
Кредитор в течение 10 секунд прошел к выходу ва-
350
гона, выпрыгнул из него и побежал, чтобы догнать
должника. Принимая, что кредитор бежит в два раза
быстрее, чем идет должник, и в пять раз медленнее,
чем двигается трамвай, рассчитайте через сколько
секунд кредитор догонит должника.
РЕШЕНИЕ ЗАДАЧ
Каждая окружность имеет два центра
Ошибка в «доказательстве» заключается в том, что
мы предположили, что окружность, проведенная че-
через точки С, М и D, пересечет стороны угла PRS
в двух точках. При проведении анализа, необходимо
уточнить рис. 20-4: окружность пройдет через вер-
вершину угла R, а тогда О совпадет с О1.
Каждый треугольник — равнобедренный
Ошибка заключается в рис. 20-5. Наши рассуждения
базировались на рисунке, о котором мы не знаем,
правильный он или нет.
Необходимо рассмотреть три вопроса: во-первых,
всегда ли пересекаются ^.ВАС и ось симметрии сто-
стороны ВС, во-вторых, где находится точка О их пе-
пересечения: внутри треугольника ABC или снаружи,
и в-третьих, всегда ли равны стороны А В и АС
сумме отрезков AF и FB и АЕ и ЕС?
На первый вопрос мы можем ответить утвердитель-
утвердительно: в неравнобедренном треугольнике биссектриса
351
Рис. 20-6
Рис. 20-1
и ось симметрии стороны ВС всегда пересе-
пересекаются.
Что касается второго вопроса, где расположена точка
пересечения О, то предположение, что она распо-
расположена вне треугольника ABC (рис. 20-6) также не
позволит нам обнаружить ошибки вJ«доказатель-
вJ«доказательстве», так как и в этом случае АВ = AF+FB и АС —
= АЕ+ЕС, т. е. мы снова приходим к равенству
АВ = АС.
Только на основании анализа рис. 20-7 мы можем
найти нашу ошибку.
Предположим, что вокруг треугольника ABC опи-
описана окружность, которая проходит через точку О
Далее рассмотрим вписанный в эту окружность че-
четырехугольник АВОС. Каждая пара противополож-
противоположных углов этого четырехугольника равняется 180°.
Из этого следует, что либо ?.АВС — острый, а
Ч.АСВ — тупой, либо наоборот. Если ^.АВС— ост-
острый угол, то OF пересечет сторону АВ, а в то же
время ОЕ (%.АСВ — тупой угол) пересечет продол-
продолжение стороны АС. В этом случае АВ = AF+FB, но
АС = АЕ—ЕС. Следовательно, мы установили, что
АВ не равняется АС, а следовательно не каждый
треугольник равнобедренный.
Кредитор и должник
Принимаем, что в течение 1 секунды должник про-
проходит 1 единицу длины. Тем самым в течение 1 се-
352
кунды кредитор пробегал две единицы длины,
а трамвай проезжал 10 единиц длины. В течение 10
секунд, когда кредитор проходил по трамваю, трам-
трамвай проехал 10 • 10 единиц. Из этого следует, что
в момент, когда кредитор выскочил из трамвая, рас-
расстояние между ним и должником составляло 10 • 10+
+ 10 = 110 единиц длины. Так как кредитор за се-
секунду пробегает две единицы длины, а должник
проходит одну, то кредитор догонит последнего через
НО л СЛ
-~—.- секунд, т. е. через 1 минуту 50 секунд.
и
СИММЕТРИЯ
АСИММЕТРИЯ
ГЛАВА 21
Симметрия — слово греческое и обозначает оно ре-
регулярную систему, гармонию между частями целого.
Признаки симметрии мы встречаем в геометрических
фигурах, в неорганической природе (кристаллы),
в растительной! мире, (расположение листьев, ле-
лепестков цветов), в животном мире (расположение
некоторых наружных органов), в строительстве, ис-
искусстве (орнамент, узоры), в рукоделье (кружева,
вышивки), в технике — одним словом везде, потому
что симметрия является структурной необходимо-
необходимостью организмов и устройств.
Что такое симметрия в геометрии — мы знаем и:!
школы, где мы изучали осевую симметрию, цеп-
тральную симметрию (на плоскости) и простран-
пространственную симметрию. Фигура может быть симметрич-
симметричной относительно другой фигуры, а также относитель-
относительно самой себя; может иметь оси, центр и плоскости
симметрии. При наличии в фигуре оси (плоскости)
симметрии, фигура состоит из пар точек, располо-
расположенных на прямых перпендикулярных оси (плоско-
(плоскости) симметрии на равных от нее расстояниях. Если
фигура имеет центр симметрии, то она состоит из пар
точек, расположенных на прямых, проходящих че-
через центр симметрии на одинаковых от него рассто-
расстояниях.
354
Рис. 21-1
У
у
У\
¦
у
-У
У
л
у
У\
У
Рис. 21-2
В целом, ограниченная фигура может иметь несколь-
несколько осей (плоскостей) симметрии, например, квадрат
имеет четыре оси симметрии (рис. 21-1), но только
один (четырехкратный) центр симметрии, в кото-
котором пересекаются все его оси симметрии.
Фигуры, которые такими свойствами не обладают,
называем асимметричными. Некоторые асимметрич-
асимметричные фигуры могут иметь другие интересные свой-
свойства.
Очень существенную роль играет симметрия в кри-
кристаллографии — науке о кристаллах и кристалли-
кристаллическом состоянии материи. Геометрическая кристалло-
кристаллография исследует положение граней кристаллов
и повторяемость одинаковых симметрично распо-
расположенных граней в, так называемых, простых фор-
формах: кубах, четырехгранниках, восьмигранниках,
ромбоидальных двенадцатигранниках, ромбоэдрах и
т. д. (рис. 21-2). Исследуется также повторение оди-
одинаковых элементов симметрии кристаллов: граней,
ребер, вершин возникающее вследствие симметрии
относительно: плоскости симметрии, дающей зер-
зеркальное отражение, оси симметрии, повторяющей
при обороте каждый элемент 2, 3, 4 или 6 раз или
центра симметрии (отражение в точке). Все возмож-
возможные сочетания элементов симметрии образуют 32
кристаллографических класса.
В структуре кристаллов встречаются также в ка-
качестве элементов симметрии плоскости скольжения
(отражение с перемещением) и винтовые оси (враще-
355
Рис. 21-3
Л/Л/А/А/
Рис. 21-4 а, б
ние с перемещением), которые образуют 230 про-
пространственных групп.
Симметрия в биологии заключается в гармоническом
распределении подобных частей тела относительно
определенной точки, относительно прямой (рис
21-3) или относительно плоскости (двухсторонняя
симметрия). Полная симметрия не встречается в жи-
живых организмах. Обычно симметрия отмечается
в общей конфигурации тела и в расположении неко-
некоторых его частей. Наружное строение человеческого
тела — симметрично. Внутреннее — нет (сердце, же-
желудок, печень). Симметрия организмов формирова-
формировалась по ходу их развития вследствие необходимости
приспособиться к условиям жизни и под действием
сил, действующих в среде, в которой развивался
и жил организм.
Исследуя сущность геометрической симметрии в ис-
искусстве, технике, изделиях рукоделья (орнамент,
узоры, кружева, художественные вырезки), можно
различить следующие фазы ее возникновения. Пред-
Представьте себе отрезок ломаной линии (рис. 21-4а)
Любой из отрезков такой ломаной не имеет с точки
зрения симметрии никаких свойств. Но, если этот ри-
рисунок мы повторим несколько раз, на определенном
одинаковом расстоянии один от другого и вдоль
прямой, то получится кайма (рис. 21-46), мотивом
которой будет этот примитивный рисунок ломаной
линии, а способ повторения этого рисунка (мотива)
называется ритмом.
356
Рис. 21-5
Рис. 21-6
Рис. 21-7 Рис 21-8
Прерывные и непрерывные бордюры в виде про-
продольных полос издавна известны и применяются,
например, при окраске стен в жилых помещениях.
Если, однако, какой-либо мотив перемещается рит-
ритмично по всей плоскости стены, то возникает узор.
Другой способ ритмичного повторения мотива за-
заключается в его повороте на определенную долю
полного угла A/4, 1/6, 1/8, ...). Нарисованный на
рис. 21-5 орнамент совмещается при его обороте на
45°, а пятиконечная звезда (рис. 21-6) при повороте
на 72°. Вращательным ритмом перемещений часто
пользуется в своих творениях природа, а также
и техника. В искусстве — перемещения можно на-
наблюдать в розетках, орнаментах, кружевах и т. п.
Наконец, третьим видом ритмичного перемещения
является одновременное линейное перемещение с по-
поворотом вокруг вертикальной оси (рис. 21-7). При-
Примером такого ритмичного перемещения в технике
является ходовой винт судна (рис. 21-8). Получен-
Полученные таким образом бордюры, узоры, розетки и ор-
орнаменты являются уже фигурами, которые могут
быть описаны на основании видов и законов сим-
симметрии.
Возникает вопрос: может ли симметрия быть источ-
источником эстетического удовлетворения, художествен-
художественных восприятий? Безусловно, да. Расширяя понятие
симметрии на цвета, звуки и движения можно, бла-
благодаря ей видеть сущность красоты природы и тво-
творений человеческих рук.
357
ЗАНИМАТЕЛЬНЫЕ Звезда шерифа
ЗАДАЧИ
Красота геометрических фигур издавна привлекала
внимание не только математиков. Их красотой поль-
пользовались, прежде всего, артисты, художники, скуль-
скульпторы и ремесленники. Особенно хорошо известна
красота квадрата, который имеет четыре равные сто-
стороны, четыре равных и прямых угла и четыре оси
симметрии. Равносторонний треугольник в равной
мере используется в искусстве, как и в рукоделье
и ремеслах. Среди многоугольников особую роль
играют звездообразные многоугольники, а, в част-
частности, звездчатый пятиугольник (рис. 21-6) — пен-
пентаграмма — тайный знак пифагорцев (в нынешние
времена — герб многих государств) и шестиконеч-
Рис. 21-9 ная звезда (рис. 21-9), так называемый щит царя
Давида. Тайну успеха пентаграммы математики объяс-
объяснили тем, что все его боковые стороны делятся
взаимно золотым сечением1^.
На рис. 21-10 вы видите звезду шерифа. Ее лучи
образованы 6 равными дугами окружности.
Попробуйте указать:
1) метод ее вычерчивания,
2) длину ее периметра,
Рис. 21-10 3) ее площадь.
') Смотри главу 9.
358
Кривая Коха или „снежинка"
Треугольник То (рис. 21-11) — равносторонний.
Каждую из его сторон мы делим на три равные части.
Среднюю часть каждой стороны заменяем двумя
сторонами равностороннего треугольника и получаем
фигуру 7\ в виде звезды. С фигурой Tt поступаем
аналогично и получаем фигуру Тг. Продолжая по-
поступать таким же образом, получаем фигуру Г3 и т. д.
Предел Т = lim Т„ называется кривой Коха. Мож-
но доказать, что длина /„ ломаной Т„ и ограниченная
ею площадь Р„ равняются:
1 7 1 p
3" ~а"~Уг
P« = Л.-1
Рис. 21-11
где Ро — площадь треугольника То, а а — длина сто-
стороны треугольника То.
Задачи со спичками
1. Составьте 3 равных квадрата из 10 спичек.
2. Составьте 6 равных квадратов из 12 спичек.
3. Составьте 4 равных треугольника из 6 спичек.
4. Составьте 8 прямых углов из 5 спичек.
5. В фигуре, составленной из 12 спичек (рис. 21-12),
передвиньте 4 спички таким образом, чтобы образо-
образовались 3 равных квадрата.
359
Рис. 21-12
Рис. 21-13
Рис. 21-14
L ! I I
L
Рис. 21-15
6. В фигуре, составленной из 24 спичек (рис. 21-13),
передвиньте 8 спичек таким образом, чтобы образо-
образовались 2 равных квадрата.
7. В фигуре, составленной из 12 спичек (рис. 21-14),
передвиньте 3 спички таким образом, чтобы образо-
образовалось 6 равных параллелограммов.
8. Из 63 спичек составлено 4 квадрата (рис. 21-15).
Передвиньте 5 спичек таким образом, чтобы образо-
образовалась фигура, напоминающая спираль.
9. Превратите неравенство на рис. 21-16 в равенство,
передвигая только две спички.
10. На рис. 21-17 вы видите составленные из 12
спичек квадрат и крест. Площадь квадрата состав-
составляет 9 с2, площадь креста — 5 с2. Составьте из 12
спичек фигуру с площадью 4 с2.
11. На рис. 21-18 вы видите правильный десяти-
десятиугольник, составленный из 10 спичек. Передвиньте
спички таким образом, чтобы образовавшийся деся-
десятиугольник имел такие же стороны, но меньшую
площадь.
Рис. 21-17
Рис. 21-18
РЕШЕНИЕ ЗАДАЧ Звезда шерифа
Рис. 21-19
1. Метод вычерчивания звезды шерифа показан на
рис. 21-19.
2. Периметр звезды равняется длине шести дуг
АтВ, т. е.
—,- • 6 = 4тсг
3. Площадь звезды равняется площади окружно-
окружности (izr2) с радиусом г и 6 площадям «углов» звез-
звезды. Площадь «угла» звезды найдем, если из пло-
площади равностороннего треугольника Атп (площадь
г2т/3
треугольника Атп равняется —.—, так как Am = г)
мы вычтем площади трех одинаковых сегментов.
Если из площади окружности (тсг2) вычтем площадь
вписанного правильного шестиугольника о —-¦— и по-
полученный результат разделим на 2, то мы получим
искомую площадь трех сегментов. После выполне-
выполнения всех этих расчетов (после расчета площади од-
одного «угла», затем шести «углов» и сложения с пло-
площадью окружности), получим
Если, например, г = 10 мм, то площадь звезды рав-
равняется 410 мм2, а ее периметр
4-3,14- 10 = \25,6мм
361
Рис. 21-20
Рис. 21-21 а, 6
Задачи со спичками
1-7. Решения — смотри на
рис. 21-20.
8. Перемещенные спички
обозначены на рисунке
B1-21 а, б) штриховой ли-
линией
9. тг = 22/7 (рис. 21-22)
=1Г
VI
Рис. 21-22
10. Прямоугольный треу-
треугольник со сторонами 3, 4-
5 с (длина спички) имеет
площадь 6 с2 (рис. 21-23о)-
Решением является фигура
(рис. 21-236) площадью 4с2.
Рис. 21-23 а, б
362
11. Десятиугольник A1BlC1DlElF1G1H1J1Kl (рис.
21-24) имеет стороны длиной 1 с, но площадь меньше
площади десятиугольника на рис. 21-18 на сумму
площадей 5 параллелограммов JlK1A1P.
Рис 21-24
О НЕЕВКЛИДОВОЙ глава 22
ГЕОМЕТРИИ
Евклид (около 300 г до н.э.)
Человек познает пространство всю свою жизнь.
Непосредственно окружающее нас пространство поз-
познается с помощью наших чувств: зрения и ощущения.
Однако, ограниченные возможности нашего ощуще-
ощущения и зрения позволяют нам познать лишь ограни-
ограниченный отрезок пространства и то лишь в известном
приближении. Свойства этого отрезка пространства,
в котором живет человек, описал Евклид в своем
монументальном труде «Начала». Этот труд изве-
известен нам в школьном изложении под названием
«Геометрия». Читатели знают, как составлены «На-
«Начала» — прежде всего, приведено небольшое число
аксиом — т.е. правд, которые мы принимаем без
доказательства, затем сформулированы первичные
понятия и, наконец, известное число постулатов. Да-
Далее, на основании сформулированных аксиом, по-
постулатов и первичных понятий, выводятся более
сложные теоремы, а из них еще более сложные и так
далее. Так возводится здание науки дедуктивньш
методом.
В системе аксиом, сформулированных Евклидом
в «Началах», имеется одна, которая наделяет осо-
особым свойством наше пространство. Эта аксиома в со-
современной редакции гласит: «Через данную точку,
не лежащую на данной прямой, можно провести не
364
л Лобачевский A792—1856)
более одной прямой, параллельной данной». Многие
ученые и философы предполагали, что эта аксиома
выводится из остальных, т. е., что можно доказать
ее с помощью других аксиом, что они и пытались
осуществить. Начиная с первого века нашей эры,
в каждом столетии было сделано несколько таких
попыток. Последние попытки делались безуспешно
еще в XIX веке. Русский математик Михаил Лоба-
Лобачевский A792—1856IJ выразил эту задачу совершен-
совершенно иначе, так, как до этого никто не пытался посту-
поступить. Лобачевский изменил в принципе содержи-
ние этой аксиомы, не изменяя всех остальных аксиом
и постулатов. Лобачевский принял, что: «через точ-
точку, не лежащую на данной прямой, можно провести,
по крайней мере две прямые, параллельные одной».
На основании таким образом измененной системы
аксиом Лобачевский вывел все теоремы, которые
встречаются в «Началах» Евклида. Так как уда-
удалось вывести все геометрические теоремы Евклида,
нигде не сталкиваясь с противоречием, то Лоба-
Лобачевский пришел к правильному выводу, что аксиома
о параллельной прямой не зависит от других аксиом,
а по сему не может быть выведена на их основании.
Мы написали выше, что Лобачевский вывел все
геометрические теоремы Евклида. Однако, справед-
справедливости ради, необходимо отметить, что это не со-
совсем верно, ибо теоремы Лобачевского не всегда
') А также венгерский математик Я. Больяй A802—1860).
365
сформулированы точно, так как у Евклида. Давайте
сравним некоторые из них:
У Евклида:
1. Через точку, не лежащую
на данной прямой, можно
провести только одну прямую
к ней параллельную и лежа-
лежащую в той же плоскости, что
и данная прямая.
2. В каждом треугольнике
сумма его трех внутренних
углов равняется тс (двум пря-
прямым углам)
3. Подобные треугольники не
обязательно должны быть
равными
4. Два перпендикуляра, вос-
восстановленные к одной из
двух параллельных пересе-
пересекают вторую
5. Если радиус окружности
увеличивается до бесконеч-
бесконечности, то его предел — пря-
прямая
У Лобачевского:
1. Через точку, не лежащую
на данной прямой, можно
провести неограниченное чи-
число прямых, не пересека-
пересекающих данную и лежащих
в той же плоскости, что
и данная, две крайние из их
числа называются прямыми,
параллельными данной
2. В каждом треугольнике
сумма внутренних углов мень-
меньше л и может стремиться
к нулю.
3. Все подобные треугольни-
треугольники равны
4. Два перпендикуляра, вос-
восстановленные к одной из
двух параллельных, не пере-
пересекают второй (расходятся)
5. Предел окружности, Ра"
диус которой увеличивается
до бесконечности, это —¦ не
прямая, а некоторая кривая:
называемая орициклом1).
1) Орицикл — кривая, которая пересекает под прямым утло»1
все прямые пучка параллельных, проходящих через ту ж<^
бесконечно удаленную точку.
366
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
6. Геометрическое место то-
точек, равноудаленных от дан-
данной прямой, является мно-
множеством двух прямых
7. Через три точки, не ле-
лежащие на одной прямой,
можно провести только одну
окружность
8. Длина окружности прямо
пропорциональна ее радиусу
6. Геометрическое место то-
точек, равноудаленных от дан-
данной прямой, — это не пря-
прямая, но некоторая кривая,
называемая эквидистантой1)
7. Через три точки можно
провести либо окружность,
либо орицикл, либо эксидис-
танту, либо прямую
8. Длина окружности не пря-
прямо пропорциональна ее ра-
радиусу, но возрастает быстрее
его.
Логические задачи, как чисто математические задачи,
требуют смекалки, настойчивости, умения найти в за-
задаче такое условие, с помощью которого можно
найти решение. А вот и примеры.
Какого цвета?
Три подруги Аня, Шура и Соня сидели в амфитеатре
одна за другой без беретов. Соне и Шуре нельзя огля-
оглядываться назад. Шура видит только голову сидящей
ниже ее Сони, а Аня видит головы обеих подруг.
г) Эквидистанта — геометрическое место точек, расположен-
расположенных по одну сторону от прямой и на одинаковом от нее рас-
расстоянии. Эквидистанта — иначе равноудаленная.
367
Из коробки, в которой находятся 2 белых и 3 черныч
берета (об этом все три подруги знают), вынули
3 берета и одели их подругам на головы, не говоря
о том, какого цвета берет; два берета неизвестного
цвета остались в коробке. Когда спросили Аню о цве-
цвете берета, который ей одели, она не сумела ответить
Шура слышала ответ Ани и сказала, что она также
не умеет определить цвет своего берета.
Может ли Соня на основании ответов своих подруг
определить цвет своего берета'
Новогодняя головоломка
Четыре друга Эдуард, Федор, Юра и Костя пошли
вместе со своими женами в клуб на новогодний бал
Сначала каждый танцевал со своей женой, но затем
пары перемешались. Варя танцевала с Эдуардом, Аля
368
с мужем Ольги, Тося с мужем Али, Федя с женой
Юры, а Юра с женой Эдуарда.
Попытайтесь распутать этот «гордиев узел» танцу-
танцующих пар и определить кто на ком женат и кто с кем
танцевал.
Логическая головоломка
На конкурсе для поступающих на философский фа-
факультет была задана следующая логическая голово-
головоломка ¦
1) Фамилии машиниста паровоза, кочегара и кон-
кондуктора — но не в том же порядке — Ковалев, Пет-
Петров, Смирнов;
2) Фамилии пассажиров: доктор Ковалев, доктор
Петров, доктор Смирнов;
3) Доктор Ковалев живет в Москве;
4) Кондуктор живет на середине пути от Москвы
до Ленинграда;
5) Пассажир, носящий ту же фамилию, что и кон-
кондуктор, живет в Ленинграде;
6) Доктор Петров зарабатывает ежемесячно 250
рублей;
7) Пассажир, который живет очень близко от кон-
кондуктора, зарабатывает ровно в 3 раза больше, чем
кондуктор;
8) Смирнов выиграл партию шахмат у кочегара.
Как фамилия машиниста?
369
Кто чей сын?
Три крестьянина Кузьма, Михаил и Иван послали
своим сыновьям Коле, Пете и Грише, которые учи-
учились в городе, несколько килограммов меда для про-
продажи. Числа килограммов меда, посланного отцами,
относятся как 1:2:3. Сыновья продали мед знако-
знакомой хозяйке по одинаковой цене за килограмм. После
получения денег, юноши пошли в кафе, где за съеден-
съеденные пирожные и выпитый кофе они заплатили вместе
столько, сколько получили от хозяйки за 1 кг меда,
причем выпало так, что доля, которую каждый из
них заплатил, была пропорциональна полученной
каждым сумме денег.
Известно что Петя заплатил в кафе 1 рубль, Коля
получил за свой мед 48 рублей и что Иван получил
от сына за проданный мед 69 рублей, а Михаил выс-
выслал своему сыну 8 кг меда. Кто был чьим сыном?
РЕШЕНИЕ ЗАДАЧ
Какого цвета?
Может. Из ответа Ани ее подружки решили, что
они обе не могут иметь на голове двух белых бере-
беретов . Они имеют либо два черных, либо белый и чер-
черный. Однако, если бы на голове Сони был белый
берет, то Шура сразу бы узнала, что у нее черный.
А так как Шура тоже сказала, что не знает какой
у нее берет на голове, то, следовательно, у Сони
на голове черный берет.
370
Новогодняя головоломка
Давайте, прежде всего, упорядочим, то что нам из-
известно из условий задачи:
1) Варя танцевала с Эдуардом;
2) Аля танцевала с мужем Ольги;
3) Тося танцевала с мужем Али;
4) Федя танцевал с женой Юры;
5) Юра танцевал с женой Эдуарда.
Прежде всего, установим, кто жена Эдуарда: это
не Варя (см. 1 и 5); это не Аля (см. 1 и 3); это не
Ольга (см. 1 и 2), следовательно, это Тося. Теперь
мы уже знаем, что Юра танцевал с Тосей (см. 5),
но по C) Тося танцевала с мужем Али, следователь-
следовательно, Юра муж Али. Затем из D) следует, что Федя
танцевал с Алей, но Аля (см. 2) танцевала с мужем
Ольги, следовательно, Федя муж Ольги. Таким об-
образом, у нас осталась лишь одна пара Варя и Костя,
которые не танцевали.
Логическая головоломка
Три пассажира, названные в B) живут в трех раз-
разных местностях C), E), и G)—D).
Доктор Петров F) — это не тот пассажир, о котором
говорится в G), так как его заработная плата не де-
делится ровно на три 250:3 = 83,333..., и именно
в этом условии таится ключ к решению всей задачи.
Доктор Петров — это также не тот, о ком говорится
в C), следовательно, доктор Петров это пассажир,
371
о котором говорится в E), а из этого следует, что
фамилия кондуктора Петров.
Теперь на основании A) фамилия машиниста либо
Смирнов, либо Ковалев, но из (8) нам известно, что
Смирнов выиграл у кочегара партию шахмат, сле-
следовательно, Смирнов это и есть машинист.
Кто чей сын?
Отношение чисел килограммов меда, посланного от-
отцами, было как 1:2:3; такое же отношение было
полученных сыновьями денег, такое же отношение
было между уплаченной каждым из них долей счета
в кафе. На основании условий задачи известно, что
Коля получил за свой мед 48 рублей, а Иван полу-
получил от сына 69 рублей после того, как тот уплатил
свою долю в кафе. Эти два числа не относятся ни
как 1:2, ни как 1:3. После того, как мы учтем сумм)
денег (х), заплаченную сыном Ивана в кафе, мы по-
получим 48 : F9+х) = 2 : 3 из чего следует, что х ~
= 3 рубля. Следовательно сын Ивана получил за
мед 69+3 = 72 рубля.
Так как Петя заплатил в кафе 1 рубль, то третий
юноша заплатил 2 рубля. Из этого следует, что хо-
хозяйка заплатила за 1 кг меда 1 +2+3 = 6 рублей,
и что Коля, чтобы получить за свой мед 48 рублей
должен был продать 8 кг, а это значит, что Коля был
сыном Михаила. Сын Ивана заплатил в кафе 3 рубля,
следовательно, зто не Петр. Сыном Ивана был Гри-
Гриша, а Петя был сыном Кузьмы.
НЕГОРДИЕВЫ
УЗЛЫ
ГЛАВА 23
Рис. 23-1
Существовал некогда во Фригии, в городе Гордион,
храм бога Зевса, около которого стояла колесница
с ярмом, привязанным к дышлу столь запутанным
узлом, что никто не мог его развязать. Но появился
великий полководец Александр Македонский, ко-
который узел этот разрубил мечом. Оракул бога Зевса
высоко оценил столь «мудрое» решение, и боги
дали Александру власть над Азией.
Так гласит легенда.
«Узлы», которыми занимается математика, нередко
также очень сложны, однако, среди них нет таких,
которые нельзя было бы решить.
Давайте познакомимся с некоторыми из них.
Вот на рис. 23-1 представлен узел Борромео. Назван
он этим именем, так как он был вышит на рукавах
мундиров вооруженных слуг итальянского рода Бор-
Борромео в эпоху Возрождения. Эти кольца нельзя разъе-
разъединить, хотя ни одна пара колец между собой не
соединена. Это очень легко проверить. Достаточно
отсоединить одно, любое из трех колец, как два
остальных окажутся ничем не соединенными. Как
видно на этом примере, взаимное проникание кривых
является также математическим вопросом.
Самая простая замкнутая в пространстве кривая не
образует узла. Часто называют ее узлом с нулевым
373
Рис. 23-2 а, 6
Рис. 23-3 а, 6
числом точек самопересечения. На рис. 23-2а мы
видим именно такую кривую. Ограниченная ею
площадь заштрихована. Мы здесь хотели бы еще
обратить ваше внимание на другой способ выделе-
выделения площади, ограниченной кривой, который пока-
показан на рис. 23-26. При этом способе можно себе
представить, что кривая показана на поверхности
шара, при этом она будет иметь совершенно другие
свойства, чем та же кривая на плоскости (рис.
23-2а).
Давайте воспользуемся таким же методом рассуж-
рассуждения для более сложного рисунка. Пусть кривая,
представленная на рис. 23-За, сделана из куска элас-
эластичной веревки. В точке самопересечения одна нить
веревки проходит под второй. Эта кривая так же
является узлом с нулевым числом точек самопере-
самопересечения, так как достаточно выполнить один пово-
поворот и точка самопересечения исчезает. Порядок уз-
узла — равняется тому минимальному числу точек са-
самопересечений, которые нельзя удалить путем транс-
трансформации. Заштрихованный рисунок 23-За имеет те
же свойства, что и рисунок 23-2а, а рисунок 23-36,
что и рис. 23-26.
После этих разъяснений можем вернуться к узлам
Борромео. Если три кольца Борромео (рис. 23-4),
образующие узел, будем считать проекцией на пло-
плоскость пространственной кривой, то точки, в кото-
которых две дуги этой кривой самопересекаются (обра-
(образуют узел), проходя одна над другой, в проекции
374
Рис. 23-4
Рис. 23-5
на плоскость будут точками самопересечения, кото-
которые иначе называются двойными точками. Как видно
на рисунке 23-1, обходя кривую, проекцией которой
на плоскости являются кольца Борромео, мы будем
проходить в пространстве двойные точки (узлы) раз
верхом, а раз низом.
На плоском рисунке эти кольца можно нарисовать
не отрывая карандаша от бумаги, и ведя его от од-
одной точки до другой, как это показано на рисунке
стрелками (последовательность прохождения точек:
1, 2,3, 4, 5,6,1, 4, 2, 6, 3, 5, 1). Узел, при обхож-
обхождении проекции которого мы проходим двойные точ-
чки раз верхом, а раз низом, называем альтерниру-
альтернирующим узлом.
На основании рисунка 23-5 мы видим, что не каж-
каждый узел альтернирующий.
На рисунке 23-6а, б показаны два способа выделения
части поверхности, ограниченной кольцами Борро-
Борромео, три кольца Борромео можно считать узлом с точ-
точками самопересечения третьего порядка.
375
15
На рисунке 23-7 показаны узлы с точками самопе-
самопересечения от 4 до 7 порядка. Мы предоставляем
читателям самостоятельно изучить эти рисунки и по-
попытаться подсчитать число самопересечений в каж-
каждом узле.
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Терпение и упорство
Просим набраться терпения и упорства. Хорошо за-
заточите карандаши. Не отрывая карандаша от бумаги,
необходимо пройти через все линии, образующие
звезду (рис. 23-8). Нарисуйте эту звезду на отдель-
отдельном листе бумаги, чтобы не портить книгу.
Рис. 23-9
Рис. 23-10
Клад
Рисунок 23-9 — это схема лабиринта. Стороны пяти
квадратов, вписанных один в другой, — это кори-
коридоры, ведущие к наименьшему внутреннему квад-
квадрату, где зарыт клад. Клад этот обладает таким свой-
свойством, что получить его может только тот, кто при-
придет за ним, пройдя все коридоры по одному разу.
Ни один коридор, даже частично, нельзя пройти
дважды.
Таким же образом необходимо возвращаться наружу
после розыска клада.
Попытайте счастья.
Уиикурсальиые фигуры
Уникурсальными фигурами мы называем такие фи-
фигуры, которые можно вычертить, не отрывая каран-
карандаша от бумаги, и которые можно обойти, побывав
дважды только в точках самопересечения.
Какие из указанных на рис. 23-10 фигур уникурсаль-
ны?
Королевские мосты
В связи с уникурсальными кривыми в истории мате-
математики известна задача, которая продолжительное
время привлекала внимание известного математика
Л. Эйлера A736).
В Кенигсберге (теперь Калининград), раскинувшемся
по обе стороны реки Прелоги, 200 лет тому назад
377
Рис. 23-11
Рис. 23-12 a, 6
было 7 мостов (рис. 23-11). И вот, тридцатилетний
математик заинтересовался, можно ли, гуляя по го-
городу, пройти через все семь мостов, но только по
одному разу.
Эйлер доказал, что это невозможно. А, впрочем,
попробуйте сами.
На цирковой арене
На цирковой арене выступал канатоходец. На высо-
высоте 3 метров от земли на 5 столбах были натянуты
канаты, по которым он должен был проходить. Ка-
Канаты были натянуты так, как это показано на рисун-
рисунке (рис. 23-12а). Канатоходец должен был пройти
по восьми канатам таким образом, чтобы по каждому
из них пройти всего один раз. И это ему всегда уда-
удавалось, хотя он и не возвращался в то же место, от-
откуда выходил. Но во время одного из выступлений
оборвался канат № 8 и осталось всего семь канатов
(рис. 23-126).
Может ли теперь канатоходец пройти все канаты,
проходя по каждому из них всего один раз?
Покажите, как ходил канатоходец, когда все канаты
были целы, и ответьте на поставленный вопрос.
Тропинки в садах
В саду Александра Ивановича тропинки проложены,
как это показано на рисунке 23-1 За, а у Бориса Бори-
378
a 5
Рис. 23-13 a, 6
7 / Л S S S
Рис, 23-14 a, 6, в
совича — как это показано на рис. 23-136. Кто из
них может обойти все свои тропинки, проходя по
каждой всего один раз?
Почтовая посыпка
Почтовая посылка имеет форму параллелепипеда.
Необходимо:
а) перевязать ее дважды в ширину и один раз в дли-
длину (рис. 23-14а), таким образом, чтобы веревка нигде
не проходила дважды;
б) перевязать ее так, как это указано на рис. 23-146
при условии, чтобы веревка нигде не проходила
дважды;
в) перевязать ее так, как это показано на рис. 23-14в,
и также при условии, чтобы веревка не проходила
дважды.
Среди георгинов
Садовник имел квадратную D X 4 м) клумбу, на ко-
которой он выращивал 16 кустов георгинов. Расстоя-
Расстояние между кустами составляло 1 м. Пока кусты еще
не расцвели, цветовод обходил все кусты, идя по
кратчайшему пути, но когда чудесные цветы распус-
распустились, садовник обходил их по самому длинному
пути. К каждому цветку он подходил только один
раз. Как выглядел самый короткий путь от куста
к кусту, а как самый длинный?
379
Задача садовника
РЕШЕНИЕ ЗАДАЧ
Садовнику поручили высадить 10 деревьев на пло-
площадке в форме равностороннего треугольника. Са-
Садовник имел два сорта деревьев: 10 акаций и 10 лип.
Чтобы внести некоторое разнообразие, садовник ре-
решил посадить несколько акаций и несколько лип,
причем так, чтобы на каждой стороне каждого из
4 равносторонних треугольников, которые при это.ч
образовались, росло не больше двух деревьев того
же сорта.
Как он это сделал?
Терпение и упорство
Смотри рис. 23-15.
Клад
Путь к кладу и обратно показан на рис. 23-16.
Рис. 23-16
Рис. 23-17
На цирковой арене
Когда все канаты были на месте, канатоходец про-
проходил по ним, как это показано на рис. 23-17. После
обрыва каната № 8 (рис. 23-12) канатоходец уже не
мог выполнить поставленной перед ним задачи.
Если какой-то канат приводит канатоходца до какого-
то столбика, то должен существовать канат, по ко-
которому канатоходец сможет пойти к следующему
столбу. Короче говоря, у каждого столба должно
сходиться четное число канатов. Если у какого-либо
столба сходится нечетное число канатов, то канато-
канатоходец не сможет обойти всех канатов и вернуться
в то же место, из которого вышел. При благоприят-
благоприятных условиях он сможет пройти по всем канатам один
раз, но не вернется в место, из которого вышел.
Так именно и происходило в нашем случае пока все
канаты были целы. На рис. 23-12а имеется одна точ-
точка, в которой сходится два каната A и 5), 2 точки,
в которых сходятся по 4 каната A, 2, 8, и 7; 5, 8,
4 и 3) и. 2 точки, в которых сходятся по три каната
B, 4 и 6; 3, 7 и 6). Канатоходец, выходя из точки А,
кончал свой маршрут в точке В (смотри рис. 23-17).
После того, как оборвался канат № 8 (рис. 23-126)
вопрос осложнился, так как точек, в которых схо-
сходится по три каната стало 4 A, 2 и 7; 5, 3 и 4; 3, 7
и 6; 2, 4 и 6), а точек, в которых сходится четное
число канатов только 2 A и 5; 4 и 7).
Следовательно, канатоходец не может обойти все
канаты по одному разу.
381
Рис. 23-18 а, б, в
Тропинки в садах
Александр Иванович.
Почтовая посылка
Смотри рис. 23-18а, б, в.
0
5
0
9
0
13
о
0
В
0
10
0
11
о
1
7
0
11
о
15
0
а
4
0
Я
0
12
о
16
о
Среди георгинов
Самый краткий путь:
1, 2, 3, 4, 8, 7, 6, 5, 9, 10, 11, 12, 16, 15, 14, 13
(рис. 23-19а).
Самый длинный путь:
5, 9, 13, 10, 7, 4, 3, 2, 1, 6, 11, 16, 12, 8, 15, U
(рис. 23-196).
Задача садовника
Садовник посадил 4 акации и 6 лип (рис. 23-20)
Рис. 23-19 а, б
(•)©(•)
© (•)(•)(§)
Рис. 23-20
ЛИНИИ ГЛАВА 24
эллипс
породояй
гипербола
Рис. 24-1
Рис. 24-2
Понятие линии в геометрической интерпретации до-
довольно сложно, а определение линии довольно труд-
трудное и сформулировано по разному в разных гео-
геометриях,
Евклид говорил, что это длина, у которой нет ши-
ширины, или что это граница поверхности. Он рассмат-
рассматривал только прямые, ломанные линии, окружности
и дуги. Аполоний B60—200 до н. э.) открыл линии —
сечения конуса — которые он назвал эллипс, ги-
гипербола и парабола (рис. 24-1). Архимед B87—212
до н. э.), который кроме математики занимался так-
также механикой и физикой, открыл спираль, т. е. ли-
линию, которую вычерчивает точка, перемещающаяся
по отрезку прямой /, равномерно вращающемуся во-
вокруг точки О (рис. 24-2).
Расширением понятия линии является ее определе-
определение как геометрического места точек пространства,
координаты которых являются функциями одной пе-
переменной, например, окружность — геометрическое
место точек, находящихся на одинаковом расстоянии
от некоторой точки, называемой центром; парабола —
это геометрическое место точек плоскости, находя-
находящихся на одинаковом расстоянии от фокуса и дирек-
триссы и т. п. Крупное открытие Декарта— коор-
координаты, пара чисел, характеризующих положение
383
Рис. 24-3
точки на плоскости — сделало возможным предста-
представлять прямые и кривые с помощью уравнений. Ока-
Оказалось, что прямую можно представить в виде урав-
уравнения первой степени с двумя переменными: ал +
¦\-by-\-c = 0; окружность с радиусом г — уравнением
х2-\-у2 = г2; эллипс — уравнением Ъгхг-\-а2уг -
= a2b2 (a, b — полуоси эллипса).
Однако определение линии как геометрического ме-
места точек не исчерпывает полностью понятия линии.
Дальнейшим расширением понятия линии есть опре-
определение, сформулированное французским матема-
математиком Мари Энмоном Камилем Жордано, которое
связывает линию с точкой, перемещающейся соглас-
согласно закону, определяемому так называемой системой
параметрических уравнений:
*=Л0; y = g(t)
где х и у — это координаты двигающейся точки,
a t — это параметр содержащийся в интервале
а^ t ^ b иначе говоря, f(t) и g(t) — это непрерыв-
непрерывные функции в интервале а< /^ Ь, например,
х = rcost, у = rsmt, г > 0, 0 < t < 2тс, является
уравнением окружности с радиусом г и центром в на-
начале системы координат (рис. 24-3).
Линия, представленная на рис. 24-4, по Жордано, —
это замкнутая кривая, т. е. кривая, начало и конец
которой совпадают. Замкнутая кривая делит поверх-
поверхность на две части: одну, находящуюся внутри крй"
вой, и вторую — наружную. Прямая, проведенная
Рис. 24-5
Рис. 24-6
из точки внутреннего пространства пересекает замк-
замкнутую кривую в нечетном числе точек, прямая, про-
проведенная из точки, лежащей снаружи — в четном
числе точек.
В том случае, если замкнутая кривая несложна, то
нетрудно определить, которая точка находится внут-
внутри кривой, а которая снаружи. Однако, если замкну-
замкнутая кривая сложная, то вопрос определения, где
находится данная точка — довольно-таки сложен.
На рис. 24-5 мы видим очень сложную замкнутую
кривую. Она изображает всадника на лошади. Чи-
Читатель может сам легко убедится, как трудно опреде-
определить, где находится данная точка: внутри или нару-
наружу кривой. Для облегчения проверки ответа на рис.
24-6 внутренняя поверхность заштрихована, а наруж-
наружная оставлена белой.
385
г?
-С
L
3-
1
rti
с.
Рис. 24-7
Рис. 24-8
На рис. 24-7 представлена кривая Пеано, а на рис.
24-8 — так называемые ковер Серпинского. Рисунки
показывают процесс построения этих кривых. Про-
Продолжая этот процесс до бесконечности, мы получим
линии, которые проходят через все точки квадрата,
что кажется парадоксом.
Соответственно степени уравнения линии, они были
названы линиями первого порядка (прямая), вто-
второго порядка (сечение конуса), третьего порядка
и т. д.
Из этого следует, что обобщение, а также уточнение
понятия линии тесно связано с алгеброй. В заклю-
заключение необходимо обратить внимание на близкое
сродство математики и искусства, на то, что сухие
строгие уравнения имеют иногда красивое и изящное
графическое изображение, напоминающее звезды,
цветы, узоры и даже ковры.
На рис. 24-9 представлены некоторые из них:
1) строфоида;
2) четырехлепестковая роза;
3) кардиоида;
4) конхоида;
5) овал;
6) лемниската.
Рис. 24-9
386
ВИНТОВАЯ ЛИНИЯ Это пространственная кривая, в виде спирали, на-
находящейся на поверхности прямого кругового ци-
цилиндра или конуса вращения (рис. 24-10), и пересе-
пересекающая все образующие цилиндра или конуса под
постоянным углом.
Если круговую цилиндрическую поверхность раз-
развернуть на плоскость, то винтовая линия перестает
^ быть непрерывной линией и превращается в несколь-
несколько отрезков прямой, расположенных на одинаковом
расстоянии друг от друга (рис. 24-106). Длину от-
отрезка винтовой линии между двумя последователь-
последовательными пересечениями той же образующей называем
шагом винтовой линии.
Винтовая конусная линия после развертывания ко-
конуса на плоскость образует отрезки подобных и по-
подобно расположенных логарифмических спиралей.
Рис. 24-10 а, б, в
ЛОКСОДРОМА
И ОРТОДРОМИЯ
Локсодрома (рис. 24-11 а, б) — это пространственная
кривая, лежащая на сфере или любой другой по-
поверхности вращения, пересекающая все меридианы
этой поверхности под постоянным углом К, а в част-
частности, пересекающая все земные меридианы под по-
постоянным углом. Путь морского судна и трасса полета
самолета имеют форму, подобную локсодроме.
На картах, составленных в проекции Меркатора,
все локсодромы имеют вид прямых линий. Локсо-
387
180°
Рис. 24-11 а, б
дрома, образующая с меридианом угол 0° или 180°
совпадает с меридианом, а образующая угол 90° сов-
совпадает с параллелью. Название «локсодрома» было
введено в математику в 1624 году голландским ма-
математиком В. Снеллиусом.
Ортодромия — пространственная кривая, которую
противопоставляют локсодроме. Ортодромия — крат-
кратчайшая линия на сфере между двумя данными точ-
точками. В морской и авиационной навигации Землю
считают шаром, вычерченная на ней ортодромия
является дугой большого круга. Судно или самолет,
который двигался бы по ортодромии должен бы
был непрерывно изменять свой курс, поэтому суда
не плывут точно по ортодромии, а по некоторой
ломанной кривой, являющейся результирующей
локсодромы и ортодромии.
388
ВЕКТОРЫ И СКАЛЯРЫ
Рис. 24-12
Уг
X, '2
Рис. 24-13
Вектор (слово происходит от латинского vehere —
тянуть) — зто направленный отрезок АВ (рис. 24-12),
т.е. две точки А и В, взятые в определенной после-
последовательности. Первую точку, т. е. А называем на-
началом вектора, а вторую, т. е. В — его концом. Век-
Вектор однозначно определен, если указаны начало,
длина (длина отрезка АВ), направление и ориента-
ориентация. Векторами являются скорость, ускорение, сила,
момент силы и т. п.
Скаляр (от латинского scaliarld) — зто величина,
каждое значение которой может быть выражено
с помощью одного отвлеченного или именованного
числа, например, длина, площадь, масса, вес, плот-
плотность, температура и т. д.
Векторы играют очень существенную роль в мате-
математике и физике.
Для нужд физики в XIX веке возникло и развилось
векторное исчисление — самостоятельная математи-
математическая дисциплина. Предметом векторного исчис-
исчисления является наука об операциях над векторами.
Введены понятия: нуль-вектора, противоположных
векторов, равенства векторов. Определены опера-
операции над векторами: сложение векторов, вычитание
векторов, умножение вектора на число, скалярное
произведение, и вектора на вектор — векторное про-
произведение. Операции над векторами обладают в прин-
принципе теми же свойствами, что и операции над чис-
числами (ассоциативность, коммутативность сложения).
Векторы можно рассматривать в системе прямоуголь-
389
Рис. 24-14
Рис. 24-15
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
ных координат. При этом вводится понятие коорди-
координат вектора: это разность между координатами
конца и начала вектора (рис. 24-13). Вектор и> имеет
координаты (*i, ух; х2, у2).
Два вектора, параллельные той же прямой, называ-
называются коллинеарными векторами, а параллельные той
же плоскости — компланарными.
Различают несколько видов векторов. Свободным
вектором называем вектор, начало которого может
находится в любой точке на любой прямой парал-
параллельной данной прямой (рис. 24-14). Скользящим
вектором называем вектор, началом которого может
быть любая точка на данной прямой (рис. 24-15).
Путем придания каждой точке данного пространс-
пространства — вектора, представляющего определенную ве-
величину, мы вводим понятие векторного поля.
Сечение куба плоскостью
Какие трехразмерные фигуры можно получить, рас-
рассекая куб одной плоскостью?
Есть ли у вас пространственное воображение?
На рисунке 24-16 вы видите октаэдр, ребро кото-
которого имеет длину 1 дм. Что необходимо сделать,
чтобы этот октаэдр превратился в тетраэдр, ребро
которого будет иметь 2 дм длины ?
7 вопросов
1. Единицей скорости является узел. Что больше
узел или км/ч ?
2. На каком расстоянии от окна необходимо дер-
держать головку спички, чтобы видеть ее под таким
углом, под которым мы видим Луну во время полно-
полнолуния. С какого расстояния мы видим под таким же
углом человека ростом 180 ом?
3. По легенде — над аркой у входа в одно извест-
известное учебное заведение виднелась надпись: «Пусть
никто не входит сюда, кто не изучал геометрии».
Где находилась эта надпись ?
4. У портного имеется кусок материала на под-
подкладку длиной 30 м. Ежедневно портной отрезает
по 5 м. В который день по очереди он отрежет по-
последний раз?
5. Когда сыну исполнилось 6 лет, его отцу было
30 лет. Сейчас отец в четыре раза старше сына.
Сколько лет сыну ?
6. Какое самое большое число можно написать с по-
помощью четырех единиц?
7. В какой системе счисления справедливо равен-
равенство: 400-344 = 1?
391
РЕШЕНИЕ ЗАДАЧ Сечение куба плоскостью
Рис. 24-17 а, б, в, г, д
На рисунке 24-17 мы видим самые элементарные
фигуры, которые можно получить после пересе-
пересечения куба плоскостью.
Есть пи у вас простраиствеииое
воображение?
На рисунке 24-16 нарисован октаэдр ABCDEF, кото-
который на рисунке 24-18а поставлен на плоскости
ADE. На рисунке 24-186 показан способ преобразо-
преобразования октаэтра в тетраэдр. Достигается это путем
присоединения к октаэдру 4 тетраэдров с ребром
1 дм: эти тетраэдры это: NFBC, KCED, ADLF и
BFAM.
Рис. 24-18 а, 6
392
7 вопросов
1. Узел, так как 1 узел равен 1,852 км/ч.
2. Луну мы видим под углом 1/2°, это значит, что,
если из точки, в которой находится наш глаз, мы
проведем две прямые, касательные двум противо-
противоположным концам диаметра луны, то угол, образо-
образованный этими прямыми, будет равняться 1/2°.
Чтобы увидеть под этим углом спичечную головку
необходимо удалить ее на расстояние 25 см. Чело-
Человека ростом 180 см мы видим под углом 1/2° с рас-
расстояния примерно 200 м.
3. Академия Платона, которая была расположена
в роще, вблизи Афин над рекой Кифизос, посвя-
посвященной мифическому герою Академу.
4. На пятый день.
5. 8 лет, отцу сейчас 32 года.
6. И11. Это число, которое имеет 12 знаков. Но
1111! (факториал) — больше!
7. В пятиричной системе счисления равенство
400—344 читается: сто минус девяносто девять.
О ТРИГОНОМЕТРИИ глава 25
Тригонометрия — это раздел элементарной мате-
математики, отличающийся от Евклидовой геометрии
тем, что решения своих задач он ищет не методам
построения, а методом расчета. Термин «тригоно-
«тригонометрия» выводится от двух греческих слов «три-
гонон» — треугольник и «метрео» — мерю. Это, ко-
конечно, не означает, что тригонометрия занимается
только треугольниками, она изучает также и другие
фигуры, ибо любую фигуру, ограниченную отрез-
отрезками прямых можно расчленить на треугольники.
Тригонометрия рассматривает не только плоские
фигуры, ограниченные отрезками прямой, но и тре-
треугольники, построенные на поверхности сферы, у ко-
которых стороны являются дугами окружностей. По-
Поэтому тригонометрия делится на прямолинейную
и сферическую.
Для того, чтобы можно было применить вычисле-
вычисления при решении треугольников необходимо было
найти соотношения между элементами треугольни-
треугольника: его углами и сторонами. Так как эти соотно-
соотношения не могут быть выражены в алгебраической
форме, то были установлены тригонометрические
величины. Древнегреческие астрономы Гиппарх (I*
век до н. э.) и Птолемей (II век нашей эры), кото-
которые ввели тригонометрию в свои астрономические
394
Рис. 25-1
С О
Рис. 25-2 а, б
расчеты, заметили, что в окружности с данным
радиусом длина хорды зависит от величины соот-
соответствующего центрального угла: большему углу
соответствует более длинная хорда и наоборот —
большей хорде — больший центральный угол (рис.
25-1: /? > а; т > п). Затем Гиппарх, а позже и Пто-
Птолемей высчитали длину хорд для центральных
углов через каждые полградуса (греки, как и вави-
лонцы, делили окружность на 360 градусов, а каж-
каждый градус — на 60 минут). Таким образом были
созданы первые в Европе таблицы тригонометри-
тригонометрических величин. Принимая во внимание, что длина
хорды зависит исключительно от величины соответ-
соответствующего ей центрального угла, тригонометричес-
тригонометрические величины были позднее названы тригонометри-
тригонометрическими функциями угла.
Древние греки не знали таких функций, которые
известны нам теперь под названием синус, косинус
и т. д. Геометрический синус угла а (отрезок ЕВ на
рис. 25-2а, б) равен половине хорды, соответствую-
соответствующей центральному углу 2а. Отрезок ОЕ— это гео-
геометрический косинус угла а. Синус и косинус были
введены индусскими астрономами примерно в IV—V
веке нашей зры. В Европу они попали благодаря
астрономическим и математическим работам арабов,
а сам термин «синус» был введен латинскими пере-
переводчиками арабских трудов в XIII—XIV веках.
В качестве единицы измерения при составлении
таблиц синусов была принята дуговая минута. Так
395
как геометрическим синусом дуги АС = 90° является
радиус окружности ОС, а центральный угол дуги AD,
длина которой равняется радиусу ОС, содержит
примерно 57°18' = 3438', было принято, что си-
синус 90° = 3438.
Индусские таблицы синусов, которые сохранились
до наших дней, менее точны, чем греческие таблицы
хорд. Они указывают величину синусов через 3345'
(т. е. через 1/24 четверть окружности). Дальнейшее
развитие тригонометрии связано с работами араб-
арабского математика Абу-ль-Вефа (X век) и работами
крупнейшего азербайджанского астронома и матема-
математика Насиреддина Туей Мухаммеда A201—1274),
который развил тригонометрию в самостоятель-
самостоятельную научную дисциплину, ввел понятие тангенса
и котангенса (на рис. 25—26 отрезок AF является
геометрическим тангенсом угла a, a CD — котан-
котангенсом угла а) и установил соотношения между
функциями того же угла:
sin а , . 1 • -г -г
"c5F = tga; ctga = 1^; s22
Европейские ученые не знали об этих работах Наси-
реддина и спустя двести лет повторили их. Впервые
это сделал немецкий астроном и матемитик РегДО-
монтан (истинная фамилия Иоганн Мюллер, 1436—"
1476). На развитие тригонометрии существенное влй'
яние оказал великий польский астроном Николай
Коперник, который сообща со своим другом Геор-
396
ДУГЕ, КАСАТЕЛЬНОЙ
К ДВУМ ЗАДАННЫМ
ОКРУЖНОСТЯМ
гом Ретиком разработал сферическую тригономе-
тригонометрию и изложил ее в введении в своем основном
труде «О вращении небесных сфер» (De revolutio-
nibus orbium coelestium). Рассчитанные им таблицы
указывали значение тригонометрических функций
через 10 секунд, а радиус (единица измерений) был
разделен не на 3438 частей, как это было у инду-
индусов, а на 10ls, что позволило высчитать значения
синуса-с 15 значащими цифрами.
Все существующие в настоящее время названия
тригонометрических функций: тангенс, котангенс,
секанс и косеканс были установлены датским мате-
математиком Томасом Финке A561—1656). Буквенные
обозначения, которые в алгебру ввел французский
математик Виет в XVI веке, в тригонометрии стали
использоваться лишь в XVIII веке. Особенно круп-
крупный вклад внес швейцарский математик Леонард
Эйлер A707—1783). Величины: sinx, cosx, tgx
и т. д. Эйлер рассматривал как функции числа х —
радиальной меры угла, придавая числу х все поло-
положительные, отрицательные и даже комплексные
значения.
На рис. 25-3 мы видим построенную дугу окружно-
окружности, касательную к двум другим окружностям, в том
случае, когда точки касания находятся по одной
397
Рис. 25-3
стороне линии центров, а на рис. 25-4 — когда
точки касания находятся одна над, а вторая под
линией центров.
Вычисление радиуса дуги касательной к двум за-
заданным окружностям проводится в следующей по-
последовательности :
Дано: гиг, — радиусы окружностей, D — длина
отрезка, соединяющего центры окружностей, и от-
отрезки х vl у (рис. 25-3 или 25-4), определяющие точки
касания искомой дуги и окружностей. Определяем
углы А и В из зависимости
cos А = —; cosB = —
г г,.
Зная углы А и В и длину D, можно решить тре-
треугольник FAB, т. е. определить стороны FA = R—r
Получаем
D
R-r
sin В
и
D
R -J
из этого находим:
DsinA
(рис. 25-3), таким же образом, используя формулу
синусов, найдем:
„ DsinA
DsinB _
Sin (A+В)
(рис. 25-4).
sin (A + B)
398
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Иногда указаны длины сторон треугольника FAB,
при этом углы А и В рассчитываем с помощью фор-
формулы косинусов:
а2 = b2jrC2— 2bc ¦ cosA, из чего
_ Ьг+сг~аг _ (Ь+с+а) ф+с-а) 1
C0SA~ We - We 1
Например, если стороны треугольника равны:
а = 7,95; 6 = 8,31; с = 9,54,
то после подстановки всех данных в последнюю фор-
формулу получим:
cos А = 0,61; а из этого А = 52°25'
Согнутый стержень
Железный стержень имеет 4 метра длины. Необ-
Необходимо его согнуть посередине таким образом, что-
чтобы образовался угол 240°. Каково расстояние между
концами согнутого стержния?
Рис 25-5
Лист металла
В кооперативе изготавливают из гофрированного
листового металла будки для разведения кроликов.
Профиль листа образован последовательно сопря-
сопряженными равными дугами окружностей (рис. 25-5).
399
На изготовление одной будки расходуется 6 метров
гофрированного металла с профилем, в котором
каждой дуге отвечает центральный угол а, при
этом 60° < я< 180°.
Кооператив сам гофрирует металл.
Сколько метров негофрированного железа нужно
для того, чтобы изготовить 100 будок.
При каком угле а расход негофрированного листо-
листового металла будет самым меньшим?
Может ли изменение величины дуги, образующей
профиль листа, дать экономию материала?
РЕШЕНИЕ ЗАДАЧ
Согнутый стержень
После изгиба стержень образовал угол (рис. 25-6),
который больше развернутого, но меньше полного.
Следовательно, соединяя концы стержня, мы не
построим треугольник, ибо угол равный или боль-
больший развернутого не может быть внутренним углом
треугольника.
Дополнительный угол (до 360°) равен 120°. Отрезок
АВ, соединяющий концы стержня, высчитываем,
исходя из зависимости:
АВ2 = АС2+ВС2-2АС ¦ ВС ¦ cosl20° =
= 4+4+8-1=12,
а из этого AB — \/l2.
400
Лист металла
2-kRo.
~шг
Отрезок АС = 2jRsiny, дуга АС =
На длине 6 м отрезок АС поместится п раз, т. е.
а
6 = 2jRsin-y-n a из этого:
3 -jp 2-xRa.
п —; Ь АС
- R%m-7r 60 sm-=-
Когда а = 60°; L = 2ж\ когда а = 180°, L = Зтг.
Следовательно, количество израсходованного ма-
материала зависит от радиуса дуги гофрирования. На
100 будок расходуется от 200 до 300 м плоского ли-
листового металла в зависимости от величины угла а.
ВАРИАЦИОННОЕ
ИСЧИСЛЕНИЕ
ГЛАВА 26
Рис. 26-1
Вариационное исчисление — это один из разделов
математики, изучающий методы определения мак-
максимума и минимума функционалов, т. е. переменных
величин, зависящих от выбора одной или несколь-
нескольких функций. Примером функционала является ве-
величина площади плоской фигуры, ограниченной
замкнутой кривой. Эта площадь зависит (является
функционалом) от кривой (от уравнения кривой),
ограничивающей эту площадь. Уже в древности было
известно, что среди всех замкнутых кривых данной
длины окружность ограничивает самую большую
площадь. Самую маленькую поверхность вращения
дает кривая, называемая цепной (рис. 26-1).
Вариационное исчисление начало развиваться в кон-
конце XVII века сначала для решения разных любопыт-
любопытных задач. Вот, например, задача, которую задал
математикам Иоганн Бернулли в 1696 году в журнале
«Вопросы ученых» (Acta Eruditorum):
«Из всех плоских и гладких кривых, соединяющих
точки А и В, не лежащие на одной вертикали, и на
одном уровне указать уравнение такой кривой, по
которой материальная точка, двигающаяся только
под действием силы тяжести (без учета трения) от
вышележащей точки А к нижележащей точке В,
затратит наименьшее время».
402
Рис. 26-2
Изопериметрические
задачи
Была это так называемая задача о брахистохроне (кри-
(кривой наикратчайшего спуска) (рис. 26-2).
Самое интересное решение этой задачи привел Яков
Бернулли A654—1705). Однако, лишь работы Л. Эй-
Эйлера превратили решение любопытных задач в са-
самостоятельное математическое исчисление.
Вычислительные методы, используемые Эйлером,
были очень сложны и поэтому их вскоре вытеснил
другой метод — «метод вариации», разработанный
Ж. Лангранжем.
Изопериметрические задачи — это основной вид за-
задач вариационного исчисления. Слово «изопери-
метрический» происходит из соединения двух гре-
греческих слов: изос — одинаковый и периметрео —
измеряю вокруг.
Простые изопериметрические задачи были уже из-
известны и решались в Древней Греции Архимедом,
Зенодором и другими. Например, уже в древности
было доказано, что из всех треугольников данного
периметра наибольшую площадь имеет равносто-
равносторонний треугольник; что среди всех четырехуголь-
четырехугольников с данным периметром наибольшую площадь
имеет квадрат; что, если квадрат и треугольник имеют
одинаковый периметр, то квадрат имеет площадь
большую, чем треугольник и т. п.
403
ХИТРОСТЬ ДИДОНЫ
Однако, общий метод решения изопериметрических
задач был найден лишь в конце XVII века. Разработ-
Разработка этого метода — заслуга двух знаменитых швей-
швейцарских математиков братьев Бернулли: Якова и Ио-
Иоганна A667—1748). Первый из них нашел решение
задачи, являющейся обобщением многих конкретных
геометрических и механических задач: «Среди всех
кривых данной длины найти ту, для которой неко-
некоторая величина, зависящая от кривой, (например,
площадь ограниченной ею поверхности), имеет мак-
максимальное или минимальное значение» A697 г.).
Позднее, примерно, в 1732 г. обширные и системати-
систематические исследования в области изопериметрических
задач проводил Л. Эйлер. Из числа польских мате-
математиков этими вопросами занимался первым Я. Бро-
жек A585—1652).
В мифологии описывается, как Дидона, царская
дочь, спасая свою жизнь, бежала из финикийского
города Тира (не забыв, однако, прихватить свою
шкатулку с драгоценностями) в Африку. Там, на
северном побережье Африки, Дидона купила у ко-
короля Нумидии Ярба «столько земли, сколько можно
опоясать кожей, содранной с вола». Ярб, не дога-
догадываясь подвоха, согласился продать «столь не-
небольшой» участок земли. Тогда Дидона велела по-
порезать содранную кожу на узенькие полоски и опо-
404
ясала ими значительную территорию в форме окруж-
окружности.
Так гласит предание. Значит Дидона знала, что при
той же длине периметра наибольшую площадь имеет
окружность, именно не квадрат, не треугольник,
а окружность. Мифология, повествуя об этом, ука-
указывает, что это происходило в IX веке до нашей эры.
Значит уже тогда ученые (очевидно, вавилонские)
решали иэопериметрические задачи.
Пусть равносторонний треугольник, квадрат, пра-
правильный шестиугольник и окружность имеют оди-
одинаковый периметр равный р. Обозначим площади
этих фигур соответственно через Р^РаРь и Р.
Используя известные нам из геометрии формулы
площади, найдем:
1р\2 Уз р
Р3 = I) • ; 4
¦^ — сторона равностороннего
треугольника
—- — сторона квадрата
Р6 = 11^1 • -7-\'6> -f- — сторона шестиугольника
Р = те 1у-| j -у радиус окружности дли-
длиной р.
После преобразования получим:
3 36 '* 16 ' б"" 24 ' Л 12,56
405
УДИВИТЕЛЬНАЯ
КРИВАЯ
Легко доказать, что: Р3 < Р4 < Р6 < Р.
Примечание: при постоянном периметре пло-
площадь выпуклого многоугольника тем больше, чем
больше сторон он имеет. Окружность — это «мно-
«многоугольник» с максимальным числом сторон, а по-
поэтому при заданном периметре окружность имеет са-
самую большую площадь.
Стоя на обочине дороги, можно иногда заметить, как
к колесу проезжающей крестьянской телеги при-
приклеился лист или кусок бумаги и вращается вместе
с ним, катясь вперед. Каждые несколько метров лист
подымается до наивысшей точки, а затем опускается
до полотна дороги и снова подымается вверх, и сно-
снова опускается. Если телега движется равномерно, то
эти подъемы и спуски происходят в одинаковых
промежутках времени.
Вычерчивает ли этот лист какую-либо кривую ? Изу-
Изучает ли математика эту кривую? А может быть это
синусоида ?
Кривая, которую вычерчивает лист или клочек бу-
бумаги, приставший к ободу колеса катящейся теле-
телеги, — это не синусоида (так как, если бы это была
синусоида — то какая-то ее часть должна бы была
находиться ниже уровня дороги), но это кривая,
которую математика уже давно и тщательно изучила.
406
Для облегчения хода наших рассуждений заменим
колесо телеги геометрической окружностью, а лист —
выбранной на ней точкой.
Рисунок 26-3 изображает катящуюся без скольжения
окружность. Качение начинается в точке А, а пол-
Рис. 26-3 ный оборот окружности заканчивается в точке В.
Из этого следует, что расстояние АВ = 2тсг, где г —
это радиус катящейся окружности. На отрезке АВ
нарисованы 4 положения катящейся окружности.
Расстояния между этими положениями равны 2тсг : 4
1т. е. yW I. Передвигаясь из положения А в поло-
положение В, точка вычерчивает кривую, которая назы-
называется циклоидой. Эта кривая уже хорошо исследо-
исследована. Мы знаем ее уравнение и знаем много интерес-
интересных и важных геометрических и технических свойств
этой кривой.
— Когда она была открыта?
До 1500 года в математике не встречается каких-
либо упоминаний о ней. Первым исследовал циклои-
циклоиду итальянский математик, физик и астроном Галилей
A564—1642), затем его ученик Эванджелиста Тор-
ричелли A608—1647), который в 1644 году издал
научный труд, посвященный циклоиде. Он привел
в нем формулу для расчета площади, ограниченной
дугой циклоиды и ее основанием. Циклоидой зани-
занимался также известный французский математик и фи-
физик Б. Паскаль. В связи с этим существует довольно-
таки забавный анекдот.
407
У Паскаля болели зубы. Однажды, когда его осо-
особенно мучила зубная боль, чтобы забыть о ней,
Паскаль начал думать о циклоиде. Случайно боль
прекратилась. Паскаль счел, что это не пустое сов-
совпадение, а особое влияние мыслей о циклоиде и при-
приступил к ее тщательному изучению. Он рассчитал,
что площадь фигуры, ограниченной одной дугой
циклоиды и ее основанием АВ (рис. 26-3) точно
в 3 раза больше площади окружности, ею образо-
образованной, т. е. равняется Зтсг2. Он рассчитал также
объем V и площадь Р тела, которое образуется при
вращении циклоиды вокрут ее основания АВ A634 г.).
Объем V равен 3-^-объема шара радиусом г, т. е.
V = 5тсг3, а площадь поверхности Р равна5 -^ площа-
64 2
ди поверхности шара радиусом г, т. е. Р = -j-7w .
Длину дуги циклоиды высчитал английский архи-
архитектор (XVII век) Кристофор Рен. Оказалось, что
длина одной дуги циклоиды составляет 8г, т. е. рав-
равна восьми радиусам окружности, которая ее обра-
образует, хотя длину окружности, образующей циклоиду?
нельзя, как известно, точно измерить с помощью ее
радиуса. Это очень примечательный факт, о котором
стоит помнить.
Механические свойства циклоиды также довольно
любопытны. Открыл их знаменитый нидерландский
математик, физик и естествовед Христиан Гюйгенс,
который в 1673 году опубликовал свой трктаат « Ма-
408
Рис. 26-4
Рис. 26-5
ятниковые часы» (Horologium Oscillatoriwn). Гюй-
Гюйгенс доказал, что часовой маятник, колеблясь, неза-
независимо от величины амплитуды колебаний, двигает-
двигается по кривой, называемой изохроной, и что изохро-
на — это повернутая выпуклостью вниз циклоида.
На рисунке 26-4 представлен маятник, подвешенный
между двумя циклоидами. Гиря маятника вычерчи-
вычерчивает точно такую же циклоиду, как те, между кото-
которыми она подвешена.
Маятники обычных часов двигаются по круговому
пути (не циклоидальному), но дуга, которую они про-
проходят, очень мала и соответствует центральной части
циклоиды, которую в средней части можно в приб-
приближении. рассматривать как дугу окружности. За-
Запомните, однако, что изохрона (рис. 26-5) — это
такая кривая, по которой материальная точка падает
в свое нижайшее положение за то же время, незави-
независимо от того, с какого места она начала падать. Ма-
Материальные точки В и С, падая по изохроне, попадут
в точку А в одно и то же время.
В начале этой главы мы упоминали о том, что швей-
швейцарский математик Иоганн Бернулли в 1696 опубли-
опубликовал задачу на нахождение кривой кратчайшего
спуска. Для решения этой задачи он предоставил ма-
математикам 1 год. Много раньше срока ее решили:
его брат Яков Бернулли, Лейбниц, Гюйгенс и Нью-
Ньютон. Полученную кривую назвали брахистохроной.
При этом оказалось, что брахистохрона является
отрезком циклоиды, находящимся между точками
409
Рис. 26-6
А и В (рис. 26-6). Необходимо, однако, помнить, что
точка должна катиться по кривой (брахистохроне),
хотя кратчайшей линией, соединяющей точки А я В
является прямая.
Давайте предположим, что через точки А и В мы
должны вычертить отрезок циклоиды. Прежде все-
всего, найдем радиус окружности, которая, катясь по
линии АС, образует циклоиду. Для этого соединим
А и В прямой и вычертим окружность произвольного
радиуса под линией АС касательно к АС. Пусть эта
окружность катиться без скольжения по АС и пере-
пересечет АВ в точке D (смотри рис. 26-6). Так как все
циклоиды имеют такую же форму, то AD так отно-
относится к АВ, как радиус данной окружности к радиусу
искомой окружности. После расчета искомого радиу-
радиуса можно вычертить отрезок дуги брахистохроны,
соединяя точки А и В.
Циклоида имеет еще и другие технические свойства.
Конструкции в форме дуги и циклоиды (о чем дога-
догадывался еще Галилей) выдерживают наибольшие наг-
нагрузки. Поэтому очень многие мосты имеют циклоид-
циклоидные арки, зубья шестерен имеют циклоидальную
форму для уменьшения трения в передаточных меха-
механизмах.
Американский инженер С. Олигви рассмотрел связь
между окружностью, прямой и циклоидой с обратной
стороны. Он поставил себе вопрос: по какой кривой
должна катиться без скольжения окружность, чтобы
взятая на ней точка вычертила своим движением
410
о
Рис. 26-7
прямую? Ответ оказался, как и предполагали, до-
довольно прост — по перевернутой выпуклостью вниз
циклоиде (рис. 26-7).
Вас, очевидно, заинтересует какой-либо несложный
метод вычерчивания циклоиды. Американский ма-
математик М. Гарднер указал в журнале « Сайентифик
Америкэн» (Scientific American), метод вычерчива-
вычерчивания циклоиды с помощью металлической консервной
банки, веревки, карандаша и небольшой дощечки.
Банку следует обвязать веревкой, которая прикреп-
прикрепляется к обоим концам дощечки. Внутри банки укреп-
укреплен карандаш, как это показано на рисунке. «При-
«Прибор» необходимо приложить к листу бумаги, при-
прикрепленному в горизонтальном положении, например,
на стенке (карандаш должен находится внизу), и по-
повернуть банку так, чтобы карандаш снова оказался
внизу.
При полном обороте банки карандаш вычертит цик-
циклоиду.
КАЧЕНИЕ
БЕЗ СКОЛЬЖЕНИЯ
1. По прямой р катится окружность радиусом г
(рис. 26-8). Пусть за один оборот окружность пере-
перемещается из положения А в положение В. Следо-
Следовательно, АВ = 2то\
2. Давайте изогнем теперь отрезок АВ в точке С
(рис. 26-9), т е. по середине отрезка АВ, и снова
411
Рис. 26-8
Рис. 26-10
перекатим нашу окружность из положения А в по-
положение В. Катящаяся из положения А в положе-
положение С окружность сделает половину оборота (тег).
Чтобы окружность могла дальше покатиться из С
в В, она должна из положения Ot переместиться
в положение О2, т. е. повернуться на угол %.DCE.
Этот угол равен Z.FCB (наружному углу ломанной
АС В).
Заметим, что ¦? DCE = -^- части полного оборота
окружности. Следовательно, катясь из С в В, окруж-
окружность сделает половину оборота, а катясь без сколь-
скольжения по ломанной АС В {АС+СВ — АВ), окруж-
окружность сделает I полный оборот плюс у- части пол-
полного оборота.
Если мы сделаем из отрезка АВ правильный шести-
шестиугольник (замкнутую кривую), и покатим окружность
по периметру шестиугольника (рис. 26-10), то на
каждой стороне окружность сделала бы 1 /6 полного
оборота, но при переходе с одной стороны на другую
она будет дополнительно делать у- часть оборота.
В шестиугольнике -^- = -?¦ оборота. Следовательно,
катясь по периметру шестиугольника, окружность
сделает два полных оборота. Из отрезка А В мы мо-
можем сделать многоугольник с любым числом сторон,
катясь по его периметру, окружность всегда сделает
на 1 оборот больше, чем при качении без скольжения
412
Рис. 26-П
по прямой АВ. Из этого следует, что сумма внешних
углов любого многоугольника равна полному углу
-=— • п = 360° (и — число сторон многоугольника).
Так как окружность можно также считать «много-
«многоугольником» с неограниченно большим числом сто-
сторон, то окружность с радиусом г, катясь до пери-
периметру другой окружности, периметр которой равня-
равняется длине отрезка АВ, сделает на 1 оборот больше,
чем при качении по прямой АВ.
А теперь мы можем приступить к решению следу-
следующей задачи. Мы имеем 2 окружности с разными
радиусами R и г. Окружность радиусом R непо-
неподвижна, а окружность радиусом г катится без сколь-
скольжения по периметру неподвижной окружности (рис.
26-11). За один полный оборот окружности радиу-
радиусом R окружность радиусом г повернется 4 раза.
Какое соотношение радиусов R:г?
R:r = 3:1, так как 2tzR — 3 • 2тсг
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Задача жестянщика
Из квадратного куска оцинкованной жести со сто-
стороной а == 15 см необходимо сделать сосуд с квад-
квадратным основанием, сверху открытый. Какова может
быть самая большая емкость сосуда?
413
Найдите это число
1. Найдите такое четырехзначное число, девятая
часть которого также четырехзначное число, запи-
записанное теми же цифрами, но в обратной последова-
последовательности.
2. Найдите другое четырехзначное число, четвертая
часть которого также четырехзначное число, запи-
записанное теми же цифрами, но в обратной последова-
последовательности.
3. Много ли таких чисел?
Рис. 26-12 а, б
Кубик
Кубик с ребром 3 дм покрашен со всех сторон в зе-
зеленый цвет. Этот кубик рассечен несколькими пло-
плоскостями (сколькими?) на 27 кубиков с ребром 1 дм.
Сколько из образовавшихся кубиков имеют 3 стенки
зеленые, сколько — две стенки, сколько — одну5
а сколько ни одной?
Маленькие вопросы по геометрии
а) Сколько углов, меньших 360° образуется на плос-
плоскости, если из произвольной точки этой плоскости
мы проведем т полупрямых (рис. 26-12а).
б) Сколько углов образуется, если из вершины угла
проведем внутри угла т радиусов (рис. 26-126).
414
РЕШЕНИЕ ЗАДАЧ Задача жестянщика
Рис. 26-13 а, б
Чтобы сосуд имел квадратичное основание, его раз-
развертка должна иметь вид, показанный на рис. 26-13а.
На рисунке 26-136 вы видите готовый сосуд. Емкость
сосуда обозначим буквой у и высчитаем по формуле:
у = {а-2х){а-2х)х
Эта функция достигает своего максимума при х = -т-
Доказательство. Рассмотрим функцию
у = {а—2х){а-2х)х.
Функция 4у достигает своего максимума при том же
значении х, что и функция у
4д> = {а~2х)(а-2хLх
Так как: (а—2х)+(а—2х)+4х — 2а (постоянное чи-
число) то произведение 4у достигает максимума, когда
зти числа равны, т. е. когда а—2х — 4х, т. е. когда
, а
а = ох, х = -г-.
о
Из этого следует, что наибольшая емкость сосуда
равняется:
2а \2 а 2а3 500
—(Г}
Найдите это число
1. Из условия задачи явно следует, что в девятой
части искомого числа первой цифрой должна быть
415
единица, а следовательно, в искомом числе первая
Цифра — это девятка.
Теперь искомое число мы можем записать следу-
следующим образом:
9000+lOOx+lOy+l
а девятую часть искомого числа:
1000+1007+10Х+9
а далее
9000+lOOx+lOj+l = A000+100^+10jc+9) • 9
Умножаем: девятью девять восемьдесят один; пи-
пишем единицу, восемь в уме. Ищем цифры десяток
(х), помня, что это также цифра сотен в искомом
числе. Найдем цифру 8.
Теперь имеем:
1000+ ... +80+9 и 9000+800+ ... +1
Без труда определим, что недостающая цифра —
это ноль. Итак, искомое число 9801, а его девятая
часть 1089.
2. Подобным же образом решим вторую задачу: ис-
искомое число 8712, а его четвертая часть — 2178.
3. Есть только два числа с такими свойствами.
Кубик
Ответ: 6 плоскостями; 8, 12, 6, 1.
416
Маленькие вопросы по геометрии
а) Каждая из т полупрямых образует с остальными
(т—1) углов, меньших, чем 360°, раз меньше
развернутого, раз — больше, например, полупрямые
а и Ь образуют углы (а, Ь) и (Ь, а). Следовательно,
всех углов т{т—1).
Если т = 5, 10 углов 5 • 4 = 20.
„ _, _ т{т—1)
б) В этом случае углов будет 2~^> "Р11 т = 5»
углов — 10.
СЮРПРИЗЫ ГЛАВА 27
КОМБИНАТОРИКИ
Прежде, чем мы укажем опеределение комбинато-
комбинаторики и формулы, которыми она оперирует, нам хо-
хочется познакомить вас с несколькими задачами из
области комбинаторики.
Задача № 1. У вас имеются ткани трех цветов: бе-
белого (б), красного (к) и зеленого (з). Сколько разных
трехцветных флагов можно сшить из этих материа-
материалов?
Комбинаторика отвечает: 6, а именно: б, к, з; б, з, к;
к, б, з; к, з, б; з, б, к; з, к, б.
Задача № 2. Цветов — пять: белый (б), красный (к),
зеленый (з), синий (с) и желтый (ж). Сколько мож-
можно из этих пяти цветов сшить разных трехцветных
флагов?
Комбинаторика отвечает: 60. Действительно, в две-
двенадцати флагах первым цветом будет белый: б, к, з;
б, к, с; б, к, ж; б, з, к; б, з, с; б, з, ж; б, ж, с;
б, ж, к; б, ж, з; б, с, к; б, с, з; б, с, ж. В следу-
следующих двенадцати флагах первым будет красный
цвет. Затем первым цветом будут по очереди зеле-
зеленый, синий, желтый, каждый в двенадцати флагах.
Задача № 3. В одном центральном учреждении име-
имеется три свободных должности: директора департа-
418
мента, начальника отдела и старшего инспектора. На
эти три должности выдвинуты 4 кандидатуры. Сколь-
Сколько троек, отличающихся друг от друга, по крайней
мере одним кандидатом, можно создать из четырех
кандидатов ?
Комбинаторика отвечает: 4. Если кандидатов обоз-
обозначим номерами от 1 до 4, то
тройки
директор
начальник
инспектор
I
1
2
3
II
1
2
4
III
1
3
4
IV
2
3
4
Итак, что же это такое комбинаторика? Это — раз-
раздел математики, который занимается расчетами числа
различного рода соединений из элементов данного
конечного множества. В комбинаторике различают
три вида соединений:
1. Перестановки — обозначаем символом Рп, в кото-
котором п — обозначает число элементов в каждом сое-
соединении. Примером вычисления числа перестановок
Р„ было решение задачи № 1.
Цветов было 3 (п — 3). Мы убедились, что
Р3 = 1 • 2 • 3 = 6
419
a ff 6 г а б г в
а 6
1
1
щ
Г
г д
1
¦
Г
¦
а в 5 г
а г 5 В а г 6 5 5 а В г 5 а г в
В общем:
Л = 1 -2-3 • ... • (n-l)-n
Например:
Р10 = 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 = 3 628 800
2. Размещения, которые обозначаем символом А ,
где п — это число всех элементов, а к — число эле-
элементов, встречающихся в каждом соединении. При-
Примером определения числа размещений было решение
задачи № 2. В этой задаче мы имели 5 элементов
(цветов) и по 3 элемента в каждом соединении; п =-
= 5, к = 3. Мы видели, что
5 В а г 5 В г a 5 г а В б г В a
A3 =
Л5
В общем
= 5 -4-3 = 60
III» Наг д Д г а А = И • (и —1) • (и—2) • (и-3) • (и—4)-... • (п—к
В г a 5 В г S а г а б В г а В б
г 5 6 а г д а В г 6 б а г В a 5
Рис.
420
27-1
т. е. равняется произведению к последовательных
натуральных чисел от и до п—к-\-1.
л
Например, А, = 6 • 5 • 4 • 3 = 360.
3. Сочетания (комбинации) — обозначаем символом
С или |") при этом п обозначает число всех эле-
элементов, а к — число элементов в каждом соедине-
соединении (к < п). Примером определения числа сочета-
сочетаний было решение задачи № 3. Сочетания должны
ИГРА В ПЯТНАДЦАТЬ
отличаться друг от друга по крайней мере одним эле-
элементом
(я) ¦ (и-1) ¦ (я-2) • . ¦ • (я-fc+l)
1 -2-3- ... -к
/4\ 4-3-2 .
например, (,| = -.— —?¦ — 4
Французский математик Э. Лукас напал на очень
интересный метод графического представления пе-
перестановок Рп. Лукас назвал свой метод «фигураль-
«фигуральным отображением». На рисунке 27-1 вы видите
фигуры, полученные Лукасом при перестановках че-
четырех элементов. Как следует из рисунка, из 4 эле-
элементов можно получить Р4 = 1 • 2 • 3 • 4 = 24 пере-
перестановки.
Любителям математических развлечений предлагаем
попробовать представить таким же образом все воз-
возможные перестановки из 5 элементов, однако, по-
порядка ради, предупреждаем, что их общее число
Р, = 1-2-3-4-5 = 120.
В некотором сродстве с комбинаторикой находится
игра, придуманная в семидесятых годах прошлого
века американцем Самуэлем Лойдом и названная
игрой в пятнадцать.
В большом сокращении игра эта заключается в сле-
следующем. На дне квадратной коробочки размерами
4x4 расположено 15 нумерованных шашек. Шест-
421
1
5
11
9
В
10
В
13
2
7
12
14
3
4
15
1
5
9
6
10
11
13
2
7
8
14
3
4
12
15
1
5
9
13
6
10
11
14
г
7
8
15
3
4
TS)
1
5
9
13
6
10
11
14
2
7
15
3
4
8
12
1
5
3
13
6
10
14
г
7
и
15
3
4
8
12
1
5
9
13
г
6
10
14
?
3
7
11
15
4
8
11
1
5
9
13
г
е
10
14
d
3
7
11
15
4
а
и
ж
Рис. 27-2 а, б, в, г, д, е, ж
422
надцатое поле — свободное. Игра заключается в по-
последовательном передвижении шашек, возможном
благодаря наличию свободного поля. Цель игры —
перевести любое начальное положение 15 шашек
в нормальное, т. е. такое, при котором шашки уло-
уложены в порядке своих номеров (Внимание: перенос
шашек не разрешается).
На рисунке 27-2 вы видите пример решения такой
задачи. На рисунке 27-2а показано начальное поло-
положение. Затем шашку 15 мы передвигаем на свободное
место внизу поля, а шашки 12, 8 и 11 передвигаем
вправо. При этом получается положение шашек,
указанное на рисунке 27-26. Теперь переместим шаш-
шашку 9 вверх, на свободное поле, а шашки 13, 14 и 15
влево, как это показано на рисунке 27-2в.
Последующие перемещения, показанные на рисунках
27-2г, д, е, приводят нас к окончательному решению,
показанному на рисунке 27-ж.
Мы предлагаем читателю выбрать другое начальное
положение 15 шашек и, передвигая их, прийти к их
натуральному размещению в коробке. Однако, не-
необходимо отметить, что число возможных переста-
перестановок из 15 элементов равняется
Р15 = 1 • 2 • 3 • 4 • 5 ¦ 6 • 7 ¦ 8 • 9 • 10 • 11 • 12-
¦ 13 ¦ 14-15 = 1 307 674 368 000
В 1879 году американский математик Джонсон раз-
разработал математическую теорию этой игры.
АНЕКДОТ Однажды 12 очень вежливых гостей встретилось на
12 СОТРАПЕЗНИКАХ званном обеде. Так как хозяин не определил зара-
заранее, где кто должен сидеть, то приглашенные начали
друг другу уступать из вежливости свои места. Один
из гостей, желая найти выход из создавшегося по-
положения, предложил бросить жребий, другой — по
профессии математик — с улыбкой предложил, преж-
прежде всего, испробовать все возможные перестановки
12 гостей за обеденным столом. Гости согласились
с этим предложением и начали испытывать возмож-
возможные перестановки, однако, вскоре так устали от не-
непрерывного пересаживания, что отказались про-
продолжать эту игру и сели за стол как попало.
После обеда, когда все уже пили кофе, математик
объяснил собравшимся, что если бы одно переса-
пересаживание продолжалось одну секунду и если бы гости
пересаживались круглые сутки, то и так для того,
чтобы испробовать все возможные варианты распо-
расположения двенадцати гостей за столом потребовалось
бы, примерно, 15 лет и 2 месяца.
— Как вы это высчитали ? — заинтересовались го-
гости.
— Очень просто, — ответил математик, — число всех
перестановок 12 гостей равняется
Р12 = 12! = 479 001 600
Принимая, что одна пересадка продолжается 1 се-
секунду, нам потребуется 479 001 600 секунд, т.е. при-
примерно 15 лет и 2 месяца.
423
л!(л-ФАКТОРИАЛ) Этот чрезвычайно полезный математический знак
был введен в математику в 1808 году.
и! = 1 -2-3 -4-5 • ... ¦ (п-2) (п-1)п;
5! = 1 -2-3 -4-5 = 120
0! =1
1! = 1
2! =2
3! =6
4! = 24
5! =120
6! = 720
7! = 5040
8! =40 320
9! =362 880
10! = 3 628 800
И! =39 916 800
12! =479 001600
13! =6 227 020 800
14! = 87 178 291 200
15! = 1307 674 368 000
16! = 20 922 789 888 000
17! =355 687 428 096 000
18! =6 402 373 705 728 000
19! =121645 100408 832000
20! = 2 432 902 008 176 640 000
21! =
22! =
23! =
24! =
25! =
любителям математики рекомендуем продолжить эти
вычисления.
|ЕРОЯТНОСТЬ ИЛИ ГЛАВА 28
ДОСТОВЕРНОСТЬ?
1. Никого не удивляет, что математика раскрывает
законы, которым подчиняются силы природы, и что
знание этих законов позволяет предвидеть разные
события, например, затмение Луны или Солнца,
появление кометы, а также рассчитать расстояния
между планетами и звездами, высчитать силу при-
притяжения на удаленных планетах и т. п.
Вполне понятно также, что математика является
орудием инженера, строящего мосты или изготовля-
изготовляющего точные приборы, что она помогает ученому,
использующему в своих работах вычислительные ма-
машины.
Однако, многие из вас очевидно очень удивятся,
узнав, что математика позволяет предвидеть, напри-
например, сколько пар чулок первого сорта находится
в среднем в пачке, содержащей 1000 пар чулок, по-
полученных торговой сетью; или: попадает ли во вра-
вражеский самолет залп из 250 винтовок; или: сколько
соответствующих стандарту лампочек накаливания
(т. е. таких лампочек, которые перегорают не раньше,
чем через 1200 часов горения) находится в каждой
тысяче изготовленных на данном заводе?
Такие события подчинены случайности, т. е. чему-
то, что не укладывается в рамки определенных за-
425
конов. Математикам удалось, однако, выразить эти
случайности в виде формул.
Блез Паскаль A623—1662)
2. Французский дворянин, некий господин де Мере,
был азартным игроком в кости и страстно хотел раз-
разбогатеть. Он затратил много времени, чтобы открыть
тайну игры в кости. Он выдумывал различные ва-
варианты игры, предполагая, что таким образом при-
приобретет крупное состояние. Так, например, он пред-
предлагал бросать одну кость по очереди 4 раза и убеждал
партнера, что по крайней мере один раз выпадет при
этом шестерка. Если за 4 броска шестерка не выхо-
выходила, то выигрывал противник.
В те времена еще не существовала отрасль матема-
математики, которую сегодня мы называем теорией вероят-
вероятности, а поэтому, чтобы убедиться, верны ли его
предположения, господин Мере обратился к своему
знакомому, известному математику и философу Б. Па-
Паскалю с просьбой, чтобы он изучил этот вопрос.
Паскаль не только сам заинтересовался этим, но и на-
написал письмо известному математику П. Ферма, чем
спровоцировал его заняться общими законами игры
в кости и вероятностью выигрыша.
Таким образом, азарт и жажда разбогатеть дали тол-
чок возникновению новой чрезвычайно существен'
ной математической дисциплины: теории вероятно-
вероятности. В разработке ее основ принимали участие мате-
математики такого масштаба, как Паскаль и Ферма >
Гюйгенс A629—1695), который написал тракта?
426
Вероятность
«О расчетах при азартных играх», Яков Бернулли
A654—1705), Муавр A667—1754), Лаплас A749—
1827), Гаусс A777—1855) и Пуассон A781—1840).
В наше время теория вероятности используется почти
во всех отраслях знаний: в статистике, синоптике
(прогноз погоды), биологии, экономике, технологии,
строительстве и т. д.
В некоторых странах, например, в Японии, теория
вероятности преподается в средних школах. У нас
элементы теории вероятности включены в новую
программу по математике для средней школы.
3. Математическую вероятность следует понимать,
как некоторую стабильную частоту какого-то слу-
случайного события. Исследование такой вероятности
и законов, которые ею управляют, являются сутью
теории вероятности.
Вероятность какого-либо события А обозначает сим-
символ Р(А). Если вероятность события А становится
достоверностью, то это записывается следующим
образом
Р(А) = 1
Если известно, что событие А, наверняка, не может
произойти, то это записывается следующим образом:
Р{А) = 0
Например, при подбрасывании монеты можно ожи-
ожидать двух разных событий (исходов): либо монета
427
Рис. 28-1
упадет «орлом» вверх, либо «решкой». Следова-
Следовательно, вероятность, что монета упадет орлом вверх
(вероятность события А) равняется 1/2. Запишем
зто следующим образом:
Р{А) = 1/2
Вероятность того, что монета упадет решкой вверх,
т. е. что произойдет событие В, также равно 1/2,
иначе говоря:
Р{В)= 1/2 = \-Р(А)
Давайте теперь рассмотрим более сложный случай.
Мы подбрасываем вверх две кости (каждая кость —
это кубик, на каждой стороне кубика имеются выре-
вырезанные очки: один, два, три, ..., шесть). Чему равна
вероятность, что сумма очков будет равняться семи?
Посмотрим, какие сочетания очков на двух костях
дают в сумме семь очков: это может быть 1 и 6, 2 и 5,
4 и 3, 6 и 1} 5 и 2, 3 и 4. Следовательно, таких соче-
сочетаний 6 (рис. 28-1).
С другой стороны нам необходимо узнать, сколько
имеется возможных сочетаний при кидании двух ко-
костей. Таких возможностей 36, а именно:
1-1, 1-2, 1-3, 1-4, 1-5, 1-6
2-1, 2-2, 2-3, 2-4, 2-5, 2-6
6-1, 6-2, 6-3, 6-4, 6-5, 6-6
Из этого следует, что вероятность получения 7 очков
428
при кидании двух костей составляет примерно (со-
(событие А-т):
' / 2 3 A 5 6 7 в 9 10 U 12 В
А„
Рис. 28-2
Если бы мы исследовали все возможные суммы оч-
очков, которые могут выпасть при кидании двух ко-
костей B, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12), и результаты
наших рассчетов представили в виде графика, то
получилась бы фигура, показанная на рисунке 28-2.
Необходимо отметить, что событий, при которых
сумма очков на двух костях не равняется 7, всего
тридцать. Вероятность таких событий, назовем их
событиями В, составляет:
к ' 36 6 '
Событие А и событие В взаимно исключаются, та-
такие события называются несовместными, они обра-
образуют полную систему событий.
Сумма вероятностей двух несовместных событий
(противоположных) равна 1.
Р{А)+Р{В) = 1 + 1=1
т. е. Р{В) = 1 —Р(А).
4. Самым простым и одновременно самым сущест-
существенным законом, используемым при вычислении ве-
вероятностей, является закон сложения. Для иллю-
иллюстрации этого закона рассмотрим следующий пример:
429
На трамвайной остановке останавливаются трамваи
№№ 3, 4, 6, 21, 32 и 34. Для того, чтобы доехать
в институт студент может ехать маршрутом 32 или
34. Принимая, что трамваи всех шести маршрутов
курсируют с однаковой частотой, подсчитать веро-
вероятность того, что первый подъехавший трамвай
будет подходящим.
Так как вероятность — это отношение числа благо-
благоприятных исходов к числу всех возможных исхо-
исходов (в этом случае возможных исходов 6), то иско-
2 1
мая вероятность РC2) или РC4) равняется—- = у,
ноу = y-f-g-, т. е. РC2 или 34) = РC2)+РC4)
В общем, если в последовательности п одиночных
взаимно исключающихся событий получается в сред-
среднем: /их раз исход Ах, а следовательно, вероятность
исхода Ах составляет —-, т2 раз исход А2, а следо-
следовательно, вероятность исхода А2 составляет
т2-, ..., тп раз исход Ап, а следовательно, вероят-
п
ность исхода Ап составляет —, то вероятность, что
произойдет, по крайней мере, одно из событий М
(i = 1, 2,...,«) можно выразить формулой:
i или Аг или ... или Ап) = Р(А1)+Р(А2) +
430
Рис. 28-2
При использовании этой формулы очень важно про-
проверить, чтобы исходы событий были взаимоисклю-
чающимися. Если мы не проследим за этим, то
могут получиться неверные результаты.
Вот пример. В мишень стреляло двое стрелков.
Мишень разделена на 5 зон (рис. 28-3). Попадание
в 1 зону квалифицируется как отличное, попадание
во вторую зону — хорошее. Первый стрелок на
100 выстрелов имеет 60 отличных попаданий (со-
(событие Ах), второй стрелок на 100 выстрелов имеет
80 отличных попаданий (событие А2)- Вычислить
вероятность попадания в зону 1, когда стреляют
одновременно оба стрелка.
Предположим, что оба стрелка выстрелили одновре-
одновременно 100 раз, т. е., что было произведено сто
двойных выстрелов. Примерно 60 выстрелов пер-
первого стрелка было отличных, этот стрелок про-
промахнулся 40 раз. Второй стрелок из 100 выстрелов
попал в первую зону 80 раз, из этого следует, что
второй стрелок из каждых 10 выстрелов попадает
восемь раз в первую зону. Следовательно, при
40 промахах первого стрелка, второй попадает в пер-
первую зону 8 • 4 = 32 раза. Из этого уже нетрудно
подсчитать, что при 100 двойных выстрелах будет
60+32 = 92 отличных попадания.
Если бы мы в этом случае хотели подсчитать веро-
вероятность на основании формулы
или А2) = Р{А1)+Р{А2)
431
то получили бы абсурдный результат
80
60
Тб0
_ 1 .
ТОО + Тб0 ~ТбО
так как вероятность события не может быть больше
единицы.
Ошибка возникла вследствие того, что мы не уч-
учли в наших рассуждениях, что события Ах и Аг
взаимно не исключаются: попадание в первую зону
первого стрелка не исключает попадание в нее вто-
второго. Несовместность событий является обязатель-
обязательным условием применения закона сложения.
432
5. Чулки изготавливаются на двух фабриках. Пер-
Первая фабрика изготавливает 80% всех пар чулок,
а вторая соответственно — 20%. На 100 пар чулок
первой фабрики в среднем 83 пары первого сорта,
а на 100 пар чулок второго завода — только 63 пары
первого сорта.
Сколько пар чулок первого сорта находится в каж-
каждой сотне, поступающей в торговую сеть ?
Как нетрудно высчитать, на каждую сотню пар чу-
чулок приходится 79 пар первого сорта, так как:
0,83 • 80+0,63 • 20 = 0,79
Следовательно, вероятность покупки чулок первого
сорта составляет 79/100.
Если бы мы, однако, купили наши чулки в магази-
магазине, где продаются чулки только первой фабрики, то
вероятность покупки чулок первого сорта состав-
составляла бы соответственно 83%. Начатом примере хо-
хорошо видно, что добавление к общим условиям, при
которых происходит какое-либо событие (покупка
чудок), какого-то нового существенного условия,
(чулки куплены в магазине, торгующем только
изделиями первой фабрики), изменяет вероятность
данного единичного события.
Добавляя новое условие, мы изменяем существен-
существенным образом набор условий и наш процесс будет
протекать иначе.
Таким образом, мы получили две разные вероят-
вероятности того же события — покупки пары чулок пер-
433
вого сорта. Каждая из них была рассчитана с учетом
разных условий. В первом случае, пока не учиты-
учитывалось дополнительное условие (покупка в мага-
магазине, продающем только изделия первой фабрики),
мы получили безусловную вероятность Р(А) = 79/100,
после введения дополнительного условия мы по-
получаем так называемую условную вероятность, ко-
которую обозначаем символом Р(А\В). Буква В обозна-
обозначает здесь дополнительное условие. Символ Р(А\В)
следует читать следующим образом: вероятность
события А, если произошло событие В. В рассматри-
рассматриваемом нами случае, оно составляет:
83
Р(А\В) =
100
6. Давайте, однако, вернемся к нашему предыду-
предыдущему примеру с чулками. Пусть из 1000 пар чулок,
находящихся в продаже, в среднем 200 пар изго-
изготовлены на втором заводе, из этого числа 126 пар —
первого сорта. Вероятность, что данная пара чулок
изготовлена на втором заводе (событие В) равняется
02
Вероятность, что данная пара чулок, изготовленная
на втором заводе, первого сорта, равна
^ = 0,63
Так как в каждой партии, состоящей из 1000 пар
чулок, 126 пар одновременно являются изделиями
434
второго завода и по качеству относятся к первому
сорту, то вероятность того, что произойдет одновре-
одновременно событие А и В равняется:
т. е. произведению Р(В) на Р(А\В). Этим мы вывели
формулу умножения. Эту формулу можно предста-
представить в виде теоремы о вероятности произведений
двух событий: вероятность одновременного по-
появления двух событий равна произведению веро-
вероятности одного из них на условную вероятность
другого при условии, что первое событие произо-
произошло.
Пример № 1. Рубашки, которые шьются в одном
кооперативе, признаются в 90% годными к про-
продаже (событие А); из 100 рубашек признанных
годными — в среднем 80 квалифицируются первым
сортом (событие В). Какова вероятность, что данная
рубашка, сшитая в этом кооперативе, окажется
первого сорта?
Ищем Р{А и В) так как для того, чтобы изделие
оказалось первого сорта, необходимо, прежде всего,
чтобы оно не было забраковано (событие А), а затем,
чтобы было заквалифицировано в первый сорт.
В соответствии с условиями задачи Р{А) = 0,90,
*) Путем изменения обозначений в формуле A) получаем фор-
формулу Р(А и В) = Р(А) ¦ Р(В\А).
435
a P(B\A) — 0,80, следовательно, на основании фор-
формулы Р(А и В) = 0,90 • 0,80 = 0,72.
При подсчете вероятности одновременного появле-
появления двух или более событий используется следующая
теорема: Вероятность одновременного появления
произвольного числа событий равняется вероят-
вероятности этих событий, при условии, что эти события
не зависят одно от другого.
Р(А и В и С и ... и К) =
= Р(А)-Р(В)-Р(С)-....Р(К) B)
Примечание. При использовании этой фор-
формулы необходимо всегда проверить, не зависят ли
события (А, В, С, ..., К) одно от другого, так же
как и при применении теоремы сложения необхо-
необходимо проверить являются ли данные события не-
несовместными.
Пример № 2. Техник обслуживает три автомата.
Вероятность того, что в течение одного часа авто-
автомат не будет нуждаться в ремонте составляет: для
первого автомата 0,9, для второго — 0,8, а для
третьего — 0,75. Какова вероятность, что в течение
часа ни один из автоматов не будет нуждаться в ре-
ремонте.
Так как автоматы работают независимо один от дру-
другого, то мы применяем формулу B). Искомая веро-
вероятность равняется:
0,9 • 0,8 • 0,75 = 0,54
436
Пример № 3. Американский бомбардировщик Б-52,
летящий в направлении Северного Вьетнама, был
обстрелян отрядом партизан, насчитивавшем 250
бойцов. Какова вероятность того, что бомбарди-
бомбардировщик будет сбит в результате залпа (одновремен-
(одновременного выстрела) из 250 винтовок.
Подсчитано, что в некоторых условиях вероят-
вероятность попадания в самолет при одиночном выстреле
составляет 0,004. Из этого следует, что вероят-
вероятность непопадания в самолет составляет 1—0,004 =
= 0,996. Вероятность непопадания в самолет при
залпе из 250 винтовок соответственно составляет
0,996 • 0,996 • 0,996 • ... • 0,996B50 раз), т. е. 0,996250
Вероятность попадания теперь составит:
р = 1-0,996250 ж 0,625
Мы видим, что вероятность попадания относитель-
относительно высока (больше 1/2).
437
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Выборка цифр
У мальчика была игрушечная типография. Кроме
букв там были и цифры: 10 отдельных типографс-
типографских знаков от 0 до 9. Эти знаки беспорядочно раз-
разбросаны в коробке. Какова вероятность, что мальчик
выберет наугад 3 таких знака, чтобы из них можно
было составить число, делимое на 9.
Примечание. Использовать
мости на 3 (глава 17).
признак дели-
Мудрый отец и неглупый сын
Сын известного американского математика получал
карманные деньги от своего отца: 10 долларов
в месяц. Однако, как-то отец сказал сыну:
— Сегодня ты не получишь своих карманных де-
денег, однако, ты можешь вышрать свои 10 долларов,
если рискнешь принять участие в игре.
— Во что, — спросил сын?
— Вот, — ответил ему отец, — пачка, в которой
находится десять десятидолларовых купюр, а здесь
пачка с десятью одно долларовыми купюрами. Как
тебе известно, десятидолларовая купюра отличается
от одно долларовой только цветом. Все эти купюры
ты разделишь на две пачки, как тебе будет угодно.
Затем я завяжу тебе глаза и одну пачку положу
в коричневую шляпу, а вторую — в черную. После
этого я перемешаю купюры в шляпах и одну шляпу
438
положу с правой стороны, а вторую с левой. Ты
должен с завязанными глазами вытянуть одну
купюру из любой шляпы, если это будет десять
долларов, то можешь себе их взять.
— А если это будет один доллар ?
— Трудно, будешь весь месяц поливать цветы в на-
нашем саду и ничего за это не получишь.
Мальчик согласился.
Как он разделил купюры на две пачки, если это
обеспечивало ему самую большую вероятность вы-
вытянуть десять долларов и каково численное значение
этой вероятности.
На боксерском ринге
Один из боксеров для того, чтобы попасть в ко-
команду, отправлявшуюся на олимпийские игры в Мек-
Мексику, должен был провести три боя в течение трех
дней подряд с двумя противниками. Две победы,
одна за другой, гарантировали ему поездку на олим-
олимпийские игры. Его противниками были два боксера:
один очень сильный (назовем его А) и второй более
слабый (назовем его В).
В какой последовательности наш боксер должен был
провести свои бои, чтобы вероятность двух после-
последовательных побед была самой большой: в последо-
последовательности А-В-А (с боксером А, затем с боксером
В и снова с боксером А) или же в последователь-
последовательности В-А-В7
439
РЕШЕНИЕ ЗАДАЧ Выборка чисел
Всех возможных сочетаний из 10 цифр по три
10-9 8 1ОП „
1 . _ =1/0. Благоприятных исходов, т. е. та-
таких, при которых сумма цифр составляет 9 или 18
(признак делимости на 9) всего И, а именно: 126,
135, 180, 234, 270, 360, 450, 189, 279, 396, 459. Сле-
Следовательно, вероятность выборки благоприятного
сочетания цифр равна 11/120.
Мудрый отец и неглупый сын
Мальчик в одну пачку положил только одну купюру
в десять долларов, а во второй — все оставшиеся
девятнадцать купюр. Таким образом, вероятность
10 долларов 10 долларов ji доллар
440
извлечения десятидолларовой купюры была 1 :2
(две шляпы — одна купюра). Если мальчик попал бы
на соответствующую шляпу, то он имел уверенность
выигрыша. Если же он попал бы в шляпу, где ле-
лежало девятнадцать купюр, то вероятность вытяги-
вытягивания десятидолларовой купюры составляла 9/19,
а одно долларовой 10/19.
На боксерском ринге
Решение этой задачи нельзя найти интуитивно или
методом угадывания. Здесь необходима помощь
математики, а точнее теории вероятности.
Пусть Р1 — вероятность победы нашего боксера
в бою с боксером А, а Р2 — в бою с боксером В. По
условиям задачи Рх < Рг. Вероятность поражения
нашего боксера в бою с боксером А равняется \—Р1,
а вероятность поражения с боксером В равняется
1— Рг. Если боксер выберет последовательность
боев А-В-А, то существуют три возможных вари-
варианта 2 последовательных побед.
I. Наш боксер побеждает во всех трех боях. Веро-
Вероятность этого события выражается числом
II. Наш боксер побеждает в двух первых боях
и проигрывает в третьем. Вероятность такого ис-
441
хода можно выразить числом:
Ш. Наш боксер проигрывает первый бой и выигры-
выигрывает во втором и третьем. Вероятность такого исхо-
исхода:
A-Р1)Р2Р1 = Р2Р1-Р2Р21
После сложения всех этих вероятностей мы полу-
получим результат Р1Р2{2—Р1). Такова вероятность, что
наш боксер выиграет два последовательных боя,
если будет бороться в последовательности А-В-А.
Подобные рассуждения в случае, если наш боксер
будет бороться в последовательности В-А-В, дадут
нам следующие результаты.
I. Вероятность выигрыша всех трех боев:
P2PtP2 = Р,Р1
II. Вероятность выигрыша только двух первых бо-
боев:
III. Вероятность выигрыша двух последних боев:
(l-P2)Pi-P2 = P1P2-PlPi
Сумма этих вероятностей равняется PiP2B—Р2)-
Такова вероятность, что наш боксер выиграет два
последовательных боя, если будет бороться в после-
последовательности В-А-В.
442
Сравнивая вероятность побед при последователь-
последовательности боев А-В-А с вероятностью побед при борьбе
в последовательности В-А-В, т. е. величины:
Р1Р2B—Р1) и Р1Р2B—Р2), мы придем к выводу,
что число Р1Р2B—Р1) больше чем Р1/>2B—Р2)
так как B—Pt) больше чем B—Р2).
Резюмируя, можно сказать, что наш боксер имеет
больше шансов выиграть два последующих боя,
встречаясь на ринге со своими противниками в по-
последовательности А-В-А, т. е. прежде всего, про-
проведя бой с боксером А, затем с боксером В и снова
с боксером А.
РАСЧЕТ ИЛИ
РИСУНОК
ГЛАВА 29
л
5
Рис. 29-1 а, б
Решая математические задачи, мы, как правило, вы-
выполняем разные вычисления. Имеются, однако, воп-
вопросы, которые значительно яснее и проще могут
быть решены с помощью рисунка. Если мы некото-
некоторые две величины представим в виде отрезков, на-
например, а и Ь, то легко можно найти такой отрезок с,
который равняется а-\-Ъ или а—Ъ или а • Ъ или а: b
(рис. 29-1 а, б).
Графическое сложение, умножение, решение урав-
уравнений и т. п., — это система конструкций, которая,
с некоторым приближением, заменяет нам вычисле-
вычисления. В графических расчетах используются также
графики функции. Графические расчеты употребля-
употребляются также довольно часто в прикладной матема-
математике и являются основной формой расчета в некото-
некоторых разделах техники, например, в графической ста-
статике. Ценность графического метода заключается,
между прочим, в его несложности и наглядности)
к его недостаткам относится сравнительно неболь-
небольшая точность. Во многих случаях, например, в инже-
инженерной практике, точность графического расчета
вполне достаточна, так как величины, которыми эти
расчеты оперируют, являются сами по себе прибли"
зительными величинами, а поэтому результаты вы-
вычислений также относительно мало точные.
444
График дбижения
минроЬуса
Рис. 29-2
А вот пример графического решения задачи:
В экскурсии, направляющейся из Курска в местность
В, удаленную на 63 км, принимает участие 30 — че-
человек. В последнюю минуту перед отправлением ока-
оказалось, что в распоряжении экскурсантов имеется
лишь один микробус на 15 мест. Поэтому было ре-
решено, что микробусом отправится первая группа
15 человек, которая выйдет из ьего на некотором
расстоянии от местности В и далее пойдет пешком,
а микробус вернется и заберет вторую группу, ко-
которая будет продвигаться из Курска пешком в на-
направлении местности В, Как необходимо организо-
организовать маршрут микробуса, чтобы все 30 человек ока-
оказались в местности В одновременно, если микробус
двигается со скоростью 30 км\ч, а средняя скорость
передвижения пешеходов принимается равной 4 км/ч.
Задачу необходимо решить графически без составле-
составления уравнений.
Графическое решение задачи показано на рисунке
29-2. Читатель сам догадается, как была вычерчена
прямая КВ.
Из графика следует, что:
1. Микробус перевез первую группу на расстояние
51 км, затратя на это 1,7 часа = 1 час 42 минуты
(точка Nj), затем вернулся за второй группой.
2. Вторую группу микробус встретил на расстоянии
12 км от Курска, через 3 часа с момента выхода (точ-
(точка Mi).
445
ФОРМУЛА И ЕЕ
ГЕОМЕТРИЧЕСКОЕ
ИЗОБРАЖЕНИЕ
A a b 8
\
III
a b
а-Ь
о с
Рис. 29-3
3. Первая группа туристов, выйдя из микробуса,
направилась в местность В. После трех часов ходьбы
она дошла до этой местности и в этот же момент ее
нагнал микробус со второй группой туристов.
4. Путешествие от Курска до местности В продолжа-
продолжалось примерно 4 часа 42 минуты.
5. Обе группы прошли пешком и проехали микробу-
сом одинаковое число километров (NtB = КМХ',
KN± = MtB).
Попытайтесь решить эту задачу путем вычислений
(полученный результат можете проверить в «Реше-
«Решениях задач»).
В школе нас учат, что:
I. (а+ЬJ = а2+2аЬ+Ь2
II. (a-bJ = a2-2ab+b2
III. (а+Ь) • (а-Ь) = а2-Ь2
Все эти формулы имеют свою геометрическую ин-
интерпретацию. Согласно формулы (I) можно из кваД"
рата со стороной а и из квадрата со стороной Ъ и из
двух прямоугольников со сторонами а и Ъ составить
один квадрат со стороной а+Ь как это показано на
рис. 29-3.
446
E b A
—1?
1
я
J
к
в
¦a
а с
Рис. 29-4
E
0
W/////,
j В
nl
Рис. 29-5
Согласно формуле (II), если из суммы площадей двух
квадратов, одного со стороной а и второго со сторо-
стороной Ь, вычтем площади двух прямоугольников со
сторонами а и Ъ, то получим квадрат со стороной
а—Ъ (рис. 29-4). Площадь фигуры ABCD = а2,
площадь EAGF = Ъ2, площадь фигуры EBCDGF =
= a2+b2, площадь прямоугольника EHJF = площа-
площади прямоугольника НВСК = а • Ъ.
Если от фигуры EBCDGF отрежем два равных за-
заштрихованных прямоугольника, то останется квадрат
со стороной а—Ъ
Формула (III) представлена графически на рисунке
29-5. Читатель сам его поймет. На этом рисунке:
АВ = ВС = CD = DA = a
AG = GF= FE= EA = b
ED=GB = a-b
BDX = a+b
ABCD = a2
AGFE = b2
EFGBCD = (a+b) (a-b)
Формула (I) выражает квадрат суммы двух чисел.
Можно указать формулу квадрата суммы трех, че-
четырех и более чисел. Например:
IV. (a+b+cJ = Q2+b2+c2+2ab+2ac+2bc
447
Hi
a b
а с
a b
V/by//
УШ
b С
а с
b с
a+b+z
Рис. 29-6
b с d
w
a b
а с
a d
a b
Ш
b с
b d
а с
be
'//p
Щ
с d
a i
bd
с d
Puc. 29-7
V. (a+b+c+dJ = a2+b2+c2+d2+2ab+2ac+
+2ad+2bc+2bd+2cd
Эти формулы очень легко вывести геометрически.
Читатель сам поймет их на основании рис. 29-6 и 29-7.
Мы предлагаем также читателю выполнить рисунки
для:
(a+b+c+d+eJ = ...
и для
(а+Ь~сJ
На основании рисунка 29-6 можно вывести еще 2 до-
дополнительных формулы, а именно
VI. (a+b+cJ = (a+bJ+2(a+b)c+c2
VII. (a+b+cJ =a2+2a(.b+c)+(.b+cJ
Попробуйте составить для них соответствующие ри-
рисунки.
На основании рисунка 29-7 можно вывести еще три
формулы. Какие?
ЛЮБОПЫТНОЕ
ТОЖДЕСТВО
аг+Ьг _ а+Ь
a3+(a-bK ~ а+(а-Ь)
(А)
Правая сторона тождества содержит те же буквы
и те же математические знаки, но не содержит пока-
448
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
зателей степени. Эту формулу можно использовать
в качестве примера недопустимых сокращений, на-
например:
253+113 _ 25+11 36 12
253+B5-11K ~~ 25+B5-И) ~ 39 ~ 13
Читатель сам проверит тождество (А) (смотри «Ре-
«Решение задач»).
га
Недопустимые сокращения
За контрольную работу Иванову поставили двойку,
хотя полученные им ответы при решении примеров
точно совпадали с ответами Петрова, который по-
получил за свою работу четверку. Иванов сократил
19
дробь -гр-, зачеркивая в числителе и в знаменателе 9,
1 49
и получил ответ -=-. Он сократил дробь -д^-, зачеркнув
в числителе и знаменателе 9, и получил ответ -5~ = -*->
о Z
_ 16 ,
при сокращении дроби -j-^ он зачеркнул о, ответ по-
1 _ 266 ,, 2
лучился т,ав дроби --?=¦ зачеркнул 66 и получил —.
Его сосед по парте, Петров, поступил несколько ина-
иначе при сокращениях дробей, хотя и получил те же
19
ответы: -^ он сократил, разделив числитель и зна-
449
менатель на 19, ^разделив числитель и знаменатель
i /¦ 266 ..л
на 16, а -тгс- разделив числитель и знаменатель на 133.
Так бывает в математике нередко: правильный от-
ответ не всегда свидетельствует о правильном ходе ре-
решения.
Игры с числами
а) 145 = 1!+4!+5!,
т.е. 1+1-2-3 -4+1 -2 -3 -4-5
б) 387 420 489 = 387+42°-489 т. е. З18
Кто не верит может проверить.
в) 1+2+3 = 1.2-3 = /13+23+33
История с алмазом
Прежде, чем мы расскажем вам зту историю, напом-
напомним, что:
1. Из нескольких прямоугольников с одинаковым
периметром самую большую площадь имеет тот, у ко-
которого стороны равны, т. е. квадрат.
2. Если слиток, например, золота стоит л рублей,
то слиток той же пробы, в 2 C,4,...) раза тяжелее
стоит соответственно в 2 C,4, ...) раза дороже. Этот
закон действителен для абсолютного большинства
товаров, но не для алмазов (бриллиантов).
450
\~ a -
b
Mm.
Урон
с
Урон
т..
, а
щ
Урон
Урон
ш
Рис. 29-8 а, 6, «
3. Алмаз, который весит в два раза больше, стоит
в 4 раза дороже, алмаз в три раза тяжелее, стоит
в 9 раз больше и т. д. Одним словом, цена алмаза
пропорциональна квадрату его веса.
Во время шлифования алмаз массой а каратов рас-
распался на две неравные части. Как велик урон, кото-
который понес гранильщик алмазов? В каком случае
этот урон самый большой?
Эту задачу лучше всего решить графически. На рис.
29-8а масса алмаза представлена в виде отрезка а,
а его ценность в виде площади квадрата со стороной
а. На рис. 29-86 мы видим стоимость частей бис,
на которые распался алмаз массой а каратов. Эта
стоимость представлена в виде квадратов с площадью
Ь2 и с2. На рисунке показана также величина урона
(два не заштрихованных прямоугольника с перимет-
периметрами равными 2Ь+2с — 2а). Как видно из рисунка
29-8в самый большой урон получается, когда эти
прямоугольники превращаются в квадраты.
Разное — „Яйцо Колумба"
Рассказ об яйце Колумба вам очевидно известен. Его
содержание сводится к следующему.
Критики Колумба упрекали его, что он берется за
Дело в принципе невыполнимое, между прочим, так-
ж е и потому, что если Земля — шар, то каравеллы
Колумба должны будут въехать на водяную гору,
что невыполнимо.
24*
451
Когда Колумб вернулся после завершения своего
успешного путешествия, его противники высказы-
высказывали мнение, что он, собственно говоря, ничего чрез-
чрезвычайного не совершил. Рано или поздно кто-ни-
кто-нибудь другой мог также пристать к неизвестному бе-
берегу. Слыша эти высказывания, Колумб попросил,
чтобы ему принесли свежее яйцо. Когда ему при-
принесли яйцо, он обратился к присутствующим:
— Кто из Вас сумеет поставить это яйцо вертикально
на столе?
Попробовали это сделать все присутствующие, од-
однако, это никому не удалось. Тогда Колумб взял
яйцо, ударил им довольно крепко в стол и таким
образом поставил яйцо вертикально.
— Так-то и я сумею, — сказал при этом один из
наиболее ярых противников Колумба.
— Так почему ты этого не сделал? — спросил Ко-
Колумб.
Из этой притчи можно вывести следующую мораль:
решение каждой задачи кажется легким, когда оно
известно.
Далее найдете несколько таких маленьких задач,
каждая из которых является в какой-то степени
«яйцом Колумба».
1. Стороны треугольника ABC имеют соответствен-
соответственно длину 18, 23 и 41 см, а стороны треугольника
DEF— 25, 33 и 58 см. Площадь каторого из треуголь-
треугольника больше?
452
Рис. 29-9
А 10 см В
Рис. 29-11
2. Три улицы пересекаются попарно, образуя пло-
площадь в виде равностороннего треугольника, как это
показано на рисунке 29-9. Найдите на этой площади
такую точку, чтобы сумма расстояний от киоска с га-
газетами, который будет установлен на этой площади,
до трех улиц, образующих площадь, была минималь-
минимальной. Где находится эта точка?
3. Иван кинул шестигранный игральный кубик. По-
После него этот же кубик кинул Гриша. Какова вероят-
вероятность, что у Ивана выпало большее количество
очков?
4. На рисунке 29-10 нарисован куб ABCDEFGH.
Какой угол образуют прямые GE и ЕА, а какой пря-
прямые GD и DB7 Ответ обосновать доказательством.
5. На озере плавало 5 уток. Охотник выстрелил
и убил двух уток. Сколько уток осталось?
6. Что больше: два деленное на 0,125, или два ум-
умноженное на 4. На ответ вам дается три секунды.
7. Вот три пилюли, — сказал врач больному, — на-
начинайте принимать сейчас и глотайте по одной пилю-
пилюле каждые полчаса. На сколько часов больному
хватит этих пилюль?
8. Вершина С треугольника ABC не поместилась
на рисунке 29-11. AD и BD — биссектрисы углов
у основания этого треугольникп — образуют прямой
угол ADB; отрезок АВ = 10 см. Какова высота тре-
треугольника ABC}
453
9. Ученик решает задачу в течение 60 минут. За
сколько минут эту же задачу могут решить 10 уче-
учеников?
10. В аллейке в ровном ряду растет 10 деревьев.
Между каждой парой деревьев стоит скамейка.
Сколько скамеек стоит между деревьями?
11. Математики издавна ищут общую формулу для
выражения простых чисел. Мы предлагаем чита-
читателям найти очень простую формулу, содержащую
только одну цифру и одну переменную х, в которой
для каждого целого и положительного значения х
получается то же простое число.
12. На стене висят часы. На их циферблате числа
от 1 до 12. Как необходимо провести линию через
циферблат часов, чтобы сумма чисел по обеим сто-
сторонам линии была одинаковой?
Сколькими линиями необходимо разделить цифер-
циферблат часов", чтобы образовались три одинаковых
суммы? Шесть одинаковых сумм?
13. У вас две окружности с разными периметрами.
Окружность В неподвижна, окружность А катится
по окружности В. Сколько раз должна обернуться
окружность А, чтобы обойти весь периметр окруж-
окружности В'?
14. Во сколько раз число 1 307 674 368 000 меньше
числа 16!?
454
Рис. 29-12
15. Как известно, ряд натуральных чисел 1, 2,
3, ..., и, ... — бесконечен. Сколько в этом ряду чи-
чисел, которые делятся на три?
16. Используя только одно действие и одну цифру,
напиши число 65 636.
17. Рассчитай периметр треугольника ОО1О2, зная,
что радиус О А = г и что окружности О1 и О2 между
собой внешне касательные, а к окружности О внут-
внутренне касательные (рис. 29-12).
РЕШЕНИЕ ЗАДАЧ
-S-2X-
5-63 КМ
Рис. 29-13
Расчет или рисунок
Расстояние от местности В до места, в котором микро-
бус высадил первую партию экскурсантов, обозна-
обозначим х (рис. 29-13).
Из условия задачи следует, что вторая группа экс-
экскурсантов должна пройти такое же расстояние пеш-
пешком (условие одновременного прибытия в местность
В). Следовательно, лшкробус встретит вторую группу
экскурсантов, проехав обратно в направлении Курска
расстояние s—2x.
Теперь можем составить уравнение. Первая группа
экскурсантов пройдет расстояния за — часов. За это
же время микробус проедет (s— 2x)-\-{s—x) км со
455
скоростью 30 км/ч, следовательно:
Л — (s-2x)+(s-x) х _ 2s-Зх
Т~ зб ' 7 зо
2,s-3x _30 _ 8'j _ 8'63 _ 17
следовательно, х = 12 км.
Микробус высадил первую группу проехав 63—12 =
= 51 км. Вторая группа прошла до того, как за нею
вернулся микробус также 12 км. Время, затраченное
экскурсией на преодоление расстояния от Курска
до^местности В, составит
12 , 63-12 „ , 51
Любопытное тождество
аъ+Ь3 (а+Ь) (a2-ab+b2)
а2+(а-ЬK ~~ [а+(а-Ь)] ¦ (a1-a2+ab+aI-2abk-bz)
(a2-ab+b2) а+Ь
[а+(а-Ь)\ ¦ (аг-аЬ+Ь2) а+(а-Ь)
Разное — „Яйцо Колумба"
1. Площади обоих треугольников равны:
Рьавс = Padef = 0
2. В любом месте, так как в равностороннем тре-
треугольнике сумма расстояний любой точки внутри
456
Рис. 29-14
треугольника от его сторон равна высоте треуголь-
треугольника. Действительно, площадь треугольника ABC
равна площади треугольников ABO, BCO, С АО (рис.
29-14), т. е.
1
1
1 .
f 3
1
из чего после деления обеих сторон нау а получим:
h ^йх+йг+йз
3. Вероятность выпадения любого номера составляет
1/6; следовательно, вероятность невыпадения этого
номера равняется 5/6. Вероятность выпадения самого
крупного номера у одного из играющих равняется
T'Z~ 12
4. Угол GEA = 60°, так как треугольник GEA рав-
равносторонний. Угол GDB — прямой, так как прямая
GD перпендикулярна грани BCDE.
5. Две убитые уткиДОстальные улетели.
6. Два деленное на 0,125, так как 2: 0,125 = 16,
а 2-4 = 8.
7. На один час.
8. Бесконечно большая, так как сумма углов у осно-
основания равняется 180°. Из этого следует, что либо
прямые АС и ВС перпендикулярны основанию АВ,
457
Рис. 29-15 а, б, в
либо одна из них образует с основанием тупой угол,
а вторая острый. Вершина С удалена в бесконеч-
бесконечность.
9. Задача не имеет смысла.
10. Девять скамеек.
11. Формула 1+1* выражает число 2 при любом
целом и положительном х.
12. Решение показано на рис. 29-15а, б, в.
13. 2 раза
14. 16 раз, так как 1 307 674 368 000 = 15!, а 16! =
= 1 307 674 368 000 • 16.
15. Столько же, сколько есть натуральных нисел,
т. е. бесконечное количество, так как под каждым
натуральным числом можно подписать число дели-
делимое на три:
1,2, 3,4, ..., и, ...
3,6,9, 12, ...,3и, ...
16. 2222 = 65 536.
17. Периметр A00i02 равен 2г так как О^Ог —
(смотри рис. 29-12).
МАТЕМАТИЧЕСКИЕ ГЛАВА 30
ФОРМУЛЫ
Математическая формула — это выражение взаимо-
взаимоотношений между величинами, обозначенными ма-
математическими знаками и символами, например, фор-
формула аг+Ъг = с2 выражает взаимоотношение между
катетами (а, Ь) и гипотенузой (с) в прямоугольном
треугольнике.
Математическая формула может также выражать
математический закон или теорему, например, фор-
формула a-\-b = b-\-a выражает комутативный закон
сложения. Мы называем алгоритмом такую формулу,
в которой указаны все операции, которые необходи-
необходимо вьшолнить, и их последовательность, для того,
чтобы решить задачу данного типа, например, ал-
-Ь±]/Ь*^4ас
горитм ^ указывает, какие действия
и в какой последовательности необходимо вьшолнить
на коэффициентах уравнения типа ахг+Ъх+с = 0,
чтобы его решить.
Формулы 2пг, то-2, 4то-2 и -=- то-3 указывают нам, как
высчитать длину окружности, ее площадь, поверх-
поверхность шара и его объем. Математики нашли очень
много формул, которые используются не только в ма-
математике, но и во многих других точных науках
и в технике. Образно выражаясь, математические
459
Рис. 30-1
формулы — это ключи, приоткрывающие врата в со-
сокровищницу тайн Природы.
Древние математики не знали формул в том виде,
в каком знаем их мы. Формулы появились лишь тог-
тогда, когда математики научились выражать числа
и другие величины буквами и соединять их знаками
действий (в XVI веке). Древние математики выра-
выражали формулы риторически, словами и в таком виде
использовали их для решения отнюдь не легких за-
задач.
А вот пример, как Птолемей (II век н. э.) рассчитал
расстояние от Земли до Луны (в современной запи-
записи). Птолемей принял, что рассуждения и рассчеты
Эратосфена (примерно 275—194 до н. э.) были вер-
верны, и на них обосновал свои рассуждения.
Предположим, что Луна К (рис. 30-1) находится над
точкой^./!/ натповерхности Земли. Геометрически это
обозначает, что Луна находится на прямой, выхо-
выходящей из центра Земли Z й проходящей через точку
М. Пусть Р — это такая точка на поверхности Зем-
Земли, с которой мы наблюдаем восход Луны в момент,
когда она находится над точкой М. Это означает,
что прямая КР — касательная к поверхности Земли
в точке Р, т.е. что AKPZ — это прямоугольный
треугольник. Ищем расстояние ZK, считая Луну
точкой в пространстве. Для упрощения наших рас-
рассуждений мы можем принять, что точки М и Р на-
находятся на экваторе. Такое положение возникает
один раз в месяц. Длину радиуса Земли ZP Птоле-
460
мей знал из расчетов Эратосфена F000 км). Централь-
Центральный угол Z измеряем по длине дуги РМ, которая
равна разности географических длин точек Р и М.
Птолемей умел вычислять географическую длину,
так как делал зто уже астроном Гиппарх (II век
до н. э.). Угол Z равнялся 89°4'12". Из таблиц Гип-
парха можно было высчитать, что cosZ = 0,0163.
Следовательно, можно было написать, что:
^- = cos 89°4'12" = 0,0163, из этого
PZ — ZK -0,0163, а из этого расстояние
PZ 6000
Вполне понятно, что полученное значение расстояния
ZK приблизительное, так как мы приняли, что ра-
радиус Земли 6000 км, а не 6370; величина cos Z также
является приблизительной.
Подобным образом можно высчитать расстояние от
Земли до Солнца.
Большое значение для исследования законов, управ-
управляющих явлениями природы, имело представление
в виде формул законов движения: прямолинейного
вертикального, криволинейного и орбитального (Ко-
(Коперник, Галилей, Кеплер), а также закона всеобщего
тяготения (Ньютон).
Анализ этих формул позволил открьпъ целый ряд
чрезвычайно интересных фактов, не предвиденных
учеными, например, из формулы Ньютона, выража-
461
ющей второй закон динамики F — т • а, где F —
это действующая сила, т — масса, а — ускорение,
формулы F = к ——- выражающей закон всеобщего
тяготения, в которой F—сила, тх и т2 — массы
взаимно притягивающихся тел, г — расстояние меж-
между ними, к — постоянная гравитация и формулы
h = ij'gt2 пути, пройденного свободно падающим те-
телом, в которой g = 9,8 м/сек2 земное ускорение, t —
время падения, можно высчитать ускорение пада-
падающего тела на любой планете, например, на Луне
или на Солнце, а также массу любой планеты, и мас-
массу Солнца. Анализируя эти формулы и сопоставляя
данные анализа с результатами наблюдений, Ньютон
пришел к выводу, что та же сила, которая вызывает
падение тела на Землю, удерживает Луну на ее ор-
орбите вокруг Земли.
Благодаря этим формулам нам известно, что грави-
гравитационное ускорение на Луне почти в 6 раз меньше,
чем на Земле. Образно выражаясь, лицо, которое
весит на Земле 60 кГ, становится на Луне несколько
«эфирным созданием», так как весит всего лишь
10 кГ. Мы знаем, что скорость, необходимая для прео-
преодоления притяжения Земли, равна 11,2 км/сек, а для
преодоления притяжения Луны достаточно лишь
2,4 км/сек. Известно нам также, что из массы земного
шара можно слепить 81 Луну и многое, многое дру-
другое.
462
КОСМИЧЕСКАЯ
СКОРОСТЬ
Рис. 30-2
Ученые и техники конструируют все более совершен-
совершенные космические корабли. На пути космических ко-
кораблей стоит, однако, прежде всего, наша матушка
Земля, которая прижимает нас к своему чреву с не-
небывалой силой, именуемой силой земного притяже-
притяжения. Человек установил, что силу эту можно прео-
преодолеть при условии, если мы отправимся в путь
с Земли на корабле со скоростью не меньшей 11,2
км/сек.
На рисунке 30-2 показаны траектории, по которым
будет двигаться корабль в поле земного притяжения
в зависимости от скорости старта. Во всех случаях
в момент старта скорость имеет горизонтальное на-
направление. Траектория пути образует окружность,
если скорость космического корабля v в момент
старта такова, что ускорение свободного падения g
равняется центробежному ускорению -г— = g. Радиус
траектории R можно в этом случае принять равным
радиусу Земли, т. е.
v =
7,93 км/сек^
Если скорость во время старта (в точке А) больше
7,93 км/сек (первая космическая скорость), но меньше
11,2 км/сек, то траектория полета выглядит как
эллипс, при этом фокус, находящийся к точке стар-
») R = 6300 км, g = 10 м1сек2 =^—км/сек2.
463
ЧЕЛОВЕК ПОКОРЯЕТ
ПРОСТРАНСТВО
та А, находится в центре Земли (на рис. 30-2 —
эллипс нарисован сплошной линией).
Если скорость во время старта равняется 11,2 км/сек
(вторая космическая скорость), то траектория поле-
полета — парабола. Если скорость в момент старта боль-
больше 11,2 км/сек у то траектория полета представляет
собой гиперболу. В двух последних случаях косми-
космический корабль покинет Землю и отправится в кос-
космическое пространство.
Здесь можно также отметить, что при скорости
меньшей 7,93 км/сек траектория пути представляет
собой отрезок дуги эллипса (на рис. 30-2 эллипс,
обозначенный пунктирной линией): более удаленный
от точки А фокус находится в центре земного шара.
При старте со скоростью значительно меньшей
7,93 км/сек траектория движения представлена в виде
дуги параболы.
60 лет тому назад человек начал стремительный штурм
пространства. Молодежь тех лет с энтузиазмом пере-
переживала первые пробные полеты и рекорды первых
летательных машин, которые были тяжелее воздуха.
Первый полет братьев Райт, состоявшийся в 1903
году, продолжался всего 59 секунд. Их машина, по-
построенная из дерева и полотна с двигателем внутрен-
внутреннего сгорания, поднялась всего на несколько десят-
десятков метров над землей и пролетела около километра.
464
С громадным изумлением и восхищением весь мир
приветствовал в 1909 году известие о перелете Бле-
рио через Ла-Манш. А первый перелет из Нью-
Йорка в Париж через Атлантический океан в 1927
году, совершенный американским летчиком Линд-
бергом, человечество признало полным покорением
воздушной стихии.
Польские летчики находились в числе первопроход-
первопроходцев воздушной стихии. В 1926 году капитан-пилот
Болеслав Орлинский совершил беспосадочный пе-
перелет Варшава-Токио, а затем вернулся из Токио
в Варшаву этим же самолетом. В 1933 году капитан-
пилот Станислав Скаржинский перелетел один в са-
самолете польской конструкции марки RWD-5-бис
через Атлантический океан из Сен-Луй в Сенегале
в Масейо в Бразилии. В 1932 и 1934 гг польские
летчики Вигура, Жвирко и Баян заняли первые
места в международных авиационных соревнова-
соревнованиях.
Современная ^молодежь является свидетелем еще
более решительного штурма человеком космического
пространства. С большим энтузиазмом и восхище-
восхищением все человечество следит за последовательными
этапами этого штурма. Большим почетом окружает
оно первых героев — победителей космоса. Челове-
Человечество верит, что еще в нашем веке космическое
пространство будет освоено в такой степени, в какой
уже освоено околоземное пространство. Но слава
героев космоса не может и не должна затмить геро-
465
мысли о мыслях
ический труд ученых-математиков, которые с колос-
колоссальной точностью высчитали скорости, орбиты и все
другие параметры старта космических кораблей, ко-
которые у электронно-вычислительных машин следи-
следили за безопасностью полета космического корабля,
а также ученых-инженеров, которые сконструиро-
сконструировали эти корабли. Героизм математиков и инжене-
инженеров заслуживает не меньшего уважения, чем ге-
героизм летчиков-космонавтов.
В своем труде: «Рассуждение о методе для хорошего
направления разума и отыскивания истины в нау-
науках» великий французский философ и ученый Де-
Декарт пишет: «...Я сравниваю тайны Природы с за-
законами математики. Я был и по сей час остаюсь
убежден, что один и тот же ключ открывает смысл
одного и другого. Когда я тщательно все взвесил,
то пришел к выводу, что все науки, которые зани-
занимаются познанием порядка и меры, принадлежат
к математике, независимо от того, ищут ли они эту
меру в числах, фигурах, звуках или других объектах.
Поэтому должна быть универсальная наука, которая
обрабатывает все, что относится к мере и порядку,
независимо от того или другого применения. Эта
наука более всего достойна называться математикой,
потому что все остальные науки являются как бы ее
частями».
466
Дополнением мысли Декарта является прекрасное
изречение французского математика, астронома и фи-
физика Лапласа A749—1827): «Анализ любого явле-
явления приводит нас к одному субстрату — переменчи-
переменчивости по закону функциональной зависимости. Все
явления, даже те, которые из-за своих минимальных
размеров казалось бы не связаны с могучими зако-
законами Природы, являются также неизбежным их
следствием, как вращение Солнца. События нынеш-
нынешнего дня связаны с минувшими деяниями, основан-
основанными на неопровержимом принципе, согласно ко-
которому ничто не происходит без причины. Эта аксио-
аксиома имеет универсальное применение. Если бы какой-
либо гениальный разум знал все силы, действующие
в настоящий момент в природе, и знал взаимосвязь
существ, из которой состоит природа, и если бы этот
разум мог охватить все это в такой степени, чтобы
все эти данные подвергнуть математическому ана-
анализу, то тогда он смог бы представить в одной фор-
формуле движение всех самых крупных небесных светил
и самых маленьких электронов».
Венцом этих высказываний может быть короткое
изречение Эйнштейна, этого «Ньютона современно-
современности», как его называли: «Математика — это продукт
человеческой мысли, независящий от опыта, однако,
великолепно соответствующий реальному миру
и прекрасно его.объясняющий».
МАТЕМАТИКА
И ПАЗИГРАФИЯ
ГЛАВА 31
Различные условия развития первобытного общест-
общества привели к возникновению различных языков.
По мере повышения культурного уровня наших пред-
предков языковые различия не только не уменьшались,
но, наоборот, увеличивались. Возрастало также чув-
чувство национального различия и привязанности к род-
родной речи. Правда, история знает такие эпохи, когда
один язык был общим почти для всех народов, за-
заселявших «весь тогдашний мир», таким был, на-
например, индоевропейский (арийский) праязык, но
это было очень очень давно. Затем многие столетия
латынь была общим языком народов, населявших
Европу, в основном, однако, она использовалась
в науке и дипломатии.
В конце XVIII века национальные языки вытеснили
латынь из областей, в которых она применялась. Од-
Однако, были люди, понимавшие значение существо-
существования международного языка. Потребность в меж-
международном языке ощущалась издавна. Издавна"де-
Издавна"делались также попытки создать нейтральный искусст-
искусственный язык, простой в своей конструкции и легкий
для усвоения. Идея эта зародилась уже в XVI веке,
однако, более серьезные проекты создания между-
международного языка относятся лишь к XVII веку. Упо-
Упоминают о них в своих сочинениях Каспар Скоттус
468
и Кегельм Дигби. Их предложения не нашли, од-
однако, сочувствия в тогдашнем обществе. Значительно
больший интерес привлек язык, составленный нем-
немцем Мартином Шлейером, и известный под именем
«воляпюк», но и его успех был кратковременным,
так как вскоре, уже в 1887 году, появился новый
искусственный международный язык, созданный
польским врачом Людвиком Заменгофом — эспе-
эсперанто, который вытеснил «воляпюк» и нашел очень
многих последователей во всем мире. Кроме эсперан-
эсперанто, имеются еще и другие искусственные междуна-
международные языки, например, идо, ило, интерлингва.
Несмотря на свою относительную популярность, эс-
эсперанто, по мнению многих специалистов, никогда
не станет истинно международным языком, по не-
нескольким причинам: прежде всего, — это искус-
искусственный, мертвый язык (т. е. язык, на котором не
говорит ни один народ). Поэтому появляются уже
идеи, пока еще в виде скромных научных предло-
предложений, принять в качестве международного языка
один из натуральных, наиболее широко распростра-
распространенных в мире языков (английский, русский, фран-
французский или немецкий). Это стало бы безусловно
крупным событием для всего человечества.
Но все это картина далекого будущего. К счастью,
вопрос международного писанного языка, языка
с международными знаками, по разному лишь про-
произносимыми в разных странах, но одинаково пони-
понимаемыми, обстоит значительно лучше. Тем более,
469
что такой писанный международный язык, собствен-
собственно говоря, уже существует, например, в математике.
Запись вида
12-5-18:3
V9
иначе будет произнесена англичанином, иначе рус-
русским и еще иначе китайцем, но каждый из них пой-
поймет ее таким же образом и таким же образом произве-
произведет вычисления. Любой человек, знакомый с мате-
математикой, напишет ответ:
/ 12
12- 5-18:3 \2=324
Дело создания международного писанного языка
математики еще не полностью завершено. В школь-
школьных учебниках и в работах ученых-математиков еще
используется язык высказываний, тем не менее, то,
что уже достигнуто, имеет громадное значение и до-
достойно восхищения. Прежде, чем были изобретены
такие знаки (символы) как:
1 ? Ч flo/o/_i__w.
1, z,, о, ..., и, /0, /00, -]-, , л, ., —,
ф, X, >, <, ||, ±, 00, ...
и буквы а, Ь, с, ... х, у, z, ...
используемые вместо цифр, прошло свыше двух
с половиной тысячелетий. Но уже в XVII веке оказа-
оказалось, что этих знаков недостаточно. Философы и ма-
математики пришли к выводу, что международный пи-
470
санный язык необходимо расширить. История куль-
культуры называет имена фамилии и труды нескольких
ученых, которые занимались этим вопросом, между
прочим, Джона Вилькинса A668 г), Афанасия Кир-
хера A669 г), и наконец наиболее заслуженного для
дела создания международного писанного языка ма-
математика и философа Г. В. Лейбница A646—1716).
Всю свою жизнь Лейбниц работал над созданием,
так называемой, пазиграфии, т.е. системы всеобщего
писанного языка. Он желал в противовес «лингва
универсалис» (международной речи) создать «ха-
«характеристика универсалис» (международную систему
обозначений) — письмо для записи мыслей и идей,
одинаково понимаемых, хотя и по разному произно-
произносимых. Однако, Лейбниц столкнулся с труднопрео-
труднопреодолимой преградой, так как пазиграфия — система
общепонятных знаков, по Лейбницу, должна была
быть разработана для всех отраслей знаний. А, сле-
следовательно, таких знаков необходимо было создать
довольно много, по крайней мере, несколько тысяч.
Чтобы уменьшить число таких знаков Лейбниц под-
подверг анализу некоторые идеи, считая их, как будто
составными, с целью разложить их на более простые.
После Лейбница к идее создания пазиграфии возвра-
возвратился во второй половине XIX века испанский посол
в Китае Дон Синбальдо де Мае, который издал
в 1863 году труд под названием «Идеография», где
была разработана система 2600 знаков, достаточных,
по мнению автора, для выражения «характеристи-
471
ки» каждой идеи. Труд этот, однако, не нашел от-
отклика и вскоре был забыт.
Самой крупной ошибкой творцов пазиграфии, как
мы уже об этом упоминали, было желание охватить
все отрасли жизни и творчества человека, которые
так разнообразны по существу и которые оперируют
столь различными формами мышления. Поэтому
ограничение пазиграфии одной областью знаний, ис-
использующей одну какую-либо форму мышления, на-
например, математикой или логикой, принесло ей боль-
больший успех. Здесь необходимо упомянуть об итальян-
итальянском ученом, профессоре университета в Турине,
умершем в 1932 году, Джюзеппе Пеано, который
создал идеографические знаки, позволяющие выра-
выразить любые математические рассуждения. В своем
сочинении «Математический формуляр» (Formu-
lario di Matematicd) Пеано доказал, что при соответ-
соответствующем анализе небольшое число знаков вполне
достаточно, чтобы без помощи слов, используя лишь
международные знаки (общепонятные) записать все
теоремы и математические рассуждения.
Работы Пеано были дополнены путем распростране-
распространения пазиграфии на логику, крупным английским
ученым Бертраном Расселем, который в 1910 году
издал вместе с Уайтхедом труд под названием « Прин-
Принципы математики» (Principia Mathematica).
Наконец, необходимо упомянуть о двух работах не-
немецкого ученого Фреге, посвященных идеографи-
идеографическому письму: «Понятийное письмо» (Begriffs-
472
schrift) и «Основные законы арифметики» (Grimd-
gesetze der Arithmetik).
А теперь давайте спустимся с высокого пьедестала
науки к повседневной жизни. Сколько сотен тысяч
писем ежедневно высылается в любой стране?
А сколько же это составит в масштабе всего мира?
Сколько тонн бумаги ежедневно исписывается во
всех странах! Нельзя ли было бы ввести в этой об-
области какую-нибудь экономию? Это вопрос номер
один!
Вопрос номер два. Нельзя ли писать письма с по-
помощью знаков, которые одинаково понимались бы
всеми народами; иначе говоря, не следовало ли бы
подумать о создании международного письма для
вьфажения мыслей и чувств нашего повседневного
бытья ?
Нам кажется, что для ведения обычной корреспон-
корреспонденции достаточно было бы 100 основных знаков,
с помощью которых и путем добавления к этим ос-
основным знакам точек или черточек и соответству-
соответствующей их записи можно выразить примерно 1000 ос-
основных понятий. Международный язык для пере-
переписки мог бы принять все знаки и символы, исполь-
используемые в настоящее время в математике и математи-
математической логике, придав им, однако, более широкое
значение, чем они имеют в настоящее время в этих
дисциплинах. Например, знак «+» (плюс) может
обозначать не только «сложить», но также «и»,
«да», «вместе», «в сумме» и т. п. То же относится
473
и к знаку «—» (минус), может он обозначать также
«нет», «без», «остаток» и т. п. Самым основным
вопросом был бы выбор основных символов, нахож-
нахождение для них достаточно простых идеограмм и опре-
определение функций дополнительных точек и черточек.
Письма, написанные с помощью такой идеографи-
идеографической письменности, читались бы получателями на
их родном языке; они были бы лаконичнее, а для
их написания потребовалось бы не более 20% бу-
бумаги, необходимой ныне для составления этих же
писем на нормальном живом языке.
Нашим читателям мы предлагаем ради развлечения
попытаться создать пазиграфическое письмо, состав-
составленное из различного рода символов и сокращений,
широко употребляемых хотя бы в школьных учеб-
учебниках. Желаем успеха!
ЮЛОТЫЕ МЫСЛИ глава 32
О МАТЕМАТИКЕ
1. Среди многих научных дисциплин, созданных че-
человеком, есть одна, которая именуется наукой. Эта
«наука» — математика, ибо по гречески /лаёг)/м
значит наука. Истинный поклонник математики
выговаривает это слово с глубоким уважением.
2. Математика может обойтись почти полностью
без слов. Для нее не существуют языковые барьеры,
ибо ее язык, как и язык музыки, понятен всему че-
человечеству.
Универсальным золотым ключом математики явля-
является уравнение. С его помощью Архимед открыл
злоупотребления при изготовлении короны для царя
Сиракуз. Эти уравнения позволили жрецам Древ-
Древнего Египта предсказывать затмения Солнца и вос-
восходы Сириуса. Ими пользовались Коперник и Га-
Галилей, Ньютон, Декарт, Эйнштейн...
3. После полного освоения важнейших естественных
наук: физики и химии, экономических наук, матема-
математика вторгается ныне в области знаний, которые рань-
раньше были для нее закрыты: в гуманитарные науки
и в искусство, вооружая их более современными и бо-
более объективными методами познания.
475
МОЛОДОСТЬ Многие утверждают, что математика — это «сухая»
И МАТЕМАТИКА наука, занимающаяся абстрактными, отвлеченными
спекуляциями, хорошая только для взрослых, что
математика не может заинтересовать молодежь, ко-
которая значительно больше увлекается такими нау-
науками, которые содержат в себе элементы приключе-
приключений или путешествий (например, география) или по-
повествуют о судьбах людей и народов (например, ис-
история) или о явлениях, происходящих в окружающем
нас мире, или же, наконец, затрагивают извечные
вопросы бытия и строения вселенной (биология,
астрономия). Так ли это на самом деле? Нам думается
что нет, так как и математика может увлечь молодежь,
может стать для нее захватывающим занятием. А вот
несколько примеров из истории: Паскаль A623—
1662) увлекался математикой с детского возраста.
В возрасте примерно 8 лет он открыл и доказал це-
целый ряд теорем Евклида. В возрасте 16 лет он напи-
написал сочинение о конических сечениях, а в возрасте
24 лет открыл закон давления жидкости и создал ос-
основы теории вероятности.
Лагранж A736—1813) в возрасте 18 лет был про-
профессором университета в Торине, годом позже ой
сформулировал общую теорию решения изоперимет-
рических задач.
Лаплас A749—1827) в возрасте 18 лет преподавал
математику в военном училище, а в 20 лет стал про-
профессором высшего учебного заведения в Париже.
476
МАТЕМАТИЧЕСКИЕ
ЗАДАЧИ
Коши A789—1857) уже в возрасте 21 года был ин-
инженером и опубликовал выдающееся сочинение по
теории чисел.
Эйлер A707—1783), родившийся в швейцарском го-
городе Базеле, имел исключительное влечение к мате-
математике. В возрасте 20 лет Эйлер был адъюнктом ака-
академии наук в Петербурге, спустя три года — стал
профессором физики, а в возрасте 26 лет — профес-
профессором математики петербурского университета.
Галуа прожил всего 21 год A811—1832). В возрасте
16—18 лет он разработал основные положения разде-
раздела алгебры, названного позднее теорией Галуа.
Абель A802—1829), один из создателей основ теории
алгебраической и эллиптической функции, доказал
невозможность решения уравнений пятой и высших
степеней. Умер в расцвете лет, в возрасте всего лишь
27 лет.
Математика не сводится, конечно, к решению задач,
но без этого трудно себе вообразить математику.
И именно, как раз то, что благодаря математическому
мышлению мы умеем решать самые разнообразные
задачи, является завлекающей силой математики.
Задача — это как будто крепость, ее решение — это
награда победителю.
Постановка и решение некоторых задач дало толчок
развитию многих математических дисциплин. Итак,
477
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
например, задача об игральных костях, поставленная
одним французским игроком перед Паскалем, дала
толчок развитию теории относительности; из задачи
об определении величины угла, образуемого каса-
касательной к кривой в любой точке этой кривой и осью
абсцисс, развилось дифференциальное и интеграль-
интегральное исчисления, а применение этих исчислений для
решения интереснейших задач, сформулированных
в 1687 году Я. Бернулли (о брахистохроне, т. е. о ли-
линии кратчайшего падения материальной точки и о, так
называемой, цепной кривой) способствовало призна-
признанию этих исчислений мощным инструментом науч-
научного исследования и побудило математиков заняться
их дальнейшим развитием, углублением и совершен-
совершенствованием. Можно сказать, что математика возникла
из задач, которые ставила жизнь, и которые не-
необходимо было решить, чтобы обуздать силы приро-
природы.
Турнир
В двух школах (назовем их А и Б) существовали
математические кружки, которые часто разыгрывали
турниры. И вот однажды кружок из школы А выс-
выслал своим «противникам» следующие две задачи
Задача № 1. Польское внешнеторговое предпри-
предприятие, занимающееся экспортом древесины, направило
478
своему представителю в Лондон зашифрованную
телеграмму следующего содержания: «Имеем на
складе Гора-Лер кубических метров сосновых досок,
Гера кубических метров дубовых досок, Лаба-роба
листов ольховой фанеры. Цены держать твердо. По
желанию можем также доставить Ирен кубических
метров дубового долготья».
Представитель имел, конечно, ключ для расшифров-
расшифровки этой телеграммы. Предлагаем вам найти этот
ключ с помощью следующих указаний:
1. Ключ — математический термин из 9 букв.
2. Каждая буква этого слова обозначает цифру.
3. Необходимо заменить каждую букву этого слова
последовательным рядом цифр от 1 до 9.
4. Ключ читатели должны составить из первых букв
слов, значение которых приведено ниже:
1) Наука о фигурах, взаимном их расположении
и размерах их частей и элементов;
2) Двадцатигранник;
3) Математический знак для обозначения действия
сложения;
4) Древнегреческий математик, автор «Начал»;
5) Одно из понятий комбинаторики;
6) Виднейший математик XVII века, один из осново-
основоположников теории вероятности, решил задачу о бра-
брахистохроне;
7) Кривая в плоскости Лобачевского, являющаяся
геометрическим местом концов секущих равного на-
наклона, проведенных из некоторой точки А прямой
479
а к прямым, параллельным ей в определенном
направлении и лежащим с ней в одной плоскости;
8) Крупнейший русский математик, основоположник
неевклидовой геометрии;
9) Счетная доска у древних греков и римлян.
Указать полный текст зашифрованной телеграммы.
Задача № 2. Из местностей М и Р, расположенных
вдоль той же дороги, вышли одновременно навстре-
навстречу друг другу два пешехода. Тот, который вышел
из М, шел в среднем со скоростью v км/ч, а тот,
который вышел из Р — шел со скоростью w км/ч.
Первый из них пришел в Р через 25 ч ходьбы после
встречи со вторым пешеходом, а второй — в М че-
через 16 ч.
Сколько времени затратил каждый из пешеходов на
преодоление расстояния от М до Р?
После получения этих задач, ребята из математичес-
математического кружка школы Б направили в школу А свои
две задачи.
Задача Ш 1. Из десяти слов, значение которых
указано ниже, необходимо взять первые буквы и со-
составить из них название одной математической дис-
дисциплины.
1) Великий математик, физик, инженер древних вре-
времен. Грек. Воевал с римлянами;
2) Два выражения, соединенные матемап ческим
знаком, бывают верные и неверные, числовые я бук-
буквенные;
3) Страна — родина математических знаков, кото-
которые используются во всем мире как учеными, так
и простыми смертными;
4) Французский математик, один из создателей
теории чисел;
5) Часть логаритма, всегда положительная или рав-
равная нулю;
6) Одна из важнейших постоянных математического
анализа;
7) Итальянский математик, имел неприятное столк-
столкновение со своим соотечественником математиком
Кардано, которого обвинил в краже своего открытия;
8) Результат многократного применения какой-либо
математической операции;
9) Крупнейший немецкий астроном, в 1971 году
праздновалось четырехсотлетие со дня его рождения;
10) Одна из декартовых координат, третья по счету.
Во второй части этого задания необходимо ответить
на ряд дополнительных вопросов, касающихся най-
найденных слов:
к 1) Когда жил математик, о котором речь, за что
он воевал и как погиб?
к 2) Какими свойствами обладают верные ...?
к 3) Где расположена эта страна? Что вы о ней
знаете ?
к 4) Назовите физический принцип, связанный
с именем этого ученого;
к 5) Какие есть логарифмы и как выражается со-
соотношение между ними?
т
к 6) Назовите ее числовое значение?
к 7) Что это было за столкновение?
к 8) Каково приложение этой операции?
к 9) Назовите основные три закона, установленные
этим астрономом;
к 10) Назовите остальные две координаты.
Задача № 2. Четверо юношей: Андрей, Борис,
Кирилл и Дмитрий влюблены (увы, как это в жизни
часто бывает, без взаимности) в четырех девушек:
Таню, Машу, Зину и Галю, которые также влюб-
влюблены без взаимности. Андрей любит девушку, влюб-
влюбленную в юношу, который любит Таню. В Машу
влюблен юноша, которого любит девушка, любимая
Борисом. Кирилл влюблен в девушку, которая любит
Диму.
Если Бориса не любит Зина, и юноша, которого
любит Галя не любит Зины, то кто любит Андрея?
L М
Рис. 32-1
Длина приводного ремня
Один механический агрегат состоит из трех одина-
одинаковых шкивов Ки К2, К3 с периметром 10 дм каж-
каждый и приводного ремня, плотно натянутого на эти
шкивы (смотри рис. 32-1).
Расстояния между центрами шкивов Кг и К2 а также
К^ и К3 равняются 30 дм; расстояние между центра-
центрами шкивов К2 и Къ составляет 40 дм.
Какова длина приводного ремня?
482
„Лунар"
В ежемесячном журнале «Сайентифик Америкэн»
в разделе «Математические игры» была опублико-
опубликована следующая задача.
В рассказе английского писателя-фантаста Уэллса
A886—1946) «Первые люди на луне» упоминается
о том, что на Луне живут разумные насекомые, ко-
которые обитают в гротах под поверхностью Луны.
Эти существа, как можно предположить, умели из-
измерять и имели, следовательно, какую-то меру дли-
длины. Пусть единица их длины называется «лунар».
Выраженный в лунарах объем Луны равен точно,
выраженной в этих же единицах, площади поверх-
поверхности Луны. Сколько метров имеет лунар, если при-
принять, что радиус Луны имеет 1728 км.
Кофе с молоком
У меня полный стакан черного кофе. Сначала я вы-
выпил одну шестую этого кофе и долил в стакан моло-
молока, чтобы стакан снова оказался полным. Затем
я снова выпил одну третью часть стакана и снова
долил молока дополна. Наконец, я в третий раз вы-
выпил половину стакана и еще один раз дополнил его
доверху молоком. И только после этого я выпил
свой стакан до дна.
Передо мной пустой стакан, а я думаю, чего я выпил
больше: кофе или молока и вообще, сколько я выпил
всего вместе?
48?
РЕШЕНИЕ ЗАДАЧ
Две цепочки
У ювелира было много серебрянных колечек. Тол-
Толщина каждого колечка в сечении равнялась 0,5 мм.
Из этих колечек ювелир сделал две цепочки, одну
длиной 32 см и 6 мм и вторую длиной 42 см и 6 мм.
Сколько всего колечек было у ювелира, если на
более длинную цепочку он израсходовал на 40 коле-
колечек больше, чем на более короткую?
Турнир
Задача № 1. 1) Геометрия; 2) Икосаэдр; 3) Плюс;
4) Евклид; 5) Размещение; 6) Бернулли; 7) Орицикл;
8) Лобачевский; 9) Акаба.
Из первых букв этих слов образуется термин ги-
гипербола.
Теперь согласно ключу, имеем следующие значения
отдельных букв: Г = 1, И = 2, П = 3,Е = 4, Р =
= 5, Б = 6, О = 7, Л = 8, А = 9. Остается только
вставить в телеграмму вместо букв эти цифры, что-
чтобы полностью ее расшифровать.
Задача № 2. Обозначим время, в течение которого
пешеходы находились в пути, t. Теперь расстояние
от М до Р можно выразить тремя следующими спо-
способами :
(f+25)w = МР A)
484
0+16) w = MP B)
(v+w)t = MP C)
Из уравнений A) и C) имеем: (t+25)v = (v+w)t;
tv+25v = tv+wt; 25я = wt;
t=**L (A)
w
Из уравнений B) и C) имеем: (f+16)w = (v+w)fs
= tv-\-wt; 16w = tv;
(B)
t
V
Сравнивая уравнения (А) и (В) получим:
w ~ v ' 16 v2 ' v ~ 4
Подставляя значение — = х в Уравнение (А) полу-
получим окончательно:
Первый пешеход прошел расстояние из М в Р за
25+20 = 45 часов, а второй за 16+20 = 36 часов.
Задача Ш 1. 1) Архимед; 2) Равенство; 3) Индия;
4) Ферма; 5) Мантисса; 6) е-число; 7) Тарталья;
8) Итерация; 9) Кеплер; 10) Аппликата.
Первые буквы этих слов образуют слово Арифме-
Арифметика.
485
к 1) Архимед жил примерно в 287—212 гг до н. э.
Защищал свой город во время осады Сиракуз римля-
римлянами, тогда же после взятия города был убит рим-
римским воином.
к 2) Верные равенства обладают свойствами реф-
рефлексивности, симметричности и транзитивности;
к 3) Индия расположена в юго-восточной части
Азии на Индийском полуострове;
к 4) Принцип Ферма — основной принцип геомет-
геометрической оптики, утверждающий, что действитель-
действительный путь распространения света из одной точки
в другую, есть тот путь, для прохождения которого
свету требуется минимальное время;
к 5) Имеются еще натуральные логарифмы, основа-
основание которых — число е.
1) N= 10я; х = lg10N
2) N=e>; 10* = <*; lgloA0*) = Ig10H;
у - x - lSloN ¦ lc N- hloN
к 6) е-число = 2,718 218...;
к 7) Тарталья имел конфликт с Кардано из-за прио-
приоритета на определение формулы решения уравнений
третьей степени;
к 8) Многочисленное, но самым основным является
применение итерации в методе последовательных
приближений при численном решении математичес-
математических задач;
486
к 9) Три закона движения небесных тел: 1) каждая
планета движется по эллипсу, в одном из фокусов
которого находится Солнце; 2) радиус-вектор от Сол-
Солнца проведенный к планете в равные промежутки
времени описывает равные площади; 3) квадраты
времен вращения планет вокруг Солнца относятся
как кубы их средних расстояний от Солнца;
к 10) Абсцисса и ордината.
Задача № 2. Пусть символ х~*у обозначает х любит
у, а символ х<-у — х не любит у.
Следовательно, имеем положение
I. .Л->?->?->Г-*?
II. ?->?->?->ЛГ->?
III. К-*7^>Д
IV. 3<г-Б
V. Г
Условие, что без взаимной любви нельзя ожидать
взаимности, позволяет нам предположить, что имеем
дело с одним замкнутым кругом, состоящим из 8 че-
человек, либо с двумя замкнутыми кругами, состоящи-
состоящими каждый из четырех человек. Предположим, что
верно это второе предположение. Из этого следует,
что поскольку К и Д принадлежат к тому же кругу
(условие III), то А и Б также должны относиться
к тому же кругу. Теперь А-*М-*Б->Т->А. Однако,
поскольку 3 иГ также принадлежат к тому же кругу,
4Я7
то становится невозможным условие V. Из этого
следует, что все восемь человек принадлежат к тому
же кругу.
Теперь мы можем уже сказать, что Таню не любит
Андрей (условие I), ни Дима (условие III), ни Кирилл,
что противоречило бы V. Следовательно, Таню лю-
любит Борис.
Далее, Андрей любит Галю, Галя любит Бориса,
Борис любит Таню, Таня любит Кирилла, Кирилл
любит Машу, Маша любит Диму, Дима любит Зину,
Зина любит Андрея.
Длина приводного ремня
Из рисунка 32-1 следует, что длина участка ремня
MN = LS = 30 дм,*а PR = 40 дм.
Так как
ХЪ + ХКг+ХКз = 180°
следовательно
* MKtL+ *NK3P+ ? SK2R =
= C60°-90° • 2-?.К:1)+C60о-90о
+ C60°-90° -2
= 360° • 3-180° -З-
= 360° • 3-180° -4 = 360°
Следовательно, длина ремня
/ = C0+30+40+10) = ПО дм.
„Лунар"
Сравнивая формулы объема шара с формулой его
поверхности получаем равенство: -у7" = ^tw2
Из этого после сокращения обеих сторон на 4тгг2
получим: г = Ъ (лунным единицам измерения), т. е.
г = 3 лунара. Следовательно, 1 лунар = 1728: 3' =
= 576 км.
Кофе с молоком
Я выпил стакан кофе и (^ + у + у = 1) стакан
молока.
Две цепочки
Разность в длине цепочек составляет 42,6 см—
—32,6 см = 10 см. Следовательно, длина внутренне-
внутреннего диаметра составляет 10 см : 40 = 0,25 см = 2,5 мм.
Вычитая из длины каждой цепочки толщину пер-
первого и последнего колечка @,5 лш+0,5 мм = 1 мм)
найдем, сколько колечек израсходовал ювелир на
"J 0 1ч АО К.
каждую цепочку: -тт-г = 130 штук; -тгг = 170 штук.
Всего у ювелира было 300 колечек.
ИНТУИЦИЯ И РАЗУМ глава 33
Кроме математики, не существует
другой надежной отрасли знания,
за исключением той;,
которая выводится
из математики.
РОБЕРТ РЕКОРД A560—1621)
Знание законов природы основано на наблюдениях.
Наблюдения вырабатывают интуицию, которая по-
помогает создавать гипотезы и решать многие вопро-
вопросы. Однако, не всегда интуитивное решение пра-
правильно. Вот пример ошибочного интуитивного ре-
решения, приведенный в книге известного американ-
американского математика Морриса Клайна «Математика
и физический мир».
Один молодой человек имеет два предложения по-
поступить на работу: учреждение А ему предлагает
вознаграждение 18 000 долларов в год, с тем, что
каждый последующий год его жалование будет уве-
увеличиваться на 2000 долларов в год. Учреждение Б
предлагает ему также 18 000 долларов в год и 500
долларов повышения зарплаты каждые полгода.
Какое из двух предложений лучше? Интуиция под-
подсказывает, что первое предложение лучше, так как
предлагает 2000 долларов в год повышения заработ-
заработной платы, а второе учреждение лишь 500 долларов
в полгода, т.е. одну тысячу в год. Однако, в данном
случае интуиция подсказывает нам неправильное ре-
решение.
Чтобы в этом убедиться, составим таблицу заработ-
заработков в учреждениях А и Б.
лоп
(.—, _
?д
Олугодие
'чреждение А
гчрежде1ше Б
1
I
9 000
9 000
IT
9000
9 500
2
I
10000
10000
II
10000
10 500
3
I
11000
11000
И
11000
11500
4
I
12 000
12000
II
12000
12 500
5
I
13 000
13 000
II
13 000
13 500
Как видно, на основании таблицы, второе учрежде-
учреждение платит во втором полугодии каждого года на
500 долларов больше, чем учреждение Л, а следо-
следовательно, предложение учреждения Б — выгод-
выгоднее.
Существуют задачи, для решения которых мы можем
воспользоваться интуицией лишь в ограниченной сте-
степени, базируя все наши рассуждения на математи-
математических умозаключениях. Вот очень древний пример
математического мышления, который использовал
известный греческий ученый астроном, географ, ис-
историк и математик Эратосфен B75—194 до н. э.). Он
принадлежал к тому немногочисленному сонму фи-
философов, которые считали, что Земля имеет форму
шара, и который решил высчитать окружность этого
шара. Будучи географом, Эратосфен знал, что Алек-
Александрия, город в котором он жил, находится к северу
от города Сиена и что расстояние между ними, в пе-
пересчете на современные меры, составляет 750 км.
Во время летнего равноденствия в полдень лучи
солнца падают в Сиене перпендикулярно к поверх-
поверхности Земли. Это означает, по мнению Эратосфена,
что солнце находится в этот момент как раз в зените.
491
на линии вертикали OBS' (рис. 33-1). В этот же
самый момент в Александрии лучи Солнца имелр
такое направление, как линия AS, наклоненная по/
некоторым утлом к вертикали ОАЕ. Так как Солнце
Япександрия ^/ о
\ /7± J- расположено очень далеко, то мы можем считать err
Гномон \ / _J^
лучи параллельными (AS\\BS). Из этого следует.
что X.EAS = %.АОВ. С помощью гномона Эратосфен
1°
высчитал, что: %.EAS = 7 у. Следовательно,
Рис. 33-1 %.АОВ = 1'-=-, столько же, как и дуга АВ. Так как
вся окружность земного шара имеет 360°, то дуга,
соответствующая центральному углу 7 -=-, является
7 -=-: 360 = -fg- частью окружности.
Следовательно, если j= часть окружности Земли имеет
длину 750 км, то вся окружность Земли составляет
750 км • 48 = 36 000 той. Это очень хорошее прибли-
приближение, как на те времена. Сегодня мы принимаем,
что длина экватора равна 40 000 км. Как мы видим
на этом примере математических рассуждений не мо-
могут заменить ни угадывание, ни интуиция.
Упоминаемый выше Моррис Клайн так пишет о ма-
математике :
«Основной причиной развития математики является
ее использование для исследований природы. Ма-
Математические понятия и методы приобретения знаний
наиболее эффективны при исследовании и объяс-
492
нении движения небесных светил, движения тел на
Земле и вблизи ее, явлений света, звука, тепла,
электричества, электромагнитных волн, строения
материи, химических реакций, строения глаза, уха
и других органов человеческого тела, а также сотен
других вопросов».
Кто-нибудь может спросить, для чего мы исследуем
Природу ?
Только ли для того, чтобы собрать лучший урожай,
плавить более высококачественную сталь, все более
уверенно и надежно водить суда и летать на самоле-
самолетах, иметь лучшую связь?
Нет, не только поэтому.
Существуют люди, которые ищут ответ на вопрос,
как возникла Вселенная? Как возникает свет и ка-
какова его природа? Существует ли какой-либо план
и организация солнечной системы? «Есть такие
люди, которые, по словам Клайна, сознают чудеса
Природы и которые стремятся познать Ее с такой
же страстью, с какой деловые люди стремятся на-
нажить капитал».
Говорят, что математика оперирует абстрактами и да-
далека от мира действительности. Такой взгляд верен
только в известной степени. Математика не имеет
исключительного права на абстракцию. Понятия
физики являются также абстрактными эквивален-
эквивалентами своих прототипов из физического мира. Хотя
математик создает все более сложные абстрактные
понятия, необходимо, однако, отметить, что абстрак-
493
ХАНОЙСКАЯ БАШНЯ
ция, которой пользуются математики, выводится из
рассмотрения явлений Природы и поэтому она по-
понятна.
Ханойской башней называется игра, изобретенная
в XIX веке французским математиком Э. Лукасом.
Публикуя свою игру под вымышленной фамилией
Клаус, ее изобретатель связал ее с экзотической, не-
нелишенной математического смысла, легендой. Легко
догадаться, что «Клаус» — это анаграмма фамилии
Лукас, образованная путем изменения последователь-
последовательности букв его фамилии.
По легенде Лукаса, на берегу священной реки Ганг,
в городе Бенарес, под куполом самого большого
храма творец мира Брахма поместил бронзовую пла-
пластину с приклепленными к ней тремя алмазными па-
палочками. На одну из них надеты 64 кружка. Самый
большой кружок — нижний, самый маленький —
верхний. Диаметры кружков уменьшаются равно-
равномерно снизу кверху. Брахма приказал жрецам пере-
перенести все кружки с первой палочки на третью с со-
соблюдением следующих условий:
1) взякий раз можно переносить только один кру-
кружок;
2) переносимые кружки можно укладывать только
таким образом, чтобы меньший кружок лежал на
большем;
494
/ II III
Кружок 11— /-»|_ 3-»i
Круток 2 \~2—I -|
III
I II
Рис. 33-2
Кружок 1
Кружок 2
Кружок 3
Рис. 33-3
3) вторую палочку можно использовать в качестве
вспомогательной палочки, однако, и на ней меньший
кружок должен лежать на большем.
Когда все кружки с первой палочки будут перене-
перенесены на третью, наступит конец мира.
Как долго будет существовать наш мир ? Сколько лет
жрецы будут переносить кружки?
Для того, чтобы отдать себе отчет, сколько же вре-
времени необходимо, чтобы перенести 64 кружка с пер-
первой палочки на третью с соблюдением указанных ус-
условий, применим метод рассуждений, который назы-
называется индукцией и который позволяет на основании
отдельных фактов делать общие выводы.
Пусть на палочке / (рис. 33-2) находятся два круж-
кружка. Перенесение этих кружков с палочки / на палоч-
палочку III показано на графике А (числа у стрелок ука-
указывают последовательность переноса).
На основании графика А видно, что 2 кружка могут
быть перенесены с палочки / на палочку III с по-
помощью трех переносов, кружок 1 переносим два
раза, кружок 2 — один раз, что записываем следу-
следующим образом:
2!+2° = 2+1 = 3
Затем на палочку /положим три кружка (рис. 33-3).
График Б показывает, сколько необходимо сделать
переносов, чтобы три кружка оказались на палочке
III.
495
Кружок 1
Рис. 33-4
Из этого графика следует, что
Кружок 1 переносим 4 раза, т. е. 22
Кружок 2 переносим 2 раза, т. е. 21
Кружок 3 переносим 1 раз, т. е. 2°
Итого, 2*+24-2° =4+2+1 =7 раз
Как выглядит перенос 4 кружков с палочки / (рис.
33-4) на палочку III, показано на графике В:
Кружок 1 переносим 8 раз, т. е. 23
Кружок 2 переносим 4 раза, т. е. 22
Кружок 3 переносим 2 раза, т. е. 21
Кружок 4 переносим 1 раз, \т. е. 2°
Итого,
= is раз
Аналогично найдем, что для переноса пяти кружков
с палочки / на палочку /// необходимо:
Кружок 1 перенести 16 раз, т. е. 24
Кружок 2 перенести 8 раз, т. е. 23
Кружок 3 перенести 4 раза, т. е. 22
Кружок 4 перенести 2 раза, т. е. 21
Кружок 5 перенести 1 раз, т. е. 2°
Итого, 24+23+22+21+2° = 31 раз
На основании метода индукции можно сделать вы-
вывод, что для переноса 64 кружков с палочки / на па-
палочку III, необходимо выполнить:
2бз+2б2+2б1 +2бо+ ... +25+24+23+22+21+2° ¦-'
= 18 446 744 073 709 551 615 переносов
Если бы на каждый перенос жрецы затратили одну
секунду, то и так для переноса всех 64 кружков был0
496
Рис. 33-5
бы необходимо затратить около пяти миллиардов сто-
столетий. Наша планета существует примерно 10 мил-
миллиардов лет, т. е. около ОД миллиарда столетий.
Поэтому мы можем спать совершенно спокойно, до
конца мира еще очень, очень, далеко...
В игре, которую Лукас назвал Ханойской башней,
на 1 палочке находится только 8 кружков (рис. 33-5).
Для нас и это число очень большое, так как при вось-
восьми кружках число переносов составит:
274-2б+25+24+23+22+21+20 = 255
Для 255 переносов не каждый из нас имеет доста-
достаточное количество свободного времени. Поэтому мы
ограничим нашу игру до 6 кружков. Кружки можно
сделать не из золота, а из картона, палочки не из
алмазов, а из твердой проволоки, пластину можем
заменить куском фанеры.
Радиусы кружков рекомендуем принять следующие
считая сверху): 2 см, 2,5 см, 3 см, 3,5 см, 4 см, 4,5 см.
Переносов необходимо выполнить:
25+24+23+22+21+2° = 63
Кружок 1 необходимо перенести 25, т. е. 32 раза
Кружок 2 необходимо перенести 24, т. е. 16 раз
Кружок 3 необходимо перенести 23, т. е. 8 раз
Кружок 4 необходимо перенести 22, т. е. 4 раза
Кружок 5 необходимо перенести 21, т. е. 2 раза
Кружок 6 необходимо перенести 2°, т. е. 1 раз
Итого 63 раза
Желаем приятного времяпровождения.
497
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Рис. 33-6
Рис. 33-7
Как переставить кружки?
В американском научном ежемесячном журнале
«Сайентифик Америкен» в разделе «Математичес-
«Математические развлечения» мы нашли маленькую, но нелег-
нелегкую для решения задачу. Вот она:
Необходимо изменить последовательность располо-
расположения пяти кружков, показанную на рисунке 33-6,
установив кружки следующим образом, как это по-
показано на рисунке 33-7.
Перемещения должны быть вьшолнены следующи.м
образом: два пальца, указательный и средний кладем
на два соседних кружка, при этом один из них дол-
должен быть белый, а второй черный, пару кружкоь
перемещаем на другое место и устанавливаем на ли-
линии, показанной на рисунке. Оба кружка должны
во время передвижения прикасаться друг к другу.
Кружок, который находится с левой стороны, дол-
должен остаться с левой стороны, кружок, который на-
находился с правой стороны, также должен остаться
с правой стороны. Разрывы в цепи кружков могу!
образоваться и оставаться после очередного пере-
перемещения. После последнего перемещения кружки
должны образовать цепь, как это показано на рисун-
рисунке 33-7.
Примечание: если бы было разрешено пере-
перемещать кружки того же цвета, то задачу можно вы-
выполнить в три перемещения. Решите эту задачу и при
этом условии.
498
Рис. 33-8
РЕШЕНИЕ ЗАДАЧ
Крест Красного Креста
Знаком организации Красного Креста является крест,
показанный на рис. 33-8. Это одновременно геомет-
геометрическая фигура, которую мы можем использовать
для увлекательного развлечения:
1) двумя разрезами разделите этот крест на 4 части
и из этих частей составьте квадрат,
2) двумя разрезами разделите крест на четыре рав-
равные части и из них сложите квадрат,
3) четырьмя разрезами разделите крест на 5 частей
и сложите из них квадрат.
Не менее любопытно преобразование двух таких крес-
крестов в один равный им квадрат. Значительно более
сложны обратные преобразования превращения квад-
квадрата в крест или другие фигуры; в технике и ремесле
мы часто встречаемся именно с таким заданием:
вырезать из квадрата крест, таким образом, чтобы не
было отходов. Этот вопрос имеет особенное значение
в том случае, когда материал, из которого делается
крест, дорогой.
Как переставить кружки
Кружки могут быть переставлены за четыре пере-
перемещения (рис. 33-9):
1) переводим кружки 3 и 4 вправо от 5, но оставляем
между ними место на два кружка,
499
Q_
10
2) переводим кружки 1 и 2 вправо от кружков 3 и 4,
таким образом, чтобы соприкасались кружки 4 и 1;
3) переводим кружки 4 и 1 в просвет между круж-
кружками 5 и 3;
Щ/Ъ (jp) 4) переводим кружки 5 и 4 в просвет между круж-
кружками 3 и 2.
Крест Красного Креста
Решение смотри на рисунке 33-10.
Рис. 33-9
\
Л
1
V
/
L
/
2
Рис. 33-10
АБСТРАКЦИЯ ГЛАВА 34
С абстракцией мы встречаемся уже на самом низком
уровне математических знаний, в арифметике. Не-
Немецкий математик Кронекер A823—1891) сказал,
что целые числа создал добрый бог, а все остальное —
человек. Эта мысль не совсемтверна. Добрый бог
создал целые именованные числа. Первобытный че-
человек использовал только именованные числа, он
говорил: я убил 5 зайцев, съел два яйца или три
гриба.
Абстрагирование чисел от вещей и предметов про-
произошло значительно позднее. Знаменитый греческий
филосов Платон понимал числа как абстрактные
понятия, оторванные от каких-либо материальных
ассоциаций, понимал их как идеи. Сегодня число
в математике является абстрактным понятием.
В повседневной жизни мы встречаемся с еще одним
существенным абстрактным понятием — нулем. Мно-
Многие из нас отождествляют понятие нуль с понятием
«ничто». Однако, нуль — это совсем не то же самое,
что «ничто». Если у кого-либо^нет сберегательной
книжки, то его счет не может равняться нулю, так
как его просто нет, в то же время лицо, у которого
имеется сберегательная книжка может иметь счет
с балансом равным нулю. В математике нуль — это
очень существенное понятие. Мы выполняем на нем
501
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
Разьезд
=ооосзо=
Рис. 34-1
все математические действия, кроме деления на нуль
Без нуля мы не смогли бы написать большинства ис-
используемых нами повседневно чисел, больших де-
девяти, например, 10, 102, 1025 и т. п. Благодаря нулю
возникла позиционная система счисления, а благо-
благодаря позиционной системе счисления оказалось воз-
возможным даже с помощью одной цифры написать
бесконечное множество чисел, 5, 55, 555, 5555...
и т. п.
Так как в математике число — это абстрактное поня-
понятие, то можно было область чисел распространить за
пределы целых и дробных чисел, ввести отрица-
отрицательные числа (—1, —15, ...), иррациональные числа
(^/2, |/5,...), комплексные числа B+|/—1, 2—]/—1
...) и другие.
Наконец стало возможным введение буквенных обоз-
обозначений вместо цифр: а, Ь, с, ..., х, у, z.
На разъезде
На одноколейной железной дороге у ремонтируемого
разъезда встретились два состава, ведомые электро-
электровозами В и С (рис. 34-1).
Каким образом, эти составы могли разъехаться, если
на разъезде могут поместиться только электровоз
и два вагона, а каждый состав состоял из электровоза
и четырех вагонов?
502
Как была осуществлена переправа?
Шли два пешехода. Они дошли до реки. У берега
находилась парусная лодка, на которой мог пере-
переправиться только один человек. Пешеходы пере-
переправились на другой берег с помощью этой лодки
и оставили ее на том же месте, где она до этого
находилась. Никаких вспомогательных средств, ве-
веревок, цепей и т. п. у пешеходов не было. Как они
это сделали?
Еще одна переправа через речку
Двое друзей отправились на экскурсию и каждый
взял с собой своего сына. В пути они должны были
переправиться через реку с помощью складной
лодки, которая могла перевезти самое большее
100 кГ. Каждый из друзей вместе с рюкзаком весит
100 кГ, а каждый из мальчиков 50 кГ. Каким образом
все переправились через речку?
jplolololo"
Рис. 34-2
Задача Лукаса
Шашки установлены так, как это показано на рис.
34-2. Белые шашки необходимо переставить на место
черных, а черные на место белых. Белые шашки
можно перемещать только вправо, а черные — толь-
только влево, при этом каждую шашку можно пере-
переместить, либо только на соседнее свободное поле,
либо на ближайшее свободное поле, находящееся
503
за одной шашкой другого цвета: белую шашку за
черную шашку и наоборот. Попробуйте зто выпол-
выполнить. Сколько необходимо выполнить перемещений?
РЕШЕНИЕ ЗАДАЧ
На разъезде
Решение показано на рисунке 34-3:
— Электровоз В въезжает на разъезд, оставляет там
два задних вагона и возвращается на свое место по
главному пути; электровоз С подал назад, освобож-
освобождая место (поз. 2);
— Электровоз С въехал на разъезд, забрал остав-
оставленные там два вагона В и вернулся к своим вагонам,
на освобожденный разъезд въехал электровоз В
с остальными двумя вагонами (поз. 3);
— Электровоз С перегоняет свои 4 вагона и два
вагона состава В по освобожденному главному пути
вправо. На освобожденное электровозом С место
въезжает с разъезда электровоз В (поз. 4);
— Электровоз С перегоняет свои 4 вагона и два
вагона состава В по главному пути за разъезд, а затем
загоняет два вагона состава В в разъезд и там их
оставляет (поз. 5);
— Электровоз С возвращается к своим вагонам
и проезжает по главному пути вправо, а электро-
Рис. 34-3 воз В забирает с разъезда стоящие там свои вагоны
и отправляется по главному пути влево (поз. 6).
Составы разъехались.
504
Как была осуществлена переправа?
Первый пешеход после переправы оттягивает парус-
парусную лодку вверх по теченшо, устанавливает соот-
соответствующим образом парус и руль и лодка сама
возвращается на другой берег. Второй пешеход
после переправы поступил таким же образом.
Еще одна переправа через речку
Переправляются два сына, затем один из них воз-
возвращается. Переправляется один из друзей, а воз-
возвращается лодкой второй сын. Затем снова пере-
переправляются оба сына, один из них возвращается,
а второй остается на другом берегу. Затем переправ-
переправляется второй друг, а возвращается на первый бе-
берег второй сын. Наконец, переправляются оба сына
вместе.
Задача Лукаса
Перестановка шашек требует, по крайней мере,
35 перемещений, которых последовательность можно
записать следующим образом: б, ч, ч, б, б, б, ч, ч, ч,
ч, б, б, б, б, б, ч, ч, ч, ч, ч, б, б, б, б, б, ч, ч, ч, ч,
б, б, б, ч, ч, б.
МЕТОД ИНДУКЦИИ глава 35
Индукция — это такой метод мышления, с помощью
которого от единичного тезиса переходим к общим за-
законам, например:
1. Вес кусочка железа, который мы погрузили в во-
воду, уменьшается, т. е. железо весит меньше, чем
перед погружением (единичный тезис),
2. Каждое тело, погруженное в воду, весит меньше,
чем до погружения (общий закон).
Закон 2, выведенный на основании единичного тезиса
1, верен, однако, это не всегда бывает так:
1. Стакан, который я держу в руке, лопнул при
быстром наполнении кипятком.
2. Каждый стакан лопается при быстролх напол-
наполнении кипятком.
Во втором примере общее правило неверно, потому
что имеются стаканы, изготовленные из специаль-
специального стекла, которые не лопаются даже при очень
быстром их заполнении кипятком. Индукция являет-
является самой повседневной, будничной формой мыш-
мышления. Как, однако, можно уберечься от непра-
неправильных выводов, сделанных на основе индуктив-
индуктивного мышления. В нашей повседневной жизни, мы
учимся избегать ошибочности выводов путем мно-
многократного повторения акта индукции, благодаря
жизненному опыту.
506
В науке, очень широко использующей метод индук-
индукции, мы избегаем делать ошибочные выводы, воспол-
восполняя обычную индукцию дополнительными умоза-
умозаключениями. Эти умозаключения состоят в следу-
следующем, если вывод верен для 1, 2, 3, ... случаев, то
мы принимает, что он верен для к случаев и дока-
доказываем, что поскольку он верен для к случаев, то
он должен быть верен и для fc+1 случая. Такой
метод мышления называем полной индукцией или ма-
математической индукцией. Выводы, сделанные без
проверки с помощью математической индукции, даже
самыми крупными математиками, неоднократно ока-
оказывались ложными. А вот примеры:
1. Известный математик Леонард Эйлер A707—
1783) предполагал, что трехчлен х2+х+41 выра-
выражает простые числа при подстановке вместо х лю-
любого натурального числа. Действительно, если вмес-
вместо х поставим 1, 2, 3, ..., 10, то получаем ряд нату-
натуральных чисел: 43, 47, 53, 61, 71, 83, 97, 113, 131,
151. Однако, этот вывод, сделанный на основании
10 единичных тезисов, оказался неверным, если,
например, вместо х подставим 40; при этом полу-
получается число 1681, которое не является простыл
числом, ибо 1681 : 41 = 41.
2. Ферма считал, что числа вида 22 +1, где п —
это натуральное число, являются простыми числами.
При подстановке вместо п чисел 1, 2, 3, 4 получаем
5, 17, 257, 65 537. Это все простые числа, но уже
507
после подстановки вместо п числа 5 получаем
- 4 294 967 297, для которого Ферма не нашел дели-
делителя и которые считал поэтому также простьш
числом. Только Эйлер доказал, что это число де-
делится на 641, а следовательно, не является простьш
числом. Из этого видно, как важно в науке приме-
применять математическую индукцию.
Доказательство, проведенное на базе метода мате-
математической индукции, должно обязательно состоять
из двух частей, из доказательства двух независи-
независимых теорем.
Теорема I. Тезис действителен для п = 1.
Теорема II. Если тезис действителен для и = к,
где к — это произвольное натуральное число, то те-
эис справедлив также и для я = к-\-1.
Если обе эти теоремы доказаны, то на основе матема-
математической индукции можно утверждать, что тезис
справедлив для любого натурального п.
Чтобы дать читателю конкретное представление
о применении метода математической индукции,
далее приводится решение нескольких задач с по-
помощью этого метода.
Задача № 1. Выпишем в порядке возрастания по-
положительные нечетные числа 1, 3, 5, ...
Первое из них обозначим — t/j, второе — и2, тре-
третье — м3 и т. д., т. е.
ut = 1, м2 = 3, и3 = 5 ...
508
Необходимо найти формулу, выражающую нечет-
нечетное число и„ с помощью ее номера п.
Решение. Первое нечетное число и, мы можем
записать в форме:
wi = 2 - 1—1 A)
Второе нечетное число и2 запишем в форме:
ы2 = 2-2-1 B)
Третье нечетное число м3 —
ы3 = 2-3-1 C)
Давайте теперь посмотрим повнимательнее на урав-
уравнения A), B) и C), можно предположить на осно-
основании этих уравнений, что для получения любого
нечетного числа достаточно из его удвоенного но-
номера вычесть единицу, т. е. что для и-ного нечет-
нечетного числа действительна формула
ип = 2и-1 D)
Докажем, что эта формула справедлива.
На основании уравнения A) констатируем, что при
л = 1, формула D) справедлива (теорема I).
Предположим теперь, что формула D) справедлива
для п = к, т. е. что нечетное число ик имеет вид
ик = 2к-\
Докажем, что формула D) справедлива также
и для нечетного числа ик+1, т. е. что
509
или:
Для получения нечетного числа ик+1 достаточно сло-
сложить нечетное число к с 2, т. е. ик+1 = ик-\-2.
Из условий щ = 2к—1, следовательно:
что и требовалось доказать (теорема II).
Задача № 2. Доказать, что сумма квадратов п пер-
первых натуральных чисел равняется
Решение
1. Для и = I теорема верна
1A+1)-B-1+1) 1 -2-3 _ 6^ _
6 6 "~ 6 ~
Для л = 2, теорема также верна
2B+1) • B ¦ 2+1) =5
=5
2. Пусть для п -- к будем иметь
32+ +к2 =
тогда для л = (/с+1) будет
520
) ¦ BА:+1)+6(Аг+1J _ (Jfc+1) ¦ BA:2+A:+6fc+6) _
6 ~" 6
_ (fc+1) • Bк2+7к+6) (к+1) -(k+2) -(lk+3)
~~~ 6 6
т.е. для n = fc+1 формула также действительна.
Задача № 3. Доказать, что сумма кубов п первых
натуральных чисел равна:
Решение
1. Для « = 1 формула верна
2. Пусть для п = к будет
тогда
_ (Аг+1J • (А:г+4А:+4) (fc+1J • (А:+2J
~ 4. 4
J
Следовательно и для п = fc+1 формула правиль-
правильна.
Задача № 4. Как известно, произведение 1 • 2 •
• ... ' п обозначаем п\ и произносим «л факториал»
(см. главу 27).
511
Докажите методом индукции, что:
Sn = 1 • 11+2-21+3 -3!+ ... +л-л!
Решение
^ = 1-11 = 1
52 = 1 • 11+2-2! = 5
53 = 1 • П+2-21+3 -3! = 23
S4= I • 1!+2-2!+3 ¦ 31+4-4! = 119
Рассматривая эти результаты, можно заменить, что:
^ = 21-1; S2 = 3!-l; 53 = 4!-!;
SA = 5\-1
Из этого можно сделать заключение, что:
Sn = (л+1)[-1
Давайте проверим правильность этой формулы:
Для п — 1 и и = 2 эта формула верна, так как
Sj = 1 . и = 2!-1
5Г2== 1 • 11+2-2! = 5 = 31-1
Пусть формула будет также верна для п = к
Sk = 1 • 1 !+2 • 2!+ ... +к ¦ к\ = (fc+l)!-l
Докажем, что при этом:
Sk+1 = 1 -11+2 -21+ ... +fc
512
Фактически:
Sk+i = Sk+(k+l)
= (fc+1)! • (fc+2)-l = (fc+2)!-l
МЕТОД ДЕДУКЦИИ
Методом дедуктивного мышления называется такая
форма мышления, при которой на основании общей
теоремы делаются единичные выводы. А вот при-
примеры :
А. 1. Каждый гражданин СССР имеет право на
труд (общая теорема),
2. Иванов — гражданин СССР, следовательно, он
имеет право на труд (единичный вывод).
Б. 1. В каждом треугольнике центр тяжести распо-
расположен в точке пересечения его медиан.
2. В треугольнике АЕС центр тяжести расположен
в месте пересечения его медиан.
А вот еще пример дедуктивного метода.
«Каждое физическое тело, погруженное в воду,
теряет в весе столько, сколько весить вода, вытес-
вытесненная этим телом»;
«Железо — это физическое материальное тело, а
следовательно, кусок железа после погружения в во-
513
ду теряет в весе столько, сколько весит вытеснен-
вытесненная этим железом вода». Дедуктивный метод про-
проявляется также и в таком суждении:
1. Каждый газ сжимаем,
2. Воздух — это газ.
3. Следовательно, воздух сжимаем.
Было установлено новое положение: «воздух сжи-
сжимаем», которого нет ни в утверждении «каждый газ
сжимаем», ни в утверждении «воздух — это газ».
При дедуктивном мышлении создаются новые утвер-
утверждения.
К дедуктивным относится и такое суждение:
1. Все одноименные правильные многоугольники
(например, квадраты) подобны;
2. Данные правильные многоугольники — одно-
одноименные;
3. Данные правильные многоугольники — подоб-
подобны.
В этом умозаключении, первое суждение — общее,
второе — частное, а третье — вывод.
Для того, чтобы можно было сделать вывод, необ-
необходимо, дабы в первом и втором суждениях был
общий термин. Таким общим термином в первом
и вторрм суждениях первого примера является тер-
термин «газ», во втором примере «одноименные пра-
правильные многоугольники».
Существом дедукции является то, что конкретный
единичный случай мы подводим под общее пра-
правило.
514
Математические умозаключения обычно дедуктив-
дедуктивны.
Дедуктивный метод впервые разработал Аристо-
Аристотель C84—322 до н. э.) в своей науке о силлогизме.
Индуктивный метод разработал английский фило-
философ XVII века Ф. Бэкон A561—1626), а в матема-
математике его широко применял уже Б. Паскаль. Разви-
Развитие наук в XVIII—XIX веках доказало, что индук-
индукции нельзя отделять от дедукции, и что оба эти ме-
метода необходимо применять параллельно.
Дедуктивная форма мышления позволила Евклиду
построить всю геометрию на основании небольшого
количества аксиом и постулатов. Заменив только
одну из этих аксиом (о параллельных прямых) на
другую, великий русский математик Лобачевский
построил новую геометрию, отличную от евклидо-
евклидовой (смотри в главе 22).
О МАТЕМАТИЧЕСКОЙ
ЛОГИКЕ
Слово «логика» выводится из греческого «X
т. е. наука о мышлении. Логикой мы называем нау-
науку о законах и формах мышления. Она считается
частью философии.
Математическая логика — это наука, которая ис-
исследует математические доказательства; она явля-
является как бы частью логики в целом, однако, с уче-
учетом специальных потребностей математики.
515
Математическое мышление имеет свои особенности,
обусловленные своеобразием математической абс-
абстракции. Сложность систем математической абстрак-
абстракции, многообразие их взаимосвязей и сама их
сущность — все это находит свое отражение в сис-
систематизации логической математики, а в частности, —
в доказательствах математических теорем. Аксиома-
Аксиоматический метод (точкой отправления которого явля-
является: система аксиом и постулатов) — это один из
наиболее всеобщих способов систематизации логи-
логической математики. Классическим примером аксио-
аксиоматической теории является создание геометрии
Евклидом.
Слова не всегда одинаково, однозначно и точно
выражают мысли и понятия. Унификация и уточне-
уточнение понятий и методов умозаключений в некоторых
отраслях математики стало безусловной необходи-
необходимостью. Поэтому в современной математике приме-
применяется метод формализации доказательств. Его сущ-
сущность можно объяснить следующим образом.
Формулировки аксиом и теорем развиваемой теории
записываются в виде формул с помощью специаль-
специальных символов, используемых наряду с известными
уже математическими знаками. Кроме этого, указы-
указывается закон выведения теорем из аксиом, или из
уже ранее выведенных теорем. Законы эти — чисто
формальные, т. е. при их использовании нет необхо-
необходимости задумываться над содержанием формул,
к которым мы их применяем и которые в результате
si d
получаем, необходимо только убедиться, что эти фор-
формулы построены из соответствующих символов
и правильно составлены.
Доказательство теоремы сводится к выведению
представляющей ее формулы, причем этот вывод —
последовательность формул, на конце которой нахо-
находится искомая формула, и в которой каждый эле-
элемент является аксиомой или может быть получен
из одного или нескольких предшествующих формул
на основании любого закона выведения. Некоторые
математики пытались выразить все математические
дисциплины без применения словесных доказа-
доказательств, только с помощью символов и формул, вы-
выведенных на основании формальных законов выве-
выведения.
Математическая логика возникла в XIX веке. Ее
создателем был англичанин Д. Буль A815—1864),
а усовершенствовали Ч. Пирс и Б. Рассел, Фреге
и Шредер, Д. Пеано, А. Н. Колмогоров, А. А. Маль-
Мальцев, А. И. Мальцев, а также польские матема-
математики Я. Лукасевич A878—1956) и А. Тарский
(р. 1902).
Из вышесказанного следует, что идея создания
знаков, которые бы заменили слова — имеющие
иногда разное значение, а следовательно, затемня-
затемняющее мысль — беспокоила ученых уже давно.
В XVII веке этими вопросами занимался создатель
дифференциального исчисления Лейбниц. Он был
убежден, что можно создать такое универсальное
527
ЗАНИМАТЕЛЬНЫЕ
ЗАДАЧИ
международное письмо. Итальянский математик Пеа-
но реализовал это убеждение Лейбница. Он на-
написал сочинение по математике, в котором нет ни
одного слова. Такое представление математики чрез-
чрезвычайно компактно, точно и лишено каких-либо
двухсмысленностей, но очень сложно при чтении
и быстро утомляет человеческий мозг (смотри гла-
ву 31).
О человеке, приговоренном к повешению
Мартин Гарднер, автор рассказов, публикуемых
в ежемесячном журнале: «Сайентифик Америкен»
под общим заглавием «Математические развлече-
развлечения» приводит очень интересную логическую голо-
головоломку.
Один американский судья судил очень опасного
преступника. В субботу вечером процесс закончился
и судья объявил приговор:
«Вы приговорены к смертной казни через повеше-
повешение. Приговор должен быть приведен в исполнение
в полдень, в один из дней следующей недели.
О дне, в котором приговор будет приведен в испол-
исполнение, вы узнаете лишь утром того дня, когда вы
будете повешены. Раньше вы об этом знать не мо-
можете».
После оглашения приговора, приговоренный отпра-
отправился обратно в камеру в сопровождении своего
518
защитника. Как только защитник и его подопечный
остались одни, защитник рассмеялся и сказал:
— Так как судья, который вас судил известен
исключительно строгим соблюдением своих приго-
приговоров, ваш приговор практически не может быть
приведен в исполнение.
— Почему?
— Сейчас попытаюсь вам это объяснить. Будущая
суббота зто последний день недели, в течение ко-
которой приговор должен быть приведен в исполне-
исполнение. Так вот, в субботу приговор не может быть
исполнен, так как об этом вы уже знали бы в пят-
пятницу после полудня, если бы вы дожили до этого
времени. Приговор не может быть приведен в ис-
исполнение в субботу, потому что об исполнении при-
приговора вы можете узнать только утром того дня,
когда приговор должен быть приведен в исполнение.
Таким образом субботу необходимо исключить. Сле-
Следовательно, последним днем, когда приговор может
быть приведен в исполнение, является пятница.
Однако, в пятницу также нельзя вас повесить, так
как в четверг после полудня (если вы до этого вре-
времени доживете), вы будете знать, что вас могут
повесить либо в пятницу, либо в субботу. Так как
суббота исключается, то остается только пятница.
Следовательно, в четверг вечером вы бы знали,
что вас повесят в пятницу. А так как в приговоре
судьи ясно сказано, что о дате казни вы можете
узнать лишь утром того же дня, следовательно,
519
и в пятницу не могут вас повесить. Пятницу можно
исключить. Таким образом, четверг становится по-
последним днем, когда могут привести приговор в ис-
исполнение, но и в четверг повесить вас не могут, так
как об этом вы будете знать в среду после полудня.
Рассуждая таким образом, мы прийдем к выводу,
что не могут вас повесить ни в среду, ни во вторник,
ни в понедельник. Остается только завтрашний день
воскресенье, но и завтра вас не могут повесить, так
как вы знаете об этом уже сегодня. Короче говоря,
мне кажется, что приговор опровергает сам
себя.
Хотя в обеих частях, из которых этот приговор
состоит, нет ничего противоречивого, тем не менее
логически рассуждая, привести его в исполнение
нельзя.
Существует несколько вариантов парадокса о чело-
человеке, приговоренном к повешению. Одним из них
является вопрос «непредвиденного» яйца. Пред-
Представьте себе десять пронумерованных коробок.
Кто-то втайне положил в одну из них яйцо. Можно
ли предвидеть, в какой коробке находится яйцо.
А может его нет ни в одной ?
Яйцо не может находится в коробке № 10, так как
вы могли бы это предвидеть после установления, что
коробки от № 1 до № 9 пустые. Оно не может быть
спрятано в 9 коробке, так как после установления,
что коробки от № 1 до № 8 пустые ... и т. д., как
в парадоксе о приговоренном к повешению. Однако,
520
яйцо действительно находиться в одной из
коробок.
Если парадокс о приговоренном или о непредвиден-
непредвиденном яйце упростить до двух дней или же до двух
коробок, то мы также не избежим беспорядка в ло-
логических рассуждениях, которые хотя и справедли-
справедливы, приводят к выводам, противоречащим практике.
Буддийский монах
Однажды, точно в час восхода солнца из буддий-
буддийского монастыря вышел монах и начал подниматься
на очень высокую гору, где на вершине в лучах
восходящего солнца блестел храм Будды. Тропинка,
по которой шел монах, была узкой и спиралью опо-
опоясывала гору. Монах восходил вверх с переменчи-
переменчивой скоростью, несколько раз останавливался, чтобы
отдохнуть и подкрепиться фруктами, которые забрал
из монастыря на дорогу. Монах достиг вершины горы
точно в час заката солнца. После нескольких суток
поста и размышлений о тщетности мира сего, монах
покинул храм точно в час восхода солнца и отпра-
отправился в обратный путь, идя по той же тропинке
и так же с переменной скоростью. Конечно, средняя
скорость спуска монаха с горы была больше, чем
средняя скорость восхождения.
Доказать без каких-либо формул и расчетов (на
здравый смысл), что на тропинке, по которой шел
монах, имеется такой пункт, в котором монах нахо-
521
дился точно в тот же самый час дня, как при вос-
восхождении, так и при спуске.
Указание для решения. Вместо одного
монаха, предположим, что одновременно в час вос-
восхода солнца один монах отправился сверху вниз,
а второй начал по той же тропинке подыматься на-
наверх.
ПРОЩАНИЕ
С КНИГОЙ
Вместо заключения
Последние слова. Заключительный аккорд. Как за-
завершить эту книгу? Автор решил закончить ее го-
головоломкой, которая подчеркнула бы ее общий ха-
характер. Расшифровать эту головоломку несложно,
если известен ключ к ней. Ключ этот вы найдете,
если хорошо приглядитесь к рисунку на следующей
странице.
Игра это не легкомысленность в ней столько же
пользы сколько и в индифферентной мудрости
источники,
которые использовал автор при подготовке к печати книги «От раз-
развлечения к знаниям». Многих из этих книг читатель не найдет
в книжных магазинах, да и не все из них окажутся в наличии на
библиотечных полках. Чтобы облегчить поиск книг, рядом с загла-
заглавием книги и фамилией ее автора указаны год издания и название
издательства, которое ее опубликовало. Среди названий книг Чи-
Читатель обнаружит труды не только математические, но и естество-
естествоведческие, технические, а также гуманитарные, которые вроде бы
не связаны с математикой. Но мы живем в эпоху, когда, с одной
стороны, происходит непрерывный процесс гуманизации математики,
а, с другой, математизации наук, казалось бы очень отдаленных от
математики. Поэтому иам кажется, что истинный любитель матема-
математики потянется и за этими книгами.
Книги на русском языке
Берман Т. Н. Число и наука о нем, 1954
Воробьев Н. Н. Числа Фибоначчи, 1951
Дынкин Е. Б., Успенский В. А. Математические беседы, Москва 1952
Колмогоров А. Н. Математика. Б.С.Э. II изд. том 26
Маркушевич А. Л. Площадь поверхностей и логарифмы, 1952
Пархоменко А. С. Что такое линия? 1954
Рыбников К. А. Очерки по истории математики XVII и XVIII вв., 1957
Книги на иностранных языках
Aaboe A.: Matematyka w starozytnoSci, PWN, 1968
Bienko W.: Zygzakiem przez matematyke., PZWS, Warszawa, 1964
Cajori P.: A history of elementary mathematics, 1910
525
Colerus E.: Od tabliczki do rozniczki, Lwow, 1938
Courant R., Robbins H.: Co to jest matematyka, PWN, Warszawa, 1962
Cundy H. M., Rollet A. P.: Modele matematyczne, PWN, Warszawa, 1967
Diaimi J.: Jan Brozek, Johaannes Broscius, PZWS, Warszawa, 1949
Dianni J., Wachulka А.: Tysiac lat polskiej mysli matematycznej, PZWS, Warszawa, 1963
Ducrocq A.: Era robotow, PWN, Warszawa, 1960
Dynkin J., Uspienski W.: Ciekawe zagadnienia matematyczne, PWN, Warszawa, 1956
Ehrenfeuchtowa A.: Ciekawy szesbian, PWN, Warszawa, 1963
Farrington В.: Nauka grecka, PWN, Warszawa, 1954
Gardner M.: Mathematical Games, Scientific American
Hadamard J.: Psychologia odkry? matematycznych, PWN, Warszawa, 1964
HogbenL.: Matematyka dla milion6w, KiW, Warszawa, 1952
Infeld L.: Albert Einstein, PWN, Warszawa, 1956
Ja&owski S.: Matematyka ornamentu, PWN, Warszawa, 1957
Jkan F.: Design of the Universe, Iskry, Warszawa, I960
Kohnogorow A. N.: О matematyce, PWN, Warszawa, 1955
Komitet Olimpiady Matematycznej: Be.de, studiowal matematyke,, 1954
Kline M.: Matematyka a swiat fizyczny, PWN, Warszawa, 1964
Kulczycki S.: Geometria nieeuklidesowa, PWN, Warszawa, 1956
Lefebvre H.: Kartezjusz, PWN, Warszawa, 1950
Lietzman W.: Gdzie tkwi bla.d? PZWS, Warszawa, 1958
Lofler E.: Ziffern und abzahlbares System, 1928
Lorentz H.: Elementy matematyki wyzszej, Mathesis, 1910
Mary slownik matematyczny, Wiedza Powszechna, Warszawa, 1967
Markuszewicz А.: О szeregach w matematyce, Wiedza Powszechna, Warszawa, 1967
Markuszewicz A.: Ci^gi rekurencyjne, PWN, Warszawa, 1955
Matematyka w swiecie wspolczesnym. «Scientific American», PWN, Warszawa, 1966
Natanson L. P.: Sumowanie nieskonczenie mafych, PWN, Warszawa, 1955
Natanson L. P.: Najprostsze zadania na maksima i minima, PWN, Warszawa, J955
Newson C. V.: Istota matematyki, PWN, Warszawa, 1967
Peter Rozsa: Gra z nieskonczonoscia., PWN, Warszawa, 1962
526
Praca zbiorowa pod red. R. Wesleya: Matematyka dla wszystkich, WNT, Warszawa, 1958
Raedemacher H., Toeplitz О.: О liczbach i figurach, PWN, Warszawa, 1956
SierpMski W.: Czym sie, zajmuje teoria liczb. Wiedza Powszechna. Warszawa, 1957
Sierpinski W.: О rozkladach liczb wymiernych na ulamki proste, PWN, Warszawa, 1957
Sierpinski W.: Trojkaty pitagorejskie, PWN, Warszawa, 1954
Sluckin W.: Mozg i maszyny, PWN, Warszawa, 1957
Sominski J. S.: Metody indukcji matematycznej, PWN, Warszawa, 1955
Steinhaus H.: Czym jest a czem nie jest matematyka. Ks. Altenberga, Lwow, 1921
Steihhaus H.: Sto zadan, PWN, Warszawa, 1958
Steinhaus H.: Orzel czy reszka, PWN, Warszawa, 1962
Steinhaus H.: Kalejdoskop matematyczny, Ks. Altenberga, Lwow, 1937
Straik D.I.: Krotki zarys historii matematyki, PWN, Warszawa, 1963
Sznirelman L.: Liczby pierwsze, PWN, Warszawa, 1954
Weizaacker C.F., Juilfs J.: Fizyka wspolczesna, PWN, Warszawa, 1960
Wilkowski R.: Elementy matematyki wyzszej dla pracuja.cych i samoukow Czytelnik,
Warszawa, 1947
Wilkosz W.: Licze,— mys"le., PZWS, Warszawa, 1951
ОГЛАВЛЕНИЕ
К ЧИТАТЕЛЮ 5
ВМЕСТО ПРЕДИСЛОВИЯ 7
Глава 1
МЫ ЖИВЕМ СРЕДИ ЧИСЕЛ 9
ЦИФРЫ РАЗНЫХ НАРОДОВ И ЭПОХ 14
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 21
Архимед и число 21
Дайте мне точку опоры я я 22.
Энергия голоса 23
Исторический анекдот 24
Вдовья копейка 26
Сколько дней? 27
РЕШЕНИЕ ЗАДАЧ 27
Глава 2
МИФ О ИРРАЦИОНАЛЬНЫХ
ЧИСЛАХ 28
ДВА ЗНАМЕНИТЫХ ИРРАЦИОНАЛЬНЫХ ЧИСЛА .... 32
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 36
Математические игры и головоломки 36
Из папирусов Ахмеса 37
Задача Диофанта 38
Головоломка Иосифа Флавия 39
Непроверенная легенда 42
Надгробный памятник Архимеда 43
РЕШЕНИЕ ЗАДАЧ 44
Глава 3
ОБ ОТРИЦАТЕЛЬНЫХ
ЧИСЛАХ 47
ГРЕЧЕСКИЕ МАТЕМАТИКИ 47
ИНДИЙСКАЯ МАТЕМАТИКА 48
ПРЕЖДЕВРЕМЕННОСТЬ ОТКРЫТИЯ
ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ 49
529
АРАБСКАЯ МАТЕМАТИКА 49
МАТЕМАТИКА В ЕВРОПЕ ЭПОХИ ФЕОДАЛИЗМА .... 51
МАТЕМАТИКА В ЭПОХУ ЗАРОЖДЕНИЯ
КАПИТАЛИСТИЧЕСКИХ ОТНОШЕНИЙ 56
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 59
Как он поделил деньги? 59
Как разделить наследство? 63
Сумеете ли вы ответить? 64
РЕШЕНИЕ ЗАДАЧ 66
Глава 4
КОМПЛЕКСНЫЕ ЧИСЛА 72
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 75
Сколько раз? 75
Испорченные часы 76
Машины часы 76
Кант и часы 76
Приказ о вылете 78
Что больше? 78
Сколько молодежи было в аудитории? 78
Курьезы, загадки, головоломки 79
РЕШЕНИЕ ЗАДАЧ 80
Глава 5
ТРИ ЗНАМЕНИТЫЕ
'ЕВНЕГРЕЧЕСКИЕ ЗАДАЧИ 89
КВАДРАТУРА КРУГА 89
УДВОЕНИЕ КУБА (ДЕЛОССКАЯ ЗАДАЧА) 95
ТРИСВКЦИЯ УГЛА 97
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 100
Геометрическая смесь 100
Задачи на построение 101
Рассчитать площадь поверхности 101
Площадь шестилепестковой розы 101
Об одной экскурсии 101
Неудачная экскурсия 102
530
Странствующий отряд 103
Математика в кухне , 103
Кто скорее? 104
Два пассажира 105
Задача Пуассона 105
Как она справилась? 106
РЕШЕНИЕ ЗАДАЧ 106
Глава 6
ВЕЛИКАЯ ТЕОРЕМА ФЕРМА 114
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 117
Сколько?
Сколько было учеников?
О пожарных и дежурствах
Напишите
Какие арифметические действия?
Что это за число?
Приключение в сберкассе
Какое это число?
Четырехзначная головоломка
Харнты и музы (древнегреческая задача)
Как они рассчитались?
Определите это число?
Сколько у кеня было денег?
Размен купюры
РЕШЕНИЕ ЗАДАЧ
Глава 7
СРЕДНЕЕ ГАРМОНИЧЕСКОЕ
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ
Прежде всего пунктуальность
Разумный бухгалтер
Виноторговец и его помощник
В сельмаге
В зоологическом магазине
Кто продает дешевле?
Учет товаров
На ферме
РЕШЕНИЕ ЗАДАЧ
531
Глава 8
ДВОИЧНАЯ СИСТЕМА 153
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 169
Увеселительная игра 169
Из дневника любителя математики 171
Хобби хроникера 173
Игра с цифрами 174
РЕШЕНИЕ ЗАДАЧ 176
Глава 9
ВИКТОРИНЫ, ТЕОРИЯ
ИНФОРМАЦИИ
И КИБЕРНЕТИКА 180
УПРАВЛЕНИЕ (ПУТЬ СОБАКИ) 185
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 190
Обман зрения при оценке величины и формы 190
12 маленьких вопросов 191
РЕШЕНИЕ ЗАДАЧ 193
Глава 10
1АГИЧЕСКИЕ КВАДРАТЫ 197
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 200
Найти трехзначное число 200
Магический треугольник 200
Шахматная доска 201
Уклончивый ответ 202
Квадратный корень из феодализма 203
Задача Киркмана 204
Числовая задача 204
Лабирин! с 42 помещениями 204
РЕШЕНИЕ ЗАДАЧ 205
Глава 11
РЯДЫ 211
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 215
Путешествие гусеницы 215
Ахиллес й черепаха 216
О ломаных линиях 218
Из окна вагона 220
Квадратный корень 220
032
Проверка железнодорожных путей 220
Путешествие господина Смита 220
РЕШЕНИЕ ЗАДАЧ 222
Глава 12
ОБ ОТНОШЕНИЯХ 225
ЗОЛОТОЙ ТРЕУГОЛЬНИК И ЗОЛОТОЙ ПРЯМОУГОЛЬНИК 227
РЯД ФИБОНАЧЧИ 230
СТАНДАРТНЫЕ ПРЯМОУГОЛЬНИКИ И ТРЕУГОЛЬНИКИ .
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ
Крест Лотарингии
Катание на санях
Сколько раз
Кубический метр
У самовара
Головоломка
Сколько страниц
Птицы и рыба
РЕШЕНИЕ ЗАДАЧ
Глава 13
»ОРИГАМИ«
ТРЕУГОЛЬНИК ПАСКАЛЯ И ПОКЕР
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ
Колдовство хитреца
Задача Льва Толстого о косарях
Валька и Иоська — логическая головоломка
РЕШЕНИЕ ЗАДАЧ
Глава 14
КАК УКЛАДЫВАЕТСЯ ПАРКЕТ
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ
Геометрия ножниц
Как разделить торт?
Деление треугольника
Деление квадрата на шестиугольники
Как разрезать?
Как разделить квадрат на половины?
Квадратный лист бумаги
Как разделить без спора?
533
Бокал сока 262
Шоколадный торт 262
Рамка из квадрата 263
РЕШЕНИЕ ЗАДАЧ 263
Глава 15
САМОЛЕТ И ВЕТЕР 268
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 272
Двукратное эхо 272
Вода и лед 272
Какова емкость бутыли? 273
Какая была температура? 273
Приводной ремень 274
Скорость езды 274
Четыре снаряда 274
Два пловца 275
РЕШЕНИЕ ЗАДАЧ 276
Глава 16
СКОЛЬКО ВЕСИТ
СТАНИСЛАВ? 281
КОРЕЦ, ЛОКОТЬ И ФУТ 284
ФАЛЬШИВАЯ МОНЕТА 288
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 290
Девять шариков 290
Задача о 12 дукатах 290
Десять вопросов 292
РЕШЕНИЕ ЗАДАЧ 293
Глава 17
О СРАВНЕНИИ 299
ДЕЛИМОСТЬ ЧИСЕЛ 301
ЧИСЛО НШХЕРЕЗАДЫ 306
ЛЮБОПЫТНЫЕ ЧИСЛА 308
ПРИЗНАК ДЕЛИМОСТИ НА 11 309
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 310
Под которым деревом находится клад? 310
Четыре загадки 311
РЕШЕНИЕ ЗАДАЧ 311
534
Глава 18
ОБ АЛГЕБРЕ 315
МЕТАМОРФОЗА СИМВОЛИКИ УРАВНЕНИЙ НА ПРОТЯ-
ПРОТЯЖЕНИИ ВЕКОВ 317
ОБ АЛГОРИТМЕ 320
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 322
Торопящийся господин 322
Два брата и Джек 323
Среди автомобилистов 324
Четыре четверки 324
РЕШЕНИЕ ЗАДАЧ 324
Глава 19
О ГЕОМЕТРИИ 328
МЕДОНОСНЫЕ АРХИТЕКТОРЫ 330
ЛИСТ МЁБИУСА 334
ТРИ РАЗА «ИН»: ИТЕРПОЛЯЦИЯ, ИНВЕРСИЯ,
ИНВОЛЮЦИЯ 335
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 338
Квадрат и прямая 338
Проверьте свою геометрическую смекалку 338
Еще о листе Мёбиуса 338
Сколько лет дяде? 339
Справедливый отец 339
Кройка и геометрия 340
Модница и поясок 340
Недружные соседи 341
Не в лоб, так по лбу 342
РЕШЕНИЕ ЗАДАЧ 342
Глава 20
ГЕОМЕТРИЧЕСКИЕ
СОФИЗМЫ 347
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 349
Каждая окружность имеет два центра 349
Каждый треугольник — равнобедренный 350
Кредитор и должник 350
РЕШЕНИЕ ЗАДАЧ 35t
535
Глава 21
СИММЕТРИЯ И АСИММЕТРИЯ : 354
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 358
Звезда шерифа 358
Кривая Коха или «снежинка» 359
Задачи со спичками 359
РЕШЕНИЕ ЗАДАЧ 361
Глава 22
О НЕЕВКЛИДОВОЙ
ГЕОМЕТРИИ 364
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 367
Каково цвета? 367
Новогодняя головоломка ( 368
Логическая головоломка 369
Кто чей сын? 370
РЕШЕНИЕ ЗАДАЧ 370
Глава 23
НЕГОРДИЕВЫ УЗЛЫ 373
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 376
Терпение и упорство 376
Клад 377
Уникурсальные фигуры 377
Королевские мосты 377
На цврковой арене 378
Тропинки в садах 378
Почтовая посылка 379
Среди георгинов 379
Задача садовника 380
РЕШЕНИЕ ЗАДАЧ 380
Глава 24
ЛИНИИ 3!-3
ВИНТОВАЯ ЛИНИЯ 387
ЛОКСОДРОМА И ОРТОДРОМИЯ ЗЬ7
ВЕКТОРЫ И СКАЛЯРЫ 3S9
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 390
Сечение куба плоскостью 390
536
Есть ли у вас пространственное воображение? 390
7 вопросов 391
РЕШЕНИЕ ЗАДАЧ 392
Глава 25
О ТРИГОНОМЕТРИИ 394
О ДУГЕ, КАСАТЕЛЬНОЙ К ДВУМ ЗАДАННЫМ
ОКРУЖНОСТЯМ 397
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 399
Согнутый стержень 399
Лист металла 399
РЕШЕНИЕ ЗАДАЧ 400
Глава 26
ВАРИАЦИОННОЕ
ИСЧИСЛЕНИЕ 402
ИЗОПЕРИМЕТРИЧЕСКИЕ ЗАДАЧИ 403
ХИТРОСТЬ ДИДОНЫ 404
УДИВИТЕЛЬНАЯ КРИВАЯ 406
КАЧЕНИЕ БЕЗ СКОЛЬЖЕНИЯ 411
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 413
Задача жестянщика 413
Найдите это число 414
Кубик 414
Маленькие вопросы по геометрии 414
РЕШЕНИЕ ЗАДАЧ 415
Глава 27
СЮРПРИЗЫ
КОМБИНАТОРИКИ 418
ИГРА В ПЯТНАДЦАТЬ 421
АНЕКДОТ О 12 СОТРАПЕЗНИКАХ 423
л! (п-ФАКТОРИАЛ) 424
Глава 28
ВЕРОЯТНОСТЬ ИЛИ
ДОСТОВЕРНОСТЬ 425
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 438
Выборка цифр 438
537
Мудрый отец и неглупый сын 438
На боксерском ринге 439
РЕШЕНИЕ ЗАДАЧ 440
Глава 29
РАСЧЕТ ИЛИ РИСУНОК 444
ФОРМУЛА И ЕЕ ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ ... 446
ЛЮБОПЫТНОЕ ТОЖДЕСТВО 448
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 449
Недопустимые сокращения 449
Игры с числами 450
История с алмазом 450
Разное — «Яйцо Колумба» 451
РЕШЕНИЕ ЗАДАЧ 455
Глава 30
МАТЕМАТИЧЕСКИЕ
ФОРМУЛЫ 459
КОСМИЧЕСКАЯ СКОРОСТЬ 463
ЧЕЛОВЕК ПОКОРЯЕТ ПРОСТРАНСТВО 464
МЫСЛИ О МЫСЛЯХ 466
Глава 31
МАТЕМАТИКА
И ПАЗИГРАФИЯ 468
Глава 32
ЗОЛОТЫЕ МЫСЛИ
О МАТЕМАТИКЕ 475
МОЛОДОСТЬ И МАТЕМАТИКА 476
МАТЕМАТИЧЕСКИЕ ЗАДАЧИ 477
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 478
Турнир 478
Длина приводного ремня 482
«Лунар» +83
Кофе с молоком 483
Две цепочки 484
РЕШЕНИЕ ЗАДАЧ 484
538
Глава 33
ИНТУИЦИЯ И РАЗУМ 490
ХАНОЙСКАЯ БАШНЯ 494
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 498
Как переставить кружки? 498
Крест Красного Креста 499
РЕШЕНИЕ ЗАДАЧ 499
Глава 34
АБСТРАКЦИЯ 501
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 502
На разъезде 502
Как была осуществлена переправа? 503
Еще одна переправа через речку 503
Задача Лукаса 503
РЕШЕНИЕ ЗАДАЧ 504
Глава 35
МЕТОД ИНДУКЦИИ 506
МЕТОД ДЕДУКЦИИ 513
О МАТЕМАТИЧЕСКОЙ ЛОГИКЕ 515
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ 518
О человеке, приговоренном к повешению 518
Буддийский монах 521
ПРОЩАНИЕ С КНИГОЙ 523
ИСТОЧНИКИ 525