ЗГопг|лярнъ1е
ПО МАТЕМАТИКЕ
<IOJ>
В.Г. БОЛТЯНСКИЙ
ОГИБАЮЩАЯ
ФИЗМАТГИЗ -1961

ПОПУЛЯРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ
ВЫПУСК 36
В. Г. БОЛТЯНСКИЙ
ОГИБАЮЩАЯ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1961

АННОТАЦИЯ
В книге на простых примерах, взятых
из области механики и геометрии и доступ-
доступных учащимся средней школы, разъясняется
понятие огибающей, играющее важную роль
в высшей математике. Эти примеры не
требуют рассмотрения никаких других функ-
функций, кроме многочленов, благодаря чему
разыскание огибающих производится весьма
простыми приемами. Книга может быть
использована в работе математических
кружков.
Болтянский Владимир Григорьевич
Огибающая
Редактор Л. Ю. Чернышева.
Техн. редактор Л. В. Лихачева.	Корректор Г. М. Алексеева.
Сдано в набор 16/Ш 1961 г. Подписано к печати 10/VII 1961 г. Бумага 84x108/32.
Физ. печ. л. 2,375. Условн. печ. я. 3,89. Уч.-изд. л. 3,72. Тираж 32 000 экз. Т-087С2.
Цена книги 11 коп. Заказ 2430.
Государственное издательство физико-математической литературы.
Москва, В-71, Ленинский проспект, 15
Типография № 2 нм. Евг. Соколовой УПП Ленсовиархоза.
Ленинград, Измайловский пр., 29.

ОГЛАВЛЕНИЕ
От автора		4
Глава I. Парабола безопасности	¦		5
1.	Движение тела, брошенного под углом к горизонту . .	5
2.	Парабола		8
3.	Парабола безопасности		10
4.	Некоторые свойства параболы		15
Глава И. Гипербола—граница зоны слышимости		19
1.	Сверхзвуковой полет самолета		19
2.	Характеристический угол		22
3.	Нахождение зоны слышимости		24
4.	Некоторые свойства гиперболы		29
Глава III. Астроида и циклоида		36
1.	Мгновенный центр вращения		36
2.	Астроида		37
3.	Циклоида		40
Глава IV. Огибающая		43
1.	Семейства линий и их огибающие		43
2.	Уравнение семейства линий		45
3.	Пересечение линий семейства		49
4.	Дифференцирование и нахождение огибающих ....	53
5.	Дискриминантная линия		58
6.	Примеры нахождения огибающих		61
7.	Эволюты и эвольвенты		71

ОТ АВТОРА
Понятие огибающей встречается в различных разделах так
называемой «высшей» математики. Нахождение огибающих
обычно производится с помощью операции дифференцирова-
дифференцирования — одной из основных операций высшей математики. Вместе
с тем понятие огибающей весьма наглядно и геометрично.
Оно может быть пояснено несложными примерами, доступ-
доступными пониманию учащихся старших классов.
В этой небольшой книге на материале механики (равно-
(равномерное и равномерно ускоренное движение, качение) рас-
рассмотрены несколько интересных примеров построения огибаю-
огибающих. В качестве огибающих появляются замечательные кри-
кривые, часто встречающиеся в математике и ее приложениях:
парабола (глава I), гипербола (глава II), астроида и циклоида
(глава III). В заключительной, четвертой главе дается объясне-
объяснение общего понятия огибающей. Здесь же указан общий
прием нахождения огибающих, в связи с чем приведено крат-
краткое описание операции дифференцирования.
Первая глава содержит материал лекции, несколько лет
назад прочитанной автором по просьбе руководителей школь-
школьных математических кружков при МГУ.
Для понимания основного материала книги достаточно
иметь знания в объеме восьми классов средней школы.
Пользуюсь случаем выразить искреннюю признательность
за советы и указания, высказанные Н. В. Ефимовым и
И. М. Ягломом.
В. Г. Болтянский

ГЛАВА I
ПАРАБОЛА БЕЗОПАСНОСТИ
1. Движение тела, брошенного под углом к горизонту
Предположим, что тело небольших размеров (материаль-
(материальная точка) свободно движется над земной поверхностью. Для
того чтобы составить правильное представление о движении
этого тела, нужно учесть действие на него всех сил, и прежде
всего силы тяжести и сил, вызываемых воздействием воз-
воздушной среды на тело. Силы, вызываемые воздействием воз-
воздушной среды, в одних случаях имеют существенное значение,
в других же случаях их влияние не столь заметно. Напри-
Например, при рассмотрении полета планера этими силами пре-
пренебречь нельзя — воздух «поддерживает» планер. При движе-
движении же артиллерийского снаряда или баллистической ракеты
влияние силы сопротивления воздуха менее значительно. На
рис. 1 приведен примерный вид траектории полета снаряда
Рис. 1.
в воздухе (сплошная линия — так называемая баллистическая
кривая) и линии, по которой летел бы снаряд под действием
одной только силы тяжести.
В дальнейшем мы будем рассматривать именно такое «упро-
«упрощенное», идеализированное движение тел под действием одной
только силы тяжести, т. е. будем пренебрегать воздействием

воздушной. среды на тело и другими менее значительными
силами (скажем, силами земного магнетизма, силами притя-
притяжения Луны, Солнца и звезд и т. п.). Силу тяжести P~mg
будем считать постоянной и направленной вертикально вниз.
Таким образом, мы принимаем, что единственной силой, дей-
действующей на брошенное тело, является сила тяжести, и что
действие ее заключается в сообщении телу ускорения g, по-
постоянного по величине и направлению.
Обозначим через L линию, по которой движется бро-
брошенное тело (траекторию его движения). В каждый момент
времени движущееся тело находится в некоторой точке этой
траектории и имеет определенную скорость движения. Ско-
Скорость является вектором (направленной величиной), причем
этот вектор касается траектории L. В данном случае это
означает, что вся траектория L расположена по одну сторону
от прямой, по которой направлен вектор скорости v (рис. 2).
Рис. 2.
Пользуясь правилом параллелограмма, можно разложить
скорость брошенного тела на две составляющие — вертикаль-
вертикальную и горизонтальную. Так как ускорение g направлено
вертикально, то оно не может изменить горизонтальной состав-
составляющей скорости; следовательно, при сделанных предположе-
предположениях горизонтальная составляющая скорости остается постоян-
постоянной в течение всего движения. Иными словами, проекция тела
на горизонтальную плоскость движется равномерно и прямо-
прямолинейно (рис. 3). Если, например, предположить, что часть
земной поверхности, над которой движется брошенное тело,
является совершенно плоской и горизонтальной, а солнце
находится в зените, то тень брошенного тела будет двигаться
по земле равномерно и прямолинейно (принимая параллель-
параллельность лучей солнца). Таким образом, движение брошенного
тела происходит в одной вертикальной плоскости. Эту
плоскость в дальнейшем мы будем предполагать совпадающей
с плоскостью чертежа.
Условимся считать положительным направлением верти-
вертикальной прямой направление вверх. Тогда вертикальная

составляющая скорости меняется с ускорением — g, т. е.
с замедлением g. Если обозначить горизонтальную- и верти-
вертикальную составляющие начальной скорости знаками vl и v®,
то составляющие скорости через t секунд после начала дви-
движения будут соответственно равны
-vl-gt.
A)
B)
Предположим, что в начальный момент времени брошенное
тело находится в точке А на высоте h0 над поверхностью
Рис. 3.
земли, которую предположим ровной и горизонтальной,
Проекцию точки А на земную поверхность обозначим через О
(рис. 4). Будем считать,
что горизонтальная со-
составляющая начальной
скорости направлена впра-
вправо. Положение, которое
занимает брошенное тело
через t секунд после на-
чала движения, обозна-
обозначим через Т, а проекции
точки Т на вертикальную
и горизонтальную пря-	рис 4.
мые, проходящие через О,
обозначим соответственно буквами В и F. Наконец, введем
обозначения OB^h, OF = х. Тогда, очевидно,
х = vlt,
C)
2 Зак. 2430. В. Г. Болтянский

так как точка F движется равномерно и прямолинейно со ско-
скоростью vrQ. Далее, AB — h — h0 есть путь, пройденный точ-
точкой В, двигающейся равноускоренно с начальной скоростью v^
и ускорением — g, так что мы имеем
и 	и 	„,Bi	 S*
или
D)
Формулы A), B) определяют скорость, а формулы C), D) —
положение брошенного тела через t секунд после начала
движения.
2. Парабола
В формулах A) — D) подразумевается, что t принимает
лишь положительные значения, так как мы рассматриваем
движение тела после момента ^ = 0, когда оно было бро-
брошено с некоторой начальной скоростью. Однако эти формулы
имеют смысл и для отрицательных значений t. Предположим,
например, что тело начало двигаться раньше интересующего
нас момента времени t — 0, а в момент t = 0 мы засекли
положение тела и его ско-
скорость и условились счи-
считать эти положение и
скорость «начальными».
Тогда движение тела до
момента t = 0 также
описывается формулами
A) — D), если в этих
формулах придавать t
отрицательные значения.
Рис- 5.	Это движение на рис. 5
показано пунктиром. Та-
Таким образом, придавая^ не только положительные, но и отри-
отрицательные значения, мы получим всю траекторию движения
тела, как вправо, так и влево от некоторой «начальной»
точки А.
Полученная кривая упирается концами в горизонтальную
прямую OD — тело падает на землю, и движение прекращается.
Предположим, однако, что в точке D, в которой тело падает
на землю, вырыта яма (рис. 5). Тогда тело будет еще неко-
некоторое время падать, и формулы A) — D) останутся справед-
8

ливымн. При этом тело будет находиться ниже прямой OD,
так что h будет принимать отрицательные значения. Таким
образом, траектория движения тела естественно продолжается
вниз от прямой OD и описывается теми же формулами
A) — D), Придавая t все большие значения, мы сможем про-
продолжить траекторию как угодно далеко. Точно так же, при-
придавая t в формулах A) — D) отрицательные и все большие
по абсолютной величине зна-
значения, мы продолжим и левую
«ветвь» кривой как угодно да-
далеко. Мы получаем кривую,
неограниченно простирающую-
простирающуюся вдаль от А обеими своими
ветвями; она называется пара- л~,
болой (рис. 6). Формулы A)—	'
D) описывают движение тела /
по этой кривой под действием /
постоянного по величине и на- /
правлению ускорения *).
Изучим на основании фор-	Рис- б.
мулA)— D) некоторые свой-
свойства рассмотренного движения тела по параболе. Из B) ясно,
в
что в момент времени t =¦ — вертикальная составляющая
скорости vB равна нулю. До этого момента времени состав-
составляющая ifi была положительна, т. е. тело двигалось вверх;
после этого момента она отрицательна — тело движется вниз.
Иначе говоря, в момент времени
t = A	E)
тело имеет наибольшую высоту подъема, а именно высоту
/гтах = /гп + -Ц^-	F)
*) Часть пространства, в котором на каждую единицу массы
действует постоянная по величине и направлению сила тяжести,
называется однородным полем тяготения. Небольшой участок
пространства над земной поверхностью можно приближенно считать
однородным полем тяготения. Движение тела происходит по кривой,
близкой к небольшой дуге параболы и прекращается при падении
тела на землю. Изучение же всей параболы, т. е. обеих ветвей
кривой, простирающихся неограниченно далеко, имеет в данной
задаче только математический смысл.
2*	9

(см. D)). Это легко подтвердить также непосредственным
вычислением:
т. e. h ^C ho-\- 9°- при любом t. Обозначим эту наивысшую
точку параболы через С. Скорость движения тела в точке С
горизонтальна. Иначе говоря, часть параболы справа от
точки С можно получить, если бросить тело из С горизон-
горизонтально вправо с соответствующей скоростью. Левая часть
параболы получится, если бросить тело горизонтально влево
с такой же скоростью. Отсюда ясно, что вертикальная прямая,
проходящая через С, является осью симметрии параболы.
В точке С парабола пересекает свою ось симметрии; эта точка
называется вершиной параболы.
3. Парабола безопасности
Рассмотрим теперь вопрос о траекториях полета снарядов,
выпускаемых из орудия, расположенного в некоторой точке О
земной поверхности. Скорость v0 вылета снаряда из канала
ствола будем считать не
зависящей от угла о,
под которым ствол ору-
орудия наклонен к линии
горизонта. Таким обра-
образом, мы должны изучить
траекторию полета сна-
снаряда, брошенного из точ-
точки О со скоростью х>п
Рис 7.	под углом ср к горизонту
(рис. 7).
В момент времени t — —— снаряд достигает вершины своей
траектории, которая, согласно F), находится на высоте
"max == olr *
10

Мы полагаем /z0 — 0, так как орудие установлено на земле;
высотой самого орудия мы пренебрегаем. Из рис. 7 видно,
что v^-^Vq и равенство vBQ = vQ достигается только в том
случае, когда да = 90°. Таким образом, самая большая высота
подъема снаряда достигается при совершенно отвесном вы-
выстреле вверх; она равна
Займемся вычислением дальности полета снаряда. Очевидно,
что высота снаряда над землей равна нулю только в двух
точках — в точке выстрела и в точке взрыва — при падении
на землю. Из D) ясно, что высота равна нулю для значе-
значений t, являющихся корнями уравнения (напомним, что Л0 = 0)
2wo
т. е. при t = 0 или t=	¦. Первый корень соответствует
моменту вылета снаряда, второй — моменту падения. Расстоя-
Расстояние от места выстрела до места взрыва равно согласно C):
Написав это выражение в виде
Ч< _ [КJ + КJ - К - «5J] _ < - К
X,
мы найдем, что наибольшая дальность полета получается
при vB0=vc0, т. е. при ср = 45°; она равна
— в два раза больше наибольшей высоты подъема.
Аналогичным образом можно показать, что для тупых углов а
(т. е. в случае, когда vrQ < 0 и, следовательно, траектория
полета снаряда располагается слева от точки О) наибольшая
дальность полета снаряда достигается при а= 135°. Впрочем,
это ясно и из соображений симметрии (рис. 8).
Интересно отметить, что при отклонении ствола орудия
от 45° вверх и вниз на один и тот же угол дальность полета
11

снаряда получается одинаковой (рис. 9, а). В самом деле
(рис. 9,6),
01 для угла 45° -j-
Vв I
о! для угла 45°
= i/B 1
о 1 для угла 45° — ?'
= VT I
° ' для угла 45°—f
Поэтому произведение vTovl для углов 45°-f"T и 45° — f
одинаково, а следовательно (см. (8)), и дальность полета
снаряда одинакова.
Р
Рис. 8.
Разберем теперь вопрос о зоне обстрела, т. е. решим
задачу о том, какую часть пространства заполняют траекто-
траектории движения снарядов при разных углах ср. Зона обстрела—•
Рис. 9.
в предположении, что все траектории расположены в одной
плоскости, — ограничена куполообразной кривой, проходящей
через точку С максимального подъема и точки Dv D2 наи-
наиболее далеких разрывов (рис. 10). Эта кривая, как мы сей-
сейчас увидим, также является параболой.
Прежде всего проведем параболу через точки С, Dx и D2,
т. е. выясним, с какой начальной горизонтальной скоростью
надо выпустить снаряд из точкиС, находящейся на высоте
12

о
kQz=z~— (см. G)), чтобы его трйектория прошла через
«о
точку D2, расположенную на расстоянии ¦— от точки О,
(см. (9)). Обозначим эту неизвестную скорость через и.
Тогда, согласно формуле D), в которой следует положить
«о
¦ув = 0 и /zo=y-, мы получим, что через t секунд после
vl gf
выстрела высота снаряда над землей будет равна -=——к~.
Рис. 10.
Момент падения на землю определится уравнением ^-	^"=0,
откуда ^ = —— (отрицательный корень отбрасываем). Из фор-
мулы C), в которой надо положить vTQ — u, заключаем, что
точка падения будет находиться на расстоянии ut — и—- от О.
Для того чтобы эта точка совпала с D2, нужно, чтобы было
«8
g
g
т. е. и = vQ. Итак, снаряд, выпущенный из
точки С горизонтально со скоростью v0, имеет траекторию,
проходящую через D2. Эту траекторию, продолженную не
только вправо, но и влево от точки С, называют параболой
безопасности, ибо, как мы вскоре увидим, она и ограничи-
ограничивает зону обстрела, а выше нее полет безопасен. Для
удобства напишем формулы, которыми определяется в момент
времени t положение и скорость воображаемого снаряда, дви-
двигающегося по параболе безопасности. Они получаются из
13

A) — D), если в них положить vBQ = (
vr = v0,
2g 2 *
=^0, Ао= „—
A0)
(И)
A2)
A3)
Снаряд, выпущенный из орудия О, будет через t секунд после
выстрела находиться в такой точке Т, проекция которой F
находится от точки О на рас-
расстоянии x — vty (см. C)).
Определим положение Т вооб-
воображаемого снаряда, при кото-
котором он будет находиться на
одной вертикальной прямой
с точкой Т (рис. 11). В таком
положении вспомогательный
снаряд будет через такое вре-
\
'¦¦N
'¦N
\ \
r
Рис. 11.
в
г мя f после выстрела из точ-
ки С, что имеем vJ' —OP —
^o
^o
— v\t (см. C), A2)), т. е. через t'=t-~- секунд. Вооб-
Воображаемый и действительный снаряды будут в это время
находиться на высотах
РГ-Н
r i —по—
Разность этих высот неотрицательна
-.2	„Л
2 от	о |~
-m-
Таким образом, точка Т всегда расположена ниже точки Т',
за исключением только момента времени t=-
когда
FT — /г7=0, т. е. точки Т и Т совпадают. Итак, траек-
траектория движения снаряда расположена ниже параболы
14

безопасности и в одной точке касается ее. Снаряд, вы-
выпущенный из орудия О под углом ср к горизонту, достигает
2
v2
v
параболы безопасности через t = —— секунд; проекция F сна-
ряда на землю будет в это время находиться на расстоянии
vl vv vl
от точки О. При изменении ср от 90° до 45° это выражение
«о
принимает все значения между 0 и ¦—¦ (котангенс меняется
от 0 до 1), так что параболы безопасности в любой ее
точке касается траектория некоторого снаряда, выпущенного
из О. Иначе говоря, стреляя из О под разными углами,
можно подбить самолет, находящийся в любой точке
параболы безопасности или ниже ее, но ни один снаряд
не залетает выше параболы безопасности, т. е. эта пара-
парабола действительно ограничивает зону обстрела.
Обратимся снова к рис. 10. Мы имеем бесконечное мно-
множество различных кривых-—парабол, являющихся траекто-
траекториями полета снарядов. Кроме того, мы видим на этом чер-
чертеже еще одну кривую — параболу безопасности,—которая
ограничивает область, заполненную траекториями снарядов,
касаясь каждой из этих траекторий. Этот факт выражают
следующими словами: парабола безопасности является
огибающей для траекторий полета снарядов *).
4. Некоторые свойства параболы
Изучим некоторые свойства параболы безопасности **).
Расстояние точки О от точки Т, в которой снаряд, дви-
движущийся по параболе безопасности, будет через t секунд
после выстрела из С, равно (см. A2), A3)):
•'2 х2 vl gfi v20
*) Читатель может перейти теперь к чтению главы II.
**) Можно показать, что и любая другая парабола будет обла-
обладать аналогичными свойствами.
15

Проведем горизонтальную прямую d, находящуюся на рас-
v% v2
стоянии —— от поверхности земли. Тогда —	h есть рас-
стояние точки Т от прямой d (рис.12). Мы получаем важ-
важО
Рис. 12.
нейшее геометрическое свойство параболы, обычно принимае-
принимаемое за определение этой кривой: парабола есть геомет-
геометрическое место точек, равноудаленных от данной точки О
и данной прямой d (рис. 13).
Точку О называют фоку-
фокусом параболы, а прямую
d — ее направляющей или
директрисой.
Выведем в заключение
еще одно свойство пара-
параболы: если MN — каса-
касательная к параболе в точ-
точке Т, a F — проекция точ-
точки Т на горизонтальную
прямую, то имеет место
равенство / FTN = / О7*М(рис. 12). Достаточно доказать
равенство тангенсов этих углов. Так как касательная MN
совпадает с направлением скорости v в точке Т (рис. 14),
то мы имеем (см. A0) — A3))
Рис. 13.
tg I FTN:
16
2?
A4)

Далее,
tg / Om = tgA80°— I O77V) = —tg
^^tgi/FTN4-/0TF)^	tg zFTN + tg
4iVL "V -j- /_ wn ) _	1 _tg Z /=Т# tg Z.OTF
или, после подстановки значений A4) и упрощения,
A5)
Таким образом, tg / ОГЖ —tg / FTyV, что и требовалось
доказать.
О	F
Рис. 14.
Доказанное свойство означает, что если из точки F вверх
направлен луч света и если парабола является зеркально
гладкой, то луч света, отразившись в точке Т по закону
Рис. 15.
«угол падения равен углу отражения», пойдет по отрезку ОТ
и пройдет через точку О. Так как это верно для любой
точки Т, то параллельный пучок световых лучей, идущих
вертикально вверх, отразившись от параболы, соберется
в ее фокусе О (рис. 15). Вращая параболу вокруг ее оси
17

симметрии, мы получим поверхность — параболоид вращения
(рис. 16), обладающую таким же свойством, т. е. получим
параболический рефлек-
рефлектор. Обратно, поместив
источник света в фокусе
параболы или рефлек-
рефлектора, мы увидим, что
после отражения лучи
Рис. 16.
Рис. 17.
света пойдут параллельным пучком. На этом свойстве пара-
параболической поверхности основано устройство прожектора
(рис. 17).

Г Л А В А II
ГИПЕРБОЛА - ГРАНИЦА ЗОНЫ СЛЫШИМОСТИ
1. Сверхзвуковой полет самолета
На высоте h над поверхностью земли со сверхзвуковой
скоростью v летит самолет. Какова в данный момент времени
область земной поверхности, в точках которой уже слышался
или слышится сейчас звук двигателя самолета? Эту задачу
(нахождение зоны слышимости) мы и хотим использовать
для построения второго примера огибающей. Поверхность
земли, над которой пролетает самолет, мы будем предпола-
предполагать совершенно ровной и плоской, а высоту h самолета и
его скорость v — постоянными.
Конечно, при такой постановке задачи имеет смысл рас-
рассматривать лишь небольшой кусок земной поверхности,
который можно приближенно считать плоским, и небольшой
отрезок времени, в течение которого самолет пролетает над
этим куском земной поверхности. Но для математического
рассмотрения задачи мы будем предполагать, что поверхность,
над которой летит самолет, является неограниченной
плоскостью и что самолет летит над этой плоскостью уже
неограниченно долгое время. Факты, которые мы таким путем
получим, будут иметь реальный смысл лишь в ограничен-
ограниченном куске плоскости, который можно считать совпадающим
с частью земной поверхности. Мы будем, однако, условно
называть всю бесконечную плоскость «земной поверхностью».
В каждый момент времени летящий самолет находится
над некоторой определенной точкой земной поверхности.
Эта точка — проекция самолета на земную поверхность —
движется равномерно со скоростью v, вычерчивая прямую
линию /, параллельную той, по которой в пространстве летит
19

самолет (рис. 18); (движение самолета мы будем изображать
происходящим справа налево).
Пусть в тот момент времени, когда мы интересуемся зоной
слышимости, самолет находится над точкой О прямой /.
Ясно, что t секунд назад самолет находился над точкой А
прямой /, которая расположена справа от точки О на рас-
расстоянии OA = vt. Точку пространства, в которой в тот
момент находился самолет, обозначим через В; она распо-
расположена на высоте h над точкой А земной поверхности.
В
Рис. 18.
Пролетая через точку В, самолет производил шум, который
стал распространяться от этой точки В во всех направле-
направлениях. Скорость распространения звука в воздухе будем обо-
обозначать через и. Тогда к моменту прохождения самолета
над точкой О, т. е. через t секунд после того, как он нахо-
находился в точке В, звук успеет из точки В распространиться
во все стороны на расстояние at. Иначе говоря, звук из точки
В успеет за это время распространиться в шаре радиуса tit
с центром в точке В. Если радиус этого шара больше чем
Л, то звук успеет дойти и до земли, причем областью
на земле, куда дойдет звук от точки В, будет круг, полу-
получающийся при пересечении рассматривающегося шара с земной
поверхностью. Из рис. 19 видно, что радиус этого круга
равен Vu2t2 — h2, а центр его находится в точке А.
Для того чтобы некоторая точка М на плоскости при-
принадлежала зоне слышимости, необходимо и достаточно, чтобы
нашлось такое положение В самолета, звук от которого успе-
успевает достичь точки М, т. е. чтобы точка М принадлежала
указанному выше кругу. Иначе говоря, взяв такие круги для
всевозможных положений самолета, мы и получим всю зону
слышимости.
20

Итак, мы приходим к следующей математической задаче.
Дана некоторая полупрямая /, исходящая из точки О, и три
положительных числа и, v, h (причем м<г»). Пусть А— про-
произвольная точка полупрямой I, a. t — такое положительное
Рис. 19.
число, что длина отрезка О А равна vt. Обозначим через КА
круг с центром в точке А и радиусом ]/ иЧ2 — /г2. Найти
на плоскости область, заполняемую всеми кругами КА,
Рис. 20.
получающимися при всевозможных положениях точки А
на полупрямой /. На рис. 20 изображены несколько таких
кругов и пунктирная линия, которая ограничивает область,
21

заполняемую этими кругами, т. е. линия, являющаяся грани-
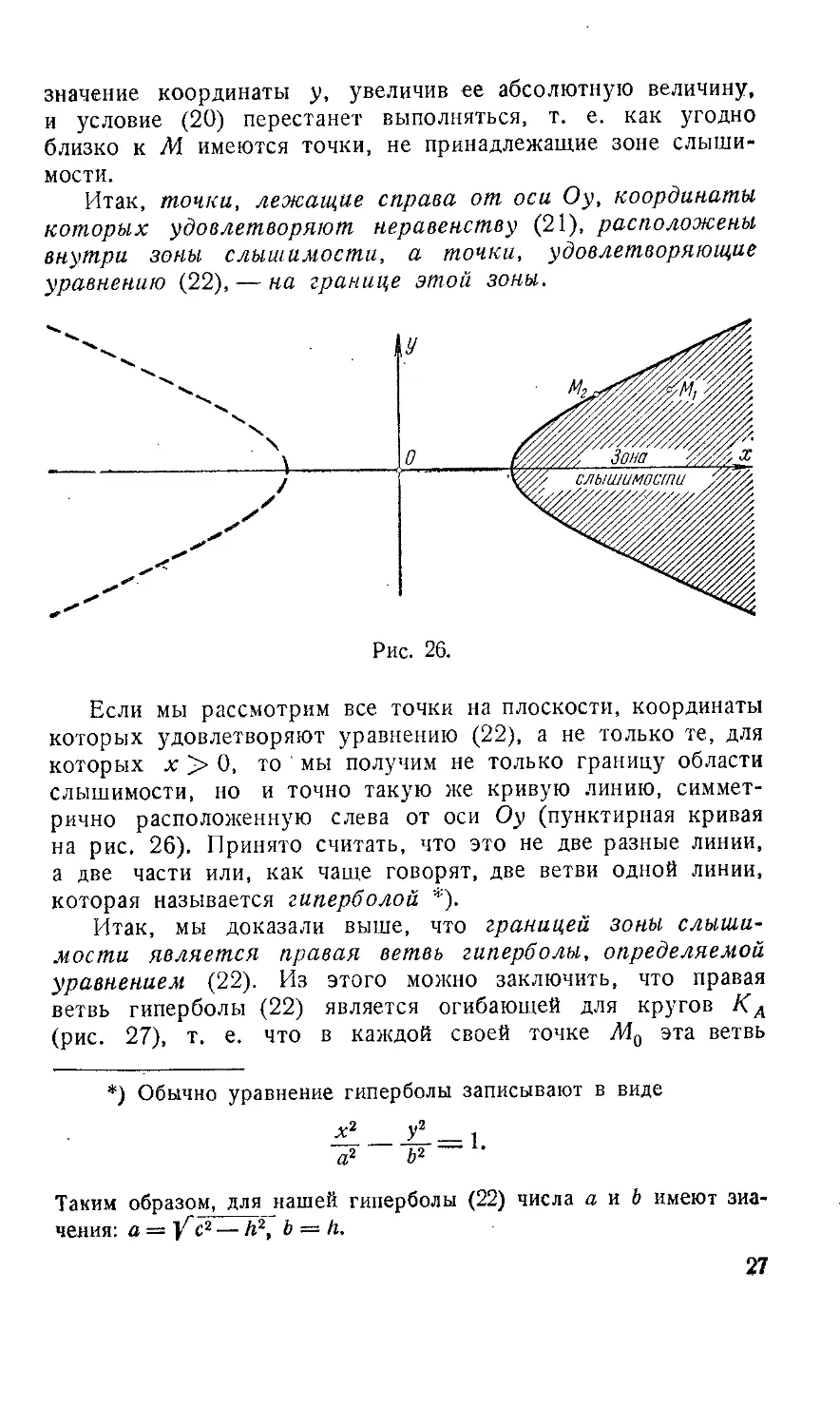
границей зоны слышимости. Из рассмотрения этого рисунка мы
можем сделать вывод, что граница зоны слышимости яв-
является огибающей для рассматриваемых окружностей.
2. Характеристический угол
Рассмотрим сначала случай, когда h = 0, т. е. когда
движение происходит по поверхности земли — «сверхзвуковой
автомобиль» вместо самолета. В этом случае радиус у иЧ2 — /г2
круга КА становится равным ut, и мы приходим к следую-
следующей задаче. Из точки А, лежащей на полупрямой / и находя-
находящейся от О на расстоянии vt, как из центра, описывается
круг КА радиуса ut (причем u<Cv). Найти на плоскости
область, заполняемую всеми кругами КА.
Решение этой задачи очень просто. Все круги КА, как
легко видеть, имеют общий центр подобия О (так как при
. „ изменении t расстояние
О A = vt и радиус кру-
круга КА, равный ut, меня-
меняются в одинаковое чис-
число раз). Поэтому область
плоскости, заполняемая
_i кругами КА, т. е. зона
слышимости, в рассмат-
рассматриваемом случае пред-
представляет собой угол SOT
с вершиной в точке О,
образованный общими ка-
касательными всех кру-
Рис. 21.	гов КА (рис. 21). Мы
можем сказать, что сто-
стороны угла 507" служат огибающей для рассматриваемых
окружностей.
Полупрямая /, очевидно, является биссектрисой угла 50Г.
Половина угла 507", т. е. угол ср между полупрямой / и
одной из полупрямых 05, ОТ, называется характеристи-
характеристическим углом или углом Маха для рассматриваемого «сверх-
«сверхзвукового автомобиля» *). Так как в треугольнике ОАЕ, изо-
*) Разумеется, о сверхзвуковом автомобиле речь шла только
для наглядности — таких автомобилей пока еще нет. Однако рас-
рассмотренное выше понятие характеристического угла имеет реаль-
22

Сраженном на рис. 21, мы имеем OA — vt, AE — ut и потому
ОЕ = V (vtf — {utf = t Vv2 — м2 , то
A6)
По этим формулам, зная скорости м, v, можно вычислить
величину характеристического угла.
ный смысл и широко используется в газовой динамике. Только там
рассматривают не движение сверхзвукового автомобиля в неподвиж-
неподвижном воздухе, а установившийся сверхзвуковой поток воздуха, в кото-
котором расположен неподвижный предмет. Характеристический угол
Рис. 22.
легко можно видеть при движении корабля в спокойной воде
(рис. 22); в этом случае речь идет не о распространении звука
в воздухе, а о распространении волн на поверхности воды (и—•
скорость распространения волн,
v — скорость корабля).
К этому же кругу вопро-
вопросов относится явление, откры-
открытое в 1934 году советскими
физиками С. И. Вавиловым и
II. А. Черенковым. Оно заклю-
заключается в следующем. Обозна-
Обозначим через и скорость распро-
распространения света в некоторой
однородной среде (например,
в прозрачной жидкости). Если
в этой среде движется со ско-
Движение
Рис. 23.
ростью v > и некоторая заря-
заряженная частица, то возникает
свечение, причем свет излу-
излучается не во все стороны, а только в направлениях, составляющих
с линией движения частицы вполне определенный острый угол
(рис. 23); угол <р. обозначенный на этом рисунке, определяется фор-
формулами A6). Это свечение и представляет собой эффект Вавилова —
Черенкова.
3 Зак. 2430. В. Г. Болтянский
23

3. Нахождение зоны слышимости
Заметим сначала, что если в некоторой системе коорди-
координат точка А имеет координаты (а, |3), а точка М — координаты
(jc, у), то (рис. 24)
MA2 = AN2 -\~ NM2 = PQ2 + NM2 =
= (OQ — OPJ + (QM — QNJ = (х — аJ + (У — ВJ.
Это соотношение, как нетрудно проверить, будет выполнено
и при любом другом положении точки М, например, если М
будет располагаться левее или
ниже точки А. Поэтому если
точка М принадлежит кру-
кругу с центром А и радиусом
R (т. е. если MA < R), то
М(х,у)
A(«,fi)
A7)
х а если точка М лежит на
окружности этого круга, то
Рис. 24.
Вернемся теперь к поставленной вначале задаче о нахожде-
нахождении зоны слышимости для самолета, летящего над землей
на высоте /г>0.
Рассмотрим систему коор-
координат, начало которой нахо-
находится в точке О, ось абсцисс
направлена по линии /, а ось
ординат — перпендикулярно к
ней (рис.- 25). Пусть, как и
прежде, А — точка полупря-
полупрямой /, находящаяся от точки О
на расстоянии OA = vt. Для
того чтобы точка М с координатами
кругу КА радиуса Yu2t2
h2
Рис. 25.
х, у принадлежала
с центром в точке А, необ-
необходимо и достаточно, чтобы выполнялось неравенство
получаемое из неравенства A7), если положить a. = vt,
-h Л2) < 0.	A9)
yu't* — й% или, иначе,
l — u2)t2 — 2vxt^\-(x2
24

Так как всевозможные круги КА как раз заполняют всю об-
область слышимости, то имеет место следующее утверждение:
точка М с координатами х, у тогда и только тогда
принадлежит области слышимости, когда существует
положительное число t, удовлетворяющее неравенству A9).
Докажем теперь следующую лемму, которая поможет нам
разобраться в условии A9).
Лемма 1. Рассмотрим квадратный трехчлен at2-\~
-\-bt-\-c, в котором коэффициенты а и с положительны.
Для существования положительного числа t, удовлетво-
удовлетворяющего неравенству afi-\-bt-\-c^Q, необходимо и до-
достаточно, чтобы были выполнены следующие условия:
1)	Ь<0,
2)	дискриминант трехчлена неотрицателен, т. е.
Ь2 — 4ас > 0.
Доказательство. Если условие 1) не выполнено, т. е.
#^>0, то при положительных t все три слагаемых в сумме
at2 ~\~bt-\-с неотрицательны (так как а к с положительны).
Следовательно, трехчлен at2 -\- Ы -\- с принимает при поло-
положительных t только положительные значения. Если не вы-
выполнено условие 2), т. е, число Ь2— Аас отрицательно, то
трехчлен также принимает только положительные значения,
так как
Таким образом, если при некотором положительном t имеет
место неравенство at2-\-bt-\-c ^0, то оба условия 1), 2)
должны выполняться.
Обратно, пусть условия 1) и 2) выполняются. Тогда
в силу условия 2) корни трехчлена at2-\~bt-\-c действи-
действительны, а так как а 5> 0 и с у> 0, то произведение корней
положительно, т. е. оба корня имеют одинаковые знаки.
Из условия 1) вытекает, что сумма корней положительна, и
потому оба корня положительны. Иначе говоря, существует
такое положительное число, что aft-\-bt-\-с = 0, что и тре-
требовалось. Лемма доказана.
Эта лемма может быть применена к трехчлену, стоящему
в левой части соотношения A9), так как в нем коэффици-
коэффициенты a = v2— м2 и с = х2 -\- у2 -f- ft2 положительны. Таким
образом, для существования положительного числа t, удов-
удовлетворяющего неравенству A9) (т. е. для того чтобы точка М
3*	25

принадлежала области слышимости), необходимо и достаточно,
чтобы были выполнены следующие два условия:
1)	2vx > 0, или, иначе, х > 0;
2)	дискриминант неотрицателен, т. е.
{2vxf — A(v2 — и2) (х2 -f у2 Ч- /г2) > 0.
Раскрыв в последнем неравенстве скобки и разделив его на
положительное число 4(v2— и2)п2, мы перепишем это нера-
неравенство в виде
¦A' *'
Наконец, обозначив число •— h через с, мы получим
Заметим, что v > и, и потому с — —h > h, т. е. число
с1 — п2 положительно.
Итак, область слышимости состоит из всех тех точек,
лежащих справа от оси Оу {т. е. удовлетворяющих
условию х > 0), для координат которых выполнено соот-
соотношение B0).
Если координаты х, у точки М удовлетворяют нера-
неравенству
> l
то, как легко понять, точка М лежит внутри области слы-
слышимости. Действительно, все точки, расположенные очень
близко к М (т. е. точки, координаты которых мало отли-
отличаются от координат точки М), также будут удовлетворять
неравенству B1); иначе говоря, точку М со всех сторон
окружают точки, принадлежащие области слышимости, а это
и означает, что точка М лежит внутри этой области (точка Мх
на рис. 26). Если же координаты л:, у точки М удовлетво-
удовлетворяют соотношению
то точка М лежит на границе области слышимости (точка М2
на рис. 26). Действительно, достаточно чуть-чуть изменить
26

значение координаты у, увеличив ее абсолютную величину,
и условие B0) перестанет выполняться, т. е. как угодно
близко к М имеются точки, не принадлежащие зоне слыши-
слышимости.
Итак, точки, лежащие справа от оси Оу, координаты
которых удовлетворяют неравенству B1), расположены
внутри зоны слышимости, а точки, удовлетворяющие
уравнению B2), — на границе этой зоны.
У
Рис. 26.
Если мы рассмотрим все точки на плоскости, координаты
которых удовлетворяют уравнению B2), а не только те, для
которых х > 0, то мы получим не только границу области
слышимости, но и точно такую же кривую линию, симмет-
симметрично расположенную слева от оси Оу (пунктирная кривая
на рис. 26). Принято считать, что это не две разные линии,
а две части или, как чаще говорят, две ветви одной линии,
которая называется гиперболой *).
Итак, мы доказали выше, что границей зоны слыши-
слышимости является правая ветвь гиперболы, определяемой
уравнением B2). Из этого можно заключить, что правая
ветвь гиперболы B2) является огибающей для кругов КА
(рис. 27), т. е. что в каждой своей точке Мо эта ветвь
*) Обычно уравнение гиперболы записывают в виде
х2
а'
Таким образом, для нашей гиперболы B2) числа а и Ь имеют зна-
значения: а = У"е2 — Л2, b = Л.
27

касается одного из кругов КА *). Для дальнейшего нам
нужно будет иметь формулы, позволяющие находить тот
круг КА, который касается огибающей в точке Мо. Выведем
эти формулы. Пусть Мо — некоторая точка, лежащая на
границе зоны слышимости, т. е. лежащая на правой ветви
Рис. 27.
гиперболы B2). Обозначим координаты этой точки через
х0 и у0. Эти координаты удовлетворяют уравнению B2), так
как точка Мо лежит на гиперболе, откуда находим
— 1
с2 —А2
далее, вспоминая формулу с — — Н, получаем
с2х2	"l2
г2 4- v2 4- ft2 — -	— — •
Ло ~ У о i ' с2 — Л2
B3)
Так как точка Мо принадлежит зоне слышимости (она лежит
на границе этой зоны), то найдется круг КА, содержащий
эту точку, т. е. найдется положительное число t, удовлетво-
удовлетворяющее неравенству (см. A9)):
(„2 _ В2) t2 _ 2vXo t + (Xl + У2 + ft*) < О,
или, что то же самое (см. B3)), неравенству
2 2
*) Читатель может перейти теперь к чтению главы III или даже
сразу главы IV,
28

Но последнее неравенство можно переписать в виде
откуда ясно, что оно выполняется только при одном
значении t, а именно при значении
t = -
vx0
обращающем в нуль выражение, стоящее в квадратных скоб-
скобках. Таким образом, существует только один круг КА, со-
содержащий точку Мо, а именно круг с центром в точке А,
отстоящей от О на расстоянии
OA — vt —
vi — i
с2 —А2
Рассматриваемая точка Мо лежит на окружности этого круга
КА, так как Мо расположена на границе зоны слышимости.
Таким образом, гипербола, ограничивающая зону слышимости,
проходит вне рассматриваемого круга КА и имеет с ним об-
общую точку Мо, т. е. касается круга КА в точке Мй.
4. Некоторые свойства гиперболы
Изобразим теперь на одном чертеже гиперболу B2) и
прямые OS, ОТ, наклоненные к оси абсцисс под углом ср
Рис. 28.
(см. A6)). Мы покажем сейчас, что вся гипербола распо-
расположена целиком в вертикальных углах SOT и S'OV
(рис. 28) и что по мере удаления от точки О гипербола
29

все более и более приближается к прямым SS' и ТР.
Для доказательства мы представим себе, что по земле со
скоростью v движется «сверхзвуковой автомобиль», а прямо
над ним (с той же скоростью v) движется самолет. Круги КА,
относящиеся к «автомобилю» и самолету, будем обозначать
символами КТ и К™и- Рассмотрим круги КТ и К а м с цент-
центром в одной и той же точке А, находящейся от О на рас-
расстоянии О А = vt. Так как радиус ]/и'Ч2 — К1 круга К дам,
очевидно, меньше, чем радиус ut круга /Сдвт, то круг /С"м
расположен внутри круга /Сдвт, и потому вся зона слы-
слышимости самолета расположена внутри зоны слышимости
«автомобиля». Следовательно, правая ветвь гиперболы B2)
расположена внутри угла SOT (рис. 28); симметричная же ей
левая ветвь расположена внутри угла S'OT'. Далее,
h2	_ Л2
at —У и'Ч1 — h2 =
ut -f У иЧг — К1
ut
Таким образом, разность радиусов кругов К%а1 и К^м де-
делается все меньше и меньше при увеличении t (т. е. при
удалении точки А от О), а это означает, что гипербола все
более приближается к прямым OS, ОТ (рис. 29).
Рис. 29.
Прямые SS' и ТТ называются асимптотами гипер-
гиперболы.
Выведем теперь уравнение прямой линии, являющейся
касательной к гиперболе. Пусть Мо — некоторая точка, ле-
лежащая на правой ветви гиперболы. Координаты этой точки
обозначим через х0 и у0. Как мы видели выше, круг КА
30

с центром в точке А, определяемой соотношением B4), ка-
касается гиперболы B2) в точке MQ (рис. 30). Но тогда ка-
касательная к кругу КА в точке MQ касается также и гипер-
гиперболы. Так как касательную к кругу мы проводить умеем,
то тем самым найден способ построения касательной к ги-
гиперболе.
— .Г
Рис. 30.
Напишем уравнение этой касательной. Для этого обозна-
обозначим через D точку пересечения касательной с осью абсцисс
AD
и рассмотрим
перпендикуляр
lADMa= I
, ,.п,,
tg / ADM0 =
треугольник ADMQ. Опустив из точки Мо
N	найдем, что
MtiN
A
на ось абсцисс, мы
и потому (см. B4))
NA OA — ON
с2 —
'о
Если мы запишем уравнение искомой касательной в виде
y — kx-\~b, то угловой коэффициент k будет равен тан-
тангенсу угла ADMQ, образованного касательной с осью абсцисс.
Этот тангенс мы только что вычислили. Таким образом, урав-
уравнение касательной имеет вид
х+Ъ.
У^Т^пг,
у0
Остается узнать, чему равна начальная ордината Ь. Так как
касательная проходит через точку /Ио, то координаты точки Мо
31

должны удовлетворять уравнению касательной, т. е.
откуда
Выражение, стоящее в скобках, равно единице, так как
точка Мо лежит на гиперболе (см. B2)). Таким образом,
окончательно находим
и потому уравнение касательной принимает вид
__^_ ( хо	Уо_\
У0 \ с2 — /г2	Л2 / *
Наконец, умножив обе части на ~, мы получим уравнение
касательной в форме, в которой его легко запомнить (ср.
уравнение гиперболы B2)):
Напомним, что B5) есть уравнение прямой, касающейся
гиперболы в точке MQ с координатами х0, у0.
Напишем теперь уравнения асимптот; это даст нам воз-
возможность установить два весьма интересных свойства гипер-
гиперболы. Угловой коэффициент к прямой S'S равен tg<p, т. е.
(см. A6))
, _ и	1	l	h
— g'f—
_„2
г~& ~~ гт*
V 1F~1 V IF
а начальная ордината b равна нулю, так как эта прямая про-
проходит через начало координат. Следовательно, уравнение
асимптоты S'S имеет вид
у = ¦ - h х.	B6)
* /С2 —/г2
Прямая 7'7 наклонена к оси абсцисс под тем же углом, 'но
ее ординаты отличаются знаком от ординат точек на
32

прямой S'S. Поэтому уравнение прямой Т'Т имеет вид
h
!— А2
х.
B7)
Пусть теперь Мо — произвольная точка гиперболы; коор-
координаты этой точки обозначим через х0, у0. Проведем каса-
касательную к гиперболе в точке Мо и обозначим точки пере-
пересечения этой касательной с асимптотами через Р, и Р2
(рис. 31). Мы хотим вычислить координаты точек Рх и Р2.
Рис. 31.
Обозначим координаты точки Рг через xlt у,. Так как
точка Pj лежит на асимптоте S'S, то ее координаты удовле-
удовлетворяют уравнению B6), т. е.
у, = ,. fe х,.	B8)
Так как, кроме того, точка Pj лежит на касательной, то ее
координаты удовлетворяют уравнению B5), т. е.
	4г = Ь	B9)
Наконец, так как точка Мо лежит на гиперболе, то (см. B2)):

— А*
А
/г2
C0)
Из трех последних соотношений нетрудно определить коор-
координаты точки Рг Именно, заменяя в соотношении B9) число уг
33

его значением B8), мы получим
хх ( *о _ ll\= 1
/с2 — й2 VyV —Л2 /г
дг0	у0
Умножив, далее, обе части этого соотношения на у , -)	¦
и воспользовавшись соотношением C0), найдем
	^м	-^о	 I у а
откуда
х\ — хй-тУо	^	•	(о1)
Совершенно аналогично можно вычислить абсциссу х2 точки Р2:
•\Гr2 	 ft2
„ 	 „	., V L "	(Ч9\
Л2 — Л0 У 0	и	'	\OL)
Из соотношений C1) и C2) мы получаем теперь
х\ х 0 = х 0 х2,	C3)
(?f2F—4)=^-А» C4)
(см. C0)).
Опустим из точек Р,, Л10, Р2 перпендикуляры P]Qi,
Л10Л/0, P2Q2 на ось абсцисс. Тогда N^ = OQj — ОЛ^0 =
= х1 — х0, Q2A/0 = ONQ — OQ2 = х0 — х2, и из соотноше-
соотношения C3) вытекает, что N0Qi^=Q2N0, т. е. /Vo — середина
отрезка Q2QV Отсюда (в силу параллельности отрезков PjQi,
MQNQ, P2Q2) вытекает, что Мо есть середина отрезка Р]Р2.
Итак, отрезок касательной к гиперболе, заключенный
между асимптотами, делится в точке касания пополам.
Дадим теперь геометрическую интерпретацию соотноше-
соотношения C4). Для этого мы вычислим площадь треугольника ОРгР2.
Опустим из точки Р2 перпендикуляр Р2Н на прямую 55'.
Тогда площадь 5Д треугольника ОРХР2 имеет следующее
значение:
\	0P @Р sin 2ср) =
sin 2<p
cos <p ) \ cos у ) 2 cos2
7Т " 	5	 (С2	А2).
/ COS2 <р ч	'
34

(см. C4)). Таким образом, какую бы мы касательную
к гиперболе на провели, она отсекает от угла между
асимптотами треугольник, имеющий всегда одну и ту же
площадь, а именно
5	.i!?|i.(c2_/z2).
Д 2 cos2 9
(Читатели, знакомые с тригонометрией, легко сообразят, что
= t _л_ и по s.^
SY /с2 А*	Л
_ j^ = t __
2 cos2tp SY /с2 — А*

ГЛАВА Ш
АСТРОИДА И ЦИКЛОИДА
1. Мгновенный центр вращения
В этой маленькой главе мы рассмотрим еще два примера
огибающих, в качестве которых у нас здесь появятся две
интересные линии: астроида и циклоида. Для исследования
мы воспользуемся понятием мгновенного центра вращения,
играющим важную роль в механике.
Рассмотрим вращательное движение плоской неизменяемой
фигуры, например вырезанной из картона, т. е. такое пере-
передвижение фигуры по плоскости, при котором некоторая точка
О (центр вращения) остается все время неподвижной, а сама
фигура поворачивается вокруг точки О (рис. 32). Любая,
Рис. 32.
Рис. 33.
отличная от О точка А движущейся фигуры описывает при
этом окружность. В каждый момент времени скорость v дви-
движения точки А направлена по касательной к этой окружно-
окружности, т. е. направлена перпендикулярно отрезку О А (рис. 33).
В механике принято считать (и это можно было бы обо-
обосновать математически), что при произвольном передвижении
по плоскости фигура в каждый отдельно взятый момент вре-
36

мени t совершает «мгновенное движение», являющееся либо
прямолинейным поступательным движением с некоторой
«мгновенной скоростью» либо вращением вокруг некоторой
точки, называемой «мгновенным центром вращения». При
этом точка О, являющаяся мгновенным центром вращения,
совсем не движется в рассматриваемый момент времени (т. е.
ее скорость равна нулю), а любая отличная от О точка А
движущейся фигуры имеет в этот момент отличную от нуля
скорость, направленную перпендикулярно отрезку О А. Таким
образом, мгновенный центр вращения есть единственная
точка движущейся фигуры, имеющая в данный момент скорость,
равную нулю, т. е. единственная «мгновенная точка покоя».
Пусть, например, круг (или какая-либо другая фигура)
без скольжения катится в плоскости по некоторой линии L
(рис. 34). Слово «катится» означает, что круг передвигается
Рис. 34.
в плоскости, касаясь в каждый момент времени линии L. Когда
же мы говорим, что круг катится «без скольжения», то имеем
в виду, что точка движущегося круга, которой он прикаса-
прикасается к линии L, не скользит по линии L, т. е. эта точка
имеет скорость, равную нулю, и потому является мгновен-
мгновенным центром вращения. Итак, если круг катится без сколь-
скольжения по неподвижной линии L, то в каждый момент
времени точка каеания круга с линией L является мгно-
мгновенным центром вращения; если обозначить точку каса-
касания через О, то любая точка А катящегося круга имеет
в рассматриваемый момент времени мгновенную скорость,
направленную перпендикулярно отрезку О А.
2. Астроида
Возьмем в качестве линии L окружность некоторого ра-
радиуса R и будем рассматривать круг радиуса 1/4 R, катя-
катящийся без скольжения по окружности L с внутренней ее сто-
стороны. Отметим на окружности катящегося круга некоторую
37

точку А и проследим траекторию движения точки А, т. е.
линию, которую вычерчивает точка А при качении круга.
С°
Рис. 35.
Если, например, в начальный момент точка А находилась на
окружности L (рис. 35, положение I катящегося круга), то
затем точка А переместится
внутрь окружности L (поло-
(положения II, III) и вновь вер-
вернется на окружность L (по-
(положение IV). В результате
точка А опишет дугу, рас-
расположенную внутри окруж-
окружности L и упирающуюся в нее
своими концами (пунктир на
рис. 35). Ясно, что между
концами этой дуги содер-
содержится ровно четверть окруж-
окружности L, ибо длина окруж-
окружности L вчетверо больше
длины окружности катяще-
катящегося круга. При дальнейшем
качении круга точка А
опишет вторую такую же
дугу, стягивающую четверть окружности, затем третью и четвер-
четвертую. В результате точка А вернется в исходное положение,
вычертив при этом замкнутую линию с четырьмя заострени-
заострениями (вершинами), вписанную в окружность L (рис. 36). Эта
линия называется астроидой. Соединив через одну вершины
38

о
астроиды, мы получим два взаимно перпендикулярных диа-
диаметра РМ и QN окружности L, делящих астроиду на четыре
равные дуги.
Рассмотрим некоторое положение катящегося круга и соот-
соответствующую точку А астроиды (рис. 37). Точку касания
катящегося круга с окруж-
окружностью L, как и прежде,
обозначим через О. Легко
понять, что дуга МО
окружности L имеет ту
же длину, что и дуга АО
окружности катящегося
круга: ведь в начальном
положении катящегося
круга точка А совпадала
с Ж, а качение происхо-
происходит без скольжения. Про-
Проведем из центра С окруж-
окружности L радиусы СМ, СО,
CN. Радиус СО про-
проходит, очевидно, через	рис 37.
центр катящегося круга и
пересекает окружность этого круга в точке D, диаметрально
противоположной точке касания О. Так как радиус катящегося
круга равен 1/4 R, то CD — DO = 1/2 R. В этот момент качения
круга мгновенный центр вращения находится в точке О, и
потому скорость движения точки А, описывающей астроиду, на-
направлена перпендикулярно отрезку О А. Но скорость движения
точки всегда направлена по касательной к той траектории,
которую эта точка описывает. Поэтому перпендикуляр к отрезку
О А, проходящий через точку А, является касательной к астрои-
астроиде в точке А. Этот перпендикуляр проходит, очевидно, через
точку D (ибо угол OAD опирается на диаметр). Итак, AD —•
касательная к астроиде. Точки пересечения этой касательной
с радиусами СМ и CN обозначим через Е и F.
Обозначим, далее, угол МСО через а. Так как дуга МО
стягивает центральный угол а, то равная ей по длине дуга АО
стягивает в окружности вчетверо меньшего радиуса централь-
центральный угол 4а, а потому вписанный угол ADO, опирающийся
на ту же дугу АО, равен 2а. Теперь из треугольника CDE
находим: /С?75 = а, а из треугольника CDF получаем:
? DCF = /_ DFC = 90° — а. Следовательно, треугольники
CDE и CDF — равнобедренные, т. е. ED^CD — DF— 1/2 R,
39

и потому EF = R. Итак, отрезок EF касательной к аст-
астроиде, заключенный между прямыми СМ и CN, равен
радиусу R окружности L.
Так как /^CEF — а, а угол а
при качении круга по дуге
MN меняется от 0 до 90°, то
с помощью этого построения
может быть получен любой
отрезок EF длины R, концы
которого лежат на сторонах
угла MCN. Иначе говоря,
астроида касается всех
прямолинейных отрезков
длины R, концы которых
лежат на двух взаимно
перпендикулярных прямых
МР и NQ, т. е. астроида
является огибающей всех
этих отрезков (рис. 38).
В главе IV (см. стр. 63) мы еще вернемся к рассмотрению
астроиды и выведем ее уравнение.
3. Циклоида
Будем теперь рассматривать круг радиуса г, катящийся
без скольжения по прямой линии L. Точка А, лежащая на
Рис. 39.
окружности катящегося круга, вычерчивает при таком движе-
движении линию, называемую циклоидой (рис. 39). Каждая «арка»
циклоиды заключает между своими концами отрезок прямой L,
имеющий длину 2w.
Рассмотрим некоторое положение катящегося круга и соот-
соответствующую точку А циклоиды. Точку касания круга с пря-
прямой L обозначим через О, а диаметрально противоположную
40

\
точку окружности — через D. В этот момент качения круга
мгновенный центр вращения находится в точке О, и потому
скорость движения точки А, описывающей циклоиду, направлена
перпендикулярно отрезку О А, т. е.
направлена по прямой AD. Так
как скорость движения направлена
всегда по касательной к линии
движения точки, то прямая AD
есть касательная к циклоиде
в точке А.
Если К — некоторая кривая,
А — ее точка и AD — касатель-
касательная к кривой К в точке А (рис. 40), то прямая линия,
проходящая, через точку А и перпендикулярная к касатель-
касательной AD, называется нормалью к кривой К в точке А. Из
рис. 39 ясно, что нормалью к циклоиде в точке А служит
прямая АО.
Отметим еще, что длина отрезка МО равна длине дуги
АО окружности, ибо качение происходит без скольжения.
Установим теперь одно важное свойство циклоиды. Рас-
Рассмотрим две циклоиды, изображенные на рис. 41. Мы дока-
Рис. 40.
Рис. 41.
жем сейчас, что любая нормаль к верхней циклоиде
ется касательной для нижней (и обратно, любая касатель-
касательная к нижней циклоиде является нормалью для верхней).
Иначе говоря, нижняя циклоида является огибающей для
нормалей, проведенных к верхней циклоиде. Если к неко-
некоторой кривой К проведены во всех ее точках нормали, то
огибающая этих нормалей называется эволютой линии К
(рис. 42). Таким образом, сформулированное выше свойство
циклоиды означает, что эволютой циклоиды является рав-
равная ей, но смещенная циклоида: эволютой верхней цик-
циклоиды на рис. 41 является нижняя.
41

Докажем это свойство циклоиды. Рассмотрим некоторое
положение круга, качением которого по прямой L образована
верхняя циклоида (рис. 43). Буквы
А, О и D имеют тот же смысл, что
и на рис. 39. Построим круг, сим-
симметричный только что рассмотрен-
рассмотренному относительно точки О, и пусть
А' и D' — точки, симметричные точ-
точкам А и D. Тогда отрезок МО имеет
ту же длину, что и дуга О А, отре-
отрезок МС имеет ту же длину (равную яг),
что и полуокружность OD; следова-
следовательно, отрезок ОС имеет ту же
длину, что и дуга AD. Иначе говоря,
отрезок D'Q имеет ту же длину, что и
дуга D'A'. Но это означает, что
точка А' лежит на нижней циклоиде,
а нижний круг на рис. 43 как раз соответствует этой точке А'.
Из доказанных выше свойств касательных и нормалей сле-
следует теперь (в силу того, что D' — мгновенный центр вра-
1}
Рис. 42.
шения при качении круга по прямой /,'). что О А' — каса-
касательная, а А'П — нормаль к нижней циклоиде. Так как
отрезки О А и О А' составляют продолжение один другого,
то мы видим, что произвольно взятая нормаль АА' к верх-
верхней циклоиде является касательной для нижней циклоиды.

ГЛАВА IV
ОГИБАЮЩАЯ
1. Семейства линий и их огибающие
Из целого ряда вопросов, рассмотренных в главах I, II и III,
мы хотим теперь выделить факты, связанные с рассмотре-
рассмотрением рис. 10, 20, 21, 38, 41. В каждом из этих случаев мы
имеем бесконечное множество кривых или, как говорят, семей-
семейство кривых — в первом случае семейство парабол, во вто-
втором и третьем случае — семейство окружностей, в двух
последних случаях — семейство прямых (на чертежах изо-
изображены, разумеется, не все линии семейства — их беско-
бесконечно много, — а лишь некоторые из них). Во всех случаях
Рис. 44.
линии рассматриваемого семейства заполняют на плоскости
некоторую область (зону обстрела в первой главе, зону слы-
слышимости во второй главе), причем кривая, ограничивающая
эту область, в каждой своей точке касается некоторой линии
семейства. Мы называем эту кривую огибающей. Так, в при-
примере, изображенном на рис. 10, мы имеем семейство пара-
парабол— траекторий снарядов. Огибающая этого семейства линий
(.парабола безопасности) в каждой своей точке касается одной
43

из линий семейства, т. е. одной из траекторий снаряда. В при-
примере, изображенном на рис. 20, мы имеем семейство окруж-
окружностей. Огибающая этого семейства линий (одна ветвь гипер-
гиперболы) в каждой своей точке касается одной из линий нашего
семейства, т. е. одной из окружностей.
Вообще, если имеется некоторое семейство линий, то
огибающей этого семейства называется такая линия,
которая в каждой своей точке касается одной из линий
заданного семейства. Приведем простые примеры. Рассмот-
Рассмотрим семейство кривых, состоящее из окружностей одного
и того же радиуса R с центрами на заданной прямой / (рис. 44).
Огибающая этого семейства состоит, очевидно, из двух парал-
параллельных прямых, находящихся на расстоянии R от прямой /.
Далее, если мы рассмотрим семейство окружностей радиуса R
с центрами на заданной окружности О радиуса г, то (при г > R)
огибающая этого семейства будет состоять из двух окружно-
окружностей радиусов r-\-R и г — R (рис. 45).
Наконец, еще один простой пример. Рассмотрим семейство,
состоящее из всех прямых, проходящих на одном и том же
расстоянии R от данной точки О (рис. 46). Очевидно, оги-
огибающей этого семейства прямых является окружность радиуса R
с центром в точке О.
2. Уравнение семейства линий
Теперь мы хотим выяснить, каким образом можно задавать
семейства линий с помощью формул. Для этого мы разбе-
разберем подробнее рассмотренные выше примеры.
Рассмотрим вновь семейство окружностей радиуса R с цен-
центрами на прямой / (рис. 44). Примем прямую / за ось абсцисс
координатной системы и проведем перпендикулярно к ней ось
ординат. Пусть А — некоторая точка прямой /; обозначим
ее абсциссу через а (ордината точки А, очевидно, равна нулю).
Согласно A8), окружность с центром в точке А и радиусом R
описывается уравнением
(х — а)
(которое получится, если в формуле A8) считать р равным
нулю), или, что то же самое, уравнением
__#2 = 0.	C5)
В уравнение C5) входит число а. При каждом а мы
получаем одну из окружностей семейства, а именно ту, центр
45

которой находится в точке с абсциссой а. Придавая числу а
всевозможные значения и каждый раз вычерчивая получаю-
получающуюся окружность, мы получим все рассматриваемое семей-
семейство окружностей. На основании этого соотношение C5) назы-
называется уравнением рассматриваемого семейства окружно-
окружностей. Величина а, входящая наряду с координатами х, у
в уравнение C5), называется параметром.
Рассмотрим теперь окружности кругов КА, которые мы
изучали в главе второй (см. рис. 20). Возьмем одну из таких
окружностей; ее центр находится в точке А с абсциссой vt,
а радиус равен у и'Ч2 — /г2. Обозначая число vt через а I так
что t — —) и вспоминая, что — = — (см. B0)), мы найдем:
Итак, радиус окружности, имеющей центр в точке А с абс-
абсциссой а, равен"!/ п'21\— 1 ]. Согласно A8), уравнение этой
окружности имеет вид
или, после раскрытия скобок,
(	^) Й2 = 0.	C6)
При каждом а это уравнение дает нам одну из окружностей
изображенного на рис. 20 семейства, а придавая параметру а
всевозможные положительные значения, мы получим все рас-
рассматриваемое семейство окружностей.
Формулы C5) и C6) позволяют нам сделать следующий
вывод. Семейство линий может быть задано с помощью
одного уравнения с тремя неизвестными х, у, а, где х, у —
координаты точек, а а — параметр (вспомогательная вели-
величина); при каждом определенном а это уравнение дает нам
одну из линий рассматриваемого семейства; придавая же
числу а. всевозможные значения и каждый раз вычерчивая
получающуюся линию, мы и получим все рассматриваемое
семейство линий.
Мы условимся уравнение семейства линий записывать
в виде
/{х.у,а) = 0,	C7)
46

где f (x, у, а) означает то, что записано в левой части
соотношения C5) или C6), или какого-либо другого анало-
аналогичного уравнения. В дальнейшем будет рассматриваться лишь
случай, когда функция / (х, у, а) является многочленом, свя-
связывающим величины х, у, а.
Однако задание семейств линий уравнением вида C7)
не всегда бывает удобным. Чтобы понять это и найти еще
один способ задания семейств линий, мы рассмотрим два сле-
следующих примера.
Возьмем семейство окружностей, изображенное на рис. 45.
Точку О мы примем за начало системы координат. Пусть
А — некоторая точка, лежащая на окружности радиуса г с цент-
центром в начале координат. Обозначим ее координаты через a, р.
Тогда числа аир удовлетворяют соотношению
= rJ.	C8)
Окружность радиуса R с центром в точке А имеет, согласно
A8), уравнение
(*_аJ_|_(у_ 0J = ^2.	C9)
Соотношения C8), C9) и определяют рассматриваемое семей-
семейство окружностей. Именно, уравнение C9) дает окружность
радиуса Re произвольным центром; соотношение же C8)
требует, чтобы этот центр лежал на окружности радиуса г
с центром в точке О. Раскрывая скобки и перенося все члены
в левую часть, мы перепишем соотношения C8), C9) в виде
—2ах—23у-)-а2-)-р2—/?2 = 0. а2-+-?2 — Г2 = О. D0)
Первое из этих соотношений содержит, кроме координат х, у,
два параметра a, j3; второе же соотношение связывает между
собой эти два параметра. В таком виде мы и будем рассмат-
рассматривать уравнение нашего семейства окружностей*).
Наконец, еще один пример. Рассмотрим траектории сна-
снарядов, изученные в первой главе (см. рис. 10). Обозначая
горизонтальную и вертикальную составляющие начальной ско-
скорости через а и р, а высоту снаряда — буквой у (вместо /г),
*) Заметим, что, разрешив второе из соотношений D0) относи-
относительно р и подставляя найденное значение в первое соотношение,
мы могли бы получить уравнение с одним параметром а, т. е. урав-
уравнение вида C7). Однако соотношения D0) более удобны, так как
не содержат корней и двойного знака, получающегося при под-
подстановке р = ± Угг — а2.
47

мы сможем описать движение снаряда формулами (см. C), D))
x — at,
Находя с помощью первого из этих соотношений значение t
и подставляя его во второе соотношение, мы получим
., — Р у Sx2
У ~~ а Х 2а2 '
или, после умножения на 2а2 и переноса всех членов в левую
часть,
gx2 — 2a[3je -f- 2a2y = 0.
Этим уравнением и определяется траектория движения снаряда.
Так как а и J3 — составляющие его начальной скорости v0,
то (см. рис. 7)
Итак, рассматриваемое семейство траекторий описывается
соотношениями
gx2 — 2а$х-\-2а.2у = 0, а2 + р2 — г>2 = 0, D1)
первое из которых содержит, кроме координат х, у, два
параметра а, {3, а второе связывает между собой эти пара-
параметры.
Формулы D0) и D1) позволяют нам сделать следующий
вывод. Семейство линий может быть задано с помощью
двух уравнений:
f(x, у, а, Р) = 0,	D2)
?(«. Р) = 0.	D3)
первое из которых содержит координаты х, у и два пара-
параметра а, C, а второе связывает между собой эти два
параметра; выбрав определенные значения параметров
а и р, удовлетворяющие соотношению D3), мы найдем
с помощью уравнения D2) одну из линий рассматриваемого
семейства; придавая же параметрам а, C всевозможные
значения, подчиненные условию D3), мы и получим все
рассматриваемое семейство линий.
48

Вообще, если мы хотим задать семейство линий с помощью
уравнения
fix, У, а,, а2, .... ат) = 0.
D4)
содержащего (кроме х, у) т параметров аь а2	ат, то мы должны
еще иметь т — 1 соотношений
gm-
между этими параметрами.
gi 0*ь <*2, .... ат) =0.
#2 («1, «2	ат) = 0,
а2. .... ат) =0
D5)
3. Пересечение линий семейства
Теперь мы переходим к вопросу о том, как, зная урав-
уравнение семейства линий, найти огибающую этого семейства.
Пусть С—огибающая некоторого семейства линий (рис. 47).
Рассмотрим какую-либо линию L нашего семейства. Она
Рис. 47.
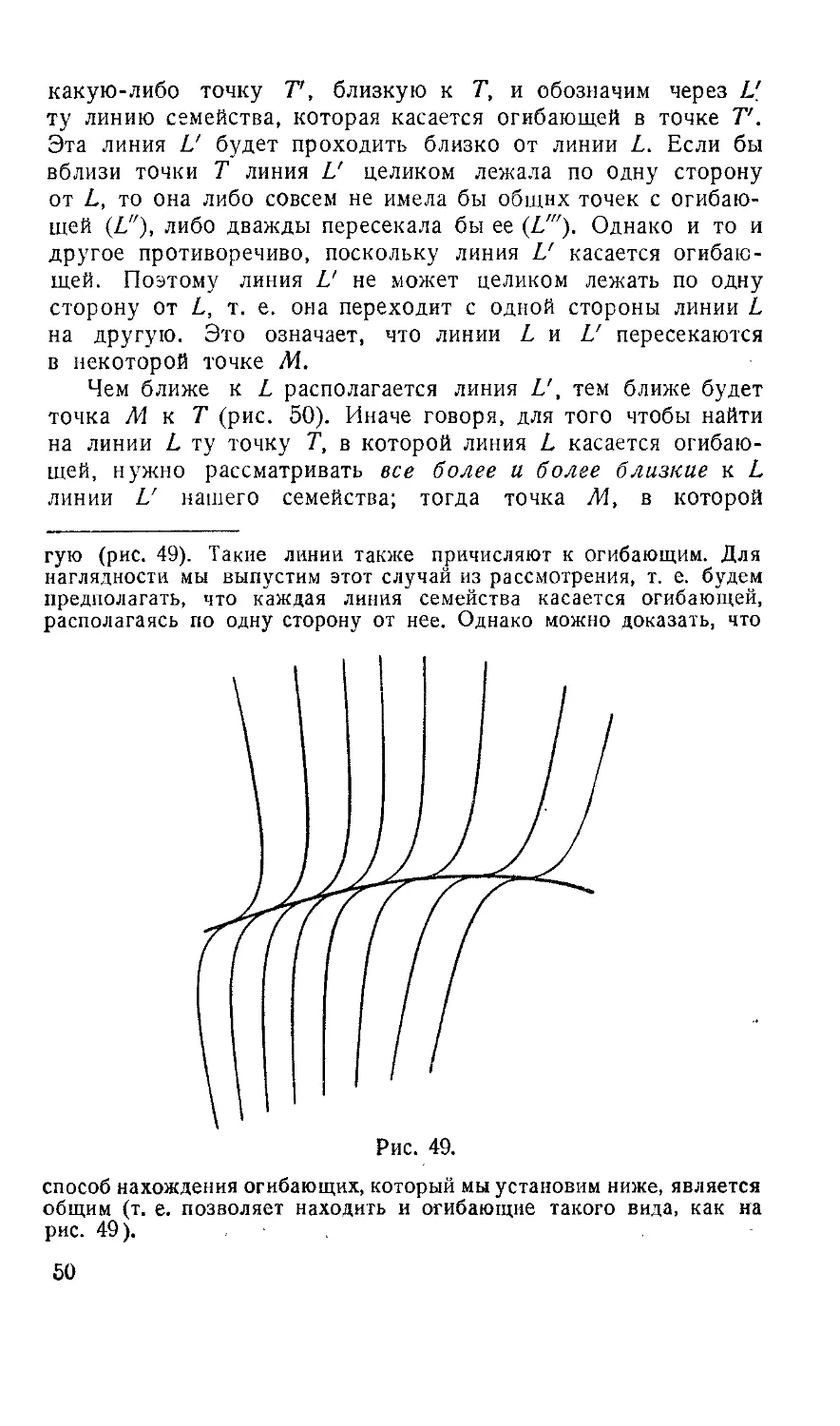
касается огибающей С (рис. 48) в некоторой точке Т, рас-
располагаясь по одну сторону *) от нее. Возьмем на огибающей
*) Следует отметить, что могут существовать линии, которых
все линии семейства касаются, переходя с одной стороны иа дру-
49

какую-либо точку V, близкую к Г, и обозначим через Ц
ту линию семейства, которая касается огибающей в точке Т.
Эта линия L' будет проходить близко от линии L. Если бы
вблизи точки Т линия L' целиком лежала по одну сторону
от L, то она либо совсем не имела бы общих точек с огибаю-
огибающей (/,"), либо дважды пересекала бы ее (//"). Однако и то и
другое противоречиво, поскольку линия U касается огибаю-
огибающей. Поэтому линия L' не может целиком лежать по одну
сторону от L, т. е. она переходит с одной стороны линии L
на другую. Это означает, что линии L и Z/ пересекаются
в некоторой точке М.
Чем ближе к L располагается линия Z/, тем ближе будет
точка М к Т (рис. 50). Иначе говоря, для того чтобы найти
на линии L ту точку Т, в которой линия L касается огибаю-
огибающей, нужно рассматривать все более и более близкие к L
линии L' нашего семейства; тогда точка М, в которой
гую (рис. 49). Такие линии также причисляют к огибающим. Для
наглядности мы выпустим этот случай из рассмотрения, т. е. будем
предполагать, что каждая линия семейства касается огибающей,
располагаясь по одну сторону от нее. Однако можно доказать, что
Рис. 49.
способ нахождения огибающих, который мы установим ниже, является
общим (т. е. позволяет находить и огибающие такого вида, как на
рис. 49).	. ¦ .
50

линия L пересекается с L', будет приближаться к искомой
точке Т. Иногда этот факт выражают словами: каждая точка Т
огибающей является точкой пересечения двух «бесконечно
близких» линий рассматриваемого семейства.
Эти рассуждения играют решающую роль при нахожде-
нахождении огибающей. Мы покажем это на примере семейства окруж-
окружностей, определяемого уравнением
C5). Возьмем две окружности L и U
нашего семейства, близко располо-
расположенные друг от друга. Обозначим
через а значение параметра, соот-
соответствующее окружности L, а через
а'—значение параметра, соответст-
соответствующее окружности L'. Числа а и
а' мало отличаются друг от друга,
так как окружности L и L' были
взяты «близко» расположенными
(вспомним, что я и а' — это абсциссы
тех точек, которые являются цент-
центрами окружностей L и ?'). Ина-
Иначе говоря, мы можем написать
a'=a-f-e, где е — очень маленькое
по абсолютной величине число. Для
того чтобы написать уравнения
окружностей L и U, мы должны параметру в уравне-
уравнении C5) придать значения а и a
(L)
Рис. 50.
?:
Первому уравнению удовлетворяют точки, лежащие на
окружности L, а второму — точки, лежащие на окружности V.
Точки пересечения этих окружностей лежат и на I и на L',
так что они удовлетворяют обоим написанным уравнениям.
Поэтому для нахождения точек пересечения нам достаточно
решить эти два уравнения совместно, как систему. Мы
оставим первое уравнение без изменения, а из второго урав-
уравнения для упрощения системы вычтем первое. Получим
D7)
Заметим теперь, что число е хотя и очень маленькое,
но обязательно отличное от нуля: ведь L и L' — это две
51

разные окружности из нашего семейства, так что а Ф а'.
Поэтому левую часть последнего уравнения можно разделить
на е, и мы получим систему
д;2 i у2_
Решив эту систему, мы получим точки пересечения линий L
и L'. Однако вспомним, что нас интересуют не сами эти
точки пересечения. Мы должны приближать линию L'
к L и найти те точки, к которым будут приближаться точки
пересечения линий L и U. Но что значит «приближать»
линию L' к L? Это значит брать число е все более близким
к нулю. Если же брать е все меньше и меньше, приближая
его к нулю, то второе уравнение D8) заменится соотношением
— 2лг-4-2а==0, т. е. «в пределе» система D8) примет вид
1 -4- У2 — 2ах + а2 — R2 = О,
'	D9)
Второе из этих уравнений показывает нам, что а — х, и
потому из первого уравнения мы находим
у2 = Я2.	E0)
Итак, точка, в которой окружность L касается огибаю-
огибающей, должна удовлетворять уравнению E0). Так как это
Прямая y-R
Прямая y—R
Рис. 51.
верно для любой окружности нашего семейства, то каждая
точка огибающей должна удовлетворять полученному
уравнению E0). Обратно, любая точка, удовлетворяющая
уравнению E0), является точкой огибающей. Это можно до-
52

казать вычислением, но еще проще увидеть геометрически:
ведь уравнение E0) распадается на два уравнения у = R и
у = — R, которые изображают две прямые, параллельные
оси абсцисс и находящиеся на расстоянии R от нее (рис. 51).
Таким образом, проведенные рассуждения помогли вывести
уравнение E0), которое и определяет огибающую.
4. Дифференцирование и нахождение огибающих
Конечно огибающую, изображенную на рис. 51, можно
было определить сразу, так как семейство окружностей было
взято очень простым. Однако тот алгебраический вывод
уравнения огибающей, который был приведен выше, никак
не использовал простоты геометрического устройства рас-
рассматриваемого семейства; точно таким же способом можно
выводить уравнение огибающей и в других случаях.
Мы повторим рассуждения в общем виде. Пусть задано
семейство линий
/(*, у, а) = 0.
Возьмем две «близкие» линии L и U из этого семейства,
для чего придадим параметру значения а и а-\-е:
(L)	f{x, у, а) = 0,
(V) f(x, у, а + е) = 0
(ср. уравнения D6)). Для того чтобы найти точку пересе-
пересечения (или точки пересечения, если их несколько) линий L
и U, мы должны решить эти уравнения совместно, как
систему. Вспомним теперь, как мы из уравнений D6) по-
получили D7): мы оставили первое уравнение без изменения,
а из второго вычли первое. Так же мы поступили и в общем
случае. Тогда мы получим систему
fix, у, а) = 0.
fix, у, а+е) — fix, у, а) = 0.
Заметим, для перехода к уравнениям D8) мы разделили
левую часть второго уравнения на е; поступим так же и
здесь:
fix, у, <х) = 0, |
f(x, у, « +0-/(¦*, у, a) ^q }	E1)
*, у, a) ^q }
53

Эта система дает нам точки пересечения линий L и U. Мы
теперь будем приближать U к L, т. е. будем брать число г
все более близким к нулю. В системе D8) при этом второе
уравнение несколько упростилось, и мы получили «в пределе»
систему D9), из которой определили огибающую. Естественно
ожидать, что в случае системы E1) второе уравнение также
перейдет в пределе в некоторое более простое уравнение,
которое и позволит определить огибающую. Вопрос о том,
какое уравнение получится в пределе из второго уравнения E1),
решается с помощью следующей леммы.
Лемма 2. Пусть f (х, у, а) — некоторый многочлен.
Расположим его по степеням а, т. е. запишем в виде
f(x, у, а) = Ро + Аа + Р2а2 + Рз(х3+ ¦••• E2)
где коэффициенты р0, рх, р2, р3 сами являются некото-
некоторыми многочленами от х, у. Тогда левая часть вто-
второго уравнения E1) является многочленом, т. е. мы можем
написать
_/(*, у, « + «)-/(*, у, «) _Гм> у_ а)+ _ E3)
где f'a(x, у, а) означает сумму всех членов, не содержа-
содержащих е, а многоточием в E3) обозначена сумма осталь-
остальных членов, каждый из которых содержит множителем
число е или некоторую его степень. При этом многочлен
f'a(x, у, а) имеет следующий вид:
f'a (х, у, a) = Pl-\- 2р2а + З^2 + • • •	E4)
Доказательство.
f(x, у, a-f s)— f(x, у, а) __
==:(Р\~\~2Р2а + 3/?3а2~Ь . • .) + члены. содержащие е. E5)
Доказанная лемма позволяет заменить систему уравнений
E1) системой
f{x, у, <х) = 0, )
/:(*. у.«)+'...=о. j	E6)
54

в которой многоточием обозначены невыписанные члены,
каждый из которых содержит множитель е. Решив систему
E6), мы и получим точки пересечения линий L и L'. Однако
вспомним, что нас интересуют не сами эти точки пересече-
пересечения. Мы должны приближать линию L' к L и найти те точки,
к которым будут приближаться точки пересечения линий L
и L'. Иначе говоря, мы должны брать число е все меньше
и меньше, приближая его к нулю. При этом второе урав-
уравнение E6) заменится соотношением
f'a(x, у, а) = 0,
так как все члены, обозначенные многоточием, содержат
множитель е и потому также будут приближаться к нулю.
Итак, в пределе система E6) примет вид
f(x, у, а) = 0,
Это означает, что точка, в которой линия L касается оги-
огибающей, должна удовлетворять соотношениям E7). Так как
это верно для любой линии нашего семейства, то каждая
точка огибающей должна при некотором значении а удо-
удовлетворять полученным уравнениям E7). Иначе говоря,
если мы исключим параметр а из уравнений E7), т. е.
найдем его значение из одного уравнения и подставим во
второе, то получим одно уравнение, уже не содержащее а
(т. е. связывающее только х и у), которому должна удовлет-
удовлетворять любая точка огибающей. Таким образом, мы получаем
следующую теорему.
Теорема 1. Каждая точка огибающей удовлетворяет
уравнению, которое получается из соотношений E7) исклю-
исключением параметра а.
]Многочлен f'a (x, у, <х), с помощью которого были по-
получены уравнения E7), называется производной многочлена
/ (х, у, а). Вычисление производной называется дифферен-
дифференцированием многочлена / (х, у, а). Как видно из формул
E2), E4), дифференцирование многочленов производится очень
просто: нужно в каждом слагаемом, содержащем множитель ай,
заменить этот множитель на kak~\ а члены, не содержащие а,
отбросить.
Укажем теперь теорему, аналогичную теореме 1, но от-
относящуюся к случаю, когда семейство линий задается урав-
уравнениями с двумя параметрами а, р (см. D2), D3)).
55

Теорема 2. Пусть семейство линий задано урав-
уравнениями D2), D3). Тогда каждая точка огибающей удо-
удовлетворяет уравнению, которое получается из соотношений
fix, у, а, р) = 0, |
E8)
исключением параметров sap.
В третьем из уравнений E8) многочлен f'a = f'(x, У> а> Р^
вычисляется дифференцированием по а (т. е. нужно, не
обращая внимания на параметр {$, найти производную, см.
E2), E4)), а многочлен f. получается из f(x, у, а, C)
дифференцированием по параметру [3. То же относится
к производным g'a и g' многочлена g(a, [3).
Для того чтобы установить справедливость формул E8), мы,
как и прежде, рассмотрим две близкие линии L и L' нашего
семейства. Пусть линия L соответствует значениям а, C, а линия
L' — близким значениям параметров а+еь Р + гь Иначе говоря,
уравнения линий L и V записываются в виде
О |
причем выбранные значения параметров удовлетворяют соотноше-
соотношению D3), т. е.
<Р> 0
= 0. /
Из второго уравнения E9) мы вычтем первое и аналогично
поступим с соотношениями F0). Мы получим:
f(x, у, a, fi)=Q,
fix, у, а+?„ ^ + ?2)_/(аг, у, а, Р) = О,
> — s (а> @ = °.
или, что то же самое:
/(¦*> У. °. P) = 0i
? (а, р) = о,	+ U{X> У'п'? + *2)~ПХ' У< п> т ~°' [ (б1)
56

Первые два из этих соотношений, рассматриваемые как система
относительно х н у, определяют точку пересечения линий L и L'.
В силу формула E3) мы можем написать:
f{x, у,а + ?„ р + ?,) — f(x, у, о, р + *») =  (/„ (¦*> У. «,
/(.Г, у, а, р + е2) —/(*, У, а, Р) = ?2 (/р (х, у, а, ?) + ...),
Таким образом, соотношения F1) переписываются в виде:
f{x, у, а, р)=0,
У.
F2)
Здесь многоточием обозначены члены, содержащие множитель
или ?2- Умножая третье из соотношений F2) на
а четвертое соотношение — на
и складывая, получим после приведения подобных членов и груп-
группировки
Число ?j -f- е| непременно отлично от нуля, так как из еj -f- e| = О
следовало бы е, = е2 = 0, н потому кривые L и V совпадали бы,
а это не так. Следовательно, на г\ -f-1% можно последнее соотно-
соотношение разделить, и мы получим
« (¦*. У. «. Р + *г) + ¦¦-)(&'?(«>$)+ ...) —
-{^(«. Р + «2) + • • -)D<*• У. »• Р) +...)"°-
Это соотношение вместе с первым из уравнений F2) и даст нам
точки пересечения линий L и Z/. Если же мы будем приближать
линию L' к L, т. е. брать числа ?i и е2 все более близкими к нулю,
то последнее соотношение в пределе перейдет в уравнение
К (*• У- «• Р) • g9 («, Р) - *« («. Р) -4 (*. У, «, р) = О,
т. е. в последнее из соотношений E8). Вместе с первым из урав-
уравнений E8) оно даст нам возможность найти ту точку, в которой
57

линия L касается огибающей. Таким образом, приписывая к полу-
полученному соотношению первые два уравнения F2), мы и найдем
систему равенств E8). Точка, в которой линия L касается огибаю-
огибающей, должна этой системе удовлетворять. Так как за L можно
принять любую из линий семейства, то любая точка огибающей
должна (при некоторых а, {») удовлетворять системе E8), что н
утверждает теорема 2.
Читатель, знакомый с понятием определителя и основными
теоремами о линейных уравнениях, сможет убедиться в справедли-
справедливости следующей теоремы. Если семейство линий определяется
уравнениями, D4), D5), то любая точка огибающей удовлетво-
удовлетворяет уравнению, которое получится, если к D4), D5) при-
приписать соотношение
= 0
(gm-\)'a
и из полученной системы равенств исключить параметры
«\, .... ат.
Эта теорема при т = 1 превращается в теорему 1, а при
т = 2 — в теорему 2.
5. Дискриминантная линия
В теоремах 1 и 2 говорится, что всякая точка огибающей
удовлетворяет уравнению, которое получится, если из соот-
соотношений E7) или E8) исключить параметры. Мы не гово-
говорили, что огибающая в точности определяется получающимся
уравнением, а лишь утверждали, что любая точка огибаю-
огибающей этому уравнению удовлетворяет. Это не случайно. Дело
в том, что линия, определяемая уравнением, которое полу-
получается, если из E7) или E8) исключить параметры, — она
называется дискриминантной линией — может, кроме оги-
огибающей, содержать ряд других точек, не принадлежащих
огибающей.
Что же собой представляет дискриминантная линия? Для
ответа на этот вопрос мы расскажем (без пояснений, хотя
все рассуждения можно провести, используя только введен-
введенное выше понятие производной), чтб может представлять
собой линия, определяемая некоторым уравнением. Пусть
f(x, у)—какой-либо многочлен относительно х, у. Геоме-
58

трическое место точек на плоскости, координаты которых
удовлетворяют уравнению
/(*. У) = 0.
называют алгебраической линией. Прямая является алгебраи-
алгебраической линией, так как ее уравнение имеет вид y = kx-\-b,
или у— kx—b = Q. Соотношения A8), B2), D1) позволяют
сделать вывод, что окружность, гипербола, парабола также
представляют собой примеры алге-
алгебраических линий.
Алгебраическую линию называют
гладкой, если в каждой ее точке
У
Рис. 52.
Рис. 53.
У
к ней можно провести касательную. Прямая, окружность,
парабола, гипербола являются гладкими линиями. Но может
случиться, что алгебраическая линия содержит особые точки,
к числу которых причисляют
точки самопересечения, са-
самоприкосновения и изолиро-
изолированные точки. Например, ли-
линия, определяемая уравнением
(х2 -\-у2J — 2а2 (х2 — у2) = О
(она называется лемнискатой
Бернулли, рис. 52), пересе-
пересекает сама себя, линия
у2 — х4 = 0	Рис. 54.
(рис. 53) имеет точку самоприкосновения в начале координат,
а линия, заданная уравнением
состоит из точек, принадлежащих прямой у — х—1=0
(т. е. у = х-\- 1), и, кроме того, точки О (начала координат),
вблизи которой нет других точек этой линии (рис. 54).
59

Рис. 55.
Всякая алгебраическая линия либо совсем не содержит осо-
особых точек, т. е. является гладкой, либо содержит лишь
конечное число особых точек, разбивающих ее на отдельные
гладкие куски, причем никаких других особых точек, кроме
перечисленных выше, алгебраическая
линия иметь не может *).
Пусть теперь нам задано семейство
алгебраических линий, определяемое
уравнением C7) или D2), D3). Если
какая-либо линия L нашего семейства
имеет точку самопересечения Т (рис. 55),
"	L' то «близкая» к ней линия L' обяза-
обязательно должна пересечь линию L
в некоторой точке М вблизи точки Т.
Поэтому рассуждения, с помощью кото-
которых мы установили теорему 1 или теорему 2, покажут нам, что
координаты точки Т удовлетворяют уравнениям E7) или E8),
т. е. точка Т принадлежит дискриминантной линии.
Итак, точки самопересечения каждой из линий семейства
должны принадлежать дискриминант-
дискриминантной линии. Точно так же и любая
изолированная точка линии L должна
принадлежать дискриминантной ли-
линии. Таким образом, дискриминант-
ная линия содержит не только оги-
огибающую, но и все особые точки
линий нашего семейства. Оказывается,
что этим уже и исчерпываются все
точки дискриминантной линии, т. е.
дискриминантная линия состоит
из огибающей и геометрического
места особых точек всех ли-
линий рассматриваемого семейства
(рис. 56). Если же мы рассматриваем
семейство линий, ни одна из которых не имеет особых точек,
то дискриминантная линия ничего, кроме огибающей, не
содержит, т. е. в этом случае дискриминантная линия сов-
совпадает с огибающей. В рассматриваемых ниже примерах все
семейства состоят из линий, не имеющих особых точек.
тек
Рис. 56.
*) Существуют еще кратные точки, которые получа-
получаются, если «изолированная» точка попадает на гладкую дугу
кривой.
60

Поэтому мы ограничимся нахождением лишь дискриминантной
линии, так как в рассматриваемых случаях она будет сов-
совпадать с огибающей, т. е. ограничимся исключением пара-
параметров из уравнений E7) или E8).
6. Примеры нахождения огибающих
Пример 1. Рассмотрим опять семейство окружностей C5),
т. е. положим
f(x, у, а) = а2 — 2ах + (х2 + у2 — Я2).
Производная этого многочлена равна
f'a(x, у, а)=2а — 2х.
Таким образом, для определения огибающей мы должны
исключить а из уравнений
а? — 2ах + (х2 + у2 — /<2) = О,
2а — 2л: = 0.
Эту же систему мы имели и раньше (см. D9)), и из нее
получили y2 = R2 (см. E0)). Таким образом, огибающая
состоит из двух параллельных прямых y = R и )i = —R
(см. рис. 51).
Пример 2. Рассмотрим теперь семейство окружностей
C6), т. е. положим
Производная этого многочлена равна
fa(x,y, a)=2a(l—§¦) —2*.
Таким образом, для определения огибающей мы должны
исключить а из уравнений
а21 1	j-) — 2ах -\- {х2 -f- у2 -(- /г2) = О,
2а fl — -^-) — 2л; = 0.
Умножая второе из этих уравнений на —у
и прибавляя к первому, получим	' ~'
61

откуда, разделив на h2 и приводя подобные члены, находим
уравнение искомой огибающей *) в наиболее простой форме
22»
f
У__	1
Л2 —
С2 _ Л	Л
Пример 3. Рассмотрим семейство траекторий D1),
т. е. положим
/ (х, у, а, р) = g-^ _ 2ар
Вычисляем производные:
*) Строго говоря, пока доказано только, что из двух перво-
первоначальных уравнений, содержащих параметр а, следует, что х и у
удовлетворяют найденному уравнению гиперболы. Верно ли обрат-
обратное, т. е. всякие ли х, у, удовлетворяющие уравнению гиперболы,
будут удовлетворять первоначальным уравнениям при некотором а?
В рассматриваемом случае в справедливости этого можно убедиться,
проводя вычисления в обратной последовательности. Такую про-
проверку эквивалентности полученного уравнения тем уравнениям
с параметрами, которые имелись первоначально, следовало бы про-
проводить и в каждом из последующих примеров. Мы этого делать
не будем.
**) Во второй главе мы получили не всю эту гиперболу, а лишь
правую ее ветвь (см. рис. 20), т. е. к уравнению этой гиперболы
было добавлено неравенство х > 0. Это происходило потому, что
Рис. 57.
по смыслу задачи мы рассматривали лишь положительные а, т. е.
не все линии семейства C6), а лишь линии, соответствующие поло-
положительным а. Если рассматривать все окружности семейства C6),
то огибающей будет вся полученная гипербола (рис. 57).
62

Последнее из уравнений E8) принимает вид (после сокраще-
сокращения на 4)
2 ^
Таким образом, для нахождения уравнения огибающей мы
должны исключить а и р из уравнений
gx2
2а2у = 0,
F3)
Умножая первое из этих уравнений на [3, а третье — на —a
и складывая, получим после приведения подобных членов
или, учитывая второе из уравнений F3),
g$x2 — av2Qx = 0.
Так как линия х = О, т. е. ось ординат, очевидно, не является
огибающей (это ясно геометрически — из рис. 10, а также
и чисто алгебраически — линия х — 0 не является решением
уравнений F3)), то можно последнее урав-
уравнение на х сократить
g$x — avl=Q, т. е. а = -Щ-х.
Подставляя это значение а в третье урав-
уравнение F3), мы получим (после сокраще-
сокращения на 82х)
У о
Рис. 58.
Это и есть уравнение искомой огибающей.
Нетрудно видеть, что эта линия совпа-
совпадает t найденной в главе I параболой безопасности. Напри-
Например, исключив t из уравнений A2), A3) (и заменив h на у),
мы и получим написанное выше соотношение.
Пример 4. Отрезок постоянной длины / скользит своими
концами по двум взаимно перпендикулярным прямым. Найдем
огибающую этих отрезков (см. рис. 38); эта огибающая, как
было сказано в главе III, называется астроидой).
Пусть MN — один из рассматриваемых отрезков (рис. 58).
Две взаимно перпендикулярные прямые, по которым скользят
63

концы отрезка, мы примем за оси координат. Обозначим
через а абсциссу точки М, а через р— ординату точки N.
Тогда, учитывая, что длина отрезка MN равна /, мы полу-
получим из прямоугольного треугольника OMN:
а2 + р2 = Л	F4)
Далее, угловой коэффициент прямой MN, т. е. тангенс
ft
угла XMN, равен — —, так как tg / XMN = — tg / OMN',
это же значение угловой коэффициент имеет и при любом
другом положении отрезка MN, т. е. при положении этого
отрезка во второй, третьей или четвертой четверти. Таким
образом, уравнение прямой MN имеет вид
или, после умножения на а,
ау + р* — сф = О.	F5)
Мы приходим к задаче нахождения огибающей семейства
прямых линий, определяемого уравнениями F4), F5), или,
что то же самое, уравнениями D2), D3), в которых
/(*, у, а, Р) = а
Вычисляем производные:
Последнее из уравнений E8) принимает вид (после сокра-
сокращения на 2)
ру — ах + а2— f = Q.	F6)
Таким образом, для нахождения огибающей мы должны
исключить а и р из уравнений F4), F5), F6). Умножая
уравнения F5) на a, a F6) на р и складывая, получим
откуда находим, учитывая соотношение F4),
Аналогично, умножая уравнение F5) на р, а F6) — на —а
и складывая, получим
64

Наконец, подставляя эти значения а и E в F4), находим
или, после сокращения на I '*,
F7)
Это и есть уравнение огибающей (т. е. астроиды).
Пример 5. На плоскости задан прямой угол. Про-
Проводятся всевозможные прямые, отсекающие от этого угла
треугольники, имеющие площадь 2. Найдем огибающую всех
этих прямых (рис. 59).
Примем стороны заданного угла за оси координат. Возь-
Возьмем одну из прямых, отсекающих от этого угла треугольник
площади 2, и пусть М,
N— точки пересечения этой
прямой с осями координат
(рис. 60). Обозначим абсцис-
абсциссу точки М через a, a
У
Рис. 60.
ординату точки N — через р. Тогда, как и выше (см. F5)),
мы найдем, что прямая MN определяется уравнением
ау + рх — ар = 0.	F8)
Однако числа i и р удовлетворяют уже не условию F4),
которое означало, что длина отрезка MN равна /, а условию
ар = 4,	F9)
которое означает, что площадь треугольника OMN равна 2
(так как ОЖ = а, ОЛГ —р, то 5доллг = ~n аР)- Таким обра-
образом, мы приходим к задаче нахождения огибающей семейства
65

прямых, определяемого уравнениями F8), F9), или, что то же
самое, уравнениями D2), D3), в которых
f(x, у, a, ф) = а,у-\~фх— оф,
g(a. р) = сф — 4.
Вычисляем производные:
Последнее из уравнений E8) принимает вид
а>у — $х = 0.	G0)
Таким образом, для нахождения огибающей мы должны
исключить а и [3 из уравнений F8), F9), G0). Из F8) и
G0)	получаем
Сокращая первое из этих уравнений на а, а второе — на р
(это возможно, так как в силу F9) а и [J отличны от нуля),
находим
р = 2у, a = 2*.
Наконец, подставляя найденные значения а и |3 в соотноше-
соотношение F9), получаем искомое уравнение огибающей
*у=1.	G1)
Любая касательная к линии G1) является одной из прямых
рассматриваемого семейства и потому отсекает от заданного
прямого угла треугольник площади 2. Как мы видели в конце
главы II, таким же свойством обладает гипербола, если ее
асимптоты взаимно перпендикулярны; такая гипербола назы-
называется равнобочной. Из этого можно заключить, что линия
G1)	также является гиперболой. Различие в записи урав-
уравнений G1) и B2), каждое из которых определяет одну
и ту же линию — гиперболу, объясняется тем, что гипер-
гиперболы G1) и B2) по-разному расположены относительно осей
координат.
Пример 6. Рассматривается окружность радиуса 1а
с центром в точке Fx и внутри этой окружности точка F2,
находящаяся от центра на расстоянии 2с. Произвольная
точка А окружности соединяется отрезком с точкой /\, и
через середину этого отрезка проводится к нему перпен-
66

дикуляр L (рис. 61). Найти огибающую семейства таких
перпендикуляров (рис. 62).
Для решения этой задачи мы примем прямую F^F2 за ось
абсцисс, а перпендикуляр к отрезку FXF2 в его середине —
за ось ординат. Тогда абсциссы точек Fl и F2 будут равны с
х	и —с. Пусть А — произвольная
точка на рассматриваемой окруж-
Рис. 61.
Рис. 62.
ности, а а и C — координаты этой точки. Для того чтобы
точка М с координатами х, у лежала на перпендику-
перпендикуляре L, проведенном через середину отрезка AF%, необходимо
и достаточно, что5ы было выполнено равенство МА = MF%,
или, что равносильно, равенство
MA2 = MF\.
Но МА2 = (х — аJ —f— (у — [ЗJ (см. стр. 24) и, аналогично,
MFi = (x-\-cf -f-y". Таким образом, уравнение перпенди-
перпендикуляра L, проведенного через середину отрезка AF2, запи-
записывается в виде
(х - ееJ + (у - J3J = (х + с? +- у\
или, после очевидных упрощений,
— 2ах — 2^у — 2сх — с2
0.
G2)
Уравнение окружности радиуса 2а с центром в точке Flt
имеющей координаты (с, 6), записывается в виде (х — сJ +
(см. A8)). Так как точка А лежит на этой
67

окружности, то ее координаты a, (D должны удовлетворять
написанному уравнению, т. е.
(а — с
G3)
или, после очевидных упрощений,
_ 2ас + с2 — 4а2 = 0.
Итак, поставленная задача сводится к нахождению огибаю-
огибающей семейства прямых, заданного уравнениями G2), G3).
Обозначая, как обычно, левую часть уравнения G2) через
/ (х, у, а, [3), а левую часть уравнения G3) через g(a, C),
мы легко напишем последнее из уравнений E8):
(а — х) р — (Р — у) (а — с) = 0.	G4)
Из уравнений G2), G3), G4) и получается уравнение
огибающей. Эта огибающая носит название эллипса; точки Fx
и F2 называются фокусами эллипса. Уравнение эллипса можно
получить, исключив параметры а и р из уравнений G2), G3)
и G4). Однако мы не бу-
будем этого делать, а выве-
выведем из соотношения G4) не-
несколько интересных геомет-
геометрических свойств эллипса.
Вспомним прежде всего,
что при выборе значений а
и р, удовлетворяющих вто-
второму уравнению E8), т. е.
s., при выборе некоторой ли-
линии L рассматриваемого се-
семейства, неизвестные х, у,
определяемые из системы
E8), представляют собой ко-
Рис. 63.	ординаты той точки Т,
в которой линия L ка-
касается огибающей. В рассматриваемом случае это озна-
означает, что если мы выберем значения а и C, удовлетворяющие
уравнению G3), т. е. выберем точку А (рис. 63) на окружности,
то неизвестные х, у, определяемые из системы G2), G4),
представляют собой координаты той точки Т, в которой
перпендикуляр, проведенный через середину отрезка AF2,
касается эллипса. Итак, координаты точки касания Т
удовлетворяют уравнению G4). Это уравнение после
68

очевидных преобразований можно переписать в виде
откуда видно, что оно определяет некоторую прямую.
Точка Т лежит на этой прямой, так как ее координаты
удовлетворяют этому уравнению. Далее, точка Ft также
лежит на этой прямой (так как ее координаты х = с, у — О,
очевидно, удовлетворяют этому уравнению); лежит на этой
прямой и точка А (ее координаты, как легко видеть, также
удовлетворяют написанному уравнению). Таким образом,
точки Flt T и А лежат на одной прямой.
Вспомним теперь, что перпендикуляр L, проходящий через
середину отрезка AF2, является касательной к эллипсу,
проведенной через произвольную его точку Т, так как эллипс
является огибающей всех таких перпендикуляров. Далее,
точки F2 и А симметричны относительно прямой L. Нако-
Наконец, точки Fv T и А, как мы доказали, лежат на одной
прямой, т. е. точка Т лежит на радиусе FXA. Итак, если
мы проведем произвольную касательную L к эллипсу, то
точка А, симметричная фокусу F2 относительно пря-
прямой L, будет лежать на окружности радиуса 1а с центром
в фокусе /y, точка Т, в которой прямая L касается
эллипса, совпадает с точкой
пересечения прямой L и радиу-
радиуса FXA.
Так как точки F2 и А симмет-
симметричны относительно прямой L, то
TF2 — ТА, и потому TF2 + TFX =
= TF1-j-TA — 2a. Таким образом,
сумма расстояний от точки Т,
лежащей на эллипсе, до его фоку-	рис_
сов равна 2а. Это верно для любой
точки, лежащей на эллипсе, так как в каждой точке эллипса
его касается одна из прямых L (ведь эллипс есть огибаю-
огибающая). Легко понять, что для точки Т', лежащей внутри
эллипса, сумма расстояний T'Fl и T'F2 меньше 2а (рис. 64),
а для точки, лежащей вне эллипса, эта сумма больше 2а.
Итак, эллипс есть геометрическое место точек на пло-
плоскости, сумма расстояний которых от двух заданных
точек, называемых фокусами эллипса, равна заданному
отрезку 2а. Это свойство эллипса обычно принимают за его
определение.
69

Далее, так как точки F2 и А симметричны относительно
прямой L, а отрезки FXT и ТА составляют продолжение
один другого, то
T = /_АТТ' = /_FX ТТ.
Это означает, что луч света, вышедший из точки F2 в на-
направлении F2T, отразившись от прямой L по закону «угол
падения равен углу отражения», пойдет далее по отрезку TFX.
Но ведь прямая L касается эллипса в точке Т, и потому
отражение луча от прямой L в точ-
точке Т равносильно отражению от
самого эллипса в точке Т. Итак,
если в одном фокусе эллипса поме-
поместить точечный источник света,
то каждый луч, отразившись от
эллипса, пойдет затем во второй
фокус, т. е. все отраженные лучи
рис gg	соберутся («сфокусируются» — от-
отсюда и название «фокус») во втором
фокусе эллипса (рис. 65). Это «оптическое» свойство эллипса
напоминает установленное в главе I свойство параболы. Ана-
Аналогичным свойством обладает и гипербола.
Заметим в заключение, что уравнение рассматриваемого
эллипса имеет вид
¦» I	У 	 1
Это уравнение можно получить из G2), G3), G4) исключе-
исключением параметров и и Р; такое исключение параметров тре-
требует не очень коротких алгебраических преобразований, и
потому мы его здесь не приводим. Обычно положительную
величину а2 — с2 обозначают через Ь2, и уравнение эллипса
записывается в виде:
-2L
b2
G5)
Замечание. Мы рассмотрели несколько примеров
нахождения огибающих, ограничиваясь при этом лишь алге-
алгебраическими линиями. Сказанное выше можно применять и
к неалгебраическим (трансцендентным) линиям. Простейшими
примерами неалгебраических линий являются синусоида, гра-
графики показательной и логарифмической функций, циклоида.
Однако при этом для нахождения огибающих надо уметь
70

дифференцировать не только многочлены, но также более
сложные функции: показательные, тригонометрические и др. *).
Кроме того, особые точки неалгебраических линий могут
иметь весьма сложное строение и их может быть бесконечно
много. Для того чтобы избежать всех этих усложнений, мы
и ограничились рассмотрением лишь алгебраических линий
и семейств.
7. Эволюты и эвольвенты
Напомним некоторые понятия, введенные в главе III
(стр. 41). Рассмотрим некоторую кривую линию К. В произ-
произвольной точке А этой кривой проведем к ней касательную AD
и перпендикуляр AN к этой касательной (рис. 40). Пря-
Прямая AN называется нормалью к кри-
кривой К в точке А. Если мы рассмот-
рассмотрим нормали кривой К, проведенные
во всех точках этой кривой, то по-
получим семейство прямых — семей-
семейство нормалей кривой К. Огибаю-
Огибающая Е этого семейства прямых назы-
называется эволютой рассматриваемой
линии К.
Проведем нормали в двух близ-
близких друг к другу точках А, А' кри-
кривой К. Пусть N, N'—те точки,
в которых эти нормали касаются
эволюты, a Q — точка пересечения
нормалей AN и A'N' (рис. 66).
Тогда в «треугольнике» AA'Q, имею-
имеющем в качестве «основания» дугу АА' линии К, углы при осно-
основании равны (они прямые, так как AN и A'N' — нор-
нормали). Если бы основание АА' было прямолинейным отрез-
отрезком, то из равенства углов при этом основании вытекало бы,
что боковые стороны AQ и A'Q равны. Однако в действи-
действительности основание АА' немного искривлено, и потому
боковые стороны AQ и A'Q лишь примерно одинаковы
AQ^A'Q.
Далее, дуга kj NN' эволюты искривлена мало (нормали AN
и A'N' образуют между собой очень маленький угол!), и
Рис. 66.
*) См. книгу «Что такое дифференцирование?» того же автора
(популярные лекции по математике, вып. 17) или статью «Инте-
«Интеграл и производная» в третьем томе «Детской энциклопедии».
71

потому длина этой дуги очень мало отличается от длины
ломаной NQN':
Таким образом,
о NN' ж NQ + QN' = (AN — AQ) -{- (A'Q — A'N') =
= (AN — A'N') + (A'Q — AQ) ^ AN — A'N'.
Замечательно, что полученное приближенное равенство
{j NN' яй AN — A'N' в действительности является точным
G6)
' = ЛУУ — A'N'.
Это доказывается на основании указанного выше приближен-
приближенного равенства при помощи интегрирования — операции,
обратной к дифференцированию и изучаемой в высшей мате-
математике. При этом равенство G6) справедливо без предполо-
п11	жения, что дуга АА' является «ма-
«маленькой».
Равенство G6) допускает очень
простое и наглядное истолкование.
Представим себе, что изготовлена
пластина в форме эволюты, и на
К эту пластину навернута идеально
тонкая, гибкая и нерастяжимая нить.
Допустим, что эта нить натянута
таким образом, что она идет по эво-
эволюте до точки N', а далее идет по
отрезку N'A' касательной к эво-
эволюте, и в этой точке А' к нити
прикреплен карандаш (рис. 67). Так
как, в силу G6), AN —о NN' +
-{-N'A', то карандаш можно пере-
переместить в точку А, причем нить
останется натянутой. Так как это
верно для любой точки А на ли-
линии К, то, двигая карандаш таким образом, чтобы
нить сматывалась с эволюты, оставаясь натянутой, мы
опишем карандашом линию К. На основании этого линию К
называют эвольвентой (разверткой) линии Е.
Итак, если Е — эволюта линии К, то К есть эвольвента
линии Е. Если мы поместим карандаш в другой точке
Рис. 67.
72

навернутой на линию Е нити, то при раскручивании нити
он опишет другую эвольвенту линии Е. Таким образом,
линии Е соответствует бесконечно много эвольвент; для
каждой из этих эвольвент линия Е является эволютой. Так
как каждая касательная к эволюте Е является нормалью ее
эвольвенты К (ведь эволюта и определяется как огибающая
семейства нормалей кривой К1), то любые две эвольвенты
линии Е имеют общие нормали, т. е. нормаль к одной эволь-
эвольвенте является нормалью и ко второй (рис. 68). При этом
длина отрезка общей норма-
нормали, заключенного между двумя
А'
JA"
Рис. 68.
Рис. 69.
эвольвентами, постоянна, т. е. АВ — А'В' — А"В" = ...
Действительно, если укрепить на нити, сматывающейся с эво-
эволюты Е, два карандаша (рис. 69), то эти карандаши опишут
две эвольвенты линии Е, и длина отрезка общей нормали,
заключенного между этими эвольвентами, будет все время
оставаться равной длине отрезка нити между карандашами.
Если нить, сматывающуюся с эволюты, закрепить в неко-
некоторой точке N линии Е, то при дальнейшем движении
карандаш опишет дугу окружности, касающуюся линии К
в точке А (рис. 70). Радиус этой окружности равен длине
отрезка нормали от точки А до точки N, в которой нор-
нормаль касается эволюты; центр окружности находится в точке N
(рис. 71). Построенная окружность называется соприкасаю-
соприкасающейся окружностью линии К в точке А. Эта окружность
наиболее близко подходит к кривой К около точки А по
73

сравнению со всеми другими окружностями. Можно сказать,
что маленькая дуга линии К около точки А ведет себя
так же, как и дуга соприкасающейся окружности; в част-
частности, искривление (кривизна) линии К вблизи точки А,
т. е. скорость поворота касательной при перемещении точки
касания по линии К, совпадает с искривлением соприкасаю-
соприкасающейся окружности. В связи с этим центр N соприкасаю-
соприкасающейся окружности называют
центром кривизны линии К
Рис. 70.
Рис. 71.
в точке Л, а ее радиус AN называют радиусом кривизны
линии К в точке А. Итак, радиус кривизны кривой К
в точке А (его обозначают через рд) равен длине отрезка
нормали от точки А до точки N, в которой нормаль касается
эволюты, а центр кривизны (точка N) лежит на эволюте.
Иначе говоря, эволюта Е кривой К является геометри-
геометрическим местом центров кривизны этой кривой. Заметим
еще, что равенство G6) выражает следующую геометри-
геометрическую теорему: длина дуги эволюты равна разности
радиусов кривизны, соответствующих концам этой дуги
(т. е. <;NN' = pA — pA,y
Таким образом, эволюта очень тесно связана по своим гео-
геометрическим свойствам с исходной кривой К- Укажем без доказа-
доказательства, каким образом, зная уравнение линии К, можно найти
уравнение ее эволюты. Пусть линия К задается уравнением
/С*, у) = 0.
Возьмем на кривой К. произвольную точку А; обозначим ее коор-
74

динаты через аир. Так как точка А лежит на линии К, то коор-
координаты a, (S этой точки удовлетворяют уравнению линии К, т. е.
/(а, р) =
G7)
В высшей математике доказывается, что нормаль к линии К, про-
проведенная в точке А, имеет уравнение
(У - Р) /« («. Р) - (* - «) /р («. Р) = 0.	G8)
Таким образом, семейство нормалей кривой К. определяется урав-
уравнением G8), содержащим параметры а, [3, которые связаны соот-
соотношением G7). Для нахождения огибающей этого семейства, т. е.
для нахождения эволюты, нужно теперь применить теорему 2.
й)
Рис. 72.
Мы ограничимся указанием без проведения вычислений
трех примеров.
Эволютой эллипса G5) является кривая
(ax)h + (by)h = (a2 — b2)*1*
(рис. 72, а и б); эта кривая получается из астроиды «растя-
«растяжением» ее в направлении оси ординат. Далее, эволютой
астроиды
(см. стр. 65) служит новая астроида, получающаяся из
75

первой подобным увеличением в два раза и поворотом на
угол 45° (рис. 73). Наконец, отметим еще, что, как мы
видели в главе III, эволютой верхней циклоиды, изображен-
изображенной на рис. 43, является нижняя. Следовательно, верхняя
Рис. 73.
циклоида является эвольвентой нижней циклоиды. На этом
основано устройство циклоидального маятника (рис. 74).
Рис. 74.
За подробностями мы отсылаем читателя к книге Г. Н. Бер-
мана «Циклоида», которая содержит много интересных фактов
из геометрии и механики, связанных с циклоидой, астроидой
и другими кривыми, получающимися при качении круга.