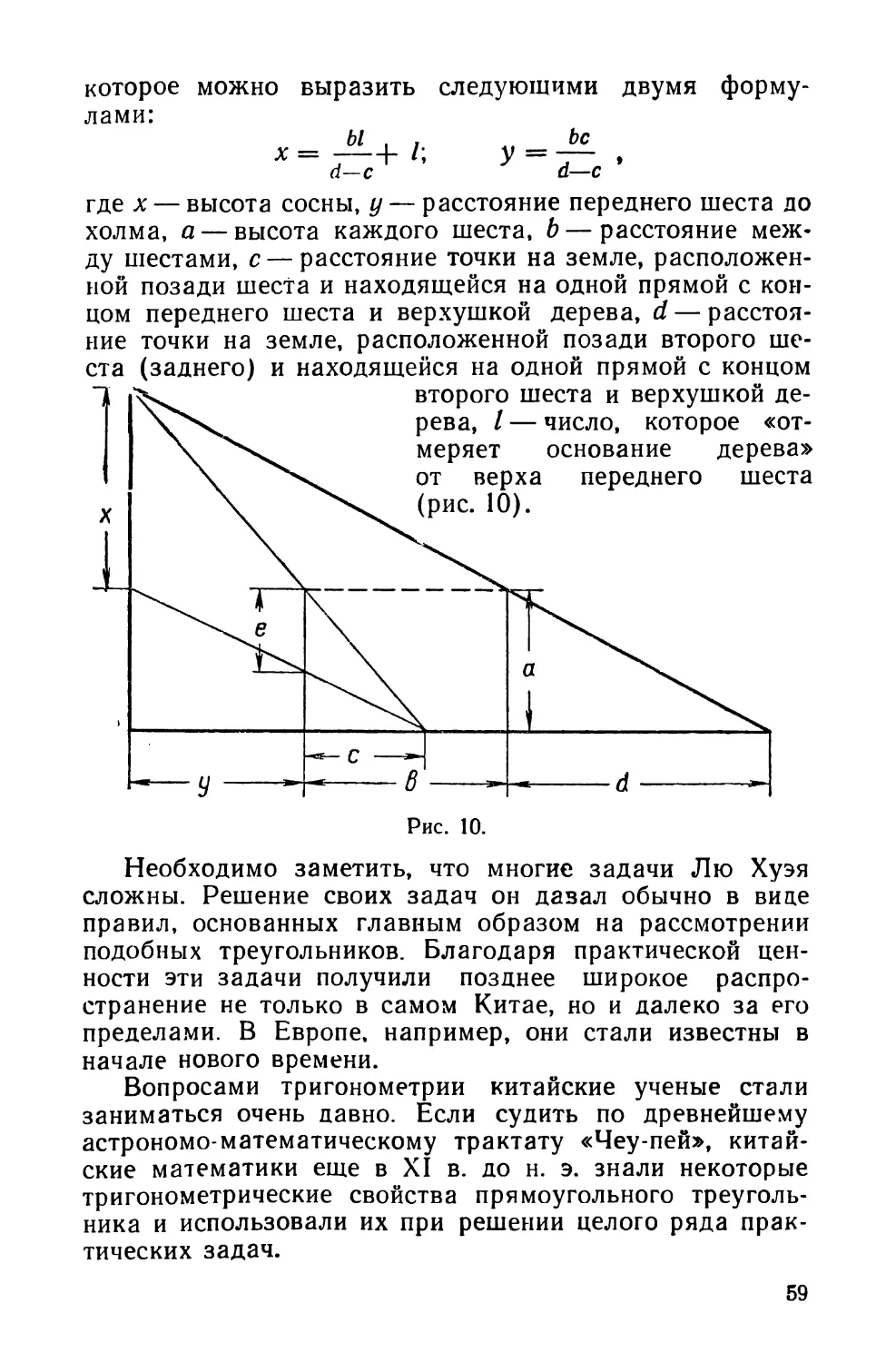
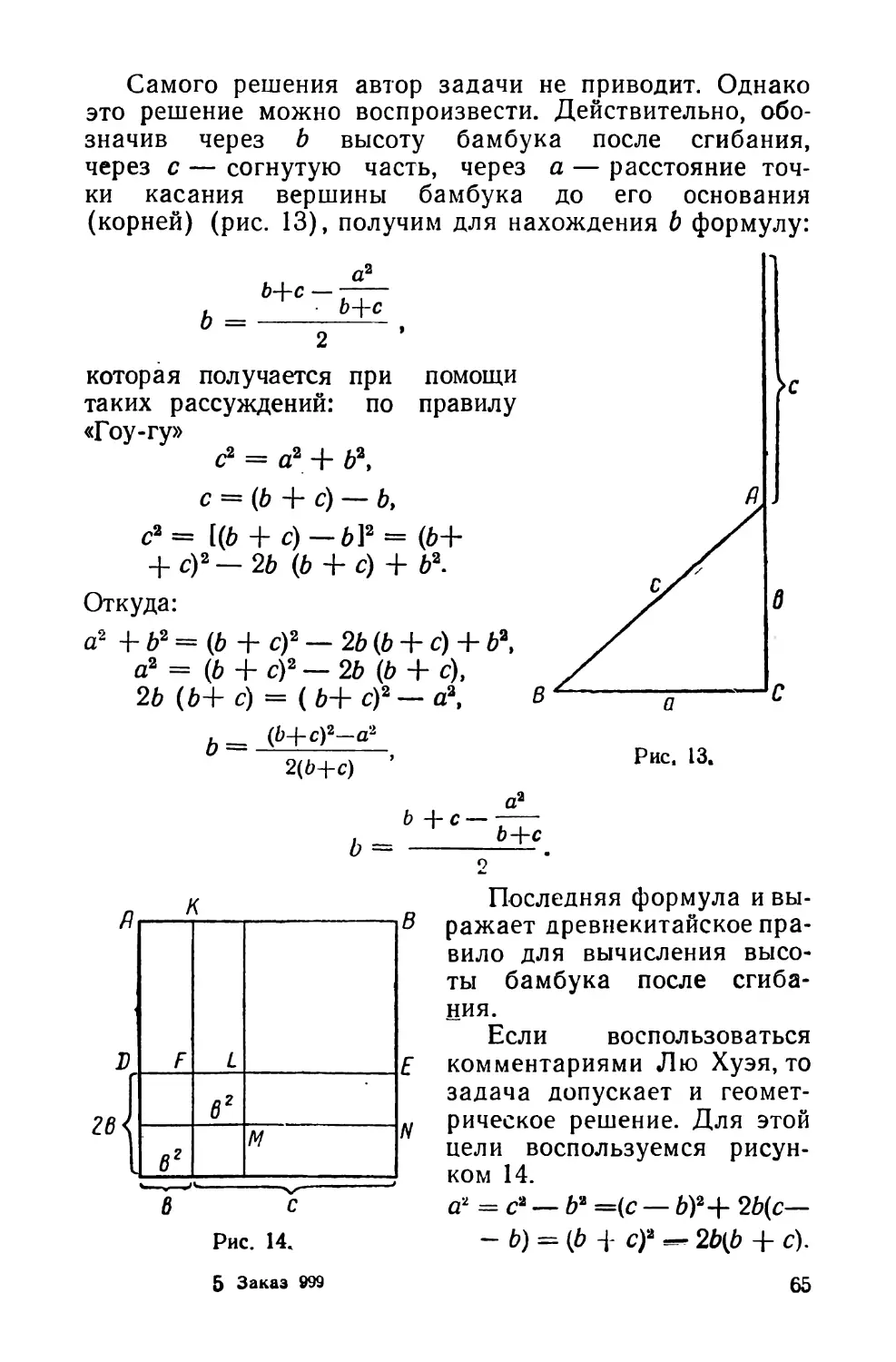
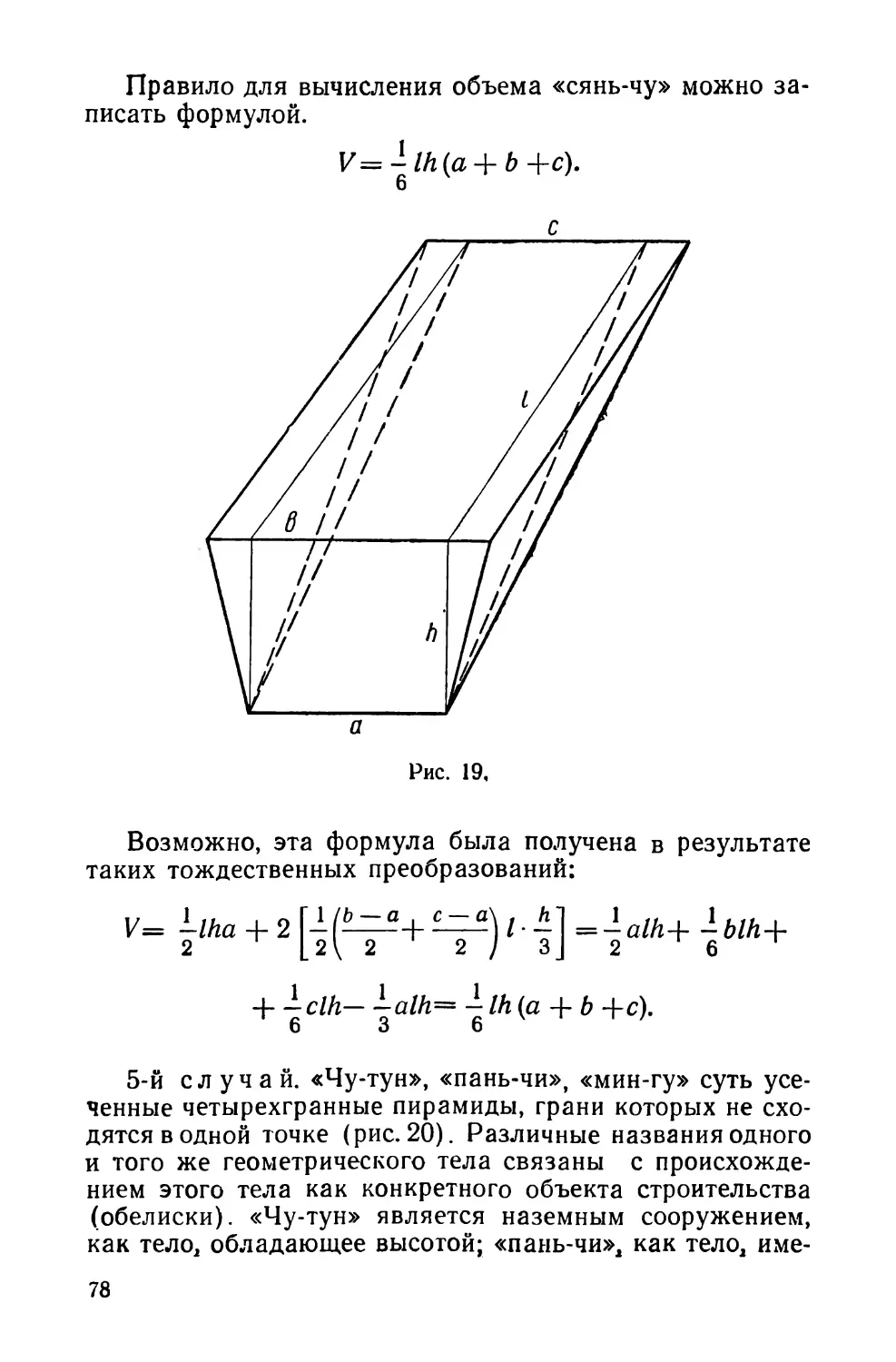
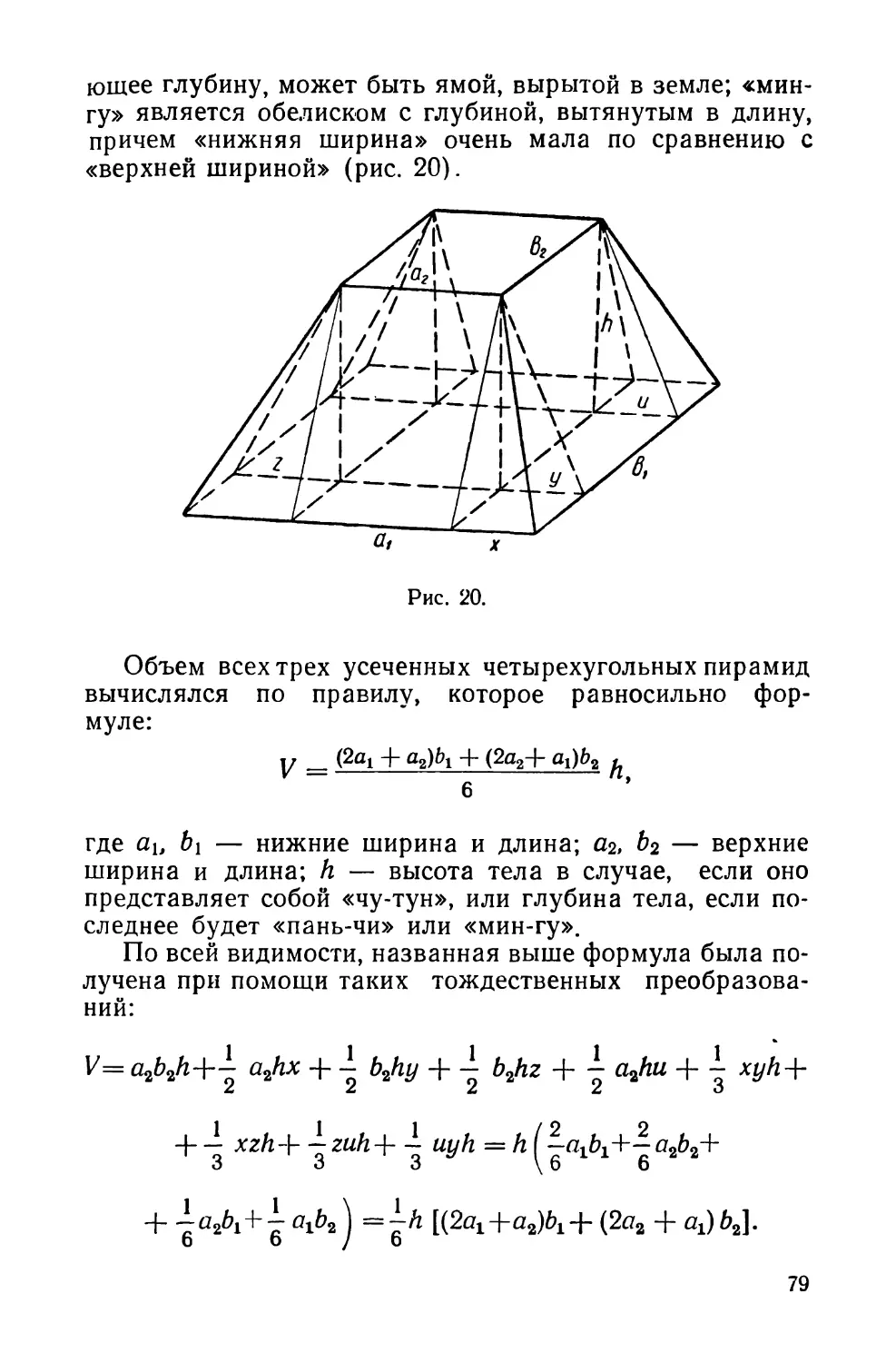
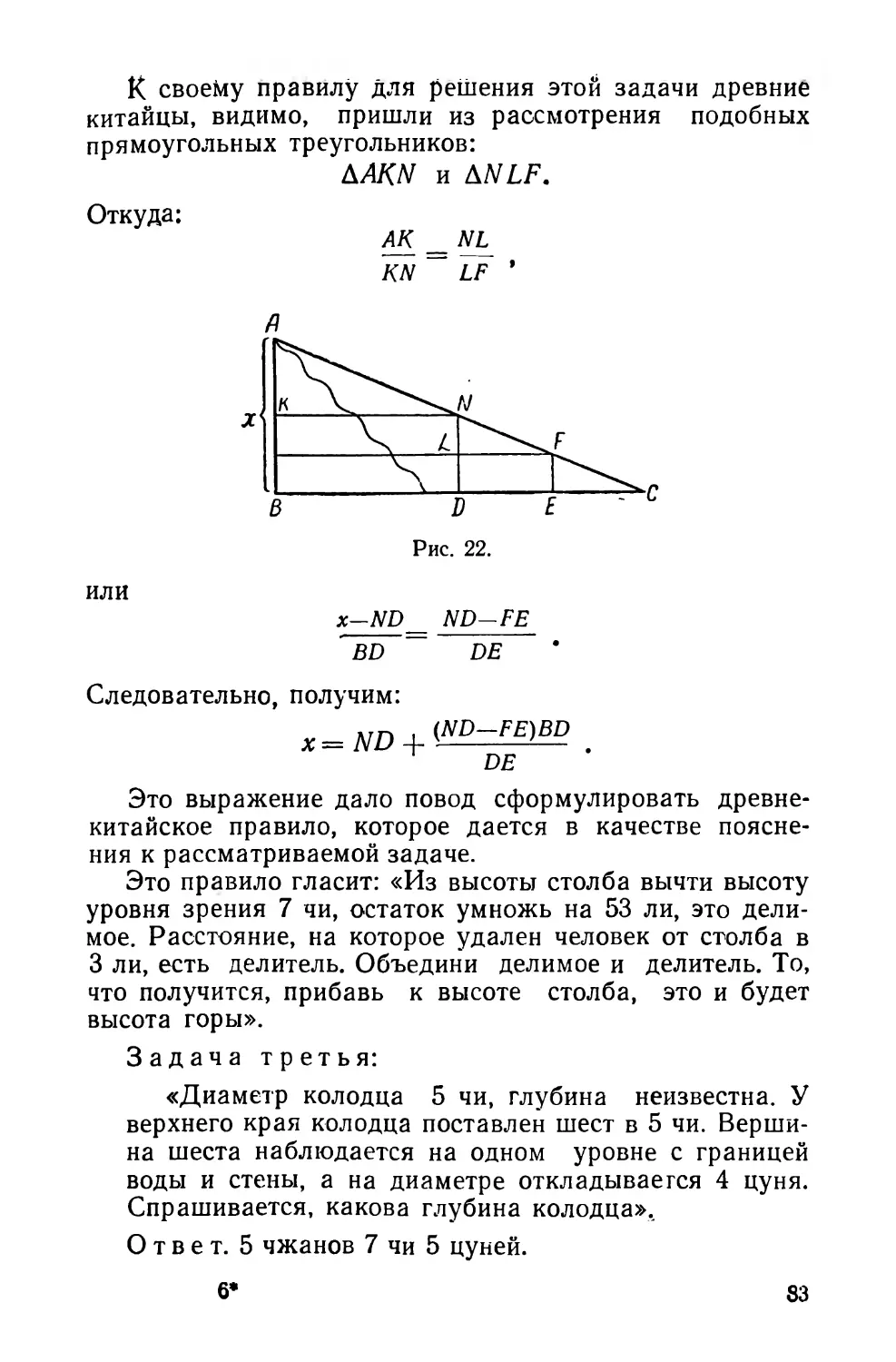
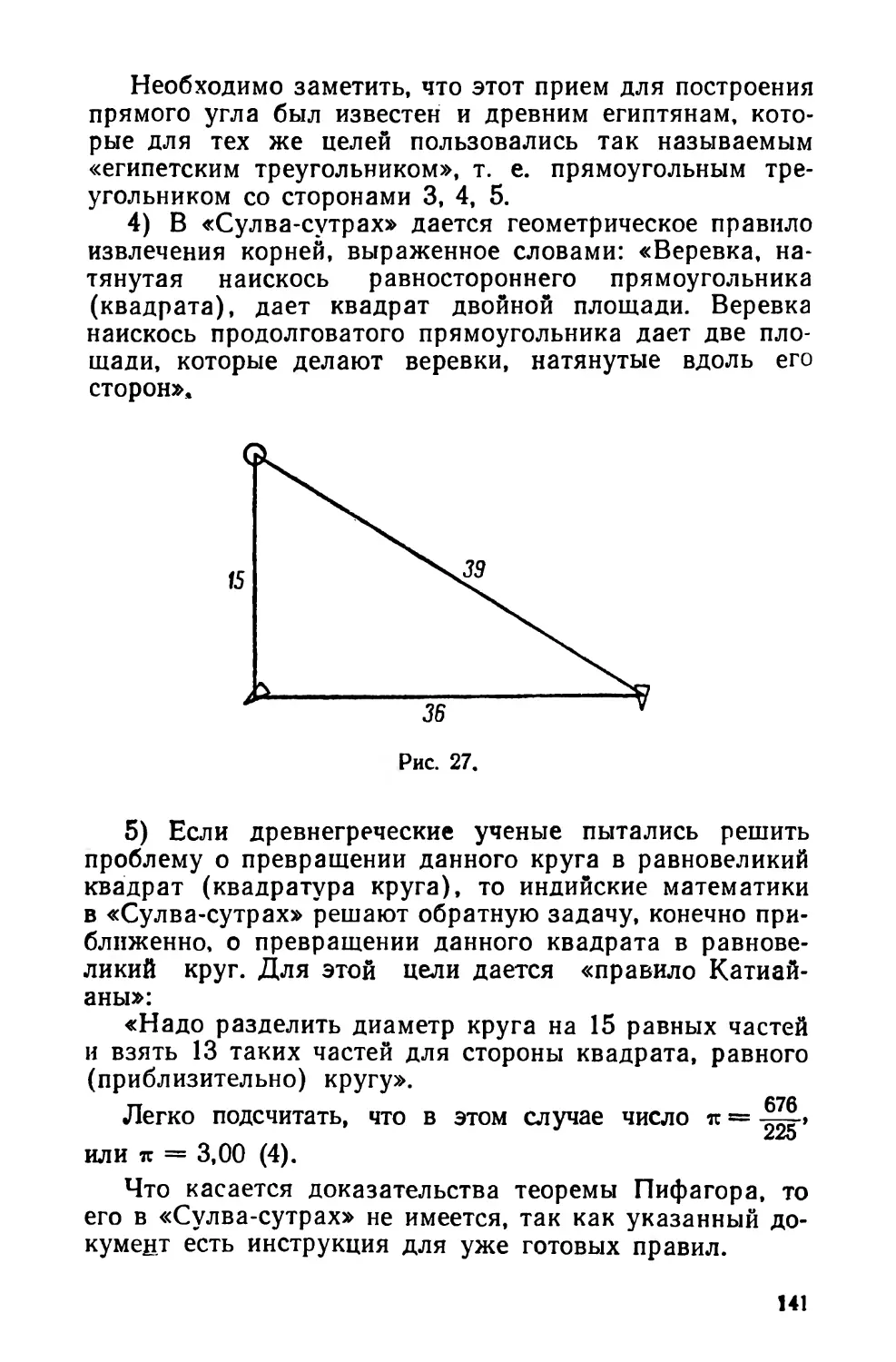
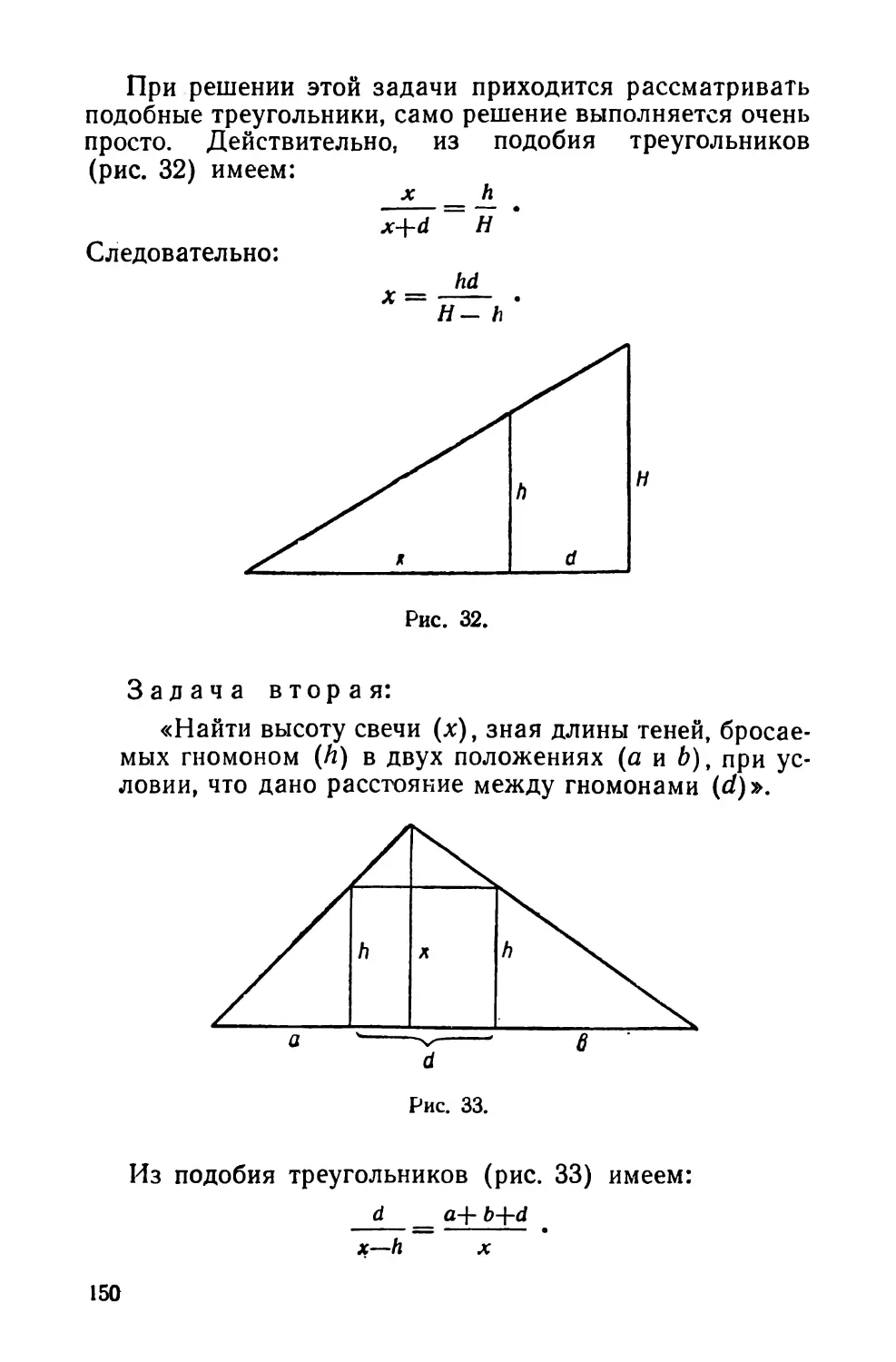
Похожие
Текст
КИТАЕ
.ЧИСТЯКОВ
УЧПЕДГИЗ-1960
|&» МАТЕРИАЛЫ ПО ИСТОРИИ МАТЕМАТИКИ В КИТАЕ И ИНДИИ «gl
МАТЕРИАЛЫ
ПО ИСТОРИИ
М АТЕМАТИ КИ
.9). Т'ИСЖЯЮоЧ?
МАТЕРИАЛЫ
ПО ИСТОРИИ
МАТЕМАТИКИ
КИТАЕ и ИНДИИ
ПОСОБИЕ ДЛЯ ВНЕКЛАССНОЙ (s^
РА БОТЫ
Joey Э aр с тб ен ног.
*Уче$н о-педагогическое иуда тел ьстбо
Ли Hucmej)ст'ёа, п^осбещения ФС.Ф.СЛР.
МОСКВА -1960
ОТ ИЗДАТЕЛЬСТВА
Настоящая книга является попыткой создания до-
ступной для широкого круга читателей популярной ли-
тературы по краткой истории развития математики в Ки-
тае и Индии.
Материал книги может быть использован для про-
ведения исторических экскурсов на уроках математики
и на внеклассных занятиях по математике.
Книга написана для учителей математики, но может
быть использована и учащимися старших классов.
Все отзывы по книге и пожелания просим направ-
лять по адресу: Москва И-18, 3-й проезд Марьиной
рощи, д. 41, Учпедгиз, редакция математики.
Of
U а с nc 6
I
КРАТКАЯ ИСТОРИЯ
МАТЕМАТИКИ
КИТАЕ
ЕП£¥=
ГЛАВА ПЕРВАЯ
КИТАЙ—СТРАНА МНОГОВЕКОВОЙ САМОБЫТНОЙ
КУЛЬТУРЫ
Китайский народ имеет многовековую богатую исто-
рию. Многие важнейшие открытия в науке и технике, сде-
ланные китайскими учеными, вошли в золотой фонд ми-
ровой науки и культуры и составляют законную гордость
китайского народа и всего прогрессивного человечества.
Считается установленным, что китайскому народу
принадлежат следующие изобретения:
L Компас. В китайских летописях II в. до н. э.
имеются записи о применении компаса, первоначально
употреблявшегося при сухопутных путешествиях; свое-
образной стрелкой для компаса служил природный маг-
нитный железняк, отшлифованный в виде ложки, кото-
рая только выпуклой частью касалась отшлифованной
поверхности медной пластинки (рис. 1).
Рис8 1. Компас периода Первой Ханьской династии.
5
Европейцы заимствовали компас из Китая и ввели его
в употребление лишь в XVIII в.
2. Сейсмограф — чувствительный прибор для за-
писи и измерения колебаний земной коры. Этот прибор
впервые в мировой науке изобрел в 132 г. н. э. выдаю-
щийся ученый-астроном Чжан Хэн. Описание первого
сейсмографа сохранилось в старинных записях биогра-
фии Чжан Хэна (рис. 2).
3. Б у м а г а. Полагают, что впервые бумагу из тряпья
и древесной коры изготовил в 105 г. н. э. Ц а й Лунь.
Значительно позднее бумага из Китая через Корею бы-
ла завезена в Японию, а через Синьцзян — в Среднюю
Азию и Персию. Искусство приготовления бумаги стало
известно в Западной Европе лишь в XII в. Первое бу-
мажное производство в Европе было организовано в
1189 г. в одном из местечек французских Пиренеев.
Интересно отметить, что само русское слово «бумага»
произошло от слова «бамбук». Дело в том, что до изобре-
тения бумаги китайцы писали на табличках из бамбука
и других материалов. По-видимому, слово «бамбук» ста-
ло синонимом того, на чем пишут. Действительно, в
XVI—XVII вв. бумага называлась «бамбак», «вамбак», а
позднее «бумаг» и, наконец, бумага».
В одной старинной китайской летописи об изобрете-
нии бумаги сохранилась следующая запись: «В древние
времена писали обыкновенно на бамбуке или кусках шел-
ка. Но так как шелк дорого стоит, а бамбук тяжеловесен,
эти два материала не были удобны. Цай Лунь придумал
употреблять в дело древесную кору, коноплю, тряпье и
рыболовные сети. В первый год эпохи (105 г. н. э.) он
сделал доклад императору относительно процесса изго-
товления бумаги и удостоился похвалы за свое искусст-
во. С этого времени бумага применяется повсеместно и
называется бумагой маркиза Цай» Ч
4. Книгопечатание. Употребление печати в Ки-
тае встречается в III—IV вв. до н. э. Первоначальные
отпечатки делались при помощи специально изготовлен-
ных деревянных рельефов, намазанных краской, что те-
перь называется ксилографией (от греческих слов «ксю-
лон» — кусок дерева, «графо» — пишу). Затем для этих
1 Е. И. К а ц п р ж а к, История письменности и книги, изд. «Ис-
кусство», 1955, стр. 24.
6
целей китайцы стали вместо
дерева употреблять бронзу и
камень. Приблизительно в
период Северных и Южных
династий текст книги высе-
кался на камне и затем пере-
печатывался на бумагу. Этот
процесс послужил началом
развития литографии, т. е.
способа печатания с плоской
поверхности камня, на кото-
рую предварительно нано-
сился рисунок.
Способ печатания под-
вижными литерами также
был впервые применен в Ки-
тае. Изобретателем этого
способа является выходец из
простого народа — кузнец
Би Шен (XI в.). В Китай- Рис. 2. Китайский сейсмограф,
ской энциклопедии XV в. о
нем сказано следующее: «Он
брал вязкую глину и вырезывал на ней письменные зна-
ки, такие, как край монеты, и для каждого знака изготов-
лял отдельную литеру, обжигал ее на огне, чтобы сде-
лать ее твердой» L
При печатании подвижными литерами Би Шэн поль-
зовался кассами, в которых содержались в определенном
порядке несколько тысяч литер, каждая из которых со-
ответствовала отдельному слову.
5. Спидометр — прибор, указывающий скорость и
пройденное расстояние. Первый спидометр, изобретенный
китайцами, служил для определения пройденного рас-
стояния. Принцип действия его был такой: когда тележ-
ка измерителя проходила одно ли (576 м), деревянные
фигурки, установленные на ней, ударяли в барабан; для
передачи движения от колес тележки к фигуркам ис-
пользовались зубчатые колеса (рис. 3).
6. Порох. Китайцы первыми научились использовать
селитру для изготовления пороха. Порох они применяли
1 Е. И. Кацпржа к, История письменности и книги, изд. «Ис-
кусство», 1955, стр. 45.
7
в X в. при изготовлении ракет для фейерверков. В начале
XV в. китайцы стали употреблять порох для стрельбы.
В Европе с порохом ознакомились лишь только в начале
XIV в.
7. Фарфор. Китай — родина фарфора. К сожале-
нию, время его изобретения и имя изобретателя до сих
пор еще не установлены. Однако имеется два предполо-
жения: согласно одному — фарфор изобретен около
VII в. до н. э., согласно другому — это изобретение от-
носится ко времени Хань, т. е. к III в. до н. э.
Уже в I в. н. э. китайский фарфор стал проникать в
соседние государства.
В VII в. н. э. через порт Кантон начался вывоз фар-
фора в Индию и Персию.
В XII в. китайский фарфор был завезен в Европу.
В середине XVIII в. после долгих напрасных попыток ев-
ропейцам, наконец, удалось раскрыть секрет производ-
ства китайского фарфора.
«Таким образом, — говорит Н. А. Фигуровский, — в
области производства фарфора человечество является в
Рис. 3, Тележка для измерения пройденного расстояния*
8
полном смысле слова учеником китайского наро-
да» Ч
Известно также, что Китай — родина производства
шелка, замечательных красителей и лаков.
Но это далеко не все. Уже в глубокой древности ки-
тайцы вели систематические наблюдения за небом, за по-
ложением и движением небесных светил.
В VII в. до н. э. китайские астрономы умели предска-
зывать солнечные и лунные затмения и установили их
периодичность повторения.
В IV в. до н. э. китайскими астрономами Гань Дэ и
Ши Шэнь был составлен первый в мире звездный ка-
талог, в котором дано описание 800 звезд (каталог Гип-
парха).
Примерно за 600 лет до н. э. в Китае продолжитель-
ность года считалась равной 365V4 дням.
К началу нашей эры китайские ученые изучили дви-
жение планет Меркурия, Венеры, Марса, Юпитера, Са-
турна и знали периоды их обращений.
До настоящего времени сохранился большой камень,
на котором китайские астрономы в 1193 г. до н. э. нанес-
ли 1140 звезд. Это была первая, нам известная, своеоб-
разная карта звездного неба. Свои наблюдения китайские
астрономы проводили в специально оборудованных, об-
серваториях, оснащенных остроумными астрономиче-
скими приборами, с помощью которых можно было на-
блюдать высоты небесных тел над горизонтом, опреде-
лять расположение светил относительно меридиана об-
серватории и т. д. Древним памятником китайской астро-
номии является в настоящее время Пекинская обсерва-
тория (общий вид дан на рис. 4) с ее оборудованием
(рис. 5, 6, 7), построенная в 1729 г. н. э. на окраине го-
рода Пекина.
В XV—XVI вв. в Китае наблюдается рост городов и
новой техники, в частности, производились большие ра-
боты в области орошения.
Об объеме китайской культуры в древности можно су-
дить Хотя бы по китайскому энциклопедическому слова-
рю, составленному в XV в. и состоящему из 11095 книг.
1 Н. А. Ф и г у р о в с к и й, Химия в древнем Китае и ее влия-
ние на развитие химических знаний в других странах. Сб. статей
«Из истории науки и техники Китая», изд. АН СССР, М., 1955,
стр. 126.
9
Рис. 4. Общий вид пекинской обсерватории.
Наряду с другими науками древнекитайский народ
занимался и вопросами философии. Ученые древнего Ки-
тая на основе растущих знаний в области естественных
Рис. 5. Секстант.
наук старались проник-
нуть в тайны природы и
объяснить их.
Так, в древних китай-
ских книгах «Го юй» и
«Цзо чжуань» говорится,
что первоэлементами
окружающего мира явля-
ются материальные суб-
станции: вода, огонь, дере-
во, металл и земля.
В древнем Китае во
второй половине первого
тысячелетия до нашей эры
было распространено фи-
лософское учение о «дао»,
которому в известной сте-
пени присущ наивный ма-
териализм и стихийно-ди-
алектический взгляд на
мир. Основоположник это-
10
го учения Лао-цзы (родил-
ся около 604 г. до н. э.)
считал, что жизнь идет не
по велению какого-то бо-
га, а по естественнонауч-
ным путям — дао. «Че-
ловек, по его мнению, сле-
дует земле. Земля следует
небу. Небо следует дао,
а д а о следует естествен-
ности» Ч
Жизнь, учил этот фи-
лософ, есть всепобеждаю-
щая сила естественности
самих вещей. Основу ми-
ра составляет всеобщий
закон дао, находящийся
среди хаоса вещей с не-
которой материальной
субстанцией ц и.
Согласно закону дао:
1) В мире нет ничего
Рис. 6. Эклиптический теодолит.
постоянного, все движется и
изменяется, переходя в свою противоположность.
2) В процессе бесконечного изменения новое всегда
преодолевает препятствие на своем пути, так как «в мире
самые слабые побежда-
ют самых сильных».
3) Мир подобен «та-
инственному соседу, к
которому нельзя при-
коснуться». «То, что
сжимают, расширяется.
То, что ослабляют,
укрепляется».
Учение Лао-цзы про-
тиворечиво. В нем есть
элементы прогрессив-
ные и консервативные.
Из его учения, напри-
1 Ян Хи н-ш у н, Из
истории китайской филосо-
фии, изд. «Знание», М.,
1955, стр. 6.
Рис. 7. Квадрант»
11
мер, логически вытекает теория пассивности и примире-
ния, так как, кто нарушит закон, тот «погибнет раньше
времени».
«Несмотря на свою историческую ограниченность,—
пишет Ян Хин-шун, — учение Лао-цзы сыграло в исто-
рии философии и культуры Китая прогрессивную роль.
Основная заслуга Лао-цзы состоит в том, что он, про-
тивопоставляя «небесной воле» закон дао, в условиях
древнего Китая впервые выдвинул гениальную догадку
о существовании всеобщего закона мира, отражающего
сущность самой природы» Ч
Активным борцом против мистики и идеализма свое-
го времени выступал выдающийся китайский материа-
лист I в. н. э. В а н Ч у н. Он считал, что мир материален
и управляется естественными законами. Человек, как и
вся природа, так же материален и состоит из той же ма-
териальной субстанции ц и. Жизнь человека сменяется
смертью, причем не может быть и речи о бессмертии ду-
ши. Наши знания составляют единство опыта и резуль-
тата.
Философское учение Ван Чуна явилось кульминаци-
онным пунктом развития материалистической традиции
в древнем Китае и оказало большое влияние на развитие
материализма в Китае в последующие века.
1 Я н X и н-ш у н, Из истории китайской философии, изд. «Зна-
ние», М., 1956, стр. 7.
(HIS?*------------- "“^Г=
ГЛАВА ВТОРАЯ
РАЗВИТИЕ АРИФМЕТИКИ И АЛГЕБРЫ
В ДРЕВНЕМ КИТАЕ
§ 1. КИТАЙСКИЕ СЧЕТЫ — СУАН-ПАН
Среди замечательных китайских изобретений по ма-
тематике прежде всего назовем китайскую счетную доску
«суан-пан» для быстрого счета и скорого выполнения
четырех арифметических действий с большими числами
вплоть до одиннадцатизначных. Изобретение суан-пана
относится к глубокой древности, полагают, что он яв-
ляется прообразом многих позднейших счетных дощатых
приборов, в том числе и наших конторских счетов. Суан-
пан, по-видимому, был в ходу тогда, когда люди еще не
пришли окончательно к десятичной системе счисления
и пользовались смесью
пятеричной системы и де-
сятеричной. Об этом го-
ворит само устройство
этого прибора. А конст-
рукция его довольно про-
ста. Как и наши счеты, он
состоит из деревянной ра-
мы, поперек которой го-
ризонтальными рядами
протянуты шнуры (прово-
локи). Далее, вдоль всей
рамы в вертикальном на-
правлении идет перего-
родка, через которую и
проходят шнуры и кото-
рая делит раму на две
неравные части, имеющие
форму прямоугольника,
причем левая шире, а пра-
вая уже (рис. 8).
Рис. 8.
13
На каждом шнуре надето семь шариков, из которых
пять находятся слева от перегородки, т. е. в широкой ча-
сти, а два — справа, т. е. в узкой части. Всего в суан-пане
десять-одиннадцать горизонтальных линий (шнуров).
Нижняя линия служит для откладывания единиц и пят-
ков, вторая — для десятков и полсотен, третья — для со-
тен и полутысяч и т. д. Поэтому стоит только набрать
пять косточек на нижней линии, как их надо сбросить и
заменить одной из двух косточек, расположенных справа
от перегородки. В свою очередь, как только наберется
этих пятерных косточек две, они сбрасываются и заменя-
ются простой косточкой на следующей высшей линии
и т. д. При счете шарики сдвигаются к продольной пере-
кладине. Например, на чертеже (рис. 8) отложено число
27 091.
В XVI в. китайский суан-пан был заимствован япон-
цами с небольшой модификацией, а именно справа от
перегородки они брали не два шарика, а всего только
един (рис. 9). Действительно, если внимательно поду-
мать, второй шарик справа от продольной перегородки,
собственно, и не нужен. Без него можно обойтись. Япон-
цы называют свой счетный прибор «сорубаном».
Что касается русских счетов, то они построены на не-
сколько ином принципе и выражают десятичную систему
счисления в чистом ее виде.
Мы часто говорим «скостить», «сбросить со счета»,
«сводить счеты», «прикидывать», «скидка», «накидка»
и т. д. Все эти обороты нашей речи появились очень давно
в результате частого использования счетов в процессе
трудовой деятельности русского народа.
Рис. 9.
14
Западная Европа стала пользоваться русскими счета-
ми совсем недавно, после того как их завез во Францию
знаменитый французский математик Понс еле (1788—
1867), который был в России в 1812 г. в качестве плен-
ного офицера.
Сначала во Франции, а потом и в других государст-
вах Западной Европы русские счеты стали широко упот-
ребляться в школах как наглядное пособие при обучении
арифметике.
§ 2. ДРЕВНЕКИТАЙСКИЙ ТРАКТАТ
«МАТЕМАТИКА В ДЕВЯТИ КНИГАХ»
Одним из древнейших китайских трактатов, дошед-
ших до нас, является «Математика в девяти книгах»
(«Цзю чжан суань шу»). Он был составлен не позднее
первого века начала нашей эры и много раз перераба-
тывался. Последняя значительная переработка с коммен-
тариями, выполненная математиком Лю Хуэем, отно-
сится к 263 г.
Написан трактат на малодоступном древнекитайском
языке, который представляет большие трудности для
чтения и перевода. На русском языке трактат частично
опубликован в 1957 г. в сборнике «Историко-математиче-
ские исследования», т. X, в переводе и с комментариями
Э. И. Березкиной.
«Математика в девяти книгах» является одной из пер-
вых китайских математических энциклопедий для земле-
меров, инженеров, астрономов и людей других профес-
сий.
Изложение трактата догматическое. Он состоит из
большого количества задач и правил к ним. Правила да-
ются сразу в готовом виде без доказательства и пояс-
нительных чертежей.
Трактат состоит из девяти довольно самостоятельных
книг, мало связанных между собой. Каждая книга долж-
на содержать в себе весь материал, посвященный какой-
либо теме.
Рассмотрим содержание трактата по книгам.
Первая книга. Измерение полей. Содержит зада-
чи на вычисление площадей полей, имеющих форму пря-
моугольника, треугольника, трапеции, круга, сектора,
сегмента и кольца.
15
Задачи расположены под такими заголовками:
1. Измерение поля (2 задачи).
2. Измерение поля в ли (2 задачи).
3. Сокращение дробей (2 задачи).
4. Сложение дробей6 (3 задачи).
5. Вычитание дробей (2 задачи).
6. Сравнение дробей (3 задачи).
7. Уравнение дробей (2 задачи).
8. Деление дробей (2 задачи).
9. Умножение дробей (3 задачи).
10. Общее измерение полей (3 задачи).
И. Измерение полей различной формы (14 задач).
Площадь прямоугольника и трапеции вычисляется по
правилам, которые мало отличаются от современных.
Правило:
Площадь круга и его части определяются при я = 3.
Общий наибольший делитель числителя и знамена-
теля, на который можно сократить дробь, древние ки-
тайцы находили с помощью особого алгоритма, который
по существу совпадал с алгоритмом Евклида (отличает-
ся от него только арифметической формулировкой).
Вторая книга. Соотношение между различными
видами зерновых культур («Су ми»). Здесь рассматрива-
ются задачи на «тройное правило», согласно которому
по трем заданным величинам определяется четвертая
пропорциональная. Книга содержит 46 задач.
Задачи даны под следующими заголовками:
1. Правило соотношения между различными видами
зерновых культур.
2. Расчет стоимости предмета.
3. Расчет, когда имеются разного рода предметы.
4. Расчет стоимости предмета каждого вида в отдель-
ности на одну монету.
В этой книге даются, например, правила для опреде-
ления цены на рис и просо, учитывая их качество и сорт.
Третья книга. Деление по ступеням («Чуй фэнь»).
Книга состоит из 20 задач и правил к ним. Начинается
она с задач на пропорциональное деление и содержит за-
дачи на простое и сложное правило.
Задачи даны с такими подзаголовками:
1. Деление по ступеням.
2. Распределение, обратное ступеням.
Здесь даны примеры деления имущества между не-
16
сколькими лицами, причем у некоторых задач числен-
ные соотношения между частями выражаются арифмети-
ческими прогрессиями.
Четвертая книга носит трудно переводимое на-
звание: Шао гуан. По-видимому, это специальный термин,
по смыслу означающий уменьшение одной из сторон пря-
моугольника с соответствующим увеличением другой,
причем площадь его остается неизменной. Книга начи-
нается с решения задач на вычисление одной из сторон
прямоугольника, если даны площадь и другая его сторо-
на. Книга заканчивается рассмотрением задачи на вы-
числение диаметра сферы при заданном ее объеме. Эта
книга содержит 24 задачи.
О характере задач можно судить по заголовкам, под
которыми они размещаются. Вот они:
1. Правило «Шао гуан».
2. Извлечение квадратного корня.
3. Извлечение квадратного корня из площади круга.
4. Извлечение кубического корня.
Книга знакомит читателя с древнейшими китайскими
алгоритмами на вычисление квадратных и кубических
корней. Распространяя этот метод на полное квадратное
и кубическое уравнения, можно прийти к так называемо-
му методу Руффини — Г орнера.
Пятая книга. Оценка работ («Шан гун»). Книга
содержит 28 задач. Все они практического содержания и
посвящены вычислению объемов параллелепипедов, пол-
ных и усеченных пирамид, цилиндров, обелисков и не-
которых призматических тел. Так, например, задача
27 формулируется так:
«Имеется амбар. Ширина 3 чжана, длина 4 чжана
5 чи; наполняющее его просо составляет 10 000 ху. Спра-
шивается, какова высота амбара»?
Приводится ответ: 2 чжана — и дается правило:
«Установи, что количество чи в 10 000 ху проса, ссыпан-
ного в амбар, есть делимое. Перемножь ширину и длину,
это делитель. Делимое и делитель объедини (т. е. пред-
ставь в виде дроби) —получишь высоту в чи».
Шестая книга. Пропорциональное распределение
(«Цзюнь шу»). Книга содержит 28 задач, среди которых
первые четыре задачи на пропорциональное распределе-
ние налога. В этой книге, так же как и в третьей книге,
имеются задачи на пропорциональное деление, на про-
2 Заказ 999
17
стое и сложное тройное правило, только с более услож-
ненными условиями и требующее довольно больших вы-
числений. В этой книге встречаются прогрессии и эле-
менты приближенных вычислений, основанные на округ-
лении чисел.
Так, в качестве примера на арифметическую прогрес-
сию может служить задача о бамбуке из девя-
ти колен.
«Имеется бамбук из девяти колен. Объем трех
нижних колен 4 шэна, четырех верхних колен 3 шэна.
Спрашивается, каковы объемы двух средних колен,
если объем каждого колена отличается от соседних
на равную величину.»
29
Ответ. Самое нижнее колено 1— шэна, следующее
66
.22 .15 «в
1 — шэна, следующее 1— шэна, следующее 1 —шэна, сле-
66 66 66
. 1 60 53
дующее 1 — шэна, следующее —шэна, следующее— шэ-
66 66 66
46 39
на, следующее - - шэна, следующее — шэна.
ио 66
Для решения этой задачи составитель трактата при-
водит правило: «4 шэна, разделенные на 3 нижних ко-
лена, составляют нижний коэффициент. 3 шэна, разде-
ленные на 4 верхних колена, составляют верхний коэф-
фициент. Из большого нижнего коэффициента вычти
верхний меньший, остаток есть делимое. Сумму половин
4 колен и 3 колен вычти из 9 колен, остаток является де-
лителем. Объедини делимое и делитель — получишь иско-
мое количество в шэнах, т. е. на столько отличается каж-
дая ступень от соседней. Нижний коэффициент, т. е. 1 с
малой половиной шэна, есть объем второго снизу колена».
Согласно этому правилу можно провести и сами не-
сложные вычисления:
4 3 7
1)------= — — разность между «верхним» и «нижним
3 4 12
коэффициентами», что составляет делимое.
2) 9 — -— —= —— составляет делитель.
2 2 2
3) — : — = —= d, т. е. то число, на какое отличается
12 2 66
каждая ступень от соседней.
18
4 1
4) Тогда восьмое колено будет составлять--= 1—шэна.
О о
Теперь без труда можно в шэнах найти и другие
восемь колен.
Седьмая книга. Избыток — недостаток («Ин бу
цзу»). Состоит из 20 задач алгебраического содержания.
Все они приводят к тому или иному уравнению с одним
неизвестным или к системе двух линейных уравнений с
двумя неизвестными. В трактате они решаются преиму-
щественно «правилом двух ложных положений».
Показательны в этом отношении задачи 18 и 19.
Задача о слитках золота (№ 18).
«Имеется 9 слитков золота и 11 слитков серебра, их
взвесили, вес как раз совпал. Переложили слиток зо-
лота и слиток серебра, золото стало легче на 13 ла-
нов. Спрашивается, каков вес слитка золота и слитка
серебра, каждого в отдельности.»
Составитель трактата приводит ответ: вес слитка
золота 2 цзиня 3 лана 18 чжу, вес слитка серебра 1 цзинь
13 ланов 6 чжу. Задачу рекомендует решать по такому
правилу; «Предположим, что вес слитка золота 3 цзиня,
тогда вес слитка серебра 2— цзиня, недостаток равен
49 в правой строке. Предположим, что вес слитка золо-
та 2 цзиня, тогда вес слитка серебра 1~ цзиня. Избы-
ток 15 в левой строке. Каждый знаменатель умножь на
количества, содержащиеся в этих строках. Избыток и не-
достаток умножь крест-накрест на предположенные нор-
мы, сложи; это делимое. Сложи избыток и недостаток;
это делитель. Объедини делимое и делитель — получишь
вес слитка золота. Знаменатель умножь на делитель, раз-
дели на него делимое — получишь вес слитка серебра.
Сократи — получишь искомую дробь».
Самого решения в трактате не дается. Их нет, как
указывалось выше, и ко всем другим задачам. Руководст-
вуясь приведенным правилом, решение задачи можно вы-
полнить при помощи таких рассуждений.
Прежде всего заметим, что 1 цзинь = 16 ланам а
1 лан = 24 чжу. Обозначим теперь вес слитка золота че-
2*
19
рез х, а вес слитка серебра через z, задача сводится к
решению системы:
(9х = Hz
|13 + 8х + г = 10z + х.
Будем решать эту систему правилом двух ложных поло-
жений:
Первое ложное положение: х1 = 3 цзи-
ням.
9х, 9-3 27 п 5 , х
z, = — = — = —=2— (цзиня).
11 11 11 И
Находим теперь «недостаток в первой строке», который
обозначим через у1:
У! =(-+8 3 + 2—W10 • 2-+ S'U 27 —-----
1 \16 П/ \ Н / 1Ы6
о7 96 __ 49
11-16 1116 ’
Второе ложное положение: х2=2 цзиням.
В этом случае z2=l цзиня и «избыток в левой строке»
будет
у2 = (^+ 1- + 8 • 2 V (10 • 1 - + 2^= 18 —--
\1б 11 1 ) \ 11 ) 11-16
_ 18_64_ =J5_.
11-16 11-16
Далее предполагается, что у1 и у2 вместе с хг и х2 записа-
ны по китайскому способу:
Х1
У2 У1
где левая колонка составляет по-китайски «левую строку»,
а правая колонка — «правую строку».
Применяя к этой таблице правило, получаем:
о. 49 3 15
11-16 ’11-16 2-494-3-15 143 о15 , ч
---------------------- =-------!----=----= 2— (цзиня).
49 15 494-15 64 64 V
11 -16+ 11-16
49+15
Следовательно,
х = 2 цзиня 3 лана 18 чжу.
20
Вес слитка серебра определяется очень просто. Для этого
делимое 143 надо разделить на произведение делителя 64
и знаменателя —. Тогда получаем:
9
X 143 13-9 117 .53, .
2 = — = -22—=------=----= 1 — (цзиня).
11 11 64 64 64
— —.64
9 9
Следовательно, окончательно: z = 1 цзинь 13 ланов 6 чжу.
Задача о рысаке и кляче (№ 19):
«Рысак и кляча движутся от Чанъаня к княжест-
ву Ци, которое удалено от Чанъаня на 3000 ли. В пер-
вый день рысак пробегает 193 ли, каждый следующий
день пробегает на 13 ли больше. Кляча в первый день
пробегает 97 ли, каждый последующий день пробега-
ет на половину ли меньше. Рысак первым достиг кня-
жества Ци, повернул обратно и в некотором месте
встретил клячу. Спрашивается, через сколько дней
они встретятся и сколько ли пробежит каждая ло-
шадь.»
Ответ: Встретятся через 15 у|удня, рысак пробежит
4534—ли, кляча пробежит 1465— ли.
191 г 191
Составитель трактата для решения этой задачи пред-
лагает такое правило: «Предположим, что через
15 дней, тогда недостаток равен 337 с половиной ли.
Предположим, что через 16, тогда избыток равен 140 ли.
Избыток и недостаток умножь крест-накрест на предполо-
женные количества, сложи; это делимое. Сложи избыток
и недостаток; это делитель. Объедини делимое и дели-
тель— получишь искомое количество дней. Если разде-
лится не до конца, то сократи на общий делитель и обоз-
начь делитель».
За п целых дней рысак пробежит:
193-Ц1934-13)4-(1934-2 • 13)4-...4- 11934-(л—1)13]=
= 193п4-134-2 • 134-...4-(п—1)13=
= 193п +13[ 14-24-...+(п-1) J = 193п4-13-п и).
21
За это же число дней кляча пробежит:
97+ (97—1)+ (97—21) +...+(97 — (n— 1 )1) =
=97п — 1 П+2+ ..+(п—1)]=97л— 1 п(п~1) (ли).
2 2 2
За указанное число дней рысак и кляча пробегут вместе:
193п + 13 - (n~1)+97n—
2 2 2
=290п+(13—1)”-(^~1>. =290п+б1(п2—п) (ли),
что должно составить 6000 ли.
Далее, придерживаясь указанного выше правила, за-
дачу продолжаем решать методом двух ложных положе-
ний.
При п = 15 недостаток равен 6000— 5662y=337-i- (ли);
при п = 16 избыток составляет 6140 — 6000 = 140 (ли).
Обозначая время встречи через х и предполагая, что
на протяжении дня скорости не менялись, получим:
15-140+ 16-337 1
х =-----------j—~15+т(дней)-
140+337 — ,У1
Теперь не составляет большого труда найти, сколько
ли пройдут рысак и кляча за 15—дней.
Из анализа решения последней задачи видно, что со-
ставитель трактата должен владеть формулой суммирова-
ния арифметической прогрессии:
1+2+3+...+л=1±^,
2
хотя в самом трактате она и не упоминается.
Восьмая книга. Китайское название этой книги:
Правило «Фан чэн». Книга содержит 18 задач на Состав-
ление определенных и неопределенных систем линейных
уравнений, решаемых китайским правилом «фан чэн», во
22
многом напоминающим известное правило Крамера, на-
званное в честь швейцарского математика Г. К р з м е р а,
который в 1750 г. дал общие формулы, выражающие не-
известные через определители, составленные из коэффи-
циентов системы. В книге рассматриваются только сов-
местные системы и объектом рассмотрения являются ис-
ключительно положительные корни. Хотя китайские уче-
ные свободно пользовались отрицательными коэффици-
ентами, отрицательных корней они не рассматривали,
считали их невозможными. Специалисты считают, что
восьмая книга является вершиной, которой достигла в
своем развитии математика Китая к началу нашей эры
(см., например, статью Э. И. Б е р е з к и н о й «О «Матема-
тике в девяти книгах», «Историко-математические иссле-
дования», вып. X, ГИТТЛ, М, 1957, стр. 434).
В качестве примера приводим следующую задачу этой
книги.
Задача о буйволах и баранах (№7):
«5 буйволов и 2 барана стоят 10 ланов, 2 буйвола
и 5 баранов стоят 8 ланов золота. Спрашивается,
сколько стоят буйвол и баран.»
13
Ответ. 1 буйвол стоит 1— ла на золота,
20
1 баран стоит — лана золота.
Эта задача решается правилом «фан чэн», с которым
мы познакомимся несколько позднее (глава III, §1).
Очевидно, вопрос сводится к системе уравнений:
( 5х + 2у=10
( 2х+5у= 8
Девятая книга (последняя). Соотношение между
катетами и гипотенузой в прямоугольном треугольнике
(правило «Гоу гу»). Она содержит 24 геометрические за-
дачи, решаемые на основании теоремы Пифагора и
свойств подобных прямоугольных треугольников. Как
правило, эти задачи в конечном счете приводят к реше-
нию уравнений второй степени с одним неизвестным. В
книге имеются задачи ( № 14, 21) на отыскание пифаго-
рейских чисел путем решения в целых числах уравнения
23
x2 4-f/2 = z2, а также задачи (№ 22—24) на вычисление
расстояний до недоступных предметов (см. V гл.)
По мнению проф. А. П. Юшкевича, после матема-
тики древнего Вавилона это первое исторически засвиде-
тельствованное широкое применение числовой алгебры в
измерительных задачах геометрии. Позднее, подчеркива-
ет он, с таким применением алгебры мы встречаемся в
Индии, а затем в сочинениях Средней Азии, Ирана и
Ближнего Востока, написанных преимущественно на
арабском языке (см. по этому вопросу А. П. Юшкевич,
О достижениях китайских ученых в области математики.
«Историко-математические исследования», вып. VIII,
ГИТТЛ, М, 1955, стр. 544—545).
§ 3. СТАРИННЫЙ КИТАЙСКИЙ ТРАКТАТ
«ДЕВЯТЬ ОТДЕЛОВ ИСКУССТВА СЧЕТА»
Это сочинение, написанное в середине XIII в. (около
1247 г.), представляет собой комментарии к более древ-
нему трактату VIII в. под названием «Таен лйн-шу». Ав-
тором этих комментариев является выдающийся китай-
ский математик Ц и н ь Ц з ю-ш а о.
Сочинение состоит из двух частей, из которых первая
посвящена математике (на ней мы и остановимся), а вто-
рая преимущественно астрономии и физике.
Первая часть, как показывает само название тракта-
та, состоит из 9 отделов. Рассмотрим содержание этой
замечательной книги.
Отдел первый содержит применение числовых
символов к предсказанию будущего.
Отдел второй посвящен приложению арифметиче-
ских правил к различного рода астрономическим вычис-
лениям.
Отдел третий заключает решение ряда задач на
вычисление различных работ. В частности, здесь приво-
дится такая задача:
«Четыре артели рабочих, состоящая каждая из из-
вестного, но неодинакового числа лиц, строят плотину.
Известен объем выполненной ими сообща работы.
Требуется определить количество работы, выполнен-
ной каждой артелью в отдельности».
Отдел четвертый занимается решением задач,
относящихся к вычислению капиталов. Здесь при реше-
24
нии многих вопросов применяются правила вычисления
процента и учета денег.
Отдел пятый содержит решение такой задачи:
«Три лица имеют по одинаковому количеству пшени-
цы, купленной в различных местах, в различных мерах.
Требуется определить количество пшеницы в единых
мерах».
Отдел шестой посвящен решению задачи:
«Из данного места выступили три полка в столицу;
известно число миль, пройденное каждым полком в день,
а также известны часы прихода полков в столицу. Тре-
буется определить расстояние места выхода полков от
столицы».
Отдел седьм-ой дает решение задачи о курьерах,
едущих с различной скоростью. В задаче требуется опре-
делить место их ночлега.
Отдел восьмой приводит решение задачи:
«Определить размеры фундамента здания, построен-
ного из четырех родов кирпичей, величина которых зави-
сит от желания строителя. Величина кирпичей дается».
Отдел девятый рассматривает решение задачи
о похищении риса тремя ворами. Задача формулируется
так:
«Из трех бочек риса одинаковой емкости похищено
тремя ворами некоторое количество риса. Общее
количество его было неизвестно, но выяснилось, что в
первой бочке остался 1 го риса, во второй— 1 шинг
4 го и в третьей — 1 го. Пойманные воры показали:
первый, что он отсыпал рис из 1-й бочки при помощи
лопаты, второй, что он пользовался деревянным баш-
маком, а третий — миской, причем они соответствен-
но брали из 2-й и 3-й бочек. Лопата, башмак и миска
найдены на месте преступления. При обмере их ока-
залось, что емкость лопаты 1 шинг 9 го, башмака —
1 шинг 7 го, миски — 1 шинг 2 го. Требуется узнать,
сколько похитил каждый вор. При этом известно, что
10 го=1 шингу, 10 шингов=1 тау, 10 тау=1 ши».
Эта задача на неопределенное уравнение, которое на-
до решать в целых числах.
В современных обозначениях задача решается так:
Пусть х — число, выражающее, сколько раз отсыпали
рис лопатой,
25
у — число, выражающее, сколько раз отсыпа-
ли рис башмаком,
z — число, выражающее, сколько раз отсыпали
рис миской.
Тогда условия задачи приводят к системе уравнений:
19x4-1 = 17^+14= 12z+ 1.
Откуда получается неопределенное уравнение:
19x=12z;
х = *2£.
19
Поскольку х, у, z суть целые числа, можно положить,
что
z = 19/.
Тогда получаем неопределенное уравнение:
17у + 13 = 228/.
Беря для / наименьшее целое значение, при котором у
будет целым, т. е. /= 14, получим:
х= 168
у = 187
z = 266.
Следовательно, первый вор похитил 3 ши 1 тау 9 шин-
гов 2 го второй — 3 ши 1 тау 7 шингов 9 го и третий —
3 ши 1 тау 9 шингов 2 го.
Книга «Девять отделов искусства счета» замечатель-
на тем, что в ней не намеками, как в математических ра-
ботах более отдаленных времен, а в развернутом виде
объясняется «метод небесного элемента», который состав-
ляет крупнейшее достижение древних китай-
ских математиков,
«Небесным элементом» китайцы называли неизвест-
ную величину «Метод небесного элемента» — это уни-
версальный китайский алгоритм отыскания корней цело-
го алгебраического уравнения вида f(x) = 0. Этим мето-
дом китайские математики решали квадратные и кубиче-
ские уравнения, а также уравнения более высоких сте-
пеней.
Сущность метода довольно простая.
26
Пусть требуется найти корень уравнения f(x) — О,
тогда согласно этому методу поступают так:
Шаг первый. Находят при помощи подбора пер-
вую цифру искомого корня уравнения f(x) = 0, пусть она
будет р.
Шаг второй. В данное уравнение[(х) делают под-
становку х = р + у и получают вспомогательное уравне-
ние:
ф(«/)=0.
Шаг третий. Снова при помощи подбора находят
первую цифру корня уравнения у(у), пусть она будет q,
что составляет вторую цифру корня х для исходного урав-
нения f(x).
Шаг четвертый. В уравнение <?(у) делают под-
становку
{/=<?+з
и получают вспомогательное уравнение
ф(з) = 0.
И т. д.
Этот процесс продолжают до тех пор, пока не будет
найдена целая часть корня Ч
Для автоматического нахождения коэффициентов
вспомогательных уравнений китайцы изобрели очень
удобную и вместе с тем простую схему, которая не тре-
бует знания общей формулы бинома Ньютона для целых
положительных чисел.
Поясним сказанное на примере. Пусть
f(x) = а4*4 + вз*3 + + с^х + а0 = 0.
Предположим теперь, что р — это первое число иско-
мого корня х, тогда после подстановки х = р + у в дан-
ное уравнение получим вспомогательное уравнение:
ф(У) = А^ + 4- Ао = 0.
1 Продолжением этого процесса можно найти и дробную часть
корня, однако этой детали в старинной китайской математической
литературе не обнаружено.
27
Для автоматического вычисления коэффициентов Ло,
Alf А2, А3, А4 служит следующая «китайская схема»:
а4+а'"3 а\=А2
____________
Д4 <73 Л3
Д4~^4
Пользуясь «методом небесного элемента» и приведен-
ной только что «китайской схемой» для коэффициентов
вспомогательных уравнений, Цинь Цзю-шао удалось для
уравнения четвертой степени
—х4+763200х1 2— 40642650000 = 0
найти его целый корень х = 840. Однако выкладки этих
вычислений получились очень громоздкими, и мы на них
не останавливаемся.
Для иллюстрации «метода небесного элемента» вме-
сте с его «китайской схемой» рассмотрим пример извле-
чения кубического корня из 17 576 или, что то же, реше-
ние кубического уравнения Ч
х3—17 576=0.
Путем подбора находится число десятков корня, что
составляет 2. Следовательно,
х=204-£/.
Далее, подставляя значение х в данное /кубическое
уравнение, получаем вспомогательное уравнение
T(0)=VW+4y +А>-
1 Этот пример позаимствован из статьи А. П. Юшкевича «О до-
стижениях китайских ученых в области математики, стр. 552. При-
мер принадлежит китайскому математику XIII в. Чжу Ши-цзе и на-
ходится в его трактате «Введение в математикуэ (1299).
28
Для определения коэффициентов Ао, Alf Л2, А3 соста-
вляем «китайскую схему»:
1+/0 .(0 (-17576
1 И1-20 И20 20 440Q.20
il/20 ./400— 957б=А
А~П1 • 20 440 20
, >/40 1200=Д
1 И 1 • 20
1 60= л2
1=Дз
Откуда вспомогательное уравнение
ф(у)=У3+60у1 2+1200//—9576= 0.
Оно и служит для определения единиц корня.
Путем подбора устанавливаем, что 6 является точным
корнем уравнения
ф(у)=0, т. е. <р(6)=0.
Следовательно, искомый корень
х = 26.
«Метод небесного элемента», открытый китайцами
еще в VII в., по существу и по форме совпадает с изве-
стным методом и схемой Горнера для приближенного вы-
числения действительных корней алгебраических уравне-
ний любой степени с числовыми коэффициентами, откры-
тыми английским математиком Горнером в 1819 г. L
1 Считая открытие «метода небесного элемента» китайскими уче-
ными как крупнейшее завоевание китайской науки, А. П. Ю ш к е-
в и ч пишет, что позднее «такой же прием мы встречаем в примене-
нии к извлечению корней любой степени из чисел в «Ключе к ариф-
метике» самаркандского математика и астронома Джемшида Гияссэд-
дина ал Каши, написанном в 1427 г. В Европе сходный с «методом
небесного элемента» прием был вновь предложен знаменитым
Ф. Виет ом, опубликовавшим его в 1600 г. Однако прием Виета
был громоздок, ибо Виет не располагал схемой вычисления вспо-
могательных коэффициентов. Способ Виета был вытеснен в конце
XVII в. более удобным методом Ньютона (также использовавшим
линейную подстановку вида х — у + р), а в XVIII — XIX вв. были
созданы различные другие методы. Но в начале XIX в. метод небес-
ного элемента, включая схему вычисления коэффициентов, был вновь
открыт почти одновременно двумя учеными: итальянцем П. Р у ф-
фини (1804, 1813) и английским ученым У. Горнером (1819) —
29
Трактат «Девять отделов искусства счета» замечате-
лен еще и тем, что в нем довольно много места уделяется
н е о п р е д е л е н н о му анализу, т. е. решению неоп-
ределенных уравнений в целых числах.
В частности, здесь дается подробный анализ решения
знаменитой задачи Сунь-цзы, жившего не позднее III в.
Эта задача формулируется так:
«Найти число, которое при делении на 3 дает оста-
ток 2, а при делении на 5 дает остаток 3, наконец, при де-
лении на 7 остаток 2».
Сам Сунь-цзы решает свою задачу по такому пра-
вилу:
«При делении на 3 остаток есть 2, поэтому возьмите
140. При делении на 5 остаток есть 3, поэтому возьмите
G3. При делении на 7 остаток есть 2, поэтому возьмите
30. Сложив их вместе, получите 233. Из этого вычтите
210, и мы получим ответ»
Задача Сунь-цзы в «Девяти отделах искусства сче-
та» решалась довольно оригинальным методом, который
мало чем отличается от современного.
Изложим суть этого метода на современном языке
сравнений * 1 2.
Прежде всего сама задача запишется так:
х = /\ (mod qty
х = r8 (mod q2)-9
x = r3 (mod q3)t
где модули q19 q2t q3 — простые числа (в задаче Сунь-цзы
ri = 2, г2 = 3, г3 = 2, qY = 3, q2 = 5, q3 = 7). Сначала
находятся вспомогательные числа Nlt N2, с таким рас-
четом, чтобы они удовлетворяли сравнениям:
и под их именами получил широкое распространение. Так называемая
«схема Горнера» повсеместно используется ныне для деления много-
члена на двучлен и в ряде стран стала предметом школьного обуче-
ния» А П. Юшкевич, О достижениях китайских ученых в области
математики. «Историко-математические исследования», вып, VIII,
ГИТТЛ, М, 1955, стр. 554.
1 А. П. Юшкевич, О достижениях китайских ученых в обла-
сти математики. «Историко-математические исследования», вып. VIII,
ГИТТЛ, М., 1955, стр. 566.
2 Изложение решения задачи Сунь-цзы заимствовано из ст.
А. П. Юшкевича <0 достижениях китайских ученых в области ма-
тематики», «Историко-математ. исслед.», вып, VIII, стр. 556—557.
30
(mod qt);
. (mod 9г);
(mod q3).
Применительно к задаче Сунь-цзы будем иметь:
35Л^ = 1 (mod 3);
217V2=1 (mod 5);
157V3=1 (mod 7).
Откуда, используя известные свойства сравнений, полу-
чим:
2Л\=1 (mod 3);
JV2==1 (mod 5);
7V3=1 (mod 7).
Далее подбором определяется, что = 2, N2 = 1, N3=l.
Общей формулой для нахождения искомых чисел является:
x=(Nt q2q3rl+N2qlq^+N^ q2r3)(mod q^qj.
Следовательно,
x=(140+63+30)(mod 105),
что равносильно уравнению:
*=233—105/,
где / — любое число.
Полагаем / = 2, неизвестное х принимает наименьшее
положительное значение, равное 23, что и составляет ис-
комый ответ (следующее возможное число можно полу-
чить, например, при /= 1, что составит 128).
Необходимо заметить, что при решении задачи Сунь-
цзы можно, конечно, и не пользоваться языком сравне-
ний и решить ее элементарными приемами, которые изло-
жены в современных курсах элементарной алгебры (см.,
например, учебник алгебры, ч. II, А. П. К и с е л е в а,
Учпедгиз, 1953, стр. 164—176).
Действительно, задача Сунь-цзы сводится к системе:
х=Зу+2
x=5z+3
x=7u+2,
или
3i/+2=5z+3=7u+2.
31
Откуда находим:
3«/=7и, t/=^.
Полагая и=3/, где t—некоторое целое число, получим:
y=7t.
Тогда
х=21/+2.
Следовательно, будем иметь:
21/+2=5z+3,
или
21/—5z=l.
Путем подбора находим одну пару корней последнего не-
определенного уравнения:
t=l, z=4.
Общие формулы корней этого уравнения будут:
/=Ц-5<7,
z=4+21(7, где 7=0, 1, 2, 3,...
Так как
х=21/+2,
то
х=23+105(/, где q=0t 1, 2, 3,...
Наименьшее значение х будет при q=0t т. е.
х= 23; при <7=1 х=128; при q=2
х=233; при 7=3 х=338. И т. д.
Метод Сунь-цзы, широко применяемый Цинь Цзю-
шао в его «Девяти главах искусства счета», является так-
же величайшим достижением древней китайской мате-
матики.
Хотя метод Сунь-цзы долгое время не был известен
европейцам, однако его задача была им известна давно.
Так, эту задачу без решения буквально приводит италь-
янский математик XIII в. Леонардо Пизанский (Фиб-
боначчи) в своей работе «Книга об абаке» (1202). Эта же
задача была известна и в России, она встречается и в рус-
ских арифметических рукописях XVII в. L
Китайские математики XI—XIV вв. знали свойства би-
номинальных коэффициентов. Полная таблица биноми-
1 См. В. В. Бобынин, Очерки развития физико-математиче-
ских знаний в России, вып. I, М., 1886, стр. 117.
32
нальных коэффициентов до 8-й степени встречается у ки-
тайского математика Чжу Ци-цзе в 1303 г. в его трак-
тате «Зеркало четырех начал».
Таблица чисел, приведенная в этом сочинении, напи-
санная нашими цифрами, имеет форму:
1
1 1
1 2 1
13 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Правило составления этой таблицы было известно ки-
тайцам значительно раньше написания трактата, о чем
говорит сам Чжу Ци-цзе, называя это правило «старин-
ным методом».
В Европе таблица биноминальных коэффициентов по-
лучила широкую известность лишь в XVII в. в результа-
те работ французского математика и физика Паскаля
(1623—1662), почему она и носит название «треугольни-
ка Паскаля», хотя лучше и справедливее было бы назвать
ее «китайским треугольником».
Китайским ученым XI—XIII вв. принадлежат замеча-
тельные исследования по суммированию арифметических
рядов. Так, в XI в. на суммирование одного ряда интерес-
ную задачу решил китайский математик Шэн ь-к о. В за-
даче требовалось определить число предметов, составляю-
щих n-слойную усеченную пирамиду, если слои имеют
форму прямоугольников, обе стороны которых последова-
тельно увеличиваются сверху вниз на единицу.
Задача, как легко видеть, сводилась к суммированию
ряда:
oft+(a+l)(6+l)+...+ Ia+(n- 1)](Н-(п-1)1,
где ab составляет число предметов в верхнем слое.
Шэнь-ко для вычисления этой суммы без всякого до-
казательства предлагает следующее правило:
a6+(a+l)0+l)+...+ Ia+(n—1)][6+(п-1)]=
= - [а(26+В)+Л(2В+6)+(В—6)1,
6
3 Заказ 999
33
где
А = а+п—1; В=Ь+п—1.
Ученым Китая XIII в. хорошо были известны правила
вычисления суммы арифметической прогрессии и ряда
натуральных квадратов. Кроме того, они владели ориги-
нальными доказательствами этих правил Ч
Кроме того, на суммирование рядов им были, напри-
мер, известны следующие правила:
1) 1+3+6+.. .+5-Ц±1)=±л(п+1)(п+2);
2 6
Sn (п 1) (п+2) ।
6 =4; п(п+1)(п+2)(л+3);
° 24
1
п
3) £ n(n+l)(n+2)(n+3)=^ л(п+1)(п+2)(п+3)(л_|_4)
1
Были ли эти результаты оригинальными открытиями
китайских математиков? На этот вопрос определенного
ответа пока что не имеется. «В настоящее время,— гово-
рит А. П. Юшкевич,— мы можем только констатировать
сходство китайских и индийских исследований по сумми-
рованию указанных рядов, естественно наводящее на
мысль о тесной связи между соответствующими иссле-
дованиями ученых обоих народов. Вопрос о первенстве
в настоящее время остается открытым» 1 2.
§ 4. СТАРИННОЕ КИТАЙСКОЕ СОЧИНЕНИЕ
«НАЧАЛА ИСКУССТВА ВЫЧИСЛЕНИЯ»
Чтобы довести историю китайской математики до
XVI в., надо рассмотреть еще одно сочинение, написан-
ное самостоятельно китайцами и опубликованное ими в
1593 г. Это сочинение носит название «Начала искусства
вычисления». На заглавном листе книги имеется изобра-
1 См. об этом подробнее в статье А. П. Юшкевича «О достиже-
ниях китайских ученых в области математики». «Историко-матема-
тические исследования», вып. VIII, ГИТТЛ, М., 1955, стр. 558—562.
2 А. П. Юшкевич, О достижениях китайских ученых в обла-
сти математики. «Историко-математические исследования», вып. VIII,
ГИТТЛ, М., 1955, стр. 559.
34
жение императорского герба б виде дракона. Важней-
шие правила, вероятно, для лучшего запоминания дают-
ся в стихотворной форме. По-видимому, это сочинение в
свое время было принято как учебное руководство в шко-
лах по элементарной математике.
Содержание книги, которое приводится ниже, по-ви-
димому, дает хорошую картину о состоянии китайской
математики вплоть до конца XVI в.
«Начала искусства вычисления» состоит из 12 книг,
содержащих ряд статей и задач по арифметике, ал-
гебре и геометрии, причем много вопросов заимст-
вовано из трактата «Математика в девяти кни-
гах».
Остановимся коротко на содержании каждой из книг
в отдельности.
Книга первая содержит:
1) Объяснение нумерации, употребляемой в Китае.
2) Таблицы мер.
3) Правила извлечения квадратных и кубических
корней.
4) Правила действия над дробями.
5) Различные действия над числами.
Книга вторая содержит:
1) Описание китайской счетной доски — суан-пана и
ее употребление.
2) Различные действия над дробями.
3) Правило пропорций.
4) Десятичные дроби.
5) Правила распределения имущества.
6) Правила на смешение.
Книга третья освещает:
1) Измерения на местности. В основном здесь повто-
ряется материал первой книги «Математики в девяти
книгах».
2) Отношение длины окружности к длине диаметра
дается в виде дроби
22
к = — .
7
3) Вычисление площадей.
4) Распределение податей и налогов.
5) Описание различных мер для измерения на мест-
ности.
3*
35
Книга четвертая — это фактически вторая кни-
га древнего трактата «Математика в девяти книгах». В
ней содержится:
1) Установление цен на различные товары.
2) Меры вместимости.
3) Правило для определения количества соли.
4) Правило плавки меди и железа.
Книга пятая — это третья книга древнего тракта-
та «Математика в девяти книгах». Она содержит:
1) Правило пропорционального деления.
2) Решение задачи Сунь-цзы, о которой довольно по-
дробно говорилось выше.
Книга шестая в основном повторяет четвертую
книгу «Математики в девяти книгах». Она содержит:
1) Арифметический треугольник.
2) Задачи на извлечение квадратных и кубических
корней.
3) Нахождение площади круга.
4) Превращение данного квадрата в круг.
5) Выражение объема шара (дается приближенно).
6) Треугольные числа.
7) Решение задачи:
«Определить стороны прямоугольного треугольника,
если известны его площадь и периметр».
Решение задачи сводилось к нахождению корней
квадратного уравнения.
8) Решение задачи:
«Найти стороны прямоугольника, если известны его
периметр и площадь».
Решение этой задачи сводилось также к нахождению
корней квадратного уравнения.
9) Численное решение некоторых уравнений третьей
степени методом небесного элемента.
10) Нахождение площадей земельных участков раз-
личных форм.
Книга седьмая содержит в основном изложение
пятой и шестой книг «Математики в девяти книгах». Она
содержит:
1) Вычисления, связанные с различными постройка-
ми из земли.
2) Вычисление вместимости башен.
3) Построение стен, пирамид, конусов и плотин.
4) Расчеты, связанные с устройством каналов.
36
5) Семь вопросов, относящихся к задаче о курьерах.
6) Пирамидальные числа.
7) Арифметические прогрессии.
8) Суммирование арифметических рядов.
9) Задачи на пропорции.
10) О распределении налогов.
Книга восьмая в основном повторяет содержание
седьмой, восьмой и девятой книг «Математики в девяти
книгах». Она содержит:
1) Различные задачи на пропорции.
2) Вычисления, связанные с различными мерами.
3) О свойствах прямоугольного треугольника.
4) Решение задачи:
«Вписать круг в прямоугольный треугольник».
Центр искомого круга находился как точка пере-
сечения биссектрис двух углов данного треуголь-
ника.
5) Задача о бамбуковой трости, сломанной ветром.
6) Определение расстояний и высот.
Книга девятая составляет материал, взятый из
различных китайских математических сочинений.
Книги десятая и одиннадцатая посвяще-
ны решению разнообразных задач.
Книга двенадцатая содержит:
1) Образование магических квадратов.
2) Различные фигуры, служащие для предсказаний.
3) Суммирование арифметических рядов.
В этой книге имеются элементы мистического содер-
жания. Дело в том, что некоторые китайские ученые при-
давали отдельным числам и фигурам толкования, свя-
занные с различного рода суевериями.
Анализ содержания только что приведенного сочине-
ния показывает, что китайская математика XVI в. стоит
примерно на уровне XIII в., который составляет, по-види-
мому, наивысшую точку развития математической куль-
туры древнего Китая.
ЪО ------’4?3fr]
О
ГЛАВА ТРЕТЬЯ
О ДРЕВНЕКИТАЙСКИХ АЛГЕБРАИЧЕСКИХ
ПРАВИЛАХ
§ 1. ПРАВИЛО «ФАН-ЧЭН»
Термином «фан-чэн» обозначают алгоритм, с по-
мощью которого вычисляются корни системы линейных
уравнений с двумя и большими неизвестными. Суть это-
го метода заключается в следующем.
Пусть нам дана система линейных уравнений:
Н biy-\~C]Z d±
k Я3*+М+^2=Ч
а3
Ьз
Сз
Требуется решить эту систему, т. е. найти неизвестные
х, у и х.
Сначала данную систему запишем китайским спосо-
бом:
#2 ^1\
^2 J
с2 (\ J
^2
Эта таблица по существу представляет собой расши-
ренную матрицу системы. Сам способ составления табли-
цы соответствует китайскому способу письма: сверху
вниз, справа налево и означает «выстраивание чисел по
направлению», или «фан-чэн».
Далее таблицу преобразуют к виду:
О 0 at
О b± bt
^3 £2
^2
38
Эта таблица соответствует такой «ступенчатой» си-
стеме:
^+b^y+c1 z=dl
Ь2у+ ^2 % ^2
c3z=d3
Откуда легко получить искомые неизвестные. Действи-
тельно, будем иметь:
z= = .
сз
Далее определяются у и х.
Лучше всего с методом «фан-чэн» ознакомиться на
конкретных примерах. Для этого рассмотрим несколько
задач из восьмой книги трактата «Математика в девяти
книгах».
Задача о снопах различных урожаев
«Из 3 снопов хорошего урожая, 2 снопов среднего
урожая и 1 снопа плохого урожая получили 39 доу
зерна. Из 2 снопов хорошего урожая, 3 снопов средне-
го урожая и 1 снопа плохого урожая получили 34 доу
зерна. Из 1 снопа хорошего урожая, 2 снопов среднего
урожая и 3 снопов плохого урожая получили 26 доу
зерна. Спрашивается, сколько зерна получили из каж-
дого снопа хорошего, среднего и плохого урожаев».
Ответ. Из 1 снопа хорошего урожая 9~ доу, из 1
снопа среднего урожая 4± доу, из 1 снопа плохого урожая
2 т Доу.
4
Для решения этой задачи (самого решения в тракта-
те не приводится) составитель сочинения и приводит
правило «фан-чэн».
Вот это правило:
«Расположи 3 снопа хорошего урожая, 2 снопа сред-
него урожая, 1 сноп плохого урожая, составляющие их
39 доу зерна с правой стороны. Расположи посредине и
слева количества снопов урожаев в таком же порядке,
как и с правой стороны. Числа среднего столбца умножь
39
на количество снопов хорошего урожая в правом столбце
и образуй остатки. И еще раз также образуй остатки до
тех пор, пока не исчерпается все до количества снопов
среднего урожая в среднем столбце. И снова образуй
остатки до тех пор, пока не исчерпается все до количест-
ва снопов плохого урожая в левом столбце. Верхнее
число есть делитель, нижнее число есть делимое, делимое
для искомого количества снопов плохого урожая. Чтобы
найти делимое для среднего урожая, нижнее составляю-
щее среднего столбца умножь на делитель и вычти дели-
мое для плохого урожая. Остаток объедини с количест-
вом снопов среднего урожая, это и будет делимое для
среднего урожая. Чтобы найти делимое для хорошего
урожая, нижнее составляющее количество правого столб-
ца также умножь на делитель, исключи делимые для
плохого урожая и среднего урожая, объедини остаток с
количеством снопов хорошего урожая, это и будет
делимое для хорошего урожая. Все делимые объе-
дини с делителем, получатся искомые количества в
Доу».
Задача сводится к решению системы уравнений:
Зх+2у+ z=39
2х+3у+ z=34
x+2y+3z=26
В китайской записи выглядит это так:
1 2 3\
2 3 2 1
3 11/
26 34 39/
Далее согласно правилу проводятся следующие пре-
образования этой таблицы:
Первый шаг. Числа среднего столбца умножь на
количество снопов хорошего урожая в правом столбце и
образуй остатки. Тогда получим:
1 6 3
2 9 2
3 3 1
26 102 39.
40
Второй шаг. И еще раз также образуй остатки до
тех пор, пока не исчерпается все до количества снопов
среднего урожая в среднем столбце.
1 3 3\ / 1 0 3\
2 7 2 1/ 2 5 2 1
3 2 1/13 111
26 63 39 / \ 26 24 39 /
Третий шаг. И снова образуй остатки до тех пор,
пока не исчерпается до количества снопов плохого уро-
жая в левом столбце. Будем иметь:
/ 3 0 3\ / 0 0 3\ / 0 0 3\
/ 6 5 2 \ -L 4 5 2 1 / 20 5 2 \
9 11/ 18 11/ 40 1 1
\ 78 24 39/ \ 39 24 39/ \ 195 24 39/
/ 0 0 3\ / 0 0 3\ / 0 0 3\
/ 15 5 2 \ / 10 5 2 \ / 5 5 2 \
I 39 1 1 / I 38 1 1 / I 37 1 1 /
\ 171 24 39/ \ 147 24 39/ \ 123 24 39/
/ 0 0 3 \
/ 0 5 2 1
36 1 1 /
\ 99 24 39 /
Четвертыйшаг. Верхнее число (36) есть делитель,
нижнее число (99) есть делимое для искомого количест-
ва снопов плохого урожая.
Пятый шаг. Чтобы найти делимое для среднего
урожая, нижнее составляющее среднего столбца умножь
на делитель и вычти делимое для плохого урожая. Оста-
ток объедини с количеством снопов среднего урожая, это
и будет делимое для среднего урожая.
Таким образом «делимое» для у будет:
24 36 — 99 _ А
5
Шестой шаг. Чтобы найти делимое для хорошего
урожая, нижнее составляющее количество первого столб-
ца также умножь на делитель, исключи делимое для пер-
вого урожая и среднего урожая, объедини остаток с коли-
чеством снопов хорошего урожая, это и будет делимое
для хорошего урожая.
41
В соответствии с этим «делимое» для х будет:
39 • 36- 99 - 2А _ в
3 “
Седьмой шаг. Все делимые объедини с делителем,
получатся искомые количества в доу.
Следовательно, будем иметь:
z =
99
36
7 = 2 ~ (доу);
А л 1 / ч
!' = S-47 (доу);
В п 1 .
Х = 7 = 9Т (Д°У)-
36 4
§ 2. ВВЕДЕНИЕ НУЛЯ
Необходимо заметить, что у китайцев к началу I в.
не было символа, изображающего нуль. Нуль обозначал
на китайской счетной доске пустое место. Поэтому в ки-
тайском правиле «фан-чэн» говорится о том, что в резуль-
тате определенных действий получилось пустое место.
Эти пустые места (нули) должны, как известно, распо-
лагаться в верхнем левом углу от главной диагонали
таблицы коэффициентов.
§ 3. ДЕЙСТВИЯ С ОТРИЦАТЕЛЬНЫМИ ЧИСЛАМИ И НУЛЕМ
Еще не позднее начала нашей эры древние китайцы
свободно владели отрицательными числами, как числами
промежуточных вычислений. Ответ задачи у них всегда
дается положительным числом. Отрицательным
корням они, по-видимому, не умели давать реального ис-
толкования. Восьмая книга «Математики в девяти кни-
гах» как раз и замечательна тем, что в ней имеются зада-
чи, решение которых требует операции с нулем и отрица-
тельными числами. Ниже приводятся две такие задачи,
взятые из упомянутого выше трактата.
Задача первая о снопах различных
урожаев:
«2 снопам хорошего урожая,3 снопам среднего уро-
жая и 4 снопам плохого урожая не хватает до 1 доу
соответственно по 1 снопу среднего урожая, плохого
42
урожая, хорошего урожая. Спрашивается, сколько зер-
на получили из каждого снопа хорошего, среднего и
плохого урожаев».
9
Ответ. Из 1 снопа хорошего урожая получили —
Zu
. 7
доу, из 1 снопа среднего урожая получили ~ ДОу, из
, 4
1 снопа плохого урожая — — доу.
К этой задаче автор трактата дает два правила:
Первое правило на установление таблицы «фан-
чэн»: «Составь таблицу «фан-чэн», установи для каждого
то, что не хватает. По способу «чжен-фу» вычисляй».
Пользуясь современными обозначениями, задача сво-
дится к системе уравнений:
2х=1—у
Зу= 1—2
4z=l— х
или в канонической форме:
2х-{- у= 1
3t/+z=l
4z+x=l
Соответствующая таблица «фан-чэн» будет:
1 0 2\
0 3 1]
4 10/
111/
С самого начала уже в таблице имеются нули (пустые
места).
Второе правило — правило «чжэн-фу», т. е. пра-
вило сложения и вычитания отрицательных чисел. Это
правило дается в таких словах: «Если одинакового назва-
ния, то вычитается, если разного названия, то прибав-
ляется; если положительное без пары, то становится от-
рицательным, если отрицательное без пары, то становит-
ся положительным».
43
Это правило для вычитания, оно в современных сим-
волах может быть записано так:
(± ±Ь)=± (а-Ь)-9 0—(+£)=—6;
(± а)-( + Ь)= ± (а+&); 0—(—6)=+&.
Для сложения правило формулируется так: «Если
разного названия, то вычитается, если одинакового на-
звания, то прибавляется; если положительное без пары,
то становится положительным, если отрицательное без
пары, то становится отрицательным».
В современной алгебраической записи все это можно
записать следующими формулами:
(±a)+(^b)=±(a—b); O+(+b)=+b;
(1 a)+(±b)= ± (а+Ь); 0+(— fe)=—b.
Вот эти правила и составляют суть правила «чжэн-
фу». «Чжэн» означает «прибавляемый», «фу» — «вычи-
таемый». Такие цифры обозначались разными цветами:
чжэн — красным, фу—черным.
Применяя правило «фан-чэн» к поставленной выше за-
даче, надо теперь от расширенной матрицы перейти к со-
ответствующим матрицам с нулями. Здесь для данной
задачи и появляются отрицательные числа (коэф-
фициенты ступенчатой системы).
Так, при преобразовании появляется «минус единица»,
т. е. (—1), как результат вычисления:
О—(+1)=—1.
Действительно, будем иметь:
1 0 2 \ / 2 0 2 \
О 3 1 \ / 0 3 1 \
4 10/ 18 10/
111/, \ 2 1 1 J,
0 0 2\
—1 3 1 \
8 1 0l
111/
В качестве примера приведем теперь задачу, когда
отрицательные числа появляются в самой расширенной
матрице.
Задача вторая о снопах различных уро-
жаев:
«2 снопа урожая А, 3 снопа урожая Б, 4 снопа уро-
жая В превышают по весу дань: вес 2 снопов уро-
44
жая А превышает дань на вес 1 снопа урожая Б, вес
3 снопов урожая Б — на вес 1 снопа урожая В, вес
4 снопов урожая В — на вес 1 снопа урожая А.
Спрашивается, каков вес каждого из снопов урожаев
Л, Б, В».
17
Ответ. 1 сноп урожая А весит — даня, 1 сноп урожая
23
Б весит даня, 1 сноп урожая В весит — даня.
23 23
К задаче дано правило: «Установи таблицу «фан-
чэн». Установи, что вещи, на веса которых превышает
дань (веса данных снопов),отрицательны. Вычисляй
по способу «чжэн-фу».
Задача сводится к решению системы:
2х=1+у
3y=l+z
4z=l+x
Ее каноническая форма будет:
2х—у=\
Аг—х=1
Соответствующая таблица будет:
О
3
Рассмотрение всех таких задач позволяет сделать вы-
вод, что отрицательные числа понадобились китайским
ученым для распространения правила «фан-чэн» на более
широкий класс задач. Вместе с тем необходимо еще раз
подчеркнуть, что в то отдаленное от нас время китайские
ученые не могли дать реального истолкования отрица-
тельным корням и поэтому их не рассматривали.
45
§ 4. О ДРЕВНЕКИТАЙСКОМ ИСТОЛКОВАНИИ
ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ
Отрицательным и положительным числам ученые да-
вали вполне конкретные истолкования. Согласно этим
истолкованиям отрицательные числа означали долг, не-
хватку монет при покупке. Отрицательные числа обозна-
чались иероглифом «фу» (вычитаемый), которыц и имел
значения: ноша, долг, недостача и т. п. Положительные
числа обозначались иероглифом «чжэн» (прибавляемый),
который и имел значения: правильный, основной, справед-
ливый и т. д. ’ "
О том, что указанное выше истолкование отрицатель-
ных чисел в древнем Китае было в ходу, можно су-
дить, например, по задаче о буйволах и баранах
(№ 8) восьмой книги трактата «Математика в девяти
книгах».
Задача формулируется так:
«Продали 2 буйволов, 5 баранов, купили 13 сви-
ней, осталось 1000 цяней. Продали 3 буйволов, 3 сви-
ньи, купили 9 баранов, как раз хватило. Продали 6
баранов, 8 свиней, купили 5 буйволов, не хватило 600
цяней. Спрашивается, сколько стоят буйвол, баран и
свинья?»
Ответ. Буйвол стоит 1200 цяней, баран — 500, сви-
нья — 300.
К задаче дано такое правило: «Составь таблицу
«фан-чэн». Установи, что 2 буйвола, 5 баранов положи-
тельны. 13 свиней отрицательны, остаток цяней положи-
телен. Еще установи, что 3 буйвола положительны, 9 ба-
ранов отрицательны, 3 свиньи положительны; еще уста-
нови, что 5 буйволов отрицательны, 6 баранов положи-
тельны, 8 свиней положительны, недостаток цяней отри-
цателен. Вычисляй по способу «чжэн-фу».
Если через х, yt z обозначим соответственно стоимость
буйвола, барана и свиньи, тогда условия задачи приво-
дят нас к системе:
' 2x+5z/ = 13z+1000
• 3x+3z=9z/
ь 6y+8z=5x—600,
46
где 1000 — остаток цяней от продажи 2 буйволов, 5 бара-
нов и покупки 13 свиней; 600 — недостаток цяней от про-
дажи 6 баранов, 8 свиней, покупки 5 буйволов.
§ 5. ДРЕВНЕКИТАЙСКИЙ НЕОПРЕДЕЛЕННЫЙ АНАЛИЗ
К НАЧАЛУ I ВЕКА НАШЕЙ ЭРЫ
Судя по восьмой книге древнекитайского трактата
«Математика в девяти книгах», ученые древнего Китая
рассматривали задачи, решение которых сводилось к
системе линейных уравнений, в которой число неизвест-
ных больше числа уравнений, т. е. занимались задачами
неопределенного анализа. В этом отношении характерна
задача об общем колодце (№ 13):
«У 5 семей имеется общий колодец. Чтобы до-
стать до поверхности воды, 2 веревкам семьи А недо-
стает 1 веревки семьи Б, 3 веревкам семьи Б недостает
1 веревки семьи В, 4 веревкам семьи В недостает 1 ве-
ревки семьи Г, 5 веревкам семьи Г недостает 1 верев-
ки семьи Д, 6 веревкам семьи Д недостает 1 веревки
семьи А. Спрашивается, какова глубина колодца и
какова длина каждого куска веревки».
Ответ. Глубина колодца 7 чжан 2 чи 1 цунь; длина
веревки семьи А — 2 чжана 6 чи 5 цуней, длина веревки
семьи Б— 1 чжан 9 чи 1 цунь, длина веревки семьи В —
1 чжан 4 чи 8 цуней, длина веревки семьи Г — 1 чжан
2 чи 3 цуня, длина веревки семьи Д — 7 чи 6 цуней.
К задаче дается правило: «Составь таблицу «фан-
чэн», вычисляй по способу «чжэн-фу». Других указаний
к рассматриваемой задаче не имеется.
Данная задача, как легко видеть, сводится к системе
из 5 линейных уравнений с шестью неизвестными. Эту
систему можно записать так:
2х+у=т
3y+z=m
4z+u=m
5u+v=m
6v+x=m
Здесь неизвестными являются х, у, z, и, о, /и. Причем
согласно ответам т берется с таким расчетом, чтобы це-
лые положительные значения х, yt zt и, v были бы наи-
меньшими.
47
Основная матрица полученной системы будет:
/ 1 0 0 0 2 \
О 0 0 3 1 \
0 0 4 10 I
0 5 10 0 I
6 10 0 0 /
\ т т т т т /
Преобразованная матрица с нулями будет:
/ 0 0 0 0 2 \
1 0 0 0 3 1 \
1 0 0 4 1 0 1
1 0 5 1 0 0 1
\ 721 1 0 0 0 /
\ 76m т т т т /
Следовательно, и _ 1 721m -76т 129 _ 148 =— tn, z=—т,
191 265
у= — т, х=^т> причем т нужно положить=721.
§ 6. КАК В ДРЕВНЕМ КИТАЕ ИЗВЛЕКАЛИ КОРНИ
В древнем Китае все вычисления производились на
счетной доске, где числа изображались при помощи счет-
ных палочек. С помощью счетной доски и счетных пало-
чек древние китайцы не только выполняли четыре
арифметических действия, но извлекали квадратные
и кубические корни. К сожалению, описания самой
счетной доски и правил четырех арифметических дейст-
вий в китайских трактатах не дается, по-видимому, все
это считалось в то далекое от нас время широко извест-
ным и не требовало особых разъяснений. Зато до нашего
времени сохранились правила вычисления квадратных и
кубических корней.
Остановимся на китайском способе извлечения квад-
ратных корней. Древние китайцы извлекали корни при-
мерно так же, как мы теперь, но все же их способ отли-
чается от нашего по форме и терминологии. На последней
т. е. на терминологии лежит печать влияния процесса
счета на китайской счетной доске. Процесс извлечения
корня на китайской счетной доске имеет много общего с
делением целых чисел. Поэтому не удивительно, что опи-
48
сание китайского способа извлечения корней со-
держит одинаковые термины с количествами деле-
ния.
Сама формулировка правила извлечения корня (квад-
ратного) такая: «Установи площадь квадрата в качестве
делимого. Возьми одну счетную палочку и шагай через
одну колонку. Обсуди «со-дэ». Первую выбранную цифру
корня умножь на «цзе-суань», это делитель. Раздели на
него. После деления удвой делитель, это фиксированный
делитель. Возврати его на одно деление— получишь уре-
занный фиксированный делитель. Внизу возврати уста-
новленную счетную палочку на шаг. Продолжай, как и
ранее. Одну выбранную цифру умножь на это. Со-дэ
прибавь к фиксированному делителю, укороти возвра-
том — получишь урезанный фиксированный дополнитель-
ный делитель. Далее, как раньше. Если извлечение корня
не выполняется полностью, то можно продолжать, как
ранее. Если делимое представлено в виде дроби, то число
долей в числителе будет фиксированным делимым. Из не-
го извлеки корень. Извлеки корень из знаменателя.
Раздели результат друг на друга. Если из знаменателя
извлечь корень нельзя, то знаменатель умножь на фикси-
рованный делитель и из этого извлеки корень. Получен-
ное объедини со знаменателем».
Дадим китайскому способу извлечения квадратного
корня алгебраическою форму.
Положим, х=УN и х = В десятичной системе
х можно представить так:
х = lOOctj + 10а2 + а3.
Тогда
N = (100^ + 10а2 + а3)я,
или
N = 10000а? + (2 • IOOoj - 10а2+100а?) + 2 • lOOa^-f-
+ 2 • 10а2а3 + а? = (Л/ — + (Вд + Сха*) -f-
+^2a3 + С-2азл
где
A^N — (lOOaJ2;
В. = 2000ах;
С, = 100;
В2 == 200а. + 20а2;
С2 = 1.
4 Заказ 999
49
Первый шаг. Выбирается первая цифра корня
ах, как наибольшее однозначное число, удовлетворяющее
неравенству:
А = Л\ — (100а,)2 > 0.
После этого счетная доска будет выглядеть так:
а1 корень
N делимое
10 000 G4 «со-дэ»
10 000 «цзе-суань»
Второй шаг. Для нахождения второй цифры кор-
ня а2 производится преобразование чисел счетной доски.
Для этой цели делимое заменяется разностью между под-
коренным выражением N и произведением делителя «со-
дэ» ЮО2^ на число аь выбранное для первой цифры квад-
ратного корня.
Далее, удваивая делитель 10000 ар получают так на-
зываемый «фиксированный делитель» 20 000 с^, а пере-
двигая последний на одну колонку вправо, получают «уко-
роченный фиксированный делитель» 2000аг В последней
строке счетную палочку сдвигают на две колонки вправо,
получается число 100, которое называют вторым «цзе-суань».
Все это оформляется такой таблицей:
а корень
At=N -(lOOaJ2 первый остаток
Я, =2000?, укороченный фиксированный целитель
С] = 100 второе «цзе-суань»
50
После этого определяют вторую цифру корня а2, как
наибольшее однозначное число, удовлетворяющее усло-
вию:
Аг — (Вх + С,а2)а2 > О,
что словами можно выразить так: сумма произведения
на него второго «цзе-суань» и укороченного фиксирован-
ного делителя, умноженная на само это выбранное число,
не превышает первого остатка.
Третий шаг. Подготовляем счетную доску для на
хождения третьей цифры искомого корня. Для этого в
таблицу вместо первого остатка помещается второй оста
ток, получаемый от «деления» первого остатка на сумму
укороченного фиксированного делителя и нового «со-дэ».
который получается путем умножения второго «цзе-су
ань» на только что выбранную вторую цифру корня.
Вместо первого «укороченного фиксированного дели
теля» ставится новый «фиксированный делитель», полу
ченный путем сложения нового делителя со вторым «со-
дэ» и передвижения результата на одну колонку вправо.
Чтобы получить третье «цзе-суань», в последней стро-
ке палочку сдвигают на две колонки вправо.
Указанное выше преобразование доски изображается
такой таблицей:
а1а2 корень
^2 второй остаток
В, второй укороченный фик- сированный делитель
С2 третье «цзе-суань>
В этой таблице:
А2 - W — (100^ + 10а2)2;
В, = (B1+Cia2)+Cp2= 200 _|_ 20а ;
10 1
с2 = = 1.
2 100
4’
61
Третья цифра а3 корня выбирается с таким расчетом,
чтобы
(^2 ^2®3®з)
ИЛИ
2V — (ЮОа, + 10а2 + а3)2 > 0.
Э. И. Березкина подчеркивает, что получение чисел
Bi и Ci в третьей и четвертой строках, в частности приме-
ненный при этом сдвиг вправо, происходит не в соответ-
ствии с формулой квадратного бинома: (а + Ь)2 = а2 +
2ab + b2t а так, как это делается при решении уравнения
х2—2V = 0 по так называемому способу Горнера.
Древние китайцы умели также извлекать и кубиче-
ские корни. Это извлечение у них также связано со счет-
ной доской и преобразованием чисел на этой доске. В са-
мом правиле много аналогии с правилом извлечения
квадратных корней.
С помощью своего алгоритма извлечения квадратного
корня древние китайцы решали, например, такую задачу:
Задача о стороне квадрата:
«Имеется площадь квадрата в 71 824 бу. Спраши-
вается, какова сторона квадрата».
Ответ. 268 бу.
Задача сводится к решению уравнения:
х2 = 71 824.
Ответ получается путем извлечения квадратного кор-
ня из 71 824. Сам процесс извлечения этого корня можно
изобразить следующим образом.
Первый шаг. Для нахождения первой цифры 2 кор-
ня числа на доске записываются так:
2 корень
71 824 делимое
20 000 «со-дэ»
10 000 «нзе-суань»
52
Первая цифра корня, это будет, как отмечалось, 2, должна
являться наибольшим числом, удовлетворяющим неравен-
ству:
(10 000 • 2) 2 <71 824.
Второй шаг. Для определения второй цифры 6
корня числа на доске преобразуют следующим образом:
10 000 • 2 = 20 000;
71 824 — 2 • 20 000 = 31 824 (1-й остаток);
20 000 • 2 = 40 000 (фиксированный делитель);
40 000 ЛЛЛЛ / v л «
—= 4000 (укороченный фиксированный
делитель).
Доска примет вид таблицы:
2 корень
31 824 первый остаток
4000 укороченный фиксирован- ный делитель
100 второе «цзе-суань»
Вторая цифра корня равна 6, так как она наибольшее чис-
ло, удовлетворяющее неравенству:
(100 6 4- 4000) 6 <31 824.
Третий шаг. Находится третья цифра 8 корня. Для
этого проделываем соответствующие преобразования чи-
сел доски:
100 • 6 = 600 (новое «со-дэ»);
4000 + 600 = 4600 (новый делитель);
31 824 — 6 4600 = 4224 (второй остаток);
^600+622 = 520 (новый укороченный фиксированный
делитель).
53
Теперь доска будет выглядеть так:
26 корень
4224 второй остаток
520 укороченный фиксирован- ный делитель
1 третье «цзе-суань»
Третьей цифрой корня будет 8, так как
(1 • 8 + 520) 8 = 4224.
Следовательно, будем иметь:
У 71824 = 268, что и служит ответом
задачи.
ГЛАВА ЧЕТВЕРТАЯ
РАЗВИТИЕ ГЕОМЕТРИИ И ТРИГОНОМЕТРИИ
В ДРЕВНЕМ КИТАЕ
Несомненные достижения китайские математики да-
лекого прошлого имели в области геометрии, особенно,
когда дело касалось решения вычислительных задач,
связанных с измерением разного рода фигур.
Еще в древнейшем трактате «Математика в девяти
книгах» имеется богатый материал, посвященный геомет-
рии. Во всяком случае, китайцы того времени имели сле-
дующие познания в области геометрии:
1) Владели практическими способами измерения зе-
мельных участков различной формы (треугольной, четы-
рехугольной, круглой и т. д.).
2) Умели приближенно вычислять площадь круга, пред-
полагая отношение длины окружности к длине диаметра
равным 3, т. е. л = 3.
Нужно отметить, что позднее китайские ученые, поль-
зуясь довольно высокой вычислительной техникой, осно-
ванной на приближенных вычислениях, дали более точные
выражения для числа л.
Так, во II в. н. э. китайский математик Чжан X э н
полагал, что л = УЧО, которым в VII в. н. э. пользовался
крупнейший индийский математик Брамагупта.
В III в. н. э. виднейший китайский математик Л ю
X у э й путем рассмотрения правильного вписанного мно-
гоугольника с 192 сторонами получил для л значение —,
50
т. е. л = 3,14.
В V в. н. э. выдающийся китайский математик Ц з у
Ч у н - ж и (430—501) для л получил приближение
дающее 7 верных значений цифр, и показал, что число л
лежит в пределах:
3,14155926 <к<3,14155927.
55
Прошло более 10 веков, когда в XVI в. это приближе-
ние было вновь переоткрыто в Нидерландах математиком
355
Адрианом Мецием. Число — в Европе назы-
вают «число Меция», а на самом деле его справедливее
было бы назвать «числом Цзу Чун-жи». В течение более
десяти веков, вплоть до XIV в., точность вычисления чис-
ла л, данная Цзу Чун-жи, была самой высокой во всей
мировой науке, и только по прошествии указанного вре-
мени эту точность числа л удалось перекрыть Джем-
шиду Гияссэддинуал Каши, который для л
нашел значение с 16 верными десятичными знаками после
запятой1 * * * * * * В.
3) Знали практические правила измерения различных
объемов, которые они применяли при построении стен,
зданий, башен, рвов и укреплений.
4) Знали теорему Пифагора и умели применять ее к
решению целого ряда практических задач.
Из древнейших китайских математико-астрономиче-
ских сочинений, дошедших до нас, где уделяется много
1 В XVI в. крупный французский математик Франсуа Виет
(1540—1603) вычисляет л с 10 десятичными знаками, исполь-
зуя для этой цели многоугольники с 251 658 240 сторонами. Соглас-
но его вычислениям л находится в границах: 3,1415926535<л<
<3,1415926536.
Далее, в этом же веке голландец Адриан Ромен опреде-
лил л с 15 десятичными знаками, для чего пришлось ему рассматри-
вать многоугольники с 251 658 240 сторонами. Эта точность в вычис-
лениях в конце XVI в. была доведена до колоссальных разме-
ров, далеко превосходящих потребность практики. Лудольф из
Кельна определил л сперва с 20 десятичными знаками, а потом
даже с 35. Вот какое значение для л он получил:
л = 3,14159265358979323846264338327950288. По завещанию самого
Лудольфа, это число записано на его надгробном памятнике и на-
зывается «числом Лудольфа».
Математики XVIII и XIX вв. далеко превзошли своих предшест-
венников и вычисляли л с очень большим числом десятичных зна-
ков. Например, М э к и н дал для л 100 знаков, Ланьи — 127, В е-
г а — 140, Д а з е — 200, Рихтер — 500, а английский математик
Шенке в 1873 г. даже дал 707 десятичных знаков.
В заключение надо отметить, что немецкий математик Лам-
берт (1728—1777) в 1771 г. впервые в науке показал, что число л
иррациональное. Позднее французский математик Лежандр
(1752—1833) показал, что и квадрат л есть также число иррацио-
нальное. Наконец, немецкий математик Линдеман (1852 —
1939) доказал, что я — несоизмеримое трансцендентное число, т. е.
не может служить корнем какого-нибудь алгебраического уравнения
с рациональными коэффициентами,
56
внимания геометрии, является трактат «Чеу-пей», напи-
санный за 1100 лет до н. э. Этот трактат дан в форме диа-
логов и состоит из двух частей, причем вторая часть боль-
ше относится к астрономии и написана, как полагают,
значительно позднее первой, именно во II в. н. э.
Все предложения первой части относятся к различным
свойствам прямоугольного треугольника. Одно из свойств
представляет собой не что иное, как теорему Пифагора
относительно прямоугольного треугольника со сторона-
ми 3, 4 и 5, и сформулирована так: «Квадрат большей
стороны прямоугольного треугольника равняется сумме
квадратов меньших его сторон».
Автору этого сочинения были известны некоторые
тригонометрические соотношения, при помощи которых
можно определять расстояние между недоступными пред-
метами. Кроме того, ему было известно также правило
нахождения площади круга, если известен радиус, причем
круг иногда рассматривался как правильный многоуголь-
ник с очень большим числом сторон. В практике имеется
также ряд вычислительных задач на приложение ариф-
метических соотношений к некоторым геометрическим во-
просам.
Что касается второй части, то она, как говорилось
выше, больше всего относится к астрономии и математике
уделяет внимания сравнительно мало. Отношение длины
окружности к длине диаметра считается здесь равным 3.
Откуда правило: «Во всех случаях, когда по диаметру
требуется найти окружность круга, диаметр умножается
на три». В одном из примеров так и говорится: «Возьми
диаметр длиною в 121— фута, умножь это число на
3, то получишь
365-
4
фута». Весьма вероятно, что это
и послужило поводом для китайцев делить окружность
не на 360 равных частей, а на 3651/4 (деление окружности
на 360° было также известно китайцам). Вполне веро-
ятно также, как полагает проф. М. Е. Ващенко-Захарчен-
ко, что это находится в тесной связи с солнечным го-
дом в 36574 дней, который был известен китайским астро-
номам 7
1 См. М. Е. В ащен ко-З а х ар чен ко, История математики.
Исторический очерк развития геометрии, т. I, Киев, 1883, стр. 351 —
376.
57
Среди задач с геометрическим содержанием обраща-
ет на себя внимание следующая:
«Доказать, что удвоенная сумма квадратов кате-
тов прямоугольного треугольника без квадрата их
разности равняется квадрату их суммы».
В современном обозначении задача сводится к дока-
зательству тождества:
2 (а2 + &2) — (а2 —62) = (а + &)2.
Автор трактата доказывал это тождество чисто гео-
метрически.
Много сделал для развития прикладной геометрии
крупнейший китайский математик III в. Л ю Хуэй, автор
многих сочинений по математике. Вопросам прикладной
геометрии он посвятил целый трактат под названием «Ма-
тематика морского острова», написанный сначала как де-
сятая глава комментариев к древнейшей книге «Мате-
матика в девяти книгах» и издававшийся позднее в ви-
де отдельной книги. Несколько странное название трак-
тата объясняется тем, что в нем решаются различные за-
дачи на определение расстояний до недоступных предме-
тов, расположенных на острове, причем точка наблюде-
ния находится вне его. Кроме того, имеется задача на вы-
числение недоступных высот, расположенных на острове,
наблюдение над которыми ведется из точек, расположен-
ных также на острове.
Вот одна из характерных задач этого сочинения Ч
«На холме растет сосна неизвестной высоты. Внизу,
на равнине, поставлены два шеста, каждый высотой в 20
футов, на одной прямой с деревом и на расстоянии друг
от друга в 50 ш^гов. Верхушка дерева и конец первого
шеста образуют прямую с точкой на земле, расположен-
ной в 7 шагах и 4 футах позади шеста и в этой точке ос-
нование дерева отмеряет 2,8 фута от верха шеста. Вер-
хушка дерева образует опять-таки прямую линию с кон-
цом заднего шеста и точкой на земле в 8 шагах и 5 футах
позади шеста. Требуется узнать высоту сосны и расстоя-
ние от переднего шеста до холма».
Лю Хуэй решает эту задачу согласно правилу,
1 См. А. П. Юшкевич, О достижениях китайских ученых в
области математики. «Историко-математические исследования», вып.
VIII, ГИТТЛ, М., 1955, стр. 564—565.
58
которое можно выразить следующими двумя форму-
лами:
Ьс
ы , .
х =-------h /;
d—c
где х — высота сосны, у — расстояние переднего шеста до
холма, а — высота каждого шеста, Ь—расстояние меж-
ду шестами, с — расстояние точки на земле, расположен-
ной
цом
ние
ста
позади шеста и находящейся на одной прямой с кон-
переднего шеста и верхушкой дерева, d — расстоя-
точки на земле, расположенной позади второго ше-
(заднего) и находящейся на одной прямой с концом
второго шеста и верхушкой де-
рева, I — число, которое «от-
меряет основание дерева»
от верха переднего шеста
(рис. 10).
Рис. 10.
Необходимо заметить, что многие задачи Лю Хуэя
сложны. Решение своих задач он давал обычно в виде
правил, основанных главным образом на рассмотрении
подобных треугольников. Благодаря практической цен-
ности эти задачи получили позднее широкое распро-
странение не только в самом Китае, но и далеко за его
пределами. В Европе, например, они стали известны в
начале нового времени.
Вопросами тригонометрии китайские ученые стали
заниматься очень давно. Если судить по древнейшему
астрономо-математическому трактату «Чеу-пей», китай-
ские математики еще в XI в. до н. э. знали некоторые
тригонометрические свойства прямоугольного треуголь-
ника и использовали их при решении целого ряда прак-
тических задач.
59
Первые сочинения по тригонометрии в Китае относят-
ся к VIII в. н. э., хотя основные начала тригонометрии
были известны гораздо раньше. Примером может слу-
жить тригонометрическое сочинение китайского ученого
Чау Чванга под названием «Арифметические класси-
ки тригонометрии Чау», написанное в начале VII в.
В XIII в. жил китайский математик Кашу Кинг,
написавший около 1300 г. первое сочинение по сфериче-
ской тригонометрии, которое, к сожалению, считается уте-
рянным. Однако, как утверждает проф. М. Е. Вашенко-
Захарченко в цитированной выше его книге по истории
математики, до нас дошло другое сочинение — конца
XVI в., в котором изложены правила и приемы, найден-
ные и изложенные Кашу Кингом. Сочинение это носит
название «Арифметические правила для сегментов и си-
нусов-верзусов».
В начале XIV в. китайский математик Лей Ин-кинг
составил сочинение «Зеркало для измерения круга», в ко-
тором дается приложение алгебры при решении некото-
рых тригонометрических задач.
В китайскую учебную литературу XVI в. из геометри-
ческого материала, который принял вполне отчетливое
выражение и форму и стал достоянием школы, входят:
1) Теория подобных треугольников.
2) Точные значения поверхностей пирамиды и конуса.
3) Точные значения объемов пирамиды и конуса.
4) Приемы, близкие к современному понятию предела,
для вычисления числа п Ч
5) Решение геометрических задач практического зна-
чения. Все эти результаты были уже известны в XIV ве-
ке, когда китайская средневековая математика достигла
своего наивысшего развития.
1 Занимаясь приближенной квадратурой круга, Лю Хуэй еще
в III в. пришел к представлению о неограниченном приближении
вписанных треугольников Sn к площади круга S. Он писал: «Чем
мельче делить, тем меньше будет недостаток. Если делить все даль-
ше и дальше, до тех пор, пока деление не станет невозможным, то
будет совпадение с окружностью и недостатка не будет». А. П. Ю ш-
к е в и ч, О достижениях китайских ученых в области математики.
«Историко-математические исследования», вып. VIII, ГИТТЛ, М.,
1955, стр. 563.
о
ГЛАВА ПЯТАЯ
О ДРЕВНЕКИТАЙСКИХ ГЕОМЕТРИЧЕСКИХ
ПРАВИЛАХ
§ 1. ДРЕВНЕКИТАЙСКИЙ ЗАКОН О КАТЕТАХ
И ГИПОТЕНУЗЕ
(«Г О У-Г У сянь ДИН ЛИ»)
Трудно указать время, когда впервые китайский на-
род стал пользоваться «законом о катетах и гипотенузе»,
т. е. теоремой Пифагора. Но достоверно известно, что тео-
ремой Пифагора китайцы пользовались очень давно.
Как свидетельствуют летописи, для прямоугольного тре-
угольника со сторонами 3, 4, 5 теорема Пифагора была
известна в древнем Китае около 2200 лет до н. э.
Если судить на основании «Математического тракта-
та о чжоу-би» («Чжоу-би суань цзин»), который является
более древним, чем «Математика в девяти книгах», то
можно сделать вывод, что теорема Пифагора в ее част-
ном случае, когда стороны равны 3, 4, 5, была впервые
высказана в XII в. до н. э. китайским ученым Шан
Гао, а в общем виде теорему Пифагора знал и приме-
нял при решении разного рода задач примерно в VII в.
до н. э. китайский ученый Чэн ь-ц з ы.
«Математический трактат о чжоу-би», несмотря на его
название «математический», является более астрономи-
ческим трактатом, в котором математические сведения
даются постольку, поскольку это необходимо для н^жд
астрономии. Термин «чжоу-би» в переводе на русский
язык означает «шест для измерения солнечной тени»,
по-видимому, он выполнял главным образом роль гномо-
на, т. е. древнейшего астрономического инструмента для
определения по его тени момента полдня и направления
полуденной линии (т. е. меридиана) в данном месте.
В «Математике в девяти книгах» теорема употребля-
ется под видом правила «Гоу-гу». Согласно этому прави-
лу можно по известной гипотенузе и одному известному
катету находить другой неизвестный катет, а также на-
ходить гипотенузу, если известны оба катета.
61
Правило Гоу-гу» формулируется так: «Умножь сам
на себя каждый из катетов, сложи, извлеки из этого
квадратный корень: это и будет гипотенуза. Так же:
умножь сам на себя вертикальный катет, вычти из умно-
женной самое на себя гипотенузы, извлеки из остатка
квадратный корень, это и будет горизонтальный катет.
Так же: умножь сам на себя горизонтальный катет, выч-
ти из умноженной самое на себя гипотенузы, извлеки из
остатка квадратный корень, это и будет вертикальный
катет».
Термины «гоу» и «гу» обозначают катеты прямо-
угольного треугольника, причем «гоу» обозначает гори-
зонтальный, обычно меньший катет, а «гу» — вертикаль-
ный и обычно больший катет. В буквальном переводе
«гоу» означает крюк, а «гу» — ребро, связка.
Правило «Гоу-гу» применяется ко всем 24 задачам
девятой книги древнекитайского трактата «Математика
в девяти книгах», поэтому и сама девятая книга назы-
вается «Гоу-гу».
Правилом «Гоу-гу» решалась, например, такая задача
девятой книги (№ 6).
Задача о водоеме:
«Имеется водоем со стороной в I чжан. В центре
его растет камыш, который выступает над водой на 1 чи.
Если потянуть камыш к берегу, то он как раз кос-
нется его. Спрашивается, какова глубина воды и ка-
кова длина камыша (1 чжан = 10 чи)».
Ответ. Глубина воды 1 чжан 2 чи, длина камыша
1 чжан 3 чи.
Правило. «Половину стороны водоема умножь са-
мое на себя, надводную часть в 1 чи умножь самое на
себя, вычти это из первого, остаток раздели на удвоен-
ную надводную часть камыша — получишь глубину во-
ды. Прибавь количество чи надводной части — получишь
длину камыша».
Самого решения в трактате не дается. Это решение
легко выполнить в общем виде при помощи таких рас-
суждений.
Обозначим длину водоема через 2а, длину камыша
через с (рис. 11). Задача заключается в нахождении
b и с.
62
Руководствуясь китайским правилом, находим фор-
мулы для определения искомых величин:
_ а2—(с—6)2.
” 2(с—Ь) ’
с=&+(с-6) = ^±^-)2.
2(с—Ь)
Самого вывода правила не дается, поэтому трудно
сказать, каким путем древнекитайские математики уста-
новили последние формулы. Однако к этим формулам
можно легко прийти обычными рассуждениями. Исходя
из условия задачи и применяя правило «Гоу-гу», т. е.
теорему Пифагора, получаем систему;
/ b = с— k
( 62= с2 — а2,
где для краткости через k обозначена известная нам над-
водная часть, равная с—Ь.
Решая эту систему, будем иметь:
, а2- /г2
ь =------
2k
а2+&2
2k '
где k = с — Ь.
Лю Хуэй, живший в III в., в своих комментариях к
«Математике в девяти книгах» делает довольно убеди-
63
тельную попытку дать объяснение, каким путем древние
китайцы получили правило, сводящееся к двум послед-
ним формулам. Он считает, что эти формулы, записанные
в словесной форме, они получили, исходя из геометриче-
ских соображений. По-видимому, древнекитайские уче-
ные в данном конкретном
случае пользовались таким
чертежом (рис. 12).
Прежде всего по правилу
«Гоу-гу» имеем:
а2 = с2 — Ь2.
Далее, из рассмотрения
чертежа пол у чается:
а2==с2_Ь2== (С_Ь)2 +
+ 2Ь (с— &),
или
а2 = (с—Ь)2 + 2Ь (с—Ь),
откуда
ь = а2-(с-Ь)2
2(с-Ь) •
Это не исключает, конечно, возможности, что к этим
формулам древние китайцы пришли несколько другим
путем. Каким же именно? Пока что на этот вопрос наука
ответить не в состоянии. Можно лишь строить гипотезы.
Одна из вероятных гипотез и есть приведенное выше
решение Лю Хуэя.
Приводим на правило «Гоу-гу» еще одну задачу.
Задача о бамбуке (№ 13 из девятой книги):
«Имеется бамбук высотой в 1 чжан. Вершину его
согнули так, что она касается земли на расстоянии 3 чи
от корня. Спрашивается, какова высота после сги-
бания».
л Н
Ответ. 4 - чи.
12
Правило. «Расстояние от корня умножь само на се-
бя, объедини с высотой. То, что получится, вычти из вы-
соты бамбука, возьми половину остатка, это и будет вы-
сота после сгибания»,
64
Самого решения автор задачи не приводит. Однако
это решение можно воспроизвести. Действительно, обо-
значив через b высоту бамбука после сгибания,
через с — согнутую часть, через а — расстояние точ-
ки касания вершины бамбука до его основания
(корней) (рис. 13), получим для нахождения b формулу:
а2
ь =-----,
2
которая получается при помощи
таких рассуждений: по правилу
«Гоу-гу»
с2 = а2 + Ь2,
с = (Ь + с) — Ь,
с2 = [(6 + с)—Ь]2 = (Ь+
+ с)2—2Ь (Ь + с) + Ь2.
Откуда:
а2 4- Ь2 = (Ь + с)2 — 2Ь(Ь +с) + b2t
а2 = (b + с)2 — 2Ь(Ь + с),
2Ь (Ь+ с) = (6+с)2— а2,
(b+c)*-d>
W+c) ’
b +с
а2
Ь+с
b =
Рис. 14.
5 Заказ 999
Последняя формула и вы-
ражает древнекитайское пра-
вило для вычисления высо-
ты бамбука после сгиба-
ния.
Если воспользоваться
комментариями Лю Хуэя, то
задача допускает и геомет-
рическое решение. Для этой
цели воспользуемся рисун-
ком 14.
а* = с2 — Ь2 =(с — Ь)2+ 2Ь(с—
- Ь) = (Ь + с)2 2Ь(Ь + с).
65
Следовательно, получаем:
a2=(Z>+c)2—2Z>(fc + c);
ь= (Ь±с?-а*
2(Ь+с)
Откуда:
а2
ь =-------^±£
2
что и нужно по древнекитайскому правилу.
Однако Э. И. Березкина в своих комментариях к рус-
скому переводу «Математики в девяти книгах» (стр. 579)
считает более вероятной, другую реконструкцию только
что рассмотренной и аналогичной ей задач. Вот ее ре-
шение.
Из условия задачи находим, что:
а2 = с2 — Ь2 = (с + Ь) (с — Ь).
Если известны а и с — Ь, то
। . а2 а2 , а2 , , , ч
с + Ь =-----; с =--------Ь; с =------ + (с — Ь) — с.
с — ь с — Ь с — ь
Откуда:
2с = —t + (с — Ь).
с— b
Итак, окончательно получаем:
а2
с = .
С 2
Если же, как у нас в последней задаче, даны а и с + Ь,
тогда:
Откуда:
2Ь = (с + Ь)----
с+ Ь
(с+Ь)- —
ь =________с-±-Ь.
2
а это и дает то правило, которое приведено в трактате.
Результат, полученный по методу Э. И. Березкиной
66
для b, сразу совпадает с древнекитайским правилом и де
требует дополнительных преобразований.
Необходимо заметить, что обе приведенные задачи,
т. е. задача о водоеме и задача о бамбуке, встречаются
также у индийского математика VII в. Брамагупты. Сле-
довательно, эти задачи умели решать и индийские уче-
ные. Кто же у кого позаимствовал? Или это совпадение
случайное. На этот вопрос ответить чрезвычайно трудно.
Этот вопрос как следует еще не изучен, и, следовательно,
в этом направлении можно делать только предположения.
§ 2. ПОЗНАНИЯ ДРЕВНИХ КИТАЙЦЕВ В ОБЛАСТИ
ПИФАГОРОВЫХ ЧИСЕЛ
Древние китайские математики знали формулы для
пифагоровых чисел и свободно ими владели. Об этом,
например, свидетельствуют китайские правила на реше-
ние ряда задач, помещенных в древнем трактате «Ма-
тематика в девяти книгах». В качестве примера приве-
дем задачу о двух путешественниках:
«Два человека находятся в одном месте. Норма
ходьбы А есть 7, норма ходьбы Б есть 3. Б идет на во-
сток. А идет 10 бу на юг, а затем идет по косому на-
правлению на северо-восток до встречи с Б. Спраши-
вается, какой путь прошел каждый из них».
Ответ. Б прошел на восток 10 с половиной бу, А про-
шел по косому направлению 14 с половиной бу, когда
догнал его.
Эту задачу древнекитайский математик рекомендует
решать по такому правилу (самого решения не дает-
ся): «7 умножь само на себя. 3 тоже умножь само на
себя, сложи и возьми половину. Возьми это в качестве
нормы ходьбы А по косому направлению. Вычти из 7,
умноженного само на себя, норму ходьбы по косому на-
правлению, остаток является нормой ходьбы на юг. 3 ум-
ножь на 7, это норма ходьбы Б на восток. 10 бу ходьбы
на юг умножь на норму ходьбы А по косому направле-
нию, 10 бу умножь на норму ходьбы Б на восток, каждое
есть делимое. Объедини (т. е. представь дробно) дели-
мое и норму ходьбы на юг — получишь для каждого ко-
личество пройденного».
б*
67
Пользуясь этим правилом, задачу можно решить до-
вольно просто.
1) Находим сначала норму ходьбы А «по косому на-
правлению»:
72±^= 29.
2
2) Находим норму ходьбы А на юг:
20.
2
3) Норма ходьбы на восток будет:
7-3 = 21.
4) Находим «делимое»: 10*29 и 10*21.
5) А прошел «по косому направлению» путь:
10 29 29 . л 1 /х ч
-----= —= 14- (бу).
20 2 2 v
6) Б прошел на восток путь:
10 21 21 1П1 /х .
-----=— = 10- (бу).
10 2 2 V
Обычным путем задача решается так: обозначим че-
рез х путь, пройденный Б на восток, через у — путь, прой-
денный А на юг, причем, по условию задачи, у = 10 бу,
Рис.
через z—путь, пройденный А «по косому направлению»,
т. е. по диагонали полученного прямоугольного треуголь-
ника (рис. 15) t
Тогда: х2 + 10а = za,
х _ 3
z + 10“ 7 *
68
Откуда находим:
z =— х — 10.
3
Далее:
Х2_|_ 102 =(7 х_
или х2 + 100 = -х2 — —7- 10х I- 100,
2 3
40х2 — 3 2-7- 10х = 0,
2х2 — 21х = 0,
х(2х — 21) = О,
2х = 21,
10L(6y).
Теперь находим г:
г = - • - — 10 =-— 10 = - = 14 — (бу).
3 2 2 2 2
При внимательном рассмотрении оказывается, что чис-
ла 29, 20, 21, которыми китайцы оперировали, по-видимо-
му, составлялись по формулам для пифагоровых чисел.
Действительно, если положить:
а2 + ₽2 а2—₽2
z = ——; г/=-------—, х = аВ,
2 * 2 г
то при всяких аир будет выполняться уравнение:
%2 + у2 = z2.
Следовательно, выражения:
g - «2+32 .
2 ’
а2—В2
у = —— ;
* 2
х = аР;
являются формулами для пифагоровых чисел.
Полагая, как этого требует задача, а = 7 и Р = 3, по
этим формулам получим:
z = “2±P1=ZM±2=29
2 2
= 72=31 20
*22
69
Х = а . р = 73 = 21.
Выходит, что древнекитайские математики знали
формулы для пифагоровых чисел и владели ими.
§30 ТОМ, КАК В ДРЕВНЕМ КИТАЕ РЕШАЛИ
КВАДРАТНЫЕ УРАВНЕНИЯ, К КОТОРЫМ ПРИВОДИЛИСЬ
НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
Древние китайцы умели решать квадратные уравне-
ния. Так, в трактате «Математика в девяти книгах» име-
ется ряд задач, решение которых сводится к нахожде-
нию корней квадратного уравнения. Для иллюстрации
сказанного рассмотрим задачу о двери (№ И де-
вятой книги):
«Имеется дверь, высота которой больше шири-
ны на 6 чи 8 цуней. Наибольшее расстояние между угла-
ми (диагональ) 1 чжан. Спрашивается, каковы ширина
и высота двери».
Ответ. Ширина 2 чи 8 цуней, высота 9 чи 6 цуней.
К задаче, как всегда, дается готовое правило:
«1 чжан умножь сам на себя, это «ши», половину избыт-
ка умножь самое на себя, удвой, вычти из «ши», возьми
половину остатка, извлеки квадратный корень, из него,
из полученного вычти половину излишка, это и будет ши-
рина двери. Прибавь половину излишка, это и будет вы-
сота двери».
Если обозначить ширину двери через х, а длину ее че-
рез у, далее положить, что у — х = т («избыток»), а диа-
гональ двери dt то задача сводится к рассмотрению си-
стемы:
fda = х2 + у2
[т = у — х
Для определения х получаем квадратное уравнение:
2х2 4- 2тх 4- т2 — d2 = 0.
Решая это уравнение обычным приемом, будем иметь:
70
Так как древнекитайские ученые отрицательных кор-
ней не рассматривали, то ширина двери у них получалась:
А это и есть то, о чем говорит вышеприведенное правило
для определения х.
Интересно заметить, что после определения х величину
у легко было бы найти из уравнения
у = х + т,
но согласно древнекитайскому правилу для определения
у дается формула:
что является положительным корнем уравнения:
2у2 — 2ту + т2 — d2 = 0.
Как замечает Э. И. Березкина, по-видимому, сами
древние китайцы решали полное квадратное уравнение
так же, как древние вавилоняне.
Если, придерживаясь условий задачи, положим:
то
У = 2
х2 4- у2 = 2г2 + 2-]2.
но \2/
Следовательно:
Откуда:
х2 + у2 = d\
2z2
71
или
Окончательно будем иметь:
Древние китайцы владели еще одним способом реше-
ния квадратного уравнения, который в настоящее время
известен как способ Горнера. Это подтверждает древне-
китайское правило к задаче о городе, обнесен-
ном квадратной стеной (задача № 20 девятой
книги):
«Имеется город в виде квадрата со стороной неиз-
вестного размера, в центре каждой стороны находятся
ворота. На расстоянии 20 бу от северных ворот име-
ется столб. Если пройти от южных ворот 14 бу и по-
вернуть на запад, пройти еще 1775 бу, то можно уви-
деть столб. Спрашивается, какова сторона города».
Ответ. 250 бу.
Правило к этой задаче гласит: «Количество бу,
пройденное от северных ворот, умножь на удвоенное
количество бу, пройденное на запад, это делимое. Сложи
с количеством бу, пройденным от южных ворот, это до-
72
полненный делитель. Извлеки квадратный корень, это и
будет сторона города».
Эту задачу можно иллюстрировать рисунком 16.
Пользуясь обозначениями чертежа, задачу можно свести
к решению квадратного уравнения:
Xе + + 4)х — 2/?/2 = О-
§ 4. ДРЕВНЕЙШИЕ ПРАВИЛА ДЛЯ ВЫЧИСЛЕНИЯ
ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
С древнекитайскими правилами для вычисления пло-
щадей плоских фигур можно познакомиться по первой
книге древнего трактата «Математика в девяти книгах».
Здесь дан ряд задач на вычисление плошадей земельных
участков, имеющих различную форму. Так, при вычисле-
нии прямоугольного поля умножалась ширина на длину.
При вычислении площади поля, имеющего форму тре-
угольника, применялось правило: «Половину ширины ум-
ножь на прямую длину (высоту)». Поле, которое имеет
форму трапеции, называется «косым полем». Для вычис-
ления площади такого поля применялось правило: «Сло-
жи обе стороны поля, раздели пополам, умножь на пря-
мую длину или на прямую ширину. И можно половину
прямой длины или ширины умножить на сложенные сто-
роны поля». Это правило дает формулу:
5 = °±_ь . h
2
где а и b — основания трапеции, a h — высота ее.
Для вычисления площадей круглых полей древние
китайцы имели четыре правила.
Первое правило. «Умножь половину обвода на
половину диаметра». Таким образом, имеем:
Второе правило. «Умножь обвод на диаметр,
раздели на 4 и возьми один раз». Следовательно, полу-
чим:
S = с-.
4
73
Третье правило. «Умножь диаметр сам на се-
бя, раздели на 4 и возьми 3 раза». Что соответствует:
S = - • 3= - d\
4 4
Здесь вместо гс взято 3, т. е. « = 3.
Четвертое правило. «Умножь обвод сам на
себя, раздели на 12 и возьми 3 раза». Это можно записать
так:
При нахождении площади круглого поля древние ки-
тайцы полагали к =3. Это, конечно, не значит, что они
не знали более точного его значения. Для более точных
вычислений они брали и более точные значения к.
Сектор круга древние китайцы называли «кри-
вым полем» и для вычисления его площади пользовались
правилом: «Диаметр умножь на обвод, раздели на 4
и возьми один раз». Таким образом, имеем формулу:
Q —
сектор круга *
Сегмент круга древними китайцами назывался
«полем в виде лука», причем основание сегмента называ-
ли тетивой, а высоту сегмента — стрелой. Например, в
древнем Китае решалась такая задача (первая книга
«Математики в девяти книгах», задача № 35):
«Имеется поле в виде лука, тетива в 30 бу, стрела
в 15 бу. Спрашивается, каково поле».
Ответ. 1 му 97 бу с половиной.
Дается правило: «Умножь тетиву на стрелу, ум-
ножь еще стрелу на себя, сложи, раздели на два и возь-
ми один раз».
Таким образом, площадь сегмента вычисляется по
формуле:
где а—основание, b — высота сегмента.
Внимательно вглядываясь в формулу площади сег-
мента, легко сделать заключение, что площадь сегмента
74
вычислялась приближенно путем вычисления площади
трапеции (рис. 17), у которой основания а и Ь и высота Ь,
т. е.
S _ с _ ° + ь ь= аЬ+^2
сегм. °тр, 2 2 *
Кроме того, древние китайцы решали задачи на вы-
числение площади «по-
ля в виде кольца». При-
мером может служить
такая задача (первая
книга «Математики в
девяти книгах», зада-
ча № 37):
«Имеется поле в ви-
де кольца, внутренний
обвод в 92 бу, внешний
обвод в 122 бу, диа-
метр кольца в 5 бу.
Спрашивается, каково
поле».
О т в е т. 2 му 55 бу.
Для решения этой и аналогичных ей задач в трактате
дается правило: «Сложи внутренний и внешний обво-
ды, возьми их половину, умножь на диаметр — получится
площадь в бу».
Соответствующая формула будет:
(R-r).
где С и с — внешний и внутренний обводы, R и г—ра-
диусы внешнего и внутреннего обвода, R— г—ширина
(«диаметр») кольца.
§ б. ДРЕВНЕКИТАЙСКИЕ ПРАВИЛА ДЛЯ ВЫЧИСЛЕНИЯ
ОБЪЕМОВ
В древнекитайском трактате «Математика в девяти
книгах» имеются задачи на вычисление объемов крепост-
ных стен, валов, плотин, каналов и других сооружений,
а также решение различных вопросов, связанных с рас-
75
четами земляных работ. Правила к решению этих задач
говорят о том, что китайцы еще в глубокой древности
умели вычислять объемы различных тел, в частности
объемы параллелепипеда, призмы, конуса, пирамиды
и т. д.
Объем параллелепипеда
Объем параллелепипеда находится по правилу пере-
множения всех его трех измерений. В древнем Китае
рассматривался также частный случай параллелепипеда
под названием квадратное «бао-дао».
Древние китайцы, например, решали такую задачу:
«Имеется квадратное «бао-дао». Сторона квад-
рата 1 чжан 6 чи, высота 1 чжан 5 чи. Спрашивается,
каков объем». (1 чжан=10 чи=100 цуням.)
Ответ. 340 чи.
Эта задача снабжена правилом: «Умножь сторо-
ну самое на себя, умножь на высоту, это и будет объем
в чи».
Квадратное «бао-дао» есть параллелепипед с квад-
ратным основанием, который, как полагает Э. И. Берез-
кина, видимо, считался «единичным», так как его боко-
вые грани представляют собой площади в 15-16 =
= 240 кв. чи, численно равные количеству кв. бу в еди-
нице площади 1 му.
Объем призмы и призматических тел
1-й случай. «Цзя-ду» — прямая призма, основа-
нием которой служит прямоугольный треугольник со
сторонами а и Л. а высота призмы / (рис. 18).
Древние китайцы объем «цзя-ду» вычисляли по пра-
вилу, которое можно выразить формулой:
v = — alh.
2
2-й случай. «Ян-ма»— пирамида, основанием кото-
рой является прямоугольный треугольник с катетами а
и /, а высота которой h является одновременно одним из
ребер. Таким образом, «ян-ма» представляет собой левое
нижнее тело (рис. 18), полученное сечением «цзя-ду»
плоскостью АВС.
76
Объем «ян-ма» фактически вычисляем по формуле:
1 it.
v = — alnt
3
3-й случай. «Бе-нао» — пирамида, основанием ко-
торой служит прямоугольный треугольник с катетами а
и h (рис. 18) s а высота пирамиды I является одновремен-
Рис. 18,
но одним из ее ребер. Как легко видеть, «бе-нао» пред-
ставляет собой верхнюю часть «цзянь-ду», отсеченную
плоскостью АВС. Китайское правило для вычисления
объема «бе-нао» сводится к формуле:
V = - ahi.
6
4-й случай. «Сянь-чу» — тело, составленное из пря-
мой призмы, основанием которой является прямоуголь-
ный треугольник с катетами I и h (рис. 19), а высота
равна а, и двух равновеликих пирамид, основанием ко-
b — а
торых является трапеция со сторонами ~ и
и высотой 1Л а высота этих пирамид равна
с — а
77
Правило для вычисления объема «сянь-чу» можно за-
писать формулой.
V=-lh(a + b+c).
6
Возможно, эта формула была получена в результате
таких тождественных преобразований:
V= -lha + 2\-(—^/-1 =-alh+ -blh+
2 [2\ 2 2 / 3j 2 6
+ — clh— —alh— —lh(a + b 4-c).
6 3 6
5-й случай. «Чу-тун», «пань-чи», «мин-гу» суть усе-
ченные четырехгранные пирамиды, грани которых не схо-
дятся в одной точке (рис. 20). Различные названия одного
и того же геометрического тела связаны с происхожде-
нием этого тела как конкретного объекта строительства
(обелиски). «Чу-тун» является наземным сооружением,
как тело, обладающее высотой; «пань-чи», как тело, име-
78
ющее глубину, может быть ямой, вырытой в земле; «мин-
гу» является обелиском с глубиной, вытянутым в длину,
причем «нижняя ширина» очень мала по сравнению с
«верхней шириной» (рис. 20).
Рис. 20.
Объем всех трех усеченных четырехугольных пирамид
вычислялся по правилу, которое равносильно фор-
муле:
у (2ai + + (2а2+ ft
6
где аь — нижние ширина и длина; Ь2 — верхние
ширина и длина; h — высота тела в случае, если оно
представляет собой «чу-тун», или глубина тела, если по-
следнее будет «пань-чи» или «мин-гу».
По всей видимости, названная выше формула была по-
лучена при помощи таких тождественных преобразова-
ний:
V= a2b2h+± a2hx + b2hy + 4 b2hz + 4 a2hu + 4 xyh+
2 2 2 2 2)
1 1 1 /22
H— xzh-\—zuh-\— uyh = ft — a2b2+
3 3 3 \ 6 6
+ = l(2a1+a2)b1+ (2a2 + ajbj.
О 0/0
79
Объем конуса
В пятой книге древнекитайского трактата «Математи-
ка в девяти книгах» имеется такая задача:
«Имеется конус. Обвод основания 3 чжана 5 чи,
высота 5 чжанов 1 чи. Спрашивается, каков объем».
Ответ. 1735 -чи.
12
В книге для решения этой задачи дано правило:
«Обвод основания умножь сам на себя, умножь на высо-
ту, разделив на 36, возьми один раз».
Таким образом, объем конуса древние китайцы вы-
числяли по формуле:
3 4л ’
причем предполагается, что 3.
Объем усеченного конуса
Усеченный конус древние китайцы называли «круглое
тин» и решали на него ряд задач. В качестве примера
приведем одну из них.
Задача об усеченном конусе (пятая книга
«Математики в девяти книгах», задача № 11):
«Имеется круглое тин. Нижний обвод 3 чжана,
верхний обвод 2 чжана, высота 1 чжан. Спрашивает-
ся, каков объем».
Ответ. 527—чи.
9
Древние китайцы решали эту задачу по такому пра-
вилу: «Перемножь верхний и нижний обводы, умножь
каждый сам на себя, все это сложи, умножь на высоту,
раздели на 36, возьми один раз».
Следовательно, объем усеченного конуса в древнем
Китае находился по формулам:
у = (Cc-f-C2H-c2)/:
36 ’
80
или, полагая к =3, получим:
у_ h Сс+С2+с2
3 4гс ’
где С и с — длины окружностей верхнего и нижнего ос-
нований, a h — высота.
§ 6. ЗАДАЧИ, ОСНОВАННЫЕ НА РАССМОТРЕНИИ
ПОДОБНЫХ ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
Древним китайцам была известна теория подобия
прямоугольных треугольников, которую они применяли
к решению целого ряда геометрических задач (смотрите
девятую книгу трактата «Математика в девяти книгах»
в переводе и с комментариями Э. И. Березкиной).
К этой категории, например, относится такая з а-
д ач а:
«Имеется горизонтальный катет в 5 бу, вертикаль-
ный катет в 12 бу. Спрашивается, какова сторона
квадрата, вписанного в этот треугольник».
g
Ответ. Сторона квадрата 3 -бу.
Древнекитайское правило к этой задаче гласит: «Сло-
жи горизонтальный и вертикальный катеты, это делитель.
Перемножь горизонтальный и вертикальный катеты, это
делимое. Объедини делимое и делитель — получишь сто-
рону квадрата в бу».
С помощью рассмотрения подобных треугольников
древние китайцы решали ряд задач практической геомет-
рии на вычисление недоступных расстояний. Как указы-
валось выше, этими вопросами в III в. особенно много
занимался Лю Хуэй в своем трактате «Математика
морского острова».
В древнекитайском трактате «Математика в девяти
книгах» вопросам практической геометрии посвящаются
последние три задачи последней книги. Рассмотрим эти
задачи.
Задачапервая:
«Столб отстоит от человека на неизвестном рас-
стоянии. Поставлены 4 столбика, которые удалены
§ Заказ 999
81
друг от друга на 1 чжан. Пусть два столбика нахо-
дятся слева от наблюдателя, сам же он находится у
правого последнего столбика и наблюдает столб на
расстоянии в 3 цуня от правого переднего столбика.
Спрашивается, на сколько удален от человека столб».
Задачу можно иллюстрировать
S рисунком 21. Решая эту задачу, ки-
\ тайский ученый, по-видимому, рас-
\ сматривал два подобных треуголь-
у ника:
\ kSAD и \ECD.
\ Откуда делался вывод, что
\ AS_ AD
\ CD“ ЕС 9
V ИЛИ
\ ЕС
\ Подставляя данные задачи, по-
/9 _______j лучаем словесную формулу:
о О1 1чжан X 1чжан
Рис. 21. х =-------------.
3 цуня
На основании этого древние китайцы давали такое
правило: «Умножь 1 чжан сам на себя, это делимое.
3 цуня есть делитель. Объедини делимое и делитель».
Задача вторая:
«Гора расположена на запад от столба. Высота ее
неизвестна. Она удалена от столба на 53 ли. Высота
столба 9 чжанов 5 чи. В 3 ли к востоку от него стоит
человек и наблюдает вершину столба на одном уров-
не с вершиной горы. Уровень зрения человека распо-
ложен на высоте в 7 чи. Спрашивается, какова высота
горы».
Ответ. 164 чжана 9 чи 6 с большей частью цуня.
К этой задаче можно дать рисунок 22.
82
К своему правилу для решения этой задачи древние
китайцы, видимо, пришли из рассмотрения подобных
прямоугольных треугольников:
&AKN и &NLF.
Откуда:
АК =
KN LF 9
x—ND_ ND—FE
BD ~ DE
или
Следовательно, получим:
x-np + <kd-fe'bd .
DE
Это выражение дало повод сформулировать древне-
китайское правило, которое дается в качестве поясне-
ния к рассматриваемой задаче.
Это правило гласит: «Из высоты столба вычти высоту
уровня зрения 7 чи, остаток умножь на 53 ли, это дели-
мое. Расстояние, на которое удален человек от столба в
3 ли, есть делитель. Объедини делимое и делитель. То,
что получится, прибавь к высоте столба, это и будет
высота горы».
Задача третья:
«Диаметр колодца 5 чи, глубина неизвестна. У
верхнего края колодца поставлен шест в 5 чи. Верши-
на шеста наблюдается на одном уровне с границей
воды и стены, а на диаметре откладывается 4 цуня.
Спрашивается, какова глубина колодца».
Ответ. 5 чжанов 7 чи 5 цуней.
6*
S3
Во всех трех последних задачах надо иметь в виду,
что 1 чжан=10 чи=100 цуням. Для составления нужного
правила решения древнекитайские математики, по всей
во в цунях».
вероятности, рассматривали два
подобных прямоугольных тре-
угольника (рис. 23):
&ABF и \FCD.
Откуда получали:
— ; x = FC — •
BF FC BF’
_ AB(BC—BF)
X~ BF
Последняя формула давала
возможность сформулировать
правило, которое и дается в
трактате: «Из 5 чи, диаметра ко-
лодца, вычти 4 цуня, что отклады-
вается на диаметре. Остаток
умножь на 5 чи, высоту шеста,
это делимое, 4 цуня, что отклады-
вается на диаметре, есть делитель.
Объедини (т. е. представь в виде
дроби) делимое и делитель, получишь искомое количест-
— do
О
ГЛАВА ШЕСТАЯ
ОТДЕЛЬНЫЕ ЗАМЕЧАНИЯ
Необходимо отметить, что Китай далекого историче-
ского прошлого нельзя мыслить отгороженным от осталь-
ного мира «китайской стеной», которой, кстати сказать,
в древнее время еще не существовало. Многие достиже-
ния китайской культуры передавались и в другие стра-
ны и в конце концов достигли Европы.
Распространению китайской культуры прошлого, по-
видимому, во многом содействовала внешняя торговля.
Известно, что шелковые ткани, производство которых в
Китае налажено с древнейших времен, занимали первое
место среди предметов вывоза. Торговые пути древнего
Китая тянулись к Индии. Вместе с китайскими шелками
в другие страны, в том числе и в Индию, проникали и
некоторые достижения китайской науки и культуры.
О связи Китая с другими странами говорит и тот
факт, что ряд китайских задач дословно повторяется в
математических рукописях других стран. Например, ки-
тайская задача Сунь-цзы о нахождении числа, которое
при делении на 3 дает остаток 2, при делении на 5 дает
остаток 3 и при делении на 7— остаток 2, почти дословно
повторяется у индийских математиков, а также в извест-
ной книге об абаке Леонардо Пизанского (1202).
Однако с XVII в. намечается резкое торможение в
развитии китайской науки и культуры, вызванное завое-
ванием Китая маньчжурами и утверждением их власти
(династия Цин), которая на долгое время сохраняет в
Китае феодальный строй.
С конца XVIII в. Китай становится объектом колони-
ального захвата со стороны ряда капиталистических
стран. С середины XIX в. такие капиталистические стра-
85
Проф. Цянь Сюэ-сянь.
ны, как Англия, США,
Франция, Япония, посте-
пенно превращают Китай
в свои колонии и приводят
науку и культуру Китая к
глубокому упадку.
И только совсем не-
давно, в связи с победой
китайской народной рево-
люции, впервые в истории
Китая созданы все необ-
ходимые условия для
успешного развития науки
и культуры в стране.
За последние 25 лет
китайскими математика-
ми написано большое ко-
личество оригинальных
работ по теоретической и
прикладной математике.
Среди современных та-
лантливых математиков
можно назвать Чень
Цзян-гун а, В а н Ф у ч-у н я, Ч э н ь Мин-д э, успешно
работающих по теории тригонометрических рядов.
По разработке идей современной геометрии работа-
ют также видные математики Китая Су Бо-цин и
Чжан Су-чэн (теория кривых), Бай Чжин-го
(теория поверхностей), Сун Цзэ-ин (обобщенные
пространства), У Да-жэнь (интегральная геомет-
рия), Янь Чжи-да (главные кинематические фор-
мулы в n-мерном пространстве), Цзян Цзе-хань
(теория многообразий), Янь Чжи-да (топологиче-
ские свойства групп Ли). В теории чисел китай-
ские математики разрабатывают преимущественно идеи
нашего советского ученого Героя Социалистического
Труда академика И. М. Виноградова. И в
этом направлении интересными и оригинальными ра-
ботами зарекомендовали себя видный ученый Китая Ху а
Ло-чен и его ученики. По современной алгебре работают
ученые В а н С я н-х а о, Цзэн Цзю н-ч ж и, СунБэнь-
ван и другие. По истории древней китайской математи-
ки много сделали Ли Янь иЦянцБао-цзун. Они да-
80
Проф. Хуа Ло-чен.
ли много ценных материа-
лов для составления исто-
рии развития математики
в Китае, в особенности
древнего периода.
Большое влияние на
интенсивное развитие со-
временной китайской ма-
тематики оказывают мате-
матические научные шко-
лы Советского Союза. В
настоящее время значи-
тельная часть советской
математической литерату-
ры переведена на китай-
ский язык, и, кроме того,
большинство преподавате-
лей китайских университе-
тов научились со слова-
рем читать математиче-
скую литературу на рус-
ском языке.
Несомненным свидетельством достижений и успехов
современных китайских ученых в области математики яв-
ляется недавнее присуждение премий. Для поощрения
дальнейшего развития науки Государственный Совет Ки-
тайской Народной Республики в 1955 г. издал постанов-
ление «О научных премиях Академии наук Китая». В
1957 г. состоялось присуждение первых премий ученым за
выдающиеся заслуги в области науки и техники. Премии
получили 34 китайских ученых. Труды этих ученых имеют
большое народнохозяйственное значение и способствуют
дальнейшему развитию научных теорий.
Первой премии удостоены три крупных математика
Китая: Цянь Сюэ-сянь, Ху а Ло-чен, У Вэнь-
ц з ю н ь.
X у а Ло-чен, имя которого известно далеко за пре-
делами Китая, удостоен первой премии за оригинальные
и очень важные открытия в области теории функций
многих комплексных переменных, что, несомненно, ока-
жет влияние на развитие теории дифференциальных
уравнений.
У В э н ь-ц з ю н ь удостоен первой премии за очень
87
Проф. У Вэнь-цзюнь.
нужные открытия в об-
ласти топологии, которая
в настоящее время состав-
ляет целую геометриче-
скую науку, весьма абс-
трактную и ценную для
дальнейшего развития ма-
тематических теорий.
Цянь Сюэ-сянь
удостоен первой премии
за разработку основ мо-
лодой науки, которая ре-
шает проблемы автома-
тического управления и
регулирования отдельных
систем.
Все эти работы полу-
чили высокую оценку не
только в Китае, но и за
рубежом.
«Мы уверены, — за-
являет китайский матема-
тик Хуа Ло-чен,— что под мудрым руководством Ком-
мунистической партии и председателя Мао Цзэ-дуна нам
удастся, изучая передовой опыт Советского Союза, в
кратчайший срок развить и укрепить нашу науку, чтобы
она играла надлежащую роль в хозяйственном и куль-
турном развитии страны» Ч
1 X у а Ло-чен, Современное положение математики в Китае,
«Вестник АН СССР», 1953, № 6, стр. 20.
a. c nt в
II
КРАТКАЯ ИСТОРИЯ
МАТЕМАТИКИ
ч?
И Н | И И
ГЛАВА СЕДЬМАЯ
ИНДИЯ—СТРАНА МНОГОВЕКОВОЙ
САМОБЫТНОЙ КУЛЬТУРЫ
Культура Индии имеет большую и богатую историю,
истоки которой уходят в седую древность. Уже в III—
II вв. до н. э. в Индии строились оросительные каналы,
городские водосточные системы и многоэтажные здания
из хорошего обожженного кирпича. В далеком прошлом
индийцы владели искусством керамического производст-
ва и пользовались гончарным кругом, успешно развива-
лось ювелирное дело.
Еще в глубокой древности в Индии были накоплены
большие знания в области грамматики, медицины, мате-
матики, астрономии, физики, химии и других наук.
Древнеиндийские астрономы делили солнечный год
на 12 месяцев и каждый месяц на 30 дней, причем через
каждые пять лет ими прибавлялся тринадцатый месяц.
Они учили, что Земля имеет форму шара и совершает
вращение вокруг своей оси. Наибольшего своего разви-
тия индийская астрономия достигла в средние века, ког-
да в индийских городах возникли астрономические обсер-
ватории, которые по своему техническому оборудованию
не уступали первоклассным средневековым обсерватори-
ям Ближнего и Среднего Востока, а также и Европы.
В средние века в Индии было хорошо налажено при-
боростроение для астрономических обсерваторий и гео-
дезических съемок. Так, в Государственном музее вос-
точных культур в Москве хранится индийская астроля-
бия, изготовленная в 1588 г. и представляющая собой
копию с более древнего образца.
Во многих областях изобразительного искусства древ-
ние индийцы достигли значительного совершенства. Вы-
соко были развиты ваяние и художественные ремесла,
91
среди которых особенно выделялись резьба по камню,
дереву и кости.
Образцы изящной древнеиндийской фресковой жи-
вописи сохранились до настоящего времени в некоторых
пещерных храмах, например в пещерном храме Аджанты,
высеченном в скале между II в. до н. э. и VII в. н. э.
В древней Индии независимо от других стран возник-
ла высокоразвитая литература. В особенности на боль-
шой высоте стояли драматургия и поэзия. Образцом вы-
сокохудожественной лирической поэзии является поэма
Калидасы «Мегхадута» («Облако-вестник»).
Древнеиндийские авторы, писавшие в большинстве
случаев на санскрите, придавали большое значение зву-
ку, поэтому их литература, как проза, так и стихи, отли-
чается музыкальностью и ритмичностью1.
Что касается философии, то еще в глубокой древности
индийские мыслители, пользуясь тогдашними достиже-
ниями науки, старались философски осмыслить окружа-
ющий мир и его развитие. Ранняя индийская философия
тесно переплетается с мифами и религиозными веровани-
ями, что отвечало интересам правящих классов того вре-
мени. Таким образом, господствующее направление в
древнеиндийской философии, тесно связанное с буддий-
ским и брахманистским богословием, было насквозь
идеалистическим.
Однако против господствующей идеалистической фи-
лософии выступали индийские философы-материалисты,
отражавшие взгляды городских низов и свободных об-
щинников. Наиболее старым индийским философским
материалистическим учением является учение «Чарва-
ка», согласно которому окружающий мир извечно мате-
риален, единственным источником познания является
чувственное восприятие, не может быть раздельного су-
ществования души и тела, бессмертия души и переселе-
ния душ.
На материалистической основе возник целый ряд на-
турфилософских атомистических систем, рассматриваю-
щих окружающие нас вещи и самого человека состав-
1 «Санскрит, — как подчеркивает Неру, — язык удивительно бога-
тый, цветистый, полный различных новых образований и в то же
время точный и строго выдержанный в рамках грамматики, изложен-
ной Панини 2600 лет назад». Джавахарлал Неру, Откры-
тие Индии. Перев. с англ., ИИЛ, М., 1955, стр. 169.
92
ленными из мельчайших частичек, обладающих опреде-
ленными свойствами и качествами.
Сторонники материалистических учений выступали
с критикой идеалистических направлений, высмеивали
брахманистские обряды, жертвоприношения и разного
рода суеверия.
Древнеиндийская философия с ее различными тече-
ниями оказала глубокое влияние на развитие философ-
ских взглядов у многих народов древности.
Наибольших успехов индийские ученые в древности
достигли в области математики. Достижения индийских
ученых в области арифметики и алгебры, как увидим
далее, оказали сильное влияние на развитие восточной,
а затем и европейской математики.
ГЛАВА ВОСЬМАЯ
РАЗВИТИЕ АРИФМЕТИКИ И АЛГЕБРЫ В ИНДИИ
§ 1. ОБ ИНДИЙСКОЙ ПОЗИЦИОННОЙ ДЕСЯТИЧНОЙ
СИСТЕМЕ СЧИСЛЕНИЯ
Расцвет математической культуры Индии относится
к V—XII вв. н. э. Заслуги индийцев в области матема-
тики, особенно арифметики и алгебры, трудно переоце-
нить. Оказывается, первоначальные основы современной
арифметики и алгебры были заложены не только в древ-
нем Китае, но и в древней Индии. Величайшим достиже-
нием древнеиндийской математики является прежде все-
го открытие позиционной системы счисления, состоящей
из десяти индийских цифр, включая и знак нуль—«су-
нья», что дословно означает «ничто» Интересно заме-
тить, что в первоначальном начертании нуль изображал-
ся точкой и лишь спустя много веков — маленьким кру-
жочком. Индийский народ первый стал употреблять де-
сятичную позиционную систему. Есть основание думать,
что эта система индийцами была изобретена в начале
I в. н. э., а первое употребление знака нуля относится
ко II в. н. э.
Великий французский математик Лаплас (1749—
1827) по поводу открытия индийских математиков писал:
«Индия дала нам остроумный метод выражения всех
чисел посредством десяти знаков, причем, кроме величи-
ны каждого знака, имеет значение и его расположение.
Эта глубокая и важная мысль кажется нам сейчас на-
столько простой, что мы не замечаем ее истинных досто-
инств, но ведь сама ее простота и большая легкость, ко-
торую она придала всем вычислениям, делают нашу
1 Арабы называли цифровые обозначения «цифрами Хинда»
(т. е. Индии), а число по-арабски называется «Хандаса», т. е. «из
Хинда». Джавахарлал Неру, Открытие Индии, перев. с англ.
ИИ Л, М., 1955, стр. 229.
94
арифметику одним из самых полезных изобретений. Мы
оценим все величие этого достоинства, когда вспомним,
что мимо него прошел даже гений Архимеда и Аполло-
ния.— двух величайших людей древности» Ч
Индийская десятичная позиционная система счисле-
ния, как наиболее удобная и простая для повседневной
вычислительной практики, была сначала воспринята так
называемой арабской математикой, а затем через нее
была перенесена в Европу. Здесь уместно заметить,
что большую роль в распространении индийской десятич-
ной позиционной системы счисления в странах Ближнего
и Среднего Востока, а также и в Европе сыграл арифме-
тический трактат знаменитого хорезмийского математи-
ка и астронома Мухамеда бен Муса ал Хорез-
м и, жившего в Багдаде в первой трети IX в. 1 2.
Только в процессе труда, как отражение свойств и
отношений реальных предметов действительного мира, и
были созданы понятия числа и натурального ряда, а так-
же учение о десятичной позиционной системе счисления.
«Понятия числа и фигуры, — писал Энгельс, — заимст-
вованы именно из действительного мира. Десять пальцев,
на которых люди учились считать, т. е. производить пер-
вое арифметическое действие, представляют что угодно,
но только не свободное творение рассудка. Для счета не-
обходимы не только объекты счета, но также уже и спо-
собность при рассмотрении этих объектов отвлекаться от
всех их свойств, кроме их числа, а эта способность — про-
дукт долгого исторического эмпирического развития» 3.
§ 2, ИЗ ИСТОРИИ ПОЗИЦИОННОЙ СИСТЕМЫ
СЧИСЛЕНИЯ
Впервые позиционной системой счисления стали поль-
зоваться древние вавилоняне. Их позиционная система
счисления была шестидесятеричной. Она просущество-
вала примерно полторы тысячи лет (до III в. до н. э.) и
1 Джавахарлал Неру, Открытие Индии, перев. с англ.,
ИИЛ, М., 1955, стр. 226.
2 См. об этом подробно в статье А. П. Юшкевича «Арифмети-
ческий трактат Мухамеда бен Муса ал Хорезми». «Труды Института
естествознания и техники», т. I («История физико-математических
наук»), изд. АН СССР, М., 1954, стр. 85—127.
3 К. Маркс и Ф. Энгельс, Сочинения, т. XIV, стр. 39.
95
оказала заметное влияние на развитие математики дру-
гих стран, включая Индию и Китай.
Вавилоняне писали палочками на глиняных пластин-
ках. Палочки имели трехгранную форму, так что при на-
жиме на глину получался клинообразный отпечаток. Та-
кой способ записи впоследствии стал называться кли-
нописью. Клинописью вавилоняне записывали и числа.
Все числа они записывали при помощи двух знаков, а
именно вертикального клина, у означавшего едини-
цу, и горизонтального клина , означавшего 10. Пер-
вые девять чисел натурального ряда у них записывались
так:
123 4567 89
Из этого видно, что каждое число до девяти включитель-
но изображалось соответствующим количеством клиныш-
ков, причем с таким расчетом, что их количество сразу
бросалось в глаза и нет нужды каждый раз их пересчиты-
вать заново.
Числа второго десятка вавилоняне записывали в та-
ком виде:
Из приведенного примера видно, что запись идет слева
направо, причем сначала идут десятки, а потом единицы.
96
В таком виде можно записать любое число до 60. Так,
число 53 запишется так:
Придерживаясь шестидесятеричной системы счисле-
ния, число 60 вавилоняне записывали символом Y , счи-
тая его единицей высшего разряда. Затем числа от 60
до 602 — 1 записывались так же, как и числа от 1 до 59, с
той только разницей, что каждый символ имел значение,
в шестьдесят раз большее. Например, число 93 записы-
валось таким образом:
Необходимо заметить также, что вавилонская шести-
десятеричная позиционная система счисления, как гово-
рят, не носила абсолютный характер, гак как в ней сим-
волическая запись числа не была однозначной. Напри-
мер, как указывалось выше, символ
означает число 93, но с одинаковым правом эта запись
может означать и число 93-60 или 602 + 33, а также вооб-
ще любое число вида 93 60 п или 60tW + 33 60tn. Не-
абсолютный характер вавилонской шестидесятеричной
позиционной системы счисления объясняется отсутствием
нуля. Оказывается, вавилоняне в течение сотен лет сов-
сем не знали нуля. Собственно, большой нужды в нуле в
то время и не было, так как древние вавилоняне практи-
чески пользовались небольшими числами примерно от 1
до 3600, где нуль в шестидесятеричной системе нужен
всего 59 раз (в десятеричной системе он встречается 917
раз), а в пределах от 1 до 59 включительно он вообще не
нужен. В VI или V в. до н. э. преимущественно в связи с
задачами астрономии появилась потребность в больших
числах, намного превосходящих 3600. Пришлось тогда
вавилонянам ввести нечто вроде нуля, который они обоз-
7 Заказ 999
97
начали символом . После этого вавилонская ше-
стидесятеричная система счисления стала ближе к абсо-
лютной. Действительно, с введением «египетского нуля»
стало вполне возможно по записи отличить, например,
число 3608 от 68. В самом деле число 3608 уже записы-
валось так:
Y £
а 68 — так:
Однако египетская шестидесятеричная позиционная
система все же не стала вполне абсолютной по той про-
стой причине, что египетский нуль никогда не ставился в
конце числа, так что по написанию нельзя отличить, на-
пример, число 3600 от 60 или от 1, так как во всех этих
случаях запись числа была одинаковой, она обознача-
лась вертикальным клинышком у т.е, единицей. 'О точ-
ном значении числа в подобных случаях приходилось до-
гадываться по смыслу соответствующего текста. Казалось
бы, чего проще число 3600 обозначать через
Y
, тогда вавилонская шестидеся-
а 60 — через у
теричная позиционная система была бы абсолютной. Од-
нако вавилоняне этого не сделали и не довели свою си-
стему до завершения.
Только индийский народ, возможно, под влиянием
позиционного счисления вавилонян создал свою деся-
тичную позиционную систему счисления уже абсолютно-
го характера, в которой нуль, как и подобает ему для од-
нозначного написания чисел, стал ставиться не только
внутри записи числа, но и в конце его.
О происхождении вавилонской шестидесятеричной по-
зиционной системы счисления имеется много гипотез,
на которых мы не будем останавливаться. Заметим толь-
ко, что согласно одной из них, по нашему мнению, более
вероятной, происхождение ее связывается с древнейшим
счетом по пальцам и суставам (И. Н. Веселовский,
И. Ю. Тимченко). Действительно, с рукой человека свя-
зано число 15, если это число рассматривать как резуль-
тат счета суставов пальцев руки, полагая, что каждый
палец содержит три сустава, не исключая и большого
пальца, утолщение которого считается как бы третьим су-
ставом его Такого счета придерживаются, например, бен-
гальцы. Они начинают счет с нижнего сустава мизинца
левой руки и, продолжая считать таким образом, закан-
чивают счет большим пальцем. Имея это в виду,
И. Ю. Тимченко полагает, что «шестидесятеричное счис-
ление могло произойти от продолжения такого счета на
правой руке, а затем на другой стороне суставов правой
и левой руки в обратном порядке» !.
Следы вавилонской шестидесятеричной системы счис-
ления сохранились и сейчас при измерении углов и вре-
мени. Действительно, до настоящего времени шестую
часть окружности принято делить на 60 градусов, градус
на 60 минут и минуту на 60 секунд.
Современные цифры
1, 2, 3, 4, 5, 6, 7, 8, 9, 0,
получившие мировое признание и распространение, по
мнению большинства ученых, индийского проис-
хождения. Но это вовсе не значит, что у самих индий-
цев они имели именно такой вид. Нужно было много ве-
ков, чтобы индийские обозначения цифр приняли, нако-
нец, современную форму. Полагают, что цифры самих
индийцев, которыми они пользовались раньше в своей
десятичной системе, произошли от первых букв числи-
тельных имен. Подтверждением этому служит то, что на
санскритском языке, которым обычно пользовались ин-
1 См. примечание И. Ю. Тимченко к книге Ф. Кэджори,
История элементарной математики, Одесса, 1910, стр. 313—316. Сам
И. Ю. Тимченко считал также вполне возможным, что шестидеся-
теричная система могла возникнуть из смешения 4-ричной и 15-рич-
ной систем счисления, встречающихся, по его словам, в Бенга-
лии,
7*
99
дийские ученые, первые девять числительных имен все
начинаются с различных букв.
Ниже приводится таблица эволюции индийских цифр,
которые в Европе неправильно назывались арабскими
(рис. 24).
1 2 3 ч 5 6 7 8 9 0
1 Г Г О в Ч V Л 9 о
1 2 $ of <v ч V 7 9 о
1 г- 6 7 X 9
5 ь 3 е б" /\ ъ 9 &
1 г 9- *7 б А 8 9 О
\ 7 Я 7 б и 8 9 0
t 2 3 4 S 6 7 8 9 0
7 2 3 4 5 6 7 6 9 0
Рис. 24.
Из анализа приведенной таблицы вытекает, что напи-
сания индийских цифр в течение веков с переходом от
одного народа к другому подвергались коренным изме-
нениям. Эти изменения настолько большие, что от форм
старинных первоначальных индийских -цифр к современ-
ным перешло очень и очень мало. Из таблицы видно, что
наиболее совершенными оказались единица, девятка и
нуль, их начертание почти не менялось. Зато потребова-
лось много веков для стабилизации 2, 4, 5 и 7. В XIII в.,
когда индийская система была известна всей Европе,
по-современному стали писаться семь цифр: 1, 2, 3, 6, 8,
9, 0. В XV в. современную форму начертания получают
4, 5 и 7. И только в XVI в. индийские цифры приняли, на-
конец, стабильную современную всем известную форму
написания:
1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
100
§ 3. РОЛЬ УЧЕНЫХ СРЕДНЕЙ АЗИИ И ЗАКАВКАЗЬЯ
В РАСПРОСТРАНЕНИИ ИНДИЙСКОЙ СИСТЕМЫ
СЧИСЛЕНИЯ
Индийская система счисления завоевала признание
не сразу. Обладая простотой и удобством по сравнению
с другими системами счисления, она «медленно, но верно»
входила в жизнь и быт народов. Сначала, как указыва-
лось выше, индийская система счисления была воспри-
нята так называемой арабской математикой, а потом че-
рез нее сделалась достоянием всей Европы. Надо при
этом иметь в виду, что арабская математика в то время
вовсе не была математикой одних только арабов. «Под
названием «арабской» науки,— пишет А. П. Юшкевич,—
неправомерно скрывались достижения ученых различных
народов, пользовавшихся в научном обиходе преимуще-
ственно, хотя и не исключительно, арабским языком, ко-
торый в мусульманском средневековом мире играл роль,
сходную с ролью латыни в средневековой католической
Европе»
В освоении и распространении индийской системы
счисления приняли участие ученые народов Средней
Азии и Закавказья — хорезмийцы, таджики, узбеки,
азербайджане и т. д. Особенно много сделал в распро-
странении указанной системы знаменитый хорезмийский
математик и астроногл Мухаммед бен Муса ал Хорезми
(коротко Алхорезми). Десятичной позиционной системе
и ее применению Алхорезми посвящает целый арифмети-
ческий трактат. Трактат начинается с заявления автора,
что он намерен изложить и показать способ счисления
индийцев посредством девяти цифр («букв»), при помо-
щи которых индийцы легко и кратко выражают любое
число, что позволяет с большой легкостью исследовать
арифметические вопросы, производить умножение и деле-
ние чисел, их сложение и вычитание и т. д.1 2.
Арифметический трактат Алхорезми состоит из трех
разделов, из которых первый посвящен объяснению ин-
1 А П. Юшкевич, О математике народов Средней Азии
в IX—XV вв., «Историко-математические исследования», вып. IV,
ГИТТЛ, М.—Л., 1951 стр. 457.
2 См. А. П. Юшкевич, Арифметический трактат Мухаммеда
бен Муса ал Хорезми, «Труды Института истории естествознания
и техники», т I, «История физико-математических наук», изд. АН
СССР, М., 1954, стр. 90,
101
дийской десятичной позиционной системы счисления, вто-
рой — правилам действий с целыми числами и, наконец,
третий — правилам действий с дробями и извлечению
квадратных корней.
Под влиянием указанной работы позиционный способ
обозначения чисел стал называться алгорифмом (ис-
каженное латинизированное прозвище Алхорезми), а сто-
ронники его — а л г о р и ф м и к а м и в отличие от а ба-
цнет о в, которые, не пользуясь индийской системой счи-
сления, все расчеты производили па счетной доске, назы-
ваемой абаком. Слово «абак» еврейского происхожде-
ния и дословно означало «пыль». Такое странное назва-
ние объясняется тем, что в глубокую старину разные на-
роды, в особенности римляне, при вычислении пользова-
лись досками, на которых был насыпан мелкий песок.
На таких досках вычерчивались вертикальные параллель-
ные линии, которые образовывали вертикальные ко-
лонки. Если счет велся десятками, то первая такая ко-
лонка слева предназначалась для единиц, вторая для де-
сятков, третья для сотен и т. д. Числа единиц, десятков,
сотен и т. д. в разные времена и у разных народов обоз-
начались по-разному. Самый примитивный способ вычис-
ления был таков: в колонках писали столько палочек
(крестиков, кружков), сколько хотели обозначить единиц.
Примерно в VI в. до н. э. вместо палочек, крестиков и
кружков стали писать в колонках цифры. Позднее эти
цифры были заменены «марками» с выгравированными
на них цифрами. С течением времени устройство абака
изменялось, вместо доски с песком стали употреблять
доску с вертикальными желобами для числовых марок
или жетонов. Уместно заметить, что чисто римский абак
был приспособлен к счету пятками, так как римляне
дольше всех народов примешивали к десятичной системе
пятеричную. Далее, сбоку у этого абака имелись неболь-
шие колонки для долей: половин, третей или же унций
(двенадцатых долей).
Средневековая арифметика Европы пользовалась
исключительно римскими цифрами, а для производства
вычислений — римским абаком. Счет на абаке имел свои
преимущества. Во-первых, с помощью абака можно про-
изводить четыре арифметических действия, а с римской
системой счисления умножение и деление практически
неосуществимо. Во-вторых, он не требовал дорогосгоя-
102
щей бумаги, производство которой в Европе было нала-
жено только в XII в., и усовершенствованных письмен-
ных принадлежностей, которые в Европе появились еще
позднее (карандаш появился лишь в XVI в.).
§ 4. О РАСПРОСТРАНЕНИИ ИНДИЙСКОЙ СИСТЕМЫ
СЧИСЛЕНИЯ В ЕВРОПЕ
Индийская система счисления, перенесенная в Европу,
встретила ожесточенное сопротивление со стороны после-
дователей римской арифметики (абацистов), которые в
то время были представителями официальной схоласти-
ческой науки в Европе. Часто на стороне абацистов про-
тив алгорифмиков (сторонников индийской системы счи-
сления и «арабской» учености) выступали отдельные
правительства. Так, например, законодательным путе^м
в 1299 г. во Флоренции в своих бухгалтерских расчетах
купцам запрещалось пользоваться индийскими цифра-
ми. Согласно указу все расчеты должны были произво-
диться с помощью римских цифр или цифр, написанных
словами.
Тем не менее алгорифмики в конце концов все же
одержали верх. Энтузиастом новой нумерации в Европе
явился итальянский математик Леонардо Пизан-
ский (Фибоначчи). Он в 1202 г. выпустил «Liber abaci»—
книгу по арифметике, основанную на индийской системе
счисления. «Девять индусских знаков,— писал Леонардо
Пизанский,— суть следующие: 9, 8, 7, 6, 5, 4, 3, 2, 1. С по-
мощью этих знаков и знака 0, который называется по-
арабски zephirum, можно написать какое-угодно число»1.
1 И. Г. Башмакова и А. П. Юшкевич, Происхождение
систем счисления. Энциклопедия элементарной математики. Книга
первая. Арифметика, ГИТТЛ, М.—Л., 1951, стр. 54.
Интересно заметить, что Леонардо Пизанский цифрой называл
только нуль, а остальные девять знаков — 1, 2, 3, 4, 5, 6, 7, 8, 9, —
по его представлению не являются цифрами. Дело в том, что индий-
ское название нуля — «сунья» (sunya) в дословном переводе па
арабский язык означает as-sifer, или в латинизированной форме
zephirum, откуда и произошло название «цифра». В том же смысле
слово «цифра» употребляет и Леонтий Магницкий в своей «Ариф-
метике» (1703); он так же, как Леонардо Пизанский, цифрой назы-
вает один только нуль. Термин «нуль» произошел от латинского
слова nullus (никакой) и стал употребляться лишь в XVI в.
Как полагает И. Ю. Тимченко, французские слова chiffre —
числовой знак и zero — нуль произошли от одного арабского слова
«сифр» (as-sifr).
103
«Liber abaci» Леонардо Пизанского пользовалась боль-
шой славой в течение нескольких столетий и являлась
животворным источником для последующих составителей
всевозможных арифметических и алгебраических трак-
татов.
В Германии, Франции и Англии индийские цифры
стали употребляться лишь со второй половины XV в.
В 1488 г. во Франции (город Страсбург) была напечата-
на книга «Об искусстве счисления» («De arte numeran-
di»), называвшаяся также «Algorismus», посвященная
индийской арифметике, в которой лишь сообщались
арифметические правила без их доказательств и числен-
ных примеров. Эта книга в течение нескольких столетий
имела большое распространение не только во Франции,
но и за ее пределами (в Италии). Полагают, что автором
этой книги является Джон Галифакс, именуемый
иногда Сакробоско, родом из йоркшира, получив-
ший воспитание в Оксфорде и живший впоследствии в
Париже, где до последних дней своей жизни занимался
преподавательской деятельностью (умер в 1256 г.).
Уже к XVII в. индийские цифры нашли повсеместное
распространение и почти полностью вытеснили старую
систему счисления. Римская нумерация стала упот-
ребляться лишь в специальных случаях, например в по-
следнее время на циферблатах часов и в обозначении
глав книг.
§ 5. О РАСПРОСТРАНЕНИИ ИНДИЙСКИХ ЦИФР В РОССИИ
Теперь остановимся на распространении индийских
цифр в России. Как полагает русский историк математики
В. В. Бобынин (1849—1919), появление в России пер-
вых арифметических рукописей относится к началу XII в.
Первая дошедшая до нас рукопись, относящаяся к этому
времени, носит название «Кирика диакона и доместника
Новгородского Антониева монастыря учение, им же веда-
ти человеку числа всех лет». Она посвящена арифметико-
хронологическим расчетам и состоит из 19 параграфов,
в которых давались сведения о календаре, позаимство-
ванные из греческих церковных книг. Большая часть ру-
кописи содержит вычисление времени (месяцев, дней, ча-
сов), прошедших от «сотворения мира» Числа в этой ру-
кописи выражались в алфавитной нумерации.
104
Во время пожара Москвы в 1812 г. погибла древней-
шая рукопись арифметического содержания, относящая-
ся к XVI в., полное название которой «Сия книга рекома
по-гречески Арифметика, а по-немецки Алгоризма, а по-
русски Цифирная Счетная мудрость».
Наиболее интересным из сохранившихся математиче-
ских памятников В. В. Бобынин считает рукопись по
арифметике XVII в., имеющую такое своеобразное преди-
словие: «Пятая мудрость в семи великих мудростех на-
рицается Арифметика. Начала мудростем: Грамматика,
Геометрия, Астрономия, Музыка. Те 4 мудрые книги. Сия
мудрость есть изыскана древними философи остропари-
мого разума нарицается Арифметика, сиречь счетная-
арифмос по-гречески счет толкуется. Без сея мудрости
ни один философ, ни доктор не может быти. По сей муд-
рости гости по государствам торгуют и во всяких това-
рех и торгех силу знают, и во всяких весах и мерах, и в
земном верстании, и в морском течении. Сия мудрость есть
многих в прикупех корысти сподобляет и честь дарует,
и ум человеческий высокопарив творит, и память укреп-
ляет, и острых острее творит в разум. И сего ради слыши
сию мудрость и вонми, яже глаголет Арифметика. Аз
есмь от бога свободная мудрость высокозрительного и
остромысленного разума и добродатное придарование
человеческое. Мною человек превосходит бессловесное не-
разумие. Аз бо есмь своима легкима крылома парю
выспрь под облаки, аще и несть мя тамо. Аз заочные, не-
видимые и предъочные дела объявляю; в солнечном же и
в лунном течении разум многим подаваю, и в морском
плавании, и в земном верстании наставляю и меру ука-
зую; и в купеческих вещех, и во всяких числех недоуме-
ние разрешаю. И всего ради отъидите от меня иже ме-
ламколиею обдержаны суть, и у которых мозги с черною
желчью смешаны, а моим учеником достоит имети суп-
тильный чистый и высокий разум» Ч
Такая мораль, как говорится, в назидание потомству
составляла неотъемлемую часть предисловий тогдашних
арифметик. Текст рукописи был на славянском языке
и написан славянскими бувами, причем цифры, как пра-
вило, употреблялись славянские.
1 В. Б ел л ю ст и н, Как постепенно люди дошли до настоящей
арифметики, М., 1914, стр. 44.
105
Индийские цифры стали вводиться с начала XVII в.
Эти цифры впервые появились в славянских книгах, ко-
торые печатались в юго-западных типографиях. «Здесь,—
по мнению В. Беллюстина, — сказывается польское влия-
ние: оно энергично воздействовало на Россию в XVII сто-
летии и много сообщило нам того, что само получило от
западноевропейской культуры» Ч
Сначала индийскими цифрами пользовались только
для обозначения страниц в книгах, а цифры, употребляе-
мые в тексте, оставались славянскими. Так, в 1611 г. в
Венеции были отпечатаны две духовные книги, в кото-
рых страницы занумерованы индийскими цифрами. В
1638 г. в России типографским путем был отпечатан
«Псалтырь», где страницы также занумерованы индий-
скими цифрами. Далее, в книге «Учение и хитрость рат-
ного строения пехотных людей», изданной в Москве
в 1647 г., индийскими цифрами были пронумерованы не
только страницы, но и чертежи в тексте и ссылки на них.
В 1702 г. вышел в свет «Юрнал об осаде Нотебур-
га» тиражом в 2000 экземпляров, причем одна по-
ловина тиража имела «числа русские», т. е. славян-
ские, а вторая половина — «циферные», т. е. индий-
ские цифры.
В 1703 г., как известно, вышла знаменитая энциклопе-
дия математики начала XVIII в.— «Арифметика» Маг-
ницкого, на титульном листе которой значилось:
«Арифметика, сиречь наука числительная. С разных
диалектов на славянский язык переведенная и во едино
собрана и на две книги разделена. В лето от сотворения
мира 7211, от рождества Бога Слова 1703. Сочинися сия
книга через труды Леонтиа Магницкого».
Весь шрифт и обозначения страниц этой книги — сла-
вянские, но все вычисления в тексте проводятся уже в ин-
дийских цифрах.
Со второй половины XVII в. индийские цифры стали
появляться на русских монетах. Так, в 1654 г. индийски-
ми цифрами были отпечатаны русские монеты достоинст-
вом в четверть червонца, предназначавшиеся главным
образом для наград и дарований. В Петровское время
индийские цифры на монетах окончательно вытесняют
славянские. После Петра I из обихода совершенно исче-
1 В. Беллюстин, Как постепенно дошли люди до настоящей
арифметики, М., 1914, стр. 44—45.
106
зают славянские цифры и славянский текст. Книги, нако-
нец, получили шрифт и форму, которые мало чем отли-
чаются от современных.
§ 6. КАКИЕ ШЕСТЬ ДЕЙСТВИИ БЫЛИ ПОЛОЖЕНЫ
ИНДИЙСКИМИ УЧЕНЫМИ В ОСНОВУ МАТЕМАТИКИ
Индийские ученые рассматривали шесть действий, ко-
торые являлись основными в их математике. Эти дейст-
вия следующие:
1) сложение, 4) деление,
2) вычитание, 5) возведение в степень,
3) умножение, 6) извлечение корня.
В настоящее время к ним присоединено еще одно дей-
ствие — логарифмирование.
Немецкий историк математик И. Тропфке считает,
что наш современный метод сложения индийского проис-
хождения. Разница только в том, что мы в настоящее
время, производя сложение «столбиком», выполняем его
справа налево, а индийцы делали наоборот — слева на-
право. Кроме того, индийцы результат сложения подпи-
сывали не под слагаемыми, как это мы делаем теперь, а
над слагаемыми L
Конечно, сложение по колонкам слева направо для
индийцев не составляло большой трудности, если иметь в
виду, что вычисления производились на досках, покрытых
цветным песком, где написанные числа легко можно бы-
ло стереть и заменить новыми.
Предположим, нужно было сложить три числа: 3759,
2720 и 1230. Тогда сложение по индийскому способу про-
изводилось так:
7 7
Л X 0 #
Я Д' Я X
Наверху появлялся искомый результат 7709. То, что
перечеркнуто, индийцами стиралось и заменялось
1 См. И. Тропфке. История элементарной математики в систе-
матическом изложении, т. I, ч. I Перев. с немец. Д. А. Бема,
Р, Э. Струве, под ред. И. И, Чистякова, М., 1914, стр. 42—43.
107
соответственно цифрой наверху. Сам механизм сло-
жения несложен и виден из анализа приведенного
примера.
Действие вычитания, как и сложения, индийцы произ-
водили слева направо, что было вполне возможно опять-
таки благодаря легкому уничтожению цифр и легкой за-
мене их новыми. Пусть, например, надо из числа 34 725
вычесть 15 871. Вычисление результата индийцы произво-
дили так:
1 8 8
X 5 4
Результат получался над уменьшаемым и был равен
18 854. Так же, как и при сложении, то, что перечеркнуто,
стиралось, и в процессе вычисления на песочной доске
оставались только цифры искомого результата.
Что касается умножения, то оно в древней Индии
выполнялось по-разному. Например, для устного счета
с частичной записью Брамагупта (индийский ученый
VII в. до н. э.) предлагал поступать так: надо сначала
вычислять отдельные произведения в уме, а потом их
складывать между собой обычным приемом. Пусть, на-
пример, требуется умножить 325 на 37; вычисление по
способу Брамагупты можно записать так:
325 30 9750
325 7 2275
12 025
Сумма чисел 9750 и 2275, равная 12 025, находилась
по правилу сложения, и результат надписывался над сла-
гаемыми, например:
1 2 0
X 1 X 2 5
X X X X
X % х X
Результат сложения, т. е. сумма, равняется 12 025.
Бхаскара, индийский ученый XII в., предлагал ум-
ножение производить по правилу «оконной решетки».
Правило это поясним на примере.
108
Пусть требуется умножить знакомые нам числа, т. е.
325 на 37. Решение оформлялось в таком виде (напоми-
нает переплеты окна):
Техника умножения очевидна. Цифры искомого ре-
зультата получаются снизу и справа; они составляют
нужное произведение 12 025.
Оригинальное правило для умножения давал в VII в
Брамагупта. Он предлагал не все множимое умножать
на отдельные разряды множителя, а отдельные разряды
множимого умножать на весь множитель. Поясним пра-
вило Брамагупты на том же примере:
1 2 0 2 5
1 8 5
7 4
1 1 1
3 2 5
3 7
3 7
3 7
Из анализа схемы видно, что искомый результат Бра-
магупта помещал сверху, данные числа внизу, причем
множитель переписывался столько раз, сколько цифр во
множимом. Сначала он умножал 3 сотни на 37, получал
111 сотен и писал их над сотнями. Аналогично он посту-
пал с десятками и единицами.
Индийские математики были виртуозами устного сче-
та, для которого у них было много так называемых «мол-
ниеносных» правил умножения. Многие из этих правил
в ходу и до настоящего времени Ч
1 См. об этом книгу В. Беллюстина «Как постепенно дошли лю-
ди до настоящей арифметики», М., 1914, стр, 89—93,
109
Довольно сложными приемами древнейшие ученые
производили деление. Этим сложным приемам следовали
и индийские ученые. Недаром много позднее в средневе-
ковых европейских школах тому, кто оказывался в состо-
янии понимать деление, давался почетный титул «доктора
абака», вроде нашего «доктора наук», и его считали чуть
ли не гением.
§ 7. ОБ ИНДИЙСКОМ СПОСОБЕ ПРОВЕРКИ ПРАВИЛЬНОСТИ
ПОЛУЧЕННОГО РЕЗУЛЬТАТА
Поскольку индийцы, как указывалось выше, все свои
вычисления производили на белых дощечках, покрытых
цветным песком, где удобно было стирать и одни цифры
заменять другими, так что в конце вычисления на дощеч-
ках оставались только данные числа и ответ, то, естест-
венно, у них возникала потребность в проверке правиль-
ности полученного результата. Для этой цели индийские
ученые изобрели «правило проверки девяткой», которое
позднее получило широкое распространение не только
в странах Востока, но и в государствах Западной Евро-
пы. Этим правилом пользуются и в настоящее время.
Приведем это правило:
Проверка сложения. Чтобы с помощью девятки
проверить правильность сложения нескольких чисел, не-
обходимо убедиться в том, что сумма остатков, получен-
ных от деления на 9 суммы цифр каждого слагаемого,
или равна остатку от деления на 9 суммы цифр числа,
полученного от сложения данных чисел, или же разность
между ними кратна 9.
Проверка вычитания. Для проверки вычитания
посредством 9 достаточно убедиться в том, что остаток,
полученный от деления на 9 суммы цифр уменьшаемого,
или равен сумме остатков суммы цифр вычитаемого
и разности при делении на 9, или разность их кратна 9.
Правило проверки 9 можно сформулировать также
для умножения и деления, рассматривая последнее как
действие, обратное первому.
В терминах современной теории чисел все эти провер-
ки девяткой можно объединить в одном правиле:
Если над числами производятся в каком-либо порядке
действия сложения, вычитания и умножения, то, произ-
водя те же действия и в том же порядке над остатками
ПО
от деления этих чисел на 9. получим число, принадлежа-
щее тому же классу вычетов по модулю 9, что и остаток
от деления на 9 результата действий над числами1.
Однако индийский способ проверки не дает полной
уверенности в правильности полученного результата.
Действительно, этой проверкой нельзя, скажем, открыть
пропуск нулей или же излишка нулей. Например, числа
203, 2030, 23 при делении на 9 дают одинаковые остатки.
Поскольку проверка числом 9 ненадежна, многие уче-
ные XVI и XVII вв. рекомендовали дополнить индийское
правило еще проверкой числом 7. Но и это некоторых не
удовлетворяло. Например, европейский ученый Фишер
в 1559 г. свои вычисления проверял с помощью 5, 6, 7,
8, 9, 11.
Эти слишком усердные ухищрения привели многих
ученых даже к отрицанию их пользы. Так, известный
французский математик Пьер Рамус (умер в 1575 г.)
заявил, что все эти старания излишни и ненужны и что
если кому требуется проверить действие, то пусть он пе-
ределает его снова, и больше ничего; так будет лучше и
в том отношении, что, проделывая снова, мы мо-
жем не только открыть присутствие ошибки, но и
исправить ее 2.
«Правило проверки девяткой» индийцы формулирова-
ли в готовом виде без теоретического обоснования.
Впервые доказательство «правила проверки девяткой»
дал Леонардо Пизанский (Фибоначчи) в своей «Книге об
абаке», опубликованной в 1202 г. (глава III, стр. 20). Но
совершенно строгое доказательство этому правилу было
дано только в XVII в. английским ученым, профессором
Оксфордского университета Джоном Валлисом
(1616—1703).
Что касается других вопросов современной школьной
арифметики, то индийцы были знакомы с простым и слож-
ным тройным правилом, с правилом простых и сложных
процентов, с правилом товарищества, задачами на сме-
шение и т. д. Кроме того, индийцы владели правилом для
решения ряда других задач, которые в настоящее время
решаются алгебраически при помощи уравнений. Среди
1 См. об этом подробнее в книге М. К. Гребенча и С. Е. Ляпина
«Арифметика», Учпедгиз, М., 1952, стр. 121 — 127.
2 См. В. Беллюстин, Как постепенно дошли люди до настоя-
щей арифметики, М., 1914, стр, 119,
111
этих правил большой популярностью у индийцев пользо-
вались «правило ложного положения» (фальшивое пра-
вило) и «правило обращения».
§ 8. ТРОЙНОЕ ПРАВИЛО
Тройное правило, которым владели индийские ученые,
высоко ценилось средневековыми математиками и назы-
валось в немецких учебниках «ключом купцов».
Оно и понятно почему. Круг задач на тройное правило
был весьма обширен. Само правило выражалось просто
и ясно, и применить это правило к решению конкретной
задачи не представляло никаких трудностей.
Еще в V в. индийский математик Ариабхата, о ко-
тором подробнее будет говориться ниже, применил трой-
ное правило к решению следующей задачи: «16-летняя
девушка-рабыня стоит 32 нишка. Что стоит 20-летняя
рабыня?»
По поводу этой задачи Ариабхата дает разъяснение,
что эту задачу следует решать с помощью обратной про-
порции. так как «стоимость живых существ (рабов и ско-
та) устанавливается сообразно их возрасту: чем старее,
тем дешевле» !.
В приложении к различным вопросам торговли «трой-
ное правило» позднее рассматривали и другие индий-
ские математики. Например, известный индийский астро-
ном и математик XII в. Бхаскара в математической
части своего астрономического сочинения подробно оста-
навливается на «тройном правиле» и его приложении к
вопросам торговли. Вместе с тем Бхаскара посвящает
целую главу задачам на смешение («Разыскания, отно-
сящиеся к смесям»). В этой же главе рассматривается
правило процентов и товарищества. Все это поясняется
на большом количестве задач и примеров. Например, в
рассматриваемой главе разбирается задача о времени
наполнения бассейна водой из нескольких источников,
которая стала популярной в учебной литературе вплоть
до самого последнего времени. Задача о бассейне
у Бхаскара формулируется так:
1 Ф. К э д ж о р и, История элементарной математики с указа-
ниями на методы преподавания. Перев. с англ., под ред с примеча-
ниями и прибавлениями И. Ю. Тимченко, Одесса, 1910, стр. 106.
112
«Определить время, нужное для наполнения бас-
сейна водой, текущей в него из нескольких источников,
если известны времена, в которые бассейн наполняется
каждым из источников в отдельности».
От индийцев «тройное правило» перешло к средне-
азиатским народам и арабам, а через них и к европейцам.
Так, в IX в. «тройным правилом» широко пользовался
среднеазиатский ученый Алхорезми и применительно
к алгебре.
Начиная с XIII в. «тройное правило» стало популяр-
ным и в Европе. Так, итальянский математик Леонар-
до Пизанский (Фибоначчи), живший, как известно, в
XIII в., в своей знаменитой книге «Liber abaci» посвящает
«тройному правилу» особый отдел, состоящий из рассмот-
рения ряда конкретных задач на вычисление стоимости
товаров.
Вот одна из таких задач:
«100 ротули (пизанский вес) стоят 40 лир. Что стоят
пять ротули?»
Леонардо Пизанский предлагает записать условие
так:
40L 100/?
К этой записи он и предлагал применить «тройное пра-
вило», согласно которому надо 40 умножить на 5 и полу-
ченное произведение разделить на 100.
В учебной европейской литературе XVI в. «тройное
правило» формулировалось так: «Задача состоит из трех
чисел и дает собой четвертое число, подобно тому, как
если поставить три угла дома, то этим самым определя-
ется четвертый угол; второе число умножить на третье и,
что получится, то разделить на первое число» L
«Тройное правило» было хорошо известно в начале
XVIII в. в России. Этому правилу в начале XVIII в. мно-
го места в своей арифметике уделял Леонтий Маг-
ницкий (1669—1739). Он, как это было тогда в моде,
распределял «тройное правило» на ряд мелких отделов
в зависимости от содержания задач, носивших замысло-
1 В Беллюстин, Как постепенно дошли люди до настоящей
арифметики, М.» 1914, стр. 164.
8 Заказ 999
113
ватые названия. Рассмотрим эти мелкие отделы по Маг-
ницкому:
1) «Тройное торговое правило». Сюда относятся зада-
чи на вычисление стоимости купленного товара.
2) «Тройное торговое правило о куплях и продажах».
Сюда входят более сложные задачи, чем в первом отделе.
3) «Тройное торговое правило в товарных овощах и
с вывескою». В этих задачах приходится, как правило, де-
лать вычеты за тару и упаковку.
4) «О прибыли и убытке».
5) «Статья вопросная-о тройном правиле». В этом от-
деле рассматриваются задачи разнообразного содержа-
ния, причем преимущество отдается задачам с обратной
пропорциональностью.
6) «Статья вопросная со временем». Здесь, как пока-
зывает название, рассматриваются задачи на определе-
ние времени, потребное для выполнения какой-нибудь
работы, совершения пути и т. д.
§ 9. ПРАВИЛО «ЛОЖНОГО ПОЛОЖЕНИЯ»
Индия наравне с Китаем является страной, где отчет-
ливое выражение приняло «правило ложного положе-
ния».
Еще в III или IV в. н. э. в Бахшалийской арифметике 1 * III
ряд задач решается «правилом ложного положения».
Примером может служить следующая задача:
«В дает вдвое больше, чем А, С — втрое больше,
чем В, D — вчетверо больше, чем С; все вместе дают
132. Сколько дал Л?»
Автор рукописи предлагает решать эту задачу «пра-
вилом ложного положения» в его частном виде, когда
искомое предполагается равным единице (решение при-
ведением к единице). Рассуждение ведется в следующем
виде: пусть неизвестное равняется единице, тогда А = 1,
В = 2, С=6, D = 24, сумма их равна 33. Теперь разделим
132 на 33. Это и будет искомым ответом, т. е. представ-
ляет то число, которое дал А.
1 Бахшалийской арифметикой называется арифметическая руко-
пись, найденная в 1881 г. при раскопках в Бахшали в северо-запад-
ной Индии. Рукопись выполнена на березовой коре и относится к
III или IV в. н. э. Ученые установили, что эта рукопись является
неполной копией более древней рукописи.
114
«Правило ложного положения» находит отчетливое
выражение и применение также в математических изы-
сканиях Бхаскары. Этим правилом он решает, напри-
мер, такую задачу:
«Если некоторое число умножить на пять, от произ-
ведения отнять его треть, остаток разделить на 10 и
1 1 1
прибавить к этому у- у и у первоначального числа,
то получается 68. Как велико это число?»
«Пусть, — говорит Бхаскара, — это число равняется
3, тогда согласно условию получим числа: 15, 10, 1 и
1 + 2+2+’=1?.
3 2 4 4
Откуда:
68:—7V 3=48.
4 /
Это и есть искомое число».
Из рассмотрения примененного решения видно, что
Бхаскара в качестве ложного значения неизвестного
предпочитает брать не единицу, как поступал автор Бах-
шалийской арифметики, а число 3. Но и здесь «правило
ложного положения» выступает в простом виде. В более
сложных задачах неизвестному приходится давать два
ложных значения.
Сущность «правила ложного положения» в самом об-
щем случае лучше всего пояснить алгебраически на при-
мере. Для этой цели возьмем
ах + b = 0.
Дадим х произвольное значение Поставим X] вместо х
в левую часть уравнения, в правой части уравнения по-
лучим вместо нуля какое-то число пь так что будем
иметь:
ахх + Ь = пи
где П1 будет ошибка правой части уравнения.
Теперь дадим х другое произвольное значение х2, тог-
да по аналогии с тем, что было выше, получим:
+ 6 = ^2,
8*
115
где «2 будет соответствующей ошибкой правой части
уравнения. Таким образом, имеем систему:
lax1 + b = nl
|ах2 -|- b = «а
тт ь
Имея в виду, что х=—“получаем следующую фор-
мулу для определения х:
х _ niXi-X^n*
rii—n* ’
которая и составляет «правило ложного положения».
В словесной записи формула выглядит так:
__ 1 погреши. х2 знач.—1 знач. х2 погреши.
1 погреши.—2 погреши.
Эту формулу индийцы применяли, например, к реше-
нию следующей задачи (XII в.):
«Пятая часть пчелиного роя села на цветок ка-
дамбы, треть— на цветок силинды, тройная разность
этих двух чисел улетела на цветок кутаджи, и толь-
ко одна-единственная пчела носится в воздухе, при-
влекаемая ароматом жасмина и пандануса. Назови
мне, красавица, число пчел!»
Обозначив через х число пчел, будем рассуждать так:
Пусть л=3 (первое ложное значение), тогда:
- + - + 3(-— + 1=3 + - .
5 3 \3 5/ 5
Первая погрешность равна 4/s.
Пусть теперь х=5 (второе ложное значение), тогда:
~ + 1+3/5_ _5\ J =5 2
5 3 \3 3
О 2
Вторая погрешность составляет — .
Следовательно, по «правилу ложного положения», когда
даются два ложных значения для искомой, будем иметь:
— • 5 3 • —
5 3 (4 — 2) 15 , с- z ч
х =---------------= -----------— = 15 (пчел).
12-10 7
5 3
116
От индийцев «правило ложного положения» под на-
званием «фальшивого правила» перешло к среднеазиат-
ским и арабским математикам, а затем через них и к
европейским математикам, причем как там, так и здесь
оно было известно, как индийское правило.
Например, среднеазиатский ученый Алхорезми (IX в.
н. э.) фальшивым правилом решал такую задачу:
1 1
«Найти такое число, что если отнять от него у и ~
его, то в остатке будет 8».
Эту задачу он фактически решал по формуле, кото-
рая была дана выше, проводя следующие рассуждения.
Пусть искомое число равняется 12, тогда остаток будет
равен 5 вместо 8, т. е. на 3 меньше. Если же положить
число равным 24, тогда остаток будет равен 10 вместо 8,
т. е. на 2 больше. Тогда:
3 -24+12 2 1Q 1
----------— 1У — .
3+2-------5
Большое место «фальшивому правилу» отводил в сво-
их работах Леонардо Пизанский (Фибоначчи) в XIII в.,
а вслед за ним и другие европейские математики.
«Фальшивое правило» было широко известно у нас на
Руси. Так, в русских математических рукописях XVII в.
оно встречается под таким затейливым названием: «Ста-
тья циферная именуется вымышленная или затейчивая.
Высоко остропамятного разума и умного приложения ее
же нении фальшивою строкою нарекоша, иже ни малым
чем погрешается» L
О «фальшивом правиле» много говорит также Леон-
тий Магницкий, который в своей «Арифметике» отводит
ему особую четвертую часть. Это правило /Магницкий по-
ясняет словами «фальшивая правила, сиречь не истин-
ная положения, зане через два не истинная положения
изобретает самое оно желаемое истинное число»2.
Вот, например, одна из задач Магницкого, которую
он решал «фальшивым правилом»:
«Спросил некто учителя: скажи, сколько у тебя в
классе учеников, так как хочу отдать к тебе в учение
1 В. Беллюстин, Как постепенно дошли люди до настоящей
арифметики, М., 1914, стр. 180,
8 Т а м же, стр. 179.
П7
своего сына. Учитель ответил: если придет еще учени-
ков столько же, сколько имею, и полстолька и чет-
вертая часть и твой сын, тогда будет и у меня учени-
ков 100. Спрашивается, сколько было у учителя уче-
ников» *.
Предположим, во-первых, что учеников было 24 (пер-
вое предположение). Тогда согласно условию задачи, со-
считаем, что составляет столько да полстолько, да чет-
верть столько, да еще один, и получится всего учеников:
24+24+12+6+1=67.
По условию же задачи, учеников должно быть 100, сле-
довательно, их недостает: 100—67 = 33 (первая погреш-
ность).
Предположим теперь, во-вторых, что учеников было
32 (второе предположение), тогда в итоге получим:
32+32+16+8+1=89,
а до 100 недоставало бы 11 (вторая погрешность).
Далее по формуле получим:
33 • 32-24 11 ч
-----------=36 (учеников),
что и составляет верный ответ задачи.
Необходимо заметить, что эта задача Магницкого
встречается в старой учебной литературе довольно часто
и иногда в другой формулировке. Например, в арифме-
тике Румовского (1760) она дается как задача о
гусях:
«Летело стадо гусей, навстречу им летит один гусь
и говорит: здравствуйте, сто гусей, а те ему отвечают:
нет, нас не сто гусей, а если бы нас было еще столько,
сколько есть, да еще полстолька, да четверть столька,
да еше ты один гусь с нами, тогда нас было бы ровно
сто гусей. Сколько их было?»
Решение дается также «фальшивым правилом».
1 Эта задача с ее подробным решением приводится в книге
проф. И. Я- Депмана «Рассказы о математике», Детгиз, Л., 1954,
стр. 60—61. Этот же материал имеется в другой его книге: «Расска-
зы о решении задач», Детгиз, Л., 1957, стр. 112—114.
Ученые Арабского халифата еще в XIII в. «фальши-
вому правилу» придали удобное механическое истолкова-
ние под названием «метода чашек весов». Так, арабский
математик ибн-А л б а н н а (1222) в своем трактате «Тал-
кис» писал:
«Метод чашек весов — геометрический и состоит в
том, что ты берешь весы указанной формы и кладешь из-
вестную величину над точкой опоры. На одну из чашек
кладешь произвольное число, прибавляешь к нему, что
дано тебе прибавить (или вычесть). Полученный резуль-
тат сравни с тем, что находится над точкой опоры. Если
ты попал правильно, то чашка весов дает известную вели-
чину. Если же ты не попал, заметь погрешность над чаш-
кой, если результат велик, и под чашкой, если резуль-
тат мал. Затем положи на другую чашку другое, произ-
вольно выбранное число и поступай подобным же обра-
зом. После этого умножь погрешность каждой из чашек
на число, положенное на другую чашку. Если обе по-
грешности положительны или обе отрицательны, вычитай
меньшую из большей, а также меньшее произведение из
большего и раздели разность произведений на разность
погрешностей. Если же одна погрешность положительна,
а другая отрицательна, раздели сумму произведений на
сумму погрешностей» L
Другой арабский математик а л-К а л ь с а д и (XV в.),
написавший в свое время трактат «Раскрытие тайны нау-
ки Габар», содержавший основы арифметики и алгебры1 2,
написал комментарии к «Талкису» ибн-Албанна. В этих
комментариях ал-Кальсади «методом чашек весов» ре-
шает следующую задачу:
«Найти число, которое, будучи взято семь раз и сло-
жено с ушестеренным числом, дает 25».
Само решение приводится в таком виде. Положим
вместо х какое-нибудь произвольное число, хотя бы 6
(правая чашка). Тогда согласно условию задачи полу-
чим:
7-6+6-6=78.
1 Г. Н. Попов, Очерки по истории математики, М.—Л., 1950,
стр. 83—90.
2 «Габар» по-арабски обозначает «пыль». Это название искус-
ству счисления присвоено потому, что арабы, как индийцы, произ-
водили арифметические выкладки на доске, посыпанной пылью или
песком.
119
Сравнивая полученное число с данным (25), найдем
погрешность:
78—25=53.
Положим теперь вместо х какое-нибудь другое про-
извольное число, например 1 (левая чашка). Тогда:
7 14-6 1= 13,
а вторая погрешность будет:
13 —25 = —12.
Применяя к полученным числовым значениям пра-
вило, сформулированное ибн-Албанной, окончательно
будем иметь:
53 1 + 12 6 .12
X = ----5----= 1 - ,
53+12 J3
что и составляет нужный ответ.
В своем арифметическом трактате «Раскрытие тайн
науки Габар» ал-Кэльсади тем же «методом чашек ве-
сов» решает такую задачу:
«Найти число, одна треть и одна четверть которого
составляют 21».
Пусть х=12 (правая чашка), тогда первая погреш-
ность будет 14. Если же х=24 (левая чашка), тогда вто-
рая погрешность составляет 7. Следовательно, по извест-
ному правилу:
14 24—7 12
х = ---------= 36,
14-7
что и составляет окончательный результат.
Необходимо заметить, что «фальшивое правило» или
«метод чашек весов» в современной школе не употребля-
ются, так как вывод его может быть сделан только ал-
гебраически и, следовательно, в арифметике он не может
быть объяснен ученикам и требует ог них прямого за-
учивания. Далее, никакой учебник не разграничивал, ка-
кие задачи можно решать «фальшивым правилом», а ка-
кие нельзя им решать. В самом деле, если применить пра-
вило к тему, к чему оно неприменимо, то выйдет «одно
печальное недоразумение». Это правило может иметь
силу только для тех задач, где вся задача сводится к ум-
ножениям и делениям неизвестного,
120
§ 10. ПРАВИЛО ОБРАЩЕНИЯ
Индийские математики часто пользовались еще одним
арифметическим правилом, которое они очень любили и
широко применяли. Это «правило обращения», или
«правило инверсии». Суть «правила обращения» заклю-
чается в следующем: если нужно найти число, которое
после ряда операций приводит к некоторому известному
числу, то для этого необходимо над этим последним чис-
лом произвести в обратном порядке все обратные опе-
рации.
Ариабхата этот метод поясняет так: «Умножение ста-
новится делением, деление умножением, то, что было вы-
игрышем, становится потерей, что было потерей, стано-
вится выигрышем; обращение» 1.
Бхаскара применяет это правило к решению следую-
щей задачи:
«Красавица со сверкающими глазами, ты, знаю-
щая истинный метод обращения, назови мне число,
3
которое, умноженное на 3, сложенное с J произведе-
1
ния, разделенное на 7, уменьшенное на у частного,
умноженное на само себя, уменьшенное на 52 после
извлечения квадратного корня, прибавления 8 и де-
ления на 10, будет равняться 2».
Решение заключается в том, что, начиная с числа 2,
производят обратные действия в обратном порядке.
Тогда:
(2-10—8)а+52= 196;
/196 = 14;
14.- .7--= 84;
2 7
84:3=28.
Это и есть искомое число.
Индийский математик Парамадисвара, один из
' Г. Ф а ц ц а р и, Краткая история математики с древнейших
времен, кончая средними веками, М„ 1923, стр. 123.
1?!
комментаторов Ариабхаты, «правилом обращения» ре-
шал такую задачу:
«Найти число, которое, будучи умножено на 3, а
затем разделено на 5, увеличено на 6, после чего из
пего извлечен корень квадратный, отнята единица и
результат возведен в квадрат, дает 4».
Следуя «правилу обращения», получим:
УТ=2; 2+1=3; 32=9; 9—6=3; 3-5=15; 15:3=5,
5 и составляет искомое число.
«Правило обращения», которым пользовались индий-
ские ученые, стало широко известно и за пределами Ин-
дии. Им позднее стали пользоваться сначала в странах
Арабского халифата, а потом и в Европе.
Например, иранский математик XVI в. БегаЭддин,
автор трактата «Сущность искусства счисления», пере-
веденного на немецкий и французский языки, использует
«метод обращения» при решении такой задачи:
«Требуется найти число, которое, будучи умноже-
но само на себя, сложено с двумя, затем удвоено,
вновь сложено с тремя, разделено на 5, наконец, ум-
ножено на 10, в результате дает 50».
Решение дается простое:
50:10 = 5; 5.5 = 25; 25 — 3 = 22; 22:2=11;
11 — 2 = 9; )/9 = 3, что и будет служить ответом.
§ 11. УЧЕНИЕ ИНДИЙСКИХ УЧЕНЫХ ОБ ОТРИЦАТЕЛЬНЫХ
И ПОЛОЖИТЕЛЬНЫХ ЧИСЛАХ
Индийские математики создали алгебру, свободно
оперирующую не только дробями, но и иррациональными
и отрицательными числами. В особенности большая их
заслуга в создании правильных представлений об отри-
цательных числах. Уже к V в. в Индии, оказывается, сло-
жилось правильное понимание отрицательных величин.
Так, индийские математики интерпретировали понятие о
положительных и отрицательных величинах преимуще-
ственно при помощи представлений об имуществе и дол-
ге. Исходя из этого, они даже знали истолкование дей-
ствий с отрицательными числами. Например, еще в VII в.
индийский математик Брамагупта указывал: «Сумма
122
двух имуществ есть имущество, двух долгов — долг, сум-
ма имущества и долга — их разность или, если они
равны — нуль. Сумма нуля и долга есть долг, иму-
щества и нуля — имущество, двух нулей — нуль».
«Меньшее вычитается из большего, имущество из иму-
щества, долг из долга, но если вычитается большее из
меньшего, значение избытка меняется. Долг,, будучи вы-
чтен из нуля, делается имуществом, имущество превра-
щается в долг».
Другой индийский математик XII в. Бхаскара пи-
сал: «Произведение двух имуществ или двух неимуществ
есть имущество; результат произведения имущества на
долг представляет избыток. То же правило имеет место
и при делении. Квадрат имущества или долга есть иму-
щество, имущество имеет два корня; один составляет
прибыль, другой долг» Ч
Индийская точка зрения в вопросах обоснования
арифметики положительных и отрицательных величин
оказала большое влияние на развитие алгебры и
явилась отправной точкой для признания отрица-
тельных величин и выработки строгих теорий в этом
направлении.
Заслуга индийских ученых в области отрицательных
величин становится более выпуклой, если вспомнить, что
в Европе еще в XVII в. находились ученые, которые от-
вергали понятия самостоятельной отрицательной ве-
личины, признавая только понятия «абсолютной» ве-
личины.
Как известно, обоснование правильного толкования
отрицательных величин и создания строгой теории в Ев-
ропе шло дальше через труды передовых ученых XVII и
XVIII вв. (Декарт, Ньютон, Эйлер, Клеро, Лаплас и дру-
гие) и нашло свое отчетливое выражение в мемуаре
датского математика К. Бесселя (1745—1818), опубли-
кованном в 1799 г. в «Трудах Датской Академии наук»,
в котором в связи с изложением геометрического истол-
кования арифметики комплексных чисел дается строгое
геометрическое истолкование арифметики положитель-
ных и отрицательных чисел* 2.
‘В Н. Молодший, Основы учения о числе в XVIII в., Учпед-
гиз, М., 1953, стр. 84—85.
2 См. там же, стр. 84—123.
123
§ 12. О ЗНАЧЕНИИ ИНДИЙСКИХ УЧЕНЫХ В РАЗРАБОТКЕ
ТЕОРИИ КВАДРАТНЫХ УРАВНЕНИИ
Теперь остановимся на значении разработки теории
квадратных уравнений индийскими учеными. Необходи-
мо заметить, что квадратные уравнения имеют длинную
историю, начало которой уходит далеко в глубь веков.
Еще древние греки построили целую геометрическую
алгебру, в которой излагались методы решения некото-
рых квадратных уравнений, получаемых из условия гео-
метрических задач. В III в. до н. э. знаменитый греческий
ученый Евклид отвел геометрической алгебре всю
вторую книгу своих «Начал» (трактат по элементарной
геометрии в 13 книгах), где собрал весь необходимый
материал для решения квадратных уравнений. Во II в.
н. э. греческий математик-инженер Гер он дал чисто ал-
гебраический способ решения квадратного уравнения.
Герон, решая уравнение
11х2 + 29х = 212-4,
сводил его к результату:
Х = 1Ь2 154-212—841—29 )•
Далее, в III в. н. э. греческий ученый Диофант, не
прибегая к геометрии, чисто алгебраическим путем решал
некоторые квадратные уравнения, причем само уравне-
ние и его решение записывались в символической форме.
В разработке общего метода решения квадратных
уравнений много сделано индийскими математиками.
Так, в XII в. н. э. индийский математик Бхаскара для
общего уравнения
ах2 + Ьх + с = О
находит решение в виде:
___ —b+Yb2 — 4ас
Х__2а ’
причем, признавая существование двух решений, он, од-
нако, отрицательных корней в расчет не принимал.
В то время, когда Диофант, избегая отрицательных
чисел, рассматривал три случая квадратных уравнений
ах2 + Ьх = с,
124
bx + с = ax\
ax2 + c = bx
раздельно и давал для них отдельные правила, индий-
ские математики все эти случаи объединяли в одном пра-
виле, рассматривая полное квадратное уравнение в са-
мом общем виде.
Уравнение (для простоты будем пользоваться совре-
менными обозначениями)
ах2 + Ьх=с.
Бхаскара решал таким путем: сначала умножал обе части
уравнения на 4а, тогда:
4а2х2 4- 4abx = 4ас.
После этого к обеим частям полученного равенства при-
бавлял по Ь2 и получал:
4а* х2 + 4abx + b2 = b2 + 4act
или:
(2ах 4- Ь)2 = Ь2 + 4ас.
Извлекая квадратный корень, имел:
2ах + b = у Ь2 4- 4act
или:
2ах = — Ь+УЬ2 4- 4ас.
Откуда:
х = —&+/ b2 + 4ас
2а
Как указывалось выше, индийские ученые дали реаль-
ное истолкование отрицательным числам, рассматривая
их чисто отвлеченно без уменьшаемого и истолковывая
их как «долг» или как выражение противоположного
направления. По их представлениям, коэффициенты
квадратного уравнения могут быть как положительными,
так и отрицательными, т. е. выражать «имущество» или
«долг». Однако признавая существование двух решений
квадратного уравнения и идя в этом направлении дальше
Диофанта, который рассматривал всегда только одно ре-
шение, индийские ученые тем не менее отвергали отрица-
тельные решения (корни). Так, Бхаскара, касаясь отри-
125
цательных значений корней, говорил, что «люди не одоб-
ряют отвлеченных отрицательных чисел» Ч
В соответствии с этим, решая квадратное уравнение:
х1 2 — 45х = 250,
Бхаскара, хотя и получает оба корня Xi = 50 и х2 =—5,
но отрицательного корня не берет, говоря, что «второго
значения в данном случае брать не следует, так как оно
не соответствует условию задачи»2.
Рассмотрим теперь задачу, при решении которой
Бхаскара признает оба корня как удовлетворяющие не
только составленному уравнению, но и самому условию:
«На две партии разбившись,
Забавлялись обезьяны.
Часть восьмая их в квадрате
В роще весело резвилась.
Криком радостным двенадцать
Воздух свежий оглашали.
Вместе сколько, ты скажешь,
Обезьян там было в роше?»
Эту задачу сам Бхаскара решал примерно так: если
обозначим число всех обезьян через х, то задача сведет-
ся к решению уравнения3:
-+0-х+ 12
64
0-ха + х + О4.
После приведения к одному знаменателю и упрощения
получим
х2— 64х
— 768.
Прибавляя к обеим частям квадрат 32, будем иметь:
ха— 64х + 322
— 768 + 1024.
После извлечения квадратного корня получается:
х—32
16.
1 Ф. К э д ж о р и, История элементарной математики с указа-
ниями на методы преподавания, Одесса, 1910, стр. 107.
2 Т а м ж е.
3 При решении этой задачи и задач, следующих за ней, для про-
стоты пользуемся современной буквенной символикой.
4 Индийские ученые имели привычку записывать левую часть
уравнения на первой строчке, а правую часть — на второй. В даль-
нейшем уравнения будем записывать в обычной современной форме.
126
«В данном случае,— говорит Бхаскара,— отрицатель-
ные единицы первой части таковы, что единицы второй
части меньше их, а потому последние можно считать и
положительными и отрицательными, и получаем двойное
значение неизвестного 48 и 16»1.
А вот другая задача, в которой из двух положи-
тельных корней Бхаскара признает только один:
«Скажи мне, сколько обезьян в стае, если квадрат
пятой части, уменьшенный тремя, спрятались в пещере
и только одна осталась на виду, взобравшись на де-
рево».
Задача сводится к решению уравнения:
3)2 + 1 = X.
\ 5
Его корнями будут Xi = 50 и х2 = 5. В заключение Бхаска-
ра делает такое замечание: «Так как у’ 5—3 есть число
отрицательное, то годится только первое решение» 2.
Но комментатор Бхаскары Кришна-Бхатт а го-
ворил: «Если бы по условию вопроса было сказано:
часть стаи вычитается из 3, то второе решение, а не
первое удовлетворяло бы условию» 3.
Вот пример еще одной задачи Бхаскары, в которой
из двух положительных корней условиям задачи удовле-
творяет только больший корень:
«Посреди сражения яростный сын Притхи схватил
некоторое число стрел, чтобы убить Карну; половину
их он употребил на собственную защиту, а учетверен-
ное количество квадратного корня — против лошадей;
6 стрел пронзили возницу Салью, 3 других прорвали
зонтик Карны, разбили его лук и знамя и только одна
последняя пронзила ему голову. Сколько было стрел
у Арджуны (сына Притхи)?»
1 Г. Н. Попов, Сборник исторических задач по элементарной
математике, ОНТИ, М.—Л., 1938, стр. 102.
2 Г. Н. Попов, Очерки по истории математики, М.—Л., 1925,
стр. 83—90.
3 Т а м ж е.
127
Уравнение, удовлетворяющее условию задачи, сле-
дующее:
- 4- 4/Г4- б + 3 +1= х.
2
После упрощения получается:
х2 — 104х + 400 = 0,
откуда:
х = 52 ± V522 — 400.
Следовательно:
х = 52 ± 48.
Таким образом, имеется два корня: Xi = 100 и х2 = 4,
причем непосредственной проверкой можно убедиться,
что условию задачи удовлетворяет только первый корень,
тогда как второй корень этому условию не удовлетворяет
и, следовательно, этот второй корень не годится.
Довольно оригинальным приемом Бхаскара решает
следующую задачу на квадратное уравнение:
«Корень квадратный из половины числа пчел пче-
линого роя полетел к кусту жасмина. Восемь девя-
тых роя осталось дома. Одна пчелка полетела за сам-
цом (трутнем), который жужжит в цветах лотоса, ку-
да он попал ночью, привлеченный приятным ароматом,
и не может оттуда выбраться, так как цветок закрыл-
ся. Скажи мне число пчел роя».
Бхаскара эту задачу решает так: положим, что число
пчел роя 2х2. Тогда корень квадратный из половины числа
пчел роя составит х, а-^ всего роя ~х2. Учитывая все это,
задача сводится к решению уравнения:
2хг = х 4- 16г2 4- 2,
9
или:
2х2 = 9л 4- 18.
Откуда:
х = 6.
И, следовательно:
2хг = 72,
что и составляет нужный ответ.
128
Невольно приходится обращать внимание на то, что
большинство задач Бхаскары, как и многие старинные
задачи других индийских авторов, часто облекались в
художественную поэтическую форму и некоторые из них
давались в стихах.
Показательна в этом отношении, например, такая з а-
дача Бхаскары о лебедях:
«Удесятеренный корень квадратный из стада лебе-
дей полетел по направлению к озеру, заметив, что
сгущаются тучи. Однако восьмая часть всех лебедей
скрылась в ненюфарах (цветущие водяные растения),
и только шесть безмятежно плещутся в волнах.
Скажи мне, юная девушка с пышной прической, сколь-
ко всех лебедей?»
Уравнение, к которому сводится задача, будет!
х = lOj/х + — %4-6.
8
Откуда получается квадратное уравнение:
и2 = 10а + -- и2 + 6, где и = )/хГ
8 г
После небольших упрощений:
7а2 — 80а — 48 = 0.
Пользуясь формулой Бхаскары, получим:
" _ 80-Ь |/ 6400 4- 1344
U 14
или:
и== 80+88^ |2
14 14
Следовательно:
х1 = и2 = 144.
Второй корень Х2 Бхаскара не берет, так как он соот-
ветствует отрицательному значению а, кроме того, дает
дробное значение для х, что не соответствует действитель-
ности (дробного числа лебедей быть не может).
В IX в. теории квадратных уравнений много внимания
9 Заказ 999
129
уделял узбекский математик Алхорезми, который
рассматривал шесть видов квадратных уравнений.
1) х2 = Ьх, 4) ха -\-Ьх=с9
2) х2 = с, 5) х2 -{-c=bx,
3) Ьх2 = с, 6) Ьх+с=х2.
Для каждого из шести уравнений в словесной форме
(буквенной символикой Алхорезми не пользовался) он
давал особое правило.
Потребовалось много-много лет, чтобы все эти шесть
уравнений, которые рассматривал Алхорезми, стали счи-
тать частными случаями одного общего уравнения.
ах2+Ьх+с=0
с универсальной формулой для его решения:
_ — b±yrb2—4ас
2а '
И это чрезвычайно важное обобщение, по-видимому,
выполнили впервые индийские ученые, среди которых
особенно выделяется Бхаскара.
В Европе попытка вывода общей формулы решения
квадратного уравнения была предпринята лишь в XVI в.
французским математиком Франсуа Виета (1540—
1603). Окончательный вывод этой формулы дал в 1630 г.
голландский математик Жи р а р (1595—1632).
§ 13. ПОПЫТКИ РЕШЕНИЯ УРАВНЕНИЙ ТРЕТЬЕЙ
И ЧЕТВЕРТОЙ СТЕПЕНЕЙ
В определенном алгебраическом анализе индийские
математики не ограничивали себя рамками одних только
квадратных уравнений и шли в указанном направлении
дальше, предпринимая попытки выработать отдельные
приемы решения уравнений более высоких степеней, а
именно третьей и четвертой.
Можно привести много старинных индийских задач,
решение которых сводится к рассмотрению уравнений
третьей и четвертой степеней.
Вот образцы таких задач.
Задача Бхаскары:
«Найти такое число, чтобы, умноженное на 12 и
прибавленное к своему кубу, оно давало сумму уше-
130
стеренного квадрата искомого числа, увеличенного
на 35».
Задачу эту Бхаскара решает довольно оригинально—
путем использования куба разности двух количеств. Ход
рассуждения его таков: согласно условию задачи состав-
ляем уравнение:
х3+ 12х = 6х2 + 35,
далее приводим его к виду:
х3 — 6х2 + 12х = 35.
Стоит теперь из левой и правой частей вычесть 8, чтобы в
левой части получился полный куб, т. е.:
(х — 2)3 = 27.
Откуда:
х — 2 = 3.
И, следовательно:
х = 5.
Бхаскара рассматривал только один корень кубиче-
ского уравнения, не подозревая, по-видимому» о сущест-
вовании еще двух его корней. Чтобы найти и другие два
корня, нужно было бы данное уравнение решить несколь-
ко иначе. Ниже приводим это решение:
х3 —6х2 + 12х — 35 = 0;
х3—5х2 —х2 + 5х 4-7х — 35 = 0; .
х2 (х —5)—х(х —5) +7 (х — 5) = 0;
(х —5) (х2 — х + 7) = 0.
Полагая
х — 5 = 0,
получим:
хг = 5.
Полагая
х2 — х + 7 = 0,
найдем еще два корня:
^2= |( 1 + Г-27); х3=^( 1 - V-27).
Последними двумя корнями, если бы он их даже и нашел,
Бхаскара не мог интересоваться, так как он не призна-
вал реального значения квадратного корня из отрица-
тельного числа. Это видно из следующего утверждения
9* 131
Бхаскары: «...квадрат положительного числа а равен
квадрату отрицательного числа, оба положительны; что
квадратный корень из положительного числа двойной,
положительный и. отрицательный, и что квадратного кор-
ня из отрицательного числа не существует, так как такое
число не может быть квадратом» 1.
Рассмотрим теперь еще одну задачу Бхаскары на
решение уравнения четвертой степени:
«Решить уравнение:
х4 _ 2%2 _ 4оох .= 9999».
Приводим, решение самого Бхаскары. Стоит только к
первой части прибавить 400х 4- 1, как она будет иметь
корнем х2 *— 1, так как:
х4 — 2х2 — 400х 4- 400х 4- 1 = х4 — 2х2 4- 1 =
= (х2— I)2.
Однако вторая часть, будучи тогда равна 400x4-10 000,
не будет иметь корня. Поэтому к первой и второй частям
данного уравнения надо прибавить
4х2 4- 400x 4- 1.
тогда каждая часть будет иметь корни. Действительно,
первая часть будет:
х* — 2х2 — 400х + 4х2 + 400х 4- 1 = х4 4- 2х2 + 1 =
= (х2 + I)2,
а вторая часть составляет:
9999 4- 4х2 + 400х + 1 = 4х2 4- 400х + 10 000 =
= (2х 4- 100)2.
Следовательно:
х2 4- 1 = 2х 4- 100;
х2 — 2х 4- 1 = 100;
(х — I)2 = 100;
х — 1 = 10;
х, = 11.
Этот корень Бхаскара и рассматривал. Остальные три кор-
ня, которые Бхаскара не рассматривал, также нетрудно
найти, если применить следующее рассуждение:
1 Ф. К э д ж о р и, История элементарной математики с указания-
ми на методы преподавания, Одесса, 1910, стр. 107—108.
(Курсив сделан нами. — В. Ч.)
132
х4 — 1 lx3 + 1 lx3 — 121x2 + j 19%2 _ i309x + 909% _
—9999 = 0;
x3(x — 11) + llx2(x— 11)+ 119x(x— 11)+ 909(x — ll)=0;
(X — 11) (x3 + 1 lx2 + 119x + 909) = 0; x— 11 = 0;
хг = 11;
x3 + llx2 + 119x + 909 = 0;
x3 + 9x2 + 2x2 + 18x + lOlx + 909 = 0;
x2(x + 9) + 2x(x + 9) + 101 (x + 9) = 0;
(x + 9) (x2 + 2x + 101) =0;
x + 9 = 0 дает x2 = — 9,
a x2 + 2x + 101 = 0 дает еще два корня: х3 и х4, которые
будут мнимыми. Но Бхаскара, как уже указывалось вы-
ше, последние три корня не признает, так как отрица-
тельные и мнимые корни, по его мнению, реального смыс-
ла не имеют.
§ 14. УЧЕНИЕ В ОБЛАСТИ ИРРАЦИОНАЛЬНЫХ ВЕЛИЧИН
Теперь остановимся на учении индийских ученых в
области иррациональных величин. Открытие иррацио-
нальных величин, как известно, принадлежит древнегре-
ческим ученым, которые проводили резкую границу, от-
делявшую величины от чисел. По их представлению, ир-
рациональная величина никогда не может быть числом.
Что касается индийских ученых, то они не замечали
разницы между величинами и числами, между рацио-
нальными и иррациональными количествами, подвергая
иррациональные количества тем же действиям, что и ра-
циональные числа.
Действительно, при решении ряда конкретных задач
индийские ученые свободно переходили от рассмотрения
чисел к рассмотрению фигур, не делая различия между
непрерывными и раздельными (дискретными) величина-
ми. И это обеспечивало им успех.
«Индийская алгебра, — говорил датский историк и ма-
тематик Г. Г. Цейтен,— похожа на алгебру Диофанта
в том отношении, что она освободилась от геометриче-
133
ского способа представления и рассматривает числа
только как таковые. Но грек Диофант требовал, чтобы
получившиеся в результате вычисления величины были
рациональными величинами, между тем как индий-
цы, менее требовательные по части логической строгости,
самым спокойным образом применяли к иррациональным
числам правила вычисления рациональных чисел; благо-
даря этому обстоятельству они были гораздо более сво-
бодны в своих алгебраических операциях. Вместо пре-
образований иррациональных величин, производившихся
Евклидом в геометрической форме, мы встречаем у ин-
дийцев прямые выкладки с иррациональными числами»
(курсив наш.— В.Ч.)\
Все сказанное выше дало право видному немецкому
математику Г. Ганкелю (1839—1873) дать высокую
оценку индийским ученым в создании современной ал-
гебры. Он писал: «... если разуметь под алгеброй прило-
жение арифметических операций к сложным величинам
всякого рода, будут ли то рациональные или иррацио-
нальные числа, или пространственные величины, то уче-
ных-браминов Индостана следует считать истинными изо-
бретателями алгебры»1 2.
Занимаясь иррациональными выражениями, индий-
ские математики сформулировали правило для приведе-
ния знаменателей дробей к рациональному виду и уни-
чтожения двойной иррациональности. Конечно, всеми эти-
ми вопросами занимался древнегреческий ученый Евклид,
но делал он это в чисто геометрической форме, избегая
чисел, а поэтому довольно сложно.
Простой подход к иррациональным выражениям поз-
волил индийскому математику Бхаскара заниматься ис-
следованием иррациональных выражений вида:
V а+ Vb.
Им было получено в простой и ясной форме тождество:
а+ V fl2~fr + fl— \Г&—Ь
1 Г. Г. Ц е й т е н, История математики в древности и в средние
века, изд. 2, подготовл. А. П. Юшкевичем, ГОНТИ, М.—Л., 1938,
стр. 185.
2 Herman Hankel, Zur Geschichte der Mathematik in Alterthum
und Mittelalter, Leipzig, 1874, p. 195.
1314
которое вошло во все современные школьные учеб-
ники» !.
В частности, тому же Бхаскаре принадлежит устано-
вление преобразования типа:___________________
V 16+V1204-y72+ 60 + 1/48 + У40+ ]/24 =
= /Г + уз~ + у Г + /6?
По-видимому, этот результат Бхаскара получил при по-
мощи обратного вычисления. Бхаскара также пользовал-
ся тождеством:
У а ± ]/F= V а-\-Ь+У abt
правильность которого устанавливается путем возведе-
ния в квадрат левой и правой частей. Наверное, из этих
соображений исходил и сам Бхаскара.
Бхаскара любил заниматься преобразованием ради-
калов и этому вопросу посвящал ряд интересных задач.
Вот одна из таких задач, которую предлагает Бхаскара:
«Показать, что
V10 + 1/24 + J/40-I-/60
= /2 +]/3'+/5».
Вероятно, доказательство Бхаскары сводилось к следую-
щему:
V l0 4-K24+/4(r+/60 =
= )Л+3+5+2/2^3 + 2j, 2+4-2)/3-5 =
-V (/2 + |/3"+ /5)1 2 = ГТ+УЗ + Г5’.
§ 15. НЕОПРЕДЕЛЕННЫЙ АНАЛИЗ В РАННИХ РАБОТАХ
ИНДИЙСКИХ УЧЕНЫХ
Индийские математики занимались решением неопре-
деленных уравнений, причем занимались не только одним
уравнением с двумя неизвестными, но также системами
1 У Евклида это тождество дается в X книге его «Начал», при-
чем чисто геометрически, в очень сложной и малопонятной форме.
135
уравнений с большим числом неизвестных. У индийских
математиков, например, встречаются задачи, где надо
найти число, которое при делении на различные данные
числа давало бы данные остатки. Есть основание думать,
что указанные задачи проникли в Индию из Китая, где
в древности рассматривались эти задачи и было найдено
общее правило решения.
Особое внимание обращали индийские математики на
решение следующих неопределенных уравнений:
1) ах + by = с\
2) ху + ах + by =с\
3) ах2 + b = у2\
4) сх ± а У х = Ь\
5) ах + by + с = ху\
6) xyzu = а(х + у + z+u\
Чтобы иметь некоторое представление об индийском
способе решения неопределенных уравнений, рассмотрим •
решение уравнения:
у2 = ах2 + 1,
которое позднее в Европе стало называться уравнением
Пеля.
Если воспользоваться современной символикой, то ин-
дийцы уравнение Пеля решали так: сначала, пользуясь
произвольными числами xv yv х2, у2, определяли bt и Ь2
с таким расчетом, чтобы выполнялись равенства:
<зх/ + bv = уу2
ах/ + Ь, = у.2,
или:
у/ — ах/ = by
у/ — ах22 = Ь2.
Путем умножения последних двух уравнений получали:
(axjx2 4- i/ji/J2 — а(Хуу2 4- хгуу)2 = b}b2.
Положив х2 = xv у2 = yv а тогда и b2 = bv последнее
уравнение приводили к виду:
а(2х1У1)* + by 2 = (ах/ 4- Уу1)2.
Разделив на Ь2, окончательно имели:
/2х|У1 . /ол/4-у/ у
\ Ь ) k by )'
1S6
Следовательно:
_ 2х,У1. _ axi2+t/ta
bi ’ у bx
Так индийские ученые получали решения в рациональ-
ных числах, удовлетворяющих данному уравнению. Да-
вая Xi и у\ произвольные значения, они добивались иног-
да того, что решения были в целых числах.
ГЛАВА ДЕВЯТАЯ
РАЗВИТИЕ ГЕОМЕТРИИ И ТРИГОНОМЕТРИИ
В ИНДИИ
§ 1. НЕСКОЛЬКО СЛОВ О РАЗВИТИИ ГЕОМЕТРИИ
ВООБЩЕ И ИНДИЙСКОЙ ГЕОМЕТРИИ В ЧАСТНОСТИ
Возникновение геометрии вызвано потребностью че-
ловека измерять землю. Слово «геометрия» буквально
означает измерение земли. Таким образом, первые гео-
метры были преимущественно землемерами. На заре сво-
его развития, несколько тысяч лет тому назад, геомет-
рия Вавилона и Египта состояла из отдельных правил и
рецептов, полученных опытным путем и предназначавших-
ся главным образом для вычисления площадей и границ
земельных участков. Геометрия того времени еще не бы-
ла научной теорией, основанной на логических доказа-
тельствах. Как наука геометрия оформилась к III в. до
н. э. благодаря упорной и настоятельной работе грече-
ских математиков (Фалес, Евклид, Пифагор и другие),
результаты которых нашли свое выражение в знамени-
тых «Началах» Евклида.
Евклид (древнегреческий ученый, жил в III в. до
н. э.) собрал в своих «Началах», состоящих из 13 книг,
различные результаты по геометрии в единую научную
систему, заполнив пробелы своими собственными иссле-
дованиями.
Насколько большой авторитет имели и имеют «Нача-
ла» Евклида, видно из того, что почти вся последу-
ющая учебная литература по геометрии или дословно
копирует Евклида, или написана под большим его
влиянием.
Индийская геометрия по значительности и характеру
хотя и уступает греческой, тем не менее она оставила
заметный след в истории математики. В особенности ве-
138
лика заслуга индийских ученых в разработке тригоно-
метрии, которая обеспечила нормальное развитие астро-
номии, давшей индийскому народу довольно точный ка-
лендарь и необходимые сведения по мореплаванию и дру-
гим прикладным вопросам.
§ 2. «СУЛВА-СУТРЫ» («ПРАВИЛО ВЕРЕВКИ»)
ДРЕВНЕЙШИЙ ПАМЯТНИК ИНДИЙСКОЙ ГЕОМЕТРИИ
Самым старым памятником индийской геометрии, ко-
торый дошел до нашего времени, являются сборники,
имеющие общее название «Сулва-сутры», в буквальном
переводе — «Правило веревки». «Сулва-сутры» пред-
ставляют собой своеобразную инструкцию о построении
жертвенников, в которой дается весьма ценный геомет-
рический материал в его приложении, т. е. связанный с
формой жертвенников, их размерами и необходимой
ориентацией. В настоящее время известны три таких
сборника. Авторами их являются Бодгайана (VI или
VII в. до н. э.), К а т и а й а н а иАпастамба (IV или
V в. до н. э.).
Судя по этим сборникам, можно сделать вывод:
1) По меньшей мере уже в VIII в. до н. э. индийским
ученым была известна теорема о квадрате гипотенузы,
т. е. известная теорема Пифагора.
В «Сулва-сутрах» эта теорема формулировалась так:
«Веревка, проведенная наискось в продольном квадрате
(прямоугольнике), образует то же, что образует вместе
каждая из мер: продольных и поперечных».
Эта же теорема в виде краткого правила еще форму-
лировалась так: «То, что образуется на двух сторонах,
равно тому, что образуется по диагонали».
2) Пользуясь соотношением между сторонами прямо-
угольного треугольника, Апастамба дает общие пра-
вила сложения и вычитания квадратов.
Первое правило Апастамбы позволяет решить
такую задачу:
«Построить квадрат, равновеликий сумме двух
данных квадратов».
Суть правила следующая: «Отрезать стороной ЕС
меньшего квадрата ECFG часть большего ABCD, т. е.
прямоугольник НВСЕ (рис. 25). Диагональ его BE дает
10*
139
столько же, сколько дают его измерения, т. е. стороны
данных квадратов. Действительно:
В£2=ВС2+£С2
Второе правило Апастамбы относится к з а-
д аче:
«Построить квадрат, равновеликий разности двух
данных квадратов».
Правило заключается в следующем: «Отрезать сто-
роной ЕС отнимаемого квадрата часть (прямоугольник
НВСЕ) от большего и провести большую из сторон НЕ
отрезанной части до встречи с другой стороной ВС. От-
резок КС—искомый» (рис. 26).
В самом деле:
КС2 = КЕ2 — ЕС2 = НЕ2 — ЕС2 = АВ2 — ЕС2.
что и требовалось по условию задачи.
3) В «Сулва-сутрах» дается правило построения
перпендикуляра к направлению восточной линии (на-
правление жертвенника). Правило поясняется приме-
ром:
«Пусть длина восточно-западной линии 36 падасов,
в обоих концах этой линии вбивают колья в землю. К
этим кольям прикрепляют концы веревки длиной в 39
падасод, на которой предварительно на расстоянии 15
падасов от одного конца сделан узел. Если теперь на-
тянуть веревку на поверхности земли, держа за узел,
то получается прямой угол на конце восточно-запад-
ной линии» (рис. 27).
140
Необходимо заметить, что этот прием для построения
прямого угла был известен и древним египтянам, кото-
рые для тех же целей пользовались так называемым
«египетским треугольником», т. е. прямоугольным тре-
угольником со сторонами 3, 4, 5.
4) В «Сулва-сутрах» дается геометрическое правило
извлечения корней, выраженное словами: «Веревка, на-
тянутая наискось равностороннего прямоугольника
(квадрата), дает квадрат двойной площади. Веревка
наискось продолговатого прямоугольника дает две пло-
щади, которые делают веревки, натянутые вдоль его
сторон»»
5) Если древнегреческие ученые пытались решить
проблему о превращении данного круга в равновеликий
квадрат (квадратура круга), то индийские математики
в «Сулва-сутрах» решают обратную задачу, конечно при-
ближенно, о превращении данного квадрата в равнове-
ликий круг. Для этой цели дается «правило Катиай-
аны»:
«Надо разделить диаметр круга на 15 равных частей
и взять 13 таких частей для стороны квадрата, равного
(приблизительно) кругу».
Легко подсчитать, что в этом случае число к«
или тс = 3,00 (4).
Что касается доказательства теоремы Пифагора, то
его в «Сулва-сутрах» не имеется, так как указанный до-
кумент есть инструкция для уже готовых правил.
141
§ 3. ОБ ИНДИЙСКОМ ДОКАЗАТЕЛЬСТВЕ
ТЕОРЕМЫ ПИФАГОРА
Доказательство теоремы встречается дважды у Бха-
скары (род. в 1114 г., год смерти неизвестен) в его
алгебраическом сочинении «Виджа-Ганита» («Вычисле-
ние корней»). Он доказывает теорему так: строит на ги-
потенузе треугольника квадрат и четыре треугольника,
равных данному, с таким расчетом, чтобы в середине
часть, не занятая треугольниками, составила квадрат со
стороной, равной разности между двумя катетами пря-
моугольного треугольника (рис. 28). Далее Бхаскара
рассуждает так: «Расположи те же части фигуры иначе,
смотри!» (Рис. 29.) Теорема, по его мнению, доказана.
Из рассуждения Бхаскары видно, что в индийском
способе доказательства существенную роль играет чер-
теж и его наглядность, основанная на утверждении, что
равносоставленные фигуры равны.
Комментатор Бхаскары Кришна к его доказатель*
ству считает нужным добавить еще: «Продолжив линию
(т. е. левую сторону бокового квадрата на рис. 29), мы
разделим фигуру на два квадрата: один — квадрат боль-
шего катета, другой—квадрат меньшего катета и сумма
их равна площади первого большого квадрата; корень
же квадратный из нее есть сторона четырехугольника» L
1 И. Ю. Тимченко, Доказательство пифагоровой теоремы у
Бхаскары. Прибавление II к книге: Ф. Кэджори, История эле-
ментарной математики с указаниями на методы преподавания,
Одесса, 1910, стр, 333—334.
142
Из приведенных выше фигур Бхаскара вывел такое
правило: «Удвоенное произведение катетов, сложенное с
квадратом их разности, равно сумме их квадратов, со-
вершенно как и для двух неизвестных количеств». В со-
временных обозначениях запись этого правила выглядит
так:
2аЬ + (а — Ь)1 2 = а2 + Ь2.
Второе доказательство теоремы Бхаскары основано
на опускании перпендикуляра из вершины прямого угла
на гипотенузу и рассмотрении полученных таким обра-
зом подобных треугольников. Умело составленные про-
порции приводят его к нужному соотношению:
с2 = а2 + 6а.
Это доказательство, вошедшее во все современные
учебники элементарной геометрии, стало известным в
Европе только в XVII в„ после того как оно было пере-
открыто английским математиком Д ж оном Валл и-
сом (1616—1703).
§ 4. СТАРИННЫЕ ИНДИЙСКИЕ ЗАДАЧИ,
РЕШАЕМЫЕ ПРИ ПОМОЩИ ТЕОРЕМЫ ПИФАГОРА
Задача о тополе:
«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола.
Поошу тебя, скоро теперь мне скажи.
У тополя как велика высота?»'
Задача поясняется рисун-
ком 30, согласно которому тополь
АВ сломлен в точке С на высо-
те 3 футов и верхушка D в новом
положении отстоит от основа-
НИЯ А на 4 фута. Требуется
узнать высоту тополя.
в
Рис. 30.
1 Стихотворный перевод выполнен В. И. Лебедевым.
У Бхаскары эта задача дается также в стихотворной форме.
143
Решение:
AB=AC-i- C/J=AC+V AC2+AD2 = 3 + /94Й6 = 34-5 =
= 8 (футов).
Задача о лотосе:
Рис. 31.
«Над озером тихим, с полфута размером,
Высится лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону. Нет
Больше цветка над водой.
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока?»
Согласно рисунку (рис. 31) за-
дачу можно сформулировать так:
«Цветок лотоса, основание кото-
рого С при отвесном положении
стебля возвышалось над водою на
Ц- фута, порывом ветра отклонил-
ся на 2 фута от прежнего положе-
ния (считая по поверхности во-
ды); при этом вершина цветка
оказалась на уровне воды. Опре-
делить глубину озера в этом месте, т. е. длину отрез-
ка АВ.
Решение: (х + —V= х2 + 22
\ 2/
или:
х? + X + 1 = ха 4- 4,
4
откуда:
х + — = 4.
4
Следовательно:
х =3у (фута).
4
Теперь подробнее остановимся на геометриях трех
крупнейших индийских математиков, а именно на геомет-
риях Ариабхаты, Брамагупты и Бхаскары, имена кото-
рых не раз уже упоминались выше.
144
§ 5. ГЕОМЕТРИЧЕСКОЕ УЧЕНИЕ АРИАБХАТЫ
Индийский астроном и математик Ариабхата
родился в 476 г. (год смерти неизвестен). Когда ему бы-
ло всего двадцать три года, он написал астрономо-мате-
матический трактат под названием «Ариабхатиам», со-
стоящий из четырех частей. Математику содержит пре-
имущественно вторая часть сочинения, носящая название
«Начала счисления». Здесь сжато излагаются матема-
тические сведения, необходимые главным образом для
астрономических вычислений, и даются они в виде правил
арифметики, алгебры, геометрии и тригонометрических
таблиц.
К геометрии из второй части относится следующее:
1. Дается определение квадрата и куба, а также вы-
ражение их плошади и объема куба, причем квадрат
определяется как прямоугольник с равными сторона-
ми.
2. Площадь треугольника полагается равной произве-
дению основания на половину высоты.
3. Площадь круга считается равной произведению по-
ловины окружности на радиус.
4. Для шара выражение объема дается неправильно,
с очень грубым приближением, а именно объем шара
16пз
считается равным —/г.
5. Дается теорема Пифагора, которая выражена поч-
ти в такой же форме, как и в «Сулва-сутрах», т. е. в
«Правилах веревки».
6. Дается приближенное вычисление отношения дли-
ны окружности к длине диаметра (десятое правило). Со-
гласно расчетам Ариабхаты
я = -—«3,1416.
20000
Само правило гласит: «Прибавь 4 к 100, умножь на 8,
приложи 62 000, это будет приблизительно длина окруж-
ности для диаметра, равного 40 000».
7. Излагается теория гномона, т. е. вопросы, связанные
с построением и вычислением на местности.
8. В двадцать первом правиле показан способ вы-
числения числа шарообразных ядер в треугольной
куче.
Д45
Способ представляет собой суммирование так назы-
ваемых треугольных чисел вида:
п (п+1)
2
по формуле:
р п(п+1)(п4-2)
£"=------S---- '
где —сумма п первых треугольных чисел. Например,
при и=4 будем иметь:
£ 4_5_6= 20
4 6
Действительно, непосредственная проверка суммы четы-
рех первых треугольных чисел дает:
Е4= 1 + 3 + 6 + 10 = 20.
9. В двадцать втором правиле дается способ нахож-
дения числа ядер с квадратным основанием, что соответ-
ствует формуле:
п(п+1)(2п+1)
1-2-3
Другая часть этого правила показывает, что Ариаб-
хате было известно соотношение:
I3 + 23 + З3 + ... + п3 = (1 + 2 + 3 + ... + п)а,
т. е. сумма кубов первых чисел равняется квадрату сум-
мы этих чисел.
§ 6. ГЕОМЕТРИЧЕСКОЕ УЧЕНИЕ БРАМАГУПТЫ
Крупнейший индийский математик Брамагупта
родился в 598 г. и умер в 660 г. Для потомства сохранил-
ся один его астрономический трактат «Брама-спутта-
сидданта» («Пересмотр системы Брамы»). Трактат со-
стоит из 20 книг, из которых математические — XII и
XVIII книги. XII книга содержит арифметику, а XVIII—
алгебру. В арифметической книге имеется целая глава
(четвертая), целиком посвященная вопросам геометрии.
Геометрическую часть сочинения Брамагупты хорошо
изложил крупнейший французский математик-геометр
М. Шаль (1793—1880) в своем объемистом трактате
146
«Исторический обзор происхождения и развития геомет-
рических методов», первый том которого посвящен гео-
метрии (имеется русский перевод, М., 1833).
М. Шаль пришел к следующим выводам:
1. Изложение всех геометрических предложений дано
Брамагуптой в очень сжатой форме и не сопровождается
никакими доказательствами.
2. Предложения даются в самой общей форме без
чертежей и числовых примеров. Правда, в примечаниях
одного из индийских комментаторов Брамагупты, по име-
ни Шатурведа, к указанным предложениям даются и
чертежи и числовые примеры.
3. Только немногие геометрические предложения Бра-
магупты даны полностью в законченном виде и, следо-
вательно, вполне понятны для читателя. Остальные пред-
ложения сформулированы неполностью, и для их пра-
вильного понимания следует прибегать к догадкам.
4. По смыслу геометрических предложений, который
им придал М. Шаль, оказалось, что сочинение имеет
целью решение следующих четырех проблем, относящих-
ся к треугольнику и четырехугольнику.
Проблема первая. Найти площадь треугольни-
ка и радиус описанного около него круга в функции трех
его сторон.
Проблема вторая. Построить треугольник, пло-
щадь которого и этот радиус выражались бы рациональ-
ными числами, причем предполагается, что стороны тре-
угольника суть также числа рациональные.
Проблема третья. Для четырехугольника, впи-
санного в круг, определить в функциях сторон: площадь,
диагонали, перпендикуляры, отрезки, образуемые при
взаимном пересечении этих линий, и диаметр круга.
Проблема четвертая. Построить четырехуголь-
ник, вписанный в круг, в котором все это — площадь диа-
гонали, перпендикуляры, их отрезки и диаметр круга —
выражалось бы рациональными числами.
Для решения этих проблем Брамагупта предваритель-
но рассматривает восемнадцать предложений, и их как
раз столько, сколько нужно. Учитывая это, М. Шаль за-
являет, что «сочинение изложено умно и точно». «Можно
даже сказать, — продолжает несколько дальше Шаль,—
что сочинение Брамагупты имеет предметом один только
из вышеприведенных вопросов (проблем), именно по-
147
следний (четвертая проблема), относящийся к вписанно-
му четырехугольнику. Три других являются тогда неиз-
бежными подготовлениями к его решению; и действи-
тельно, все они имеются при полном решении вопроса о
четырехугольнике»
После решения указанных выше четырех проблем (им
посвящено 18 первых параграфов), Брамагупта излагает
следующий геометрический материал:
1. Приводится древняя ошибочная египетская теоре-
ма: площади треугольника (как частного случая четы-
рехугольника) и четырехугольника равны половине про-
изведения полусумм противоположных сторон.
2. Дается совершенно верная теорема, выражающая
площадь треугольника или вписанного четырехугольника
в функции сторон. Эта теорема читается буквально так:
«Написав четыре раза полусумму сторон, из нее последо-
вательно вычитают стороны и затем перемножают; квад-
ратный корень из этого произведения есть точная пло-
щадь фигуры».
Приведенная теорема есть не что иное, как известная
формула Герона Александрийского и ее обобщение на
случай описанного четырехугольника.
Действительно, согласно индийскому правилу, сфор-
мулированному Брамагуптой, для треугольника со сто-
ронами а, b и с имеем:
S =/р (р — а) (р — 6) (р — с),
где р Это и есть формула Герона.
Для описанного же четырехугольника со сторонами а,
6, с и d получим:
s =v?<7 —а) (<? —6) (9 — С) (<?—</).
где q =----------. Это и есть индийское обобщение фор-
мулы Герона1 2.
1 Шаль, Исторический обзор происхождения и развития гео-
метрических методов, М., 1883. стр. 90.
2 О жизни древнегреческого ученого Герона имеются отрывоч-
ные сведения. Известно, что он жил в Александрии около III и II вв.
до н. э. Некоторые историки математики, например Кантор, счи-
тают, что Герои Александрийский жил в I в. н. э.; другие историки,
например Мари, полагают, что он жил во II в. до н. э. (около
148
3. Устанавливается предложение: «Если d — диаметр
и г—радиус круга, то на практике окружность равна
3d и площадь Зг2; но для получения более точных значе-
ний надо взять длину окружности, равной d /10, а пло-
щадь круга r*V 10»-
Таким образом, Брамагупта получает, что для прак-
тических целей отношение длины окружности к диамет-
ру к = /ТО = 3,62.
4. Формулируется предложение: «В круге полухорда
равняется квадратному корню из произведения двух от-
резков перпендикулярного к ней диаметра».
5. Рассматривается предложение: «Стрела, т. е. мень-
ший отрезок диаметра, перпендикулярного к хорде, рав-
на полуразности между диаметром и корнем квадратным
из разности квадратов диаметра и хорды. В двух пере-
секающихся кругах, вычитая из двух диаметров отрезок,
равный сумме двух стрел, соответствующих общей хорде
кругов, умножая остатки на этот отрезок и разделяя про-
изведение на сумму остатков, получим по порядку обе
стрелы».
6. Дается предложение: «Квадрат хорды, разделен-
ный на учетверенную длину одного из отрезков и увели-
ченный на тот же отрезок, равен диаметру».
7. В V отделе дается измерение призмы, пирамиды и
практический метод приближенного измерения некото-
рых других тел.
8. Наконец, в последнем отделе решаются две задачи
при помощи гномона (вертикального шеста).
Задача первая:
«Зная высоту свечи (Н), высоту гномона (h) и рас-
стояние между их основаниями (d), найти длину тени
(х), бросаемой гномоном».
155 г. до н. э.). Известно также, что он был выдающимся ученым-
инженером. Занимался вопросами геодезии, т. е. науки, изучающей
размеры и форму Земли, дающей методы изображения земной по-
верхности на планах и картах, устанавливающей способы измерений
на местности
Математические работы Герона Александрийского составляют эн-
циклопедию античной прикладной математики. Его работы до эпохи
Возрождения оказывали большое влияние на развитие математики и ее
приложений в Европе. Мы находим их следы в Риме, на Западе в
средние века и даже пожалуй в Индии. Однако обобщения теоремы
Герона, т. е. распространение ее на любой вписанный четырехуголь-
ник, выполненное Брамагуптой, в работах самого Герона не имеется.
149
При решении этой задачи приходится рассматривать
подобные треугольники, само решение выполняется очень
просто. Действительно, из подобия треугольников
(рис. 32) имеем:
х_____Л
x-\-d “ Н
Следовательно:
hd
х~ Н- h'
Задача вторая:
«Найти высоту свечи (х), зная длины теней, бросае-
мых гномоном (А) в двух положениях (а и Ь), при ус-
ловии, что дано расстояние между гномонами (d)».
Из подобия треугольников (рис. 33) имеем:
d _ а+ Ь-И '
x—h х
150
Следовательно:
или окончательно:
й(а + b + d)
Х~ а+Ь •
9. В последнем же отделе приводится правило для по-
строения прямоугольного треугольника в рациональных
числах. Это правило формулируется так: «Если а есть
- 1 /л2
один катет треугольника и Ь— какое-либо число, то -Ч— —
— Ь) будет другим катетом, а — ( —+ 6] станет гипотену-
зой».
Действительно, правило это основано на тождестве,
если, конечно, иметь в виду теорему Пифагора:
§ 7. ГЕОМЕТРИЧЕСКОЕ УЧЕНИЕ БХАСКАРЫ
О геометрии Бхаскары уже частично говорилось вы-
ше, в связи с индийским доказательством теоремы Пи-
фагора. Дополнительно о самом Бхаскаре и его геомет-
рии можно сказать следующее.
Знаменитый индийский математик и астроном Бха-
скар а-а к а р и я родился, как указывалось выше, в
1114 г. (год смерти неизвестен). Приставка «акария»
означает «мудрец», «ученый». Примерно в 1150 г. он из-
дал трактат «Сидданта-сиромани» («Венец системы»).
Введение к нему содержит арифметику — «Лилавати»,
что буквально означает «прекрасная», и алгебру —
«Виджа-Ганита» («Вычисление корней»). Полагают, что
«Лилавати» было имя дочери Бхаскары. Из-за простоты
и ясности стиля, доступного пониманию юношества, ма-
тематические сочинения Бхаскары еще до сих пор исполь-
зуются в санскритских школах.
Геометрия Бхаскары размещается главным образом
в VI—IX главах его сочинения «Лилавати».
151
Так, глава VI содержит плоскую геометрию. Изложе-
ние мало чем отличается от Брамагупты, а если и отли-
чается, го только незначительными дополнениями.
Следующие четыре геометрические главы (VII—X)
относятся к измерению объемов тел при решении раз-
личных практических вопросов. Изложение во многом
копирует Брамагупту.
Наконец, последняя глава (XI) носит название «Тень
гномона» и занимается вопросами измерения при помо-
щи теней. Такого рода задачи, как мы видели выше,
встречаются также и у Брамагупты.
Согласно исследованиям Шаля геометрический мате-
риал Бхаскары разделяется на пять частей. Первая
часть относится к треугольнику вообще. Вторая часть
относится к прямоугольному треугольнику. Третья
часть составляет учение о произвольном четырехуголь-
нике. Четвертая часть заключает в себе некоторые
предложения, относящиеся к кругу. Наконец, в последней,
пятой части находятся правила для измерения объ-
емов и глава эб употреблении гномона.
В первой части дается выражение перпендикуляра в
треугольнике и площади треугольника через его стороны.
Во второй части рассматриваются построение прямо-
угольного треугольника в рациональных числах и неко-
торые другие вопросы, относящиеся к прямоугольному
треугольнику.
В третьей части вычисляются различные линии в про-
извольном четырехугольнике по данным четырем сторо-
нам и одной диагонали.
Все эти части не связаны между собой, и каждая
представляет из себя отдельное исследование.
Однако по сравнению с Брамагуптой Бхаскара, яв-
ляясь его учеником, в геометрических исследованиях де-
лает шаг назад, так как он некоторые верные и изящные
теоремы Брамагупты, относящиеся к вписанному четы-
рехугольнику, не понял и признавал их ложными. Это
обстоятельство даже дало Шалю повод сделать заклю-
чение, что после Брамагупты математика пришла в упа-
док и сочинения этого геометра перестали быть понят-
ными Ч
1 См. М. Шаль, История геометрии, т. II, примечания, М.»
1883, стр. 146«
152
Как пример приводим следующее неверное толкова-
ние Бхаскарой верного геометрического предложения
Брамагупты. Вот его слова: «Полусумма сторон пишется
четыре раза, из каждой отдельно вычитаются стороны и
составляется произведение остатков. Квадратный корень
из этого произведения будет площадь неточная (раз-
рядка наша. — В. Ч.) для четырехугольника, но то ч н а я
(разрядка наша. — В. Ч.), как было доказано, для тре-
угольника».
«Это и есть, — говорил Шаль, — формула Брамагуп-
ты, которую Бхаскара списал, не поняв ее и не заметив,
что здесь речь идет о четырехугольнике, вписанном в
круг. Вот почему он говорит, что это неверно для четы-
рехугольника, и дальше доказывает, что нелепо искать
площадь четырехугольника, в котором известны только
стороны, потому что из тех же сторон, говорит он, мож-
но составить много различных четырехугольников» Ч
Несмотря на указанные выше недостатки геометриче-
ской части сочинений Бхаскары, в ней есть много поучи-
тельного и интересного. В особенности большую ценность
составляют задачи. Вот некоторые из них.
Задача первая:
«Зная длины тип двух палок бамбука, верти-
кально воткнутых в землю на известном расстоянии,
вычислить длину перпендикуляра к земле, опущен-
ного из точки пересечения прямых, соединяющих ко-
нец одной палки с основанием другой, и отрезки, опре-
деляемые основанием этого перпендикуляра на соеди-
няющей основания двух палок».
Обозначая через h длину перпендикуляра, через d —
расстояние между основаниями палок, х и у — отрезки
(рис. 34), правило Бхаскары можно записать так:
й = у=^~ .
т+п т + п т + п
3 адача втор ая:
«Найти прямоугольный треугольник, в котором
гипотенуза выражалась бы тем же числом, что и
плошадь».
1 М. Шаль, История геометрии, т. II, М., 1883, стр. 134.
11 Заказ 990
153
Решая эту задачу, Бхаскара исходил из тождества:
[(m2 +л2)х] 2=[(т2—п2)х]2+(2тпх)а,
в котором (т2 + п2)х принимает за гипотенузу, а (т2 —
— п2)х и 2тпх — за катеты. Имея ввиду условие задачи, по-
лучал:
(т2 4- п2)х = тпх\т2 — п2).
Откуда:
Рис. 34.
Затем он без труда вычислял катеты искомых треуголь-
ников, а следовательно, находил и сам треугольник.
Задача третья:
«Найти высоту кругового сегмента, если известны
диаметр круга и основание сегмента».
Если обозначить длину диаметра через d, основание
сегмента АВ положить равным а, а высоту сегмента обо-
значить через х (рис. 35), тогда:
у = x(d — х) = dx — ха,
или:
х2 — dx + — =0.
4
Откуда без труда находится х, т. е. искомая высота
сегмента.
Бхаскара решает так же задачу на вычисление сторон
правильных вписанных в круг многоугольников с 3, 4, 5,
6, 7, 8 и 9 сторонами и приходит к выводу, что при диа-
154
метре круга, равном 2000, стороны упомянутых много-
угольников соответственно равны:
1732—, 1414 -, 1175 —, 1000, 867—, 765 —и 683- .
20 60 30 12 30 20
Автор прибавляет:
«Для разных других
диаметров получатся
другие стороны, как
мы покажем это в трак-
тате «Sphaerica», в от-
деле о построении сину-
сов». Для вычисления
поверхности и объема
сферы Бхаскара фор-
мулирует следующие
два правила:
Правило пер-
вое. «Четверть диамет-
ра, умноженная на ок-
ружность, есть пло-
щадь круга. Эта пло-
щадь, помноженная на
4, есть поверхность
сферы».
Правило второе. «Пусть D будет диаметр кру-
3927
га; Р1 2-^^-есть довольно приближенная величина площади
круга; D2 — есть грубая мера, употребляемая в практике;
14
D3 1 D3 * , 1
— ----есть мера объема сферы»1.
Легко подсчитать, что в последних двух случаях число
22
к = — (знаменитое архимедово приближение). Действи-
7
тельно:
D2.H = £2 22.
*14 4*7’
D3 лз — 22
2*2 21“ 6*7’
«Следующее правило, — писал Бхаскара, — достав-
ляет весьма удобный способ находить хорды с грубым
приближением» 2.
1 М. Шаль, История геометрии, т. II, М., 1883, стр. 141.
2 Т а м же, стр. 142.
11*
155
Правило Бхаскары (для определения хорд):
«Пусть будет с окружность, а — дуть, Ь — диаметр, С —
хорда; тогда будем иметь:
а(с—а)
4
«Эта приблизительная формула,— замечает М. Шаль,—
весьма любопытна; было бы интересно знать, каким обра-
зом индийцы пришли к ней» Ч
Приведенную выше формулу для вычисления хорд
Бхаскара рассматривал на примере. Так, если диаметр
равен 240, то хорды дуг в 20, 40, 60, 80, 100, 120, 140,
160 и 180 градусов равны 42, 82, 120, 154, 184, 208, 226,
236, 240.
Бхаскара дает также правило для определения дуг,
если дана ее хорда. Вот это правило:
«Формула, определяющая дугу а в функции хорды С
для окружности с и диаметра D:
4 4D+C
Эту формулу Бхаскара получил из предыдущей форму-
лы, решая буквенные уравнения второй степени.
В главе XI, посвященной вычислению расстояний по-
средством тени гномона, Бхаскара решает такой вопрос,
которого нет у Брамагупты: «Гномон освещен двумя раз-
ными светящимися точками; если известны разность те-
ней и разность их гипотенуз, то можно определить самые
тени». Решение этого вопроса приводится к решению
следующей задачи:
«Построить треугольник, зная его перпендикуляр,
разность отрезков, образуемых перпендикуляром на
основании, и разность двух других сторон».
По правилу Бхаскары, искомые отрезки будут равны:
4/12 >
da— ьа 1
1 М. Шаль, История геометрии, т, II, М., 1883, стр. 142,
156
где h — высота или перпендикуляр треугольника, 8 —
разность отрезков и d — разность сторон.
Некоторые вопросы алгебры Бхаскара, как он сам вы-
ражался, решал геометрическим способом. Например,
чтобы решить в рациональных числах неопределенное
уравнение второй степени:
ах + Ьу + с = ху,
Бхаскара прибегал к чертежу, на котором выяснял гео-
метрическое значение этого уравнения, и, исходя из это-
го уравнения, показывал, что оно может быть приведено
к виду:
(х —ь) (у— а) = ab + с.
Далее он заключал, что при произвольном п для ра-
циональных величин х и у должны взять выражения:
х = 6+п; у = а с .
Несмотря на ряд ошибочных положений, допущенных
Бхаскарой в его алгебраическом трактате «Виджа-Гани-
та», тем не менее в этом сочинении «есть несколько гео-
метрических вопросов, решенных посредством вычисле-
ния, и несколько правил алгебры, доказанных при по-
мощи геометрии. Все эти вопросы исследованы с заме-
чательным изяществом и точностью.
В некоторых вопросах, которые могли быть решены
различным образом, автором избран самый простой спо-
соб решения. Можно подумать, что читаешь какое-ни-
будь место из «Arithmetica universalis», где Ньютон дает
столь основательные советы относительно выбора неиз-
вестных» L
Показательны в этом отношении следующие рассуж-
дения Бхаскары. Так, желая, например, определить осно-
вание косоугольного треугольника со сторонами 13 и 5,
площадь которого равна 4, он делает замечание, что
если за неизвестное примем искомое основание, то при-
дем к квадратному уравнению. Но если будем искать пер-
пендикуляр, опущенный на одну из данных сторон из
противоположной вершины, и отрезки, образуемые на
1 М. Шаль, История математики, т. II, М.» 1883, стр. 143.
157
этой стороне, то получим искомое основание через про-
стое извлечение квадратного корня. Искомое основание
4 («Виджа-Ганита», § 117) Ч
§ 8. ВКЛАД ИНДИЙСКИХ УЧЕНЫХ В ТРИГОНОМЕТРИЮ
Переходим теперь к краткой истории тригонометрии
и укажем, какой замечательный вклад в эту науку внес-
ли индийские ученые.
На заре своего развития тригонометрия выступала
главным образом как наука о решении плоских и сфери-
ческих треугольников. Об этом говорит и само слово
«тригонометрия», которое буквально означает «измере-
ние треугольника». Действительно, термин тригономет-
рия состоит из двух греческих слов: «тригоном», что
означает «треугольник», и «метрейн», что означает «из-
мерять». И лишь значительно позднее границы ее рас-
ширились, и она стала наукой о тригонометрических функ-
циях и их приложениях.
Тригонометрия, как и всякая другая наука, выросла
из потребностей человеческой практики. Задачи морепла-
вания, требовавшие по звездам определять правильный
курс корабля, а также земледелия, требовавшие введе-
ния точного календаря, обусловили развитие астроно-
мии, а с ней и тригонометрии. Тригонометрия как прак-
тическая наука, по-видимому, возникла в Греции, а за-
тем дальнейшее ее развитие связано с деятельностью ин-
дийских, китайских и среднеазиатских математиков.
Так, еще во II в. до н. э. древнегреческий астроном
Гиппарх составил первые тригонометрические табли-
цы (таблицы хорд) и дал начало вычислительной триго-
нометрии. Этими таблицами много лет спустя пользова-
лись и другие астрономы, в частности, ими пользовался
в своей книге «Великое построение» (Альмагест) зна-
менитый греческий астроном Клавдий Птолемей,
(вторая половина II в. н. э.), автор докоперниковской ге-
лиоцентрической системы мира.
Успешное развитие тригонометрии в связи с задача-
ми астрономии наблюдается в Индии в период с V по
XII в. н. э. Индийские ученые впервые в науке стали упо-
треблять линию синуса как половину хорды и составили
1 М. Шаль, История математики, т. II, М., 1883, стр. 143—144.
158
первые тригонометрические таблицы синусов (полухорд).
Им были известны способы приведения синуса и коси-
нуса тупого угла к функциям острого угла, а также
основная формула тригонометрии:
sin2 а + cos2a = 1.
Интересно заметить, что слово «синус», которым мы
пользуемся теперь, индийского происхождения. История
этого слова такова. Величину полухорды (синуса) индий-
ские ученые сначала называли «архаджива», что бук-
вально означает «половина тетивы лука», а потом стали
просто называть «джива», что буквально означает «тети-
ва лука». В арабской транскрипции слово «джива» писа-
лось «джиба», что созвучно арабскому слову «джайб»,
которое дословно означает «пазуха». Слово «пазуха» и
было переведено на латинский язык словом «синус». По-
скольку латинский язык считался общепризнанным на-
учным языком в Европе, то термин «синус» нашел там
широкое распространение и сохранился до настоящего
времени.
Точно так же термин «косинус» произошел в конеч-
ном счете от индийского слова «котиджива», которым
пользовались индийские ученые для обозначения линии
косинуса.
Что касается техники составления индийскими учены-
ми первых таблиц синусов, то она очень проста и прин-
ципиально отличается от греческого способа составления
таблиц хорд.
Устройство таблиц синусов у Ариабхаты дано в 12-м
правиле его трактата «Ариабхатиана» (V в.). Таблица
эта следующая. Приводим ее с некоторым пропуском.
Дуги Синусы Разности
0 0
1 225 225
2 449 224
3 671 222
4 890 219
5 1105 215
22 3409
23 3431 22
24 3438 7
159
Чтобы понять, в чем тут дело, посмотрим, на каком
принципе она построена. Ариабхата, подобно вавилонянам
и грекам, делил окружность на 4 . 90 • 60 = 21 600 рав-
ных частей, или минут. Далее, из соотношения 2кг =
= 21 600 находил, чему равняется радиус г. Полагая, что
к = 3,1416, он с большим приближением находил, что ра-
диус:
21600 _ 21600
2к — 2 3,1416
3438 минутам.
Уместно заметить, что здесь прямолинейный отрезок
(радиус) измеряется частями кривой. Этот факт сильно
отличает индийских ученых от греческих, которые никог-
да не брали дугу для измерения прямолинейного отрезка.
Затем Ариабхата делил квадрант на 24 равные части,
в результате чего каждая такая часть у него равнялась
225 минутам, или 3°45'. После этого Ариабхата приступал
к построению самой таблицы.
Принимая sin 90° за радиус, он получал:
sin 90° = sin 24 = 3438 ',
что и стоит в последней строке вышеприведенной таблицы
синусов. Далее Ариабхата вычислял sin 30°. Действитель-
но:
sin 30е = -г = 1719', т. е. sin 8 = 1719'
2
(этот результат в таблице пропущен).
Применяя соотношение
sin245° + cos245° = г2
и имея в виду, что sin 45° = cos 45°, Бхаскара получал:
.sin 45° = |/^ = 2431
или:
sin 7 = 2431'.
Пользуясь двумя соотношениями:
sin^O0 + cosW = г2 и cos 60° = sin 30°,
получал, что:
sin 60'
— = 2978',
4
160
или, что то же:
sin 16 = 2978'.
Пользуясь найденными значениями синусов 90°, 60°,
45° и 30°, Бхаскара вычислял синусы половинных углов
по формуле:
sinvers 2а = 2sin2a,
или, что то же:
1 — sin 2а = 2sin2a.
Действительно, из sin 45° получал sin 22°30' и sin 11°15',
а из sin 30° — sin 15°, sin 7°30' и sin 3° 45'.
Затем он вычислял дополнительные к ним синусы, а
именно:
sin 67°30'; sin 78°45'; sin 75°; sin 82°30'; sin 86°15'.
Повторяя эту процедуру дальше, Ариабхата получал
синусы половин этих дуг, затем дополнительных к ним,
потом половин последних дуг и т. д.
Таким образом Ариабхата составил приведенную вы-
ше таблицу синусов всех углов, разнящихся друг от дру-
га на 3°45', выражая каждый синус равной ему по дли-
не дугой.
Поскольку таблица синусов составлена Ариабхатой
для углов, отличающихся друг от друга на 3°45z, то сину-
сы промежуточных углов приходилось находить с по-
мощью интерполяции. Для этого индийским ученым слу-
жила интерполяционная формула:
sin а — sin& = (sin b — sin с) — —’
225
при условии, что:
а— b = Ь — с = 3°45'.
Бхаскара-акария в своем трактате «Сидданта-сиро-
мани» указал еще на другой способ составления табли-
цы синусов для всех дуг через каждый градус. Отправ-
ными соотношениями у него являются два случая:
sin 1° = 60 и sin (a ± д)
sin<2 сочЬ co>a
Пользуясь этими формулами и имея в виду, что
sinl° 60 10
~~г 3438 — 573
161
cosl0 _j___1_
r “ 6569 ’
он получил основное равенство:
sin (a+l°)=(sina--^-)+^ ,
6569 7 “ 537 ’
с помощью которого и составляется нужная таблица.
Тригонометрии как обособленной от астрономии на-
уки в Индии в то время, по-видимому, еще не существо-
вало, так как таких трактатов или не было, или они не
дошли до нас. Однако для астрономических нужд индий-
ские ученые решали плоские и сферические треуголь-
ники. Что касается плоских и сферических косоугольных
треугольников, то они решались посредством разложе-
ния на прямоугольные треугольники, т. е. вопрос сводил-
ся к уже рассмотренным случаям.
Народы Средней Азии и Закавказья, входившие в так
называемый Арабский халифат и писавшие книги на
арабском языке, творчески восприняли математическую
культуру Индии, включая и исходные положения триго-
нометрии. Индийскому названию синуса «джива», как
указывалось выше, они дали арабское название «джиба»
и, пополнив арсенал тригонометрических терминов, полу-
чили ряд новых замечательных результатов.
Руководствуясь задачами практики, которые выдви-
гались астрономией, географией и геодезией, ученые
Средней Азии и Закавказья впервые стали рассматри-
вать все шесть тригонометрических линий, а именно си-
нус, косинус, тангенс, котангенс, секанс и косеканс.
В XIII в. трудами крупнейшего азербайджанского ма-
тематика и астронома Насирэддина Туси тригоно-
метрия впервые выделяется из астрономии как самостоя-
тельная наука и в таком виде излагается в его сочинении
«Трактат о полном четырехстороннике» («Шаклул-
Гита»).
Надо заметить, что, излагая тригонометрию как само-
стоятельную математическую дисциплину, Насирэддин
Туси в этом отношении почти на два века опередил немец-
кого ученого Региомонтана (1436—1476), основопо-
ложника тригонометрии в Европе.
Первые значительные работы по тригонометрии в Ев-
ропе относятся к XIV и XV вв. Так, в XIV в. английский
162
ученый Брадвардин (1290—1349) первый в Европе
ввел понятия котангенса и тангенса под названиями «пря-
мой тени» и «обратной тени». Далее, в XV в. немецкий
ученый Региомонтан (настоящее имя и фамилия
Иоганн Мюллер) в своем сочинении в пяти книгах «О
треугольниках всех видов» впервые в Европе, независимо
от астрономии, излагает тригонометрию, как самостоя-
тельную науку. В XVI в. известный французский матема-
тик Франсуа Виет (1540—1603) использовал три-
гонометрию для решения кубического уравнения. Он по-
ложил начало буквенным обозначениям в тригонометрии
и получил формулы синуса и косинуса кратных углов.
Дальнейшие успехи в области тригонометрии связаны
главным образом с трудами знаменитого петербургского
ученого Леонардо Эйлера (1707—1783). Заслуги
его в этой области трудно переоценить. Он внес ясность
в недоработанные до него вопросы и продвинул тригоно-
метрию далеко вперед. Эйлер уже рассматривал триго-
нометрию как науку о тригонометрических функциях и
придал ей современный вид.
ЗАКЛЮЧЕНИЕ
В настоящей книге рассмотрены некоторые материа-
лы по истории развития математики в Китае и Индии,
причем объектом рассмотрения был главным образом
древний период ее развития. Древняя математика этих
народов, как мы убедились, отличается самобытностью
и оригинальностью научных результатов, что подчерки-
вает и без того высокую их культуру в то время.
Математическая культура двух великих народов Ки-
тая и Индии развивалась, конечно, не изолированно друг
от друга, а во взаимодействии на основе международных
торговых, культурных и других связей. Известно, что
Китай в древние времена вывозил шелк в Индию, а Ин-
дия торговала с Китаем слоновой костью, перцем и дру-
гими пряностями.
Сухопутная торговля велась через северные проходы в
Гималаях и вдоль старых караванных путей Средней
Азии. Велась также значительная морская торговля через
острова Юго-Восточной Азии, главным образом с южно-
индийскими портами.
«В течение тысячи и более лет, — пишет Джавахарлал
Неру,— общения между Индией и Китаем обе страны
кое-чему научились друг у друга не только в области
мышления и философии, но также и в области искусств и
практических наук. Вероятно, влияние Индии на Китай
было сильнее, чем влияние Китая на Индию, что весьма
прискорбно, ибо Индия вполне могла бы с пользой для
себя позаимствовать у китайцев немного их здравого
смысла и с его помощью обуздать свои экстравагантные
фантазии. Китай много взял у Индии, но он был всегда
достаточно силен и уверен в себе, чтобы брать это по-
своему и как-то вплетать в ткань своей жизни» 1.
Именно только культурными связями этих народов
можно объяснить, почему некоторые старинные китай-
ские задачи повторяются в их дословном выражении у
’Джавахарлал Неру, Открытие Индии, ИИЛ, М., 1955,
стр. 206.
164
индийских математиков, и наоборот, замечательные до-
стижения индийцев в области математики, например де-
сятичная позиционная система счисления и истолкование
положительных и отрицательных чисел как имущества и
долга, встречаются у китайских ученых.
Необходимо заметить, что ученые Индии и Китая в
своем многогранном творчестве владели математической
теорией, основанной на дедуктивных доказательствах, но
она у них проявлялась в трактатах, если так можно вы-
разиться, в неявной форме, оставаясь в большинстве слу-
чаев секретом ученого, и о ней можно лишь только до-
гадываться по готовым результатам, сформулированным
в окончательном виде в тех или иных готовых математи-
ческих правилах.
Вычислительная математика нужна была индийцам и
китайцам для удовлетворения прежде всего и ранее все-
го потребностей хозяйственной жизни, развития астроно-
мии и календаря.
Бросается в глаза общность математической пробле-
матики Китая и Индии. Как те, так и другие много зани-
мались вопросами приближенных вычислений, задачами
неопределенного анализа, решением уравнений высших
степеней и систем алгебраических уравнений приложе-
нием алгебры к геометрии и вычислительной тригономет-
рии и т. д.
«Такая общность, — говорит А. П. Юшкевич,— яви-
лась прямым следствием сходства главных условий обще-
ственной жизни — постепенной смены рабовладельческо-
го строя строем феодальным; эта общность усиливалась
благодаря торговым, политическим и культурным связям
между восточными государствами. Возможно, что здесь
имело место и влияние традиций, восходивших еще к
древневавилонской математике» 1.
Вычислительное направление в математике, культиви-
руемое в Китае и Индии, в особенности через Индию,
оказало большое влияние в XIII в. на математику на-
родов стран Арабского халифата, живших на территории
Азербайджана, Узбекистана, Таджикистана, Ирана и не-
которых стран Востока, а через них в XIV в. и на моло-
дую европейскую математическую науку.
1 А. П. Юшкевич, О достижениях китайских ученых в об-
ласти математики. «Историко-математические исследования», вып.
VIII» ГИТТЛ, 1955, стр. 568—569.
165
Рекомендуемая литература
(на русском языке)
В. Беллюстин, Как постепенно люди дошли до настоящей
арифметики, М., 1914 и Учпедгиз, 1941 г.
Дж. Бернал, Наука в истории общества. Перев. с англ.
А. М. Вязьминой, Н. М. Макаровой, Е. Г. Панфилова. Общая редак-
ция Б. М. Кедрова, И. В. Кузнецова, изд. ИИ Л, М., 1956, стр. 735.
В. В. Бобынин, Древнеиндийская математика и отношение
к ней Греции. «Известия Казанского физико-математического обще-
ства», т. XXII, 2-я серия, 1917.
М. Е. В а щ е н к о-З ахарченко, Исторический очерк мате-
матической литературы индийцев, Киев, 1882.
М. Е. В а щ е н к о-З ахарченко, Характер развития матема-
тических наук у различных народов древнего и нового мира до
XV в., Киев, 1882.
М. Е. В а щ е н к о-З ахарченко. История математики. Исто-
рический очерк развития геометрии, Киев, 1883.
И. Я. Депман, Рассказы о математике, Детгиз, Л., 1954.
И. Я. Депман, Рассказы о решении задач, Детгиз, Л., 1957.
Е. М. Жуков (гл. редактор) и др., Всемирная история, в де-
сяти томах, т. II, Госполитиздат, М., 1956.
«Индия», опубликовано в 18-м томе второго издания Большой
Советской Энциклопедии, Государственное научное издательство
«БСЭ», стр. 32—97.
«История философии», т. I, под ред. М. А. Дынника, М. Т. Иов-
чука, Б. М. Кедрова, М. Б. Митина, С. В. Трахтенберга, изд. АН
СССР, М., 1957.
А. Н. Колмогоров, Математика. Статья в Большой Совет-
ской Энциклопедии, изд. 2-е, т. 26, стр. 468—469.
«Китай», опубликовано в 21-м томе второго издания Большой
Советской Энциклопедии, Государственное научное издательство
«БСЭ», стр. 463.
А. А. Колосов, Книга для внеклассного чтения по матема-
тике для учащихся VIII класса, Учпедгиз, М., 1958, стр. 208.
Б. А. Кордемский, Очерки о математических задачах на
смекалку, Учпедгиз, М., 1958, стр. 116.
Ф. К э д ж о р и, История элементарной математики с указания-
ми на методы преподавания. Перев. с англ., под ред., с примеча-
ниями и прибавлениями И. Ю. Тимченко, Одесса, 1910.
В. И. Лебедев, Кто изобрел алгебру, М., 1916.
Г. Лоренц, Элементы высшей математики. Перев. с дополне-
ниями, изменениями и историческими очерками развития математи-
ческого анализа В. П. Шереметевского, т. I, М., 1919, стр. 784.
166
К. А. Малыгин, Элементы историзма в преподавании матема-
тики в средней школе. Пособие для учителей, под ред. проф.
И. Я. Депмана, Учпедгиз, М., 1958, стр. 240.
В. Н. М о л о д ш и й. Очерки по вопросам обоснования матема-
тики. Пособие для учителей математики, Учпедгиз, М., 1958, стр. 230.
В. Н. Молодший, Основы учения о числе в XVIII в., Учпед*
гиз, М., 1953.
Джавахарлал Неру, Открытие Индии. Перев. с англ.,
ИИЛ, М., 1955.
Г. Н. Попов, Очерки по истории математики, М.—Л., 1925,
стр. 163.
Г. Н. Попов, Памятники математической старины в задачах,
Гиз, М.—Л., 1929.
Г. Н. Попов, Сборник исторических задач по элементарной
математике, ОНТИ, 1938, стр. 214.
М. Рой, История индийской философии. Перев. с бенгальского
М. С. Андронова, И. С. Колобкова, Г. Н. Шестопаловой и А. Ф. Иса-
енковой. Вступительная статья В. В. Бродова, редактор Ф. Н. Грец-
кий, ИИЛ, М., 1958, стр. 548.
Л. В. Симоновская, Г. Б. Эренбург, М. Ф. Юрьев,
Очерки истории Китая. Пособие для учителей, Учпедгиз, М., 1956,
стр. 424.
И. Г. Спасский, Происхождение и история русских счетов.
«Историко-математические исследования», вып. V, ГИТТЛ, М., 1952,
стр. 269—420.
И. Т р о п ф к е, История элементарной математики в системати-
ческом изложении, т. I. Перев. с немецк. Д. А. Бема и Р. Э. Струве,
под ред. И. И. Чистякова, М., 1914, стр. 146.
Г. Ф а ц ц а р и, Краткая история математики с древнейших
времен, кончая средними веками. Перев. с итальянок. С. А. Гала-
шина, изд. «Колос», М., 1923, стр. 214.
А. Филиппов, Великий счет, Одесса, 1922.
X у а Л о-к э н, Современное положение математики в Китае,
«Вестник Академии наук СССР», 1953, № 6, стр. 14—20.
Г. Г. Ц е й т е н, История математики в древности и в средние
века, изд. 4, подготовленное А. П. Юшкевичем, ГОНТИ, 1938,
стр. 231.
В. Д. Чистяков, Математические вечера в средней школе,
Учпедгиз, М., 1958.
М. Шаль, Исторический обзор происхождения и развития гео-
метрических методов, т. I. История математики, стр. 307, т. II. При-
мечания, стр. 428.
Ф. И. Щ е р б а т с к и й. Научные достижения древней Индии.
Отчет о деятельности Российской Академии наук за 1923 г., Л., 1924.
А. П. Юшкевич, Достижения китайских ученых в области
математики. «Историко-математические исследования», вып VIII,
ГИТТЛ, 1955, стр. 539—572.
А. П. Юшкевич, О новых работах в СССР по истории мате-
матики. «Историко-математические исследования», вып. XI, Гос. изд.
физико-математической литературы, М., 1958, стр. 11_62.
Я н Ю н-г о, История древнекитайской идеологии Перев. с ки-
тайск. Ф. С. Быкова, Д. Л. Веселовского, Т. Е. Мытарова. Ппедисло-
вие к книге Ян Юн-го, ИИЛ, М„ 1957.
ОГЛАВЛЕНИЕ
Часть первая
Краткая история математики в Китае
Глава I. Китай—страна многовековой самобытной куль-
туры ............................................. . б
Глава II. Развитие арифметики и алгебры в древнем Ки-
тае 13
Глава III. О древнекитайских алгебраических правилах . 38
Глава IV. Развитие геометрии и тригонометрии в древнем
Китае.................................... 55
Глава V. О древнекитайских геометрических правилах 61
Глава VI. Отдельные замечания .......... 85
Часть вторая
Краткая история математики в Индии
Глава VII. Индия — страна многовековой самобытной куль-
туры ................................................ 91
Глава VIII. Развитие арифметики и алгебры в Индии . . 94
Глава IX. Развитие геометрии и тригонометрии в Индии 138
Заключение..................................... 164
МАТЕРИАЛЫ ПО ИСТОРИИ МАТЕМАТИКИ В КИТАЕ И ИНДИИ
Редактов ЧД. И.у Сидорова
Обложка худо^шкъ/ Н. Н. Румянцева
Рисунки художник^О. М. Шухвостова
Художественный редактор И Л Волкова
Техн, редактор В. И. Корнеева
Корректор Р. Б. Берман
Сдано в набор 10/XI 1959 г. Подписано к печати 29/1II 1960 г.
84Х1087з2. Печ. л. 10.5 (8,61). Уч.-изд. л. 7.36. Тираж 10 тыс. экз. А03430.
Заказ № 999
Учпедгиз. Москва. 3-й проезд Марьиной рощи, 41.
Полиграфкомбинат Саратовского совнархоза,
г. Саратов, ул. Чернышевского. 59.
Цена без переплета 2 руб., переплет 80 коп.
Цепа 2 р. КО h