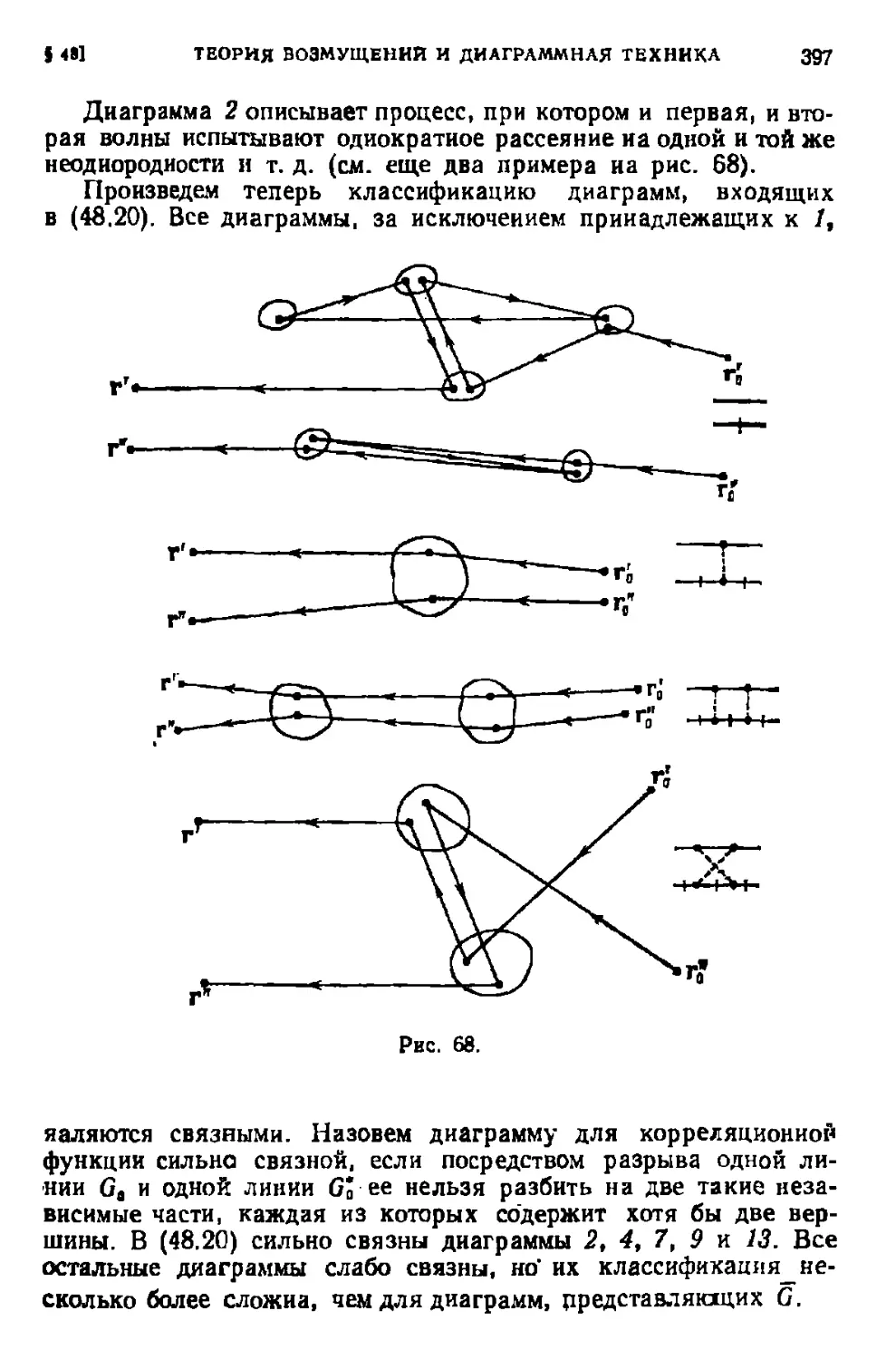
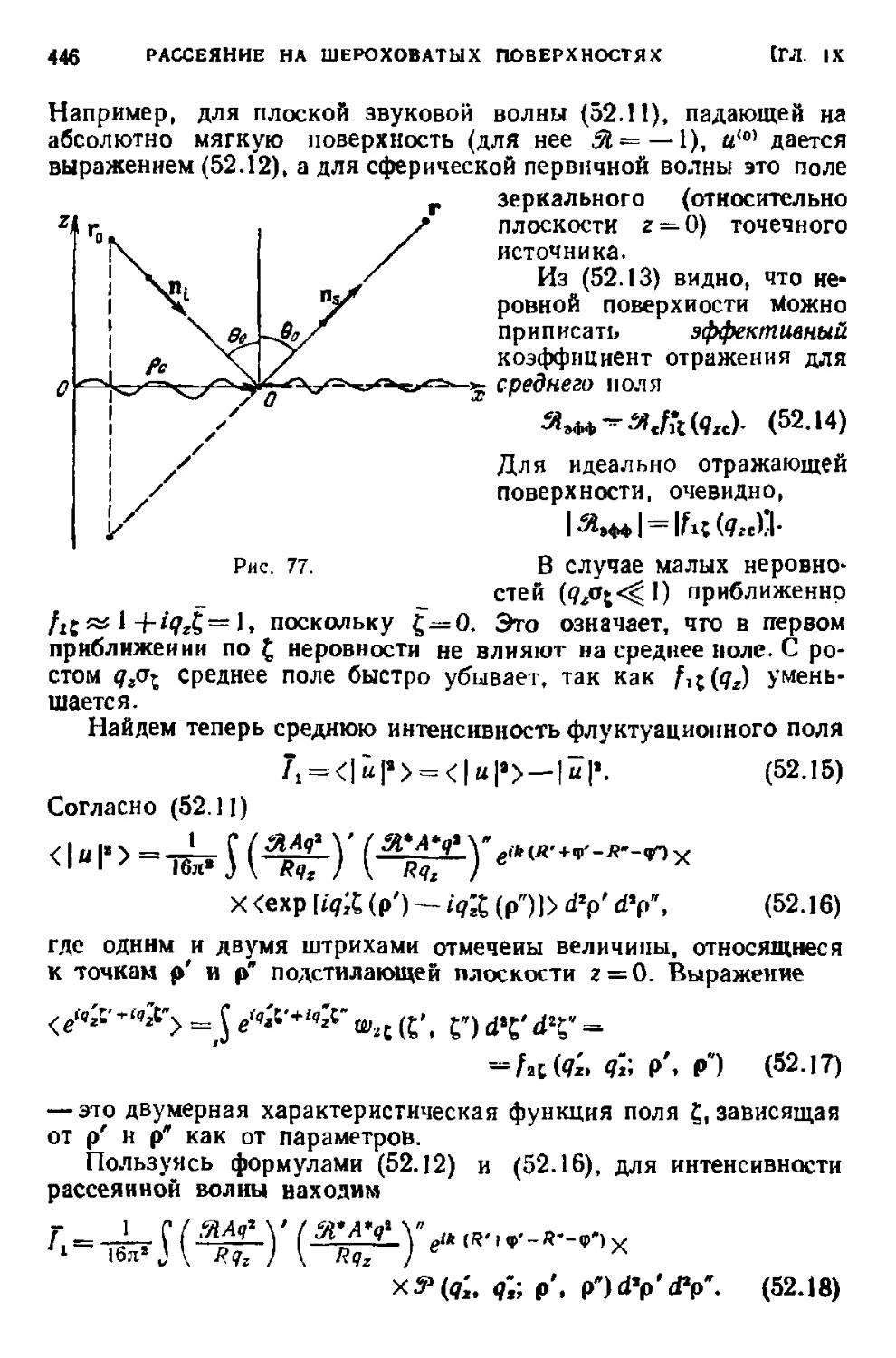
Текст
Введение
в статистическую
радиофизику
ЧАСТЬ II
С. М. РЫТОВ, Ю. А. КРАВЦОВ, В. И. ТАТАРСКИЙ
СЛУЧАЙНЫЕ ПОЛЯ
ИЗДАНИЕ ВТОРОЕ. ПЕРЕРАБОТАННОЕ
И ДОПОЛНЕННОЕ,
под общей редакцией С. М. РЫТОВА
Допущено Министерством высшего и среднего
специального образования СССР
в качестве учебного пособия для студентов
физических специальностей высших учебных заведений
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1978
32.841
P 05
УДК 538.3
20407—179
100-79
Наука
Главная редакция
физико-математической
1978
ОГЛАВЛЕНИЕ
От редактора б
Глава I
Общие сведения о случайных полях
S 1. Основные понятия 7
§ 2. Пространственные корреляционные функции комплексных слу
чайных полей • 10
§ 3. Пространственные спектральные разложения для однородных
случайных полей 16
§ 4. Локально однородные случайные поля 21
§ 5. Квазиоднородные поля 26
§ 6. Пространственно-временные спектральные разложения случайных
полей 27
§ 7. Функциональный метод описания случайных полей 33
Задачи 44
Глава 11
Излучение и дифракция случайных волновых полей
§ 8. Основные типы статистических волновых задач 58
§ 9. Случайные волны в неограниченной однородной среде 62
§ 10. Дифракция плоской волны на безграничном хаотическом экране 71
| 11. Дифракция случайных полей в простейших оптических системах 87
5 12. Возбуждение полей случайными источниками 102
Задачи ИЗ
Глава III
Тепловое электромагнитное иоле
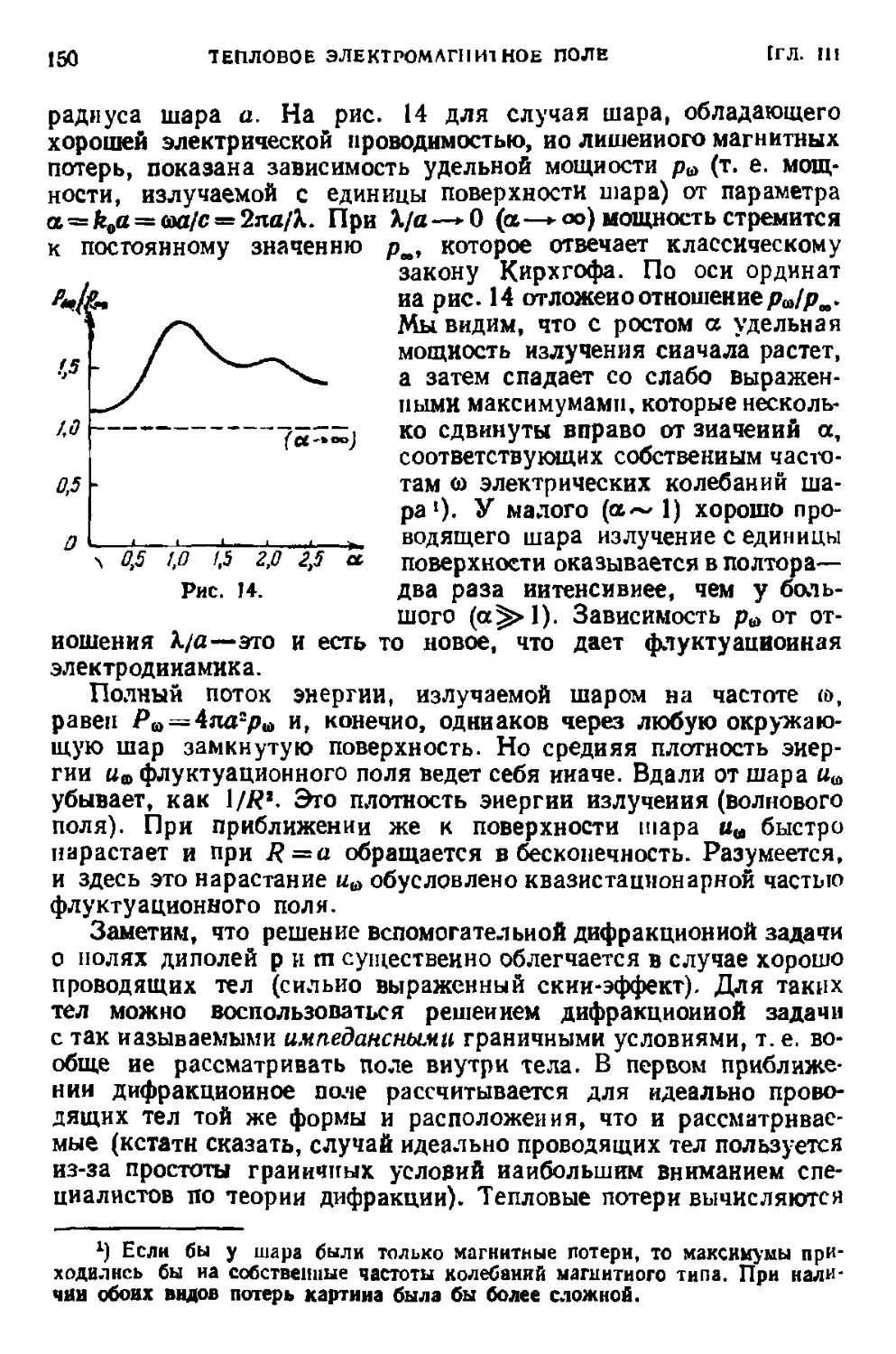
§ 13. Предварительные замечании 123
| 14. Стохастические уравнения Максвелла 127
§ 15. Равновесные тепловые флуктуации в непрерывных диссипативных
системах -. 130
§ 16. Корреляция сторонних тепловых источников в электродинамике 13S
§ 17. Обобщенный закон Кирхгофа 139
§ 18. Примеры применений обобщенного закона Кирхгофа 145
J 19. Волноводная форма закона Кирхгофа 153
| 20. Тепловое излучение н антенны 158
§ 21. Равновесное тепловое поле. Равновесная форма ФДТ 164
1*
4 ОГЛАВЛЕНИЕ
§ 22. Тепловое поле в гиротролньис телах 16?
§ 23. Тепловое поле в среде с пространственной дисперсией 172
Задачи 18S
Глава IV
Теория однократного рассеяния волн
§ 24. Метод малых возмущений iQi
§ 25. Средняя интенсивность рассеянного поля 197
§ 26. Эффективный поперечник рассеяния. Границы применимости при-
ближения однократного рассеяния 208
§ 27. Пространственная корреляция н вероятностные распределения
рассеянного поля 215
§ 28. Рассеяние на нестационарных неоднородностях 220
§ 29. Рассеяние импульсных и модулированных сигналов 229
§ 30. Рассеяние электромагнитных волн 233
§ 31. Рассеяние на дискретных вкраплениях 241
Задачи 251
Глава V
Распространение волн в средах с крупномасштабными
случайными иеоднородностями.
Метод геометрической оптики
§ 32. Уравнения геометрической оптики 256
§ 33. Флуктуации эйконала 261
§ 34. Флуктуации углов прихода, боковых смещений луча и группового
запаздывания волны 271
§ 35. Флуктуации уровня 279
§ 36. Флуктуации параметров волн в турбулентной тропосфере .... 286
§ 37. Среднее поле н функция когерентности 290
Задачи 292
Глава VI
Метод плавных возмущений
§ 38. Обоснование параболического урввнения 297
§ 39. Закон сохранения энергии в приближении параболического урав-
нения 306
§ 40. Метод плавных возмущений 308
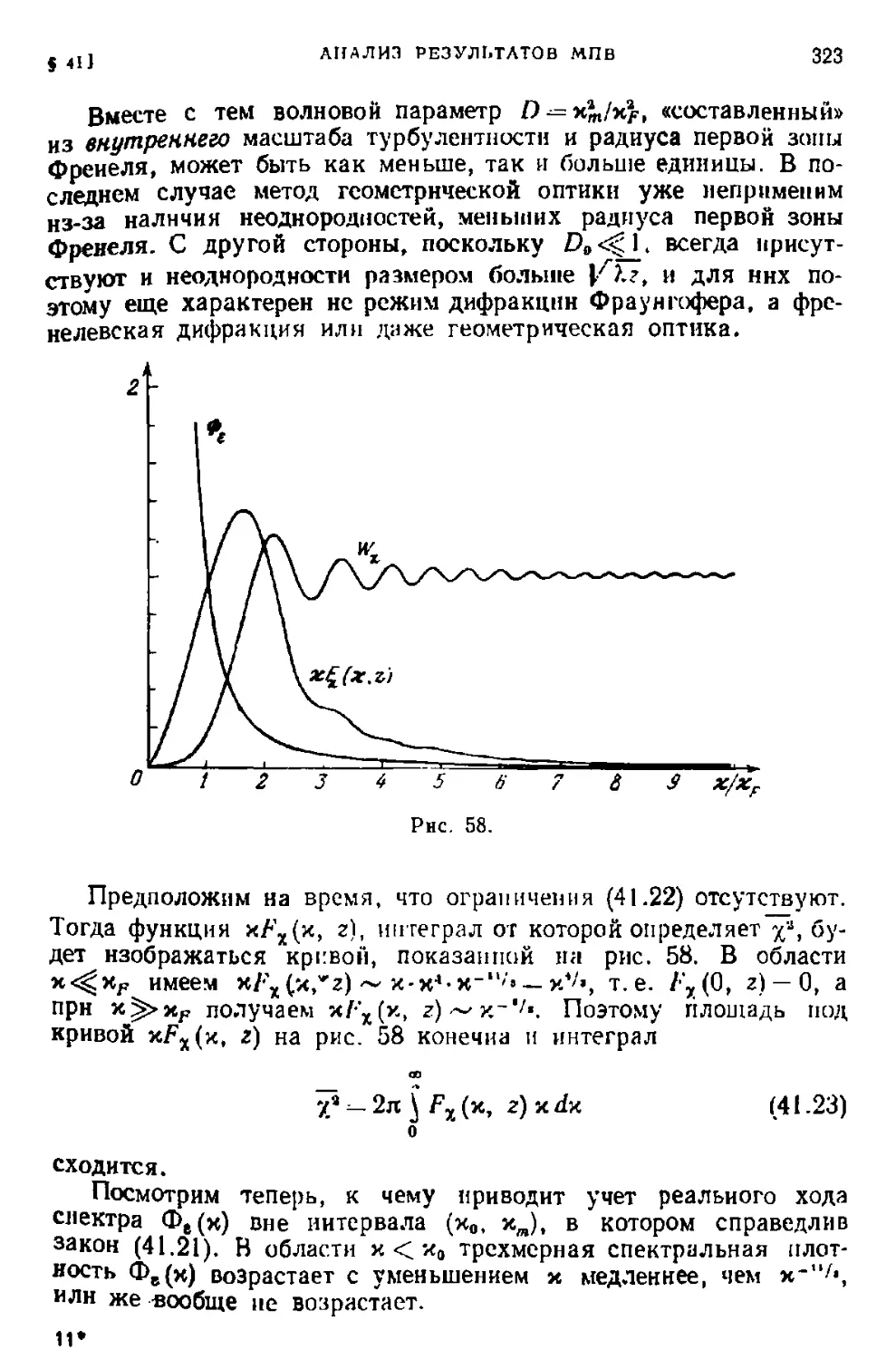
§ 41. Анализ результатов МПВ 316
§ 42. Распределение вероятностей флуктуации амплитуды и фазы. За-
кон сохранения энергии н границы применимости МПВ 330
Задачи 336
Глава VII
Приближение марковского процесса
в задаче о распространения волн
в среде со случайными неодиородностямн
§ 43. Обоснование марковского приближении 342
§ 44. Уравнения для статистических моментов волнового поля в при-
ближении марковского случайного процесс» 349
ОГЛАВЛЕНИЕ 5
§ 45. Среднее поле и функция когерентности второго порядка .... 355
§ 46. Функция когерентности четвертого порядка н флуктуации интен-
сивности 364
§ 47. Учет конечности продольного радиуса корреляции флуктуации е
и границы применимости марковского прнближепия 372
Задачи 379
Глава VIII
Элементы общей теории многократного рассеяния воли
§ 48. Теория вовмущеннй и диа|раммная техника для среднего поля
и функции корреляции 385
§ 49. Среднее поле точечного источника в неограниченной случайно-не-
одпоиодной среде 401
§ 50. Функция когерентности поля. Оптическая теорема и уравнение
переноса излучения 413
Задачи 426
Глава IX
Рассеяние иа шероховатых поверхностях
§ 51. Рассеяние на малых неровностях. Метод возмущений ,-„._. . . . 429
§ 52. Рассеяние иа крупномасштабных неровностях. Метод Кирхгофа 442
§ 53. Дополнительные замечания. Другие подходы 451
Задачи 455
Литература 456
ОТ РЕДАКТОРА
Вторая часть книги, посвященная теории случайных полей,
построена в соответствии с тем же принципом, чго и первая
(случайные процессы): математическая теория излагается в тес-
ной связи с приложениями к физическим задачам, выбор кото-
рых ограничен вопросами, имеющими самостоятельное значение
и интерес. Вместе с тем эти вопросы позволяют довольно широ-
ко осветить различные методы теории случайных полей, главным
образом корреляционной теории.
Выбраны две физические проблемы — излучение и распростра-
нение скалярных и векторных воли в случайно-неоднородных
средах и равновесные поля теплового происхождения.
Первой проблеме уделено наибольшее место. Рассмотрено рас-
сеяние волн преимущественно на флуктуациях непрерывной не-
однородной среды, но затронуты также случаи и дискретных рас-
сеивателей (вкраплений), и случайно-неровных границ раздела
(шероховатых поверхностей).
В вопросах, касающихся тепловых полей, упор сделан на
обобщение и различные формы флуктуационно-диссипационной
теоремы применительно к распределенным системам, сплошным
средам и телам.
Каждая глава сопровождается задачами, предназначенными,
как и в ч. I, для упражнений и для дополнительных сведений по
теории.
Главы I (кроме § 7), II, IV, V и IX написаны Ю. А. Крав-
цовым, глава III—СМ. Рытовым, §7 главы I н г лавы VI — VIII —
В. И. Татарским.
С. М. Рытое
Глава I
ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ
§ 1. Основные понятия
В части I этой книги мы, почти без исключений, имели
дело с однопараметрическими случайными функциями s(a),
причем в";большинстве приложений параметра являлся *квре-
менем I. Если же речь идет о случайной функции более чем
одного параметра, ? (а, р, ...), то ее называют обычно случай-
ным полем (в пространстве параметров а, C, ...), Мы сразу же
ограничимся случаем, когда параметров всего четыре: время
t и точка пространства т = (х, у, г). Можно, конечно, назы-
вать ? d г) полем В четырехмерном пространстве, но в нереля-
тивистских задачах привычнее и нагляднее говорить о перемен-
ном (зависящем от t) поле в трехмерном пространство (х, у, г).
В свою очередь случайное поле может описываться не одной,
а N функциями Ъ'п (t, г), t"=I,2 N, и называется тогда
//-мерным случайным полем, подобно Л^-мерной случайной функ-
ции |1" (t), f = 1, 2, ..., N. С чисто математической точки ярения
компоненты ?l" (t, г) Смогут быть чем угодно и даже не обяза-
ны обладать одинаковой размерностью. Например, флуктуации
плотности жидкости р, давления р, температуры Т п скорости v
образуют в совокупности шестимерное случайное поле. Но осо-
бый физический интерес представляют, конечно, те случаи, ког-
да величины ?(" (t, г) одноразмерны и обладают определенными
трансформационными свойствами при ортогональных преобразо-
ваниях координат в пространстве х, у, г, т. е. являются сово-
купностью компонент тензора какого-либо ранга. При таком под-
ходе целесообразнее говорить в приведенном примере о четырех
полях — трех скалярных (р, р и Т) и одном векторном (v).
Ряд определений и свойств, введенных и' установленных'ра-
нее в ч, I для случайггьгх функций одного параметра, естествен-
ным образом обобщается и на случайные поля, зависящие
8 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ 1ГЛ. 1
от многих параметров, в частности, на пространственно-времен-
ные случайные поля, зависящие от х, у, г, t. Эти (зачастую до-
вольно очевидные) обобщения касаются и вопроса о том, что
означает полное задание случайного поля.
Обозначим для краткости через Q = (t, г) точку в четырех-
мерном мире. Полное задание одномерного случайного поля ? (Q)
означает, что известны все его n-мерные, или, как иногда гово-
рят, л-точечкые (п —1,2, ...), плотности вероятностей, т. е.
для любого числа п произвольно выбранных точек Qv известны
функции
и*{Ei, ¦¦-. U«i ••• <*L =
= P{Sv<5@v)<?v+4v (V = l,2 л)}, A.1)
где Р {?<;i (Q) < i + dg} — вероятность того, что случайная ве-
личина | (Q) приняла значение, лежащее в интервале A,% + dJI).
Аналогично, полное, статистическое задание (описание) ЛГ-мерно-
го поля |(г> (Q) дается совокупностью «Химерных плотностей веро-
ятностей
{u + ^v). v-1,2 п, i = l, 2 N}.
A.2)
Эти плотности вероятностей, разумеется, должны быть подчине-
ны условиям неотрицательности, симметрии, согласованности и
нормировки (ч. I, § 14).
Очевидным образом распространяется на случайные поля и
понятие статистической однородности. Одномерное случайное по-
ле 5 называется однородным (в узком смысле), т.е. стационарнымг)
по ( и однородным по х, у, z, если все /(-мерные плотности ве-
роятности а>„ инвариантны относительно преобразования транс-
ляции Q—*Q I-8Q:
Ъ I-«v. v=1,2,...,«}-
<?(<?v)<?v + ^v, v^l,2,...,n}. A.3)
Если речь идет о Л'-мерном случайном поле |';' и указан-
ной инвариантностью относительно сдвига 6Q обладают все
«jV-мерные плотности вероятностей wnN, то говорят об однород-
ных и однородно связанных (в (Э-пространстве) полях J"'1 (I— 1,2,...
..., N).
Понятие пространственной однородности для случайных по-
лей (инвариантность плотностей wa no отношению к простран-
х) Полное описание случайного ноля достигается также при помощи харак-
теристических функционалов, о которых пойдет речь в §7.
2) Однородность по времени принято называть стационарностью.
§ll ОСНОВНЫЕ ПОНЯТИЯ
9
ствениому сдвигу г—>г + бг) является естественным обобщением
понятия стационарности для случайных функций времени
(ч. I, § 16). Но многомерность пространства параметров х, у, г, t
открывает новые возможности, а именно: поле может быть по
части параметров однородным, а по остальным — неоднородным.
Например, наряду с полями, однородными в Q-пространстве,
иногда приходится иметь дело со стационарными, но простран-
ственно, неоднородными полями или же однородными, но нестацио-
нарными полями. В волновых задачах часто встречаются поля,
однородные только на определенных поверхностях, скажем на
плоскости или на сфере.
Зная многомерные плотности вероятностей, можно вычислить
моменты случайного поля ? любого порядка. В общем случае
эти моменты будут функциями координат: Qv={tv, rv). Во мно-
гих вопросах наибольший интерес представляют наиниэшие мо-
менты (первого и второго порядка), с которыми оперирует кор-
реляционная теория случайных полей. Основные понятия этой тео-
рии те же, что и в корреляционной теории случайных функций.
Среднее значение случайного поля g (Q) (момент первого по-
рядка) вычисляется при помощи одномерной плотности вероят-
ностей да^!)'):
<?«?)> = $?*,«)<«. A.4)
Флуктуациониую часть случайного поля |, т. е. величину |—<|>,
мы по-прежнему будем обозначать волнистой чертой сверху:
1^?-<?> = |-1- A-5)
Смешанный момент второго порядка В| вычисляется при по-
мощи двумерной плотности вероятностей a>,(?j, ?,):
. Я8(<г„ Q1)-<1(Q1)E(Q,)>=SSEiE,»,Ei, Wd-l^u. A.6)
Через нее же выражается и функция корреляции (точнее, функция
автокорреляции):
QJ-<?(<?,)><? «?,)>• A.7)
Для случайных полей с нулевым средним значением функции
Bi(Q1, QJ = <i(Q,)i(Q2)> и ts(Qi, Q.) совпадают. Дисперсия
') Операция статистического усреднения обозначена здесь посредством
угловых скобок, но иногда, если это будет удобнее, мы будем пользоваться,
как н в ч, 1, прямой чертой сверху, так что <|> =з |.
10 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ (ГЛ. I
случайного поля ?>[?], т. е. средний квадрат флуктуации, равна
z>[E] = oi(Q)-<S'(Q)> = <[E(Q)-<6(<2)>]'>==1>e(<?, <?)• О-в)
51, Многомерное поле ?"' (Q) в рамках корреляционной теории
характеризуется совокупностью средних значений <?"' ((?)> и
матрицей моментов второго порядка с элементами
A.9)
или, что равносильно, — корреляционной матрицей с элементами
lf B)>. (МО)
Для краткости аргументы d и Qs здесь заменены просто своими
номерами 1 и 2. Диагональные элементы корреляционной мат-
рицы представляют собой функции автокорреляции ^A,2), а
недиагональные—функции взаимной корреляции -ф/ь A,2) полей
|(Л и ?(*>
Наряду с вещественными случайными нолями 1(Q), о кото-
рых шла речь выше, часто приходится рассматривать также комп-
лексные поля
где | = Ке?иг|=1т ?—вещественные функции в Q-пространстве.
Полное статистическое описание комплексного случайного поля
?(<?) осуществляется заданием 2гс-мериых плотностей вероятно-
стей Н1„ EХ, ..., 6„; т)а т|„) (п = 1,2, ...), через которые
выражаются вероятности
(ц, v=l,2. ...,»»
аналогично A.1). Через а)гп можно выразить любые моменты
комплексного случайного поля ? и, в частности, его низшие мо-
меиты. Последние представляют для рассматриваемых далее за-
дач наибольший интерес, так что мы лишь изредка будем вы-
ходить за пределы корреляционной теории случайных полей.
§ 2. Пространственные корреляционные [функции
комплексных случайных полей
Рассмотрим сначала случайные поля, зависящие только от
пространственных координат, т. е. не зависящие от времени.
К полям, зависящим также от времени, мы обратимся в § 6.
Итак, пусть одномерное комплексное случайное поле зависит
только от г:
«2] ПРОСТРАНСТВЕННЫЕ КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ Ц
По определению корреляционная (автокорреляционная) функция
комплексного поля ? равна
<C(r1)><E'(r,)>. B.1)
Положив здесь rj = г2 = г, получкм дисперсию в точке г:
I ^(r, г). B.2)
Многие свойства пространственной корреляционной функции
¦*Mri> га) имеют аналоги в теории случайных процессов (ч. I,
§§ 14, 17, 18 и 38). Перечислим кратко эти свойства.
Корреляционная функция ^(г^ г2) является эрмитовой:
%(<-!, г2) = ^(г2, г,), B.3)
как это непосредственно следует из определения B.1). В част-
ном случае вещественного случайного поля (? = ?*) корреляци-
онная функция симметрична:
%(i-i, r,) = i|>t(ra) rx). B.4)
Далее, квадрат модуля ^(г,, г2) никогда не превышает про-
изведения дисперсий оК^) и сг| (г2):
, г,). B.5)
Из B.5) вытекает, в частности, что коэффициент корреляции
(иначе—нормированная корреляционная функция), определяемый
как
К-(г 1-)--= фг<г''г'> — 4>t(rj. га)
^2, r.) ' [1-Ь>
ие превышает но модулю единицы:
Mfftfo.rJKl. B.7)
Из неотрицательности величины (| J |(r)u(r)dv 2) следует,
что корреляционная функция ^(г^ га) является положительно
определенной, т. е.
J J фЕ (rt, г.) и (г,) и» (г,) dV% > °. <2.8)
v
где u(r)—произвольная комплексная функция, aV—произволь-
ная область интегрирования, для которых интеграл B.8) суще-
ствует.
12 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ [ГЛ. I
Взаимной корреляционной функцией двух комплексных полей
(л (г) и v(r) называется величина
W"*!. г2)=<Й(г1)>(г2)>. B.9)
Квадрат модуля \J,>v не превышает произведения дисперсий oj,
и oV.
IIVvfr.-rJI'^aJMoSd-,), B.10)
что аналогично B.5). Как следствие этого, взаимный коэффициент
корреляции
^у(Г1.г,)-О11(Г1)Оу(Г1, B.11)
по модулю не превышает единицы: | Kuv ] ^ 1. Существенно, что,
в отличие от автокорреляционных функций, взаимная функция
корреляции xlVv не обладает ни свойством эрмитовости B.3), ни
положительной определенностью B.8), но при этом ^^г,, г2) —
= ЧЧи(г„га).
Наряду с iff (rt, га) иногда полезно ввести еще одну автокор-
реляционную функцию комплексного поля:
Ч>;(, г,) = 4 W ?(г,)>, B.12)
которая ранее (ч. I, § 38) была названа второй корреляционной
функцией. В отличие от ijij (i^, г2), т. е. от первой функции кор-
реляции, определенной выражением B.1), значение случайного
поля ?(г2) входит в B.12) без комплексного сопряжения. Вторая
корреляционная функция симметрична относительно своих ар-
гументов, ^е(г2, r1) = ^j(r1, rs), а для вещественного поля ? она
совпадает, очевидно, с ^(iv r2).
Черед первую и вторую функции корреляции i))j (r^ rs) и
Фе(г1> ги) можно выразить автокорреляционные функции веще-
ственной и мнимой частей комплексного поля ? = |-i щ:
а также их взаимную функцию корреляции:
'fei fa. г,) = <1 (гг) т) (г,)> = 4'п5 (г„ г,).
Заметим, что симметрии относительно аргументов rt и г3 у функ-
ции <pin, вообще говоря, нет. Используя очевидные соотношения
%0V г,) = 1|>|(rlf r2) + ^(rIr г,) —/^(r,, r,)-f «
1, г2)— трп(г,, г,)+»Фел(г1.
§2] ПРОСТРАНСТВЕННЫЕ КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ 13
получаем следующие выражения для компонент корреляционной
матрицы вещественных полей ? (г) и ц (г):
0\, га) - V, Re \% (гг, г,) + |s (Г1, г2)],
Г1, га)],
ft (г,, га) - г|)с (iv г„)], ( ' ;
^ „ r2)].
От аналогичных формул C8.3) в ч. I формулы B.14) отличаются
только тем, что вместо моментов времени t и f в них фигури-
руют радиусы-векторы ri и г2.
В случае статистически однородного (в широком смысле)
случайного поля ? инвариантность относительно сдвига г—>-г + 6г
должна выполняться только для среднего значения и для мо-
ментов второго порядка. Иными словами, должно быть
<?(г)> = <? (г+ 6г)>, B.15)
¦Фс («-1 •«¦») = *Е («"! + Sr, r2 -4- 6г). B.16)
Условие B.15) означает, что <J> = const, т. е. среднее зна-
чение является постоянной величиной. Положив в B.16) 6г = — г2,
находим, что ^(r,, r^^i^fa — гг> 0), т. е. корреляционная функ-
ция i|:j статистически однородного поля зависит только ог раз-
ности i\—г2, но не от г, и г2 порознь. Для краткости вместо
1|>е(г,—г2, 0) принято писать просто il'f(r):
^(г)=<Ё(г1)Г(г1-г)>. ч B.17)
Подобным же образом (только без комплексного сопряжения)
записывается и вторая корреляционная функция т^(г).
Дисперсия статистически однородного поля постоянна:
tr|= < 15(г) 1г> = 4>с (°)» B.18)
а общие свойства B.3), B.5) и B.8) корреляционной функции
для статистически однородных полей принимают следующую
форму, аналогичную соотношениям для стационарных случайных
процессов:
B-19)
B-20)
J dV, ] *г,фс(r.-rj а (г,) и« (г2)> 0. B.21)
V V
Согласно B.19)
Im г|5Е (— г) = — Im фс (г).
]4 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ [ГЛ. I
т. е. вещественная часть ipj четна по г, а мнимая — нечетна.
Четность функции i|)j (r) автоматически влечет за собой ее ве-
щественность.
Вторая корреляционная функция, симметричная по своим
аргументам, для однородных полей становится четной: ij)j(—г) =
= ф;(г). Для частного случая, когда четна не только вторая,
ио и первая корреляционная функция, выражения B.14) при-
нимают вид
(г) + Re фс (г)] 1|) (г) = V [tk (r) Re ^ (r)J
Из этих соотношений следует, что вещественная' и мнимая части
| и г| комплексного статистически однородного поля J = |-fir|
тоже статистически однородны и, кроме того, однородно связаны.
Статистически однородные поля, у которых 1|>е(г) и ift(r)
зависят только от модуля (но не от направления) вектора г =
= Г! — га, соединяющего точки rt и г2,
B.23)
i|>i (г) = V, |Ч>5 (г) + Re фс (г)], 1|)„ (г) = V, [tk (r) - Re ^ (r)J,
где г = | г | = V^xa + У1 + г!1> называются статистически изотроп-
ными. Полноправного аналога изотропных полей в теории слу-
чайных процессов указать нельзя. Ограниченную аналогкю можно
провести лишь со стационарными вещественными процессами, для
которых функция корреляции четна: if (т) = гр(|т|).
Для изотропных случайных полей корреляционная функция
всегда четна и, следовательно, всегда вещественна. Из B.22)
следует, что если поле ? изотропно, то поля i = ReJnr] = ImJ
изотропны и изотропно связаны между собой.
Примерами корреляционной функции однородного и кзотроп-
ного случайного поля ? могут служить корреляционная функция
в виде гауссовой кривой
Tpt(r)=a\e-w B.24)
и экспоненциальная функция корреляции
ifE(r) = o|e-'-/'. B.25)
В обоих примерах / — радиус корреляции поля, т. е. расстояние
r = |rj — г, |, на котором ^(г) уменьшается примерно вдвое «о
сравнению с дисперсией а\. Для полей с функцией корреляции
произвольного вида эффективный (или интегральный) радиус
корреляции обычно определяется как
'.фф=-т| *:(')*• = j\Kt(r)dr. B.26)
* О П
S2] ПРОСТРАНСТВЕННЫЕ КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ J5
У гауссовой функции корреляции B.24) 1,^=вУ1/1п1, а у эк-
споненциальной функции B.25) /,фф = /.
Иногда встречаются корреляционные функции, имеющие оп-
ределенный масштаб изменения, но для которых эффективного
радиуса корреляции не существует из-за расходимости интеграла
в B.26). Так обстоит дело, например, для функции корреляции
вида
*С (Г)
Хотя понятие радиуса корреляции (как и времени корреля-
ции для случайных процессов) часто оказывается полезным,
универсальное его определение, пригодное для флуктуации про-
извольного вида, дать нельзя. Корреляционные функции часто
обладают не одним, а несколькими характерными масштабами,
как, например, быстро осциллирующая корреляционная функция
с плавно меняющейся огибающей, или же корреляционные функ-
ции анизотропных полей, к которым мы и перейдем.
У статистически однородных, но анизотропных полей функции
корреляции зависят не только от модуля, но и от направления
вектора г = г1—г,, как, скажем, в следующих двух примерах:
B.27)
B.28)
Анизотропные поля, очевидно, не имеют аналога в теории
случайных процессов. Расстояния, иа которых значения анизо-
тропного случайного поля становятси иекоррелнроваинымк, раз-
личны по разным направлениям. Так, для анизотропной гауссовой
корреляционной функции
[?(? ? ?)] B.29)
которая является частным случаем функций вида B.28), вели-
чины а, Ь и с характеризуют масштабы пространственной кор-
реляции в направлениях х, у я г. Масштаб / для функций вида
B.27) характеризует радиус корреляции в направлении, перпен-
дикулярном плоскости ах+ $у+-уг = 0, тогда как в самой этой
плоскости (и в параллельных ей) корреляция простирается до
бесконечности.
Иногда вместо статистической анизотропии говорят об аниэо-
мерии случайных полей. Термин «анизомериыё флуктуации»
удобен в некоторых задачах электродинамики и теории упругости,
в которых речь идет о статистически анизотропных флуктуациях
параметров в анизотропных же средах, но пользоваться им нам
почти не придется.
16 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ (ГЛ. I
Наряду с моментами первого и второго порядков, можно
ввести и высшие моменты комплексного случайного поля ?. При-
нято определять (т +поточечный момент В„^ „ (момент (/n-f п)-го
порядка) следующим образом:
Вя,„<1,2 m+») = <S(l)...?(m)C*(/n+l)...?•(»»+«)>. B.30)
Поле ? входит под знак усреднения т раз, а комплексно со-
пряженное поле ?*—п раз. Для краткости вместо координат г,
здесь снова написаны только номера точек /, например, t,(m)
вместо ?(гя) и т. д. Моменты второго порядка В и В запишутся
в этих обозначениях следующим образом:
ВA,2) = Ви1A,2), ?A,2) =/?,,„ A,2). B.31)
Некоторые простые свойства моментов ВЯ]Я вытекают непо-
средственно из определения. Так, очевидно, что В„<п(\, ...,п;
п, ..., 1)^0. При перестановках внутри первой A, ...,т) и
второй (от + 1, ..., т + п) групп аргументов момент Вт,п не ме-
няется, а комплексное сопряжение приводит к следующим изме-
нениям в порядке следования аргументов и индексов:
[Bm,n(U ...,т+п)]* = Вп,я(/п + п> .... 1). B.32)
Эрмиговость В и симметрия В представляют собой частные
случаи этого тождества.
§ 3, Пространственные спектральные разложения
для однородных случайных полей
Запишем формальное разложение флуктуационной компоненты
одиородкого случайного поля g (г) в трехкратный интеграл Фурье:
S<r)= l Ше""с1*к. C.1)
-ао
Здесь ?(к)—пространственная спектральная амплитуда (или,
короче k-амплитуда) поля ?, которая выражается через" ? (г) при
помощи обратного преобразования Фурье:
«о
= B5)T J Ur)e-'"d>& C.2)
— CD
Иногда вместо ? (к) используется более краткое обозначение ?к.
Спектральное разложение C.1) мы назвали формальным по-
тому, что для неубывающей на бесконечности функции, какой
является однородное случайное поле 1(г), трансформанты Фурье
5 3] ПРОСТРАНСТВЕННЫЕ СПЕКТРАЛЬНЫЕ РАЗЛОЖЕНИЯ 17
? (к) не существует. Для того чтобы придать спектральным раз-
ложениям таких случайных полей обычный математический смысл,
следовало бы предположить, что поле однородно в большой, но
конечной области V, вне которой оно достаточно быстро убывает
до нуля, и переходить к бесконечным размерам области V лишь
иа последнем этапе расчетов, уже после статистического усред-
нения. Мы не будем, однако, пользоваться здесь такого рода
приемами (как мы не делали этого в аналогичной ситуации и
для спектральных разложений стационарных случайных процес-
сов), а будем считать, что интегралы C.!) и C.2) существуют
в смысле вероятностной сходимости, а именно — в среднем квад-
ратичном (ч. I, § 40).
Согласно C.1) функция корреляции однородного случайного
поля i|.'E (ri — ги) Равиа
GO
ti ОЧ-г,,) = $ $ <? (к') ?' (к")> eW.-if.) d'k' d'k". C.3)
Спектральные амплитуды ? (к') н ?* (к") оказываются дельта-
коррелированными по к. В самом деле, в силу C.2)
Введем здесь новые переменные интегрирования г = г, — г2,
R = (г, + га)/2, для которых d3r1d3r2 = d3rd3R. Учитывая, что
после интегрирования по R получаем
<?(к');*(к")> = Фс(к')в(к'-к"), C.4)
где
фе(к) = B^5 J *t(Oe-'kr#r. C.5)
Подставляя же C.4) в C.3), находим
^ C.6)
Функция Ф;(к) называется пространственной спектральной
плотностью (^.-плотностью) или, короче, пространственным
1 спектром случайного однородного поля ?(г) и аналогична спек-
тральной плотности (ш-плотности) g(m) в теории стационарных
случайных процессов. Соотношение C.5) представляет собой обоб-
щение теоремы Хинчина (ч. I, § 41) на случайные поля. Заме-
тим, что наряду с трехмерными спектральными разложениями
18 ОЁЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ trfl. 1
иногда удобно использовать также одномерные и двумерные
спектральные разложения (см. задачи 2—4 в конце главы). Не-
трудно убедиться, что пространственный спектр Ф;(к) является
вещественной и неотрицательной величиной. Вещественность
Ф^(к) вытекает из B.19), а неотрицательность—из положитель-
ной определенности корреляционной функции.
В отличие от Фс(к) взаимный пространственный спектр
отвечающий взаимной корреляционной функции. %iV (г) ДОУХ ком-
плексных полей ц (г) и г1 (г), в общем случае является комплексной
величиной.
Для четных корреляционных функций i|^ (— г) = i|je (г), в част-
ности для функции корреляции вещественного или изотропного
поля, спектральная плотность тоже четна, Ф; (— к) = Ф; (к). В этом
случае -ф; (г) и Ф& (к) связаны косинус-преобразованием Фурье:
S>: (г) = I ФЕ (k) cos кг d*k, C.8)
jk? I *(г) cos kr d'r-
В частном случае изотропного однородного случайного поля,
для которого i|>j(r) = i|>j(r), пространственная спектральная плот-
ность зависит только от модуля вектора к. Для того чтобы это
показать, перейдем в C.5) к полярным координатам (г, 9, ф)
с полярной осью, направленной по вектору к. Тогда кг = &r cos в
и мы получаем
2я Я "=
iqi \ sin В d6\ tyi(r)e-ikrmer2dr =
К о
2п** ) s п г
Зависимость Ф^ только от к позволяет записать C.6) и C.8)
в более простом виде, а именно через однократный интеграл
по к. Вводя сферические координаты в пространстве волновых
векторов к (с полярной осью «о вектору г), после интегрирова-
ния по угловым переменным получаем
C.11)
$3] ПРОСТРАНСТВЕННЫЕ СПЕКТРАЛЬНЫЕ РАЗЛОЖЕНИЯ 19
Приведем в качестве примера значение пространственного
спектра ФЕ (ft) однородного и изотропного случайного поля с гаус-
совой функцией корреляции B.24):
a>E(fc) = Bn)-'/.ay3e-V.w, C.12)
и с экспоненциальной функцией корреляции B.25):
(ЗЛЗ)
Эти выражения можно получить при помощи любой из формул
C.5), C.9) или, что проще всего, C.10).
Из этих примеров видно, что «неопределенность» (ширина)
спектра Ak обратно пропорциональна радиусу корреляции слу-
чайного поля: Afc~!//. Но I характеризует «неопределенность»
(ширину) Аг корреляционной функции, которая существенно
отличается от нуля лишь при г^;Дг~/. В результате для изо-
тропных случайных полей можно формулировать соотношение
неопределенностей (т. е. размытостей)
Л/гДг>1, C.14)
которое является аналогом соотношения Д<оД01 для случай-
ных процессов (ч. I, § 44). Согласно C.14) коротко коррелиро-
ванным полям (Дг ~ / мало) отвечают широкие пространственные
спектры (Д& велико), тогда как при больших радиусах корре-
ляции ширина спектра мала.
Для анизотропных полей неопределенности (радиусы корре-
ляции) по разным направлениям неодинаковы, и для них вместо
одного неравенства (в.14) выполняются сразу три неравенства:
ДЬ,Дг*55 1, Akfir^l, Д/^Дг^Зэ]. C.15)
Для иллюстрации этих соотношений можно привести про-
странственный спектр, отвечающий гауссовой корреляционной
функции B.29):
^{ y C.16)
Ширина этого спектра по осям kx, ky, fer обратно пропорцио-
нальна соответственно величинам а, & и с, которые характери-
зуют масштаб изменения корреляционной функции B.29) по осям
х, у я г.
Для существования Ч';(г). т. е. для существования интеграла
в правой части C.8) и C.11), необходимо, с одной стороны,
чтобы с ростом k спектральная плотность Ф;(к) убывала быст-
рее ?'. С другой стороны, при k—>-0 у спектра ФЕ (к) допустимо
наличие степенной особенности вида fe~a с a < 3.
20 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ [ГЛ. I
В тесной связи с условиями существования корреляционной
функции находится вопрос о требованиях, которым должен под-
чиняться спектр дифференцируемых случайных полей. Так же,
как и в теории случайных процессов (ч. I, § 19), можно убедить-
ся, что необходимое и достаточное условие существования (разу-
меется, в среднем квадратичном) первых пространствениых произ-
водных, например yj (r), сводится к существованию величины
<XZ A4) VC* (г«)> = - Aih (Г1-г,). C.17)
Если подставить сюда спектральное разложение C.6) и поло-
жить rt = r2 = r, то условие существования у? запишется в виде
<|VS(r)|2> = -A^(O)= \ fe4Dc(k)d»fe<oo. C.18)
- да
Это условие допускает при k—>-0 степенные особенности вида
Ф^(к)~ k~a более высокого порядка, чем это требуется для
существования i|)E(r): интеграл C.18) сходится, если ос < 5, тогда
как для сходимости интеграла C.6) допустимы лишь а< 3. В то
же время условие C.18) предъявляет более жесткое требование
к скорости убывания Ф((к) при k—>«. Необходимо, чтобы
Ф^ (к) с ростом k убывало, как й~й с ц > 5 (для существования
г|)Е (г) необходимо лишь (х > 3). Последнему условию не удовлетво-
ряет, например, случайное поле с экспоненциальной функцией
корреляции B.25), поскольку его спектральная плотность C.13)
убывает на бесконечности недостаточно быстро (как fe~4). Сле-
довательно, такое поле недифференцируемо.
Еще более жесткие требования при k —>- 00 предъявляет
к Ф(,(к) существование у случайного поля производных п-го
порядка. Из условия <| \% (г) |2> < о° следует, что должно вы-
полняться неравенство
<oo, C.19)
так что с ростом k спектр ФЕ (к) должен убывать быстрее, чем
ft~3~2". Очевидно, для бесконечно дифференцируемого поля Ф^(к)
должно уменьшаться при k—>-оо быстрее любой отрицательной
степени к, например, экспоненциально. Таким является, напри-
мер, случайное поле с гауссовой корреляционной функцией B.24).
Примером спектра, спадающего более медленно (чем по эк-
споненте), но быстрее любого l/k", может служить функция
Фг (k) = С ехр {— (In feJ} = Ck~i" \
для которой при любом конечном т
[k)dk =Клехр { \ \ < °° ,
$.(] ЛОКАЛЬНО ОДНОРОДНЫЕ СЛУЧАЙНЫЕ ПОЛЯ 21
§ 4. Локально однородные случайные поля
Случайное комплексное поле ? (г) можно характеризовать не
только корреляционной функцией B.1), но и так называемой
структурной функцией, которая представляет собой средний
квадрат модуля приращения флуктуацнонной компоненты ? (r)
поля ?(г):
l-e(r2)p>. D.1)
Очевидно, прн rt = r2 структурная функция обращается в нуль,
Если структурная функция ?>s(rt, г2) и приращение среднего
поля /;(]-!, r2) = <S(r1)> —<J(r2)> зависят только от разности
i"i — г2:
0;(«V r^-ZJj^-r,), /jfo, гг)=/Е(Г1-г,), D.2)
то такие поля называют локально однородными. Понятие локально
однородных полей ввел А. Н. Колмогоров [3, 4], а термин «струк-
турная функция» был предложен позднее А. М. Обуховым. Усло-
вия локальной однородности налагают определенные ограничения
на моменты приращений ? (г), т. е. разностей значений поля
в двух точках г, и г2, а не на моменты самих этих значений
?(гх) и ?(г2). В силу полной аналогии таких полей со случай-
ными процессами со стационарными (первыми) приращениями
(ч. I, § 56) можно было бы назвать локально однородное поле
также случайным полем с однородными приращениями, ио это
название не получило распространения.
Требованию однородности величины/>(г,, г2) = <? (г,)> — <?(гг)>
можно удовлетворить, ^только если среднее поле линейно зави-
сит от г: <?(r)> = <a>r + const, где а—произвольный вектор,
который может быть н не случайным. Действительно, при ли-
нейной зависимости <?(г)> от г имеем
ЫГ1> |) = <а>(г1— г,) = /;(!-!—г„).
Если у поля существует корреляционная функция iftfo, г2) =
= <?(г1)?»(г,)>, то, согласно D.1),
?>?>!• «¦*) = *t(«-I. Г,) + +t (Г„ Г2)-1|)Е(Г1. Г,)-¦?(!¦„ Г,). D.3)
В частности, для однородного поля ?(г) имеем из D.3)
+t<r)l. D.4)
Важным преимуществом структурной функции является то, что
эна может сохранять смысл и в том более общем случае, когда
корреляционной функции не существует. Ситуация здесь такая
же, как для случайных процессов (стационарные процессы пред-
22 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ [ГЛ. I
ставляют собой частный случай процессов со стационарными
прнращеинями). Аналогия становится еще более полной, если
речь идет о локально однородных и изотропных полях. Под этим
понимаются случайные поля, у которых Dj(r) и /;(г) зависят
только от модуля вектора г = гх—г2:
/t(r)-ft(r). D.5)
Второе из этих условий удовлетворяться, если <а> = 0, т. е.
вектор а обладает изотропным распределением в пространстве.
В приложениях и, в частности, в теории атмосферной турбу-
лентности часто можно считать равным нулю сам вектор а. Так
или иначе, среднее значение локально однородного и изотроп-
ного поля постоянно: <?> = const. Для однородного и изотроп-
ного случайного поля равенство D.4) принимает вид
Ot (О = 2 [ifc @)—ifr5 (r)]. D.6)
причем D^(r) и ф^@ вещественны. Если i|'t(r) при г—>«> исче-
зает, то ?>j (оо) = 2i|)? @), что позволяет выразить ifj (г) через ?*j (r):
W V[D()lDt(r)]. D.7)
Важное свойство структурной функции состоит в том, что на
нее не влияют большие по пространственной протяженности
флуктуации ?, т. е. флуктуации с характерным размером 1^>г =
~ \г1—г,|. Обусловленные такими флуктуациями возмущения
практически одинаковы в точках г1 и г2, разность f(r,)— ?(г2)
для них мала и, соответственно, мал их вклад в D^(r). Корре-
ляционная же функция в равной мере учитывает флуктуации
любого масштаба. Именно поэтому использование структурной,
а не корреляционной функции оказывается физически оправдан-
ным в тех случаях, когда крупномасштабные флуктуации поля
не сказываются на иктересующнх нас явлениях. Это вовсе не
означает, что такие флуктуации отсутствуют. Напротив, нх доля
в результирующих флуктуационных возмущениях может быть
даже велика, но для наблюдаемых явлений они несущественны.
Примером может служить статистическая теория развитой
турбулентности Г', 2], т. е. такого вихревого движения газа или
жидкости, в котором присутствуют вихри с очень широким диа-
пазоном размеров I. Наиболее интересными по своим внутренним
закономерностям здесь оказываются вихри, значительно усту-
пающие по размерам тем наиболее крупным вихрям (размера Lo,
так называемого внешнего масштаба турбулентности), которые
порождены первичным потоком и еще сильно зависят от его
геометрических и кинематических особенностей. Именно для
субдиапазона 1<^LO A. H. Колмогоров ввел понятие локальной
однородности случайного поля и предложил для его статисти-
54] ЛОКАЛЬНО ОДНОРОДНЫЕ СЛУЧАЙНЫЕ ПОЛЯ 23
ческого описания функцию ?>g, которая просто исключает крупно-
масштабные неоднородности из рассмотрения.
Тем самым, предположение об однородности, если оно де-
лается для ?>?, гораздо менее обременительно, т. е. оно позво-
ляет охватить класс случайных полей (локально однородные
поля) более широкий, чем такое же предположение для фс (одно-
родные поля).
Обратимся к пространственным спектральным разложениям
локально однородных полей. По аналогии со спектральными раз-
ложениями для процессов со стационарными случайными при-
ращениями (ч. I, § 56) имеем
DE(r)=2 \ Ф;(к)A— coskr)d3fe. D.8)
Интеграл D.8) сходится, если при k—> () спектр Ф(,{к) имеет
степенную особенность вида k~a с а < 5, тогда как существова-
ние $i{r) обеспечено лишь при а < 3.
Формула обращения разложения D.8) в случае^локально од-
нородных полей получается несколько, [более сложным путем,
чем для однородных^ полей, Сначала^надо продифференциро-
вать D.8) по г и только после этого применить обратное пре-
образование Фурье. Мы получаем тогда, что
D.9)
Для изотропного поля, переходя в D.8) и D.9) к сферическим
координатам и учитывая, что k\E>i(r) = кгD' (г)/г (штрих обозна-
чает производную по г), находим
D.10)
— krcoskr)Di(r)dr. D.11)
Рассмотрим в качестве примера локально однородного и изот-
ропного поля пространственные флуктуации диэлектрической
проницаемости е турбулентной атмосферы. Структурная функ-
ция этих флуктуации
B.W-<l*«(fJ-*»WI^
подчиняется при достаточно больших г «закону двух третей»
Колмогорова—Обухова [1]:
?>e(r)«CirV., />/„, D.12)
24
ОВЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ
(ГЛ. I
где Се—так называемая структурная постоянная, a i0—внутрен-
ний масштаб турбулентности1). При малых, же г, т. е. г<^/0,
структурная функция нарастает по квадратичному закону:
Л.(г)«СУ.-'/т\ г^1„. D.13)
Внутренний масштаб /„ входит в формулы D.12) и D.13) так,
что значения обоих асимптотических выражений одинаковы при
Пггг13
О L
Рис. 1.
r~l0. Соответствующие графики показаны на рис. 1 пунктир-
ными кривыми, а сплошной линией изображен реальный ход
структурной функции De(r).
Подобрать слекгр, отвечающий реальному ходу структурной
функции De(r), можно из следующих соображений. Для степен-
ной структурной функции
D^^&r*, 0<|x<2,
пространственная спектральная плотность равна [1]
так что «закону двух третей»
Ф (k) = Г ¦('/^° "/
) отвечает спектр
> = 0,033C|fe-"/..
D.14)
D.15)
D.16)
Для того чтобы получить квадратичный ход De (г) при малых
значениях г<^,1„, следует подавить спектральную плотность D.16)
1) В противоположность внешнему масштабу Ц внутренний масштаб /„ —
это наименьший размер вихрей. Возмущения с / < /0 уже ламинарны.
§ 41 ЛОКАЛЬНО ОДНОРОДНЫЕ СЛУЧАЙНЫЕ ПОЛЯ 25
при больших значениях fe^>l//0. Физически эта операция ото-
бражает диссипацию турбулентных вихрей из-за вязкости, когда
их масштаб l/fe становится малым (\lk<^.ta). Подавление плотно-
сти D.16) при больших к можно осуществить, например, путем
введения множителя е т, т. е. полагая
Ф„(Ь) =0,033C!fe-"/'e-*v'u. D.17)
Получаемая отсюда структурная функция Ds{r) будет обладать
требуемой асимптотикой D.12), D.13), если параметр обреза-
иия хт взять равным б,92/70. Она хорошо описывает турбулент-
ное поле при не слишком больших значениях г—не превышаю-
щих внешнего масштаба турбулентности Lo. В действительности
же при rp>L0 структурная функция «насыщается» (см. рнс. 1)
и стремится к конечному значению, которое удобно записать
в виде
De(™)=ClLlh. D.18)
Если значение Lo вводится таким путем, то кривая D.12) пере-
секает уровень DB—De(oo) как раз при r=La. Согласно D.6)
предельное значение D.18) равно 2а\—удвоенному среднему
квадрату флуктуации: C|Z-o'* = 2o|.
В результате мы приходим к тому, что структурную функ-
цию DB(r) можно аппроксимировать на отдельных интервалах г
следующими функциями:
?) (г) = { О!/»=2а!(гД,„)'Ч lu<r<*LQ, D.19)
I ^ 1
Ограниченность структурной функции при г —> оо можно от-
разить и в D.17), заменив множитель k'"l> на (k2 + ««)""¦'', где
xo-=2n/Lo —волновое число, отвечающее внешнему масштабу тур-
булентности. При такой замене, т. е. при спектральной плотно-
сти
Фе (k) = 0,033Cj (fe2 + х|)- "/«<Г*!/К«, D.20)
значения интегралов D.8) и D.10) будут конечны при любых г.
Конечно, поведение флуктуации е в реальной турбулентной
атмосфере подчинено более сложным закономерностям, чем при-
веденные здесь аппроксимации. Тем не менее формула D.20)
достаточно хорошо описывает пространственный спектр турбу-
лентных флуктуации г во многих задачах радиофизики.
Систематическое изложение вопросов, относящихся к стати-
стической гидродинамике, можно найти в монографиях [1, 2].
2G ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ 1ГЛ. I
§ 5. Квазиоднородиые поля
Идеализация реальных неоднородных случайных полей при
помощи рассмотренных выше локально однородных полей, описы-
вающих довольно специальный вид уклонений от однородности,
далеко не всегда применима. Поэтому особое значение приобре-
тает рассмотрение н других специальных случаев нарушения
однородности. Сюда относится, в 'частности, класс полей, не-
однородность которых в определенном смысле пространственно
медленна, или, иначе говоря, плавна, а в остальном произвольна.
Это так называемые статистически квазиоднородные поля, т. е.
поля с плавно меняющимися статистическими характеристиками —
средними значениями, дисперсиями и т. д. Очевидно, они пред-
ставляют собой пространственный аналог квазистационарных
случайных процессов, рассмотренных в ч. I, § 67.
Согласно B.6) в общем случае корреляционная функция свя-
зана с коэффициентом корреляции К% соотношением
которое в координатах г = г2 — г2 и R = (r1 + r2)/2 принимает вид
R). E.1)
Если /;—радиус корреляции поля ? (масштаб изменения Kj(r, R)
по разностному аргументу г = г1—г,), а L — характерный масштаб
изменения дисперсии <з\, среднего поля <?> н коэффициента кор-
реляции /<? по аргументу R, то для квазиоднородных полей
выполняется неравенство
В силу F.2) можно заменить в формуле E.1) произведение
a?(R + r/2) ffj(R—г/2) на а\. Такая замена безусловно справед-
лива внутри сферы радиуса г^^; что же касается пространства
вне этой сферы, то там значение множителя при К^ несущест-
венно, так как Ki(r, R)—>-0 при г^>^- Таким образом, мы при-
ходим к следующему выражению для функции корреляции квази-
однородного поля:
г|);(г, R) = a|(R)ATt(r, R). E.3)
Поскольку квазиоднородность представляет собой нарушение
строгой однородности, дельта-корреляция спектральных ампли-
туд S(k) теперь уже не имеет места, подобно тому как нет
дельта-корреляции для со-амплитуд в случае квазистационарных
случайных процессов (ч. I, § 57).
Рассматривая спектральные разложения'таких процессов (ч. I,
§ 57), мы выяснили, однако, что в случае квазистационарных
процессов определенный физический смысл приобретает мгновен-
S 61 ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ РАЗЛОЖЕНИЯ 2?
ный частотный спектр g (<a, t), получающийся при спектральном
разложении функции корреляции i|) (т, t) только по «быстрой»
переменной x = tt —12. To же справедливо и для квазиоднород-
ных полей. Записав преобразование Фурье только по разностной
переменной г = г1 — гг:
ift(r, R)= ] Ф;(к, R)eikr*ft, E.4)
можно рассматривать величину
Ф;(к, R)-^ J 1>с(г, R)e-'w*r E.5)
как локальную пространственную спектральную плотность, ко-
торая медленно меняется от одной точки R к другой (с харак-
терным масштабом L§>/[).
Естественно, напрашивается сочетание обоих видов нарушения
пространственной однородности, т. е. локальной одирродности
и квазиоднородности. Такого рода поля можно было бы назвать
локально квазиоднородными, определив их как поля, первые при-
ращения которых квазиоднородны. Примером локально квазиодно-
родното (и изотропного) поля может служить рассмотренное
в [1] поле флуктуации диэлектрической проницаемости г (г)
в плавно неоднородной по высоте г турбулентной атмосфере.
§ 6. Пространствеино-времеииые спектральные разложения
случайных полей
До сих пор мы отвлекались от временной зависимости слу-
чайных полей с тем, чтобы оттенить особенности, обусловленные
зависимостью полей от нескольких пространственных координат
и отсутствующие у однопараметрических случайных функций.
Конечно, при учете зависимости случайных полей также от
времени возникает ряд новых возможностей в отношении раз-
личных комбинаций пространственных и временных статистиче-
ских свойств поля ?(<, г) (стационарности по t, однородности
по г и разных видов отклонений от стационарности и однород-
ности), о чем мы уже упоминали в § 1. Однако использование
четырехмерных (пространственно-временных) гармонических раз-
ложений ? (t, г) с формальной стороны осуществляется довольно
очевидным образом н соответствующие обобщения вряд ли тре-
буют подробного описания. Мы приведем лишь некоторые наи-
более важные соотношения и формулы, которые понадобятся нам
в дальнейшем.
28 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ (ГЛ. I
Запишем для флуктуации одномерного случайного поля ? (/, г)
четырехмерное спектральное разложение:
I (t, г) = \\ ? (со, к)е' <кг-м'> d<ad»k, F.1)
где ?(со, к)—сок-амплитуда (точнее, амплитудная плотность) поля,
иногда обозначаемая ?»к. В отличие от ч. I, где в гармонических
разложениях процессов вводился временной фактор е*', в дан-
ной части книги зависимость от времени мы будем описывать
множителем е~ш, так как при рассмотрении волновых явлений
удобнее оперировать с пространственным гармоническим мно-
жителем «ikr, а не е-'кг. В связи с этим при использовании тех
или иных комплексных выражений нз ч. I надо заменять в них
ш на —ш.
У однородного и стационарного случайного поля спектраль-
ные амплитуды ? ((о', к') и ? (со", к") дельта-коррелироваиы как
по со, так н по к:
<?(<в', к') С* (to", k")> = Gt,<co', к'N(со' —со")сЗ(к' —к"). F.2)
Здесь Ge(cu, к) — пространственно-временной спектр поля (или
сок-плотность), который всегда неотрицателен. Иногда представ-
ляют этот спектр в виде GE (со, k) = |?юк |2, но следует помнить,
что это лишь иное обозначение множителя при дельта-фуикциях.
Пространственно-временная корреляционная функция ^(т, г)
связана с сок-плотностью Gj(<o, к) преобразованием Фурье:
= 5SG?(ffl. к)е(<•"-«')dted'fe F.3)
— х
(обобщение теоремы Хинчина). Обратное преобразование Фурье:
GE (со, к) = ^ JJ VZ (т, г) е-' <*-«> dx d'r. F.4)
— х
В случае четной корреляционной функции, W (— т, — г) = V (т, г),
экспоненту в этих разложениях можно заменить на cos (kr—сот).
Через сок-плотность Gj(co, к) можно выразить как простран-
ственный Ф^(к), так и временной (частотный) g(,(w) спектры
случайного поля-.
= ] G:(co, k)Ao= J YE@, T)e-tkrd'r, F.5)
gt(сй)= J Gc(co, k)d*k= I Vt(r, O)e'mdx. F.6)
§61 ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ РАЗЛОЖЕНИЯ 29
В качестве примера рассмотрим поле с так называемыми
«замороженными» неоднородностями, т. е. поле, в котором все
временные изменения ?(t, г) обусловлены только перемещением
пространственных возмущений х (г) с постоянной скоростью V.
Если покоящееся однородное случайное поле v (r) описывается
пространственной корреляционной функцией tyv(r), то при не-
релятивистских значениях скорости1) ?(/, r) = v(r — W), и тогда
Vt(T,r) = i|>v(r-VT). F.7)
Подставляя F.7) в F.4), находим простую связь между ик-
плотиостью Gj(co, к) «замороженного» поля ?(/, г) и простран-
ственной спектральной плотностью Фу (к) покоящегося поля v (r):
Gt(o), k)=O>v(kN>> — kv). F.8)
При помощи F.5) и F.8) легко убедиться, что
Ф5(к)=Ф„(к), F.9)
т. е. пространственные спектры полей ?(/, г) и v (г) совпадают.
Что же касается временного спектра флуктуации ?(/,г)„ то из
F.6) н F.8) находим
gE(co)= j dkn J ^ХФ,(^|, kxN(co-V) =
где fey и kx—продольная и поперечная (по отношению к век-
тору скорости v) составляющие волнового вектора к. Выражение
F.10) упрощается в случае изотропного поля v(r), когда
<Dv(?|l, kx) = fIiv(l/'ft|i + fe'i). Переходя в F.10) к полярным коор-
динатам и вводя вместо fej_ новую переменную интегрирования
x = ]/(co/t'J + fe^, получаем
со
§ ®()*d* F.H)
I e> l/o
Дифференцируя F.11) по со, нетрудно выразить пространственный
спектр замороженного изотропного поля Ф^A1) = Фу(к) через
частотный спектр g^ (со):
F.12)
2) Об особенностях релятивистского случая см. в задаче 7.
30 ОБЩИЕ СВЕДЕНИЙ О СЛУЧАЙНЫХ ПОЛЙХ 1ГЛ. [
Формулы типа F.11) п F.12) часто используются при анализе
полей, которые можно с достаточной точностью считать заморо-
женными.
Сказанное выше относительно спектральных разложений одно-
мерных полей легко переносится на многомерное поле ?"'('> г)
(i= 1, 2, . . ., п). Наиболее простыми свойствами обладают поля
однородные и однородно связанные (в широком смысле) в прост-
ранстве Q = (t, г).
В случае векторного тюля ?'¦> элементы корреляционной матри-
цы Ч"$ трансформируются при ортогональных преобразованиях
координат как компоненты я-мерного тензора второго ранга,
т. е. можно говорить о корреляционном тензоре векторного поля.
Для однородных и изотропных векторных полей доказан ряд
изящных теорем, часть которых сформулирована в задачах
8—10.
Разложение многомерного случайного поля t,u>(t,r) в инте-
грал Фурье имеет вид, аналогичный F.1); при этом для одно-
родного и стационарного цоля выполняется равенство
<?,-(»'. к')?/(а>", к")> = 0;-5'(<»', к') 6(ш' — со")8(к' — к"), F.13)
которое естественно приводит к обобщению теоремы Хинчина
на многомерные пространственно-временные поля:
4$ (т. г) = JJ Gty (<a, k) e<<кг-ш" dm d'k F.14)
с обратным преобразованием
ч^. г)е-'*<-»'Ыт<1»г. F.15)
Корреляционная матрица многомерного поля Vft положи-
тельно определена. Отсюда вытекает, что диагональные компо-
ненты матрицы (ok-плотности вещественны и неотрицательны:
G'jjj^io, k)>0. Недиагональные же элементы в общем случае
комплексны.
Отметим теперь следующее существенное обстоятельство. Об-
ласть интегрирования по со и к в разложениях Фурье самих
полей, равно как н нх корреляционных функций F.3) и F.14),
вообще говоря, четырехмерна. Но в том случае, когда рассмат-
риваемые поля удовлетворяют некоторым динамическим уравне-
ниям (в частности, волновым уравнениям) в однородной и ста-
ционарной среде, свободной от источников (т. е. сами уравнения
однородны), то со н к уже не независимы, а подчинены так на-
зываемому дисперсионному уравнению:
Д(а>,к) = 0. F.16)
j6} ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ РАЗЛОЖЕНИЯ 31
Это уравнение следует из требования, чтобы плоская монохро-
матическая волна exp (tkr—Uot) была собственной волной, т. е.
была частным решением динамических уравнений.
Говоря на геометрическом языке, дисперсионное уравнение
описывает в пространстве (о), к) некую трехмерную гиперповерх-
ность—дисперсионную поверхность, — которая может быть и
многолистной (например, а анизотропной среде). Вие точек этой
гиперповерхности cok-амплитуды полей равны нулю, а значит,
равны нулю и спектральные плотности в F.3) и F.14). Другими
словами, ?A)(к>, k) и С$'(ю, к) содержат множителем дельта-функ-
цию б[Д(о), к)] и, соответственно, снижается кратность инте-
гралов Фурье: они распространяются фактически толька на дис-
персионную поверхность (всю или ее участки), т. е. на м и к,
удовлетворяющие дисперсионному уравнению. Уже в следующей
главе мы непосредственно столкнемся с этим обстоятельством.
В тех случаях, когда стационарное поле ? (t, г) является,
как функция от t, эргодшеским (ч. I, § 20), угловые скобки
в предыдущих выражениях можно трактовать (в смысле вероят-
ностной сходимости) как усреднение по времени, т. е. считать,
например, что для произвольной детерминированной функции
практически справедливо равенство
т
</[Е(«, r)]>= lira ЩГ$\= liln W \
причем для получения средних по ансамблю путем временного
усреднения можно с достаточной точностью ограничиваться ко-
нечными Т, существенно превышающими время корреляции
7>W F-18)
Наряду с эргодичностью по времени, можно ввести понятие
пространственной и пространственно-временной эргодичности.
Так, для однородных пространственно эргодических полей сред-
ние по ансамблю «совпадают» в смысле сходимости по вероят-
ности со средними по пространству. Практически это означает,
что_ для произвольной детерминированной функции / можно счи-
тать справедливым равенство
= lim 4-^КС г)]*»", (б-19)
где V—пространственная область, по которой ведется усредне-
ние. Предельный переход V—>-оо опять-таки может быть при-
остановлен на областях V, поперечник [которых L велик
по сравнению с радиусом корреляции lz, т. е. выполняется
32 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ ГГЛ. I
неравенство, аналогичное F.18):
д ~ У'/ф./Е. F.20)
О пространственно-временной эргодичности стационарных и
однородных полей говорят тогда, когда имеет место сходимость
по вероятности как при Т—>-оо,таки при V—>-°°, что практи-
чески означает одновременное выполнение равенств F.17) и F.19).
Возможны также случаи, когда поле ? (t, г) является эргоднче-
ским только по части пространственных аргументов, например
только в плоскости (х, у) или только на поверхности сферы.
Наконец, иногда удобно пользоваться понятием квазиэргоди-
ческих полей, которые находятся по отношению к эргоднческим
полям в таком же положении, как квазиоднородные поля по
отношению к однородным. Иными словами, эти поля являются
эргоднческими лишь в объемах, малых по сравнению с харак-
терными масштабами L- изменения статистических характеристик
поля (среднего значения, дисперсии и т. д.). В отличие от F.19),
область пространственного усреднения для квазиэргодических
нолей должна быть ограничена сверху масштабом Lj, но при
этом должно по-прежнему выполняться неравенство F.20). Сле-
довательно, о квазиэргоднчности полей можно говорить лишь
при таких условиях, когда можно ввести объем усреднения V,
который удовлетворял бы двухстороннему неравенству
k^V'^k. F.21)
В феноменологической физике V называют обычно «физически
бесконечно малым объемом». Этот объем должен быть, с одной
стороны, достаточно малым, чтобы в его пределах исследуемые
поля были статистически однородными (в механике и электро-
динамике сплошных сред обычно требуется лишь постоянство
в объеме V средних полей), а с другой — настолько большим,
чтобы в пределах V поле t, испытывало достаточно много про-
странственных флуктуации.
В физике сплошных сред под 1^ следует понимать среднее
расстояние между источниками возмущений, которыми могут
быть отдельные молекулы, дислокации, вкрапления и т. д. Если
п — концентрация молекул (или других возмущающих объектов),
то /j ~я-'Л , н тогда неравенство V1''^-/; принимает вид пК^> 1,
что и отвечает большому числу молекул в физически бесконечно
малом объеме V. Прн выполнении этого неравенства усреднение
по ансамблю молекул можно заменять усреднением по малой
пространственной области V. Таким образом, в макроскопической
физике существенно используется предположение о пространст-
венной квазиэргодичности тех или иных полей, характеризующих
состояние сплошных сред.
$ 7] ФУНКЦИОНАЛЬНЫЙ МЕТОД 33
§ 7. Функциональный метод описания случайных полей
Как мы знаем, полное описание вещественной случайной
величины ? дается ее характеристической функцией щ(и) =
= <ехр Aи%У>, при помощи которой можно найти как плотность
вероятностей 1, так и моменты разного порядка, а также ку-
мулянты.
Для W-мерной случайной величины ? = {|„ ..., \N) характе-
ристическая функция имеет вид <р$ (и) = <ехр (?«?)>, где и? =
= 2 ujlj и тоже содержит всю информацию о совокупности
случайных величин ?; (ч. I, § 9).
Прн рассмотрении общих вопросов, обсуждаемых в данном
параграфе, целесообразно отказаться на время от ограничения"
числа параметров, от которых зависят интересующие нас функ-
ции, и'вернуться от четырех координат х, у, г, t к п-мерному
пространству параметров х= {хг хп). Пусть 5 (*ц • • •. хп) =
= |(х)—вещественное случайное поле в этом пространстве
(в частном случае единствеииого параметра, я=1, мы будем,
как и ранее, обычно считать, что параметр х является временем t).
Рассмотрим теперь другой, по существу равносильный, но во
многих задачах более удобный н лаконичный способ задания
случайных функций—при помощи так называемых характери-
стических функционалов. Убедимся прежде всего, что полное
вероятностное описание поля |(х) дается характеристическим
функционалам
ФГя]-(ехр{|55(ж)и(х)&}), dx = dXl...dxn. G.1)
Здесь а(х)—произвольная функция, для которой интеграл в G.1)
сходится при всех возможных реализациях ? (х). Функция а (х)
заменяет дискретную совокупность переменных u = {Uj, ..., ик},
от которых зависит характеристическая функция для .jV-мернон
случайной величины !={ii, .... ?яЬ Подчеркнем, что «функцио-
нал Ф|"«] Должен быть известен для любой функции и (х).
Зная Ф\а], можно получить характеристическую функцию
для любой совокупности случайных величин 5, = | (х,) ?.N=
= |(хд.). Для этого достаточно взять в качестве аргумента «(х)
функционала Ф[и] фуикцяю вида
Тогда
2 С. м. Рытоя я др. 1. II
34 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ [ГЛ. I
и функционал Ф[и] превращается в характеристическую функ-
цию ^-мерной случайной величины {t,t |д,}, т. е. значений
поля J (х) в N точках xL Хд,:
Но характеристическая функция ф(а,, ...,и#) позволяет, как
мы знаем, найти Л^-мерную плотность вероятностей wN (?,, ..., i,N).
Тем самым, ясно, что характеристический функционал Ф[и] одно-
значно определяет плотности wN(?,,, ...,lN) при любом N к при
любом выборе точек xt, ...,хЛ-, т. е. полностью определяет слу-
чайное поле ? (х).
Зная функционал Ф[и], мы можем найти также моменты
(в частности, корреляционные функции) и другие статистические
характеристики случайного поля |(х). Однако для этого необхо-
димо уметь дифференцировать функционал ®[uj по функциональ-
ному аргументу и (х). Поэтому часть этого параграфа будет по-
священа чисто математическим вопросам, касающимся функ-
ционалов.
Прежде всего дадим оби^ее определение функционала. Мы
говорим, что функционал задан, если установлено правило, по
которому каждой функции, принадлежали области определения
функционала, сопоставлено число, называемое значением функцио-
нала на этой функции. Приведем некоторые примеры функцио-
налов:
FN\u] = \ АЛ,(х„ ..., хЛ,) и (х2) ... и (xN) dx,... dxN,
Фо [и] = ехр {—72 \ 11|> (х,, х.) и (х,) и (ха) dx, dx,) .
Здесь FJu]—линейный функционал, FN[u] функционал ЛГ-й
степени, Фо[«]—гауссов функционал (ниже будет показано, что
Фо[«] — характеристический функционал для гауссовых случай-
ных полей). Отметим, что функционал зависит от вида функции
и (х) в целом ¦ (т. е. от ее поведения во всем пространстве х),
в силу чего в обозначении F \и\ мы не пишем явно зависимости
и от ее аргумента х. В тех случаях, когда на эту зависимость не-
обходимо указывать, мы будем отмечать аргумент функции и
тильдой: F\u (x)]. Однако прн такой записи следует иметь в виду,
что сам функционал F не зависит от х (подобно тому как в тен-
зорной алгебре веллчипа дгй«6 не зависит от «немого» индекса
k — индекса суммирования).
Рассмотрим значения одного и того же функционала F для
двух различных «значений» его аргумента, а именно для функций
„j ФУНКЦИОНАЛЬНЫЙ МЕТОД 35
к(х) и а(х) + ба(х). Будем прн этом считать, что функция 6а (х)
отлична от нуля лишь в некоторой области Дх вокруг точки х„.
Функциональной (или вариационной) производной функционала
F [и] в точке х0 называется предел
+faWM {72)
6ulXo1
конечно, при условиях, что этот предел существует и не зависит
ни от вида 6и (х), ни от способа стягивания к нулю объема
области j Ax|, ни от закона, по которому стремится к нулю
максимум модуля функции 6а (х). Приведем некоторые примеры.
Найдем функциональную производную линейного функцио-
нала F, [и] ~ J А (х') и (х') dx' в точке х„. Имеем
F,[u +8и]- I А (х') [а (х') +бы (х')] dx',
fJtt + Su-J — FJu]- J Л (х') бы (х') dx',
так что
f
Ах Ах
Применяя теорему о среднем к интегралу в числителе, находим
где точка Xj принадлежит Д-окрестности точки х0. Переходя
к пределу при | Ах /—>-0, получаем
^"л(хХх')^' = Л(х0). G.3)
Такимjже образом производится дифференцирование и более
сложных функционалов (см. задачу 13).
Выберем в качестпе ба(х) функцию ба (х) = Хб(х—х0) (как и
ранее, 6 (х—х„) = 8 (дс, — х01)... б (х„—О)- Тогда j 6« (x') dx' = X
и, согласно G.2),
G-4)
Зб ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ (ГЛ. 1
Формула G.4) сводит операцию вычисления функциональной
производной к обычному дифференцированию.
Приведем теперь формальные правила функционального диф-
ференцирования, аналогичные обычным правилам.
Если At и А% не зависят от и, то
Далее,
^^Мф^И^^ф.М+ф.М^. G-6)
Пусть /(г)—функция от г. Рассмотрим функционал вида tp[и] =
= f{F[u\) (функция от функционала). Тогда
где f = ~7бг —обычная производная функции f по ее аргу-
менту. Формулы G.5)—G.7) непосредственно следуют из G.4).
Наконец, положив в G.3) А (х') = 8(х'—xj, получаем
Формулы G.5)—G.8) позволяют, ие прибегая к формальному
определению G.2) операции функционального дифференцирова-
ния, дифференцировать большинство функционалов, с которыми
приходится встречаться в конкретных задачах. В частности, из
G.5) следует, что можно производить дифференцирование
функционалов под знаком интеграла или производной.
В качестве еще одного примера найдем функциональную про-
изводную от гауссова функционала:
-ЭД- - шехр: {-¦HJ *» *'>" (*'>«
В соответствии с G.7) получаем
На основании G.5) дифференцируем под знаком интеграла, ис-
пользуя при этом формулы G.6) и G.8):
х.) [в Оч-х)и(х.) +
'. x)]u(x')dx'.
ФУНКЦИОНАЛЬНЫЙ МЕТОД 37
В данном примере можно считать, что г|> (х„ х,) = ф (ха, х,),
так как несимметричная часть ij) (х„ ха) не вносит вклада в функ-
ционал, поскольку .интеграл от произведения несимметричной
функции на симметричную и (xj и (ха) равен нулю. Поэтому полу-
ченную производную можно записать короче:
Функционал Ffa+y] можно разложить в функциональный
ряд Тейлора по v(x) (см., например, [1J, приложение I):
... G.9)
Подобно операторной записи формулы f (x+l)=exp <l-^i [ (х)
для обычного ряда Тейлора, удобно записать и формулу G.9)
в операторном виде:
В фигурных скобках мы имеем степенное разложение экспоненты,
так что
^^^ G.10)
Вернемся к характеристическому функционалу G.1) и подей-
ствуем иа него оператором — -* Выполняя дифференцирова-
ние под знаком среднего, находим
} G.Л)
Таким образом, оператор у Сц.ху , действуя иа Ф [а], вводит под
знак усреднения множитель ?(х'). Повторяя эту операцию, при-
ходим к* формуле
x')). G.12)
38 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ [ГЛ. I
Если теперь положить здесь и = 0, то получим
G.13)
:,)...!/v чч_± в"ф_М
Таким образом, моменты G.13) случайного поля ?(х) мож-
но находить как значения функциональных производных харак-
теристического функционала при нулевом значении его аргу-
мента.
Если разложить экспоненту в G.1) в ряд и записать k-ю
степень интеграла в виде ft-кратного интеграла, то получится
формула
представляющая собой разложение характеристического функ-
ционала Ф[и] в функциональный ряд Тейлора.
Рассмотрим теперь функционал в[и] = 1пФ[«], так что Ф[а] =
= ехр{0[и]}. Разложение в [и] в ряд Тейлора определяет куму-
лянтные (илн корреляционные) функции различных порядков:
..dxk. G.15)
Кумулянтная функция fe-ro порядка (k=l, 2, ...) определена
формулой
G.16)
<* вн(х,)...ба(хй)
аналогичной формуле для кумулянтов случайной величины. Из
G.13) и G.16) вытекает связь между моментными и кумулянт-
ными функциями (см. задачу 16). В частности,
Выше мы рассмотрели несколько примеров функционалов
общего вида. Обратимся теперь к примерам характеристических
функционалов.
1) Пусть 1(х)—нормальное случайное поле. Обозначим через &
интеграл
Тогда характеристический функционал Ф0[и] запишется в виде
7] ФУНКЦИОНАЛЬНЫЙ МЕТОД 39
1нтеграл от гауссовой случайной функции является гауссовой
лучайной величиной, что позволяет сразу же написать плотность
ироятностей для 3:
4з выражения для З очевидно, что параметры 5 в о' =
=<{3—J?)j> = <(.JT> этого распределения выражаются следую-
цнм образом:
о» = 5 5 % (х1( х2) и (зц) и (х,) dxj dxa.
Вычисляя теперь <ехр (t'J?)>, получаем известный результат-.
а подстановка выражений для J? и а2 дает
Фо[uj = ехр|i j|(х)а (х)dx-
-yjj%(x,, ^«(^«(^dx.dx.J.. G.18)
Отсюда следует, что
вс[ц]-1пФЛ«] =
= i5Hx)u(x)dx-V255t5(x.. x2)u(x1)u(x!!)dx1ix2. G.19)
Сопоставление G.19) с G.15) показывает, что для гауссовых
случайных полей все кумулянтные функции выше второго по-
рядка равны нулю.
Центральные моменты нормального случайного поля обладают
следующими свойствами (ч. I, задача 6 к гл. II):
<!,--• I,*+i> = О, |,н= !(*,),
<fi-••!»*>= S <L,lo;>.• • ^Jc^. G29)
где р. п. под символом 2 означает, что суммирование произво-
дится по всем возможным разбиениям индексов 1, 2, ...,2k на
пары. Нетрудно подсчитать, что число слагаемых в сумме, вхо-
дящей в G.20), равно Bfe—1I! = 1-3-5.. ,Bfc—1). Например,
при fe=2
40 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ (ГЛ. I
Аналогичная формула для шестого момента содержит ^слагае-
мых. Определения гауссова поля G.18) и G.20) равносильны
(см. задачу 17).
2) Пуассоновское случайное поле строится следующим образом.
Рассмотрим сначала конечную область V пространства парамет-
ров х={х1, ..., х„\. Пусть т—случайная величина, распреде-
ленная по закону Пуассона Р (т) = (т)яе~т1/п\, где т—среднее
значение т. Выберем в V случайным образом т точек xlt ..., хя,
считая, что плотность вероятностей для координат каждой из
этих точек равна V'1 при xk?V и нулю вне V н что коорди-
наты всех т точек статистически независимы. Возьмем, далее,
т случайных величин А1г ¦.., Ат, взаимно независимых и имею-
щих одинаковую плотность вероятностей w (А), а значит, и
характеристическую функцию %(Х). Пусть g(x)—фиксированная
детерминированная функция. Пуассоновское случайное поле мы
определим теперь формулой
SW=2Mrf(x-x*). G.21)
Согласно построению в G.21) содержатся следующие случайные
параметры: «амплитуды» Ак, положения «центров» хк и число
слагаемых т. Мы распространяем здесь на случай поля в п-мер-
ном пространстве параметров х то, что в ч. I было сделано для
однопараметрнческих случайных функций, т. е. для случайных
процессов'(см., в частности, ч. I, гл. II).
Характеристический функционал случайного поля G.21) имеет
вид (см. задачу 18)
O[ttJ = exp{v J[x(Jg(x-x')u(x)dx)-l]dx'}, G.22)
где v = m/V—средняя плотность случайных точек. Область V
в G.22) можно считать н неограннчениой (V—>-оо, т—<-<» при
v = m/V = const).
Из G.22) нетрудно вывести кумулянтные функции пуассо-
новского случайного поля (см. задачу 19). Они имеют вид
x)dx. G.23)
Гауссово случайное поле можно получить из пуассоновского,
если определенным образом устремить в бесконечность v, умень-
шая в то же время «амплитуды» А (см. задачу 20).
При решении многих физических задач возникает необходи-
мость вычисления величин вида <g(x)i?[|]>, где R [I] — некото-
рый функционал от случайного поля g (x). Выведем, следуя ра-
боте [5], полезную формулу, позволяющую находить эту величину.
$ 7] ФУНКЦИОНАЛЬНЫЙ МЕТОД
Рассмотрим среднее значение выражения
где T) = ti'(x)—некоторая детерминированная функция. Восполь
зовавшксь формулой G.10) для ряда Тейлора, представим функ
ционал R[l + r\]B виде
R [ч + у = exp { J dx' |(x') -g^} « [t,].
Тогда
Разделив и умножив это равенство на оператор
(он коммутирует с входящим в G.24) оператором), получаем
. G.25)
Введем функционал Q, зависящий от функции и(х) и кроме того,
являющийся обычной функцией параметра х:
G.26)
где в последнем сомножителе неслучайная величина R [тг]] вве-
дена под знак усреднения. Снова воспользовавшись формулой
G.10), получаем
С его помощью можно записать G.25) в виде
или, внося неслучайный оператор под знак среднего,
42 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ [ГЛ. ]
Поскольку функционал R зависит лишь от суммы ц + Е, можно
заменить оператор дифференцирования по ц оператором диффе-
ренцирования по §. Таким образом,
причем здесь уже можно приравнять вспомогательную функцию
ч\ нулю. Это приводит к окончательной формуле, полученной
В. И. Кляцкиным [5]:
[L?] G.27)
Функционал Q[x, u\ можно, согласно G.26), G.11) и G.1),
выразить через логарифм характеристического функционала поля
Ъ, (х) следующим образом:
ОГ* .,1- ' ' 6Ф М
Воспользуемся теперь разложением G.15) функционала 0
по кумулянтным функциям. Дифференцируя G.15), получаем
с учетом результата задачи 13
S flPTj!
Заменив здесь ы(х,) на — fie и подставив результат в G.27),
находим
х'х> х*-х)х
Рассмотрим частный случай гауссова поля %(х), у которого
Фа = 11'4= • • • =° и, следовательно, в G.29) остаются только два
первых слагаемых с i|\(x) = J(x) и i)J(x, x') = if|(x, х'):
)Л\ G.30)
Формула G.30) была получена К. Фуруцу [6J, Е. А. Новиковым
[7] и М. Д. Донскером [8].
j7j ФУНКЦИОНАЛЬНЫЙ МЕТОД 43
Укажем, как изменятся некоторые из предыдущих формул,
если рассматривать совокупность N случайных полей (#-меркое
поле) ?i(x). •••,5дг(х). Характеристический функционал опреде-
ляется тогда формулой
S J и„(х) 6»W<fa}). G-31)
Формулы G.5)—G.7) сохраняют прежний вид, но с заменой
в них б/бц(х) на 6/5цу(х). Вместо G.8) теперь справедлива
формула
eJ| G.32)
Формула Фуруцу—Новикова G.30) принимает вид
WЁА(х')>(б|^?))^'. G.33)
В заключение сформулируем свойства однородности и изо-
тропности случайных полей на языке характеристического
функционала. Статистическая однородность поля g (x) (в узком
смысле) означает, что <\ (х, + xj ... g (%k -f x,)> = <g (x:)... \ (хл)>.
Используя это равенство, можно записать разложение G.14)
в виде
X «(х,)... u (xft) dx,
или, после замены переменных х/ + х„ = Х;) в виде
Xu(x|—х„)... u(x'k—x
Но, как легко видеть, в правой части получился функционал
Ф[и(х— х0)]. Таким образом, для статистически однородных полей
Ф[и$] = Ф[ц(х-х,)], G-34)
т. е. характеристический функционал не меняется, если его
аргумент и рассматривается в смещенной точке.
Аналогичным образом, если /?х = х' означает преобразова-
ние поворота в пространстве параметров, то статистическая
44 ОБЩИБ СВЕДЕНИЯ О СЛУЧАЙНЫЙ ПОЛЯХ 1ГЛ. I
изотропность поля ?(х) выражается равенством
Ф [и (х)] = Ф [и (?"»х)]. G.35)
Возможны случаи, когда поле статистически однородно или
изотропно не по всем координатам jc,, ..., х„, а лишь в отно-
шении некоторой их части, т. е. в некотором подпространстве
параметров х. Тогда инвариантность Ф[«] должна иметь место
при преобразованиях трансляции (вектор х„ в G.34)) или пово-
рота (оператор R в G.35)), осуществляемых только в этом под-
пространстве.
Приведем в качестве примера характеристический функционал
статистически однородного гауссова поля, у которого 1 = 0.
Для него
Ф[й]=ехр{— '/> J] ?sC*i—x,)u(Kj) u(x1)dxldxij. G.36)
Ясно, что G.34) здесь выполнено. Если рассматриваемое поле
статистически изотропно, то вместо G.36) будет
Ф [«] = ехр {- V, J J 4* (| х(-х„ |) и (х.) и (х2) dx, dx2} . G.37)
Как уже было сказано, этот параграф посвящен в основном
правилам оперирования с функционалами и выводу ряда важ-
ных соотношений и формул. Примеры использования функцио-
нального метода при решении конкретных задач рассматриваются
в некоторых из последующих глав. В задаче 22 функциональ-
ный метод применен для вывода приведенного в ч. I уравнения
Эйнштейна—Фоккера C6.15) для вероятностей перехода слу-
чайного отклика дискретной динамической системы иа гауссовы
дельта-коррелированные по времени воздействия.
Задачи
1. Найти пространственную спектральную плотность для анизотропного
однородного случайного поля с гауссовой корреляционной функцией общего
вида
% (г) *=о| ехр | — Vs 2 a'Jxix/ \ •
где Xi=x, xt—y, Xs — г и Det||a;/|! Ф 0.
Отает.
где \A-,j'.: — \Щ)\~Х—матрица, обратная матрице ||ос,-у{|. В частном случае,
когда корреляционная функция имеет вид B.29), пространственный спектр
лается выражением C.16).
ЗАДАЧИ 4S
2. Доказать следующее неравенство для статистических моментов порядка
n) комплексного поля ? (г):
<?„,иA n; n 1)В„.„(л+1 2л; 2л, ..., я + 1). A)
Решение. Неравенство следует из того, что при любом комплексном X
< \К A) ¦ ¦ ¦ С («)+? (л+ 1)... С Bл) | «>3*0.
Если положить
Я. = а[В„,„A 2л)]»,
где а вещественно, то неравенство (I) представляет собой условие неотрица-
тельности квадратичного по а трехчлена. Частный случай A) при я=1—это
неравенство
аналогичное B.20).
3. Если провести в пространстве какую-либо прямую лннню н рассмат-
ривать значения однородного'и изотропного Поля ? (г) только на этой пря-
мой, то получится случайная функция одной пространственной переменной —
координаты, отсчитываемой вдоль этой прямой. Обозначим ее через г. Можно
записать разложение корреляционной функции if»(г) в одномерный интеграл
Фурье:
со
J zdk,
где Yr(*)—одномерная спектральная плотность, выражающаяся через
посредством обратного преобразования Фурье:
lSr j I'd*) cos fcrdz. A)
Показать, что трехмерный пространственный спектр Ф* (А) однородного изо-
тропного поля ? (г) связан с одномерным спектром у- {k) соотношением
Указание. Надо продифференцировать {\)'по к н сравнить результат
с формулой (ЗЛО).
Формула B) удобна для расчета трехмерного спектра в тех довольно
•шогочислениых случаях, когда интеграл A) для у. (*) вычисляется проще,
«ей интеграл C.10) для Ф»(А). Примерами могут служить'даже простые
корреляционные функции B.24) н B.25).
Формула B) используется также для нахождения трехмерного спектра
случайного изотропного поля по одномерному спектру V; (*)• полученному по
»кспернментально измеренной одномерной корреляционной функции 1Ь(г).
4.'Пусть, как и в предыдущей задаче, г — координата, отсчитываемая
вдоль какого-либо выбранного направления в пространстве, а случайное поле
Ь(г) однородно в плоскости г = const. Вводя в плоскости г = const двумер-
иы8 вектор р — (х, у), так что г = (р, г), можно записать корреляционную
46 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ [ГЛ. I
Функцию поля С (г) а виде
1|)С(р, г,-г,) = <?(рь z,I*(Pi-P. *s)>-
Эту функцию можно разложить в двумерный интеграл Фурье:
от
*,—*,)= 5 h&±' Zl~*i) «Р (ЛдР) <Р*|., A)
где к^ = (?л, Ау). Функция /у (k^, zx—г2) называется двумерной спектральной
плотностью поля или просто двумерным (пространственным) спектром.
Показать, что для однородного и изотропного случайного поля дву-
мерный спектр Fr(k^t zt—z2) и трехмерный спектр Ф*(к) связаны между собой
соотношениями
F%(kv Zi-ZjH J ф? ( V kl + k'x) cos *Л*1-*2) d*i. B)
Решение. Формула B) следует из сопоставления A) с трехмерным
разложением C.5), если учесть вещестаеииость корреляционной функции тк (г)
для изотропного поля. Обращая B), находим
Формула 13) получается отсюда при Ьг^0. Отметим, что Ф{(У А|+А^) как
функция от Az имеет характерный масштаб ftj_. В силу этого нз B) следует,
что fj(*j_, Z] — г2) сосредоточена в области
Ах|г,-г2| <2я. . D)
5. Выразить спектральное разложение корреляционной функции поля,
изотропного в плоскости z —const, в виде однократного интеграла.
Решение. В общем случае корреляционная функция if. (х, у) — \|>, (р)
и ее двумерный спектр F.(-xx, xB) — Л(") связаны прямым и обратным
преобразованиями Фурье:
Lf A)
В случае изотропного поля имеем ф^(р) — ifj(p) и F^(pt)=-F^(jt). Переход
в формулах A) к полярным координатам (соответственно в р-и «-пространст-
вах) с последующим интегрированием по углоаым переменным приводит
к прямому и обратному преобразованиям Ганкеля:
00 «
^(p) = Zn^Fi(x)J,(Kp)KdK, Fj.OO^-.^f ^(pJ-Mxplpdp, B)
° О
где р= У&-\-у", ¦л — \ xl-- щ, а /0~нулевая бесселева функция.
ЗАДАЧИ
47
6. Найтн частотный спектр g^(a>) замороженного поля ?(г,г), если
соответствующее покоящееся случайное поле v (ri обллдает гауссовой прост-
ранственной корреляционной функцией i|>v(r)~ &1 ехр {—rs/2(a}.
Ответ.
7. Найти корреляционную функцию, пространственно-временной, прост-
ранственный н частотный спектры замороженного поля ?(/, г) при реляти-
вистских значениях скорости и, если изаестна функция корреляции i|>v(r)
(нли пространственный спектр <Dv(k)) соответствующего покоящегося поля v (г).
Отает. Если скорость и направлена по оси я, то в соответствии с пре-
образованием Лоренца
, kz)8(a-tixv
-v*Jc*. ky, кг),
Отметим, что если покоящееся поле v (г)^ изотропно, то замороженное поле
?(f, г) статистически анизотропно.
8. Пусть а (г) и Ь(г)—изотропные и изотропно связанные случайные
векторные поля. Найти общиД вид корреляционного тензора <оа («i) *Р (га)>
в этом случае.
Решение. Для построения корреляционного тензора однородных и
изотропных векторных полей мы располагаем только скалярными функциями
от р ^= | ri — га |, единичным вектором р/р и
единичным тензором бар. Поэтому общий
внд корреляционного тензора будет
"' " (Г,!
A)
Выбор 'скалярных коэффициентов в (I) в
форме F н в—F обусловлен тем, чтой(р)
и F (р)^описыввют при атом продольную и
попер&шую корреляции. Действительно,
рассмотрим корреляцию между а-компонеп-
тями в„ и ba. Если точки ri и г» лежат на
пряиов, парзллельной оси ха. т. е. р—ра,
то (рис. 2, а)
(продольная корреляция). Если же вектор p = ri—гг перпендикулярен оси ха
то ра«=0 (рис. 2,6) н
(поперечная корреляция).
18 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ 1ГЛ. 1
Вместо F (р) и в (р) можно ввести две другие скалярные функции, положив
Сопоставление A) и B) показывает, что
i ). C)
где штрих означает производную по р.
9. Показать, что для однородного и изотропного потенциального поля
а (г) (rota = 0) продольная и поперечная функции корреляции F (р) и G(p),
введенные в предыдущей задаче, связаны соотношением (А. М. Обухов)
<?<р) = [Р^(рI'. О
а для соленоидального поля (diva = 0)—соотношением (Т. Карман)
F(P)=^[p'<J(p)l'. B)
Решение. Пусть а = —>р<р—потенциальное поле, a ifip (p)—корреля-
ционная функция потенциала ф(г). Тогда
т. е. в формуле B) предыдущей задачи ?/=0, V= — фф. Следовательно, по
формулам C) той же задачи f (р)=—V и С=К", откуда и вытекает A).
Рассматривая солеиоидальиое поле, уыножиы div a (ri) = 0 на а (га)и про-
ведем статистическое усреднение, используя соотношение B). задачи 8. Это.
приводит к условию V (У + ДК) = 0, откуда с точностью до постоянной, ко-
торую всегда можно включить в U, имеем 1/ + ДУ = 0. Отсюда следует, что,
Согласно формулам C) задачи 8
f = -V— V", G = — — V,
Р Р
что эквизалентно B).
10. Покааать, что при условии однородности и изотропности векторное'
соленоидальное поле а (г) не коррелиронано со скалярным полем <р (г)
(A.M. Обухов) н с векторным потенциальным полем Ь(г)=— \"Р(г).
Решение. Для однородных и изотропных полей корреляционная функ-
ция <<р (г,) а* (г,)> должна быть вектором, параллельным р:
<ф Ci) а* М> = Я (Р) ¦? - В (р),
где II (f)—скалярная функция. Поскольку для солепоидального поля diva = 0,
должно быть
V» <ф (гi) а* (г«)> = - di vp В (р)=О,
т. е. вектор В должен быть соленоидальным (уа означает дифференцирование
по га). В отсутствие источников единственное допустимое решение есть В = 0,
Задачи 49
что и означает некоррелированность скалярного и соленоидальиого вектор-
ЯОГО полей. Отсюда вытекает также некоррелированность солекоидальиого и
потенциального векторных полей:
<*в (гО А (г,)> = —щ «р (г,) «4 (г,)> = - ^?-'=0.
Н. О флуктуация* с корреляционными функциями типа B.24) и B.25)
говорят как об одномасштабных флуктуанионных полях, имея в виду, что
доведение ф (г) характеризуется только одним масштабом / (п ространствен-
ВЫЙ спектр таких флуктуации содержит, разумеется, множество масштабов,
сосредоточенных в области k^.\/t). Реальные функции корреляции часто
имеют много характерных масштабов (при этом говорят о многомасштабных
фдуктуациях). Иногда удобно аппроксимировать такие функции суперпози-
цией гауссовых функций корреляции, т. е. записывать коэффициент корре-
ляции в виде [9J
о
подчиняя, конечно, весовую функцию / (а) условию нормировки
рбычный гауссов коэффициент корреляции К {р) = е~р'^!' получается отсюда
ири /(а)=6(а—/Й).
Найти весовую функцию / (а), отвечающую:
а) экспоненциальному коэффициенту корреляции егТ11\
б) локально однородной и изотропной модели турбулентных флуктуации
диэлектрической проницаемости воздуха; коэффициент корреляции для таких
флуктуации в соответствии с D.19) имеет асимптотические выражения
Ответ.
при а < („ и a > Ц,
Lo~ i* при io<;a<;Lo.
12. В ч. 1, § 47 было выведено выражение для функции корреляции ян-
тенсивностей двух нормальных комплексных колебании d (t) и ?г {() в пред-
положении, что ti = ?2 = 0- Получить аналогичное выражение для случая,
когда среднее значение случайного поля ?((, г) отлично от нуля.
Ответ. В обозначениях /„, = |?и|а, гДе im = i{tm, гт), т~ 1, 2, функ-
ция корреляции интенснвностей есть
il>,(l,2) = </,/i|>-717, = <7i7s>,
где
1=1-7= \\ |2-< 11\Ь + fit» + к. с).
50 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ [ГЛ. 1
Используя ре»ультаты задачи 2 к гл. VI ч. I, получим
При ?i=?j=0 отсюда следует формула
которая в случае $? = 0 принимает вид ip/(l, 2) = | i|>j(l,2)|a
13. Пусть Fii[u\—функционал N-& степени:
Показать, что
а) значение Ftf\u] вависнг только от симметричной по всем аргументам
части функции А;
в) в случае симметричной функции А
( аналог формулы -g—^=NxN-1 J.
Указание. Задачу полезно решить тремя способами: исходя из опре-
деления (Т.2), при помощи формулы G.4) и при помощи правил G.5)—G.8).
14. Найтн вариационную производную функционала действия классичес-
кой механики
Решение. Дифференцируя под знаком интеграла, получаем
6 (dxwy _r,dx(x) Ь dx(i)
dt ] dx bx{t) dx '
На основании G.7)
Так как пронаводная dx(x)/dx есть предел отношения ' ~ , можно
на основании G.5) внестк операцию функционального дифференцировании
под знак d/dx, после чего использовачь G.8):
Для второго слагаемоги в S[x], используя G.7) и G.8), получаем
ЗАДАЧИ
В результате
= - т IJ 4?± 8 (т- О Л- JI" (х W) 8 (т- ОЛ,
откуда
gg—
Принцип наименьшего действия , ,.]=0 Дзет уравнение движения т*=—V'(x).
15. Найти j для функционала
8*@
Ответ.
&S[x] = dL d dL
т. е. вариационная производная представляет собой левую часть уравнения
Эйлера—Лагранжа.
Для получения этого результата следует использовать формулы G.5)—¦
G.8), подобно тому как это сделано в предыдущей задаче.
16. Вывести формулу для tyn(Xi, xa, х3), аналогичную формуле G-17) для
Ответ. _
*а (xi, х2, х,) = <1 (х,) I (х,) | (х,)>-|
-i(x.,:
17. Исходя из выражений G.20) для центральных моментов гауссова слу-
чайного поля 5 (х), получить характеристический функционал для флуктуа-
ции 1(х).
Решение. Согласно G.14) имеем
Ф|[«] = 1 +?Й Г <1 (х,).. .f (x
причем, в силу G.20), в этой сумме присутствуют только члены с &^2/тг:
Используя теперь вторую формулу G.20), получаем
SS ОВЩИВ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ !ГЛ. 1
Интеграл кратности Bм) распадается на произведение т двукратных интег-
ралов, отличающихся друг от друга лишь обозначением переменных интегри-
рования. Каждый из двукратных интегралов имеет вид
/= $ $ <|(х')I(х")> и (х') и (х") <Ы dx".
Следовательно, каждый из членов внутренней суммы равен /м, а так как
сумма содержит всего 12т—1I1 членов, функционал Ф| [и] равен
или, поскольку Bm)! = Bm)!!Bm—!)H = 2«/nl Bm— I)!!,
Таким образом,
Ф| [«] = ехр (-1/2
Очевидно, эта формула является частным случаем G.18), отвечающим ну-
левому среднему значению, как это и должно было получиться дли 1=1—?,
поскольку <?> =¦ 0. Тем самым доказана эквивалентность определений гауссова
случайного поля прн помощи равенств G.20) и при помощи характеристи-
ческого функционала G.18).
18. Найти характеристический функционал пуассоновского случайного
поля {7.Щ.
Рье ш е н и е. По определению пуассоновского поля
Ф М = ({(ехР | l J dx ф) 2/bS (»-»*)})л).)я-
где каждая изуг ловых скобок с индексом внизу означает усреднение по
соответствующим случайным величинам. Очевидно,
Ф [«] = (((Дехр [1Ак
Выполним усреднение по Ак. Так как <ехр{(.4А>.}>^=*(>.), где хA) — ха-
рактеристическая функция для Ак, находим
Далее произведем усреднение по х^. Оно сводится к интегрированию каждого
сомножителя по xs с весом V~l по области V:
С S '<х~х^ и W dx)
ЗАДАЧИ 53
фбов здесь выражение в кэадратиых скобках через а. Последнее усред-
вение (по распределению Пуассоиа для т) дает
Таким образом, получаем
Ф[«] = ехр ( т [V-1 [ х([ g(x~ х')к(х)**Л dx' — 1 |) ,
что, в силу тождества
,-v-j,.*.
можно записать в виде
Вводя v=m/y—средиее число случайных точек в единице объема, приходим
К формуле G.22).
19. Исходя из формулы G.22), получить кумулянтные функции пуассо-
ковского случайного поля.
Решение. Имеем
Подстановка разложения характеристической функции
дает
т
?^ J[ Jg (х-х-) и (х)
Запишем А-ю степень интеграла в виде А-кратиого интеграла и изменим
рядок интегрирования по х их; (/ = 1,2, ..., А):
=2XT
Сравнивая это выражение с G.15). получаем, что
54 ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ 1ГЛ. 1
_ 20. Показать, что если А имеет гауссово распределение вероятностей и
/) = 0, то при v—>», А2—> <) и чА~% = const пуассоновское случайное поле
стремится к гауссову. Показать, что аналогичный результат можно полу-
чить, если считать, что А имеет плотность вероятностей ш(Л) = BЛо)Х
Хехр {— | А |/Л0}, т. е. нормальность распределения вероятностей для ампли-
туд несущественна.
Указание. Воспользоваться формулой G.23) для кумулянтов пуассо-
новского случайного поля.
21. Исходя из G.27), получить формулу для вычисления среднего значе-
ния от произведения пуассоновского случайного поля |(дг) на функционал
Решение. Согласно G.22)
6 [и] = v $ [х ( $ g(х"-х')«(х-) dx") -1 ] dx'.
Действуя на это равенство оператором —т—г— , найдем
О [х, и] = у j dx' x' ( J g(x'-x') и (х") dx"'\ g(x-x').
Но
х (Я,) = С е'м ш (A) dA, 4- х' (>.) = Г eiXAw (A) A dA.
J l J
1 С
Полагая X. — — \ dx* g (x*—x') „ .. , получаем
В результате формула G.27), с учетом операторной записи функционального
ряда Тейлора G.10), принимает вид
22. Пусть .Х;(х, г)—детерминированные функции, fi(x, t)—случайные
гауссовы функции (п+1) переменных (х, t), причем
<Л> = 0, </((». ОЫ*'. <')> = 2f,*(x, x', О* ('-О- (•)
Пусть функции |( @ подчинены системе динамических уравнений
^=Х.-E@. 0+Ы& @.0 B)
с начальным условием ?('@) = |(.
Вывести дифференциальное уравнение для плотности вероятностей ш(х, t)sss
^<л(К0—х)> решения уравнений B).
Решение. Продифференцируем w(x, <) по t:
и подставим сюда dli(t)fdt нз уравнений B):
ЗАДАЧИ 55
Последнее выражение — результат вынесения ^— [за скобку и за знак сред*
него, поскольку единственный сомножитель, зависящий от х,— это дельта.
функция. Используя равенство
получаем
где мы вынесли за знак среднего неслучайный множитель Х[ (х, t). Так как
<6 F@—х)> = ю(х, t), получаем уравнение
где
Q,(x. t)=*<tt(x, ЦЦЦ{)-х)>. D)
Уравнение C) не является замкнутым, так как кроме искомой функции w
в него входят еще неизвестные функции Q,-. Далькейшая задача состоит в том,
чтобы выразить Q; через ш. Используем для этого .формулу Фуруцу—Нови-
кова G.33), которая в нашем случае и с учетом A) имеет вид
</.•(*. OR Ш>=</<(*. ')><«> Ь
Для того чтобы получить Qi (х, t), надо, согласно D), положить R [/] =
= 6(| (г)—х). Это эполне законное равенство, поскольку 5(()i будучи реше-
нием системы уравнений B), является функционалом от /;.
Чб айти 4Я/6/ б
ур () фу /;
Чтобы найти <4Я/6/й>, обратимся снова к уравнениям B). Проинтегри-
ровав их по t, находим
t
F)
Отсюда видно, что %j(l) зависит от значений /*(т), принимаемых только на
интервале OaSt«sr Поэтому
°. если f<0«mf>t. G)
Формула G) показывает, что решения системы уравнений B) удовлетворяют
принципу динамической причинности. Запишем F) в виде
6/@ = 6?+ $ Л $ Л6 (? (т)-х) U,-(»
56
ОБЩИЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ПОЛЯХ
[ГЛ. I
н применим к »тим выражениям оператор 6/о/у(х', г'), где 0 < г* < t:
Первое слагаемое в фигурной скобке проинтегрируем по частям. Во втором
же слагаемой учтем, что, согласно G.32),
и используем при интегрировании наличие этих дельта-функций. В результате
Но, в силу условия причинности G), At /*' >|1|~^ "Р" х ^ ''' чт0 поаволявт
заменить нижний предел интеграла по т иа V:
Тогда переход к пределу при t'—>t обращает интеграл в нуль и мы полу-
чаем точную формулу
^O. (8)
являющуюся следствием динамических уравнений B).
Вернемся к формуле (б) для Qi- Так как при i' > / в силу G) имеем
(т7-\=0, интегрирование по V в E) происходит в пределах @, /). При выпол-
t
ненни интегрирования по f следует учесть, что \ 6(t—(')«' = !/,, поскольку
фигурирующая здесь дельта-фуикция предполагается пределом четной корре-
ляционной функции. Поэтому
-,
Так как R If] — б A (г) — х), имеем
*'. 0
S6 (I @-х)
*/*(*'. О"
ЗАДАЧИ 57
Усредняя это равенство, получаем формулу
с учетом которой выражение (9) принимает вид
Записывая ннтегранд в виде
-f>* (х, х', 0д~ [и (х, 0 в (х-х')]
4г ^^ '>ш <х- г» 6 С-*''1 +aff*(x;X-<) to (x, t) 6 (х-х'),
получаем
Таким образом, функция Q/ (х, () выражена через искомую плотность
вероятностей го (х, (), после чего C) становится вамкнутым уравнением:
dw(x, t) , dAjjx, t)w__d*Ftk{x, x, t)w
где введено обозначение
А,(х, t) =
Глава II
ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ
СЛУЧАЙНЫХ ВОЛНОВЫХ ПОЛЕЙ
§ 8. Основные типы статистических полковых задач
Среди разнообразных случайных полей, с которыми имеет
дело статистическая радиофизика, волновые поля занимают цент-
ральное место. Мы тоже сосредоточим внимание на волновых
(в первую очередь электромагнитных) полях и ограничимся при
этом только линейными и неквантовыми, задачами'). Весьма
широкий класс таких задач можно сформулировать следующим
образом.
Пусть распространение волн той или иной физической при-
роды (электромагнитных, упругих, поверхностных и т. д.) опи-
сывается линейным пространственно-временным оператором L
(обычно дифференциальным, реже—интегро-дифференциальным),
так что волновое поле «^удовлетворяет уравнению
?и = 9, (8.1)
где функция q (t, г) описывает источники волн. Поля и и q могут
быть и многокомпонентными (в частности, векторными), и тогда
L—операторная матрица (в частности, тензор). Во многих зада-
чах пространственная область, в которой рассматривается поле
и, выделенная некоторой поверхностью 50, не содержит источ-
]) Укажем некоторые обзоры н монографии по нелинейным волновым
задачам и по квантовой статистике излучения. Статистическим явлениям
в нелинейной оптике посвяшены книга [1] и обзор [2]. Обширные исследо-
вания ведутся по теории слабой турбулентности — явлению, которое проис-
ходит во многих ситуациях, в том числе в случае волн в плазме [3, 4J, на
поверхности жидкости [4, 5], в активных распределенных системах и т. д.
Статистические вопросы нелинейной акустики рассмотрены в книге [45].
Вопросы квантовых флуктуации электромагнитного поля, ставшие особенно
актуальными в связи с развитием лазерной техники, освещены в работах
[6-10].
S8J ОСНОВНЫЕ ТИПЫ СТАТИСТИЧЕСКИХ ЗАДАЧ 59
ников (д =-0), а задано первичное волновое поле и„, приходящее
в эту область извне. Тогда уравнение (8.1) однородно:
?,и = 0, (8.2)
но на So заданы значения первичного поля (илн его производ-
ных), например:
v^uo(t,T)\r,s.. (8.3)
(Обычно в этом случае говорят, что на So заданы «виртуаль-
ные» источники поля.) Искомым является здесь рассеянное или
дифракционное поле, т. е. это задачи теории дифракции.
При наличии внутри поверхности So границ раздела между
разными средами или телами (поверхности раздела S) поле и
должно удовлетворять еще определенным граничным условиям.
Если поверхность So не замкнута или же охватывает все про-
странство, так что волны от реальных источников, расположен-
ных в конечной области, могут уходить в бесконечность, то
должны также выполняться известные условия излучения (на
достаточно больших расстояниях от источников должны суще-
ствовать только убегающие волны).
В задачах прикладного характера часто представляет инте-
рес измерение излученного или дифракцнонного поля—для полу-
чения информации об источниках поля, о рассеивающих телах
или о среде, в которой распространяются волны. Тогда в опи-
санную схему может быть включен еще приемник излучения1),
а также разного рода помехи как внешнего (по отношению
к приемнику), так и внутреннего происхождения. Отклик прием-
ника w будет зависеть и от измеряемого поля и, и от помех Jj:
w=w(u, I), (8.4)
где а)— в общем случае нелинейный оператор.
Все, что было сказано в ч. I, § 33 об обыкновенных стохас-
тических дифференциальных уравнениях, теперь, когда мы рас-
сматриваем случайные поля, переносится на уравнения в част-
ных производных. Статистические волновые задачи ставятся
теми же уравнениями и условиями, что и динамические, но
теперь это будут стохастические уравнения и условия, т. е.
уравнения и условия для отдельных реализаций случайного
поля и. Другими словами, фигурирующие в задаче параметры,
функции н операторы теперь случайны (все или их часть) и,
соответственно, заданы своими распределениями вероятностей.
1) Под приемником подразумевается все измерительное устройство в це-
лом, например 'радиоантенна вместе с усилительным трактом н регистрирую-
щим устройством или фотодетектор с измерительными приборами н т. п.
60 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ 1ГЛ. II
Поэтому гораздо большее разнообразие возможностей для про-
странственно-временных полей (по сравнению с процессами во
времени) в равной мере затрагивает как динамические, так и
статистические задачи.
В соответствии с описанной постановкой динамической вол-
новой задачи случайными могут быть
1) источники поля (реальные или виртуальные, так что можно
различать заданную «статистику источников» q и «статистику
первичного поля» v);
2) свойства среди (задана «статистика среды», ачзначит, опе-
ратора L);
3) форма и положение границ раздела S (задана «статистика
границ»);
4) условия приема и регистрации волн (заданы «статистика
приемника»—оператора w и «статистика помех» \).
К этим четырем основным статистическим схемам, которые
мы назовем первичными, фактически сводится постановка подав-
ляющего большинства задач статистической волновой теории.
Конечно, возможны задачи и смешанного типа, например о теп-
ловом излучении в случайно-неоднородной среде [11], но пока
таких задач рассмотрено немного (краткий их обзор приве-
ден в [12]).
Если бы мы располагали точным решением динамической
задачи, например некоторым интегральным представлением иско-
мого поля и в виде
u = Gq, (8.5)
где Gq= L-*q—решение неоднородного уравнения (8.1), записан-
ное, скажем, через функцию Грина, учитывающую все гранич-
ные и другие условия, то вычисление моментов поля свелось
бы к [усреднению произведений вида аA)мB) ... и (я) по сов-
местному распределению всех фигурирующих в задаче случай-
ных параметров и функций, характеризующих статистику источ-
ников, среды, граинц раздела н т. д. Но в реальных ситуациях
этот идеал осуществляется не часто, например, в задачах о воз-
буждении полей случайными источниками, которые рассматри-
ваются в дайной главе. Чаще же всего мы не умеем находить
точное решение прн любых детерминированных функциях и, тем
самым, прн произвольных реализациях всех случайных величин
и функций, в силу чего приходится уже на этапе решения дина-
мической задачи обращаться к разного рода приближенным мето-
дам. Зги разнообразные методы н приемы приурочены в конк-
ретным особенностям задачи.
Флуктуации случайных параметров и функций могут быть
(в каких-то характерных масштабах) большими и малыми, плав-
§8] ОСНОВНЫЕ ТИПЫ СТАТИСТИЧЕСКИХ ЗАДАЧ g|
ными, медленными и, наоборот, резкими, быстрыми; корреляция
может быть сильной, «далекой», или же слабой, «короткой», и
т. п. Эти различия требуют использования разных приближен-
ных подходов и приводят к многочисленным вторичным статис-
тическим схемам, связанным уже с теми или иными приближен-
ными методами решения.
Следует заметить, что во многих случаях, в особенности когда
нас интересуют только моменты поля, этап отыскания динами-
ческого решения (для последующего вычисления моментов) опу-
скается и речь идет о выводе уравнений и условий для самих
моментов (исходя из уравнений и условий для поля и). Однако
и в такой постановке практически нельзя обойтись без макси-
мально возможного упрощения исходных уравнений для и, зара-
нее учитывающего особенности флуктуации и характер детерми-
нированных функций.
Выделенные выше четыре первичные статистические схемы
отражают лишь фактически часто встречающееся разделение пара-
метров и функций, входящих в условия задачи, на детермини-
рованные и случайные. Остановимся коротко на этих схемах и
укажем некоторые примеры относящихся к ним задач.
В схеме 1), если присутствуют реальные источники, мы имеем
дело с неоднородным уравнением (8.1), в котором статистически
задана правая часть q. Однородные граничные условия детермини-
рованы. Задач такого типа много и в радиофизике, и в оптике,
и в акустике. Они охватывают, в частности, статистическую
теорию антенн и теорию тепловых флуктуации в распределенных
системах.
С виртуальными случайными источниками мы сталкиваемся,
очевидно, во всех задачах о дифракции случайных (иначе—час-
тично когерентных) полей1), когда однородное уравнение (8.2)
н все необходимые условия детерминированы, за исключением
случайного первичного поля и„. Такие задачи типичны прежде
всего для оптики (формирование оптического и голографического
изображений, действие интерферометров и др.), но с ними при-
ходится иметь дело н в радиодиапазоке (в частности, в радиоастро-
номии), и при дифракции рентгеновских волн.
Задачи типа 1) мы рассмотрим в данной главе, но тепловые
флуктуации в распределенных системах, ввиду важности и спе-
цифичности этого круга вопросов, мы выделяем в самостоятель-
ную (следующую) главу.
Схема 2) охватывает проблему распространения и дифракции
волн в случайно-неоднородных средах (случайный оператор L). Эти
') Применительно к волновым гшлям термины «случайный» я «частично
когерентный» равнозначны.
62 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ [ГЛ. '
вопросы представляют большой интерес для радиосвязи, лазер
ной связи, гидроакустики, радиоастрономии, диагностики плазм!
и т. п., и им уделена поэтому половина данной части книги.
К схеме 3) относятся волновые задачи при наличии тел
имеющих случайную форму или занимающих случайное положе
ние. Речь может идти, в частности, о граничных поверхностя:
со множеством случайных неровностей (так1 называемые шеро
ховатые или статистически неровные поверхности). Различны'
методы расчета^ рассеяния волн на таких поверхностях рассмот
реиы в гл. IX.
В задачах о телах, занимающих случайное положение в про
странстве, речь может идти о рассеянии как на одном ил]
немногих телах, так и на очень большой совокупности дискрет
ных вкраплений (осадки, туман, аэрозоли и т. п.). Последня]
весьма общая задача требует, вообще говоря, учета многократ
ного рассеяния. Мы ограничимся ее рассмотрением лишь в при
ближении однократного рассеяния (§ 31).
Наконец, схема 4) охватывает многочисленные задачи прием;
и обработки информации о волновых полях при наличии помех
Если статистические свойства поля и, помех % н оператора w, опи
сывающего приемник, известны, то, в соответствии с (8.4), в прин
цнпе можно рассчитать статистические характеристики отклик;
приемника w.
Однако более ^важным и вместе с тем более сложным явля
ется другой вопрос—о выборе оптимального (в каком-то опре
деленном смысле) способа приема при наличии помех, т. е. воп
рос о нахождении оптимального оператора w. Примером задач:
такого типа может служить проблема восстановления форм!
объекта по его изображению, представляющая первостепенны!
интерес для оптики, радиоастрономии, радиолокации, гидроакус
тики и т. д. Эта проблема оптимального приема случайных поле]
требует привлечения идей и методов теории информации — воз
можно, даже в большей степени, чем вопросы обработки слу
чайных процессов. Но, как и в ч. I, мы не будем углублятьс:
в эти проблемы, поскольку они ближе по своему характер;
к «радиоматематике», а не к радиофизике. Ряд вопросов опти
мального приема и пространственной фильтрации рассматри
вается в работах [13—20].
§ 9. Случайные волиы в неограниченной однородной среде
Задачи возбуждения полей случайными источниками (реаль
ными или виртуальными), отнесенные нами к статнстнческо
схеме 1), принадлежат к тем весьма немногочисленным пробле
мам статистической волновой теории, которые допускают, и
jgj СЛУЧАЙНЫЕ ВОЛНЫ В ОДНОРОДНОЙ СРЕДЕ дЗ
существу, универсальный подход. Это обусловлено тем, что
поле и связано с источниками линейным детерминированным
оператором, который, в принципе, может быть обращен.
При возбуждении поля реальными источниками в силу (8.5)
любые моменты поля могут быть получены усреднением произ-
ведений вида u(l)uB) ... и(я) лишь по ансамблю случайных
источников q. В частности, для двух низших моментов имеем
= G1GJ<G1G,*>. (9-1)
В случае виртуальных источников, когда в соответствии
с (8.3) заданы значения v первичного поля (или его производ-
ных) на некоторой поверхности So, а искомое поле выражается
через v при помощи линейного детерминированного оператора &'¦
u = &v, (9.2)
искомые моменты и связаны с известными моментами о линей-
ными соотношениями, подобными (9.1):
<и> = ?<»>, <u1ui> = ^1S>t<v1v'2>< ... (9.3)
Соотношения вида (9.1) или (9.3), в принципе, дают полное
решение статистических задач схемы 1), поскольку совокуп-
ность всех статистических моментов однозначно определяет всю
совокупность я-мерных плотностей вероятностей случайного
поля. Однако эта формально простая процедура фактически
реализуема крайне редко. Удобные для физического анализа
выражения для моментов поля и в большинстве случаев удается
получать только для низших моментов и лишь при использо-
вании тех или иных приближений для обратных операторов
G или S*. Получение же плотности вероятностей поля осущест-
вимо обычно лишь при условиях, когда применима центральная
предельная теорема.
С необходимостью прибегать к различным приближениям мы
сталкиваемся даже в простейшем 'случае скалярного волнового
поля в однородной безграничной среде, когда мы располагаем
сравнительно простыми точными выражениями для операторов
G и 9*. Приведем относящиеся к этому случаю и необходимые
для дальнейшего динамические соотношения и выясним на при-
мере скалярного поля ряд свойств случайных волновых полей.
В последующих параграфах мы обратимся к конкретным радио,
физическим задачам, относящимся к схеме 1).
В однородной и стационарной среде без дисперсии и погло-
щения скалярное поле и удовлетворяет волновому уравнению
(t,T)~.q(t, r), (9.4)
64 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ [ГЛ. И
где с—скорость распространения волн, a q—поле случайных
источников. Решение уравнения (9.4), удовлетворяющее усло-
виям излучения на бесконечности, имеет, как известно, вид
«со—^Г""**0*''- (9-5)
где /J = |r—г'|. Это частный случай линейной, связи (8.5) поля
с источниками.
Во многих задачах удобнее рассматривать ие само случай-
ное поле и (t, г), а его спектральную амплитуду
ОБ
«(»,г) = ^г J u(t,t)^'dt, (9.6)
- ОБ
которая, в силу (9.4), удовлетворяет уравнению
Ди(<в, г) +Jfe3w (со, г) = ?Кг), k = <s>/c, (9.7)
где g (to, г)—спектральная амплитуда q(t, r). Для спектральных
амплитуд решение (9.5) принимает вид
Здесь введена функция Грина для неограниченной однородной
среды
O(r,r') = -^-^, R = |r-r'|, (9.9)
удовлетворяющая уравнению
G = 6(r—г').
При помощи (9.8) легко записать выражения для всех моментов
поля.
Если источники сосредоточены в ограниченной области, ска-
жем в пределах сферы радиуса а, а нас интересует поле и
в дальней (фраунгоферовой) зоне распределения источников, то
формулы (9.6) и (9.8) упрощаются, так как можно воспользо-
ваться приближенным выражением функции Грина. Пусть начало
координат помещено в центр области, занятой источниками.
Тогда при r^>toJ расстояние i? = |r—г'| в формуле (9.9) можно
приближенно заменить на г—(пг') в показателе экспоненты и
на г в знаменателе, что и приводит к фрауигоферову прибли-
жению. В этом приближении (9.8) принимает вид
и(<о,г)«—-^ J<?(<», r')e-ik"r'd>r', r^>ka\ (9.10)
где п = г/г единичный вектор в направлении на точку наблю-
дения.
I g] СЛУЧАЙНЫЕ ВОЛНЫ Е ОДНОРОДНОЙ СРЕДЕ 65
Приведем теперь динамические соотношения для того случая,
когда заданы виртуальные источники. Будем исходить из фор-
мулы Грина, которая связывает спектральную амплитуду поля
й((о, г) внутри области, ограниченной поверхностью So, со спект-
ральной амплитудой граничного поля v(<s>, r'):
].. (9.11,
Здесь /? = |г—г'|—расстояние от точки наблюдения до точки
г', лежащей на поверхности So, по которой ведется интегриро-
вание, a djdN означает дифференцирование в направлении внеш-
ней нормали N к So. Граничные значения и(ш, г') и dv(a>, r')/cW,
как известно, должны быть заданы математически непротиворе-
чивым образом. Поэтому двучленная формула Грииа (9.11) может
быть использована лишь в тех случаях, когда из каких-либо
дополнительных соображений вытекает связь (точная или при-
ближенная) между граничным полем v и его нормальной произ-
водной dv/dN.
Особым является случай, когда поверхностью So служит
плоскость, замкнутая полусферой бесконечно большого радиуса.
В этом случае, которым мы и ограничимся, двучленная фор-
мула (9.11) сводится к одночленной.
Если на плоскости г=0 задано само поле и(ш, р) ^ ы (о>, г) |^=0,
где р = (х, у) — двумерный вектор, то интеграл по бесконечно
удаленной сфере обращается в нуль, и тогда в полупростран-
стве г > О
в(в,г)=и(Ш,р,г) = --^ J t»(a>,p')^-(^)dy, (9.12)
Если же на плоскости 2 = 0 задана нормальная производная
dv(a>, р)/дг = ди (to, т)/дг |г=0, то
Таким образом, в случае плоской границы г —0 достаточно
задания на So либо самого поля и, либо его нормальной произ-
водной ди/дг.
Другой метод расчета полей в полупространстве г > 0 вос-
ходит к Релею и основан на разложении полей по плос-
ким волнам. Представим граничное поле v (<а, р) двумерным
3 С. И. Рытов в др. ч. Ц
66 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ 1ГЛ. II
интегралом Фурье:
со
v((o, р)= \ v(u>, х) exp (ixp) <Рх, (9.14)
— »
где к = (х„ х„)—двумерный волновой вектор, а а(<в, х)—оме-
амплитуда граничного поля, связанная с v (<в, р) обратным пре-
образованием Фурье:
»(«. Х)=4Н5- J и(ю> Р)ехр{—i«p)dap.
—«>
В полупространстве г > 0 каждая пространственная гармо-
ника граничного поля v (ю, х) exp (ixp) порождает плоскую соб-
ственную волну о(ш, х) exp (ixp-И'Р2) (напомним, что множитель
e~iat опущен), которая удовлетворяет волновому уравнению при
условии, что
Таким образом, в случае волнового уравнения для однородной
и изотропной среды дисперсионная поверхность (см. § 6) пред-
ставляет собой в четырехмерном пространстве (to, k) трехмерный
конус с осью по и и вершиной в начале координат. В соответ-
ствии с этим дисперсионным уравнением в свободной от источ-
ников области г > 0 возможны при заданном х собственные
волны двух типов—в зависимости от того, вещественна или
мнима г-компоиента р волнового вектора к:
(9.15)
При к < k компонента р вещественна и мы имеем бегущие
волны. При х > k, когда период осцилляции на границе 2я/%
меньше длины волны X = 2n/k, соответствующей частоте ш, ком-
понента р мнима и получаются неоднородные волны. Они экспо-
ненциально ослабевают с удалением от границы z = 0. Практи-
чески уже при z'Si'K остаются только бегущие волны.
Результирующее волновое поле и (<в, г) = и(<в, р, г), удовлет-
воряющее граничному условию «(со, г)|г=0 ==о(<о, р), выражается
суперпозицией плоских волн обоих типов:
и (at, р, г)= J »(<o, x)exp(txp \-ipz)dht. (9.16)
Аналогичное представление поля нетрудно записать ихв том
случае, когда на плоскости 2 = 0 задана производная по нор-
мали duldz.
jj] СЛУЧАЙНЫЕ ВОЛНЫ В ОДНОРОДНОЙ СРЕДЕ 67
Формула Грина (9.12) и разложение по плоским волнам (9.16),
разумеется, эквивалентны друг другу. В дальнейшем мы будем
пользоваться той из них, которая быстрее ведет к окончатель-
ному результату. Любая из них позволяет выразить моменты
и(а>, г) через моменты и(ш, р).
При вычислении моментов поля при помощи приведенных
выше формул часто приходится рассматривать те или иные част-
ные случаи. Перечислим наиболее существенные из них. При
l т.е. в волновой зоне, для ядра в формуле (9.12) имеем
При выполнении неравенств |р— p'[<^z и fc|p— р'|4<^г3
справедливо так называемое френелевское приближение, в кото-
ром R = V z2 + (p — р'J заменяется на г + (р—р'J/2г в показа-
теле экспоненты и на г в знаменателе предыдущей формулы;
при этом формула Грина (9.12) принимает вид
ОБ
в(ш, Р,г)=|? J о(«, P')exp(ift^el2)dy. (9.17)
— со
Наконец, в зоне Фраунгофера, z^>ka*, где а—-радиус области,
в которой граничное поле и ((о, р) отлнчно от нуля, имеем
-№&!р]#р'. (9.18)
Обратимся теперь к некоторым свойствам моментов и спект-
ров волновых полей Статистические моменты волновых случай-
ных полей часто называют функциями когерентности, так как
соответствующие коэффициенты корреляции служат количест-
венной мерой когерентности этих полей (ч. I, §§ 47 и 48). Тер-
мины «время когерентности», «длина когерентности», «степень
когерентности» являются в отношении волновых полей синони-
мами «времени корреляции», «радиуса корреляции», «коэффи-
циента корреляции». В связи с этим мы предпочитаем и в этой
части книги говорить о теории случайных волн, а не о «теории
когерентности», рассматривая последнюю просто как одао из
приложений общей теории случайных полей. Однако мы не будем
избегать и терминов «функция когерентности» или «степень
когерентности», которые уже прочно вошли в физический обиход.
Смешанный момент волнового поля u{t,t) порядка т-\-п
(функция когерентности порядка т-\-п) определяется соотноше-
нием вида B.30) и вместо Вя- „ обычно обозначается Гя, „. Корре-
ляционная теория случайных волн ограничивается рассмотрением
68 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ [ГЛ. II
моментов лишь первого и второго порядков: среднего поля <и>
(функции когерентности первого порядка Г,=э<к>) и_двух сме-
шанных моментов второго порядка, называемых первой и второй
функциями когерентности второго порядка:
B)>-=ГA,2),
B)>^ГA,2). { Щ
Последние связаны с первой и второй функциями корреляции
поля формулами
(920)
фA, 2) = <и A)иB)> = ГA, 2)>-<и(!)><« B)>
(как обычно, здесь ы = и —<«>).
Для зависимости волновых полей от времени мы примем
комплексное представление в виде аналитического сигнала*)
да
н(/, г) = $«(<в, г)е-""'Ао, (9.21)
о
где спектральная амплитуда и (<в, г) тождественно равна нулю
для отрицательных частот, а для oi^O равна удвоенной спект-
ральной плотности исходного вещественного поля «,.(/, г)=
=Rett(/, г).
Если поле и (i, r) является как функция / аналитическим
сигналом и стационарно, то среднее значение поля <«> и его
второй смешанный момент Г равны нулю (ч. I, § 38).
Без предположения об аналитическом сигнале среднее зна-
чение стационарного поля может быть отличным от нуля и
представляет собой некоторую функцию mtHto от г, удовлет-
воряющую уравнению Лапласа Д«(г)=О. Так как такие стати-
ческие детерминированные поля нас не интересуют, можно и
в этом случае рассматривать только флуктуации и = и,— и, т. е.
считать, что п = 0. Что касается нестационарных и, в частности,
монохроматических полей (—е~'ш'), то для них среднее поле и
Г, вообще говоря, отличны от нуля.
Энергетические величины (интенсивность, плотность энергии,
плотность ее потока) квадратичны по полю, в силу чего их
средние значения можно выразить через статистические моменты
первого и второго порядков (ч. 1, § 47 и задача 1).
') Еще раз напомним, что при разложении в интеграл Фурье по t мы
берем здесь и далее функцию е~'ш<, а не <?<ю', как в ч. I. Поэтому поле и
как функция I аналитично теперь не в верхней, а в нижней полуплоскости
комплексного премени t.
g) СЛУЧАЙНЫЕ ВОЛНЫ 6 ОДНОРОДНОЙ СРЕДИ 69
Из высших моментов наибольший интерес представляет момент
аетвертого порядка
Г,,, A, 2, 3, 4) = <и (!) и B) и» C) и* D)>, (9.22)
герез который выражается, в частности, корреляционная функ-
ция флуктуации интенсивности комплексного поля /=|«|2:
г|>,A,2) = <7AOB)> = Г2,аA,2; 2, 1)-7A) ГB), (9.23)
причем /A) = <|иA)|*> = ГA, 1). Если поле и нормально, то
все высшие моменты выражаются через первый (и) и вторые
(Г и Г) моменты. Функция корреляции интенсивности для этого
случая приведена (в несколько иных обозначениях) в задаче 12
к гл. I.
Выражения для моментов поля мы получали выше, исполь-
зуя динамические решения для и. Как уже было отмечено,
существует и другой способ нахождения моментов — из уравне-
ний, которым подчиняются сами статистические моменты. В рас-
сматриваемой задаче о возбуждении полей реальными источни-
ками, которая в общем случае описывается уравнением (8.1)
С детерминированным оператором L и с детерминированными
граничными условиями, уравнения для вторых моментов легко
получить простым перемножением левых н правых частей (8.1),
взятых в разных пространственно-временных точках. Так, вто-
рой момент ГA,2) = <иA)и*B)> удовлетворяет уравнению
lll 2)>, (9.24)
которое становится однородным в области, свободной от источ-
ников.
В рамках схемы 1), когда динамическое решение задачи для поля
и известно, находить моменты из уравнений типа (9.24) обычно
гораздо менее удобно, чем по формулам типа (9.1) или (9.3).
Волновые уравнения для моментов представляют здесь интерес,
пожалуй, лишь в том отношении, что из них очевидны волно-
вые свойства самих моментов и, соответственно, можно говорить
о распространении и дифракции этих моментов почти в том же
смысле, что и для поля иг). Одно из важных волновых свойств
статистических моментов поля и состоит в том, что их значения
на некоторой поверхности So определяют поведение моментов
во всем объеме, ограниченном поверхностью So, подобно тому
как это имеет место для самого поля.
1) Однако в тех случаях, когда мы не располагаем решением динамиче-
ской задачи, уравнения для моментов, получаемые из уравнений для и,
приобретают самостоятельную ценность (гл. VI—VIII).
70 излучение и Дифракция случайных Полей [гл. и
Как уже было отмечено в § 6, в рассматриваемом случае волно-
вого уравнения для однородной и стационарной среды дисперсион-
ная гиперповерхность представляет собой конус х* = <ог/с! э k* или
|»e| = fe. Поэтому спектральная плотность G((o,k) в разложении
Фурье корреляционной .функции однородного и стационарного
поля F.3) содержит множитель 6A*1—ft):
0(a.1x) = /(<B,nN(|x|-fc). (9.25)
где /(to, п)—функция частоты со и направления п=х/%.
В коэффициенте при дельта-функции можно выделить мно-
житель k~*:
G (со, *) =. У (to, n) fe-?8 (к — k). (9.26)
Величина 3 (со, п) носит название лучевой интенсивности или
яркости и играет большую роль в теории переноса излучения
(гл. VIII). Связь этой величины с функцией корреляции можно
установить, подставив (9.26) в F.3) и положив d?K = xs dv,do (n)
(Л>(п)—элемент телесного угла). Выполнив интегрирование пох,
получаем искомое соотношение (r = Tj— г4> t = t±—12):
УA,т) = Цэ (со, n) ft-s6 (х—k) exp [i (да — a>0] *2 ^ do (n) dco =
= 1 d(o§ 3 (to, n)exp[i(Jisnr —(oO)rfo(n). (9.27)
о
При г — 0 и t — 0 эта формула дает дисперсию поля
се
о? = <| м !*>=? @, 0) = J da § 3 (a>, n) do (n). (9.28)
о
Из последнего выражения видно, что лучевая интенсивность
3 (со, п) описывает распределение энергии по (положительным)
частотам и по углам, т. е. представляет собой частотно-угловой
спектр поля. В частности, изотропному полю отвечает лучевая
иитеисивность, ие зависящая от углов (общее выражение для
функции корреляции в этом случае дано в задаче 2). Заметим,
что угловым спектром часто называют также двумерное разло-
жение функции корреляции в интеграл Фурье:
F (to; «х, г) =щг J i|) (<в; р, г) ехр (— Ыхр) d?p, hl = (хх, ку).
(9.29)
Как показано в задаче 4, при малой ширине углового спектра
величина F (<о; Хх, z) пропорциональна лучевой интеисивностк
(при г = 0 эти величины отличаются лишь множителем k~2).
j 10] ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ НА ХАОТИЧЕСКОМ ЭКРАНЕ 71
При помощи (9.27) можно оценить минимальный радиус кор-
реляции /„ свободного волнового поля. Пусть ю,^—максималь-
ная частота волн, еще заметно представленных в спектре Э (<*, п).
В силу (9.27) радиус корреляции поля 1и можно оценить из
условия ftmax (n, г) 251, что приводит к оценке
, > 1 ,
лтах
Иными словами, радиус корреляции случайного волнового поля
не может быть меньше минимальной длины волны, имеющейся
в спектре колебаний. Строго говоря, эта оценка относится
к случаю изотропного поля, когда лучевая интенсивность не
зависит от п. Оценки продольного и поперечного радиусов кор-
реляции поля для случая, когда его лучевая интенсивность
сосредоточена в узком конусе, даны в задаче 3.
Описанные выше свойства статистических моментов и спект-
ральных плотностей характерны не только для скалярных, но
и для векторных случайных полей. Мы не будем приводить
здесь векторные аналоги рассмотренных выражений для полей
и их моментов, поскольку в принципе они не выходят за рамки
общих соотношений (9.1) и (9.3). Отметим только, что статисти-
ческие характеристики поляризации плоских квазимонохроматн-
ческих волн мы уже рассмотрели в ч. I, § 49. Введенная там
матрица поляризации характеризует статистическую связь раз-
ных компонент поля в одной и той же точке в один и тот же
момент времени (см. также [13, 14, 211 и [22]). Общий вид
корреляционной матрицы стационарного, однородного и изотроп-
ного поля приведен в задаче 6, а в задаче 5 указана связь
энергетических характеристик поля с корреляционной матрицей
поля и с матрицей лучевых интенсивностей.
§ 10. Дифракция плоской волны
на безграничном хаотическом экране
Первичное поле на границе рассматриваемой области может
флуктуировать как из-за флуктуации в его источниках (нахо-
дящихся вне данной области), так и в результате случайных возму-
щений, внесенных в первоначально детерминированную первичную
волну при ее распространении. Примером может служить прохож-
дение этой волны через случайно-неоднородную среду или слой
такой среды. Если толщина этого слоя достаточно мала, то его
можно рассматривать как бесконечно тонкий экран. Примени-
мость общих методов расчета поля в области, на границе кото-
рой S, задано случайное поле (§ 9), конечно, не связана с тем,
по каким причинам флуктуирует поле на границе. Существенно
лишь то, что статистика этих флуктуации известна,
72 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ ГГЛ. И
Начнем с простейшей задачи о прохождении плоской мо-
нохроматической волны через плоский безграничный хаотический
экран, следуя в основном работе [23]1).
1. Основные соотношения. Пусть монохроматическая
нолна ип(р, г)е~ш падает на безграничный экран, расположен-
ный в плоскости z — 0. Экран пространственно модулирует па-
дающую волну в соответствии со своей функцией пропускания
f (p) — комплексной функцией, модуль которой описывает ампли-
тудную модуляцию, а аргумент—фазовую. Граничное поле«(р),
т. е. поле непосредственно за экраном 2 = 0, есть
Для краткости мы опускаем множитель е~ш, а также аргумент ш
в спектральных амплитудах.
Если падающая волна плоская н распространяется по нор-
мали к экрану, то ц„(р, г) = е'*г, так что
у(р) = /(р) A0.2)
— поле на граничной плоскости 2 = 0 просто равно функции
пропускания, и, соответственно, статистика i>(p) в случае хао-
тического экрана та же, что у f(p). Формулы (9.12) и (9.16)
позволяют связать статистические моменты* поля и (г) = и (р, г)
за экраном (т. е. в области г > 0) с моментами граничного поля
о(р). Найдем первый и второй моменты поля и (г) в простей-
шем случае статистически однородного хаотического экрана,
для которого
</ (р)> . /, = const, о} = < | f |2> = < | /-/, |«> = const,
а корреляционная функция зависит только от разностей коор-
динат:
В силу A0.2) имеем
<v> = vo = fe, oj = oj, ФЛр' —p")=i|v(p' —p").
Для среднего поля за экраном по формуле (9.12) находим
2) В этой работе суммированы результаты и предшествующих исследова-
ний [24—26], относящихся преимущественно к прохождению радиоволн через
случайно-неоднородную ионосферу. Более полный список литературы по по-
следнему вопросу содержится в обзоре 127].
I it] ДИФРАКЦИЙ ПЛОСКОЙ ВОЛНЫ НА ХАОТИЧЕСКОМ ЭКРАНЕ 73
Интеграл легко вычисляется и равен —2л exp (ikz). Таким об-
разом, среднее поле за экраном—это плоская волна
н = иое«*. (Ю.З)
амплитуда которой «0 равна средней прозрачности /0.
Для нахождения функции корреляции воспользуемся выра-
жением (9.16), из которого следует, что
% (ft. гп Ра. га) = <» (ri) "* (Г*)> =
= $jj d'W&v," <u(x')«*(s*")>exp (Ы'р,,— ix"p2 + ip'z1—ip"zx), A0.4)
где p' и р" даются выражением (9.15) соответственно при х = и
и и = к". Но для однородного граничного поля
<5(х')в* (*")> = F, (х') S (х'-х"), A0.5)
где Fv(«.)—двумерная спектральная плотность, через которую
выражается корреляционная функция граничного поля:
A0.6)
— 00
Подставляя A0.5) в A0.4), находим
да
Ч>« = Ч>„ (Pi— Р„. ^, г,) = 5 F, (к) exp Wx (р^р.) + i (pzl~p*z,)\ d2K.
(Ю.7)
Таким образом, полг и (р, г) статистически однородно в плос-
костях г = const, что является следствием однородности' v (p) в
плоскости г = 0. Из сравнения A0.7) с двумерным спектраль-
ным представлением
*b(Pi—P*. ги гг)= ^о(и, Zl z^explixjpi — р2)]й!х A0.8)
следует, что пространственная спектральная плотность есть
FB (x; zlf г,) = Fv (и>ехр [i (pz1—p*z.i)\ =
exp[il/"fe«—хМг^—г,)]. x2<fe2,
Спектральные составляющие c«>t (неоднородности граничного
поля v{p) меньше длины волны) порождают в полупространстве
z>0 неоднородные волны, ослабевающие при удалении от эк-
рана по экспоненциальному закону. Для точек наблюдении г1
74 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ [ГЛ. II
и г2, удаленных от экрана уже на несколько длин волн (гь
приближенно
Р Ы-г 2i~/f.(*)«P['l'*r=*1(*i-*.)I. *'<fe' A09)
А,(и, г„ z2)~j ^ yC>k\ [ '
Подставляя A0.9) в A0.8), получаем для корреляционной
функции выражение
¦4>«(P.S)= S F,(и)ехр[«ир + iW—xaUd*x, (Ш10)
х</6
где p = Pj-—р2, ^=га — г2. Из A0.10) видно, что при zli|
случайное поле и (р, г) становится статистически однородным не
только в поперечных плоскостях г = const, но и в продольном
направлении г.
Используя формулу A0.10), рассмотрим частные случаи мел-
комасштабных и крупномасштабных флуктуации граничного
поля v (р).
В случае мелкомасштабных флуктуации, когда радиус кор-
реляции граничного поля lv мал по сравнению с длиной вол-
иы Л, т. е. при klv<<^\, можно принять, что спектральная плот-
ность Р„ (к) практически постоянна в круге и^?и приближен-
но равна Fv@)=sFe. Тогда из A0.10) получаем
Ф«(Р. ?) = F0 \ exp(ixp + ^)d4 ft^l. A0.11)
Поперечная функция корреляции, т. е. функция корреляции в
плоскости г = const, перпендикулярной к направлению распрост-
ранения, получается из A0.11) при ? = zi — га = 0:
где ij—функция Бесселя первого порядка. При увеличении р
отношение J1 (ftp)/p проходит в первый раз через нуль Лри
fep = 3,83, т. е. при р«0,61Х. Таким образом, уже на расстоя-
ниях в несколько X от экрана поперечный радиус корреляции
поля /j_ — величина порядка длины волны, т. е. значительно
больше радиуса корреляции lv в плоскости z = 0: /j_i^/
Из выражения для продольной функции корреляции
следует, что продольный радиус корреляции /„ тоже порядка
длины волны: /ц~Я,^>/„. Таким образом, в случае мелкомас-
штабных флуктуации на экране как поперечный, так н продоль-
J101 ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ НА ХАОТИЧЕСКОМ ЭКРАНЕ 75
ный радиусы корреляции поля при удалении от экрана увели-
чиваются и при г^>Х достигают значений порядка длины волны.
Вместе с тем происходит уменьшение дисперсии флуктуации,
т.е. их сглаживание. Действительно, при помощи A0.11) находим
Но
так что
В пределе при klv-*-0 (очень мелкие неоднородности экрана)
флуктуационное поле и вообще исчезает, так как столь мелкие
неоднородности порождают за экраном только неоднородные
(экспоненциально спадающие) волны.
Обратимся теперь к крупномасштабным неоднородностям
граничного поля (klv^>l). Такие флуктуации порождают бегу-
щие волны, в силу чего оии особенно важны в приложениях-.
Мы уделим им поэтому основное внимание.
В случае крупномасштабных флуктуации граничного поля
двумерный спектр Fv(%) сосредоточен в узком интервале зна-
чений к*гх,,~ \jlv<^k. Это позволяет разложить продольное
волновое число p = J/fe'—иа в формуле A0.10) в ряд Тейлора
по степеням иа и ограничиться двумя первыми членами:
Кроме того, не совершая заметной ошибки, можно раздвинуть
пределы интегрирования в A0.10) до ±оо, и тогда
*« (Р. О »в«В $ /=¦„(х) exp <ixp—iK«5/2ft) d*»t (ft/B>l). A0.12)
— OB
Нетрудно убедиться, что сделанные допущения эквивалентны
использованию для поля и (р, г) френелевского приближения
(9.17).
Положив в A0.12) ? = 0, получаем поперечную функцию кор-
реляции:
(см. A0.6)). Таким образом, поперечная функция корреляции
волнового поля и равна функции корреляции граничного поля
76 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ [ГЛ. I!
и не меняется при удалении от экрана. Тем самым и попереч-
ный радиус корреляции такой же, как в плоскости экрана:
Сохранение поперечной функции корреляции, отмеченное
впервые в работе [24], означает сохранение и дисперсии (о? = ст5),
и поперечной функции когерентности. В самом деле, учитывая
закон изменения среднего поля A0.3), имеем для волны, не ог-
раниченной в поперечной плоскости,
^Х (P. z) — <" (Ри г) и* (Рз> г)У = Ф-L (р) + и (Pi> г) "* (Рг< г)=
= itJ,,(p) + |o0|»=rB(p). A0.14)
Прн p = pt—ра = 0 отсюда вытекает постоянство средней интен-
сивности при удалении от экрана:
7„ (г) = <| и |!> = Г^ @) = <| v |8> = const.
Следует подчеркнуть, что сохранение <фх, Т± и / при удалении
от плоскости г — 0 не имеет места для статистически неоднород-
ного экрана и для иеплоской падающей волны, а более высокие
моменты поля не сохраняются даже для плоской волны и ста-
тистически однородного экрана.
Продольная функция корреляции ^„(^ получается из A0.12)
при р = 0:
Ф и @ = е"с \ F,, (x) e-iK'№ dlK.
- 00
Заметное уменьшение модуля функции ij)||(?) по сравнению с
максимальным значением фц@) = а? наступает при t,~2k/xl,
когда подынтегральная экспонента начинает осциллировать в
пределах интервала y.^.y.v^-\)Iv, в котором сосредоточен спектр
Fv(x). Отсюда можно оценить продольный радиус корреляции/„:
т. е. 1„ в klv^>l раз больше поперечного масштаба l±~lv.
Можно сказать, что продольная корреляция флуктуации поля
исчезает тогда, когда радиус первой зоны Френеля ]f% | z,—гх\ —
= V*-I?l для отрезка |g| = |гг—га| становится больше попереч-
ного радиуса корреляции: V Ы „ ~\v.
Проиллюстрируем сказанное о соотношении между продоль-
ным и поперечным масштабами корреляции примером, в котором
функция корреляции поля вычисляется точно. Пусть у поля на
экране корреляционная функция гауссова: ¦$„(?) = о\ехр\1— р*/2/у.
10] ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ НА ХАОТИЧЕСКОМ ЭКРАНЕ 77
Для нее
F,,(x) = aj; ехр[— кЧ
и простой расчет по формуле A0.12) дает
*« (Р. Е) = °2?е'*:ехр [- р»у/2?] = уф, (р) ехр {A -
Где -у=[1+'?/^'У"'- Характерный масштаб изменения |i])n| имеет
порядок /±~/в B поперечном направлении и fn~A/J|>^f в про-
дольном. Поверхности равных значений | 1|>„ | имеют при этом
форму овалоидов, сильно вытянутых вдоль оси г.
2. Прохождение плоской волны через фазовый
хаотический экран. Так называют прозрачный экран с
функцией пропускания /(p) = exp[(S(p)J, где S —вещественная
Случайная функция, т. е. экран модулирует только фазу, но
оставляет неизменной амплитуду (и, следовательно, интенсив-
ность) волны. В полупространстве г > 0 фазовый экран вызы-
вает в прошедшей волне-как фазовую, так н амплитудную моду-
ляцию. Последнюю можно наблюдать, например, на листе бумаги
при прохождении света через оптически неоднородное или не-
ровное (скажем, обычное оконное) стекло, если отодвинуть
бумагу на некоторое расстояние от стекла.
Фазовый экран часто используется в качестве модели для
описания ряда явлений как в оптике, так и в радиофизике.
Например, линза с оптическими неоднородностямн модулирует
главным образом фазу проходящей световой волны. Такое же
действие оказывает ионосфера Земли на проходящие через нее
радиоволны УК.В-диапазона. Модель фазового экрана применяют
также (хотя и с меньшими основаниями) при анализе мерцаний
радиоволн, посылаемых внеземными радиоисточниками и прохо-
дящих через статистически неоднородную межпланетную или
¦межзвездную среду.
Если на неограниченный плоский фазовый экран падает
плоская волна и„ = е1к
экрана z = 0 равно
v (р) = ехр [iS (р)] «„ |г=0 == ехр [LS (p)].
Выясним, как связаны статистические моменты поля прошедшей
волны с функцией корреляции фазы
4>s (Р) = <S(Pi)S(Ps)> = a%Ks (р),
где а|—- дисперсия, a Ks(p)—коэффициент корреляции фазы.
Предположим, что флуктуации S статистически однородны в
плоскости г = 0, имеют нулевое среднее значение E = 0) и под-
чиняются нормальному закону распределения вероятностей.
78 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ 1ГЛ. II
_ Учитывая, что для нормально распределенной величины а с
се = О справедлива формула <?*'"> = ехр (—аа/2), находим
Tv (р) = <v (Pl) v* (ps)> = <ехр {([S (Pl)-S (p,)]}> =
= exp|--i<[S(Pl)-S(p2)]2>}.
Но при S = 0 средний квадрат разности фаз — это структурная
функция фазы Ds(p), связанная с корреляционной функцией
t|>s(p) соотношением D.6). Поэтому
Г„(р) = ехр [-V2Ps(p)] = exp [ф5 (p)-i|>s (O)J = exp \a% [Ks (p)-Ill-
Среднее значение и поперечную функцию когерентности поля
за экраном можно найти по формулам A0.3) и A0.14):
п= voeila = ехр {— al/2 + ikz},
причем поперечная функция корреляции равна
*i(p) = ^(p) = exp{a2s[^s(p)-l]}-e-"s. AO,i5)
Если флуктуации фазы на экране слабы (сг^<^1), то из (ТО.15)
еем
имеем
т. е. при малых флуктуациях фазы поперечная функция корре-
ляции поля во всем полупространстве г>0 совпадает с \))s(p).
В случае же больших дисперсий фазы (crj^> 1) среднее значе-
ние поля va = e~"sli пренебрежимо мало по сравнению с едини-
цей, а величина ехр {о| [Ks (р) — 1]} заметно отличается от нуля
только при малых р. Учитывая это, пренебрежем в A0.15) чле-
_ 2
ном е s и разложим коэффициент корреляции /fs(p) в ряд Тейлора.
Считая для простоты флуктуации фазы на экране изотроп-
ными, имеем
где штрихом обозначено дифференцирование по р (линейный по
р член в разложении A0.17) отсутствует, так как случайное поле
фазы S(p) предполагается дифференцируемым, Л^@)=0). В ре-
зультате получаем
'/*> ? (о|§>1), A0.18)
101 Дифракция плоской еолны на хаотическом экране ?<j
це учтено, что значения в нуле вторых производных Ks@) и
"s @) = cisKs (U) отрицательны.
Из A0.18) видно, что корреляция исчезает при p^|o$/Cs@) (-'/.;«
ils/as, где /s-~|/Cs(O)l"'/*~радиус корреляции фазы. Поэтому
ля поперечного радиуса корреляции получаем оценку
Il~ hit's iPs>\)-
аким образом, при trs^>l радиус корреляции примерно в as
аз меньше корреляционного масштаба фазы ls. Нетрудно по-
ять, с чем связано это различие масштабов 1± и ls.
При смещении вдоль экрана на расстояние порядка радиуса
орреляцни ls фаза S изменяется на величину AS ~ as, совер-
иив при этом не более одной осцилляции. В то же время гра-
[ичное поле о (р) = e's испытывает на том же расстоянии р ~ ls
7римерно п <— as/n осцилляции, откуда и следует, что l± ~ Zj/n~
l<h
s/s<h
Приведенные выше соотношения используются, например, при
мтерпретации данных о прохождении ультракоротких радио-
эолн от внеземных источников через ионосферу Земли [23—26],
} которой имеются неоднородности электронной концентрации.
При определенных условиях можно считать, что поле v (p) на
выходе из ионосферы испытывает только фазовые флуктуации.
Если дисперсия фазы <з% мала. по сравнению с единицей, то
пространственная функция корреляции поля на поверхности
Земли совпадает, согласно (ГО.16), с функцией корреляции фазы
¦ф5(р), которая определенным образом связана с функцией кор-
реляции ионосферных неоднородностей. Следовательно, прио|<^1
можно непосредственно измерить корреляционную функцию фазы
волны, прошедшей через ионосферу, и судить о неоднородностях
ионосферы.
Значительно сложнее интерпретировать данные наблюдений
при ajSg>l. В этом случае функция корреляции изотропного
поля фх(р) связана с г|M (р) соотношением A0.18), при помощи
Которого можно оценить лишь величину | ift @) | ~ а%/1^. Допол-
нительные сведения о as и ts можно извлечь из данных об от-
носительных флуктуациях интенсивности волны (см. ниже), но и
с привлечением этих данных добиться однозначной интерпрета-
ции трудно.
Дело в том, что ионосферные неоднородности расположены
не на фиксированной высоте, а распределены (причем неравно-
мерно) на высотах от 100 до 400 и более километров над уров-
нем Землн. Кроме того, эти неоднородности имеют широкий
Диапазон горизонтальных масштабов (от 1^.1 до 1^ 500 км), их
действие часто маскируется сильно" фокУсирую1щши~~образВва-
ниями («ионосферными линзами») и т. д. Поэтому наблюдения
флуктуации поля на Земле позволяют оценивать только грубые
§0 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ [ГЛ. II
характеристики ионосферных иеоднородностен: их горизонталь-
ные масштабы, степень анизотропии (неоднородности, как пра-
вило, вытянуты вдоль линий магнитного поля Земли), вероят-
ную высоту их расположения, а также среднюю скорость пере-
мещения (дрейфа) неоднородностей [28, 29].
3. Флуктуации амплитуды и фазы за безгра-
ничным фазовым экраном. Во многих приложениях, в
частности в задачах радиосвязи и радионавигации, представляют
самостоятельный интерес статистические характеристики ампли-
туды и фазы волны. Для их вычисления кроме первой функции
корреляции комплексного поля фх (р) = <й (pt, г) и* (рг, г)>, кото-
рая в случае плоской волны и статистической однородности экра-
на не меняется при удалении от последнего, необходима и вторая
корреляционная функция фх (р) = <и (plt г) и (р3, г)>.
Закон преобразования второй функции корреляции при /уда-
лении от экрана можно получить при помощи френел^вского
приближения (9.17), которое применимо к полям именно-'с круп-
номасштабными неоднородпостями на границе. Используя (9.17)
и опуская для краткости аргумент га, находим
, *) =
00
И - (Р'-Р")ехр |,-^[(Pl_p') }
A0.19)
где ijv (р) = <о (p.,) w (р1 — р)>—вторая корреляционная функция
поля на экране. Введем новые переменные интегрирования § =
= р' — р" и T| = (p'-fp")/2. Интеграл по ц легко вычисляется,
при этом зависимость от Р! + ра из A0.19) выпадает и остается
лишь зависимость от pL — р2. Переобозначив в оставшемся инте-
грале | через р' и pt—ра через р, получаем
а
¦j. (Р. ^ ^~ I *. (р') ехр [§¦ (р- р')«] dy. A0.20)
Таким образом, вторая корреляционная функция преобразуется
почти так же, как и само поле: отличие от (9.17) заключается
лишь в том, что в A0.20) входит удвоенное расстояние от экрана 2г.
Последующие выкладки упростятся, если вместо флуктуацион-
ной; части поля и ввести вспомогательную случайную величину
а^ие''1", о. — 0, которая представляет собой комплексную ам-
плитуду флуктуации поля. Первая и вторая корреляционные
функции этой величины преобразуются по формулам, аналогичным
ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ НА ХАОТИЧЕСКОМ ЭКРАНЕ 81
{10.13) и A0.20):
k С
Asitz J
A0.21)
A0.22)
В отличие от A0.20), в A0.22) не входит множитель е*"".
Кроме того, удобно нормировать средний квадрат пцля на
экране v (р) к единице:
<|y|*>=,a? + li.'0|*=l. A0.23)
Такая нормировка отвечает непоглощающим и неотражающим
экранам, поскольку падающая волна единичной интенсивности
/n = |*'te|2= I порождает за экраном волну с той же средней
интенсивностью:
Это условие, очевидно, выполнено
для чисто фазового экрана.
Свяжем теперь величину а с ам-
плитудой А и фазой S волны
и — Ае-?+1кг, распространяющейся за
экраком. Имеем
u(p, z)=A(p, z)exp
Рис. 3.
где va без ограничершя общности можно считать вещественной
величиной. Разделяя а на вещественную (а') и мнимую (а") части,
находим, что
откуда
A0.24)
На рис. 3 показаны соответствующие векторы на комплексной
плоскости амплктуды U = Aels.
Задача о нахождении из A0.24) статистических характеристик
амплитуды Л и фазы S решается до конца в двух частично пе-
рекрывающихся случаях: при слабых флушуациях поля на
экране, когда \а'\ и \а"\ малы по сравнению с единицей, и во
фраунеоферовой зоне, когда величины а' н а" распределены по
нормальному закону. Эти случаи и будут рассмотрены ниже.
Исследуем сначала флуктуации амплитуды и фазы при слабых
флуктуациях. Пренебрегая малыми членами порядка !«'|3и |а"|»,
82 излучение и Дифракция случайных полей 1гл_ п
и учитывая, что в силу A0.23) о1 + (а')г + {а")г = 1, при помощи
A0.24) получаем средние значения А и S:
7=1->/,<а">, S = -<a'a">, A0.25)
а также выражения для корреляционных функций (p = Pj—ра):
<ЫР, z)=<A(Pl,z) А(р„ z)>=i&(p, г),
ife (p, z) = <S(Pl, z)S(p2, 2)> = ^°а (р, г), A0.26)
z)>=i|&(p, 7),
где i|Jf/(p, г), I, / = 1,2—корреляционные функции вещественной
и микмой частей комплексного случайного поля а. В общем слу-
чае они выражаются через первую и вторую функции корреляции
Ф„(р, г) и \\>а (р, г) при помощи формул B.14). Однако, если
^а(р, г)—четная функция р, то справедливы более простые
формулы B.22):
1/(Ф + Кеф) фЬ = 1/(ФКеф) 0
Таким образом, посредством формул A0.25) и A0.26) первые
два момента амплитуды и фазы выражены через первую н вторую
корреляционные функции комплексного поля а. Последние же
преобразуются при удалении от экрана в соответствии с выра-
жениями A0.21) и A0.22), чем и решается поставленная задача [23].
В частном случае фазового экрана с начальной фазой S, рас-
пределенной по нормальному закону, имеем
V')'*P>1. (Ю.28)
Ob
. *)=ш J Шр)созУ?^<гу, A0.29)
где i|>!(p)—корреляционная функция фазы 6 плоскости г = 0.
Для гауссовой корреляционной'функции фазы
^(р)=а|ов-Р1/«'| A0.30)
эти интегралы легко вычисляются и, в частности, при р = С
дают
(ю.зг
где D = D(z) = 2z/kl%. Величину D называют вслед за Г, С. Го
реликом [43] волновым параметром. Этот параметр показывает
101 ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ НА ХАОТИЧЕСКОМ ЭКРАНЕ S3
во сколько раз площадь первой зоны Френеля л /
превышает по порядку величины «площадь» одной неоднородности
л/ я/|, т. е. сколько неоднородностей умещается в этой зоне.
В зависимости от значения волнового параметра можно выделить
трн области дистанции z (которые тоже называют зонами): ближ-
нюю (D<^1), френелевскую (D~l) и фраунгоферову (D^>1)
зоны (по отношению к отдельной неоднородности). Для каждой
нз них характерны определенные особенности флуктуации.
В ближней зоне (D<|;1) преобладают, естественно, фазовые
флуктуации: aj^crj я: ст|0. При удалении от экрана амплитудные
флуктуации нарастают, а фазовые уменьшаются, причем в пре-
деле D—уса (фраунгоферова зона) дисперсии амплитуды и фазы
выравниваются:
<^.sU»=V2<. A0.32)
Корреляция между А и S пренебрежима в ближней и дальней
зонах н максимальна при D ~1.
Обратимся теперь к флуктуациям в зоне Фраунгофера (D^>1)
при произвольных (не обязательно слабых) флуктуациях поля
на экране. При D§5>1 в пределах первой зоны Френеля с ради-
усом у Яг, которая только и существенна для интегрирования
в (9.17), умещается много неоднородностей поля на экране.
В силу центральной предельной теоремы теории вероятностей
закон рчспределення величин а' и а" приближается поэтому
к нормальному.
Нормализация этих величин обусловлена «фильтрующим» дей-
ствием свободного пространства и имеет такую же природу, как
н нормализация временных сигналов на выходе узкополосных
фильтров (ч. I, § 50). Действительно, преобразование случайного
поля по формуле (9.17) вполне аналогично преобразованию слу-
чайных процессов, причем аналогом импульсной функции в иа-
шем случае является разностное ядро преобразования (9.17),
которое и осуществляет фильтрацию с эффективной шириной
полосы пространственных частот Ди~ Vkjz~ (Яг)"'/>. С ростом
дистанции г эта полоса сужается и при г^>Щ (т. е. в дальней
зоне, D^> 1) становится значительно уже первоначальной ширины
пространственного спектра к„~ \/1о. При этих условиях и про-
исходит нормализация поля м(р, г).
То обстоятельство, что а' и а" в дальней зоне распределены
по нормальному закону, дает возможность найтн плотности ве-
роятностей амплитуды н фазы и вычислить моменты этих величин.
По существу, речь идет о хорошо изученной задаче о статистике
огибающей А и фазы S сигнала и(р, г) = Ae!S*ik!:— (у„Л- а)е"",
представляющего собой сумму гармонического колебания i\eikz и
гауссова шума « = ««'**.
84 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ [ГЛ.
Для гауссовых величин закон распределения вероятностен
полностью характеризуется только низшими моментами—средними
значениями и функциями корреляции. В нашем случае а'=а" = О,
а функции корреляции я^, ijft и i)^ выражаются через первую
н вторую функции корреляции комплексного поля а посредством
формул A0.27). В зоне Фраунгофера эти формулы существенно
упрощаются, поскольку прн D^> 1 вторая корреляционная функ-
ция •фд (р, г) пренебрежимо мала по сравнению с первой. В ре-
зультате при Ь^>1 имеем
•Ф& (Р. г) = i|& (р, г) = V, % (Р), 4>f, (P, г) = 0, A0.33)
т. е. в зоне Фраунгофера поля а и а" некоррелированы, а нх
автокорреляционные функции одинаковы н отличаются коэффи-
циентом 7а от первой функции корреляции поля на экране. Как
следствие этого, функции ijifi н if» и связанные с ними стати-
стические характеристики амплитуды и фазы не зависят от рас-
стояния до экрана: с ростом дистанции г они остаются такими
же, как на «входе» в дальнюю зону г^Ы%.
Определение статистических моментов амплитуды и фазы при
известной (гауссовой) статистике а' и а" проводится таким же
образом, как н в ч. I, §§ 25 и 44 (см. также [30, 31]).
4. Флуктуации интенсивности за безгранич-
ным фазовым экраном. При рассмотрении флуктуации
интенсивности обычно интересуются их функцией корреляции
(P = Pi — Pa)
ф/(р,г)= </-(Pl, г) 1~(р1,г)> = <Цр1,г)Цр„г)>-7» A0.34)
и так называемым индексом мерцаний E:
A035)
который характеризует относительные флуктуации интенсивности.
Если принять, как и выше, что 7=1, то
Ь (Р, *) = </ (р„ г) / (р„ г)>-1, A0.34')
Р* (г) = </» (г)>-1 = о? (г). A0.35')
Как и прн анализе амплитудных н фазовых флуктуации, рас-
четы % и р удается довести до конца лишь в двух частично
пересекающихся предельных случаях—4цля слабых флуктуации
и дляИфраунгоферовой зоны. '
Используя результаты п. 3, легко показать, что в случае
слабых флуктуации
Ф/(Р. г)=41|)д(р, г),
Ра (г) = 4cr,f (г).
ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ НА ХАОТИЧЕСКОМ ЭКРАНЕ 85
Таким образом, флуктуации интенсивности меняются прн удале-
нии от экрана по тому же закону, что и флуктуации амплитуды.
При D^l (зона Фраунгофера) J3a(z) стремится к предельному
значению
pL = 2a|0> а|0^1, A0.36)
независимо от вида функции корреляции фазы на экране.
При расчете чр, в дальней зоне ф^\) воспользуемся фор-
мулой из задачи 12 к гл. I, которая справедлива для полей,
распределенных по нормальному закону. Прн D^>1 имеем
$, = е>шФ„«О, так что Г A, 2) = ы (I) и B) и
ЫР>г)ЧГя(рIа-|"|*=|ГЛРI2-Ы*- (Ю.37)
Так как мы приняли, что Гв@) = / = 1, для индекса мерцаний
в дальней зоне (г —>• <») получаем
Р1,-^р1 = *,@)=1-|с„|1. A0.38)
Согласно этим формулам функция корреляции интенсивности ijjj
й индекс мерцаний Р2 при D§->1 уже не зависят от г.
В частном случае фазового экрана с гауссовыми флуктуацнями
фазы, когда v0 — е""^2, а ^„(р) дается выражением A0.15), по-
лучаем
SV(f>) = e~2<l|<4exp[2i|>°s(p)l-l}, P*=-1-е'***. A0.39)
При о!о<С 1 последнее выражение переходит, как и следовало
ожидать, в формулу A0.36). В другом частном случае—экран
с нулевым средним полем (ио~О) — выражения A0.37) и A0.38)
принимают особенно простой вид:
^(р)Чг,(р)|2 = |чир)I2, Р-^1-
Аиалнз флуктуации в общем случае наталкивается на значи-
тельные математические трудности. Если флуктуации поля на
экране не малы и точка наблюдения не удалена во фраунгофе-
рову зону по отношению к отдельной неоднородности, то расчет
индекса мерцаний сводится, в рамках френелевского приближе-
ния (Э. 17), к вычислению интеграла
хехр [-Ц (р! + р|- pj-pj)] d'Pl. . .i'p4- 1, A0.40)
86
ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ
где
Г!,2'"' A, 2, 3,4) = <о (Pl) v (Pl) и' (р3) о» (р4)>
— смешанный момент четвертого порядка. Для произвольных
функций Г?'"A,2, 3,4) значения интегралов вида A0.40) можно
находить лишь численными методами. Рассмотрим полученные
таким путем в [32] результаты для фазового экрана.
Если фазовые флуктуации распределены по нормальному за-
кону, то
Г'2-»A, 2, 3,4) = <ехр {/ [S (Pl) + 5 (pJ-S (p,)-S (Pl)]}> =
= exp {- [2o|0—Ф^-^.-^а-
где %ft = fs(P(—P*)—значения функции корреляции фазы S при
р = р,~рк, a ff|0—дисперсия фазы. На рис. 4 показаны полу-
ченные в [32] графики зависимости индекса мерцаний р от вол-
нового параметра D = 2z/kl% для
гауссовой функции корреляции
фазы A0.30) и для значений дис-
персии о|0 от 0,1 до 5.
Поведение этих кривых нам
уже частично известно: в зоне
Фраунгофера (D> I) pa = K =
= 1 — e~2°'s«, а при слабых флук-
туацнях фазы (ff|0<^l) р =
^2a|0Da/(l +D2). Новым является
наличие при' а%0 > 1 максимумов
(За прн промежуточных значениях
О^1.Д^я величины максимумов
Р2 при сильных флуктуаииях фа-
зы (oio^l) B [32], а также в
[33], где было проведено качест-
венное рассмотрение вопроса, дана оценка PLax^ 1по|0. Более
аккуратные расчеты, проделанные в [34, 35] для функции кор-
реляции фазы i))s(p) произвольного вида, привели к следующему
асимптотическому значению р„ах при а|0^> 1:
Рис. 4.
/4 f\? rf / fi\
Здесь у — численный коэффициент, равный -тг-—.st ;, а /, =
=^ | j"Cs @) I"*'1'— величина порядка радиуса корреляции фазы. Для
гауссовой функции корреляции A0.30) у = 72> l,-=h- Эти оценки
указывают на логарифмическое «насыщение» индекса мерцаний
fem с ростом ff|0.
^ц] ДИФРАКЦИЯ Ё ОПТИЧЕСКИХ СИСТЕМАХ 87
Максимум индекса мерцаний приходится, согласно [32—35],
на расстояние гт, равное
Формула A0.41), как и самый факт появления максимумов,
допускает простую геометрическую интерпретацию: флуктуации
интенсивности максимальны там, где волны за фазовым экраном
фокусируются. Действительно, в приближении геометрической
оптики фокусировка происходит на расстоянии гт~ 1/v от фазо-
вого экрана, где v — кривизна фазового фронта. По порядку ве-
личины v~-r (тгг] (х—°Дна из координат в плоскости г = 0) н
-fab —jr ¦ Следовательно, zm ~ 1/v ~ kls/oso, что совпадает
с A0.41). Очевидно, чем больше дисперсия фазы а$„, тем ближе
к экрану расположена зона фокусировок.
Эффект фокусировки волн и обусловленные им максимумы
индекса мерцаний характерны, очевидно, только при условии,
что на экране хорошо выражены именно фазовые флуктуации.
Если же на экране флуктуирует только амплитуда, то дифрак-
ция приводит не к увеличению, а, наоборот, к сглаживанию
флуктуации интенсивности, т. е. к уменьшению индекса мерца-
ний. Примеры такого сглаживания рассмотрены в задачах 7 и 8.
Сглаживание флуктуации интенсивности происходит также в том
случае, когда на фазовый экран падает не плоская волна, а волна
от источника конечных угловых размеров [32].
§11. Дифракция случайных полей
в простейших оптических системах
В предыдущем параграфе мы рассмотрели одну из простейших
статистических дифракционных задач — дифракцию детерминиро-
ванной плоской и монохроматической волны на бесконечном и
статистически однородном хаотическом экране. Здесь мы обра-
тимся к дифракции случайных полей на детерминированных объ-
ектах. В основном мы будем иметь в виду слабо расходящиеся
волновые пучки, чаще всего встречающиеся в оптических и ква-
зиоптических системах.
1. Прохождение случайной волны через отвер-
стие в экране. Теорема Ван-Циттерта — Цернике.
Пусть и(со, р) = ип (со, г)|г=0— спектральная амплитуда поля, соз-
даваемого каким либо источником в плоскости 2 = 0. Если
поместить в этой плоскости непрозрачный экран с отверстием S,
вырезающим пучок волн конечного диаметра, то непосредственно
за экраном образуется поле «на выходе» и„ (со, р), которое в
88 Излучение и Дифракция случайных Полей [гл. п
приближении Кирхгофа равно1)
( v (ш, р) на S,
"о К Р)=| q вне s
Это поле можно записать через функцию пропускания отверстия:
считая, что
на S,
с О'-2)
вне о.
В случае плавных (в масштабе длины волны) флуктуации
граничного поля V (со, р) для вычисления поля за отверстием
можно воспользоваться френелевским приближением (9.17), кото-
рое с учетом A1.1) дает
м(р')v <¦«>• ?">ехР fir(Р-р'
Среднее по ансамблю источников значение v (со, р) равно нулю,
вследствие чего и
<«(», г)> = 0. A1.4)
Вычислим поперечную функцию когерентности дифракционного
поля, т. е. функцию когерентности в плоскости г — const. В со-
ответствии с A1.3) имеем
Г± (са, ри р2, г) = <ц (w, pu г) и* (со, р2, г)> =
М(р')М (р") Г„ (м, р' — р") X
хехр {-§ [(Р1-Р'J-(Р2"Р")!]} dy dy, A1.5)
где Г0((в, р'—р") — пространственная функция когерентности гра-
ничного поля v (а, р), которое предполагается статистически одно-
родным. Пространственно-временные функции когерентности полей
u(t, т) и v{t, р) связаны с Гх(ео, рг, р2, г) и Г„(со, р'—р") преоб-
разованиями Фурье, например:
00
г±(т> Pi, P2, г) = 1 гх(ю. Pi. P2. г)е-шйш. A1.6)
о
') Приближение Кирхгофа применимо, как известно, при условии, что
размеры отверстия а велики по сравнению с длиной волны, а^л.
|jj] ДИФРАКЦИЯ В ОПТИЧЕСКИХ СИСТЕМАХ 89
1$ силу A1.4) все эти функции когерентности совпадают с соот-
ветствующими функциями корреляции.
Не конкретизируя вида функции когерентности (корреляции)
граничного поля, интеграл A1.5) можно вычислить в двух
предельных случаях — при больших и малых размерах отверс-
тия а по сравнению с радиусом корреляции /„ (но всегда при
)
При a^t.lv {малое отверстие) функция когерентности гранич-
ного поля Г„ практически постоянна в пределах отверстия и ее
можно вынести за знак интеграла со значением Tv (со, 0) =7^,A»).
В результате1)
ri(Pi. Рг, г)=7„иЛ1(р1, г)и"м(р81 г), A1.7)
где поле иц(р, г) дается выражением
§]Y A1.8)
и представляет собой дифракционное поле за отверстием при
нормальном падении на него плоской волны единичной амплитуды.
Коэффициент корреляции при дифракции на малом отверстии
равен
Г±(Р1, Рг, z)ал (pi, г)и*м(рг. г)
i, ра, г) = yv^ (p
(pi] pi_ г) v^ (р8_ рг= = YUM (Pl, г) | | uM (PaT^Jl '
Так что j ATj_<J = 1 ¦ Это означает, что случайная волна, прошед-
шая через малое отверстие), порождает пространственно коге-
рентное поле. До создания лазеров пропускание света через
малое отверстие (наряду с использованием малых источников
света) было практически единственным способом получения про-
странственно когерентн(Л"о света. Этим способом пользуются и
в настоящее время, если не требуется высокой интенсивности
поля.
Обратимся к другому предельному случаю а'^>lv (широкое
отверстие). Прежде всего отметим, что вблизи отверстия имеется
область, в которой функция корреляции будет такой же, как
и в отсутствие непрозрачного экрана. Форму и размеры этой
области можно оценить, используя спектральное представление.
Ширина двумерного спектра Fv(x) случайного поля v имеет по-
рядок иг,~1//г, или, в пересчете на углы, 8~xJk~X/lv. Сле-
довательно, если точки наблюдения г\ и г2 находятся внутри
') Начиная с формулы A1.7), мы опускаем аргумент (О всюду, где это не
Может привести к недоразумениям.
90
ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ
1ГЛ. II
конуса с основанием а и углом при вершине б (рис. 5), то поле
<вде почувствует» влияния краев диафрагмы. Для всех точек
внутри этого конуса поперечная функция корреляции будет та-
кой же, как у граничного поля:
ра, г) = Г„(р!—ра).
Рис.
Предельная дистанция глр, на
которой еще справедливо это соот-
ношение, оценивается как1)
гч~-у~-^~*а/.. (П.9)
При а^>/„ эта дистанция отвечает
дальней зоне по отношению к раз-
меру неодиородиостей lv, так как
и ближней зоне по отношению к размеру отверстия а:
гпр ^ Jv^ sz 1
ka* a ^
Отсюда, в частности, следует практически важный вывод, что
распределение флуктуации поля за отверстием нормализуется
еще в ближней зоне апертуры а.
Вычислим интеграл (П-5) при г^>гпр. Для этого перейдем
к новым переменным | = р'— р" и т) = (р'+р")/2 и обозначим
полусумму (Pi + p2)/2 через р+, а разность pj—pa—через р.
Тогда A1.5) принимает вид
Г±(р, Р+, г) =
хехр |-^[1т,-г,р_
Область интегрирования по \ ограничена здесь неравенством 5<
^1а<^.а, так как при \~&lv функция корреляции Г„(|) близка к
нулю. В то же время т]*€а, поскольку при г\>а обращается внуль
произведение М (т\-\-%/2) М (г\—1Ц2)я*М* (tj) =Ai (r\). Поэтому пер-
вое слагаемое в показателе экспоненты ограничено сверху не-
равенством k\,t\lz^kalj2 ~ гпр/г. При г^>гпр этим слагаемым
') Если lv^.a, то в качестве гпр следует брать величину гпр~в, так
как в этом случае ширина углдвого спектра 6 сравннша с nJ2,
5 til ДИФРАКЦИЯ В ОПТИЧЕСКИХ СИСТЕМАХ 9)
можно пренебречь, и тогда интегралы по ? и г] разделяются
X
- со
j #|Г„<5)ехр(--!*l?±-). (НЛО)
Ж(
чл
*ехр[*(н-|^
Точно такое же выражение можно получить и непосредст-
венно из формулы (9.18) для поля во фраунгоферовои зоне:
A1.11)
Однако приближение A1.11) справедливо только в дальней зоне
z^ka*, а формула A1.10) применима и на гораздо меньших
дистанциях z §5> znp ~ fea^,- Иными словами, функция когерент-
ности (П. 10) формируется еще в ближней зоне по отношению
к отверстию.
Зависимость функции когерентности A1.10) от поперечных
координат p = pj — р2 и P+ = (Pt + p2)/2 определяется произведе-
нием трех сомножителей. Множитель перед интегралом
exp {ikpp+lz} = exp {ik (p? —pi)/2z} к, exp {ik (^— г2)}
возникает просто из-за того, что сферические волны, покидаю-
щие отверстие, ие согласованы с плоской формой поверхности
z = const, на которой рассматривается корреляция поля. Если
взять корреляцию на сфере г = const, этот множитель обратится
в единицу.
Интеграл по г\ в A1.10), зависящий только от разности р =
= р1—р2, характеризует поле когерентного источника с распре-
делением амплитуды А1(т|). При размере отверстия а угловая
ширина диаграммы направленности такого излучателя имеет по-
рядок h/a, а линейная ширина центрального дифракционного
лепестка в плоскости z = const равна Др —• Xz/a. Отсюда для
поперечного радиуса корреляции сразу же следует, что
где y~aJ2 — угловой размер отверстия из точки наблюдения.
Как и ширина дифракционных лепестков, поперечный радиус
корреляции возрастает по мере удаления от плоскости г = 0.
Увеличение радиуса когерентности геометрически объясняется
ИЗЛУЧЕНИЕ И ДИФРАКЦИЙ СЛУЧАЙНЫХ ПОЛЕЙ
1гЛ. it
тем, что при удалении от отверстия фазовые фроиты всех эле-
ментарных сферических волн можно считать (с точностью до Я)
совпадающими иа все большей площади.
Второй интеграл в A1.10) определяет пространственное рас-
пределение средней интенсивности дифракционного поля. Поло-
жив в A1.10) р = 0 н учитывая, что интеграл по т\ при р = 0
равен площади отверстия S, имеем
Г,(8)ехр(—Й^
(,,.13)
По предположению масштаб lv изменения функции Г„ мал по
сравнению с поперечником отверстия а. Поэтому ширина рас-
пределения интенсивности 7а в плоскости 2 = const, составляю-
щая р+ -~ 'kzjly (угловая ширина имеет порядок p+lz~'kjl!/~\/ktv),
велика по сравнению с поперечным радиусом корреляции lL
Таким образом, мы имеем здесь дело с примером квазиоднород-
ного (в плоскости г = const) поля. В данном случае все реали-
зации дифракционного поля за отверстием представляют собой
быстрые пространственные осцилляции с масштабом /j_ и с раз-
махом порядка "|/„(р) (рис. 6.).
Если разделить функцию когерентности A1.10) иа среднюю
интенсивность дифракционного поля, то мы получим коэффи-
ДИФРАКЦИЯ Й ОПТИЧЕСКИХ СИСТЕМАХ 93
циент поперечной пространственной корреляции поля
где величина
представляет собой нормированное к единице (JF @) = 1) преоб-
разование Фурье от М (ц) и одновременно—диаграмму направ-
ленности отверстия при нормальном падении на него плоской
монохроматической волны. В частном случае круглого отверстия,
когда Л1(р) = 1 при р<а и обращается в нуль вие этого круга,
где Jl(y.d) — функция Бесселя первого порядка.
В пределе, когда радиус корреляции граничного поля /„ мал
по сравнению с длиной волны, интеграл по | перестает зави-
сеть от р+:
ос
J i\
Через Sv здесь обозначена эффективная площадь когерентности
граничного поля:
^-y-f Гг,A)*5= Г КАЪ)П, (П.15)
которая по порядку величины равна 1%. В результате при
is<^X из A1.10) вытекает так называемая теорема Ван-Цшп-
терта — Цернике-
Г.(Р, Р+, Z)^^exp («ffii) J ^(p')exp (--iM-)dy. A1.16)
Входящую сюда величину
•f(p')=^-7"AM(p') (U -17)
называют приведенной интенсивностью.
Согласно теореме Ваи-Циттерта—Цернике модуль поперечной
Функции когерентности Гх зависит от разности р = р,—Р2 так
94 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ ИГЛ. II
же, как и поле в зоне Фраунгофера, создаваемое полностью
когерентным источником с распределением амплитуды, пропор-
циональным J (р'). От обычных дифракционных формул выра-
жение A1.16) отличается в двух отношениях. Во-первых, квад-
ратичная по полю величина Гх обратно пропорциональна квад-
рату (а не первой степени) расстояния. Во-вторых, это выражение
вместе с исходйой формулой A1.10) применимо, как уже отме-
чалось, на дистанциях г^>г|ф, причем в рассматриваемом пре-
деле lv^a величина гпр сравнима с а, тогда как диаграмма
когерентного источника с поперечником а формируется на зна-
чительно больших дистанциях z^kcP^z^^ а.
Обычно теорему Ван-Циттерта—Цернике A1.16) получают
путем формального введения дельта-коррелированных флуктуа-
ции граничного поля, полагая в A1.5) или в (НЛО)
r.(P-p') = /"e(p')8(p'-p')S., A1.18)
при этом в выражении (П. 16) для приведенной интенсивности
вместо произведения IVM (р') возникает переменная интенсив-
ность /„ (р'). Источник с независимыми значениями поля в сколь
угодно близких точках называют пространственно некогерентным.
Представление о пространственно некогерентном источнике
является идеализацией, имеющей ограниченную область приме-
нимости. Дело в том, что поле бегущих волн по самой своей
природе не может быть дельта-коррелированным в пространстве,
поскольку (§ 9) масштаб изменения поля 1„ ие может быть
меньше длины волны А1). Поэтому в рассматриваемой поста-
новке задачи (дифракция случайного поля на отверстии) переход
к пределу /„—>-0 является, строго говоря, незаконным, что ста-
вит справедливость вывода теоремы Ван-Циттерта—Цернике на
основе A1.18) под сомнение. С теоремой (П.16) мы встретимся
еще в одном важном случае, а именно в задаче об излучении
поля системой точечных независимых источников, к которой мы
обратимся в § 12. Смысл приведенной интенсивности в этой за-
даче будет, разумеется, иным, чем в A1.17).
Результаты, полученные выше для пространственной корре-
ляции спектральных амплитуд, в случае квазимонохроматиче-
ского поля сохраняют силу и для самих полей. В самом деле,
х) Заметим попутно, что отождествление приведенной интенсивности A1.17)
со средней интенсивностью поля в отверстии Iv (р) ведет к тому же выводу.
Такое отождествление возможно при ?2А'„/4я2= 1, а это означает, что 5„ = Х2,
что противоречит принятой в A1.18) гипотезе о дельта-корреляции, по ко-
торой Sv~ ll<^,\z.
{Ill ДИФРАКЦИЯ В ОПТИЧЕСКИХ СИСТЕМАХ 95
согласно A1-6) пространственная корреляционная функция равна
во
rj.(t = O, р„ ps, г)=^Гл.(ш, Pl, p2, г)е*«Ж*|т=о =
-^-) . A1.19)
Для квазимонохроматического поля функция Г„(м, 1) сосредо-
точена в узкой полосе частот Дсо вблизи частоты «„. Поэтому
приближенно (fe0 = ajc)
Гл.(т = О, Pl, ps, z) =
(^)f (^) , A1.20)
где
— пространственная функция корреляции граничного поля, а
Дсо,4*—эффективная ширина полосы частот.
Переход от A1.19) к A1.20) возможен при выполнении не-
равенства
физический смысл которого заключается в том, что разность
хода воли от разных частей отверстия должна быть мала по
сравнению с длиной когерентности lk = стА ~ с/Дш. Простые
оценки показывают, что для выполнения неравенства A1.21) до-
статочно условия квазимонохроматичности (Дсо^ю,) и условия
Р+=€й, которое требует, чтобы «центр тяжести» точек наблюде-
ния р+= V2(Pi"l"Pj He выходил за пределы размеров отвер-
стия а.
2. Фокусировка случайных волн. Дифракционную
картину в фокусе линзы можно получить из предыдущих ре-
зультатов при помощи простых преобразований, поскольку поде
96 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ [ГЛ. II
в фокальной плоскости линзы подобно полю отверстия на бес-
конечности.
Пусть в отверстии непрозрачного экрана иаходитси тонкая
линза с главным фокусным расстоянием F. Действие линзы можно
описать, введя под знак интеграла в (Н.З) фазовый множитель
ехр{— [fe'22F}
A1.22)
В главной фокальной плоскости z = F показатель экспоненты
упрощается и поле ы (р, F) выражается просто преобразованием
Фурье от М (р') v ((>'):
kexp
A1.23)
От фраунхоферова приближения A1.11) для поля отверстия
(без линзы) выражение A1.23) отличается только заменой г на F,
так что формулы для функций корреляции повторяют соответ-
ствующее выражения из п. 1. Так, при a<S;/„ (малое отверстие)
распределение интенсивности в фокальной плоскости оказывается
таким же, как и для пространственно когерентной плоской
волны. В противоположном случае a^>lv (большое отверстие)
распределение интенсивности может быть получено из A1.13):
Размер фокального пятна в этом случае дается выражением
рф — XF/lv, т. е. оно в a/tv раз больше, чем для детерминиро-
ванного поля плоской волны (Рф — XF/a). Однако интенсивность
в центре дифракционной картнны теперь равна
что примерно в SIS,, ~ {a/lvy раз меньше, чем при когерентном
освещении (малое отверстие). Разумеется, полная интенсивность,
полученная интегрированием /„ по всей плоскости z — F, в обоих
случаях одинакова и равна полной «входной» интенсивности
7VS.
ДИФРАКЦИЯ В ОПТИЧЕСКИХ СИСТЕМАХ
97
Как и при дифракции на отверстии, распределение интен-
сивности для квазимоиохроматического поля оказывается прак-
тически таким же, как и для строго монохроматической волны.
Более того, в, оптике даже в случае белого света, у которого
Дв>~соо, распределение интенсивности в плоскости z = F лишь
незначительно отличается от соответствующей картниы для моно-
хроматического поля. Именно поэтому при рассмотрении задач
oj формировании оптического изображения допустимо пренебре-
жение эффектами, обусловленными временной некогереитиостью
поля [21, 36].
3. О роли пространственной когерентности
освещения в|форм ир овани к оптического изобра-
жения. Рассмотрим простейшую оптическую систему, содер-
жащую только одну тонкую линзу (рис. 7). Полупрозрачный
г-г,
объект, например диапозитив, характеризуемый комплексным
коэффициентом пропускания f(pt), расположен в предметной
плоскости г=—zL. При освещении этого объекта слева плоской
монохроматической волной ulniU = Uin(p, г) непосредственно за
объектом создается поле
«i(Pi)-/(PiWPi). o(Pi) = «ln(P, г) I—.,. (H.24)
где pt — радиус-вектор точки в предметной плоскости.
В плоскости г = 0, где расположена линза, образуется иоле
u»a(Pi) (Ра—вектор в плоскости 2 = 0), которое вофренелевском
приближении (9.17) равно
"»<р.>~йг! "<(р')ехр ГУНd3p"
«На Выходе» линзы возникает поле
и. Ы = «и, (Р,) М (рО ехр (- ^ff) ,
* С. М. Pmjoj и др. ч, II
A1.26)
98 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ ГГЛ. II
где множитель М(ра), равный нулю вне лиизы и единице на
линзе, описывает действие ограничивающей линзу диафрагмы,
а множитель ехр {— ikpl/2F}— действие линзы с фокусным рас-
стоянием F.
Наконец, пересчет поля A1.26) от линзы к плоскости изобра-
жения z = 2, также может быть произведен во фреиелевском
приближении:
^i^) (П.27)
Выражения A1.24)—A1.27) связывают поле и (р) в плоскости
изображения с коэффициентом пропускания f(Pj), характери-
зующим объект, и с первичным полем а (р,), свойства которого
определяются источником света. Не рассматривая собственно
оптический аспект задачи, уделим основное внимание особен-
ностям формирования изображения в зависимости от степени
пространственной когерентности освещения полупрозрачного
объекта.
С этой целью примем с самого начала, что плоскости пред-
мета и изображения сопряжены в смысле геометрической оп-
тики, т. е. 1/г, + 1/г2= 1/F. Подставив последовательно A1.26),
A1.25) и A1.24) в A1.27), получаем
)M (Ра)ехр [_(-fcpa(i+-ei.) + ^-g.
Интегрирование по ра дает
где S—площадь отверстия, а через !FM(x) обозначена норми-
рованная к единице (#"ж@)=1) трацсформаита Фурье от М(р)
(см. A1.14)). В результате
и(Р) =
ДИФРАКЦИЯ В ОПТИЧЕСКИХ СИСТЕМАХ 99
Выражение A1.28) представляет собой частный случай более
общей формулы
и (Р) = S в (Р,) f (р.) & (Р, р.) *р„ (! 1.29)
которая принадлежит к соотношениям типа (9.2) и в рассматри-
ваемой задаче связывает поле в предметной плоскости произ-
вольной оптической системы с облучающим полем v (ft) и функ-
цией пропускания объекта /(р,). Функцию ^?(р, р,) называют
аппаратной функцией системы. Характерный масштаб изменения
аппаратной функции в плоскости изображения (т. е. по р) — это
радиус дифракционного пятна, отвечающего точечному объекту,
а .масштаб изменения <? по аргументу pi определяет размер
области в плоскости предмета, дающей заметный вклад в поле
в' данной точке плоскости изображения. Иными словами, это
предел разрешения оптической системы.
В рассматриваемом случае однолинзовой системы с круглой
диафрагмой аппаратная функция равна
i- ft'S exp [ik (Zl + г2 + р2/2га -±- pj/2zi)] 2Jt (xa) .., ~m
где х = /г|р/га + р1/г1|. Согласно A1.30) точечному объекту, по-
мещенному в точку р10, отвечаег дифракционное пятно с центром
В точке р„ — —PjjZj/Zj. Отношение z,/zL характеризует увеличе-
ние данной системы, а знак минус отвечает перевернутому
изображению. Так как функция Бесселя Jl(xa) первый раз
обращается в нуль приха = 3,83, характерным масштабом аппа-
ратной функции по р может служить радиус первого темного
.кольца Эйри в дифракционном изображении точечного объекта,
равный—^-г2 ж 0,61 Я-^-, тогда как масштаб изменения по р,
(с точностью до множителя порядка единицы — это релеевский
предел разрешения) равен 6==0,61Х~.
При анализе свойств изображения мы будем исходить из об-
щей формулы A1.29), а частный вид этой формулы A1.28)
используем только для иллюстрации общих выводов. Согласно
A1.29) при освещении объектов частично когерентным светом
средняя интенсивность поля в плоскости изображения равна
где
—пространственная функция когерентности первичного поля.
Для заданного объекта (функция / фиксирована) характер
распределения интенсивности в предметной плоскости зависит
4»
IUO ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ *1ОЛЁЙ [ГЛ. II
от соотношения между радиусом когерентности первичного поля lv
(это характерный масштаб изменения функции когерентности Г„),
размером области разрешения б (характерный масштаб изменения
аппаратной функции по pt) и размером наиболее мелких дета-
лей объекта рш1п. Соотношение между pmin и 6 определяется
характеристиками соответственно объекта и оптического прибора.
Если считать эти величины заданными, то воздействовать на
изображение можно, только менян /.„ т. е. меняя характер об-
лучения.
Рассмотрим предельные случаи /„^Pmm. б и 4<СРш«. 6,
которые принято называть соответственно когерентным и неко-
герентным освещением предмета. При когерентном освещении
(/„§?>Рты, б) можно считать, что в области, существенной для
интегрирования в A1.3!) (в этой области обе функции ^?(р, р')
и S?* (р, р") отличны от нуля, так что |р'— р"|^6), функция
когерентности Г„(р'—р") практически постоянна (поскольку
|_р' — p'l^S-^'o). Вынося ее за знак интеграла со значением
/„, где /„ = Г„@)— интенсивность облучающего поля, получаем
\
A1.32)
Такую же формулу можно получить, разумеется, и непосредст-
венно из A1.31), если считать первичное поле v (px) когерентным
на всей плоскости предмета. Из приведенного вывода видно, что
требование когерентности на всем предмете является излишним:
для справедливости A1.32) достаточно, чтобы первичное поле v (p)
было когерентным лишь в пределах области разрешения 6.
В другом предельном случае некогерентного освещения A„<^.
<€$, Pmin) существенная для интегрирования область в A1.32)
ограничена площадью когерентности с линейными размерами
I р' — р" | =? lv. В пределах этой площади функции f* (p") и ??* (р, р")
можно приближенно заменкть соответственно на /* (р') н &* (р, р'),
и в результате получим
/(Р)не«ог= ] |/(р'M»(Р, РТ^Р' I Tv((.'-p")dY.
-ОО -СО
Внутренний интеграл равен 7VSV, где, подобно A1.15), введена
площадь когерентности Sv, равная интегралу от коэффициента
корреляции первичного поля Kv = Tvllv.
Таки{д образом, распределение средней интенсивности в пло-
скости изображения при некогерентном освещении дается выра-
жением
7;J[^(p,p1)|2d2p1. A1.33)
ДИФРАКЦИЯ В ОПТИЧЕСКИХ СИСТЕМАХ 101
Формально это выражение можно получить из A1.31), считая,
j«K и в A1.18), первичное поле дельта-коррелированным.
формулы A1.32) и A1.33) существенно отличаются друг от
друга. Можно сказать, что при когерентном (в указанном выше
смысле, т.е. при lv^>6, pmin) освещении происходит преобразо-
вание самого комплексного коэффициента пропускания /(р,) (с пе-
редаточной функцией у 7^i?(p, p,)), а при некогерентном осве-
щении (/„<§: 6, pmin) преобразуется квадрат модуля \j(pl)\i (с пе-
редаточной функцией lvSv\f?{p, pJI2). Отсюда следует, в част-
ности, что при некогерентном освещении изображение не зависит
от фазы комплексной функции пропускания /, тогда как коге-
рентное освещение может выявить резкие вариации фазы/даже
при |/1 = const. Например, если на некоторой линии в плоскости
предмета фаза скачком меняется на я, a |/| = const, то, как
еледует из A1.32), в плоскости изображения на соответствующей
(сопряженной) линии интенсивность Т(р)тт обратится в нуль и
ныувидим там темную полосу. Правда, при плавном (в масштабе 8)
изменении модуля и аргумента коэффициента прозрачности, т. е.
при рШш^>6, оба вида освещения дают практически одинаковое
изображение, так как в обоих случаях распределение интенсив-
ности в плоскости изображения /(р) пропорционально |f(Pi)|2.
Укажем еще на два различия между когерентным и некоге-
рентным освещением. Во-первых, при одинаковой интенсивности
освещения lv интенсивность и плоскости изображения при коге-
рентном свете будет больше, чем при некогерентном, поскольку
Ширина углового спектра у некогереитнэго облучения больше,
Чем у когерентного. Во-вторых, в предельных случаях освещения
возникают различия и в величине разрешающей способности:
при некогерентном освещении размер наименьших различимых
по Релею деталей несколько меньше (примерно на 30%), чем
при когерентном. Это различие связано просто с тем, что вхо-
ЙЯщнй в формулу A1.33) квадрат модуля |,??(р, pjl" меняется
В1 функции от координаты р, круче, чем сама аппаратная
функция ^?(р, pj в формуле A1.32). В результате при разре-
шении двух точечных объектов с центрами в точках pi и
Pi провал между горбами в распределении интенсивности в пло-
скости изображения получается более глубоким, если световые
колебании в точках р[ и р", некогереитиы. Провал можно сде-
лать еще глубже, если добиться отрицательной корреляции
освещающего поля в точках р[ и Pi (отрицательные значения
может принимать, например, функция когерентности вида 2i, (x)/x,
отвечающая равномерно светящемуся диску или же пучку света,
пропущенному через малое круглое отверстие). Этот красивый
по своей идее способ увеличения разрешающей способности дает,
однако, весьма незначительный выигрыш (всего лишь на несколько
102 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕП (ГЛ. II
процентов) по сравнению с некогерентным облучением. Более
подробно этот вопрос рассмотрен в книге [21J.
Возникающие в оптике статистические задачи, конечно, не
исчерпываются приведенными примерами. Среди других проб-
лем упомянем пространственную фильтрацию, статистические
вопросы, связанные с несовершенством оптических систем и с
зернистостью фотоматериалов, нсгюльзование оптических систем
для корреляционного анализа и т. д. С этими и некоторыми
другими приложениями можно познакомиться по работам [13—22].
Многие идеи, развитые первоначально в оптике, нашли приме-
нение и в радиотехнике [37].
§ 12, Возбуждение полей случайными источниками
Флуктуации поля, возбуждаемого случайными источниками,
представляют интерес для многих разделов физики. Здесь мы
остановимся на излучении радиоантенн со случайными вариа-
циями токов d раскрыве и рассмотрим особенности излучения
большого числа независимых источников.
1. Статистика поля, излученного большой ан-
тенной, Причиной флуктуации поля, излученного антенной, мо-
гут быть случайные отклонения амплитуд и фаз токов в апертуре
ог заданных значений, обусловленные различными факторами.
Главными из них являются неровности антенного зеркала, раз-
брос параметров излучающих вибраторов, случайные отклонения
в системах возбуждения и т. Д. Определенную роль играют также
деформации антенн при изменении температуры нли из-за ветро-
вых нагрузок. Рассмотрим одну из моделей антенны с флуктуа-
циями токов.
Если размеры плоской антенны велики по сравнению с дли-
ной волны, а токи в раскрыве монохроматические (~е-'ш') и
имеют только одну компоненту, скажем jx, то в направлениях,
не сильно отклоняющихся от нормали к плоскости раскрыва
z = 0, можно считать, что электрическое поле имеет только ком-
поненту ?х, удовлетворяющую уравнению
AF 4-fe2F • 4дц'* i
иЕд:Т'< Е.\- " /х-
Таким образом, с учетом иных обозначений (а — Ех, q— ^г"Ы
задача сводится к уже рассмотренной скалярной задаче (9.7),
имеющей решение (9.8).
В случае антенн с плоским раскрывом токи сосредоточены
в плоскости z = 0, т.е. объемный интеграл (9.8) превращаетси
в поверхностный. Сохраняя для плотности поверхностных токов
ВОЗБУЖДЕНИЕ ПОЛЕЙ СЛУЧАЙНЫМИ ИСТОЧНИКАМИ ЮЗ
обозначение q, получаем
P'>-V-d2p'. RHr-O. A2.1)
где для краткости опущен аргумент ы, а интегрирование рас-
пространяется на площадь раскрыва S.
Обычно представляет интерес поле в дальней (фраунгоферо-
вой) зоне z^-ka1, где а—поперечник раскрыва. Можно поэтому
воспользоваться приближением фраунгоферовой дифракции, т. е.
формулой (9.10), которая в данном случае (поверхностные источ-
ники, излучение сосредоточено в узком конусе около оси г)
принимает вид
]
Здесь р = (х, у)—координаты точки наблюдения на удаленной
плоскости г = const. Ограничимся нахождением среднего значе-
нии к пространственной функции корреляции поля, излученного
большой антенной, имея в виду лишь основные эффекты, к ко-
торым приводят флуктуации токов в антеннах. Систематическому
изложению вопросов статистической теории антенн посвящена
книга [38].
Как и в § 11, удобно ввести функцию М (р), которая равна
единице на раскрыве S н обращается в нуль вне S (см. A1.2)):
что позволяет раздвинуть пределы интегрирования в A2.2) до
бесконечности:
«(Р. г) =
A2.3)
Среднее но ансамблю реализаций токов значение ноля дается
интегралом
"{р> г>=тЬ"ехР ['* (z + f)] J »(Р')М (Р'> ех
который можно представить в виде
^ , A2.4)
104 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ [ГЛ. II
где qm — максимальное значение среднего тока в раскрыве, а
? А (к)— нормированная к единице (FA@) = \) диаграмма на-
правленности антенны:
f ^ A2.5)
причем паправлеиие на точку наблюдения (х, у) в плоскости
? = cortst задается вектором K — kp/z — (kx/z,kylz). Наконец,
Чп.
— нормировочный множитель, значение которого близко к пло-
щади раскрыва (SA = S при q = const).
Функция корреляции поля в плоскости г = const (попереч-
ная функция корреляции) выражается двукратным интегралом
л, Р2. г) = <и(р1г)п* (р„ г)> =
И
A2.6)
где *f,j(p'> р") = <9 (р')9* (р")>—функция корреляции тока. Во-
обще говоря, флуктуации тока в раскрыве статистически неодно-
родны, что связано с краевыми эффектами; вследствие взаимного
влияния элементов излучающей системы статистика токов на
краях раскрыва может отличаться от статистики в середине
антенны. Однако в случае больших антени, размеры которых а
велики по сравнению с радиусом корреляции токов lq, краевым
эффектом можно пренебречь н считать, что на всем раскрыве
%(Р',Р")&%(Р' — Р"), 1«<а.
Принимая модель мелкомасштабных (lq<^а) флуктуации тока
в раскрыве, мы можем воспользоваться изложегшыми в § 11
приемами вычисления интегралов типа A1.5). Если обозначить
p = pj —р2, р+ = (р1 + р4)/2, то A2.6) примет вид
ехр DЕЯ) *„ j Кд © ехр
A2.7)
где ajj =--<| </12> — дисперсия, а К,,—коэффициент корреляции
флуктуации тока,
ВОЗБУЖДЕНИЕ ПОЛЕЙ СЛУЧАЙНЫМИ ИСТОЧНИКАМИ |05
Первый интеграл в A2.7) равен SoF^f-—), где S—площадь
раскрыва, а ?м дается выражением A1.14). Эта величина не-
сколько отличается от диаграммы антенны A2.5), но при
a"=*const qFm = 3~а- Второй интеграл (по \) тоже можно записать
в виде произведения двух множителей:
^ K,(S)exp(-i^jd^=S,r,(^±-), A2.8)
— ос
где
—эффективная площадь когерентности токов, а еГв(и)—нор-
мированная к единице (ёГ?(О) = 1) диаграмма направленности
флуктуационных токов.
С введением этих обозначений корреляционная функция tjjj_
принимает вид
р.. г) = ехр [л*±-)$^ ТЯ (i) Гч {^-) • A2.9)
Эту формулу можно рассматривать как обобщение теоремы Ван-
1Д.иттерта—Цернике на случай конечного радиуса корреляции
источников. При дельта-коррелированных флуктуациях «F,= l,
и тогда A2.9) отличается от A1.16) только обозначениями.
Отсюда следует, что пространственное распределение дисперсии
Йэля определяется сравнительно широкой (с угловым раствором
«v Я//,) диаграммой 3"?:
^(^) A2.10)
тогда как пространственный коэффициент корреляции поля за-
висит от диаграммы JThl;
Цоследняя имеет угловую ширину ~ Х/а, меньшую, чем ширина
Xfl* флуктуационной диаграммы Wq, поскольку a^>lq- Попереч-
ный радиус корреляции 1± оказывается таким же, как в A1.12),
i. e. /j_ ~ Хг/а.
Пространственное распределение средней интенсивности /„
1«ожно получить при помощи A2.4) и A2.10):
1
106
ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ
[ГЛ. II
Здесь первое слагаемое описывает вклад среднего поля, а вто-
рое— вклад флуктуацнонного поля. На рис. 8 показана зависи-
мость 1а от р+ для различных соотношений между этими сла-
гаемыми в предположении, что полная мощность, подводимая
к антенне, постоянна, т. е.
|9m|a + a2, = consts<2>
В отсутствие флуктуации, когда оя = (
невозмущеиную интенсивность
A2.12)
и | qm | = Q, мы имеем
пропорциональную квадрату модуля диаграммы направлен-
ности WА. Ширина этой диаграммы, скажем расстояние между
се нулями, составляет Хг/а (кривая 1 на рис. 8). При малых
Рис.
возмущениях появляется флуктуационная компонента, пропор-
циональная угловому спектру флуктуации lT9(ftp+/z) н имеющая
ширину Др+ ~ Xz/lq^-kz/a. Эта составляющая приводит к «замы-
ванню» нулей (или минимумов) регулярной диаграммы (кри-
вая 2 на рис. 8) и к росту бокового излучения, т. е. излучения
вне центрального максимума. Вместе с тем несколько умень-
шается вклад регулярной составляющей поля, так как прн
неизменной мощности, подводимой к антенне, величина |<?m|2
уменьшается по сравнению с Qa: |gm|a = <22—о%.
Распределение интенсивности в плоскости г=const в случае
примерного равенства регулярной и флуктуационной компонент
в центре диаграммы изображает кривая 3 на рнс. 8. Согласно
ii?! ВОЗБУЖДЕНИЕ ПОЛЕЙ СЛУЧАЙНЫМИ ИСТОЧНИКАМИ 107
— / 5S
A2.11) равенство |u|" = aj достигается при aJ = Qa( 1 ?-
при этом квадрат среднего значения тока |gOT|! = Qs—aj мал
по сравнению с Q2, т.е. |9„|2«—r-Q'^Q1- При столь боль-
ших возмущениях говорят о разрушении диаграммы направлен-
ности антенны.
С дальнейшим ростом флуктуации регулярное слагаемое в
A2.11) ставовнтся пренебрежимо малым и распределение сред-
ней интенсивности уже совсем не похоже на иевозмущеииое
распределение A2.13):
Ширина диаграммы излучения здесь порядка Хг//?, а максимум
интенсивности в Sq/S раз меньше, чем в отсутствие флуктуации.
Уменьшение интенсивности в направлении максимума излу-
чения удобно характеризовать величиной коэффициента направ-
ленного действия (к. н. д.), который показывает, во сколько раз
интенсивность поля в центре главного лепестка диаграммы
больше, чем у ненаправленной антенны, излучающей ту же мощ-
ность. Вычислим средний к. н. д. антенны <С> при сделанных
Выше допущениях. Очевидно, если Go —к. н.д. невозмущенной
антенны, то
Так как
для величины <G>/GC с учетом A2.12) получаем
При малых возмущениях токов в раскрыве (t,,<^Q) средний
к. н.д. антенны мало отличается от Сг„: <G>»G,,A—<%/(}*) (на-
помним, что Sg<^.S). Уменьшение среднего к. н. д. вдвое на-
ступает уже при заметных флуктуациях, когда aj ~ VjQ3. При
сильных же флуктуациях, когда aQ—>Q, а регулярная состав-
ЛйЮщая тока \qK\ = \fQ*—oj стремится к нулю, получаем
108 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ [ГЛ. и
Таким образом, при сильных флуктуациях к.н.д. антенны тем
меньше, чем больше неоднородностей N — S/S^ содержит раскрыв:
<,G> = GjN. Учитывая, что G0~S/X*, соотношение A2.15) можно
записать иначе;
Отсюда видно, что если радиус корреляции lq сравним с длиной
волны Я, то 5?«/|~-?.а и <0>~1. Иными словами, при силь-
ных (oq"$>\qm\) и мелких (/?~Я) флуктуациях излучение ан-
тенны полиостью теряет направленность.
В статистической теории антени возможны и многие другие
задачи. Например, может представлять интерес направление
центрального лепестка диаграммы направленности, уровень бо-
кового излучения, статистика амплитуды и фазы и т. д. Эти
вопросы достаточно полно освещены в монографии [38]. Отметим,
что при исследовании статистики излучения антенны основная
трудность заключается, по-видимому, не в вычислении тех или
иных интегралов, входящих в выражения для моментов поля,
а в физически обосиованиом задании статистики флуктуирующих
по раскрыву антенны токов. Ясно, что предсказать эту стати-
стику только из теоретических соображений невозможно. В то
же время прямые измерения статистических характеристик со-
пряжены со значительными трудностями, в частности, из-за
того, что при внесении в антенну измерительных зондов распре-
деление токов в ней меняется. Косвенное же нахождение флук-
туации путем измерения полей, излученных антенной, тоже не
дает исчерпывающего решения проблемы: такие измерения под-
вержены влиянию дополнительных посторонних факторов (рас-
положенные рядом предметы и постройки, неровности местности
и т. д.), не говоря уже о том, что измерения поля сложны сами
по себе как в ближней, так и в дальней зонах.
2. Статистика поля, излученного системой не-
зависимых источников. Для простоты будем считать вол-
новое поле скалярным, а источники-—точечными. Если ;-й точеч-
ный источник движется по траектории г=г7- (f), а его интенсив-
ность меняется по закону (вообще говоря, случайному) Qt (t), то
для системы N точечных источников правая часть волнового
уравнения (9.4) запишется в виде
Q(t, г) = 2Q/(OS[r-г,(<)].
В результате поле излучения (9.5) будет выражаться суммой
. 1г
I г—
ВОЗБУЖДЕНИЕ ПОЛЕЙ СЛУЧАЙНЫМИ ИСТОЧНИКАМИ
109
В которой |г — Гу(<)| — расстояние от точки наблюдения до /-го
Источника.
Не интересуясь средним значением поля, которое в подав-
ляющем большинстве задач равно нулю, вычислим простран-
ственно-временную функцию когерентности, сначала—для си-
стемы неподвижных источников (г, = const). В силу A2.16)
Г(Л г'; Г, г") = <«(/', г') <*•(<". «¦")> =
|r'-iy||r*-r,|
f]& угловые скобки означают усреднение по ансамблю положе-
ний источников, а черта сверху—усреднение по ансамблю реа-
лизаций случайных процес-
Выражение A2.17) при-
нимает особенно простой вид
|йпя системы независимых и
финиковых источников. Для
такой системы при \Ф1
одинаковую для всех Рис- 9-
|фодессов Q/ ({) корреляцион-
ную функцию обозначить через MpQ (t) (предполагается стационар-
ность этих процессов), то двойная сумма A2.17) превратится в
"'одинаковых слагаемых:
Г
Щи т=^—1г, а 8=1^ — R |—|гг —R|—разности хода отисточ-
Ййка, находящегося в точке R до точек наблюдения rt и га
#нс. 9).
Усреднение по положениям гшточннков можно представить
% виде интеграла по объему с весовой функцией w(R), которая
Надставляет собой плотность вероятностей для радиуса-век-
WpaR:
или, если ввести среднюю концентрацию источников n(R)=Nw{R),
г.<*; г, rJ = tk>$itl-l7*-*\«™*«- A2Л8)
ПО ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ ГГЛ. и
В частном случае, когда источники распределены по объему V
равномерно, п = Л//К = const.
Временная функция когерентности может быть получена из
A2.18), если положить г1 = г2 = г. Тогда s = 0 и
Отсюда видно, что коэффициенты временной корреляции поли
и источников совпадают: Ки (т) =Kq (т), т. е. временная коге-
рентность излученного поля оказывается такой же, как у источ-
ников. Это естественно, так как при неподвижных источниках
изменения поля обусловлены только изменениями функций Qj (t).
Обращаясь к пространственной корреляции излученного поля,
рассмотрим некоторые частные случаи.
Если размеры «облака» источников малы по сравнению со
средней длиной волны излучения Х„, L~Vl/a<^.h0, то можно
считать задержку s/c в формуле A2.18) постоянной величиной,
равной sjc=(\rl — Ra\—\T,—R0\)/c = (r1—rs)/c, где Ro-0 —
центр объема V. Для точек наблюдения гх н г,, лежащих вне
объема V, тогда находим
1 Лх> ¦",. Тг) Dп)г,л,
где учтено, что J n(R)d*R = N. При т = 0 отсюда получается
пространственная функция когерентности излучателя малых
размеров:
Согласно A2.19) поле пространственно когерентно внутри
шарового слоя толщины сх„, где хк — время корреляции источ-
ников. Таким образом, пространственный радиус корреляции 1К
совпадает в данном случае с длиной когерентного цуга схк.
Иначе обстоит дело для больших (по сравнению с %„) объе-
мов V. Соответствующие закономерности проще всего установить
при помощи величины Г„ (ш; г^ г2), являющейся преобразова-
нием Фурье по времени от Г„ (т; г,, г2)'). Для функции] коге-
рентности A2.18) имеем [44J
1 Г1
Гя(о>; г,, г,)—^ ^ Г.(т, rlf ra)^dx =
') В оптике эту величину называют взаимной спектральной интенсив-
ностью, так как она относится к взаимной функции когерентности Г„(т; п, ц),
характеризующей статистическую евяэь поля в двух точках.
ВОЗБУЖДЕНИЕ ПОЛЕЙ СЛУЧАЙНЫМИ ИСТОЧНИКАМИ Ц1
Здесь /г = ш/с, а
— спектральная плотность процесса Q(t).
Непосредственно из вида формулы A2.20) можно заключить,
что если размеры «облака» источников L велики по сравнению
с длиной волны X, а точки г1 и г2 находятся внутри облака,
то смещение любой из точек гх или г2 на % приведет к суще-
ственному изменению величины Г„, так как под интегралом
имеется быстро осциллирующая функция e'ks. Отсюда следует,
Что внутри большого (L^>%) облака излучателей пространствен-
Йый радиус корреляции сравним с длиной волны1):
По мере удаления точек наблюдения от облака должно, оче-
андно, происходить некоторое упорядочение интерференционной
Картины—хотя бы из-за того, что волиы будут приходить теперь
только из ограниченного телесного угла. Это упорядочение
проявляется в увеличении пространственного радиуса корреля-
ции вдали от системы излучателей, подобно вытекающему из
теоремы Ван-Циттерта—Церпике ун»личению 1и для дифракцион-
ного поля отверстия (§ 11). Теорема Ван-Циттерта—Цернике
Мржет быть сформулирована и для системы независимых излуча-
телей, но вывод оказывается несколько сложнее, чем в задаче
О,дифракции случайного поля.
Приведем только окончательный результат. Пусть точки тг
и г2 лежат в плоскости г = const, при этом гь г = (рь 2, г). У век-
тора R тоже оыделнм продольную (г') н поперечную (р') коор-
динаты: R —(р', г'), dsR — d~p'dz . Если расстояние от облака
?елико по сравнению с его поперечником (г^-L), а точки наблю-
дения расположены ие слишком далеко от оси г (рь ,<^г), то
формула A2.20) принимает вид
ГЛ<»; р, р+. г) =
*) Простая иллюстрация: от брошенного в воду камня расходятся волны
правильной круговой формы. Если же бросить пригоршню камней, то интер-
ференция круговых волн создает в месте падения камней беспорядочную кар-
тину гребней и впадин, сменяющих друг друга при смещении примерно иа
Длину волны в любом направлении.
112 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ 1ГЛ. П
где р —р, р2, р+=(Pi + p2)/2- Это соотношение эквивалентно
A1.16), если под приведенной (к плоскости г' = 0)интенсивностью
понимать величину
^(р')-=4^е<з(«>К(е'>. С2-22)
где
— число излучателей, приходящихся на единицу площади в пло-
скости 2 = 0.
Теорема Ван-Циттерта—Церннке сохраняет силу и в случае
движущихся источников, но спектральная плотность gQ(a>), вхо-
дящая в определение приведенной интенсивности A2.22), а также
в формулы A2.20) и A2.21), должна быть усреднена по всем
возможным значениям доплеровского смещения частоты, возни-
кающего из-за движения источников. Иными словами, в форму-
лах A2.20)—A2.22) нужно произвести замену
—flj>, A2.23)
где угловые скобки обозначают усреднение по распределению
доплеровского сдвига И^ — ию^/с, пропорционального лучевой
скорости Уц =(m, v), т=-(г—R)/|r—R |.
Замена A2.23) справедлива при условии, что «длина свобод-
ного пробега» источника 1сва6 (т. е. длина, на которой заметно
меняется скорость излучателя, или же расстояние, проходимое
источником за время корреляции излучаемого сигнала) мала по
сравнению с расстоянием |г—R| до точки наблюдения: /св(,й^5
<?5|г—R |. В подавляющем большинстве практически интересных
случаев это условие выполнено.
В качестве конкретного выражения для спектральной плот-
ности ge(G>) укажем на результаты расчетов, проведенных в ч. I
(задача 11 к гл. VI) для луассоновского импульсного процесса,
состоящего из следующих друг за другом отрезков экспонен-
циально затухающих синусоидальных цугов. Этот процесс может
служить моделью излучения атомов, возбуждаемых ударами
соседей. Окончательная формула для спектральной плотности
(формула A) в указанной задаче) имеет вид
где пг—средняя частота соударений, у — радиационная ширина
линий излучения и одновременно показатель затухания импуль-
сон вида Q (t) = А ехр {— (у+ша) t + ф}, А —случайная амплитуда
Со средним квадратом А1, E — случайная фаза, распределенная
ЗАДАЧИ 513
равномерно в интервале @, 2я), а <а0—частота излучения в си-
стеме отсчета, в которой осциллятор покоится. В случае мак-
свелловского распределения скоростей частиц формула A2.24),
в зависимости от соотношения между шириной линии излучения
я, + Т и среднеквадратнчным доплеровским уширениемащ=-|/Щ,
дает либо гауссову (при о^^п^ + у), либо лоренцеву (при
o@^n1-)-'v) форму линии излучения.
Теорема Ван-Циттерта — Цернике допускает обобщение еще
в одном направлении. Спектральная плотность A2.24) соответ-
ствует модели, в которой излучают атомы только одного сорта
н только на одной частоте. Между тем в реальных нагретых
газах могут содержаться атомы многих сортов, излучающие на
многих частотах; в плотном облаке многие световые импульсы
поглощаются другими атомами, не достигнув наблюдателя, и
т, д. Все эти эффекты можно учесть в теореме Ван-Циттерта —
Цернике, если под J (p) понимать сумму приведенных интенсив-
ности, отвечающих различным линиям излучения:
J (Р) = 2j Jm (P) = 4^» 2j ^ ^ """' ^'
VI
Спектр каждой из этих линий излучения характеризуется
собственной частотой излучателя &f\ силой осциллятора А%т,
радиационной шириной ут и средним числом столкновений п?".
Величина п\т (р) определяет тогда эффективную поверхностную
концентрацию излучателей, импульсы от которых в состоянии
выйтн из объема V. Разумеется, если излучатели распределены
не в объеме, а на поверхности, то при расчете следует с самого
¦начала ввести вместо объемной концентрации п (R) поверхност-
ную концентрацию rcs(p) (см., например, [39]).
Задачи
1. Выразить среднюю плотность звуковой энергии в жидкости W — '/грв8 +
?3~ ViPp2 и средний вектор Уыова (плотность потока энергии) оУ ~ pv через
функцию когерентности потенциала скорости и через лучевую интенсивность.
Решение. Выразив давление р н скорость v через потенциал скорости
Эф
9J с = (Вр)~1'2 —скорость звука, р — средняя плотность, fl—сжимаемость
К*Цкости. Если u(t,r) — комплексный потенциал скорости (аналитический
<?ЙГКал), отвечающий вещественному потенциалу 4>(t, г): (р-^1?е«, то W н 3*
114 ИЗЛУЧЕНИЕ к ДИФРАКЦИЯ СЛУЧАЙНЫХ НОЛЕЙ [ГЛ. И
записываются через и следующим образом:
Усреднение этих выражений дает
old - ) A)
<=f> = — у Re \jf V2 [Г„ A, 2) f ГвA, 2))\
Символом 2—>¦ 1 здесь обозначен предельный переход <2—> tu г2—>ri, ко-
торый следует делать после вычисления временных и пространственных про-
изводных. Заметим, что эакои сохранения div<ff -\-dW/dt = 0, который должен
выполняться и для средних значений <IF> и i^fy, при подстановке в него
выражений A) можно рассматривать как своеобразное уравнение сохранения
для функций Г„ и Г„.
Если поле и стационарно, то и = 0, Г = 0, и тогда
Если поле и к тому же и однородно, то его корреляционная функция ^д (I, 2)
имеет внд (9.27), что позволяет выразить <Й7> и <<5Р> через лучевую интен-
сивность:
"§
Я (ю, n)do(n),
> = -?¦ \ k% da ф п 3 {at, n) do (n).
Для изотропного случайного звукового поля, очевидно, (of>~O. Для квази-
монохроматического звукового поля (спектр сосредоточен вблизи частоты со0)
множигель k2 в написанных выражениях можно вынести за знак интеграла
со значением &о—о)«/с2.
2. Найти общий вид функции корреляции изотропного, однородного и
стационарного скалярного волнового поля.
Решение. Лучевая интенсивность 3 (to, fi) для изотропного поля не
зависит от направления: 3 (to, n) = ^ (со), так что корреляционная функция
(9.27) выражается однократным интегралом:
поскольку
злдлчи П5
3. Оценить продольный и поперечный радиусы корреляции волнового
поля, лучевая интенсивность которого 3 (о>, п) сосредоточена в узком конусе
направлений с раствором 9<^1.
Решение. Пусть ось г отвечает направлению, по которому лучевая
интенсивность максимальна. Записав единичный вектор п в виде
при п^ ^Р<С ' имеем пг~У 1 —п\ да 1 —лх/2, так что (nr) ss г — xUn\z -\-
-j- (ij_1 Р). <? (ю> п) ~ 3 (со, Hj_, 1) и Корреляционная функция (9.27) прини-
мает вид
V(t, г) =
= \ daexpiikz— iat) ? 3 (со, n_j_, l)exp(ifti^p—~ kn \z Ыо(п), A)
о
где р — (JC, у). Поперечный A^) и продольный Aц) радиусы корреляции оце-
ниваются из условий Ikn.p!^], \kaj_z\^.t, если подставить в них л . к В.
В результате находим
±~ кв~ в ' n~W~W (~'
4. Установить связь между лучевой интенсивностью и двумерным спект-
ром (9.29) в случае узкого углового спектра [40].
Решение. В узком конусе 1 п. |^C6<g;l выполняется приближенное
соотношение do (n) я йпх йпу, которое можно представить d эквивалентной
форме do (n) = k~2 dnx dXy=-k~^d^v., , если ввести двумерный волновой вектор
ti^ — kn^ — (knx, krty). Формула A) предыдущей задачи принимает тогда вид
двумерного спектрального разложения:
V(t,T)= \ rfraexp(|-fa — Ш) f *? (ю, n±> l)exp f ix±p—^
Сравнение этого разложения с разложением
T(/,r)=(J da f F(a; их, z) exp (ix^p—le
6 -»
обратным (9.29), показывает, что
(
5. Выразить среднюю плотность электромагнитной энергии и средний век
тор Пойнтинга в вакууме через матрицу лучевых интеиснвностей tfaai кото
рая вводится аналогично (9.26):
при этом, подобно (9.27),
fap'C г) =
116 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ [ГЛ. II
Здесь Gaj'—матрица спектральных плотностей, представляющая собой преоб-
разование Фурье корреляционной матрицы свободного статистически однород-
ного электромагнитного поля
Решение. Рассматривая случай стационарного и однородного электро-
магнитного поля с нулевым средним значением и учитывая, что в вакууме
/Н|аНЕ|з, имеем
Но при Ё = 0 в силу A)
3 т
<| Е 1«> = 2 Т$ @, 0)=\de><$3 (ш, n) do (n),
а = 1 о
где введена лучевая интенсивность
В результате имеем
>=g^ С 4o if ST (», n) do (n).
о
Среднее значеине вектора Пойнтинга
можно получить, используя спектральные разложения для Е и Н и соотно-
шение Ншх=[пЕоие]:
<&У = ^ Re
-• о
X <[Ей-х' [п"Бв-х»Ц> exP [i (к' - к') г - ? (a' - со')], C)
где п'=х"/и". Раскрывая двойное векторное произведение, получаем выра-
жение
Вследствие дельта-корреляции спектральных амплитуд вектор п* можно заме-
нить на п'=х'/х', но в силу поперечности электроиагинтиого поля (п'Еш.х,)=0.
В результате, с учетом B), имеем
з
<...>= Sn'G^O»', х')8(и'—©')«(*'—«*) =
а=1
= п'Э (о), п)А-«8(ю' — ш")б(х'—х*)8(н' — А).
Подставляя это выражение в C), получаем
if ((о)^пЭ(о), n)do(n). D)
ЗАДАЧИ Ц7
Легко видеть, что электромагнитные формулы для <W> и <^Р> отличаются
от акустических выражений (см. задачу 1) только множителем 1/8л вместо
р*'/2.
Из D) следует, что величина ^-пЗ(ю, п) имеет смысл потока энергии
через единичную площадку в единичный телесный угол в расчете на единич-
ный.частотный интервал. Именно так вводится лучевая интенсивность (яркость)
в феноменологической теории переноса излучения [41, 42].
в. Построить корреляционную матрицу Ч^' для изотропного, однород-
ного и стационарного электромагнитного поля.
Решение. Входящая в формулу A) предыдущей задачи матрица Зар
в случае изотропного поля должна иметь вид
Кроме того, в силу поперечностн электромагнитных воли в свободном прост-
ранстве матрица ?ag должна удовлетворять условиям
Это возможно только при <? = — У, н тогда
где s = 4л sin kr/kr, а штрихом обозначено дифференцирование по г. Лучевая
интенсивность 3=2заа в данном случае равна 2ff5(o>) и, следовательно,
не зависит от направления; при этом, в соответствии с результатами задачи 5,
<Sf>~0, a <W>= [ p(a,)du>.
о'
7. Вычислить индекс мерцаний в дальней зоне для амплитудио-фажшого
экрана с логарифмически нормальным законом распределения вероятностей
Поля.
Решение. Пусть и —ex+tSi, где фаза S и уровень % распределены по
нормальному закону, так что ?—логарифмически нормальное поле. Предпо-
ложим, что S^O н <SX> = 0. В силу нормировки A0.23) "х= — <4- В ре-
•ультате
v0 - < e"+'s> - е*+ ''* «*~+lS>'> = f '/¦(<^+ox).
Следовательно, в дальней зоне
Э* = PL = 1 — | ^'„ I4 = 1 — ехр {—
[18 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЙ [ГЛ. II
В случае чисто амплитудных флуктуации (cjs^O) квадрат индекса мерцаний
в дальней зоне равен р1^,—1—е х, тогда как на самом экране |12^^=^
= « х — I. Очевидно, go > 1 > pi, т. е. амплитудные флуктуации за экраном
сглаживаются.
8. Пусть поле в плоскости экрана вещественно и распределено по нор-
малыкму закону. Показать, что квадрат индекса мерцаний в дальней зоне
вдвое меньше, чем на экране.
Решение. В дальней зоне, согласно A0.38), [Й= = 1 —11'„ |*. На
экране же
(,* = рЦ = <«'> _ 1 = р
Но для вещественного нормального случайного поля <i'*> — 3
Поэтому, с учетом нормировки Сту + ио=1, имеем
т. е. р"!> = '/аРо- В этой и предыдущей задачах fil < Й, потому что поле и
порождает за экраном помимо амплитудных еще и фазовые флуктуации, кото-
рые, очевидно, не влияют иа величину флуктуации интенсивности.
9. Вывести из френелевскоги приближении (9Л7) соотношение (Ш.13),
согласно которому при падении плоской волны корреляционная функция за
бесконечным экраном i|)j_ (p) совпадает с функцией корреляции граничного
поля iMp).
Решение. Во френелевском приближении
Вводя обозначения p = pL—р2, Р+= (pi + P2)/2, | = {р' — р"), Л^СР' —р")/2,
получаем выражение
Интеграл по v\ здесь вычисляется точно и равен (-т— ) $(|—р), что и прн-
водит к соотношению т|з^ (р, г) *1\. (Р)-
10. Найти закон изменения среднего значении и функции корреляции
сферической волны, прошедшей через неограниченный статистически однород-
ный хаотический экран.
Решения. Пусть слева от плоскости z^Q, в которой расположен
экран, находится источник, излучающий сферическую волну
exp {i*| г — го|}/[г—го|.
где го^(О, —г„) (рнс. 10). Если /(р) — комплексная функция пропускания
экрана, то граиичппе поле в плоскости г~0 равно
exp I
Задачи
119
Подставим это выражение для поля в формулу Грина (9.12) и, зафиксировав
точку наблюдения г=(р, г), разложим показатель экспоненты в ряд по сте-
пеням отклонения в = р'—рст перемытой р' от стационарной точки рёт =
_ рг/(г + г0), лежащей на луче, соединяющем точку наблюдения с источни-
ком. Все предэкспоиенциальные множители, кроме f (p), заменим стационар-
ными значениями, т. е. значениями при р' = рст.
Получившуюся приближенную формулу
и (р, г) ~ ¦
/(рст+6)ехр/
(I)
можно назвать френелевским приближением для сферической волны. Здесь
Из A) находим среднее поле
представляющее собой сферическую волну с амплитудой /, и функцию кор-
реляции поля в плоскости 1 —- const:
ехр
, (Pi. Ра, г) =
, г) = -
Ь Р
где p = pi—Р2, р+ = (рН~р>)/2. Аналогичное выражение получается и для
функции когерентности.
В отличие от рассмотренного в § 10 случая плоской волны, функция
корреляции сферической волиы, прошедшей через экран, не сохраняется.
В частности, радиус корреляции
171
поля в плоскости г = const растет
при удалении от экрана пропор-
ционально расстоянию от источ-
ника /ы = ?j. —^t—?t где //—радиус
корреляции функции пропускания
f. Роль волнового параметра в дан-
ной аадаче играет величина Z)c^ —
= 2L/ktj, которая при г —>¦ оо
стремится к конечному пределу
&mtx =2zo/?if. Легко понять, что
приОтах^|, когда радиус первой зоны Френеля }fXzz0/(z-{-z0) при любых
z меньше размера неоднородностен на экране //, поле сферической аолиы
за экраном не нормализуется даже на бесконечности.
И. Найти распределение интенсивности поля в дальней зоне ограничен-
ного хаотического экрана.
Решение. Поле в зоне Фраунгофера определяетси выражением A1.11),
в котором под v нужно понимать граничное поле v(p) = /(p) и„, возникаю-
щее при падении плоской волны un=eikz иа хаотический экран с фупкцией
пропускания /(р). Распределение интенсивности в дальней зоне можно вычис-
лить из A1.11) так же, как это было сделаио в § 12 для поля A2.3), воз-
бужденного антенной с флуктуирующими токами. Учитывая, что выражение
02.3) переходит в A1.11) при замене q—> — 2ikv, по аналогии с распределе-
Рис. 10.
120 излучение и Дифракция случайных полей
нием интенсивности A2,11) можно написать
1гл. и
; величины оФ и $v вводятся по аналогии с A2.8).
Заметим, что подобное же распределение интеисивиости (с заменой z—>F)
получнгся в фокальной плоскости линзы, поставленной непосредственно после
ограниченного хаотического экра-
на, В обоих случаях при переходе
от слабых флуктуация (ov <§; v)
к сильным {ov^>v) распределе-
ние интенсивности трансформи-
руется так же, как на рис. 8.
12. Найти средний коэффи-
циент направленного действия пя-
= *¦ рнболнческой зеркальной антенны
^ с пологими ггеровиостямк.
Решение, Пусть z ~ p2/2F~—
уравнение невозмущеиного пара-
6 it : Г\ Г* ¦ & I — \ __
олонда, аг-с
(
2=0
VI I
г=р/2Т^-Цр)
Рис. II.
д, р/+1(р)ур
нение зеркала при наличии неров-
ностей ?(р). Облучатель, помещен-
ный в фокусе параболоида (рнс.
11), посылает на зеркало сфери-
ческую волну, которая после отра-
жения превращается в искаженную
плоскую волну. При плавных (в масштабе Я) неровностях зеркала искажение
поля в апертуре можно учесть введением фазового множителя exp (i'S(p)]-^
—ехр [22??(р)| BА?—дополнительный набег фазы, обусловленный неровностя-
ми). Тем самым задача сведена к расчету дифракции поля с граничным значе-
нием на апертуре ч(р) = ехр [2|°??(р)].
Если высота неровностей ? (р) распределена по нормальному аакону, то
oS-l-iFl^l-r'*10?;
при этом для малых неровностей
а для больших неровностей
где /f—радиус корреляции неровностей, а величина 4ft!a| играет туже роль,
что и дисперсия фазы as в теории фазового экрана.
Используя для расчета к. и. д. формулу A2.14), в которой, с учетом пре-
дыдущей задачи, можно заменить 5?, o"J, | q \г и <22 = o-|-f | q I2 соответственно
иа Sv, c%, |о|2 н ol-\-|и|г=1, получаем
121
(здесь, кроме того, учтено, что Sj — S при i> = const). В предельных случаях
имеем
C = G0(l— oji) ж G0(l— 4?2О;) (*оЕ<1),
или, если принять во внимание оценку Sv ~ /' ~ i|/(*<t>.J.
A)
B)
Качественный ход зависимости
б ф
нормированного
среднего к. н. д.
ток кривой отвечает первой формуле
{!), а конечный — формуле B). Из ри-
унка видно, что заметное уменьшение
к. н. д. начинается со значений ко, ~ 1,
tu е- при о,-—1/&~Л/2л, что согла-
суется с инженерным критерием глад-
кости зеркал о"^ < Х/8. Для больших
зеркальных антенн современных ра-
даотелескопов величина Oj может быть
доведена примерно до сантиметра. В
!сйответствии с критерием а^ < ^/8
.резкое снижение эффективности таких
Авгеин происходит при переходе от
сантиметрового к миллиметровому
диапазону воли.
!3. Оценить продольный радиус корреляции
Статистически независимых источников.
Решение. Расположим точки наблюдения fi и Г2 на оси г: п — (О, О, ;
1"«.=@, 0, г). Для входящей в формулу A2.20) разности хода s имеем
поля, созданного облаком
s = |r1-R|-|r2-R|-=K(z + ?-2'J + p"-/(z-/J + p'2, A)
ГД« переменные интегрирования р' и г' меняются в пределах объема V, заня-
того источниками: jp'J^i, ] 2 | j^ZZ,. Прн анализе продольной корреляции
рассмотрим три характерные зоны.
;_ В ближней зоне (z^L) можно ожидать малости /ц по сравнению с L, что
возволяет разложить A) в степенной ряд по t и ограничиться только липей-
жыи членом:
При всех значениях р' н г' множитель при 5 не превышает единицы. Поэтому
Присутствие множителя exp(ifts) под знаком интеграла в A2.20) проявится
Ж)Шь при ??^>1. Следовательно, продольный радиус корреляции может быть
оценен из условия А? — I, т. е.
C)
В промежуточной зоне (?<^ z<^!??2) отношения z'/z и р'/г малы по
сравиевию с единицей, в результате чего выражение B) упрощается и
122 ИЗЛУЧЕНИЕ И ДИФРАКЦИЯ СЛУЧАЙНЫХ ПОЛЕЯ (ГЛ. II
принимает вид
¦'('-¦&)¦
Первое слагаемое в D) не зависит от переменных интегрирования н его
можно не принимать во внимание прн рассмотрении корреляции, так как
|е'*^| = 1. Второе слагаемое по модулю не превышает велнчниы ??'/2г2. Из
условия kXyfjz* — 1 получаем оценку
1 E)
Эта оценка аналогична формуле B) из задачи 3 для продольного радиуса кор-
реляции однородного случайного поля с шириной углового спектра 8 — а/2.
Можно сказать, что в данном случае ширина углового спектра в опреде-
ляется видимым углоаым размером облака источников у — L/г.
В дальней зоне B^>*?.*) величина ks для всех о' и г' отличается от S?
ие более чем на я. Поэтому в дальней зоне е'** гД, а продольный радиус
корреляции увеличивается до бесконечности:
/|=»oo B>ALa|, F)
что отвечает полностью сформировавшейся диаграмме излучения в зонеФраун-
гофера.
Глава III
ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
§ 13. Предварительные замечания
Тепловое электромагнитное поле создается в результате хао-
тического теплового движения заряженных микрочастиц (элек-
тронов, ионов п т. п.), из которых построены тела. Уже отсюда
ясно, что интенсивность теплового поля должна возрастать с по-
вышением температуры, подобно тому как с ростом температуры
убыстряется брауновское движение или усиливаются тепловые
шумы в электрических цепях. Но в макроскопической электро-
динамике электромагнитное поле рассматривается не как сумма
полей отдельных микрочастиц, а как поле макроскопических же
источников, описываемых, например, объемными плотностями
заряда и тока. Применительно к тепловому электромагнитному
полю это означает, что его источниками являются пространст-
венно-временные флуктуации заряда и тока в физически беско-
нечно малых элементах объема тел. Чаще всего масштабом ма-
лости таких объемов служит при спектральном описании поля
интересующая нас длина волны, но аналогичную роль могут
играть и размеры тел или их неоднородностей, расстояния между
телами и т. п. Если физические и геометрические условия задачи
допускают выделение таких физически бесконечно малых эле-
ментов объема, то можно пользоваться уравнениями макроско-
пической электродинамики, т. е. уравнениями Максвелла.
Мы уже рассматривали тепловые флуктуации электрических
величин, но в квазистационарной области, т. е. для электриче-
ских систем, размеры которых / много меньше длины волны
Я: Z<^Al). Состояние таких систем можно описать конечным
числом интегральных функций времени — сил токов через сечения
проводов, зарядов на сосредоточенных емкостях и т. п. При по-
мощи теоремы Найквнста и обобщающей ее флуктуаииомно-дис-
сипационпой теоремы (ФДТ) мы получили в ч. I, § 54 выраже-
ния для вторых моментов термодинамически равновесных флуктуа-
ции таких интегральных величин. Мы уже знакомы, таким
') Не следует смешивать кваэистациоиарноетъ в этом элехтродинамичг-
™*>m Смысле со статистической кваэистацнонзрностью случайных процессов.
124 тепловое Электромагнитное поле [гл. ш
образом, с корреляционной теорией электрических тепловых
флуктуации в квазнстациоиарных цепях, т. е. в случае/-^Х.
Но существует и совсем иная область явлений, для которых
теория тепловых электромагнитных полей была развита уже
давно, причем при прямо противоположных условиях, когда все
характерные размеры тел / велики по сравнению с длиной волны:
/^>Х. Это классическая теория теплового излучения, созданная
Г. Кирхгофом, Л. Больцмаиом и рядом других выдающихся фи-
зиков копна прошлого века. Ее завершило в 1900 г. открытие
М. Планком закона, дающего спектральное распределение энер-
гии равновесного теплового излучения, заключенного в полости
достаточно больших размеров: 1^>Х. Другие законы этой теории
(например, законы Кирхгофа) тоже опираются на асимптотиче-
ское описание электромагнитного поля в приближении геометри-
ческой оптики, пригодном только для достаточно коротких воли.
Исторически это произошло потому, что классическая теория
теплового излучения развивалась прежде всего для оптического
диапазона.
Общая флуктуационная электродинамика полей теплового про-
исхождения, основанная на уравнениях Максвелла (понимаемых,
конечно, как стохастические уравнения), должна быть, очевидно,
свободна от ограничений, касающихся соотношения между раз-
мерами тел / н длиной волны Я. Она должна охватывать, наряду
с иайквистовской теорней тепловых шумов в квазистационарных
цепях (/ <^ X) и классической теорией теплового излучения
A^>Х), также промежуточную область 1~Х, в которой оба пре-
дельных подхода неприменимы. Такая общая теория тепловых
электромагнитных нолей была построена сравнительно недавно [1],
и в данной главе излагаются ее основы. Для краткости мы
будем далее называть случайное электромагнитное поле тепло-
вого происхождения просто флуктуационным полем.
Прежде чем перейти к систематическому изложению, остано-
вимся на двух вопросах, которые легко могут возникнуть после
сказанного выше. Одни из них можно поставить следующим
образом: почему в классической теории теплового излучения
речь идет не вообще о тепловом флуктуационном поле, а именно
об излучении, т. е. только о волновом поле?
Это вполне резонный вопрос, потому что флуктуации заряда
и тока в каждом элементе объема тела порождают не только
разбегающуюся электромагнитную волну, но и так называемое
ближнее квазистационарное поле. Известно, однако, что оно
убывает с расстоянием R от своего «точечного» источника гораздо
быстрее, чем волновое поле,— не как 1/R, а как 1/Я2 и \IRS,
простираясь лишь на расстояния порядка X. Кроме того, это
ближнее поле в среднем за период не создает потока энергии.
Именно поэтому классическая теория теплового излучения, инте-
||Л] ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 125
ресующаяся только переносом «лучистой» энергии и только до-
статочно короткими волнами (X<^0> просто игнорирует блнжиее
флуктуационное поле. Она не может поэтому правильно описать
флуктуационное поле, например, в полости, размеры которол
невелики или тем более малы по сравнению с длиной волны.
Равным образом она оставляет без внимания особенности тепло-
вого поля на малых расстояниях (/<=А.) от поверхности нагре-
того тела. Между тем нетрудно понять, в чем заключаются эти
особенности и каково нх происхождение.
Внутри нагретого тела, в каждом элементе его объема про-
исходят непрерывные тепловые флуктуации плотностей заряда
и тока, непрерывное электрическое «кишение», если воспользо-
ваться образным выражением М. А. Леонтовнча. Сумма волновых
полей этих источников дает вне тела его тепловое электромаг-
нитное излучение, описываемое законом Кирхгофа. Сумма же
ближних полей (от приповерхностных элементов объема) создает
квазиспищионарное тепловое поле, которое как бы выстилает
поверхность любого тела. Это поле сосредоточено около поверх-
ности, в слое толщины порядка Я, так что на расстояниях 1^>Х
им можно пренебречь, но прн I—>-0 его напряженность неогра-
ниченно возрастает. В этом, конечно, нет никакого парадокса,
так как на удалениях от поверхности порядка межатомных рас-
стояний макроскопическое описание поля уже становится непри-
годным.
Хотя квазистациоиарное флуктуационное поле не участвует
в создании потока энергии, его наличие проявляется вполне
наблюдаемым образом, например, в молекулярных силах сцеп-
леиня между телами (см. § 21).
Использование приближения геометрической оптики ограни-
чивает классическую теорию теплового излучения не только тем,
что она не учитывает квазистационарного флуктуационного поля,
но и тем, что от нее ускользают дифракционные явления в самом
излучении.
Другой законный вопрос касается того, представляет ли ин-
герес область /~Я, т. е. тот случай, когда размеры тел срав-
нимы с длиной волны.
При своем зарождении радиотехника использовала метровые
н даже сантиметровые волны, возникающие при колебательном
искровом разряде. Весьма быстро, однако, она била вынуждена
перейтн к очень длинным (километровым) волнам, после чего —
уже с электронными лампами в генераторах и усилителях—на-
чался длительный процесс настоящего технического освоения
все более коротких волн. Постепенно этот путь привел к деци-
метровому диапазону, а затем—к сантиметровым и миллиметро-
вым волнам и, соответственно, к радиотехническим устройствам,
У которых все (или некоторые) размеры сравнимы с длиной
126 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 1ГЛ. III
волны, т. е. к не квазистациопарным распределенным волновым
системам. Такого рода устройства (волноводы, объемные резона-
торы, рупорные и зеркальные антенны и т. п.) составили предмет
так называемой электродинамики сверхвысоких частот (СВЧ).
По мере повышения чувствительности и точности применяемых
радиотехнических методов естественно приобрели остроту вопросы,
касающиеся тепловых шумов и в распределенных системах. Таким
образом, если говорить о нуждах радиотехники, то развитие
обще» флуктуационной электродинамики было стимулировано
проблемой тепловых шумов в диапазоне СВЧ. Однако физиче-
ские результаты флуктуационной электродинамики, конечно, не
исчерпываются ее радиотехническим» приложениями. Например,
одним из основных ее следствий ивляется обобщение такого
фундаментального закона, как кирхгофовскнй закон излучения,
на общий случай произвольного соотношения между размерами
тел и длиной волны (§ 17).
Заметим кстати, что закон Кирхгофа, строго говоря, отно-
сится уже к неравновесным условиям. Ведь речь идет об излу-
чении нагретого тела в окружающую более холодную среду,
т. е. температура не одинакова во всем пространстве. Если
теряемая телом энергия не компенсируется, то процесс даже
нестационарен: тело «высвечивается» н остывает. Разумеется, не-
трудно создать н стационарные условия, поддерживая темпера-
туру тела постоянной путем подвода энергии от какого-либо
стороннего источника, как это происходит, скажем, в лампочке
накаливания. Ясно, однако, что и такое стационарное состояние
все равно термодинамически неравновесно: в теле происходит
одностороннее преобразование энергии н протекают явления
переноса (например, связанные с теплопроводностью). В этих ус-
ловиях применение равновесных законов (в том числе ФДТ)
уже не вполне строго, но оно оправдано, если, как часто бывает,
роль явлений переноса еще невелика.
Последнее замечание, которое уместно здесь сделать, касается
функций распределения вероятностей флуктуационного поля.
Казалось бы, нахождение этих функций — более сложная задача,
чем вычисление моментов, но во многих случаях дело обстоит
как раз наоборот. Флуктуацнонное поле слагается нз множества
микрополей, порожденных флуктуацнямн заряда и тока в разных
элементах объема. Если эти вклады можно считать статистиче-
ски независимыми и «равноправными» по величине (например, по
их доле в суммарной дисперсии), то в силу центральной пре-
дельной теоремы теории вероятностей суммарное поле будет
гауссовым. Тем самым, для его полного статистического описания
достаточно знать только функции корреляции его напряженно-
стей (поскольку средние значения этих напряженпостей равны
нулю).
4] СТОХАСТИЧЕСКИЕ УРАВНЕНИЯ МАКСВЕЛЛА 127
§ 14. Стохастические уравнения Максвелла
Исходные уравнения Максвелла
+ J rotE = С41)
необходимо, как известно, дополнить так называемыми материаль-
ными уравнениями, связывающими индукции D и В с напряжен-
ностямн Е и Н. Эти уравнения описывают электродинамические
свойства среды и могут быть в общем случае нелинейны. Однако
если задача о тепловых флуктуациях ставится макроскопическими
уравнениями (а именно так она ставится во флуктуационной
электродинамике) и если мы интересуемся только термодина-
мически равновесными флуктуациями, то макроскопическая не-
линейность системы не играет роли, т. е. достаточно пользо-
ваться линеаризованными уравнениями. Это обстоятельство было
разъяснено ранее для дискретных систем (ч. I, § 54), но оно
остается в силе н для распределенных систем. Другими сло-
вами, сохраняя полную общность, мы можем исходить из линеари-
зованных материальных уравнений. Последние можно было бы
взять наиболее общими, учитывающими наличие неоднородности
и анизотропии среды, временную и пространственную диспер-
сию, а также движение среды. Однако для упрощения выкладок
и для более четкого выделения принципиальных моментов мы
ограничимся случаем неподвижной и поначалу изотропной среды,
обладающей только временной нелокальностью (частотной дис-
персией). В этом частном случае среду можно описать мате-
риальными уравнениями вида (см. сноску на стр. 173)
D(/, г)- $ в(/-Г, г)Е(Г, г)Я\
;:
B(f, г)= $ (I (*-/', г)Н(Г, г) Л',
где е и у.—диэлектрическая н магнитная проницаемости.
Переходя к стохастическим максвелловскнм уравнениям, вве-
дем теперь в правые части уравнений A4.1) случайные сторонние
источники, которые «вызывают» тепловые флуктуации напряжен-
иостей поля и всех связанных с ними электродинамических вели-
чин. Эти распределенные источники играют здесь такую же
Вспомогательную роль эквивалентных ланжевеновских «сил», как
интегральные э. д. с. Найквиста в электрических цепях с сосре-
доточенными параметрами (ч. I, § 54).
Флуктуационные источники можно выбнрать различным обра-
зом, в частности в виде объемных плотностей электрических (jf)
128 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ [ГЛ. Ill
и магнитных (jM)токов1). Стохастические уравнения Максвелла
примут тогда вид
Можно было бы воспользоваться вместо токов сторонними индук-
циями Ю и ЯЗ, положив
что, как мы увидим далее, оказывается в некоторых случаях
целесообразным. Поля флуктуационных источников je и jm (равно-
как и Ю, ЯЗ) мы будем считать стационарными во времени.
Обратим внимание на вытекающее из A4.3) уравнение ба-
ланса энергии (теорему Пойнтинга), которое мы запишем для пол-
ного поля г). Умножив первое уравнение A4.1) на Е, второе—на
— Н; сложив результаты н взяв интеграл по объему V, ограничен-
ному поверхностью 2, получаем
где
dUidt — скорость изменения заключенной в объеме V электромаг-
нитной энергии, a Q—диссипируемая в этом объеме мощность.
Интеграл в левой части равенства пропорционален потоку
энергии (потоку вектора Пойнтинга) через поверхность 2, так
что для полного поля он обращается в нуль. Поэтому dilldt^Q
представляет собой не что иное, как диссипируемую в объеме V
мощность. После усреднения по ансамблю случайных «сил» j,
и )„, если учесть, что для полного и стационарного поля
dibyidt—Q, мы получим для средней днссипируемой мощности
выражение
«?> = — С <Ej, + Н 1Я> dV. A4.5)
2) Использование магнитных токов янляется, конечно, лишь формальный
приемом, но для многих задач оно удобно (см., например, |2]|.
') Напомним, что полным называется в электродинамике поле, равное
нулю за пределами некоторой замкнутой поверхности 2. Возможность по-
строения такой поверхности обусловлена либо наличием идеально отражаю-
щих оболочек, либо достаточио быстрый убыванием поля на бесконечности
(поверхность ? могкет быть частично или целиком бесконечно удаленной).
j,D] СТОХАСТИЧЕСКИЕ УРАВНЕНИЯ МАКСВЕЛЛА 129
Нас будут интересовать спектральные амплитуды стационар-
ных во времени электродинамических величин, т. е. простран-
ственные поля трансформант Фурье
ТО
) = -L J E(<, r).el<*<dt.
и аналогично для Н, D, В, j, j, и ]т. Для спектральных ампли-
туд уравнения A4.3) принимают вид
rotH = --»ftD + -^j,, rot E = iftB — -^]-я, A4.6)
где k = s>lc, а материальные уравнения A4.2) —вид
D(o), r)-e(ft), г)Е(о), г),
В (о), г) = ц(ш, г)Н(о), г), ( ' '
где
И». г) J ~ J И- (т, г) /
е (ш, г) \ л е (т, г) 1
{(=[ , [ \e!mdi. A4.8)
Заметим, что член 4nj/c мы объединили в A4.6) с членом ikD.
это означает включение электрической проводимости в е или,
точнее, в ее мнимую часть е" (е=е' + г'е"). Вводя ц(ц = ц'+/(а")
можно учесть и магнитные потери.
Система неоднородных линейных уравнений A4.G), A4.7) од-
нозначно определяет спектральные амплитуды папряженностей и
индукций флуктуационного поля при заданных граничных усло-
виях и (если это нужно) условиях на бесконечности, а также,
^зумеется, при заданных случайных источниках ]", (ш, г) н jm(to, r).
Таким образом, это задача со случайными источниками (схема 1
;Щ) классификации, введенной в § 8), вероятностные свойства
которых должны быть известны. Так как уравнения линейны,
ДЛЯ нахождения вторых (гг-х) моментов флуктуациоииого поля
надо знать только вторые же (л-е) моменты источников. Эти вто-
рые моменты, если речь идет о флуктуациях около состояния
термодинамического равновесия, полностью определены (как
;¦ в случае сосредоточенных систем) флуктуационно-диссипациоп-
ИОй теоремой (ФДТ), которую нетрудно распространить и на
распределенные системы (поля). Поэтому мы теперь оставим на
время уравнения Максвелла и обратимся к указанному обобще-
нию ФДТ.
130 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЙ ПОЛЕ 1ГЛ. in
§ IS. Равновесные тепловые флуктуации
в непрерывных диссипатнвиых системах
В ч. I, § 54 была приведена формулировка ФДТ для диск-
ретных систем, состояние которых описывается совокупностью
какого-то конечного числа п обобщенных координат qf {t). При
помощи этой дискретной формы ФДТ можно получать резуль-
таты, относящиеся и к распределенным системам,— либо косвен-
ным путем, как сделано в задаче 1, либо используя искусствен-
ную дискретизацию непрерывной системы, например разбиение
пространства, занимаемого полем, на малые ячейки и замену
дифференциальных операторов разностными. Именно с помощью
последнего способа дискретная ФДТ применена к стохастическим
уравнениям Максвелла в книге [3], гл. 13. Однако представляет
больший интерес получить общую форму ФДТ для непрерывных
систем, состояние которых описывается случайными нолями —
функциями Времени и точки пространства. Такое обобщение,
удобное для приложений теоремы к полям равновесных тепловых
флуктуации любой физической природы —как электромагнитным,
так и механическим (в аэро- и гидродинамике, теории упруго-
сти), температурным и энтропийным, и т. п.,—можно осуществить
следующим образом [4].
Пусть флуктуации в распределенной системе, занимающей
объем V, описываются стационарным и однородным нолем \ (t, г).
Для простоты мы берем случай одномерного поля1). Обобщение
на многомерное поле |(" (t, г) (г — 1, 2, ...) легко может быть
получено, и соответствующий результат будет далее приведен.
Пусть /(/, г)—объемная плотность поля обобщенной силы, со-
пряженной в лагранжеиом смысле с обобщенной координатой
I (/, г), причем спектральные амплитуды ? (со, г) и / (ш, г) свя-
заны между собой посредством линейных пространственных опе-
раторов А и Л~1:
?(», г)=Л/(о>, г), /К г) = Л-Ч(й>, г). A5.1)
А н Л~1—взаимно обратные операторы, т. е. их произведение
равно единичному оператору ? (ЛЛ — Л-1Л = ?), который остав-
ляет функцию неизменной (?/(г) = /(г)). В приложениях обычно
задан оператор Л~1, являющийся большей частью дифференци-
альным.
F-сли, например, мы имеем дело с волновым уравнением
^Р . г),
L) Одномерного в сиыеле числа описывающих что функций |.
jjj] ТЕПЛОВЫЕ ФЛУКТУАЦИИ В НЕПРЕРЫВНЫХ СИСТЕМАХ 131
частное решение которого равно, как известно,
|«,r)-J/(<--f-,r')^ (Л=|г-г'|),
то для спектральных амплитуд получаем (ft —<о/е)
(A + fcJ)?((o, г) = —4л/((о, г),
?(*, г) =
Таким образом,
Допустим теперь, что мы располагаем полной ортонормиро-
ванной системой вещественных функций фу (г), определенной для
области V:
$
Разложим l(t, г) н /(*,г) по функциям фу (г):
2 2. A5.3а, б)
1(.J
или в спектральной форме:
К», г)-Si/И Фу (г). /(», г) = S//И ФУ (г), A5.4а,б)
где
и аналогично для /,(«>). Заметим, что согласно A5.2) и A5.3)
средняя мощность, диссипируемая в объеме V под действием
силы f(t, г), записывается в виде
<^f)). A5.5)
Принимая 5/ @ за те дискретные переменные, которые опи-
сывают флуктуации в рассматриваемой системе, естественно
распространить дискретную ФДТ на спектральные амплитуды
I/ (<о) н /у (со). Единственное допущение, которое необходимо при
этом сделать, заключается в том, что ФДТ остается в силе для
бесконечного множества дискретных переменных |/ (/). Опираясь
на это допущение, мы и найдем теперь пространственные функ-
ции корреляции для спектральных амплитуд \ (о>, г) и /(<т>, г).
132 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ |ГЛ. 111
Как связаны между собой спектральные амплитуды ?/(<о) и
fy (ш)? Подставив A5.3а, б) в первое уравнение A5.1), получаем
Умножим это равенство слева на <ру(г) и проинтегрируем по
объему V. Учитывая A5.2), находим'
|, (и) - ? fh (и) J ф, (г) ЛФ* (г) *r ^ S«/* (•) /* (•)¦ A5-6а)
где величины
5Лг)ат A5.7а)
представляют собой, очевидно, не что иное, как коэффициенты
разложения функции Яф»(г) по базисным функциям фу (г), т.е.
Точно такие же операции.над вторым уравнением A5.1) при-
водят к обратной A5.6а) системе уравнений:
A5.66)
где
ад1 (ш) = j 4V (г) Л~1Ф* (г) d*ri A5.76)
т. е. а^1—коэффициенты разложения по фу (г) функции Л~>фА(г):
Л~1Фд (г) = ^ ссу^фу (г). A5.86)
Величины A5.7а, 6), являющиеся коэффициентами в уравнениях
A5.6а, 6), связывающих ?у(ь>) и //(ю), образуют, таиим образом,
элементы бесконечномерной матрицы обобщенной восприимчи-
вости {ад.1} и обратной ей матрицы {aJk\.
Дискретная ФДТ дает следующие выражения для спектраль-
ных плотностей переменных |у (I) и ланжевеновских сил ft (t)
(ч. I, E4.18) и E4.22); отметим, что перед правыми частями
теперь стоит знак минус, поскольку мы пользовались ранее
спектральным разложением с е1*', а в данной иниге перешли
к разложению по е~*"'):
A5.9а)
<// (») П (»)> = - ?&*2 («в/*- «7». A5-96)
fit! ТЕПЛОВЫЕ ФЛУКТУАЦИИ В НЕПРЕРЫВНЫХ СИСТЕМАХ 133
где в(ш, У)—средняя энергия квантового осциллятора:
формулами A5.9а, б) мы теперь и воспользуемся.
Согласно A5.4а) и A5.9а)
(ш, г) 5» (ев, г')> = ^ <lj (») И Н> q>/ (г) q>* (г')=
При помощи A5.8а) можно записать это выражение в виде
,<|(to, г) 6» (со, г')> =--^ЦярЯ {Ф/ (г') Aq,j (г)-ь (г)Л'Ф/ (г)},
причем оператор А действует на функции точки г, а А'—на
функции точки г'. Поэтому оба они могут быть выиесеиы за
знак суммы, которая оказывается тогда разложением дельта-
функции от г—г' по базисным функциям:
В результате
<|(о.,г)|«(о..г')> = -^1-)(Л-Л«)б(г-г'). A5.11а)
Совершенно аналогичным путем при помощи A5.46), A5.96)
В A5.86) получается пространственная функция корреляции для
ьяектральной амплитуды силы /((о, г):
Поскольку дельта-функция зависит лишь от разности р=г—г',
Оба оператора А и А' можно выразить через компоненты р.
Равным образом можно и дифференциальные операторы А'1 к
и* (первый содержит ?, а второй \') записать через опера-
«Ч» Vp= V = — V'.
Формулы A5.11а, б), в которых уже никак ие проявляются
форма н размеры области V, и представляют ФДТ для одно-
мерного однородного поля 5 (t, г) и соответствующего ему поля
«ижевеновской силы [(t, г).
Обобщение полученного результата на многомерное поле, т. е.
на случай системы однородных и однородно связанных между
«обой полей |V) (<,!¦), почти очевидно. Вместо уравнений A5.1)
134 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 1ГЛ. Ill
теперь будут системы линейных уравнений
&">(«, г)-2 *,»/*(», г),
* A512)
0
где AJlt и Aji—элементы прямой и обратной операторных мат-
риц, а вместо выражения A5.5) для мощности, развиваемой
силами /<¦" (t, г), будет сумма
A5.13)
Наконец, окончательные формулы A5.11а, б) заменяются на кор-
реляционные матрицы спектральных амплитуд |Vi (и, г) и
Г" Кг):
A5.14а)
(», г) /*• (о., г')> - - ^?2 (Л,/*-Л>)8 (р), A5.146)
где по-прежнему р = г—г'.
Итак, в распределенных системах, как и в дискретных, ФДТ
выражает корреляционные функции (матрицы) ю-амнлитуд1)
совершенно регулярным образом. Эти функции однозначно опре-
делены видом операторов Ajk и Aj}, т. е. самими линеаризован-
ными макроскопическими уравнениями рассматриваемой системы.
Если это уравнения Максвелла, то формулы A5.14) позволяют
найти пространственную корреляцию напряженностей флуктуа-
цнонного поля н тех сторонних полей (индукций илн токов),
которые «создают» флуктуацнонное электромагнитное поле. Если
же мы имеем дело, например, с уравнениями теории упругости,
то при помощи тех же формул A5.14) определяется корреляция
тепловых флуктуации деформаций и температуры, равно как и
соответствующих сторонних напряжений и источников тепла [5J
и т. д. Более точно: корреляционные матрицы флуктуационных
и сторонних тепловых полей определяются антиэрмитовыми
частями соответствующих линейных операторов, или иначе
говоря, обусловлены диссипативными свойствами системы.
В отсутствие поглощения энергии, т. е. в отсутствие диссипа-
') А тем самым и сох-амплитуд, если ш-амилитуды разложить в прост-
ранстоенные интегралы Фурье (см. задачу 6).
jjj] КОРРЕЛЯЦИЯ СТОРОННИХ ТЬПЛОВЫХ ИСТОЧНИКОВ ]35
ции, операторы или операторные матрицы будут эрмитовыми и
разности, стоящие в правых частях любой из формул, выража-
ющих ФДТ, обращаются в нуль. Это означает, что в среде (илн
участке среды), ие обладающей потерями, сторонних источников
флуктуации нет и, следовательно, нет и вклада от такого участка
среды по флуктуацношюе поле. В формулах A5.11а) и A5.14а)
учтен только этот вклад, и он в данном случае тоже обращается
в нуль. Но флуктуационное поле может создаваться источниками,
локализованными вне- данного нелоглощающего объема среды,
т.. е. может приходить в этот объем извне. Поэтому корреляци-
онные функции флуктуационного поля, вообще говоря, отличны
от нуля и в тех областях пространства, где среда ие обладает
поглощением.
§ 16. Корреляция сторонних тепловых источников
в электродинамике
Вернемся к спектральным уравнениям Максвелла A4.6),
исключив из них при помощи материальных уравнений A4.7)
индукции D и В:
rotH = -(fceE+-^-je, rotE = «sjiH—^-j,,. A6.1)
Состояние рассматриваемой системы—флуктуационного электро-
магнитного поля—описывается 6-вектором иапряженностей
|</>г={Е, Н}. Каков при этом б-вектор сопряженных с g</i по
Лагранжу сторонних сил /W?
Согласно общему выражению A5.13) средняя дисенпируемая
мощность <Q> равна (со знаком минус) сумме произведений
координат на скорости изменения сил. Сопоставляя с A5.13)
формулу A4.5), нетрудно усмотреть, что [сторонние токи j, и
|я ие являются сопряженными «силами» для «координат» \Ч>=
={Е, Н}. Если же воспользоваться сторонними индукциями ©
и- SB и подставить в A4.5) выражения A4.4), то мы получим
Для <Q> формулу как раз вида A5.13):
Таким образом, для напряженностей |^> = {Е, Н} «силами» явля-
ются величины /У> = {Ю/4я, 89/4я} и общие формулы A5.14а, б),
выражающие ФДТ, следует применять именно к таким |'/> и /'¦".
Разумеется, получив корреляционную матрицу для спект-
ральных амплитуд сторонних индукций О и SB, мы тотчас же
сможем написать такую матрицу и для спектральных амплитуд
136 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
сторонних токов, поскольку, в силу A4.4),
[ГЛ. III
A6.2)
Подставив A6.2) в A6.1), запишем уравнения A6.1) в ком-
понентах:
где fe = o)/c, а знак О обозначает круговую перестановку индек-
сов 1, 2, 3. Сопоставление этих шести уравнений со второй
группой уравнений A5.12), где, как мы помиим, надо положить
EV» = {Е, Н}, р = {е/4я, ЯЭ/4л} (/ = 1 6),
дает нам матрицу операторов ^^(V)".
1 °
V v
е
¦л
3
0
у
s —V»
Vi
1 0
Р=1,
•
• j_
• 4п
\ j
i
/ ;
2,3).
/ °
т -V.
*V v,
1
V»
0
—Vi
— вар
-v,\
0 /
Транспонированная комплексно сопряженная матрица, завися-
щая от v', будет
Учитывая, что V' — — V (поскольку операторы действуют на
функцию от г—г'), получаем
в-в*
(а, р- 1,2,3).
Ц.161 КОРРЕЛЯЦИЯ СТОРОННИХ ТЕПЛОВЫХ ИСТОЧНИКОВ 137
Наконец, подстановка этого результата в формулу A5.146),
выражающую ФДТ для ланжепсновскнх сил, даст нам корреля-
ционные функции сторонних индукций О и й$:
Г) (е-«•) 6аР »(г-г'),
(|1-|1'N„!6(г-г'), A6.3)
<Da(u>(rK?5(o,.r')> = 0.
В более общем случае анизотропной или гиротропиой среды,
описываемой тензорами проницаемостей еав и цар, мы получили
бы те же формулы A6.3), но с заменой диагональных тензоров
tbaf и (i6aP на еар и (iap, a e*6ae и ц'6а() на е|а и ц^.
Пользуясь A6.2) и A6.3), нетрудно написать корреляцион-
ные функции сторонних токов. Мы приведем эти функции сразу
для случая анизотропной среды 1):
</..(». г) Аэ(«, г')>= - **в?; П(ИаР-^) б(г-г'), A6.4)
</«(», О/m(l К Г')> = О.
Менее формальный вывод этих формул дан в задаче 2.
Итак, электрические и магнитные источники флуктуацион-
яого поля пространственно не корродированы между собой,
а радиус пространственной корреляции тех и других порознь
равен нулю (дельта-функция б (г—г')). Для сред без простран-
ственной дисперсии, которыми мы здесь и ограничиваемся, этот
1Ц>следний результат представляется очевидным. Действительно,
фактический радиус корреляции источников теплового поля
В таких средах может быть только микровеличиной (порядка,
Например, межатомных расстояний), и поэтому в макроскопи-
яеекой теории, рассматривающей среду как сплошную, он и
должен быть равен нулю. Напротив, в средах с пространствен-
ной дисперсией материальные уравнения нелокальны не только
ло t, но и по г, т. е. вместо A4.2) будут уравнения, содер-
жащие операторы как по t, так и по г'). Это приводит к
1) Формулы A6.4) были получены Л. Д. Ландау и Е. М. Лнфшнцем |3|
при помощи ФДТ в ее дискретной форме. На основе непрерывной формы ФДТ
формулы вида A6.4) были выведены в [4]. В дальнейшем, независимо от
"Мученной в D] обшей непрерывной формы ФДТ. формулы вида A6.4) выво-
дили многие авторы (см., например, ссылки [23, 55—62) а книге [6]).
') Соответственно уравнения A4.7) тоже ие будут алгебраическими, а
оУДУт содержать пространственные операторы. Алгебраическими будут лишь
Уравнения для их-амплнтуд.
138 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ [ГЛ. Ill
отличному от нуля радиусу корреляции источников флуктуаци-
онного поля, имеющему тот же порядок величины, что и размер
области нелокальности в материальных уравнениях (см. [6J,
Для кусочно-однородных сред, т. е. при наличии резких гра-
ниц раздела между средами, формулы A6.3) и A6.4) справед-
ливы (нз-за дельта-корреляции) вплоть до самых границ раздела.
При наличии же пространственной нелокальности положение
меняется: вблизи от границ раздела, а именно в слое, толщина
которого порядка радиуса корреляции, поля сторонних источ-
ников неоднородны (их корреляционные функции зависят от г
и г' в отдельности, а не от разности г—г') и анизотропны даже
в том случае, когда сама среда изотропна.
Мы смогли, используя теорему A5.146), сразу написать кор-
реляционные функции источников флуктуационного поля только
потому, что входящие в A5.146) операторы А^\ нам известны из
самих уравнений Максвелла. Иначе обстоит дело с корреляцией
скоордннат», т. е. напряженностей флуктуационного электро-
магнитного поля Е и Н. Для того чтобы написать корреляцион-
ные функции Е и Н, надо, согласно A5.14а), знать обратные
операторы Д*э, т. е. надо «обернуть» уравнения Максвелла,
выразив Е н Н через j, и jn (или О н »). Другими словами,
надо решить неоднородные уравнения Максвелла, считая рас-
пределение источников }е н jn произвольным, но заданным и
налагая граничные условия, отвечающие дайной конкретной за-
даче.
Если краевая задача решена, то тем самым мы получаем
операторы Аа» (обычно в виде интегралов, распространенных
иа области пространства, в которых сторонние токи }е и )т
отличны от нуля) и можем воспользоваться тогда «готовой» тео-
ремой A5.14а). Можно поступить и иначе: составить из полу-
ченных решений для Е и Н интересующие нас билинейные ком-
бинации и усреднить их. Под кратные интегралы, выражающие
вторые моменты нанряжениостей, войдут при этом корреляци-
онные функции сторонних токов ]е и jn, вместо которых
надо будет подставить уже полученные выражения A6.4). Оба
способа вполне правомерны, и ряд флуктуационных элект-
родинамических задач был решен именно таким путем [1,
7, 8].
Однако в обоих указанных вариантах это трудоемкий и не-
экономный путь, так как для каждой конкретной задачи его
надо проделывать заново. Попытаемся поэтому выяснить, к чему
приводит ФДТ, если применить ее к решению уравнений Макс-
велла, записанному в общей интегральной форме—через функ-
ции Грина.
I 17) ОБОБЩЕННЫЙ ЗАКОН КИРХГОФА |39
§ 17. Обобщенный закон Кирхгофа
Функции Грина представляют собой решения краевой задачи
с элементарными точечными источниками поля. Введем их в нашем
электродинамическом случае следующим образом.
Пусть j0,—детерминированный электрический ток, сосредо-
точенный в некоторой точке А (г = гл) и направленный по
постоянному единичному вектору 1:
jo, = 16(r-r,,). A7.1)
Можно считать ток ]„ поляризационным, т. е. рассматривать
источник как точечный электрический диполь с моментом
р=—1/гсо1). Решение уравнений Максвелла, т.е. напряженности
электромагнитного поля, создаваемого в данной системе тел и
сред источником A7.1), мы обозначим через Ео, (г, гА, 1),
Н„ (г, гд, I) я для краткости будем называть это детерминиро-
ванное поле дифракционным. Напряженности Е0(, н Ног и явля-
ются функциями Грина.
Наша цель состоит в том, чтобы выразить напряженности Е
и Н флуктуациониого поля, порождаемого случайными распре-
деленными токами )е и }п, через эти токи и через функции
Грина Е0(. и Ное. Проще всего сделать это при помощи электро-
динамической теоремы взаимности, которая связывает «накрест»
напряженности и источники двух различных полей 1 и 2 в одной
и той же системе тел и сред.
Пусть имеются два распределения сторонних электрических
и магнитных токов j,,, j]m и jae, j,,,, которые создают при про-
чих одинаковых условиях поля Et, Н, и Е2, Н, соответственно.
Теорема взаимности выводится весьма просто (при очень широ-
ких допущениях) из двух систем уравнений Максвелла — одной
для поля и источников 1 и другой для поля и источников 2
(см., например, [6]). Она гласит, что
S (E.l«-HJ«)*r = J (EJ.l-H,J.l)*r1 A7.2)
V V
где V—объем полного поля. Фактически интегралы в A7.2)
распространяются только на те области пространства, в кото-
рых сторонние токи отличны от нуля.
*) Плотность поляризационного тока равна dP/dt. где Р—объемная плот-
ность поляризации. Для точечного диполя с моментом р имеем Р —рб (г—г^),
так что jlc=?-6(r—г/0. а Для спектральных амплитуд )ае = — ("сор в (г—гд).
При р= — l/ico мы получаем A7.1).
140 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 1ГЛ. Ill
Отождествим теперь в теореме A7.2) интересующее нас флук-
туационное поле с полем 1:
!« = !.. 1., = ].. Е! = Е. "i = H- С7-3)
а вспомогательное дифракционное поле — с полем 2:
]„ = 1в(г-гД J., = 0. Е.-Е,., На = Н0,;
формула A7.2) дает тогда
= \ {Е.. (г, гл, 1) U (г)-Н„ (г. г,. 1) jB (г)} d?r, A7.4)
\/
т.е. именно то, что нам нужно: компонента по направлению 1
электрической напряженности флуктуационного поля в точке А
выражена через распределение случайных токов и через функ-
ции Грина — напряженности детерминированного поля, создавае-
мого электрическим диполем, направленным по 1 и находящимся
в точке А.
Для того чтобы получить аналогичное выражение для ком-
поненты магнитного флуктуационного поля, надо, сохраняя A7.3),
воспользоваться в теореме взаимности A7.2) другим полем 2,
а именно дифракционным полем Евя, НОш, которое создается
магнитным точечным током
]оя = 16(г-г,,)
или, что то же, магнитным диполем с моментом т=—1/гсо,
помещенным в точку А:
Мы получаем тогда из A7.2)
A7.5)
Линейные относительно j, и jm выражения A7.4) и A7.5)
позволяют получать теперь любые моменты напряженностейфлук-
туационного поля, если нам известны моменты того же порядка
для токов ]е и Jn. В частности, мы заведомо можем вычислить
вторые моменты компонент флуктуацнонпого поля, поскольку
вторые моменты сторонних токов дает нам A6.4).
Найдем, например, среднее значение произведения ?/,@^1,(г,).
Полагая в A7.4) 1-=1„ гд = Г! и записывая скалярные произве-
дения векторов в компонентах (ab = uaba, где по дважды вхо-
|j?f] ОБОБЩЕННЫЙ ЗАКОН КИРХГОФА ]41
дящим индексам производится суммирование от 1 до 3), имеем
= $<?о«х(Г, Г„ 11)/«а(г)-Яога(г, Г„ IJ^aW}^. A7.G)
Полагая в A7.5) 1^12, г^ = г3, получаем
Я/,(г.) =
= -${?„,„з(г', г„ 1,)й(г')-Я„тЭ(г', г„, ls)/mp(r;)}d»r'. A7.7)
Для краткости мы далее опустим аргументы г„ lt в Ем, Ное
ц аргументы г2, 12 в Ео„, Н0|Я. Умножив A7.6) на выражение,
Комплексно сопряженное A7.7), и взяв среднее по равновес-
ному ансамблю случайных источников j, и jn, находим
>,)> =
= — J J {?ога (г) E'omfi (Г') </,„ (Г) /*|)(Г')> +
+ Htea (Г) Я^шр (Г') <1ка (г) /^р (г')> —
— Еат (г) Н'„„ф (г') </„ (г) /^р (г')> —
-Нио. (г) ?*„тр (г') </т« (г) /i (r')>} d»r d»r'.
Согласно A6.4) последние два члена интегранда равны нулю
* силу некоррелированности электрических и магнитных сто-
ронних токов; корреляционные же функции токов в первых двух
членах содержат б (г—г'), что позволяет сразу выполнить ин-
тегрирование по г'. В результате
' Г)
A7.8)
Но величина
1т. (г) = —~ {E^Elnp (e.,-efc) + l/«eWi* (H«s-^a)} A7.9)
¦Представляет собой не что иное, как спектральную объемную
Йяотность смешанных тепловых потерь (электрических+ магнит-
Вых) в точке г1). Интеграл от qem> (г) по г—это спектральная
х) Поясним понятие ссмешанных» потерь на примере изотропной среды,
обладающей только электрическими потерями, когда Еар — [е'-|-? ] бар
• И«в = (*'6аВ' гДе 8' и С'—вещественные проницаемости, о—электрическая
проводимость. Формула A7.9) принимает для такой среды вид
Чет' (г)--- 1/s"E0eEom, </j.m — (qm*)*.
Си. продолжение примечания на следующей странице.)
142 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 1ГЛ. 111
плотность потерь во всем объеме среды (фактически во всех
областях, где есть диссипация энергии, т. е. еоР—е1аф0 и (или)
Пав—P-ia?*0):
Q,,n. A4, К; г,, У = $ q,m. (г) d»r. A7.10)
Конечно, q,m» и Qem' зависят от координат и направлений то-
чечных источников вспомогательных дифракционных полей, в дан-
ном случае—электрического диполя с моментом p——\l/im
в точке rt и магнитного диполя с моментом m = —12/М) в точке г3.
Из A7.8)—A7.10) следует, что
<?,>,)Я,',(¦-,)> = -|-вК T)Qem.(tlt I,; r2, 12). A7.11)
Аналогичный расчет при помощи формул A7.4), A7.5) и
A6.4) функций корреляции компонент Е нлн компонент Н при-
водит к следующим результатам:
<?,, (г,) Е\, (г,)> =-|в (о., Т) Qm. (rt, lt; г„ la), A7.12)
<Я(,(г1)Я;,(г,)> = -|в(о>, VQ^.^, 1,; г„ 1а). A7.13)
В формулу A7.12) входят смешанные потери дифракционных
полей от двух электрических диполей (р, = — \jirn в точке г,
и ра=—1,/йо в г2), а в A7.13)—от двух магнитных диполей
(ш,= — \Jia в г, и та = — 1а//<о в г,). Не смешанные, а собст-
венные потери дифракционного поля одного источника опреде-
ляют среднеквадратичное значение какой-либо одной компоненты
флуктуационного поля в одной и той же точке. Например, по-
лагая в A7.12) г,^=га = г и Ij — 1, = 1, получаем
< | Е, (г) |«> = |- 0 (со. Т) О», (г, 1; г, 1), A7.14)
Мы назвали эти потерн «смешанными», так как они обусловлены полями от
двух разных источников. Посмотрим на том же примере, как такие потери
возникают.
Как известно, мгновенная объемная плотность джоулева тепла есть
q(t, г) — а(г)Е'A, г). Для гармонического поля Е(/, г) = >/г[Ь(а>, г)е^ +
+ Е*(а>, г)е'<>>'] в среднем по периоду Г — 2я/ю имеем
«?(<«, г) = Vae (г)! Я (ш, г)|*.
Если поле Е представляет собой суперпозицию двух полей (E = Ei+Ej), то,
очевидно,
где <7л«(<», ¦>) = '/i°|Eil>i ?22«(o>, г) = Vi" 1Е»|l—потери каждого из полей Ei
и Еа в отдельности, а ^н»(<в, r)=1/«fEiEj, ^«(ш, г) = I/»<fEiEa—смешанные
тетери полей Е^ н Еа.
J17J ОБОБЩЕННЫ*! ЗАКОН КИРХГОФА |43
т. е. сюда входят собственные потери дифракционного поля, со-
здаваемого электрическим диполем с моментом р=—1/ift), нахо-
дящимся в точке г.
Формулы A7.11)—A7.13) можно назвать кирхгофовской фор-
мой ФДТ, потому что они представляют собой прямое обобще-
ние закона Кирхгофа классической теории теплового излучения.
Этот закон связывает, как известно, интенсивность теплрэого
излучения тела в каком-либо направлении с поглощением в этом
теле при падении на него плоской волны с обратным направ-
лением распространения (можно сказать, что это волна от бес-
конечно удаленного точечного источника). Обобщение касается
сразу трех сторон дела.
Во-первых, мы можем теперь находить средние значения про-
изведений любых компонент Е и Н, а не только тех, которые
определяют плотность энергии и ее поток (поток вектора Пойн-
тинга)—две величины, которыми только и интересуется клас-
сическая теория излучения.
Во-вторых, мы можем вычислять не только средние произ-
ведения компонелт, взятых в одной и той же точке (г, = г,),
что требуется для расчета плотности энергии и ее потока, но
и пространственные функции корреляции флуктуационного поля
(*хФ г.) •
- И D-третьих, что наиболее существенно, D формулах A7.11 )—
A7.13) нет никаких ограничений для соотношения между дли-
ной волны X и характерными масштабами задачи / (размерами
тел, радиусами кривизны их поверхностей, расстояниями от
тела до точки наблюдения и т. п.). Иначе говоря, в отлнчие
от классической теории теплового излучения, связанной усло-
виями применимости геометрнческой оптики, мы можем вычис-
лять теперь вторые моменты флуктуационного поля—как вол-
новой его яасти (с учетом всех дифракционных явлений), так
и неволновой (квазистапионариой)—при любом соотношении А, и/.
Необходимо остановиться на преимуществах, которые дает
обобщенный закон Кирхгофа и в отношении вычислительной
йороны дела. Конечно, для нахождения вспомогательных ди-
фракционных полей (функций Грина) по-прежнему необходимо
решать обычными методами соответствующие краевые электро-
динамические задачи. Однако эти задачи проще тех, о которых
Говорилось в конце предыдущего параграфа. Для формул A7.11)—
A7.13) надо находить решения однородных уравнений Максвелла,
обладающие дипольными особенностями в заданных точках г:
и г„ а не решения неоднородных уравнений с заданным, но
произвольным распределением сторонних токов j, н ]„. Более
того, во многих случаях можно использовать уже известные
Функции Грина, т. е. готовые решения задач с точечными источ-
никами (например, классической задачи А. Зоммерфельда о поле
144 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ (ГЛ. 111
диполя, расположенного над плоской границей поглощающей
среды).
Наконец, далеко не всегда необходимо вычислить напря-
женности дифракционных полей. Ведь в формулы A7.11)—A7.13)
входят, в конечном счете, не эти напряженности, а тепловые
потери дифракционных полей. Во многих практически интерес-
ных случаях эти потери можно с достаточной точностью по-
лучить приближенными методами. Сюда относится, например,
случай хорошо проводящих тел (сильный скип-эффект), случай
тел, больших по сравнению с Л или, наоборот, малых по срав-
нению с X (хотя бы по некоторым своим размерам, как это
имеет место для тонких проводов). Далее мы приведем несколько
примеров применения обобщенного закона Кирхгофа и заодно
проиллюстрируем предельный переход к результатам классиче-
ской теории теплового излучения. В заключение же этого па-
раграфа сделаем еще два общих замечания.
Первое касается распространения обобщенного законя Кирх-
гофа A7.11)—A7.13) на случай неравномерно нагретых тел. Если
градиенты температуры достаточно малы, так что 6 = 0 (г) —
настолько плавная функция, что роль неравновесных процессов
еще пренебрежимо мала, то, очевидно, учет неравномерного
нагрева сведется к тому, что в (г) надо оставлять под интегра-
лом по объему. Вместо произведения 6Q, в формулах A7.11)—
A7.13) надо при таких квазиодцородных условиях писать
j6dQ,, где dQ, = q,dlr—тепловые потери дифракционного поля
в элементе объема d'r рассматриваемого тела.
Второе замечаиие касается нулевых колебаний. Во все формулы
корреляционной теории равновесных и квазиравиовесных флук-
туациоиных полей входит множителем средняя энергия осцил-
лятора в(о>, 7"), содержащая слагаемое А<о/2—энергию так
называемых нулевых колебаний (см. A5.10)). Слагаемое в A5.10),
зависящее от температуры Т и обращающееся в нуль при Т — 0,
соответствует так называемому черному излучению. Только эта
часть обычно и рассматривается, когда речь идет об излучении,
т. е. о потоке энергии, поскольку лишь она ивляется в таких
случаях наблюдаемой величиной. Между тем в формулах типа
A7.11) содержится поток энергии и нулевых колебаний. Когда
и почему его не следует учитывать?
Дело в том, что при выводе формул типа A7.11)—A7.13)
сделано неявное допущение, что рассматриваемое тело является
единственным источником флуктуацнонного поля. В действитель-
ности же нулевые колебания существуют и в отсутствие дан-
ного тела, так как оии создаются всеми телами без исключении,
в том числе и абсолютно холодными G* = 0). Можно сказать, что
по отношению к нулевым колебаниям всегда имеет место равно-
ПРИМЕРЫ ПРИМЕНЕНИЯ ЗАКОНА КИРХГОФА
146
весное состояние, т. е. нулевые колебания -это всегда стоячие
волны и, соответственно, любой поток энергии этих колебаний
ВСЮДУ гасится встречным потоком той же интенсивности1).
Поэтому в любых формулах, относящихся к потоку энергии
(но не к ее плотности!), следует удерживать лишь ту часть
9(й>, Т), которая относится к черному излучению, вычитая поток
энергии нулевых колебаний, который всегда компенсирован при
любом окружении данного тела.
РнС- |3-
§ 18. Примеры применений обобщенного закона Кирхгофа
Рассмотрим в качестве первого примера случай полупро-
странства г < 0, заполненного поглощающей однородной и изо-
тропной средой с прошщаемостями е„ ц,, над коюрым (г > 0)
среда тоже однородна н изотропна, но проз-
рачна (проницаемости виц вещественны)
(рис. 13). Как мы знаем, для нахождения
вторых MONreHTOB флуктуационного поля
в какой-либо точке прозрачной среды надо
вяать дифракционные лоля Ео„ Нф, н ЕОл|,
Н»я элементарных электрического и магнит-
Вйго диполей с моментами р— — l,/io> н
ад=— li/ш, помещенных в эту точку {\1 и
>,—единичные векторы). Решение этой клас-
сической задачи можно найти в любом
учебнике по распространению радиоволн
^подробное изложение см., например, в монографиях [9, 10]).
.Потери дифракционного поля Е„ = Е„ -4- Еоя>, Но = H,f + НОя в
Поглощающем полупространстве г < 0 проще всего вычислить
Как поток энергии через границу г —0 в это полупространство:
r J
о
На плоскости г —0 мы ввели в A8.1) полярные координаты
f и <р, причем диполи находятся на высоте h над началом
Отсчета г —0. Ясно, что Qo будет зависеть только от ft и, ко-
йечтю, от ориентации диполей I, и 1а.
Разные выражения для Q01 отвечающие различным ориеита-
цням I, и I,, определят по формулам A7.11)—A7.14) средние
значения произведений соответствующих компонент флуктуацион-
иого поля. Если, скажем, направить \ по оси .v и положить
') Разумеется, гасится в среднем, т. е. гасятся средние значения встреч-
Вых потокок. Пели интересоваться флуктущиями потока энергии, то в ни»
¦восят вклад и нулевые колебания.
14В ТЕПЛОВОС ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ |ГЛ. Ill
m —0, то мы получим <|?л.|2>; если направить lL по оси х,
а |3 по оси у, то соответствующее Qo даст <ЕхНу> и т. д.
Отличными от нуля оказываются только следующие моменты1):
зависящие уже только от высоты h точки наблюдения над гра-
ницей раздела.
Зная моменты A8.2), нетрудно составить выражения для
спектральных плотностей (по ш > 0) электрической и магнитной
энергий флуктуационного поля в прозрачной среде (с в и ц, ие
зависящими от ш, т. е. в отсутствие дисперсии) и для г-компо-
ненты вектора Пойнтинга:
A8.3)
Как и моменты A8.2), величины A8.3) выражаются одно-
кратными интегралами от 0 до оо по некоторой переменной р,
причем расстояние h точки наблюдения от границы г = 0 вхо-
дит в подынтегральные выражения только через экспоненту
ехр[—(q-\-q*)h], где q = V p*~ k* , a k—волновое число в про-
зрачной среде (k — kt У ец , ko — u>/c). Тем самым, интегралы по р,
выражающие величины A8.3), распадаются на два существенно
различных слагаемых. 1) Интегралы по интервалу р от 0 до k.
Здесь q чисто мнимое, q^-q* = O, и эта доля в величинах A8.3)
не зависит от h. Это волновая часть флуктуационного поля.
2) Интегралы по интервалу р от k до оо, где q вещественно и
положительно; соответствующие вклады в ы«а(/г) и Ыти(Л) убы-
вают с удалением от границы z = 0, а в потоке энергии &а,г эта
часть вообще отсутствует, так как в подынтегральное выраже-
ние для <5"шг входит еще и множитель q—q*, который при ве-
щественном q обращается в нуль. Это квазистационарное флук-
туацнонное поле, не дающее вклада в поток энергии.
Для волнового поля, если в качестве переменной интегриро-
вания ввести вместо р угол 9 между волновым вектором к и
плоскостью z —0, так что p = ks\x\Q, величины A8.3) приводятся
1) Подробно вес вычисления приведены в [6|, § С
ПРИМЕРЫ ПРИМЕНЕНИЙ ЗАКОНА КИРХГОФА
147
К ВИДУ
я/г
-^-^^f- f [1-Я (в)] sine d9, A8.4)
b
^2 = 2пЭошл8 \ [1— .51 (в)] cos 9 sin 9 d9. A8.5)
6
Здесь л = У гц—показатель преломления прозрачной среды,
«от и 3<>ш — -^ «ош—соответственно плотность энергии и интен-
сивность равновесного излучения в вакууме, а Я(в)—полусумма
френелевских коэффициентов отражения (по энергии) при угле
падения плоской волны 0 и при двух ее поляризациях—с элек-
трическим вектором, параллельным плоскости падения и пер-
пендикулярным к ней:
A8.6)
{N = 1/в1ц1/к|1 — относительный показатель преломления). В A8.6)
вошла полусумма 5? и и fltj_, так как в рассматриваемой за-
даче обе поляризации совершенно равноправны.
Сопоставление A8.5) с общим выражением нормальной к по-
верхности компоненты вектора Пойнтиига &ш через интенсив-
ность аЫ8, ф):
6<л/2
(p)cos6do-=
8, ф) cos G sin8 dO,
показывает, что в нашем случае, т. е. в случае излучения полу-
пространства, заполненного однородной и изотропной погло-
щающей средой, интенсивность q/u не зависит от угла ф и
равна (закон Кирхгофа)
Эш(О) = Э„шп» [1—51(9)]. A8.7)
Отсюда можно перейти к случаю бесконечного пространства,
аполиенного прозрачной средой с показателем преломления л,
росто положив 51 = 0. Тогда получается закон Клаузиуса,
148
ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
!ГЛ. III
связывающий равновесные интенсивиостя в прозрачной среде и
в вакууме:
Тот же переход к 5?= О дает, согласно A8.4),
т. е. половину плотности энергии ЫощЛ* равновесного излучения
в прозрачной среде, как и должно быть, поскольку мы выде-
лили из этого излучения односторонний поток энергии (в сто-
рону z > 0).
Для квазистационарного поля квадратуры, выражающие плот-
ности энергии uj? и «",„, сложнее, и можно дать лишь прибли-
женные их оценки.
Если kh гораздо больше величин
— VN*— 1 и — \/ N1— 1
то
т. е. убывание плотностей энергии с удалением от границы
(с ростом h) происходит по закону \/h*. На расстояниях Л, при
которых
J^gEL) A8.8)
плотность энергии квазистационарной части теплового поля уже
пренебрежимо мала по сравнению с постоянной в полупрост-
ранстве г>0 плотностью энергии волновой части поля A8.4).
Напротив, иа малых расстояниях h преобладает квазистацио-
нарное поле, так что малые зазоры и полости, для которых
условие A8.8) не выполнено, практически заполнены именно
квазистационарным флуктуационным полем.
При малых kh с точностью до членов порядка l/(Wt)9 полу-
чаются оценки
Отсюда видно, что при наличии только электрических потерь
(ц.; — 1тц! = 0) плотность электрической энергии ujg растет с
уменьшением h, как 1/А1, а магнитной ы™ш—лишь как 1/Л*
(а в случае, когда Ej=Ime1 = O,—наоборот). Интеграл от uff —
= ujg + "mm по любому конечному объему, прилегающему к гра-
нице раздела, тоже расходится. Как уже было сказано в § 16,
|)«] ПРИМЕРЫ ПРИМЕНЕНИИ ЗАКОНА КИРХГОФА |49
jro результат принятой нами дельта-корреляции сторонних источ-
ников в поглощающей среде. Если бы мы взяли нелокальную
среду, и которой, тем самым, сторонние флуктуациониые токи
,р<5ладалн бы некоторым отличным от нуля радиусом корреля-
ции а, то плотность ы&в оставалась бы при Л-^-0 конечной, до-
стигая значения порядка иш/(каK.
Современная усилительная техника в диапазоне СВЧ вполне
позволяет поставить прямой опыт, выявляющий сильное иа-
.растание квазистационарного флуктуациоппого поля вблизи по-
верхности нагретого проводящего тела, но, к сожалению, таком
Опыт пока не осуществлен.
В рассмотренном примере мы получили для нолновой части
доля классический закон Кирхгофа A8.7), так как в случае бес-
конечного полупространства этот закон справедлив для любой
длины волны. Правда, для достаточно малых расстояний h от
Йрверхности среды были прослежены эффекты, выходящие за
рамки классической теории теплового излучения (наличие квази-
«пгациоиарного флуктуационпого ноли). Но особый интерес пред-
ставляют приложения общей теории к таким задачам, где клас-
сическая теория вообще неприложима, так как размеры тел не
Слишком велики по сравнению с длиной волны. Тогда н в вол-
Вовой части теплового поля должна проявиться новая законо-
мерность— зависимость характеристик волнового поля от отно-
Ц|ения 1/Х, где I — характерный размер (выше это было расстояние
Ь от границы). Приведем пример, иллюстрирующий сказанное,—
|Епловое излучение равномерно нагретого шара.
Общий метод остается прежним: надо найти вспомогательное
цифракцнонное) поле диполей с моментами р = —lL/i<a и m —
у— 1,/«ш, находящихся в какой-либо точке прозрачной среды
(ЮЩествепные проницаемости к и ц), окружающей тар, который
^полнен средой с комплексными проннцаемоггями е: и >и1. Реше-
яе этой краевой задачи (с обычными условиями непрерывности
тенциальных компонент Ео и Н„ па поверхности шара и
овием излучения на бесконечности) нетрудно получить в виде
¦Ядов по фундаментальным векторным функциям шара. Потери Qo
Рефракционного поля в шаре можно вычислить затем как поток
(Ьергии внутрь шара через его поверхность1). Напомним, что
л1Ь всех таких, по сути дела, неравновесных задачах («высвечи-
Цбние» нагретого тела) предполагается, что внутри тела каким-то
Йуразом поддерживается квазиравновесное состояние н, в част-
JfDCTH, постоянная температура.
Мы приведем только один результат — зависимость среднего
Ректора 1 !ойнтинга флуктуационпого поля нагретого шара от
*) Подробное изложение расчета см. в [6j, § 7, где таким же путем ре-
а задача и для бесконечного круглого цилиндра.
150 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ ГГЛ. Ill
радиуса шара а. На рис. 14 для случая шара, обладающего
хорошей электрической проводимостью, ио лишенного магнитных
потерь, показана зависимость удельной мощности ра (т. е. мощ-
ности, излучаемой с единицы поверхности шара) от параметра
a=kaa = e>a/c = 2na/X. При Я/о—0 (а—> «>) мощность стремится
к постоянному значению ри, которое отвечает классическому
закону Кирхгофа. По оси ординат
иа рис. 14 отложено отношение рш/р„.
Мы видим, что с ростом а удельная
мощность излучения сначала растет,
а затем спадает со слабо выражен-
ными максимумами, которые несколь-
ко сдвинуты вправо от значении а,
соответствующих собственным часто-
там и электрических колебаний ша-
ра')• У малого (а~ 1) хорошо про-
, водящего шара излучение с единицы
0,5 1,0 1,5 г,о 2,5 а, поверхности оказывается в полтора—
Рис. 14. два раза интенсивнее, чем у боль-
шого (а^>1). Зависимость р0 от от-
ношения к/а—это и есть то новое, что дает флуктуаииоиная
электродинамика.
Полный поток энергии, излучаемой шаром на частоте <е>,
равен Ра — 4ла*рш и, конечно, одинаков через любую окружаю-
щую шар замкнутую поверхность. Но средняя плотность энер-
гии иа флуктуационного поля ведет себя иначе. Вдали от шара иа
убывает, как 1/Я». Это плотность энергии излучения (волнового
поля). При приближении же к поверхности шара ыи быстро
нарастает и при R=a обращается в бесконечность. Разумеется,
и здесь это нарастание ио обусловлено квазистационарной частью
флуктуационного поля.
Заметим, что решение вспомогательной дифракционной задачи
о полях диполей р и m существенно облегчается в случае хорошо
проводящих тел (сильно выраженный скии-эффект). Для таких
тел можно воспользоваться решением дифракционной задачи
с так называемыми импедансными граничными условиями, т. е. во-
обще ие рассматривать поле внутри тела. В первом приближе-
нии дифракционное паче рассчитывается для идеально прово-
дящих тел той же формы и расположения, что и рассматривае-
мые (кстати сказать, случай идеально проводящих тел пользуется
из-за простоты граничных условий наибольшим вниманием спе-
циалистов по теории дифракции). Тепловые потери вычисляются
!) Если бы у шара были только магнитные потерн, то максимумы при-
ходились бы иа собственные частоты колебаний магнитного типа. При нали-
чии обоих видов потерь картина была бы более сложной.
jlSj ПРИМЕРЫ ПРИМЕНЕНИЯ ЗАКОНА КИРХГОФА 151
затем интегрированием по поверхности тела поверхностной плот-
ности джоулева тепла. На элементе dS поверхности тела по-
глощается тепло
| /|L, A8.10)
где ?'—вещественная часть импеданса, а Яо, (тангенциальная
компонента Но) берется из решения дифракционной задачи для
идеально проводящего тела.
Другой приближенный способ вычисления потерь Q, дифрак-
ционного поля применим в тех случаях, когда, во-первых, все
характерные размеры тела (включая радиусы кривизны его по-
верхности) велики по сравнению с длиной волны Я и с глубиной
проникновения поля внутрь тела и, во-вторых, моменты флук-
туационного поля ищутся лишь вдали от тела—иа расстояниях,
значительно превышающих Я. Соответственно точечные источники
дифракционного поля тоже помещаются иа таких расстояниях.
Кроме того, предполагается, что форма тела такова, что в при-
ближении геометрической оптики лучи, выходящие из точечного
источника, испытывают на границе тела лишь однократные отра-
жения.'
*. Перечисленные условия позволяют считать, что в ближай-
шей окрестности каждого элемента поверхности тела поле уда-
лонного точечного источника имеет структуру плоской волиы,
а значит, полное дифракционное поле у поверхности можно
вайти, пользуясь френелевскими коэффициентами отражения (для
каждой из поляризаций и с локальным значением угла падения
первичной волны). Так как, по предположению, многократных
отражений иет, а преломленная волна поглощается, не доходя
До других участков поверхности тела, потери Qo дифракционного
поля равны просто суммарной мощности преломленных в тело
Фолн, причем интеграл берется по «освещенной» части поверх-
ности тела.
Ряд примеров использования обоих приближенных методов
'расчета потерь Qo (т. е. применение формул сильного скин-
яффбкта и применение френелевских отражательных формул) при-
веден в монографии [6J.
Остановимся теперь на случае, когда излучение тела, нахо-
дящегося в свободном пространстве (для простоты—в вакууме),
^нтересует нас только в волновой зоне этого тела, т. е. на рас-
стояниях R^>l*/X, где /—размеры тела. Помещая диполи р и m
taa столь большом расстоянии, мы можем считать, что в области,
йавятой телом, приходящая волна —плоская. Если моменты р
Щ п (т. е. орты I, и 12) взять взаимно ортогональными и образую-
IWam с R ортогональную правовинтовую связку (рис. 15), то
ЗВапряжеиности в падающей иа тело волне будут различаться
152 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 1ГЛ. Ш
только знаком:
Еи--Е„,-Е,. Н„ = -НОЯ^НО> A8.11)
т. е. падающая волна линейно поляризована (по IJ, а ее ампли-
туда (при p = l/i(o) равна \Et\ = 2n/cXR.
В силу A8.11) формулы
A7.4) и A7.5) дают для наиря-
женностей теплового поля в
точке R выражения
mi
A8.12)
где К —объем тела, а индексы 1 и 2 обозначают компоненты
по ортам lt и 1,. По формулам A7.11)—A7.13) мы получаем
поэтому, что
Соответственно поток энергии (вектор Пойитинга) излучения
тела (с поляризацией lt и в направлении R) будет
а>, T)Q,, A8.13)
а поток в телесный угол do, т. е. через площадку R*do, нахо-
дящуюся на расстоянии R от тела, составит
dPm=^RR%do=~e{o>, T)Q,R'do. A8.14)
Индекс © указывает, как обычно, что речь идет о спектре по
частотам а>^0.
Выразим теперь потери Qo дифракционного поля в теле через
так называемый эффективный поперечник поглощения:
°»ФФ — — •
^1'
Таким образом, о,фф—это та площадь фронта падающей на тело
плоской волиы, поток энергии через которую равен поглощае-
мой телом мощности Qo (на поляризации 1,). Подставив в
значение \Е„], находим
ВОЛНОВОДНАЯ ФОРМА ЗАКОНА КИРХГОФА 153
Наконец, внося это выражение для <?„ в A8.14) и удвоив ре-
зультат (для учета обеих независимых поляризаций), получаем
A8.15)
Таков поток энергии теплового излучения тела в дальней зоне
В телесный угол do в направлении Л и па частоте со.
Если тело представляет собой перпендикулярную к R плас-
тину, размеры которой гораздо больше Я, то о.фф = Л2, где
2—площадь пластины, а А—ее коэффициент поглощения. Тогда
A8.16)
ft соответствии с классической теорией теплового излучения.
§ 19. Волноводная форма закона Кирхгофа
При рассмотрении передачи электромагнитных сигналов по
волноводам представляет интерес спектральная интенсивность
епловых «шумов», т. е. мощность теплового излучения, нере-
осимая по волноводу в спектральном интервале (со, со + Ла).
Шловое поле может создаваться стенками самого волновода,
[кнми-лнбо антенными устройствами, к которым он присоединен
№ль, рупор), рефлекторами, диафрагмами, аттенюаторами н т. п.
азовем для краткости любую систему таких элементов излуча-
елем. Разумеется, флуктуационное волновое поле в волноводе
оке может быть представлено как суперпозиция бегущих (докри-
ческих) собственных волн волновода, или так называемых
бственных мод.
"На основании формулы A7.11)—A7.13) нетрудно заранее
«двидеть, что мощность теплового излучения, посылаемая в
ЫШовод любым излучателем иа какой-либо л-й моде и иа
Стоте и, будет связана с коэффициентом поглощения этого
(иучателя, когда на него падает n-я собственная волна часто-
(о. Соответствующую формулу, названную волноводной формой
Нона Кирхгофа ([1], §17), легко получить как при помощи
оремы взаимности, так и на основе принципа детального рав-
*есия ([6], §9). Мы приведем только второй способ вывода,
"~" сказать, не предполагающий заранее выполнения теоремы
«имности.
¦ В ч. I, §54 было показано, что произвольный излучатель,
|Гласованный с линией (волноводом, коаксиалом) на часто-
>' со^О, посылает в лниию в интервале частот (ш, ш+Ло)
154 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ [ГЛ. Ш
МОЩНОСТЬ х)
Если согласованный излучатель возбуждает только одну (л-ю)
собственную волну, то это равенство должно выполняться и для
Данной волны, т. е. для каждой моды и частоты, на которых
излучатель согласован, имеем
ЯШЯ=5Г. A9.1)
П +
^ rtm
я~.-*—
к
С
11
I ain
Рассмотрим следующую равновесную
jj- fl- J^ ^Z систему. Между двумн сечениями ре-
т " "т гулярного волновода, показанными
Рис. I6. пунктиром на рис. 16, расположен не-
который несогласованный излучатель
М (причем рассогласование, вообще говоря, различно по обе сто-
роны от М).
Введем для М коэффициенты поглощения n-й волны А* и коэф-
фициенты ее трансформации (п—*т) при отражении от М (Rtml и
при прохождении через занятую М область (D^), где индексы
плюс и минус означают падение первичной n-й волны на М со-
ответственно слева и справа. Из закона сохранения энергии имеем
1= UlRU l,
A9.2)
Штрих около знака суммы должен напоминать, что суммирование
распространяется только на те т-е волны, которые на частоте ю
являются бегущими (докритическими).
Пусть но обе стороны от излучателя М находятся черные
излучатели, т. е. тела, которые имеют ту же температуру, что и
М, и согласованы с волноводом (при дайной частоте со) на каж-
дой из рассматриваемых бегущих волн. Обозначим через Pffl±
мощности, излучаемые М на n-й волне вправо и влево (рис.16).
Принцип детального равновесия требует, чтобы встречные потоки
энергии на этой волне были одинаковы (как справа, так и слева
') Разумеется, под в (со, 7") надо понимать здесь только энеотию черного
излучения (§17). Если же речь идет о неквантовой области йох^кГ, то
в (<а, Т) = кТ без каких-либо оговорок.
jisl волноводнля форма закона Кирхгофа 1В5
от М):
<19-3>
Умножая A9.2) на в/2п и вычитая из соответствующих ра-
венств A9.3), получаем
{ A9.4)
что и является искомым результатом.
При выполнении принципа взаимности матрицы R и D обла-
дают симметрией:
и мы получаем тогда из A9.4)
т. е. мощность, излучаемая М направо (налево), определяется
коэффициентом поглощении М при падении n-й волны справа
^(слева).
В отсутствие трансформации типов воли, когда матрицы R и
D диагональны, получаем из A9.4)
A9.6)
Выполнение принципа взаимности (?>+=О~) или же полная ие-
Эроэрачиость излучателя М (DJ = 0) снова приводят к A9.5).
Заметим, что посколькуР±п—неотрицательные величины, из
{J9.6) следует, что для любого тела или системы М
$. е. доля энергии, поглощенная и пропущенная при облучении
ijM в одном направлении, всегда не меньше, чем доля энергии,
прошедшая через М при облучении во встречном направлении.
156
ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
1ГЛ. 11!
Если материальные уравнения для тел, составляющих излу-
чатель М, локальны, то можно перейти к квазиравновесному
случаю, считая температуру Т функцией точки, и пользоваться
средним значением Э(ш, Т), взвешенным по локальной величине
джоулевых потерь внутри тел:
тогда A9.5) запишется в более общем виде:
pS.=?aI(»). A9?)
Значения величии А± (со) определяются, конечно, всей структу-
рой поля, создаваемого в излучателе М падающей на него п-й
волной, а не только его поглощаю-
щими элементами (см. задачу 4).
Согласно A9.5) какое-либо
удовлетворяющее принципу вза-
имности тело излучает, находясь
в волноводе, следующие полные
мощности в интервале частот До:
Я»
—
k
/¦
1
/
/
i
1
/
/
i
=¦&?' *?
A9.8)
Сумма беретси по всем докрити-
г
Рис. 17.
ческим волнам, число которых
при разных значениях со различно. Рис. 17 иллюстрирует фор-
мулу A9.8) на примере одностороннего излучения хорошо про-
водящей поперечной перегородки в прямоугольном волноводе.
Мощность Яш (в некотором произвольном масштабе) показана в
функции параметра ?=2а/Я, где о—меньшая сторона прямо-
угольного сечения. С ростом § (повышением со) все большее
число собственных Е- и //-волн переходит в разряд бегущих.
Из-за того, что перегородка обладает только электрическими по-
терями и лишена магнитных, коэффициенты поглощения Е- и И-
воли ведут себя при переходе через критические частоты раз-
лично: для Я-волм они плавно нарастают (от нуля при крити-
ческой частоте), а для f-волн они начинаются с острых пиков,
расположенных вплотную к критической частоте. Эти пики и
дают сильные выбросы Ры, которые в принятом масштабе дале-
ко выходят за пределы чертежа. Пунктиром на рисунке показан
тот ход Ри(?), который получился бы при экстраполяции на
область малых | классического закона Кирхгофа. Непримени-
мость этого асимптотического закона вполне очевидна.
I 19] ВОЛНОВОДНАЯ ФОРМА ЗАКОНА КИРХГОФА 157
Следует отметить, что для любой совокупности воли, распро-
страняющихся в одном измерении (например, по радиальному
направлению в случае излучения шара), можно представить из-
лучаемую мощность в виде A9.8), т. е. в виде суммы по взаим-
но ортогональным модам. Таким образом, называя формулы типа
A9-8) валноводной формой закона Кирхгофа, мы несколько су-
жаем область их применимости. Однако это оправдано, так как
именно волноводы дают реальную возможность выделять волны
отдельных типов (Е и Н) и номе-
ров, тогда как при излучении
тел в свободное пространство пред-
ставляет интерес лишь вся вхо-
дящая в A9.8) сумма, причем
'сумма бесконечная (ввиду отсут-
ствия критических частот).
Волиоводная форма закона
Кирхгофа справедлива не только
в бесконечном регулярном волно- Рис. 18.
воде, но и в том" случае, когда
рзлучатель (система тел) М находится на конце полубесконечного
-Волновода. Пусть, например, к концу волновода присоединен
рупор, перед которым и (или) внутри него расположены любые
*ела Л*а(сс=1, 2, ...) с температурами Та (рис.18). Под излу-
чателем М надо понимать всю систему тел Мя, заключенную
внутри замкнутой поверхности, охватывающей левое полупрост-
ранство и достаточно удаленной от конца волновода, т. е. пере-
секающей его там, где уже существует одномерная совокупность
взаимно ортогональных собственных воли регулярного волново-
да (сечение 2 на рис. 18). Мощность теплового излучения, по-
Сылаемого системой тел М в волновод на л-й собственной вол-
Вё, запишется в том же виде A9.7):
J>Sn=-JLSe.4i1(«>), A9.9)
где суммирование распространяется на все тела МЛ (включая,
?оиечио, и рупор, если в нем есть джоулевы потери).
Напомним, что Аш(®)—это поглощенная телом Ма доля мощ-
ти л-й волны, падающей справа через! сечение 2, т. е. при
всего устройства в передающем режиме. При этом часть
ности излучается в окружающее пространство. Простое рас-
дение показывает, однако, что можно и эту часть включить
1^A9.9). Действительно, допустим, что среда, заполняющая про-
" раиство, охваченное замкнутой поверхностью, и окружающая
па Ма, обладает сколь угодно малым поглощением. Если при
вся мощность, излучаемая в передающем режиме, в конеч-
счете поглощается средой, то последнюю можно рассматри-
158 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ [ГЛ. Ill
вать как одно из тел Ма. Таким образом, один из членов сум-
мы A9.9) будет относиться к среде, а роль соответствующего Aj,
будет играть так называемый энергетический коэффициент излу-
чения, т. е. доля мощности падающей справа п-я волны, излу-
ченная рассматриваемой системой в непоглощающую среду.
§ 20. Тепловое излучение и антенны
Как известно, существуют разные виды аитенп, например:
тонкие (проволочные) антенны, широко применяемые в радиове-
щании и связи на коротких и более длинных волнах, зеркальные
антенны, используемые в радиоастрономии и для связи на ультра-
коротких и еще более коротких волнах, и др. В любой антенне
происходят тепловые флуктуации в материале антенны и возни-
кает обусловленное этими флуктуациями собственное тепловое
излучение антенны. Но во многих случаях представляют интерес
не только эти собственные шумы и излучение, но и воздействие
на антенну (а значит, и на последующие каналы) флуктуациоп-
ных полей внешних нагретых тел и сред. Мы остановимся на
этих наведенных тепловых шумах и только на тонких антеннах ').
Внешнее флуктуациониое поле наводит в проводах антенны
токи, которые и представляют основной интерес, так как обыч-
но именно они являются здесь непосредственно измеряемыми
величинами. В принципе, если корреляционная функция падаю-
щего на антенну теплового излучения известна, моменты наве-
денного тока можно найтн, используя формулы теории возбуж-
дения антенн. Однако такого рода расчеты связаны с трудностями,
которые обусловлены в первую очередь тем, что флуктуационное
поле не обладает дельта-корреляцией вдоль проводов антенны.
Эти трудности можно в значительной мере обойти, если вновь
воспользоваться функцией Грина и теоремой взаимности.
В теории тонких антеии удобно и принято оперировать ие со
сторонними токами, а со сторонними полями и э. д. с. Целесооб-
разно поэтому соответствующим образом видоизменить и теоре-
му взаимности. Запишем «электрическую часть» этой теоремы
A7.2):
$Е]„*г=$Е.].*г, B0.1)
и заменим сторонние токи j, и j0(,— цгт(мкшсцфлуктуацио1жого(Е)
и вспомогательного дифракционного (Ео) полей на—напряжен-
') Теория, позволяющая рассчитывать собственное тепловое излучение ан-
тени, развита в книге F). в <>§ 10 и 11—для зеркальных антенн, а в § 12 —
специально для тонких антенн. § 13 указанной книги посвящен наведенным
тепловым шумам в антеннах и содержит более обширный материал, чем при-
водицый ниже в данном параграфе.
$20] ТЕПЛОВОЕ ИЗЛУЧЕНИЕ И АНТЕННЫ 159
ности сторонних полей соответственно К и Ко- Так как в спек-
тральном представлении j, = — i(oO/4n, a O = eK, где е = е' +
-f-j — (в'—вещественная проницаемость, а—проводимость),
ш
имеем
-т?к, !..= -¦?¦ К.. B0.2)
где вторая формула—для дифракционного тока ]„,,—разумеется,
аналогична первой. Если обозначить плотности токов, наведен-
ных в антенне полями Е и Е„ соответственно через j и j0, то и
для них будет
1=-ТгЁ. J.=—?-Е.. B0.3)
Из B0.2) и B0.3) следует, что Ejoe = Koj и E0L = Kj0, так что
теорема B0.1) принимает вид1)
$КЖЖОЛ-'-$К(г)].(г)*г. B0.4)
Именно такая форма теоремы взаимности—с напряжеиностями
сторонних полей и плотностями наведенных токов—чаще всего
используется в случае тонких проводов (в том числе в теории
проволочных антеин), а также в квазистациоиарной области (в том
числе в теории цепей с сосредоточенными параметрами).
При применениях B0.4) надо знать корреляционную функцию
компонент стороннего флуктуационного поля К (г). Ее нетрудно
получить из первого равенства B0.2) и первой формулы ФДТ
A6.4), причем мы ограничимся случаем изотропного материала
проводов, когда 6
/.« (г) ft (О> =
= --|-в(а), Г)(-^-|)баЭ6(г-г'). B0.5)
Более того, если речь идет, как в нашем случае, о металли-
ческих проволоках, то обычно можно пренебречь токами смеще-
ния внутри этих проволок и считать, что е да t -^. Тогда
<*„ (г) Ц (г')> = У?2М (г-г'). B0.6)
Пусть нас интересует наведенный флуктуационный ток /
в некотором сечении какого-либо из проводов, входящих в со-
') Для последующего нам удобнее обозначить переменную интегрирования
в левой части иначе, чем а правой; поэтому мы и ввели г'.
160 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 1ГЛ. Ill
став антенны. Сечеиие 2 этого тонкого (квазилинейного, как го-
ворят в электродинамике) проводника, вообще говоря, может
меняться по длине провода s, ио, по условию, всюду имеет ли-
иейные размеры, малые по сравнению с длиной волны X в окру-
жающей непроводящей среде. Кроме координаты s, отсчитываемой
по оси провода, введем еще радиус-вектор р, лежащий в плоскости
поперечного сечения провода. Таким образом, dfr'—d'p'ds'.
Для того чтобы выразить ток / (s) через К, допустим, что
вспомогательное стороннее поле К„(г) действует только в по-
перечном сечении провода с координатой s'—s, на всем сечении
постоянно и направлено по оси провода (орт s):
-«)• B0-7>
Очевидно, &а—это интегральная сторонняя э. д. с, приложен-
ная в сечеиии с координатой s:
$ K,s ds' = g,.
Коль скоро К, имеет вид B0.7), интеграл в левой части B0.4)
равен
ir теорема взаимности B0.4) дает
#,/W=U (г)],<*)*/-. B0.8)
При помощи этой формулы нетрудно получить теперь сред-
ний квадрат модуля флуктуационного тока / (s). Умножая B0.8)
на комплексно сопряженное равенство и усредняя, получаем
$ S <Ка (г
г) ft (ОЛ1 *''•
Подставив сюда функцию корреляции B0.6) стороннего теплово-
го поля К, находим
где
Л?0 = ||Е.|»*г=-^-^ B0.10)
— джоулевы потери тока, вызываемые сосредоточенной в сече-
иии s вспомогательной э. д. с. ?с. Очевидно, равенство B0.9)
J20] ТЕПЛОВОЕ ИЗЛУЧЕНИЕ И АНТЕННЫ ]61
представляет собой модифицированную форму обобщеииого зако-
на Кирхгофа A7.14). Оио позволяет ие решать неоднородную
краевую задачу о флуктуациониом поле Е в материале антенны,
а сводит нахождение < | / (s) |*> к вычислению квадратуры, если
известно решение задачи о вспомогательном поле Е„ дельта-за-
питываемой антенны, т. е. о поле, возбуждаемом э. д. с. ?,,
приложенной в интересующем иас сечении s.
Если ZM (s)—входной импеданс антенны по отношению к э. д. с,
включенной в сечение s, то gt = ZM(s) /0(s). гДе
/.(•)-$/« (P. s)^P
— полная сила «дифракционного» тока в этом сечении. Можно
ввести аналогичным образом эквивалеитную тепловую э. д. с. ?(s)
в сечении s, определив ее через импеданс ZBX (s) и полный флук-
туационный ток:
B0.11)
Таким образом, ?(s) = gj(s)/It(s), т. е., согласно B0.8),
)dT. B0.12)
Таково выражение эквивалентной тепловой э. д. с. в сечении s
в общем случае, когда обусловливающее ее стороннее поле К (г)
произвольно распределено в объеме проводов антенны. В силу
B0.9) средний квадрат модуля ?(s) равен
B0.13)
Следует подчеркнуть, что ?(s) не представляет собой флук-
туационной э. д. с, распределенной вдоль провода. Формула
B0.11) вводит (по сути дела, формально) для каждого сечеиия s
свою сосредоточенную в этом сечении э. д. с. <#(s), смысл ко-
торой состоит только в том, что она обеспечивает правильное
значение флуктуационного тока в том же сечении.
Однако в случае квазистационарной цепи, когда в каждой ее
ветви полная сила тока / и входной импеданс цепи ZBI не зави-
сят от s, э. д. с. ? тоже не зависит от s, т. е. может быть
включена в любое сечеиие данной ветви. Если к тому же цепь
имеет всюду одинаковую температуру F=const), то ? можно ото-
ждествить с локальной найквистовской э. д. с. е того двухполюс-
ника, который получается при размыкании рассматриваемой вет-
вк цепи. При этих условиих (квазистациоиарности и равновес-
4СМ. РытовТ» id. ц. II
162 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ (ГЛ. Ill
ностн) B0.13) переходит в формулу Найквиста:
<1«(«)Г>-4в-^г-1вЛ.| B0.14)
где #э—энергетическое (активное) сопротивление двухполюсника:
Вернемся х антенной формуле B0.13) и рассмотрим два ил-
люстрирующих ее примера.
1. Антенна в поле равновесного излучения.
Пусть антенна находится в свободном пространстве, заполнен-
ном прозрачной средой со всюду одинаковой температурой
F=const).
Включенная в каком-то сечении s антенны вспомогательная
э. д. с. &„ создает дифракционное поле антенны, которое отнюдь
не локализовано только в проводах антенны или в их ближай-
шей окрестности. Напротив, это поле содержит и излучаемые
антенной волиы, так что джоулевы потери Q, имеют место как
в материале самой антенны, так и в любых проводищих телах,
оказавшихся на пути излучаемых воли. Пока мы предположим,
что таких тел нет (свободное пространство) и, следовательно,
мощность, отдаваемая э. д. с. ?л, расходуется только на нагре-
вание самой антенны и на излучение, причем во всякой антенне,
отвечающей своему назначению, подавляющая доля приходится
именно на излучение.
Предполагая, что среда обладает исчезающе малой проводи-
мостью, и пренебрегая тепловыми потерями в самой антенне, мы
можем считать, что полные потери <20 дифракционного поля просто
равны мощности излучения Р„. Последняя записывается обычно
в виде Р, = /?i(s)|/, (s)|V2, где Rz—так называемое сопротив-
ление излучения антенны, зависящее, конечно, от того, в каком
сечеиии s включена э. д. с. ?0. Таким образом,
О IMs)!1. B0.I5)
При 6 = const формула B0.13) имеет вид
= 2в(?0/п |/„ (s) I1. Подставив сюда B0.15), получаем
а спектральная плотность флуктуационной э. д. с. по положи-
телоным частотам вдвое больше:
A (s) = 2 < | ё (s) |«> = j &RS (s). B0.16)
$201 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ И АНТЕННЫ 1§3
Из вывода ясно, что этот результат справедлив для любой
сколь угодно сложной антенны в свободном пространстве, если
только относить Rz и А'ш к одному и тому же сечению антенны.
2. Тепловые шумы, наводимые удаленными те-
лами. Если тело находится на достаточно большом расстоянии R
от антенны, точнее—в ее фраунгоферовой зоне, и размеры тела
тоже малы по сравнению с зоной Френеля, то в области про-
странства, занятой телом, можно считать антенное поле супер-
позиций плоской волны и дифрагированного телом вторичного
поля. Обозначая, как н в § 18, эффективный поперечник погло-
щения тела для падающей на него плоской но л ни соответствую-
щей поляризации через оЭфф, можно записать поглощаемую те-
лом мощность в виде Qa — оЭфф<#°0, где <У0 — модуль вектора ПоГш-
тиига первичной волны. Связь fft с полной мощностью
/*в = А?х | /01"/2, излучаемой антенной, дается известным соотно-
шением
где G—функция направления, называемая приведенным коэффи-
циентом направленности антенны и описывающая угловое рас-
пределение излучаемой мощности Ро (среднее значение G по еди-
ничной сфере равно единице: -^?Gdo=\). Таким образом,
Согласно B0.13) средний квадрат эквивалентной тепловой э. д. с,
создаваемой рассматриваемым телом в сеченин s антенны, равен
(на ш > 0)
А*ад'^^. B0.17)
Здесь предполагается, что тело обладает всюду одинаковой тем-
пературой (в = const). Если в поле излучения антенны находится
несколько тел с различными температурами и на разных уда-
лениях от антенны, то
%?1?!^#^- B0.18)
Для абсолютно черных тел эффективное сечение совпадает
с геометрическим @»** = 0, предполагается, что линейные раз-
меры а гораздо больше длины волны X) и, следовательно, o^^/R* =
¦=а/#* = о, где о—телесный угол, под которым тело видно из
места расположения антенны. Формула B0.18) запишется тогда
164 ТВПЛОВОЕ ЭЛЕКТРОМАГНИТНОВ ПОЛЕ СГЛ. Ill
в виде
или даже
(при условии, что do^X4R'). Если температура всех тел оди-
накова, то мы получаем
При сплошном заполнении периферии черными телами со всюду
одинаковой температурой (черная оболочка) мы возвращаемся
к формуле B0.16).
§ 21. Равновесное тепловое поле. Равновесная форма ФДТ
До сих пор мы рассматривали главным образом неравновес-
ные задачи—о поле, создаваемом нагретыми телами в окружа-
ющей среде1), которая считалась либо прозрачной (и поэтому
не вносящей никакого вхлада в тепловые потери вспомогатель-
ного дифракционного поли), либо настолько холодной, что ее
собственным флуктуациониым полем можно было пренебречь.
В этом параграфе мы обратимся к случаю, когда во всем объеме
полного поля температура одинакова, т. е. будем рассматривать
равновесное флуктуацнонное поле. Если, в частности, речь идет
о телах, охруженных прозрачной средой, не заключенной в иде-
альную зеркальную оболочку, то мы будем предполагать, что
на достаточно больших расстояниях поле ограничено полно-
стью поглощающей оболочкой, имеющей ту же температуру, что
и нагретые тела.
Общие формулы A7.11) — A7.13) для пространственных кор-
реляционных функций спектральных амплитуд флуктуационного
поля, создаваемого равномерно нагретыми телами, можно объе-
динить в одну формулу, если обозначить через А н В какие-ли-
бо две из шести компонент Е и Н. Тогда вместо A7.11)—A7.13)
можно написать
<A(rl)B'{ri)>= ±|в(ш
х) Напомним, что состояние самих нагретых тел необходимо предполагать
при этом квазиравновесным.
,,,] РАВНОВЕСНОЕ ПОЛЕ. РАВНОВЕСНАЯ ФОРМА ФДТ 165
Верхний знах отвечает случаю обеих электрических или обеих
магнитных компонент, нижний —одной элехтрической и другой
магнитной; Quab»—смешанные потери дифракционного поля, соз-
даваемого единичными точечными источниками соответствую-
щего типа, помещенными в точках тг и г,.
Кирхгофовская форма ФДТ B1.1) справедлива, конечно, и
для равновесного поля, но под Qcab. надо понимать теперь сме-
шанные потери дифракционного поля во всем занимаемом им про-
странстве. Это обстоятельство позволяет существенно упростить
выражение для Q0/is«. воспользовавшись так называемой комп-
лексной леммой Лоренца. Эта лемма, в известном смысле анало-
гичная теореме взаимности, отличается от последней тем, что она
связывает «накрест» поле одной системы источников с комп-
лексно сопряженным полем другой системы источников.
Написав, как и при выводе теоремы взаимности A7.2), две
системы уравнений Максвелла A6.1)--одну для поли и источ-
ников I, другую для поля и источников 2,—умножим уравне-
ния первой системы соответственно на —HJ н EJ, а комплексно
сопряженные уравнения второй системы иа — Н, и Et и сложим
результаты. Это приводит к равенству
^ .HJ-H.BJ).
При интегрировании этого равенства по всему объему V полно-
го поля интеграл от div обращается в нуль и мы получаем лем-
му Лоренца:
. B1.2)
Выражение, стоящее в левой части B1.2), если учесть, что
Clct = eap?1p, Dif—t.itaEia (и аналогично для В, и В,), представ-
ляет собой не что ниое, как смешанные тепловые потери QM<
полей 1 и 2 во всем пространстве (см. A7.9), A7.10)), и, значит,
B1.3)
Этим результатом леммы Лоренца мы теперь и воспользуемся
применительно х дифракционным полям, создаваемым единич-
ными точечными источниками.
166 ТЕПЛОВОВ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ (ГЛ. III
Возьмем случай, когда А и В в B1.1)—компоненты электри-
ческой напряженности теплового поля Е. Тогда
J.-J«=»l,e(r-r1). 1, = 1„ = 1,в(г-г,), jmi = jm! = O
и B1.3) дает
««.(Г!, 1,; г„ У—V.{l,Ei(rl) + l,E0l(ri)}. B1.4)
Но из обычной теоремы взаимности A7.2) следует, что в этом
же случае
Исключая из B1.4) при помощи последнего равенства либо Ео1,
либо Ещ, можно записать потери QK. в следующих двух формах:
<?«.(¦•„ I,; г„ l1) = -V,Re{l1E,,(r1)} = -V.Re{lsE,1(r1)}.
Подстановка этих выражений в A7.12) дает
<?,,(г,) Е\ (г,)> =. - ±8 (со, Г) Re [\fin (г,)} =
= -±в(», ^Re^E^r,)}. B1.5)
Применение B1.3) к случаю двух компонент магнитной на-
пряженности теплового поля Н приводит к аналогичному выра-
жению для Qmm. и, в соответствии с A7.13), к результату:
<Н,, (rj hi, (r,)> = -10 К Т) Re {1,Н01 (г,)} ^
Наконец, в случае, когда А—компонента Е, а В—компонента
Н, мы получаем Qm, и нз A7.11) следует, что
<E,,(Tl) H'lt (r,)> - - ie («о, T) Im {I.E., (r,)} =
?„(г;)}1 B1.7)
т. е. корреляционные фуихцин между электрической и магнит-
ной напряженностями чисто мнимые.
Формулы B1.5) — B1.7) показывают, что с точностью до мно-
жителя—в/л корреляционные функции равновесного поля совпа-
дают с вещественными или мнимыми частями соответствующих
функций Грина. Эти формулы можно назвать равновесной формой
ФДТ. Она избавляет от необходимости вычислять после нахож-
дения вспомогательного дифракционного поля его тепловые
потери. Достаточно взять вещественную нли мнимую часть самих
иапряжеиностей этого поля. Вместе с тем линейная связь между
вторыми моментами теплового поля и напряженностями дифрак-
|ltI РАВНОВЕСНОЕ ПОЛЕ. РАВНОВЕСНАЯ ФОРМА ФДТ 167
двойного поля сразу же позволяет использовать аппарат теории
аналитических функций комплексного переменного при нахож-
дении тех или иных интегральных (по спектру) эффектов в рав-
новесном поле, т. е. при интегрировании корреляционных функ-
ций теплового поля по частоте о>.
Располагая функциями корреляции спектральных компонент
флуктуационного поля и зная, в частности, средние значения
произведений этих компонент в одной точке, мы имеем возмож-
ность находить не только средние плотности энергии и ее потока,
ио и другие средние билинейные величины. Мы можем, напри-
мер, вычислить средние значения компонент максвелловского
тензора натяжений, т. е. найтн механические (пондеромоторные)
силы, с которыми равновесное поле действует на тела. Сказан-
ное относится как к квазиравновесным полям, когда в нашем
распоряжении обобщенный закон Кирхгофа B1.1), так н к равно-
весным, когда можно пользоваться равновесной формой ФДТ
B1.5) и B1.6). Однако этя интересные физические применения
указанных теорем [61 не имеют прямого отношения к радиофи-
зике, и поэтому мы ограничимся лишь немногими замечаниями.
На первый взгляд может показаться странным, что даже
в равновесном случае флуктуационное электромагнитное поле
обусловливает действие сил на тела (в том числе н на идеальные
проводники). Но ничего удивительного здесь нет просто потому,
что, говоря о равновесии, мы постоянно имели в виду только
тепловое равновесие, т. е. одинаковую во всей рассматриваемой
системе температуру Т (в частности, Т' = 0). Это вовсе не исклю-
чает действия электродинамических сил, которые либо уравно-
вешены внешними связями, либо вызывают перемещение тел
К механически равновесной конфигурации. Поэтому нет ничего
удивительного и в том, например, что равновесное поле в полу-
пространстве над идеальным плоским зеркалом оказывает на это
зеркало давление, спектральная плотность которого в случае
недиспергирующей среды равна
Как всегда, член Й<о/2 в в(о>, Т) (т. е. нулевые колебания) дает
при интегрировании по и расходящееся выражение. Однако эта
Часть давления компенсируется «нулевым» давлением поля по
Другую сторону от зеркала, где равновесное излучение может,
Вообще говоря, иметь другую температуру. Результирующая
сила, действующая на зеркало, определяется разностью давле-
ний по обе стороны и не содержит в данном примере вклада
Нулевых колебаний.
Это не означает, что нулевые колебания вообще не создают
Вондеромоторных сил. В случае плоского зеркала геомстричес-
168 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ [ГЛ. III
кие условия симметричны, одинаковы по обе стороны от зеркала.
Если же взять, скажем, образованный двумя идеальными зерка-
лами двугранный угол (рис. 19), то структура «нулевых» стоячих
волн внутри угла и вие его будет различна. В результате полу-
чается, что даже при Т = 0 иа зеркала действует «схлопываю-
щнй» интегральный (по о>) момент. Интегрирование по <в надо
при этом распространять ие до о>=оо, а лишь до некоторой
частоты (i>m<^0 (о—проводимость; нера-
' венство является условием того, что при
нормальном скин-эффекте металл еще
можно считать идеально проводящим).
Разумеется, флуктуационное электро-
^нс# 1Э- магнитное поле порождает силы, дейст-
вующие и на поглощающие тела. Более
того, поскольку поверхности таких тел «выстланы» слоем ближнего
(квазистационарного) теплового поля, сильно нарастающего при
приближении к поверхности, эффект механического взаимодей-
ствия (сил сцепления) становится особенно большим в случае
малых зазоров между поверхностями тел. На такого рода явле-
ния обратил внимание Е. М. Лнфшиц, исследовавший их в ра-
боте 17] (см. также [11], [12] и § 18 в [6]).
Теория макроскопических сил сцепления строилась раиее на
основе элементарного закона ван-дер-ваальсовых сил попарного
взаимодействия между атомами или молекулами, что заранее
ограничивало результат случаем разреженных сред. Чисто фено-
менологическая теория, основанная на флуктуационной электро-
динамике, снимает это ограничение. Напротив, исходя из выра-
жения для макроскопической силы сцепления, можно в случае
разреженных сред сделать обратное заключение—о законе
попарного взаимодействия отдельных нейтральных атомов и
молекул. Такой путь, как это ни парадоксально на первый
взгляд, оказывается проще, чем прямой квантовомеханический
расчет для двух нейтральных частиц, при котором закон взаимо-
действия получается лишь в высоких порядках при вычисле-
ниях методом возмущений.
§ 22. Тепловое поле в гвротропиых телах
Многие среды (ферриты, плазма), находясь в достаточно силь-
ном постоянном (во времени) внешнем магнитном поле В,, ста-
новятся гирошропными1)- Это означает, в частности, что в одно-
!) Под «достаточно сильным» понимается ноле, модуль напряженности ко-
торого Во существеыио больше стандартов иапряжсиностей флуктуациошюго по-
ля. Поэтому при линеариаации уравнений Максвелла относительно этих флук-
туаиноныых полей сохраняет смысл учет зависимости параметров среды от В„.
JJ2) ТЕПЛОВОЕ ПОЛЕ В ГИРОТРОПНЫХ ТЕЛАХ 169
родной среде и однородном поле Во собственными волнами явля-
ются монохроматические волиы с круговой (правой и левой)
поляризацией, т. е. только эти волны распространяются без
изменения вида поляризации. Если же в среду впущена, ска-
жем, линейно поляризованная волна, то по мере распростра-
нении ее плоскость поляризации будет, вообще говоря, повора-
чиваться вокруг направления распространении—за счет раз-
ницы фазовых скоростей волн с правой н левой круговой поля-
ризацией, на хоторые можно разложить линейно поляризованную
волну.
В то время как в анизотропных средах тензоры проницае-
мостей симметричны:
ш, г),
Пор (<», Г) = Цра (Ш, Г),
в гиротропной среде, будучи функциями Во, они обладают сим-
метрией с переменой знака В,:
еац К г, В,) = е&а (to, г, — В„),
Цар(Ш, Г, В,) = цЭа(ш, Г, —В,).
Тем самым, для гиротропных сред обычная теорема взаимности
A7.2) несправедлива. Ее заменяет равенство, связывающее
«макрест» источники и напряженности поля 1 в среде, находя-
щейся в магнитном поле B0(jrt, ]„,, Ev HJ, и источники и
напряженности поля 2 в той же среде, но с обращенным внеш-
ним магнитным полем—В„. Будем отмечать электромагнитные
величины, относящиеся к полю 2 в такой «обращенной среде»,
значком «тильда» (jea, ]„,, Ё,, Н„). Вместо A7.2) для гнротрои-
иой среды выполняется теорема
B2.1)
Формулы A6.4) для корреляционных функций сторонних
токов справедливы, конечно, и в гиротропной среде, но обоб-
щенный закон Кирхгофа B1.1), дающий корреляцию напряжен-
ностей флуктуационного поля, уже теряет силу, так как при
выводе этого закона была использована теорема взаимности
A7.2).
Если повторить весь вывод, но опираясь на равенство
B2.1), то мы придем к следующему результату, обобщающему
формулы B1.1) на случай гиротропиых сред:
< А (г,) В* (г,)> = ± | в (а, Т) QMS., B2.2)
170 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 1ГЛ. III
а при достаточно плавном пространственном изменении темпе-
ратуры—
^,T)dQtAB.. B2.3)
Таким образом, корреляция спектральных амплитуд флуктуа-
ционного поля в гиротропиой среде, находящейся во внешнем
магнитном поле В, (г), определяется тепловыми потерями вспо-
могательного дифрахциониого поля в обращенной среде, т. е.
потери надо вычислять при изменении знака внешнего магнит-
ного поля (В„ (г)—>—В„ (г)) ¦)• Формулы B2.2), B2.3) универсаль-
ны в том смысле, что они не налагают никаких ограничений ни
иа размеры и форму тел, ни на их электрические и магнитные
свойства, включая и гиротропию, зависящую также от интен-
сивности и конфигурации постоянного (во времени) подмагни-
чивающего поля В„.
Формулы B2.2), B2.3) облегчают решение флуктуацкониых
задач для гиротропных тел в не меньшей степени, чем формулы
B1.1) в отсутствие гиротропии. Разумеется, необходимое для
вычисления тепловых потерь решение вспомогательной дифрак-
ционной задачи связано, вообще говоря, с большими труднос-
тями, чем для негиротропных тел и сред. Достаточно указать,
что даже нахождение .френелевских коэффициентов отражения
плоской волны от однородного гнротропного полупространства
представляет собой при произвольной ориентации однородного
же поля В„ чрезвычайно громоздкую задачу. Обычно здесь огра-
ничиваются поэтому лишь частными случаями (поле В, перпен-
дикулярно или параллельно границе, первячиая волна падает
нормально). Круг точно решаемых дифракционных задач, т. е.
допускающих нахождение точных функций Грина, ограничен для
гиротропных тел еще более жестко, чем для тел изотропных, но
это лежит в природе вещей, а не в методе решения флуктуа-
ционных задач. Нахождение статистических характеристик теп-
лового поля в принципе столь же просто.
Естественно, что все формулы, выводимые на основе обобщен-
ного закона Кирхгофа, претерпевают при рассмотрении гиро-
тропных тел такое же изменение, какое содержится в B2.2). Так,
например, для потока энергии теплового излучения в телесный
угол do в волновой зоне гиротропного тела вместо формулы
A8.15) будет теперь
^n B2.4)
1) Не только обобщенный, но и классический закон Кирхгофа для гнрот-
ропиых сред долгое время оставался нензвестным. Закон B2.3) был получен
М. Л. Левиным лишь в конце 50-х годов, а опубликован еще позднее, в кни-
ге [в].
|j2] ТЕПЛОВОЕ ПОЛЕ В ГИРОТРОПНЫХ ТЕЛАХ ]71
где 0,44,—эффективный поперечник поглощения данного тела при
обращенном поле —В,. Волновода а я форма закона Кирхгофа
A9.5) тоже заменится на
Ряд примеров применения формул B2.2)—B2.5) см. в книге F1,
§§ 21-23.
Что касается равновесной формы ФДТ (§ 21), то для нее при
наличии гиротропия дело обстоит следующим образом. Формулы
B1.5) —B1.7) были получены при помощи обобщенного закона
Кирхгофа B1.1) и комплексной леммы Лоренца, т. е. результата
B1.4). Лемма Лоренца справедлива для любых сред с линейными
материальными уравнениями, но B1.1) заменяется в случае
гиротропных сред на B2.2). Поэтому, например, вместо формулы
(см. B1.5))
<?,, (г,) Е\. (г,)> = - ± в («, Т) {l,Ei (г,) + 1,Е01 (г,)}
мы получим теперь
<?i,(rj?;.(r,)>- -^вК Г) {1,6;, (г1) + 1,Е01(г,)}, B2.6)
где справа входят функции Грина в обращенной среде.
Но из теоремы B2.1), т. е. из обобщенной на гиротропиые
среды теоремы взаимности, следует, что при рассматриваемых
точечных источниках
A B2.7)
При помощи этого равенства можно исключить из B2.6), скажем
6«i (rj, что дает
<?,,(!•,)?;, (г,)> = - ±в (», Т) 1, {Б;, (г,) + Ё01 (г,)}. B2.8)
Это смешанная форма корреляционной функции, содержащая
функции Грина как в исходной среде, так и и среде с обращен-
ным подмагничивающим полем. При В, = 0 формулы смешанного
тяпа (в частности, B2.8)) непосредственно переходят в получен-
ные ранее формулы для иегиротропных тел (в частности, B1-5)).
Можно также, пользуясь B2.7), заменить в B2.6) обе напря-
женности с тильдами на напряженности в исходной среде (без
обращения В,), и тогда
<Сл(г1) ?,'. (г,)> = - ^9 (<о. Г) {ltt'tl (г,) + I.E., (г,)}. B2.9)
Аналогично формулам B2.8) н B2.9) записываются н функции
Для компонент Н, и взаимные функции корреляции между ком-
поиеитамя Е и Н.
172 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ [ГЛ. III
Таким образом, в случае равновесного поля гиротропность
не вносит никаких принципиальных усложнений. Как и для
иегиротропиых тел, надо знать только функции Грина, хотя их
фактическое вычисление, конечно, значительно сложнее, чем для
изотропных тел.
Ясно, что наличие гиротропиости не должно нарушать уни-
версальную снязь между интегральным излучением и поглоще-
нием одного и того же тела, вытекающую из второго начала
термодинамики. Если, например, тело окружено достаточно уда-
ленной абсолютно черной оболочкой с той же температурой,
что и у тела, то тепловое равновесие между телом и оболочкой
должно иметь место независимо от того, обладает тело гиротро-
пией нли иет. Это значит, что интегральная (по телесному углу)
суммарная (по обеим поляризациям) интенсивность излучения
тела должна быть в обоих случаях одкиакова (Я» = Ли). Но
в отсутствие гиротропии, согласно A8.15),
а при ее наличии, согласно B2.4),
Из равенства Ра=Ра следует, что
§§*,**&>¦ B2.10)
Точно так же суммарное излучение тела, находящегося в вол-
новоде между двумя черными пробками, влраао и влево
ие должно зависеть от наличия гкротропии, т. е. должно быть
Р<ь = Ра- Суммируя выражения A9.4) по всем номерам п бегу-
щих воли, получаем
т.п
Конечно, в двойных суммах~по т и п эти индексы можно пере-
ставлять. Поэтому
р.-Pi+Ъ-&*?,'№+ля.
п
Из равенства Ра — Ри вытекает соотношение, аналогичное B2.10):
АЯ. B2.11)
j23] ПОЛЕ В СРЕДЕ С ПРОСТРАНСТВЕННОЙ ДИСПЕРСИЕЙ 173
§ 23. Тепловое поле в среде
с пространственной дисперсией
До сих пор мы ограничивались материальными уравиениями
A4.2), описывающими среду (вообще говоря, неоднородную)
н отсутствие пространственной ,'дисперсии: индукции D и В
в точке г зависели от свойств и предыстории как среды (от е
н ц), так и поля (ыапряжениостей Е и Н) только в той же
точке г. Если же состояние среды в точке г зависит от пре-
дыстории (в чем заключается временнйя иелокальность) не только
в этой же точке, ио и в некоторой ее окрестности (простран-
ственная келокальность), то материальные уравнения надо брать
более общего вида:
+ » + ао
D(i!,r) = J at' I t(t — V, г, r')E(*', r')d'r',
В(/,г)= J at' $И< —''. г. г')Н(<', t')d?r'.
-00 -00
Зависимость ядер е и ц от разности t—V отражает стационар-
ность интересующих нас процессов, т. е. предполагает неиз-
менность свойств среды во времени (если бы среда менялась
во времени, то в и ц зависели бы от t и V порознь). Зависи-
мость е и ц от г и г' отвечает пространственно неоднородной
среде. В однородной среде ядра е и ц зависят только от раз-
ности р = г—г'. Если область простраиствеиной нелокальное™
стягивается в точку, то
B(i — /', г, г')—-в(< — V, гN(г—г'),
и аналогично для ц. Материальные уравнения B3.1) тотчас же
переходят при этом в локальные уравнения A4.2)х).
В B3.1), как и в A4.2), имеются в виду изотропная и не-
гиротропная среды. Для анизотропной или гиротропиой среды
соотношение между D и Е устанавливается тензором диэлектри-
') Состояние среды в момент / в точке г может зависеть только от собы-
тий, которые находятся внутри обращенного в прошлое светового конуса
с вершиной в «точке» (I, г). Иначе говоря, это события, которые предшест-
вуют моменту / по времени и создают поля, распространяющиеся не быстрее
света в вакууме (принцип причинности). Таким образом, интегрирование по
/' и г' в B3.1) и в последующей формуле B3.2а) в бесконечных пределах
предполагает, что функции е, ц и р.ар обращаются вые указанного конуса
в нуль. Это налагает определенные ограничения и на их аж-амплитуды,
« именно устанавливает определенную связь между вещественными и мни-
мыми частями этих функций. В отсутствие пространственной дисперсии такая
связь выражается формулами Крамерса—Кронига ([3], § 62), а при ее нали-
чии—более общими формулами [13].
174 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 1ГЛ. III
ческой проницаемости еаВ (а, E=1, 2, 3), так что первое урав-
нение B3.1) заменяется на
Do(/, г) - I df \ ^(i-f, r, r')?p(<', r')dV. B3.2а)
Что касается второго уравнения B3.1), то из общих соображе-
ний следует, что введение еще одного тензора fiaf было бы из-
лишиим. Дело в том, что при введении D — Е+4пР и В=Н +4яМ
мы описываем состояние среды поляризацией Р и намагниче-
нием М, разбивая для этого индуцированные в среде токи и
заряды иа «сорта» (связанные и свободные заряды с соответст-
вующими поляризационным током и током проводимости, а кроме
того, молекулярные амперовы токн). Но в нелокальной среде
проще и естественнее включить в D все виды наведенного тока,
так что
В = Н, B3.26)
а для D справедливо материальное уравнение B3.2а). Конечно,
определения D н В (т. е. их связь с микрополями и микрото-
ками) при этом иные, чем в B3.1), так что при отсутствии про-
странственной дисперсии уравнения B3.2а, б) не переходят
н B3.1).
Возможность полного описания среды материальными урав-
нениями B3.2а, б) показывает, что достаточно одного тензора еар
при цар = ва9 (подробней см. [8. 14J). Заметим, что в толще
нелокалькой среды, даже если она однородна и изотропна, тен-
зор еа9 (/—/', r, г') в B3.2а) не вырождается в диагональный,
а имеет общий для данного случая вид:
еа|> (т, р) = (баР —^-) е, (т, р) + -^ е, (т, р), B3.3)
где т = < — С, р^-г—г', т. е. содержит две независимые ска-
лярные функции в, и е, — поперечную и продольную (по отно-
шению к р) диэлектрические проницаемости. Отсюда ясно, что
для однородной и изотропной нелокальной среды допустимы
материальные уравнения и вида B3.1), поскольку в них тоже
фигурируют только две независимые скалярные функции е (т, р)
н Р(т> р)- О связи между е,, в, и в, р. мы скажем несколько
дальше.
Выше мы не случайно подчеркнули, что выражение B3.3)
для Сар относится к толще среды, т. е. к областям, достаточно
удаленным от ее границ. Прн приближении к границе среды
еаР ие может оставаться функцией только разности р = г—г',
так как направление по нормали к границе становится выде-
ленным. Иначе говоря, прилегающий к границе слой с толщи-
fill ПОЛЕ В СРЕДЕ С ПРОСТРАНСТВЕННОЙ ДИСПЕРСИЕЙ 175
ной порядка радиуса нелокальности неоднороден н анизотропен
по своим электродинамическим свойствам. Это в особой степени
усложняет электродинамическую часть задачи, т. е. нахождение
вспомогательных дифракционных нолей (функций Грииа) или
же плотности их джоу левых потерь, если необходимо учитывать
и указанный приграничный слой. Что же касается собственно
флуктуациоииой частя задачи, то в ней все обстоит так же, как
и в случае локалькых сред, поскольку и обобщенный закон
Кирхгофа A7.11)—A7.13), и равновесная форма ФДТ B1.5) —
B1.7) справедливы при любой форме материальных уравнений.
Мы ограничимся далее простейшим случаем однородной и
изотропной нелокальной среды, причем среды неограниченной,
когда во всем пространстве можно пользоваться как ед (т, р)
в форме B3.3), так и скалярами е(т, р), ц(т, р). Целесообразно
при этом перейти к трансформаитам Фурье как по т, так и по р:
«>. *) е*Р I-' («я-яр)]*> Ас, B3.4)
и аналогично для р. (т, р). Такое же преобразование Фурье для
тензора еар(т, р) содержит под интегралом трансформаиту
B3.5)
где е, (<о, ») и е,(ш, .х)—поперечная и продольная (по отноше-
нию к к) проницаемости, конечно, не являющиеся преобразова-
ниями Фурье от е, (т, р} и в,(т, р) в B3.3). Связь скалярных
функпий е (ш, х) и ц (<в, х) с функциями е, (ш, х) и г1 (ш, х) очень
проста [8]:
е(<о, х) = е((ш, х), B3.6)
Вторая из этих формул показывает, что |i (со, х) не может обра-
щаться в нуль.
Целесообразность использования при указанных условиях
пространственно-временных трансформант Фурье (шх-амплитуд)
или пространственных трансформант Фурье от спектральных
амплитуд, вытекает из того, что при этом все линейные уравне-
ния для полей превращаются в алгебраические линейные урав-
нения для их шх-амплитуд. В частности, уравнения Максвелла
A4.6), если мы полагаем
, х)ехр[—Ца>(~xr)]dtod»x B3.7)
176 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ [ГЛ. III
и аналогично для Н, нндукцкй D, В и сторонних токов j0, Jn, при-
нимают для юх-амплитуд следующий вид (аргументы со и х мы
для краткости опускаем):
«[xH] = -.V> + ^j,,
• [xEj = i*,B-^Jel
а материальные уравнения-дли сох-амплитуд, полученные нэ B3.1)
с учетом B3.4) и B3.7) (среда однородна!), сводятся к соотно-
шениям
D (ш, и) = 8 (ш, х) Е (ш, и), В (ш, х) = ц (ш, х) Н (ш, х). B3.9)
Наличие пространственной дксперсии отражено в том, что е и
ц зависят от х (для изотропной среды они зависят только от
я=]к|).
Алгебраическую форму принимает и ФДТ. В общем случае
многомерного флуктуациониого поля %W(t,T) и сопряженного
по Лагранжу силового поля /Vl (t, г) операторные уравнения
A5.12) переходят для спектральных амплитуд в результате про-
странственного преобразования Фурье в алгебраические урав-
нения
Е<"(», *)=2Л/*(-й». ix)/<*>, х),
* B3.10)
р К х) = 2 Л7*1 (- *». «) S1*' (». н),
а вытекающие из ФДТ выражения для корреляционных матриц
шх-амплитуд g1'1 и /^' имеют вид (см. задачу 6)
(ш, х')> ^ G^ (ш, х) 6 (х—х') =
-x'), B3.11)
и, x) 6 (x-x') =
)}6(x-x'), B3.12)
где Оу4(ш, х)—шх-плотности. Преобразование Фурье этих плот-
ностей по v. дает, конечно, спектральные плотности. Например,
g% (ш, р) = <SW (ш, г) ?<*>• (ш, г')> =
- х) ?'*" (ш> х')> ехр [I («г—х'г1)] *хd'x' =
ш« х) 6 (н—к') ехр [I (чг—хг')] Ле d*x' «=
ш, х) ехр (Ыр) йы (р = г—г'). B3.13)
jj3l ПОЛЕ В ВРЕДЕ С ПРОСТРАНСТВЕИИОЯ1ДИСПЕРСИЕЯ 17?
Применим равенство B3.11) к уравнениям Максвелла B3.8).
Исключив при помощи материальных уравнений B3.9) индукции
D и В, получаем
Для того чтобы воспользоваться формулой B3.11), надо разре-
шить эти уравнения относительно Е и Н. Детерминант уравне-
ний B3.14) равен ?>=#ецД«, где
B3.15)
Пусть среда однородна. Так как ц (<в, х) не может обращаться
в нуль, дисперсионное уравнение ей = 0 распадается на два:
либо е(ш, х) = 0 (продольные волны), либо Д (ш, х) = 0 (попереч-
ные волны). Решение уравнений B3.14) есть
или в компонентах
, аЭ^* "*„ B3Л6)
где
г. v. к»!
Е.е)\ л{Е.т)
— __ГГ е_.1 _Г.?-7_ I B3 17)
Здесь eOYp—полностью антисимметричный единичный тензор
третьего ранга (е1!3 =1), а по дважды входящему в B3.16) ин-
дексу р, конечно, производится суммирование. Заметим, что
в силу B3.15)
___ ¦ - '
Де
Поэтому элементы диагональных квадратов матрицы B3.17) можно
записать и в другом виде:
178 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ [ГЛ. III
Согласно § 16 величины С/4л — — j./ito и »/4я = — \Jto яв-
ляются для полей Е и Н обобщенными силами, так что введен-
ные в B3.16) коэффициенты А—это именно те коэффициенты AJk,
которые входят в формулу B3.11). Применяя эту формулу,
получаем для ож-плотиостей G'Jff (<о, х) е> <?в (ю, к) EJ (<о, к)>
и т. д. следующие выражения:
-^)-gP-K. с.}, B3.186)
4~^) • B3-18В)
Из B3.18в) мы видим, что, в отличие от сторонних токов J,
и 1„, компоненты Е и Н взаимно коррелированы, но только их
ортогональные компоненты, так как е„-^ = 0 при <х=р\ Первые
члены в формулах B3.18а, б), содержащие в знаменателях Д,
определяют корреляцию поперечного (по отношению к х) поля,
т. е. иапряженностей ЕХ = Е—Е„ н НХ = Н—Н,, а вторые
члены—корреляцию продольного поля Е „ = к (хЕ)/ч*, и анало-
гично для Н„. Между собой поперечные и продольные напря-
женности не коррелнрованы (в силу чего G = GX + G|,).
Остановимся в заключение настоящего параграфа на флук-
туациях полного тока в среде, под которым понимается ток, со-
стоящий из всех «видов» электрического тока, за исключением
вакуумного тока смещения. В рамках микроскопической теории
полный ток—это сумма конвекционных токов, обусловленных
движением любых (не подразделяемых иа «виды») микрозарядов,
усредненная по физическн бесконечно малым объемам среды. При
таком усреднении лоренцевых уравнений для микрополей ей h
мы получаем для Е=ё и В—h (волнистая черта—усреднение
по физически бесконечно малому объему) макроскопические урав-
нения следующего вида:
Здесь через jn обозначена объемная плотность полного тока, а
штрих над В поставлен для того, чтобы не смешивать эту
магнитную индукцию, включающую и стороннюю магнитную ни-
дукцию, с индукцией В в ураннениях A4.3), в которых сторон-
ний магнитный ток выделен. Объемные плотности полного за-
ряда н полного тока связаны, конечно, уравнением непрерыв-
ности
^ O. B3.20)
JJ3] ПОЛЕ В СРЕДЕ С ПРОСТРАНСТВЕННОЙ ДИСПЕРСИЕЙ |79
Именно эти полные плотности представляют интерес в ряде задач,
в частности, в задачах о флуктуациях в плазме.
Установим прежде всего связь величии В' н )„ с величинами,
фигурирующими в стандартной симметричной форме уравнений
Максвелла. Запишем уравнения B3.19) н B3.20) для сох-амплитуд:
,ft,B\ B3.21)
B3.22)
Сопоставление вторых уравнений B3.21) и B3.8) показывает,
что В' = В—tj^J,,, в силу чего первое уравнение B3.21) прини-
мает вид
Вычитая отсюда первое уравнение B3.8), получаем
I»5"!—'^(D-E)-^KJ + i[x(B-H)J. B3.23)
Отсюда непосредственно видно, что полный ток слагается из
стороннего электрического тока (первый член), наведенного по-
ляризационного тока (второй член, включающий, конечно, и ток
проводимости) и электрических токов, обусловленных сторонним
магнитным током (третий член) и наведенным намагничением
(последний член, включающий и магнитную проводимость).
Нетрудно записать полный ток в функции только электриче-
ской напряженности Е. Для этого достаточно подставить в B3.23)
вытекающие из B3.8) выражения для сторонних токов Ь и ]а.
Это дает
или в компонентах
Следонательно, сом-плотности полного тока j, и электричесиой
напряженности Е связаны соотношением
х).
Подставке сюда выражение B3.18а) для 0$'н выполнив сумми-
рование по дважды входящим в правую часть индексам у и в,
180 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ [ГЛ. III
находим
-^)-^-к.с]. B3.24)
Для еж-плотности флуктуации полного заряда р. единицы объема
среды, в соответствии с уравнением непрерывности B3.22) и
результатом B3.24), получаем
0^ К х) _ ^ С® (со, к) - »??«! (-L-±) . B3.25)
В флуктуации полного тока B3.24) вносят вклад как попе-
речные, так и продольные волны, ио флуктуации объемной плот-
ности полного заряда B3.25) связаны только с продольными
волнами: в знаменателе выражения для G<p<i) содержится только
е (ш, х), а Л (ш, х) не входит. Мкожитель х1 в B3.25) подчеркивает
большую роль мелкомасштабных флуктуации. Из-за того, что
в однородной среде е—функция только х = |х|, преобразование
Фурье B3.13), дающее спектральную плотность флуктуации, при-
нимает для заряда р„ вид
(P = |r-r'|)- B3.26)
В задаче 7 формулы B3.24) и B3.25) применены к простой
модели среды, обладающей пространственной дисперсией н пред-
ставляющей интерес для описания флуктуации в ионосферной
плазме.
Сделаем несколько дополнительных замечаний в заключение
этой главы.
В § 20 мы отметили, что теория случайных полей, обуслов-
ленных равновесными тепловыми флуктуациями, относится к ста-
тистической схеме 1), т. е. имеет дело с задачами, в которых
известна статистика случайных источников поля. Тем не менее
мы выделили тепловые поля в отдельную главу, указав не только
на их важность, ио и иа специфичность. Последняя заключается
именно в том, что в данном круге задач статистика источников
не задается извне, а определяется самими динамическими урав-
нениями задачи. Говоря точнее, функции корреляции сторонних
(ланжевековских) сил определены антиэрмитовыми частями тех
детерминированных линейных операторов, через которые записы-
ваются динамические уравнения. В этом и состоит флуктуационно-
диссипацнонная теорема (§ 15).
J23J ПОЛЕ В СРЕДЕ С ПРОСТРАНСТВЕННОЙ ДИСПЕРСИЕЙ ]8|
Если же речь идет о существенно неравновесных тепловых
флуктуацнях нлн вообще о полях нетеплового происхождения,
то статистика источников обычно не определена видом са-
мих уравнений, а должна быть задана—либо формально, либо
на основе статистического исследования микроскопических мо-
делей.
Другое замечание касается универсальности различных форм
ФДТ. Мы рассматривали в этой главе электромагнитные тепловые
поля, хотя опирались на ФДТ, которая применима к равновесным
тепловым флуктуациям любой физической природы (§ 15). Для
электромагнитных полей были получены другие формы ФДТ —
кирхгофовская (§§ 17, 18), волноводпая (§ 19), равновесная
(§ 21),—более прозрачные физически, более «экономные» по про-
цедуре решения конкретных задач и обладающие более широкими
возможностями в отношении охвата задач, поддающихся решению.
Естественно возникает вопрос о том, являются ли эти формы ФДТ
столь же физически универсальными, как и исходная «канони-
ческая» ее форма A5.14).
Все, что нам понадобилось учесть в электродинамике для
получения указанных форм ФДТ, сводится к электродинамиче-
ской теореме взаимности A7.2) или B2.1) и комплексной лемме
Лоренца B1.2). Можно поэтому ожидать, что для любых равно-
весных (и квазиравновесных) флуктуационных полей, для кото-
рых справедливы теорема взаимности и аналог леммы Лореица,
будут верны и перечисленные формы ФДТ. Анализ этого вопроса
показывает, что дело обстоит именно так [15], и отсюда выте-
кает ряд интересных следствий.
Например, кирхгофовская форма ФДТ и, в частности, фор-
мула A8.15) полностью справедливы для акустических волн.
Тепловые потери обусловлены здесь вязкостью и теплопровод-
ностью среды. Представим себе, что тело, обладающее такими
потерями, погружено в «прозрачную» жидкость, т. е. жидкость
с малым поглощением продольных волн. Послав на тело плоскую
волну частоты со (скажем, в звуковом или ультразвуковом диа-
пазоне), мы можем найти эффективный поперечник поглощения
тела о,фф (прн данной ориентации тела). Формула A8.15), в ко-
торой можно, конечно, положить в = кТ, определяет тогда поток
энергии продольных волн частоты со, излучаемых телом в телес-
ный угол do, в направлении, противоположном направлению
прихода вспомогательной плоской волны. Хотя физический ме-
ханизм тепловых флуктуации в теле (флуктуации плотности,
температуры, скоростей макрочастиц) совершенно иной, чем
в электродинамике, гвызвучи ванне» нагретого тела в окружающую
«прозрачную» среду происходит по такому же закону, как и
«высвечивание» на электромагнитных волнах, а нменио по закону
Кирхгофа.
182 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ [ГЛ. Ш
Задач ¦
I. С учетом реакции излучения уравнение движения упруго связанного
электрона имеет при малых его скоростях | г | «^ с вид
m"r-^H maJr=f(O-=eE(O, A)
где е н ш—заряд и масса электрона, с—скорость света в вакууме, а0—соб-
ственная частота осциллятора. Пусть Е@—напряженность электрического
поля равновесного излучения. Применив ФДТ к уравнению A), иайти спек-
тральную плотность энергии этого излучения (по положительным частотами),
т. е. величину (электрон находится в вакууме)
Решение. Уравнение движения (I) в спектральной форме есть
г (ш) = а (ш) !(ш),
где
B)
Спектральная плотность компоненты Ex(t) — fx(l)le флуктуациоиного поля
по 0) > 0 равна
^ C)
гае <|k(о>)|'>—спектральная плотность силы fx(t) по ш от —«в до +»•
Согласно дискретной ФДТ < | fx (o>) |»> выражается через обобщенную воспри-
имчивость а(ш) следующим образом:
(это формула A5.96) в частном случае едниственной переменной). Из B) — D)
следует, что
й1'1
Заметим, что R«(l/a(o>)} ие играет роли, и поэтому электрон мог бы быть
и свободным (Qe=0).
Для того чтобы получить спектральную плотность энергии электромагнит-
ного поли, достаточно учесть, что равновесное излучение в неограниченном
пространств изотропно, в силу чего
<|?лг11>=<|?„|1> = <|?«1>>.
и что его магнитная энергии равна электрической:
Поэтому
т. е. мы получили формулу Планка.
ЗАДАЧИ (83
2. Формулы A6.4) для корреляционных функций сторонних токов можно
получить и более физическим путей, чем использованный в $ 16, опираясь на
классический закон Кирхгофа и принцип детальною равновесия. Последний
требует, чтобы для двух одинаково нагретых тел 1 к 2 мощность Qii, погло-
каеиая телом I на излучения тела 2, была иа каждой частоте <а равна мощ-
ности Си, поглощаемой телом 2 из излучения тела 1. Пользуясь этим, вы-
вести формулы A6.4) из рассмотрения обмена энергией между телом н пластиной
(ряс. 20). разнесенными на столь большое расстояние R, что их размеры го-
раздо меньше радиуса j/ХЯ первой зоны Френеля (т. е. они находятся во
фраунгоферовой зоне друг дру-
га). Вместе с тем размеры
пластины настолько больше дли-
ны волны X, что излучение ,<<slsl3 #¦
пластины можно вычислять по лчх>жччм
клессическону закону Кирх-
гофа.
Решение. Подсчитаем
прн указанных условиях мощ- "ис- 20-
вости <2Т и Qn, поглощаемые
телом и пластиной иа частоте ш.
Пусть А —коэффициент поглощения иластяны и S—ее площадь (ЛЯ>?>Х').
Поглощаемая пластиной мощность есть
(р *у /|\
I Vl№ \')
где ifг—^-компонента аектора ПоЛнтнвга теплового излучения тела. Для af,
на одной поляризации мы имеем выражение A8.13), так что прп учете обеих
нееависямых поляризаций &'г—-^-<\Е1\1>. Подставив сюда Ег ив A8.12) я
записывая скалярные произведения аекторов в компонентах, получаем в соот-
ветствии с A), что
<?- -^ \ \ (?*« « Я« С) </«х (г) ih <О> +
-//oo(r) ?Je (r1) <jma (r) /;p (r')>} d>r d>r'. B)
Теперь подсчитаем QT—мощность, поглощаемую телом из излучения пла-
стины. Так как ее размеры велики по сравнению с X, для интенсивности из-
лучения пластины в телеснмЛ угол do, ось которого направлена иа тело,
справедлива формула A8.16).
Сопоставим выражение A8.16) с мощностью, нэлучаемой в тот же телесный
угол do единичным точечным источником (электрическим диполем в точке М
с моментом p = l/iu, лежащим в плоскости пластины):
Мы видим, что пластана излучает в
раз больше точечного источника. Следовательно, во столько же раз больше
¦ мощность Qt no сравнению с мощностью Qo, поглощаемой телом из
184 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ !ГЛ. III
излучения точечного источника:
Потери же <20 дифракционного поля, создаваемого электрическим диполем,
равны
-ejj + йю(г) //о'р(г) (uo|J-|i
С г)
чт to?
+ Hta (г) /Уов(г) (ца(>—ЦЭ») \ &'• C)
Выражения B) и C) должны быть раены друг другу. Почленное сравне-
ние подынтегральных выражений дает формулы A6.4). Однозначность резуль-
тата следует из того, что равенство интегралов должно иметь иесто при
любой форме, величине и расположении тела и пластины (конечно, не нару-
шающих условий XJ?^>2^>XS).
Следует заметить, что при данном выводе формул A6.4) надо понимать
под в (о>, Т) только ту часть средней энергии осциллятора, которая зависит
от температуры. Энергия нулевых колебаний 1ш/'2 не должна учитываться,
поскольку рассматривается обмен энергией посредством излучения (§ 17).
3. В волноводе между двумя черными излучателями с температурой Го
находится тело с температурой Т Ф То. Найти поток энергии флуктуационного
поля па я-й собственной волне волновода и показать, что при любых Т и Го
нулевые колебания из этого потока выпадают.
Решение. Поток энергии, скажем, справа от тела равен собственному
излучению тела (PJn) плюс отраженное телом излучение правого излучателя
[ -g-i- V" Rmn ) плюс прошедшее излучение левого излучателя / -~ V' Din }
\ /и / \ m J
и иинус встречный поток излучения справа (вд/2п):
в.
Согласно A9.3)
Но нулевая энергия ta/2 из разности В—в0 выпадает, т. е. встречные по-
токи энергии нулевых колебаний взаимно уничтожаются при любых Т и Го-
Имен но потому, что эти колебания никогда на участвуют в переносе энергии,
член ?ш/2 в В (ш, Т) можно отбрасывать во всех случаях, когда речь идет
о (среднем) потоке энергии.
ЗАДАЧИ 18R
4. Найти мощность, излучаемую в идеальный волновод на волне с по-
стоянной распространения к излучателем, состоящим из поперечной идеально
отражающей перегородки и поперечной же полупрозрачной пластинки, отстоя-
щей от перегородки на расстояние / (рис. 21). Пластяика предполагается
тонкой, т. е. ее толщина мала по сравнению с длиной
волны в ее материале, так что интерференции внутри
пластинки можно не учитывать и характеризовать плас-
тинку вещественными амплитудными коэффициентами от-
ражения (г) и пропускания(d).Прмэтом г%+<Р+а—1,
где а—энергетический коэффициент поглощения плас-
тинки. „ .,
9 Рис. 21.
Решение. Излучаемая мощность Р = ^— А, где
А — 1— Si (излучатель в целом непрозрачен), Я— энергетический коэффи-
циент отражения шлучателя. Если справа падает волна «-<*«, то в результа-
те первого отражения от пластинки и последующих многократных повторных
отражений прошедшей через нес волны между пластинкой и идеально отра-
жающей перегородкой, амплитуда отраженной излучателем волны будет
d"
Следовательно,
г+
d«
»—2rcoa2Af
Or / поглощение зависит осцилляторио с периодом, равным половине
длины волиы Л=2л/А, н с иаксимунамн на ревонансных длинах резонатора,
образуемого перегородкой н пластинкой. При уменьшении прозрачности
пластинки (d—'О) получаем Л=а. Если же коэффициент отражения от пла-
стинки г*—И (при этом с необходимостью d—>0, а—>-0), то А—"О.
Б. Формула Найквнста для спектральной плотности тепловой э. д. с. е(!)
в двуполюснике с импедансом Z (ш) имеет вид
<1 ё"(ш)|»> = — в (в), 7") ReZ (о>).
Для хороших проводников часто заменяют ReZ sa омическое сопротивление R.
При каких условиях эта замена законна? Ведь при переходе от проводника
к идеальному диэлектрику (проводимость а—>Он соответственно R—,. да)
получается неограниченное нарастание э. д. с. Как уже было отмечено в ч. 1,
§ 54, этот кажущийся парадокс возникает при забвении того, что замена ReZ
на R законна лишь для столь хороших проводников, внутри которых можно
пренебречь током смещения по сравнению с током проводимости. Ясно, что
прн а—*0 зго условие рано или поздно нарушается. Вывести формулу для
<|ё(о>)|*> в тонкой проводе с учетом тока смещения.
Решение. Если прн выводе формулы B0.9) для <| / (s) |*>, а значит,
и ири выводе выражения B0.13) для <|#(s)|'> не пренебрегать током сме-
щения в проводе, т. е. пользоваться общим выражением B0.5) для корреляции
компонент теплового поля, то результатом снова будут формулы B0.9) и
B0.13), но, в отличие от B0.10), теперь
dQ0^-lbJl <* .
40 2о 1 +(ея>/4ло)»
Следовательно, для квазистационарной (/„ ие зависит от s) равновесной
F=const) цепи энергетическое сопротивление, определенное равенством,
186
ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
(ГЛ. Ш
аналогичным B0.15), равно
р » с
Смысл этого выражения лучше всего пояснить переходом к предельному
случаю слабого скин-эффекта в проводе из однородного материала (е' н с
постоянны). Тогда /0=/о/2 и для участка провода длины /
формула A) иринимает вид
п Я
где R = l/aE—омическое сопротивление, а С = е'2/4я(—внут-
ренняя емкость данного участка провода. Таким обрвэом, ft,
представляет собой в этом случае активное сопротивление
Рис. 22. ЛС-ячейкн (рис. 22) и прк tf-^>« получаем *, = (?. Замена
А, на А справедлива лишь при условии (КСш)* <g 1.
в. Пользуясь формулами A5.11а, б), получить корреляционные функции
вж-амплитуд полей |(г, г) н /(Л г) в неограничен ной однородной среде, т. е.
амплитуд в пространственных разложениях Фурье
ш, г)
m, x)exp(t*r)d»x, /(ш,г)
f (и, н) ехр (»мг)
Решение. Проведем сначала расчет функции корреляции для ож-ам-
плитуды f(t, r):
С учетом A5.116) имеем
</(«, к) Г («а. *')> =
(«». г) /• (и. г')> ехр (-
+ 00
= - '^ Г Я (Я"" - А'1) б(г-г') ехр (-тг -I M)*r*Y. (I)
Представим д«льта-фуикцвю в виде интеграла Фурье:
7
1 7
— о»
Поскольку ve'pr=fpe*r» действие линейного оператора A~l(v) на ^ даст
ЗАДАЧИ 187
где A~l(lp)—функция р, получающаяся при замене v—>-i'p в операторе
Я-1^). Аналогично1),
— »
тах что A) приникает вид
+¦ эо
X JJ exp{i[(P—к) г—(р—х
Интегралы по г и г' дают BлI6 (р—х)8 (р—я'), после чего интегриро-
вание по р приводит к искомому результату:
-х')- B)
Можно получить функцию корреляции для ? (ш. ж) таким же путем (поль-
зуясь формулой A5.11а)), а можно сделать это и иначе—исходя на того,
что g(o), х) = Л(—ioi, i'x)/(a>, ж). Полагая х' =х в множителе прн
в (к—к'), имеем
х) ?*
Уравнения A5.1) (если явным образом записать зависимость операторов
А и Д-1 от — to) принимают для шх-амплитуд вид
5(ш, и) = А(—/и, (х)^(ш, х), /(ш, >с) = Д-1( — fra, Г>с)?(ш, х).
Первьш из них мы только что воспользовались при выводе C), а из второго
видно, что уравнение
А-Ц — to, (x)--O D)
]) В связи с этой н последующнмн формулами необходимо сделать одно
разъяснение. Знак комплексного сопряжения » понимается адесь и далее в
обычном смысле, т. е. как замена (на —/во всех аргументах вещественной
функции от —/ш, |'х, ip и т. д. В книге [6] использовано другое (и менее
удачное) обозначение: знак » означает там комплексное сопряжение только
в спектральной амплитуде, т. е. в вещественной функции от lea я г, и сво-
дится, таким образом, к замене —ш—> +|'ш. Поэтому в [6] выражение для
Д'(у')в(г—г') содержит под интегралом функцию А~х'(—ip). Звеадочка
означает изменение знака в ш, а в аргументе —/р анвк минус записан явно.
Обычное обозначение, принятое н данной книге, конечно, проще.
188 ТНПЛОНОБ ЭЛЕКТРОМАГНИТНОЕ ПОЛН [ГЛ. П1
представляет собой дисперсионное уравнение вадачн. Из C) ясно, что любой
интеграл по н и х", содержащий <5 (ш, «)?*(ш, х')>, сразу же сводится к
интегралу только по н (из-за наличия б(х — ж')), а последний часто может
быть взят вычетами в полюсах функции А (—Но, ix), т. е. в нулях функции
A~1{ia, ix), или, иначе говори, при значениях х, являющихся корнями дис-
персионного уравнения D).
Нетрудно воспроизвести расчеты, проделанные при выводе формул B)
и C), для случая многомерных однородных полей ?'¦" (t, г) и /<Л {t, г), исполь-
зуя при этом формулы A5.14а, б). Это приводит к корреляционным матрицам
B3.11) и B3.12) для вох-амплнгуд.
7. Для продольных поли, длинных по сравнению с радиусом нелокаль-
ности a(ka<^\), не слишком разреженная плазма, состоящая нз электронов,
ионов разного сорта и нейтральных атомов и молекул, может быть хорошо
описана в так называемом квазигидродинамическом приближении. Уравнения
гидродинамики надо писать при этом для всех видов частиц, но мы ограни-
чимся простейшей моделью одножидкостной (электронной) плазмы, т. е. бу-
дем считать ноны неподвижным1).
Тогда линеаризованное уравнение движения электронной жидкости (газа)
запишется в виде
m-^- + mvv^—-у- V Р—еЕ, A)
где m—масса электрона, е—абсолютная величина его заряда, N-^средняя
Концентрация электронов, р — переменная часть давления:
(у — отношение Пуассона, 9 — кТ—энергетическая температура электронного
газа, Л'—переменная часть концентрации). В уравнение (I) введено также
«трение»—через эффективное число соударений в единицу времени (v). Плот-
ность электронного тока (в данной модели это и полный ток) в линейиом при-
ближении равна J=—Nev, а переменная часть плотности заряда есть рф —
= —Ne (средние плотности электронного и ионного зарядов скомпенсированы,
т. е. плазма квазииейтральна). Поэтому линеаризованное уравнение непре-
рывности будет
-^-+tfdivv=0. C)
Найти для описанной моделн плазмы спектральную плотность флуктуа-
ции электронной концентрации.
Решение. Согласно B3.25) для нахождения qx-плотности флуктуа-
цнй рф достаточно знать продольную диэлектрическую проницаемость е (ш, к).
Для шх-амплитуд (N, р, v, ?~ехр[ — i(mt — кг)]), исключая из A) — C)
все величины, кроме v=—MNe, получаем следующее уравнение для полного
тока ] (в компонентах):
где ш,—плазменная (электронная) частота:
1) О более общих случаях и, в частности, о двужидкостной модели (эле-
ктроны и один сорт ионов), причем модели неравновесной (температуры эле-
ктронов и ионов различны), см. в [14, 16].
ЗАДАЧИ 189
Удобно ввести обозначения
Х = а?/ш', Z=v/«,, a=Yyd,
где
'=-=;Vиг
— так называемый дебаевский радиус (или радиус экранирования электричес-
кого поля, см. [16]). В этих обозначения* уравнение дли ] принимает вид
{\+izYY)ja-
откуда
toJf
+ а Ух-к
Электрическая индукция Da—e.a$E^ связана с полным током ] соотно-
шением D = E — 4nJ/ia]), так что
Выражение в фигурных скобках—это диэлектрическая проницаемость
еар (ш, х). Она легко преобразуется к вкду
Л
1 + JZ /Х-х«а1
откуда следуют выражении для поперечно* и продольпой проницаемостей:
Таким обрааон, в рассматриваемой модели Et не обладает пространствен-
ной дисперсией (не зависит от х). Пространственвав же дисперсия g/=e воз-
никает нз-за члена с ур в A), т. е. обусловлена упругостью электронного
газа.
Согласно выражению D) для е имеем
I I _ 2iZX'>'
г) Это ясно нз первого уравнения B3.21), если записать его в виде
i[xB] = — i*0D.
190 ТЕПЛОВОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ [ГЛ. III
Подставив это в формулы B3.25) н B3.26), получаем, что шх-плотность флук-
туации электронной концентрации N= — рф/е есть
а ее спектральная плотность равна
x3sinxp
f x3
о
Интеграл в F) легко вычисляется. Из-аа четности интегранда лох можно
взять половину значения интеграла в пределах ± оо. Записав далее sin хр
в виде (е"*" — e~iKp)l2i, изменим знак х в интеграле с е~'*р. Это просто
удваивает первый интеграл (с е'хр) и дает
J (I-^-x"a'X
Замыкание пути интегрирования в верхней полуплоскости комплексного у.
сводит интеграл к вычетам в полюсах к—k и х= —к*, где * — корень дис-
персионного уравнения к (и, х)- 0, лежащий в первом квадранте плоскости х:
G)
Окончательный результат:
Nmv «~*"р
Х , ... 1
Как это видно уже из F), g( > (и, 0)-^оо. Эта особенность прн р = 0,
вполне очевидная в (8), обусловлена недостаточно быстрым убыванием 1/е— 1/е*
к нулю при возрастании к. Однако само гидродинамическое описание спра-
ведливо лишь для ха <^ I, т. е. для пространственных гармоинк флуктуации .V
с длинами волн 2д/ч = Л:>а. Поэтому брать значении р^а нет смысла.
В этой области х фазоваи скорость продольных волн становнтси одного по-
рядка с тепловой скоростью электронов и, как показывает кинетическое рас-
смотрение, происходит сильное затухание продольных волн. Гидродинами-
ческая модель не учитывает этого затухания, обусловленного тепловым
движением зарядов ([14], § 2). Отметим в связи со сказанным, что, напри-
мер, в слое F ионосферы, если принять Л^ = Б-1О* см, Т — 300 К и Y = 31).
т, = 4-10' Гц, а =а 0,3 см.
В диапазоне частот и > а>е(Х < 1) и при 2^ I — X кз G) имеем при-
ближенно
1-Х
X
) Основанием для такого выбора у является кинетическое рассмотрение
([«*]. § 2).
ЗАДАЧИ 191
т. е. *'^>*\ и основную роль в (8) играет член с sin«?p. Спектральная
нлотность (8) представляет собой в функции от р медленно затухающее коле-
бавие. Напротив, прн <л < <ле(Х > I) и Z^X—l значения f и *• меняются
нестамя:
так что экспонента затухает гораздо быстрее, чем аа период колебания 2л/*'.
В окрестности ше, т. е. при X а 1 и | \—X\^Z, имеем
4/F
Заметим в заключение, что, ограничившись в рамках гидродинамической
модели опнсаниси состояния электронного гааа переменными v, p И R, мы
исключили тем самым из рассмотрения флуктуации его температуры Т&=Т—Т.
Глава IV
ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН
§ 24. Метод малых возмущений
В этой и последующих главах мы займемся флуктуациями
волн, распространяющихся в случайно-неоднородных средах, т.е.
по классификации § 8 задачами типа 2).
Случайные неоднородности реальных сред влияют на характе-
ристики волн, распространяющихся в этих средах, и возникающие
при этом явления чрезвычайно разнообразны. Мерцание звезд и
флуктуации радиоизлучения от внеземных, источников, замирания
(федниги) радиоволн и релеевское рассеяние света, ушнренне
лазерных пучков в тропосфере и рассеяние звука в море—это
лишь немногие примеры наблюдаемых эффектов. Исследованием
такого рода эффектов занимается статистическая теория распро-
странения и рассеяния воли.
Задачи о распространении волн в средах с флуктуирующими
параметрами решаются, как правило, приближенными методами.
Дело в том, что соответствующие дифференциальные уравнения
содержат в коэффициентах случайные функции точки (а возможно,
и времени), описывающие неоднородную среду. Точное решение
такой параметрической задачи означало бы, что мы в состоянии
написать, например, функцию Грина для любых реализаций
входящих в уравнения случайных функций, что практически
никогда не осуществимо1). Это и вынуждает обращаться к при-
ближенным методам. Характер приближения зависит, разумеется,
от постановки задачи—слабо или сильно флуктуируют параметры
среды, каково соотношение между длиной волны и размерами
неоднородностей, какова геометрия задачи (длина трассы, ширина
волнового пучка) и т. д. При всем разнообразии конкретных
') Если не говорить о тех весьма частных случаях, когда среда описыва-
ется специального вида детерминированными функциями, зависящими от ко-
нечного числа случайных параметров.
5 24] МЕТОД МАЛЫХ ВОЗМУЩЕНИИ [93
условий значительная часть задач типа 2) может быть решена
при помощи небольшого числа разработанных к настоящему
времени приближенных методов.
Если относительные флуктуации параметров среды достаточно
слабы, а рассеянное поле мало по сравнению с нолем первичной
волны, то применяется метод малых возмущений. Анализ полей,
рассчитанных в первом порядке теории возмущений, составляет
содержание теории однократного рассеяния, которой н посвя-
щена данная глава.
При нарушении условий применимости теории однократного
рассеяния (флуктуации в среде недостаточно слабы, рассеянное
поле не мало) необходимо принимать во внимание двух-, трех-
и т. д. кратное рассеяние поля, т. е. нужно строить теорию с
учетом многократного рассеяния волн. В случае слабых, но
крупных (по сравнению с длиной волны) неоднородностей мно-
гократно рассеянные волны лишь незначительно уклоняются от
направления распространения первичной волны. В таких условиях
многократное рассеяние эффективно описывается методом геомет-
рической оптики (МГО) и примыкающими к нему более общими ко-
ротко-волновыми асимптотическими методами теории дифракции —
методом плавных возмущений (МПВ) и методом параболического
уравнения (МПУ). Последние три метода мы рассмотрим в
гл. V—VII.
Другая возможность учета многократного рассеяния волн
основана на приближенном суммировании рядов теории возму-
щений (в основном при помощи методов, развитых первоначально
в квантовой электродинамике). При таком подходе удается, в
частности, рассмотреть не только слабые, но и сильные флуктуации
среды. Однако при этом необходимо, чтобы неоднородности были
мелкомасштабными. Элементы теории многократного рассеяния
изложены в гл. VIII.
Начнем с простейшей постановки задачи: волновое поле
и (t, г) будем считать скалярным и монохроматическим (и (t, г) =
— и (г) ?"'<"'), а неоднородности среды—не меняющимися во вре-
мени и покоящимися1). Хотя при скалярной постановке задачи
не охвачена поляризация, она достаточна для ряда общеволно-
вых явлений, таких, как интерференция и дифракция. К поля-
ризационным эффектам в рассеянии электромагнитных волн мы
обратимся в § 30.
При указанных выше условиях распространение волны в
неоднородной среде описывается уравнением Гельмгольца
= О, B4.1)
*) В этой главе мы будем в основном придерживаться монографии [1J.
Библиография по вопросам теории однократного рассеяния содержится также
в обзоре [2|.
7 С. М. Рытое и др. «. II
194 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. IV
где й„ = ш/с—волновое число в невозмущенной среде или в слу-
чае электрического ноля —в вакууме. Функцию в (г), описываю-
щую неоднородность среды, мы будем называть (диэлектрической)
проницаемостью, имея в виду в основном электромагнитное поле.
Для случайно-неоднородной среды проницаемость в (г) можно
представить в виде
е(г)=8(г)+8(г), B4.2)
где е—среднее (но ансамблю реализаций среды) значение в,
а е—флуктуации проницаемости. Уравнение Гельмгольца при-
нимает при этом вид1)
Аи (г) -I-й?[в(г)+ е(г)] и (г) -0. B4.3)
Общих методов решения даже такого простого волнового
уравнения не существует. Наиболее распространенным из при-
ближенных методов является метод возмущений: флуктуации е
считаются достаточно слабыми, а волновое поле и (г) ищется в
виде ряда по степеням е(г), или, что то же—но степеням ае<^е.
Чтобы построить такой ряд, удобно перейти от дифференциаль-
ного уравнения B4.3) к эквивалентному интегральному
уравнению.
Пусть и» (г)—ноле первичной волны, удовлетворяющее не-
возмущениому уравнению Гельмгольца, т. е. уравнению B4.3)
при е — 0:
Дйо(г)+Л-?(г)ио(г)-О. B4.4)
Обозначим через О (г, г') невозмущенную функцию Грина, ко-
торая удовлетворяет уравнению для точечного источника
AG(r, г') !-*;e"(r)G(r, г') = 6(г, г'). B4.5)
Разумеется, первичное поле ы„ и функция Грина G удовлетво-
ряют необходимым граничным условиям. Решение неоднородно-
го уравнения
&u + k$u = F (г)
выражается через функцию Грина следующим образом:
и(г) = н„(гL- $G(r, r')F(r')d3r'. B4.6)
•) Рассеяние звукопых волк в турбулентной среде описывается более
сложным скалярным уравнением, чем B4,3), поскольку распространение со-
провождается нелинейным взаимодействием звуковых волн н гидродинамических
турбулентных движений. Упрощенное описание достигается путем линеариза-
ции исходных нелинейных уравнений гидродинамики но отношению к слабым
звукоаым возмущениям. Связанные с этим особенности рассеяния звука рас-
смотрены в [1J.
§ 24] МЕТОД МАЛЫХ ВОЗМУ1ЦЕНИИ (§5
Записав исходное уравнение B4.3) в форме
Ди+*?«-= — *fcu = F(r) B4.7)
и используя B4.6), получаем следующее интегральное уравнение
для волнового поля:
и(г)-«0(г)-Г^С(г, r>(r')u(r')dV, B4.8)
где интегриронамие распространяется, очевидно, на область V,
занятую неоднородностями е(г). Уравнение B4.8) эквивалентно
исходному дифференциальному уравнению B4.3), но учитывает
(через функцию G) и все граничные условия задачи.
Ряд теории возмущений строится путем итерирования интег-
рального уравнения B4.8). Чтобы получить первую итерацию,
запишем значение поля в точке г —г':
и (г') - «, (г')-kl \ G (г', г") ё (г") и (г") d'r",
и подставим это выражение в правую часть B4.8). Это дает
и (г) - и, (г) -kl $ G (г, г> (г') u0 (r') dV +
+ ki $ С (г, г')ё (г1) dV J С (г', г") ё (г") и (г") dV\ B4.9)
Записав зна^^еиие поля к (г) в точке г = г" и подставив его в
правую часть B4.9), получим вторую итерацию. Повторяя такую
операцию, мы и получим бесконечный ряд теории возмущений:
+ kt Ц G (г, г') G (г', г")в (г') Ё (г") и„
", г'")в(г')ё(г")8(г'")х
»r"d«r'"-f... B4.10)
В математике этот ряд называется рядом Неймана для интеграль-
ного уравнения B4.8), а в физике—борцовским разложением1).
Первый член борновского ряда B4.10) — первичное поле и„(г).
Второе слагаемое,
«х (г) = -к\ У G (г, г') е (г') «0 (f')dV, B4.11)
') М. Бори впервые применил теорию визмущеинй в задаче о рас-
сеянии в квантовой механике. Правда, задолго до М. Борма метод возму-
щений в сходной форме был примечен Релесм прн рассмотрении рассеяния
света на прозрачных телах. В оптике н теперь говорят о релеевском, а ие о
борновском рассеянии света.
196 ТЕОРИЯ ОДНОКРАТНОГО РЛССЕЯНИЯ ВОЛН [ГЛ. IV
описывает однократно рассеянное поле. Оно порождено непосред-
ственно первичным полем «0 (г) и линейно относительно возму-
щений е(г). Третье слагаемое в B4.10) можно представить в
форме, аналогичной B4.11):
«. (г) = -k% \ G (г, г') I (г') их (г') d?r'. B4.12)
Это—двукратно рассеянное поле, порожденное уже не первичным,
а однократно рассеянным полем. Двукратно рассеянное поле в
свою очередь возбуждает трехкратно рассеянные волны us и т. д.
Таким образом, ряд теории возмущений B4.10) представляет со-
бой разложение рассеянного поля i^ — u—u,, no кратности рас-
сеяния:
uts=u — ul> = u1 + u2 + u1+... B4.I3)
Из самого способа построения этого ряда видно, что л-й его
член, описывающий л-кратное рассеяние, содержит под знаком
л-кратного интеграла произведение е(г1)...е(г„). Отсюда следует,
что для вычисления даже среднего значения поля инадо знать
для е моменты <s(rj).. .е(гП)> любого порядка. При произволь-
ной статистике е нахождение таких моментов само по себе пред-
ставляет сложную задачу, но если даже она и разрешима (как,
например, в случае нормального распределении), то остается
еще открытым вопрос о методах суммирования усредненных рядов
теории возмущений. В общей постановке этот вопрос будет ос-
вещен в гл. VIII. Здесь же, как сказано, мы ограничимся более
простой задачей нахождения статистических характеристик поля
в приближении однократного рассеяния (так называемое первое
борцовское или, чаще, просто борновское приближение).
В этом приближении флуктуации е предполагаются настоль-
ко малыми, что в разложении B4.13) можно ограничиться первым
членом их. С выражениями такого типа мы уже встречались в§ 12
при рассмотрении возбуждения полей случайными источниками.
В данном случае в качестве заданных источников?^) выступает
правая часть уравнения B4.7) с и0 вместо и: <7(r) — —AJe(r) цо(г).
Таким образом, в приближении однократного рассеяния задача
о распространении волн в случайно-неоднородных средах (задача
типа 2)) сводится к задаче типа 1)—возбуждению полей задан-
ными случайными источниками..
Согласно B4.11) рассеянное поле и3аих является линейным
функционалом от флуктуации е. Поэтому и все моменты поля и,
линейно же выражаются через моменты е того же порядка.
В частности, у однократно рассеянного поля а, среднее значение
равно нулю, поскольку <е(г)> = 0, а корреляционная функция
tpn (ri> ra)= <ui (ri) "i (га)> линейно выражается через функцию
J 25] СРЕДНЯЯ ИНТЕНСИВНОСТЬ ]9?
корреляции неоднородиостей ^„(г', г"):
1-х. О = % И ° <Г1- т">С* <г" г") «• С') "°(г"> х
r")d'r'd*r'. B4.14)
Выражение B4.14) и аналогичные квадратуры для высших
моментов рассеянного поля и1 в принципе дают полное статисти-
ческое решение задачи в рассматриваемом борновском прибли-
жении. Однако этот математический результат еще нуждается
в физическом истолковании.
§ 25. Средняя интенсивность рассеянного поля
Для того чтобы лучше уяснить основные закономерности рас-
сеяния, сделаем ряд допущений, которые упрощают анализ, но
вместе с тем сохраняют общность, достаточную для многих при-
ложений теории. Допущения сводятся к следующему.
а) Среда в среднем однородна, т. е. с,— const.
б) Первичное поле и„(г) представлнет собой ненаправленную
сферическую волну с центром в точке г0:
Цо (Г) ^ ^| eik i '-'- i, B5.1)
где ft—волновое- число в однородной среде: k — koy e =— j/ e .
в) Функция Грина G(r, r') описывает ноле точечного источника
в неограниченной однородной среде:
-¦ B5.2)
г) Поле флуктуации е статистически квазиоднородно, т. е.
корреляционная функция е имеет вид (§ 5)
ц,е(г\ г") s<i (r') i(r")> =\|:«,(p, R), B5.3)
где р —г'—г", R —(r'-fr")/2 и зависимость фе (р, R) от R «мед-
ленна», т. е. масштаб Le изменения tye по аргументу R сущест-
венно больше, чем характерный масштаб 1Е (радиус корреля-
ции е) по разностному аргументу р. Спектральная плотность
таких флуктуации, определяемая выражением
з, R)exp(— ixp)d3p, B5.4)
— медленная функция R, т. е. она мало меняется на рассто-
яниях порядка I, .
Д) Наконец, будем считать, что случайные неоднородности
заполняют ограниченный объем К и в этом объеме содержится
|9Я ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ИОЛН [ГЛ. IV
много неодиородностей. Последнее условие можно записать в виде
неравенства
V~/,»>/!, или L ~ V1'1 > U , B5.5)
где L — поперечный размер области, занятой неоднородностямн.
Предположение о конечности рассеивающего объема необходимо
для обеспечения малости однократно рассеянного ноля, тогда
как неравенство B5.5) принято лишь дли упрощения расчете».
Конечность рассеивающего объема удобно учитывать при по-
мощи обрезающей функции
( 1 внутри V,
Введя ее. иод знак интеграла в B4.11), можно распространить
интегрирование на все пространство. Для первичной сферической
волны B5.1) и функции Грина свободного пространства B5.2)
однократно рассеянное поле B4.11) запишется в виде
пг^7Го1IлМг>)Е"(г':1^'' B5-7)
Б дальнейшем мы обратимся к некоторым более общим по-
становкам задачи (учет временных изменении е, расчет поляри-
зационных характеристик электромагнитного поля и др.). Вместе
с тем мы будем иногда вводить частные допущения (плоская
первичная полна, статистически однородные флуктуации и т. д.).
Здесь же, исходя из B5.7), мы получим выражения для функции
корреляции я, в частности, для средней интенсивности рассеян-
ного ноля.
Согласно B5.7) пространственная функция корреляции поля
равна
ФЖ. г.) - -- "°^jj \ ^ М (г') М (г") тЬ (р, R)X
- я,
X ехР('*<1Г|--г'| -|Г2 —Г"| —|г'—Г„| —|Г*—Г„!)} ^:,г'^,г» B5 8)
От выражения B4.14) эта формула отличается только тем, что
в ней конкретизированы вид первичного поля и вид функции
Грина.
Перейдем в B5.8) к переменным интегрирования р — г' — г",
R = (r' + r")/2, откуда г' — R-f p/2, r" = R —р/2, причем d'r'd'r" =
=rf9p d'R.
; 26] СРЕДНЯЯ ИНТЕНСИВНОСТЬ |99
Формула B5.8) принимает вид
B5.9)
где
(| g? )
/| о о \ B5.10)
?,=fc(|r'-r,|-|i"-r,|)-*(|R-r,+-f— R-r,—§¦).
Все последующие упрощения формулы B5.9) основаны на том,
что функция корреляции неоднородной среды 1ре (p, R) стано-
вится при р^> U очень малой. Мы можем поэтому воспользоваться
разложением модуля вектора |г—р| в ряд Тейлора по степеням
малого отношения р/г:
^), B5.11)
где п = г/л, а рх — перпендикулярная к п составляющая век-
тора р: р^ = р—п(пр).
Применим разложение B5.11) к каждому из слагаемых, вхо-
дящих в ^ и V,. Для 4'j получаем
Здесь
s = |r,-R|-|r,-R| B5.I3)
— разность хода от «точки рассеяния» R1) до точек наблюде-
ния Tj и r3; nsl и ns,—единичные векторы, направленные на
точки rt и г„ (рис. 23):
а рХ1 н pia—перпендикулярные к nsl и nsl составляющие век-
тора р.
х) Тнчиее, от «центра тяжести», т. е. от точки, лежащей посередине между
точками рассеяния г' и г", раздвинутыми на иалое расстояние (J^'B .
200
ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН
[ГЛ. IV
Выясним условия, при которых в B5.12) можно пренебречь
квадратичными и кубичными по р членами. Фактическая область
Рис. 23.
интегрирования по р выделена неравенством р^/е- Требуя ма-
лости квадратичных членов в B5.12) по сравнению с я при
р ~ 1е , получаем неравенство
ри
|r,-R| Лр
B5.15)
которое заведомо будет выполнено, если оно справедливо для
каждого из слагаемых:
8|rli2-Ri
Смысл же последних неравенств заключается в том, что точки
наблюдения г, и г2 должны находиться во фраунгоферовой зоне
по отношению к неоднородностям размера U '¦
kll
8л
ll
B5.16)
Ясно, однако, что неравенство B5.16) следует рассматривать как
достаточное условие пренебрежения высшими степенями р, по-
скольку в B5.15) входит разность двух примерно одинаковых
по величине, слагаемых. Если точки наблюдения совмещены
(г1 = гг), то левая часть B5.15) обращается в нуль и квадратич-
ные члены в разложении B5.12) просто отсутствуют. Вместо
B5.15) следует потребовать в этом случае малости (по сравнению
с я) уже не квадратичных, а кубичных членов:
Это неравенство налагает на расстояния | г,_ 2 — R | ограничение
VWi- B5.17)
$ 25! СРЕДНЯЯ ИНТЕНСИВНОСТЬ 201
В случае крупных неоднородностей Aе^>Х) условие B5.17) зна-
чительно слабее условия B5.16), согласно которому точки наб-
людения должны находиться во фраунгоферовой зоне отдельной
неоднородности (размер ~ 1г). Напротив, при /е<\ неравен-
ство B5.17) сильнее условия B5.16). Для неоднородностей, раз-
меры которых сравнимы с длиной волны, оба условия B5.16)
и B5.17) равносильны.
Что касается слагаемого Ч^, то разложение этой величины
содержит только нечетные степени р. Поэтому при выполнении
аналогичного B5.17) условия
|R-ro|>^'r7IЛ, B5.18)
позволяющего отбросить кубичные члены разложения, имеем
где
MR)=-|fE?r B5.Ш)
— единичный вектор в направлении распространения первичной
волны в точке R (рис. 23). В результате
] B520)
В знаменателе подынтегрального выражения B59) и в про-
изведении /W(R | р/2)Л1 (R—р/2) мы просто пренебрежем р. Для
такого упрощения знаменателя достаточно, чтобы обе точки наблю-
дения г, и г, и точка излучения г„ отстояли от точки рассея-
ния R не меньше, чем на 1е . Замена же произведения М (R + р/2) х
XM(R —р/2) па jW(R) или, что то же, па М (R) пригодна во
всем объеме V, за исключением приграничного слоя толщины
порядка /в . Совершаемая при этой замене относительная ошибка —
порядка отношения объема пограничного слоя L4e к полному
объему V~L», т. е. порядка /?,'L<^1 (см. B5.5)).
При сделанных допущениях формула B5.9) принимает вид
¦.Ci. Г,)- —ffi)I-Jj Ir.
где введено обозначение
Q (R) = * { V. [п„ (R)+nfi (R)] -п,- (R)} . B5.22)
Согласно B5.4) интеграл по р можно выразить через спект-
ральную плотность квазиоднородных флуктуации:
Со
$ Ф. (Р, R) ехр (—iQp) d'p = 8л»Фе (Q, R), B5.23)
202 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ПОЛИ [ГЛ. IV
так что окончательно получаем
¦« (г., г,)
Анализ этой функции корреляции мы отложим до § 27, а здесь
рассмотрим только пространственное распределение средней ин-
тенсивности
7'1(г) = <|«1(г)|г>-ф„(г, г). B5.25)
При совмещении точек наблюдения (i^ -г4 —г, так 4tos = 0)
вектор Q B5.22) переходит в так называемый вектор рассеяния
q(R)-ftfn,(R)-n,.(R)J- B5.26)
В результате средняя интенсивность будет
Как видно отсюда, волны, рассеянные отдельными элементами
объема d*R, складываются некогерентно, т. е. складываются их
интенсивности: выражение под интегралом (конечно, вместе с ко-
эффициентом, вынесенным в B5.27) из-под интеграла) представ-
ляет собой среднюю интенсивность dl1 поля, рассеянного элемен-
том объема d'R.
Формулу B5.27), выведенную для сферической' первичной
волны B5.1), нетрудно распространить па волны другой формы.
Величина /0(Я) = | А |"/| R—г01!—это интенсивность сферической
волны в точке R. Записав B5.27) в виде
*™, B5.28)
мы получаем выражение, справедливое для любого первичного
поля, если его структура в пределах одной неоднородности раз-
мера /с практически ие отличается от структуры сферической
волны. Последнее означает, что и пределах отдельной неоднород-
ности амплитуду поля и радиус кривизны RKt волнового фронта
можно считать постоянными, причем радиус Якр должен удов-
летворять еще неравенствам вида B5.18), т. е. #вр^>|Л|Л.
Таким образом, мы можем применить выражение B5.28) и к
плоской первичной волне
иг--А<>е""Чг. B5.29)
§25]
СРЕДНЯЯ ИНТЕНСИВНОСТЬ
203
для которой /0 — |/t0|2 = coast (в отличие от B5.19), единичный
вектор П;, указывающий направление распространения первич-
ной волны, здесь постоянен во всем пространстве), и к направ-
ленной сферической волне
».— Л/.(п,)г|г_г<| B5.30)
(/o(ni)—диаграмма направленности излучателя), для которой
Наиболее существенная особенность формул B5.27) и B5.28)
заключается в том, что они отражают селективный характер
рассеяния. Пусть 6 — угол между волновыми пекторамн падаю-
щей (к,) и рассеянной (ks) волн, называемый углом рассеяния.
Очевидно,
B5.32)
Этому значению q отвечает простраиствеиная гарйоиика возму-
щений е'чг с длиной волны
Л - 2" — *
*~ q ~~ 2 sin @/2) '
B5.33)
а направление нормали к фронту параллельно лектору q, т. е.
параллельно (п,—п,) (рис. 24). Следовательно, равенство B5.33) —
это условие Вульфа—Брегга, опреде-
ляющее пространственный период той
гармоники, на которой волна дифра-
гирует под углом 0.
Разумеется, пространственный
спектр флуктуации я (г) содержит
бесконечный набор таких гармоник
(объемных «дифракционных реше-
ток») со всевозможными периодами
и ориентациями. Селективность рас-
сеяния заключается в том, что в
заданном направлении п, дают вклад
волны, рассеянные лишь на выде-
ленной решетке—с пространствен-
ным периодом B5.3.3) и с ориентацией, отвечающей закону от-
ражения (в точке R) первичной волны из точки г0 в точку г.
Интенсивность этой гармоники пропорциональна спектральной
плотности Фе (q), которая и фигурирует в B5.27) и B5.28).
Рис. 24.
204 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛИ [ГЛ. IV
При обратном рассеянии, когда ks — — к,, так что вектор
рассеяния равеЕ! q - —2k,, a 9 —я, рассеяние обусловлено гар-
моникой с периодом А, = Я./2, т. с. г. периодом, равным половине дли-
ны волны падающего излучения. Обратное рассеяние наблюдают
в очень многих случаях, например в радио- и гидролокации, когда
источник и приемник излучения расположены в одной точке.
Рассеяние мод произвольным
углом часто используется в
оптике при изучении неодно-
родиостей в прозрачных ма-
териалах.
При уменьшении угла
рассеяния 6 период Л? уве-
личивается. Значения Ад и
X равны друг другу при
9^= л/3. При дальнейшем
уменьшении 9 пространст-
венный период рассеивающей
решетки Л, превышает ). и
Рис. 25. для рассеяния вперед (9—«-О)
величина q обращается в
нуль, а Лч—в бесконечность. Это означает, что рассеяние впе-
ред обусловлено наиболее крупными объемными возмущениями
с пространственными масштабами Л?^>Я.
Формула B5.28) упрощается для столь малого рассеивающего
объема, что в его пределах величины <De(q, R), /0(R) и !/|г— R |а
практически постоянны. Вынося их из-под знака интеграла со
значениями, соответствующими, скажем, центру О рассеивающего
объема (R — 0), получаем
Здесь q0 — q @) — ft (nsl) —n/0) — вектор рассеяния, отвечающий
центру рассеивающего объема, a ni0=r/r и п,„-— г„/г0—единич-
ные векторы, направленные из О (рис. 25).
Замена множителя 1/|г—R |* на 1 /г' возможна прн очевидном
условии, что точка наблюдения удалена на расстояние, значи-
тельно превышающее поперечный размер L рассеивающего объема:
B5.35)
Если падающая волна сферическая, то переход от точного выра-
жения для интенсивности Io (R) = | А |*/| R—г01" к приближенному
значению /„ @) = | А |V; требует выполнения такого же неравен-
ства и для расстояния до источника: г,^>1.
Что касается замены Фс (q, R) постоянным значением Ф8 (q0,0),
то для этого необходима, во-первых, статистическая однородность
f 25] СРЕДНЯЯ ИНТЕНСИВНОСТЬ 205
флуктуации в пределах V (масштаб /.е должен быть больше попе-
речника L) и, во-вторых, малость изменения (в пределах объема V)
вектора q по сравнению с характерным масштабом изменения
спектра Фе (q, 0), равным 1/1е:
B5.36)
По порядку величины Aq ~ kAn, или k An, (Ans и Дп, —вариации
направлений падающей и рассеянных волн в пределах V). Оче-
видно, Ani~Ljr, так что неравенство B5.36) сводится к условию
LU/l. B5.37)
Поскольку ограничения для расстояния г0 до источника сфери-
ческой волны формулируются аналогичным образом, мы будем
далее говорить только о неравенствах, относящихся к расстоя-
нию г до точки наблюдения.
В случае мелкомасштабных неоднородностей AС<^.\) из двух
неравенств B5.35) н B5.37) более жестким, очевидно, является
первое, тогда как для крупномасштабных неоднородностей (/е^> Я.)
минимальное расстояние до точки наблюдения ограничено уело-,,
вием B5.37). Обозначив через rmin меньшщ&из величин L и Lljh, /
можно записать оба неравенства/B*5^5Т н B5.37) в виде
RT, ил\. B5.38)
Обычно упрощенное выражение B5.34) выводят в предполо-
жении, что точка наблюдения находится во фраунгоферовой зоне
всего объема V. Для этого в выражении B5.7) (нли в аналогич-
ном ему выражении для плоской первичной волны) разлагают
модуль разности |г—г'| в ряд по степеням г' и пренебрегают
квадратичным слагаемым kr\/2r непосредственно в функции
Грина B5.2). Это н приводит к фраунгоферову приближению
f e-"*r'M(r')e(r')<iV'. B5.39)
Выражение для средней интенсивности, вычисляемое при помощи
B5.39), значительно проще, чем в общем случае, а именно сов-
падает с B5.34). Однако условие
нли
которое необходимо для фраунгоферова приближения B5.39), го-
раздо жестче, чем условие B5.38), достаточное для применимо-
сти B5.34).
Во многих прикладных задачах измеряется не само рассеян-
ное ноле Hi (г), а сигнал на выходе приемной антенны. Если
206
ТКОИИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ИОЛН
ИЛ. IV
центр приемной апертуры расположен в точке г, то выходной
сигнал а представляет собой поле и, (г + р), проинтегрированное
по апертуре 2 с весовой функцией Ь(р), которая описывает
распределение тока в антенне в передающем режиме:
^?"(гМ$ Ul(T + p)b(p)d'(>. B5.41)
Интегрирование по апертуре (волнистая черта), разумеется, не
равносильно статистическому усреднению.
Подставим в B5.41) рассеянное поле B5.7), не конкретизируя
пока вида первичной волны uo(r):
^f-L'Af (T')l(r')Uv(r')d?rf. B5.42)
где
Величину |г-f-p — г' | разложим в ряд Тейлора по р:
'1 = 1Г—г'| + п> i 21 г—г' Гр*—(*)*]-< •••> B5.43)
г г'
|Г_Г» | —единичный вектор, направленный из точки рас-
сеяния г' в центр приемной апертуры г (рнс. 26).
Пусть d—наибольший размер приемной антенны, так что
в пределах ее апертуры i>*id, и пусть выполнено условие
Й!<§|г —г'| (точка г' лежит во фраун-
гоферопой ^оне антенны, где уже сфор-
мировалась диаграмма направленности).
Тогда в показателе экспоненты в B5.42)
можно ограничиться двумя первыми чле-
нами разложения B5.43), а в знаменателе
,п. подынтегрального выражения—первым
членом этого разложения. Выполнив ин-
тегрирование по р, находим
B5.44)
где
Рис. 2G.
h КО - \Ь (р) exp (ifeibp) <Pp B5.45)
— диаграмма направленности приемной янтениы. Максимальное
значение |/, Aь)| удобно нормировать к единице. Если весовая
функция 6(р) симметрична относительно центра р = 0, то макси-
мум |/, (nj)j достигается при ns'p = 0, т. е. при ориентации век-
тора щ по нормали к плоскости антенны.
i 25] 1
СРЕДНЯЯ ИНТЕНСИВНОСТЬ
207
От исходной формулы B5.7) выражение B5.44) отличается
тем, что под интегралом появился диаграммный множитель /, (п,).
При малых по сравнению с длиной волны размерах приемной
антенны (kd<^ 1) этот множитель Eie зависит от направления п,,
и мы возвращаемся тогда к формуле B5.7).
Взяв в качестве первичной направлеш1ую сферическую волну
B5.30), получаем для v выражение
V-
,«<|г-г| + |'-г,|)
М <Х') | г_г.,, г-_Га | /. (n}) h (К) е (г')d?r\ B5.46)
которое, если ввести обозначение
4я |
можно записать в виде
г—г' || г'—го| '
''-'• 1)ё (г') d»r'.
B5.47)
B5,48)
Заметим, что в рассматриваемом случае, когда излучение и
прием осуществляются наиравлешшмн антеннами, область инте-
грирования в B5.46) илн
B5.48) остается конечной и
тогда, когда неоднородности
е (г) заполняют все простран-
ство, т. е. М (г') всюду равно
единице. Специальное огра-
ничение величины занятого
неоднородностями объема
теперь излишне, так как про-
изведение диаграммных мно-
жителей спадает практичес-
ки до нуля вне области пе-
ресечения центральных
(главных) лепестков обеих
диаграмм (рис. 27).
Располагая выражением B5.46), нетрудно^ычиелнть среднюю
интенсивность сигнала на выходе антенны /„«з<|и'|>. В отли-
чие от B5.27), под знак интеграла теперь войдет множитель
1/()М)|а
Рис. 27.
B5.49)
208 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. IV
При использовании остронаправленных передающих и прием-
ных антенн интенсивность рассеянного поля удобно характери-
зовать величиной эффективного рассеивающего объема. Обозначим
через q0 вектор рассеяния k(nia—п,0),- отвечающий точке пере-
сечения максимумов диаграмм направленности, которую естест-
венно принять за начало координат, и запишем B5.49) в форме,
аналогичной выражению B5.34) A, — \А\Чг\):
- _
57»
Множитель
, B5.51)
определенный нз сравнения B5.49) и B5.34), и представляет
собой эффективный рассеивающий объем.
Величина V^^, как следует нз B5.51), зависит от многих
факторов: от расстояний до источника и приемника, от формы
диаграмм направленности антенн и от вида спектра Фе(ч, R).
При использовании остронаправленпых антенн, если область
пересечения диаграмм целиком лежит в рассеивающем объеме,
величины jW(R) h rrj\ R — г, ||г—R| можно с хорошим прибли-
жением принять равными единице, и тогда
ds/?' B552)
Эта формула часто используется при расчетах интенсивности
радиоволн, рассеянных в тропосфере и нижней ионосфере [1J.
§ 26. Эффективный поперечник рассеяния.
Границы применимости приближения
однократного рассеяния
Для скалярного монохроматического поля и (г), удовлетво-
ряющего уравнению Гельмгольца B4.1), в случае прозрачной
среды, т. е. вещественной проницаемости е (г), выполняется соот-
ношение
и*Д«—«Ди* = 0, или div(«*v«—«V«*) —0, B6.1)
которое вытекает непосредственно из B4.1). Из B6.1) следует,
что величину
V«). B6.2)
I 2в] ЭФФЕКТИВНЫЙ ПОПЕРЕЧНИК РАССЕЯНИЯ 209
удовлетворяющую в прозрачной среде закону сохранения
div^ = O, B6.3)
можно при подходящем выборе нормировочного множителя а
интерпретировать как плотность потока энергии').
Найдем среднюю плотность потока энергии однократЕЮ рас-
сеянного поля
Дифференцируй выражение B5.7), получаем
B6.5)
Единичный вектор п'ж=в(т—г')/|г—г'|, направленный из точки
рассеяния г' в точку наблюдения г, можно при помощи разло-
жения B5.1!) преобразовать к виду
¦ ^jp, ~ ¦•„> —. r'j.~r'-n,0(ni(Ir'), B6.6)
где по-прежнему nst = t/r. Принимая, что точка наблюдения г
достаточно далека от рассеивающей области (г ^> L), имеем
|гх|«^г и nj«n,0. Кроме того, при r^>L заведомо выполнено
неравенство fe^>|r—г'|~». В результате выражение B6.5) сильно
упрощается:
Т«! (г) « ifensou, (г),
а формула B6.4) дает
^rI«anJO<|u1|4> = an,07. B6.7)
Зная ifv нетрудно найти эффективный поперечник (сечеине)
рассеяния а единичного объема в единичный телесный угол и на-
правлении п3г).
По определению
B6.8)
2) Для звуковых волн, если и—потенциал скорости, множитель и равен
ра'/2с (р—плотность жидкости, с—скорость звука), а для электромагнитных
полей а—с/8я, где с — скорость электроиагпитной волпы, если под и пони-
мать напряженность электрического поля.
*) Для эффективного поперечинка рассеяния часто используется сокраще-
ние ЭПР.
210
ТЕОРИЯ ОДНОКРАТНОГО РАСС.КЯНИЯ ВОЛН
[ГЛ. IV
где dPx—средняя мощность, рассеиваемая в телесный угол do
в наЕфавлении п„ V — рассеивающий объем, а \^„\—модуль плот-
ности потока энергии в первичной волне. Через 6 и <р обозна-
чены полярный и азимутальный углы, отвечающие направлению
п, (рис. 28).
Мощность dP1 равна
г do,
B6.9)
аях = | ^г jra do =
или, поскольку при выполнении условия B5.38) средняя интен-
сивность /j дается выражением B5.34),
B6.10)
Плотность же потока энергии в перничной волне, будь то пло-
ская, сферическая или направленная сферическая волна, сог-
ласно B6.2), равна (по модулю)
|<5ро| = а/о@), так что B6.8) дает
о (в, (r-)-=V,nft{Ct>B(q). B6.11)
J3§ В соответствии со свойствами
преобразования Фурье пространст-
венный спектр B5.23) практически
не зависит от q, если корреляцион-
ная функция ij>e(p) отличается от
нуля только в малой области p»S /е<сЯ..
В этом случае мелкомасштабных ие-
однородностей рассеяние изотропно:
Рис.Г28.
о (в,
const = 7iiftS<De@). B6.12)
Напротив, в случае крупномасштабных неоднородностей (е^)
спектральная плотность Фе(ц) быстро уменЕ.шается с ростом q,
т. е. с ростом угла рассеяния 8, что отвечает преимущественному
рассеянию вперед. Сектор углов 9, в котором-сосредоточено излу-
чение, неожно оценить из условия qle^\ или9^1/6/в. Ниже мы
проиллюстрируем этн особенности рассеяния несколькими при-
мерами.
Величину B6.8) Етзывают также дифференциальным сечением
рассеяния—в отличие от полного поперечника рассеяния
ао^^а(в, (f)do^l/2nk\^4>e((i)do, B6.13)
который представляет собой отношение средней полеюй рассеян-
ной мощности P1 = r1j)afido к плотности потока энергии в
5 26] ЭФФККТИБНЫЙ ПОПЕРЕЧНИК РАССЕЯНИЯ 211
первичной волне в расчете на единицу объема:
Как а, так и а, имеют размерность обратной длины, сечение же
рассеяния всего объема V, равное dV, измеряется в единицах
площади.
Согласно B6.8) и B6.9) для средней плотности_ потока рас-
сеянной энергии с?! и для средней интенсивности 11 имеем
^i-TSI^olVote, ч>). Л=-^Л^(в, ф). B6-15)
В оптике а @, ф) обычно называют индикатрисой рассеяния,
причем чаще всего имеется в виду величина /(9, ер)—значение
а (в, ф), отнесенное либо к максимальному значению поперечника
аша1, либо к полному сечению а0:
,@, ф) = !!??) „ли /(в, Ф)«^. B6.16)
Полный поперечник рассеяния а0 непосредственно связан
с ослаблением первичной волны за счет рассеяния (так называе-
мой жстинкции). Представим себе малый цилиндр с осью вдоль
волнового вектора первичной волны Vi = kni. Объем цилиндра
равен dV — dzdi, где dS—площадь поперечного ссчення цилин-
дра, a dz— его длина. Мощность, приносимая первичной волной
на передний торец цилиндра, равна P = \"S>C \a"L, а на заднем торце
она изменена до значения P+dP, где dP = — dPlt a dPv -мощ-
ность, рассеянная объемом dV, равная, согласно B6.14),
dP, = а„\ V „ | dV = а01 <S1 d2 dz = Pa, dz. B6.17)
Следовательно,
dP^~ dP, = — Paadz,
т.е. мощность первичной волны уменьшается по экспоненциаль-
ному закону Р -^ е'"'г. По такому же закону уменьшается н
плотность потока энергии:
К„|~«-**. B6.18)
Ослабление в е раз происходит на путийв=1/а0, который назы-
вается длиной, жстинкции (а„ называют также коэффициентом
экстинкции). Произведение т = аог, где г— путь, пройденный
волной в рассеивающей среде, называют оптической толщиной
(т= 1 на пути z = da).
212 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛИ ГГЛ. IV
Теория однократного рассеяния строится в предположении,
что амплитуда первичной волны иа, а. стало быть, и плотность
потока энергии <У0 практически постоянны в пределах рассеи-
вающего объема. Согласно B6.18) это справедливо, если оптиче-
ская толщина, отвечающая размерам рассеивающего объема
L~V113, мала по сравнению с единицей:
B6.19)
Условие B6.19) можно записать и в форме
B6.20)
т. е. полное сечение рассеяния всего объема 20^a0V должно
быть мало по сравнению с площадью порядка V, вырезаемой
объемом V нз фронта первичной волны.
Приведем несколько примеров вычисления поперечника рас-
сеяния а (в, ф).
1. Неоднородности с изотропной гауссовой
корреляционной функцией:
Ыг)=о1е"''- B6.21)
Пространственная спектральная плотность флуктуации в рассмат-
риваемом случае равна (см. C.12))
], B6.22)
так что для эффективного поперечника рассеяния единичного
объема по формуле B6.11) находим
с (в) - -^L exp[-2W.s!n« G3в)]. B6.23)
Полный поперечник рассеяния а0 вычисляется интегрированием
стF) но единичной сфере (do = sined6d(p) и равен
A_гг*1\ B6.24)
Условие B6.19) применимости приближения однократного
рассеяния принимает в случае B6.21) вид (для простоты пола-
гаем е = 1, так что k = k0)
B5.25)
Это условие ограничивает величину произведения дисперсии
I 26]
ЭФФЕКТИВНЫЙ ПОПЕРЕЧНИК РАССЕЯНИЯ
213
флуктуации а\ на k0L. С ростом дисперсии а\ или с увеличением
L неравенство B6.25) рано или поздно нарушается. Функция
/Т
W (kje) при /го/? — >0 растет, как у —{kjt)~'. а при у,-.»
убывает, как 2 |/ 2/лй„/е. Следовательно, чем больше радиус кор-
реляции /е, тем жестче ограничена величина а'гкаЬ. Поэтому рас-
сеяние иа крупных неоднородностях описывается борновским
приближением лишь на сравнительно малых дистанциях. Увелн-
z чение же L требует учета многократного
рассеяния. Соответствующие методы будут
рассмотрены в гл. V—VII.
Рис. 29.
2. Обратное рассеяние на анизотропных (аннзо-
мерных) флуктуациях с гауссовой корреляцион-
ной функцией:
-|1.) . B6.26)
у, г)-
Спектральная плотность таких флуктуации дается выражением
C.1$i|. Будем считать, что Ь > а, т. е. что большая ось эллипсо-
идальных неоднородностеи направлена по оси г.
Пусть волновой вектор первичной волны к,- лежит в плоско-
сти (х, г) н составляет угол ф с осью х (рис. 29), так что
k( = (fecosi|), 0, fcsini|>). При обратном рассеянии q — —2k, и,
следовательно.
exp [— 2k' {a* cos»i|; +62 sin* if)]. B6.27)
214 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. IV
Рассмотрим зависимость сечения обратного рассеяния оойр от
угла i|:, который иногда называют ракурсным углом. При i|> = 0
(так называемое «ракурсное условие») волновой вектор первич-
ной волны к, перпендикулярен к большой оси неодиородностей.
Индикатриса рассеяния выражается формулой
/ (¦) - gjg = exp \-2k* (б'-а*) sin»*}. B6.28)
Она имеет максимум при Ц =0 (рис. 30) и минимум при i|>= ± л/2
(к,- параллелен большой оси неодиородностей).
Этот эффект (так называемой ракурсной чувствительности)
особенно отчетливо выражен при сильно вытянутых неодиород-
ноотях, когда kVb2—aa^> 1. В этом случае индикатрису B6.28)
можно аппроксимировать выражением
/ (i|)) х- ехр {—2k* {b*—а2) у*}, B6.29)
т. е. узкой гауссовой кривой с шириной
А-ф — l/kVb'—аг<^1. B6.30)
3. Рассеяние на турбулентных флуктуацнях
в атмосфере. В инерционном интервале волновых чисел
2яД.о<^q<^2п//0, соответствующем колмогоровскому закону 2/3
(§ 4), спектральная плотность турбулентных флуктуации описы-
вается степенным законом
<S>s(q) = AC\q~"l>, A -=0,033. B6.31)
Для такого спектра поперечник рассеяния единицы объема в еди-
ничный телесный угол равен (полагаем е = 1)
а (в) = 2-'l-nAQk;'h (sin Ч?)-"'- = 0,016^',/' (sinЧ,&)'"'•¦ B6.32)
Полный поперечник рассеяния оказывается в этом случае
бесконечным, так как интеграл
я
a, = ^ado = 2nja(
расходится при малых углах рассеяния в. Объясняется ето тем,
что выражение для спектральной плотности B6.31), отвечающей
инерционному интервалу 2n/La<^q<^.2n/lt, непригодно при малых
значениях q — 2ks\n1/fi. Расчет полного сечения рассеяния для
другой модели спектра D.20), принимающего при q-+0 конеч-
ные значении, приведен в задаче 2.
f 271 ПРОСТРАНСТВЕННАЯ КОРРЕЛЯЦИЯ 215
§ 27. Пространственная корреляция
и вероятностные распределения рассеянного поля
Возвращаясь к выражению B5.24) для функции простран-
ственной корреляции рассеянного поля, обратим внимание иа
сходство этой формулы с формулой A2.20), которая описывает
пространственную корреляцию поля системы независимых излу-
чателей. В обеих формулах зависимость от координат точек на-
блюдения г1 н г8 входит через один и тот же подынтегральный
множитель exp {iks)/\ гх—R | |г,— R |, где
sHrj-RI-lr.-RI. B7.1)
Это не случайное совпадении. Как уже было отмечено (§ 24),
нахождение однократно рассеянного поля — задача, относящаяся
к схеме 2), т. е. к распространению волн в случайно-неоднород-
ной среде, фактически сводится к задаче типа 1), к возбужде-
нию полей заданными случайными источниками. Согласно B4.11)
эти источники непрерывно распределены по объему V- Однако,
в силу конечности радиуса корреляции 1е неодиородностей е, не-
прерывное распределение источников равносильно конечному
числу (порядка V/l\) дискретных некоррелированных источников.
Именно в этом и лежит причина сходства формул B5.24) и A2.20).
Опираясь на это сходство, можно сделать ряд качественных
н количественных заключений о характере пространственной
корреляции рассеянного поля. Так, можно утверждать, что вну-
три рассеивающего объема, а также вблизи него (т. е. при r^L)
радиус корреляции поля /„ порядка длины волны X, если неод-
нородности мелкие Aг<§.\), и порядка /е, если /е§>Я. Оба утверж-
дения вытекают из оценки
1,~К'У. B7.2)
где у—видимый угловой размер области, занятой источниками.
В самом деле, в случае мелкомасштабных неодиородностей,
которые рассеивают изотропно, угол у сравним с я, так что
1п ~ Я/я ~ Я. Крупномасштабные же неоднородности нмеюх^зкую
индикатрису (у~Я//е), ширина которой определяет эффективный
угловой размер области, занятой источниками. В результате
здесь ln~\iy~le.
По мере удаления от рассеивающего объема происходит неко-
торое упорядочение поля, что выражается в увеличении масшта-
бов пространственной корреляции. При r^>L угловой размер
рассеивающего объема v становится величиной порядка Llr<^ 1,
и в результате поперечный (по отношению к направлению рас-
сеяния п,) радиус корреляции превышает Длину волны в r/L раз:
/j. - Xr/L. B7.3)
216 ТКОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН |ГЛ. IV
При приближении к началу фраунгоферовой зоны, r~kLt, по-
перечный радиус корреляции увеличивается до диаметра рас-
сеивающего объема, lx~L, а прн r^>kU превышает L.
Что касается продольного радиуса корреляции lt, то его
можно оценить поформулам задачи 13 к гл. II: в пределах ближней
зоны рассеивающего объема (r<^fe/.a)
<»-?-? ('¦<«-•), B7-4)
ио, начиная с расстояний r~kl>, корреляция простирается до
бесконечности:
/,,-оо (/>&/.•)• B7.5)
Сказанное можно частично проиллюстрировать на примере
пространственной функции корреляции B5.24) при условиях,
что точки наблюдения находятся в зоне Фраунгофера, r^>feL2,
а рассеивающий объем заполнен статистически однородными
флуктуациямн. При этих предположениях можно заменить ks
приближенным значением
feswfer, — kr., f /гАпД, B7.6)
где Дп,=-п„ —п„— гг/г,—г,//1,, и вынести за знак интеграла
в B5.9) вес множители, кроме Af(R) и е'к1м**:
*. (rlf г,) = Я*»И'* ®°lSsLeik (,,-,,) f M (R) е1ьА«.*#х. B7.7)
^ Л2Ло ^
- Si
Мы заменили здесь произведение |г, — R] [r2 — R| на г' ¦= (т^т^Н,
сделав дополнительное предположение о малости расстояния
между точками наблюдения |г,—гг| по сравнению с расстоя
ннем г от центра рассеивающего объема до «центра тяжестн»
точек наблюдения.
Интеграл п B7.7) представляет собой дельтообразную функ-
цию. Если ввести обозначение
Kj, B7.8)
— 00
то формула B7.7) примет вид
)"'-'l> An,,. B7.9)
Функция 6v{k) равна V/8n* прн х —0 и, в соответствии со свой-
ствами преобразования Фурье, спадает до малых значений при
х2;2л/?, где L — поперечник объема V. При V—> °о она перехо-
дит в б (х).
$ 27] ПРОСТРЛМСТВЕН.НАЯ КОРРЕЛЯЦИЯ 217
Разделив корреляционную функцию B7.9) иа среднюю интен-
сивность B5.34), получаем коэффициент корреляции
K/()/() V
Поскольку 6и(йДп,) заметно отличается от нуля только при
к | Лп51 sg 2n,'L, значения рассеянного ноля в точках г, и г, ста-
новятся некоррелированными при &ns^2n/kL — XiL.
Величина |Дп,| приблизительно равна углу Дв между единич-
ными векторами ni4 и ns. (рис. 23), так что полученная оценка
определяет «угол корреляции»
Л6К~1. B7.11)
Но вместе с тем А0к ~ lxir> так чт0 Для поперечного радиуса
корреляции из B7.11) следует прежняя оценка B7.3).
Что касается продольной корреляции, то при расположении
точек наблюдения на одной прямой, когда Ап,=0, коэффициент
корреляции дается выражением
/Г, (г.. г„)-в'*"'-Ч
т. е. равен по модулю единице при любых г, и гг, лежащих
в дальней зоне. Это означает, в согласии с B7.5), что для
амплитуды рассеянного поля i41^|uI| продольный радиус кор-
реляции бесконечен, („—оо, а разность фаз полей в точках г,
и г,, лежащих па одной прямой, равна разности оптических
путей fe (г, — г2).
Обратим внимание иа то, что в формулу B7.10) входят только
геометрические параметры задачи г и /., а также длина волны
первичного поля К, но не входят статистические характеристики
флуктуации ё. Это говорит о том, что корреляционные харак-
теристики рассеянного ноля вытекают из чисто динамических
соображений и лишь косвенно связаны со статистическим опи-
санием.
Действительно, синусоидальная дифракционная решетка ко-
нечной длины L и с периодом Л, дает и направлении 9 (см.
B5.33)) волновой пучок конечной угловой ширины А0~ЛД..
Поскольку в спектре флуктуации представлены различные про-
странственные гармоники, рассеяние на данный угол обусловлено
не только той объемной решеткой, которая точно удовлетворяет
условию Вульфа — Брегга B5.33), ио и близкими по размерам
и ориентациям решетками, для которых рассматриваемое направ-
ление лежит в пределах главных дифракционных максимумов
ширины Д9~ А//.. Таким образом, пока угловое расстояние между
точками наблюдения меньше A6~a/L, рассеяние обусловлено
2|8 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. IV
вполне определенной группой дифракционных решеток. Напротив,
при AQ-^XlL поля, рассеянные в направлениях nJ1 = r,/r1 н
ns, = ra/r2, обусловлены уже различными группами решеток (с не-
перекрывающимися главными максимумами), что и приводит к
исчезновению пространственной корреляции.
Обратимся тенерь к вероятностным распределениям рассеян-
ного ноля. В приближении однократного рассеяния поле uL (г)
выражается интегралом B4.11) от произведения некоторой де-
терминированной функции на случайную функцию к (г'). По-
скольку линейные размеры L рассеивающего объема по предпо-
ложению велики по сравнению с радиусом корреляции /е флуктуа-
ции е, можно утверждать, что в силу центральной предельной
теоремы теории вероятностей закон распределения для рассеян-
ного поля близок к нормальному.
Найдем параметры, характеризующие совместные функции
распределения вещественной и мнимой частей комплексного ноля:
и,.(г)-1](г) + М(г). B7.12)
Так как величины {/, = {/(гу) и Vk = V{rk) распределены но
нормальному закону, достаточно получить матрицу вторых мо-
ментов этих величин, которая совпадает с корреляционной
матрицей, поскольку среднее значение рассеянного поля, а значит,
и средние значения <?/у> и <Ук> равны нулю. Билинейные сред-
ние <.UjVb> можно выразить тогда через корреляционные функ-
ции комплексного поля
¦.(«/. г») = <И1(гу)иГ(г,)>,
+.(«>. г») ==<«! (г,) «i(rj>. [ ¦ '
Первая из этих функций была вычислена в § 25 н рассмотрена
выше. Покажем, что вторая корреляционная функция ij>n почти
всюду мала по сравнению с tyu. С этой целью оценим величину
<ы! (г)> = ¦»(:„ (г, г) в зоне Фраунгофера. Согласно B5.39),
M{r')d>r'
~ JT^S1 Я d'p dSR M (R + P/2)M(R-p/2He(p) г'2"lR- B7.14)
Заменяя M (R 4 p/2) M (R—p/2) на Af(R), получаем
<«J C)> = Dt,o)8 Bл)" Фе @) 6V Bq), B7.15)
где функция 6V. (>t) определена выражением B7.8).
I j7] ПРОСТРАНСТВЕННАЯ КОРРЕЛЯЦИЯ 219
При рассеянии вперед (q = 0) средний квадрат поля <nj>
с точностью до фазы совпадает со средней интенсивностью
/1 = <|и1|2>, поскольку 6K@) = V/8nJ. Однако при \2q\^2n/L
значения функции 6vBq) резко уменьшаются по сравнению
с 6к@), т. е.
|<й?(г)>КЛ-<|«!(г)|>, qssn/L. B7.16)
Так как q — 2&sin l,-afl, неравенство qs>ajL выполняется вне
узкого конуса с раствором 6~^/2L, откуда и следует, что при
рассеянии па не слишком малые углы F^)./2/,)
.i- B7.17)
Практически это означает, что вне указанного конуса вторую
корреляционную функцию г|:„ можно положить равной нулю:
UO. rt)«0. B7.18)
Этот результат получен для дальней зоны рассеивающего
объема (r^>kL2), но в ближней зоне (г<^.kl.s) on справедлив и
подавно. Действительно, если разбить рассеивающий объем на
отдельные элементы с линейными размерами, малыми но срав-
нению с /., но большими по сравнению с радиусом корреляции
кеоднородностей, и поместить точку наблюдения в зону Фраун-
гофера каждого из таких элементов, то результирующий средний
квадрат поля <uj> можно получить, суммируя выражения типа
B7.15), поскольку флуктуации е в различных элементах стати-
стически независимы. Ясно, что суммирование величин, содер-
жащих осциллирующий множитель е'"кг, может привести только
к уменьшению <«;> по сравнению с /, = <|и,|2> даже внутри
конуса с углом раствора 6-~Я/2?.
Воспользовавшись этим, применим для вычисления моментов
<l//Vt> формулы B.14), которые при равенстве нулю второй
корреляционной функции дают
- V, Re ф„ (г„ г,),
<V\l/,> = - <иу,> = ¦/, Im 1>, (г,, г,). V'-1*'
Положив в B7.19) г,-=г2 —г, находим, в частности, что
<J/2>--<Va>-1/a/i, <t/(r)V(r)>=,0. B7.20)
Последующие вычисления статистических моментов амплитуды
и фазы производятся так же, как в ч. 1, §§ 25 и 44.
220 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. IV
§ 28. Рассеяние на нестационарных неоднородностях
1. Временная функция корреляции! Поле, рассеян-
ное на неоднородностях e(t, г), зависящих от времени, создает
на выходе антенны отклик, аналогичный B5.48):
)r'. B8.1)
В отличие от B5.48), мы восстановили здесь множитель е~""',
который для краткости ранее опускали. Волновое возмущение,
возникающие при рассеянии в точке г', достигает точки наблю-
дении г за конечное время At — |г — г' \>с (для простоты считаем,
что е=1). Поэтому иод интеграл входят значения е не в мо-
мент /, а в предшествующий момент V ¦ t—At. Функция З1 (г')
по-прежнему дается выражением B5.47).
Вычислим временную корреляционную функцию рассеянного
поля п предположении, что флуктуации t статистически одно-
родны и стационарны, так что простраиственио-временная кор-
реляционная функция неоднородностей зависит лишь от разно-
стных (пространственных и временных) переменных:
iM*', г'; *", О = <8(<\ Ов(<", n>-W-t\ <¦'-"•")• B8.2)
Из B8.1) сразу же видно, что временная корреляционная функ-
ция отклика на выходе антенны
тоже зависит только от разности t — tf— Г:
со
% (т) = е-!™\ J 5> (г') S" (r") eiV <¦"• г'>^е (т—Дт, г'- г") d*r' 6?r",
B8.3)
где
Таким образом, в случае стационарных флуктуации е отклик
v(t), как и само рассеянное поле u, (t), является стационарным
случайным процессом.
Входящая в B8.3) величина
Дт=(|г'-г|-|г"-г|)/С
представляет собой разность временных задержек возмущений,
пришедших из точек г' и г". В силу того, что пространственная
корреляция неоднородностей простирается на расстояния
|г'—г"|^с/е> разность задержек Дт фактически не превышает
времени Ulc, за которое волна проходит одну неоднородность
$28] РАССЕЯНИЕ НА НЕСТАЦИОНАРНЫХ НЕОДНОРОДНОСТЯХ 22]
). Интервал Дтобычно значительно меньше те—времени
корреляции флуктуации е:
Дт~/8/с<те. B8.4)
Поэтому без большой ошибки можно при этом условии поло-
жить в B8.3) Дт = 0, и тогда
¦С
^(г) ^e-'<<"l$ 93 (г') у" (г")е™"'¦ Г">х|)е(т, г' — r")d'r'd'r'. B8.5)
Выражение B8.5) отвечает так называемому квазистационар-
ному приближению, при котором считается, что рассеяние на
отдельных неоднородностях происходит так, как если бы не-
однородности покоились, а зависимость i|>e от времени восста-
навливается уже в окончательной формуле B8.5).
Дальнейший анализ временных флуктуации целесообразно
провести отдельно для следующих двух случаев: а) в среднем
покоящаяся случайно-неоднородная среда и б) случайно-неодно-
родная среда, перемещающаяся в среднем равномерно со ско-
ростью v, которую принято называть скоростью дрейфа.
2. Рассеяние в отсутствие регулярного дрей-
фа. Для среды, в среднем неподвижной, можно почти без
изменений повторить выкладки § 25, т. е. перейти к переменным
интегрирования R — (г,-|та)/2, р = г,— гг и разложить показа-
тель экспоненты ^(г', г") в ряд по степеням р:
) d?p i|>E-(t, p) exp (t qp) =
QO
-^8nse-im \ d3iI?|55(R)^e(T, q), B8.6)
где
Фе(т, ч)-=^з J *e(t, p)exp(— («p)d3p B8.7)
— пространственное преобразование Фурье корреляционной функ-
ции $#(т, р), a q = q(R) — вектор рассеяния, отвечающий точке R.
Из выражения B8.6) следует, что время корреляции отклика
на выходе антенны того же порядка, что и у флуктуации в.
Тот же результат можно выразить и в спектральной форме,
222 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ПОЛИ [ГЛ. IV
написав спектральную плотность стационарного процесса v (t):
CD
* j *P*B(*. p) exp J((«-со) T-tqp]. B8.8)
-да
Учитмнан, что пространс-шсшт-иременной спектр ф.чуктутшй к
выражается формулой
GR(Q, *)=щ; ] dx J d»pi)v(T, р)ехр (iQ-r-ixp),
— ос — »
можно представить частотный спектр сигнала у(?) в виде
^ B8.9)
Спектр флуктуации Се(Й, «) обычно сосредоточен в окрестности
нулевой частоты И«0, спектр же рассеянного сигнала #„(П)
расположен вблизи частоты первичной волны <>>• Как следует
из B8.9), частотный спектр рассеянного поля получается сум-
мированием пространственно-временного спектра неодиородностей
Geffi — to, q(R)] по рассеивающей области с Бесовой функцией
Если условия задачи позволяют пренебречь изменением пектора
рассеяния q в пределах области интегрирования (согласно B5.38)
это возможно при г^>г„\п — min(Z., Lljh)), то Ge\Q—w, q(R)]
можно вынести за знак интеграла со значением при q -q0, где
q0 —ft(ni0—п/0) —вектор рассеяния, отвечающий центру рассеи-
вающей области. В результате частотный спектр поля оказы-
вается пропорциональным Ge(Q — to, q0):
ffr(^) = 8n»Gs(Q-co, q0) J |
|*LAl! B8.10)
где Vett—эффективный рассеивающий объем. Таким образом,
при r^>rmin можно находить форму спектра флуктуации е не-
посредственно по измеренным значениям #., (Й). В случае же
протяженных рассеивающих областей, когда спектры. ?„(и) и
Ge связаны между собой интегральным соотношением B8.9), рпре-
деление формы G8(Q) по измерениям gv(Q) затруднительно.
S 28] РАССЕЯНИЕ НА НЕСТАЦИОНАРНЫХ Н1ЮДНОРОДНОСТЯХ 223
Спектр комплексной огибающей 91 (/) сигнала w(/) = 9((/)e-'w(
сосредоточен в окрестности нулевой частоты, поскольку g*(Q) =
= gv(Q4,-io). В частности, при г>гш1п, когда gv(Q) дается
выражением B8.10), имеем
3. Рассеяние при наличии регулярпогодрейфа.
Нахождение функции корреляции поля, рассеянного на дрей-
фующих неодиородиостях, несколько сложнее, чем при v = 0.
При рассмотрении этого вопроса мы следуем результатам Г. С. Го-
релика и его сотрудников [3—6], а также анализу, приведен-
ному в [1].
Пусть 1|>дР(т, р)—функция корреляции неодно роди осте ft
в сопровождающей системе координат, т. е. в системе, равно-
мерно перемещающейся вместе со средой со скоростью v.
В неподвижной системе координат, связанной с наблюдателем,
функция корреляции, очевидно, равна
Подставим это выражение в формулу B8.5) и введем новые
переменные интегрирования R н р', равные
'—r"—vt. B8.12)
В этих переменных функция корреляции сигнала v (t) будет
p')x
xexp|W'(T, p', R)]d*pd'R, B8.13)
где
р рЧ vt |\
Поскольку корреляционная функция $1р(т, р') спадает прак-
тически до нуля при р'зз/,., разложим V в степенной ряд по р'
и ограничимся первыми двумя членами разложения:
Ч"(т, р', Я)-=Ф(т, R)-q'(x, R)p'+... B8.14)
224 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. I
Здесь
Ф(т, R)~-V(x, 0, R)-fc(|r— R — vx/21 -I -
-IR + VT/2—г„|-|г—R-bvt/2|-|R—vt/2-r,,|),
+ VT/2_re|
г—R I vt/2 . R—vt/2—г, \
"t|R-w/2-r0| )'
Если подставить в B8.13) приближение B8.14), справедливое
при выполнении довольно слабых условий типа B5.18), то интег-
рирование по р' дает
1|!„(т) = 8я»е-"« \ d'tf^+^V^""^^, q'), B8.15)
где 5*.| ^ 5* (R ± vt/2), а функция
ос
Фд, (т, х) - gij j *„ (т, р) exp (.-*p) J»p B8.16)
— ос
представляет собой пространственное преобразование Фурье кор-
реляционной функции неоднородностей в сопровождающей си-
стеме координат.
Выражение B8.15) сложнее, чем B8.5). Во-первых, под знаком
интеграла теперь содержится дополнительный экспоненциальный
множитель е'ф('•¦>. Во-вторых, вектор рассеяния q' и произве-
дение P+Pt, заменяющее теперь |^(R)|a, зависят от т. Однако
если допустить, что источник первичного поля и приемный пункт-
удалены от рассеивающей области иа расстояния, превышающие
ее поперечник (r^>L и ra^>L), то формула B8.15) упрощается.
В последующих оценках мы будем писать неравенства, относя-
щиеся только к г. Аналогичные неравенства должны выполняться
и для /•„.
Прн Rs:L произведение5*+S"Lстремится к нулю. Следователь-
но, в области R^.1., существенной для интегрирования в B8.15),
отношение Rir<?. 1 в силу принятого допущения r^>L. По той же
причине в B8.15) существенны только значения vti^L. Имея
это в виду, разложим показатель экспоненты O(t,_R) в стенеи-
иой ряд по малым параметрам /?/г<:?/г<^1 н от./r^L/r<^ 1:
Ф(т, R)- -
J гв] РАССЕЯНИЕ НА НЕСТАЦИОНАРНЫХ НЕОДНОРОДНОСТЯХ 225
Здесь у—вектор, имеющий размерность частоты и пропорцио-
нальный скорости дрейфа v:
v = т [п„ [та,.П + То К [vn,0]J. B8.18)
Вектор q' мы тоже разложим в ряд, ио лишь по перемен-
ной т:
q'(T,R) = q(R) |-ftO[(^)*], q(R) = ft(n,-n,) B8.19)
(член, линейный по т, здесь отсутствует).
Ниже мы убедимся, что условие r^>L достаточно для того,
чтобы сохранить в B8.17) два первых члена, а в B8.19)—только
первый член разложения. Если это сделать, то B8.15) прини-
мает вид
^(т) = 8я»е-'<т+ч»;'>т I ?+?'_ ехр((Ы?т)Фдр(т, q)<f'tf. B8.20)
Разумеется, при v —*0 это выражение переходит в формулу
B8.5), полученную в отсутствие дрейфа.
С ростом т значение интеграла в B8.20) уменьшается по
трем причинам. Во-первых, уменьшается произведение 5>+Р1,
которое стремится к нулю при Hx-^L. Во-вторых, экспонен-
циальная "функция exp((fcvRt) начинает заметно осциллировать
в пределах существенной для интегрирования области. В-третьих,
уменьшается функция Фдр(т, q), которая описывает временную
корреляцию флуктуации в сопровождающей системе координат
и стремится к нулю при т—>-оо.
Из условий »t~Z. и kyRx^.kvL-i/r ~ I находим два харак-
терных интервала времени, отвечающих первым двум факторам
"/ ъ B8.21)
It S4*> ——— S^/
1 * kvL ~vL '
Характерное же время изменения функции Ф,р(т. q), т. е. вре-
менной интервал корреляции неоднородностей н сопровождаю-
щей системе координат, мы обозначим через тп. По существу,
это «время жизни» неоднородностей. Меньшее из трех перечис-
ленных значений т определяет, очевидно, время корреляции тж
сигнала:
т^пппК.Тз/т,}. B8.22)
При V—-0 (отсутствие дрейфа) т, и т., бесконечно возрастают,
а т„ = т,.
226 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. IV
Применим формулу B8.20) к анализу частного случая рас-
сеяния на замороженных иеодиородностях, которые в сопрово-
ждающей системе координат не зависят от времени (тя = оо).
4. Рассеяние на замороженных неодиородно-
ст я х. Очевидио, в лабораторной системе координат, отиосительно
которой не метающиеся со времелем неоднородности дрейфуют
со скоростью v, флуктуации проницаемости е (t, r) обладают
свойством
ё(/,г) = в(/ —т, г —vt), B8.23)
т. е. в точку г в момент времени t приходит возмущение е (Г, г'),
которое в предшествующий момент /' = /—т находилось в точке
г' = г—vx и переместилось за время г со скоростью v в точку г.
Как сказано, «время жизни» неодиородностей т3 в сопрово-
ждающей системе координат формально бесконечно: т.3 = оо.
Практически же замороженными можно считать неоднородности,
для которых
т,>т„ г,. B8.24)
При выполнении этого условия функцию Фдр(т, q) в B8.20)
можно положить равной Фдр@, q)=^B (q), поскольку значение
интеграла в B8.20) сделается малым раньше, чем начнется
уменьшение ФДр(т., q). Таким образом, для замороженных ие-
одиородностей
V)
^„(т) = 8л»е-<<»<-9.7>т f .р+$>_*ехр(|Ы*т)Ф,(ч)*#. B8.25)
Поведение этой функции корреляции существенно зависит от
соотношения между т, и т2. Согласно B8.21) они сравнимы
друг с другом при г ~kU. В ближней зоне, где r<^kLl и одно-
временно, по условию, г5>>/,, выполняется неравенство тг<^т,.
Следовательно, время корреляции в ближней зоне совпадает с т2:
(Z.< r <*/.). B8.26)
Напротив, в дальней (фраунгоферовой) зоне, где г^>W.', время
корреляции совпадает с тр которое значительно меньше тг:
тк-т,~Г./о (г>/г/.!). B8.27)
Нетрудно убедиться, что в обеих зонах отбрасывание «лиш-
них» слагаемых в разложениях B8.17) и B8.19) вполне оправ-
дано. Например, в ближней зоне, где г<l:kLl и t.k = ts, четвер-
тый член разложения B8.17) по порядку величины равен
* ( ' V ' '
f 3S] РАССЕЯНИЕ НЛ НЕСТАЦИОНАРНЫХ НЕОДНОРОДНОСТИ* 227
т. с. меньше произведения двух малых параметров. Но он мал
и в дальней зоне, где r^>feia и тж —т„ так что
Отметим, что при нарушении условия замороженное™ B8.24),
т. е. при т,; т,^т3, отбрасывание «лишних» членов является
тем более оправданным, чем меньше т3 по сравнению с т, и т,.
Иными словами, единственное условие применимости формулы
B8.20) выражается неравенством r^>L.
Рассмотрим теперь Солее детально поведение корреляционной
функции B8.25) в ближней и дальней зонах.
Для ближней зоны выражение B8.25) можно упростить, если
учесть, что Ихt?.vra~ rikL<^.L, а при vx<^.L произведение !Р+3>1
приближенно равно |^(R)|2. Таким образом, здесь
i|>e(T) = e~'(aHq'*it j I^WPexptifcvRTjaMqJd3/?. B8.28)
— <»
Для вычисления интеграла, конечно, надо конкретизировать
вид спектра <I>e(q) и весовой функции |5'(R)|*. Однако спек-
тральный анализ выражения B8.28) можно провести и без кон-
кретизации этих функций.
Выполнив временное преобразование Фурье B8.28), находим
спектральную плотность сигнала v(t):
ее
g,(Q)=&*» J |s»(R)|»Oe(qN(Q—<B-q,v-ftvR)tf>/?. B8.29)
— оо
Согласно B8.29) каждому элементарному объему d'R отвечает
спектральная линия на частоте Q — to + q0v+ftvR и с «интен-
сивностью» 8ла (^5(Я)|аФе(ч). Суперпозиция этих линий и обра-
зует частотный спектр gv№). Смещение частоты линии И —
— ю-f q,v-t-fcvR относительно частоты первичного поля ш обу-
словлено эффектом Доплера.
Доплеровский сдвиг частоты
содержит два слагаемых, из которых первое одинаково для
всех точек рассеивающей области, тогда как второе меняется
от точки к точке в силу изменения вектора q (R) внутри рассеи-
вающего объема1).
*) Более точное выражение доплеровского сдвига: йд = vq(R). Выраже-
ние, приведенное выше, содержит только первые члены тейлоровского раз-
ложения но R.
228 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛИ [ГЛ. IV
Ширина частотного спектра AQ определяется, очевидно, раз-
ностью доплеровских смещений частоты иа краях рассеивающего
объема R~L:
ДО х ДЦ, ~ kvL ~ коЦг, B8.30)
что, как и следовало ожидать, согласуется с оценкой ширины
спектра ДО ~ 1/т„ ~ 1/тг. Оценке' B8.26) можно дать и другую
интерпретацию. Как было показано в § 27, величина r/kL пред-
ставляет собой в случае неподвижных неоднородностей попереч-
ный радиус корреляции ноля 1Х, т. е. пространственный масштаб
интерференционной картины, образующейся в результате нало-
жения рассеянных волн. При дрейфе замороженных неоднород-
иостей интерференционная картина будет пробегать мимо точки
наблюдения со _скоростью v, так что характерное время флук-
туации поля ljv~rjkoL как раз совпадает с т., = т,.
Оценка B8.26) пригодна, строго говоря, только при r^>L'.
Если, несмотря иа это, применить ее к случаю г ~ L, когда
точка наблюдения находится вблизи рассеивающей области, то
мы получим, что т„~ l/ftu~A./i». Это ие противоречит и оценке
т„~/х/к, поскольку вблизи рассеивающего объема l± ~ Я
(см. § 27).
Иные закономерности наблюдаются в дальней зоне, для ко-
торой, согласно B8.27), время корреляции т., равно времени
t.j ~ L/v пребывания отдельной неоднородности в рассеивающем
объеме. В дальней зоне показатель экспоненты в формуле B8.25)
мал но сравнению с единицей, а Фг(ч)«(^е(Ч|). так что кор-
реляционная функция поля дается выражением
1j,s(T)=e-'(m+<'^8n3Oe(qf) \ 55+55lds/?. B8.31)
— се
Для вычисления интеграла необходима, как и в B8.28), кон-
кретизация вида функции 5s (R). В предельно ндеализнрованном
случае, когда функция 5* (R) = S't = const внутри куба с ребром L
и равна нулю вне этого куба, а скорость дрейфа v перпенди-
кулярна к одной из граней куба, имеем
f
О при |t|>Z./|v|.
Более сложным закономерностям подчинено рассеяние на
блуждающих неодиородностях, когда поле скоростей состоит из
общей скорости дрейфа v и случайной компоненты v, т. е.
j 29] ИМПУЛЬСНЫЕ И МОДУЛИРОВАННЫЕ СИГНАЛЫ 229
v = v + v. Некоторые аспекты этого случая рассмотрены в [I]
и [3-6].
5. Флуктуации интенсивности. В § 27 уже было
отмечено, что однократно рассеянное поле распределено по гаус-
сову закону с нулевым средним значением. Для такого поля
функция корреляции интенсивности
7п<-*). /.-К.
выражается через квадрат модуля корреляционной функции поля
(см. задачу 12 к гл. I):
¦i(*) = l*.WI'- B8-32)
Отсюда следует, что характерное время пульсаций интенсивно-
сти несколько меньше (в 1,5—2 раза, в зависимости от вида
¦»(T))i чем вРемя корреляции самого сигнала v(l). Соответ-
ственно частотный спектр флуктуации интенсивности
ев
J B8.33)
несколько шире, чем gv(Q).
§ 29. Рассеяние импульсных и модулнровапных сигналов
Рассеяние немоиохроматнческих воли обладает рядом инте-
ресных особенностей. Мы ограничимся частным, но важным
случаем квазимонохроматических сигналов, которые часто ис-
пользуются и в оптике, и в акустике, и в радиофизике. Пред-
ставив такой сигнал в пиде произведения медленно меняющейся
¦(вообще говоря, комплексной) амплитуды Э1(<) на е~ш (несущая
частота ш), мы должны, очевидно записать сигнал па выходе
антенны аналогично формуле B5.46), выведенной для монохро-
матической волны, но с заменой постоянной амплитуды А на
переменную амплитуду Ш (I — b'jc) с запаздывающим аргументом
F' = |г'—гв| + |г—г'|). Если восстановить еще временной фак-
тор е-"", опущенный в B5.46), то для квазимонохроматического
сигнала получим
B9.1)
Для упрощения последующих выкладок введем безразмерную
амплитуду a(/) = St(O/9L, где Щп = тах|И@1. а через Э> (г')
обозначим произведение неосциллирующих множителей, отли-
230 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН ГГЛ. IV
чающееся от B5.47) заменой А на 3(т. В этих обозначениях
B9.1) запишется в виде
у@ = е-'ш' j S>{T')a(t—~)eck'>''i(r')d>r', B9.2)
откуда для временной функции корреляции следует выражение
(г")в ( ^)
хЫт, г'—i")d3r'd»r", B9.3)
где г-—<! — ?3. Для общности здесь учтена возможная зависи-
мость флуктуации е от времени, а именно введен временной
аргумент т в функцию корреляции tyt. Процесс v(l), конечно,
нестационарен, 1|>„ зависит порознь от ^ и tr Оценим интервал
корреляции v(t) в случае одиночного импульса (периодическая
последовательность импульсов рассмотрена в задаче 5).
Пусть a it)— прямоугольный импульс длительности Т (а@—1
при |(|<Г/2 и равно нулю при |/|>Г/2). Ясно, что при Т,
превышающем время корреляции неодиородностей те, время кор-
реляции v (t) совпадает с те. В противоположном же предельном
случае Г<^ге время корреляции будет порядка Т, поскольку
произведение a(/j — b'lc)a'(tl—b"/c) обращается в нуль при
l'i~'il>^ Для любых значений г' и г".
Более детальный анализ выражения B9.3) возможен в пред-
положении, что пространственная длина импульса сТ велика
по сравнению с радиусом корреляции неодиородностей 1е. В этом
случае можно выполнить интегрирование по разностному аргу-
менту р = г'—г", как это неоднократно делалось в предыдущих
параграфах. В результате
|J(|).(т, q)dHt, B9.4)
где fl = |r—R|+|R-ro|.
В отличие от случая монохроматической первичной волны,
средняя интенсивность /„ = <|о|2> зависит теперь от времени:
= ФД<. 0-8*' J |5»(«)|«fo(t—f)|*Ot@, q)d'R. B9.5)
§ 29] ИМПУЛЬСНЫЕ И МОДУЛИРОВАННЫЕ СИГНАЛЫ 231
Величина /„ меньше, чем в случае монохроматического сигнала
той же амплитуды, поскольку под знаком интеграла появился
множитель |а|'^1. Этот множитель отличен от нуля внутри
эллипсоидального слоя, для внутренних точек которого имеем
|/—Я/с К Г/2, или в развернутой форме
r/2). B9.6)
Фокусы ограничивающих слой эллипсоидов (рис. 31) совпадают
с точками наблюдения (г) и излучения (г„), а размеры эллипсо-
идов с течением времени увеличиваются. Эллипсоидальный слой
B9.6) можно назвать им- . ...
пульсным объемом. Область, ..' ¦ ¦/.
принадлежащая в данный
момент одновременно им-
пульсному объему B9.6) и
эффективно рассеивающей
области V^, как раз и оп-
ределяет величину интенсив-
ности /„.
Толщина импульсного
объема 6 наиболее просто Рис. 31.
выражается при обратном
рассеянии, когда г — г0 и эллипсоидальный слой B9.6) вырож-
дается в сферический. Как ясно из B9.6), Ь^-сТ/2, т. е. толщи-
на импульсного объема равна половине 71ространственной длины
импульса. В общем случае выражения для б довольно сложны,
но для не очень длинных импульсов (гТ<<?|г—го|) толщина 6
определяется простой формулой [1J:
6 = c772sin(e/2), B9.7)
где 9—угол рассеянии (рис. 31). При рассеянии назад (9 — п)
из B9.7) получается прежний результат б = сТ/2. Отмстим, что
эллипсоид \t — В/с| = const расширяется со скоростью г/о нормали
vn = с/2 sin (9/2).
Временной ход Iv(t) существенно зависит от соотношения
между толщиной импульсного объема б и поперечником рассеи-
вающей области L. В случае длинного импульса F^>1 или
Т ^ BL/c) sin (9/2) происходит монотонное увеличение lv(t), пока
весь рассеивающий объем не окажется внутри импульсного
объема B9.6). Время нарастания Iv(t) до максимального значе-
ния /шах по порядку величины равно Ljvn = (Llc) 2 sin @/2). В те-
чение такого же времени происходит уменьшение /„ (i) до нуля
при выходе из рассеивающей области заднего фронта импуль-
сного объема. Между стадиями нарастания н убывания интен-
232 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. IV
сивность Jv(t) постоянна н равна средней интенсивности моно-
хроматического сигнала бесконечной длительности. Если
— sin-!j-<7\ B9.8)
т. е. времена нарастания н спадания малы по сравнению с дли-
тельностью сигнала Г, то рассеянный импульс практ71ческн без
искажений повторяет форму излученного импульса.
Неравенство B9.8) можно представить и в другом виде, если
ввести ширину полосы частот сигнала
Это условие ограничивает ширину полосы пропускания каналов
связи, использующих рассеяние. Прн передаче и приеме микро-
волновых сигналов при помощи остронаправленных антенн,
когда размеры рассеивающего объема атмосферы L порядка не-
скольких десятков километров, полоса пропускания Дсо оказы-
вается достаточной для передачи телевизионных сигналов
(Д/ = Дсо/2я~ 10е Гц).
В противоположном пределыюм случае 6<^L или
T<^BL/c)sin(9/2) {короткий импульс) «время входа» импульса
в рассеивающую область, а также «время выхода» из нее имеют
порядок длительности импульса: bivn ~ Т. Время'же, в течение
которого импульсный объем находится внутри ^рассеивающей
области, приближенно равно LjvnKs BL/c)sin@/2). Для короткого
импульса это время значительно превышает длительность сиг-
нала Т, т. е. короткий первичный импульс при рассеянии
существенно растягивается—в общем случае примерно
в BL/c7)sin(8/2) раз, а при обратном рассеянии — в 2L/cT раз.
Следует отметить, что, несмотря на существенное растягивание
рассеянного сигнала по сравнению с первичным импульсом,
время корреляции по-прежнему остается величиной порядка Т.
Это вытекает как из изложенных выше общих соображений, так
н из выражения
(b)« (* = *!-*.). B9.10)
которое, как можно показать прн помощи B9.4), связывает
в случае коротких импульсов функцию корреляции поля со
средней интенсивностью /„ и «коэффициентом корреляции»
I 36] РАССЕЯНИЕ ЭЛЕКТРОМАГНИТНЫХ ПОЛИ 233
огибающей первичного импульса
? И (О И* С—г) Л
B9.11)
Из B9.10) ясно, что в случае коротких импульсов рассеянное
поле представляет собой квазнстационарный случайный процесс
с переменной дисперсией lv(t) и с коэффициентом корреляции
Як(т) в"'"*- Коэффициент корреляции огибающей /Си (т) обра-
щается при г>Г в нуль, откуда и следует, что время корре-
ляции рассеянного поля порядка Т.
§ 30. Рассеяние электромагнитных волн
При рассеянии электромагнитных воли (как и при рассеянии
поперечных упругих волн) возникают два новых эффекта, кото-
рые отсутствуют в скалярной задаче. Во-первых, рассеяние
сопровождается изменением поляризации волны, а во-вторых,
если речь идет об анизотропной среде, может происходить транс-
формация одних типов поляризации в другие. Мы рассмотрим
однократное рассеяние электромагнитных воли лишь в изотроп-
ной недиспергирующей среде, в которой могут распространяться
волны только одного типа, а именно поперечные электромаг-
нитные волны.
1. Рассеяние монохроматических электромаг-
нитных волн на покоящихся иеодпороди остях
В изотропной среде. В этом случае уравнения .Максвелла
rotH-i-f-, rotE^-l^L C0.1)
с dt ' с fit K '
Нужно решать совместно с материальным уравнением для изо-
тропной недиспергирующей среды
D = eE. C0.2)
Материальное уравнение C0.2) исключает из рассмотрения
не только рассеяние в анизотропных средах (об особенностях
такого рассеяния см., например, в [7]), но и рассеяние на
анизотропных флуктусщиях в изотропной среде (так называемые
флуктуации анизотро77ии). Такие флуктуации возникают, напри-
мер, в вязких жидкостях из-за случайных поворотов молекул,
если последние оптически анизотропны (см. [8] и обзор [9]).
234 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ 6ОЛН 1гЛ. IV
Пусть монохроматическая волиа распространяется в среде
с постоянной средней диэлектрической проницаемостью вис по-
коящимися неоднородностями:
е=ё-"-ё(г), e"=const, <ё> = 0. C0.3)
Уравнения Максвелла принимают внд (А.ззю/с)
rolH-Hfc.eE ifc.eE, rot E —jfc0H =0, C0.4)
а их решение может быть представлено при слабых флуктуациях
<(ё)Ъ<^(е)а рядами теории возмущений
E = E0-fE, + E2-..., H-H.-H.-I-H, |- ... C0.5)
При этом первичное /юле Ео, Но удовлетворяет однородным
уравнениям
rotH0-1-«VE0 = 0, rotE0 — ifc,Ho = 0, C0.6)
а однократно рассеянное поле—неоднородным уравнениям
•1*оёЕ1 = — ift,eE0, rolE,— ife0Hl = 0. C0.7)
Уравнения для последующих приближений получаются из C0.7)
при последовательных заменах Е„^Е„,.„ Н„- >Н„+1.
Рассеянные моля Е, и Н, можно найти, используя известные
функции Грина, т. е. решение задачи о возбуждении электромаг-
нитных воли точечным электрическим источником }, —1,6 (г—г').
В волновой зоне, т. е. при R — |г—г'|^>Х, элементарный источник
создает поля
где п;= (г— r')/|r —r'|^=R/# — единичный вектор, направленный
из г' в г.
Используя C0.8), решение неоднородных уравнений C0.7)
можно представить в виде
о»
Е> <г>^тг 1 M(r')^e(r')[n;[Eo(r')n;]jdv\
Ч C0-9)
tOKEfr'lK'
Так как существенно новое по сравнению со скалярной задачей
касается только поляризации рассеянного поля, рассмотрим
f 301 РАССЕЯНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН 235
простейший случай, когда точка наблюдения расположена в зоне
фраунгофера рассеивающего объема (r^W,1), а первичное поле
представляет собой плоскую волну:
Ea{r)--Aeelk'r, k,-=fen, -*,j/Tn,. C0л0)
Здесь е — вектор поляризации первичной волны, вообще говоря —
комплексный. Будем считать его нормированным к единице
условием ее*—1. В силу поперечности волн, распространяю-
щихся в изотропной среде, вектор поляризации е перпендикулярен
к направлению распространения п,. Простой расчет с использо-
ванием разложений вида B5.11) дает для однократно рассеянных
полей Е, и Н, выражения
Е, (г) = -*^Г Ко [en,.]] j M (г') ё (г') e-
C0.11)
Н,(r)=klVlAre'kr К„е] j М(г')I(r-)e-<*"'d>r\
где nJ0 —г/г—единичный вектор, направленный п точку г из
центра рассеивающей области, a qo = fc(n,o —п/0) — вектор рассе-
яния, отвечающий центру этой области. Для упрощения записи
мы опустим ниже индекс 0 у векторов п,0, п/0 и q0.
Легко видеть, что поля Е^ и Н^ отличаются от скалярного
поля
*^lj>-^dV, C0.12)
вычисленного прн тех же допущениях, только множителями:
Е.О-ИКММг), Н1(г) = /Г[п,е]«1(г). C0.13)
Следовательно, в приближении однократного рассеяння прн де-
терминированной поляризации е первичной волны любые средние
билинейные величины, составленные из компонент нолей Е,
и Н„ могут быть выражены через функцию корреляции скаляр-
ного поля ^„(r,, ra) = <u, (rt) uf (гг)>. Если же поляризация пер-
вичного поля случайна, то усреднения по направлениям е и по
ансамблю пеоднородностей 8 производятся раздельно в силу ста-
тистической независимости этих величин. Иными словами, и прн
случайной поляризации первичной волны средние от билинейных
комбинаций компонент Ej и Hj можно выразить через ipB нлн /,.
Рассмотрим примеры.
236 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. IV
2. Средний вектор Пойитинга и эффективный
поперечник рассеяния. Среди билинейных комбинаций,
составленных из компонент Е, и Н„ важную роль играет вектор
Пойнтинга
S 1k l]). C0.I4)
Учитывая, что Hj = ye [n,Ej], и используя выражение B5.34)
для Т1 — < | их |s >, находим
C0.15)
Заметим, что в отличие от исходных формул C0.11), это выра-
жение применимо не только в зоне Фраунгофера г^>*1\ но и
на гораздо меньших расстояниях г^>гШ1П = тш \L, LljX)
(см. B5.38)).
Введем, как и в § 26, эффективный поперечник рассеяния
единицы объема в единичный телесный угол о — \ Ух \ гг1 \ Уо \ V, где
|<S%| = су е\А |*/8я—модуль плотности потока энергии первич-
ной волны. При помощи C0.15) находим
fe). C0.16)
где оск — «скалярный» поперечник рассеяния B6.12). Множитель
V = | [п, [en,]] |» = |е - n, (en,) |» = 1 - (п,е)» C0.17)
связан с особенностями рассеяния электромагнитных волн по
сравнению со скалярной задачей и может быть назван поляриза-
ционным. Вычислим у для некоторых частных случаев.
Для линейно поляризованной первичной волны е—вещественный
единичный вектор. Если х — угол между е и ns (рис. 32), то
•y=sin3x- Таким образом, для линейно поляризованной первичной
волны
a = oCKsin!x- C0.18)
Множитель sin'x обращается в нуль в направлениях, коллииеар-
ных с е, что связано с дипольным характером рассеяния электро-
магнитпых волн в каждом элементе рассеивающего объема.
Произвольн ую эллиптически поляризованную волну можно пред-
ставить, как известно, в виде суммы двух линейно поляризованных
колебаний, сдвинутых по фазе на л/2. Пусть большая ось эл-
f 30]
РАССЕЯНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
237
лнпса поляризации направлена вдоль орта е^ а малая—вдоль
орта е,. Векторы ej и е, ортогональны к направлению распро-
странения п;, так что еХ1 е, и п,- образуют ортогональную связку.
При эллиптической поляризации
где /», и р,—вещественные коэффициенты, удовлетворяющие, в
силу принятой нами нормировки ее*=1, условию р\-\ pi=l.
Рис. 32.
Рис. 33.
Поляризационный множитель -у для волн эллиптической поля-
ризации равен
7=1—Pi (n,e,)«-/»3 (nse2)« = 1 -р\ cos'Xl-p? cos«x,, C0.20)
где Xi и %t—углы между Еектором п^ и ертами е, ие, (рис. 33).
Подставляя C0.20) в C0.16) и учитывая, что р\-\-р\—\, по-
лучаем
о = (р\ sin» xi + р\ sin'z,) o«- C0.21)
В отличие от линейно поляризованной первичной волны,
сеченне C0.21) никогда не сбргщается в нуль, потому что
sin'x, и silica не мсгут обратиться в нуль одновременно.
Из C0.13) следует, что в направлениях п, = ±е, и п^ = ±е,
рассеянное поле поляризовамно линейно—в силу уже отмечен-
ного дипольиого характера рассеяния. В других направлениях
рассеянное поле поляризовано по эллипсу. Параметры эллипса
поляризации могут быть найдены из выражений C0.13), если в
них подставить C0.19).
В частном случае круговой поляризации волны, когда
Pj= 1/1^2, pt—-±l/V2 (плюс отвечает правой, а минус—левой
поляризации), находим из C0,20)
238 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН ГГЛ. IV
В силу взаимной ортогональности векторов еи е, и п, имеем
cos*x1 + cos*Xi+cosie= 1, так что для волн„ поляризованных по
кругу,
V= I— V,(l — cos»e) = V,0 +eos»6). C0.22)
Таким образом, у зависит здесь только от угла рассеяния в,
т. с. имеет азимутальную симметрию.
Если в точке наблюдения г измеряется интенсивность рассе-
янных волн какой-либо одной поляризации, то плотность потока
энергии будет, очевидно, меньше плотности полного по-
тока C0.15) и, соответственно, уменьшится величина эффектив-
ного сечения рассеяния а.
Пусть измеряется поток энергии, переносимой компонентой
?A,= (NE,I где N—единичный и, вообще говоря, комплексный
вектор, перпендикулярный к направлению рассеяния n,: (Nn,)^0.
Вектор N описывает поляризационные характеристики приемной
антенны в случае радиоволн или анализатора в случае световых
волн. Из C0.13) следует, что
так что роль поляризационного множителя у играет теперь
величина
Гл-= / (N [п, [en,]]) |*=|(Ne)-(NnJ (en,) |»-1 (Ne) |«.
Нетрудно убедиться в том, что v.v^V. если поляризационные
характеристики приемной антенны «согласованы» с поляризацией
оассеяниого излучения, т. е. антенна принимает волну C0.13).
В остальных случаях ук < у.
3. Рассеяние неполярнзованного (естествен-
ного) света. С небольшими изменениями полученные резуль-
таты переносятся и на частично поляризованные поля (ч. I, § 49),
когда компоненты первичного поля Е„ случайны. Усреднение по
этим величинам можно проводить, как уже было отмечено, не-
зависимо от усреднения по реализациям флуктуации е. Рассмот-
рим простой, но важный случай неполяризбеанной волны.
Разложим напряженность электрического поля первичной вол-
ны на ортогональные компоненты по ортам е, и е,:
В случае неполяризованиой волны амплитуды Л, н At статисти-
чески независимы, имеют нулевые средние значения и одинако-
вые дисперсии:
>, C0.23)
где I5J* —|Д,|'-|-| Д,'|2—полная интенсивность.
} 30) РАССЕЯНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН 239
Сечение рассеяния неполярнзоваиной волны можно найти из
следующих простых соображений. Если бы первичная волна била
линейно поляризована вдоль орта eXt то, согласно C0.21), сечение
рассеяния равнялось бы а — а, = a^sm2 х, даже при флуктуирую-
щей амплитуде А1. При линейной же поляризации вдоль е, мы
имели бы а = а4=гаС|15т2х2. Поскольку в неполяризованной волне
поток энергии делится поровну между двумя ортогональными
компонентами, полное сечение рассеяния должно быть равно
полусумме Uj и а2:
<J«i = V, К +<*,) = V, (sin2 х, + sin" x.) Сек-
Но коэффициент прн аСЕ здесь такой же, как и в случае рас-
сеяния волны с круговой поляриза7и!ен, и, следовательно, он
равен (l+cosa6)/2 (см. C0.22)). Таким образом,
"«„-i^V. C0.24)
Множитель g (9) — A - Ь cos2 9)/2 называют релеевской индикатрисой
рассеяния. Уменьшение g@) до значения 1/t при 6= ± л/2 объя-
сняется тем, что в этом направлении вклад в рассеянное поле
дает только одна компонента первичной волны, т. е. рассеянное
поле оказывается линейно поляризованным.
Выражение для степени поляризации Р (б) рассеянного поля
можно получить но формуле D9.18) из ч. I:
P = у 1 —(ТТ^рт^р . C0.25)
где Jo» = <EaEl> — элементы поляризационной матрш(ы в пло-
скости, перпендикулярной к направлению распространения. Про-
стые вычисления дают принадлежащее Релею выражение
Из C0.26) видно, что Р — 0 прн 0 — 0 или л, т. е. поле Е,
сохраняет естественную поляризацию при' рассеянии вперед и
назад. При рассеянии под прямым углом @— ± я/2) степень по-
ляризации равна единице, а в других направлениях рассеянное
поле поляризовано частич77О @ < Р < 1).
4. Частотны н спектр рассеянного поля. Некоге-
рентное рассеяние электромагнитных волн в
изотропной п л азме. Прн неоднородностях к, зависящих от
времени, отлнчня рассеяния электромагнитных волн от анало-
гичной скалярной задачи тоже могут быть учтены введением в
результаты скалярной теории поляризационного множителя у —
— 1— (п^е)а. Так, например, в отсутствие регулярного дрейфа
240 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. IV
неоднородностей и при г ^> rmit[ частотный спектр рассеянного
поля
= ii I <Е, (О ЕГ (<-*)>«"**: C0.27)
- »
в случае сферической первичной волны может быть получен ум-
ножением спектра B8.10) на у:
ёв(П) - V "**' *Ц°ФФ G. (а. -Q, q), C0.28)
где Gj(<o, х)—<ох-плотность флуктуации диэлектрической про-
ницаемости.
Применим формулу C0.28) к так называемому некогерентнО'
му рассеянию электромагнитных волн в плазме. Первоначально
предполагалось, что рассеяние волн в плазме происходит на сво-
бодных электронах, находящихся в тепловом движении, благо-
даря чему ипте71сивности полей, рассеянных отдельными элек-
тронами, складываются некогерентно (отсюда и возник термин
«некогереитное рассеяние»). В дальнейшем выяснилось, однако,
что существенную роль в этом явлении играют коллективные
процессы '). Мы ограничимся вычислением интенсивности высоко-
частотного ноля, рассеянного в изотропной плазме, опираясь
на макроскопическую теорию тепловых флуктуации (гл. III).
В § 31 мы вернемся к рассмотрению некогерентного рассеяния
в рамках теории рассеяния на отдельных частицах.
В макроскопической электродинамике свойства изотропной
холодной плазмы описываются на высоких частотах (<о^>ш,)
диэлектрической проницаемостью
-1 "• 1
где е, т и N—соответственно заряд, масса и концентрация элек-
тронов. Таким образом,
*, ё е^_^, C0.29)
откуда следует связь между сох-плотностями в и i\f:
G(<0 х)- <30-30)
J) Возможность наблюдать некогерентное рассеяние радиоволн в ионо-
сферной плазме была указана У. Е. Гордоном в 1958 г., а первые наблюде-
ния этого явления осуществил в том же году К. Л. Боулс (см. [10]). Анали-
зу коллективных процессов в плазме посвящены многие работы (см., напри-
мер, (Щ).
§81] РАССЕЯНИЕ НА ДИСКРЕТНЫХ ВКРАПЛЕНИЯХ 241
Подставляя это выражение для G8 в формулу C0.28), получаем
0„@-<в, q), C0.31)
где ге = е*/тсг—классический радиус электрона. Спектр флук-
туации электронной концентрации GN, как было показано в за-
даче 7 гл. III, пропорционален температуре Т и средней кон-
центрации электронов N. Таким образом, спектр рассеянного
поля gE пропорционален полному числу электронов /VE = NV, на-
ходящихся в объеме V.
Из C0.31) следует, что спектр рассеянного поля gE сосредо-
точен в окрестности частоты первичной волны а>, а его форма
полиостью определяется видом спектра флуктуации GN(v>, x).
Поэтому частотный спектр рассеянного сигнала gF(Q) позволяет
судить о свойствах и состоянии плазмы. Основанный на этом
метод диагностики широко применяется для анализа не только
ионосферной, но и лабораторной плазмы («метод некогерентного
рассеяния»).
§ 31. Рассеяние иа дискретных вкраплениях
1.Поле, рассеянное отдельной частицей. Наря-
ду с рассеянием на объемных неоднородностях, большой инте-
рес представляет и рассеяние на совокупности большого числа
тел (частиц, вкраплений и т. д.), случайно расположенных и
(или) случайно ориентированных в пространстве. Это очень об-
щая задача, имеющая широкие приложения во многих областях
физики.
Строго говоря, проблема рассеяния на системе многих тел
относится к статистической схеме 3) (§ 8). Но если дискрет-
ные рассеиватели имеют сравнительно небольшие размеры и рас-
йоложены достаточно редко, то дифракционная задача может быть
решена в приближении однократного рассеяния, которое основа-
но на допущении, что каждое вкрапление рассеивает падающую
волну так, как если бы других вкраплений не было.
Приближение однократного рассеяния сводит задачу для ди-
скретных рассен вате лей, как н в случае непрерывных неодно-
родностей, к схеме 1), т. е. к излучению полей случайными источ-
никами. В данном случае речь идет о совокупности дискретных
Источников, статистика которых задана статистикой положений
(и ориентации) рассеивателей. Как мы увидим, «внешние» зако-
номерности однократного рассеяния на-дискретных вкраплениях
to иа непрерывных неоднородностях среды (пространственная кор-
реляция, частотный спектр и т. д.) во многом сходны.
Рассмотрим и здесь упрощенную постановку задачи, а имен-
Яо рассеяние монохроматической волны на совокупности непод-
242 ТЕОРИЯ ОДНОКРАТНОГО РАССКЯНИЯ ВОЛН [ГЛ. IV
вижных частиц, размеры которых малы по сравнению с длиной
волны, причем точка наблюдения находится в зоне Фраунгофера
объема V, занятого частицами.
Для малых частиц рассеянное поле можно рассчитывать в
диполыюм приближении. Пусть р — электрический дипдльный
момент частицы, возникающий под действием электрического
поля Е.
р = яЕ, C1.1)
где а—тензор поляризуемости частицы. Для частиц, малых по
сравнению с длиной волны, а можно вычислить, считая ноле Е
статистически однородным. Сводка формул для некоторых сим-
метричных тел приведена, например, в монографин [12], посвя-
щенной рассеянию волн на малых частицах.
Для сферических частиц из изотропного материала, а также
для частиц произвольной формы, но с диэлектрической проница-
емостью, близкой к единице, поляризуемость я является скаляром:
р^аЕ. C1.2)
В качестве электрического поля а формуле C1.2) следует
брать так называемое действующее поле Ед, которое отличается
от ноля первичной волны Е„ тем, что включает также совокуп-
ное поле соседних рассейвателей. В приближении однократного
рассеяния (борновское приближение) Ед практически ие отли-
чается от поля первичной волны Ео, которое для простоты мы
будем считать полем плоской волны Ео — Аее'к'Т'ш. Тогда
р --¦ аЕд « яЕ0 = яЛее""г'-'ш', C1.3)
где г' — радиус-вектор частицы, а е — вектор поляризации пер-
вичной полны.
Волновое поле, излучаемое в вакууме отдельным диполем с
моментом C1.3), может бычь рассчитано по формуле C0.8), если
подставить туда —/wp вместо 1Х (множитель е~ш, как обычно,
опускаем):
Здесь Я = |г — г'|, ns' —(г —г')/|г —г'| —единичный вектор, нап-
равленный из точки г' в точку наблюдения г. Магнитное поле
рассеянной волны в волновой зоне дается выражением
H^KE.bKeJfe^""^-1'1'^. C1.5)
2. Среднее значение однократно рассеянного
поля. Пусть в объеме V находятся N одинаковых частиц с цент-
рами в точках г' — rm (m=l, 2 N). В приближении одно-
f 31] РАССЕЯНИЕ НА ДИСКРЕТНЫХ ВКРАПЛЕНИЯХ 243
кратного рассеяния ноле в точке наблюдения г представляет со-
бой сумму полей, рассеянных отдельными частицами:
Е, (г) = К Z К [enт]]«А "Р «**- + **.) _ C1.6)
где Rm^\r— rm|, a nm^-(r —rj/| г—rj — единичный вектор, на-
правленный от т-п частицы в точку наблюдения г. При учете
двукратного рассеяния в качестве Ед надо взять сумму первич-
ного ноля Е„ и однократно рассеянного ноля C1.6) и т. д.
Заметим, что при учете двукратного рассеяния пренебреже-
ние в действующем поле Е„ квазистационарным полем индуци-
рованных диполей, ближайших к точке г, т. е. пренебрежение
полем Е|1В~осЕо/|г—г' \г по сравнению с Е„, налагает опреде-
ленное ограничение на среднее расстояние между частицами р. Из
условия ЕКВ<^ЕО следует неравенство а/р3<^1, илн поскольку
пр'»1, где п — средняя концентрация частиц, неравенство
тх<^1. C1.7)
При выполнении этого условия возможно как р > Я, так и р < )..
Облако частиц, удовлетворяющее нераиепстну C1.7), можно наз-
вать разреженным (конечно, в электродинамическом смысле),
в отличие от конденсированной среды, в которой па~5>\.
Поместим начало координат в центр рассеивающего объема
V ~ L', заполненного частицами. Для точек наблюдения г, вы-
несенных в зону Фраунгсфера объема V (г^>kL2), мсжно исполь-
зовать разложение B5.11):
подставив
где q = ftn
|г—г„|«г —п,гЖ1 не-
которое в C1.6), получим
N
Ег=8, X, е
т= 1
j—k,=ft(n, —п;)—вектор
-fqr»f
рассеяния, а
C1.8)
C1.8а)
— поле, рассеянное одной частицей, помещенной в начале коор-
динат, т. е. в центр области V.
Для нахождения статистических моментов однократно рас-
сеянного поля нужно задаться законом распределения случай-
ных координат гт—(хт, ут, гт), а если частицы движутся, то и
244
ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН
[ГЛ. IV
законом распределения скоростей vm = {pmx, vny, vmz). Для рас-
чета среднего значения и функции корреляции рассеянного по-
ля необходимы только одночастичная (а>,) и бинарная (wt) плот-
ности вероятностей. Примем, что все частицы и все нх пары
равноправны, т. е. функции а>,(гя) и ^(г,,, г,) ие зависят от
индексов переменных ги и г,.
Усредняя C1.8) по положению частиц гя, получаем среднее
поле, рассеянное /V частицами:
N
Е,С) = *i( L e'iVm) = «iW С «"'"в, (г) ^=8,^D), C1.9)
где
C1.10)
— характеристическая функции одночастичного распределе-
ния [^(г).
Интенсивность среднего поля \Es\a, т. е. когерентная состав-
ляющая интенсивности, равна
/.„r = |EJ|» = |81|«JV'|/1(q)|>. C1.11)
Когерентная составляющая отличается от интенсивности |6i|a по-
ля, рассеянного одной частицей, множителем W|/i(Q)|*' T- е-
/ког пропорциональна квадрату числа частиц. Величину л|/\(ч)|
можно назвать эффективным числом когерентно рассеивающих
частиц:
|(J)| C1.12)
При рассеянии вперед (8 = 0, q = 0), когда /, (q) = /, @) = 1, коге-
рентно излучают все частицы (WKor = Ы) и при этом
(Ё.)« = (^«J» = Nklea^e'». C1.13)
При рассеянии под углом JVKor резко падает, поскольку харак-
теристическая функция /\ (q) сравнима с единицей только при
q^2n/'L или, что то же, при углах рассеяния, лежащих внутри
конуса 6^.X/L<^.\ (оценки скорости убывания #ког с ростом в
даны в задаче 7).
3. Средняя интенсивность. Согласно C1.8) средняя
интенсивность однократно рассеянного поля 7t = <|Ei|1> равна
C1.14)
I Si] РАССЕЯНИЕ НА ДИСКРЕТНЫХ ВКРАПЛЕНИЯХ 245
Выделим нз двойной суммы, содержащей /Vs членов, N слагае-
мых cm — /, каждое из которых равно единице, а остальные
N'—# слагаемых с тФ1 усредним при помощи бинарной плот-
ности вероятностей wt. В результате получим
N)f1(q)], C1.15)
где
? J$ >-'<i<r'-r-WdV\ C1.16)
/>(Qi- 4s)~бинарная характеристическая функция. Фактически
/,(q) — это характеристическая функция распределения относи-
тельных координат. В самом деле, если заменить в C1.16)
ш, (г', г") d*r' far"на W, (р, R) d»pd'R, где р = г' — г", R = (г' + г")/2,
н выделить интегрирование по R, то
Вычитая из C1.15) интенсивность когерентной составляющей
поля C1.11), получаем среднюю интенсивность некогерентного
рассеяния
) —|Л(ЧI*]}- C1-17)
Если положения частиц статистически независимы, т. е.
tti,(r', т") = 0)! (r')tt)j (г"), то /,(q)—|^(ч)|' = 0 и второе слага-
емое в C1.17), пропорциональное N' — #, обращается в
нуль. Следовательно, слагаемое, пропорциональное N*—N,
описывает рассеяние на частицах, положения которых кор-
редарованы между собой, и его можно рассматривать как
характеристику коллективных эффектов при рассеянии:
Первое же слагаемое в C1.17) описывает рассеяние на незави-
симых частицах:
L. = l в^АГ 11-|/.D)PJ- C1-19)
Так как /^ @) =/, @) = 1, при рассеянии вперед F = 0) оба сла-
гаемых в C1.17) обращаются в нуль, Гктт@) = 0. Но это имеет
место только в приближении однократного рассеяния. Можно пока-
зать, что уже при учете двукратного рассеяния Тшт@) ф 0.
Исключив из рассмотрения рассеяние вперед, т. е. в узкий
конус с раствором б^Х/i, можно пренебречь в формуле C1.19)
246 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН 1Г.1. IV
слагаемым |Л(Ч)|а<^' (см- задачу 7), что дает
/„„«IS.I'iV, C1.20)
т. е. сумму ннтенсивностей волн, рассеиваемых независимыми
частицами. Если, как чаще всего бывает в приложениях теории,
N^>1, то в C1.18) можно пренебречь N по сравнению с N', и
тогда
/««, ** I в? |» JV [?, (q) —| /, (q) П = | «! I» Af" v (q). C1.21)
Представив бинарную функцию распределения ш3 в виде.
w,(r', r') = wl(r')w,{r')l\+ii(rr, r")], C1.22)
можно связать разность v = /a — |/,|' с величиной ц, которая об-
ращается в нуль для частиц с независимыми координатами
г' и г":
v (q) ^ J С [ш, (г', г") — ш, (г') wl (r")J е-'ч <'¦-¦"№/•' d*r" =
= I J ш, (г') wl (г") |г (г', г") е-'" fr'-^dV dV. C1.23)
Если радиус корреляции Zw, т. е. характерный масштаб из-
менения \i по разностной переменной р = г' — г", мал по сравнению
с поперечником облака L (одновременно L является масштабом
изменения ^(г) и ц по аргументу R = (r'-|-r")/2), то в пределах
сферы р = |г'—г"|^/№ произведение wl (r') wl (r") можно прибли-
женно заменить на a?(R), после чего в C1.23) можно выпол-
нить интегрирование по р. Это дает
Ч, R)d*R, C1.24)
где
— преобразование Фурье ц(р, R) по аргументу р. Таким образом,
q, tyd>R. C1.26)
4. Средний вектор Пойнтинга. Эффективный
поперечник рассеяния. Поскольку в зоне Фраунгофера
^, = -ST Re [Е.НГ] = -кг п. | Е,|- = -^- п,/„ C1.27)
для среднего значения вектора Пойнтинга ^ке1«,г, отвечающего
флуктуационной (некогерентной) компоненте поля, имеем
«^веког = J^ nt Лге«ог = ^ пs (^"«еэ + Лю») ¦ C1.28)
S 31] РАССЕЯНИЕ НА ДИСКРЕТНЫХ ВКРАПЛЕНИЯХ 247
Обозначим через а, поперечник рассеяния отдельной частицы
в единичный телесный угол. Согласно C1.8а)
j3"o = -§jj-Re[EoHJ]—вектор Пойнтиига первичного поля, <У,
поток энергии поля C1.4), рассеянного одной частицей, а у—
поляризационный множитель C0.17). Подставляя в C1.28) вы-
ражения C1.20) и C1.26) и учитывая C1.29), получаем для
суммарного поперечника рассеяния aN системы N частиц в еди-
ничный телесный угол выражение
] C1.30)
Вводя среднюю концентрацию частиц
n(r) = Nw1(T) C1.31)
и учитывая, что N = Jra(r)dV, можно представить выражение
C1.30) в виде
\ (q, R)] d»R; C1.32)
при этом подынтегральное выражение интерпретируется как се-
чение рассеяния единичного объема:
О=0н« + Омод. C1.33)
где первое слагаемое
o^^aji C1.34)
отвечает рассеянию в пренебрежении корреляцией между поло-
жениями частиц, а второе слагаемое
o«o* = <vMn)X(q. R) C1.35)
—рассеянию с учетом попарной корреляции положений частиц.
В зависимости от конкретных условий соотношение между
этими слагаемыми может меняться в широких пределах. Ясно,
например, что при малой средней концентрации п преобладает
слагаемое сг„ез, а с ростом п—слагаемое акол; при этом оказы-
вается, что рассеяние на системе частиц с коррелированными
положениями может быть описано как рассеяние на макроско-
пических (объемных) неоднородиостях (см. ниже, раздел 5). При
рассеянии электромагнитных волн в квазииейтральной плазме
248 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. IV
коллективное рассеяние и рассеяние на независимых частицах
могут быть сравнимы по величине.
5. Переход к сплошной среде. При макроскопическом
рассмотрении диэлектрическая проницаемость разреженного
(в смысле неравенства C1.7)) облака частиц равна
е=1 + 4яла, C1.36)
где а — поляризуемость частицы, а п — макроскопическая концен-
трация частиц, являющаяся, вообще говоря, случайной величи-
ной. Тем самым,
е--е-| в, е—1+4япа, ё — 4iukx. C1.37)
Постараемся установить, каковы те статистические характе-
ристики е (или п), при которых макроскопическое описание рас-
сеяния, т. е. описание на языке флуктуации е, дает те же ре-
зультаты, что и микроскопическое рассмотрение. Говоря о ста-
тистических характеристиках е, мы будем иметь в виду только
моменты е и <fe.
В силу C1.31) в качестве среднего значения е(г) следует,
очевидно, взять
ё(г)=^ 1+4п<хЛ/а>,(г) = 1-; 4ясш(г). C1.38)
Среднее поле, рассчитанное при помощи C1.38) в борновском
приближении для зоны Фраунгофера, совпадает с C1.9).-
Для нахождения i))e отождествим сечеиие C1.33), вычислен-
ное для системы частиц, с сечением C0.16), описывающим рас-
сеяние на непрерывных объемных неоднородностяк. Приравнивая
эти два выражения, учитывая C1.29) и сокращая на укк\/2,
получаем
| ll(q, R). C1.39)
Корреляционная функция ^(р, R) получается отсюда преобра-
зованием Фурье по q:
iMp, R)-$<P.(q, R)exp(iqp)d»? =
=-|- па* С exp (iqp) d'q + Dпап)г Г Фйехр (iqp) d'q.
Интеграл в первом слагаемом правой части равен 8л'6 (р), а ин-
теграл во втором члене, согласно C1.25), равен ц(р, R):
p, R)J. C1.40)
Учитывая, что е = 4япа, получаем из C1.40) корреляционную
функцию концентрации частиц:
) C1.41)
S 31] РАССЕЯНИЕ НА ДИСКРЕТНЫХ ВКРАПЛЕНИЯХ 249
Первые слагаемые в C1.40) и в C1.41) связаны с дискрет-
ностью рассеивателей. Дельта-функция б(р) появляется в ре-
зультате замены реальных частиц точечными диполями. При
конечных размерах частиц вместо б(р) появилась бы дельтооб-
разная функция, спадающая практически до нуля на расстояниях
порядка размера частиц. Второе слагаемое, обусловленное кор-
реляцией положений, напротив, описывает особенности рассеяния
на коллективе частиц. При достаточно большой концентрации
частиц я3) это слагаемое становится основным, и тогда можно
рассматривать рассеяние на системе частиц с коррелированными
положениями как рассеяние на объемных макроскопических
иеоднородностях сплошной среды с корреляционной функцией
фв = DлапM ц (р, R).
Условие, при котором можно при любых умах рассеяния
пренебречь «дискретным» слагаемый aHM »° сравнению с членом
ах0„ имеет вид
8яап(Фц)ш1п>1, C1.42)
гДе (Фц)т1а — минимальное,(по q) значение спектра. При выпол-
нении же неравенства 8п'п (Ф^)™, <^ 1 можно пренебречь кол-
лективными эффектами. Если ни одно из этих неравенств ие
выполняется во всем диапазоне изменения угла рассеяния
0<9<л, то надо нользоваться_либо полным сечением C1.33),
либо, определив из условия 8л*пФ„~1 граничный угол 8гр, поль-
зоваться различными предельными формулами при 8 > вгр и
о < егр.
6. О иекогерентном рассеянии в плазме. Этот
вопрос мы уже затрагивали в § 30. Здесь мы рассмотрим рас-
сеяние на свободных электронах в плазме под другим углом
зрения, а именно как пример явления, в котором, в силу осо-
бенностей парной корреляции, коллективное рассеяние оказы-
вается пропорциональным не второй, а первой степени концен-
трации электронов Ne.
Двумерная плотность вероятностей w2(r1} r,) в случае плазмы,
находящейся в равновесии при температуре 7", выражается рас-
пределением Больцмана:
wt(tx, г,) = const-ехр Г_"»^-
где & = кТ—температура, выраженная в энергетических едини-
цах, а Uu(rlt T,) — Olt(rl — г,) —эффективная потенциальная
г) Совместимой, однако, с условием 4лла<^ 1, при котором можно не учи-
тывать вклада кваэистяцисшарного поля. Учет /-*кп припел бы к формуле
Лпрентца —Лиренца |13].
250 ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. IV
энергия электрона, находящегося в точке г2, в поле другого
электрона, расположенного в точке г,.
Предположим, что частицы равномерно заполняют большой
объем V, так что шг (г) = const — l/V, и рассмотрим случай, когда
энергия взаимодействия двух электронов Uia мала по сравнению
с энергией теплового движения В = кТ. Тогда приближенно
двумерная плотность будет равна
C1.43)
Сравнивая C1.43) с формулой C1.23), в которой нужно поло-
жить ш1=1/К, получаем для функции ц, характеризующей кор-
реляцию положений электронов, приближенное выражение
В случае изотропной плазмы 1/1, = е<р1„ где tp12—дебаевский
потенциал, отличающийся от кулоновского потенциала е/\т1—гг|
экспоненциальным множителем ехр {—| г,—Tt\ld}, где d =
— (в/8яегА/г)'/1 — дебаевский радиус (радиус экранирования)
[14], а Л^„ — средняя концентрация электронов. Таким образом,
Преобразование Фурье этой функции, равное
обратно пропорционально концентрации Ne, так что для попе-
речника коллективного рассеяния по формуле C1.35) находим
В результате суммарный поперечник рассеяния C1.33) оказы-
вается равным
или, учитывая, что поперечник рассеяния отдельной частицы
а1=7^оО?|1 в случае электрона равен уг^ — уеЧш'с1,
C1.45)
В предельном случае коротких волн (qd^>\) из C1.45) сле-
дует, что _
C1.46)
ЗАДАЧИ 251
Таким образом, суммарный эффект при рассеянии коротких волн
на тепловых флуктуациях электронной концентрации оказывается
таким же, как при рассеянии на N свободных электронах. Это
связано с независимым характером движения электронов в пре-
делах области Ar~\/q<^.d, целиком лежащей внутри сферы де-
баевского радиуса d.
В противоположном случае, когда длина волны Aq=2n/q
много больше дебаевского радиуса, движение электронов уже
нельзя считать независимым от движения ионов. В этом случае
сечение рассеяния будет
o = V2V^ (qd<^\), CI.47)
т. е. вдвое меньше, чем в C1.46).
Задачи
1. Показать, что полный поперечник рассеяния единичного объема а в
случае мелкомасштабных флуктуации (*'е<й1) равен
}Ц j С)
- <Ю
а в случае крупномасштабных флуктуации (А/е^>1) —
Решение. Формула A) сразу же следует из определения B6.13), так
как при kle <^ 1
В случае же А/е^-1 надо учесть, что существенный вклад в B6.13) дают
только малые углы рассеяния в^С 1/?/е<^; 1. Вводя переменные интегрирова-
ния Xi = *6cos(p, и2 = *в5тф и учитывая, что при малых углах рассеяния
Фе^) я; Фе(><1. Ks, 0) и do — sinedftdtp ~-p- dxidKj, получаем формулу B).
2. Оценить полный поперечник рассеяния а0 световых волн в случае тур-
булентных флуктуации со спектральной плотностью <Ьл{х) = ЛСЦхг+х1)-;
не имеющей особенности при х—>-0 (х0 = 2я/10 — волновое число, отвечающее
внешнему масштабу турбулентности ?„).
Решение. В оптическом диапазоне длина волны X мала по сравнению
с внутренним масштабом турбулентности 10. Поэтому для расчета о, можно
воспользоваться формулой B) предыдущей задачи, что дает (при Л — 0,033)
252
ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН
1ГЛ. IV
В приземном слое атмосферы при Я—510"* см, /-о — 1 м и С\— 10~1ь см"*'1
для длины экстннкции d,—1/о0 получаем оценку ds~20 м. Это означает, что
в задачах распространения света в приземном слое атмосферы применимость
борновского приближения ограничена дистанциями такого порядка,
3. Оценить, пользуясь B7.3), поперечный радиус корреляции поля прн
обратном рассеянии, считая, что размеры рассеивающего объема L ограничены
шириной диаграммы излучающей антенны v (Рис- 34).
Решение. Главный лепесток диаграммы выреза-
ет участок слоя с поперечными размерами L — гу. Пи
формуле B7.3) имеем 1^~1/у. Но у — I'd, где d—
размер антенны. Поэтому l,~~d, т. е. прн ' обратном
рассеяинн полеречный радикс корреляции поля порядка
диаметра антенны d.
4. На рассеивающий объем V, расположенлый вбли-
зи идеально отражающей плосности г = 0, падает плос-
кая волна Ле''*шг. Найти среднюю интенсивность рас-
сеянного поли в зоне Фраунгофера, предполагая, что
поверхность г = 0 абсолютно жесткая, так что гранич-
ди
ное условие имеет вид -^у = 0.
oN z—o
Р е ш е я и е. Полное первичное поле, удовлетворяю-
щее граничному условию, имеет вид ио= A(eihmr l c'frm*r),
рис 34 гДе m* — единичная нормаль к фазовому фронту отра-
женной волны Un%~—тг)- Функция же Грина для
абсолютно жесткой поверхности равна
ikR p elk
' ' R'
где R — | г — r' |, R* — | г — r'*|, a r'* — радиус-вектор зеркально отраженного
источника г', так что г'* — {*', у', —г'}.
Подставляя «« и G в формулу B4,11) и используя разложения типа
B5.12), находим, что в зоне Фраунгофера
-4^ f
(О
Отдельные слагаемые в A) отвечают четырем возможным видам рассеяния,
схематически показанным на рис. 35. Соответствующие векторы рассеяния
равны
q^fcfn— m), qa-i(n —m*), qs —A(n'—m), q4=-6 (n*— m*),
где через п* обозначен вектор, «зеркальный» по отношению к единичному
вектору n — r/г, направленному из центра рассеивающего объема в точку
наблюдения (л*— —пг).
Выражение для средней нитенсивиостн /t — <] "i |*>, вычисляемое при по-
мощи A), содержит 16 слагаемых, но существенную роль играют только
четыре из них [15]:
B)
Задачи
253
Остальными 'менами можно пренебречь (нх нужно учитывать только при
mz ¦ у О или м,—»0, т.е. при малых углах скольжения перзичиой или рас-
сеянно': волн). В случае крупномасштабных неоднородностей существенный
вклад п B) дают только слагаемые с q = q, и q — q3, которые отвечают, как
это видно из рис. 35, рассеянию иа малые углы.
Рис. 35.
5. Найти функцию корреляции рассеянного поля, если первичное излуче-
ние представляет собой периодическую последовательность коротких импуль-
сов, повторяющихся с периодом 7"„.
Решение. В случае покоящихся неодцородностен рассеянный сигнал
в момент 1 + 7*11 был бы в точности таких же, как и в момент (, н мы имели
бы периодическую no % — ll—/, корреляционную функцию, составленную из
слагаемых вида B9.10):
где Ка(П— коэффицнеит корреляции огибающей отдельного импульса B9.11).
При рассеянии же на неоднородностях 7.-1A, г), меняющихся во аре-
ыени, корреляция сигналов в моменты времени ; и /-f 7"„ будет неполной,
потому что за время Т„ рассеивающая среда изменяется. В этом случае из
254
ТЕОРИЯ ОДНОКРАТНОГО РАССЕЯНИЯ ВОЛН
[ГЛ. IV
B9.1) и B9,4) можно получить, что
= 2
где
/-В/с) |2Фе(тГ„,Ч) <*</?.
Очевидно, /о @ совпадает со средней интенсивностью /„(')> которая дается
выражением B9.5).
Зависимость функции корреляции т?г, (t, t — т) от т при фиксированном t
схематически показана на рис. 36 в предположении, что Тп$.-Т. Ширина
отдельных максимумов ^v определяется длительностью импульсов Т, а рас-
стояние между максимумами равно Тп. Высота отдельных максимумов lm
уменьшается с ростом m в соответствии с временным ходом Фе(т7*п, q).
Следовательно, по убыванию максимумов с ростом m можно судить о времени
корреляции неоднородностей [16].
6. Пусть рассеивающий объем облучается двумя первичными волнами с
разными частотами m-i и ьц. Найти интервал частотной корреляции рассеян-
ного поля в зоне Фраупгофера.
Решение. Обозначив через iti(ti>i, г) и Ui(o>2, г) соответствующие этим
волнам рассеянные поля, которые в зоне Фраунгофера даются выражением
B5.39), для коэффициента частотной корреляции находим
i, г)иГ(т8,г)> 8я»
===^-=у-
i) h (cos)
Дю
где Дсо — ш1 — coj, о>(и)—дельтообразная функция, определенная соотноше-
нием B7.8), a q = —(п^— п,-) — вектор рассеяния на средней частоте co^fc»,-]
-f-(i>i)/2. Интервал частотной корреляции До) можно оценить из неравенства
Дев. ... 2л /Асо \
— |Ч|^—г~> ПРИ выполнении которого функция 0/ —q еще заметно от-
лнчается от нуля. Учитывая B5.32), получаем, что
. ?~-21Ш не
U>^~Lq~Lsin(ej2)'
т. е. интервал коррелниии совпадает с шириной полосы частот B9.9), в кото-
рой каналы связи, использующие рассеяние, могут работать без искажений |1].
7. Выяснить, как меняется число когерентно рассеивающих частиц при
изменении длины волны в случае облака частиц, равномерно распределенных
в объеме шара, и в случае непрерывного плавного (в масштабе длины волны)
распределения.
Решение. Для частиц, равномерно распределенных в объеме шара
радиуса а,
aij (г) = const = -р-= С/з^о3) -1,
так что по формулам C1.10) и C1.12) получаем
При qa^>\, т. е. при в^Х/а, NK0T убывает пропорционально (ад)~
ЗАДАЧИ 255
Еще более быарое (экспоненциальное) убывание NKOr с ростом qa про-
исходит при учете размытых границ облака рассеиоателей. Пусть плотность
вероятностей t»i(r) плавно спадает от центра облака к периферии с характер-
ным масштабом изменения а, равным по порядку величины радиусу облака
(о^>Л). Учитывая, что шах ш,--1/а3, и используя известные свойства интег-
ралов Фурье [17], для модуля характеристической функции f, (q) получаем
оценку
., 1 к I 4nosin(8/2)\ .,
l/i(q)l~-«—-teas,nte/2)e»p( j^-'J. A)
Отсюда следует, что при рассеянии назад F-=-л, q — 2k) величина NKBT со-
ставляет ничтожно малую долю от N уже прн ка^ 10, т. е. при о^ 1,6?..
Легко объяснить, почему число когерентно рассеивающих частиц умень-
шается с ростом ka. Рассмотрим слон толщины tf<s?X, в котором qrh = const
с точностью до величин порядка d/X<^. 1 (слой ориентирован перпендикулярно
к вектору рассеяния q). Частицы, находящиеся в этом слое, рассеивают
падающее излучение синфазно (когерентно). Для каждого такого слоя можно
подобрать другой тонкий слон, излучающий в противофазе (для зтого он
должен быть удален на нечетное число полуволн Л?) н частично гасящий
излучение первого слоя. Гашение было бы полным, если бы оба слоя содер-
жали одинаковые числа частиц. Однако, в силу случайного положения частиц
в пространстве, каждая пара слоев дает малый некомпенсированный остаток.
Сумма таких остатков и оценивается формулой A).
Глава V
РАСПРОСТРАНЕНИЕ ВОЛН
В СРЕДАХ С КРУПНОМАСШТАБНЫМИ
СЛУЧАЙНЫМИ НЕОДНОРОДНОСТЯМИ
МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
§ 32. Уравнения геометрической оптики
В этой и двух последующих главах мы рассмотрим прибли-
женные методы решения задач о прохождении волн через среды
с крупными случайными неоднородностями, характерные размеры
которых /в велики по сравнению с длиной волны Я. Как мы
уже знаем, при этом рассеяние на большие углы (и, в частно-
сти, рассеяние назад) пренебрежимо мало. В результате флук-
туации волнового поля определяются преимущественно теми
неоднородностямн, которые лежат на пути волны, т. е. в окрест-
ности луча, соединяющего источник н точку наблюдения. Обычно
говорят поэтому не о рассеянии, а о распространении волн в
случайно-неоднородных средах с крупными неоднородностями.
Задачи такого типа, как и задачи о рассеянии воли, рассмот-
ренные в предыдущей главе, относятся, по классификации § 8,
к статистическим проблемам типа 2).
Существуют три основных приближенных метода, используе-
мых для решения задач о флуктуациях коротковолновых (>.<^^)
полей в случайно-неоднородной среде: метод геометрической
оптики (МГО), метод плавных возмущений (МПВ) и метод пара-
болического уравнения (МПУ).
Сначала мы рассмотрим наиболее простой и наглядный из
них — метод геометрической оптики. Первые расчеты по флук-
туациям волн в средах с крупными неоднородностямн были
проведены именно при помощи МГО ([1, 2] и др.; библиографию
см. в [3—5]). Простота метода связана с тем, что, в отличие
от метода плавных возмущений и метода параболического урав-
нения, приближение геометрической оптики не учитывает ди-
фракционных эффектов, в силу чего область его применимости,
конечно, уже, чем у МПВ и МПУ. Однако в своей области
метод геометрической оптики обладает определенными достоин-
ствами. Во-первых, при помощи МГО удается исследовать ряд
эффектов (таких, как влияние регулярной рефракции и усиление
флуктуации поля в окрестности каустик), которые труднее опи-
сать при помощи двух других методов. Во-вторых, некоторые
результаты МГО сохраняют силу п за пределами области его
применимости. Это относится к расчетам флуктуации фазы и
5 321 УРАВНРНИЯ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ 257
направления распространения волн (но не к флуктуациям ампли-
туды). Указанные достоинства немало способствовали тому, что
метод геометрической оптики широко применялся, несмотря на
успехи, достигнутые при помощи МПВ и МПУ. Можно добавить
еще, что приближение геометрической оптики послужило эври-
стической основой при разработке обоих указанных асимптоти-
ческих методов, учитывающих дифракционные эффекты.
Напомним коротко вывод уравнений геометрической оптики
для простейшего случая скалярной монохроматмеской волны,
распространяющейся в среде с неподвижными непрерывными
неоднородностями. Пусть проницаемость е(г) в уравнении
Гельмтольца
Auffc'e(r)u = O C2.1)
мало меняется на длине волны ^ (X|Vb|<^e— плавно неодно-
родная среда). В этих условиях естественно предположить, что
поле и в каждой точке приближенно имеет структуру плоской
волны:
u=*Aets = Ae""*, C2.2)
где амплитуда А и градиент фазы VS—медленные (в масштабе \)
функции координат.
Воспользовавшись медленностью изменения А и VS, нетрудно
получить уравнения для Л и S или для величины q> = S/ft, ко-
торая представляет собой фазовый путь волны и называется
эйконалом').
Предложенный Дебаем способ вывода уравнений для ампли-
туды А и эйконала <р состоит в следующем. Разложим ампли-
туду А в ряд по обратным степеням волнового числа1):
. C2.3)
Коэффициенты Лт в этом разложения в общем случае комп-
лексны и поэтому дают вклад и в фазу результирующего поля.
Подставив ряд C2.3) в уравнение Гельмголыш и приравняв
нулю коэффициенты при одинаковых степенях k, получаем
') Иногда эйконал ф тоже называют фазой, по ми будем употреблять
термин «фаза» только для безразмерной величины S — ?ф.
а) Строго гопоря, разложение следует проводить по безразмерному малому
параметру n~l/WEl где U~ t./\ vepj? X—характерный масштаб неоднород-
ностей (см , например, F|). Однако разложение по степеням 1/* фактически
означает именно разложение по степеням ц=1/Ме.
? С. м. Рыто» и ло. ч. II
268 МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ [ГЛ. V
систему уравнений для ф, Ло, At, А„ ...:
(ft') (Yq>)"-«, C2.4)
(k) 2(Тф ХА„) + Л„Дф-=0, C2.5)
iip = — ДЛ„, C2.5а)
Уф = — ДЛ,.!, C2.56)
Уравнение C2.4) носит название уравнения эйконала, а после-
дующие уравнения для Л„ (л = 0, 1, 2, ...) называют уравне-
ниями переноса для амплитуд соответственно нулевого, первого
н га-го приближений. Обычно ограничиваются нулевым прибли-
жением МГО, оставляя в разложении C2.3) только член Ло.
Последующие члены в C2.3) отбрасывают ие только из-за слож-
ности их вычисления, ио главным образом потому, что ряд
C2.3) является асимптотическим1), а для асимптотических раз-
ложений, как известно, увеличение числа учитываемых членов
не всегда ведет к улучшению аппроксимации.
Уравнению эйконала C2.4) отвечают характеристики (лучи),
на которых функционал j Vsds экстремален (принцип Ферма).
Уравнения лучей можно записать в различных формах. Для
наших целей их удобно представить в виде [3, 4]
17 = *' "I—йГ*в-*(**»)]. <32-6)
где ds—элемент длины луча, a t—касательный к лучу единич-
ный вектор, который одновременно является и нормалью к фа-
зовому фронту S = fcq> = const. Так как |Vq>| = p/"e, имеем
t
Если тем или иным способом решение лучевых уравнений C2.6)
найдено, то уравнение эйконала C2.4) и уравнения переноса
C2.5) могут быть проинтегрированы вдоль лучевых траекторий.
Эйконал ф находится по формуле
C2-7)
') Ои сходится к точному решению уравнения Гельмгольца, если одно-
временно с увеличение» числа членов устремить волновое число k к беско-
нечности или, точнее, если безразмерный малый параметр р,~ 1//Ые устремить
к нулю.
i 321 УРАВНЕНИЯ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ 259
а амплитуда А„ — из условия сохранения интенсивности / — У г А\
в бесконечно тонкой лучевой трубке сечеиин dS (рис. 37):
/ д.2 = VI A\dZ - const. C2.8)
Последнее соотношение вытекает непосредственно из уравнения
переноса C2.5), если записать последнее в виде
div (А\ Т<р) = div (J/1 А\\) = div (/t) =- О
и проинтегрировать по объему между двумя сечениями беско-
нечно тонкой лучевой трубки.
Одно из условий применимости МГО состоит в требовании
плавности изменения параметров среды:
C2.9)
В гл. VI, § 38 мы убедимся, что переход к геометрическому
приближению (т. е. пренебрежение всеми членами в C2.3), кроме
нулевого) допустим при условии
малости радиуса первой зоны
Френеля j/XL (L— дистанция,
пройденная волной) по сравнению
с характерным масштабом неод- ^«j
породностей /в:
C2.10) Рис- 37'
При выполнении этого условия можно пренебречь дифракцион-
ными эффектами, которые в рамках МГО проявляются именно
в первом порядке по n^=l/We-
Обратимся теперь к случайно-неоднородной среде. Получить
аналитическое решение уравнения эйконала C2.4) или уравне-
ний лучей C2.6) при произвольной зависимости проницаемости в,
от координат невозможно. Это вынуждает к здесь при решении
статистических задач прибегать к приближенным методам и в
первую очередь—^к методу возмущений'. Пусть г (г) =е(г) + е(г),
причем флуктуационная компонента е мала по сравнению с
регулярной: ак<^«. Представим эйконал в виде ряда
Ф-Ф. + Ф. + Ф.+ --- . C2.11)
предположив, что <р0 удовлетворяет «невозмущснпому» уравнению
эйконала
(Vq>,L-I C2.12)
н | Vcp! I ~ <те -^ I Vq>o|. I V<p,|~°KI,V(p,| и т.д. Подставляя ряд
B3.11) в уравнение эйконала C2.4) и учитывая C2.12), получаем
260 МКТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ [ГЛ. V
дли поправок q>,, фа, ... следующие линейные уравнения:
ф1) = Е, no i«
Решения этих уравнений можно выразить в квадратурах,
если известны невозмущенны ii эйконал ц:„ и не возмущенные
лучи ro = ro(i) и td^tofs), удовлетворяющие лучевым уравне-
ниям C2.6) при е = е. Заметим, что в нулевом приближении
Vf, - У е t,, где t0 — drjds—единичный вектор, касательный
к невозмущенпому лучу г —ro(s). Тогда уравнение C2.13) для
поправки первого порядка ср,, которой обычно и ограничиваются
чри расчетах, принимает вид
2(ГФ„ГФ1) = 2/Г(иФ1) = 2/Г^ = 8~, C2.14)
откуда следует, что
s
^^'. C2.15)
о
Интегрирование здесь ведется вдоль невозмущенного луча
r = ro(s), т.е. под знак интеграла входят функции e^e[re(s')J
и ?-¦?[!•„ (s')].
В простейшем случае плоской волны, распространяющейся
вдоль оси z в однородной (в среднем) среде с е — const, невоз-
мущенное значение эйконала ф равно фо = Ке г; при этом лучи
представляют собой прямые, параллельные оси г:
х„ (s) — const, у„ (s) = const, zt(s) = s.
В этом случае
j7
2К
C2.16)
Для приземной атмосферы, а также для ионосферы в случае
ультракоротких радиоволн можно считать ,что еж 1, и тогда
z
tPx^V.S^.jr, z')dz'. C2.17)
о
Аналогичным образом, как мы увидим далее, можно развить
теорию возмущений для амплитуды, направления распростране-
ния волн, отклонений луча от невозмущенной траектории и т.д.
§ 33] ФЛУКТУАЦИИ ЭЙКОНАЛА 261
Применяя метод возмущений для расчета флуктуации ампли-
туды it фазы волн, мы используем малость флуктуации про-
ницаемости:
сте<?, C2.18)
и отбрасываем члены второго порядка малости относительно ос.
Условия, при которых можно пренебречь членами второго
порядка малости, сводятся к требованию малости дисперсии
уровня амплитуОы х = 1п(Л/.4°):
^Ш-г)')-<-!!><1, C2.19)
что эквивалентно (при малых стх) условию ол<^.А. Заметные
флуктуации уровня х наступают, очевидно, там, где лучи начи-
нают пересекаться и образуют случайные фокусы и каустики [7].
Поэтому условие C2.19) фактически ограничивает интенсивность
флуктуации CTg и дистанцию L такими значениями, при которых
образование каустик еще маловероятно.
Приведенные условия применимости имеют характер доста-
точных условий. Что же касается необходимых условий, то
здесь можно высказать только качественное соображение, состо-
ящее в том, что дифракционные эффекты слабее влияют на
поведение фазы, чем амплитуды, вследствие, чего пределы при-
менимости расчетов фазы могут оказаться более широкими.
И действительно, сравнение с методом плавных возмущений
показывает (§41), что некоторые результаты геометро-оптического
приближения, относящиеся к статистическим характеристикам
фазы и углов прихода, справедливы (с точностью до коэффи-
циента порядка единицы) за пределами, устанавливаемыми нера-
венствами C2.10) и C2.19). Неравенства же. C2.9) и C2.18)
должны выполняться в любом случае.
Ниже мы проведем расчеты различных характеристик слу-
чайной волны (флуктуации фазы и уровня волны, статистика
углов прихода и боковых смещений лучей, определение среднего
поля и его функции когерентности), которые нужны для решения
как прямых, так и обратных задач статистической теории рас-
пространения волн. Результаты данной главы (как и двух после-
дующих глав) применимы к анализу широкого круга физических
явлений (см., например, [3—5]).
§ 33. Флуктуации эйконала
В первом приближении теории возмущений для эйконала <р
имеем <р л; <р0 + <рг Среднее значение поправки первого поряд-
ка ф, равно нулю, ч>! = 0, так что в принятом приближении
флуктуационная компонента эйконала ф = ф— tp совпадает с ф^
262
МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
а корреляционная функция равна
*»(»i. г,) = <ф (г,) ф (г,)> = <ф1 (г,) ф, (г,)>. C3.1)
Корреляционная же функция фазы S = feq> равна, очевидно,
r1). C3.2)
Начнем с наиболее простого случая. Пусть плоская волна
е**г распространяется в статистически однородной среде со сред-
ним значением диэлектрической проницаемости <Г— 1. Используя
C2.17), получаем для функции корреляции эйконала выражение
wvrj^ui&i&bfPi-p., *'-о. (зз.з)
о о
где г, = (р,, Zj) и г, = (р„ za)— радиусы-векторы точек наблюдения,
а ^—корреляционная функция флуктуации г. Перейдем в C3.3)
к новым переменным интег-
рирования ^¦¦^¦г'—г" и т) =
= (z' + z")/2. В этих пере-
менных
V-
\ ч
/->
1
1
-z,jl
где 2—область интсгрирова-
Рнс' 38' НИЯ В ПЛОСКОСТИ (g, 1\). ЕСЛИ
z, > Zj, то эта область имеет
иид параллелограмма, показанного на рис. 38.
Существенный вклад в интеграл C3.4) дает только узкая
полоса —/е^?^'а (на рис. 38 она заштрихована), в пределах
которой корреляционная функция яре заметно отличается от нуля.
Поэтому пределы интегрирования по ? можно сделать бесконеч-
ными, а интеграл по г\ брать от 0 до гд:
О
Здесь учтено, что функция ф, четна по ?. При г, < г, мы по-
лучили бы аналогичное выражение с г2 вместо г1. Таким образом,
C3.5)
i 33] ФЛУКТУАЦИИ ЭЙКОНАЛА 263
где z< = min jz,, Zj[ —меньшая из величин г, и г,, а р = р, —р,.
В частности, для изотропных флуктуации
!>фЛ, г,)»-¦?¦[¦.(Vv4Tl)«. C3.6)
b
Корреляционную функцию эйконала можно выразить н через
пространственный спектр флуктуации е. Подставив в C3.5)
спектральное разложение
н выполнив интегрирование по ?, находим
Фф (г„ г,) = -^ | Фе (к±, 0) exp (iXj.p) <?хх. C3.7)
Если флуктуации е изотропны, то Ф8(хх, 0
— ^е (хх) и переход к полярным координатам х = | их | = KxJ + xj,
a = arctg(xv/xx) с последующим интегрированием по угловой
переменной а дает
% (""к г.) = лаг< J Фе (х) Ja (кр) х dx, C3.8)
о
где ^0(х)—функция Бесселя нулевого порядка.
Дисперсия эйконала aj,, получающаяся из C3.5) или C3.7)
при р — 0 и z, — г, = z, линейно растет с увеличением дистанции г:
<о ос
В случае изотропных флуктуации
<4 W = 1J *е (С) « = л»г J Фе (х) х А.У.. C3.10)
о о
Интеграл от г|)е в этих выражениях равен произведению диспер-
сии флуктуации <т| на эффективный интегральный радиус кор-
реляции ;8фф = \ Ке @, 0 d?. Поэтому C3.9) можно представить
о
также в виде
264
МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
1ГЛ V
Если, например, функция корреляции i]:e имеет гауссову форму
Ыр)=а!е-р>К, _ C312)
то эффективный радиус корреляции /8фф равен \fn/2lt и
Рассмотрим продольную корреляцию эйконала, считая, что
точки наблюдения т1 и г, расположены на одном и том же луче
@)
C3.14)
Из этого выражения видно, что продольная функция корреляции
не меняется с ростом большей из величин г, и г,. Отсюда не
следует, однако, что при продольном разнесении точек наблю-
дения сохраняется также и коэффициент корреляции Л",. В самом
деле, из C3.14) находим
2< --.
^ V
мри
при
зависимости Кг, от г, при фиксированном значении г1
показан на рис. 39, из которо-
го ясно, что продольная корре-
ляция ф (а следооательно, и фазы
S) простирается па расстояния по-
рядка пройденного пути, т. е.
Иными линейными масштаба-
ми характеризуется поперечная
корреляция эикоцала. Считая, что
точки наблюдения разнесены толь-
ко в поперечном направлении
р р
l — z, — L), для поперечной функции корреляции имеем
C3.15)
а при изотропных флуктуациях ё
C3.16)
S 3;fl ФЛУКТУАЦИИ ЭГЖОНАЛА 265
Из выражений C3.15) и C3.16) следует, что поперечная корре-
ляция простирается на расстояния порядка /„—радиуса корре-
ляции диэлектрической проницаемости, т. с. lL ~ 1е. Это не-
посредственно видно и на примере гауссовой корреляционной
функции C3.12), для которой
*х (р, L) -^ LUd\e'P'''Jl = o^We-^'l C3.17)
В дальнейшем нам понадобится также поперечная структур-
ная функция эйконала
) <[П>! (Pl Ц-Ф, (Р,. L)\*>,
которая выражается через поперечную корреляционную функ-
цию i))^ (если она существует) следующим образом:
Di (РД) - 2[^ @, /.)-*! (р, Ц] -L 1 fe @, 9-^ (Р,
о
Но согласно D.7)
¦.(Р. ?)-
и поэтому
ОС
]" C3.18)
В отличие от C3.15), эта формула пригодна не только для одно-
родных, но и для локально однородных случайных полей е, когда
корреляционной функции i|re не существует. Для «локально
однородных и изотропных полей вместо C3.18) имеем
)=y С [^(КрЧ^5)-^(?)]<«• C3.19)
Приведем также аналогичное C3.8) выражение для DL через
пространственный спектр флуктуации:
DL(p,L) -2n*L\or.(K)[\-JlI(KP)\xdx. C3.20)
о
Эти формулы понадобятся в § 36 при анализе флуктуации эйко-
нала в турбулентной атмосфере.
Мы рассмотрели флуктуации плоской волны в статистически
однородной среде. Но, оставаясь в рамках метода геометрической
266 МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ГГЛ. V
оптики, нетрудно получить характеристики флуктуации ненло-
ских (в первую очередь сферических) волн, учесть регулярную
рефракцию_волны, обусловленную изменением средней прони-
цаемости е(г), и отказаться от статистической однородности
флуктуации е, ограничившись квазиоднородностью. Эти возмож-
ности, собственно rqeopH, и составляют преимущество МГО по
сравнению с другими асимптотическими методами—МП В и МПУ,
в которых указанные обобщения либо приводят к слишком
сложным выражениям, либо вообще неосуществимы.
Проведем качественное рассмотрение некоторых обобщений,
используя результаты, полученные выше для плоской волны
(разумеется, количественные
выводы должны опираться на
* исходное выражение C2.15)).
Рассмотрим два невозмущен-
ных луча, отвечающие иеплос-
кой волне (рис. 40). Обозначим
р tf) через /., и Ц длины этих лучей,
' приходящих в точки наблюде-
ния г, и г,, через t01 н t0,—
единичные векторы вдоль этих лучей, а через 6—вектор, соеди-
няющий точку на одном луче с ближайшей к ней точкой на
другом луче. Для краткости мы будем называть 6 «расстоя-
нием» между лучами. В рассмотренном выше случае плоской
волны величины Z,, и Lt были расстояниями от начальной плос-
кости z = 0 до точек наблюдения г, и г,, векторы t01 и t,, были
равны друг другу и направлены по оси г, а расстояние между
лучами в совпадало с поперечным разнесением точек наблюде-
ния 8 — р = р,—р,. Поэтому выражение C3.5) в новых обо-
значениях запишется следующим образом:
где /.< {, ,}
Главная особенность неплоской волны заключается в том,
что расстояние между лучами 6 является переменной величи-
ной, зависящей от пройденного волной пути s. Если попереч-
ное разнесение точек наблюдения мало по сравнению с длинами
лучей Lx и L2, то дистанцию s удобно отсчитывать вдоль неко-
торого среднего луча, приходящего, скажем, в точку (г,-(-г,)/2.
При этом единичные векторы t0l и t0, приближенно можно счи-
тать равными единичному вектору t, вдоль среднего луча (на
рис. 40 средний луч показан пунктиром). Чтобы получить пра-
вильный результат при переменном расстоянии между лучами,
33] ФЛУКТУАЦИИ ЭЙКОНАЛА 267
нужно заменить в формуле C3.21) L< на $ ds и рассматривать
о
X, как единичный вектор вдоль среднего луча. Для функции
корреляции нсплоской волны в статистически однородной среде
с е — 1 мы получим тогда
L< «
f U . C3.22)
Совместив точки наблюдения г, и г„ т. е. положив Z., =
—La=L и 6(s) —0, находим из C3.22) выражение для днспер-
син эйконала:
CD
$ C3-23)
Отсюда видно, что дисперсия эйконала о}, не зависит от вида
первичной волны и, в частности, одинакова для плоской, сфе-
рической н цилиндрической волн.
Используя C3.22), рассмотрим поперечную функцию корре-
ляции эйконала расходящейся сферической волны, полагая, что
источник и точки наблюдения находятся внутри случайно-не-
однородной [среды (флуктуации в слое конечной толщины рас-
смотрены в задаче 1, а особенности флуктуации фазы сходя-
щейся сферической волны — в задаче 2). Пусть точки наблюдения
г, и г, расположены на одинаковом расстоянии L от источника.
Если р = Г!—г,—поперечное расстояние между точками наблю-
дения, то текущее расстояние между лучами 6 (s) линейно
меняется от нуля при s = 0 до р прн s = L:
Следовательно, для сферической волны
№ (P. L) = ^ f ds U, (p L + u) d?. C3.24)
&ry формулу можно записать иначе, если учесть, что
C3-2б)
268 МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ [ГЛ. V
где 1|з5л(р, L) — поперечная функция корреляции плоской волны
C3.15). Отсюда следует полезная формула
L I
(рг- *-) = f«*vt"(». «• <33-26)
которая связывает функции корреляции эйконала сферической
и плоской воли.
В случае изотропных флуктуации параметров среды, когда
1|>фл зависит от р "¦ | р |, функция корреляции эйконала сфериче-
ской волны тоже будет зависеть только от р и выражение
C3.26) можно записать в форме
Из этой формулы, как и из C3.24), следует, что радиус кор-
реляции эйконала у сферической волны больше, чем у плоской,
поскольку при одинаковом конечном расстоянии р текущее
расстояние 6(s) между расходящимися лучами меньше, чем
между параллельными. Очевидно, для сходящейся сферической
волны будет справедливо обратное соотношение (см. задачу 2).
Рассмотрим конкретный пример вычисления t|>J.*. В случае
гауссовой корреляционной функции флуктуации г, когда ф™
дается выражением C3.17), для ^ получаем
где
— интеграл ошибок.
На рис. 41 коэффициенты корреляции эйконала показаны
кривой / для плоской волиы: ft{J,"(p) — exp (— р*/2/}) — и кри-
вой 2 для сферической волны: К"$ (р) - Кя/2 (/,/р) Ф (р//„). Из
рисунка видно, что уровень Kv=l/t достигается при р—1,18/,
в случае плоской волиы и при р = 2,40/,в случае .сферической,
т. е. поперечный радиус корреляции эйконала сферической
волны примерно в два раза больше, чем у плоской.
Обобщение C3.22) на случай среды с постоянной средней
диэлектрической проницаемостью е, отличной от единицы, осу
ществляется просто изменением масштабов в у в раз, т. е.
i 33] ФЛУКТУАЦИИ ЭЙКОНАЛА
заменой dsdr на dsdZ^iE:
ч. г,) =
о о
+«К-
269
C3.28)
Эта формула, однако, остается справедливой и тогда, когда в
медленно (в масштабе радиуса корреляции 1е) меняется вдоль
среднего луча: e = e[ro(s)]. Сам средний луч под действием ре-
гулярной рефракции становится при этом криволинейным, так
Рис. 42.
что направление касательного к нему единичного вектора t0
зависит теперь от s: to = to(s).
Наконец, можно отказаться и от предположения о статистиче-
ской однородности флуктуации среды и рассмотреть более общую
модель статистически квазиоднородных флуктуации. Функция
корреляции квазноднородного поля е имеет вид (§ 5)
r'-r', R), C3.29)
причем здесь дисперсия a'i(R) и коэффициент корреляции
УСе(г' — г", R) медленно (в масштабе /е) зависят от координаты
центра тяжести R =(г' —г")/2. При подстановке C3.29) в C3.28)
значения R следует брать на невозмущенном среднем луче
R =ro(s), а разность г —г" целесообразно представить в виде
суммы 6 (s) +10 (s) I, где 6 (s) — поперечное, а t0 (s) ? — продольное
расстояние между точками г' и г", лежащими на соседних лучах
(рис. 42). В итоге для функции корреляции эйконала имеем
<
jj e l
C3.30)
Под L< здесь подразумевается меньигая из длин криволинейных
лучей Lx и L2. Дисперсия получается из C3.30) при L^^L^ — L
270 МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ |ГЛ. V
н 6 = 0:
C331>
Внутренний интеграл в C3.31) представляет собой эффектив-
ный радиус корреляции:
В общем случае анизотропных флуктуации /афф зависит не
только от положения точки г0 (s) на луче, но и от направления
луча to(s) в этой точке. Записав дисперсию эйконала в виде
заключаем, что наиболыпии_ вклад в oj, дают те участки луча,
иа которых величина a\lxii.lz .максимальна. Отсюда, в частности,
следует, что флуктуации эйконала усиливаются по мере умень-
шения средней диэлектрической проницаемости е. Такое усиле-
ние флуктуации происходит, например, в ионосфере в области
отражения радиоволн, излученных с Земли (см. задачу 4).
Рассмотрим некоторые особенности поведения поперечной
(относительно невозмущепного луча) функции корреляции эйко-
нала, считая, что точки наблюдения г, и г, лежат на одном и
том же невозмущениом фазовом фронте <ро = const:
C3.33)
Очевидно, основной вклад в интеграл C3.33) дают тс участки
траектории, на которых расстояние между лучами минимально,
т. е. участки наибольшего сближения лучей (с этим мы уже
сталкивались при сопоставлении флуктуации в сферической и
плоской волнах в среде с е = const). Влияние расстояния между
лучами иа функцию корреляции эйконала можно проиллюстри-
ровать на примере наклонного падения плоской волны на отра-
жающий [слой С i = F(z). На рис. 43, а и 43,6 показаны две
34]
ФЛУКТУАЦИИ УГЛОВ. СМЕЩЕНИЙ И ЗАПАЗДЫВАНИЯ
271
amst ¦
пары лучей при разнесении точек наблюдения г, и т. на оди-
наковое расстояние р, по один раз — перпендикулярно к пло-
скости чертежа (рис. 43, а), а другой раз — в плоскости чертежа
(рис. 43, б). В_ первом случае оба луча параллельны друг другу и
расстояние б _между ними всюду равно расстоянию р между
точками наблюдения. Во . втором жел случае, когда лучи лежат
в одной плоскости, расстояние б всюду меньше р и даже обра-
щается в нуль в точке пересечения лу-
чей. Ясно, что величина радиуса кор-
реляции эйконала больше именно во
втором случае, когда лучи сближают-
ся. Различие радиусов корреляции в
случаях а и б означает, что регуляр-
ная рефракция приводит к анизотро- у
пни (аннзомерии) флуктуации эйконала,
в плоскости, поперечной к лучу.
В рассмотренном примере лучи,
отраженные от плоского слоя, обра-
зуют каустику, которая касается лу-
чей в точках нх поворота. Строго го-
воря, применение метода геометрической
оптики в этом случае незаконно, пос-
кольку на каустике, как известно, ам-
плитуда волны, вычисленная в прибли-
жении геометрической оптики, равна бесконечности в силу обраще-
ния в нуль сечения лучевой трубки dS, в формуле C2.8). Этот
недостаток метода геометрической оптнки можно, однако, испра-
вить, используя для описания поля вблизи каустики более
совершенные асимптотические методы, которые обеспечивают ко-
нечность поля на самой каустике, а вдали от нее дают сумму
падающей н отраженной волн вида Ие'*» [8]. В результате вдали
от каустики корреляционная функция эйконала отраженной
волны определяется тем же выражением C3.33), что н для па-
дающей волны. В непосредственной же близости к каустике при-
ближение геометрической оптики, разумеется, непригодно.
Рис. 43.
§ 34. Флуктуации углов прихода, боковых смешений луча
и группового запаздывания волны
1. Флуктуации углов прихода. Углы прихода
волны определяются направлением нормали к фазовому фронту,
которое в изотропной ^среде совпадает с направлением единич-
ного вектора t-=V<p/Ke, касательного к лучу. Найдем отклоне-
ние этого вектора от невозмущенного положения to = V<Po/' е.
272
МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
[ГЛ. V
С точностью до первого приближения включительно имеем
t_ УФ _ У(фо + <Р1-и-¦¦)
у
Но согласно C2.14) ё - 2 У ё (t0V9i), так что
t я* t, +_^_[vTl —t. (t. ТФ,)],
У е
и поправка первого порядка к направлению невозмущенного
луча t0 оказывается равной
4
У
C4.1)
где Vi — оператор поперечного (по отношению к невозмущенному
лучу) дифференцирования.
Согласно C4.1) вектор t, перпендикулярен к t, и лежит в
плоскости, касательной к невозмущенному фазовому фронту
Ф„ = const. Пусть а и 0 —
два единичных ортогональ-
ных вектора в этой плоскос-
ти, составляющие вместе с
вектором t0, касательным к
певозмущенному лучу, ор-
тогоналг.пый репер (а, 0, t,).
Вектор \t можно разложить
па две составляющие — по
направлениям а и 0:
С точностью до членов вто-
рого порядка малости углы
прихода луча 0а и Йр, от-
Рис 44. считываемые от направле-
ния невозмущенного луча t,
(рис. 44), равны соответственно t\a и t^:
q ^ , 1 . . [ дц>1 л ^ 1 5<Fi
Отсюда следует, что средние значения углов прихода в обеих
взаимно ортогональных плоскостях (t0, а) и (t0, P) равны нулю,
9а-=Вр=0, поскольку ф, = 0, а элементы корреляционной мат-
рицы этих углов даются выражением
I d2t|> i (Pi, Pa)
^ajl (Pi. Pj) = <6a (Pi) Op (Pa)> '¦= ~ лОлгг до,я ' C4.2)
5 34] ФЛУКТУАЦИИ УГЛОВ, СМЕЩЕНИЙ И ЗАПАЗДЫ11АНИЯ 273
Эту формулу можно немного упростить, сслн учесть, что
флуктуации эйконала в плоскости, касательной к невозмущен-
ному фазовому фронту, квазиоднородны: поперечная функция
корреляции эйконала -ф, (р,, P2) = t|u(Pp р~) «быстро» (с мас-
штабом ~/Е) зависит от разностного аргумента р —р,—р„ и
«медленно» (с масштабом /.е^>/Е)—от координаты «центра тя-
жести» р+ —- (р, -f р„)/2. Поэтому при переходе н формуле C4.2)
от переменных р, и р2 к переменным pup, мы можем диффе-
ренцировать только по разностной переменной р -р,—р,. Опу-
ская для краткости второй аргумент р+ у ф^ и -ф_, получаем
C4-3)
Второй вариант этого соотношения сохраняет силу не только
для квазноднородпых, ио и для локально однородных флуктуа-
ции е, когда корреляционной функции ^р не существует.
Выберем орты а и Р так, чтобы при малых р структур-
ная функция DL имела вид D_ ж сар? — Cppji. Тогда флук-
туации углов прихода 0а и 0р, взятые в одной и тон же точке
наблюдения, т. с. при р — 0, оказываются некоррелированными:
I с)гП . @)
^^0 (^Р) C4-4)
Дисперсии же этих углов даются выражениями
и в общем случае анизотропных флуктуации ^йконала различны.
В частности, эти дисперсии неодинаковы в случае отражения
плоской волны от плоского слоя, в котором к--в(г) (рис. 43):
даже при изотропных флуктуациях 8 флуктуации угла прихода-
в плоскости чертежа меньше, чем в перпендикулярной плоскости.
При распространении плоской и сферических волн в статис-
тически однородной и изотропной среде флуктуации эйконала
в плоскости, перпендикулярной к лучу, изотропны: D± (р) = Ojjp).
В этом случае, в соответствии с общими свойствами изотроп-
ных векторных случайных полей (см. задачу 4 к гл. I), корре-
ляционный тензор ifan выражается через единичный тензор fiaP
и симметричный тензор р«рр/р* (считаем, что 7—1):
Здесь i);c| —поперечна я,, a i|>^ —продольная функции корреляции
изотропного двумерного векторного поля в-={9а, 6Э} = {tla, tlf,\
274 МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ [ГЛ. V
(термины «поперечная» и «продольная» функции корреляции
относятся здесь к компонентам корреляционного тензора, а не
к корреляции вдоль и поперек луча). Из сравнения C4.6)
с C4.3) находим
Эти функции связаны соотношением
которое является очевидным следствием потенциальности век-
тора e«t, — Т<р!- Дисперсии углов 6а и Ор для изотропных
флуктуации е одинаковы:
<ela> = <e'f,> = ^=D"x(O). C4.8)
Для плоской волны, когда ?>х дается выражением C3.19),
для продольной и поперечной функций корреляции имеем
C4.9)
о о
В частности, если функция корреляции имеет гауссову форму
C3.12), то
Ч>1 (р) - =г+х (Р). til (Р) = ^| (l ~f.) +i (P).
где 1)>х(р) = о^ехр(—р4/2/|), а о% дается выражением C3.13).
Аналогичным путем можно вывести формулы и для сфериче-
ской волны. Укажем на полезное соотношение между диспер-
сиями углов прихода плоской и сферической волн'):
=1/,<в^>гз, C4.10)
1) Считается, как и при высоде C3.26), что источник сферической волны
расположен внутри случайно-неоднородной среды и об* волны (плоеная н
сферическая) проходят в среде одинаковый путь L.
S 34] ФЛУКТУАЦИИ УГЛОВ, СМЕЩЕНИЙ И ЗАПАЗДЫВАНИЯ 275
которое легко вывести, используя C3.26):
[¦1 @)]* = § J dy iff (W) |p-o = [¦! 1@)]™ \y'dy=~ [¦! @)]-.
о о
Таким образом, дисперсии углов прихода сферической волны
в три раза меньше, чем у плоской волны, прошедшей тот же
путь в среде. Качественно это можно объяснить различием в
величине поперечного радиуса корреляции (напомним, что у
сферической волны lL 'больше, так как лучи идут в среднем
ближе друг к другу, чем а плоской волне).
На опыте обычно фиксируются не сами углы 9а илн 0g, a
некоторые другие величины, при помощи которых затем и оп-
ределяются 9а и 9р (и большинстве случаев — приближенно). Так,
на интерферометре, ориентированном вдоль оси а и имеющем
базу ра, измеряется разность фаз AS (ра) = k Дер (ра). Если отнести
эту разность фаз к электрической длине базы kpa, получится
величина
которая при малых ра, а именно при (ia<$.lt, совпадает с
В соответствии с этим дисперсия
при малых р может служить мерой <9|>, поскольку при Ра^/,
<в1>»«/,в;@),
что совпадает с C4.8)
2. Статистика боковых смещений луча. Луч
в среде, содержащей случайные неоднородности, представляет
собой извилистую пространственную кривую. Вычислим средне-
квадратичное смещение луча от его невозмущенного положения,
ограничившись для простоты случаем плоской волны, распро-
страняющейся в статистически однородной среде.
Запишем для траектории луча r(s) ряд теории возмущений
по е: r(s) = ro(s)-| r1(s) + rs(s)+... Для поправки первого по-
рядка q = rx из уравнений лучей C2.6) имеем (при е=1)
L L I
SS' C4.11)
откуда видно, что в первом порядке теории возмущений луч
смещается только в поперечном по отношению к невозмущен-
ному лучу направлении: если волна распространяется вдоль
оси г, то вектор q содержит только х- и ^-компоненты.
276 МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ [ГЛ. V
Подставив в C4.11) значение сра из C2.17) и интегрируя по
частям, находим
If L
0 0 0
C4.12)
Составим корреляционную матрицу боковых смещений луча
". C4.13)
где <ja и (jB—компоненты вектора q по двум взаимно перпен-
дикулярным направлениям а и р" в плоскости г = const. Выра-
жение C4.13) можно упростить, перейдя в нем к переменным
интегрирования ? — г'—г" и т\ - (г' -j- z")/2. Повторив рассужде-
ния, использованные при выводе C3.5), получаем
<34'14'
Если флуктуации е изотропны, то изотропным будет и дву-
мерное векторное поле q. Элементы корреляционной матрицы
C4.14) в этом случае принимают вид, аналогичный C4.6):
где продольная и поперечная функции корреляции боковйх
смещений луча даются выражениями
C4.15)
Можно убедиться, что прн изотропных флуктуациях е взаимно
ортогональные компоненты боковых смещений ?a(p,) и 9з(ра) при
Pj — p, не коррелированы между собой
«/а<7е> = Ф5э @) = 0,
{ 31) ФЛУКТУАЦИИ УГЛОВ, СМЕЩЕНИЙ И ЗАПАЗДЫВАНИЯ 277
а средине квадраты qa и qp равны друг другу:
^- C4.16)
В частности, в случае изотропной гауссовой корреляционной
функции флуктуации проницаемссти C3.12) имеем
C4.17)
Если волна неплоская, но среда по-прежиему статистически
однородна и е=1, корреляционная матрица боковых смещений
C4.13) приводится к виду
^*?«^«. C4..8)
где, как н ранее, 6(s) — текущее расстояние между лучами, за-
висящее от поперечного разнесения точек наблюдения р. В част-
ном случае сферической волны Ь — ps/L, так что -5г- =-г*г и
можно написать
lJ?j3^ C4.14
Для среднего квадрата смещения qa получаем отсюда
d?. C4.20)
0 о
Но интегрирование по s дает /,3/30, и поэтому
— средний квадрат бокового смещения луча в сферической вол-
не в 10 раз меньше, чем в плоской.
Расчеты флуктуации углов прихода и боковых смещений
лучей можно было бы провести, опираясь на иной подход, раз-
витый в [4] и заключающийся в том, что случайные отклонения
и повороты луча можно прн определенных условиях описать
как марковский процесс, возникающий под действием случайных
«толчков», обусловленных градиентами диэлектрической прони-
278 МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ [ГЛ. V
цаемости (ч. I, §§ 30 и 36). При таком подходе задача сводится
к решению уравнения Эйнштейна — Фоккера для совместной
плотности вероятностей поперечных смещений н направлений
луча. В случае плоской волны, распространяющейся в статисти-
чески однородной и изотропной среде, решением уравнения
Эйнштейна —Фоккера является нормальный закон распределе-
ния, причем вторые моменты, полностью характеризующие нор*
мальное распределение, совпадают с вычисленными выше. Поэтому
рассмотрения статистики лучей при помощи уравнения Эйн-
штейна— Фоккера мы здесь не проводим. Отметим только, что
границы применимости такого подхода были установлены в [9,10],
а распространение метода на среды с регулярной рефракцией
было дано в работах [11 —13].
3. Флуктуации группового пути. Групповой путь 2
в однородной и изотропной среде определяется выражением
C4.22)
где
— групповая скорость волны. Очевидно, отношение Sic пред-
ставляет собой время распространения сигнала. В случайно-пре-
ломляющей среде групповой путь 2, а следовательно, и время
распространения сигнала испытывают флуктуации. Дисперсию
флуктуации группового пути можно вычислить методом возму-
щений. Ограничимся случаем, когда e = const, т.е. регулярная
рефракция отсутствует. Разлагая" 2 в ряд по малым флуктуа-
циям е, получаем для поправки первого порядка J?, к невоз-
UVf)
мущениому значению группового пути ¦^«——^~^>—-L выражение
Интегрирование ведется, конечно, вдоль невозмущенного луча.
В недиспергирующей среде как е, так и ё ие зависят от
частоты. В этом случае
l=r<& = q>i, C4.24)
е
т. е. возмущение группового пути Sx совпадает с возмущением
эйконала q>t. Это является следствием равенства групповой и
i 35) ФЛУКТУАЦИИ УРОВНЯ 279
фазовой скоростей в недиспергирующей среде, так что все ска-
занное в § 33 относительно флуктуации эйконала без каких-либо
изменений переносится и на флуктуации группового пути. В част-
ности, для дисперсии группового пути, в соответствии с C3.12),
имеем
L «
о* - < =- -I- Г ds С «Iv | U; г, (s)] dZ,. C4.25)
в о о
Важным частным случаем диспергирующей среды является
изотропная холодная плазма, для которой е и е даются выра-
жениями C0.29). Подстановка C0.29) в C4.23) приводит к выра-
жению (при ё = coast)
в котором под знак интеграла входит 1/е" вместо 1/е 'в выра-
жении C2.15) для эйконала <р,. Учитывая это, можно записать
выражение для дисперсии группового пути в плазме, аналогич-
ное C3.31), ио с заменой 1/е на 1/(к)8:
I. *>
C4.27)
Ясно, что дисперсии a> и а\ могут совпасть лишь при е я? 1,
т. е. в случае достаточно высокочастотных воли, для которых
§ 35. Флуктуации уровня
Как мы уже указывали, уровнем амплитуды или просто
уровнем называют величину
где А' — некоторая постоянная величина той же размерности,
что н А, например амплитуда невозмущенной волны. Найдем
функцию корреляции уровня х-
Уровень % удовлетворяет уравнению
2?у„Уф + Лф = 0, C5.1)
которое непосредственно пытекает из уравнения переноса C2.5).
Представим х в виде ряда по е:
X = Xt + X.-rX,+ ..., C5.2)
2Я0 МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ [ГЛ. V
гДе Хо — невозмущенное значение уровня, т. е. решение уравнения
0. C5.3)
Подставляя ряд C5.2) и аналогичное разложение C2.11) для
эйконала ср в урапнение C5.1) и учитывая C5.3), для поправки ул
получаем
2Y<p,Vx, +<41 + 2VX.Vq>,-0. C5.4)
В этом уравнении можно приближенно заменить ^Чч и Дфх на
Yiq>L и Ai<f,, где Vx = V —10 (t0Y) и \L -~\\ — операторы попе-
речного дифференцирования. Действительно, по порядку величины
в то время как |V:iiPil= -jnr 1 = -g-1e 1 — °в- Поскольку нас инте-
ресуют дистанции /., большие по сравнению с радиусом корре-
ляции неоднородностей 1е, можно считать, что I V г Ф, I <^ J V л_ф11-
Нодобным же образом можно показать, что | А „ фа | «^ j A i_rpx J.
В результате уравнение C5.4) принимает вид
2WXi + A:.'P, +2Vj.XoV.jp, = 0. C5.5)
У плоской и ненаправленной сферической волн V.:Xo~0, по-
скольку на фазовом фронте ф„ — const амплитуда таких волн
постоянна и последнее слагаемое в C5.5) исчезает. Этим слагае-
мым можно пренебречь и во многих других случаях, например
в случае волнового пучка или направленной сферической волны
с шириной луча а, превышающей радиус корреляции неодно-
родностей /е. В самом деле, по порядку величины
откуда следует, что третье слагаемое в C5.5) примерно в IJa
раз меньше, чем второе. Пренебрегая членом с Yj_Xo и учитывая,
что
запишем уравнение для %г в следующей форме:
Решение уравнения C5.6) имеет вид
ь1 у е
$ 35] ФЛУКТУАЦИИ УРОЗНЯ 281
так что поперечная корреляционная функция уровня ifx(P" L) —
:-<Xi(Pi. 4Xi(Pa> Ц> выражается через корреляционную функ-
цию эйконала 4\р(г'> г) таким образом:
Ml
C5.8)
Здесь г'—r'(s') и г" -r"(s") -лежат на невозмущенных лучах,
приходящих и точки наблюдения г{ и г, (рис. 45), a AL и Дх ---
поперечные операторы Лапласа по переменным г' и г". Ограни-
чимся анализом флуктуации уровня для плоской и сферической
волн, распространяющихся в статистически однородной среде
с i-1.
Согласно (.43.5) корреляционная функция эйконала плоской
волны %{г',.т") равна
OS
%(т', r")-^Ue(P, Qdt. C5.9)
b
где s<—меньшее из двух расстояний s' и s", a p = const — рас-
стояние между двумя параллельными лучами, приходящими в
точки г, и г,. Подставляя C5.9) в C5.8), получаем
тЫе.Ч JJ *<&'&•" f аЬ.(р. Q<%- C5.Ю)
о- о
Двукратный интеграл в C5.10) легко вычисляется:
о
так что для плоской волны
Щ^рД)^- C5.11)
Таким образом, флуктуации уровня нарастают пропорциональ-
но кубу пройденной волной дистанции L, тогда как поперечная
282 МЕТОД ГЕОМЕТРИИ ЕСКОЯ ОПТИКИ (ГЛ. V
корреляционная функция эйконала плоской волны C3.15) растет
пропорционально L:
оо
J C5.12)
Заметим, что если интеграл в C5.11) выразить через i|>x, T0
корреляционная функция уровня плоской волны запишется в виде
Ъ(р. Ц = т5А1ЧМ-(Р. ?)¦ C5-13)
Эта формула упрощает вычисление tf>x, если известна корреля-
ционная функция эйконала ty±.
Корреляционную функцию уровня можно выразить также
через спектральную плотность флуктуации диэлектрической про-
ницаемости:
. Ц=Цг J *i<M*i, 0)АР*хх. C5.14)
— OS
Полагая в C5.11) или C5.14) р = 0, получаем два варианта
формулы для дисперсии уровня амплитуды:
Ж" J «хФ«(*х, 0)Л«х. C5.15)
В случае изотропных флуктуации е функция корреляции
уровня зависит только от модуля расстояния р между точками
наблюдения:
или в иной форме
OS
J C5.17)
В частности, для гауссовой корреляционной функции C3.12)
расчет по любой из формул C3.16) нли C3.17) дает
fx (р)= °х ( 1—7i~+"g"'7r)e~ *• C5.18)
где
!-?• C519)
t 35] ФЛУКТУАЦИИ УРОВНЯ 283
Полезно отметить, что отношение дисперсии уровня а\ к дис-
персии фазы a| = ft3a5> по порядку величины равно
JL
*ч{
т.е. определяется квадратом волнового параметра D-—L/kll~
~ (V А?//Е)*. Но в области применимости геометрической оптики
выполняется условие J/"XZ.<^/E C2.10), при котором волновой
параметр мал (размер первой зоны Френеля мал по сравнению
с размером неоднородностей). Поэтому в пределах применимости
метода геометрической оптики флуктуации уровня должны быть
малы по сравнению с флуктуациямн фазы:
C5.21)
Это позволяет в ряде случаев, например при вычислении в рам-
ках геометрической оптики среднего поля и функции когерент-
ности, пренебречь амплитудными флуктуациямн по сравнению
с фазовыми (§ 37).
Обратимся еще раз к выражению C5.14), которое можно рас-
сматривать как двумерное разложение функции корреляции в
интеграл Фурье. Следовательно, величина
*1ф (*1. °) C5.22)
представляет собой двумерную спектральную плотность флук-
туации уровня амплитуды. В случае изотропных флуктуации
Fx (*х, L) = Fх (кх, L) = Згх!Ф, (хх). C5.23)
Входящий в C5.23) множитель Xj. приводит к ослаблению вклада
крупномасштабных (хх -*¦ 0) составляющих спектра флуктуации е.
Это означает, что в приближении геометрической оптики флук-
туации амплитуды обусловлены в основном мелкомасштабной
частью спектра флуктуации проницаемости е. Наличие в C5.23)
множителя хх позволяет пользоваться этой формулой и в слу-
чае локально однородных и изотропных нолей, когда простран-
ственный спектр Ф„ (х) может иметь при к -*¦ 0 степенную осо-
бенность вида к~а с а. < 5.
Следует специально отметить, что обращение двумерной спект-
ральной плотности Fx(xjl, L) в нуль при хх—«-О эквивалентно
равенству
«
Bя)«/>х@)= J *е(р)*р = О, C5.24)
284 МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ [ГЛ. V
которое is случае изотропных флуктуации принимает вид
Ь0. C5.25)
Соотношения C5.24) и C5.25) тесно связаны с законом сохране-
ния энергии. Подробно этот вопрос рассмотрен is § 46, где по-
казано, что в случае плоской волны интеграл от флуктуацион-
иой компоненты /—/--/, взятий по всей плоскости, равен нулю:
\ 7 (р, г) tfp -= 0 C5.26)
- OS
(заметим, что встречающийся иногда вывод соотношения C5.26)
с использованием свойства пространственной эргодичности
\ / (р, L)d'fi — /2 некорректен). Но, поскольку 1 = \А\"~
— | /4O|VX « | /4J'A +2%), при малых флуктуациях уровня
(когда только и можно пользоваться приближением геометриче-
ской оптики) имеем
так что из C5.26) вытекает закон сохранения для %:
\ х(р,г)с*гр-=О. C5.27)
— ОС
Умножая C5.27) на %((>', г) и усредняя, получаем C5.24).
Из C5.24) следует, что функция корреляции уровня обяиа-
тельно должна наряду с положительными значениями принимать
и отрицательные. Это можно видеть и на частном примере среды,
у которой флукт>ация р имеет гауссову корреляционную функ-
цию: выражение C5.18) в этом елч'чае отрицательно в интервале
Несколько сложнее вычисляется функция корреляции уровня
амплитуды сферической волны. Пусть источник и точка наблю-
дения находятся в статистически однородной среде. Согласно
C3.22)
*f "
*9*(r',r") = 4- \" ds fi|)eF + ?t0)d?, C5.28)
о с
причем текущее расстояние между лучами, приходящими в точки
§ .151 ФЛУКТУАЦИИ УРОВНЯ 288
г' и г", равно (рис. 45)
Дифференцирование C5.28) дает
А1ЛЖ* («•', О ^4" J ^ (т? )*\ Д1+«F"•' '«О^' C5-29)
и в результате по формуле C5.8) находим
'- . ? . 5< °°
Ъ1*(р, /.)--if-^- Г^ (' sMsfAi^F-I-?t0)dg. C5.30)
I) 0 о 0
Текущее расстояние между лучами 6 здесь можно выразить
через расстояние р = т1 — г2 между точками наблюдения г, и iy
6-ps/Z..
Упростим выражение C5.30), воспользованшись соотношением
L L s< L
^ J
которое легко доказывается повторным интегрированием по
частям. В нашем случае
О
н поэтому
L
Полученный результат можно представить в иной форме, если
учесть, что внутренний интеграл равен корреляционной функции
плоской волны C5.11), умноженной на 24/L*:
J«" ("г) *. C5-32)
кли если ввести безразмерную переменную интегрирования
V = slL:
, Z-) = 3 J V2(l— ?)а Фхл (YP) dY' C5.33)
о
286 МЕТОЛ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ (ГЛ. V
При р=0 отсюда следует универсальная связь между диспер-
сиями уровня в плоской и сферической волнах. Поскольку
i
3 1 . . * , 4 Ч« J__ 1
дисперсия уровня сферической волны в 10 раз меньше, чем у
плоской:
i
К (L)Y* = 4>j* @, L) - з j т1 A - v)• ¦№@) <h = -/о К?)W
C5.34)
Эго соотношение, как и выведенные ранее соотношения C4.10)
н C4.21) для дисперсий углов прихода н боковых смещении
луча, универсально, разумеется, только в области применимости
приближения геометрической оптики.
Множитель 72A—ЧУ — S*{L—sY/L* в формулах C5.33) и
C5.34) определяет относительный вклад различных участков
луча в суммарный эффект флуктуации уровня амплитуды сфе-
рической волны. Появление этого множителя, который обра-
щается в нуль в начале (s = 0) и в конце (s — L) трассы, связано
с фокусировкой и дефокусировкой на неоднородиостях среды,
т. е. с их линзовым действием. Известно, что линза, помещен-
ная вблизи точечного источника света или вблизи точки наблю-
дения, не влияет на интенсивность сферической волны. Линзо-
вым же эффектом объясняется и относительная малость флуктуа-
ции сферической волны по сравнению с плоской: неоднород-
ности, расположенные в начале трассы, практически не влияют
на величину флуктуации амплитуды сферической волны, тогда
как именно этн неоднородности сильнее всего сказываются на
флуктуациях плоской волны.
§ 36. Флуктуации параметров волн
в турбулентной тропосфере
Применим общне формулы геометрнческой оптики к расчету
флуктуации параметров волн в турбулентной тропосфере. Для
тропосферы с хорошей степенью точности можно принять е—1,
а флуктуации е считать локально однородным и изотропным
полем (§ 4). Прн этих условиях структурная функция эйконала
плоской волны дается выражением C3.19) или C3.20).
Подставим в C3.20) спектральную плотность D.17):
''•ехр(— хЧК,), C6.1)
i 36] ФЛУКТУАЦИИ В ТУРБУЛЕНТНОЙ ТРОПОСФЕРЕ 287
где С% — структурная постоянная, х„, —5,92//0, а /„ — внутренний
масштаб турбулентности. Интеграл C3.20) от такого простран-
ственного спектра выражается через вырожденную гипергеомет-
рическую функцию 1F1 (см. [3], § 42):
Dx(p, L) = 2. 2
Если заменить эту функцию ее асимптотическими значениями
при малых и больших значениях ее третьего аргумента, то для
Dj_ (p, L) получаются следующие предельные выражения:
Аналогичные предельные выражения для D± (p, L) можно иайти
н непосредственно из C3.19), если распространить грубую аппро-
ксимацию для DE(r), полученную интерполяцией предельных
значений D.12) и D.13), справедливых соответственно при r^>lt
и г<^1„, на область г~/0:
D'^-{cV^. r<l0. C6-4>
Проделав указанные выкладки, мы увидим, что найденный ре-
зультат отличается только заменой коэффициента 0,82 на единицу.
Формула C6.3) дает при малом разнесении точек наблюде-
ния квадратичную зависимость структурной функции от р. При
больших же р поведение D± описывается степенным законом
«пять третей». Неограниченное нарастание DL сростом р соответ-
ствует бесконечному значению дисперсии эйконала а% (L) —
= ifx @, L) —^UDx (oo, L). Конечно, в действительности диспер-
сия а^, ограничена, поскольку при р—>х структурная функция
Dx(p. 1-) «насыщается». Дли грубой оценки,} с\ примем для
De(p) аппроксимацию D.19):
!С- = const, г>С C6-5)
где Z,o—внешний масштаб турбулентности (по сравнению с D.19)
мы пренебрегаем здесь участком г <! ?„, который вносит несу-
щественный вклад в alp).
Поскольку $e{r)=[De(oo) — De(r)]/2, из C6.5) находим
^«(Г)*\О, rt>L,, C66)
288 МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ [ГЛ. V
где сг|^\|)е @) = l/,C|Z.o''—дисперсия диэлектрической проницае-
мости. Оказывается, что функция корреляции C6.6), получен-
лая интерполяцией предельных значений при г«^/.о и r^>L0 на
промежуточную область г ~ Lo, не является положительно опре-
деленной (спектральная плотность Фе для C6.6) принимает отри-
цательные значения). Тем не менее, используя C6.6) для вычис-
ления корреляционной функции фазы, мы можем рассчитывать
на получение качественно правильных результатов при r<^La
и r'^>L0. Оправданием этому служит то, что приводимые ниже
формулы C6.7) и C6.8) могут быть получены и более строгим
путем. I
Подставляя C6.6) в C3.if), получаем корреляционную функ-
цию фазы:
\ C6.7)
В частности,
\
- C6.8)
Таким образом, средний квадрат флуктуации эйконала опреде-
ляется длиной трассы, внешним масштабом турбулентности и
дисперсией флуктуации o'i~ 42Clf-'J', а функция корреляции эй-
конала обращается в пуль при р > Lo.
Положив в C6.8) С?—10~" см-'>'\ L = l км, Z,o — 1 м, полу-
чаем для дисперсии эйконала сг^, типичное значение Стф ~ 2-10 8 см2.
Типичное же значение дисперсии фазы a2s — k'cfip составляет 3-102
на длине волны X — 5-10см (оптический диапазон) и 3-10"«
прн >. — 0,05 см (субмиллнметровые волны).
Статистические характеристики углов прихода луча могут
быть рассчитаны при помощи формул § 34. В частности, при
помощи C6.3) для дисперсии угла прихода <й^> по формуле
C4.5) находим
<9i>.l?!^p.0,82CJ.Z,/o'/-. C6.9)
Подобно структурной функции фазы, функция корреляции
уровня тоже может быть выражена (при помощи C5.14)) через
гипергеометрическне функции [3]. В частности, согласно [3],
для спектра C6.1) дисперсия уровня равна
о{^0,8СЦЧ;''', C6.10)
S 36] ФЛУКТУАЦИИ В ТУРБУЛЕНТНОЙ ТРОПОСФЕРЕ 289
а коэффициент корреляции уровня Кх(р) — г)>х(Р. L)ja\ (L) ведет
себя так, как показано на рис. 46, взятом из [3J, причем хя—
-=5,92//0. Как видно из рисунка, коэффициент корреляции Kx(t>)
припимает отрицательные значения, как это и должно быть для
плоской волны.
Структурную функцию эйконала сферической волны можно
рассчитать при помощи формул C3.26) или C3.27). В предель-
ных случаях р<^К и р^>/„ для нее получаются выражения [3]
Что же клсается дисперсий углов приходи к уровня амплитуды
сферической волны, то для них справедливы соотношения C4.10)
и C5.34), показывающие, что
дисперсия угла прихода в три
раза, а дисперсия уровня амп-
литуды сферической волны в
десять раз меньше, чем у плос-
кой волны. Дисперсия бокового
смещения в сферической волне
тоже в десять раз меньше, чем
в плоской (см. C4.21)). о i г 3
Общее, ограничение МГО— Рис. 46.
неравенство C2.10) —в случае
турбулентной атмосферы сводится к условию малости радиуса
первой зоны Френеля по сравнению с внутренним масштабом
турбулентности:
VXL<^U. C6.12)
В приземном слое атмосферы, где l0 ~ 1 см, и в оптическом диа-
пазоне (к = 5-10~6 см) неравенство C6.12) ограничивает дистан-
цию L значениями порядка 200 м. Однако из дифракционных
расчетов (см. § 41) следует, что некоторые результаты прибли-
жепвя геометрической оптики оказываются справедливыми иа
гораздо больших дистанциях.
Отчасти это объясняется тем, что в спектре турбулентности
C6.1) мелкомасштабные неоднородности с у.~^у.т представлены
слабее, чем крупные неоднородности с х^хт. Поэтому, когда
с ростом дистанции размер первой зоны Френеля станет срав-
ним с внутренним масштабом 1„ и неравенство C6.12) нару-
шится, для большей наст» неоднородностсй еще будет выпол-
нено неравенство KXZ?<^;/, позволяющее применять геометриче-
скую оптику для более крупных неодиорэдностей, с масштабом
1>1„. Эгн крупные неоднородности влияют главным образом на
фазу волны, а не на ее амплитуду. В результате флуктуации
'3 СМ. Рытов> др. ч.;и
290 МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТМКИ (ГЛ. V
фазы в турбулентной среде выражены (по отношению к флуктуа-
циям уровня) сильнее, чем в среде с одномасштабными неодно-
родностями. Действительно, согласно C6.8) и C6.10) отношение
дисперсий уровня и фазы по порядку величины равно
По сравнению с C5.20) здесь появился малый множитель
(/„/?„)'/• «^1, который и отражает возросший вклад крупных
масштабов в флуктуации фазы (о роли крупных и мелких неодно-
родностей при учете дифракции см. также § 41).
§ 37, Среднее поле и функция когерентности
В первом приближении геометрической оптики флуктуации
фазы и уровня волны распределены по нормальному закону,
поскольку обе величины выражаются в этом приближении инте-
гралами от е (илн от производных г), причем на пути интегри-
рования L луч встречает много неодиородиостей. Нормализация
фазы и уровня при этих условиях является следствием цент-
ральной предельной теоремы.
Если флуктуации фазы S a; S, = fop, и уровня x^Xi подчи-
няются нормальному закону, то поле
и = elSi*x, e'5'+*-e's'+*i = «oe's'+*' C7.1)
(uo — eis>+x'—невозмущенное поле) распределено по логарифми-
чески нормальному закону. Учитывая, что в зоне применимости
геометрической оптики дисперсия уровня о|_значителыю меньше
дисперсии фазы а% (см. C5.20) и C6.13))/можно при вычисле-
нии моментов поля а пренебречь флуктуациямн уровни, т. е.
положить
uxuoeis>. C7.2)
Воспользовавшись формулой
<е'5> = е- '/.«'>, C7.3)
которая справедлива для любой нормальной величины | с 5 = 0,
находим из C7.2)
« = «„«>'*.> = гу>-°*/2 =исе-*Ч/2,
или, учитывая выражение C3.31) для дисперсии (Хф,
«-«.«р}-^^?*!».; ,.«!«}
!Uoexp'(—T\a(s)"ds J. C7.4)
о
j 37J СРЕДНЕЕ ПОЛЕ И ФУНКЦИЯ КОГЕРЕНТНОСТИ 291
Величина
ос
| C7.5)
выступает здесь как коэффициент ослабления среднего поля
вдоль луча, т. е. как коэффициент экстинкцни. Согласно C7.4)
среднее ноле убывает тем быстрее, чем больше дисперсия флук-
туации а\.
В статистически однородной среде коэффициент экстинкции
постоянен и среднее поле затухает по экспоненциальному закону
u^u^-'''aL. C7.6)
При е = 1 и для статистически однородных флуктуации коэффи-
циент экстинкцин C7.5) записывается в ниде
что совпадает с. полным поперечником рассеяния единичного
объема а,, который определяет затухание поля в приближении
однократного рассеяния (см. задачу f к гл. IV).
Функцию когерентности поля Г,,^, r,) = <u(rx) и* (г,)> можно
вычислить при помощи C7.2) н C7.3). Приведем выражение для
поперечной функции когерентности, когда точки г, и г, распо-
ложены на фазовом фронте (р = г,—г,):
Г« (Р. Ц as | и, Is <е' ts«<'>)-s> <'•))> = | u01!в"'/• <ls> №••-«• <r«»iv =
= /.txp[-VIOe(p, Ц\, C7.8)
где /,s=|uo|a—интенсивностьяевозмущенного поля, a Ds(p, L)—
=k'Dim(p, ^ — поперечная структурная функция фазы. В случае
статистически однородной среды (е=1) D± определяется выра-
жениями C3.19) нлн C3.20), а выражения дли Dx в турбулент-
ной атмосфере приведены в предыдущем параграфе. В частном
случае плоской полны, распространяющейся в турбулентной
среде (структурная функция дается C6.3)), функция когерент-
ности равна ,
0JVj. P<1,- { '
Функция корреляции поля равна
s(P-«_1j- C7.10)
292 МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ] [ГЛ. V
Прн слабых флуктуациях фазы, когда о$<^1, корреляционные
функции (а следовательно, и радиусы корреляции) фазы н самого
поля совпадают: \|>а (р)« ij>5 (р). Если же Os^>l, то вторым сла-
гаемым в формуле C7.10) можно пренебречь, и тогда
*. (р, L) ж Г.(р, L) ^ I,e-'UDs^L\ C7Л)
Радиус корреляции поля можно оценить (прн о|^>1) из усло-
вия i|>« (p, L) «г Vi'o или из эквивалентного уравнения Ds (p, L) »
я;2In2—1,4. Поскольку структурная функция фазы Ds=*ft*D,
пропорциональна пройденному волной расстоянию, радиус кор-
реляции (когерентности) поля с ростом 1. уменьшается. Напри-
мер, если плоская волна распространяется в турбулентной тро-
посфере, а расстояние между точками наблюдения р лежит в инер-
ционном интервале i,^>p^>/0, то при помощи первой из формул
C7.9) для радиуса корреляции поля /„ находим
В данном случае он уменьшаете!! с ростом дистанции, как!""'*.
В дальнейшем мы убедимся, что выражения C7.6) дли сред-
него ноля и C7.8) для функции когерентности сохраняют силу за
пределами применимости приближении геометрической оптики,
когда флуктуации уровня не малы и когда нельзя пренебречь
дифракционными эффектами. Как уже было сказано, это связано
с тем, что в случае крупномасштабных иеоднородностен наруше-
ние пространственной когерен шости ноля происходит в первую
очередь за счет фазоиых флуктуации, тогда как флуктуации
амплитуды (уровня) играют меньшую роль.
Задачи
I. В общем сяучас поперечная функция корреляции эйконала дастся вы-
ражением C3.33). В простейшем случае, когда флуктуации статистически
однородна, а средняя диэлектрическая проницаемость постоянна, невозмущен-
ные лучи можно считать прямыми линиями, расходящимися от источника.
Найти поперечную функцию корреляции эйконала сферической полны,
прошедшей через случайно-преломляющий слой конечной толщины (рис. 47).
Решение. Если /.,—толщина слоя, a Rt—расстояние от источника до
слоя, то расстояние между лучами меняется по закону 6(s)-~ps/(#i— Lj),
а интегрирование по 5 в CJ.33) нужно проводить в пределах от Ях — #o/cos9
До R\-rl-i — (Ro I Lo)/cos 0, где 0—угол падения среднего луча иа слой, Тогда
R. о
или, если учесть C3.25),
ЗАДАЧ!!
293
Эти формулы допускают предельный переход к случат плоской волиы (/?„ —> да,
т. е. бесконечно удалени-ш источник^ и к случаю источника сферической волны,
находящегося на границе слоя (#„—> 0).
Выражения такого типа позволяют рассчитывать, например, флуктуации
фазы ультракоротких радиоволн, прошедших через статистически неоднород-
ную ионосферу. Во многих случаях флуктуяциями амплитуды (уровня) можно
пренебречь, заменяя ионосферу эквивалентным фазовый экраном, и тогда легко
вычислить функцию корреляции поля на выходе из ионосферы. Дальнейшая
эволюция поля на пути от ионосферы до поверхности Земли подчиняется за-
кономерностям дифракции волн в свободном пространстве (§ 10).
Рис. 48.
2. Пусть на 1мучайно-меод1К>родное полупространство г > 0 палает сходя-
щаяся сферическая волна с фокусом в точке г —Г (рис. 48). Найтн функции
корреляции эйконала в плоскости г —const.
От d с т.
f
. *<F,
p
[uF/iz-F) p 'I
\ 4>Mrf ')*>'+¦ fit1 !¦')*>'
3 „ p • ¦ j > «• j.
Иа этих выражений следует, что в сходящейся сферической волне раднус кор-
реляции меньше, чем в плоской, и стремится к нулю при г—> F (разумеется,
непосредственно в области фокуса приведенная формула непригодна). После
прохождения фокуса радиус корреляции начинает увеличиваться н в пределе
*§>F формула A) описывает флуктуации эйконала расходящейся сферической
во,1шы.
3. Найти поперечную функцию корреляции эйконала плоской волны в среде
с анизотропными флухтуацнямн ё, описываемыми гауссовой корреляционной
функций вида B.29)'с масштаСгми а и Ь^-с (cf> Ь).
Ответ. Если большая ось Неоднородностей а лежит в плоскости (у, г)
и наклонена под углом у к направлению распространения волиы (ось г), то
по формуле C3.15) имеем
у.
' 2 (a3 sin3 y-f ft" cos31
294
МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
1ГЛ. V
2 К 2
6s cos3
Прн изменении угла у от 0 до п/2 масштаб корреляции эйконала по оси у,
равный /,= J^a'sin'y ; b2cos2y, меняется от Ь(при у^О) доа (при у — "/2),
тогда как масштаб корреляции по оси х остается постоянный, 1Х~Ь.
4. Вычислить дисперсию эйконала волиы, отраженной от плоско-слоистой
?реды с линейным законом изменения средней диэлектрической проницаемости
e=Ei—e2z (рис. 49, а) и со статистически однородными флуктуациями е.
Реше II н е. Пусть случайные неоднородности расположены выше уровня
г=Л."Для статистически однородных флуктуации по формуле (АЧ.32) имеем
L L
г "е'эФФ Г ds с>Лм> С ds ...
°ф" 2—j-.,-,^—§—J et—егг^)' ()
о ' ^s" о
где L—длниа дуги луча от входа до выхода из слоя (рнс. 49, б). Для вычис-
ления интеграла A) надо зиять зависимость г от текущей дляны луча s. Если
в—угол падения луча па слой, а п^шву е (ft) = V^e, -е^Л -коэффицнепт про-
ломлеиин в начале слов, то уравнение луча удобно записать через параметр
[81:
дс (т) = дг0 -I T/70sin9, г(т) ft-f n0tcose — 8iT2/4,
причем е [z (т)] — п\—е2тл0соз04-е|т|/4. Точкам поворота лучей отвечает уро-
вень гпо, — Л- По cos2 0/е,, отстоящий от начала слоя г—Л иа расстояние
Переходя в A) к интегрированию по т(йт — dsjye) в пределах от нуля
до t=4n0cos 6/е2, что отвечает возвращению луча на начальный уровень z = Л,
получаем
^ 1+cose
ЗАДАЧИ
295
При помощи этой формулы можно оценить толщину слоя
рый дает пятидесятипроцеитный вклад в о^>:
, Д sin 0A— sinB) nic
Л ~~2 cos»в f Л-гпов "¦ i
гпов—А', кото-
При начальной наклоне луча 9 — 45° находим отсюда Л' — 0/214, т. е. поло-
вину дисперсии эйконала n!v дает примерно пятая часть слоя, априО — 30° —
шестая часть (Л'— 4/6). Таким образом, меньшая часть слоя, прилегающая
к точке поворота г — гпов (средняя проницаемость на луче в (г) здесь мини-
мальна), даст примерно такой же вклад в дисперсию эйконала, как и осталь-
ной слой.
S. Вывести общую формулу для поперечной функции корреляции уровня
с учетом регулярной рефракции.
Ответ. Пусть &х,-(ц) и fl*i(sa) —приращения координат ж,-(s,) и x/,(sa)
двух точек на одном и том же невозмугденном луче при переходе на близкий
соседний луч с сохранением длин Si и s2. Если ввести обозивчения
6x/(S.)
= min {s't s"\.
i. a-const
где (;—компоненты единичного вектора, касательного к нсвозмущенноыу лучу,
то при помощи C5.7) н C3.22) получаем для поперечной корреляционной функ-
ции уровня формулу
в которой но повторяющимся индексам производится суммирова!ше.
6. Если волна дважды проходит через один н те же'неоднородности (на-
пример, в результате отражения or препятствия), то возникают своеобразные
аффекты двукратного прохождения [14]. Напри-
мер, для плоской волны, прошедшей в случайно-
неоднородной среде путь L в прямом и обратном
направлениях, дисперсия фазы «двое больше, чем
для волны, прошедшей дистанцию 2Л в той же сре-
де, но в одном направлении. Найти дисперсию
офд, фазы сферической волны, отраженной от
плоскости, удаленной от источника па расстояние
L (рис. 50).
Решение. Пусть источник расположен в
начале координат. При Г— 1 флуктуации фазы
жащей в плоскости г — 0, выражаются суммой
Рнс. 60.
точке г — (р, г),
(П
первое слагаемое которой соответствует прямому," а второе—обратному пути
296 МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ [ГЛ. V
ооллы. Статистическое усреднение A) даст (при L^-tF)
L *
<4д„(!>. L) - j'rfr! j ^,@, ?)+Ч>« ("Х • ?)] <*»• B)
"о о
При р — О, когда точка наблюдения совмещена с источником.
ОфДВ @, t)-2ij Фе @, «<*С~4оф(/.)-2афB1), C)
о
где Сф(г) представляет собой, в соответствии с (^3.9), дисперсию фазы при
однократном прохождении дистанции г. Двукратное увеличение а%д0 (О, I.) по
сравнению с Оф B1) обусловлено корреляцией флуктуации фазы на прямом
и обратном пути. Пели же прямой н обратный лучн проходят большую часть
пути через разные неоднородности (т. е. р^>/?), то второе слагаемое а B) ста-
новится пренебрежимо малым по сравнению с первым, и тогда
оФД,(р, L) 3i2a\[L)~<%BL), p>/8-
Корреляция флуктуации интенсивности на прямом я обратном пути приводит
н к другому интересному эффекту — усилению обратного рассеяния [15].
Глава VI
МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ
§^38. Обоснование^нараболического'уравнения
Мы уже говорили о том, что в случае длин волн Я, малых
по сравнению с размерами 1е неоднородностей диэлектрической
проницаемости, рассеянные волны концентрируются в узком те-
лесном угле с раствором 6 порядка А,//е<^1, т. е. распростра-
няются практически в том же направлении, что и первичная
волна. В силу этого становится существенным многократное рас-
сеяние.
Одним нз приближенных методов, учитывающих многократное
рассеяние, является метод геометрической оптики (гл. V), но он
полностью игнорирует дифракционные эффекты и ограничен усло-
вием V^L^lf,. Если это условие нарушается, т. е. расстояние L,
проходимое волной в неоднородной среде, достаточно велико:
L^>(l\jX)=s.LR, то дифракционные эффекты становятся сущест-
венными. Это можно пояснить следующим качественным рассу-
ждением. Если неоднородность размера /е освещается плоской
волной, то и размер ее геометрической «тени» на любом расстоя-
нии L равен 1В. Однако дифракция приводит к «расплыванию»
резких границ тени на величину порядка VXL (это размер пере-
ходной области свет—тень при дифракции на краю непрозрач-
ного экрана). Ясно, что дифракцией можно пренебречь лишь
при условии УЛ<^/В (см. C2.10)). Это условие зачастую до-
вольно жестко ограничивает длину трассы L.
Как мы видели в § 36, для света в турбулентной атмосфере
уже при L л; 200 м имеет место равенства VJX = le, т. е. гео-
метрическая оптика становится неприменимой на расстояниях
порядка нескольких сотен метров.
В гл. V уже были упомянуты более общие приближенные
методы решения дифракционных задач, связанные с примене-
нием параболического уравнения, которые, с одной стороны,
используют, как и МГО, малость параметра Х//Е, но вместе с тем
учитывают н дифракционные эффекты. Это — метод плавных
298 М1:ТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ [ГЛ. VI
возмущений (МПВ) и метод параболического уравнения (МПУ).
В этом параграфе мы выведем параболическое уравнение, причем
двумя способами, проясняющими разные стороны МПУ. Урав-
нения МПВ будут затем получены из параболического уравне-
ния (§ 40).
Будем исходить из скалярного уравнения Гельмгольца
Аи-\ k'[\ гё(г)]ы^-0, C8.1)
где кг — —?-е—квадрат среднего волнового числа (предпола-
гается, что f.--const), а е = [е(г)— е]/б- относительная величина
флуктуации диэлектрической проницаемости, так что <е> = 0.
Приведем сначала простейший вывод параболического уравне-
ния, основанный на наглядных соображениях.
Пусть неоднородная среда занимает полупространство z>0
и на него падает плоская волна и — Д, exp(iTiz). Так как мы
предположили, что 1е^>Х, то рассеянные волны распростра-
няются в основном ннеред, и волна, отраженная от неоднородной
среды, слаба по сравнению с падающей волной. Будем искать
поле и в среде в виде
u(p, z) = i>(p, z)exp(iftz), p = (x, у). C8.2)
Здесь и(р, х)— амплитуда волны (вообще говоря, комплексная).
Если бы среда была однородной (е = 0), то амплитуда v не за-
висела бы от координат. В неоднородной среде можно ожидать,
что функция v (р, г) и ее производная по z будут мало меняться
на протяжении длины волны, так как изменения v связаны
только с наличием неодиородностей, а их размеры велики по
сравнению с ).. Поэтому должны выполняться условия
5?
\dv
(быстрое изменение и в зависимости от z уже описывается мно-
жителем exp (ifcz)). Условия C8.3) могут выполняться лишь в том
случае, когда поле, рассеянное назад, мало. Действительно,
если поле и содержит и обратную волну Лехр(—ikz), то это
означает, что в амплитуде и присутствует слагаемое вида
А ехр (—2ifez), быстро меняющееся на расстояниях порядка I.
Таким образом, условия C8.3) уже предполагают, что ампли-
туда А обратной полны достаточно мала по сравнению с ампли-
тудой прямой волны.
f 38] ОБОСНОВАНИЕ ПАРАБОЛИЧЕСКОГО УРАВНЕНИЯ 299
Подставив C8.2) в C8.1), получаем уравнение
Но в силу второго неравенства C8.3) можно пренебречь членом
d'v/dz' по сравнению с членом 2ikdv/dz, что н приводит к па-
раболическому уравнению для амплитуды v:
+*'"(р Z)V° C84)
Уравнение параболического типа впервые было использовано
М. А. Леонтовичем при решении детерминированной задачи о диф-
ракции радиоволн вокруг Земли [1J. Приведенное обоснование
уравнения C8.4), конечно, весьма нестрого. Рассмотрим поэтому
другой его вывод, где более отчетливо выявятся те величины,
которыми нужно пренебречь, чтобы получить C8.4) из C8.1) [2].
Уравнение C8.1) вместе с необходимыми для него граничными
условиями эквивалентно следующему интегральному уравнению:
и (г) = и0 (г) -k* $ G (г —г') ё (г') и (г') d?r'. C8.5)
Здесь ы0 (г) — первичная волна (волна в отсутствие нсоднородностей
среды), удовлетворяющая уравнению Дио + йгыо = О, a G(r—г') —
функция Грина:
G(r-r') = -to|r'_t,|«P<ffe|'—г'1}. C8.6)
удовлетворяющая уравнению AG+ft2G = 6'(r— г') и условиям
излучения на бесконечности.
Пусть падающая волна имеет вид и„ (р, z) = A exp (ikz). Разо-
бьем область интегрирования по г' в C8.5) на два участка —
О < г' < г н г' > г:
г
и (г) = ut (г)—ft* С dz' f d*p'G (г- г') I (г') и (г') -
i J
-k* I dz' I d'p'G (г -г') Ё (г') и (г'). C8.7)
г
Рассмотрим первый из интегралов. Он является суммой слагае-
мых вида
du+ (г) = — кЮ (г —г')ё (г') и (г') dz' dy,
причем для каждого нз этих слагаемых г > г'. Велпчина'^ы +
представляет сферическую волну (множитель G (г—г')) с центром
в точке г' и амплитудой —fc2e (г') и (г') dz'dtp', определяемой рас-
сеянием волны и (г') на неоднородности е (г'). Прн этом продоль-
300
МЕТОД ПЛЛППЫХ ВОЗМУЩЕНИЙ
[ГЛ. VI
о
ная координата точки рассеяния г' всегда меньше z — продольной
координаты точки наблюдения. Это означает, что все источники
сферических волн в первом интеграле C8.7) расположены в слое
п ^ '' '" ' т. е. рассеянные волны, учитываемые этим слагаемым,
п приходят в точку наблю-
дения с той же стороны,
что и падающая волна.
Точно так же легко
убедиться в том, что вто-
рой интеграл в'C8.7) сум-
мирует все волны, прихо-
дящие в точку г из области
г' > г. Ясно, что для того,
чтобы попасть в точку г
из области г' > г, волна
хотя'бы один раз должна
испытать рассеяние назад
(рис. 51, а).
Если, однако, выпол-
няется условие Я<^/е, то,
как мы знаем, при каждом
акте рассеяния основная
часть рассеянной энергии
сосредоточивается в узком
телесном угле вблизи пер-
воначального направления
распространения волны.
1} этом случае можно ожи-
дать, что интенсивность
волны, испытавшей хотя
Рис. 51. бы одно обратное рассея-
ние, будет малой по сравне-
нию с интенсивностью волны, которая испытала то же общее число
рассеяний вперед. На этом основании мы можем пренебречь вто-
рым слагаемым в уравнении C8.7) и записать его в виде л)
г
и"» (г) - и, (г)—к' \ да' \ d'p'G (г - г')е (г') «<•' (г'). C8.8)
о
В приближении, описываемом уравнением C8.8), которое должно
удовлетворяться при любом z = z, в каждую точку приходят
волны только n:i области г' < г. Это означает, что при переходе
от уравнения C8.7) к уравнению C8.8) мы отбрасываем не только
') Смысл верх него индекса @) в C8.8) разъяснен ниже.
j 381 ОБОСНОВАНИЕ ПАРАБОЛИЧЕСКОГО УРЛВНЬНИЯ 301
волны, изображенные на рис. 51, я, но и волны того типа, кото-
рый изображен на рис. 51, б, где волна приходит справа п одну
из промежуточных точек г,. Единственный тип волн, который
учитывается в уравнении C8.8), соответствует рис. RI, в. Здесь
не только в точку г, но и в каждую из промежуточных точек
волна приходит слева. В этом легко убедиться, если записать
формальное решение уравнения C8.8) в виде итерационного ряда.
Таким образом, уравнению C8.8) удовлетворяют лить те волны,
которые на пути распространения в слое @, г) не испытали ни
одного акта обратного рассеяния. Это отмечено верхним индек-
сом 0 п обозначении и'01. .Можно показать [2], что полное волно-
вое поле и разбивается на сумму полей ит, иаУ, ul!1 где
«<"—волна, испытавшая / актов обратного рассеяния.
Уравнение C8.8) можно упростить и дальше, если более после-
довательно учесть условие >.<^.1е. Как мы знаем, характерный
угол рассеяния па неоднородности масштаба /е имеет порядок
0~V'e- Если первоначально падающая волна распространялась
вдоль оси г, то после перлого же акта рассеяния она будет рас-
пространяться под углом порядка 8 к оси г. Это'означает, что
в C8.8) отношение поперечной составляющей вектора г—г' к его,
продольной составляющей имеет порядок величины в, т. е.
Используя малость этого отношения, можно применить раз-
ложение |г — г'| в ряд Тейлора:
Функция Грина 0 содержит в показателе экспоненты фазовый
набег k\r—г'|. Подставить вместо |г—г'| приведенное разложе-
ние и ограничиться в нем лишь первыми двумя членами можно,
если выполняется условие
"Если, согласно C8.9), подставить сюда |р—р'|~ ). (г—г')//е, то
мы приходим к ограничениям1)
C8.11)
т) Отиетнм, ЧТО в силу условия ^^'е величина Лг/4 должна Сыть малин
не 1го сравнению с единицей, как в МГО, а по сравнению с большим пара-
метром (/еД)'. Таким образом, первое из неравенств C8. II) может выполняться
И » том случае, когда условия применимости МГО нарушаются.
302 МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЯ |ГЛ. VI
при выполнении которых функцию Грина C8.6) можно заменить
на ее френелевское приближение
"fc} C8.12)
СВ знаменателе функции Грина с относительной ошибкой порялкя
X//,, сказывающейся лишь на амплитуде, можно взять только пер-
вый член разложения C8.10).)
Подставляя в C8.8) приближенную формулу C8.12) для функ-
ции Грння, приходпм к уравнению
«<«(р, г)-«„(р, г) +
2! ^ fig'f )', О.
которое уже эквивалентно параболическому уравнению C8.4).
Чтобы убедиться в этом, используем аналогичную C8.2) подста-
новку uln(p.z)—v(p, ?)exp(ifezl. В такой же форме пред-
стапим и падающую волну: и„ (р, г) -- А„ (р) exp (ikz). Отметим, что
в силу уравнения Д«о 4-fe*«n = 0 амплитуда А„ (о) падающей волны
удовлетворяет условию Л LA, (р)=0, где Л , — д*1дх* + д'/ду*. Тогда,
после сокращения на общий множитель exp(/fcz), получим
" (Р. *)-'г
C8.13)
Чтобы перейти к дифференциальному уравнению для о, следует
продифференцировать C8.13) по г. Прн дифференцировании ин-
теграла по верхнему пределу возникает, однако, неопределен-
ность—значение заключенного в квадратные скобки выражения
при г' = г. Чтобы установить, к чему стремится это выражение,
введем временно обозначение а* = /(г—г')'к. Тогда оно при-
мет вид
и мы узнаем в нем двумерную гауссову плотность вероятностей,
соответствующую дисперсиям а по обеим осям. Но прн а—-О
гауссова плотность вероятностей стремится к дельта-функции,
так что
§ 38J ОБОСНОВАНИЕ ПАРАБОЛИЧЕСКОГО УРАППРНПЯ 303
Дифференцируя C8.13) по г и используя последнюю формулу,
получаем
Теперь учтем, что выполняется легко проверяемое непосред-
ственным дифференцированием соотношение
Используя его и вынося оператор Aj. за знак интеграла, полу-
чим, с учетом C8.13), уравнение
H = -?;(rMr) + iAj>-A,). C8.14)
Но, как отмечалось, ДхЛ„ = 0, в силу чего последнее уравнение
совпадает с параболическим уравнением C8.4).
В процессе вывода уравнения C8.14) мы установили, что
переходить в C8.8) ко фреиелевскому приближению для функции
Грнна можно лишь при выполнении условий C8.11). Однако мы
не выяснили еще, когда можно пренебрегать волнами, рассеян-
ными назад. Легче всего это сделать, воспользовавшись форму-
лой B6.11) для эффективного поперечника рассеяния из единицы
объема (мы рассматриваем простейший случаи статистически
изотропных флуктуации):
!) C8.15)
о задней полусфере
<<, < ф < ), у эффективный поп
рассеяния назад из единицы объема:
Если проинтегрировать C8.15) по задней полусфере (л/2 <
<6<я, 0 < ф < 2л), то мы получим эффективный поперечник
рассеяния назад из единицы объема:
я/2
Интегрируя по ф и вводя вместо в новую переменную интегри-
рования х = 2k sin VA находим
2*
$ C816>
Эффективный поперечник сто6р равен той доле энергии падающей
волны, которая за счет рассеяния преобразуется в обратную
волну, когда прямая полна проходит единичное расстояние. Если
304 МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ 1ГЛ. VI
пренебречь уменьшением энергии падающей волны за счет этого
рассеяния, то на мути г в энергию обратной волны перейдет доля
энергии, равная cr^z (заметим, что, пренебрегая потерями энер-
гии прямой иолны, мы завышаем энергию обратной волны).
Поэтому условие, необходимое для того, чтобы пренебречь обрат-
ным рассеянием и тем самым отбросить второй интеграл в C8.7),
можно записать в виде сОбРг<5$1, или
n'k'z J Фе (х) х d* <g: 1. C8.17)
ft VT
Обратим внимание на следующее обстоятельство. Если бы мы
интегрировали формулу C8.15) по всем углам (Ог^б^Сл), то
получили бы полный эффективный поперечник рассеяния а0 (по
всем направлениям) и вместо C8.17) пришли бы к неравенству
2k
с„г = Ti'k'z $ Фв (х) х dx <^ 1, C8.18)
о
т. е. к условию применимости борновского приближения. Мы ви-
дим, что условие C8.17) всегда является менее жестким, чем
C8.18). Если в области х>А]^2 функция Фе(х) мала по срав-
нению с ее значением в области x<fe^2, то условие C8.18)
может нарушаться, даже если C8.17) выполняется.
Пусть, например, 1|>Е(г) = а|ехр (—ra/2aa). Тогда (§3) Фе(х) =
=Bя)-'/аа|а3ехр(—каяа/2) и, выполняя интегрирование в C8.17),
получаем
yrnc\k'zae-k'at A — е-*1) <^ 1. C8.17а)
Условие же применимости борновского приближения C8.18) в этом
случае имеет вид (см. B6.19))
C8.18а)
Если ka^>\ (крупномасштабные неоднородности), то условие
C8.18а) будет а|/гагя<5;1, тогда как из C8.17а) получаем
olk2za<^.exp(k2d'/2), т. е. параметр a\k'za ограничен сверху не
единицей, а большим числом ex p (fe2aa/2) *).
С другой стороны, если выполняется условие применимости
борновского приближения C8.18), то заведомо выполняется к
') Если помимо условия ка^>1 выполняется также условие каг^>г, прн
которим результаты дифракционного расчета совпадают с расчетами по МГО,
то многократное рассеяние вперед оказывается тем не менее учтенным. Отсюда
видно, что и МГО учитывает многократное рассеяние вперед.
f 381 ОБОСНОВАНИЕ ПАРАБОЛИЧЕСКОГО УРАВНЕНИЯ 305
условие C8.17). В этом случае пренебрежимо мала роль много-
кратного рассеяния вообще, в том числе и роль обратного рас-
сеяния.
В качестве второго примера рассмотрим спектральную плот-
ность Фг (х) = АС\у.-":' ехр (— xa/Xm)i соответствующую флуктуа-
циям диэлектрической проницаемости, обусловленным турбулент-
ностью (см. 4.17)).
Трехмерная спектральная плотность такого вида применима
в области и > 2я/?,0, где La — внешний масштаб турбулентности.
Пользуясь этой спектральной плотностью, нельзя оценивать гра-
ницы применимости борцовского приближения, так как в области
х < 2л/Л„ она неверна. Если, однако, k^>'2n/L0, то рассеяние
назад обусловлено лишь той частью пространственного спектра
неоднородности, которую приведенная формула описывает. В этом
случае, оценивая интеграл C8.17), можно получить следующее
условие применимости параболического уравнения:
В атмосфере Земли, например, С|~ 10~" см-*/>, хя ~ 10' см.
Если к~ 10* см (видимый свет), то последнее условие приводит
к ограничению z<§10" км, которое заведомо выполняется, так
как путь светового луча в атмосфере Земли по порядку вели-
чины не может превышать 103 км.
Суммируем результаты этого параграфа. Если выполняются
условия
2ft
J
к VY
то распространение волны в случайно-неоднородной среде можно
описывать при помощи параболического уравнения
для медленно меняющейся комплексной амплитуды, связанной
с волновым полем и формулой ц (р, г) — ехр (ikz) v (p, г). Прибли-
жение параболического уравнения учитывает многократное рас-
сеяние воли вперед и не учитывает обратного рассеяния. Дифрак-
ция при использовании МПУ учитывается в приближении Фре-
неля. Важной особенностью параболического уравнения является
то, что оно первого порядка по г. Поэтому на плоскости г--const
достаточно ставить только одно граничное условие.
ЯОГ« МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ 1ГЛ. VI
§ 39. Закон сохранения энергии
в приближении параболического уравнения
Исходное волновое уравнение
Ди + ?'[1 + ё(г)]а = 0, C9.1)
из которого было получено, уравнение C8.4) для о(р, г), имеет
интеграл энергии B6.2), B6.3):
div^ = 0, C9.2)
<У = -^-(и*Ум — u V«%) = Im (a* V«) C9.3)
(для упрощения дальнейших формул мы приняли входящий
в B6.2) коэффициент а равным к). Вектор <У представляет собой
плотность потока энергии волны.
Пусть u = Aexp(iS), где Л —амплитуда н S—фаза полны.
Тогда для У легко получить формулу
& = A*\S. C9.4)
Выразим теперь <У через v. Если комплексную амплитуду v
представить в форме v — А ехр(iS"), то нз выражения и = иехр(ikz)
получаем соотношение
S = kz+S' C9.5)
между полной фазой S и фазой S' медленной функции v. Согласно
C9.5)
и закон сохранения энергии C9.2) принимает вид
l[A'(fe+^)]+ViH»VxS'] = O. C9.6)
В приближении параболического уравнения имеем
Умножив это уравнение на и*:
н вычитая из него комплексно сопряженное уравнение
{ 391 ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ 307
получаем
+ \(v*Vv t>Vtf*) = O, C9.7)
где мы использовали формулу и*Дхи — v&1v* = Vi_(y*\\v—t
Соотношение C9.7), полученное в приближении параболического
уравнения, заменяет закон сохранения C9.2). Подставим в C9.7)
о = /4ехр (iS'), что дает
¦? (kA») + Vi. (A1 V±S') = 0. C9.8)
Сравнение C9.8) с C9.6) показывает, что из компоненты <Уг
плотности потока энергии прн переходе к параболическому урав-
нению выпадает величина A*dS']dz. Следовательно, должно вы-
полняться неравенство
as'
или
C9.9)
Неравенство C9.9) означает, что фаза S' должна мало меняться
на длине волны в направлении осн г. Это неравенство не является
дополнительным ограничением, а вытекает из уже использован-
ного при выводе C8.4) условия X<j/e. Действительно, чисто
геометрический набег фазы волны уже учтен слагаемым kz
в C9.5). Поэтому слагаемое S' связано только с наличием неод-
нородностей. Но характерные размеры последних велики по срав-
нению с длиной волны, в силу чего неравенство C9.9) удовлет-
воряется.
Уравнение C9.8) можно интерпретировать еще и иначе. Вели-
чина A'— vv* =uu**al пропорциональна плотности энергии
волны. Разделив C9.8) на k, имеем
§ = 0, К=А'Ц^. C9.10)
Уравнение C9.10) аналогично закону сохранения энергии в не-
стационарном поле. В C9.10) координата г выступает в роли
времени, а энергия распространяется в плоскости (х, у). Если
проинтегрировать C9.10) по некоторой площадке 2, лежащей
в плоскости г = const н ограниченной замкнутым контуром $?,
то получим
^1 dxdy+ ^d\\<f'Ldxdy = 0.
Применяя ко второму слагаемому теорему Гаусса для двумерного
случая, находим
308 МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ [ГЛ. VI
Таким образом, изменение энергии, сосредоточенной на площадке
2, связано с потоком энергии через контур &, ограничиваю-
щий X.
Рассмотрим частный случай, когда неоднородности диэлектри-
ческой проницаемости статистически однородны и плоскостях
z = cunst, а падающая волна — плоская. Из соображений симмет-
рии очевидно, что все усредненные величины могут зависеть
в этом случае только от г и не зависят от поперечного радиуса-
вектора р. Усредним уравнение C9.8):
Так как (A'V^S'y не зависит от р, имеем Vi<^'ViS'> = 0
и, значит,
,Чы видим, что для плоской волны, распространяющейся
в среде, статистически однородной в плоскостях г —const, выпол-
няется равенство
Ш' -йп»' = Л» = А\ = const. C9.11)
Этот результат строго вытекает из C9.8), но он оказывается
приближенным, если исходить из точного уравнения C9.6). Дей-
ствительно, усредняя C9.6), мы получили бы
откуда видно, что равенство C9.11) справедливо с относительной
погрешностью порядка Я./7С.
§ 40. Метод плавных возмущений
Параболическое уравнение C8.4)
2ik^ + ALv+k*l(p, г) о = 0,
д> д' D01>
Р = {*. У). AL-ajr+ijr.
определяющее комплексную амплитуду v, связанную с волновым
полем и формулой и (р, г) = exp (ikz) v (р, г), в общем случае, как
и исходное уравнение Гельмгольца C8.1), не. может бьпь решено
точно. Поэтому и для уравнения D0.1) приходится использовать
приближенные методы решения. В этом параграфе мы рассмотрим
так называемый метод плавных возмущений (МПВ), предложен-
ный С. М. Рытовым в детерминированной задаче о дифракции
j <0] МЕТОЛ ПЛАВНЫХ ВОЗМУЩЕНИЙ 309
света на ультразвуковой волне [3] н примененный для решения
статистических задач А. М. Обуховым [4]. МПВ приспособлен в
первую очередь для исследования таких параметров волны, как
ее фаза и уровень.
Представим комплексную амплитуду t' (p, г) в виде
>1„схр(Ф(р,г)). D0.2)
откуда Ф — ln(v,'Aa). Здесь S'— S—ki (см. C9.5)) — отклонение
фазы от регулярного ее набега fez в отсутствие иеоднородностей,
а 1п (Л/Л,,) з= у — уровень. Таким обрядом,
Подставив D0.2) в D0.1), получим уравнение
^ )* f k4(p, 2)=- 0 D0.3)
для комплексной фазы Ф. Уравнение D0.3), в отличие от D0.1),
нелинейно, но случайная функция е входит в него ие в качестве
Коэффициента, а аддитивно.
Будем искать решение уравнения D0.3) в виде ряда
Ф-Ф^Ф^Н-..., D0.4)
«редполагая, что Ф; имеет порядок малости ае = т/ <еа>, Фа — по-
рядок о\ и т. д. Подставив D0.4) в D0.3) и приравнивая нулю
группы членов одинакового порядка малости, получаем следую-
щую систему уравнении последовательных приближений:
21*^!-|-А1Ф1--*'1(р, г), D0.5а)
2ift^l-Ai®, = -(VJ.©J', D0.56)
2ifc^ -I-ЛлФ3 = -2УхФ,¦ \LO,, D0.5b)
Рассмотрим при помощи этих уравнений задачу о флуктуа-
Циях уровня и фазы волны п статистически однородной случай-
ной среде, заполняющей полупространство г > 0, если из области
*<0иа нее падает плоская волиа и (р, г) — Л0ехрA7гг). Поскольку
*<Ы пренебрегли обратным рассеянием, на границе г = 0 должно
быть непрерывным только поле и, ио не ди/дг:
"(Р, 0) = Л„, v(p,0) = A,, Ф(р, 0) = 1п^-^ = 0.
ЗЮ МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ (ГЛ. VI
Таким образом, граничные условия ко всем уравнениям D0.5)
имеют один и тот же вид:
ф,(р, О)=о. г = 1, 2, ...,
а сами уравнения различаются только правыми частями. Поэтому
решение любого из этих уравнений можно представить в виде
Ф((Р> z)= Ыг'\ dsp'K(p—р', г—г')/,(р', г'), D0.6)
где К—функция Грина оператора 2ifeg- + A_i_, a ft — правая часть
соответствующего уравнения для Ф(.
Фактически удается вычислить лишь несколько первых чле-
нов ряда D0.4) (обычно используется только первое приближение,
а следующий член Ф2 служит лишь для оцевки погрешности).
Для того чтобы Ф мало отличалось от Ф,, необходимо, чтобы
правые части уравнений D0.5) достаточно быстро убывали
с ростом номера /, т. е. необходимо потребовать виполнения
неравенства
I Vj.®ila<Sfes0ei или \\\±Ф,\г<^.сЕ. D0.7)
Условие D0.7) означает, что изменения Ф, на поперечных
расстояниях порядка длины волны X должны быть малыми по
сравнению с сте (сама величина Ф, имеет тот же порядок малости,
что и е). Таким образом, условие D0.7) требует достаточной
плавности изменения ф,. В связи с этим и сам метод, основан-
ный riS использовании теории возмущений для комплексной фазы
Ф, получил название метода плавных возмущений (ЛШВ).
Входящая в D0.6) функция Грина имеет вид (см. задачу 2)
D0.8)
Оиа отличается от функции Грина уравнения Гелыигольца, взя-
той в приближении Френеля (см. C8.12)), лишь отсутствием
множителя exp(t'6(z—г')).
В дальнейшем вместо формулы D0.6) мы будем пользоваться
соответствующей формулой, связывающей траисформанты Фурье
по поперечным иоординатам:
ф< (Р. г) = J <р, (х, г) exp (txp) d'x,
h (Р. г) = \ ц, (х, г) ехр (гхр) <ftc.
j 40) МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ 311
Эквивалентная D0.6) формула имеет вид (см. задачу 2)
Z
Ф, (*. г) « Jj j exp (_ 'VB7Z'') !Ч (к. г') Л'. D0.9)
Рассмотрим первое приближение Ф,. Согласно D0.5а) /, (р, г) =
=—k*i(p, г) и из D0.9) получаем (опустим индекс 1 в ср,)
<р(х, г)=-^
о
где е(х, z)—случайная двумерная амплитуда Фурье диэлектри-
ческой проницаемости в(р, г). Перейдем теперь к уровню- % =
= Re<t> и фазе 5'- 1тФ.
Так как
Ф (р, г) = f ер (х, г)ехр (ixp) d?x,
Ф* (р, г) — Г ф* (х, г) ехр (— ixp) d2x = \ ф* (—х, г) exp (ixp) d«x,
можно написать
D0.11)
S'(p.z) =
= j S'(к, г)схр (ixp) *x-*^-'=J ф<"-')-ф;(-"^) ехр (гхр) *х,
D0.12)
причем спектральные амплитуды уровня и фазы выражаются
через ф(х, г) следующим образом:
Х(«,*)=ф(м-1)+Г(~'''1)' S'(x,2) = -S^ibVHiLil. D0.13)
Найдем ф*(—х, г). Так как поле е(р, г) вещественно, имеем
е*(—х, г') ~--е(х, г'), и поэтому из D0.10) получаем
Ф\(-к. ^-T-Jexpif^HgP^}^*'*'><**'¦ D0.14)
Подставляя D0.10) и D0.14) в D0.13), находим
х, z')dz\ D0.15)
440.16)
312 МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ (ГЛ. VI
Усредняя эти формулы, получим у.л — SJ = O (здесь мы вос-
становили индекс 1, так как средние значения уровня и фазы
равны пулю только в первом приближении). Во втором прибли-
жении в формулах, аналогичных D0.15) и D0.16), вместо е (х, г)
фигурировала бы спектральная плотность величины (Vx^i)*
(см. D0.56)), среднее значение которой не раино нулю. Тем
самым и величины Yi и S» оказались бы отличными от нуля.
На вычислении этих средних мы остановимся позднее. Если же
нас интересуют средние квадратичные величины, например
Xs, S'\ то формулы D0.15) и D0.16) достаточны для их расчета
(учет членов второго порядка в % (х, г) привел бы к членам
третьего порядка малости в <xs>, малым но сравнению с основ-
ным членом).
Рассмотрим корреляционную функцию уровня '/ в плоскости
г — const. Из D0.11) имеем
^х (Pi. Ps! г) = <Х (Pi, г) % (рг, г)> =
J J р. + ^р,)] <х (*!, г) х (*»¦ г)>. D0.17)
Таким образом, для расчета i^ необходимо знать функцию кор-
реляции спектральных компонент, входящую в D0.17). Исполь-
зуя D0.15), получаем
<X(*i. *) X (*..*)> =
Sin
D0.18)
Но для статистически однородной случайной среды справедлива
формула
<?(*„ zJeK, za)> = 6(x1 + xs)Fe(x1, 2,-г,), D0.19)
где двумерная спектральная плотность FB сосредоточена в области
|х||г,—гг|<2л D0.20)
(см. задачу 4 к гл. I).
Из D0.19) и D0.18) следует, что
<X(*i.z)x(*,.2)> = 6(xl + xJ)/7J((x1,2), D0.21)
где
1-2!). D0.22)
i 40]
МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ
3K
Еслк подставить D0.21) в выражение D0.17) для tyx, то получим
• D0.23)
Ми видим, что функция Fx(x, г) предстапляет собой двумерный
(в плоскости г — const) пространственный спектр флуктуации
уровня.
Формулу D0.22), связывающую двумерные плотности флук-
туации уровня и флуктуации е, можио существенно упростить,
если использовать свойство функции Fe, выражаемое неравен-
ством D0.20). Для этого сначала введем в D0.22) новые
А
z
переменные интегрирования г' -» (г, + гг)/2, 1 = гг—г,. Для этих
переменных уравнения границ области интегрирования будут
z' = jL?/2, г' = г±(?/2), и D0.22) примет вид
,(х,0. D0-24)
Область интегрирования 2 изображена па рис. 52.
В силу D0.20) в области, существенной для интегрирования
по ?, справедливо неравенство кС, < 2я. Поэтому члены >cJ?/4fe
в аргументах синусов можно оцепить в чтой области следующим
образом:
4* ^ к 4,
поскольку максимальное волновое число хт, ограничивающее
-область, где сосредоточена функция Fe(x, Q, по предположению
мало по сравнению с волновым числом fe. Следовательно, с точ-
ностью до поправок порядка малости y.Jk можно вообще отбро-
сить члены ±x2?/4ft в аргументах синусов, н D0.24) переходит
314 МЕТОЛ ПЛАВНЫХ ПОЗМУЩВЦИЙ [ГЛ. VI
тогда в формулу
Fx (х, г) = ? J dz' di sin' [*'% г<)] Fe(x, ?)• D0.25)
Рассмотрим спектральную плотность Fx(x, г) при таких х,
которые удовлетворяют условию
хг>1. D0.26)
Это неравенство означает, что характерные поперечные масштабы
пеоднородностей урони я, которые мы хотим рассмотреть, малы
по сравнению с длиной трассы г Bя/х<^г). Для таких значе-
ний х область, существенная для интегрирования по ?, ограни-
чена в силу D0.20) неравенством |?| < 2я/х<?:г. Следовательно,
из всей области интегрирования, изображенной на рис. 52,
существенной является лишь узкая полоса ширины 2л/х<^?
вблизи оси ь=0 (па рис. 52 она указана горизонтальной штри-
хоикой). Вне этой полосы функция Fe(x, ?) пренебрежимо мала,
что позволяет добавить к области интегрирования 2 дополни-
тельные участки, изображенные на рис. 52 вертикальной
штриховкой, т. е. расширить область интегрирования 2 до бес-
конечной (по ?) полосы 0 < г' < г (аналогичные соображения
использовались в § 33, рис. 38). Так как в добавляемой области
интегрирования функция Ft пренебрежимо мала (например, она
убывает там с ростом J экспоненциально, как в случае степен-
ных спектров Фе), то допускаемая при этом погрешность несу-
щественна. В результате описанного преобразования мы получаем
из D0.25) выражение
Z СО
Fx (х, z) - ? J sin* [Х>(^г<)] dz' J Fe (x, 0 dj. D0.27)
Но функция F,(x, ?) удовлетворяет равенству (см. формулу C)
в задаче 4 к гл. I)
со
J /•„ (х, 1) dt, = 2лФе (х, О), D0.28)
— 00
где Ф, (х, 0)—трехмерная спектральная плотность флуктуации е,
аргументом которой является двумерный вектор (х, 0). Исполь-
зуя это равенство и вычисляя первый из входящих в D0.27)
интегралов, получаем окончательную формулу для Fx:
Fx[x, г)-^-г [l --Lsin^] Фе(х, 0). D0.29)
{ 401 МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ 315
Эта формула получена для области xz^>\, т.е.
Однако в области -х.<^У1ф функция 1 j-sin-^ стремится
к нулю, как х1. Поэтому, если Vk/z^z'1 (т.е. Vkz"§>\), то
практически во всей области, где сосредоточена функция D0.29),
условие хг^>\ хорошо выполняется. Поэтому ограничение
xz^l, использованное при выводе D0.29), несущественно, если
выполняется условие
означающее, что на длине трассы укладывается много длин воли.
Остановимся еще на одном чисто формальном обстоятельстве,
которое, однако, в дальнейшем будет использовано. При выводе
формулы D0.29) мы предположили, что FK(x, z) является «острой»
функцией ? практически для всех представляющих интерес зна-
чений х. Фактически мы неявным образом заменили функцию
Ft{x, г) на дельта-функцию 6(?). Убедимся, что при замене
Fe (х, 0 ¦— 2яФе (х, 0) 6 (?) г F?* (х, г) D0.30)
мы сразу же получаем из D0.22) формулу D0.29). Действительно,
подставляя D0.30) в D0.22) и выполняя интегрирование но г3,
мы получаем формулу D0.27), в которой использован интеграл
D0.28).
Подобно тому, как, исходя из формулы D0.15), мы подсчи-
тали двумерную спектральную плотность флуктуации уровня,
можно вычислить и двумерную спектральную плотность фазы
fs(*i г). если исходить из формулы D0.16). Не приводя вычис-
ления (см. задачу 3), дадим окончательный результат:
Fs(x, z) = ^[] +^ь\п^]фе{х, 0). D0.31)
Корреляционная функция флуктуации фазы в плоскости г -const
выражается через функцию Fs(x,z) обычным образом:
Фл (Р. г) = S Fs (х, z) exp (ixp)d»x. D0.32)
Если иоле е(р, г) статистически изотропно в плоскостях
г —const или в трехмерном пространстве, то ч|)е(р, г) — фе(р, г)
и трехмерная спектральная плотность Фе(хх, ху, xz) имеет вид
Фв(К*?Ч х\, х]). В этом случае Фе(х, 0) — Фе(х, 0), т. е. зависит
лишь от модуля двумерного вектора х. Из формул D0.29) н
D0.31) при этом. следует, что спектральные плотности Fx(x,z)
и Fs(x, г) тоже зависят лишь от х = |х| и, значит, случайные
поля i н S' статистически изотропны в плоскостях г —const.
Формулы, выражающие корреляционные функцни т)зх и ifis через
316 МЕТОД ПЛАВНЫХ ПОЗМУЩЕНИЯ [ГЛ. VI
F% и Fs, принимают мри этом вид
се
Фх (Р. *) = ~ J Jo (хр) A - -гг sin ^) Ф« (х. 0) к 4», D0.33)
. D0.34)
где J0(x) — функция Бесселя.
Структурная функция фазы Ds(p, z) —<[5'(Pi, г)- S'(Pi + P. г)]2>
пыражается в этом случае интегралом
, г) = л«А»г^[1 -/„(хр)] U -f-*- sin^) Фе(у., ())х dx. D0.35)
§ 41. Анализ результатов МП В
Проанализируем полученные в предыдущем параграфе резуль-
таты. Рассмотрим функцию
Wx(H,z)=\-~s\n^, D1.1)
т.е. множитель, переводящий Фе (х, 0) в Fx(x, г). Разлагая
синус в ряд Тейлора, получаем
Таким образом, в области
или
функция Wx(x) пропорциональна х1. Характерное волновое число
xf -У k/г — ^2я/Яг соответствует по порядку велнчины радиусу
первой зоны Френеля У%.г. В области х^>х^ функция Wx пере-
стает зависеть от х и стремится к единице. График функции
Wx(x, г) изображен на рис. 53. Что касается функции
Ws{x,z) = \+±smv^, D1.3)
фигурирующей в D0.31), то при х=0 она равна 2, а при x^>xF
стремится, как и Wx, к единице (рис. 53).
Вид функции Фе(х, 0) может быть различным и разных за-
дачах, но мы предположили, что волновое число хп, соответ-
ствующее размеру наименьших неоднородности среды, всегда
мало по сравнению с волновым числом излучения к, и поэтому
АНАЛИЗ РЕЗУЛЬТАТОВ МПВ
317
в области х > хи функция Фс (х, 0) пренебрежимо мала. Что же
касается величины y-m'nF — [/rx'mz;k= У2л\г/11, то она зависит от
отношения радиуса первой зоны Френеля к размеру наименьших
неоднородноетей диэлектрической проницаемости. Как мы пом-
ним, величину D -x5,/xj~ Xzjll
принято называть волновым па-
раметром (§ 10).
Рассмотрим сначала случай
^1 Т. 0. J?B<^Xf ПЛИ
(рис. 54). Как уже от-
мечалось, в этом случае спра- '. Щ,
ведлива геометрическая оптика.
Во всей области, где сосредо-
точена функция Фе(к, 0), мож-
D^1 й
(
но при D<^1 с ; достаточной
степенью точности ограничить-
ся первыми членами разложе-
ний Wx(x,z) и Г4.(х, г), т. е.
считать, что
Ws(x, г)«2. D1.4)
Для двумерных простран-
ственных спектров уровня и
фазы формулы D0.29) и D0.31)
дают при этом
Fs(x,
3
Рис.
—в-
f
53.
Фе(К
;, 0).
x/xF
D1
•5)
Таким образом, как уже было показано в гл. V, в области при-
менимости геометрической оптики средний квядрат флуктуации
уровня растете расстоянием, как г3, а средний квадрат флуктуа-
ции фазы—как г. Волновое число k ие входит в формулу для
fx(x. г), т. е. в геометро-оптнческом пределе флуктуации уровня
ие зависят от длины волны.
Средний квадрат флуктуации уровня выражается через Fx
ври помощи формулы^
^ J D1.6)
Отсюда видно, что вклад компонент спектра, соответствующих
крупномасштабным неодкороднестям, которым отвечают малые
Значения х, подавляется множителем и*, обращающимся в нуль
316
МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИИ
[ГЛ. VI
при у,— 0. Основной вклад в хг вносит часть спектра, отвеча-
ющая мелкомасштабным неоднородностям. В этой области произ-
Vn x/xF
Рис. 54.
Рис. 55.
ведение х'Ф, (х, 0) имеет максимум. В связи с этим и поперечный
радиус корреляции для флуктуации % имеет порядок величины /„
(рис. 55).
5 41] АНАЛИЗ РЕЗУЛЬТАТОВ МПВ 319
формулу D1.6) можно представить также в виде
(см. задачу 5). В этой форме выражение для хг Уже было полу-
чено в гл. V при помощи МГО (см. C5.11)).
Для среднего квадрата флуктуации фазы нз D0.31) и D1.4)
находим
~~ '" ' D1.8)
Здесь основной вклад обусловлен той же частью спектра неод-
иородностей, для которой ФЕ(х, 0) максимально. Таким образом,
амплитудные и фазовые флуктуации обусловлены разными участ-
ками спектра неоднородности диэлектрической проницаемости.
Формулу D1.8) можно представить также в виде (см. за-
дачу 5)
(С
~~ " " D1.9)
что отвечает формуле C3.9) для эйконала q> = S'/k, полученной
при помощи МГО. Мы видим, таким образом, что найденные
при помощи МПВ формулы переходят в предельном случае D<^cl
(^>.г<^0) в соответствующие формулы приближения геометри-
ческой оптики.
Рассмотрим теперь другой предельный случай D^>1, соот-
ветствующий фраунгоферовой дифракционной зоне.
Если трехмерный спектр Фе (х) обладает несколькими харак-
терными масштабами хп (п — 1, 2, ...), то мы будем считать, что
условие D = xJ/Kff §> 1 выполнено для наименьшего из этих вол-
новых чисел х,, т. е. область пространства, в которой рассмат-
ривается поле, отвечает фраунгоферовой зоне для неоднородно-
стей всех масштабов, присутствующих в среде.
Взаимное расположение кривых Wx, Ws и Фе для этого слу-
чая показано на рис. 56. Мы видим, что в большей части
области, существенной для интегрирования, Wx я; Ws» 1.
Поэтому, если трехмерная спектральная плотность Фе(х, 0) не
имеет неинтегрнруемой особенности в нуле (и, значит, изменение
в нуле весовой функции Wx(x, z) не играет роли), можно счи-
тать, что
Fx(x, 2)»Fs(x, г)х~Фе(у., 0), Dp-X. D1.10)
320
МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ
[ГЛ. VI
Таким образом, в предельном случае больших D спектральные
плотности флуктуации амплитуды и фазы оказываются примерно
одинаковыми, в силу чего примерно одинаковы н корреляцион-
ные функции:
i|>x (р, г) я; i|)s (р, г) я; i^i f exp (ixp) Фе (x, 0) dxx, D Ss> 1. D1.11)
Для средних квадратов флуктуации уровня и фазы при ?)^> 1
получаем
~~ '* " D1.12)
дли
Что
Отметим, что формула для среднего квадрата флуктуации
фазы в случае D ^> 1 отличается от формулы D1.8), справедли-
вой при D<§\, только вдвое меньшим коэффициентом. Ч
касается флуктуации уровня, то здесь при переходе к случаю
?>^>1 меняется вид зависимости х2 от z: nPl< О<^1, согласно
D1.6), %*<yza, тогда как х2л5г ПРИ D~^>1. Иначе говоря, при
постепенном увеличении г величина %г сначала (в зоне геомет-
рической оптики, где D ~ Яг/г|«^ I) растет, как г», а затем (во
фраунгоферовой зоне, когда величина кг/1% становится большой)
рост 5са замедляется до линейного:
%*-¦¦< ;>
%*-¦
при
5 41] АНАЛИЗ РЕЗУЛЬТАТОВ МПВ 321
Рассмотрим в качестве примера среду, у которой корреля-
ционная функция флуктуации диэлектрической проницаемости
описывается гауссовой кривой
W)^olexp{— rV2a'}, D1.14)
а соответствующая трехмерная спектральная плотность имеет вид
Размер неоднородностеи характеризуется здесь единственным
масштабом а.
Несложный расчет приводит для такого спектра ФЕ (х) к сле-
дующим выражениям для у* и S'* (см. задачу 6):
D1.16)
, D1.17)
где ?> = 2г/Ля2. При D—*0 можно использовать разложение
arctgD — D—D'/3+..., что приводит, в согласии с D1.6) и
D1.7), к кубической зависимости у.а от г:
а для S'1, в согласии с D1.8), — к линейной зависимости:
75 D1.19)
В случае же D^>1 членами ±arctgD/D в D1.16) н D1.17)
можно пренебречь, и тогда, в соответствии с D1.12), получаются
примерно одинаковые выражения для хг и S1':
D1.20)
Графики функций х1 и $''> отнесенных к V2nal (fea)*/16 в за-
висимости от D приведены на рис. 57.
Следует отметить, что формулы того же вида, что и D1.18)—
D1.20), справедливы и в более общем случае, когда трехмерная
спектральная ллотность иеоднородиостей Фе(х) всюду ограничена
(Фе(х)<С) и имеет максимум в точке х = 0. Исходя из общих
формул D1.6), D1.8) и D1.12), можно показать, что при D^1
Г1 ~ о! (*/'«)•, S^-otfc'/eZ,
11 С. М. Рытое в др. ч. II
322
а при D ^>
МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ
[ГЛ. VI
где /s—радиус корреляции флуктуации е.
Рассмотрим теперь другой пример, который не укладывается
в общие предельные соотношения D1.10)—D1.12). Мы имеем в
О I г J 4 S В 7 Л
Рис. 57.
виду степенной спектр, соответствующий флуктуациям диэлек-
трической проницаемости, вызываемым турбулентностью:
Фв(х)^-у/С|х-п/.. D1.21)
Здесь ,1 ж 0,033, а С\ — структурная характеристика, входящая
в «закон 2/3» для флуктуации диэлектрической проницаемости.
В действительности спектр Фг (х) является степенным лишь в
ограниченном диапазоне волновых чисел
х.<^х<^х„, х„ = 2я/?„ кя=2я//., D1.22)
где U н Z-o—соответственно внутренний и внешний масштабы
турбулентности. Однако но многих практически интересных слу-
чаях волновой параметр D0 = h;/hJ-, «составленный» из радиуса
первой зоны Френеля и внешнего масштаба турбулентности 1.0,
ик превышает единицы даже на достаточно больших дистан-
циях г').
]) Например, при распространении света в атмосфере типичные значения
радиуса первой зоны Френеля ис превышают несколько десятков сантиметров,
тогда как внешний масштаб турбулентности Lo порядка нескольких .меаров.
На дистанциях в несколько сотен километров Do остается малым по сравне-
нию с единицей.
S 4IJ
АНАЛИЗ РЕЗУЛЬТАТОВ МПВ
323
Вместе с тем волновой параметр D — y^/ttf, «составленный»
из внутреннего масштаба турбулентности и радиуса первой зоны
Френеля, может быть как меньше, так и больше единицы. В по-
следнем случае метод геометрической оптики уже неприменим
из-за наличия неоднородностей, меньших радиуса первой зоны
Френеля. С другой стороны, поскольку Do<^±< всегда присут-
ствуют и неоднородности размером больше У).г, и для ннх по-
этому еще характерен не режим дифракции Фраунгофера, а фре-
нелевская дифракция или даже геометрическая оптика.
Предположим на время, что ограничения D1.22) отсутствуют.
Тогда функция х/''х(х, г), интеграл от которой определяет ^», бу-
дет изображаться кривой, показанной на рис. 58. В области
x<^kf имеем к/'х(х,"г) ~ х-к1-к-"'' — *'/., т.е. /'х@, г) — 0, а
при х^>хр получаем и/-'х(х, г) ~ у.-''-. Поэтому площадь под
кривой xFx(x, г) на рис. 58 конечна и интеграл
y.dx.
D1.23)
сходится.
Посмотрим теперь, к чему приводит учет реального хода
спектра Фе(к) вне интервала (н0, хт), в котором справедлив
закон D1.21). В области х < х0 трехмерная спектральная плот-
ность Фе(к) возрастает с уменьшением х медленнее, чем у.'',
или же вообще не возрастает.
И»
324 МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ [ГЛ. VI
Поэтому, если х„<^у.р, то в области х < х„ произведение
xWxH>8 уже мало и не влияет существенно на значение интег-
рала D1.23). Следовательно, если «реальная» функция Фе(х) в
области у. < х0 уменьшится по сравнению с чисто степенной
функцией D1.21), то это заметным образом не повлияет на зна-
чение интеграла D1.23). Таким образом, если х<,-^у.р, то откло-
нения «реального» спектра ФЕ(и) от чисто степенного можно
не учитывать.
Равным образом, если х„^>нр, то точка х,„ лежит уже в той
области, где произведение kFx<0,, мало и убывает с ростом н,
так что интеграл
\ 3;tK-'" D1.24)
при больших х„ настолько мал, что его вкладом в полный ин-
теграл D1.23) тоже можно пренебречь. Поскольку интеграл от
произведения «реального» спектра на Wx отличается в высоко-
частотной части спектра от интеграла с чисто степенным спектром
на малую величину D1.24), этой разницей при кт^>кР тоже
можно пренебречь.
Итак, если выполняются условия х„ <^xf<^zm, то при рас-
чете ](а можно считать, что Фе(и) ~ х~"'> при всех я, и в этом
случае подстановка D1.21) в D0.33) дает
00
Замена переменной интегрирования K^zjk — t'1 приводит этот ин-
теграл к виду
J(/I)(!?!)--/.tf. D1.26)
Полагая р=0 (напомним, что У„@) —1), получаем для
Ха = г|?х(О, г) выражение
X* = NCWWI; щ<^кр<^*„, D1.27)
где N—числовая константа, равная
V.d*«0,077. D1.28)
I 4il АНАЛИЗ РЕЗУЛЬТАТОВ МПВ. 325
Степенная зависимость %г от г (показатель 1]/6) оказывается
промежуточной между предельными случаями ~%' ~ г3 и х"'~2,
соответствующими зоне геометрической оптики и зоне Фраунго-
фера. Это обусловлено тем, что при Ho<^xf<^xm • всегда суще-
ствуют неоднородности, для которых точка наблюдения находится
в зоне дифракции Френеля.
Расстояние р между точками наблюдения входит в D1.26)
лишь в комбинации рУкг=У 2пр1\/Г).г. Это означает, что ра-
днус корреляции флуктуации уровня имг-от порядок величины
VT7z. График корреляционной функции A1.26) приведен па
рис. 59 (см. III]).
Обратимся к флуктуациям фазы. Если подставить трехмерную
спектральную плотность вида D1.26) в формулу D0.34) и не при-
нимать во внимание ограничений
D1.22), то интеграл в D0.34)
будет расходиться в точке х —0.
Это обусловлено тем, что, в от-
личие от Wx(x., г), несовая функ-
ция Ws(x, г) не обращается
в нуль при х--0. Таким обра-
8ом, роль компонент спектра, от-
вечающих крупномасштабным не-
одяородностям, пренебрежимо
Малая для амплитудных флуктуа-
диН, оказывается для флуктуа- р зд
ний фазы не меньшей, чем роль
мелкомасштабных компонент. Это
не позволяет экстраполировать спектральную плотность вида
D1.21) на область к<х„- Для расчета величины S'" необходимо
знать истинную трехмерную спектральную плотность в указанной
области волновых чисел, т. е. надо учитывать влияние крупных
кеоднородностей. Простейший способ учета «насыщения» флук-
туации в области крупных масштабов состоит в замене спектра
D1.21) спектром D1.15), который не имеет особенностей при
я—>-0. Оценка дисперсии эйконала, отвечающая такому спектру,
уже была ранее получена при помощи МГО (см. C6.8)).
Рассмотрим теперь структурную функцию фазы Ds(p, г) в
плоскости г— const. Здесь мы уже можем ожидать, что крупно-
масштабные неоднородности (с размерами, много большими р)
ие будут играть роли, так как они дают одинаковый вклад в
набеги фаз но обоим лучам и поэтому выпадают из разности
S (Pi, г)—S'(pt, г). В формуле D0.35) это находит отражение
¦ том, что множитель 1—Уо(ир) в области х<^р-' велет себя
как н1. Поэтому, если подставить степенной трехмерный спектр
D1.21) в формулу D0.35) и не учитывать ограничении D1.22),
326 МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ (ГЛ. V]
то мы получим сходящийся интеграл
Ds(p. 2)-лда'г[[1-ЛЫ|(| hj^-sin-^-)*-'/,**. D1.29)
о
Особенность в нуле имеет здесь вид х2-";> — х~*'\ т.е. является
интегрируемой. Повторяя рассуждения, проведенные при обосно-
вании формулы D1.24), можно убедиться в том, что при выпол-
нении условий
*о «^ 1 /р «^ хя или /0 <?; р <* ^и D1.30)
справедлива формула D1.29). В этих рассуждениях волп'.-иое чи-
сло 2л/р будет играть ту же роль, что ки в предыдущем случае,
так как весовая функция [1—./о(хр)]W'.s^-, -г) при и<*2л/|1
имеет вид Xs, а при н^>2л/|) она приблизительно постоянна.
Сдела» в интеграле D1.29) замену переменной хр = t, получаем
7e-sin-^-)/-I"d/. D1.31)
Исследование этого интеграла (см. задачу 7) приводит к следую-
щим результатам. Если /0<^Р<«??о и fep35s>z, то
Ds[p. z) = '2MClk2zp''; M-:^Jt\[\—J,(t)]t-b'dix0J3, D1.32)
а при kp'<^z
Ds(p. г)=-МС*к*гр':т: D1.33)
Чтобы найти вид функций i)"x(|>, г) и Dsifi, 2) при р^
необходимо учесть, что трехмерная спектральная плотность Фе(н)
в области и;$>чш быстро убывает. Лля области |i<^/n можно
получить формулы (см. задачу 8)
% (р, г) - ? (г) [1 -а, {,.//.)' ~ ¦ ¦ ¦ J, D1.34)
D.S.(P, г)-а2(р//„J+... D1.35)
В заключение данного параграфа выведем ряд найденных выше
основных формул при помощи простых рассуждений качествен-
ного характера (разумеется, мы не получим числовых коэффи-
циентов, входящих в эти формулы).
Рассмотрим сначала флуктуации фазы. Как мы убедились
выше, для нх расчета достаточно использовать приближение гео-
метрической оптики, так как учет дифракционных эффектов при-
водит лишь к изменению числовых коэффициентов. Возьмем луч
j 4|] АНАЛИЗ РЕЗУЛЬТАТОВ МПВ 327
длины z. Если масштаб иеодиородностей равен /е, то на луче
укладывается N~zjlt независимых иеоднородностей. После про-
хождения одной неоднородности произойдет набег фазы волны,
равный lt — V^tmljiy I +-S-), т.е. случайная компонента этого
набега равна по порядку величины /„fee. Так как случайные ве-
личины е, отвечающие различным неодиородностям, статистически
независимы, для суммарного среднего квадрата набега фазы имеем
5'* ~ N {1еке)г = у- l\k*a\ — a\k*ltZ, что соответствует формуле
D1.19).
Оценим теперь в том же приближении геометрической оптики
флуктуации амплитуды. Их можно рассматривать как результат
случайных фокусировок и дефокусировок. Пусть по-прежнему
неоднородность имеет размер /е, а отклонение диэлектрической
проницаемости от средней равно е. Как известно, фокусное рас-
стояние линзы, ограниченной сферической поверхностью с радиу-
сом R, равно F — nR/(n — я), где п — показатель преломления
линзы, а п —окружающей среды. Поэтому для рассматриваемой
неоднородности фокусное расстояние будет порядка 1;~1г1е, а
угол отклонения луча а (рис. 60) имеет порядок a~(lt/F) ~ е. Из-
менение диаметра упавшего па «линзу» пучка составит на рас-
стоянии 2 позади нее величину Дй = га~ге. Но амплитуда вол-
ны А связана с диаметромJ пучка d соотношением A*d* — АЦ%,
откуда ЛА/А-^ —\d/d. Если
рассматривать только слабые
флуктуации интенсивности,
то фокусное расстояние F
очень велико \\ d для z<^F
будет порядка /е, т. е. А~Аи
и, тем самым,
%~4- D1.36)
Мы подсчитали относительное изменение амплитуды, вызванное
действием одной «линзы». Суммарная оптическая сила I,/7 не-
скольких слабых «линч», расстояние между которыми мало по
сравнению с их фокусными расстояниями, равна сумме оптических
сил составляющих, так что суммарное изменение амплитуды будет
— — У* i^_
А» 1 lti
328 МЕТОД ПЛАВНЫХ ВОЗМУЩЕНПГ) [ГЛ. VI
Среднее значение этой суммы равно нулю, а для среднего квад-
рата получаем
где N я> г/1г — среднее число неоднородностей на дистанции г.
В итоге
что соответствует формуле D1.18).
Возьмем теперь случай, когда в среде присутствуют неодно-
родности различных размеров, причем в соответствии с трехмер-
ной спектральной плотностью D1.21), которой отвечает струк-
турная функция ?)е(р) = С|р*/', неоднородность размера / харак-
теризуется флуктуацией диэлектрической проницаемости ё;~СвГ'>.
Рассмотрим сначала амплитудные флуктуации. Согласно фор-
муле D1.36)
Мы видим, что эффект тем больше, чем меньше неоднородность.
Если размер наименьших неоднородностей /„ удовлетворяет усло-
вию la^>\^Xz (и поэтому дифракционными эффектами можно пре-
небречь), то и качестве / в D1.37) следует взять 1а. Число таких
неоднородностей на пути распространения волн равно N— г/'1я,
и суммарный средний квадрат флуктуации амплитуды будет равен
по порядку величины
- D|-38)
Пусть теперь /„«^j/Хг, но вместе с тем ^Я?<^/.0, где Z.o —
внешний масштаб неоднородностей. Это означает, что имеются
неоднородности с размерами / > \^Xz, к которым применима
геометрическая оптика, а значит, и формула D1.37). В то же
время к неоднородностям, размер которых I лежит в интервале
(/0, 1/Тг), геометрическая оптика неприменима и их действие
необходимо рассматривать с учетом дифракционных эффектов.
В данном случае роль дифракции сводится к тому, что лннзы
с размерами, меньшими V\z, уже перестают фокусировать или
дефокусировать полпу, а в обоих случаях создают расходящиеся
пучки с углом раствора порядка X//. Следовательно, неоднород-
ности с размерами, меньшими (/лг, можно вообще не учитывать.
t 4.1
АНАЛИЗ РЕЗУЛЬТАТОВ MlIB
.129
Действие же более крупных неоднородностей по-прежнему опи-
сывается формулой D1.37). Поэтому окончательную формулу мы
можем получить прямо из D1.38), если заменим в ней размер /„
на размер наименьших неоднородностей, которые еще способны
фокусировать (или дефокусировать) волну, т.е. на V~\z. В ре-
зультате получаем формулу
L^\'Tz^>h, D1.39)
которая соответствует D1.27).
Перейдем теперь к флуктуациим разности фаз в двух точках
с координатами (р,,.г) и (р„ г), отстоящих друг от друга на
расстояние р = |р1—р2|.
z=0
ё,
Az
Рч<
A
•
. fil.
Рассмотрим два луча, приходящих в точки (р„ г) н (р2, г),
н выберем слой среды такой толщины Дг, чтобы на протяжении
Дг величины e(pt, г) мало менялись. Этот участок трассы вносит
сдвнг^фаз AS ~ k Де (р) Дг, где Де(р) — разность значений е на
лучах (рис. 61). Здесь возможны следующие два случая.
Если р^/0, то оба луча находятся в пределах одной неод-
нородности размера /0 и мы можем выбрать Дг~/0- Тогда для
участка длины U имеем AS? — fe2 [Ле (р)]а <5- Но Аеа (р) — это струк-
турная функция t. Как было указано в гл. I, § 4, если р<^/0.
ToDe(p)~C2(p/7u)Yo'1~C&-'.'-(>! и, следовательно, AS\~Clk4^p4l
Число независимых неоднородностей на пути г в этом случае
АГ~2//0, так что суммарный средний квадрат разности фаз равен
eSI~CifcVtf'T-~Cifc1/J1V*, P^'o- D1.40)
'о
Пусть теперь /.о^р^-'о- В этом случае основной влад в AS
вносят неоднородности с размерами порядка р. Действительно,
более мелкие неоднородности обладают меньшими значениями к, а
более крупные вносят одинаковый вклад в сдвиг фазы обоих
лучей' и поэтому несущественны для разности фаз AS. Мы можем
Поэтому выбрать Дг~р, и тогда
AS,-
330 МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ 1ГЛ. V
(поскольку Де (p)~Cepv>)- Полный средний квадрат разности
фаз, вызванной всеми Л'~г/р неоднородностями, будет иметь по-
рядок величины
6S>~CJfe»pi/l-|-~C|feV'''Z. D1.41)
что соответствует формуле D1.32).
Из приведенных качественных рассуждений видно, что основ-
ные формулы МП В для турбулентной среды можно получить из
геометро-оптического анализа, если только учесть дополнительно,
что неоднородности с масштабами, меньшими радиуса первой
зоны Френеля, несущественны для амплитудных флуктуации.
Что же касается предельного случая D^>1, которому соот-
ветствуют формулы D1.20), то здесь геометрическая оптика уже
полностью неэффективна. Формулы D1.20) тоже можно получить
путем качественных рассуждений, но при этом необходимо поль-
зоваться чисто дифракционным понятием эффективного попереч-
ника рассеяния для зоны фраунгоферовой дифракции [6J.
§д42. Распределение вероятностей флуктуации
амплитуды и фазы. Закон сохранения энергии
и границы применимости МПВ
Исследуем законы распределения вероятностей для уровня
н фазы волны. Если при расчете комплексной фазы Ф можно
ограничиться первым приближением Ф., то, согласно D0.5а)
и D0. G),
Z
t>i(P, z) = -fc'$dV \dz'K{p—p', 2—z')?(p', г'), D2.1)
о
где функция К определяется формулой D0.8). Отсюда для
уровня у. и фазы S' следуют формулы
2
Xi(P. z) = -*«Jdy $&'Де/С(р-р'. г-г')е(р', г'), D2.2а)
S[(p, г) = —fc'Jdy $<fc'Im/C(p—р', г—г')в(р', г'). D2.26)
о
Для того чтобы найти законы распределения вероятностей % и
S', можно было бы, пользуясь этими формулами, найти моменты
<Xi>. <S'in>, <XiSi"> и по ним построить плотности вероятностей
для х. S' и совместную плотность вероятностей для (хг/, S[).
Такой путь, однако, слишком сложен.
I ,2| РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ 331
В конце предыдущего параграфа нам удалось получить испов-
ные формулы для средних квадратов флуктуации уровня и фазы,
исходя из простых качественных соображений, причем неодно-
родная среда разбивалась па отдельные объемы, вносившие ста-
тистически независимые вклады в х и S'. Аналогичное разбие-
ние можно провести и в формулах D2.2), представив интегралы
как суммы интегралов по слоям (г,, zni), продольные размеры
которых Аг значительно превышают радиус корреляции флук-
туации диэлектрической проницаемости (Аг^>/8). При этом мы
получим для % и S' формулы, имеющие внд
Х'2Л S' -25"", D2.3)
в которых отдельные слагаемые можно приближенно считать
статистически независимыми. Если размер Аг [можно выбрать
так, что будут выполняться соотношения
то на протяжении пути волны число независимых слагаемых
в формуле D2.3) будет велико: /У = г/Дг^>1. В этом случае вели-
чины х и S' оказываются представленными в виде сумм большого
числа статистически независимых слагаемых и в силу централь-
ной предельной теоремы их можно считать распределенными по
нормальному закону.
Приведенное рассуждение весьма нестрого. В действительно-
сти вклады отдельных слоев не являются полностью некоррели-
рованными, так как неоднородности, примыкающие к границам
этих слоев, вносят коррелированный вклад в соседние члены
сумм D2.3). Далее, us некоррелированности отдельных слагае-
мых, входящих в суммы D2.3), еще не следует их статистическая
независимость. Позтому строгое обоснование утверждения о стрем-
лении законов распределения для у. и S' к нормальным должно
опираться на пределвные теоремы для линейных функционалов
от случайных функций1) (см., например, [7]). Мы не будем,
1) Например, для случайных процессов 5@ условия, при которых рас-
пределение вероятностей интеграла т)= Г | (f) / (() dt стремятся к пормалмкшу
при увеличении интервала Aг, /,), включают и так называемое условие силь-
ного перемешивания:
р
(I
-¦>
t)<*t )
;Ш МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИИ [ГЛ. VI
однако, углубляться в этот вопрос. Отметим, что эксперимен-
тальные данные хорошо подтверждают вывод о нормальности
распределений вероятностей для % и S' в тех случаях, когда
применимо первое приближение МПВ [8].
Амплитуда А волны связана с уровнем х формулой
Х = 1п-г, D2.4а)
откуда
Л = Л„ехр(х). D2.46)
Как следует из D2.4а), логарифм амплитуды распределен по
нормальному закону, откуда вытекает, что сама амплитуда имеет
логарифмически нормальное распределение. Легко найти мо-
менты А". Для этого представим % в виде % = % + %¦ Как уже
отмечалось выше, величина х в первом приближении МПВ равна
нулю и для ее расчета необходимо использовать второе прибли-
жение. Формула D2.46) принимает вид А = Л„ехр(х)ехр (х).
Отсюда
Так как для нормальной случайной величины п%, среднее зна-
чение которой равно нулю, справедлива формула
то для А" получаем
D2.5)
При распространении плоской волны в статистически однород-
ной среде имеет место закон сохранения А' — const = А'О (см. C9.11)).
Полагая в D2.5) п = 2, получаем
Отсюда и из равенства Л3 = Л? следует, что должно выполняться
соотношение
Х = -о*. («.6)
являющееся следствием закона сохранения энергии.
Разумеется,' величину х можно было бы найти и непосред-
ственно из второго приближения уравнений МПВ. Такой расчет
проведен, например, в работе [9], и его результат согласуется
с равенством D2.6).
{ 42] РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ 333
Если подставить D2.6) в формулу D2.5), то она принимает
вид
^^Ц] D2.7)
Найдем средний квадрат флуктуации интенсивности / — Л*. Оче-
видно, 7=- Л5- Л}. Для 7*=-Л1 получаем из D2.7) П^АУ*.
Поэтому дисперсия интенсивности О; = /а —(/)а будет
o) = Ai(eia*-l) . D2.8)
Отметим, что интенсивность / = Ла = АЦе2* имеет, как и ампли-
туда, логарифмически нормальное распределение.
Рассмотрим теперь вопрос о границах применимости МПВ.
Прежде всего, поскольку уравнения МПВ получены из прибли-
женного параболического уравнения C8.4), условия применимо-
сти последнего необходимы и для применимости МПВ. Но урав-
иения МПВ решены нами лишь в первом приближении, поэтому
следует выяснить условия, при которых поправки к величинам
о?, S' , Ds(p) и т. д., найденные из второго приближения, будут
малыми. Соответствующие расчеты проведены в целом ряде работ
{см., например, [9,10]), результаты которых сводятся к сле-
дующему.
Прежде всего, должно выполняться условие малости флук-
туации уровня, найденных в первом приближении МПВ:
х!<^1. D2.9)
При выполнении этоСЬ условия поправки второго приближения
X величине о% будут несущественными. Например, если трехмер-
ная спектральная плотность флуктуации е имеет чисто степен-
ной вид, как в случае турбулентных неоднородностей, то для
Величины о\ (с учетом следующих приближений МПВ) справед-
лива формула
! Jg M+ ¦ ¦¦ =/(Й). D2.10)
Причем ffrF)«?! при 5с!<^1.
Если же мы интересуемся величиной D$(p, г), то для нее
1в случае степенных спектров) с учетом следующих приближений
МПВ имеет место формула
Ds(p, z)=--Dsl(p, z)+ai[Dsl(p, z)]'+..., D2.11)
В которой DSl (р, г) — структурная функция фазы, найденная
» Первом приближении МПВ. Поэтому условием применимости
3»+ МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ [ГЛ. VI
МПВ для начисления Ds(p, г) служит неравенство
Dsi(p, г)<1. D2.12)
Следует подчеркнуть, что условия D2.9) и D2.12) независимы:
возможны такие соотношения между параметрами задачи, когда
одно из них выполнено, а другое нет. В этом случае первое
приближение MI IB пригодно для расчета одной величины, но
непригодно для расчета другой. Ограничение D2.12) является,
по-видимому, излишне жестким. Расчеты, проведенные в при-
ближении параболического уравнения (гл. VII), приводят к зна-
чительно более слабому ограничению величины Ds (р, г), чем
D2.12). _
Важно отмстить также следующее. Если условие Ул<^1 на-
рушено, например у.'«1, то учет второго приближения не спа-
сает положения, так как, согласно D2.10), при этом все члены
ряда становится существенными.
В области применимости МПВ, в силу условия aj^rl, мы
можем разложить экспоненциальные множители и формулах для
А" в ряды и ограничиться их первыми членами. Например, вме-
сто D2.8) можно написать
A=e«i-lfbtol D2.13)
В связи с этим возникает следующий вопрос. Так как МПВ
применим лишь в случае слабых флуктуации уровня (к ампли-
туды) волны, то имеет ли он преимуществе! по сравнению с ме-
тодом малых возмущений?
Если поле к (г) искать в виде и — и„ + и1+..., то флуктуации
амплитуды Л и фазы 5 можно выразить через и„ и «,: А/Ао —
= Re(u,/«,l), 6'= Im (A,/и„). Поэтому, зная вторые моменты для
Re и, и Im и„ можно найти соответствующие величины для ам-
плитуды н фдны. Формулы для амплитудных и фазовых флук-
туации, найденные таким путем, совпадают с полученными из
уравнении первого приближения МПВ, за исключением того, что
вместо la А следует подставить In Л04- А/Ло, т. е. учесть первый
член разложения In Л в ряд по .4/Л0.
Если же обратиться к законам распределения вероятностей
для амплитуды, то здесь выводы, получаемые при помощи обоих
сравниваемых способов, будут отличаться коренным образом.
Применив к амплитудным флуктуациям теорию возмущений,
мы находим для закона распределения вероятностей амплитуды
обобщенный закон Релея (ч. I, формула B5.3)). Для этого за-
кона распределения отношение <Л'>/Л? =4—'-=0,27, т.е. боль-
42J
РАСПРЕДЕЛЕНИЕ ИЕРОЯТНОСТЕЙ
335
шие флуктуации амплитуды не находят объяснения. В то же
время МПВ приводит к логарифмически нормальному закону
распределения для А, при котором такого ограничения нет. Хотя
формально должно выполняться неравенство D2.9), фактически
оказывается, что формулы для а\, получаемые в первом прибли-
жении МПВ, хорошо согласуются с экспериментальными данными
Рис. f.2.
вплоть до значений с$^1 [8, И]. Законы распределения вероят-
ностей для А, полученные экспериментально лри oj^l, тоже
хорошо согласуются с логарифмически нормальным распределе-
нием, и их нельзя аппроксимировать распределением Релея.
Однако в области, где рассчитанная при помощи МПВ вели-
чина а\ превышает единицу, экспериментальные данные резко
расходятся с результатами расчета. Сопоставление измеренных
и рассчитанных при помощи .МПВ результатов приведено на
рис. 62 [8]. На этом рисунке по вертикальной оси отложены
измеренные значения ах, а по горизонтальной оси — значения
0оея у х?, вычисленные в рамках первого приближения МПВ
с использованием независимо полученных (из микрометеорологи-
ческих измерений) величин С\.
_ Из сказанного ясно, что для описания области, в которой
Х*>1, необходимо использовать методы расчета, выходящие за
рамки теории малых возмущений и МПВ.
jt36 метод плавных возмущений [гл. vi
Задачи.
1. Функция Грина G(r) удовлетворяет уравнению
ДО (г) | «5 (г)-6 (г) A)
и условию излучения на бесконечности. Вывести для О (г) двумерное спек-
тральное разложение.
Решение. Подставив в A) трехмерное разложение Фурье
G(r)-G(p, г)- J d*x Jj dpg(x, p) exp {i (хрН-рг)}, B)
получаем уравнение
откуда следует, что
В знаменателе подынтегрального выражения введена бесконечно малая
(в - -*-|-0) мнимая добавка, соответствующая затуханию юлны (ImA>0) н
приводящая при вычислении интеграла C) к функции Грина, отвечающей
расходящимся волнам.
Если выполнять в C) интегрирование по р, то мы получим искомое раз-
ложение функции G (г) в двумерный интеграл Фурье. Рассмотрим интеграл по р:
— э>
Полюсы Pi.»—i Vk*— х'н« расположены как в верхней полуплоскости
(ImPi > 0), так и в нижней (Imp. < 0). Ксли г > О, то контур интегрирова-
ния можно замкнуть бесконечной полуокружностью в верхней полуплоскости
комплексного переменного р, и вычет в верхнем полюсе дает
е'Р,* _ _ ехр {<' Ук1—х'г}
Pi-Pa "' V^=Ti
причем
у - _ 2Л1-^- - - Ж "'' '>г„ ~ '' . (S)
(выбор знака в нижнем равенстве обеспечивает выполнение условия Im р, > О
как лри к* > х1, так и при к* < х>). Подставляя E) в C), получаем, что
нри г > О
X
0 (р'г» -w I «•* »р{'^р+^;-^1} р г > 0. F)
— 30
Аналогично вычисляется интеграл н при г < 0. когда вычет надо брать в по-
люсе Pi- Окончательная формула, охватывающая оба случаи, отличается от (б)
заменой г на \г\.
ЗАДАЧИ 3,47
i. Найтн функцию Грнна К (р. 2) уравнения D0.5).
Решение. Будем искать решение уравнения
2ift-^.+ALO-/(p. г)
с начальным условней Ф(р, 0)_о в виде двумерного интеграла Фурье
Ф(р, z)=jj exp(ixp)if (x, z)d«x. B)
Подставляя в A) такое же разложение и для функции /(р, г):
/ (р'_ г) - ^ ехр (*яр) ц (х, г) &х.
f
получаем
1 I xlz\
Умножая это уравнение на ^ехр< — jjr f и интегрируя по г от 0 до г
с учетом граничного условия <р(к, 0)=0, находим
\[^Щ. D)
Подстановка D) в B) дает
j{'V!^~g')|(x, г')-
Чтобы получить окончательное выражение для Ф, нздо воспользоваться
обратным преобраэованнем Фурье для ц(х, г') (вторая формула C)):
Ф(Р'
Взяв интеграл по к, получаем формулу вида D0.6), в которой /С(р, г) опре-
деляется формулой D0.8).
3. Найти двумерную пространственную спектральную плотность /^{х, г)
флуктуации фазы D0.16).
Решение. Как и для флуктуации уровня (см. D0.21)), имеем
. г). A)
338 МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИИ [ГЛ. VI
Из D0.16) следует, что
<S (ч. г) S (х\ г» = Т J d2' J dz" cos
Xcos
а так как, согласно D0.19),
<е(х, г')е(х', г*)> = 6(и4 х')^е(и, /—г"),
получаем следующую связь между спектральными плотностями fs и /"с:
«, г'-г'). C)
Еслн'воспользоваться теперь эффективной двумерной спектральной плот-
ностью D0.30):
^(и, г'—г')^2лФе(х, 0)8(г'—г*),
то формула C) принимает вид
г
FS&, г) = ^Фс(И> 0) Ccos» ["' (г2~г>)] ^',
что после вычисления интеграла приводат'к выражению D0.31).
4. Найти корреляционные функций флуктуации уровня н фазы для точек
наблюдения, разнесенных как в поперечном, так и в продольном направлении.
Решение. Исходя из формулы C.11), получаем
й р», гг) =
= J <P*! J d3)*, exp [i (xjpi + «rf),)] <x (xj, ?j) x (иа, га)>. A)
Используя формулы D0.15), D0.19) и D0.30), находим, далее,
i. Ji)X(«.. г,)> = -^ J d/ j* dz' 3in ^ Kl (г1~г>) I x
о о
х,, 0)8(г'-2') =
if 5(«1 + х.)Фе(хь0) Г"
где г< = т1п(г1, гг). Подстановка B) в A) дает
*x(pi. г,; Pi, г,) = ^-|(РхФе(х, 0) exp [i»t (Pj—Р*I X
ЗАДАЧИ 339
Формула для функции корреляции фазы i|)S отличается от C) лишь заменой
синусов на косинусы:
+S(Pi- гь Р«- ^> = V I <Ркфе(я-
х!(г2 —г'I
-4*—J ¦
С'., Г"а(г, —г)|
х J d2' cos [ ^ j cos
Вычислив интегралы по z' и используя равенство 11ъ(%1~22)—г< =
l/>l*i~~zs|> находим
*х. S<f •- г'' Р>- г=) = —4~^ \ ^чФ?(и.
L-p2)] X
Здесь верхние знаки относятся к \)?х, нижние—к т^$.
При Zj —г2 = г формула E) переходит в формулы D0.29) и D0.31). Заме-
тим, что корреляционные функции, определяемые формулой E), зависят лишь
от pi—рг, т. е. инвариантны-по отношению к одновременным сдвигам обеих
точек наблюдения в плоскостях г — г^ н г = г2 на одну и ту же величину.
Вместе с тем в E) входит как Bt—га), так и (Zj-fzj). Таким образом, флук-
туации уровня н фазы статистически однородны по поперечным координатам,
но не являются статистически однородными но продольной координате.
5. Вывести формулу D1.7) из D1.6) и D1.9) из D1.8).
Решение. Проинтегрируем разложение Фурье
^ $ Фв(и, р) ехр [/ (хр+р
- СС - 00
по г в пределах (—»', со):
J J J x. р)ехр(|«р).2яб(р) =
^2л f
или, учитывая четность фв(р, z) пи г,
("ф8(«, 0)exp(ixp)d2x=i-Гфе(р, г)<Ь. A)
-со О
Действуя на это равенство оператором Aj_ н [принимая во внимание, что
Д5 1), находим
СО IX
f х4Фе (х, 0) ехр (Ыр)й"-л=~ С д^1|)с (р, г) Лг.
340 МЕТОД ПЛАВНЫХ ВОЗМУЩЕНИЙ [ГЛ. VI
Положим здесь р = 0; тогда
х'фе(х, 0)<Рк=
Подставляя это равенство в D1.6), получаем D1.7).
Положив р = 0 в формуле A), получаем
=_L t ^ @, г) dz.
Подстановка этого равенства в D1.8) приводит к формуле D1.9).
6. Найти средние квадраты флуктуации уровня и фааы для частного слу-
чаи гауссовой корреляционной функции флуктуации диэлектрической прони-
цаемости:
Решение. Найдем x'^+xCi г)- Полагая в D0.33) р = 0, получаем
B)
где х! —xJ-J-Xj. Полагая в D1.15) хг = 0 и подставляя Фе(х, 0) в B), по-
лучим
' о
Произведем замену переменной интегрирования, положив xsa8/2 = '- Тогда
для х5 получям
Г Г,
О
где введен волновой параиетр_О = 2г1ка*.
Рассмотрим входящий в х* интеграл
Очевидно, при Я = 0 имеем /@) —0. Далее,
СС jo /
/' (D) = J cos Dt e-'dt - Re J е- u + W)' it = Re 1HJfO--fTToi •
ЗАДАЧИ 341
откуда
Следоватсльно,
Средний квадрат флуктуации фазы получается отсюда просто переменой
знака перед вторым слагаемый.
7. Найти асимптотические формулы для структурной функции фазы D1.31)
для предельных случаев *р'<^г и Ар3^8>г.
Решение. Наиболее существенный вклад в иитеграл D1,31) даег область
/~1. так как при <^>1 мал множитель <"'¦", а при : <^ I мал множитель
!1 — Уо @1- Если при (— I справедливо неравенство kp'/z^l, то
??|
где Л1—числовая постоянная. Если же *<>2/z;>l, to при / — 1 имеем
I . / t'z \ ; t*z
Гп^/|
П—МО] (i-r-т^- sin ^-)г''-лй 2 f [1-
Именно поэтому коэффициенты в формулах для Ds(p, г) в случаях *ps<^z
и %is^>z отличаются в два раза.
8. Ограничиваясь случаем статистически изотропнш флуктуации е, найтн
вид функций if»(p, г) и Ds(f>, г) при p<-g/0, где /0- размер наименьших
неоднородиостей диэлектрический проницаемости.
Решение. Будем исходить из формул D0.33) и D0.36):
(I)
B)
Так как функция Ф! (х, П) пренебрежимо мала при к>хя~2я//0, основной
вклад в интегралы A) и B) дает область х < 2л/1а. Если р<^/„, то и этой
области хр < 2яр//0 <^ 1. Поэтому можно воспользоваться первыми членами
степенного разложения Л(хр) = 1— х*р'/*+ ••¦ Подстановка этого разложе-
ния в A) и B) и приводит к формулам D1.34) и D1.35).
Глава VII
ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА В ЗАДАЧЕ
О РАСПРОСТРАНЕНИИ ВОЛН В СРЕДЕ
СО СЛУЧАЙНЫМИ НЕОДНОРОДНОСТЯМИ
§ 43. Обоснование марковского приближения
Во всех рассмотренных в гл. IV—VI приближенных спосо-
бах описания распространения волн в случайво-веодвородных
средах использовалось предположевие о малости флуктуации
диэлектрической проницаемости. Оно либо лежало в самой ос-
нове способа (метод малых возмущений для точного волнового
уравневия), либо вводилось потому, что без него нельзя было
продвинуться в решении приближенных уравнений (геометриче-
ская оптика, метод плавных возмущений). Только при этом
предположении удавалось выразить с помощью указанных ме-
тодов в явном приближенном виде волновое поле в случайной
среде или его амплитуду и фазу через г. Для нахождения ста-
тистических характеристик различных параметров волны надо
было лишь выполнить усреднение полученных выражений или
их комбинаций. Разумеется, использование в той или иной
форме теории возмущений по е налагает на границы примени-
мости этих методов довольно жесткие ограничения. Например,
ни одни из рассмотренных выше методов решения стохастиче-
ского волнового уравнения не позволяет дать адекватное описа-
ние сильных флуктуации волнового поля.
В ч. I книги для анализа физических задач, описываемых
системой обыкновенных дифференциальных уравнений со слу-
чайными коэффициентами, был применен аппарат марковских
случайных процессов. При этом в ряде случаев удавалось по-
лучить уравнение непосредственно для распределений вероят-
ностей или для усредненных величин—моментов и т. п. В случае
динамических систем, подверженных случайным параметрическим
воздействиям (см. задачу 22 к гл. I), для применения аппарата
марковских случайных процессов оказалось необходимым выпол-
нение следующих условий.
} 43] ОБОСНОБАНИЕ МАРКОВСКОГО ПРИБЛИЖЕНИЯ 343
Во-первых, должен выполняться принцип динамической при-
чинности: решение в некоторый момент времени должно функ-
ционально зависеть лишь от предшествующих по времени значе-
ний случайных коэффициентов.
Во-вторых, время корреляции случайных воздействий (т. е.
случайных функций, входящих в уравнения) должно быть малым
по сравнению с наименьшим характерным временем отклика
динамической системы. В этом случае возможна аппроксимация
корреляционных функций случайных воздействий дельта-функ-
цнями от времени.
При выполнении обоих условий оказалось возможным полу-
чить замкнутое уравнение для плотности вероятностей состояния
динамической системы. Прн гауссовых дельта-коррелированных
коэффициентах это было дифференциальное уравнение Эйнш-
тейна—Фоккера. Если динамическая система к тому же линей-
на, то можно получить замкнутые уравнения н для моментов
(ч. I, §§ 36, 37 и задача 7 к гл. V, а также задача 22 к гл. I
данной книги).
Аппроксимация марковским случайным процессом использует,
в отличие от теории возмущений, другой малый параметр—отно-
шение то/т, т. е. времени корреляции воздействий т0 ко времени
корреляции отклика т. Нулевому приближению по этому пара-
метру н отвечает марковское приближение. Для законности такой
аппроксимации, разумеется, могут потребоваться также ограни-
чения интенсивности флуктуации параметров, но возникающие
при этом неравенства содержат и параметр то/т, так что огра-
ничения интенсивности флуктуации оказываются менее жесткими.
Можно ли применить теорию марковских процессов к задаче
о распространении волн в случайно-неоднородной среде, т. е.
к задаче о случайных поля»}
Прежде всего, само понятие марковского процесса предпола-
гает наличие упорядоченной, переменной (аналогичной времени),
без наличия которой невозможно формулировать основное свой-
ство таких процессов—возможность представления многоточеч-
ной плотности вероятностей в виде произведения вероятностей
перехода. Ясно, что упорядоченную переменную можно ввести
лишь в отношении одной координаты. Следовательно, можно
надеяться описать распространение волны как марковский слу-
чайный процесс либо в одномерной задаче (например, для слу-
чайно-неоднородной слоистой среды), либо же в том случае,
когда одна из координат физически выделена по отношению
к другим (например, при распространении плоской волны нлн
узконаправленного пучка излучения).
Далее, если из трех пространственных переменных удастся
выделить одну, играющую в указанном выше смысле роль вре-
мени, то по этой координате должно выполняться условие
344 ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА [ГЛ. VII
динамической причинности, т. е. рассматриваемое волновое поле
должно функционально зависеть лишь от предшествующих1) (по
данной координате) значений случайного параметра. В общем
случае волновое поле не удовлетворяет этому требованию, так
как в неоднородной среде присутствуют волны, рассеянные как
вперед, так и назад (§ 38), а наличие воли, рассеянных назад,
обусловлено теми неоднородностями среды, которые расположены
за точкой наблюдения.
Тем не менее для одномерного уравнения Гелыигольца
описывающего распространение скалярной волны в слоистой
среде, можно ввести -функцию
удовлетворяющую уравнению первого порядка
«.=
и «начальному» условию (т. е. граничному условию, например,
при г = 0). В таком случае значения R (г) функционально за-
висят лишь от e(J) при 0^?<г, так что условие причинности
для R выполнено и эту функцию можно аппроксимировать мар-
ковским случайным процессом, если радиус корреляции для
ё(г) достаточно мал (см., например, [1]).
Однако для волн в среде, содержащей трехмерные неодно-
родности, не удается ввести аналогичную функцию, для которой
выполнялся бы принцип причинности. Здесь переход к аппрок-
симации распространения волны марковским случайным процес-
сом возможен лишь в том случае, когда законно пренебрежение
волнами, рассеянными назад.
Как мы установили в § 38, приближение параболического
уравнения как раз и соответствует пренебрежению рассеянными
назад волнами. Кроме того, в МПУ имеется физически выде-
ленная координата—вдоль направления распространения волны,,
падающей на неоднородную среду. Таким образом, в приближе-
нии параболического уравнения переход к аппроксимации рас-
пространения волиы в среде со случайными неоднородностямн
марковским процессом, вообще говоря, возможен, но необходимо
еще предварительно выяснить, каково соотношение между харак-
l) Мы будем пользоваться термином «предшествующий» не только для
временной, но и для любой другой координаты, играющей а указанном выше
смысле роль времени.
I 43] ОБОСНОВАНИЕ МАРКОВСКОГО ПРИБЛИЖЕНИЯ 345
терными продольными масштабами флуктуации е н флуктуации
волнового поля V.
Существенное математическое отличне неодномерной задачи
о распространении волн в случайно-неоднородных средах от
задач, рассмотренных в ч. I, заключается в том, что динами-
ческое уравнение является теперь уравнением в частных произ-
водных. Вместо случайной величины (илн случайного вектора)
мы имеем здесь прн каждом фиксированном значении г двумер-
ное случайное поле и(р, г). Распределения же вероятностей слу-
чайного поля полностью задаются, как мы знаем, характерис-
тическим функционалом (§ 7). Поэтому уравнение Эйнштейна —
Фоккера в интересующих иас случаях должно определять не
функцию, а функционал. В связи с этим оно существенно слож-
нее, чем для динамических систем с конечным числом степеней
свободы: вместо уравнения в обычных частных производных оно
оказывается уравнением с функциональными производными. Для
того чтобы упростить свою задачу, мы ограничимся поэтому
выводом уравнений для моментов поля о(р, г).
Как мы убедились на примере динамических систем с конеч-
ным числом степеней свободы, замкнутые уравнения для мо-
ментов можно получить из уравнения Эйнштейна—Фоккера только
в случае линейных систем. Поскольку параболическое уравнение
C8.4) линейно, можно н здесь надеяться на получение замкну-
тых уравнений для моментов. В отличие от C8.4), исходное
уравнение МПВ D0.3) нелинейно, и поэтому получить из соот-
ветствующего функционального уравнения Эйнштейна—Фоккера
замкнутые уравнения для моментов комплексной фазы Ф не уда-
ется (несмотря на то, что решение уравнения D0.3) для Ф удов-
летворяет условию причинности).
Перейдем теперь41к оценкам продольных радиусов корреляции
флуктуации различных параметров поля. При этом мы будем
основываться на результатах, полученных в гл. VI при помощи
МПВ.
Продольный радиус корреляции флуктуации фазы и интен-
сивности (или уровня) можно оценить, исходя из качественных
соображений, развитых в конце § 41. Мы видели, что фаза волны
определяется всеми неоднородностями, которые пересекает при-
ходящий в точку наблюдения луч. Для оценки можно считать,
что различные неоднородности вносят в фазу независимые вклады
AS*. Набег фазы вдоль луча, прошедшего через п неоднород-
л
ностей, равен S — 2 AS,,. Для другой точки наблюдения, лежа-
п'
щей на том же луче, набег фазы будет S' = 2 AS*. Если п'>п,
34b ПРИБЛИЖЕННЕ МАРКОВСКОГО ПРОЦЕССА [ГЛ. VII
п'
то S' = 5-f- 2 &$к и. следовательно,
SS7=(s(s+ jg AS»)) =5*;
поскольку 5Д5л=0 при ft>n. Коэффициент корреляции равен
поэтому
/"Ж
Но мы видели (см. D1.17)), что S'coz, где г—длина дистанции,
пройденной волной в неоднородной среде. Отсюда следует, что
Ks = VH? = VTd^:. D3.1)
Эту формулу можно получить и более строго при помощи МГО
или МПВ (см., например, формулу C3.14) и задачу 4 к гл. VI).
Если зафиксировать г< = г и положить г> = г + ?, то, согласно
D3.1),
Г„(~. -) ' D3.2)
Таким образом, продольный радиус корреляции фазы имеет
порядок величины г, т. е. он во много раз больше радиуса
корреляции неоднородностей диэлектрической проницаемости.
Но, как мы уже убедились ранее, это н есть то необходимое
условие, которое позволяет переходить к приближению марков-
ского случайного процесса.
Оценим теперь продольный радиус корреляции флуктуации
уровня. В конце § 41 мы подсчитали порядок величины фокус-
ного расстояния характерной неоднородности с размером lt и
отклонением диэлектрической проницаемости от сред1|его значе-
ния, равным е:
Если е<^1, то F^te. В области применимости МПВ все
«линзы» можно считать слабыми, т. е- Р^>г. В этом случае к
амплитудным флуктуациям допустимо применить те же сообра-
жения, которые только что были использованы при оценке про-
дольного радиуса корреляции фазы. Если же условие F^>z не
выполняется, то [точка наблюдения может попадать в область
фокусировки излучения, где флуктуации интенсивности не малы.
Однако при ё<^1 мы имеем и в этом случае F^>lt, так что
} 431 ОБОСНОВАНИЕ МАРКОВСКОГО ПРИБЛИЖЕНИЯ 347
протяженность по оси г «области влияния» каждой неоднород-
ности намного превышает размер самой неоднородности.
Анализируя амплитудные флуктуации, следует учесть и тот
случай, когда размер неоднородностей мал по сравнению с ра-
диусом первой зоны Френеля: /в<^|/"?.г. Здесь уже нельзя
использовать геометрическую оптику, а необходимо привлечь
для оценок основные положения теории дифракции. Как мы
знаем, дифракция ва неоднородности размера /е начинает суще-
ственно проявляться па расстоянии порядка zA — l\j"K от нее.
Поэтому фокусирующее действие неоднородностей возможно лишь
на расстояниях, не превышающих гя. Таким образом, «область
влияния» неоднородности имеет продольный масштаб гА и усло-
вие 2д^>/е, при котором можно использовать приближение мар-
ковского случайного процесса, принимает вид (/?М)^>/Е, т. е.
Ь<1
Как мы видим, для слабых флуктуации и крупномасштабных
неоднородностей продольный радиус корреляции амплитудных
флуктуации оказывается во всех рассмотренных случаях боль-
шим по сравнению с размерами неоднородностей, что и необхо-
димо для применимости приближения марковского случайного
процесса.
Разумеется, приведенные качественные соображения не могут
служить строгим обоснованием марковского приближения, и
границы его применимости будут более последовательно рас-
смотрены ниже (§ 47). Все же следует подчеркнуть, что нам
нигде ие пришлось делать предположение о малости флуктуации
амплитуды волны. Поэтому можно надеяться, что марковское
приближение окажется пригодным н для описания сильных
флуктуации поля„ если только допустимо пренебречь волнами,
рассеянными назад.
Проводя в гл. VI конкретные расчеты флуктуации фазы и
уровня при помощи МПВ, мы уже пользовались аппроксимацией
корреляционной функции 8 дельта-функцией. R § 40 была при-
менена формула D0.30):
F,(m, t)-*F|"*(*е. ?)-2яФ,(*е, 0)8E), D3.3)
и было показано, что подстановка F|** вместо FB приводит при
расчете спектров флуктуации амплитуды н фазы к правильным
результатам, если выполнены условия
Поскольку корреляционная функция 1|>8(р, ?) связана с двумер-
ной спектральной плотностью Fe(x, ?) формулой
)=$Л(и, Oexp(«*ep)d«4,
34S ПРИБЛИЖЕНИЕ МАРКО&СКОГО ПРОЦЕССА 1ГЛ VII
легко установить, что замена D3.3) эквивалентна следующей
замене корреляционной функции:
Ъ(Р. ?)—Ц*(Р. О-ч»(Р)«@, D3.4)
где
А (р) = 2я $ Фе (х, 0) ехр (±«хр) &г% D3.5)
(в силу четности Л(р) можно использовать любой знак показа-
теля экспоненты).
Рассмотрим интеграл от i)>e (p, г) по продольной координате ?.
Используя трехмерное спектральное разложение
Ъ (P. S) = I С>е (и, Р) ехр [I (чр +
и интегрируя его по ? в бесконечных пределах, получаем
$ Ф. (Р, Оd? = I Фе (х, р) ехр ((кр) d*v dp \ е'Л dt, =
-ос -а,
= $Фе (к, р) ехр (txp) • 2яб (р) d«xdp = 2я$ Ф8 (х, 0) ехр (»хр) d*x =
= А (р).
С другой стороны, интеграл по ? от аппроксимирующей корре-
ляционной функции ^^(р, Б) = /4(рN(?) тоже дает функцию
Л (р), так что справедливо равенство
5 tb(p. t)«- J «**(Р. 0Л-=-4(р). D3.6)
-во -»
В дальнейшем часто будет встречаться комбинация
Я(р) = -j- И @) - Л (р) J = 2 J [1 -cos up] Фе (н(/.О) Ле. D3.7)
Функция #(р) зависит от двумерного вектора р и выражается
при помощи двумерного преобразивания Фурье через трехмерную
спектральную плотность Ф„(х, 0).
Если случайное поле 8(р, г) является гауссовым, то для его
полного статистического описания достаточно задания корреля-
ционной функции 8 и, в частности, эффективной корреляционной
функции вида D3.4). Однако если не предполагать нормальности
поля е(р, г), то необходимо задавать и более высокие моменты
<ё(р1, г,)...ё(ря, г„)>.
Для гауссова поля е(р, г) из дельта-коррелированности по г
вытекает, что при любых г1фг1 случайные величины е (рх, г,) и
8 (р„ г,) статистически независимы. Но для негауссовых полей
{ 441 УРАВНЕНИЯ ДЛЯ СТАТИСТИЧЕСКИХ МОМЕНТОВ 349
некоррелированность еще не влечет за собой независимости.
Оказывается, что для иегауссовых полей е (р, z) условие, ана-
логичное D3.4), при котором для "моментов случайного волнового
поля v (р, г) можно получить замкнутые уравнения, формулируется
следующим образом. Пусть гг (t = l, ¦.., п) н г) (/ = 1, .... т)
удовлетворяют при любых С, / условиям
*,<*,,, г)>г„.
Тогда совокупности случайных величин i(p/t г,) н е(р}, zj)
должны быть статистически независимы. Аналогом дельта-корре-
лированности здесь является то, что при любом сколь угодно
малом «зазоре» между переменными обеих групп уже наступает
их полная статистическая независимость.
Известно, что совместные кумулянты для нескольких случай-
ных величин обращаются в нуль, если среди этих величин
имеется хотя бы одна, статистически независимая от остальных.
Поэтому совместные кумулянты для е(р,, z,) и e(pj, z'j) должны
обращаться в нуль. С другой стороны, для негауссовых случай-
ных велнчин высшие кумулянты должны быть отличными от
нуля. Отсюда следует, что кумулянты для случайных величин
е(р,, г,) должны иметь вид дельта-функций по переменным г,-:
¦.(Pi. zi". P.. г,; ...; р„, г„) =
= Л(Р! р„, 21N(Z,-ZlN(Z3-?I)...6(zn-2n_1). D3.8)
Случайные функции е(р, г), удовлетворяющие этому условию,
мы н будем называть дельта-коорелированными ло г.
§ 44. Уравнения для статистических моментов
волнового поля в приближении марковского
случайного процесса
В соответствии с изложенными выше соображениями рассмот-
рим теперь приближение параболического уравнения
2,-**^+Ait4p> *)+W(p, z)v(p, г)-О, D4Л)
t»(p, O) = t»0(p),
считая е(р, г) случайной функцией, дельта-коррелироваиной
по г.
Получим сначала уравнение для о(р, г) [2]. Для этого при-
меним тождественное преобразование
-^f ё(р,
350 ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА (ГЛ. VII
при помощи которого уравнение D4.1) можно записать в следу-
ющей форме:
, г)- D4.2)
Проинтегрируем это уравнение в пределах от 0 до г, обозначив
переменную интегрирования в правой части через г', а затем
умножим обе его части на
В результате с учетом равенства
получим
j ).*'). D4.3)
В правой части D4.3) под знак интеграла входит произведение
( t- \
двух случайных величин Axf(p, г') и expl 1/tik j s(p, C)<SJ-
Так как о (р, г') функционально зависит лишь от предшествую-
щих по г значений в(р, ?')> где 0<t'<z'ta в экспоненту вхо-
дят только последующие значения е(р, Q при ?^г', для дель-
та-коррелированных по z случайных функций е(р, г) эти два
сомножителя статистически независимы. Поэтому, усредняя
уравнение D4.3), получаем соотношение
2ikv(p, Z)_2ift(exp(|("i(p, t)«)wp) =
). г'), D4.4)
j.,41 УРАВНЕНИЯ ДЛЯ СТАТИСТИЧЕСКИХ МОМЕИТОВ 351
представляющее собой замкнутое уравнение относительно функ-
ции о (р. г).
В уравнение D4.4) входит функции
Я (г, г'; р)=(ехр^| ё(р, »<)). D4.5)
Она известна, если заданы статистические характеристики слу-
чайной функции е.
Рассмотрим частный случай, кода в (р, г)—гауссово случайное
поле. В этом случае величина a=j e(p, ?)d? является гауссо-
г'
вой со средним значением, равным нулю. Следовательно,
т(?)] <44-6>
Найдем а\ используя формулу D3.4):
г' г'
Л @) \ dCt J dW (Ь-Ы = (г-г') Л @).
В результате получаем для Р выражение
>(г, г') = ехр [_^1 (,_«•)] . D4.7)
где введено обозначение Ло()
Подставив D4.7) в уравнение D4.4), находим
, 2)-2ifeexp [-^i г] 0,(р) =
= - J Л' ехр [-^ (г-г'I ДАо (р. г'). D4.8)
о
После умножения D4.8) иа ехр A/,ЬМ„г) и дифференцирования
по г получаеиГ"равенство
= -ехр(^-г)дх"о(р, г).
352 ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА [ГЛ. VII
из которого вытекает искомое дифференциальное уравнение для
среднего значения v:
|+^-;?Л^<Р. г)=0. D4.9)
Решением этого уравнения мы займемся позднее, а сейчас
обратимся к выводу аиалогвчных уравнении для моментов лю-
бого порядка
Г,,.я = <о(р;, 2)...о(рА, *)»* (pi, г)...хГ(р'т, г)>. D4.10)
Прежде всего выведем дифференциальное уравнение для слу-
чайной функции
7 = о(р[, z)...v(p;, z)tf (р\, г).. .V(р'т, г). D4.11)
Запишем для этого уравнение D4.1) для о(р[, г), обозначив
через AJ поперечный лапласиан Д'х по координатам х„ ух
точки pi:
2lk
Умножим это уравнение на a(pj, г) у (pi, z)...v(p'n, г)х
xo*(pi, г)..,а*(рт, г). Так как этот множитель ие зависят
от pi, его можно внести под знак Д,, что дает
d^^ p[, гO=0. D4.12)
Записав уравнение D4.1) для v(pi, г) и домиожив его на
"(Pi. г)о(р;, г)...о»(р"т, г), получим
D4.13)
Уравнения для о (pi, г), .... о (р„, г) имеют аналогичный вид.
Взяв уравнение, комплексно сопряженное D4.1)с
^= О,
запишем его для .о* (pi, z) и, домножив на v(pl, z)...v(p'n, z)x
Хо*(р;, z)...V(p'a, г), получим
—AW—*'в(рТ. z)v=O. D4.14)
Аналогичные уравнения справедливы также для o*(pl, г), ...
*(; )
I 44] УРАВНЕНИЯ ДЛЯ СТАТИСТИЧЕСКИХ МОМЕНТОВ 353
Сложив теперь все уравнения, начиная с D4.12), получаем
уравнение для случайной функции у:
D4.15)
где введены обозначения
1=д;+...+д;-д^-...-д;,
(i(z) = e(ft, г)-Ь...+е(Р;, z)-?(ft, г)—...—ё(р^, г). D4.16)
Уравнение^ D4.15) отличается от D4.1) только заменами
v—*у, Дх—>?, е—^[^. Поэтому, проделав такие же преобразо-
вания, как и при переходе от D4.1) к D4.2), D4.3) и D4.4),
мы получим уравнение для у = Тп, т, аналогичное D4.4):
в,я(р;, р\, 0) =
^((?)).я(Р;, р5, г'). D4.17)
Уравнение D4.17)—замкнутое, а входящая в него функция
Р,(г, г') = ( ехр(% J ц (Р;, Рр, О^) D4.18)
язвестна, если заданы статистические свойства в(р,. г).
Рассмотрим, как и для о (р, г), гауссово случайное поле е. Тогда
Pi (г, г') определяется формулой
J J| . D4.19)
Учитывая, что
л m
t*(Pa. PP. 0=2 8 (Pi. 0— 2 8 {Pi, 9,
получаем
<R(pi. Pp, J,)n(p^ P». C)>= 2 2 <~e(p'a, Е,)ё(рр, W>-
-222 <5(pt.«i(ps.w>+ 2 2
12 С. М. Рнтов «"др. ч. II
354 ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА [ГЛ. VII
Согласно D3.4)
<ё(Ра,
так что
где
«...~2 iil (Pi-Pi)-
5 Ь p".-Pp)- D4.20)
5
Следовательно,
/>1(г1г') = ехр(-^<гя.я(г-г')|. D4.21)
Подставим D4.21) в уравнение D4.17), затем умножим обе
его части на expA/«feI-Qn.mz) и продифференцируем по г. В ре-
зультате получим уравнение
дГ
.. .Г... exp (V.A'Q,, «г) =
которое, с учетом выражения D4.16) для ?, приводится к сле-
дующему окончательному виду:
+ ТГв..«Г...-О. D4.22)
«Начальное» условие к уравнению D4.22) имеет форму
г»..(р« pJT, о)=v.(Pj)...о.(р;)«г(pD...о!(р;>.
При «i=l, m = 0 из формулы D4.20) следует, что
<?1..= Л@) = Л„ D4.23)
а для Г1#,=зо(р, г) из D4.22) получаем прежнее уравнение D4.9).
Запишем еще уравнение для момеита Г,,, =<w(pi, z) и'(р", г)>,
т. е. для поперечной функции когерентности. Полагая в D4.20)
п = т=\, получаем
Qi. 1 = 2Л @)-2Л (pi-pi) = 2яЯ (pI-pD,
gij|gl СРЕДНЕЕ ПОЛЕ И ФУНКЦИИ *U1 |!НЕНТНО1ЛИ 355
где использовано обозначение D3.7). Уравнение D4.22) прини-
мает при л = т = 1 вид
-р")Г,,1 = 0. D4.24)
Решение этого уравнения будет подробно рассмотрено в следую-
щем параграфе. Функция взаимной когерентности Г,, , играет
важную роль при описании статистических свойств излучения.
В частности, при р" —р' она переходит в среднюю интенсивность
волны: ritl(p\ р', г)-<Ир', г) |«> = </(р\ г)>.
Наконец, запишем уравнение для момента четвертого порядка
Г,,, = <v (pi, г) v (pi, г) в* (рГ, г) v* (pj, z)>.
Полагая rt = m = 2, с учетом четности функции А (р) получаем
из формулы D4.20)
= 2я [Н (Pi —р^) + Л (pl-p,-) +Я (pj-pl) + Л (pi-rt)-
-Я(й-р;)-я(р;-рЭ].
Уравнение D4.22) принимает в этом случае вид
-рЭ-Я(К-р;)-Я(рГ-рЭ1Г,.1 = 0. D4.25)
Момент Г,,, связан с флуктуациями интенсивности волны. Иссле-
дованию их свойств будет посвящен § 46.
Совокупность всех уравнений D4.22) эквивалентна одному
уравнению с функциональными производными для совместного
Характеристического функционала случайных полей v(p, г) и
f*(p, z) (см. [22]). Это уравнение и является аналогом уравнения
Эйнштейна — Фоккера для рассматриваемой здесь задачи.
§ 45. Среднее поле и функция когерентности
второго порядка
1. Среднее поле. Среднее поле о(р, г) подчиняется полу-
ченному в предыдущем параграфе уравнению D4.9):
12»
356 приближение марковского Процесса (гл. vii
Нетрудно получить решение этого уравнения. Заметив, что
запишем уравнение D5.1) в следующем виде:
^ [е*м.г/»у] —1 Дх [e*Wv] = 0. D5.2)
Рассмотрим поле ш(р, г) в однородной среде. Уравнение для
него получается из D5.1), если положить А„ = 0:
*^0, »(р.0) = Ц,(р). D5.3)
Сравнивая D5.3) с D5.2),]_мы видим, что эти уравнениями на-
чальные условия к ним) "совпадают. Тем самым совпадают н
функции ехр {Ч,кгА„г\ v (р, г) и w (p, г), подчиненные этим урав-
нениям, т. е. имеет место равенство
v(р, г) = ехр (- ??¦ г) ш(р, г), D5.4)
которое связывает среднее поле и(р, г) с нолем ш(р, г), созда-
ваемым тгли же истопниками на плоскости г--0, ио в одно-
родной среде. Таким образом, влияние случайных неодиородно-
стек среды проявляется в том, что среднее поле экспоненциально
затухает.
Этот результат нетрудно понять, если сравнить коэффициент
экстинкцин k'AjB в формуле D5.4) с его значением, полученным
в борновском приближении. Последнее определяется формулой
B6.13):
2л я
о,=^ f d9 f sin e de Фе;( 2fejsin 4 )j,
которая сразу записана здесь для статистически иэотропшйх
флуктуации диэлектрической проницаемости. Выполнив интегри-
рование по <р и введя вместо 6 новую переменную интегрирова-
ния x = 2fcsinF/2), приводим формулу для о, к виду
2»
Но_в интересующем нас случае крупномасштабных неоднород-
ностей функция Фе (х) пренебрежимо мала в области 'л > 2k,
в силу чего можно, практически не меняя значения интеграла,
j*^] Среднее Поле и функция когерентности 35?
отодвинуть верхний предел в бесконечность:
00
а0 = nlk* \ Ф, (х) х dv. D5.5)
(эта формула была получена в задаче 1 к гл. IV).
Сравним это выражение с величиной feM0/8, где, согласно
D3.5),
00
А„ = 2я J Фе (х) d2x = 4л8 \ Фс (х) х dx.
о
Мы находим, что
00
^^J i-o0. D5.6)
Для интенсивности среднего поля |и|« из D5.4) и D5.6) полу-
чается следующий закон убывания с ростом г:
|»(p, tJI-e^w. D5.7)
Отсюда ясно, что убывание среднего поля можно целиком объяс-
нить перекачкой энергии из упорядоченной составляющей поля
в его неупорядоченную (флуктуирующую) часть. Например, в слу-
чае падающей плоской волны, когда i>0 — const и w(p, г) — const,
формула D5.7) принимает вид
ЙР, г)|« = |о.|'ехр{-а.г}. D5.8)
В то же время средняя интенсивность поля, как мы установили
в § 39, в этом случае постоянна:
<| ц* |> = | Ио [" = const. D5.9)
Комбинируя формулы D5.8) и D5.9), получаем
<\Ъ\г> = фг\>-\Ъ\' = \0о\'{\-е-''*). D5.10)
Мы видим, что интенсивность флуктуациониой части поля нарас-
тает по мере углубления волны в неоднородную среду, и на
расстояниях г^а^1 практически вся интенсивность волны свя-
зана с ее случайной компонентой.
2. Функция когерентности второго порядка. Рас-
смотрим теперь функцию когерентности второго порядка Гь,.
Для нее в предыдущем параграфе было получено уравнение
D4.24). Преобразуем это уравнение.
358 ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА [ГЛ. VII
Введем на плоскости г = const координату р+ центра тяжести
точек р', р" и относительную координату р:
p+=v,(p'+p"). р=р'-р*.
Тогда
а1 а д
Если ввести обозначения ГЬ1(р', р', г) = Г,,1 (р+ +Р/2, р* —
— р/2, г) = Г(р, р+, г), то уравнение для Г, получаемое из D4.24)
путем перехода к новым переменным, будет
Уравнение D5.11) можно решить при помощи преобразова-
ния Фурье по переменной р4:
Г(р, р+, г)-Jv(P. P. г)ехр({рр+)*р. D5.12)
Подставив это в D5.11), получаем для у уравнение
Используем операторную запись для ряда Тейлора')
/(Р+Р,)=ехр(р,?)/(Р) D5.14)
н преобразуем сумму первых двух членов в уравнении D5.13):
Уравнение D5.13) можно записать поэтому в виде
или, если умножить этот результат слева на Оператор
(&) •-¦ виде
, р, г)]. D5.15)
>) Разложив expip, —j. в ряд, получаем обычную форму записи ряда
Тейлора.
СРЕДНЕЕ ПОЛЕ И ФУНКЦИЯ КОГЕРЕНТНОСТИ 369
я формулу D5.14) и полагая в ней р, — рг/к, можно
уравнение D5.15) еще и следующим образом:
T'P'2)- D5Л6)
Решение этого уравнения относнтельно функции у(р+рг/к, р, г)
где у101 (Р> Р) = 7 (Р> Р> 0)—значение функции у прн г = 0. Если
заменить р на р—pz/fe, то решение примет вид
Т(Р. Р. г) =
. D5.17)
' )
Подставив D5.17) в D5.12), получаем
D5.18)
Остается лишь выразить здесь трансформанту Фурье yie) через
функцию Г<в>(р, р+) = Г(р, pt, 0). Согласно D5.12)
v@) (р. р) -я? JexP (-*й) г'0) (р- pi) d'p;-
Поставив это разложение в D5.18), находим
Г(Р. Р+. 2)=i
Для того чтобы придать правой части этого равенства более
симметричный вид, введем вместо р новую переменную интегри-
рования р' = р—(рг/fe), <Pp = A'd'p /г". Тогда окончательно имеем
¦г(р. р+, г)=4-^5<рР'*Р;г»'(р'. р;)х
(р1 + р'A-4
D5.19)
360 ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА [ГЛ. VII
Мы получили решение уравнения D5.11) в самом общем слу-
чае—для произвольной функции Я(р) н произвольной функции
Г"» (р, р+) на границе [4—6J.
Рассмотрим частный случай падения на неоднородную среду
плоской волны. Тогда Г1*'(р, р+) = const = /, и в D5.19) можно
выполнить интегрирование по р+, что приводит к появлению
множителя Dя'г'/А') 6 (р—р'). После этого выполняется интегри-
рование н по р', в результате чего получаем
Г (Р. Р+, г) = /, ехр [- 5? Я (р)] =Г (р, г). D5.20)
Естественно, в случае плоской волны, распространяющейся в ста-
тистически однородной среде, Г не зависит от координаты центра
тяжести р+. Полагая в D5.20) р=0 и учитывая, что Я@)=0,
получаем
Г@, р+, 2)-<о(р+, *)f*(p+, г)>-=7(р+, *) = /„.
Равенство /"=/0 для плоской волны мы уже получали в § 39.
Как мы знаем, функция Я (р) возрастает при увеличении
своего аргумента. Поэтому функция Г с ростом р уменьшается.
Можно ввести некий характерный масштаб р*, для которого
Г(р*. г) уже мало по сравнению с Г@, г), определив этот мас-
штаб, скажем, как корень уравнения
^ЯЫ=1. D5.21)
Если расстояние р между точками наблюдения мало по сравне-
нию с рл, то Г(р, г)/Г@, г)« 1 и значения полей в этих точках
сильно коррелированы. Если же р^>р*. то Г«0 и значения
полей оказываются пространственно некоррелированными. Таким
образом, масштаб pk является пространственным радиусом кор-
реляции лолей, или радиусом когерентости. Ясно, что рк умень-
шается с увеличением г. Если, например, Н (р) ~ Clp''>, Kav это
имеет место для турбулентной среды, то
I
Этот результат уже был получен в § 37 при помощи МГО.
Обратимся теперь к общему случаю, когда Гм) не является
nocTOHHHofiJвеличиной (например, Г(" может быть отлично от
нуля лишь в некоторой области р*, что соответствует ограни-
ченному волновому пучку). Рассмотрим интеграл от Г по пере-
менной р+. Интегрируя выражение D5.19), получаем под инте-
гралами по р' н р\ множитель Dn*z'/fcsN(р—р'), что позволяет
выполнить интегрирование также по р' и приводит к следующему
I 4б] СРЕДНЕЕ ПОЛЕ U ФУНКЦИЯ КОГЕРЕНТНОСТИ 351
соотношению:
Jr(f>. f>+, *)d»p+ = exp{-^z//(P)} jr">(P, P;)*p;. D5.22)
Таким образом, усредненная по сечению пучка функция коге-
рентности второго порядка ведет себя так же, как функция
когерентности плоской волны.
Полагая в D5.22) р=0 и учитывая, что #@)=0, Г@, pf, г) =
= /((>+¦ О),чполучаем закон сохраневня
S 7(Р+. *)*Р+ = 5 /„ (p+)d»p+- D5.23)
Равенство D5.23) показывает, что флуктуации диэлектрической
проницаемости приводят лишь к перераспределению средней
интенсивности в плоскости г = const; интеграл же от этой интен-
сивности по плоскости z = const сохраняется.
Формула D5.19) позволяет рассчитывать распределения сред-
ней интенсивности и степени когерентности для волновых пучков
в Случайно-неоднородных средах (см. задачу 1).
3. Связь с уравнением переноса излучения. Оста-
новимся теперь иа связи полученных результатов с так назы-
ваемым уравнением переноса излучения (УПИ), которое приме-
няется для расчета энергетических характеристик нзлученвя
(в том числе теплового) в рассеивающих средах и широко исполь-
зуется во многих задачах астрофвзики и геофизики. Обычно
УПИ обосновывается феноменологически.
Рассмотрим абсолютную величину плотности потока энергии
|d<S"| в телесный угол do с вершиной, расположенной в точке R,
и осью, направленной вдоль единичного вектора п:
\d<ST\ = 3(R, n)do. D5.24)
Введенная таким образом величина 3 носит название яркости
или лучевой интенсивности. Мы уже рассматривали ее в § 9 для
однородной среды (см. формулу (9.26)). Значение 3 (R', п) в точке
R'=R + n<# отличается от Э (R, п) да счет двух факторов.
Первый нз них —ослабление излучения на пути dl из-за погло-
щения и рассеяния в другие направления: ДЭ11) = — a3dl. Коэф-
фициент ослабления (экстннкции) а равен сумме коэффициентов
рассеяния и поглощения. Второй фактор—прирост потока энер-
гии в направлении л из-за рассеяния потоков энергии, перво-
начально распространявшихся в других направлениях:
A3w = <p3(R, n')f(n—n')do(n')dl.
(Здесь /(п—п')—отнесенное к единице объема сечение рассеяния
при изменении направления от п' до п). Тогда ДЗ =^ДЗШ + Д31а>,
362 Приближение марковского процесса [гл. vii
что приводит к уравнению
^, n')/(n-n')do(n').
где -?¦—производная по направлению п, которую можно запи-
сать в виде -gj* =n-jD"- В результате получаем УПИ
D5.25)
Рассмотрим теперь случай крупномасштабных неоднородно-
стей, когда, как мы знаем, индикатриса рассеяния сильно вы-
тянута вперед, т.е. функция /(п—п) заметно отлична от нуля
лишь при п'«п. Будем также считать первоначальный пучок
излучения узконаправленным, так что функция 3(R,n) заметно
отлична от нуля лишь в узком конусе направлений около оси г и
То же относится и к вектору n': "z~l, |n, |<<cl, поскольку
рассеяние происходит лишь на малые углы. Интеграл в формуле
D5.25) распространяется на единичную сферу, но основной вклад
в него дает лишь небольшая область вблизи оси г. Воспользо-
вавшись этим, можно заменить интегрирование по сфере интегри-
рованием по касательной плоскости, перпендикулярной к оси г:
Это приближенное равенство выполняется в силу того, что функ-
ция 3(R; 1, п'±) отлична от нуля лишь при |n'i|<^l и, значит,
далекие от полярной оси части сферы, равно как я далекие*
части касательной плоскости, ие вносят н интеграл заметного
вклада.
Далее,
„ d3 дЭ , „ _ _ дЗ , =«
П"ЗГ=Л*7+ nJ-"-i.?jeW+llj-
где R = {p+,«}, Vi=^-=^—. Поэтому в случае крупномас-
штабных неодиородностей и узконаправленных пучков излу-
чсиня можно записать УПИ в так называемом малоугловом
ц СРЕДНЕЕ ПОЛЕ И ФУНКЦИЯ КОГЕРЕНТНОСТИ 363
Приближении [4, 5]:
00
j" ( ')(Dl. D5.26)
Покажем теперь, что полученное из феноменологических со-
ображений уравнеиве D5.26) тесно связано с уравнением D5.11)
для функции Г(р, р+, г).
При решении уравнения D5.11) мы вводили преобразование
Фурье функции Г(р, р+, г) по переменной р+. Введем теперь
тршисформаиту Фурье от Г по разностной переменной р:
Г (р, р+, г) = J ехр (<хр) F (р+, х, г) Ас. D5.27)
Умножив уравнение D5.11) на ехр (tap) и интегрируя по р, по-
лучаем с учетом формулы D3.7).
= 0.D5.28)
Используем формулу D3.5) с тем, чтобы преобразовать член,
содержащий А (р):
if- J ехр (<хр) А (Р) Г (р, р+, г) d'p =
-^ Jехр [«(х-х')р] Ф. (х'( 0) Г (р, р+, г) *р <Ы =
(x-V, O)f(p+, x',r)dV.
В результате уравнение D5.2$ принимает вид
J"+"JST+—j^F =\ -2"Фг(>«—*'> 0)f (p+, x', z)dV. D5.29)
Сравнивая уравнения D5.29) и D5.26), мы видим, что если по-
Яожнть x/fe = niF F(р+, х, г) = Э(р+1 п±| г) и сРч' = й'сРл'1, то
уравнение D5.29) совпадет с уравнением D5.26), в котором
коэффициенты аи/ принимают значения
а^^р. /(n.L—ni)«=^O.(*(nj.—ni), 0). D5.30)
Легко показать, что интеграл от /, взятый по всем направ-
лениям рассеяния, равен а. Это означает, что истинное погло-
щение отсутствует и введенный выше коэффициент ослабления а
совпадает с коэффициентом рассеяния, т. е. с полным эффектив-
ным поперечником рассеяния из единицы объема.
364 ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА [ГЛ. VII
Обращаясь к формуле D5.6), мы убеждаемся, что a=a0, т. е.
эффективный поперечник рассеяния а из единицы объема во
все направления—это именно та величина о„, которая фигури-
ровала в формуле для ослаблевия когерентной составляющей
поля. Что же касается /(tij.—п^), то в этой величине мы узнаем
найденный в гл. IV эффективный поперечник рассеяния в еди-
ничный телесный угол из единичного объема (см. B6.8), B6.11)).
Таким образом, уравнение для функции Г, полученное из
параболического уравнения для поля, описываемого в марковском
приближении, оказывается эквивалентным малоугловому прибли-
жению УПИ. Эта связь впервые была установлена в работе [7].
Связь между Г и 3 дается следующей, вытекающей из D5.27),
формулой:
Г (р, р+> г) = ft' Jexp (ikn±P) 3 (р+1 tix, г) *nL. D5.31)
В гл. VIII мы получим полное уравнение переноса D5.25)
из уравнения для функции когеревтности поля в более общем
случае, исходя не из параболического уравнения, а из уравнения
Гельмгольца.
Отметим, что приведенное выше решение уравнения для Г,
выражаемое формулой D5.19), позволяет, в силу соотношения
D5.31), одновременно найтн в аналитической форме и решение
УПИ в малоугловом приближенви. Именно для этой задачи оно
и было первоначально получено в работах [4, 5].
§ 46. Функция когерентности четвертого порядка
и флуктуации интенсивности
Запишем снова уравнение D4.25) для четвертого момента
Г,,, (р|, р'г\ pi, Р»\ г) = <о(р;, г) v (pi г)в* (pi, г) V (р,'( г)>.
Оно имеет вид
,-0. D6.1)
Как мы уже указывали, функция Г,,, связана с флуктуациямн
интенсивности волны. Действительно, если совместить точку pi
с pi, а точку pi с ра, то получим
!. г)о (Рг. г)о*(р
W] ФЛУКТУАЦИИ ИНТЕНСИВНОСТИ 365
Поэтому корреляционная функция флуктуации интенсивности
может быть выражена через Г,,, и Г,,,:
<Mf>i. <»,)<<Р.)(«.»(ft) fo)
= Г,,,(р„ Pt: Pi. P.. *)—Г,., (Pi, P,. г)Г1.,(р1, Р„ г).
Если нас интересуют только флуктуации ивтенсивностн, то, ка-
залось бы, можио не рассматривать четырехточечиый момент Г9>„
а ограничиться частным случаем двухточечного момента, который
получается из Га,, при попарном слияиии'точек р[ с р^ и pi с р?.
Однако в уравнении D6.1) произвести такое слияние нельзя,
тан как при этом войдут, помимо функции r,i2(pl, pj; pi, pj, г),
еще йовые неизвестные функции [А^Г.^Ср,', pj; р,', pj, z)]p-=p;.
Поэтому даже для исследования флуктуации интенсивности необ-
ходимо рассматривать полное уравнение D6.1).
Введем новые переменные:
D6.2)
(p1-pI)—V4P,
P» = P+—VJP!—p,)—'ЛР-
Легко установить, что при этом АН AJ—A[—AJ— 2(VP+VP+ VPlVPl).
Момент Г,,„ выраженный через аргументы р+, р, р,, р,, z, мы
будем обозначать через Г4(р+, р, р,, р„ г). Уравнение D6.1)
в новых переменных принимает следующий вид:
с(десь F (с учетом четности функции Я(р)) записывается в виде
+ Н (р, + р/2) + И (р,- Р/2)-Я (р, + pt)-// (Pl-p,). D6.4)
. Рассмотрим сначала простейший случай, когда иа неоднород-
ную среду падает плоская волна. В этом случае можно принять
*4 (Р+, р, р„ р„ 0) = 1. Так как мы рассматриваем статистичеснн
однородные флуктуации в, ясно, что Г4 не может зависеть от р+,
поскольку совместный сдвиг всех четырех точек наблюдения
иа одну и ту же величину приводит к физически тождествен-
ной ситуации. Таким образом, vp+r4 = 0 и уравнение D6.3)
366 приближение марковского процесса [гл. vii
упрощается:
^=!vPlVp.r,-^F(Pl, p,,p)IV
D6.5)
Г4(Р„ Р„ Р, 0)=1.
Здесь теперь отсутствуют производные и по р, так что эту
переменную можно рассматривать как параметр и выбирать ее
значение произвольно. Выберем р = 0, н тогда, согласно D6.4)
и D6.5),
P.. 0) = f (р„ р,) =
р1)> D6.6)
^—Г Ъ.*р.Г. -*?-F(ft. ft) Г. (Pl, ft, г),
Г. (Pi. ft.0) = l. D6.7)
Так как p = p| + pi—pt—ft, равенство р=0 означает, что
pi—Pi=pi—pj, т. е. точки pi, p?, pi, pj расположены в вер-
шинах параллелограмма, сторонами которого являются векторы
/V
р„ р, (рис. 63). Слиянию точек й с р! н pi с р", соответствует
обращение в нуль аргумента р, функции Г4.
Так как
Г. (Л. Р., г)=(«(Р+-|
функция Г4(р,, р„ z) обладает, очевидно, следующими свой-
ствами симметрии:
r«(Pi, Р„ г) = Г«(р„ р„ z),
D6.8)
Г.(Р1. —р,, г) = Г*,(р1, р„ г).
Рассмотрим предельный случай |р,|—><», р, = const. Это
означает, что две пары точек (pi, pi) и (р^, р5) бесконечно раз-
двигаются при неизменных расстояниях внутри каждой пары,
Щ ФЛУКТУАЦИИ ИНТЕНСИВНОСТИ 367
ЯЬИО, тго корреляции между полями в точках (pi, р\) и (pj, pi)
ыйтаны при этом исчезать, т. е.
Ы r4(plf Р„ z) = <«(pl, г)«•(ft. z)><»(pJ, г)о*(ft. «)> =
(^)(^Ь) D6.9)
В силу симметрии относительно перестановки р,^р, функция Г4
обладает аналогичным свойством н при | р,} —> оо. В частном
случае плоской волны функции Г не зависят от Vi(pi-T-Pi) и
Vi(P« + P») и формула D6.9) принимает внд
I'm Г4(р„ р«, г) = (Г(р„ г))\
pt-» ™
D6.10)
Ига Г.(Р» Р.. г) = (Г(р„ г))«.
Pi-»™
Проанализируем теперь следствия из закона сохранения
энергии, приводящие к некоторым ограничениям вида функции Г,.
KiK мы убедились выше (см. уравнение C9.7)), точным следст-
вием параболического уравнения является закон сохранения
рцергнн
}
D6.11)
.где /(р, г) = |о(р, г)|'. Рассмотрим распространение ограннчен-
|юго волнового пучка, для которого |»(р, г)\—»0 при |р|—»оо.
Проинтегрировав D6.11) по плоскости z = const и используя
теорему Гаусса для двумерного случая, получаем
где (#*n|p=s—компонента плотности потока энергии по направ-
лению вектора п=р/р, взятая на окружности бесконечного ра-
Двуса. Но в силу ограниченности пучка v—>0 при р—>ю, так
что ^„Ip^jo =0, н мы получаем закон сохранения
CD
J / (р, г) d"p = const = J / (р, 0) d»p. D6.12)
— о»
В левой части этого равенства фигурирует случайная интенсив-
ность У (р, г) = /(р, z) + /(p, г). Усредняя D6.12), пркходнм
к формуле
$7(Р, 0)d»p = J/(p,O)d»P, D6.13)
368 ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА 1ГЛ. VII
которая была уже получена выше из уравнения для Г
(см. D5.23)). Вычитая D6.13) из D6.12), получаем равенство
)d»p = O, D6.14)
физический смысл которого весьма прост: случайные отклонения
интенсивности от средней, имеющие различные знаки, всегда
взаимно компенсируются, так что флуктуации вызывает лишь
перераспределение интенсивности по поперечному сечению пучка.
Отметим, что равенство D6.14) уже было использовано в гл. V
(формула 35.25)) для объяснения равенства вулю интеграла от
корреляционной функции уровня.
Возводя D6.14) в квадрат и усредняя, имеем соотношение
которое при замене переменных р = р'—р" и р+= V, (р'4-р")
можно записать в виде
$1>#(|>+1р,2)*р+*р = 0. D6.15)
Отсюда следует, что корреляционная функция флуктуации ин-
тенсивности обязательно должна иметь отрицательный участок.
В случае плоской волны справедливо равенство, аналогич-
ное D6.15):
J 0, D6.16)
однако его вывод несколько более сложен в связи с тем, что
поле о(р, г) не убывает при р—> <». Равенство D6.16) можно
получить непосредственно из уравнения D6.7). Введем для этого
функцию
X(plf Р„ г) = Г4(Р„ Р„ г)-Р(р„ г). D6.17)
Если р, = 0, то Г4@, р„ 2) = </(Р;, г)/(Р;, г)>, Г"@, z) = 7»,
а К@, ра, г) =1(з, (р„ г)—корреляционная функция интенсивно-
сти. Кроме того, при р,—+<х> функция К, согласно D6.10), обра-
щается в нуль. Привлекая уравнение D5.11) для функции Г
(в этом уравнении в случае плоской волны <ЗаГ;дрдр+ = 0), не-
трудно установить, что К. удовлетворяет уравнению
^ . D6.18)
Если проинтегрировать это уравнение по р, в бесконечных пре-
делах, то, в силу отмеченного выше предельного соотношения
lim K"(Pl> P»i •?) = (), интеграл от первого члена правой части
Hi— *>
j 4в] ФЛУКТУАЦИИ ИНТЕНСИВНОСТИ 369
D6.18) обращается в нуль, т. е. получается
[>«. г)*Ра = — ^4~J F (ft. Pi)^C(Pi. Р«. г)*р,—
_^ir»(Pl> г) C[F(Pl. p,)-2«(p1)Jd»pa. D6.19)
Так как F (р„ р,)—2Я(р1)^-^0 прнр,—>«>, интеграл от второго
слагаемого в правой части D6.19) сходится. Положим теперь
в D6.19) р, = 0. В силу равенств F@, pJ = O, Я@)=0 мы по-
лучаем дифференциальное уравнение
Решение этого уравнения с начальным условием J г|),(ра, O)dap,=O
(при г = О^флуктуаиии интенсивности отсутствуют) выражается
равенством D6.16).
Отметим, что из формулы D6.14), справедливой для ограни-
ченных пучков, можно получить аналогичные D6.15) соотноше-
ния для моментов произвольного порядка.
Аналитического решения уравнения D6.7) для Г4 получить
не удается. В настоящее время получены численные решения
этого уравнения, соответствующие двум моделям флуктуации
диэлектрической проницаемости среды—со спектральными плот-
ностями вида Ф)!(ч)~ехр{—х'/'/2} [8] и Фе(х)~ х-"/. [9—11].
В обоих случаях средний квадрат флуктуации интенсивности
р*=[7*—(/)']/(/)* с ростом г насыщается. Численные результа-
ты, полученные для степенного спектра флуктуации е, удовлетво-
рительно согласуются с экспериментальными результатами.
Для области сильных флуктуации, где р»да 1, получены асимп-
тотические решения уравнения D6.7) [13—16]. Не приводя
довольно громоздких вычислений, необходимых для вывода соот-
ветствующих асимптотических формул, опишем основные резуль-
таты, полученные в указанных работах.
Формальное решение уравнения D6.7) можно записать в виде
предела при iV—к» 4УУ-кратного интеграла, соответствующего
замене непрерывной случайной среды, заполняющей слон @, г),
на N фазовых экранов, расположенных на расстоянии г/N друг
от друга. В области сильных флуктуации в этом бесконечно-
кратном (так называемом континуальном) интеграле появляется
большой параметр fTz/p*, равный отношению радиуса первой
зоны Френеля к радиусу ногерентиостн р», определяемому фор-
мулой D5.21). Этот параметр имеет ясный физический смысл.
В случае р„^У"}а когерентным образом складываются только
поля, рассеянные неоднородностями, разнесенными на расстояние,
меньшие р^. Поэтому при рд<^:]/Тг радиус когерентности играет
370 ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА [ГЛ, VII
такую же роль, как радиус первой зоны Френеля в случае
При Kte/p*^> 1 асимптотическая формула для р"'(г) имеет вид
г
Р« (г) ж 1 + п I (z—г')ЧЬ' $ <1*чх«Фе(«, 0) X
о
D6.20)
Корреляционная функция ^(р, г) обладает двумя характерными
масштабами. Одним из ннх является рк, другим—отношение
ro = z/ftpt. Первый из ннх с ростом г уменьшается, а второй —
растет. В первом приближении
^}... D6.21)
Для случая турбулентной среды, Когда Фг(х) = ^С|х""/«, фор-
мула D6.20) принимает вид
р« (г) = I + 0,861 да)"*/. + ..., D6.22)
где pj = 4x' = 0,307CJft'/<z"/i—средний квадрат относительных
флуктуации интенсивности, найденный при помощи МПВ (см.
D1.27), D1.28) и D2.13)). Корреляционная функция D6.21)
в этом случае равна
*,(Р. z) = exp {-0.729С8к»гр*/.Ц-.... D6.23)
а масштабы р* н г0 по порядку величины равны
Следует отметить, что функция D6.21) не удовлетворяет усло-
вию D6.16). Это связано с тем, что отрицательный участок функ-
ции фг при р?^>1 располагается в области больших значений
р^>г„. Так как для статистически изотропных флуктуации ра-
венство D6.16) записывается в виде
CD
$Ф/(Р. z)pdp = 0,
то ясно, что значения фДр, г) при больших р входят в интеграл
с большим весом р. Поэтому достаточно очень небольших по
абсолютной величине отрицательных значений ф/. чтобы равен-
ство D6.16) удовлетворялось. Но эти малые значения ф, ие
описываются первыми членами асимптотического разложения,
ФЛУКТУАЦИИ ИНТЕНСИВНОСТИ
371
Цк что для выполнения равенства D6.16) необходимо учитывать
вдвдующие малые члены в D6.21).
В заключение этого параграфа сопоставим результаты числен-
HfgX расчетов [11] с приведенными выше асимптотическими фор-
мулами для случая степенного спектра Ф8(х) = ^С|к""/». На
Рис. 65.
рве. 64 приведена полученная в результате этих расчетов крн-
вая p = f(P0) (крнвая /)• Там же показаны кривая 2, построенная
по формуле D6.22), а также усредненные экспериментальные
данные (крнвая 3). На обороте обложкн данной книги—на фор-
*Ще приведено распределение интенсивности света п области
СИЛЬНЫХ флуктуации [23].
372 ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА [ ГЛ. VI
На рис. 65 приведены точки, полученные путем численных
расчетов функции ^(р, г), а также кривые, построенные по
асимптотической формуле D6.23). Из рисунка видно, что с уве-
личением параметра (}„ результаты все лучше согласуются между
собой.
§ 47. Учет конечности продольвого радиуса
корреляции флуктуации в
и границы применимости марковского приближения
До сих пор мы предполагали, что случайную функцию е (р, г)
можно считать дельта-коррелированной по г, опираясь на ка-
чественный анализ, проведенный в § 43. Однако у нас пока нет
количественных оценок, из которых можно было бы получить
поправки к результатам марковского приближения, связанные
с конечностью продольного радиуса корреляции е. Рассмотрим
теперь более общий метод вывода уравнений для моментов вол-
нового поля, позволяющий учесть конечность продольного ра-
диуса корреляции е, но сразу же ограничимся при этом случаем,
когда е—нормальное случайное поле.
Будем исходить из параболического уравнения
АВ(р Z) + ye(p, г)»(р, г), ^ ^
и выведем систему уравнений для среднего поля и. Усредняя
D7.1), получаем уравнение
dv
которое не замкнуто, поскольку содержит, наряду с искомой
функцией v, новую неизвестную функцию <ei>>. Так как е —
гауссова случайная функция, a v—функционал от нее, можнс
применить для нахождения <еи> формулу Фуруцу—Новикова
G.30), которая в данном случае имеет вид
<ё(р, z)ti(p, z)> =
. г)Цр\ Z')>(|^L). D7.з;
Верхний предел интегрирования здесь равен г, так каи
6u(p, z)/6e(p', z') = 0 при г' > г в силу условия причинности.
47] ГРАНИЦЫ ПРИМЕНИМОСТИ МАРКОВСКОГО ПРИБЛИЖЕНИЯ 373
которое мы рассмотрели в § 43. Обозначив
Ш
запишем уравнение D7.2) с подставленным в него значением D7.3)
для <во> в следующем виде:
+ '¦§ Jd*' J*p'<e>, г)'г{р', z')>S, (р, г; р', г'). D7.4)
Это уравнение, как н D7.2), не замкнуто.
Найдем теперь уравнение для функции S,. Для этого подей-
ствуем на равенство D7.1) оператором б/6ё(р', г'). Где г' < г:
Здесь отброиден член у 6 (р—р')б(г—z')ti(p, г), возникающий
при дифференцировании е(р, г), так как 6(г—г') = 0 при'г>г'.
Усредним уравнение D7.5):
Й^(Р. г; Р\ г') =
=24Др5,(р, г; р', »') + ?(«(р, г) ff' ^), г>г'. D7.6)
Но би/бе тоже является функционалом от е, в силу чего длн
вычисления этой величины можно снова применить формулу
фуруцу—Новикова:
Введем обозначение
Отметим, что функция S, не меняется при перестановке аргу-
-ментов (р'( /)^t(p', z^. Подставляй D7.7) в D7.6), находим
й
2
^ ^&" Jd«p" <¦ (Р. г) 5(Р". О>S8(Р. г; р', г'; р", г"), г> г'. D7.8)
374 ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА [ГЛ. VII
Ясно, что использованный процесс можно продолжить н полу-
чить в результате бесконечную цепочку уравнений для функ-
ций v и Sn.
Рассмотрим граничные условия к уравнению D7.8) и анало-
гичным уравнениям для ?>„. Так как само уравнение справед-
ливо прн г>г', граничное условие должно ставиться прн г — г'.
Иными словами, нам надо найтн St(p, г'; р', г'). Проинтегрируем
для этого уравнение D7.1) по г, после чего применим оператор
6/бв(р', г'):
Так как 6о(р, ?)/бё(р', г') —0 прн ?<z', нижний предел инте-
грирования в первом интеграле можно заменить на г'. Второй
же интеграл вычисляется, и в результате мы приходим к формуле
6о (р, г)
6в(р', г')
Положив здесь г' = г (при этом интеграл обращается в нуль),
мы получаем
¦). D7.9)
Это равенство является точным следствием уравнения D7.1).
Усредняя D7.9) и полагая г' = г, получаем граничное условие
к уравнению D7.8):
SAP, г'; р\ *')-*в(р-р'M(р,О. D7.10)
Из формулы D7.9) можно получить граничные условия н для
функции St. Для этого применим к D7.9) оператор б/бв (р*, г"),
усредним результат н положим затем г = г'\
S,(p, г'; (.', г'; р", O = S,(p, z'; p", г"; р', г')-
= y6(p-p')S1(p, г'; р", г"). D7.11)
ГРАНИЦЫ ПРИМЕНИМОСТИ МАРКОВСКОГО ПРИБЛИЖЕНИЯ 375
изводя п-кратное функциональное дифференцирование фор-
мулы D7.9), можно аналогичным путем получить граничное ус-
ловие для функции Sn+1.
До сих пор мы не делали предположения о дельта-коррели-
рованности ё. Если сделать это предположение в уравнении D7.4),
т. е. положить в нем
<в(р, г)в(р'. «')> —¦г**(Р.2; р'.г') = А(р-р')в(г-г'), D7.12)
то интеграл по г' в D7.4) вычисляется и мы получаем
причем при интегрировании б-функции появляется множитель »/«•
Но функция Sj (p, z; p', г) при совпадающих значениях продоль-
ной координаты нам уже известна нз-формулы D7.10); подстав-
ляя ее в интеграл, получаем замкнутое уравнение для и:
^-¦^Aj>-kjA@)v{p, г), D7.13)
Которое совпадает с полученным в § 44 уравнением D4.9). Таким
образом, если предположить дельта-коррелнрованность е в пер-
вом нз уравнений нашей цепочки, то оно замыкается, так что
остальные уравнения оказываются излишними.
Сделаем теперь следующий шаг: в первом уравнении нашей
цепочки оставим точную корреляционную функцию, а прибли-
жение дельта-коррелнрованности используем лишь во втором
уравнении вида D7.8). Тогда интеграл по г" вычисляется, и
в результате мы получаем уравнение
pM(p—p")Sa(P, г; Р', г'; Р", г). D7.14)
Если заменить в D7.11) г' на г, г" на г' к поменять местами
р' и р", то мы получим необходимое нам значение
S,(p, г; р\ г'; р\ z) = ^6(p-p«)S1 (p, г; р', г').
После этого уравнение D7.14) становится замкнутым, принимая
внд
' г>г- D7.15)
IF
Теперь мы имеем уже систему из двух уравнений D7.4) н D7.15),
а остальные уравнения цепочки можно не использовать.
Ясно, что если в первых (/г—1) уравнениях мы используем
точное значение корреляционной функции ij!c, а замену D7.12)
376 ПРИБЛИЖЕНИЕ МАРКО&СкОГО ПРОЦЕССА 1ГЛ. VII
совершим лишь в n-м уравнении, то получим замкнутую систему
из п уравнений, которая будет тем точнее, чем больше д.
Рассмотрим подробнее случай л = 2. Сначала нужно решить
уравнение D7.15) с начальным условием D7.10). Нетрудно про-
верить, что решение имеет вид
D7.16)
Подставив это выражение для S, в D7.4), получаем уравнение
для Ъ:
о
Xexp{'Vglff —^(г- г')}^(р-р', г-г')и(р', г'); D7.17)
его легко решить, если воспользоваться преобразованием Лапласа
по г и преобразованием Фурье по р. Мы, однако, не будем этого
делать, а ограничимся выяснением условий совладения решения
уравнения D7.17), которое мы будем называть уравнением вто-
рого марковского приближения, с решением уравнения D7.13).
Уравнение D7.13) получается из D7.17), если продольный
масштаб /,, функции $8(р— р', г—г'?мал по сравнению с мас-
штабами по г других сомножителей. Как мы выяснили в § 45
(см. D5.4)), характерный масштаб функции t»(p', г') имеет поря-
док величины (feM,)-1. Тот же масштаб входит и в множитель
ехр{—V«feM0(z—г')} в D7.17). Поэтому необходимо, чтобы вы-
полнялось условие
<l. D7.18)
Если это условие выполнено, то под знаком интеграла в
D7.17) можно заменить о(р', г') на t»(p', г) и считать, что
ехр {—г1,к*А,(г—г')}&1. Тогда это ураввение примет следую-
щий вид:
р', г-г')и(р'.г). D7.19)
В области |р— p'|^>K(z— г')/к функция
ир! ГРАНИЦЫ ПРИМЕНИМОСТИ МАРКОВСКОГО ПРИБЛИЖЕНИЯ 377
выстро осциллирует. Если характерный масштаб функции i|>e по р,
который мы обозначим через ti, велик по сравнению с У {г—z')lk~
му1„/к, то множитель -фв(р— р*. г—г') мало меняется на ха-
рактерном масштабе функции f н его можно счтитать постоян-
ным. Что касается функции »(р', г), то ее характерный попе-
речный масштаб имеет порядок размера пучка а. Поэтому при
выполнении условий
a>KTjfe, l.^Vhlk D7.20)
произведение \J)?(p—р', г—z')t»(p', г) можно заменить на
$в@, г—г')и(р, г), после чего интеграл по р' вычисляется и
дает единицу. Таким образом, при выполнении условий D7.20)
уравнение D7.19) еще более упрощается:
^ Jt,(O, z-z')dz'. D7.21)
о
Наконец, если
z>fu, D7.22)
то верхний предел интегрирования в D7.21) можно заменить на
бесконечновть, н тогда, с учетом равенства
мы получаем из D7.21) уравнение первого марковского при-
ближения D7.13).
Интересно отметить, что даже уравнение D7.21) дает для v
более точное выражение в области г^.1„, чем первое марковское
приближение. Например, в случае плоской падающей волны ре-
шение уравнения D7.21) имеет вид
При г<^1„ можно на всем участке интегрирования считать
4>e@, QssiMO, 0) = <r|, и тогда D7.23) дает
5(z)-o1exp{-*4»V8} B</„). D7.24)
Если же г^>/,|, то в формуле D7.23) можно считать
$ (* - 0 Ч'е @, 0 < * * S * @. 0 <Ч = Л.2/2,
378 ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА [ГЛ. VII
н мы получаем
п(г) = в0ехр{-<!М|1г/8} (z>/,,). D7.25)
В первом же марковском приближении мы при всех г получаем
для плоской волны формулу D7.25).
Остановимся на условиях D7.18), D7.20) и D7.22) применимо-
сти марковского приближения для среднего поля и. Первое из ус-
ловий D7.20) означает, что продольный масштаб корреляции
in должен быть мал по сравнению с дистанцией feaa, на кото-
рой начинает проявляться дифракция на апертуре пучка. Второе
условие тоже можно записать в виде 1Л <^fe/j_> так чт0 масштаб I „
должен быть мал н по сравнению с дифракционной длиной, со-
ответствующей поперечным размерам неоднородностей. Условие
D7.18) означает, что ослабление среднего поля на масштабе 1„
должно быть малым (напомним, что согласно формуле DЯ.6)
&М0/4 = <т0 — коэффициент рассеяния), или, иначе говоря, ln <^d=
=aj', где й^длииа экстинкцни. Наконец, условие D7.22) озна-
чает, что /и должно быть мало по сравнению с длиной трассы.
Мы видим, что все четыре условия можно формулировать как
ограничения сверху величины продольного масштаба корреляции
диэлектрической проницаемости. При этом условие D7.18) озна-
чает ограничение и величины ol. Действительно, А,~а\1л, так.
что неравенство D7.18) можно записать еще и в виде
<№/!,< 1. D7.18а)
Отметим, что полученные условия применимости марковского
приближения не ограничивают сверху длины дистанции г, в от-
личне от любого из ранее рассмотренных методов, использующих
теорию возмущений по е.
Мы рассмотрели уравнения более высоких приближений для
среднего поля. Подобным же образом можно получить уравнения
второго и более высоких приближений для произвольных мо-
ментов Г„, „ [20]. Мы не будем приводить здесь этих уравнений,
а изложим лишь некоторые качественные соображения и выводы
работы [20].
Если обратиться к уравнению D4.15) при n=m=l, т. е.
к уравнению для функции i>(pi, z) о* (pi, z), то в него входит
в качестве случайного коэффициента только разиость в (р^, z) —
— e(pj, г). При замене е—«-в + const эта разность не меняется.
Отсюда следует, очевидно, что крупномасштабные неоднородности
не сказываются на произнеденииы^р/.г)!!* (р,,г). Поэтому и условия
применимости марковского приближения для функции Г не могут
содержать таких величин, как а\, 1и и 1±, которые зависят от
ЗАДАЧИ 379
Поведения спектра флуктуации диэлектрической проницаемости
ц? области малых волновых чисел.
Условия применимости марковского приближения для Г
имеют вид
klt^>l, kz| Vi.H(р) |<^ 1, z^-p. D7.26)
Здесь /„—масштаб наименьших неоднородностей диэлектрической
проницаемости. Второе из условий D7.26) ограничивает вели-
чину, характеризующую интенсивность флуктуации 8. Если
вспомнить, что радиус когерентности поля определяется из усло-
вия к1гН(рк) ~ 1 (см. D5.21)), то второму условию D7.26) можно
придать вид
fep*^>l-i D7.27)
Таким образом, применимость марковского приближения требует,
чтобы радиус когерентности всегда оставался много большим
длины волны.
Задачи
1. Найти распределение средней интенсивности по поперечному' сечению
пучка излучения, у которого в плоскости г—О поле имеет вид
I р3 ' |"Ав! I
(гауссов пучок с эффективным радиусом а и с расстоянием от плоскости z — О
до центра излучения, равным F) [6]. Рассмотреть частный случай, когда
Н (р)= jpCjP*'3, что соответствует турбулентным флуктуация» диэлектрической
проницаемости.
Решение. Средняя интенсивность /(р+, г) может быть получена из
функции Г при р = 0. На основании D5.19) инеем поэтому
7(р+-г)=S? J *? J dip+Tm (р/> р'+)х
i^(p+-p;)-^jW(p'A-l))cJ. B)
Подсчитаем функцию Г<°>, используя начальное условие A) для поля:
/1одставим C) в B) и выполним интегрирование по р+. В результате полу-
таем формулу
[гл. vit
«(*)= Vl + JftfO/z+l/FI. E)
Формула D) справедлива при любом виде функции Н (р). Если Н (р) = рС\р'*, то
380 Приближение марковского процесса
где введено обозивчеиие
и формула D) после перехода к полярным координатам принимает вид
Интеграл no q> равен 2л./0(*р'р+/г), так что для 1 получаем выражение
7(Р+. г)=*!^|ехр{-^ P'-^C»*V}^ (^) РФ- F)
Введен /g(z)—интенсивность на оси пучка в однородной среде, т. е.
при С, = 0:
Отношение7(р+, z)/Iu(z) можно записать в виде
Если ввести безразмерную переменную интегрирования (ер12а)'-1, то G)
запишется так:
- -
Из (8) следует простая формула для интенсивности иа осн пучка:
где
ЗАДАЧИ
381
Параметр " пропорционален структурной функции фазы на базе 2o/g (г). Раз-
д4Гая «-' или e-ut'l% в ряды, нетрудно получить для /(и) разложения
—ц)п = 1 -0,94ц+0,75и»—0,56и8+ ¦ ¦., A0)
л=0
Второе иа них представляет собой асимптотическое разложение f (и) при боль-
ших и. График функции /(и) приведен иа рис. 66.
Щ
1.0
0,6
0,2
4 6
Рис. 66.
Согласно D5.23) интеграл от / (р+, г) по поперечному сечению пучка не
зависит от z. Уменьшение средней интенсивности на оси пучка можно объяс-
нить его уширеннем. Если определить эффективную площадь пучка при по-
мощи равенства
A2)
то иа закона сохранения D5.23) будет следовать, что
7@, г) S3w (г) =П@, 0) S,M @).
Праваи часть этого равенства не зависит от иеоднородностей среды. Поэтому,
если записать A2) для однородной среды, в которую посылает излучение
тот же источник (т. е. то же распределение поля на плоскости 2 = 0), то мы
получим равенство
/о (г
U) = Г@, 0) Stw @),
(! 3)
где /о (г) и 5^ф (г) — интенсивность на оси пучка и его эффективная площадь
в однородной среде.
Из A2) и A3) следует, что
5,ФФ(г)_ 1,(г) 1_
ФГГ@,и /W ()
Если и>1, то, согласно A1), /(и) я 1,!и~#/< и
382 приближение марковского процесса [гл. vn
Например, при F — oo (коллимиреваниый пучок) g1 (г) — 1 + *%*/*'• Если
г<$.ки- (ближняя зона источника), то ga(z) и к'а^/г1, и тогда
Если же ф кФ (фраунгоферова зона источиика), то g' « 1 и
2. Случайный радиус-вектор «центра тяжести» распределения интенсив-
ности пучка в его поперечном сечении определяется формулой
6=4 •
Выразить средний квадрат \* через функцию когерентности Г,.
Решение. Интеграл в знаменателе является постоянной детерминиро-
ванной величиной. Обозначая его через Р, получаем
Г = Р"» $ $ *р; <Ppi PlPG </ (Pi. г) / (pi, г)>.
Но
</ (p't, г) I (р'г, г)> = <*(р^, гI(р;, г)р*(р', г)о»(р^, г» ,
т. е. в формуле для Г, следует положить Р][ —р^ и р," —р.^, что эквивалентно
для новых переменных р+, р, р,, р, (см. D6.2)) равенствам ра — 0, р-0.
При STOMp^ = p+ + V:Pb Рг' = Р+—VsPi. P[Pi=fi—V<Pj и
f«(P + . P. Pi. Pj. г) = Г,(р+, 0, pv 0, г).
Следовательно,
V = P-* 11 dV«Ppi (P'+-V,P!) Г, (p+, 0, р„ О, г).
8. Фотодетектор, представляющий собой диск радиуса R, реагирует на
интеграл от интенсивности света / (р, г). Найти закон убывания относитель-
ных флуктуации фототока J при увеличении R в случае, хогда падающая
плоская световая волна распространяется в статистически изотропной слу-
чайно-неоднородной среде.
Решение. Мгновенное значение фототока равно
J^-*\l(p,z)<Pp. A)
где а—чувствительность фотодетектора, ? — круг радиуса Ft. Усредняя A),
имеем У = а?2. Из (!) следует также, что
так что относительные флуктуации J/J выражаются формулой
ЗАДАЧИ 383
B) в квадрат и усредняя, получаем
.4,, (p, -р„ г). C)
о«. ^4 V = Jj- J d«Pl Г
ft» ф7 — корреляционная функция, деленная на G)а. Вводя функцию
f 1 при р € 2,
0 при p#S, ЖН° в^клтп ° в вида
а»
И dVdVM (Pi) ^ (Pi) т|=/ (Pi-Pi» г).
нлн, после введения новых переменных интегрирования p = pi—pi и p'^
¦/ &>¦ *) rflP j « (P-P') Л1 (p') d'p'. D)
ОФоввачим через /(р) функцию
о»
/%(Р) =4" J *• (Р-Р') « (Р') <Рр'- E)
Тогда D) записывается в виде
°1
F)
Из определения М следует, что произведение /2 равно площади пересе-
2*1™* Двух кругов радиуса R, центры которых раздвинуты на расстояние р.
Эденеатариыа расчет приводит к формуле
,..,.._( — arccos-^ ^- V^l — (р/2/?)' при р < 2R,
\ 0 при р > 2R.
8 силу статистической изотропности флуктуации (т. е. if/ тоже зависит только
от Р=|Р|) можно записать F) в виде одиократиого интеграла;
•"•ссмотрим случай, когда /? намного превышает радиус коррелянни флук-
ТУ*ив. Тогда функция 1|>/ (р, г) быстро спадает етце при таких значениях р,
opt которых ftp) ие успевает заметно измениться. Разложим / (о) в ряд
"мора по степеням р/2/?:
384 ПРИБЛИЖЕНИЕ МАРКОВСКОГО ПРОЦЕССА [ГЛ. VII
и подставим это разложение в G):
2ft 2R
2 Г 4 Г
" "вг \ ¦/& z)p4P"~;Jd3 ) *'^>1 г)Р*^Р"Ь--- (8)
в о
Первый интеграл можно эаписвть в форме
2R
S-M-
О О 3R
tR
что приводит к формуле
2R
J )р'Ф + - (9)
Но интеграл в первом члене'в силу D6.1С) равен нулю, и поэтому в разло-
жении (9) член с ?~* исчезает. Таким образом, флуктуации фототока убы-
вают с ростом R быстрее, чем R-*:
tR
0
A0)
А
Заметим, что при больших р функция tp/(p, г) отрицательна, так что о'ЭгО-
Убывание в' с ростом К более быстрое, чем /?-*, объясняется тем, что
на ллощвдн фотодетехтора 2 = л/?* при больших R происходят почти полнав
компенсация положительных н отрицательных флуктуации интеисивпости.
Глава VIII
ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ
МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН
§ 48. Теория возмущений и диаграммная техника
для среднего поля И функции корреляции
В этой главе мы рассмотрим некоторые общие вопросы тео-
рии многократного рассеяния волн. С частным случаем такой
теории мы уже встретились в гл. VII, где была очерчена теории
распространения волн в приближении марковского случайного
процесса, учитывающая многократное рассеяние волн, но лишь
при условиях, когда рассеяние происходит практически только
вперед. Если, однако, длина волны недостаточно мала по срав-
нению с размерами неоднородностей, то, как мы помним, ста-
новится существенным рассеяние не только на малые, а на любые
углы. Если, кроме того, неоднородная среда достаточно про-
тяженна, то и в этом более общем случае роль многократного
рассеяния может сделаться значительной.
Мы уже упоминали о том, что многократное рассеяние воз-
можно как на совокупности дискретных рассеивателей (элект-
роны в плазме, частицы аэрозоля в атмосфере и т. д.), так и
на непрерывных неоднородностях, например па флуктуациях
диэлектрической проницаемости сплошной среды. Теория много-
кратного рассеяния для этих двух случаев строится несколько
различно, хотя и имеет много общего. Мы ограничимся здесь
методически более простой теорией многократного рассеяния
на непрерывных неоднородностях. Что касается теории рассеяния
на дискретных вкраплениях, то первоначальные сведения о ней
Можно найти, например, в обзоре [1].
Кроме того, мы будем рассматривать лишь наиболее
простую постановку задачи, когда распространение волны опи-
сывается скалярным волновым уравнением. Здесь следует заме-
тить, что в случае крупномасштабных неоднородностей скалярная
постановка задачи позволяла хорошо описать многие законо-
мерности распространения также и векторных (электромагнит-
ных) волк, тогда как при произвольном соотношении между
Длиной волны и размерами неоднородностей это уже не так,
'3 С. М. Рыто» а др. ч. II
386 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. VIII
поскольку при многократном рассеянии происходят сильные
изменения поляризации. Тем не менее мы ограничимся скаляр-
ным волновым уравнением, так как уже в этом простейшем
случае четко выявляется специфика многократного рассеяния.
Наконец, мы ограничимся задачей о распространении волн
в безграничной среде, в которой флуктуации показатели пре-
ломления являются гауссовым случайным полем. Последние два
предположения делаются только для упрощения излагаемой
теории, но ие являются обязательными.
Рассмотрим первоначально задачу о среднем поле точечного
источника, находящегося в некоторой точке г0 неоднородной
среды. Случайная функция Грина, т. е. поле такого точечного
источника в данной среде, удовлетворяет волновому уравнению
Z(r)G(r, r0) = AG(r,r0H Аг[1+ё(г)]О(г, го) = 6 (г-г„) D8.1)
(где Л—лапласиан по переменной г), а также условию излучения
при | г—г01—»¦ оо.
Запишем ряд теории возмущений для этой задачи, который
получается нз формулы B4.10), если считать в ней и,(г) =
= Ge(r,r0), где
—функция Грина однородной среды («свободного пространства»).
Подставляя D8.2) вместо и0 в B4.10), получаем ряд
О (г, г„) =G, (г, ro)-ft« $ G0(r, г,)I (rt)Go (rv г,)d»r, +
+(-*')'$Ge(r, rjSfrJC.Jr,, г,)ё(г,) X
X Go (г„ r0) d'r, d'r. + (- ft')» $ G, (r, rj ё (rj Go (г„ г,) х
X ё (г,) G, (г„ г,) в (г.) Go (г„ г„) d>rid>rtd'rt + ... D8.3)
Заметим, что функция G, (г, г„) симметрична, т. е. удовлетворяет
равенству G0(r, г„) = Go (г„, г). Покажем, что такому же равенству
удовлетворяет н функция G (г, г,). Действительно, используя
симметрию фувкцнн G,, можно записать интеграл во втором
слагаемом D8.3) в виде
5 Go (г, ОI (г,) 0„ (г„ г.) d>r1 = J Ge 04, re) I (r.) Ge (г, г,) d'r, =
= 5Go(ro,r1);(r1)G0(r1, r)d»/v
Такое же преобразование можно проделать и в следующем
Pjfl ТЕОРИЯ ВОЗМУЩЕНИЙ И ДИАГРАММНАЯ ТЕХНИКА 387
хватаемом:
$.<?,.(г, rt) в (г,) G. (Г1> г,) ё (rj G. (г„ гв) d% <*»г, =
== J Gg (r01 r1);(r,)Ci(ri.»1i)«(ri)Cf(rI>r)*r1*rI-
= $ Ов («-в. <Ч) ё(г.) Ge (г„ rj е"(г,) G. (г„ г) d»r, d»r,.
Здесь мы изменили обозначения переменных интегрирования
(г,^г,). Ясно, что подобным же образом можно преобразовать
любой член ряда D8.3), в силу чего и имеет место равенство
G(r,r0) = G(r0,r), D8.4)
выражающее теорему взаимности: в произвольной линейной
неоднородной среде поле не меняется, если точку расположения
источника и точку наблюдения поменять местами.
Рассмотрим теперь среднюю функцию Грина. Усредняя D8.3),
следует учесть, что для гауссова поля ё <ё(г1)... е(г,п_,)> = 0,
а.Дря четных моментов справедлива формула G.20):
<ё (г,) ... ё(!¦„,)> = 2 Ъ> (г„, г,) ... т|>е(гт, гв), D8.5)
р. п.
причем сумма в правой части распространена на все возможные
разбиения множества точек гг ..., г.м на пары (ra,,rBt) (поря-
док следования внутри каждой пары ие имеет значения). Так,
например, согласно D8.5)
(г,)>^(г„ г,)^е(г3, г,) +
+ *.(«¦„ ОЫГ,, Г,)+Ц>е(Г1. «\Не(Г„>,). D8.6)
а в формуле для <ё(г,) ... е(га„)> будет Bп —1I! слагаемых.
Усредняя D8.3) с учетом D8.5), получаем
ff(f,r,)=G.(r, г„) +
+** S G, (г, tt) С„ (rx: rs) Ge (г„ г.) фе (г„ г„) d»ri d'rt +
+*• I Ge (г, rj Ge (г,, г,) Go (г„ га) G, (г„ г.) Ge (г„ г0) X
X fro <гх, г,) Ч)в (Г„ r4) +i|;e(Г!, г,) %(г2, г4) +
г.)ij>, (г„ r,)\d*rx ... d'r4 + • • • D8.7)
Чтобы наглядно представить себе структуру этого ряда,
введен графическое изображение входящих в него элементов.
Такого рода графики (диаграммы) были введены Р. Фейнманом
в квантовой электродинамике и получили затем распространение
в самых различных областях теоретической физики. Это объяс-
няется нх лаконичностью по сравнению с аналитической записью
13»
38Й ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. VIII
и упрощением выкладок. Разумеется, оперирование этой «диаг-
раммной техникой» требует известного навыка.
Сопоставим функции G0(tj, r,) отрезок прямой линии, концам
которой приписываются координаты Tj н г,:
Множителю fe4i)>E (г,, г,) сопоставим пунктирную линию с двумя
точками па концах:
Точки rJt г,, в которых сходятся линии, изображающие Go и i|>e,
будем называть вершинами диаграммы. Условимся, что по коор-
динатам всех внутренних вершин производится интегрирование.
Число таких вершин в диаграмме будем называть порядком
диаграммы.
Приведенные правила соответствия позволяют сопоставить
каждому члену ряда D8.7) диаграмму Фейнмана. Так, первый
член в правой части D8.7) изображается диаграммой
а второму члену этой формулы соответствует график
Заметим, что, поскольку по координатам tlt г, внутренних вер-
шин производится интегрирование, аналитическое выражение,
изображаемое диаграммой, не зависит от координат внутренних
вершин. В связи с этим мы не будем в дальнейшем отмечать
эти координаты на диаграммах. Третьему слагаемому в D8.7)
соответствуют следующие три диаграммы:
.-"'¦¦ /"-.
го
Неусредненный член порядка 2я ряда теории возмущений дли G
имеет вид
ft'» \ 00 (г, rj 00 (г,, г,) ... 00 (г,„, г„) i (rJ ... е (г,„) *г, ... &гп.
Щ4Л ТЕОРИЯ ВОЗМУЩЕНИЙ И ДИАГРАММНАЯ ТЕХНИКА 389
Поэтому диаграммы порядка 2п содержат 2л 4-1 линий функций
Грина Go и 2п внутренних вершнн г„ ..., г,„. Так как при
усреднении множитель <е (г,) ..."г (г,„)> распадается на сумму
Bп—1I1 слагаемых, в которых аргументы га, ..., г,„ объеди-
Няются попарно всеми возможными способами, при усреднении
возникает Bя—1I! диаграмм порядка 2л, в которых 2п вершин
Соединяются между собой попарно пунктирными линиями всеми
возможными способами. Наконец, введем графическое изобра-
жение для самой средней функции Грина в неоднородной среде:
Тогда ряд D8.7) можно представить графически следующим
образом:
г
¦—-)¦
¦О'"'' + -
,-
"\ '* *—ч \
8
?!
lit
1 - /
1
3
12
".""¦ДЛ
15
7
+ —*-
¦' '• '»— +
Ю
:У;Ч' + D8.7а)
+ ^"У4'4-1-
т да /¦?
г<7
Здесь, помимо написанных в D8.7) членов, представлены еще
все 15 членов шестого порядка (диаграммы с шестью вершинами).
Соответствие между диаграммами Фейнмана н аКалитическими
выражениями является взаимно однозначным. Мы можем ие только
составить по аналитическому выражению соответствующую диаг-
рамму, но и обратно—восстановить по диаграмме аналитическую
форму записи. Например, диаграмме 19 из D8.7а) соответствует
член ряда 0"", равный
О' (г, г0) -А" \ О,(г, г,) 0. (rlt г,) Go (г„ г,) С, (г„ г4) X
X 00 (г4, г.) 00 (г6, г.) 0в (г„ г0) ф, (г„ г,) х
X % (г„ г4) iK (г„ г,) d*rx ... d*r,. D8.8)
390 элементы теории многократного рассеяния иолн 1гл. vin
Некоторые из диаграмм, входящих в D8.7а), содержат в ка-
честве фрагментов диаграммы более низкого порядка. Например,
диаграмма 3 содержит в качестве фрагмента диаграмму 2, диаг-
рамма 19 содержит диаграмму 4. Этим можно воспользоваться
и для сокращения аналитических выражений. Например, можно
записать слагаемое G'1" (г, г0) в виде
б<»> (г, re) = ft« I Ge (г, г,) G«> (г,, г,) С„ (г4, г„)«, (г,, г.) d'r, d'r,,
D8.9)
где
G<" (г„ г,) = к' \ Go (ги г!) Go (г;, r^) Go (ri, rj) х
х g0 (г;, r;) g0 (г;, г,) ^ (К, г;) ф, (г;, о <л-[... d*r\. D8.1 о)
Легко убедиться, что подстановка D8.10) в D8.9) приводит
после изменения обозначений переменных интегрирования к вы-
ражению D8.8).
Прежде чем развивать дальше технику преобразований диаг-
рамм Фейимана, остановимся па их физической интерпретации.
Диаграмма / из D8.7а) описывает распространение волн нз
точки г, в г без рассеяния (как в однородной среде), Диаг-
рамма 2 описывает следующий процесс: волна распространяется,
как в однородной среде, из точки г„ в точку г,. Здесь проис-
ходит первое рассеяние, после чего рассеянная волна распро-
страняется в точку г,, в которой происходит второе рассеяние.
Двукратно рассеянная волна достигает точки наблюдения г.
Распространение описывается множителями G, (r, rj 0„ (rlf г,) х
хО„(г,,г0). Наличие в диаграмме 2 корреляционной функции
^('n'l) указывает на то, что оба рассеивателя (в точках г,
и г2) коррелированы, т. е. оба рассеяния фактически произошли
на одной и той же неоднородности.
Рассмотрим теперь диаграммы второго порядка, т. е. диаг-
раммы 3—5. Все они содержат одно и тоже произведение функ-
ций Грина
«о (г. rt) Go (г,, г,) G, (г„ г.) Ge (г„ г,) С„ (г„ г.).
Это означает, что волна в точку г пришла после рассеяния
в точке г„ в точку гх—после рассеяния в точке г, и т. д., а пер-
вому рассеянию в точке г, подвергалась первичная волна Go (г,, г0).
Таким образом, все эти диаграммы описывают четырехкратное
рассеяние. В чем же состоит различие между процессами, кото-
рые описываются этими топологически различными диаграммами?
В диаграмме 3 линии корреляционных функций соединяют точ-
ку г, с г, и точку г8 с г,. Это означает, что обе точки г, и г,
принадлежат одной неоднородности, а обе точки г, и г,—другой.
ТЕОРИЯ ВОЗМУЩЕНИЙ И ДИАГРАММНАЯ ТЕХНИКА
ЗУ1
Таким образом, процесс, описываемый диаграммой 3, заклю-
чается в том, что сначала происходит свободное распростране-
ние волны от источника к первой неоднородности, затем—дву-
кратное рассеяние на ней, затем—свободное распространение
двукратно рассеянной волны до второй неоднородности, после
чего—двукратное рассеяние на второй неоднородности. Диаграм-
ма 4 тоже описывает четырехкратное рассеяние на двух нсодно-
родностях, но последовательность рассеяния здесь иная. Сначала
Рис. 67.
происходит рассеяние иа первой неоднородности (в точке г.),
'затем однократно рассеянная волна распространяется до второй
неоднородности и рассеивается на ней (в точке га), яатем дву-
кратно рассеянная волна снова возвращается к первой неодно-
родности и рассеивается иа ней (в точке г„ которая соединена
пунктирной лиикей с точкой г,), после чего трехкратна рассеян-
ная волна снова рассеивается на второй неоднородности (в точке г,)
в достигает точка наблюдения. Схематически последовательность
рассеяний на двух неодиородностях изображена на рис. 67.
Представление решения уравнения D8.1) в виде совокупности
диаграмм D8.7а) полезно не только из-за наглядности, но и по-
тому, что оно позволяет преобразовывать ряд теории возмуще-
ний, используя топологические признаки входящих б решение
392 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. VIII
диаграмм. При этом удается выразить сумму ряда D8.7) через
сумму некоторой бесконечной подпоследовательности этого же
ряда. Чтобы осуществить такое сведение, произведем сначала
классификацию входящих^ в D8.7а) диаграмм.
Назовем входящую в <Т диаграмму слабо связной, если ее можно
разделить на две отдельные диаграммы, разорвав какую-либо
одну линию Go. В формуле D8.7а) слабо связными являются
диаграммы 3, 6—9 и 12. Остальные диаграммы назовем сильно
связными B, 4, 5, 10, 11, 13—20 в формуле D8.7а)). Диаграммы,
получающиеся из слабо связной диаграммы путем разрыва ли-
ний Go, в свою очередь могут оказаться сильно или слабо связ-
ными. Если среди «вторичных» диаграмм есть слабо связные,
то и их можно путем разрыва какой-либо одной сплошной линии
разбить на более простые диаграммы. Продолжая этот процесс,
мы придем в конечном счете к некоторому количеству сильно
связных диаграмм. Назовем число сильно связных диаграмм,
на которое может быть разбита слабо связная диаграмма, пока-
зателем связности исходной диаграммы. Возвращаясь к фор-
муле D8.7а), можно сказать, что диаграммы 3, 7—9 и 12 имеют
показатель связности 2, а диаграмма 6—показатель связности 3.
Сильно связным диаграммам можно приписать показатель связ-
ности, равный 1.
Отберем из ряда D8.7а) все сильно связные диаграммы. Так
как каждая из диаграмм начинается и оканчиваетси линией Go,
то сумму всех сильно связных диаграмм можно представить
в виде
—<О>— » D8.11)
где введено обозначение
В аналитической форме D8.11) имеет вид
ё^ьносв) (г. h) - J Go (r, r') Q (г', О G, (г\ г„) d»r'dV, D8.11 a)
«481
ТЕОРИЯ ВОЗМУЩЕНИЙ И ДИАГРАММНАЯ ТЕХНИКА
393
где
Q (г'( г") = ft'G0 (г', г") i|=e (г\ г") + к' $ Go (г;, г,) Go (г„ г,) х
xG0(r2> т")% (г', г,)Ч>е Оч, г")«Рг1<Рг,+
+ ft» J Go (r', r,) Go (г„ г,) Со (г„ г") Ц>, (г', г") х
Х4>е (г1Э г,) d»rtd»r, + ... D8.12а)
Функция Q носит название яд/за массового оператора (это назва-
ние заимствовано из квантовой теории поля).
Рассмотрим теперь сумму всех диаграмм с показателем связ-
ности, равным 2. Каждая из них имеет вид
D8.13)
— какие-либо диаграммы, принадлежащие
где VS^* н *
правой части D8.12Х Так как при построении ряда D8.7а) переби-
раются все возможные способы попарного объединения вершин,
ясно, что сумма всех возможных членов вида D8.13) равна
где <3> —полная сумма D8.12).
Точно так же сумма всех диаграмм с показателем связности 3
имеет вид
и т. д. Таким образом, мы можем представить среднюю функ-
цию Грина в виде диаграммного ряда
D8.14)
Соответствующая формула отличается от исходного ряда D8.7а)
лишь перегруппировкой его членов.
394
ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. VIM
Убедимся теперь в том, что ряд D8.14) является решением
следующего уравнения:
которое носит название уравнения Дайсона. В аналитической
форме D8.15) имеет вид
G (г, г.) = G, (г, г,) + $ О, (г, г,) Q (г,, г,) G (г„ г.) d»r,d*r,. D8.15а)
Для того чтобы показать, что D8.14) есть решение уравнения
D8.15), найдем это решение, пользуясь последовательными ите-
рациями. Это можно делать как в аналитической форме, так и
в графической, которой мы и воспользуемся. Подставляя выра-
жение D8.15) для G в правую часть D8.15), получаем
Снова подставляя в правую часть этого уравнения правую часть
D8.15), получим
Ясно, что, продолжая итерации, мы придем к ряду D8.14). Как
сказано, те же выкладки можно было бы проделать и в аналити-
ческой форме, если исходить из уравнения D8.15а). При этом
мы придем к разложению D8.14), записанному в аналитическом
виде. Мы не будем приводить здесь указанные выкладки, ио
советуем читателю проделать их самостоятельно, что, несомненно,
подкрепит его доверие к графическим преобразованиям диаграмм.
Уравнение D8.15а), если считать в нем функцию Q извест-
ной, представляет собой линейное интегральное уравнение отно-
сительно G, которое во многих случаях может' быть решено
(см. следующий параграф). При этом получается явное выраже-
ние С_через Q, т. е. сумма ряда D8.7а) выражается через вели-
чину С<с"льио св), являющуюся некоторой подпоследовательностью
того же ряда.
1491 теория возмущении и диаграммная техника 395
В действительности функция Q точно не известна. В каче-
стве этой функции можно использовать сумму нескольких пер-
вых членов ряда D8.12) или же выразить Q через некоторую
новую функцию, подчиненную нелинейному интегральному урав-
нению. Последний путь, однако, слишком сложен, и его мы
касаться не будем (см. монографию [2]).
Обратимся теперь к корреляции двух полей, создаваемых то-
чечными источниками, расположенными в точках г' н г":
<G (г', Г;)С* (г", г;» = Г(г'. г'; г;, г;). D8.16)
Для того чтобы найти Г, следует перемножить два ряда вида
D8.3) и после этого произвести усреднение—задача более гро-
моздкая, чем рассмотренная выше. Ее можно несколько облег-
чить, если ввести диаграммные обозначения для входящих в D8.3)
еще-ке усредненных величин. Будем изображать множитель
— k*e{t) в аиде косого Крестика, а функцию G (г, го)^в виде
волнистой линии; при усреднении этих величин мы должны полу-
чать введенные выше элементы:
D8.17)
-/f-!7rl— *' <-' -X х > = •—•
г \ г, г,/ г, г,
Разложение D8.3) изобразитси при этом бесконечной суммой
диаграмм следующего вида:
Если усреднить D8.3а), то диаграммы с нечетным числом крес-
тиков исчезнут и, в соответствии с правилами усреднения, мы
получим снова разложение D8.7а).
Запишем теперь аналогичное разложение для G* (г', rj). Оно
отличается от D8.3а) заменой функции С„ на GJ, что мы будем
отмечать, перечеркивая соответствующую линию:
D8.18)
Мы должны перемножить теперь разложения D8.3а) и D8.18).
после чего усреднить результат. При перемножении отдельных
слагаемых из D8.3а) и D8.18) будем помещать сверху элементы,
принадлежащие D8.3а), а снизу—принадлежащие D8.18). Напри-
мер, усредненное произведение третьего члена из <48.3а) на
396
ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. VII!
третий член из D8.18) примет вид
_ ^ D8.19)
Поясним этот результат. При усреднении произведения
в (г,) в (г,) е (г,) ? (г.) возникают, согласно D8.5), три слагаемых,
которым соответствуют в правой части D8.19) три диаграммы.
В первой из них усредняется произведение множителей е, при-
надлежащих G(r', rj) и G*(r", г„). Возникающая при этом диаг-
рамма состоит из двух независимых кусков, ие соединяемых
какими-либо линиями (несвязная диаграмма). Очевидно, всякая
несвязная диаграмма такого типа представляет собой один из
членов произведения С (г', т'а) GJ (г", г'„), а сумма всех несвязных
диаграмм равна этому произведению.
Если ввести для <G (r', r'0)G*(r", rj)> графическое обозначение
то результат перемножения и усреднения рядов D8.3а) и D8.19)
изобразится в виде
D8.20)
Здесь приведены все диаграммы четвертого порядка 3—10 и
только три из диаграмм шестого порядка.
Остановимся на физической интерпретации этих диаграмм.
Диаграмме / в D8.20) соответствует распространение волны
с учетом многократного рассеяния пз точки т'о в г' и из точки
г; в г", причем на обоих путях распространения рассеяние про-
исходит на разных неоднородностях (рис. 68).
S4S1
ТЕОРИЯ ВОЗМУЩЕНИИ И ДИАГРАММНАЯ ТЕХНИКА
397
Диаграмма 2 описывает процесс, при котором и первая, и вто-
рая волны испытывают однократное рассеяние на одной и той же
неоднородности и т. д. (см. еще два примера на рис. 68).
Произведем теперь классификацию диаграмм, входящих
в D8.20). Все диаграммы, за исключением принадлежащих к /,
Рис. 68.
являются связными. Назовем диаграмму для корреляционной
функции сильно связной, если посредством разрыва одной ли-
нии G, и одной линии G; ее нельзя разбить на две такие неза-
висимые части, каждая из которых содержит хотя бы две вер-
шины. В D8.20) сильно связны диаграммы 2, 4, 7, 9 к 13. Все
остальные диаграммы слабо связны, но' их классификация^ не-
сколько более сложна, чем для диаграмм, представляющих G.
398 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. V1I1
Каждая из сильно связных диаграмм оканчивается четырьмя
линиями Go и Go, т. е. имеет вид
D8.21)
или в аналитической форме
Г(с.ль,о «> {T't г.. г;, гЭ = J Go (г', г,) Go (г3, г') о; (г", г,) х
хО;(г„ rl)/f (г„ г„; г,, rt)d'ri.. .d'rt. D8.21a)
Функцию К называют ядром оператора интенсивности. Диа-
граммное представление К имеет вид
В том случае, когда иа верхнем или на нижнем уровне присут-
ствует только одна вершина, в аналитическом выражении для К
содержится множитель 6 (г,—г3) или 6 (г,—г4). В аналитической
форме диаграммный, ряд D8.22) записывается следующим образом:
* (Г1. Гг, Г„ Г4) = й^в(Г1> Г,)в(Г1-Г1)в(г,-Г1) +
+ J feH|>« A4. г.) % (г,, г.) GJ (г„ г,) GJ (г., г4) 8 (Г1 - г,) d*r, +
+ ЛЧ. (rlf г,)*, (г„ т.) Go (Fi, г,) в; (г„ г4) +
+ $ *»Ф« (rt, г,)фе (г6) г,) G.fo, г,) О0(г„ г,) 8 (г,—r«)d>r.+... D8.22а)
(здесь выписаны слагаемые только до четвертого порядка вклю-
чительно).
Рассмотрим теперь возможные типы слабо связных диаграмм.
1. Слабо связная диаграмма может содержать всего один нз
сильно связных элементов, входящих в К, но быть слабо связ-
ной за счет того, что одна (нлн несколько) из внешних линий G,
или GJ _заменена на элементы, принадлежащие средней функции
Грииа G или G*. В D8.20) к этому типу относятся диаграммы
3, 5, 8 и 10. Все они принадлежат к совокупности диаграмм
вида
1* Г, Г, rl
Например, диаграмма 3 в D8.20) получается, если в К выби-
рается элемент .—. , в & (г4, гД—элемент нАс, а в остальных
% 48]
ТЕОРИЯ ВОЗМУЩЕНИЙ It ДИАГРАММНАЯ ТЕХНИКА
399
функциях G, G*—элемент Go. Очевидно, сумма всех диаграмм
этого типа равна D8.23).
2. Слабо связные диаграммы, содержащие два сильно связ-
ных элемента из К, в сумме равны
D8.24)
К этой совокупности диаграмм в D8.20) относятся диаграммы
6 н 12.
Аналогично, диаграммы, содержащие m сильно связных эле-
ментов из К, в сумме равны
Отсюда следует, что ряд D8.20) можно представить в виде
D8.25)
•^¦^^
аналогичном представлению D8.14) для G.
Подобно тому, как из D8.14) следует уравнение Дайсона
D8.15), из D8.25) легко получить так называемое уравнение
Бете—Солпшпера:
"лнГ-аГ Dв.«)
г"
Действительно, если решать [уравнение D8.26) последователь-
ными итерациями, мы получим ряд D8.25):
В аналитической форме уравнение D8.26) имеет вид
Г (г', г"; г;, r^ = G(r', r;)G'(r", r".) +
+ \ С(г', Г1)О'(г", г,) К (г,, г,; г„ г,)х
хГ(г„ r4; rifldT,...^, D8.26а)
40.0 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. VIII
Следующие два параграфа этой главы будут посвящены исследо-
ванию среднего поля и функции когерентности Г. Относительно
материала, изложенного в данном параграфе, следует сделать
одно замечание общего характера.
Фактически мы нигде не использовали до сих пор конкрет-
ного вида функции Со (г', г") и весь проведенный анализ опи-
рался на разложение D8.3). Это разложение представляет собой
решение следующего интегрального уравнения:
G (г'( г") = в„ (г', r")-ft' J Go (г', г,) I (г,) G (г,, г") dV. D8.27)
Вообще говоря, мы могли бы рассматривать это уравнение с
произвольной функцией Go в качестве исходной и пришли бы
в результате к тем же диаграммным рядам и тем же уравне-
ниям D8.15) и D8.26). Кроме того, размерность пространства,
в котором раднусом-вектором является г, тоже не играет роли.
Поэтому и г можно рассматривать как вектор в n-мерном про-
странстве с произвольным п.
К уравнению вида D8.27) могут быть сведены весьма разно-
образные физические задачи. Например, в задаче о параметри-
ческих колебаниях осциллятора со случайной частотой ш =
= ai>y 1 +8@. где е(/)—случайный процесс, стохастическая
функция Грина G (/, /„) удовлетворяет дифференциальному урав-
нению
и начальным условиям G @, /0) = 0, G@, /0) = 0. Эту же задачу
можно сформулировать в виде интегрального уравнения вида
D8.27):
G(t, t0) = Go(t, д-Ш;$Оо(<, i')l(f)G{i', ta)df,
где
здесь в—функция скачка.
В качестве другого примера, также сводящегося к интеграль-
ному уравнению вида D8.27), укажем задачу о рассеянии волн
на поверхности со случайно распределенным импедансом [17].
Ряд других примеров можно найти в обзоре [18] и моногра-
фии [19].
Другими словами, развитый выше аппарат относится к весьма
широкому кругу задач, описываемых линейными интегральными
уравнениями со случайным ядром гауссова типа.
i 49] СРЕДНЕЕ ПОЛЕ ТОЧЕЧНОГО ИСТОЧНИКА 40|
Отметим также, что наряду с диаграммной техникой часто
используется и теория возмущений в операторной форме (см.
обзор [5J), которая также позволяет получать приближенные
уравнениядля статистических моментов решеияя уравнения D8.27).
§ 49. Среднее поле точечного источника
в неограниченной случайно-неоднородной среде
Рассмотрим уравнение Дайсона D8.15а):
д (г, г.) = G. (г, г.) + J <?„ (г. г,) Q (г„г.) 5 (г,. г.) *г, *г,. D9.1)
Если применить к нему оператор D-|-?а), то, в силу равенства
(A + ft!)G0(r, г,) = в(г-г,), D9.2)
мы получим уравнение
AG (г, г„) + кЮ (г, г0) -1 Q (г, г') G (г', г.) 0>г' = б (г-г,). D9.3)
Из сравнения D9.3) с D9.2) видно, что, в отличие от Go, функ-
ция G удонлетворяет не дифференциальному, а интегро-днффе-
ренциальиому уравнению. Уравнение вида D9.3) получается,
например, из уравнений Максвелла в том случае, когда связь
между электрической индукцией D и напряженностью поля Е
н изотропной среде имеет пространствеино нелокальный характер:
D (г) а Е (г) + 4лР (г), Р(г) = J х (г, г') Е (г') d»r',
где Р—поляризация, а %—поляризуемость среды. Действительно,
из уравнений Максвелла rot Е = ikH, rot H = — ikD мы получаем
тогда для напряженности Е уравнение
ДЕ +fe'E + 4я*' J х («•• г') Е (О *'¦' = grad d'V E.
Сравнивая это уравнение с D9.3), мы виднм, что величину
можно трактовать как поляризуемость среды с пространствен-
ной дисперсией. Найденный результат легко понять и с физи-
ческой точки зрения, поскольку он выражает тот факт, что сред-
нее поле в иекоторой точке г зависит и от окружающих эту точку
неоднородностей.
Рассмотрим статистически однородную среду, т. е. предпо-
ложим, что \|>е (г!, г,)=\|)е (г,—г,). Если обратиться к разложе-
нию D8.12а) для Q (г,, г,), то легко убедиться, что в этом слу-
чае ядро Q тоже зависит только от г,—г,, т. е. Q = Q (^ — rj.
402 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ: VIII
Наконец, поскольку функция Грина Go (г, г0) тоже зависит лишь
от разности своих аргументов, ясно, что и средняя функция Гри-
на в неоднородной среде имеет вид С (г, ro) = G(r— г„). При этих
условиях уравнение D9.1) можно разрешить относительно G, вос-
пользовавшись преобразованиями Фурье
Go (г —1\) = $ g0 (к) ехр [IX (г — г,)] d»x,
G (г —г,) = \ g (*) ехр [Ы (г - г,)] d'n, D9.4)
Q (r,-r,) = $<?(*) ехр [in (г, - г,I d»x.
Для ga (к) имеем выражение
ft M = ai'tif-ч'-цо) ' D9-5)
В знаменатель этой дроби введена бесконечно малая мнимая
добавка to, обеспечивающая при вычислении интегралов D9.4)
присутствие только расходящихся волн. Величину го можно,
конечно, рассматривать как бесконечно малое поглощение
(fe — fe+V,«o).
В рассматриваемом случае уравнение D9.1) имеет вид
G(r-ro) =
= G0 (г-!•„)+ [ Ga{r-tr) Q (r.-r.JGtr.-r.JdV^'r,. D9.6)
т. е. двукратный интеграл представляет собой теперь двойную
свертку. Поэтому при преобразовании Фурье он дает произведе-
ние трансформант Фурье н уравнение D9.6) приводит к чисто
алгебраическому уравнению
IМ = g0 (к) + (8я«)« gt (и) q (я) ?(к). D9.7)
Разрешая это уравнение относительно g, получаем с учетом D9.5)
Подставив D9.8) в D9.4) и выразив ?(х) при помощи обратного
преобразования Фурье через Q (г), мы получаем формулу
Л«. D9.9)
которая в явном виде выражает G через Q.
Хотя формула D9.9) является точной, выражение для Q
известно лишь в виде ряда, просуммировать который в общем
случае не удается. Поэтому формула D9.9) полезна лишь в том
J49] СРЕДНЕЕ ПОЛЕ ТОЧЕЧНОГО ИСТОЧНИКА 403
отношении, что она позволяет по тому или иному приближен-
ному выражению для Q получить соответствующее приближе-
ние для G.
Одно из простейших приближений, которое в дальнейшем
будет рассмотрено подробнее,—так называемое приближение
Бурре—заключается bJjom, что для Q берется первый член ряда
D8.12а), т. е. полагается
Q~qff~=*'so(TrrM>e(rrr!>' D9. !0)
Соответствующее приближение С, для G мы будем изображать
графически как
Если в D.8.14) подставить вместо Q диаграмму_D9.10), то полу-
чится следующее диаграммное представление 6~t:
/S /-^.
D9.11)
Следовательно, подстановка D9.10) в D9.9) и последующее вы-
числение интеграла позволяет найти С1> т. е. просуммировать
ряд D9.11).
Если случайно-неоднородная среда не только статистически
однородна, но _и статистически изотропна, то, очевидно,
Q(r')=Q(r') и G(r—г„) = С(|г—го|). В этом случае формула
D9.9) может быть еще более упрощена посредством перехода
к сферическим координатам (как по г', так и по к) и выполне-
ния интегрирования по всем угловым переменным. В резуль-
тате D9.9) преобразуется к виду
"¦ *'-xJ ~~ ^ Q (/¦') sin (x/) /¦' <tr'
Я = 1'-г„|.
Уравнение Дайсона D9.1) можно преобразовать к виду,
в котором вместо функции Грина невозмущенной среды Go будет
фигурировать уже частично просуммированная бесконечная под-
последовательность ряда для G [3, 4J. Тгкое преобразование
Позволяет улучшить сходимость ряда для G. Для его осуществле-
ния запишем сначала уравнение Дайсоиа в операторном виде.
404 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН ?ГЛ. VIII
Введем для этого линейные интегральные операторы М, Мс и Q
с ядрами G, Go и Q:
,Л (г) - j С„ (г. г.)/(г,)*г„
Запись (Л?/) (г) означает, что функция / преобразуется опера-
тором М в функцию (М[), значение которой берется в точке г.
Если умножить D9.1) на /(г„) и проинтегрировать по г0, то
полученное равенство можно записать в следующей оператор-
ной форме:
Mf=*MJ+McQMf.
Так как это равенство справедливо при любой функции f,
его можно записать и как уравнение для оператора М:
M = Mt + MtQM = Mt$+QM)- D9.1а)
В предыдущем параграфе было показано, что функция
G(r', г") (еще не усредненная) симметрична: G(r', r") = G(r", r').
После усреднения это равенство, естественно, сохраняется:
3(r', r") = G(r*,r').
В операторном виде последнее равенство означает, что транспо-
нированный оператор М1 совпадает с М:
ЛГ=М. D9.13)
Из симметрии функции Go вытекает такое же равенство и для
оператора Ма:
AfJ = Af0. D9.14)
На диаграммном языке равенство D9.13) означает, что каждая
диаграмма, входящая в ряд для G, либо симметрична относи-
тельно вертикальной оси, проходящей через центр диаграммы,
либо, если она несимметрична, входит в G в сумме с другой
диаграммой, которая получается из исходной несимметричной
диаграммы путем отражения относительно вертикальной оси.
Например, в D8.7а) входят симметричные диаграммы /—б, 10,
13 и 17—20 и пары несимметричных диаграмм G, Р), (8, 12),
A1, /5), {14, 16). _
Из симметрии G(r', r*) следует, что и Q{r', r") = Q(r", r'),
так как диаграммы для Q имеют тот же тип симметрии, что и
S 49] СРЕДНЕЕ ПОЛЕ ТОЧЕЧНОГО ИСТОЧНИКА 405
диаграммы для G. Следовательно,
QT=<?. D9.15)
Известно, что при транспонировании произведения операторов
порядок их следования меняется на обратный: (ЛВС...I =
= ...СТДТЛТ. Применим операцию транспонирования к уравнению
D9.1а). С учетом D9.13)—D9.15) получаем уравнение
a. D9.16)
Предположим, что нам известно какое-либо приближенное
решение М1 уравнения D9.16), соответствующее некоторому
приближенному выражению.Qu т. е. известно решение уравнения
Л ! ??!) Л?,. D9.16)
Мы всегда можем получить такое решение, если подставим в D9.9)
некоторое приближенное выражение <?, вместо неизвестного точ-
ного выражения Q (например, используем в качестве Q, при-
ближение Бурре). Умножим операторное уравнение D9.1а) слева
на оператор A + Af^):
Учитывая в правой части последнего равенства формулу D9.16),
получаем отсюда
Наконец, перенося член Мх QiM в правую часть этого равенства,
запишем его в форме
Q—Ql)M. D9.17)
Уравнение D9.17) аналогично уравнению Дайсона D9.1а),
но вместо М„ в ием фигурирует оператор Mlt а вместо Q—раз-
ность (Q—Q,). Ясно, что если норма оператора Q—Q, меньше
нормы исходного оператора Q, то итерационный ряд уравнения
D9.17) будет сходиться быстрее, чем исходный.
Применив операторное равенство D9.17) к дельта-функции,
получим соответствующее уравнение для ядер операторов М,
М1У Q и Qt:
0 {г, г.) = GL (г, г„) + J G, (г. г,) [Q (г„ г,)-Q, (rlt r,)]x
xG(r2, OdV.d'r,. D9.17a)
В случае статистически однородной среды уравнение D9.17а)
можно решить при помощи преобразования Фурье. В спектраль-
1-((№>)¦ в,?*)? (*)-<?.(*»'
406 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. VII]
ной форме, т. е. для траисформант Фурье, решение имеет вид,
аналогичный D9.8):
?* D9'18)
Описанную процедуру улучшения сходимости ряда для G
можно повторять. Например, мы можем задать приближенное
выражение для Q—Q, = Qt и, используя формулу D9.18), найти
соответствующее выражение для G2.
Обратимся теперь к более подробному рассмотрению при-
ближения Бурре для статистически изотропных флуктуации е.
Из формулы D9.12), в которой вместо Q(r) использовано
приближение D9.10), получаем
»
GiW-япв 7^-^ • <4919>
-"«> *»—х1-;-— \ <|>е(r)e'*rsinxrdr+lo
KoJ
Для лучшего уяснения этого результата рассмотрим сначала
частный пример, когда 1|;в('")=«^ехр(—аг), где а = /«— радиус
корреляции флуктуации е. При таком виде фг интеграл, входя-
щий в знаменатель подынтегрального выражения в D9.19), легко
берется. Чтобы вычислить затем интеграл по к, будем считать к
комплексным. Тогда контур интегрирования можно замкнуть
бесконечной полуокружностью в верхней полуплоскости % и
значение интеграла сведется к сумме вычетов в полюсах, лежа-
щих в области Im х > 0.
В рассматриваемом примере корни знаменателя легко вычи-
сляются; они равны
m о<5Ий D9.20)
—2/4)»
Для упрощения дальнейших вычислений рассмотрим достаточно
малые флуктуации, когда |6|<^1, что выполняется при условии
В этом случае
(a—2ife)>,
и
f 491 СРЕДНЕЕ ПОЛЕ ТОЧЕЧНОГО ИСТОЧНИКА 407
Потребуем, чтобы, наряду с D9.21), выполнялись условия
позволяющие приближенно извлечь квадратный корень из D9.22)
и записать лежащий в верхней полуплоскости корень х, в виде
Заметим, что три ограничения D9.21) и D9.23) можно объе-
динить в одно:
Воспользовавшись очевидным неравенством
мы несколько усилим последнее ограничение, заменив его на
требование
j в» . I. а аЧ
1 п Ш(
при котором все три неравенства D9.21) и D9.23) будут выпол-
нены. Последнее же ограничение сводится, очевидно, к тому, что
?<4 = кЧМ^1. D9.25)
Что касается второго корня ха, то при 16|<^1 он равен
. D9.26)
Если теперь взять вычеты подынтегрального выражения в ин-
теграле по х D9.19) в полюсах к, и к„ то для Gl{R) получится
выражение
Проанализируем это выражение.
Функция G, описывает две расходящиеся волны, причем
амплитуда' второй волны много меньше, чем первой. Сравним
коэффициенты ослабления обеих волн, т. е. Imx1 и *
lmxi k*al
1ти8~"а!(а1+4*г) '
408 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН 1ГЛ. VIII
В силу условия D9.21) это отношение мало, т. е.
Таким образом, вторая волна в D9.27) не только мала по ампли-
туде, но и затухает значительно быстрее основной волиы (зату-
хание второй шолны происходит иа длине порядка размера не-
однородностей a-1 = /e). Поэтому с достаточной точностью можно
считать, что
D9.28)
Это выражение отличается от Со лишь заменой веществен-
ного k на комплексное Kj (причем Imxj >0), т. е. среднее поле
экспоненциально затухает. Кроме того, и вещественная часть х4
отличается от fe: Rex, > fc.
Оба эти результата легко объяснить: наличие иеоднородностей
приводит к перекачке энергии волны из детерминированной
компоненты поля в случайную, т. е. к ослаблению среднего
поля. Кроме того, неоднородности увеличивают фазовый путь
лучей, что эквивалентно увеличению вещественной части волно-
вого числа.
Отметим, что в силу условия D9.25) относительные изменения
волнового числа малы:
D9.29)
Это позволяет провести исследование приближения Бурре, опи-
сываемого формулой D9.19), в общем виде, без конкретизации
корреляционной функции фе-
Полюсы х„ подынтегрального выражения в D9.19) являются
корнями уравнения
=0. D9.30)
При этом основной интерес представляет тот, лежащий в верхней
полуплоскости к, корень х, уравнения D9.30), который имеет
наименьшую мнимую часть, поскольку остальные корни дают
малые и быстро затухающие вклады в G,. Но в силу условия
D9.29) роль интегрального члена в D9.30) мала, и если им
пренебречь, то мы получим xB = fc-f''o. а интересующий нас
корень х, будет близок к этому значению. Следовательно, урав-
нение D9.30) можно решать последовательными итерациями:
в нулевом приближении я, =fe, а уравнение первого приближе-
ния получится, если в интегральный член D9.30) подставить
49] СРЕДНЕЕ ПОЛЕ ТОЧЕЧНОГО ИСТОЧНИКА 409
**—*n + fe* J *« (r) e"" sin fer dr = 0. D9.31)
a
Решая это уравнение и считая интегральный член малым, полу-
чаем для эффективного волнового числа ?„фф = х, выражение
ее во -,
-± <\ sin2krЪ(г)dr + i±§sin* kr%{r)drl D9.32)
Удобно выразить fesW) через спектральное разложение функцин
1|>«(г), которое для статистически изотропных флуктуации опре-
деляется формулой C.11):
i),,(r) = -iiC©8(K')sin(x'r)x'dx'. D9.33)
о
Подставим D9.33) в D9.32) н изменим порядок интегрирования
по г и х'. С учетом формул
'sinsxcosi* , я а/ ,. (л/2 при 0>6,
получаем после выполнения интегрирования по г
+ 1^*|'фе(х)хйх
D9.34)
В рассматриваемом приближении усредненная функция
Грнна, согласно D9.19), равна
Таким образом, мы пришли к тому, что при R^>lt средняя
функция Грина имеет тот же вид, что и в однородной среде,
410 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. VIII
но с заменой исходного волнового числа k на fe>M). Величину
Аафф/Ь можно трактовать как эффективный показатель прелом-
ления случайно-неоднородной среды. Согласно D9.34)
4 $ V2A *J D9.36)
2*
Из этих формул видно, что л, > 1 при любом виде спект-
ральной плотности Фе(к) Гтак как In (jj^jj)* > Ol , а п, всегда
положительно. Объяснение этому уже было дано выше при
обсуждении результатов расчета с корреляционной функцией
г|>е~ехр(—or).
Согласно D9.34) коэффициент ослабления среднего поля по
мощности равен
¦гк
у = 2 1ш (*8М,) = я'*1 $ Фв (х) кdx. D9.37)
о
Легко убедиться в том, что эта величина совпадает с коэффи-
циентом рассеяния сг„, вычисленным в борновском приближении
для статистически изотропных флуктуации е (см. B6.13)):
Принимая здесь 2fesin@/2) = x за новую переменную интегри-
рования, мы получаем правую часть D9.37), т. е. Y=o«-
Если обратиться к случаю крупномасштабных иеоднородио-
стей, т. е. считать, что k^>Hm, то верхний предел интегрирова-
ния в D9.37) можно заменить на бесконечиость и эта формула
перейдет в полученную ранее в марковском приближении фор-
мулу D5.6). В выражении D9.36) для п1 можно при &^
считать, что
и, следовательно,
S «I СРЕДНЕЕ ПОЛЕ ТОЧЕЧНОГО ИСТОЧНИКА 411
По порядку величины в этом случае имеем
т. е. изменение (по сравнению с волновым числом для однород-
ной среды) действительной частн волнового числа мало по срав-
нению с изменением его мнимой части.
Остановимся теперь на вопросе о границах применимости
приближение Бурре. В качестве первого приближения мы рас-
смотрели ядро массового оператора Q в приближении D9.10).
Возьмем теперь следующее приближение для Q, в которое вклю-
чим следующую бесконечную подпоследовательность диаграмм
из точного ряда для Q:
D9.38)
Таким образом, функция Qt отличается от <3, тем, что содержит
вместо G, среднюю функцию Грина Gp найденную в приближе-
нии Бурре:
И в этом случае полюсы функции Грина будут определяться
уравнением, аналогичным D9.30), но под знаком интеграла
вместо е'*г будет фигурировать е'*»*Фг:
у? = k* + -?¦ j фе (г) e'W sin кг dr. D9.39)
о
Мы уже знаем, что в первом приближении корень этого уравне-
ния равен »1 = А,фф. Поэтому в правую часть D9.39) вместо х
можно подставить найденное выше fe
45" *l+i? J *¦(г) е*"*фГ sin (fe>*»r) *• D940)
Нам следует теперь сравнить это выражение с
mkr dr. D9.41)
о
Положим Л»фф = * + ДА, где согласно D9.29) \bk\<$.k- Тогда
1/А 1/А—ДЙ/А5. Подставим это значение l/fe,t» в D9.40) и
412 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН (ГЛ. VIII
после этого вычтем D9.41) из D9.40). Заменяя сннус по формуле
Эйлера на разность экспонент, получаем
Чтобы оценить эту разность, снова воспользуемся модельной
корреляционной функцией ^(г)—о*ехр(—аг). Интегралы прн
этом легко берутся н выражение х|—xf приводится к виду
1 ' ~ L(o-2«) (о-2(*8фф) в (a-2i*) J "
Так как мы оцениваем разность у%—*\ с точностью до величин
первого порядка по ДА, можно положить в квадратных скобках
kk и тогда
или, поскольку к\—xj = (x,—kJ (х,4-х,)»2&(х,—н,),
Для того чтобы найденный в приближении Бурре сдвиг Д& имел
смысл, необходимо потребовать малости по модулю по сравве-
нню с |Д/г| поправки следующего приближения к,—х2, т. е.
<49-43>
Но это условие совпадает со вторым условием D9.23) и заведомо
выполняется, если удовлетворено условие D9.25), при котором
были выведены основные формулы в приближении Бурре. Таким
образом, можно считать, что полученные выше в приближении
Бурре формулы для G справедливы прн выполнении условия
где U—радиус корреляции случайного поля е.
Следует отметить, что оценка D9.43) получена из сравнения
приближения Бурре не с точным решением, которое неизвестно,
а со следующим приближением (правда, включающим, как это
видно нз D9.38), бесконечное число диаграмм для Q). Поэтому
это условие нельзя считать достаточным, во оно являете и необ-
ходимым.
$ ВО] ФУНКЦИЯ КОГЕРЕНТНОСТИ ПОЛЯ 413
Помимо приближения Бурре известен еще целый ряд дру-
гих приближенных решений, а также ряд более сложных урав-
нений (в том числе и нелинейных) для средней функции Грина.
Более подробно с ними можно ознакомиться по работам [2, 4—6J,
а дальнейшие литературные ссылки можно найти в обзоре [7].
С работами, посвященными применению теории многократного
рассеяния к различным задачам распространения электромагнит-
ного излучения в случайно-неоднородных средах, можно ознако-
миться по обзору [8].
§ 50. Функция когерентности поля.
Оптическая теорема и уравнение переноса излучения
Выше было получено уравнение Бете—Солпитера D8.26а)
для функции когерентности
Г (г', г"; г;, r;) = <G(r',ri)G*(r', г;)>
поля двух точечных источников; оно имеет вид
Г (г', г"; г;, r;)-G(r',r;)G«(r*, гЭ +
+ $ G (г*, г,) G» (г", г,) К (г„ г,; г„ г4) Г (г8, г,; rj, Q X
X d»rl... d°r,. E0.1)
Разумеется, от него нетрудно перейти и к уравнению для функ-
ции когерентности поля и (г), создаваемого в неоднородной среде
произвольным распределением объемных источников /(г). Поле
ц(г) выражается через /(г) формулой
Отсюда следует, что среднее поле равно
u(r) = jG(r,ro)/(r0)d'ro, E0.2)
а функция когерентности поля получается усреднением произ-
ведения ц(г')и%(г*):
= J <G (г', г;) G (г\ гЭ> / (О /• (гЭ d»r; d'rl =
= J Г (г', г"; г;, rj) / (г» /• (rj) d'r'o d'rl
Поэтому, если умножить уравнение E0.1) на /(ri);*(rj) н цро-
интегрировать по т'е и т'с, то результатом будет уравнение
^ r-, ra)x
X К(г„ г,; г,, г4) Г„ (г„ г4) d'r,.... d>rit E0.3)
414 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. V!»
определяющее функцию когерентности поля, возбуждаемого
произвольным детерминированным распределением источни-
ков / (г).
В отличие от уравнения Дайсоиа, уравнение Беге—Солпи-
тера E0.1) не удается разрешить относительно Г.
В этом параграфе мы займемся исследованием связи между
уравнением Бете—Солпитера и УПИ—феноменологическим урав-
нением переноса излучения D5.25). Выше, в § 45, такая связь
была установлена в том частном случае, когда для описания
распространения волн использовалось приближение параболи-
ческого уравнения, а для УПИ — малоугловое приближение.
Теперь задача ставится в общем случае, но для ее упрощения
мы ограничимся статистически однородной случайной средой,
а функцию когерентности Г (г', г") будем рассматривать только
в области, свободной от источников, т. е. там, где ;(г) = 0.
Преобразуем сначала E0.3) в интегро-диффереициальное
уравнение. Для этого вспомним, что функции G удовлетворяет
уравнению D9.3), которое мы запишем в виде
fi(r)G(r, г') = 8(г-г'), E0.4)
где D(r) — оператор Дайсона:
D(r) = j? + *'-Qr, E0.5)
a Qr — массовый оператор, т. е. интегральный оператор с ядром
Q (г, г'):
Qr/(r)-SQ(r,r')/(r')dV\
Если применить оператор б(т) к формуле E0.2), то в силу
E0.4) получим
а значит, в области, свободной от источников, справедливо
уравнение
6(г)п(г) = 0. E0.6)
Применим теперь оператор б (г') к уравнению E0.3). С уче-
том E0.6) и E0.4) находим
Й(г')Г„(г', г-) =
= J G* (г", О К (г', г,; г„ г4) Г. (г„ rjd'r, d*r, d?rt. E0.7)
Точно так же, если применить к E0.3) оператор ?)' (г"), то
с учетом уравнений, комплексно сопряженных с E0.4) и E0.6),
S ВО] ФУНКЦИЯ КОГЕРЕНТНОСТИ ПОЛЯ 415
получим
О'(ОГ„(г'.О=
= $ G (г', г,)К (г„ г"; г„ г.) Г„ (г„ rj *r, *г, #г.. E0.8)
Вычтем уравнение E0.8) из E0.7). Если обозначить при этом
через г, переменные интегрирования г, в E0.7) и г, в E0.8),
то эта разность запишется в виде
г'. г") = J [О* (г", го)АГ(г'. iy, г„ О-
-G (г'( г,)/С (г0> г"; г.. г.)] Г„ (г„ г4) d'rt d'r, d>rt. E0.9)
Но согласно определению E0.5)
-J d»ro[Q (г', г.) Г. (г.. r')-Q'(f, го)Г„(г', г,)]. E0.10)
Введем теперь, как уже неоднократно делалось, новые пере-
менные R = i/J(r' + O и г=г'—г". Тогда A'—A" = 2vRV,. Функ-
цию Г„, выраженную через переменные R, г, будем обозначать
через r(R, г):
r(R,r)-rB(R-|-V.r. R-V,r).
Перейдя к новым переменным и подставив E0.10) в E0.9) с уче-
том статистической однородности среды (G (г', г") = G (г'—г"),
Q (г', О = Q («¦'—г")), находим
2v«V,r(R, г)—
-J*r.[Q(R+f-r.)r(."+?-¦?. r.-R + |)-
'r.dV,. E0.11)
Выполним в различных слагаемых E0.11) замены перемен-
ных интегрирования, принимая каждый раз за независимую
переменную аргумент той из функций Q, Q', G* или G, которая
входит в данное слагаемое, и, кроме того, обозначая R'—Va (гз+г*)
416 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. VIII
и г' = г,—г4. Уравнение E0.11) принимает после этого внд
2v«V,r(R, r)-J [Q (г')Г (r—? . г-г")-
- Q* (г") Г ( R —?, г + г")] А* =
(
X Г (R'( r') d'R' d'r' d*r". E0.12)
Отметим, что E0.12)—это точное следствие уравнения Бете—
Солпитера.
Рассмотрим связь уравнения E0.12) с законом сохранения
энергии, который во всякой области, свободной от источников,
записывается в виде (см. C9.2))
где
Усредняя эти выражения, получаем
div<<iSp{R)> = 0, E0.13)
<& (R» = 27j<»'(R) V««(R)-«(R) V*u*(R)>.
Средняя плотность потока энергии <<9°> может быть выражена
через функцию T(R,r). Действительно, дифференцируя по г
равенство
T(R, r) = <u(R+r/2)u'(R—r/2)>,
находим
V,r(R, г) = V,<u* (R—г/2) V«« (R + г/2) —
—и (R + r/2) V«u* (R—г/2)>.
Полагая здесь г = 0, получаем
так что
<^(R)>= (tt)-l[V,r(R, r)Jr=0. E0.14)
Вернемся к уравнению E0.12). Если положить в нем г = 0, то
для величины 2V«V,T(R, г), используя E0.14) и E0.13), получим
2V«V,r(R, r)|r=0 = 2v
; во] функция когерентности поля 417
Поэтому уравнение E0.12) принимает при г = 0 вид
R-r"; R' + T, R'—4) —
-r, R; R'+T, R'~t)] r(R'' r')d*r'd*R' d'r".
E0.15)
Обратим теперь внимание на следующее. Функция Г в E0.15).
зависит от выбора поля источников / (г), тогда как функции
Q, G и К от выбора /(г) не зависят. Поскольку соответствую-
щим выбором источников можно произвольно изменить функ-
цию Г, не меняя функций Q, G и К, уравнение E0.15) должно
выполняться тождественно относительно Г. Записав левую часть
E0.15) в виде трехкратного интеграла:
[f-R') а (»•+»•)-
-Q«(r")8(R—T~R')8(r"—r')]r(R', r')d"r'd!>R'd3r",
подставив это выражение в E0.15) и приравняв коэффициенты
при T(R', г') в левой и правой частях, получаем
q (-о б (R-R'+4)-Q'(r')a (r-r' -y) =
= J [с (О К (R-r", R; R'+Y' R'-j)-
R-r*; R'+T, R'~t)] d'r"- E0-16>
Это равенство, связывающее среднюю функцию Грина с ядрами
массового оператора н оператора интенсивности, носит назва-
ние оптической теоремы [9].
Физический смысл оптической теоремы заключается в сле-
дующем. Ослабление среднего поля выражается через 1тАвфф>
т. е. через Im Q, ио вызывается оно не поглощением (среда
прозрачна), а' рассеянием, которое описывается оператором К»
Поэтому между этими величинами должна существовать опреде-
ленная связь. Эта связь и выражается оптической теоремой.
Заметим, что, когда для G, Q и К используются какие-либо
приближенные выражения, оии должны удовлетворять соотно-
шению E0.16), так иак в противном случае может возникнуть
противоречие с законом сохранения энергии.
Вернемся к уравнению E0.12). Нашей следующей задачей
будет преобразование этого уравнения в УПИ.
14 С. М. Рытов н ар. ч. II
418 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. VIII
Воспользуемся приближением D9.38) для Q:
Q(r) = *4>.(»K(r), E0.17)
где G—средняя функция Грииа в приближении Бурре. Для
оператора интенсивности используем первый член разложения
/СК, V, '.. r«) = *4*t('i—*,) 6 Ci-r,) 6 (',-».)• E0.18)
Такая аппроксимация ядра оператора интенсивности носит
название «лестничного» приближения. Объясняется это название
тем, что если в разложении D8.25) использовать лишь первый
член ряда D8.22) для К, то диаграммное представление функ-
ции Г будет иметь вид слестниць»:
Подставив E0.17) и E0.18) в уравнение E0.12), получаем
= *' J {8 (г') ft,, (г')-Ц,,(г-г')]Г (R —у. г-г')-
( —у, r+r')Jcf/. E0.19)
Прежде всего, отсюда видно, что прн г=0 правая часть
обращается в нуль, т. е. в рассматриваемом приближении закон
сохранения энергии н оптическая теорема удовлетворяются
(иными словами, приближения E0.17) в E0.18) согласованы
между собой н не вызывают нарушения закона сохранения
энергии). Кроме того, как видно из E0.19), в уравнение для
Г входят лишь разности ф,(г')—ф, (г ± г'), которые можно выра-
зить через структурные функции Z>,(r). Это означает, что крупно-
масштабные неоднородности не влияют на функцию когерент-
ности поля (напомним, что в приближении марковского случайного
процесса дело обстояло точно так же, § 45).
Очевидно, необходимым условием применимости приближен-
ного уравнения E0.19) должно быть полученное в предыдущем
параграфе условие применимости приближения Бурре. Рассмот-
рим в этой связи характерные масштабы функции F(R, r) по
обоим ее аргументам.
Как мы знаем нз предыдущего параграфа, среднее поле экспо-
ненциально убывает по мере удаления от источника, причем
характерный масштаб убывания равен (Im AlW,)"" ^d. Так как
ослабление среднего поля обусловлено рассеянием иа неодно-
родиостях, то ясно, что тот же масштаб d будет характерным
продольным масштабом функции Г по переменной R. Характер-
$ 50) ФУНКЦИЯ КОГЕРЕНТНОСТИ ПОЛЯ 419
иым поперечным масштабом Г по R может являться диаметр
пучка излучения или же характерное расстояние, на котором
заметно меняются такие усредненные характеристики среды, как
а\ или радиус корреляции /„.
Что касается характерного масштаба г„ функции F(R,r) no
разностной переменной г, то ои может быть порядка либо радиуса
корреляции /а неоднородностей
среды, либо радиуса первой |фГгП-*(г-г'I
зоны Френеля (что имело место '« , « '
в области применимости МПВ),
либо быть еще меньше (как при
рассмотренных в гл. VII силь-
ных флуктуациях поля). Во вся-
ком случае, всегда можно счи-
тать, что гк, намного меньше,
чем характерный масштаб d
функции Г по переменной R.
Такое соотношение между
масштабами функции Г можно рис
использовать для того, чтобы
еще несколько упростить уран-
нение E0.19). Действительно, разность | % It')—ф„ (г ± г') | при
г «г4 заметно отлична от нуля лишь при г < {1„ + г)~ (/,+/¦»)
(рис. 69). Но, нак мы предположили, величина (/«-+¦ г») мала по
сравнению с характерным масштабом d фуииции F(R, r) по
переменной R. Это означает, что в E0.19) можно считать
r^R—y,r±r')<wr(R, r±r'). Тогда уравнение E0.19) при-
нимает вид
2v«V,r(R, г) = А*^ G (г')[фв(г')—^(г—r')J Г (R, t-r')d'r'-
Сделаем во втором интеграле замену переменной интегрирования
г'-*-г'. Так"как G*(—r') = G*(г') и ф.(— г')=ф.(г'), полу-
чим урани
чим уравнение
, г) = *$ [G(r')-G'(г')] X
X [Ь (r')-ib (r-r')J Г (R, r-r') d»r'. E0.20)
В случае, если п(г) = О (тогда T(R, г) совпадает с корреля-
ционной функцией поля), уравнение E0 20) эквивалентно урав-
нению переноса кзлучеиия. Убедимся в этом. Введем трансфер-
14»
420 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. Vfl!
манту Фурье функции T(R, г) по разностной переменной1):
ПИ. r) = J/(R, x)exp(/xr)d»x, E0.21)
5, r)exp(—txr)d»r. E0.22)
Для облегчения перехода к трансформантам Фурье я урав-
нении E0.20) вычислим предварительно трехмерную спектраль-
ную плотность средней функции Грина G, которую мы возьмем
в приближении
^li E023)
где k,^ = kl + ikl и Aji^fcj. Как_ нетрудно убедиться, спектраль-
ная плотность разности G(r)—G* (г) равна
z(K) = z(x)-^^[6(r')-G-(r')Iexp(-(Hr')*r' =
тгтт- E0.24)
Покажем, что в силу неравенства k,^.ky функцию E0.24) можно
приближенно заменить на дельта-функцию. Максимум модуля
фуикцни г (х) соответствует х = х0 = У/?—ftj, причем в этой точке
2(xo)=l/8n»i7j1A,. Вместе с тем при jc' = fe|—А*=р 2*!*,, т. е. при
к « х„ =F ft,, получаем z (х0 =f ft,) = Vsz (к0). Таким образом, г (х)
падает в два раза при сдвиге аргумента от х„ на малую вели-
чину k,— [mkttli/—\ld. Легко проверить, далее, что
-С
п J
Поэтому, если (как мы уже предположили) масштаб d велик по
сравнению с масштабами функции фе(г') и T(R, г—г') по г',
то функцию
я (*»_*|-,
сосредоточенную в узком интервале Ах ~ 2к„ можно заменить
на 8(ftJ—&g—х1); тогда получим
а) Если и / 0, то предварительно следует вычесть из Г произведение
средних полей с тек, чтобы брать трансформанту Фурье от корреляционной
функции (си. [10] и задачу I).
§ БО] ФУНКЦИЯ КОГЕРЕНТНОСТИ ПО.ЧЯ 421
Используя формулу 6 (х'—xg) = & iK~K°]^{к + Хо) и учитывая,
что й(х + хо) = 0 (поскольку х>0 и х„ > 0), можно написать
8
а если учесть малость fea, то
Я№**ШЕГ- <50-25>
Теперь легко выполнить преобразование Фурье уравнения
E0.20). Подставив в него выражение
5 (r')-G' (г') = J ^^
и разложение E0.21), после несложных вычислений с учетом
формулы
J ^ (г') exp ((xr')dV = 8я»Фв (х)
получаем
2г V« j exp (ixr) x/ (R, к) d3x =
= — — ("d3xexp(ixr)/-(R, и) f d?*'6 (х' — <г,)Фе(х' — х) +
x'exp(ix'rN(x'— ftj fd»v./(R, х)Ф,(х'—х).
Меняя в последнем интеграле обозначения переменных интегри-
рования, »п*'| и приравнивая коэффициенты при exp (ixr), по-
лучаем уравнение
пр члене в правой части этого уравнения введем по пе
ременной интегрирования-х' сферичесиие координаты, положив
х' = х'п', где п' — единичный вектор. Тогда d*x' — v/'dv-'do(n')
и уравнение принимает вид
422 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССВЯНИЯ ВОЛН 1ГЛ. VI11
Будем искать его решение в следующем виде:
/(R, x) = 6(x-ft1M'(R, n)-^-, E0.27)
где х = хп.
Подстановка E0.27) в E0.26) дает для 3 (R, п) следующее
уравнение:
чп6(ч—ft,) V*3(R, n)= — 2^1б(ч—ft,) 3(R, n)x
, п')Ф,(хп—ч'п).
Так как имеет место равенство ф(хN(х—ft,) = q> (ft,) 6 (х—ft,),
можно везде заменить ч н ч' на ft,, после чего сравнение коэф-
фициентов при дельта-функциях приводит к уравнению
. n) +
i(n—n')K(R. n')rfo(n'). E0.28)
где учтена четность функции Фе.
Это уравнение представляет собой не что иное, как УПИ D5.25),
причем коэффициент ослабления равен
06=§ Т- ф« (*'"'>л ("')• Eа29)
а эффективное сечение рассеяния нз единицы объема в единич-
ный телесный угол имеет вид
а (п, п') =^Ф.(*, (п-п')). E0.30)
Действительно, с использованием этих обозначений уравнение
E0.28) принимает стандартную форму УПИ [14J:
п V«J (R, п) = — аЭ (R, п) + §а (л, л1) 3 (R, n')do (п'). E0.31)
Из сопоставления E0.29) и E0.30) видно, что
a=<f)o(n,n')do(n'), E0.32)
т.е. все ослабление поля обусловлено рассеянием. Сравнение
формулы E0.30) с полученной в борновском приближении фор-
мулой B6.13) показывает, что значение о, определяемое выра-
жением E0.30), отличается от значения в бориовском прибли-
жении заменой ft на ft,. Мы виделн, что отлнчие ft, от ft обуслов-
f 60] ФУНКЦИЯ КОГЕРЕНТНОСТИ ПОЛЯ 423
лено влиянием миогократного рассеяния. Однако в рассмотренном
в § 49 приближении отличие ft, от ft мало, и, если Ф, (х) —
достаточно плавная функция, этим отличием можно пренебречь.
Принципиально важная сторона полученных результатов
заключается в следующем. В феноменологической теории пере-
носа излучения, яркость, или лучеваи интенсивность, Э никак
ие связана с параметрами, описывающими волновое поле. Теперь
мы получили возможность установить эту связь. Комбинируя
формулы E0.21) и E0.27), находим, что
Г(Я, r)=-jj-fe""(x—A,) J(R, n)x«A«do(n),
или, после интегрирования по х,
E0.33)
Таким образом, лучеваи интенсивность представляет собой угло-
вой спектр функции когерентности. Положив в E0.33) г = 0, мы
получаем формулу, связывающую среднюю интенсивность Г—
=<|'"|1>=-r(R, 0) с лучевой интенсивностью:
7(R) =^> 5 (R, n)da(n). E0.34)
Далее, продифференцировав E0.33) по г, положим затем г=0:
Подставляя это выражение в E0.14) и пренебрегая разницей
между ft и fcj, получаем среднюю плотность потока энергии:
<<Р(Ю> = <f пЭ(R, n)do(n), E0.35)
Таким образом, через J(R, n) можно выразить все основ-
ные характеристики волнового поля: плотность энергии (интен-
сивность), плотность потока энергии и функцию когерентности1).
Разумеется, свести точное уравнение Бете—Солпитера к УПИ
возможно отнюдь не всегда. В общем случае функция когерент-
ности T(R, r) разлагается в интеграл Фурье вида E0.21), в ко-
тором присутствуют плоские волны exp (ixr) с произвольными
значениями х. Лишь в том случае, когда в этом разложении
|х| =ft, справедлива формула E0.33).
11алее, при выводе УПИ мы использовали приближение Бурре
для G и ограничились только первым членом разложения опе-
') Отметин, что в § 9 были приведены аналогичные формулы для слу-
чайного волнового поля в однородной среде.
424 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. VIII
ратора интенсивности («лестничное» приближение). Правда, более
подробный анализ показывает, что второе из этих приближений
справедливо тогда же, когда и первое (т. е. когда справедливо
приближение Бурре), так что оба верны при необходимом условии
fe'/|a'«^l. E0.36)
Наконец, при переходе от уравнения E0.19) к E0.20) было
сделано предположение о малости характерного масштаба функ-
ции T(R, г) по переменной г по сравнению с ее характерным
масштабом по R. Оказывается, однако, что для выполнения этого
предположения тоже необходимо условие E0.36).
Тем не менее возможны и такие ситуации, когда УПИ заве-
домо неприменимо. Так обстоит дело, например, в том случае,
когда нас интересует обратное рассеяние. В УПИ производится
некогерентное сложение рассеянных воли (сложение интеиснв-
ностей), что особенно наглядно проявляется при феноменологи-
ческом выводе этого уравнения (§ 45). Но при рассеянии назад
рассеянная волна проходит точно через те же неоднородности,
что н падающая, в силу чего существенны фазовые соотношения
между этими волнами. В результате УПИ оказывается непри-
годным для описания рассеяния назад [12, 13]. Существенную
роль при таком рассеянии играют «циклические» диаграммы
(например, диаграммы 7 и 13 в формуле D8.20)).
Мы ограничились весьма упрощенной задачей о распростра-
нении скалярного волнового поля в статистически однородной
случайной среде. Более общий случай статистически неоднород-
ной среды рассмотрен в работе [10]. В работе [11] УПИ выве-
дено для электромагнитного поля, причем с учетом простран-
ственной и частотной дисперсии.
Остановимся еще на одной стороне вопроса, постансвка кото-
рого даже не возникала в феноменологической теории переноса
излучения [14]. Речь идет о дифракционном содержании УПИ.
Как мы видели, УПИ эквивалентно уравнению E0.20) для функ-
ции когерентиостн F(R, r), которое в свою очередь получено
нз волнового уравнения. Поэтому, если известно аналитическое
выражение функции 3 (R, п), то при помощи формулы E0.33)
можно восстановить функцию Г, которая должна содержать ин-
формацию и о дифракционных эффектах (см. задачу 2). Здесь
возникает вопрос о том, как следует формулировать граничные
условия к УПИ, чтобы при обратном переходе к Г (R, г) полу-
чить описание дифракционных эффектов. Этот и ряд других
вопросов о взаимосвязи теории когерентности с теорией переноса
излучения анализируются в работах [15, 16].
Подведем некоторые итоги. Общая теория многократного рас-
сеяния охватывает случаи ие только крупных, но и мелких
неоднородностей. В рамках этой теории получены приближенные
$ 50] ФУНКЦИЯ КОГЕРЕНТНОСТИ ПОЛЯ 425
замкнутые уравнения для моментов поля, вывод которых факти-
чески основан иа частичном суммировании рядов теории воз-
мущений. При этом в рамках общей теории многократного рас-
сеяния удается вывести все уравнения, полученные различными
приближенными методами, и, что еще важнее, указать границы
применимости такнх методов. Существенным достижением теории
можно считать «статистико-волиовое» обоснование УПИ и уста-
новление дифракционного содержания этого уравнения. Здесь
получены н другие важные результаты. В частности, удается
вывести УПИ с учетом трансформации когерентной составляю-
щей поля в некогерентную (см. задачу 1, где соответствующее
уравнение выводится для скалярных волн, и работу [II] для
электромагнитных волн). При вычислении когерентного поля
одновременно решается и задача об определении эффективного
показателя преломления случайной среды.
В рамках теории многократного рассеяния можно получить
прнблнжеиные замкнутые уравнения не только в случае сплош-
ной случайно-неоднородной среды, ио и для моментов волнового
поля, рассеянного на совокупности большого числа дискретных
вкраплений (дифракция иа телах, занимающих случайное поло-
жение н случайно ориентированных). Здесь также удается вы-
вести УПИ (см. например, [20, 21J) и установить микроскопи-
ческий смысл феноменологических параметров, входящих в это
уравнение. Оказывается, что сечение рассеяния единичного объема
в общем случае не совпадает с сечением рассеяния одной ча-
стицы, умноженным иа концентрацию частиц: при больших кон-
центрациях проявляются так называемые коллективные Еффскты
J22J, вызванные падением на данную частицу не только прямых
волн, но и волн, рассеянных другими частицами.
Что касается перспектив дальнейшего развития теории мно-
гократного рассеяния, то, во-первых, можно ожидать, что она
приведет к решению задачи о распространении воли в среде с
не малыми флуктуациями диэлектрической проницаемости (это
имеет место, например, в плазме, если частота электромагнитной
волны близка к плазменной частоте, или в жидкостях вблизи
критической точки).
Кроме того, имеется широкий круг практически интересных
задач, несомненно относящихся.к теории многократного рас-
сеяния, но усложненных многочислеинымн дополнительными фак-
торами. Здесь можно упомянуть дифракцию частично когерентных
полей в случайно-неоднородной среде, рассеяние воли на шерохо-
ватой поверхности, окруженной случайно-неоднородной средой,
дифракцию волн в случайно-неоднородной среде при наличии
дискретных вкраплений, теплсвое излучение случайно-неодно-
родных сред и т. д. (см. сбзор [23J и цитированную в нем ли-
тературу).
426 9ЛВМВНТЫ ТЕОРИИ МНОГОКРАТНОГО РАССЕЯНИЯ ВОЛН [ГЛ. VIII
Задача
I. Исхода из уравнения F0.19), получить УПИ для случая, когда сред»
лее поле и не равно нулю'
Р;ешен;не. Введем ^обозначение F (R, r) = «(R4-r/2)u»(R—г/2) и под-
ставим BE0.19)r(R,r)^,(R,r)+F(R,r), где 4M^O=<u(R+r/2)u«(R-r/2)>.
Из уравнения E0.6) легко получить, что
-j . r-r1) -
)} (I)
С учетом этого уравнения находим после подстановки в E0.19) r^i
следующее уравнение для 1?,:
(R. r) = *« J jSaO№, (r')-*, (r-r')] *« (R-^-, r-r') -
-y, r+r')|dV. B)
Пренебрегая, как и при переходе от E0.19) к E0,20), величиной г'/2 в ар-
гументах Ч>, и Р, получаем уравнение, обобщающее E0.20):
t-i')^R, r-r')d»r'. C)
Введем траисформанты Фурье
«. (R. г) = \ f (R. и) «р (ixr) <l»x.
F (R. ') = i /.(R. н)ехр(<нг)<Л(.
Выполняя иреобраэование Фурье уравнения C) и учитывая формулы E0.24),
E0.25), получнм
К'Ф,(«-«') [/(R, h'L
Если искать решение этого уравнения в виде
. и). «=хп,
ЗАДАЧИ
то это приводит и следующему уравнению для 3:
:, п) =—аЗ (R, п) + $о(п, п') 3 (R, п')*>(п') +
487
(здесь использованы те же обозначения, что и в E0.29) н E0.30)).
Уравнение F) отличается от стандартного УПИ E0.31) наличием допол-
нительного (последнего) слагаемого, описывающего трансформацию когерент-
ной части поля в иекогерентную. Формула E0.33) теперь справедлива ие для
Г, а для функции корреляции:
iMR,r) = $ff(R. и) «'*'"*> (п). G)
2. Плоская волна «„ (г) падает на объем V, анутрн которого в (г) ф 0.
Размер объема V мал по сравнению с длиной экстникции й, так что рассея-
ние волны и, (г) на неоднород-
ностях можно описывать в бор-
иовском приближении. Полу-
чить решение задачи о рассея-
нии, исходя из УПИ, выведен-
ного в предыдущей задаче, н
пренебрегая различием между
Ь н *i.
Решение. Поскольку рас-
свивающий объем мал по срав-
нению с d, энергия рассеянного
поля значительно меньше энер-
гни падающей волны. Поэтому
в УПИ (формула F) предыдущей
задачи) можно пренебречь членами, описывающими экстинкцкю и рассеяние
некогерентного ноли, т. е. в правой частя остается только последний член:
(*п-н'. R)/, (R. нО d*'. (!)
Здесь специально выделена зависимость Фе от R, так как флуктуации в
не являются статистически однородными. Так как размер рассеивающего
объема мал по сравнению с й, можно считать, что и (г) — и„ (г) — Uo«f*n»r, где
п0—единичный вектор вдоль направления распространения первичной волны,
a Ug—ее амплитуда. Тогда (обозначения те же, что и в предыдущей задаче)
F(R. r) = |U,|«eip(iftn.r),
MR. *)=
р <• 7П
Подставляя B) в A), получаем уравнение
п-*п,. К).
C)
Функция Ф„ отлична от нуля только внутри рассеивающего объема V. Так
как п ЧцЗ (R, л) =g7ff, где -я— производиаи по направлению единич-
ного вектора п (рис. 70), то очевидно, что решение уравнения C) имеет
428 ЭЛЕМЕНТЫ ТЕОРИИ МНОГОКРАТНОГО РДССГЯНИЯ ВОЛН [ГЛ. VIII
следующий вид:
а>
g(R, n)=^ — ^""''ф,. (*("-"¦)¦ R п()Л. D)
п
Найдем теперь i|'B(R, г), воспользоваршись формулой G) задачи I:
+»(R. r) =^ *'*"*> (n) \ '2"'' Ф? (* (п—п.), R-nl) dl. E)
и
Введем новую переменную интегрирования г'¦¦ —п/, представляющую совой
радиус-вектор точки R—п/, проведенный нз точки R. Тогда <2V' —Pdldoin),
т. е. <(.'do(n) = —tj-:=—tj-• Формула E) принимает внд
В гл. IV эта формула била получена в приближении однократного рас-
сеяния, и, как ясно из проведенного там вывода, оиа полностью учнтыоаег
дифракционные эффекты. Таким образом, данная задача непосредственно под-
тверждает, что УПИ описывает дифракционное поведение поля.
Глава IX
РАССЕЯНИЕ НА ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ
§ 51. Рассеяние на малых неровностях.
Метод возмущении
Поверхности реальных тат всегда в той или иной степени
неровны, в силу чего отражение и преломление волн на этих
поверхностях сопровождаются явлениями, которые отсутствуют
в случае идеально гладких границ раздела. Разумеется, степень
«гладкости> определяется в первую очередь соотношением между
длиной волны и геометрическими параметрами неровностей.
Одна и та же поверхность, «идеально» гладкая для радиоволн
или звука, может быть шероховатой для света или ультразвука.
Неровности могут изменяться со временем (морское волне-
ние, тепловые флуктуации формы поверхности), но могут быть
и практически неизменными '-.(рельеф суши или морского дна,
поверхность бумаги, матового стекла, вообще твердого тела).
Наконец, как и для объемных неодпородностей среды, сами
задачи об отражении и преломлении волн на неровных поверх-
ностях или о дифракции н рассеянии па них могут быть и
детерминированными, и статистическими. Последние возникают,
как обычно, в тех случаях, когда нас интересует не какой-то
конкретный, «индивидуальный» вид неровной понерхности, а
характеристики ансамбля таких поверхностей. Со статистическим
ансамблем приходится иметь дело при наличии большого числа
неровностей на облучаемом участке поверхности (шероховатые
поверхности), но возможны, конечно, и такие ситуации, когда
речь идет о малом количестве неровностей. Например, нас может
интересовать рассеяние от некоторого единичного выступа на
плоскости, ансамбль же состоит из реализаций с выступами
разного вида, причем геометрические и (или) физические харак-
теристики выступа случайны (подчинены определенным вероят-
ностным распределениям).
Рассеяние волн на телах, имеющих случайную форму или
занимающих случайное положение, мы отнесли в § 8 к задачам
430 РАССЕЯНИЕ НА ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ [ГЛ. IX
типа 3). Обычная постановка задач этого типа состоит в том,
чтобы найти статистические характеристики рассеянного поля
по заданной статистике неровностей, но часто возникает необхо-
димость н в решении обратной задачи—по статистике рассеян-
ного поля определить свойства поверхности.
Характер рассеяния определяется многими факторами. Кроме
размеров неровностей и длины волны падающего излучения,
играют роль и размеры рассеивающей площади, и способ ее
облучения, а также поляризация первичной волны, отражающие
и преломляющие свойства вещества и т. д. В зависимости от
соотношения между различными параметрами применяют те или
иные приближенные методы расчета рассеянного поля. Мы рас-
смотрим только два наиболее простых и часто применяемых
метода—метод малых возмущений и метод Кирхгофа. Сведения
о более общих методах, учитывающих многократное рассеяние,
можно найти в монографии [I] и в обзорной статье [2].
Пусть шероховатая поверхность задана уравиеннем г =
— ?(х, г/) = ?(р). Примем, что <?> = 0, т. е. ограничимся случаем
в среднем плоской поверхности, уклонения от которой описы-
ваются случайным полем ?(р). Если поверхность z = ?(p) пред-
ставляет собой границу двух сред, то на ней должны выпол-
няться соответствующие «двусторонние» граничные условия.
Например, если ы, и и,—потенциалы акустической скорости
в первой и второй средах, то для звуковых волн на границе
должно выполняться равенство нормальных компонент скорости
fgrr«=g^, N — нормаль к поверхности) и равенство давлений
(p1u1=p!ua, где р! и р,— плотности сред). В электромагнитной
задаче на граиипе должны быть непрерывны тангенциальные
компоненты напряженностей Et и //,. Рассеянные волны рас-
пространяются при этом в обеих средах.
Рассматривая для простоты скалярные волны, мы упростим
постановку задачи еще в одном отношении: будем считать, что
распространение волн возможно лишь в одной среде, т. е. по-
верхность г = ?(р) либо «абсолютно мягкая» (на пей и = 0), либо
«абсолютно жесткая» [ш*"®)- В обоих случаях происходит
полное отражение. В электромагнитной задаче этому соответ-
ствует идеально проводящая поверхность (?, = 0) и поверхность
идеального магнетика (Я, = 0).
Итак, для абсолютно мягкой поверхности граничное условие
имеет вид
«Is = «(P. *)|,= t(p) = 0, E1.1)
а для абсолютно жесткой —
i 51] РАССЕЯНИЕ НА МАЛЫХ НЕРОВНОСТЯХ 431
причем единичный вектор внешней-нормали N имеет компо-
ненты
(Nj., tf2)=(aVj? -a). a = [l -{-(ViCI]-1". E1.3)
Vi = f^, щ\ — поперечный оператор дифференцирования.
Строгих методов решения волнового уравнения со случай-
ными граничными условиями E1.1) или E1.2) не существует,
и задачу удается решить лишь приближенно, при определенных
ограничениях, налагаемых на размеры и форму неровностей.
Мы рассмотрим ниже два случая таких ограничений, при кото-
рых и приложимы два упомянутых метода. А именно—мы рас-
смотрим поверхности, неровности которых в масштабе длины
волны Я либо малы и пологи, либо плавны. В первом слу-
чае применим метод малых возмущений, а во втором—метод
Кирхгофа.
Пологость неровностей означает, что наклоны поверхности
в среднем невелики, т. е.
<(Vi.?)'>~a|/Z|V^l, E1.4)
где о|=<{;г>—средний квадрат уклонения от невозмущениой
поверхности г = 0, а /;—характерный размер неровностей. Ра-
зумеется, это неравенство, справедливое для среднего квадрата,
при расчетах используется еще до усреднения.
Малость неровностей означает, что моменты <?"> малы по
сравнению с соответствующими степенями длины волны, <?*>^Х.И,
в частности,
о(<4*-'- E1.5)
В результате для малых и пологих неровностей можно исполь-
зовать разложение как граничного условия, так и искомого
решения по степеням малых параметров ?А <^ 1 и | Vj.? \~<*t/lf^\ •
в чем и состоит метод малых возмущений.
В случае плавных неровностей величина уклонения J не
ограничивается, а условие пологости заменяется требованием
малой кривизны (плавности) неровностей: радиусы кривизны
поверхности RKf должны быть велики по сравнению с \:
или kRKt^>l. E1.6)
Соответственно неоднородности должны обладать и ри ?г>Я боль-
шой протяженностью в направлениях х и у (крупномасштабные
неровности). При этих условиях применимо кирхгофово прибли-
жение: поле в окрестности каждой точки поверхности прибли-
женно представляется суммой падающей волны н волны, отра-
женной от соприкасающейся плоскости в этой точке; при этом
используются локальные значения «плоских» коэффициентов отра-
432 РАССЕЯНИЕ НА ЩЕРОХОНАТЫХ ПОВЕРХНОСТЯХ [ГЛ. IX
жения (в электромагнитной задаче — френелевских коэффициен-
тов). Под падающей волной можно понимать не. только первичную
волну, но и волны, попадающие на данный участок поверхности
в результате отражения от других ее участков. Простейшим
является случай, когда многократные отражения отсутствуют.
Для плавных неровностей отношение cj'/j может и не быть
малым. В принципе метод Кирхгофа применим и в этом случае
крутых неровностей (a^'/^l). Ясно, однако, что с ростом кру-
тизны неровностей многократные отражения будут все более
существенными. Учесть их, пользуясь методом Кирхгофа, очень
трудно. Для того же, чтобы ими можно было пренебречь, опять-таки
требуется даже в случае крупномасштабных неровностей опре-
деленная их пологость. Она нужна еще и для того, чтобы можно
было пренебречь затенениями одних элементов поверхности
другими, хотя учет затенений осуществить легче, чем учет мно-
гократных отражений. Таким образом, в отличие от метода воз-
мущений, наклон неровностей |Vj_?| не является в методе Кирх-
гофа малым параметром. Пологость требуется лишь для упрощения
задачи, т. е. в той мере, в какой это нужно для пренебрежения
многократными отражениями и затенениями. Метод Кирхгофа
мы рассмотрим в § 52, а сейчас обратимся к случаю малых
неровностей.
Как сказано, в основе метода возмущений лежит разложение
искомого поля и и граничных условий в ряды по степеням малых
параметров ?Д ~ ас/Я <g 1 и | Vj_S | — cE//;<-gl. Такой подход был
впервые предложен еще Релеем для случая синусоидальных
неровностей и был применен затем Л. И. Мандельштамом к ста-
тистической задаче о рассеянии света на неровностях, обуслов-
ленных тепловыми флуктуациями поверхности жидкости [3].
Пусть U (г) — первичное монохроматическое поле, падающее
на шероховатую поверхность (множитель e~imt для краткости
опускаем). Запишем решение уравнения Гельмгольца в виде ряда
и(г)-?/(гН-2«>(г). E1-7)
п-0
где п-й член ряда имеет порядок (а;/Я)" нли (а;/^)". Этот ряд
представляет собой разложение по кратности рассеяния.
В случае абсолютно мягкой поверхности граничное условие
E1.1), разложенное по степеням J, принимает вид
здесь и далее нижним индексом 0 отмечены значения поля и его
производных по г при г = 0. В данном случае Vj.? в граничное
условие не входит, так что требование пологости E1.4) для
§ 61] РАССЕЯНИЕ НА МАЛЫХ НЕРОВНОСТЯХ 433
абсолютно мягкой поверхности является излишним и в разло-
жении E1.7) используется только один малый параметр а^/Х<^1.
Подставив E1.7) в E1.8), получаем граничные условия (уже
на плоскости г = 0, которую иногда называют подстилающей)
для последовательных приближений поля:
«$ + ?„ <).
и?'-г-[!(«'"+У)] С-О,
Таким образом, нахождение n-кратно рассеянного поля ulB)(r)
сводится к рассмотренной в § 9 задаче о волновом поле, имею-
щем заданное значение u)(p) = Uo"^jj|n)(p, 0) на плоскости
г — Q. Это заданное значение известно, коль скоро известны по-
лученные одно за другим предшествующие приближения от и"" до
u(n-i) Случайный характер граничных значений и"' обусловлен
присутствием в E1.9) случайной функции ?(р).
Для фактического нахождения поля в n-м приближении можно
воспользоваться либо формулой Грина (9.12), либо методом Релея
(разложение по плоским волнам—формулы (9.14)—(9.16)); для
плоской границы z = 0 оба подхода эквивалентны. Проведем рас-
четы по формуле Грина (9.12), которая для полей нулевого н
первого приближения дает следующие выражения (здесь г™ {р, г},
EU0)
В рассматриваемом случае, когда на плоскости z = 0 заданы
сами поля, вычисление иш) (г) имеет смысл как .для ограничен-
ного участка площади 2 этой "плоскости, так и для всей беско-
нечной плоскости. Если берется конечная площадка, то в пред-
положении, что ее размеры велики по сравнение с длиной
волны, мы можем воспользоваться гипотезой Кирхгофа о том,
что формулы E1.10), написанные для бесконечной плоскости,
остаются в силе и на рассматриваемой площадке конечных раз-
меров, и надо только ограничить область интегрирования в E1.10)
пределами площадки. Пусть на шероховатую поверхность под
углом 0, к оси z падает плоская волиа
U (г) - А ехр (/fen.r) = A exp [ik (nip + п'гг)] =
-=Aexp[tk(n'±p — zcos90)], E1.11)
'5 СМ. Рытов и др. ч. II
434
РАССЕЯНИЕ НА ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ
[ГЛ. IX
где n,-=(ni, л,) —единичный вектор в направлении распростра-
нения падающей волны, причем «J= — cos90 (рис. 71). В случае
бесконечной поверхности ясно и без расчета по первой из фор-
мул E1.10), что в пулевом приближении мы имеем зеркально
отраженную волну
Ц(о)(г) =—И ехр \ik (п'хр- п\г)\ = — А ехр [ik(п{р + г cos 9,I. E1.12)
Если площадка имеет конечные размеры, то по гипотезе Кирх-
гофа вблизи площадки поле
ит тоже представляет собой
зеркально отраженную волиу
E1.12), ио иа достаточны^
удалениях от площадки поле
и101 превращается в направ-
ленную сферическую волну
с максимумом интенсивности
в направлении зеркального
отражения.
Поле нулевого приближе-
ния ut0)(r) представляет для
нас интерес лишь в той ме-
Рнс 71. ре, в какой оно определяет
нелнчнну однократно рас-
сеянного поля иш. Из E1.11) и E1.12) следует, что
и, стало быть, в соответствии с E1.10),
E1.13)
Второй вариант этой формулы относится к случаю kz^>\, когда
точка наблюдения удалена от плоскости г—0 по меньшей мере
на несколько длин волн.
Среднее значение поли uul равно нулю, а расчет его средней
интенсивности /, = <|ца)|4> во многом сходен с вычислением /,
в случае рассеяния на объемных иеоднородностях. В предполо-
жении о статистической однородности флуктуации ?(р) при
помощи E1.13) находим
р' —р") 1 !*(«'— R")\x
E1.14)
¦ Ml
РАССЕЯНИЕ НА МАЛЫХ НЕРОВНОСТЯХ
435
где i|>t(p'—P") ~ ^» (Р*) S(Р*)> —функция корреляции иеровностей,
#' <=j/"z*-Hp—р')''> Я" = Vrz* ~ (р—р')*. Введем новые перемен-
ные интегрирования 1 —р' — р", т| = (р' + р")/2 и разложим R' и
R" в ряды Тейлора по разностной переменной ?. Наличие под
интегралом функции корреляции ^(S) = ipt(p'—P"). быстро спа-
дающей до нуля при ?^> /с,
позволяет ограничиться в этих z
разложениях первыми членами.
А именно при Ы\1г% <^ 1 ') можно
Г1иближенно заменить R' и R'
знаменателе подынтегрально- '
го выражения на jR, = | г—1| | =
= V^z* + (p—ч)е, а разность
R'—R" в показателе—на — пЦ.
Через п, = RJRi обозначен еди-
ничный вектор в направлении
от точки рассеяния т| на плос-
кости г = 0 к точке наблюдения
г = (р, г), а через п^—поперечная составляющая этого вектора:
()
Далее, распространив пределы интегрирования по ? до бес-
конечности (это возможно, даже если площадка 2 конечна, но
велика по сравнению с радиусом корреляции /;), находим
+: (I) exp [ife (ni-
где
E1.15)
— преобразование Фурье функции корреляции, т. е. двумерный
пространственный спектр неоднородностей; qi —k(n'x—n'L) — по-
перечная компонента вектора рассеяния q = fe(n,-—п,) (рис. 72).
В результате в E1.14) остается только интеграл по г):
•) Заметим,'что это неравенство слабее, чаи условие ft/{/z<^l, отвечаю-
щее удалению точки наблюдения во фраунгоферову зону отдельной неодно-
родности.
15*
436 РАССЕЯНИЕ НА ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ 1ГЛ. IX
который распространяется на всю плоскость г = 0 илн только
на ее часть 2, если шероховатая поверхность имеет конечные
размеры.
Согласно E1.16) каждый элемент поверхности d'r\ = dl, с цент-
ром в точке т| даст в суммарную интенсивность 1L вклад
.) | Л 1»-^ , E1.17)
где «! = «//},. = cos9—косинус угла между вектором n,— R,/R4
и осью z (рис. 71). Формула E1.16) отражает, таким образом,
избирательный характер рассеяния: в ладанном направлении as
рассеивает только определенная «гармоника» неровностей, отве-
чающая вектору рассеяния Чх = *(п1 — nL)> что полностью ана-
логично селективности рассеяния на объемных неоднородностях
(см. § 25). В частности, при нормальном падении первичной
волны, когда п'г = —I, п^=- 0 и qx = fenl, длина волны «активной»
гармоники неровностей A^ — Sn/q^ равна A/ni = A/sin0. При
рассеянии в направлении зеркального отражения, когда п^ —п^
н qj. = O, Л, обращается в бесконечность. Наконец, при обрат-
ном рассеянии (п^ — — п^_, qj. = — 2/jrij.)
Л -=
* 2knlx 2sin00°
Величина
E1.18)
т. е. коэффициент при \A^dLlR\ в формуле E1.17), пред-
ставляет собой сечение рассеяния единичной площадки абсолютно
мягкой поверхности в направлении п5. В отличие от объемного
рассеяния, сечение E1.18) безразмерно. Формула E1.16), запи-
санная в виде
EЫ9)
явно выражает некогерентность волн, рассеянных отдельными
элементами шероховатой поверхности, их сложение по интенсив-
ности. В рассматриваемом случае абсолютно мягкой поверхно-
сти сечение E1.18), содержащее множитель (fij/t5)' = cos2 0, cos39,
обращается в нуль при скользящих углах падения и отражения,
т. е. прн 8, 80—»-я/2. Именно поэтому интеграл E1.19) сходится
даже при интегрировании по всей плоскости г = 0.
Если рассеивающая поверхность имеет конечную площадь 2
и в пределах этой площади величины aM(qx) и Ry практически
f «I) РАССЕЯНИЕ НА МАЛЫХ НЕРОВНОСТЯХ 437
ПОСТОЯННЫ, ТО
Л-141'0:^. E1.20)
Условие постоянства а„ (q.J и R^ в пределах площадки 2 с мак-
симальным размером L записывается, как нетрудно установить,
в виде
если ft<$^ (мелкомасштабные неровности),
... _..
если ';§>^ (крупномасштабные неровности).
Случай абсолютно жесткой поверхности отличается тем, что
рассеянное поле уже в первом приближении зависит не только
от ?, но и от ViS- Из E1.2) и E1..4) следует, что на границе
должно быть
Подставляя сюда разложение E1.8), находим
Таким образом, для последовательных приближений поля, в от-
личие от E1.9), получаются граничные условия, содержащие Vi?:
dU\ n
Для нахождения полей и1 по заданным на плоскости г = 0
значениям нормальной производной 1-з—) можно воспользо-
ваться формулой Грина (9.13):
.^' E..23,
E1.24)
Пусть на шероховатую поверхность падает плоская волна
E1.11). Ясно, что в непосредственной близости к площадке
регулярно отраженна» волна и101, удовлетворяющая первому из
граничных условий E1.22), подчиняется законам зеркального
отражения и записывается в виде
и"» = А ехр life (n^p — n*z)|.
438 РАССЕЯНИЕ НА ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ [ГЛ. IX
Тогда выражение в фигурных скобках 8 E1.24) равно
Среднее значение этой величины равно нулю, а функция кор-
реляции 1|Э/(!) = </(р')/*(р")> выражается через 4; A) следую-
щим образом:
1», ft) = 41 А |» exp (i*niS) [ik «V j.) - fe> (n-J]' ^t (D- E1 -25)
(дифференцирование Vj. здесь производится no | = p' — p").
Подсчитаем среднюю интенсивность рассеянного поля
7» ° чИ 5 *' {p'-pl е'**У *р'dy- E126)
Как и ранее, целесообразно перейти к новым переменным инте-
грирования |=р'_р" и г] =- (р' — р")/2 н заменить приближенно
е"<«'-«")//?'/?" на ехр(— tftn'j_j)/#f. Используя E1.25), запишем
выражение для 7t в виде
/. = "^ j|-^г f exp (-/qj) [t* (niVj.) -f к'- («i)'p tj A) d2|.
Внутренний интеграл выражается через двумерную спектраль-
ную плотность неровностей Fi(x):
Но 4i = fe(ni — n^), и поэтому
f-*(niqJ4-fe»(nf)T = fel[(niL-(n'1.)f-(ninl)] =
= **[! -("'>!)]'¦
В результате имеем
7^4Mr^jiizK^l!^ld4 E1.27)
Это выражение можно представить в форме E1.19), если
ввести сечение рассеяния единичной абсолютно жесткой пло-
щадки
o»Di) = «Ф -KnsJ]»/4 (Чх). E1-28)
которое отличается отсечения рассеяния мягкой площадкиE1.18)
другим множителем при /•'t(qJ_). Этот множитель [1 —(n'j.n^)]1
(а тем самым и сечение аж) не стремится к нулю при скользя-
щих углах, падения и отражения, так что нитеграл E1.27),
взятый по всей плоскости г —0, расходится. Разумеется, интен-
сивность реального рассеянного поля не может обращаться
в бесконечность. Расходимость связана лишь с примененным
i 611 РАССЕЯНИЕ НЛ МАЛЫХ НЕРОВНОСТЯХ 439
методом расчета, а именно с использованием первого приближе-
ния. Расходимость интеграла в E1.27) в этом приближении
влечет за собой появление бесконечностей и в последующих
приближениях, но интенсивность суммарного поля 0 = 2"""
п
должна оставаться конечной.
Указанную расходимость можно устранить, применяя усовер-
шенствованные формы теории возмущений, учитывающие зате-
неиия и многократное рассеяние уже в нулевом приближении.
Не вдаваясь в подробности, отметим только, что при учете
затенений и многократного рассеяния (о которых кратко будет
сказано в § 53), в отличие от E1.28), сечение рассеяния аж
обращается в нуль при скользящих углах падения и рассеяния,
т. е. при 60- *п/2 или 0—>-л/2 (когда п'г—> () или п\—>О), а
при умеренных значениях углов 80 и 0 сечение совпадает с E1.28).
Таким образом, расчет интенсивности рассеянного поля по фор-
муле E1.27) правомерен лишь для площадок конечных размеров.
Переход же к бесконечным пределам требует использования
более точного выражения для (^(q).
Рассмотрим угловую зависимость сечення рассеяния а для
мягкой и жесткой границ на примере шероховатой поверхности
с изотропной гауссовой функцией корреляции неровностей
которой отвечает спектральная плотность
Если положить n, = (sin 80, О," —cos 0O), n^ — (sin 9 cos ф,
sin6siti(p, cos9), то по формулам E1.18) и E1.28) находим
1 cos*-в, cos2 6 1
I A— sin00sin9cos(p)a J
^.(sin*eo4-sin28—2 sin 0„ sin 8 cos ф)
При малых kit (мелкомасштабные неровности) угловая зави-
симость определяется предэкспоненциальными множителями; при
этом рассеяние происходит в широкий сектор углов с раствором
порядка 90°. Зависимость сечений ам и аж от угла 8 (прн фикси-
рованных значениях угла падения В, и азимутального угла <f)
показана на рис. 73, а и 73, б. Пунктиром на рис. 73, б по-
лзай истинный ход индикатрисы аж@) с учетом многократного
'ассеяния.
440
РАССЕЯНИЕ НА ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ
[ГЛ IX
При &С^>1 форма диаграммы рассеяния определяется в основ-
ном экспоненциальным множителем, одинаковым для а„ и аж.
Максимальное значение а приходится в этом случае на направ-
ление зеркального отражения в = в0, tp = O, а убывание интен-
Рис. 7а.
сивности в е раз происходит при угловом отклонении от
максимума примерно на Д0~1/&/? (рис. 74).
Нетрудно подсчитать, что при М;^>1 и для углов падения,
не слишком близких к скользящему (cosв0 ^> I/«/;), отношение
полной интенсивности поля, рас-
сеянного единичной площадкой,
2я я/г
/
(т(в)
к полной интенсивности падающе-
го на эту площадку излучения
/„ = | A Y coseo приближенно равно
Отсюда видно, что с ростом высоты
неровностей <jj условие /п<^ /„, поз-
воляющее ограничиться первым
приближением теории возмуще-
ний, рано или поздно нарушается.
На практике чаще приходится встречаться не с рассмотрен-
ной постановкой задачи о рассеянии на шероховатых поверх-
ностях (плоская первичная волна, в среднем плоская рассеи-
вающая площадка), а со случаем, когда облучение большой
(практически бесконечной) шероховатой поверхности произво-
дится волновым пучком—коллимированным или расходящимся.
Именно так обстоит дело в радиолокации и гидролокации, а
также в лабораторных экспериментах по рассеянию света. Путем
незначительного видоизменения расчетов нетрудно обобщить вы-
5 ЯП РАССЕЯНИЕ НА МАЛЫХ НЕРОВНОСТЯХ 441
ражшие E1.19) и на этот случай, учитывая также и возможное
искривление подстилающей поверхности.
Пусть на шероховатую поверхность падает квазиплоская
волна и = Аеи"*, амплитуда которой А и локальный волновой
вектор k, = ftV(p практически постоянны в масштабе радиуса
корреляции неровностей /;. Пусть уравнение поверхности задано
в параметрической форме:
г (а. Р)=7(а, Р) + ?(а, P)N0(a, Р), E1.30)
где r = r(a, P)—уравнение невозмущенной (подстилающей) по-
верхности 20, а ?.(«• P)N0(a, P)—случайные смещения но нор-
мали к 2„ (рис. 75). Если радиус кривизны подстилающей
поверхности велик по срав-
нению с длиной волны X и
с радиусом корреляции /;,
то малый элемент поверх-
ности dS, на который
падает квазкплоская волна
Ae""f, рассеивает так же, "'"
как и элемент плоской
поверхности, касательной
к 20. Обозначим через п;
градиент эйконала падаю»-
щей волны в точке рассея- '
ния Р, лежащей на 20 Рис. 75.
(n, = k,/ft = Vq>), а через
п^ — единичный вектор в направлении от Р на точку наблю-
дения Q (рис. 75). Если под п^ и п[ понимать компоненты
векторов п,- и ns> касательные к 2„, а под 7?, — расстояние
между Р и Q, то средняя интенсивность рассеянного поля за-
пишется в виде
E1.31)
где сечение a(q±) определяется спектром неровностей Pj в ок-
рестности точки рассеяния Р. Пределы интегрирования опре-
деляются размерами либо рассеивающей площадки, либо облу-
чаемой области, т. е. области, где амплитуда первичной волны
заметно отличается от нуля. Формула E1.31), как и выражение
E1.19), применима при условии Я^УЩ- При fe/j^>l это
условие слабее условия 41*^>к1\, означающего удаление точки
наблюдения вофраунгоферову зону отдельной неровности. В слу-
чае же ft/:<^l формулы E1.19) и" E1.31) справедливы уже при
удалении на расстояния R, ~ X от шероховатой поверхности.
442 РАССЕЯНИЕ НА ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ [ГЛ. IX
§ 52. Рассеяние на крупномасштабных неровностях.
Метод Кирхгофа
В акустике, оптике и радиофизике часто интересен случай
не малых, а больших неровностей, когда зеркальное отражение
практически отсутствует. Примером может служить рассеяние
дециметровых и сантиметровых радиоволн на поверхности взвол-
нованного моря или отраженке звуковых волн от морского дна.
Эта задача была впервые достаточно полно исследованаМ. А.Иса-
ковичем [4], который применил для ее решения метод Кирхгофа.
Мы будем следовать в основном оригинальной работе [4], а также
работе [5], где сняты некоторые ограничения, принятые в ряде
предшедствующих публикаций.
Для интересующего нас теперь случая больших неровностей
воспользуемся формулой Грина (9.13). Пусть на поверхность
падает локально плоская скалярная волна
и = А(т)е^^>, E2.1)
которую мы описываем в приближении геометрической оптики.
Это может быть, в частности, плоская нли сферическая волна
(направленная или ненаправленная). Мы будем предполагать,
что ни для падающей волны, ни для рассеянной нет затенений
каких-либо элементов поверхности. Очевидно, сколь бы плавной
поверхность ни была, это условие исключает слишком малые
углы скольжения как для падающей волны, так и для направ-
ления наблюдения.
Как известно, при падении плоской волны U (г) на плоскую
границу раздела отраженное поле и (г) и его нормальная про-
изводная du/dN связаны на этой границе с U и dU/dN точными
соотношениями
* $-, E2.2)
где Я — коэффициент отражения, зависящий от угла падения.
В соответствии с принципом Кирхгофа мы принимаем, что гра-
ничные условия E2.2) приближенно справедливы для локально
плоской волны E2.1), падающей на локально плоскую по-
верхность 2, т. е. на поверхность с плавными неровностями.
Разумеется, под Я следует понимать в этом случае локальный
коэффициент отражения.
Подставляя E2.2) в формулу Грина (9.11), для вторичного
(рассеянного) поля цвтор = ц(г) получаем
где R — \г—г'|—расстояние от точки наблюдения г = (р, г)
до точки г' = (р', г'), лежащей на неровной поверхности г'=
L
§52 РАССЕЯНИЕ НЛ КРУПНОМАСШТАБНЫХ НЕРОВНОСТЯХ 443
= ?(р'). Преобразуем это выражение к виду, удобному для ста-
тистического усреднения. Для простоты рассмотрим случай,
когда подстилающей поверхностью является плоскость z' = ? = 0.
Прежде всего, перейдем в E2.3) к интегрированию по под-
стилающей плоскости г'=0: если a — \:V\ + (Vj.?)* , то dS —
= d2,,/a = dap'/a. Вводя нормальный к поверхности 2 вектор
N, = N/ot с компонентами (—V^.?, 1), имеем
E2.4)
(оператор дифференцирования \' действует на координаты точки
г' = (р'. г')).
Далее, пусть точка наблюдения г удалена от 2 на расстоя-
ние, которое превышает и длину волны Я, и высоту неровностей:
kz^>], z^>o"j. Тогда можно дифференцировать в E2.4) только
быстро осциллирующую экспоненциальную функцию ett<*f|0, пре-
небрегая производными от медленных функций А (г) и \,R:
(NiV')(
A dt^lz:) «ik-J e" <«*') (N,V) (R + Ф) -
^ _,ь iPx«\ /м -\ - _^_ -(* (Л+ф) Г /п I Г Г^ -4- а 1 /52 "Л
о * V4J. • xb/ I "itj' ^^^л•.«^^
где
q ^= — feV' </? т ф) = *1(п, — п() E2.6)
— вектор рассеяния. Величина п,- = v'<f представляет собой ноп-
маль к фазовому фронту падающей волны, а единичный вектор
указывает направление из точки г' на точку наблюдения г.
Учитывая, что для пологих неровностей VxS^l и рассеяние
на таких неровностях происходит в направлениях, близких
к направлению зеркального отражения (в этом направлении
п^=п^ и q._ — 0), заменим скалярное произведение (N,q) =
=—(qj.ViE)-|-?j просто на qz. В результате имеем
и = -± §.Щг Ае" «*« d»p'. E2.7)
Все величины под интегралом относятся к точке неровной
поверхности г' = {р', ц(р')}. Чтобы выделить в явном виде за-
висимость от возмущения ?(р'), разложим подынтегральные
функции в ряды Тейлора по С, причем в медленных функциях Я,
444
РАССЕЯНИЕ НА ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ
ГГЛ. IX
qz, А и \/R ограничимся нулевым приближением, а в показа-
теле экспоненты учтем еще и линейный по ?(р') член:
exp \i
exp {ik {R + <р) lt=0 — iq&
E2.8)
Локальный коэффициент отражения 5i|;=0 отвечает здесь на-
правлению зеркального отражения, в котором п^=п^, qj. = O,
и является уже детерминированной величиной. Для френелев-
ских коэффициентов отражения, меняющихся (если исключить
случай полного отраже-
ння) в функции угла паде-
ния медленно, это при-
ближение вполне оправ-
дано, поскольку в дан-
ном направлении nf рас-
сеивают только такие
участки поверхности 2
(дающие «блики»), которые
наклонены под одним и
тем же определенным уг-
лом (рис. 76).
Пренебрегая линейны-
ми членами в медленных
амплитудных функциях и квадратичными — в показателе экспо-
ненты, мы совершаем относительную ошибку, не превышающую
ka\lD, где D — либо радиус кривизны фазового фронта падающей
волны, т. е., по существу, расстояние до источника, либо рас-
стояние до точки наблюдения R. Требуя, чтобы выполнялось нера-
венство
Рис. 76.
D
E2.9)
означающее, что источник и точка наблюдения должны нахо-
диться в зоне Фрауигофера по отношению к масштабу неров-
ностей а», после подстановки E2.8) и E2.7) находим
Qi~ae z*d?p , E2.10)
где значения величин qz, A, R, <р, $Я взяты на плоскости г = 0.
Более аккуратный расчет, при котором член (q^VaJ) в фор-
муле E2.5) не отбрасывается, а преобразуется путем интегри-
рования по частям [4|, приводит к выражению
5 52] РАССЕЯНИЕ НА КРУПНОМАСШТАБНЫХ НЕРОВНОСТЯХ 445
которое отличается от E2.10) заменой qz на q*!qz. В выражениях
E2.10) и E2.11) все величины являются функциями точки г'=
— {р', Of подстилающей плоскости г = 0, а не точки г' —{р',
&р')\ неровной поверхности 2, как в E2.7).
Наличие возмущения ?(р') в показателе экспоненты придает
некоторое сходство рассматриваемой задаче с задачей о про-
хождении волны через фазовый экран [б], но следует помнить,
что при рассеянии на шероховатости случайный набег фазы —</z?
зависит (через qz) от 'направлений первичной и отраженной
волн.
Переходя к статистической части задачи, мы сразу обратимся
к случаю не малых qzt,. Нелинейная зависимость поля и от t,
означает, что для нахождения моментов и (г) необходимо знать
уже не моменты случайного поля ? (р') того же порядка, а его
функции.распределения.
Согласно E2.11) среднее значение и равно
]
Величина
где K>ij(?)—плотность вероятностей отклонений, представляет со-
бой характеристическую функцию поля ? (р). Если это поле одно-
родно, то f,i(qz) зависит от р' лишь неявно—через локальное
значение z-компоиенты вектора рассеяния"?,.(р'). Таким образом,
'l»)'- E212)
Поскольку и определяется характеристической функцией ?,
формула E2.12) легко распространяется на случай, когда не-
ровность поверхности представляет суперпозицию независимых воз-
мущений ? = 2?v- Функция fL ;(</x) равна тогда произведению
V
соответствующих характеристических функций.
Применив для вычисления E2.12) метод стационарной фазы
E], можно показать, что
E2.13)
где нижний индекс «с» означает, что Я. и qt берутся в стационар-
ной точке рс, отвечающей зеркальному лучу, приходящему в точку
наблюдения г (рис. 77). Через ц(|1)(г) обозначено значение ин-
теграла E2.11) при ? — 0, т. е. поле волны, отраженной от под-
стилающей плоскости z = 0 по законам геометрической оптики.
446
РАССЕЯНИЕ НА ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ
[ГЛ. IX
Например, для плоской звуковой волны E2.11), падающей на
абсолютно мягкую поверхность (для нее Э1 =—1), а<0) дается
выражением E2.12), а для сферической первичной волны это поле
зеркального (относительно
плоскости z — 0) точечного
источника.
Из E2.13) видно, что не-
ровной поверхности Можно
приписать эффективный
коэффициент отражения для
среднего поля
5?*И — &Jh (Як)- E2-14)
Для идеально отражающей
поверхности, очевидно,
Рис. 77. В случае малых неровно-
стей (^о;<^1) приближенно
/,;s« I +iqzt,— \, поскольку ?—0. Это означает, чго в первом
приближении по ? неровности не влияют на среднее ноле. С ро-
стом qfli Среднее поле быстро убывает, так как fxi(qz) умень-
шается.
Найдем теперь среднюю интенсивность флуктуациоиного поля
7, = <|"|2> = <|«|1>-|й|«. E2.15)
Согласно E2.11)
X <ехр \iq? (р') — iqll (p"))> dy d'p",
E2.16)
где одним и двумя штрихами отмечены величины, относящиеся
к точкам р' и р" подстилающей плоскости г=0. Выражение
= /.t(<7« <7«; P'. P") E2.17)
— это двумерная характеристическая функция поля 5, зависящая
от р' и р" как от параметров.
Пользуясь формулами E2.12) и E2.16), для интенсивности
рассеянной волны находим
l; p'
. E2.18)
РЛССР.ЯНИК НА КРУПНОМАСШТАБНЫХ НЕРОВНОСТЯХ 447
р 5s здесь обозначена разность двумерной характеристической
функции E2.17) и произведения одномерных характеристических
функций:
Ля*, я",; (>'. p"W*(<?;. -91: р', Р")-Гч(яд/.:(?)• E2.19)
Эта разность обращается в нуль при большом (по сравнению с ра-
диусом корреляции неровностей /;) разнесении точек р' и р*, по-
скольку при |р' — р"|^>': значения ?(р') и ?(р") становятся
некоррелированными, а двумерная характеристическая функция
f%l распадается иа i-.роизведение одномерных характеристическкх
функций. Ниже мы убедимся на одном из примеров, что область,
где 5s заметно отличается от нуля, в действительности даже меньше,
чем круг |р' —р"|^/{.
Воспользуемся указанным свойством функции 5s для прибли-
женного вычисления интеграла E2.18). Перейдем отр' и р" к пере-
менным | = р' -— р" и t) = (р' + Р")/2. Разность ft (R' + ф') — k(R" -f ф")
в показателе экспоненты разложим в ряд Тейлора по \, сохранив
в нем только линейный член:
*(/г'+ф')—*(«" + 9")t=««*(V.i'? + Vi4'M = —qxt E2.20)
В предэкспоненциальном же множителе положим % — 0 (т. е.
р' = р" = т|) и, кроме того, заменим# q'z и q\ в аргументах З1 зна-
чением qz в «центре тяжести» т)=(р' + р")/2, т. е. положим q',ta
«"?i«9iD)- Тогда
где R1 = (p\y, F, ^(^(П) ?,(ч) Р Р)
Распространив, далее, пределы интегрирования по % в E2.18)
до бесконечности, получаем формулу некогерентного рассеяния
(сложения ллтепсивностей)
в которой величина
E2.22)
имеет смысл сечения рассеяния единичной площадки.
Область применимости выражения E2.21) определяется теми
приближениями, которые были сделаны при его выводе. Наиболее
жестким оказывается условие
E2.23)
448 РАССЕЯНИЕ НА ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ 1ГЛ. I."
при выполнении которого можно отбросить кубичный член в раз-
ложении E2.20) (квадратичный член и вообще слагаемые четных
степеней в этом разложении отсутствуют). Здесь R — расстояние
от точки ц иа плоскости z = 0 до точки наблюдения или до источ-
ника, alp—характерный масштаб изменения 5* по переменной ?.
В случае малых неровностей, когда
E2.24)
характерный масштаб lp совпадает, очевидно, с радиусом корреля-
ции неровностей /j. В противоположном предельном случае qpi^> 1
масштаб 1р по порядку величины равен tyq&i. В этом можно
убедиться, скажем, на примере двумерного нормального распре-
деления
для которого
S1(I, n) = e-''"c[e'7'otJCi:(» _ l]. E2.26)
Оценка lp~ Ifjqjai выводится отсюда так же, как н аналогичная
оценка 1а~ /j/as в случае фазового экрана (см. § 10), причем роль
фазового набега as = V <Sa> в данном случае играет «фазовая
высота» неровностей q,csl [6].
В обоих предельных случаях ^2а^<^1 и qza^^>l величина
VW.\ значительно меньше, чем расстояние Ы\, начиная с которого
точка наблюдения находится в фраунгоферовой зоне отдельной
неровности. Таким образом, формула иекогерентного рассеяния
E2.21) становится справедливой еще до удаления точки наблю-
дения и источника во фраунгоферову зону отдельной неров-
ности [5].
Сечение рассеяния а существенно при расчете энергетических
характеристик поля как при рассеянии иа площадке конечных
размеров, так и в случае неограниченной неровной поверхности.
Вычислить интеграл E2.22) точно удается лишь в немногих слу-
чаях, обычно он оценивается приближенно. Рассмотрим некоторые
частные случаи.
1. В случае малых неровностей ((^oj^l), когда, в соот-
ветствии с E2.24), 5s л> 9^A), сечение а выражается через
трансформанту Фурье корреляционной функции ^с(|), т.е.
521 РАССЕЯНИЕ НА КРУПНОМАСШТАБНЫХ НЕРОВНОСТЯХ 449
пропорционально спектральной плотности E1.15):
E2.27)
Для абсолютно жесткой и абсолютно мягкой поверхностей (\М\ = I)
это выражение эквивалентно результатам теории возмущений (см.
задачу 1), поскольку в направлениях, близких к направлению
зеркального отражения, q x. |^| = 2fe|п'г\.
2. При вычислении интеграла E2.22) в противоположном слу-
чае неровностей, больших по сравнению с длиной звуковой волны
(<7го-?^> 1), можно использовать то обстоятельство, что основной
вклад в E2.22) вносит область малых g, а второе слагаемое в вы-
ражении E2.19) при <7zaj§>l пренебрежимо мало по сравнению
с первым, и, следовательно,
*(S, Ч);«/*(?.. -?.. Р'. р') = «Г"*':'-">. E2.28)
Вычислим в качестве примера сечение рассеяния а для не-
ровностей, распределенных по нормальному закону E2.25) и изо-
тропных в плоскости г — 0. Изотропность поля ? означает, что
коэффициент корреляции зависит только от модуля вектора ?:
Ki = K^(l). Разлагая /(с в формуле E2.26) в ряд Тейлора и пре-
небрегая единицей по сравнению с экспонентой в квадратных
скобках, получаем для 5s приближенное выражение
5> «ехр {М- К\ @) I*} . E2.29)
Подстановка E2.29) в E2.22) дает после интегрирования
Этой формулой можно пользоваться в случае неровностей, об-
ладающих единственным пространственным масштабом (радиусом
корреляции) lt~[—Kt@)]~1/2. Если же коэффициент корреляции
убывает не монотонно, а имеет осциллирующий характер (как,
например, в случае морского волнения), то, наряду с окрестностью
точки | = 0, надо учитывать вклад и других точек, в которых 51
имеет локальные максимумьЦпример такого расчета приведен в[4]).
3. Для высоких неровностей (qza^^> 1), обладающих единствен-
ным радиусом корреляции, сечение рассеяния можно рассчитать
и без предположения о нормальном распределении [7, 8]. Полагая,
как и ранее, что основной вклад в интеграл E2.22) вносит окрест-
ность точки 1 = 0, разложим разность ?' — ?" в формуле E2.28)
в ряд Тейлора по | = р' — р":
450
РАССЕЯНИЕ НА ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ
IX Л. I.
Тогда 51 яа<ехр{— iq? Vj.J
TW
E2.31)
где вектор ve-vj; характеризует случайные наклоны неровной
поверхности. Но <ехр(гаг)> = Д.(а) —это характеристическая
функция v, связанная с функцией распределения наклонов wv(v)
преобразованием Фурье:
/v(a)-= $ exp(iav)a\-(v)dav,
-ел
так что обратное преобразование дает
—iav)d«o.
E2.32)
Если ввести в E2.31) новую переменную интегрирования а —
= q&, то, в соответствии с E2.32), сечение а можно выразить
через Wv(nLlq,):
0,4
E2.33)
Таким образом, сечение а пропорционально вероятности такого
наклона, прн котором происходит зеркальное отражение. Сечение
максимально при Ях = 0> поскольку wv(v) имеет максимум прн
v = Vxe = 0 (наиболее вероятная
ориентация элементов неровной
поверхности—параллельная плос-
кости z = 0), а увеличение qj.
приводит к уменьшению о, в со-
ответствии с тем, что большие
наклоны менее вероятны.
Если, неровности распределе-
ны по нормальному закону и изо-
тропны в плоскости г = 0, то фор-
мула E2.33), как легко убе-
диться, переходит в E2.30). От-
метим еще, что формулы E2.30)
и E2.33) соответствуют вычислению сечения рассеяния E2.22)
в приближении геометрической оптики. Это ясно уже из того,
что обе формулы не содержат длины волны, поскольку отношения
jqz H я!Яг не зависят от Я.
г з
Рнс. 78.
J 53) ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ- ДРУГИЕ ПОДХОДЫ 451
4.. Для изотропного поля ?, распределенного по нормальному
закону с гауссовым коэффициентом корреляции /Cj (p) =е~р /а/^,
в работе [9] было получено точное выражение для сечения а
в направлении зеркального отражения (qj_ — 0):
а,= -gx e-"^i\Ei(q^l)—C—2 ln?,oj. E2.34)
Здесь С = 0,577 — постоянная Эйлера, a Ei (z)— интегральная экс-
понента (о3 при ч±фО выражается в виде бесконечного ряда).
График нормированного сечения 8жта/| Я \'ql4 в зависимости от
q2a^ показан на рис. 78. Сначала а, растет, как а\, в соответствии
с первым приближением метода малых возмущений. Прн До; я; 1
сеченне достигает максимума, а прн больших До{ убывает по за-
кону I/a;. Разумеется, полное (проинтегрированное повеем углам)
сечение рассеяния продолжает расти прн до;—«¦<», но при этом
происходит пространственное перераспределение рассеянного из-
лучения, сопровождающееся уширением индикатрисы рассеяния
и Уменьшением о3.
§ 53. Дополнительные замечания. Другие подходы
В большинстве работ по рассеянию на -шероховатых поверх-
ностях используются, как уже было сказано, метод возмущений
н метод Кирхгофа. Приведем некоторые результаты, полученные
этими методами, и укажем также на другие подходы к проблеме,
основываясь в первую очередь на монографии [1], в которой
подробно освещены затрагиваемые здесь вопросы, а также на
обзоре [2].
1. Рассеяние электромагнитных волн отличается от
скалярного случая только учетом поляризации. Для первичной
волны, заданной в приближении геометрической оптики, вывод
динамических соотношений в принципе не отличается от ска-
лярной задачи, но выкладки становятся более громоздкими, по-
скольку вместо (9.13) следует пользоваться векторным вариантом
формулы Грина. Креме того, при расчетах по методу Кирхгофа
необходимо учитывать различие локальных френелевских коэф-
фициентов отражения для двух ортогональных поляризаций поля
падающей волны.
Наиболее простые формулы получаются при рассеянии на иде-
ально проводящей поверхности. В частности, выражение для элект-
рического вектора рассеянней волны при применении метода Кирх-
гофа можно получить из формулы E2.11), положив в ней Я = 1 и
заменив скаляр q* вектором е0^2 — 2q (eoq), где е„ — единичный
вектор поляризации первичной волны. С этой заменой можно
452 РАССЕЯНИЕ НА ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ [ГЛ. IX
вывести затем формулы для средних значений иапряженностей
и для билинейных характеристик рассеянного электромагнитного
поля (средней интенсивности, среднего вектора Пойнтинга, эле-
ментов поляризационной матрицы). На расстояниях R^X^klpOT
неровной поверхности для билинейных характеристик оказыва-
ются справедливыми формулы некогерентного рассеяния типа
E2.21), разумеется, с заменой интенсивности /0 = |Л|г более слож-
ным выражением, зависящим от е„. Существенно, однако, что в
подынтегральные выражения для билинейных величин будет
входить сеченне E2.22), вычисленное при скалярной постановке
задачи, так что результаты скалярной теории можно непосредст-
венно использовать и в теории рассеяння электромагнитных волн.
Например, дисперсия /,=-<]Е|5> поля электромагнитной волны,
рассеянной на неровной поверхности, определяется форму-
лой E2.21), если понимать под а величину в = уаск, где стск
дается выражением E2.22),
а у = 1—|qeo|V9'—поляри-
зационный множитель.
2. Учет затен ен ий в
методе Кирхгофа. Мы
уже указывали иа то, что
Рис. 79. с увеличением высоты не-
ровностей и с уменьшением
угла скольжения рано или поздно начинается затенение от-
дельных элементов поверхности: часть шероховатой поверх-
ности оказывается неосвещенной (рис. 79), а часть освещен-
ных участков не будет вндна из точки наблюдения. Нетрудно
оценить диапазон углов скольжения ijj, в котором еще можно не
учитывать эффект затенения: очевидно, если /j—размер неров-
ностей, a cij—их среднеквадратичная высота, то затенениями мож-
но Пренебречь при УСЛОВИИ ф^СТ;//;.
Вследствие затенений отдельных элементов поверхности проис-
ходит уменьшение сечения рассеяння о по сравнению со значением,
даваемым выражением E2.22). Величина фактора ослабления
определяется отношением площади освещенной части поверхности
к полной поверхности, причем освещенные участки можно выде-
лить, исходя из простых геометрических соображений: на осве-
щенных участках падающий луч пересекает неровную поверх-
ность один раз, тогда как затененным участкам отвечает трех-,
пяти- и т. д. кратное пересечение. Таким образом, дело сводится
к нахождению вероятности того, что луч пересечет заданную
случайную поверхность только один раз. Несмотря на простоту
постановки задачи, ее решение оказывается довольно сложным.
Результаты исследований этого вопроса (и ряда других аспектов
проблемы) суммированы в книге [1].
$53] ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ. ДРУГИЕ ПОДХОДЫ 453
3. Рассеяние при наложении мелкомасштабных
и крупномасштабных неровностей (комбинирован-
ный подход). Реальные поверхности часто содержат как мелкие
(W;<^1), так и крупные (Wc^> 1) неровности. Такие поверхности
можно рассматрваать как крупномасштабные образования, на
которые наложена мелкая рябь («шероховатый рельеф»). В то
время как у крупных неровностей диаграмма рассеяния срав-
нительно узкая, мелкие неровности рассеивают практически во
все стороны и их влияние в направлении зеркального луча
пренебрежимо мало. Но под малыми углами скольжения рас-
сеяние обусловлено именно мелкомасштабной компонентой. Оиа
же определяет форму спектра рассеянного поля в направлениях,
не совпадающих с зеркально отраженным лучом. Эти и некоторые
другие соображения позволяют качественно объяснить ряд экспе-
риментальных данных, в частности, особенности рассеяния на
взволнованной морской поверхности..Однако теоретический ана-
лиз рассеяния волн на поверхности типа «шероховатый рельеф»
наталкивается на определенные трудности: исследование здесь
не может быть проведено ни методом возмущений (поскольку
высота крупных неровностей не мала), ни методом Кирхгофа
(поскольку имеется мелкомасштабная компонента).
Б. Ф. Курьянов [10] предложил комбинированный метод рас-
чета, в котором в качестве пулевого приближения взяго кирхго-
фово решение; типа E2.11), отвечающее плавным крупномасштаб-
ным неровностям, а влияние мелкой ряби учтено а первом порядке
теории возмущений, причем обгЬтипа неровностей считаются
статистически независимыми. Этот метод был разпнт в дальнейшем
в работах A1, 12]. Несколько иной подход применен в [13, 14],
где использована формула сложения пптенсивностей полей, рас-
сеянных мелкомасштабными неровностями.
Возможности комбинированного подхода ограничены диумя
условиями: во-первых, результаты расчета не должны зависеть
от способа разбиения отклонения t,{x) на независимые части
ц (х) 'II т) (х), и, во-вторых, должны выполняться условия при-
менимости метода возмущений для расчета рассеяния на мелко-
масштабной компоненте. Оказывается, что эти требования удов-
летворяются не для всех видов волнения [1].
4. Учет многократного рассеяния. Как в методе
Кирхгофа, так и в методе малых возмущений (если ограничи-
ваться первым приближением) рассматриваются только однократно
рассеянные (или однократно отраженные) поля. Это допустимо,
пока неровности достаточно пологи и сравнительно невысоки.
С ростом высоты неровностей о; и (или) с увеличением кх наклона
О; Д; необходимо учитывать многократное рассеяние волн.
Учет многократного рассеяния удобно осуществить на основе
интегрального уравнения для функции Грина [1]. Если линеа-
454 РАССЕЯНИЕ НА ШЕРОХОВАТЫХ ПОВЕРХНОСТЯХ [ГЛ. IX
ризовать интегральное уравнение по возмущению ?, то из него
можно вывести уравнение Дайсона для средней функции Грина
<G> и уравнение Бете—Солпитера для функции когерент-
ности <С(г,, го)С*(г2, г„)>. Оба уравнения можно далее решить
приближенно, первое—в приближении Бурре, а второе—в лест-
ничном приближении. Как и в случае объемного рассеяния, эти
способы решения указанных уравнений эквивалентны приближен-
ному (частичному) суммированию бескоиечного ряда теории воз-
мущений.
Описанный подход оказался весьма эффективным при решении
ряда задач, в частности при рассмотрении волноводон с шерохо-
ватыми стенками. Здесь удается вычислить коэффициенты зату-
хания нормальных волн, коэффициенты трансформации из одной
моды в другую и вывести уравнение переноса излучения в вол-
новоде, учитывающее взаимную трансформацию волн [1J. Кроме
того, при учете многократного рассеяния можно обосновать
и уточнить так называемые «нелокальные» граничные условия
для среднего поля, которые были ранее выведены иным спо-
собом [1J.
5. Крутые и е рови остн. Несмотря на значительные успехи
теории рассеяния волн на плавных шероховатых поверхностях,
трудной задачей остается случай рассеяния иа плавных, но кру-
тых неровностях, к которому нельзя подойти при помощи су-
ществующих приближенных методов. Вполне естественны поэто-
му попытки модельного описания подобных неровностей—либо
в виде хаотически разбросанных по плоскости полусфер, полуци-
линдров и т. д. (типичная модель такого рода описана, например,
в [15J), либо и ниде плоских площадок со случайным распределе-
нием наклонов. Вторая модель широко используется, в частности,
в оптических расчетах отражения света как при помощи метода гео-
метрической оптики [16, 17], так и с поправками на дифракцию,
которая учитывается введением индикатрис рассеяния элементар-
ных площадок [18].
Модельному описанию присуши, по крайней мере, два недо-
статка. Во-первых, область применимости результатов, получен-
ных при помощи конкретных моделей, сильно ограничена. Во-
вторых, погрешности результатов, возникающие из-за упрощающих
предположений при расчетах, с трудом поддаются оценке. Тем
не менее к модельному описанию крутых неровностей прибегают
довольно часто — просто в силу отсутствия более общих методов.
Более того, иногда прибегают к моделированию не формы по-
верхности, а самого закона рассеяния, т. е. функции ст(9, <р).
Наиболее известной моделью такого рода является закон. Лам-
берта, согласно которому о F) —const- cosU. Этот простой закон,
однако, принадлежит к числу наименее обоснованных —как ¦
теоретической, так и с экспериментальной точек зрени;.
ЗАДАЧИ 455
Задачи
1. Показать, что в случае крупномасштабных неровностей (М.^>1) сечения
рассеяния, вычисленные по методу возмущений для абсолютно мягкой и абсо-
лютно жесткой поверхностей, практически одинаковы.
Решение. npirWji^l спектр ^(Ч^) заметно отличается от нуля
только в узком интервале I qx] ^ 1//^, т. е. в окрестности направления зер-
кального отражения, для которого qj=ft(n^—л^) = 0. В этом интервале
п!|. я ПХ' н П0ЭТОМУ множители (л^)» в E1.18) и A—п'^п^I в E1.28)
приближенно совлвдают и равны (n'z)a — cos400. В результате
2. Оценить поперечный радиус корреляции поля, рассеянного на поверх-
ности с мелкомасштабными неровностями (Ы,<$.\), в двух случаях: 1) точка
наблюдения удалена от неровной поверхности иа расстояние Ri, большее
диаметра освещенной площадки, и 2) диаметр освещенной площадки L опре-
деляется шириной диаграммы направленности облучателя v — tyd («i —попереч-
ник антенны).
Решение. В первом случае, в соответствии с теоремой Ван Циттерта —
Церникс, поперечный радиус корреляции 1± определяется величиной угла
АО — L/R,, под которым видна рассеивающая площадка с расстояния А?ь
1Х ~ Х/ЛО — XRilL. В частиости, если Дв — 1, то /j. — X.
Во втором случае L~yRt~-i.Raldt где i?0—расстояние мсж*у облучате-
лем и центром освещенного пятна па поверхности. Поперечный радиус корре-
ляции на расстоянии R% от центра освещенного пятна равен поэтому 1Х —
— i.Rj/L — dRi/Ro. При рассеянии назад, когда Ri~Rt, радиус корреляции
совпадает с диаметром антенны, lj_~d, хак и в случае рассеяния на объем-
ных исоднородностях (см, задачу 3 к гл. IV},
3. Оценить поперечный (по отношению кэеркальиому лучу) радиус кор-
реляции рассеянного поля в случае крупномасштабных неровно:тей поверх-
ности.
Решеняе. Оценки радиуса корреляции проще Rcero получить, нсполь-
зуя результаты, найденные для фазового экрана |6|. Пели плоская волна
падает нормально иа бесконечную поверхность с радиусом корреляции не-
ровностей /j ^> Л к среднеквадратичным отклонением а., то отраженная волна
оказывается промоделированной по фазе с дисперсией с| = BАо.J В соот-
ветствии с п. 2 в § 10 имеем при этем 1а ~ 'г при 2*о> <^ 1 (малые неров-
ровностн) л lux /j/2*oc при 2*o-j ^> 1 (высокие неровности).
Если шероховатая поверхность облучается не плоской аолной, то при-
веденные оценки справедлнвы тольио иа малых расстояниях от илсскости z-0.
На больших же расстояниях 1„ будет увеличиваться (или уменьшаться) в соот-
ветствии с изменением сечения лучевых трубок, отвечающих зеряально отра-
женным (от плоскости г—0) лучам. Например, если на шероховатую поверх-
пость падает сферическая волна, то
,. = |i-/E при
где /?х—расстояние от точкн зеркального отражения до точки наблюдения,
a Ra — от точки зеркального отражения до источника.
ЛИТЕРАТУРА
К главе I
1. Татарский В. И. Распространение поли в турбулентной атмосфере.-:-М.:
Наука, 1967.
2. Монин А. С, Яглом А. М. Статистическая гидромеханика. ч.1. — М.; Наука,
1965, ч. 11, 1967.
3. Колмогоров А. И. Кривые н гильбертовом пространстве, инвариантные по
отношению к однопараметрической группе движении.—ДАН СССР, 1940,
т. 26, с. 6.
4. Колмогоров А. Н. Спираль Винера и некоторые другие интересные кривые
в гильбертовом пространстве.—ДЛИ СССР, 1Я40, т. 26, с. 115.
5. Кляцкип В. И. Статистическое описание динамических систем с флуктуи-
рующими параметрами.—М.: Наука, 1975.
6. Furutsu К- Он Statistical Theory of Electromagnetic Waves in a Fluctua-
ting Medium.-J. Res. NBS, 1963, v. 67, p. 303.
7. Новиков Е. А. Функционалы и метод случайных сил в теории турбу-
лентности.— ЖЭТФ, 1964, т. 47, с. 1919.
8. Donsker М. D. On Function Space Integrals.— Proc. of a Conference on the
Theory and Applications of Analysis in Function Space—Cambridge. Л1. I. T.
Press, I9fi4, p. 17—30.
9. Виноградов А. Г., Коавиов Ю. А., Фейзулин 3. И. Флуктуации сигнала
от источника, движущегося в мнигомасштабной случайно-неоднородной
среде.—Радиотехника и электроника, 1974, т. 19, с. 1758.
К г л а в е 11
1. Ахманов С. А., Чиркин А. С. Статистические явления в нелинейной оп-
тике.—М.: Изд. МГУ, 1971.
2. Ахманов С. А. Взаимодействие случайных волн в нелинейных средах.—
Изо. вузео: Радиофизика, 1974, т. 17, с. 541.
3. Цытович В. Н. Теория турбулентной плазмы.—М.: Атомнздат, 1971.
4. Кадомцев В. Б., Канторович В. М. Теория турбулентности п гидродина-
мике и плалме. — Изв. вузов: Радиофизика, 1974, т. 17, с. 511.
5. Филпипс О. М. Динамика верхнего слоя океана. — М.: Мир, 1969-
6. Мандель //., Вольф Э. Когерентные свойства оптических полей. — УФН,
1965, т. 87, с. 491, ч. I; т. 88, с. 347, ч. II; т. 88, с. 619, ч. III.
7. Глаубер Р. Дж. Оптическая когерентность и статистика фотонов.—
В сб.: Квантовая оптика и квантовая радиофизика. — М.: Мнр, 1966, с. 91.
8. Кяаудер Пж., Сударшан Э. Основы квантовой оптики.—М.: Мир, 1970,
9. Перина Я- Когерентность света. —М.: Мир, 1974,
10. Лоудон Р. Квантовая теория света. — М,: Мир, 1976.
11. Рыжов Ю. А. Тепловое излучение в хаотически неоднородной прозрачной
среде. —ЖЭТФ, 1970, т. 59, с. 218.
ЛИТЕРАТУРА 457
12. Кравцов Ю. А., Рытое С. М., Татарский В. И. Статистические проблемы
в теории дифракции,— УФН, 1975, т. 115, с. 239.
18. Нейл Э. О. Введение в статистическую оптику. — М.: Мир, 196G.
14. Строук Дж. Введение в когерентную оптику и голографию.— М.: Мнр,
1У67.
15. Шестов II. С. Выделение оптических сигналов на фене случайных по-
мех.—М.: Сов. радио, 11N7.
16. Зверев В. А., Орлов Е. Ф. Оптические анализаторы. — М: Сов. радио, 1971.
17. Ван-дер-Люгт А. Когерентная оптическая обработка информации.—
ТИИЭР, 1974, т. 62, с. 5.
18. Кловский. Д. Д., Сойфер В. А. Обработка пространсгненно-временных
сигналоп.—М.: Связь, I97G.
19. Передача информации по каналам, содержащим статистически неодно-
родные среды./Под ред. В. И. Сифорова, А. В. Просина.—М.: Наука, 1976.
20. Бакут П. А., Устинов Н. Д., Троицкий И. Н., Свиридов К. Я. Методы
обработки световых полей при наблюдении объектов через турбулентную
среду: обзор.—Зарубежнан радиоэлектроника, 1976, вып. 7, с. 15, ч. I,
вып. 0, с. 3, ч, [[; 1977, вып. I, с. 3, ч. Ill; вып. 3, с. 55, ч. IV.
21. Норн .VI., Вольф Э. Основы оптики.—М.: Наука, 1970.
22. Beran М. J., Parrent С. В. Theory of Partial Coherence. —N. Y., 1964.
23. Денисок И. Г. О дифракции волн на хаотическом экране.—Изв. вузов:
Радиофизика, 1961, т. 4, с. 630.
24. Booker П. С, Ratclifje J. A , Schinn D. II. Diffraction from an Irregular
Screen with Application lo Ionospheric Problems. — Phil. Trans. Roy Soc,
1950, v. A 242, p. 579.
25. Hmish A. Tlie Diffraction of Radio Waves in Passini; through a Phase-
Changing Ionosphere. — Proc. Roy. Soc, 1951, v. A 209, p. 81.
26. Fejcr J. A. The Diffraction of Waves Passing through an Irregular Ref-
racting Medium.—Proc. Roy. Soc, 1953, v. A 220, p. 453.
27. Барибаненкоа 10. П., Кравцов Ю. А.,.Рытое С. М., Татарский В. И.
Состояние теории распространения волн в случайно-неоднородной среде. —
УФН, 1970, т. 102, с. 3.
28. Ерухимов .7. /И., Максимеико О. И. Исследования нсодиородностей ионо-
сферы при помощи МС.З.—В сб.: Дрейфы и неоднородности в ионосфере. -
М.: Наука, 197,4, с. 41.
29. Briggs Б. Н., Ionospheric Irregularities and Radio Scintillations.-- Contemp.
Phys., 1975, v. 16, p. 469.
30. Дьяков Ю. Е. Некоторые статистические характеристики огибающей и
фазы нестационарного гауссового процесса,—Радиотехника и электро-
инка, 1963, т. 8, с. 1812. '
31. Всехсвятская И. С. Статистические характеристики сигналов, отражен-
ных от ионосферы.—М,: Наука, 1975.
32. Альбер Я- И., Ерухимов Л. М., Рыжов В. А., Урядоа В. П. О статисти-
ческих свойствах флуктуации интенсивности болны за хаотическим экра-
ном.—Ияв. вузов: Радиофизика, 1968, т. И, с 1371.
33. Salpeler Е. ?. Interplanetary Scinlillalinnv - Astrophys. J., !S(i7, v. 147,
p. 433,
34. Шишов В. И. Дифракция воли па сильно преломляющем фазовом эк-
ране.—Изв. вузов: Радиофизика, 1971, т. 14, с. 85.
35. Якушкин И. Г. Флуктуации интенсивности поля плоской волиы за хао-
тическим фазовым экраном. —Изв. вузов: Радиофизика, 1974, т. 17,
с. 1350.
36. Франсон М., С.юнский С. Когерентность в оптике. — М.: Наука, 1967.
37. Зверев U. А. Раднооптикл. М.: Сов. радио, 197Г).
38. Шифрин Я- С. Вопросы статистической теории антенн.—М.: Сов. радио,
1970.
458 ЛИТЕРАТУРА
39. Курьянов Б. Ф. Пространственная корреляция полей, излученных слу-
чайными источниками на плоскости. — Акустич. ж., 1964, т. 9, с. 441.
40. Долин Л. С. О лучевом описании слабо неоднородных волновых полей. —
Изв. вузов: Радиофизика, 1964, т. 7, с. 559.
41. Чандрасекар С. Перенос лучистой энергии.—М.: ИЛ, 1953.
42. Железняков В. В. Радиоизлученне Солнца н планет. — М.: Наука, 1964.
43. Горелик Г. С. Колебания и волны. — 2-е изд.—М.: Физматгнз, 1959.
44. Кравцов К). А., Татарский В. И. Статистические явлении при днфрак-
цнн волн.: Лекции ия IV Всес. школе по дифракции и распространению
волн. — Рязань: Изд. Рязанского радиотехнического института, 1976.
45. Руденко О. В., Солуян С. Я. Теоретические основы нелинейной акус-
тнкн. —М.: Наука, 1975.
К главе 111
1. Рытое С. М. Теория электрических флуктуации н теплового излучения,—
М.: Изд. АН СССР, 1953.
2. Вайншпгсйн Л. А. Электромагнитные волны.—М.: Сов. радио, 1957.
3. Ландау Л. Д., Лифшиц Е. М. Электродинамика сплошных сред. — М.:
Гостехиэдат, 1957.
4. Рытое С. М. О тепловых флуктуациях в распределенных системах. —
ДАН СССР, 1956, т. ПО, с. 371.
5. Рытое С. М. Корреляционная теория тепловых флуктуации в изотроп-
ной среде. —ЖЭТФ, 1957, т. 33, с. 166.
6. Левин М. Л., Рытое С. М. Теория равновесных тепловых флуктуации
в электродинамике.—М.: Наука, 1967.
7. Лифшиц Е. М. Теория молекулярных сил притяжения между твердыми
телами. —ЖЭТФ, 1955, т. 29, с. 94.
8. Силин В. П., Рухадзе А. А. Электромагнитные свойства плазмы и плаэмо-
подобных тел. — М.: Госатомиздат, 1961.
9. Гринберг Г. А. Избранные вопросы математической теории электрических
и магнитных явлений.—М.: Изд. АН СССР, 1948.
10. Фейнберг Е. Л. Распространение радиоволи над земной поверхностью. —
М.: Изд. АН СССР, 1961.
11. Диялошинский И. Е., Лифшиц Е. М., Пилшевский Л. П. Ван-дер-Вааль-
совы силы в жидких пленках.—ЖЭТФ, 1959, т. 37, с. 229; Общая тео-
рия Ван-дер-Ваальсовых сил. —УФН, 1S61, т. 73, с. 381.
12. Абрикосов А. А., Горькое Л. П., Дзялошинский И. Е. Методы квантовой
теории поля в статистической физике. — М.: Физматгиз, 1962.
13. Леонтович М. А. Обобщение формул Крамерса—Кроннга на среды с про-
странственной дисперсией. —ЖЭТФ, 1961, т. 40, с. 907.
14. Шафранов В. Д. Электромагнитные волны в плазме. — В сб.: Вопросы
теории плазмы.—М.: Госатомиздат, 1963, вып. 3.
15. Левин М. Л., Рытое С. М. «Кирхгофовская» форма флуктуационно-
диссипативной теоремы дли распределенных систем.—ЖЭТФ, 1973, т. 65,
с. 1382.
16. Гинзбург В. Л. Распространение электромагнитных волн в плазме. —
2-е изд.—М.: Наука, 1967.
К главе IV
1. Татарский В. И. Распространение ноли в турбулентной атмосфере.—
М.: Наука, 1967.
2. Барабаненков Ю. И., Кравцов Ю. А., Рытое С. М., Татарский В. И.
Состояние теории распространения волн в случайно-неоднородной среде.—
УФН, 1970, т. 102, с. 3.
ЛИТЕРАТУРА 459
3. ГореПк Г. С. К теории рассеяния радиоволи на блуждающих неодно-
родностях. — Радиотехника и электроника, 1956, т. 1, с 695.
4. Горелик Г. С. О влиянии корреляции рассенклтелей на статистические
свойства рассеянного излучения. —Радиотехника н электроника, 1957,
т. 2, с. 1227.
5. Родак М. И., Францсссон А. В. О применении теории турбулентности
к рассеянию радиоволн иа блуждающих неоднородностях. —Радиотех-
ника и электроника, 1959, т. 4, с. 398.
6. Родак М. И. О рассеянии немонохроматического излучения на блуждаю-
щих неоднородностях.—Радиотехника и электроника, 1960, т. 5, с. 1370.
7. Денисов Н. Г. Дифракция электромагнитных волн в гиротропном слое,
содержащем статистические неоднородности. —Изв. вузов: Радиофизика,
1960, т. 3, с. 393.
8. Рытое С. М. Корреляционная теория рассеяния света.—ЖЭТФ, 1957,
т. 33, с. 514, 679.
9i Вихренко В. С. Теория деполнриэованного молекулярного рассеииия
соета. — УФН, 1974, т. ИЗ, с. 627.
10. Некогерентное рассеяние радиоволн: Сб. переводных статей./Под ред.
В. А. Рудакова.— М.: Мир. 1965.
11. Ахиежр А. И., Axuejep И. Л., Половин Р. В. и др. Коллективные коле-
бании в плазме.—-М.: Атомнздат, 1964.
12. Ван-дер-Хюлст. Рассеяние света малыми частпшши. —М.: ИЛ, 1961.
13. Ворн М., Вольф Э. Основы оптики. — М.: Наука, 1970.
14. Гинзбург В. Л. Распространение электромагнитных ваш в плазме. —
2-е изд.-М.: Наука, 1967.
15. Денисов Н. Г. О рассеянии волн в условиях полного отражения. — Изв.
вузов: Радиофизика, 1961, т. 7, с. 378.
16. Горышник Л. Л., Кравцов Ю. А. Корреляционная теория рассеяния радио-
волн в полярной ионосфере.--Геомагнетизм и аэрономия, 1959, т. 9, с. И8.
17. Мигдал А. Б., Крайнов В. П. Приближенные методы квантовой меха-
ники.— М.: Наука, 1966.
К главе V
1. Красильникое В. А. О распространении звука в турбулентной атмосфере.—
ДАН СССР, 1945, т. 47, с. 486.
2. Bergman Р. G. Propagation of Radiation in a Medium with Uandom lnlio-
mogeneities.— Phys. Rev., 1946, v. 70, p. '186.
3. Татарский В. И. Распространение оолн в турбулентной атмосфере.— М.:
Наука, 1967.
4. Чернов Л. А. Распространение волн в среде со случайными неодчородно-
стими.—М.: Паука, 1975.
5. Барабаненкоа Ю. Н., Кравцов Ю. А., Рытое С. М-, Татарский В. И.
Состояние теорнн распространения волн в случайно-пеоднородной среде.—
УФН, 1970, т. 102, с. 3.
6. Рытое С. М. О переходе к геометрическому приближению в электроди-
намике сплошных сред, —ДАН СССР, 1938," т. 18, с. 283.
7. Кранцоа Ю. А. Сильные флуктуации амплитуды световой волны и веро-
ятность образования каустик.—ЖЭТФ, 19иЛ т. 55, с. 798.
8. Кравцов Ю. А. О двух новых асимптотических методах в теории распро-
странения воли в неоднородных средах.— Лкустнч. ж., 1968, т, 14, с. 1.
9. Кляцкин В. И., Татарский В. И. О диффузии лучей в среде со случай-
ными неоднородностями.—Изв. вузов: Радиофизика, 1971, т. 14, с. 706.
10. Кляцкин В И. Статистическое описание динамических систем с флукту-
ирующими параметрами.— М.: Наука, 1975.
11. Денисов Н. Г. Рассеяние волн в плоскослонстой среде.— Изв. вузов: Ра-
диофи!ика, 1958, т. 1, с. 34.
450 ЛИТЕРАТУРА
12. Голынский С. Л!., Гусев В. Д. Статистика лучей в неоднородной изотроп-
ной среде.— Радиотехника и электроника, 1970, т. 21, с. СЗО.
13. Голынский С. М., Гусев В. Ц. Траектории лучен в рефрагнрующей рас-
сеивающей среде.— Раднотехпньа и =.иектрони>а, 1Ь76. т. 21, г. 1303.
14. Денисов II. Г., Ерухи.чов Л. М. Статистические Свойства флуктуации
фазы при полном отражении волн от ионосферного слоя.— Геомагнетизм
и аэрономии, I960, т. 6, с. 695.
15. Виноградов А. Г., Кравцов Ю. А., Татарский В. И. Эффект усиления
обратного рассеяния на телах, помещенных в среду со случайными неод-
иородностями. - Изв. вузов: Радиофизика, 1973, т. 16, с. 1064.
К главе VI
1. Фейнберг. К. Л. Распространение радиоволн вдоль земной поверхности.—
М.: Изд. ЛИ СССР, 1961.
2. Осташев В. В., Татарский В. И. Ряд по кратности обратного рассеяния
в задачах о распространении воли в неоднородных средах.— Изв. вузов:
Радиофизика, 1978, т. 21, с. 714.
3. Рытое С. М. Дифракция света на ультразвуковых волнах.— Изв.
АН СССР: Сер. физ.. 1937, вып. 2, с. 223.
4. Обухов А- М. О влиянии слабых неоднородности атмосферы на распро-
странение звуки и света.— Изв. АН СССР: Сер. геофнз., 1953, вып. 2,
с. 155.
5. Горелик Г. С. Колебания и волны. 2-е изд.— М.: Фнзматгнз, 1959,
6. Татарский И. И. Теория флукт5ационнмх явлений при распространении
волн в турбулентной атмосфере.— М.: Изд. ЛН СССР, 1959.
7. Ибрагимов И. А.. Линник Ю. В. Независимые и стационарно связанные
величины.— М.: Наука, 1%5.
8. Гурвич.А. С, Кон А. П., Миронов В. Л.. Хмелеецов С. С. Лазерное из-
лучение в турбулентной атмосфере.— М.: Наука, 1976.
9. Татарский В. II. Второе приближение в задаче о распространении воли
в среде со случайными неоднородиостямн.— Изв. вузов: Радиофизика,
1962, т. 5, с. 490.
10. Писарева В. II. О границах применимости метода плавных возмущений в
задаче о распространении излучения через среду с кеоднородностями.—
Акустич. ж., 1960, т. 6, с. 87.
И. Татарский В. И. Распространение волн в турбулентной атмосфере.— М.:
Наука, 19E7.
К главе VII
1. Кляцкин В. И., Татарский В. И. К статистической теории распростра-
нения волн в случайных слоистых средах.— Изв. вузов: Радиофизика,
1977, т. 20, с. 1040.
2. Кляцкин В. И. О пределах применимости приближения марковского слу-
чайного процесса в задачах, связанных с распространением света вереде
со случайными иеоднородностяни показателя преломления.— ЖЭТФ, 1969,
т. 57i с. 952.
3. Татарский В. И. Распространение коротких волн г, среде со случайными
неоднородпостями в приближении марковского случайного процесса: Пре-
принт ООФАГ, 1970.
4. Долин Л. С. О рассеянии светового пучка в слое мутной среды.— Изв.
вузов: Радиофизика, 19G4, т. 7, с. 380.
5. Вгеттсг //., Random Volume Scattering,- J. Res. NBS, 1964, v. fi8, p. C67.
6. Кляцкин В. П., Татарский В. И. К теории распространения световых
пучков в среде со случайными неоднородностями.— Изо. вузов: Радиофи-
зика, 1970, т. 13, с. 1061.
ЛИТЕРАТУРА 461
7. Долин Л. С. Уравнения для корреляционных функций волнового пучка в
хаотически неоднородной среде.— Изв. вузов: Радиофизика, 1968, т. 11,
с. 840.
8. Дагкесманская И. М., Шишов В. И. Сильные флуктуации интенсивности
при распространении волн в статистически однородных и изотропных
средах.—Изв. вузов: Радиофизика, 1970, т. 13, с. 16.
У. Rrgsm W. P., Fourth Moment of a Wave Propagating in a Random Me-
dium.—J. Opt. Soc. Am., 1972, v. 62, p. 966.
10. Елепов Б. С, Михайлов Г. А. Методы Монте-Карло для оценки корре-
ляционной функции сильных флуктуации света в турбулентной среде.—
ЖВМ и МФ, 1976, т. 16, с. 1264.
11. Гуреич А. С, Елепов Б. С, Покосов В. В., Сабельфелд К- К., Татар-
ский В. И. Пространственная структура сильных флуктуации интенсив-
ности света в турбулентной среде.— Изв. вузов: Радиофизика, 1979, т. 22,
вып. 2.
12. 1'урвич А. С, Кон А. И., Миронов В. Л., Хмелевцов С. С. Лазерное
излучение в турбулентной атмосфере.- М.: Наука, 1976.
13. Oochetashvily К- S., Shishou V. I., Multiple. Scattering of Light in a Tur-
bulent Medium,—Opt. Acta, 1971, v. 18, p. 767.
14. Гочелашеили К- С, Шишов В. И. Насыщенные флуктуации интенсивности
лазерного излучения D турбулентной среде.— ЖЭТФ, 1974, т. ОС, с. 1237.
15. Якушкин И. Г. Асимптотическое вычисление флуктуации интенсивности
поля в турбулентной среде при больших длинах трассы.—Изв. вузов:
Радиофизика, 1975, т. 18, с. 1660.
16. Заворютный В. У., Кляцкин В. И., Татарский В. И. Сильные флукту-
ации интенсивности электромагнитных волн в случайно-неоднородных
средах.—ЖЭТФ, 15,77, т. 73, с. 481. :
17. Кляцкин В. И., Татарский. В. И. О приближений параболического урав-
нения в задачах распространения волн в среде со случайными пеоднород-
ностями.— ЖЭТФ, HI70, т. 58, с. 024.
18. Фрадкин Е. С. Метод функции Грина в теории квантовых полей и кван-
товой статистике.—Труды ФИАН, 1965, т. 29. с. 7.
19. Fradkin E. S. Application of Functional Methods in a Quantum Held
Theory and Quantum Statistics. II.—Nucl. Phys., 1966, v. 76, p, 588.
20. Фейнман Р., Хиббс А. Квантовая механика и интегралы по траекториям.—
М.: Мир, 1968.
21. Кляцкин В. И., Татарский В. И. Новый метод последовательных при-
ближений в задаче о распространении волн в случайных средах.— Изв.
вузов: Радиофизика, 1!O1, т. D, с. 1400.
22. Татарский В. И. Распространение спета в среде со случайными неодно-
родностями показателя преломления в приближении марковского случай-
ного процесса.—ЖЭТФ, 1Г6У, т. 56, с. 2106.
23. Гуреич А. С, Каллистратова М. А., Мартвель Ф. Э. Исследооание
сильных флуктуации интенсивности света в турбулентной среде при малом
волновом параметре.— Изв. вузов: Радиофизика, 1977, т. 20, с. 1020.
К главе VIII
1. Барабаненков Ю. Н. Многократное рассеяние волн на ансамбле частиц и
теория переноса излучения.— УФН, 1У75, т. 117. с. 49.
2. Татарский В. И. Распространение воли в турбулентной атмосфере.— М.:
Наука, 1967, гл. 5.
3. Алексеев В. Н., Комиссаров В. М. Флуктуации звукового полк в случайио-
иеодиородной среде.— Труды Акустического института, 1Г68, вып. 4, с. 27.
4. Налбамдян О. Г., Татарский В. И. Сопоставление диаграммных и ана-
литических методов приближенною решения линейных стохастических
уравнений.— Изв. вузов: Радиофизика, 1977, т. 20, с. 549.
462 ЛИТЕРАТУРА
5. Апресян Л. А. Методы статистической теории возмущений.— Изв. вузов:
Радиофизика, 1ЭТ4, т. 17, с. 165.
6. Татарский В. И. Некоторые методы решения стохастических д
ииальных уравнений—Изв. вузов: Радиофизика, 1974, т. 17, с.
7. Барабаненков Ю. И., Кравцов Ю. А., Рытое С. М., Татарский .В. И.
Состояние теории распространения волн в случайно-неоднородной спеде.—
УФЫ, 1S70. т. 102, с. 3.
8. Рыжов Ю. А., Тамойкин В. В. Излучение и распространение электро-
магнитных волн D хаотически неоднородных средах.— Изв. вузов: Ра/ШО-
физика, 1970,- т. 13, с. 356.
9. Барабаненков Ю. И., Финкельберг В. М, Оптическая георема в теории
многократного рассеяния волн,—Изв. вузов: Радиофизика, 1С68, т. 11,
с. 719.
10. Барабаненков Ю. И., Виноградов А. Г., Кравцов Ю. А., Татарский В. И.
Применение теории многократного рассеяния волн к выводу уравнения
переноса излучения для статистически неоднородной среды.— Иэь. вузов:
Радиофизика, 1972, т. 15, с. 1&52.
П. Апресян Л. А. Уравнение переноса излучения с учетом продольных волн. ¦—
Изв. вузов: Радиофизика, 1973, т. 16, с 461.
12. Барабаненков 10. И., О волновых поправках к уравнению переноса для
направления рассеяния «назад».— Изв. вузов: Радиофизика, 1973, т. 16,
с. 88.
13. Виноградов А. /'., Кравцов Ю. А., Татарский В. И. Эффект усиления
обратного рассеянии на телах, помещенных в среду со случайными иеод-
ыородностями—Изв вузов: Радиофизика, 1973, т. 16, с. 19К4.
14. Чандрасекар С. Перенос лучистой энергии.— М.: ИЛ, 1953.
15. Овчинников Г. П., Татарский В. И. К вопросу о соотношении теории
когерентности и уравнения переноса излучения.— Изв. вузов: Радиофи-
зика, 1972, т. 15, с. 1419.
16. Апресян Л. А. О применении уравнения переноса излучения для описания
свободного электромагнитного поля—Изв. вузов: Радиофизика, 1975,
т. 18, с. 1870.
17. Басе Ф. Г , Фукс И. М. Рассеяние воли на статистически неровной
поверхности.— М.: Наука, 1972.
18. Кляикин В. И., Татарский В. И. Приближение диффузионного случай-
ного процесса в некоторых нестационарных статистических задачах фи-
зики.-УФН, 1973, т. ПО, с. 499.
19. Кляикин В. И. Статистическое описание динамических систем с флуктуи-
рукщями параметрами.— М.: Наука, 1975.
20. Финкельберг В. М. Распространение волн в случайной вреде. Метод кор-
реляционных групп,—ЖЭТФ, 1967, т. 53, с. 401.
21. Барабаненков Ю. И., Финкгльбврг В. М. Уравнение переноса излучения
для коррелированных рассеивателей.—ЖЭТФ, 1967, т. 53, с. 978.
22. Рожнбсрг Г. В. Вектор-параметр Стокса (матричные методы учета поля-
ризации излучения а приближении лучеоой оптики).— УФН, 1955, т. 56,
с. 77.
23. Кршцов Ю. А., Рытое С. М., Татарский В. И. Статистические проблемы
в теории дифракции.—УФН, 1975, т. 115, с 239.
К г л а ве IX
1. Басе Ф. Г., Фукс И. М. Рассеяние волн на статистически неровной
поверхности,— М.: Наука, 1972.
2. Шмелев А. Б. Рассеяние ноли статистически неровными поверхностями.—
УФН, 1972, т, 106, с. 459.
3. Мандельштам Л. И. Полное собрание трудов.— Изд. ЛИ СССР, 1948,
т. 1, с. 246.
ЛИТЕРАТУРА 463
4. Исакович М. А. Рассеяние воли от статистически шероховатой поверх-
ности.—ЖЭТФ, 1952, т. 23, с. 305. Труды Акустического института,
1969, вып. 5, с. 152—251.
5.. Кравцов Ю. А., Фукс И. М., Шмелев А. Б. Последовательное применение
метода Кирхгофа к задаче о рассеянии звуковой волны на поверхности
со случайными неровностями.— Изв. вузов: Радиофизика, 1971, т. 14,
с. 854.
6. Тамайкин В. В., Фрайман А. А. О статистических свойствах поля, рас-
сеянного шероховатой поверхностью.— Изв. вузов: Радиофизика, 1968,
т. 11, с. 56.
7. Чаевский Е. В. Энергетические характеристики поля, рассеянного шеро-
ховатой площадкой.— Изв. вузов: Радиофизика, 1965, т. 8, с. 1128.
8. Barrick D. E. Relationship between Slope Probability Density Function
and the Physical Optic Integral in Rough Surface Scattering.— Proc. IEEE,
1968, v. 56, p. 1728.
9. Чаевский Е. В. Рассеяние волн площадкой с нормальным распределением
случайных отклонений.— Изв. вузов: Радиофизика, 1966, т. 9, с. 400.
10. Курьянов Б. Ф. Рассеяние звука на шероховатой поверхности с двумя
типами неровностей.— Акустнч. ж., 1962, т. 8, с. 325.
11. Калмыков А. И., Островский И. Е., Розенберг Л. Д., Фукс И. М. О вли-
яния структуры морской поверхности на пространственные характеристики
рассеянного ею радиоизлучения.— Изв. вузов: Радиофизика, 1965, т. 8,
с. 1117.
12. Фукс И.М. К теории рассеяния волн взволнованной поверхностью моря.—
Изв. вузов: Радиофязика, 1966, т. 9, с. 876.
13. Семенов Б. И. Пряближенный расчет рассеяния электромагнитных волн
поверхностью типа шероховатого рельефа.— Радиотехника и электроника,
1966, т. 11, с. 1351.
14. Семенов Б. И. Расчет рассеяния электромагнитных волн поверхностью
типа шероховатого рельефа для произвольных углов наблюдения.— Радио-
техника и электроника, 1970, т. 15, с. 595.
15. Burke J. E., Twersky V. Scattering and Reflection by Elliptically Striated
- Surfaces, —J. Acoust. Soc. Am., 1966, v. 40, p. 883.
16. Reuse V. A. Polarisation Studies of Light Diffusely Reflected from Ground
and Etched Glass Surfaces.—J. Opt. Soc. Am., 1950, v. 40, p. 55.
17. Гершун А. А., Попов О. И. К вопросу о рассеянии света матовыми стек-
лами.—Светотехника, 1955, вып. 1, с. 3.
18. Полянский В. К-, Рвачев В. П. Рассеяние света при отражении от ста-
тистически распределенных микроплощадок. Дифракционное рассмотре-
ние.—Опт. и спектр., 1967, т. 22, с. 279.