НОВОЕ
В

Ю. И. Алимов,

ЖИЗНИ,

НАУКЕ,
ТЕХНИКЕ

Серия
«Математика,
кибернетика»,
№ 3, 1980 г.

Издается

доктор технических наук,
профессор

АЛЬТЕРНАТИВА
МЕТОДУ
МАТЕМАТИЧЕСКОЙ
СТАТИСТИКИ

ежемесячно
с

1967

г.

Издательство
«Знание»
Москва
1980

22.172
А50

Scan+DjVu: AlVaKo
24/02/2023

Алимов Ю. И.
А50

Альтернатива
статистики.

методу математической

М., «Знание», 1980.

64 с.
(Новое в жизни, науке, технике.
Серия
«Математика, кибернетика», 3, Издается ежемесячно с
1967 г.).
Рассказывается о фундаментальном принципе естественных
требовании многократной воспроизводимости
—

наук
предсказываемого

принципа
концепций
анализируются

экспериментального результата. С точки зрения
прослеживается логика построения исходных

прикладной теории вероятностей
типичные

Излагается

положения

альтернатива
математическое

этим

этого

и

критически
математической статистики.

положениям,

нашедшая

оформление в подходе Р. Мизеса.
Брошюра рассчитана на широкий круг
интересующихся математической статистикой.

свое

читателей,

22.172

20204

© Издательство «Знание»,

1980 г.

ПРЕДИСЛОВИЕ
ее

В последнее время и математики и те, кто применяют
в своей практической деятельности, часто выражают

озабоченность тем, что математические модели во многих
случаях оказываются заметно оторванными от реальности.
Из-за этого отрыва недостаточно эффективно используется

труд высококвалифицированных специалистов и
дорогостоящее машинное время. Критика
порой весьма
—

резкая

—

такого состояния дел все чаще встречается не

монографиях, предназначенных для
учебниках и научно-популярных изданиях
[1—4]). Показательно, что в учебнике [3]
цитируется из дидактических соображений статья Д.
Шварца под названием «О пагубном влиянии математики на
только в статьях и

специалистов, но и в
(см., например,

науку».

Нередко далекими от реальности оказываются, в
частности, модели, предлагаемые математической статистикой.
Специально условиям

и границам применимости
вероятностно-статистических
методов
посвящены
брошюры
В. Н. Тутубалина [5—7], опубликованные в серии
«Математика, кибернетика». Много внимания уделено подобным
вопросам и в учебнике [8], написанном тем же автором. По
своей «ограничительной» направленности настоящая
брошюра примыкает к этим публикациям.
Сразу же подчеркнем, что брошюра ни в коей мере не
направлена против статистики как таковой. (Под
статистикой мы подразумеваем любые усреднения или другую

«совокупную» обработку экспериментальных данных с
получения их прогнозируемых интегральных
характеристик; относительно этих характеристик
предполагаем, что они будут затем измеряться для аналогичных
экспериментальных данных в предстоящих опытах, и,
таким образом,
правильность статистического прогноза в
целью

1*

3

самом

деле

совсем

не

последняя

Речь

будет проверяться экспериментом.)

Мы такжа

против использования математики в статистике!
без математики попросту немыслима.

ниже

пойдет

именно о математической

руководство по этой дисциплине, легко
убедиться, что под математической статистикой
подразумевают далеко не всякое использование математики в
статистике. Если присмотреться, математическая статистика
статистике. Взяв любое

весьма

это

—•

дисциплина, обладающая своим
Отличительной чертой ее метода

специфическая

характерным

методом.

домысливание ровно одного «этажа» вероятностей,
называемых доверительными вероятностями, или уровнями
значимости, сверх тех, которые действительно измеряются
в эксперименте. И вот с таким специфическим подходом
является

не соглашаться. Можно применять математику
статистике и несколько иначе, чем это предписывается
математической статистикой.
можно

На

практике давно

статистической

используются

в

принципы

обработки

экспериментальных данных, не
к
доверительным вероятностям и потому чуждые
апеллирующие
устоям математической статистики. В физической

примеру, такую запись измеренной
вакуумной поправки к магнитному моменту электрона:
0,0011609±0,0000024. Здесь фигурирует только
максимальная погрешность измерений. В последнее время
физики стали иногда указывать не максимальную, а среднеквадратическую погрешность измерения последних цифр
экспериментального результата (обычно в круглых
скобках). Например, для скорости света в вакууме
мы

литературе

указывается

находим,

величина

к

с=2,9979250(10)-108 м/с. Существенно,

что

среднеквадратическая погрешности здесь
действительно измерялись в отличие от доверительных
которыми оперирует математическая
вероятностей,
максимальная

и

статистика.

математической статистики активно велась
И все же физики, наверное, и в наши
удержались бы от улыбки, если бы им сказали,

Пропаганда

в течение многих лет.
дни

не

например, что,

обработав результаты

измерения скорости
предписаниям математической статистики,
получаем следующее: с попадает в такой-то
доверительный интервал с доверительной вероятностью Р=0,99,
и в эдакий, более узкий, соответственно с вероятностью
/>=0,95.
Ссылки на физиков будут встречаться и ниже. Именно
света

4

согласно

в

физике были

естествознания,

заложены основы современного точного
именно

здесь

накоплен

наибольший

опыт

сложного и тонкого
высокая
культура
данных. С другой

фундаментальным

экспериментирования и сложилась
трезвой обработки экспериментальных

стороны,

именно

физика

подала другим

прикладным дисциплинам пример
математизации, который, как это теперь часто признают,
оказался не совсем хорошим. Непосредственно к этому
вопросу мы вернемся в конце брошюры.
Главная цель настоящей брошюры
рассказать о
принципах такой обработки данных, при которой
воздерживаются от упоминания о доверительных вероятностях. Эти
принципы появились даже раньше математической
статистики, собственно говоря, одновременно с появлением
и

—

количественных

экспериментальных результатов
эти принципы получили
отражение в теории вероятностей с большой задержкой
в
процессе развития того подхода к математическому
оформлению теории вероятностей, который связывают с именем
Р. Мизеса. Мизесовский подход живо обсуждается не одно
десятилетие, ему были посвящены и статьи автора [9, 10],
а также учебные пособия [11—13].
Связь мизесовского подхода с принципами и приемами,
альтернативными методу математической статистики,
весьма органична. Поэтому содержание настоящей брошюры в
значительной мере сводится к последовательному—хотя,
данного
разумеется, лишь схематичному—изложению
подхода. Такое изложение в литературе, доступной
первых

в

Однако

естествознании.

—

широкому кругу читателей, пока отсутствует.
В настоящей брошюре внимание сосредоточено на
вопросах интерпретации и практического применения
теоретико-вероятностных понятий. В отличие от решений
проблем любые ответы на такого сорта
вопросы всегда в значительной степени спорны. Читатель,
конечно же, должен иметь это в виду. Ниже излагается
подход, заметно отличающийся от той позиции, которую
занимают
стандартные руководства и большинство работ
по теории вероятностей и математической статистике.
чисто математических

Повторим, что излагаемая нами точка зрения отнюдь не нова.

Крайний вариант
Ф. Дж. Анскомба

ее

хорошо выражают, например, слова

(цитируем по брошюре [14, с. 43] серии
«Математика, кибернетика»): «Недопустимо отождествлять
«статистику» с абсурдным явлением, общеизвестным под
именем «математическая

статистика».
5

Глава 1. ВВОДНЫЕ ЗАМЕЧАНИЯ
О ПРОГНОЗИРОВАНИИ

Конечной

целью

фундаментальных,

и

прикладных

—

прогноз результатов предстоящих
экспериментами мы подразумеваем не
исследовательские,

поисковые

устройств

и
исследований
надежный
(под
экспериментов
—

естественнонаучных

опыты,

и систем,

и

но

а в понятие

является

только

эксплуатацию различных
прогноза включаем

приборов, устройств, систем
д.). Прогнозирование в форме требования
воспроизводимости публикуемого результата было принято
если

проектирование

всевозможных

и т.

—

в качестве конечной цели и
угодно, по определению
отличительной черты естественных наук еще пр.; их зарождении.
В этом требовании заключено, пожалуй, главнейшее
—

отличие

естественных

наук

от

магии.

К сожалению, приходится констатировать,
как

конечная

что

прогнозирование
естественнонаучных теорий
отчасти ускользало и ускользает от внимания даже самих
ученых. Видимо, отсюда проистекает наблюдаемое иногда
цель

увлечение такими расплывчатыми формулировками целей
научного исследования, как «объяснение» или «раскрытие
сущности» явлений. Примером тому может служить
отмеченная— не
без едкости—в [15] склонность химиков
«объяснять» с высокой точностью явление постфактум
посредством обильного введения в формулы подгоночных
параметров. Подбором должного количества таких
параметров всегда можно добиться идеального совпадения
расчетной и эмпирической кривых
только не до того,
—

как

в

эксперименте.
предложена формула для
количественного показателя Р ценности теории P~(klri)—1,
число величин, которые можно предсказать с
здесь k
последняя

А. И.

получена

Китайгородским [15]

—

помощью

оцениваемой теории,

а

п—число

подгоночных

параметров теории. Согласно этой формуле ценность
теории равна нулю, если для объяснения эксперимента вводят
ровно столько параметров, сколько величин измеряется
в эксперименте. Ценность теории значительна, если &>/г.
Разумеется, читатель вправе видеть в данной формуле
шутку, но эта шутка из тех, что содержат большую долю
истины.

Несколько избыточное подчеркивание идеи прогноза,
имеющее место в новейшей дисциплине
прогностике
[16], должно быть, является реакцией на упомянутое ча—

6

стичное забвение этой

фундаментальной идеи. В этой
конкретной области

связи еще раз отметим, что в любой

естественнонаучного исследования прогнозирование

ни

в

коем

случае не является новинкой и здесь за многие годы
накоплен большой и трудно доставшийся специфический опыт
прогнозирования. Едва ли возможно создание какой-то
общей и притом в самом деле
принципиально новой
теории прогнозирования. В то же время
содержательной
унификация терминологии, связанной с
прогнозированием, несомненно, может сыграть некоторую положительную
роль.
Научный прогноз имеет форму гипотезы следующего
типа: возпроизведение в эксперименте определенных
контролируемых условий U всегда приведет к одному и тому
в
же
результату V.
пределах оговоренной точности
Контроль условий эксперимента U и получение
результата V означают не что иное, как измерение определенных
■—

—

—

—

физических величин, за которыми мы оставим обозначения
U и V. Процедуру измерения величин U и V (их так
называемое
с

операциональное

определение)

достаточной аккуратностью,

иначе

следует оговаривать

сколько-нибудь

убедительная экспериментальная проверка прогноза окажется
невозможной. Прогноз охарактеризованного нами типа

прогнозом U-+V (« от U к V»),
научного прогноза U-+V зачастую
представляет собой внутренне сложный и, скорее всего, не

условимся называть

Формулирование

поддающийся эффективной алгоритмизации процесс,

в

переплетаются эмпирические и теоретические
изыскания. Заключительная же проверка (верификация)
сформулированного прогноза всегда носит эмпирический
характер и состоит в многократном воспроизведении
условий эксперимента U и измерении получаемых
котором

тесно

V, или, как
вероятностей,

результатов

■—

это принято писать в литературе по теории
в

проведении серии

однородных

испытаний.

Только многократное постоянное получение
устойчивых, т. е. близких друг к другу, результатов в длинной
серии однородных испытаний служит в естественных
науках окончательным обоснованием надежности прогноза
(/->]/. Это обоснование нельзя, конечно, считать
непогрешимым, поскольку оно тоже представляет собой всего лишь
прогноз «как было, так и будет», издавна связываемый с
понятием

ное

эмпирической индукции [17]. Эмпирико-индуктив-

обоснование

от такового в

надежности

прогноза

в

науке

повседневной жизни, собственно,

отличается
не

принци7

пом

действия,

ний

величин

а отмеченными выше

аккуратностью измере*
многократностью повторения
однородных проверочных испытаний.
В книге [18], прямо относящейся к предмету нашего

{/, V

и

разговора, для многократно проверенного прогноза

выразительный термин перманентность.

применен

можно сказать, что конечной целью
естественнонаучного исследования является отыскание

Воспользовавшись последним,

новых

перманентностей. Мы уже

сложность

такого

поиска,

внешне

отмечали
же

он

образом. Многократно

внутреннюю
следующим
достаточно высокой

выглядит

воспроизводя с
контролируемые условия
эксперимента U{, измеряют в качестве результата испытания
некоторую величину У1# При этом нередко убеждаются в
отсутствии перманентности иг-+Уъ т.е. в том, что

точностью одни

значения

Vi

и те же

заметно

меняются

от

к

испытания

не

испытанию,

взирая на стабильность условий Ult а значит, не поддаются
прогнозированию с нужной точностью. Затем многократно
воспроизводят, вообще говоря, другие условия U2 и
измеряют в качестве результата испытания другую величину
У2. Не обнаружив перманентности U2-+V2, переходят к

U3
(г, /=1, 2, ...)

величинам

Vs

и

и т. д.

Варьирование

Ut

и

Vj

иногда

по

величин

иногда осуществляют совместно,

Например, порою варьируют Uu оставляя
характер величины Vx с тем, чтобы с помощью
более детального контроля и улучшенной стабилизации
так
их
сказать,
условий эксперимента

отдельности.
неизменным

—

рафинирования

■—

сделать

предсказуемыми

значения

именно

данной

физической величины Vx. С другой стороны, часто
варьируют Vj при фиксированных условиях (/1#
При благоприятном исходе поиска в конце концов
находят некую
перманентность U-+V.

исследователя

удовлетворяющую

Предсказуемую

величину

V

часто

именуют

детерминированной (при контролируемых
условиях U). Исход поиска иной раз оказывается и
неслучайной

или

неблагоприятным.

Найденная перманентность

в

подавляющем

относительной: измеренные
значения величины V обычно совпадают в разных
испытаниях при стабильных
контролируемых условиях U только
большинстве

случаев бывает

всего лишь

приблизительно, обнаруживая некоторое рассеивание.
Таким образом, все или почти все физические величины
оказываются, с точки зрения экспериментатора, случайными,
т. е.
8

точно

не

предсказуемыми величинами,

а

эпитет

«не-

случайная» обычно
вообще-то случайна,
к

испытанию

ли когда

бы

присваивается величине,
но

меняет

свои

значения

которая
от

испытания

Объективная реальность вряд
было виделась экспериментатору жестко

незначительно.

то ни

детерминированной. Трудно согласиться с встречающимися
в литературе (например, [19]) утверждениями, что в связи
с появлением
применением

статистики

квантовой механики и широким
в XX веке у естествоиспытателей

в

целом

происходит мучительная смена детерминистической
картины мира (парадигмы) картиной вероятностной.
По-видимому, драматическая смена парадигм имела место в основном
у теоретиков, находившихся в силу склада их натуры на
значительном удалении от эксперимента. Даже
механика
Ньютона, часто трактуемая как опора и наиболее яркое
воплощение детерминизма, доставляет далеко не жестко

детерминистическую картину механических явлений,
учитываются неизбежные погрешности измерений (см.,

если

например, [20], [21,

часть 2]).
Приведенные соображения

ностей

нам

послужат

относительно

точкой для

отправной

перманентвсего

дальнейшего изложения. В главе 2

мы шаг за шагом проследим
построения исходных концепций теории
заняв при этом, как уже указывалось в
позицию того,
предисловии,
кто,
применяя теорию вероятностей
(в дальнейшем для краткости мы будем называть его

логику
вероятностей,

прикладником), обязан сравнивать

результаты расчетов

с

экспериментальными результатами. Глава 2, по сути дела,
и будет изложением альтернативы методу математической
статистики, которое завершится в главах 3 и 4 его прямым
анализом и выводами. В последних главах попутно
обсуждаются исторические корни математической статистики.

Глава 2.

ИСХОДНЫЕ КОНЦЕПЦИИ
ПРИКЛАДНОЙ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Случайные

величины

и

их

моменты.

серия испытаний,

пусть проводится

Итак,

заключающихся

в

воспроизведении одних и тех же контролируемых

условий

эксперимента U

X.

и в

измерении некоторой

Предельно лаконичный протокол серии
испытаний

имеет

вид

конечной

величины

таких

однородных

числовой

последовательности

{X

(*)}?

-

[X (1),

X (2),

...,

X

(m),

...,

X

(N)}.
9

Здесь

и всюду далее применяются следующие обозначения!
номер испытания (следуя Р. Мизесу, мы будем

s—

отождествлять
с

рамках теории вероятностей номер испытания
испытанием); X (s)—значение величины X,

в

самим

измеренной

в

испытании s\

m

и

N

■—

соответственно текущее
и общее количество

данный момент)
(рассматриваемое
проведенных испытаний.
в

Пусть по мере увеличения количества m=l, N
испытаний мы анализируем протокол { X
целью предсказать значение величины X (s) в

проведенных
с

(s)}?

(т+1)-м испытании.
Хорошо известно, что попытки предсказывать нередко
кончаются неудачей: в последовательности {X (s)}?
зачастую не удается подметить четкой и подтверждающейся
закономерности, даже если т велико. Простейший поиск
предстоящем

[/->!/ осуществляют

перманентности

от

путем перехода

V±=X (s)

в данной
ситуации
исходной непредсказуемой величины

«вторичной»

к

величине

V=V

(m)=Mm [X]t

где

S=» 1

Величину Мт [X], которая, вообще говоря, тоже
непредсказуема, называют эмпирическим средним случайной
величины X (s) для серии из т испытаний. Переменная
отношению к

Мт [X].
через

т

роль номера нового
вторичного по
s
испытания, состоящего в измерении величины
Протокол этих вторичных измерений обозначим

играет здесь

■—

—

{Мт[Х]}?.

Обращаем

внимание на то, что в

непредсказуемых величин X (s) и Мт[Х] у
выписаны
номера соответствующих испытаний, так
в
и
эксперименте всякая измеряемая величина
именно
появляется
предсказуемая и непредсказуемая
функция от номера испытания.

обозначениях

нас

как

■—

—

Как

{Мт[Х]}?

показывает

анализ

как

последовательностей

эмпирическое среднее непредсказуемой ве
личины X (s) довольно часто (хотя и не всегда!)
действительно обнаруживает
должную устойчивость в том
конце концов ощутимо
смысле, что разброс значений Мт[Х] в
уменьшается по мере возрастания т:
(1)
MJX] ~Л1 IX] при N^m^m,,, где W»me.
то
Здесь М [X]
некоторая константа, а те
,

—

—

наименьшее количество
10

испытаний,

начиная с

которого,

по мнению

исследователя, уже постоянно соблюдалось

равенство (1). Обычно получается,

что

приближенное
ше>1. Напомним,

через N обозначено общее количество проведенных
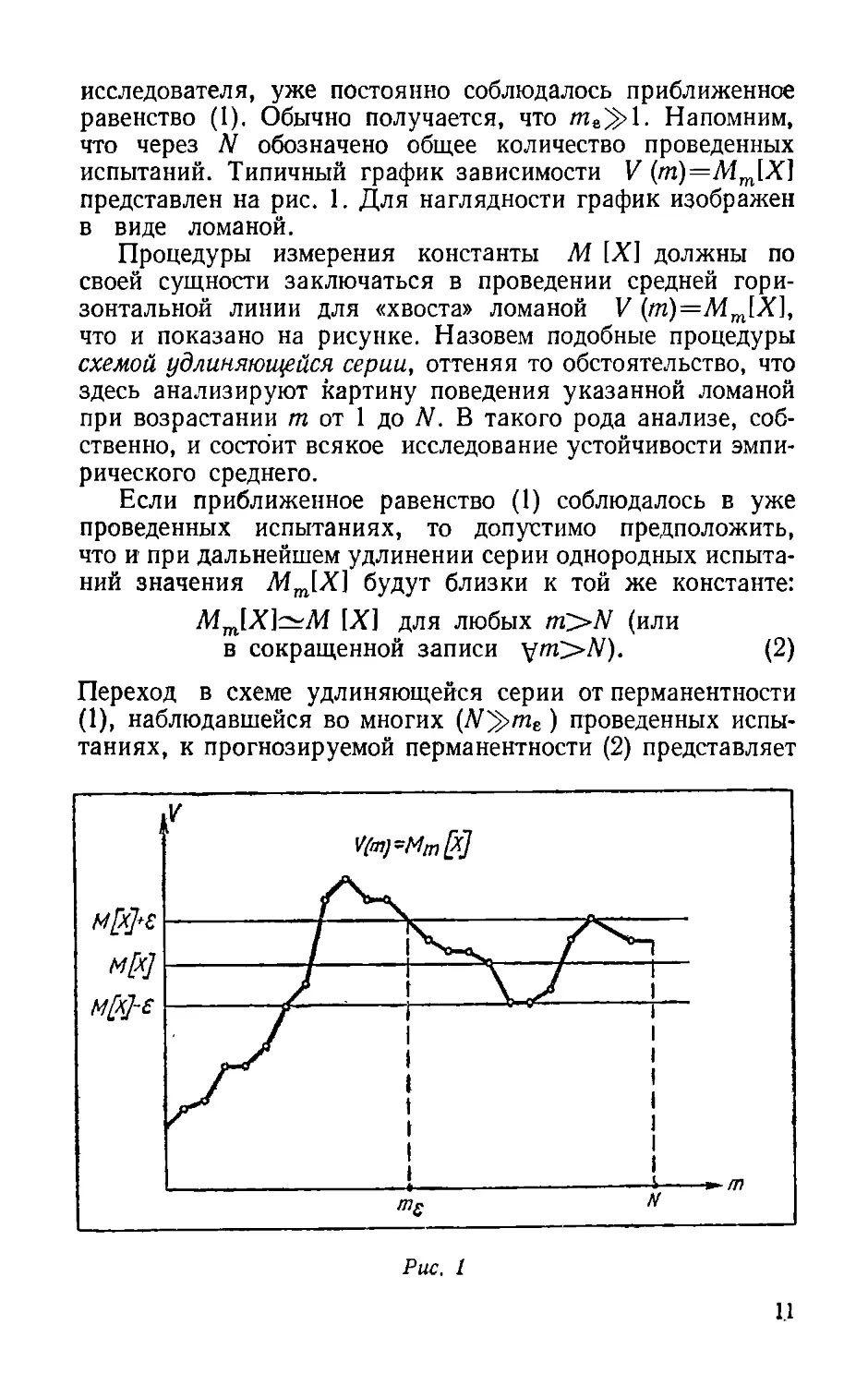
испытаний. Типичный график зависимости V
(т)=Мт[Х]
представлен на рис. 1. Для наглядности график изображен
в
ломаной.
виде
Процедуры измерения константы М IX] должны по
своей сущности заключаться в проведении средней
горизонтальной линии для «хвоста» ломаной
V (т)=Мт[Х]у
что

что

и

показано

на

рисунке. Назовем подобные процедуры

схемой

оттеняя то

здесь

поведения

удлиняющейся серии,
анализируют картину

при возрастании
собственно,

т от

обстоятельство, что
указанной ломаной

1 до N. В такого рода анализе,

и состоит всякое

исследование устойчивости
эмпирического среднего.
Если приближенное равенство (1) соблюдалось в уже

проведенных испытаниях, то допустимо предположить,
при дальнейшем удлинении серии однородных
испытаний значения Мт[Х] будут близки к той же константе:
что и

Мт1Х]^М [X]
в

для любых m>N

сокращенной

записи

ym>N).

(или
(2)

Переход в схеме удлиняющейся серии от перманентности
(1), наблюдавшейся во многих (N>me) проведенных
испытаниях, к прогнозируемой перманентности (2) представляет

Рис. 1
1J

собой

разновидность

было,

заключения

эмпирико-индуктивного

будет».
Константа М IX], вблизи которой группировались

«как

так

и

Мт[Л1 к концу серии проведенных испытаний и
которую принимают в качестве приближенной оценки
значений
Мт[Х] на будущее, как раз и является, с точки
зрения прикладника, тем, что называют математическим
ожиданием случайной величины X (s). Короче говоря,
математическое ожидание
это прогнозируемая грубая
оценка эмпирического среднего.
Более точная оценка могла бы выглядеть как прогноз
значения

—

\Мт[Х]—М [Х]\

(3)

ym>N

<е,

интервала (М [X]—е, М [X]+e)t в котором, судя по
наблюдавшемуся при N^m^m& поведению ломаной V (т)
=Мт [X], значения Л1т[Х], видимо, будут оставаться
и впредь (см. рис. 1). Интервальные оценки типа (3) для
=

эмпирического

среднего

возникают с

неизбежностью,

как

придать ясный смысл приближенным
равенствам (1),
(2) и выражению «должная устойчивость».
Устойчивость эмпирического среднего или каких-либо
других усредненных характеристик протокола измерений
только

пытаются

называют статистической

часто

измерений). Мы

(результатов

далее

устойчивостью

будем

постоянно

пользоваться

удобным общим термином, указывая, в случае
надобности, об устойчивости каких именно усредненных

этим

характеристик идет речь.
Проводить на глаз
на

среднюю

прямую

линию

V=M [X]

по-разному.
графике
можно по-разному реализовать
Соответственно,
схему
удлиняющейся серии в программах для ЭВМ.
можно

одном

и

Неоднозначность в результатах таких

М [X]

несколько

том же

измерений

математического

удивлять. Результаты измерения
любой физической величины абсолютно однозначными, как
правило, не бывают.
Мы и далее будем говорить об измерении
математического ожидания, однако это всего лишь удобное сокращение:
оператор математического ожидания М, в отличие от

ожидания

не

должна

оператора Мт
эмпирического среднего, символизирует у нас
не просто измерение или вычисление, а главным образом
исследование

статистической

устойчивости

и

прогнозирование.

Математическое ожидание М [X]
первым

12

начальным

моментом

случайной

называют также
величины

X (s). На

Мт

практике операторами
описанном

выше

или

{Xk (s)}?,

и

смысле

где

на

и

М

часто

действуют

последовательности

к (s)=X (s)—M [X].

в

вида

Тем

{Xk(s)}™

самым

измеряют начальные М [Xk] и центральные М [°Xk] моменты
Л-го порядка (для не слишком больших значений k>\).
Все сказанное об М [X] относится в своих существенных
чертах
Мы
математического

к

и

моментам

обсудили
ожидания

высших
порядков.
процедуры измерения

такие
и

моментов

вообще,

Всюду дальше
процедуры. Применительно

статистическими.

такие

которые именуют

имеются

в

виду

только

к ним нет никакого

смысла говорить, например, о математическом ожидании
дисперсии каждого отдельного измерения случайной
величины X (s); любые моменты усредненно характеризуют

(s)}T

или

весь

целом. Можно сказать, что
при
роли случайной величины
выступает весь протокол как единое целое, но не результат
каждого отдельного измерения.
Нестатистические же процедуры измерения
математических ожиданий, в частности экспертные оценки,
наверное, небесполезны, однако с точки зрения метрологии они
выглядят не очень серьезно.
о
наличии
статистической
Вопрос

длинный

протокол {X

в

статистическом подходе в

весьма
устойчивости
актуален в приложениях
теории вероятностей. Обсудим его подробнее.
В литературе встречаются высказывания типа «если
испытания

однородны,

Данное

то

статистическая

устойчивость

проверяемо, очевидно, лишь
тогда, когда под однородностью испытаний подразумевают
стабильность контролируемых условий эксперимента. Но
в этом случае оно, вообще говоря, ложно уже оттого, что
налицо».

высказывание

ряд существенных
незамеченным.

Так,

факторов может оказаться
лаборатории Э. Резерфорда

однажды в

эксперимента с
(теперь оно называется

результаты

новым

радиоактивным веществом

стали форменно хаотичными,
хотя условия эксперимента были такими же, как и раньше.

Исследователи

не

радоном)

сразу догадались,

что

новое вещество

—

все ранее открытые радиоактивные вещества
газообразными не были. Условия эксперимента были
газ;

дополнительно

рафинированы (устранили сквозняки, перестали
чихать), и только после этого
статистическая
устойчивость восстановилась.
поблизости курить и

Любой

экспериментатор

всегда

может

столкнуться

в

13

своей

работе

подобными замаскированными факторами,

с

осложняющими жизнь. В силу этого объективного
обстоятельства именно выходную характеристику эксперимента

—

наличие статистической устойчивости,
входную
характеристику— постоянство контролируемых условий £/—<
приходится считать на практике окончательным
а не его

достаточной однородности испытаний. Иными словами,
приходится считать приемлемыми разве что инверсные

критерием

высказывания

типа «если

статистическая

устойчивость

налицо, то испытания однородны».

Допущение
принадлежит

попросту уже
математически.

посылку

о

должной статистической устойчивости

интуитивным посылкам, которые
строго логически или
Наиболее убедительно обосновывать эту

к тем

исходным

не из чего выводить

можно

эмпирической

только

чисто

Такая

с

—

помощью

индукции.

На практике довольно

пренебрегая

эмпирически

часто

полагают

анализом последовательности

М

[X]=MN[X],

{Мт[Х]}?.

упрощенная процедура измерения математического
которую мы назовем схемой фиксированной

ожидания,

серии, является отступлением

от

эмпирической

идеи

индукции и означает отказ от исследования статистической
устойчивости.

Схема

определенное значение

фиксированной

М [X]

и

серии доставит
тогда, когда рассмотрение всей

{Л1т[Х]}^

не выявило бы должной
последовательности
статистической устойчивости (1), например, тогда, когда
ломаная V (т)=Мт[Х]
неуклонно поднимается с ростом

т

(монотонный тренд).
Мы сейчас вернулись

к

тому,

что должная

устойчивость (1) наблюдается

статистическая

серия

проведенных

испытаний

не

была

всегда,

длинной;

даже

если

ответ

на

устойчивости может быть
как положительным, так и отрицательным. При отсутствии
должной статистической устойчивости (1) нет оснований
вопрос о

оценивать

наличии статистической

значения

М IX]. Это означает,
математического

вопрос

Мт[Х]
что в

с помощью одной константы
данной ситуации понятие

неприменимо. Таким образом,
статистической устойчивости вполне
следующей более острой форме: применимо

ожидания

о наличии

резонно ставить и в

к данной случайной величине понятие математического
ожидания? В общем случае речь пойдет о применимости и

ли

других, более сложных теоретико-вероятностных понятий,
словом, о самой применимости теории вероятностей к рас14

сматриваемым

конкретным

непредсказуемым

величинам.

Попутно заметим, что в обычном русском языке и в
философском лексиконе слово «случайность» очень давно
очень широко употребляется для обозначения
непредсказуемости как таковой, без обязательной связи с теорией
вероятностей. Слово «случайность» в данном широком
смысле

прочно

вошло в

обиход вообще

и

задолго до того, как

известной за
пределами узкого круга математиков; по всей видимости,
оно укоренилось даже до появления слова
«непредсказуемость».
Придерживаясь общелитературных норм, мы
только что применяли словосочетание «случайная

вероятностей

теория

величина»

в

качестве

точного

сколько-нибудь

синонима

словосочетания

величина».

«непредсказуемая

Между

стала

тем

математики

стали

постоянно

случайной величиной

называть

функцию, измеримую
нормированной меры (см., например, [8]). Такая «узурпация»
общелитературных слов для обозначения чисто
относительно

объектов породила в данном случае значительную
путаницу, причем сразу в двух различных аспектах: с

математических

одной стороны,

будто

многим стало казаться,

любая

быть успешно
непредсказуемость
описана в теоретико-вероятностных терминах, а с другой,
у многих создалось впечатление, что теория вероятностей
органически применима только к непредсказуемым
случайность,

т. е.

может

—

величинам.

Действительно, под влиянием математической
литературы в инженерных и естественнонаучных интерпретациях
теории вероятностей под случайной величиной
нередко
стали

подразумевать только такую непредсказуемую
которая демонстрирует статистическую
устойчивость и потому принадлежит к сфере серьезных
применений теории вероятностей. Более того, следуя математикам,
под случайной величиной здесь стали подразумевать
величину,

такую непредсказуемую величину, к которой применимо
прикладной теории вероятностей
понятие распределения
вероятностей. Однако эту узко
интерпретацию словосочетания «случайная
специальную
величина»
волей-неволей
путать с его
продолжают
широким общелитературным смыслом, поскольку
именно

самое сложное понятие

последний,

как и всякое языковое явление,

—

упразднить

не так-то

у читателей литературы по
прикладной теории вероятностей и математической статистике
просто. Вот

и

возникает

15

(в особенности у начинающих)
применимы
широком смысле,

дисциплины
в

ко всем
т.

иллюзия того,

без

исключения

е.

что эти

случайным

—-

величинам.
непредсказуемым
И, таким образом, важнейший вопрос об эмпирическом
обосновании применимости
теоретико-вероятностных
понятий к рассматриваемым конкретным непредсказуемым
величинам порою полностью выпадает из поля зрения.
С другой стороны, читатель, постоянно наталкиваясь в
—

математических текстах на словосочетание

«случайная

величина», начинает думать, что математические
предложения теории вероятностей как-то непосредственно

непредсказуемым величинам, а то и только к ним. На
эти предложения являются обычными
математическими
теоремами, относящимися к самым обычным
функциям и не имеющими ни малейшего
к

относятся

самом деле

формально-логического отношения к
к

обыденному

непредсказуемым

понятию

и

величинам и

вообще

философской категории

«случайность».

Этот второй аспект путаницы дает в конечном счете
основной эффект, что и первый: у прикладника
притупляется чувство личной ответственности за применение
теоретико-вероятностных понятий и предложений к

тот

же

рассматриваемым конкретным непредсказуемым величинам.
Проблему перевода математических предложений теории
вероятностей на язык эксперимента мы еще затронем ниже.
Вдобавок этот второй аспект затрудняет понимание того,
быть может,
что при моделировании случайных величин
в отличие от прямого их воспроизведения
необходимо
максимально устранять всякий элемент случайности,
—

—

точнее, непредсказуемости. Такая метрологически жесткая
установка представляет собой прямое следствие из
фундаментальнейшего естественнонаучного требования

публикуемого результата.
В последнее время для обозначения непредсказуемости,
вообще говоря, не вписывающейся в рамки
теоретико-вероятностных понятий, стали употреблять термин
воспроизводимости

«неопределенность»

(см., например, [8,

с.

145]).

К сожалению,

это

устранит вышеозначенную путаницу. Ибо если под
случайностью подразумевать только непредсказуемость,
сопровождающуюся статистической устойчивостью и,
стало быть, всерьез «вписывающуюся» в теорию вероятностей,
вряд

то

ли

неясно,

как

«неслучайная

толковать

употребительное

величина»:

то

ли

детерминированная величина,

то

ли,

16

это

словосочетание

предсказуемая,

наоборот,

величина

столь

непредсказуемая,

что

вероятностей
Наверно, было бы

теория

статистической
здесь

устойчивости нет

и

неприменима.

хорошо условиться выделять
величины, к которым применима теория вероятностей, какимнибудь специализированным эпитетом, не нагруженным
обыденными ассоциациями и не оттеняющим вовсе
необязательное свойство непредсказуемости.
Например, можно

говорить о стохастических или вероятностных величинах,
зачастую и делается.
Во избежание смещения акцентов мы сейчас
подчеркнем, что о статистической устойчивости вполне допустимо
что

говорить и применительно к неслучайным, т. е. хорошо
предсказуемым величинам. Ведь ничто в принципе не
запрещает
рассматривать эмпирическое среднее, допустим
периодической величины X (s), равной нулю при четных s
и единице— при нечетных. Другое дело, что на практике

устойчивости обычно
убедятся в своей
неспособности предсказывать величину X (s) точно. Такой поиск
перманентности, осуществляемый по принципу «лучше
прогнозировать что-нибудь, чем ничего», мы и описали
выше. Между тем легко представить себе ситуацию, когда
к исследованию статистической

приступают

только после того,

как

ограничиваются исследованием только статистической
устойчивости, несмотря на то, что есть принципиальная или
даже реальная возможность точно предсказывать и самую
величину X (s). Получение точного прогноза может
оказаться слишком дорогим, а то и попросту ненужным делом.
Следовательно, непредсказуемость величин отнюдь не
является
обязательным условием применимости к ним
теории вероятностей. Важно, чтобы величина X (s)
в длинной серии испытаний и
многократно
демонстрировала статистическую устойчивость. Поэтому оба
конкурирующих эпитета
«непредсказуемая» и
«случайная»
в применении к величине X (s) мы будем далее
измерялась

—

—

—

опускать

всюду, где они представляются
к делу. А так будет почти всегда.

не

относящимися

понятно, не относятся к
не безобидная вещь
И все же язык

Терминологические вопросы,
наиболее важным.

—

Неудачные термины и выражения, казалось
бы, давно обретшие узко специальный смысл, могут
исподволь деформировать восприятие и оценку того или иного
научного исследования. В учебнике [8], например,

даже в науке.

указано, что название «теория игр» известной математической
дисциплины оставляет желать лучшего, поскольку на са2 «Математика»

№ 3

17

мом деле здесь

обычных

изучают

смыслах

этого

Видимо, лучше было бы

нечто не очень похожее на

игры в

употребляющегося

широко

остановиться

на

слоБа.

менее

нагруженном

ассоциациями специализированном термине, скажем,
встречающемся в технической литературе названии
«теория матричных игр». Перечень не совсем удобных
терминов можно было бы продолжить. Так, название
«планирование эксперимента» представляется, пожалуй,
чересчур широким и слишком много обещающим для той
на

довольно

специфической дисциплины, за которой оно
Образцы терминов, свободных от мешающих

закрепилось.

ассоциаций,

дают нам,

к

примеру,

(в прошлом
или физический термин
сочетание звуков).
«мартингал»

В

—

связи с

математический термин

исключительно

«кварк»

предпринятым

(вообще

обсуждением

загадочное
языковых

вопросов здесь же коснемся и обычных для

литературы

математической

типа

среднее

—

выражений
приближенная оценка

статистике
это

упряжи)

элемент

по

«эмпирическое

математического

тому, чтобы
ожидания
применимость
собой разумеющейся или, другими словами, считать

ожидания».

Подобные выражения располагают

считать
само

понятия

к

математического

математическое ожидание как бы непременно
объективно
существующим. Между тем, с точки зрения прикладника,
наиболее объективно существуют именно эмпирические
средние, измеренные в объективно поставленных
экспериментах. Математическое ожидание как физическая,

измеряемая величина появляется несколько позже
более субъективная приближенная оценка этих
эмпирических средних в прошлом,
Причем

появляется

не всегда,

а

а главное
в

—

в

т. е.

как

будущем.

идеале лишь тогда,

когда

с

правдоподобием установлена и
прогнозируется статистическая устойчивость.
Таким образом, наличие статистической устойчивости
(в частности, устойчивости (1) эмпирического среднего)

достаточным

проведенных испытаниях, как и наличие любой другой
перманентности £/->V, к сожалению, не вытекает с
непреложностью из стабильности контролируемых условий
эксперимента. Вместе с тем весь опыт естественных наук
в

показывает,
результата

что для повышения

обусловленный
18

максимально

эксперимента, иначе к неизбеж»
рассеиванию результата добавиться еще и вклад,

возможного числа

ному

воспроизводимости

необходимо обеспечивать стабильность

условий

неряшливостью.

Искусственное

внесение

непредсказуемости в эксперимент, осуществляемое при
называемой рандомизации, а также при случайном
поиске экстремума и в некоторых вычислениях по методу

так

Монте-Карло, бросает, надо думать, чрезмерно смелый
вызов естественнонаучной традиции.
Что же касается прогноза статистической устойчивости
(например, прогноза (2)), то он не является непреложным
следствием ни из стабильности контролируемых условий
эксперимента, ни даже из статистической устойчивости в
уже проведенных испытаниях: будущее есть будущее.
Повторим, что здесь имеет место эмпирико-индуктивное
заключение «как было, так и будет». В соответствии с общей

идеей эмпирической индукции прогноз (2)

правдоподобней,
ломаной

«хвост»

серии

чем

при

экспериментального

(т)=Мт [X].

V

естественным

N>me

фундаментальную

тем

образом

воплощает

эту

результата.

иногда

m,

выглядит

слабо колебавшийся
Схема удлиняющейся

многократной проверки

идею

события.

Вероятность
s=l,

был

длиннее

Проводя

лишь тем,

интересуются

испытания

происходит или

не

происходит при определенных контролируемых
условиях эксперимента U некоторое событие Л.Можно считать,
что в подобных ситуациях в каждом испытании измеряют

XA(s),

которую удобно полагать
наступило, и равной
О— в противном случае. Будем называть величину XA(s)
индикатором события Л, а последовательность {XA(s)}™—
двоичную величину
равной

1,

событие Л

если

в

испытании s

протоколом-индикатором.
повторим вкратце все,

общего

этой

индикатор
в

то

в

сот(Л)

не

поддается

с

Мт[ХА ]

общему
Обратим

величины

от

к

(относительной)

определением

их

индикатора

эмпирическое

оказывается

испытаний,

тех

точному
переходят

часто

которое обозначают символами
частотой события А
испытаний. Это название обусловлено тем, что

из т

среднее
к

индикаторам
X (s)

Мт[ХА ],

и называют

соответствии

количества

к

сказано о величинах

перманентности

исходной непредсказуемой

серии

в

XA(s)

поисках

эмпирическому среднему
типа

Применительно
было

вида.

Если

предсказанию,

что

количеству

в

равным отношению
которых наступало событие Л,

т.

что событие полностью
индикатором; событие Л называют
случайным (в любом—широком или узком смысле), если
случайна величина XA(s). Словом, в рамках прикладной

представлено

2*

внимание на то,

здесь

своим

19

случайные события являются
специфической разновидностью

теории вероятностей
иным,

случайных

как

весьма

не

чем

величин.

Для

исследования устойчивости частоты сот(Л)
прибегнуть к эмпирической индукции в форме
схемы удлиняющейся серии. В случае обнаружения должной
устойчивости частоты можно измерить математическое
ожидание М 1ХА], называемое в данной обстановке
необходимо

(статистической) вероятностью Р (А) события А. С

точки

это
прикладника, вероятность Р (А)
прогнозируемая доля тех испытаний в их длинной серии, в которых
событие А наступит. Короче говоря, вероятность

зрения

—

—

прогнозируемая

грубая

оценка частоты для

это

т>1.

Подчеркнем, что вероятность, как и математическое ожидание

вообще, стоит всерьез вводить в игру только тогда, когда
вопрос о наличии статистической устойчивости решен
положительно. Ясно, что статистическую вероятность не
запрещено измерять и для предсказуемого события. Важно,
чтобы в наличии была длинная серия испытаний.
На практике часто ограничиваются схемой
фиксированной серии, отказываясь от анализа последовательности
{(от(А)}^ и полагая Р (Л)2^со^(Л). Тем самым
от исследования статистической устойчивости.
Статистическая вероятность усредненно характеризует

отказываются

всю длинную серию рассматриваемых испытаний в целом.
Если речь идет о статистической вероятности, полностью
лишено смысла говорить о вероятности наступления
события в каждом отдельном испытании.

Должная устойчивость

любой другой вид статистической
устойчивости, к сожалению, не вытекает с непреложностью из
стабильности контролируемых условий эксперимента.
Остановимся на вероятностях редких событий,
характерных, например, для проблемы надежности. Если Р (Л)~
~10~п то это означает, что событие А наступает в среднем
один раз на 10" испытаний. Для измерения вероятности
какого бы то ни было события, очевидно, необходимо
провести настолько много испытаний, чтобы это событие

частоты,

как

и

,

наступило не один, а несколько раз. Следовательно, для
необходимо провести
измерения вероятности порядка Ю~п
испытаний.
порядка 10n+1
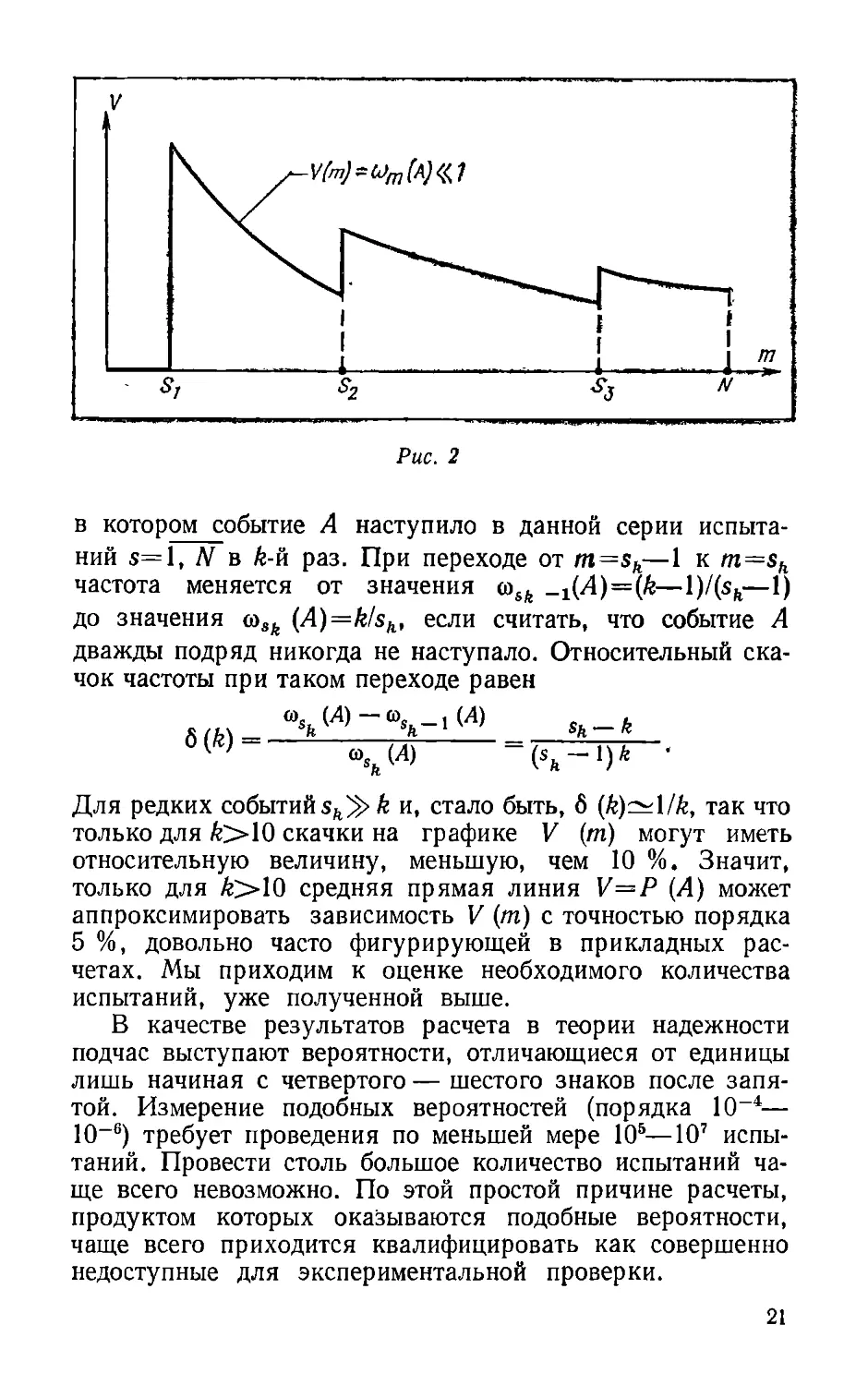
Эти простые соображения можно несколько уточнить,
обратившись к схеме удлиняющейся серии и учитывая
примерный вид зависимости V (т)
сот(Л) для редкого собы*
тия А (см. рис. 2). Обозначим через sk номер испытания,
=

20

Рис. 2

в

котором событие А

испытаний s=l, N
частота

до

наступило в

данной серии

k-й раз. При переходе
меняется
значения
от
cosfe
в

значения

(oSk

(A)=klsh,

если

m=sh—1 к m=sk
_Х(Л)=(^—l)/(sh—1)

от

считать,

что

событие А

дважды подряд никогда
наступало. Относительный
скачок частоты при таком переходе равен
не

<\(Л)-%-1(Л)
%3)

6(h)-

Для

редких событий

только для

£>10

относительную
только

для

sh^>k

скачки на

величину,

sk

—

k

к-1)*

быть, 6 (£)~1/£, так что
графике V (т) могут иметь

и, стало

меньшую,

£>10 средняя прямая

чем

линия

10 %. Значит,
V=P (А) может

аппроксимировать зависимость V (т) с точностью порядка
5 %, довольно часто фигурирующей в прикладных
расчетах. Мы приходим к оценке необходимого количества

испытаний, уже полученной

выше.

В

качестве результатов расчета в теории надежности
подчас выступают вероятности, отличающиеся от единицы
шестого знаков после
лишь начиная с четвертого
запятой. Измерение подобных вероятностей (порядка 10~4—
10~6) требует проведения по меньшей мере 105—107
испытаний. Провести столь большое количество испытаний
чаще всего невозможно. По этой простой причине расчеты,
—

оказываются

продуктом

которых

чаще всего

приходится

недоступные для

подобные вероятности,

квалифицировать как совершенно
экспериментальной проверки.
21

Распределение
Моменты

являются

наиболее

вероятностей.

часто

измеряемыми усредненными
характеристиками
непредсказуемых величин. Однако во
многих
практических задачах недостаточно измерять и
прогнозировать только моменты. Например, нередко
требуется прогнозировать такой количественный показатель,
как процентное содержание в
партии деталей, у которых
значение определенного параметра X (s) (здесь s— номер
детали) попадает в назначенный промежуток [а, Ь]. В

подобных случаях, в сущности, требуется предвидеть, как в
среднем будут распределены между возможными
значениями величины X
(s) частоты реализации этих значений в
серии предстоящих испытаний. Так и возникает понятие

распределения

распределения.
верог.т чостгй, или кратко
В теоретических исследованиях и при вычислениях
наиболее удобно задавать распределение величины X (s)
—

функцией распределения
Fx{x)=P(X(s)^x),vx.
Под

знаком вероятности здесь выписано то неравенство,
выполнение которого в испытании s означает наступление
рассматриваемого события. Подобная запись применяется
ниже и к частотам.

Идеальная процедура измерения

следующим образом. Для ряда
возрастающих значений т находят и сравнивают между
собой эмпирические функции распределения

Fx (x)

функции

выглядит

Fm(x)

=

aJX (s)^x),yx.

Если конфигурация ступенчатых кривых

стабилизируется,
для

т>1 кривой

ступенчатой,

то

эти

Fx(x), которая
В

Fm(x)

с

приближенно

кривые

может

быть

ростом

т

оценивают
и

реализуется
непрерывной.
эмпирическая индукция в форме схемы удлиняющейся серии.
это простоС точки зрения прикладника, кривая Fx(x)
линия
оценивающая
напросто
регрессии, приближенно
устойчивую эмпирическую зависимость Fm(x) для длинной
серии проведенных, а главное—будущих испытаний.
Подчеркнем, что при отрицательном ответе на вопрос об
и

таком виде здесь

—

устойчивости функции Fm(x) понятие распределения
вероятностей оказывается неприменимым к данной
непредсказуемой величине X (s). С другой стороны, ничто в
принципе
величины

22

не

мешает

X (s).

измерять

Fx(x)

и

для

неслучайной

Зная
вероятность

функцию распределения,

попадания

Р

назначение

слово «оценить»
о

в

любой

можно

оценить

промежуток

(4)

(а<Х (s) ^b)=Fx(b)-Fx (а),у6>а.

Формула (4)
основное

X (s)

выражает,

если можно так сказать,

функции

распределения. Мы употребили

потому,

приближенных

что

оценках

практике речь идет все
прогнозах. С позиций

на

—

же

запись равенства (4) как точного выглядит всего
общепринятой условностью.
Пользуясь случаем, заметим, что экспериментальная

прикладника,
лишь

проверка любого равенства, записанного как точное
равенства, выражающего закон сохранения энергии),

(скажем,

доказывает, строго говоря, лишь то, что оно выполняется в
некотором

дела,

не

приближении. В естественных науках, по сути
выполняется или не
вопрос ребром

ставят

■—

интересуются тем, с какой
именно точностью он выполняется в эксперименте. Так, в
настоящее время эксперимент позволяет ручаться за
относительную точность выполнения закона сохранения энергии
в ядерных реакциях,
равную 10~6, тогда как, допустим,
законы Менделя выполняются в эксперименте гораздо
выполняется

данный закон,

а

(см., например, [7, 9, 10]).
Распределение вероятностей является самой полной
характеристикой, которая
прогнозируемой
рассматривается в прикладной теории вероятностей. Зная
распределение величины X (s), можно, в частности, оценить любой
ее момент. Например, для начальных моментов
справедлива формула
менее точно

Ш [X*]

=

x*fx (x) dx,

J

(5)

—со

где под интегралом фигурирует плотность распределения
fx (x)=dFx(x)/dx. Моменты М [Xk], найденные по формуле
это те самые моменты, которые получаются как
(5),
—

результат действия оператора М прямо на
последовательность {Xk(s)}T.
Вовсе не обязательно вводить
только

формулами

типа

(5),

моменты

т. е.

через посредство
распределений. На практике зачастую не располагают протоколом
такой длины, чтобы можно было всерьез измерить
распределение, и тогда поневоле ограничиваются измерением
моментов. Так что фактически моменты часто выступают и
в качестве самостоятельных усредненных
характеристик,

23

связываемых в обязательном порядке с понятием
распределения.
В литературе встречаются настоятельные рекомендации
измерять именно функции распределения на том основании,
что стабилизация функций
Fm(x) с ростом т всегда более
заметна, нежели стабилизация гистограмм
эмпирических
плотностей распределения. Между тем это отличие
функций распределения от плотностей сродни преимуществу
нечувствительного прибора, дающего малое рассеивание
результатов измерений, перед прибором чувствительным, у
которого рассеивание в тех же условиях значительно
больше как раз из-за чувствительности.
Статистическая независимость.
Величины Хх (s),
Xn(s)
Некоррелированность.

не

—

...,

называют статистически независимыми тогда и только
тогда,

когда

справедливо

тождество
п

F{*i>

...»

*п)-

П Fxt(xt),

V*i.

.-.

(6)

*п.

1 = 1

В левой
распределения

части здесь стоит совместная

данных

выполнения

функция

равная вероятности одновременного
неравенств Xi(s)^xt для i=l, п. В

величин,
всех

функцию распределения
n-мерной. Определение статистической независимости

инженерной литературе такую
называют

можно

дать

и

на

языке

событий

независимостью

плотностей

Л£,

независимость

статистическую

...,

их

распределения. Под
подразумевают
индикаторов XAl(s),

Ап

...,

ХЛп (s), функции распределения которых, естественно,
можно рассматривать на общих основаниях. Правда, свойство
независимости

вероятностей,

событий
а

Допущение
весьма охотно,

о

обычно

формулируют

на

языке

функций распределения.
статистической независимости принимают
поскольку при этом совместная п-мерная
не

функция распределения оказывается выраженной через
одномерные функции распределения. Измерить же п
одномерных функций распределения намного проще, чем
измерить одну n-мерную. Однако не следует упускать из
виду, что статистическая независимость, к сожалению, не
вытекает с непреложностью из кажущейся,
интуитивной
независимости
рассматриваемых величин. Здесь имеется
полная аналогия с тем фактом, что из стабильности
контролируемых
вытекает

24

условий эксперимента, вообще
устойчивость.

статистическая

говоря,

не

Для идеальной эмпирической проверки статистической
все-таки
необходимо измерить я-мерную
функцию распределения, что в соответствии с изложенной
независимости

статистической

трактовкой распределений требует
устойчивости л-мерной эмпирической функции
распределения.
Таким образом, о статистической независимости можно
исследования

говорить

с полным основанием только после того,

установлена

статистическая

F

При
(хъ

статистической

...,

хп)

характеризует

{Хг(8))?9

как

устойчивость.
трактовке функция распределения

...,

длинные

протоколы

m»l

{Xn(s))T;

(7)

целом. Соответственно к протоколам в целом относится и
свойство (6), так что полностью лишено смысла говорить
о статистической независимости величин в каком-либо
отдельном их измерении. Точнее суть дела передавал бы

в

термин
мы и

«статистическая

будем прибегать

независимость

протоколов».

К

нему

ниже в самые ответственные моменты

изложения.

Более простым, нежели статистическая независимость,
глобальным свойством протоколов (7) является (попарная)

некоррелированность
означает

величин

справедливость
М

X±(s),

...,

Xn(s)>

которая

равенств

[ВД,]=0,

(8)

у1Ф1.

Основная
задача
прикладной
теории вероятностей в принципе та же, что и любой
другой математизированной
естественнонаучной теории:
по прогнозируемым эвристическим путем исходным
величинам
V вычислять некоторые вторичные величины W
в отыскании оператора W=0 (V) заключается собственно
математическая часть теории. С точки зрения практики,
вычисление
вторичных величин W означает их
теоретическое

прогнозирование,
осуществляемое с привлечением
математики. Такое прогнозирование зачастую существенно
экономнее прямого экспериментального исследования

величин

W. Ясно,

оказывается

исходных

что

величин

Подчеркнем,

эффективно лишь тогда, когда
удачным эвристический прогноз

оно

достаточно

V.

прогноз исходных величин всегда
эвристическим, интуитивным. Ведь в любой теории
неизбежны некие начальные посылки,
которые попросту
что

является

уже

не

из

чего

выводить

формально

по

четким

правилам
25

(между прочим, это простое обстоятельство
удивительно часто упускают из виду). В прикладных теориях
начальные интуитивные посылки, принимаемые на основе
анализа экспериментальных данных, образуют так
называемый эмпирический базис теории. Природа вещей такова,

логики

что тщетно надеяться как-то вычислить или обосновать
чисто математически достоверность этих базисных посылок.
Самый

надежный способ эвристического прогнозирования
исходных величин, равно как и заключительной проверки
теоретических прогнозов, доставляет неоднократно
упоминавшаяся выше эмпирическая индукция. Математический
аппарат

прикладной теории

выполняет

функции

своего

рода надстройки над эмпирическим базисом, позволяя по
исходным величинам вычислять величины вторичные.
Естествоиспытатели издавна сравнивают математику с
жерновами, перемалывающими то, что в них засыпают.
Вместе с тем математические понятия обычно участвуют
и в описании эмпирического базиса теории. Математика,
несомненно, является тем языком, без которого трудно
подступиться хотя бы к постановке и обсуждению
большинства современных практических задач,
не говоря уже об их

эффективном решении.
В прикладной теории

вероятностей роль исходных
прогнозируемых величин V играют такие усредненные
характеристики исходных непредсказуемых величин X (s),

как

вероятности, распределения. Вторичными же
прогнозируемыми величинами W здесь являются
аналогичные
усредненные характеристики некоторых вторичных
непредсказуемых величин Y (s), связанных известным
образом с величинами X (s). Собственно математическая часть
основной задачи прикладной теории вероятностей
моменты,

состоит в

переходе

от известного исходного

оператора Y=q

(X)y

связывающего непредсказуемые величины, к производному
оператору W=y (V), связывающему величины,
поддающиеся прогнозированию. Простым примером служит
рассмотренный выше случай, когда исходный оператор

собой
W=M [Xk], то

представлял

функцию ф (X)=Xk.
производный оператор

(5).
Предельные

Если

V=fx (x),

a

определяется

равенством

теоремы теории
решают более трудные варианты основной
задачи теории вероятностей. Они рассматривают ансамбль
исходных величин Х1 (s),
Xn(s) в предположении, что
л-^-оо, почему теоремы и называют предельными. В качествероятностей

...,

26

ве

вторичной

деталей, сумма

величины

Yn(s)

=

выступает,

если отвлечься от

X1(s)+...+Xn(s).

Относительно ансамбля исходных величин в
центральной предельной теореме (ЦПТ) предполагают следующее:

1)

Xi(s),

величины

при любом п\
2) рассеивание

...,

Xn(s)

независимы

всех этих величин возле своих

ожиданий примерно

математических

статистически

одинаково.

Условия тех предельных теорем, за которыми
закрепилось название «законы больших чисел» (ЗБЧ), в целом

отсутствует требование 2, а также допускается
с математической точки зрения
ослабление
требования 1 вплоть до замены его требованием
мягче.

В

них

заметное

—

—

некоррелированности (8). При всем этом, с точки зрения
прикладника, условия ЦПТ и ЗБЧ практически совпадают. На
практике считают допустимым применять ЦПТ всякий
раз,
когда есть интуитивные основания применять ЗБЧ.
В заключении ЦПТ утверждается в общих чертах то,

Yn(s)fY~n

что при п->оо распределение величины
имеет

нормальному. Заключение ЗБЧ
характер: утверждается, что при п-^оо

приближается

неограниченно

аналогичный

к

распределение величины
вырожденному,

Yn(s)/n

неограниченно
распределению постоянной
величины (равной в данном случае нулю). С практической
стороны ЦПТ полностью перекрывает законы больших
чисел, доставляя количественные оценки там, где ЗБЧ в
основном устанавливают лишь существование предела. В

приближается к

ходе доказательства
тоже

получаются

неравенства

т. е.

законов

к

больших чисел, надо сказать,

количественные оценки с помощью

Чебышева, но эти оценки намного грубее тех,
центральной предельной теоремой.

что

доставляются

неравенство Чебышева в практических расчетах
нецелесообразно.
Итак, с принципиальной стороны предельные теоремы
решают ничем особенным не выделяющиеся разновидности
основной задачи теории вероятностей. В начальный период
Применять

развития теории вероятностей принципиальное значение
предельных теорем сильно преувеличивали, что
обусловливалось не совсем логичной их интерпретацией. Подобные

преувеличения
и

встречаются

статистическая

не

до

конца

(ослабленный вариант—в
облегчить

изжиты

и

поныне:

нет-нет

современной литературе утверждения,
устойчивость имеет место в силу ЗБЧ

в

обсуждение

соответствии

данного

с

да
что

ЗБЧ). Чтобы

примечательного обстоятель27

ства в главе

3, сформулируем сейчас частный случай ЗБЧ

теорему Бернулли,
эмпирическим терминам. Для
удобства
формулировку теоремой 1.

по возможности не

Теорема 1.

Пусть

прибегая

ссылок назовем

выполнены

—

к

нашу

следующие

два

условия:

1)

математические ожидания двоичных

XAn(s)

...,

2)
независимы

одинаковы: М

XAl(s),

величины

при любом

величин

XA|(s),

[XAi]=p, у/;
XAn(s)

...,

статистически

п.

Тогда справедливо равенство

limW|^rn(s)-/>|<e)=l,
\\
|
/

у8>0,

П-+оо

Yn(s)=X1{s)+...+Xn{s).
Иногда математические ожидания М [ХА] называют
здесь
продольными средними рассматриваемого ансамбля
величин, а функцию Yn(s)/n—его поперечным средним.
Теоремы, устанавливающие в том или ином смысле
где

близость

между продольными

называют

эргодическими.

и

поперечными средними,

Теорема 1

<—

простейшая эргодиче-

ская

теорема.
Мизесовский

подход. До сих пор мы
рассматривали теоретико-вероятностные понятия лишь
с прагматических
позиций прикладника. К
нестрого
строгому построению математического аппарата теории
вероятностей подходят по-разному. При мизесовском подходе
—

не

выбирать исходные понятия математической
предельно близкими к тому, с чем имеют дело в

стесняются

теории

эксперименте.

собственно,

Исходные

математические

понятия

здесь,

совпадают с рассмотренными выше понятиями

{X (s)}™, эмпирического среднего Мт[Х]у
распределения
сот(Л), эмпирической функции
Fm{x). Правда, в математическом контексте протокол
протокола
частоты

называют

конечной

числовой

последовательностью,

а

под

такие

эмпирическими подразумевают
усредненные
характеристики, которые вычислены именно для конечной
последовательности.
Словом, все начинается здесь с рассмотрения
вещественных функций X (s) вещественного аргумента s=l, 2,

...

выбирать в качестве «теоретического двойника»
случайной физической величины какие-либо более
абстрактные функции. Происходит, так сказать, арифметизация
теории вероятностей. Об этой главной черте мизесовского
и с

2&

отказа

подхода

к

оформлению теории
неодобрительно как об

математическому

вероятностей порою

отзываются

излишнем натурализме. С таким же успехом можно попрекать
теоретическую механику тем, что она выбирает в качестве
исходного объекта изучения функции вещественного

аргумента /.
Мизесовским «теоретическим двойником» допущения о
должной устойчивости эмпирического среднего является
о

постулат

существовании предела
MlX]

=

для идеализированного протокола

последовательности

традиционной
применяющейся в

Ньютона

и

бесконечной числовой

(9)

как четкое математическое

уже

неконечной математики,

понятие в стиле
систематически

■—

Равенством

{X (s)}i°.

математическое ожидание вводится

(9)

hmMjX]

науках со времен
равенстве прямо, хотя и
математических понятиях эмпирико-

Лейбница. В

естественных

этом

отражена в
индуктивная схема удлиняющейся серии.
Мизесовское определение (9) понятия математического
ожидания критиковали как неприменимое к объективной
реальности, данной нам в эксперименте, на том
основании, что количество испытаний на практике всегда
схематично,

ограничено.

Подобная критика

в

равной мере

относится

ко

всем

применениям понятия предела в естественных науках,
например, к понятию мгновенной скорости в механике.
Ответ на такую поверхностную критику давался не раз.
Разумеется, перейти к пределу в эксперименте
невозможно. С точки зрения прикладника, предельный переход
это удобный иероглиф, хорошо отражающий идею (но не
более) реальных процедур измерения и прогнозирования,
о которых прикладнику всегда приходится помнить. Можно
сказать, что предельный переход дает весьма схематичное
—

описание этих
построения

строгих

и

процедур, удобное прежде всего для
одновременно достаточно простых

математических теорий. Без предельных переходов многие строгие
теории из числа ориентированных на приложения
уподобились бы геометрии точек конечных диаметров и прямых
линий конечных толщин, которую пробовали строить, но
оставили,

как

неудобную

в

обращении.

Частным случаем постулата (9) является мизесовское
определение вероятности как предела частоты.
Соответственно,
функции распределения вероятностей вводятся в
29

строгой

мизесовской теории

равенствами

типа

^(x)=lim FJx),

(10)

m-»oo

где сходимость может пониматься в смысле разных метрик.
Таким образом, объектом изучения мизесовской теории

{X(s)}~'—в

последовательности

последовательности

бесконечные

оказываются

вероятностей

{XA(s)}i°,

—

для

числовые

двоичные

частности,
которых

постулировано

(9), (10). При этом

существование пределов вида

вовсе не

обязательном порядке распределения.
Можно ограничиваться рассмотрением моментов, т. е.
постулатами типа (9).
Подчеркнем, что здесь имеют дело с самыми обычными
предписывается вводить в

числовыми

последовательностями, для которых
постулируются вполне определенные математические свойства.

в
смысле
случайности
непредсказуемости
формально не имеет никакой связи с этими
последовательностями и свойствами. Другими словами, математический

аппарат

—

—

Категория

мизесовской

вероятностей, впрочем,

теории

как

вариантов данной теории (об этом уже
говорилось выше), не имеет ни малейшего формально-логического
отношения к непредсказуемости
это самая обычная
математика.
Особенность рассматриваемого нами теоретикои всех иных

—

вероятностного
внимание

во

постулатами типа

Так,

что здесь в

только

статистическая

...,

Xn{s)y

принимают

свойства, которые

их

—

задаются

оно

(6) в мизесовской
глобальное свойство функций

независимость
это

на

заданных

Как таковое,

чисел.

конечном счете

(9), (10).

теории вероятностей

Xi(s),

те

последовательностей

числовых

изучения

в том,

заключается

множестве

сходно

со

всеми

натуральных

другими

свойствами функций, например с их
или линейной независимостью.
Более точно суть
дела передавало бы здесь выражение «статистическая
глобальными

ортогональностью

последовательностей»,

независимость
мы

которого
статистической независимости протоколов
некоррелированность (8) представляет собой

когда

использовали,

ортогональность счетномерных

эмпирический
говорили

аналог

о

(7). Кстати,
не что
—

векторов

иное,

как

последовательностей

{^(5)}Г,..., {Хп(8)}Т.
Выше отмечалось,
прикладника

понятие

него

30

что даже с точки

математического

понятия

вероятности

и

зрения
и производные от
распределения вероятностей

ожидания

отнюдь ке намертво связаны с

категорией случайности.

усредненные характеристики в принципе
и
а
возможно
кое-когда
практически
целесообразно
измерять и для предсказуемых величин. Так что введение
этих
усредненных характеристик для обычных числовых
последовательностей ни с какой стороны не выглядит
экстравагантным.
Мы заостряем внимание на такого рода вопросах с целью
лишний раз напомнить, что любая прикладная теория
расчленяется на два различных по своему характеру блока:
математический аппарат и интерпретацию этого аппарата.
Данные блоки как раз и сравнивают с жерновами и
засыпкой. Для успешного применения прикладной теории
необходимо отчетливо разграничивать эти блоки. В
противном случае будет непонятно, за что в выводах теории
Названные
—

—

отвечает математический аппарат с его высокой четкостью,
а что порождено гораздо более расплывчатыми правилами
интерпретации.

Прикладник

должен достаточно ясно представить

себе,

теоремах, входящих в
математический блок теории, а затем лично провести интерпретацию
их
условий и заключений, никому не передоверяя эту
работу. В то же время доказательства теорем можно
полностью отнести к компетенции математиков, следуя идее
разделения труда. Все это справедливо и для прикладной
что

именно

доказано

в

вероятностей.
Думается, что различать,
вероятностей жернова, а где

теории

где

в

прикладной теории

было бы намного
бы при изложении математического блока этой
теории избегали терминов «испытание», «событие» и
«случайная величина», явно перегруженных ассоциациями,
и вообще старались бы не
упоминать о случайности. В
математическом
тексте,
по-видимому, лучше не упоминать
и о
некоррелированности: корректнее говорить об
ортогональности. Математические результаты всегда желательно
легче,

засыпка,

если

на нейтральном для прикладника языке с
тем, чтобы не навязывать заранее интерпретаций. К

формулировать
примеру,

математический

Компетенция
примерно столь же
в

вопросах

руководствах для
применением математических
и «интеграл», а не говорят
теплоемкостях, площадях и т.

анализ

прикладников излагают
терминов «производная»
исключительно о
скоростях,

даже

в

с

математиков по части

п.

интерпретаций

ограничена, как и компетенция прикладников
строгой математики.
31

Повторим,

что

прикладник может вполне осознанно
интерпретировать теоремы, по-видимому, только при ясном
понимании

их

основного

Достигнуть

чисто

математического

нужных для
теоретико-вероятностных теорем в общем-то не
труднее, чем разобраться в теоремах из втузовского курса
анализа. Например, в сформулированной выше теореме 1 с
математической точки зрения имеют дело, конечно же, не
со случайными величинами или событиями, а с ансамблем
статистически независимых двоичных последовательностей
содержания.

такового

понимания

практики

(будучи

стеснены

предшествующим контекстом, мы
теореме 1 на термине «двоичные величины»,
опустив, однако, эпитет «случайные»). В логичной
это
интерпретации двоичные последовательности
остановились

в

<—

протоколы-индикаторы набора Лх,
событий. Величина

Ап независимых и равновероятных
это количество всех тех
Yn(s)
набора, которые наступили в

...,

*—

событий из указанного
испытании s, а вторичная вероятность Р в заключении теоремы 1
оказывается при такой трактовке самой обычной
статистической вероятностью. Таким образом, в логичной
интерпретации теорема 1 непосредственно относится к некоторому

набору
событию

исходных событий

Аъ

...,

Лп,

а не к

Отметим, что условие 2 в теореме 1 можно
некоррелированностью двоичных величин, т. е.
ортогональностью

последовательностей

{XAl(s)}?,

математической стороны, теорема
формы

одному

Л.

...,

Бернулли

ЗБЧ, например, теорема Чебышева

заменить

{^ап (s)}T
и

.

С

другие

в своих сильных

вариантах представляют собой не что иное, как теоремы об
ортогональных функциях. Таковыми они, вероятно, и
должны с самого начала преподноситься прикладникам. По
нашим
содержание

наблюдениям, «выудить»
ЗБЧ

это математическое

по теории
стандартных руководств
вероятностей, стремящихся оперировать исключительно
эмпирическими
терминами, представляется для прикладников
из

(притом не только для начинающих) довольно сложным
делом. Неясность же в этом вопросе поддерживает
застарелые иллюзии насчет большого принципиального и
практического

значения

Резюмируем.
угодно,

ЗБЧ.
точки

зрения прикладника, предельные
уж важной чертой мизеподхода, а представляют собой средство и, если
издержки строгой формализации. Главная черта

переходы
совского

С

не

являются

слишком

мизесовского подхода состоит в том,
32

что здесь с самого на-

берут все так, как оно есть на самом деле в
Неудивительно, что в инженерной и физической
литературе вводят математическое ожидание равенством
(9) нередко без ссылок на Р. Мизеса. Мизесовский подход

чала

эксперименте.

лишь

предоставляет, так сказать, права гражданства в
теории вероятностей тем давным-давно известным эмпирико-индуктивным схемам обработки данных, которые
восходят к

самим основам естественнонаучного метода с его

требованием многократного воспроизведения
Сравнение с аксиоматикой

В этой широко известной аксиоматике теории

Колмогорова.

вероятностей
случайной

результата.

в

качестве

«теоретического двойника»

выбирается измеримая функция Х((о),
абстрактном вероятностном пространстве й.

величины

на

заданная

Мизесовский подход, скорее всего, не может быть
полностью уложен в рамки аксиоматики Колмогорова, так как
точку со практически невозможно отождествить с номером
s испытания, если s пробегает счетное множество значений.
Невозможность обусловлена свойствами понятия меры.
Основная теоретическая проблема в мизесовском
подходе состоит, по-видимому, в том, чтобы найти
конструктивные теоремы существования числовых
последовательностей

{X(s)}i°,

для которых имеет место нужная

(10) к наперед заданной функции распределения.
Эта проблема пока решается только для слабой
сходимости
[22]. В аксиоматике Колмогорова имеется
сходимость

теорема существования: для любого согласованного
семейства функций распределения существует
вероятностное
пространство Q и набор функций Х1(со), Х2(со),...,

следующая

coeeQ,

для

совпадает

семейство

которых
с

функций

согласовалным

заданным

распределения
семейством. Данная

теорема не решает вышеуказанной теоретической проблемы
хотя бы потому, что пространство Q непохоже на
множество натуральных чисел s= 1,2,
Мизесовский подход нуждается в особой разработке
теоретико-числовыми методами, не свойственными
аксиоматике Колмогорова. Высказывалось мнение, что этот
подход страдает органической нестрогостью. Между тем это
не так, о чем свидетельствуют, в частности,
упомянутые
теоремы существования [22]. При желании можно вполне
строго оформить основы мизесовского подхода и в виде
...

Противопоставление

четкого

свода

подхода

аксиоматическому

целиком

основано

аксиом.

на

методу

в

теории

мизесовского

вероятностей

недоразумении.
33

итоги.
Выше отстаивалась
В
каждой
зрения.
практической задаче, к
которой всерьез привлекают теорию вероятностей,

Подведем
следующая точка
решению

набор исходных величин, многократно
измеряемых в эксперименте] непредсказуемость этих величин
не является ни достаточным, ни необходимым условием
имеется

свой

применимости к ним теоретико-вероятностных понятий.
Действительно необходимым условием эффективного
применения
теории вероятностей является статистическая

устойчивость, т.
характеристик исходных
по

е.

устойчивость усредненных

величин.

этим

Теория вероятностей

позволяет

усредненным
характеристикам аналогичные характеристики других,
вторичных
величин, если известен оператор, связывающий вторичные
величины с исходными. При этом гарантируется, что
рассчитанные
разумеется, без ошибок
вторичные
усредненные характеристики будут устойчивы в нужной степени,
рассчитать

исходным

—

если

достаточно

—

устойчивы

исходные

усредненные

Однако теория вероятностей не может дать
никаких
гарантий относительно исходной статистической
устойчивости. Полных гарантий здесь вообще дать нельзя,

характеристики.

так как на практике речь идет о прогнозах. Можно лишь
что
об
допущения-прогнозы
устойчивости
утверждать,

оправдываются чаще, когда
эмпирической индукции.

они

принимаются

на

основе

Далее, при проведении теоретико-вероятностных
часто принимают допущение о статистической
независимости длинных протоколов. Согласно определению (6)
о
статистической независимости можно говорить только
расчетов

как принято допущение о должной
статистической устойчивости (точнее, об устойчивости n-мерной
эмпирической функции распределения).
Таковы логика введения и соотношение двух наиболее

после того,

фундаментальных концепций прикладной теории
вероятностей
концепций статистической устойчивости
результатов измерений и статистической независимости
—

протоколов

измерений.
При введений

этих

фундаментальных концепций

нам

представился случай официально привлечь к делу
понятие независимости испытаний, являющееся между тем

так и не

одним

Был

из

основных

понятий

математической

статистики.

разговор об однородности испытаний, т. е.
стабильности контролируемых условий эксперимента U, но в
формулы, с участием которых вводились обе фундаментальные
34

условия U не

концепции,
надеяться

на введение

вошли.

условий U

в

Видимо,

нельзя

количественные

и

понятия,

и предложения теории
вероятностей, как бы она
строилась. Слишком разнообразны эти условия в
разных приложениях теории вероятностей, и подчас они очень
сложны. Самым подробным отчетом о проведенной серии
испытаний, который под силу «переваривать» теории
вероятностей, является предельно лаконичный протокол,
где от каждого испытания остались лишь его номер s
да результат измерения.
Для того чтобы сформулировать

формулы
ни

определение независимости испытаний, апеллирующее
к такому протоколу, необходимы какие-то
нетривиальные идеи. Ниже мы коснемся этих идей, отсутствовавших
в
классической теории вероятностей и составляющих
«высший слой» мизесовского подхода.
Выходит, понятия статистической устойчивости и
статистической независимости величин не нуждаются для
своего введения в понятии независимости испытаний.
только

Наоборот,
вводиться

последнее
на

их

понятие

каким-то

образом

должно

основе.

Глава 3. КРИТИЧЕСКИЙ

АНАЛИЗ МЕТОДА

МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Определения
статистикой

просмотрев
из

того, что понимают под математической

(МС),

разноречивы,
размеров

почтенных

обычных

в

чем

легко

коллекцию

убедиться,
[23].

определений: «Математическая

Вот

одно

статистика

—

наука, исследующая количественные соотношения
массовых явлений. При этом к области математической
статистики

относятся

те

количественные

отражают специфические черты
массовых. Математическая статистика

соотношения,

этих

явлений

тесно

которые

как

связана

с

теорией

вероятностей, предельные теоремы которой
больших чисел и другие
образуют теоретическую
—

закон

основу
вопросов. Методы математической
статистики
универсальны и приложимы к самым различным
областям знания: общественной, экономической,
—

решения

многих

ее

технической, биологической и т. д.»
В первой же фразе процитированного определения и
во всей книге [24], из которой оно взято, а также в ряде
других руководств видна тенденция отождествлять МС
с любыми приложениями математических символов и по35

нятий

к

статистике.

К тому располагает сам термин
наподобие того, как располагают

«математическая статистика»

к чересчур широким толкованиям упомянутые выше
термины «теория игр» и «планирование эксперимента».
В настоящей брошюре МС трактуется более узко.
Сопоставив между собой разные руководства по этой
дисциплине, можно еыявить не только отличия, но и более или
менее определенное смысловое ядро, общее для большинства
руководств. Мы подразумеваем под МС именно такое ядро,
поскольку, надо полагать, в нем и сосредоточены наиболее
характерные черты метода МС. Кстати, с этих позиций

[24 ]

книга
определения

—

за вычетом процитированного нами
раз представляется руководством не

—

как

по

МС,

опубликована
просто
серии
«Математическая статистика для экономистов». В [24 ]
обстоятельно рассказано о понятиях статистики, т. е. о
по

а

хотя

статистике,

она

и

в

всякого

рода усредненных характеристиках, против
которых вряд ли уместно выдвигать какие-либо
общие принципиальные возражения. В главе 2 мы тоже
рассказывали о том, что понятия статистики служат
прообразом и «метрологически обеспеченной» интерпретацией
теоретико-вероятностных понятий. Ясно, что
использования

практическую полезность теории вероятностей также вряд ли
отвергать в принципе.
Ниже критикуется только специфическая манера
использования
теории вероятностей, характерная для МС.

уместно

Истоки

этой

манеры

охарактеризованы

в

третьей фразе

это
законы
определения МС
больших чисел, а точнее, их исторически первые
интерпретации, на удивление прочно вошедшие в традицию.
Альтернатива общей установке
математической статистики. Во всех

процитированного

руководствах по
определении,

МС,

нами

—

процитированном выше
дать
следующая общая установка

а не только в

сквозит

—

универсальную теорию измерения усредненных характеристик.
От этой теории надеются получить ответ на вопрос,
достаточна ли проведенная серия испытаний для измерения

нужной усредненной характеристики
точностью и надежностью.

с

требуемыми

Последний вопрос короче

так:
представительна ли имеющаяся выборка? На
пути МС развилась в обширную и изрядно сложную
дисциплину.
Между тем простые соображения естественнонаучного
здравого смысла, изложенные нами в главе 2, заставляют

формулируют

этом

36

самой возможности построения такого рода
и сложной
теории, которая в самом деле
бы очень полезной. Дело в том, что едва ли
как-то всерьез «вычислить» или «обосновать

сомневаться

в

универсальной
оказалась
возможно

математически»

бы

какого

надежность

начальных

посылок

ни

—

являются

прогнозами

и

было прикладного расчета. На практике
посылки
засыпка в жернова
математики

начальные

всегда

точность

то

неких

по

—

необходимости

перманентностей. В

интуитивными
естественных

науках

издавна принято подтверждать перманентности не
сложными теоретическими построениями и выкладками,

а

убедительной демонстрацией многократно воспроизведенных
результатов эксперимента, т. е. эмпирической индукцией.
Таким

альтернатива общей установке МС
прикладных задачах всемерно
воздерживаться от теоретизирования на этапе принятия
начальных посылок-прогнозов, концентрируя усилия на эмпирико-индуктивном обосновании правдоподобности этих

образом,

состоит в том,

прогнозов.

чтобы

в

Сколько-нибудь

бывает полезна

сложная

математическая

в статистических задачах

оснастка

что потом

разве
вторичных усредненных
характеристик по уже надежно спрогнозированным исходным
характеристикам.
Усомнившись в реалистичности общей установки МС,
мы можем ожидать, что анализ логической структуры и
практического содержания типичных понятий и
на

этапе

утверждений этой
Наш

—

вычисления

анализ

дисциплины

будет

выявит

касаться

не

в

них

уязвимые

математических

места.

тонкостей,

кардинального для практики вопроса: каким
ставить
эксперимент для верификации, т. е.
проверки соответствия типичных утверждений МС
объективной реальности? Объявить эти утверждения не
подлежащим «примерке» хотя бы к мысленному эксперименту
значило бы исключить их из компетенции естественных
наук. Мы приступаем к примерке, оставаясь на тех же
метрологически жестких позициях, которые были заняты
нами с самого начала: любое математическое ожидание,
в частности любая вероятность, трактуется статистически.
Начнем с разбора истоков МС.
а

лишь

образом

надо

Традиционные интерпретации
предельных теорем. Возьмем в качестве примера
традиционную формулировку теоремы Бернулли. Для
удобства

ссылок

эту формулировку
сравнить теорему 2 с

назовем

Рекомендуем сразу

же

теоремой 2.
теоремой 1.
37

Теорема 2.

Пусть проводится

п

испытаний,

в

наступить или не наступить
которых
некоторое событие Л, и пусть Yn— количество наступлений
события А в этой серии испытаний. Пусть, далее,
может

из

каждом

выполнены следующие два

Р

1) вероятность

условия:

(А)

события А

в

испытании

каждом

равна р\

2)

испытания

Тогда

независимы.

для вероятности

(11)

Р(п,е)=Р(\<*п(А)-р\<г)
на

чем

(on(A)=Yn/n

что частота

того,

е,

отклонится

от

не

р

более,

справедливо равенство

(12)

HmP(n, e)=l, уе>0.
П-»оо

В теореме 2 говорят об одном многократно наблюдаемом
событии А и, следовательно, с математической точки
зрения

—

об одной двоичной последовательности

{ХА(5)}Г

протоколе-индикаторе
идеализированном
(если, конечно, слова «испытание» и «событие»
в

—

события

этого

понимают

буквальном, обыденном смысле). Этим теорема

заметно

2
ансамбль
где
1,
теоремы
фигурирует
последовательностей, или в интерпретации

отличается

двоичных

от

—

набор событий А19

...,

Ап.

В теореме 2 налицо две
МС

независимость

—

вероятности частоты

соп(Л)

фундаментальные

испытаний
к

и

сходимость

вероятности Р

концепции
по

(А). Обсудим

концепций.
Независимость испытаний. В МС

традиционные разъяснения этих

если
стабильны
называют
иногда
независимыми,
условия эксперимента. Выше отмечалось, что стабильность
контролируемых условий эксперимента U не всегда
обеспечивает саму применимость
теории вероятностей и что
U
не
вообще
условия
могут входить в количественные

испытания

формулы

и предложения теории вероятностей, как
строилась.
Менее легковесные определения, даваемые здесь МС,
сводят независимость п испытаний к статистической
независимости п величин. Это, безусловно, необходимо сделать,

понятия,

бы

она

если

ни

стремиться

представить теорему 2 в

качестве одной

интерпретаций теоремы 1. В МС такое сведение считают
тривиальной задачей, которая сразу решается, если
из

положить,

38

что каждое испытание

порождает случайную

величи-

(см., например, [25]). Тогда п испытаний породят
случайных величин, и статистическая независимость
последних будет означать независимость п испытаний.

ну

п

Однако каждое отдельное испытание s, понимаемое как
измерение величины X, порождает все же не случайную
число X (s).
величину, а только
одну ее реализацию
В роли случайной величины, точнее, объекта, к которому
применимы понятия математического ожидания или
вероятности, выступает при статистическом подходе весь
—

длинный

протокол

измерений
как

последовательность
все испытания

{X

всего

порождают

(s)}?,

одну

т.

е.

числовая

теореме 2
двоичную случайную

целое.

единое

Так,

в

величину.
Если позволительно так выразиться, волюнтаризм
соответствия
«п испытаний
п
в
величин»
случайных
счете
конечном
в
ясных
МС
оборачивается отсутствием
—

правил для эмпирической проверки независимости
испытаний в ситуации, когда сначала располагают одним
протоколом, скажем, одним протоколом-индикатором {XA(s)}?t
как в теореме 2. Неясно, какому правилу надо следовать,
чтобы перейти от одного исходного протокола к ансамблю

{Xjn(r)}T, j=~n,

(13)

V"

протоколов с тем, чтобы проверить их статистическую
независимость, руководствуясь определением (6), и таким
способом действительно проверить независимость п
из п

испытаний.

Итак,
испытаний

—

что

можно

где

что

соответствие

«п

представляет собой

в МС не
домысливание ансамбля случайных величин
сначала ведут речь об одной случайной величине,

величин»

как

главное,

одну

утверждать,

случайных

иное,

там,
а

п

на

самом

случайную

деле

в эксперименте только
Подобное домысливание

имеют

величину.

—

одна из характерных черт метода МС. Таким силовым
приемом, конечно, удается свести на словах теорему 2 к схеме,
по которой построена теорема 1. Но в результате остаются
по

не только
условия традиционных
предельных теорем, где непременно
независимые испытания (измерения, опыты), но

существу

неясными

формулировок
фигурируют

поскольку и для последних не
правил эмпирической проверки; в
традиционных комментариях к законам больших чисел нет
достаточно четких
разъяснений и того, что представляет
сходимость по вероятности.
и

их

предлагают

заключения,
ясных

собой

39

Сходимость

вероятности. Обратимся
теоремы 2. Для того, чтобы проверить в
эксперименте наличие сходимости (12), нужно измерить
вторичную вероятность Р (я, е). Значит, нужно
организовать
длинную серию вторичных испытаний, каждое из
которых состояло бы в проверке выполнения неравенства
типа того, что довольно условно указано под знаком
к

по

заключению

вероятности в формуле (И). Для этого необходимо иметь не
одну серию-выборку, состоящую из п испытаний, как это
может показаться при чтении формулировки теоремы 2,
а много выборок по п испытаний. Обозначим эти выборки,
точнее их протоколы, через 5(г, n), r=l, Q,
где г
номер
количество наступлений события
выборки. Пусть Yn(r)
их частота в выборке 5(г, п).
Л, a (urn(A)=Yn(r)/n
Назовем процедуру формирования многих
выборок схемой
многих серий, тогда как рассмотренные в главе 2 схемы
удлиняющейся и фиксированной серии станем называть
схемой одной (удлиняющейся или
для контраста
—

—

—

фиксированной)

серии.

Подсчитав обычным образом для серии
вторичных испытаний частоту

r=l, Q

coQ(n, e)=(oQ( |согп(Л)—р|<е),

(14)

измерить вероятность Р (п, е),
руководствуясь в идеале схемой одной удлиняющейся
Такое измерение схематически формализуется по

можно в самом деле

как

серии.

Мизесу

предельный переход
P(nt e) lim coQ(n, e).

(15)

=

теорему 1, можно видеть, что теорема 2
чертах сводится к ней, если выборка 5
представляет собой поперечное сечение ансамбля

Перечитав

существенных

S(r, n)

Вот

выборок

из

и

=

(г, п)
(13);

{Xjn (г) |/ =17^},

получается, что правил для

одной исходной

в

формирования

последовательности

{XA(s)}T

в

МС не дают, коль скоро не дают правил для формирования
ансамбля (13). Этот ансамбль, а с ним и выборки 5 (г, п)
в МС попросту домысливают. Можно считать и так: здесь
домысливают много

40

выборок 5 (г, п),

таких, что после объе-

динения чисел Xjn (г),
в последовательности

стоящих в

статистически независимый ансамбль

абстрагируются

возможности

выборках

по

эксперимент

схеме

j-x

местах,

получается
В МС вообще

(13).
факта,

от того

сходимости по вероятности

верификации

на

{Xjn(r) |r=l,2, ...}

по

что для

необходимо проводить

серий. Даже

многих

грамматически
традиционные формулировки законов больших чисел,
как и формулировка теоремы 2, построены так, будто дело
касается только одной серии из п испытаний.
Соответственно в МС никогда не выписывают аргумент г вторичных
случайных величин типа Yn(r) или (огп (А)
(сравните
все

в этом смысле довольно условную
традиционную запись (11)
с нашей «неиносказательной» записью (14).
—

Две

—

конкурирующие

математические

статистической

модели

Таким

устойчивости.

образом,

в

традиционных
предельных теорем
комментариях к ним нет ясных
правил для верификации ни условий, ни заключений этих
теорем. Именно это и породило в свое время иллюзию того,
что законы больших чисел решают не ординарный вариант
основной математической задачи теории вероятностей, а
и в

формулировках

теоретически выводят устойчивость средних из
однородности испытаний. От подобной иллюзии окончательно
отмежевались

вероятностей

современные

руководства

по

отождествляют

со

частоты

(12),

а

о

в

сходимостью

заключениях

не

теории

МС; подборку соответствующих выдержек

публикациях автора [9, 13].
Данное обстоятельство находит отражение, в
том, что статистическую устойчивость в МС
найти

можно

в

и

и

законов

частности,

по вероятности,
фигурирующей в
больших чисел. Так, устойчивость
МС отождествляют со сходимостью

события А в
мизесовской модели устойчивости
Р

{А)

=

\\т

(16)

сот(Л)

т-»оо

обычно

не

упоминают.

между собой сходимость по
вероятности и схема многих серий в принципе неспособны
дать завершенное описание феномена статистической
устойчивости. В них налицо логическое зацикливание,

Между

являющееся еще

Зацикливание

тем тесно связанные

одной характерной чертой

состоит

в

метода МС.

следующем.

Измерение первичной вероятности Р (А) по схеме
серий заключается в таком оценивании близости
первичных выборочных частот согп (А) к определенной
многих

кон-

41

станте,

предполагает

которое

(я, е). Последнее

вероятности Р
оценивании

насколько

того,

измерение

вторичикой

же, в свою очередь, состоит в
близки к определенной

вторичные частоты coQ (n, е). Следовательно, мы
приходим в принципе к такой же задаче, с какой начинали,
только теперь все будет технически значительно труднее,
так как вторичные испытания г намного сложнее первичных
испытаний s. Назовем это обстоятельство первым
парадоксом математической статистики.
константе

Если, проявляя упорство, подвергнуть вторичные
частоты точно
к

придем

отличаются от

такому

рассмотрению, как и первичные, то
что вторичные частоты
константы-вероятности Р (п, г) менее,

же

вероятности того,

вторичной

чем на ра. То есть мы придем уже к серии

испытаний. И

так

далее,

А. Н. Колмогоров
такое

вполне

но

раз,

освободиться
обратиться

этого

этому поводу заметил: «При желании
повторять неограниченное число

можно

понятно,

от

Другими

это

в

не

на

позволит

кроме

зацикливание схемы многих

примитивном, грубом

как

(12)

ни

было

совсем

понимании

на практике
разорвать логическое

серий, обратившись

к схеме

мизесовской модели устойчивости

от

нам
этапе

последнем

словами, вполне понятно, что

выхода,

к

что

необходимости

к вероятностям
термина».

иного

т. е.

по

рассуждение

серий серий
популярной статье [26]

ri

под знаком предела в

вероятностей.

(15)

или

одной серии,

частот.

(16)

нет

В отличие

нет каких

бы

то

Если хотите, мизесовское

вероятности как раз и есть обращение к вероятностям
примитивном, грубом понимании этого термина.
По здравому смыслу, разрыв логического
зацикливания, названный А. Н. Колмогоровым «последним этапом»,
необходимо произвести так, чтобы вероятности самого
высокого
ранга,
фигурирующие в математической модели
определение
в

данного конкретного эксперимента, в самом деле
измерялись бы в этом эксперименте; по-видимому, трудно
оправдать домысливание вероятностей хотя бы одного лишнего

ранга.
Тем не менее
основ метода МС,
сейчас внимание

1) Как
(12)

в

определении

предельные
подчеркивают

42

домысливание составляет одну из
этому мы еще раз вернемся. Обратим
на следующие три факта:
мизесовском определении (16), так и в
и

к

сходимости по вероятности участвуют

переходы.
лишь

такое

Однако сторонники МС обычно

трудности,

возникающие при физической

ин-

терпретации мизесовского (между прочим, более простого)
предельного перехода.
2) Согласно формуле (14), вторичные частоты и
вероятности можно найти только после того, как
измерена
первичная вероятность р=Р(А)\ назовем это обстоятельство
вторым парадоксом МС. Для измерения Р (А) теперь уж
с
полной очевидностью виден единственный путь
—

одной серии,

к схеме

к

т. е.

обращение
вероятности. Следовательно,

определению

к

мизесовскому
этому поистине

неизбежному определению пришлось бы обращаться при
Р (п, е)
измерении вторичной
вероятности

реальном

даже

дважды.

Логическое зацикливание

3)

не

от

зависит

совершенно
независимости испытаний.

отсутствующей
структурный недостаток

Внесение

МС,

в

в

схеме

истолкования

не в

в

это

истолкование

состоянии

схемы многих

серий

многих
понятия

ясности,

исправить

серий, заключающийся

в

переходе от первичных вероятностей к более сложным
вторичным вероятностям.
Из традиционных формулировок законов больших чисел
МС заимствовала не только модель статистической
устойчивости, но и наиболее характерные черты всего метода
в целом. Мы их, собственно, уже рассмотрели при анализе
теоремы 2. Теперь «пройдемся» по ним специально,

обсуждение

подразделив

1°

—

3°.
1°. Постулат

несколько

условно

—

на

пункты

—

о

существовании

вероятностей
случайных величин. В

распределения

для

исходных

условия

теоремы

2 входит допущение о существовании вероятности события
А (пусть в не совсем понятном смысле).
Аналогично во
всей МС начинают, как правило, с того, что постулируют

существование,

вероятностей
величин.

для

а

то

и

конкретный

рассматриваемых

вид распределения

непредсказуемых

Отсюда выражения: «Рассмотрим выборку

распределения

Fx (*)». Затем

плотности

или

распределения

из

ставят задачу оценивания

функции

«объективно существующего»
вероятностей. Эта задача послужила и
параметров

служит поводом для

разработки

довольно внушительного

математического
По
о

такой

теория

оценок

Р.

Фишера,

руководстве [25] для экономистов
«Именно теория оценок позволяет научно подойти

которой, например,

сказано:
к

аппарата.
схеме построена
в

обработке выборочных

статистических

наблюдений

и

43

применить

в каждом

конкретном случае

дает возможность извлечь из

тот

выборочных

метод,

который

данных максимум

и обеспечить наиболее точные и
свойствах генеральной совокупности».

нужной информации
надежные

о

выводы

Так построены,

в

частности,

метод максимального

правдоподобия, теория доверительных интервалов, теория
и

статистик

порядковых

многочисленные

концепции

(например, теория
автоматических системах).

более

дуального

специальные

управления

в

В результате в МС, образно говоря, на большой
проходят мимо самого трудного и интересного
места
эмпирического исследования статистической
устойчивости. Вопрос о том, применимо ли к данной конкретной
непредсказуемой величине понятие распределения
вероятностей или хотя бы понятие математического ожидания,
как бы и не ставится.
более осторожный подход, при
Альтернативу
скорости

—

—

сосредоточивается на эмпиперво-наперво
рико-индуктивном обосновании прогноза о статистической
котором внимание

устойчивости,
Приведем в

—

[2 ]

по

малом

мы

обрисовали

в

главе

2.

этой связи критическое замечание из статьи
поводу вычисления доверительного интервала при
числе опытов:
Ю. Л.)
«Для этого (вычисления.
—

довольно тонкий аппарат, основанный на
допущении, что нам известен закон распределения
случайной величины (нормальный). И опять возникает вопрос;

разработан

откуда, собственно, это известно? И с какой точностью?
И какова, наконец, практическая ценность самого
«продукта»
доверительного интервала? Мало опытов
а

—

—

значит,

мало

при

этом

информации, и
доверительный

не так

меньше,

вероятность
С наших
и

наше

плохо.

немного

уж важно, тем более,
произвольно».

что

и

А будет ли
больше или

доверительная

назначена

относительно

откуда

дело

интервал

позиций
мягкой

представляется еще
сомнений. Можно добавить:

такое замечание

формой

насколько точно

известно,

что в

конкретной ситуации вообще уместно говорить

вероятностей? Последний
излишней осторожностью разве

статистической физики,

вопрос
что в

данной
о

распределении
представляется

фундаментальных разделах

где

рассматриваются
колоссальные коллективы частиц и огромные количества
сравнительно простых актов
Стабильность объекта
скажем,
44

в

взаимодействия между

частицами.

изучения там несравненно выше, чем,
технике или экономике. И там для проверки-

следствий

из принимаемых гипотез можно поставить
достаточной
чистоты, точности и повторяемости, а
эксперимент
строго говоря, лишь это делает позволительным введение

в

гипотезы таких

реального

понятий, которые

сами

далеки

от

эксперимента.

Допустим

все же, что распределение вероятностей
рассматриваемых непредсказуемых величин существует. Но
и тогда, следуя
[2], можно не разделять высокого мнения
о теории оценок,
выраженного в нашей цитате из [25].

Ведь теория
информации

не

оценок

просто

из

позволяет

извлечь

выборочных

максимум

как это

данных,

может

показаться, скажем, при чтении [25].
Принимается еще
постулат о виде распределения вероятностей. Этот постулат

отражает реальность лишь с какой-то точностью, на
эмпирическую оценку которой теория оценок отнюдь не
нацеливает. Выводы же теории оценок и сама теория, вообще
говоря, меняются, если изменять постулируемое
распределение.

Поэтому

полагалось

бы вычислить,

к

какой размытости

параметров приведет ожидаемая
постулируемого распределения. Данная задача
дает повод для развития еще более тонких и внушительных
для проведения
теорий или по меньшей мере
в

искомых

оценках

размытость

—

трудоемких

на

ЭВМ.

Тут

мы

подчеркнем, что оценить
размытость распределения всерьез, т. е. путем
аккуратного эксперимента, наверно, не проще, чем прямо оценить
экспериментальным путем искомые параметры
распределения.
расчетов

Кроме

того,

теория

информации,

оценок

извлекает

не

абсолютный

а

максимум в смысле некоторых
специфических критериев. Их практическая полезность
не бесспорна. Наконец, эта теория опирается на постулат
о независимости испытаний. С ним, как мы видели, тоже
максимум

не

все

ладно.

Таким
что

образом,

теория оценок

можно

не

позволяет

обработке наблюдений. Надо

соглашаться
очень

уж

с

[25]

в

том,

научно подойти

к

руководства по МС
вообще не упускают случая отождествлять эту
действительно непростую дисциплину с научным подходом в
статистике. Здесь мы еще раз процитируем статью [2]:

«Математический аппарат

имеет

сказать,

некое

гипнотическое

свойство,

безоговорочно

верить своим
расчетам, и тем больше верить, чем «кудрявее»
примененный аппарат, чем больше времени своего и машинного

и исследователи часто склонны

45

потрачено

и

чем

место

первое

сложности

по

отзываются

больше бумаги

правдоподобия,

максимального

(например,

точности доставляемых

в

Так,

исписано».

о

методе

пожалуй,

занимающем,

получаемых уравнений,
как об оптимальном

[25])

нередко
в смысле

им оценок.

Научный подход прежде всего предполагает создание
в любой прикладной теории интуитивно убедительного
эмпирического базиса. Сложность, строгость и стоимость
математического

аппарата

—

так

математической

сказать,

с
надежностью
должны сообразовываться
надстройки
базиса. Это издавна применяемое прагматическое правило
—

метко

названо

в

[2 ] принципом равнопрочности

прикладного

элементов

исследования.

всех

Теория

оценивания,
МС, едва ли в

составляющая значительную часть всей
должной мере удовлетворяет данному принципу.
о
2°. Постулат
существовании

вероятностей

распределения

оценок.

выборочных

для

Домысливание

В теореме 2 говорят об одной выборке
подразумевают много таких выборок. При
этом рассматривают вторичную случайную величину согп(Л),
и
ее
г=1,2,
распределение вероятностей. Аналогично
во всей МС обычно переходят от исходной X (s) к вторичной
многих

выборок.

объема

/г,

но

...

величине <хгп

[X], являющейся выборочной оценкой

искомого
величины

параметра
X (s). При

а

[X ] распределения вероятностей

этом

постулируют существование,

а

то

и

конкретный вид распределения вероятностей величины
В терминах этих вторичных распределений
агп [X].
выражаются, скажем такие свойства выборочных оценок, как
несмещенность, состоятельность, эффективность.
Допустим, по существу задачи всерьез интересуются
величиной аГп [X], а не просто параметром
соответственно проводят эксперимент по схеме

а

[X ],

и

серий,
выборок. (По такой
схеме проводилась, например, усиленная верификация
законов
Менделя, обсуждавшаяся в [7, 9, 10]). В этом
случае роковой
разницы между исходной и вторичной
случайными величинами, видимо, нет, так что по поводу
вторичных распределений можно лишь повторить все
реально получая большое

многих

количество

сказанное в постулате 1° относительно первичных
распределений.
Но чаще всего фактически интересуются только

параметром

а

обработав
45

[X ]. В МС обычно
как

единое

целое

aN [X ],
имеющийся протокол

находят его оценку
весь

{X (s)}". Напомним,

через N мы в главе 2
проведенных
испытаний, а обработку упомянутого типа назвали схемой
фиксированной серии. Применение этой схемы в МС
домысливанием
многих
сопровождают
выборок 5 (г, ЛО,

г=2,3,
единственной

что именно

обозначать общее

условились

тогда как,

...,

количество

повторяем,

реальной выборкой S (1,

имеют дело с

A/)={X(s)}f

.

Путем

такого

погружения исходной задачи в схему многих
с непременным участием
стараются найти
1° и допущения о «независимости п испытаний»

мысленного

серий
постулата

—

—

*N[X]=a*N [X]. При этом
оптимальную оценку
погружении как раз и впадают в логическое зацикливание с его
двумя парадоксами.
Альтернатива такова: за пределами статистической
физики вести речь по возможности только о тех случайных
a

величинах, которые действительно измеряются в длинных
Соответственно ссылаться только на
сериях испытаний.
действительно
измеряемые
теоретико-вероятностные
характеристики. Их измерение выполнять по схеме одной

фиксированной) серии.
процедуры оценивания в МС рассчитаны
домысливание многих серий; обычно не

удлиняющейся (а

Интересно,
именно
разъясняют,

на

как

не

что

пользоваться

этими

процедурами, когда

берут несколько выборок S (г, я), r=l,Q(N=Qn).
Например, метод максимального правдоподобия даст тут

действительно

оптимальных

несколько
за

что

же

из

этих

боролись,

оценок

а*п [X]t

оценок

r=

1,Q. Неясно,

расчеты,— какая
оптимальная? Данный метод, если

выполняя

самая

сложные

присмотреться, исходит из того, что первая и единственная
самая вероятная как раз в нужном нам смысле.
выборка
Наверное, было бы правильней связать название такого
—

метода

Не

с

максимумом

менее

оптимизма.

странно при наличии нескольких

выборок

выглядит и

концепция доверительного интервала, допустим,
частоты согп(Л),
для вероятности Р
r=

1,Q

(А). Найдя выборочные
доверительной вероятностью

и задавшись

5s,

можно

рассчитать соответствующее количество доверительных
так сказать
доверительную полосу
интервалов
—

iiPiir),

РМ\г=Щ

переменного сечения. Что
Теория ручается здесь только
допущениях

(постулат 1°

плюс

(17)

затем с ней делать, неясно.

за то, что

при принятых
допущение о «независимости

п
47

испытаний»)
{А)^(рх{г),

тех г из (17),
для
процент
которых
р2 (г)),
равен 3M00 для Q->oo.
Относительно же доверительного интервала (рх (г),
р2 (г)),
действительно вычисляемого на практике по первой и
единственной выборке, вообще ничего определенного сказать,
видимо, нельзя, поскольку он является всего лишь одним
из сечений полосы (17).
В руководствах по МС все это либо не разъясняется,
либо разъясняется крайне бегло, без выписывания
В результате у многих, кто вычисляет
аргумента л
доверительный интервал
{р1 (1), /?2 (1)), последний, вероятно,

Р

с таким фиксированным интервалом (plt p2),
который попадает SM00 процентов частот соГГ1 (Л),
г=1, Q для Q->oo. Однако между двумя этими

ассоциируется

в

интервалами на самом деле нет ничего

замечанию

процитированному

доверительный

что

интервал вообще

который в нем ищут.
3°. Постулат
как

так

центральным,

о

он

не имеет того смысла,

независимости

является для МС

испытаний

общего. Таким образом, к
из
[2] можно еще добавить,

позволяет

в

известном

смысле

выразить вторичные

через первичные и тем самым связывает воедино
постулаты 1° и 2°. После внесения ясности в постулат 3°
он вряд ли может считаться элементарным и

распределения

что

нестеснительным,

и

мы

Выбор

обсудим в следующей главе.
порогов различения,

интуитивный по самой своей сути и неизбежный при проверке и
сравнении между собой различных статистических гипотез,
МС обойти, естественно, не может. Она лишь смещает
этот

выбор

«кудрявым»

математическим

по

направлению к неизмеряемым в реальном
обставляя его тем самым
величинам,
эксперименте
аппаратом.

Пусть, например, проверяют,

согласуется ли
эмпирическая функция распределения Fn (х)
гипотетической функцией Fx (x). Здесь для сравнения
измеренная

необходимо выбрать метрику
Если
р (Fn(x), Fx W)<P°,
установленным,
гласил

МС это,

различения

некоторого

в

р°

и

р
то

согласие

нет.
случае
сущности, и делается,
—

противном
в

порог

с

функций
р°.

различения
считают

В критериях
только порог

со-

находят, можно сказать, путем решения
где выбираемой величиной
ср (р°)=Р°,

уравнения

является Р°
уровень значимости критерия. По своему
смыслу Р° представляет собой вторичную
вероятность,
к которой приходят, опираясь на постулаты 2°,
3°.
—

48

Подчеркнем, что выбирать Р° нисколько не легче, чем
выбирать р°, и, таким образом, особой пользы от этого
смещения не видно. Вред же можно усмотреть в том, что
создается иллюзия, будто надежность испытания гипотезы
за счет привлечения якобы нестеснительных
постулатов и применения солидной математики. Ведь для
чтобы
того,
уравнение,
решить упомянутое
приходится
повышается

обращаться

к

внушительным таблицам, за которыми стоит
и непростая теория, что ее в
руководствах
обычно даже и не приводят. К тому же измерять
вторичные вероятности, с тем чтобы верифицировать
результаты расчета, в данных условиях явно не под силу,
поскольку здесь испытывают затруднения и с измерением
гораздо более простой первичной функции распределения
Fх (х). Сказанное относится к любым доверительным
вероятностям.
Проблема представительности
выборок, на которую МС главным образом и нацеливает
свой математический аппарат, по всей видимости, должна
быть чистосердечно отнесена к неформальной по самой
своей сути проблеме
выбору исходных интуитивных
настолько тонкая

—

посылок.

О

неформальном

подходе с большим подъемом

[4].
Альтернативу методу МС

говорят в мини-пьесе

образом. Для

следующим

здесь можно сформулировать
того, чтобы наиболее

выборки объема п
необходимо взять несколько
убедительно

убедительно подтвердить представительность
относительно

параметра

S (г,

выборок

а

п), г=1, Q

[X],
и

arn [X]~afen[X],
равенства
yr, k < Q.
Высказывая прогноз «как было, так и будет», можно
что такая перманентность сохранится
затем предположить,
продемонстрировать

наличие

будущих выборок S (г, п). Этот прогноз
правдоподобней, чем больше Q. В терминах
и
обучающей
проверочной выборок это означает, что
суммарный объем последней должен намного превосходить
Можно сказать еще и так:
объем обучающей выборки.
и

для

выглядит

всех

тем

наличный

протокол

{X (s)}f необходимо разделить

подвыборок объема n=N/Q
настолько
грубые усредненные

и

одной удлиняющейся серии,

удлинение

несколько

на

прогнозировать
лишь
характеристики
<*гп IX ], чтобы упомянутое равенство действительно
выполнялось (подобная прямая демонстрация
представительности выборок близка по своему смыслу и к описанной нами
схеме

происходит

шагами

если

Ат=п).
49

Q

Величину

и

порог различения при демонстрации
упомянутого равенства следует принимать, руководствуясь
прецедентами, на откровенно интуитивном уровне в
терминах измеряемых величин, без «призывания в свидетели»
неизмеряемых доверительных вероятностей и интервалов,
расчет которых, порою отождествляемый в МС (например,
в

сборнике [16])
не

с

процедурой верификации,

безобидных постулатах

основан

на

равно приводит к
логическому зацикливанию.
Такой эмпирико-индуктивный подход как раз и
воплощал бы, ни много ни мало, фундаментальный принцип
естественных наук—требование многократной повторяемости
эксперимента и убедительной воспроизводимости его
результата. Более обстоятельно все это обсуждалось в
далеко

и

все

публикациях автора [9—13].

Глава 4. МИЗЕСОВСКИЕ

ФОРМАЛИЗАЦИИ
ПРЕДСТАВЛЕНИЯ О НЕЗАВИСИМЫХ
ИСПЫТАНИЯХ

Обсуждая традиционную формулировку теоремы Бернулли
(у нас
теорема 2), мы пришли к выводу, что для
—

прояснения
необходимо

понятия

указать

независимости

четкое

правило,

последовательности

бы

ансамбль

последовательностей

{Xjn (г)}Г,
о

{ХА (s)}?

статистически

правило должно
представления

по

/= 1,

как-то

независимости

испытаний здесь

которому

из

одной исходной

для любого п

формировался

независимых

Само собой разумеется,
отражать интуитивные
/г.

что

испытаний.

Приемлемой

для интуиции основой при построении
таких правил может служить общая идея Мизеса считать
испытания s независимыми, если протокол
очень
прогнозированию

иррегулярным,

(так

игры,
назван

т. е.

называемый
системы

плохо

{X (s)}?

выглядит

поддающимся

принцип

невозможности

угадывания). Подобный

системы

протокол был

Мизесом
иррегулярным коллективом (испытаний).
с 20-х годов различные варианты

Начиная
формализации

понятия иррегулярного коллектива развивали многие
авторы, в том числе А. Вальд, В. Феллер, А. Черч, Г. Рейхенбах. К данной проблеме имеет отношение и
алгоритмическая
А. Н. Колмогорова
концепция
вероятности

50

(1963 г.),
по

хотя эта

концепция,

лишь косвенно

видимо,

идеей прогнозирования. Исходную библиографию
данной проблеме можно найти, например, в [27 гл. 31.
Мы остановимся на двух простейших формализациях
с

связана

иррегулярного коллектива, по-видимому,
большинства практических задач.

понятия
достаточных

для

Формализация

Ж.

по

Биллю

и

А. Г. Постникову [22 ]. Рассмотрим двоичную
последовательность
идеализированный
—

протокол-индикатор {ХА (s)}T события Л.
вероятность Р

(l)=lim

com

Пусть существует мизесовская
(Л), которую удобно назвать

т-юо

безусловной вероятностью единицы.
Представим себе следующую идеализированную
члена

процедуру прогнозирования очередного
последовательности

{ХА (s)}i°. Допустим,
единичными

последовательности

на

гусеницу, вычленяющую

перемещаем по этой
как бы я-звенную

шагами

своем

каждом

шаге

п)={ХА (г-1+/)|/=га. г=1,2,

S (г,
объема

мы

Здесь

...

выборку
(18)

номер шага.
Фиксируем
определенную комбинацию бп-1 из п—1 двоичных цифр, например,
при п=3 любую из комбинаций 00, 01, 10, 11. Подсчитаем
п.

г

—

мизесовскую условную вероятность Р

(l^^)

следования

выборки-гусеницы S (г, п) в
рассматриваемой комбинациии 8П_Х. Для этого найдем при r=l, Q
количество \iQ (б^^) всех тех положений гусеницы, в

единицы в А1-м звене

которых

она

комбинацию

положений,

накрывает

8n_lf

своими

в

«Q(l|fin-l)

=

звеньями

|л^(1|вл_1)тех

которых при этом условии в n-м
единица. Потом вычислим частоту

стоит

и

первыми п—1

а также количество

звене

гусеницы

^Q(l|Sn-l)/^Q(Sn-l)
lim coQ (l^^). Теперь

найдем предел Р (l|6ri_1)

=

Р (1|вл.х) и Р (1).
На практике такая процедура осуществлялась бы
подсчет частот сот (А) и coQ (1 \6п^9 исследование их

сравним

устойчивости

и

сравнение между

собой

в

как

процессе удлинения

чтобы выяснить, не
какой-либо из 2п~1 различных
комбинаций бп_! с явно повышенной частотой.
Обнаружение в прошлом, а главное, оправдывающийся прогноз такой
перманентности означали бы устойчивое повышение ирореального протокола
следовала

ли

{XA(s)}T

единица

с

тем,

за

51

угадываний того, наступит или не наступит событие
в очередном предстоящем испытании s.

цента

А

Отправляясь

комбинации

термина

«иррегулярный

{XA(s)}1°°

последовательность

по

единицы

совпадают:

Р

Это

мизесовского

Биллю—Постникову, если для любой
бд^при любом п условная и безусловная

иррегулярной
вероятности

от

назовем

коллектив»,

(1|б„_1)=Р (1), v«»-i.

(19)

п.

что при естественной
функции
«перекос» в тех случаях, когда
не существует выигрышной стратегии
Р
основанной
только на измерении
угадывания,
вероятностей
Р (\\8n-i) и Р (1). В этом смысле здесь воплощен мизесовский принцип невозможности системы игры.
Так, периодическая последовательность {001 Г}

как

и

раз

означает,

(учитывающей

штрафа

(1)4^=0,5)

(штрихом

период)

выделяем

(19)

условие

неиррегулярна, потому что
л=2. Уже при п=3 имеем:

выполняется лишь для

Я(1|00)=Р (1|01)=1, Р (1|П)=Я (1|Ю)=0,
тогда как Р (1)=0,5.
Например, для периодической
последовательности [28 ]
{11111000001000110010100111010110'}
условие (19) нарушается только при м>5. Машина,
запрограммированная на проверку условия (19) только для
сочла бы эту последовательность иррегулярной.
п < 5,

Объединим
двоичные

числа,

в

{Xjn(r)}T

одну последовательность

стоящие

в

выборках (18)

XJn(r)=XA(r-l+j)9 r-1,2,

j-x

на

местах:

}=~п\

...,

(20)

выборка

S (г, п) представляет собой, очевидно, поперечное
ансамбля последовательностей (20). Определение
(19) эквивалентно требованию статистической
независимости последовательностей (20) при любом п. Таким
образом, здесь реализована программа формирования из одной
исходной последовательности целого ансамбля
сечение

статистически

сдвигами

независимых

Заметим,
исходной

дискретов влево.

что

последовательностей.

последовательности

последовательности

(20)

{XA(5)}f

Следовательно, иррегулярность

никову последовательности

{ХА (s)}?

являются
на

по

/—1

Биллю—Пост,

означает

статистическую независимость ее сдвигов. Это определение
особенно

легко

общего
52

распространить

вида.

на

Мотивировка

{X (s)}T
выборок-гусениц

последовательности
о

помощью

вида

(18)

только

сохраняется,

появляются распределения

вместо

вероятностей.

В

вероятностей
[22]

имеются

конструктивные теоремы существования иррегулярных
последовательностей. Об этих теоремах мы упоминали в главе
2
в пункте, специально посвященном мизесовскому
подходу.
Формализация по А. Коуплэнду [27].
—

Выборки-гусеницы (18)
перемещались по
протоколуиндикатору единичными шагами, и поэтому соседние
выборки пересекались. В ряде практических задач более
естественно формировать непересекающиеся выборки.
Простейший закон формирования таких выборок сводится к
на

отрезки

я:

S (г,

Приняв
на него

п)={ХА(п (г-1)+/)|/=1~}, г=1,2,

{ХА (s)}T

Билля

...

(21)

(21), можно мотивировать опирающееся
иррегулярности по Коуплэнду для

закон

понятие

последовательности
в

{ХА (s)}J°

последовательности

разрезанию

длины

в точности так, как это

Постникова.

Приходим

делалось

к

определению
вида (19) с тем отличием, что теперь комбинацию бп_4
должна накрывать своими первыми звеньями гусеница вида (21).
Таким образом, иррегулярность по Коуплэнду
полностью
аналогична
иррегулярности по Биллю
модели

—

—

Постникову,

только

протоколу

не

В

гусеница

Коуплэнда перемещается

единичными

[22 ] доказано,

что

а

шагами,

шагами

последовательность

по

величины

п.

иррегулярна

по

тогда и только тогда, когда она иррегулярна по

Коуплэнду
Постникову.
Общие замечания

Биллю

—

формализация
иррегулярная по Биллю

х.

о

рассмотренных

Последовательность,

Постникову или Коуплэнду,
простейшим примером интуитивно мотивированной
строгой математической модели протокола таких
—

является

испытаний, которые

и

можно назвать независимыми и одинаковыми

(одинаковыми потому, что распределения вероятностей
всех формируемых последовательностей
{Х;-п(г)}Г
совпадают).
Представление о плохой предсказуемости одного
исходного протокола здесь действительно сведено довольно
естественным способом к требованию статистической
независимости
ансамбля протоколов. В итоге дается такая
трактовка независимости
достаточно ясное

испытаний, при которой

правило для количественной

имеется

эмпирической
53

проверки этой

измерению

в соответствии

независимости

статистической
Таким
независимость

Проверка сводится к
вероятностей, коль скоро к их
с (6) сводится эмпирическая
проверка

независимости.

измерению статистических

образом,

испытаний

после

с

протоколов.

четкого

очевидностью

оформления
оказывается

понятием,

производным от понятия статистической устойчивости,
что
мы и
еще при подведении итогов,в
предположили
Так что постулат 3° никак не может служить
главе 2.
посылкой, из которой логически выводилась бы
статистическая устойчивость, по крайней мере, понимаемая в
согласно схеме одной серии.
неизбежном изначальном смысле
—

Постулат 3°

даже

в

простейшем

оформлении

четком

1°

2°. Поэтому
верификация любых утверждений МС будет нацелена не на
измерение искомых параметров а [X ] первичного
распределения, а на проверку постулата 3°. Измерение же параметров

оказался

а

явно

сложнее,

чем

постулаты

[X ], ради которых вроде бы

при

и

создается

и

МС,

составит

небольшую и, так сказать, вступительную
обстоятельство можно назвать
Данное
работы.

этом лишь

часть

парадоксом МС.

третьим

Например, верификация

результатов расчета
интервала для вероятности Р (А) неизбежно
начиналась бы с измерения этой вероятности по схеме одной
серии (второй парадокс МС). Только после этого следует
перейти к схеме многих серий, с тем чтобы найти
доверительного

(17) и
o)q (Р (А)^(р1 (г), р2 (г))).

=

таки

=

частоту
вторичную
<oQ
опятьЗатем надо измерить
одной серии
вероятность P=\im (oQ, что

полосу

доверительную
по

схеме

—

—

Q-+oo
сделать

труднее,

МС). Наконец,
вероятностью дь.
со

схемой

как

Р (А) (первый парадокс
измерить
следует сравнить Р с доверительной
Все этапы данной процедуры, связанные

многих

верификация

Р

(А)

о

независимости

измеряют

Ясно,
тогда,

чем

что

когда в

серий, в самом деле суть не что иное,
постулата 3°: ведь искомую вероятность

в

самом начале.

рассмотренные формализации представления
п испытаний
применимы всерьез лишь
самом деле проводят много раз по п

испытаний, т. е. имеют весьма длинный протокол. За пределами
статистической физики это условие чаще всего трудно
выполнимо.
Словом, альтернатива методу МС состоит здесь
чтобы постулат 3° вводить в игру исключительно
Б4

в

том,
после

как

того,

искомые

надежно измерены

параметры

а

[X1

само

или

первичное распределение вероятностей.
Уточнение традиционных
на
основе
формулировок
предельных
теорем
понятия
коллектива.
иррегулярного
Пользуясь понятием иррегулярности по Биллю
Постникову, можно сформулировать, например, следующую
—

интерпретацию

теоремы Бернулли, относящуюся к одному
исходному протоколу и допускающую количественную
эмпирическую проверку как своих условий, так и
заключения. Согласно изложенному выше проверка целиком
сводится к измерению статистических вероятностей по схеме

одной серии.
Теорема

3. Пусть проводятся испытания,

результате которых получен
последовательность

протокол-индикатор

Пусть

{XA(s)}?.

выполнены

в

—

следующие

два условия:

1) для
р=Р (Л)

последовательности

Нт сот

=

{XA(s)}T

существует предел

(Л);

т-юо

2)

испытания независимы в том смысле,

{ХА (5)}Г

последовательность

иррегулярна

по

что

Биллю

—

Постникову.

Пусть,
вида

далее,

o)Q

(n, е)

|соГ71(Л)—Р (Л)|

неравенства

(18)

при r=l,

Q.

<

—

8

частота
для

выполнения

серии

выборок-гусениц

Тогда

lim Р (я, е)=1, у8>0,
П-+оо

где
Р

(п, e)=lim o)Q (я, е).

С математической точки зрения теорема 3 является
к ансамблю статистически

теоремой 1, примененной
независимых

последовательностей (20). В теореме 3

постулировать

и

Сравнивая теорему 2

с

можно

Коуплэнду.
теоремой 3, видим, что

иррегулярность

по

в

последней достигнута полная ясность во всех вопросах,
остающихся без ответа при анализе традиционных формулировок

предельных теорем. Теорема 3
претендует

на «математическое

устойчивости
в

с

очевидностью

не

обоснование» статистической

сот (А)^.Р (Л), ут3>1> которая выступает здесь
О нетривиальявно оговоренного условия 1.

качестве

55

условия 2 мы только что говорили. Эмпирическая
проверка условия 2 невозможна без предварительной
проверки условия 1. Чтобы оттенить это, мы расположили
условия теоремы 3 именно в таком порядке, а раньше
аналогично обошлись с теоремой 2. Во всех традиционных
ности

формулировках теоремы Бернулли принят обратный
порядок записи условий. Это лишний раз подтверждает,
во

всех

по

МС

руководствах
элементарным
отождествляя ее, в сущности,
считают самым

независимость

и нестеснительным

с

кажущейся

что

испытаний

условием,

независимостью

испытаний, которая определяется контролируемыми
эксперимента U. Мы уже отмечали, что
теории вероятностей не имеют ни малейшей
формально-логической связи с условиями U.
Из условий 1 и 2 в теореме 3 выводится
условиями
количественные

понятия

дополнительное описание свойств последовательности
терминах

вторичной

вероятности

Р

(я, е),

{ХА ($)}Г

в

сопряженное,

с

точки

зрения прикладника, с логическим зацикливанием.
Итак, после прояснения традиционных формулировок
предельных теорем получается нечто отличное от
каковыми представлялись эти
фундаментальных предложений,
теоремы в начальный период развития теории
вероятностей. Так происходит из-за того, что обнажается
нетривиальность

эмпирической проверки

независимости

предельных теорем. Сходную
метаморфозу претерпевают все утверждения МС, опирающиеся
постулат 3е. С «зависимыми испытаниями», например
марковскими, дело принимает подобный же оборот.
За пределами MG с ее основными постулатами 1°

испытаний и заключений

—

понятие

важные

коллектива

иррегулярного
применения. Но это,

как

находит

на

3°

действительно

говорится,

уже другая

повесть.

Укажем только, что иррегулярность по Биллю
Постникову трудно обойти стороной в задачах, где в самой
постановке фигурируют сдвиги функций. Такая ситуация
налицо, к примеру, в тех версиях теории массового
обслуживания, которые лучше всего подходят для обычного
«безансамблевого»
[30].
моделирования [29, с. 224, 270],
—

Упомянем

еще задачу вычисления усредненных по времени
характеристик сигналов на выходе линейных стационарных
динамических систем (сдвиги там присутствуют в интеграле

свертки), когда строят «безансамблевую» статистическую
теорию случайных сигналов (см., например, [31 ]). Мы
применяем кавычки потому, что здесь все равно появляется
56

ансамбль,
функции, в
Биллю

но

это

ансамбль сдвигов одной исходной

Иррегулярность

последовательности.

частности,

по

Постникову

служит в отмеченных задачах
вариантом кониепции белого шума. Для моделирования
«безансамблевого» белого шума, по-видимому, представляют
—

интерес нормальные периодические системы [28].
Один пример из классической
статистической физики (вместо заключения
нашему

о мизесовском

рассказу

подходе). Обсудим

к

в

терминах
пространственном

мизесовского подхода старую задачу о
линейном осцилляторе, пребывающем в тепловом
равновесии с газообразным термостатом:
частица А притягивается
к неподвижной точке О с силой, пропорциональной вектору

ОА. Свободное
эллипсу

с

частотой

движение частицы А совершается по
v, не зависящей от параметров

обращения

эллипса, которые меняются после каждого соударения
частицы А с какой-либо частицей термостата (обозначим
последнюю

через

Считаем

В),

упругими, парными,

Повторим,

что

а

все

основа

соударения

частицы

мгновенными,

одинаковыми.

мизесовского

подхода

состоит не

предельных переходах, а, пожалуй, в том простом
обстоятельстве, что здесь выписывают и аккуратно
интерпретируют все аргументы рассматриваемых величин. В
в

становится ясным

физический

которых ведут речь.

смысл всех

итоге

усреднений,

о

Мы будем рассматривать скорость

частицы А как функцию и от номера s=..., —1,0,1,
соударения частицы А с частицами термостата. Пусть

...

это

будет

после
соударения. Обозначим через v (s)
скорость частицы В непосредственно перед этим
соударением. Таким образом, рассматриваемые средние для частиц

скорость сразу

А

и В

это

—

пребывания,
трехмерного
смысл

средние

на

скажем, скорости и

пространства

скорость

(s)

Скорость
извлечение из

(s)

скоростей

относительной доли
и

соударение.

одно

тех

в

имеет

соударений,

соответственно
после

которых

попадает именно в данную область.
v

(s)

представляет собой

как

бы случайное

колоссального коллектива

{Ms,)| s~...,-1,0,1,...}, /=1,2,
Здесь i

...

номер частицы,
термостата.
номер соударения i'-ой частицы с другими
рассматриваем скорость непосредственно перед соуда-

скоростей
aSj
частицами;

Вероятность

данной области

частиц

—

—

57

рением.
невозможности
ния

Отправляясь от

мизесовского принципа
игры, постулируем совпадение распределе.

системы

случайной

величины

v

(s)

с

распределениями,

Такая разновидность
тривиальна, нежели
иррегулярности
обе рассмотренные выше модели, но, вероятно, приемлема
для интуиции. Тут не так уж плохо выражена идея хаоса
и сильного перемешивания в большом рое частиц.
одинаковыми

каждой

из

величин

v-t

(st)

.

коллектива еще менее

Пусть

суть материальные точки, а
частицы А и В обменяются
Тогда
соударения
центральны.
при соударении скоростями и, следовательно, распределение
все

частицы

—

скорости

и

(s) осциллятора совпадает с распределением
(s). Таким образом, в силу принятого «постулата

скорости v
средние кинетические энергии Е иф
иррегулярности»
осциллятора и любой частицы термостата совпадают.
Напомним, что имеются в виду средние на одно соударение.
Предположение о центральности соударений здесь
несущественно, и его можно заменить обычным допущением о
равноправности всех направлений, по которым происходят
соударения.

Предположим далее, что соударения настолько редки,
что частица А успевает сделать между двумя
последовательными соударениями много витков по своей
орбите. В этом случае логично постулировать
равномерность распределений и статистическую независимость
местоположений (точнее
фаз) тех двух точек на
эллиптической орбите, в которых произошли два
последовательных соударения частицы А,
«включившие» и
эллиптической

—

«выключившие»
средних

именно эту орбиту. Отсюда следует равенство
кинетической и потенциальной энергий осциллятора.

Пусть

теперь

Допущение

частицы

имеют

конечный

диаметр

а.

о

редкости соударений сразу приводит в этом
случае к более интересным, если можно так выразиться,
негиббсовским следствиям. Дело в том, что эллиптическая
орбита теперь не геометрическая линия, а «бублик»
тороидальная трасса. И медленная частица В не сможет
(попросту не успеет за максимальное отведенное ей время
к линии, описываемой
T=\/v) проникнуть коси трассы
Л.
частицы
^медленности
центром
скорость
Критерий
—

—

—

v

(s)

не должна

превосходить

по

модулю величину

порядка av.

Стало быть,
Б8

из-за наличия

тороидальной трассы

возни-

кают своего рода кинематические ограничения, вследствие
которых медленные частицы В бьют только по тем точкам
частицы Л,
которые лежат вдали от оси трассы. Этот
«эффект пропеллера» в среднем меняет условия обмена
энергией между частицами А и В. Медленные частицы В
забирают при соударениях у частицы А в среднем меньше,
а отдают ей больше кинетической энергии, чем
при
отсутствии тороидальной трассы, т. е. при а=0.
Для быстрых
же частиц В все остается по-прежнему.
Мы говорим об эффекте пропеллера, опираясь на

следующую аналогию: слабо брошенный предмет не может
быть разрублен быстро вращающимся винтом. Предмет
сравнительно благополучно отскочит как бы от сплошного
диска, не успев проникнуть внутрь трассы винта, где
только и можно забрать у винта хорошую порцию вращательной
кинетической энергии. Такой эффект пропеллера может
усилиться, если оболочки винта и предмета мягкие.
В итоге зависимость Е (Ф) пойдет выше «гиббсовской»
Е (#)={К
зависимости
Превышение должно становиться
более существенным по мере

уменьшения

ft,

т. е.

температуры термостата, поскольку при этом увеличивается доля
медленных частиц В. Это означает, что теплоемкость
dE (ft)/dft осциллятора с уменьшением ft где-то будет
падать. Может появиться и конечная энергия Е

(0) нулевых
определяемая характерным параметром av.
Заметим, что средние кинетическая и потенциальная
энергии осциллятора совпадают на прежних основаниях. В
таком стиле можно рассмотреть и двумерные (но не
одномерные!) осциллятор и термостат.
колебаний,

Обращаем
Если

внимание на то, что

пользоваться

мизесовским

эффект пропеллера груб.
языком

с

его

проводимых усреднений и
«безансамблевой» направленностью, то мимо этого эффекта
прямо-таки трудно пройти. Его приходится иметь в виду
всякий раз, когда в движении молекул имеются
периодические или квазипериодические составляющие, а
температура настолько низка, что становится ощутимым время,
затрачиваемое молекулами в их поступательном движении
на
покрытие расстояний, равных по порядку величины
скрупулезностью

в

выяснении

смысла

диаметру атомов, из которых состоят молекулы. Так
обстоит дело, например, при подсчете теплоемкости
двухатомного

газа.

Правда,

мгновенными, объяснить

этим

если

считать

соударения

эффектом

зависимость теплоемкости не

здесь температурную
удается, поскольку в отличие
59

осциллятора у «гантели», состоящей из двух жестко
скрепленных шариков-атомов, угловая скорость не
фиксирована, а меняется, так сказать, синхронно с температурой
термостата. Однако спад теплоемкости здесь все же можно
от

наложив

получить,

разным

на

определенные ограничения

взаимодействия

потенциала

атомов

вид

(принадлежащих

к

молекулам). Потенциал

должен быть таким, чтобы
возрастало с уменьшением скорости

время соударения
сближения w соударяющихся

Интересно,

что

для

атомов

необходимо

этого

быстрее,
наличие

l/w.

чем

сил

притяжения, а не только отталкивания.

Соображения, сходные с изложенными, нам удалось
работе [32]. Но, как нам кажется, именно

найти только в
использование

Заметим,

немизесовского
в

к

языка,

сожалению,

не

[32]

достаточно далеко.
что руководства по статистической физике почему-то

позволило

продвинуться

без оговорок утверждают, что спад теплоемкости
конечную энергию нулевых колебаний классическая

предсказывать

не

в

и

физика

состоянии.

ЗАКЛЮЧЕНИЕ
Альтернативу методу математической

статистики,
обрисованную выше, можно в немногих словах охарактеризовать
так: в прикладных исследованиях, точнее за пределами

фундаментальной физики,
от

в

введения

исходные

по

возможности

посылки

воздерживаться

таких

теоретико-вероятностных величин,

которые не измеряются в натурных
называемый численный эксперимент
сравнивает между собой две модели
машинную и «бумажную»,
но не модель с реальностью). Объекты изучения в
экспериментах (так

—

экономике,

социологии

и

даже

слишком сложны и

в

современной

технике

чаще

нестабильны для построения

всего

их

моделей, исходя из удаленных от эксперимента общих
принципов, характерных для основ физики. Здесь, так

полезных

сказать,

рентабельны оперативные феноменологические
претензий на фундаментальность. В со-1

модели без особых

ответствии

с

принципом равнопрочности всех элементов
исследования здесь следует с
настороженностью
относиться
к
привлечению сложной математики.
Закончим цитатой из Н. Винера [33], которого трудно
отнести к противникам математизации: «Успехи
математической физики вызвали у социологов чувство ревности к
прикладного

60

силе ее методов,

чувство, которое едва ли сопровождалось
интеллектуальных истоков этой

пониманием

отчетливым

силы... Подобно тому,
как
некоторые отсталые народы
заимствовали у Запада его обезличенные, лишенные
национальных примет, одежды и парламентские формы,
смутно веря, будто эти магические облачения и обряды смогут
их сразу приблизить к современной культуре и технике,
так и экономисты принялись облачать свои весьма
неточные

идеи

дифференциального

данных

в

информацию

строгие формулы интегрального и
исчислений... Как ни труден отбор надежных
физике, гораздо сложнее собрать обширную
в

или

экономического

характера, состоящую
данных... В
этих

из

слишком точных

Приписывать

социологического

серий однородных
безнадежно добиваться

многочисленных

обстоятельствах

определений

таким

величин, вступающих в игру.
по

особую

бесполезно,

величинам какую-то

точность

бы ни был предлог, применение точных
слишком

как

вольно

обман

и

самой своей сути

неопределенным

формул

определяемым величинам
пустая трата времени».

есть

и, каков

к этим

не

что

иное,

ЛИТЕРАТУРА
M

1. Блехман И. H.j
к о

Я* Г.

ы ш к и с

математика.

Прикладная

Предмет,

А.

Д.,

Панов-

логика, особенности

Киев, «Наукова думка», 1976. 270 с.
2. Грекова И.
Методологические особенности
математики на современном этапе ее развития.—

подхода.

прикладной

философии», 1976, № 6,
3. Веников
процессы

в

1979, № 3,

Переходные электромеханические

М., «Высшая школа», 1978, 540 с.
Под знаком интеграла.— «Знание

системах.

М.

—

с. 43—44.

5. Тутубалин
естествознании.

«Вопросы

104—114.

В. А.

В ы с о т с к и й

4.
сила»,

электрических

с.

В.Н.

М., «Знание», 1972, 48

Теория

вероятностей

в

с.

Статистическая обработка рядов
6. Тутубалин
В.Н.
наблюдений. М., «Знание», 1973, 64 с.
61

7.

Тутубалин В. Н.

(вероятностно-статистические

1977, 64

Границы применимости
и

методы

возможности). М., «Знание»,

их

с.

В. Н.
8. Тутубалин
1972, 230 с.

Теория вероятностей. Mti МГУ,

О проблемах приложения теории
Ю. И.
9. А л и м о в
вероятностей, рассмотренных в работах В. Н. Тутубалина.—
«Автоматика», 1978, № 1, с. 71—82.

с.

вероятностей.— «Автоматика*,

теории

в

№ 4,

случайных величин, векторов и процессов.
Свердловск, изд-во УГЛИ, 1976, 104 с.

моментов

пособие.

Измерение

Элементы теории эксперимента.

Ю. И.

11. Алимов

Ю. И.

вероятностей

распределений вероятностей. Учебное пособие.

13.
Опытная

и

изд-во

У ПИ,

Элементы теории эксперимента.
1977,

Ю. И.

Алимов

80 с.

Элементы теории эксперимента.

утверждений математической
Свердловск, изд-во У ПИ, 1978. 92 с.

проверка

пособие.
14.

Д

Т ь ю к и

математика.— В

«Знание»,

1977,

с.

У.

ж.

сб.:

Анализ данных,

статистики.

вычисления

«Современные проблемы

Учебное

на ЭВМ

математики»,

М.,

41—64.

15. Китайгородский
«Знание», 1978. 64 с.

32

Учебное

12. Алимов

Свердловск,

т.

1979,

103—110.

Измерение

и

Еще раз о реализме и фантастике

Ю. И.

10. Алимов

приложениях

Молекулярные силы. М.г

А, И,

16.

Прогностика. Терминология,

17.

Индукция. Статья

92, М., «Наука», 1978,

вып.

с.

10.

в

Большой

Советской Энциклопедии,
с. 263—264.

М., «Советская энциклопедия», 1970,

18. Нейман Ю.

Вводный

курс

теории

вероятностей

и

математической статистики. М., «Наука», 1968, 448 с.
19. Н а л и м о в В. В.
Язык вероятностных
представлений.— «Автоматика», 1979, № 1, с. 62—74.
20. Б р и л л ю э н Л. Научная неопределенность и
информация. М., «Мир», 1966, 272 с.

21. Б

В
с.

о р н
М.
Размышления
162—187.

кн.:

Непрерывность, детерминизм,
и

воспоминания

реальность.—

физика. М., «Наука», 1977,

22. Постников А. Г.
Арифметическое моделирование
случайных процессов. Труды Математического ин-та им. В. А. Стеклова, т.

23.

57, М., изд-во АН СССР, 1960, 84 с.
Н и к и т и н а Е. П.,
Ф р е й д л и н а

А, В.
Коллекция определении
изд-во МГУ, 1972, 46 с.

х о

термина

В. Д.,
Яр«статистика», М.,

24. В е н е ц к и й И. Г,
Вариационные ряды и их
характеристики. М., «Статистика», 1970, 160 с.
25. Боярский Э. А. Порядковые статистики. М.,
«Статистика», 1972. 120 с.

26. Колмогоров

Математика,
СССР, 1956,
62

ее
с.

А. Н.

содержание,

252—281.

Теория вероятностей.— В

методы

и

значение.

М.,

изд-во

кн.:

АН

27. Кнут Д.

Искусство программирования для ЦВМ,

М,5 «Мир», 1977, 724
28. Коробов
и

их

Сер.

приложение

мат.,

Н. М.

к оценке

1951, № 1,

29. Боровков
массового

т.

2,

с.

т.

Нормальные периодические системы
сумм

15,

с.

А. А.

обслуживания.

М.,

дробных долей.— Изв. АН СССР.

17—46.
Вероятностные процессы

«Наука»,

1972, 368

в

теории

с.

30. А л и м о в Ю. И.,
Мучник В. Л.
Неравенства и
в
«безансамблевой»
вероятностные
пространства
счетномерные
мизесовской теории массового обслуживания.— В кн.: Обобщенные
функции и векторные меры. Труды Ин-та математики и механики
УНЦ АН СССР, вып. 31. Свердловск, 1979, с. 75—89.
31. Алимов Ю. И, О временном статистическом описании

случайных
с.

сигналов.— «Автоматика

и

телемеханика»,

1969, № 8,

16—30.

32. J a f f e G. Uber die Ung Ciltigkeit des Gleichverteilungsatzes
bei Oszillatoren und Rotatoren.— «Annalen der Phisik», 1924, b. 74,
c, 628—660.
33. Винер Н. Творец и робот, М., «Прогресс», 1966, 104 с.

СОДЕРЖАНИЕ

Предисловие

.

t

.......

.

1. Вводные замечания о прогнозировании
2. Исходные концепции
прикладной теории
вероятностей
Глава 3. Критический анализ метода математической
статистики
Глава 4. Мизесовские формализации представления о
Глава
Глава

.........

независимых

Заключение
Литература

испытаниях

......

...........

..,.,.

.....

Юрий Иванович АЛИМОВ
АЛЬТЕРНАТИВА МЕТОДУ МАТЕМАТИЧЕСКОЙ
СТАТИСТИКИ
Главный отраслевой редактор В. П. Демьянов
*
Редактор Г. Г. Карвовский. Мл. редактор Т. Г. И н
такова. Обложка
художника Л. П. Р о м а с е н к о.

Худож. редактор М. А. Бабичева. Техн. редактор
А. М. Красавина. Корректор И. В. Сорокина
ИБ 2472
»
набор 16.01.80 г. Подписано к печати 18.02.80 rt Т-05 437,
Формат 84Х108'/з2. Бумага № 3. Гарнитура литературная.
Печать высокая, Бум, л, 1, Печ, л. 2: Усл. печ: л. 3,36.
Уч.-изд. л, 3,53 Тираж 35 350 экз. Заказ 3196&
Цена 11 коп. Издательство «Знание». 101835, ГСП, Москва, Центр,
проезд Серова, д. 4. Индекс заказа 804303

Сдано

полиграфический комбинат Союзполиграфпрома
Государственного комитета СССР по делам издательств,

Чеховский

полиграфии

и

книжной

торговли<

г,

Чехов

Московской

области

35
50
60
61