Текст
Engineering Optimization
Methods and Applications
G. V. REKLAITIS
Chemical Engineering
Purdue University
A. RAVINDRAN
Industrial Engineering
University of Oklahoma
К. M. RAGSDELL
Aerospace and Mechanical Engineering
University of Arizona
A Wiley-Interscience Publication
JOHN WILEY AND SONS
New York • Chichester • Brisbane • Toronto • Singapore
1983
Г. Рек л ей тис. АРейвиндран, К.Рэгсдел
Оптимизация в технике
В 2-х книгах
1
Перевод с английского
канд. техн, наук В. Я. Алтаева, В. И. Моторина
люсква
«МИР»
1986
ББК 22.18
Р36
УДК 519.6
Реклейтис Г., Рейвиндран А., Рэгсдел К.
Р36 Оптимизация в технике: В 2-х кн. Кн. 1. Пер. с англ.—
М.: Мир, 1986.— ООО с., ил.
Монография известных американских специалистов посвящена прикладные
аспектам теории математического программирования Рассматриваются методы ли-
нейного, целочисленного и нелинейного программирования, используемые для реше-
ния задач оптимизации технических систем, а также вопросы реализации соответ-
ствующих алгоритмов с помощью ЭВМ Изложение иллюстрируется многочислен-
ными примерами решения конкретных инженерных задач оптимизации. В русской
переводе выходит в двух книгах.
Для инженеров-конструкторов, специалистов в области проектирования техни-
ческих систем и устройств, а также преподавателей, аспирантов и студентов техни-
ческих вузов
2109000000—304
₽ 041 (01)—86
154—86, ч. 1
ББК 22. И
Редакция литературы по информатике и электронике
© 1983 John Wiley & Sons, Inc. All rights reserved
Authorized translation from English languag
edition published by John Wiley & Sons, Inc.
© перевод на русский язык, «Мир», 1986.
Предисловие к русскому изданию
Методы оптимизации эффективно применяются в самых различ-
ных областях человеческой деятельности. Особенно значительные
мнихи достигнуты при проектировании и анализе больших техни-
ческих систем. Ускоренные темпы внедрения теоретических разра-
Сннок в инженерную практику в существенной степени обусловлены
широким распространением и интенсивным совершенствованием
средств вычислительной техники.
В настоящее время для инженера ^знание методов оптимизации
является столь же необходимым, как знание основ математического
тылпза, физики, химии, теории сопротивления материалов, радио-
электроники и ряда других дисциплин, ставших традиционными.
О.чнако большинство публикаций, посвященных теоретическим и
прикладным аспектам математического программирования, как
правило, охватывают узкий круг вопросов и требуют от читателя
фундаментальной математической подготовки.
11 щание на русском языке книги Г. Реклейтиса, А. Рейвиндрана
и К. Рэгсдела окажет несомненную помощь инженерам при изуче-
нии методов оптимизации и их практическом использовании. В мо-
ши рафии последовательно излагаются методологические и вычисли-
тельные основы построения нелинейных оптимизационных моделей
технических систем. Авторам удалось четко систематизировать раз-
нообразные приемы и методы, используемые для решения задач
нелинейного программирования, раскрыть их специфические осо-
бенности, сопоставить достоинства и недостатки. Отличительной
•icpioii книги является ее практическая направленность. С большим
нед.п огическим мастерством описаны обязательные этапы оптими-
кщнонного исследования, которые, как правило, не рассматрива-
нием в обычных курсах нелинейного программирования: определе-
ние границ моделируемой технической системы, выбор приемлемого
уровня моделирования, построение целевой функции и модели в це-
пом, интерпретация оптимального решения и др. Значительный
птерес представляет сравнительный обзор алгоритмов условной
ошимизации в соответствии с критериями вычислительной эффек-
11ИП1ОСТИ и робастности [гл. 12].
Следует отметить, что многочисленные рекомендации по изуче-
нию дополнительной литературы содержат в основном ссылки на
рнбогы зарубежных авторов. Однако советские математики внесли
6 ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
существенный вклад в развитие теории нелинейного программирова-
ния. Из недавно вышедших в свет книг читателю можно рекомендо-
вать следующие работы: Немировский А. С., Юдин Д. Б. Слож-
ность задач и эффективность методов оптимизации.— М.: Наука,
1979; Кузнецов Ю. Н., Кузубов В. И., Волощенко А. Б. Матема-
тическое программирование.— М.: Высшая школа, 1980; Поляк Б.Т.
Введение в оптимизацию.— М.: Наука, 1983.
Книга может быть использована как учебное пособие и практи-
ческое руководство по применению методов оптимизации. Она будет
доступна и полезна широкому кругу читателей: инженерам, эко-
номистам, специалистам по математическому обеспечению ЭВМ,
преподавателям, аспирантам и студентам высших технических учеб-
ных заведений.
Канд. техн, наук В. Д. Алтаев, В. И. Моторин
Посвящается Джанин, Буване, Дженет
Предисловие
Эта книга посвящена вопросам практического применения мето-
дов оптимизации. Основное внимание уделяется методам и алгорит-
мам, используемым в инженерных приложениях при проектирова-
нии, эксплуатации и анализе функционирования технических объек-
тов. Главным образом рассматриваются методы оптимизации, ориен-
тированные на решение задач с непрерывными переменными, огра-
ничениями, содержащими действительные функции, и единственной
действительной целевой функцией, т. е. математические методы,
часто объединяемые в рамках теории нелинейного программирова-
ния. При этом дается обзор всех наиболее важных типов методоз
оптимизации, начиная от методов минимизации функции одной
переменной и кончая методами, применяемыми для решения нели-
нейных задач условной оптимизации большой размерности. Рас-
сматриваются не только классические методы, значение которых
определяется причинами исторического характера и ролью в даль-
нейшем развитии оптимизации, но также и перспективные новые
методы, примером которых может служить метод решения последо-
вательности задач квадратичного программирования.
Авторы стремились к тому, чтобы читатель получил ясное пред-
ставление о логической структуре излагаемых методов и о важней-
ших предположениях, на основе которых они разработаны, а также
об их сравнительных преимуществах и недостатках. Доказательства
и математические выкладки приводятся только в тех случаях, когда
они служат для пояснения основных шагов или свойств рассматри-
ваемых алгоритмов Как правило, при отсутствии доказательства
дается ссылка на соответствующий источник, а объем книги исполь-
зуется для обоснования и разъяснения ключевых аспектов построе-
ния различных математических схем. Таким образом, наша главная
цель заключается в том, чтобы информировать инженера о приклад-
ных возможностях методов оптимизации, а не в том, чтобы подго-
товить специалиста по математическому обеспечению ЭВМ. Поэтому
значительное внимание уделено таким практически важным вопро-
сам, как построение модели, ее реализация, подготовка к решению,
выбор первого приближения к экстремальной точке, выбор страте-
гии оптимизации и т. д. Одна из основных глав (гл. 13) посвящена
методике проведения оптимизационных исследований, в другой
главе (гл. 12) приведены результаты сравнительного анализа из-
8
ПРЕДИСЛОВИЕ
вестных программ решения оптимизационных задач на ЭВМ; в гл. 14
на трех конкретных примерах описан опыт практического приме-
нения методов оптимизации в технике. Значительная часть каждой
главы отведена примерам использования этих методов авторами
в области химической технологии, организации производства и ма-
шиностроения. Несмотря на то что имеется ряд полезных книг,
содержащих подробное изложение теоретических и вычислительных
аспектов нелинейного программирования, данная монография яв-
ляется, по-видимому, единственной в своем роде работой, которую
отличают отмеченные выше особенности: достаточно полный обзор
современных методов нелинейного программирования, неформаль-
ный подход к изложению материала и ориентация на изучение при-
кладных возможностей методов оптимизации в технике.
Работа над книгой продолжалась в течение восьми лет. За это
время материал книги использовался при чтении курса лекций по
оптимизации в технике для студентов последнего и аспирантов пер-
вого годов обучения в Университете Пурдью. Этот курс читался
в течение одного семестра; для большей части слушателей он ока-
зался первым последовательным изложением методов оптимизации.
Математическая подготовка студентов основывалась на универси-
тетских курсах математического анализа и линейной алгебры.
Таким образом, от читателя не требуется каких-либо иных знаний
в области математики. Существенное влияние на структуру книги
и методику изложения материала оказал опыт авторов, приобре-
тенный при чтении телевизионного цикла лекций по оптимизации
в технике, который передавался по местной телевизионной сети для
студентов-иностранцев и дипломированных инженеров. Поэтому
есть основания полагать, что книга может служить учебным посо-
бием как для обычных лекционных курсов, так и для телевизионных
циклов лекций, краткосрочных курсов повышения квалификации,
а также для самостоятельной работы.
Занятия по изучению материала книги были организованы
в соответствии с двумя различными программами. Первая из них
представляет собой обычный лекционный курс, рассчитанный на
45 пятидесятиминутных лекций в течение одного семестра. Вторая
программа предусматривает 30 лекций и 15 семинарских занятий.
В первом случае содержание книги можно излагать последовательно
в порядке нумерации глав, за исключением гл. 14. Во втором случае
гл. 1, 13 и 14, а также дополнительные практические примеры ре-
комендуется обсуждать на семинарах, материал гл. 2—10 и гл. 12 —
излагать в лекциях. При этом гл. И и разд. 8.3 и 9.4 приходится
обычно опускать из-за недостатка лекционного времени. Домашние
задания в обоих случаях должны включать ряд задач, приведенных
в заключительной части каждой главы и предназначенных для
решения как с помощью, так и без помощи ЭВМ. Решение задач на
ЭВМ можно осуществлять, используя программы OPTLIB, ОРТ и
BIAS, описание которых дано в гл. 12.
ПРЕДИСЛОВИЕ
9
Заметное влияние на подбор и структуру материала книги ока-
вали советы и предложения наших коллег и наставников по соот-
ветствующим дисциплинам. Число таких сознательных или неволь-
ных «участников» этой работы слишком велико, чтобы можно было
упомянуть здесь каждого из них. Проф. Дон Филипс, работавший
вместе с нами в Университете Пурдью, внес значительный вклад
в первый вариант конспектов лекций, послуживших исходным ма-
териалом для написания книги. Курс лекций и их конспекты полу-
чили одобрение бывших деканов наших факультетов: Лоуэлла Б.
Коппела, Уилбура Мейера, Р. У. Фокса и А. Г. Лефевра. Проф.
Ф. Кейхан и проф. К- Нопф, д-р Ф. У. Аренс, д-р Дж. А. Габри-
ель, д-р Р. Рут, д-р Е. Сандгрен, д-р П. В. Сарма, Брэд Овертерф
и Мохайндер Суд, а также П. К. Эсуаран, Дж. Поузи и Б. Нельсон
внесли целый ряд поправок и улучшений. Мы признательны также
нашим студентам, настойчиво проработавшим различные варианты
рукописи, за многочисленные вопросы и просьбы о пояснении тех
или иных результатов. Их подчас острые, но, как правило, справед-
ливые критические высказывания служили отличным стимулом
к совершенствованию материала книги. Наконец, хотелось бы вы-
разить благодарность редактору книги Фрэнку Серра и его пред-
шественнику Мейеру Кутцу за их настойчивость и терпение. Мы
благодарны нашим женам и детям, позволившим нам тратить время
на написание книги, за поддержку в течение всей работы.
Г. Реклейтис
А. Рейвиндран
К. Рэгсдел
Уэст-Лафайетт, Индиана,
лето 1983 года
Глава 1
Методологические основы
оптимизации
Данная книга является введением в теорию оптимизации и зна-
комит с приложениями этой теории к решению ряда задач, возни-
кающих в инженерной практике. В наиболее общем смысле теория
оптимизации представляет собой совокупность фундаментальных
математических результатов и численных методов, ориентированных
на нахождение и идентификацию наилучших вариантов из множества
альтернатив и позволяющих избежать полного перебора и оценива-
ния возможных вариантов. Процесс оптимизации лежит в основе
всей инженерной деятельности, поскольку классические функции
инженера заключаются в том, чтобы, с одной стороны, проектиро-
вать новые, более эффективные и менее дорогостоящие технические
системы и, с другой стороны, разрабатывать методы повышения
качества функционирования существующих систем.
Эффективность оптимизационных методов, позволяющих осу-
ществить выбор наилучшего варианта без непосредственной про-
верки всех возможных вариантов, тесно связана с широким исполь-
зованием достижений в области математики путем реализации
итеративных вычислительных схем, опирающихся на строго обосно-
ванные логические процедуры и алгоритмы, на базе применения
вычислительной техники. Поэтому для изложения методологиче-
ских основ оптимизации требуется привлечение важнейших резуль-
татов теории матриц, элементов линейной алгебры и дифференциаль-
ного исчисления, а также положений математического анализа.
Математические понятия и конструкции используются в настоящей
книге не только для того, чтобы повысить уровень строгости пред-
ставления материала, но и потому, что они составляют- терминоло-
гическую базу изложения, которая позволяет упростить описание
и определение структурных элементов рассматриваемых вычисли-
тельных процедур и облегчить их понимание.
Поскольку размерность инженерных задач, как правило, до-
статочно велика, а расчеты в соответствии с алгоритмами оптими-
зации требуют значительных затрат времени, оптимизационные ме-
тоды ориентированы главным образом на реализацию с помощью
ЭВМ. Однако несмотря на то, что изложение методологических
принципов ведется в книге с учетом указанной ориентации, авторы
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ
И
не сочли целесообразным подробно останавливаться на вопросах,
связанных с составлением программ для ЭВМ и программированием.
Главное внимание в книге уделяется математическим и логическим
построениям, лежащим в основе исследуемых методов, факторам,
обусловливающим выбор тех или иных аналитических схем, а таю
же рассмотрению важнейших прикладных аспектов теории.
1.1. Необходимые условия для применения
оптимизационных методов
Для того чтобы использовать математические результаты и чис-
ленные методы теории оптимизации для решения конкретных инже-
нерных задач, необходимо установить границы подлежащей опти-
мизации инженерной системы, определить количественный критерий,
на основе которого можно произвести анализ вариантов с целью
выявления «наилучшего», осуществить выбор внутрисистемных пе-
ременных, которые используются для определения характеристик
и идентификации вариантов, и, наконец, построить модель, отра-
жающую взаимосвязи между переменными. Эта последовательность
действий составляет содержание процесса постановки задачи ин-
женерной оптимизации. Корректная постановка задачи служит
ключом к успеху оптимизационного исследования и ассоциируется
в большей степени с искусством, нежели с точной наукой. Искусство
постановки задач постигается в практической деятельности на при-
мерах успешно реализованных разработок и основывается на четком
представлении преимуществ, недостатков и специфических особен-
ностей различных методов теории оптимизации. По этим причинам
изложение материала книги сопровождается большим количеством
практических примеров, заимствованных из специальной литера-
туры, а также построенных авторами на основе собственного инже-
нерного опыта. Кроме того, наряду с описанием оптимизационных
методов в книге освещаются вопросы, касающиеся их относительных
преимуществ и недостатков; в ряде случаев приводятся результаты
расчетов, подтверждающие обоснованность сделанных выводов, и
даются ссылки на соответствующие публикации.
Последующие подразделы посвящены более подробному рас-
смотрению этапов постановки задачи, которое завершается
в разд. 1.2 анализом формулировок нескольких практических
задач.
1.1.1. Определение границ системы
Прежде чем приступить к оптимизационному исследованию,
важно четко определить границы изучаемой системы. В данном
контексте система предстает как некоторая изолированная часть
реального мира. Границы системы задаются пределами, отделяю-
щими систему от внешней среды, и служат для выделения системы
12
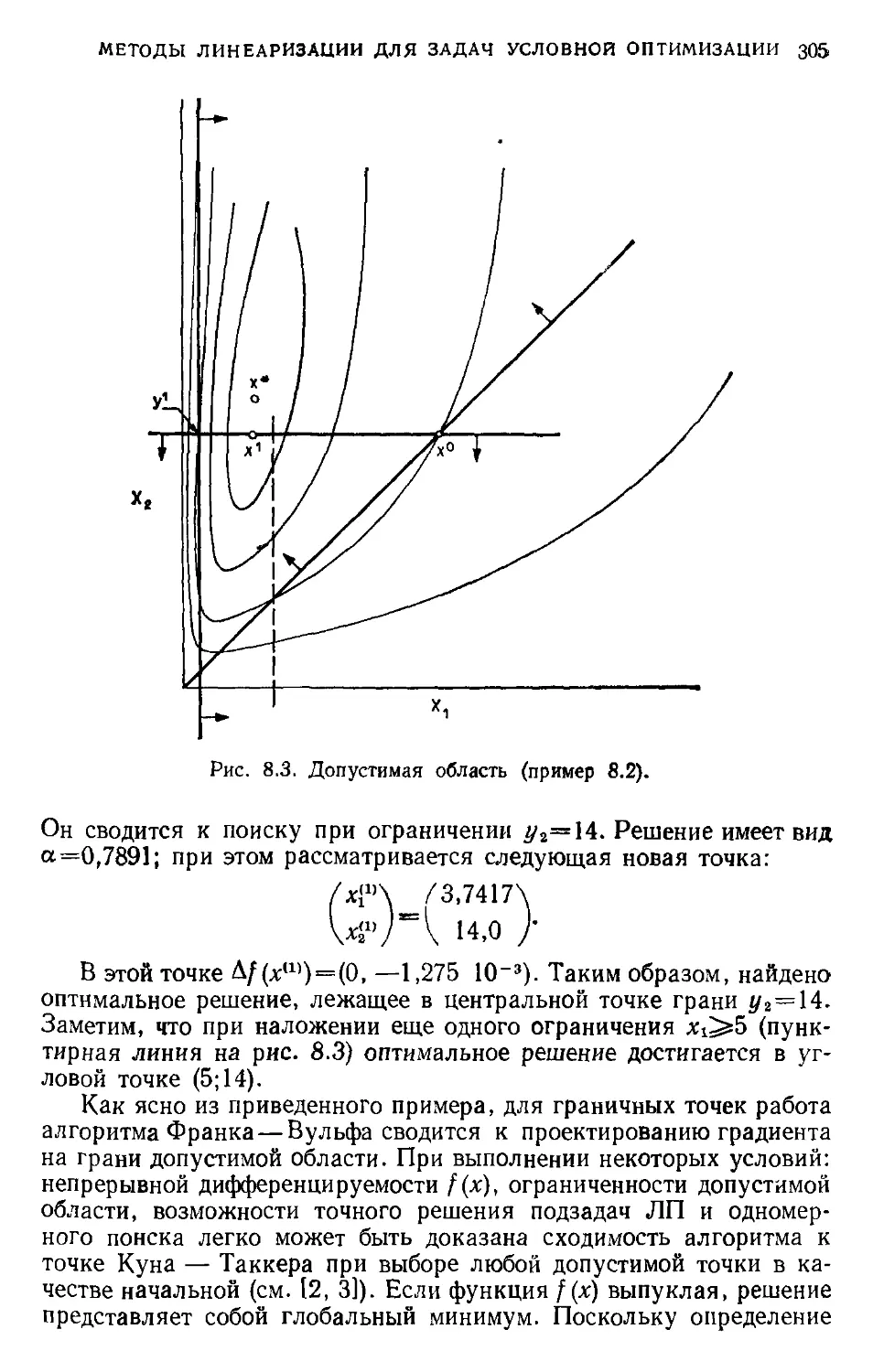
ГЛАВА I
из ее окружения. При проведении анализа обычно предполагается,
что взаимосвязи между системой и внешней средой зафиксированы
на некотором выбранном уровне представления. Тем не менее,
поскольку такие взаимосвязи всегда существуют, определение гра-
ниц системы является первым шагом в процессе приближенного
описания реальной системы.
В ряде случаев может оказаться, что первоначальный выбор
границы является слишком жестким. Для более полного анализа
данной инженерной системы может возникнуть необходимость рас-
ширения установленных границ системы путем включения других
подсистем, оказывающих существенное влияние на функционирова-
ние исследуемой системы. Предположим, например, что на промыш-
ленном предприятии имеется красильный цех, в котором готовые
изделия поступают на поточную линию и окрашиваются в различ-
ные цвета. На первой стадии изучения красильного цеха можно
рассматривать его изолированно от других цехов предприятия.
Однако анализ может показать, что оптимальный размер партии
изделий и последовательность нанесения красителей в существен-
ной степени зависят от особенностей функционирования производ-
ственного цеха, в котором выпускаются готовые изделия. Таким
образом, возникает необходимость принять решение о расширении
границ системы путем включения в нее производственного цеха.
Разумеется, расширение границ системы повышает размерность и
сложность многокомпонентной системы и, следовательно, в значи-
тельной мере затрудняет ее анализ. Очевидно, что в инженерной
практике следует, насколько это возможно, стремиться к разбиению
больших сложных систем на относительно небольшие подсистемы,
которые можно изучать по отдельности. Однако при этом необхо-
димо иметь уверенность в том, что такая декомпозиция не приведет
к излишнему упрощению реальной ситуации.
1.1.2. Характеристический критерий
Если подлежащая исследованию система определена и ее границы
установлены, то на следующем этапе постановки задачи оптимизации
необходимо осуществить выбор критерия, на основе которого можно
оценить характеристики системы или ее проекта, с тем чтобы вы-
явить «наилучший» проект или множество «наилучших» условий
функционирования системы. В инженерных приложениях обычно
выбираются критерии экономического характера. Однако спектр
возможных формулировок таких критериев весьма широк; при
определении критерия могут использоваться такие экономические
характеристики, как валовые капитальные затраты, издержки
в единицу времени, чистая прибыль в единицу времени, доходы от
инвестиций, отношение затрат к прибыли или собственный капитал
на данный момент времени. В других приложениях критерий может
основываться на некоторых технологических факторах, например,
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ
13
когда требуется минимизировать продолжительность процесса про-
изводства изделия, максимизировать темпы производства, миними-
зировать количество потребляемой энергии, максимизировать ве-
личину крутящего момента, максимизировать нагрузку и т. п.
Независимо от того, какой критерий выбирается при оптимизации,
«наилучшему» варианту всегда соответствует минимальное или мак-
симальное значение характеристического показателя качества функ-
ционирования системы.
Важно отметить, что независимо от содержания оптимизацион-
ных методов, рассматриваемых в настоящей книге, только один
критерий (и, следовательно, характеристическая мера) может ис-
пользоваться при определении оптимума, так как невозможно по-
лучить решение, которое, например, одновременно обеспечивает
минимум затрат, максимум надежности и минимум потребляемой
энергии. Здесь мы опять сталкиваемся с существенным упрощением
реальной ситуации, поскольку в ряде практических случаев было
бы весьма желательным найти решение, которое бы являлось «наи-
лучшим» с позиций нескольких различных критериев.
Один из путей учета совокупности противоречивых целевых уста-
новок состоит в том, что какой-либо из критериев выбирается в ка-
честве первичного, тогда как остальные критерии считаются вто-
ричными. В этом случае первичный критерий испрльзуется при
оптимизации как характеристическая мера, а вторичные критерии
порождают ограничения оптимизационной задачи, которые уста-
навливают диапазоны изменений соответствующих показателей от
минимального до максимального приемлемого значения. В част-
ности, в примере с красильным цехом различными служащими фир-
мы, которой принадлежит промышленное предприятие, могут быть
выбраны следующие критерии.
1. Управляющий красильным цехом отдает предпочтение про-
екту, согласно которому производственный процесс протекает
с минимальными изменениями в ассортименте изделий и исполь-
зуемых красок. При этом максимизируется количество изделий,
окрашиваемых в единицу времени.
2. Руководитель отдела сбыта заинтересован в реализации
проекта, в соответствии с которым объемы складских запасов изде-
лий всех видов и окрасок максимальны. В этом случае минимизи-
руется продолжительность интервала времени между получением
заказа от потребителя и его выполнением.
3. Руководитель фирмы отдает предпочтение проекту, в соот-
ветствии с которым объемы складских запасов минимальны, с тем
чтобы уменьшить капитальные издержки на хранение изделий.
Нетрудно видеть, что эти критерии не могут быть реализованы
при оптимизации одновременно. Приемлемым компромиссом явля-
ется выбор в качестве первичного характеристического показателя
качества функционирования системы подлежащего минимизации
показателя суммарных затрат в единицу времени с последующим
14
ГЛАВА 1
учетом необходимых вторичных условий, к числу которых отно-
сится поддержание объемов складских запасов изделий всех видов
в заранее установленных границах, а также ограничение количества
изменений в ассортименте изделий и используемых красок в тече-
ние недели.
В заключение отметим, что для применения рассматриваемых
в книге методов необходимо сформулировать оптимизационную зада-
чу, которая обладает единственным характеристическим критерием.
За последние годы разработан ряд методов решения мультикритери-
альных оптимизационных задач различных типов, однако обсуж-
дение этого нового и постоянно совершенствуемого аналитического
аппарата выходит за рамки данной книги. Заинтересованный чита-
тель может обратиться к недавно вышедшим в свет специальным
работам [1, 2].
1.1.3. Независимые переменные
На третьем основном этапе постановки задачи оптимизации осу-
ществляется выбор независимых переменных, которые должны
адекватно описывать допустимые проекты или условия функциони-
рования системы. В процессе выбора независимых переменных
следует принять во внимание ряд важных обстоятельств, которые
рассматриваются ниже.
Во-первых, необходимо провести различие между переменными,
значения которых могут изменяться в достаточно широком диапазо-
не, и переменными, значения которых фиксированы и определяются
внешними факторами. Так, в примере с красильным цехом виды
изделий и сорта применяемых красок зафиксированы технологиче-
скими спецификациями или заказами потребителей, т. е. относятся
к числу параметров системы. С другой стороны, порядок окраски
изделий в различные цвета с учетом ограничений, накладываемых
на количество видов изделий и объемы складских запасов, пред-
ставляется независимой переменной, значения которой могут варьи-
роваться при заданной производственной программе.
Далее важно провести различие между теми параметрами сис-
темы, которые могут предполагаться постоянными, и параметрами,
которые подвержены флуктуациям вследствие воздействия внешних
или неконтролируемых факторов. В частности, в примере с красиль-
ным цехом поломки оборудования и прогулы рабочих могут ока-
зать весьма заметное влияние на процесс производства в цехе.
Ясно, что существенные изменения этих важных параметров систе-
мы должны быть приняты во внимание при постановке задачи про-
изводственного планирования, если требуется, чтобы составленный
оптимальный план был реалистичным и выполнимым.
Во-вторых, при постановке задачи следует учитывать все основ-
ные переменные, которые влияют на функционирование системы
или качество проекта. Например, если при проектировании газо-
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ
15
хранилища рассматривать высоту, диаметр и толщину стенок ци-
линдрического газгольдера как независимые переменные, но исклю-
чить возможность использования компрессора для повышения ра-
бочего давления, то получится проект весьма низкого качества. Для
выбранной и фиксированной величины давления, разумеется, можно
определить размеры газгольдера, обеспечивающие его наименьшую
стоимость. Однако если включить в число независимых переменных
давление, при котором хранится газ, и ввести в характеристический
критерий стоимость компрессора, то можно получить проект, реа-
лизация которого,требует меньших полных затрат из-за уменьшения
необходимого объема газгольдера. Следовательно, независимые
переменные должны выбираться таким образом, чтобы все важней-
шие технико-экономические решения нашли отражение в формули-
ровке задачи. Исключение возможных альтернатив в общем случае
приводит к получению субоптимальных решений.
Наконец, еще одним существенным фактором, влияющим на вы-
бор переменных, является уровень детализации при исследовании
системы. Очень важно ввести в рассмотрение все основные незави-
симые переменные, но не менее важно не «перегружать» задачу боль-
шим количеством мелких, несущественных деталей. Например, при
проведении предварительного анализа производственного процесса,
включающего большое число различных видов оборудования—
сосудов высокого давления, колонн, насосов, компрессоров и тепло-
обменников,— обычно явным образом не учитываются несуществен-
ные особенности конструкции того или иного устройства. Теплооб-
менник может быть с достаточной для поставленных целей полнотой
охарактеризован как размерами площади поверхности теплопере-
дачи, так и перепадами давления в трубах и корпусе аппарата.
Переменные, имеющие непосредственное отношение к конструкции
аппарата,— количество и размеры труб, число проходов труб через
корпус, частота расположения перегородок и размеры корпуса —
рассматриваются, как правило, при исследовании каждого отдель-
ного устройства. При выборе независимых переменных целесооб-
разно руководствоваться правилом, согласно которому следует
рассматривать только те переменные, которые оказывают суще-
ственное влияние на характеристический критерий, выбранный для
анализа сложной системы.
1.1.4. Модель системы
После того как характеристический критерий и независимые
переменные выбраны, на следующем этапе постановки задачи необ-
ходимо построить модель, которая описывает взаимосвязи между
переменными задачи и отражает влияние независимых переменных
на степень достижения цели, определяемой характеристическим
критерием. В принципе оптимизационное исследование можно про-
вести на основе непосредственного экспериментирования с системой.
16
ГЛАВА 1
Для этого следует зафиксировать значения независимых внутри-
системных переменных, реализовать процедуру наблюдения за
функционированием системы в этих условиях и оценить значение
характеристического показателя качества функционирования систе-
мы, исходя из зарегистрированных характеристик. Затем с помощью
оптимизационных методов можно скорректировать значения неза-
висимых переменных и продолжить серию экспериментов. Однако
на практике оптимизационные исследования проводятся, как пра-
вило, на основе упрощенного математического представления сис-
темы, которое носит название модели. Применение моделей обуслов-
лено тем, что эксперименты с реальными системами обычно требуют
слишком больших затрат средств и времени, а также в ряде случаев
оказываются связанными с риском. Модели широко используются
при инженерном проектировании, поскольку это открывает воз-
можности для реализации наиболее экономичного способа изучения
влияния изменений в значениях основных независимых переменных
на показатель качества функционирования системы.
В самом общем представлении структура модели включает ос-
новные уравнения материальных и энергетических балансов, соот-
ношения, связанные с проектными решениями, а также уравнения,
описывающие физические процессы, протекающие в системе. Эти
уравнения обычно дополняются неравенствами, которые определяют
область допустимых значений независимых переменных, позволяют
определить требования, накладываемые на верхние или нижние
границы изменения характеристик функционирования системы, и
установить лимиты имеющихся ресурсов. Таким образом, элементы
модели содержат всю информацию, которая обычно используется
при расчете проекта или прогнозировании характеристик инженер-
ной системы. Очевидно, что процесс построения модели является
весьма трудоемким и требует четкого понимания специфических
особенностей рассматриваемой системы. В последующих главах
вопросы конструирования моделей будут рассмотрены более под-
робно. Здесь же целесообразно ограничиться констатацией того
факта, что модель представляет собой некоторый набор уравнений
и неравенств, которые определяют взаимосвязь между переменными
системы и ограничивают область допустимых изменений пере-
менных.
Из вышеизложенного следует, что задача в виде, пригодном для
применения оптимизационных методов, объединяет характеристи-
ческую меру, множество независимых переменных и модель, отра-
жающую взаимосвязь переменных. Поскольку требования, предъ-
являемые к оптимизационным задачам, являются весьма общими и
носят абстрактный характер, область приложения методов оптими-
зации может быть достаточно широкой. Действительно, рассматри-
ваемые ниже методы находят применение при решении самых раз-
личных задач науки и техники, включая задачи оптимального про-
ектирования структурных элементов систем и процессов, планиро-
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ
17
вания стратегий капитальных вложений, компоновки сетей склад-
ских помещений, определения оптимальных маршрутов движения
грузового транспорта, планирования в здравоохранении, дислока-
ции вооруженных сил, проектирования механических узлов и ряд
других задач. В данной книге основное внимание уделяется инже-
нерным приложениям. Некоторые из приложений такого рода
вместе с постановками соответствующих задач рассматриваются
в следующем разделе.
1.2. Применение методов оптимизации
в инженерной практике
Теория оптимизации находит эффективное применение во всех
1 направлениях инженерной деятельности, и в первую очередь в сле-
дующих четырех ее областях:
1) проектирование систем и их составных частей;
> 2) планирование и анализ функционирования существующих
- систем;
3) инженерный анализ и обработка информации;
4) управление динамическими системами.
В данном разделе кратко рассматриваются типичные приложе-
ния методов оптимизации в каждой из первых трех перечисленных
областей.
Такая важная область инженерной деятельности, как управ-
ление динамическими системами, также допускает применение
методов оптимизации, однако анализ соответствующих примеров
требует от читателя специальной подготовки и выходит за рамки
этой книги.
При рассмотрении приложений методов оптимизации при проек-
тировании и анализе функционирования систем следует иметь
в виду, что оптимизация — всего лишь один этап в процессе фор-
мирования оптимального проекта или условий эффективного функ-
ционирования системы. Вообще говоря, указанный процесс, как
показано на рис. 1.1, является циклическим и включает синтез
(определение) структуры системы, построение модели, оптимизацию
параметров модели и анализ полученного решения. При этом опти-
мальный проект или новый план функционирования системы строит-
ся на основе решения серин оптимизационных задач, способствую-
щего дальнейшему совершенствованию структуры системы. Для
краткости изложения рассматриваемые в данном разделе примеры
иллюстрируют лишь один цикл процесса проектирования и связаны
главным образом с подготовкой к этапу оптимизации. Такую ориен-
тацию примеров не следует интерпретировать как подчеркивание
ведущей роли оптимизационных методов в инженерном проектиро-
вании и в процессе анализа систем. Несмотря на то что методы теории
оптимизации отличаются универсальностью, их успешное приме-
18
ГЛАВА 1
Инженерное
проектирование
I
Определение потребностей
и установление лимитов
ресурсов
Постановка задачи
Построение модели
Анализ
।
Рычнсленил U
Рис 1 1. Этапы процесса инженерного проектирования.
нение в значительной степени зависит от профессиональной подго-
товки инженера, который должен иметь четкое представление о спе-
цифических особенностях изучаемой системы. Основная цель рас-
смотрения приводимых ниже примеров заключается в том, чтобь
продемонстрировать разнообразие постановок оптимизационных
задач, возникающих в процессе проектирования и анализа, на фоне
общности их формы.
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ
19
1.2.1. Использование методов оптимизации
при проектировании
Сфера применения оптимизационных методов в инженерном про-
ектировании достаточно широка: от проектирования отдельных
структурных элементов технических систем до проектирования узлов
оборудования и составления предварительных проектов промыш-
ленных предприятий в целом. Для того чтобы использовать методы
оптимизации, необходимо разработать «принципиальную схему»
функционирования системы или выявить ее структуру; тогда задача
оптимизации сводится к выбору таких значений переменных, харак-
теризующих размеры отдельных устройств и режимы их работы,
которым соответствует наилучшее значение характеристического
показателя качества функционирования системы.
Пример 1.1. Проектирование системы снабжения кислородом
Описание задачи. Кислородный конвертер, используе-
мый в производстве стали, представляет собой химический реактор
периодического действия, который потребляет чистый кислород.
Процесс функционирования конвертера — циклический. Руда и
D,
Скорость
потребления
фунт 02
час
F
—— Время - >
Цикл потребления кислорода, пример 1.1.
о < t <
Рис 1.2.
{Do при
Dj при
< t < /2,с повторением в каждом цикле длины t2
флюс загружаются в реактор, взаимодействуют в течение определен-
ного периода времени, а затем продукты взаимодействия выводятся
наружу. Этот циклический процесс связан с периодическими изме-
нениями скорости потребления кислорода. Как показано на рис. 1 2,
каждый цикл состоит из временного интервала длины tlt на котором
расход кислорода в единицу времени невелик и равен Do> и времен-
ного интервала (£2—G), которому соответствует высокая скорость
потребления Dx. Используемый в конвертере кислород производится
на специальной установке в соответствии с распространенным тех-
нологическим способом, который позволяет получать кислород из
20
ГЛАВА 1
воздуха путем охлаждения и дистилляции. Кислородные установки
отличаются высоким уровнем автоматизации и, как правило, имеют
постоянную производительность. Для того чтобы соединить непре-
рывно действующую кислородную установку с циклически функцио-
нирующим конвертером, необходимо разработать проект простой
системы управления запасами (рис. 1.3), состоящей из компрессора
и резервуара для хранения кислорода. Рассмотрим возможные
Рис. 1.3. Проект системы снабжения кислородом, пример 1.1.
проекты. В самом простом случае производительность кислородной
установки можно выбрать равной D15 наибольшей скорости потреб-
ления кислорода. В течение интервала времени, которому соответ-
ствует низкий расход кислорода, излишек газа придется выпускать
в атмосферу. С другой стороны, можно выбрать кислородную уста-
новку с такой производительностью, которая позволила бы в тече-
ние одного цикла получать количество кислорода, требуемое для
обеспечения нормальной работы конвертера. В интервале времени,
когда расход газа невелик, излишек кислорода под давлением на-
капливался бы в резервуаре для последующего использования в те-
чение интервала времени, которому соответствует высокая скорость
потребления. Все промежуточные проекты отличаются от рассмот-
ренных различными сочетаниями запасов и потерь кислорода. За-
дача заключается в том, чтобы выбрать оптимальный проект.
Постановка задачи. Изучаемая система состоит из
установки для производства кислорода, компрессора и резервуара
для хранения газа. Характеристики кислородного конвертера и
цикла потребления кислорода предполагаются заданными, так как
определяются внешними по отношению к системе факторами. Ха-
рактеристический показатель качества проекта естественно выбрать
в виде полных затрат в единицу времени, которые включают затраты
на производство кислорода (постоянные и переменные), затраты на
эксплуатацию компрессора, а также постоянные издержки, свя-
занные с приобретением компрессора и резервуара для хранения
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ
21
кислорода. Основными независимыми переменными являются про-
и шодительность кислородной установки F (кг О2/ч), проектная
мощность компрессора Н (л. с.), проектная емкость резервуара
(м3) и максимальное давление в резервуаре р (Н/м2). Предпола-
1ается, что кислородная установка является стандартной и поэтому
полностью характеризуется своей производительностью. Кроме
ни о, предполагается также, что резервуар отвечает требованиям
обычного проекта и предназначен для хранения кислорода.
Модель системы включает основные соотношения, с помощью
которых можно описать взаимосвязи между независимыми перемен-
ными.
Пусть /макс— максимальное количество кислорода, запасенного
и резервуаре; используя скорректированное уравнение газового
состояния, получим
К=(/макс/М)(7?Т/р)г, (1.1)
1 де R — универсальная газовая постоянная, Т — температура газа
(предполагается постоянной), z— коэффициент сжимаемости, М. —
молекулярный вес кислорода.
Из рис. 1.2 следует, что максимальное количество кислорода,
которое должно быть запасено в резервуаре, равняется площади,
ограниченной кривой потребления между точками tx и t2, Dx и F.
Таким образом,
lMailc=(D1-F)(t2-t1). (1.2)
Подставив выражение (1.2) в (1.1), получим
у (Pi—F)(t2—ti) RT /141
v — M p z- U
Конструкция компрессора должна обеспечивать управление
потоком газа, обладающим скоростью (Dt—F) (t2—и повыше-
ние давления газа до максимального значения р. В предположении,
что газ идеальный, а процесс сжатия изотермический, имеем [3J
Я = (Pi^F)_(y.2-(i)_ RT 1п_^ ,
р0 v '
где — переводной коэффициент, k2— коэффициент полезного дей-
ствия компрессора, ра— начальное давление кислорода.
Уравнения (1.3) и (1.4) необходимо дополнить неравенством,
устанавливающим, что производительность кислородной установки
F не должна быть меньше средней скорости потребления кислорода,
т. е. неравенством
Р (it— ti) (। 5)
Кроме того, максимальное давление в резервуаре должно превышать
начальное давление кислорода:
Р>Ро- (1.6)
22
ГЛАВА 1
Характеристический показатель качества проекта включает
затраты на производство кислорода:
Ci (долл./год) —ai+a^F, (1.7)
где и а2— эмпирически определяемые параметры для установок
рассматриваемого типа, связанные с затратами на топливо, воду и
рабочую силу.
Капитальные затраты на приобретение резервуара для хранения
кислорода находятся с помощью следующей степенной зависимости:
С2 (долл.)=5, УЧ (1.8)
где и Ьг— эмпирически определяемые постоянные, отражающие
специфические особенности конструкции резервуара. Капитальные
затраты, связанные с приобретением компрессора, вычисляются
с помощью аналогичной формулы:
Сз(долл.)=&3//йп (1.9)
Затраты на эксплуатацию компрессора приближенно описывают-
ся выражением bd^H, где Ь&— затраты на эксплуатацию компрессора
единичной мощности в единицу времени. Таким образом, функцию
полных издержек можно записать в следующем виде:
Полные годовые затраты — a1+a2F+d{b1Vb!jrb3ffbi}-}-Nbii1H,
(1.Ю)
где N — число циклов потребления кислорода, реализуемых в те-
чение года, d — весовой коэффициент.
Задача оптимизации заключается в том, чтобы минимизировать
функцию (1.10) путем соответствующего выбора значений F, V,
Нир, удовлетворяющих уравнениям (1.3) и (1.4), а также неравен-
ствам (1.5) и (1.6).
Решение сформулированной задачи в существенной степени за-
висит от выбора параметров цикла (IV, ЕЕ, Dt, Л и t2), стоимостных
параметров (alt а2, Ьг—Ьъ и d) и физических параметров (Т, ра, k2,
г и /И).
В принципе эту задачу можно решить путем исключения V и Н
из формулы (1.10) с помощью (1.3) и (1.4); в результате получается
задача с двумя переменными. Если затем изобразить линии уровня
функции полных затрат на плоскости с координатами F и р, а также
учесть неравенства (1.5) и (1.6), то можно найти точку минимума.
Однако методы, рассматриваемые в последующих главах книги,
позволяют получить решение с гораздо меньшими затратами труда.
Более подробно вопросы, связанные с решением задач с различными
значениями параметров, освещены в работе [4].
В примере 1.1 представлена постановка задачи предварительногс
проектирования системы, состоящей из нескольких агрегатов. Сле-
дующий пример иллюстрирует процесс проектирования отдельногс
структурного элемента системы.
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ
23
Пример 1.2. Проектирование нагруженной балки
Описание задачи. Балка А крепится на жесткой опоре
В с помощью сварного соединения. Балка изготавливается из стали
марки 1010 и должна выдерживать нагрузку F=6000 фунт. Размеры
балки выбираются таким образом, чтобы полные затраты были ми-
нимальными. Схематический чертеж системы приведен на рис. 1.4.
Рис. 1.4. Нагруженная балка, пример 12.
Постановки задачи. Определение границ системы
в данном случае является тривиальной задачей. Система состоит из
балки А и сварного шва, необходимого для прикрепления балки
к опоре В. Независимыми, или управляемыми, переменными служат
размеры h, I, t и b, которые показаны на рис. 1.4. Длина балки L
предполагается равной 14 дюйм. Для удобства записи представим
введенные переменные как компоненты неизвестного вектора х:
х=[х1( х2, х3, x]4T=[h, I, t, b]T.
Характеристическим показателем качества проекта служат за-
траты на построение сварной группы. Основными стоимостными ха-
рактеристиками такой группы являются (1) затраты на подготови-
тельные работы, (2) затраты на сварочные работы и (3) стоимость
материалов, т. е.
F (х)=с0+с1+с2,
где F (х) — функция затрат, с0— затраты на подготовительные рабо-
ты; Ci— затраты на сварочные работы, с2— стоимость материалов.
Затраты на подготовительные работы с0. Решение о проектиро-
вании рассматриваемого структурного элемента в виде сварного
узла было основано на наличии аппарата для сварки прямолиней-
ным швом у заказчика проекта. Далее предположим, что все устрой-
ства, необходимые для установки и поддержания балки в положе-
нии, удобном для проведения сварочных работ, также имеются
в наличии. В этом случае затраты с0 можно не учитывать при по-
строении модели.
Затраты на сварочные работы сг. Предположим, что сварка
будет проводиться аппаратом, при использовании которого полные
расходы составляют 10 долл./ч (включая эксплуатационные расходы
п издержки на техническое обслуживание и текущий ремонт). Далее
пусть сварочный аппарат накладывает один кубический дюйм свар-
24
ГЛАВА 1 .
кого шва за 6 мин. Тогда затраты на сварочные работы равны
- _ / 1 л ДОЛЛ- W 1 Ч \ / g мин \ 17 _ 1 /долл. \ 17
. 1 \ 4 ) \60 мин ) \ дюйм3/ 'w \дюйм3/ ®”
где Vw— объем сварного шва в кубических дюймах.
Стоимость материалов с2.
Сг = С3Уш+с4УЯ,
где с3 = стоимость / объем сварного шва = (0,37)-(0,283) (долл./
/дюйм3); с4 = стоимость / объем балки = (0,17)-(0,283) (долл./
/дюйм3); Vb — объем балки А в кубических дюймах.
Из геометрических соотношений следует, что
Vu,=2(1/2/i2/)=/i2/, Vg—tb(L+l).
Имеем
c2=c3h2l+c4lb (L+l).
Следовательно, функция затрат принимает следующий вид:
F (x)=h4+c^l+c4tb (L+l), (1.11)
или (если выразить ее через переменные х)
F (х)=(1 +c3)x?x2+c4x3x4(L+x2). (1.12)
Заметим, что все комбинации значений х4, х2, х3 и х4 могут ока-
заться допустимыми, если балка выдерживает заданную нагрузку.
Необходимо построить несколько функциональных соотношений
между управляемыми переменными, позволяющих сузить область
их допустимых значений. Эти соотношения, записанные в форме
неравенств, представляют модель системы. Сначала приведем эти
неравенства, а затем интерпретируем их. Имеем
gi(x)=Tf7—т(х)>0,
g2(x)=sd—о(х)>0,
g3(x)=x4—Xi>0,
g4(x)=x2>0,
g6(x)=x3>0,
ge(x)=Pc(x)-F>0,
g, (х) =%!—0,125>0,
ge(x)=0,25—б (х)^0,
(1-13)
(1.14)
(1-15)
(1-16)
(1-17)
(1-18)
(1-19)
(1.20)
где Tj— расчетное напряжение в сварном шве при сдвиге; х(х) —
максимальное напряжение в сварном шве при сдвиге, функция х;
<jd— расчетное нормальное напряжение для материала балки;
о(х) — максимальное нормальное напряжение в балке, функция х;
Рс(х) — критическая нагрузка на балку, функция х; б (х) — вели-
чина прогиба конца балки, функция х. Для того чтобы завершить
построение модели, необходимо ввести в рассмотрение несколько
формул из теории сопротивления материалов.
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ
25
Напряжение в сварном шве ч(х). В соответствии с работой [5]
напряжение в сварном шве можно разложить на две составляющие
т' и т", где т'— первичное напряжение в плоскости поперечного
сечения сварного шва, а т"— вторичное напряжение при кручении:
При этом
M = F[L+(x2/2)],
^={4+[^]Т ’
J = 2 {о,7О7хЛ [4 + >
где М — момент силы F относительно центра тяжести сварной груп-
пы, J — полярный момент инерции сварной группы. Напряжение
т в сварном шве вычисляется в соответствии с формулой
т(х)=[(т')2+2тЧ" cos 0+(т")211/2,
где cos 0=хг/2/?.
Напряжение при изгибе балки о(х). Можно показать, что мак-
симальное напряжение при изгибе равно
a(x)=6FL/x4X3.
Критическая нагрузка на балку Рс(х). С ростом отношения tlb~
=х8/х4 наблюдается тенденция к потере устойчивости балки. Те
комбинации значений х3 и х4, при которых возможна потеря устой-
чивости, необходимо исключить из числа допустимых. В работе {6]
показано, что для балок, близких к прямоугольным, критическая
нагрузка приближенно описывается следующим выражением:
/Г.
где Е — модуль Юнга = 30X10’ фунт/дюйм2, /=(1/12) х3х4, <х =
= (1/3) Gxsx4, G — модуль сдвига = 12X10* фунт/дюйм2.
Прогиб балки б(х). Чтобы вычислить величину прогиба, пред-
положим, что балка представляет собой консоль с вылетом L. Тогда
6 (х)=(4/?£3)/(£х1х4).
Остальные неравенства интерпретируются следующим образом:
g3>0 устанавливает практическую невозможность получения свар-
ного шва, ширина которого превышает ширину балки, a g4^0 и
g5^0 отражают требования неотрицательности х2 и х8. Заметим,
что неотрицательность х4 и х4 следует из неравенств g3^0 и g-^O-
Ограничение g6^0 гарантирует, что критическая нагрузка на балку
не будет превышена. Неравенство отражает тот факт, что фи-
26
ГЛАВА 1
зически невозможно сделать сварной шов, ширина которого меньше
некоторого порогового значения.
Наконец, параметры zd и ad, фигурирующие в gr и g2, зависят
от материала конструкции. Для стали марки 1010 соответствующие
значения этих параметров равны ^=13 600 фунт/дюйм2 и od =
=30 000 фунт/дюйм2.
Оптимизационная задача проектирования включает функцию
затрат (1.12) и сложную систему неравенств, которая получается
путем подстановки приведенных выше формул в (1.13) — (1.20).
При этом все функции оказываются выраженными через четыре не-
зависимые переменные.
Данная задача достаточно сложна и, как легко видеть, не может
быть решена графическим способом. Однако оптимальный проект
нетрудно получить с помощью численных методов, рассматриваемых
в последующих главах.
Более подробное обсуждение этой задачи и методов ее решения
можно найти в [7].
1.2.2. Использование методов оптимизации
при планировании и анализе функционирования систем
Вторая важнейшая область применения оптимизационных мето-
дов в инженерной практике связана с совершенствованием суще-
ствующих систем и разработкой производственных планов для мно-
гопродуктовых технико-экономических процессов. Задачи анализа
функционирования систем обычно возникают в тех случаях, когда
требуется адаптировать существующую производственную систему
к новым условиям функционирования, отличным от тех условий,
которые были предусмотрены проектом этой системы. Причины,
порождающие требования такого рода, как правило, связаны с не-
обходимостью
1) увеличения общего объема выпуска продукции;
2) использования других видов сырья и расширения ассорти-
мента изделий;
3) совершенствования технологических операций, отличающихся
низким уровнем проектных решений.
В связи с решением указанных задач требуется выбрать новый
температурный режим, давление или характеристики потока; уста-
новить дополнительное оборудование; разработать новые техноло-
гические операции. Методы оптимизации в производственном пла-
нировании ориентированы главным образом на составление про-
грамм производства нескольких видов продукции на отдельном
предприятии, а также на координирование производственных пла-
нов предприятий, которые связаны хозяйственными отношениями.
Поскольку в таких приложениях предполагается, что основное обо-
рудование установлено и функционирует, предметом исследования
являются только функции переменных затрат. Возникающие при
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ
2/
Рис 1 5. Схема к задаче планирования нефтеперерабатывающего производства,
пример 1.3.
этом задачи чаще всего можно сформулировать с помощью линейных
и квазилинейных моделей. В качестве иллюстрации этого класса
приложений оптимизационных методов рассмотрим задачу плани-
рования производства нефтепродуктов.
Пример 1.3. Планирование производства нефтепродуктов
Описание задачи. В процессе переработки сырой нефти
производится определенное количество бензиновых полупродуктов,
которые затем последовательно смешиваются с целью получения
двух видов топлива для двигателей внутреннего сгорания — обыч-
ного топлива и топлива высшего качества. Для каждого полупро-
дукта известны значение показателя его эффективности, максима ть-
ный выход и фиксированная цена единицы объема полупродукта.
Для каждого вида топлива установлены минимальное значение
показателя эффективности и продажная цена, а также известны
удельные затраты на смешивание топлива. Минимальный уровень
производства обоих видов топлива определяется договорными обя-
зательствами. Остальное произведенное топливо и неиспользован-
ные полупродукты могут быть реализованы посредством свободной
продажи по известным ценам. Требуется составить оптимальный
план производства топлива в течение заданного периода времени.
Постановка задачи. На схеме, изображенной на
рис. 1.5, показано что исследуемая система включает ряд бензц-
28
ГЛАВА 1
новых полупродуктов, технологическую операцию смешивания и
два вида жидкого моторного топлива. Процессы переработки нефти
и производства полупродуктов исключены из рассмотрения наряду
с подсистемами управления запасами и распределения сырой нефти,
полупродуктов и конечной продукции. Поскольку оборудование,
необходимое для выполнения операции смешивания, к началу пла-
нового периода установлено и функционирует, следует рассмотреть
только стоимостные характеристики производственного процесса.
Характеристическим показателем качества функционирования
системы в данном случае является чистая прибыль, реализуемая
в течение планового периода. Чистая прибыль состоит из дохода от
продажи топлива и полупродуктов за вычетом затрат на смешивание
и производство полупродуктов. Независимые переменные выражают
величины потоков по ориентированным дугам, изображенным на
рис. 1.5. Таким образом, с каждым из полупродуктов ассоциированы
три переменные. Одна из переменных выражает количество полу-
продукта, направляемого на производство обычного топлива, вто-
рая — количество полупродукта, направляемого на производство
топлива высшего качества, и третья — количество полупродукта,
поступающего в свободную продажу.
Итак, для каждого полупродукта с номером i
xt— количество полупродукта, используемого для производства
обычного топлива,
yt— количество полупродукта, используемого для производства
топлива высшего качества,
2,-— количество полупродукта, направляемого в свободную про-
дажу.
С каждым видом производимого топлива в свою очередь ассоции-
рованы две переменные, одна из которых представляет количество
топлива, продаваемого по договорам, а другая — количество топ-
лива, поступающего в свободную продажу.
Таким образом, для каждого вида топлива с номером /
Uj— количество топлива, продаваемого по договорам,
Vj— количество топлива, поступающего в свободную продажу.
В модель следует включить балансовые соотношения для каждого
полупродукта и каждого вида топлива, ограничения, связанные
с технологической операцией смешивания и позволяющие учесть
заданные уровни эффективности двух видов топлива, а также огра-
ничения, вытекающие из наличия договорных обязательств.
1. Балансовое соотношение для полупродукта с номером i
записывается в виде неравенства
*i+y i+Zi^ctj, (1.21)
где а(-— выход полупродукта i за плановый период.
2. Балансовые соотношения для конечной продукции имеют
следующий вид:
ui + yi> = + (1-22)
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ
29-
3. Технологические ограничения, связанные с операцией сме-
шивания, записываются в виде
+ 2₽г-Уг->Т2(«2 + Уг). (1.23).
где значение показателя эффективности полупродукта i, а у,-—
минимальное значение показателя эффективности топлива вида /.
4. Ограничение, обусловленное договорными обязательствами,
для топлива вида / задается неравенством
«Z>6Z, (1.24)
где 6у— минимальный объем производства топлива вида /, преду-
смотренный договорами.
Характеристический показатель качества функционирования
системы (чистая прибыль) определяется выражением
2е/1>и/ + 2 сГи/ + 2 c™zi~ 2с<4’ (xz + Уг + —
—2 е*5’ (Xf + yt), где
i
с)11 — продажная цена единицы конечной продукции вида / в соот-
ветствии с договорами; с)2’ — рыночная цена единицы конечной
продукции вида /; с<3) — рыночная цена единицы полупродукта i;
— затраты на производство единицы полупродукта I; с<-” —
технологические затраты на смешивание в расчете на единицу полу-
продукта г.
С учетом данных, приведенных в табл. 1.1, задача планирования
принимает следующий вид:
минимизировать 40u1+55u2+46ui+60y2+ 621+82 24-7,5234-7,5021+
+2025—25 (X14-Z/1)—28 (х2+у2)—29,50 (х3+у3)—35,50 (х4+//4)—
—41,50 (х5+у5)
при следующих ограничениях:
ограничения типа (1.21):
Xi+yi+Zi^X 10\
x2+y2+z2s^4x 10\
х3+у3+г3^4х 103,
X4-\~yt~\~Zt^5X 105,
^5+ys+z5<5x 10s;
ограничения типа (1.22):
Х1+х2+х3+л:4+хв=«14-ц1,
У^У^Уз^Уь+Уь—иг+из}
ограничения типа (1.23):
70х1+80ха+85х34-90х4+99х5>85 («i+щ),
70i/1+80z/2+85z/3+90//4+99z/5>95(tz2+u2);
30
ГЛАВА I
ограничения типа (1.24):
ut^5 X 105, u2>4X10\
Таблица 1.1. Данные для примера 1.3
Номер полупродукта Выход полу- продукта а.» баррель/пе- риод Показатель эффективности Продажная цена cj.3> Затраты на производство 44) Технологиче- ские затраты г(&) i
1 2-1(Р 70 30,00 24,00 1,00
2 4. Ю> 80 35,00 27,00 1 ,00
3 4-10= 85 36,00 28,50 1,00
4 5-10’ 90 42,00 34,50 1 ,00
5 5-10’ 99 60,00 40,00 1,50
Вид топлива Минимальный объем произ- водства Максимальное значение по- казателя эф фектнвности v/ Продажная цена, долл /баррель
по ^оговорам ,(1) / рыночная -(2) /
обычное (1) 5-10' 85 40,00 46,00
высшего качест- 4.10’ 95 55,00 60,00
ва (2)
Кроме того, все переменные должны принимать неотрицательные
значения; в противном случае решение задачи может и не иметь
«физической» интерпретации. В целом задача оптимизации включает
19 переменных и 11 ограничений, а также условия неотрицательности
переменных. Заметим, что все фигурирующие в модели функции
являются линейными относительно независимых переменных.
Вообще говоря, в процессе нефтепереработки производится зна-
чительно большее количество различных полупродуктов и видов
конечной продукции, чем это предполагалось в рассмотренном
примере. Кроме того, в ряде практических ситуаций целесообразно
ввести дополнительные переменные, отражающие динамику управ-
ления запасами, а также расширить модельные построения на не-
сколько последовательных плановых периодов. В последнем случае
каждая переменная должна быть снабжена вторым индексом, на-
пример:
— количество полупродукта i, используемое для производ-
ства обычного топлива в плановом пециоде k.
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ
31
При этом размерность результирующей модели производственного
планирования существенно возрастает. На практике решение задач
такого типа с числом переменных, превышающим тысячу, осуще-
ствляется на основе специальных алгоритмов.
1.2.3. Использование методов оптимизации для анализа
и обработки информации
Еще одна широкая область применения оптимизационных мето-
дов в инженерной практике связана с задачами инженерного анали-
за, в частности с задачами нелинейного регрессионного анализа.
Среди наиболее общих проблем, возникающих в процессе разработки
инженерных моделей, можно выделить проблему определения пара-
метров некоторой полуэмпирической модели на основе заданного
множества экспериментальных данных. Такого рода задачи обра-
ботки информации, или задачи регрессионного анализа, путем не-
сложных преобразований приводятся к виду оптимизационных за-
дач, поскольку выбор значений параметров модели осуществляется
в соответствии с критерием качества описания имеющихся данных
с помощью этой модели.
Предположим, что некоторая переменная у зависит от некоторой
независимой переменной х, а связь между ними задается уравне-
нием y=f (х, 01, 02), в котором фигурируют два параметра (Д и 02.
Для того чтобы определить соответствующие значения 0j и 02,
необходимо провести серию экспериментов, в каждом из которых
задается значение независимой переменной х и регистрируется зна-
чение зависимой переменной у. Результатом серии из N экспери-
ментов является множество пар чисел (yt, х{), i = l.N. Затем
на основе полученной информации делается попытка подобрать зна-
чения и 02 таким образом, чтобы обеспечить хорошую точность
описания экспериментальных данных с помощью функции f. Наибо-
лее часто используемая на практике мера качества описания экспе-
риментальных данных определяется так называемым критерием
наименьших квадратов, в соответствии с которым требуется мини-
мизировать функцию
/V
^(0п ег)= 2 kT-Ж.. е„ е2)р. (1.25)
i= 1
Разность yt—f(xh 0Ь 02) между зарегистрированным значением
у{ и теоретическим значением f(xh 6Х, 02) показывает, насколько
точно выбранная модель описывает имеющиеся данные, и называ-
ется остатком. Сумма квадратов остатков по всем эксперименталь-
ным точкам является мерой точности описания данных. Действи-
тельно, если значение L(Qit 02) равно нулю, то сделанный выбор
0! и 02 обеспечивает точное описание, поскольку экспериментальные
данные совпадают с теоретической кривой. Таким образом, задачу
32
ГЛАВА 1
описания данных можно рассматривать как задачу оптимизации,
в которой требуется найти значения параметров 61 и 62, минимизи-
рующие функцию L(9i, 62).
Пример 1.4. Нелинейная регрессия
Описание задачи. Известно, что соотношение между
давлением, молярным объемом и температурой реальных газов отли-
чается от аналогичного соотношения для идеального газа, которое
записывается в виде
(1.26)
Pv=R Т,
где Р— давление (атм), v — молярный объем (см8/г-моль); Т —
температура (К), R — универсальная газовая постоянная
(82,06 атм-см3/г-моль-К).
Полуэмпирическое уравнение Редлиха — Куонга [3]
р____________________ RT________а_____
— и — Ь Tlliv(v + b)
ориентировано на то, чтобы скомпенсировать отклонение свойств
реального газа от свойств идеального газа, и содержит параметры
а и Ь, значения которых определяются на основе экспериментальных
данных. В табл. 1.2 приведены результаты измерений давления,
Таблица 1.2. Результаты измерений давления, молярного объема
и температуры углекислого газа
Номер эксперимента Р, атм и, см3/г«моль т, к
1 33 500 273
2 43 500 323
3 45 600 373
4 26 700 273
5 37 600 323
6 39 700 373
7 38 400 273
8 63,6 400 373
молярного объема и температуры углекислого газа (СО2), которые
используются при расчете нелинейной регрессии для оценивания
значений а и Ь.
Постановка задачи. Значения параметров а и b
находятся путем минимизации суммы квадратов остатков (1.25).
В данном случае эта функция имеет следующий вид:
_ RTi ।_______а 12
vi~b T^Vi(vt+b) J ’
(1-27)
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ
33
где Р(— результат измерения давления в эксперименте с номером
i, а остальные два слагаемых в скобках представляют соответствую-
щие члены уравнения (1.26) в условиях эксперимента с номером i
и зависят от параметров а и Ь. Например, слагаемое суммы, которое
соответствует первому эксперименту, равно
/по 82,06 (273) а \а
500 — 6 "г (273) V2(500; (500 + &J '
Функция (1.27) представляет собой функцию двух переменных,
которая подлежит минимизации путем соответствующего выбора
значений независимых переменных а и Ь. Если бы уравнение Ред-
лиха — Куонга точно описывало имеющиеся данные, то минималь-
ное значение функции (1.27) равнялось бы нулю. Однако наличие
экспериментальных ошибок в результатах измерений, а также от-
дельные упрощения, принимаемые при построении уравнения, при-
водят к тому, что изучаемая модель лишь приближенно описывает
свойства углекислого газа, и, следовательно, функция (1.27) не
обращается в нуль в точке оптимума. В частности, оптимальным
значениям а=6,377 • 10’ и Ь—29,7 соответствует сумма квадратов
остатков, равная 9,7» 10"2.
Кроме задач регрессионного анализа в инженерной практике
возникает множество других задач, которые можно формулировать
и решать как задачи оптимизации. Отметим ставший классическим
подход к определению равновесного состава химической смеси [3].
Известно, что равновесным состоянием замкнутой системы, началь-
ное состояние которой задано, при фиксированной температуре и
фиксированном давлении является такое состояние, при котором
свободная энергия Гиббса принимает минимальное значение. В ра-
боте [8] показано, что задача определения равновесного состава
смеси может быть сформулирована как задача минимизации нели-
нейной функции при ограничениях, образованных системой линей-
ных уравнений вместе с условиями неотрицательности переменных.
Другая классическая инженерная задача, которую можно сфор-
мулировать и решить как задачу оптимизации, связана с определе-
нием величин установившихся токов в электрической цепи, состав-
ленной из активных сопротивлений [9]. Если известны величины
сопротивлений и полный ток в цепи, то значения токов через сопро-
тивления можно определить путем решения задачи минимизации
полной потери мощности в цепи (72/?) с учетом линейных ограниче-
ний, которые обеспечивают выполнение закона Кирхгофа для каж-
дого узла цепи.
1.3. Структура оптимизационных задач
Несмотря на то что прикладные задачи, рассмотренные в преды-
дущем разделе, относятся к совершенно разным областям инженер-
ной практики и представляют различные системы, они имеют общую
2 № 1826
34
ГЛАВА I
форму. Все эти задачи можно классифицировать как задачи мини-
мизации вещественнозначной функции f (х) А'-мерного векторного
аргумента .х=(х1, х2, . . , xN), компоненты которого удовлетворяют
системе уравнений hk(x)=6, набору неравенств а также
ограничены сверху и снизу, т. е. х)и’ ^х^х^. В последующем
изложении функцию /(х) будем называть целевой функцией, урав-
нения /rfc(x)=0 — ограничениями в виде равенств, а неравенства
gy(x)^0 — ограничениями в виде неравенств. При этом предпола-
гается, что все фигурирующие в задаче функции являются веще-
ственнозначными, а число ограничений конечно.
Задача общего вида:
минимизировать /(х)
при ограничениях
(х) = 0, 1, , К,
gj^x^Q, j = \..........J,
х\Е7> Аэ х{ x-L>, i = 1, ..., N
называется задачей оптимизации с ограничениями или задачей
условной оптимизации. В частности, в примерах 1.1, 1.2 и 1.3 рас-
смотрены задачи условной оптимизации. Задача, в которой нет огра-
ничений, т. е.
J = K = 0и
х)77’ = — x-L> = оо, i = 1, ..., N,
называется оптимизационной задачей без ограничений или задачей
безусловной оптимизации. В примере 1.4 представлена задача без
ограничений.
Задачи оптимизации можно классифицировать в соответствии
с видом функций /, hk, gj и размерностью вектора х. Задачи без
ограничений, в которых х представляет собой одномерный вектор,
называются задачами с одной переменной и составляют простейший,
но вместе с тем весьма важный подкласс оптимизационных задач.
Задачи условной оптимизации, в которых функции Лли g}- являются
линейными, носят название задач с линейными ограничениями.
В таких задачах целевые функции могут быть либо линейными,
либо нелинейными. Задачи, которые содержат только линейные
функции вектора непрерывных переменных х, называются задачами
линейного программирования; в задачах целочисленного программиро-
вания компоненты вектора х должны принимать только целые зна-
чения. Одна из задач линейного программирования рассмотрена
в примере 1.3 (разд. 1.2).
Задачи с нелинейной целевой функцией и линейными ограниче-
ниями иногда называют задачами нелинейного программирования
с линейными ограничениями. Оптимизационные задачи такого рода
можно классифицировать на основе структурных особенностей не-
линейных целевых функций. Если /(х) — квадратичная функция,
то мы имеем дело с задачей квадратичного программирования; если
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ 35
f(x) есть отношение линейных функций, то соответствующая задача
носит название задачи дробно-линейного программирования, и т. д.
Деление оптимизационных задач на эти классы представляет зна-
чительный интерес, поскольку специфические особенности тех или
иных задач играют важную роль при разработке методов их реше-
ния. В последующих главах рассматриваются методы, которые
можно использовать для решения таких задач.
1.4. Некоторые замечания о книге
в целом
В книге изложены методологические основы анализа задач как
условной, так и безусловной оптимизации. Главное внимание здесь
уделено общим методам, которые применимы к решению задач с
непрерывными переменными, действительными функциями, вхо-
дящими в ограничения, и единственной действительной целевой
функцией. Задачи, включающие целочисленные или дискретные
переменные, рассмотрены лишь кратко. Кроме того, исключены
оптимизационные задачи, содержащие функциональные уравнения
и структурные элементы стохастической природы, а также модели
с переменной структурой. Этот материал представляет значительный
интерес, однако является весьма сложным и поэтому должен быть
освещен в специальных работах. Авторы стремились к изложению на
достаточно высоком уровне математической строгости; вместе с тем
подробные доказательства математических результатов в тексте
отсутствуют, за исключением тех случаев, когда они служат для
разъяснения приемов построения алгоритмических структур. До-
казательства используемых результатов можно найти, руковод-
ствуясь ссылками на литературные источники. Важно подчеркнуть,
что изложение материала книги ориентировано в первую очередь
на построение и пояснение системы понятий, лежащих в основе
изучаемых математических конструкций.
Одна из целей написания данной книги заключается в том, чтобы
продемонстрировать возможности применения методов оптимизации
к решению инженерных задач. В связи с этим значительная часть
материала посвящена рассмотрению конкретных примеров из ин-
женерной практики, обсуждению вариантов постановок задач и
анализу вычислительных методов, которые облегчают решение
прикладных задач. Кроме того, особое внимание уделено вопросам
эффективности вычислений, тесно связанным с проблемой выбора и
использования тех или иных методов при определенных условиях.
В гл. 2 исследуется простейшая задача оптимизации, а именно
задача безусловной оптимизации с одной переменной. Полученные
результаты затем обобщаются на случай многомерной задачи безу-
словной оптимизации. В гл. 4 анализируются задачи и методы ли-
нейного программирования. Гл. 5 посвящена исследованию нели-
2*
36
ГЛАВА 1
нейных задач с ограничениями и анализу условий оптимальности
для этих задач. В гл. 6—10 излагаются методы решения задач с огра-
ничениями. Гл. 6 знакомит с методами преобразования задач услов-
ной оптимизации в задачи без ограничений, гл. 7 — с методами пря-
мого поиска. В гл. 8 и 9 рассматривается важный класс методов,
использующих процедуру линеаризации. В гл. 10 исследуются
методы, основанные на квадратичной аппроксимации. Методы, ис-
пользуемые при решении задач со специальной структурой, описы-
ваются в гл. 11. Далее, в гл. 12, приводятся результаты сравнитель-
ного анализа методов оптимизации с точки зрения эффективности
вычислений. Книга завершается обзором методических рекоменда-
ций по проведению оптимизационных исследований (гл. 13) и под-
робным обсуждением трех конкретных примеров из инженерной
практики (гл. 14).
Литература
1. Zeleny М., Multiple Criteria Decision Making, McGraw-Hill, N.Y., 1982.
2. Vincent T. L., Grantham W.J., Optimality in Parametric Systems, Wiley, N.Y.,
1981.
3. Bett K.E., Rowlinson J.S., Saville G., Thermodynamics for Chem cal Engineers,
MIT Press, Cambridge, Massachusetts, 1975.
4. Jen F. C , Pegels С. C., Dupuis T. M., Optimal Capacities of Production Facili-
ties, Management Sci., 14B, 570—580 (1968).
5. Shigley J E., Mechanical Engineering Design, McGraw-Hill, N. Y., 1973, p. 271.
6. Timoshenko S., Gere J., Theory of Elastic Stability, McGraw-Hill, N.Y., 1961,
p. 257.
7. Ragsdeil К. M., Phillips D. T., Optimal Design of a Class of Welded Structures
using Geometric Programming, ASME J. Eng. Ind. Ser. В , 98, (3), 1021—1025
(1975).
8. White W. B., Johnson S. M., Dantzig G. B., Chemical Equilibrium in Complex
Mixtures, J. Chem Phys , 28, 251—255 (1959).
9 Hayt W. H., Kemmerly J. E., Engineering Circuit Analysis, McGraw-Hill, N. Y.,
1971. Ch. 2.
Глава 2
Функции одной переменной
Задача оптимизации, в которой характеристическая мера задана
функцией одной переменной, относится к наиболее простому типу
оптимизационных задач. Тем не менее анализ задач такого типа
занимает центральное место в оптимизационных исследованиях как
теоретической, так и практической направленности. Это связано не
только с тем, что именно такие задачи обычно решаются в инженер-
ной практике, но и с тем, что одномерные методы оптимизации часто
используются для анализа подзадач, которые возникают при реа-
лизации итеративных процедур, ориентированных на решение мно-
гомерных задач оптимизации. Важность теоретических и приклад-
ных оптимизационных задач с одной управляемой переменной
обусловила разработку большого числа алгоритмов их решения.
Классификация методов решения одномерных задач по существу
основывается на различных предположениях и допущениях отно-
сительно природы и свойств функции f(x).
2.1. Свойства функций одной переменной
Согласно наиболее простому определению, функция [ (х) пред-
ставляет собой правило, которое позволяет каждому значению х
поставить в соответствие единственное значение y=f(x). В этом
случае х носит название независимой переменной, ay — зависимой
переменной. Рассмотрим множество Sc.R, где R — множество всех
действительных чисел. Мы можем определить соответствие (или
преобразование), с помощью которого каждой точке x£S приписы-
вается единственное числовое значение. Такое соответствие назы-
вается скалярной функцией f, определенной на множестве S.
Когда множество S=R, мы имеем дело со всюду определенной
функцией одной переменной. Если S есть некоторое подмножество
множества R, то функция f определена в ограниченной области.
Например,
/(х)=х3+2х2—х+З для всех x£R
38
ГЛАВА 2
есть всюду определенная функция, тогда как функция
f(x)=xs+2x2—х—3 для всех х € S= {х|—5^х<5}
определена в ограниченной области. В теории оптимизации f назы-
вается целевой функцией, aS— допустимой областью, множеством
точек, удовлетворяющих ограничениям, или областью допустимых
значений х.
Ряд физических процессов можно описать (или построить моде-
ли этих процессов) с помощью непрерывных функций, т. е. функций,
которые обладают свойством непрерывности в каждой точке х,
принадлежащей областям их определения. Однако в инженерных
Затраты
БТЕ
Электрический
дуговой разряд,
лазеры и Т п.
Печь прямого
нагрева
Пар высокого
—--------„ давления
Пар низкого
-давления----------------
Температура
Рис 2.1. Разрывная функция.
приложениях нередки и такие случаи, когда приходится использо-
вать разрывные функции. Например, если мы строим график функ-
ции, которая измеряет затраты на сообщение некоторой системе
количества тепла, равного 1 БТЕ J), при различных температурах
системы, то в результате получаем кусочно-непрерывную кривую,
изображенную на рис. 2.1. Затраты описываются разрывной функ-
цией температуры системы; однако температура системы может при-
нимать все значения в диапазоне от 200 до 3000 градусов по шкале
Фаренгейта.
Разумеется, не всегда необходимо, чтобы область допустимых
значений независимой переменной х содержала все действительные
числа из рассматриваемого интервала. Вполне возможны случаи,
когда переменная принимает только дискретные значения. Напри-
мер, если мы строим график функции, представляющей зависимость
стоимости погонного фута трубы от ее диаметра, то естественно
ограничиться лишь последовательностью точек, изображенных на
рис. 2.2, поскольку количество установленных размеров выпускае-
мых промышленностью труб-конечно."
Примечание. Важно иметь в виду, что непрерывные функции
обладают следующими свойствами:
1) сумма или произведение непрерывных функций является
непрерывной функцией;
*’ Британская тепловая единица; 1 БТЕ = 252 кал.— Прим, перев.
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
ЗЕ
2) отношение двух непрерывных функций является функцией,
непрерывной во всех точках, в которых знаменатель отношения не
обращается в нуль.
Очевидно, что в зависимости от того, является ли исследуемая
функция непрерывней или разрывной, а также в зависимости oi
структуры допустимой области для реализации процедуры поиска
Стоимость
трубы
Длина
а футах
1 1-1______।---1-------
1 1-1/2 2 3 4
Диаметр, дюйм
Рис. 2.2. Дискретная функция.
точек оптимума функции следует использовать различные методы.
Необходимо отметить, что метод, эффективный при анализе непре-
рывных функций, может оказаться неэффективным при исследова-
нии разрывных функций, хотя обратное не исключается.
В дополнение к перечисленным выше свойствам можно также
классифицировать функции в соответствии с их формой, определяю-
щей топологические свойства функций в рассматриваемом интервале.
Рис. 2.3. Монотонно возрастающая
функция.
Рис. 2.4. Монтонно убывающая функ-
ция.
Монотонные функции. Функция f(x) является моно-
тонной (как при возрастании, так и при убывании), если для двух
произвольных точек хг и х2, таких, что х^Ха, выполняется одно из
следующих неравенств:
/(Xi)^/(x2) (монотонно возрастающая функция),
/(х0>/(х2) (монотонно убывающая функция).
На рис. 2.3 представлен график монотонно возрастающей функции,
а на рис. 2.4 — график монотонно убывающей функции. Заметим,
что монотонная функция не обязательно должна быть непрерывной.
На рис. 2.5 изображен график функции, которая монотонно
убывает при х</0 и монотонно возрастает при х^О. Функция до-
40
ГЛАВА 2
стигает своего минимума в точке х—х* (начале координат) и моно-
тонна по обе стороны от точки минимума. Такие функции называют-
ся унимодальными.
Рис. 2.5. Унимодальная функция.
Определение
Функция fix) является унимодальной на отрезке в том
и только том случае, если она монотонна по обе стороны от един-
ственной на рассматриваемом интервале оптимальной точки х*.
Другими словами, если х*— единственная точка минимума f (х)
на отрезке а^х^Ь, то /(х) оказывается унимодальной на данном
интервале тогда и только тогда, когда для точек хх и х2
из x*^Xi^x2 следует, что f(x*)^f (xJCf (xf)>
и
из x*>Xi>x2 следует, что f (х*)^/(х1)^/:(х2).
Непрерывная Разрывная
Рис. 2.6. Унимодальные функции.
Дискретная
Как показано на рис. 2.6, унимодальная функция не обязательно
должна быть непрерывной. Унимодальность функций является
исключительно важным свойством, которое широко используется
в оптимизационных исследованиях. Вопросы, связанные с этим
свойством функций, рассматриваются в разд. 2.3.
2.2. Критерии оптимальности
При анализе оптимизационных задач, как правило, возникают
два общих вопроса.
1. Вопрос анализа «в статике». Как определить, представляет
ли данная точка х* оптимальное решение задачи?
2. Вопрос анализа «в динамике». Если х* не является точкой
оптимума, то какая последовательность действий приводит к полу-
чению оптимального решения?
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
41
В этом разделе основное внимание уделяется решению вопроса
анализа «в статике», а именно построению множества критериев
оптимальности, позволяющих определить, является ли данное ре-
шение оптимальным.
Определения
Функция f(x), определенная на множестве S, достигает своего
глобального минимума в точке х** gS в том и только том случае,
если
(х) для всех xgS.
Функция / (х), определенная на множестве S, имеет локальный ми-
нимум (относительный минимум) в точке х* g S в том и только
том случае, если
/(х*)^/(х) для всех х, удаленных от х*
на расстояние, меньшее е,
т. е. если существует е>0, такое, что для всех х, удовлетворяющих
условию |х—х*|<е, выполняется неравенство f(x*)^f(x).
Замечания
1. Аналогичные определения глобального максимума и локаль-
ного максимума можно получить путем замены знака неравенства
на противоположный.
2. Если функция обладает свойством унимодальности, то ло-
кальный минимум автоматически является глобальным минимумом.
X, х2 х3 х„ х5
Рис. 2.7. Локальные и глобальные оптимумы.
3. Если функция не является унимодальной, то возможно нали-
чие нескольких локальных оптимумов; при этом глобальный мини-
мум можно определить путем нахождения всех локальных оптиму-
мов и выбооа наименьшего из них.
42
ГЛАВА 2
На рис. 2.7 точка %!— точка глобального максимума, х2— точка
локального минимума, х3— точка локального максимума, —
точка глобального минимума, а х6 можно рассматривать и как точку
локального минимума, и как точку локального максимума.
Идентификация оптимумов в случае фун-
кции одной переменной. Предположим, что функция
f (х) одной переменной х определена на открытом интервале (а, Ь)
и n-кратно дифференцируема на этом интервале. Если %*— внут-
ренняя точка интервала, то теорема Тейлора позволяет записать
изменение функции / при переходе от точки х* к точке (х*+е)
в следующем виде:
и*-< L. »•+ т 5 L. ,.+ +
(2|>
где через Оп + 1(г) обозначена сумма членов, в которых степень е
равна (п+1) и выше. Если х*— локальный минимум функции f на
(а, Ь), то по определению должна существовать е-окрестность точки
х*, такая, что для всех х из этой окрестности выполняется нера-
венство
/ (%)>/(%*)• (2.2)
Из неравенства (2.2) следует, что
р I I (е2) I I I (Е") I I п /Р\ л /о
При достаточно малом е первое слагаемое доминирует над осталь-
ными, а так как е можно выбрать и положительным, и отрицатель-
ным, то неравенство (2.3) будет выполняться только в том случае,
если
5-1,.,.=°- м
Рассуждая аналогичным образом, нетрудно установить, что нера-
венство (2.3) будет справедливым только тогда, когда
<25>
Эта же схема анализа применима и в случае локального максимума,
стой лишь разницей, что знак неравенства (2.2) требуется заменить
на противоположный. Мы получили следующий общий результат,
который можно сформулировать в виде теоремы.
Теорема 2.1
Необходимые условия того, что х* является точкой локальногс
минимума (максимума) дважды дифференцируемой функции f на
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
43
открытом интервале (а, Ь), выражаются следующими соотношениями:
2. ^-| >0 «0).
dx2 [ххх* '
Эти условия являются необходимыми, т. е. в случае, когда они не
выполняются, точка х* не может быть точкой локального минимума
(максимума). С другой сторо-
ны, если эти условия выполня-
ются, мы не имеем гарантии,
что х* является точкой локаль-
ного минимума (максимума).
Рассмотрим например, функцию
/(х)=х3, график которой пред-
ставлен на рис. 2.8. Эта функ-
ция удовлетворяет необходимым
условиям наличия как локаль-
ного минимума, так и локаль-
ного максимума в начале коор-
динат, однако не имеет ни мак-
симума, ни минимума при
х* -0.
Рис. 2.8. Точка перегиба.
Определения
Стационарной точкой называется точка х*, в которой
Л|
dx
= 0.
Если стационарная точка не соответствует локальному оптиму-
му (минимуму или максимуму), то она является точкой перегиба,
или седловой точкой.
Для того чтобы провести различие между случаями, когда ста-
ционарная точка соответствует локальному минимуму, локальному
максимуму или является точкой перегиба, необходимо построить
достаточные условия оптимальности.
Теорема 2.2
Пусть в точке х* первые (и—1) производные функции обращаются
в нуль, а производная порядка п отлична от нуля.
(1) Если п — нечетное, то х*— точка перегиба.
(2) Если п — четное, то х*— точка локального оптимума.
Кроме того,
(а) если эта производная положительная, то х*— точка локаль-
ного минимума;
(б) если эта производная отрицательная, то х*— точка локаль-
ного максимума.
44
ГЛАВА 2
Доказательство
Утверждение теоремы нетрудно доказать с помощью разложения
в ряд Тейлора, представленного равенством (2.1). Поскольку поря-
док первой отличной от нуля производной равен п, формулу (2.1)
можно переписать в следующем виде:
f № + <0-f (х‘) = 5 L=x. + 0в+1 (8). (2.6)
Если п — нечетное число, то правая часть (2.6) может принимать
как положительные, так и отрицательные значения в зависимости
от того, является ли величина е положительной или отрицательной.
Это означает, что в зависимости от знака е разность /(х*4-е)—f(x*)
либо положительная, либо отрицательная. Следовательно, функция
не достигает в точке х* своего минимального или максимального
значения, т. е. х*— точка перегиба.
Далее рассмотрим случай, когда п — четное число. При этом ве-
личина е" всегда положительная, а знак правой части (2.6) опреде-
ляется первым слагаемым, если е — достаточно малая величина.
Таким образом, если величина (dnf/dxn)\x-x* положительная, то
/(х*+е)—/(х*)>0 и точка х* соответствует локальному минимуму.
Аналогичные рассуждения нетрудно провести также и для локаль-
ного максимума.
Для того чтобы применить теорему 2.2 к функции f(x)=x3, гра-
фик которой изображен на рис. 2.8, вычислим
=0, -Й1 =о, -Й1 =6.
ах [х=о ах2 |х=о ах3 |х=о
Так как порядок первой отличной от нуля производной равен 3
(нечетное число), точка х=0 является точкой перегиба.
Замечание
Выше предполагалось, что рассматриваемая функция диффе-
ренцируема или что ее первая производная существует и непрерыв-
на. Однако если функция не является дифференцируемой во всех
точках области определения, то даже необходимое условие наличия
оптимума, позволяющее идентифицировать стационарные точки,
может не выполняться в точке оптимума. Например, рассмотрим
кусочно-линейную функцию
( х при х -С 2,
f (х) = | 0
4 ( 4—х при х^2.
Эта функция непрерывна во всех точках действительной оси, но не-
дифференцируема при х=2. Функция достигает максимума в точке
х=2, которая не является стационарной в соответствии с данным
выше определением.
Пример 2.1
Рассмотрим функцию
/(х)=5х°—36х5+(165/2) х4—60х3+36,
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
45
определенную на всей действительной оси. Первая производная
этой функции равна
= 30х«— 1 80л1 + ЗЗОх3— 180х2 = ЗОх2 (х — 1) (х—2) (х—3).
Ясно, что первая производная обращается в нуль в точках х=0,
1, 2, 3, и, следовательно, эти точки можно классифицировать как
стационарные. Вторая производная функции равна
= 150х*—720х3 + 990х2—ЗбОх.
Вычислив значения второй производной в четырех точках х=0,
1, 2, 3, получим
X 1 (X) 8 1 /Г\-
0 36 0
1 27,5 60
2 44 —120
3 5,5 540
Отсюда следует вывод, что х=1, 3 — точки локальных минимумов,
а х—2 — точка локального максимума. Чтобы идентифицировать
точку х=0, вычислим третью производную
-^.|^ц = (600х3 — 2160х2+1980х— 360) |^о = —360.
Так как эта производная отлична от нуля и имеет нечетный порядок,
то точка х=0 является не точкой оптимума, а точкой перегиба.
Следующий вопрос, к рассмотрению которого мы переходим,
связан с определением глобального максимума или минимума функ-
ции одной переменной. Поскольку глобальный оптимум является
локальным, можно вычислить все локальные оптимумы и выбрать
из них наилучший. Алгоритм, основанный на этом простейшем
подходе, приводится ниже.
Максимизировать /(х) при ограничении as^xs^b,
где а и b — установленные границы изменения значений перемен-
ной х.
Так как функция исследуется на заданном интервале, нетрудно
заметить, что проверку наличия локального оптимума необходимо
проводить не только в стационарных точках, но и в граничных
точках интервала.
Шаг 1. Приравнять df/dx=0 и найти все стационарные точки.
Шаг 2. Выбрать все стационарные точки, которые располо-
жены в интервале [а, &]. Обозначим эти точки через х1( х2, . . . , xN.
46
ГЛАВА 2
Проверку наличия локального оптимума следует проводить только
на множестве указанных точек, дополненном точками а и Ь.
Шаг 3. Найти наибольшее значение f(x) из множества f(a),
f(b), f(x1), ... , f(xN). Это значение соответствует глобальному
максимуму.
Примечание. При построении алгоритма мы не пытались клас-
сифицировать стационарные точки как точки локального минимума,
точки локального максимума или точки перегиба, поскольку для
этого требуется вычисление производных высших порядков. Для
определения глобального оптимума легче вычислить соответствую-
щие значения функции и выбрать из них максимальное.
Пример 2.2
Максимизировать f(x)=—х3+Зх24-9х+10 на интервале —2^
зфс^4. Имеем
—Зх2 + 6х + 9 = 0.
ах 1 1
Решая это уравнение, получаем две стационарные точки х=3 и
х——1, которые расположены внутри заданного интервала.
Для того чтобы найти глобальный максимум, вычислим значения
f(x) в точках х=3, —1, —2 и 4:
/(3)=37, /(—1)=5,
/(—2)=12, f(4)=30.
Таким образом, точка х=3 соответствует максимальному значению /
на интервале [—2, 4].
Вместо перебора всех стационарных точек и соответствующих
значений функции можно воспользоваться специальными процеду-
рами, позволяющими найти глобальный оптимум с меньшими за-
тратами времени при условии, что функция обладает определенными
свойствами. В заключительной части разд. 2.1 было дано определе-
ние унимодальной функции, для которой локальный оптимум яв-
ляется глобальным. К сожалению, определение унимодальной функ-
ции не позволяет непосредственно проверить, является ли функция
унимодальной. Однако в теории оптимизации выделяется важный
класс унимодальных функций, а именно класс выпуклых и вогнутых
функций, которые допускают проверку такого рода. Основные
свойства выпуклых и вогнутых функций приведены в приложении Б.
Пример 2.3
Исследуем свойства функции
/(х)=(2х+1)2(х—4),
/'(х)=(2х+1) (6х—15),
/”(х)=24(х-1).
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ 47
При х<1 имеем /"(х)^0, и, следовательно, функция является вог-
нутой в указанной области. Если же х^1, то /"(х)^0, т. е. функ-
ция является выпуклой в этой области.
Заметим, что функция имеет две стационарные точки х=—1/2 и
х=5/2. Поскольку f'\—1/2')<.О, функция обладает локальным мак-
симумом при х=—1/2. В точке х=6/2 вторая производная Г(5/г)>0,
и, следовательно, функция достигает в этой точке локального ми-
нимума. Если ограничить допустимую область неравенством xs^l,
то f(x) имеет глобальный максимум при х=—Vj, так как /(х)—
вогнутая функция (в данной области) и х——V2 — точка локаль-
ного максимума. Аналогично если ограничить допустимую область
неравенством х^1, то /(х) достигает глобального минимума при
х=5/2. Однако если переменная х изменяется на всей действительной
оси от —оо до Н~оо, то функция / (х) не имеет конечного глобального
максимума или минимума.
Пример 2.4. Задача управления запасами
Многие фирмы создают запасы производимых товаров для удов-
летворения будущего спроса. Среди причин, обусловливающих
содержание запасов в определенном объеме, можно отметить нера-
циональные потери времени и средств, связанные с их непрерывным
пополнением. С другой стороны, пополнение запасов через продол-
жительные промежутки времени приводит к образованию чрезмер-
но больших запасов, которое требует необоснованных капитальных
затрат и значительно повышает стоимость хранения запасов. Опре-
деление оптимального объема запасов представляет собой классиче-
скую задачу оптимизации, для решения которой часто используется
так называемая модель определения наиболее экономичного размера
заказа.
В рамках этой модели спрос предполагается постоянным и рав-
ным X единиц товара в год. Частое пополнение запасов нецелесооб-
разно, так как стоимость выполнения одного заказа составляет
К долл, независимо от его размера. Первоначальная стоимость еди-
ницы товара равна с долл. Хранение излишних запасов также не-
целесообразно, поскольку стоимость хранения единицы товара от-
лична от нуля и составляет h долл, в год. Для того чтобы упростить
задачу, предположим, что спрос удовлетворяется немедленно (т. е.
задолжениые заказы отсутствуют), а пополнение осуществляется
сразу же, как только запасы иссякают.
Рис. 2.9 иллюстрирует изменение объема запасов с течением
времени. В точке А объем запасов равен В; затем объем запасов
начинает уменьшаться со скоростью X единиц товара в единицу вре-
мени и достигает нулевого значения в точке С. В это время посту-
пает новая партия товара, и объем запасов восстанавливается.
Треугольник АВС представляет один цикл управления запасами,
который повторяется во времени. Задача заключается в том, чтобы
определить оптимальный размер заказа В и продолжительность
48
ГЛАВА 2
интервала времени между заказами С — А. Обозначим соответ-
ствующие переменные через Q и Т.
Поскольку Т есть величина промежутка времени, в течение ко-
торого при скорости расходования X истощается запас Q, имеем
7'=Q/X. Таким образом, задача сводится к нахождению оптималь-
ного значения Q. Заметим, что когда Q мало, переменная Т также
принимает малое значение. При этом частота заказов велика, что
о₽е н Рис. 2.9. Циклы управления запасами,
обусловливает большие затраты на выполнение заказов и относи-
тельно малые издержки хранения запасов. С другой стороны, нали-
чие большого объема запасов (Q велико) приводит к увеличению
затрат на хранение запасов и одновременно к снижению издержек,
связанных с выполнением заказов на товары. Одна из основных задач
управления запасами состоит в определении оптимального значе-
ния Q, которому соответствует минимум суммы полных годовых
затрат.
Получим аналитическое выражение для функции полных годо-
вых затрат (затраты/цикл X количество циклов/год).
Количество циклов (заказов)/год=1/7’=Х^,
Затраты/цикл = Затраты на выполнение заказов +
+ Затраты на хранение запасов =
=(K+cQ)+[(Q/2) hT] =
=/<+cQ4-(/iQ2/2X).
Примечание. Затраты на хранение запасов в течение цикла рав-
ны затратам на хранение Q/2 единиц товара в течение интервала
времени Т.
Таким образом, подлежащая минимизации функция полных
затрат есть
f (Q)=(WQ)+Xc+(/iQ/2),
f(Q)=(-XK/Q2)+(/i/2),
f"(Q)=(2WQ3)>0 при всех Q>0.
Отсюда следует, что f(Q) — выпуклая функция и если существует
положительное значение Q*, такое, что /'(Q*)=0> т0 Q* минимизи-
рует /(Q).
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
4»
Решив уравнение /'(Q)=0, получим
Q» = /2Wi> 0.
Таким образом, оптимальный размер заказа равен
Q* = /2Wi.
При этом Т*— интервал времени между заказами =К2/<Ж.
Величина Q* известна в теории управления запасами как наиболее
экономичный размер заказа.
2.3. Методы исключения интервалов
В разд. 2.2 рассматривался вопрос анализа «в статике», который
заключается в том, чтобы определить, является ли данное решение
оптимальным. Для этого были построены необходимые и достаточ-
ные условия оптимальности решения. Далее мы переходим к изу-
чению вопроса анализа «в динамике», связанного с нахождением оп-
тимального решения. С этой целью ниже рассматривается ряд одно-
мерных методов поиска, ориентированных иа нахождение точки
оптимума внутри заданного интервала. Методы поиска, которые-
позволяют определить оптимум функции одной переменной путем
последовательного исключения подынтервалов и, следовательно,
путем уменьшения интервала поиска, носят название методов;
исключения интервалов.
В разд. 2.1 было дано определение унимодальной функции. Уни-
модальность функций является исключительно важным свойством.
Фактически все одномерные методы поиска, используемые на прак-
тике, основаны на предположении, что исследуемая функция в до-
пустимой области по крайней мере обладает свойством унимодаль-
ности. Полезность этого свойства определяется тем фактом, что для
унимодальной функции f(x) сравнение значений f(x) в двух различ-
ных точках интервала поиска позволяет определить, в каком ид
заданных двумя указанными точками подынтервалов точка опти-
мума отсутствует.
Теорема 2.3
Пусть функция f унимодальна на замкнутом интервале
а ее минимум достигается в точке х*. Рассмотрим точки хг и х2,
расположенные в интервале таким образом, что а^х^х^Ь.
Сравнивая значения функции в точках и х2, можно сделать сле-
дующие выводы.
1. Если f (%!)>/ (х2), то точка минимума f(x) не лежит в интерва-
ле (а, х^, т. е. х* С (xlt b) (рис. 2.10).
2. Если f (х,)</(х2), то точка минимума не лежит в интервале
(х2, Ь), т. е. х* С (а, х») (см. рис. 2.10).
50
ГЛАВА 2
Доказательство
Рассмотрим случай, когда f (А)>/(х2). Пусть утверждение тео-
ремы неверно, т. е. a^x*^Xi. Поскольку х*— точка минимума,
то по определению f(x*)^f (х) для всех х £ (а, Ь). Получаем двойное
неравенство
/(Х*)</(Х1)>/(Х2) при X*<Xj<X2.
Это неравенство не может выполняться, так как унимодальная функ-
ция f(x) должна быть монотонной по обе стороны от точки х*. Таким
Рис 2.10 Графические иллюстрации к теореме 2.3.
образом, получено противоречие, доказывающее утверждение тео-
ремы. Аналогичные рассуждения справедливы также в случае,
когда /(Xj)</(x2).
Примечание. Если f (xt)=f (х2), то можно исключить оба крайних
интервала (а, х^ и (х2, Ь)\ при этом точка минимума должна распо-
лагаться в интервале (xt, х2).
Согласно теореме 2.3, которую иногда называют правилом ис-
ключения интервалов, можно реализовать процедуру поиска, позво-
ляющую найти точку оптимума путем последовательного исключе-
ния частей исходного ограниченного интервала. Поиск завершается,
когда оставшийся подынтервал уменьшается до достаточно малых
размеров. Заметим, что правило исключения интервалов устраняет
необходимость полного перебора всех допустимых точек. Несом-
ненным достоинством поисковых методов такого рода является то,
что они основаны лишь на вычислении значений функций. При этом
не требуется, чтобы исследуемые функции были дифференцируемы;
более того, допустимы случаи, когда функцию нельзя даже записать
в аналитическом виде. Единственным требованием является воз-
можность определения значений функции f (х) в заданных точках х
с помощью прямых расчетов или имитационных экспериментов.
Вообще в процессе применения рассматриваемых методов поиска
можно выделить два этапа:
этап установления границ интервала, на котором реализуется
процедура поиска границ достаточно широкого интервала, содер-
жащего точку оптимума;
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
51
этап уменьшения интервала, на котором реализуется конечная
последовательность преобразований исходного интервала с тем,
чтобы уменьшить его длину до заранее установленной величины.
2.3.1. Этап установления границ интервала
На этом этапе сначала выбирается исходная точка, а затем на
основе правила исключения строится относительно широкий интер-
вал, содержащий точку оптимума. Обычно поиск граничных точек
такого интервала проводится с помощью эвристических методов
поиска, хотя в ряде случаев можно также использовать методы
экстраполяции. В соответствии с одним из эвристических методов,
который был предложен Свенном [1], (/г+1)-я пробная точка опре-
деляется по рекуррентной формуле
xk+1 k = Q, 1, 2, ...,
где х0— произвольно выбранная начальная точка, Д — подбирае-
мая некоторым способом величина шага. Знак Д определяется путем
сравнения значений /(х0), /(х0+1Д1) и /(лг0—IДI). Если
/(х„-1Д|)>/(х0)>/(х0+|Д|),
то, согласно предположению об унимодальности, точка минимума
должна располагаться правее точки х0 и величина Д выбирается
положительной. Если изменить знаки неравенств на противопо-
ложные, то Д следует выбирать отрицательной. Если же
/(х0-|Д|)>/(х0к/(х„+1Д|).
то точка минимума лежит между х0—|Д| и х0+1А1 и поиск гранич-
ных точек завершен. Случай, когда
/(х0~ |Д1К/(Хо)>/(Хо+1Д|),
противоречит предположению об унимодальности. Выполнение
этого условия свидетельствует о том, что функция не является уни-
модальной .
Пример 2.5
Рассмотрим задачу минимизации функции /(х)=(100—х)~ при
заданной начальной точке хо=ЗО и величине шага |Д|=-5.
Знак Д определяется на основе сравнения значений
/(х0) =/(30)=4900,
/(х0+1Д|)=/(35)=4225,
/(х0— |Д|)=/(25)=5625.
Так как
/(Хо-|Д|)>/(Хо)>/(Хо+1Д|).
то величина Д должна быть положительной, а координата точки
минимума х* должна быть больше 30. Имеем х1=х04-Д=35. Далее
х2=х1+2А=45, /(45)=3025</(Х!),
52
ГЛАВА 2
откуда х*>35.
х3=ха+22А=65, /(65) = 1225</(х2),
откуда х*>45.
Х4=х3+23А = 105, /(105)=25</(х3),
откуда х*>65.
xs=x4+24A=185, / (185)=7225>/(х4),
следовательно, х*<185. Таким образом, шесть шагов вычислений
х* позволили выявить интервал 65^х*^185, в котором располо-
жена точка х*. Заметим, что эффективность поиска граничных точек
непосредственно зависит от величины шага А. Если А велико, то
получаем грубые оценки координат граничных точек, и построен-
ный интервал оказывается весьма широким. С другой стороны, если
А мало, для определения граничных точек может потребоваться
достаточно большой объем вычислений.
2.3.2. Этап уменьшения интервала
После того как установлены границы интервала, содержащего
точку оптимума, можно применить более сложную процедуру умень-
шения интервала поиска с целью получения уточненных оценок
координат оптимума. Величина подынтервала, исключаемого на
каждом шаге, зависит от расположения пробных точек хг и хг внутри
интервала поиска. Поскольку местонахождение точки оптимума
априори неизвестно, целесообразно предположить, что размещение
пробных точек должно обеспечивать уменьшение интервала в од-
ном и том же отношении. Кроме того, в целях повышения эффек-
тивности алгоритма необходимо потребовать, чтобы указанное от-
ношение было максимальным. Подобную стратегию иногда назы-
вают минимаксной стратегией поиска.
Метод деления интервала пополам. Рас-
сматриваемый метод позволяет исключать в точности половину
интервала на каждой итерации. Иногда этот метод называют трех-
точечным поиском на равных интервалах, поскольку его реализация
основана на выборе трех пробных точек, равномерно распределен-
ных в интервале поиска. Ниже приводится описание основных шагов
поисковой процедуры, ориентированной на нахождение точки ми-
нимума функции f(x) в интервале (а, Ь).
Шаг 1. Положить хт=(а+Ь)/2 и L=b—а. Вычислить значе-
ние f(xm).
Шаг 2. Положить %i=a+L/4 и xt=b—LH. Заметим, что точ-
ки хт и х2 делят интервал (а, Ь) на четыре равные части. Вычис-
лить значения {(xj и /(х2).
Шаг 3. Сравнить f(xj и f(xm).
(1) Если f (Х1)</(хт), исключить интервал (хт, Ь), положив Ь—хт,
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
53
< редней точкой нового интервала поиска становится точка Xj. Сле-
довательно, необходимо положить xm=Xi.
I (ерейти к шагу 5.
(2) Если f (Xi)>f (хт), перейти к шагу 4.
Шаг 4. Сравнить f(x2) и f(xm).
(I) Если f (х2)</(хт), исключить интервал (а, хт), положив а=хт.
Гак как средней точкой нового интервала становится точка х3.
положить хт=х2. Перейти к шагу 5.
(2) Если f (х2)>/(хт), исключить интервалы (a, xj и (х2, Ь). Поло-
жить a=Xi и &=х2. Заметим, что хт продолжает оставаться средней
ючкой нового интервала. Перейти к шагу 5.
Шаг 5. Вычислить L=b—а. Если величина |£1 мала, закон-
чить поиск. В противном случае вернуться к шагу 2.
Замечания
I. На каждой итерации алгоритма исключается в точности по-
ловина интервала поиска.
2. Средняя точка последовательно получаемых интервалов всег-
да совпадает с одной из пробных точек Xi, х2 или хт, найденных на
предыдущей итерации. Следовательно, на каждой итерации тре-
буется не более двух вычислений значения функции.
3. Если проведено п вычислений значения функции, то длина
полученного интервала составляет (1/2)п/2 величины исходного
интервала.
4. В работе [2] показано, что из всех методов поиска на равных
интервалах (двухточечный, трехточечный, четырехточечный и т. д.)
I рехточечный поиск, или метод деления интервала пополам, отли-
чается наибольшей эффективностью.
Пример 2.6. Метод деления интервала пополам
Минимизировать /(х)=(100—х)2 в интервале 60^x^150. Здесь
«=60, д=]50 и £=150—60=90.
хт=(60+150)/2=105.
Итерация 1
х1=а+(£/4)=60+(90/4)=82,5,
x2=b—(£/4)=150—(90/4)=127,5,
f (82,5)=306,25>/ (105)=25,
/(127,5)=756,25>/(105).
Таким образом, исключаются интервалы (60, 82,5) и (127,5, 150).
Длина интервала поиска уменьшается с 90 до 45.
Итерация 2
а=82,5, ft=127,5, хт=105,
£=127,5—82,5=45,
Х!=82,5+(45/4)=93,75,
х2=127,5—(45/4) = 116,25,
f (93,75) =39,06>/ (105) =25,
f (116,25) =264,06>/(105).
54
ГЛАВА 2
Таким образом, интервал неопределенности равен (93,75, 116,25)-
Итерация 3
а=93,75 6=116,25, хт=105,
L=116,25—93,75=22,5,
%!=99,375, х2 = 110,625,
/(Xi)=0,39</(105)=25.
Таким образом, исключается интервал (105, 116,25). Новый ин-
тервал неопределенности равен (93,75, 105), его средняя точка есть
99,375 (точка на итерации 3). Отметим, что за три итерации (шесть
вычислений значения функции) исходный интервал поиска длины
90 уменьшился до величины (90) (1/2)3=11,25.
Поиск с помощью метода золотого сече-
ния. Из проведенного выше обсуждения методов исключения ин-
тервалов и минимаксных стратегий поиска можно сделать следую-
щие выводы.
1. Если количество пробных точек принимается равным двум,
то их следует размещать на одинаковых расстояниях от середины
интервала.
2. В соответствии с общей минимаксной стратегией пробные
точки должны размещаться в интервале по симметричной схеме
таким образом, чтобы отношение длины исключаемого подынтервала
к величине интервала поиска оставалось постоянным.
0|-----------------©--------©----------------—I 1
Рис. 2.11. Поиск с помощью метода золотого сечения.
3. На каждой итерации процедуры поиска должно вычисляться
только одно значение функции в получаемой точке.
Руководствуясь этими выводами, рассмотрим симметричное рас-
положение двух пробных точек на исходном интервале единичной
длины, которое показано на рис. 2.11. (Выбор единичного интервала
обусловлен соображениями удобства.) Пробные точки отстоят от
граничных точек интервала на расстоянии т. При таком симметрич-
ном расположении точек длина остающегося после исключения ин-
тервала всегда равна т независимо от того, какое из значений функ-
ции в пробных точках оказывается меньшим. Предположим, что
исключается правый подынтервал. На рис. 2.12 показано, что
оставшийся подынтервал длины т содержит одну пробную точку,
расположенную на расстоянии (1—т) от левой граничной точки.
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
55
Для того чтобы симметрия поискового образца сохранялась,
расстояние (1—т) должно составлять т-ю часть длины интервала (ко-
юрая равна т). При таком выборе т следующая пробная точка раз-
мещается на расстоянии, равном т-й части длины интервала, от
правой граничной точки интервала (рис. 2.13).
Ф
-(1-т)
Рис. 2.12. Интервалы, полученные методом золотого сечения.
Отсюда следует, что при выборе т в соответствии с условием
1—т=т2 симметрия поискового образца, показанного на рис. 2.11,
сохраняется при переходе к уменьшенному интервалу, который
изображен на рис. 2.13. Решая это квадратное уравнение, получаем
т=(—1 ±К5)/2,
откуда положительное решение т=0,61803... . Схема поиска, при
которой пробные точки делят интервал в этом отношении, известна
О
ir
Рис. 2.13. Симметрия золотого сечения интервала.
под названием поиска с помощью метода золотого сечения. Заметим,
что после первых двух вычислений значений функции каждое по-
следующее вычисление позволяет исключить подынтервал, величина
которого составляет (1—т)-ю долю от длины интервала поиска.
Следовательно, если исходный интервал имеет единичную длину, то
величина интервала, полученного в результате У вычислений зна-
чений функции, равна тЛ'~1. Можно показать, что поиск с помощью
метода золотого сечения является асимптотически наиболее эффек-
тивным способом реализации минимаксной стратегии поиска.
Пример 2.7. Метод золотого сечения
Опять рассмотрим задачу из примера 2.6, в которой требуется
минимизировать f(x)=(100—х)2 в интервале 60^x^150.
Для того чтобы перейти к интервалу единичной длины, проведем
замену переменной, положив ш==(х—60)(90. Таким образом, задача
принимает следующий вид:
минимизировать f (ш)=(40—90ш)4
при ограничении
56
ГЛАВА 2
Итерация 1. Д=(0, 1); Lx=l. Проведем два первых вы-
числения значений функции:
Ш1=т=0)618, f (йУ1)=244,0,
ш2=1—т=т2=0,382, f (w 2)=31,6.
Так как f(w2)<Zf(Wi) и ш2<Ш1, интервал исключается.
Итерация 2. /2=(0, 0,618); Е3=0,618=т. Следующее вы-<
числение значения функции проводится в точке
ш3=т—т2=т(1—т)=т3=0,236, f (ш3)=352.
Так как f(w3)>f(w2) и ш3<од2, интервал ui^ui3 исключается. i
Итерация 3. /3=(0,236, 0,618), L3=0,382=x2. Следующее)
вычисление значения функции проводится в точке, расположенной
на расстоянии т X (длина полученного интервала) от левой гра-
ничной точки интервала, или на расстоянии (1—т) х (длина ин-
тервала) от правой граничной точки. Таким образом,
ш4=0,618—(1— т) L3=0,618—т2Т3=
=0,618—т2(т2)=0,618—т4=0,472,
/(ш4)=6,15.
Так как f (од4)<7(ui2) и ui4>ui2, интервал ш^и>2 исключается.
В результате получен следующий интервал неопределенности:
0,382^ш^0,618 для переменной w, или 94,4^x^115,6 для перемен-
ной х.
Если в процессе поиска проведено шесть вычислений значений
функции, то длина результирующего интервала для переменной w
равна
т^1 = т5==0,09,
что соответствует интервалу длины 8,1 для переменной х. Для срав-
нения напомним, что в аналогичной ситуации метод деления интер-
вала пополам привел к получению интервала длины 11,25.
В общем случае если правая и левая граничные точки интервала
неопределенности (обозначим их через XR и XL) известны, то ко-
ординаты всех последующих пробных точек, получаемых в соответ-
ствии с методом золотого сечения, можно вычислить по формулам
w = XR—т" или w= XL-f-T"
в зависимости от того, какой подынтервал был исключен на преды-
дущей итерации — левый или правый. В приведенных выше форму-
лах через т" обозначена n-я степень т, где п — количество вычисле-
ний значений функции.
Поиск с помощью метода золотого сечения может быть окончен
либо исходя из заданного количества вычислений значений функ-
ции (и, следовательно, величины интервала неопределенности),
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ 57
либо по достижении относительной точности искомого значения
функции. Наиболее предпочтительным является использование
обоих критериев одновременно.
2.3.3. Сравнение методов исключения интервалов
Ниже проводится сравнение относительных эффективностей рас-
смотренных методов исключения интервалов. Обозначим длину
исходного интервала неопределенности через Llt а длину интервала,
получаемого в результате N вычислений значений функции,— через
Ln. В качестве показателя эффективности того или иного метода
исключения интервалов введем в рассмотрение характеристику
относительного уменьшения исходного интервала FR (?V)=LJV/LI.
Напомним, что при использовании метода деления интервала
пополам и метода золотого сечения длина получаемого интервала
составляет Л.1(0,5)Л//2 и £-1(0,618)^“' соответственно. Следовательно,
относительное уменьшение интервала после М вычислений значений
функции равно
FR (N) — (для метода деления интервала пополам;
((0,618)Л'~1 для метода золотого сечения.
Для сравнения рассмотрим также метод равномерного поиска,
в соответствии с которым оценивание функции проводится в N
равноотстоящих друг от друга точках [при этом интервал Li де-
лится на (АНО равных интервалов длины LJtN+V)]. Пусть х*—
точка, в которой наблюдается минимум функции f(x). Тогда точка
истинного минимума f (х) оказывается заключенной в интервале
откуда Ln=2L1/(N+1). Следовательно, для метода равномерного
поиска
FR (W)=2/(7V-|-1).
В табл. 2.1 представлены значения FR (N), соответствующие вы-
бранным N, для трех методов поиска. Из таблицы следует, что поиск
Таблица 2.1. Величины относительного уменьшения интервала
Количество вычислений значений функции
Метод поиска
/7 = 2 /7 = 5 Л/=10 W=I5 /V«20
Метод деления интервала 0,5 0,177 0,031 0,006 0,0009
пополам
Метод золотого сечения 0,618 0,146 0,013 0,001 0,0001
Метот равномерного поиска 0,667 0,333 0,182 0,125 0,0?5
58
ГЛАВА 2
с помощью метода золотого сечения обеспечивает наибольшее от-s
носительное уменьшение исходного интервала при одном и том же
количестве вычислений значений функции. С другой стороны, можно
также сравнить количества вычислений значения функции, требуе-
мые для достижения заданной величины относительного уменьшения
интервала или заданной степени точности. Если величина FR(M)=
=Е задана, то значение N вычисляется по следующим формулам:
для метода деления интервала пополам
N=2 In (£)/1п (0,5),
для метода золотого сечения
М = 1+Пп(Е)/1п(0,618)1,
для метода равномерного поиска
tf=(2/E)—1.
В табл. 2.2 приведены данные о количествах вычислений значений
функции, необходимых для определения координаты точки мини-
мума с заданной точностью. Следует еще раз подчеркнуть, что метод.
Таблица 2.2. Требуемые количества вычислений значений функции !
Заданная точность
Метод поиска
Е = 0,1
Е = 0 05
Е = 0,001
Метод деления интервала 7
пополам
Метод золотого сечения 6
Метод равномерного по- 19
иска
9 14 20
8 11 16
39 199 1999
золотого сечения оказывается более эффективным по сравнению
с остальными двумя методами, поскольку он требует наименьшего
числа оцениваний значения функции для достижения одной и той
же заданной точности.
2.4. Полиномиальная аппроксимация
и методы точечного оценивания
Применение методов исключения интервалов, которые рассмат-
ривались в предыдущем разделе, накладывает единственное требо-
вание на исследуемую функцию: она должна быть унимодальной.
Следовательно, указанные методы можно использовать для анализа
как непрерывных, так и разрывных функций, а также в случаях,
когда переменные принимают значения из дискретного множества.
Логическая структура поиска с помощью методов исключения ин-
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
59
тервалов основана на простом сравнении значений функции в двух
пробных точках. Кроме того, при таком сравнении в расчет прини-
мается только отношение порядка на множестве значений функции
и не учитывается величина разности между значениями функции.
В данном разделе рассматриваются методы поиска, которые позво-
ляют учесть относительные изменения значений функции и как
следствие в ряде случаев оказываются более эффективными, чем
методы исключения интервалов. Однако выигрыш в эффективности
достигается ценой введения дополнительного требования, согласно
которому исследуемые функции должны быть достаточно гладкими.
Основная идея рассматриваемых методов связана с возможностью
аппроксимации гладкой функции полиномом и последующего ис-
пользования аппроксимирующего полинома для оценивания коор-
динаты точки оптимума. Необходимыми условиями эффективной реа-
лизации такого подхода являются унимодальность и непрерывность
исследуемой функции. Согласно теореме Вейерштрасса об аппрок-
симации [3], если функция непрерывна в некотором интервале, то
ее с любой степенью точности можно аппроксимировать полиномом
достаточно высокого порядка. Следовательно, если функция уни-
модальна и найден полином, который достаточно точно ее аппрок-
симирует, то координату точки оптимума функции можно оценить
путем вычисления координаты точки оптимума полинома. Согласно
теореме Вейерштрасса, качество оценок координаты точки оптиму-
ма, получаемых с помощью аппроксимирующего полинома, можно
повысить двумя способами: использованием полинома более высо-
кого порядка и уменьшением интервала аппроксимации. Второй
способ, вообще говоря, является более предпочтительным, поскольку
построение аппроксимирующего полинома порядка выше третьего
становится весьма сложной процедурой, тогда как уменьшение ин-
тервала в условиях, когда выполняется предположение об унимо-
дальности функции, особой сложности не представляет.
Методы оценивания с использованием квадратичной
аппроксимации
Простейшим вариантом полиномиальной интерполяции является
квадратичная аппроксимация, которая основана на том факте, чтс
функция, принимающая минимальное значение во внутренней точке
интервала, должна быть по крайней мере квадратичной. Если же
функция линейная, то ее оптимальное значение может достигаться
только в одной из двух граничных точек интервала. Таким образом,
при реализации метода оценивания с использованием квадратичной
аппроксимации предполагается, что в ограниченном интервале
можно аппроксимировать функцию квадратичным полиномом, а за-
тем использовать построенную аппроксимационную схему для оце-
нивания координаты точки истинного минимума функции.
60
ГЛАВА 2
Если задана последовательность точек хъ х2, х3 и известны соот
ветствующие этим точкам значения функции flt /2 и /3, то можнс
определить постоянные величины ал, ах и а2 таким образом, что зна-
чения квадратичной функции
q (x)=a0+ai(x—Xi)+n2(x—xj (х—х2)
совпадут со значениями /(х) в трех указанных точках. Перейдем
к вычислению q(x) в каждой из трех заданных точек. Прежде всего,
так как
(^i)=?(xi)=a0,
имеем а0=Л-
Далее, поскольку
(x2)=q (x2)=f1+a1(xi—xi),
получаем П1=(/2—Л)/(х2—х2).
Наконец, при х=х3
f3=f(x3)=q(x3)=f1+(f2—f1)/(x2—x1) (х3—xi)+a2(x3—Xi) (ха—х2).
Разрешая последнее уравнение относительно а2, получаем
а - 1
2 Хз—Х2\Х3—*1 *2 —*!/
Таким образом, по трем заданным точкам и соответствующим зна-
чениям функции можно оценить параметры а0, а2 и а2 аппроксими-
рующего квадратичного полинома с помощью приведенных выше
формул.
Если точность аппроксимации исследуемой функции в интервале
от Xi до х3 с помощью квадратичного полинома оказывается доста-
точно высокой, то в соответствии с предложенной стратегией поиска
построенный полином можно использовать для оценивания коорди-
наты точки оптимума. Напомним, что стационарные точки функции
одной переменной определяются путем приравнивания к нулю ее
первой производной и последующего нахождения корней получен-
ного таким образом уравнения. В данном случае из уравнения
g = а± + а2 (х—х2) + а2 (х—xj == 0
можно получить
х=(ха+х1)/2—(ai/2a2).
Поскольку функция /(х) на рассматриваемом интервале обладает
свойством унимодальности, а аппроксимирующий квадратичный
полином также является унимодальной функцией, то можно ожи-
дать, что величина х окажется приемлемой оценкой координаты точ-
ки истинного оптимума х*.
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
61
Пример 2.8. Поиск с использованием квадратичной аппроксима-
ции
Рассмотрим процедуру оценивания координаты точки минимума
функции
/(х)=2х2+(16/х)
в интервале 1^х^5. Пусть хх=1, х3=5, а хг есть средняя точка
интервала, т. е. х2=3. Вычислим соответствующие значения функ-
ции:
/1=18, /2=23,33, /З=53,2.
Для того чтобы оценить х, необходимо найти значения парамет-
ров и «2 аппроксимирующей функции. Имеем
_ 1 (53,2—18 8 1 _ 46
Й2~5—3\ 5—1 3f~15-
Подстановка этих значений в формулу для х позволяет получить
х=(3+1)/2—(8/3)/[2 (46/15)1 = 1,565.
Точный минимум достигается при х* = 1,5874.
Метод последовательного оценивания с использованием квадра-
тичной аппроксимации
Этот метод, разработанный Пауэллом [4], основан на последова-
тельном применении процедуры оценивания с использованием квад-
ратичной аппроксимации. Схему алгоритма можно описать следую-
щим образом. Пусть хх— начальная точка, Дх — выбранная вели-
чина шага по оси х.
Шаг 1. Вычислить x^Xj+Дх.
Ш а г 2. Вычислить j (хх) и /(х2).
Ш а г 3. Если /(%!)>/(х2), положить х3=Х1Ч-2Дх. Если /(xj^
^/(х2), положить x3=xt—Дх.
Ш а г 4. Вычислить/(х3) и найти
Емии= min {/,,/2, /3},
Хмин = точка х/( которая соответствует Емии.
Шаг 5. По трем точкам хь х2, х3 вычислить х, используя фор-
мулу для оценивания с помощью квадратичной аппроксимации.
Шаг 6. Проверка на окончание поиска.
(а) Является ли разность Емии — /(х) достаточно малой?
(б) Является ли разность Хмин — х достаточно малой?
Если оба условия выполняются, закончить поиск. В противном
случае перейти к шагу 7.
62
ГЛАВА 2
Ш а г 7. Выбрать «наилучшую» точку (Хмин или х) и две точки
по обе стороны от нее. Обозначить эти точки в естественном порядке
и перейти к шагу 4.
Заметим, что при первой реализации шага 5 границы интервала,
содержащего точку минимума, не обязательно оказываются уста-
новленными. При этом полученная точка х может находиться за
точкой х3. Для того чтобы исключить возможность слишком боль-
шого экстраполяционного перемещения, следует провести после
шага 5 дополнительную проверку и в случае, когда точках находится
слишком далеко от х3, заменить х точкой, координата которой вы-
числяется с учетом заранее установленной длины шага.
Пример 2.9. Метод Пауэлла
Рассмотрим задачу из примера 2.8:
минимизировать f (х) = 2х2 + (16/х).
Пусть начальная точка Xj=l и длина шага Дх=1. Для проверки на
окончание поиска используются следующие параметры сходимости:
Разность значений х | ^- 9 щ-2 I Разность значений f I q . п_3
f
X
Итерация I
Шаг 1. x3=Xx+Ax=2.
Ш а г 2. f (Xi) = 18, /(х2)=16.
Шаг 3. /(xi)>/(x2), следовательно, положить х3=1+2=3.
Шаг 4. /(х3)=23,33, ГМИн= 16, Хмии=х2.
Ш а г 5.
16—18 _
+ = -^- = -2,
„ _ 1 (23,33-18 1 5,33 . _ . ссс
+ 3__2 । з___I — 2 1 —4,665,
х— !.( 2) _______. с . 1 _.
2 2 (4,665)“ 1,Э + 4,665“ '
f(x) = 15,210.
Шаг 6. Проверка на окончание поиска:
(a) | = 0,0519 > 0,003.
Следовательно, продолжаем поиск.
Ш а г 7. Выбираем х как «наилучшую» точку, a Xi=l и х2=2 —
как точки, которые ее окружают. Обозначаем эти точки в естествен-
ном порядке и переходим к итерации 2, которая начинается с шага 4.
Итерация 2
Шаг 4. х1=1, /1 = 18, х2=1,714, А=15,210=Гиик, Хи11н=х2,
Х3 = 2, />=16.
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
63
“1- 1,714-1 -
л 1 (16—18 . о nn0J 1,908 с
О2— 2—1,714 ) 2—1 3’908)f — о,286 — 6,67 ’
— 2,714 •—3,908 . аС7 । л оло i сел
х==~2-----2(^=1,357 + 0,293= 1,650,
f(x)= 15,142.
Ш а г 6. Проверка на окончание поиска:
115,210—15,1421 П лл.г х Л ЛЛ, , ,
(а) ----,о------ =0,0045 > 0,003 (условие не выполняется).
I 10,14Z |
Шаг 7. Выбираем х как «наилучшую» точку, а Хх=1 и х2=
= 1,714 — как точки, которые ее окружают.
Итерация 3
Ш а г 4. Xi=l, Л=18, х3=1,65, /2= 15,142=FMI1n, ХМИ11=л'2>
х3=1,714, /3= 15,210.
Шаг 5.
15,142—18 . оО7
“>=-ns=i------4'397’
» “ 1,7.4-..вВ0 1ТЙСТ-<-Ч'397) } = 7'647'
~_ 2,65 (—4,397) , «125
Х 2 2 (7,647)
/(*) = 15,123.
Ш а г 6. Проверка на окончание поиска:
(а)
(б)
15,142—15,123
15,123
1,65—1,6125
1,6125
= 0,0013 < 0,003,
= 0,023 < 0,03.
Следовательно, поиск закончен.
2.5. Методы с использованием производных
Все рассмотренные в предыдущих разделах методы поиска осно-
вываются на предположениях об унимодальности и в ряде случаев
о непрерывности исследуемой целевой функции. Целесообразно
предположить, что если в дополнение к условию непрерывности
ввести требование дифференцируемости функции, то эффективность
поисковых процедур можно существенно повысить. Напомним, что
в разд. 2.2 установлено необходимое условие существования ло-
кального минимума функции в некоторой точке г, согласно которому
первая производная функции в точке z должна обращаться в нуль,
т. е. f (z)=df/dx\x=z=0.
64
ГЛАВА 2
Если функция f(x) содержит члены, включающие х в третьей
и более высоких степенях, то непосредственное получение аналитиче-
ского решения уравнения f'(x~)=6 может оказаться затруднитель-
ным. В таких случаях используются приближенные методы последо-
вательного поиска стационарной точки функции f. Прежде всего
опишем классическую поисковую схему, ориентированную на на-
хождение корня нелинейного уравнения. Эта схема была разрабо-
тана Ньютоном и позднее уточнена Рафсоном [5].
2.5.1. Метод Ньютона — Рафсона
В рамках схемы Ньютона — Рафсона предполагается, что функ-
ция f дважды дифференцируема. Работа алгоритма начинается
в точке хь которая представляет начальное приближение (или на-
чальную оценку) координаты стационарной точки, или корня урав-
нения /'(х)=0. Затем строится линейная аппроксимация функции
/’(х) в точке Xj, и точка, в которой аппроксимирующая линейная
функция обращается в нуль, принимается в качестве следующего
Рис 2.14. Метод Ньютона — Рафсона (сходимость).
приближения. Если точка хк принята в качестве текущего прибли-
жения к стационарной точке, то линейная функция, аппроксими-
рующая функцию f'(x) в точке хк, записывается в виде
? (х; хк) = /' (хк) + /" (хк) (х—хк). (2.7)
Приравняв правую часть уравнения (2.7) нулю, получим следующее
приближение:
xk+i = xk [/ (xk)/f (*&)]
Рис. 2.14 иллюстрирует основные шаги реализации метода Ньютона.
К сожалению, в зависимости от выбора начальной точки и вида
функции алгоритм может как сходиться к истинной стационарной
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
65
точке, так и расходиться, что отражено на рис. 2.15. Если начальная
точка расположена правее х0, то получаемые в результате последова-
тельных приближений точки удаляются от стационарной точки г.
Рис. 2.15. Метод Ньютона — Рафсона (отсутствие сходимости).
Пример 2.10. Метод Ньютона — Рафсона
Рассмотрим следующую задачу:
минимизировать f(x)=2x3+(16/x).
Для того чтобы определить стационарную точку функции /‘(х),
воспользуемся методом Ньютона — Рафсона, положив Хх=1:
f (х) == 4х—(16/х2), Г(х) = 4 + (32/х3).
Итерация 1. Хх=1, f (xi)=—12, /"(х1)=36, х2=1—
—(—12/36)= 1,33.
Итерация 2. х2=1,33, —3,73, /"(хг) = 17,6,
х8=1,33— =^= 1,54.
Итерации продолжаются до тех пор, пока не будет выполняться не-
равенство I/'(xft) Ке, где е — заранее установленная величина до-
пустимого отклонения.
2.5.2. Метод средней точки
Если функция f(x) унимодальна в заданном интервале поиска,
то точкой оптимума является точка, в которой /'(х)=0. Если при
этом имеется возможность вычислять как значения функции, так и
ее производной, то для нахождения корня уравнения /'(х)=0 можно
воспользоваться эффективным алгоритмом исключения интервалов,
на каждой итерации которого рассматривается лишь одна пробная
точка. Например, если в точке z выполняется неравенство f'(z)<Z.O,
то с учетом предположения об унимодальности естественно утверж-
дать, что точка минимума не может находиться левее точки г. Дру-
гими словами, интервал xsCz подлежит исключению. С другой сто-
роны, если f'(z)>0, то точка минимума не может находиться правее
z и интервал x^z можно исключить. Приведенные рассуждения ле-
жат в основе логической структуры метода средней точки, который
иногда называют поиском Больцано.
3 № 1 826
66
ГЛАВА 2
Определим две точки LuR таким образом, что f'(L)<ZO и /'(/?)>0.
Стационарная точка расположена между L и R. Вычислим значе-
ние производной функции в средней точке рассматриваемого интер-
вала z=(L+R)/2. Если f'(z)>0, то интервал (г, R) можно исключить
из интервала поиска. С другой стороны, если /'(z)<0, то можно
исключить интервал (L, г). Ниже дается формализованное описа-
ние шагов алгоритма.
Пусть имеется ограниченный интервал и задан параметр
сходимости е.
Шаг 1. Положить R=b, L=a; при этом /'(а)<0 и /'(Ь)>0.
Шаг 2. Вычислить z=(R+L)/2 и f'(z).
Ш а г 3. Если закончить поиск. В противном случае,
если /'(z)<0, положить L=z и перейти к шагу 2. Если f'(z)>0, по-
ложить R=z и перейти к шагу 2.
Следует отметить, что логическая структура поиска в соответ-
ствии с изложенным методом исключения интервалов основана лишь
на исследовании знака производной независимо от значений, кото-
рые эта производная принимает. В следующем подразделе рассмат-
ривается метод секущих при реализации которого рассматри-
ваются как знак производной, так и ее значения.
2.5.3. Метод секущих
Метод секущих, являющийся комбинацией метода Ньютона и
общей схемы исключения интервалов, ориентирован на нахождение
корня уравнения f'(x)—O в интервале (а, Ь), если, разумеется, такой
корень существует. Предположим, что в процессе поиска стацио-
нарной точки функции f(x) в интервале (а, Ь) обнаружены две точки
L и R, в которых знаки производной различны. В этом случае алго-
ритм метода секущих позволяет аппроксимировать функцию f'(x)
«секущей прямой» (прямой линией, соединяющей две точки) и най-
х> В отечественной литературе этот метод известен также под названием
«метод хорд».— Прим, перев.
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
67
ти точку, в которой секущая графика f'(x) пересекает ось абсцисс
(рис. 2.16). Таким образом, следующее приближение к стационарной
точке х* определяется по формуле
7_ о___
If'
Если |/'(z)l^e, поиск следует закончить. В противном случае
необходимо выбрать одну из точек L или R таким образом, чтобы
знаки производной в этой точке и точке z были различны, а затем
повторить основной шаг алгоритма. Например, в ситуации, изобра-
женной на рис. 2.16, в качестве двух следующих точек должны быть
выбраны точки z и R. Легко видеть, что в отличие от метода средней
точки метод секущих основан на исследовании не только знака, но
и значений производной в пробных точках и поэтому в ряде случаев
позволяет исключить более половины интервала поиска (см.
рис. 2.16).
Пример 2.11. Метод секущих
Опять рассмотрим задачу из примера 2.10:
минимизировать / (х)=2х2+(16/х) в интервале 1<х^5.
£, , . df (х) . 16
f (%) = -ДА-Д = 4х--.
' ' ' dx хг
Итерация 1
Ш а г 1. R=5, L=l, f (R)—19,36, 12.
Ш а г 2
2___5_________19,36 _ 9 53
2 (19,36-j- 12)/4 ~'3<3
Ш а г 3. f (z)=7,62>0; положить R=2,53.
Итерация 2
Шаг 2
г = 2,53 — {7 62_|_ 12>/1,53 = 1 *94-
Шаг 3. /'(z)=3,51>0; положить R = l,94. Итерации продол-
жаются до тех пор, пока не будет выполняться неравенство \f'(z)\^e.
2.5.4. Метод поиска с использованием кубичной
аппроксимации
В соответствии с рассматриваемым методом подлежащая мини-
мизации функция f аппроксимируется полиномом третьего порядка.
Логическая схема метода аналогична схеме методов с использовани-
ем квадратичной аппроксимации. Однако в данном случае построе-
ние аппроксимирующего полинома проводится па основе меньшего
числа точек, поскольку в каждой точке можно вычислять значения
как функции, так и ее производной.
з*
68
ГЛАВА 2
Работа алгоритма начинается в произвольно выбранной точке
хх: находится другая точка х2, такая, что производные /'(%i) и Г(хг)
имеют различные знаки. Другими словами, необходимо заключить
стационарную точку х, в которой /'(х)=0, в интервал между Xj и х2.
Аппроксимирующая кубичная функция записывается в следующем
виде:
/(x)=a0+fli(x—Xi)+a2(x—Xj) (х—х2)+а3(х—х1)2(х—х2). (2.8)
Параметры уравнения (2.8) подбираются таким образом, чтобы зна-
чения f (х) и ее производной в точках хх и х2 совпадали со значениями
/(х) и f’(x) в этих точках. Первая производная функции /(х) равна
= aj + а2 (х—Xj) + a2 (х—х2) +
т«3 (х—Xi)2+ 2«3 (х—х,) (х— х3). (2.9)
Коэффициенты а0, аи а2 и а3 уравнения (2.8) определяются по из-
вестным значениям /(х^, /(х3), /'(х2) и f'(x2) путем решения следую-
щей системы линейных уравнений:
f2 = f(x2)=a, + al (х2 — Xj),
f'i = f Ui) = «i + «2Ui—x2),
f2 = f (-^2) 4“ ^2 (X2 ^1) H- @3 C^2
Заметим, что данная система легко решается рекурсивным ме-
тодом. После того как коэффициенты найдены, действуя по анало-
гии со случаем квадратичной аппроксимации, можно оценить коор-
динату стационарной точки функции f с помощью аппроксимирую-
щего полинома (2.8). При этом приравнивание к нулю производной
(2.9) приводит к квадратному уравнению. Используя формулу для
вычисления корней квадратного уравнения, запишем решение,
определяющее стационарную точку аппроксимирующего кубичногс
полинома, в следующем виде:
если р < О,
х2—р(х2— хг), если 0 р 1,
х(, если р > 1,
(2.10)
где
/2Ч-к>—г
/г — fi 2а>
г = (^) + « + Л’
_( (<2—Ш1УЗ, если ху < хг,
W ( — (z2—fif2)l/2, если хх > хг.
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
69
Формула для w обеспечивает надлежащий выбор одного из двух
корней квадратного уравнения; для значений р, заключенных в ин-
тервале от О до 1, формула (2.10) гарантирует, что получаемая точка
х расположена между Xi и х2. Затем снова выбираются две точки для
реализации процедуры кубичной аппроксимации — хи одна из
точек или х2, причем значения производной исследуемой функции
в этих точках должны быть противоположны по знаку, и процедура
кубичной аппроксимации повторяется.
Приведем формализованное описание алгоритма. Пусть заданы
начальная точка х0, положительная величина шага А и параметры
сходимости ох и е2.
Шаг 1. Вычислить /'(х0).
Если f(xo)<O, вычислить хк+1=хк+2*Д для значений К=0,
1......
Если f(x0)>0, вычислить хк+1=хк—2^А для значений К=0,
1......
Шаг 2. Вычислить значения /'(х) в точках хк+1 при К=0,
1, 2, ... вплоть до точки хм, в которой /'(хм-1) f(x5i)C0. Затем
положить Х1=хЛ1_1, х2=хм. Вычислить_ значения Л, /2, К и f2.
Ш а г 3. Найти стационарную точку х аппроксимирующего ку-
бичного полинома, пользуясь формулой (2.10).
Ш а г 4. Если /(х)</(хг), перейти к_шагу 5. В противном слу-
чае вычислять х по формуле x=x+V2(x—xj до тех пор, пока не
будет выполняться неравенство /(хХ/(Хх).
Шаг 5._Проверка_на окончание поиска.
Если If (x)|^ei и |(х—Х1)/х|<е2, поиск закончить. В противном
случае положить либо
(a) x2=Xi и Хх=х, если f (х) f (xt)<0,
либо
(б) Хх=х, если f'(x) f (х2)<0.
Затем перейти к шагу 3.
Заметим, что шаги 1 и 2 реализуют процедуру поиска границ
интервала по эвристическому методу, причем изменение знака про-
изводной используется в качестве критерия перехода через точку
оптимума. На шаге 3 проводятся вычисления координаты точки
оптимума аппроксимирующего полинома. Шаг 4 ассоциирован с
проверкой того факта, что полученная оценка действительно явля-
ется улучшенным приближением к точке оптимума. В случае когда
значения производной вычисляются непосредственно, метод поиска
с использованием кубичной аппроксимации, безусловно, оказыва-
ется более эффективным по сравнению с любым из представленных
выше методов поиска. Однако если значения производной вычисля-
ются путем разностного дифференцирования, то предпочтение сле-
дует отдать методу Пауэлла, основанному на квадратичной аппрок-
симации.
70
ГЛАВА 2
Пример 2.12. Поиск с использованием кубичной аппроксимации
и производных
Опять рассмотрим задачу, в которой требуется
минимизировать / (х) =2х2+16/х.
Пусть начальная точка х0=1 и длина шага Д=1. В качестве пара-
метров сходимости используем
е^Ю-2 и е2=Зх10-2,
, df . 16
f (*) =-г- :: 4х-х-.
' v ' dx х2
Итерация 1
Шаг !./'(!)=—12<0. Следовательно, Xi=l + 1=2.
Ш а г 2. /'(2)=4.
Так как f'(i) f'(2)=—48<0, стационарная точка расположена между
1 и 2. Положим хг=1, х2=2. Тогда /1 = 18, /2=16, f[=—12, /2=4.
Шаг 3.
z=J/1(18—16)+(—12)+4=—2,
и/=+[4-(—12)(4)]^=(52)‘/г=7,211,
4 + 7,211-(-2) _
Н— 4— (—12)4-2 (7,211) °’
х= 2—0,4343 (2—1) = 1,5657.
Шаг 4. f (1,5657)=15,1219</ (Xj) = 18. Следовательно, продол-
жаем поиск.
Ш а г 5. Проверка па окончание поиска.
/'(1,5657)=—0,2640; поиск не закончен.
Так как /'(х) /'(х2)=(—0,2640) (4)<0,
положим х1=х=1,5657.
Итерация 2
Ш а г 3
z= 0^(15,1219—16) + (—0,2640) + 4 = -2,3296,
да = +[(2,3296)2 — (—0,2640) (4)]1'2 = 2,5462,
_ 4 < 2,5462 —(—2,3296) _ q
* 4 —(—0,2640)+ 2 (2,5462) и’ чои’
х=2—0,9486(2—1,5657)= 1,5880
Шаг 4. /(1,5880) = 15,1191</(х1) = 15,1219. Следовательно,
продолжаем поиск.
Ш а г 5. Проверка на окончание поиска:
/'(1,5880) = 0,0072 < 10~2,
11,5880—1.56571 ПП|Я, ,п_,
|---| = 0,0140 <3x10 *.
Поиск закончен.
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
71
Заметим, что при тех же самых исходных точках x^l и х2~2
метод Пауэлла в примере 2.9 позволил получить оценку х=1,714,
тогда как метод с использованием кубичной аппроксимации привел
к оценке х=1,5657. Точная координата точки минимума равна
1,5874, что указывает на преимущество полиномиальной аппрок-
симации более высокого порядка.
2.6. Сравнение методов
С помощью теоретических выкладок можно показать, что такие
методы точечного оценивания, как метод Пауэлла или метод поиска
с использованием кубичной аппроксимации и производных, су-
щественно эффективнее методов исключения интервалов, среди ко-
торых выделяется метод золотого сечения. В частности, известно,
что применение схемы поиска с использованием квадратичной ап-
проксимации позволяет достигнуть асимптотически суперлинейной
скорости сходимости к точке истинного минимума, т. е. отклонение
(£+1)-й оценки от истинной координаты точки минимума пропор-
ционально отклонению Л-й оценки, возведенному в степень а>1
(как показано в [61, а=1,3). Для сравнения отметим, что если при
реализации метода золотого сечения в качестве k-й оценки коорди-
наты точки истинного минимума берется координата средней точки
интервала, полученного в результате k вычислений значения функ-
ции, то отклонение этой оценки от точной координаты линейно
убывает при переходе от k-й к (й+1)-й итерации. Это означает, что
в случае, когда интервалы сходимости сравнимы между собой, метод,
основанный на квадратичной аппроксимации, сходится быстрее, чем
любой из методов исключения интервалов. Разумеется, сделанный
вывод справедлив лишь в предположении, что интервалы сходи-
мости сравнимы между собой, а исследуемая функция является
достаточно гладкой и унимодальной.
Результаты численных экспериментов, представленные в спе-
циальной литературе, не подтверждают преимущества методов с ис-
пользованием производных и квадратичной аппроксимации или
метода исключения интервалов над остальными методами. Если
для вычисления значений целевой функции требуется значительное
машинное время, то, по мнению авторов работы [7], предпочтитель-
нее использовать стратегию поиска, основанную на модификации
метода Пауэлла. Это мнение подтверждается результатами вычис-
лительных экспериментов, проведенных Химмельблау 181, который
сравнил указанную стратегию поиска со схемой поиска по методу
золотого сечения и показал, что модифицированный метод Пауэлла
требует меньшего количества вычислений значения функции для
достижения заданной точности при оценивании координаты точки
минимума. Если необходимо получить решение с очень высокой
степенью точности, то лучшими оказываются методы поиска н<;
основе полиномиальной аппроксимации. С другой стороны, извест-
72
ГЛАВА 2
но, что при исследовании мультимодальных или быстро изменяю-
щихся функций метод Пауэлла сходится значительно медленнее,
чем методы исключения интервалов. Таким образом, если очень
важно добиться надежной работы алгоритма, то целесообразно
выбрать метод золотого сечения. Поэтому поисковые методы типа
метода Пауэлла следует использовать совместно с методом золотого
сечения, переход к алгоритму которого осуществляется в тех слу-
чаях, когда реализация соответствующих итераций на ЭВМ свя-
зана с определенными трудностями. Читатель также может обра-
титься к книге Брента 19], в которой проведен анализ относительной
эффективности различных методов поиска.
Сравнительное исследование трех методов точечного оценива-
ния, а именно метода средней точки, метода Пауэлла и метода по-
иска с использованием кубичной аппроксимации, было проведено
в соответствии с учебной программой по университетскому (Purdue
University) курсу теории оптимизации. Перечисленные методы ис-
пользовались для решения задачи минимизации функции /(х)=
=sin*x при различных значениях k. Кроме того, для сравнения
был также использован метод золотого сечения как наилучший из
методов исключения интервалов.
Для оценки эффективности выбранных методов использовались
три характеристики: время, затраченное на получение решения,
точность решения и чувствительность к изменениям параметра схо-
димости. Первые две характеристики исследовались путем варьи-
рования значений показателя степени k на множестве нечетных чисел
от 1 до 79. Следует отметить, что для всех значений k минимум функ-
ции достигается в точке х* =4,71239; при этом /(х*)=—1,0. Однако
с увеличением k степень гладкости функции, которая обладает уз-
кими впадинами в окрестности точки минимума, уменьшается. Это
обстоятельство приводит к понижению точности и замедлению схо-
димости методов точечного оценивания.
Проверка методов на чувствительность проводилась путем варьи-
рования значений параметра сходимости. Как и ожидалось, в резуль-
тате исследований установлена тенденция к увеличению затрат време-
ни на решение задачи с ростом k, которая особенно ярко проявляется
при реализации метода средней точки вследствие резкого увеличения
модуля градиента функции в окрестности точки минимума. Однако
возрастание показателя степени k не оказывает заметного влияния
на продолжительность поиска с помощью метода золотого сечения.
Аналогично точность решения, измеряемая как относительная (в
процентах) ошибка оценивания координаты точки истинного ми-
нимума, падает с ростом k для всех трех методов — метода средней
точки, метода Пауэлла и метода поиска с использованием кубичной
аппроксимации. Однако метод золотого поиска оказывается весьма
нечувствительным к изменениям крутизны функции. Исследования
также показали, что чувствительность всех четырех выбранных ме-
тодов к изменениям параметра сходимости минимальна.
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
73
2.7. Заключение
В этой главе были представлены необходимые и достаточные
условия оптимальности решения задач безусловной оптимизации
с целевыми функциями одной переменной. Показано, что необходи-
мое условие наличия оптимума в данной точке заключается в том,
что данная точка должна быть стационарной, т. е. первая производ-
ная функции должна обращаться в нуль в этой точке. Для того чтобы
проверито, соответствует ли стационарная точка минимуму, мак-
симуму или является точкой перегиба, используются производные
второго и более высоких порядков. Затем были рассмотрены вопро-
сы, связанные с получением оптимальных решений на основе мето-
дов поиска, которые носят название методов исключения интервалов
и ориентированы на нахождение точки оптимума в заданном интер-
вале. Показано, что алгоритм поиска по методу золотого сечения,
вообще говоря, является наиболее предпочтительным вследствие
высокой вычислительной эффективности и простоты реализации.
Методы исключения интервалов основаны на процедуре простого
сравнения значений функции в двух пробных точках; при таком
сравнении используется только отношение порядка на множестве
значений функции. Для того чтобы учесть величину разности между
значениями функции, разработан ряд так называемых методов то-
чечного оценивания, позволяющих определить точку оптимума
с помощью квадратичной или кубичной аппроксимации целевой
функции. В условиях когда выполняется предположение о том, что
интервалы сходимости сравнимы между собой, а исследуемая функ-
ция является достаточно гладкой и унимодальной, методы точечного
оценивания сходятся значительно быстрее, чем методы исключения
интервалов. Однако при исследовании мультимодальных или быстро
изменяющихся функций наиболее надежным оказывается метод зо-
лотого сечения. В заключение сформулированы рекомендации, в со-
ответствии с которыми методы поиска с использованием квадратич-
ной аппроксимации типа метода Пауэлла, вообще говоря, следует
применять совместно с методом золотого сечення, переход к алго-
ритму которого реализуется в тех случаях, когда выполнение соот-
ветствующих итерационных циклов на ЭВМ сопряжено с определен-
ными трудностями.
Контрольные вопросы и задачи
2.1. Что такое точка перегиба, и как ее идентифицировать?
2.2. Как проверить, является ли функция выпуклой или вогнутой?
2.3. В чем состоит свойство унимодальности функций и в чем
заключается важное значение этого свойства при решении
задач оптимизации с одной переменной?
2.4. Пусть данная точка удовлетворяет достаточным условиям
существования локального минимума. Как установить, яв-
ляется ли этот минимум глобальным?
74
ГЛАВА 2
2.5. Сформулируйте условие, при выполнении которого метод
поиска, основанный на полиномиальной интерполяции, может
не привести к получению правильного решения.
2.6. Являются ли методы исключения интервалов в целом более
эффективными, чем методы точечного оценивания? Почему?
2.7. При реализации поисковых методов рекомендуется прини-
мать решение об окончании поиска на основе проверок как
величины разности значений переменной, так и величины
разности значений функции. Возможна ли ситуация, когда
результат одной из проверок указывает на сходимость к точке
минимума, тогда как полученная точка в действительности
минимуму не соответствует? Поясните ответ рисунком.
2.8. Заданы следующие функции одной переменной:
(a) f (х)=хъ+х1—(х3/3)+2,
(б) /(л-)=(2х+1)2(х—4).
Для каждой из заданных функций найдите
(1) интервал(ы) возрастания, убывания;
(2) точки перегиба (если таковые имеются);
(3) интервал(ы), в котором (в которых) функция вогнута,
выпукла;
(4) локальные и глобальный максимумы (если таковые име-
ются);
(5) локальные и глобальный минимумы (если таковые име-
ются) .
2.9. Паром, который должен курсировать через канал, конструи-
руется с таким расчетом, чтобы с его помощью можно было
перевозить заданное количество груза в тоннах (L) в течение
дня (рис. 2.17). Пусть стоимость парома без двигателей прямо
Левый' 1 п А Правый
берег^ --u------1 берег
Рис. 2.17. Схема к задаче 2.9.
пропорциональна грузоподъемности парома (/), а стоимость
двигателей прямо пропорциональна произведению грузоподъ-
емности на скорость движения парома (у) в кубе. Покажите,
что полная стоимость парома минимальна в том случае, когда
стоимость парома без двигателей в два раза превышает стои-
мость двигателей. (Временем погрузки и разгрузки можно
пренебречь, т. е. считается, что паром курсирует без остано-
вок.)
2.10. Лесной пожар распространяется в узкой долине шириной
2 мили со скоростью 32 фут/мин (рис. 2.18). Содержать на-
ступление огня можно путем построения заградительной
противопожарной перегородки, пересекающей лес по всей
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
ширине долины. Один рабочий может построить 2 фута пере-
городки в минуту. Затраты на транспортировку каждого ра-
бочего к месту событий и обратно составляют 20 долл.; оплата
труда каждого рабочего составляет 6 долл, в час. Стоимость
квадратной мили леса равна 2000 долл. Сколько рабочих сле-
3ai разительная
52 фут/мин огня ы-2мили противопожарная
1 перегородка
Рис. 2.18. Схема к задаче 2 10
дует послать на борьбу с огнем, чтобы полные издержки были
минимальны?
2.11. Рассмотрите задачу безусловной оптимизации с целевой функ-
цией одной переменной f(x). Пользуясь приведенными в таб-
лице данными о значениях производных порядка 1, 2, 3, 4
в точках xt (i=l, 2, . . . , 10), идентифицируйте каждую из
точек (установите, оказывается ли она точкой максимума,
минимума, перегиба или не является точкой оптимума; ука-
жите случаи, когда нельзя сделать определенный вывод
и т. д.).
vi 1' (лр (X,-) Г U,.) Г" (Х()
Л1 0 + Нет данных Нет данных
х2 0 0 + Нет данных
Хэ 0 — Нет данных Нет данных
х4 — — Нет данных Нет данных
•*5 0 0 — Нет данных
Ч 0 0 0 —
х: 0 0 0 0
х8 0 0 0 +
+ + Нет данных Нет данных
л10 0 — + —
2.12. Установите, какие из следующих функций являются выпук-
лыми или вогнутыми:
(а)
(б) 7(х)=е х,
(в) /(х) = 1/х2,
(г) f(x)=x+logx при х>0,
(д) /(*)== 1x1,
(е) /(х)==х log х при х>0,
(ж) f (х)=х2\ где k — целое число,
(з) f (x)=x2ft+1, где k — целое чиёло.
76
ГЛАВА 2
2.13. Исследуйте функцию
[(х)=х'л—12х+3 в интервале —4^x<J4.
Найдите локальные минимумы, локальные максимумы, гло-
бальный минимум и глобальный максимум / в заданном интер-
вале.
2.14. Установите области, в которых следующая функция выпукла
или вогнута:
f(x) = e'<
Найдите глобальный максимум и глобальный минимум этой
функции.
2.15. Рассмотрите модель одного цикла управления запасами скоро-
портящихся товаров, в которой
спрос описывается случайной величиной с плотностью вероят-
ности f, т. е. Р (величина спроса ^x) = ^g/(x) dx;
отсутствие запасов влечет за собой экономические потери;
С — стоимость единицы товара;
р — величина потерь, обусловленных отсутствием запасов
(включая потери дохода и так называемого неосязаемого
основного капитала);
г — продажная цена единицы товара;
I — ликвидационная стоимость единицы товара, не продан-
ного к концу периода.
Задача заключается в том, чтобы определить оптимальный
размер заказа Q, который максимизирует ожидаемую величи-
ну чистого дохода за период. Ожидаемый чистый доход равен
П (<?) = / ^0 (Q—*) f W dx~
lq(x—Q)f(x)dx—CQ,
5»
0 xf (х) dx.
(а) Покажите, что n(Q) — выпуклая функция QQssO).
(б) Объясните, как определить оптимальный размер заказа,
пользуясь результатом, полученным в п. (а).
(в) Вычислите оптимальный размер заказа для следующего
конкретного примера:
С=2,50 долл., г=5,00 долл., /=0,
р=2,50 долл., /(х) = 1/400 при
100^x^500; =0 в противном случае.
Указание. Воспользуйтесь правилом Лейбница для диффе-
ренцирования под знаком интеграла.
2.16. Предп >пожим, что проводится одномерный поиск на основе
(а) метода золотого сечения и (б) метода средней точки с исполь-
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
77
зованием производных, вычисляемых с помощью разностного
дифференцирования. Какой из методов, по всей вероятности,
окажется более эффективным? Почему?
2.17. Реализуйте процедуру одномерного поиска точки оптимума
функции
f (х)=Зх2+(12/х3)—5 в интервале 1/2;Сх;С5/2,
используя (а) метод золотого сечения, (б) метод деления ин-
тервала пополам, (в) метод поиска с использованием квадра-
тичной аппроксимации, (г) метод поиска с использованием ку-
бичной аппроксимации и производных. В каждом случае про-
ведите по четыре вычисления значения функции. Сравните
результирующие интервалы поиска, полученные с помощью
перечисленных выше методов.
2.18. Найдите точку минимума функции
/(х)=(10х3+Зх2+х+5)2.
Заданы начальная точка х=2 и длина шага Л=0,5.
(а) Воспользуйтесь методом исключения интервалов: поиск
границ интервала эвристическим методом и шесть итераций
по методу золотого сечения.
(б) Воспользуйтесь методом оценивания на основе квадратич-
ной аппроксимации: три итерации по методу Пауэлла.
2.19. Найдите вещественные корни уравнения (с точностью до
одного знака после запятой)
/ (х) =3000— 100х2—4х5—6х“=0,
используя (а) метод Ньютона — Рафсона, (б) метод средней
точки, (в) метод секущих. Полезно также написать программу
для мини-ЭВМ, реализующую перечисленные методы поиска.
2.20. (а) Объясните, как можно преобразовать задачу 2.19 в нели-
нейную задачу безусловной оптимизации с одной переменной,
(б) Напишите программу для ЭВМ, реализующую поиск по
методу золотого сечения, и используйте ее для решения задачи
оптимизации, о которой идет речь в п. (а). Сравните получен-
ное решение с решением задачи 2.19.
2.21. В результате экспериментов установлено, что траектория дви-
жения космического тела описывается следующим уравнением
[101:
f (х)=4х3+2х—Зх2+ех/2.
Найдите корень уравнения f(x)—0 с помощью любого из мето-
дов с использованием производных.
2.22. Пользуясь любым из методов одномерного поиска, минимизи-
руйте’следующие функции с точностью до одного знака после
78
ГЛАВА 2
запятой [101:
(а) /(х)=3х4+(х—I)2 в интервале [0, 4];
(б) f (х)=(4х) (sin х) в интервале 10, л];
(в) f(x)=2(x—З^+е0'5*2 в интервале (0, 100).
2.23. В структуре капитальных вложений на развитие химического
завода важное место занимают затраты на приобретение и
монтаж труб, а также затраты на установку насосного обо-
рудования. Рассмотрите проект трубопровода длиной L фут.,
который должен обеспечивать подачу жидкости со скоростью
Q галлон/мин. Выбор наиболее экономичного диаметра трубы
D (дюйм.) осуществляется на основе минимизации функции
затрат на приобретение труб, насосов и прокачивание жид-
кости. Известно, что функция затрат в единицу времени в слу-
чае, когда трубопровод состоит из труб, изготовленных из
углеродистой стали, и центробежного насоса с электродвига-
телем, может быть описана следующим выражением:
f = 0,45/. + 0.245Z.D1'5 + 325 (hp)^ + 61,6 (hp)0^ + 102,
J 03 J 02,08
где Zip = 4,4 x 10-8^+l,92x 10-^-.
Сформулируйте соответствующую задачу оптимизации с од-
ной переменной для проектирования трубопровода длиной
1000 фут., который должен обеспечивать подачу жидкости
со скоростью 20 галлон/мин. Диаметр трубы должен быть
заключен в пределах от 0,25 до 6 дюйм. Решите эту задачу с
помощью метода золотого сечения.
Литература
1 Swann W. Н., Report on the Development of A Direct Search Method of Opti-
mization, ICI Ltd., Central Instr. Res. Lab., Res Note, 64/3, London, 1964.
2. Kiefer J., Optimum Sequential Search and Approximation Methods Under
Minimum Regularity Assumptions, J. Soc. Ind. Appt. Math., 5(3), 105—125
(1957).
3. Bartie R., Elements of Real Analysis, Wiley, N. Y., 1976.
4. Powell M. J. D., An Efficient Method for Finding the Minimum of a Function
of Several Variables Without Calculating Derivatives, Computer J., 7, 155—162
(1964)
5. Raphson J., History of Fluxion, London, 1725.
6. Kowalik J., Osborne M. R., Methods for Unconstrained Optimization Problems,
American Elsevier, N. Y., 1968.
7. Box M. J., Davies D., Swann W. H., Nonlinear Optimization Techniques,
I. С. I. Monograph, Oliver and Boyd, Edinburgh, 1969
8. Himmelblau D. M.: Applied Nonlinear Programming, AIcGraw-Hill, N. Y.,
1972. [Имеется перевод' Химмельблау Д. М. Прикладное нелинейное про-
граммирование.— М., Мир, 1975.]
9. Brent R. Р., Algorithms for Minimization without Derivatives, Prentice-Hall,
Englewood Cliffs, New Jersey, 1973.
10. Phillips D. T., Ravindran A., Solberg J. J., Operations Research: Principles
and Practice, Wiley, N. Y., 1976.
Глава 3
Функции нескольких переменных
В данной главе рассматриваются фундаментальные понятия и
конкретные методы, используемые при поиске безусловных мини-
мумов функций нескольких переменных. Изложение основано на
материале гл. 2, поскольку одномерные методы играют весьма важ-
ную роль при исследовании функций нескольких переменных.
Сначала рассмотрим вопрос анализа «в статике» с использова-
нием положений линейной алгебры и дифференциального исчисле-
ния (приложение А), а также условия, которые (в достаточно общих
возможных ситуациях) позволяют идентифицировать точки опти-
мума. Такие условия используются для проверки выбранных точек
и дают возможность выяснить, являются ли эти точки точками ми-
нимума, максимума или седловыми точками. При этом задача вы-
бора указанных точек остается вне рамок проводимого анализа;
основное внимание уделяется решению вопроса о том, соответствуют
ли исследуемые точки решениям многомерной задачи безусловной
оптимизации, в которой требуется
минимизировать / (х), x^RN, (3.1)
при отсутствии ограничений на х, где х — вектор управляемых
переменных размерности N, / — скалярная целевая функция. Обыч-
но предполагается, что xt (для всех значений 1=1, 2, 3, . . . , N)
могут принимать любые значения, хотя в ряде практических при-
ложений область значений х выбирается в виде дискретного мно-
жества. Кроме того, часто оказывается удобным предполагать, что
функция f и ее производные существуют и непрерывны всюду, хотя
известно, что оптимумы могут достигаться в точках разрыва / или
ее градиента
V/=[A _а/_Г (32)
' I дх, ’ дх2 ’ дх3 ’ ’ dx/vj '
Следует помнить, что функция f может принимать минимальное
значение в точке х, в которой f или V/ претерпевают разрыв. Кроме
того, в этой точке v/ может не существовать. Для того чтобы по-
строить систему конструктивных критериев оптимальности, необ-
ходимо (по крайней мере на первой стадии исследования) исклю-
80
ГЛАВА 3
чить из рассмотрения подобные ситуации,'которые весьма усложня-
ют анализ. Наконец, в ряде случаев приходится ограничиваться
лишь идентификацией локальных оптимумов, поскольку нелинейная
целевая функция / не всегда обладает свойством выпуклости (см.
приложение Б) и, следовательно, может оказаться мультимодальной.
На рис. 3.1 изображены линии уровня функции Химмельблау
/(х) = [х! + х2-Пр+[х1 + х|-7р. (3 3)
Нетрудно видеть, что эта функция имеет четыре различных
минимума.
Далее перейдем к вопросу анализа «в динамике», который форму-
лируется следующим образом: если точка х,0) не удовлетворяет
функция Химмель&лау:
f(х) =( х“ +11) <(«, +х’-7)
Пинии
уровня
А 5,000
В 20,000!
С 35,000'
D 50,000
Е 65,000
F 60,000
G 95,000
Н 110,000
I 125,000
J 140,000
условиям, налагаемым упомянутыми выше критериями оптималь-
ности, то как получить «хорошее» новое приближение к реше-
нию х*? Попытка дать ответ на этот вопрос приводит к необходи-
мости рассмотрения ряда методов, описание которых составляет
значительную часть данной главы. Рассматриваемые методы клас-
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
81
сифицируются в соответствии с тем, используется ли информация
о производных исследуемых функций. Глава завершается обсужде-
нием относительных преимуществ методов и обзором результатов
вычислительных экспериментов.
3.1. Критерии оптимальности
Здесь рассматриваются условия, которые позволяют характе-
ризовать (т. е. классифицировать) точки пространства управляе-
мых переменных. Критерии оптимальности необходимы для рас-
познавания решений и, кроме того, составляют основу большинства
используемых методов - поиска решений. Рассмотрим разложение
Тейлора для функции нескольких переменных:
f (х) = f (х) + Vf (х)г Ах + 73 Ахг VY (х) Ах + О3 (Ах), (3.4)
где х — точка разложения из пространства RN\ \х—х—х — вели-
чина изменения х; Af(x)—AZ-мерный вектор-столбец первых произ-
водных f(x), вычисленных в точке х; V2f(x) = Hy(x) — симметриче-
ская матрица порядка jVxjV вторых частных производных /(х),
вычисленных в точке х. (Эту матрицу часто называют матрицей
Гессе. Ее элемент, расположенный на пересечении i-й строки и
/-го столбца, равен d'^/dx^Xj.) О3(Ах) — сумма всех членов разло-
жения, имеющих порядок по Ах выше второго. Пренебрегая члена-
ми высших порядков (т. е. исключая О3(Ах)), определим величину
изменения целевой функции /(х), соответствующего произвольному
изменению х:
А/ (х) = / (х) — f (х) = V/ (х)г Ах + 72 Ахг v'7 (х) Ах. (3.5)
Напомним, что по определению во всех точках из окрестности точки
минимума целевая функция принимает значения, которые превы-
шают минимальное, т. е. имеет место неравенство
А/=/(х)-/(х)>0. (3.6)
Точка х является точкой глобального минимума, если неравенство
(3.6) выполняется для всех х С RN', такие точки будем обозначать
через х**. Когда формула (3.6) справедлива лишь в некоторой 6-
окрестности точки х, т. е. для всех х, таких, что |[х—%7[<6 при
заданном 6>0, то х есть точка локального минимума, или х*. Если же
= /«-/(%)< О, (3.7)
то х есть точка максимума (локального или глобального в соответ-
ствии с данными выше определениями). Исключение знака равен-
ства из формул (3.6) и (3.7) позволяет определить точку строгого
минимума или максимума. В случае когда А/ принимает как поло-
жительные и отрицательные, так и нулевые значения в зависимости
от выбора точек из 6-окрестности, точка х представляет собой сед-
ловую точку.
ГЛАВА 3
82
Вернемся к равенству (3.5) и вспомним о выдвинутом ранее
предположении о том, что/(х), Vf(x) и V2/ (х) существуют и непре-
рывны для всех х С Как следует из формулы (3 5), для того чтобы
знак Д/ не менялся при произвольном варьировании Дх, градиент
V/ (х) должен быть равен нулю, т. е. х должна быть стационарной
точкой. В противном случае разность Д/ может принимать положи-
тельные или отрицательные значения в зависимости от знаков
Г/(х) и Дх. Таким образом, точка х должна удовлетворять условию,
стационарности
Vf(x) = O, (3.8)
и формула (3.5) принимает следующий вид:
Д/ (*) = *4 Дх7 у2/ (х) \х. (3.9)
Очевидно, что знак А/(х) определяется квадратичной формой
Q (х) = Дхг V2/ (х) Дх (3.10)
или Q(z)=zTAz.
Из линейной алгебры известно (см. приложение А), что
А — положительно определенная матрица, если Q(z)>0 для
любых г;
А — положительно полуопределенная матрица, если Q(z)^0
для любых z;
А — отрицательно определенная матрица, если Q(z)<0 для
любых z; (3.11)
А — отрицательно полуопределенная матрица, если Q(z)=C0
для любых z;
А — неопределенная матрица, если Q(z)>0 для некоторых z
и Q(z)<0 для остальных г.
Из (3.11) следует, что стационарная точка х есть
точка минимума, если У2/(х)— положительно полуопределенная
матрица;
точка максимума, если у2/(х)— отрицательно полуопределен-
ная матрица; (3-12)
седловая точка, если У2/(х)—0 — неопределенная матрица.
Кроме того, может оказаться полезным провести анализ стационар-
ной точки х в несколько ином аспекте. Рассмотрим стационарную
точку х вместе с окружающей ее 5-окрестностью и векторами, исхо-
дящими из точки х (рис. 3.2). При этом
х = х + а$(х). (3.13)
Путем соответствующего выбора а и s можно построить все точки х
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
83
из окрестности точки х. Подстановка (3.13) в (3.9) дает формулу
А/ (х) = (а2/2) sT V2 / (х) s. (3.14)
Теперь с помощью (3.11) и (3.12) можно классифицировать s(x)
как направление спуска, направление подъема или направление
общего вида. Если направление спуска найти не удается, то х
Рис. 3.2. Окрестность стацио-
нарной точки
является точкой локального минимума х*, что соответствует случаю,
когда V2/(x) — положительно полуопределенная матрица.
Ниже формулируются необходимые и достаточные условия су-
ществования минимума функции нескольких переменных.
Теорема 3.1. Необходимые условия
Для наличия в точке х* локального минимума необходимо, что-
бы выполнялось равенство
V/(x*)=0 (3.15а)
и матрица V2/(x*) была положительно полуопределенной, (3.156)
Теорема 3.2. Достаточные условия
Если
V/(x») = 0 (3.16а)
и матрица Г2/(х*) положительно определена, (3.166)
то х* есть точка изолированного (строгого) локального минимуме
/(X).
Доказательства этих теорем непосредственно следуют из прове-
денного выше обсуждения и предоставляются читателю в качестве
упражнений. Обычно приходится довольствоваться нахождением
локального минимума; вместе с тем если можно показать, чтс
xrV2/(x)x^0 для всех х, то /(х) называется выпуклой функцией,
а локальный минимум оказывается глобальным.
84
ГЛАВА 3
Пример 3.1. Критерии оптимальности
Рассмотрим функцию
/ (х) = 2x1 + 4хгх2— ЮхрСа + xl,
линии уровня которой изображены иа рис. 3.3. Требуется классиф!
пировать точку х=Ю, 01г.
f (х) = 2х1г+4х,х^-10х,хг+ х|
-2,40 -1,20 0,00 1,20 2/0
Линии
уровня
А -40,000
В -30,000
С -20,000
D -10,000
Е 0,000
F 10,000
G 20,000
Н 30,000
I 40,000
J 50,000
Х1
Рис. 3.3. Линии уровня нелинейной функции двух переменных из примера 3.
Решение
^- = 4х1 + 4х’—10хг,
-^-= 12Х1Х|—Юх^Зха,
V/(x) = [0, 0]Г.
Следовательно, точка х — стационарная.
дх2 ~
d2f .
дх, дх2
_¥L_4
дх2 ~ ’
24х1х2±2= +2,
12х2 — 10 = —10.
Следовательно,
_Л(,-. и Г+4 —10
V7 W — W — [______________iq _[_ 2
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
85
Матрица V2/(x) является неопределенной, так как квадратичная
форма zTHfz принимает положительное значение при z=(0, 1) и
отрицательное значение при z=(l, 1) (см. приложение А). Поэтому
х представляет собой седловую точку, что и отражено на рис. 3.3.
3.2. Методы прямого поиска
В этом и последующих разделах данной главы рассматривается
вопрос анализа «в динамике» для функций нескольких переменных,
т. е. исследуются методы и алгоритмы, позволяющие на итерацион-
ной основе получать оценки х*— вектора управляемых переменных,
которому соответствует минимальное значение функции /(х). Ука-
занные методы применимы также к задачам максимизации, в кото-
рых целевую функцию следует заменить на —/(х). Методы, ориен-
тированные на решение задач безусловной оптимизации, можно
разделить на три широких класса в соответствии с типом используе-
мой при реализации того или иного метода информации.
1. Методы прямого поиска, основанные на вычислении только
значений целевой функции.
2. Градиентные методы, в которых используются точные значе-
ния первых производных /(х),
3. Методы второго порядка, в которых наряду с первыми про-
изводными используются также вторые производные функции /(х).
Ниже рассматриваются методы, относящиеся к каждому из пере-
численных классов, поскольку ни один метод или класс методов не
отличается высокой эффективностью при решении оптимизационных
задач различных типов. В частности, возможны случаи, когда про-
исходит переполнение памяти ЭВМ; в других ситуациях вычисление
значений целевой функции требует чрезмерных затрат времени;
в некоторых задачах требуется получить решение с очень высокой
степенью точности. В ряде приложений либо невозможно, либо
весьма затруднительно найти аналитические выражения для произ-
водных целевой функции. Поэтому если предполагается использо-
вать градиентные методы, следует применить процедуру разностной
аппроксимации производных. В свою очередь это приводит к необ-
ходимости экспериментального определения длины шагов, позво-
ляющего установить надлежащее соответствие между ошибкой
округления и ошибкой аппроксимации. Таким образом, инженер
вынужден приспосабливать применяемый метод к конкретным ха-
рактеристикам решаемой задачи.
Методы решения задач безусловной оптимизации отличаются
относительно высоким уровнем развития по сравнению с другими
методами нелинейного программирования. В специальной литера-
туре представлены достаточно полные обзоры наиболее эффектив-
ных методов. Отличным примером такого обзора может служить
книга Мюррея [1]. В данном разделе речь идет о методах прямого
поиска, для реализации которых требуются только значения целе-
86
ГЛАВА 3
вой функции; в следующем разделе рассматриваются градиентные
методы и методы второго порядка. Здесь предполагается, что f(x',
непрерывна, a Vf (%) может как существовать, так и не существовать
поскольку соответствующие числовые значения не используются
Однако следует отметить, что методы прямого поиска можно приме-
нять для решения задач, в которых V/ существует, и они чаете
используются в тех случаях, когда V/ представляет собой сложную
векторную функцию управляемых переменных. Наконец, в этом г
последующих разделах предполагается, что функция f(x) унимо-
дальна в рассматриваемой области. Если же изучаемые методы
применяются для анализа мультимодальных функций, то приходит-
ся ограничиваться идентификацией локальных минимумов.
Многомерные методы, реализующие процедуру поиска оптиму-
ма на основе вычисления значений функции, с общих позиций
можно разделить на эвристические и теоретические. Эвристические
методы, как это следует из названия, реализуют процедуры поиска
с помощью интуитивных геометрических представлений и обеспечи-
вают получение частных эмпирических результатов. С другой сто-
роны, теоретические методы основаны на фундаментальных матема-
тических теоремах и обладают такими операционными свойствами,
как сходимость (по крайней мере при выполнении некоторых опре-
деленных условий). Ниже подробно рассматриваются три метода
прямого поиска:
1) поиск по симплексу, или 52-метод;
2) метод поиска Хука — Дживса;
3) метод сопряженных направлений Пауэлла.
Первые два из перечисленных методов относятся к категории
эвристических и реализуют принципиально различающиеся стра-
тегии поиска. В процессе поиска по 52-методу последовательно опе-
рируют регулярными симплексами в пространстве управляемых
переменных, тогда как при реализации метода Хука — Дживса
используется фиксированное множество (координатных) направле-
ний, выбираемых рекурсивным способом. Метод Пауэлла основан
на теоретических результатах и ориентирован на решение задач
с квадратичными целевыми функциями; для таких задач метод
сходится за конечное число итераций. К числу общих особенностей
всех трех методов следует отнести относительную простоту соответ-
ствующих вычислительных процедур, которые легко реализуются
и быстро корректируются. С другой стороны, реализация указанных
методов может требовать (и часто требует) более значительных за-
трат времени по сравнению с методами с использованием производ-
ных. Здесь не рассматриваются методы, основанные на идее исклю-
чения интервалов (гл. 2), в частности методы, предложенные Бок-
сом, Дэвисом и Свенном (21, а также Кролаком и Купером [3],
поскольку такие методы в значительной степени уступают другим
известным методам.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
87
3.2.1. Метод поиска по симплексу (S2-метод)
Первые попытки решения оптимизационных задач без ограниче-
ний на основе прямого поиска связаны с использованием одномер-
ных методов оптимизации. Как правило, при реализации таких
методов допустимая область определения показателя качества
функционирования системы (целевой функции) заменяется дискрет-
ным множеством (решеткой) точек пространства управляемых пере-
менных, а затем используются различные стратегии уменьшения
области, которая содержит решение задачи. Часто эта процедура
оказывается эквивалентной равномерному поиску в узлах решетки
и, следовательно, непригодной для решения задач с числом пере-
менных, превышающим 2. Более полезная идея заключается в выбо-
ре базовой точки и оценивании значений целевой функции в точках,
окружающих базовую точку. Например, при решении задачи с дву-
мя переменными можно воспользоваться квадратным образцом,
изображенным на рис. 3.4. За-
тем «наилучшая» из пяти иссле-
дуемых точек выбирается в ка-
честве следующей базовой точ-
ки, вокруг которой строится
аналогичный образец. Если ни
одна из угловых точек не имеет
преимущества перед базовой,
размеры образца следует умень-
шить, после чего продолжить
поиск.
Этот тип эволюционной опти-
мизации был использован Бок-
сом 14] и другими исследователями для анализа функционирования
промышленных предприятий, когда эффект варьирования значений
Пробная точка
Базовая точка
Рис. 3 4 Квадратный образец (частный
случай кубического образца).
переменных, описывающих производственные процессы, измеряется
с ошибкой. В задачах большой размерности вычисление значений
целевой функции проводится во всех вершинах, а также в центре
тяжести гиперкуба 15, т. е. в точках так называемого кубического
образца. Если количество переменных (размерность пространства,
в котором ведется поиск) равно N, то поиск по кубическому образцу
требует 2ЛЧ~1 вычислений значения функций для одного образца.
При увеличении размерности задачи необходимое количество вы-
числений значения целевой функции возрастает чрезвычайно быст-
ро. Таким образом, несмотря на логическую простоту поиска по
кубическому образцу, возникает необходимость использования
более эффективных методов прямого поиска для решения возникаю-
щих на практике задач оптимизации.
*> Гиперкубом называется куб в JV-мерном евклидовом пространстве, т. е.
множество S=(x=(X!, х2, ., /=1, 2,. . ., JV), где а и & —
заданные числа.— Прим, перев.
88
ГЛАВА 3
Одна из вызывающих особый интерес стратегий поиска положе-
на в основу метода поиска по симплексу, предложенного Спендли,
Хекстом и Химсвортом [5]. Следует отметить, что указанный метод
и другие подобные методы не имеют отношения к симплекс-методу
линейного программирования, а сходство названий носит случай-
ный характер. Процедура симплексного поиска Спендли, Хекста и
Химсворта базируется на том, что экспериментальным образцом,
содержащим наименьшее количество точек, является регулярный
симплекс. Регулярный симплекс в AZ-мерном пространстве пред-
ставляет собой многогранник, образованный А7+1 равностоящими
друг от друга точками-вершинами. Например, в случае двух пере-
менных симплексом является равносторонний треугольник; в трех-
мерном пространстве симплекс представляет собой тетраэдр. В алго-
ритме симплексного поиска используется важное свойство симплек-
сов, согласно которому новый симплекс можно построить на любой
грани начального симплекса путем переноса выбранной вершины на
Рис. 3.5. Построение нового симплекса.
а — начальный симплекс; х'11, xf2), х<3); б — новый симплекс; х<2>, х<3>, х<4>.
надлежащее расстояние вдоль прямой, проведенной через центр
тяжести остальных вершин начального симплекса. Полученная та-
ким образом точка является вершиной нового симплекса, а выбран-
ная при построении вершина начального симплекса исключается.
Нетрудно видеть, что при переходе к новому симплексу требуется
одно вычисление значения целевой функции. Рис. 3.5 иллюстрирует
процесс построения нового симплекса на плоскости.
Работа алгоритма симплексного поиска начинается с построения
регулярного симплекса в пространстве независимых переменных и
оценивания значений целевой функции в каждой из вершин симп-
лекса. При этом определяется вершина, которой соответствует
наибольшее значение целевой функции. Затем найденная вершина
проецируется через центр тяжести остальных вершин симплекса в
новую точку, которая используется в качестве -вершины нового
симплекса. Если функция убывает достаточно плавно, итерации
продолжаются до тех пор, пока либо не будет накрыта точка мини-
мума, либо не начнется циклическое движение по двум или более
симплексам. В таких ситуациях можно воспользоваться следую-
щими тремя правилами.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
89
Правило 1. «Накрытие» точки минимума
Если вершина, которой соответствует наибольшее значение це-
левой функции, построена на предыдущей итерации, то вместо нее
берется вершина, которой соответствует следующее по величине
значение целевой функции.
Правило 2. Циклическое движение
Если некоторая вершина симплекса не исключается на протя-
жении более чем М итераций, то необходимо уменьшить размеры
симплекса с помощью коэффициента редукции и построить новый
симплекс, выбрав в качестве базовой точку, которой соответствует
минимальное значение целевой функции. Спендли, Хекст и Химс-
ворт предложили вычислять М по формуле
Л4=1,65АМ-0,05№,
где А/ — размерность задачи, а М округляется до ближайшего
целого числа. Для применения данного правила требуется уста-
новить величину коэффициента редукции.
Правило 3. Критерий окончания поиска
Поиск завершается, когда или размеры симплекса, или разности
между значениями функции в вершинах становятся достаточно ма-
лыми. Чтобы можно было применять эти правила, необходимо за-
дать величину параметра окончания поиска.
Реализация изучаемого алгоритма основана на вычислениях
двух типов: (1) построении регулярного симплекса при заданных
базовой точке и масштабном множителе и (2) расчете координат
отраженной точки. Построение симплекса является достаточно
простой процедурой, так как из элементарной геометрии известно,
что при заданных начальной (базовой) точке х<0) и масштабном мно-
жителе а координаты остальных А/ вершин симплекса в АЛмерном
пространстве вычисляются по формуле
f x^' + Sj, если /тМ,
\ х“' + 62, если / = I,
(3-17)
для i и /=1, 2, 3....N.
Приращения и <32, зависящие только от А/ и выбранного мас-
штабного множителя а, определяются по формулам
(JV-H)1,2 + N —И
АГ/ 2 ]
. ~(JV+i)1/2~ila
’ |_ JV/ 2 J
(3.18)
(3.19)
Заметим, что величина масштабного множителя а выбирается ис-
следователем, исходя из характеристик решаемой задачи. При а=1
ребра регулярного симплекса имеют единичную длину.
У (J
ГЛАВА 3
Вычисления второго типа, связанные с отражением относи-
тельно центра тяжести, также представляют несложную процедуру.
Пусть х(у) — точка, подлежащая отражению. Центр тяжести осталь-
ных М точек расположен в точке
= (32°)
, t = о
1 =# /
Все точки прямой, проходящей через №’ и хс, задаются формулой
х = х<л + 7. (хс — x{J}). (321)
При 7.-0 получаем исходную точку x{J'\ тогда как значение 7ъ=1
соответствует центру тяжести хс. Для того чтобы построенный симп-
лекс обладал свойством регулярности, отражение должно быть сим-
метричным. Следовательно, новая вершина получается при 7.=2.
Таким образом,
^нов = 2%с ^предыдущ • (3.22)
Проиллюстрируем вычислительную схему метода следующим при-
мером.
Пример 3.2. Вычисления в соответствии с методом поиска по
симплексу
Минимизировать /(%)=(!—хг)2+(2—х2)2.
Решение. Для построения исходного симплекса требуется
задать начальную точку и масштабный множитель. Пусть +0) =
=10, 0)г и а=2. Тогда
61 = [£-+1 1а = 1,9318,
L 2/2 J
1а = 0,5176.
2К 2 J
Используя эти два параметра, вычислим координаты двух осталь-
ных вершин симплекса:
=[0+0,5176, 0+1,93181г=[0,5176, 1,93181г,
х(21=[0+1,9318, 0+0,5176И=[1,9318, О,5176И,
которым соответствуют значения целевой функции, равные/(х<1)) =
=0,2374 и /(х2)=3,0658. Так как f (х((”)=5, необходимо отразить
точку х<0) относительно центра тяжести двух остальных вершин
симплекса
2
= ТХ<2’).
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
91
Используя формулу (3.22), получаем
х<(3> _ ЛД1> I __£«»
х^== [2,4494, 2,4494]г.
В полученной точке /(х3) =2,3027, т. е. наблюдается уменьшение
целевой функции. Новый симплекс образован точками х11’, х(2) и
хи>. В соответствии с алгоритмом следует отразить точку х(2), ко-
торой соответствует наибольшее значение целевой функции, отно-
сительно центра тяжести точек х(1) и х(3). Итерации продолжаются
до тех пор, пока не потребуется применение правил 1, 2 и 3, которые
были сформулированы выше.
Изложенный выше алгоритм 52-метода имеет несколько очевид-
ных преимуществ.
1. Расчеты и логическая структура метода отличаются сравни-
тельной простотой, и, следовательно, соответствующая программа
для ЭВМ оказывается относительно короткой.
2. Уровень требований к объему памяти ЭВМ невысокий, мас-
сив имеет размерность (М+1, У+2).
3. Используется сравнительно небольшое число заранее уста-
новленных параметров: масштабный множитель а, коэффициент
уменьшения множителя а (если применяется правило 2) и параметры
окончания поиска.
4. Алгоритм оказывается эффективным даже в тех случаях,
когда ошибка вычисления значений целевой функции велика, по-
скольку при его реализации оперируют наибольшими значениями
функции в вершинах, а не наименьшими.
Перечисленные факторы характеризуют метод поиска по симплек-
су как весьма полезный при проведении вычислений в реальном
времени.
Алгоритм обладает также рядом существенных недостатков.
1. Не исключено возникновение трудностей, связанных с мас-
штабированием, поскольку все координаты вершин симплекса за-
висят от одного и того же масштабного множителя а. Чтобы обойти
трудности такого рода, в практических задачах следует промасшта-
бировать все переменные с тем, чтобы их значения были сравнимыми
по величине.
2. Алгоритм работает слишком медленно, так как полученная
на предыдущих итерациях информация не используется для уско-
рения поиска.
3. Не существует простого способа расширения симплекса, не
требующего пересчета значений целевой функции во всех точках
образца. Таким образом, если а по какой-либо причине уменьшается
(например, если встречается область с узким «оврагом» или «хреб-
том»), то поиск должен продолжаться с уменьшенной величиной
шага.
Модифицированная процедура поиска по симплексу, разрабо-
танная Нелдером и Мидом [6], частично устраняет некоторые из
92
ГЛАВА 3
Рис. 3.6. Растяжение и сжатие симплекса.
в — нормальное отражение (0=а=|), < f (хиов.) < /1£)> б —растяжение (9=v > I),
f (*нов.) <f ll>> а —сжатие (6=0 < 0), f (хНов.) > Ч*нов.) > t(fn> г —сжатие
(0 = 0 >0), < f (хнов.) <
перечисленных недостатков. Нетрудно заметить, что хотя формула
для определения вершин регулярного симплекса оказывается весьма
удобной при построении исходного образца, однако веских основа-
ний для сохранения свойства регулярности симплекса в процессе
поиска нет. Следовательно, при отражении симплекса существует
возможность как его растяжения, так и сжатия х>. При расчетах
по методу Нелдера и Мида используются вершины симплекса хм
(которой соответствует наибольшее значение целевой функции
/1Л)), х& (которой соответствует следующее по величине значение
целевой функции /(£’) и хи} (которой соответствует наименьшее
значение целевой функции /1г)). Напомним, что отражение вершины
симплекса осуществляется по прямой
х = x(k> + X (хс—хш),
или х = хм + (1 -ф0) (хс—х{,,}). (3.23)
При 0=1 имеет место так называемое нормальное отражение симп-
лекса, поскольку точка хиов располагается иа расстоянии Их,,—х(/)|)
от точки хс. Если —1^0<1, то наблюдается сжатое отражение, или
сжатие симплекса, тогда как выбор 0>1 обеспечивает растянутое
отражение, или растяжение симплекса. На рис. 3.6 приведены воз-
можные варианты отражения. Три значения параметра 0, исполь-
По этой причине процедуру Нелдера и Мида иногда называют методом
поиска по деформируемому многограннику.— Прим, перев.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
93
зуемые при нормальном отражении, сжатии и растяжении, обозна-
чаются через а, р н у соответственно. Реализация метода начинается
с построения исходного симплекса и определения точек х1Л), х1г>,
xil> и хс. После нормального отражения осуществляется проверка
значений целевой функции по критерию окончания поиска в точках
отраженного симплекса. Если поиск не закончен, то с помощью те-
стов, приведенных на рис. 3.6, выбирается одна из операций —
нормальное отражение, растяжение или сжатие. Итерации продол-
жаются, пока изменения значений целевой функции в вершинах
симплекса не станут незначительными. В качестве удовлетвори-
тельных значений параметров а, 0 и у Нелдер и Мид рекомендуют
использовать а=1, 0=0,5 и у=2.
Результаты отдельных численных экспериментов показывают,
что метод Нелдера — Мида обладает достаточной эффективностью
и высокой надежностью в условиях наличия случайных возмущений
или ошибок при определении значений целевой функции. В 1969 г.
Бокс и Дрейпер [7] утверждали, что этот метод является «наиболее
эффективным из всех известных методов последовательной оптими-
зации». В 1972 г. Паркинсон и Хатчинсон [81 исследовали влияние
выбора параметров а, 0, у и способа построения исходного симплек-
са на эффективность поиска. Они установили, что ориентация исход-
ного симплекса в отличие от его формы является существенным фак-
тором, влияющим на процедуру поиска, и предложили использо-
вать значения параметров (а, 0, у)=(2, 0,25, 2,5). Такой выбор
параметров позволил обеспечить хорошую работу алгоритма при
повторении последовательных растяжений симплекса.
3.2.2. Метод поиска Хука — Дживса
Изложенные выше методы поиска основаны на различных опе-
рациях над образцами, составленными из пробных точек. Несмотря
на то что в предыдущем подразделе основное внимание было уделено
геометрическому расположению пробных точек, совершенно ясно,
что основная цель построения множества таких точек заключается
в определении направления, в котором должен вестись поиск. Рас-
положение пробных точек влияет лишь на чувствительность на-
правления поиска к изменениям топологических свойств целевой
функции. В частности, уравнение для вычисления координат отра-
женной точки
*нов.=*(/) + Мхс — X1'’)
четко устанавливает, что множество отраженных точек описывается
вектором, определяющим некоторое направление в пространстве
управляемых переменных. Остальные элементы логической струк-
туры поиска связаны лишь с выбором такой величины шага X, ко-
торая позволяет достигнуть заметного «улучшения» значений целе-
вой функции. Если же главная задача работы с образцом, состав-
94
ГЛАВА 3
ленным из пробных точек, состоит в определении направления по-
иска, то стратегию поиска по симплексу можно усовершенствовать
путем непосредственного введения множества векторов, задающих
направления поиска. Простейший подход заключается в том, чтс
поиск ведется на основе рекурсивного перебора направлений из
произвольно заданного множества. С другой стороны, можно по-
строить стратегию поиска, в рамках которой одно или несколькс
направлений поиска уточняются на каждой итерации, что позво-
ляет согласовать систему направлений поиска с глобальной топо-
логией целевой функции. Для того чтобы гарантировать возможность
проведения поиска по всей рассматриваемой области, в обоих слу-
чаях целесообразно наложить требование линейной независимости
направлений поиска, которые должны образовывать базис в до-
пустимой области определения f(x). Например, легко убедиться
в том, что нельзя вести поиск оптимума функции трех переменных
с использованием двух направлений поиска. Отсюда следует, чтс
все рассматриваемые методы прямого поиска используют по мень-
шей мере N независимых направлений поиска, где N — размер-
ность вектора х.
Элементарным примером метода, в рамках которого реализуется
процедура рекурсивного перебора на множестве направлений поис-
ка, является метод циклического изменения переменных, в соответ-
ствии с которым каждый раз меняется только одна переменная. При
таком подходе множество направлений поиска выбирается в виде
множества координатных направлений в пространстве управляемых
переменных задачи. Затем вдоль каждого из координатных направ-
лений последовательно проводится поиск точки оптимума на основе
методов решения задач оптимизации с одной переменной. Если це-
левая функция обладает свойством сферической симметрии, такой
поиск обеспечивает получение решения исходной задачи. Однако
если линии уровня функции искривлены или растянуты (что весьма
часто имеет место в возникающих на практике задачах), то итерации
могут превратиться в бесконечную последовательность уменьшаю-
щихся шагов и процедура поиска становится неэффективной. Кроме
того, как показал Пауэлл [9], изменение координатных направле-
ний поиска (или направлений поиска из любого заданного множе-
ства) в циклическом порядке может не только оказаться неэффектив-
ным, но и привести к отсутствию сходимости к точке локального
оптимума даже при бесконечном числе итераций.
Конструктивные попытки повышения эффективности этого ме-
тода были связаны с тем обстоятельством, что поиск, периодически
проводимый в направлении d{i}=xw—позволяет существен-
но ускорить сходимость. Это обстоятельство было положено в осно-
ву модифицированного метода, разработанного Хуком и Дживсом
110] и являющегося одним из первых алгоритмов, в которых при
определении нового направления поиска учитывается информация,
полученная на предыдущих итерациях. По существу процедура
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
95
Хука — Дживса представляет собой комбинацию «исследующего»
поиска с циклическим изменением переменных и ускоряющегося
поиска по образцу с использованием определенных эвристических
правил. Исследующий поиск ориентирован на выявление характера
локального поведения целевой функции и определение направлений
вдоль «оврагов». Полученная в результате исследующего поиска
информация затем используется в процессе поиска по образцу при
движении по «оврагам».
Исследующий поиск. Для проведения исследующего
поиска необходимо задать величину шага, которая может быть раз-
личной для разных координатных направлений и изменяться в про-
цессе поиска. Исследующий поиск начинается в некоторой исходной
точке. Если значение целевой функции в пробной точке не превы-
шает значения функции в исходной точке, то шаг поиска рассматри-
вается как успешный В противном случае необходимо вернуться
в предыдущую точку и сделать шаг в противоположном направлении
с последующей проверкой значения целевой функции. После пере-
бора всех N координат исследующий поиск завершается. Получен-
ную в результате точку называют базовой точкой.
Поиск по образцу. Поиск по образцу заключается
в реализации единственного шага из полученной базовой точки вдоль
прямой, соединяющей эту точку с предыдущей базовой точкой.
Новая точка образца определяется в соответствии с формулой
Xpft+1) = xlW + (Xм —x1*"1’). (3.24)
Как только движение по образцу не приводит к уменьшению целе-
вой функции, точка х(£+и фиксируется в качестве временной базо-
вой точки и вновь проводится исследующий поиск. Если в резуль-
тате получается точка с меньшим значением целевой функции, чем
в точке хш, то она рассматривается как новая базовая точка хи+1>.
С другой стороны, если исследующий поиск неудачен, необходимо
вернуться в точку ха) и провести исследующий поиск с целью вы-
явления нового направления минимизации. В конечном счете воз-
никает ситуация, когда такой поиск не приводит к успеху. В этом
случае требуется уменьшить величину шага путем введения неко-
торого множителя и возобновить исследующий поиск. Поиск завер-
шается, когда величина шага становится достаточно малой. После-
довательность точек, получаемую в процессе реализации метода,
можно записать в следующем виде:
х<Л) текущая базовая точка,
х(*-о предыдущая базовая точка,
Хр + 1) точка, построенная при движении по образцу,
xlft+1) следующая (новая) базовая точка.
Приведенная последовательность характеризует логическую струк-
туру поиска по методу Хука — Дживса.
J6
ГЛАВА 3
Метод поиска Хука — Дживса
Шаг 1. Определить:
начальную точку х(0),
приращения Дп i=l, 2, 3, .... N,
коэффициент уменьшения шага а>1,
параметр окончания поиска е>0.
Ш а г 2. Провести исследующий поиск.
Ш а г 3. Был ли исследующий поиск удачным (найдена ли точ-
ка с меньшим значением целевой функции)?
Да: перейти к шагу 5.
Нет: продолжать.
Ш а г 4. Проверка на окончание поиска.
Выполняется ли неравенство ||Дх|]<е?
Да: прекратить поиск; текущая точка аппроксимирует точку оп-
тимума х*.
Нет: уменьшить приращения по формуле
Дг=Дг/а, i=l, 2, 3, .... IV.
Перейти к шагу 2.
Ш а г 5. Провести поиск по образцу:
х‘*+1> = х*+(х(*) —х'*-1’).
Ш а г 6. Провести исследующий поиск, используя х'*+1> в ка-
честве базовой точки; пусть х(А+1) — полученная в результате точка.
Ш а г 7. Выполняется ли неравенство /(х(/!+1))<;/(х(*))?
Да: положить xlft-1)=xlW, x(ft)=x<s+1).
Перейти к шагу 5.
Нет: перейти к шагу 4.
Пример 3.3. Поиск по методу Хука — Дживса
Найти точку минимума функции
f (х) = 8х? + 4х,х2 5х),
используя начальную точку х'0)=[—4, —4]г.
Решение. Для того чтобы применить метод прямого поиска
Хука — Дживса, необходимо задать следующие величины:
Дх — векторная величина приращения = [1, 1]г,
а — коэффициент уменьшения шага = 2,
е — параметр окончания поиска = 10-4.
Итерации начинаются с исследующего поиска вокруг точки х10),
которой соответствует значение функции f (х10>)=272. Фиксируя х2,
дадим приращение переменной хх:
х2=—4,
хг=—4+1 ->/(—3, —4)=200</(х(0))Успех.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
97
Следовательно, необходимо зафиксировать х,=—3 и дать прираще-
ние переменной х2:
Xi=—3,
х2=—4+1 /(—3, — 3) = 153<200-> Успех.
Таким образом, в результате исследующего поиска найдена точка
х(1) = [-3, —3]г, /(х(1») = 153.
Поскольку исследующий поиск был удачным, переходим к поиску
по образцу:
= х'1’ + (х(1) —х(0)) = [—2, — 2\т,
Далее проводится исследующий поиск вокруг точки х102), который
оказывается удачным при использовании положительных прираще-
ний переменных х, и х2. В результате получаем точку
х12’ = [—1, — 1]г, /(х(2,)=17.
Поскольку / (х(2))</ (х(П), поиск по образцу следует считать успеш-
ным, и х(2) становится новой базовой точкой при следующем про-
ведении поиска по образцу. Итерации продолжаются, пока умень-
шение величины шага не укажет на окончание поиска в окрестности
точки минимума х*=[0, 01г. Последовательные шаги реализации
метода показаны на рис. 3.7.
Из примера 3.3 следует, что метод Хука — Дживса характери-
зуется несложной стратегией поиска, относительной простотой
вычислений и невысоким уровнем требований к объему памяти ЭВМ,
который оказывается даже ниже, чем в случае использования ме-
тода поиска по симплексу. Благодаря этому алгоритм Хука —
Дживса находит широкое применение во всех областях инженерной
практики; особенно эффективны его варианты с использованием
штрафных функций, которые рассматриваются в гл. 6. Однако
необходимо отметить, что основанный на циклическом движении по
координатам алгоритм в ряде случаев может заканчивать работу
преждевременно, а при наличии значительных нелинейных эффек-
тов вырождается в последовательность исследующих поисков без
перехода к ускоряющемуся поиску по образцу.
Известен целый ряд подходов к усовершенствованию метода
Хука —Дживса. В частности, Бендлер и Мак-Дональд [11] моди-
фицировали процедуру Хука — Дживса путем введения дополни-
тельных правил увеличения и уменьшения приращений переменных,
а также правила уменьшения шага по образцу, которое применяется
в тех случаях, когда обычный шаг оказывается неудачным. Экспе-
рименты, проведенные авторами данной книги, позволили дорабо-
тать другую фазу реализации алгоритма, которую иногда называют
использованием образца. Если движение по образцу приводит к
успеху, имеются определенные основания для того, чтобы полностью
4 № 1826
98
ГЛАВА 3
f Ы = вх’+ 4 х, х2+ 5 *2
Линии
уровня
А 10,000
В 40,000
С 70,000
О 100,000
Е 130,000
F 160,000
Б 190,000
Н 220,000
I 250,000
J 280,000
Рис. 3.7. Итерации поиска по методу Хука — Дживса в примере 3.3
использовать возможности поиска вдоль прямой, определяемой
образцом, или по крайней мере увеличить длину шага по образцу
Такие действия часто позволяют существенно ускорить сходимость
метода. Эмери и О’Хаган [12] изменили фазу исследующего поиска
путем введения системы ортогональных направлений поиска, ориен-
тация которой случайным образом меняется на каждой итерации.
Розенброк [131 разработал метод, в котором, как и в методе Хука —
Дживса, новое направление поиска определяется с учетом информа-
ции, полученной на предыдущих итерациях. Однако (в отличие от
метода Хука—Дживса) подход, предложенный Розенброком, осно
ван на непрерывном изменении множества векторов, используемых
при исследующем поиске, с помощью процедуры ортогонализации
Другой метод, изложенный в работе Свенна [14] и иногда называе-
мый методом поиска Дэвиса, Свенна и Кемпи, опирается на страте-
гию поиска, подобную стратегии Розенброка. При его реализации
поиск ведется не с помощью фиксированных шагов по каждому из
выбранных направлений, а вдоль каждой прямой, заданной одним
из направлении 11. Каждый из перечисленных методов прямоте
т> Методы Розенброка и Дэвиса, Свенна, Кемпи более подробно изложены т
кни1е Химмельблау [69], переведенной на русский язык.— Прим, перев.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
99
поиска обладает рядом преимуществ перед остальными при реше-
нии задач определенного типа. Вместе с тем вопрос о том, являются
ли дополнительные усложнения метода Хука — Дживса оправ-
данными, по-видимому, остается открытым. Если же существует
возможность реализовать более сложный алгоритм, то предпочтение
следует отдать методу Пауэлла, превосходство которого над рас-
смотренными выше эвристическими методами несомненно.
3,2.3, Метод сопряженных направлений Пауэлла
Наиболее эффективным из алгоритмов прямого поиска является
метод, разработанный Пауэллом [15], в особенности его модифици-
рованные варианты, предложенные Зангвиллом [16] и Брентом [171.
При работе этого алгоритма информация, полученная на предыду-
щих итерациях, используется для построения векторов направлений
поиска, а также для устранения зацикливания последовательности
координатных поисков. Метод ориентирован иа решение задач с
квадратичными целевыми функциями и основывается на фундамен-
тальных теоретических результатах.
Задачи с квадратичными целевыми функциями занимают важ-
ное место в теории оптимизации по двум причинам.
1. Квадратичная функция представляет простейший тип нели-
нейных функций, для которых может быть сформулирована задача
безусловной оптимизации (линейные функции не обладают внутрен-
ними оптимумами). Следовательно, если с помощью того или иного
метода успешно решаются задачи оптимизации с целевыми функция-
ми общего вида, то такой метод должен оказаться эффективным при
решении задач с квадратичными функциями.
2. В окрестности точки оптимума любую нелинейную функцию
можно аппроксимировать квадратичной функцией (поскольку ли-
нейный член разложения Тейлора обращается в нуль). Следова-
тельно, работа алгоритма при решении задач с квадратичными функ-
циями позволяет получить определенное представление о сходи-
мости алгоритма в случае, когда минимизируется функция общего
вида.
Основная идея алгоритма заключается в том, что если квадра-
тичная функция /V переменных приведена к виду суммы полных
квадратов, то ее оптимум может быть найден в результате реализа-
ции W одномерных поисков по преобразованным координатным на-
правлениям.
Процедура преобразования квадратичной функции
q (х) = а-\-Ьтх-\- 1/2хтСх (3.25)
к виду суммы полных квадратов эквивалентна нахождению такой
матрицы преобразования Т, которая приводит матрицу квадратич-
ной формы к диагональному виду. Таким образом, заданная квад-
А*
100
ГЛАВА 3
f (х) = 4х^+3х^-4х,хг-гх1
-2,00 -1,00 0,00 1,00
2,00
”1
Линии
уровня
А 0,500
В 5,500
С 10,500
D 15500
Е 20,500
F 25,500
6 30,500
Н 35,500
I 40,500
J 45,500
Рис. 3.8. Линии уровня квадратичной функции с перекрестными членами.
ратичная форма
Q(x) = xTCx (3.26)
путем преобразования
х = Тг (3.27)
приводится к виду
Q (х) = zTVCTz = zrDz, (3.28)
где D — диагональная матрица, т. е. элементы D отличны от нуля
только при 1=/.
Пусть tj — j-ii столбец матрицы Т. Тогда преобразование (3 27)
позволяет записать каждый вектор х в виде линейной комбинации
вектор-столбцов tf,
х — Tz = t}zY Z2z2 + ... -р- (д Zfj. (3.29)
Другими словами, вместо координат вектора х в стандартной коор-
динатной системе, определяемой множеством векторов е(,), исполь-
зуются координаты вектора в новой координатной системе, заданной
векторами tj. Кроме того, система векторов t} соответствует главным
осям рассматриваемой квадратичной формы, поскольку матрица
квадратичной формы приводится к диагональному виду. Такая си-
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
101
Рис. 3.9. Линии уровня квадратичной функции без перекрестных членов.
туация возникает, если квадратичную функцию с перекрестными
членами, линии уровня которой изображены на рис. 3.8, записать
в новой координатной системе, оси которой совпадают с большой и
малой осями квадратичной функции (см. рис. 3.9).
Итак, с помощью преобразования переменных квадратичной
функции строится новая система координат, совпадающих с глав-
ными осями квадратичной функции. Следовательно, одномерный
поиск точки оптимума в пространстве преобразованных переменных
г эквивалентен поиску вдоль каждой из главных осей квадратичной
функции. Так как направления главных осей определяются векто-
рами tj, одномерный поиск проводится в направлениях, заданных
этими векторами. Проиллюстрируем вышеизложенное примером.
Пример 3.4. Преобразование к виду суммы квадратов
Рассмотрим функцию
f (х) = 4х? + Зх22—4х1х2 + хх
и преобразование
/з^з, -Х2 ~ ^2»
102
ГЛАВА 3
ИЛИ
1
0
Ч2
1
Преобразованная квадратичная функция принимает следующий вид:
f (г) = 4г? + 2г? ф- г2.
Заметим, что это преобразование не является единственным, по-
скольку система векторов tj не удовлетворяет условию ортонорми-
рованности. В частности, нетрудно проверить, что преобразование
1 0
Х~ г/з 1 Z
также приводит матрицу квадратичной формы к диагональному
виду. Задавая начальную точку хо=[О, 01г и два столбца матрицы
преобразования
= ок, ;г=[1/8, 1]г,
можно найти точку оптимума [—8/1в, —1/8]г в результате проведе-
ния двух последовательных поисков в направлениях и t2- Поиск
в направлении по формуле
A-<i> = A-<0) + Wi
позволяет получить значение Х=—V8 и точку —Vs, ОН.
Далее из точки х(1) проводится поиск в направлении t2. Получаем
значение Х=—V8 и решение х(2) = [—8/16, —V8]r.
Из рассмотренного примера и предыдущего изложения следует,
что если система векторов tj, j=l, . . . , М, или система сопряжен-
ных направлений, построена, то точку оптимума квадратичной функ-
ции можно найти в результате реализации в точности N одномерных
поисков, которые проводятся вдоль каждого из N направлений tj,
3=1, . . . , N. Таким образом, нерешенными остаются лишь воп-
росы, связанные с построением системы векторов tj. Если матрица
С известна, то матрицу преобразования Т можно найти с помощью
метода Гаусса — Жордана (как это выполнено в приложении А).
Метод Гаусса — Жордана позволяет представить матрицу С в виде
произведения
C = PrDP, откуда (3.30)
(P-1)rC(P~l) = D и Т = р-\ (3.31)
Однако матрица С (или ее оценка) в данном случае неизвестна, по-
скольку речь идет о построении метода решения задач безусловной
оптимизации с целевой функцией f(x), при реализации которого
используются только значения функции и не используются значе-
ния первых и тем более вторых производных. Тем не менее и в этом
случае можно определить систему сопряженных направлений на
основе следующего элементарного свойства квадратичных функ-
ций.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
103
Свойство параллельного подпространства
Пусть заданы квадратичная функция q(x), две произвольные не-
совпадающие точки х(1) и х(2), а также направление d. Если точка
г/'1’ минимизирует q(x(1'+Zd), а точка у‘'л минимизирует <7 (х(2)+^ф,
то направление (г/(2>—z/(1)) сопряжено с d.
Рис. 3.10 иллюстрирует сформулированное свойство для случая
двух переменных. Нетрудно видеть, что поиск, проводимый из точ-
ки z/(1) или у{2} в направлении (z/2)—обеспечивает получение
Рис. 3.10. Сопряженные направления на плоскости.
точки минимума. Таким образом, в случае двух переменных реа-
лизация трех одномерных поисков позволяет построить систему
сопряженных направлений и, кроме того, найти точку оптимума
квадратичной функции. Прежде чем продолжать алгоритмические
построения, докажем теорему о свойстве параллельного подпро-
странства.
Напомним, что по определению С-сопряженные направления
задаются системой вектор-столбцов матрицы Т, которая приводит
матрицу С к диагональному виду:
TrCT = D. (3 32)
Поскольку все внедиагональные элементы D равны нулю, отсюда
следует, что
если j = k, (3.33)
0, если /#=&,
где tt — i-й столбец матрицы 7’. Таким образом, мы получили воз-
можность дать более удобное, эквивалентное и, по-видимому, более
конструктивное определение сопряженности направлений.
104
ГЛАВА 3
Сопряженные направления
Пусть С — симметрическая матрица порядка ДГхМ; направле-
ния s(1), s<2), s<8), .... r^N, называются С-сопряженными,
если эти направления линейно независимы и
stn TCstJ> = 0 для всех 1=/=/. (3.34)
Опять обратимся к квадратичной функции общего вида
q (х) = а + bTx + (г/2) хт Сх.
Точки прямой, исходящей из х11) в направлении d, задаются форму-
лой
х = xll> -|- Kd.
Минимум д(х) вдоль направления d определяется путем нахожде-
ния значения X*, при котором dg/dX=O. Вычислим эту производную
по правилу дифференцирования сложной функции:
-§- = ^--^- = (&r + xrC)d. (3.35)
По предположению теоремы минимум достигается в точке у{1’, сле-
довательно,
[(z/(i>)rC + &r]d = O. (3.36)
Аналогично, так как минимум q(x) при движении из точки х<2)
в направлении d достигается в точке у(2), имеем
[(z/<2,)rC + &r]d=0. (3.37)
Вычитая (3.36) из (3.37), получаем
G/l2) —*/(l))rCd = 0. (3.38)
В соответствии с данным выше определением направления d и
(г/12'—г/(1)) оказываются С-сопряженными, и свойство параллельного
подпространства для квадратичных функций доказано.
Пример 3.5. Минимизация на основе свойства параллельного
подпространства.
Опять рассмотрим квадратичную функцию q (х) = 4х2+3х2 —•
—4х1х2+х1. Пусть заданы две точки х(1) = [0, 01г, х’2) = [1,01г и
направление d=[l, 1]г. Первый поиск проводится вдоль прямой
х=[0, 0]г+Х [1, 1]г
и приводит к точке г/11) = [—х/6, —1/в]г(^*=—1/6). Второй поиск
проводится вдоль прямой
х = [1, 1]г
и позволяет получить точку f/'2)=[1/6, —S/61T(^*=—6/в). Согласие
свойству параллельного подпространства, направление
- 7вР =Г/в, -7аГ
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
105
сопряжено с d=[l, 1 ]г, т. е. по определению
[1, 1]С[*/а. -2/з]г = 0.
Выше отмечалось, что в случае двух переменных оптимум q(x)
можно найти путем проведения поиска вдоль прямой, заданной
направлением Q/l2)—Этот факт нетрудно проверить, поскольку
минимум q(x) вдоль прямой
х = [-1/6, -ЧвГ + ЧЧз. -2/з]г
достигается в точке х*=[—3/16, —VsF (V =—х/16), которая сов-
падает с полученным ранее решением.
В рассмотренных выше построениях для того, чтобы определить
сопряженное направление, требовалось задать две точки и некото-
рое направление. Это не слишком удобно при проведении расчетов,
поэтому предпочтительнее строить систему сопряженных направле-
ний, исходя из одной начальной точки, что легко осуществить при
помощи единичных координатных векторов е11), е<2), е<3), .... eGV).
(Здесь рассматривается процедура построения сопряженных на-
правлений в случае двух переменных, которая допускает очевидное
обобщение для W-мерного пространства.) Пусть е(1) = [1,0И и е(2| =
= [0, 1)г. При заданной начальной точке х(0) вычислим значение
X10’, которому соответствует минимум / (х<о)+Х1о)е(1)). Положим
х(1) = + Х(о) е11»
и вычислим значение Х<1), которому соответствует минимум/(х(1)+
+Z,ll)el2)). Положим
х‘2) = х(1) + Х(1)е<2).
Далее вычислим значение V2), минимизирующее f (xl2)+Z,(2)ell)), и
положим
х<3> = х<2,+
При этом направления (х1з)—х11)) и е11) оказываются сопряженными.
Для того чтобы убедиться в этом, рассмотрим рис. 3.11. Заметим,
что точка х(1) найдена в результате поиска из точки х10) в направле-
нии е11), а точка х<8) получена при поиске из точки х<2) в направлении
е11’. Следовательно, направления е11) и (х1з)—х11)) являются сопря-
женными согласно свойству параллельного подпространства. Да-
лее если на следующей итерации провести поиск в направлении
(х(3)—х11)), то процедура поиска будет охватывать два сопряженных
направления, и поскольку/(х) предполагается квадратичной функ-
цией двух переменных, в результате будет найдено решение х*.
Проведенное на основе свойства параллельного подпространства
построение рассмотрено для случая, когда число сопряженных
направлений равняется двум. Однако это построение естественным
образом обобщается на случай задач более высокой размерности.
В частности, нетрудно показать, что если точка у{1} найдена в ре-
зультате поиска из точки х11) вдоль каждого из М (<(V) сопряжен-
106
ГЛАВА 3
X.
Рис. 3.11. Построение сопряженных направлений из одной точки.
ных направлений, а точка у<2> получена в результате поиска из
точки х<2) вдоль каждого из тех же М сопряженных направлений
s(1), s<2>, s<3), . . . , slAI), то вектор (t/<2)—yw) задает направление,
сопряженное со всеми выбранными М направлениями. Это утверж-
дение известно как обобщенное свойство параллельного подпростран-
ства. Используя указанное свойство, можно обобщить метод по-
строения сопряженных направлений, последовательные шаги реа-
лизации которого отражены на рис. 3.11 на случай пространства
управляемых переменных более высокой размерности. Рис. 3.12
иллюстрирует построение сопряженных направлений в трехмерном
пространстве.
Как показано на рис. 3.12, сначала поиск осуществляется вдоль
трех координатных направлений е(1), е(2) и е1з); затем эти направле-
ния последовательно заменяются вновь построенными сопряженны-
ми направлениями. Серия одномерных поисков из точки х1о) про-
водится в направлении е(3), затем е11), е(2) и снова е18); в результате
построены сопряженные направления е(8) и (х(4)—х(1)). Направле-
ние е11) заменяется новым направлением поиска, которое на рис. 3.12
обозначено цифрой 4. Следующая серия поисков проводится в на-
правлении 4, затем е(2), е(3> и снова 4. Согласно обобщенному свой-
ству параллельного подпространства, новое направление (х<8)—x(S)),
обозначенное на рисунке цифрой 5, сопряжено не только с 4, но и
с е<8). Следовательно, направления е<8\ (х<4)—х(1)) и (х<8)—х<5))
образуют систему взаимно сопряженных направлений. Поэтому
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
10J
Рис. 3.12 Построение сопря-
женных направлений в трех-
мерном пространстве
если провести дополнительный поиск из точки х18’ в направлении
(х'8>—хФ)(т. е. в направлении 5 на рисунке), то будет найдена точка
xw, в которой должен достигаться оптимум квадратичной функции
трех переменных/(х), поскольку поиск последовательно осуществля-
ется в трех взаимно сопряженных направлениях. Таким образом,
в трехмерном случае для нахождения точного (если, разумеется,
оперировать недесятичными дробями) оптимума квадратичной функ-
ции требуется провести девять поисков вдоль прямой с использо-
ванием только значений функции. Алгоритм легко обобщается и
в случае Димерного пространства требует проведения последователь-
ности № одномерных поисков, которая приводит к получению точки
оптимума квадратичной функции. Ниже представлены шаги обоб-
щенного алгоритма.
Метод сопряженных направлений Пауэлла
Шаг 1. Задать начальную точку х1о) и систему М линейно не-
зависимых направлений; возможен случай, когда s<n=eu>, 1 = 1, 2,
3......N.
108
ГЛАВА 3
Ш а г 2. Минимизировать f(x) при последовательном движении
(М+1) направлениям; при этом полученная ранее точка минпму-
берется в качестве исходной, а направление s{N} используется
по
ма
как при первом, так и последнем поиске.
Шаг 3. Определить новое сопряженное направление с по-
мощью обобщенного свойства параллельного подпространства.
Ш а г 4. Заменить s(1) на sl2) и т. д. Заменить slM сопряженным
направлением. Перейти к шагу 2.
Для того чтобы применить изложенный метод на практике, его
необходимо дополнить процедурами проверки сходимости и линей-
ной независимости системы направлений. Проверка линейной неза-
висимости особенно важна в тех случаях, когда функция f(x) не
является квадратичной [16, 17].
Из способа построения алгоритма следует, что в случае, когда
целевая функция квадратична и обладает минимумом, точка мини-
мума находится в результате реализации М циклов, включающих
шаги 2, 3 и 4, где N — количество переменных. Если же функция
не является квадратичной, то требуется более чем М циклов. Вместе
с тем можно дать строгое доказательство того, что при некотором
предположении метод Пауэлла сходится к точке локального мини-
мума с суперлинейной скоростью (см. данное ниже определение).
Скорость сходимости. Рассматриваемый метод по-
зволяет построить последовательность точек xlft), которая сходится
к решению х*. Метод называется сходящимся, если неравенство
^<1. где (3.39)
е<« = дш_ х*, (3.40)
выполняется на каждой итерации. Поскольку при расчетах обычно
оперируют конечными десятичными дробями, даже самый эффектив-
ный алгоритм требует проведения бесконечной последовательности
итераций. Поэтому в первую очередь интерес представляют асимпто-
тические свойства сходимости изучаемых методов. Будем говорить,
что алгоритм обладает сходимостью порядка г (см. [18, 19]), если
И |1 е(& + 1>Д ______________________q .о д,.
где С — постоянная величина. Из формулы (3.39) следует, что при
г=1 имеет место неравенство С^1. Если г=1 или г=2, то алгоритм
характеризуется линейной или квадратичной скоростью сходимости
соответственно. При г=1 и С=0 алгоритм характеризуется супер-
линейной скоростью сходимости.
Пример 3.6. Метод сопряженных направлений Пауэлла
Найти точку минимума функции
f (х) = 2х[ + 4xtx’— 1 Qxax2 + xl,
если задана начальная точка х(0)=[5, 2]г, в которой /(х10))=314.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
109
Ш а г 1. sll)=[l, OR, s<2)=[0, 1R.
Шаг 2. (a) Найдем такое значение X, при котором
f(xw + Xsl2))—> min.
Получим Х*=—0,81, откуда
х(1) = [5, 2]г—0,81 [0, 1]г = [5, l,19]r, f (х(1)) = 250.
(б) Найдем такое значение X, при котором f (x'^-J-Xs*1’)-> min.
Х* = —3,26, х121 = [1,74, 1,19]г, / (х(2))= 1,10.
(в) Найдем такое значение А., при котором /(x<2,+Xsl2)) -► min.
Я* = — 0,098, xl” = [l,74, l,092]r, f (x(3>) = 0,72.
Шаг 3. Положим st3)=x<3)—xll)=[—3,26, —0,0981г. После
нормировки получим
sl3’ = 15r = [-°.99955, -0,03]Л
Положим sll) =s(2>, s(2)=st3) и перейдем к шагу 2 алгоритма.
Ш а г 4. Найдем такое значение X, при котором /(xt3)+Xsl2))-►
min.
Х* = 0,734, х“> = [1,006, 1,070]т, f (xu)) = — 2,86.
Примечание. Если бы f(x) была квадратичной функцией, то
полученная точка являлась бы решением задачи (если пренебречь
ошибкой округления). В данном случае итерации следует продол-
жить до получения решения.
Направления поиска, полученные в процессе реализации метода,
показаны на рис. 3.13.
Результаты вычислительных экспериментов позволяют утверж-
дать, что метод Пауэлла (дополненный процедурой проверки линей-
ной зависимости направлений) отличается по меньшей мере столь
же высокой надежностью, как и другие методы прямого поиска, и
в ряде случаев является значительно более эффективным. Поэтому
проблема выбора алгоритма прямого поиска часто (и обоснованно)
разрешается в пользу метода Пауэлла.
Здесь заканчивается рассмотрение методов прямого поиска ре-
шений в задачах безусловной оптимизации. В следующем разделе
описываются методы, основанные на использовании производных.
3.3. Градиентные методы
В предыдущем разделе рассматривались методы, позволяющие
получить решение задачи на основе использования только значений
целевой функции. Важность прямых методов несомненна, поскольку
в ряде практических инженерных задач информация о значения*
целевой функции является единственной надежной информацией,
по
ГЛАВА 3
Х2
f(x)=2x’+4x,x’-1Ox1x2+x|
4,0
3,0
2,0
1,0
0,0
Линии
уровня
А -3,000
В -1,000
С 1,000
О 3,000
Е 40,000
F120,000
6200,000
Н280,000
1360,000
х<о>
Рис. 3.13. Решение задачи из примера 3.6 по методу сопряженных направлений
Пауэлла.
которой располагает исследователь. С другой стороны, при исполь-
зовании даже самых эффективных прямых методов для получения
решения иногда требуется чрезвычайно большое количество вы-
числений значений функции. Это обстоятельство наряду с совер-
шенно естественным стремлением реализовать возможности нахож-
дения стационарных точек [т. е. точек, удовлетворяющих необходи-
мому условию первого порядка (3.15а)] приводит к необходимости
рассмотрения методов, основанных на использовании градиента
целевой функции. Указанные методы носят итеративный характер,
так как компоненты градиента оказываются нелинейными функция-
ми управляемых переменных.
Далее везде предполагается, что f(x), Vf(x) и V2/(x) существу-
ют и непрерывны. Методы с использованием как первых, так и вто-
рых производных рассматриваются лишь кратко и главным образом
в их связи с более полезными методами. Особое внимание уделяется
подробному изложению методов сопряженных градиентов, в основе
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
111
которых лежит введенное выше понятие сопряженности направле-
ний, и так называемых квазиньютоновских методов, которые анало-
гичны методу Ньютона, но используют лишь информацию о первых
производных. Предполагается, что компоненты градиента могут
быть записаны в аналитическом виде или с достаточно высокой точ-
ностью вычислены при помощи численных методов. Кроме того,
рассматриваются способы численной аппроксимации градиентов.
Все описываемые методы основаны на итерационной процедуре,
реализуемой в соответствии с формулой
X<A+l> = X<A>-|-a<A>s(X<A>), (3.42)
где хш — текущее приближение к решению х*; а{к} — параметр,
характеризующий длину шага; s(x<,!l)=s<ft) — направление поиска
в (V-мерном пространстве управляемых переменных хь 1=1, 2,
3, . . . , N. Способ определения s(x) и а на каждой итерации свя-
зан с особенностями применяемого метода. Обычно выбор alftl
осуществляется путем решения задачи минимизации /(х) в направ-
лении s(x(fc)). Поэтому при реализации изучаемых методов необхо-
димо использовать эффективные алгоритмы одномерной миними-
зации.
3.3.1. Метод Коши [20]
Предположим, что в некоторой точке х пространства управляе-
мых переменных требуется определить направление наискорейшего
локального спуска, т. е. наибольшего локального уменьшения це-
левой функции. Как и ранее, разложим целевую функцию в окрест-
ности точки х в ряд Тейлора
f(x)=f(x) + Vf(x)rAx + ... (3.43)
и отбросим члены второго порядка и выше. Нетрудно видеть, что
локальное уменьшение целевой функции определяется вторым сла-
гаемым, так как значение/(х) фиксировано. Наибольшее уменьше-
ние f ассоциируется с выбором такого направления в (3.42), кото-
рому соответствует наибольшая отрицательная величина скаляр-
ного произведения, фигурирующего в качестве второго слагаемого
разложения. Из свойства скалярного произведения следует, что
указанный выбор обеспечивается при
s(x) = —V/(x), (3.44)
и второе слагаемое принимает вид
— aV/(x)rV/(x).
Рассмотренный случай соответствует наискорейшему локальному
спуску. Поэтому в основе простейшего градиентного метода лежит
ГЛАВА 3
112
формула
х(А+п = хм_ау[ (3 45)
где а — заданный положительный параметр. Метод обладает двумя
недостатками: во-первых, возникает необходимость выбора подхо-
дящего значения а, и, во-вторых, методу свойственна медленная
сходимость к точке минимума вследствие малости V/ в окрестности
этой точки.
Таким образом, целесообразно определять значение а на каждой
итерации
= хи»_а(А> V^XU>). (3.46)
Значение вычисляется путем решения задачи минимизации
f(xlA+n) вдоль направления V7(xtw) с помощью того или иного ме-
тода одномерного поиска. Рассматриваемый градиентный метод
носит название метода наискорейшего спуска, или метода Коши,
поскольку Коши первым использовал аналогичный алгоритм для
решения систем линейных уравнений.
Поиск вдоль прямой в соответствии с формулой (3.46) обеспечи-
вает более высокую надежность метода Коши по сравнению с про-
стейшим градиентным методом, однако скорость его сходимости
при решении ряда практических задач остается недопустимо низкой.
Это вполне объяснимо, поскольку изменения переменных непосред-
ственно зависят от величины градиента, которая стремится к нулю
в окрестности точки минимума, и отсутствует механизм ускорения
движения к точке минимума на последних итерациях. Одно из глав-
ных преимуществ метода Коши связано с его устойчивостью. Метод
обладает важным свойством, которое заключается в том, что при
достаточно малой длине шага итерации обеспечивают выполнение
неравенства
/(x(ft+n)^/(x,w). (3.47)
С учетом этого свойства заметим, чго метод Коши, как правило, по-
зволяет существенно уменьшить значение целевой функции при
движении из точек, расположенных на значительных расстояниях
от ючки минимума, и поэтому часто используется при реализации
градиентных методов в качестве начальной процедуры. Наконец,
на примере метода Коши можно продемонстрировать отдельные
приемы, которые используются при реализации различных гради-
ентных алгоритмов.
Пример 3.7. Метод Коши
Рассмотрим функцию
f (х)—+4xjX 2 4- 5xi
и используем метод Коши для решения задачи ее минимизации.
Решение. Прежде всего вычислим компоненты градиента
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
ИЗ
Рис. 3.14. Итерации по методу Коши с использованием метода
интерполяции.
Линии
уровня
А 10,000
В 40,000
С 70,000
О 100,000
Е 150,000
F 160,000
G 190,000
Н 220,000
I 250,000
J 280,000
квадратичной
Для того чтобы применить метод наискорейшего спуска, зададим
начальное приближение
х<0| = [10, 10]г
и с помощью формулы (3.46) построим новое приближение
x'li —— а(01 у/U10’)-
Таблица 3.1. Результаты вычислений по методу Коши
k 4* Лк) 2 f
1 -1,2403 2,1181 24,2300
2 0,1441 0,1447 0,3540
3 —0,0181 0,0309 0,0052
4 0,0021 0,0021 0,0000
114
ГЛАВА 3
Рис. 3.15. Блок-схема метода Коши.
Выберем а<0) таким образом, чтобы min; а<0)=0,056. Сле-
довательно, х(1) = [—1,20, 2,161г. Далее найдем точку
хт = х(1)— а’11 V/ (х(1)),
вычислив градиент в точке х(й и проведя поиск вдоль прямой.
В табл. 3.1 представлены данные, полученные при проведении ите-
раций на основе одномерного поиска по методу квадратичной интер-
поляции [21, 22]. Последовательность полученных точек изображена
на оис. 3.14.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
115
Несмотря на то что метод Коши не имеет большого практического
значения, он реализует важнейшие шаги большинства градиентных
методов. Блок-схема алгоритма Коши приведена на рис.’ 3.15. За-
метим, что работа алгоритма завершается, когда модуль градиента
или модуль вектора Дх становится достаточно малым.
3.3.2. Метод Ньютона [23]
Нетрудно видеть, что в методе Коши применяется «наилучшая»
локальная стратегия поиска с использованием градиента. Однако
движение в направлении, противоположном градиенту, приводит
в точку минимума лишь в том случае, когда линии уровня функции f
представляют собой окружности. Таким образом, направление,
противоположное градиенту, вообще говоря, не может служить
приемлемым глобальным направлением поиска точек оптимума
нелинейных функций. Метод Коши основывается на последователь-
ной линейной аппроксимации целевой функции и требует вычисления
значений функции и ее первых производных на каждой итерации.
Для того чтобы построить более общую стратегию поиска, следует
привлечь информацию о вторых производных целевой функции.
Опять разложим целевую функцию в ряд Тейлора
f (х) = f (хм) + V/ (х(*>)г Ах +1/2 Дхг V2/ (хм) Дх + 0 (Ах3).
Отбрасывая все члены разложения третьего порядка и выше, полу-
чим квадратичную аппроксимацию /(х):
f(x; хм) — f (хм) + Vf (хм)т Дх-ф */2 ^хт У2[(хм) Дх, (3.48)
где / (х; хм) — аппроксимирующая функция переменной х, по-
строенная в точке х(А). На основе квадратичной аппроксимации
функции f (х) сформируем последовательность итераций таким
образом, чтобы во вновь получаемой точке х(А+,) градиент аппрок-
симирующей функции обращался в нуль. Имеем
V/(x; xM) = yf(xM) + V2f(xM)kx==0, (3.49)
откуда Дх = — V2/ (х(А))-1 Vf (хм). (3.50)
Последовательное применение схемы квадратичной аппроксимации
приводит к реализации оптимизационного метода Ньютона по
формуле
х<л+» = х‘*) —^(х'^-^Нх1*)), (3.51)
использование которого демонстрируется на следующем примере.
Пример 3.8. Метод Ньютона
Опять рассмотрим функцию из предыдущего примера:
f (х) = 8х[ -ф 4XjX2 -ф 5х2, откуда
V/(x) = [16X1 + 4x5, 10х5-ф4Х1_|г,
_.,г, . г, Г16 41
?-/(х) = Я = |_ 4 10 .
116
ГЛАВА 3
При х<0)=[10, 10]г из формулы (3.51) получаем
х(1’ = [10, 2^ Лб][200’ 14°1г
и. следовательно,
х(1) = [10, Ю]г —[144°- 14W = [O, °F.
что совпадает с точным решением.
Таким образом, задача минимизации квадратичной функции
решается с помощью одной итерации по методу Ньютона (при любой
начальной точке).
Свойства сходимости. Анализ свойств сходимости
метода Ньютона представляет значительный интерес. Мангасариан
124] показал, что при выполнении некоторого (достаточно общего)
условия регулярности /(х) метод Ньютона обнаруживает квадра-
тичную скорость сходимости, т. е. выполняется неравенство
||е‘*+1> КСЦе1*’ ||2. (3.52)
где постоянная С связана с обусловленностью матрицы Гессе V2/.
Легко видеть, что метод Ньютона сходится всякий раз, когда выбор
х(0) осуществляется в соответствии с условием
||е (х<0>) || < 1/С. (3.53)
Квадратичная скорость сходимости объясняется тем обстоятель-
ством, что метод основан на квадратичной аппроксимации. При
минимизации произвольных функций целесообразно предположить,
что в случае выбора начальной точки, удовлетворяющей неравен-
ству Це (х10>)||>1/С, применение метода не приведет к получению
решения. Заметим, что алгоритм не обладает свойством убывания
значений целевой функции от итерации к итерации. Чтобы показать
это, предположим, что текущее приближение х не является стацио-
нарной точкой (т. е. V/(x)^=0), и найдем проекцию направления
поиска по методу Ньютона на направление, задаваемое градиентом
в точке х. По определению направление поиска называется направ-
лением спуска, если имеет место неравенство
V/ (х)г s (х) < 0. (3.54)
Таким образом, из формулы (3.51) следует, что должно выполняться
неравенство
— V/(х)г Vs / (^-у V/(х) < 0. (3 55)
Нетрудно видеть, что в случае, когда матрица vY(x) положительнс
определена, это условие выполняется, т. е. направление поиска пс
методу Ньютона оказывается направлением спуска. Однако если
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
117
в некоторой точке V2/(x) отрицательно определена, то указанное
направление является направлением подъема, а в случае неопреде-
ленности матрицы Гессе однозначный вывод сделать нельзя.
3.3.3. Модифицированный метод Ньютона
Опыт показывает, что при исследовании неквадратичных функ-
ций метод Ньютона не отличается высокой надежностью. В самом
деле, если точка х(0’ находится на значительном расстоянии от
точки х*, шаг по методу Ньютона часто оказывается чрезмерно
большим, что может привести к отсутствию сходимости. Метод
можно довольно просто модифицировать, с тем чтобы обеспечить
уменьшение целевой функции от итерации к итерации и осу-
ществлять поиск вдоль прямой, как в методе Коши. Последователь-
ность итераций строится в соответствии с формулой
x(ft+1) = х'к'—а(И V2 / (xM)~l Vf (3.56)
Выбор осуществляется таким образом, чтобы
f (х<А+1)) —► min;
это гарантирует выполнение неравенства
Такой метод носит название модифицированного метода Ньютона
и в случаях, когда вычисление точных значений первых и вторых
производных не сопряжено с существенными трудностями, оказы-
вается надежным и эффективным. Однако при использовании моди-
фицированного метода Ньютона на каждой итерации возникает
необходимость построения и решениялинейного уравнения, содер-
жащего элементы матрицы Гессе V2f(x).
3.3.4. Метод Марквардта
Рассматриваемый метод является комбинацией методов Коши и
Ньютона, в которой удачно сочетаются положительные свойства
обоих методов. Вместе с тем при использовании метода Марквардта
требуется информация о значениях вторых производных целевой
функции. Выше было отмечено, что градиент указывает направление
наибольшего локального увеличения функции, а движение в на-
правлении, противоположном градиенту, из точки х’01, располо-
женной на значительном расстоянии от точки минимума х*, обыч-
но приводит к существенному уменьшению целевой функции. С дру-
гой стороны, направления эффективного поиска в окрестности точки
минимума определяются по методу Ньютона. Простая идея объеди-
нения методов Коши и Ньютона была положена в основу алгоритма,
разработанного Марквардтом [25] в 1963 г. В соответствии с этим
118
ГЛАВА 3
методом направление поиска определяется равенством
s (xw) = — [Н(*> + А1*’!]'1 V/ (х(А)). (3.57)
При этом в формуле (3.42) следует положить а(*’=+1, поскольку
параметр А позволяет не только изменять направление поиска, но и
регулировать длину шага. Символом 1 здесь обозначена единичная
матрица, т. е. матрица, все элементы которой равны нулю, за исклю-
чением диагональных элементов, равных +1. На начальной стадии
поиска параметру А<0) приписывается большое значение (например,
10*), так что
[Н(0> + А(0>1]-1 = [А(«>1]-1= I. (3.58)
Таким образом, большим значениям А(0) соответствует направление
поиска s (х10)) ->—V/(xW)). Из формулы (3.57) можно заключить,
что при уменьшении А до нуля s(x) изменяется от направления,
противоположного градиенту, до направления, определяемого по
методу Ньютона. Если после первого шага получена точка с мень-
шим значением целевой функции (т. е. / (х<1>)<С/(xt0>)), следует вы-
брать А(1)<А1о) и реализовать еще один шаг; в противном случае
следует положить А<О’=|ЗА<<П, где 1, и вновь реализовать преды-
дущий шаг. Ниже представлены шаги алгоритма.
Алгоритм Марквардта
Шаг 1. Задать х<0) — начальное приближение к х*; М —
максимальное (допустимое) количество итераций; е — параметр
сходимости.
Шаг 2. Положить /г=0, А(0) = 10*.
Шаг 3. Вычислить компоненты
Шаг 4. Выполняется ли неравенство
II V/ (х‘«) || < 8?
Да: перейти к шагу 11.
Нет: перейти к следующему шагу.
Шаг 5. Выполняется ли неравенство
Да: перейти к шагу 11.
Нет: перейти к следующему шагу.
Шаг 6. Вычислить s(xlft)) =—[Hu,4-A(A>I]_,vf (xft).
Шаг 7. Положить x<A+1)=x(ft)+s(x<ft>).
Шаг 8. Выполняется ли неравенство f (x‘A+1))</(x‘ft’)?
Да: перейти к шагу 9.
Нет: перейти к шагу 10.
Шаг 9. Положить A<ft+1)=V2А(А) и k—k+\. Перейти к шагу 3.
Шаг 10. Положить A<ft)=2A(A). Перейти к шагу 6.
Шаг 11. Печать результатов и останов.
Метод Марквардта характеризуется относительной простотой,
свойством убывания целевой функции при переходе от итерации
к итерации, высокой скоростью сходимости в окрестности точки
минимума х*, а также отсутствием процедуры поиска вдоль прямой.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 119
Главный недостаток метода заключается в необходимости вычисле-
ния Hlft) и последующего решения системы линейных уравнений,
соответствующей (3.57). Этот метод широко используется при ре-
шении задач, в которых f(x) записывается в виде суммы квадра-
тов г), т. е.
f (X) = ft (Х)+П (%)+.••+ Гт W- (3.59)
Именно такая задача рассматривалась Марквардтом. Пауэлл [26]
и Бард [27] на основе вычислительных экспериментов показали, чтс
метод Марквардта отличается высокой эффективностью при реше-
нии задач такого типа.
3.3.5. Методы сопряженных градиентов
В предыдущих подразделах рассматривались методы Коши и
Ньютона. Отмечалось, что метод Коши эффективен при поиске на
значительных расстояниях от точки минимума х* и плохо «рабо-
тает» в окрестности этой точки, тогда как метод Ньютона не отли-
чается высокой надежностью при поиске х* из удаленной точки,
однако оказывается весьма эффективным в тех случаях, когда х1*’
находится вблизи точки минимума. В этом и последующих подраз-
делах рассматриваются методы, которые обладают положительны-
ми свойствами методов Коши и Ньютона и основаны на вычислении
значений только первых производных. Таким образом, эти методы,
с одной стороны, отличаются высокой надежностью при поиске х*
из удаленной точки х* и, с другой стороны, быстро сходятся в ок-
рестности точки минимума.
•Методы, позволяющие получать решения задач с квадратичными
целевыми функциями приблизительно за N шагов при условии ис-
пользования недесятичных дробей, будем называть квадратично
сходящимися. Среди таких методов можно выделить класс алгорит-
мов, в основе которых лежит построение сопряженных направлений.
Выше было сформулировано условие сопряженности для системы
направлений s(ft), k=l, 2, 3, ..., r^N, и симметрической матрицы С
порядка NXN. Была также установлена связь между построением
указанных направлений и преобразованием произвольной квадра-
тичной функции к виду суммы полных квадратов; сделан вывод
о том, что последовательный поиск вдоль каждого из М направле-
ний, обладающих свойством С-сопряженности, позволяет найти
точку минимума квадратичной функции N переменных. Рассмот-
рена процедура определения системы сопряженных направлений
с использованием только значений целевой функции. Ниже для
получения сопряженных направлений применяются квадратичная
аппроксимация /(х) и значения компонент градиента. Кроме того,
') Задачи такого типа возникают, например, в регрессионном анализе,—
Поим, пеоев.
120
ГЛАВА 3
потребуем, чтобы рассматриваемые методы обеспечивали убывание
целевой функции при переходе от итерации к итерации.
Пусть в пространстве управляемых переменных заданы две
произвольные несовпадающие точки х(0) и х(1). Градиент квадратич-
ной функции равен
Vf(x) = V<?(x) = Cx + &=g(x). (3.60)
Обозначение g(x) введено здесь для удобства записи формулы.
Таким образом,
£(х(0>) = Сх(0> + &,
g (х11>) = Сх(1) -|- b.
Запишем изменение градиента при переходе от точки х(0) к точке
хЦ):
Ag (%) = g (х’1’) — g (х(0)) = С (х(1)— х(0)), (3.61)
Ag (х) = САх.
Равенство (3.61) выражает свойство квадратичных функций, кото-
рое будет использовано ниже.
В 1952 г. Эстенс и Штифель [28] предложили эффективный ите-
рационный алгоритм для решения систем линейных уравнений, ко-
торый по существу представлял собой метод сопряженных градиен-
тов. Они рассматривали левые части линейных уравнений как ком-
поненты градиента квадратичной функции и решали задачу мини-
мизации этой функции. Позже Флетчер и Ривс [29] обосновали
квадратичную сходимость метода и обобщили его для случая не-
квадратичных функций. Фрид и Метцлер 130] продемонстрировали
(допустив, однако, некоторые неточности) возможности использо-
вания метода для решения линейных систем с разреженной матри-
цей коэффициентов. (Определение разреженной матрицы см. в при-
ложении А.) Они подчеркнули простоту реализации метода по срав-
нению с другими, более общими алгоритмами, что является особен-
но важной характеристикой с позиций нашего изложения.
Рассмотрение метода будем проводить в предположении, что це-
левая функция является квадратичной:
f (х) = q (х) = а + Ьтх +1 /2хгСх,
а итерации проводятся по формуле (3.42), т. е.
Х(/г+1) _ xik) _|_ s (£<*)).
Направления поиска на каждой итерации определяются с помощью
следующих формул:
к- 1
s'*’ = — g<*> + 2 Y(/)s(n. (3.62)
1 = 0
s‘°> = —g<0), (3.63)
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
121
где Так как после определения системы направлений
проводится последовательный поиск вдоль каждого из направлений,
полезно напомнить, что в качестве критерия окончания одномерного
поиска обычно используется условие
V/ (xlft+1,)rsiw = 0. (3.64)
Значения у(,), i'=l, 2, 3, k—1, выбираются таким образом,
чтобы направление s(fc) было С-сопряжеио со всеми построенными
ранее направлениями поиска. Рассмотрим первое направление
s(l> _ _g(l> | у(0>s(0) _ _ gll)_y(O>g(O)
и наложим условие его сопряженности с s(0)
s(i>rCs(o> = oi
откуда [gll) + 'V11” g(0)]rCs('” = 0.
На начальной итерации
s(0) = Дх/а(0);
следовательно,
[gll> + v«»g«»]T с [ Дх/а(0>] = 0.
Используя свойство квадратичных функций (3.61), получаем
[Я(1>+ Т‘О,^1О>]Г = (3.65)
откуда
Y10’ = - (Ag^y^g'O)). (3.66)
Из уравнения (3.65) следует, что
g<l> Tg<l> _|_ y<0>g.<0> Tg<l>_g<V Tg<0>_y«»g«» Tg<0> _ о
При соответствующем выборе a(n) и с учетом формулы (3.64) имеем
gin т gw = о
Таким образом,
T(0, = k(1,il2/kl0,lia- (3.67)
Далее определим следующее направление поиска
$(2) — - g-(2> _j_ y(0>s(0> _|_ y(l> ^(1>
и выберем yl0) и yll) таким образом, чтобы выполнялись условия
s(2)TCs(0) = 0 и s(2)7'Cs(1) = 0,
т. е. условия С-сопряженности направления s(2) с направлениями
sl0) и s(1). С помощью формул (3.61) и (3.64) можно показать (это
предоставляется читателю в качестве упражнения), что здесь
у(0) =0, а в общем случае у(/)=0, i—0, 1, 2, .... k—2, при любом зна-
чении k. Отсюда следует, что общая формула для направлений по-
иска может быть записана в виде, предложенном Флетчером и Рив-
сом:
s1*1 + [ ||g(*) |]2/|| g"*-» ||a] s1*’1». (3.68)
122
ГЛАВА 3
Если f(x) — квадратичная функция, для нахождения точки ми-
нимума требуется определить М—1 таких направлений и провести
М поисков вдоль прямой (при отсутствии ошибок округления).
Если же функция /(х) не является квадратичной, количество на-
правлений и соответствующих поисков возрастает.
Некоторые исследователи на основе опыта проведения вычис-
лительных экспериментов предлагают после реализации каждой
серии из N или М+1 шагов возвращаться к начальной итерации
алгоритма, положив s(x)=—g(x). Это предложение остается пред-
метом для изучения, поскольку при минимизации функций общего
вида в ряде случаев влечет за собой замедление сходимости. С дру-
гой стороны, циклические переходы к начальной итерации повы-
шают надежность алгоритма, так как вероятность построения ли-
нейно зависимых направлений уменьшается. Если полученное на-
правление оказывается линейной комбинацией одного или не-
скольких полученных ранее направлений, то метод может не при-
вести к получению решения, поскольку поиск в соответствующем
подпространстве уже проводился. Однако следует отметить,
что на практике такие ситуации встречаются достаточно редко.
Метод оказывается весьма эффективным при решении практических
задач, характеризуется простотой однопараметрической вычисли-
тельной схемы и небольшим объемом памяти ЭВМ, необходимым для
проведения поиска. Относительно невысокий уровень требований
к объему памяти ЭВМ делает метод Флетчера — Ривса (ФР) и его
модификации особенно полезным при решении задач большой
размерности.
Пример 3.9. Метод Флетчера — Ривса
Найти точку минимума функции
/(х)=4х2+3х|—4XiXs+xi,
если х(П) = [0, 0]г.
Решение
Шаг 1. V/(x)=[8xi—4х2+1, 6х2—4xi)r,
s«» = —v/(x(0)) = —[1, О]7.
Шаг 2. Поиск вдоль прямой:
х(1> = х10> —а10’ V/ (х‘0)) —> а(0) = %,
xll>=[o, оу-%[i, оу=[-7g, оу.
Ш а г 3. 6=1:
s(i,=-[o, i][i, оуч-г. l/.y.
Шаг 4. Поиск вдоль прямой:
x(2) = x(1>+a(1)s(1) _>а(1> = 1/41
^>=[-1/в, oy-vj1/.., 1/2]г=[—3/1в, -1/8у,
V/(xl2)) = [0, 0]г.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
123
Таким образом, х(2)=х*. Решение получено в результате прове-
дения двух одномерных поисков, поскольку целевая функция квад-
ратичная, а ошибки округления отсутствуют.
Миль и Кентрелл [31] обобщили подход Флетчера и Ривса,
предложив формулу
х‘*+1> = хм +а(л> + (х‘А-г>)}, (3.69)
где a(W и ylft) — параметры, значения которых определяются на
каждой итерации. Этот метод, известный как градиентный метод
с памятью, очень эффективен по числу необходимых для решения
задачи итераций, но требует большего количества вычислений зна-
чений функции и компонент градиента, чем метод Флетчера —
Ривса. Поэтому алгоритм Миля и Кентрелла оказывается полезным
лишь в тех случаях, когда оценивание значений целевой функции
и компонент градиента не связано с какими-либо трудностями.
Напомним, что рассмотрение метода Флетчера — Ривса прово-
дилось в предположении квадрэтичности целевой функции и от-
сутствия ошибок округления в процессе поиска вдоль прямой. Од-
нако при реализации ряда методов сопряженные направления оп-
ределяются без учета одного из указанных предположений (или даже
обоих предположений). Среди таких методов наибольшего внима-
ния, по-видимому, заслуживает метод, разработанный Полаком и
Рибьером [32] в 1969 г. Метод основан на точной процедуре прове-
дения поиска вдоль прямой и на более общем предположении об
аппроксимации целевой функции. При этом
V ||g(x(»-1,)|P
(3.70)
где, как и прежде,
Ag (x(W) = g (x(ft)) — g(x(k~1}). (3-71)
Если a — параметр, значение которого определяется в результате
поиска вдоль прямой, и у — параметр, значение которого вычис-
ляется по формуле (3.70), то метод сопряженных градиентов По-
лака — Ривьера реализуется с помощью следующих соотношений:
X(ft+1> _ %(А> _|_аОг)5 (x(fc)),
s (x(ft)) = — V/ (xlft)) + y(ft)s (x(ft-1)). (3.72)
Легко видеть, что единственное различие между методами Пола-
ка — Рибьера и Флетчера — Ривса заключается в способах выбора
параметра у.
Известны и другие подобные методы, которые также основаны
на проведении точных вычислений при одномерном поиске и на
более общей (чем квадратичная) аппроксимации целевой функции
(см., например, [33, 34, 35]). Краудер и Вульф [36] в 1972 г., а затем
Пауэлл [37] доказали, что методы сопряженных градиентов обла-
124
ГЛАВА 3
дают линейной скоростью сходимости при отсутствии периодиче-
ского возврата к начальной итерации. Указанные возвраты осу-
ществляются в соответствии со специальной процедурой, которая
прерывает процесс построения векторов направлений поиска, а
далее вычисления продолжаются по аналогии с построением s(x(0)).
Выше отмечалось, что по ряду причин наличие процедуры возврата
к начальной итерации повышает устойчивость работы алгоритма,
так как позволяет избежать построения линейно зависимых векто-
ров направлений поиска. Пауэлл [38] доказал, что метод Полака —
Рибьера также характеризуется линейной скоростью сходимости
при отсутствии возвратов к начальной итерации, однако имеет не-
сомненное преимущество перед методом Флетчера — Ривса при
решении задач с целевыми функциями общего вида и обладает ме-
нее высокой чувствительностью к ошибкам округления при прове-
дении одномерных поисков.
Вопросы разработки эффективных процедур и методов, обеспе-
чивающих возврат к начальной итерации и при этом обладающих
малой чувствительностью к ошибкам округления, остаются предме-
том активных исследований. Бил [39] предложил метод сопряжен-
ных градиентов, аналогичный стандартной процедуре Флетчера —
Ривса, но вместе с тем не использующий направление вдоль гра-
диента при возвращении к начальной итерации. Он показал, как
на основе анализа направления, полученного непосредственно
перед возвращением к начальной итерации, можно уменьшить
объем необходимых вычислений при решении задач, требующих
нескольких возвратов. Пауэлл [38] исследовал стратегию Била,
а также другие стратегии возврата к начальной итерации и пред-
ложил использовать процедуру возврата либо после проведения
каждой серии из N шагов, либо при выполнении неравенства
| g (х»)г g (х'*’1») | > 0,2 (| g (х‘*>) ||2. (3.73)
Он продемонстрировал, что стратегию Била, дополненную услови-
ем (3.73), можно успешно применять как вместе с формулой Флет-
чера — Ривса, так и с формулой Полака — Рибьера, и провел ряд
вычислительных экспериментов, результаты которых подтверж-
дают превосходство метода Полака — Рибьера (с возвратом).
Шэнно [40] исследовал влияние ошибок округления при проведе-
нии поисков вдоль прямой и различных стратегий возврата на
эффективность методов сопряженных градиентов. Он показал, чтс
стратегия Била (с использованием соответствующей двухпарамет-
рической формулы), дополненная предложенным Пауэллом усло-
вием возврата, приводит к существенному уменьшению требуемой
точности одномерного поиска и, следовательно, к значительному
повышению эффективности полной вычислительной схемы метода
сопряженных градиентов. Шэнно также представил численные ре-
зультаты, которые указывают на преимущество метода Полака —
Рибьера с использованием процедур возврата и округления при
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
125
поисках вдоль прямой. В работе [41] продемонстрирована ведущая
роль методов сопряженных градиентов при решении задач нелиней-
ного программирования большой размерности.
3.3.6. Квазиньютоновские методы
Эти методы подобны методам, рассмотренным в подразд. 3.3.5,
поскольку также основаны на свойствах квадратичных функций.
В соответствии с изложенными выше методами поиск решения осу-
ществляется по системе сопряженных направлений, тогда как ква-
зиньютоновские методы обладают положительными чертами метода
Ньютона, однако используют только первые производные. Во всех
методах указанного класса построение векторов направлений поис-
ка осуществляется с помощью формулы (3.42), в которой s(x{k})
записывается в виде
s(x(W) = —А’*'?/ (%<*>), (3.74)
где AlS) — матрица порядка МхМ, которая носит название мет-
рики. Методы поиска вдоль направлений, определяемых этой фор-
мулой, называются методами переменной метрики, поскольку мат-
рица А изменяется на каждой итерации. Более точно метод пере-
менной метрики представляет собой квазиньютоновский метод,
если в соответствии с ним перемещение пробной точки удовлетво-
ряет следующему условию:
Ax = C-!Ag. (3.75)
К сожалению, в специальной литературе не выработаны единые
и твердые рекомендации по использованию приведенных выше тер-
минов [42]; мы будем считать их взаимозаменяемыми, поскольку
они несут одинаково важную информацию об особенностях разра-
ботки и реализации рассматриваемых методов.
Для аппроксимации матрицы, обратной матрице Гессе, восполь-
зуемся следующим рекуррентным соотношением:
А‘*+1> = А1А’ + А'4’, (3.76)
где А!?’— корректирующая матрица. Матрица А(А) будет исполь-
зоваться в формулах (3.74) и (3.42). Задача заключается в том, что-
бы построить матрицу А’*’ таким образом, чтобы последователь-
ность А(0), А(1), А(а), ..., Alft+1) давала приближение к Н~’ =
—V7(^*)-1; при этом для получения решения х* требуется один
дополнительный поиск вдоль прямой, если f(x)— квадратичная
функция. Как неоднократно подчеркивалось выше, имеются опре-
деленные основания полагать, что метод, обеспечивающий нахож-
дение оптимумов квадратичных функций, может привести к успе-
ху при решении задач с нелинейными целевыми функциями общего
вида.
Вернемся к важному свойству квадратичных функций (3.75)
126
ГЛАВА 3
и предположим, что матрица С-1 аппроксимируется по формуле
= (3.77)
где Р — скалярная величина. Наиболее предпочтительным является
приближение, удовлетворяющее (3.75), т. е.
Дх‘« = А1'”Дг<А>. (3.78)
/
Однако ясно, что построить такую аппроксимацию невозможно,
поскольку для того, чтобы найти Д§(Л), необходимо знать матрицу
Alft). Здесь используются следующие обозначения:
Дх‘*> = х‘*+1’—х1», (3 79)
Д§(/г) = g (х(А;+,))—g(xM). (3.80)
С другой стороны, можно потребовать, чтобы новое приближе-
ние удовлетворяло формуле (3.75):
Дх‘й> = |ЗА(*+1) Д£1*’. (3.81)
Подставляя выражение (3.76) в (3.81), получаем
AM\gM = 1/рДх‘*> — А(Л)Д£(*>. (3.82)
С помощью непосредственной подстановки можно убедиться,
что матрица
С ~ Н yT^gM J гт^
является решением этого уравнения. Здесь у и г — произвольные
векторы, т. е. формула (3.83) определяет некоторое семейство ре-
шений. Если положить
у = Дх(4> и г = А(*)Д§(А’, (3.84)
то получим формулу, реализующую известный и широко приме-
няемый метод Дэвидона — Флетчера — Пауэлла (ДФП) [43, 441:
А^> = Аи-1) | A<^-W<-1)Ag'ft-1)rA^-i> 3 85
‘ Ag(A-l) Д£(Я-1)ТД(Я-1)Д£(/г-1) ' ' ' '
Можно показать, что эта рекуррентная формула сохраняет свойства
симметрии и положительной определенности матриц. Поэтому
если А(0)—симметрическая положительно определенная матрица,
то матрицы А(1), А(2), ... также оказываются симметрическими и
положительно определенными при отсутствии ошибок округления;
обычно удобно выбирать А<0) = 1.
Первая вариация f(x) равна
Д/(х) = у/(х^)гДх. (3.86)
Используя формулы (3 42) и (3.74), получаем
Д/ (Х) = — V/ (xM)TaMAMvf (хм), (3.87)
откуда
Д/ (х) = — (Xм)1 (хм), (3.88)
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
127
и неравенство f (x(fc+1))</ выполняется при любых значениях
a(W>0, если Аи) — положительно определенная матрица. Таким
образом, алгоритм обеспечивает убывание целевой функции при
переходе от итерации к итерации. Метод Дэвидона — Флетчера —
Пауэлла в течение ряда лет продолжает оставаться наиболее ши-
роко используемым градиентным методом. Он отличается устойчи-
востью и успешно применяется при решении самых различных за-
дач, возникающих на практике. Основным недостатком методов та-
кого типа является необходимость хранить в памяти ЭВМ матрицу
А порядка NxN.
Пример 3.10. Метод Дэвидона — Флетчера — Пауэлла
С помощью метода Дэвидона — Флетчера — Пауэлла найти
точку минимума функции
/(x)=4x?+3x^—4xixa+x1,
если х(о) = [О, 0]г.
Решение
Шаг 1. Положим s(0) =—V/(x(0>)=—[1, 0]г.
Ш а г 2. Поиск вдоль прямой приводит к результату, получен-
ному в примере 3.9, x(l)—I—1/е> 0]г.
Шаг 3. Л=1, А(1)=А(0)+А‘°>,
д ,0) _ А*с°>Ах<0>г _ At0|Ag<0)Ag(0) ГА(О)
с ~ Ax<0>TAg<0> AgWTA(0)Ag(0) ’
Дх10) = [-’/8, од-[0, 0]’-=[—Ve, О]Д
Л£(0) = [0, -11, ог=[-1, 4К,
АГ = - А£” = А(1,= [—1/в, 0 [—Vs. 0 Г7в 01 0 0j 0,325 2/ L '6 ч- [-1 7ь- 4/5. Vs, 0] , 4]г 4/ '5 2/ 'Б ч [о YJi-i. 414-1, v2][j \ 1-1. 41 [о ?]l-i.‘Ы7 -7J vj ’ J f
s<i) = _Aa>vZ(A.(1)) = _p/5) 2/б]т
Шаг 4. Поиск вдоль прямой:
х(2> = хш + aa> = 6/iei
х(2, = [-7е. 0]г-ь/1в р/5, 76Г = [-71«. -1/в]г.
что совпадает с полученным ранее решением.
Интересно отметить, что в примерах 3 9 и 3.10 методы Флет-
чера — Ривса и Дэвидона — Флетчера — Пауэлла порождают одни
и те же направления поиска, которые оказываются Н-сопряжен-
128
ГЛАВА 3
ными:
s(i)THs(o> = [1/4) 1/J
6 D. о]г=о-
Заметим также, что матрица А(А> стремится к Н-1:
4 6J -|//8
Дх = х‘«—х‘1) = [—«/16, - 1/8]г-[-%, 0]г = [—-1/8]г,
А£ = £(2,-£(1, = [°- 0J7- [0, 1/2]г=[0, -1/2]г,'
д(1 > _ I—X/16' 1/slr L—1/i6< —1 /в}
С [—Vie. - 1/в]г[0, -1/г]Т
ГО,325 0,4] ,0 _1/1Г[0 1, , [0,325 0,4]
[0,4 0,8]'°’ /21 ~~'2‘[о,4 0,8]
[О, -‘/21
0,325
0,4
ГО,325 0,4] г0 т
0,4 0,8] 1 ’ /2)
Г 0,2 0,4]_Р/18 %]
[0,4 0,8J -[‘/в ‘/..Г
Таким образом, А(2) = Н-1 (х*). После опубликования работы Дэ-
видона [431 были разработаны другие методы переменной метрики,
отличающиеся выбором р, у и z в (3.83). Общая трудность реализа-
ции методов такого типа связана с тем, что матрица А(А+П в ряде
случаев становится плохо обусловленной (определение плохо обус-
ловленной матрицы см. в приложении А) и возникает необходимость
возврата к начальной итерации с пересмотренной метрикой.
Другой метод, предложенный Бройденом [45], Флетчером [46]
и Шэнно [47], получил широкую известность благодаря рекомен-
дациям Пауэлла [48]. Метод Бройдена — Флетчера — Шэнно
(БФШ) реализуется в соответствии с рекуррентной формулой
А1й+1> = |
№
I
Ax<*>Ag<*> г ] Ах<»>Ах<*>Т
Дх<й> rAg(»> J + Ax>»>rAg‘*>
(3.89)
К числу главных преимуществ этого метода следует отнести не
всегда обязательную необходимость возврата к начальной ите-
рации алгоритма и относительно слабую зависимость от точности
вычислений при проведении одномерного поиска.
Улучшение методов переменной метрики и методов сопряжен-
ных градиентов в настоящее время осуществляется весьма близ-
кими путями. Следовательно, все замечания, сделанные выше пс
поводу методов сопряженных градиентов, в некоторой степени
справедливы для методов переменной метрики. Отметим, что Дэ-
видон [49] предложил ряд модифицированных процедур, в которых
не требуются точные вычисления при проведении поисков вдоль
прямой. Позже Пауэлл [50] установил свойство квадратичной
сходимости этих методов при отсутствии одномерных поисков. По-
видимому, метод переменной метрики в условиях квадратичной
сходимости и отсутствия трудоемких операций одномерного поискг
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
129
может отличаться как устойчивостью, так и быстродействием при
решении задач с целевыми функциями общего вида. Эти вопросы
были также рассмотрены Голдфарбом [51]. Вообще, возврат к на-
чальной итерации метода Дэвидона — Флетчера — Пауэлла (при
А = 1) обычно осуществляется после реализации N шагов алгорит-
ма. Как правило, такие действия носят профилактический характер,
I оскольку в ряде случаев можно сделать большее число шагов до
возврата. Необходимость возврата к начальной итерации можно
обосновать путем анализа обусловленности получаемых матриц.
Однако следует иметь в виду, что наряду с повышением степени
надежности (или устойчивости) алгоритмов переменной метрики
возвраты чаще всего замедляют процесс приближения к точке оп-
тимума, так как не позволяют использовать имеющиеся оценки
производных второго порядка.
В работах [40, 52, 53] проведены обширные исследования связи
между методами сопряженных градиентов и методами переменной
метрики. Шэнно рассматривает методы сопряженных градиентов
как методы переменной метрики с отсутствием «памяти». Боль-
шинство авторов придерживается тон точки зрения, что эти два
класса методов обладают гораздо более существенным сходством,
чем это представлялось ранее. Кроме того, ясно, что многие вари-
анты метода переменной метрики отличаются рядом общих особен-
ностей при решении практических задач [54, 551, наличие которых
заставляет проводить оценку трудоемкости дополнительных вы-
числений, связанных с реализацией более сложных методов. Шэнно
и Фуа 156, 57] представили обширные числовые результаты, кото-
рые свидетельствуют в пользу относительно простой рекуррентной
формулы Бройдена — Флетчера — Шэнно.
Описание программной реализации на Фортране некоторых
наиболее полезных методов дано в работах 153, 58]. Следует отме-
тить, что методы переменной метрики широко используются при
разработке методов решения задач условной оптимизации. В ра-
боте [59] предложен алгоритм, объединяющий метод обобщенного
приведенного градиента *) и метод Дэвидона — Флетчера — Пау-
элла, тогда как Рут [60] применил метод Дэвидона — Флетчера —
Пауэлла при расчетах по методу множителей Лагранжа. В работах
Хэна [61] и Пауэлла [62] исследуются вопросы эффективности ме-
тодов переменной метрики при решении задач с ограничениями.
Наконец, значительное количество работ посвящено вопросам
применения методов переменной метрики к решению задач большой
размерности. Как было отмечено выше, в настоящее время наилуч-
шим средством решения таких задач являются методы сопряженных
градиентов. Достигнуты определенные успехи при решении задач,
в которых матрица Гессе разрежена [63—66]. Одна из трудностей
х) В отечественной литературе используется также термин «условный гра-
диент».— Прим, перев.
5 № 182а
130
ГЛАВА 3
использования методов переменной метрики связана с тем обстоя-
тельством, что часто известна лишь степень разреженности некото-
рой оценки матрицы Н-1, а ие матрицы Н.
3.3.7. Обобщенный градиентный алгоритм
Сходство методов сопряженных градиентов и квазиньютонов-
ских методов дает основание для разработки обобщенного алго-
ритма, в основе которого лежит использование ряда рассмотренных
выше методов. Таким алгоритмом является обобщенный градиент-
ный алгоритм.
Обобщенный градиентный алгоритм
Шаг 1. Задать М — максимальное (допустимое) количество
итераций; /V — количество переменных; х(0) — начальное прибли-
жение к х*; ех — параметр сходимости алгоритма; е4 — параметр
сходимости для поиска вдоль прямой.
Шаг 2. Положить £=0.
Шаг 3. Вычислить компоненты V/(x(W).
Шаг 4. Выполняется ли неравенство ||V/(xlA,)|j ех?
Да: печать «сходимость: градиент»; перейти к шагу 13.
Нет: перейти к следующему шагу.
Ш а г 5. Выполняется ли равенство fc>A4?
Да: печать «окончание поиска: £=Л4»; перейти к шагу 13.
Нет: перейти к следующему шагу.
Шаг 6. Вычислить s(xw).
Шаг 7. Выполняется ли неравенство
Да: перейти к шагу 9.
Нет: положить s(x(W) =—V/(x(*’)-
Печать «возврат: неудачное направление». Перейти к шагу 9.
Ш а г 8. Найти такое значение а1й>, при котором /(х1й)+
4-а1й)х(х(й)))->1шп (используя параметр е2).
Шаг 9. Положить х1й+1>=х(й,+а(й)$(х(й)).
Шаг 10. Выполняется ли неравенство f(x(A+1))<f(х(й))?
Да: перейти к шагу 11.
Нет: печать «окончание поиска: нет уменьшения функции», перейти
к шагу 13.
Шаг 11. Выполняется ли неравенство ||Дх||/||х(й,ПСе1?
Да: печать «окончание поиска: нет продвижения к решению»;
перейти к шагу 13.
Нет: перейти к шагу 12.
Шаг 12. Положить k=k+l. Перейти к шагу 3.
Шаг 13. Останов.
В описанном алгоритме можно использовать различные методы
путем определения соответствующих направлений поиска на шаге 6.
Вычисления, требуемые для реализации того или иного метода,
проводятся по приведенным выше формулам. Отдельные шаги ал-
горитма (в частности, шаг 7) не соответствуют случаю, когда при-
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
131
меняется метод Коши, однако алгоритм этого метода подробно рас-
сматривался ранее. Можно было бы ввести в алгоритм процедуру
возврата к начальной итерации для метода Флетчера — Ривса, но
вместе с тем тесты, включенные в алгоритм, обеспечивают обнару-
жение любых трудностей, ассоциированных с необходимостью воз-
врата при расчетах по методу сопряженных градиентов.
На шаге 7 можно реализовать дополнительную проверку в со-
ответствии с предложениями Била и Пауэлла относительно возвра-
та к началу алгоритма. Кроме того, повышению эффективности ал-
горитма способствует включение в шаг 8 дополнительных процедур,
предложенных Дэвидоном, Пауэллом и Шэнно. Отметим, что в про-
цессе одномерного поиска следует по возможности избегать точных
вычислений; проведенные авторами данной книги эксперименты
показывают, что на выполнение операций поиска вдоль прямой
тратится весьма значительная часть общего времени счета по про-
грамме.
3.3.8. Численная аппроксимация градиентов
При рассмотрении градиентных методов предполагалось, что
элементы градиента Vf(x) и матрицы Гессе VVW можно вычис-
лить с достаточной степенью точности. Новейшие методы обладают
такой положительной характеристикой метода Ньютона, как вы-
сокая скорость сходимости в окрестности точки минимума, и вместе
с тем в них не используются значения вторых производных (V2/(x)).
Во многих возникающих на практике задачах получение аналити-
ческого выражения для градиента оказывается весьма затрудни-
тельным. В качестве примера можно рассмотреть случай, когда зна-
чения /(х) определяются в результате имитационного экспери-
мента. Кроме того, даже построение аналитических выражений не
исключает возникновения ошибок. Следовательно, хотя бы для
того, чтобы иметь возможность проверять аналитические выраже-
ния, целесообразно разработать аппроксимационную схему для
получения числовых оценок компонент градиента. Простейшим
вариантом такой схемы может служить аппроксимация с помощью
конечной разности вперед
df(x) I = НЙ-ее^) —/(х) _ 9Q.
дх; [х=х е
Такая аппроксимация непосредственно основывается на определе-
нии частной производной и при достаточно малых значениях е
дает весьма точные оценки. Выбор е осуществляется в зависимости
от вида /(х), координат точки х и точности (длины машинного сло-
ва) ЭВМ. Заметим, что в пределе при стремлении е к нулю аппрок-
симация становится точной, однако этот факт не может служить ре-
комендацией по выбору е. Величина е должна выбираться доста-
132
ГЛАВА 3
точно большой, чтобы числитель выражения (3.90) был отличен
от нуля. Если же е оказывается меньше, чем минимальная точность
расчетов на ЭВМ, то числитель обращается в нуль. Кроме того, не
следует выбирать величину е слишком большой, поскольку в этом
случае разрывается связь с предельным переходом. Другими сло-
вами, при больших е получаем «хорошие» числа с позиций точности
расчетов на ЭВМ, но плохие оценки производных.
За счет дополнительного вычисления значений функции можно
повысить точность аппроксимации путем использования централь-
ной конечной разности:
df (х) I _ = /(х+ее«'>)—Дх+egt») (3 9В
Для одной и той же ЭВМ при заданных f(x), х и е такая аппрокси-
мация оказывается более точной, однако при этом используется
дополнительное значение функции. Отметим, что в ряде случаев
повышение точности аппроксимации за счет дополнительного вы-
числения значений функции не является оправданным.
Стьюарт [67] предложил процедуру вычисления е на каждой
итерации по методу Дэвидона — Флетчера — Пауэлла. Его метод
основан на оценивании ошибки аппроксимации с помощью раз-
ности (3.90) и ошибки, обусловленной вычитанием почти равных
чисел, которые фигурируют в числителе (3.90) при малых значе-
ниях е. Среди достоинств метода Стьюарта следует отметить то, что
он не требует дополнительных вычислений значений функции.
Вместе с тем Гилл и др. [68] показали, что указанный метод может
приводить к получению неточных оценок е, и предложили другой
подход, в соответствии с которым требуется вычислять 2М значений
функции для того, чтобы оценить N значений 8. Однако этот метод
необходимо реализовать лишь в начальной точке х(0). Результаты
вычислительных экспериментов подтверждают преимущество под-
хода Гилла, который основывается на уточненных оценках соответ-
ствующих ошибок.
3.4. Сравнение методов и результаты
вычислительных экспериментов
Исследования, проведенные в последние годы, позволили на
теоретической основе рассмотреть сходимость методов, изложенных
в предыдущих разделах. Вместе с тем значительная часть сведений
об эффективности применения указанных методов к задачам с целе-
выми функциями общего вида получена в результате проведения
вычислительных экспериментов. Очень часто изложение нового ме-
тода в той или иной публикации сопровождается кратким сравни-
тельным обзором результатов соответствующих вычислений. В ряде
случаев тестовые задачи выбираются таким образом, чтобы подчерк-
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
133
путь положительные характеристики нового метода. Этот способ
представления материала несколько ограничивает степень обосно-
ванности публикуемых результатов.
Химмельблау (см. [69, гл. 51) приводит численные результаты
реализации ряда методов. Полученные им данные представляют
значительный интерес, поскольку Химмельблау не является сто-
ронником того или иного метода. Он характеризует каждый метод
(прямого поиска или градиентный) в соответствии с его устойчи-
востью, количеством требуемых вычислений значений функции и
количеством необходимого для реализации алгоритма машинного
времени при решении ряда тестовых задач. Устойчивость метода
отражает успех в получении оптимального решения с заданной
точностью для широкого круга задач. Химмельблау делает вывод,
что методы Бройдена — Флетчера — Шэнно, Дэвидона — Флет-
чера — Пауэлла и метод прямого поиска Пауэлла лучше осталь-
ных методов. Более подробные сведения можно найти в книге
Химмельблау.
Аналогичное, но менее полное исследование выполнено Сард-
жентом и Себастьяном в работе [701, где приведены результаты
применения градиентных методов, в том числе алгоритмов Брой-
дена — Флетчера — Шэнно, Дэвидона — Флетчера — Пауэлла и
Флетчера — Ривса. Они изучали влияние параметра сходимости
для одномерного поиска, частоты возвратов к начальной итерации,
положительной определенности матрицы Гессе для квазиньютонов-
ских методов и точности вычисления компонент градиента. Полу-
ченные ими результаты указывают на превосходство квазиньюто-
новских методов (в частности, метода Бройдена — Флетчера —
Шэнно) при решении задач с функциями общего вида. Сарджент
и Себастьян отмечают также, что точность расчетов на ЭВМ оказы-
вает более заметное влияние на реализацию квазиньютоновских
методов, чем на реализацию методов сопряженных градиентов.
Это позволяет сделать вывод о том, что при расчетах на микро-
ЭВМ (подобных тем, которые иногда используются в управлении
технологическими процессами) метод Флетчера — Ривса может ока-
заться наиболее эффективным.
Карпентер и Смит [711 исследовали относительную эффектив-
ность вычислений по методу Ньютона для задач специальной струк-
туры. Они сделали вывод, что для рассматриваемого круга задач
методы Дэвидона —- Флетчера — Пауэлла и метод Ньютона обла-
дают преимуществом перед методом прямого поиска Пауэлла, а
метод Дэвидона — Флетчера — Пауэлла превосходит метод Нью-
тона при решении задач большой размерности. Несколько позже
Шэнно и Фуа [40, 56, 57] провели подробный анализ методов со-
пряженных градиентов и переменной метрики на основе вычисли-
тельных экспериментов. Полученные ими результаты весьма за-
труднительно изложить в краткой форме (читателю следует обра-
титься к указанным выше работам); однако можно отметить, что
134
ГЛАВА 3
результаты указывают на преимущество метода Бройдена — Флет-
чера — Шэнно перед остальными методами.
Здесь, по-видимому, нецелесообразно уделять значительное вни-
мание теоретическим вопросам проведения вычислительных экспе-
риментов. С другой стороны, необходимо упомянуть о наличии оп-
ределенных правил проверки алгоритмов 172], а также отметить,
что числовые результаты, представленные в литературе примерно
до 1977 г., следует использовать с известной осторожностью. Оцен-
ки эффективности тех или иных алгоритмов, полученные на основе
анализа только количества вычислений значений функции, могут
привести к неверным выводам, что подчеркивалось в работе Миля
и Гонсалеса [73].
Авторы данной книги провели ряд вычислительных экспери-
ментов для того, чтобы продемонстрировать относительные возмож-
ности реализации методов Коши, Флетчера — Ривса, Дэвидона —
Флетчера — Пауэлла и Бройдена — Флетчера — Шэнно на ЭВМ
CDC-6500 с обычной точностью. Возврат к начальной итерации по
методу Флетчера — Ривса осуществлялся после каждой серии из
Таблица 3.2. Критерии окончания поиска
1 k>M 3. || у/ (%<«') || <вх
||Дх|| 4. vH-v(*,)7s(*(A’)>0
2 iiW*”
5. f(x(A + 1>) >/(%>«>)
У+1 шагов; критерии окончания поиска представлены в табл. 3.2.
В табл. 3.3 приведены результаты исследования функции Розен-
брока (рис. 3.16):
/(х)=100(х2—xJ2. (3.92)
которая обычно используется при анализе градиентных методов.
Результаты получены с помощью различных методов поиска вдоль
прямой; во всех случаях применялась процедура численной аппрок-
симации градиента. Заметим, что комбинация «метод Коши/метод
деления интервала пополам» обеспечивает нахождение наиболее
точного значения /, однако при этом требуются наибольшие затраты
машинного времени. Самым эффективным по количеству вычисле-
ний значений функции оказывается метод Бройдена — Флетчера —
Шэнно с использованием кубичной аппроксимации. Отметим, что
метод Коггинса представляет собой один из вариантов метода квад-
ратичной интерполяции [21].
Табл. 3.4 содержит результаты анализа задачи, связанной с ми-
нимизацией инерции зубчатой передачи [74]. Эта задача (рис. 3.17)
была включена Изоном и Фентоном в число тестовых задач для срав-
нения различных алгоритмов. Ее целевая функция записывается
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
135
Рис. 3.16. Линии уровня функции Розенброка.
в следующем виде:
/(х) = /12 + хН
1 г 2
1 4“ Х2
2
*1X1 + 100 )
(Х1Х2)4 JI \ 10 ) '
(3.93)
Отметим, что в данном случае алгоритм Флетчера — Ривса с ис-
пользованием кубичной аппроксимации является наиболее эффек-
тивным как по затратам машинного времени, так и по количеству
вычислений значений функции.
В табл. 3.5 приведены результаты исследования функции Вуда
[75] (рис. 3.18):
/(х)=100(х2-х2)2+(1-х1)2+90(х4-х!)2+(1-х3)2+
+ 10,1[(ха— 1)2+(х4— 1)21+19,8(х2— 1)(х4— 1). (3.94)
Опять комбинация метода Флетчера — Ривса с методом кубичной
аппроксимации оказывается наиболее эффективной. Следует отме-
Таблица 3.3. Результаты исследования функции Розенброка (х(0) =[—1,2, 1,0^г)
Метод Метод
деления интервала пополам золотого сечения Коггинса кубичной аппроксимации
Коши 1J0E-10/7,47/38424 “> 1.25Е-10/1,382/4066 8, ЗОЕ-8/1 ,074/3570 6,19Е-9/2,631/10685
Флетчера—Ривса 3.24Е-6/0,18/988 5,91 Е-6/0,57/805 5,96Е-5/0,109/370 2,77Е-7/0,059/273
Дэвидона — Флетчер а — Пау- 2,45Е-8/0,173/977 2,39Е-8/0,133/656 6,6Е-8/0,115/331 4,ЗЕ-8/0,063/239
элла Бройдена— Флетчера— 5,6Е-8/0,169/932 3.6Е-8/0,161/740 2,1Е-8/0,115/315 3.9Е-9/0,065/204
Шэнно
ГЛАВА 3
Нх*)/время/К. Ф . где К. Ф.-количество вычислений значений функции при проведении поиска; время-количество секунд работы
центрального процессора до окончания поиска; / (*•)=/ (х) в момент завершения поиска
Таблица 3.4. Результаты решения задачи (№ 10) Изона и Фентона (х(0> = [0,5, 0.5]7")
Метод
Метод деления интервала пополам золотого сечеиия Коггинса кубичной аппроксимации
Коши Флетчера—Ривса Дэвидона— Флетчера— Пау- элла Брондена— Флетчера— Шэнно 1,744/0,299/1026 ’» 1,744/0,066/249 4,744/0,056/232 1,744/0,055/226 1,744/0,219/688 1,744/0,053/199 1,744/0,051/184 < 1,744/0,051/176 1,744/0,181/312 1,744/12,21/28141 1,744/0,09/208 1,744/0,087/195 1,744/0,091/171 1,744/0,025/92 1,744/0,079/262 1,744/0,043/133
а) / (х*)/время/К Ф
Таблица 3.5. Результаты исследования функции Вуда (л<°>=|— 3, —1, —3, ~1]Г)
Метод
Метод деления интервала пополам золотого сечення Коггинса кубичной аппроксимации
Коши Флетчера—Ривса Дэвидона — Флетчера — Пау- элла Бройдена — Флетчера — Шэнно 3.74Е-9/13,466/39503” I .ЗЕ-10/0,401/1257 3,9Е-9/0,810/2404 2,2Е-9/0,759/2054 1,77Е-8/10,70/29/692 1,2Е-8/0,311/942 3.7Е-9/0,684/1895 2,0Е-9/0,652/165О 2,95Е-9/5,844/12,392 2,9Е-8/0,571/1468 2,9Е-9/0,403/747 2,0Е-9/0,444/723 8,36Е-6/7,89/20,007 2,0Е-7/0,083/244 9,5Е-10/0,298/727 2,ЗЕ-9/0,240/410
а‘ f (х*)/Время;К Ф ’
w
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
138
ГЛАВА 3
Рис. 3.17. Линии уровня функции Изоиа и Фентона.
тить, что представленные в этом разделе данные не в полной мере
согласуются с другими опубликованными результатами. В первую
очередь это касается метода Флетчера — Ривса, результаты реали-
зации которого оказались значительно лучше результатов, полу-
ченных другими авторами. По-видимому, окончательные выводы
можно будет сделать только после проведения дополнительных
вычислительных экспериментов.
3.5. Заключение
В данной главе изложены методы исследования функций несколь-
ких переменных в задачах оптимизации. Сформулированы необхо-
димые и достаточные условия существования минимума функции
нескольких переменных. Вместе с тем большая часть главы посвя-
щена рассмотрению методов поиска оптимумов. Некоторые методы
включены по причинам исторического характера, другие методы
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
13
Функция Вуда: (xs=x4=1)
»(х) = 100(хг-х;Л(1-х,Л90(х4-х’Л(1-х3)г+10,1[(к3-1)г+ (х4-1)‘]*19,6(хг-1)(х4-1)
Рис. 3.18. Линии уровня функции Вуда
являются наиболее эффективными из разработанных к настоящем}
времени. Рассмотрены методы, в которых используются только зна-
чения f(x), значения f(x) и Vf(x), значения /(х), v/(x) и V2/(x)-
Достаточно подробно освещены вопросы, связанные с важным по-
нятием сопряженности направлений; изложены методы сопряжен-
ных градиентов и квазиньютоновские методы. Разумеется, прове-
денное обсуждение не является полным, и многие полезные методы
не рассмотрены из-за ограниченного объема книги. Глава завер-
шается кратким анализом алгоритмов и результатов вычислитель-
ных экспериментов.
Контрольные вопросы и задачи
3.1. Объясните, почему направления поиска, которые исполь-
зуются в алгоритме прямого поиска, например в алгоритме
Хука — Дживса, должны быть линейно независимыми.
Сколько направлений следует использовать в данном случае?
140
ГЛАВА 3
3.2. Опишите две ситуации, в которых метод поиска по симплексу
оказывается более предпочтительным, чем метод сопряженных
направлений Пауэлла.
3.3. Почему квадратичные функции используются как основа
для построения алгоритмов нелинейной оптимизации?
3.4. В чем состоит полезность свойства параллельного подпрост-
ранства, которым обладают квадратичные функции?
3.5. В чем заключается свойство убывания целевой функции при
переходе от итерации к итерации? Почему выполнение этого
свойства необходимо для построения эффективного алгоритма?
Укажите один алгоритм, обладающий этим свойством, и один
алгоритм, который этим свойством не обладает.
3.6. Почему положительная определенность матрицы AUi) явля-
ется необходимым условием при решении задач минимизации
с помощью квазиныотоновских методов?
3.7. Поясните связь метода Марквардта с методами Коши и Нью-
тона. Какому из трех перечисленных методов следует отдать
предпочтение?
3.8. Возможно ли получение одинаковых точек при использовании
методов Дэвидона — Флетчера — Пауэлла и Флетчера —
Ривса для решения задачи с квадратичной целевой функцией,
если в обоих случаях начальная точка одна и та же?
Если возможно, то при каких условиях? Если невозможно,
то почему?
3.9. Поясните понятие квадратичной сходимости. Укажите один
алгоритм, обладающий свойством квадратичной сходимости,
и один алгоритм, который этим свойством не обладает.
3.10. Покажите, что функция
/ (х) =ЗХ1+2х^+хз—2XiX2—2xix34-2x2x3—6xj—4ха—2х3
является выпуклой.
3.11. Найдите и классифицируйте стационарные точки функции
f (х)=2х?4-4Х1Х2—1 0xiX24-X2,
линии уровня которой изображены на рис. 3.19.
3.12. Проведите анализ определенности следующих квадратичных
форм:
Qi (х) =х?4-2хг—3x5—бХ1Х24-8Х1Х3—4х2х3,
Q2(x)=2axIx2+2bx2x3+2cx3xl,
Q3(x)=xf4-5x|4-3x|4-4x1x2—2х2х3—2xtX3.
3.13. Воспользуйтесь методом Гаусса — Жордана для преобразо-
вания следующей квадратичной формы к виду суммы полных
квадратов'
Q (x)=x54-2xjx24-4x1x34-3xa4-2x2x3 5х3.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
141
Рис. 3.19 Линии уровня функции из задачи 3.11.
Линии
уровня
А -40,000
В -30,000
С -20,000
D -10,000
Е 0,000
F 10,000
G 20,000
н 30,000
I 40,000
J 50,000
Покажите, что эта квадратичная форма положительно опре-
делена.
3.14. Пусть в точке х—х градиент V/(x)=0. Что можно сказать
о точке х, если
(a) f(x) — выпуклая функция?
(б) f(x) — вогнутая функция?
(в) V2/(x) — неопределенная матрица’
(г) матрица V2f(x) положительно определена?
(д) матрица V2/(x) отрицательно определена?
3.15. Контрпример Пеано. Дана функция
f (х) = (х,— o-xi) (х,—а2х22),
где й! и а2 — постоянные коэффициенты.
(а) Охарактеризуйте точку х=[0, (Ж.
(б) Покажите, чго максимальное значение ?(х) на множестве
142
ГЛАВА 3
точек кривой, заданной уравнением
xi = l/3 (al + al) xl,
достигается в начале координат.
(в) Нарисуйте несколько линий уровня этой функции
в окрестности начала координат.
3.16. В результате поиска минимума функции
/(х)=1х?+(х24-1)а1 1)21
найдены следующие точки:
(а) хш = [0, О]7',
(б) х<2)=[0, 1Р,
(в) х<3> = [0, —1И,
(г) х“>=[1, 1И.
Классифицируйте полученные точки.
3.17. Пусть требуется переправить 400 ярд3 сыпучего материала
через большую реку. Для перевозки груза необходимо пост-
роить контейнер. Известны следующие данные: стоимость
каждого рейса на противоположный берег реки и обратно
равна 4,2 долл.; стоимость материалов для изготовления дна
контейнера составляет 20,00 долл /ярд2; боковых стенок
контейнера — 5,00 долл./ярд2, крышки контейнера —
20,00 долл /ярд2.
Сконструируйте контейнер таким образом, чтобы минимизи-
ровать полные затраты на перевозку груза.
3.18. Рассматриваются функция Розенброка
/(х) = 100(х2-х21)2+(1-х1)2
и начальная точка
х«”=[—1,2, 0]г.
Найдите точку х*, которой соответствует минимальное зна-
чение /(х*), пользуясь:
(а) методом поиска по симплексу Нелдера и Мида (проведите
четыре итерации), затем при начальной точке х(0) прове-
дите счет по программе SPX из библиотеки программ
OPTLIB [22] или по другой подходящей программе по
вашему выбору;
(б) методом Хука — Дживса (программа PS в OPTLIB);
(в) методом сопряженных направлений Пауэлла (программа
PCD в OPTLIB).
3.19. На рис. 3.20 изображен бункер для хранения зерна.
Требуется выбрать значения параметров h, d и «р таким об-
разом, чтобы бункер имел заданный объем (о* = 10 м3), а его
стоимость была минимальной. Основание бункера изго-
тавливается из деревянных плит стоимостью С2=1 долл./м2,
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
143
а остальная часть бункера — из листового металла стои-
мостью Сг=1,5 долл./м’. Воспользуйтесь ограничением на
объем бункера для того, чтобы исключить одну переменную
Рис. 3.20. Бункер для хранения зерна
из целевой функции, и решите получаемую в результате за-
дачу с двумя переменными с помощью метода поиска по об-
разцу (0=30°). Указание. Полезно попытаться описать гео-
метрическую форму бункера с помощью другого (эквивалент-
ного) множества управляемых переменных.
J.20. На рис. 3.21 схематически изображена система подачи газа
по трубам [761, в которой компрессорные станции располо-
жены на расстоянии L миль друг от друга. Суммарные затраты
Рис. 3.21. Схема газопровода.
на эксплуатацию газопровода в течение года определяются
функцией
C(D, Plf L, г) ==7,840’^+ 450 000+ 36 9000 +
. (6,57) (108) , (772) (10е) . ...
+ —- l—-+-—т—~(г *) (д°лл-/г°д). (О
где D — внутренний диаметр труб, дюйм; Pi — давление на
выходе компрессора, фунт/дюйм’; L — расстояние между
компрессорными станциями, миля; г=Рг1Р2 — отношение
давлений на выходе и входе компрессора.
Предположим, что расход газа в единицу времени можнс
описать функцией
Г (р2 ГР 11/4
(фу H/ч.), (2)
144
ГЛАВА 3
где /=0,008D_,/i— коэффициент трения. Пусть расход газа
составляет 100X10’ фут3/день. Воспользуйтесь формулой (2)
для исключения переменной Рг из (1). Затем с помощью ме-
тода поиска по симплексу Нелдера и Мида и метода сопря-
женных направлений Пауэлла найдите такие значения пара-
метров системы, которым соответствует минимум суммарных
эксплуатационных затрат в единицу времени.
3.21. Найдите координаты точек минимума функции Химмельблау
(рис. 3.1)
f(x) = (х? + ха— 11 )2 + (х, + xl — 7)2
с точностью до трех десятичных знаков. Воспользуйтесь ме-
тодом Хука — Дживса при поиске из следующих начальных
точек:
х11) = [5, 5]г, х<2) = [5, — 5]г, х13) = [0, 0]т,
х(4’ = [—5, —5]г, х(5) —[5, 0]г.
3.22. Заданы текущее приближение к решению х1*’ и направление
поиска s(x(A>). Итерации проводятся по формуле (3.42).
Покажите, что
а*._ vg(x<A))rs(x>A’),
s (x<A))r Cs (х(А))
если целевая функция квадратичная:
f (х) = q (х) = а + Ьтх + */гх’Сх.
3.23. Определите размеры прямоугольного контейнера открытого
типа (без крышки), стоимость которого минимальна. (Пусть
v* = 10 м3.)
3.24. Заданы функция ^(x)=8x12+4x1x2+5xi, начальная точка
х('”=110, 10т] и два линейно независимых направления
if10’— Vg (х("’) = [200, 140]г, dw = [7, —10]г.
Определите новое направление поиска (S(n=dU)+pnAg11’),
сопряженное cd'"’. Используйте эти направления при поиске
точки х*: сначала проведите поиск в направлении S<0>=d(0>,
затем из полученной точки минимума проведите поиск в на-
правлении S(1). Сравните 8(1> с направлением, полученным
по методу Флетчера — Ривса.
3.25. Найдите направление, ортогональное вектору
Sj = [-L,---------------х = [0, 0, 0]г.
[ /з V3 Y3 J 1 J
Найдите также направление s2, сопряженное с Sj в той же точ-
ке при условии, что целевая функция равна
/ (х) =Xj+2xJ—Х!Ха | Зх,’—2х1х3 С х%.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
145
3.26. Определите и классифицируйте стационарные точки функции
/(х)=х?—XiX2+x|—2xi+3x2—4.
3.27. Изон показал, что задача выбора (с целью минимизации инер-
ции передачи) передаточных отношений в понижающей зуб-
чатой передаче, образованной тремя прямозубыми цилиндри-
ческими колесами и имеющей суммарное передаточное число
10, эквивалентна задаче минимизации функции (3.93). Вос-
пользуйтесь методами Хука — Дживса, Коши и Флетчера —
Ривса для нахождения приближенных значений координат
точки х* при хм —10,5 0,5]г.
3.28. Заданы функция
/(х) = 100 (хг-х?)2+(1- Xi)2
и две первые точки, полученные в процессе поиска точки ми-
нимума функции f:
х<0>-= [—1,2, 1]г, х11> = [—1,3, 1,07]г.
Определите направление поиска из точки х11), пользуясь
следующими градиентными методами: (а) методом Коши,
(б) модифицированным методом Ньютона, (в) методом Флет-
чера — Ривса, (г) методом Марквардта (Х(1) = 100).
3.29. Исследуйте влияние — параметра сходимости для поиска
вдоль прямой — на процедуры расчетов по методам Флет-
чера — Ривса, Дэвидона — Флетчера — Пауэлла и Брой-
дена — Флетчера — Шэнно. Используйте каждый из пере-
численных методов для решения задачи минимизации функции
Вуда (3.94) при х(0)=[—3, —1, —3, — Нг. Положите ea=aej,
a =0,01, 0,1, 1 и 10; при этом значение параметра сходимости
алгоритма et следует выбирать в зависимости от характеристик
используемой ЭВМ. Примечание: для ЭВМ CDC-6500 можнс
выбрать е1=10-1.
3.30. Рассмотрите задачу 3.19, в которой речь шла об определении
параметров геометрической формы бункера для хранения
зерна. Исследуйте влияние отношения cjci на оптимальную
форму бункера. В частности, найдите оптимальные решения
при с2/с!=0,5, 1,5 и 3 и проиллюстрируйте ответы рисунками.
Какие общие выводы можно при этом сделать?
3.31. Проведите три итерации в соответствии с методом Коши, мо-
дифицированным методом Ньютона и методом Дэвидона —
Флетчера — Пауэлла для минимизации функции Пауэлле
/ (х)=(Х1+ 10хг)2+5 (х3—х4)2+(х2—2х3)4+ 10 (х4—х4)4
при х(0) = 13, —1,0, 1 И.
3.32. В процессе проведения экспериментов инженер устанавли-
вает наличие функциональной зависимости некоторой вели-
чины Q от переменной t. Он имеет определенные основана
146
ГЛАВА 3
полагать, что существует физический закон, отражающий
связь между Q и t в форме
Q(/)=a sin t+b tg t+c.
Инженер хочет определить «наилучшие» значения коэффи-
циентов а, b и с, используя результаты п проведенных экспе-
риментов (G, Of, ta, Q.a, h, Q3‘. •••; in< Qn)- Принимая во внима-
ние несовершенство экспериментальной установки и неточ-
ность уравнения связи, он не ожидает полного совпадения
расчетных данных с экспериментальными и вводит в рассмот-
рение величины
e^Qi-Qdi),
после чего пытается найти минимум функции
Докажите, что для нахождения оптимальных значений а,
Ь и с инженер должен решить систему линейных уравнений.
Указание-, сначала покажите, что задача, стоящая перед ин-
женером, эквивалентна задаче безусловной минимизации
выпуклой функции.
3.33. Из теоретических соображений известно, что связь между
зависимой переменной у и переменной X можно описать двух-
параметрической функцией
t/(x)=feix/(l + fe2x).
Значения параметров fe, и k2 определяются в соответствии
с критерием наименьших квадратов на основе следующих
экспериментальных данных:
1,0 1,05
2,0 1,25
3,0 1,55
4,0 1,59
Найдите /г, и k2, используя метод переменной метрики Брой-
дена — Флетчера — Шэнно.
3.34. Покажите, что yw,=0, i=0, 1, 2.....k—2, если компоненты
сопряженного градиента вычисляются по формуле (3.62),
s(0>=—gl0>, итерации проводятся по формуле (3.42), а функ-
ция /(х) квадратичная.
Литература
1. Murray W. (ed.), Numerical Methods for Unconstrained Optimization, Acade.
mic Press, London, 1972.
2. Box M. J., Davies D., Swann W H., Non-Linear Optimization Techniques.
1CI Monograph 5, Oliver and Boyd, Edinburg, 1969.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
147
3 Krolak Р., Cooper L , An Extension of Fibonaccian Search to Several Variables,
ACM, 6, 639—641 (1963).
4. Box G. E. P., Evolutionary Operation- A Method for Increasing Industrial Pro-
ductivity, Appl. Stat., 6, 81—101 (1957).
5. Spendley W., Hext G. R., Himsworth F R., Sequential Application of Simplex
Designs in Optimization and Evolutionary Operation, Technometrics, 4, 441—461
(1962).
6. Nelder J. A., Mead R., A Simplex Method for Function Minimization, Com-
puter}., 7, 308—313 (1965).
7. Box G. E. P., Draper N. R., Evolutionary Operation, Wiley, 1969.
8. Parkinson J.M., Hutchinson D., An Investigation into the Efficiency of Va-
riants on the Simplex Methods, in Numerical Methods for Non-Linear Optimi-
zation (F. A. Lootsma, Ed), Academic Press, London, 1972, pp. 115—135
9. Powell M. J.D., On Search Directions for Minimization Algorithms, Math.
Prog., 4(2), 193—201 (1973).
10. Hooke R., Jeeves T. A., Direct Search of Numerical and Statistical Problems,
J. ACM, 8, 212—229 (1966).
11. Bandler J. W., McDonald P. A., Optimization of Microwave Networks by Ra-
zor Search, IEEE Trans. Microwave Theory Tech., 17, 552—562 (1969).
12. Emery F. E., O’Hagan M. O., Optimal Design of Matching Networks for Micro-
wave Transistor Amplifiers, IEEE Trans. Microwave Theory Tech., 14, 696—698
(1966).
13. Rosenbrock H. H., An Automated Method for Finding the Greatest or Least
Value of a Function, Computer J., 3(3), 175—184 (1960).
14. Swann W. H., Report on the Development of a New Direct Search Method of
Optimization, ICI Ltd., Central Instr. Res. Lab., Res. Note, 64/3, 1964.
15. Powell M. J. D., An Efficient Method for Finding the Minimum of a Function
of Several Variables Without Calculating Derivatives, Computer J., 7, 155—162
(1964).
16. Zangwill M. I., Minimizing a Function without Calculating Derivatives, Com-
puter J., 10, 293—296 (1967).
17. Brent R. P., Algorithms for Minimization without Derivatives, Prentice-Hall,
Englewood Cliffs, New Jersey, 1973.
18. Gill P. E. Murray W., Wright M. H., Praclical Optimization, Academic Press,
N. Y„ 1981, p. 57.
19. Fletcher R., Practical Methods of Optimization, Vol 1; Unconstrained Opti-
mization, Wiley, N. Y , 1980, p. 17.
20. Cauchy A., Method generale pour la resolution des systemes d’equations simul-
tanees, Compt. Rend. Acad. Sci., 25, 536—538 (1847).
21. Coggins G. F., Univariate Search Methods, Imperial Chemical Industries Ltd.,
Central Instr. Res. Lab., Res. Note 64/11, 1964.
22 Gabriele G. A., Ragsdell К. M., OPTL1B- An Optimization Program Library,
Purdue Research Foundation, January 1977.
23 Ragsdell К. M , Root R. R., Gabriele G. A., Newton’s Method- A Classical
Technique of Contemporary Value, ASME Design Technol. Transfer Conf.
Proc., N. Y. October, 1974, p. 137.
24. Mangasarian O. L, Techniques of Optimization, ASME paper 71-vibr.-l 18,
ASME Design Automat. Conf , Sept. 8—10, 1971.
25 Marquardt D. W., An Algorithm for Least Squares Estimation of Non-Linear
Parameters, SIAM J., Il, 431—441 (1963).
26 Powell M. J. D., Problems Related to Unconstrained Optimization in: Numeri-
cal Methods for Unconstrained Optimization, Academic Press, N. Y., 1972,
Chap. 3, p. 29.
27. Bard Y., Nonlinear Parameter Estimation, Academic Press, N. Y., 1974. [Имеет-
ся перевод. Бард Й. Нелинейное оценивание параметров.— М : Статистика,
1979 1
28. Hestenes М. R., Stiefel Е , Methods of Conjugate Gradients for Solving Linear
Systems, NBS, Res. Y., 49, 409—436 (1952).
148
29
30
31.
32
33.
34.
35
36
37.
38
39
40
41.
42
43
44
45
46.
47
48.
49.
50
51.
52.
53
54
55
ГЛАВА 3
Fletcher R., Reeves С. M., Function Minimization by Conjugate Gradients,
Computer J7, 149—154 (1964).
Fried I., Metzler J., SOR vs Conjugate Gradients in a Finite Element Discreti-
zation, Int J. Numerical Methods Eng , 12, 1329—1342 (1978)
Miele A., Cantrell J W , Study on a Memory Gradient Method for Minimiza-
tion of Funtions, JOTA, 3 (6), 459 (1969).
Polak E., Ribiere G., Note sur la convergence de methods de directions conjugess,
Rev. Fr. Inform Rech. Operat, 16, 35—43 (1969)
Davison E J , Wong P., A Robust Conjugate-Gradient Algorithm which Mini-
mizes L-Functions, Automatica, 11, 297—308 (1975)
Boland W R , Kamgnia E R , Kowalik J S., A Conjugate Gradient Optimi-
zation Method Invariant to Nonlinear Scaling, JOTA, 27(2), 221—230 (1979)
Boland W. R., Kowalik J S , Extended Conjugate-Gradient Methods with Res-
tarts, JOTA, 28(1), 1—9 (1979)
Crowder H. P., Wolfe P., Linear Convergence of the Conjugate Gradient Met-
hod, IBM J. Res Develop , 16, 431—433 (1972).
Powell M J. D., Some Convergence Propel ties of the Conjugate Gradient Met-
hod, Math Prog., II, 42—49 (1976)
Powell M J. D., Restart Procedures for the Conjugate Gradient Method, Math
Prog., 12, 241—254 (1977)
Beale E. M L , A Derivation of Conjugate Gradients, in. Numerical Methods
for Non-Linear Optimization (F. A Lootsma Ed.), Academic Press, N Y.,
1972, pp 39—43
Shanno D F , Conjugate Gradient Methods with Inexact Searches, Math. Oper.
Res , 3(3), 244—256 (1978)
Gabriele G. A , Ragsdell К M., Large Scale Nonlineai Programming Using
the Generalized Reduced Gradient Method, А5Л4Е J Meeh. Des., 102(3), 566—
573 (1980).
Avriel M , Nonlinear Programming Analysis and Methods, Prentice-Hall, Eng-
lewood Cliffs, New Jersey, 1976, p. 322
Davidon W. C., Variable Metric Method fur Minimization, AEC Res. Develop
Rep., ANL-599, 1959.
Fletcher R., Powell M. J. D., A Rapidly Convergent Descent Method for Mini
mization, Computer J., 6, 163 (1963).
Broyden G. G., The Convergence of a Class of Double-Rank Minimizatior
Algorithms, J Inst Math. Appl., 6, 76—90, 222— 231 (1970).
Fletcher R., A New Approach to Variable Metric Algorithms, Computer J.,
13, 317—322 (1970).
Shanno D. F , Conditioning of Quasi-Newton Methods for Function Minimization,
Math. Comp., 24, 647—657 (1970)
Powell M. J. D., A View of Unconstrained Optimization, IMA Conf. «Optimiza-
tion in Action», January 1975.
Davidon W. C., Optimally Conditioned Optimization Algorithms without Line
Searches, Math. Prog., 9, 1—30 (1975).
Powell M. J. D., Quadratic Termination Properties of Davidon’s New Variable
Metric Algorithm, Math Prog, 12, 141 —147 (1977).
Goldfarb D., Generating Conjugate Directions without Line Searches Using
Factorized Variable Metric Updating Formulas, Math. Prog., 13, 94—110 (1977)
McCorniik G P , Methods of Conjugate Directions versus Quasi-Newton Methods,
Math Prog., 3(1), 101—116 (1972).
Shanno D. F., Phua К H., A Variable Method Subroutine for Unconstrained
Nonlinear Minimization, Manage. Inform Syst. Rep., 28, The University of
Arizona, 1979
Dixon L. C. W„ Quasi-Newton Algorithms Generate Identical Points, Math.
Prog., 2 (3), 383—387 (1972)
Dixon L C. W , Quasi-Newton Algorithms Generate Identical Points 11: The
Proofs of Fourth New Theorems, Math Prog., 3(3), 345—358 (1972).
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
149
56. Shanno D. F., Phua К. Н., Matrix Conditioning and Nonlinear Optimization,
Math. Prog., 14, 149—160 (1978).
57. Shanno D. F., Phua К. H., Numerical Comparison of Several Variable-Metric
Algorithms, JOTA, 25(4), 507—518 (1978).
58. Shanno D. F., Phua К. H , Algorithms 500 Minimization of Unconstrained Mul-
tivariate Functions (E4), ACM Trans. Math. Software, 2(1), 87—94 (1976).
59. LaFrance L. J. Hamilton J F., Ragsdell К. M., On the Performance of a Com-
bined Generalized Reduced Gradient and Davidon-Fletcher-Powell Algorithm:
GRGDFP, Eng. Optimization, 2, 269—278 (1977).
60. Root R. R., Ragsdell К. M., Computational Enhancements to the Method of
Multipliers, ASME J. Meeh. Des., 102(3), 517—523 (1980).
61. Han S. P., Superlinearly Convergent Variable Metric Algorithms for General
Nonlinear Programming Problems, Math Prog., 11, 263—282 (1976).
62. Powell M. J.D., The Convergence of Variable Metric Method for Nonlinear
Constrained Optimization Calculations, in Nonlinear Programming 3 (O L
Mangasarian, R R. Meyer, and S M Robinson, Eds ), Academic Press, N Y.,
1978, pp. 27—64.
63 Toint Ph. L., On Sparse and Symmetric Matrix Updating Subject to a Linear
Equation, Math. Comp , 31 (140), 954—961 (1977).
64 Powell M. J. D., Toint Ph L , On the Estimation of Sparse Hessian Matrices,
SIAM J. Sumer. Anal., 16 1060—1074 (1979)
65 Shanno D. F., On Variable-Metric Methods for Sparse Hessians, Math. Comp.,
34 (150), 499—514 (1980).
66. Shanno D. F., Computational Experience with Methods for Estimating Sparse
Hessians for Nonlinear Optimization, JOTA, 35(2), 183—193 (Oct. 1981).
67. Stewart G. W., A Modification of Davidon’s Method to Accept Difference Appro-
ximations of Derivatives, J ACM, 14, 72—83 (1967).
68. Gill P. E., Murray W., Saunders M. A., Wright M. H., Computing Finite-Dif-
ference Approximations to Derivatives for Numerical Optimization, Stanford
Systems Optimization Lab Tech. Rep. SOL80-6, 1980.
69. Himmelblau D. M., Applied Nonlinear Programming, McGraw-Hill, N. Y.,
1972, p. 190. [Имеется перевод- Химмельблау Д. М Прикладное нелинейное
программирование — М.- Мир, 1975.1
70. Sargent R. W. Н., Sebastian D. J., Numerical Experience with Algorithms
for Unconstrained Minimization, in: Numerical Methods for Non-Linear Opti-
mization (F. A. Lootsma, Ed.), Academic Press, N. Y., 1971, Ch. 5, p. 45.
71. Carpenter W. C., Smith E. A., Computational Efficiency in Structural Opti-
mization, Eng. Optimization, 1(3), 169—188 (1975). •
72. Growder H., Dembo R. S , Mulvey J. M., On Reporting Computational Experi-
ments with Mathematical Software, ACM Trans. Math. Software, 5(2), 198—203
(1979).
73. Miele A., Gonzalez S., On the Comparative Evaluation of Algorithms for Mat-
hematical Programming Problems, in Nonlinear Probramming III (Mangasarian,
Meyer, and Robinson, Eds ) Academic Press, N. Y., 1978, pp. 337—359.
74. Eason E. D., Fenton R. G., A Comparison of Numerical Optimization Methods
for Engineering Design, J. Eng. Ind., Trans. ASME, 96(1), 196—200 (1974)
75. Colville A. R., A Comparative Study of Nonlinear Programming Codes, Tech.
Rep. 320-2949, IBM New York Scientific Center, 1969
76. Sherwood T. K., A Course in Process Design, MIT Press, CambridgeMassachusetts,
1963. d. 84.
Глава 4
Линейное программирование
Задачами линейного программирования называются оптимиза-
ционные задачи, в которых ограничения представляются в виде ра-
венств или неравенств и целевая функция линейна. Методы линей-
ного программирования (ЛП) широко используются для решения
различных военных, экономических, промышленных и организа-
ционных задач. Главными причинами столь широкого применения
методов ЛП являются доступность математического обеспечения
для решения задач ЛП большой размерности и возможность анализа
решений задач ЛП при вариации исходных данных (анализа чувст-
вительности).
В работе [1] отмечается, что линейное программирование пред-
ставляет собой наиболее часто используемый метод оптимизации
(74% от общего числа применяемых оптимизационных методов).
Около четверти машинного времени, затраченного за последние
годы на проведение научных исследований, было отведено решению
задач ЛП и их многочисленных модификаций (см. работу [2]).
4.1. Разработка моделей линейного
программирования
Термин «разработка» означает построение моделей ЛП практи-
ческих задач. Построение моделей не следует рассматривать как
науку, скорее это искусство, которое постигается с опытом. Разра-
ботка модели ЛП включает следующие основные этапы: определе-
ние переменных задачи, представление ее ограничений в виде ли-
нейных уравнений или неравенств; задание линейной целевой
функции, подлежащей минимизации или максимизации. Приведем
некоторые примеры, иллюстрирующие основные этапы разработки
модели ЛП.
Пример 4.1. Задача технического контроля
В отделе технического контроля (ОТК) некоторой фирмы рабо-
тают контролеры разрядов 1 и 2. Норма выработки ОТК за
8-часовой рабочий день составляет не менее 1800 изделий. Контролер
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
151
разряда 1 проверяет 25 изделий в час, причем не ошибается в 98%
случаев. Контролер разряда 2 проверяет 15 изделий в час; его точ-
ность составляет 95%.
Заработная плата контролера разряда 1 равна 4 долл, в час,
контролер разряда 2 получает 3 долл, в час. При каждой ошибке
контролера фирма несет убыток в размере 2 долл. Фирма может
использовать 8 контролеров разряда 1 и 10 контролеров разряда 2.
Руководство фирмы хочет определить оптимальный состав ОТК,
при котором общие затраты на контроль будут минимальными.
Разработка модели. Пусть xt и х2 обозначают коли-
чество контролеров разрядов 1 и 2 соответственно. Число контро-
леров каждого разряда ограничено, т. е. имеются следующие огра-
ничения:
Xi<8 (разряд 1),
х2^10 (разряд 2).
Ежедневно необходимо проверять не менее 1800 изделий. Поэтому
выполняется неравенство
8-25хх+8- 15x2=200xi+120хг>1800,
или 5xi+3x2^45.
При построении целевой функции следует иметь в виду, что расходы
фирмы, связанные с контролем, включают две составляющие:
1) зарплату контролеров и 2) убытки, вызванные ошибками конт-
ролеров. Расходы на одного контролера разряда 1 составляют
4 долл.+2-25-0,02 =5 долл./ч.
Расходы на одного контролера разряда 2 равны
3 долл.+2-15-0,05=4 долл. 50 цент./ч.
Следовательно, минимизируемая целевая функция, выражающая
ежедневные расходы на контроль, имеет вид
Z=8 (5xi+4,50х2)=40xi+36х2.
Можно сформулировать следующую задачу ЛП:
минимизировать Z=40xx+36x2
при ограничениях Xi«^8, х2<10,
5х!+Зх2^45,
хх>0, х2>0.
Пример 4.2. Планирование работы гидроэнергетического комп-
лекса
На рис. 4.1 представлен гидроэнергетический комплекс, состоя-
щий из двух водохранилищ и двух гидроэлектростанций, каждая
из которых использует свое водохранилище. Горизонт планирова-
ния работы комплекса разбит на два периода. При наполнении од-
ного из водохранилищ избыток поступающей воды удаляется через
152
ГЛАВА 4
водосброс, который также можно использовать для сброса воды
в целях защиты от наводнений. Вода, проходящая через водосброс,
не влияет на производство электроэнергии.
Предполагается, что 1 килоакр-фут (КАФ) воды на электростан-
ции А преобразуется в 400 МВт-ч электроэнергии. Для станции В
Рис 4.1. Гидроэаергосистема.
аналогичный показатель равен 200 МВт-ч. В течение одного перио-
да станция А может произвести 60 000 МВт-ч электроэнергии, стан-
ция В — 35 000 МВт- ч электроэнергии Цена 1 МВт- ч электроэнер-
гии равна 20 долл, при условии, что общий объем ее реализации не
превосходит 50 000 МВт-ч. Каждый МВт-ч сверх 50 000 МВт-ч
имеет цену в 14 долл. Необходимые дополнительные данные о при-
токе воды в водохранилища приведены в следующей таблице (еди-
ница измерения 1 КАФ).
Хранилище А Хранилище В
Полезный объем 2000 1500
Прогнозируемый приток воды
период 1 200 40
период 2 130 15
Минимально допустимый объем воды 1200 800
Объем воды в начале периода I 1900 850
Построим модель линейного программирования для определения
оптимального режима функционирования системы, максимизирую-
щего общий доход от продажи электроэнергии.
Разработка модели. На этом примере показывается,
как при решении задач с помощью методов ЛП можно использовать
нелинейные целевые функции определенного вида. Причина нели-
нейности целевой функции состоит в том, что цена электроэнергии
зависит от общего объема ее производства. Нелинейность хорошо
видна на графике зависимости общего дохода от объема продаваемой
анергии (рис. 4.2). Эта функция является кусочно-линейной, по-
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
153
скольку она линейна в областях (0,50 000) и (50 000, оо). Разбивая
общее количество продаваемой электроэнергии на две части, одна
из которых продается по цене 20 долл, за 1 МВт-ч, а другая — по
,14 долл за 1 МВт-ч, можно свести целевую функцию к линейной.
Рис. 4.2. Продаваемая электроэнергия, МВт-ч.
Целесообразно сначала построить модель функционирования
системы в течение первого периода, а затем перейти ко второму
периоду. Для этой цели необходимо ввести следующие переменные:
РН1 — количество электроэнергии (в МВт-ч), продаваемой по цене
20 долл, за I МВт-ч;
PL1 — количество энергии (в МВт- ч), продаваемой по цене 14 долл,
за 1 МВт-ч;
ХА1 — объем воды (в КАФ), направляемой на станцию А;
ХВ1 — объем воды (в КАФ), направляемой на станцию В;
SA1 — объем воды (в КАФ), сбрасываемой из хранилища А;
SB1 — объем воды (в КАФ), сбрасываемой из хранилища В;
ЕА1 — объем воды (в КАФ) в хранилище А в конце периода 1;
ЕВ1 — объем воды (в КАФ) в хранилище В в конце периода 1.
Общее количество энергии, производимой в течение периода 1,
равно 400ХА1+200ХВ1, а общее количество энергии для продажи
составляет PH1+PL1. Следовательно, условие баланса производи-
мой энергии записывается следующим образом:
400XAl+200XBl=PH14-PLl.
Поскольку максимальное количество энергии, продаваемой по бо-
лее высокой цене, равно 50 000 МВт-ч, выполняется неравенство
PH 1^50 000. Мощность станции А, выраженная в единицах объема
воды (КАФ), составляет 60 000/400=150. Поэтому ХА1^150. Ана-
логично XBls^87,5.
Условие водного баланса для хранилища А можно записать
в следующем виде:
Вода, направляемая на станцию А + Сбрасываемая вода +
Конечный объем воды в хранилище А = Начальный объем
воды в хранилище А + Прогнозируемый приток воды.
154
ГЛАВА 4
Таким образом,
XA1+SA1+ЕА1 = 1900+200=2’00.
Поскольку емкость хранилища А равна 2000 КАФ, а минимально
допустимый объем воды составляет 1200 КАФ, то возникают допол-
нительные ограничения:
ЕА1<2000, ЕА1>1200.
Аналогично для хранилища В получаем
XBl+SBl + EBl=850+40+XAl+SAl,
800<ЕВ1<1500.
Теперь легко построить модель для периода 2, введя соответст-
вующие переменные: РН2, PL2, ХА2, ХВ2, SA2, SB2, ЕА2, ЕВ2.
Ограничения, связанные с производством энергии в течение
периода 2, имеют следующий вид:
400XA2 + 200XB2=PH2+LH2,
РН2 <50 000,
ХА2<150,
ХВ2<87,5.
Условия водного баланса можно записать в виде
XA2+SA2+EA2=EAl + 130,
1200<ЕА2<2000,
XB2+SB2+EB2=EB1 + 15+XA2+SA2,
800<ЕВ2<1500.
Кроме приведенных выше ограничений имеются условия неотри-
цательности переменных.
Максимизируемая целевая функция, выражающая общий доход
от продажи электроэнергии, задается следующей формулой:
Z=2O(PH1+PH2)+14(PL1+PL2).
Таким образом, окончательно в модели имеются 16 переменных и
20 ограничений, не считая требования неотрицательности перемен-
ных.
4.2. Графическое решение задачи линейного
программирования с двумя переменными
В разд. 4.1 были приведены примеры, показывающие, каким об-
разом можно сформулировать некоторые практические задачи как
задачи ЛП. Далее необходимо найти оптимальное решение постав-
ленной задачи ЛП. В настоящем разделе описывается графическая
процедура решения задач ЛП с двумя переменными. На практике
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
155
задачи такой размерности обычно не встречаются, однако рассмат-
риваемый графический метод хорошо иллюстрирует некоторые ос-
новные понятия, используемые при решении задач ЛП большой
размерности.
Пример 4.3
Напомним формулировку задачи технического контроля из при-
мера 4.1:
минимизировать Z=40x,+36x2
при ограничениях Xi^8, х2^10,
5xl+3x2^45,
Xi^O, х2^0.
В этой задаче требуется найти значения переменных х, и х2, удов-
летворяющие всем ограничениям и обеспечивающие минимальное
значение целевой функции. В качестве первого шага решения сле-
дует определить все возможные неотрицательные значения перемен-
ных Xi и х2, которые удовлетворяют ограничениям. Например, ко-
ординаты точки Xi=8, х2=10 положительны и для этой точки вы-
полняются все ограничения. Такая точка называется допустимым
решением. Множество всех допустимых решений называется до-
пустимой областью. Решение задачи ЛП состоит в отыскании наи-
лучшего решения в допустимой области. Лучшее допустимое ре-
шение задачи ЛП называется оптимальным. В рассматриваемом
примере оптимальное решение представляет собой допустимое ре-
шение, минимизирующее целевую функцию 40xi+36x2. Значение
целевой функции, соответствующее оптимальному решению, назы-
вается оптимальным значением задачи ЛП.
Для изображения допустимой области следует начертить гра-
фики всех ограничений. Все допустимые решения лежат в первом
квадранте, поскольку значения переменных неотрицательны. В
силу ограничения 5xl+3x2^45 все допустимые решения (xlt х2)
задачи располагаются по одну сторону от прямой, описываемой
уравнением 5х,+3х2=45. Нужную полуплоскость можно найти,
проверив, удовлетворяет ли начало координат рассматриваемому
ограничению. Прямую 5xi+3x2=45 удобно провести, соединяя
пару подходящих точек (например, Xi=0, х2=15 и х1=9, х2=0).
Поскольку начало координат не удовлетворяет ограничению,
нужная полуплоскость отмечена стрелкой, направленной перпен-
дикулярно прямой. Аналогичным образом представлены ограни-
чения Xi^8 и х2<Д0. На рис. 4.3 допустимая область (АВС) заштри-
хована. Ясно, что в допустимой области содержится бесконечное
число допустимых точек. Нужно найти допустимую точку с наимень-
шим значением Z.
Если заранее зафиксировать значение целевой функции Z=
=40xi+36x2, то соответствующие ему точки будут лежать на не-
которой прямой. При изменении величины Z эта прямая подвер-
гается параллельному переносу. Рассмотрим прямые, соответст-
J56
ГЛАВА 4
Рис. 4 3. Графическое решение задачи из примера 4.3.
вующие различным значениям Z, имеющие с допустимой областью
хотя бы одну общую точку. Начальное значение Z положим равным
600. При приближении прямой к началу координат значение Z
уменьшается. Если прямая имеет хотя бы одну общую точку с до-
пустимой областью АВС, ее можно смещать в направлении начала
координат. Ясно, что для прямой, проходящей через угловую точ-
ку А с координатами хх=8, х2=1,6, дальнейшее движение невоз-
можно. Точка А представляет собой наилучшую допустимую точку,
соответствующую наименьшему значению Z, равному 377,6. Следо-
вательно, Xi=8, х2= 1,6 — оптимальное решение и Z=377,6 — оп-
тимальное значение рассматриваемой задачи ЯП.
Таким образом, при оптимальном режиме работы ОТК необхо-
димо использовать восемь контролеров разряда 1 и 1,6 контролеров
разряда 2. Дробное значение х2 = 1,6 соответствует использованию
одного из контролеров разряда 2 в течение неполного рабочего дня.
При недопустимости неполной загрузки контролеров дробное зна-
чение обычно округляют, получая приближенное оптимальное
целочисленное решение Xi=8, х2=2.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
157
Единственность оптимального решения.
В примере 4.3 решение Хх=8, х2=1,6 — единственная допустимая
точка с минимальным значением Z. Другими словами, значения Z,
соответствующие другим допустимым решениям, больше 377,6.
В силу этого для рассматриваемой задачи решение %i=8, х2=1,6
называется единственным оптимальным решением.
Неединственность оптимального реше-
ния. Для некоторых задач ЛП может существовать несколько до-
пустимых решений со значениями целевой функции, равными оп-
тимальному значению задачи. В таких случаях все эти допустимые
решения оптимальны и говорят, что задача ЛП имеет альтернатив-
ные оптимальные решения.
Пример 4.4
Максимизировать Z=x1+2x2
при ограничениях Xl+2x2^10. Xi+x2^1,
х2^4, х^О, х2^0.
Допустимая область показана на рис. 4.4. Проведены прямые,
соответствующие значениям Z=2, 6, 10. Оптимальное значение
целевой функции равно 10, причем соответствующая прямая Xj+
+2х2=10 содержит отрезок ВС, лежащий на границе допустимой
области. Поэтому все точки на отрезке ВС представляют собой опти-
мальные оешення.
158
ГЛАВА 4
Неограниченный оптимум. Для некоторых за-
дач ЛП не существует оптимального решения. Другими словами,
для любого допустимого решения можно найти другое допустимое
решение, которому соответствует лучшее значение целевой функ-
ции. В примере 4.4 такое положение возникнет, если опустить огра-
ничение В этом случае удаление от начала координат
вызывает рост целевой функции и максимум Z равен фоо. Если не
существует конечного оптимума, говорят, что задача ЛП имеет
неограниченный оптимум.
В практических задачах такая ситуация, конечно, не встреча-
ется, поскольку в противном случае можно было бы получить бес-
конечный доход при конечном запасе ресурсов. Если в какой-либо
практической задаче получено подобное решение, то это обычно
означает, что одно из ограничений (или несколько) задачи было
пропущено на этапе построения модели. При наличии этого ограни-
чения значения целевой функции не могли бы возрастать до беско-
нечности.
Вывод. В примере 4.3 оптимальное решение было единствен-
ным и достигалось в вершине А допустимой области. В примере 4.4
получились различные оптимальные решения, среди которых на-
ходились вершины допустимой области В и С. В обоих случаях
одна из вершин была оптимальным решением. В действительности
это свойство выполняется для всех задач ЛП.
Свойство 1
Если в задаче линейного программирования существует опти-
мальное решение, то по крайней мере одна из вершин допустимой
области представляет собой оптимальное решение.
Симплекс-метод решения задачи ЛП основывается на этом фун-
даментальном свойстве. Допустимая область задачи ЛП обычно
состоит из бесконечного числа точек, однако оптимальное решение
всегда можно найти путем перебора конечного числа ее вершин.
Так, в примере 4.4 с целевой функцией
Z=Xj4-2x2
допустимая область имеет следующие вершины: А (1, 0), В (10, 0),
С (2, 4), D(0, 4) и Е(0, 1). Вычисляя значения Z, легко убедиться,
что Z(A)=1, Z(B)=10, Z(C)=10, Z(Z))=8, Z(E)=2. Поскольку
максимальное значение Z достигается в вершинах В и С, согласно
свойству 1, обе они представляют оптимальные решения.
4.3. Задача линейного программирования
в стандартной форме
Задача ЛП в стандартной форме с т ограничениями и п пере-
менными имеет следующий вид:
максимизировать или минимизировать Z = с1х1 ф- с8х8 -j-... ф снх„
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
159
при ограничениях
Gii^i + «12*2 + • • • + а1пх„ =
®21*1 4“ Огг*2 4" • • • 4" = b2.
omi*i 4- ат2х2 + ... 4- атпхп = bm,
xt 0, х2 > О ... х„ О,
&1>0, 62>0 ... 6,л>0.
Задачи ЛП в стандартной форме можно записать в компактных мат-
ричных обозначениях следующим образом:
максимизировать или минимизировать Z — cx
при ограничениях Ах = Ь, х^О, 6^0,
где А — матрица размерности тХп, х— вектор-столбец размер-
ности nXl, b — вектор-столбец размерности mxl, ас— вектор-
строка размерности 1Х/г.
Обычно А называется матрицей коэффициентов, х — вектором
переменных, b — вектором ресурсов, с — вектором оценок задачи
ЛП.
При решении задачи ЛП симплекс-методом требуется, чтобы за-
дача была представлена в стандартной форме. Однако не все задачи
ЛП имеют стандартную форму. Часто ограничения имеют вид не
равенств, а неравенств. В некоторых задачах не все переменные
можно считать неотрицательными. Таким образом, первый этап
решения задачи ЛП состоит в приведении ее к стандартной форме.
4.3.1. Преобразование неравенств
Ограничения в виде неравенств можно преобразовать в равенства
при помощи введения так называемых остаточных или избыточ-
ных переменных. Например, неравенство вида
х14-2х24-Зх3+4х4<25 (4.1)
можно преобразовать в равенство при помощи введения остаточной
переменной St:
x14-2x24-3x34-4x44-S1=25.
Переменная Si неотрицательна и соответствует разности правой г
левой частей в неравенстве (4.1). Аналогично неравенство вида
2xi4~x2—Зх3)>12
можно преобразовать в равенство путем введения избыточной пере-
менной S2:
2xi4-x2—Зх3—S 2= 12.
J 60
ГЛАВА 4
Следует подчеркнуть, что дополнительные переменные столь же
необходимы, как и исходные переменные задачи. Дополнительные
переменные могут принимать положительные значения, а их зна-
чения в оптимальном решении позволяют судить о том, являются ли
•ограничения в виде неравенств активными.
4.3.2. Преобразование неограниченных
по знаку переменных
В некоторых случаях возникает необходимость рассмотрения
переменных, принимающих как положительные, так и отрицатель-
ные значения. Поскольку переменные задачи ЛП в стандартно?!
форме предполагаются неотрицательными, неограниченные пере-
менные следует заменить разностью двух неотрицательных. Напри-
мер, если Sj — неограниченная переменная, то используется сле-
дующая замена переменных-
s, = S]* — sp, S|+ 0, sf 0.
Значение s4 может быть положительным пли отрицательным в за-
висимости от соотношения величин sj и sf.
Для иллюстрации рассмотрим следующую задачу ЛП, записан-
ную в нестандартной форме.
Пример 4.5
Максимизировать Z—х,—2х2+Зх3
при ограничениях Х|+х»+х3^7, (4.2)
х,— х2+х3>2, , (4.3)
Зх,—х2—2х3 =—5, (4.4)
ХЬ Х2^0,
где х3 — переменная, не ограниченная по знаку.
Преобразуем эту задачу к стандартной форме.
1. Заменим х3 на х4—х6, где х4, х6^0.
2. Умножим обе части уравнения (4.4) на —I.
3. Введем дополнительные переменные х6 и х7 в ограничения
(4.2) и (4.3) соответственно.
4. Припишем нулевой коэффициент переменным х6 и х7, целевая
функция при этом не меняется.
Таким образом, рассматриваемая задача сводится к следующей
задаче ЛП в стандартной форме:
максимизировать Z=x,—2х2+3х4—Зх6
при ограничениях Xi+x2+x4—х5+хв=7,
х4—х24 х4—х6—х7=2,
— Зх,+х2-г2х4—2х,=5,
Хь х2, х4, xft, х», х7^0.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
161
Используя стандартную форму задачи ЛП в матричных обозна-
чениях:
максимизировать Z=cx
при ограничениях Ах=6, х^О,
можно сформулировать основные определения следующим образом.
1. Допустимое решение представляет собой неотрицательный
вектор х, для которого выполняются ограничения Ах=6.
2. Допустимая область, обозначаемая через S, состоит из всех
допустимых решений. Формально это определение можно записать
в следующем виде:
S={x|Ax=6, х^О}.
Если допустимая область S пуста, задача ЛП называется противо-
речивой.
3. Оптимальным решением называется такой допустимый век-
тор х°, для которого соответствующее ему значение целевой функ-
ции (сх°) больше, чем для любого другого допустимого решения.
Таким образом, вектор х° является оптимальным решением задачи
тогда и только тогда, когда х° £ S и сх°^сх для всех х С S
4. Оптимальное значение задачи ЛП представляет значение це-
левой функции, соответствующее оптимальному решению. Если
Z0 — оптимальное значение, то Z°=cx".
5. Неединственность оптимального решения. В том случае,
когда задача ЛП имеет более одного оптимального решения, гово-
рят, что у нее имеются различные оптимальные решения. При этом
существует более одного допустимого решения со значениями целе-
вой функции, равными оптимальному (Z0).
6. Единственность оптимума. Говорят, что оптимальное реше-
ние задачи ЛП единственно, если не существует других оптималь-
ных решений.
7. Неограниченный оптимум. В том случае, когда задача ЛП не
обладает конечным оптимумом (т. е. max Z->+oo или min Z->—оо),
говорят, что задача имеет неограниченный оптимум.
4.4. Основы симплекс-метода
Рассмотрим общую задачу ЛП с т ограничениями и п перемен-
ными, записанную в стандартной форме
максимизировать Z=c1x1+c2x2+ . +спхп
при ограничениях о11х1+а12х2+...+а1,!х„=/>1,
021^1+^22^2+ ...-\-а2пхп=Ь2,
П:т1-3£'1 + Пп12-3£'а+- * *+пш„ Х,( Ьгп,
xlt х2, ..., х„^0.
6 № 1826
162
ГЛАВА 4
Как правило, число уравнений задачи меньше числа переменных
(т. е. m<Zn), поэтому множество ее допустимых решений бесконечно.
Следовательно, выбор наилучшего допустимого решения, максими-
зирующего Z, нетривиален.
Известен классический метод решения систем линейных урав-
нений, называемый методом Гаусса — Жордана (см. приложение
В). Основная идея этого метода состоит в сведении системы т урав-
нений с п неизвестными к каноническому или ступенчатому виду
при помощи элементарных операций над строками. При использо-
вании первых т переменных (х1; ..., хт) каноническая система имеет
следующий вид:
Х1 + а1, ,л+ 'хт+ 1 + • • • “й! Дт " ' 4*^4,— ^1,
xr Н- аг, »1+ Ал+1Н- • • • 4- arsxs 4- • • • 4" arnxn ~br< (S1)
Хт + ага. т + А + 1 4- • • • Т°иА~ • • • ^~атпхп = ^т-
Переменные xlt ..., хт, входящие с единичными коэффициентами
только в одно уравнение системы и с нулевыми — в остальные, на-
зываются базисными или зависимыми. В канонической системе
каждому уравнению соответствует ровно одна базисная перемен-
ная. Остальные п—т переменных (хт+1, ..., хп) называются неба-
зисными или независимыми переменными.
При записи системы в каноническом виде все ее решения можно
получить, присваивая независимым переменным произвольные зна-
чения и решая затем получающуюся каноническую систему относи-
тельно зависимых переменных. Для приведения системы к канони-
ческому виду можно использовать два типа элементарных опера-
ций над строками.
1. Умножение любого уравнения системы на положительное или
отрицательное число.
2. Прибавление к любому уравнению другого уравнения систе-
мы, умноженного на положительное или отрицательное число.
Определение
Элементарное преобразование представляет собой последовате-
льность элементарных операций над строками, в результате кото-
рой коэффициент при некоторой переменной становится равным
единице в одном из уравнений системы и нулем в остальных урав-
нениях.
Определение
Базисным решением системы в каноническом виде называется
решение, полученное при нулевых значениях небазисных пере-
менных.
Например, в системе (S1) одно из базисных решений задается
как Xi=&i, ..., хт=Ьт, хт+1 = ..,=х„=0. Если bi..bm к тому
же неотрицательны, то полученное решение называется допустимым
базисным решением.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
163
Определение
Базисное решение называется допустимым базисным решением,
если значения входящих в него базисных переменных неотрица-
тельны.
В системе (S1) для удобства записи в качестве базисных ис-
пользуются первые т переменных. В действительности для полу-
чения канонической системы уравнений и базисного решения любые
т из п переменных можно выбрать в качестве базисных Это озна-
чает, что максимальное число базисных решений задачи ЛП с т
ограничениями и п переменными, записанной в стандартной форме,
конечно и выражается следующим образом:
/ п \ _ п 1
\т) т ! (л —т) I
Каждое допустимое базисное решение по определению является
базисным решением. Следовательно, максимальное число допусти-
мых базисных решений также ограничено приведенной величиной.
В конце разд. 4.2 указывалось, что если задача ЛП обладает
оптимальным решением, то хотя бы одна из вершин допустимой об-
ласти оптимальна. Можно доказать, что любая вершина допустимой
области соответствует некоторому допустимому решению системы
ограничений. Поэтому оптимальное решение задачи ЛП можно
найти путем перебора допустимых базисных решений. Такой про-
цесс будет конечным, поскольку число допустимых базисных ре-
„ ( п\
шении не превосходит величины ( I.
Интуитивный подход к решению задачи ЛП, обладающей опти-
мальным решением, состоит в нахождении при помощи метода Га-
усса — Жордана всех возможных допустимых базисных решений
и последующем выборе решения, которому соответствует наилуч-
шее значение целевой функции. Однако при решении задач ЛП
симплекс-метод оказывается более эффективным, так как при этом
анализируется лишь часть всех допустимых базисных решений.
Ниже приводится подробное описание симплекс-метода.
Симплекс-метод разработан Дж. Данцигом. Он представляет
собой итеративную процедуру решения задач ЛП, записанных в
стандартной форме. При этом требуется, чтобы система ограниче-
ний-равенств была приведена к каноническому виду, что дает воз-
можность легко находить допустимое базисное решение. Алгоритм
симплекс-метода включает следующие основные шаги:
1. Выбор начального допустимого базисного решения.
2. Переход от начального решения к другому допустимому ба-
зисному решению с лучшим значением целевой функции. На этом
шаге исключаются из рассмотрения все допустимые базисные ре-
шения, которые хуже текущего решения. В силу этого обстоя-
тельства симплекс-метод гораздо эффективнее упомянутого выше
«прямого» подхода к решению задач ЛП.
А*
164
ГЛАВА 4
3. Продолжение поиска допустимых базисных решений, улуч-
шающих значение целевой функции. Если некоторое допустимое
базисное решение нельзя улучшить, оно является оптимальным,
и алгоритм симплекс-метода завершает свою работу.
Рассмотрим шаг 2 симплекс-метода в предположении, что ба-
зисное решение, задаваемое системой (S1), допустимо. Пусть до-
пустимое базисное решение задано в следующем виде:
Базисные переменные = Ь; 0, i = 1, 2, ..., т,
Небазисные переменные лу = О, j — m+\, .;.,п.
Множество базисных переменных называется базисом и обозна-
чается через хв. Вектор коэффициентов при базисных переменных
обозначается через св. Для начального базиса
xa = (x1, св = (с1, ...,ст).
Поскольку небазисные переменные равны нулю, значение целевой
функции Z, соответствующее начальному допустимому базисному
решению, равно _
Z = свхв — Cj&j + • • • + cmbm.
Симплекс-метод дает возможность проверить существование допус-
тимого базисного решения с большим значением Z. Для этого сна-
чала проводится проверка оптимальности рассматриваемого реше-
ния. Если оно не оптимально, симплекс-метод позволяет перейти
к смежному допустимому базисному решению с большим (или по
крайней мере не меньшим) значением Z.
Определение
Смежное допустимое базисное решение отличается от рассматри-
ваемого только одной базисной переменной.
Для получения смежного допустимого базисного решения симп-
лекс-метод превращает одну из базисных переменных в небазисную
и вводит одну из небазисных переменных в базис. Необходимо
выбрать базисную и небазисную переменные так, чтобы замена
одной из них на другую давала максимальное приращение целевой
функции.
В любом допустимом базисном решении базисные переменные
положительны, а небазисные равны нулю. Следовательно, превра-
щение небазисной переменной в базисную приводит к увеличению
ее значения от нуля до некоторой положительной величины. Вво-
димая в базис переменная должна давать улучшение значения Z.
Для выбора вводимой в базис переменной следует присвоить неба-
зисной переменной значение, равное единице, и вычислить измене-
ние целевой функции.
Для иллюстрации рассмотрим небазисную переменную xs.
Пусть ей присвоено значение, равное единице; исследуем получае-
мое при этом изменение целевой функции. Заметим сначала, что,
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
165
поскольку рассматриваются только смежные допустимые базисные
решения, остальные базисные переменные по-прежнему равны ну-
лю, так что систему (S1) можно переписать в следующем виде:
Х1 + alsxs— ^1»
хг +arixs = brt (S2)
xm + a,nsxs = bm.
Из системы (S2) при возрастании xs от 0 до 1 получаем новое решение
xi = bi—ais, t = l..............т,
xs — 1, Xj = 0, j = т 4- 1, ..., п, j =jf= s.
Новое значение целевой функции равно
2= 2 c, (F,—+
< = 1
Обозначим через cs приращение величины Z, получающееся при уве-
личении значения xs на единицу. Таким образом,
cs = Новое значение Z—Старое значение Z=i
= 2 с, (bi—als) + cs — 2 cfit =
i= 1 i=l
= CS— 2 сД-г
i = 1
Величина cs называется относительной оценкой небазисной
переменной xs, тогда как cs является исходной оценкой xs в целе-
вой функции. Если 4\>0, то можно добиться увеличения значения
целевой функции Z, вводя переменную xs в базис. Уравнение (4.5),
определяющее относительную оценку, известно под названием
правила скалярного произведения.
Правило скалярного произведения
Относительная оценка небазисной переменной Xj, обозначаемая
через с,, равна
Су = Су СВ?Р
где св соответствует оценкам базисных переменных, a Р, представ-
ляет собой /-й столбец в канонической системе, соответствующей
рассматриваемому базису.
166
ГЛАВА 4
Условие оптимальности
Если относительные оценки небазисных переменных допусти-
мого базисного решения задачи максимизации отрицательны
или равны нулю, то решение оптимально.
Ясно, что если с7О0 для всех небазисных переменных, то любому
смежному допустимому базисному решению соответствует значе-
ние целевой функции, не превосходящее уже достигнутого. Отсюдг
следует, что в рассматриваемой точке имеется локальный макси-
мум. Поскольку целевая функция Z линейна, локальный максимум
совпадает с глобальным. _
С целью пояснения предположим, что с*=шах с7>0 и, следо-
вательно, начальное допустимое базисное решение неоптимально.
Поскольку величина cs положительна, при увеличении значения
небазисной переменной xs на единицу Z возрастает на cs. Чем боль-
ше увеличение значения xs, тем больше приращение величины Z,
поэтому необходимо, чтобы значение xs было возможно большим.
С другой стороны, при увеличении xs значения остальных базисных
переменных также меняются, и их новые значения находятся и:
системы (S2):
х, — Ь,-— а.-,х„ /=1......т. (4.6)
Если als<Z0, то xt возрастает вместе с xs, а при als=0 значение х,
не меняется. Однако если а(5>0, переменная xt убывает с ростом х,
и становится отрицательной при неограниченном увеличении xs,
а решение—недопустимым. Таким образом, максимальное допус-
тимое значение xs определяется следующим правилом:
maxxj = _min |&2/а;5]. (4.7)
> 0
Пусть ’ br/ars= min
^>°
Следовательно, при увеличении xs до br/ars базисная переменная х,
первой среди базисных переменных обращается в нуль и заменяется
в базисе переменной xs. Переменная xs становится новой базисной
переменной в r-й строке, причем новое допустимое базисное реше-
ние имеет вид
— als(brlars) при всех i, (4.8)
= br/ars,
Xj — О для всех остальных небазисных переменных,
/ = т + 1, .... п, / 7^s.
Поскольку при увеличении xs на единицу приращение Z состав-
ляет cs, для нового решения общее приращение Z равно
( cs) $>riars) > 0.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
167
Уравнение (4.7), на основании которого определяются базисные
переменные, выводимые из базиса, носит название правила мини-
мального отношения. При использовании симплекс-метода вычис-
ление относительных оценок всех небазисных переменных теку-
щего допустимого базисного решения (4 8) и проверка его оптималь-
ности проводятся до тех пор, пока не будут выполнены условия
оптимальности.
Проиллюстрируем теперь на примере основные шаги симплекс-
алгоритма.
Пример 4.6
Используем симплекс-метод для решения следующей задачи:
максимизировать Z=3xx4-2x2
при ограничениях —хх+2хг <4,
Зхх+2х3 =^14,
— %2 ^^3,
хх^0, х2^0.
Приведение задачи к стандартной форме при помощи дополнитель-
ных переменных дает:
максимизировать Z=3xx-\-2x2
при ограничениях —хх4-2х2+х3=4,
Зхх-|-2х2+х4-14,
хх х2-]~ х5=3,
Xt^O, х2^0, *з>0, х4^0, х5^0.
В допустимом базисном решении системы уравнений в канониче-
ском виде базисными переменными являются хв, х4 и хь. Последо-
вательные итерации симплекс-метода удобно представить в ком-
пактном виде, используя таблицу для записи ограничений и целевой
функции. При этом вспомогательные вычисления (например,
с использованием правила скалярного произведения, правила ми-
нимального отношения и элементарных преобразований) можно
проводить при помощи стандартных процедур. Использование таб-
личной формы записи делает симплекс-метод более удобным и эф-
фективным при реализации на ЭВМ.
Элементы таблиц представляют собой коэффициенты задачи
(в табл. 1 содержится начальное допустимое базисное решение для
примера 4.6). Заметим, что для каждого ограничения записаны
лишь коэффициенты при входящих в него переменных. Коэффи-
циенты целевой функции с, находятся над коэффициентами соот-
ветствующих им переменных х}. Понятие базис обозначает сово-
купность базисных переменных начальной таблицы (х3 для ограни-
чения 1, х4 для ограничения 2 и х5 для ограничения 3), а символом
св обозначена совокупность значений оценок переменных с, базиса.
Из табл. 1 легко находится начальное допустимое базисное реше-
ние: х3=4, х4=14, х6=3, хх=х2=0. Значение целевой функции Z
168
ГЛАВА 4
задается скалярным произведением вектора св и вектора правых
частей уравнений:
/ 4 \
Z=(0, 0, 0) 14 =0.
\3 /
Для проверки оптимальности найденного допустимого базисного
решения следует вычислить относительные оценки переменных
(пользуясь правилом_ скалярного произведения). Заметим, что от-
носительные оценки с3, с4, съ будут нулевыми, поскольку соответст-
вующие переменные — базисные. Небазисные переменные хх и х2
Таблица 1
св CJ Постоянные
3 2 0 0 0
Базис *1 *2 х3 Х4 *5
0 хз -1 2 1 0 0 4
0 хА 3 2 0 1 0 14
0 xs ф -1 0 0 1 3
С -строка 3 2 0 0 0 2 = 0
имеют положительные относительные оценки. Следовательно, рас-
сматриваемое допустимое базисное решение неоптимально. Неба-
зисная переменная х, имеет наибольшую относительную оценку,
поэтому ее следует ввести в базис.
Для определения переменной, выводимой из базиса, применя-
ется правило минимального отношения (4.7). Вычисляются соот-
ветствующие отношения для всех ограничений с положительным
коэффициентом при х^.
Номер строки Базисная переменная Отношение
1 Хз 00
2 х} 14/3
3 X/, 3/1
Заметим, что для первой строки это отношение не вычисляется (оно
принимается равным сю), поскольку коэффициент при хх в строке 1
отрицателен. Это означает, что можно неограниченно увеличивать
хх, причем при этом значение х3 остается положительным. С другой
стороны, из значения 14/3 для отношения во второй строке следует,
что xi станет равным нулю при возрастании хх до 14/3. Аналогично
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
!(>')
если Xi возрастет до 3, то хь обратится в нуль. Минимальное отно-
шение равно 3, поэтому при возрастании хх от 0 до 3 первой средн
базисных переменных обратится в нуль х6; опа заменится в базисе
переменной xt. Третья строка называется ведущей строкой, а коэф-
фициент при Xj в ведущей строке называется ведущим элементом
(в табл. 1 он обведен кружком). Элементарное преобразование при-
водит к системе с новыми базисными переменными х3, х4 и х,:
1) прибавить ведущую строку (строку 3) к первой, чтобы исклю-
чить переменную хх;
2) умножить ведущую строку на (—3) и прибавить ее ко второй
строке, чтобы исключить хх.
Для проверки оптимальности полученного в табл. 2 допустимого
базисного решения необходимо вычислить вектор относительных
оценок (строку с). Это можно выполнить, пользуясь правилом
скалярного произведения. С другой стороны, новую строку с можно
вычислить, применяя элементарное преобразование Относительная
Таблица 2
Базис с Постоянные
3 2 0 0 0
л| *2 *з х4 *5
0 х3 0 1 1 0 1 7
0 *4 0 ® 0 1 -3 5
3 Х| 1 -1 0 0 1 3
С •строка 0 5 0 0 -3 Z = 9
оценка переменной хх должна быть равна нулю, поскольку хх вошла
в базис. Равенства нулю можно добиться, умножая третью строку
на —3 и прибавляя ее к строке с. В результате автоматически полу-
чается новая строка с табл. 2.
Рис. 4.5 графически иллюстрирует переход от табл. 1 к табл. 2.
Символами ABCDE обозначена допустимая область примера 4.6.
Пунктирные прямые соответствуют значениям целевой функции
Z=3 и Z=9. Допустимое базисное решение, представленное в табл 1,
соответствует вершине А. Из рассмотрения строки с в табл I
видно, что для увеличения Z в базис можно ввести любую из пере-
менных хх или х2. На рис. 4.5 видно, что увеличение любой из них
вызывает рост значения Z. В пределах допустимой области значе
ние Xi можно увеличить не более чем на три (точка В). Эта величина
и составляет минимальное отношение, задаваемое симплекс-мего-
дом. Следовательно, табл. 2 соответствует точке В на рис. 4.5.
Строка с табл. 2 все еще содержит положительный элемент, чк
указывает на возможность введения в базис небазисной перемен-
170
ГЛАВА 4
ной х2, улучшающей значение целевой функции. Применяя пра-
вило минимального отношения, находим минимум из набора (7/1.
5/5, оо). Переменная х2 должна занять место базисной переменное
х4. В табл. 3 представлено следующее допустимое базисное решение
полученное после выполнения элементарной операции. Поскольку
в табл. 3 все элементы строки с неположительные, она оптимальна.
Оптимальное решение имеет следующий вид: %i=4, х2=1, х3=6,
zd=0, х6=^0, а оптимальное значение Z равно 14.
Таблица 3
св Базис с> Постоянные
3 2 0 0 0
*1 Х2 *3 л4 xs
0 *3 0 0 1 8 у 6
2 *2 0 1 0 J. 5 1
3 1 0 0 1 5 2 5 4
С -строка 0 0 0 -1 0 Z= 14
Неединственность оптимума. Небазисная пере-
менная х5 в табл. 3 имеет нулевую относительную оценку. Следова-
тельно, изменение хБ не приведет к изменению значения целевой
функции. Таким образом, переменную хь можно ввести в базис,
причем для соответствующего допустимого базисного решения зна-
чение целевой функции Z также равно 14. По определению любое
Таблица 4
св Базис 3 с) 0 Постоянные
2 0 0
*1 хг *3 Х4 *5
0 0 0 i 8 ~ i 1 К
2 Х2 0 1 1 8 8 0 V
3 ч 1 0 _ 1 4 1 0
С -строка 0 0 0 -1 0 7=14
допустимое решение, для которого соответствующее значение Z
равно оптимальному, также оптимально. Следовательно, в данном
случае у задачи ЛП имеются различные оптимальные решения.
Одно из них получается, если переменную хь ввести в базис. Соглас-
но правилу минимального отношения, из базиса необходимо
вывести переменную х3; при этом получается оптимальная табл. 4.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
171
Ей соответствует оптимальное решение, отличное от первоначаль-
ного: хх=5/2, х2=13/4, х3=0, х4=0, х6=15/4.
Итак, если в оптимальной таблице имеется небазисная пере-
менная с нулевой относительной оценкой (с;), то оптимальное ре-
шение неединственно. На рис. 4.5 переход от табл. 2 к табл. 3 при
помощи симплекс-метода соответствует движению вдоль ребра ВС
допустимой области. Поскольку целевая функция Z равна 3Xi+
+ 2х2, ясно, что угловые точки С и D, а также все точки отрезка CD
являются оптимальными.
Основные шаги вычислительного процесса
Основными шагами процесса вычислений в соответствии с сим-
плекс-методом в табличной форме применительно к задаче макси-
мизации являются следующие.
Шаг 1. Записать задачу в стандартной форме.
Ш а г 2. Заполнить первоначальную таблицу с использованием
начального допустимого базисного решения. (Процедура отыскания
такого решения описывается ниже.) _
Шаг 3. Вычислить вектор относительных оценок (строки с)
при помощи правила скалярного произведения.
172
ГЛАВА 4
Ш а г 4. Если все оценки с, неположительные, текущее допу-
стимое базисное решение оптимальное. В противном случае не-
обходимо ввести в базис небазисную переменную с наибольшим
значением с;.
Шаг 5. Определить при помощи правила минимального от-
ношения переменную, выводимую из базиса.
Ш а г 6. Применить элементарное преобразование для получе-
ния нового допустимого базисного решения и новой таблицы.
Шаг 7. Вычислить новые относительные оценки с использо-
ванием элементарного преобразования или правила скалярного
произведения. Перейти к шагу 4.
Итерацией симплекс-метода называется выполнение шагов 4—7
описанного процесса. На каждой итерации получаются новая таб-
лица и улучшенное допустимое базисное решение. Число допусти-
мых базисных решении, просматриваемых при использовании сим-
плекс-метода, представляет собой важную характеристику эффек-
тивности этого метода.
4.4.1. Задачи минимизации
Для решения задач минимизации можно использовать два под-
хода.
Подход 1. Преобразование задачи минимизации в эквива-
лентную задачу максимизации путем умножения целевой функции
на —1 и последующего применения симплекс-метода к задаче
максимизации.
Подход 2. Напомним, что относительные оценки в строке с
представляют изменение Z при увеличении небазисной переменной
на единицу. Отрицательный коэффициент в строке с указывает на
уменьшение Z при увеличении соответствующей небазисной пере-
менной. Следовательно, для задач минимизации в базис должны
вводиться небазисные переменные с отрицательными cJt посколь-
ку они улучшают целевую функцию. Если все коэффициенты в стро-
ке с неотрицательные, текущее решение оптимальное. Таким обра-
зом, для решения задач минимизации можно использовать семь ша-
гов алгоритма, изменив шаг 4 симплекс-метода.
Модифицированный шаг 4. Если все коэффициенты
в строке с положительны или равны нулю, текущее допустимое ба-
зисное решение оптимальное. В противном случае необходимо
ввести в базис небазисную переменную с наименьшим (т. е. отри-
цательным и максимальным по абсолютной величине) значением
относительной оценки.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
173
4.4.2. Неограниченный оптимум
Говорят, что задача линейного программирования имеет неогра-
ниченный оптимум, если у нее нет конечного оптимального реше-
ния. В таком случае целевая функция стремится к 4~оо для задачи
максимизации и к —оо для задачи минимизации.
При использовании симплекс-метода для решения задачи с не-
ограниченным оптимумом при помощи правила минимального
отношения невозможно определить, какая переменная должна быть
выведена из базиса. В этом случае все коэффициенты в ограниче-
ниях при вводимой в базис переменной неположительные. Такая
ситуация возникает, если в уравнении (4.7) нет ни одного конеч-
ного отношения и вводимая в базис небазисная переменная может
неограниченно возрастать, не нарушая множество ограничений.
Отюда следует, что у задачи ЛП нет конечного оптимального ре-
шения.
Таблица 5
СВ Базис С! Постоянные
2 3 0 0
Х1 *3 Х4
0 хз -2 0 1 0 6
3 х2 -3 1 0 1 4
С -строка 11 0 0 -3 Z= 12
Пример 4.7. Рассмотрим табл 5, представляющую собой симп-
лексную таблицу некоторой задачи максимизации. Можно ввести
небазисную переменную в базис, поскольку ^>0. Однако пра-
вило минимального отношения оказывается неприменимым, по-
скольку в столбце, расположенном под переменной хг, нет положи-
тельных элементов. Это означает, что с увеличением хг базисные
переменные хг и х3 также растут. Следовательно, переменная
может неограниченно увеличиваться. Рассматриваемая задача ЛП
имеет неограниченный оптимум. При возрастании хг на единицу
значение Z возрастает на 11 единиц, поэтому Z может неограни-
ченно увеличиваться. Наличие неограниченного максимума при
решении практических задач свидетельствует об ошибках при раз-
работке модели ЛП, в частности о пропуске некоторых существен-
ных для задачи ограничений.
4.4.3. Вырожденность и зацикливание
Допустимое базисное решение, в котором одна или более базис-
ных переменных равны нулю, называется вырожденным допусти-
мым базисным решением. Допустимое базисное решение, в котором
174
ГЛАВА 4
все базисные переменные положительны, называется невырожден-
ным
Вырожденность может присутствовать в первоначальной фор-
мулировке задачи (если некоторые правые части равны нулю);
она может также возникать при симплексных вычислениях. Послед-
нее происходит, когда по крайней мере две строки имеют одинако-
вые значения минимального отношения, вычисляемого по пра-
вилу (4.7).
При вырожденности допустимого базисного решения минималь-
ное отношение может оказаться нулевым. В этом случае изменение
базиса не влияет на значение целевой функции. В действительности
встречаются задачи, в которых несколько итераций симплекс-ме-
тода не приводят к улучшению значения Z. Это означает, что вы-
полняются трудоемкие вычисления с симплексными таблицами, не
дающие реального эффекта. Естественно, что при таких условиях
вычислительная эффективность симплекс-метода снижается. Еще
более важен вопрос, возможно ли выполнение неограниченного
числа итераций си мп леке-метода без продвижения к оптимуму.
Имеются примеры, показывающие, что теоретически такая ситуа-
ция возможна. В этом случае вычисления по симплекс-алгоритму
зацикливаются и не приводят к оптимальному решению. Это явле-
ние носит название классического зацикливания или просто зацикли-
вания. В практических задачах зацикливания не происходит, не-
смотря на вырожденность некоторых промежуточных решений.
Однако описаны случаи, когда при реализации на ЭВМ симплекс,
метод не давал оптимального решения. Такая ситуация возникала
в основном в силу особенностей программного обеспечения сим-
плекс-метода. Это явление в работе [3] названо машинным зацик-
ливанием, поскольку оно возникает из-за особенностей конкретных
ЭВМ. При решении таких задач на ЭВМ других типов всегда ока-
зывалось возможным добиться сходимости к оптимуму.
4.4.4. Метод искусственных переменных
Наличие начального допустимого базисного решения канони-
ческой системы уравнений представляет собой необходимое условие
применимости симплекс-метода. Без этого невозможно построить
начальную симплексную таблицу. Для получения системы в кано-
ническом виде, обладающей допустимым базисным решением, су-
ществует специальный метод. Сначала задача ЛП приводится к
стандартной форме, в которой все переменные неотрицательные,
ограничения имеют вид равенств, правые части неотрицательные.
Затем для каждого ограничения проверяется существование соот-
ветствующей базисной переменной. Если ее нет, вводится новая
переменная, играющая роль базисной для данного ограничения.
После проверки всех ограничений получается система в канони-
ческом виде, поскольку каждому ограничению соответствует своя
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
175
базисная переменная и появляется возможность заполнить началь-
ную симплексную таблицу. Вводимые таким образом переменные
не имеют отношения к задаче ЛП в исходной постановке, а служат
лишь для приведения системы ограничений к каноническому виду,
который необходим при использовании симплекс-алгоритма. Такие
переменные называются искусственными в отличие от управляемых
переменных задачи. В оптимальном решении искусственные пере-
менные должны обращаться в нуль, поскольку в противном случае
ограничения задачи будут нарушены. Проиллюстрируем способ
использования искусственных переменных на следующем примере.
Пример 4.8
Минимизировать Z=—3xi+x2+x3
при ограничениях х4—2х2+х3^11,
—4х1-\-х3-[-2хз^'3,
2хл—х3——1,
х,2й0, х^О, х3^0.
Сначала задача преобразуется к стандартной форме:
минимизировать Z=—3x1-f-x2-f-x3
при ограничениях хг—2х2Н-х3+х4 = 11, (4 9)
—4х1Н-х2+2х3—х6=3, (4.10)
—2х1+х3=1, (4.11)
х,^г0, х2^0, х32>0, х435=0, х5^0.
В уравнении (4.9) дополнительная переменная х4 — базисная.
Поскольку в других уравнениях нет базисных переменных, вводятся
искусственные переменные хв и х7, являющиеся базисными для урав-
нений (4.10) и (4.11) соответственно. Для сохранения стандартной
формы задачи переменные хв и х, предполагаются неотрицатель-
ными. Тогда получается следующая вспомогательная система:
Xi—2х2+х3+х4 = 1 1,
•—4х1+х2+2х3—х6+х6=3,
—2xi+x3+x7 = 1,
Xj^O.....х,^0.
Вспомогательная система имеет следующее допустимое базисное
решение: Xi=x2=x3=0, х4=11, х6=0, х6=3, х, = 1. Это решение
недопустимо для первоначальной задачи, поскольку искусствен-
ные переменные хв и х7 положительные. С другой стороны, любое
допустимое базисное решение вспомогательной системы, в котором
хв и х7 равны нулю, допустимо для исходной задачи. Таким обра-
зом, необходимо добиться обращения в нуль искусственных пере-
менных. Этого можно достигнуть при помощи двухэтапного сим-
плекс метода.
176
ГЛА*А 4
4.4.5. Двухэтапнцщ симплекс_метод
В случае введения искусстц^ннь[х переменных применяется
двухэтапныи симплекс-метод, т е. задача решается /два этапа.
та п 1. На этом этапе ах^дится начальное допустимое ба-
зисное решение первоначальной 3 Другими словами, произ-
водится исключение искусствен^ пе е^нных. с этой цРелью
рассматривается искусственная целева£ функция>
равная сумме
искусственных переменных, котор^ мини7ЙЗируегс£ при помощи
симплекс-метода. 1 * 1
Задача ЛП, рассматриваемая Ч „ этапе, применении
двухэтапного симплекс-метода к за * 4 8 формулируется
следующим образом (через W обо^ / ц^евая
функция).
Задача этапа 1
^иниЧизировать
при ограничениях ^х2+х3+х4=И.
9 1 । а:2-(—2хз—х5-+-х6==3,
,^з+х, = 1.
..., х7>0.
Исходная целевая функция Z=-3* + + на этапе j не _
ривается. к
Если минимальное значение всг,шогательной 3
лю, то все искусственные перемену обращаютСЯ в Нуль и полу-
чается допустимое базисное решеннач‘альной 3 у (Примеч\.
ние-. если сумма неотрицательных гц еменных равна ю £0 каж.
дая переменная также тождествен^ а } д/лее 3
ется этап 2. ‘ r J
Если минимальное значение вейомогательной и положн.
тельное, то по крайней мере одна из искусственных переменных
также положительная, что свидет^ 0 противоречивости
начальной задачи, и вычисления г,рекраУща1отся/
Э т а п 2. На этом этапе довуст^оеРбазисное реШение, найден-
ное на этапе 1, улучшается в соо>ветствии с £левой ф fi
исходной задачи ЛП. Другими слов% 0ПТИмальная таблица этапа
1 превращается в начальную таблиц этапа 2 изменя-
ется целевая функция. Для поиска оптимальногно ешения приме.
няется симплекс-метод1). г г
4.5. Решение задач лп на эвм
Многие практические задачи сводНтся к за линейного про-
граммирования с сотнями ограничен и тысячами управляемРш
переменных. Ясно, что их следует Решать при ПОмощи цифровых
1) Полное решение задачи примера 4.8 h
метода приведено в монографии [4, с. 51— П0М0Ш'И двухэтапного симплекс
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
177
вычислительных машин. Симплекс-метод в табличной форме пред-
ставляет собой итеративную процедуру, применимую к любой за-
даче ЛП, что делает его удобным для реализации на ЭВМ.
4.5.1. Машинные программы
Многие фирмы, специализирующиеся по выпуску ЭВМ и разра-
ботке математического обеспечения для больших компьютерных
систем, предоставляют машинные программы для решения задач
ЛП. Такие программы различаются по стоимости, удобству обра-
щения с ними, сложности и другим характеристикам. Необходи-
мость решения задач ЛП большей размерности привела к разра-
ботке очень сложных вариантов программ решения задач ЛП, на-
зываемых системами математического программирования (напри-
мер, IBM MPSX-370, CDC APEX III, Management Systems MPS-111).
Они снабжены мощными средствами обработки данных, аналити-
ческими средствами и дают возможность решать задачи с числом
ограничений порядка 8—16 тысяч и практически неограниченным
числом переменных. При помощи системы MPS-III была успешно ре-
шена задача ЛП с 50 тыс. ограничений.
Задачи линейного программирования с 5 тыс. и более ограниче-
ний следует рассматривать как задачи большой размерности. Воз-
можность успешного решения таких задач зависит от их структуры
и других специфических особенностей.
Встречающиеся на практике задачи ЛП обычно содержат от
500 до 1500 ограничений и несколько тысяч переменных. Задачу
с такими параметрами можно без труда решить при помощи любой
из функционирующих вычислительных систем, снабженных мате-
матическим обеспечением для решения задач ЛП. Если пользова-
телю приходится часто решать задачу ЛП, то экономически целе-
сообразно приобрести соответствующий пакет программ. Если же
такая необходимость возникает редко, то выгоднее воспользоваться
услугами квалифицированного местного ВЦ или арендовать тер-
минал, связанный с крупным вычислительным центром, распола-
гающим математическим обеспечением для решения задач ЛП. Ис-
черпывающий обзор характеристик современных программ реше-
ния задач ЛП, включающий информацию об управлении входными
данными, содержится в работе [5]. В работе [6] дается обзор вычис-
лительных алгоритмов для систем математического программиро-
вания. В качестве основного метода решения задачи ЛП во всех
коммерческих программах используются симплекс-метод и егс
многочисленные модификации. В работе [7] подробно рассмотрены
вопросы математического обеспечения задач ЛП, включая програм-
мы генерации матриц и выдачи данных.
178
ГЛАВА 4
4.5.2. Реализация симплекс-метода на ЭВМ
На раннем этапе развития математического обеспечения задач
ЛП при реализации симплекс-метода на ЭВМ проводились вычис-
ления над всеми элементами симплексной таблицы, как описанс
в предыдущих разделах. При таком подходе требовался быстрый
доступ ко всем элементам симплексной таблицы, что возможно лишь
при условии хранения полной таблицы в оперативной памяти ЭВМ.
При решении задачи ЛП большой размерности хранить в оператив-
ной памяти всю симплексную таблицу невозможно, вследствие чего
решение таких задач оказалось малоэффективным и дорогостоящим.
Поэтому потребовались усовершенствования симплексного метода,
которые позволили более эффективно организовывать вычисли-
тельный процесс на ЭВМ. В настоящее время во всех программах
для решения задач ЛП используется модифицированный симплекс-
метод, весьма эффективный при реализации на ЭВЛ4.
В модифицированном симплекс-методе используются те же ос-
новные идеи, что и в обычном симплекс-методе, однако при его
реализации нет необходимости пересчитывать всю симплексную
таблицу на каждой итерации. В связи с этим требуются меньшие
вычислительные ресурсы и время, поскольку информация, необ-
ходимая для перехода от одного допустимого базисного решения
к другому, формируется на основе анализа первоначальной системы
уравнений. В настоящее время во всех программах для решения
задач ЛП используется модифицированный симплекс-метод. По-
скольку при реализации модифицированного метода требуется
меньший объем оперативной памяти, появляется возможность ре-
шения задач большей размерности. Для детального ознакомления
с модифицированным симплекс-методом и его преимуществами сле-
дует обратиться к работе [4]. Имеется также ряд упрощенных ва-
риантов реализации симплекс-метода на ЭВМ. Один из них осно-
ван на правиле выбора переменной, вводимой в базис. Обычно ма-
шинные программы реализации симплекс-метода не производят
вычисления всех элементов строки с для определения небазисной
переменной, которая должна войти в базис. Такие вычисления мо-
гут потребовать больших затрат машинного времени при решении
задачи большой размерности, содержащей несколько тысяч неба-
зисных переменных. Как правило, относительные оценки вычис-
ляются последовательно до получения первой положительной
оценки; соответствующая переменная вводится в базис, что поз-
воляет избежать дальнейших вычислений элементов строки с. Та-
кая стратегия может привести к росту числа итераций при решении
задачи, однако выигрыш во времени ла каждой итерации обычно
компенсирует рост их числа.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
179
4.5.3. Вычислительная эффективность симплекс-метода
Как неоднократно указывалось специалистами в области мате-
матического программирования, с теоретической точки зрения сим-
плекс-метод нельзя считать эффективным, поскольку на каждой
его итерации происходит переход к смежному допустимому базис-
ному решению (т. е. изменяется только одна базисная переменная).
Интуиция подсказывает, что алгоритм, анализирующий несмежные
решения (т. е. заменяющий несколько базисных переменных на
каждой итерации), должен работать быстрее. Тем не менее ни один
из вариантов симплекс-метода при этом не дает ощутимого выиг-
рыша во времени вычислений. В силу этого обстоятельства
симплекс-метод считается наилучшей процедурой для решения
задач ЛП. В работе [81 дается обзор модификаций симплекс-
метода.
Вычислительную эффективность симплекс-метода можно оце-
нить при помощи следующих двух параметров: (1) числа итераций
(допустимых базисных решений), необходимых для достижения
оптимального решения, и (2) общих затрат машинного времени,
требуемого для решения задачи. Проводились многочисленные ис-
следования зависимости вычислительной эффективности от числа
ограничений и числа переменных задачи.
Опыт решения большого числа практических задач показывает,
что число итераций при решении задачи ЛП в стандартной форме
с т ограничениями и п переменными обычно заключено между т
и 3/п, среднее число итераций равно 2m. На практике можно рас-
сматривать величину 2(т+п) как верхнюю границу числа итера-
ций, хотя встречаются задачи, для которых эта закономерность
нарушается.
Установлено, что требуемое для решения машинное время ме-
няется приблизительно пропорционально кубу числа ограничений
задачи (т3). Например, если задача А имеет вдвое больше ограни-
чений, чем задача В, то машинное время решения задачи А будет
примерно в восемь раз больше.
Число ограничений задачи влияет на вычислительную эффек-
тивность сильнее, чем число переменных. Поэтому не рекомен-
дуется увеличивать число ограничений; следует отбрасывать из-
лишние ограничения при разработке модели ЛП.
Новый алгоритм, предложенный советским математиком Хачия-
ном [9], вызвал большой интерес. Он представляет собой важное
теоретическое достижение, однако, вероятно, мало перспективен
для реализации на ЭВМ [101.
180
ГЛАВА 4
4.6. Анализ чувствительности в линейном
программировании
Коэффициенты целевой функции и ограничений во всех задачах
ЛП задаются в качестве исходных данных (параметров) модели.
Оптимальное решение, получаемое симплекс-методом, зависит от
значений исходных коэффициентов. На практике значения этих
коэффициентов редко известны с абсолютной точностью, поскольку
многие из них являются функциями некоторых неконтролируемых
параметров. Например, будущие потребности, стоимость сырья
или энергоресурсов невозможно предсказать совершенно точнс!
Следовательно, решение практической задачи нельзя считать за
конченным, если найдено оптимальное решение. I
Любое изменение в исходных данных меняет условия задачи ЛП,
что в свою очередь может изменить найденное оптимальное реше-
ние при изменении начальных данных. Эта информация получается
в результате выполнения анализа чувствительности. Кроме того,
анализ чувствительности необходим по следующим причинам.
1. Некоторые параметры задачи ЛП, такие, как финансовые
средства, запасы сырья, производственные мощности, можно ре-
гулировать. Анализ чувствительности позволяет оценить влияние
изменений этих параметров на оптимальное решение. Если обнару-
живается, что оптимальное решение (отношение прибыли к затра-
там) можно значительно улучшить за счет небольших изменений
заданных параметров, то целесообразно провести эти изменения
Например, если при увеличении рабочего времени за счет сверх-
урочных работ приращение дохода превышает дополнительные
затраты на оплату труда, то сверхурочные работы экономически оп-
равданы.
2. Во многих случаях оценки параметров получаются путем ста-
тистической обработки ретроспективных данных. Например, таким
образом оценивается ожидаемый сбыт, строятся прогнозы цен и
затрат. Полученные в результате оценки, как правило, не могут
быть точными. Если удается определить, какие параметры в наи-
большей степени влияют на значение целевой функции, то целесо-
образно увеличить точность оценок именно этих параметров, что
позволяет повысить надежность рассматриваемой модели и полу-
чаемого решения.
Проиллюстрируем практическое использование анализа чувст-
вительности на конкретном примере.
Пример 4.9
Предприятие выпускает три вида продукции, для производства
которой необходимы такие ресурсы, как физический труд, сырье
и управленческий труд. Прибыль на единицу каждого вида продук-
ции составляет 10, 6 и 4 долл, соответственно. В течение рабочего
дня можно использовать 10 ч физического труда, 600 фунтов сырья
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
181
и 300 ч управленческого труда. Для определения оптимальной
производственной программы поставлена и решена следующая за-
дача ЛП:
максимизировать Z=10%i+6x2+4x3
при ограничениях Х14~х2+*з ^100 (труд),
10хг4-4х24-5х3с:б00 (сырье),
2х14-2х2+6х3^300 (управление).
Xi, х2, х3^0,
где Xi, х2, х3 обозначают ежедневное производство продукции видов
1, 2 и 3 соответственно.
В табл. 4.1 приведено решение задачи примера 4.9, полученное
на ЭВ1М. Отметим, что оптимальное решение предусматривает про-
изводство продукции только вида 1 (33,33 единицы в сутки) и вида 2
(66,67 единицы в сутки).
Теневые (неявные) цены определяют приращение максимального
дохода при использовании дополнительной единицы некоторого
ресурса. Использование физического труда дает максимальный
Таблица 4.1
Оптимальное решение: «i==33,33, х2 = 66,67, х3 = 0 Оптимальное значение
целевой функции: Теневые цены: Маргинальные оценки: максимальная прибыль = 733,33 долл.
для строки для строки для строки ДЛЯ Ху=0, 1 =3,33 долл., 2 = 0,67, 3 = 0 для х, = 0, для лг3 = 2,67
Диап азоны изменения коэффициентов целевой функции
Переменная Нижняя граница Текущее значение Верхняя граница
Х1 6 10 15
Хг 4 6 10
Хд 00 4 6,67
Диапазоны изменения правых частей
Строка Нижняя границ» Текущее зкач ние Верхняя сраиица
1 60 100 150
2 400 600 1000
3 200 300 00
182
ГЛАВА 4
выигрыш, так как приносит дополнительную прибыль в 3 долл.
33 цент, на каждый дополнительный час рабочего времени. Тене-
вые цены ресурсов применимы только при условии, когда измене-
ния количества ресурсов не выходят за указанные в таблице гра-
ницы правых частей. Другими словами, рост прибыли на 3 долл.
33 цент, на каждый дополнительный час физического труда проис-
ходит до тех пор, пока общие затраты физического труда не превы-
шают 150 ч. Предположим, что имеется возможность увеличить
ресурс физического труда на 25% за счет сверхурочных работ, что
требует дополнительных затрат 50 долл. Для определения целе-
сообразности применения сверхурочных работ вычислим чистый
прирост максимальной прибыли при использовании 25 ч сверхуроч-
ного времени- (25) X (3,33)=83 долл. 25 цент. Применение сверхуроч-
ных работ экономически оправдано, поскольку получаемый при-
рост прибыли превышает дополнительные расходы на оплату этих
работ. Важно отметить, что при изменении любой из правых частей
оптимальное решение также изменяется. Тем не менее оптимальная
номенклатура выпуска не меняется, пока правые части изменяются
в определенных пределах. Таким образом, при указанных условиях
будет выпускаться продукция только видов 1 и 2, хотя количест-
венные соотношения могут измениться.
Представленные в табл. 4.1 интервалы изменения коэффициен-
тов целевой функции определяют чувствительность оптимального
решения по отношению к изменениям удельной прибыли по трем
видам продукции. Приведенные данные показывают, что оптималь-
ное решение не изменится, пока удельная прибыль по продукции
вида 1 сохранится в пределах от 6 до 15 долл. Разумеется, макси-
мальная прибыль при этом будет меняться. Например, если удель-
ная прибыль по продукции вида I возрастает с 10 до 12 долл., то
оптимальное решение не меняется, а максимальная прибыль уве-
личивается до 733,33+(12—10) (33,33)=799 долл. 99 цент.
Следует отметить невыгодность производства продукции вида 3.
Значение ее маргинальной оценки показывает, насколько снижается
максимальная прибыль при выпуске единицы этой продукции.
Поэтому дальнейшее снижение вклада продукции вида 3 в функцию
прибыли не влияет на оптимальное решение и величину максималь-
ной прибыли. Для того чтобы производство этого вида продукции
стало выгодным, необходимо иметь удельную прибыль по ней в
6 долл. 67 цент, (приведенная стоимость -f- маргинальная оценка).
Одновременные изменения нескольких параметров [11]
В результате анализа чувствительности определяются границы
изменения коэффициентов целевой функции и правых частей при
условии, что зафиксированы все параметры, кроме рассматривае-
мого. Тем не менее можно применять анализ чувствительности и
в случае одновременного изменения нескольких параметров. Это
достигается за счет использования следующего правила 100% •
Правило 100% (для коэффициентов целе-
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
183
вой функции)
2бС//АС/^1, (4.12)
/
где 6с; — фактическое изменение коэффициента целевой функции
при переменной х}-, а Дс^ — граница, полученная в результате ана-
лиза чувствительности. Если неравенство (4.12) выполняется, тс
оптимальное решение задачи ЛП не меняется.
Например, если предположить, что удельная прибыль по про-
дукции 1 снизилась на 1 долл., а удельная прибыль по продукции
2 и 3 возросла на I долл., то легко заметить, что эти изменения
удовлетворяют правилу 100%, поскольку 6ct=—1, Дсх=—4, бс2=
= 1, Дс2=4, бс3=1, Дс3=2,67
" +l+i+0«<L
Таким образом, оптимальное решение не изменится, а максималь-
ная прибыль изменится на (—1)хЗЗ,33+1 Хбб,67+1 ХО=33,34
(долл.)
Правило 100% (для правых частей ограни-
чений)
(4-13)
1
где бй, — фактическое изменение правой части i-ro ограничения,
а Ай, — границы, полученные в результате анализа чувствитель-
ности. Если неравенство (4.13) выполняется, то соотношение объе-
мов производства различных видов продукции в оптимальном ре-
шении остается неизменным, теневые цены также не меняются,
а оптимальное решение и величина максимальной прибыли изме-
няются. Очевидно, что изменение максимальной чистой прибыли
можно определить, используя теневые цены.
Рассмотрим в качестве примера следующие одновременные из-
менения: уменьшение затрат физического труда на 10 ч, рост ко-
личества сырья на 100 фунтов и уменьшение затрат управленче-
ского труда на 50 ч. Имеем 6йх=—10, 6й2 = 100, бй3=—50, тогда
как Дй1=—40, Дй2=400, Дй3=—100. Правило 100% выполняется,
поскольку
—10 100 —50 >
—40 + 400 + —100 ~ 1
Следовательно, оптимальное соотношение видов продукции остается
прежним, хотя очевидно, что оптимальное решение изменится.
При этом изменение максимальной чистой прибыли можно опреде-
лить с использованием теневых цен:
Изменение оптимального дохода = (3,33) (—10) + (0,67) (100) —
— (0) (50) = 33,70 долл.
184
ГЛАВА 4
П римечание. Нарушение правила 100% не обязательно приво-
дит к изменению оптимального решения задачи ЛП, т. е. нера-
венство (4.12) может не выполняться, а оптимальное решение при
этом сохраняется в прежнем виде.
4.7. Приложения
Модели линейного программирования широко применяются
при решении военных, экономических, промышленных и социаль-
ных задач. Согласно опубликованному в 1976 г. обзору [I], линей-
ное программирование является наиболее часто (в 74% случаев)
применяемым методом оптимизации. В работе [2] отмечено, что
около четверти машинного времени, затраченного в последние годы
на проведение научных исследований, было отведено на решение
задач ЛП и их многочисленных модификаций. К числу главных
пользователей моделей ЛП большой размерности относятся нефтя-
ные фирмы, применяющие их для решения задач переработки
нефти, распределения и транспортировки нефтепродуктов. Здесь
невозможно провести исчерпывающий обзор приложений ЛП, по-
скольку за последние 20 лет их число стало огромным. Можно по-
советовать читателям обратиться к учебникам [12, 13J, посвящен-
ным приложениям ЛП в различных областях: промышленности,
розничной торговле, сельском хозяйстве, защите окружающей сре-
ды и других. В этих работах рассматривается также практический
опыт применения моделей ЛП во многих областях.
В монографиях Ill, 14, 15] описаны различные машинные реа-
лизации алгоритмов решений задач ЛП, применяемых в промышлен-
ности, а также особенности соответствующего математического
обеспечения. В книге [16] имеется хорошая библиография по при-
менениям ЛП; представленные в ней работы распределены по об-
ластям приложений (например, сельское хозяйство, угледобыча,
воздушные перевозки, производство чугуна и стали, производство
бумаги, нефти, железнодорожный транспорт). В обзоре [171 также
содержится библиография по приложениям ЛП. Для ознакомления
с более современными практическими приложениями ЛП можно
обратиться к журналам Interfaces, AIIE Transactions, Decision
Sciences, European Journal of Operational Research, Management
Science, Operations Research, Operational Research (U. R.), Naval
Research Logistics Quarterly, OpSearch (India) за последние
годы.
4.8. Развитие идей линейного программирования
В этом разделе кратко рассмотрены некоторые важные вопросы
линейного программирования, а именно теория двойственности,
двойственный симплекс-метод и целочисленное программирование.
Для более подробного ознакомления с этими вопросами полезно
обратиться к работам [4, 18, 191.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
185
4.8.1. Теория двойственности
Теория двойственности представляет собой весьма важное как
с чисто теоретической, так и практической точки зрения направле-
ние линейного программирования. Основной идеей теории двойст-
венности является то, что для каждой задачи ЛП существует не-
которая задача ЛП, решение которой тесно связано с решением
прямой. Между решениями прямой и двойственных задач имеется
ряд важных соотношений, полезных при исследовании общих
свойств оптимального решения задачи ЛП и проверке оптимальности
допустимого решения. Кроме того, оптимальное двойственное ре-
шение может интерпретироваться как набор оценок ресурсов, фи-
гурирующих в ограничениях, т. е. теневых цен. Последнее обстоя-
тельство играет важную роль в анализе чувствительности (разд. 4.6).
Кроме того, понятие двойственности и различные теоремы двойст-
венности используются при изучении актуальных вопросов мате-
матического программирования. В работе (4] приведено полное
изложение теории двойственности и ее приложений.
4.8.2. Двойственный симплекс-метод
Двойственный симплекс-метод представляет собой модифика-
цию симплекс-метода, использующую теорию двойственности. В ря-
де случаев двойственный симплекс-метод обладает определенными
преимуществами по сравнению с обычным. Он используется при
анализе чувствительности, параметрическом программировании,
решении задач целочисленного программирования, во многих ва-
риантах симплекс-метода и при решении некоторых задач нелиней-
ного программирования. Подробное описание этого метода можно
найти в книге 14].
4.8.3. Целочисленное программирование
При решении многих практических задач ЛП требуется найти
целочисленные значения некоторых переменных. Например, не-
возможно использовать дробное число рабочих для производства
дробного числа автомобилей. Задачи ЛП, требующие целочислен-
ности переменных (или некоторой части переменных), называются
задачами целочисленного линейного программирования. Как пра-
вило, решение таких задач трудоемко, обходится дорого и требует
больших затрат машинного времени. На практике часто применя-
ется способ, состоящий в решении задачи целочисленного програм-
мирования как задачи ЛП при помощи симплекс-метода. Значения
некоторых переменных в получающемся оптимальном решении
могут оказаться целыми, а для остальных переменных произво-
дится округление до ближайшего целого так, чтобы не нарушались
ограничения задачи. Обычно этот способ дает хорошее целочислен-
ное решение, достаточно близкое к оптимальному целочисленному
186
ГЛАВА 4
решению. Если значения целочисленных переменных велики, тс
он оказывается весьма эффективным. Иногда в формулировке за-
дачи предполагается, что переменные принимают значение 0 или I,
т. е. являются булевыми. В этом случае необходимо применять дру-
гие методы, позволяющие находить оптимальное целочисленное
решение, поскольку округление дает очень плохой результат.
В гл. 11 рассмотрены некоторые из этих методов и ряд их практиче-
ских приложений.
4.9. Заключение
В этой главе рассмотрены задачи линейного программирования’
представляющие специальный класс задач оптимизации, в которых
ограничения задаются линейными функциями и целевые функции
также линейны. Модели линейного программирования (ЛП) позво-
ляют просто получать численные решения и широко применяются
в различных областях. Описан симплекс-алгоритм, используемый
для решения общих задач ЛП. Кроме того, рассмотрены вопросы
анализа чувствительности решений задач ЛП. Возможность прове-
дения анализа такого рода представляет собой одну из основных
причин успешного практического применения методов линейного
программирования. Аппарат ЛП используется также при решении
задач целочисленного и нелинейного программирования.
Контрольные вопросы и задачи
4.1. В чем состоит различие между симплекс-методом и методом
полного перебора допустимых вершин области, задаваемой
ограничениями?
4.2. Какова роль правила минимального отношения в симплекс-
методе?
4.3. Как при помощи симплекс-метода определить, что задача ЛП
имеет неограниченный оптимум?
4.4. Какова роль правила скалярного произведения в симплекс-
методе?
4.5. Что такое искусственные переменные и для чего они служат?
В чем их отличие от остаточных (избыточных) переменных?
4.6. Опишите систематическую процедуру отыскания допустимых
решений линейной системы неравенств.
4.7. Что такое анализ чувствительности и для чего он применя-
ется?
4.8. Что такое теневые цены? Какова их практическая польза?
4.9. Когда и с какой целью применяется «правило 100%»?
4.10. Как прибавление постоянной К к целевой функции задачи
ЛП отразится на ее оптимальном решении, оптимальном
значении целевой функции?
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
187
11. Для производства двух продуктов А и В необходимы два хи-
мических процесса. На производство единицы продукта А
требуется процесс I в течение 2 ч и процесс 2 в течение 4 ч.
Процесс 1 можно использовать в течение 16 ч в сутки, про-
цесс 2 — круглосуточно (24 ч). При производстве продукта В
в качестве побочного получается также продукт С. Некото-
рую часть этого побочного продукта можно продать, а остаток
уничтожается. Удельная прибыль по продукту А равна
4 долл., по продукту В — 10 долл. Удельная прибыль по
продукту С составляет 3 долл., а затраты на его ликвида-
цию — 2 долл. По прогнозу возможность сбыта продукта С
составляет пять единиц. При выпуске единицы продукта В
выход продукта С равен двум единицам.
Определите оптимальное суточное производство продуктов
А и В (с учетом С), обеспечивающее максимальную прибыль
от их реализации.
12. Рассмотрите задачу планирования производства некоторой
продукции в течение четырех недель. Стоимость производства
единицы продукции равна 10 долл, в течение первых двух
недель и 15 долл, в течение второй пары недель. Необходимо
удовлетворить недельные потребности в продуктах, которые
равны 300, 700, 900 и 800 ед. соответственно. Максимальное
производство данной продукции в одну неделю составляет
700 ед. Кроме того, в течение второй и третьей недель фирма
Запасы
сырья,
баррель/неделя
Сырье
Максимальный
спрос на продукцию,
баррепь/неделя
100 000
100000
100000
200 000
Бензин
Соляровое масло
-*> Керосин
170000
85 000
85 000
Смазочное масло „__
-----—20 000
Рис 4.6. Технологическая схема процесса.
имеет возможность применять сверхурочные работы. При ис-
пользовании сверхурочных работ недельная продукция может
возрасти на 200 ед., однако стоимость производства единицы
дополнительной продукции выше на 5 долл. Стоимость хране-
ния единицы продукции равна 3 долл. Как спланировать
производство продукции, чтобы минимизировать общие про-
изводственные затраты? Сформулируйте соответствующую
задачу ЛП.
188
ГЛАВА 4
4.13. На нефтеперерабатывающий завод поступают четыре сорта
сырой нефти, из которых производятся четыре вида нефтепро-
дуктов: бензин, керосин, соляровое масло и смазочное масло.
Запасы сырья, а также спрос на продукты ограничены.
На рис. 4.6 изображена технологическая схема процесса.
В табл. 4.2 указаны цены на готовую продукцию, сырье и
размеры выхода продукции.
(а) Постройте модель планирования нефтепереработки, мак-
симизирующую прибыль.
(б) Предполагая, что указанные в таблице максимальные
потребности в продукции являются минимальными, пост-
ройте модель планирования нефтепереработки, миними-
зирующую издержки при удовлетворении спроса.
Таблица 4.2. Прибыль, затраты, выход
1 2 3 4 Цена продукции, долл /баррель
Производство топлива Производство смазки
Выход продукции (в баррелях на
баррель сырья)
Бензин 0,6 0,5 0,3 0,4 0,4 45,00
Соляровое масло 0,2 0,2 0,3 0,3 0,1 30,00
Керосин 0,1 0,2 0,3 0,2 0,2 15,00
Смазочное масло 0 0 0 0 0,2 60,00
Прочее а) 0,1 0,1 0,1 0,1 0,1
Затраты на сырье, долл./баррель 15,00 15,00 15,00 25,00 25,00
Эксплуатационные расходы, 5,00 3,50 7,50 3,00 2,50
долл./баррель
а) «Прочее» относится к технологическим потерям
4.14. Фирма выпускает три продукта: А, В и С. На производство
единицы продукта А требуется затратить 1 ч труда ИТР, 10 ч
физического труда и 3 фунта сырья. Для единицы продукта В
соответствующие показатели равны 2 ч, 4 ч и 2 фунт., для
продукта С—1 ч, 5 ч и 1 фунт. Ресурсы составляют 100 ч
труда ИТР, 700 ч физического труда и 400 фунт, сырья. При
оптовых закупках покупателю предоставляются скидки, так
что прибыли от продажи продукции изменяются следующим
обпазом:
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
189
Продукт А Продукт В Продукт С
Продажа, ед Удельная прибыль, долл Продажа, ед. Удельная прибыль, долл Продажа, сд Удельная прибыль, долл
0—40 10 0—50 6 0—100 5
40—100 9 50—100 4 Более 100 4
100—150 8 Более 100 3
Более 150 7
Например, если продается 120 ед. продукта А, то первые
40 ед. приносят по 10 долл, прибыли; следующие 60 — по
9 долл., а остальные 20 — по 8 долл. Сформулируйте задачу
линейного программирования, решение которой определяет
наиболее доходный производственный план.
4.15. Исследователь производит измерения некоторой величины Q,
интересуясь ее зависимостью от времени t. Его цель — на
основании п наблюдений (tlt Qi), Q2)> • ••, (С,, Qn) устано-
вить функциональную зависимость вида
Q(t)=at3+bt2+ct+d.
Известно, что значения коэффициентов a, b, с, d неотрица-
тельные и в сумме дают единицу. Ошибки наблюдений опре-
деляются по формуле
Нужно найти наилучшие возможные значения коэффициентов
а, Ь, с и d, используя следующие критерии:
т
критерий I: минимизировать Z=2 1е*1;
критерий 2: минимизировать max et,
где et — величина ошибки в t-м эксперименте. Покажите, чтс
задача, рассматриваемая исследователем, сводится к задаче
ЛП при использовании любого из двух критериев.
4.16. В механической мастерской установлены один сверлильный
и пять фрезерных станков, предназначенных для производст-
ва узлов, состоящих из деталей двух типов: 1 и 2. Произво-
дительность станков выражается следующим образом:
Производительность станков, шт /мин
Деталь
сверлильный фрезерный
1
2
3
5
20
15
J 90
ГЛАВА 4
Загрузка станков должна быть равномерной, так чтобы раз-
ница во времени работы любых двух станков не превышала
30 мин в день (предполагается, что загрузка фрезерных стан-
ков равномерная). Считая, что рабочий день длится 8 ч,
составьте такое расписание обработки деталей на станках,
при котором дневное производство готовых узлов макси-
мально.
4.17. Фирма производит растворитель особого состава в двух ва-
риантах, отличающихся по чистоте. Растворитель в обоих
вариантах продается в упаковке вместимостью I галлон.
Чистота растворителя А выше, чем В, прибыль по А состав-
ляет 40 цент./галлон, по менее чистому продукту В—30 цент./
/галлон.
Время производства продукта А в два раза превышает
время производства продукта В. При условии выпуска одного
продукта В фирма может производить его в количестве 1000
галлонов в день. По техническим условиям при выпуске
обоих продуктов общее производство не превышает 800 гал-
лонов в день. Контракт предусматривает, что каждый день
должно производиться не менее 200 галлонов продукта В.
Найдите оптимальные объемы выпуска продуктов А и В
при условии, что всю производимую продукцию можно реа-
лизовать. Решите задачу при помощи симплексных таблиц
Проверьте полученное решение при помощи графического
метода.
4.18. Преобразуйте следующую задачу ЛП к стандартной форме:
минимизировать Z=—Зх3+4хг—2х3+5х4
при ограничениях 4xt—х2+2х3—х4 =—2,
Х1Ч- х 2+Зх з—x4s~/ 14,
—2%)+Зх2 —xs4-2x4>2,
Xt^O, х2^0, х3^04, х4 не ограничена по знаку.
4.19. Рассмотрите следующую систему двух уравнений с пятью
неизвестными:
Xj+2%3-1- 10х34-4х4—2х5=5,
Х1+х2+4хз+Зх4+х5=8,
хь х2, .... х^0.
(а) Приведите ее к каноническому виду относительно базис-
ных переменных (хп х2)- Запишите базисное решение.
Допустимо ли оно? Почему?
(б) Каково максимально возможное число базисных решений?
(в) Найдите методом проб и ошибок каноническую систему,
дающую допустимое базисное решение.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
191
4.20. Рассмотрите следующую задачу ЛП:
максимизировать Z=2x4—х2+х3+х4
при ограничениях —х1+х24-х3+х,=1,
Xt-i-xs+x4— 2,
2x1-]-x2-|-x3-|-x'e=6,
xlt хв^0.
(а) Запишите начальное допустимое базисное решение.
(б) Найдите допустимое решение, в котором небазисная пе-
ременная Xi обратится в единицу (а переменные х2 и *3
останутся нулевыми). Каково результирующее изменение
значения целевой функции? t
(в) Насколько может возрасти переменная %!, не нарушая
ограничения?
(г) Найдите новое допустимое базисное решение, получаю-
щееся при значении х4, вычисленном в п. (в)
(д) Оптимально ли новое допустимое базисное решение? По-
чему?
4.21. Решите следующую задачу при помощи симплекс-метода:
максимизировать Z=x1+3x2
при ограничениях Xi^5, х1Н-2х2^10,
х2^4, Xi, х2^0.
Изобразите допустимую область в координатах (х1г х2).
Проследите за движением от одного допустимого базисного
решения к другому на графике в соответствии с последова-
тельностью шагов симплекс-метода.
4.22. Решите следующую задачу ЛП:
минимизировать Z=%i—Зх3+2х3
при ограничениях —2^х^3,
0<х2<4, 2<х3<5.
4.23. Решите следующую задачу при помощи симплекс-метода:
минимизировать Z=3x1-j-x2+x3+xi
при ограничениях —2x4+2x2+a:3=4,
3%i+x2+x4=6,
xit х2, х3, х4^0.
Найдите альтернативное оптимальное решение, если оно су-
ществует.
4.24. Решите следующую задачу при помощи симплекс-метода:
максимизировать Z=x1+2x2+3x3+4x4
при ограничениях х1+2х2+2х3+Зх4^20,
2х1+х2+Зх3+2х4<20,
Xi, ..., х4>0.
Единственно ли оптимальное решение? Почему?
192
ГЛАВА 4
4.25. Проверьте при помощи симплекс-метода, что у следующей
задачи нет оптимального решения:
максимизировать Z=%i+2x2
при ограничениях —2xi+%2+x3^2,
^2 Х3^^ i >
Xi, х2, х3^0.
Используя заключительную симплекс-таблицу, постройте до-
пустимое решение со значением целевой функции, превышаю-
щим 2000.
4.26. Рассмотрите задачу ЛП в стандартной форме:
минимизировать Z=cx
при ограничениях Ах=Ь, х>0.
Пусть векторы и х(2> представляют собой оптимальные
решения этой задачи. Покажите, что тогда вектор х(Х) =
=Х%(1)+(1—Х)х(2) также оптимален для любого X, заключен-
ного между 0 и 1. (Примечание. Этот результат очень важен
в линейном программировании. Исходя из найденной пары
оптимальных решений задачи ЛП можно получить бесконеч-
ное число оптимальных решений, варьируя X между 0 и 1.)
4.27. В приведенной ниже таблице задачи максимизации не из-
вестны значения шести величин «1, а2, а3, р, р1( р2 (считается,
что искусственные переменные отсутствуют).
Базис *1 Хг *3 Xi х3 х6 Постоянные
*3 4 «1 1 0 а2 0 3
Xi -1 -5 0 1 - 1 0 2
Х(, «3 -3 0 0 -4 1 3
с-строка Pl 0 0 -3 0
х1(...,х4>0
Укажите, при каких ограничениях на неизвестные парамет-
ры («1, а2, (х3, р, р1( р2) справедливы следующие утверждения
о таблице:
(а) Текущее решение оптимальное и оптимальное решение
неединственное.
(б) Текущее решение недопустимое. (Укажите переменную,
по которой оно недопустимо.)
(в) Одно из ограничений несовместное.
(г) Текущее решение представляет собой вырожденное до-
пустимое базисное решение. (Какая переменная вызывает
вырожденность?)
(д) Текущее решение допустимое, однако задача не имеет ко-
нечного оптимума.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
193
(е) Текущее решение является единственным оптимальным
решением.
(ж) Текущее решение допустимое, однако при замене перемен-
ной хе на Xi значение целевой функции возрастает. Как
изменится значение целевой функции после применения
элементарного преобразования?
4.28. Руководство фирмы, выпускающей изделия трех видов —
А, В и С с использованием трех станков, Ml, М2 и М3, желает
определить оптимальный календарный план производства,
максимизирующий общую прибыль. При производстве изде-
лия А используются станки Ml, М2 и М3, для производства
изделия В требуются станки Ml и М3, а для изделия С исполь-
зуются станки Ml и М2. Цены изделий А, В и С равны 4, 2
и 5 долл, соответственно. Сформулирована следующая за-
дача ЛП:
максимизировать Z=4xi+2x2+5x3
при ограничениях Х!+2х2+х3^430 (станок 1),
Зх1+2х3^460 (станок 2),
*1+4x2^450 (станок 3),
х1( х2, х3^0,
где через хь х2, х3 обозначены объемы производства изделий
А, В и С соответственно, а ограничения соответствуют произ-
водительностям станков. Решение задачи, полученное на
ЭВМ, имеет следующий вид:
Оптимальное решение Xt = 0, х2 — 100, х3 — 230
Оптимальное значение целевой функции max Z— 1350
Теневые цены 1,0, 2,0; 0,0 для ограничений
1, 2 и 3 соответственно
Маргинальные оценки 3,0; 0, 0 для переменных х2,
хя соответственно
(а) Вследствие роста затрат на сырье, используемое при про-
изводстве изделия С, удельная прибыль от него упала
до 4 долл,. Определите новое оптимальное решение и мак-
симальную прибыль.
(б) Предположим, что имеется возможность увеличить про-
изводительность одного из станков. Производительность
какого станка следует увеличить? Почему?
(в) За счет улучшения конструкции удалось увеличить удель-
ную прибыль от изделия А до 6 долл. Выгодно ли пос-
ле этого его производство? Объясните почему.
(г) Предположим, что при дополнительных затратах в раз-
мере 250 долл, можно добиться роста производительности
станка 2 на 200 мин. Выгодно ли это? Объясните почему.
(д) Из-за увеличения затрат на потребляемую станками
энергию удельные прибыли от изделия А, В и С упали
Г № 1826
194
ГЛАВА 4
Диапазоны изменения коэффициентов целевой функции
Пер менная Нижняя границу Текущее значение Верхняя граница
Xi QQ 4,0 7,0
*2 0 2,0 10,0
*3 2,333 5,0 00
Диапазоны изменения правых частей
Строка Нижняя I рапипя Текущее значение Верхняя г раница
1 230 430 440
2 440 460 860
3 400 450 00
соответственно на 2,0; 0,50 и 1,0 долл. Как это отразится
на оптимальном решении и максимальной прибыли?
Литература
1 Fabozzi Е, J., Valente J., Mathematical Programming in American Companies:
A Sample Survey, Interfaces, 7 (1), 93—98 (Nov. 1976).
2. Steen L. A. Linear Programming Solid New Algorithm, Science Ne^s, 116,
234—236 (Oct. 6, 1979).
3 Gass S. I., Comments on the Possibility of Cycling with the Siiplex Method,
Oper. Res., 27(4), 848—852 (1979).
4. Phillips D T., Ravindran A., Solberg J. J., Operations Research: Principles
and Practice, Wiley, N. Y., 1976.
f>. Orchard-Hays W., On the Proper Use of a Powerful MPS, in: Optimization Met-
hods for Resources Allocation (R. W. Cottle, J. Krarup, Eds.), English Univer-
sities Press, London, 1974, pp. 121 —149.
(5 . White W. W., A Status Report on Computing Algorithms for Mathematical
Programming, Comput. Sure., 5(3), 135—166 (1973).
7. Ravindran A., Linear Programming, in: Handbook of Industrial Engineering
(G. Salvendy, Ed.), Wiley, N. Y., 1982, ch. 14.2.1 —14.2.11.
8 Barnes J. W., Crisp R. M., Jr., Linear Programming A Survey of General
Purspose Algorithms, Amer. Inst. Ind. Eng. Trans., 7(3), 212—221 (1975)
9 Хачиян Л. Г., Полиномиальный алгоритм в линейном программировании,
ДАН СССР, 1979, т. 224, № 5.
10 Dantzig G. В., Comments on Khachian’s Algorithm for Linear Programming,
Tech Rep. SOL 79-22, Department of Operations Research, Stanford Universi-
ty, Stanford, CA, 1979
11. Bradley S. P., Нах A. C., Magnanti T. L., Applied Mathematical Programming,
Addison-Wesley, Reading, MA, 1977.
12 Gass S. I., An Illustrated Guide to Linear Programming, McGraw-Hill, N. Y.
1970.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
195
13. Salkin Н. М , Saha J., Studies in Linear Programming, North Holland/Ameri-
c^n Elsevier, N. Y., 1975.
14. Driebeek N. J., Applied Linear Programming, Addison-Wesley Reading, MA,
1969.
15. Daellenbach H. G., Bell E. J., User’s Guide to Linear Programming, Prentice-
Hall, Engelwood Cliffs, NJ, 1970.
16. Gass S., Linear Programming, 4th ed., McGraw-Hill, N. Y. [Имеется перевод-
Гасс C. Линейное программирование.— M.: Физматгиз, 1961.]
17. Gray Р., Cullinan-James С., Applied Optimization — A Survey, Interfaces,
6(3), 24—41 (May 1976).
18 Dantzig G. B., Linear Programming and Extensions, Princeton Univ. Press,
Prenceton, N. J., 1963. [Имеется перевод: Данциг Дж. Линейное программи-
рование, его применения и обобщения.— М.: Прогресс, 1966.]
19. Murty К. G., Linear and Combinatorial Programming, Wiley, N. Y., 1976.
Глава 5
Критерии оптимальности
в задачах с ограничениями
В гл. 2 и 3 были рассмотрены необходимые и достаточные усло-
вия оптимальности решений оптимизационных задач без ограниче-
ний. Однако ряд инженерных задач связан с оптимизацией при
наличии некоторого количества ограничений на управляемые пере-
менные. Такие ограничения существенно уменьшают размеры об-
ласти, в которой проводится поиск оптимума. На первый взгляд
может показаться, что уменьшение размеров допустимой области
должно упростить процедуру поиска оптимума. Между тем, напро-
тив, процесс оптимизации становится более сложным, поскольку
установленные выше критерии оптимальности нельзя использовать
при наличии ограничений. При этом может нарушаться даже ос-
новное условие, в соответствии с которым оптимум должен дости-
гаться в стационарной точке, характеризующейся нулевым гра-
диентом. Например, безусловный минимум функции /(х)=(х—2)а
имеет место в стационарной точке х=2. Но если задача минимиза-
ции решается с учетом ограничения х^4, то будет найден условный
минимум, которому соответствует точка х=4. Эта точка не является
стационарной точкой функции f, так как /' (4)=4. В данной главе
исследуются необходимые и достаточные условия оптимальности
решений задач с ограничениями. Изложение начинается с рассмот-
рения задач оптимизации, которые содержат только ограничения
в виде равенств.
5.1. Задачи с ограничениями
в виде равенств
Рассмотрим общую задачу оптимизации, содержащую несколь-
ко ограничений в виде равенств:
минимизировать/(хь х2, ..., xN)
при ограничениях (%!, х2, ..., xN)=0, k—i, ..., К.
Эта задача в принципе может быть решена как задача безусловной
оптимизации, полученная путем исключения из целевой функции
К независимых переменных с помощью заданных равенств. Наличие
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ 197
ограничений в виде равенств фактически позволяет уменьшить
размерность исходной задачи с N до W—/С. Поскольку при этом
возникает задача безусловной оптимизации, то для идентификации
точки оптимума можно использовать методы, изложенные в гл. 2
и 3. В качестве иллюстрации рассмотрим следующий пример.
Пример 5.1
Минимизировать f(х)=х1х2х3
при ограничении h-l(x)=xx+x2+x3—1=0.
Исключив переменную х3 с помощью уравнения /ii(x)=0, получим
оптимизационную задачу с двумя переменными без ограничений
min f (xv хг)=ххх2 (1 — х,—х2).
Для идентификации точки оптимума исследуемой функции можно
использовать один из методов, представленных в гл. 3.
Метод исключения переменных применим лишь в тех случаях,
когда уравнения, представляющие ограничения, можно разрешить
относительно некоторого конкретного набора независимых пере-
менных. При наличии большого числа ограничений в виде равенств
процесс исключения переменных становится весьма трудоемкой
процедурой. Кроме того, возможны ситуации, когда уравнение не
удается разрешить относительно переменной. В частности, если
в примере 5.1 ограничение /ii(x)=0 задать в виде
h, (х) = ХуХ3 + x2Xj + х^Ху — 0,
то получить аналитическое выражение какой-либо из переменных
через другие не представляется возможным. Таким образом, при
решении задач, содержащих сложные ограничения в виде равенств,
целесообразно использовать метод множителей Лагранжа, описа-
ние которого дается в следующем разделе.
5.2. Множители Лагранжа
С помощью метода множителей Лагранжа по существу устанав-
ливаются необходимые условия, позволяющие идентифицировать
точки оптимума в задачах оптимизации с ограничениями в виде па-
венств. При этом задача с ограничениями преобразуется в эквива-
лентную задачу безусловной оптимизации, в которой фигурируют
некоторые неизвестные параметры, называемые множителями Ла-
гранжа.
Рассмотрим задачу минимизации функции N переменных с уче-
том одного ограничения в виде равенства:
минимизировать f(xt, х2, ..., xN) (5.1)
при ограничении h^Xy, х2, ..., Хд,)=0. (5.2)
В соответствии с методом множителей Лагранжа эта задача преоб-
198
ГЛАВА 5
разуется в следующую задачу безусловной оптимизации:
минимизировать L (%; v)=f (х)—vh1(x). (5.3)
Функция L (х; V) называется функцией Лагранжа, v — неизвест-
ная постоянная, которая носит название множителя Лагранжа.
На знак v никаких требований не накладывается.
Пусть при заданном значении безусловный минимум функ-
ции L(x\ v) по х достигается в точке х=х° и х° удовлетворяет урав-
нению fti(x°)=0. Тогда, как нетрудно видеть, х° минимизирует (5.1)
с учетом (5.2), поскольку для всех значений х, удовлетворяющих
(5 2), /ij(x)=0 и min Е(х; u) = min/(x).
Разумеется, необходимо подобрать значение v=va таким обра-
зом, чтобы координата точки безусловного минимума х" удовлетво-
ряла равенству (5.2). Это можно сделать, если, рассматривая v как
переменную, найти безусловный минимум функции (5.3) в виде
функции v, а затем выбрать значение V, при котором выполняется
равенство (5.2). Проиллюстрируем это на конкретном примере.
Пример 5.2
Минимизировать /(x)=Xi+*i
при ограничении ht (x) = 2xj+x2—2=0.
Соответствующая задача безусловной оптимизации записывается
в следующем виде:
минимизировать L(x\ v)=x2-t~x2—v(2xt+x2—2).
Решение. Приравняв две компоненты градиента L к нулю,
получим
dL/dx1—2x1—2v=0 ->xj=v,
dL/dx2=2x2—ц=0->х°=ц/2.
Для того чтобы проверить, соответствует ли стационарная точка
х° минимуму, вычислим элементы матрицы Гессе функции L(x; v),
рассматриваемой как функция х,
(х, v) — Q 2 I ’
которая оказывается положительно определенной. Это означает,
что L (х; v) — выпуклая функция х. Следовательно, координаты
xf=v и х’=ц/2 определяют точку глобального минимума. Оптималь-
ное значение v находится путем подстановки значений х“ и х2 в урав-
нение 2xi+x2=2, откуда 2v+v/2=2 или ц°=4/5. Таким образом,
условный минимум достигается при х?=4/5, х’=2/5 и равен min /(х) =
= 4/s-
При решении задачи из примера 5.2 мы рассматривали L(x; v)
как функцию двух переменных Xj и х2 и, кроме того, предполагали,
что значение параметра v выбрано так, чтобы выполнялось ограни-
чение. Если же решение системы
dL/dxj~Q, j=l, 2, N,
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ 199
в виде явных функций v получить нельзя, то значения х и v нахо-
дятся путем решения следующей системы, состоящей из 1 урав-
нений с Д+1 неизвестными:
dL/dXj—Q, /=1, 2, .... Д, /it(x)=0.
Для нахождения всех возможных решений данной системы можно
использовать численные методы поиска, рассмотренные в гл. 3
(например, метод Ньютона). Для каждого из решений (Д’; и°) сле-
дует вычислить элементы матрицы Гессе функции L, рассматри-
ваемой как функция х, и выяснить, является ли эта матрица поло-
жительно определенной (локальный минимум) или отрицательно
определенной (локальный максимум).
Пример 5.3
Минимизировать /(х)=х1+%2
при ограничении
Решение
L(x; v)=Xt+xi—v(xl+xl— 1),
dL/dxi =1—2их1=0,
дЬ1дхг =1—2их2=0,
ЛДх) — х?+х%—1=0.
Эта система трех уравнений с тремя неизвестными имеет два
решения: ___
(Д11; У1) = (-1/К2 , -1/К2 ; -К 1/2),
(Д2>;о2) = (1//2, 1/Г2 ;/Т/2).
Матрица Гессе функции L(x; v), рассматриваемой как функция х,
равна
Вычислив элементы матрицы Н для каждого из двух решений, на-
ходим, что матрица
ДДД1’; +) =
V2
0
0
/2.
положительно определена,
а матрица
/Д(Д2); +) =
’-/2
0
0
-/2
отрицательно определена.
Следовательно, (Д2); о2) соответствует максимуму функции L, рас-
сматриваемой как функция х; оптимальное решение х?=Д[ = 1/К2.
[Заметим, что (Д1’; щ) соответствует минимуму LJ
Здесь необходимо подчеркнуть, что если мы рассмотрим L как
функцию трех переменных, а именно переменных xt, х2 и V, то точки
(xll); 01) и (Д2); о2) не окажутся точками минимума или максимума
200
ГЛАВА 5
L как функции х и V. На самом деле они являются седловыми
точками функции L(x; и). Вопросы, связанные с седловыми точ-
ками, рассматриваются ниже в данной главе.
Метод множителей Лагранжа можно распространить на случай,
когда задача имеет несколько ограничений в виде равенств. Рас-
смотрим общую задачу, в которой требуется
минимизировать f (х)
при ограничениях hk(x)=0, fe=l, 2, ..., /С.
Функция Лагранжа принимает следующий вид:
к
L(x, v) = f(x) — 2 vkhk.
k= I
Здесь v1; v2, vk — множители Лагранжа, т. e. неизвестные
параметры, значения которых необходимо определить. Приравни-
вая частные производные L по х к нулю, получаем следующую
систему N уравнений! с N неизвестными:
dL (х; v)_Q
dxi '
dL (х\ v) _ п
дх* ’
dL 0
дхх
Если найти решение приведенной выше системы в виде функций
вектора v оказывается затруднительным, то можно расширить
систему путем включения в нее ограничений в виде равенств
hi (х)=0,
Я2 (х) =0,
hK(x)=Q.
Решение расширенной системы, состоящей из М+К уравнений
с М+К неизвестными, определяет стационарную точку функции L.
Затем реализуется процедура проверки на минимум или максимум,
которая проводится на основе вычисления элементов матрицы
Гессе функции L, рассматриваемой как функция х, подобно тому,
как это было проделано в случае задачи с одним ограничением.
Для некоторых задач расширенная система /V+ft уравнений
с М+К неизвестными может не иметь решений, и метод множителей
Лагранжа оказывается неприменимым. Следует, однако, отметить,
что такие задачи яа практике встречаются достаточно редко.
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ 201
5.3. Экономическая интерпретация
множителей Лагранжа
Множители Лагранжа рассматривались выше как параметры,
значения которых выбираются таким образом, чтобы выполнялись
ограничения задачи. С экономической точки зрения множители
Лагранжа интерпретируются как неявные (теневые) цены ресурсов,
определяемых ограничениями; оптимальные значения множителей
Лагранжа играют важную роль в анализе чувствительности реше-
ний. Для того чтобы пояснить эту интерпретационную схему, рас-
смотрим следующую оптимизационную задачу с двумя перемен-
ными и одним ограничением в виде равенства:
минимизировать f(xlt х2)
при ограничении hi(Xi, x2)=bi,
где постоянная величина (ц характеризует наличие некоторого ре-
сурса.
(5.4)
(5.5)
L(x; v1)=f(x)—v1[hi(x)—b1].
Предположим, что стационарная точка функции L соответствует
глобальному минимуму.
дЬ _ df dhi __л
d-t] dxt Vl dxt '
dL dj dhi n
ox% дх^ дх%
Пусть — оптимальное значение множителя Лагранжа, ах" —
оптимальное решение задачи. Далее, пусть минимум функции
L(x; при Vj=Vi достигается в точке х=х", причем hi(x°)=&i и
f(x°)=L(x°; и?)=/°. Очевидно, что оптимальные значения (х°; и?)
связаны функциональной зависимостью с величиной bi, задающей
границу наличия дефицитного ресурса.
Изменения f° (оптимального значения /), обусловленные изме-
нениями bi, описываются частной производной df°!dbi. По правилу
дифференцирования сложной функции имеем
df» __ df» dxi df° дх?
dbi - дх° ^bi “Г" дх° d6i ’
Дифференцируя обе части ограничения hi(x)~bi=0, получаем
дх? дх? О
dxi ^1 "Г” дх? dbi
Умножим обе части равенства (5.7) на п? и вычтем из (5.6):
Г Г э/° v« д1г> I дх?
дх? 1 дх? J dbi
(5 6)
(5-7)
df°
dbi
(5-8)
202
ГЛАВА 6
Так как х° и удовлетворяют уравнениям (5.4) и (5.5), равенстве
(5.8) приводится к виду
dp/db^^. (5.9J
Таким образом, из формулы (5.9) следует, что скорость изменения
оптимального значения f, вызываемого изменением blt определя-
ется оптимальным значением множителя Лагранжа yj. Другими
словами, величина изменения оптимального значения целевой фун-
кции, обусловленного единичным увеличением правой части огра-
ничения, т. е. величина, которая в гл. 4 определена как неявная
цена, задается'множителем Лагранжа. В зависимости от знака
п? значения /" при изменении bi могут увеличиваться или умень-
шаться.
В случае когда рассматривается оптимизационная задача с Л
ограничениями и N переменными, в которой требуется
минимизировать f(x)
при ограничениях hk(x)=bk, /г=1, 2, .... X,
пользуясь аналогичной схемой рассуждений, можно показать, чтс
= fe=l, 2, ..., К.
dbk ’
5.4. Условия Куна — Таккера
В предыдущем разделе было установлено, что множители Лаг-
ранжа можно использовать при построении критериев оптималь-
ности для задач оптимизации с ограничениями в виде равенств.
Кун и Таккер обобщили этот подход на случай общей задачи нели-
нейного программирования с ограничениями как в виде равенств,
так и в виде неравенств. Рассмотрим следующую общую задачу не-
линейного программирования:
минимизировать f(x) (5.10)
при ограничениях gj (х)^0, / = 1, 2, ..., J, (5.11)
hk(х)=0, k=l, 2, ..., К, x=(xlt х2, xN). (5.12)
Определение
Ограничение в виде неравенства gy(x)^0 называется активным,
или связывающим, в точке х, если gj(x)=0, и неактивным, или
несвязывающим, если gy(x)>0.
Если существует возможность обнаружить ограничения, ко-
торые неактивны в точке оптимума, до непосредственного решения
задачи, то эти ограничения можно исключить из модели и тем самым
уменьшить ее размеры. Основная трудность заключается при этом
в идентификации неактивных ограничений, предшествующей ре-
шению задачи.
Кун и Таккер построили необходимые и достаточные условия
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ
203
оптимальности для задач нелинейного программирования, исходя
из предположения о дифференцируемости функций /, gs и hk. Эти
условия оптимальности, широко известные как условия Куна —
Таккера, можно сформулировать в виде задачи нахождения решения
некоторой системы нелинейных уравнений и неравенств, или, как
иногда говорят, задачи Куна — Таккера.
5.4.1. Условия Куна — Таккера и задача Куна — Таккера
Найти векторы х^хц, п(1хл и уахк)> удовлетворяющие следую-
щим условиям:
J к
V (х) — 2 «/ Vg/ (х) - 2 (х) = 0,
1=1 А— 1
^«>0, /=1,2......J,
hk(x) = 0, fe=l,2, .. .,К,
Ujgj (х) = 0, /=1,2,...,./,
и7>0, /=1,2,...,./.
(5.13)
(5 14)
(5.15)
(5.16)
(5 17)
проиллюстрируем условия Куна—Таккера на
Прежде всего
примере.
Пример 5.4
Минимизировать /(х) = х,—х2
при ограничениях Xj4-x2 = 6, xt—1^0,
^ + 4<26.
Решение. Записав данную задачу в виде задачи нелиней-
ного программирования (5.10) — (5.12), получим
V/(x) = (2x1, -1),
« = (1,0),
V&(x) = (—2х„ —2х2),
Vft[(x) = (l, 1).
/(х) = ^~Х2,
gA (X) = Xj— 1,
£2(х) = 26 —х* — х2,
/г1(х) = х, + х2 —6,
Уравнение
принимает
(5.13), входящее в
следующий вид:
и
дх,- 1дх,- и*дх.-
состав условий Куна — Таккера,
Й/i 1 л • , п
— ^,«-=0, / = , 2,
1 дх / ’ ' ’ ’
откуда
2хх—Ui+2x1U2—Vi =0,
— 1+2x2u2—1д=0.
Неравенства (5.14) и уравнения (5.15) задачи Куна — Таккера
в данном случае записываются в виде
Xi—1^0, 26—Xj—х2^0, Хх+хз—6=0.
204
ГЛАВА 5
Уравнения (5.16), известные как условие дополняющей нежесткости,
принимают вид
м1(х1—1)=0, м2(26—х2—х2)=0.
Заметим, что на переменные и и2 накладывается требование не-
отрицательности, тогда как ограничение на знак отсутствует.
Таким образом, для задачи из примера 5.4 условия Куна —
Таккера записываются в следующем виде:
2х,—«j + 2х1и.1 — Uj = 0,
—1 4- 2хгиг—vt — 0,
— 1 >0,
26—х";— х2 0,
Xj -Т хг—6 = 0,
м, (%1 — 1) = 0,
и2 (26 — X, — х2) = 0,
Uj^O, м2^0, ограничений на знак нет.
5.4.2. Интерпретация условий Куна — Таккера
Для того чтобы интерпретировать условия Куна — Таккера,
рассмотрим задачу нелинейного программирования с ограничения-
ми в виде равенств:
минимизировать /(х)
при ограничениях /rfe(x)=0, fe=l.К.
Запишем условия Куна — Таккера
V/(x) — ЦикЧкц(х) = 0, (518)
hk(x') — 0. (5.19)
Далее рассмотрим функцию Лагранжа для задачи нелинейногс
программирования с ограничениями в виде равенств
L (х; у) = / (х) — 2 vkhk W •
К
Для этой функции условия оптимальности первого порядка запи-
сываются в виде
V,. (х) = ?/(х) — 2^ W = 0,
V, (v) = /ift (x) = 0.
Нетрудно видеть, что условия Куна — Таккера (5.18) и (5.19)
совпадают с условиями оптимальности первого порядка для задачи
Лагоанжа.
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ 205
Рассмотрим задачу нелинейного программирования с ограни-
чениями в виде неравенств:
минимизировать f (х)
при ограничениях gj(xy^O, j=l, J.
Запишем условия Куна — Таккера
v/ (х)—2 vgy w = о,
I
£/(х)>0, M7g7(x) = 0, u7>0.
Соответствующая функция Лагранжа имеет вид
L(x; u) = f(x) — ^Ujgj (х).
Условия оптимальности первого порядка записываются как
V/(х) — ^Uj Vgj (х) = 0, (5.20)
gr/(x) = 0, /= 1, .... J.
Заметим, что Uj— множитель Лагранжа, соответствующий ограни-
чению /. В разд. 5.3 было показано, что Uj представляет неявную
цену, ассоциированную с ограничением /; другими словами, вели-
чина Uj отражает изменение минимального значения целевой функ-
ции f (х), вызываемое единичным приращением правой части /-го ог-
раничения.
Если предположить, что /-е ограничение является неактивным
(т. е. ^у(х)>0), то и,=0 и Ujgj(x)=G. С другой стороны, если /-е
ограничение активное (т. е. £7(х)=0), то соответствующая неявная
цена Uj не обязательно равна нулю, однако Ujgj(x)—Q, так как
g,(x)=0. Таким образом,
H/<?j(x)=0 для всех значений /=1, .... J.
Для того чтобы определить знак Uj (неявной цены, ассоциирован-
ной с ограничением £>(х)^0), следует увеличить правую часть
ограничения от 0 до 1. Ясно, что при этом область допустимых
решений сужается, поскольку любое решение, удовлетворяющее
ограничению g7(x)^l, автоматически удовлетворяет неравенству
gi(x)^Q. Следовательно, размеры допустимой области уменьша-
ются, и минимальное значение / (х) улучшить невозможно (так как
вообще оно может только возрастать). Другими словами, неявная
цена Uj, ассоциированная с /-м ограничением, должна быть неотри-
цательной, что соответствует условиям Куна — Таккера.
5.5. Теоремы Куна — Таккера
В предыдущем разделе построены условия Куна — Таккера
для задач условной оптимизации. С помощью метода множителей
Лагранжа получено интуитивное представление о том, что условия
206
ГЛАВА 5
Куна — Таккера тесно связаны с необходимыми условиями опти-
мальности. В данном разделе рассматриваются строгие формули-
ровки необходимых и достаточных условий оптимальности решения
задачи нелинейного программирования.
Теорема 5.1. Необходимость условий Куна—Таккера
Рассмотрим задачу нелинейного программирования (5.10) —
(5.12). Пусть f, gn h — дифференцируемые функции, а х* — допус-
тимое решение данной задачи. Положим I={j\gj(x*)=O}. Далее
пусть Vgj(x*) при /С / и vhk(x*) при fe=l, ..., К линейно неза-
висимы. Если х*— оптимальное решение задачи нелинейного про-
граммирования, то существует такая пара векторов (u*, и*), что
(х*. и*, о*) является решением задачи Куна — Таккера (5.13)—
(5.17).
Доказательство этой теоремы здесь не приводится; заинтересо-
ванный читатель может обратиться к книге Базара и Шетти [1,
гл. 4].
Условие, согласно которому Vg;(x*) при j£l и yhk(x*) при
й=1, ..., К должны быть линейно независимыми, известно как ус-
ловие линейной независимости и по существу представляет собой
некоторое условие регулярности допустимой области, которое поч-
ти всегда выполняется для встречающихся на практике задач опти-
мизации. Однако вообще проверка выполнения условия линейной
независимости весьма затруднительна, так как требуется, чтобы
оптимальное решение задачи было известно заранее. Вместе с тем
условие линейной независимости всегда выполняется для задач
нелинейного программирования, обладающих следующими свой-
ствами.
1. Все ограничения в виде равенств и неравенств содержат
линейные функции.
2. Все ограничения в виде неравенств содержат вогнутые функ-
ции, все ограничения-равенства — линейные функции, а также
существует по крайней мере одна допустимая точка х, которая рас-
положена во внутренней части области, определяемой ограниче-
ниями-неравенствами. Другими словами, существует такая точка х,
4Togy(x)>0 при /=1..... J и hk(x)=0 при fe=l, ..., К-
Если условие линейной независимости в точке оптимума не вы-
полняется, то задача Куна — Таккера может не иметь решения.
Пример 5.5
Минимизировать /(x)=(xi—3)24~х|
при ограничениях gi(x)=(l—хх)3—х2^0,
g2(x)=xl>0,
g-3W=*2>0.
Решение. На рис. 5.1 изображена область допустимых ре-
шений сформулированной выше нелинейной задачи. Ясно, что оп-
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ 207
тимальное решение этой задачи есть Xi = l, х2=0 и /(х*)=4. Пока-
жем, что условие линейной независимости не выполняется в точке
оптимума.
Рис. 5.1. Допустимая область в задаче из примера 5.5.
Так как gi(x*)=0, gi(x*')'>Q и gs(х*)=0, то /={1, 3}. Далее
V^(x*) = [-3(l-x1)8, -1Ь»А. = (0, -1),
Vgs(x*) = (0, 1).
Легко видеть, что векторы Vgt(x*) и Vgs(x*) линейно зависимы,
т. е. условие линейной независимости в точке х*=(1, 0) не выпол-
няется.
Запишем условия Куна—Таккера и проверим, выполняются
ли они в точке (1,0). Условия (5.13), (5.16) и (5.17) принимают сле-
дующий вид:
2(Xi — 3)—uf [—3 (1 —Xj)2] — и2 = 0, (5.21)
2х2—иг (—1) — мя = 0, (5.22)
xi)S — *s] = °. (5-23)
и2х1==0, (5.24)
м3ха = 0, (5.25)
Kj, и2, и3^0. (5.26)
При х* = (1, 0) из уравнения (5.21) следует, что и2=—4, тогда как
уравнение (5.24) дает и2=0. Следовательно, точка оптимума не
является точкой Куна — Таккера.
Заметим, что нарушение условия линейной независимости не
обязательно означает, что точка Куна — Таккера не существует.
Для того чтобы подтвердить это, заменим целевую функцию из
примера 5.5 функцией f (х)=(Х\—1)2-Тх2. При этом оптимум
по-прежнему достигается в точке (1, 0), в которой условие
линейной независимости не выполняется. Условия Куна — Так-
кера (5.22) — (5.26) остаются неизменными, а уравнение (5.21)
208
ГЛАВА 5
принимает вид
2 (х,—1)—и, [—3 (1—Xj)2]—«2=0.
Нетрудно проверить, что точка х* = (1, 0), и*=(0, 0, 0) является
точкой Куна — Таккера, т. е. удовлетворяет условиям Куна —
Таккера.
Теорема о необходимости условий Куна — Таккера позволяет
идентифицировать неоптимальные точки. Другими словами, тео-
рему 5.1 можно использовать для доказательства того, что задан-
ная допустимая точка, удовлетворяющая условию линейной неза-
висимости, не является оптимальной, если она не удовлетворяет
условиям Куна — Таккера. С другой стороны, если в этой точке
условия Куна — Таккера выполняются, то нет гарантии, что най-
дено оптимальное решение нелинейной задачи. В качестве примера
рассмотрим следующую задачу нелинейного программирования.
Пример 5.6
Минимизировать /(х) = 1—х2
при ограничении —1^х^3.
Решение. Здесь g'1(x)=x+1^0, g2(x)=3—x?ss0.
Запишем условия Куна — Таккера:
2х—иг Д и2 = 0, (5.27)
—1 ^х^З, (5.28)
«j (х Т-1) = 0, (5.29)
м2 (3 — х) = 0, (5.30)
и2 7> 0. (5 31)
Так как ограничения содержат линейные функции, условие линей-
ной независимости выполняется во всех допустимых точках. Легко
видеть, что х=3 — точка оптимума. Рассмотрим допустимое ре-
шение х=2. Для того чтобы доказать его неоптимальность, прове-
рим выполнение условий Куна—Таккера (5.27) — (5.31). Из
уравнений (5.29) и (5.30) следует, что «i=u2=0; однако значения
х=2; «1=м2=0 не удовлетворяют уравнению (5.27). Следовательно,
по теореме 5.1 точка х=2 не может быть оптимальной.
С другой стороны, решение х=м1=и2=0 удовлетворяет системе
(5.27) — (5.31) и, следовательно, определяет точку Куна — Так-
кера, однако оптимальным не является. Согласно теореме 5.1, ус-
ловия Куна — Таккера должны выполняться в точке оптимума
х=3. Нетрудно проверить, что решение х=3, «1=0, м2=6 удовлет-
воряет условиям Куна — Таккера.
Следующая теорема устанавливает условия, при выполнении
которых точка Куна — Таккера автоматически соответствует
оптимальному решению задачи нелинейного программирования.
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ 209
Теорема 5.2. Достаточность условий Куна — Таккера
Рассмотрим задачу нелинейного программирования (5.10) —
(5.12). Пусть целевая функция f (х) выпуклая, все ограничения в
виде неравенств содержат вогнутые функции gj(x), j=\, ..., J, а
ограничения в виде равенств содержат линейные функции hk(x),
k=\, ..., К- Тогда если существует решение (х*, и*, V*), удовлет-
воряющее условиям Куна — Таккера (5.13) — (5.17), то х*—оп-
тимальное решение задачи нелинейного программирования.
Строгое доказательство достаточности уЛовий Куна—Так-
кера можно найти в книге [2].
Если условия теоремы 5.2 выполняются, то нахождение точки
Куна — Таккера обеспечивает получение оптимального решения
задачи нелинейного программирования. Теорему 5.2 можно также
использовать для доказательства оптимальности данного решения
задачи нелинейного программирования. В качестве иллюстрации
опять рассмотрим пример 5.4:
минимизировать f(x)=Xj—х2
при ограничениях gi(x)=Xi—1^0,
g2 (х) =26—Xj—х^>0,
hx (х) =х1+х2—6 =0.
С помощью теоремы 5.2 докажем, что решение х’ = 1, х2=5 является
оптимальным. Имеем
V/(x) = (2xlt —1)
и Ну (х) =
’2 О’
0 0
Так как матрица НДх) положительно полуопределена при всех х,
функция f (х) оказывается выпуклой. Первое ограничение в виде
неравенства содержит линейную функцию gi(x), которая одновре-
менно является как выпуклой, так и вогнутой. Для того чтобы
показать, что функция g2(x) является вогнутой, вычислим
Vg2 W = (—2xi, —2х2) и Hg2 (х) =
—2 0'
0 —2
Поскольку матрица Н#2(х) отрицательно определена, функция
g2(x) является вогнутой. Функция /гДх) входит в линейное ограни-
чение в виде равенства. Следовательно, все условия теоремы 5.2
выполнены; если мы покажем, что х* = (1, 5) — точка Куна — Так-
кера, то действительно установим оптимальность решения х*.
Условия Куна — Таккера для примера 5.4 имеют вид
2Х[ — и1-\-2х1и2 — п1 = 0, (5.32)
— 1 + 2х2м2— п1 = 0, (5.33)
хх-1>0, (5.34)
26 — xl—х^>0, (5.35)
- х1 + х2 — 6 = 0, (5.36)
clO
ГЛАВА 5
Ui(Xj—1)=0, (5.37)
«2 (26 —xj —х2) = О, (5.38)
ии (5.39)
Точка х*=(1, 5) удовлетворяет ограничениям (5.34) — (5.36) и,
следовательно, является допустимой. Уравнения (5.32) и (5.33)
принимают следующий вид:
# 2—«14-2«2—yr = 0,
— 1 + 10«2—^1=0.
Положив и1=0, получим м2=0,1 и М!=2,2. Таким образом, реше-
ние х*=(1, 5), «* = (2,2, 0,1) и «i=0 удовлетворяет условиям
Куна — Таккера. Поскольку условия теоремы 5.2 выполнены, то
х*=(1, 5) — оптимальное решение задачи из примера 5.4. Заметим,
что существуют также и другие значения «н и2 и «п которые удов-
летворяют системе (5.32) — (5.39).
Замечания
1. Для встречающихся на практике задач условие линейной
независимости, как правило, выполняется. Если в задаче все
функции дифференцируемы, то точку Куна — Таккера следует
рассматривать как возможную точку оптимума. Таким образом,
многие из методов нелинейного программирования сходятся к точке
Куна — Таккера. (Здесь уместно провести аналогию со случаем
безусловной оптимизации, когда соответствующие алгоритмы
позволяют определить стационарную точку.)
2. Если условия теоремы 5.2 выполнены, точка Куна — Таккера
в то же время оказывается точкой глобального минимума. К сожа-
лению, проверка достаточных условий весьма затруднительна, и,
кроме того, прикладные задачи часто не обладают требуемыми
свойствами. Следует отметить, что наличие хотя бы одного нелиней-
ного ограничения в виде равенства приводит к нарушению предпо-
ложений теоремы 5.2.
3. Достаточные условия, установленные теоремой 5.2, можно
обобщить на случай задач с невыпуклыми функциями, входящими
в ограничения в виде неравенств, невыпуклыми целевыми функ-
циями и нелинейными ограничениями-равенствами. При этом ис-
пользуются такие обобщения выпуклых функций, как квазивыпук-
лые и псевдовыпуклые функции. Заинтересованный читатель может
обратиться к книге Мангасариана [2, гл. 9 и 10).
5.6. Условия существования седловой точки
При обсуждении условий оптимальности Куна — Таккера (разд.
5.4 и 5.5) предполагалось, что целевая функция и функции, входя-
щие в ограничения, являются дифференцируемыми. Далее рассмат-
риваются критерии оптимальности для недифференцируемых функ-
ций при наличии ограничений.
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ 211
Определение
Говорят, что функция f(x, у) имеет седловую точку (х*, у*),
если f(x*, y)^f(x*, y*)^f(x, у*) для всех х и у.
В определении седловой точки подразумевается, что х* миними-
зирует функцию fix, у*) по всем х, а у* максимизирует функцию
/(х*, у) по всем у. Рассмотрим, например, функцию /(х, у)=х2—
—х+2у, определенную для всех действительных значений х и не-
отрицательных значений у. Нетрудно проверить, что функция имеет
седловую точку х* =2, у* —4, так как
/(2, y)^f(2, 4)^f(x, 4) для всех значений у^О и всех действительных
значений х.
Обратимся к методу множителей Лагранжа, изложенному в
разд. 5.2. Этот метод используется при решении задач условной
оптимизации, которые записываются в следующем виде:
минимизировать /(х)
при ограничениях hfl(x)=0, fe=l, .... К-
Определим функцию Лагранжа
Л(х, у) = /(х)~ 2иА (*)•
Предположим, что при v=v* минимум L (х; у*) достигается в точке
х=х*, причем йА(х*)=0. В соответствии с методом множителей
Лагранжа известно, что х* есть оптимальное решение задачи не-
линейного программирования. Можно показать, что (х*, и*) —
седловая точка функции Лагранжа, т. е.’
L(x*; y)^L(x*; v*)^L(x; v*)
при любых х и и.
Рассмотрим общую задачу нелинейного программирования:
минимизировать /(х)
при ограничениях gj (х)^0, /=1, ..., J, х £ S-
Множество S может вводиться для того, чтобы учесть дополнитель-
ные ограничения на управляемые переменные, например, в тех
случаях, когда все управляемые переменные должны принимать
только целые значения или значения из некоторого дискретного
множества.
Задача Куна— Таккера о седловой точке формулируется сле-
дующим образом: найти такой вектор (х*, и*), чтобы неравенство
Л(х*; «)^£(х*; ц*)^Л(х; и*)
имело место для всех ц^О и всех xg S. При этом
L (х; и) = f (х) — 2 ujgj (х).
212
ГЛАВА 5
Теорема 5.3. Достаточные условия оптимальности
Если (х*, и*)—решение задачи Куна — Таккера о седловой
точке, то х* есть оптимальное решение задачи нелинейного про-
граммирования.
Доказательство этой теоремы приводится в работе Мангасариа-
на [2, гл. 3].
Замечания
1. В теореме 5.3 не требуется выполнения предположений
о выпуклости или вогнутости соответствующих функций.
2. Теорема 5.3 не опирается на условие регулярности допустимой
области.
3. Учет нелинейных ограничений-равенств в виде hh(x)—0,
k=l, ..., К, можно осуществить путем переопределения функции
Лагранжа:
L(x; и, v) = Дх) — 'ZiUjgj (х) — 2^Л(х)-
/ *
Здесь переменные vh, k=l, К, не ограничены по знаку.
4. Теорема 5.3 устанавливает лишь достаточные условия опти-
мальности. В связи с этим следует отметить, что встречаются такие
задачи нелинейного программирования, в которых седловые точки
не существуют и которые в то же время обладают оптимальными
решениями.
Существование седловых точек. Несколько теорем устанавли-
вают необходимые условия оптимальности, которые гарантируют
существование седловой точки при отсутствии предположения о
дифференцируемости соответствующих функций. Однако формули-
ровки таких теорем базируются на предположениях о выполнении
условий регулярности допустимой области и выпуклости функций.
Теорема 5.4. Необходимые условия оптимальности
Пусть х* минимизирует f (х) при ограничениях g,(x)^0, /=1,
.... J, xgS. Предполагается, что S — выпуклое множество, /(х) —
выпуклая функция, a g,(x) — функции, вогнутые на множестве S.
Предполагается также, что существует такая точка x£S, в кото-
рой g,(x)>0 для всех /=1, 2, ..., J. Тогда существует такой вектор
множителей ц*^0, что (х*. и*) является седловой точкой функции
Дагранжа
L (х; и) = u/gf (х)
I
и неравенство
£(х*; tz)^L(x*; u*)^Z.(x; и*)
выполняется для всех х g S и и^О.
Доказательство этой теоремы имеется в работе Лэсдона
[3, гл. Н.
Несмотря на то что теорема 5.3 вместе с задачей Куна — Так-
кера о седловой точке позволяет вывести достаточные условия он-
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ 213
тимальности без использования свойств дифференцируемости и
выпуклости функций, определение седловой точки в задаче Куна —
Таккера о седловой точке, вообще говоря, сопряжено со значитель-
ными трудностями. Следующая теорема обеспечивает некоторое
упрощение вычислений, связанных с нахождением седловой точки.
Теорема 5.5
Вектор (х*, и*), где и х* £5, определяет седловую точку
в задаче Куна — Таккера о седловой точке тогда и только тогда,
когда выполняются следующие условия:
(1) х* минимизирует L (х; и*) по всем x£S;
(2) ^(х*)>0 для / = 1, ...,
(3) Ujgj(x*)=0 для /=1.. J.
Доказательс1во см. в книге Лэсдона [3, гл. 1).
Условие (1) теоремы 5.5 связано с нахождением точки безуслов-
ного минимума функции; при этом можно использовать какой-либо
из методов прямого поиска, изложенных в гл. 3, если, разумеется,
значение и* априори известно. Для одновременного определения
значений и* их*, удовлетворяющих также требованиям (2) и (3),
можно воспользоваться методом проб и ошибок. Один из методов
такого рода, разработанный Эвереттом [4], носит название обоб-
щенного метода множителей Лагранжа. Теоремы 5.3 и 5.5 лежат
в основе многих релаксационных методов лагранжевского типа,
ориентированных на решение задач нелинейного программирова-
ния большой размерности [31. Важно отметить, что существование
седловых точек характерно не для всех задач нелинейного програм-
мирования; седловые точки имеются лишь в тех задачах, которые
отвечают условиям теоремы 5.4.
5.7. Условия оптимальности второго порядка
В разд. 5.4—5.6 рассматривались необходимые и достаточные
условия первого порядка, называемые условиями Куна — Так-
кера. Эти условия применимы к задачам условной оптимизации и
формулируются через градиенты целевой функции и функций, вхо-
дящих в ограничения. Необходимые и достаточные условия оп-
тимальности второго порядка для задач с дважды дифференцируе-
мыми функциями были построены Мак-Кормиком [5]; данный раз-
дел отводится изложению полученных им основных результатов.
Рассмотрим следующую задачу нелинейного программирования.
Задача 31.
Минимизировать / (х)
при ограничениях g/(x)^0, /=!,2,
МА) = 0.
xG
214
ГЛАВА 5
Условия Куна — Таккера первого порядка записываются в следую-
щем виде:
V/(x) — ЧёДх)— (х) = 0, (5 40)
gy(x)>0, /=1......J, (5 41)
hk(x) = 0, k= 1, . . К, (5 42)
Uygy(x)=0, /=1, J, . (5.43)
/=1, ,J- (5.44)
Определения
Точка х соответствует допустимому решению задачи нелиней-
ного программирования, если g/(x)^0 для всех / и hk(x)=0 для
всех k.
Точка х* представляет собой точку локального минимума в за-
даче нелинейного программирования, если х* соответствует допус-
тимому решению и /(х*)^/(х) для всех допустимых х из некоторой
малой окрестности 6(х*) точки х*.
Точка х* представляет собой точку строгого (единственного или
изолированного) локального минимума, если х* соответствует до-
пустимому решению задачи и f (х*)</ (х) для всех допустимых
х=/=х* из некоторой малой окрестности б(х*) точки х*.
Точка Куна — Таккера в задаче нелинейного программирования
определяется вектором (х*, и*, V*), удовлетворяющим соотношениям
(5.40) — (5.44).
Прежде всего обсудим основную идею построения условий
оптимальности второго порядка. В целях упрощения рассмотрим
следующую задачу нелинейного программирования с ограниче-
ниями в виде равенств:
минимизировать /(х)
при ограничениях /ife(x)=0, k=l, 2, ..., К-
Запишем условия Куна — Таккера первого порядка
VfW-S^VAft(x)=0. (5.45)
Пусть точка х удовлетворяет условиям первого порядка. Для того
чтобы проверить, является ли она точкой локального минимума,
воспользуемся разложением в ряд Тейлора каждой из функций f
и hh в точке х
Д/ (х) = f (х + Дх) — f (х) =
= ?/ (х) Дх-|- 1/2^хТ Hz Дх-| О (Дх), (5.46)
Д/1А (х) = hk (х + Дх) — h!t (х) =
= \hk (х) Дх + 1/г ^х1 Hfc Дх + 0 (Дх), (5.47)
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ 215
где через О(Дх) обозначены малые слагаемые более высокого по-
рядка по Дх, Hft — матрица Гессе функции hk(x), вычисленная
в точке х. Умножим равенство (5.47) на множитель Куна — Так-
кера vk и просуммируем по всем fe=l, К. Вычитая полученное
уравнение из (5.46), получаем
Д/ Й)~2Х А/г* (*).= [v/(x) —2 ик Wk (x)j Ax +
+ 1/гЬхт |’H/— Дх + О(Дх). (5.48)
Для того чтобы точка (х+Дх) была допустимой, должно выпол-
няться требование
Д^(х)=0. (5.49)
С учетом предположения о выполнении в точке х условия ли-
нейной независимости из теоремы о необходимости условий Куна —
Таккера следует, что
V/(x) — 2^ W = 0. (5.50)
k
Подстановка выражений (5.49) и (5.50) в (5.48) приводит к урав-
нению
Д/(х) = 1/2Дх^Н/-2^Н^ Дх+О(Дх). (5.51)
Для того чтобы точка х соответствовала локальному минимуму,
необходимо, чтобы неравенство Д/(х)^0 выполнялось для любых
допустимых перемещений Дх в окрестности х. Используя уравне-
ния (5.49) и (5.51), запишем это условие в следующем виде:
Дх^ГН/—2v*HJ Дх>0 (5.52)
L и j
для всех Дх, удовлетворяющих уравнениям
ДЛДх)=0, fe = l, ..., К. (5.53)
Используя формулу (5.47) и пренебрегая членами второго и
более высоких порядков по Дх, преобразуем (5.53) к виду
A/zfe(x)= V/it (x)Ax=0.
Таким образом, с учетом предположения о выполнении в точке х
условия линейной независимости необходимые условия того, чтобы
точка х являлась точкой локального минимума, можно сформули-
ровать следующим образом.
1. Существуют такие множители vh, /е=1, ..., К, что (х, V) есть
точка Куна — Таккера.
216
ГЛАВА 5
2. Неравенство Ах7'[Н/—SvhHfe]Ax>0 выполняется для любых
к
&х, удовлетворяющих уравнениям
V/1& (х)Ах=0, k=\, К.
Аналогично необходимое условие того, чтобы точка х была точкой
строгого локального минимума, задается неравенством
А/(х)>0,
которое должно выполняться для всех допустимых Ах в окрест-
ности точки х. Отсюда следует, что неравенство
Ахг [Н,—Дх>0
должно выполняться для любых Ах, удовлетворяющих уравнениям
yhk (х)Ах=0, k=l, .... К. (5.54)
Обратимся к формальным утверждениям, устанавливающим необ-
ходимые и достаточные условия оптимальности второго порядка
для задач нелинейного программирования с ограничениями в виде
равенств и неравенств.
Теорема 5.6. Необходимые условия оптимальности второго по-
рядка
Рассмотрим задачу нелинейного программирования в виде 3.1.
Пусть f,gwh — дважды дифференцируемые функции, х*— допус-
тимое решение нелинейной задачи, а множество активных в точке
х* ограничений определяется множеством 7= {/lg,(x*)=0}. Далее
предположим, что Vg7(x*) при / £/ и yZife(x*) при Л=1, 2.К
линейно независимы. Тогда необходимые условия того, чтобы точка
х* была точкой локального минимума в задаче нелинейного про-
граммирования, формулируются следующим образом.
1. Существует такой вектор (и*, и*), что вектор (х*, и*, v*) оп-
ределяет точку Куна — Таккера.
2. Для каждого вектора уахю, удовлетворяющего системе урав-
нений
Vg/(x*)y = 0, j£l, (5.55)
Vhk (х*) у = 0, fe=l,2, ...К, (5.56)
выполняется неравенство
yTHL (х*; и*, о*) у > О, где (5.57)
j к
L (х; «, У) = f(x) — 5 ujgj- (х) — 2 vkhk (х),
i-i k=1
a Hz(x*; u*, v*) есть матрица Гессе, образованная значениями вто-
рых частных производных L по х в точке (х*; и*, и*).
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ 21/
Проиллюстрируем теорему 5 6 конкретным примером, в кото-
ром необходимые условия оптимальности первого порядка вы-
полняются, тогда как условия второго порядка показывают, чтс
исследуемая точка не является оптимальной.
Пример 5.7 [5]
Минимизировать f(x)=(xi—1)2+х2
при ограничении gi(x) =—Xj+x^O.
Предположим, что требуется проверить, является ли точка х* =
= (0, 0) точкой оптимума.
Решение
V/(x) = [2(Xi—1), 2х2],
VgiW=(-l, 2хг), /={!}
Так как Vgi(x*) = (—1, 0), условие линейной независимости в точ-
ке х* выполняется. Запишем условия Куна — Таккера первого
порядка:
2 (хх—1)4-и1=0,
2х2—2хд/1=0,
Mi (—Xi+x|)=0, «!>().
Точка х* = (0, 0) и Uj=2 удовлетворяет приведенным выше усло-
виям Следовательно, (х*; «*)=(0, 0, 2) — точка Куна — Так-
кера, т. е. х* удовлетворяет необходимым условиям оптимальности
первого порядка, которые установлены теоремой 5.J. Другими сло-
вами, без дополнительного исследования невозможно сделать вы-
вод о том, соответствует ли точка (0,0) оптимальному решению за-
дачи нелинейного программирования.
Для того чтобы проверить, является ли (0, 0) точкой локаль-
ного минимума в данной задаче нелинейного программирования,
воспользуемся необходимыми условиями оптимальности второго
порядка. Первая часть утверждения теоремы 5.6 выполняется,
так как (х*; и*) — точка Куна — Таккера. Завершая проверку
условий второго порядка, вычислим матрицу
14 / .Г2 0 1
НДх;и) = ^0 2-2uJ- 0ТКУда
Ht(x*,«*) = [o __4 .
Требуется проверить выполнение неравенства
Т Г2 °]
У [о —4]У>0
для всех у, удовлетворяющих уравнению
f Ui\
Vgi (**) у = 0 или (—1,0) ( , = 0.
218
ГЛАВА 5
Другими словами, неравенство (5.57) необходимо рассмотреть
только для векторов (ih, у2) вида (0, у2). Имеем
/о Г2 °1Г°
[о —4] [z/2
= —4y2i < О ПРИ
всех
Таким образом, точка х*=(0, 0) не удовлетворяет необходимым
условиям оптимальности второго порядка и, следовательно, не
является точкой локального минимума в задаче нелинейного про-
граммирования.
Достаточные условия
Если некоторая точка удовлетворяет необходимым условиям
второго порядка, сформулированным в теореме 5 6, то она оказы-
вается точкой Куна — Таккера и может рассматриваться как воз-
можная точка локального минимума. Для того чтобы окончательно
подтвердить факт соответствия этой точки минимуму, следует вос-
пользоваться достаточными условиями оптимальности второго по-
рядка. Разумеется, в тех случаях, когда нелинейная задача удов-
летворяет предположениям теоремы 5.2 (теоремы о достаточности
условий Куна — Таккера) точка Куна — Таккера автоматически
является точкой глобального минимума. Однако, согласно теореме
5.2, целевая функция должна быть выпуклой, а функции, входящие
в ограничения в виде неравенств и равенств, должны быть вогну-
тыми и линейными соответственно. Эти предположения являются
весьма жесткими и не выполняются для ряда возникающих на прак-
тике задач оптимизации. В таких случаях полезными оказываются
достаточные условия второго порядка, при выполнении которых
точка Куна — Таккера является точкой локального минимума.
Теорема 5.7. Достаточные условия оптимальности второго по-
рядка
Достаточные условия того, чтобы точка х* была точкой стро-
гого локального минимума в задаче нелинейного программирования
вида 31, где f, g, и hk — дважды дифференцируемые функции, фор-
мулируются следующим образом.
1. Существует такой вектор (и*, и*), что вектор (х*; и*, и*) оп-
ределяет точку Куна — Таккера.
2. Для каждого ненулевого вектора yaxN>, удовлетворяющего
системе уравнений и неравенств
Vg/(^*)^ = O, /€/. = {/|g/(x*) = 0, ы,->0}, (5.58)
Vg/(x*)y>0, /e/2={J|g,(x*) = 0, u* = 0}, (5.59)
\hk (x*) у == 0, k = 1,2, . . ., К, f/7^0, (5.60)
выполняется неравенство
yrHL (х"; и*, v*) у > 0.
(5.61)
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ 214
Примечание. Множество /=/ill/2 содержит номера всех ак-
тивных в точке х* ограничений.
Сравнивая теоремы 5.6 и 5.7, нетрудно заметить, что достаточ-
ные условия лишь немногим отличаются от необходимых условий
и не требуют выполнения дополнительных предположений о свой-
ствах функций. Основное различие заключается в том, что уравне-
ние (5.55) не должно выполняться для всех активных ограничений,
а неравенство (5.57) превращается в строгое неравенство.
Замечание
В ограничениях на вектор у, налагаемых с помощью формул
(5.58) и (5.59), учитывается величина множителя и*. Хан и Манга-
сариан [61 дали эквивалентную формулировку теоремы 5.7 без ис-
пользования множителя Куна—Таккера и*. Они показали, что
формулы (5.58) и (5.59) эквивалентны следующим неравенствам:
V/(x* )«<(),
Vgj(**)l/>0 для / с /= {/lg/(x*)=0}.
Ниже приводится пример использования достаточных условий
оптимальности второго порядка.
Пример 5.8
Минимизировать /г(х)=(х1—1)2+х2
при ограничении gi(x)=—Xi+(х2/5)^0.
Данная задача незначительно отличается от задачи из примера 5.7.
Предположим, что требуется проверить, будет ли точка х* = (0, 0)
точкой локального минимума. Заметим, что область S = {xlgi
^0} не является выпуклым множеством. Например, точка (0,2, 0),
расположенная между двумя допустимыми точками (0,2, 1) и (0,2,
—1), не принадлежит допустимой области.
Запишем условия Куна — Таккера для данной задачи;
2 (л-д — 1) + = 0,
2х2— = 0,
«1 [—ATi + (л:2/б)] = о, «!>0.
Точка х* = (0, 0), и, =2 удовлетворяет условиям Куна — Так-
кера. Согласно теореме 5.1, можно сделать вывод, что х*=(0, 0)
удовлетворяет необходимым условиям наличия минимума. Однако
нельзя утверждать, что х*— точка локального минимума, посколь-
ку функция gi(x) в нарушение предположений теоремы 5.2 (о до-
статочности условий Куна — Таккера) является выпуклой.
Используя достаточные условия второго порядка, найдем мат-
рицу
Г2 0 1
HL(x*;u*) = ^0 12|.
Вектор y=(yt, у2), удовлетворяющий условиям (5.58) и (5.59), как
и в примере 5.8, записывается в виде (0, у2). Неравенство (5.61)
220
ГЛАВА Б
принимает вид
Г2
(°. У*) [ о
при всех г/2=#0.
Таким образом, по теореме 5.7 х*=(0, 0) — точка строгого локаль
ного минимума.
Фиакко [7] обобщил теорему 5.7 и построил достаточные услови:
наличия слабого (нестрогого) минимума.
5.8. Заключение
В данной главе рассмотрены необходимые и достаточные условия
оптимальности для задач условной оптимизации. Изложение нача-
лось с обсуждения условий оптимальности Лагранжа для заца^
с ограничениями в виде равенств. Затем были введены в рассмотре-
ние ограничения в виде неравенств и построены условия оптималь-
ности Куна — Таккера, т. е. условия первого порядка, исполь-
зующие градиенты целевой функции и функций, входящих в огра-
ничения.
Показано, что условия Куна — Таккера являются необходи-
мыми, если соответствующие функции дифференцируемы, а огра-
ничения удовлетворяют некоторому условию регулярности, из-
вестному под названием условия линейной независимости. Усло-
вия Куна — Таккера становятся достаточными условиями наличия
глобального минимума, если целевая функция выпуклая, ограни-
чения-неравенства образованы вогнутыми функциями, а ограниче;
ния в виде равенств содержат линейные функции. Рассмотрены
также условия оптимальности, связанные с существованием седло-
вых точек функции Лагранжа. Эти условия применяются для ис-
следования недифференцируемых функций.
В случаях когда необходимые условия Куна — Таккера вы-
полняются в нескольких точках, следует воспользоваться необхо-
димыми условиями второго порядка, которым должна удовлетво-
рять точка локального минимума. Отметим также, что достаточные
условия Куна — Таккера выполняются при весьма жестких пред-
положениях. В связи с этим рассмотрены достаточные условия вто-
рого порядка, формулировка которых не требует предположений
о выпуклости и вогнутости соответствующих функций и о линей-
ности ограничений-равенств. Как необходимые, так и достаточные
условия оптимальности второго порядка дополняют условия Ку-
на — Таккера и, следовательно, оказываются полезными при су-
жении множества возможных точек оптимума.
Контрольные вопросы и задачи
5.1. Поясните трудности, которые возникают при использовании
метода множителей Лагранжа для решения задач с неотри-
цательными переменными.
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ 221
5.2. В чем состоит значение условия регулярности допустимой
области?
5.3. Что такое седловая точка? Какую роль играет решение за-
дачи о седловой точке в условной оптимизации?
5.4. При выполнении каких условий существуют седловые точки
в задачах нелинейного программирования?
5.5. Укажите основные направления использования необходимых
и достаточных условий оптимальности второго порядка.
5.6. Рассматривается задача минимизации функции f(x) в допус-
тимой области S. Пусть v/(x)=/=0 для всех xgS. Что можно
сказать о свойствах оптимального решения этой задачи?
5.7. С помощью метода множителей Лагранжа решите следующую
задачу:
минимизировать z=xj+xl+xj
при ограничениях х1+2х2+Зх3=7,
2хг-[-2х2-^х3=9/2.
Объясните (двумя или тремя способами), почему указанный
метод обеспечивает получение оптимального решения.
5.8. Примените метод множителей Лагранжа для нахождения то-
чек глобального минимума и глобального максимума функ-
ции
/(%)=Х2--*1
при ограничении х,+х2 = 1.
На знаки xt и х2 ограничения не наложено.
5.9. Найдите кратчайшее расстояние от точки (1, 0) до параболы
у2=4х:
(а) путем исключения переменной у;
(б) с помощью метода множителей Лагранжа.
Объясните, почему процедура (б) в отличие от процедуры
(а) приводит к получению решения задачи.
5.10. Дана следующая задача:
минимизировать f (х) = (xj—3)2+ (х2+4)2+с5а:«
при ограничениях Xi+x2+x:3^l,
Хъ х2, х3>0.
(а) Запишите условия Куна — Таккера для этой задачи.
(б) Покажите, что выполнение условий Куна — Таккера
оказывается достаточным для существования оптималь-
ного решения данной задачи.
(в) Используя результаты пп. (а) и (б), докажите, что х=
= (1, 0, 0) есть точка оптимума.
5.11. Рассмотрите следующую задачу нелинейного программиро-
вания:
минимизировать Z=Xi+2x22
при ограничениях х?+*г^5,
2xi—2х2=1.
222
ГЛАВА 5
(а) Сформулируйте эквивалентную задачу Куна — Таккера.
(б) Используя результат и. (а), сделайте выводы о следующих
решениях задачи: (1) х(1)=(0, 0); (2)х(2)=(1, 1/2); (3) х(3> =
=(1/3, —1/6). Проверьте сделанные выводы. Дайте ссылку
на какую-либо теорему, которая подтверждает ваши
выводы.
5.12. Рассмотрите задачу нелинейного программирования, в ко-
торой требуется
минимизировать /(х) = 1—2xi—4xjX2
при ограничениях х1+4х1х2^4,
Xi^O, х2^0.
(а) Покажите, что допустимая область в данной задаче не-
линейного программирования не является выпуклым
множеством.
(б) Запишите условия Куна'—Таккера для данной задачи
нелинейного программирования.
(в) Положите </i=xt и у2=Х1Х2. Запишите данную задачу
через переменные (t/i, у2). К какому классу задач матема-
тического программирования принадлежит полученная
задача? Покажите, что допустимая область в преобразо-
ванной задаче оказывается выпуклым множеством. Ре-
шите преобразованную задачу и найдите оптимальные зна-
чения (f/j, у2). Вычислите соответствующие значения (хь
х2).
(г) Докажите, что в точке х выполняется условие линейной
независимости (покажите это аналитически).
(д) Используя теорему о необходимости условий Куна —
Таккера, докажите, что х представляет возможную точку
оптимума.
(е) Оказываются ли условия Куна — Таккера достаточными
для того, чтобы показать, что х доставляет оптимальное
решение задачи нелинейного программирования? Почему?
Объясните.
5.13. Рассмотрите следующую задачу нелинейного программиро-
вания:
максимизировать г=а1х1-\-х2
при ограничениях х?+х2^25,
Xi—х2^1, Xj>0, х2^0.
(а) Запишите условия Куна — Таккера.
(б) Покажите, что условия Куна — Таккера являются необ-
ходимыми и достаточными.
(в) Используя результат п. (б), определите область значений
й1, для которой решение Xi—4, х2—3 оптимально.
КРИТЕРИИ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ 223
5.14. (а) В чем заключается практическое значение (1) теоремы
о необходимости условий Куна — Таккера и (2) теоремы
о достаточности условий Куна — Таккера? Объясните,
какие предположения положены в основу применения
этих теорем.
(б) Сформулируйте условия Куна— Таккера для следующей
задачи, а затем упростите их и запишите в окончательном
виде.
Максимизировать z=3x?—2х2
при ограничениях 2хг-}-х2=4,
х?+х£С40,
На знак хг не наложено ограничение.
5.15. Рассмотрите следующую задачу нелинейного программиро-
вания:
Л'
максимизировать г = 2 xj
N ?
при ограничениях gCD,
х.-^О для всех значений /,
где Kj и D — положительные постоянные.
(а) Запишите условия Куна — Таккера.
(б) Покажите, что решение системы, образованной усло-
виями Куна — Таккера, является оптимальным реше-
нием задачи нелинейного программирования.
(в) Пользуясь результатом п. (б), найдите оптимальное ре-
шение задачи нелинейного программирования.
5.16. Дана следующая задача-
минимизировать ^(х)=х]+х|
при ограничении (Xj—1)’—х2=0.
(а) Покажите графически, что оптимальное решение имеет
место при Xi = l, х2=0.
(б) Примените метод множителей Лагранжа к решению дан-
ной задачи. Объясните, почему этот метод не приводит
к успеху.
5.17. Дана задача нелинейного программирования, аналогичная
задаче 5.6. Проверьте, выполняются ли необходимые и доста-
точные условия оптимальности второго порядка в возмож-
ной точке оптимума х.
5.18. Рассмотрите следующую задачу нелинейного программиро-
вания:
минимизировать f (х) = 0,2х^/а 4-0,05х2—3Xj—5х2
при ограничении 0,9х1+0,5х2 = 100.
224
ГЛАВА 5
Пользуясь условиями Куна — Таккера и условиями опти-
мальности второго порядка, проведите анализ следующих
точек:
(а) xt=l0l,94, х2=16,508;
(б) Xi=84,l, х2=48,62;
(в) Xi = l 11,111, х2=0;
(г) Xi=0, х2=200.
Примечание. Функция f не является выпуклой.
Литература
1 . Bazaraa М. S., Shetty С. М., Nonlinear Programming' Theory and Algorithms,
Wiley, N. Y., 1979 [Имеется перевод: Базара M., Шетти К. Нелинейное про-
граммирование Теория и алгоритмы.— М.: Мир, 1982 t
2 Mangasarian О. L., Nonlinear Programming, McGraw-Hill, N. Y., 1969.
3 . Lasdon L. S., Optimization Theory for Large Systems, Macmillan, N Y., 1979.
[Имеется перевод первого издания' Лэсдои Л. С. Оптимизация больших си-
стем.— М.. Наука, 1975.1
4 Everett Н , Generalized Lagrange Multiplier Method for Solving Problems of
Optimum Allocation of Resources, Oper lies., 11, 399—471 (1963)
5 McCormick G P., Second Order Conditions for Constrained Optima, ,57/144 J.
Appl. Math, 15, 641—652 (1967).
6 Han S. P., Mangasarian O. L., Exact Penalty Functions in Nonlinear Programming,
Math. Programming, 17, 251—269 (1979).
7 Fiacco A V , Second Order Sufficient Conditions for Weak and Strict Constrained
Minima, S/M J. Appl. Math., 16, 105—108 (1968).
Глава 6
Методы оптимизации на основе
преобразования задачи
В этой главе начинается рассмотрение методов решения задач
нелинейного программирования следующего вида:
минимизировать / (х), x£RN, (6.1)
при ограничениях gj (х) > 0, /=1,2,3...J, (6.2)
ЛЛ(х) = 0, 6=1,2, 3, ..., К, (6.3)
х!(> < Х( *7', t= 1,2,3, ..., N. (6 4)
Предполагается, что для вектора х*, являющегося решением этой
задачи, известно некоторое начальное приближение х101, возможно
недопустимое, т. е. не удовлетворяющее соотношениям (6.2) — (6.4).
С помощью рассматриваемых далее алгоритмов в пространстве
RN строится конечная последовательность точек х‘п, /=0, 1, ....
Т, которая начинается с заданной точки х(01 и заканчивается точ-
кой хт, дающей наилучшее приближение к х* среди всех точек
построенной последовательности. В качестве x(tl, 1=1, 2, 3, ..., Т,
берутся стационарные точки так называемой штрафной функции —
целевой функции вспомогательной задачи безусловной минимиза-
ции. С помощью штрафной функции исходная задача условной
минимизации преобразуется в последовательность задач безуслов-
ной минимизации. Конкретные методы, основанные на указанной
общей схеме, определяются видом штрафной функции, а также пра-
вилами, по которым производится пересчет штрафных параметров
по окончании очередного цикла безусловной минимизации. Штраф-
ная функция, позволяющая ограничиться решением лишь одной
задачи безусловной минимизации, называется точной.
Условия оптимальности, установленные в предыдущей главе,
составляют основу рассматриваемых методов и дают аппарат для
их исследования. В том, что вспомогательные функции, учитываю-
щие ограничения, бывают полезны, можно убедиться хотя бы на
примере функции Лагранжа. Эта функция, во-первых, позволяет
дать удобную формулировку условий оптимальности (см. гл. 5).
Во-вторых, функция Лагранжа используется в ряде методов, на-
пример в известном методе Эверетта [1], в котором безусловная
минимизация чередуется с последовательным оцениванием множи-
3 № 1826
226
ГЛАВА 6
телей Лагранжа. Известно, что это оценивание сопряжено с опре-
деленными трудностями вычислительного характера. Тем не менее
указанные факты наталкивают на мысль использовать безусловную
минимизацию вспомогательных функций с учетом ограничений для
итеративного отыскания точки условного минимума. Идея преоб-
разования задачи с ограничениями в надлежащим образом пост-
роенную последовательность задач без ограничений представляется
заманчивой главным образом в связи с наличием эффективных и
надежных методов безусловной минимизации. При этом, конечно,
мы надеемся отыскать условный минимум с приемлемой точностью
путем решения относительно небольшого числа не слишком слож-
ных подзадач.
Методы штрафных функций классифицируются в соответствии
со способами учета ограничений-неравенств, поскольку ограниче-
ния-равенства учитываются во всех методах более или менее оди-
наково. В зависимости от того, являются ли элементы последова-
тельности хг допустимыми или недопустимыми точками, говорят
о методах внутренней или внешней точки соответственно. Если х*
содержит точки обоих типов, метод называют смешанным.
6.1. Понятие штрафной функции
Штрафная функция определяется выражением
Р(х, fl)=f(x)+Q(/?, g(x), h(x)), (6.5)
где R — набор штрафных параметров, а так называемый штраф Q
является функцией R и функций, задающих ограничения. Как уже
отмечалось, методы штрафных функций классифицируются в соот-
ветствии со способами учета ограничений-неравенств. В любом слу-
чае, однако, С определяется так, чтобы допустимые точки задачи
имели преимущество перед недопустимыми в отношении безуслов-
ной минимизации штрафной функции. Методы внутренней точки
связаны с такими й, при которых стационарные точки функции
Р(х, R) оказываются заведомо допустимыми. Эти методы называют
также методами барьеров, поскольку здесь штраф как бы создает
вдоль границы допустимой области барьер из бесконечно больших
значений функции Р. Очевидно, любой метод, основанный на пре-
образовании задачи условной минимизации в последовательность
подзадач безусловной минимизации, может представлять интерес
лишь при выполнении следующих требований.
1. Решения подзадач должны стремиться к решению исходной
задачи нелинейного программирования: Пт х(/)=х*.
2. Сложность минимизации Р (х, R) должна быть того же по-
рядка, что и для функции /(х). Даже при наличии исчерпывающего
теоретического обоснования сходимости метод будет не особенна
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 227
полезен, если подзадачи безусловной минимизации с чрезвычайно
большим трудом поддаются решению.
3. Правило пересчета 7?u+l) = F (R<ty) должно быть простым.
В самом деле, естественно требовать, чтобы объем вычислений,
связанных с пересчетом штрафных параметров, был мал по сравне-
нию с объемом вычислений, затрачиваемым на решение подзадач
безусловной минимизации. (Примечание. В действительности такая
точка зрения спорна, если функции, входящие в задачу, сложны.
В этом случае большие усилия, затрачиваемые на пересчет штраф-
ных параметров, могут оказаться оправданными.)
6.1.1. Основные типы штрафов
В этом разделе описываются широко используемые типы штрафов
и различные процедуры учета ограничений при переходе к задачам
безусловной минимизации. Прежде всего рассмотрим квадратичный
штраф, используемый для учета ограничений-равенств (рис. 6.1):
fi=R{/i(x)}2. (6.6)
При минимизации этот штраф препятствует отклонению величины
h(x) от нуля (как в сторону положительных, так и в сторону отри-
цательных значений). Легко видеть, что при увеличении R стацио-
нарная точка соответствующей штрафной функции Р(х, R) приб-
лижается к х*, поскольку в пределе h (х(Г|)=0. Отметим, что в дан-
ном случае Q непрерывна и имеет непрерывные производные.
Рио. 6.1. Квадратичный штраф.
Переходя к ограничениям-неравенствам, рассмотрим несколько
различных типов штрафа. По-видимому, простейшим среди них
является бесконечный барьер, изображенный на рис. 6.2. Соответ-
ствующее выражение принимает бесконечно большие значения в не-
допустимых точках и нулевое значение в допусичмых точках.
О А
228
ГЛАВА 6
В данном случае штрафная функция Р (х, R) разрывна (и, разуме-
ется, недифференцируема) на границе допустимой области. Строго
говоря, машинная реализация бесконечных штрафов невозможна,
однако можно в качестве «бесконечности» использовать большое
положительное число, допускающее запись в имеющейся ЭВМ.
я
----------- + 03
-------о|--------------------- дМ
Рис. 6.2. Бесконечный барьер.
В 12, 3] (см. также [4]) этот штраф использовался в форме
£2= Ю20 (6-7)
/ е J
где J — множество индексов нарушенных ограничений, т. е.
£у(х)<0 при j£J. (6.8)
Другим широко используемым типом штрафа является логариф-
мический штраф (рис. 6.3):
Q——R In lg(x)J. (6.9)
Рис. 6.3. Логарифмический штраф.
Этот штраф положителен при всех х, таких, что 0<Zg(х)< 1, и от-
рицателен при g(x)>l. В данном случае как бы вводится искус-
ственная дискриминация точек допустимой области: внутренним
точкам отдается предпочтение перед граничными точками. Отрица-
тельных значений штрафа можно было бы избежать, положив Й=С
для х, таких, что£(х)>1, однако при этом у градиента ГР появи-
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 229
лись бы разрывы в прилегающей к границе части допустимой об-
ласти. Логарифмический штраф — это барьерная функция, не оп-
ределенная в недопустимых точках (т. е. для х, таких, что g(x)<S)).
Поэтому в тех случаях, когда приходится иметь дело с недопусти-
мыми точками (например, когда заданное начальное приближение
х(0' не является допустимым), требуется специальная процедура,
обеспечивающая попадание в допустимую область. Вопреки утверж-
дениям, содержащимся в некоторых работах, недопустимые точки
могут появляться в процессе минимизации барьерной функции, на-
пример как результат слишком большого первого шага при одно-
мерном поиске. В связи с этим должны быть предусмотрены спе-
циальные меры по предотвращению подобной ситуации либо ее
обнаружению и устранению. Итерационный процесс начинается
Рис. 6.4. Штраф, задаваемый обратной функцией.
из допустимой начальной точки при положительном начальном
значении R (скажем, при /? = 10 или /? = 100). После решения каж-
дой подзадачи безусловной минимизации параметр R уменьшается
и в пределе стремится к нулю.
Штраф, заданный обратной функцией (рис. 6.4),
Q=R [l/g(x)] (6.10)
не имеет отрицательных значений в допустимой области. Этот
штраф, как и предыдущий, является барьером; в этом случае также
возникают трудности, связанные с появлением недопустимых точек.
Необходимость предотвращения этой ситуации очевидна, поскольку
в недопустимых точках штраф принимает отрицательные значения.
В допустимых точках вблизи границы значения штрафа положи-
тельны и быстро убывают при продолжении от границы внутрь до-
пустимой области. На самой границе Р(х, R) и VP не определены.
Итерации начинаются с начальной допустимой точки при положи-
230
ГЛАВА 6
тельном значении /?, причем в процессе вычислений в пределе
стремится к нулю.
Рассмотрим, наконец, штраф типа
квадрата срезки (рис. 6.5):
Я = R <g (х)>2,
I а, если
<а> = < о
( 0, если
где
а С) 0,
а > 0.
(6.Н)
(6-12)
Заметим прежде всего, что этот штраф внешний, и стационарные
точки функции Р(х, R) действительно могут оказаться недопус-
тимыми. С другой стороны, недопустимые точки не создают в дан-
ном случае дополнительных сложностей по сравнению с допусти-
мыми: различие между ними состоит лишь в том, что в допустимых
Рис. 6.5. Штраф типа квадрата срезки.
и граничных точках штраф равен нулю. Штраф типа квадрата срезки
весьма удобен, в частности, тем, что функция Р(х, R) определена
и непрерывна всюду. Вычисления проводятся с положительным R;
после решения очередной подзадачи безусловной минимизации R
увеличивается. Приведем несколько простых примеров использо-
вания рассмотренных штрафов.
Пример 6.1. (Квадратичный штраф)
Рассмотрим задачу:
минимизировать f(х)=(Х]—4)2+(х2—4)2
при ограничении /i(x)=Xj+x2—5=0.
Используя квадратичный штраф, введем штрафную функциюг)
Р(х, /?) = (xL—4)2+(х2—4)2+(1//?)(х1+х2—5)2. (6.13)
*) Во избежание недоразумений следует иметь в виду, что авторы использу-
ют две формы записи коэффициента при квадратичном штрафе' R [см. (6 6)] и
1/R [см. (6.13)]. В первом случае R в процессе решения устремляют к оо, во вто-
ром— к нулю [см. табл. 6.Ц.— Прим, перев.
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 231
Из уравнений, определяющих стационарную точку функции
Р(х, R),
g = 2(x1-4)+(A)(xl + x.-5)-0,
+ </, +л,_5) -0.
находим координаты этой точки в зависимости от R:
x1=x2=(10+8R)/(4-(-2R). (6.14)
Переходя в этом выражении к пределу, получаем
lira [(10 + 8Я)/(4 + 2Я)]= 10/4 = 2,5. (6.15)
R—► 0
Таким образом, метод сходится к точке х* — [2,5; 2,5]г с /(х) = 4,5,
являющейся решением (рис. 6.6).
Рис. 6 6. Двумерная задача минимизации с ограничениями-равенствами.
В табл. 6.1 приведены координаты стационарных точек штраф-
ной функции Р(х, R) для различных значений R. На рис. 6.7—6 9
представлены линии уровня этой функции при различных значе-
ниях R', видно, что при R -> 0 они сближаются с линиями уровня
функции h(x). Такое изменение формы линий уровня — важный
фактор, непосредственно связанный со сходимостью метода.
Обсудим данный пример подробнее. Рассмотрим стационарную
точку функции Р (х, 1). Эта точка уже довольно близка к х*, а имен-
но х) х1П=[3, 3]т, причем /(х(П)=2 и /i(x(t,) = 1. Во многих при-
В данном случае под х(/> авторы подразумевают стационарную точку функ-
ции Р (х, 1).~Прим, перев.
232
ГЛАВА 6
Таблица 6.1. Координаты стационарных точек
квадратичной функции штрафа
я 1/Я К)
00 0 4,0000 0,0000
10 0,1 3,7500 0,7500
1 1 3,0000 3,0000
0,1 10 2,5714 4,2857
0,01 100 2,5075 4,4776
0 00 2,5000 4,5000
кладных задачах такое приближенное решение может считаться
вполне удовлетворительным, однако в общем случае величина не-
вязки й(х), как правило, неудовлетворительна. Возникает вопрос,
как изменить штрафную функцию, чтобы ее стационарная точка
Рис. 6.7. Линии уровня квадратичной штрафной функции при /?=1.
приблизилась к х*. Заметим, что в точно вычисленной стационар-
ной точке функции Р(х, 1) значение целевой функции /(х) меньше
оптимального из-за нарушения условия h(x)=0. При этом соот-
ношение между значениями / (х) и h (х) связано с величиной R (в дан-
ном случае R — \). По существу R играет роль весового коэффици-
ента, определяющего относительную значимость ограничения и
целевой функции. Ясно, что при уменьшении R стационарная точка
функции Р(х, R) будет смещаться в сторону более точного выпол-
нения ограничения /i(x)=0 и тем самым приближаться к х* (это
Р(х,10) = (х1-4Л(ха-4)г + 10(х,+ хг-5)г
Линии
уровня
А 5,000
В 20,000
С 35,000
□ 50,000
Е 65,000
F 80,000
G 95,000
Н 110,000
I 125,000
J 140,000
Рис. 6.8. Линии уровня квадратичной штрафной функции при /?=10.
Линии
уровня
А 50,000
В 300,000
С 550,000
D 800,000
Е 1050,000
F 1300,000
G 1550,000
Н 1800,000
I 2050,000
J 2300,000
Рис. 6.9. Линии уровня квадратичной штрафной функции при /?=100.
234
ГЛАВА 6
подтверждается, в частности, данными табл. 6.1). По-видимому,
если бы можно было положить 7?=0, точное решение соответствую-
щей подзадачи на безусловный минимум совпало бы с решением
исходной задачи. Выбрать 7? равным нулю, разумеется, нельзя, но
можно взять его достаточно малым. Вопрос теперь сводится к тому,
насколько малым должно быть 7?.
Из табл. 6.1 видно, что при R =0,01 точная минимизация штраф-
ной функции позволяет найти решение с двумя верными знаками.
Однако аналитически находить точный минимум удается лишь
в редких случаях, и обычно для безусловной минимизации штраф-
ной функции приходится использовать уже известные методы по-
иска при отсутствии ограничений. Возникает соблазн выбрать сразу
столь малое 7?, чтобы суммарная погрешность, складывающаяся
из отклонения стационарной точки от решения и из погрешности
нахождения этой стационарной точки, не выходила за рамки требо-
ваний к точности. Такое намерение наталкивается, однако, на впол-
не ощутимые трудности, связанные с тем, что форма линий уровня
функции Р(х, R) зависит от R. Вследствие того что линии уровня
штрафной функции с уменьшением R становятся все более вытяну-
тыми, сложность безусловной минимизации резко возрастает. По-
этому более предпочтительной становится стратегия многоэтапного
последовательного приближения к решению, состоящая в следую-
щем. Начав с относительно большого R, например с R = 100, находят
точку минимума функции Р (х, 100). Затем уменьшают R, например,
до 10 и находят точку минимума функции Р (х, 10), используя ранее
полученную точку в качестве начальной. R уменьшают до тех пор,
пока не окажется, что элементы итерационных последовательностей
х(/>, /(х(/>), а также Р(х(П, R) изменяются от шага к шагу достаточ-
но мало. Применяя подобную стратегию, рассчитывают на то, что
всякий раз близость вновь определяемой точки безусловного мини-
мума к предыдущей, используемой в качестве начальной, послужит
компенсацией за возрастание сложности минимизации, обуслов-
ленное уменьшением R. В действительности так и бывает, если R
уменьшается достаточно медленно. Однако в последнем случае уве-
личивается число итераций, и общее время, затрачиваемое на полу-
чение решения, нередко оказывается весьма большим. В этом и
состоит основная трудность, присущая методу штрафных функций.
Немало усилий было затрачено на поиск таких правил пересчета
R, которые обеспечивали бы эффективность вычислительного про-
цесса в целом.
Рассмотрим теперь штрафы, учитывающие ограничения в форме
неравенств. В этом случае возникают примерно те же трудности,
что и в случае ограничений-равенств.
Пример 6.2. (Штрафы, учитывающие ограничения-неравенства)
Заменим ограничение-равенство задачи из примера 6.1 на
неравенство
g (х) =5—Xi—х2>0.
(6.16)
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 235
При этом решение х* задачи останется прежним. Для полученной
задачи запишем штрафную функцию, наиболее близкую к той, ко-
торая рассматривалась в случае ограничения-равенства, т. е.
используем штраф типа квадрата срезки. Имеем
Р(х, R)=f (x)+R<g(x)>2 (6.17)
или в данном случае
Р(х, /?) = (х1-4)2+(х2—4)2+7?<5-х1—х2>2. (6.18)
Уравнения, определяющие стационарную точку функции, имеют
вид
|| = 2(х1-4)-|-2/?<5-х1-х2> (-1) = 0,
-|^ = 2(х2—4)4-2Я<5—хг—х2> (—1) = 0,
откуда, подобно предыдущему, следует
xt=x2. (6.19)
С учетом этого получаем
(хх—4)—/?<5—2xi>=0. (6.20)
Предположим, что аргумент оператора срезки равен нулю,
больше или меньше нуля, и проанализируем результаты. В частно-
сти, положив 2X1^5, будем иметь
(Xi—4)—R (5—2xi)=0
или, что то же самое,
х1=(5Д4 4)/(2Д+1). , (6.21)
Отсюда lim Xi—2,5 (сделанное предположение при этом не нару-
Я-.-0
шается). Следовательно, стационарная точка функции Р(х, 1) имеет
вид х(/)=[3, 31г, причем /(х(/,)=2, g-(x</f)=—1 и Р(х, 1)=3. При
изменении R от 0 до оо стационарная точка функции Р(х, R) пере-
мещается вдоль отрезка прямой, соединяющего точку [4,4]гбезуслов-
ного минимума функции /(х) с точкой [2,5; 2,5]г ее условного мини-
мума. При любом (конечном) R соответствующая стационарная
точка недопустима, так что мы действительно имеем дело с методом
внешней точки.
Сопоставляя формулы (6.21) с (6.15), видим, что при использо-
вании квадратичного штрафа и штрафа типа квадрата срезки траек-
тория движения к решению задачи одна и та же (в предположении,
что штрафная функция минимизируется точно). На рис. 6.10—6.12
изображены линии уровня функции Р(х, R) при /? = 1, 10 и 100
соответственно.
Используем теперь применительно к той же задаче с ограниче-
нием-неравенством логарифмический штраф, т. е. положим
Р(х, R)=f(x)-R In [gr(x)J, (6.22)
236
ГЛАВА 6
Рис. 6.10. Линии уровня штрафной функции со штрафом типа квадрата срезки
при 7?=1.
или в данном случае
Р(х, 7?) = (х1—4)2—R In (5—Xi—х2). (6.23)
Условия стационарности принимают вид
^=2и,_4)+Л[5_!_ ]=о,
g-=:2(x2-4) + K t-J-x И0’
откуда jq—Xj.
С учетом этого имеем
2(х,—4)+[/?/(5—2x01=0. (6.24)
Отсюда приходим к уравнению
2х2—13х,+20—(/?/2)=0, (6.25)
один из корней которого дает координату искомой стационарной
1 очки:
х, = “/4 — */« К9+ 4/? (6.26)
(второй корень соответствует недопустимой точке и поэтому должен
быть отброшен). Устремляя 7? к нулю, получаем в пределе
х‘'> = х7’= lim х1(7?) = 2,5, /(х(1’)=4,5.
Я-++0
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 237
Линии
уровня
А
в
с
□
Е
F
G
Н
)
3,500
8,500
9,500
12,500
15,500
18,500
21,500
24,500
27,500
50,500
Рис. 6.11. Линии уровня штрафной функции со штрафом типа квадрата срезки
при 7?=10.
Линии
уровня
А 3,500
В 6,500
С 9,500
□ 12,500
Е 15,500
F 18,500
G 21,500
Н 24,500
I 27,500
J 30,500
Рис. 6.12. Линии уровня штрафной функции со штрафом типа квадрата срезка
при 7?=100.
23b
ГЛАВА 6
Таблица 6.2. Координаты стационарных точек логарифмического
штрафа
R *1 = /(х) Д(х) ?(х, Д)
100 -1,8059 67,4170 8,6118 -215,3133 -147,8963
10 1,5000 12,5000 2,0000 -6,9315 5,5685
1 2,3486 5,4542 0,3028 +1,1947 6,6489
0,1 2,4835 4,5995 0,0034 + 0,3411 4,9406
0,01 2.4983 4,5100 0,0034 т 0,0568 4,5668
0 2,5000 4,5000 0.0000 0,0000 4,5000
Опять, как и в предыдущих случаях, метод оказывается сходящим-
ся по крайней мере в предположении, что безусловная минимизация
проводится точно. В табл. 6.2 приведены координаты стационарных
Х8
Р(х, R] =(х,-4)2+(хг-4) -100 1п(5-х,-х2]
Линии
уровня
А -100,000
В - 70,000
С -40,000
О -10,000
Е 20,000
F 50,000
G 80,000
Н 110,000
I 140,000
J 170,000
Х1
Рис. 6.13. Линии уровня логарифмической штрафной функции при 7?=Ю0.
точек функции Р(х, R) для различных значений R, а на рис. 6.13—
6.15 показано, как зависят от R линии уровня этой функции. Как
видно из табл. 6.2, значения Р (х(/), R) изменяются немонотонно:
сначала они возрастают, а затем убывают. Этот эффект связан с на-
личием у логарифмического штрафа отрицательных значений.
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ
Р(х,10)=(х,-41+(х2~4)-101п [5-х,-х4]-
Линии
уровня
А 9,000
В 10,000
С 11,000
□ 12,000
Е 13,000
F 14,000
G 15,000
Н 16,000
I 17,000
J 18,000
Х1
Рис. 6 14 Линии уровня логарифмической штрафной функции при 7?=К
Линии
УРОВНЯ
А 9,000
В 10,000
С 11,000
D 12,000
Е 13,000
F 14,000
G 15,000
Н 16,000
I 17,000
J 18,000
Рис. 6.15. Линии уровня логарифмической штрафной функции при 7?=1.
240
ГЛАВА 6
Наконец, применим штраф, задаваемый обратной функцией.
Имеем
Р(х, R) = f(x) + R [-J^] , (6.27)
или в данном случае
Р(х, R) = (Х1-4^+ (хг-4Г + /? [5^_ J • (б-28)
Исследуем стационарные точки функции Р(х, R) при различных
значениях R
= 2 — 4) + [(5_Х1_Х2)2] = 0,
^=2 (х2—4) + Г-=-----5---?21 = О,
дхг 42 ' ' L(5 —*1—*г) J
откуда Xi—x2 и
4х3—36х*+105xj— 100 4- (/?/2) =0. (6.29)
Для определения стационарных точек нужно найти корни полу-
ченного уравнения. В табл. 6.3 приведены координаты стационар-
ных точек функции Р(х, R), полученные при различных значениях
Таблица 6.3. Координаты стационарных точек штрафа,
задаваемого обратной функцией
R х, “ х2 /(х) 8(х) Я/8(х) P(x,R)
100 0,5864 23,3053 3,8272 26,1288 49,4341
10 1,7540 10,0890 1,4920 6,7024 16,7914
1 2,2340 6,2375 0,5320 1,8797 8,1172
0,1 2,4113 5,0479 0,1774 0,5637 5,6116
0,01 2,4714 4,6732 0,0572 0,1748 4,8480
0,001 2,4909 4,5548 0,0182 0,0549 4,6097 ,
0 2,5000 4,5000 0,0000 0,0000 4,5000
R с помощью алгоритма численного отыскания корней [51. На
рис. 6.16—6.18 показаны линии уровня этой функции при различ-
ных R. Опять убеждаемся в том, что точно найденные стационарные
точки штрафной функции сходятся к х* при R 0.
Рассмотренные примеры демонстрируют, с одной стороны,
принципиальную возможность использования традиционных мето-
дов штрафных функций, а с другой стороны — их общие недостатки.
Имеется в виду то отмеченное выше обстоятельство, что сходимость
метода связана со степенью вытянутости линий уровня штрафной
функции, а это в свою очередь увеличивает вероятность того, чтс
используемые методы поиска при отсутствии ограничений окажутся
неэффективными. Напомним, что данное выше описание метода
штрафных функций основывалось на предположении, что все под-
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 241
Рис. 6.16. Линии уровня штрафной функции со штрафом, задаваемым обратной
функцией, при R= 100.
задачи безусловной минимизации могут быть решены с достаточной
точностью. В тех случаях, когда в этом нет уверенности, фактически
ставится под сомнение практическая эффективность метода в целом.
6.1.2. Выбор штрафного параметра
При использовании любой из рассмотренных выше штрафных
функций требуется выбрать начальное значение параметра 7? и из-
менять 7? после решения каждой подзадачи безусловной минимиза-
ции с тем, чтобы обеспечить сходимость последовательности стацио-
нарных точек х<п. Ясно, что 7? следует выбирать так, чтобы при
переходе от одной подзадачи к другой весовые коэффициенты в огра-
ничениях, учитываемых с помощью внешних штрафов (и, вообще
говоря, нарушенных), увеличивались, а весовые коэффициенты
в ограничениях, учитываемых с помощью внутренних (барьерных)
штрафов, уменьшались. При этом необходимо установить, как
именно будет изменяться 7? при переходе от одной подзадачи к дру-
242
ГЛАВА 6
Рис. 6.17. Линии уровня штрафной функции со штрафом, задаваемым обратной
функцией, при /?=10.
гой. Например, для обычного квадратичного штрафа, учитываю-
щего ограничения-равенства, представляется целесообразным на-
чинать с /?=0, т. е. с безусловной минимизации функции f (х), а за-
тем последовательно увеличивать R на некоторое &R либо исполь-
зовать возрастающие степени какого-либо числа (скажем числа 10).
В результате получаемые стационарные точки будут все точнее и
точнее удовлетворять ограничениям. Вычислительные эксперимен-
ты показывают, что точно найденная стационарная точка х(<) (R)
перемещается вдоль некоторой гладкой траектории к точке х*.
В работах (6—9] предлагается аппроксимировать траекторию х<п (Л?),
с тем чтобы использовать точку, полученную с помощью аппрокси-
мации при /?=01), в качестве улучшенного начального приближе-
ния х(<+1> при решении следующей подзадачи безусловной миними-
зации. Конечная цель применения этого приема — максимально
увеличить R. Как показывают численные эксперименты [10], наи-
лучшие результаты дает квадратичная аппроксимация.
См. сноску на стр. 230. — Прим, перев.
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 243
Линии
уровня
А 0,000
В 3,000
С 8,000
D 9,000
Е 12,000
F 15,000
G 18,000
Н 21,000
I 24,000
J 27,000
Рис. 6 18. Линии уровня штрафной функции со штрафом, задаваемым обратной
функцией, при /?=1.
Указанный прием экстраполяции хотя и позволяет несколько
усовершенствовать исходную схему метода штрафных функций, не
может компенсировать, однако, той деформации линий уровня функ-
ции Р(х, R), которая происходит при пересчете R. На самом деле
именно эта деформация и обеспечивает сходимость метода (при точ-
ном решении вспомогательных подзадач). С другой стороны, для
любой из рассмотренных выше штрафных функций пересчет пара-
метра R, имеющий целью обеспечить сходимость метода, автомати-
чески приводит к ухудшению обусловленности вспомогательных
подзадач. Этот факт (легко усматриваемый из приведенных выше
рисунков) отмечается во многих работах, в частности в (11, 12].
Как показано в [12], часть собственных значений матрицы V2P (х, R)
зависит от величины 1/R (их число равно М — числу активных огра-
ничений в х*). При этом обусловленность матрицы V2P(x, R) не-
ограниченно ухудшается, когда R стремится к нулю. Тем самым
становится все труднее решать вспомогательные подзадачи, и пре-
рывание вычислительного процесса может происходить не в резуль-
тате достижения заданной точности, а вследствие того, что исполь-
244
ГЛАВА 6
зуемый метод безусловной минимизации не дает возможности найти
решение очередной подзадачи. Подчеркнем, что указанные труд-
ности имеют вычислительный характер, поскольку в предположе-
нии, что все вычисления ведутся точно, удается теоретически обо-
сновать быструю сходимость метода.
6.2. Алгоритмы и программы
Построение эффективных алгоритмов на основе метода штраф-
ных функций не представляет особых трудностей. Ниже описывается
простейший алгоритм, в котором используется штрафная функция.
Шаг 1. Задать значения /V, J, К, 81, е2, е3, х101 и где
gj— параметр окончания одномерного поиска,
е2— параметр окончания процедуры безусловной минимизации,
е3— параметр окончания работы алгоритма,
х,0>— начальное приближение для х*,
— начальный вектор штрафных параметров.
Ш а г 2. Построить Р(х, /?)=/(х)+й (/?, g(x), й(х)).
Шаг 3. Найти х1,+1), доставляющее минимум функции Р (х<,+1),
при фиксированном В качестве начальной точки исполь-
зовать х1П, а в качестве параметра окончания шага — константу е2.
Ш а г 4. Проверить, выполняется ли условие |/>(х,/+1), —
Р(х'п, В случае если оно выполняется, положить
х1/+1)=х7' и закончить процесс решения; в противном случае
перейти к следующему шагу.
Ш а г 5. Положить в соответствии с ис-
пользуемым правилом пересчета, после чего перейти к шагу 2.
Разумеется, хорошая программа, реализующая подобный алгоритм,
должна быть более разветвленной и включать ряд дополнительных
шагов. Например, при принятии решения об окончании процесса
наряду с последовательностью, указанной на шаге 4, целесообразно
использовать последовательности x<n, P<n, g(xi1r), /i(x<n) и /(х,п).
По-видимому, впервые штрафная функция упоминается в работе
113], однако по существу современный этап развития методов пре-
образования начался с появления «искусственных поверхностей
отклика» 114]. Важное значение имели также работы [7, 15, 161, с ко-
торыми связано создание SUMT — первого комплекса программ для
решения задач нелинейного программирования, нашедшего широ-
кое применение (подробнее об этом будет сказано ниже). Несколько
позже в работе [171, где метод штрафных функций рассматривался
в общем виде, были получены условия сходимости для штрафов
различных типов. По-видимому, наиболее полно метод исследован
в работах [18—20], в которых, в частности, детально проанализиро-
ваны достоинства и недостатки различных штрафов в связи с их по-
ведением на границе допустимой области. Представляет интерес
и проведенное в 121] сравнение метода штрафных функций с другими
методами условной оптимизации. По указанным выше причинам
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 245
следует ожидать возникновения трудностей при использовании того
или иного метода одномерного поиска (гл. 2) для минимизации
функции Р(х, R) вдоль заданного направления, поскольку \Р (х, R)
принимает очень большие значения вблизи границы. Чтобы пре-
одолеть эту трудность, выявленную в ряде работ, в [22] предложен
специальный метод минимизации, ориентированный на штрафные
функции. В рамках настоящего краткого обзора названы лишь не-
которые важнейшие публикации. С гораздо большей полнотой исто-
рия развития метода штрафных функций отражена в работах
[4, 23—27].
Широко используется ряд комплексов программ, основанных
на методе штрафных функций. К ним относятся SUMT и OPTISEP,
краткая характеристика которых дается ниже, а также пакет про-
грамм COMPUTE II фирмы Gulf Oil [29] и пакеты, описанные в [29]
и [30]. Каждый из них предоставляет в распоряжение пользователя
целый набор штрафных функций и методов безусловной оптимиза-
ции. Рекомендации по использованию стандартного набора штраф-
ных функций, вытекающие из сравнительного анализа их свойств,
даны в работе [31]. Наконец, оценить подход в целом помогают раз-
нообразные приложения [32], в частности те из них, которые свя-
заны с применением метода штрафных функций при проектировании
теплосистем [33, 34].
Двумя наиболее широко используемыми пакетами программ,
основанными на методе штрафных функций, являются, по-видимо-
му, SUMT [35] и OPTISEP [31. Соответствующая информация спра-
вочного характера и результаты решения тестовых задач приведены
в [36]. Существуют по крайней мере две версии SUMT: версия 1967 г.,
использующая функцию вида
Р (X, R) = fix) + R £ [ -Lj ] + ± £ [hk (X)]’ (6.30)
7=1 J k=1
и версия 1970 г., основанная на штрафной функции
j к
P(x,R) = f(x)-R^ ln[gz(x)]4-l-S. [М*)]\ (6.31)
7=1 k=1
где положительный штрафной параметр R стремится к нулю, моно-
тонно убывая от итерации к итерации. При решении тестовых задач
в работе [36] (см. гл. 12) использовалась версия 1970 г., известная
как SUMT-IV. В этой версии реализованы четыре различных алго-
ритма, использующие общую штрафную функцию (6.31), но разли-
чающиеся правилами пересчета R и применяемыми методами безу-
словной минимизации. В частности, пользователь может выбрать
процедуру безусловной минимизации с помощью метода градиент-
ного типа, метода ДФП, а также одного или двух вариантов моди-
фицированного метода Ньютона. При этом после решения каждой
246
ГЛАВА 6
вспомогательной подзадачи производится увеличение штрафного
параметра R и, кроме того, используется описанный выше прием
экстраполяции. Чтобы подробнее ознакомиться с этими вопросами,
читатель может обратиться к руководству для пользователей па-
кета SUMT-1V.
Методы штрафных функций, реализованные в пакете OPTISEP,
различаются главным образом применяемыми в них способами бе-
зусловной минимизации. В качестве штрафной функции использу-
ется либо
J к
Р(х,/?) = /(х)+102<- 2\<gj (х)> |+ 1Оао 2 1М*)|. (6-32)
/ = [ k= 1
либо (6.30). Программа SEEK1 работает с (6.32) и использует пря-
мой поиск по методу Хука и Дживса. По окончании работы алго-
ритма в окрестности хт случайным образом выбирается несколько
пробных точек, и, если хотя бы одна из них позволяет уменьшить
значение функции Р(х, R), поиск начинается заново. Программа
SEEK3 работает с (6.30), т. е. со штрафной функцией из SUMT в
версии 1967 г., причем (6.31) применяется для выбора допустимой
начальной точки. И в этом случае вспомогательные подзадачи ре-
шаются методом Хука и Дживса, a R уменьшается при переходе
от одной подзадачи к другой путем умножения на постоянный мно-
житель, меньший единицы. Программа SIMPLX использует (6.30)
в комбинации с методом прямого поиска по симплексу. В программе
DAVID штрафная функция (6.30) минимизируется методом Давидо-
на — Флетчера — Пауэлла, использующим информацию о гради-
енте. Наконец, в программе MEMGRD используется выражение
(6.30), а также градиентный метод с памятью, предложенный Милем;
этот метод является обобщением метода сопряженных градиентов
Флетчера — Ривса. Входные данные для всех программ задаются
в одном и том же формате.
6.3. Метод множителей
Ухудшение обусловленности вспомогательных подзадач в обыч-
ной схеме метода штрафных функций существенно ограничивает
практическую применимость метода; в частности, он не может вы-
держать конкуренцию с методами линеаризации (рассматриваемы-
ми в гл. 8 и 9). В ряде работ (важнейшими из которых являются
[37—42]) предложены непараметрические схемы метода штрафных
функций, явившиеся попыткой хотя бы отчасти поправить поло-
жение.
Особый интерес представляет метод центров Хьюарда, в соот-
ветствии с которым максимизируется функция
j
Р (х, т) = [1 — f (х)] Il gy (х), (6.33)
I = 1
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 247
где т — параметр «отсечки», определяемый для каждой итерации,
т. е. при решении каждой подзадачи. Например, можно задавать
«отсечку» на Ай итерации метода по формуле Tu,=f (хи~и), где
х(,-п— точка безусловного максимума, полученная на предыдущей
итерации. Таким образом, т пересчитывается по ходу вычислитель-
ного процесса. В работе [27] показано, что при этом максимизация
произведения (6.33) эквивалентна минимизации непараметрической
штрафной функции
P(x) = -lnJ/(xl''1’)-/(x) -£lng;(x). (6.34)
Отсюда можно сделать следующий важный вывод (см. [27]): не-
смотря на свою внешнюю привлекательность, непараметрические
методы штрафных функций в точности эквивалентны обычным па-
раметрическим методам (типа SUMT) со специальным правилом
пересчета R. Это вполне согласуется с результатом работы [431,
согласно которому скорость сходимости метода центров примерно
та же, что и у методов типа SUMT.
Привлекая к дальнейшим рассуждениям функцию Лагранжа
L (х, и, и) = f (х) —2 ujSj (х)—2 vkhk (х)' (6.35)
i k
вспомним о той роли, которую играет эта функция в условиях опти-
мальности (см. обсуждение условий Куна — Таккера в гл. 5).
Речь идет о том, что, используя функцию Лагранжа, мы не можем
минимизировать ее по х, и, v с целью получения (х*, и*, V*), по-
скольку указанный вектор является не точкой минимума функции
L, а ее стационарной (более точно, седловой) точкой. Оказывается,
что если определенным образом модифицировать функцию Лагранжа
(например, добавив к ней квадратичное штрафное слагаемое), то
полученная в результате функция будет достигать своего безуслов-
ного минимума в точке Куна — Таккера исходной задачи. Ниже
рассматривается метод модифицированной функции Лагранжа,
называемый также методом множителей, который позволяет избе-
жать той нежелательной деформации поверхностей уровня, которая
свойственна методу штрафных функций.
6.3.1. Штрафная функция
Рассмотрим функцию
P(X,O,T) = f (х) +
J к
+ R 2 {<£7 (X) + оу>2-о?} + R 2 {\hk (х)+<|2-тП, (6 36)
/ — 1 k —1
где R — постоянный весовой (нормирующий) коэффициент (в прин-
ципе R может зависеть от номера ограничения, но не должен зави-
сеть от номера итерации), а угловые скобки означают операцию
248
ГЛАВА 6
срезки, определение которой было дано выше. Параметры о7- и
входящие в (6.36), играют принципиально иную роль, чем /?, осу-
ществляя сдвиг штрафных слагаемых. Этот сдвиг итеративно уточ-
няется, в результате чего процесс сходится к решению при не очень
жестких требованиях к задаче. Рассматриваемый далее метод был
разработан в [44, 451. Он близок к тому варианту метода множите-
лей, который появился ранее в [46] в качестве обобщения метода
Пауэлла — Хестенса, предложенного в [47, 48] для задач с ограни-
чениями в виде равенств. Ниже будет показано, что метод множи-
телей имеет определенное сходство с методом Эверетта [1], однакс
при его использовании приближения для множителей Лагранжа
(а и т) получаются автоматически в результате очень простых вы-
числений. Учитывая тот факт, что/? не меняется от итерации к ите-
рации, условимся опускать этот параметр в последующих выклад-
ках. Компоненты векторов а и т меняются по ходу вычислений,
однако в процессе решения каждой вспомогательной подзадачи
безусловной минимизации оба этих вектора остаются постоянными.
При переходе от одной подзадачи к другой векторы о ит пересчи-
тываются по определенным правилам (см. ниже), и, таким образом,
штрафная функция изменяется. Начальная точка х<0) не обязатель-
но должна быть допустимой, а начальные значения множителей
удобно (но совершенно необязательно) выбирать нулевыми: а=т=0.
При соблюдении последнего условия первая вспомогательная под-
задача минимизации оказывается той же самой, что и в методе штраф-
ных функций, использующем рассмотренные выше внешние штрафы.
6.3.2. Формулы пересчета множителей
Обозначим через х1П точку минимума штрафной функции, ис-
пользуемой на Ли итерации, т. е. функции
j
Р (х, Ф”, т">) = f (х) + Я 2 {<£/ (X) + [аур} +
‘' к
+ я 2 {[М*)-^2-[^’]2}- (6 37)
k= 1
При переходе к (/+1)-й итерации множители пересчитываются по
формулам
а(/+1> = <^(х«') + а/)>, /=1.2,3..J, (6.38)
Ч/+1’ = М*и’) + ^’, Л=1,2, 3....К. (6.39)
Из-за наличия в формуле оператора срезки векторы а не имеют по-
ложительных компонент, тогда как компоненты векторов т могут
иметь любой знак. Каждый из этих векторов определяет сдвиг аргу-
мента соответствующего штрафа, причем формулы пересчета таковы,
что в результате изменения сдвига при переходе к новой подзадаче
штраф за нарушение ограничений возрастает, и вследствие этого
стационарные точки х(П приближаются к допустимой области.
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 249
6.3.3. Геометрические свойства штрафной функции
Из формулы (6.37) не видно, как сказывается пересчет множи-
телей а и т на форме поверхностей уровня функции Р(х, а, т). Это
можно понять, анализируя выражение для ГР(х) — матрицы Гессе
этой функции. Начнем с выражения для градиента. Используя опре-
деление срезки, находим
VP (х) = V/ (х) + 27? 2 (<gj (х) + ау> Vgj (х)] +
/ = 1 \ /
К
+ 27? 2 {[^s (х) + т4] (х)}. (6 40)
к = 1
Повторное дифференцирование дает матрицу вторых производных:
ГР (X) = v7 (х) + 27? ,2 J <g, (х) + oy>V2 gj (x)+[Vg7(x)]2 j' +
+ 27? 2 {[hk (x) + rft] Vhk (x) + [Vftft «}. (6 41)
i<= i
Известно, что радиус кривизны поверхности уровня функции Р(х)
определяется матрицей V2P(x). В том случае, когда функции-огра-
ничения g(x) и й(х) линейны, имеем
j к
ГР (х) = Г[ (х) + 27? 2 {Vgj (х)}2 + 27? 2 {V(х)}\ (6.42)
/=1 k —1
т. е. матрица v2P (х) не зависит от о и т. Это означает, что в случае,
когда ограничения линейные, поверхности уровня не меняют форму
от итерации к итерации, а лишь сдвигаются относительно поверх-
ностей уровня функции /(х). Таким образом, сходимость метода не
сопровождается нежелательной деформацией поверхностей уровня
функции Р(х) и не связана с неограниченным увеличением штраф-
ных параметров. В случае когда ограничения нелинейны, форма
поверхностей уровня Р (х) меняется, однако это изменение второго
порядка (а не первого, как в методе штрафных функций).
6.3.4. Критерий окончания работы алгоритма
Для контроля за сходимостью метода используют последова-
тельности х(П, о(П, т<г), /(xin), g(x<n) и Л(х1П). При этом предпо-
лагается, что применяемый алгоритм безусловной минимизации
всякий раз позволяет найти стационарную точку и после этого за-
кончить итерацию па основе некоторого критерия. Останов основ-
ного процесса происходит, когда члены по крайней мере одной из
перечисленных последовательностей перестают изменяться при
пересчете множителей и последующей безусловной минимизации.
Как будет ниже показано, точка хт, получаемая в результате оста-
нова, является точкой Куна — Таккера.
250
ГЛАВА 6
Заметим, что градиент штрафной функции в результате безуслов-
ной минимизации должен в конце обратиться в нуль. Далее,
согласно формулам (6.38) и (6.39), величины <gr7-(x<f))+o/’> и
[/ih(xinH-Tp)] принимаются за о(,+1) и т(/+1) соответственно. Рас-
смотрим величины аг, gj(xITy), тгл и /гй(хг), предполагая, что они
являются пределами соответствующих последовательностей. Из
формулы (6.39) видно, что предельное значение т<Г) может суще-
ствовать лишь в том случае, если /ih(x<n)=0. Аналогично в силу
(6 38) для существования предельных значений о(Г) и gj(x{T}) не-
обходимо, чтобы выполнялись условия
&(х|П)>0 Hof’ = 0, (6.43)
либо gj(xm)=Q и а'л^0. (6.44)
С учетом этого, подставляя хт в качестве аргумента в выражение
(6 40) для градиента, получаем
VP (хт) = V/ (х‘л) + 2Р 2 (х(П) + 2/? 2 4Г> Vhk (х‘л) = 0,
: — t * I,_ t
(6.45)
^.(х(Г’;>0, /=1,2,3,...,/, (6.46)
(Дл) = 0, /=1,2,3,...,/, (6.47)
af’<0, /=1,2,3.......J, (6.48)
Мх‘г,) = 0, £=1,2,3, (6.49)
Легко видеть, что соотношения (6.45) — (6.49) представляют собой
условия Куна — Таккера для точки х1Г). Таким образом, получен-
ная предельная точка оказывается точкой Куна — Таккера. Да-
лее, как видно из формулы (6 45), соответствующие значения мно-
жителей Лагранжа могут быть найдены по формулам
uj = — 2/?а/>, (6.50)
vft =— 2Рт^’, (6.51)
т. е. по существу без каких-либо дополнительных вычислений. От-
метим, что в ряде работ (см., например, 149, 50]) данный метод рас-
сматривается как метод множителей Лагранжа в пространстве двой-
ственных переменных.
6.3.5. Свойства метода множителей
Перечислим основные свойства метода множителей.
1. Метод сходится к точке Куна — Таккера: lim х<ъ=х*. Это!
факт был установлен ранее при единственном предположении о том,
что удается решить вспомогательные задачи безусловной миними-
зации. Свойства вспомогательной целевой функции и характер из-
менения параметров а и т дают основания считать, что при этом
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 251
вспомогательные подзадачи не становятся столь плохо обусловлен-
ными, как в методе штрафных функций. Анализ ситуации приводит
к следующему заключению.
2. При не слишком больших 7? задача минимизации Р(х, R) по х
почти столь же сложна, как и задача минимизации функции f(x).
3. Правила пересчета <т и т простые и практически не требуют
дополнительных вычислений.
Попытки использовать более сложные способы уточнения мно-
жителей предпринимались в работах [51—53]. Однако оказалось,
что уменьшение числа итераций, нужных для получения решения,
как правило, недостаточно для компенсации того объема вычисле-
ний, который дополнительно тратится на выполнение самих итера-
ций. Впрочем, как уже отмечалось, справедливость подобных вы-
водов находится в сильной зависимости от относительной трудоем-
кости вычисления функций, входящих в задачу. В работе [51] ис-
следован также вариант метода множителей, использующий «внут-
ренние» штрафы; показано, что этот вариант не только обладает
основными достоинствами рассмотренной здесь схемы (основанной
на внешнем штрафе), но и генерирует итерационную последователь-
ность xw, состоящую из допустимых точек.
Можно указать и на недостатки рассмотренного метода. Один
из них состоит в том, что элементы итерационной последовательности
xt0 приближаются к х*, находясь почти всегда вне допустимой об-
ласти. К недостаткам следует отнести и отсутствие правил выбора
R (этот вопрос рассматривается в разд. 6.3.6). Следует напомнить,
что в основе обоснования метода лежит допущение о возможности
эффективно решать вспомогательные подзадачи безусловной мини-
мизации. Укажем в связи с этим на работу [53], где доказана гло-
бальная сходимость метода для задач выпуклого программирования
и предложен критерий окончания вычислений при приближенном
решении вспомогательных подзадач, гарантирующий ту же скорость
сходимости, что и при точном их решении.
Пример 6.3. (Та же задача, что в примере 6.1)
Рассмотрим задачу с ограничениями-равенствами, которая фигу-
рировала в примере 6.1:
минимизировать /(х) = (х,— 4)2 +(х2 —4)а
при ограничении h (х) = х1 ф- х2—5 = 0.
Имеем
Р (х, т) = (Xj — 4)2 + (х2—4)2 + (1 /R) (х, ф- х2—5 ф- т)2 — (1 /R) та,
ЭР 9
== 2 (Xj 4) ф-(Xj ф-х2— 5-f-т) = 0,
ар 9
•^- = 2(х2 — 4) + -£- (х, Ф-х2 — 5 ф-т) = 0.
Отсюда х1 = ха = (5ф- 4R — т)/(2ф- R). (6.52)
252
ГЛАВА 6
Таблица 6.4. Результаты вычислений с использованием
метода множителей
1 7 *1 ~хг /М ?(л,т)
0 0 3,0000 2,0000 3,0000
1 1,0000 2,6667 3,5556 4,3333
2 1,3333 2,5556 4,1728 4,4814
3 1,4444 2,5185 4,3896 4,4979
4 1,4818 2,5062 4,4629 4,4997
— 1,5000 2,5000 4,5000 4,5000
При /? = 1 полученные соотношения принимают вид
Xi=x2=3—(т/3). (6.53)
Пересчитаем множитель т по формуле (6.39) и используем (6.52) для
точного вычисления точки безусловного минимума функции Р (х, т)
по х. Результаты соответствующих вычислений приведены
Рис 6.19. Линии уровня штрафной функции, используемой в методе множителей
при т—1.
в табл. 6.4. Из таблицы видно, что определяемое по ходу процесса
минимальное значение Р(х, т) возрастает с увеличением номера ите-
рации. Таким образом, функция Р(х, т) минимизируется по х г
одновременно максимизируется по т, т. е. фактически ищется ее
седловая точка. Линии уровня Р(х, т) при нескольких различный
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 253
Р(х,т)=(х1-4Л(х2-4)г+(х1+хг-5+-^-)-(^-)’
Линии
уровня
А 5,000
В 10,000
С 15,000
О 20,000
Е 25,000
F 30,000
G 35,000
Н 40,000
I 45,000
J 50,000
в методе множителей
Рис. 6.20. Линии уровня штрафной функции, используемой
при т= 1319.
Линии
уровня
А 5,000
В 10,000
С 15,000
D 20,000
Е 25,000
F 30,000
G 35,000
Н 40,000
I 45,000
J 50,000
Рис. 6.21. Линии уровня штрафной функции, используемой в методе множителей
пои т=1.5
254
ГЛАВА 6
значениях т представлены на рис. 6.19—6.21. В соответствии с тем,
что ограничение рассматриваемой задачи линейно, форма линий
уровня Р(х, т) не меняется в зависимости от т.
6.3.6. Выбор R и масштабирование переменных задачи
По-видимому, трудности, возникающие при применении рас-
сматриваемых в этой главе методов к решению прикладных задач,
чаще всего связаны с неудачным масштабированием. Задачу назы-
вают плохо масштабированной, если абсолютные значения перемен-
ных и функций, входящих в эту задачу, сильно различаются между
собой. При плохом масштабировании может оказаться, что процесс
минимизации реально воздействует лишь на часть переменных (или
ограничений), что в ряде случаев приводит к преждевременному
окончанию работы любого алгоритма.
В гл. 13 будет рассмотрен метод, предложенный в работе [54],
в рамках которого автоматически осуществляется изменение мас-
штаба переменных задачи, в результате чего обусловленность под-
задач минимизации улучшается. Аналогичные процедуры в схеме
метода штрафных функций предлагались ранее в [55, 56], тогда как
работа [54] ориентирована на построение эффективных алгоритмов,
реализующих метод множителей. Заметим, что хотя указанные
процедуры, улучшающие обусловленность, рассматривались в рам-
ках методов преобразования, их можно применять и в сочетании
с любыми другими методами. При использовании методов преоб-
разования обусловленность играет особенно важную роль, и здесь
масштабированию переменных стоит уделить достаточное внимание.
6.3.7. Учет ограничений на значения переменных
В большинстве схем методов, основанных на преобразовании
задачи, специфика ограничений (6.4) не используется: двусторонние
ограничения на значения переменных учитываются как общие
ограничения-неравенства. Соответственно каждая из переменных
задачи добавляет в систему неравенств еще два ограничения. Ко-
нечно, эти ограничения очень просты, но все же целесообразнее
учитывать их непосредственно. Другими словами, нужна процедура,
в которой алгоритмически учитываются ограничения на значения
переменных и не увеличивается размерность задачи за счет увели-
чения числа ограничений. Эта процедура должна позволять обна-
руживать, что значения той или иной переменной находятся на
своей границе (или уже вышли за нее), и фиксировать значения соот-
ветствующих переменных на их границах. При этом должны разре-
шаться любые допустимые изменения значений переменных (т. е.
не приводящие к нарушению заданных ограничений).
Этим требованиям можно удовлетворить многими различными
способами. В частности, можно по-разному действовать в случае,
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 255
когда некоторые ограничения на значения переменных оказываются
нарушенными. Поскольку обычно при реализации методов безуслов-
ной минимизации на каждом шаге осуществляется движение в не-
котором направлении, можно начать двигаться в обратном направ-
лении до тех пор, пока все переменные не окажутся в пределах своих
границ. При этом сохраняется направление поиска безусловного
минимума, но требуется находить нуль некоторой функции, что
бывает связано со значительными вычислительными затратами.
Более примитивный и дешевый способ состоит в том, чтобы одновре-
менно вернуть все переменные, нарушающие ограничения, на соот-
ветствующие границы. В этом случае направление движения при
поиске безусловного минимума изменяется, но тем не менее, как
показывает опыт, такой способ оказывается наилучшим.
Другая проблема, связанная с предыдущей,— учет линейных
ограничений. Можно ожидать, что линейность хотя бы части огра-
ничений позволит сделать вычисления более экономными. Для
этого имеются следующие основания. Во-первых, за счет улучше-
ния геометрических характеристик вспомогательной целевой функ-
ции должна ускориться сходимость. Во-вторых, можно добиться
Рис. 6.22. Нагруженная балка.
большей эффективности алгоритма одномерного поиска, поскольку
в линейном случае очень просто определяется момент выхода на
границу. В численных экспериментах, проводимых с методом мно-
жителей [54], применялась нормировка, а ограничения на значения
переменных учитывались в рамках алгоритма, однако попыток по-
высить эффективность за счет линейности ограничений не делалось.
Пример 6.4. Расчет нагруженной балки
Опять рассмотрим задачу расчета нагруженной балки [57]
(рис. 6.22), постановка которой была дана в гл. 1.
£56
ГЛАВА 6
Будем решать данную задачу с помощью процедуры BIAS (581,
реализующей метод множителей. В этой процедуре используются
простые формулы пересчета множителей, применяется нормировка
и в рамках алгоритма учитываются ограничения на значения пере-
менных. Целевая функция задачи та же, что и выше, но три огра-
ничения (g4, g5 и gi) включены в совокупность ограничений на зна-
чения переменных. При этом задача принимает вид
минимизи ровать f (х) = (1 -фс3) х4х2 + с4х3х4 (L + хг) (6.54)
при ограничениях gv (х) = та—т (х) О,
g2(x)=od—ff(x)>0,
g3 (x) = xt—xt>0,
gt (x) = Pc(x)—F^Q,
g3 (%) = 0,25—DEL x 0
и 0,125 Xj Ю,
0,100<x2< 10,
0,100<x3< 10,
(6.55)
(6.56)
0,100sCx4<C 10,
где x=\h, I, t, b]T, c3=0,10471 долл./дюйм3, c4=0,04811 долл./дюйм1.
Нижняя граница значений х4 связана с постановкой задачи,
а нижние границы значений хг, х3 и х4 вводятся, чтобы не допус-
тить обращения этих переменных в нуль, поскольку функции, вхо-
дящие в ограничения, не определены для нулевых значений пере-
менных. Пронормируем ограничения, разделив их на целые степе-
ни числа 10. Показатели степени подберем так, чтобы значения ле-
вых частей пронормированных ограничений в точке х<0>=[1, 7, 4,
2]J попадали в интервал 10, 101. Получим
f (х(0)) = 15,81545 (долл.),
gi (х‘0)) = 8,6785Е —01,
g2(xw,)= 1,4250Е-)-00,
£3(х<°‘) = 1,0000Е + 00,
gr4(x‘°‘)=l,8319E + 00,
g6(x<»') = 2,3285E — 01.
Поскольку точка х10’ допустима и К=0, первая вспомогательная
подзадача безусловной минимизации решается методом Давидо-
на — Флетчера — Пауэлла (ДФП) без дополнительной нормировки.
Новые нормирующие коэффициенты приведены в табл. 6.5, где
величины а,} относятся к ограничениям, а т]г— к переменным.
В табл. 6.6 приведены решения вспомогательных подзадач безу-
словной минимизации, найденные методом ДФП. Окончательное
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 257
Таблица 6.5. Нормирующие коэффициенты в задаче
расчета нагруженной балки
о / 1 2 3 4 5
0,8724 0,5324 0,9649 1,6730 7.2657
1,0000 0,2704 0,1441 3,90
решение, полученное с помощью данной процедуры, имеет вид
х‘г' = [0,2444, 6,2187, 8,2915, 0,2444]г
при f (х*Г)) = 2,38>116 долл.,
ё1 (х‘л) = —6.5386Е—07,
gi (x‘n) = — 1.5824Е—07,
gs (х‘г’> = _ 2.6740Е — 06,
gt (xl7)) = 8.7002Е — 08,
£5(х(П) = 2,324Е —01.
Результаты показывают, что реализация метода позволяет быстро
достичь окрестности решения, но для получения требуемой точно-
сти решения потребовались дополнительные итерации. Заметим, что
Таблица 6.6. Решения задачи расчета нагруженной балки
методом ДФП
Итерации Число шагов по методу ДФП
(О хг *1 Х4 f(x) Р(х, о)
1 0,2544 5,7098 8,3347 0,2417 2,3184 2,3482 27
2 0,2567 5,6319 8,2979 0.2435 2,3182 2,3476 36
3 0,2470 6,1130 8,2909 0,2444 2,3727 2,3804 44
4 0,2450 6,1937 8,2913 0.2444 2,3792 2,3810 64
5 0,2444 6,2177 8,2915 0,2444 2,3811 2,3811 71
6 0,2444 6,2187 8,2915 0,2444 2,3811 2,3811 76
ограничения 1—4 выполняются почти точно, что представляется
естественным. Хотя для получения результата хватило шести ите-
раций метода множителей (шести подзадач безусловной минимиза-
ции), следует отметить, что для этого потребовалось вычислить 1173
раза целевую функцию и 1177 раз функции, задающие ограничения.
Приведенные результаты были получены при /?=20; примерно та-
кой же эффективностью метод обладает при произвольном R из
интервала [10, 100). При больших значениях R количество итераций
метода множителей обычно оказывается меньшим, а число шагов
по методу ДФП на каждой итерации увеличивается. Если значение
R оказывается слишком малым, метод перестает работать. Так,
например, при /? = 1 останов в программе BIAS произошел после
258
ГЛАВА 6
выполнения 14 итераций метода множителей, что соответствовало
57 итерациям метода ДФП. При этом только в двух ограничениях
невязки стали малыми, а значение переменной ха вообще осталось
равным я!/”. Здесь видна связь между нормировкой и выбором R.
Работа в этом направлении пока далека от завершения.
6.3.8. Программы, реализующие метод множителей
Существуют, разумеется, и другие программы, реализующие
метод множителей. В работе [59], например, представлены резуль-
таты численных экспериментов, проводившихся с использованием
по крайней мере 12 различных программных реализаций метода.
В программе ACDPAC [60] используется модифицированная функ-
ция Лагранжа [46]. Специальным образом здесь учитываются как
двусторонние ограничения на значения переменных, так и линей-
ные ограничения. В работе [61] вспомогательные подзадачи реша-
ются методом сопряженных градиентов в одном из известных его
вариантов. В программе GAPFPR [62] штрафная функция та же,
что в [48], причем ограничения-неравенства преобразуются в ра-
венства с помощью дополнительных переменных. В этой программе
для решения подзадач применяется квазиньютоновский метод со
специальным учетом линейных ограничений. В программе VF01A
используются множители в форме, предложенной Флетчером
[63], и применяется квазиньютоновский метод для решения вспо-
могательных подзадач. Наконец, отметим работу [64], где описаны
три близкие друг другу программы SALQDR, SALQDF и SALMNF.
В них используется модифицированная функция Лагранжа и учи-
тываются неравенства с помощью дополнительных переменных.
В зависимости от конкретной версии применяются те или иные ме-
тоды безусловной минимизации, а значения производных вычисля-
ются либо аналитически, либо численно. Некоторые дополнитель-
ные сведения об этих и других программах можно найти в гл. 12.
6.4. Заключение
В этой главе рассматривались методы, основанные на преобра-
зовании задачи. Основное внимание было уделено методу модифи-
цированной функции Лагранжа (методу множителей). Было отме-
чено, что обычные типы штрафов — логарифмический, обратный и
штраф типа срезки — просты как в теоретическом, так и практиче-
ском отношении. Наряду с этим было показано, что обязательным
следствием неограниченного увеличения штрафного параметра R
является плохая обусловленность подзадач безусловной миними-
зации, проявляющаяся в сильной деформации соответствующих
поверхностей уровня. Избежать этого можно с помощью метода
множителей, вычислительная схема которого представляется более
удобной. Исследование метода проиллюстрировано (и в ряде случаев
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 25?
существенно дополнено) рассмотрением примеров. Перечислены
наиболее простые и удобные из существующих программных реали-
заций методов преобразования (о них вновь пойдет речь в гл. 12).
Контрольные вопросы и задачи
6.1. Перечислите основные отличия метода множителей от других
методов, основанных на преобразовании задачи, например
метода штрафных функций.
6.2. При каких условиях кривизна поверхностей уровня вспомо-
гательной целевой функции в методе множителей не меняется
от итерации к итерации?
6.3. Имеется ли необходимость в разработке модификации метода
множителей, которая является методом внутренней точки?
Почему’
6.4. Предположим, что задача
минимизировать f (х)
при ограничениях £/(х)^0, / = 1,2, ...,J,
решается путем последовательной безусловной минимизации
одной из следующих двух штрафных функций:
j
Pl (X, R) = f(x) + R 2 <gj (*)А
I — I
где R пробегает положительную возрастающую последова-
тельность значений, и
/ j
Рг (х, R,<f) = f(x) + R 2 <gj (х) + oz>2 — R 2
/=i t=i
где R фиксировано, а сходимость достигается путем пересчета
оу после решения каждой подзадачи безусловной минимиза-
ции. Перечислите относительные достоинства и недостатки
соответствующих методов, а также различия в их вычисли-
тельных схемах.
6.5. Дана задача:
минимизировать / (х) = 100 (х2—х?)Ч-(1—ху)2
при ограничениях g\(x)=Xi + 1^0,
gi(x) = \—х2^0,
g3(x)=4x2—Xj—1>0,
gt(x) = 1 —0,5X1—х2^0.
Запишите для этой задачи штрафные функции, используя:
1) логарифмический штраф; 2) штраф, задаваемый обратной
функцией; 3) форму штрафа для метода множителей. Иссле-
дуйте каждую из функций в точках х10)=4—1, 1]г и хи>=
О*
ГЛАВА 6
160
-I-0,5, 0,5]т, обратив внимание на встречающиеся при этом
сложности.
6.6. Пусть при решении задачи с ограничениями в виде неравенств
(g,(x)^0, /=1, 2,3, . . . , J) получена начальная внутренняя
точка. Объясните, в каких методах (внутренней или внешней
точки) можно использовать следующие штрафные функции
и почему:
(a) P(x;/?)=/W+/?SWx)}-2;
(б) Р(х, R)=f(x)+/?[min{0, minlg/x)]}2].
i
6.7. Даны задача
минимизировать / (х) = (хх—1)2+(х2—I)2
при ограничениях gi(x)=x1+xt—1^0,
g2(x) = l—Xi>0, ,
g3(x) = l—х2>0
и штрафная функция вида
Р(х, Т?) = /(х) + /?£
(а) Найдите зависимость координат стационарных точек
функции Р(х, /?) от /?.
(б) Покажите, что скорость сходимости метода зависит от
g2 и g3.
(в) Ускорится или замедлится сходимость, если отбросить
ограничения, задаваемые с помощью g2 и g3?
6.8. Выбрав по своему усмотрению один из методов преобразова-
ния, найдите с точностью до трех десятичных знаков решение
задачи
минимизировать f (х)=х|+х|+х3
при ограничениях gi(x) = l—х2_1х3^г0,
g2(x)=Xi—х3>0,
h1(x)=x1—хЦ-х2х3—4=0,
0<х2СЗ, 0<х3СЗ.
6.9. Как известно, локальными характеристиками поверхности
служат кривизна К и радиус кривизны R. Пусть поверхность
представляет собой линию уровня функции двух переменных
f(x), отвечающую значению /. Найдите связь между V2/(x)
и К.
6.10. Подумайте, как можно использовать соотношение, найденное
в задаче 6.9, в качестве характеристики того или иного штрафа.
6.11. Задача об описанном контуре минимальной длины. На плос-
кости даны три круга (рис. 6.23). Требуется так разместить
1ЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 261
эти круги в положительном квадранте, чтобы описанный во-
круг них прямоугольник имел минимальный периметр. При-
веденная формулировка очевидным образом обобщается на
случай любого числа произвольных плоских фигур. Эта
простая задача имеет и практическое значение. Одной из ее
постановок является оптимизация размещения элементов
электронных схем. Другая постановка связана с выбором
шаблона для штамповки металлических деталей.
Рис. 6.23. Задача об описанном контуре минимальной длины.
Переменными оптимизации здесь являются координаты
(х, у) центров круга, а целевой функцией — периметр описан-
ного прямоугольника: f(х)~2(А+В), где А и В — длины
его сторон. Для того чтобы круги оставались внутри положи-
тельного квадранта, вводятся ограничения вида gj(x)=xa—
—Ra^0, а для того чтобы не допустить взаимных пересече-
ний, постулируется, что сумма расстояний между центрами
кругов не меньше, чем сумма их радиусов:
ё/ (*) = {(*а—хь)2 + (Уа — УьУ}г/2 — (Ra + Rb) > 0.
Конкретные числовые значения радиусов указаны на рис. 6.24.
(а) Сформулируйте соответствующую задачу нелинейного про-
граммирования.
(б) С помощью одного из методов, основанных на преобразо-
вании задачи, найдите описанный прямоугольник с ми-
нимальным периметром.
(в) Выпукло ли в данном случае допустимое множество?
(г) Насколько вероятно, что в качестве решения будет полу-
чена точка локального условного минимума?
262
ГЛАВА 6
(д) Проверьте полученное в п. (б) решение, передвигая пс
листу бумаги кружочки соответствующих радиусов и ис-
пользуя линейку.
Рис 6.24. Задача об описанном контуре минимальной длины при R—5, 10, 15.
6.12, Определение узловых точек для шарнирного механизма. На
рис. 6.25 схематически изображен плоский четырехзвенный
механизм. Требуется установить такое соотношение между
Рис. 6 25. Задача синтеза зависи-
мости между углами
углами 0 и Ф, чтобы получить аппроксимацию заданной функ-
ции у<1(х). В частности, нужно определить три узловые точки
%1, х2, х3, доставляющие минимум квадрату ошибки аппрок-
симации.
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 262
Рассмотрим кривые аппроксимируемой функции yd(x)
и аппроксимирующей функции у^(х), представленные на
рис. 6.26, и график соответствующей ошибки аппроксимации
E(x)—yd(x)—у (х), приведенный на рис. 6.27. Чтобы при
Рис 6 26. Расположение узловых течек
заданных xL, хн, yL, ун установить зависимость между вход-
ными и выходными величинами с помощью полученного в ра-
боте [66] уравнения
F(</>)=7?iCos 0—/?2cos ф+/?3—cos(0—Ф)=0,
где Ri=d/c, Rt—d/a, R3 = (a2—b2+c2+d2)/2ca, полагаю!
Е (х)=0 в точках xlt х2 и х3. Кроме того, считаются заданными
линейные соотношения 0=Cjx+c2 и ф=с3у+с4.
Рис. 6.27. Ошибка аппрокси-
мации.
(а) Сформулируйте задачу определения узловых точек как
задачу нелинейного программирования.
(б) Пусть yd(x) = l/x, xz = l, хн=2, yL=\, ун=0,5, так чтс
0 =90x4-60 и Ф=—180//4-240. Найдите узловые точки xL,
х2 и х3 при х10’ —11,15, 1,50, 1,85]г.
264
ГЛАВА 6
6.13. Дана задача (рис. 6.28)
минимизировать f (х) = (х—2)2, х g R1,
при ограничении /i(x)=x—3=0.
Очевидно, ее решением является х*=3, причем /(х*) = 1,0.
Получите выражения для (а) квадратичной штрафной функ-
ции и (б) формы штрафа для метода множителей, которые соот-
ветствуют линиям уровня, изображенным на рис. 6.29 и 6.30.
1 (х) =(х-2)а
Рис. 6.28. Одномерная задача условной минимизации.
6.14. Используя один из методов штрафных функций, решите за-
дачу (3.18) (не прибегая к исключению одной из переменных
с помощью ограничения на объем).
6.15. (а) Используя метод множителей, решите задачу (3.19) (не
прибегая к исключению одной из переменных с помощью
ограничения на расход).
(б) Исследуйте возможность решения подзадач методами гра-
диентного типа, обратив внимание на возникающие при
этом трудности.
Литература
1 . Everett М., Generalized Lagrange Multiplier Method for Solving Problems ol
Optimum Allocation of Resources, Oper, Res , 11, 399—471 (1963)
2 . Siddall J. N., Analytical Decision-Making in Engineering Design, Prentice-Hall,
Englewood Cliffs, NJ, 1972.
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧЕ
Рис. 6.30. Штрафная функция, используемая в методе множителей,
266
ГЛАВА 6
3 Siddall J. N., Opti-Sep: Designer’s Optimization Subroutines, McMaster Uni-
versity, Canada, 1971.
4 . Lootsma F. A , A Survey of Methods for Solving Constrained Minimization Prob-
lems via Unconstrained Minimisation, in: Numerical Methods for Nonlinear
Optimization (F. A. Lootsma, Ed ). Academic Press, N. Y., 1972, pp. 313—348.
5 Ragsdell К M , Root R. R., Gabriele G A , Subroutine ZERO, in MELIB:
A Subroutine Library for Mechanical Engineers, 1975.
6 . Fiacco A. V., McCormick G P., Computational Algorithm for the Sequential
Unconstrained Minimization Technique for Nonlinear Programming, Manage.
Sci., 10, 601—617 (1964).
7 . Fiacco A. V , McCormick G. P , Nonlinear Programming Sequential Unconstra-
ined Minimization Techniques, Wiley, N. Y., 1968. [Имеется перевод Фиакко
A , Мак-Кормик Г. Нелинейное программирование Методы последователь-
ной безусловной оптимизации. М.. Мир, 1972 ]
8 . Lootsma F A., Extrapolation in Logarithmic Programming, Philips Res Rep ,
23, 108-116 (1968).
9 Lootsma F. A , Boundary Properties of Penalty Functions for Constrained Mi-
nimization, Philips Res. Rep. Suppl., 3 (1970).
10 Fletcher R , McCann A P., Acceleration Techniques for Nonlinear Programming,
in Optimization (R. Fletcher, Ed ), Academic Press, N. Y., 1969, pp. 203—214.
11 Murray W., Ill-Conditioning in Barrier and Penalty Functions Arising in Con-
strained Nonlinear Programming, in Proceedings of the Sixth Symposium on
Mathematical Programming, Princeton, NJ, 1967.
12 Lootsma F. A , Hessian Matrices of Penalty Functions for Solving Constrained
Optimization Problems, Philips Res. Rep., 24, 322—331 (1969)
13 . Cotirant R., Variational Methods for the Solution of Problems of Equilibrium
and Vibrations, Bull. Am. Math Soc , 49, 1—23 (1943).
14 Carroll C. W., The Created Response Surface Technique for Optimizing Nonlinear
Restrained Systems, Oper Res , 9, 169—184 (1961).
15 . Fiacco A. V , McCormick G. P., The Sequential Unconstrained Minimization
Technique for Nonlinear Programming, a Primal-Dual Method, Manage. Sci.,
10, 360-366 (1964).
16 Fiacco A V., McCormick G. P., Computational Algorithm for the Sequential
Unconstrained Minimization Technique for Nonlinear Programming, Manage,
Sci., 10, 601—617 (1964).
17 Zang'.1,ill W. I , Nonlinear Programming via Penalty Functions, Manage Sci.
13(5), 344—358 (1967).
18 Lootsma F. A., Logarithmic Programming’ A Method of Solving Nonlinear Pro-
gramming Problems, Phillips Res Rep , 22, 329—344 (1967).
19 . Lootsma F A., Constrained Optimization via Penalty Functions, Philips Res.
Rep., 23, 408—423 (1968).
20 . Lootsma F. A., A Survey of Methods for Solving Constrained-Minimization
Problems via Unconstrained Minimization, in. Optimization and Design (M. Av-
riel, H Rijckaert, D J. Wilde, Eds ), Prentice-Hall, Englewood Cliffs, NJ,
1973, pp 88—118.
21 . McCormick G P., Penalty Function versus Non-Penalty Function Methods for
Constained Nonlinear Programming Problems, Math. Prog., 1 (2), 217—238
(1971).
22 Lasdon L. S., An Efficient Algorithm for Minimizing Barrier and Penalty Fun-
ctions, Math. P/og., 2 (1), 65—106 (1972)
23 Moe J., Penalty-Function Methods, in Optimum Structural Design Theory and
Applications (R. H. Gallagher, О. C., Zienkiev,icz, Eds.), Wiley, N Y., 1973,
ch. 9.
24 Ryan D. M., Penalty and Barrier Functions, in: Numerical Methods for Constrai-
ned Optimization (P. E. Gill, W. Murray, Eds.), Academic Press, N Y., 1974,
pp 175—190.
25 . Fox R L., Optimization Methods for Engineering Design Addison-Wesley, Re-
ading, MA, 1971.
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
МЕТОДЫ ОПТИМИЗАЦИИ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЗАДАЧИ 267
Himmelblau D М , Applied Nonlinear Programming McGraw-Hill N Y ,
1972, ch 7, p 299 [Имеется перевод Химмельбтау Д М Прикладное нели-
нейное программирование — М Мир, 1975 ]
Ах riel М , Nonlinear Programming Analysis and Methods, Prentice-Hall, Eng-
lewood Cliffs, NJ, 1976
Gulf Oil Corporation, Compute 11, a General Purpose Optimizer for Continuous
Nonlinear Models—Description and User s Manual Gulf Computer Sciences
Incorporated Houston, TX, 1972
Afimiwala К A , Program Package for Design Optimization, Department of
Mechanical Engineering, State University of Nev, York at Buffalo, 1974
Lili S , The University of Liverpool Computer Laboratory E04HAF, Numeri-
cal Algorithms Group, Document no 737, 1974
DeSilva В M E , Grant G N C , Comparison of Some Penalty Function Ba
scd Optimization Procedures for the Synthesis of a Planar liuss, Intern J Nu-
merical Methods Eng, 7(2), 155—173 (1973)
Brocken J , McCormick G P , Selected Applications of Nonlinear Programming,
Miley, N Y, 1968
Gupta В D , Rao S S , Optimum Design of Air Conditioned Buildings, ASA'IE’
J Meeh Des , 102(3), 476—480 (1980)
Rao S S Gupta В D , Application of External Distributions m the Design
of Thermal Systems ASME J Meeh Des , 102, (3) 481—491 (1980)
Mx lander W C , Holmes R L , McCormick G P , A Guide to SUMT—Version
4, Research Analysis Corporation Feb 1974
Sandgren E , The Utility of Nonlinear Programming Algorithms Ph D Dis
sertation, Purdue University 1977 available from University Microfilm, 300 N
Zeeb Road Ann Arbor, MI, Document n 7813115
Koualik J Nonlinear Programming Procedures and Design Optimization,
Acta Poly tech. Scand 13, 1966
Fiacco A V, McCormick G P, The Sequential Unconstrained Minimization
Technique Without Parameters, Oper Res 15, 820—827 (1967)
Fiacco A V Sequential Unconstrained Minimization Methods for Nonlinear
Programming, Thesis Northwestern University, 1967
Rosenbrock H H , An Automatic Method for Finding the Greatest or Least Value
of a Function, Computer J , 3 175—184 (1960)
Hoard P , Resolution of M thematical Programming with Nonlinear Constra-
ints by the Method cf Centres in Nonlinear Programming (J Abodie, Ed),
Noith-Holland, Amsterdam, 1967 pp 207—219
Staha R L , Documentation for Progiam Comet, A Constrained Optimization
Code, The University of Texas Austin TX, 1973
Lootsma F A , Convergence Rates of Quadratic Exterior Penalty Function Met
hods for Solving Constrained Minimization Problems, Piuhps Res Rep , 29'
(1) (Feb 1974)
Schuldt S В , A Method of Multipliers for Mathematical Programming Problems
with Equality and Inequality Constraints, JOTA, 17 (1/2) 155—162 (1975)
Schuldt S В , Gabriele G A , Root R R , Sandgren E , Ragsdell К M , Appli
cation of a New Penalty Function Method to Design Optimization, ASMEJ
Ing hid , 99 (I), 31—36 (Feb 1977)
Rockafellar R T , A Dual Approach to Solving Nonlinear Programming Prob-
lems by Unconstrained Optimization, Math Programming 5(3) 354—373 (1973)
Powell M J D A Method for Nonlinear Constraints in Minimization Problems,
in Optimization (R Fletcher Ed) Academic Press London, 1969, pp 283—298
Hestenes M R , Multiplier and Gradient Methods, JOTA, 4(5) 303—320 (1969)
Gould F J Howe S , A New Result on Interpreting Lagrange Multipliers and
Dual Variables Dept Statistics, University of North Carolina, Chapel Hill,
NC 1971
Gill P E Murray К , The Computation of I agrange-Multiplier Estimates for
Constrained Minimization, Math Programming, 17 (I), 32—60 (1979)
268
51.
52
53
54.
55.
56
57.
58.
59.
60.
61.
62.
63.
64
65.
ГЛАВА 6
Root R. R., An Investigation of the Method of Multipliers, Ph. D. Dissertation,
Purdue University, Dec. 1977.
Bertsekas D P., On Penalty and Multiplier Methods for Constrained Minimiza-
tion, in Nonlinear Programming, Vol. 2 (O. L. Mangasarian, R. R. Meyer, S. M.
Robinson, Eds.), Academic Press, N. Y., 1975, pp. 165—192.
Kort В W., Rate of Convergence of the Method of Multipliers with Inexact Mi-
nization, in Nonlinear Programming, Vol. 2 (Mangasarian, Meyer, Robinson,
Eds.), Academic Press, N. Y., 1975, pp. 193—214.
Root R. R., Ragsdell К. M., Computational Enhancements of the Method of
Multipliers, ASME J. Meeh. Des., 102(3), 517—523 (1980).
Keefer D. L., Gottfried X. X., Differential Constraint Scaling in Penalty'Fun-
ction Optimization, AIIE Trans., 2 (4), 281 (1970).
Keefer D. L , Simpat: A Self-Bounding Direct Search Method for Optimization,
7 & EC Proc. Des. Develop., 12, 92 (1973).
Ragsdell К. M., Phillips D. T., Optimal Design of a Class of Welded Structures
Using Geometric Programming, ASME J Eng. Ind. Ser. B, 98(3), 1021—1025
(1976).
Root R. R., Ragsdell К. M., BIAS; A Nonlinear Programming Code in Fortran
JV-L’sers Manual Purdue Research Foundation, June 1976.
Schittkowski К , Nonlinear Programming Codes Information, Tests, Performan-
ce, Lecture Notes in Economics and Mathematical Systems, Vol. 183, Springer-
Verlag, Berlin, 1980.
Best M J , Bowler A. T., ACDPAC: A Fortran IV Subroutine to Solve Diffe-
rentiable Mathematical Programmes — Users Guide—Level 2.0, Res. Rep.
OORR75-2S, Dept, of Combinatorics and Optimization, University of Waterloo,
Ontario, Canada, 1978-
Best MJ., Ritter K., An Accelerated Conjugate Direction Method to Solve
Linearly Constrained Minimization Problems, J, Computer Syst. Sci., 11 (3),
295—322 (1975)
Newell J S., Himmelblau D. M., A New Method for Nonlinearly Constrained
Optimization, AIChE J., 21 (3), 479—486 (1975).
Fletcher R., An Ideal Penalty Function for Constrained Optimization, in: Non-
linear Programming, Vol. 2 (O. L. Mangasarian, R. R. Meyer, S. M. Robinson,
Eds.), Academic Press, N. Y., 1975
Gill P. E., Murray W., (Eds.), Numerical Methods for Constrained Optimizati-
on, Academic Press, N. Y.. 1974
Freudenstein F., Approximate Synthesis of Four-Bar Linkages, Trans. ASME,
853—861 (Aug. 1955).
Глава 7
Методы прямого поиска
в задачах условной оптимизации
При обсуждении методов преобразования и метода множителей
Лагранжа в гл. 6 использовались построения, не требующие деталь-
ного рассмотрения функций, входящих в ограничения. Единствен-
ное структурное различие, которое учитывалось, определялось
лишь видом используемых ограничений (равенства или неравенства).
В методах, рассматриваемых в этой и нескольких последующих
главах, напротив, в процессе оптимизации ограничения учитыва-
ются в явном виде. В этой главе основное внимание уделяется мето-
дам прямого поиска, т. е. приемам отыскания точек оптимума, когда
в процессе поиска используются только целевая функция и ограни-
чения. Как и в случае задач безусловной оптимизации, необходи-
мость разработки этих методов связана с тем, что в технических
приложениях часто приходится сталкиваться с задачами, в которых
функции разрывны или недифференцируемы. В подобных случаях
применимы методы, использующие лишь значения самих функций.
Ниже рассматриваются методы, основанные на применении
идей, процедур, приемов, алгоритмов прямого поиска, описанных
в гл. 3, и методы, основанные на случайном выборе пробных точек.
Поскольку эти методы строятся на интуитивных соображениях, не
подкрепленных строгой теорией, и, следовательно, не гаранти-
руются их сходимость и получение оценок скорости сходимости,
они, по существу, являются эвристическими. Несмотря на это, они
позволяют получать достаточно хорошие (но не обязательно опти-
мальные) решения. Кроме того, в силу своей логической простоты
эти методы легко реализуемы. Начнем рассмотрение с краткого об-
суждения вопросов «подготовки» задач с ограничениями для реше-
ния методами прямого поиска.
7.1. Подготовка задачи к решению
Общая задача условной оптимизации содержит ограничения
в виде неравенств или равенств, а также верхние и нижние границы
значений переменных. Интуитивно ясно, что для произвольной
допустимой точки х° можно так видоизменить схему метода безуслов-
ной оптимизации, что точки, получаемые на последующих итера-
270
ГЛАВА 7
циях, оказываются допустимыми. Например, если пробная точка и
не удовлетворяет какому-либо ограничению-неравенству, то можно
заменить ее другой, изменяя величину шага так, чтобы это неравен-
ство оказалось выполненным. Ограничения в виде равенств достав-
ляют больше трудностей, поскольку даже если х° и v удовлетворяют
ограничениям-равенствам, то точки на прямой
х=х°+а(и—х°) для 0^а^1
не обязательно им удовлетворяют, за исключением случая линей-
ных ограничений-равенств. Если и к тому же недопустимая точка,
то, оперируя лишь значениями входящих в ограничения функций,
трудно изменить ее координаты так, чтобы добиться выполнения
нелинейных ограничений-равенств. Проблема в данном случае
сводится к нахождению решения системы уравнений
/ih(x)=0, fe=l, К
путем использования лишь значений функций и подбора зна-
чений координат v так, чтобы найденное решение было лучше, чем
базовая точка х°. Трудности получения допустимой точки в задаче
с ограничениями в виде равенств приводят к тому, что по существу
все методы прямого поиска требуют, чтобы ограничения задачи
были заданы только в виде неравенств. Следовательно, ограничения
в виде равенств должны быть явно или неявно исключены перед ре-
шением задачи.
Вторая, не менее существенная проблема заключается в том, что
алгоритмы методов прямого поиска обычно начинают работать с до-
пустимой точки. Во многих технических приложениях начальная
допустимая точка может быть выбрана на основе априорных сведе-
ний о моделируемой системе или об условиях ее функционирования.
Однако когда это не удается, приходится применять специальные
методы нахождения допустимой точки.
7.1.1. Исключение ограничений в виде равенств
Простейший способ исключения ограничения в виде равенства
заключается в решении его относительно одной из переменных с по-
следующим исключением этой переменной путем подстановки полу-
ченного выражения в соотношения, описывающие задачу. При этом
следует помнить, что верхние и нижние границы значений исклю-
чаемых переменных сохраняются в задаче в виде ограничений-нера-
венств.
Пример 7.1
Рассмотрим задачу
минимизировать/(х)=х?+4х|+%з ।
при ограничениях /i/xJ—Xj+x’—2—0,
—
0<х2<2, 0<%з<2.
МЕТОДЫ ПРЯМОГО ПОИСКА В ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 271
Из первого ограничения %! можно выразить через х2, т. е. %i =
=2—х|. После подстановки выражения хг через х2 целевая функция
принимает вид
f(x2l x3) = (2-x2)4-4x2+x2s.
Поскольку значение должно находиться в определенных гра-
ницах, необходимо выполнение неравенств
—1<2—х£С1.
Задача уменьшенной размерности теперь примет вид
минимизировать (2 — х2)24х;1 + х,
при ограничениях 1 -С х2 «С К 3, 0 х3 2.
Отметим, что если не учитывать границ значений переменной xj,
то оптимальным решением последней задачи будет х2=х3=0. От-
сюда Xi=2, что противоречит условиям исходной задачи.
При реализации методов решения задач с ограничениями в виде
равенств обычно нет необходимости производить алгебраическую
подстановку. Вместо этого удобнее и надежнее включать в програм-
му вычисления целевой функции и ограничений в виде неравенств
выражение, получаемое при решении уравнений-ограничений отно-
сительно какой-либо неизвестной, как определение этой перемен-
ной В этом случае можно сохранить значения зависимых перемен-
ных с тем, чтобы позднее вывести их на печать, и минимизиро-
вать вероятность ошибок при алгебраических подстановках.
Несмотря на то что подстановка является самым простым спосо-
бом исключения ограничений в виде равенств, не всегда оказыва-
ется возможным ее осуществить. Во многих случаях подстановка
либо алгебраически недопустима, либо непосредственное решение
уравнения относительно одной из переменных затруднительно.
Тогда можно осуществить исключение ограничений-равенств неяв-
ным образом, решая численно уравнения относительно зависимых
переменных при заданных значениях независимых оптимизирующих
переменных. Численные методы исключения ограничений в виде
равенств требуют большого числа вычислений, особенно когда числе
зависимых переменных велико, но с этим приходится мириться,
если применяются методы прямого поиска.
Пример 7.2. Задача
минимизировать / (x)=xix2x3
при ограничениях h1(x)=x1+x2+x3—1=0,
/т4(х) =x?x3+x2xj+x^1xl—2=0,
’ 0<х,<1/2) 0<х2<1/2
содержит два ограничения в виде равенств и, следовательно, имеет
две зависимые и одну независимую переменные. Ясно, что уравне-
272
ГЛАВА 7
ниеЛ1(х)-0 можно разрешить относительно хъ что дает Xj=l—х2—х3.
После подстановки задача принимает вид
минимизировать /(х2, х3)=(1—х2—х3) х2х3
при ограничениях (1—х2—х3)гх3+х2х3+х7’(1—х2—х3)—2=0,
0^1—Х2—Хв<?/2, О^Хз^’/а.
Получить из оставшегося уравнения выражение для одной перемен-
ной, например х3 через х2, затруднительно. Вместо этого для
каждого возможного значения независимой переменной х2 можно
численно найти соответствующее значение х3 каким-либо методом
вычисления корней многочленов. Отметим, что в неравенства, содер-
жащие х3, теперь входят неявные функции от независимой перемен-
ной х2. Таким образом, поскольку переменные х3 и х2 связаны между
собой функциональной зависимостью x3=q(x2), ограничения при-
нимают вид
0^ 1 —х 2—q (х 2)^ V 2,
0^7(Х2Х’/2.
Проверить их выполнимость можно только после решения урав-
нения.
Вообще при большом числе ограничений-равенств оказывается
удобным использовать методы упорядочения уравнений и декомпо-
зиции для выбора независимых переменных и эффективные вычисли-
тельные методы решения систем уравнений. Обсуждение этих мето-
дов выходит за рамки настоящей книги. Читателю следует обра-
титься к работам, в которых рассматриваются решения систем урав-
нений [1, 2], или к прекрасному обзору, сделанному Сарджентом
13].
7.1.2. Определение начальной допустимой точки
Следуя терминологии линейного программирования, задачу
поиска допустимой начальной точки часто называют этапом I ме-
тода. Обычно используются следующие три способа отыскания до-
пустимой точки: случайный поиск, минимизация штрафной функции
при отсутствии ограничений и последовательная минимизация при
наличии ограничений. В этом разделе кратко рассматривается толь-
ко первый из перечисленных способов. Два других описаны в гл. 13.
Теоретически простейший способ получения начальной допусти-
мой точки состоит в генерировании с помощью датчика псевдослу-
чайных чисел (такая программа имеется в программном обеспече-
нии большинства вычислительных систем) пробной точки и в про-
верке ее на допустимость подстановкой в ограничения. По заданным
верхним и нижним границам каждой переменной подсчитываются
x^x^’ + z-i (х'/71 — х'Ч), i=l,...,]V, (7 1)
МЕТОДЫ ПРЯМОГО ПОИСКА В ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 273
где rt— случайные числа, равномерно распределенные на интервале
(О, 1). Если х—N-мерный вектор, то гг генерируется N раз, и коор-
динаты Xi вычисляются по формуле (7.1). Полученная точка прове-
ряется на допустимость вычислением функций, входящих в огра-
ничения задачи. Процесс продолжается, пока не будет найдена точ-
ка, удовлетворяющая всем ограничениям. Поскольку вероятность
получения подобным способом точки, одновременно удовлетворяю-
щей системе ограничений в виде равенств, ничтожно мала, удобнее
использовать форму задачи, в которой ограничения-равенства ис-
ключены. Описанным способом, естественно, определяются толькс
независимые переменные. Но даже при этом случайный выбор может
потребовать значительных затрат машинного времени. Следова-
тельно, для задач большой размерности или с узкой допустимой
областью необходимо использовать другие способы поиска допусти-
мой точки. Они описаны в гл. 13.
7.2. Использование методов поиска для решения
задач безусловной оптимизации
В этом разделе мы кратко остановимся на трудностях, которые
могут встретиться при попытках использования методов прямого
поиска, описанных в гл. 3, для решения задач с ограничениями.
Всюду в дальнейшем предполагается, что ограничения в виде ра-
венств исключены одним из способов, изложенных в 7.1.1. Мы под-
робно рассмотрим только один метод прямого поиска, а именно метод
комплексов, поскольку он широко используется в технических при-
ложениях.
7.2.1. Трудности, встречающиеся при решении задач
с ограничениями
В принципе каждый из трех основных методов прямого поиска,
рассмотренных в гл. 3, можно модифицировать для решения задач
с ограничениями в виде неравенств. Действительно, прежде чем
зафиксировать какую-нибудь точку, можно подставить ее в огра-
ничения задачи и, если хотя бы одно из них нарушается, взять дру-
гую допустимую точку. На практике, конечно, необходимо исполь-
зовать специальные правила, позволяющие в процессе вычислений
переходить от недопустимых точек к допустимым. В противном слу-
чае алгоритм, реализующий метод прямого поиска, может не толькс
иметь невысокую скорость сходимости, но и преждевременно обры-
ваться.
Рассмотрим сначала применение метода сопряженных направ-
лений. Пусть заданы начальная точка и множество направлений
поиска dt, i=l, . . . , N. Метод включает процедуру одномерного
поиска вдоль каждого из этих направлений, в результате чего
определяются сопряженные направления и улучшается значение
274
ГЛАВА 7
Рис. 7.1. Преждевременная остановка алгоритма при использовании метода
сопряженных направлений.
целевой функции. При наличии ограничений в виде неравенств
поиск вдоль какого-либо из заданных направлений может привести
к тому, что решение одномерной задачи оптимизации окажется не-
допустимым. Ясно, что этого можно избежать, ограничив поиск
вдоль фиксированного направления точкой пересечения луча с гра-
ницей области. Но в этом случае нельзя гарантировать возможность
построения сопряженных направлений, и вычисления могут свес-
тись к поиску вдоль направлений, принадлежащих фиксированному
множеству. На рис. 7.1 показано, что в этом случае может произой-
ти преждевременное окончание процесса. Одномерная оптимизация
вдоль лучей dj и d2, выходящих из х(П, либо выводит из допустимой
области, либо дает точку с худшим значением целевой функции.
Следовательно, в поиск обрывается. Очевидно, единственный вы-
ход из создавшегося положения состоит в изменении множества
направлений поиска. Например, можно взять в качестве направле-
ния луч, параллельный линии g'2(x)=0. Приемы, подобные этому,
предложены Дэвисом (см. [41 в гл. 5) и другими, но, как правило:
МЕТОДЫ ПРЯМОГО ПОИСКА В ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 275
для их реализации требуется информация о градиентах функций,
входящих в ограничения
Аналогичные приемы можно использовать при нахождении
оптимума методом поиска, включающим два основных этапа: «ис-
следующий поиск» и «поиск по образцу». В задачах с ограничениями
каждый из этих этапов (или оба) может приводить к недопустимой
Рис. 7 2. Сдвиг точки при «поис-
ке по образцу».
точке; поэтому в алгоритм метода требуется ввести некоторые допол-
нительные правила. Как показано на рис 7 2, если в результате
«поиска по образцу» получена недопустимая базовая точка, то мож-
но уменьшать шаг, например вдвое, до тех пор, пока ие будет найде-
на допустимая точка. Аналогично недопустимые точки, получаемые
Рис. 7.3. Исключение недопусти-
мых точек при исследующем поиске
при исследующем поиске, могут рассматриваться как точки с очень
большим значением целевой функции и поэтому должны быть от-
брошены (рис. 7.3). В итоге может оказаться, что при любом «ис-
следующем поиске» получаются либо недопустимые точки, либо
точки с худшими значениями целевой функции. В этом случае ис-
следующий поиск можно возобновить с уменьшенной величиной
шага. Однако, как и для метода сопряженных направлений (см.
рис. 7.1), возможна ситуация, когда уменьшение Щага поиска не
дает улучшения. Тогда следует проводить поиск вдоль направлений,
параллельных ограничивающей поверхности. Клингман и Хим-
мельблау [5], а также другие авторы (см. [6], гл. VII, а также [4])
дают рекомендации по реализации этого приема. Во всех случаях
276
ГЛАВА 7
требуется информация о градиентах целевой функции и функций,
входящих в ограничения. Но эксперименты показывают, что методы,
описанные в гл. 8—10, оказываются более предпочтительными,
если имеется информация о градиентах.
Основной вывод, который можно сделать из краткого рассмотре-
ния применения методов прямого поиска к задачам с ограничения-
ми, состоит в том, что несложный прием уменьшения шага поиска,
когда принятый шаг приводит к недопустимой точке, обеспечивает
получение допустимой пробной точки. Безусловно, требуется, чтобы
поиск начинался с допустимой точки и чтобы последующие базовые
точки оставались допустимыми; это обеспечивает возможность сокра-
щения шага на каждом этапе. С другой стороны, если множество
направлений поиска не корректируется, то движение вдоль огра-
ничивающих поверхностей исключается и результаты оказываются
неудовлетворительными. Эту трудность можно преодолеть суще-
ственным расширением множества направлений поиска или пере-
ходом к процедурам случайного поиска направлений. Ниже при-
водится эффективный алгоритм, позволяющий применить прямой
поиск по симплексу к решению задач с ограничениями-неравен-
ствами.
7.2.2. Метод комплексов
При реализации метода прямого поиска по симплексу последо-
вательно порождаются точки симплекса в пространстве поиска,
затем симплекс преобразуется путем проектирования «худшей»
точки вдоль прямой, проходящей через центр тяжести остальных
точек симплекса. В задачах с ограничениями в виде неравенств
новая точка может оказаться недопустимой, и тогда ее можно сдви-
гать по направлению к центру тяжести, пока она не станет допусти-
мой. Очевидно, что такая процедура может привести к нарушению
свойства регулярности симплекса, но как показали Нелдер и Мид,
это не обязательно дает плохие результаты. Однако построение
исходного симплекса затруднительно, поскольку, каким бы ни был
размер регулярного симплекса а, велика вероятность, что некото-
рые его вершины будут недопустимыми. Конечно, с помощью под-
ходящих корректировок можно обеспечить допустимость всех его
вершин, но это снова может привести к нарушению свойства регу-
лярности. Кроме того, точки необходимо определять не одновре-
менно, а последовательно, с помощью формулы для построения регу-
лярного симплекса. Эти соображения привели к модификации мето-
да поиска по симплексу, предложенной Боксом [7] и получившей
название метода комплексов.
Бокс предложил строить множество пробных точек Р случайным
образом и последовательно. Приемы генерации случайных точек
приведены в разд. 7.1.2. С учетом заданных верхней и нижней гранив
значений переменных х'у’ и генерируются псевдослучайные
МЕТОДЫ ПРЯМОГО ПОИСКА В ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 277
числа Г/, равномерно распределенные на отрезке (0, 1), после чего
соответствующие координаты точки определяются с помощью фор-
мулы (7.1). Для получения точки в AZ-мерном пространстве требуется
AZ случайных чисел. Каждая полученная точка проверяется на
допустимость, и если какое-нибудь из ограничений нарушается, то
она сдвигается к центру тяжести уже построенных точек до тех пор,
пока не получится допустимая точка. Общее число точек Р должно
быть, конечно, не меньше W-Н, но может быть и большим.
После того как множество из Р точек построено, в каждой из
них вычисляется целевая функция и точка с наибольшим значе-
нием функции отбрасывается. Новая точка получается путем отра-
жения исключаемой точки через центр тяжести остальных точек.
Если х*— исключаемая точка их — центр тяжести остальных то-
чек, то новая точка определяется как
хт — х-|-а (х—Xs).
Параметр а задает расстояние отражения: при а=1 имеет место
равенство ||хот—х|| = ||х—xR||; а>1 соответствует растяжению,
а<1 — сжатию.
Когда найдена новая точка, вычислены значения целевой функ-
ции и функций, входящих в ограничения, возможны следующие
случаи.
1. Новая точка допустимая, и значение целевой функции в ней
не совпадает с максимальным значением на всей совокупности точек.
В этом случае выбираем точку с максимальным значением функции
и вновь выполняем операцию отражения.
2. Новая точка допустимая, и значение функции в ней совпадает
с максимальным значением. Вместо того чтобы производить отра-
жение, передвинем эту точку на половину расстояния до ранее
найденного центра тяжести (в противном случае возможно зацикли-
вание).
3. Новая точка недопустимая. В этом случае уменьшаем в два
раза расстояние до вычисленного ранее центра тяжести. Процедура
поиска продолжается, пока многогранник не будет стянут в центр
тяжести в пределах заданной точности и(или) пока разница между
значениями целевой функции в вершинах не станет достаточно ма-
лой.
Бокс [7] провел численные эксперименты по описанному алго-
ритму и на основе их анализа рекомендует выбирать а = 1,3 и
«2AZ; с другой стороны, Байлс приводит в работе [8] хорошие ре-
зультаты, полученные при P=AZ+2. В большинстве случаев следуют
рекомендации Бокса, согласно которой если новая точка выходит
за границы значений переменных, то соответствующая координата
полагается равной граничному значению. Выбор а большим еди-
ницы компенсирует сжатие комплекса, обусловленное сокращением
в два раза расстояния до центра тяжести. Большое число вершин
278
ГЛАВА 7
используется для предотвращения «уплощения» и вырождения комп-
лекса, когда поиск проводится вблизи границы допустимой области.
Использование границ значений переменных в процессе поиска
также позволяет избежать излишнего сжатия комплекса.
Ниже дается полное описание алгоритма.
Алгоритм метода комплексов
Заданы начальная строго допустимая точка х°, параметр отра-
жения а и параметры окончания вычислений ей 6
Шаг 1. Построение начального комплекса, состоящего из Р
допустимых точек. Для каждой точки р— 1, . . . , Р—1
(а) случайным образом определить координаты xf;
(б) если хр— недопустимая точка, найти центр тяжести х уже
найденных точек и положить
хр = хР+1/2 (х—хР),
повторять процедуру до тех пор, пока хр не станет допустимой;
(в) если хр— допустимая точка, повторять (а) до тех пор, пока
Р=Р,
(г) ВЫЧИСЛИТЬ f(XP) для р=0, . . . , Р—1.
Шаг 2. Отражение комплекса:
(а) выбрать точку xR, для которой
/(x«) = max/(xP) = FMaKC;
(б) найти центр тяжести х и новую точку
хт = х + а (х — xR)\
(в) если хт—недопустимая точка и f (х'я)^Рмакс, уменьшить
в два раза расстояние между хт и центром тяжести х, продолжать
поиск, пока f (хт)<Рпллр,
(г) если хи—допустимая точка и/(хга)</7макс, перейти к шагу 4;
(д) если хт— недопустимая точка, перейти к шагу 3
Ш а г 3. Корректировка для обеспечения допустимости.
(а) если х-"<х-£), положить х^—х^-,
если х™>х(Р\ положить х'’1=х^'1\
(б) если хт— недопустимая точка, уменьшить в два раза рас-
стояние до центра тяжести; продолжать до тех пор, пока хт не ста-
нет допустимой точкой.
Шаг 4. Проверка условий окончания вычислений:
(а) положить
T=~^^f(xP) и х = -^^хр,
(б) если 2 (/ (хР) — /)2 е и 2 (хР — ХУ
р р
вычисления прекратить; в противном случае перейти к шагу 2а.
Отметим, что для выполнения шага 1 необходимо задать границы
МЕТОДЫ ПРЯМОГО ПОИСКА В ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 279
значений всех переменных. Если эти границы нельзя определить
естественным образом из постановки задачи, нужно провести оцен-
ки интервалов возможных значений переменных. Эти оценки следует
включить в ограничения задачи; для обеспечения эффективности
вычислений эти интервалы должны быть как можно короче.
Подробные вычисления с использованием метода комплексов
иллюстрируются следующим примером.
Пример 7.5
Требуется спроектировать прямоугольную конструкцию в форме
параллелепипеда с открытой передней стенкой. Конструкция долж-
на иметь объем 16 000 фут 3, но периметр ее основания не должен
превышать 220 фут Глубина не должна быть больше 60 фут, а ши-
рина — 80 фуг. Кроме того, ширина не должна превышать утроен-
ной глубины, а высота — 2/3 ширины. Стоимость гофрированного
материала, из которого изготовляются крыша и три стенки кон-
струкции, составляет 1 долл за квадратный фут Требуется опре-
делить размеры конструкции таким образом, чтобы минимизировать
стоимость материалов.
Постановка задачи
Введем (рис. 7.4) переменные: х,— глубина (в футах), х2— ши-
рина (в футах), х3— высота (в футах). Стоимость материала будет
стоимость крыши
стоимость задней стенки
стоимость боковых стенок
30^!X2 долл.
ЗОх2х3 долл.
2 (ЗОх|Х3) долл.
включать:
Таким образом, целевая функция имеет вид
/ (х)=30xjX g+30х 2х з+60ххх з.
Условие на объем конструкции задает ограничение в виде равенства
х'1ХгХ3=16 000 фут*.
280
ГЛАВА 7
Условия на линейные размеры задают ограничения в виде нера
венств
2(xi+x2)^220 фут,
х 2<3Xi,
Х3<2/3Х2.
Границами изменения переменных являются следующие:
0=Cxi^60 фут.
0^х2^70 фут.
В стандартной форме записи задача будет иметь вид
минимизировать I (х) = 30х,х2 4- 30х2х,бОх^х,
при ограничениях hx (х) = ххх2х3—16 000 = 0,
gxx =110— х, —х2 > 0,
g'2(x)=3x1—х2>0,
£з (х) = 73х2 —х3>0,
0 sC х, -С 60,
О CJ х2 -С 70,
0< х3.
Для решения этой задачи методом комплексов необходимо ис-
ключить ограничения в виде равенств. В данном случае это можнс
сделать непосредственно, решая уравнение hx(x)=0 относительнс
одной из переменных, например х3:
х3= 16- 103/xiX2.
Используя это соотношение для исключения х3, приведем задачу
к виду
f , 48-104 . 96. Ю4
минимизировать j (х) = 30ххх2 -|------1------
Xi х%
при ограничениях gx (х) = 110—хх — х2 0,
gg(x) = 3x1—х2>0,
/ х 2, 16-ТО3
g3 х) = 78х2 ——— > о,
*1*2
0 < хх < 60,
0 х2 -С 70.
Заметим, что g3 нелинейно зависит от хх и х2. Кроме того, по-
скольку уже имеются верхние и нижние границы для хх и х2, для
применения метода комплексов нет необходимости в специальном
введении границ значений переменных.
Решение. Чтобы алгоритм метода комплексов начал рабо-
тать, возьмем точку х(1’ = (50, 50) как начальное допустимое при-
МЕТОДЫ ПРЯМОГО ПОИСКА В ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 281
ближение. Поскольку задача имеет размерность два, то необходимо
построить еще три точки. Каждая из них может быть получена из
соотношений
х;*’= 0 + 60гг, х^ = 0 + 70^,
где Г1 и г2— случайные числа, равномерно распределенные на ин-
тервале (0, 1).
Предположим, что датчик псевдослучайных чисел генерирует
Г1=0,5 и г2=0,9. Тогда х(2| = (30; 63). Так как это допустимая точ-
ка, то ее необходимо запомнить как вторую вершину.
Предположим, что генератор случайных чисел дает теперь
следующую пару: Г1=0,1 иг2=0,15. Тогда х(3) = (6; 10,5).
Как видно из рис. 7.5, точка х<3) недопустимая. Чтобы получить
допустимую точку, сдвинемся в направлении к центру тяжести уже
282
ГЛАВА 7
найденных допустимых вершин х(1) и х<2). Так как
х = Чг (х(1) + х<2)) = (40; 56,5),
то х(3> = '/2 (X13* + X) = (23, 33,5).
Эта точка допустимая и, следовательно, запоминается.
Наконец, положим ri=0,9 и r2=0,33; тогда х(4) = (54; 23,1) также
является допустимой точкой. Имея четыре допустимые начальные
вершины, вычисляем значения целевой функции для каждой из
них и переходим к первой основной итерации метода.
Номер итерации Xj 1 W
1 50 50 . 103,8-108
2 30 63 87,94 103
3 23 33,5 72,64 103
4 54 23,1 87.87-103
Из таблицы видно, что л'11— наихудшая из всех точек и должна
быть исключена из рассмотрения.
Новая возможная точка находится при величине шага а=1,3:
х16’ = х+ 1,3 (1-х‘») = (39^7) +
(/ЯЧ А7\ /^Л\ I
+ КЗД-(5о)Н17’03’ 26’69>-
Однако в точке х(5) ограничение g3 не выполнено. Сдвигаем точку
в направлении к центру тяжести и получаем
х(5> = 1/г (Х(5> + 7) (26,35; 33,28)
— допустимую точку со значением целевой функции /(х(5’)=«
— 73,37-103, которое меньше, чем вхш.
Теперь множество вершин состоит из точек х(2), х'3’, х(4) и х(5>.
Наихудшей из них является х(2), в которой /(х(2))=87,94-108. Цент-
ром тяжести остальных вершин будет х=(34,45; 29,96), и новая
точка х161 получается после двух последовательных сдвигов к центру
тяжести. Тогда х(6’ = (34,81; 27,28) с f(x‘e’)=77,47-103. На рис. 7.5
видно, что вершины х(3), х(4), х(5) располагаются примерно вдоль
кривой g3(x)=0- Последующие итерации приводят к оптимальному
решению х*=(20; 40). Однако, как следует из результатов расчетов,
приведенных в табл 7.1, вершины имеют тенденцию располагаться
вдоль кривой g3(x)=0, вследствие чего поиск существенно замед-
ляется.
МЕТОДЫ ПРЯМОГО ПОИСКА В ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 283
Таблица 7.1.
Номер X] А-7 /М, ХЮ” Замененная вершина
7 23,84 32,69 72,880 4
8 17,63 36,978 72,747 6
9 19,91 34,75 72,491 5
10 18,99 35,85 72,478 7
11 21,61 33,96 72,497 8
12 19,25 35,73 72,437 3
13 19,02 35,77 72,484 11
14 18,80 36,11 72,483 9
15 18,94 35,94 72,475 13
16 19,245 35,62 72,459 14
17 19,476 35,46 72,437 10
18 20,021 35,44 72,349 15
19 20,021 35,44 72,349 16
20 20,842 35,08 72,331 12
21 21,359 35,14 72,309 17
22 21,603 35,08 72,321 18
23 21,471 35,04 72,323 19
24 21,684 35,105 72,319 20
25 21,650 35,197 72,206 23
26 21,625 35,299 72,293 22
7.2.3. Обсуждение
Хотя метод комплексов не требует непрерывности функций,
определяющих задачу, так как не использует значения производ-
ных, строго говоря, необходимо, чтобы допустимая область была
выпуклой (см. определение в приложении А). Это условие оказы-
вается существенным при нахождении центра тяжести (шаги 16 и
26) и сдвиге допустимой, но неудовлетворительной по значению
целевой функции точки. В первом случае предполагается, что центр
тяжести — выпуклая комбинация допустимых точек — тоже будет
допустимой точкой. Как показано на рис. 7.6, а, это может оказать-
ся неверным, если допустимая область невыпуклая. Аналогично
при невыпуклой области сдвинутая точка может оказаться недопу-
стимой, даже если центр тяжести — допустимая точка (рис. 7.6, б).
Следовательно, для невыпуклых областей метод комплексов рас-
ходится. На практике метод широко используется и дает хорошие
результаты для выпуклых задач, поскольку ситуации, описанные
выше, встречаются редко.
Из анализа примера 7.5 следует, что сходимость метода комплек-
сов существенно замедляется, если пробные точки располагаются
вдоль границы. Действительно, в примере 7.5 при любом разумном
критерии остановки вычислений можно оказаться на значительном
расстоянии от оптимума. Эта ситуация довольно типична для метода
284
ГЛАВА 7
комплексов, и поэтому используется специальный прием, при кото-
ром вычисления несколько раз прерываются при выполнении ка-
кого-либо критерия остановки и затем вновь возобновляются.
Наилучшее из полученных решений запоминается и используется
в качестве начальной точки при возобновлении вычислений. Кри-
терием полного окончания вычислений может служить заданное
число прерываний. Описанный прием в целом улучшает сходимость
Рис. 7.6. Последствия невыпуклости допустимой области.
метода. Конечно, ни этот, ни любой другой эвристический прием
не может гарантировать во всех случаях сходимость метода к ло-
кальному оптимуму. Хотя метод, вообще говоря, сходится медлен-
но, он в большинстве случаев приводит к лучшей точке по сравнению
с начальной точкой и поэтому находит широкое применение в тех-
нических приложениях.
Свенн в своем обзоре ([61, гл. 7) приводит многочисленные улуч-
шенные варианты основного алгоритма Бокса, предложенные раз-
личными авторами. Они включают дополнительные правила рас-
ширения/сжатия, использование метода центра тяжести и его мо-
дификаций для случаев, когда центр тяжести не допустим, проце-
дуры построения симплексов без случайных выборок, а также ква-
дратичную интерполяцию. В целом эти модификации основной схе-
мы алгоритма не дают значительных улучшений. Если представля-
ется необходимым использовать более сложный алгоритм, то по
сравнению с эвристическим методом следует отдать предпочтение
методам, описанным в гл. 9 и 10.
7.3. Методы случайного поиска
Применение случайных выборок для нахождения допустимой
начальной точки с использованием метода комплексов целесооб-
разно рассматривать как развитие методов прямого поиска, пол-
ностью или частично основанное на идеях случайного поиска. Дей-
МЕТОДЫ ПРЯМОГО ПОИСКА В ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 285
ствительно, после опубликования в 1958 г. работы Брукса [9] в
технической литературе стали появляться рекомендации по ис-
пользованию методов случайного поиска, начиная с совсем простых
процедур совместных выборок до более сложных вычислительных
схем, включающих последовательные выборки и эвристические ме-
тоды спуска. В этом разделе будет кратко описано несколько при-
меров методов, использующих случайные выборки. Хотя подобные
методы могут оказаться эффективными в окрестности оптимума,
они непригодны, если требуются более точные оценки решения.
7.3.1. Прямые выборочные процедуры
Наиболее простой способ генерации точек посредством выбороч-
ных процедур основан на использовании формулы (7.1). После про-
верки каждой из этих точек на допустимость вычисляется значение
целевой функции, которое сравнивается с наилучшим значением,
полученным к данному моменту. Если исследуемая точка дает луч-
шее значение, то она запоминается, в противном случае отбрасыва-
ется. Процесс прекращается либо после' заданного числа итераций,
либо по исчерпании установленного машинного времени. Описан-
ная процедура относится к типу так называемого совместного по-
иска и, как хорошо известно, непригодна для оценок функций.
В работе 110] указано, что для получения 90%-ного доверительного
интервала величиной еДх'^’—х'^’), где0<е<1, для переменной
Xi совместный случайный поиск требует
N
2,3 П ег1
i = 1
испытаний. При М=5 и ег =0,01 число испытаний будет примерно
равно 2,3-101", что исключает возможность непосредственного ис-
пользования метода совместного поиска.
Некоторого улучшения можно достичь группировкой выборок
в серии. Наилучшая точка в каждой серии используется как на-
чальная точка следующей серии, точки которой выбираются из
интервала меньшей величины. Ниже описывается один из возмож-
ных способов реализации этого подхода (см. НН), когда пользова-
тель задает количество серий Q и количество точек Р в каждой из
них.
Выборки с уменьшением интервала. Даны: начальное допустимое
решение х°, оценка величины начального интервала г°, где
х"—1/2г(0)^х<;(х(0’+1/2г(0)), и параметр е, определяющий уменьше-
ние интервала (0<е<1). Для каждой из серий, начиная с <?=1,
нужно выполнить следующие действия.
Шаг 1. Для i=l, . . N вычислить х^—х^+г^-1, где г —
случайная величина, равномерно распределенная на интервале
(—1/а, V2)-
286
ГЛАВА 7
Ш а г 2. Если хр — недопустимая точка и p<ZP, повторить
шаг 1. Если хр — допустимая точка, запомнить и /(хр), и если
р<Р, повторить шаг 1. Если р=Р, найти среди всех допустимых
точек хр точку с наименьшим значением f(x?) и положить ее рав-
ной хч.
Шаг 3. Уменьшить интервал, полагая z?=(l—е) г?*1.
Шаг 4. Если q>Q, закончить вычисления. В противном слу-
чае увеличить q и продолжить вычисления, начиная с шага 1.
В работе [111 величина г полагалась равной 0,05 и каждая серия сос-
тояла из 100 точек. Число серий выбиралось в соответствии с же-
лаемым уменьшением интервала значений переменной. При 20С
сериях начальный единичный интервал сводился к интервалу дли-
ной
(1—0,05)200^3,5-10-5
за 2-10' испытаний. Для простой задачи небольшой размерности,
в которой каждая проверка допустимости и подсчет значения целе-
вой функции требуют не более 10~3 с работы центрального процес-
сора, общие затраты времени можно считать приемлемыми. Для
более реальных задач, например задач имитационного моделиро-
вания, описанный алгоритм может оказаться слишком дорогостоя-
щим.
Пример 7.6. Распределение топлива в силовых установках [11!
Каждый из двух электрических генераторов может работать на
жидком топливе и газе или в любом их сочетании. Суммарная мощ-
ность, развиваемая обоими генераторами, должна составлять
50 МВт. Потребление газа ограничено 10 ед./ч. Желательно выб-
рать схему работы каждого генератора так, чтобы минимизировать
потребление жидкого топлива.
Согласно кривой, отражающей эксплуатационные характеристи-
ки генератора 1, затраты топлива на обеспечение выходной мощно-
сти МВт составляют
w^-1,4609 +0,15186 Xj+0,00145 х(, (7.2)
1^=1,5742+0,1631 ^+0,001358 (7.3)
где Wi и zo2— затраты жидкого топлива и газа в час соответственно.
Аналогично для генератора 2 затраты топлива на обеспечение
выходной мощности х2 МВт составляют
у, =0,8008+0,2031 х2+0,000916 х\, (7.4)
у2=0,7266+0,2256лг2+0,000778 х2, (7.5)
где ь/i и уг— затраты жидкого топлива и газа в час соответственно.
По эксплуатационным характеристикам генераторов может из-
меняться в диапазоне
18CXJC30, (7.6)
а - в диапазоне
14<х2С25. (7.7)
МЕТОДЫ ПРЯМОГО ПОИСКА В ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 287
Предположим, что разные виды топлива могут комбинироваться
аддитивным образом, т. е для любого значения выходной мощно-
сти х* любая линейная комбинация топливных компонент
hitth (%*)-+ (1 —(х*г),
где , также дает мощность, равную xj. Подобное предполо-
жение верно и для генератора 2.
Задача теперь формулируется следующим образом: требуется
определить мощность каждого генератора Xi и х2 и доли использо-
вания разных видов топлива и Х2 так, чтобы минимизировать об-
щее потребление жидкого топлива:
/=Х,ьу1(х1)+Х2у1(х1)
при ограничении на использование газа
(1—2ч>2(Х1)+(1—Х2) у2(л2ХЮ, (7.8)
ограничении на суммарную мощность
Xi+x2=50 (7.9)
и ограничениях на переменные (7.6) и (7.7), а также
OCXxCl и 0^2<1. (7.10)
Используя равенство (7.9), можно исключить переменную хг
и свести исходную задачу к задаче, содержащей три переменные,
одно нелинейное неравенство (7.8), неравенства (7.10) и
25^X1^30;
последнее получается из (7.6), (7.7) и (7.9)
В работе [11] показано, что при начальном решении
Zi=20, ^=1/2, Х2=1/2
и оценках границ начального интервала
гх=20, z2=l,0, z3=l,0
решение с точностью 0,1% достигается при реализации 55 серий по
100 пробных точек в каждой. Для получения точности в 0,01%
необходимо 86 серий или 86 000 пробных точек. Оптимальное ре-
шение имеет вид
/=3,05 ед. кол. нефти/ч,
Х!=30, х2=20,
Х2=0 и Х2=0,58.
Очевидно, что количество пробных точек 5500 итераций для ре-
шения задачи с целевой функцией и единственным нелинейным
ограничением третьей степени слишком велико. Кроме того, тре-
бование дополнительных 3100 пробных точек для повышения точ-
ности на один знак непциемлемо.
288
ГЛАВА 7
Сходимость описанного выше эвристического алгоритма, ос-
нованного на непосредственном уменьшении интервалов значе-
ний переменных при переходе от серии к серии, можно улучшить,
используя другие функции распределения случайных переменных*
Так, в работах [12,13] предлагается использовать формулу
x? = 7z + zz(2r-l)\
где х — текущее наилучшее решение, zt— допустимый интервал
значений xt и г — случайная величина, равномерно распределенная
на интервале (0, 1).
Когда k=\, хР становится случайной величиной, равномерно
распределенной на интервале (хг—гг, хг+гг). При /г=3, 5,‘7 и т. д.
распределение хр( все более и более концентрируется вокруг
Xi. Следовательно, k можно использовать как регулирующий пара-
метр, сжимающий или расширяющий область поиска. В работе
[12] рекомендуется увеличивать k на две единицы, если получено
заданное число точек, улучшающих значение целевой функции,
и, наоборот, уменьшать k на две единицы, если при заданном числе
испытаний не происходит требуемого улучшения целевой функции.
Преимущество такого подхода состоит в том, что число испытаний
между корректировками изменяется в соответствии с результатами
вычислений.
Дальнейшее уточнение подобных методов представлено в работе
[141. Новые точки генерируются путем выборок из нормального
распределения с центром в наилучшей текущей точке х и дисперсией,
которая рассматривается как параметр, корректируемый эвристи-
ческим методом. Так, в частности, дисперсия уменьшается в три
раза после каждого улучшения или увеличивается в два раза после
100 неудачных испытаний. Эмпирические данные, приведенные в
работах [12] и [14], свидетельствуют о том, что подобные методы
подходят для задач небольшой размерности и при невысоких тре-
бованиях к точности решения, например в 1%. Эффективность этих
методов существенно снижается, когда требуется большая точность.
Например, при увеличении точности на один знак число итера-
ций увеличивается в три раза [14]. Применение подобных методов
для нахождения оптимального решения в имитационной модели хи-
мического процесса с шестью переменными описано в работе [131.
Для получения оптимального решения понадобилось несколько
сотен прогонов имитационной модели, несмотря на то что начальное
приближение было вполне удовлетворительным. В целом все име-
ющиеся сведения о применении описанных выше простых процедур
случайных выборок позволяют сделать вывод об их непригодности
для решения задач большой размерности и задач, в которых тре-
буется высокая точность.
МЕТОДЫ ПРЯМОГО ПОИСКА В ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 289
7.3.2. Комбинированные эвристические процедуры
Для повышения эффективности методов случайного поиска
различные авторы предлагают ряд более сложных адаптивных или
эвристических алгоритмов, которые позволяют включить некото-
рые элементы методов спуска в общую схему поиска. К их числу
относятся простые методы случайного спуска [11], более сложные
адаптивные методы с уменьшаемым интервалом значений перемен-
ных и тщательно разработанные процедуры частичного перебора
[16]. В этом разделе кратко рассматриваются лишь два типичных
алгоритма. В технической литературе приводится много данных о
применении подобных алгоритмов, но в большинстве случаев там
отсутствуют контрольные тесты, позволяющие оценить их срав-
нительную эффективность (см., например, обзор в работе [17]).
Рассматриваемые алгоритмы не превосходят другие по своим вы-
числительным характеристикам и демонстрируют лишь определен-
ный подход к решению описываемых задач.
В адаптивном алгоритме случайного поиска с переменным шагом
[16], первоначально разработанном для задач без ограничений,
случайные выборки используются для определения направления
поиска, а длина шага находится в соответствии с достигаемым улуч-
шением целевой функции. Точнее, если две последовательные ите-
рации дают улучшение целевой функции, величина шага увеличи-
вается в раз. Если же М последовательных итераций не дают
улучшения, то величина шага уменьшается в раз. В схематиче-
ском виде и с учетом необходимых модификаций, позволяющих учи-
тывать ограничения задачи, алгоритм описывается следующим обра-
зом.
Адаптивный алгоритм случайного поиска с переменным шагом.
Даны параметры aJ, af и М и начальная допустимая точка х°.
Начальная величина шага а полагается равной 1, а т — число
испытаний, не дающих улучшения,— принимается равным 0.
Шаг 1. Получить случайный вектор d единичной длины и по-
ложить x(i)=x(0)4-ad.
Шаг 2. Если х(1)—допустимая точка и f(xw)<.f(х<0>), по-
ложить y=xw+as (х*п—х(0)) и перейти к шагу 3. В противном слу-
чае принять т=т+\ и перейти к шагу 4.
Шаг 3. Если у — допустимая точка и f(y)<f (х'0’), положить
a=a5a, хм=у и перейти к шагу 5. В противном случае перейти
к шагу 1.
Шаг 4. Если т>М, положить a=afa, т=0 и перейти к ша-
гу 5. В противном случае сразу перейти к шагу 5.
Шаг 5. Перейти к шагу 1, если не выполнено условие окон-
чания вычислений.
Рекомендованные в работе [161 значения параметров: ссл=1,618,
3^=0,618 и Л1=ЗАГ, где АГ — размерность задачи.
Численные эксперименты с некоторыми алгоритмами случай-
10 № 182А
290
ГЛАВА 7
ного поиска 118], в том числе и с вышеописанным, показывают, что
в случае безусловной оптимизации адаптивный алгоритм случай-
ного поиска эффективен на начальной стадии вычислений для задач,
содержащих не более 10 переменных. Для получения решения с
большей точностью линейная (в среднем) скорость сходимости ал-
горитма оказывается недостаточной. Хотя сравнение алгоритмов,
описанных в работах [11, 12 и 14], не производилось, более после-
довательный характер адаптивных прямых методов поиска позво-
ляет их считать более предпочтительными.
Противоположностью описанного алгоритма является комбина-
торный эвристический алгоритм, разработанный для решения за-
дач проектирования машин и механизмов. Основная идея этого
алгоритма состоит в дискретизации интервалов значений незави-
симых переменных и реализации случайного поиска на полученной
дискретной решетке, узлы которой представляют собой возможные
значения переменных. Решетка получается в результате разбиения
интервала значений каждой независимой переменной. Поиск значе-
ния переменной осуществляется на этой фиксированной решетке
путем квазислучайных процедур, проводимых отдельно для каж-
дой переменной. Описание алгоритма приводится ниже.
Комбинаторный эвристический алгоритм
Шаг 1. Построить случайную допустимую начальную точку
х° и положить FM„H=f(x°). Для каждой переменной i, i=l, 2, . . .
. . ., М выполнить следующую последовательность вычислений.
Шаг 2. Провести оптимизацию по i-й переменной, зафикси-
ровав остальные.
(а) Выбрать случайным образом возможные значения i-й пере-
менной для нахождения q дополнительных допустимых точек с луч-
шим значением целевой функции по сравнению с текущей базовой
точкой. Если такие точки получить не удается, повторить шаг 2 для
переменной £+1.
(б) Определить наилучшее из q допустимых решений и положить
значение целевой функции равным Тмп.
(в) Произвести «упреждающий» поиск.
(1) Для каждого из q допустимых решений, найденных на шаге
2(a), провести случайный выбор одного из q возможных значений
переменной (i+1) для определения допустимого значения этой
переменной, дающего лучшее значение целевой функции по
сравнению с Ткпа.
(2) Выбрать наилучшую из q допустимых точек. Зафиксиро-
вать значение переменной i, соответствующее этой точке, как
оптимальное.
(г) Если i=N, перейти к шагу 3. В противном случае выполнить
шаг 2 для переменнной (i+1).
Шаг 3. Провести случайный поиск для определения наилуч-
шего значения переменной N при фиксированных значениях дру-
МЕТОДЫ ПРЯМОГО ПОИСКА В ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 291
гих переменных, соответствующих текущим базовым точкам. Най-
денную точку принять за новую базовую точку, а значение целевой
функции в ней — за новое значение Fmii.
Шаг. 4. Перейти к шагу 2 с i=l, если не выполнены условия
окончания вычислений.
В качестве критерия окончания вычислений можно использо-
вать, например, тот факт, что целевая функция не улучшается. Ав-
торы алгоритма утверждают, что q, т. е. число «упреждающих»
точек, должно лежать между 3 и 5.
Необходимо обратить внимание на то, что после отыскания
случайной начальной точки дальнейший поиск состоит в случай-
ном выборе одного возможного значения для каждой переменной из
дискретного множества значений. При этом случайный поиск сво-
дится к последовательному выбору одного из возможных значений
переменных и позволяет исключить трудоемкий поиск па всем ди-
скретном множестве в пространстве переменных. Случайные про-
цедуры подобного типа разбиения интервала (0,1) на равные подын-
тервалы реализуются так, чтобы каждому возможному значению
переменной соответствовал один подынтервал. Далее выбирается
то дискретное значение переменной, которому соответствует подын-
тервал, содержащий полученную реализацию случайной величины,
равномерно распределенной на интервале (0, 1). Дальнейшие усовер-
шенствования комбинаторного эвристического алгоритма описаны
в работе [20]. Они включают переупорядочивание переменных, более
разработанные «упреждающие» процедуры и приемы уменьшения
числа переменных.
Разработчики комбинированного эвристического алгоритма при-
водят данные о его применении к различным задачам проектирова-
ния машин и механизмов. В частности, даются примеры разработки
привода с плавно регулируемой скоростью, записывающего устрой-
ства, сдвоенной кулисной передачи и зубчатой передачи с двойным
зацеплением [20, 21]. В этих примерах применение алгоритма обе-
спечило улучшение конструкций по сравнению с описанными ранее
в технической литературе. Хотя отдельные примеры использования
алгоритмов подобного типа свидетельствуют об их преимуществе
по отношению к алгоритмам одновременного случайного поиска,
пока нет достаточных оснований для более обстоятельного сравни-
тельного анализа.
7.3.3. Обсуждение
По имеющимся разрозненным данным о вычислительных экспе-
риментах можно сделать вывод, что алгоритмы случайного поиска
целесообразно использовать либо для задач небольшой размерно-
сти, либо как вспомогательный прием для определения «хорошей»
начальной точки при применении более сложных методов оптими-
зации. Известно, что любые процедуры случайного поиска, охва-
292
ГЛАВА 7
тывающего большую часть допустимой области, существенно
улучшают возможности обнаружения окрестности глобального
оптимума. Проведены исследования с целью использования этого
обстоятельства для решения многоэкстремальных задач безусловной
оптимизации [22—24]. Однако накопленный в этой области опыт
свидетельствует о том, что выборочные методы следует использовать
только для обнаружения окрестности минимума, тогда как теорети-
чески обоснованные методы целесообразно применять для улуч-
шения получаемых приближенных оценок.
Алгоритмы случайного поиска, описанные в данном разделе,
в которых используются адаптивные эвристические процедуры,
представляются более эффективными, поскольку они минимизируют
обращение к одновременным выборкам. Вообще последовательные
выборочные процедуры более эффективны, чем процедуры, реализу-
емые одновременно, так как позволяют использовать накопленную
информацию. Выборочными процедурами, подобными приведенным
в работе [11], в которых последовательно производится сокращение
допустимой области, следует пользоваться с осторожностью, с тем
чтобы эвристические правила сокращения допустимой области не
привели к потере самого оптимального решения. В принципе это
возможно, поскольку многие или большинство пробных точек в
одной серии могут оказаться недопустимыми. В этом случае базо-
вая точка следующей серии выбирается из очень небольшого числа
допустимых точек и дальнейший поиск может производиться в об-
ласти, не содержащей оптимального решения. Чтобы избежать это-
го, в подобных алгоритмах необходимо контролировать число до-
пустимых точек, полученных в одной серии, и увеличивать количе-
ство испытаний в серии, если число допустимых точек мало.
Хотя исчерпывающих сведений о применении методов случай-
ного поиска нет, из опубликованных данных можно сделать вывод,
что эти методы эффективны при решении существенно нелинейных
многоэкстремальных задач небольшой размерности. Для задач
большей размерности с большим числом нелинейных ограничений
гораздо более эффективными оказываются методы, изложенные в
следующих трех главах.
7.4. Заключение
В этой главе основное внимание сосредоточено на методах оп-
тимизации, основанных на вычислении значений целевой функции
и ограничений. Поскольку при реализации этих методов трудно
обеспечить выполнение ограничений в виде нелинейных равенств,
последние необходимо тем или иным способом исключить. Кроме
того, рассмотренные методы требуют предварительного нахождения
хотя бы одной допустимой точки. Для решения этой задачи можно
воспользоваться случайным поиском. Все алгоритмы, описанные
в данной главе, можно разделить на две группы. К первой группе
МЕТОДЫ ПРЯМОГО ПОИСКА 3 ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 293
относятся алгоритмы, основанные на методах прямого поиска для
задач безусловной оптимизации; ко второй — алгоритмы, построен-
ные на идеях случайного поиска. Показано, что алгоритмы, реа-
лизующие поиск на фиксированном множестве направлений, могут
преждевременно обрываться. Чтобы избежать этого, необходимо их
модифицировать и включить в множество направлений нормали к
ограничивающим поверхностям. Распространение прямого поиска по
симплексу на задачи с ограничениями требует введения лишь не-
значительных изменений. Трудности возникают только в тех слу-
чаях, когда допустимая область невыпуклая.
Алгоритмы методов случайного поиска включают широкий класс
вычислительных процедур, начиная с простейшего метода проб и
ошибок и кончая существенно более сложными процедурами, в ко-
торых сочетаются случайные выборки с различными эвристическими
и адаптивными приемами. Показано, что последовательные случай-
ные выборки всегда предпочтительнее одновременных и некоторые
способы последовательного уменьшения интервалов значений пере-
менных вполне оправданы. Простейшие методы случайного поиска
применимы к задачам небольшой размерности и в тех случаях, когда
не требуется высокая точность вычислений. В конце главы в ка-
честве иллюстрации показано, как могут использоваться случай-
ные методы в сочетании с эвристическими приемами. При использо-
вании адаптивного алгоритма с переменным шагом случайным обра-
зом выбирается направление поиска, а величина шага определяется
из эвристических соображений. В случае комбинаторного эвристи-
ческого алгоритма производится построение решетки на интервалах
значений независимых переменных с последующим случайным по-
иском на ней. Некоторые экспериментальные данные свидетель-
ствуют, о том, что применение подобных алгоритмов эффективно
для существенно нелинейных задач небольшой размерности. По
всей видимости, наилучшими областями применения методов слу-
чайного поиска являются определения достаточно хорошей началь-
ной допустимой точки и окрестности глобального решения для мно-
гоэкстремальных задач.
Контрольные вопросы и задачи
7.1. Почему необходимо исключить ограничения в виде равенств
при использовании методов прямого поиска?
7.2. Почему можно использовать штрафную функцию для нахожде-
ния допустимой точки в задаче с ограничениями в виде нера-
венств?
7.3. Какова причина использования более чем /V 4-1 точки в алго-
ритме комплексов?
7.4. Почему необходима выпуклость для успешного применения
алгооитма комплексов?
294
ГЛАВА 7
7.5. Почему в алгоритме комплексов используется процедура воз-
врата?
7.6. Какие факторы необходимо учитывать при выборе числа точек
в каждой серии при случайном поиске с уменьшением интер-
вала?
7.7. Возможен ли пропуск минимального решения при использо-
вании случайного поиска с уменьшением интервала? Если да,
то по какой причине и как можно этого избежать?
7.8. Какие параметры изменяются в адаптивном случайном алго-
ритме с переменным шагом?
7.9. Покажите, что множество точек, удовлетворяющих ограниче-
нию gi(x)=xf—х2^0, выпуклое. Пусть ограничение пере-
писано в виде равенства с введением дополнительной перемен-
ной. Будет ли выпуклым множество точек, удовлетворяющих
ограничениям
gi (х)=х2—х2+х3=0,
gi (х)=х3>0.
7.10. Являются ли выпуклыми множества, определяемые ограни-
чениями
a) gi(x)=^i+x2—1 =0, б) gi(x)=Xt—1<0,
g2(х)=2—xf—xl > 0, g2(x)=xi+x2—2>0?
7.11. Является ли выпуклой допустимая область
Х1 + Х2+Х3=1 ,
х* + х2<1,
•Гз+*! > 1?
Обоснуйте ответ.
7.12. Дана задача
минимизировать /(х)=х?+х|+х|
при ограничениях gL(x) = l—хг'х-^О,
gi(x)=Xi~ х3>0,
/i!(x)=x!—х\ +х2хэ—4=0,
0ССС5, ОС-чСЗ, ОСхзСЗ.
Какие преобразования необходимо выполнить, чтобы можно
было использовать метод комплексов? Приведите окончатель-
ную форму задачи.
7.13. Дана задача
минимизировать f(x)=—XiX?x3/81
при ограничениях hj (х)=х,’-}-х^-|-ха—13=0,
h2 (х) =х2х~1/2—1 =0,
х(С0.
МЕТОДЫ ПРЯМОГО ПОИСКА В ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 295
(а) Перепишите задачу в форме, пригодной для использо-
вания метода комплексов. Будет ли множество допустимых
точек выпуклым?
(б) Оцените верхние и нижние границы значений независи-
мых переменных при использовании метода комплексов.
(в) Найдите начальную допустимую точку.
7.14. При решении задачи
минимизировать /(х)=3(ха—4)2—2хх
при ограничениях gi (х) = 10—х|—х|>, 0
g2(x)=9—х?— (х2—4)2>0,
0СхгД4, 0Сх2С4
методом комплексов получены следующие точки:
X1 x2 f W
1 2,0 2,0 8
2 0,5 3,0 2
3 0,6 1,1 24,03
4 2,3 2,1 6,23
Полагая а = 1,3, выполните две итерации метода комплексов.
Изобразите результаты графически.
7.15. Дана задача
минимизировать f(x)=3xl—2ха
при ограничениях gi(x)=2xi+x2^4,
g2(x)=xl + х2<40.
(а) Оцените верхние и нижние границы значений переменных
и найдите начальное допустимое решение.
(б) Составьте программу для случайного поиска с уменьше-
нием интервала и найдите решение задачи. Возьмите
е=0,05 и 100 серий по 50 точек в каждой.
7.16. Решите задачу
минимизировать /(х) = (хх — 1)а + (*i — ха)3 + (ха —-xs)2
при ограничениях ht (x) = xt (1 + x£)4-xj— 4 — 3]/ 2=0,
0<хг<3
методом комплексов, используя ЭВМ [/*=0,032567; см Miele
et al., J. Optim. Theory Appl., 10, 1 (1972).]
7.17. Решите задачу
минимизировать f(x) = (x,—1)2 + (x4—xa)24- (x3 — 1)2 +
+ (•'V-1 )4 + (хь [)
при ограничениях (x) = xfxt + sin (x4 — x,)_— 2|/ 2 = 0,
h2 (x) = x2 xaXi—8 — ]/ 2 — 0
296
ГЛАВА 7
с помощью адаптивного алгоритма случайного поиска, ис-
пользуя ЭВМ [/(х*)=0,24149, см. Miele et al., J. Optim. Theory
Appl., 10, 1 (1972)1.
7.18. Для разработки конструкции водонепроницаемых переборок
минимального веса для танкера требуется решить следую-
щую оптимизационную задачу (Kvalie et al., Tech. Rep.,
Norwegian Technical Institute, Trondheim, Norway, 1966):
минимизировать f(x) = ’ 2 \ 7
xi~ Ha — x2)
при ограничениях g4(x) — xtxi (OAxyA-1/^)—
—8,94 [x4 + (xl — x2W2] > 0,
g2 (x) = x2x4 (0,2xi + 7l2x3)—
— 2,2(8,94 [Xj-Hxl—x22)i/2jp/3>o,
g3 (x) = x4— 0,0156X1 — 0,15^ 0,
g4 (x) = x4 — 0,0156x3— 0,15^0,
g5 (x) = x4—1,05>0,
g« (x) = x3—x2>0.
Переменные xf соответствуют линейным размерам перебо-
рок: Xi— ширина, х3— глубина, х3— длина и х4— толщина,
(а) Найдите начальное допустимое решение с помощью слу-
чайных выборок при заданных границах значений пере-
менных.
(б) Решите задачу методом случайного поиска (/*=6,84241).
Литература
1 Wait R., The Numerical Solition of Algebraic Equations, Wiley, N. Y., 1979.
2 Westerberg A W., Hutchinson H. P., Mo ard R. L., Winter P., Process Flow-
sheeting, Cambridge University Press, Cambridge, England, 1979.
3 Sargent R. W H., A Review of Methods for Solving Nonlinear Algebraic Equati-
ons, Proceedings Conference, in: Foundations of Computer Aided Process Design
(R.S. H. Mah, W. D. Seider, Eds.), Vol. 1, Engineering Foundation, N. Y.,
pp. 27 -76, 1981
4 Box M. J., Davies D., Swann W. H., Nonlinear Optimization Techniques,
ICI Monograph No. 5, Oliver & Boyd, London, 1969.
5. Klingman W R., Himmelblau D. M., Nonlinear Programming with the Aid
of a Multiple Gradient Summantion Technique, J ACM, 11, 400—-415 (1964).
6. Gill P. E., Murray W. (Eds.), Numerical Methods for Constrained Optimizati-
on, Academic Press, London, 1974
7. Box M. J., A New Method of Constrained Optimization and a Comparison with
Other Methods, Computer J., 8, 42—52 (1965).
8. Biles W. E., Optimization of Multiple Response Simulation Models, Universi-
ty of Notre Dame, Final Report, ONR-Contract N0014-76-C-1021, Oct. 31, 1978.
9. Brooks S. H„ A Discussion of Random Methods for Seeking Maxima, Oper.
Res., 6, 244—253. (1958).
10. Spang H A , A Review of Minimization Techniques for Nonlinear Function,
SIAM Rev., 4, 343-3o5 (1962),
МЕТОДЫ ПРЯМОГО ПОИСКА В ЗАДАЧАХ УСЛОВНОЙ ОПТИМИЗАЦИИ 29?
11. Luus R., Jaakola Т. Н. I., Optimization by Direct Search and Systematic Re-
duction of the Size of Search Region, AlChE J., 19, 760—766 (1973).
12. Heuckroth M. W., Gaddy J. L., Gaines L. D., An Examination of the Adaptive
Random Search Technique, AlChE J., 22, 744—750 (1976).
13 Doering F. J., Gaddy J. L., Optimization of the Sulfuric Acid Process with a
Flowsheet Simulator, Computers Chem. Eng., 4, 113—122 (1980).
14. Goulcher R., Casares Long J. J., The Solution of Steady State Chemical Engine-
ering Optimization Problems using a Random Search Algorithm, Computers
Chem. Eng, 2, 33—36 (1978).
15. Martin D. L., Gaddy J. L., Process Optimization with the Adaptive Randomly
Directed Search, in: Selected Topics in Computer Aided Process Design and Ana-
lysis (R. S. H. Mah, G V. Reklaitis, Eds.), CEP Symp. Ser., Vol. 214, Ameri-
can Institute of Chemical Engineers, N. Y., 1982.
16. Schumer M. A., Steiglitz K., Adaptive Step Size Random Search, IEEE Trans.,
AC-13, 270—276 (1968).
17 Jarvis R. A., Optimization Strategies in Adaptive Control: A Selective Survey,
IEEE Trans. Syst., Man, and Cybern., 5, 84—94 (1975).
18 Schrack G., Borowski N., An Experimental Comparison of Three Random Se-
arches, in Numerical Methods for Nonlinear Optimization (F. A. Lootsma, Ed.),
Academic Press, N. Y., 1972.
19 Lee T. W., Freudenstein F., Heuristic Combinatorial Optimization in the Ki-
nematic Design of Mechanisms: Part 1. Theory, J. Eng. Ind Trans. ASME,
1277—1280 (1976).
20. Datseris P., Principles of a Heuristic Optimization Technique as an Aid in De-
sign—An Overview, ASME Tech. Paper, 80-DET-44, Sept. 1980.
21. Lee T. W„ Freudenstein R., Heuristic Combinatorial Optimization in the Ki-
nematic Design of Mechanisms, Part 2: Applications, J. Eng. Ind. Trans. ASME,
1281 — 1284 (1976).
22. Mockus J., On Bayesian Methods of Optimization, in: Towards Global Optimi-
zation (L. C. W. Dixon, G. P. Szego, Eds.), North-Holland, Amsterdam, 1975.
23 Zilinskas A., On Statistical Models For Multi-Modal Optimization, Math. Ope-
rationforsh. Stat. Ser. Stat., 9, 255—266 (1978).
24 Devroye L. P., Progressive Global Random Search of Continuous Functions,
Math. Programming, 15, 330—342 (1978).
Глава 8
Методы линеаризации
для задач условной оптимизации
В предыдущих главах были подробно рассмотрены два наиболе<
изученных в теории оптимизации класса задач: задачи без ограни
чений и задачи с линейными ограничениями. Для этих классов зада'
разработаны весьма эффективные, надежные и теоретически обо
снованные алгоритмы. Поэтому представляется естественным, чт<
в большинстве случаев для решения задач с нелинейными ограниче
ниями используются методы, разработанные для упомянутых клас
сов оптимизационных задач. В гл. 6 описан подход к решению об
щей задачи условной оптимизации, основанный на ее сведении i
параметрической задаче без ограничений. Задача условной оптими
зации решается при этом при помощи методов безусловной оптими
зации как последовательность задач без ограничений. В данной i
последующих главах рассматривается основанный на линеаризацш
подход, который позволяет свести общую задачу к задаче с линей
ними ограничениями. Использование линеаризации дает возмож
ность применять методы линейного программирования либо для ре
шения последовательности задач ЛП, либо для итеративного вы
полнения тех или иных операций симплекс-метода.
Все методы рассматриваемые в данной главе, основываются н<
разложении нелинейной функции f{x) общего вида в ряд Тейлор:
до членов первого порядка в окрестности некоторой точки х°:
f (x)=/(x°)4-V/(x°) (х—х°)+О (|1х—х«||)2.
Член второго порядка малости О(||х—х°||)2 почти всегда отбрасы
вается, и функция /(х) аппроксимируется в точке х0 линейной функ
цией, обозначаемой следующим образом:
/ (х; х°) = /(х°) 4- V7(x°) (х—х°).
Точка х° называется точкой линеаризации. Следует иметь в виду
что линеаризацию следует использовать с большой осторожностью
поскольку в большинстве случаев она дает весьма грубое прибли
жение. Тем не менее такое приближение часто применяется ка:
при оптимизации, так и для других целей. Методы оптимизации
рассматриваемые в этой главе, различаются в основном по спосо
бам обращения к процедуре линеаризации и оценивания ошибок
возникающих при использовании линеаризации.
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 299
8.1. Непосредственное использование
последовательности задач ЛП
Наиболее простым способом линеаризации является замена об-
щей нелинейной задачи на задачу, получаемую при помощи лине-
аризации всех функций, фигурирующих в исходной задаче. По-
скольку при этом все функции, входящие в задачу, заменяются на
линейные, получается задача ЛП, которую можно решать при по-
мощи методов ЛП. Очевидно, что получаемое таким образом ре-
шение является лишь некоторым приближением к решению исход-
ной задачи; тем не менее, если принять некоторые меры предосто-
рожности, найденное значение целевой функции будет лучше зна-
чения в точке линеаризации. Сначала рассматривается задача с ли-
нейными ограничениями и описываются дополнительные вычисле-
ния, необходимые для обеспечения эффективной непосредственной
линеаризации. Затем рассматривается общая задача нелинейного
программирования (НЛП).
8.1.1. Случай линейных ограничений
Задача НЛП с линейными ограничениями имеет следующий вид:
минимизировать f{x)
при ограничениях Ах=О, х^О.
Она отличается от задачи ЛП в стандартной форме нелинейностью
целевой функции f(x). Так же как для задачи ЛП, допустимая об-
ласть является многогранником, т. е. геометрическим телом, обра-
зованным пересечением полуплоскостей. Поскольку функция f(x)
нелинейная, оптимальное решение может не совпадать с вершиной
или угловой точкой допустимой области. Кроме того, если f(x)
не выпуклая, задача НЛП с линейными ограничениями может иметь
несколько локальных минимумов. Рассмотрим с учетом этих особен-
ностей последовательность действий при формулировке и решении
линеаризованной в некоторой допустимой точке х" задачи НЛП с
линейными ограничениями.
Ясно, что задача вида
минимизировать f (х; х°)
при ограничениях Axs^ft, х^О
представляет собой задачу ЛП и поэтому имеет оптимальное ре-
шение в допустимой угловой точке (при условии, что допустимая
область ограничена). Весьма важен вопрос о соотношении между
решением линеаризованной задачи х* и решением исходной задачи
х*. Заметим, что при решении линеаризованной задачи получается
единственное решение (если не принимать во внимание случай не-
единственности оптимума в задаче ЛП), тогда как исходная задача
300
ГЛАВА 8
может иметь несколько локальных минимумов. Выбор точки ло-
кального минимума вблизи х* зависит от выбора начальной точки
линеаризации. Следовательно, при невыпуклой целевой функции
нельзя быть уверенным в том, что найдено приближение к глобаль-
ному минимуму. Однако даже в случае выпуклой функции f(x)
нет гарантии, что точка ~х* хорошо «приближает» х*. Истинное ре-
шение х* может лежать внутри допустимой области, а точка х*
должна быть угловой. Из этого следует, что и в случае выпуклой
функции / (х) для получения хорошего приближенного решения х*
необходима дополнительная корректировка х*.
Заметим, что в силу допустимости точек х", х* имеет место нера-
венство
/(х"; х°) > / (х*; х°).
Следовательно, если воспользоваться формулой для /, то получится
следующее неравенство:
/(х°)> f(x») + v/(x“) (х*-х°),
или V/(х°) (х* — х°) < 0.
Очевидно, что вектор (х*—х°) задает направление спуска. Как
отмечалось при рассмотрении задач оптимизации без ограничений,
использование направления спуска в качестве направления поиска
эффективно лишь при применении специальных правил изменения
шага или одномерного поиска. Заметим, что одномерный поиск из
точки х° в направлении (х*—х°) приводит к точке х*. Поскольку х*
является угловой точкой допустимой области и х° допустима, все
точки на отрезке прямой между ними допустимы (так как допусти-
мая область выпуклая). Более того, поскольку х* представляет
собой угловую точку, точки прямой, лежащие вне этого отрезка,
недопустимы. Таким образом, одномерный поиск должен произво-
диться на следующем отрезке прямой:
х=х°+а(х*—х°), 0^а^1.
Следовательно, решение задачи ЛП, не дающее хорошего прибли-
жения к оптимуму, позволяет получить важную информацию: оп-
ределить направление поиска и точку пересечения соответствую-
щего луча с границей допустимой области.
В результате решения задачи
минимизировать /(х°+<х(х*—х0)), O^a^l,
находится допустимая точка х1, такая, что
/(Х1)</(Х«).
Поскольку величина Vf(xl) вообще не равна нулю, полученная
точка х1 может служить точкой линеаризации для построения сле-
дующей аппроксимации. Решение последовательности задач ЛП
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 301
и одномерный поиск продолжаются до тех пор, пока последова-
тельные оптимумы л40, получаемые при помощи одномерного поис-
ка, не станут достаточно близкими (т. е. расстояние между ними не
станет меньше заранее выбранной малой величины). Ниже описан
соответствующий алгоритм Франка — Вульфа [1].
Алгоритм Франка — Вульфа
Заданы х° и два числа е>0 и б>0.
Шаг 1. Вычислить у/(х1(|). Если ||V/(х(П)||^е, то прекра-
тить вычисления. В противном случае перейти к шагу 2.
Шаг 2. Решить следующую задачу ЛП:
минимизировать V/(xtn)f/
при ограничениях Ау^.Ь, у^О.
Пусть «/(П — оптимальное решение этой задачи.
Шаг 3. Найти а(/), представляющее собой решение задачи
минимизировать / (xtn + a (y{t) — х(П))
при 1.
Шаг 4. Вычислить
+11 =х“>+а‘1) (уи>—х«>).
Шаг 5. Проверить близость к решению. Если
||х«+1»—х«’||<б|| х«+»||
и И(х(,+П)-/ (^’Ж е(|/(%«+>') ||,
то прекратить вычисления. В противном случае перейти к шагу 1.
Заметим, что в формулировке подзадачи ЛП опущены постоян-
ные члены целевой функции f(x, х(П)-
Рис. 8.1. Схема многоступенчатого компрессора (пример 8.1).
Пример 8.1. Оптимизация многоступенчатого компрессора
Изображенный на рис. 8.1 трехступенчатый компрессор пред-
назначен для сжатия газа, поступающего под давлением 1 атм в
количестве N моль/ч, до давления в 64 атм. Предполагается, что
сжатие двустороннее и адиабатическое; после каждой его стадии
газ охлаждается до начальной температуры Т. Требуется выбрать
значения давления на промежуточных стадиях процесса, миними-
зирующие потребление энергии.
302
ГЛАВА 8
(k~1)/k—NRT( -Л
W^NRT
Решение. Для двустороннего адиабатического сжатия с ох-
лаждением до начальной температуры Т работа газа дается форму-
лой
k \ ( ^*вых
Рвх
где k= Ср!Cv — коэффициент Пуассона, R— универсальная газо-
вая постоянная.
При трехступенчатом сжатии полная работа газа определяется
формулой
где a—k—l/k, х,— выходное давление на первой ступени, х2—
выходное давление на второй ступени.
Если для рассматриваемого газа а=1/2, то при фиксированных Т
и N оптимальные давления и х2 можно получить, решая следую-
щую задачу:
минимизировать f(х) = xj/4 + (x^xj1^ + (64/х2)’^4
• при ограничениях Xj^l, хг^х1г 64 ^х2
(при этом требуется, чтобы выбранные давления монотонно уве-
личивались от входа к выходу).
Сформулированная задача является задачей НЛП с линейными
ограничениями. Ее можно решить при помощи алгоритма Франка —
Вульфа. Допустим, что в качестве начальной оценки используется
допустимое решение Xj=2, х2=10. Градиент /(х) в точке х’ равен
Д = 0,25х~3/4 (1 — х'/4х“1/2) = — 3,83-10-2,
= 0,25х-3/4 (х- Vi—(64)’/4 x-V2) = — 2,38 - IO"3.
(JX2 2\1 2 /
Считая, что эти значения не удовлетворительны, переходим к
шагу 2. Решаем следующую задачу ЛП:
минимизировать —3,83- 10~2yi—2,38-10-3#2
при ограничениях у^\, Уг^Уи 64^у2.
Очевидно, что минимум достигается при наибольших возможных
значениях yt и у2 (у?=у2=64).
Шаг 3. Одномерный поиск вдоль прямой
/хД /2\ //64\ /2\\
\xJ = к Ю/ \iojj
при O^a^l. Используя метод интерполяции, находим, что опти-
мум достигается при а=0,02732.
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 303
Шаг 4. Новая точка:
Как видно из рис. 8.2. точка х(1) является внутренней точкой до-
пустимой области. Поскольку полученное приближение к решению
Рис. 8.2. Допустимая область (пример 8 1).
неудовлетворительно, переходим к шагу ] следующей итерации.
Шаг 1. v/(xu>)=(3,97-10-3; —4.56-10-3).
Шаг 2. Подзадача ЛП имеет следующий вид:
минимизировать 3,97- —4,56- 10~3у2
при ограничениях у^\, Уг^Ук 6^у2.
Минимум достигается в угловой точке с наименьшим возможным
г/i и наибольшим возможным уг', таким образом, r/l1>=64.
Шаг 3. Поиск вдоль прямой
/хД / 3,694 А (( 1 \ ( 3,694 \\
^х J “ <11,475 ) + \\64V1,47577
при O^a^l, минимизирующем /(х(а)).
304
ГЛАВА S
Оптимальное значение достигается при а =0,06225.
Шаг 4. Новая точка:
( 3,694 \ / — 2,694\ ( 3,526\
) = V1,475j+ °>06225(ч 52,525 ) = \14,745/ ’
Из рис. 8.2 видно, что рассматриваемая точка лежит внутри допу-
стимой области еще достаточно далеко от оптимума. Следует про-
должить выполнение итераций, что приводит к рассмотрению точек
х‘»>=(3,924; 15,069),
х<4>=(3,886; 15,710).
Процесс продолжается до тех пор, пока не будет достигнута задан-
ная точность приближения к решению.
Из рис. 8.2 видно, что в случае оптимума, лежащего внутри до-
пустимой области, алгоритм Франка — Вульфа весьма похож на
градиентный метод оптимизации при отсутствии ограничений. Зигза-
гообразная траектория, подобная траектории на рис. 8.2, типична
для обычного градиентного метода. Если решение лежит на границе
допустимой области и в качестве начальной точки также выбрана
граничная точка области, то процесс приближения к решению сво-
дится к последовательному применению процедуры одномерного
поиска на гранях допустимого многогранника.
Пример 8.2
Предположим, что компрессорная система предыдущего примера
удовлетворяет дополнительному ограничению
х2<И4 атм.
Получим новое оптимальное решение, исходя из начальной оценки
х’ = (14, 14).
Решение. Как видно из рис. 8.3, заданная начальная точка
является угловой в новой допустимой области. В точке х° имеем
V/(x°) = (16,7.10-»; — 8,25-Ю-3).
Соответствующая подзадача ЛП имеет следующий вид:
минимизировать 1,67 • —8,25 - Ю-3«/2
при ограничениях i/i^l, i/2^i/i, 14^i/2.
Решение получается при наименьшем возможном значении у-,
и наибольшем возможном значении у2. Таким образом, «4=1 и
«4=14.
Одномерный поиск на шаге 3 проводится вдоль прямой
(хЛ /14\ // I \ Г14\\
S
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 305
Рис. 8.3. Допустимая область (пример 8.2).
Он сводится к поиску при ограничении #2=14. Решение имеет вид
«=0,7891; при этом рассматривается следующая новая точка:
/хР’Х /3,74174
к 14’° )'
В этой точке А/(х,1))=(0, —1,275 10-3). Таким образом, найдено
оптимальное решение, лежащее в центральной точке грани j/2=14.
Заметим, что при наложении еще одного ограничения (пунк-
тирная линия на рис. 8.3) оптимальное решение достигается в уг-
ловой точке (5; 14).
Как ясно из приведенного примера, для граничных точек работа
алгоритма Франка — Вульфа сводится к проектированию градиента
на грани допустимой области. При выполнении некоторых условий:
непрерывной дифференцируемости f(x), ограниченности допустимой
области, возможности точного решения подзадач ЛП и одномер-
ного поиска легко может быть доказана сходимость алгоритма к
точке Куна — Таккера при выборе любой допустимой точки в ка-
честве начальной (см. 12, 3]). Если функция f(x) выпуклая, решение
представляет собой глобальный минимум. Поскольку определение
306
ГЛАВА 8
направления спуска зависит от угловых точек, трудно дать оценку
скорости сходимости алгоритма к оптимуму. Однако ясно, что ско-
рость сходимости не может быть больше, чем у обычного градиент-
ного метода.
Заметим, что при условии выпуклости целевой функции /(х)
для алгоритмов Франка — Вульфа (а также любых алгоритмов, в ко-
торых используются подзадачи с линеаризованной целевой функци-
ей) после решения каждой подзадачи можно получить очень удоб-
ную оценку разности между достигнутым и истинным значениями
целевой функции. Напомним, что для выпуклой функции /(х),
линеаризованной в точке х,п, выполняется неравенство
f (х) > / (х“>) + V/ (х<г>) (х—х'<») = f(x\ х(/>).
для всех х. Отсюда следует, что для всех допустимых точек
min f (х) min ~f (х; х(/)) = fх(()).
Поэтому х<0) представляет собой нижнюю оценку значения
/(х) в точке минимума. С другой стороны, /(f/U)), а лучше /(х(/ + 1))
служит верхней оценкой минимального значения /(х). Таким обра-
зом, на каждой итерации разность
может служить в качестве оценки улучшения целевой функции.
Ее удобно использовать в качестве критерия останова на шаге
5 алгоритма Франка — Вульфа.
После краткого изложения метода непосредственной линеари-
зации для задач НЛП с линейными ограничениями перейдем к рас-
смотрению общего случая.
8.1.2. Общая задача нелинейного программирования
Рассмотрим общую задачу НЛП
минимизировать f (х)
при ограничениях gj (х)> 0, j=1, ..., J,
(х) = 0, k=\, .. .,К,
x\U) xt $L\ i = 1, ..., N.
При некоторой заданной оценке решения х<0 использование не-
посредственной линеаризации приводит к следующей задаче:
минимизировать / (х1П) + V/ (х1П) (х—х'г>)
при ограничениях gf(xin) + Vgf (xl“) (х — х“') 0, /=1,
hk (x,n) + (л‘) (х — х“’} = 0, k = 1..К,
хЧ x\L>, i = 1, .... У.
Эта задача представляет собой задачу ЛП. Решая ее при помощи
методов ЛП, находим новое приближение хи+1). Заметим, что если
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 307
x(t) — допустимая точка исходной задачи, то нет уверенности, что
новая точка х((+1) будет допустимой. В действительности в случае
нелинейных функций, входящих в ограничения, точка x(t+1) обыч-
но недопустима. Если х,г+1)— недопустимая точка, то оптимальное
значение линеаризованной целевой функции, удовлетворяющее
неравенству
f (х(,+1); х»>) < xtn),
может не быть точной оценкой истинного оптимума. Для сходимости
к оптимуму достаточно, чтобы для последовательности точек {x(f)},
полученных в результате решения последовательности подзадач
ЛП, выполнялось следующее условие: значения целевой функции
и невязки по ограничениям в х(г+1) меньше их значений в точке х(/).
Из следующего примера видно, что это условие может удовлетво-
ряться при непосредственном применении метода последовательной
линеаризации.
Рис. 8.4. Допустимая область (пример 8.3).
а — ограничения, б — линеаризованные ограничения.
Пример 8.3
Рассмотрим следующую задачу:
минимизировать f (х) = х? х|
при ограничениях g\(x) = x?—х2^0,
(х) = 2—х,—х| = 0,
72 > -ч > Vs, 3 > х2 > 0.
Из рис. 8.4, а видно, что допустимая область задачи состоит
из точек кривой /i!(x)=0, лежащих между точкой (2, 0), определяе-
мой ограничением х2^0, и точкой (1, 1), определяемой ограниче-
нием gi(x)^0. В результате линеаризации задачи в точке х° = (2, 1)
308
ГЛАВА 8
получаем следующую задачу ЛП:
минимизировать / (х; х°) = 5 + 4(х1— 2) + 2(ха—1)
при ограничениях ^(х; х°) = 3 + 4(х1— 2)—(х2—1)25=0,
hj (х; х°) — —1—(хх—2)— 2(х2—1) = 0,
3>х2>0.
Из рис. 8.4, б видно, что допустимая область получаемой задачи
ЛП представляет собой отрезок прямой 3—х2—2хг—0, ограничен-
ный точками (2,5; 0), (11/9; 8/9). Линии уровня линеаризованной
целевой функции представляют собой прямые с наклоном —2,
тогда как линии уровня целевой функции исходной задачи — ок-
ружности с центром в начале координат. Ясно, что решением лине-
аризованной задачи является точка х(1) = (11/9; 8/9).
В этой точке имеем
g-1(x‘1>)=0,6049>0,
h1(x‘1>)=—0,0123=^=0,
так что ограничение в виде равенства нарушается. Производя но-
вую линеаризацию в точке х(1), получаем следующую задачу:
минимизировать f (х; хш) = 2,284 + 2,444 (xj—п/9)+
+ 1,778 (ха—%)
при ограничениях (х; хП)) = +0,6049+ 2,444 (Xj—и/9)—
-(х2-“/9)>0,
Мх; х(1)) = — 0,0123—(х, —п/9) —
-1,778 (х2-%) = 0,
/2 > -Vi > 1/2, 3 > х2 > 0.
Новое решение лежит на пересечении прямых gi(x-, х(1))=0 и
/ц(х; х(1,)=0 и имеет координаты х(а)=(1,0187; 0,9965). Ограниче-
ние в виде равенства все еще нарушается Ih^x™)——0,0117],
но уже в меньшей степени. Если провести еще две итерации, то по-
лучим очень хорошее приближение к решению х*=(1, 1). Из при-
веденной ниже таблицы последовательных значений функций /,
g и h видно, что значения целевой функции и функции h монотонно
улучшаются. При этом значение g(x) остается допустимым во всех
промежуточных точках.
Монотонность, имеющая место в рассмотренном примере, ха-
рактерна для задач, функции которых являются «умеренно» нели-
нейными. Она теряется при появлении более выраженной нелиней-
ности. В этом случае при линеаризации целевой функции и решении
соответствующей задачи ЛП часто получается значение целевой
функции, худшее, чем предыдущее. Аналогично при линеариза-
ции ограничений и решении задачи ЛП невязка по ограничениям
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 309
Итерации f g h
0 5 3 — l.o
1 2,284 0,605 —0,0123
3 2,00015 3,44 10-* — 1,18 10-»
Оптимум 2,00 0,0 0,0
также может возрасти. В случае возникновения подобных ситуаций
алгоритм перестает сходиться. Это явление иллюстрируется сле-
дующим примером.
Пример 8.4
Предположим, что решение задачи примера 8.3 начинается
с точки х’=(1,9999; 0,01). В этой точке
/(х“)=3,9997,
gr (х°)=3.9995>0,
Поэтому она допустима. Линеаризованная подзадача имеет следую-
щий вид (после приведения подобных членов):
минимизировать —3,9997+3,9998xi+0,02х2
при ограничениях 3,9998%!—х2—3,9996>0,
—Хх—0,02х2+2,0001 = 0,
3>Х2>0.
На рис. 8.5 графически представлены линеаризованные ограниче-
ния и решение линеаризованной подзадачи — точка х(1, = (1,9401; 3).
При переходе от х° к хц) значение линеаризованной целевой функ-
3)0
глава а
ции уменьшилось с f(xn; х°)=3,9997 до /(х(1); х°)=3,8203. Однако
значение истинной целевой функции не улучшилось:
f(x°)=3,9997, /(xtl,)= 12,764.
Невязки по ограничениям в новой точке равны
gi(x(1’)=0,764>0, h1(xw)= —8,9401(1’=^0.
Таким образом, результаты итерации свидетельствуют о расходи-
мости процесса.
Правило изменения шага. Из примера 8.4 видно, что линеари-
зация не гарантирует в общем случае сходимости алгоритма к оп-
тимуму. Она дает хорошее приближение в достаточно малой ок-
рестности базовой точки, но это приближение становится плохим на
большом расстоянии от этой точки, особенно в случае «сильной» не-
линейности рассматриваемой функции в окрестности базовой точки.
Налагая ограничения на возможные изменения переменных, можно
добиться использования линейного приближения лишь в окрест-
ности базовой точки. При этом в любой линеаризованной подзада-
че в окрестности базовой точки хш на значения переменных х,-
накладываются следующие ограничения:
—— хр i=l, • ••, N,
где б,-— соответствующим образом выбранный параметр шага. Сле-
дует выбирать 6Z таким образом, чтобы значение целевой функции
исходной задачи уменьшалось, а невязки по ограничениям сокра-
щались на каждой итерации. Выполнение последних требований га-
рантирует сходимость алгоритма. К сожалению, такое правило из-
менения шага часто приводит к резкому уменьшению скорости схо-
димости.
Пример 8.5
Пусть в подзадаче, рассмотренной в примере 8.4, значения пере-
менных бх и б2 ограничены величиной 0,5. По существу это
эквивалентно введению дополнительных ограничений
1,9999—0,5<х<0,5+1,9999,
0,01—0,5<х2<0,5+0,01.
Эти ограничения задают квадрат с центром в базовой точке х°
(рис. 8.6). Решение задачи с учетом введенных ограничений совпа-
дает с точкой х, полученной при пересечении прямой й(х; х°)=0
и прямой х2=0,51.Она имеет следующие координаты: х=(1,9899;
0,51). Значение целевой функции равно /”(х)=4,2198, а левые части
ограничений в точке х равны gi(x)=3,450>0,/ij(x)=—0,25^0.
Заметим, что при сокращении невязок по ограничениям по срав-
нению с начальной точкой значение целевой функции ухудшилось.
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 311
Это обстоятельство указывает на необходимость дальнейшего умень-
шения величин 6Z. Можно проверить, что для улучшения значения
целевой функции необходимо положить 61=62==0,05. При этом ре-
шение будет иметь следующий вид:
х=(1,9989; 0,05), /(х)=3,9992,
gi^-S^SO^, М*)=~0,0025.
Рис. 8.6. Допустимая область
(пример 8.5).
Как видно, полученное по сравнению с базовой точкой Xй улучше-
ние весьма незначительно.
Из рассмотренного примера хорошо видны трудности, возникаю-
щие при использовании описанной модификации метода непосред-
ственной линеаризации. При нали-
чии «сильных» нелинейностей для
обеспечения сходимости приходится
выбирать столь малый шаг, что сходи-
мость становится очень медленной.
Общая эффективность вычислений при
этом значительно уменьшается.
Алгоритм, используемый при ре-
шении задачи из примера 8.5 пред-
ложен в работе [4]. Впоследствии пред-
лагались другие реализации этого ал-
горитма [5, 6] (см. также 17]). Прог-
рамма, описанная в работе [4], назы-
вается МАР; она использует спе-
циальную эвристику для выбора вели-
чин 6г на каждой итерации. Програм-
ма фирмы IBM, называемая РфР II,
применима только к задачам с огра-
ничениями в виде неравенств, посколь-
ку в ней выбор 8t осуществляется
на основе оценок ошибки линейного
описанная в работе [5], отличается тем, что в ней используются
оценки остаточного члена разложения Тейлора до членов первогс
порядка. Эта программа также может применяться только при ре-
шении задач с ограничениями в виде неравенств. В нее введен специ-
альный параметр, позволяющий регулировать величину поправки
при решении последовательных задач ЛП. Доказана сходимость
этого алгоритма при вогнутых функциях gj(x) и выпуклой целевой
функции.
Использование штрафных функций. Заметим, что логическая
схема ограничения величины шага в рассмотренных выше методах
решения обладает определенным сходством со стратегией одномер-
ного поиска минимума некоторой штрафной функции
Р(х, р)=/(х)+рй (g, h, х)
приближения. Программа,
312
ГЛАВА 8
в направлении, задаваемом вектором x(t + 1>—x,tj. Таким образом,
можно построить двухшаговый алгоритм, являющийся аналогом
алгоритма Франка — Вульфа. На первом шаге формулируется и
решается задача ЛП и получается новая точка х. На втором шаге ре-
шается следующая задача одномерного поиска:
минимизировать Р(х(а), р),
гдех(а)=а(х—xU))4-x(t), а^О
(при подходящем выборе параметра р). При этом следовало бы ис-
пользовать процедуру корректировки штрафного параметра и,
возможно, процедуру нахождения точного минимума штрафной
функции свести к поиску подходящего приближения.
Методы такого типа исследовались в работе [8]. Типичный ва-
риант этого метода состоит из двух основных этапов. Ниже приво-
дится описание этих этапов. Считаются заданными е>0 и параметр
величины шага 6.
Этап проверки
Если в точке x(t) величина штрафного члена й удовлетворяет нера-
венству H(g, h, х)>е, то перейти к этапу I. В противном случае
перейти к этапу II.
Этап I
Шаг 1. Линеаризовать в х(/) и получить решение х задачи ЛП.
Шаг 2. Если й (g, h, х)<й (g, h, x<f)), то положить xu+1)=x
и перейти к этапу проверки. В противном случае уменьшить 6
(например, положить 6=6/2) и перейти к шагу 1.
Этап II
III а г 1. Линеаризовать и получить решение х задачи ЛП.
Ш а г 2. Если Р(р, x)<ZP(p, х(/)), положить х<г+1,=х, уве-
личить штрафной параметр и перейти к этапу проверки. В про-
тивном случае уменьшить 6 и перейти к шагу 1.
Алгоритм завершает свою работу, когда величины (||х—xU)||) и
]Р(р,х)—Р(р, x(t))l оказываются достаточно малыми.
Пример 8.6
Предположим, что описанный метод применяется для решения
задачи из примера 8.3 с начальной точкой х11>=(1,9899; 0,51), полу-
ченной в примере 8.5, и 6 = 1/2. Пусть е = 10-2,
£2(g, h, x)=h?4-[min(g1(x), 0)12.
В точке х’1’ имеем й=^ = 1/16>10-2. Следовательно, результат
этапа проверки требует перехода к этапу I.
Шаг 1. Соответствующая точке х'11 задача ЛП имеет вид
минимизировать 3,9798 Ах1+1,02Ах2
при ограничениях 3,45+3,9798Ах2—Ах2^0,
—0,25—Axi— 1,02Ах4=0,
—^^(Axi, Дх2Х3/4.
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 313
Решение: х=(1,4899; 0,7551).
Шаг 2. В точке х имеем g(x) = l,4647 ий1(х)=—6,007-10-4.
Таким образом,
Q(g,/i,x)=3,6-10-3<Q(g, h, =
Поэтому х(2’ =х. Этап проверки показывает, что Q(g, h, х)<10-4,
и указывает на необходимость перехода к этапу II.
Шаг 1. Задача ЛП для точки х<4):
минимизировать 2,9798Ах1+1,5102Ах2
при ограничениях 1,4647+2,9798Axj—Ах2^0,
-6,007-10-»— Ах!— 1,5102Ах2=0,
—ЧгССАхь АхгХ1/^
Решение: х=(1,1369; 0,9889).
Ш а г 2. Для х имеем
/(х)=2,2703, бДх^О.ЗОЗб, йДх)- —0,1147.
Следовательно, Р (102, х)=3,586>Р (102, х'4')=3,150. Необходимо
уменьшить величину шага 6 в два раза и повторить шаг 1 с —
+(Axi, Дх2)^У4. Для решения х—{ 1,2399; 0,8809) имеем /(х) =
—2,31327; g2(x)=0,6565 и ?ъ(х)=—0,01582. Поэтому
Р(102; х)=2,338<Р(102; х’4');
полагаем х<3)=х, увеличиваем р до 1000 и переходим к этапу про-
верки. _
Путем решения еще одной задачи ЛП находим точку х=(1,0215;
0,9958), для которой
Р(103; х)=2,210<Л(102; +’)<+ (103; х'3’).
Следовательно, х<4,=х. На следующей итерации получается очень
близкая к оптимуму оценка х(б) = (1,00019; 0,99991).
Заметим, что удалось избежать излишнего сокращения вели-
чины параметра 6 и ускорить сходимость, используя в качестве ме-
ры близости к оптимуму штрафную функцию. При использовании
штрафных функций метод непосредственной линеаризации стано-
вится более эффективным, однако их применение не гарантирует в
общем случае сходимости к оптимуму. Она доказана лишь в случае
линейных ограничений 18]. При этом требуется, чтобы для решений
последовательных подзадач ЛП сх11+1>=х(,) не существовало Ах==0,
для которого
V/- Ах<0,
Vgy-Ax>0, j=l, . . ., J,
Vhk-^x=0, k—l,
и следовательно, должны выполняться условия Куна — Такие-
оа [81.
314
ГЛАВА 8
8.1.3. Обсуждение и приложения
Несмотря на усовершенствование вычислительной схемы метода
последовательного решения подзадач ЛП [8, 9], основным недостат-
ком метода является необходимость решения последовательности
задач ЛП. Применение такого метода допустимо в тех случаях,
когда линейность задачи нарушается небольшим числом нелинейных
членов. Хорошей мерой нелинейности является число переменных,
по которым хотя бы одна функция, входящая в задачу, нелинейна.
Метод последовательного решения подзадач ЛП широко применя-
ется в различных практических областях для задач с относительно
малым числом нелинейных переменных. Например, в работе [10]
сообщается об успешном применении двумя нефтяными фирмами
такого подхода для решения задач развития нефтяного производ-
ства. Решались задачи с 4932 линейными и 400 нелинейными пере-
менными. Фирма Marathon Oil использовала систему Р</>Р II как
подмодель иерархической модели процесса переработки нефти.
Начальные данные для работы системы генерировались при помо-
щи 20 имитационных моделей [10]. Подобный подход применялся
также для задач смешивания нефтяных фракций и задач оптимиза-
ции производственных процессов, разбивающихся на несколько вре-
менных периодов. В последнем случае линеаризованные подзадачи
имели до 10 000 переменных. Однако для решения последователь-
ных подзадач ЛП потребовалось в среднем лишь 23 итерации по сим-
плекс-методу, поскольку число нелинейных переменных было мало
[10]. Сообщение об аналогичных результатах содержится в работе
[11]. Следующий пример иллюстрирует типичное приложение опи-
санного метода к задаче по переработке нефти с малым числом не-
линейных переменных.
Пример 8.7. Задача смешивания
Для получения конечного продукта при перегонке нефти и при-
готовлении угольных смесей часто возникает необходимость смеши-
вания нескольких видов сырья на промежуточных стадиях процесса.
Это бывает обычно обусловлено ограниченностью емкостей для хра-
нения компонентов, а также необходимостью совместной транспор-
тировки исходных продуктов. На рис. 8.7 представлена упрощен-
ная схема процесса смешивания фракций. В этой системе [12] сна-
чала смешиваются два потока сырья: 1Д с содержанием серы 3%
и Vi с содержанием серы 1 %. Полученная смесь смешивается в двух
различных пропорциях с третьим потоком сырья F, имеющим 2%
серы; при этом получаются два вида конечной смеси.
Первая смесь должна производиться в количестве не более ЮС
баррелей в час, причем содержание серы не должно превосходить
2,5%; для второй смеси аналогичные показатели равны 200 барре-
лям в час и 1,5%. Стоимость сырья для потоков 1, 2 и 3 равна 6.
16 и 10 долл, за 1 баррель соответственно. Продажная цена смесей
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 315
составляет 9 и 10 долл, за 1 баррель соответственно. Требуется опре-
делить размеры потоков, максимизирующие доход. Пусть
Р(— выход смеси i-ro вида (в баррелях в час),
Ft— величина потока сырья третьего вида, используемого в
смеси i-ro вида,
Смеситель
Рис. 8.7. Схема к примеру 8.7.
Vt— величина потока промежуточной смеси, используемой в
i-й смеси,
X— содержание серы в промежуточной смеси.
Условия баланса для потоков:
1++У2=1++У2,
Ft+V^Pr,
f2+v2=p,.
Условия баланса по содержанию серы:
0,03^+0.01 У2=х(У1+У2),
о.огг^хР^.огбРь
0,02Р2+хУ2<0,015Р2.
Кроме того, имеются ограничения на выход смесей:
PfClOO, Р 2<200.
Содержание серы в промежуточной смеси определяется содержанием
серы в ее компонентах, поэтому
0,01<х^0,03.
Целевая функция в данном случае линейная:
9Р1+10Р2—61+—16У2—10F.
316
ГЛАВА 8
Задачу оптимизации можно записать в следующем виде:
максимизировать f — 9P1-ir \0Р2—6Vt— 16Г2—10F
при ограничениях —V2 = 0,
h2 = 0,03 + 0,01V2 — ~х (Vi + Г2) = О,
h^F. + V'-P^V,
^ = /?2+v2-p3=o,
^ = 0,025^! —0,02^ —xVj^O,
g, = 0,015P2 — O,O2F2 —xV2 > 0,
иР2<100, P2 < 200,
0,01 <x<0,03.
Заметим, что единственными нелинейностями задачи являются
члены вида xV\ и хУ2 в h2, gt и g2; в остальном она линейна. При
заданном значении х задача становится линейной. Полученное реше-
ние задачи ЛП можно использовать для корректировки значения х;
процесс решения задачи следует продолжать до получения удовлет-
ворительного приближения. В работе (12] отмечается, что такая
рекурсивная процедура решения характеризуется низкой надеж-
ностью и имеет различные локальные решения, поскольку допусти-
мая область невыпуклая в силу характера функции h2. В работе
(12] указано, что для этой задачи имеются три точки Куна — Такке-
ра.
1. Седловая точка х=0,02; величины потоков нулевые.
2. Локальный максимум х=0,03, Pt = 100, Р=И=50, остальные
потоки равны нулю. Величина дохода для этой точки составляет
100 долл, в час.
3. Глобальный максимум с х=0,01, Г2=/?2==100, Р2=200, ос-
тальные потоки равны нулю. Доход составляет 400 долл, в час.
Описанная выше итеративная процедура может сходиться к
любой из этих трех точек в зависимости от выбора начального зна-
чения х. Однако применение предложенного в работе [8] подхода
приводит к глобальному максимуму независимо от выбора х [13].
При этом требуется решение двух или трех подзадач ЛП. Этот ре-
зультат следует рассматривать как весьма удачный; однако неясно,
почему применение стратегии последовательного решения подзадач
ЛП приводит к глобальному максимуму. В практических приложе-
ниях для задачи смешивания следует использовать метод после-
довательного решения подзадач ЛП, поскольку число потоков сырья,
промежуточных и окончательных видов смесей и число их характе-
ристик обычно намного больше, чем в рассмотренном примере, и
количество локальных максимумов велико.
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 317
Можно сделать вывод, что метод, основанный на последователь-
ном решении подзадач ЛП, хорошо подходит для решения задач
НЛП большой размерности с умеренной степенью нелинейности.
Он особенно эффективен при использовании штрафных функций,
предложенных в работе [8]. В то же время при применении этого-
метода в случае существенно нелинейных задач приходится значи-
тельно уменьшать величину шага; скорость сходимости к оптиму-
му при этом весьма низкая. Методы, подобные описанному, носят
название градиентных методов с малой длиной шага.
Существуют три способа усовершенствования методов непосред-
ственной линеаризации.
1. Глобальная аппроксимация нелинейных функций задачи
при помощи кусочно-линейных функций.
2. Применение последовательных линеаризаций на каждой ите-
рации для уточнения допустимой области.
3. Использование линейного приближения для отыскания на-
правления спуска.
В последующих разделах подробно рассматриваются этн три
способа. Показывается, что первые два подхода применимы только
к достаточно узкому классу задач, тогда как третий приводит к
весьма общим и эффективным алгоритмам.
8.2. Сепарабельное программирование
При помощи метода сепарабельного программирования, раз-
работанного в работе [14], удается преобразовать нелинейные задачи
оптимизации определенного типа к задаче, содержащей только ли-
нейные функции. Получаемые таким образом задачи решаются при
помощи специальной модификации симплекс-алгоритма. Обос-
нованием такого метода служит то обстоятельство, что в качестве
хорошего приближения нелинейной функции на большом отрезке
можно использовать ее кусочно-линейную аппроксимацию. Послед-
няя получается, если разбить отрезок на подынтервалы и построить
линейное приближение рассматриваемой функции на каждом из
подынтервалов.
В этом разделе сначала рассматривается использование этого ме-
тода для функций одной переменной, а затем для функций многих
переменных. Анализируются также изменения, которые необходимо
ввести в стандартные методы ЛП для эффективного решения поту-
чаемых линейных подзадач. Рассматриваются некоторые практиче-
ские применения сепарабельного программирования.
8.2.1. Функции одной переменной
Кусочно-линейные аппроксимации функций одной переменной
легко построить. Рассмотрим произвольно определенную на ин-
тервале О^х^а непрерывную функцию /(х). Предположим, что на
318
ГЛАВА 8
этом интервале построена сетка, имеющая узловх’*’, А=1, . . К-
График кусочно-линейной аппроксимации/(х) функции /(х) можно
построить, соединяя отрезками точки (xlft), и (х<А+1),
где /(*’=/(х<А)). На рис. 8.8 представлены графики /(х) и /(х).
Уравнение прямой, проходящей через точки (x(ft), и (xlft+1),
записывается следующим образом:
Д/г 4-1)_ ДЙ)
Нх) = ^’ + ^й5=^(х-х(й). (8.1)
С каждым подынтервалом x(ft)^x^x<ft+1) можно связать уравнение
подобного типа. Следовательно, функция /(х) аппроксимируется
при помощи (К—1) линейных функций, причем каждая из них слу-
жит в качестве приближения на своем подынтервале.
Рис. 8.8. Кусочио-линейная аппроксимация.
Удобно записывать совокупность рассматриваемых линейных
«функций в более общем виде. Заметим сначала, что любое значение х
в интервале xlft)^x^x<A+1) можно записать как
х= X(ft)x(W + X(K+1)x(ft+n, (8 2)
где Х<м, X<ft+1) — неотрицательные числа, сумма которых равна
единице:
Подставим выражение для х в формулу (8.1)
f (x) = f (х'*>) +^=gr[X<*^>x’^1’-(l-l‘*>)x<»>].
Поскольку 1—Хш =Xlft+1,( то отсюда следует, что
f (х) = f (х<и) + X'ft+1’ (/<*+!> — /<*)) =,
= + (8.3)
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 31<>
Следовательно, присваивая определенные значения двум пере-
менным X, соответствующим некоторому подынтервалу х, можно
получить любое значение х на интервале х<1)^х^х(*) и значение
аппроксимации f(x) в точке х. Поскольку любое значение х лежит
только на одном подынтервале, лишь две переменные X, соответ-
ствующие этому подынтервалу, могут отличаться от нуля. Значе-
ния остальных переменных X должны равняться нулю. Следователь-
ер, К—1 уравнений (8.2) и (8.3) можно переписать в следующем удоб-
ном виде:
к к
х = 2 Х^х'*’, f (х) = 2 где (8.4)
t=i k=i
к
(i) = h
k= i
(2) Xl*>>0, fc=l, .... Я,
(3) X<''X('> = 0, />i+l; t = l.К — 1.
Условие (3) выражает тот факт, что не более двух переменных Х('>
должны быть положительными; если положительны, например,
X*/’ и Xl,), j>i, то должно выполняться условие /=»-Н, т. е. XV’ и
Xli) должны быть соседними. Выполнение последнего требования
гарантирует, что в качестве приближения к /(х) рассматриваются
точки, лежащие на кусочно-линейном графике (рис. 8.8). Действи-
тельно, если Х(1>>0, Х(2)>0, Х(3) = . . ,=Х16)=0, то точка, получае-
мая при решении уравнений (8.4), лежит на отрезке АВ, принадле-
жащем графику функции /(х). Если же Х(1)=/=0, Х(3)=/=0, Х<2,=Х<4> —
=Х(5) =Х<6) =0, то соответствующая точка лежит на отрезке АС,
не принадлежащем графику аппроксимации. Наконец, если Х(3)>0,
то в соответствии с условием (1) Х<3) = 1 и решение уравнений дает
точку С, лежащую на пересечении графиков f(x) и /(х).
Использование кусочно-линейных аппроксимаций приводит к
росту размерности задачи. Приближение /(х) функции /(х), пред-
ставленное на рис. 8.8, построено при введении шести новых пере-
менных (X) и пары линейных условий (8.4), (1). Увеличение точности
аппроксимации требует рассмотрения новых узлов сетки и введе-
ния дополнительных переменных X.
Точность приближения также сильно зависит от выбора узлов
сетки. Удобно выбирать положения узлов сетки на основании рас-
смотрения графика функции. Узлы сетки обычно целесообразно
располагать вблизи точек перегиба (как С на рис. 8.8 ), причем в
областях быстрого изменения функции (т. е. в областях с большими
значениями производной) узлы сетки должны располагаться более
тесно. Таким образом, узлы сетки должны вообще располагаться
неравномерно.
320
ГЛАВА 8
8.2.2. Сепарабельные функции нескольких переменных
Описанный выше метод кусочно-линейной аппроксимации обоб-
щается только на случай функций нескольких переменных специ-
ального вида. Такие функции называются сепарабельными.
Определение
Функция /(х), зависящая от AZ-мерного вектора переменных х,
называется сепарабельной, если она представляется в виде суммы
функций, каждая из которых зависит только от одной из Д/ пере-
менных. Таким образом,
N
1= 1
Например, функция
f (х) = Xi + е*‘ -f- х?'»
сепарабельная, а функция
f (х) = Xi sin (х2 4- Xg) 4- х^ех‘
таковой не является.
Условие сепарабельности функций, при котором возможно при-
менение метода кусочно-линейной аппроксимации, является весьма
жестким. Однако класс нелинейных сепарабельных функций не
слишком узок. Кроме того, некоторые функции, не являющиеся
сепарабельными, при помощи специальных приемов можно пре-
образовать к сепарабельному виду.
Например, произведение XiX2 можно переписать в виде х| — х?,
полагая
Х3 == /а (Xi 4~ == (^1 -^з)* (8.5)
Обобщенное произведение с положительными at
N
сП xia{
I— 1
заменяется на величину у следующего вида:
N
In (у) = In (с) 4- 2 at In (xz).
t= 1
Кусочно-линейная аппроксимация для сепарабельной непре-
рывной функции / (х) нескольких переменных строится следующим
образом. Интервал значений каждой переменной хг разбивается
при помощи сетки с /(г узлами. Таким образом, на интервале x*L>^
Сх^х^' значений переменной х( (xJL> — заданная нижняя гра-
ница хг, а х\и> — верхняя граница) рассматривается последователь-
ность точек
x\U} = х‘1> < х^2’ < ... < х‘'> < ... < х'л-' = Х^’.
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 321
Записывая для удобства можно следующим об-
разом представить выражение для аппроксимирующей функции:
К. К, KN
1 w = 2 w fr + s +... + 2 ww,
*=/ k= 1 k=i
где
Ki
х.^^хГ, t = l.............N,
k= i
причем при всех i=l, N
Ki
(i) S/(*’= i,
(2) X;*’>0, fc==l......Kt,
(3) X'/’X'/’ = 0, />/+!; i=l,2.......Kt—\.
При помощи описанной процедуры нелинейная функция f(x)
заменяется на кусочно-линейную функцию/(х). Ясно, что если тре-
буется построить очень хорошее приближение для /(х), то число уз-
лов сетки должно быть большим. Следовательно, число переменных
также будет велико. Таким образом, линейность достигается за счет
существенного роста размерности задачи.
Пример 8.8
Рассмотрим функцию
/(х)=Л(х1)+/2(х2)=(1-(1-х1П+(0,1х!),
заданную в прямоугольнике 0^хг^2, О^х^З.
Пусть построена аппроксимация Д (Xj) путем деления интервала
0^х^2 на три части, причем узлы сетки соответствуют значениям
Xi=0; 0,5; 1,5; 2,0. Таким образом,
х, = OXJ” + 0,5Х'2’ + 1,5Х'4’ + 2, OX'4’,
h (A) = Л (0) X'1’ + f 1 (0,5) M2i + h (1,5) M31 + h (2,0) X'4’ =
== OX!1 ’ + 0,875X',2’ +1,125X;J’ + 2,OX'4’.
Аналогично для построения аппроксимации /2(х2) выбираются пять
узловых точек 0; 1; 2; 2,6; 3. Значения /2 в них равны 0; 0,1; 1,6;
4,57; 8,1 соответственно. Поэтому
1 Сч, х2) = 0Х'1’ + 0,875Х'2’ + 1,125Х'3’ + 2,0Х'4’ +
+ 0Х'" +0,1 Хр + 1,6Х<3’ + 4,57Xi * ’ + 8,1 Х‘25’,
где Xj = OX'1’ + 0,5Х'2’ + 1,5Х'4’ + 2,0Х;4’,
х2 = OXJ1 ’ + 1Хр + 2Хр + 2,6Х'4 + ЗХр’.
Величины Хр удовлетворяют следующим ограничениям:
4 о
2^V’=1, 2М*»1, х^’ >0;
Л=1 k-l
322
ГЛАВА 8
при этом только два соседних X'** и два соседних Х^> могут быть
положительными. Например, набор величин
Х<2' = 0,4, А{3’ = 0,6, X'1’ = X'4’ = О,
Х<3’ = 0,5, Х!/’= 0,5, X'1’ = Х'2> = X'5’ = О
задает точку х=(1,1; 2,3) и следующее значение аппроксимации:
/(1,1; 2,3)=4,11. Точное значение функции равно /(1,1; 2,3) =3,8.
8.2.3. Решение сепарабельных задач методами
линейного программирования
Решение задачи НЛП с сепарабельными левыми частями огра-
ничений и сепарабельной целевой функцией при помощи кусоч-
но-линейной аппроксимации, подобной использованной в примере
8 8, можно свести к решению задачи ЛП большой размерности с
переменными Х(*'. Полученную задачу ЛП можно решить при по-
мощи подходящих машинных программ ЛП. В связи с наличием
условия (3) при этом требуется некоторая модификация процедуры
симплекс-метода. Такую модификацию осуществить нетрудно бла-
годаря тому, что в симплекс-методе только базисные переменные
могут принимать ненулевые значения. При вводе некоторой
переменной в базис проверяется, что единственной ненулевой ба-
зисной переменной Х)*’, связанной с той же переменной xt, что
и вводимая в базис переменная, является соседняя с ней перемен-
ная. Если это условие не выполняется, то рассматриваемую перемен-
ную нельзя ввести в базис и нужно выбрать другую переменную для
ввода в базис. Описанная модификация симплекс-метода носит наз-
вание симплекс-метода, дополненного правилом ограниченного ввода
в базис. Напомним, что условие (3) и правило ограниченного ввода
в базис нужны для получения точек, требуемых при построении
кусочно-линейных аппроксимаций.
Проиллюстрируем использование сепарабельного программи-
рования для решения задачи НЛП при помощи построения кусочно-
линейной аппроксимации на следующем примере.
Пример 8.9
Максимизировать /(х)=х4-Еха
при ограничениях gj(x)=9—2х*—3x^0,
Xi>0, х2>0.
Поскольку левая часть ограничения и целевая функция сепара-
бельные, можно записать
/(Х)=Л(Х1)+/2(Х2),
gi (x)=gii(Xi)+gi1!(X2),
где /i(Xi)=x’i, /г(^2)=Х21
gnUi)=~2x2, £12(х2)=—Зх2.
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 323
Поскольку /2 и gl3 линейные, нет необходимости строить их ку-
сочно-линейные аппроксимации. Дляи £п построение аппрокси-
маций необходимо. Предполагается, что рассматриваемые аппрокси-
мации строятся на отрезке О^х^З и в качестве узлов сетки вы-
бираются четыре равноотстоящие точки. Данные, необходимые для
построения кусочно-линейной аппроксимации, можно представить
следующим образом:
k 1 ' И’) «..(4й)
1 0 0 0
2 1 1 —2
3 2 16 —8
4 3 81 — 18
Таким образом, для Д (хх) аппроксимацией будет функция
h (*,) = (0) х;" + (i) v> + (16) x;3' + (81) x<%
а для gufxi) — функция
gn (xj = (0) X‘” — 2X‘2' — 8ХД — 18X<4’,
причем выполняется ограничение: X1,'1 -f- Xlp -J- X1;”X’f’ = I.
Следовательно, соответствующая задача ЛП имеет следующий вид:
максимизировать f (х) = Хр -)- 16Х{” 81X)4’ -(-х?
при ограничениях 2Хр + 8Х(3’ 18Х'.4’ 4-Зха + х3 = 9,
XV’ + Xp’ + X'^ + Xr =1,
хр, х2, х3^о.
Переменная х3 представляет собой дополнительную переменную,
необходимую для преобразования неравенства в равенство. Далее
данные задачи записываются в виде таблицы и проводятся вычис-
ления симплекс-методом.
св Базис
. 1 16 81 1 0 0
X® X?1 Х<4> *2 хз Х<’>
0 *3 2 8 18 3 1 0 9
0 1 Ф 1 0 0 1 1
1 16 81 1 0 0 0
324
ГЛАВА 8
Из строки Cj видно, что переменная Х‘4’ должна войти в базис,
а из правила минимального отношения следует, что переменную
х3 нужно вывести из базиса. Однако, поскольку переменные Л]4’ и
Х'/* не являются соседними, X)4’ нельзя ввести в базис. Таким обра-
зом, надо найти следующий по величине элемент строки С7. Сле-
дующим кандидатом на ввод в базис является переменная X)-”; по
правилу минимального отношения из базиса необходимо вывести
X'1'.
Действуя подобным образом, находим оптимальное решение
с базисными переменными Х'/^ОД и Х)4)=0,1. Соответствующее
оптимальное значение Xi равно
х1=0(0)+1(0)+2(0,9)+3(0,1)=2,1.
Таким образом, оптимальное решение рассматриваемой задачи
сепарабельного программирования равно х* =(2,1; 0) с/(х*) =22,5.
Легко проверить, что точное оптимальное решение задается сле-
дующим образом:
х*—(2,12; 0), /(х*)=20,25.
Заметим, что если отбросить правило ограниченного ввода в базис
при рассмотрении таблицы, то Х/> войдет в базис, а х3 выйдет из
него. Следующая таблица в этом случае будет иметь вид
Св Базис С
1 16 81 1 0 0
4 Х<4> х2 хз Д’>
81 Х<4’ 1 9 4 9 1 1 6 ) 18 0 1 2
0 А',1’ 8. 9 5 9 0 _ j. 6 1_ 18 1 1 7
С -8 -20 0 -12,5 -4,5 0 40,5
Очевидно, что оптимальным решением является следующее-
X'/’ ==Х‘14’ = 1/2 с /=81/2=40,5. Однако получаемое таким образом
приближение неудовлетворительно, поскольку
х1=0(72)+1(0)+2(0)+3(1/2) = 1,5,
а в точке (1,5; 0) истинная целевая функция имеет значение
/(1,5; 0) = (1,5)4-0=5,0625.
Таким образом, отбрасывание правила ограниченного ввода в ба-
зис приводит к рассмотрению точек, не лежащих на отрезках, ис-
пользуемых при построении аппроксимации, и, следовательно, к ре-
шению задачи ЛП, не имеющему содержательной интерпретации.
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 325
Однако для некоторых классов задач сепарабельного програм-
мирования правило ограниченного ввода в базис можно ослабить.
В работе [15] доказано (теорема 11.3.1), что правило ограниченного
ввода в базис всегда выполняется для оптимального решения зада-
чи сепарабельного нелинейного программирования следующего
вида:
N
минимизировать 2 ft (xi)
i= 1
N
при ограничениях 2 gji(xi)^bj, /=1, .... J,
х,->0, i=I, N,
если
1) для всех i функция (Xj) строго выпукла или линейна,
2) для всех i и j функция gJt вогнута или линейна.
Эти условия допускают простую проверку и весьма полезны на
практике, поскольку используют выпуклость функций одной пере-
менной.
8.2.4. Обсуждение и приложения
Точность решения задачи, полученного методом сепарабель-
ного программирования, не превосходит точности ее аппроксима-
ции. Кроме того, допустимость решения можно гарантировать толь-
ко при линейности или вогнутости всех компонент gjt сепара-
бельных функций gj- Для повышения точности решения п прибли-
жения его к допустимому можно использовать следующие приемы:
1. Увеличение числа узловых точек, что ведет к повышению
точности аппроксимации. Однако при этом сильно увеличиваются
размерность задачи и число необходимых итераций, поскольку не-
обходимо следить за выполнением правила выбора базиса.
2. Итеративное локальное уточнение аппроксимаций всех функ-
ций. Первоначальное решение задачи находится путем выбора не-
которого грубого приближения. Далее рассматривается более точ-
ная сетка, отличающаяся от первоначальной только в окрестности
полученного решения. Задача снова решается, и процесс уточнения
аппроксимации повторяется до получения достаточно точного ре-
шения. При таком способе действий число узлов сетки может со-
храняться, если допустить неоднократное решение промежуточных
задач ЛП.
Обычно более предпочтительным является второй прием. Следует
заметить, что локальное итеративное улучшение аппроксимаций
в некоторых случаях может приводить к сходимости в точке, отлич-
ной от оптимума, и его необходимо проводить с осторожностью. Во-
обще решение, полученное при помощи сепарабельного программи-
рования, представляет собой только локальный минимум. Сходи-
мость к глобальному минимуму можно гарантировать только в слу-
чае выпуклой целевой функции и выпуклой допустимой области.
326
ГЛАВА 8
Метод сепарабельного программирования нельзя применять к
общим задачам НЛП. Он подходит для решения задач, которые
в основном линейны, а отклонения от линейности представляются
сепарабельными функциями. Если не требуется высокой точности
решения задачи, приближенное решение можно получить при по-
мощи однократного решения подзадачи ЛП, построенной в резуль-
тате кусочно-линейной аппроксимации. Благодаря этому многие
рассматривают сепарабельное программирование как метод, весь-
ма эффективный на практике (16]. Многие приложения сепарабель-
ного программирования относятся к моделям планирования нефте-
перерабатывающего производства 117]. Следующий пример иллю-
стрирует одно из подобных приложений.
Пример 8.10. Требования к содержанию тетраэтилсвинца [17, 18)
Одна из важнейших нелинейностей, фигурирующих в моделях
перегонки нефти, связана с нелинейной зависимостью октанового
числа бензиновой смеси от количества добавляемого в нее тетра-
этилсвинца (ТЭС). Зависимость октанового числа от концентрации
Рис 8.9. Зависимость октанового числа от концентрации ТЭС (пример 8.10).
ТЭС приведена на рис. 8.9. На практике принимается, что октановое
число смеси равно объемному среднему октановых чисел ее компо-
нентов, если последние измеряются при концентрации ТЭС, совпа-
дающей с концентрацией ТЭС смеси.
Предположим, что требуется смешать N компонентов с ТЭС для
получения бензина с заданным октановым числом. Концентрация
ТЭС не может превышать 3 см3 на галлон. Для каждого компонента
существует зависимость октанового числа от концентрации ТЭС,
подобная изображенной на рис. 8.9. Пусть
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 327
хп — величина потока n-го компонента в галлонах в день;
у — величина выхода бензиновой смеси в галлонах в день;
z — концентрация ТЭС в смеси, см3 на галлон;
гп (г) — октановое число п-то компонента по исследовательскому
методу при концентрации ТЭС, равной г;
тп (г) — октановое число n-го компонента по моторному методу
при концентрации ТЭС, равной г;
г, т — минимальное допустимое октановое число смеси по
исследовательскому (моторному) методу;
w — объем используемого ТЭС, см3 в день.
Из условия баланса потоков следует, что %хп=у.
п
Из предположения об октановых числах смеси получается, что
^rn(z)xn^ry, ^mn(z)xn^my. (8.7)
п п
Кроме того, w=zy, целевая функция зависит от w. Заметим, что
ограничения (8.7) нелинейные, поскольку гп и тп зависят от г.
Рис. 8.10. Кусочно-линейная аппроксимация зависимости октанового числа от
концентрации ТЭС.
Для кривых на рис. 8.9 можно построить кусочно-линейные аппрок-
симации, как на рис. 8.10, где использована сетка с четырьмя уз-
лами. Это приводит к рассмотрению следующих уравнений:
4
г — а1'к1 a3ks -j- (8.8)
rп (г) = глЛ1 + гпЛа + гпзЧ + гп4^4>
тп (?) = т пА1 + m-nzh + -i-m (8-9)
328
ГЛАВА 8
Ограничение (8.7) переписывается в виде соотношения
N
2 Хп лА1 Гп2^2 + ^яЗ^З + n'Al) ГУ>
п — I
(8 Ю)
содержащего нелинейные члены х„Хг.
Пусть r(“’=max xn i(rni) и представляет собой разумную
верхнюю границу величины производства бензина у. Используя
формулы (8.5), приведенные в разд. 8.2, можно записать
1
Ui ~ 2
I N
П— 1
. А'
У Гп,Хп + ^1 - l’=1..........4>
(8.11)
Поскольку
1’ 0 У Г111ХП 1»
(8-12)
Ограничение (8.10) принимает теперь следующий вид:
1=1 1=1
(8 13)
Наконец, можно кусочно-линейно аппроксимировать величины
ut, Vt и их квадраты на отрезках, определяемых формулами (8.12).
Например, при пяти равноотстоящих узлах получаем
ui — OP/i + + 1/2Р;з + + Pfs> (8 14)
u? = 0pn + v lep <2 + ЧК + 9/»Pm + P/3. (8.15)
2Po=l. (8.16)
Аналогичные переменные уц требуются для величин и(.
Таким образом, при использовании четырех узлов для концен-
трации ТЭС и пяти узлов для переменных uit vt вводятся 52 пере-
менные:
ut, vt, Kt, i = l..4,
Ры, Уц, i = l....4;/=1, . . ., 5.
Были введены следующие ограничения: соотношения (8.8) и ус-
ловие нормировки N уравнений вида (8.9), восемь уравнений вида
(8.11) и 24 уравнения вида (8.14)—(8.16). Общее число уравнений
составляет 34+М, имеются также ограничения (8.12). Может по-
казаться, что линейность достигнута слишком дорогой ценой.
Однако сеточные методы хорошо зарекомендовали себя на практике,
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 329
поскольку условия такого типа обычно составляют весьма малую
часть систем ограничений больших моделей процесса нефтеперера-
ботки, которые в остальном линейны [17, 181.
8.3. Методы отсекающих плоскостей
В разд. 8.2 изложены два подхода к использованию линейных
аппроксимаций для решения нелинейных задач. В некотором смы-
сле описанные методы представляют собой крайние случаи при
линеаризации нелинейных задач. При применении метода непо-
средственной линеаризации используется одна линеаризация для
каждого нелинейного ограничения. Оказывается, что такой способ
аппроксимации эффективен в окрестности базовой точки, однако
он становится ненадежным при удалении от нее. Таким образом,
для сходимости этого метода необходимо накладывать жесткие огра-
ничения на величину шага на каждой итерации, что приводит к
медленной сходимости. С другой стороны, используемая в сепара-
бельном программировании кусочно-линейная аппроксимация дает
хорошие приближения во всей области определения каждого огра-
ничения. Однако этот метод можно применять только к задачам
сепарабельного программирования. Кроме того, его точность сильно
зависит оттого, насколько густо расположены узлы сетки. Следова-
тельно, для получения хороших локальных приближений необхо-
димо использовать сетку с большим числом узлов или итеративную
процедуру уточнения аппроксимаций.
Из вышеизложенного ясно, что желательно построение алгорит-
ма, использующего довольно грубые аппроксимации левых частей
ограничений для достижения окрестности оптимальной точки и стро-
ящего более точные аппроксимации в этой окрестности, которые
позволяют приблизиться к оптимуму. При таком способе нет не-
обходимости тратить усилия на построение хороших аппроксимаций
на далеких от оптимума итерациях. Это служит в значительной
мере обоснованием рассматриваемых в данном разделе алгоритмов.
8.3.1. Основной алгоритм отсекающих плоскостей
Ограничимся пока рассмотрением задачи следующего вида:
(1) минимизировать f (х)
при ограничениях gfy(x) 0, /=1. .-.,7,
sC Xj sC x(U), i = 1, ..., N.
Область F в в пределах которой лежат все допустимые решения
задачи (1), определяется ограничениями в виде неравенств. Пред-
полагается, что F ограничена и непуста. Рассматриваемый ниже ал-
горитм позволяет получить решение задачи путем решения после-
довательности подзадач. Указанные подзадачи строятся при помощи
330
ГЛАВА 8
последовательных уточнений грубого первоначального приближения
допустимой области, получаемых при наложении новых ограниче-
ний. Вид этих ограничений зависит от решения, полученного на
предыдущей итерации.
Если область F непуста и ограничена, простейшим приближе-
нием к F служит содержащий F гиперкуб, т. е. множество Z®, зада-
ваемое следующими неравенствами
Z° = {х: xf' i = 1, ..., N},
где величины x[Ll и х\и>, если они не фигурируют в формулировке
задачи, выбираются так, чтобы гарантировать F<^Z°. Полученное
приближение к F представляет собой допустимую область для сле-
дующей первой подзадачи:
минимизировать f (х)
при ограничении х g Z0.
Для оптимального решения задачи х’1’ существуют две возмож-
ности: точка х<п может быть допустимой, т. е. х(1>£ F; она может
быть также недопустимой, т. е. xU)fZ°, но xu’^F. Для первого
случая получено решение задачи, поскольку из включений xw £ F<z
cZ° следует, что х(1) представляет собой точку минимума для исход-
ной задачи. Во втором случае для получения допустимой точки не-
обходимо улучшить рассматриваемое приближение F. Заметим, что
при помощи точки х11’ можно получить информацию об истинном
оптимуме. Представляется вероятным, что оптимум лежит в наи-
более близкой к х(1) части F. Таким образом, именно эту часть F
нужно исследовать при получении улучшенной аппроксимации F.
-----Х1 ----►Ь,
<4--------*--------* bt
а б
Рис 8.11. а — аппроксимация допустимой области гиперкубом; б — отсекающие
плоскости.
Для построения улучшенной аппроксимации в окрестности точ-
ки хш необходимо изменить границу обл-асти Z® вблизи х(1) таким
образом, чтобы она приблизилась к границе F. Этого можно до-
биться, налагая дополнительные ограничения, при выполнении
которых из Z® будет удалена окрестность точки хш. В результате
добавления этих «отсекающих» ограничений точка минимума в но-
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 33f
вом приближении допустимой области должна оказаться ближе к
F, чем точка х(1). На рис. 8.11, а дается иллюстрация этого поло-
жения. Область F здесь заштрихована, a Z0 представляет собой пря-
моугольник, задаваемый неравенствами tZi^Xi^&i, a2^x2^b2. Пусть
х(1>— точка оптимума в Z0 для некоторой целевой функции /(х),
например /(х) =—Xi—х2. Можно улучшить текущее приближение к
F в окрестности х(1), введя нелинейные ограничения вида р-1,(х)^0,
«отсекающие» окрестность точки х(П (рис. 8.11, б). Если обозна-
чить через Hw множество
Д(1) = {х: рР> (х)>0},
то новое приближение Z(1) к допустимой области можно представать
в следующем виде:
Очевидно, что Z(l) содержится в Z(o>.
Меньшая область Z*1’ представляет собой допустимую область
для следующей подзадачи:
минимизировать /(х)
при ограничении xgZ(i).
Оптимальное решение х<2) этой подзадачи может быть оптималь-
ным решением исходной задачи; в противном случае оно дает воз-
можность введения следующего множества линейных неравенств,
позволяющих построить еще меньшую область Z(2). Разумно пред-
положить, что при продолжении описанного процесса находится
допустимая точка х, представляющая собой точку минимума /(х)
на F, если на каждом его шаге отбрасывается ненужная часть Z<0).
Описанная процедура является основой метода отсекающих пло-
скостей.
Для того чтобы из описанной общей схемы получить конкретную
модификацию метода отсекающих плоскостей, необходимо уточнить
два момента. Первый состоит в выборе численной процедуры для
решения промежуточных подзадач с линейными ограничениями.
Второй относится к методу построения множества отсекающих пло-
скостей на каждой итерации. Далее рассматривается вариант ме-
тода, предложенный в работе [19] (а также независимо в [20]).
Следует рассматривать этот алгоритм, известный как метод отсе-
кающих плоскостей Келли, как один из классических методов нели-
нейного программирования.
8.3.2. Алгоритм Келли
Алгоритм отсекающих плоскостей Келли предназначен для ре*
шения задач следующего вида:
N
(II) минимизировать НХ) = 2СЛ
332
ГЛАВА 8
при ограничениях gy(x)^0, /—1. •••, J,
X(iL> Х{ Х;У), I = 1, . . . , Л7,
где gj— вогнутые функции. Такая задача, в которой целевая функ-
ция линейная, эквивалентна задаче I, поскольку в случае нелиней-
ной f(x) задача (II) сводится к задаче (I). Действительно, для этого
достаточно ввести новую переменную х0 и еще одно ограничение
х0>/(х).
Таким образом, получается следующая задача:
минимизировать х0
при ограничениях gj (х) 0, / = 1, J,
х^'^х^х^’, 1 = 1........JV,
представляющая собой частный случай задачи (II). Очевидным пре-
имуществом рассматриваемой формулировки является то обсто-
ятельство, что при рассмотрении линейных отсечений промежуточ-
ные подзадачи оптимизации представляют собой задачи линейного
программирования. Следовательно, при использовании метода Кел-
ли можно решать промежуточные задачи при помощи стандартных
алгоритмов ЛП.
Отсечения, используемые в алгоритме, строятся при помощи ло-
кальной линеаризации нарушаемых ограничений следующим об-
разом. Пусть х(1> — оптимальное решение задачи
минимизировать f (х)
при ограничении xgZ°
и xll>^F. Поскольку х11) не лежит в F, одно из ограничений должно
нарушаться в точке х(1). Пусть нарушается k-e ограничение:
gft(x(1))<0.
При помощи локальной линеаризации любого нарушающегося
в точке х(1) ограничения gy(x)^0,
gj (х; х11’) = gj (xll)) + V gj (x‘n) (x—хш),
можно добиться исключения точки х11’ из допустимой области.
Для этого достаточно записать следующее неравенство (/' — лю-
бое, для которого нарушается ограничение):
gy(x; х11,)>0.
Чтобы убедиться в этом, достаточно заметить, что, поскольку
gj (х(1))<С0, точка х11) не удовлетворяет линеаризованному неравен-
ству. Таким образом, при построении Л11’ в принципе возможна
линеаризация всех ограничений, нарушающихся в точке х11’. На
практике такой способ ведет к рассмотрению ограничений, являю-
щихся излишними. С учетом этого обстоятельства при построении
Д11) Келли предложил осуществлять линеаризацию того из ограни-
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 333
чений, которое нарушается в точке х(1) наиболее сильно. Таким обра-
зом, при построении улучшенной аппроксимации в методе Келли
используется только одно дополнительное неравенство на каждой
итерации.
Изложив основные моменты метода Келли, опишем последова-
тельность действий при его работе.
Метод отсекающих плоскостей Келли
Заданы: задача в виде (II), некоторый алгоритм ЛП, положитель-
ное 8>0 (точность решения) и начальные границы допустимой об-
ласти
Z° = {х: х'л’х(-х'^’, i = l, ..., А/},
так что Z°^>F.
Ill а г 1. Решить задачу ЛП:
минимизировать 2СЛ
при ограничении x£Z°.
Пусть х(1)— оптимальное решение этой задачи. Для k=l, 2, . . .
выполнить следующую последовательность шагов.
Шаг 2. Найти такое т, что
—gm(*lft,)=max[—£7(х(И), 0:/=1, ..., У].
Если gm(xw)>—е, то прекратить вычисления. В противном слу-
чае перейти к шагу 3.
Шаг 3. Построить отсекающие плоскости следующего вида:
Pik} (*) = gm (х; х‘*>) = gm (х1*’) 4- Vgm (х(*>) (х—хш).
Пусть — полупространство = {х : рм (х)^0}. Решить
задачу ЛП:
минимизировать 2СЛ
при ограничении х g Z{k~l> n Я‘А>.
Оптимальное решение обозначить через х(*+1).
Шаг 4. Положить Z‘»>=Z(»-i> п FFk>, k=k-\-\. Перейти к
шагу 2.
Пример 8.11
При помощи метода Келли требуется решить следующую задачу:
минимизировать f (x)=Xi—х2
при ограничениях gt(x)=2xi—х] —1^0,
g2(x)=9—0,8х? —2х2>0,
х^О, х2>0.
Как видно из рис. 8 12, допустимая область этой задачи лежит в
прямоугольнике О^Схц^б, 0^х2^4. Заметим, что gi и g2— вогну-
тые функции.
334
ГЛАВА 8
Зафиксировав некоторое малое 8>0, перейдем к шагу 1 алго
ритма, полагая Z° = {x : О^х^б, 0с4х2С4}.
Шаг 1. Найдем минимум функции
f(x) ——Xi—х2
при ограничениях 0^х^5, 0^7х2^74.
Очевидно, что решением является точка х11) = (5,4).
0 1 2 з ' 4 5 6
Рпс. 8 12. Допустимая область (пример 8.11).
Шаг 2. Поскольку g1(xll))=—7,g2(xll)) =—19, наиболее силг
но нарушается ограничение g2(x)^0. Перейдем к шагу 3.
Шаг 3. Отсекающая плоскость задается при помощи линеа
ризации ёг(х) в точке х11), так что
(х) =i2 (х; х(1>) = —19—8 (Xj—5) — 2 (х2—4).
Таким образом, необходимо добавить ограничение
—19—8(Х!—5)—2 (х2—4)>0.
Заметим, что точка л11) не удовлетворяет этому ограничению. 'Ге
перь следует решить вторую подзадачу:
Ш а г 1.
Минимизировать —Xi—х2
при ограничениях 29—8xj—2х2^0, ФСх^СБ, 0^х2^4.
Оптимальная точка: х12’=(2,625; 4).
Шаг 2. ^(х‘!>)=—11,75, я2(х(2))=—4,5125.
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 335
Ясно, что первое ограничение нарушается сильнее, причем ве-
личина невязки велика, поэтому необходимо продолжать выпол-
нение итераций алгоритма.
Шаг 3. Уравнение отсекающей плоскости имеет следующий
ВИД'
Р(2’ (x)=g1(x; х‘2,) =
= —11,75+2 (Xi—2,625)—8 (х2—4)=0.
Она отделяет точку х12’ от допустимой области F.
Третья промежуточная подзадача ЛП:
минимизировать —хх—х2
при ограничениях 29—8xi—2х2^0,
15-J-2X!—8х2^0,
0Сх!<5, 0jCx3<C9.
Оптимальное решение: х13)=(2,971; 2,618).
Выполнение итераций продолжается до тех пор, пока ограни-
чения не удовлетворятся с предписанной точностью 8. Точка х* =
=(2,5; 2,0) представляет собой точное решение.
Результаты выполнения последовательных итераций можно за-
писать в следующем виде:
Номер подзадачи /fe) 1 2 1 цЩ
1 5 4 —9,000
2 2,625 4 —6,625
3 2,971 2,618 —5,589
4 2,343 2,461 —4,804
5 2,516 2,050 —4,566
00 2,500 2,000 —4,500
Из рассмотрения таблицы следует, что движение к оптимуму проис-
ходит с ростом значения целевой функции на каждой итерации.
Причина этого состоит в последовательном сокращении допустимой
области подзадач, что приводит к росту оптимальных решений под-
задач.
8.3.3. Вычислительные аспекты алгоритма Келли
Основной алгоритм Келли с успехом использовался в различных
областях. Он зарекомендовал себя как очень эффективный при ре-
шении специального класса задач нелинейной оптимизации, так
называемых обобщенных задач геометрического программирования
(см. гл. 11). Важным преимуществом метода Келли (общим для всех
336
ГЛАВА 8
методов линеаризации) является сохранение при его применении
любой линейности или «почти линейности» в первоначальной фор-
мулировке задачи. Кроме того, весьма немаловажно, что решаемая
на каждой итерации подзадача представляет собой задачу ЛП, для
решения которой разработаны эффективные методы. Поскольку каж-
дая подзадача ЛП отличается от предыдущей лишь на одно ограни-
чение, в этой ситуации весьма эффективен упомянутый в гл. 4
двойственный симплекс-метод. Оптимальную таблицу предыдущей
подзадачи нужно лишь незначительно изменить при добавлении
нового ограничения для исключения некоторых коэффициентов при
базисных переменных. Получаемое допустимое двойственное реше-
ние можно использовать в качестве начального для проведения ите-
раций при решении следующей подзадачи.
Несмотря на высокую эффективность процесса последователь-
ного решения подзадач ЛП, основной метод Келли имеет ряд недо-
статков как теоретического, так и практического характера (к
счастью, некоторые из них удается устранить). Генерация алгорит-
мом последовательности недопустимых точек представляет собой
наибольший недостаток. По этой причине нельзя прекращать вы-
числения при достижении «хорошего» приближения к решению.
Важным теоретическим недостатком является требование выпук-
лости допустимой области F. Сходимость к оптимальному решению
можно гарантировать, только если область F выпуклая, хотя при
помощи метода Келли был решен ряд невыпуклых задач. Выпуклость
области F требует вогнутости левых частей gy(x) всех ограничений
задачи. Напомним, что значение локально линеаризованной вогну-
той функции всегда больше значения самой функции; таким обра-
зом, для фиксированной точки w и переменной точки х выполняется
следующее неравенство-.
g-(x)Cg(w)+Vg-(ay) (x—w).
Если точка х удовлетворяет неравенству gj (х)^0, то для любой точки
w выполняется также неравенство
(w)+vgj(w) (x—w).
Другими словами, если левые части gj(x) всех ограничений пред-
ставляют собой вогнутые функции, область, задаваемая линеари-
зованными ограничениями, содержит допустимую область F ис-
ходной задачи. Следовательно, порождаемая алгоритмом Келли
последовательность аппроксимаций Z(*’ допустимой области F
представляет собой семейство вложенных множеств, каждое из ко-
торых включает допустимую область F:
Z°z;Z(1,Z)Zl2,=>... =>Zl*>Z)F.
Если выполняется это свойство вложенности, то при рассмотре-
нии последовательных отсечений не происходит потери части допу-
стимой области F, которая возможна при ее невыпуклости.
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 337
Третий недостаток метода Келли, имеющий практический ха-
рактер, состоит в непрерывном росте размерности подзадач ЛП на
каждой итерации. Кроме того, последовательные отсекающие пло-
скости при приближении к оптимуму почти совпадают, что затруд-
няет решение соответствующих задач ЛП, поскольку строки таб-
лицы становятся приближенно линейно зависимыми. Использова-
ние процедур отбрасывания отсекающих плоскостей позволяет
уменьшать число отсечений. При этих процедурах необходимо со-
блюдать некоторые предосторожности, поскольку может быть вне-
сена неустойчивость в итеративный процесс решения подзадач.
В частности, допустимо отбрасывать только ограничения, не явля-
ющиеся активными для оптимального решения предыдущей под-
задачи [21, 22]. В работах [21,22] предложена следующая процедура
отбрасывания отсечений.
Пусть Р обозначает множество индексов отсекающих плоскостей,
рассматриваемых на итерации t.
Шаг 4 метода Келли следует заменить на следующий шаг.
Шаг 4а. Определить множество D отсекающих плоскостей,
которые необходимо отбросить. В множество D включить те и только
те i Ё/* U {0> для которых выполняются следующие два условия:
р('> (х«+1>) > 0( > Е),
+ (х-Д,
затем включить I в D. Положить /(/+1) = /'и {/}—D.
Шаг 46. Положить
Z/ + J = Z" А {х: р01 (х) >0,
/ = /+1,
и перейти к шагу 2.
Описанная процедура позволяет отбрасывать ограничение, по-
рожденное на предыдущих итерациях, при условиях, что оно не
является активным в точке х1(+1) и значение /(х) в достаточной сте-
пени улучшилось с момента введения этого ограничения. Послед-
нее условие гарантирует монотонный рост целевой функции. Если
допустимая область выпуклая, рассматриваемая процедура схо-
дится к оптимуму [21, 22]. Для ее реализации удобно применять
двойственный симплекс-метод, который обычно используется для
решения подзадач ЛП.
Пример 8.12
Рассмотрим применение модифицированного метода Келли для
решения следующей задачи:
минимизировать Зхц+хз
при ограничении g(x) = l— (хх—2)2—(х2—5)3^0.
338
ГЛАВА 8
Пусть в качестве начального приближения к F выбрано множество
Z°= {х : 0^Xi^5, 0ё7х2^7}.
Оптимальным решением первой подзадачи является точка х(1,=0
с /(х11))=0. Вторая подзадача содержит ограничение
—28+4X1+10к3>0
и имеет следующее решение:
х(2’=(0; 2,8), /(х12,)=2,8.
Выполняем еще три итерации с сохранением всех предыдущих от-
секающих плоскостей. Пятая подзадача имеет следующий вид:
минимизировать Зхг + хг
при ограничениях р(1)(х) =—28 + 4хх + 10х2 О,
р12) (х) = —20,16 + 4xt + 4,4х2 0,
р(3) (х) = —7,024 + 4х1 + 0,84х2 0,
р“> (х) = —13,422 + 2,038х1 + 2,62хг>0,
0^х2^5, 0sCx2^7.
Применим к этой подзадаче процедуру отбрасывания ограниче-
ний. Поскольку все предыдущие отсечения сохранялись, /= {1,2,3}.
Оптимальное решение пятой подзадачи ЛП: х15,=(0,813, 4,491)
с /(х15’)=6,930. Можно выполнить шаг 4а.
Проверяем выполнение описанных выше условий для всех
1 = 1. 2, 3, 4.
Для 1 = 1 . р11) (х<5’)=20,162>0,
f(x(5))=6,903>/(xll))+p(l) (х(1))=0+(—28).
Таким образом, £>={!}.
Для i=2 : р(2> (х1з’)=2,852>0,
f(x(=>)=6,930>f(x(2’)+p(2>(xl2>)=2,8+(—784), поэтому D = {1,2}
Для i=3: р<3> (х+)=0,0.
Для i = 4: р(4’(х16))=0,0.
Следовательно, /+={1, 2, 3} (J {4}—{1, 2} = {3,4}.
Ш а г 46
Z15’ = {х: 0 + + 5, 0^х2^7}п
Г) {х: р13’ (х)>0, р‘4»(х)>0}.
В результате шага 4 были отброшены две предыдущие отсекающие
плоскости. Возвращаемся к шагам 2 и 3. Уравнение следующей от-
секающей плоскости:
р<?>(х)=-7,170 +2,374х1+1,018х2=0.
Шестую подзадачу можно записать в виде
минимизировать 3xi+x2
при ограничениях р(3)(х)^0,
р(4’ (х)>0,
р(5> (х)^0,
0<х,С5, 0s£x2sS7.
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 339
Решение этой задачи: xlS) = (0,5427; 5,778) с /(х(в,)=7,406 Выпол-
няется шаг 4. После проверки плоскостей из множества (3; 4; 5}
выполнение итераций продолжается.
Рис. 8 13 Допустимая область (пример 8.12).
Результаты следующих шести итераций приведены ниже в таб-
лице, а на рис. 8.13 они представлены графически.
Как видно из вышеизложенного, при использовании критерия
отбрасывания лишних отсечений не возникло необходимости рас-
смотрения более трех отсекающих плоскостей в каждой подза-
Номер подзадачи 1 ,,(П 2 !(?'»)
6 0,5427 5,778 7,406 3, 5
7 0,8069 5,162 7,582 5, 6
8 0,9501 4,828 7,678 5, 7
9 1,052 4,590 7,746 5, 8
10 1,030 4,721 7,813 8, 9
11 1,058 4 658 7,831 9, 10
12 1,048 4.692 7,836 10, 11
00 1,051 4,684 7,838 —
340
ГЛАВА 8
даче. При применении немодифицированного метода Келли, сох-
раняющего все порожденные ранее ограничения, двенадцатая под-
задача содержит все 11 порожденных ранее неравенств.
Заметим, что, хотя число отсекающих плоскостей при использо-
вании процедуры отбрасывания уменьшается, остается проблема,
связанная с почти параллельностью этих плоскостей (см. рис. 8.13).
При приближении отсекающих плоскостей к допустимой области
ограничения становятся все более и более близкими, например
pw и pV. Следовательно, оказывается затруднительным при по-
мощи численных методов точно определить точку пересечения отсе-
кающих прямых. Решение этой проблемы пока не найдено.
8.3.4. Обсуждение
Можно доказать, что алгоритм отсекающих плоскостей Келли
сходится при выполнении некоторых общих условий, включающих
требование вогнутости левых частей ограничений как при исполь-
зовании процедуры отбрасывания ограничений [21], так и без нее
[2]. Поведение отсекающих плоскостей в методе Келли сильно на-
поминает поведение траектории градиентного метода безусловной
оптимизации. Это хорошо видно на примерах из данного раздела.
Показано, что для некоторых специальных случаев алгоритма отсе-
кающих плоскостей скорость сходимости линейна 131. Поскольку
скорость сходимости алгоритма отсекающих плоскостей существен-
но зависит от конкретных особенностей отсечений, невозможно дать
оценку скорости сходимости алгоритма в общем случае.
В работах [23, 24] рассмотрены другие модификации методов от-
секающих плоскостей. При использовании этих методов вводятся
«более глубокие» отсечения для построения лучших приближений
допустимой области. Читателю следует обратиться к работам [22,
23, 24] для подробного ознакомления с этими методами.
8.4. Заключение
В данной главе описаны три основных способа применения
линейных аппроксимаций для решения задач с нелинейными огра-
ничениями: решение последовательности подзадач ЛП, глобаль-
ная аппроксимация при помощи кусочно-линейных функций и ап-
проксимация с использованием линеаризации сильно нарушаемых
ограничений. При подходе, основанном на непосредственной лине-
аризации, решение задач ЛП используется только для отыскания
направления, в котором поиск осуществляется на основе методов,
изложенных в гл. 2 Применяемый для решения задач с линейными
ограничениями алгоритм Франка — Вульфа можно рассматривать
как комбинацию решения последовательности задач ЛП и проце-
дуры одномерного поиска. При использовании метода, основанной
на рассмотрении последовательности подзадач ЛП для решения за
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 341
дач с нелинейными ограничениями, возникает необходимость кор-
ректировки решений задач ЛП для достижения допустимости. Пра-
вило ограничения величины шага, рассмотренное в работе [4], обе-
спечивает допустимость промежуточных решений и сходимость к
оптимуму, но скорость сходимости оказывается при этом весьма
низкой. Более эффективен метод штрафных функций. Даже усовер-
шенствованный метод последовательного решения подзадач ЛП
эффективен только для задач с малым числом нелинейных перемен-
ных.
В методе сепарабельного программирования используются ку-
сочно-линейные аппроксимации сепарабельных нелинейных функ-
ций в областях их определения. При таком подходе происходит су-
щественный рост размерности задачи. Если требуется более точное
решение задачи, то необходимо осуществлять корректировку узлов
сетки, с помощью которой строится аппроксимация. В случае не-
выпуклой допустимой области следует решать получаемую задачу
ЛП с учетом правила ограниченного ввода в базис, обеспечиваю-
щего порождение нужных при построении аппроксимации точек.
Сепарабельное программирование эффективно при решении задач
с сепарабельными левыми частями, не слишком сильно отклоняю-
щимися от линейности. Такие ситуации часто встречаются в при-
ложениях, связанных с планированием.
Был рассмотрен также класс методов отсекающих плоскостей.
Эти методы основаны на построении последовательных линейных
аппроксимаций допустимой области в окрестности решения. Дви-
жение к решению при этом происходит извне допустимой области.
В алгоритме Келли отсекающие плоскости служат для отбрасывания
части предыдущей аппроксимации допустимой области. Такой способ
применим только при решении задач с ограничениями в виде нера-
венств и выпуклой допустимой областью. Последовательность под-
задач ЛП может быть эффективно решена при помощи специальных
методов ЛП. В частности, существует процедура отбрасывания от-
секающих плоскостей, которые становятся излишними в процессе
построения дальнейших отсечений. Методы отсекающих плоскостей
чувствительны к ограничениям точности численного решения под-
задач, которые возникают из-за того, что последовательно вводимые
отсекающие плоскости в окрестности точки оптимума почти парал-
лельны. Несмотря на это, методы отсекающих плоскостей эффектив-
но применялись для решения трудных задач специальной структу-
ры. В настоящее время ведутся дальнейшие исследования этих ме-
тодов.
Контрольные вопросы и задачи
8.1. Почему в алгоритме Франка — Вульфа необходим одномер-
ный поиск? Почему начальная ючка должна быть допусти-
мой?
ГЛАВА 8
342
8.2. По какой причине в методе непосредственной линеаризации
Гриффита — Стюарта необходимо накладывать ограничения
на величину изменения переменных?
8.3. Опишите метод, при помощи которого можно найти начальную
допустимую точку для алгоритма Франка — Вульфа.
8.4. Объясните, каким образом итерации алгоритма Франка —
Вульфа могут сходиться к внутренней точке допустимой обла-
сти, тогда как любая подзадача ЛП имеет решение в угловой
точке ее допустимой области.
8.5. Напомним, что при применении метода последовательного
решения подзадач ЛП, использующего штрафные функции,
производится только грубая минимизация штрафной функции.
Что произойдет, если подзадачу ЛП также решать только при-
ближенно? Может ли хватить одной итерации симплекс-ме-
тода для каждой подзадачи? Объясните.
8.6. Опишите в общих чертах метод последовательного решения
подзадач ЛП, использующий штрафные функции, при при-
менении которого из штрафной функции исключаются линей-
ные неравенства и ограничения на переменные. Укажите пре-
имущества такого метода.
8.7. При решении каких задач следует предпочесть сепарабельное
программирование методу решения последовательных подза-
дач ЛП?
8.8. В чем состоит правило ограниченного ввода в базис, почему
оно необходимо и в каких случаях его можно отбросить?
8.9. Пусть для приближения функции f(xn) построена некоторая
сетка. Есть ли необходимость использовать ту же сегку для
построения приближений других функций, зависящих от х„?
Объясните.
8.10. Опишите в общих чертах два метода отсекающих плоскостей,
предназначенных для решения задач с ограничениями в виде
нелинейных равенств. Укажите их относительные преимуще-
ства.
8.11. Объясните, как следует поступать с линейными ограничениями
при использовании метода отсекающих плоскостей. Что про-
исходит в случае линейных ограничений в виде равенств?
8.12. Какова цель добавления нового ограничения на каждой ите-
рации алгоритма Келли?
8.13. Каковы преимущества использования процедуры отбрасы-
вания отсечений совместно с рассмотрением нескольких новых
отсечений на каждой итерации?
8.14. Докажите или опровергните, что при использовании метода
Келли для выпуклых задач целевая функция монотонно воз-
растает, а невязка по ограничениям монотонно убывает.
8.15. Постройте отсекающую плоскость в точке х=(1, 2) для сле-
дующего нелинейного неравенства: g(x)= х&ь+х&^К).
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 343
8.16. Рассмотрите следующую задачу:
минимизировать /(х)=1/3 (Xi+3)s+x3
при ограничениях З^х^!, 2^х3^0.
(а) Постройте кусочно-линейную аппроксимацию кубиче-
ского члена целевой функции на всем отрезке изменения
Xi, используя сетку с четырьмя узлами.
(б) Необходимо ли применять правило ограниченного ввода
в базис при решении получаемой задачи ЛП? Объясните.
(в) Решите полученную задачу ЛП. Сравните ее решение с
точным решением исходной задачи.
8.17. Рассмотрите следующую задачу:
минимизировать f(x)=(xI—2)2+ (х2—2)а
при ограничениях gt(x)=3—х,—х3^0,
g2 (х) = 10xi—х2—2^0,
х2^0.
(а) Можно ли принять в качестве начальной точки при ис-
пользовании алгоритма Франка — Вульфа точку г° =
=(0, 0)? Почему?
(б) Решите задачу при помощи алгоритма Франка — Вульфа,
выбирая в качестве начальной точку х° = (0,2; 0).
8.18. Рассмотрите следующую задачу:
максимизировать f (x)=2xt—3(х2—4)2
при ограничениях gi(x) = 10—х~—х^О,
g2(x)=9—х2—(х— 4)22&0,
Xi>0.
(а) Вычислите точку, получаемую на следующей итерации
градиентного метода с малой длиной шага (3 = 1), если
в качестве начальной выбрана точка х° = (2; 2).
(б) Повторите те же вычисления, что и в п. (а), для начальных
точек х“=(0; 1) и (1; 3).
8.19. Рассмотрите задачу из примера 8.9 с новой целевой функцией:
максимизировать f {х)~х1^+х2.
(а) Покажите, что при использовании сепарабельного про-
граммирования нет необходимости в применении правила
ограниченного ввода в базис.
(б) Решите задачу ЛП, получаемую при использовании тех
же узловых точек, что и в примере 8.9.
8.20. Постройте отсекающую плоскость в точке x0=(p<3/3, |/"3/3)
для заданного множества ограничений
g(x)=x;+x2—1^0,
1,5>Х!^0
344
ГЛАВА 8
и покажите, что она отсекает часть допустимой области.
[Указание: рассмотрите точку (1; 0).]
8.21. Продолжите с пятой итерации решение задачи примера 8.12,
используя процедуру отбрасывания отсечений, при которой
отбрасывается любое отсечение, являющееся избыточным в
новой точке. Представьте результаты последующих трех-
четырех итераций графически и объясните наблюдаемые яв-
ления.
8.22. (а) Постройте кусочно-линейную аппроксимацию следую-
щей функции:
х2)=х2+хг1+2(х2+2)-2
на отрезках V^x^C5/.,, —1^х2^1, используя сетку с
пятью узлами для Xi и с четырьмя узлами для х2.
(б) С помощью симплекс-метода минимизируйте аппроксими-
рующую функцию в указанной выше области.
8.23. Рассмотрите следующую задачу:
максимизировать f (x)=x1-\-x2i
при ограничениях gi(x)=25—х2—х^О,
g2 (х)=9—х?—х2>0,
5>Х!>0, 10>х2>0.
(а) Сформулируйте и решите первую подзадачу, возникающую
при использовании метода отсекающих плоскостей Келли.
(б) Найдите уравнение отсекающей плоскости в точке, полу-
ченной в результате выполнения п. (а).
(в) Сформулируйте и решите вторую подзадачу и найдите
следующее отсечение.
8.24. Допустим, что при помощи метода Келли ищется цешение
следующей задачи:
минимизировать f(x)=—Xi—х2
при ограничениях gi(x)=25—х2—х2^0,
g2 (х) -^9—2xj—x2S5sO,
Xi^O, x2S5sO.
(а) Верно ли, что при использовании алгоритма нужно по-
разному рассматривать ограничения gi и g2?
(б) Как обобщить полученное наблюдение?
8.25. Покажите, что при помощи сепарабельного программирования
можно решить следующую задачу.
минимизировать /(x)=Xi j-х^+х^
при ограничениях 64x72x24Xge^l,
хг>0.
В предположении, что значения всех переменных не превос-
ходят десяти, сформулируйте задачу сепарабельного програм-
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 345
мирования, используя сетку с пятью узлами для всех пере-
менных.
8.26. Пусть дана следующая задача НЛП:
минимизировать / (х) — х; + хЦ- xj
при ограничениях gi(x) = l—x^Xg^O,
gt (x) = Xj — x3>0,
hi (x) = Xj—Xj + x2x3 — 4 = 0,
0<^x1^5, 0^x2^3, 0 x3 ^3.
Выполните одну итерацию модифицированного алгоритма
последовательного решения подзадач ЛП, описанного в ра-
боте [8], с х°=(4; 2; 2), 6 = 1, е=10-3.
8.27. Можно ли решить задачу 8.26 при помощи метода отсекаю-
щих плоскостей? Если нет, переформулируйте ее таким обра-
зом, чтобы это стало возможным. Верно ли, что получаемая
задача является выпуклой? Сделайте чертеж допустимой об-
ласти для проверки ответа.
8.28. Переформулируйте задачу примера 8.7 в виде, пригодном
для использования метода сепарабельного программирования.
Используйте сетку с пятью узлами для потоков и с четырьмя
узлами для смесей. Можно ли решить получаемую задачу
при помощи стандартной программы ЛП? Необходимо ли
внести какие-либо изменения в такую программу?
8.29. (а) Постройте кусочно-линейную аппроксимацию функции
/(х) = 10 sin х
на отрезке 0^х^2л, используя сетку с девятью узлами,
(б) Какова максимальная величина ошибки полученного
приближения?
(в) Покажите, что при использовании симплекс-мегода для
минимизации полученной кусочно-линейной аппроксими-
рующей функции находится решение, совпадающее с
одной из узловых точек.
8.30. Рассмотрите следующую задачу:
минимизировать f (х)=х;+х; +х!
при ограничениях xix2x3=9,
Х;+хК6,
Х'з+х^Л, Xi, х2>0.
В каком виде необходимо представить эту задачу для решения
методом отсекающих плоскостей Келли? Можно ли решить
эту задачу методом Келли?
8.31, Объясните, что произойдет при использовании метода отсе-
346
ГЛАВА 8
кающих плоскостей Келли в следующей задаче:
минимизировать /(x)=(Xj—V2)2+(x2— I)2
при ограничениях 4—х2—2x^0,
—2==С(х1, х2)<2.
[Указание: постройте сначала грубое приближение.)
8.32. Рассмотрите следующую задачу:
минимизировать —х2)2+х2
при ограничениях Xj+x2^l,
Х1+2х2^3,
х,>0, х2>0,
с начальной точкой х° = (3; 0).
(а) Выполните три итерации алгоритма Франка — Вульфа.
(б) Представьте задачу в виде, пригодном для решения при
помощи метода отсекающих плоскостей. Выполните три
итерации этого метода.
(в) Используйте чертеж допустимой области для объяснения
разницы в поведении траекторий, полученных в результате
выполнения пунктов (а) и (б).
Литература
1 Frank N., Wolfe Р., An Algorithm for Quadratic Programming, Naval Res.
Log. Quart., 3, 95—110 (1956).
2 Zangwill W. 1., Nonlinear Programming, Prentice-Hall, Englewood Cliffs,
NJ, 1969. [Имеется перевод- Зангвилл У. И. Нелинейное программирование.
Единый подход.— М.. Советское радио, 1973.]
3 Wolfe Р., Convergence Theory in Nonlinear Programming, in Integer and Non-
linear Programming (J. Abadie, Ed.), North-Holland Amsterdam, 1970.
4 Griffith R. E., Stewart R. A., A Nonlinear Programming Technique for Opti-
mization of Continuous Processing Systems, Manage. Sci , 7, 379—391 (1961)
5 Smith H. V., A Process Optimization Programm for Nonlinear Systems, Pop 11,
7090 H9 IBM UD21, SHARE General Program Library, 1965.
6 Graves G. W., Development and Testing of a Nonlinear Programming Algorithm,
Aerospace Corporation, Rep. No. ATR-64 (7040)-2, June 1964.
7 Clasen R. J., Graves G. W., Lu J. Y., Sortie Allocation by a Nonlinear Program-
ming Model for Determining a Munitions Mix, Rand Corporation Rep. R-1411-
DDPAE, March 1974.
8 Palacios-Gomez F. E., The Solution of Nonlinear Optimization Problems Using
Successive Linear Programming, Ph. D. Dissertation, School Business Adminis-
tration, The University of Texas, Austin, TX, 1980.
9 Beale E. M. L., Nonlinear Programming Using a General Mathematical Pro-
gramming System, in: Design and Implementation of Optimization Software
(H. J. Greenberg, Ed.), Sijthoff and Noordhof, Netherlands, 1978.
10 Lasdon L. S., Warren A D., Survey of Nonlinear Programming Applications,
Oper. Res., 28, 1029—1073 (1980).
11 Baker T. E., Lasdon L. S. Successive Linear Programming at Exxon, Working
Paper 81/82-2-8, Graduate School of Business, The University of Texas, Austin,
TX, July 1982.
12 Haverlv C. A., Studies of the Behavior of Recursion of the Pooling Problem,
SIGMAP Bull.. 25, 19—28 (Dec. 1978).
МЕТОДЫ ЛИНЕАРИЗАЦИИ ДЛЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ 347
13 Lasdon L. S., Warren A. D., Sarkar S., Palacios-Gomez F. E., Solving the
Pooling Problem using Generalized Reduced Gradient and Successive Linear
Programming Algorithms, SIGMAP Bull , 77, 9—15 (July 1979).
14 Miller С. E., The Simplex Method for Local Separable Programming, in Recent
Advances in Mathematical Programming (R. Graves, P. Wolfe, Eds ), McGraw-
Hill, N. Y„ 1963.
15 . Bazaraa M. S., Shetty С. M., Nonlinear Programming Theory and Algorithms,
Wiley, N. Y., 1979. [Имеется перевод. Базара M , Шетти К. Нелинейное
программирование Теория и алгоритмы.— М.: Мир, 1982.J
16 . Beale Е. М. L., Advanced Algorithmic Features for General Mathematical Pro-
gramming Systems, in Integer and Nonlinear Programming (J. Abadie, Ed.),
North-Holland, Amsterdam, 1970.
17 . El Agizy, Applications of Separable Programming to Refinery Models, ORSA
36th National Meeting, Nov. 1969
18 Kawatatoni T. K.., Ullman R. J., Dantzig G. B., Computing Tetraethyl-lead
Requirements in a Linear Programming Format, Oper. Res., 8, 24—29 (1960).
19 , Kelley J E., The Cutting Plane Method for Solving Convex Programs, SIAM
J., 8, 703—712 (1960).
20 . Cheney E. W., Goldstein A. A., Newton’s Method of Convex Programming and
Tchebycheff Approximation, Numer Math., 1, 253—268 (1959)
21 . Topkis D M„ Cutting Plane Methods without Nested Constraint Sets, Oper.
Res., 18, 404—413 (1975).
22 . Eaves В. C., Zangwill W. 1., Generalized Cutting Plane Algorithms, SIAM.
J. Control, 9, 529—542 (1971)
23 Veinott A. F., Jr , The Supporting Hyperpiane Method for Unimodal Program-
ming, Oper. Res., 15, 147—152 (1967).
24 . Elzinga J., Moore T. G., A General Cutting Plane Algorithm for the Convex
Programming Problem, Math. Programming, 8, 134—145 (1975).
ОГЛАВЛЕНИЕ
Предисловие к русскому изданию....................................... 5
Предисловие.......................................................... 7
Глава 1. Методологические основы оптимизации....................... 10
1.1. Необходимые условия для применения оптимизационных методов 11
1.2. Применение методов оптимизации в инженерной практике ... 17
1 3 Структура оптимизационных задач ........................... 33
1 4. Некоторые замечания о книге в целом ...................... 35
Литература..................................................... 36
Глава 2. Функции одной переменной.................................. 37
2 1. Свойства функций одной переменной......................... 37
2 2. Критерии оптимальности.................................... 40
2 3. Методы исключения интервалов ............................. 49
2 4. Полиномиальная аппроксимация н методы точечного оценивания 58
2 5. Методы с использованием производных....................... 63
2.6. Сравнение методов......................................... 71
2 7. Заключение................................................ 73
Контрольные вопросы и задачи ............................... . 73
Литература................................................ ... 78
Глава 3. Функции нескольких переменных ............................ 79
3 1. Критерии оптимальности.................................... 81
3.2. Методы прямого поиска.................................... S5
3.3. Градиентные методы ...................................... 109
3 4. Сравнение методов и результаты вычислительных экспериментов 132
3.5. Заключение............................................... 138
Контрольные вопросы и задачи ................................. 139
Литература.................................................... 146
Глава 4. Линейное программирование ................................ 150
4 1. Разработка моделей линейного программирования............ 150
4 2 Графическое решение задачи линейного программирования с
двумя переменными............................................ 154
4 3. Задача линейного программирования в стандартной форме . . 158
4 4. Основы симплекс-метода................................... 161
4 5 Решение задач ЛП на ЭВМ .................................. 176
4 6. Анализ чувствительности в линейном программировании . . . 180
4.7. Приложения................... ........................... 1?4
4.8. Развитие идей линейного программирования ................ 184
ОГЛАВЛЕНИЕ
349
4 9. Заключение............................................... 18&
Контрольные вопросы и задачи................................. 186
Литература..................................................... 194
Глава 5. Критерии оптимальности в задачах с ограничениями .... 196
5 1. Задачи с ограничениями в виде равенств.................. 196
5 2. Множители Лагранжа....................................... 197
5 .3 Экономическая интерпретация множителей Лагранжа.......... 201
5 .4. Условия Куна—Таккера.................................... 202
5 5. Теоремы Куна—Таккера.................................... 205
5 6 Условия существования седловой точки ................... 210
5 7. Условия оптимальности второго порядка .................. 213
5 8. Заключение............................................... 220
Контрольные вопросы и задачи ................................ 220
Литература..................................................... 224
Глава 6. Методы оптимизации иа основе преобразования задачи .... 225
6 1. Понятие штрафной функции................................. 226
6 2. Алгоритмы и программы ................................... 244
6. 3 Метод миожителей........................................ 246-
6 4. Заключение .............................................. 258
Контрольные вопросы и задачи ................................ 259
Литература..................................................... 264
Глава 7. Методы прямого поиска в задачах условной оптимизации . . . 269
7 1. Подготовка задачи к решению ............................. 269
7 2. Использование методов поиска для решения задач безусловной
оптимизации................................................... 273
7. 3. Методы случайного поиска ............................... 284
7 4. Заключение............................................... 292
Контрольные вопросы и задачи .................................. 293
Литература..................................................... 296
Глава 8. Методы линеаризации для задач условной оптимизации . . . 298
8 1. Непосредственное использование последовательности задач ЛП 299
8. 2. Сепарабельное программирование.......................... 317
8. 3. Методы отсекающих плоскостей ........................... 329
8 4. Заключение............................................... 340
Контрольные вопросы и задачи .................................. 341
Литература..................................................... 346