Автор: Силадьи М.
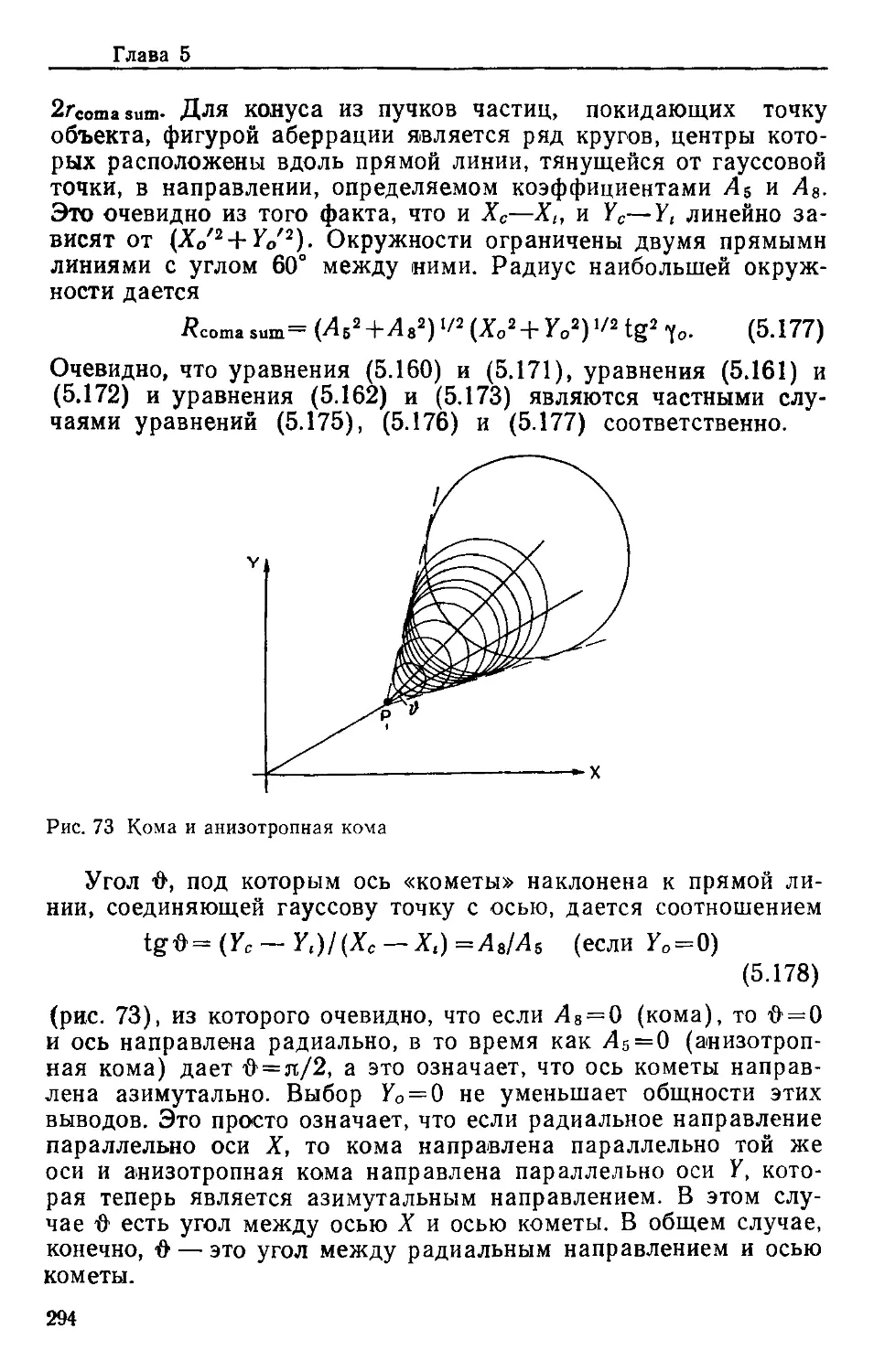
Теги: электронные и ионные явления физико-математические науки оптика
ISBN: 5-03-001634-1
Год: 1990
Текст
М.Силадьи
ЭЛЕКТРОННАЯ
И ИОННАЯ
Издательство «Мир»
ELECTRON
AND ION OPTICS
Miklos Szilgyi
University of Arizona
Tucson, Arizona
PLENUM PRESS NEW YORK AND LONDON
М.Силадьи
ЭЛЕКТРОННАЯ
И ИОННАЯ
ОПТИКА
Перевод с английского
канд. физ.-мат. наук
И. М. Ахмеджанова и Ф. В. Пригары
и В. В. Овчарова
Москва «Мир» 199О
ББК 22.833
С36
УДК 537.533
Силадьи М.
Электронная и ионная оптика: Пер. с англ. — М.: Мир,
С36 1990. — 639 с, ил.
ISBN 5-03-001634-1
Монография американского физика посвящена электронной и ион-
нон оптике, которая находит все более широкое применение при созда-
создании ускорителей элементарных частиц, электронно-лучевых приборов,
спектрометров, установок для субмикроиной литографии. Математиче-
Математический аппарат ориентирован на моделирование процессов на ЭВМ.
Принципы моделирования основаны на аналогии между световой гео-
геометрической оптикой и законами движения заряженных частиц в элек-
электростатическом и магнитном полях.
Для научных работников, инженеров и аспирантов, специализирую-
специализирующихся в области электронно-лучевых приборов, ускорителей элемен-
элементарных частиц и полупроводниковой микролитографии.
2302030500—400
С 121-90 ББК 22.833
041@1)—90
Редакция литературы по физике и астрономии
ISBN 5-03-001634-1 (русск.) © 1988 Plenum Press, New York
ISBN 0-306-42717-6 (англ.) © перевод на русский язык, Ах-
меджанов И. М., Пригара Ф В
Овчаров В. В., 1990
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Книга, предлагаемая вниманию советского читателя, написа-
написана профессором Аризонского университета Миклошем Силадьи
и представляет собой один из трех томов серии «Микроприбо-
«Микроприборы. Физика и технология изготовления», выпускаемой издатель-
издательством «Плинум Пресс», США. Она посвящена важному на-
направлению физической электроники — электронной и ионной оп-
оптике, основу которой составляют процессы формирования и
движения пучковых заряженных частиц в электрических и маг-
магнитных полях. Автор является одним из ведущих в мире спе-
специалистов в этой области. Особенно большой известностью
пользуются его научные труды по разработке методов автома-
автоматизированного проектирования, синтеза и оптимизации фокуси-
фокусирующих устройств электронной и ионной оптики.
Бурное развитие электронной и ионной оптики начиная
с 20-х годов нашего столетия во многом объясняется потребно-
потребностями новых направлений науки и техники, таких, как ядерная
физика, физика высоких энергий, СВЧ-радиоэлектроника, эле-
элементный и структурный анализ материалов. В результате были
созданы принципиально новые приборы, позволившие получить
уникальные сведения об окружающем нас мире как фундамен-
фундаментального, так и прикладного характера. В настоящее время
электронная и ионная оптика не утратила своей актуальности
и продолжает развиваться. Большое стимулирующее влияние
при этом оказывают новые ее приложения в микроэлектрони-
микроэлектронике, диагностике материалов, обработке поверхностей. Доста-
Достаточно сказать, что решение одной из важнейших задач совре-
современной микроэлектронной технологии — освоение субмикронно-
субмикронного диапазона — трудно представить без диагностического и
технологического оборудования на основе электронных и ион-
ионных зондов.
Существенный вклад в оптику пучков заряженных частиц
внесли отечественные исследователи, что отмечено автором
книги, который хорошо знаком с трудами советских ученых.
К сожалению, основные наиболее обширные по охвату моно-
монографии, посвященные этому предмету (читатель найдет соответ-
соответствующие ссылки в библиографическом списке), были изданы
у нас в стране достаточно давно, в 40-е — 60-е годы.
Предисловие к русскому изданию
Быстрый прогресс в области электронной и ионной оптики,
связанный прежде всего с развитием плодотворных компьютер-
компьютерных методов расчета, расширением технических возможностей,
а также потребности в подготовке квалифицированных специа-
специалистов диктуют необходимость издания новых учебных пособий.
Книга М. Силадьи является хорошим примером современного
введения в предмет. Она начинается с уравнений Максвелла,
вариационных принципов классической механики, вывода урав-
уравнений движения заряженных частиц, далее подробно рассмат-
рассматриваются различные вопросы функционирования фокусирую-
фокусирующих, отклоняющих, формирующих электронных и ионных опти-
оптических устройств. Особое внимание уделено методам расчета
электрических и магнитных полей, теории аберраций, компью-
компьютерным методам расчета и оптимизации параметров линз. Сле-
Следует отметить, что вопросы применения анализируемых уст-
устройств автором не рассматриваются. Это вполне оправданно,
так как при необходимости можно обратиться к имеющейся
специальной литературе. Книга содержит богатую библиогра-
библиографию, насчитывающую более 400 наименований. В целом ее
отличает удачное сочетание подробного изложения физических
основ предмета, практических методов и новейших результатов.
Книгу проф. М. Силадьи можно рекомендовать как учебное
пособие студентам старших курсов, инженерам, научным со-
сотрудникам, желающим понять основы электронной и ионной
оптики и применять их на практике.
И. М. Ахмеджанов
Ютке, Габору ш Золтану в благодарность
за то время, которое должно было при-
принадлежать им
ПРЕДИСЛОВИЕ
Электронная и ионная оптика базируется на аналогии меж-
между световой геометрической оптикой и движением заряженных
частиц в электромагнитных полях. Впечатляющее развитие
электронной микроскопии со всей ясностью демонстрирует воз-
возможность формирования изображения заряженными частицами,
длина волны которых гораздо меньше, чем у видимого света.
С развитием новых приложений, таких, как ускорители эле-
элементарных частиц, электронно-лучевые трубки, анализаторы
заряженных частиц, микроволновая техника, сканирующие ана-
аналитические приборы, технологии мощных пучков и т.д., пред-
предмет оптики пучков заряженных частиц был расширен и вклю-
включает в себя формирование прецизионных зондов. Основной за-
задачей здесь является концентрация как можно большего числа
частиц в как можно меньшем объеме.
Технология интегральных микросхем является хорошим при-
примером возрастающей важности этой области знании. Основной
тенденцией современной микроэлектроники является повышение
уровня интеграции и усложнение топологии микросхем. Нали-
Наличие дифракционных ограничений в оптическом диапазоне и тех-
технологические проблемы использования рентгеновских лучей
склоняют выбор в пользу технологий на основе пучков заряжен-
заряженных частиц. С их помощью возможно прямое формирование
рисунка на подложке с управлением от компьютера без исполь-
использования фотошаблонов. Особенно большие возможности сфо-
сфокусированные ионные пучки открывают в субмикронной облас-
области. Поэтому технологии на основе электронных и ионных пуч-
пучков с наибольшей вероятностью будут играть очень важную
роль в ближайшие двадцать лет или около того.
По различным вопросам теории и применения электронной
и ионной оптики опубликовано множество книг. Эта книга за-
задумана как замкнутое систематическое и исчерпывающее на
настоящий момент введение в рассматриваемую область. Чи-
Читатель сможет найти здесь вывод наиболее важных соотноше-
соотношений, понимание которых абсолютно необходимо при намерении
сколь-нибудь серьезно работать с пучками заряженных частиц
и соответствующей техникой, но которые в большинстве книг
обычно приводятся без доказательств. Особое внимание уделе-
Предисловие
но современным компьютерным методам. Книга может служить
учебником для инженеров, научных сотрудников, студентов
старших курсов, желающих понять основные принципы элект-
электронной и ионной оптики и применять их при конструировании
и/или работе с приборами и оборудованием такого типа.
Автор вполне сознает всю трудность достижения поставлен-
поставленной цели. В одном томе едва ли можно охватить даже основ-
основные теоретические принципы и наиболее важные применения.
Поэтому рассмотрение ограничено главными вопросами и по-
последними результатами исследований, включая принадлежащие
автору. На протяжении всей книги особое внимание уделяется
связи излагаемого материала с практическими применениями,
однако мы не пытались рассматривать сами применения. Биб-
Библиография насчитывает более 400 основных наименований,
включая публикации, содержащие последние достижения в этой
области. Вследствие ограниченности объема книги список лите-
литературы весьма далек от полного.
Для изучения книги не требуется предварительного знаком-
знакомства с физической электроникой. Необходимая вводная инфор-
информация дана в гл. 1. Теоретический материал выводится из ос-
основополагающих принципов. Однако существенная роль мате-
математического аппарата в рассматриваемом предмете предпола-
предполагает хорошее знание читателем техники вычислений (включая
векторный анализ).
Автор работает в данной области с 1958 г. Возможность
суммировать основные собранные знания доставила огромное
удовольствие. Эти знания приобретены благодаря общению
с многими людьми. Автор особенно благодарен профессорам
В. М. Кельману, С. Я- Явор и А. Д. Сушкову, а также незаб-
незабвенному Деннису Габору. Исследовательская работа в послед-
последние три года поддерживалась Национальным научным фондом.
Автор высоко ценит непрерывную поддержку со стороны
Т. Триффета, декана Аризонского университета, стимулирую-
стимулирующую инициативу редакторов этой серии и качественную работу
издательства «Плинум Пресс». Книга никогда не была бы за-
закончена без поддержки, терпения и любви семьи.
Миклош Силадьи
Тусон, Аризона
Глава 1
ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
1.1. Введение
Электронная и ионная оптика представляет собой одно из
направлений физической электроники и занимается проблема-
проблемами формирования потоков заряженных частиц, управления ими,
а также вопросами их применения. В самом названии отражен
тот факт, что движение заряженных частиц в электромагнит-
электромагнитных полях во многом подобно поведению световых лучей в не-
неоднородных оптических средах. Электронная и ионная оптика —
это обширнейшая область знаний с относительно короткой
историей. Хотя аналогия между классической механикой и гео-
геометрической оптикой была установлена Гамильтоном еще в пер-
первой половине прошлого столетия, миру пришлось ждать почти
сто лет, прежде чем в 1926 г. X. Буш [1] доказал возможность
формирования электронно-оптических изображений. Список
приложений электронной и ионной оптики велик. Электронно-
Электроннолучевые трубки и мониторы, электронные микроскопы, ускори-
ускорители частиц, масс-спектрометры, микроволновые генераторы и
усилительные лампы, а также электронно-лучевые технологии
(такие, например, как сварка, сверление, плавка, резка, очист-
очистка, легирование) — все это хорошо известные классические
приложения. Электронные и ионные микрозонды, анализаторы
энергии, электронные спектрометры и ионные имплантаторы от-
относятся к сравнительно недавним практическим результатам
этого быстро развивающегося направления. Без электронной
и ионной оптики сегодня нельзя обойтись в аналитической хи-
химии и при исследовании поверхностей. Новые приложения раз-
разработаны в области синтеза и преобразования энергии. Возра-
Возрастающее значение этой области недавно отмечено Американ-
Американским физическим обществом, при котором учреждена специаль-
специальная тематическая группа по физике пучков и частиц. Электрон-
Электронной и ионной оптике посвящены тысячи статей и множество
книг [2—51 Ь].
Данная книга начинается с уравнений Максвелла, а также
некоторых основных понятий классической механики и геомет-
геометрической оптики, которые составляют основу для дальнейшего
изложения (гл. 1).
В гл. 2 рассмотрены уравнения движения заряженных ча-
частиц в электрическом и магнитном полях, а также траекторные
Глава 1
уравнения. Даны решения для некоторых простых случаев, вве-
введено понятие электронно-оптического показателя преломле-
преломления.
В гл. 3 представлены различные методы определения элект-
электрических и магнитных полей. Глава не может заменить курс
по электромагнетизму, но в то же время в ней дан обзор прак-
практических, в первую очередь численных, методов расчета полей.
Такие методы абсолютно необходимы при конструировании
любых электронных или ионных оптических систем.
В гл. 4 обсуждаются фокусирующие свойства аксиально-
симметричных полей. Дана общая теория формирования изо-
изображения, представлены электронные и ионные линзы, рассмот-
рассмотрено приближение тонкой линзы.
Гл. 5 посвящена теории аберраций. Ее изучение может быть
сопряжено с некоторыми трудностями для начинающих чита-
читателей. Однако аберрации приводят к наиболее жестким ограни-
ограничениям характеристик приборов, основанных на использовании
потоков частиц. И поэтому понимание причин и природы воз-
возникновения аберраций абсолютно необходимо для вычисления
аберрационных коэффициентов и работы с ними при поиске
способов уменьшения и компенсации аберраций.
В гл. 6 рассмотрены некоторые численные методы расчета
траекторий частиц и аберрационных коэффициентов.
В гл. 7 и 8 дан детальный обзор соответственно электроста-
электростатических и магнитных линз. Большое внимание уделено как
аналитическим моделям, так и конкретным реализациям линз.
Гл. 9 занимает особое место. В ней представлены наиболее
разработанные методы оптимизации и автоматизированного
проектирования электронных и ионных оптических систем. Из-
Изложенные методы проектирования могут быть широко исполь-
использованы в практической работе.
В гл. 10 рассмотрены мультипольные линзы. Они являются
основными оптическими элементами ускорительной техники,
а также находят применение в системах коррекции аберраций
н в отклоняющих элементах различных зондовых приборов.
Собственно отклоняющие системы являются предметом изу-
изучения гл. 11. Здесь рассмотрены дефлекторы и призмы электро-
электростатического и магнитного типов.
В гл. 12, посвященной проблеме пространственного заряда,
обсуждаются способы создания высокоинтенсивных пучков за-
заряженных частиц и методы управления ими. Основными лими-
лимитирующими факторами здесь являются уширение пучка и уве-
увеличение разброса по энергиям частиц, вызванные пространст-
пространственным зарядом.
Каждая глава заканчивается кратким резюме.
На протяжении всей книги используется система единиц СИ.
ю
Предварительные замечания
Приступим теперь к краткому изложению информации, не-
необходимой для изучения этой книги.
1.2. Электромагнитные поля
Мы собираемся изучать движение заряженных частиц
в электромагнитных полях, поэтому прежде всего необходимо
знать природу этих полей. Электромагнитные поля в вакууме
полностью описываются двумя векторами Е и В. Как напря-
напряженность электрического поля Е, так и магнитная индукция В
являются векторными функциями пространственных координат
и времени:
E = E(R,0 [В/м], B=B(R,0 [В-с/м2],
где R — радиус-вектор, t — время.
1.2.1. Уравнения Максвелла
В наиболее простом виде законы электромагнетизма форму-
формулируются через соотношения между двумя этими векторами и
двумя другими величинами, описывающими заряды и токи.
Самой изящной записью этих соотношений являются уравнения
Максвелла, которые можно представить в следующем ви-
виде [52]:
divE = p/e0, A.1)
rotE = — дЪ/dt, A.2)
divB = 0, A.3)
где p(R, t) —суммарная плотность заряда в единицах (А-с/м3),
J (R, t)—вектор суммарной плотности тока в единицах (А/м2),
Е0 = 8,85-10~12 А-с/(В-м)—электрическая постоянная, цо =
,=4л-10~7 Гн/м — магнитная постоянная и с = 299 792 458 м/с —
скорость света в вакууме. В такой форме уравнения Максвелла
не зависят от выбранной системы координат.
Уравнение A.1) представляет собой закон Гаусса, уравне-
уравнение A.2)—закон Фарадея, уравнение A.3)—закон магнитно-
магнитного потока, уравнение A.4) дает обобщенный закон циркуляции.
Дивергенция и ротор векторного поля V в обобщенной кри-
криволинейной ортогональной системе координат определяются как
divV= (l/hrhthz) E (д/dqt) (hihifaVtlhi), A.5)
и
Глава 1
' = A/ЛААз)
Аае2 hses
d/dq2 dldq3
A.6)
соответственно. Здесь q\, q2, q3 — обобщенные криволинейные
ортогональные координаты; ei, е2, ез — соответствующие еди-
единичные векторы; Vi, V2, V3 — компоненты вектора V; hu А2,
A3 — коэффициенты Ламе (метрические коэффициенты), харак-
характеризующие данную систему координат. Они определяются со-
соотношением:
(ds)*=*hht4dqty, A.7)
которое выражает абсолютную величину элемента длины ds
при одновременном приращении всех трех координат. Это вы-
выражение справедливо в том случае, когда единичные векторы
взаимно ортогональны. Если известна связь криволинейных
координат с декартовыми, то коэффициенты Ламе могут быть
вычислены с помощью соотношения
А,-2, = (dx/dq,J + {dyldqiJ + (дг/dqiJ. A.8)
Легко видеть, что в декартовой системе координат (<7i=*,
Цилиндрические координаты г, a, z выражаются через де-
декартовы следующим образом:
* = rcosa, y = r sin а, г—г. A.9)
Подставляя их в уравнение A.8), получаем коэффициенты
Ламе:
А, = 1, А2 = г, А3 = 1. A.10)
Можно также ввести скалярный потенциал и. и векторный
потенциал А, которые удовлетворяют следующим соотноше-
соотношениям:
Е= — gradu — dAldt, A.11)
B = rotA, A.12)
где градиент скалярного потенциала в обобщенных ортогональ-
ортогональных криволинейных координатах имеет вид
gradu = Z(ei/hi)du/dqi. A.13)
1=1
Наконец, сила, действующая на частицу с зарядом Q, дви-
движущуюся во внешнем электромагнитном поле со скоростью v,
12
Предварительные замечания
называется силой Лоренца и определяется выражением
F = Q(E+vXB). A.14)
1.2.2. Статические поля
Если поля, заряды и токи не изменяются во времени, урав-
уравнения Максвелла существенно упрощаются. Уравнение A.2)
принимает вид
rot E=0, A.15)
а уравнение A.4) —
rotB=|i0J. A.16)
В этом случае уравнения A.1) и A.15) определяют напряжен-
напряженность электрического поля, в то время как магнитная индук-
индукция определяется уравнениями A.3) и A.16). В случае стати-
статических полей электрические и магнитные составляющие явля-
являются независимыми друг от друга и напряженность электриче-
электрического поля определяется только скалярным потенциалом:
Е= — gradu. A.17)
Подставляя это выражение в уравнение A.1) приходим к урав-
уравнению Пуассона:
divgrad«=—р/ео, A-18)
где как и, так и р являются только функциями координат. При
р = 0 уравнение A.18) называется уравнением Лапласа. В обоб-
обобщенных ортогональных криволинейных координатах
wCfw) <М9>
Поэтому в декартовых координатах уравнение Пуассона прини-
принимает вид
а в цилиндрических с учетом коэффициентов Ламе (уравне-
(уравнение A.10)) —
При отсутствии токов в рассматриваемом пространстве маг-
магнитное поле становится безвихревым и, следовательно, можно
13
Глава 1
ввести магнитный скалярный потенциал «>, определяемый соот-
соотношением
В = —(xgrada A.22)
(ц — магнитная проницаемость) и удовлетворяющий уравнению
Лапласа
divgrad«=0. A.23)
1.2.3. Теорема Стокса
В заключение сформулируем теорему Стокса: циркуляция
любого вектора V по произвольной замкнутой кривой Г равна
интегралу по поверхности от нормальной составляющей ротора
вектора V:
&X-ds = JrotV-dS, A.24)
где dS— вектор элемента поверхности, направленный перпен-
перпендикулярно элементу поверхности.
1.3. Основы классической механики
Движение заряженной частицы определяется законами клас-
классической механики. Естественно, что волновая природа частиц
является существенным ограничением при характерных разме-
размерах, сравнимых с длиной волны де Бройля:
% = hjmv, A.25)
где А = 6,62-10~34 Дж-с — постоянная Планка, a m и v — соот-
соответственно масса и скорость частицы. Такие размеры встреча-
встречаются на практике и соответствующие дифракционные ограниче-
ограничения будут рассмотрены в разд. 5.6.1. Однако при анализе дви-
движения частиц волновой природой можно пренебречь, так как
электромагнитные поля не претерпевают существенных измене-
изменений на расстояниях, сравнимых с длиной волны де Бройля.
1.3.1. Принцип Гамильтона;
уравнения движения Лагранжа
Рассмотрим теперь основные законы, описывающие траекто-
траекторию движения классического объекта во внешних полях. Со-
Согласно принципу Гамильтона, интеграл действия
*в
/= I Ldt A.26)
имеет экстремальное значение относительно малых вариаций
истинной траектории [53]
б/ = 0. A.27)
14
Предварительные замечания
Здесь tk и гв определяют ин-
<2U<-—~~/ тервал времени \в—*а, в тече-
течение которого происходит дви-
движение, a L — функция Лагран-
жа (лагранжиан). Ее выраже-
выражение для заряженной частицы,
движущейся в электромагнит-
электромагнитном поле, будет дано в разд.
Рис 1. Вариация траектории частицы. 2.1. Вариацию можно предста-
представить следующим образом. Рас-
Рассмотрим движение частицы из точки А в точку В (рис. 1) вдоль
траектории A), начавшееся в момент времени га и закончив-
закончившееся в момент времени te. В произвольной точке вектор dR
направлен по касательной к траектории. Введем небольшое от-
отклонение от истинной траектории, т. е. представим, что частица
движется из точки А в точку В вдоль траектории B). Эта тра-
траектория определяется в произвольной точке вектором 6R (ва-
(вариация радиуса-вектора). Так как лагранжиан зависит как от
R, так и от v, его вариация дается выражением
6l=(dL/<3RNR+(<3L/dvNv. A.28)
Но
поэтому
dL g _ dL с
dv dv d
Интеграл и его вариация не зависят друг от друга. В самом
деле, варьируя уравнение A.26), имеем
= \{L+bL)dt,
что дает
б/= J 8Ldt = O. A.31)
*А
Подставляя уравнения A.28) и A.30) в A.31), получаем
I %-tr (*)] * * + (# «).-..-(**).-... - •>•
A.32)
Заметим, что вариация 8R обращается в нуль на обоих концах,
поэтому второй и третий члены обращаются в нуль. Отсюда
15
Глава 1
следует, что оставшийся интеграл всегда должен быть равен
нулю. Это условие приводит к уравнению движения Лагранжа
в векторной форме
4 (*)-*-«• с-33»
Можно также представить лагранжиан как функцию обоб-
обобщенных криволинейных координат qi и их производных по вре-
времени t (обобщенных скоростей qi). Тогда, повторяя такую же
процедуру для вариации
получаем систему трех уравнений Лаграижа в скалярной фор-
форме:
Вектор скорости определяется выражением
\=dRldt, v2=(ds/dt)\ A.36)
a ds дается уравнением A.7), поэтому компоненты скорости
в криволинейных координатах имеют вид
vi-htqi (i= 1,2,3), A.37)
где точка обозначает дифференцирование по времени.
1.3.2. Принцип Мопертюи
Полная производная функции Лагранжа имеет вид
dL __dL dL dR dL dv ,. „_
Используя соотношения A.36) и уравнение Лагранжа A.33),
можно записать
Лк-у±
I¥"v dt V
-Из уравнений A.38) и A.39) получаем
d fv dL т\ v d f dL\ dL dv dL dL
Если функция Лагранжа не зависит явно от времени, то
v-^— L-const. A.41)
16
Предварительные замечания
Тогда из принципа Гамильтона (уравнение A.31)) имеем
*н в
б J v (dL/dv) Л = б J {dL/dv) dR = 0. A.42)
'л А
Пусть
dL/dv = P, A.43)
назовем эту величину обобщенным импульсом. Окончательно
получаем
в
>$P-dR = O. A.44)
А
Это соотношение и является математическим выражением прин-
принципа Мопертюи — одного из фундаментальных принципов
электронной и ионной оптики.
1.4. Краткий обзор геометрической оптики
Существует глубокая аналогия между классической геомет-
геометрической оптикой и электронно-ионной оптикой. Это будет по-
показано в разд. 2.6. Для того чтобы понять указанную анало-
аналогию, необходимо прежде всего познакомиться с принципом
Ферма. Это позволит использовать понятия геометрической оп-
оптики для описания электронно-ионных оптических элементов.
Поэтому необходимо также познакомиться с основами геомет-
геометрической оптики.
1.4.1. Принцип Ферма; показатель преломления
Вся геометрическая оптика основана на принципе Ферма
[10], который можно сформулировать как
A.45)
где ds — элемент траектории, определяемый уравнением A.7),
а п — показатель преломления среды, в которой распространя-
распространяется свет. Луч света распространяется по тому пути, вдоль
которого интеграл A.45) экстремален (см. рис. 1). Вообще го-
говоря, п зависит от пространственных координат.
Свет, падающий на плоскую границу раздела двух сред
с показателями преломления щ и Яг соответственно, частично
17
Глава 1 __^^_____
проникает из среды A) в среду B). Изменение направления
распространения называется преломлением. Угол падения I от-
относительно нормали к поверхности связан с углом преломле-
преломления г (рис. 2) формулой Снелля
Jh. A.46)
sin г % '
Схема, показанная на рис. 2, соответствует случаю п.2>пи т.е.
луч отклоняется к нормали при переходе в среду с более высо-
высоким показателем преломления. Так как
п = фР, A.47)
где vp — фазовая скорость (скорость распространения монохро-
монохроматической световой волны), фазовая скорость меньше в опти-
оптически более плотной среде (т.е. в среде с более высоким пока-
показателем преломления).
1.4.2. Аксиально-симметричная линза
Рассмотрим один из наиболее часто используемых оптиче-
оптических элементов, а именно аксиально-симметричную линзу
(рис. 3). Линза состоит из произвольного материала с перемен-
переменным показателем преломления (например, сложной системы
различных стекол), ограниченного двумя поверхностями враще-
вращения относительно оптической оси. Если эта ось совпадает
с осью z цилиндрической системы координат, то основой при
анализе является плоскость (г, z) и основные соотношения не
зависят от координаты а. Рис. 3 представляет собой сечение
оптической системы, симметричное относительно вращения
вокруг оси 01. Показатель преломления слева от линзы (про-
(пространство объектов) равен пи а справа от линзы (пространст-
(пространство изображений) равен я2.
Пусть луч света падает на линзу со стороны пространства
объектов параллельно оптической оси. В пространстве объектов
его траектория является прямолинейной вследствие постоянст-
постоянства показателя преломления.
На поверхности линзы луч ис-
испытает преломление, причем
направление движения внутри
линзы может многократно ме-
меняться (столько раз, сколько
раз изменяется показатель
преломления). Луч покинет
линзу под некоторым углом
к оптической оси и будет дви-
Рис. 2. Преломление света. гаться ВДОЛЬ Прямой В Прост -
18
Предварительные замечания
ранстве изображений. Если линза является собирающей, эта
прямая пересечет оптическую ось в точке F2, которая называет-
называется фокусом пространства изображений. В случае же рассеива-
рассеивающей линзы оптическую ось пересечет продолжение траектории
в обратном направлении. В так называемом гауссовом прибли-
приближении все лучи, падающие на линзу со стороны пространства
объектов параллельно оптической оси, пересекают ось в одной
и той же точке F2 независимо от их расстояния 00' относитель-
относительно оси и траектории в линзе. Обратное также верно: любой луч,
входящий со стороны пространства изображений через фокус,
покинет линзу в пространстве объектов параллельно оптической
оси. Естественно, что расстояние от оси будет функцией угла
падения. Таким образом, расположение фокусов является важ-
важной общей характеристикой линзы.
Рдс. 3. Кардинальные точки аксиальио-аимметричиой линзы.
Рассмотрим теперь луч, падающий на линзу со стороны про-
пространства изображений параллельно оси. Он опишет сложную
траекторию внутри линзы и покинет ее по прямолинейной тра-
траектории, которая (в случае собирающей линзы) пересечет ось
в фокусе пространства объектов Fb Любой луч, падающий со
стороны пространства объектов и проходящий через точку Fu
покинет линзу в пространстве изображений параллельно оси.
Так как ничего неизвестно об истинных траекториях лучей
внутри линзы, но в то же время известно, что происходит в фо-
фокусах по обе стороны от нее, целесообразно выделить две плос-
плоскости, перпендикулярные оптической оси. Продолжим два пря-
прямолинейных отрезка траектории луча, падающего параллельно
оптической оси со стороны пространства объектов. Они пере-
пересекутся где-то внутри линзы в точке Я2'. Построим плоскость,
19
Глава 1
проходящую через точку Н2' перпендикулярно оптической оси.
Эта плоскость называется главной плоскостью пространства
изображений. Она пересекает оптическую ось в точке Н2, ко-
которая называется главной точкой пространства изображений.
Можно показать, что продолжения всех лучей, падающих на
линзу параллельно оптической оси со стороны пространства
объектов, пересекаются с продолжениями соответствующих
лучей, выходящих из линзы со стороны пространства изобра-
изображений, в той же самой главной плоскости Н2Н2• Таким обра-
образом, положение главной точки является еще одной очень важ-
важной характеристикой оптического элемента.
Аналогичным образом можно показать существование глав-
главной плоскости Н\Н\ и главной точки Н\ пространства объек-
объектов. Продолжения прямолинейных отрезков траектории, изна-
изначально параллельной оптической оси в пространстве изображе-
изображений, пересекутся в главной плоскости пространства объектов.
Зная координаты двух главных точек и двух фокусов, мож-
можно построить изображение любого предмета, даваемое линзой.
Эти четыре характеристики (кардинальные точки линзы) одно-
однозначно определяют оптические свойства аксиально-симметрич-
иой линзы в гауссовом приближении.
Расстояние между фокусом и соответствующей главной
точкой называется фокусным расстоянием. Фокусное расстояние
положительно для собирающей лиизы и отрицательно для рас-
рассеивающей. Таким образом, фокусное расстояние в пространст-
пространстве объектов определяется как fi = FxH\, а в пространстве изо-
изображений— f2=F2H2 (см- Рис- 3, соответствующий собираю-
собирающей линзе). Фокусные расстояния могут быть различными в за-
зависимости от показателей преломления с обеих сторон линзы,
а именно:
ЫЛ = Ла/я,, A.48)
поэтому fi = f2 только в случае п2 = П\.
Еще одна важная пара точек, которая характеризует тол-
толстую линзу, — узловые точки. Они определяются следующим
образом: если луч падает со стороны пространства объектов под
таким углом к оптической оси, что его продолжение пересекает
ось в узловой точке пространства объектов N\, то луч, выходя-
выходящий в пространстве изображений, будет иметь то же направле-
направление, т. е. луч будет как бы выходить из узловой точки простран-
пространства изображений N2 под тем же углом к оптической оси.
В этом случае угловое увеличение равно единице.
Положения узловых точек определяются фокусными рас-
расстояниями:
FiN1=fi, N2F2=fi. A.49)
20
Предварительные замечания
Расстояние между узловыми точками равно расстоянию между
главными точками: #i#2=AfiiV2. Если фокусные расстояния
одинаковы, то узловые точки совпадают с соответствующими
главными точками.
Рассмотрим теперь плоский предмет 00', расположенный
лерпендикулярно оптической оси на расстоянии р слева от
главной плоскости пространства объектов. Луч, падающий на
линзу со стороны пространства объектов параллельно оптиче-
оптической оси через точку О', пересечет ось в пространстве изобра-
изображений в фокусе F2 и затем пересечется в точке /' на расстоя-
расстоянии q справа от главной плоскости пространства изображения
с лучом, входящим в линзу через точки О' и Л и выходящим
параллельно оси. Точка / является изображением точки О',
а отрезок //' — изображением предмета 00'. Это вытекает из
того, что в гауссовом приближении изображение плоского пред-
предмета также является плоским и перпендикулярным к оптичес-
оптической оси.
Легко видеть, что треугольники O'FiO и tf/Fitfi подобны
так же, как и треугольники H'2F2H2 и I'FzL Увеличение линзы
дается соотношением:
M = -II'fOO'=-(q-fa)ff2=-hHp — fi)<0. A.50)
(Увеличение отрицательно, так как изображение перевернуто.)
Отсюда сразу следует формула Ньютона для толстой линзы,
связывающая расстояния до предмета р с расстоянием до изо-
изображения q через фокусные расстояния:
Л/Р + Ы<7 = 1. A-51)
Увеличение можно переписать в виде
М- hqlhP- A-52)
Особенно удобным является случай, когда главные плоско-
плоскости столь близки, что расстоянием между ними можно прене-
пренебречь; тогда можно использовать приближение тонкой линзы,
что существенно упрощает вычисления.
Заключение
В этой главе кратко суммированы основные понятия, необ-
необходимые для изучения книги. Начав с введения о содержании,
мы затем привели уравнения Максвелла A.1) — A.4), описы-
описывающие поведение электрических и магнитных полей. Введена
обобщенная криволинейная ортогональная система координат
как удобный способ записи уравнений в любых координатах,
подходящих для решения поставленной задачи. Уравнение A.14)
2!
Глава 1
определяет силу Лоренца, действующую на заряженную части-
частицу, движущуюся в электромагнитном поле. Далее рассмотрен
частный случай статических полей и сформулирована теорема
Стокса (уравнение A.24)).
Введены некоторые основные понятия классической меха-
механики. Исходя из принципа Гамильтона A.27), выведены урав-
уравнения движения Лагранжа A.33), A.35), откуда в свою оче-
очередь получен принцип Мопертюи A.44). В заключение мы на-
напомнили читателю принцип Ферма A.45), ввели определение
показателя преломления и рассмотрели процесс формирования
изображения в аксиально-симметричной толстой оптической
линзе.
Далее мы рассмотрим движение заряженной частицы в
электрическом и магнитном полях.
Глава 2
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ
В ЭЛЕКТРИЧЕСКОМ И МАГНИТНОМ
ПОЛЯХ
2.1. Лагранжиан
Чтобы иметь возможность воспользоваться уравнениями
Лагранжа A.33) и A.35), необходимо определить форму ла-
лагранжиана L. Сила, действующая на заряженную частицу, оп-
определяется уравнением A.14). С другой стороны, общее выра-
выражение для силы дается законом движения Ньютона
i|=jL{mv) = F, BЛ)
где p = mv—-импульс частицы,
m = m0l(l — v2c2I'2 B.2)
есть релятивистская масса частицы (то — масса покоя). Под-
Подставляя выражение для силы Лоренца A.14) и уравнения
A.11), A.12) в уравнение B.1), получаем соотношение
B.3)
ов А
grad(A-v) = (A-V)v+(v-V)A+AXrotv+vX rot A, B.4)
Как известно из векторного анализа, для любых векторов А
и v выполняется соотношение
где
V = £(etlhi)dldqi B.5)
есть символический векторный оператор набла, позволяющий
записать выражения A.13), A.5) и A.6) в следующем виде:
grad«=V«, B.6)
divV=V-V, B.7)
rotV=VXV. B.8)
(Указание: Чтобы убедиться в справедливости соотношений
B.7) и B.8), необходимо принять во внимание зависимость
единичных векторов е,- от координат qi.)
Поскольку в частных производных дифференцирование вы-
выполняется при постоянной скорости, (A-V)v = 0 и rotv = 0. Сле-
Следовательно,
23
Глава 2
(d/dt) (mv) = Q [— grad и — дА/dt+igrad (A ■ v) — (v • V) A].
B.9)
Полная производная А по времени связана с частной произ-
производной соотношением
d\/dt=dAldt+(v-V)\. B.10)
Подставляя соотношение B.10) в B.9), получаем
(d/dt) (mv+QA)=Qgrad(A-v — и). B.11)
Левая часть последнего соотношения представляет собой пол-
полную производную по времени, а правая часть — сумму частных
производных. Следовательно, соотношение B.11) примет вид
уравнения Лагранжа A.33), если сделать подстановку
dL/dv = mv + QA = P, B.12)
где Р — обобщенный импульс, то
— и). B.13)
Непосредственно видно, что в отсутствие магнитного поля обоб-
обобщенный импульс совпадает с обычным импульсом частицы.
Теперь можно переписать уравнение Лагранжа A.33) в виде
dPldt=dLfdR. B.14)
Уравнение B.14) является наиболее общей формой уравне-
уравнения движения заряженной частицы в электромагнитном поле,
независящей от выбора координат.
Теперь мы близки к тому, чтобы найти вид лагранжиана
в нашем случае. В самом деле, нам уже известны частные про-
производные лагранжиана как по радиусу-вектору R, так и по век-
вектору скорости v.
Из уравнения B.14) следует, что функция Лагранжа имеет
размерность энергии. Следовательно, ее частная производная
по скорости v имеет размерность импульса (p = mv). Легко
получить векторную производную требуемого типа, если лагран-
лагранжиан содержит скалярный квадрат вектора v (t>2=v-v) и его
скалярное произведение с вектором А. Поскольку А и зави-
зависят только от координат, но не от скорости, лагранжиан дол-
должен содержать член QA>v и другой член, частная производная
которого по v даст т\. Легко видеть, что последний член равен
— т0с2A —у2/с2)'/2.
С другой стороны, частная производная лагранжиана по
радиусу-вектору R определяется соотношением B.13). Так как
вектор скорости не зависит от радиуса-вектора в явном виде,
достаточно прибавить—и к члену (A-v), чтобы полученный
24
Движение заряженных частиц в электрическом и магнитном полях
лагранжиан удовлетворял уравнениям B.12) и B.13). Оконча-
Окончательное выражение для лагранжиана заряженной частицы, дви-
движущейся в произвольном переменном электромагнитном поле,
имеет вид
L=— m0c2(l — u2/c2)'/2 + Q(A-v — u). B.15)
гергии
B.16)
Полная механическая энергия частицы равна сумме энергии
покоя и кинетической энергии:
Тогда кинетическая эиергия может быть записана в виде
№kin = /noc2[(I -v2fc2)-^- 1]. B.17)
Первый член разложения этого соотношения в ряд Тейлора по
степеням v/c дает выражение для кинетической энергии в слу-
случае малых скоростей (и^Сс)
Wkln*mov2/2. B.18)
Первый член функции Лагранжа B.15) также можно раз-
разложить в ряд Тейлора по степеням v/c, что дает приближенное
выражение
— m0c2(l — trVc2I/2»— moc2 + mov2l2. B.19)
Подставляя последнее соотношение в B.15) и опуская постоян-
постоянную энергии покоя (в уравнениях движения используются
только производные L), получаем выражение для лагранжиана
в случае малых скоростей
2 — u). B.20)
В отсутствие магнитного поля соотношение B.20) принимает
вид
L = Wkln— Wpot B.21)
(см. уравнение B.27)).
2.2. Сохранение энергии
Умножая (скалярно) основное уравнение B.3) на вектор
скорости v, получим соотношение
v(d/dt)[{l — u2/c2)-1/2m0v]=Qv.(F+vXB) = QvE. B.22)
Левая часть полученного соотношения может быть преобразо-
преобразована следующим образом:
v(d/dt} [A — v2/c2)-l'sm0v] =
= v*(d[dt) [A — v^c^-^mo] +
25
Глава 2
= {d/dt) [ A — v2/c2) -v2m0c2]. B.23)
В случае статических (независящих от времени) полей справед-
справедливо соотношение A.17) и правую часть уравнения B.22) мож-
можно преобразовать к виду
v-E=— vgrad«= — (dR/dt) {du/dR)= — du/dt. B.24)
Подставляя соотношения B.23) и B.24) в B.22), получаем
d[maC2(l — у2/с2)-1/2]=— Qdu. B.25)
Интегрируя последнее соотношение, получаем
/п0с2A — v2/c2)-V2 — m0c2(l — ио2/с2)-1/2 =
= -Q(«-«0), B.26)
где v0, v; uo, и — начальные и конечные значения скорости и по-
потенциала соответственно. Потенциальная энергия заряженной
частицы, движущейся в статических полях, равна
№Pot = Q«, B.27)
а ее кинетическая энергия определена соотношением B.17).
Следовательно, уравнение B.26) можно записать в виде
Wkin—Woun=Wo pot — WpoU B.28)
где Wo Kin, Wo pot — начальные значения кинетической и потен-
потенциальной энергий частиц соответственно. Непосредственно вид-
видно, что полная энергия частицы постоянна:
Wt = Wun+ Wpoi=W0 кш + №о pot=const. B.29)
(это очень важное соотношение представляет собой закон со-
сохранения энергии для заряженной частицы, движущейся в ста-
статических полях; если частица ускоряется, то ее потенциальная
энергия уменьшается и обратно.)
Уравнение B.29) непосредственно следует из A.41), если
в последнее уравнение подставить выражения для обобщенного
импульса и лагранжиана B.12) и B.15) соответственно.
В случае малых скоростей уравнение B.26) упрощается:
mo(v2 — vo2)/2=—Q(u — Uo). B.30)
2.2.1. Движение свободных частиц.
Зависимость скорости от потенциала
Уравнение B.26) выражает энергетический баланс для заря-
заряженной частицы. Прежде всего следует отметить, что он совер-
совершенно не зависит от магнитного поля. Стационарное магнитное
26
Движение заряженных частиц в электрическом и магнитном полях
поле не оказывает никакого влияния на величину скорости ча-
частицы. Так как сила Лоренца пропорциональна vXB, она
всегда перпендикулярна к направлению движения и может
изменить только направление движения, но не величину ско-
скорости.
Существует однозначное соответствие между скоростью
частицы v и электростатическим потенциалом и. Определим на-
начальное значение потенциала ы0 таким образом, чтобы соответ-
соответствующее значение скорости равнялось нулю (и=0). Тогда
по — потенциал тех точек пространства, в которых скорость
частицы обращается в нуль. Как следует из уравнения B.26),
абсолютная величина скорости в этом случае может быть пред-
представлена в виде следующей функции потенциала:
o=»c|l —[]
B.31)
Поскольку частица может увеличить скорость, только переме-
переместившись в область с меньшей потенциальной энергией, величи-
величина Q(u—и0) всегда отрицательна: положительные заряды ус-
ускоряются при движении в область с меньшим потенциалом, от-
отрицательные— при движении в область с более высоким потен-
потенциалом. Согласно соотношениям B.17) и B.26), кинетическая
энергия частицы равна
Wkm=— Q{u — ыо)>0. B.32)
Если заряженной частицей является электрон или однозаряд-
однозарядный ион, разность потенциалов (и—ыо) дает энергию частицы,
выраженную в электрон-вольтах. Масса покоя электрона со-
составляет /по=9,1О9-1О-31 кг, его заряд Q = 1,602-109 Кл, а
его энергия покоя равна тоС2 =0,5089 МэВ. Энергия покоя про-
протона в 1836,1 раза больше (934,4 МэВ). Поэтому, если Q(u —
— «о) мало по сравнению с энергией покоя в уравнении B.31),
можно ограничиться первым членом разложения в ряд Тейлора:
t» = [— 2Q(« — ыо)//по]1/2. B.33)
Это выражение, разумеется, непосредственно вытекает из от-
отношения B.30). Отметим, что знак ыо обычно противоположен
знаку и. В этом можно убедиться, рассматривая источник час-
частиц с фиксированным нулевым потенциалом. Поскольку части-
частицы покидают источник, обладая некоторой положительной ки-
кинетической энергией, из уравнения B.32) следует Qu0>0, т.е.
«о положительно для положительно заряженных частиц и отри-
отрицательно для отрицательных ионов или электронов. С другой
стороны, и — ио<.О для положительно заряженных частиц
27
Глава 2
Таблица 1
Увеличение скорости и релятивистской массы в зависимости от потенциала
для электронов и протонов
Электрон Протон
Потенциал
\и—и„\. В
1
10
10»
103
Ю4
10s
10»
10*
10»
Скорость
V, М/С
5,93110s
1,875,10е
5,930-10е
1,873-107
5,845-107
1,643-10»
2,816-10»
2,988-10»
2,99175-10»
Увеличение
массы, mlma
1,000002
1,000020
1,000196
1,001965
1,019649
1,196495
2,964949
20,649487
197,494868
Скорость
v, м/с
1,384-104
4,377-«104
1,384-105
4,377-105
1,384-106
4,377-Ю6
1,383-107
4,342-107
1,283-10»
Увеличение
массы, mlm0
1,000000001
1,000000011
1,000000107
1,000001070
1,000010702
1,000107018
1,001070176
1,010701764
1,107017638
и и—Ыо>-О для электронов, следовательно, тот же знак дол-
должен иметь и и. Начальное значение потенциала Ио отвечает
в этом случае фиктивной поверхности позади источника.
Уравнение B.31) представляет скорость в виде функции
электростатического потенциала. Если потенциал изменяется,
скорость изменяется вместе с ним. Это же уравнение может
быть использовано для определения скорости в наиболее три-
тривиальном случае движения свободных частиц в отсутствие по-
полей. В этом случае потенциал является постоянным (но, вооб-
вообще говоря, не равным «о). Подставляя его значение в B.31)
или B.33), можно вычислить величину скорости, которая так-
также является постоянной (постоянно и направление скорости:
свободная частица движется по прямой). Результаты вычисле-
вычислений в случае электрона и иона водорода (протона) представ-
представлены в табл. 1. Релятивистские массы частиц легко вычислить,
подставляя соотношение B.31) в B.2):
B.34)
Численные значения отношения т/то для электрона и протона
также представлены в табл. 1. Согласно уравнению B.33),
в нерелятивистском приближении скорость протона при том же
значении потенциала в A836,1)'Л = 42,8 раза меньше, чем ско-
скорость электрона. По мере возрастания энергии различие в ско-
скоростях становится меньше.
Как легко видеть, в случае малых значений разности потен-
потенциалов скорость пропорциональна (ы—щ)'1' в соответствии
с B.33), а масса не отличается существенно от массы покоя.
Однако в случае достаточно высоких значений разности потен-
потенциалов следует использовать уравнение B.31). Изменение
28
Движение заряженных частиц в электрическом и магнитном полях
массы в этом случае становится существенным. На практике
релятивистские эффекты должны приниматься во внимание при
более чем 2%-ном изменении массы, что отвечает отношению
а/с« 0,2. Следовательно, нерелятивистское приближение явля-
является достаточным вплоть до энергий порядка 10 кэВ для элек-
электронов и порядка 10 МэВ для однозарядных ионов. В области
более высоких энергий скорость постепенно приближается к
скорости света. Так, например, для электронов с энергией
100 МэВ у/с = 0,999987, но для ускорения заряженной частицы
до скорости, в точности равной скорости света в вакууме, по-
потребовалась бы бесконечная энергия.
Обычный энергетический диапазон электронной оптики —
1—100 кэВ, так что в большинстве приложений можно прене-
пренебречь релятивистскими эффектами. Мы приведем общие урав-
уравнения движения релятивистских частиц, но в большинстве по-
последующих глав книги применяется нерелятивистское прибли-
приближение. Мы покажем, однако, что в случае чисто магнитного
поля нерелятивистские уравнения остаются действительными
и в области больших скоростей, если только заменить потен-
потенциал его релятивистским аналогом B.89). Это важно, посколь-
поскольку магнитные линзы чаще используют для фокусировки и пре-
преломления электронных пучков с энергией порядка 100 кэВ, при
которой уже существенны релятивистские эффекты. Электро-
Электростатическая оптика применяется в случае ионных пучков с
энергиями ниже релятивистского предела. Таким образом, наш
подход удовлетворяет требованиям большинства приложений.
2.3. Уравнения движения
Теперь дадим вывод релятивистских уравнений движения
частицы в электромагнитном поле, описываемом векторами Е
и В.
Прежде всего подставим в лагранжиан B.15) компоненты
векторов А и v в общей ортогональной системе криволинейных
координат [см. A.37)], представив лагранжиан в следующей
скалярной форме:
(
B.35)
Частные производные L имеют вид
|
X hhiqi'dhi/dqi+Q[hqid(Ajhj)ldqi — duldqi], B.36)
29
Глава 2
£ /V] Q,. B.37)
(Потенциалы и коэффициенты Ламе зависят только от коорди-
координат.) Учитывая соотношение B.2) и используя компоненты
импульса р, запишем полученные выражения в виде
dL/dqi = S pjqfdh,/dqi+Q [ 2 <j/d (Л/А/) /dqt — ды/d?*],
B.38)
B.39)
■отсюда
(j h I ^ф ^ + Q 2 q B-40)
Подставляя соотношения B.38) и B.40) в уравнения Ла-
гранжа A.35), получаем
dt ^ hi £* dqj 4J hi jLi r/4j dq.
Q_ • Г о A th f fi (A h \\ d r)ii
ж ^ I J J v \ i'"l) I V C/M /л j 4 v
ft/ ^^м^ I @Q i @Q 4 I Л/ vQ {
i=i
Здесь мы изменили порядок суммирования. Вместо того чтобы
начинать суммирование с /=1, мы начинаем с j=i. При этом
не следует забывать циклический характер индексов: например,
если ;=3, то /+1 = 1 и т.д.
Выполнив суммирование, получим
dt
[^^]}^^. ,2.42,
Отметим, что
B.43)
В наших новых обозначениях уравнение A.6) дает
frnt A1 ' Гд(А,ч.«Л/+») 3(А, + 1Л;+1I B 44)
(rotA),-_ л.+1Л.+1 у dq,+i dq, + 2 J- ^.^
30
Движение заряженных частиц в электрическом и магнитном полях
Уравнение B.42) можно теперь записать в виде
dp£_i ( д,- dh. qi+l dhj+A ( eg dh- *qi+2 dhi+2\
dt t/''41U,+i^+1 ^ % )~tPl + l\hi+tdqut h< dqi )
= Q [ht+iQt+i (rot A)/+1—hi+2qi+2 (rot A),+1 - (grad u),] =
(При написании двух последних равенств использованы соот-
соотношения A.12), A.13) и A.17).) Последнее равенство пред-
представляет собой i-ю компоненту Q(E+vXB). Но лагранжиан
получен из уравнения B.3), так что первая строка уравнения
B.45) должна быть t-й компонентой dpjdt. Почему она выгля-
выглядит столь сложно? По той причине, что производная вектора
импульса по времени содержит производные единичных векто-
векторов наряду с производными криволинейных координат. В самом
деле, вектор импульса можно записать в криволинейных коор-
координатах следующим образом:
Р = 2 eipi, B.46)
его производная по времени есть
dpfdt= L (bdpildt+pideifdt), BA7}
i
где
deildt = U qidti/dqj. B.48)
Частные производные dei/dq/ являются векторными функциями
коэффициентов Ламе. Наконец, производная вектора импульса
по времени сводится к выражению
(p) B.49)
1=1
где 1-я компонента вектора dp/d,t дается уравнением B.45).
Почему следует использовать уравнения Лагранжа? По той-
причине, что они более удобны в том случае, когда некоторые
из координат qi не входят в лагранжиан явным образом. Тогда
dLldqi = Q и, как видно из уравнения A.35), соответствующая
компонента обобщенного импульса dLfdqi^const Это обстоя-
обстоятельство может существенно упростить систему уравнений. Мы
используем такую возможность прн описании оптических
свойств аксиально-симметричных электрического и магнитного
полей в гл. 4.
Отметим, что левая часть уравнения B.45) действительна
и в случае переменных полей, а замена Е на —grad и справед-
справедлива только для статических полей.
Глава 2
Подставляя индексы i=l, 2, 3 в уравнение B.45), приходим
к релятивистским уравнениям движения в произвольной орто-
ортогональной системе криволинейных координат:
dqt Ai дъ/р**~\1ь dqa hx dq
,-h,q^t), B.50)
q2 dh2 qi dht \ . I q2 dh2 g3 dh3 \ _
А1 dqi h2 dq%)Pl't\h3 dqs ha дцг)Р*~
dt \1 qi q%)\3 qs цг)
= Q(£, + ArfA-Ai?A). B-51)
dps j_( Яз_ dh3 qi dhi \ ( q3 dh3 q2 дйа \ _
+U Г )Pl + \~h2~~dqT h^-dq^JP^-
,). B.52)
Преимущество этих уравнений сложного вида в их универ-
универсальности. Посредством подстановки соответствующих коорди-
координат и коэффициентов Ламе их легко преобразовать в систему
уравнений, применимую для какой-либо конкретной системы
координат.
Выбор системы координат зависит от вида симметрии, при-
присущей конкретной задаче. Так, в случае зеркальной симметрии
применима декартова система координат, в то время как ак-
аксиально-симметричной задаче более адекватна цилиндрическая
система координат. Очень важен правильный выбор системы
координат, поскольку это позволяет свести трехмерную задачу
к двухмерной или даже одномерной задаче. В самом деле, ак-
аксиальная симметрия означает, что поля не зависят от азиму-
азимутального угла а. В таком случае распределение полей во всем
пространстве может быть представлено их распределением
в любой плоскости, отвечающей фиксированному углу а. Если
система обладает сферической симметрией, то ситуация упро-
упрощается в еще большей степени. В таком случае выбором сфе-
сферической системы координат задачу можно свести к одномер-
одномерной, поскольку все величины зависят только от радиальной
координаты R.
В электронных микроскопах и аналогичных приборах фоку-
фокусирующие системы обычно обладают аксиальной симметрией,
но для преломления пучков и изменения их формы использу-
используются системы с мультипольной симметрией. В будущем могут
появиться системы с другими типами симметрии, так что рас-
рассмотрение уравнений движения в общем виде представляется
нам необходимым.
Релятивистские уравнения движения не выглядят простыми
даже в декартовой системе qi=x, Цч=у, qz—'z (коэффициенты
32
Движение заряженных частиц в электрическом- и магнитном полях
Ламе Л1 = Л2 = Лз=1). Компоненты импульса включают в себя
релятивистскую массу, которая в свою очередь зависит от всех
трех компонент скорости B.1) н B.2). Таким образом, мы име-
имеем систему трех связанных друг с другом дифференциальных
уравнений:
,= (Qlm0) (Ex + yBz — zBy), B.53)
,= (Q/m0) (Ey + zBx — х'вг), B.54)
2)]-'/*z} =
,= (Q/m0) (Ея+хВу—уВх). B.55)
В области малых скоростей /n=mo = const и уравнения дви-
движения упрощаются, поскольку в этом случае
dpldt=modv/dt. B.56)
В декартовой системе координат нерелятивистские уравне-
уравнения движения имеют вид
B-58)
Это система из трех связанных друг с другом дифференциаль-
дифференциальных уравнений, решение которой может представлять трудно-
трудности, если компоненты полей зависят от координат сложным об-
образом.
В цилиндрической системе координат следует сделать под-
подстановку q\=r, <72=а, <7з=2 в уравнениях B.50) — B.52). Коэф-
Коэффициенты Ламе в этом случае даются соотношением A.10). Ре-
Релятивистские уравнения движения принимают следующий вид:
(dfdt) {[I -A/
= (Q/m0) {E,+raB, — zBa), B.60)
(djdt) {[I - A/с2) (г2+г2а2+г2)]-^га} +
33
Глава 2
= (Q/mo) (Ea + zBr - гВг), B.61)
= (Q/ото) (£г + /-Ва — riB,.). B.62)
В области малых скоростей полученные уравнения упроща-
упрощаются:
ePr I da V Q / т, , ..г, da „ dz
d f da\ . dr da 1 d f % da \ Q f p „ dz n dr \
HT\rdt)+~dT~dT~T~dT\r ~dTj~W\a+r~dT~~!:~d7j'
B.64)
B.65)
Последняя система содержит связанные друг с другом диффе-
дифференциальные уравнения, которые являются нелинейными даже
в случае однородных полей.
Решение этих систем уравнений в общем виде затруднитель-
затруднительно. К счастью, в большинстве ситуаций, представляющих прак-
практический интерес, уравнения движения могут быть существенно
упрощены. Наиболее важные численные методы их решения
будут изложены в гл. 6.
2.4. Траекторные уравнения
Решение уравнений движения дает временную зависимость
координат частицы qi=qi(t) в процессе ее движения. Это озна-
означает, что известна траектория частицы, заданная в параметри-
параметрическом виде, причем время t играет роль параметра. В боль-
большинстве приложений, однако, представляет больший интерес
описание траектории в явном виде. С этой целью одна из коор-
координат (обычно<7з) выбирается в качестве независимой перемен-
переменной, а две другие координаты представляются в виде функции
от <7з- Тогда мы получим два уравнения для двух проекций
траектории на две взаимно перпендикулярные плоскости. Реше-
Решение этих уравнений дает qi и q2 в виде функций от q3. Чтобы
осуществить такое преобразование, следует дифференцирование
по времени заменить дифференцированием по <7з- Это можно
34
Движение заряженных частиц в электрическом и магнитном полях
сделать, используя уравнение A.36) и затем выражая ds через
dq3. Из уравнения A.7) следует
(*)■]'"• <266>
Подставляя последнее соотношение в уравнение A.36), полу-
получаем
dt v ds (Afoa+A2V+/i3I/2d?3 • У ' )
где штрих означает дифференцирование по q3. Полученное вы-
выражение следует использовать каждый раз, когда дифференци-
дифференцирование появляется в уравнениях движения.
Теперь i-я компонента релятивистского импульса (t=l, 2, 3)
дается выражением
р, -
причем скорость частицы v определена соотношением B.31).
Из уравнений B.67) и B.68) следует выражение для первой
производной импульса
dp, _ _ mov d Г А,ч>A-р«/с»)-1/» dq,l .„ fiq.
dt W+ftW+A»1" d?3 [(Aj^+^+A»1'1 ^ J' K
С учетом уравнений B.67) — B.69) и обозначения
B.70)
уравнение B.45) приобретает вид
£ -oVc*)-1'» X
i+idqi+1
). B.71)
Запишем первый член последнего уравнения в развернутом
виде:
(d/dq3)[(hiV/H) A - o*/cs)-'/V] =
= (А,о/Я) A — о^с^-'/^/Ч (v/H) (I — o2/c2)-'/2/i«V+
+ hiqi'(d/dq3)[(v/H) (I - oVc8)"]. B.72)
Учитывая, что
9з'=1, 9з" = 0 B.73)
35
Глава 2
по определению, и помня о цикличности обозначений индексов,
после ряда преобразований из уравнения B.71) можно полу-
получить следующее уравнение для t = 3:
G = (d/dq3) [{vl Н) A-у2/с2)- !/■] = (Q/m0h3) (h^B.-h^B, + HEJv)—
£&)&] <2-74)
Уравнения B.71) и B.72) дают
+ [hi/hi + A - ^/c2I'3 tfG/y] q't +
г
fav) A - у2/с2)^2 (HE.-fv + hi+1q'i+iBi+3- hi+2q'MBi+1),
B.75)
где Н и G определены уравнениями B.70) и B.74) соответст-
соответственно, а
есть полная производная /г,. Подставляя сначала t=l, получаем
2I/г (Я£х/у + Л2^В3 - A3B2). B.76)
Подставляя i=2 в уравнение B.75), получим
B.77)
Уравнения B.76) и B.77) представляют собой релятивист-
релятивистские уравнения траектории в обобщенной ортогональной кри-
криволинейной системе координат [54].
Соответствующие нерелятивистские уравнения могут быть
легко получены из уравнений B.76) и B.77), если опустить все
36
Движение заряженных частиц в электрическом и магнитном полях
члены v2/c2 и использовать уравнение B.33) для определения
скорости.
В декартовой системе координат уравнение B.70) приобре-
приобретает вид
Н={\ + х'2 + у'2у!\ B.78)
и уравнение B.74) дает
G,= (Q/m0) (x'By — y'Bx+HEJv). B.79)
Подставляя эти выражения в уравнения B.76) и B.77), по-
получим релятивистские уравнения траектории в декартовых ко-
координатах:
x"={Qlmov)[{\ — w2/c2)
Х[A +х"+у") (Ех - xfE,)/v -
— {l+xfi)Bg + yf(x'Bx+Bt)], B.80)
y"=(Q/mov)[(l — у2/с2)
A+у'*)Вх-х'(у'Ву + Вг)]. B.81)
Разумеется, эти же уравнения могут быть получены и непосред-
непосредственно из релятивистских уравнений движения B.53)—B.55)
в декартовой системе координат [55], что и предлагается сде-
сделать читателю в качестве полезного упражнения.
В цилиндрической системе координат имеем
y\ B.82)
G= (Q/m0) (r'Ba - ra'Br + HE2!v). B.83)
Подставляя эти выражения в уравнения B.76) и B.77), легко
получить релятивистские траекторные уравнения в цилиндриче-
цилиндрической системе координат в следующем виде:
г" — ra'2=(Q/mov)[(l — v2/c2) A + г'* + г2а'*)]1/2Х
Х[A+/-/2 + /-2а/2)'/2(£, — r'Ez)lv— (l + r/2)Bo +
+ га'{г'Вг + Вг)], B.84)
ra"+2r'a'~{Q/m0v)] A — у2/с2) A +г'2 + /-2а/2)]1/2Х
Х[A + г/2 + /-2а/2I/2 (Е* — ra'Ez)lv+ (I +r2a'2)Br —
— г'(га'Ва+Вг)). B.85)
Эти уравнения также могут быть получены непосредственно
из релятивистских уравнений движения в цилиндрической си-
системе координат B.60) —B.62).
37
Глава 2 _—
Отметим, что правые части уравнений B.80) и B.84), так
же как и уравнений B.81) и B.85), полностью совпадают, если
заменить х на г, у на а, х' на г', у' на га'. Левые части этих
уравнений, однако, различны.
2.5. Релятивистский потенциал
Рассмотрим подробнее релятивистские траекторные уравне-
уравнения B.76) и B.77). Как мы знаем, скорость частицы v выра-
выражается уравнением B.31) через потенциал и. Подставим теперь
потенциал из уравнений B.31) и B.34) в выражение, содержа-
содержащее скорость v и появляющееся в обеих частях траекторных
уравнений, так же как и в соотношении для G B.74). Учиты-
Учитывая, что абсолютная величина импульса частицы равна p = mv,
причем масса определена уравнением B.2), и используя обо-
обозначение
B.86)
получим
plmo = v(l— w2/c2)->/2 = c(l— S)[l — A— S)-2]1'^
= c[(l — SJ — l]i/» = c(— 2S + S2)'/2==
= c[—25A—S/2)]'/2. B.87)
Отметим, что нерелятивистская скорость (уравнение B.33))
связана с S соотношением
v = c(—2Sy'2. B.88)
Напомним также, что нерелятивистские уравнения движения
могут быть получены из релятивистских, если отбросить чле-
члены с а2/с2. В этом случае p/mo = v.
Если сравнить релятивистское выражение B.87) с нереляти-
нерелятивистским B.88), то легко заметить, что первое может быть
получено из второго заменой S на S(l— S/2). Из уравнения
B.86) видно, что разность электрических потенциалов и — и0
следует заменить «релятивистским потенциалом»
(и — ыо)ге1 = С" — «о)[1 — <2(ы — «0)/2т0с2]. B.89)
Абсолютная величина импульса релятивистской частицы теперь
дается выражением
р=[— 2Qmo(u — ыо)ге1]1/2. B.90)
В области малых скоростей релятивистский потенциал мож-
можно заменить обычным потенциалом, уравнение B.90) упроща-
упрощается и сводится к уравнению B.33). Поскольку Q(«—«о)<О
38
Движение заряженных частиц в электрическом и магнитном полях
для любой частицы, абсолютная величина релятивистского по-
потенциала всегда больше, чем абсолютная величина обычного
потенциала.
К сожалению, каждый раз, когда компонента электрическо-
электрического поля Е появляется в релятивистских уравнениях траектории,
она снова делится на v, так что в присутствии электрического
поля простая замена потенциала его релятивистским аналогом
не приводит к преобразованию нерелятивистских траекторных
уравнений в релятивистские. Использование релятивистского
потенциала не упрощает траекторных уравнений в этом случае,
но простое выражение по-прежнему можно использовать.
В случае чисто магнитного поля, однако, уравнения не со-
содержат скорости в сочетаниях, отличных от рассмотренного
выше. В этом случае как электростатический, так и релятивист-
релятивистский потенциалы постоянны, и, следовательно, абсолютная ве-
величина импульса также является постоянной, как и следовало
ожидать. Мы приходим к очень важному выводу: в случае чи-
чисто магнитного поля нерелятивистские уравнения всегда можно
использовать, учитывая, что в случае больших скоростей элек-
электростатический потенциал следует заменить релятивистским.
Этот прием существенно упрощает уравнения и облегчает их
решение.
2.6. Электронно-оптический показатель
преломления
До сих пор мы интересовались только движением и траекто-
траекториями отдельных частиц. Теперь можно сделать следующий
шаг.
Вспомним принцип Мопертюи (уравнение A.44)). Подынте-
Подынтегральное выражение P-dR, где Р — обобщенный импульс, опре-
определенный уравнением B.12). С учетом определения вектора
скорости и ее абсолютной величины A.36) можно записать
P-dR=pds+QA-evds, B.91)
где ds — элемент длины и ev — единичный вектор в направлении
скорости, которое совпадает с направлением изменения радиу-
радиуса-вектора.
Если теперь подставить последнее соотношение в уравне-
уравнение, выражающее принцип Мопертюи A.44), и сравнить полу-
полученное выражение с принципом Ферма A45), то легко заме-
заметить, что оба уравнения имеют один и тот же вид. В самом де-
деле, если подставить
B.92)
39
Глава 2
в качестве выражения для показателя преломления, то оба
уравнения окажутся тождественными. (Напомним, что абсо-
абсолютная величина импульса определена уравнением B.90).) Это
означает, что пучок заряженных частиц, движущийся в элект-
электромагнитном поле, ведет себя точно так же, как световой луч
в преломляющей среде, если электронно-оптический показатель
преломления, определенный уравнением B.92), равен опти-
оптическому показателю преломления в каждой точке пространства.
Это чрезвычайно важное замечание, влекущее за собой мно-
множество следствий. Прежде чем перейти к ним, исследуем струк-
структуру электронно-оптического показателя преломления. (Термин
является традиционным и применяется к любой заряженной
частице с импульсом р и зарядом Q.)
1. Прежде всего отметим,
что п является функцией как
«(R), так и A(R). Поскольку
поле обычно изменяется не-
непрерывно, показатель прелом-
преломления является непрерывной
функцией координат. (Внезап-
(Внезапное изменение электростати-
электростатического потенциала можно по-
получить, применяя тонкую
фольгу или мелкие решетки в
качестве поверхностей разде-
раздела между областями с разным потенциалом, но практическая
полезность такого подхода сомнительна; см. разд. 5.6.2.)
2. Если есть только электростатическое поле, то электронно-
оптический показатель преломления в точности равен импульсу
частицы, определенному уравнением B.90). Следовательно, п
пропорционально квадратному корню из абсолютной величины
релятивистского потенциала. Это означает, что скорость части-
частицы тем больше, чем больше я. Как мы видели (уравнение
A.47)), в случае света ситуация противоположна.
3. При наличии магнитного поля электронно-оптический по-
показатель преломления зависит не только от полей, но также и
от мгновенного направления движения частицы. В этом слу-
случае п не только неоднородно (зависит от точки пространства),
но и неизотропно (зависит от направления).
Непосредственно видно, что соотношение Снелля A.46)
применимо и в случае электронной и ионной оптики. Предста-
Представим себе двойной слой тонкой фольги на границе двух областей
с разными потенциалами щ и «2 в отсутствие магнитного поля.
Единственной силой, действующей на частицу, падающую на
двойной слой, является электростатическое поле Е, направлен-
направленное перпендикулярно поверхности (рис. 4). (Рисунок относится
40
■hi
Рис. 4. Преломление частиц на двой-
двойном электростатическом слое.
Движение заряженных частиц в электрическом и магнитном полях
к случаю положительно заряженных частиц с |u2|>|ui|.
В случае отрицательно заряженных частиц с тем же соотноше-
соотношением между потенциалами поле будет направлено в противопо-
противоположную сторону, ио сила действует в том же направлении.)
Под действием этой силы компонента импульса частицы, пер-
перпендикулярная поверхности раздела, изменится, а параллель-
параллельная компонента останется неизменной:
jt?i,,=jt?isin£=p2u=j02Sinr. B.93)
Следовательно,
sini
sin
> _ рз__ »г __ Г (»2—uo)telyi* B 94)
г pi tii L («l —«o)rel J
в соответствии с уравнением A.46). Разумеется, в случае ма-
малых скоростей релятивистские потенциалы можно заменить
электростатическими потенциалами.
Наиболее важное следствие введения электронно-оптиче-
электронно-оптического показателя преломления заключается в возможности не-
непосредственного применения геометрической оптики к движе-
движению пучков заряженных частиц в электромагнитных полях.
Можно говорить о фокусировке пучков заряженных частиц по-
полями, подобно тому как говорят о фокусировке световых лучей
оптическими линзами. Можно построить электростатические и
магнитные линзы и ввести для них кардинальные точки, ука-
указанные в разд. 1.4.2. Хотя такого рода линзы физически от-
отличаются от оптических линз, основные принципы их дейст-
действия остаются теми же. Наиболее важное практическое
различие заключается в том, что в электронных и ионных лин-
линзах показатель преломления изменяется непрерывно, в то время
как в собственно оптических линзах показатель преломления
почти всегда изменяется дискретно. Вследствие этого практи-
практически любое распределение полей может представлять собой
электронный и ионный оптический элемент. Более того, зависи-
зависимость показателя преломления от направления движения час-
частиц в световой оптике отсутствует. Таким образом, возможно-
возможности электронной и ионной оптики значительно богаче.
Пучки заряженных частиц можно не только фокусировать
электромагнитными полями, но также отклонять, изменять их
форму, т. е. можно управлять ими любым возможным способом.
Могут быть использованы системы с различной симметрией.
Оставшаяся часть книги будет посвящена наиболее важным
способам осуществления этой программы.
Аналогия между световой оптикой и электронно-ионной оп-
оптикой позволяет использовать не только оптическую термино-
терминологию (для описания пучков частиц), но и громадный опыт
41
Глава 2
создания оптических приборов, накопленный на протяжении
столетий. Электронный микроскоп едва ли смог появиться, если
бы не было оптического микроскопа.
2.7. Частицы в однородных полях
В качестве практического примера использования траектор-
ных уравнений рассмотрим движение заряженных частиц в од-
однородных электростатическом и магнитном полях внутри плос-
плоских конденсаторов, длинных соленоидов и между полюсами
относительно сильных магнитов. Такие поля можно использо-
использовать для отклонения пучков, а также для определения скорости
л относительного заряда частиц.
2.7.1. Плоский конденсатор
Простейшим электронно-ионным оптическим элементом яв-
является конденсатор с параллельными обкладками (рис. 5).
Электростатическое поле внутри такого конденсатора однород-
однородно. Однако вблизи его краев
— l * поле становится слабее и из-
изгибается в окружающее про-
пространство, поскольку теорети-
теоретически поле исчезает только на
бесконечном расстоянии от
конденсатора. Если расстоя-
Рис. 5. Плоско-параллельный кон- ние между обкладками рав-
денсатор. но d, то поле внутри конден-
конденсатора практически однородно
до расстояния d от края. Неоднородную внешнюю часть поля
можно заменить ограниченным однородным полем. Таким об-
образом, реальный конденсатор можно заменить идеальным с эф-
эффективной длиной, несколько большей, чем реальная длина L.
Такой идеальный конденсатор нереализуем, поскольку одно-
однородное поле не может внезапно исчезнуть. Однако такая прос-
простая модель является хорошим приближением при описании ре-
реального прибора. (Разумеется, конденсатор является трехмер-
трехмерным прибором: его длина может быть определена в любом
направлении, перпендикулярном однородному электростатиче-
электростатическому полю Е.)
Эффективная длина широко используется в электронно-ион-
электронно-ионной оптике с целью замены трехмерных оптических элементов
длины L двухмерными объектами с другой (эффективной) дли-
длиной, оказывающими приблизительно такое же воздействие на
пучок частиц (см. разд. 3.1.3.2).
42
Движение заряженных частиц в электрическом и магнитном полях
После такого упрощения достаточно однородного электро-
электростатического поля Е для описания воздействия плоского кон-
конденсатора на заряженную частицу. Направим ось х декартовой
системы координат вдоль поля и используем координату z в ка-
качестве независимой переменной (рис. 5). Подставляя Ех — Е
и Еу=Ег = Вх = Ву = Вг~0 в релятивистские траекторные урав-
уравнения B.81), получаем у"=0, а это означает, что у'=уо' =
=const. Проекцией траектории на плоскость yz является пря-
прямая, определяемая начальным наклоном уо''. Если начальная
скорость не имеет составляющей по оси у, то проекция траек-
траектории на указанную плоскость отсутствует, поскольку отсутст-
отсутствует сила, действующая вдоль оси у. В этом случае траектория
целиком лежит в плоскости xz. В общем случае г/' = г/о', н урав-
уравнение B.80) дает следующее выражение для проекций траек-
траектории на плоскость xz:
x"l=(QE/m0v2)(l-v2/c2)i/2(l+y0'2+x'2). B.95)
Выражая скорость через ее компоненты (уравнение A.37)) и
производные по времени через производные по z, получим
v2,=x2+y2 + z2 = z2(l+x'2 + y'2). B.96)
В направлении z не действует никакая сила, так что z-компо-
нента импульса является постоянной:
moz{\ — v2/c2)-V2 = pz0 = const. B.97)
Уравнение B.96) можно переписать в виде
v2= (р2го/т2о) A — и2/с2) A+х'2 + у'2), B.98)
причем из последнего уравнения можно найти v2 и подставить
полученное выражение в уравнение B.95). В результате полу-
получим:
х"= (QE/cp%o[m\c2+p2zO(l+yo'* + x'2)y'2. B.99)
вает проекцию
сать в виде
= (QE/cp2z0)dz.
Это дифференциальное уравнение описывает проекцию траекто-
траектории на плоскость xz. Его можно переписать в виде
B.100)
Интегрируя уравнение B.100) при начальных координатах ча-
частицы (х0, Уо, z0) и начальном наклоне траектории в плоскос-
плоскости xz, равном Хо', получим
= (QEfcpz0)(z—z0), B.101)
43
Глава 2
где
Z) = arcsh{^oV[mV2 + p2zo(l + «/o'2)]-1/2} =const B.102)
и arcsh — функция, обратная гиперболическому синусу. Из по-
последнего уравнения находим
рг0[т%с2+р2г0 A +Уо") ]-w*dx~
= sh[(Q£/cpz0) (z~-zo)+D]dz. B.103)
Интегрируя, вновь получаем
х — х0 = (c/QE) [т2ос2+р2гО A +Уо") ] •/» х
X{ch[QE/cpz0)(z — zo)+D] — chD}. B.104)
Отметим, что
= {1+р>гоХо/а[таоС*+раго(\+у0'2)]-1}1'*, B.105)
x'=xlz=pxlpz, y'=ylk=pylpz. B.106)
Следовательно,
B.107)
О. B.108)
Отметим также, что полный начальный импульс может быть
представлен в виде
р2о = Р2хо + р2уо+р2го. B.109)
С учетом этих замечаний конечный результат (уравнение
2.104)) можно переписать в следующем виде:
х — хо,= (c/QE) < (m2oc2+p2yO+p2zO) ^ X
Xch{ (QE/cpz0 (z — zo)+arcsh[pxO (m20c2+p2y0+p2z0)-1^]} —
— (mV2+P2oI/2>. B.110)
Можно заметить, что решение релятивистских траекторных
уравнений является достаточно сложным даже в этом элемен-
элементарном случае.
В случае малых скоростей уравнение B.110) существенно
упрощается. В самом деле, если импульс мал по сравнению
с ШоС, то члены, стоящие в левой части уравнения B.101), ма-
малы, так что член, стоящий в правой части уравнения, также
должен быть малым. Это означает, что аргумент гиперболиче-
гиперболического косинуса в уравнении B.110) мал и функцию можно за-
заменить двумя первыми членами ее разложения в ряд Тейлора:
сЬл;«1+л;2/2 B.111)
44
Движение заряженных частиц в электрическом и магнитном полях
для малых х. Кроме того, для малых значений аргумента об-
обратный гиперболический синус можно заменить его аргументом.
Учитывая эти упрощения, подставляя p = ntov для импульса
и пренебрегая членами w2/c2, из уравнения B.110) получим, что
в случае малых скоростей
х — хо = (QE/2mQv2z0) (z — z0J + {vx0lvz0) (z — z0).
B.112)
Эту простую параболическую зависимость легко получить непо-
непосредственно из нерелятивистских траекторных уравнений.
В этом случае траектория подобна траектории брошенного кам-
камня (постоянное гравитационное поле). Отметим, что уравне-
уравнения B.110) и B.112) приводят к бесконечным значениям х,
если 2-компонента начальной скорости равна нулю. Это обстоя-
обстоятельство является следствием процедуры вывода уравнений
траектории: замена времени координатой z в предположении,
что частица движется в направлении z. Если же начальная
скорость в этом направлении отсутствует, то это предположение
недействительно. Таким образом, полученные траекторные
уравнения можно использовать только в том случае, когда
2-компонента скорости отлична от нуля.
2,7.1.1. Отклонение частиц электростатическим полем. Наи-
Наиболее важным практическим применением плоского конденсато-
конденсатора в электронной и ионной оптике является использование его
для отклонения заряженных частиц. Рассмотрим частицу, дви-
движущуюся параллельно оси z с начальной скоростью v0 и вхо-
входящую в идеальный конденсатор (рис. 5) вблизи одного из его
краев (zo=—L/2). Ее отклонение kxL на другом краю конден-
конденсатора (z=L/2) в случае малых скоростей определяется урав-
уравнением B.112). Следует подставить u*o=O, vzQ = v0 и (z—zQ) =
= L. Кроме того, начальную скорость можно связать с ускоряю-
ускоряющим напряжением (уравнение B.33)), а абсолютная величина
однородного электростатического поля определяется соотноше-
соотношением
B.113)
где AU— отклоняющее напряжение на конденсаторе. В итоге
получим
AxL = QEL2/2m0v20 = — AUL2/4d(u — u0). B.114)
Аналогичным образом, наклон траектории у выхода из конден-
конденсатора определяется первой производной соотношения B.112)
в этой же точке. Первая производная равна
x'=QE(z — zo)l(mov2zo) + vxo/vzo. B.115)
45
Глава 2
После соответствующей подстановки получаем
= — AUL/2d(u — и0) B.116)
Уравнения B.114) и B.116) верны для всех пучков незави-
независимо от их начальных расстояний Хо от средней плоскости кон-
конденсатора. Следовательно, параллельный пучок останется па-
параллельным и после отклонения. К сожалению, из-за краевых
эффектов это неверно для реальных конденсаторов. В получен-
полученных уравнениях содержится тем не менее очень ценная инфор-
информация. Как легко видеть, ни величина отклонения, ни наклон
траектории не зависят от отношения заряда частицы к массе.
Электроны или ионы разных масс отклоняются на одну и ту
же величину, если они ускорены одинаковым напряжением
(скорости сами по себе различны для разных частиц). И одна
и та же электростатическая отклоняющая система может быть
использована для любой заряженной частицы, что очень удоб-
удобно при работе с ионными пучками.
Отрицательные знаки в уравнениях просто означают, что
для положительного отклонения (в положительном направлении
оси координат х) AU/(u—и0) всегда отрицательно. В самом
деле, для положительно заряженной частицы ускоряющее на-
напряжение отрицательно; для электрона и отрицательного иона
отклоняющее напряжение отрицательно.
Если известен наклон траектории у выхода из конденсато-
конденсатора, то легко вычислить полное отклонение частицы у мишени,
расположенной на расстоянии / от конденсатора в области, сво-
свободной от поля. Частица движется по прямой линии, определяе-
определяемой наклоном х' L. Полное отклонение равно
'L=— AUL(L + 2l)/4d(u — и0). B.117)
Эффективность отклонения определяется величиной Ax/AU, т.е.
отклонением, создаваемым единичным отклоняющим напряже-
напряжением. Она зависит от геометрических размеров системы и мо-
может быть увеличена посредством уменьшения ускоряющего на-
напряжения.
2.7.1.2. Простой анализатор скорости. Если ^-компонента на-
начальной скорости противоположна по направлению электроста-
электростатической силе, то для положительно заряженной частицы
ио<О, а для отрицательно заряженной частицы ио>0. Электро-
Электростатическое поле в этом случае будет замедлять частицу до тех
пор, пока она не столкнется с электродом или же не изменит
направление движения и будет ускорена по направлению к про-
противоположному электроду.
Пусть положительно заряженная частица начинает движе-
движение от отрицательного электрода с наибольшим абсолютным
значением потенциала, причем лс-компонента ее скорости на-
46
Движение заряженных частиц в электрическом и магнитном полях
правлена к другой обкладке. Сможет ли она достичь этой обк-
обкладки? Это произойдет в том случае, когда ^-компонента ско-
скорости достаточно велика, чтобы противодействовать электроста-
электростатической силе, пока частица пройдет расстояние — d в направ-
направлении х (рис. 5). Изменение направления движения происходит
в точке с х' = 0. Из уравнения B.115) можно определить соот-
соответствующую координату
z — 20 = — moVxoVzolQE. B.118)
Подставляя полученное выражение вместе с соотношением
х—х0——d в уравнение B.112) и принимая во внимание уравне-
уравнение B.113), найдем, что частица может достичь противополож-
противоположной обкладки при условии, что
B.119)
Полученное условие не зависит от двух других компонент ско-
скорости. Следовательно, в случае i>j,o = Uzo = O, когда частица дви-
движется перпендикулярно обкладкам, ее начальная кинетическая
энергия должна быть больше QAU. Частицы с меньшей кине-
кинетической энергией будут остановлены (и ускорены в противопо-
противоположном направлении), прежде чем они достигнут противопо-
противоположной обкладки.
Если имеется источник частиц с разными кинетическими
энергиями, то можно измерить распределение частиц по энер-
энергиям (скоростям), непрерывно изменяя напряжение на конден-
конденсаторе и измеряя ток, проходящий через положительную пла-
пластину с наибольшим потенциалом. Очевидно, что при любом
значении A.U этот ток пропорционален числу частиц с началь-
начальной энергией, превышающей QAU.
2.7.2. Однородное магнитное поле
Длинные соленоиды и относительно сильные магниты также
представляют собой простые электронно-оптические и ионно-оп-
тические элементы, поскольку магнитные поля внутри соленои-
соленоида и вдали от краев магнитных полюсов практически однород-
однородны. Разумеется, однородное магнитное поле является такой же
идеализацией, как и однородное электрическое поле. На прак-
практике всегда приходится учитывать краевые эффекты. Посредст-
Посредством введения эффективной длины реальное поле всегда можно
заменить однородным полем, оказывающим приблизительно та-
такое же воздействие, как и исходное поле.
Пусть вектор индукции однородного магнитного поля ориен-
ориентирован в положительном направлении оси z, а частица входит
в область поля с произвольной начальной скоростью v. Как мы
знаем (разд. 2.2.1), магнитное поле не может изменить величи-
47
Глава 2
ну скорости, так что v=const. Скорость определена уравне-
уравнением B.33) для любых значений ускоряющего напряжения, но
при больших скоростях следует использовать релятивистский
потенциал (уравнение B.89)).
Подставляя Ех=Еу = Ег=Вх = Ву = 0 и Вг=В в нерелятивист-
нерелятивистские уравнения B.80) и B.81), получаем
*",= (QB/mov) A+х'*+у'2)^2у\ B.120)
y" = -(QB/mov) A+х'2+у'2У'2х'. B.121)
Это система из двух нелинейных дифференциальных уравне-
уравнений. Их решение, однако, элементарно. Легко заметить, что
х'х"=—у'у", B.122)
или, что эквивалентно,
d(x'2+y'2)=0. B.123)
Следовательно,
x/2+y/2=x0/2+y0/2 = const. B.124)
Последнее очевидно, поскольку v = const и отсутствует сила,
направленная вдоль магнитного поля {z=zQ = const). Уравне-
Уравнение B.124) непосредственно следует из уравнения B.96). Ис-
Используя обозначение
Di= (QB/mov) (l + xo'2+yo'2)l'2 = QB/mQzo, B.125)
первые интегралы уравнений B.120) и B.121) можно записать
в виде
x' — x'0=Dl(y — y0), B.126)
y' — yro = -Dl(x — xo), B.127)
где индекс 0 относится к начальному положению и начальному
наклону траектории частицы. Определяя dz из общих уравне-
уравнений, найдем
— yo)]dy=[y'o — Dx{x — xo)]dx. B.128)
Интегрирование последнего уравнения дает
Di[(x — хоJ+ {у — у2о)]/2=у'о(х — х0) — х/о(у — Уо).
B.129)
Последнее соотношение можно переписать в виде
B.130)
или
(х — хсJ+(у — ycJ=R2. B.131)
48
Движение заряженных частиц в электрическом и магнитном полях
(хо'2+уо'2) B.132)
Это уравнение окружности радиуса
R = (xo'2+ J/o/2I/2ADi
с центром в точке с координатами
xc=Xo+y/olD1=xo+ (m0Zo/QB)yr0, B.133)
Ус=уо — x'0IDi=yu — (m0zoIQB)x/0. B.134)
Отметим, что QB/m0 имеет размерность частоты. Введем обо-
обозначение
<oc=\Q\B/m.
B.135)
Используя это последнее выражение вместе с уравнением
B.67) и обозначая компоненты скорости в плоскости ху по-
посредством
1/2, B.136)
из уравнений B.132) — B.134) получаем выражение для ра-
радиуса
R = vojac=mvoj \Q\B
и координат центра окружности
Ус = У о — Х0/<ос*= У о — Rxofvo±.
B.137)
B.138)
B.139)
Подобные треугольники на рис. 6 позволяют убедиться
в том, что это действительно координаты центра окружности
радиуса R, если Хо и уо являются координатами произвольной
точки окружности.
Поскольку в общем случае г-компонента скорости (в на-
направлении, перпендикулярном плоскости ху) отлична от нуля,
действительная траектория —
винтовая линия. Ее проекцией
на плоскость ху является ок-
окружность, показанная на
рис. 6. Поскольку отсутствует
сила, параллельная магнитно-
магнитному полю, в направлении z тра-
траектория наращивается с по-
постоянной скоростью vzo-
Этот результат не должен
вызывать удивление. В самом Рис 6 КругОвая траектория в одно-
деле, из уравнения A.14) еле- родном магнитном поле.
49
Глава 2
дует, что сила Лоренца перпендикулярна как вектору индукции
магнитного поля, так и вектору скорости. В нашем случае аб-
абсолютные величины обоих векторов постоянны и В имеет токъ-
ко г-компоненту. Следовательно, постоянная сила всегда дей-
действует в плоскости ху и направлена перпендикулярно компонен-
компоненте скорости в этой плоскости. Иными словами, это центростре-
центростремительная сила, приводящая к равномерному движению по
окружности в плоскости ху. Поскольку центростремительная
сила равна силе Лоренца, можно записать соотношение
mv20JR=\Q\v0±B, B.140)
эквивалентное уравнению B.137). Поскольку уравнение B.137)
отвечает равномерному движению по окружности, непосредст-
непосредственно видно, что «вс имеет физический смысл угловой частоты.
Это циклотронная частота. Если известна частота, то легко вы-
вычислить период:
T = 2nac = 2nm/\Q\B. B.141)
Таково время, затрачиваемое на один оборот по окружности.
За это время частица проходит расстояние
h = vz0T B.142)
в направлении z, где иго — компонента начальной скорости.
Если отсутствует составляющая скорости, параллельная
магнитному полю, то радиус траектории однозначно определя-
определяется магнитной индукцией, ускоряющим напряжением и отно-
отношением заряда частицы к ее массе. Подставляя уравнения
B.135), B.33) и B.89) в уравнение B.137), получаем
RB={— Bmo/Q)(« — ыо)[1 — Q(« — ио)/2тос*]У'2.
B.143)
Сравнивая последнее выражение с соотношением B.87), можно
видеть, что RB пропорционально импульсу частицы:
RB=p/\Q\. B.144)
Для нерелятивистских электронов уравнение B.143) дает
= 3,37- Ю-6 (и — и0) '/2[В • с/м]. B.145)
Например, требуется магнитная индукция 0,0337 Вс/м2, чтобы
электрон, ускоренный напряжением 10 кВ, вращался по окруж-
окружности радиусом 1 см.
2.7.2.1. Длинные магнитные линзы. Наиболее очевидное при-
применение однородного магнитного поля основано на том факте,
что частицы движутся по винтовой траектории, пройдя расстоя-
расстояние h = vz0T, возвращаются к одной и той же силовой линии.
50
Движение заряженных частиц в электрическом и магнитном полях
Если облучить тонкий объект, расположенный в однородном
магнитном поле перпендикулярно силовым линиям, пучком ча-
частиц, движущихся параллельно магнитному полю, то частицы
подвергнутся рассеянию и слегка расходящиеся пучки частиц
с равными скоростями будут испущены каждой точкой объекта.
Если расхождение невелико, то можно считать, что компоненты
скорости, параллельные полю, равны, в то время как компо-
компоненты скорости, перпендикулярные полю, немного различаются.
Тогда различные частицы, испущенные одной и той же точкой,
будут двигаться по слегка отличающимся винтовым траектори-
траекториям; но все они возвратятся к их общей силовой линии, пройдя
равные расстояния h. Это верно для любой точки объекта.
Следовательно, на расстояниях nh от объекта (где п — целое
число) возникнут его действительные изображения. Увеличение
изображений равно единице. Такая линза выглядит довольно
странно, поскольку она не собирает в фокусе параллельный пу-
пучок, но может формировать
изображения. Отметим, что
величина h зависит от отноше-
отношения заряда частицы к ее мас-
массе. Следовательно, фокусиро-
фокусирование различных частиц про-
происходит на разных расстояни-
расстояниях, что является важной осо-
особенностью магнитных линз.
Следует также отметить,
что отчетливые изображения
могут быть получены только
при помощи пучков, движу-
движущихся вблизи силовых линий. Если расхождение существенно,
то значения h могут значительно различаться для разных час-
частиц в одном и том же пучке. В результате изображение будет
искажено. Это типичный пример аберрации линз — одной из
труднейших проблем электронной и ионной оптики.
Длинные магнитные линзы будут рассмотрены более под-
подробно в разд. 4.10.1.3.
2.7.2.2. Отклонение частиц магнитным полем. Рассмотрим
частицу, движущуюся параллельно оси х с начальной скоро-
скоростью v0 и входящую в область однородного магнитного поля,
параллельного оси z (рис. 7) с одной из сторон (дсо=0). Ее от-
отклонение AyL на другой границе поля (x=L) определяется урав-
уравнением B.130). Следует подставить Wj,o = O, vxq = v0 и (х—х0) =
— L. В итоге получим
B.146)
Рис. 7. Отклонение частиц магнитным
полем.
51
Глава 2
В соответствии со знаком силы Лоренца A«/L отрицательно для
положительно заряженной частицы (см. рис. 7). Наклон траек-
траектории на выходе из области локализации поля определяется
первой производной у по х. Последнюю можно найти из уравне-
уравнения B.128):
dy\ _ L/R _ LQB /.
l m»v» V
Полное отклонение на мишени, расположенной в области, за
пределами поля, иа расстоянии / от границы области однород-
однородного магнитного поля, дается выражением
B.148)
Обычно £■<#. В этом случае разложение последнего выраже-
выражения в ряд Тейлора и пренебрежение членами меньше (L/RJ
дают
Ay== — L(L + 2l)/2R = — (QBLf2m0v0) (L+21). B.149)
Подставляя в полученное выражение ускоряющий потенциал
из соотношения B.33), получим отклонение в случае малых
скоростей
B.150)
2[-2mo(u-uo)/Q]1/2
Как можно видеть, отклонение частицы в магнитном поле за-
зависит от отношения ее заряда к массе частицы. В этом заклю-
заключается фундаментальное различие между магнитными и элект-
электрическими отклоняющими системами. Разброс отношений
Q/mo представляет собой серьезное препятствие в том случае,
когда требуется отклонить пучок различных ионов одной и той
же системы. С другой стороны, магнитное поле может быть
использовано для разделения частиц. Эффективность отклоне-
отклонения в случае магнитного поля определяется отношением Ау/В
и также может быть увеличена уменьшением ускоряющего на-
напряжения.
2.7.3. Одновременное действие однородных
электрического и магнитного полей
Другим важным применением однородных полей является
масс-спектроскопия (определение отношения заряда к массе
для различных ионов в пучке). В масс-спектрометрах обычно
применяется сочетание статических электрических и магнитных
полей. В простейшем случае как те, так и другие поля однород-
52
Движение заряжеиных частиц в электрическом и магнитном полях
ны. В этом случае траектории
медленных частиц могут быть
определены аналитически.
Произвольно направленные
постоянные векторы Е и В оп-
определяют плоскость. Выберем
прямоугольную систему коор-
координат таким образом (рис.8),
чтобы указанная плоскость
совпала с плоскостью xz, a
вектор магнитной индукции В
был параллелен положитель-
положительному направлению оси z(Bz=
= fi=const). В этом случае
вектор напряженности элект-
электрического поля Е имеет две
компоненты (£*=const и Ег=
= const), причем Еу = Вх = Ву = 0. Единственная сила, действую-
действующая в направлении г, обусловлена Ег, и интегрирование урав-
уравнения B.59) дает
Рис. 8. Проекция циклоиды в произ-
произвольно ориентированных электроста-
тичеоком и магиитиом полях.
z=zo+QEztfmo,
z=г0+2о t+ QEzt2/2m0,
B.151)
B.152)
где z0 и z0 — начальные значения гиг соответственно. Решим
это квадратное уравнение и представим t в виде функции г.
Используя уравнение B.96) и подставляя выражение t(z)
в уравнение B.151), получим
\ B.153)
Теперь можно использовать траекторные уравнения B.80) и
B.81). Их нерелятивистскую форму можно в рассматриваемом
случае записать в виде
= (Q/mo)[(Ex — x'Ez)l'z2+yfB!z],
(y'Ez/z2+x'Btz),
B.154)
B.155)
где z определено уравнением B.153) в виде функции от г.
Чтобы решить эту сложную систему дифференциальных
уравнений, используем
u=Bz/Ez
в качестве новой безразмерной переменной. Тогда
dz= (m0Ez/QB2)udu,
B.156)
B.157)
53
Глава 2
и после перехода от дифференцирования по г к дифференциро-
дифференцированию по и систему дифференциальных уравнений B.154) н
B.155) можно записать в виде
d4 m0Ex dy .
du* ~ da'
Последняя система легко интегрируется:
BЛ60)
где индекс 0 обозначает начальные значения переменных. Урав-
Уравнение B.156) дает
ио = Вго/Ег. B.162)
Из уравнения B.157) следует
ie/(oc, B.163)
где сое — циклотронная частота, определенная соотношением
B.135). Аналогичным образом
)o = ir0/oc. B.164)
Теперь необходимо проинтегрировать систему дифференци-
дифференциальных уравнений B.160) и B.161). Определяя du из обоих
уравнений, найдем
[(Ех/Ва>с) (u — u
= [Уо/а>с— (х — xo)]dx. B.165)
Интегрируя последнее уравнение на интервале от начальной
точки до текущей точки траектории, получим
(Ех/Вас) S (и — uQ)dy=уо{х — Хо)/ас —
-хо(у — уо)/ас— (х — хоу/2—(у — уоу/2. B.166)
С другой стороны, интегрирование по частям дает
у и—ио
S (и — uo)dy=(u — ио) (у — уо) —- I (y — yo)d(u — uo).
Уо 0
B.167)
54
Движение заряженных частиц в электрическом и магнитном полях
Теперь подставим соотношение B.160) в правую часть уравне-
уравнения B.159). Интегрирование полученного уравнения с после-
последующей подстановкой соотношения B.161) дает
и—«о
— S (y
Ви — и0у—(х — х0). B.168)
Подставляя полученное соотношение в уравнение B.167), най-
найдем
у
\ (и — uo)dy= (и — ыо) (у — уо) +х0 (ы — Ыо)/сос +
#0
+ {Ех/2Ва>с) (и — иоJ—(х — х0). B.169)
Последнее выражение следует подставить в уравнение B.166).
Используя соотношения B.156) и B.162), вернемся к независи-
независимой переменной г. Переменную z можно заменить на время t
в соответствии с соотношением B.151). После некоторых ал-
алгебраических преобразований получим
(х — хсJ+(у — ycJt=R2. B.170)
Полученное соотношение совпадает по форме с соотношением
B.131), описывающим траекторию в однородном магнитном
поле (в отсутствие электрического поля). Различие заключает-
заключается в том, что теперь параметры имеют сложный вид:
/ас, B.171)
xt/B, B.172)
R= [xQ2+ (Уо + Ех/ВJу/2. B.173)
Непосредственно видно, что в случае Ех=0 полученные вы-
выражения дают те же результаты, что и соотношения B.137) —
B.139). Это означает, что, когда электрическое поле парал-
параллельно магнитному, проекция траектории на плоскость ху бу-
будет такой же окружностью, как и при отсутствии электрическо-
электрического поля. Траектория снова имеет форму винтовой линии с тем
отличием, что теперь имеется ускорение (или замедление) в на-
направлении оси 2, так что поступательное движение идет в на-
направлении z с переменной скоростью г, определяемой соотноше-
соотношением B.151).
Ситуация существенно меняется, однако, при наличии ком-
компоненты электростатического поля Ех, перпендикулярной векто-
вектору магнитной индукции В. В этом случае не только меняются
радиус окружности и координаты ее центра, но, кроме того,
величина ус зависит от времени. Окружность смещается вдоль
55
Глава 2
оси у, и проекция траектории на плоскость ху является нало-
наложением равномерного движения и движения по окружности.
Результирующая кривая является трохоидой. В зависимости от
величины и направления начальной скорости частицы трохоида
может иметь петли или точки поворота или же иметь вид глад-
гладких колебаний. Если начальная скорость не имеет составляю-
составляющей в плоскости ху, то трохоида превращается в циклоиду.
Последний случай показан на рис. 8 для х0 = г/о = z0 = 0. Как мы
вскоре покажем, в отдельных случаях трохоида может вырож-
вырождаться в прямую, параллельную оси у.
Траектория зависит также от г-компоненты электростатиче-
электростатического поля (см. выше). (На рис. 8 показана только проекция
траектории на плоскость ху.) Поскольку центр окружности дви-
движется параллельно оси у с постоянной скоростью — Ех/В
(уравнение B.172)) и в то же время движется вдоль оси z с по-
постоянным ускорением (уравнение B.152)), проекция траекто-
траектории центра окружности на плоскость yz является параболой.
Последний результат, возможно, покажется удивительным
новичку. В самом деле, естественно было бы ожидать, что
центр окружности будет смещаться в направлении электриче-
электрического поля, но не в перпендикулярном направлении. Чтобы по-
понять этот эффект, необходимо разобраться в природе силы Ло-
Лоренца.
Рассмотрим для простоты движение в плоскости ху. Для
этого положим Ег=0 и vz0=0. В этом случае отсутствует сила,
действующая в направлении оси 2, и траектория совпадает с ее
проекцией на плоскость ху. Рассматриваемый случай является
достаточно общим, поскольку добавление г-компоненты элект-
электрического поля и начальной скорости не изменит проекции
траектории на плоскость ху. Из выражения для силы Лорен-
Лоренца A.14) непосредственно следует, что ее электрическая ком-
компонента направлена вдоль оси х и приводит к изменению
^-компоненты скорости. Это в свою очередь приводит к изме-
изменению ^-компоненты скорости из-за действия магнитной компо-
компоненты силы Лоренца. Магнитная компонента силы является
причиной постоянного смещения траектории вдоль оси у. Если
Ех и В положительны, дрейф происходит в отрицательном на-
направлении оси у независимо от отношения заряда частицы
к ее массе.
Чтобы представить себе наглядно описанную картину, пред-
предположим, что мы движемся вдоль оси у с постоянной скоростью
w= — }Ex/B. B.174)
В нашей движущейся системе координат электрическая компо-
компонента силы Лоренца отсутствует. В самом деле, скорость части-
56
Движение заряженных частиц в электрическом и магнитном полях
цы v представляет собой сумму векторов относительной ско-
скорости частицы Vrei в движущейся системе координат и скорости
самой системы координат (w), но
wXB=-i£,, B.175)
чем и компенсируется электростатическая составляющая силы
Лоренца. Единственной оставшейся составляющей силы будет
(v—w) X В. Разумеется, сумму скоростей следует также подста-
подставить и в уравнение движения B.1). Но производная постоянной
скорости w равна нулю, так что относительная скорость (v—w)
появится в обеих частях уравнения B.1). Это означает, что
в движущейся системе координат траекторией частицы являет-
является окружность. Радиус окружности определяется соотноше-
соотношением B.137), в которое следует подставить в данном случае
относительную скорость, так что w следует вычесть из у-компо-
ненты скорости. Именно к такому результату приводит уравне-
уравнение B.173). Координаты центра окружности определяются со-
соотношениями B.138) и B.139), причем снова w следует вы-
вычесть из «/-компоненты скорости. Наконец, в исходной системе
координат центр окружности движется вдоль оси у с постоян-
постоянной скоростью w. Эти изменения полностью отражены в соотно-
соотношениях B.171) и B.172).
Отметим, что циклотронная частота ©с остается неизменной
и по-прежнему определяется только магнитным полем в соот-
соответствии с соотношением B.135). Время, необходимое для пол-
полного оборота по окружности, также остается неизменным. По-
Последнее определяется соотношением B.141) и не зависит от
электрического поля и начальных условий. Траектория имеет
периодический характер с «длиной волны»
L^wT=2nExIBac B.176)
(см. рис. 8). Это означает, что пучок частиц с различными по
величине и направлению скоростями, испущенный из точки,
расположенной на расстоянии х от плоскости yz, соберется
вновь в одной точке на расстоянии L от источника в направле-
направлении оси г/, если отношение заряда к массе одинаково для всех
частиц. Этот фокусирующий эффект является точным, посколь-
поскольку он не ограничен малостью дисперсии угловых скоростей.
Теперь легко видеть, что траектория является прямой, если
начальная скорость частицы в точности равна w. В этом случае
сила Лоренца равна нулю и начальная скорость частицы, на-
направленная вдоль оси у, остается постоянной. Формально это
вытекает из уравнений B.171) —B.173), которые дают хс~х0,
t # 0
57
Глава 2
2.7.3.1. Определение масс и другие приложения. В ионно-лу-
чевой технологии важно уметь отделять нейтральные частицы
и определять их точные массы или энергии.
В первых масс-спектрометрах использовались однородные
электростатическое и магнитное поля. Знаменитый метод пара-
параболы Томсона [56] сводится к отклонению частиц в однород-
однородных электростатическом и магнитном полях, параллельных
друг другу. Пусть ось х декартовой системы координат направ-
направлена параллельно напряженностям обоих полей, а заряженная
частица входит вдоль оси z в область поля. Отклонения на ма-
малые углы в направлении х обусловлены электростатическим
полем, а в направлении у—магнитным полем. Отклонения
определяются для разных скоростей частиц уравнениями
B.117) и B.150) соответственно. В случае малых отклонений
соответствующие эффекты независимы. Исключая ускоряющий
потенциал из обоих уравнений, получим
(A!/) BЛ77)
Это соотношение означает, что частицы с одинаковым отноше-
отношением заряда к массе, но с различными скоростями отклоняются
описанным сочетанием полей таким образом, что их треки на
мишени, перпендикулярной начальным скоростям частиц, обра-
образуют параболу. Отдельные точки параболы отвечают частицам
с разными начальными скоростями, но сама парабола опреде-
определяется только полями, геометрией системы и отношением заря-
заряда частицы к ее массе. Частицы с различными отношениями
заряда к массе образуют разные параболы. Следовательно, из-
измеряя коэффициент перед квадратичным членом в уравнении
параболы, можно определить отношение заряда частицы к ее
массе.
В масс-спектрометре Астона впервые была получена прост-
пространственная фокусировка ионов с различными начальными ско-
скоростями [57]. В этом приборе электростатическое и магнитное
поля разделены в пространстве.
Масс-спектрометр может быть построен также на основе
скрещенных полей. Как мы видели, такая система обеспечивает
теоретически идеальную фокусировку и вполне соответствует
требованиям спектроскопии. Такого рода спектрометр называ-
называется трохотроном [58]. Трохоидальные траектории частиц мож-
можно также использовать в монохроматорах [59].
Недостатком таких приборов является трудность поддер-
поддержания строгой однородности электростатического поля в боль-
большом объеме, так что совершенствование приборов происходило
и в других направлениях (см. гл. 11)
58
* xjxlx
IX |х|х в
4x|x
Движение заряженных частиц в электрическом и магнитном полях
Особый случай прямолинейной траектории использован
в простом фильтре Вина [50], состоящем из плоского конден-
конденсатора с наложенным однородным магнитным полем (рис. 9).
Магнитное поле на рисунке направлено вдоль оси г, а электри-
электрическое поле — в отрицательном направлении оси х. Согласно
соотношению B.174), скорость должна быть направлена в по-
положительном направлении оси у. Напряженности полей выби-
выбираются таким образом, чтобы для данной скорости w выполня-
выполнялось соотношение B.174), так что частицы со скоростями, близ-
близкими к w, двигаясь по прямой, проходят через диафрагму, рас-
расположенную за конденсатором. Если же начальная скорость
частицы заметно отличается от w по величине или направле-
направлению, то частица будет отклонена полями и не пройдет через
диафрагму. Следовательно, пучок частиц справа от диафрагмы
будет содержать частицы с одинаковыми скоростями. Такой
прибор называется монохроматором. Это приспособление мож-
можно использовать для измерения скорости частицы.
Одновременное действие
взаимно перпендикулярных и
однородных электростатичес-
электростатического и магнитного полей ис-
используется и в других прибо-
приборах. Магнетрон [11]—это
микроволновая трубка, в ко-
которой электроны движутся по
КВазиТрОХОИДальныМ ТраектО- Рис. 9. Фильтр Вина.
риям в поле цилиндрического
конденсатора, сочетающегося с продольным магнитным полем.
Хотя электростатическое поле в этом случае неоднородно, фор-
форма траекторий в основном остается прежней с тем различием,
что теперь траектории наматываются на цилиндрическую по-
поверхность. Скрещенные поля также могут быть использованы
в электронных умножителях [9] для удаления слабых электрон-
электронных токов.
2.8. Законы подобия
В заключение этой главы мы рассмотрим проблему, являю-
являющуюся фундаментальной для практического проектирования.
Пусть проектные данные отвечают определенному набору пара-
параметров, описывающих некоторые условия. Вопрос заключается
в том, как преобразовать эти данные для случая иных условий.
Иными словами, как использовать имеющиеся разработки, если
параметры изменены.
Чтобы ответить на поставленный вопрос, рассмотрим урав-
уравнения движения в общем виде. Поскольку простые законы по-
подобия можно получить только в случае малых скоростей,
59
Глава 2
в этом разделе мы ограничимся нерелятивистскими частицами.
В этом случае из уравнений A.36) и B.3) вытекает уравнение
движения в векторной форме:
d2R/dt2= (Q/m0) [E+ (dR/dt) X В]. B.178)
Рассмотрим две установки с разными электростатическим
и магнитным полями, имеющие разные размеры. Обозначим со-
соответствующие величины индексами а и Ь соответственно. Оче-
Очевидно, уравнение B.178) справедливо для обеих установок, так
что можно записать
d2Ra/dta*= (Q/m0) [Ea+ (dRa/dta) XВа], B.179)
d2Rb/dtb2 = (Q/mo) [E6+ (dRb/dtb) XBb]. B.180)
Предположим, что существуют линейные масштабные соотно-
соотношения между соответствующими величинами параметров:
Rb=kRRa, Еь = /г£Еа> ub=kBba, tb=ktta, B.181)
где коэффициенты kR, kE, кв и kt являются масштабными мно-
множителями. Под «соответствующими» величинами подразумева-
подразумеваются величины, определенные в соответствующих точках (на-
(например, в точках, где потенциалы достигают максимальных
значений).
Теперь выясним, какого рода соотношения между коэффи-
коэффициентами должны выполняться для того, чтобы траектории в
обоих случаях были подобны [11, 16]. Подставляя соотноше-
соотношение B.181) в B.180), получим
{kRlkEkt2)d*Raldta2= {Qlmo)[ba+{kKkBlkEkt) (dRa/dta) XBa].
B.182)
Это соотношение эквивалентно уравнению B.179), если по-
потребовать
kt=l/kB=(kR/kE)l/2. B.183)
Это означает, что для сохранения формы траектории, т. е. что-
чтобы обеспечить геометрическое подобие решения Rb{tb) уравне-
уравнения B.180) и решения \Ra(ta) уравнения B.179), необходимо
потребовать выполнение двух соотношений B.183). Исполь-
Используя уравнения A.17) и B.181), последние соотношения можно
записать в виде
R2B2/u = const, B.184)
T2u/R2 = const, B.185)
где R— расстояние между соответствующими точками, и —
электростатический потенциал в соответствующих точках, В —
60
Движение заряженных частиц в электрическом и магнитном полях
соответствующая компонента плотности магнитного потока
в соответствующих точках и Т — время движения между соот-
соответствующими точками. Отметим, что соотношения B.184) и
B.185) получены для случая, когда имеются как электростати-
электростатическое, так и магнитное поля, но они остаются в силе и в от-
отсутствие одного из полей. Частные случаи чисто электростати-
электростатического или чисто магнитного полей будут рассмотрены более
подробно ниже.
Из общих законов подобия, выраженных соотношениями
B.184) и B.185), непосредственно вытекает несколько след-
следствий.
1. Наличие масштабного фактора для времени kt означает,
что подобные траектории проходятся, вообще говоря, за разное
время. Соответственно различаются и скорости частиц. Из со-
соотношений A.36), B.181) и B.183) следует выражение для
масштабного фактора скорости
kv = Vb/Va = (kRkE) 1/2. B.186)
Из соотношений B.33) и B.184) следует, что
RBfv = const. B.187)
Последнее соотношение следует также из уравнений B.183)
и B.186) и подтверждается соотношением B.137) для однород-
однородных магнитных полей.
2. Если изменить линейные размеры системы в kR раз, оста-
оставив потенциалы неизменными, то напряженности электрических
полей изменятся в kE=l/kR раз. Из уравнения B.183) видно,
что плотность магнитного потока следует изменить в &в=1/&#
раз, чтобы форма траектории не изменилась. Время прохода из-
изменится в kt=kR раз, в то время как скорость останется неиз-
неизменной.
3. Изменим линейные размеры в kR раз, оставив напряжен-
напряженность электростатического поля неизменной. В этом случае
плотность магнитного потока следует изменить в &в = &я-'А раз.
Время прохода и скорость изменятся в kt=kv—kR'' раз. Тот же
результат будет получен и в отсутствие электростатического
поля.
4. Если плотность магнитного потока остается неизменной
или магнитное поле отсутствует, то время прохода также оста-
остается неизменным, а электростатическое поле и скорость изме-
изменяются по тому же закону, что и линейные размеры: kE=kv —
=kR. В этом случае электростатический потенциал следует из-
изменить в kR2 раз, чтобы форма траектории осталась неизмен-
неизменной.
Глава 2
5. Оставив линейные размеры неизменными, можно полу-
получить те же уравнения движения и неизменные траектории, если
изменить в kE раз электростатическое поле и потенциал и в
kB2 = kE раз плотность магнитного потока. Масштабный фактор
для времени в этом случае равен kt=kE~k, а для скорости kv —
=£е'\ поскольку скорость пропорциональна квадратному кор-
корню из электростатического потенциала. Чрезвычайно важное
следствие заключается в том, что в отсутствие магнитного поля
пропорциональное изменение всех электродных потенциалов
оставляет траекторию неизменной, т. е. только отношения потен-
потенциалов, а не их величины, влияют на форму траектории.
6. Очевидно, что все величины, имеющие размерность дли-
длины (например, фокусное расстояние, коэффициенты аберрации
и т.п.), изменяются вместе с радиусом-вектором R. Следова-
Следовательно, безразмерные величины, такие, как коэффициент абер-
аберрации, отнесенный к фокусному расстоянию (см. разд. 5.7.4),
являются масштабно-инвариантными и могут служить универ-
универсальными параметрами для характеристики электронно-оптиче-
электронно-оптических и ионно-оптических приборов.
7. Изменение отношения заряда частицы к ее массе Q/mo
приводит к тому же эффекту, что и одновременное изменение
электростатического и магнитного полей в kE раз (см. уравне-
уравнение B.178)). Но в этом случае уравнение B.183) дает kE=kB—
= l/kR, так что распределение потенциалов остается неизменным,
как и в случае 2. Единственное различие заключается в том,
что соотношение B.186) в этом случае недействительно: ско-
скорость изменяется пропорционально ItE1'. Если положить kR = \,
то мы получим еще одно важное следствие: траектории частиц
с разными отношениями заряда к массе в электростатическом
поле одинаковы. Кроме того, траектории положительно заря-
заряженных частиц совпадут с траекториями электронов, если из-
изменить знаки всех электродных потенциалов. В магнитном поле
это не так: частицы с одинаковыми по величине, но разными по
знаку отношениями заряда к массе будут отклоняться в проти-
противоположных направлениях.
8. В ненасыщенных магнитных полях линейный интеграл от
плотности потока пропорционален числу возбуждающих ампер-
витков N1 (см. уравнение C.233)). В этом случае соотношение
B.184) можно записать в виде
-'/2 = const. B.188)
Траектории в магнитных полях остаются подобными, если все
размеры магнитной цепи изменяются в одинаковое число раз
и выполняется соотношение B.188). Это позволяет измерять
62
Движение заряженных частиц в электрическом н магнитном полях
магнитные поля посредством масштабных моделей при усло-
условии, что в обоих случаях поле создается одними и теми же
магнитными материалами.
9. Другой важный закон подобия [11] вытекает из соотно-
соотношений A.1), A.17), B.85) и того факта, что плотность тока J
связана с плотностью заряда р и скоростью v соотношением
J = pv. B.189)
В случае плотного пучка частиц, когда нельзя пренебречь про-
пространственным зарядом самого пучка, траектории остаются не-
неизменными, если сохраняется первеанс
= /и-з/2 = const, B.190)
где / — полный ток в пучке (см. гл. 12).
Заключение
Мы рассмотрели основные законы движения заряженных
частиц в электрическом и магнитном полях. Сначала мы опре-
определили лагранжиан частиц (уравнение B.15)). Закон сохране-
сохранения энергии позволил представить скорость частицы в виде
функции потенциала (уравнение B.31)). Затем были получены
релятивистские уравнения движения B.50) — B.52) в обобщен-
обобщенной ортогональной криволинейной системе координат. Были
рассмотрены частные случаи уравнений движения в декартовой
(уравнения B.53) —B.55) и цилиндрической B.60)—B.62)
системах координат. Уравнения движения были затем преобра-
преобразованы в траекторные уравнения B.76) —B.77), B.80), B.81)
и B.84) — B.85) соответственно. Мы ввели релятивистский по-
потенциал (уравнение B.89)) и показали, что он позволяет ис-
использовать нерелятивистские уравнения в магнитных полях да-
даже в случае высоких энергий частиц. Затем был введен элект-
электронно-оптический показатель преломления (соотношение B.92))
и установлены аналогии между геометрической оптикой, с одной
стороны, и электронной и ионной оптикой, — с другой. Были
определены траектории частиц в однородных электростатиче-
электростатическом и магнитном полях посредством точного решения траек-
торных уравнений. В качестве практических примеров рассмот-
рассмотрены плоские конденсаторы, длинные магнитные линзы, элект-
электростатические и магнитные отклоняющие системы, простые ана-
анализаторы масс и скоростей. Наконец, были приведены законы
подобия электронной и ионной оптики (соотношения B.183) —
B.188) и B.190)).
Глава 3
ОПРЕДЕЛЕНИЕ ЭЛЕКТРИЧЕСКИХ
И МАГНИТНЫХ ПОЛЕЙ
Мы научились вычислять траектории частиц в однородных
лолях, но реальные поля никогда не бывают однородными (да-
(даже в плоском конденсаторе поле неоднородно на краях). Преж-
Прежде чем начать изучение движения частиц в полях сложной кон-
конфигурации, необходимо научиться определять распределения
таких полей в пространстве. (Поля, меняющиеся со временем,
рассматриваться не будут.)
Электростатические поля обычно формируются системой
электродов с заданным потенциалом, а магнитные поля — ка-
катушками индуктивности, по которым течет ток, либо постоян-
постоянными магнитами. Для более высокой концентрации полей в ма-
малых областях в большинстве случаев катушки окружают фер-
ферромагнитным материалом. Можно выделить три основных типа
задач, возникающих при поиске распределений полей.
1. Если в рассматриваемой области токи отсутствуют, то
статические поля описываются скалярным потенциалом, и тогда
«еобходимо решать уравнение Пуассона A.18) или уравнение
Лапласа A.23) с потенциалами, заданными на поверхностях
электродов, полюсных наконечников, либо постоянных магнитов
(граничная задача Дирихле). Если пренебречь влиянием токов,
создающих магнитные поля, электрическими и магнитными
полями, создаваемыми самими пучками заряженных частиц
(см. гл. 12), считать проницаемость магнитного материала бес-
бесконечно большой, а эффекты насыщения пренебрежимо малы-
малыми, то в принципе нет различия между электростатическими и
магнитными полями, так как распределение скалярных потен-
потенциалов в обоих случаях определяется уравнением Лапласа и
граничными условиями. Большинство методов, представленных
в этой главе, пригодны для определения таких потенциальных
полей.
2. В присутствии магнитных материалов с конечной прони-
проницаемостью вблизи насыщения, либо если нельзя пренебречь
влиянием токов, необходимы специальные приемы. Этот прак-
практически очень важный случай будет детально рассмотрен
в разд. 3.1.4.
€4
Определение электрических и магнитных полей
3. Если магнитное поле создается токами, оно определяется
векторным потенциалом, и тогда необходимо решать уравне-
уравнение Максвелла A.16). Так как токи обычно протекают в катуш-
катушках индуктивности простой формы, найти распределение маг-
магнитного поля в этом случае относительно просто (см.
разд. 3.1.5).
Следует особо отметить, что учет эффектов пространствен-
пространственного заряда делает задачу определения поля очень сложной
даже в простейших случаях. Для решения этой задачи необхо-
необходимо знать распределение частиц по координатам и скоростям.
Это требует одновременного решения уравнений Максвелла и
траекторных уравнений. Как будет видно в гл. 12, это весьма
трудно. Поэтому в большинстве случаев разработчик старается
разделить задачу на две: сначала определяются распределения
нолей без учета пространственного заряда, а эффекты, связан-
связанные с пространственным зарядом, учитываются позднее, в про-
процессе расчета оптических Характеристик. Этот подход обосно-
обоснован тем, что пространственный заряд можно рассматривать как
особый тип аберрации: он не вносит существенных возмущений
в распределение полей, но в тоже время заметно меняет оптиче-
оптические характеристики.
Ниже мы дадим краткий обзор различных аналитических,
аналоговых и численных методов определения распределений
полей.
3.1. Аналитические методы
3.1.1. Разложение потенциалов и полей в ряды
Рассмотрим сначала произвольный электростатический или
магнитный скалярный потенциал m(R) как функцию простран-
пространственных координат. Для дальнейшего рассмотрения удобно
представить и в виде ряда.
Начнем с цилиндрической системы координат, определенной
соотношениями A.9) и A.10). Уравнение Лапласа имеет вид
A21) при р=0. Эта система координат очень удобна, так как
потенциал является периодической функцией координаты а
с периодом 2я. Поэтому его можно представить в виде ряда
Фурье [16]:
СО
u{r,a,z) = £ [am(r, z) cos та+bm (r, z) sin ma], C.1)
m=0
где ат и bm — коэффициенты Фурье, являющиеся функциями г
и z. Определим их. Для этого продифференцируем и по всем
65
Глава 3
координатам и подставим производные в уравнение Лапласа
A.21) при р = 0. В результате
Так как это уравнение справедливо для любых значений а, оба
выражения в скобках должны быть равны нулю. Поэтому име-
имеем два дифференциальных уравнения:
д2ат , 1 дат т2 д2ат п ,,, п>
дл2 г дг л2 "■ dz2 v
дг6/я , 1 д&т т2 , ' дгЬт п ,о An
определяющие для каждого т неизвестные функции ат и Ьт.
Будем искать эти функции в виде разложений в ряд по степе-
степеням г с коэффициентами, зависящими только от г:
am{r,z) =I1Ami{z)rm+\ C.5)
t = 0
bm(r,z) = LBmi{z)rm+l. C.6)
1 = 0
Эти степенные ряды имеют несколько странную форму. За-
Зачем нам нужна сумма (/ra+t) в качестве степеней г? Ниже бу-
будет ясно, что этот выбор приводит к относительно простой фор-
форме решения.
Вычисляя частные производные выражения C.5) и подстав-
подставляя их в C.3), имеем
(=0
— m*]Amlrm+i-*+A"mirm+l}=0. C.7)
Более удобно иметь выражение, содержащее только одну сте-
степень г. Этого можно достичь, если заменить i на (i+2) в пер-
первом члене суммы и начать суммирование с i = —2. Тогда
| (t + 2) {2т + 1+2)Ат{1+2)Гт+1 + £ Л|/Я1(г»+' = 0. C.8)
(=-2 ,=0
Это уравнение справедливо только в том случае, если коэффи-
коэффициенты при всех степенях г равны нулю. Однако можно заме-
заметить, что при i=—2 первый член исчезает для любых значе-
значений Ат0. В случае t = — 1 имеем
Л „1=0. C.9)
66
Определение электрических и магнитных полей
(По этой причине мы выбрали «странную» форму степенных
рядов.) Остальные коэффициенты должны удовлетворять ре-
рекурсивному соотношению
Немедленно замечаем, что вследствие C.9) и C.10) все ко-
коэффициенты с нечетным вторым индексом равны нулю:
ЛтBй+1)=0 F=0,1,2,...). C.11)
Начнем теперь с £=0. Обозначим
Am0 = Um C.12)
и, подставляя в C.10), получаем
Am2 = —U"m/4(tn+l). C.13)
Полагая 1=2 в уравнении C.10) и подставив в C.13), находим
следующий коэффициент:
,,iv
л Ч-™ f 3 14Л
т4 42х2(/п+1)(т + 2) ^ '
Легко видеть, что общее выражение имеет вид
^ ^0,U2,...). C.15)
Аналогично из уравнения C.6) получаем
Bm{2k+i) = 0 (k=0, 1,2,...) C.16)
и, обозначая
Bm0 = Wm, C.17)
имеем
iwBft)
^«u,-(-D*4*«c+i)c+a)-(«+*)(*a0' 1( 2> ■••)- (ЗЛ8)
Подставляя C.11)—C.18) в C.5) и C.6), заменяя суммиро-
суммирование по i суммированием по k и затем подставляя в C.1), по-
получаем конечный результат
и(г, а, г)- ££ ^щт+т \T() + T{)
m=°fe=° C-19)
В этом соотношении все три переменные разделены. Как мы
увидим ниже, метод разделения переменных является одним из
67
Глава 3
нескольких подходов к аналитическому определению распреде-
распределений потенциалов. Таким образом, произвольное распределе-
распределение потенциала представлено бесконечным набором функций
Um(z) и Wm(z), зависящих только от координаты z. Если из-
известны все эти функции и все они бесконечно дифференцируе-
дифференцируемы, то мы знаем распределение потенциала по всему простран-
пространству.
Физический смысл этих функций зависит от вида симметрии
в решаемой задаче. Применим соотношение C.19) к различ-
различным типам симметрии. В данном случае рассмотрим простой
случай аксиальной (или осевой) симметрии. Аксиальная сим-
симметрия означает, что потенциал симметричен относительно
оси z, т. е. не зависит от угла а. Зависимость от а можно уст-
устранить, полагая т = 0. Тогда, заменив Uo на U в C.19), полу-
получаем выражение
{' )==h—^—
= U (г) - U" (г) г2/4 + (/IV B) г*/64 - (/VI (г) г6/2304 +-..., C.20)
включающее только одну функцию U(z), физический смысл
которой очевиден. В самом деле, полагая г=0, получаем рас-
распределение потенциала вдоль оси симметрии u(o,z) и видим,
что
£/(z)=u@,z). C.21)
Другими словами, если известно аксиальное распределение
U (г) вращательно-симметричного электростатического или маг-
магнитного поля и это распределение является бесконечно диффе-
дифференцируемой функцией, то можно определить поле во всем про-
пространстве с помощью разложения в степенной ряд C.20). Един-
Единственно, что для этого необходимо знать — аксиальное распре-
распределение потенциала. Это очень важный момент, и мы еще не
раз к нему вернемся. Детальное обсуждение будет проведено
в разд. 9.8.
Рассмотрим теперь, как преобразуется соотношение C.19)
при переходе к декартовой системе координат. Используя фор-
формулу Муавра для комплексных показателей степени
(х + jy)m = [r(cosa+j sina)]m =
= rm(cosma+/sin ma), C.22)
где /'= (—1)'/! — мнимая единица, получаем
m*
cos ma-X 47(m-H)i cos-"'asin*Gr, C.23)
68
Определение электрических и магнитных полей
где
* _ fm/2, если т четное,
\ (т— 1)/2, если т нечетное,
L^__COs»-*'-1asinl'+1a, C.25)
где
т/2 — 1, если т четное и тфО,
т** = 0, если т = 0, C.26)
(т—1)/2, если т нечетное.
Используя эти выражения вместе с соотношениями A.9), свя-
связывающими декартовы и цилиндрические координаты, перепи-
перепишем C.19) в виде
СО 00
и(х и г)=У У±г1)*«'.(*!+Як~
т=0 k-0
1)' m! j-я-21-1 ,.2i+l
(«-2/-l)! * У J"
I TV7C2&) (z\ Sr (—1)' m! j-я-21-1 ,.2i+l ГЧ 97\
itS Bf+l)l(«-2/-l)! * У J" ^ }
Это общее выражение для произвольного распределения по-
потенциала в декартовой системе координат. Оно по-прежнему
зависит от Um и Wm, являющихся функциями координаты г.
Выведенное соотношение весьма громоздко, но его можно упро-
упростить при наличии какой-либо симметрии.
Существует бесконечное разнообразие различных сочетаний
типов симметрии. Соотношения C.19) и C.27) включают все
возможные случаи. Например, электронная или ионная оптиче-
оптическая колонна, используемая для микротехнологии ИС, может
состоять из электростатических и (или) магнитных аксиально-
симметричных и мультипольных линз, дефлекторов, бланкирую-
щей системы, масс-анализатора и т. п. Кроме того, необходимо
принять во внимание возможные отклонения от симметрии, вы-
вызванные разъюстировкой и дефектами сборки. Таким образом,
если мы хотим рассмотреть всю колонну в целом или только
совокупность аксиально-симметричных линз и двух взаимно
перпендикулярных отклоняющих полей, необходимо начать
с полученных общих выражений. Ниже будет видно, как нали-
наличие различных типов симметрии приводит к существенному
упрощению этих соотношений.
69
Глава 3
Аксиально-симметричное распределение потенциала C.20)
легко получить из C.27), приравняв нулю все коэффициенты
Um и Wm, за исключением [/о-
3.1.1.1. Планарные поля. Если потенциал не зависит от од-
одной из декартовых координат, имеем двумерное или планарное
поле. Для такого поля общая картина силовых линий является
неизменной в плоскостях, перпендикулярных выбранной коор-
координате. Ввиду того что координата z является выделенной в со-
соотношении C.27) и мы обычно выбираем эту координату как
направление распространения частиц, можно выделить два важ-
важных типа планарных полей.
В первом случае потенциал не зависит от одной из коорди-
координат х или у. Выпишем последовательные члены соотношения
C.27) для первых значений m и k. Получим следующее выра-
выражение для членов, содержащих степени х и у не выше четвер-
четвертой:
и(х, у, z) = Uo+ £/,*+ W,y+ (£/2 - £/о74)х2 —
— (U2 + U0"/4)y2+2W2xy+ (£/3 - £/,"/8)*3 +
+ CW3 — WflWy — C£/s + f//78) xy2 —
(f/4 - £//712+ £/,>'v/64)x* +
)x*y+ (f/0IV/32 - 6U,)x2y2 -
(£/,,>v/64+ £/2712+ £W+ .... C.28)
Потребуем теперь, чтобы потенциал не зависел от коорди-
координаты х. Тогда коэффициенты при всех членах, содержащих
любую степень х, должны равняться нулю:
Uh=Ui=W2=Wt = 0, £/а = £//74,
U73= ^,724, U, = £//712 — £/0lv/64,= £/0IV/192 и т. д.
C.29)
Принимая эти соотношения во внимание, упростим C.28):
и (у, z)=U0+ W,y - £/oV/2 - Wy4G + UolvyV24 +....
C.30)
Легко обобщить это выражение и включить отсутствующие
члены высшего порядка:
Аналогичное выражение можно получить для планарного поля,
не зависящего от координаты у.
70
Определение электрических и магнитных полей
Это примечательный результат. Простой факт отсутствия
зависимости потенциала от координаты х позволяет устранить
все функции, кроме двух, из бесконечного набора функций раз-
разложения в ряд. Физический смысл оставшихся двух функций
легко понять. В самом деле, очевидно, что
Uo(z)=u{0,z), C.32)
- C-33)
Соотношение C.32) аналогично C.21), и обозначение £/0 сохра-
сохраняется только для того, чтобы отделить этот случай от аксиаль-
аксиально-симметричного. Величина £/о обозначает распределение по-
потенциала в плоскости xz, что эквивалентно распределению по-
потенциала вдоль оси z, так как потенциал не зависит от х. W\
представляет собой поперечную компоненту поля вдоль этой же
оси (с отрицательным знаком), и в случае электростатического
поля это не что иное, как отклоняющая компонента. Таким об-
образом, произвольное планарное поле полностью определяется
соответствующими аксиальными распределениями потенциала
и отклоняющей компоненты поля.
Читатель, сомневающийся в справедливости вывода соотно-
соотношения C.31), может вывести его, начав с простого разложения
в ряд
СО
и (у, г) =LVl(z)yt. C.34)
Коэффициенты Vi могут быть определены из уравнения Лапла-
Лапласа A.20) в декартовых координатах при р = 0 и д2и/дх2 = 0.
С учетом C.32) и C.33) легко получается выражение u(y,z) в
виде C.31).
Если планарное поле симметрично относительно плоскости
xz, то имеет место соотношение
и(у,г)=и(— у, г). C.35)
Поэтому нечетные степени у должны отсутствовать при разло-
разложении в ряд (Wi=0). Тогда потенциал симметричного планар-
ного поля имеет вид
= U0(z)-U;(z)yV2 + Ulv(z)yV24- + ... . C.36)
Весьма поучительно сравнить этот ряд с выражением C.20)
для аксиально-симметричного потенциала. Как видно, оба вы-
выражения имеют одинаковую структуру, но с различными коэф-
71
Глава 3 __
фициентами. Этого и следовало ожидать: оба поля симметрич-
симметричны, но с разными типами симметрии.
Планарно-симметричное поле полностью определяется рас-
распределением потенциала в плоскости симметрии.
В случае антисимметричного потенциала разность потенциа-
потенциалов между любой точкой (у, г) и соответствующей точкой @, z)
в плоскости симметрии в точности равна аналогичной разности
потенциалов с другой стороны плоскости симметрии, но взятой
с обратным знаком:
и(у, г) - к (О, z) =_[и(-у,2) - «(О, г)]. C.37)
Это означает, что только нечетные члены, содержащие у, оста-
остаются в соотношении C.31). Поэтому (за исключением распре-
распределения потенциала в плоскости антисимметрии) в разложении
остаются только отклоняющие компоненты. В случае электро-
электростатического поля это чисто отклоняющее распределение по-
потенциала. Простейшим примером антисимметричного поля яв-
является плоский конденсатор, показанный на рис. 5 (yz — плос-
плоскость антисимметрии).
Есть также второй особый случай планарного поля, когда
потенциал не зависит от координаты г. В этом случае коэффи-
коэффициенты U и W в C.27) являются постоянными, все производные
равны нулю F = 0) и соотношение существенно упрощается.
Важным приложением этого случая является планарное мульти-
польное поле (разд. 3.1.1.3).
Используя соотношения A.17) и A.22), легко выписать все
компоненты электростатического и магнитного полей, если за-
заданы соответствующие скалярные потенциалы в форме рассмот-
рассмотренных выше степенных рядов. Это и будет сделано для акси-
аксиально-симметричного поля.
3.1.1.2. Аксиально-симметричное поле. Нам уже известно
разложение в ряд аксиально-симметричного скалярного потен-
потенциала. Если и — электростатический потенциал, то из выраже-
выражений A.10), A.13), A.17) и C.20) легко найти компоненты про-
произвольного аксиально-симметричного электростатического поля
в виде степенных рядов от радиуса с коэффициентами, содер-
содержащими производные от аксиального распределения потенциа-
потенциала. В результате
F —_iii —V (~\)k+
дг ~t?x kH
= U" (г) r/2~Ulv (z) r3/16 + —.... C.38)
72
Определение электрических и магнитных полей
2
= — U' (г) + U" (г) г2/4 —L'v (г) г*/64 + — C.40)
Рассмотрим точку z=0 на оси г. На небольшом расстоянии
Az от этой точки аксиальный потенциал представляется рядом
Тейлора
U(Az)=U@)+AzU'@) + {AzJU"@)/2+.... C.41)
Дифференцируя это выражение дважды и подставляя в первый
член выражения C.20), получаем выражение для потенциала
на небольшом расстоянии Лг от оси. Если потенциал в точке с
координатами Ar, Az равен аксиальному потенциалу в точке.
2 = 0, получаем форму эквипотенциальной линии U@) из
и (Ar, Az) U@)=U @) + AzU' @) +
+ (AzJU"@)/2— (ArJ£/"@)/4. C.42)
Это уравнение гиперболы в меридиональной плоскости rz. Та-
Таким образом, эквипотенциальные поверхности представляют со-
собой гиперболоиды в окрестности оси г, за исключением следу-
следующего случая.
Если поле отсутствует в точке @,0), его z-компонента долж-
должна быть равна нулю. Тогда соотношение C.40) дает £/'@)=0,
и, подставляя в C.42), получаем уравнение эквипотенциальной
линии в простой форме
Ar/A2=2'/2. C.43)
Это означает, что в такой седловой точке эквипотенциальные
линии образуют двойной конус с половинным углом, равным
arctg 21/2 = 54°44'08" (рис. 10). Как видно из C.42), при от-
отклонении от седловой точки потенциал возрастает в любом на-
направлении вдоль оси z и спадает вдоль г, если f/"@)>0. (Для
отрицательных значений £/"@) справедливо обратное.)
Интересно отметить, что в симметричном планарном поле эк-
эквипотенциальные линии пересекаются в седловой точке под уг-
углом 90°. Чтобы показать это, необходимо подставить выражение
C.41) и его вторую производную в C.36).
Если подставить магнитный скалярный потенциал о» вместо
и и его аксиальное распределение Q(z) вместо U(z) в уравне-
уравнение C.20), то можно получить компоненты магнитной индукции
В, используя уравнение A.22). В этом случае удобнее исполь-
использовать аксиальное распределение B(z) собственно магнитной
73
Глава 3
индукции, чем аксиальное распределение скалярного потенциа-
потенциала. Эти две величины связаны соотношением
C.44>
Компонентами магнитной индукции являются
C.45)
C.46)
C.47)
Эти выражения справедливы даже в том случае, если магнит-
магнитная индукция генерируется токами. Как мы видим, аксиаль-
аксиальное распределение магнитной индукции однозначно определяет
поле во всем пространстве.
Рис. 10. Эквипотенциальные линии
в окрестности седловой точки акси-
ально-симметричиого электростати-
веского поля.
Рис. 11. Комбинированная электро-
статическая и магнитная мультиполь-
ная система.
3.1.1.3. Мультипольные поля. Рассмотрим теперь один из
важных типов полей, характеризующихся наличием N одина-
одинаково расположенных плоскостей симметрии или антисимметрии.
В принятой нами системе обозначений эти плоскости перпенди-
перпендикулярны плоскости ху. Поскольку такие поля всегда можно
построить с помощью набора электродов и полюсов, они назы-
называются мультипольными полями. Обычно они используются как
фокусирующие, отклоняющие и корректирующие элементы в
электронной и ионной оптике (см. гл. 10 и 11).
74
Определение электрических и магнитных полей
Типичное мультипольное поле показано на рис. 11. Система
состоит из четырех электродов и четырех магнитных полюсов.
Сплошными и штриховыми линиями показаны соответственно
электростатические и магнитные силовые линии. Система име-
имеет две выделенные плоскости ху и yz, являющиеся плоскостя-
плоскостями симметрии для электростатического поля и антисимметрии
для магнитного.
Так как электроды и полюса имеют конечную длину, муль-
польное поле, вообще говоря, может быть описано только в
трех измерениях. Наличие симметрии, однако, позволяет упрос-
упростить общее выражение C.19). В самом деле, для системы из
N одинаково расположенных плоскостей симметрии (если xz—
одна из них) имеем
u(r, a, z)=u(r, — a, z), C.48)
u(r,a,z)=u(r,a±2nl/N,z) A=1, 2,.... N— 1). C.49);
Отметим, что предположение о наличии плоскостей симметрии
несколько произвольно. Например, магнитное поле на рис. 11
имеет только плоскости антисимметрии. Однако фактически су-
существующую симметрию всегда можно учесть. Поэтому наш
выбор плоскости xz в качестве плоскости симметрии будет ис-
использован только как рабочая гипотеза для демонстрации при-
применения симметрии с целью упрощения выражений.
Вследствие C.48) степенной ряд не может содержать нечет-
нечетных функций от а. Поэтому члены, содержащие sin (та), исче-
исчезают. Далее, подстановка C.49) в остающиеся члены выраже-
выражения C.19), содержащие а, дает
cosma=cos(mad-2nml/N), C.50)
откуда следует, что ml/N должно быть целым числом. Это бу-
будет заведомо выполнено, если положить
m=nN (га = 0, 1, 2, ...). C.51)
С учетом этого соотношения можно переписать выражение
C.19) для мультипольного поля, содержащего N плоскостей
симметрии, следующим образом [61]:
и [г, a, z) = 2- 2-
= 2 AnN(r, z)rnNcosnNa, C.52)
f!=0
75
Глава 3
где
4(„л/+1) ~*~ 32 («Л/+1) («Л/+2)
384(я#+1)(яЛ/+2)(яЛ/ + 3) "■" 6144 ;«
& (г)
122880 (nN + l) (nN+2) (nfll +3) {nN -\-4) (nN + 5)
^1 (г)
"*■ 2949120 (nN+l) (nN + 2) (яЛ'н 3) ( + ) ( + ) ( + )
C.53)
Первый член До (г, г) ряда C.52) дает аксиально-симмет-
аксиально-симметричную компоненту потенциала C.20). (Напомним, что в C.20)
Uo было заменено на U.) Присутствие этой компоненты неуди-
неудивительно. В самом деле, аксиально-симметричное поле имеет
бесконечное число плоскостей симметрии, перпендикулярных
плоскости ху. Оно имеет более высокую симметрию, чем муль-
типольное поле с конечным числом Af плоскостей симметрии.
Поэтому общее выражение для мультипольного поля должно
включать специальный случай аксиально-симметричного поля.
Естественно, это не означает, что каждое мультипольное поле
содержит аксиально-симметричную компоненту. Если эта ком-
компонента отсутствует, имеем U0(z) =const.
Выпишем следующие шесть коэффициентов Апы'-
— г10 Uxx (z) /88473600 + — ..., C.54)
A2(r,z)=U2(z)— r*U2"(z)/\2 + r*U2iV(z)/384 ~
— r*U2vl (z)/23040+r8£/2VI11 B) /2211840 —
— r10 U2X (z) /309657600 + — ..., C.55)
— r*U3vl (z) /46080+r8£/3VI u(z) /5160960— + ..., C.56)
(z)/80640+r8t/4VIU (z)/10321920— + ..., C.57)
A5(r, z) = Ub{z) — r*Ub"(z)l24 + r*UbiV(z)ll3U -
~r6i/5vl B)/129024 + —..., C.58)
A6(r, z) =Us(z) — r*U6"(z)/28 + r*Us™(z)/1792 -
— r6f/6VI {z) /193536 + — .... C.59)
76
Определение электрических и магнитных полей
Определение функции ипн(г) в общем случае серьезная про-
проблема. В простых практических случаях можно использовать
аппроксимацию (см. разд. 3.1.3.1).
Легко видеть, что
гя*=[х2+у2)к. C.60)
Можно также, подставив A.9) и C.51) в C.23), получить
rnNcosnNa— V (—')' ("W)l яу-а/„и C 6П
Г СОьЛ/va-^ * У {>iOl)
^ Bi)!(nJV—2i)! * У
где {nN)* определено соотношениями C.24) и C.51). Подстав-
Подставляя эти выражения в C.52), получаем распределение потен-
потенциала мультипольного поля в декартовых координатах. Следу-
Следующие специальные случаи соотношения C.61) будут особенно
полезны:
/•cosa=*, C.62)
г2 cos 2a=х2 — у2, C.63)
г cos За=*3 — Зху2, C.64)
r4cos4a=x4 — 6х2у2+у\ C.65)
r5cos 5a=*5 — 10х*у2+5ху*. C.66)
г6 cos Fа) =х6 — у6— 15 (ху — х8^), C.67)
г7 cos Gа) =л? — 2lx5y2+35xY — 7ху6, C.68)
г8 cos (8а) =xs+ys — 28{х6у2+х2у6) +70хАу\ C.69)
г9 cos (9а) =х9 — 36х7у2+ 126х5у* — 84х3у6+9ху\ C.70)
г10 cos A0а) =х10 — у10 — 45 (хйу2 — х2у&) +210 (х?у* — х*у*),
C.71)
г 11 cos A1 а) = х11 — 55х V+330х7у4 —
— 462хУЧ 165х3^8 — 11 л#10, C.72)
/-12 cos A2a) =xl2+y12 — 66 (х1Оу2+х2у10) +
+ 495 (xV+*Y) — 924^6, C.73)
г14 cos A4а) =х14 — ^14 — 91 (х1 V — х2У12) +
+1001 (xlY — л:4^10) — 3003 (* V — хву8), C.74)
г15 cos A5а) =х15 — 105х1У + 1365х'V — 5005х9ув +
C.75)
C-76)
77
Глава 3
г18 cos A8а)=л:18 — у18 — 153 (х16у2 — х2у1*) +
+ 3060(л:14г/4 — х4г/14) — 185б4(д:12г/6 — х6у12) +
+ 43 758 (х1 V — хау10), C.77)
г20 cos B0а) =л:20 + г/20
2) — 184 756л:1 V0. C.78)
г21 cosB1a) =х21 — 210х™у2 + 5985х17у* — 54 264л:15#6 +
+ 203 490х13г/8 — 352 716л:пг/10 + 293 ЭЗОхУ2 —
— 116 280л:7#14+20349л:!У6 — 1330л:3^18 + 21дс^20, C.79)
г22 cos B2а) =х22 — у22 — 231 (х20у2 — х2у20) +
— *У8) — 74613 (л:16^6 — х6у16) +
— х*уы) — 646 646(д:12г/10 —л;10»/12), C.80)
г24 cos B4а) =хи+уи — 276 (х22у2+х2у22) +
+ 735471 (xl6ys+xsy16) — 1 961
+ 2 704 156л:1 V2 C.81)
и т. д. Для симметрии третьего порядка, например, мы должны
использовать значения nN-=0, 3, 6, 9, 12, 15, 18, 21, 24 и т. д.
Заметим, что вышеприведенные выражения содержат не все
возможные значения nN от 1 до 24, так как 13, 17, 19 и 23 яв-
являются простыми числами, они понадобятся только в том слу-
случае, если а) JV=1, а п простое число, либо б) л=1, а N простое
число. Ввиду того что обычно используется не более 10—12 чле-
членов разложения, первый случай встречается не часто. Второй
случай относится к симметриям 13, 17, 19-го порядка, имеющим
небольшое практическое значение.
Вышеприведенные выражения выглядят не очень привлека-
привлекательно, но являются весьма полезными. Возьмем, к примеру,
симметрию 2-го порядка (jV = 2). Уравнения C.52), C.20),
C.55), C.57), C.59), C.60), C.63), C.65) и C.67) дают сле-
следующее общее выражение для членов, включающих шестую
степень координат хну:
и (х, y,z)=A0 (r, z) +A2 (r, z) r2 cos 2a+
+Л4 (г, z) r4 cos 4a+A6 (r, z) r6 cos 6a+ ... =
= £/o(z) - Uu"{z) {x2+y2)IA+U0"(z) (x2+y2J№-
- U0^(z) (x2+y2)*/2304 + U2(z) (x*—y2) —
— U2"(z) (л:4 — #4)/12+£/2]vB)
+ UA(z) (л:4 — 6x2y2+y*) — UA"(z) (x2+y2) {х* —
+ U6 (z) [Xе - y6 - 15л:У (х2-у2)]+... . C.82)
78
Определение электрических и магнитных полей
В отсутствие аксиальной симметрии члены, содержащие
Uо (z) и соответствующие производные, отсутствуют. Кроме то-
того, если система имеет две дополнительные плоскости антисим-
антисимметрии (рис. 12), взаимная замена координат х и у должна
изменить знак потенциала. Поэтому C4(z) и соответствующие
производные должны равняться нулю. В этом случае соотно-
соотношение C.82) упрощается до [62J
]х*уЦх2 — у2)+..., C.83)
где
К6 B) = U6 (z) + U2iv (z) /384. C.84)
Из C.65) — C.81) легко видеть, что в этом особом случае не
только Л4, но и все Ain члены с индексом, кратным 4, исчезают
из C.52). Функции U2(z) и Къ{г) могут быть определены чис-
численными методами или (в некоторых простых случаях) анали-
аналитически.
Разложение в степенной ряд C.52) существенно упрощает-
упрощается, если потенциал не зависит от координаты z (планарное
мультипольное поле). В этом случае коэффициенты АП]>т(г, z)
(и соответствующие функции C/nw(z)) являются в точности по-
постоянными. Тогда имеем для случая N — 2
+ U6 [*• - у6 ~ 15*у (х2 - у2) ]+.... C.85)
Постоянные могут быть определены из геометрии и условий
подключения электродов или полюсов (см. разд. 3.1.3.2).
Проанализируем теперь физический смысл выражения C.52).
Мы уже видели, что член, соответствующий п = 0, описывает
аксиально-симметричную компоненту поля. Что представляют
собой остальные члены? Соответствующие потенциалы можно
записать в виде
U (Г, a, Z) | „jv=m=const = 4m(r, z)rm COS ШО.. C.86)
Если для простоты снова ограничиться планарным полем, то
Ат постоянно и сечение поля при любом фиксированном значе-
значении z определяется эквипотенциальными линиями rmcos(ma) =
= const. Выражения для левой части этого уравнения даются
соотношениями C.62) — C.81) для различных значений т.
79
Глава 3
Если m=l, из C.86) и C.62) имеем и(х,у) =AiX. Это —
уравнение распределения потенциала бесконечно^ плоского
конденсатора (диполя).
Для т = 2 соотношения C.86) и C.63) дают
и(х,у)=А2(х2 — у2). C.87)
Это распределение потенциала индуцируется идеальным квадру-
полем, т. е. четырьмя идентичными бесконечными гиперболиче-
гиперболическими поверхностями с чередующимися положительными и от-
отрицательными потенциалами (рис. 13).
\
Рис. 12. Квадруполь с двумя пло- Рнс. !3. Идеальный квадруполь
скостями антисимметрии (штриховые (сплошные линии — эквипотеициаль-
линии). ные, штриховые-—силовые линии).
Этот процесс можно продолжить для любых других значений
га. Распределение потенциала вида C.86) всегда может быть
получено с помощью 2га бесконечных гиперболоподобных по-
поверхностей с чередующимися высоким и низким потенциалами.
(Заметим, что в предельном случае, га=1, поверхности вырож-
вырождаются в две параллельные плоскости.) Сечение такой системы
для 2т = 8 показано на рис. 14. Из-за наличия восьми полюсов,
она называется октуполем. Аналогично 2т = 6 соответствует
гексаполю (или секступолю), 2т=10 — декаполю, 2/п=12 — до-
декаполю и т. п. Так как т — tiN, можно считать, что данное зна-
значение га соответствует N=m и л=1. Теперь можно рассмотреть
первый член ряда C.52) при различных N. Мы только что ви-
видели, что с помощью 2N бесконечных поверхностей с чередую-
чередующимся потенциалом можно всегда воспроизвести распределения
потенциала, соответствующие первому члену. Поэтому назовем
такие распределения идеальными 2N мультиполями. Они иде-
идеальны в том смысле, что не содержат гармоник выше п=1.
Бесконечный плоский конденсатор является идеальным дипо-
диполем, а система из четырех бесконечных гиперболических по-
80
Определение электрических и магнитных полей
верхностей — идеальным квадруполем. В общем случае система
с N плоскостями симметрии всегда может быть представлена
2N электродами или полюсами. Если они имеют форму и по-
потенциал, определяемые уравнением C.86), то высшие гармони-
гармоники исчезнут при разложении распределения потенциала в ряд
C.52). Если же 2N полюсов имеют N плоскостей симметрии, но
не соответствуют идеальным характеристикам, при разложении
распределения потенциала в ряд возникнут высшие гармоники.
Например, квадрупольная система, показанная на рис. 15, име-
имеет бесконечный набор высших гармоник, так как форма элект-
электродов весьма далека от идеальной, приведенной на рис. 13. На
самом деле даже последняя не является идеальным квадрупо-
Рис. 14. Октуполь.
Рис. 15. Квадруполь.
лем из-за конечности электродов. Вследствие того что бесконеч-
бесконечные поверхности не могут быть реализованы на практике, иде-
идеальные 2М-мультиполи реально не существуют, а могут быть
только аппроксимированы с той или иной точностью (см. разд.
3.1.3.3). Высшие гармоники возникают также из-за неидеально-
неидеальности конструкции мультипольных элементов.
Высшие гармоники соответствуют мультиполям высших по-
порядков. Согласно вышеизложенному, л-й член в C.52) для за-
заданного N можно интерпретировать как первый член 2пЫ-мулъ-
типоля (или единственный член идеального 2гаЛг-мультиполя).
Например, второй член разложения в ряд квадруполя (N=2)
соответствует идеальному октуполю BnN = 8), третий член —
идеальному додекаполю BnJV=12) и т. п. Некоторые из этих
мультипольных компонент можно устранить введением допол-
дополнительной симметрии (например, октупольная компонента исче-
исчезает из симметрично-антисимметричного квадруполя, показан-
показанного на рис. 12).
Глава 3
Рис. 16.
поля.
Еще одни пример квадру-
Означает ли это, что необ-
необходимо 2JV электродов или по-
полюсов для создания 2#-муль-
типоля? Положительный ответ,
казалось бы, очевиден. Одна-
Однако истинный ответ — нет. Рас-
х смотрим, например, два элект-
электрода, показанные на рис. 16.
Система имеет две плоскости
симметрии? Конечно. Тогда
это квадруполь. Где же недо-
недостающие два полюса? Они в
эквипотенциальной картине.
Так как потенциал обращает-
обращается в нуль на бесконечности,
эквипотенциальные линии ав-
автоматически формируют квадрупольную картину (с высшими
гармониками). На самом деле нет необходимости даже в двух
электродах при формировании квадруполя. Две симметрично
расположенные щели в одиночном цилиндрическом электроде
дадут аналогичный эффект в окрестности щелей [63J. Можно
создать даже систему квадруполей, вырезая щели конечной
длины в разных плоскостях. Были предложены интересные
мультипольные системы, состоящие из малого числа электро-
электродов, некоторые из них будут показаны ниже (см. рис. 38).
Основная характеристика 2М-мультиполя не количество по-
полюсов, а наличие N плоскостей симметрии в распределении по-
потенциала [64J. Мы увидим в разд. 3.1.3.3, каким образом на ос-
основе этого факта можно достичь отличной аппроксимации иде-
идеальных мультиполей.
3.1.2. Аналитическое вычисление
аксиально-симметричных потенциальных полей
Подавляющее большинство фокусирующих элементов, ис-
используемых в электронной и ионной оптике, создают аксиально-
симметричные электростатические и (или) магнитные поля, ко-
которые могут быть описаны скалярными потенциалами. Нам уже
известно их представление в виде рядов (разд. 3.1.1.2). Попы-
Попытаемся вычислить такие поля с помощью точных аналитических
методов.
3.1.2.1. Разделение переменных. Цилиндрическая система ко-
координат удобна для вычисления аксиально-симметричных по-
полей, так как их потенциалы не зависят от координаты а. Поэто-
82
Определение электрических и магнитных полей
му уравнение Лапласа A.21) в отсутствие пространственного
заряда можно записать в виде
JLJL ( ди \ д%и — П (Ч 88\
г дг V дг ) + дг2 ~ V • /
Будем искать решение этого уравнения в виде произведения
двух функций Д(г) и Z(z), каждая из которых зависит от одной
переменной. Записывая
и (г, z)t=R (r) Z (z) + const, C.89)
разделяем переменные г и z. Дифференцируя это выражение и
подставляя в C.88), получаем
Мы приравняли обе части уравнения — &2=const, так как одна
из них зависит только от г, а другая — только от z. Равенство
возможно только в том случае, если каждая из частей равна од-
одной и той же постоянной величине. Вообще говоря, k2 может
быть любым числом. Тогда уравнение C.90) распадается на
Два:
■g-*«Z = 0, C.91)
(*'J+*'+W* = 0. C.92)
Решение уравнения C.91) есть
, C.93)
где постоянные интегрирования Ah и Bh могут быть определе-
определены из граничных условий (естественно, они зависят от k).
Уравнение C.92) является особым случаем уравнения Бес-
Бесселя:
х2у"+ху' + (х2 — п*)у=0 C.94)
(штрих обозначает дифференцирование по х, а л — любое чис-
число) при x=kr, y = R и п = 0. Общее решение уравнения C.94)
есть
у (х) = din (х) + С2/_„ (х), C.95)
где
/ /у)-У (-1
Глава 3
есть функция Бесселя первого рода л-го порядка, Г — гамма-
функция, Ci и Сг — постоянные интегрирования. J^n(x) можно
вычислить с помощью этого же ряда путем замены п на —п.
В общем случае Jn(x) и J-n(x) являются независимыми реше-
решениями. Однако если п — целое число, то
/-*(*).= (—1 )»/„(*). C-97)
Это означает, что решения уравнения C.94) зависят друг от
друга. Поэтому, если п — целое число, то второе решение урав-
уравнения C.95) должно быть заменено другой функцией Nn(x)
(функцией Неймана л-го порядка). В нашем особом случае п =
= 0 необходимо положить С2 = 0 для всех k, так как N0(kr)
стремится к бесконечности при г—0 (потенциал не может иметь
бесконечное значение). Получаем
R(r)=ClkJ0(kr). C.98)
Подставляя C.93) и C.98) в C.89), имеем
u(r, z) = {Ckek*+Dke-k*)l0{kr) -fconst, C.99)
где Ck и Dh — новые постоянные, подлежащие определению из
граничных условий. Так как для целых v
r(v+l)=v!, C.100)
имеем
Z У 64 -*«/2304 + -....
v=o l '
C.101)
Сравните это выражение с общим выражением разложения
в ряд C.20) для аксиально-симметричных полей. Вас не удив-
удивляет их сходство? Вероятно, нет, так как оба ряда относятся к
одному классу полей. Какое различие между ними? Выражение
C.20) можно использовать только в том случае, если известно
аксиальное распределение потенциала. Если это простой поли-
полином, бесконечный ряд автоматически обрезается (высшие про-
производные от аксиального распределения потенциала обраща-
обращаются в нуль). С другой стороны, постоянные в C.99) зависят
от граничных условий, и функция Бесселя всегда дает беско-
бесконечный ряд C.101). Конечно, можно предположить, что грани-
границей является ось симметрии, тогда оба выражения становятся
идентичными. Это будет продемонстрировано на примере прос-
простой гармонической функции, взятой в качестве аксиального рас-
распределения потенциала. Мы увидим, что в этом случае степен-
степенной ряд C.20) дает функцию Бесселя.
£4
Определение электрических и магнитных полей
Если k — вещественно, во избежание бесконечных значений
потенциала можно использовать C.99) как решение для поло-
положительных kz только при С;{=0, либо для отрицательных kz
при Dft = 0. Далее решение распространяется на все пространст-
пространство с учетом симметрии. В общем случае в отсутствие дополни-
дополнительной симметрии относительно плоскости 2=0 следует счи-
считать k мнимой величиной:
/г=/и, C.102)
где /=(—1I/2— мнимая единица, и — вещественно. Используя
модифицированную функцию Бесселя
/„(*)=/-"/„(/*), C.103)
можно записать
и (г, z) = [Gx cos az+Fx sin xz]/0 {кг) -fconst, C.104)
где Gx и F»— новые постоянные интегрирования.
Выражение C.104) является решением уравнения Лапласа
для аксиально-симметричного поля. Однако оно не является об-
общим, это всего лишь решение для произвольно выбранного зна-
значения х. Общее решение получим, если построим суперпозицию
решений, соответствующих каждому возможному значению х.
Так как х может принимать любое вещественное значение, для
этого необходимо взять интеграл по всем значениям к от минус
до плюс бесконечности:
и (г, z) = $ [
C.105)
Наличие общего выражения не исключает применения более
простых. В простых случаях возможно построение таких конфи-
конфигураций электродов или полюсов, которые полностью описыва-
описываются простым выражением C.104). Рассмотрим, например, пе-
периодическое поле, заданное аксиальным распределением потен-
потенциала
U(z) = U0cosBnz!p), C.106)
где р — период поля. Дифференцируя эту функцию 2v раз, под-
подставляя производные в C.20) с учетом C.101) и C.103), полу-
получаем распределение потенциала во всем пространстве
v = 0
C.107)
Сопоставляя это выражение с C.104), можно заметить их иден-
идентичность при условии к = 2п/р, GX=UO и /?х=0. Форму электро-
85
Глава 3
дов (полюсов), производящих такое распределение потенциала,
легко получить из C.107) приравниванием и (г, z), заданным
значениям потенциала. Некоторые специальные формы электро-
электродов приведены в [42, p. 310J.
Этот пример показывает, что отдельные конфигурации элект-
электродов (полюсов) могут приводить к единственному значению и.
К сожалению, это имеет место не слишком часто. В частности,
аксиальное распределение потенциала от периодической систе-
системы электродов (например, последовательности одинаково рас-
расположенных цилиндрических электродов с чередованием пони-
пониженного и повышенного потенциала) можно представить только
бесконечным рядом Фурье с бесконечным набором дискрет-
дискретных к. Соответственно интегрирование в C.105) можно заме-
заменить суммированием, но для описания распределения потенциа-
потенциала одного значения к недостаточно.
Выражение C.105) можно использовать для вывода другой
общей формулы. Простая связь синуса, косинуса и экспонен-
экспоненциальной функции (формула Эйлера) позволяет переписать
C.105) в виде
со
u(r,z) = $ G(к)exp[jx.z]Iо(xr)dx +const. C.108)
—со
Так как интегрирование ведется от минус до плюс бесконечнос-
бесконечности, нет необходимости включать сюда отрицательную экспонен-
экспоненту, и мы имеем только одну постоянную интегрирования G(x).
Модифицированная функция Бесселя нулевого порядка может
быть также представлена интегралом [16]
/о (хг) = A/я) I exp[— xr cos G] Д>. C.109)
о
Подставляя в C.108), имеем
C.110)
Полагая г=0 в этом выражении, приходим к аксиальному рас-
распределению потенциала:
со
U(z) = S G(и)exp[jxz]d% + const. C.Ill)
■—oo
Это выражение прямо следует из C.108).
Так как порядок интегрирования в C.110) может быть из-
изменен, а оба выражения C.110) и C.111) содержат одинаковые
постоянные, из двух последних выражений следует
«(r,z) = (l/n)S£/(z+/rcosG)<flK C.112)
о
86
Определение электрических и магнитных полей
Это выражение полностью эквивалентно разложению в степен-
степенной ряд C.20) и представляет тот же важный факт: аксиально-
симметричное поле полностью определяется своим распределе-
распределением потенциала вдоль оси. (Заметим, что Ь — просто перемен-
переменная интегрирования и не имеет физического смысла.) Хотя вы-
выражение C.112) изящнее, чем бесконечный степенной ряд
C.20), его практическое значение ограничено трудностью чис-
численного представления комплексного аргумента функции акси-
аксиального распределения потенциала (более детальное обсужде-
обсуждение приводится в разд. 9.8).
Рассмотрим простой пример поля с аксиальным распределе-
распределением потенциала
U{z)=Az\ C.113)
Это поле нарастает с увеличением z до бесконечности, но всег-
всегда можно установить верхний предел потенциала, ограничив
поле электродом (полюсом), расположенным в точке с конеч-
конечной г-координатой. Подстановка этого выражения в C.112) и
последующее интегрирование дают
u(r,z) = (Ajn) S (z+jrcosftJdu=A(z2 — r2/2). C.114)
о
Эквипотенциальные поверхности представляют собой гипербо-
гиперболоиды, и потенциал в точности описывается выражением C.42).
Поле исчезает в седловой точке г = 2 = 0 (см. рис. 10).
Разделение переменных — весьма общий метод. И хотя он
не может быть использован в любой системе координат, в боль-
большинстве случаев ведет к упрощению решения.
3.1.2.2. Трудности аналитических вычислений (электростати-
(электростатическое поле двух цилиндров одного диаметра). Попытаемся ис-
использовать результаты предыдущего раздела для аналитическо-
аналитического расчета очень простого аксиально-симметричного фокусиру-
фокусирующего элемента. Он состоит из двух бесконечно длинных и тон-
тонких коаксиальных цилиндров одинакового радиуса R, разделен-
разделенных зазором s. Левый цилиндр имеет потенциал Уь правый —
V2 (рис. 17). В случае магнитного поля система состоит из
симметричных полюсов в ненасыщенном состоянии с внутрен-
внутренним радиусом R и зазором s. Требование бесконечной протя-
Рис. 17. Два цилиндра одинакового
диаметра, разделенные зазором s.
87
Глава 3
женности не является жестким, если источник и мишень распо-
расположены внутри цилиндров и имеют одинаковый с ними потен-
потенциал. Никакая реальная система не может быть бесконечно
тонкой, но влиянием конечной толщины можно пренебречь, по
крайней мере для малых значений s/R. Таким образом, рассмат-
рассматриваемая система очень проста и может быть использована на
практике.
Вследствие симметрии относительно плоскости 2=0, прохо-
проходящей по середине зазора между цилиндрами, имеем
u(r,0) = (Vl + V2)/2. C.115)
Подставляя это соотношение в C.105), сразу видим, что Gx=0,
а постоянная дается выражением C.115). Это отражает тот
факт, что распределение потенциала является нечетной функци-
1
1
1
J
u(R,z)
1
1
«1
5
, Z
Рис. 18. Распределение потенциала
системы из двух цилиндров вдоль
границы (г=#).
Рис. 19. Распределение потенциала
системы из двух цилиндров вдоль
оси.
ей координаты z, если ось z сдвинута на (Fi-j-F2)/2 (рис. 18 и
19). Тогда распределение потенциала упрощается до
и (г, z) = $ FJ0 (xr)sin kzcIk+
V2)/2.
C.116)
Теперь необходимо определить коэффициенты FK из граничных
условий. Здесь-то и начинаются неприятности. В самом деле,
значения потенциала вдоль цилиндрических поверхностей изве-
известны. Но что происходит в зазоре? Совершенно ясно, что абсо-
абсолютное значение напряженности поля максимально на концах
цилиндров, поэтому потенциал должен там резко измениться.
Крутизна изменения потенциала минимальна в середине зазо-
зазора (штриховая линия на рис. 18). А каково точное распределе-
распределение вдоль цилиндрической поверхности в зазоре? Его можно
измерить, но способов расчета не существует.
Таким образом, мы столкнулись с серьезной трудностью.
При использовании аналитического метода основой является
88
Определение электрических и магнитных полей
либо измерение, либо предположение о характере распределе-
распределения потенциала в зазоре. Попробуем использовать простое до-
допущение и посмотрим, можно ли получить решение в замкнутой
форме.
Возьмем для простоты линейное распределение в зазоре. Это
весьма далеко от реальности, но зато просто. Тогда имеем сле-
следующие граничные условия при r=R:
(Vlt если 2< — s/2,
(Vl + VJ/2 + {V,-Vl)z/s, если — s/2<z<s/2,
У2, если z^s/2.
C.117)
В то же время u(R, z) должно удовлетворять и выражению
C.116)
u(R,z)= lFJ0(%R)s\n%zd%+ (Vi + V*)l2. C.118)
—оо
Выпишем интеграл Фурье для нечетной функции u(R, г) — (Fi+
+ V2)I2:
и (R, z) = B/я) f sin иг<М [u(R, t) —
— (Vl + V2)j2]sinxtdt+(Vi + V2)l2. C.119)
Второй интеграл вычислим, используя C.117):
s/2
S(F2 — Vl)(t/s)sin(Kt)dt +
l[{ — Vi)l2]s\n{xt)dt. C.120)
s/2
Интегрирование от s/2 до бесконечности равносильно интег-
интегрированию от s/2 до нуля и затем от нуля до бесконечности. По-
Последний интеграл от синуса не определен. Однако его можно
вычислить с помощью следующего приема [36]:
Iе-»' sm{%t)dt= lim Ги/(а2 + и2)] =1/х.
о а->-о о а->о
C.121)
Выполняя интегрирование в C.120) и принимая во внимание
C.121), получаем
= [(V2 — F,)/x2s)]sin(xs/2). C.122)
89
Глава 3
Подставим теперь полученное выражение в C.119) и учтем, что
интегрируемая функция четна по к. Тогда можно записать
u(R, z) = ^^- ] ^^sin(xz)dx + (V1 + V2)/2. C.123)
Сравнивая это выражение с C.118), имеем
fl)i=sin(xs/2) (V2 — Vi)lnsa2. <3.124)
Теперь подставим значение F* в C.116) и вновь учтем четность
подынтегрального выражения по %. В результате получаем рас-
распределение потенциала [16]:
/0 МУУ2> sin™d* +
о
Используя новую переменную
т = хЯ, C.126)
можно записать распределение потенциала вдоль оси
U (г) - Ш^М ] sin (тда) «g^ Л + (Vl + F2)/2. C.127)
о
Это и есть окончательный результат вычисления. Так как
да
(x.s/2) sj
Г sin (x.
J "
о
C.128)
о
на границе (/■=/?) соотношение C.125) дает потенциал электро-
электродов.
К сожалению, интегралы C.125) и C.127) можно найти
только численными методами. Поэтому упрощение распределе-
распределения потенциала в зазоре между цилиндрами не оправдано: чис-
численный результат можно получить и при более реалистичной
аппроксимации. Может быть, даже линейное приближение
слишком сложно. Но что может быть проще?
Если цилиндры очень близко расположены друг к другу,
можно считать, что распределение потенциала вдоль границы
описывается ступенчатой функцией, принимающей значение Vi
при z<0, Vi при 2>0 и резко меняющейся при г=0. Опустим
обсуждение обоснованности такого допущения. Вместо этого по-
90
Определение электрических и магнитных полей
смотрим, поможет ли оно вообще. В предельном случае (s=0)
выражение C.125) приобретает вид
и(г, г)-li^L]/'ffffi»d* + (Vl + V,)/2. C.129)
о
На оси оба соотношения C.127) и C.129) дают
2. C.130)
Даже в этом очень простом случае интегралы не выражают-
выражаются в элементарных функциях. Если мы хотим иметь формулу
для аксиального распределения потенциала, необходимо исполь-
использовать некоторое приближение. Распределение потенциала вдоль
оси имеет форму, показанную на рис. 19. Оказывается [65J, что
выражение C.127) можно аппроксимировать следующим выра-
выражением:
в
U (z
предельном
и и
:>-(V,-
случае
;) = (]/,-
(s = 0)
v2
1 2(
оно
+ 1/
-V1} ch[coB+s/2)/K]
os/R nch[o)(z—s/2)/R] '
упрощается:
2(V2 — Fi)th(©2/i?).
C.132)
Совершенно очевидно, что эта функция имеет свойства кривой,
показанной на рис. 19. Мы определим значение постоянной ©
из условия, что наклон кривой при 2 = 0, вычисленный с по-
помощью соотношений C.130) н C.132), должен быть одинако-
одинаковым. Дифференцируя по z оба выражения и приравнивая значе-
значения производных в точке z = 0, получаем
a>=Bln)Jlo-1(x)dr= 1,318 C.133)
о
Сравним выражения C.131) и C.132) с численным значени-
значением интеграла C.130) и точным численным решением задачи ме-
методом конечных разностей (см. разд. 3.3.2) и методом зарядо-
зарядовой плотности (см. разд. 3.3.4). Выражение C.132) является
точным при сравнении с C.130). Различие не превышает 1%.
Однако, если сравнить первые и вторые производные, обнару-
обнаружится, что при больших z относительные ошибки достигают 32,4
и 25,7% соответственно [36]. Ситуация даже ухудшится, если
отбросить линейное приближение и сравнить результаты с чис-
численными расчетами. Итоги сравнения с численными решениями
показаны в табл. 2. Мы видим, что для s/R = 0,2 абсолютное
91
Глава 3
Таблица 2
Сраввенне приближенных выражений C.131) и C.132) с численными
решениями для аксиального распределения потенциала от двух цилиндров
одинакового диаметра методом конечных разностей [114] и методом
зарядовой плотности*
s/«=0,02
s/«=0,2
Z/R C.132)
C.131) Сил. C.131) Сил [66] [114] C.131) Сил. C.131) Сил
0,0 1,5 0,5 0,5 0,5 0,5 0,5 0,5 0,5 0,5 0,5 0,5
0,2 0,3710 0,3710 0,3710 0,3717 0,3715 0,3717 0,3714 0,3861 0,3933 0,4138 0,4293
0,5 0,2108 0,2108 0,2108 0,2119 0,2129 0,2134 0,2130 0,2364 0,2494 0,2913 0,3236
1,0 0,0666 0,0666 0,0666 0,0672 0,0704 0,0711 0,0709 0,0825 0,0926 0,1303 0,1630
2,0 0,0051 0,0051 0,0051 0,0051 0,0059 0,0065 0,0066 0,0066 0,0083 0,0130 0,0192
4,0 0,0000 0,0000 0,0000 0,0000 —0,0004 0,0001 0,0001 0,0000 —0,0004 0,0001 —0,0002
аСсылка [66] и наши собственные данные, обозначенные «Сил». Потенциалы элек-
электродов выбрэиы в виде V, = l н V2=0.
расхождение между различными численными методами не пре-
превышает 10~3, но соотношение C.131) ведет к серьезным ошиб-
ошибкам, так как распределение потенциала не столь круто, как
предсказывается линейной моделью. Этими погрешностями
можно пренебречь в случае очень малого зазора, но они быстро
нарастают, когда зазор между цилиндрами становится сравни-
сравнимым с их диаметром. И хотя некоторого улучшения можно дос-
достичь [66], выбрав другое значение <о, остается тот факт, что мы
используем распределение потенциала сложной системы элект-
электродов, а не изначальной двухцилиндровой линзы.
Имеются два источника ошибок:
1. Недостаточно оправданное предположение о линейном рас-
распределении потенциала в зазоре.
2. Аппроксимация несобственных интегралов аналитическими
функциями.
Поэтому применение эмпирических аналитических формул,
основанных на предположении о линейном распределении по-
потенциала между цилиндрами многоэлектродных систем [67, 68],
является проблематичным. Аналитические выражения оправда-
оправданы только в тех случаях, если они: а) представляют правильное
распределение потенциала; б) ведут к строгим решениям для
фокусирующих свойств (см. модели линз в гл. 7 и 8), либо
в) дают возможность провести быстрые приближенные вычис-
вычисления.
Точность результатов можно повысить для аппроксимации
распределения потенциала в зазоре, используя полиномы более
высокого порядка [69], либо бесконечные ряды, содержащие
корни от функций Бесселя нулевого порядка. Однако, по наше-
92
Определение электрических н магнитных полей
му мнению, поля в электронных и ионных оптических системах
на основе цилиндрических электродов или полюсов следует оп-
определять либо с помощью измерений (разд. 3.2), либо с помо-
помощью численных методов (разд. 3.3).
3.1.2.3. Поле круговой апертуры. В ряде случаев аналитиче-
аналитические методы можно применять для определения аксиально-сим-
аксиально-симметричных полей. Один из них — поле отдельной круговой апер-
апертуры радиуса R с потенциалом Vo, расположенной между дву-
двумя областями с однородными полями Ei и Е2 (рис. 20). Нали-
Наличие однородных полей, конечно же, является приближением, но
всегда можно считать поле однородным на больших расстояни-
расстояниях от апертуры. Поэтому в от-
отсутствие других электродов
(полюсов) в окрестности
апертуры такое допущение
оправдано. При этих услови-
условиях можно вывести строгое вы-
выражение для распределения
потенциала апертуры [70J.3to
выражение будет использова-
использовано затем для вычисления рас-
распределений потенциала более
сложных систем.
Расчет основан на пра-
правильном выборе системы ко-
координат. Рассмотрим сначала
Рис. 20. Распределение потенциала
круговой апертуры, разделяющей два
однородных электростатических поля.
гиперболу во вращающейся
плоскости rz цилиндрической
системы координат с фокусом
F в точке с координатами r=R и 2=0 (рис. 20). Ее уравнение
г2/А2 —22/Б2=1, C.134)
где
Введем новую переменную v так, что
B=VR
Тогда уравнение C.134) можно переписать в виде
r2/(l — v2) — 22/v2=#2.
C.135)
C.136)
C.137)
Рассмотрим теперь эллипс в той же плоскости с фокусом в
той же точке. Его уравнение
Ь2 = \, C.138)
93
Глава 3
где
a2 — b2=R2. C.139)
Введем новую переменную ц:
b = nR. C.140)
Тогда уравнение C.138) можно переписать в виде
г2/A + ц2)+22/ц2=Д2. C.141)
Очевидно, что параметры v и ц определяют семейства гипер-
гипербол и эллипсов, вращающихся вокруг оси симметрии z и фак-
фактически являющихся конфокальными гиперболоидами и сопря-
сопряженными конфокальными эллипсоидами вращения. Выберем
эти ортогональные поверхности в качестве координатных. Так
как каждое значение v представляет гиперболоид, а каждое
значение ц — эллипсоид, наши новые координаты будут просто
Л7 И |Х.
Перепишем C.137) и C.141) в виде
rV— 22A— v2)=flV(l — v2), C.142)
г2ц2+22A + ц2)=Д2ц2A + ц2). C.143)
Это дает линейную систему уравнений относительио г2 и z2. Ре-
Решая ее и извлекая квадратные корни, получаем выражения ци-
цилиндрических координат как функцию новых координат:
V2)]'/2, C.144)
C.145)
Нам также нужны обратные функции; |x(r, z) легко полу-
получается как решение квадратного уравнения C.141):
jx= {ll2(r2lR2+z2[R2 — 1)
+ 4z2//?2]1/2}1/2. C.146)
Величина v(r, z) получается немедленно из C.145) и C.146).
Так как ц вещественно, в уравнении C.146) необходимо вы-
выбрать значение выражения в квадратных скобках с положитель-
положительным знаком. Мы можем также формально учесть знак z в ц,
выбирая положительные значения ц для положительных z и от-
отрицательные значения ц для отрицательных z.
Покажем теперь, что поверхность электрода совпадает с по-
поверхностью v = 0. Электрод расположен в плоскости z=0 при
r^sR. Тогда C.141) дает
г2 = #2A + ц2)>/?2. C.147)
С другой стороны, из C.145) следует v = 0 при г=0.
94
Определение электрических и магнитных полей
Аналогично для z=0 C.137) дает
г2=Д2A—v2)<#2. C.148)
Из уравнения C.145) следует ц = 0. Это означает, что отверстие
в электроде совпадает с поверхностью ц = 0.
Запишем теперь уравнение Лапласа в новых координатах.
В принципе это можно сделать, заменив частные производные
относительно цилиндрических координат на производные отно-
относительно новых координат. Рекомендуем читателю обратиться к
литературе [36J, чтобы оценить все удовольствие от этого
упражнения. Мы же поступим иначе. Выведем частный случай
из общих принципов. Соответственно начнем с соотношения
A.19). Наши новые координаты
?1 = Ц, ?2 = а, <73 = v. C.149)
Используя A.8), A.9), C.144) и C.145), получаем коэффици-
коэффициенты Ламе:
, C.150)
— v2), C.151)
). C.152)
Подставляя эти выражения в A.19) с учетом аксиальной сим-
симметрии (ди/да = 0), можно тотчас записать уравнение Лапласа
в новых координатах
= 0. C.153)
Это уравнение идеально подходит для разделения перемен-
переменных. В самом деле, подставляя
tt=M(n)JV(v)+ const, C.154)
немедленно получаем
1=0. C.155)
Так как каждый член зависит только от одной переменной, они
оба должны быть постоянны. Обозначим постоянную через К-
Тогда можно записать следующие два уравнения:
C.156)
C.157)
Для вычисления К воспользуемся требованием однородности
поля при больших абсолютных значениях г, т. е. потенциал
должен быть пропорционален г. Поскольку величина v ограни-
95
Глава 3
чена соотношением C.136), большие значения z означают боль-
большие значения ц. В наиболее общей форме М и М, удовлетворя-
удовлетворяющие этим условиям, записываются в виде
М = ц/([г), где /(ц)-»-т=const при ц-»-оо, C.158)
N=nv, где п—const. C.159)
Для больших значений z подстановка этих соотношений в
C.156) и C.157) немедленно дает К=2. Найдем теперь функ-
функцию fin). Дифференцируя дважды соотношение C.158), под-
подставляя в C.156) и учитывая, что /С=2, получим
A + ц2) A1Г+2П+2]х(]хГ+П -2^=0, C.160)
где штрих обозначает дифференцирование по ц. Это уравнение
можно переписать в виде
и после простого интегрирования
/'=С,/[ц2A + ц2)]. C.162)
Интегрируя еще раз, имеем
f (и) = С2 — й/ц — й arctg ц, C.163)
где ci и с2 — постоянные интегрирования. Можно видеть, что
это выражение становится постоянным при больших ц.
Подставляя C.163) в C.158) и затем используя C.159) и
C.154), получаем распределение потенциала
C.164)
где Ci = rtc2, Сг = —спи а Сз—неопределенная постоянная из
уравнения C.154), значение которой легко найти. В самом деле,
потенциал электрода, соответствующего поверхности v = 0, pa-,
вен Vo- Отсюда С3 = Vo-
Найдем теперь значения двух других постоянных. Так как
мы условились, что знак ц будет соответствовать знаку z в
C.145), можно переписать C.164) в виде
C.165)
В пределе больших положительных и отрицательных значений
z получаем
lim u= lim (Clz/R + C2znl2R), C.166)
откуда
lim du/dz = Cl/R + C2n/2R = — E2, C.167)
lim dujdz= d/R — C2n/2^ = —£,. C.168)
■96
Определение электрических и магнитных полей
Из этих уравнений немедленно получаем значения постоянных:
C,//?=-(£i + £2)/2, C.169)
С,/Л,-(£, — £,)/я. C.170)
Подставляя эти выражения в C.165) и используя только
положительные значения ja, получаем конечную формулу для
распределения потенциала круговой апертуры:
u(r,z) = V0— (£! + £2)г/2 +
+ A/я) (Е1 - Е2) \z\ A/n + arctg ц), C.171)
где ц определяется уравнением C.146).
Вдоль оси (г = 0) имеем ц=|г|//? и соотношение C.171)
упрощается:
U(z)=VQ — (E1+E2)zl2 +
+ (/?/я) (Ei — E»)[l+(zlR)arctg(zlR)]. C.172)
Подставляя z=0 в C.171), получаем и(г, 0) = У0 только при
|л=т^0. Этого следовало ожидать, так как значение ц = 0 соответ-
соответствует отверстию, а не электроду. В отверстии (r<R) необхо-
необходимо использовать соотношение C.164) и C.170). Подставляя
ц = 0, получим
u(r,0)=V0+(El — E2)Rv/n. C.173)
Из C.137) при 2 = 0 следует
v=(l__rS/fl2)l/2. C.174)
И окончательно, подставляя в C.173), имеем
и (г, 0) = Vo+ (Ei - Ел) (R2 - г2) /л. C.175)
Это выражение обеспечивает u(R, О) = Уо. Для центра отверс-
отверстия получаем из C.172) и C.175)
C.176)
Если напряженности поля Ех и Е2 направлены противопо-
противоположно, то седловая точка формируется со стороны более сла-
слабого поля, как отмечалось в разд. 3.1.1.2. Если Ei = —£2, то сед-
седловая точка имеет координату 2 = 0. Эквипотенциальные линии
для этого случая показаны на рис. 21.
В случае одинакового направления полей эквипотенциальные
линии могут пересекать апертуру, но не будут пересекаться друг
с другом. Интересен случай, соответствующий отсутствию поля
с одной стороны апертуры. Рис. 22 дает картину эквипотенци-
эквипотенциальных линий для £2 = 0.
97
Глава 3
Как будет видно в разд. 7.8, одиночная апертура является
важным элементом катодной линзы, применяемой в эмиссион-
эмиссионных системах. Она может также служить основой для упрощен-
упрощенных моделей более сложных систем.
3.1.2.4. Быстрое вычисление полей от двух и большего числа
круговых апертур. Мы знаем теперь, как вычислить поле еди-
единичной круговой апертуры. А нельзя ли применить принцип су-
суперпозиции для получения картины поля от любого числа таких
апертур? Ответ представляется отрицательным, так как прин-
принцип суперпозиции обычно применим только для неизменных
электродов (полюсов). Введение новых электродов изменит
распределение зарядов, и результирующее поле может сущест-
существенно отличаться от исходного.
Рис. 21. Эквипотенциальная картина Рис. 22. Эквипотенциальная картина
одиночной апертуры для случая Ег= одиночной апертуры для случая Е2=0.
Рассмотрим простой пример двух круговых апертур одина-
одинакового радиуса Д, разделенных расстоянием s. Пусть потенциал
одного электрода Vu другого —V2 (рис. 23), и пусть на боль-
больших расстояниях слева и справа от системы поля отсутствуют.
Это обеспечивается дополнительными трубками с такими же
потенциалами, как у соответствующих апертурных электродов
(см. разд. 7.1). Размеры этих трубок здесь не учитываются. Ес-
Если i?<Cs, можно предположить, что поле между электродами
(исключая собственно области апертур) является постоянным и
его абсолютная величина
£=(Vi — V2)/s. C.177)
Чтобы использовать принцип суперпозиции, необходимо рас-
рассмотреть две одиночные апертуры с нулевым полем по одну сто-
сторону и постоянным с другой в каждом случае. Это означает, что
98
Определение электрических и магнитных полей
постоянные поля простираются до бесконечности в обе стороны
и мы никогда не получим требуемого поля.
Как ни странно, все же можно воспользоваться суперпози-
суперпозицией двух одиночных апертур, если применить выражение
C.172) только для определения формы решения, а постоянные
вычислить позже, используя для этого параметры объединенно-
объединенного поля. Так как апертуры расположены на расстояниях ±s/2
от плоскости z=0, в C.172) необходимо подставить z±s/2 вме-
вместо z. Объединяя постоянные, получаем суперпозицию двух по-
полей
U (z)t=A+z{B + C arctg[B+s/2)/#] +
+ D arctg[(z - sl2)IR]}+ (s/2) {C arctg[ (z+s[2)/R] -
-D arctg[(z —s/2)JR]}. C.178)
Распределение потенциала аналогично показанному на рис. 19.
Для бесконечно больших положительных значений z потенциал
стремится к V2, для отрицательных z к Vi, а при z = 0 он равен
AЛ+Кг) /2. Соответственно
A+[B+(C+D)nl2]z+(C — D)ns/4 = V2, C.179)
A+[B—(C+D)nl2]z — (C — D)ns/4 = VU C.180)
А+ (C+D) (s/2)avctg[(s/2R)] = (Vi+V2)l2. C.181)
Отсюда имеем
A=(Vi+Vi)/2, B = 0, C= — D=(V2—Vt)l(ns). C.182)
Подставляя эти значения в C.178), получаем распределение по-
потенциала вдоль оси системы двух апертур
U(z) = (Vl + V2)/2+(V2~Vl)cp(z)l2, C.183)
где
<p(z) = (lM)[Bz/s+l)arctgBz/s+l)/B/?/s) —
— Bz/s— l)arctgBz/s — l)/BR/s)]. C.184)
Это выражение обеспечивает заданное значение потенциала
при z=0 и приближается к потенциалу электродов на больших
расстояниях от центра. А как насчет других областей? Есть
еще две точки, где легко проверить точность этого метода.
В предположении R<^s потенциалы в центрах апертур опреде-
определяются выражением C.176) следующим образом:
U(s/2) = V2 + ERIn, C.185)
£/(—s/2) = Vi — ER/n. C.186)
Подставляя C.177), с учетом C.183) имеем
ф(±«/2),=±B/я)(я/2 — R/s). C.187)
99
Глава 3
С другой стороны, C.184) дает для тех же точек
<p(±s/2)=±B/n)arctg(s//?). C.188)
Сравнивая выражения C.187) и C.188), можно заметить, что
они дают одинаковый результат, если использовать первые два
члена разложения в ряд Тейлора функции арктангенса для
больших s/R. Суперпозиция потенциалов двух раздельных апер-
апертур удовлетворяет истинному распределению потенциала при
значениях z, определяемых C.179) — C.181). При всех осталь-
остальных значениях z распределение потенциала C.184) является
только приближением. Но первоначальная формула C.172) так-
также является приближенной. Она справедлива только для малых
значений R/s, для которых соотношения C.187) и C.188) дают
практически одинаковый результат. Но которое из них точнее в
случае больших R/s? Очевидно, что погрешность возрастает с
увеличением R/s. Относительная разность между arcig(s/R) и
(n/2—R/s) равна 0,19% для R/s = 0,2, 3,25% для R/s=0,5 и
11,43% для R/s = 0,75.
К счастью, распределение
потенциала двух апертур яв-
является одной из немногих за-
дач теории потенциала, для
которой возможно строгое ре-
решение. Решение дается интег-
интегральным уравнением [71] и
здесь воспроизводиться не бу-
будет. Это дает, однако, воз-
возможность сравнить наши ре-
Рис. 23. Две круговые апертуры. зультаты со строгим решени-
решением, справедливость которого
не ограничена малыми R/s. Сравнивая значения функ-
функций распределения потенциала в центрах апертур, вычис-
вычисленные из соотношений C.187) и C.188), с результата-
результатами строгих вычислений, находим, что относительные по-
погрешности составляют соответственно—1,7 и 1,6% для R/s =
= 0,5. Для случая R/s = 0,75 относительные погрешности рав-
равны— 8,4 и 3,3% соответственно. Таким образом, соотношение
C.187) дает заниженные значения потенциала. И хотя значе-
значения, следующие из C.188), несколько завышены, они более точ-
точны по сравнению со значениями, получаемыми из C.187).
Строго вычисленные функции ф(г) наряду с вычисленными из
C.184) показаны на рис. 24 для двух различных значений R/s.
Очевидно, ф@)=0 и ф(г) приближается к 1 для достаточно
больших 2 и тем быстрее, чем меньше R/s.
Итак, суперпозиция распределений потенциалов нескольких
независимых апертур — быстрый и относительно точный метод
100
Определение электрических н магнитных полей
D 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0
2z/s
Рис. 24. Функции ф(г) потенциала для двух различных значений парамет-
параметра R/s (сплошные линии). Символы представляют те же функции, вычисленные
по приближенной формуле C.184); квадраты — #/s=0,5; ромбы — R/s=0,75.
получения распределений потенциалов в сложных системах
электродов (полюсов). Этот подход применялся для вычисле-
вычислений как электростатических [72], так и магнитных полей [50].
3.1.3. Аналитическое вычисление мультипольных
полей
Общее разложение в ряд C.52) мультипольных потенциалов
содержит бесконечный набор функций £/njv(z) в противополож-
противоположность аксиально-симметричному случаю, где единственной та-
такой функцией является аксиальное распределение потенциала
в уравнении C.20). Поэтому ситуация существенно усложняет-
усложняется вследствие, вообще говоря, трехмерного характера мульти-
польного поля. Отсюда следует, что в общем нельзя строго вы-
вычислить функции распределения потенциала. Например, квад-
рупольное поле двух скрещенных щелей, показанных на рис. 25,
можно вычислить только приближенно [73J. Область примене-
применения аналитических методов ограничена упрощенными моделя-
моделями, которые могут удовлетворительно описать только свойства
либо бчень коротких, либо длинных мультиполей.
3.1.3.1. Короткие мультиполи. Для коротких
удобно [61] выбрать распределение Гаусса
мультиполей
C.189)
101
Глава 3
при аппроксимации функций £/пдг, появляющихся в соотношении
C.52). Здесь Ummax представляет максимальное значение функ-
функции при z=0, а ат — параметр, характеризующий т-ю компо-
компоненту потенциала. Подставляя z~am, имеем
Um(am) = иттяхе-1'* = 0,Ш5иттзх. C.190)
Используя это соотношение, можно определить значения Um max
и От с помощью приближенных вычислений [74] или измерений
[75J. k-я производная от Um(z) дается выражением
, C.191)
где Нъ. — полином Эрмита степени k. Таким образом, в C.54) —
C.59) можно подставить
^# C.192)
C.193)
15), C.194)
-420г»/а*, + 105),
C.195)
Um (г) = ^ф. (г"/оЙ -45г»/<й f 630г«К - 3150гЧвт +
От
+ 4725zaAU-945). C.196)
Эти выражения могут быть полезны при выводе картины
трехмерного поля короткого мультиполя. Можно также исполь-
использовать другие модели (например, колоколообразную, сходную с
гауссовой, но использующую другую функцию). Однако в дан-
данном случае необходимо полагаться на экспериментальное, либо
численное определение распределения потенциала.
Для мультиполей средней длины
можно использовать составную
гауссову модель: модельная
функция является прямоугольни-
прямоугольником, переходящим на концах в по-
полугауссово распределение.
3.1.3.2. Длинные мультиполи.
Если мультипольная система
может рассматриваться как плос-
плоская (длина существенно боль-
Рис. 25. Квадруполь на основе ше поперечных размеров и се-
скрещенных щелей. чение постоянно), аналитические
102
Определение электрических н магнитных полей
методы более полезны, чем для коротких мультиполей. В этом
случае можно снова использовать принцип эффективной длины
(см. разд. 2.7.1). Определим действие мультиполя как интег-
интеграл от распределения его поля F(r, a, z), взятый вдоль оси ко-
координат z от минус до плюс бесконечности. Здесь F(r, a, z) -—
функция, характеризующая действие мультиполя (или любого
оптического элемента). Для мультиполя это может быть потен-
потенциал или поперечная компонента поля. Далее предположим,
что действие реального мультиполя эквивалентно действию тео-
теоретического с постоянным полем и эффективной длиной Ьец.
Это так называемая прямоугольная модель, так как сложная
зависимость распределения поля от координаты z заменена про-
простым прямоугольником с длиной Left и высотой F(r, а, г), где
zm — некоторое заданное значение координаты z. Приравнивая
действия двух систем, получаем
Left = lF(r,a,z)dz/F(r,a,zm). C.197)
—со
Заметим, что эффективная длина определяется здесь как функ-
функция точки (г, а) в плоскости z=zm, где проводится вычисление.
В самом деле, эффективная длина изменяется с расстоянием от
оси и соответственно может существовать более чем одна эф-
эффективная длина для трехмерного мультиполя, например, для
каждой компоненты поля [62J. Для наших целей, однако, эф-
эффективная длина будет определена просто в начале системы ко-
координат. Принцип эффективной длины мы используем также в
случае аксиально-симметричной линзы.
Таким образом, для прямоугольной модели все зависимости
от г исчезают, и соотношение C.53) упрощается до постоянного
значения. Поэтому можно записать
A nN = U'nN = anN/RnN = const, C.198)
где R — некоторый характеристический радиус, который опре-
определяется реальной конструкцией мультипольной системы. Тогда
соотношение C.52) можно переписать в виде
и (г, а) = 1 anfl(r/R)n»cosnNa. C.199)
Используя соотношения C.62) — C.81), можно привести это вы-
выражение к декартовым координатам.
Рассмотрим следующий пример. Весьма важный с практиче-
практической точки зрения цилиндрический вогнутый 2Ы-мультиполь со-
состоит из 2N идентичных длинных электродов (полюсов), имею-
имеющих знакопеременные потенциалы W и —W и одинаково распо-
расположенных по цилиндрической поверхности радиуса /?. Такая си-
103
Глава 3
стема имеет N плоскостей симметрии и N плоскостей антисим-
антисимметрии. Поперечное сечение 12-полюсной системы показано на
рис. 26 для более общего случая двух плоскостей симметрии
(четыре различных потенциала в каждом квадранте плоскости
ху). В нашем случае Vi = V3 = W и V^=Vi =—W, но мы опреде-
определим коэффициенты апх в уравнении C.199) как функции четы-
четырех потенциалов и угловых расстояний 2е между каждыми дву-
двумя соседними электродами и затем подставим потенциалы для
нашего специального случая (решение для общего случая пона-
понадобится в следующем разделе). Затем снова сделаем обобще-
обобщение, перейдя от 12-полюсника к 2Л"-мультиполю.
Мы уже знаем (разд. 3.1.2.2), что предположение о линей-
линейном распределении потенциала между электродами (при г=Я)
ведет к существенным ошибкам, и поэтому используем более
реалистичное распределение [76]. Представим потенциал сле-
следующими функциями |[64]:
@<а<п/12-е),
и (Я, о) =
(я/12—е<а<я/12 + е),
V2 + V3)/2 + [(V3 - V2)/n] arcsin (а - я/4)/е
(я/4 — е ^а^я/4 + е),
V3 (я/4 + е^а ^5я/12 — е),
(V, + V4)/2 + [(l/4- V3)/n] arcsin (а-5я/12)/е
Eя/12-
V,
C.200)
Так как потенциал периодичен по координате а с периодом
я, коэффициенты Фурье а2п в C.199) могут быть определены
соотношениями
Я/2
$
/
Я2П=D/я)= $ и(/?,«)cos2/гсм/а,
о
я/2
)l
/
ao=B/n)lu(R,a)da.
C.201)
C.202)
(Вследствие двойной симметрии следует рассматривать только
первый квадрант плоскости ху.)
Функция u(R, а) определяется выражением C.200). Теперь
необходимо выполнить интегрирование. Интегрирование по
частям после нескольких элементарных преобразований дает
104
Определение электрических н магнитных полей
Р+8
(J-e
arcsin [ (а — Р) /е] cos 2nada = A /2п) {л sin 2Щ cos 2пг —
— 2sin2n$\ [I— (a — pJ/e2]-1/2X
о
X cos[2rae (a — P)/e]d(a — p)/e}. C.203)
Можно доказать для любого значения а, что
\ {\—x2)-l'2cosaxdx=(nl2)J0(a), C.204)
где /о (а) — функция Бесселя от аргумента а первого рода ну-
нулевого порядка. Используя это выражение, легко получаем иа
Рнс. 26. Вогнутый цилиндрический 12-полюсник.
C.203) результат интегрирования в виде
р+в
в
arcsin Г (а —
8
cos2naofa =
= (п/2й) sin 2«p [cos 2пе — /о Bпе) ]. C.205)
В этом выражении (J представляет различные значения преде-
пределов интегрирования, возникающие при использовании выраже-
выражения C.200) для представления U(R, a) в различных секторах
мультиполя между 0 и л/2.
Мы тотчас замечаем, что для я = 0 интеграл равен нулю.
Поэтому вычисление коэффициента а0 тривиально: в подынтег-
подынтегральное выражение в C.202) входят только постоянные члены.
Выполняя интегрирование от сектора к сектору, получаем
l6. C.206)
105
Глава 3
При вычислении интеграла C.201) для определения коэф-
коэффициента а2п в общем виде мы снова идем от сектора к секто-
сектору и используем в каждом из них выражение C.205). Эта про-
процедура несколько длиннее, но результат прост:
а2п= B/ля) [(Vi — V2)sinпф+ (V2 — K3)sinmt/2 +
+ (V3 — F4)sin5mx/6]/oBne). C.207)
В нашем специальном случае Vi = Vs =— V2 = — V4 = W. Под-
Подставляя эти значения в C.206) и C.207), получаем яо = О и
ain= (*W/nn) J0Bne) sin nn/2[2 cos пл/3—1]. C.208)
Немедленно видим, что ain — Q для всех четных значений, а так-
также для п=\, 5, 7, 11, 13, 17, 19 Ненулевые члены ограниче-
ограничены значениями га = 3, 9, 15, 21, ...=3B&+1), где & = 0, 1, 2,
3, — Но для этих членов выражение C.208) упрощается:
Это выражение ясно показывает, что симметрично-антисиммет-
симметрично-антисимметричный 12-полюсник имеет гармоники только 6, 18, 30, 42-го и
т. д. порядков.
Для обобщения на случай 2,А/-мультиполя необходимо прос-
просто заменить 6 на N, чтобы достичь конечного результата:
^$^ 0. C.210)
Естественно, можно было вывести это выражение непосредст-
непосредственно, без частных случаев и обобщений [61J. Читатель может
попытаться проделать это в качестве упражнения.
Интересно сравнить полученный результат с выражением
C.199). Как видно, члены, являющиеся целыми кратными N,
теперь не входят в выражение. Причина этого в наличии N
плоскостей антисимметрии в дополнение к N плоскостям сим-
симметрии, для которых было первоначально выведено соотноше-
соотношение. Мы уже встречались с частным случаем такой ситуации
для симметрично-антисимметричного квадруполя. Так как для
квадруполя N=2, наличие двух дополнительных плоскостей ан-
антисимметрии приводит к отсутствию Л4ь-членов. Именно это мы
получили выше из соотношения C.83).
3.1.3.3. Идеальные мультиполи. Как мы видели в разд.
3.1.1.3, распределения потенциалов идеальных мультиполей не
содержат никаких гармоник выше п=\ в выражении C.52). Со-
Соответствующее распределение потенциала поэтому имеет вид
u(r, a, z) = ^^1^—-U^(z)cosNa + A9(r. г), C.211)
106
Определение электрических и магнитных полей
где Ло(г, г)—аксиально-симметричная компонента потенциа-
потенциала. Для планарных мультиполей из-за отсутствия зависимости
от координаты z это выражение упрощается:
и{г, а),=яо + aN (r/N)K cos No. C.212)
Здесь ay определяется соотношением C.198). Соотношение
C.212) также прямо следует из C.199) при га = 0 и 1.
Идеальные мультиполи представляются электродами (полю-
(полюсами) с бесконечными гиперболоподобными поверхностями, оп-
определяемыми выражением C.86). Естественно, реализовать та-
такие поверхности невозможно. Но можно ли хотя бы приблизить-
приблизиться к ним?
Рассмотрим 2М-мультиполь с N дополнительными плокостя-
ми антисимметрии. Как мы видели в предыдущем разделе, на-
наличие плоскостей антисимметрии ведет к исчезновению всех,
членов, целых кратных N. Поэтому симметрично-антисимметрич-
симметрично-антисимметричные квадруполи имеют только 2, 6, 10-ю и т. д. гармоники.
Использование дополнительных плоскостей антисимметрии,
таким образом, ведет к существенному улучшению картины по-
поля по сравнению с обычным 2УУ-мультиполем. Однако можно
достичь еще большего улучшения. В самом деле, если рассмот-
рассмотреть простую конфигурацию полюсов в виде вогнутого цилинд-
цилиндра, легко видеть, что соответствующий выбор углового смеще-
смещения полюсов 2е может привести к исключению одной из высших
гармоник. Так как обычно приходится работать в окрестности
оси z системы, желательно избавиться от второй гармоники. Как
следует из C.210), это достигается, когда
a8w = /oC№s)=O. C.213)
Решение этого трансцендентного уравнения дает оптимизирован-
оптимизированные значения 2eopt, для которых вторая гармоника исчезает.
Уравнение C.213) имеет бесконечный набор решений
3We0Pt = 2,4048, 5,5201, 8,6537 и т.д. C.214)
Однако можно использовать только те решения, для которых
угловые зазоры между электродами не перекрываются. Поэтому
2вт„ = я/Л7, C.215)
и можно использовать только первое решение. Оптимизирован-
Оптимизированные значения угловых зазоров табулированы в табл. 3 для зна-
значений N от 1 до 6. Отметим, что предположение о линейном из-
изменении потенциала в зазоре между электродами вогнутого ци-
цилиндрического квадруполя [77] ведет к «оптимальному» углово-
угловому зазору 60° против значения 45°56', полученного здесь. Тща-
Тщательные измерения, выполненные на аналоговой резисторной це-
107
Глава 3
Таблица 3
Оптимальные значения угловых зазоров 2eopt,
при которых вторая гармоника
г^-мультиполя исчезает
2/V 2е„.„
2 91°51'
4 45°56'
6 30°37'
8 22° 58'
10 18°22'
12 15°19'
пи (см. разд. 3.2.2.2), подтвердили результаты наших вычисле-
вычислений.
Естественно, при использовании другой геометрической кон-
конфигурации необходимо оптимизировать другие параметры. Зна-
Значительное количество работ было посвящено этой проблеме для
различных конфигураций, особенно для квадруполей. Обычно
используются четыре цилиндрических стержня [78J, но в то же
время предлагались и весьма сложные поверхности [79] для
компенсации отсутствующих частей неограниченных гиперболи-
гиперболических поверхностей. В результате всегда получается четырех-
полюсная конфигурация со стремящейся к нулю додекапольной
компонентой, но ненулевыми а\о, ац и т. д. коэффициентами.
Существенное улучшение картины поля возможно только в
том случае, если отбросить аналитический подход и попытаться
использовать метод синтеза [64J. Начнем с идеального распре-
распределения потенциала и попробуем воспроизвести его безотноси-
безотносительно к количеству полюсов. В самом деле, как мы видели в
разд. 3.1.1.3, наиболее важной характеристикой квадруполя яв-
является не количество полюсов, а наличие в точности двух вза-
взаимно перпендикулярных плоскостей симметрии с добавлением
двух плоскостей антисимметрии, гарантирующих отсутствие
4п-х членов. В таком случае следует простое решение: набор
большого количества простых электродов с определенным по-
потенциалом лучше аппроксимирует идеальный квадруполь, чем
система из четырех сложных электродов. Чем больше количест-
количество электродов (полюсов), тем лучше аппроксимация идеально-
идеального квадруполя. Ниже мы покажем, что, используя всего 12
электродов, можно воспроизвести квадруполь, высшие гармони-
гармоники которого начинаются с 14-й.
Рассмотрим еще раз 12-полюсную конфигурацию на рис. 26.
Так как идеальный квадруполь имеет одну компоненту (я = 1)
в C.199). распределение его потенциала при r = R должно за-
108
Определение электрических и магнитных полей
висеть от а как U cos Bа), где U — потенциал электрода при
x=R. Центры четырех электродов в первом квадранте плоскос-
плоскости ху соответствуют а = 0, 30, 60, 90°. Таким образом, для фор-
формирования распределения, соответствующего идеальному квад-
руполю, их потенциалы должны составлять Vi = U, \г = U/2,
Уз =—U/2 и F4 =—U. Конечно, эта система не является иде-
идеальным квадруполем, так как только эти четыре точки удов-
удовлетворяют соответствующему распределению потенциала. Одна-
Однако мы убедимся, что она является очень хорошей аппроксима-
аппроксимацией идеального случая. Подставляя значения электродных по-
потенциалов в C.207), получаем
2ne). C.216)
Отсюда видно, что а2п = 0 для всех четных п, а также для п =
= 3B*+ О. где £=0, 1, 2 Остаются только члены 2п=2, 10,
14, 22, 26 и т. д. Выбирая 2е = 27°33', избавляемся от коэффи-
коэффициента йю, так что первой из оставшихся высших гармоник яв-
является 14-я. Эта гармоника соответствует 28-полюснику, эффект
от которого весьма мал. Для выбранного выше значения 2е по-
получаем из C.216) «2 = 0,901 U, ai4 = 0,049i/, а22=0,007 U и
Я2б = 0,016£/. Следует также помнить, что в соотношении C.199)
зависимость высших членов от г столь сильна, что можно суще-
существенно уменьшить влияние этих членов небольшим уменьшени-
уменьшением области локализации пучка. Можно с уверенностью сказать,
что ошибки, возникающие вследствие приближенных вычисле-
вычислений, и в особенности из-за погрешностей при изготовлении и юс-
юстировке, превышают эффект от этих высших гармоник.
Тем не менее можно улучшить степень приближения к иде-
идеальному квадруполю, используя большее количество электродов
(полюсов). Мы задаем потенциалы на электродах равными зна-
значениям потенциалов идеального квадруполя в центрах соответ-
соответствующих электродов. Можно показать, что в общем случае,
если имеется М электродов, первыми тремя ненулевыми коэф-
коэффициентами будут а2, ам+2 и аШ-2.
Например, если М=20, то оптимальный угловой зазор меж-
между электродами 2е = 15°19/ и первые ненулевые коэффициенты
имеют следующие значения: й2 = 0,966 U, a22=0,021 U и азв =
= 0,008 U.
Отметим, что форма электродов не столь важна, как их ко-
количество. Оно определяет точность аппроксимации идеального
поля. Форма электродов (полюсов) влияет только на фактичес-
фактические численные значения коэффициентов. Единственное необхо-
необходимое условие для расположения электродов — наличие двух
взаимно перпендикулярных плоскостей симметрии. Система, по-
показанная здесь, очень проста по конструкции: разрезая вдоль
металлический цилиндр на несколько частей и используя дели-
109
Глава 3 ____
тель напряжения, можно очень близко аппроксимировать иде-
идеальный электростатический квадруполь. Результаты также не-
непосредственно применимы к магнитным полюсам. Железный
сердечник типа статора мотора с обмоткой, имеющей косину-
соидальное распределение витков [80J, может обеспечить столь
же полезную конфигурацию.
Естественно, таким же путем можно аппроксимировать не
только квадрупольные, но и мультипольные поля. Этот подход
имеет дополнительное преимущество: мультипольная система
может использоваться разными способами. Например, 12-по-
люсная система, рассмотренная здесь, может быть также ис-
использована как комбинированный квадруполь-октуполь-доде-
капольный элемент для фокусировки пучка и одновременной
коррекции аберраций 3-го и 6-го порядков [64] (см. разд.
10.5.2). Эта система может также применяться как одиночный
гексаполь, октуполь или додекаполь.
Для демонстрации вышеприведенного утверждения рассмот-
рассмотрим суперпозицию потенциалов квадруполя U, октуполя V и
додекаполя W на электродах со следующими электродными по-
потенциалами: Vi = U+V+W, V2=—pV—W, Vz = — pV+W и F4 =
=—U-\-V—W, где p = const @<р<1). Подставляя эти потен-
потенциалы в C.206) и C.207), получаем мультипольные коэффици-
коэффициенты как функции электродных потенциалов и угловых зазоров
2е. Очевидно, что аксиальный потенциал исчезает только при
р=1/2, и мы будем иметь 2, 6, 10, 14, 18, 22-й и т. д. коэффици-
коэффициенты для симметрично-антисимметричного квадруполя, 4, 8, 12,
16, 20-ю и т. д. компоненты для октуполя и 6, 18-ю и т. д. ком-
компоненты для симметрично-антисимметричного додекаполя. Если
теперь выбрать угловое расстояние, при котором 18-я додека-
польная компонента исчезает, то будем иметь квадруполь-окту-
польную систему в суперпозиции с практически идеальным до-
декаполем.
3.1.3.4. Метод конформных преобразований. Для планарных
полей имеется другой мощный метод аналитического определе-
определения распределений потенциала. Плоскость ху декартовой систе-
системы координат является также плоскостью определения комп-
комплексной переменной
w = x+iy. C.217)
Рассмотрим произвольную комплексную функцию f(w). Она
всегда может быть выражена в виде
f(w)~f(x + iy)=u(x,y)+tv(x,y), C.218)
где и и v — действительные функции. Таким образом, для каж-
каждого значения комплексного числа w существует другое комп-
110
Определение электрических и магнитных полей
лексное число f(w), которое может быть представлено в другой
декартовой координатной плоскости uv. Взаимно однозначное
соотношение C.218) между точками плоскости ху и точками
плоскости uv называется отображением одной плоскости на
другую.
Если функция f(w) однозначна и дифференцируема, она на-
называется аналитической функцией. Функция f(w) является ана-
аналитической в том и только в том случае, если выполнены усло-
условия Коши — Римана
ди dv ди dv f
Обычно это имеет место для всех физически разумных функций.
Для аналитических функций углы между пересекающимися кри-
кривыми в плоскости ху сохраняются и между соответствующими
кривыми в плоскости uv. Поэтому ортогональные семейства
кривых (например, эквипотенциальные и силовые линии) в од-
одной плоскости останутся ортогональными при отображении в
другую плоскость, хотя и могут быть совершенно искажены в
целом. Преобразование этого вида называется конформным
отображением или конформным преобразованием.
Рассмотрим, например, функцию
/(ш) = Уш2. C.220)
Легко убедиться, что оба условия C.219) выполнены в этом
случае
Из простого дифференцирования соотношения C.219) сле-
следует, что обе функции и{х, у) и v(x, у) удовлетворяют уравне-
уравнению Лапласа. Поэтому обе они являются потенциальными
функциями. Это очень важное заключение. Оно означает, что
можно построить бесконечное количество потенциальных функ-
функций, взяв просто действительную и мнимую части любой ана-
аналитической функции. Трудность, естественно, заключается в
удовлетворении заданным граничным условиям.
Рассматривая наш пример снова, видим, что для функции
C.220)
и=>У(х* — у*), C.221)
v = 2Vxy. C.222)
Уравнение C.221) в точности совпадает с уравнением C.87) для
эквипотенциальных линий идеального квадруполя. Уравнение
C.222) представляет другой набор неограниченных гипербол
(набор силовых линий). Преобразование C.220) отображает
параллельные и взаимно перпендикулярные прямые линии и —
= const и v = const в плоскости uv в два набора ортогональных
111
Глава 3
гипербол в плоскости ху (см. рис. 13). В предельном случае и = 0
и 5 = 0 гиперболы вырождаются в прямые линии х=±у и jr=O,
г/ = 0 соответственно. Таким образом, эквипотенциальные линии
в седловой точке @, 0) пересекаются под прямым углом. Это
общее свойство планарных полей в отличие от аксиально-сим-
аксиально-симметричных полей с углом пересечения 54°44' (разд. 3.1.1.2).
Метод конформных преобразований основан на отображе-
отображении плоскости ху в плоскость uv с помощью аналитических
функций, решении задачи в этой плоскости (нахождении потен-
потенциала как функции координат и и v), что преобразует сложную
задачу в другую, с более простыми граничными условиями,
и последующем обратном преобразовании решения в плоскость
ху. Обычный подход заключается в исследовании различных
преобразований и последующем поиске задач, которые могут
быть решены с помощью этих преобразований. Таким образом,
функция f(w)=\nw решает задачу о нахождении потенциала
бесконечной заряженной нити, / (до) = 1/до позволяет найти поле
двух параллельных заряженных нитей, с противоположными
зарядами f(w)=w3/2, определить поле заряженного прямого
угла и т. п. Это не очень эффективный путь, в особенности если
вспомнить, что он применим только к планарным полям. Тем не
менее этот метод оказался весьма полезным при конструирова-
конструировании мультиполей, ограниченных прямыми линиями [79]. Метод,
используемый для решения задач этого типа, называется пре-
преобразованием Шварца — Кристофеля.
Прежде чем закончить этот раздел, хотелось бы упомянуть
еще об одной возможности вычисления планарных полей. Как
следует из ортогональности пары и(х, у) и v(x, у), если одна
из функций симметрична, то другая антисимметрична, т. е. ес-
если и(х, у)=и(х, —у), то v(х, y)=—v(x, —у). Тогда, записы-
записывая C.218) дважды (для у и —у) и используя вышеприведен-
вышеприведенные условия, получаем для распределения потенциала, симмет-
симметричного относительно плоскости xz:
u(x,y) = [f(x+iy)+f(x-iy)]/2 C.223)
и для распределения потенциала, антисимметричного относи-
относительно той же плоскости:
v(x,y)=-i[f(x+iy) -f(x-iy)]/2. C.224)
Используя эти общие соотношения, можно сразу получить урав-
уравнения C.221) и C.222) из C.220).
112
Определение электрических и магнитных полей
3.1.4. О роли магнитных материалов
Аналитические методы, обсуждавшиеся до сих пор, одинако-
одинаково применимы к электростатическим и магнитным полям при
условии, что удовлетворены все требования, представленные во
введении к гл. 3. Совершенно ясно, что магнитные поля, инду-
индуцируемые токопроводящими катушками без магнитных мате-
материалов, требуют другого подхода (см. разд. 3.1.5). В присутст-
присутствии ферромагнитных материалов, однако, следует быть осто-
осторожным.
Магнитные поля в присутствии ферромагнетиков состоят из
двух компонент: одна индуцируется возбуждающей катушкой,
другая — намагниченностью самого материала. Намагничен-
Намагниченность ферромагнитных материалов, однако, зависит не только
от текущего состояния, но и от всей предыстории'. В результате
зависимость магнитной индукции В от возбуждающего тока /
(кривая намагничивания) не только существенно нелинейна, но
и обнаруживает гистерезис. Кривые намагничивания и гистере-
гистерезиса чувствительны к химической структуре материалов тех-
технологии их создания и предыстории использования.
Теория магнетизма весьма далека от предмета рассмотрения
настоящей книги. Читатель может обратиться по этому вопро-
вопросу к литературе [52]. Мы ограничимся только поверхностным
обзором некоторых практических моментов.
В каждой точке кривой намагничивания относительная маг-
магнитная проницаемость цг может быть определена как отношение
магнитной индукции в присутствии материала к магнитной ин-
индукции в его отсутствие. При малых возбуждающих токах отно-
относительная магнитная проницаемость в основном зависит от ма-
материала и его предыстории. При более высоких уровнях воз-
возбуждающего тока относительная магнитная проницаемость про-
проходит через максимум и может достигать очень больших зна-
значений в широком диапазоне возбуждающих токов. При еще
больших возбуждающих токах кривая намагничивания изгиба-
изгибается: магнитный материал достигает насыщения. В этой облас-
области кривая намагничивания становится линейной с очень малым
наклоном, соответствующим единичной относительной прони-
проницаемости, и при дальнейшем росте возбуждающего тока уве-
увеличения намагниченности не происходит.
Магнитная линза обычно представляет собой аксиально-сим-
аксиально-симметричный электромагнит или постоянный магнит. Через полюс-
полюсные наконечники проходит канал для пучка частиц (рис. 27).
Поле концентрируется в зазоре между полюсными наконечни-
наконечниками. Мы увидим в гл. 8, что желательно повысить концентра-
концентрацию поля как можно больше для увеличения оптической силы.
По этой причине применяются ферромагнитные материалы.
ИЗ
Глава 3
В сильных полях, однако, использование ферромагнитных ма-
материалов становится все менее и менее эффективным для кон-
концентрации поля. Вследствие насыщения намагниченность ма-
материала не может превысить определенное значение.
Как следствие, максимальное поле на полюсах нельзя уве-
увеличить за счет роста возбуждающего тока или уменьшения
размеров. Распределение поля уширится вдоль оси, и полем во
внешнем по отношению к полюсам канале нельзя пренебрегать.
Поэтому следует избегать насыщения в магнитных системах
везде, за исключением собственно полюсов. (В некоторых спе-
специальных конструкциях, особенно при необходимости использо-
использования сверхсильных полей, насыщение допускается. Мы обра-
обратимся к этому случаю ниже.)
Ферромагнитные материалы не
представляют особых сложностей
прн условии, что магнитный ска-
скалярный потенциал можно считать
постоянным на поверхности мате-
материала. В этом случае, как мы виде-
видели во введении к этой главе, потен-
потенциал поля однозначно определяется
уравнением Лапласа и распределе-
нием потенциала на границах. И
Рис. 27. Железная магнитная практически нет различия между
вычислением магнитного и соответ-
соответствующего электростатического по-
поля. Таким образом, например, электростатическое поле двух
цилиндров (разд. 3.1.2.2) полностью эквивалентно магнитному
полю двух полюсов.
Этот простой подход, однако, применим только при следую-
следующих условиях:
1) влиянием любых токов можно пренебречь;
2) относительная проницаемость магнитного материала мо-
может считаться бесконечной;
3) материал ненасыщен.
Так как первые два допущения никогда не могут быть пол-
полностью удовлетворены, применение скалярного магнитного по-
потенциала для определения магнитных полей является прибли-
приближением, хотя и во многих случаях весьма хорошим.
Что необходимо для того, чтобы гарантировать правомоч-
правомочность использования этого приближения?
1. Влиянием токов можно пренебречь, если они хорошо эк-
экранированы от области прохождения пучка (см. магнитную лин-
линзу, показанную на рис. 27). Данному условию трудно удовлет-
удовлетворить, когда границы возбуждающих обмоток близки к полю-
полюсам. Это имеет место, когда необходимы толстые обмотки для
44
Определение электрических и магнитных полей
получения токов, достаточных для возбуждения сильных маг-
магнитных полей. В этом случае требуются дополнительные экра-
экранирующие материалы, и поэтому возрастает роль второго усло-
условия.
2. Ферромагнитные материалы с очень высокой (до 106) от-
относительной магнитной проницаемостью широко доступны. Так
как отношение тангенциальных составляющих магнитной ин-
индукции на границе раздела железо — воздух равно относитель-
относительной магнитной проницаемости, в случае очень высокой прони-
проницаемости тангенциальная составляющая В практически равна
нулю на воздушной стороне раздела. Тогда нет необходимости
вычислять поле внутри материала. Погрешность, возникающая
при этом приближении, по оценке [79] пропорциональна 1/цг-
3. Насыщения можно избежать, используя относительно ма-
малые возбуждающие токи, либо ферромагнетики с высокой плот-
плотностью насыщающего тока. В этих случаях магнитная индук-
индукция, возбуждаемая током, приблизительно пропорциональна то-
току. Фактически удовлетворение требования бесконечной прони-
проницаемости автоматически ведет к удовлетворению и этого требо-
требования. В самом деле, в режиме насыщения относительная про-
проницаемость близка к единице. Мы считаем отсутствие насыще-
насыщения самостоятельным требованием только потому, что прони-
проницаемость переменна: насыщение может возникать даже в мате-
материалах с очень высокой проницаемостью при больших возбуж-
возбуждающих токах. Такие токи требуются при создании сверхсиль-
сверхсильных полей для управления пучками частиц высоких энергий.
С другой стороны, очень слабые возбуждающие токи также та-
таят опасность: тогда магнитная индукция почти полностью оп-
определяется существенно нелинейной остаточной намагниченно-
намагниченностью материала. В этих случаях необходимо учитывать при
вычислениях свойства ферромагнитных материалов.
Чтобы связать разность магнитных потенциалов между по-
полюсами с возбуждающим током, необходимо использовать за-
закон циркуляции Ампера. Его легко вывести из уравнений Мак-
Максвелла A.4) и теоремы Стокса A.24). Намагниченность М учи-
учитывается добавлением эквивалентной объемной плотности тока:
JM = rotM C.225)
к плотности тока свободных зарядов J/ в уравнении A.4). Тог-
Тогда для зависящих от временн полей имеем
C.226)
и, вводя вектор напряженности магнитного поля
= В/ц0 — М=В/ц, C.227)
115
Глава 3
где
Ц = ЦгЦо C.228)
есть магнитная проницаемость, получаем из уравнений Макс-
Максвелла
rotH=Jf. C.229)
Записывая теперь теорему Стокса для вектора напряженности
магнитного поля Н и подставляя rot H из C.229), получаем за-
закон циркуляции Ампера:
H-ds=$Jf-dS=./V/, C.230)
где Л/7— полный ток, протекающий через контур Г (см. разд.
1.2.3). Закон циркуляции Ампера гласит, что циркуляция векто-
вектора Н по любому замкнутому контуру пропорциональна полному
току, протекающему через контур. Полный ток записан в не-
нестандартном виде, N1, так как обычно контур включает в себя
катушку с N витками, через каждый из которых течет ток /.
Тогда полный ток равен количеству ампер-витков.
Из уравнений A.22) и C.227) следует, что разность магнит-
магнитных потенциалов между двумя произвольными точками Р\ и Рг
определяется выражением
?H-ds = «i — «2, C.231)
Pi
где <й1 и «2 — значения потенциала в соответствующих точках.
Вспомним также, что скалярный магнитный потенциал можно
вводить только при постоянной проницаемости. В этом случае
можно прямо вычислить разность магнитных потенциалов ©i—
—юг между полюсами. Так как нормальная составляющая плот-
плотности магнитного потока непрерывна на границе раздела желе-
железо—воздух и при очень высоких значениях относительной про-
проницаемости величиной Н в ферромагнитном материале можно
пренебречь, с помощью соотношений C.230) и C.231) записы-
записываем
ом — й>2=#/. C.232)
(Эта формула основана на предположении о гипотетической
граничной поверхности, исключающей токи, принимаемом для
обоснования концепции скалярного магнитного потенциала
[81J. несмотря на то что мы учитываем эффекты, связанные с
наличием токов.) Так как полюса расположены очень близко к
116
Определение электрических и магнитных полей
оси (рис. 27), соотношения C.231) и C.232) дают для компо-
компоненты плотности потока
°bB*dz=noNI. C.233)
—DO
Здесь пределы интегрирования бесконечны, так как поле кон-
концентрируется на полюсах (это допущение, естественно, неспра-
несправедливо для насыщенных материалов).
Предположение об отсутствии сколь-нибудь значительной на-
напряженности поля в материале означает, что индуцированный
магнитный потенциал сконцентрирован в зазоре между полюс-
полюсными наконечниками. Это падение магнитного потенциала долж-
должно составлять по крайней мере 95% суммарного числа ампер-
витков обмотки. Наше допущение также предполагает, что си-
силовые линии магнитного поля перпендикулярны поверхности
полюсных наконечников, т. е. поверхности, как и требуется, эк-
эквипотенциальны для магнитного поля.
Первые вычисления распределений поля ненасыщенных маг-
магнитных линз основывались на представлении полюсов в виде
бесконечно длинных цилиндров, оканчивающихся бесконечно
протяженными параллельными плоскостями, перпендикулярны-
перпендикулярными оси зазора [82, 83J. Аксиальное распределение поля (и та-
таким образом, действие линзы), в основном, зависит от одного
параметра: отношения ширины зазора к диаметру канала s/D.
Реальная форма магнитной системы не влияет существенно на
распределение поля. Действие такой простой конструкции мо-
может быгь смоделировано соленоидом длины .9 с тем же коли-
количеством ампер-витков и приблизительным диаметром 2D/3. Та-
Такой эквивалентный соленоид [84] является хорошим приближе-
приближением при s/D>0,2.
Для достижения максимальной концентрации поля в окрест-
окрестности зазора необходимо улучшение конструкции, так как усло-
условия насыщения сильно зависят от формы полюсных наконечни-
наконечников. Было установлено, что наилучший путь устранения насы-
насыщения заключается в формировании конического сужения по-
полюсных наконечников [85] путем увеличения сечения за зазо-
зазором, так что поток утечки замыкается без насыщения (рис. 28).
Тогда для любой заданной величины s/D можно определить
конический угол, минимизирующий насыщение.
Если диаметр Dx торцевых поверхностей полюсных наконеч-
наконечников много больше диаметра канала D, то влиянием краевых
потоков на полюсах можно пренебречь, плотность потока в за-
зазоре считать постоянной и формула C.233) упрощается до
тривиального соотношения
C.234)
117
Глава 3
между магнитной индукцией и возбуждающим током. Для ко-
конических поверхностей можно использовать очень простую ана-
аналитическую модель [86J. Полюсные наконечники заменяются
двойным конусом (рис. 29), и на конических поверхностях для
обеспечения разности потенциалов N1 поддерживаются потен-
потенциалы N1/2 и —N1/2 соответственно. Сферические координаты
qi=R, ^2=8 и <7з=ос (R—абсолютная величина радиуса-векто-
радиуса-вектора) особенно удобны для вычисления распределения потенциа-
потенциала. Они определяются соотношениями
JC=i?sin8cosa, «/=./? sin 8 sin a, z=R cosO. C.235)
Отсюда с помощью A.8) определяются коэффициенты Ламе
Ai==l, ht = R, /i3=/?sin0, C.236)
Рис. 28. Сужающиеся магнитные полюсные наконечники.
и уравнение Лапласа A.23) можно записать, используя A.19),
в виде
I д f г,. да>\ , 1 д I . г, да>\ , 1 д2а> л /о О0_.
Очевидно, благодаря аксиальной симметрии зависимость от ази-
азимутальной координаты а отсутствует. Так как конические по-
поверхности предполагаются эквипотенциальными, двухконусная
модель не содержит какой-либо естественной единицы длины.
Поэтому распределение скалярного потенциала не должно зави-
зависеть от изменения масштаба радиуса-вектора R. Как следствие,
зависимостью потенциала от R можно пренебречь. Тогда урав-
уравнение C.237) упрощается до
.О, C.238)
C.239)
из которого при интегрировании тотчас получается
118
Определение электрических и магнитных полей
Постоянные интегрирования сх и с?, могут быть определены из
значений потенциала на конических границах свободного прост-
пространства между полюсными наконечниками. Вследствие симмет-
симметрии можно записать (см. рис. 29)
(й(90)=^//2, ш(я/2),=0. C.240)
Тогда C.239) принимает вид
Таким образом, эквипотенциальные поверхности являются ко-
коническими. Силовые линии магнитного поля являются дугами
окружностей, которые пересекают эквипотенциальные поверхно-
поверхности под прямыми углами. Магнитная индукция имеет только
0-компоненту. Она определяется из A.22), A.13) и C,241):
Можно видеть, что магнитная
индукция уменьшается по ме-
мере удаления от центра систе-
системы полюсных наконечников.
Она достигает максимима на
поверхностях, а минимума в
плоскости симметрии, перпен- Рис 29. Модель полюсного наконеч-
дикулярной ОСИ Z И проходя- иика в виде двойного конуса
щей через центр системы. Си-
Силовые линии идут от больше-
большего потенциала к меньшему. Знак минус в C.242) согласуется с
соотношением C.232), требующим уменьшения потенциала
вдоль оси при положительном возбуждающем источнике.
Представленная модель является слишком упрощенной. Ко-
Конические полюсные наконечники не имеют общего острия и за-
зазором между ними нельзя пренебречь. Однако можно показать
[86J, что эта модель дает хорошее приближение для больших
конических углов полураствора 8о. Так как этот угол должен ле-
лежать между 50 и 70° для поддержания плотности потока на
приемлемо низком уровне [84], модель может применяться для
быстрого конструирования систем магнитных линз. Приближен-
Приближенная картина силовых линий поля показана на рис. 28. Она со-
состоит из двух областей: почти однородного поля в зазоре и кру-
кругового поля между коническими поверхностями. Тогда можно
вычислить магнитные сопротивления параллельной части зазо-
зазора и конической поверхности полюса. Они, как магнитные эле-
элементы, соединены параллельно, поэтому для получения обрат-
обратной величины полного магнитного сопротивления следует сло-
119
Глава 3
жить соответствующие обратные величины. Так как магнитное
сопротивление R№ связано с потоком <р простым соотношением
C.243)
легко оценить поток через полюса и среднюю магнитную индук-
индукцию в полюсах.
Вычисления показывают, что для малых значений 80 маг-
магнитная индукция сначала возрастает, прежде чем начать умень-
уменьшаться по мере продвижения вдоль полюсного наконечника в
аксиальном направлении. Этот эффект особенно значителен при
s/Z?i>0,3. Поэтому, если мы хотим работать вблизи насыщения,
желателен большой угол наклона (8о=7О°).
Описанный метод совершенно непригоден при малых кони-
конических углах, либо когда диаметр торца полюсного наконечни-
наконечника D\ становится сравнимым с зазором s. В этих случаях с не-
неизбежностью необходимо рассматривать всю магнитную систе-
систему. Детализированное рассмотрение различных подходов при
практическом конструировании линз (включая линзы на осно-
основе постоянных магнитов) можно найти в литературе [87, 88J.
Для очень сильных линз необходимы высокие значения маг-
магнитной индукции. Это с неизбежностью ведет к уровням воз-
возбуждающих токов и размерам полюсных наконечников, попада-
попадающим в область режима насыщения. При Л^/> 1000 s (зазор вы-
выражен в миллиметрах) следует быть готовым к учету насыще-
насыщения. Если большая катушка практически полностью экраниру-
экранируется массивной ферромагнитной системой, аксиальная составля-
составляющая магнитной индукции будет почти полностью определять-
определяться намагниченностью полюсных наконечников. Однако когда
относительная проницаемость падает ниже 100, в вычислениях
следует строго учитывать геометрию магнитной системы и об-
обмоток. Железные поверхности не являются более эквипотенци-
эквипотенциальными, и падения магнитного потенциала в различных час-
частях материала следует аккуратно вычислять. Если только ма-
малые области полюсных наконечников достигают насыщения, лин-
линза может хорошо работать [85J, даже с некоторым улучшением
по сравнению с ненасыщенным режимом [89]. В этом случае
удобно характеризовать распределение магнитной индукции ее
максимальным значением и полушириной (расстоянием, на ко-
котором индукция уменьшается вдвое по сравнению с максиму-
максимумом). Эти величины могут быть выражены через уровни воз-
возбуждающих токов и геометрические параметры полюсных на-
наконечников. Этот подход делает возможным использование
простых моделей магнитных линз (см. гл. 8) для анализа элект-
электронно-оптических свойств при не очень высоких значениях маг-
магнитной индукции.
120
Определение электрических и магнитных полей
В некоторых особых случаях дуализм электромагнитного по-
поля может быть использован при аналитических вычислениях.
Это свойство позволяет преобразовать задачу вычисления маг-
магнитного поля в математически эквивалентную задачу расчета
электростатического поля. Таким путем могут рассматриваться
сложные магнитные поля [90, 91J, но метод пригоден только в
том случае, если соответствующая электростатическая задача
решается аналитически.
Из вышеприведенного анализа ясно, что не существует об-
общего аналитического метода, позволяющего учесть все харак-
характеристики магнитной системы. В случае сложных магнитных
линз положение обмотки и распределение плотности тока в ней
следует также принимать во внимание. При необходимости де-
детального анализа магнитных линз необходимо применять как
измерения, так и численные методы. Мы рассмотрим такой под-
подход ниже в настоящей главе.
3.1.5. Аналитическое вычисление магнитных
полей, индуцируемых токами
Характеристики линз на основе ферромагнитных материалов
ограничиваются нелинейными свойствами этих материалов, тог-
тогда как ограничивающим фактором не содержащих ферромаг-
ферромагнитных материалов линз является максимальный ток, поддер-
поддерживаемый обмоткой. В отсутствие магнитных материалов ана-
аналитическое вычисление магнитных полей, индуцируемых про-
проводниками с током, относительно просто. Закон Био — Савара
дает несложную формулу для вычисления магнитной индукции.
3.1.5.1. Закон Био — Савара. Если магнитное поле индуци-
индуцируется током, магнитный векторный потенциал А может быть
определен из соотношения A.12). Векторный потенциал выра-
выражается через распределение плотности тока J хорошо известной
формулой
C.244)
где R — радиус-вектор точки Р, в которой мы хотим определить
векторный потенциал (рис. 30), Rs —радиус-вектор элемента
объема dV, и интегрирование следует вести по всему объему
V, где есть токи. Если токи / текут в проводниках постоянного
сечения S в направлениях, определяемых вектором ds в каждой
точке системы проводников, можно заменить объемный интег-
интеграл линейным с помощью простого соотношения
C.245)
121
Глава 3
Используя A.12), C.244) и C.245), получаем для магнитной
индукции
[— Rs|-'ds. C.246)
Здесь мы учли, что ротор берется в точке Р, а интегрирование
должно проводиться по линиям тока Г. Эти две операции явля-
являются взаимно независимыми, поэтому можно поменять их по-
порядок. Так как следует вычислить ротор от произведения ска-
скаляра и вектора, можно использовать тождество
rot(/|R— Rsj-Jds) =/|R— R,|-irot(ds) +
+ (grad/|R— Rs|-')Xds. C.247)
И вновь, так как вектор ds не связан с точкой Р, соответству-
соответствующий ротор равен нулю. На практике /=const (через сложную
Рис. 30. Элемент индукции согласно Рис. 31. Магнитное поле прямоли-
закону Био — Савара. нейного проводника.
систему проводников протекает один и тот же ток). Оставшийся
градиент легко вычислить
grad(l/|R-Rs|)-grad(|R-Rs|)/(R-RsJ =
,=— (R-RS)/|R — Rs|3. C.248)
Используя эти соотношения, получаем окончательную форму
закона Био — Савара в виде
BSdB=((i0//4n)SdsX(R-Rs)/|R—Rs|3- C.249)
Как можно видеть, магнитная индукция выражается в виде
суммы элементарных вкладов от каждого бесконечно малого
элемента тока. Это точное соотношение. Оно позволяет вычис-
вычислить магнитную индукцию, создаваемую любой системой про-
проводников с током. Конечно, не всегда возможно выполнить ин-
интегрирование в замкнутой форме, но аналитические решения
122
Определение электрических и магнитных полей
существуют для ряда важных практических случаев. Ниже мы
выведем некоторые из них.
3.1.5.2. Поле прямолинейного проводника. Простейшим слу-
случаем является прямолинейный проводник с постоянным током/,
протекающим в направлении оси z (рис. 31). Очевидно, что на-
направление вектора dB перпендикулярно плоскости рисунка и
вектор направлен от нас в соответствии с правилом правой ру-
руки независимо от расположения элемента тока /ds и точки Р.
Таким образом, направление вектора В будет таким же после
интегрирования вдоль проводника. Так как уже известно на-
направление вектора В, можно вычислить его абсолютное значе-
значение. Из рис. 31 с очевидностью следует, что
|dsX (R— Rs) | =r2dp/cos2p, C.250)
|R—R,|,=r/cosp, C.251)
где г — расстояние между проводником и точкой Р. Тогда
C.249) дает
В = е„ (цо//4зтг) $ cos fJdfi =
Pi
= еа(цо//4яг) (sin §2 — sin §,), C.252)
где еа — единичный вектор в азимутальном направлении (поле
вокруг прямолинейного проводника направлено по замкнутым
окружностям), Pi и §2 — угловые координаты концов проводни-
проводника а и 6 соответственно.
Для бесконечно длинного проводника Pi = —я/2 ир2 = л/2, и в
результате получается хорошо известная формула
C.253)
3.1.5.3. Поле круговой петли. Следующий пример является
очень важным. Магнитное поле, индуцируемое током, проте-
протекающим через круговую петлю, является простейшей магнитной
линзой. Так как аксиальное распределение поля однозначно оп-
определяет поле во всем объеме, мы ограничимся определением
поля только вдоль оси петли.
Рассмотрим петлю радиуса а, поддерживающую постоянный
ток / и расположенную в плоскости, перпендикулярной оси z
(рис. 32). Тотчас видно, что совокупность векторов dB сформи-
сформирует коническую поверхность с вершиной в точке Р. Соответст-
Соответственно аксиальные компоненты векторов будут иметь одно на-
направление, а радиальные компоненты попарно взаимно скомпен--
сируются (одна пара таких элементов показана на рисунке). По-
Поэтому результирующий вектор магнитной индукции В будет
иметь только аксиальную составляющую Вг в соответствии со
123
Глава 3
вторым правилом правой руки. Так как элемент тока в этом
случае всегда перпендикулярен вектору (R—Rs) и
dBz = adB(a2 + z2)-V2, C.254)
из C.249) получаем выражение для аксиальной составляющей
магнитной индукции:
Вг (г) =\йВг = ^-— &ds = ^^— . C.255)
гК ' J z 4я(а2+г2K/2Х 2(а2 + г2K/2 V '
Отсюда видно, что индукция достигает максимума в центре
петли, где
Вг тах = Вг @) = щЩй. C.256)
Магнитная индукция медленно спадает от центра и обращает-
обращается в нуль на бесконечности (см. рис. 57).
•2
Рис. 32. Магнитное поле петли. Рис. 33. Тонкий соленоид.
3.1.5.4. Поле тонкого соленоида. Вычислим теперь аксиаль-
аксиальное распределение магнитной индукции, создаваемой соленои-
соленоидом длины / и радиуса а, состоящего из N витков с током /. Ис-
Искомое поле можно считать суперпозицией полей от N петель,
рассмотренных в предыдущем разделе. Перепишем соотноше-
соотношение C.255) в обозначениях рис. 32:
Bz=(nol/2a)sm34. C.257)
Если расстояние между витками достаточно мало, можно ввес-
ввести линейную плотность тока N1/1. Тогда магнитная индукция йВг
в точке Р, созданная петлей длины dz на расстоянии z от цент-
центра, есть
dBz= (\к>Ы1/21а) sin3 fdz. C.258)
Рассматривая малый интервал х, замечаем, что
sin у dz,=adf/sin f, C.259)
и C.258) преобразуется к виду
dBz= (noNI/21) sin fdf. C.260)
124
Определение электрических и магнитных полей
Теперь необходимо взять интеграл от ^1 до ^2 (углы между
осью z и линиями, соединяющими концы соленоида с точкой
Р), чтобы получить суммарное значение магнитной индукции в
точке Р (рис. 33):
Bz(z) = (\ioNI/2l) (cos -у, — cos f2), C.261)
где
cosYi=(//2 + 2)[(//2 + zJ + a2]-1/2, C.262)
cosf2=— A/2 — z)[{l/2 — zJ + a2]-'/2. C.263)
Магнитная индукция имеет максимальное значение в центре
(z = 0):
Вгтлх=Вг@) =ЦоЫ1A2 + 4а2)-1'* C.264)
и медленно спадает до нуля на бесконечности.
Соленоид может служить моделью симметричной железной
полюсной линзы (см. разд. 3.1.4).
Рис. 34. Катушка конечных размеров.
Для очень длинных соленоидов значения cosfi = l и cosf2=
=—1 являются хорошими приближениями, и тогда получается
простое соотношение для магнитной индукции однородного по-
поля внутри длинного соленоида:
C.265)
Заметим, что вследствие конечных размеров проводников ко-
количество витков нельзя увеличить выше определенного преде-
предела. Поэтому на практике применяются многослойные катушки.
3.1.5.5. Поле многослойной катушки. Магнитную индукцию
многослойной катушки легко получить исходя из результата
для тонкого соленоида [92J. Сечение катушки конечных разме-
размеров показано на рис. 34. Можно считать, что она состоит из ко-
конечного числа тонких соленоидов, намотанных послойно один
на другой, начиная с радиуса Г\ и кончая радиусом г2. Если об-
125
Глава 3
мотка однородна в радиальном и аксиальном направлениях и
общее число витков равно N, то плотность тока постоянна и оп-
определяется количеством ампер-витков на единицу площади се-
сечения катушки. Тогда магнитная индукция, создаваемая слоем
радиуса г в точке Р на оси, может быть определена из C.261) в
обозначениях рис. 34 в виде
<Ш(z) = „. **°^7 . . (cos a - cos P) dr. C.266)
£{fi— I'll •
Индекс 2 опущен, так как известно, что в осевых точках маг-
магнитная индукция имеет только аксиальную составляющую. Что-
Чтобы найти полную магнитную индукцию в точке Р, полученное
соотношение необходимо проинтегрировать от п до г2. Интегри-
Интегрирование проще выполнить в угловых переменных. Рассматривая
углы а и [1, тотчас имеем
Л]= B+ Ц2)da/cos2a = B— 1/2)dp/cos2 § C.267)
и суммарное распределение магнитной индукции дается выра-
выражением
— G 1l\\n
-B-//2) in tg(Pi/2+Jl/4)
где ai, <X2, §1 и §2—предельные значения углов а и § соответ-
соответственно (рис. 34). Соотношение C.268) можно преобразовать
к виду
В (Z) -
D \z>-
1-sin a2)(l +sinai)
-B
поскольку
sina=r[r2+(z + //2J]-i/2,
C.270)
sin §=r[r2+B-//2) 2]~i/2
{для предельных значений вместо г следует подставить г{ и г2).
Если линейные размеры обмотки малы по сравнению с радиу-
126
Определение электрических и магнитных полей
сом катушки, из C.269) можно вывести приближенное выраже-
выражение в форме C.255), т. е. получается «эквивалентная петля» для
катушки с «эквивалентным радиусом» а с учетом физических
размеров обмотки [16]. Такие формулы могут быть использова-
использованы только для быстрой оценки свойств катушки. Так как соотно-
соотношение C.269) является строгим и относительно простым, его
следует использовать при всех вычислениях распределений маг-
магнитной индукции от катушек конечных размеров.
Можно точно определить распределение магнитной индукции
от прямоугольных катушек [93J, конических катушек [94] и да-
даже катушек с переменным сечением.
3.1.5.6. Поле плоской катушки. Плоская спиральная магнит-
магнитная линза (рис. 35) также может быть использована как фоку-
фокусирующий элемент [84]. Аксиальное распределение магнитной
индукции такой катушки может быть определено из C.255) ин-
интегрированием. В самом деле, если создать обмотки из N вит-
витков, расположенных один на другом, и ввести линейную плот-
плотность тока в радиальном направлении [NII(r2—п)], то можно
записать выражение для полной магнитной индукции в точке Р
в виде
Максимальное значение магнитной индукции равно
C.272)
Соотношение C.271) является частным случаем C.269) для
/ = 0, но этот факт замаскиро-
замаскирован неопределенной формой
предельного случая.
Сравнивая C.264) и C.272),
можно видеть, что для задан-
заданной линейной плотности тока —
плоская катушка всегда обес-
обеспечивает большую максималь- 8
ную магнитную индукцию, чем 8
соленоид, так как отношение §
r2/ri может быть очень высо- Рис. 35. Плоская лииза.
127
Глава 3
ким. Очевидно, что поле плоской катушки также гораздо силь-
сильнее сконцентрировано. Мы обсудим электронно-оптические
свойства такой катушки в разд. 8.4.2.4.
Закон Био — Савара можно также применить для вычисле-
вычисления многих других распределений магнитного поля. Среди них
особенно важными являются тороидальное и седловое откло-
отклоняющее ярмо [95, 96J.
3.2. Измерение полей и аналоговые методы
Мы уже убедились, что аналитический подход можно ис-
использовать только в некоторых благоприятных случаях. В об-
общем случае следует полагаться на измерения либо численные
расчеты. И хотя современные цифровые компьютеры позволя-
позволяют выполнить полный анализ (и даже синтез!) практически лю-
любой электронной или ионной оптической системы, важность
прямых измерений по-прежнему трудно отрицать. Только экспе-
эксперимент может окончательно подтвердить правильность прове-
проведенных вычислений.
Для достоверного определения сложных магнитных полей,
особенно в присутствии насыщенных материалов, измерения
просто необходимы. Прямые измерения электростатических по-
полей весьма затруднительны в вакууме (и даже в воздухе)
вследствие пренебрежимо малой проводимости среды. Поэтому
для этих целей были разработаны аналоговые методы. Благо-
Благодаря простоте и эффективности эти методы определения полей
не могут быть полностью отвергнуты даже в эпоху всеобщего
распространения цифровых компьютеров по следующим при-
причинам:
1. Процесс решения с помощью аналогового метода позво-
позволяет лучше понять проблему, чем решение той же за-
задачи с помощью цифрового компьютера. Аналоговые компьюте-
компьютеры до сих пор используются для построения траекторий пучков
в ускорителях частиц. Подстраивая узлы аналогового компью-
компьютера, конструктор может непосредственно наблюдать влияние
непрерывных изменений при возбуждении линзы на форму
пучка.
2. Хотя автор полностью верит в огромные возможности циф-
цифровых компьютеров и искусственного интеллекта (см. гл. 9), он
также уверен в том, что инженерная и научная изобретатель-
изобретательность вряд ли может быть заменена машинами, сколь бы доро-
дорогими и сложными они не были. Талантливый инженер, снаб-
снабженный резисторной сетью и программируемым калькулятором,
может состязаться с посредственным коллегой, даже если по-
последний располагает суперкомпьютером.
3. Численные вычисления трехмерных полей требуют гро-
громадных вычислительных ресурсов. Поэтому измерение полей с
428
Определение электрических и магнитных полей
очень низкой симметрией (например, коротких квадруполей)
гораздо дешевле численных расчетов.
4. Наконец, большой объем превосходных работ, выполнен-
выполненных за многие годы развития электронной и ионной оптики ты-
тысячами упорных исследователей, занятых долгими измерениями
и утомительными ручными вычислениями, полностью оправдан
тем, что их более счастливые преемники должны по крайней
мере иметь представление об использованных методах.
Поэтому далее мы кратко рассмотрим методы измерения
магнитных полей, а также аналоговые методы определения по-
полей.
3.2.1. Измерение магнитных полей
Данное краткое введение в различные методы измерения
магнитных полей не может претендовать на детальное описание,
поэтому интересующимся читателям рекомендуем обратиться к
специализированной литературе [97].
3.2.1.1. Электромагнитная индукция. Согласно уравнениям
Максвелла A.2), магнитное поле, изменяющееся во времени, ге-
генерирует электрическое поле. Аналогично, если небольшая ка-
катушка перемещается в постоянном магнитном поле, которое под-
подлежит измерению, на ее концах наведется электродвижущая си-
сила. Электродвижущая сила ё> пропорциональна производной во
времени от магнитного потока ф и может быть легко измерена.
Катушка может перемещаться в магнитном поле раскачивани-
раскачиванием, вращением, вибрацией и т. д.
Если измерительная катушка присоединена к баллистичес-
баллистическому гальванометру, то электродвижущая сила вызовет ток i в
цепи с сопротивлением R и индуктивностью L. Тогда
8=— dy/dt = iR + Ldi/dt. C.273)
Интегрируя это выражение по временному интервалу Т, в тече-
течение которого движется катушка, получаем
Ф1 — Фа=# S idt+L{i2 — h) =Rq, C.274)
о
где индексы «1» и «2» относятся к началу и окончанию движе-
движения катушки соответственно (ток имеет нулевое значение в оба
момента), q — полный заряд, прошедший через цепь. Этот заряд
непосредственно измеряется баллистическим гальванометром,
а магнитный поток просто связан с индукцией y = NSBn, где
N — количество витков, S — площадь охватываемая катушкой,
Вп — нормальная по отношению к катушке составляющая маг-
магнитной индукции (для небольшой катушки магнитную индук-
индукцию можно считать постоянной внутри измерительной катуш-
129
Глава 3
ки). Измеряя компоненты индукции в трех взаимно перпендику-
перпендикулярных направлениях, можно определить распределение вектора
магнитной индукции.
Естественно, размер измерительной катушки должен быть до-
достаточно мал при измерении распределения сильно неоднородно-
неоднородного магнитного поля. Это имеет особенно большое значение, ког-
когда измерения должны проводиться в условиях насыщения на ре-
реальном магните, а не на его увеличенной модели вследствие су-
существенно нелинейного характера насыщения. Для повышения
чувствительности необходимо увеличить количество витков. Но
в этом случае необходимо определить эффективную площадь
катушки путем калибровки в хорошо известном однородном по-
поле (например, в соленоиде).
Как точность, так и чувст-
чувствительность измерения могут
быть повышены при исполь-
использовании двух вращающихся
катушек: одна в измеряемом
—t^^^^^^"' поле, а другая в опорном од-
п ос tC?l++++C++++ нородном поле. Измерение
Рис. 36. Эффект Холла. г
^ основано на точном уравнове-
уравновешивании двух электродвижущих сил путем изменения то-
тока в опорном соленоиде. Относительная точность такого метода
очень высока @,01%), но при этом требуется очень хорошая
взаимная экранировка двух полей. Указанную трудность мож-
можно устранить использованием электростатического опорного по-
потенциала.
3.2.1.2. Эффект Холла. Эффект Холла является следствием
силы Лоренца [уравнение A.14)], действующей на заряженную
частицу в магнитном поле. Пусть кристалл помещен в магнит-
магнитном поле В (рис. 36). Если через него протекает ток плотно-
плотностью J в направлении, перпендикулярном В, то сила Лоренца,
действующая на носители, заставит их отклониться вверх. В за-
зависимости от знака носителей на верхней поверхности кристал-
кристалла образуется отрицательный или положительный поверхност-
поверхностный заряд (отрицательный для электронов и положительный
для дырок), а на нижней поверхности — заряд противоположно-
противоположного знака. Поверхностный заряд приведет к образованию разно-
разности потенциалов V между двумя поверхностями, которая мо-
может быть точно измерена. Поверхностные заряды будут накап-
накапливаться до тех пор, пока сила Лоренца в точности не уравно-
уравновесится электростатической силой между двумя слоями. В рав-
равновесии результирующее электростатическое поперечное поле
составит
E=V/d=vdrmB = JB/nQ, C.275)
!30
Определение электрических и магнитных полей
где d — толщина кристалла (в вертикальном направлении),
«drift — дрейфовая скорость носителей, an — их концентрация.
Таким образом, разность потенциалов зависит от геометричес-
геометрических размеров кристалла, внешней магнитной индукции, плот-
плотности тока и концентрации носителей. Поэтому эффект Холла
широко применяется для определения как концентрации, так и
знака носителей в полупроводниковых кристаллах.
Очевидно, что для данного материала с известной концент-
концентрацией носителей этот эффект можно использовать для опре-
определения магнитной индукции. Ясно, что для повышения чувст-
чувствительности необходимо использовать материал с низкой кон-
концентрацией носителей. Так как коэффициент Холла
C.276)
пропорционален подвижности носителей, в качестве датчиков
Холла предпочтительны материалы с высокой подвижностью но-
носителей, такие, как InAs и InSb. Датчик Холла может иметь
очень малые размеры, что определяет возможность точных из-
измерений. Препятствием является сильная температурная зави-
зависимость коэффициента Холла.
3.2.1.3. Пермаллоевые и висмутовые датчики. Пермаллой —
это ферромагнитный материал на основе особого Ni—Fe спла-
сплава. Он легко переводится в состояние насыщения, и индукция
насыщения может быть легко обращена небольшим изменением
магнитного поля. Разность в значениях индукции равна удвоен-
удвоенной индукции насыщения. Возбуждение обычно обеспечивает-
обеспечивается переменными токами в двух пермаллоевых датчиках, соеди-
соединенных параллельно, а измеряются высшие гармоники, вызы-
вызываемые внешним полем. Этот принцип позволяет проводить из-
измерения с относительной точностью лучше 0,1%.
Действие висмутового датчика гораздо проще. Хорошо изве-
известно, что электрическая проводимость висмута существенно за-
зависит от внешнего магнитного поля, в котором находится мате-
материал. Если температура висмутового проводника поддержива-
поддерживается строго постоянной, возможны достаточно точные измере-
измерения распределения внешнего поля.
3.2.1.4. Магнитный резонанс. Наиболее точные методы изме-
измерения магнитных полей основаны на эффекте магнитного резо-
резонанса. Если атомная система помещена во внешнее магнитное
поле, не столь сильное, чтобы разрушить саму систему, поле
вызовет изменения в энергетической структуре системы. По-
Появятся новые энергетические уровни, и расстояние Д№ между
соседними уровнями соответствует определенной частоте шр:
haPl2n. C.277)
131
Глава 3
Эта частота лежит обычно в микроволновом диапазоне. Если
теперь облучить материал фотонами той же частоты, возникнет
резонансное поглощение: энергия системы изменится на вели-
величину AW. Так как
a>P=gQB/2m0, C.278)
где g (фактор Ланде) — количественная характеристика состоя-
состояния системы, измерение частоты немедленно дает величину маг-
магнитной индукции. Фактор Ланде можно вычислить квантовоме-
ханическими методами. Он в точности равен единице для си-
системы с чисто орбитальным моментом и в точности равен двум
для системы с чисто спиновым моментом. В более сложных слу-
случаях g лежит между единицей и двойкой.
Такие же рассуждения справедливы и для ядерных систем.
Тогда в C.278) то — масса протона, а величина g больше при-
примерно в 2,79 раза по сравнению с предыдущим случаем. В ре-
результате резонансная частота будет в 660 раз меньше, чем для
электронов. Но измерение частоты по-прежнему обеспечивает
очень высокую точность (относительная ошибка порядка 0,01%)
определения магнитной индукции в широком диапазоне величин.
Ядерный магнитный резонанс также может быть использован
для измерения градиентов магнитных полей.
Существуют и другие методы измерения магнитных полей.
Можно измерить силу, действующую со стороны поля на про-
проводник с током, и отсюда вычислить значения магнитной индук-
индукции. Более точный подход заключается в измерении отклонения
полей пучка электронов. Естественно, этот метод в основном
применим только к однородным полям.
3.2.2. Аналоговые методы
Как уже говорилось, аналоговые методы будут представле-
представлены кратко, в основном из исторического интереса. Читателей,
интересующихся деталями, отошлем к литературе [98J.
3.2.2.1. Электролитическая ванна. Проводимость в электро-
электролите определяется законом Ома
J = oE, C.279)
где о — проводимость среды. В стационарном случае уравнение
неразрывности (сохранения заряда) принимает форму
divJ = 0. C.280)
В случае однородного электролита проводимость постоянна.
Подставляя C.279) и A.17) в C.280), приходим к уравнению
132
Определение электрических и магнитных полей
Лапласа A.18) при р = 0. Отсюда тотчас следует, что если гра-
граничные условия одинаковы, распределение потенциала в элек-
электролите будет таким же, как в вакууме. Благодаря конечной
проводимости электролита это распределение в электролите го-
гораздо легче измерить, чем в вакууме. Измерения обычно осу-
осуществляются с помощью измерительного моста и всегда на пе-
переменном токе (в противном случае электролит разлагался бы
вследствие электролиза). Более того, так как уравнение Лапла-
Лапласа линейно, как потенциалы, так и геометрические размеры
можно изменять по нашему усмотрению.
Дополнительное преимущество состоит в том, что симметрия
моделируемой системы может быть легко использована в элект-
электролитической ванне. Следует только вспомнить метод изобра-
изображений в электростатике. Если заменить эквипотенциальную по-
поверхность реальной проводящей поверхностью, естественно, ни-
ничего не изменится в распределении потенциала. Однако теперь
можно забыть обо всех зарядах, индуцированных полем, если
они расположены вне проводящей поверхности, так как, уста-
устанавливая ее потенциал равным значению, созданному на экви-
эквипотенциальной поверхности этими зарядами, мы фактически за-
заменяем их поверхностью. Поэтому, например, заряд вблизи про-
проводящей поверхности будет эквивалентен этому заряду и дру-
другому заряду такой же величины, но противоположного знака,
расположенному вне поверхности на таком же расстоянии от
нее, но без физического присутствия проводника. Если поверх-
поверхность проводника плоская, она будет автоматически действо-
действовать как плоскость антисимметрии для распределения поля.
На изолирующих границах нормальная составляющая плот-
плотности тока равна нулю, поскольку ток никогда не протекает
через изолятор. Поэтому заряд вблизи изолирующей границы
эквивалентен исходному заряду и такому же заряду, распо-
расположенному вне изолирующей поверхности на том же расстоя-
расстоянии от нее. Если изолирующая поверхность плоская, она дей-
действует как плоскость симметрии для распределения поля.
Согласно этому правилу, можно вводить в электролитиче-
электролитическую ванну проводящие и изолирующие поверхности для созда-
создания плоскостей симметрии и антисимметрии. И таким образом,
нет необходимости создавать полную модель системы электро-
электродов. Используя все имеющиеся типы симметрии, малую часть
системы можно использовать для воспроизведения всей систе-
системы с помощью таких поверхностей. Это особенно удобно при
измерении мультипольных полей. Стенки и дно электролитиче-
электролитической ванны являются естественными плоскостями симметрии
либо антисимметрии в зависимости от их материала. Поверх-
Поверхность электролита также является изолятором, который можно
использовать как плоскость симметрии.
133
Глава 3
Таким путем легко моделировать специальные системы элек-
электродов, используемых в электронной и ионной оптике. Напри-
Например, планарное поле может быть просто смоделировано в мел-
мелкой электролитической ванне с изолирующим дном. Короткие
электроды, расположенные перпендикулярно обеим поверхно-
поверхностям, отобразятся бесконечное число раз в обеих поверхностях,
таким образом, создавая модель бесконечно длинной системы.
Аналогично аксиально-симметричная система может быть мо-
моделирована клинообразной электролитической ванной. Линия
пересечения наклонного дна и поверхности электролита образу-
образует ось симметрии. В этом случае в электролите можно исполь-
использовать простые электроды в форме секторов. Они будут авто-
автоматически продолжены двумя поверхностями и сформируют
тело вращения. Периодические поля можно моделировать, по-
помещая один элемент в электролит и используя отображающие
свойства поверхностей. К сожалению, преимущество использо-
использования стенок электролитической ванны как отображающих по-
поверхностей превращается в недостаток, когда моделируется
единичная открытая система: в этом случае поверхности явля-
являются существенным фактором, возмущающим распределение
поля. Возмущения, вызванные стенками, могут быть существен-
существенно уменьшены, если материалом стенок является специально
подобранный для этих целей полупроводник.
Могут быть созданы такие модели со сложными границами.
Так как «вычисления» автоматически осуществляются моделью,
сложность граничных условий не составляет проблемы. Элек-
Электролитическая ячейка может также моделировать очень слож-
сложные, несимметричные трехмерные системы, численный расчет
которых требует длительного времени и больших объемов
памяти.
Естественно, что магнитные поля можно моделировать ана-
аналогичными методами, если допустимо применение магнитного
скалярного потенциала. Возможно даже моделирование маг-
магнитных полей в присутствии токов. Пространственный заряд
можно также моделировать либо использованием электролити-
электролитической ванны с переменной глубиной, либо инжекцией дополни-
дополнительных токов.
Электролитическая ванна служила основой автоматического
построителя траекторий, который вычерчивал траектории час-
частиц в полях, измеряемых в ванне.
3.2.2.2. Резисторная сеть. Электролитическая ванна является
непрерывной моделью, но возможно также построение дискрет-
дискретных моделей для определения распределений потенциалов. Это
на шаг ближе к численным методам, которые мы собираемся
обсудить в разд. 3.3.
134
Определение электрических и магнитных полей
Прежде всего преобразуем дифференциальное уравнение
Лапласа в уравнение конечных разностей. Для простоты ис-
используем уравнение A.20), записанное в декартовых коорди-
координатах. По определению.
д2и ,. Г ди , . 4 . ди ,
lim I lim [и(х + Ах, у, z) — u(x, у, z)]/Ax —
A*-* 0 \Д*->.0
lim [и (х, у, z) — и (х — Ах, у, z)]/Ax\!Ax =
д*-»-о | /
= lim [u(x -\-Ax, y, z) — 2u(x, у, г) + ы(л:—Ax, y, z)]/{Ax)*.
д*-»-о
C.281)
Аналогично
~= lim [u(x, y + Ay, z) — 2u(x, y, z) + u(x, y — Ay, z)]/(AyJ
иУ Ay—*-0
C.282)
дги
-^2-= lim [u(x, y, z + Az) — 2u(x, y, z) + u(x, y, z — Лг)]/(ДгJ.
uz Дг-»-0
C.283)
Подставляя эти выражения в A-20) при р = 0 и полагая, что
Ax = Ay—Az=8 очень малы, но конечны, получаем
и{х+8, у, z) + и(х, у+ 8, z) +u{x, у, z + 8) +
= 6u{x,y,z). C.284)
Математическое обоснование этого допущения будет дано
в разд. 3.3.2. Соотношение C.284) означает, что потенциал в лю-
любой произвольной точке с координатами х, у, z есть среднее
арифметическое шести значений потенциала, измеренных в шести
эквидистантных точках в окрестности данной.
Представим теперь, что имеется шесть резисторов с одина-
одинаковым сопротивлением между этой и каждой соседней точкой.
Тогда, согласно закону Ома, ток, текущий из каждой соседней
точки к нашей, равен разности потенциалов между ними, де-
деленной на сопротивление. С другой стороны, алгебраическая
сумма этих токов в данной точке должна равняться нулю (за-
(закон Кирхгофа). В результате мы приходим к уравнению для по-
потенциала, в точности такому же как C.284). Это означает, что
цепь резисторов с одинаковыми сопротивлениями между точка-
точками пересечения (узлами) сетки является моделью распределе-
распределения потенциала в декартовой системе координат. Соединяя
узлы, соответствующие электродам в реальной системе, и под-
135
Глава 3
держивая на них заданные потенциалы, мы создаем распреде-
распределение потенциала, эквивалентное распределению потенциала в
реальной системе. Потенциалы в узлах можно измерить с по-
помощью измерительного моста либо цифрового вольтметра,
причем эти измерения легко автоматизировать.
Точность метода зависит от размера ячейки и в большей
степени от формы границ и граничных условий. Естественно,
чем больше элементов в цепи (чем меньше размер ячейки для
данной задачи), тем точнее аппроксимация непрерывной зада-
задачи. На границах, однако, ситуация более критична по двум
причинам. Мы уже знакомы с первой причиной: границы цепи
действуют как отображающие поверхности, которые можно ис-
использовать при наличии симметрии, но для открытых систем
это серьезный возмущающий фактор. Изменяя значение сопро-
сопротивлений, можно сконструировать специальные сетки с квази-
квазибесконечными границами [99J, Вторая причина связана с дис-
дискретным характером метода. Легко смоделировать прямоли-
прямолинейные границы, однако в случае криволинейных границ, не
проходящих точно через узлы, возникают проблемы. В резуль-
результате распределение потенциала плоского конденсатора может
быть моделировано с относительной погрешностью лучше чем
0,1%, но погрешность для цилиндрического конденсатора может
достигать 4% [100]. (Конечно, цилиндрический конденсатор
можно моделировать с очень высокой точностью, используя
цепь для цилиндрических координат, описанную ниже.) Можно
аппроксимировать криволинейные границы, опуская некоторые
узлы и используя только те, которые очень близки к границе,
но тогда возникает дополнительная ошибка из-за проникнове-
проникновения поля через промежутки, созданные опущенными узлами.
Более удачный подход заключается в использовании многоэле-
многоэлементной резисторной сетки и аппроксимации искривленных гра-
границ плоскими поверхностями, соединяющими узлы, наиболее
близко расположенные к контуру электрода. Очевидно, что
ошибки максимальны в окрестности резких краев и электродов
с малым радиусом кривизны. Если требуется очень высокая
точность для моделирования электродов, не совпадающих с уз-
узлами, можно ввести специально подобранные шунтирующие со-
сопротивления [101]. Пространственный заряд также можно
учесть, инжектируя токи в резисторные узлы.
Строить трехмерные резисторные сетки неудобно. Для пла-
нарных, аксиально-симметричных и любых других систем, опи-
описываемых двумя координатами, можно использовать двумерные
сетки. Резисторные сетки для пленарных систем представляют
частный случай трехмерной сетки, если используются декарто-
декартовы координаты. В этом случае резисторная сеть существенно
упрощается и даже может быть заменена листом специальной
136
Определение электрических и магнитных полей
резистивной бумаги. Электроды просто рисуются на поверхно-
поверхности бумаги. Планарная система может быть также описана
в полярных координатах, особенно удобных для моделирования
длинных цилиндрических электродов. Для этого случая значе-
значения сопротивлений должны быть подобраны особо. Далее мы
покажем, как следует конструировать резисторную сетку для
аксиально-симметричных потенциальных полей [16].
Уравнение Лапласа в цилиндрических координатах имеет
для этого случая форму C.88) и может быть записано в виде
^. + 1JL + ^=;O. C.285)
Выражения для вторых частных производных можно записать
так же, как в случае C.281) — C.283). Первая производная бу-
будет иметь вид
ди/дг = lim [и (r+Аг, г)—и (г — Дг, z) ]/2Ar. C.286)
Дг^О
Заменяя бесконечно малые величины на очень малые, но ко-
конечные значения Ar=Az = 6, получаем следующее дифференци-
дифференциальное уравнение:
A + б/2г)ы(г+б,г) + A — 8/2r)u(r— 6,z) +
+ u(r,z+8)+u(r,z — 8)=4u(r,z). C.287)
Это выражение имеет сингулярность на оси. Поэтому в окрест-
окрестности оси следует использовать трехмерное уравнение C.284).
Однако вследствие аксиальной симметрии для этой области
можно записать
Ы(б, 0, 2) =«(— б, 0, 2) =Ы@, б, 2) =Ы(О, — б, Z) = «F,Z).
C.288)
Подставляя х=у = 0 в C.284) и учитывая C.288), получаем
дифференциальное уравнение в окрестности оси
4«(б, z) +u@, z+8)+u@, 2 — 6) =6ы@, z). C.289)
Рассмотрим двухмерную резисторную сетку (рис. 37). Со-
Сопротивления в радиальном направлении обозначены Ry, в ак-
аксиальном— R'ij, где i и / — радиальные и аксиальные коорди-
координаты соответственно с r=ib и z=j8. Способ нумерации очеви-
очевиден из рисунка. Тогда для узла (т,п) закон Кирхгофа можно
записать в виде
(Mm+l, п — U.m,n)IRm+\, п+ (Ыт-1, п — Um,n)IRm,n-\-
+ {Um,n+\ —Umtn)IR'm,n+ (Um,n-\ ~ Um,n) IR'm, n-\ =0.
C.290)
137
Глава 3
Чтобы это уравнение было пригодно для моделирования поля
в областях вне оси, оно должно быть пропорционально C.287).
Для точки с координатами т, п последнее уравнение можно
переписать в виде
(l + l/2ftl)Um+l,n-\-(l ~ l/2m)Um-l,n +
+ «m, n+l + Wm, n-1 — 4«m,n = 0. C.291)
Эти два уравнения пропорциональны друг другу, если
R'm,n = R'm,n-i={\ + \l2m)Rm+l,n=(\ — 1/2т)Дт,п=1/ат,п,
C.292)
где ат,п — коэффициент пропорциональности.
Если теперь записать эти же уравнения для узла (т+\,п),
получим
K'm+l, n = R'm+i, „_i= [1 + 1/2 (m+ l)]Rm+2, „ =
= [1 — 1/2 (m+1 )]£„+,, я=1/ат+,.я. C.293)
Выражая Rm+i,n с помощью C.292) и C.293), видим, что
A + 1/2ш)ат,я = [1 — 1/2 (т+1) ]ат+1, я. C.294)
Отсюда следует, что
am+i,n/(m+l) =amjm=A = const C.295)
не зависит от значений тип.
На оси (тп = 0) уравнение C.290) должно быть пропорцио-
пропорционально C.289). Последнее уравнение можно переписать в виде
4«i,n+«o, n+1+Mo, и-1 — 6ыо,п = О. C.296)
Поскольку как сопротивление, так и потенциал должны быть
аксиально-симметричны, имеем
Ri,n=Ro,n, Ы1,я = и-1,я. C.297)
Тогда C.290) и C.296) пропорциональны при т = 0, если
R'o,n = R'o,n-i = 2Ri,n=\/bn=\/b = const C.298)
из-за очевидной независимости сопротивлений от п.
Выражая Rm+i,n из C.292) и C.295), подставляя т=0 и
сравнивая значения /?,,„ со значениями из C.298), получаем
Ь=Л/4. C.299)
Заметим также из C.298), что Ь однозначно определяется вы-
выбором аксиального сопротивления R'o (индекс п можно опус-
опустить, так как сопротивление не зависит от п). Благодаря акси-
аксиальной симметрии, достаточно построить цепь только для поло-
положительных значений т. Тогда каждый аксиальный резистор не-
138
Определение электрических и магнитных полей
обходимо заменить двумя параллельными с удвоенным сопро-
сопротивлением (по одному с каждой стороны оси z), и, когда мы
отбросим часть цепи, соответствующую /п<0, останутся сопро-
сопротивления только на положительной стороне (т>0). (Это
можно сделать, так как вследствие симметрии ток не протекает
через ось.) Поэтому аксиальное сопротивление необходимо
удвоить. Удобнее оставить это удвоенное значение равным R'o
и выразить через него другие сопротивления, поделив их на 2.
Тогда из C.292), C.295), C.298) и C.299) получим
C.300)
C.301)
Rm+1, п-1
Rm->2, n
"mti.n
Rm4, n
R'm.n
m+1
n-1
n+1
Рис. 37. Резисторная сетка для опре- Рнс. 38. Мультиполи, еконструиро-
делеиия аксиальио-симметричных по- ванные с помощью резисторной сет-
лей.
ки: а — квадруполь, б — квадруполь-
октунюль, в — квадруполь, г — гек-
саполь.
Как видно, сопротивления равномерно уменьшаются с увеличе-
увеличением расстояния от оси, но остаются неизменными вдоль оси.
Подсоединяя дополнительные сопротивления утечки к узлам
этой цепи, можно построить цепь, пригодную для моделирова-
моделирования мультипольных полей [102].
Мы широко использовали обычные многоэлементные пла-
нарные резисторные цепи при конструировании мультипольных
линз [100, 103—107]. Цепь содержала более 6500 резисторов
и обеспечивала вполне достаточную точность. Поперечные се-
сечения некоторых сконструированных таким образом мультипо-
лей показаны на рис. 38, а—38, г; конструкции представляли
собой:
139
Глава 3
а) квадруполь, сформированный двумя цилиндрами, причем
внутренний содержит две симметрично расположенные продоль-
продольные щели (разд. 3.1.1.3),
б) квадруполь — октуполь с квадрупольным потенциалом U
и октупольным потенциалом V,
в) квадруполь с прямыми электродами для исследования
влияния формы электродов на аберрации пятого порядка,
г) гексаполь, сформированный двумя цилиндрами, причем
внутренний содержит три продольные щели.
Целью конструирования являлось определение геометриче-
геометрических параметров, соответствующих заданным коэффициентам
мультипольного разложения. Так как все линзы окружены
замкнутыми металлическими камерами, границы цепи не влия-
влияли на измерения и была достигнута высокая точность. Линзы
были успешно применены для уменьшения размеров пятна и
увеличения эффективности отклонения в катодных трубках, для
улучшения разрешения электронных спектрометров и масс-
спектрометров, а также для компенсации аберраций в элект-
электронных зондах.
Аксиально-симметричная резисторная сеть была использо-
использована при конструировании периодической электростатической
фокусирующей системы для высокоинтенсивных электронных
пучков [108]. Интересная особенность этой работы заключает-
заключается в вычислении сложной комбинации коэффициентов Фурье
на основе прямых измерений распределения потенциала в цепи.
Магнитные поля также можно моделировать с помощью це-
цепей. В отсутствие токов и насыщения можно прямо использо-
использовать магнитный скалярный потенциал, поверхности полюсов
эквипотенциальны и нет различия между электростатической и
магнитной задачами. Однако эффекты, связанные с анизотропи-
анизотропией и нелинейностью материала, могут быть также учтены ис-
использованием переменных сопротивлений, либо инжекцией тока
в узлы. Можно моделировать и векторный магнитный потенци-
потенциал. Резисторная цепь была применена [109] для определения
распределения магнитной индукции в сильно насыщенных маг-
магнитных линзах. Сверхпроводящие экраны могут моделировать-
моделироваться размыканием некоторых граничных сопротивлений.
3.2.2.3. Другие аналоговые методы. Из предыдущего раздела
мы видели, что задача о распределении потенциала может мо-
моделироваться электрическим током в среде. Существует мно-
множество других процессов, описываемых уравнением Лапласа:
безвихревое течение жидкости, стационарное распределение
тепла, деформация эластичной мембраны. Последний широко
использовался на ранних стадиях развития электронной опти-
оптики для создания пленарных полей. Дополнительным преиму-
140
Определение электрических и магнитных полей
ществом этого метода является возможность использования
мембран для моделирования траекторий частиц: путь неболь-
небольшого шарика, катящегося без трения под воздействием грави-
чации по поверхности мембраны, соответствует пути заряжен-
заряженной частицы в планарном потенциальном поле, моделируемом
мембраной.
3.3. Численные методы
Как мы видели, всего лишь в нескольких случаях можно ис-
использовать изящные аналитические методы. Прямые измерения
распределения поля в большинстве случаев слишком громозд-
громоздки. По мере распространения цифровых компьютеров опреде-
определение электростатических и магнитных полей, используемых в
электронной и ионной оптике, стало преимущественно вычисли-
вычислительной задачей. Определение поля обычно требует решения
задачи со сложными граничными условиями. Универсального
рецепта для решения этой задачи не существует, но в то же
время есть ряд мощных методов. Далее мы детально рассмот-
рассмотрим наиболее важные численные методы вычисления полей.
3.3.1. Точность
Прежде чем приступить к каким-либо вычислениям, необ-
необходимо понять возможности и ограничения численных методов.
Ни один компьютер не способен выполнить абсолютно точные
вычисления. Пусть точное значение искомой величины есть w,
а вычисленное — w0, тогда Aw = w0—w — абсолютная погреш-
погрешность вычисления, a Aw/w=(w0—w)/w — относительная погреш-
погрешность. Следует быть внимательным при определении этих по-
погрешностей, так как очень маленькая абсолютная погрешность
может сопровождаться огромной относительной и обратно. На-
Например, при замене w=lO~s на Wo = O абсолютная погрешность
составляет всего—Ю-8, а относительная—100%. С другой сто-
стороны, относительная погрешность при записи числа на восьми-
восьмиразрядном калькуляторе весьма мала и составляет 10~6%, но
может привести к огромной абсолютной погрешности, если чис-
число очень велико. Необходимо всегда определить заранее, до вы-
выбора численного метода, хотим ли мы минимизировать относи-
относительную или абсолютную погрешность (или обе). Для наших
целей обычно (но не всегда) важнее уменьшить относительную
погрешность. Трудность заключается в том, что точное значе-
значение w неизвестно (поэтому мы хотим его вычислить). Следова-
Следовательно, в большинстве случаев можно только оценить точность
вычислений. Конечно, всегда можно рассмотреть простую зада-
задачу, допускающую аналитическое решение, и сравнить два ре-
141
Глава 3
зультата. К сожалению, этот метод можно использовать только
с большими предосторожностями, так как упрощения неизбеж-
неизбежны в простых случаях. Более предпочтительный подход состоит
в том, чтобы оценить погрешность в наихудшем случае и счи-
считать, что точность последующих вычислений существенно
выше.
Погрешности можно разделить на следующие основные ка-
категории:
1) погрешности, связанные с существом задачи (внутренне
присущие ошибки);
2) погрешности, вызванные способом записи чисел в компью-
компьютере (погрешности округления);
3) погрешности численного метода (погрешности аппрокси-
аппроксимации). Рассмотрим кратко каждую категорию.
3.3.1.1. Погрешности, связанные с природой задачи. Рас-
Рассмотрим следующую систему линейных алгебраических уравне-
уравнений: 2х+6г/ = 8 и х + у=6. Ее решение х = 7 и у =— 1. Уменьшим
теперь коэффициент при у во втором уравнении на 0,00002. Тог-
Тогда оно примет вид х+0,99998# = 6, а решение будет х=6,99997
и у=—0,99999. Другими словами, абсолютная погрешность
0,00002 в коэффициенте вызывает погрешность того же порядка
величины в результате.
Преобразуем первое уравнение к виду 2х+5,99999г/ =
= 8,00001. Тогда система будет иметь такое же решение х=7 и
у = — 1. Изменим снова коэффициент перед у на 0,00002. Первое
уравнение системы принимает вид 2х + 6,00001 у = 8,00001. Раз-
Различие столь мало, что, казалось бы, решение должно остаться
почти неизменным. Вы уверены? Как ни странно, но теперь ре-
решение х=у=\. А, может быть, это и неудивительно? В самом
деле, система двух линейных алгебраических уравнений пред-
представляет две прямые линии. Решение системы дает координаты
точки пересечения этих двух прямых. Первая наша система
представляла две линии с совершенно разными наклонами,
и поэтому небольшое изменение наклона одной из них не при-
приводит к существенному изменению результата. Ситуация во
втором случае совершенно иная. Теперь две линии почти па-
параллельны. Изменение, даже незначительное, наклона одной
из них может привести к существенному смещению точки пере-
пересечения.
Если обобщить малую погрешность в решении первой зада-
задачи на решения всех систем линейных алгебраических уравне-
уравнений, то это приведет к огромной ошибке. Итак, в зависимости
от существа задачи одна и та же погрешность в коэффициенте
может практически не влиять на погрешность решения в одном
случае и дать огромную погрешность в другом.
142
Определение электрических и магнитных полей
Как будет видно в гл. 9, внутренне присущие погрешности
имеют и положительную сторону. Тот факт, что совершенно
различные электроды могут создавать почти одинаковые акси-
аксиальные распределения потенциала, поможет при синтезе элект-
электронных и ионных оптических систем.
3.3.1.2. Погрешности записи чисел в компьютере. Запись чи-
чисел с плавающей точкой, используемая в цифровых компьюте-
компьютерах, характеризуется тем, что плотность чисел в окрестности
нуля гораздо выше, чем в окрестности больших чисел. В самом
деле, существует столько же положительных чисел между ми-
минимально возможным числом и единицей (отрицательная экс-
экспонента), сколько между единицей и максимально возможным
числом (положительная экспонента). Вследствие этого абсо-
абсолютная точность записи чисел максимальна в окрестности
нуля и намного ниже для больших чисел, но относительная
точность примерно постоянна во всем числовом диапазоне. По-
Поэтому относительные погрешности, связанные с записью чисел
в компьютере, могут быть легко оценены.
Проблема с записью чисел заключается в том, что такое
число, как 2/3, очень просто выразить в математических обозна-
обозначениях, но в компьютере оно превращается в 0,6666666....
В представлении с плавающей точкой мантисса должна ограни-
ограничиваться либо простым усечением, либо округлением ее зна-
значения до ближайшего числа с допустимым числом знаков. Хотя
округление и приводит к меньшим ошибкам, чем усечение, оно
имеет место в каждом элементарном акте вычислений, поэтому
в ходе продолжительной численной процедуры ошибки округле-
округления могут накапливаться до неприемлемо большой величины.
С другой стороны, ошибка округления не зависит от числен-
численной процедуры. Она представляет собой просто разность между
математически точным результатом некоторой вычислительной
процедуры и результатом той же процедуры, выполненной
компьютером.
Ошибка округления может быть весьма значительной. Что-
Чтобы продемонстрировать это, рассмотрим процедуру сложения
нескольких чисел различного порядка величины. Если начать
с наибольшего слагаемого, то можно заканчивать процедуру,
вообще не производя никакого сложения. В самом деле, если
разность порядков величин двух чисел больше, чем число зна-
знаков мантиссы, то их сумма просто совпадает в компьютере с
большим из этих чисел. Можно повторить процесс сложения с
тысячей других чисел малой величины, ничего не добавляя в
действительности. С другой стороны, если начать с маленьких
чисел, они будут сложены друг с другом, причем их сумма мо-
может оказаться достаточной для того, чтобы повлиять на значе-
143
Глава 3
ние много больших чисел. Поэтому разумно вычислять суммы
рядов в обратном порядке, начиная с наименьших членов.
Рассмотрим другой пример. Вычислите A,47-108 + 2,19-
•107) — A,69-108+105) с точностью до трех знаков. Результат —
нуль. Изменяя порядок вычислений, получим —200 000.
Эти примеры показывают, что коммутативный и ассоциатив-
ассоциативный законы алгебры могут не выполняться при численных рас-
расчетах. Части ошибок удается избежать, если всегда придержи-
придерживаться следующего правила: никогда не вычитать число из чис-
числа приблизительно той же величины. Если не следовать данно-
данному правилу, можно столкнуться с ситуацией, когда при вычита-
вычитании все значащие цифры взаимно уничтожат друг друга и ре-
результат будет представлять собой разность двух ошибочно
округленных чисел. Вычитания легко избежать, если использо-
использовать следующее тождество:
Необходимо также быть аккуратным при возведении в сте-
степень. Общее правило состоит в том, чтобы избегать его. Обыч-
Обычно точность выражения АХА выше, чем А2. Причина в том, что
возведение в степень производится с использованием логариф-
логарифма, что дает гораздо меньшую точность, чем простое умноже-
умножение. Однако есть ряд исключений. Если число, очень близкое
к единице, возводится в огромную степень, лучше использовать
операцию возведения в степень: ошибки округления многократ-
многократно повторенных операций умножения могут привести в сово-
совокупности к такой огромной ошибке, что окончательный резуль-
результат не будет иметь ничего общего с правильным.
Еще одно предостережение: используйте лишь те значащие
цифры, точность которых гарантирована. Предположение о том,
что точность тем больше, чем больше знаков в мантиссе, явля-
является широко распространенным заблуждением. Например, пере-
перемножая два числа, заданных с точностью до трех знаков,
в числе — результате произведения не следует использовать бо-
более трех знаков. Действительно, 0,393x0,998 = 0,392, а не
0,392214, поскольку 0,393 может означать любое число от
0,3925 до 0,3934, и соответственно точный результат может ле-
лежать между 0,391715 и 0,3926132 (как видим, даже третья циф-
цифра может оказаться неверной). Поэтому округление является
не только источником ошибок, но и необходимой защитой от не-
некорректного использования лишних цифр.
Наконец, опыт показывает, что использование арифметики
с одинарной точностью обеспечивает достаточную точность вы-,
числений лишь в некоторых тривиальных случаях. Всегда, ког-
когда есть возможность, используйте двойную точность!
144
Определение электрических н магнитных полей
3.3.1.3. Погрешности, обусловленные численными методами.
Каждый численный метод основывается на некотором прибли-
приближении и в большинстве случаев на дискретизации непрерывной
задачи. Точное решение обычно выражается в виде интеграла
или бесконечного ряда, в то время как мы аппроксимируем
это решение конечным числом членов. Это неизбежно влечет
за собой погрешность аппроксимации. Чем меньше число сла-
слагаемых, тем больше погрешность. К сожалению, увеличение
числа учитываемых членов не всегда оказывается полезным по
двум причинам:
а) сходимость ряда может быть настолько медленной, что
для достижения желаемой точности потребовалось бы неприем-
неприемлемо большое число членов;
б) чем больше добавляется слагаемых, тем большей стано-
становится ошибка округления или усечения (см. выше); оптималь-
оптимальное количество учитываемых членов должно определяться от-
отдельно для каждой задачи.
Требования к точности, предъявляемые практикой, обычно
не очень высоки: мы должны быть вполне удовлетворены, если
можем предсказать размер пятна и плотность тока хорошо
сформированного пучка с относительной точностью 10%. Про-
Проблема состоит в том, что при определении этих величин необхо-
необходимо произвести несколько различных вычислений подряд. При
расчетах обычных устройств сначала вычисляют распределение
полей, затем траектории, аберрации и, наконец, размер пятна
и плотность тока. В последующих вычислениях используются
содержащие погрешность результаты предыдущих вычислений.
В большинстве случаев очень трудно проследить распростране-
распространение ошибок и оценить необходимую точность вычислений рас-
распределения поля, требуемую для достижения желаемой точно-
точности окончательного результата. Из-за двух- или даже трехмер-
трехмерного характера поля его вычисления являются обычно наиболее
сложными. Поэтому естественно попытаться достичь макси-
максимально возможной точности этих расчетов в рамках имеющих-
имеющихся вычислительных ресурсов (время и память).
3.3.2. Метод конечных разностей
Определение потенциала методом конечных разностей осно-
основывается на дискретизации уравнения Лапласа. В результате
непрерывное дифференциальное уравнение заменяется систе-
системой алгебраических уравнений, которую легко решить.
Общий принцип описан в разд. 3.2.2.2. Заменяя бесконечно
малые величины в определении производной конечными значе-
значениями, мы вводим практически линейные соотношения между
значениями потенциала в соседних узлах сетки с конечными
145
Глава 3
размерами ячеек. Чтобы обосновать эту процедуру, рассмотрим
разложение потенциала в окрестностях некоторой произволь-
произвольной точки с координатами х, у, z в ряд Тейлора:
и(х + Ах, у + Ау, z + Az) = u(x, у,
+ ЬхАу
где Дл;, Ау и Az — малые, но конечные разности между коорди-
координатами выбранной точки и координатами некоторой точки в ее
окрестности. Хотя члены высших порядков в данном выраже-
выражении опущены, не следует забывать об их существовании. Они
составляют малую поправку, которой можно пренебречь, если
конечные разности действительно очень малы. Частные произ-
производные должны быть вычислены в точке (х, у, z). Используя
теперь C.302) в случае Дг/ = Дг=0, можно написать два выра-
выражения для изменения потенциала: одно для положительного
приращения координаты х, а другое для отрицательного (зна-
(знаки « + » и «—» соответственно):
и (х±Ах, y,z)=u (х, у, z) ± (ди/дх) Ах+
(д2и/дх2) (АхJ/2+ ... . C.303)
Складывая два уравнения, мы сразу получаем выражение
C.281) для второй частной производной по х, но без операто-
оператора «lim». Это означает, что пренебрежение высшими степенями
разложения в ряд Тейлора в точности эквивалентно замене диф-
дифференцирования линейной операцией вычисления конечных раз-
разностей. Естественно, что погрешность такой замены в точности
равна погрешности, обусловленной отбрасыванием членов выс-
высшего порядка.
> Можно написать еще два выражения для случая Ax = Az=0
и получить C.282), а также два выражения для Ах = Ау = 0 и
получить C.283). В результате можно убедиться, что формула
C.284) представляет собой трехмерное конечно-разностное
уравнение Лапласа для произвольной точки (х, у, z) при Ах =
= Дг/ = Д2=б. Это выражение является точным для второй сте-
степени б включительно в связи с тем, что в соответствующем ряду
Тейлора были отброшены члены всех степеней выше второй.
Такие же рассуждения справедливы для полей с осевой
симметрией. В этом случае выражение C.287) может быть ис-
использовано для точек, лежащих вне оси z, a C.289)—для осе:
вых точек с той же точностью. Естественно, метод будет рабо-
работать также и для любого другого типа симметрии.
146
Определение электрических и магнитных полей
Чтобы начать вычисления, следует прежде всего покрыть
всю область дискретной решеткой (расчетной сеткой). Способ
дискретизации не определен однозначно, поскольку можно сво-
свободно выбирать решетку по своему вкусу, и, кроме того, конеч-
конечная ширина ячейки может быть переменной. Очевидно, что от
нашего выбора зависит точность вычислений. Теперь напишем
линейное уравнение для потенциала в каждом узле в данной
области. Уравнения вблизи ее границ будут содержать значе-
значения потенциала, определенные из граничных условий. Наконец,
нужно решить систему N линейных алгебраических уравнений
и получить распределение потенциала в N точках, расположен-
расположенных внутри области.
Существует несколько способов повышения точности вычис-
вычислений:
1. Увеличение плотности узлов путем уменьшения размера
ячейки.
2. Использование переменного размера ячейки. Локальная
плотность узлов определяется с помощью грубой оценки опу-
опущенных в конечно-разностных уравнениях членов высокого по-
порядка. Так, большая плотность узлов нужна вблизи острых кро-
кромок границы. Две решетки разной плотности должны быть на-
наложены так, чтобы узлы грубой решетки являлись одновремен-
одновременно узлами более плотной решетки. Значения потенциала в уз-
узлах плотной решетки, лежащих между узлами грубой решетки,
могут быть определены с помощью интерполяции.
3. В случае искривленных границ узлы регулярных реше-
решеток могут оказаться за пределами области. Тогда можно дефор-
деформировать часть решетки вблизи границы [ПО], формируя не-
нерегулярную решетку, что является частным случаем интерполя-
интерполяции. Поскольку почти всегда (за исключением некоторых элект-
электронных и ионных источников) решетка является регулярной в
области самого пучка, необходимая точность обычно достигает-
достигается без приложения чрезмерных усилий. В случае источников
благодаря значительным различиям в размерах анода и катода
применима сферическая система координат, в которой размер
.ячейки увеличивается с ростом радиальной координаты [111].
4. В случае открытых систем можно использовать подход,
аналогичный введенному при анализе резисторных цепей, когда
соответствующим выбором решетки с переменным шагом уда-
удается компенсировать влияние внешних областей. Область, про-
простирающаяся на бесконечность, также может быть заменена
подходящим образом выбранной областью сшивки [112], со-
содержащей всю информацию об области, простирающейся от
границы до бесконечности. Тем не менее трудности моделиро-
моделирования открытых систем остаются большим недостатком метода
конечных разностей.
147
Глава 3
(г)
ww»
s w-
NE
5. Можно произвольно уве-
увеличить число учитываемых в
расчетах соседних узлов, по-
повышая тем самым точность
вычислений. Поскольку фор-
формулы тем сложнее, чем боль-
больше число учитываемых узлов,
это число не должно быть
слишком большим. Наиболее
часто используется девятито-
девятиточечная формула, которая ос-
основывается на учете восьми
узлов плоской решетки, бли-
PB) UJ
Рис. 39. К выводу девятиточечных
формул метода конечных разностей.
жайших к произвольному узлу, вместо четырех (рис. 39). По-
Поскольку в трехмерных расчетах нам пришлось бы в этом случае
рассматривать 26 узлов вместо шести, этот подход практически
может быть использован лишь в двумерных задачах. В даль-
дальнейшем мы выведем девятиточечные формулы как для плоских,
так и для аксиально-симметричных полей.
Метод основан на сохранении членов более высокого порядка
в разложении в ряд Тейлора потенциала. Выпишем ряд C.302)
до членов четвертого порядка включительно. Для двух пере-
переменных получим
и(х+ Ах,
24+ ... . C.304)
Применим это выражение к четырем соседним узлам, обо-
обозначенным точками на рис. 39, и просуммируем значения потен-
потенциала в этих точках, полагая Ах — Ау = 8. Получим
" —б. У)+и(х, у-\-8)-\-и{х, «/-б) =
Теперь запишем потенциалы в четырех угловых узлах, обозна-
обозначенных на рис. 39 крестиками, и, суммируя, получим
и (лг-f б, у-\- 8)->ги(х — б, у-f б) -f и(х + б, у — б) -{-и(х — б, у — б) =
_ 4-_ \&+ {w+gyT) 8'6 + d^W8+ ■■■■
C.306)
И8
Определение электрических н магнитных полей
Из уравнения Лапласа A.20) для планарных полей следует
д*и д2и дЫ д*и д*и ди „
dxi + ду* ~ дх* + дх*ду2 ~ ду* + дх2 ду* ~ '
где второе и третье равенства получаются двукратным диффе-
дифференцированием уравнения Лапласа по х и у соответственно.
Отсюда следует, что
+
я мы получаем из C.305), C.306) и C.308) пятиточечную фор-
формулу для планарных полей:
х — 8,у)+и(х,у — б)] +
— 8)+и(х — 8, у+ 8) +
— 8,у — 8)=20и{х,у). C.309)
Очевидно, что пятиточечная формула, эквивалентная C.284)
для планарных полей и учитывающая только четыре соседних
узла, может быть получена тем же способом, что и частный
случай, когда ряд Тейлора обрезается на членах второго по-
порядка. Действительно, тогда C.305) немедленно дает
и(х+8, у) +и(х — 8, у) +и(х, у+8)+и(х, у — б) =4ы(х, у).
C.310)
Выведем теперь девятиточечную формулу для аксиально-
симметричных полей. Как выражение C.304), так и рис. 39 мо-
могут быть использованы и в этом случае, если заменить х на z
и у на г. Кроме того, положим Дг=Дг = б и упростим запись,
используя индексы для обозначения географических направле-
направлений к соседним узлам и частных производных потенциала. Так,
например, u(z—б, r+б) будет записано в виде uNW и
d4uf(dr3dz) —в виде urrrz- Разумеется, все частные производные
должны вычисляться в заданной точке P(r,z).
Применение формулы C.304) ко всем восьми соседним уз-
узлам с учетом сделанных замен даст восемь уравнений для по-
потенциала в этих узлах. Комбинируя эти уравнения, можно по-
получить простые соотношения между частными производными.
Нам понадобятся следующие комбинации:
uN = иР + 8ur+82urr/2 + б3Ыггг/6 + 8*urrrr/24 +... , C.311)
us = up — 8ur+82Urr/2 — 63Urrr/6 + 64«rrrr/24 —+..., C.312)
+ 8*uZzzz/12+ ... , C.313)
+б3(мггг+Ыггг/3) +
.. , C.314)
149
Глава 3
) — б3
+ ... . C.315)
Из этих выражений немедленно следует
C.316)
C.317)
— uN) = 2b3urzz, C.318)
+ US) =84Urrzz.
C.319)
Уравнение Лапласа C.285) и его двукратное дифференци-
дифференцирование по г и по z дают следующие соотношения:
C.320)
jr — ЫГ/Г2 = О, C.321)
— 2ыгг/г2 + 2ыг/г3 = 0, C.322)
C.323)
Величина иГГг может быть выражена через иг и потенциал
в некоторых узлах с помощью C.316). Аналогично иГГгг можно
исключить, используя C.317). Величины urzz и urrzz заданы вы-
выражениями C.321) и C.322) соответственно. Тогда уравнения
C.321) и C.322) содержат лишь две неизвестные величины:
иг и игг- Эти уравнения составляют линейную алгебраическую
систему относительно указанных величин. Решение этой систе-
системы элементарно.
Нам нужна еще величина uzz. Ее можно определить из урав-
уравнений C.313), C.323), C.318) иC.319). Теперь у нас есть все
компоненты уравнения Лапласа C.320). Подставляя в него
выражения для ur, urr и игг, получим длинное выражение, со-
содержащее только г, б и девять значений потенциала. В резуль-
результате некоторых упрощений нетрудно получить девятиточечную
конечно-разностную формулу для аксиально-симметричных рас-
распределений потенциала [113]:
(96г2 + 48бг+ЗОб2 + 2363/3r) uN +
+ (96г2 — 486г+3062 — 23б3/3/-)ы5 +
+ B4r2+126r+962 + 1363/2r) {uNe+unw) +
+ B4г2— 12бг + 9б2— 1363/2r) (uSe+uSw) +
р. C.324)
(Читателю рекомендуется самостоятельно проделать вычисле-
вычисления и проверить эту важную формулу.)
150
Определение электрических и магнитных полей
Поскольку уравнение C.324) содержит сингулярность в точ-
точке г=0, оно не может быть использовано для вычисления по-
потенциала вдоль оси z. В этой области, однако, мы можем ис-
использовать разложение в степенной ряд C.20), что значительно
упрощает вычисления. Заметим также, что в силу осевой сим-
симметрии достаточно учитывать лишь «северные» соседние узлы
(см. нижнюю часть рис. 39).
Дифференцируя уравнение C.20), выразим все частные про-
производные, необходимые для разложения потенциала в ряд Тей-
Тейлора, через осевое распределение потенциала U(z) и его про-
производные. (Нам еще понадобится степенное разложение C.304),
поскольку осевое распределение потенциала неизвестно.) Сле-
Следует напомнить, что все производные должны быть вычислены
в точке Р(z), лежащей на оси. Из C.20) сразу следует
.. . C.325)
Уравнения C.313) и C.20) дают
uE+uw=2uP + 82U" (z) +84Ulv {z)/\2 + ... . C.326)
Наконец, из C.314) и C.20) получаем
uNE + uNW = 2uP + 82U"(z)/2 — 1384£/IVB)/96+ ....
C.327)
Легко видеть, что
34uN + 5(uE+uw) + 7(uNE+uNW) =58up. C.328)
Это конечно-разностная формула, справедливая для точек, ле-
лежащих на оси. Естественно, она не зависит от радиального рас-
распределения U(z).
В справедливости соответствующих пятиточечных формул
(C.287) для неосевых точек и C.289) для осевых) легко убе-
убедиться, подставив в них разложения для потенциала с точ-
точностью до членов второго порядка с использованием уравнения
Лапласа C.320). (Будьте внимательны при анализе C.289).
Необходимо показать, что вдоль оси urr = ur/r. Это можно сде-
сделать, разлагая иг в ряд Тейлора в радиальном направлении с
помощью C.20).)
Для вычисления распределения потенциала можно исполь-
использовать и другие девятиточечные формулы [114]. Например,
можно использовать точки ЕЕ, WW, NN и SS вместо точек NE,
NW, SE и SW (см. рис. 39). Вычислительная сетка может быть
даже сформирована из треугольников или любых других пра-
правильных или неправильных геометрических фигур.
Сохранение членов более высокого порядка в разложении в
ряд Тейлора позволяет использовать решетки с большей шири-
шириной ячеек и, таким образом, уменьшать количество узлов при
151
Глава 3
решении определенной задачи. Цена, которую приходится за это
платить, — усложнение систем уравнений.
3.3.2.1. Методы решения систем алгебраических уравнений.
Построив вычислительную сетку и записав уравнения для всех
узлов, можно приступать к численному решению большой си-
системы линейных алгебраических уравнений прямыми, либо ите-
итерационными методами.
Наиболее известный прямой метод решения больших систем
линейных алгебраических уравнений — приведение Гаусса с об-
обратной подстановкой. Процедура решения системы п линейных
алгебраических уравнений методом гауссова приведения состо-
состоит из п—1 шагов. На каждом шаге уравнения, кратные очеред-
очередному уравнению системы, вычитаются из остальных уравнений
с тем, чтобы исключить одну переменную. Обратная подстанов-
подстановка заключается в решении последнего оставшегося уравнения
для последней переменной, затем предпоследнего уравнения от-
относительно предпоследней переменной и т. д. до тех пор, пока
не решено первое уравнение относительно первой переменной.
Поскольку число уравнений обычно очень велико, но каждое со-
содержит не более девяти переменных, большинство элементов
матрицы системы равно нулю. Это позволяет расставить урав-
уравнения таким образом, чтобы матрица системы приняла «лен-
«ленточный» вид, т. е. чтобы все ненулевые элементы были сгруппи-
сгруппированы вблизи ее диагонали. Тогда система решается довольно
просто. Подробное описание этого метода и различные вариан-
варианты его усовершенствования можно найти в литературе [115].
Хотя прямые методы и требуют большего объема машинной
памяти, чем итерационные методы, они «чище» в том смысле,
что не содержат проблемы сходимости. Благодаря доступности
больших компьютеров прямые методы становятся все более при-
пригодными для решения практических задач.
Разработано множество итерационных методов решения си-
систем уравнений (линейных и нелинейных). Их общая идея за-
заключается в том, что сначала выбирается некоторое начальное
приближение, а затем строится последовательность векторов
(компонентами которых являются неизвестные величины), схо-
сходящаяся к точному решению. Поскольку на каждом этапе необ-
необходимо сохранять лишь последние приближения значений по-
потенциала, экономия объема памяти получается весьма ощути-
ощутимой. В силу этого до последнего времени при решении больших
систем уравнений использовались почти исключительно лишь
итерационные методы.
Наиболее известный итерационный метод — алгоритм Гаус-
Гаусса — Зейделя. Его основной принцип состоит в решении &-го
уравнения относительно k-k компоненты нового вектора с ис-
152
Определение электрических и магнитных полей
пользованием последних вычисленных величин в качестве зна-
значений всех остальных компонент этого вектора. Начиная с про-
произвольно заданного набора значений потенциала, мы поочеред-
поочередно корректируем каждое из них, выражая через остальные с по-
помощью соответствующей пяти- или девятиточечной конечно-раз-
конечно-разностной формулы. Последние исправленные величины всегда
используются при коррекции следующей неизвестной. Процеду-
Процедура повторяется до тех пор, пока при очередном повторении зна-
значение потенциала останется неизменным в пределах точности
вычислений. Новые значения потенциала могут вычисляться
все одновременно (одновременный сдвиг), однако требуемый
объем памяти меньше, если изменения производить непосредст-
непосредственно в каждом узле (последовательный сдвиг). Можно пока-
показать, что с каждой итерацией значения приближаются к точно-
точному решению независимо от выбора начального приближения
для узловых потенциалов. Недостатком метода является его
медленная сходимость.
Сходимость может быть существенно повышена при исполь-
использовании метода релаксации. Суть метода очень проста. Если
значение потенциала в некоторой точке после k-й итерации есть
u(ft) и использование пяти- или девятиточечной формулы дает
u*(*+i) для следующей итерации, возьмем
и<*>] C.329)
вместо м*(*+1>. Принимая 0<Си><1, можно получить сходимость
в тех случаях, когда метод Гаусса — Зейделя не сходится. Это
случай нижней релаксации: мы используем меньшую разность
между двумя итерациями, чем дает конечно-разностная форму-
формула. Так как мы уже знаем, что в данном случае итерации схо-
сходятся, но очень медленно, хотелось бы ускорить сходимость.
Поэтому выбираем w>\ и тем самым увеличиваем шаг сле-
следующей итерации (верхняя релаксация). Поскольку обычно ис-
используется способ последовательного^ сдвига, данный метод на-
называется последовательной верхней релаксацией (ПВР).
Очень важно правильно выбрать значение параметра верх-
верхней релаксации w. Очевидно, w = \ для обычного итерационно-
итерационного алгоритма без верхней релаксации. Ясно также, что выбор
слишком большого значения параметра w означал бы полное
пренебрежение конечно-разностным методом. Для каждой за-
задачи существует своя оптимальная величина w, при которой
итерации сходятся быстрее всего. Можно показать [116], что
это оптимальное значение зависит только от конфигурации
электродов и размера ячейки (обычно оно растет с уменьшени-
уменьшением размера ячейки). Оно не зависит от начального приближе-
приближения для потенциала и номера итерации k. Интересно, что су-
существует теоретическая возможность определить точное значе-
153
Глава 3
ние wopt в каждом расчете, но это требует более трудоемких
вычислений, чем собственно решение уравнения Лапласа. Од-
Однако оптимальное значение может быть найдено аналитически
для простых конфигураций, и затем на основе этих вычислений
можно оценить wopt для реальных задач. Обычно 1<ш<2.
Естественно, разностные методы могут использоваться вне
зависимости от вида симметрии задачи. Наряду с осесиммет-
ричными фокусирующими полями могут быть вычислены много-
многополюсные и отклоняющие поля. Кроме того, может быть учтено
влияние пространственного заряда. Однако вычисления значи-
значительно усложняются при решении трехмерных задач. В настоя-
настоящее время это направление активно развивается [117—119].
Метод конечных разностей может быть использован даже в
том случае, если рассматриваемая область содержит материа-
материалы с различными свойствами. Для значений потенциала в уз-
узлах, соответствующих пересечению поверхностей этих материа-
материалов с расчетной сеткой, могут быть получены необходимые раз-
разностные уравнения. Хотя эти уравнения нелинейные, их можно
решить, используя подходящие вычислительные методы.
Выше мы познакомились со всей основной информацией, не-
необходимой для использования конечно-разностного метода. Чи-
Читатель, интересующийся подробным освещением данного вопро-
вопроса, может обратиться к специальной литературе [ПО, 115, 116,
120, 121].
3.3.3. Метод конечных элементов
Метод конечных разностей основывается на замене уравне-
уравнения Лапласа набором линейных алгебраических уравнений, свя-
связывающих друг с другом значения потенциала в узлах расчет-
расчетной сетки. Эта связь может быть установлена и другим спосо-
способом. В методе конечных элементов используется расчетная сет-
сетка, состоящая из треугольных элементов переменных размеров,
покрывающих всю область, для которой необходимо найти ре-
решение уравнения в частных производных. Затем аппроксими-
аппроксимируемая вариация потенциала на каждом таком элементе неко-
некоторым образом связывается с положением угловых узлов, и
строится функционал (интегральная величина, определенная на
множестве функций), минимизация которого по значениям по-
потенциала в узлах треугольников эквивалентна решению уравне-
уравнения в частных производных [122]. Эти два подхода математи-
математически эквивалентны, поэтому любая задача, сформулированная
в виде уравнения в частных производных, может быть перефор-
переформулирована в виде вариационной задачи. Конечно-разностная
процедура аппроксимирует решение задачи в форме уравнения
154
Определение электрических и магнитных полей
в частных производных, в то время как метод конечных элемен-
элементов решает ту же задачу на основе вариационного подхода.
Пусть потенциал меняется линейно внутри каждого треуголь-
треугольного элемента. Тогда линейные функции могут быть состыкова-
состыкованы так, что полученное распределение потенциала будет непре-
непрерывным во всей области. Вклад в функционал от каждого эле-
элемента может быть выражен через потенциалы в узлах. Мини-
Минимизация функционала дает тогда систему линейных алгебраи-
алгебраических уравнений относительно этих потенциалов. Решая эту
систему одним из методов, описанных в предыдущем разделе,
получим искомое распределение потенциала.
Поскольку определение поля есть непрерывная задача,
сформулированная в виде уравнения в частных производных,
первое, что мы должны сделать, — это найти вариационный
принцип, приводящий к построению нужного функционала. Нам
уже известны некоторые вариационные принципы (принцип Га-
Гамильтона и принцип Мопертюи были введены в разд. 1.3). Мы
знаем также, что в состоянии устойчивого механического рав-
равновесия должна быть минимальна потенциальная энергия,
в термодинамической системе при постоянных объеме и темпе-
температуре минимальна свободная энергия и т. д. Поэтому естест-
естественно выбрать в качестве функционала, используемого при рас-
расчетах полей, интеграл от величины, имеющей размерность
энергии.
Энергия электромагнитного поля в наиболее общем случае
(при наличии среды) может быть выражена в виде [52]
Х^= A/2) S(eE-E+B-B/n)dF, C.330)
где е и fi — диэлектрическая и магнитная проницаемости сре-
среды соответственно. Интегрирование ведется по всему простран-
пространству. Если принцип минимума энергии применим в данном слу-
случае, он означает, что поле стремится принять такую конфигура-
конфигурацию, что соответствующая ей энергия минимальна.
Попробуем сначала найти функционал, соответствующий
уравнению Пуассона A.18); затем напишем функционал также
и для магнитного поля. Реальное электромагнитное поле, удов-
удовлетворяющее уравнениям Максвелла, будет заменено тогда со-
соответствующим функционалом, таким, что его первая вариа-
вариация по параметру, удовлетворяющая граничным условиям, рав-
равна нулю. Это эквивалентно минимизации функционала по мно^
жеству возможных значений некоторого параметра. В случае
потенциального поля таким параметром может быть значение
потенциала в некоторых точках. Отсюда сразу ясно, что метод
конечных элементов может быть использован при решении лю-
любой задачи, если поля Е и В внутри конечных элементов мож-
155
Глава 3
но выразить через их значения в угловых точках элементарных
треугольников.
Умножив A.18) на первую вариацию потенциала бы и про-
проинтегрировав по всему пространству, получим
(divgradu —р/ео)бЫ7=О. C.331)
Ниже мы попытаемся вынести вариационный оператор б за
знак интеграла. Тогда мы получим функционал с первой вариа-
вариацией, равной нулю. Применим прежде всего тождество
div(/v)=/divv+vgrad/ C.332)
(где f — произвольный скаляр, v — произвольный вектор) к f —
= бы и и = grad и. Имеем
divgrad «6u=div[grad ubu] —grad ugrad(8м). C.333)
Подставляя C.333) в C.331) и применяя теорему Гаусса
-dS C.334)
(интеграл от дивергенции любого вектора по объему V, заклю-
заключенному внутри поверхности S, равен интегралу от нормальной
компоненты этого вектора по поверхности S) к вектору
(grad ubu), получим
S p8udV/e0 — S grad и grad(8u)dV = — & grad и 6udS.
v v Jg
C.335)
Поскольку в задаче о потенциале задано его значение на по-
поверхности (граничное условие типа Дирихле), вариация потен-
потенциала на поверхности равна нулю и интеграл но поверхности
обращается в нуль. Используем также тот факт, что вариация
пространственной плотности заряда есть нуль и операции варь-
варьирования и интегрирования выполняются независимо. Поэтому
вариационный оператор может быть вынесен за знак интегра-
интеграла. Кроме того, заметим, что
6[(grad uJ]l=2grad u8(gradu) =2 grad «grad бы,
C.336)
так как варьирование и дифференцирование также выполня-
выполняются независимо. Тогда мы получим другой интеграл, в кото-
котором оператор варьирования может быть вынесен вперед. Учи-
Учитывая все это, получим окончательный результат:
6$ [eo(grad«J/2 — 9u]dV=8Wu = 0, C.337)
156
Определение электрических и магнитных полей
где интеграл Wu— функционал, минимизируемый таким рас-
распределением потенциала u(R), которое удовлетворяет уравне-
уравнению Пуассона A.18) и граничным условиям. Подставляя A.17)
и р = 0, можно убедиться, что уравнение C.337) эквивалентно
уравнению C.330) в электростатическом случае .без пространст-
пространственного заряда.
Уравнение C.337) с р = 0 может быть использовано также
для магнитостатического потенциала. Однако если магнитное
поле создастся током, а также в случае насыщения следует ис-
использовать другие функционалы. Для магнитных полей, созда-
создаваемых током, применение процедуры, аналогичной предыду-
предыдущей, к уравнениям A.12) и A.16) дает [123]:
0, C.338)
где Wa — функционал и ц — конечная проницаемость ненасы-
ненасыщенного магнитного материала. Если присутствуют различные
материалы, то магнитная проницаемость является функцией
координат, но не зависит от плотности потока. В случае J = 0
это уравнение эквивалентно магнитной части соотношения
C.330).
Можно также написать функционал для насыщенных маг-
магнитных материалов. Так как магнитная проницаемость теперь
зависит от магнитной индукции, необходимо заменить первое
слагаемое в C.338) интегралом следующим образом:
$($HdB — i-A)dV=8WH = 0, C.339)
v о
(г)
где Wh — функционал и В* — текущее значение магнитной ин-
индукции. Уравнение C.339) может быть использовано для любой
кривой намагничивания и даже для составных магнитных це-
цепей. Легко показать, что это выражение применимо также и для
ненасыщенных материалов. В этом частном случае подстанов-
подстановка C.227) и A.12) опять приводит к C.338).
Несомненным преимущест-
преимуществом метода конечных элемен-
элементов перед методом конечных
разностей является простота
постановки граничных усло-
условий и рассмотрения сложных
электродных или полюсных
конфигураций, обусловленная
возможностью произвольно
изменять как форму элемен- Рис. 40. Конечные элементы.
157
Глава 3
тов, так и их плотность, подгоняя их края к границам и увели-
увеличивая точность на критических участках.
Рассмотрим вначале метод конечных элементов на примере
двумерного электростатического поля, а затем распространим
его на случай осевой симметрии, включая магнитные поля с то-
токами и ферромагнитными материалами.
Покроем плоскость ху (или rz) маленькими треугольника-
треугольниками. Один из них показан на рис. 40. Полагая линейной зависи-
зависимость потенциала от угловых значений внутри треугольника,
можно написать
и(х,у),=а + Ьх + су, C.340)
где a, b и с — постоянные, определяемые угловыми значениями
потенциала. Если эти величины равны щ, и2 и щ в точках
Р\{%\, У\), Рг{х2, Уг) и Рз(*з. Уз) соответственно, то можно запи-
записать уравнения в каждой точке, и решение системы уравнений
дает
C.341)
3 — yi)+u3(yi — y2)]/2S, C.342)
— x2) + u2 (*i — x3) + ыз (x2 — xi)] /2S, C.343)
где
S= [*i (Уа — Уз) +x2 (y3 — yi) +хз (yi — y2)]/2. C.344)
Заметим, что S есть площадь треугольника. Такая запись озна-
означает, что на потенциал в некотором узле влияют только сосед-
соседние узлы.
Теперь можно выразить вклад этого треугольного элемента
в функционал через узловые значения потенциала. Эти узловые
потенциалы будут параметрами, по которым необходимо мини-
минимизировать функционал. Поэтому потребуем, чтобы
4^ = 4^=... ^=...=-^- = 0, C.345)
диг ди.2 ou.fr дин
где W — минимизируемый функционал, k=l, 2,..., N и Af —
число узлов расчетной сетки, заключенных внутри границ.
Уравнение C.345) имеет смысл системы N уравнений, которая
может быть решена каким-либо численным методом (см.
разд. 3.3.2.1).
С помощью A.6) и A.13) нетрудно записать функционал
в любой системе координат. Для осесимметричных систем ин-
интегрирование по объему может быть заменено на интегрирова-
интегрирование по всей площади поля. Подставляя соответствующие выра-
выражения для дифференциальных операций и элемента объема,
158
Определение электрических и магнитных полей
получим из C.337) и C.338) следующие выражения для акси-
аксиально-симметричных функционалов:
°/2~р(л'z)u(r'
где интегрирование производится по всей площади, занимаемой
полем в плоскости гг. Во втором функционале Л — азимуталь-
азимутальная компонента векторного потенциала, поскольку две другие
компоненты исчезают для аксиально-симметричного поля. (По
той причине, что эти две компоненты не фигурируют в выраже-
выражениях для радиальной и аксиальной компонент магнитной ин-
индукции, удобно положить их равными нулю. В результате этого
выбора условие divA = 0 автоматически выполняется, что легко
проверить, используя A.5).) По этой причине в функционале
появляется только азимутальная компонента плотности тока.
Как мы видели в разд. 3.1.5, аксиально-симметричные поля дей-
действительно создаются азимутальными катушками.
Вклад в функционал конечного треугольного элемента пред-
представляет собой аналогичный двойной интеграл по площади эле-
элемента. Можно вычислить эти вклады, используя линейное соот-
соотношение C.340) и заменяя х на z и у на г (рис. 40). Диффе-
Дифференцируя затем C.340) по г и г, подставляя для «и Л их зна-
значения в центре масс треугольника (равные в точности одной
третьей суммы трех угловых значений), полагая, что как про-
пространственная плотность заряда, так и плотность тока постоян-
постоянны внутри конечного элемента, и заменяя dr dz на площадь
треугольника 5, получим из C.346) и ,C.347) вклады конечно-
конечного элемента в функционалы:
C.348)
C.349)
где Ь, с и S определены формулами C.342) — C.344) и ц, — маг-
магнитная проницаемость материала, заключенного внутри данно-
данного конечного элемента. Дифференцируя теперь C.348) по узло-
узловым значениям скалярного потенциала щ (t = l, 2, 3) и C.349)
по узловым значениям векторного потенциала Лг (t=l, 2, 3),
получим (не забывая, что Ь и с — функции потенциала), что
C.350)
— z!+1 + 2S/3r)}/yL—2nrSJa/3. C.351)
159
Глава 3 ^
Здесь индексы i + l и i + 2 следует понимать как циклические
в соответствии с тем, как было введено в связи с B.41).
Чтобы удовлетворить всем условиям C.345), необходимо
продифференцировать функционал по узловым потенциалам.
Так как на каждый узловой потенциал влияют только конечные
элементы с общей вершиной в данном узле, вклад этих конеч-
конечных элементов в функционал должен быть минимизирован по
потенциалу в этом узле, в то время как значения потенциала
в других узлах полагаются фиксированными. Поэтому условия
C.345) принимают вид
k + n
+i = 0 (*=1, 2, ..., АО, C.352)
k + n
= 0 (*=1, 2, .... N), C.353)
где k — индекс рассматриваемого узла и / — индекс одного из п
угловых узлов, влияющих на потенциал в k-u узле (см. рис.40).
Следует соблюдать осторожность при суммировании: какД№ц,
так и AWA различны для разных конечных элементов; именно
поэтому они имеют индекс /.
Поскольку в C.350) и C.351) b и с являются функциями
узловых потенциалов (включая потенциал в k-м узле), подста-
подстановка этих выражений в C.352) и C.353) соответственно дает
следующие линейные соотношения для каждой узловой точ-
точки /V
k + n
Hgmum = q, C.354)
m—k
k + n
2 CmAm = p, C.355)
где gm, Gm, p и q — коэффициенты при соответствующих членах
в C.350) и C.351). Эти уравнения устанавливают связь между
каждым узловым потенциалом и потенциалами соседних узлов.
Особо следует рассматривать узлы, лежащие на оси и гра-
границах. Прежде всего конечные элементы с узлами, расположен-
расположенными на оси, могут лежать только в положительном радиаль-
радиальном направлении относительно этих узлов. Кроме того, Л=0
на оси. В этом можно убедиться, анализируя г-компоненту ак-
аксиально-симметричного распределения магнитной индукции,
определенного с помощью A6) и A.12). Это уже использова-
использовалось в C.347). Поскольку Вг не может быть бесконечно велико,
векторный потенциал на оси должен быть нулевым. На грани-
160
Определение электрических и магнитных полей
цах для потенциала используются соответствующие граничные
значения. На поверхности раздела различных магнитных мате-
материалов следует использовать соответствующие значения магнит-
магнитной проницаемости для каждого конечного элемента.
Уравнения C.354) и C.355), записанные для каждого внут-
внутреннего узла, образуют систему N линейных алгебраических
уравнений для N узловых потенциалов. Эту систему можно ре-
решать методом исключения Гаусса или любым другим методом
из обсужденных в предыдущем разделе.
В случае насыщения необходимо использовать функционал
Wh, определенный в C.339) [123]. Так как намагничивание не-
нелинейно, то и уравнения, полученные на основе этого функцио-
функционала, также нелинейны. Система нелинейных алгебраических
уравнений также может быть решена численными методами.
Очень важно правильно выбрать форму и плотность конеч-
конечных элементов. Они должны заполнять все магнитные материа-
материалы и возбуждающие обмотки. Плотность должна быть наиболь-
наибольшей в критической области полюсных наконечников, где требу-
требуется максимальная точность. Удобно выбирать элементы таким
образом, чтобы линии их границ совпадали с границами магнит-
магнитных цепей.
Возможность полного описания нелинейных магнитных по-
полей, несомненно, является наивысшим достижением применения
метода конечных элементов в электронной и ионной оптике.
Кроме того, уравнения данного метода автоматически учиты-
учитывают локальные изменения магнитной проницаемости; они мо-
могут быть выражены через векторные потенциалы с тем, чтобы
включать в расчет катушки возбуждения; форма конечных
элементов может быть подогнана к самой сложной форме гра-
границ и т. д. Следовательно, в рамках метода можно полностью
анализировать целые магнитные системы.
Метод конечных элементов успешно применялся при проек-
проектировании магнитных и электростатических линз [123] и откло-
отклоняющих систем [96]. Проектировались сверхпроводящие маг-
магнитные линзы, а также электростатические линзы для холодно-
эмиссионных пушек и фильтров энергии электронов. В магнит-
магнитных линзах, работающих в режиме насыщения, были найдены
необычные распределения осевых потоков, обусловленные боль-
большим потоком утечки вблизи оси.
Очевидным недостатком метода конечных элементов являет-
является его относительно низкая точность (особенно в критической
области, прилегающей к оси), обусловленная предположением
о линейной зависимости потенциала от узловых значений. Точ-
Точность может быть повышена при использовании членов более
высокого порядка в C.340). Этот подход, однако, не только
сложен сам по себе, но и приводит к дополнительным трудно-
161
Глава 3 -
стям [ПО]. Поэтому ошибка дискретизации в данном методе
обычно выше, чем в методе конечных разностей.
Вследствие того что весьма обременительно использовать ме-
метод конечных разностей в случае сложных границ, а преиму-
преимущества метода конечных элементов вполне очевидны в случае
нелинейных магнитных материалов, но, с другой стороны, точ-
точность метода конечных разностей существенно выше, последо-
последователи и противники обоих методов иногда сталкиваются друг
с другом почти с религиозным пылом. По нашему мнению, вы-
выбор между двумя методами должен зависеть от конкретной за-
задачи. Очевидно, метод конечных элементов больше подходит
для нелинейных магнитных задач, в то время как методу конеч-
конечных разностей следует отдавать предпочтение при вычислении
электростатических полей.
Существует, однако, гораздо более существенный недоста-
недостаток, в равной степени ограничивающий возможности обоих ме-
методов: они эффективны только для закрытых систем.
В разд. 3.3.2 отмечалось, что наиболее серьезные проблемы в
методе конечных разностей возникают при попытке вычислить
распределение поля в открытой системе. К сожалению, это спра-
справедливо и для метода конечных элементов. Если фокусирую-
фокусирующий или отклоняющий элемент не окружен экраном, в вычис-
вычислениях появляются большие ошибки. Действительно, оба метода
требуют введения граничных условий всюду вокруг интересую-
интересующей области. Для открытой системы приходится вводить неко-
некоторую функцию потенциала вдоль открытых границ. Если, на-
например, положить потенциал нулевым на открытой границе, то
условие, справедливое на бесконечности, перемещается ближе
к самой системе. Это может внести очень серьезные ошибки.
Мы уже обсуждали в разд. 3.1.2.2 ограничения, свойственные
другим способам введения граничного потенциала. Всегда мож-
можно, конечно, предположить наличие эквипотенциального экрана
вокруг системы, но такое дополнение неизбежно исказит поле
открытой системы. Поэтому предположения такого рода ведут
к существенным отличиям формулировки задачи от первона-
первоначальной.
Можно было бы использовать один из подходов, упомянутых
в связи с методом конечных разностей, чтобы преодолеть эту
трудность (конечные элементы переменного размера, области
сшивки и т. д.). Можно сначала определить распределение по-
потенциала в рамках простой модели с нулевым потенциалом на
удаленной границе, а затем использовать сложную модель с вы-
вычисленным в первом случае потенциалом на близкой границе
[124]. Существуют и другие нерешенные проблемы (например,
разрывы на границах конечных элементов и т. п.). Хотя сейчас
в преодолении этих трудностей и наблюдается некоторый про-
162
Определение электрических и магнитных полей
гресс [125, 126], мы все-таки весьма скептически оцениваем
возможность использования данного метода для решения задач
с открытыми границами. По мнению автора, интегральный ме-
метод (см. следующий раздел), вообще говоря, превосходит как
метод конечных разностей, так и метод конечных элементов.
Чтобы оценить точность метода при вычислении магнитного
поля, полезно сравнить результаты вычислений криволинейного
интеграла C.230) для распределения поля с реальным
числом ампер-витков. Сравнение аксиального распределения
поля в случае простой петли тока, вычисленного в рамках ме-
метода конечных элементов, с точным результатом C.255) обна-
обнаруживает расхождение 10%, что, безусловно, слишком много.
Дополнительная информация о методе конечных элементов
может быть найдена в литературе [ПО, 115, 121—123, 127,
128].
3.3.4. Метод зарядовой плотности
(интегральный метод)
Интегральный метод вычисления полей введем сначала для
задач об электростатическом потенциале. В дальнейшем будут
показаны пути распространения этого метода на задачи о вы-
вычислении магнитных полей.
В оригинальном варианте [129] этот метод основывался на
том простом факте, что в статическом случае поле выталкива-
выталкивается из любой области, занятой проводником. Заряды распре-
распределяются по поверхностям всех проводников таким образом,
что все эти поверхности эквипотенциальны. Если потенциалы
проводников (электродов) создаются извне, это эквивалентно
созданию определенных распределений заряда на электродах.
Можно считать, что эти заряды являются источниками электро-
электростатического распределения потенциала в пространстве, окру-
окружающем электроды, в том числе и потенциалов самих электро-
электродов. Если бы мы могли заменить потенциалы электродов эти-
этими поверхностными распределениями заряда на электродах, не-
нетрудно было бы рассчитать потенциал в любой точке просто на
основе принципа суперпозиции, не прибегая к использованию
сложных расчетных сеток, как в методах конечных разностей
или конечных элементов. Кроме того, мы сэкономили бы огром-
огромное количество машинного времени и машинной памяти, по-
поскольку потенциал в заданной точке может быть точно вычис-
вычислен без необходимости двигаться шаг за шагом от электродов
к заданным точкам в ходе утомительной процедуры, накапли-
накапливая ненужную информацию. Например, в случае аксиально-сим-
аксиально-симметричных фокусирующих элементов нужно знать лишь распре-
распределение потенциала вдоль оси. Метод зарядовой плотности
163
Глава 3
позволяет точно вычислить это распределение, вообще не рас-
рассматривая точки, не лежащие на оси. Сразу же ясно, что дан-
данный метод не требует замкнутых границ. Поэтому наиболее
серьезная проблема как конечно-разностного метода, так и ме-
метода конечных элементов здесь не возникает.
Соотношение между потенциалом и распределением заряда
устанавливается выражением, весьма похожим на формулу
C.244), которая определяет связь между магнитным векторным
потенциалом и распределением плотности тока. Электростати-
Электростатический потенциал в произвольной точке Р, заданной радиусом-
вектором R, есть суперпозиция потенциалов, созданных всеми
элементарными зарядами dq, расположенными внутри объ-
объема V в точках, заданных радиусами-векторами Rs. Поэтому
d[q(Rs))
| R —R.I ' C.356)
где распределение элементарных зарядов может быть выраже-
выражено через пространственную плотность заряда р, поверхностную
плотность заряда о или линейную плотность заряда К. В соот-
соответствии с этим, полагая, что плотность заряда однозначно оп-
определена радиусом-вектором малого элемента, расположенного
в месте нахождения заряда, получим
d[q(Rs)]=p(Rs)dV=a(Rs)dS=k(Rs) ds, C.357)
где dV, dS и ds — элементы объема, поверхности и длины соот-
соответственно. Можно использовать рис. 30, если только заменить
токи на заряды. Равенство C.356) представляет собой решение
уравнения Пуассона A.18) и обладает большей общностью,
чем требует формулировка данной задачи, поскольку содержит
пространственные заряды наряду с поверхностными и линейны-
линейными зарядами. Можно немедленно заключить, что метод приго-
пригоден также и для решения тех задач о вычислении потенциала,
в которых нельзя пренебречь пространственным зарядом.
Вернемся теперь к решению первоначальной задачи. Рас-
Расстояние между элементом заряда и точкой наблюдения в де-
декартовых координатах равно
| R - R,| =[(* - xs)*+ (У - ysJ+ (z - ZsYY'2, C.358)
а элемент объема равен
dV = dXsdysdzs. C.359)
С использованием этих выражений вместе с C.356) любая за-
задача о вычислении потенциала может быть решена элементар-
элементарно. Действительно, рассмотрим конфигурацию п электродов
произвольной формы. Тогда потенциал в точке Р дается выра-
выражением
164
Определение электрических н магнитных полей
1=1 S;
где интегрирование должно выполняться по поверхностям всех
электродов.
Трудность состоит в том, что в этом уравнении неизвестны
как и, так а. Однако, поскольку потенциалы электродов зада-
заданы как набор значений V,- ( t=l, 2,..., п), мы можем сразу
написать п уравнений, в которых неизвестно лишь распределе-
распределение заряда. К сожалению, этот подход не приближает к реше-
решению задачи, так как электроды могут быть весьма протяженны-
протяженными, и поэтому мы не знаем, как выбрать те точки на их поверх-
поверхностях, в которых следует положить потенциалы равными
заданным. Более того, поскольку поверхностная плотность за-
заряда меняется вдоль поверхностей электродов, пришлось бы ре-
решать систему сложных интегральных уравнений, что могло бы
оказаться невыполнимым с вычислительной точки зрения.
Нужен гораздо более простой подход. Разделим поверхность
каждого электрода на элементы, конечные, но достаточно ма-
малые для того, чтобы можно было считать, что поверхностная
плотность заряда неизменна в пределах границ каждого эле-
элемента. Тогда, если число элементов на t-й поверхности равно
п.
mi, можно записать N= 2 m,- уравнений вида
4^|т^7Г (/=1' 2' ■•• N] [ф1)- C-361)
Здесь Vj — значения потенциала на каждом граничном элемен-
элементе (имеется не более п различных величин) R, и R,- — радиусы-
векторы центров элементов (разные индексы нужны для того,
чтобы отличать рассматриваемый элемент / от всех остальных
элементов i) и Si — площадь г'-го элемента. Если эти площади
недостаточно малы, плотность поверхностного заряда в преде-
пределах каждого элемента можно еще считать постоянной, но при
этом следует провести интегрирование в пределах поверхно-
поверхности элемента, соответствующего радиусу-вектору, чтобы ре-
результат соответствовал середине каждого элемента.
Уравнения C.361) образуют большую систему линейных ал-
алгебраических уравнений, однозначно определяющую распреде-
распределение поверхностной плотности заряда. Обратная подстановка
этого распределения в C.360) дает потенциал в любой точке
пространства. Таким образом, распределение плотности заряда
осуществляет связь между потенциалами электродов и распре-
распределением потенциала во всем пространстве.
165
Глава 3
Уравнения C.361) могут быть записаны в следующей форме:
V,- = Д Gnat (/ = 1,2,..., N; 1Ф}), C.362)
где Gi — aRi и GJ;— коэффициент, связывающий t-ю поверхност-
поверхностную плотность заряда с /-м потенциалом. Этот коэффициент за-
зависит только от геометрической конфигурации системы электро-
электродов. Решение этой системы может быть получено любым из
прямых или итерационных методов, описанных в разд. 3.3.2.1.
Можно получить частные выражения для коэффициентов
Gti, если система электродов обладает тем или иным типом сим-
симметрии. Поскольку особый интерес представляет аксиальная
симметрия, рассмотрим этот случай более подробно. Будем ис-
исходить из основного уравнения C.356). Переход к цилиндриче-
цилиндрической системе координат дает
| R — Rs|,= [r* + rs2 — 2rrscos(as — a) + (z — zsJ]'/2, C.363)
dV=rsdrsdasdzs. C.364)
Следует производить интегрирование по всем значениям угла
as, поскольку потенциал образуется зарядами, распределенны-
распределенными по цилиндрическим поверхностям. Однако результат не мо-
может изменяться при изменении величины а, если система акси-
аксиально-симметрична. Удобно выбрать а=я. Тогда C.363) можно
переписать следующим образом:
ssm2as/2 ) + (z —zsJ]1/2- C.365)
Подставляя C.357), C.364) и C.365) в C.356), получим сле-
следующее выражение для аксиально-симметричного распределе-
распределения потенциала u(r, z), созданного распределением плотности
пространственного заряда p(rs, zs):
Л/2 qo оо
Г Г Г («. zs)rsdrsdzsd{asl2)
/
U(r 2) = _L Г Г Г
' яв0 J J J
_ 1 С Г
О -ос О
р (rs, Zs) К (т) rs drs dzs
-00 6
где
Л/2
Я(т) = $ A — Т2 sin2 B)-'/2dB C.367)
о
есть полный эллиптический интеграл первого рода и
T2 = 4rrs/[ (r+rs) 2+ B - zsJ]. C.368)
Заметим сразу, что вдоль оси (г = 0) т=0 и соответственно
/С@) =я/2. С другой стороны, в точках, где расположены заря-
заряды (r — rs, z=zs), имеем т2=1 и эллиптический интеграл стано-
становится бесконечно большим (сингулярность).
166
Определение электрических н магнитных полей
Аксиально-симметричная система электродов всегда может
быть представлена в виде кольцевых зарядов. Кольцевой за-
заряд— это заряд qi, равномерно распределенный по кольцу ра-
радиуса rst, расположенного при zs,-. Для такого кольца как rsu
так и zSi — постоянные. Теперь для линейной плотности заряда,
определенной в C.357), можно написать
U = SS Р (»"». z») drsdzs = qil2nrsi. C.369)
Подставляя в C.366) и суммируя по всем кольцевым зарядам,
получим простое выражение для распределения потенциала,
образованного кольцевыми зарядами qi (г=1, 2,..., N):
N
Здесь %i — значение т, вычисленное из C.368) с подстановкой
rs = rSi и zs = zSi. Полученное уравнение может быть использова-
использовано для определения поверхностных зарядов а* из потенциалов
электродов V,- с помощью подстановки r = rf и z=z,- для ради-
радиальных и аксиальных координат элементов поверхностей элек-
электродов. Поскольку поверхностная плотность заряда а, связана
с зарядом qi элементарным соотношением C.357), коэффициен-
коэффициенты G,-/ уравнения C.362) прямо получаются из C.370):
где Si — площадь г-го кольца и
т2ц = 4пп![ {п + г,У+ {г,- — г,J]. C.372)
Для открытого металлического электрода имеются две экви-
эквипотенциальные поверхности (по одной с каждой стороны элек-
электрода). Однако если толщина электрода пренебрежимо мала,
то можно просто удвоить площадь поверхности и рассматривать
обе стороны электрода как одну заряженную поверхность.
Эллиптический интеграл C.367) может быть весьма точно
вычислен с помощью полиномиального приближения [130]:
+ F0+6,ri + 62гJ + 63тK + 64тL) In A/rj), C.373)
где
4 = 1 — T2,
ao= 1,38629436112 60 = 0,5
a 1 = 0,09666344259 fr, = 0,12498593597
a2 = 0,03590092383 b2 = 0,06880248576 C.374)
az = 0,03742563713 Ьъ = 0,03328355346
a4 = 0,01451196212 64 = 0,00441787012
167
Глава 3
Ошибка этого приближения меньше 2-10~8. (Ошибка для т = 0
меньше 10~n.) В окрестности т=1 (сингулярность) можно ис-
использовать
Шп[/С(т)] = lim[(l/2)lnA6/Ti)]. C.375)
Т1 O
Вычисления можно начинать при произвольно заданном рас-
распределении плотности заряда. Тогда разность между заданны-
заданными и вычисленными потенциалами электродов может служить
основой получения улучшенных значений поверхностной плот-
плотности заряда (итерация). По окончании вычислений относи-
относительная ошибка на электродах может быть менее 0,04%, за ис-
исключением кромок электродов, где ошибка обычно несколько
выше [66].
Для достижения большей точности желательно выбирать
меньшие размеры элементов в тех местах, где сильнее всего из-
изменяется плотность заряда, например вблизи зазоров между
электродами. Однако, если плотность поверхностных элементов
слишком велика, точность падает из-за ошибок округления.
Обычно требуется несколько сотен элементов для вычисления
распределения потенциала в практически важных случаях с точ-
точностью 0,1%. Аккуратность необходима также для того, чтобы
обходить сингулярность эллиптического интеграла при т=1.
Точность может быть повышена с помощью аппроксимации
плотности заряда непрерывной функцией вместо функции, те-
терпящей разрывы на границах элементов.
Время, необходимое для работы программы, вычисляющей
плотность заряда, приблизительно пропорционально квадрату
числа элементов поверхности. Требования к объему памяти от-
относительно умеренные по сравнению с методами конечных раз-
разностей и конечных элементов, которые требуют вычислений по-
потенциала в каждой точке расчетной сетки.
Метод плотности заряда применялся к расчетам электроста-
электростатических систем различных конфигураций [44, 66, 96, 131],
включающих трехмерные поля [132], пространственный заряд
[133, 134] и даже диэлектрические среды [135].
Этот метод имеет очевидные преимущества по сравнению с
методами конечных разностей и конечных элементов:
1) он применим к системам с открытыми границами без ка-
каких бы то ни было предположений относительно распределе-
распределения потенциала вдоль этих границ,
2) он требует гораздо меньшего объема памяти, так как по-
потенциал вычисляется лишь в тех областях, где это действитель-
действительно необходимо.
Усовершенствования метода, направленные на уменьшение
ошибок округления и обход сингулярностей, изложены в лите-
литературе [136, 137, 137а].
163
Определение электрических и магнитных полей
С магнитными полями дело обстоит просто, если может
быть использован скалярный магнитный потенциал. Тогда мож-
можно приписать электродам потенциалы в соответствии с C.232)
и решать эквивалентную электростатическую задачу, не заду-
задумываясь о физическом смысле магнитных «зарядов». Как обыч-
обычно, ситуация усложняется при наличии магнитных материалов,
однако в этом направлении также наблюдается некоторый про-
прогресс [ПО, 138]. Если отделить вклад в магнитное поле Н,обу-
Н,обусловленный токами, от вклада индуцированной намагниченно-
намагниченности [139], то скалярный магнитный потенциал останется приме-
применимым для последнего, и используя A.22) и C.227), можно на-
написать интегральное выражение для потенциала, как функции
вектора намагниченности М. Поэтому, вычислив М, можно най-
найти скалярный потенциал, который в свою очередь определяет
вклад намагниченности в вектор магнитного поля Н. Вклад то-
токов легко может быть вычислен по закону Био — Савара
C.249). Таким образом, мы найдем суммарное поле, вычисляя
в основном вектор намагниченности и скалярный потенциал.
В этом методе, являющемся комбинацией методов конечных
элементов и плотности заряда (интегральный метод конечных
элементов), только катушка и магнитная цепь делятся на ко-
конечные элементы [124], а потенциал вычисляется только в ин-
интересующей области. Поскольку вся информация концентриру-
концентрируется в относительно малом объеме, для сильно неоднородных
магнитных материалов матрица является очень плотной, что
служит источником локализованных ошибок. Другая сложность
состоит в том, что в общем случае скалярный потенциал опре-
определяется системой нелинейных интегро-дифференциальных
уравнений, численное решение которой весьма затруднено.
Можно также учесть намагничивание по аналогии с выраже-
выражением для электростатического поля A.1), в котором электро-
электростатическое поле Е формально заменяется вектором намагни-
намагниченности М и плотность заряда заменяется фиктивной магнит-
магнитной «плотностью заряда». Другая возможность состоит в ис-
использовании магнитного векторного потенциала.
В заключение посоветуем читателю использовать метод за-
зарядовой плотности для всех вычислений электростатических по-
полей. В случае нелинейных магнитных задач, особенно для си-
систем с замкнутой границей, предпочтительнее выглядит метод
конечных элементов. Если границы открыты и требуется высо-
высокая точность, следует использовать интегральный метод конеч-
конечных элементов.
169
Глава 3
3.3.5. Численное дифференцирование
и интерполяция
3.3.5.1. Дифференцирование. Для того чтобы использовать
распределение потенциала при траекторных расчетах, необхо-
необходимо уметь вычислять все компоненты электростатического и
магнитного полей. Поскольку поля связаны с потенциалом
уравнениями A.17), A.22) и A.13), либо уравнениями A.12)
и A.6), задача сводится к численному дифференцированию рас-
распределения потенциала по всем координатам. В следующих
двух главах мы увидим также, что и производные потенциала
более высокого порядка могут понадобиться как для расчета
хода лучей, так и для вычисления коэффициентов аберрации.
Может показаться, что вычисление этих производных — простая
задача. Многократно используя формулы C.281) — C.283) и
C.286), можно вычислить производные любого порядка про-
простым вычитанием друг из друга потенциалов в соседних узлах.
Однако, если вспомнить, что говорилось об этом в разд. 3.3.1.2,
становится понятным, что такой процедуры следует избегать,
если мы заботимся о точности. Действительно, при вычислении
производной высокого порядка мы несколько раз вычитаем
друг из друга разности между разностями потенциала, что не-
неизбежно приводит к уменьшению точности по мере увеличения
порядка производной.
Как мы видели в разд. 3.3.2, точность может быть повыше-
повышена сохранением членов более высокого порядка в разложении
в ряд Тейлора. Здесь можно пойти по тому же пути. Вычислим
первую производную потенциала и(Щ по некоторой координа-
координате q, полагая, что потенциал задан в виде трехмерного числово-
числового массива, созданного в ходе работы некоторой вычислитель-
вычислительной процедуры.
Прежде всего напишем ряды Тейлора для потенциалов на
малых расстояниях ±6, ±26 и ±36 от произвольной точки с
координатой q (две другие координаты можно положить посто-
постоянными, поскольку мы хотим дифференцировать только по q):
u(q±8)=u(q)±W (q) б + и" (q) 62/2±и'" (q) 63/6 +
+ miv(<7N724±mv(<?N5/120 + mvi(<?N6/720±... , C.376)
u(q±28) =u(q)±2u' (q)8 + 2u" (?N2±4m'" (?)83/3 +
+ 2miv(<7N4/3±4mV(<?N5/15 + 4mvi(<?N6/45±... , C.377)
и (<7±36) = и (q) ±3uf (q) 6 + 9«" (q) 62/2±9«'" (q) 63/2 +
+ 27«iv(?N4/8±81«v(<?)85/40 + 81mvi(<?)86/80±... C.378)
Штрихи означают дифференцирование по q и производные
должны вычисляться в точке с координатой q.
170
Определение электрических и магнитных полей
Очевидно, что, если используются только линейные по б
члены, формула C.376) немедленно переходит в C.286). Как и
в разд. 3.3.2, пренебрежение членами высшего порядка эквива-
эквивалентно замене дифференцирования линейной конечно-разност-
конечно-разностной операцией.
Если требуется более высокая точность, нужны дополнитель-
дополнительные члены в разложении Тейлора. Сохраняя квадратичные и
кубические члены, из C.376) и C.377) получим
u(q + 8) — u(q — 8)*2u'(q)8 + u'"(q)b3/3, C.379)
«(<?+2б) — u(q — 28)<*4u'(q)8+8u'"(q)83/3. C.380)
Исключая из этих уравнений u"'(q), получим более точное вы-
выражение для первой производной:
— [и (q+ 28) —и (q —28)]}/128. C.381)
Можно повысить точность, используя все уравнения
C.376) —C.378). Тогда имеем
u{q + 8) — u(q—8)=2uf(q)8+W"(q)83/3 + uv(q)85/60,
C.382)
u(q+28) — и (q — 28) =4u' (q)8 +
u(q+38) — u(q — 38) =6u' (q)8 + 9ur" (q)8* + 8luv (q)8s/20,
C.384)
откуда следует еще более точное выражение для первой произ-
производной:
u'(q)={45[u(q+8)— и(q~8)]-9[и(q + 28) -
— u(q — 26)] + u(q+38) ~ и(q— 38)}/608. C.385)
Дальнейшее повышение точности может быть достигнуто со-
сохранением еще большего числа членов в разложении в ряд Тей-
Тейлора, однако это приведет к накоплению ошибок округления.
Поэтому не имеет смысла использовать формулы сложнее, чем
C.385).
Производные более высоких порядков могут быть получены
или повторным использованием формул C.381) и C.385), или
непосредственно на основе преобразований рядов Тейлора
C.376) — C.378). Например, оставляя члены до четвертой степе-
степени включительно, из C.376) и C.377) получим
u{q+8)+u(q — 8)*2u(q)+u"(q)82 + uw (q)8*ll2,
C.386)
171
Глава 3
u{q+28)+u{q — 28)&2u(q)+4u"(qN2 + 4ulv
C.387)
откуда имеем следующее выражение для второй производной:
«"(<7) = {16[и(<7 + 6)+и(<7-6)] — [u(q+28) +
+ u(q~28)]—30u(q)}ll282. C.388)
Менее точные выражения C.281) — C.283) прямо получаются
из C.386), если пренебречь членами четвертого порядка (мы
уже видели это на примере формулы C.303)).
Чтобы использовать вышеприведенные формулы для произ-
производных, необходимо знать значения потенциала в точках с ко-
координатами q, q±8, q±28 и q±38. Проблемы не возникает,
если координата q соответствует узловой точке расчетной сетки
или точке, где действительно вычислялся потенциал, и б равно
размеру ячейки или шагу независимой переменной. Однако си-
ситуация полностью меняется, если это не так. Тогда приходится
интерполировать, чтобы найти нужные значения потенциала по
его значениям в узлах. Процедура интерполяции должна как
минимум иметь такую же точность, как и процедура вычисления
самого потенциала.
Предположим, что потенциал задан для п+ 1 различных зна-
значений независимой переменной q (обычно q — одна из коорди-
координат при фиксированных значениях двух других координат, на-
например когда задано распределение потенциала вдоль оси z
цилиндрической системы координат). Таким образом, имеется
п+1 пара величин ш—qt (г' = 0, 1, 2,..., п). При этом всегда
можно построить полином степени п, принимающий значе-
значение Ui при аргументе, равном qt для любых L Действительно,
полином степени п имеет п+ 1 коэффициент и может аппрокси-
аппроксимировать п+1 заданное значение функции. Коэффициенты яв-
являются простыми функциями узловых значений потенциала. Од-
Однако процедура вычисления коэффициентов может быть весьма
сложной, так как приходится решать систему из п+1 урав-
уравнения.
3.3.5.2. Интерполяция Лагранжа. Может быть использовано
много различных приемов интерполяции, упрощающих вычисле-
вычисления [115], но все они дают один и тот же интерполяционный
многочлен для данного набора пар величин. Одним из простей-
простейших подходов является метод полиномов Лагранжа. Основная
идея состоит в использовании вместо одного полинома п раз-
различных полиномов степени п, составленных так, что вычисление
коэффициентов становится несложным. Для этого построим по-
полиномы так, чтобы они были равны единице при определенном
значении qt независимой переменной q и нулю при всех прочих
172
Определение электрических и магнитных полей
заданных значениях q/ (/ = 0, 1, 2,..., i—1, i+l,..., n). Легко
видеть, что полиномы
(Я—<?о) (.Я—Ях) ■■■ (Я—Я1-1)(Я—Я1+1) ••■ (Я—Яп) /о qqq\
= 7 w \ / w \ 7 Т io.oozf)
удовлетворяют этому требованию для любого i от нуля до п.
Тогда неизвестное значение зависимой переменной u(q) может
быть аппроксимировано суммой
C-390)
которая является теперь непрерывной функцией на всем интер-
интервале между q0 и qn. Очевидно, что C.390) дает узловые значе-
значения и (qi) для каждого узла.
Линейная интерполяция является частным случаем при
п~\. Для нее получаем из C.389) и C.390) известную фор-
формулу
где <7о и qi — координаты двух узлов, между которыми мы стро-
строим интерполяцию.
Для квадратичной интерполяции нужно три узла. Подстав-
Подставляя /г=2 в C.389) и C.390), получаем
и (а
и (а) 4
(qo-qi) (qo-qi) U Uo> + (qi-q0) (qi~
Аналогично может быть записана кубическая интерполяци-
интерполяционная формула для и = 3 и т. д. Теперь всегда можно продиффе-
продифференцировать п раз полученную таким образом непрерывную
функцию и найти производные, необходимые для вычисления
полей.
К сожалению, полиномиальная интерполяция имеет один
серьезный недостаток. Чем больше п, тем сильнее интерполяци-
интерполяционные кривые осциллируют около точного значения. Поэтому
высшие производные не могут быть получены этим методом с
приемлемой точностью.
173
Глава 3
3.3.5.3. Интерполяционный импульс. Одним из возможных
способов повышения точности интерполяции является исполь-
использование более сложных приемов, таких, как, например, поли-
полиномы Чебышева. Можно предложить более простой способ: дис-
дискретный набор данных заменяется на непрерывную функцию с
помощью интерполяционного импульса с минимальным интер-
интерполяционным шумом Г140]. Нетрудно показать, что произволь-
произвольная функция u(q) лучше аппроксимируется по формуле C.390),
если заменить в ней Li(q) на «интерполяционный импульс»
обладающий тем же свойством, что и Li(q): он равен единице
при q=qi и нулю при q = q, (/=0, 1, 2,..., i—I, i+1,..., п).
Однако принципиальное различие состоит в том, что если ис-
использовать в C.390) It(q), то аппроксимация будет улучшать-
улучшаться с ростом п. Например, в простейшем случае постоянной
функции относительиая ошибка этого метода составляет 0,167%
для п=10, но только 0,002% для «= 100. Аналогичные результа-
результаты получаются и для других функций. Непрерывная функция,
полученная из интерполяционных импульсов, может быть про-
продифференцирована любое необходимое число раз.
3.3.5.4. Кубический сплайн. Бесспорно лучшим является
принципиально другой способ замены дискретного набора дан-
данных гладкой функцией. Механические сплайны (гибкие полоски
эластичного материала) используются чертежниками с давних
пор. Если расположить сплайн так, чтобы он проходил через
все точки, соответствующие данным, в интервалах он примет
форму, минимизирующую его потенциальную энергию. Его фор-
форма может быть задана кусочной кубической кривой с непрерыв-
непрерывными первой и второй производными. Нетрудно показать, что
если кривизна сплайна равна нулю на обоих концах (естест-
(естественный сплайн), то он имеет наименьшую возможную кривизну
на всем своем протяжении. Таким образом, естественный
сплайн — наиболее гладкая интерполяционная функция. Если,
как и раньше, имеется л+1 точка, сплайн будет состоять из
п кубических выражений: по одному на каждый из п интерва-
интервалов, между соседними узлами. Для k-ro интервала (рис. 41)
имеем
«а (<7) = Ak+Bk {q — <7а_,) + Ck (q — qk-iJ + Dk (q — qk~iK.
C.394)
174
Определение электрических и магнитных полей
Здесь qk-i — координата левого конца &-го интервала {k=l,
2,..., п). Конечно, коэффициенты Ak, Bk, Ck и Dk различны
для разных интервалов. Таким образом, вместо того чтобы ис-
искать одну функцию для всей области, мы здесь используем
п различных функций, т. е. 4и коэффициентов вместо п+\.
Естественно, мы теперь имеем разные выражения для рас-
лределения потенциала и его производных во всех п интерва-
интервалах. Однако очень легко обеспечить непрерывность сплайна
вместе с его первой и второй производными в каждом из п—1
узлов, где кубические полиномы сшиваются друг с другом. Ус-
Условия непрерывности могут быть записаны в следующем виде:
=Uk{qk), C.395)
=й'4Ы, C.396)
и"*+1
C.397)
Рис. 41. Аппроксимация кривой кубическим сплайном.
(Штрихами обозначается дифференцирование по q.) Третья
производная постоянна и различна для разных интервалов, по-
поэтому она не может быть непрерывной. Производные более вы-
высоких порядков равны нулю внутри интервалов и не определе-
определены в узлах.
Подставляя формулу C.394), ее производные и qk—qk-\ = b
в уравнения неразрывности, получим 3(п—1) уравнений для ко-
коэффициентов:
A 3, C.398)
C.399)
C.400)
где k=\, 2,..., п—1. Еще п+1 уравнений получим, если подста-
подставим узловые значения u(qi) для всех узлов £=0, 1, 2,..., п
в C.394) с соответствующими значениями k. Полное число
уравнений будет 4п—2. Так как имеется всего 4п коэффициен-
коэффициентов, два из них остаются неопределенными. Именно сейчас сле-
следует решить, будет ли использоваться естественный сплайн
(и тогда нужно приравнять вторую производную нулю на обоих
175
Глава 3
концах сплайна), или выгоднее использовать две оставшиеся
степени свободы для других целей, например чтобы задать на
концах первые производные.
Собственно конструирование сплайна является простой и
стабильной процедурой. Нужно решить систему An линейных
алгебраических уравнений для коэффициентов. Если оба сво-
свободных коэффициента используются на одном конце сплайна,
то его построение тривиально, поскольку можно постепенно
двигаться от этого узла к другому, определяя три коэффициен-
коэффициента из условий непрерывности, а четвертый — из значения потен-
потенциала в очередном узле для каждого интервала. Процедура
усложняется, если, как это обычно и бывает, два свободных ус-
условия используются на разных концах. Тогда приходится ре-
решать систему уравнений целиком, что, впрочем, не составляет
проблему даже для очень больших значений п. Уравнения всег-
всегда могут быть расположены таким образом, что соответствую-
соответствующая матрица будет симметричной и «трехдиагональной», т. е.
все ненулевые члены будут расположены в ней на диагонали
и двух прилегающих к ней «линиях». В этом случае система
элементарно решается любым прямым методом, например ме-
методом приведения Гаусса с обратной подстановкой (см.
разд. 3.3.2.1).
После того как построен сплайн, дифференцирование стано-
становится элементарным действием. Первая, вторая и третья про-
производные формулы C.394) могут быть непосредственно рассчи-
рассчитаны при надлежащем выборе индекса k в зависимости от ин-
интервала, в котором расположена точка q.
Сплайн также может быть использован для аппроксимации
кривых, т. е. для моделирования кривой, заданной в графиче-
графическом виде или в виде сложной функции, более простым, легко
дифференцируемым аналитическим выражением. В этом случае
необходимо иметь в виду, что полученные на основе сплайна
производные не совпадут с производными исходной кривой
-(даже в узлах), но это обычно имеет место для всех методов
аппроксимации кривых.
Преимущества метода сплайнов над интерполяцией много-
многочленами очевидны. Второй метод удовлетворительно работает
лишь для малого числа узлов, тогда как сплайн легко постро-
построить на огромном количестве интервалов, и при этом он будет
оставаться очень гладкой функцией с непрерывными первой и
второй производными. Его недостатками являются разрывность
третьей производной и неопределенность высших производных.
Однако как мы увидим в следующих главах, эти производные
обычно вообще не нужны. Поэтому можно считать кубический
сплайн лучшей интерполяционной функцией, имеющейся в на-
нашем распоряжении. Он будет использоваться в гл. 9 как инстру-
176
Определение электрических и магнитных полей
мент для решения одной из наиболее важных проблем электрон-
электронной и ионной оптики.
Задача интерполяции и дифференцирования становится бо-
более сложной, если производные необходимо вычислить в неко-
некоторой произвольной точке, не только не совпадающей ни с од-
одним из узлов, но и не лежащей на какой-либо из линий расчет-
расчетной сетки. Известно несколько способов ее решения. Один иа
них, метод Эрмита [ПО], представляется весьма эффективным
для двумерной интерполяции. В трехмерном случае интерполя-
интерполяция может оказаться гораздо сложнее. К счастью, большой нуж-
нужды в ней не возникает, поскольку в большинстве случаев доста-
достаточно одномерных интерполяций, построенных одновременно
вдоль взаимно перпендикулярных линий сетки, особенно в слу-
случае осевой симметрии, когда вся информация содержится в рас-
распределении потенциала (или поля) вдоль оси.
Заключение
Эта глава очень большая. Ее объем оправдывается объемом
работы, необходимой для вычисления полей. Такие расчеты со-
составляют одну из наиболее утомительных процедур при конст-
конструировании электронных или ионных оптических систем. Глава
делится на три основных раздела: аналитические методы, из-
измерения и численные методы.
Аналитические методы перечислены в разд. 3.1. Сначала
были выписаны разложения в ряд для потенциалов и полей.
Формула C.19) является наиболее общим выражением для
разложения в ряд произвольного трехмерного распределения по-
потенциала в цилиндрических координатах, а C.27) — в декарто-
декартовых. Выражение C.20) написано для частного случая аксиаль-
аксиально-симметричного распределения потенциала. Затем были рас-
рассмотрены общие свойства плоских, аксиально-симметричных и
мультипольных полей. Обсуждались специальные методы вы-
вычисления как аксиально-симметричных, так и мультипольных
полей (разделение переменных, конформные преобразования
и т. д.). Было рассчитано распределение потенциала, созданно-
созданного двумя цилиндрами одинаковых диаметров с круглой апер-
апертурой. Мы ознакомились с процедурой, позволяющей быстро
рассчитать поле, созданное системой апертур. Затем было вы-
вычислено распределение потенциала, созданного цилиндрическим
вогнутым 2ЛГ-мультиполем, и найдено решение задачи об идеаль-
идеальных мультиполях. Трудности аналитических вычислений были
проиллюстрированы на практических примерах. Мы останови-
остановились на особых свойствах магнитных материалов, после чего
использовали закон Био — Савара C.249) для вычисления по-
177
Глава 3
лей прямолинейного проводника, замкнутой петли, тонкого со-
соленоида, многослойной и плоской катушек.
Содержание разд. 3.2 составляют измерения магнитных по-
полей и аналоговые методы определения полей. Здесь были пред-
представлены основные методы измерения магнитного поля, осно-
основанные на электромагнитной индукции, эффекте Холла, исполь-
использовании пермаллоевых и висмутовых датчиков и явления маг-
магнитного резонанса. Затем мы кратко ознакомились с методами
электролитической ячейки, резисторных цепей и другими ана-
аналоговыми методами.
Наиболее важная часть главы — разд. 3.3. Здесь были изло-
изложены численные методы определения полей. Мы начали с об-
обсуждения проблемы точности. Было объяснено; что представля-
представляют собой ошибки округления, аппроксимации и внутренне прису-
присущие ошибки. Мы подробно рассмотрели три основных метода
численных расчетов полей. Выражение C.324) —это девяти-
девятиточечная формула метода конечных разностей в случае акси-
аксиально-симметричных распределений потенциала. Метод конеч-
конечных элементов основывается на вариационных уравнениях
C.337) — C.339). Наиболее удачным подходом к численным
расчетам полей является метод зарядовой плотности. Его ос-
основное уравнение — уравнение C.360). Поверхностная плот-
плотность заряда может быть определена в аксиально-симметрич-
аксиально-симметричном случае из C.370). Кроме того, обсуждались наиболее важ-
важные прямые и итерационные методы решения систем уравнений,
фигурирующих во всех трех основных методах. Наконец, были
рассмотрены методы численной интерполяции и дифференциро-
дифференцирования. Формула C.385) является достаточно точным выраже-
выражением для численного дифференцирования. Интерполяция может
осуществляться при помощи полиномов Лагранжа C.389), ин-
интерполяционного импульса C.393) или кубического сплайна
C.394), причем последний способ — наилучший.
Глава 4
ФОКУСИРОВКА В АКСИАЛЬНО-
СИММЕТРИЧНЫХ ПОЛЯХ
Наиболее часто используемыми элементами электронной и
ионной оптики являются линзы, служащие для фокусировки
пучков заряженных частиц. Они эквивалентны обычным акси-
аксиально-симметричным оптическим линзам, основные свойства ко-
которых были рассмотрены в разд. 1.4.2. Существование элект-
электронно-оптического коэффициента преломления (разд. 2.6) обес-
обеспечивает возможность создания электронных и ионных линз на
основе близкой аналогии между обычной оптикой и движением
пучков заряженных частиц в электромагнитных полях. В гл. 3
уже обсуждались основные свойства аксиально-симметричных
электростатических и магнитных полей, а также основные ме-
методы их вычисления. В данной главе будет проведено деталь-
детальное исследование их фокусирующих свойств.
Всюду в этой главе будет использоваться цилиндрическая
система координат г, a, z. Как известно, аксиальная симметрия
означает, что все характеристики полей зависят только от кцрр-
динат г и z (поля и их потенциалы не зависят от азимутальной
координаты а).
4.1. Теорема Буша
Будем исходить из релятивистского лагранжиана. Подстав-
Подставляя в B.35) цилиндрические координаты и их коэффициенты
Ляме (формула A.10)) и вспоминая обсуждение формулы
C.347), приведшее к заключению, что в аксиально-симметрич-
аксиально-симметричных полях только азимутальная компонента A(r,z) магнитно-
магнитного векторного потенциала отлична от нуля, получим
L=— m0c2[l — {га + г*а* + г*I
+ Q[raA(r,z)-u(r,z)]. D.1)
Заметим сразу, что лагранжиан не содержит явно координа-
координату а. Как было показано в разд. 2.3, в этом случае сохраняет-
сохраняется соответствующая компонента обобщенного импульса. Урав-
Уравнение B.39) дает тогда вместе с B.2) и B.67)
dL/da=r[mora A — t>2/c2)-'/2 + QA {r, z)] =
= m0r2a'v A — v2/ci)-1'2/H+QrA (r, z) =C = const, D.2)
179
Глава 4
где v и Я определяются из B.31) и B.82) соответственно. По-
Постоянную можно определить в любой точке траектории. Наибо-
Наиболее удобно использовать исходную точку, обозначенную индек-
индексом 0. Тогда С — начальное значение азимутальной компонен-
компоненты обобщенного момента, равное
oA (rOl z0). D.3)
Из D.2) можно видеть, что С=0, если частица пересекает ось г
в некоторой точке своего движения.
Уравнение D.2) немедленно дает азимутальную компонен-
компоненту га скорости заряженной частицы или азимутальный «на-
«наклон» а'. Имеем
»«-га= [С — QrA (г, г)] A — o2/c2I/2/m0r. D.4)
Запишем теперь теорему Стокса (формула A.24)) для вектор-
векторного потенциала А на окружности радиуса г с центром, лежа-
лежащим на оси, принимая во внимание A.7) и A.12). Получим
Ads = $ А {г, г)гёа = 2лгА (г, z) =
°
7
= SrotA.ds= $B-ds=cp= 2n\ Bzrdr, D.5)
где ф—поток сквозь круг. Отсюда получаем для абсолютной
величины магнитного векторного потенциала
А (г, г) =Ф/2яг= A/r) j Bzrdr. D.6)
Дифференцируя это выражение по г, сразу же видим, что акси-
аксиальная компонента магнитной индукции равна
Вг=А1г+дА1дг, D.7)
что следует также из A.12) и A.6). Из этих же уравнений по-
получаем радиальную компоненту в виде
Br = —dA/dz D.8)
и Ва = 0. (Эти выражения уже использовались в C.347).)
Если теперь обозначить поток в исходной точке через фо, то
D.4), D.3) и D.6) дают
а = (<2/2тог*я)A -У*/сГ2 (<Р.-<р) + «оfro/0'{|l^ff|! . D-9)
180
Фокусировка в аксиально-симметричных полях
откуда ясно, что основной причиной изменения азимутальной
компоненты скорости является магнитное поле. Это совершенно
естественно, поскольку только магнитный член лоренцевой
силы (формула A.14)) может иметь азимутальную компонен-
компоненту в аксиально-симметричных полях. Это не означает, однако,
что в электростатических полях а постоянно. Как хорошо видно
из D.9) и B.2), в аксиально-симметричных электростатических
полях постоянен момент импульса, тг2а, но как а, так и азиму-
азимутальная компонента скорости га изменяются при движении час-
частицы, если не равна нулю начальная компонента скорости в ази-
азимутальном направлении. Этот результат следует также из
B.61) и может быть записан в виде d(mr2a)ldt=0. В нереля-
нерелятивистском случае а зависит от электрического поля только че-
через изменение г.
Уравнение D.9) называется теоремой Буша [1].
Для однородного магнитного поля, ориентированного в по-
положительном направлении оси z (разд. 2.7.2), можно написать
5z = B = const и D.6) дает
А(г)=Вг/2. D.10)
Подставляя D.3) и D.10) в D.4) и принимая во внимание, что
абсолютная величина скорости не может меняться в чисто маг-
магнитном поле, получим
г2а — го2ао = ±(йс(го2 — г2)/2, D.11)
где wc — циклотронная частота, определенная так же, как в
B.135), а знак соответствует знаку заряда частицы. Заметим,
что в выражение для циклотронной частоты входит релятивист-
релятивистская масса.
Уравнение D.11) представляется слишком сложным для та-
такого простого случая. Причина состоит в том, что здесь го мо-
может иметь любое значение. Обычно, однако, можно выбрать
систему координат таким образом, что траектория частицы бу-
будет винтовой линией вокруг оси г. Тогда радиальное расстояние
частицы от оси z будет постоянным (г=го), и мы получим оче-
очевидный результат, что азимутальная скорость постоянна (а =
= а0).
4.2. Основное траекторное уравнение
Выведем основное траекторное уравнение для заряженной
частицы, движущейся в аксиально-симметричном поле. Диффе-
Дифференциальное уравнение для азимутальной координаты а полу-
181
Глава 4
чено в предыдущем разделе. Действительно, уравнение D.2)
сразу дает
где С определено в D.3). Члены, содержащие скорость, можно
выразить через релятивистский потенциал B.89), используя
B.87) и B.90):
A — v2/c2I/2/v = mo/p — [—2Q(u — Uo)rei/'«o]~I/'2. D.13)
Теперь нужно воспользоваться релятивистскими уравнения-
уравнениями траектории в цилиндрических координатах B.84) и B.85).
Однако уравнение B.85) оказывается лишним, поскольку D.12)
уже дает простое уравнение для а'. Это дает ощутимый выиг-
выигрыш, так как уравнение B.85) весьма сложно. Такое упроще-
упрощение является следствием использования лангранжевого форма-
формализма. Однако это еще не все. Легко заметить, что единствен-
единственное оставшееся уравнение B.84) также может быть существен-
существенно упрощено подстановкой а из D.12). Компоненты электриче-
электрического поля берутся из A.17), A.10) и A.13), а компоненты
магнитной индукции определяются уравнениями D.7) и D.8).
Вспомним также, что для аксиально-симметричных полей Еа =
= Ва=0. Уравнения B.13), B.89) и D.13) используются для
того, чтобы вырааить скорость через релятивистский потенциал.
Здесь следует быть внимательным и помнить, что Q(u—ы0) —
всегда отрицательная величина, что не должно быть потеряно
при манипуляциях с корнями. Принимая все вышесказанное во
внимание, получим следующее выражение для B.84):
d?r _ „_ Я2 \ [C-QrAjr, г)]2
dzi 2 (и — uo)rel / QtfV3
i f 1 Q (и —"о) 1 ( ди , ди
Конечно, Н все еще содержит первую производную азимуталь-
азимутальной компоненты, но, к счастью, удастся избавиться также и от
нее. Для этого введем фиктивный «потенциал»:
W (г, 2) =-[и (г, 2) - и,]ге1 + (Q/2m.) [A (r, z)- C/Qr]*. D.15)
Подставляя сюда С из D.2) и используя D.13), напишем
W=(u — ио)га1A— г2а/2/Я2). D.16)
Выражая Я2 из B.82) и перегруппировывая члены в D.16), по-
получаем
rV2-[(u- «o)rei- W] A + г")ЛР. D-17)
182
Фокусировка в аксиально-симметричных полях
откуда следует
Я2/2(ы-и0)ге1=A+г'2)/2№. D.18)
Выражение D.15) указывает, что W не зависит от а'. Поэтому
после подстановки D.18) в D.14) последнее не будет содержать
а' и его можно непосредственно использовать для определения
r(z). Можно еще упростить это уравнение, подставляя B.89)
в D.15) и дифференцируя W последовательно по г и по z:
dW_ СА С* Г. Q(u—uo)\du C—QrAdA .. .q.
дг mor* Qmor3'i~l moc* J dr mor dr ' V*-iy'
dW \ t Q(u-uJ-\du C-QrAdA . 9n
dz ~ [l m0c2 J dz ' mor dz ' ^-^'
Подставляя уравнения D.18) — D.20) в D.14), получаем окон-
окончательно релятивистское траекторное уравнение для аксиаль-
аксиально-симметричных полей в общем виде:
1 + г'2 ' uw — r'^-\, D.21)
,г)\ dr dz
где W и С определены в D.15) и D.2) соответственно. На-
Начальные условия заданы в некоторой точке г0) где г = г0 и г'—
= г'о.
В случае малых скоростей уравнение не изменяется, только
релятивистский потенциал заменяется электростатическим по-
потенциалом в D.15) и можно пренебречь членом в D.2), содер-
содержащим v2/c2.
Для чисто магнитных полей u = const, но уравнения остают-
остаются неизменными. Однако они существенно проще для электро-
электростатических полей, где Л = 0 и С отлично от нуля, только если
имеется ненулевая азимутальная компонента начальной скоро-
скорости. Уравнение D.21) тогда сводится к следующему реляти-
релятивистскому уравнению траектории для электростатических полей:
£! 1 + ''2 /Г, <?("-«„) I (ди ,ди\ С* \
or2 \| тос* \ \ dr dz J
dz* (o)rel + /Qo \| о \ \ J Q
D.22)
Для малых скоростей и в отсутствие азимутальной компо-
компоненты скорости (С = 0) уравнение становится еще проще:
ди , du
(
dz2 2(и—ио)\дг дг
Отсюда следует одно важное свойство: в электростатиче-
электростатических полях траектория нерелятивистской частицы с нулевым уг-
угловым моментом не зависит от отношения массы к заряду этой
частицы. Следовательно, одно и то же электростатическое поле
183
Глава 4
может использоваться для фокусировки и электронов, и различ-
различных ионов (естественно, полярность потенциалов электродов
должна изменяться на противоположную для частиц разных
знаков).
Уравнения D.12) и D.21) полностью описывают траекторию
частицы с зарядом Q и массой покоя то, движущейся с произ-
произвольной скоростью в аксиально-симметричных электрическом и
магнитном полях. Поскольку уравнение D.21) содержит толь-
только функции координат гиг, оно не зависит от координаты а и
описывает проекцию траектории на плоскость гг. Если эта про-
проекция найдена, можно подставить функцию r(z) в D.12) и най-
найти зависимость a(z). Такое разделение переменных дифферен-
дифференциального уравнения является следствием аксиальной симмет-
симметрии. Если бы ее не было, уравнения B.84) и B.85) остались
бы связанными и очень сложными.
Хотя и удалось разделить уравнения, они все еще остаются
достаточно сложными. Действительно, даже наиболее простое
из них, уравнение D.23), справедливое в очень частном случае
нерелятивистских траекторий с С = 0 в аксиально-симметричных
электростатических полях, представляет собой нелинейное диф-
дифференциальное уравнение второго порядка, для решения кото-
которого необходимо как минимум знать потенциал u(r,z) во всей
области, где проходит пучок. Хотя возможно и численное реше-
решение такого уравнения (см. гл. 6), дальнейшие упрощения необ-
необходимы для более глубокого понимания сути физических про-
процессов.
4.3. Уравнение параксиальных лучей
Введем теперь ряд упрощений. Рассмотрим сначала только
«параксиальные» траектории, лежащие вблизи оси z, движение
по которым происходит главным образом в аксиальном направ-
направлении. Теория параксиальных лучей носит название гауссов-
ской диоптрики.
Первое предположение означает, что в степенном разложе-
разложении в разд. 3.1.1 мы будем пренебрегать всеми членами, содер-
содержащими г в степени выше первой. Поэтому параксиальную тео-
теорию иногда называют теорией первого порядка. Тогда из
C.20), C.38) и C.40) имеем
и(г,2)«£/(г), du/dr*—rU"(z)/2, du/dz*U'(z), D.24)
где U(z)—аксиальное распределение потенциала, определенное
в C.21). Аналогично из D.6) и C.47) получаем, что
Л(г,2)«гВB)/2, D.25)
184
Фокусировка в аксиально-симметричных полях
где B(z) — аксиальное распределение магнитной индукции,
введенное в C.44). Обратите внимание на аналогию между
D.10) и D.25): в случае однородного магнитного поля соотно-
соотношение D.25) справедливо на любых расстояниях от оси.
Необходимо отметить, что первое предположение будет ис-
использоваться только в той области, где существует поле. Вне
поля траектории представляют собой прямые линии, которые
могут быть продолжены сколь угодно далеко от оси, даже если
они являются параксиальными в поле.
Второе предположение состоит в том, что радиальной и ази-
азимутальной компонентами скорости можно пренебречь по срав-
сравнению с аксиальной компонентой. Поэтому наклоны траектории
как в радиальном, так и в азимутальном направлении пренебре-
пренебрежимо малы (r'<Cl и ra'<Cl), и выражение B.82) сводится к
Я«1. Тогда соотношения D.2), D.13), D.24) и D.25) дают
С = г8о,' {-2Qm0 [U (г.) - U0]iel}4> + Qr$B (zo)/2, D.26)
где U(го) и B(z0) —осевые значения потенциала и индукции со-
соответственно в начальной точке, a Uo — осевой потенциал в точ-
точке, в которой скорость частицы равна нулю (см. обсуждение,
предваряющее B.31)). Заметим, что С является выражением,
квадратичным по малой величине Го, поэтому оно может по-
появиться в наших уравнениях, только будучи поделено на дру-
другую малую величину.
Соотношения D.12), D.13), D.25) и D.26) образуют диффе-
дифференциальное уравнение для азимутальной координаты вблизи
оси (параксиальная область):
da/d2 = {-2Qm0 [U (z)-C/0]rei}-1/Sf [C/r*-QB (z)/2]. D.27)
Подставим теперь D.24) и D.25) в D.15), D.19) и D.20).
Пренебрегая величинами, содержащими г и го в степени выше
первой, получим
W*t[U(z) - I/olrei, D.28)
,4.29,
(«О)
Подстановка этих соотношений в D.21) при опускании ма-
малой величины г'2 дает уравнение параксиальных лучей для ре-
релятивистских траекторий в аксиально-симметричных электро-
электростатических и магнитных полях:
185
Глава 4
^-gg^l-ag^_|1_Q[l/Wrl/,]|[ft/,(,)ya+f>I/><
dz* 4m0 Qm^ \ж Ш? f1'" w'-T'" ^j ^ 3^
2[f/(z) —f/olrel
Уравнения D.27) и D.31) полностью определяют траекто-
траекторию заряженной частицы в таком поле. Сначала нужно решить
D.31) и получить функцию r(z), а затем подставить ее в урав-
уравнение D.27), непосредственным интегрированием которого мож-
можно теперь определить положение меридиональной плоскости,
в которой в данный момент расположена частица:
а B) -а0 = J {-2Qm0 [U (z) - U0]tel}-«> [C/r> (z) - QB (Z)/2] dz.
Отсюда видно, что в параксиальной области траектория лю-
любой заряженной частицы полностью определяется распределе-
распределением потенциала вдоль оси, двумя его первыми производными
и осевым распределением магнитной индукции.
В вышеприведенных соотношениях [U (z)—U0]rei вычисля-
вычисляется при помощи подстановки осевого потенциала вместо
u(r, z) в B.89). Естественно, при малых скоростях релятивист-
релятивистский потенциал можно заменить просто на осевой потенциал,
а членом Q[U(z)—U0]fm0c2 пренебречь.
В параксиальном случае можно записать теорему Буша,
если подставить D.25) в D.3) и D.4). Получим
2(l-uo2/c2)-}. D.33)
Уравнение параксиальных лучей D.31) все еще остается не-
нелинейным дифференциальным уравнением. Оно становится ли-
линейным только при С=0, т. е. если траектория пересекает ось,
либо если как азимутальная компонента скорости, так и маг-
магнитная индукция обращаются в нуль в одной и той же точке.
(Существует также и третья возможность: приравнивая С к
нулю, можно рассчитать значение оы/, при котором уравнение
параксиальных лучей становится линейным. Однако практиче-
практическое значение этого случая весьма ограниченно.)
Указанные ограничения являются очень серьезными. По-
Поскольку нам хотелось бы получить общие важные заключения
на основе уравнения параксиальных лучей, попытаемся линеа-
линеаризовать его при любом значении С.
186
Фокусировка в аксиально-симметричных полях
Введем новые переменные:
D.34)
где £ — мнимая единица и (J(z) —разность между азимутальной
координатой a(z) и ее значением при том же z в случае С = 0.
Переменная ш(г) является комплексной, причем ее модуль и
аргумент равны r(z) и p(z) соответственно. Дифференцируя
D.34) по z и принимая во внимание D.27) и D.35), получим
d$/dz=C{-2Qmo[U(z) - 1/0],.1}-1'*Ля =
]. D.36)
Теперь можно выразить г (г) через новые переменные из D.35)
и продифференцировать дважды по гс учетом D.36). Резуль-
Результатом будет
г (z) = w (г) ехр [— фг], D.37)
dr/dz = (cto/cte) ехр [ — $ (г) ] —
— (iC/»(z)){-2Qmo[I/(z) - I/0]rei}-1/2exp[*p(z)],
D.38)
)ехр [-£P(Z)] -g^gj^
I
D.39)
Подставляя эти выражения в D.31), окончательно получаем
уравнение параксиальных лучей для комплексной переменной
в виде:
dz* 4т^""^> V ЩР2 ) L W dz
2[U (z)-U0]Tel
(i74o)
Отметим, что это уравнение в точности совпадает с D.31), если
подставить w(z) вместо r(z) и положить С=0. Это как раз то,
что нам нужно: убирая член, содержащий С, мы преобразовали
уравнение в линейное дифференциальное. Как мы увидим в сле-
следующем разделе, этот факт может иметь далеко идущие по-
последствия.
187
Глава 4
Начальные условия получаются из D.34) и D.35). Имеем
P(zo)=O, D.41)
"Ж |г= го = «о + (Q/2) {-2Qm0 [£/ (z0) - U0]rel}~ «* В (z0), D.42)
w(zo)=ro> D.43)
= г; + fr, <ai + QB B0) {-2Qmo[C/ (г.) - £/,],„}" */»/2>. D.44)
Уравнение D.40) вместе с D.34) и D.35) полностью опреде-
определяет траекторию релятивистской частицы в аксиально-симмет-
аксиально-симметричном поле. Решив его (обычно с помощью одного из числен-
численных методов, описанных в гл. 6), можно вернуться к исходным
переменным, используя D.34) и
r={[Re(ra»)]2+[Im(t0)]2}1/2> D.45)
P = arctg[Im(z<y)/Re(uy)], D.46)
где Re(w) и lm(w)—вещественная и мнимая части комплекс-
комплексной функции w(z) соответственно.
В частном случае С = 0 мы имеем [5 = 0, поэтому w(z) =
— r(z), и мы возвращаемся к исходному уравнению для вещест-
вещественной переменной r(z).
Уравнение D.40) становится очень простым в случае чисто
магнитных полей, когда релятивистский потенциал постоянен и
правая часть уравнения содержит только один член. Для элек-
электростатических полей уравнение сложнее, однако, если частица
не имеет азимутальной компоненты начальной скорости, необ-
необходимости в использовании комплексной переменной w(z) не
возникает.
В случае малых скоростей релятивистский потенциал заме-
заменяется на электростатический, а членом, содержащим /Пос2 в
знаменателе, пренебрегают.
С точки зрения численных расчетов предпочтительней иметь
дело с дифференциальными уравнениями, не содержащими пер-
первой производной зависимой переменной. Это всегда выполняет-
выполняется для D.40) в случае магнитных полей. Поэтому, если удастся
преобразовать уравнение к такому виду, структура уравнения
будет одинаковой для электростатического и магнитного полей.
Воспользуемся следующим преобразованием:
a (z) = w (z) | [U (z) - С/о] rei 11/4- D.47)
Выражая отсюда w(z) и дифференцируя дважды по г, полу-
получаем
188
Фокусировка в аксиально-симметричных полих
| [U(г)-U,U I'61* {1 -9Ж^1М} W W °(г)/4, D.48)
=F 5/41 [I/ (г) - £/.],„-•
+ 1/21 [t/ (z) - C/.]rcl |-»/« {1 - Q t^-^1 [ V (г) §-
-(Q/m0c2)| [£/ (г) — £/„]«, -•/* С/'* (г) а (г), D.49)
где верхний и нижний знаки соответствуют положительному и
отрицательному значению релятивистского потенциала.
Подставляя эти выражения в D.40), приходим к простому
уравнению
D.50)
где
Т(г)-]
3C/'2(z)
l6[i/B)—i/0
ilrel
8m0
QU'*(z)
c2 [U (z) — U0]r
el 8/П0
QS2(z)
[U(z)-U0]rei '
- 0
D.51)
всегда положительно, так как знаки заряда и потенциала про-
противоположны. Заметим, что в этом уравнении появляется собст-
собственно релятивистский потенциал, а не его модуль.
Такая форма уравнения параксиальных лучей имеет еще
одно явное преимущество: уравнение не содержит второй произ-
производной электростатического потенциала. В разд. 3.3.5.1 мы ви-
видели, что высшие производные могут быть определены числен-
численно лишь с ограниченной точностью.
Очевидно, что в случае малых скоростей второе слагаемое
в D.51) пренебрежимо мало по сравнению с первым. Поэтому
для нерелятивистских частиц уравнение D.50) может использо-
использоваться совместно с
Г/-ч 3(/'2(z) QB*(z)
8m,K/(z)-l/eI
Отсюда следует, что параксиальная траектория нерелятивист-
нерелятивистской частицы не зависит от отношения заряда к массе. Поэтому
189
Глава 4
траектории электронов и ионов с разными массами одинаковы,
•если совпадают начальные условия. Естественно, для положи-
положительных ионов знаки всех электродных потенциалов должны
изменяться на противоположные по сравнению со случаем элек-
электронов и отрицательных ионов. Заметим, что при обратном пре-
преобразовании o(z) в r(z) через D.47), D.37), D.34) и D.32)
зависимость от Q/nto исчезает, даже если начальная скорость
имеет азимутальную компоненту (СфО). Это ясно также из
D.26) и D.31). Очевидно, кроме того, что скорость частицы за-
зависит от отношения заряда к массе даже для С = 0.
Начальные условия для D.50) могут быть получены из
D.43), D.44) и D.47):
£/0]rei|1/4, D-53)
+ (г,/4) | [U (г.) - £/.]reI |-3/* U' B.) {1 - Q [U (z0) - £/o]/moC*}. D.54)
Решив уравнение D.50), легко получить функции r(z) и а (г),
описывающие траекторию, подстановкой o(z) в D.47), w(z) в
D.45) и D.46) и, наконец, 0(г) в D.34).
Поскольку D.40) и D.50)—линейные дифференциальные
уравнения, пропорциональные изменения размеров электродов
и магнитов могут приводить к пропорциональным изменениям
траектории, если электродные потенциалы и токи возбуждения
остаются неизменными.
Кроме того, в нерелятивистском случае уравнение D.40)
линейно по электростатическому потенциалу и квадратично по
магнитной индукции. Вследствие этого пропорциональное из-
изменение всех электродных потенциалов не изменит траектории,
если магнитная индукция одновременно изменяется пропорцио-
пропорционально квадратному корню из масштабного множителя изме-
изменения потенциалов. Если нет магнитного поля, уравнение
D.40) в нерелятивистском случае однородно по потенциалу,
поэтому траектории определяются отношениями потенциалов
электродов, а не абсолютными значениями этих потенциалов.
Это не так для релятивистских скоростей: уравнение D.40) не-
нелинейно по потенциалу и траектории определяются самими по-
потенциалами, а не их отношениями.
Эти выводы полностью соответствуют законам подобия, по-
полученным в разд. 2.8.
4.4. Формирование изображения с помощью парак-
параксиальных лучей
Уравнение параксиальных лучей, записанное в форме
D.40) или D.50), представляет из себя линейное однородное
дифференциальное уравнение второго порядка. Предположим,
190
Фокусировка в аксиально-симметричных полих
что Wi(z) и w2(z)—два частных линейно-независимых реше-
решения уравнения D.40), определенные начальными условиями.
Вспомним, что w(z)—комплексная функция, содержащая в
соответствии с D.34) и D.35) как радиальную r(z), так и
азимутальную а (г) компоненты траектории. Однако, если
С=0, в D.40) может быть подставлена функция w(z) =r(z)
(это следует также из D.31)). Поскольку уравнение D.40)
имеет один и тот же вид для w(z) при СфО и для г (г) при
С=0, можно выбрать две вещественные функции л(г) и r2(z),
удовлетворяющие уравнению во втором случае для любых двух
частных решений wt(z) и W2(z), удовлетворяющих этому же
уравнению в первом случае. Тогда общее решение может быть
записано в виде
w(z)=ciri(z)+c2r2(z), D.55)
где С| и с2 — произвольные постоянные. Так как w(z) являет-
является комплексной функцией, а г{ (г) и г2 (г) вещественны, посто-
постоянные, естественно, должны быть комплексными. Подставляя
сюда начальное значение аксиальной координаты zo и принимая
во внимание D.43), можно выразить с2 в виде
c2=[ro — clr(zo)]/r2(zo), D.56)
где ri(zo), r2(zo) и г о — значения частных и общего решений
соответственно, взятые в начальной точке zo. Подставляя D.56)
в D.55), получаем общее решение в виде
М\ D'57)
Как видим, при фиксированных zo и z величина w будет раз-
разной при разных значениях постоянной С\. Однако, если сущест-
существует такое z=z,, при котором множитель при Ci равен нулю,
т. е.
r2(zi)/r2(zo)=rl(zi)/r1(zo)=M, D.58)
тогда для этого частного значения z=z» D.57) сводится к
rt. D.59)
Это означает, что величина w(zi) вещественна и ее значение
не зависит от С\, т. е. разные лучи, выходящие из точки Ро с
координатами z0, r0 под разными углами к оси, соответствую-
соответствующими разным направлениям начальной скорости и потому раз-
разным значениям с\, встретятся опять в точке Pi с координатами
<i, rt, как показано на рис. 42.
В силу простого соотношения D.59) г, — линейная функция
Го, т. е. изменение го приведет к пропорциональному изменению
191
Глава 4
Г;. Другими словами, значение функции w(z) в точке Zi в М
раз больше, чем в z0, поэтому М называют увеличением, , при-
причем оно всегда вещественно, так как вещественны г0 и r-t. Если
лучи выходят из точки на оси (го = 0), то г, = 0, следовательно,
они снова пересекутся на оси. Увеличение может быть положи-
положительным и отрицательным. В последнем случае изображение
перевернуто в меридиональной плоскости.
Как следствие, можно утверждать, что произвольное акси-
аксиально-симметричное поле представляет собой линзу, поскольку
оно приводит к формированию изображения, действуя на па-
параксиальные частицы: точка Я,- является образом точки Ро-
Такое соответствие между точками называется стигматическим
изображением. В силу линейности D.59) можно также сказать,
что отрезок ZiPi является изображением линейного объекта
гоРо. Аналогично если есть плоский объект, перпендикулярный
Рис. 42. Образование изображения.
оси в точке z0, то аксиально-симметричное поле создаст плос-
плоское увеличенное (или уменьшенное) изображение этого объек-
объекта, расположенное в точке z,- и перпендикулярное оси. Изобра-
Изображение будет геометрически подобно предмету. Положение изо-
изображения определяется уравнением D.58), поэтому его назы-
называют уравнением изображения. Оно выражает самое общее
свойство аксиально-симметричных полей.
Поскольку w(zi) вещественно, p(z,)=0. Мы знаем, что
$(z) есть разность между ос (z) при определенном значении С
и a{z) при С=0. Это означает, что для координаты изображе-
изображения Zi азимутальная координата равна ее значению при С = 0,
и уравнение D.32) дает
<— «о— (Q/2) S(-2Qmo[{/ (г) -
В (г) dz. D.60)
Это уравнение вращения изображения. Действительно все час-
192
Фокусировка в аксиально-симметричных полях
тицы, вышедшие из точки Ро, снова встретятся в точке Р„ при-
причем азимутальная координата этой точки однозначно определе-
определена в D.60) и не зависит от направления начальной скорости
частицы, хотя азимутальные координаты частиц с разными на-
начальными скоростями (разные значения С) будут отличаться в
ходе их движения по траектории до ее пересечения с осью в
точке изображения. Поскольку значение интеграла зависит
только от положений предмета и изображения, изменение ази-
азимутальной координаты будет одним и тем же для всех точек
изображения. Это означает, что изображение целиком будет
повернуто без каких-либо искажений в плоскости изображения
на угол, определенный соотношением D.60). Если предмет
линейный и перпендикулярен оси, то изображение будет нахо-
находиться в меридиональной плоскости rz, но сама эта плоскость
будет поворачиваться в соответствии с D.60). Поэтому всегда
можно использовать меридиональную плоскость для того, что-
чтобы определить положение и размер изображения, помня, что
эта плоскость поворачивается при формировании изображения.
Отметим, что вращение изображения имеет место только в
магнитных полях.
Таким образом, каждая точка предмета будет представле-
представлена соответствующей точкой изображения. Для определения
координат изображения достаточно рассмотреть две различные
траектории, выходящие из соответствующей точки предмета.
Они снова пересекутся в точке изображения. Поскольку коор-
координаты изображения всегда вещественны, можно выбрать тра-
траектории с С = 0, что существенно упрощает вычисления.
В ходе приведенного обсуждения мы подчеркнули зна-
значение основной теоремы электронной и ионной оптики, полу-
полученной впервые Бушем [1] в 1926 г. Интересно, что первая
электронная линза была изготовлена Е. Вихертом еще в
1899 г. Д. Габор повторил это открытие в 1924 г.. Вскоре по-
появились последователи, а в 1931 г. М. Кнолль и Е. Руска пост-
построили первый электронный микроскоп. Спустя два года Е. Рус-
ке удалось показать, что электронный микроскоп имеет более
высокое разрешение, чем его оптический прототип. Последую-
Последующие десятилетия засвидетельствовали ошеломляющий прогресс
в данной области. Появились новые приложения, такие, как
катодно-лучевые трубки, микроволновые генераторы и генера-
генераторные лампы, ускорители частиц, спектрометры, различные
электронно- и ионно-лучевые устройства и технологии, что по-
потребовало создания новых подходов, лучше сформированных и
более мощных пучков. В наше время сложнейшие аналитичес-
аналитические инструменты наряду с электронно- и ионно-лучевой лито-
литографией и тестированием определяют основные стимулы к
дальнейшему развитию. Но всему этому положило начало от-
193
Глава 4
крытие кажущейся простой способности аксиально-симметрич-
аксиально-симметричных полей создавать изображение.
Необходимо, однако, иметь в виду, что доказательство спра-
справедливо только для параксиальных частиц. Лучи, выходящие
из точки объекта в разных направлениях, соберутся в одной
точке изображения, только если траектории остаются близкими
к оптической оси и если малы их наклоны. Иначе справедли-
справедливым будет только нелинейное уравнение D.21), в результате
чего лучи с разными начальными наклонами сформируют «изо-
«изображения» в разных точках, поэтому изображение будет раз-
размытым. Это составляет проблему аберраций, которая будет
подробно рассмотрена в следующей главе.
4.5. Формула Гельмгольца — Лагранжа
Рассмотрим луч, выходящий из точки на оси (го = 0) под опре-
определенным углом "fo (рис. 43). Мы показали, что этот луч опять
пересечет ось в точке Zi, образуя изображение точки z0. Угол
между траекторией в точке изображения и осью равен у{. От-
Отношение
G = tg-Y.-/tg-ro D.61)
называется угловым увеличением. Так как луч однозначно задан
начальными условиями, можно считать его частным решением
r\{z) уравнения параксиальных лучей D.40). Тогда, поскольку
ro = ri(zo) —0, имеем из D.56) с2 = 0, и различные лучи пучка
будут характеризоваться разными значениями с, в D.55), со-
соответствующими разным углам ^о. Тогда D.55) и D.61) дают
' ^4^ D.62)
G ^4
w (г») r[(z0)
для всех лучей независимо от величины сь
Так как оба частных решения г, и г2 должны удовлетворять
уравнению D.40), можно записать его дважды: один раз, под-
подставляя r\ (z) вместо w(z), и затем, подставляя r2(z) вместо
zo(z). Далее умножим первое уравнение на г2, второе уравне-
уравнение на т\ и вычтем второе уравнение из первого. В результате
получим
2 [U(z)-UeU(rlr2-rir;)+\ I -QlU<$rU']} V (z)x
X(rir2-r1r;) = 2{[t/(z)-f/0]rel}i.'«(d/d?)<{[f/(z)-f/0]rel}i/»x
x(rir,-r1r;)> = 0, D.63)
откуда следует, что
{[U(Z) - (/0]rel}1/2(/V2-/-l/-'2)=COnst. D.64)
194
Фокусировка в аксиально-симметричных полях
Если некоторая величина постоянна вдоль траектории, ее
значение в z0 должно быть равно значению, вычисленному в
zt. Учтем также D.58) и D.62), а также тот факт, что по оп-
определению ri(z0) =ri(z;) =0. Получим еще одно очень важное
соотношение:
GM
1/2
\IUB,))-Uo)!el
D.65)
Это уравнение эквивалентно теореме Гельмгольца — Ла-
гранжа в обычной оптике, поэтому оно называется формулой
Гельмгольца — Лагранжа. Заметим, что D.65) остается спра-
справедливым и для непараксиальных лучей, если только заменить
тангенсы на синусы в D.61) (соотношение Аббе). Очевидно,
что для малых углов оба выражения дают один и тот же ре-
результат.
Важным следствием этой
теоремы является то, что, по-
поскольку угловое увеличение G
отрицательно, если луч пере-
пересекает ось дважды (если
fo>0, то f/<0), увеличение
М также должно быть отри-
отрицательным. Это означает, что
электронно-оптическое изоб-
изображение перевернуто в мери-
меридиональной плоскости. Если
Рис. 43. Угловое увеличение; реаль-
реальные и асимптотические предмет и
изображение.
луч пересекает ось несколько
раз, последующие изображе-
изображения всегда перевернуты отно-
относительно предыдущих, поэто-
поэтому увеличение n-го изображения может быть выражено с по-
помощью D.59) в виде
Мп=(— l)"r(z,n)/ro,
D.66)
где zin — осевая координата n-го изображения. Здесь мы рас-
рассматриваем только положительные значения г в соответствии
с определением цилиндрической системы координат. Таким об-
образом, общее увеличение может быть положительным или от-
отрицательным, как уже отмечалось. Вообще говоря, мы должны
отличать r(z)>0 как радиальную координату от функции r(z),
как решения дифференциального уравнения D.31) или D.40),
которая может иметь любой знак. В последнем случае мы рас-
рассматриваем r(z) как траекторию в меридиональной плоскости.
Именно в этом смысле и было определено увеличение в D.58)
и D.59).
195
Глава 4
Другим важным следствием D.65) является то, что для по-
получения сильно уменьшенного изображения, необходимого для
диагностики высокого разрешения, желательно создавать в об-
области изображения потенциалы много большие, чем в об-
области объекта. Если это неосуществимо, то приходится исполь-
использовать большое угловое увеличение, что является весьма не-
неблагоприятным с точки зрения аберраций.
4.6. Кардинальные элементы
Вспомним теперь о том, что говорилось в разд. 2.6 о близ-
близкой аналогии между геометрической и электронно-ионной оп-
оптикой. Поскольку такая аналогия существует, и мы только что
показали, что аксиально-симметричные поля действительно мо-
могут создавать изображения предметов, вполне естественно при-
применить классическую терминологию геометрической оптики
(разд. 1.4.2) к электронным и ионным линзам.
Однако при этом следует соблюдать осторожность. Дейст-
Действительно, оптическая линза, изготовленная из какого-либо ма-
материала (обычно специальных сортов стекла), имеет вполне
определенные четкие границы во всех направлениях. Поэтому
линза всегда ограничена двумя поверхностями вращения во-
вокруг оптической оси (см. рис. 3). В разд. 2.6 мы видели, что
электронно-оптический коэффициент преломления всегда явля-
является непрерывной функцией пространственных координат. Дей-
Действительно, его величина обусловлена действием электрическо-
электрического и магнитного полей, которые не могут резко изменяться в
однородной среде. Поэтому очень сложно определить границы
электронной или ионной линзы. Если не рассматривается сам
источник, пучок должен выйти из источника или предыдущей
линзы и затем как-то войти в поле следующей линзы. Анало-
Аналогично, если только мишень не располагается внутри линзы, пу-
пучок должен покинуть поле линзы, чтобы затем отклониться и
сфокусироваться другой линзой и т. д. По этим причинам очень
трудно заключить линзу в пределах четко определенных фи-
физических границ.
Тогда как же можно использовать оптическую терминоло-
терминологию? Прежде всего попробуем ввести две плоскости, перпен-
перпендикулярные оптической оси, следующим способом: несмотря на
то что поле теоретически существует во всем пространстве,
оно настолько мало вне этих плоскостей, что траектории прак-
практически прямолинейны, так же как и в области, где поле отсут-
отсутствует. Ограничивающие плоскости могут быть определены ма-
математически заданием малой величины е, характеризующей
отклонение траектории от прямой асимптоты. Если действи-
действительное отклонение меньше, чем е, считается, что частица рас-
196
Фокусировка в аксиально-симметричных полях
положена вне линзы. Таким образом, фиктивные «границы»
служат цели ограничения действия линзы между ними.
Сразу же замечаем, что определение границ линзы возмож-
возможно не всегда, так как асимптомы могут и не существовать.
Рассмотрим, например, случай однородных полей. За исключе-
исключением тривиального случая, когда начальная скорость направ-
направлена точно вдоль силовых линий, в таком поле траектории не
имеют прямолинейных участков. Если частица покидает об-
область, заполненную полем, она должна пересечь область неод-
неоднородного поля, так как однородное поле не может иметь рез-
резкую границу.
Можно показать [16], что необходимым и достаточным ус-
условием существования асимптот является сходимость интеграла
со
\T{z)z4z,
—со
где функция T(z) определена в D.51). Если асимптоты не су-
существуют, кардинальные элементы определить трудно.
В силу сказанного, определение кардинальных элементов
(разд. 1.4.2) требует особой осторожности. Посмотрим внима-
внимательно на рис. 43. Штриховые линии обозначают «границы»
линзы, за которыми траектория аппроксимируется ее асимпто-
асимптотой. Мы видим, что и объект z0, и изображение г,- расположе-
расположены внутри линзы. Это означает, что продолжения асимптот
пересекут ось не в точках, соответствующих объекту и изобра-
изображению, а в каких-то других точках zo* и 2,* соответственно
(асимптотические предмет и изображение). При этом асимпто-
асимптотические углы f0* и f'* соответствуют углам ^о и ^-
Как определить в данном случае кардинальные элементы?
На рис. 44 показан луч, входящий в поле линзы в пространстве
Рис. 44. Реальные и асимптотические кардинальные элементы в пространстве
изображений.
197
Глава 4
объектов (слева от линзы) параллельно оси. Согласно опти-
оптической аналогии, это соответствует объекту на минус бесконеч-
бесконечности и изображению в фокусе F2. Так как в этом случае
r(z;)=0, формула D.59) дает М = 0 (нулевое увеличение). Ес-
Если же, однако, последовать процедуре, описанной в разд. 1.4.2
(рис. 3), мы заметим, что фокус определяется пересечением
прямолинейного участка траектории с осью. Здесь можно по-
поступить аналогично, продолжая асимптоту в пространстве изо-
изображений в обратном направлении. Эта прямая линия пересе-
пересечет ось в асимптотическом фокусе F2*. Теперь, если мы захо-
захотим определить главные плоскости, у нас есть выбор: исполь-
использовать касательную к траектории в реальном фокусе F2 или
асимптоту, проходящую через F2*. Тогда с помощью процеду-
процедуры, описанной в разд. 1.4.2, можно определить положения дей-
действительных (#2#г')> либо асимптотических (Н2*Н2*') главных
плоскостей. В соответствии с этим фокусное расстояние в про-
пространстве изображений может быть определено как f2 = H2F2,
f2* = H2*F2* (рис. 44).
Рис. 45. Реальные и асимптотические кардинальные элементы в пространстве
объектов.
Рис. 45 демонстрирует аналогичные результаты, получен-
полученные в том случае, когда фокус расположен в пространстве объ-
объектов для фокуса F\, главной плоскости Н\Н{' и фокусного
расстояния fi = F[Hi, а также их асимптотических эквивалентов
Z7,*, #!*#,*' и f]* = Fi*Hl*. В этом случае ro = 0, a Af-^oo (бес-
(бесконечное увеличение).
Приведенные рассуждения показывают, что существование
различных действительных и асимптотических кардинальных
элементов обусловлено тем, что толстая линза может быть до-
198
Фокусировка в аксиально-симметричных полях
статочно сильной, чтобы настолько искривить траекторию, что
она пересечет ось до того, как выйдет за пределы поля линзы.
Отсюда следует, что мы будем называть линзу слабой, если
падающий параллельный пучок сходится в фокусе за предела-
пределами линзы. В этом случае между действительными и асимпто-
асимптотическими кардинальными элементами нет никаких различий.
Поэтому асимптотические кардинальные элементы применимы
и к действительным объектам и изображениям, расположен-
расположенным вне линзы, и к «асимптотическим» объектам и изображе-
изображениям, определенным выше.
Отметим, что иногда в литературе для того, чтобы указать
положение кардинальных элементов, используется расстояние
до каким-либо образом определенной плоскости. Это удобно,
когда линза симметрична в осевом направлении относительно
плоскости, пересекающей ось в геометрическом центре линзы.
В этом случае расстояние от центра до фокуса называется
«средним фокусным расстоянием».
Даже увеличение может быть определено двумя различны-
различными способами. Поскольку как размеры предмета, так и разме-
размеры изображения оказываются отличными от действительных
размеров, если использовать асимптоты, их отношение (асимп-
(асимптотическое увеличение) также будет отличаться от действи-
действительного увеличения. В обозначениях рис. 46 действительное
увеличение определяется как M = Plzl/Pozo, тогда как асимпто-
асимптотическое увеличение равно M* = Pi*z*jPo*zo*.
На самом деле знание действительных кардинальных эле-
элементов мало что дает, если предмет или его изображение, или
оба они расположены в поле линзы. В этом случае на части-
частицы действует лишь часть поля, зависящая от положений объ-
объекта и изображения. Если предмет движется, изменяется дей-
действующая часть поля. Соответственно придется определять
фокусное расстояние (и все кардинальные элементы) отдельно
для каждого положения предмета с тем, чтобы иметь возмож-
возможность использовать формулу Ньютона A.51). При этом вычис-
вычисления не проще, чем непосредственное использование уравне-
уравнения изображения D.58). Вообще говоря, это уравнение и со-
соотношение Гельмгольца — Лагранжа D.65) являются единст-
единственными математическими выражениями, которые можно ис-
использовать для установления связи между предметом и изо-
изображением.
К счастью, в большинстве случаев электронные и ионные
линзы используются в многоэлементных колоннах, где линзы
формируют последующие изображения предыдущих промежу-
промежуточных изображений. Таким образом, если колонна сконструг
рована так, что соблюдены подходящие рабочие интервалы
между изображениями и «границами» линз, то для любой лин-
199
Глава 4
Рис. 46 Образование реального и асимптотического изображения
зы как «предмет», так и изображение расположены за преде-
пределами линзы и в ее действии будет участвовать все поле. Тогда
действительные и асимптотические характеристики совпадают
и кардинальные элементы могут быть использованы без огра-
ограничений для построения изображения. Конечно, это возможно,
только если линзы не являются слишком сильными (см. выше).
Для электростатических линз так чаще всего и бывает, пото-
потому что для создания очень сильной линзы понадобились бы
слишком высокие напряжения, что нежелательно в связи с
опасностью электрического пробоя и сложностью работы с вы-
высоковольтными источниками питания. Кроме того, помещение
объекта или изображения (мишени) в поле линзы, привело бы
к значительному искажению поля. Конечно, с источниками де-
дело обстоит несколько иначе, но и в этом случае можно исполь-
использовать понятие рабочего интервала. Наиболее важным исклю-
исключением является объектив магнитного электронного микроско-
микроскопа, где объект помещен глубоко в поле очень сильной линзы
для достижения возможно большего увеличения. По этой при-
причине действительные характеристики линзы иногда называют-
200
Фокусировка в аксиально-симметричных полях
ся свойствами объектива в отличие от проективных свойств, ис-
используемых как другое название асимптотических характерис-
характеристик.
Даже если необходимо использовать реальные характерис-
характеристики, можно применять понятие о кардинальных элементах. Не-
Нетрудно показать [16], что для магнитных линз всегда можно
определить кардинальные элементы, не зависящие от положе-
положения предмета в пределах небольшого интервала (соприкасаю-
(соприкасающиеся кардинальные элементы). В то же время соприкасаю-
соприкасающиеся кардинальные элементы будут отличаться для двух да-
далеких друг от друга положений предмета. Для электростатиче-
электростатических линз соприкасающиеся кардинальные элементы могут быть
определены при выполнении дополнительного условия. Поэто-
Поэтому их применимость весьма ограниченна. Однако существуют
поля, для которых соприкасающиеся кардинальные элементы
не зависят от положения предмета. Это так называемые нью-
ньютоновские поля, для которых формула Ньютона A.51) справед-
справедлива и тогда, когда предмет и изображение располагаются в
поле линзы. Примером ньютоновского поля является колоколо-
образная модель Глазера (8.25).
4.6.1. Асимптотические кардинальные элементы
Из приведенного обсуждения становится ясно, что наи-
наибольший интерес представляет определение асимптотических
кардинальных элементов, введенных на рис. 44 и 45. В D.55),
для построения общего решения уравнения параксиальных лу-
лучей были использованы два частных решения. Теперь, вместо
того чтобы, как раньше, считать т\ (z) лучом, пересекающим
дважды ось, положим, что ri(z) соответствует лучу, приходя-
приходящему из пространства изображений параллельно оси, a r2{z) —
лучу, приходящему из пространства объектов параллельно оси.
Будем называть их главными лучами. Поскольку уравнение па-
параксиальных лучей D.40) линейно, любое его решение может
быть построено как линейная комбинация этих частных реше-
решений.
Главные лучи пересекают ось в пространстве объектов (Fi)
и в пространстве изображений (F2) в соответствующих дейст-
действительных фокусах (см. рис. 45 и 44). Очевидно, что все ос-
остальные лучи, проходящие параллельно оси на малом расстоя-
расстоянии от нее, пересекут ось в тех же точках. Докажем, что асим-
асимптоты всех этих лучей пересекутся соответственно в переднем
(Fi*) и заднем (F2*) асимптотических фокусах.
Асимптоты в пространстве объектов (rObj(z)) лучей
D.67>
20U
Глава 4
при произвольном С\ могут быть записаны в виде
) = (Z — Fi')r'obi = Ci (Z —./V)r'lobJ =
+ (z — a)r'obj = ci(ri(a) + (z — a)r'lobi), D.68)
где г1оь](г)—асимптота частного луча, г'ощ и г'юь] — посто-
постоянные наклоны асимптот в пространстве объектов для общего
и частного лучей соответственно и a — осевая координата пе-
передней границы поля. Отсюда координата переднего асимпто-
асимптотического'фокуса определяется с помощью условия robj(/7i*) =
= 0, что дает
Fi*=a — n(a)/r'iobj. D.69)
Положение переднего асимптотического фокуса не зависит от
произвольной постоянной си следовательно, он один и тот же
для всех лучей, проникающих в линзу из пространства изобра-
изображений параллельно оси.
Аналогично для лучей
r(z)=c2r2(z) D.70)
Тфи произвольных с2 можно определить координату заднего
асимптотического фокуса
F2* = b-r2(b)/r'2im, D.71)
где Ь — осевая координата задней границы поля и г'Гхт — по-
постоянный наклон асимптоты в пространстве изображений для
частного луча, входящего в линзу параллельно оси из прост-
пространства объектов. Положение заднего асимптотического фоку-
фокуса не зависит от произвольной постоянной с2, т. е. оно одина-
одинаково для всех лучей, входящих в линзу из пространства объ-
объектов параллельно оси. На этом доказательство закончено.
Определим теперь положение асимптотических главных
плоскостей. Из рис. 45 следует, что асимптотическое переднее
фокусное расстояние равно
D.72)
откуда с помощью D.69) можно определить координату перед-
передней асимптотической главной плоскости. Мы видим, что ни
fi*, ни Я!* не зависят от произвольной постоянной С\. Анало-
Аналогично из рис. 44 следует формула для асимптотического задне-
заднего фокусного расстояния:
H2*F2*=F2* — H2* = h* = —r2(a)r'2im, D.73)
202
Фокусировка в аксиально-симметричных полях
а координата задней асимптотической главной плоскости оп-
определяется из D.73) и D.71). Ни /2*, ни Я2* не зависят от
ПРОИЗВОЛЬНОЙ ПОСТОЯННОЙ С2.
Применим теперь D.64) к плоскостям г —а и z = b. Имеем
U(a) - f/0]rei'}I/2[r/I(a)r2(a) ~ n(a)r'2(a)] =
D.74)
Из рис. 44 и 45 следует, что
r'i(b)=r'2(a)=0, r'^aj-r'iobj, r'2(&) =r'2im. D.75)
Подставляя D.72), D.73) и D.75) в D.74) и принимая во
внимание B.94), получаем очень важное соотношение между
фокусными расстояниями:
h*lf2*={[U(a) - U0]tei/[U(b) - C/0]rei}1/2 =
= ni/n2=M*G*. D.76)
(Последнее равенство будет доказано ниже.) Это равенство
идентично равенству A.48) световой геометрической оптики.
Отсюда следует, что нужно знать только одно фокусное рас-
расстояние, другое всегда может быть определено из D.76). Не-
Необходимо помнить, однако, что это простое соотношение спра-
справедливо только для асимптотических фокусных расстояний и
несправедливо для реальных, поскольку D.72) и D.73) отно-
относятся к асимптотическим величинам. Если потенциалы с обеих
сторон линзы равны, то переднее и заднее асимптотические
фокусные расстояния также равны между собой. Это имеет
место для однопотенциальной электростатической линзы (см.
разд. 4.7) и для любой магнитной линзы.
Покажем теперь справедливость формулы Ньютона A.51)
для асимптотических предмета и изображения. Даже если
предмет z0P0 и изображение г,-Р,- и, более того, асимптотичес-
асимптотический предмет zo*Po* и асимптотическое изображение Zi*Pi* рас-
расположены внутри поля (рис. 46), все еще остается справедли-
справедливым утверждение о том, что треугольники P0*Fi*z0* и
Hi*'Fi*Hi*, а также треугольники H2*'F2*H2* и P,*F2*2X* по-
попарно подобны. Следовательно, асимптотическое увеличение
определяется выражением
. fl—g*
где р* и q* — асимптотические расстояния до предмета и изо-
изображения соответственно. Отсюда следует, что
203
Глава 4
fi*lp* + f2*/q* = l, D.78)
M*=—q*f1*/p*f2*. D.79)
Соотношения D.78) и D.79) не отличаются от A.51) и A.52).
Следовательно, асимптотические предмет и изображение мож-
можно описать с помощью ньютоновской формулы толстой линзы,
так же как и в световой геометрической оптике.
Однако если мы хотим рассматривать действительные пред-
предметы и изображения, то можно использовать только уравнение
изображения D.58) и формулу Гельмгольца — Лагранжа
D.65), т. е. придется решать уравнение параксиальных лучей
D.40) отдельно для каждого положения предмета, если только
поле не принадлежит к ньютоновскому классу.
Если асимптотический предмет расположен на передней
асимптотической главной плоскости, то р* = 0 и D.77) дает
Af* = 1 и q* — Q. Другими словами, асимптотическое изображе-
изображение будет расположено на задней асимптотической главной
плоскости и его высота будет равна высоте предмета. Мы го-
говорим, что асимптотические главные плоскости отображаются
друг в друга с единичным увеличением.
Вернемся теперь к последнему равенству в D.76). Заметим,
что соотношения D.65) и D.76) похожи. Однако равенство
D.65) в том виде, в котором оно записано, не справедливо для
асимптотических величин zo* и z,-*, так как оно было выведено
с помощью двух лучей, один из которых пересекает ось в точ-
точках Zo и z,. Если просто подставить асимптотические величины,
то придем к неверному результату, поскольку асимптоты не
обязательно пересекают ось в тех же точках. Другими словами,
D.65) будет справедливым для асимптотических величин,
только если как предмет, так и изображение расположены вне
поля. Тогда между асимптотическими и реальными величинами
нет различия, U(a) =U(z0), U{b) = U(z,), и D.65) принимает
вид D.76).
Если теперь предмет, изображение или они оба находятся
в поле, необходимо соблюдать осторожность. Используем, как
и раньше, те же два луча, но применим D.64) при z—a и
г = Ь. Итак, rx{z) есть луч, пересекающий ось в точках, где
расположены предмет и изображение (рис. 43), а в качестве
Гг(г) выберем луч, входящий в линзу со стороны предмета па-
параллельно оси (рис. 44). (Имейте в виду, что Т\ (z) имеет раз-
разный смысл в D.67) — D.75).) Тогда справедливы следующие
тождества:
г'\ (а) = т\ (а) / (а — z0*),
204
Фокусировка в аксиально-симметричных полях
г/,F)=г,F)/(Ь-г,*). г'2(а)=0, г'2F)
С другой стороны, по определению асимптотическое угловое
увеличение равно G* = r/F)/г/(а), и асимптотическое увеличе-
увеличение М* определено в D.77). Используя D.71) и D.73) вместе
с рис. 43 и 44, после элементарных преобразований приходим к
fi*f2* = G*M*. Это запись формулы Гельмгольца — Лагранжа,
которую следует использовать для асимптотических величин.
Различие между D.65) и D.76) состоит в том, что для реаль-
реальных величин потенциалы следует брать в точках предмета и
изображения, тогда как в асимптотическом случае они долж-
должны вычисляться на границах поля, а не в точках, где располо-
расположены асимптотические предмет и изображение, если они нахо-
находятся внутри поля. Это очень важный момент, поскольку фор-
формула Гельмгольца — Лагранжа широко используется в обеих
формах.
Рис 47. Инвертированное расположение узловых точек.
Рассмотрим теперь узловые точки. Как мы знаем из
разд. 1.4.2, они определяются для луча с единичным угловым
увеличением (рис. 3), как пересечения продолжений асимптот
с осью. Рассмотрим сначала параллельный пучок лучей, при-
приходящий из пространства предметов под определенным углом
1 к оси (рис. 47). Можно считать, что этот пучок выходит из
внеосевой точки, бесконечно удаленной в отрицательном на-
направлении оси, поэтому он будет сфокусирован в лежащей на
задней фокальной плоскости точке Р, радиальная координата
которой определяется пересечением асимптоты, проходящей
через Fi*, с задней асимптотической главной плоскостью (см.
рис. 47). Разные лучи выйдут из линзы в пространстве изобра-
изображений под разными углами, но один луч обязательно выйдет
205
Глава 4 .
под углом ^ к оси. По определению пересечение входящей
асимптоты этого луча с осью есть передняя узловая точка N\,
а пересечение выходящей асимптоты с осью — задняя узловая
точка N2. Теперь заметим, что в силу указанного выше свойст-
свойства взаимного единичного проектирования главных плоскостей
луч, направленный в точку передней главной плоскости, про-
продолжит свой путь из точки задней главной плоскости, располо-
расположенной на том же расстоянии от оси. Следовательно, H2*N2--
= #i*JVi и расстояние между узловыми точками равно расстоя-
расстоянию между главными плоскостями:
Ha*H1* = N2Nl. D.80)
Рассмотрим теперь подобные треугольники N2F2*P и
Fi*Hi*Hi*'. Очевидно, что
Лда=/Л D.81)
Справедливо также
Fi*F2* = fl* + Hl*H2*+f2* = Fl*Nl + N1N2 + N2F2*. D.82)
Подставляя сюда D.80) и D.81), получаем
Л*#1=/а*. D-83)
Соотношения D.81) и D.83) полностью эквивалентны соот-
соотношению A.49) в световой геометрической оптике. Заметим,
что D.81) и D.83) могут также быть получены из D.76) и
D.77) при G* = l, p* = NtHi* и q*=H2*N2. '
Узловые точки можно использовать для графического по-
построения изображения. При этом один из главных лучей заме-
заменяется на луч, проходящий через точку на конце линейного
предмета, направленный в точку Л^ и выходящий из N2 под
тем же углом у. Пересечение этого луча с главным лучом оп-
определяет точку на конце линейного изображения.
Для магнитной или однопотенциальной электростатической
линзы, когда переднее и заднее фокусные расстояния одинако-
одинаковы,- D.81) и D.83) дают N2F2* = Fl*N1. Поскольку N2F2* =
=h*—H2*N2 и Fi*Ni = fi* + Hi*Nu отсюда следует, что при рав-
равных фокусных расстояниях Hi*N] = H2*N2 = 0, т. е. узловые точ-
точки совпадают с главными.
Теперь рассмотрим луч r(z), направленный в узловую точку
Ni (рис. 48). Из D.47) ясно, что асимптота кривой a(z) также
пройдет через эту точку, хотя и под другим углом к оси. По-
Поскольку T(z) (в D.51)) всегда положительно, из D.47) и D.50)
следует, что вторая производная a{z) всегда имеет знак, проти-
противоположный знаку r(z), и равна нулю, если r(z)=0. Следова-
Следовательно, кривая a(z) всегда вогнута к оси и имеет точку переги-
перегиба при r(z)=a(z)=0. Очевидно, что эта точка Q должна быть
206
Фокусировка в аксиальио-симметричиых полях
расположена слева от узловой точки Ni. Луч r(z) выйдет из
линзы, приближаясь к асимптоте, выходящей из второй узло-
узловой точки JV2. Асимптота к кривой a(z) также выходит из той
же точки под другим углом к оси. Две асимптоты к лучу r(z)
имеют одинаковый наклон, но это не обязательно для двух
асимптот o(z). Так как кривая а (г) должна быть вогнутой к
оси, точка пересечения Q должна быть расположена правее
узловой точки N2. Из двух названных условий вытекает, что N2
расположена слева от N\, т. е. узловые точки следуют в обрат-
обратном порядке. Но тогда из D.80) следует, что главные плоскос-
плоскости также следуют в обратном порядке.
о-Ы
г(г>
Рис. 48. Скрещивающиеся узловые точки.
Мы уже приняли это во внимание на рис. 46 и 47. На этих
рисунках ясно показано, как построить асимптотическое изоб-
изображение любого асимптотического предмета, если известно по-
положение асимптотических кардинальных плоскостей. Простей-
Простейший способ состоит в том, чтобы, следуя рис. 46, рассмотреть
две прямые, проходящие через конец линейного предмета: од-
одна параллельна оси, другая направлена к переднему асимпто-
асимптотическому фокусу. Пересечения этих линий с соответствующи-
соответствующими асимптотическими главными плоскостями определяют на-
начальные точки двух прямых, первая из которых проходит че-
через задний асимптотический фокус, а вторая параллельна оси.
При этом нужно быть внимательным, помня, что главные плос-
плоскости расположены в обратном порядке.
Отметим, что доказательство обратного порядка главных
плоскостей справедливо, если внутри линзы нет промежуточ-
промежуточного изображения. В случае когда луч пересекает ось более
одного раза, асимптотические главные плоскости могут следо-
следовать в любом порядке.
207
Глава 4
Осевая координата изображения может быть определена из
D.78), но ее также можно найти графически с помощью
рис. 47, даже если мы имеем дело с точечным предметом. Рас-
Рассмотрим произвольный луч, пересекающий ось в точке А, рас-
расположенной в пространстве объектов. Как найти изображение
этой точки Л'? Очевидно, что пересечение В прямолинейного
продолжения луча с передней асимптотической главной плос-
плоскостью отображается в точку В', лежащую на той же высоте
в задней асимптотической главной плоскости, откуда асимпто-
асимптотический луч проходит через точку Р на задней асимптотичес-
асимптотической фокальной плоскости до пересечения с осью в точке Л'.
Таким образом, задача сводится к определению положения
точки Р. Это точка, где пересекаются все лучи, параллельные
спереди от линзы выбранному лучу, принадлежащая задней
фокальной плоскости. Но мы знаем, что асимптотический луч,
проходящий через передний асимптотический фокус Fi* под
тем же углом к оси, что и наш луч, после пересечения с перед-
передней главной плоскостью должен быть продолжен параллельно
оси. Точка пересечения этой параллельной линии с задней
асимптотической фокальной плоскостью есть точка Р.
Есть и другое важное следствие того факта, что функция
а (г) всегда вогнута в сторону оси. Рассмотрим снова луч
г2(г), входящий в линзу спереди параллельно оси (рис. 44).
Согласно D.54), кривая a2{z) будет также линией, параллель-
параллельной оси спереди от линзы. Войдя в поле линзы, она может изо-
i нуться только к оси, следовательно, она может либо пересечь
ось где-либо внутри линзы, либо покинуть линзу в виде прямой
линии, направленной в сторону оси. То же самое имеет место
для луча ri(z), входящего в линзу сзади параллельно оси
(рис. 45). Так как луч r(z) пересекает ось в той же точке, что
и кривая o(z), мы доказали, что в отсутствие пространственно-
пространственного заряда не существуют аксиально-симметричные ограничен-
ограниченные в пространстве рассеивающие линзы, т. е. невозможно
сконструировать линзу, ограниченную спереди и сзади прост-
пространством, не содержащим поля, которая преобразовывала бы
пучок, параллельный оси, в параллельный или расходящийся
пучок без пересечения пучка с осью внутри линзы. Единствен-
Единственным «исключением» является тривиальный случай нулевого по-
поля (линза вообще отсутствует), когда параллельный пучок,
очевидно, не изменяется. Важно, что это доказательство при-
применимо только в случае аксиально-симметричных линз, и толь-
только если пучок приходит извне линзы, границы которой можно
определить. Любой электронный или ионный источник будет
создавать расходящиеся пучки, если не использовать специаль-
специальные фокусирующие поля. Очевидно также, что расходящийся
пучок может быть создан с помощью собирающей ограничен-
208
Фокусировка в аксиально-симметричных полях
ной линзы, если ее силы достаточно, чтобы лучи пересекли ось
до того, как они выйдут из линзы. В этом случае асимптотиче-
асимптотическое фокусное расстояние становится отрицательным. Очень
интересен специальный случай ограниченной телескопической
линзы — преобразователя размера пучка, — которая изменяет
диаметр пучка, не собирая и не рассеивая его. Ее асимптоти-
асимптотическое фокусное расстояние бесконечно велико. Вследствие до-
доказанной выше теоремы внутри такой линзы всегда есть крос-
кроссовер (рис. 49).
Рис. 49. Преобразование диаметра пучка телескопической лиизой.
4.7. Электронные и ионные линзы
Из содержания разд. 4.4 ясно, что любое аксиально-симмет-
аксиально-симметричное электростатическое и(или) магнитное поле является
фактически линзой. Электростатические поля создаются элек-
электродами, на которых поддерживаются необходимые потенциа-
потенциалы. Для создания магнитных полей используются катушки с
током, обычно окруженные ферромагнитными материалами,
или постоянные магниты. Способы практической реализации
электронных и ионных линз многообразны, как сама жизнь.
Единственные ограничения — аксиальная симметрия и практи-
практическая осуществимость (реализуемые интенсивности поля, ис-
исключение возможности электрического пробоя между электро-
электродами, разумные размеры катушек и т. д.).
Линзы могут быть классифицированы с самых разных то-
точек зрения. Например, можно говорить об электростатических,
магнитных или комбинированных линзах; ограниченных линзах
или линзах, погруженных в поле в зависимости от того, можно
или нет определить границы линзы; сильных или слабых лин-
линзах в соответствии с тем, расположен ли фокус внутри или вне
ее; толстых или тонких линзах (разд. 4.9); симметричных или
асимметричных линзах в зависимости от наличия перпендику-
209
Глава 4
лярной к оси плоскости симметрии геометрической конфигура-
конфигурации линзы (а иногда и распределения поля в ней).
Линзы можно также классифицировать по числу электродов
и полюсов.
Наиболее важное казалось бы свойство, а именно: исполь-
используется ли линза для электронов или для ионов, в действитель-
действительности не вызывает трудностей при рассмотрении. Действитель-
Действительно, различие между ними состоит только в различном отноше-
отношении заряда к массе. Как известно, уравнение параксиальных
лучей D.40) содержит эту величину только для магнитных
линз или быстрых частиц. В нерелятивистском случае траекто-
траектория в электростатических линзах остается одной и той же для
любых частиц. Поэтому для фокусировки ионов следует ис-
использовать электростатические линзы. Единственное в этом
случае различие между положительно заряженными и отрица-
отрицательно заряженными частицами состоит в том, что знаки всех
электродных потенциалов должны быть обращены, если требу-
требуется фокусировать частицы другого знака.
Подробная классификация магнитных линз сравнительно
проста. Они могут быть длинными или короткими, изготовлен-
изготовленными из сверхпроводящих материалов или постоянных магни-
магнитов. Если используются ферромагнитные материалы, то они
могут находиться в насыщенном или ненасыщенном состоянии.
Магнитные линзы будут подробно рассмотрены в гл. 8.
В классических текстах по электронной оптике электроста-
электростатические линзы объединяются в группы в соответствии с соот-
соотношениями потенциалов их электродов. Называется пять ос-
основных разновидностей:
1. Однопотенциальные линзы, имеющие одинаковые посто-
постоянные потенциалы в пространстве объектов и изображений.
2. Иммерсионные линзы с различными постоянными потен-
потенциалами на разных сторонах.
3. Одноапертурные линзы с однородным полем по крайней
мере с одной стороны.
4. Катодные линзы, в которых поле спереди резко пропада-
пропадает на источнике заряженных частиц.
5. Линзы из фольги, состоящие из тонкой металлической
пленки, прозрачные для частиц и обеспечивающие разрывы в
распределении поля.
Если потенциалы с двух сторон линзы не равны, линза мо-
может работать в ускоряющем или замедляющем (тормозящем)
режимах. Частным случаем замедляющей линзы является
электронное (ионное) зеркало, образованное сильной замедля-
замедляющей линзой, потенциал которой меняет знак в некоторой
точке оси, заставляя частицы двигаться в обратном направле-
направлении.
210
Фокусировка в аксиально-симметричных полях
Приведенная классификация электростатических линз без-
безусловно полезна, и мы рассмотрим подробно первые четыре
основных типа в гл. 7 {линзы из фольги будут упомянуты в
разд. 5.6.2). Однако нам кажется, что огромное многообразие
возможных распределений поля гораздо богаче такого упро-
упрощенного подхода. Как будет показано, электростатические
линзы характеризуются осевым распределением потенциала,
а не свойствами электродов.
4.8. Системы линз
Использование асимптотических кардинальных элементов
упрощает построение изображений в электронно-ионно-оптиче-
ских системах, состоящих из нескольких линз, следующих друг
за другом в осевом направлении и формирующих промежуточ-
промежуточные изображения предмета в «дрейфовых» интервалах между
ними, не содержащих поля. Тогда, как мы знаем, асимптотиче-
асимптотические изображения не отличаются от действительных. Необхо-
Необходимо помнить, однако, определение границ линзы, данное в
разд. 4.6. Если поля двух сложных линз перекрываются, при-
приходится рассматривать эти две линзы как одну.
Для того чтобы построить последнее изображение предме-
предмета, необходимо использовать процедуру, описанную в разд.
4.6.1, последовательно для всех линз системы. Промежуточное
изображение, созданное n-й линзой, является предметом для
(п+1)-й линзы, где п — порядковый номер линзы в системе.
Это число обычно невелико; в большинстве случаев (электрон-
(электронные микроскопы, микропроекционное оборудование и т. д.) ис-
используется не более трех линз. Однако в некоторых приложе-
приложениях (например, ускорителях частиц) число последовательных
фокусирующих элементов может быть очень большим. Даже
для систем, состоящих только из двух-трех линз, для учета
вклада каждой отдельной линзы системы удобно использовать
матричный формализм.
4.8.1. Матрица переноса
Рассмотрим снова луч, соответствующий общему решению
в виде D.55), где гх(г) и г2(г)—лучи, параллельные оси со-
соответственно в пространстве изображений и в пространстве
объектов (рис. 44 и 45). Отметим, что такой выбор rx(z) и
г2(г) отличается от использованного в D.55). Тогда уравнение
падающей асимптоты для произвольной осевой координаты
Z\ в пространстве изображений (рис. 50) есть •
rob] (zi) =c, (zi — /V)n (b)/h* + c2r2 (a), D.84)
211
Глава 4
а выходящая асимптота при произвольном значении осевой ко-
координаты z2 справа от линзы задана соотношением
rim(z2) =— c2 (z2 — F2*)r2 (a)/f2* + clr1 (b). D.85)
Постоянные наклоны асимптот определяются в соответствии с
D.72) и D.73) как
r'obj = С1Л0Ы = cin {b)/fi\ D.86)
Соотношения D.84) — D.87) можно записать в матричной
форме следующим образом:
J~\ -rt(a)/n
r1 (b)
0
D.88)
D.89)
Рис. 50. К определению матрицы переноса.
Обращая матрицу в D.88), получим следующее матричное вы-
выражение для коэффициентов С\ и с2 как функций rObj(zi) и г'оы'-
,сЛ Jl/гЛа) -b-FiyrMyr^MS
\cj \ 0 ПЫЬ) А г'ощ У D"90)
Подставляя это выражение в D.89) и перемножая матрицы,
получим
Пт
- т
)
. D.91)
Матрица, появляющаяся в этом выражении, есть матрица
переноса, связывающая положение и наклон асимптоты к про-
произвольному выходящему лучу при z=z2 с соответствующими
величинами для падающего луча при z=Zi [141]. Ясно, что
212
Фокусировка в аксиально-симметричных полях
матрица переноса не зависит от Г\{Ь), Гг(а), с\ и Сг, а только
от положения кардинальных элементов и значений гх и z2.
Обратите внимание на.размерности элементов матрицы перено-
переноса. Мы будем использовать эту матрицу в следующем разделе
для упрощения анализа линзовых систем.
Детерминант матрицы переноса равен /i*//2*.
В частном случае, когда Z\=zo* и z2—Zi* есть соответствен-
соответственно координаты асимптотических предмета и изображения, мы
можем использовать D.77) и получим
WU} D92)
Это уравнение формально содержит D.59) и D.76) для луча,
пересекающего ось в точках предмета и изображения. В слу-
случаях нулевого и бесконечного увеличения следует быть внима-
внимательным: в D.92) появляются неопределенности типа «нульХ
X бесконечность».
Матрица переноса в D.92) содержит нулевой элемент. Это
отражение того факта, что величина п* не зависит от /•<,*',
т. е. все лучи, выходящие из одного и того же точечного пред-
предмета, снова встретятся в одной и той же точке изображения
независимо от их начального наклона. Это наиболее важная
информация, содержащаяся в D.92).
Вообще говоря, каждый элемент матрицы переноса D.91)
может иметь нулевое значение. Присутствие нулевого элемента
означает, что некоторая характеристика выходящего луча не
зависит от какой-то характеристики входящего пучка. Пусть
матрица переноса записана в виде
fmlt m12
/71 = 1
\m21 /n22/
тогда mi2 = 0 соответствует случаю образования изображения,
как было показано выше. Условие тп = 0 означает, что rim(z2)
не зависит от rObj(zi), т. е. радиальная координата на выходе
из линзы не зависит от радиальной координаты на входе. Это
имеет место, когда Z2 = /72*, т. е. на задней фокальной плоскос-
плоскости, где сходятся в одну точку все лучи с заданным слева от
линзы одинаковым наклоном. Аналогично т22 = 0 означает, что
Г\т' не зависит от г'оь], что, естественно, имеет место при Zi =
= F\*, когда все лучи с разными наклонами, проходящие через
одну точку, лежащую в передней фокальной плоскости, выходят
из линзы параллельно друг другу и их наклоны зависят только
от радиальной координаты точки пересечения луча с этой
плоскостью (см. рис. 47 в направлении справа налево). Нако-
Наконец, если /п21=0, то r'im не зависит от rObj(Zi). Частным случа-
213
Глава 4
ем является телескопическая линза (рис. 49), которая преоб-
преобразует диаметр пучка, не изменяя его наклона, т. е. осуществ-
осуществляет конечное «увеличение» при единичном угловом увеличе-
увеличении, не образуя изображения на каком-либо конечном рассто-
расстоянии от линзы. Ясно, что асимптотическое фокусное расстояние
телескопической линзы должно быть бесконечно большим, что
следует как из выражения D.92), так и из рис. 49. Это, конеч-
конечно, не так для действительного фокусного расстояния: как бы-
было показано в разд. 4.6.1 внутри телескопической линзы всегда
есть точка кроссовера.
При Zj = tfi* и 22 = tf2* имеем из D.72), D.73) и D.91):
Ч rim / \—1//2 /1//2/Ч robj /
где, очевидно, имеются в виду продолжения асимптот до пере-
пересечения с главными плоскостями. Видим, что
rim(H2*)=robi(Hi*), D.94)
как и ожидалось, в соответствии с единичным увеличением при
взаимном отображении главных плоскостей (см. рис. 50). Вто-
Второе равенство, содержащееся в D.93), выражает простое соот-
соотношение между наклонами двух асимптот:
r'im=- Tobj (#l*)//2* + rWl*/f2*. D.95)
Это соотношение прямо вытекает также из рис. 50 при исполь-
использовании D.78).
Наконец, очевидно, что в не содержащем поля дрейфовом
интервале длиной l = z%—z\ две асимптоты неотличимы друг от
друга, и для общей асимптоты имеем
Ч V Г\о 1Д г' )■ D-96)
Здесь / может иметь любое вещественное значение. Отрица-
Отрицательное значение / соответствует движению назад: (z2<zi).
Преимущество матричного формализма состоит в том, что
матрицы содержат всю информацию о линзах и свойства сис-
систем линз легко могут быть получены простым умножением
матриц.
4.8.2. Система из двух толстых линз
Рассмотрим систему, состоящую из двух толстых электрон-
электронно-ионных линз. Поскольку мы будем использовать асимптоти-
асимптотический подход, не обязательно знать, где проходят границы
линз. Линзы полностью характеризуются их асимптотическими
214
Фокусировка в аксиально-симметричных полях
Рис 51. Системы двух толстых линз: а — Fi">F/; б—P\"<F2'.
кардинальными плоскостями. Обозначим кардинальные эле-
элементы первой линзы одним штрихом, а второй — двумя штри-
штрихами (рис. 51). Для простоты опустим звездочки, но будем
помнить, что все величины асимптотические. Например, /У оз-
означает заднее асимптотическое фокусное расстояние первой
линзы, Н\" — осевую координату передней асимптотической
главной плоскости второй линзы и т. д. Предположим, что
фокусные расстояния обеих линз положительны.
Если известны все кардинальные элементы обеих линз, ис-
используя метод, описанный в разд. 4.6.1 (см. рис. 46), нетрудно
построить промежуточное изображение zmPm, а затем резуль-
215
Глава 4
тирующее изображение z,P,- предмета zoPo, но мы не будем ис-
использовать этот метод. Вместо этого попытаемся найти карди-
кардинальные элементы всей системы, как если бы это была одна
линза, используя кардинальные элементы двух линз. Будем
использовать два асимптотических луча: входящий в систему
через точку Ро параллельно оси из пространства объектов и
выходящий через точку Р, параллельно оси в пространстве
изображений. Ясно, что если Ро и Р, — точки на концах пред-
предмета и изображения соответственно, тогда два луча пересекут-
пересекутся в этих двух точках, а также в концевой точке промежуточ-
промежуточного изображения Рт. Как будет показано ниже, эти лучи
определяют также положение кардинальных элементов систе-
системы.
Рассмотрим сначала асимптотический луч, приходящий со
стороны предмета параллельно оси. Когда он пересекает зад-
заднюю главную плоскость первой линзы (Я2'), его направление
изменяется в сторону правого фокуса первой линзы /V. Далее
он распространяется прямолинейно до пересечения с перед-
передней главной плоскостью второй линзы (Н\"), где он отобража-
отображается в точку, находящуюся на той же высоте в задней главной
плоскости второй линзы (Я2"). Направление его дальнейшего
распространения определяется с помощью описанного выше
метода, иллюстрируемого рис. 51, а и 51,6. Проведем прямую,
параллельную лучу, через передний фокус второй линзы F\".
В точке ее пересечения с передней главной плоскостью второй
линзы начинается параллельная оси линия, пересечение кото-
которой с задней фокальной плоскостью второй линзы определяет
точку, где сходятся все асимптотические лучи, входящие во
вторую линзу параллельно друг другу. Следовательно, эта
точка определяет направление асимптотического луча к (или
от) оптической оси. По определению этот луч или его продол-
продолжение в обратном направлении пересечет ось в точке правого
фокуса системы F2 и выйдет из системы через точку Pi. Пере-
Пересечение продолжений падающей и выходящей асимптот опре-
определит положение задней главной плоскости системы (Я2).
Асимптотический луч, входящий в систему из пространства
изображений параллельно оси, изменит направление в точке
пересечения с передней главной плоскостью второй линзы Я/'
и будет повернут к левому фокусу второй линзы F\". Он пере-
пересекает заднюю главную плоскость первой линзы Я2', отобража-
отображается с единичным увеличением на переднюю главную плоскость
первой линзы Н\, а затем его направление определяется с по-
помощью параллельного луча, проведенного через правый фокус
первой линзы /V. Этот луч пересекает заднюю главную плос-
плоскость первой линзы и продолжается параллельно оси до пере-
пересечения с передней фокальной плоскостью первой линзы. Точ-
216
Фокусировка в аксиально-симметричных полях
ка пересечения определяет окончательное направление исход-
исходного луча. Этот луч или его продолжение в обратном направ-
направлении пересекает ось в переднем фокусе системы F\ и встре-
встречается с первым асимптотическим лучом в точке Ро. Пересече-
Пересечение продолжений падающей и выходящей асимптот даст поло-
положение передней главной плоскости системы Н\.
Очевидно, положение всех четырех кардинальных элемен-
элементов системы F\, F2, Hi и Я2 может быть определено аналити-
аналитически, повторным использованием соотношений между различ-
различными параметрами системы. Это требует терпения и осторож-
осторожности. Однако можно определить кардинальные элементы чис-
чисто формально, используя матрицу переноса D.91).
Применим D.91) для передней асимптотической фокаль-
фокальной плоскости fi* и задней асимптотической фокальной плос-
плоскости Fz* произвольной линзы. Получим следующее соотно-
соотношение между радиальными координатами и наклонами:
D.97)
Построим теперь матрицу переноса между передней асимпто-
асимптотической фокальной плоскостью первой линзы и задней асимп-
асимптотической фокальной плоскостью второй линзы. Ясно, что
матрицу можно построить в три этапа. Сначала напишем мат-
матрицу переноса между двумя фокальными плоскостями второй
линзы, затем — матрицу переноса для дрейфового пространст-
пространства между правой фокальной плоскостью первой линзы и левой
фокальной плоскостью второй линзы и, наконец, матрицу пе-
переноса между двумя фокальными плоскостями первой линзы.
Опуская звездочки, используя D.96) и D.97) с l — F\"—F2' и
выполняя матричное умножение, получим
О /Л/1 Fl-ft\( 0 n\(robi(Fd\_
о До 1 " -- - ' - —■ '-
о \/r
robJ(F0\
Отметим, что мы предположили наличие дрейфового интерва-
интервала между /V и F\", т. е. невозмущенных асимптот между зад-
задней фокальной плоскостью первой линзы и передней фокаль-
фокальной плоскостью второй линзы. Для действительных лучей это
предположение справедливо, только если обе фокальные плос-
плоскости находятся за пределами поля линзы.
Можно получить другое матричное соотношение между эти-
этими величинами, непосредственно используя D.91) для системы
линз в целом с Zi = Fx' н Z2 = F2". Подставляя эти значения и
217
Глава 4
сравнивая компоненты матриц в D.91) и D.98), получаем
четыре соотношения:
- (F"a - F2)/f2=-f/r2, D.99)
- l/f*= (F"i - F*)/(№), D.100)
(Frx-Fi)lh=-riir*. D-101)
(F'l — F1)(F — F2)/f2 + h = 0, D.102)
где /i и /2 — переднее и заднее асимптотические фокусные
расстояния системы соответственно.
Равенство D.100) сразу дает заднее асимптотическое фо-
фокусное расстояние системы. Мы видим, что оно отрицательно,
если правый фокус первой линзы расположен слева от левого
фокуса второй линзы. Это означает, что задняя фокальная
плоскость системы находится слева от задней главной плос-
плоскости (см. рис. 51,а). Система имеет положительные фокус-
фокусные расстояния, только если Fi"</V. Этот случай проиллюст-
проиллюстрирован на рнс. 51,6. Если Fi" = F2", фокусные расстояния ста-
становятся бесконечно большими (телескопическая система).
Подставляя D.100) в D.99) и D.101), находим положения
передней и задней фокальных плоскостей системы в виде
Fi=F\ — /'if 2/ (F"i - F'i), D.103)
"l - F'2) D.104)
соответственно.
Наконец, получим переднее асимптотическое фокусное рас-
расстояние системы из D.99) — D.102):
-F'a). D.105)
Переднее фокусное расстояние имеет тот же знак, что и зад-
заднее, т. е. если /V, например, лежит слева от Fi", то передняя
главная плоскость Hi расположена слева от F\. Заметим так-
также, что переднее фокусное расстояние системы выражается че-
через передние фокусные расстояния двух линз, в то время как
заднее фокусное расстояние системы явно зависит от задних
фокусных расстояний линз. Хотя, конечно, переднее и заднее
фокусные расстояния легко могут быть выражены друг через
друга с помощью D.76).
Таким образом, зная положение фокальных плоскостей и
фокусные расстояния, мы определили все четыре кардинальных
элемента комбинированной системы, выразив их через карди-
кардинальные элементы отдельных линз. Отметим, что главные плос-
плоскости системы не перекрещиваются (передняя расположена
слева от задней), если главные лучи пересекают ось более од-
одного раза. Благодаря наличию промежуточного изображения
218
Фокусировка в аксиально-симметричных полях
результирующее изображение не перевернуто относительно
предмета (рис. 51,а). В этом случае оба фокусных расстояния
системы отрицательны и из D.78) мы видим, что при положи-
положительном расстоянии до предмета расстояние до изображения
будет отрицательным, т. е. изображение будет располагаться
слева от задней главной плоскости. Следовательно, либо глав-
главная плоскость находится за пределами поля, либо асимптоти-
асимптотическое изображение оказывается в поле, либо имеет место и
то и другое. Как указывалось выше, увеличение положитель-
положительно. Если фокусные расстояния системы положительны, проме-
промежуточное изображение не формируется, главные плоскости пе-
перекрещены, изображение перевернуто и при положительном
расстоянии до предмета расстояние до изображения также по-
положительно (рис. 51,6). В этом случае первая линза формиру-
формирует виртуальное изображение за предметом, которое в свою
очередь преобразуется в действительное изображение второй
линзой. Заметим, что на рис. 51,6 передний фокус системы
расположен справа от заднего фокуса (F2<Fi).
На рис. 51, а и 51,6 главные плоскости очень далеко отсто-
отстоят друг от друга. Это весьма часто имеет место для систем,
состоящих из двух линз. Точное положение главных плоскостей
определяется соотношениями D.72), D.73), D.100) и D.103) —
D.105).
Обозначим электронно-оптические коэффициенты преломле-
преломления слева от системы, справа от системы и между двумя лин-
линзами соответственно пь п2 и пт. Тогда D.76) дает:
M'i = n«/«i' r*/f"i = nalnm. D.106)
Отношение двух фокусных расстояний системы можно тогда
выразить с помощью D.100), D.105) и D.106) в виде
D.107)
что вытекает также непосредственно из D.76).
Вводя оптическую силу [16] системы, определенную в
D.76) как
Д=п2//2=Я1//ь D.108)
имеем
D.109)
D.110)
для оптических сил первой и второй линз соответственно.
Введем теперь расстояние d между задней главной плос-
плоскостью первой линзы и передней главной плоскостью второй
линзы. По определению
-F'2. D.111)
219
Глава 4
Подставляя D.111) в D.100) или в D.105) и принимая во
внимание D.106) и D.108) — D.110), получим формулу сложе-
сложения оптических сил
D=Dr+D" — dD'D"\n
илн
или
D.112)
Оптическая сила системы несколько меньше суммы оптиче-
оптических сил ее элементов (если они обе положительны). Насколь-
Насколько меньше? Это зависит от двух параметров: расстояния
между главными плоскостями и потенциала в свободном от
поля промежутке между двумя линзами. Таким образом, вы-
выбирая очень большим расстояние между двумя линзами и (или)
очень слабым потенциал между ними, можно получить в ре-
результате слабую линзу из двух сильных линз или даже отри-
отрицательную оптическую силу, если промежуточное изображение
формируется, как изображено на рис. 51, а. Если между зад-
задней фокальной плоскостью первой линзы и передней фокальной
плоскостью второй линзы есть дрейфовое расстояние {F\"~>
>/V), оптическая сила линзы всегда отрицательна.
Интересно рассмотреть частный случай, когда оптическая
сила одной линзы равна оптической силе второй линзы, но
имеет другой знак (D'=—D"). Тогда D.112) дает D =
=dD' /nm>0 независимо от порядка следования линз. Это —
важный результат: система двух линз равной силы, из кото-
которых одна собирающая, а другая рассеивающая, всегда облада-
обладает суммарным фокусирующим эффектом. (Отрицательная оп-
оптическая сила не противоречит теореме о невозможности соз-
создания рассеивающей линзы. Асимптотическое фокусное рас-
расстояние может быть отрицательным, если главная траектория
пересекает ось внутри линзы (см. рис. 52 и обсуждение в кон-
конце разд. 4.6.1).)
Рис. 52. Линза с отрицательным фокусным расстоянием.
220
Фокусировка в аксиально-симметричных полях
Варьируя расстояние d, можно также изменять увеличение
системы. Используя D.108), можно переписать D.77) в следу-
следующем виде:
M=l/(l—pD/n1). D.113)
Очевидно, что при фиксированном положении предмета, изме-
изменяя параметр d, можно изменять как расстояние до предмета
р, так и оптическую силу D и таким образом устанавливать
увеличение.
Если система состоит из трех или более линз, повторным
использованием D.112) всегда можем вычислить оптическую
силу, и, следовательно, фокусные расстояния системы. Мы за-
заключаем, что формирование асимптотических электронных и
ионных изображений обладает групповым свойством: последо-
последовательные операции формирования изображений всегда могут
быть заменены одной операцией формирования изображения
единой системой.
4.9. Приближение тонкой линзы
В очень слабых линзах расстояние между границами линзы
мало по сравнению с обоими фокусными расстояниями. Тогда
можно считать линзу тонкой в том смысле, что ее поле заклю-
заключено в сравнительно узкой области. В этом случае направле-
направление траектории лишь слегка изменяется внутри линзы, и ее
действие может быть аппроксимировано более или менее рез-
резким изл!енением наклона траектории в том месте, где распо-
расположена тонкая линза. Это грубое приближение позволит не-
несколько глубже рассмотреть общие свойства линз без необхо-
необходимости решать уравнение параксиальных лучей.
Очевидно, что в случае тонкой линзы все параметры дейст-
действительны; поэтому асимптотические и реальные величины не
отличаются друг от друга, и звездочки везде могут быть опу-
опущены.
Выведем сначала выражения для фокусных расстояний тон-
тонкой линзы. Удобнее исходить из уравнения D.50), которое бо-
более компактно, чем D.40). Можно также показать [9, 20], что,.
используя функцию a(z), которая всюду обращена выпук-
выпуклостью от оси, мы получим более точное выражение, чем npir
непосредственном использовании г (г). Проинтегрируем D.50)
от z=a до произвольного z внутри поля линзы. В приближении
тонкой линзы пренебрежем изменением о внутри линзы, т. е,
предположим, что эта величина имеет значение а (а) под зна-
знаком интеграла. Тогда имеем
5 D.114)
22 k
Глава 4
Если теперь рассмотреть луч г%{г), параллельный оси в
пространстве объектов, график соответствующей функции
>02BО, очевидно, также будет параллелен этой оси, поскольку
лотенциал в этой области постоянен. Принимая во внимание
этот факт и формулу D.47), получим из D.114) для w(z) =
= r(z) и 2 = Ь, что
r2(a)\[U(a) — U0]rei\l/4\T(z)dz. D.115)
Аналогично имеем
а а
D.116)
для луча r\(z), параллельного оси в пространстве изображе-
изображений.
Тогда из рис. 44 и 45, а также из D.47), D.72), D.73),
D.115) и D.116) следует, что переднее и заднее фокусные
расстояния тонкой линзы могут быть выражены в виде
D.117)
D.118)
соответственно, где T{z) определено D.51) в релятивистском и
D.52) в нерелятивистском случае. Так как оптическая сила
тонкой линзы определяется просто интегралом от функции
T(z), электростатический и магнитный члены в T(z) соответст-
соответствуют двум отдельным аддитивным величинам в выражении для
оптической силы. Это не так, однако, для толстых линз. В не-
нерелятивистском случае оптическая сила электростатических
линз не зависит от отношения заряда к массе частицы. Для
магнитных линз при равных потенциалах оптическая сила для
электронов в 1836,1 раза больше, чем для протонов.
Заметим, что оба фокусных расстояния положительны в
•соответствии с теоремой, доказанной в разд. 4.6.1 о неосущест-
неосуществимости рассеивающей линзы, и с тем фактом, что в тонкой
линзе многократные пересечения по определению невозможны.
Естественно, D.117) и D.118), как и ожидалось, удовлетворяют
равенству D.76).
222
Фокусировка в аксиально-симметричных полях
Приближение тонкой линзы справедливо только для слабых
линз, т. е. линз малой оптической силы. В соответствии с этим
D.117) и D.118) можно использовать, только если они дают
в результате маленькие значения. Эти значения несколько боль-
больше, чем реальные оптические силы слабых толстых линз.
Действительно, так как a(z) всегда обращено вогнутой сторо-
стороной к оси, всегда справедливо, что |oi(z) | < |oi(fc) | и
|огB) | <|ог(а) |. Поэтому D.115) и D.116) и, следовательно,
D.117) и D.118) дают завышенные значения.
Определим теперь положения полюсов. Проинтегрируем
D.114) еще раз и упростим двойной интеграл с помощью ин-
интегрирования по частям. Получим:
D.119)
а
Заметьте, что переменные z и % независимы.
Из этого соотношения становится ясным сам смысл приб-
приближения тонкой линзы. Мы получили выражение для пере-
переменной величины a(z), используя для той же величины посто-
постоянное значение в правой части уравнения. Это типичный при-
пример метода последовательных приближений. В ходе этой про-
процедуры, предположив сначала, что a(z) не изменяется внутри
линзы, и интегрируя D.50) дважды, получаем лучшее прибли-
приближение для функции o(z). Подставляя это приближение в пра-
правую часть D.119), можно снова провести вычисления и полу-
получить следующее приближение и т. д. Эта процедура обычно
очень быстро сходится, но она не имеет большого практичес-
практического значения, так как существуют вполне доступные и очень
точные численные методы решения уравнения параксиальных
лучей (см. гл. 6). В указанном выше смысле D.117) и D.118)
можно рассматривать как первые шаги вычислений фокусных
расстояний методом последовательных приближений [16].
Подставляя теперь D.119) для луча, параллельного оси
слева от линзы, с z=b, а также D.115) в D.71) и принимая
во внимание D.47), получаем следующий результат для поло-
положения правого фокуса в пространстве изображений:
— =—£ . D.120)
\T{z)dz $ Г (г) Л
225
Глава 4
Аналогично, рассматривая луч, параллельный оси в прост-
пространстве изображений, заменяя а на Ь в D.119), беря в качестве
верхнего предела z — а и подставляя D.47) и D.116) в D.69),
получаем положение в пространстве объектов:
ь ь
1 — J (a— z)T{z)dz <\jzT(z)dz— I
Л = а-о1(а)/о1(а) = а —ь =—ь • D.121)
\T{z)dz
Положение главных плоскостей определяется соотношения-
соотношениями D.72) и D.73). Подставляя в них D.117), D.118), D.120)
:и D.121), получим
ъ , D.122)
dz
\T{z)
ъ
\T(z)dz
• D-123)
Расстояние между главными плоскостями может быть полу-
получено вычитанием D.122) из D.123) с использованием D.76),
D.117) и D.118). Получаем
D.124)
Как видим, главные плоскости отстоят друг от друга даже у
тонких линз. Так как фокусные расстояния различаются, толь-
только если различны потенциалы с разных сторон от линзы, глав-
главные плоскости не совпадают только в этом случае. При увели-
увеличении разности потенциалов фокусное расстояние уменьшается;
следовательно, расстояние между главными плоскостями мо-
может быть сложной функцией отношения потенциалов справа и
слева от линзы. Это расстояние не может быть больше нуля,
т. е. либо главные плоскости совпадают (в случае равных по-
потенциалов с обеих сторон линзы), либо стоят в обратном по-
порядке (перекрещиваются), как показано в разд. 4.6.1.
524
Фокусировка в аксиально-симметричных полях
Вводя координату «центра тяжести» распределения поля
с помощью
zc= I zT(z)dz/ \T{z)dz, D.125)
а а
видим из D.122) и D.123), что главные плоскости сдвину-
сдвинуты относительно центра тяжести, если только не равны потен-
потенциалы с обеих сторон линзы. Так как T(z) зависит от разности
потенциалов V(b)—U(а) квадратично, то чем больше эта раз-
разность, тем меньше сдвиг. Мы знаем, что T(z)>0 и Ъ>а. Сле-
Следовательно, если U(b)>U(a), то как Нь так и Н2 меньше
zc. В случае U(b)<U(a) как Ни так и Н2 больше zc. Это оз-
означает, что главные плоскости всегда сдвинуты в сторону мень-
меньшего потенциала. Это также верно и для толстых линз.
Как упоминалось в разд. 1.4.2, в световой геометрической
оптике считается, что фокусирующее действие тонкой линзы
сосредоточено в ее центральной плоскости. Из вышесказанного
ясно, что это не так в электронной и ионной оптике: главные
плоскости тонкой линзы могут не совпадать и быть сдвинуты-
сдвинутыми в сторону меньшего потенциала.
Если потенциалы с обеих сторон линзы равны, имеем #i =
= H2 = zc, т. е. в этом случае обе главные плоскости располо-
расположены в центре тяжести распределения поля. Удобно поместить
в эту точку начало координат. Если распределение поля тоже
симметрично относительно центра тяжести, он расположен в
центре линзы (в точности посередине между плоскостями z = a
и z = b) и обе главные плоскости совпадают тогда с плоскостью
Z — 0. Действие линзы сосредоточено в этой плоскости. В этом
случае узловые точки также совпадают с главными (см. разд.
4.6.1), следовательно, луч, проходящий через центр тяжести, не
изменит своего направления. Это свойство тонкой линзы очень
удобно для графического построения изображений.
Как было сказано выше, приближение тонкой линзы спра-
справедливо только для слабых линз. В то же время большая раз-
разность потенциалов слева и справа от линзы означает, что лин-
линза— сильная (см. гл. 7). Следовательно, даже в общем слу-
случае можно считать, что главные плоскости расположены очень
близко одна к другой, и можно заменить их одной плоскостью
с осевой координатой Н. Эта плоскость проходит через центр
тяжести распределения поля линзы, если разность потенциалов
настолько мала, что сдвигом главных плоскостей по отношению
к центру тяжести можно пренебречь. (Сдвиг пропорционален
степени 1/4 отношения потенциалов.) Тогда можно полагать,
что действие линзы сконцентрировано в плоскости zc. Рис. 53
показывает основной принцип приближения тонкой линзы. Как
225
Глава 4
видим, концентрация действия линзы приводит к резкому из-
изменению направления луча при пересечении плоскости Н, от
которой измеряются фокусные расстояния, а также расстояния
до предмета и изображения.
Снова повторим, что приближение тонкой линзы имеет
значение только для очень слабых линз, когда оба фокусных
расстояния намного превосходят толщину линзы, определенную
как расстояние (Ь—а) между двумя границами поля линзы,
а разность потенциалов спереди и сзади от линзы не очень ве-
велика. Только в этом случае можно считать, что расстояние
между главными плоскостями пренебрежимо мало, и даже пре-
пренебречь сдвигом главных плоскостей относительно центра тя-
тяжести.
Здесь следует отметить, что физическая «тонкость» линзы
не обязательно означает применимость приближения тонкой
линзы. Действительно, в разд. 7.3.1.3 мы увидим, что даже
двухцилиндровая электростатическая линза с бесконечно ма-
малым зазором между электродами может быть очень сильной,
если достаточно велико напряжение между электродами.
Рис. 53. Приближение тонкой линзы.
Если мы знаем фокусные расстояния линзы, нетрудно вы-
вычислить изменение наклона любой траектории в плоскости
z = H, вызванное действием этой линзы. Действительно, D.76)
и D.78) в обозначениях рис. 53 дают
D.126)
где r{H)—радиальная координата произвольного луча, пере-
пересекающего ось в точке zo, при z = H. Очевидно, изменение на-
наклона пропорционально оптической силе линзы.
4.9.1. Системы тонких линз
Действие тонкой линзы, сосредоточенное в плоскости Н,
может быть выражено следующими двумя соотношениями:
г{Ь)=г{а)=г{Н), D.127)
226
Фокусировка в аксиально-симметричных полях
-r (a) If 2. D.128)
Равенство D.128) прямо следует из D.126), D.127) и D.76).
В матричном виде
'гF)\ / 1 0\{г{а)}
(
Формула D.129) полностью эквивалентна формуле D.93),
которая была записана для двух главных плоскостей, отобра-
отображающихся друг на друга с единичным увеличением и изменя-
изменяющих направление луча так же, как и тонкая линза.
Если с обеих сторон тонкой линзы расположены два дрей-
дрейфовых интервала: слева — длиной U и справа — длиной /2,
можно представить матрицу переноса системы в виде произве-
произведения трех матриц: mdrift2, rn.\ms и я^гть где mdrim и
mdriit2 — матрицы переноса слева и справа от линзы соответст-
соответственно, a miens — матрица переноса линзы. Из D.96) и D.129)
получаем, что
1 U\f 1 о VI /Л
—1//2 —IJh + fJh )'
Обратите внимание на порядок, в котором следуют матрицы.
Выражение несколько упрощается, если /i = 0 или /2 = 0. Если
дрейфовые интервалы отсутствуют, т — miens. Детерминант
матрицы переноса, как и ожидалось, равен /i/f2-
Для оптического изображения U =р — расстояние до предме-
предмета, I2 = q — расстояние до изображения и, используя D.77) и
D.78), сразу получаем D.92) из D.130).
Заметим также, что D.130) содержит четыре параметра:
'ь U, f\ и f2. Соответствующим выбором этих параметров мат-
матрица в D.130) может быть превращена в любую матрицу
размерами 2x2, например в матрицу переноса толстой линзы.
Это означает, что любая толстая линза может быть заменена
на совокупность тонкой линзы и двух дрейфовых интервалов.
Докажем, что эта замена эквивалентна введению главных
плоскостей.
Сравним матрицу переноса D.130) с матрицей толстой лин-
линзы D.91). Элемент т21 одинаков в обеих матрицах. Это очень
важно, поскольку доказывает, что фокусные расстояния тонкой
линзы равны соответствующим фокусным расстояниям толстой
линзы. Мы должны сравнить еще два элемента (четвертые эле-
элементы не добавят ничего нового, так как их значение опреде-
227
Глава 4
лено значением детерминанта, равным fi//2). Сравнивая ком-
компоненты тп и т22, с помощью D.72) и D.73) получим, что
/2 = 22 —F2 + f2=z2 —Я2, D.131)
Wi— z,+ F, = tf, —2,. D.132)
Следовательно, /i — расстояние произвольной точки Zi в прост-
пространстве объектов до передней главной плоскости Ни а 12 —
расстояние произвольной точки z2 в пространстве изображений
до задней главной плоскости Я2. Так как и /ь и /2 по опреде-
определению должны быть положительны, это представление кор-
корректно, только если Z\ лежит слева от Яь a z2— справа от Яг.
Таким образом, разложение матрицы переноса толстой лин-
линзы на три более простые матрицы приводит к весьма нагляд-
наглядному представлению: фокусные расстояния тонкой линзы рав-
равны фокусным расстояниям толстой линзы, а два дрейфовых
интервала определяют положение произвольных точек в прост-
пространстве объектов и изображений по отношению к соответству-
соответствующим главным плоскостям толстой линзы. Толстая линза за-
заменяется тремя простыми элементами, но при этом изменение
координаты луча r(z) внутри линзы учитывается соответствую-
соответствующим выбором дрейфовых интервалов.
Матрица переноса толстой линзы может быть разложена и
другим способом: на простые матрицы, соответствующие двум
тонким линзам и дрейфовому интервалу d между ними. Если
обозначить характеристики передней и задней тонкой линзы
соответственно одним штрихом и двумя штрихами, для матри-
матрицы переноса получим следующее выражение:
1 0\/1 d\f 1 0
1/r. f,/f;^ {
l-d/П
n(n-wuffij ■ D'133)
Используя D.107), нетрудно убедиться, что детерминант
этой простой матрицы опять равен fi/fz. Сравним теперь ком-
компоненты этой матрицы с компонентами матрицы переноса в
D.91). Так как матрица переноса связывает заданную выход-
выходную плоскость второй линзы с заданной входной плоскостью
первой линзы и по определению тонкой линзы координаты
этих плоскостей Н" и Н' соответственно, необходимо подста-
подставить Z\ = H' и z2 = H" в D.91). После ряда упрощений прихо-
приходим к D.103), D.104) и D.112), так же как и в случае толс-
толстых линз. Это означает, что между добавлением в систему тол-
толстой или тонкой линзы нет никакой разницы.
228
Фокусировка в аксиально-симметричных полях
Мы также можем прямо последовать логике вывода матри-
матрицы переноса D.98). Тогда подставим Z\ — F\ и Z2 = F2" и напи-
напишем матрицу переноса в виде произведения трех матриц. Пер-
Первая из них — матрица переноса второй тонкой линзы, окружен-
окруженной двумя дрейфовцми интервалами h = fi" и I2=f2" (так как.
мы считаем, что для тонкой линзы #i" = #/') Вторая — собст-
собственно матрица переноса дрейфового интервала с l = F\"—F2'.
Третья — матрица переноса первой тонкой линзы, окруженной
двумя дрейфовыми интервалами U = f/ и I2 = f/. Подставляя
эти величины в соответствующие формулы D.96) и D.130),
сразу получим произведение трех матриц, в точности совпада-
совпадающее по форме с D.98). Это снова доказывает, что можно не-
непосредственно использовать формулы для комбинации линз
D.99) — D.113).
Используя теперь D.103), D.104) и D.112) вместе с D.72)
и D.73), легко вычислить расстояние между двумя главными
плоскостями (#2—Hi) комбинированной линзы. Если предпо-
предположить, что две исходные линзы являются тонкими, а потен-
потенциал везде вне поля линз одинаков, то fi' = f2' = f, fi"=f2f =
= /", fi = f2 = f, Hi'=H2' = H', Hi" = H2" = H" и d = H"—Hr. Отсю-
Отсюда следует, что Fl' = H'—f/, Fx" = H"—\", F2' = H' + f', и .F2"=
— H"+f". Подставляя эти величины в соответствующие фор-
формулы, получим
Я2 - Hi = d*/[d-(/'+/")]• D.134)
Мы видим, что главные плоскости комбинированной линзы
всегда отстоят друг от друга. Это означает, что комбинация
тонких линз уже не является тонкой линзой. Действительно,
в случае постоянного потенциала вне поля линзы мы получили
бы из D.124) нулевое расстояние между главными плоскостя-
плоскостями, если бы линза была тонкой. Естественно, результат ока-
оказался иным. Если бы это было не так, то можно было бы за-
заменить длинную последовательность далеко отстоящих друг от
друга тонких линз одной тонкой линзой, но это бессмыслица.
Комбинация двух тонких линз эквивалентна одной толстой
линзе. Этот факт можно использовать для представления одной
толстой линзы двумя тонкими.
Расстояние между главными плоскостями может иметь лю-
любой знак. Они перекрещены, только если d<f' + f". В этом слу-
случае D.112) дает положительные результирующие фокусные
расстояния (см. рис. 51,6). Если расстояние между линзами
d больше суммы двух фокусных расстояний, то у результирую-
результирующей линзы — отрицательные фокусные расстояния, и передняя
главная плоскость расположена спереди от задней (см.
рис. 51, а). Если d=f' + f", то главные плоскости отстоят бес-
229
Глава 4
конечно далеко друг от друга (телескопическая линза, см.
разд. 4.10.3.1).
Интересно сравнить две модели толстой линзы друг с дру-
другом. Пусть расстояние между двумя тонкими линзами d равно
разности между выходной и входной координатами z2—Z\
(рис. 54). С другой стороны, для модели одной линзы D.131)
и D.132) дают
d=z2 — zl = ll + l2 + H2 — Я,. D.135)
Сравнение матриц переноса в D.130) и в D.133) приводит к
D.112), которое означает, что фокусные расстояния каждой
из двух тонких линз должны быть равны соответствующим
фокусным расстояниям комбинированной толстой линзы, экви-
эквивалентной системе двух тонких линз. Получим следующие два
соотношения эквивалентности:
h/f2=d/f'2, li/fa=nld/(nmra). D.136)
Равенства D.112), D.135) и D.136) дают четыре соотношения
между параметрами. Отсюда расстояние между главными пло-
плоскостями с помощью D.106) может быть выражено в виде:
d • D-137)
сводящееся к D.134), если все потенциалы вне полей линз оди-
одинаковы. Знак #2—#i полностью соответствует рис. 51, а и
рис. 51,6.
Если заданы параметры толстой линзы (/2, d и отношения
потенциала), соответствующая двухлинзовая модель может
быть рассчитана с помощью D.135) — D.137). Ее практический
смысл, однако, невелик, так как, если известны кардинальные
элементы толстой линзы, мы не нуждаемся в упрощенной мо-
модели. Наоборот, можно разделить поле линзы на отдельные уз-
узкие области и, рассматривая их как тонкие линзы, вычислить
характеристики толстой линзы, как комбинированной линзы,
построенной из этих тонких линз [36]. Однако удобнее и гораз-
гораздо точнее прямые расчеты свойств толстой линзы, основанные
на решении уравнения параксиальных лучей.
4.10. Примеры фокусирования параксиальных
лучей
В этом разделе для иллюстрации принципов, изложенных
в гл. 4, будут рассмотрены некоторые практические примеры.
Детальное обсуждение аксиально-симметричных линз содер-
содержится в гл. 7—9.
230
Фокусировка в аксиально-симметричных полях
4.10.1. Параксиальные траектории в однородных
полях
Мы уже рассматривали движение заряженных частиц в од-
однородных электростатическом (разд. 2.7.1) и магнитном
(разд. 2.7.2) полях. В данном разделе вычислим в этих полях
параксиальные траектории и сравним их с результатами, по-
полученными в более общих случаях. Поведение параксиальных
частиц в однородных полях имеет важное значение, так как
эти поля составляют основу простейших моделей линз.
4.10.1.1. Однородное электростатическое поле. Это простей-
простейшее распределение поля. При аксиальной симметрии необхо-
необходимо, чтобы поле было направлено вдоль оси z. Осевое распре-
распределение потенциала есть
U(z)=U(zo)-E(z-Zo), D.138)
следовательно, U'(z)=—Е и U"=0. Рассматривая нереляти-
нерелятивистский случай с нулевой азимутальной компонентой началь-
начальной скорости (С = 0) и подставляя В = 0 и формулу D.138) и
ее производные в уравнение параксиальных лучей D.31), по-
получим
г" — Er'l2[U (Zo) — U0 — E(z — Zo)]=0. D.139)
Решение этого дифференциального уравнения с начальными
условиями r(zo)=ro и r'[Zo)—ro' несложно. Первое интегриро-
интегрирование дает
Так как мы знаем из B.112),
что траектория частицы в одно-
однородном поле представляет собой
параболу, ось которой парал-
параллельна направлению поля, отно-
отношение r'lr0' должно быть поло-
положительным на той ветви парабо-
параболы, где расположена начальная
точка, и отрицательным для то-
точек, принадлежащих другой вет-
ветви. Мы должны также иметь в
виду, что для положительно за-
заряженных частиц потенциал
должен быть отрицательным и ,_ t _,
обратно, следовательно, траек- Рис 54. Сравнение двух моделей
тория должна поворачивать в толстой лннзы.
231
Глава 4
обратном направлении в точке, где разность потенциалов
U(z)—Uo становится равной нулю. Это имеет место в вершине
параболы, где г'-^-сю (эта точка, однако, исключается нами из
рассмотрения, поскольку бесконечный наклон траектории вы-
выходит за рамки параксиального приближения). Очевидно, для
ускорения поле должно быть положительным для положитель-
положительно заряженных частиц и отрицательным для отрицательно
заряженных частиц. Это означает, что в обоих случаях абсо-
абсолютная величина потенциала увеличивается вдоль оси z, поэто-
поэтому \т'\го'\<.\, т. е. наклон траектории в ускоряющем поле
уменьшается и на бесконечности траектория становится парал-
параллельной полю.
Второе интегрирование следует производить с большой ос-
осторожностью, помня о том, что произведение заряда на потен-
потенциал — всегда отрицательная величина. В результате имеем
r(z) — ro = Br'o/E)([U(zo) — Uo]±
±(Q/\Q\){U(zo) - U0][U(zo) - U0-E(z-Zo)]y2>.
D.141)
Опять знак плюс относится к той ветви параболы, на которой
лежит начальная точка, знак минус — к другой ветви. Следо-
Следовательно, при z=zo имеем в правой части этого соотношения
сумму двух членов, равных по абсолютной величине. Знак пер-
первого слагаемого определяется знаком потенциала в начальной
точке. Во втором слагаемом фигурирует абсолютная величина
потенциала, а знак определяется знаком заряда. Поэтому зна-
знаки слагаемых всегда противоположны, а их сумма, как мы и
ожидали, равна нулю. Следует предупредить читателя, что ма-
малейшая небрежность в знаках заряда и потенциала может при-
привести к серьезным ошибкам. Поэтому мы всегда стараемся
писать все соотношения так, чтобы не возникало никаких раз-
разночтений.
Формула D.141) следует также непосредственно из B.112)
Из сравнения этих двух соотношений видны особенности па-
параксиального приближения. Прежде всего необходимо заме-
заменить координату х на z и z на г в соответствии с аксиальной
симметрией поля. Затем мы замечаем, что tv0 /vZo = r0', и заме-
заменяем Vz0 на абсолютное значение начальной скорости vo, кото-
которое может быть выражено через потенциал в начальной точке
с помощью B.33). Эти подстановки сразу дают D.141). Как
видно, единственное различие между двумя соотношениями со-
состоит в том, что в случае параксиального приближения рас-
рассматриваются только траектории с малым наклоном, и поэто-
поэтому пренебрегается радиальной компонентой начальной скоро-
скорости по сравнению с осевой. В результате область параболиче-
232
Фокусировка в аксиально-симметричных полях
ской траектории, близкая к вершине, исключается из рассмот-
рассмотрения в параксиальном приближении. Это важное замечание.
Оно означает, что вблизи излучателя заряженных частиц, где
поле чаще всего перпендикулярно его поверхности и в беско-
бесконечно малой области, может считаться однородным, паракси-
параксиальное приближение применимо, только если начальные ско-
скорости не направлены под большими углами к оси. Поскольку
обычно это требование не выполняется, при параксиальном
анализе эмиссионных систем необходимо соблюдать осторож-
осторожность (см. разд. 7.8.3).
Удовлетворяются ли основные условия формирования изо-
изображения в аксиально-симметричных полях в однородном элек-
электрическом поле? Сравнивая D.14Ц с D.55), видим, что в дан-
данном случае r2(z) =ro/c2 = const и формула D.58) дает единич-
единичное увеличение. Поскольку ri(zD)=0, положение изображения
определяется уравнением /i(z») =0. Его решением является точ-
r(z)
r,(z)
Рис. 55. Параболические траектории в однородном электростатическом поле.
ка, в которой кривая rx(z) пересекает ось. Но ri(z)=[r(z) —
—Го\1го —парабола с осью, параллельной оси z, пересекающая
ось z в точке zo. Очевидно, что она не может пересечь ось в
какой-либо иной точке (рис. 55). Так как мы имеем только
одно пересечение и увеличение, равное единице, точка изобра-
изображения Zi совпадает с точкой предмета го. Таким образом, од-
однородное поле не способно выполнять функции электростатиче-
электростатической линзы.
Хотелось бы еще раз напомнить о том, что однородное поле
не имеет границ в смысле, упомянутом в разд. 4.6. Вся траек-
траектория находится в поле, и никакая ее часть не может считаться
линейной. Поэтому даже если бы данное поле могло создать
настоящее изображение, введение кардинальных элементов бьь
ло бы невозможно. Тем не менее оказывается возможным ис-
использовать однородное электростатическое поле как строитель-
строительный материал для моделей электростатических линз (см,
разд. 7.2.2).
Глава 4
4.10.1.2. Скошенные лучи. Если поля нет (£=0), в D.141)
появляется сингулярность; следовательно, мы должны рас-
рассмотреть этот случай отдельно. Конечно, если отсутствует
азимутальная компонента начальной скорости, то С=0, и так
как в этом случае потенциал постоянен, уравнение параксиаль-
параксиальных лучей D.31) сводится к г"=0 с элементарным решением
r(z)l=ro+r/o(z — zo). D.142)
Как мы знаем, траектория в данном случае представляет пря-
прямую линию.
Однако решение не столь тривиально при ао'Ф®. Тогда
постоянная С имеет ненулевое значение, определенное D.26),
и уравнение D.31) становится нелинейным. В таком простом
случае это вызывает недоумение. К счастью, нет необходимо-
необходимости решать это уравнение. Вместо этого используем D.40),
которое в данном случае имеет вид w" = 0 с начальными усло-
условиями D.43) и D.44). Поскольку В = 0, решением будет
w(z),=ro+ (r'o+iroa'o) (z — zo). D.143)
Отсюда с помощью D.34), D.45) и D.46) непосредственно
получаем функции r(z) и a(z) для скошенного луча в области,
не содержащей поля, в следующем виде:
r{z),= {[ro + rfo{z — zo)]2+[roao(z — zo}2}1'2, D.144)
arctg^;;?pz)). D.145)
В частном случае ао' = 0 получаем D.142) и a(z) =ao = const.
Соотношения D.144) и D.145) иллюстрируют редко заме-
замечаемое свойство уравнения параксиальных лучей. В случае
скошенных лучей (лучей с ненулевыми компонентами началь-
начальной скорости в азимутальном направлении) СфО даже в от-
отсутствие магнитного поля и, более того, даже в отсутствие ка-
какого-либо поля вообще. Вследствие этого прямолинейная тра-
траектория не может быть описана линейными членами в мериди-
меридиональной плоскости. Как мы уже знаем, величина г2а' в этом
случае постоянна (см. D.27)), но это не означает, что г либо
а — линейная функция z. (С помощью преобразования к де-
декартовым координатам через A.9) легко убедиться, что траек-
траектория прямолинейна.) Можно заключить, что использование
цилиндрической системы координат не является лучшим спосо-
способом описания скошенных лучей даже в случае аксиально-сим-
аксиально-симметричных полей.
Конечно, мы могли бы вывести D.144) и D.145), непосред-
непосредственно решая нелинейное дифференциальное уравнение D.31),
а затем интегрируя D.32). Читателю рекомендуется сделать
234
Фокусировка в аксиально-симметричных полях
это и сравнить затраченные усилия с теми, которые необходи-
необходимы при использовании комплексной функции w(z). Такое срав-
сравнение очень ясно покажет преимущества последнего метода.
Даже не нужно вычислять величину С, достаточно решить
дифференциальное уравнение D.40) с начальными условиями
D.43) и D.44). После того как решение найдено, мы должны
использовать D.34), D.35) и D.46) и получить функции r(z)
и а (г). Этот подход может использоваться для любого поля с
осевой симметрией.
В предыдущем разделе мы определили параксиальные тра-
траектории в однородном электростатическом поле только для
случая С=0, но мы должны помнить, что хотя постоянная С
и не зависит от электрического поля, но она зависит от на-
начального азимутального наклона луча. Следовательно, полное
решение должно включать эту величину через начальные усло-
условия.
4.10.1.3. Однородное магнитное поле. Следующий пример —
длинная магнитная линза, образованная магнитным полем, на-
направленным вдоль оси z. Имеем В (z) = Вй = const, и в отсутст-
отсутствие электростатического поля U(z) = U = const. В этом случае,
вообще говоря, СфО, поскольку предмет всегда расположен
внутри поля. Как и раньше, вместо того чтобы решать нели-
нелинейное дифференциальное уравнение D.31), будем использо-
использовать комплексное уравнение D.40). Обозначая
—QB02/Sm0(U- f/0)rei = V>0, D.146)
упрощаем дифференциальное уравнение
w"+k02w = 0 D.147)
с начальными условиями D.43) и D.44). Последнее в данном
случае может быть переписано в виде
, D.148)
где ko~>0 и знак в скобках совпадает со знаком заряда части-
частицы. Решением является функция
w (z) = г0 cos k0 (z — Zo) + [r'olh + ir» {a'o/k0± 1) ] X
Xsin k0{z — zo). D.149)
Отсюда и из D.45) сразу следует
r(z) = {[rocosk0(z — zo) + (гу^о) sin £0 (z — z0) ] 2 +
+ r2o{a'olkQ±IJ sin2 k0(z — zo)У'2. D.150)
Из D.34) и D.46) получаем азимутальную координату
235
Глава 4
,, + ro(a'/kt±\)sink0(z—z0)
D.151)
Это выражение также следует из D.26), D.32) и D.150), но
получить его таким способом гораздо сложнее.
Очевидно, D.150) и D.151) удовлетворяют всем начальным
условиям. В случае ао' = 0 и очень малых значений ko{z—zo)
функция D.151) может быть аппроксимирована выражением
D.152)
откуда очевидно, что положительно заряженная частица будет
отклоняться в отрицательном азимутальном направлении в со-
соответствии с направлением силы Лоренца A.14).
Из D.150) и D.151), а также непосредственно из D.26)
и D.27) следует
a' = =pk0 + rl(a'0±k0)/r\ D.153)
что соответствует D.11) вместе с B.90), B.135), D.146) и
параксиальному приближению (z-компонента скорости аппрок-
аппроксимируется полной абсолютной величиной скорости). Особый
интерес представляют следующие частные случаи:
1. Если го = 0 (в этой точке величина аог не определена),
или ао/ = +й0, то D.26) дает С = 0 и мнимая часть решения ис-
исчезает. В этом случае D.153) дает a' — 4zkQ = con5t.
2. Если ао' = 0, то а' = +/гоA — го2/г2).
3. В случае однородного поля ось симметрии может быть
выбрана, где угодно. Удобно выбрать ее так, чтобы она совпа-
совпадала с осью винтовой траектории (см. разд. 2.7.2). Тогда, оче-
очевидно, го' = 0, и в азимутальном направлении ориентирована
полностью компонента начальной скорости, перпендикулярная
оси. Очевидно также, • что начальное значение г должно быть
равно радиусу винтовой линии R. Из соотношения B.137) сле-
следует, что в параксиальном приближении это требование экви-
эквивалентно равенству а,0' = +2йо. Если подставить это значение
вместе с го' = 0 в D.150), то, как и ожидалось, получим г =
= г0. Тогда D.153) дает а'=ао', что соответствует циклотрон-
циклотронной частоте B.135). Это означает, что все результаты, полу-
полученные в разд. 2.7.2, справедливы и в параксиальном прибли-
приближении, причем единственное отличие состоит в том, что в по-
последнем случае перпендикулярная к полю компонента скорости
считается малой по сравнению с продольной компонентой. Это
условие уже использовалось в разд. 2.7.2.1, где рассматрива-
рассматривалась длинная магнитная линза. Очевидно, все, что здесь гово-
236
Фокусировка в акснально-симМетричных полях
рилось, прямо следует также из решения уравнения паракси-
параксиальных лучей.
Действительно, исследование D.150) показывает, что при
любых z, для которых kQ(z—zo) =nn(n= 1,2,...), так же как
и при z=zo, r=ro независимо от г0' и ао'- Это означает, что в
этих точках лучи с разными начальными компонентами скорос-
скоростей пересекаются, т. е. формируются изображения предмета,
расположенного при z0 (рис. 56). Расстояние h между предме-
предметом и изображением и, значит, между любыми двумя соседни-
соседними изображениями равно
h = zln — гцп-ц^гп —z0 = n/ko> D.154)
что полностью соответствует B.141) и B.142). Это означает,
что изображения не увеличены и не перевернуты. Не расходится
ли этот результат с общей теорией аксиально-симметричных
линз?
Рис. 56. Действие длинной магнитной линзы.
Прежде всего заметим, что если подставить D.154) в
D.151), получим
a(Zin) — a(z,(rt_i)) =a(z,i) — ао=пл, D.155)
что означает, что каждый раз, когда луч проходит расстояние
h между соседними изображениями, меридиональная плос-
плоскость поворачивается на угол я. Другими словами, изображе-
изображение перевернуто в меридиональной плоскости, как того требует
теория фокусирования параксиальных лучей, но это компенси-
компенсируется вращением меридиональной плоскости.
Можно получить тот же результат, используя уравнение
изображения D.58). Рассмотрим главный луч при С=0. Тог-
Тогда из D.149) исчезает мнимая часть и w(z) можно заменить
на r(z). В соответствии с обозначениями формулы D.58), обо-
обозначим часть решения, пропорциональную косинусу, как r2(z),
а часть с синусом — r\{z). Поскольку в точках, где расположе-
расположены изображения, r1(zin)=0, сразу приходим к D.154). Под-
Подставляя
■ zo = nn/ko
D.156)
237
Глава 4
в D.58), получим увеличение л-го изображения в виде
Afn=cosfwt=(— 1)" D.157)
в полном согласии с D.66). (Вспомним, что увеличение опре-
определяется во вращающейся меридиональной плоскости.)
Хотелось бы еще раз отметить, что в данном случае не
имеет смысла введение кардинальных элементов, так как не-
невозможно определить границы однородного поля.
Если поле отсутствует (Bo = ko = O), следует перейти к пре-
пределу в выражениях D.150) и D.151), что приводит для ско-
скошенных лучей в области, не занятой полем, к D.144) и D.145).
4.10.2. Одновитковая магнитная линза
Теперь рассмотрим еще один очень простой пример: круг-
круглая петля радиуса а с током /. Так как ток течет в азимуталь-
азимутальном направлении, магнитное поле аксиально-симметрично.
Следовательно, петля с током является магнитной линзой.
Рис. 57. Распределение магнитной индукции для одновитковой линзы и в пря-
прямоугольной модели.
Осевое распределение индукции дается C.255). Попробу-
Попробуем сначала рассмотреть данный случай, считая линзу тонкой.
Подставляя в D.51) В {г) и Bmax{z) из C.255) и C.256), со-
соответственно получаем
(z/aJ]\ D.158)
где
k2 = _
/ [8m0 ( U — Uo) rel] .
D.159)
Поскольку поле слабеет по мере удаления от центра петли и
теоретически равно нулю на бесконечности, удобно вычислять
интеграл вдоль всей оси в интервале —oo<z<oo, понимая,
что поле практически нулевое при |z|/a>5 (рис. 57). Кромето-
го, для магнитных линз £/=const и из D.117), D.118) и
Фокусировка в аксиально-симуетричных полях
D.158) получаем фокусное расстояние одновитковой линзы в
приближении тонкой линзы:
l//=l//, = l//2=]r(z)rfz=3nafe2/8. D.160)
-—оо
Для вращения меридиональной плоскости при прохождении
частицей тонкой линзы из D.32), D.159), C.255) и C.256) при
С = 0 следует:
Aa==FJfe1 [B(z)/BmiK)dz = ^F2ak, D.161)
—оо
где верхний знак следует использовать для положительно за-
заряженных, а нижний — для отрицательно заряженных частиц.
Подставив k из D.159) с помощью C.256) вместе со значе-
значениями констант для электронов в D.160) и D.161), получим
— U0)rJQ]'1/2 =
f/0)rei]1/2. D.163)
Отметим некоторые важные особенности этого результата.
Оптическая сила пропорциональна квадрату тока, деленному
на энергию частиц. Поворот изображения пропорционален
корню из этой величины. В гл. 8 мы увидим, что соотношения
D.162) и D.163) сохраняют свой вид даже для линз с желез-
железными сердечниками: первое — в некотором приближении, а
второе — в точности.
Рассмотрим численный пример. Если пропускать ток / =
= 100 А через круглую петлю радиусом а = 10см (это можно
сделать, например, используя вместо одной петли катушку и
умножая ток одного витка на число витков в катушке) для
электронов с энергией 1 кэВ, из D.162) и D.163), получим f =
= 98 см и Да = 34°. Действительно, фокусное расстояние боль-
больше длины области, занятой полем, интенсивность которого мо-
может быть практически измерена, следовательно, мы имеем де-
дело со слабой линзой. (Обратите внимание, что для такой сла-
слабой линзы поворот довольно велик.) Для того чтобы таким
способом создать сильную линзу, требуются весьма большие
токи: петля с током практически всегда является слабой лин-
линзой, что позволяет использовать приближение тонкой линзы.
Для увеличения оптической силы необходим больший ток,
следовательно, нужно заменить одну петлю на катушку конеч-
конечных размеров. Чем больше требуемый ток, тем длиннее лин-
линза, и рано или поздно фокус окажется внутри поля линзы.
Дальнейшим увеличением числа ампер-витков можно заставить
239
Глава 4
частицы пересечь ось более одного раза. В результате асимп-
асимптотическое фокусное расстояние может стать очень большим и
даже отрицательным. Решение проблемы заключается в кон-
концентрации поля в очень узкой области при использовании
ферромагнитных материалов (см. гл. 8).
Естественно, для сильных линз D.162) не справедливо. При
больших токах оптическая сила не может быть квадратичной
функцией тока, иначе можно было бы увеличивать 1/f, просто
повышая ток. В случае сильной линзы мы вынуждены опреде-
определять фокусное расстояние интегрированием уравнения парак-
параксиальных лучей D.31) с магнитной индукцией из C.255).
Даже для такого простого распределения поля нельзя най-
найти решение уравнения параксиальных лучей в замкнутом виде.
Здесь мы не будем решать уравнение численно, а вместо этого
используем более простой и наглядный подход. Как мы увидим
в разд. 8.3.1, простейшей моделью магнитной линзы является
прямоугольная модель, в которой действие линзы аппроксими-
аппроксимируется действием однородного поля в слое заданной конечной
толщины (эффективная длина), резко спадающего до нуля на
границах слоя. Конечно, мы знаем, что такого поля не может
быть, но для грубой оценки параметров толстой линзы такая
тривиальная модель оказывается вполне подходящей.
Понятие эффективной длины уже использовалось в этой
книге (разд. 2.7.1 и 3.1.2.2) и было определено в C.197).
В качестве функции F(z) следует использовать функцию T(z),
так как именно T(z), согласно E.40), определяет траекторию.
Подставим D.158), zm = 0 и Г@)=/г2 в C.197) и получим
]T(z)dz=j B*(z)dz/B2max = C/8)я/а.
D.164)
Сравнивая это соотношение с D.160), мы видим, что эф-
эффективная длина выбирается так, чтобы полученное распреде-
распределение поля давало ту же оптическую силу, что и у тонкой
линзы. Как мы объяснили выше, эта величина характеризует
также и реальную линзу. Для магнитных линз требуется интег-
интегрирование величины B2(z), а для нерелятивистских электроста-
электростатических линз — [U'(z)/[U(z)—Uo]]2 в интервале между гра-
границами поля. Распределение магнитной индукции реальной
линзы показано на рис. 57. Там же для сравнения показаны
его квадрат и распределение поля в рамках прямоугольной
модели эффективной длины из D.164).
Мы могли бы определить эффективную длину множеством
других способов. Например, можно потребовать, чтобы враще-
вращение изображения в прямоугольной модели было таким же, как
и в реальной линзе. Формула D.161) показывает, что в этом
240
Фокусировка в аксиально-сим'метричных полях
случае нужно интегрировать индукцию B(z), а не ее квадрат.
В нашем случае эффективная длина тогда была бы равна
2а. Преимущество этого варианта в том, что поворот изобра-
изображения в толстой и тонкой линзах одинаков. Однако более
весомы преимущества интегрирования функции T(z), и в силу
этого придется смириться с неудобствами, вызванными непра-
неправильными значениями вращения изображения (в нашем случае
прямоугольная модель дает Да, =+Зяа&/8 вместо +2а&).
Применим теперь решение уравнения параксиальных лучей
D.150), полученное для однородного магнитного поля, к пря-
прямоугольной модели. Будем рассматривать случай С = 0 (теперь
это возможно, поскольку поле ограничено в пространстве),
когда исчезает мнимая часть решения. Подставляя ko = k, ro'~
= 0 и zo = —Lettl2, получаем решение для главного луча г2(г),
входящего в линзу из пространства объектов параллельно оси,
в виде
r2 (г) = го cos [AB) + Le«/2]. D.165)
Отсюда с помощью D.73) и D.76) вычисляем оптическую
силу толстой линзы 1//:
l//=l//i = l//2= r'2(Le,f/2)/r2(-Le,f/2)=A:sin(fcLeff).
D.166)
Формулы D.71), D.73), D.165) и D.166) дают координату
задней главной плоскости:
Ha = LeII/2—[l — cos(*Leii)]/[ftsin(fcIeH)]. D.167)
При обычных значениях kLeu эта величина, как и ожидалось,
отрицательна. Так как поле симметрично относительно плоско-
плоскости z=0, то Н\ = —Н2, и расстояние между скрещенными глав-
главными плоскостями равно М—#2 =—2#2.
В приближении тонкой линзы из D.51), D.118), D.124) и
D.159) имеем
(l//)thin= $ k4z = k2LeiU (H2 — Я,)Шп=0. D.168)
-'-eff/2
Эти соотношения следуют также из D.166) и D.167) в
предельном случае kLen^l. Поскольку sinx<A;, сравнение
D.166) и D.168) показывает, что A/f) < A/f) thin- Именно это
и ожидалось: оптическая сила, вычисленная в приближении
тонкой линзы, всегда больше ее реальной величины (см. разд.
4.9). Оптическая сила реальной линзы ограничена ее макси-
максимальным значением (в прямоугольной модели A//)тах = £),
тогда как формула для тонкой линзы дает сколь угодно боль-
241
Глава 4
шую оптическую силу для больших Left (где уже само прибли-
приближение тонкой линзы неприменимо).
Если теперь подставим Len из D.164) в D.168), мы придем
к D.160). Это неудивительно, так как мы выбрали эффектив-
эффективную длину именно так, чтобы обеспечить ту же оптическую си-
силу, что и у тонкой линзы.
4.10.3. Системы линз
Уделим теперь внимание некоторым практическим приложе-
приложениям материала, изложенного в разд. 4.8.2 и 4.9.1.
4.10.3.1. Телескопическая система. В разд. 4.8.1 мы видели,
что если какой-нибудь элемент матрицы переноса равен нулю,
возникают интересные частные случаи. Там же были исследо-
исследованы все четыре возможности. Случай телескопической линзы
(тл21 = 0) упоминался даже несколько раз (см. рис. 49). Сейчас
мы построим систему, состоящую из двух тонких линз и экви-
эквивалентную одной телескопической линзе.
I
к
-•i
d
—'i
Рис. 58. Телескопическая система двух линз.
Используем матрицу переноса D.133) и приравняем
нулю. Это сразу дает
d = f'2+f"i D.169)
в качестве условия телескопичности системы. Оно означает,
что расстояние между главной плоскостью первой линзы в
пространстве изображений и главной плоскостью второй линзы
в пространстве объектов должно быть равно сумме заднего
фокусного расстояния первой линзы и переднего фокусного
расстояния второй линзы. Сравнение с D.111) показывает, что
это эквивалентно условию Fi"=F2', но тогда формулы D.100)
и D.105) дают для комбинированной системы бесконечно боль-
большое асимптотическое фокусное расстояние, что является кри-
критерием телескопической системы. Из D.137) мы видим также,
что в этом случае и расстояние между главными плоскостями
бесконечно велико. Кроме того, из D.133) ясно, что /лц =
= —fi"/f2/<0, т. е. луч, входящий в систему параллельно оси,
242
Фокусировка в аксиально-симметричных полях
должен, как и предсказывалось в разд. 4.6.1, пересечь ось меж-
между линзами (рис. 58).
4.10.3.2. Увеличение системы линз. Для практического ис-
использования систем линз наибольшее значение имеет реализа-
реализация двух следующих возможностей: 1) изменения увеличения
в широком диапазоне варьированием электрических парамет-
параметров при фиксированных положениях предмета и всех линз и
2) достижения очень больших увеличений или уменьшений.
Здесь мы вкратце рассмотрим вторую проблему, остановив-
остановившись подробнее на вопросах, связанных с уменьшением. Есте-
Естественно, выбор числа линз и их взаимного расположения зави-
зависит от назначения устройства. Однако мы должны напомнить,
I
I
I
I
I
-5 -4 -3 -2 -1
-2
-4
-6
-8
Рис. 59. Зависимость увеличения от расстояния до предмета и оптической
силы.
что чем меньше линз используется, тем короче оптическая ко-
колонна, а это значит, что гораздо проще практическая реализа-
реализация системы (больше механическая стабильность, проще юс-
юстирование, меньше число источников питания, если использу-
используются электростатические линзы и т. д.). Поэтому всегда пред-
предпочтительней применять линзы с изменяемыми рабочими па-
параметрами (и малыми аберрациями!)
Прежде чем исследовать увеличение системы, коснемся во-
вопроса об увеличении одной линзы. Формула D.77) свидетель-
свидетельствует о гиперболической зависимости асимптотического уве-
увеличения М от параметра рЦ\ (рис. 59). Для того чтобы линза
формировала действительное изображение, расстояние до пред-
предмета р должно быть больше фокусного расстояния fu и обе
эти величины должны быть положительны (сплошная кривая).
Другая ветвь гиперболы (штриховая кривая) будет использо-
использоваться только в связи с системами линз. Мы видим, что абсо-
243
Глава 4
лютное значение увеличения падает с ростом величины рЦ\.
Это означает, что при фиксированном расстоянии до предмета
абсолютное значение увеличения падает, по мере того как рас-
растет оптическая сила линзы. С другой стороны, соотношение
D.77) содержит линейную зависимость увеличения от qlfo,
поэтому если фиксировано расстояние до изображения q, то
абсолютное значение увеличения растет с увеличением оптиче-
оптической силы. (Естественно, поддержание расстояния до предме-
предмета или изображения постоянным — трудновыполнимая задача,
так как, изменяя интенсивность поля в линзе, мы изменяем не
только оптическую силу, но и положение главных плоскостей.)
Рассмотрим систему, состоящую из двух линз, расположен-
расположенных на таком большом расстоянии d друг от друга, что форми-
формируется промежуточное изображение (рис. 51,а). Тогда полное
увеличение равно произведению увеличений двух линз. Из
D.79) имеем
M—qq D по)
По определению
q'+p"=d, D.171)
а расстояние до предмета р' может быть выражено через рас-
расстояние до предмета p = H\—z0 для комбинированной системы
с помощью D.72), D.73), D.101) и D.106) — D.112) в виде
p'=H\-z0 = p + f\-n + F\-F^p-dUirrL D.172)
Расстояния до изображения q' и q" могут быть выражены че-
через расстояния до предмета р' и р" с помощью D.78). Прини-
Принимая во внимание все эти соотношения, из D.170) получаем
увеличение в виде D.113).
Формула D.113) равно справедлива для положительных и
отрицательных значений оптической силы, и теперь можно ис-
использовать обе ветви гиперболы на рис. 59. Предположим, что
/?>0. Тогда при положительной оптической силе (промежуточ-
(промежуточное изображение не формируется) мы по-прежнему должны
использовать сплошную кривую, но, если расстояние между
линзами d становится настолько большим, что оптическая сила
становится отрицательной и появляется промежуточное изо-
изображение, следует использовать штриховую кривую. Часть
этой кривой при М>\ соответствует случаю 0<р//]<1 (вирту-
(виртуальное изображение). Особенно интересен интервал 0<jW<1
(D<0). Он используется в двухлинзовых проекционных умень-
уменьшающих системах.
244
Фокусировка в аксиально-симметричных полях
В двухлинзовой системе можно зафиксировать значение
р' и оптическую силу первой линзы. Для формирования сильно
уменьшенного изображения p'lh' должно быть по возможности
больше. Добавление второй линзы эффективно усиливает
уменьшение, если d выбрано настолько большим, что и вели-
величина p"lf\" тоже велика.'Тогда произведение двух увеличений
действительно может быть очень малым положительным чис-
числом. В D.113) pD может иметь очень большую отрицательную
величину; поэтому результирующее увеличение очень мало.
Из D.112) и D.172) имеем
Plfi = {din) (I ~ P'lf'i) + A + f'*iri)pWx. D-173)
Для больших d величина p/fi действительно меньше нуля, и ее
модуль линейно растет с увеличением d.
Fi/Нг
н'г
Рис. 60. Система двух линз с коллимированным пучком.
Важный и интересный частный случай изображен на рис. 60.
Точечный предмет расположен в левом фокусе первой линзы
/Y. Тогда лучи, испускаемые предметом в разных направлени-
направлениях, выйдут из первой линзы в виде коллимированного пучка.
После прохождения второй линзы, которая по крайней мере в
принципе может быть расположена сколь угодно далеко от
первой, лучи сойдутся в правом фокусе второй линзы F2".
Рассчитаем увеличение этой системы. Поскольку в этом
случае p'=f\', q ->оо, р"-»—оо и q"=U", прямо воспользовать-
воспользоваться выражением D.170) нельзя. Однако можно использовать
D.113), которое дает с помощью D.106) —D.112) и D.173),
что увеличение не зависит от d и равно
M=—f"i/f'2=— («if)/(f i) ■ D.174)
Увеличение в этом случае всегда отрицательно, в том числе
при сколь угодно больших d.
245
Глава 4
Заключение
В данной главе были рассмотрены основные свойства акси-
аксиально-симметричных полей, формирующих изображения. Мы
начали главу теоремой Буша D.9), которая определяет ази-
азимутальную компоненту скорости заряженной частицы в акси-
аксиально-симметричном поле. Затем мы вывели основное траек-
торное уравнение D.21) и перешли к гауссовской диоптрике,
записав уравнение параксиальных лучей D.31). Это уравнение
можно упростить, написав его в комплексном виде D.40) или
D.50). Затем была доказана способность аксиально-симмет-
аксиально-симметричных полей формировать изображения. Мы ввели кардиналь-
кардинальные элементы и выяснили отличия действительных параметров
линзы от асимптотических. Наиболее важными соотношениями
являются уравнение изображения D.58), формула Гельмголь-
ца — Лагранжа D.65) и D.76), формулы увеличения D.77) и
D.79) и формула Ньютона D.78). Затем была вкратце изложе-
изложена классификация электронных и ионных линз, после чего мы
рассмотрели системы линз, введя матричный формализм.
Матрица переноса D.91) может быть использована при конст-
конструировании систем линз. Было показано, что приближение тон-
тонкой линзы представляет удобный инструмент для быстрой
оценки параметров слабых линз в первом приближении. Опти-
Оптическая сила тонкой линзы определяется выражениями D.117)
и D.118). Среди практически значимых примеров, заключаю-
заключающих эту главу, как наиболее важные следует выделить одно-
однородные электростатическое и магнитное поля, простую маг-
магнитную линзу и двухлинзовую уменьшающую проекционную
систему.
Глава 5
ТЕОРИЯ АБЕРРАЦИЙ
Действие аксиально-симметричных электронных и ионных
линз описывается параксиальной теорией (теорией первого по-
порядка). Однако на практике траектории всегда имеют конеч-
конечные смещения z и конечные наклоны т' относительно оси. Даже
если они невелики, пренебрежение в разложении в ряд члена-
членами высших порядков, необходимое для вывода уравнения па-
параксиальных лучей, приводит к ошибке. Следовательно, парак-
параксиальная теория всегда неточна. В действительности изображе-
изображением точечного объекта будет не одна определенная точка,
а размытое пятно, образованное пересечением различных лу-
лучей с разными наклонами в разных точках изображения. Эти
лучи пересекают гауссову (параксиальную) плоскость изобра-
изображения в различных точках, поэтому «изображение» — не точ-
точка, а пятно конечных размеров, которое может иметь даже не-
неправильную форму. Это явление называется геометрической
аберрацией. Пример такого эффекта был рассмотрен в разд.
2.7.2.1, когда мы исследовали действие длинной магнитной
линзы. Было установлено, что четкое изображение может быть
получено, если только траектории частиц близки к силовым
линиям поля. В противном случае различные частицы будут
сфокусированы по-разному и изображение будет размытым.
Можно было бы предположить, что можно устранить гео-
геометрические аберрации, уменьшая сечение пучка. Однако этот
подход невозможно реализовать практически, так как, заклю-
заключая пучок в очень узкую область вокруг оси, мы также огра-
ограничивали бы ток пучка. Кроме того, уменьшение апертуры
пучка вызывает увеличение ошибки, обусловленной дифракци-
дифракцией. Поскольку для большинства приложений необходим значи-
значительный ток пучка, нам придется разобраться в природе гео-
геометрических аберраций и научиться с ними бороться (причи-
(причины, по которым мы говорим об аберрациях во множественном
числе, будут объяснены ниже).
Ошибки могут также возникать из-за того, что частицы в
пучке могут иметь различные скорости. Так как частицы, по-
покидая источник, имеют разные начальные скорости (энергети-
(энергетический разброс), они характеризуются также различными зна-
значениями и0 (потенциал точки, в которой скорость равна ну-
247
Глава 5
лю). В результате различные частицы опять будут сфокусиро-
сфокусированы в разных точках, даже если предположить, что паракси-
параксиальное приближение является точным. Этот эффект называется
хроматической аберрацией, поскольку он эквивалентен явлению
световой оптики, когда коэффициенты преломления различны
для фотонов с разной частотой (цветом). Хроматическая абер-
аберрация возникает также вследствие колебаний напряжения, вы-
вызванных нестабильностью источника питания.
Другим источником искажений изображения является про-
пространственный заряд. Из-за сил электростатического отталки-
отталкивания частицы с одноименными зарядами не могут быть сфо-
сфокусированы в точку. Вследствие этого даже в параксиальном
приближении и в отсутствие разброса по энергиям идеальное
точечное изображение может быть получено, только если ток
пучка пренебрежимо мал.
Наконец, необходимо упомянуть практические проблемы,
связанные с разъюстировкой, неоднородностью материалов,
несовершенством механической обработки и т. п.
Аберрации играют в электронной и ионной оптике чрезвы-
чрезвычайно важную роль. На практике они ограничивают возможно-
возможности пучковых приборов. Поэтому данная глава посвящена вве-
введению в теорию аберраций. Влияние пространственного заряда
будет рассмотрено отдельно (гл. 12).
5.1. Метод характеристических функций
Начнем с принципа Ферма (уравнение A.45)). Вводя вари-
вариационную функцию [16, 20J
K=nds/dq3, E.1)
где п — показатель преломления, ds — элемент пути, qz—обоб-
qz—обобщенная криволинейная независимая переменная, уравнение
A.45) можно переписать в виде
\ q=b, E.2)
А
В
где SAB=lKdq3 — характеристическая функция, или точечный
А
эйконал. Подставляя B.70) и B.92) вместе с A.36), A.37) и
B.67) в уравнение E.1), получаем
E.3)
где импульс p — mv определяется из уравнений B.2) и B.90).
Ясно, что К является функцией обобщенных криволиней-
248
Теория аберраций
ных координат и их производных по дз. Так как лагранжиан
L есть функция тех же координат и их производных по време-
времени, естественно, что подынтегральное выражение в принципе
Гамильтона (уравнения A.26) и A.27)) есть Ldt, в то время
как в принципе Ферма — K.dq3. Поскольку оба принципа выра-
выражают одно и то же и их- структура идентична, к уравнению
E.2) можно применить ту же процедуру, что использовалась
при выводе уравнений Лагранжа A.35) из A.27). Заменяя
в них лагранжиан L вариационной функцией К и время — ко-
координатой <7з, получим уравнения Эйлера:
*(*К)-*К=0 A = 1,2,3). E.4)
Отсюда легко выводятся общие уравнения для траекторий
B.76) и B.77) [54]. Вычислим сначала частные производные
К. Так как импульс зависит только от координат (через по-
потенциал и, см. уравнение B.90)), сразу же видим, используя
B.70) и E.3)
dKldq'i=muv{\ — vt/c^-VWiq'i/H+QhiAt. E.5)
Частная производная К по координате qi несколько сложнее.
Из B.31), B.70), B.89), D.13) и E.3) получаем
дК _ QH ди
dq\ ~~ v dqt +
+ (tnov/H) A — v2/c2)-^ (ftl(?i2 dhjdq, + Kq'j> dhjdq{ + h3 dhjdqi) +
+ Q2?/(d/u7/)(M/)- E-6)
Теперь можно применить уравнения Эйлера E.4). Исполь-
Используя A.6), A.12), A.13) и A.17) и выражая некоторые полные
производные через частные, приходим для t = 3 к уравнению
B.74). Подставляя теперь в уравнение E.4) i=\ и i—2 и ис-
используя B.74), после ряда алгебраических преобразований по-
получим релятивистские траекторные уравнения в обобщенных
криволинейных координатах.
Вернемся теперь к вариационной функции К и напишем
выражение для нее в аксиально-симметричных полях. Из-за
сложности предстоящих вычислений будем рассматривать толь-
только нерелятивистские частицы. Теория аберраций может быть
распространена и на релятивисткий случай. Сложность состо-
состоит лишь в большом объеме вычислений. К счастью, для реля-
релятивистских частиц используются в основном магнитные поля,
на что указывалось еще в разд. 2.2.1, а при этом наибольшая
сложность сопряжена с введением постоянного релятивистско-
249
Глава 5
го потенциала. Таким образом, вполне достаточно рассмотреть
теорию аберраций в нерелятивистском приближении. Иногда
под релятивистской аберрацией понимают погрешность, обус-
обусловленную зависимостью массы частицы от ее скорости, т. е.
разность между величинами, вычисленными с учетом релятиви-
релятивистских эффектов в первом приближении и без такого учета.
Другой важный момент состоит в том, что даже в случае
аксиально-симметричных полей необходимо рассмотреть лучи,
распространяющиеся во всевозможных направлениях. Как бы-
было показано в разд. 4.10.1.2, цилиндрическая система коорди-
координат не очень удобна для вычисления асимметричных траекто-
траекторий. Поэтому мы будем использовать декартову систему коор-
координат.
Наконец, необходимо отметить, что в ходе последующих вы-
выкладок мы ограничиваемся траекториями, в разложении кото-
которых можно пренебречь степенями смещения г и наклона г',
большими четвертой. Как будет показано, это эквивалентно
теории третьего порядка, справедливой для относительно боль-
большой, но также конечной ширины пучка. В параксиальном при-
приближении рассматриваются лишь очень узкие пучки, для кото-
которых наклон любой траектории, т. е. тангенс угла между тра-
траекторией и оптической осью, может быть заменен самим углом.
Для довольно большого угла у = я/4 параксиальное приближе-
приближение дает относительную погрешность 21,46%. Приближение
третьего порядка заключается в том, что используется следую-
следующий член разложения в ряд Тейлора tg7»T + 'Y3/3 + lY6/7,5. В на-
нашем примере относительная погрешность уменьшается до
5,31%- Последующее усложнение (теория пятого порядка)
дало бы относительную погрешность всего 1,33%, но это при-
приближение слишком сложно и потому выходит за рамки книги.
Как мы знаем из разд. 3.3.3, в аксиально-симметричном по-
поле магнитный векторный потенциал имеет только азимуталь-
азимутальную компоненту, поэтому его абсолютная величина А равна
величине этой компоненты. Используя A.9) и D.6) и сохраняя
два члена в C.47), получим следующие выражения для декар-
декартовых компонент векторного потенциала аксиально-симметрич-
аксиально-симметричного поля:
(y) {{
«- (y/2)[B°(z) -В"(г) (х2 + у2)/8]. E.7)
Ау^А cosa=Ax/r* (х/2) [В(г) — В"-(г) (хя+у*I«\.
E.8)
Очевидно, Аг=0. Теперь выразим импульс через электростати-
электростатический потенциал с помощью B.33) или B.90) и рассмотрим
250
Теория аберраций
три члена в уравнении C.20) для u(r, z), принимая во внима-
внимание A.9). Получим
р = mQv= [— 2Qm0 (и — ы0) ]1/2 =
= {— 2QmQ[U(z) - г/0— U"(z) (х*+у2)/4 +
+ U™(z)(x2+y2J/Q4]}1'2. E.9)
Подставляя qx = x, q2—y, q% = z и h\=h2 = h%=\ вместе с B.78)
и E.7) — E.9) в уравнение E.3), заменяя квадратные корни на
соответствующие разложения в ряд Тейлора и сохраняя только
члены до четвертого порядка малости включительно, получаем
вариационную функцию в виде
E.10)
где верхние индексы обозначают степень малости соответству-
соответствующих членов, и
~{— 2Qmo[U(z) — t/0]>1/2. E.11)
2- (x*+y2)U"(z)/8[U{z) - Uo] +
+ QB(z)(xy'-x'y)/2, E.12)
( (*2+У2J luiV(z)- lU"(z)]2 \ -
_
16{U(z)-U0] (X +У
. E.13)
Рассмотрим теперь уравнения Эйлера в декартовых коор-
координатах. Поскольку Кт зависит явно только от координаты
г, оно не входит в уравнения Эйлера для t=l, i—2. ЕЬли те-
теперь рассматривать лишь малые х, х', у и у', то, подставляя в
уравнения E.4) /СB) вместо К и записав их для qi=x и Цч=у,
получим два связанных дифференциальных уравнения. Связь,
очевидно, возникает из-за члена ху'—х'у в E.12). Так как ко-
коэффициент при этом члене пропорционален В (г), связь всегда
есть при наличии магнитного поля. Для упрощения уравнений
будем использовать новую систему координат X, Y, z, поверну-
повернутую относительно прежней на угол •& вокруг оси z, как пока-
показано на рис. 61. Если исходная система координат связана с
цилиндрической системой координат г, а, г в соответствии с
A.9), а новая система координат соответствует цилиндричес-
цилиндрическим координатам г, (}, z, то имеем
E.14)
251
Глава 5
наряду с
X=rcos$, y=
E.15)
Дифференцируя A.9) и E.15) по z, используя E.14) и произ-
произведя ряд простых преобразований, получим следующие соотно-
соотношения между старыми и новыми координатами:
E.16)
E.17)
E.18)
ху' — x'y=XY' —
Рис. 61. Повернутая система координат X, У, z.
Подставляя эти соотношения в E.12), получаем следующее
выражение для КB) в новых координатах:
#<*>,= {К°&*/2 — /С<°>£/" (z)/8[U(z) — Uo] +
+ QWB (z)/2} (Ха + У2) + /С<0) (Х/2 + У'2)/2 +
+ [K<°W+QB(z)/2] (XY' — X'Y). E.19)
Если подставить это выражение в уравнение Эйлера E.4),
то снова получим систему связанных дифференциальных урав-
уравнений, но теперь коэффициент при члене, осуществляющем
связь уравнений, содержит производную угла ■& по z. Очевидно,
что, выбирая
<К = — QB(z)/2Ki0K E.20)
можно избавиться от этого члена. Подставляя E.11) в E.20)
и интегрируя, получаем угол поворота новой системы коорди-
252
Теория аберраций
нат относительно старой:
ft(z) — fl.(zo),= — (Q/2) l{—2Qmo[U(z) — Uo]}1/2B(z)dz.
E.21)
Если предположить, что начальное значение Ф равно начально-
начальному значению a(#(z0) =ао), т. е. частица начинает движение в
плоскости Xz, и сравнить E.21) с D.32), то увидим, что
G(z).=a(z)|c-o, E-22)
и из D.34) сразу следует E.14). Это очень важное наблюде-
наблюдение. Оно означает, что если выбрать угол поворота новой сис-
системы координат в соответствии с E.22), то азимутальная коор-
координата [} соответствующей цилиндрической системы координат
будет полностью совпадать с функцией $(z), введенной в
D.35) в качестве аргумента комплексной функции w(z). В со-
соответствии с этим координаты X и У представляют собой про-
просто вещественную и мнимую части функции ш:
X=Rew, Y = lmw. E.23)
Тогда движение в плоскости Xz соответствует, очевидно, слу-
случаю С — О. Действительно, если С=0, то а = # и [} = 0 на протя-
протяжении всего времени движения частицы.
Если магнитное поле отсутствует, то угол поворота новой
системы координат относительно старой будет постоянным, и
мы имеем |J = a—ао- (Как нам уже известно, вращение изобра-
изображения происходит только под действием магнитного поля.)
В этом случае нет необходимости во вращении системы коор-
координат при движении частицы, так как связь между двумя
дифференциальными уравнениями отсутствует. Безусловно, С
по-прежнему может иметь ненулевое значение, а значит, дви-
движение может происходить в комплексной плоскости.
Так как уравнение параксиальных лучей D.40) является
линейным дифференциальным уравнением, оно может быть
заменено двумя идентичными уравнениями: одно — для веще-
вещественной части X и другое — для мнимой части У. Докажем
теперь, что уравнения Эйлера E.4), содержащие функцию
К{2\ действительно дают эти два уравнения. Подставляя
E.20) в E.19), получаем следующее окончательное выражение
для /С<2>:
Y '2)/2- [•^Ф + ul"lu\] (*2 + П/8. E.24)
Дифференцируя это выражение по X, X', У и У и подставляя
в уравнения Эйлера E.4), получим два дифференциальных
2ЕЗ
Глава 5
уравнения: одно — для X и одно — для Y. Оба они, как и пред-
предполагалось, идентичны уравнению D.40).
Подставим теперь соотношения E.16) — E.18) и E.20) в
уравнение E.13) и получим член четвертого порядка в вариа-
вариационной функции в виде:
+d{X2+Y2) (ХГ— X'Y)+e(X'* + Yfi){XY' — X'Y) +
+ l(XY' — X'Y)\ E.25)
где
т
\2
Qm°
2[U (z)-U0][U (Z> 2m0
)/2 + Q2B(z)B"{z)}, E.26)
= [2Qm0U"(z) — Q2B2(z)]/16/C(°)> E.27)
c=— /C@>/8, E.28)
Q I QB4z) в„ У{г)В{г)\ & т
16 \2mo[U(z)-Uo] + a (Z> U(z)-Uoi' (' >
e=QB(z)/4, E.30)
l=—Q2B2(z)/8K@K E.31)
a /C@> определяется выражением E.11). Заметим, что три по-
последних члена в E.25), содержащие (XY'—X'Y), присутствуют
только тогда, когда есть магнитное поле.
Вернемся к характеристической функции. Согласно E.10),
вариационная функция К может быть аппроксимирована тремя
слагаемыми. Подставляя эти слагаемые в E.2), получаем ха-
характеристическую функцию в виде
SAb = S% + S% + S%. E.32)
Если теперь вычислить вариацию характеристической функ-
функции для интервала между точками объекта и изображения в
декартовых координатах и параксиальном приближении (толь-
(только два члена в E.32)), но не фиксируя конечных точек [20J,
повторение процедуры, использованной для получения уравне-
уравнений Эйлера, даст
254
z0 z0
Теория аберраций
z0
где принимается 6z = 0, так как положения плоскостей объекта
и изображения фиксированны. Если бы мы зафиксировали са-
сами конечные точки, было бы 65 = 0, следовательно, члены в
квадратных скобках должны исчезать в соответствии с урав-
уравнениями E.4) и получаем
65 = т (zt) ЬХ (Zi) + п (zt) б Y (z,) —m(z0) 6Х (z0) —
-n(zo)8Y(zo), E.34)
где
т=дК/дХ', п=дК/дГ. E.35)
Естественно, вариация точечного эйконала является функцией
лишь координат конечных точек.
Теперь можно приступить к расчетам аберраций. Вычисле-
Вычисления могут производиться одним из двух существенно различ-
различных методов.
Если используется метод траекторий [142], то аберрации
третьего порядка получаются при подстановке в уравнения
Эйлера E.4) трех членов разложения функции К (уравнение
E.10)). Затем параксиальное решение, полученное с использо-
использованием только двух членов в выражении для К, вычитается из
более точного решения четвертого порядка. Разность и являет-
является аберрацией. Этот подход относительно прост, но требует
большого объема вычислений для получения коэффициентов
аберрации (см. разд. 5.2) и взаимосвязь между ними не выгля-
выглядит достаточно естественно. Поэтому метод траекторий здесь
использоваться не будет.
Альтернативным подходом является метод характеристиче-
характеристических функций [16, 20J. Хотя основная идея этого метода более
трудна для понимания, он изящнее метода траекторий и абер-
аберрационные коэффициенты появляются в этом методе более ес-
естественно.
Будем считать траекторию третьего порядка возмущением
параксиальной траектории, обусловленным добавлением чле-
члена /СD> к параксиальному приближению для вариационной
функции К. (Очевидно, что этот подход может быть распрост-
распространен и на случай хроматической аберрации. Тогда изменение
вариационной функции будет пропорционально параксиальной
вариационной функции по потенциалу (см. разд. 5.3).) Таким
образом, необходимо определить возмущение характеристичес-
255
Глава 5
кой функции. Так как мы имеем дело только с малыми возму-
возмущениями (теория возмущений первого порядка), то предполо-
предположим, что воздействия разных возмущений могут линейно на-
накладываться друг на друга. Но тогда возмущение характерис-
характеристической функции 5D> может быть записано в виде суммы двух
компонент: возмущение траектории в невозмущенном поле и
возмущение поля при невозмущенной траектории. Первая ком-
компонента определяется вариацией характеристической функции
E.34), куда следует подставить 8Х=Х<-4) и 6У=УD), так как
вариацией координаты является именно разность между ее
значениями в рамках теории третьего порядка и в параксиаль-
параксиальной теории. Вторая компонента — это характеристическая
функция, т. е. интеграл от возмущения /СD) вдоль невозмущен-
невозмущенной параксиальной траектории. Следовательно, можно напи-
написать
— т (Zo) Х<4> (г») — п (Zo) У<4> (Zo) + { K^dz. E.36)
Заметим, что верхние индексы обозначают возмущенные вели-
величины, тогда как члены без верхних индексов соответствуют не-
невозмущенным значениям.
Вариация этого выражения может быть записана в виде
= т (zi) 6XW (Zl) + хD> (z,.) gm (z«) + п (zt) б У<4> (zt) +
+ У<4> {zt) 8п (zi) — т (Zo) 8Х<4> (zo) — Х<4> (z0) 6m (z0) —
E.37)
С другой стороны, если применить принцип линейной суперпо-
суперпозиции непосредственно к уравнению E.34), получим следую-
следующее выражение для той же величины:
•)+/гD>(г,-NУ<4>(г0 —
o)8X«)(z0) — /Z<4>(ZoNy<4>(Zo) =
,=mW(Zi)8X(Zi) +m(ZiNXW(Zi) + я<4> (z() 6У (z,-) +
+ n(Zi)8YW(Zi) —m^(zo)8X(zo) — m (z0) 8X^(z0) —
— nW(zo)8Y(zo) ~n(Zo)8Y^(zo). E.38)
Сравнивая E.37) и E.38) и вводя обозначение
S*= $' KS^dz, E.39)
256
Теория аберраций
получаем соотношение первого порядка для возмущения в
виде
— У<4> (Zi) Ьп (zi) — m<4>
(zo) +
zo) Ш (zo) + F<4> (z0) бл (z0). E.40)
Заметим, что в правой части этого сложного выражения при-
присутствуют вариации лишь невозмущенных величин. Четыре
возмущенные переменные, вычисленные на концах интервала,
являются коэффициентами при этих вариациях.
Теперь можно задать траекторию, фиксируя ее положение
и наклон в плоскости объекта или изображения. Можно также
использовать смешанные граничные значения, например, зада-
задавая положение в обеих плоскостях, либо положение в одной
плоскости, а наклон — в другой. Начнем с того, что будем ис-
использовать плоскость объекта как исходную, задавая на ней
смещение и наклон траектории. Это означает, что в этой плос-
плоскости параксиальная траектория совпадает с возмущенной.
Тогда можно приравнять все вариации при z = zo нулю и E.40)
сведется к
— XW(Zi)8m(Zi) — F<4>(z/Nn(zi). E.4I)
Это выражение определяет геометрические аберрации в плос-
плоскости изображения.
5.2. Геометрические аберрации
Рассмотрим два линейно-независимых решения уравнения
параксиальных лучей g(z) и h(z), удовлетворяющих следую-
следующим условиям (рис. 62):
Рис. 62. Два решения уравнения параксиальных лучей.
257
Глава 5
£(Zo),= l, A(zo)=0,
E.42)
g'(zo)=0. h'(zo) = l.
Тогда вещественная X(z) и мнимая Y(z) части комплексного
общего решения w (z) могут быть записаны в виде
X(z).=Xog(z)+X'oh(z), E.43)
Y(z)=Yog(z) + Y'oh(z) E.44)
соответственно, где все величины
Xo = X(zo), X'o = X'{zo), Y0=Y(z0), Y'o=Y'(zo) E.45)
должны быть малы, чтобы были удовлетворены допущения га-
гауссовой диоптрики, несмотря на большие начальные значения
g(z0) и h'(Zo), заданные в E.42).
Из E.41) следует, что
E.46)
), E.47)
t E.48)
М. E.49)
Из уравнений E.43) и E.44) имеем
(г,-) ЗУ (zt) , . ,с
Г"^ ff(z,), E-
о о
exto) _. ax(ZQ „ar(ZQ _
зг0 av' ах0
Вспоминая, что члены без верхних индексов соответствуют не-
невозмущенным величинам, и используя уравнения E.35), E.24),
E.43) и E.44), можно записать
258
Теория аберраций
m (zt) = m<2> (zt) =dKW (zi)ldX\=Kw (zi)Xr (zi) =
= ff<°>(z/) [Xog7(z,) + X'oh'(zt)], E.53)
n(z() =nW(z<) =dK^(zt)/dYr = Kw(Zi) Y'(zt) =
= /C@' (z,-) [Yog' (Zi) + J"oA' (z() ], E.54)
откуда
= K™(Zi)h'(Zi), E.56)
Подставляя теперь E.50) — E.52) и E.55)—^E.57) в уравнения
E.46) —E.49), получаем
(г,-) g (zt) -X" (Zi) KM (zt) g' (г(), E.58)
(z/)A'(z,.), E.59)
W; = яD> (г,-) g (zt) - Уи) (г,) /С0 (zt) g' (zt), E.60)
g! = n^ (z() h (zt) - Г<" (zt) /C'»' (z,-) h' (z{). E.61)
Решая эту систему четырех алгебраических уравнений относи-
относительно ХD) (Zi) и УD) (г») и принимая во внимание уравнения
D.58), D.64) и E.42) и тот факт, что A(z«)=0, по определению
получаем
= [h (z/) dS*/dX0-g (z^ dSVdX'oy{K'(zt) [h' (z,)g(zt)^g' (z,) A(z,)]} =
(
= [A (zt) dS*/dY0 - g (z^ dS*/dY'0]/{Ka (Zi) \h' (z^ g (zi) -
9^™- E-63)
Напомним, что эти величины представляют собой разности
между величинами третьего порядка и параксиальными значе-
значениями переменных X(z) и Y(z). Для их вычисления необходимо
знать частные производные функции S* по Х</ и У</. Функция
5* определена в E.39). Подставляя E.25) в E.39), можно
записать
259
Глава 5
5*= i[ ( ( )( )
+ d(Х2 + Y2) (XYr — X'Y) +e(X'2+ Y'2) (XV — X'Y) +
+ l(XV — X'Y)*]dz, E.64)
где все коэффициенты а, . . . , l являются функциями z и выра-
выражаются через осевые распределения потенциала и магнитной
индукции с помощью E.11) и E.26) — E.31).
Теперь необходимо подставить сюда X(z), Y(z) и их произ-
производные по z из E.43) и E.44), а затем найти частные произ-
производные от 5* и подставить их в E.62) и E.63), принимая во
внимание E.11). Необходимые для этого преобразования три-
тривиальны, но их так много, что выполнение этой задачи можно
считать серьезным достижением.
Очевидно, что результатом является функция начальных
значений Хо, Хо', Yo и Yо', Получаем, что
X0 — A8YO)(XO'2+YO'2) +
6Yo)(XoX'o + YoY'o) +
A7Y0) (Х2О+ Y*o) +
о) (XoVo — X'oYo), E.65)
Y0'i) +
+ BASY'O + 2A2YO + Л6Л'о) (Х„Х'О+ YOY'O) +
+ (AiVo + AiYo + A1Xo) (X2o+ Y2O) +
+ BA8Y'O + A6YO) (XOY'O - X'oYo), E.66)
где все коэффициенты Аи ■ ■ ■ , As представляют собой опреде-
определенные интегралы по z от объекта до изображения. Они упро-
упрощаются с помощью выражения
которое непосредственно следует из D.64). Имеем
Л, = — 4М{— 2QmQ[U(zo) — ио]У1/2
E.68)
A2 = -M{-2Qm0[U(zo) — £/<,]} ~1/2Х
х] 4(ag2h2 + bgg'hh' + cg'4'2) —
— l(U(zo) — U0)l(U(z) — U0)]dz, E.69)
230
Теория аберраций
= — 2М{— 2Qmo[U{zo) — £/0]}-'/2Х
X l'[2ag2h2 + b(g*h'2 + g'2h2) + 2cg'2h'2 +
+ l(U(zo) - U0)/(U(z) - U0)]dz, E.70)
= — 2M{— 2Qm0[U(zo) — У0]}
X J [2ag3/* — bgg'+ (gh'+g'h) + 2cg'*h']dz, E.71)
= — 2M{—2Qm0[U(zo) — Уо]}/2Х
X l[2aghs + bhh'(gh'+g'h) + 2cg'h'*]dz, E.72)
Л6 = — 2М i {—2Qmo[U(z) — U0}}-{
E.73)
A7 = -M]l{-2Qm0[U(z) — uo]}-v3(dg* + eg'3)dz, E.74)
zo
A8 = — Ml{—2Qm0[U(z) — f/0]}-1/2(d/i2 + e/i/2)rf2. E.75)
zo_
Геометрические аберрации 61 и 6У действительно являются
величинами третьего порядка по начальным значениям Хо, Хо',
Yo и Yo'. Коэффициенты Аи ..., As при разных комбинациях
этих начальных значений называются коэффициентами геомет-
геометрических аберраций. Отметим их симметрию по функциям g(z),
h(z),g'(z) и Л'(г).
Мы могли бы рассчитать геометрические аберрации множе-
множеством различных способов. Уже упоминался альтернативный ме-
метод траекторий. Кроме того, выбор решений g (z) и h (z) урав-
уравнения параксиальных лучей с начальными условиями E.42)
был произвольным. В литературе встречаются и иные пары ре-
решений, используемые при вычислениях аберраций. Вместо пары
решений, заданных их смещениями и наклонами в плоскости
объекта, можно использовать пару решений, определенных их
смещениями в двух плоскостях [16], или одно решение, опре-
определенное смещением и наклоном в плоскости предмета, и дру-
другое решение, определенное смещениями в двух плоскостях [142].
Вторая плоскость обычно определяется апертурой, используемой
для ограничения луча, как, например, в электронном микроско-
микроскопе, где изменение апертуры используется для устранения неко-
некоторых геометрических аберраций. В результате могут получать-
получаться различные наборы коэффициентов. Однако любая пара
261
Глава 5
линейно независимых частных решений уравнения параксиаль-
параксиальных лучей, очевидно, может быть представлена в виде линейной
комбинации любой другой пары таких частных решений. Таким
образом, всегда возможно выразить один набор аберрационных
коэффициентов через любой другой набор.
Возможны также другие определения коэффициентов абер-
аберрации [26, 143]. Однако подход, изложенный здесь, является
вполне достаточным для того, чтобы охватить почти все прак-
практически важные частные случаи. Вероятно, единственные ис-
исключения — это электронные и ионные источники и электронные
зеркала. В первом случае частицы вылетают со скоростями,
близкими к нулю, и поэтому коэффициенты аберрации могут
достигать очень больших значений. Во втором случае они имеют
бесконечные значения в тех точках траекторий частиц, где по-
потенциал равен Uо- Вычисление аберраций источника осложня-
осложняется еще и тем, что распределение начальных скоростей может
быть довольно сложным; тем, что нельзя пренебрегать прост-
пространственным зарядом; ток и другие параметры пучка, как це-
целого, могут быть столь же существенны, что и аберрации и т. д.
Аберрационные коэффициенты в E.68) — E.75) относительно
компактны. Однако эти выражения имеют серьезный недоста-
недостаток. Как видно из E.26), функция a(z), фигурирующая в пер-
первых пяти аберрационных коэффициентах, содержит четвертую
производную осевого распределения потенциала. Как известно,
численные расчеты производных высших порядков очень неточ-
неточны. Необходимо, следовательно, преобразовать выражения для
аберрационных коэффициентов таким образом, чтобы они не
содержали производных распределения потенциала выше пер-
первого порядка. Это можно сделать с помощью интегрирования
по частям. Здесь снова понадобится ряд элементарных преоб-
преобразований, требующих большого терпения. Фактически, интег-
интегрирование по частям может применяться произвольное число
раз и в любых комбинациях, и, следовательно, аберрационные
коэффициенты могут быть записаны в разной форме. Некоторые
из этих форм будут рассмотрены при выводе коэффициента
сферической аберрации. Однако в этом вопросе важнее понять
физическое значение аберраций, чем погружаться в хитроумный
лабиринт элементарных математических преобразований.
Прежде всего необходимо заметить, что все коэффициенты
аберрации представляют собой определенные интегралы, взятые
вдоль оптической оси от предмета до изображения. Они явля-
являются функциями распределения поля, образующего линзу, и мо-
могут быть вычислены на основе реальных или мнимых траекто-
траекторий. Очевидно, не имеет значения, расположен ли предмет или
изображение в поле линзы или вне его. (Необходимо соблюдать
осторожность при использовании модифицированных выраже-
962
Теория аберраций
ний из учебников, приведенных, как правило, без доказательст-
доказательства. Они могут быть справедливы только с некоторыми ограни-
ограничениями, связанными с тем, что некоторыми членами пренебрег-
пренебрегли во время интегрирования по частям.)
Из гл. 4 известно, что если и предмет, и изображение распо-
расположены вне поля линзы, асимптотические величины совпадают
с реальными. Очевидно, что это справедливо и для аберраций.
Аберрационные коэффициенты, приведенные выше, являются
реальными величинами. Если нас интересуют асимптотические
аберрации, то реальные коэффициенты могут быть использова-
использованы только в том случае, если и предмет, и изображение распо-
расположены вне поля линзы, иначе асимптотические коэффициенты
должны определяться независимо. Это будет сделано в разд. 5.4.
Заметим также, что все коэффициенты аберрации сильно
зависят от увеличения не потому только, что увеличение присут-
присутствует в них в явном виде, но большей частью потому, что пре-
пределы интегрирования будут изменяться, если изменится и увели-
увеличение (и, следовательно, положение предмета и (или) изобра-
изображения). Это очень важное наблюдение. В большинстве
классических работ по электронным линзам аберрации рас-
рассматривались только для очень больших увеличений. Однако,
вообще говоря, знание конкретного реального аберрационного
коэффициента при заданном увеличении слабо помогает при
оценке того же коэффициента для другого увеличения. Как
будет показано, ситуация с асимптотическими аберрациями на-
намного благоприятнее.
Очевидно также, что структура приведенных выше аберра-
аберрационных коэффициентов такова, что при рассмотрении сингу-
сингулярных случаев нулевого и бесконечного увеличений (главные
лучи) необходима особая тщательность. Эти случаи будут по-
подробно проанализированы в частном случае сферической абер-
аберрации. В связи с этой проблемой хотелось бы отметить тот
факт, что в уравнениях E.65) и E.66) аберрации записаны как
функции начальных значений Хо, Х„', У о и У</, так как X(z)
и Y(z) были выражены в E.43) и E.44) через эти величины.
Однажо как было упомянуто выше, возможны любые другие
способы выбора пары решений уравнения параксиальных лучей.
Если определять решения в плоскости изображения, то это рав-
равносильно направлению движения от изображения к предмету.
Тогда аберрации возникнут в плоскости предмета и будут функ-
функциями начальных значений в плоскости изображения. Соответ-
Соответственно будем иметь другой, хотя и аналогичный, набор абер-
аберрационных коэффициентов («обратные» коэффициенты в отли-
отличие от представленных здесь «прямых» коэффициентов).
Для того чтобы понять физический смысл аберрационных
коэффициентов, все они будут исследованы один за другим
263
Глава 5
путем приравнивания к нулю всех коэффициентов, за исключе-
исключением одного, рассматриваемого в данный момент. Так как вра-
вращающаяся система координат была «ведена таким образом, что
частица начинает свое движение в плоскости Xz (см. обсужде-
обсуждение после уравнения E.21)), мы можем поместить точечный
объект на оси абсцисс координатной системы (Уо = 0) без поте-
потери общности. В этом случае Хо есть расстояние от объекта до
оси в плоскости объекта, и выражения E.65) и E.66) станут
несколько проще, но по-прежнему будут содержать все коэф-
коэффициенты. Просто взглянув на эти соотношения, замечаем, что
их различные части описывают разные зависимости от началь-
начальных значений.
5.2.1. Сферическая аберрация
Если единственным ненулевым коэффициентом является Аи
из E.65) и E.66) получаем, что
6X(zi)=A1Xo'(Xo'2 + Yo'*), 6Y(zt)=AlYo'(Xo'a+Yo'2).
E.76)
Эти же выражения получатся, если подставить Хо = Уо = 0, т. е.
Ai — единственный аберрационный коэффициент, который от-
отвечает за возникновение аберраций в том случае, даже если
предмет расположен на оптической оси. Так как выражения в
E.76) не зависят от Хо и Уо, эта аберрация должна быть оди-
одинаковой для всех точек объекта. Для точки на оптической оси
можно формально написать,
)]2}1/2=i4, (Xo'2+ УО'2K/2. E.77)
Строго говоря, для осевой точки объекта Уо' = 0, так как для
этой точки С=0 и движение частицы происходит в меридио-
меридиональной плоскости. Тем не менее удобно рассматривать кони-
конический пучок частиц, которые покидают точку объекта под раз-
разными углами у к оптической оси, ограниченными условием
Хо'2+Уо/2 <tg2To, E.78)
где уо — максимальное значение угла f. Его принято называть
половинным углом аксептанса пучка. Таким образом, фактиче-
фактически рассматривается пакет лучей, для каждого из которых су-
существует своя меридиональная плоскость во вращающейся сис-
системе координат, в которой происходит движение. Для того что-
чтобы избежать путаницы, сохраним конечное значение для Уо в
соотношениях E.76) — E.78). Это можно обосновать, рассмот-
рассмотрев сначала только то сечение конуса, для которого У" = 0, и
264
Теория аберраций
восстановив затем конус, вращая это сечение вокруг оси. Ко-
Конечно, результат при этом не изменится. Соотношения E.77)
и E.78) дают следующее радиальное смещение для траектории
конического щучка, наиболее удаленной от центральной оси:
si=Ai tg3 чо=
tg3 4o=
где
Cso=Al/M
E.79)
E.80)
есть коэффициент сферической аберрации, связанный с объек-
объектом, а
8rso = 8rsi/M = С so tg3 fo.
E.81)
Так как параксиальный луч, выходящий из точки объекта,
пересекает ось в точке изображения, 8rst является разностью
между радиальным смещением удаленного луча и смещением
параксиального луча в гауссовой плоскости изображения. В ре-
результате изображение точечного объекта будет не точкой, а дис-
диском радиуса \8rsi\ с центром в точке гауссова изображения.
Будем называть этот диск диском сферической аберрации в
плоскости изображения (название «сферическая аберрация» взя-
взято из световой оптики). Другими словами, фигура аберрации
в этом случае представляет собой круг радиуса \8rsi\, пропор-
пропорционального кубу начального наклона наиболее удаленного лу^
ча (аберрация третьего порядка). Далее будет показано, что
Cso — неотрицательная величина. Так как увеличение является
отрицательной величиной, 8rSi всегда отрицательно при поло-
положительных Yo (рис. 63). Это означает, что непараксиальный
луч пересекает ось раньше параксиального луча (рис. 64).
Рис. 63. Сферическая аберрация.
265
Глава 5
Аналогично можно объяснить физический смысл 8rso. Это —
радиус диска сферической аберрации в плоскости объекта, оп-
определяемый в E.81), как искаженный объект конечной величи-
величины, заменяющий идеальный точечный объект и увеличенный
идеальной линзой, в результате чего возникает искаженное
изображение. Заменяя точечный объект таким диском, мы за-
заменяем аберрацию линзы аберрационным диском в плоскости
объекта. Можно доказать это несколько иначе. Поскольку
E.79) определяет аберрационное изображение точечного объ-
объекта, расположенного на оси, и сферическая аберрация не за-
зависит от положения объекта, аберрационное изображение точки
с координатой г0 в плоскости объекта, полученное с помощью
наиболее удаленного луча в пучке, можно записать в виде
Рис. 64. Непараксиальные лучи.
Mro + 8rSi. Выбирая ro = — 8rso, можно заставить наиболее уда-
удаленный луч пересечь гауссову плоскость точно на оси (рис. 65).
Сравнивая рис. 63 и рис. 65, видим, что наиболее удаленный
луч, выходящий из точки на оси, пересекает плоскость изобра-
изображения в точке 8rsi, в то время как наиболее удаленный луч,
начинающийся при —8rso, пересекает плоскость изображения
на оптической оси. Лучи, выходящие из промежуточных точек,
очевидно, пересекут где-нибудь аберрационный диск в плоско-
плоскости изображения. Это можно интерпретировать как отображе-
отображение аберрационного диска в плоскости объекта в аберрацион-
аберрационный диск в плоскости изображения.
Эти рассуждения приводят к очень важному заключению.
Бели начать с плоскости изображения и двигаться в обратном
направлении к плоскости объекта, то можно непосредственно
получить аберрационный диск в плоскости объекта. Так как
сильно увеличивающая линза в прямом направлении является
сильно уменьшающей линзой в обратном направлении и обрат-
обратно, этот подход позволяет рассмотреть предельные случаи ну-
266
Теория аберраций
левого и бесконечного увеличений. Это также означает, по край-
крайней мере в принципе, что одна и та же линза может быть ис-
использована как для получения увеличенного изображения, так
и в качестве уменьшающей в приборах высокого разрешения.
Прежде всего, воспользовавшись соотношениями D.61) и
D.65), получим
E-82)
где
= MCS0 (tg Yo/tg
E.83)
есть коэффициент сферической аберрации, связанный с изобра-
изображением. (Отметим симметрию выражений E.81) и E.82).)
Рис. 65. Аберрационный диск в плоскости объекта.
Если двигаться в обратном направлении от плоскости изоб-
изображения, E.43) и E.44) необходимо заменить на
X(z)=Xig*(z)+X'ih*(z), E.84)
Y(z)=Yig*(z) + Y'ih*(z), E.85)
где
Xi=X(zt), X'i =
с начальными условиями
E.86)
E.87)
и результат, по аналогии с уравнением E.79), есть
6reo=i4i*tg8Yi, E.88)
где «обратный» коэффициент А\* определяется аналогично
E.68) как
267
Глава 5
г0
X S (aft** + ЬА«А*'2 + ch*'*)d{-z) = (AJM*)
E.89)
так как увеличение теперь равно 1/М и
A*(z)=A*'(zo)A(z). E.90)
Используя D.65) и E.87), получаем
[ft"(zo)]«=[A"(zo)/A" (*,)]« =
,-) - Uo]2/[U(zo) - f/o]2, E.91)
откуда с помощью E.80) выражение E.89) преобразуется к
виду
Al*=M*Cso[U(zi) - U0]3'*/[U(zo) — f/o]3/2. E.92)
Сравнивая это выражение с E.83), имеем
Csi=MAl*. E.93)
Теперь, подставляя уравнение E.93) ib уравнение E.88), видим,
что наши результаты соответствуют определениям E.81) н
E.82).
Когда мы движемся в прямом направлении, начав от объек-
объекта, конечный наклон луча h(z) будет h'(zi)=hi. С другой сто-
стороны, когда мы движемся в обратном направлении, начав от
изображения, конечный наклон луча А* (г) будет h*'(z0) =h0*'.
Уравнение D.65) дает
h'lh'-h'ih"- ' Г
П{1П0 - Не /П„ - ж |
г[) _Uq
где, согласно E.42) и E.87), ho' = h'{zo) = \ и A<*' = A*'(z,-)= —1.
Подставляя это в E.83), получаем
CsiICso=M (ho'/h'K =Af (ho*'lhi*'y =
-^ | U(z:)-U0\ -{K) | t/(^) —i/0 J ' E'95)
так как
h!ho*' = —\ E.96)
Вводя обозначение
f, [A B) ] = aA4 + ft A2A/2 + ch'\ E.97)
видим из E.90) и E.96), что
268
Теория аберраций
Fs [h* (z) ] == ah*4 + bh*2h*'2 + ch*'4 = (Ao*') 4Fs[h (z) ] = Fs[h (z) ]/A,-'4.
E.98)
Тогда для вычисления коэффициентов сферической аберра-
аберрации в прямом направлении выражение E.80) с учетом E.68)
и E.97) можно записать в виде
Cso = -4{~2Qm0[U(Zo) — U0]}~V2 $Fs[h(z)]dz. E.99)
Соотношение E.95) дает
Cs^-4{-2Qm0[U(zc) — ио]}-^(^1)~4 { Fjh(z)]dz.
го
E.100)
Если нужно вычислить аберрационные коэффициенты для
движения в обратном направлении, используем E.93) вместе с
E.89) и E.98), что дает
Csi^ — 4{-2Qmo[U(Zi) - Uo]}-^Fs[h*(z)]dz. E.101)
го
Из E.95) получаем
С*о = — 4{— 2QmQ[U(z0) — Vо]}-(h0*')-4 {F'.[A*(z)]dz.
го
. E.102)
Естественно, вычисления для обоих направлений должны давать
один и тот же результат, что очевидно из равенства E.98).
5.2.1.1. Нулевое и бесконечное увеличение. Теперь мы можем
рассмотреть предельные случаи нулевого и бесконечного уве-
увеличения. В случае нулевого увеличения удобнее использовать
прямое направление. Причина в том, что обычно вычисление
коэффициентов аберрации производится одновременно с расче-
расчетом луча, так как обе численные процедуры требуют знания
одних и тех же осевых распределений поля. Таким образом,
в начале вычислений обычно не известно положение фокальной
точки до тех пор, пока для ее определения не рассчитана тра-
траектория .какого-либо отдельного луча. Однако с другой стороны,
в этом случае объект рааположен на —оо, т. е. невозможно вы-
выполнить интегрирование функции Fs[h(z)], соответствующей
движению в прямом направлении, которая имеет бесконечные
значения всюду внутри линзы. Что же можно сделать в данном
случае?
Решением этой дилеммы является использование главного
луча r2 (z) (рис. 66), введенного в гл. 4. Он идет от объекта,
269
Глава 5
расположенного на —°о, к передней границе поля линзы (г —а)
параллельно оси и пересекает ее в заднем фокусе линаы F?,
который в данном случае является изображением. Очевидно,
h*{z)lr2{z)=hi*'lr'2i = —\lr'*{F2), E.103)
таким образом «обратная» аберрационная функция может быть
переписана в виде
Fs[h* (z)]= [r'2 (F2) ] -*Fs[r2 (z) ]. E.104)
(Напомним, что F2 — аксиальная координата фокуса, в то вре-
время как Fs — аберрационная функция.) Подставляя E.104) при
zo = a и Zi=F2 в формулу E.101), получаем выражение для ко-
коэффициента сферической аберрации, связанного с изображени-
изображением при нулевом увеличении:
С3«м=0) = — 4{-2Qmo[U(F2) - U0}}-^[r'2{F2)]~4X
X?Fs[r2(z)]dz. E.105)
а
Теперь задача решена: функция Fs[r2(z)] вычислена в прямом
направлении, и интегрирование производится начиная с конеч-
конечной координаты 2 = а. Заметим, что результат не зависит от на-
начального смещения г2(а), так как и числитель (подынтеграль-
(подынтегральное выражение), и знаменатель пропорциональны четвертой
степени этой величины.
Соотношение E.83) дает бесконечно большой коэффициент
сферической аберрации, связанный с объектом, при нулевом
увеличении
CSO(m=o) —*- оо. E.106)
Согласно E.82), диск сферической аберрации имеет конеч-
конечные размеры в плоскости изображения, но, поделив его радиус
на нулевое увеличение, найдем, что, хотя уо = 0, аберрационный
диск бесконечно велик в плоскости объекта.
Умея вычислять в прямом направлении коэффициент абер-
аберрации, связанный с изображением, при нулевом увеличении,
разумно (но не обязательно) вычислить также CSi в прямом на-
направлении при малых увеличениях (см. E.100)). Естественно,
при любом конечном увеличении все четыре соотношения
E.99) — E.102) в равной степени обоснованы.
В случае бесконечного увеличения предпочтительнее обрат-
обратное направление. Мы не можем начать с бесконечности, так как
функция Fs[h*(z)] бесконечно велика всюду внутри линзы. По-
Поэтому будем использовать главный луч r\ (z) (рис. 67). Он про-
проходит от изображения, расположенного на бесконечности, до
границы линзы со стороны изображения (z = b) параллельно
270
Теория аберраций
оси и пересекает ее в переднем фокусе Fi, который теперь яв-
является объектом. Так как
h(z)/ri(z),=h/olrfio = l/r'i(Fi), E.107)
можем записать
Fs[h{z)] = [rr1{Fi)]-4Fs[r1(z)]. E.108)
Подставляя это выражение при zo = Fi и 2, = Ь в формулу E.99),
получаем коэффициент сферической аберрации, связанный с
объектом, при бесконечном увеличении в виде
Cso«>=— 4{— 2Qm0[U(F{) — £/o]}-1/2[r', (F,)]-4X
x\Fs[ri{z)]dz. E.109)
Функция Fs[ri(z)] вычислена в обратном направлении, и интег-
интегрирование производится до конечной координаты z = b. Началь-
Начальное смещение Г\(Ь) не влияет на результат.
а г2
Рис. 66. Нулевое увеличение.
Рис. 67. Бесконечное увеличение.
Из E.83) получается бесконечно большой коэффициент сфе-
сферической аберрации, связанный с изображением при бесконеч-
бесконечном увеличении
Csloo —► оо. E.110)
В силу E.81) диск сферической аберрации конечен в плос-
плоскости объекта, но, умножая его радиус на бесконечное увеличе-
увеличение, находим, что, хотя fi=0, аберрационный диск бесконечно
велик в плоскости изображения.
Для конечного увеличения все четыре соотношения E.99) —
E.102) одинаково справедливы, но при больших увеличениях
для вычисления CSo обычно используют метод движения в об-
обратном направлении (см. 5.102)).
Из E.106) и E.110) следует, очевидно, что при малых уве-
увеличениях Cso убывает с ростом абсолютного значения
увеличения, в то время как при больших \М\ величина С si воз-
возрастает вместе с абсолютным значением увеличения. Обычно
271
Глава 5
(но не всегда), эта тенденция сохраняется для всего диапазона
значений М, и тогда Cso>CSOoo и Csj>Cs,(m=o)-
5.2.1.2. Другие способы записи коэффициента сферической
аберрации. Подставляя выражения E.11), E.26) — E.28) и
E.68) в E.80), можно записать коэффициент сферической абер-
аберрации, связанный с объектом, в виде
Cso= A/32) \'{[U(z) - U0]/[U(zo) - f/0]}1/2X
X({[U"(z)-QB*(z)/2mo]4[U(z)-U0]-U™(z) +
+ 2QB{z)B"(z)/mo}h4(z) +
+ [8U" (z) — 4QB2 (z)/m0] h2 (z) h'2 (z) +
(z) - U0]h'<(z))dz/[U(z) — Uo]. E.11)
Сейчас мы покажем, как это выражение может быть преоб-
преобразовано с помощью интегрирования по частям. Используя тож-
тождество U"dz = d(U') и тот факт, что h(zo) =h(Zi) = 0, легко по-
получаем, что
\\[U{z) - U0]/[U(zo) - f/o]}1/2X
XB2(z)U"(z)h*(z)dz/[U(z) —U0]2 =
= - l{[U(z) - U0]/[U(zo) - U0]}^U'(z) [U(z) - £70]-2X
XDB2(z)h3h'+{2B(z)B'(z) —
— 3B2(z)U'{z)/2[U(z) — U0]}h4)dz. E.112)
При следующем интегрировании используем вначале Ulvdz =
= d{U'"), затем вновь проинтегрируем по частям, используя
U'"dz = d(U") и тот факт, что h(z) является решением уравне-
уравнения параксиальных лучей D.40) и, следовательно,
h"={[QB*(z)l4mo-U"(z)/2]h —
-U'(z)h'}/{2[U(z)-U0]}. E.113)
Тогда имеем
Z{{[U(z)-UQ]/[U(zo)-U0]}^X
— Uo] =
U0]/[U(zo) - U0]}^U"(z)[U(z) - f/0]-2X
272
Теория аберраций
+ l2[U(z) —U0
В следующем интеграле начнем с B"dz=d(B'). Получим
*i{[U(z)-U0]/[U{zo)-U0]y/>X
X В (г) В" (г) Л4 (г) dz[U (г) — Uo] =
= - U[U(z) - U0]/[U(zo) -
о
X({B'*(z)-B(z)B'(z)U'(z)/2[U(z)-U0]}h* +
+ AB(z)B' (г) h*h'}dz/[U (z) — Uo]. E.115)
Используя h'dz — dh и уравнение E.113), получим
[(U (z) - UQ)/(U (z0) - Uo)] ^ h" (z) dz =
X {[3QB2 (г)/8т0 - 3U" (z)/4] A2A'2-U' (z) hh'3} dz. E.116)
В процессе интегрирования по частям появились неудобные
новые члены. От них можно избавиться повторным интегриро-
интегрированием по частям. Например, мы можем использовать U"dz =
= d(U') и получить
' {[U (z) - U0]/[U (z0)- и0]}^ V- (z) U" (z)h* (z)dz/[U (z)-Uof =
[ ЪЦ'Нг) .4 41/'» (г) ,,
X\6[U(z)-U0Vn ~3[t/(Z)-t/opft
Аналогично, начиная с того же соотношения и используя
E.113) и E.117), можно доказать, что
J {[[/ (г)- U0]/[U (z0) -Uo]}4* U' (г) U" (z) A3 (z)h'(z)dz/[U (z)-Uof=
= - A/2) f {[t/(z) - U0]/[U (ze) - £/„]} i/* X
273
zo
Глава 5
*(z)U'*(z) 5t/'«(z)
A
8m0[t/(z)-t/0p
+
3[t/B)-t/0]3 +[U(z)-UB]*nf
При следующем интегрировании начнем с B'dz=dB, исполь-
используем E.112) и E.113) и придем к
{[С/ (г) - U0]/[U (г0) - £/„]} ^ В (г) В' (г) h3 (г) ft' (г) dz/[U (г) - £/.] =
го
;;2(г) В(г)В(гI/(г)> л4
8[t/B)-t/0]2 "•" 2[1/(г)—l/ol f
+ 352 (z) h2h'2)dz/[U (г) - f/0]. E.119)
Окончательно, используя h'dz = dh и E.113), получаем
5 {[U (z) - U0]/[U (z0) -17.]}v. I/' (z) h (z) А'» (г) <fc/[l/ (z) -t/J =
= - A/2) J {[[/ (z) - £/0]/[£/ (z0) - t/0]}i/« x
fj QB*(z)U'(z) U'(z)U»(z) \ ,
X\\im(>[U(z)-UB) 2\U(z)-U0) (ПП +
-U0\. E.120)
Подставляя E.112) и E.114) —E.120) в формулу E.111) и
затем используя снова E.112), получим выражение для коэф-
коэффициента сферической аберрации, впервые выведенное О. Шер-
цером [142]:
и &~ и° 11/2 hidz ! ЧТ"* <?\/л I 5{;'4 (г)
11/2 hidz ! ЧТ."*
* (z)/(8m8) + Q[t/B)~0(/°'g2(Z)^+ 3Q5(zM'(z)t/'(z)/m0-
35QB2 (z) t/'2 (z) 2Q5^ (г)
16mo[L'B)-t/o]i" m0
35QB2 (z) t/'2 (z) 2Q5^ (г) У (г) /t' )
i" m0 /if'
В этом выражении первые четыре члена используются в
электростатическом случае, следующие три — в случае магнит-
274
Теория аберраций
ных линз и последние три, если присутствуют и электростати-
электростатическое, и магнитное поля. Заметим, что для чисто магнитного-
поля коэффициент аберрации для релятивистских скоростей
имеет ту же форму, что и при замене электростатического по-
потенциала релятивистским потенциалом (см. B.89)).
Выражение E.121) не содержит неудобных производных
высших порядков от осевых распределений потенциала и маг-
магнитной индукции; поэтому оно наиболее часто используется .на
практике для вычисления коэффициента сферической аберра-
аберрации. Формулы E.99)—E.102) позволяют достаточно просто вы-
вычислять коэффициенты, связанные с объектом или изображени-
изображением, как в прямом, так и в обратном направлении.
В особых обстоятельствах может оказаться необходимым
преобразование этого выражения к другому виду, например к
выражению, не содержащему Ы', и т. п. Как было показано,
это можно всегда сделать, если терпеливо применять сложное
интегрирование по частям до тех пор, пока мы не придем к же-
желаемому виду. Однако подчас эта задача просто внушает страх
своей сложностью. Поэтому полезно знать о существовании
другого, более общего и простого подхода, требующего, одна.ко,
некоторой математической интуиции [144]. Метод основан на
внимательном исследовании аберрационного интеграла, в ре-
результате которого формируются производные различных комби-
комбинаций переменных. Эти производные умножаются на произволь-
произвольные постоянные и прибавляются к подынтегральному выраже-
выражению. Подбирая определенные значения постоянных, можно
преобразовать аберрационный интеграл в различные формы без
каких-либо трудоемких вычислений. Мы продемонстрируем этот
метод, начав с выражения E.111).
Нам будут нужны следующие десять производных (в первых
пяти из них используется уравнение E.113)):
X [QB* (z)/Bm0) - U" (г)] - jj^]} , E.122)
±<{[U (г) - UB]/[U (z0) - £/„]}»/■ U' (z) h*h'*/[U (г) -£/„]> =
= {\U (г) - U0]/[U (z0) - Uo]} V« B[^'ff^o]2 [QB*(z)/Bmo)-U" (z)]+
, E.123)
275
^ <{[U (г) - (/„]/[£/ (z0)- £/„]}i/« U" (z) h°h'/[U (г) - £/„]> -
Глава 5
= {[U (г) -U0]/[U (z0)- £/„]}»/* (Цу1\г1ио? [QB2(z)/Bm0)- £/"(z)]+
E.124)
<{[£/ (г) - U0]/[U (z0) - Uo]} 4*[U (z) - Uo] U'* (z) h3h'> =
B) - t/0]/[f7 B0) - UB]yi> (Чу'A}{г_1ув]3 [QB*(z)/Bmo)-U" (z)} +
y (г) fy]3/ +[f;
U'(z)U"(z)
z)-UQ]/[U (z0) - U0]}V* S2 (z) A»A'/[[/ (z)-f70]> =
)-^о]}1/2Dw
2Д(г)В'(г)
z) - f/0]/[t/ (z0) - £/„]}*/« f/'" (z) AV[£/ (*)-*/.]> =
,4({[I/ (z) -U0]/[U (O"«/.]}^
'"(z)\
1/]3 (
1/0]3
2[(У(г)— t/0]4l
^•({[t/ (Z) -
276
Теория аберраций
В(г)В'(г)Ц'(г)\., 45 (г) В' (г) ,ч
2[1/(гI/р /Л + 1/(гI/ Г
Умножим соотношения E.122) — E.131) на постоянные &ь
г. •••« &ю соответственно и прибавим их к E.111) в форме
(правая часть минус левая часть) =0, где /=1, 2, . .., 10
(равенства E.126), E.130) и E.131) умножаются еще на Q/m0).
При интегрировании все производные в левой части исчезают,
так как h(z0) =h{zi) =0. В результате получим
{[U (z)-U0]/[U (Zo)-
X
QB(z)B'(z)U'(z)
. E.132)
Естественно, это выражение сводится к E.111) при ki = k2 =
= ... = feio = 0. Для того чтобы получить иное выражение, необ-
необходимо решить, ка<кие из 21 члена должны исчезнуть, и прирав-
приравнять их коэффициенты к нулю. Если количество опускаемых
членов выбрано правильно, то коэффициенты ku k2, ..., ki0
будут определены однозначно. Например, замечаем, что выра-
выражение E.121) содержит только десять слагаемых. Если мы по-
положим коэффициенты других 11 членов E.132) равными нулю,
277
Глава 5
то получим систему 11 очень простых алгебраических уравне-
уравнений, одно из которых — избыточное. Ее решение дает следую-
следующие десять коэффициентов:
fti = —16, k2l=— 8, /г3 = — 4, ki = — 5, ks = 4,
&6=1, &7=1/2, fee 1/6, fe9 = 5/2, fe10 2.
E.133)
Подставляя эти коэффициенты в E.132), действительно прихо-
приходим к E.121).
В особых условиях бывают полезны другие способы записи.
Например, если отсутствует электростатическое поле, формула
E.132) содержит всего шесть членов, в которых, однако, встре-
встречаются только три коэффициента (ku fe5 и kw). Если подходя-
подходящим образом убрать три слагаемых, то можно определить эти
коэффициенты. Потребуем, чтобы остались лишь члены, содер-
содержащие /г4. Имеем тогда
ft, = —16, *в = Ю/3, feio = —5/3. E.134)
и оставшиеся слагаемые образуют следующее выражение для
коэффициента сферической аберрации магнитной линзы:
E.135)
Здесь используется релятивистский потенциал B.89). Это вы-
выражение очень удобно для поиска распределений магнитной ин-
индукции, дающих низкую сферическую аберрацию (см. разд.
8.2.3).
Как было показано, вывод различных форм коэффициентов
аберрации является скучной и утомительной работой. Все от-
отдельные операции вычислений элементарны, но объекты опера-
операций очень громоздки. Это типичная компьютерная задача. Дей-
Действительно, компьютеры способны выполнять алгебраические
преобразования, интегрирование по частям и другие элементар-
элементарные операции яе только численно, но также и в символьной
форме. Когда требуется вычислить релятивистский коэффици-
коэффициент или коэффициент аберрации высшего порядка, естественно
использовать для этого компьютер. В случае нетрадиционных
линз это даже более удобно [146] (мультиполи, высокочастот-
высокочастотные поля, линзы с необычной симметрией), так же как и в слу-
случае сложных линзовых систем, детекторов и других элементов
электронной оптики.
278
Теория аберраций
5.2.1.3. Теорема Шерцера. Воспользуемся еще раз уравне-
уравнением E.132), чтобы доказать одну из наиболее важных теорем
электронной и ионной оптики. Выберем произвольные коэффи-
коэффициенты так, чтобы исчезали 2-й, 4-й, 7-й, 9-й, 14-й, 17-й, 20-й и
24-й члены уравнения. Это дает семь независимых уравнений
для десяти коэффициентов. Выберем оставшиеся три коэффи-
коэффициента так, чтобы получить следующий выбор:
^=—16, k2. 8, кг=— 4, £4=— 5/2, ks=2,
E.136)
k6 = l, Л7-1/2, къ=—13/8, £9 = 2. Л10 = —2.
Подставляя эти коэффициенты в E.132), получим
€so= A/32) 'i {[£/(z) - U0]/[U(zo) - f/0]}1/2X
o
I 5U{z) 5U'*{z)U"(z) 65Uri(z) Q2B*(z)
\2[U(z)—U0]2 [U(z)-U0]3 +№[U(z)-U0]i + 2ml[U(z)-U
2QB'*(z) 53QB*(z)U'*(z) 5QB (z) B' (z) U' (z)\ ,4
mo[U(z)-UQ] \6mo[U(z)-Uo]3'r m0 [U (z)-(/0]2 /
t/'(z)t/'(z) 3t/'»(z) 4Qg(z)g'(z) , 4Qfl» (г) t/'(г)
4QB»(*)
которое можно переписать в следующем виде:
!x
г/(г)_г/о"^ г/(г>—г/0 л [и (г)-
^A'/A) i w'(z) ^2|
5B (г) t/' (г)
32me[l/B)-l/0J»
Проанализируем полученное выражение. Так как Q/[U(z) —
—Uo] всегда отрицательно, легко видеть, что Cso никогда не
может быть отрицательной величиной. Это утверждение и яв-
является теоремой Шерцера [142].
279
Глава 5 ^^^
Каковы применения этой теоремы? Так как коэффициент
сферической аберрации зависит от электростатического потен-
потенциала и распределения магнитной индукции, невозможно найти
другое аксиально-симметричное распределение с аналогичными
свойствами (отсутствие пространственного заряда, непрерыв-
непрерывность распределений аксиального поля, стационарные поля),
которое компенсировало бы сферическую аберрацию данного
распределения. Компенсация сферической аберрации возможна
только при использовании других видов симметрии или некото-
некоторых упомянутых выше соображений, опущенных при рассмотре-
рассмотрении условий формирования изображения аксиально-симметрич-
аксиально-симметричными линзами [147].
Так как невозможно скомпенсировать сферическую аберра-
аберрацию и, «роме того, она не зависит от положения точки объекта
в плоскости объектов (это утверждение справедливо, даже если
точечный объект расположен на оси), то сферическая аберра-
аберрация является наиболее важной из всех геометрических аберра-
аберраций. Она является одним из основных факторов, ограничиваю-
ограничивающих разрешение электронных микроскопов, так же как и размер
электронного и ионного зондов. Естественно, что ее уменьшение
являлось одной из наиболее важных задач электронной и ион-
ионной оптики с самых ранних дней ее существования.
Важно отметить, что теорема Шерцера не утверждает, что
коэффициент сферической аберрации всегда положителен. Сум-
Сумма квадратичных членов неотрицательна, но всегда существует
возможность, что она равна нулю. Будет ли она действительно
равна нулю или нет — весьма спорная проблема, к которой мы
вернемся ниже. Однако несомненно, что уменьшение сфериче-
сферической и других аберраций путем соответствующего выбора по-
полей, формирующих изображение, в пределах практически реа-
реализуемых значений является основной задачей, решения кото-
которой необходимо добиваться. Это будет предметом обсуждения
гл. 9.
5.2.1.4. Диск минимального рассеяния. Как следствие теоре-
теоремы Шерцера и уравнения E.79), удаленный луч всегда пересе-
пересекает оптическую ось ближе к объекту, чем параксиальный (см.
рис. 64). Рассмотрим различные лучи, пересекающие оптиче-
оптическую ось в непосредственной близости от гауссовой плоскости
изображения z = zi (рис. 68). Для простоты аппроксимируем все
лучи в этой области прямыми линиями [20], как если бы мы
заинтересовались только их асимптотическим поведением. Это
можно показать в грубом приближении, но при этом необходи-
необходимо также предполагать постоянное распределение плотности
тока в пучке, что сводит на нет любые дальнейшие изыскания
с учетом реального хода лучей.
280
Теория аберраций
Согласно вышеуказанным условиям, учитывая уравнения
E.43), E.76) и E.80), предполагая Уо/ = 0 и используя затем
уравнения D.65) и E.42), можно записать уравнение главного
луча как функцию осевой координаты z в следующем виде:
X (г) + 6Х (г) «AfCsoXo'z — Xo'h' (zt) (zi — z) =
=MCS0X0'3 - [Xo'{Zi — z)/M][(U(zo) —
)-Uo)]^. E.139)
Для граничного луча необходимо заменить XJ на tg fo
[X (г) + 8Х (z)]out « MCS0 tg3Yo- (£-
MCsotgs-y0A
Рис. 68. Диск минимального рассеяния.
Этот луч пересекает ось в точке z = z(^o), определяемой из ус-
условия
Zl—z(Yo)= M*CS0 tg«Уа [
Уt, E-141)
где использованы уравнения D.65) и E.83). Тогда координату
z(Xo') точки пересечения главного луча с оптической осью
можно записать как
Zi -z{Xo') = (Xo/2/tg2 Чо) [zi - z(T,)]. E.142)
Так как по определению X/^tgfo, главный луч пересекает ось
в точке, которая всегда ближе к гауссовой плоскости, чем точка
пересечения граничного луча.
Продолжим поиск минимального поперечного сечения пучка.
Оно будет определяться пересечением граничного луча с кау-
каустической поверхностью, где максимальное радиальное смеще-
смещение различных лучей наименьшее (диск минимального рас-
рассеяния).
281
Глава 5
Приравнивая уравнения E.139) и E.140), находим осевую
координату, при которой главный луч пересекает граничный луч:
z-z-M*C ФУ°
Z, z-MLsotgyo_x;>[U(Zo)Ue\
[^l}1'2- E-143)
Смещение обоих лучей в этой точке равно
Х(г) + 8X(z) = [X(z)+8X(z)]0Ut =
= — MCsoX'otg4o(Xro + tg4o). E.144)
Как видно на рис. 68, существуют четыре точки пересечения,
две из которых имеют положительные и различные по значению
смещения и еще две с другой стороны оси z с теми же абсолют-
абсолютными значениями и зависят от начального знака исходных на-
наклонов. Также можно видеть, что абсолютные значения коор-
координат точек пересечения вблизи гауссовой плоскости меньше,
чем абсолютные значения координат точек пересечения вблизи
плоскости объекта. Меньшие значения координат точек пересе-
пересечения соответствуют разным знакам Хо' и tg *{<>■ Эти точки оп-
определяют плоскость минимального рассеяния для значения
Хо'= (Xo')opt, при котором смещение имеет максимальное зна-
значение. Для большей ясности на рис. 68 показан только этот
«предельный главный луч», но читатель может легко убедиться
сам, что все другие главные лучи действительно лежат внутри
каустической поверхности.
Максимальное абсолютное значение \X(z)+8X(z)\max сме-
смещения, наблюдающегося при осевой (координате z=zOpt, опре-
определяется как
(^o)oPt = -(tg>)/2. E.145)
Подставляя это значение в E.144) и E.143) и используя E.79)
и E.141), получим
\X(z)+8X(z)\max=\MCSotg3^\/4=\8rsi\/4, E.146)
zj —zoPt=C/4)[z, —z(f0)] E.147)
соответственно. Диск минимальною рассеяния расположен в
трех четвертях расстояния точки пересечения граничных лучей
от плоскости и имеет радиус в четыре раза меньше, чем абер-
аберрационный диск в плоскости изображения. Поэтому естествен-
естественно в зовдовых системах поместить мишень в плоскости наи-
наименьшего рассеяния, где размеры зонда намного меньше, чем
в гауссовой плоскости.
282
Теория аберраций
Интересно отметить, что подстановка уравнения E.145) в
E.142) дает для координаты пересечения предельного главного
луча с осью
zi — г [ (Х'о) Opt] = [Zi — z(To)]/4. E.148)
Очевидно, что диск минимального рассеяния может быть
аналогично введен и в пространстве объектов. Его радиус ока-
оказывается в четыре раза меньше, чем радиус аберрационного
диска в пространстве объектов.
В случае нулевого увеличения для определения радиуса дис-
диска минимального рассеяния необходимо использовать уравне-
уравнения E.82) и E.146). Для бесконечного увеличения может быть
использован только диск в пространстве объектов.
5.2.2. Астигматизм
Теперь рассмотрим случай, когда ненулевым коэффициентом
является только А2 в уравнениях E.65) и E.66). Тогда имеем
8X(Zi) =2А2(Х2оХ'о + Хо¥о¥'о),
E.149)
6У B,) =2Л2 (XoYoX'o + Y*OY'O).
bX{zi) и 8Y(zt) связаны между собой линейно:
). E.150)
Это означает, что если мы имеем конус частиц, покидающих
точку объекта с координатами Хо, Yo при различных углах j0,
определяемых значениями Хо' и Yo' и ограничиваемых уравне-
уравнением E.78), то разные частицы будут пересекать гауссову плос-
плоскость вдоль прямой линии в радиальном направлении: эта ли-
линия и является фигурой аберрации. Если точка предмета рас-
расположена в меридиональной плоскости Xz (Уо = 0), то эта линия
параллельна оси X FУ0 = 0). Линия продолжается в обоих на-
направлениях от гауссовой точки изображения, соответствующей
Xo'=Yo' = 0. Длина линии пропорциональна tg^o и квадрату
расстояния между точкой объекта и оптической осью. Эта абер-
аберрация называется астигматизмом. Очевидно, что астигматизм
(подобно всем другим геометрическим аберрациям, исключая
сферическую) отсутствует, если объект расположен на оптиче-
оптической оси.
Можно показать [16], что астигматический пучок, идущий
из конуса, как описано выше, имеет эллиптическое поперечное
сечение. Эллипс вырождается в две прямые линии в двух плос-
плоскостях, образуя взаимно перпендикулярные меридиональные и
сагиттальные изображения соответственно. Между ними суще-
283
Глава 5
ствует круговое изображение. В специальном случае, .когда обе
линии и круг совмещаются в одной точке, мы говорим о стиг-
стигматическом изображении (взаимно однозначное соответствие
между точкой объекта и точкой изображения). Этот случай
реализуется в параксиальном приближении. Однако отклонения
от осевой симметрии, вызванные дефектами изготовления или
неоднородностями материала, создают астигматизм даже для
параксиальных лучей (см. разд. 5.6.4).
Наконец, отметим, что в некоторых учебниках [9, 36] опре-
определение астигматизма отличается от определения, данного
здесь.
Коэффициент астигматизма определяется уравнением E.69).
Заметим, что, за исключением последнего члена, это уравнение
совпадает с уравнением E.68), если в последнем h4 заменить
«a g2h2, h2h'2 заменить на gg'hh' и h'4 заменить на g'2h'2. Вы-
Выполнив эти преобразования и введя дополнительный член, по-
получаем из уравнений E.80) и E.111)
= (М/32) $ {[U(z)-U0]/[U (г0)-ио\
X
I ( U"* (г) QB* (г) и" (г) Q*B4z) UIV (г)
2QB(z)B"{z)\ | 2U"(z)
Можно исключить член, содержащий четвертую производную
потенциала, проинтегрировав его по частям. Процедура анало-
аналогична той, что применена для производной уравнения E.114).
Однако для сохранения симметрии формы коэффициентов абер-
аберраций разных типов целесообразно сохранить именно эту форму
записи.
5.2.3. Кривизна поля
Если оставить только один коэффициент Л3, то уравнения
E.65) и E.66) дают
8X{Zi)=A3X'o(X*o+Y*o),
E.152)
284
Теория аберраций
Это уравнение окружности радиусом
E.153)
Таким образом, в этом случае фигура аберрации — круг с цент-
центром в точке гауссова изображения. Его радиус пропорционален
tgfo и квадрату расстояния от точки предмета до оптиче-
оптической оси.
Можно показать [16], что при этом типе аберрации плос-
плоскость предмета точно отображается на искривленную поверх-
поверхность, касающуюся гауссовой плоскости в точке изображения
первого порядка. Отсюда название этой аберрации — кривизна
поля. Эта аберрация может быть полностью компенсирована,
если вместо плоского используется слегка искривленный экран
или мишень. Аналогично искривленная поверхность объекта
может давать гауссову плоскость, как плоскость идеального
изображения. Поверхность может быть как выпуклой, так и
вогнутой в зависимости от коэффициента кривизны поля.
Кривизна поля играет важную роль в конструировании от-
отклоняющих систем. Ее коэффициент определяется уравнением
E.70). Сравнивая уравнения E.69) и E.70), видим, что А3
можно получить из уравнения E.69), заменяя в нем Agg'hh' на
2(g2h'2Jrg'2h2) и умножая последний на —2. Соответственно
преобразуем уравнение E.151), чтобы получить
= (Л1/32)
/| U»* (г) QB*(z)U"(z)
Х \\[U(z)-U0]2 /пв[У(г)-Ув]»/^[У(г)-1/о1»
2QB(z)B"(z)\ \ 2U"(z) QB*(z) \
U0]\ s" -Г*\и(г)—иа ma[U (г)—11а] f
X (*■*'■+ *'*■)+ ^S'^~4Q[^\-^pZ))dz. E.154)
Заметим, что в случае астигматизма длина линии аберрации
пропорциональна тем же величинам, что и радиус аберрацион-
аберрационного круга в случае кривизны поля. Таким образом, эти две
аберрации очень похожи друг на друга. Если обе они присутст-
присутствуют одновременно, то фигурой аберрации является эллипс.
Существуют две искривленные поверхности (меридиональная
и сагиттальная поверхности изображения), вдоль которых изоб-
изображение точечного объекта вырождается в две взаимно перпен-
перпендикулярные линии. Где-то между этими двумя поверхностями
находится третья поверхность, на которой «изображение» явля-
285-
Глава 5
ется окружностью. Но ни линии, ни окружность не находятся
на гауссовой плоскости.
Разность между коэффициентами А2 и А3 называется коэф-
коэффициентом Петцваля. Используя уравнение E.67), из уравне-
уравнений E.151) и E.154) имеем
А2- Л3= (М/8) ]' {[U(z) - U0f[U(zo) - £/0]
X{2Q[U(z0) — Uo]B*(z)/mo— [U(z0) — U0]U"(z)}dz.
E.155)
Как видим, коэффициент Петцваля не зависит ни от луча g,
ни от луча h. Для системы, у которой отсутствует астигматизм,
коэффициент Петцваля пропорционален кривизне поверхности,
на которой изображение является резким [16]. Если с помощью
.•подходящего выбора полей, формирующих изображение, сделать
коэффициент Петцваля равным нулю, тогда А2 = А3 и на плос-
плоской поверхности образуется резкое изображение.
5.2.4. Дисторсия
Если оставить только коэффициент Ац, то из уравнений
E.65) и E.66) имеем
E.156)
Так как эта аберрация не зависит ни от Хо', ни от У</, она име-
имеет место даже в случае бесконечно узкого пучка, нарушая
линейное соотношение между объектом и изображением (ди-
сторсия). Однако для данной точки объекта изображение оста-
остается точкой (стигматическое изображение), таким образом,
.фигура аберрации в этом случае является точкой. Точка изоб-
изображения не расплывается, а только смещается от гауссовой
точки на расстояние
E.157)
(Будьте внимательны: здесь бп не является радиусом круга.)
Смещение происходит в радиальном направлении и пропорцио-
пропорционально кубу расстояния между точкой предмета и оптической
осью.
Очевидно, что дисторсия наиболее существенна в случае
проекторов и дефлекторов, когда луч может находиться далеко
от оптической оси. Это можно компенсировать выбором подхо-
подходящим образом искривленной поверхности, на которой форми-
формируется изображение.
286
Теория аберраций
Существуют два вида дисторсии в зависимости от знака ко-
коэффициента Л4. Так ка« увеличение отрицательно, положитель-
положительная аберрация уменьшает расстояние между точкой изображе-
изображения и осью. Таким образом, положительный коэффициент Л4
приводит к бочкообразной дисторсии (рис. 69), в то время как
в случае Л4<0 имеет место подушкообразная дисторсия
(рис. 70).
Коэффициент дисторсии определяется уравнением E.71).
Из сравнения уравнений E.70) и E.71) видно, что вычислить
А4 можно, заменяя g2h2 на g3h, (g2h'2+g'2h2) на gg' (gh'+g'h),
VJ\ /
J
Рис. 69. Бочкообразная дисторсия.
Рис. 70. Подушкообразная дисторсия.
g'2h'2 на g'3h' и опуская последний член в уравнении E.70).
Осуществляя эти преобразования в уравнении E.154), получим
х
Х
({
{[U(z)-U0]/[U(zo)-U0]}^x
QB2(z)U"(z) .
\{U(z)-U0]*-
2QB(z)B°(z) { .
/по[/7(г)-/7о]|й
\U(z)-U0'
0]2 U(z)-U0
QB*(z)
X
. E.158)
5.2.5. Кома
Следующим коэффициентом является As. Из уравнений
E.65) и E.66) имеем
E.159)
287
Глава 5
Из этого следует, что
\ЬХ(г,) -2AbXo{Xo'*+Yo'z)Y +
+ [8Y(Zl) — 2Л5Уо(Хо'2 +
= [А,(Хо>+УоаУ'2(Хо'а+У
Это уравнение окружности радиусом
с переменными координатами
2 = гаеотл. E.160)
и центром в точке
E.161)
Центр смещен в радиальном направлении от гауссовой точки
изображения на расстояние 2/-СОта.
■*- х
Рнс 71 Кома
Таким образом, для конуса лучей, образованного частицами,
выходящими из точки объекта Хо, Yo, фигурой аберрации явля-
является набор окружностей. Их центры расположены вдоль прямой
линии, простирающейся от гауссовой точки в радиальном на-
направлении. Так как расстояния между центрами окружностей
и гауссовой точкой равны их диаметрам, то окружности огра-
ограничены двумя прямыми линиями с углом 60° между ними. Фи-
Фигура аберрации выглядит как комета (рис. 71), отсюда проис-
происходит и название кома. Заметим, что, поскольку увеличение
отрицательно, рис. 71 соответствует отрицательному значению
коэффициента А5.
Радиус наибольшей окружности дается как
E.162)
■288
Теория аберраций
который пропорционален расстоянию от точки объекта до оси
и квадрату угла аксептанса пучка. Очевидно, что самой яркой
точкой фигуры аберрации является ее вершина.
Коэффициент А5 дается уравнением E.72). Он может быть
легко выведен из уравнения E.71), если g н h поменять места-
местами. Тогда из уравнения E.158) имеем
5 = (М/32)
/( Ц'»(г) QB*(z)U"(z) Q*B*(z) ЦП (г)
HW(z)-U0]* ma[U(z)-U0]^
4m* [U (г)- l/,]« t/ (г) _ t
2QB(z)B"(z) \-.^3|oJ 2^"(г) QBHz) \
-UoU
(z)-Uo mo[U(z)
Xhh' (gh' + g'h)~\-l6g'h'3)dz. E.163)
5.2.6. Анизотропные аберрации
Пока мы рассмотрели пять различных типов геометрических
аберраций: сферическую аберрацию, астигматизм, ■кривизну
поля, дисторсию и кому. Фигуры аберраций — это окружности,
прямые линии или точки, и они всегда ориентированы (или сме-
смещены) в радиальном направлении. Эти электронные/ионные
оптические аберрации являются аналогами геометрических
аберраций световой оптикн.
Коэффициенты аберрации являются сложными функциями
осевого потенциала и распределений магнитной индукции, так
же как и лучи g и h, определенные граничными условиями урав-
уравнения E.42). Полное исследование уравнений E.111), E.151),
E.154), E.158) и E.163) совместно с уравнением параксиаль-
параксиальных лучей D.40), решения которых появляются в коэффициен-
коэффициентах аберрации, демонстрирует следующие свойства:
1. Аберрации чисто электростатических линз не зависят от
отношения заряда частицы к ее массе. Изменение знака элект-
электростатического потенциала также не влияет на аберрации.
Заметим также, что электростатический потенциал в магнитных
членах всегда появляется вместе с зарядом; таким образом,
в случае изменения знака электростатического потенциала зна-
значение коэффициентов аберрации остается неизменным.
2. Магнитная индукция и ее производные всегда появляются
в комбинациях четных степеней. Таким образом, изменение в
направлении или знаке магнитного поля не влияет на абер-
аберрации.
289
Глава 5
Если теперь посмотреть на оставшиеся три коэффициента
(уравнения E.73) — E.75)), то можно заметить, что их свойства
существенно отличаются. Во-первых, эти коэффициенты содер-
содержат только функции d и е, и, как показывают уравнения E.29)
и E.30), эти функции появляются только тогда, когда присутст-
присутствует магнитное поле. (Естественно, это не означает, что элект-
электростатическое поле должно отсутствовать. Таким образом,
ошибочно в этих коэффициентах автоматически рассматривать
электростатический потенциал как постоянную.)
Заметим также, что в уравнениях E.29) и E.30) магнитная
индукция и ее вторая производная появляются только в нечет-
нечетных степенях-. Таким образом, изменение направления или зна-
знака магнитного поля будет вызывать изменение знака этих ко-
коэффициентов. То же происходит и при изменении знака заряда.
Это свойство находится в полном соответствии с анизотропной
природой электронно-оптического коэффициента преломления в
магнитных полях (разд. 2.6). Действительно, если направление
магнитного поля изменить на противоположное, то частицы
будут вращаться в противоположном направлении и траектория
станет необратимой. Поэтому эти аберрации называются анизо-
анизотропными. Они не имеют аналога в световой геометрической
оптике.
Ниже будет показано, что анизотропные фигуры аберрации
всегда связаны с отклонением в азимутальном направлении,
вызванным магнитным полем.
5.2.6.1. Анизотропный астигматизм. Прежде всего рассмот-
рассмотрим случай, когда в уравнениях E.65) и E.66) ненулевым ко-
коэффициентом является только А6. Тогда имеем
E.164)
8Y(Zi) =А6[(ХО2 - Yo2)Xo'+2XoYoYo'].
Это дает окружность радиуса
8ri=Ae(Xo2 + Yoz)(Xo'2 + Yo/2)i'2<A(i(Xo2 + Yo2)tg'io.
E.165)
Поэтому фигурой аберрации в этом случае является круг с
центром в гауссовой точке изображения. Его радиус пропорцио-
пропорционален tg^o и квадрату расстояния от оптической оси до точки
объекта.
Эта аберрация называется анизотропным астигматизмом.
Однако заметим, что уравнения E.153) и E.165) отличаются
друг от друга только коэффициентами, поэтому анизотропный
астигматизм определяется кривизной поля, а не астигматизмом.
290
Теория аберраций
Различие между кривизной поля и анизотропным астигматиз-
астигматизмом проявляется не в фигуре аберрации, а в пути, по которому
лучи подходят к этой фигуре: в урав«ении E.152) нет смешан-
смешанных членов, но в уравнении E.164) как 8X(Zi), так и 6У(г,)
зависят как от Хо', так и от Уо', из чего следует, что лучи будут
отклоняться. Очевидно, анизотропный астигматизм (так же как
и другие две анизотропные геометрические аберрации) отсутст-
отсутствует, если объект расположен на оптической оси.
Коэффициент анизотропного астигматизма определяется
уравнением E.73). Подставляя функции d и е из уравнений
E.29) и E.30) соответственно, получаем
X ({яц^Л+Д'W -Vm^} «*-4*(»^К EЛ66)
Фигуры аберрации астигматизма, кривизны поля и анизо-
анизотропного астигматизма полностью характеризуются одинаковы-
одинаковыми величинами: квадратом расстояния от оси до точечного объ-
объекта и половинным углом аксептанса пучка. Таким образом,
по существу эти три аберрации могут рассматриваться вместе.
Если все из них присутствуют одновременно, фигура аберрации
становится эллипсом с произвольной ориентацией.
5.2.6.2. Анизотропная дисторсия. Оставим теперь только ко-
коэффициент Л7. Тогда из уравнений E.65) и E.66) имеем
-Л7У0(Х02 + У02),
E.167)
A7Xo(Xo* + Yo2).
Эта аберрация называется анизотропной дисторсией. Подобно
дисторсии, она не зависит ни от Хо', ни от У</. Таким образом,
она имеет место даже для бесконечно узкого пучка, разрушая
линейную связь между объектом и изображением. Для данной
точки объекта изображение остается точкой (стигматическое
изображение). Фигурой аберрации является точка, изображение
которой не размыто, но сдвинуто от гауссовой точки на рас-
расстояние
E.168)
где бг/ — не радиус круга, а расстояние. Уравнение E.168) име-
имеет ту же структуру, что и уравнение E.157). Различие в том,
что теперь сдвиг имеет место не в радиальном, а в азимуталь-
291
Глава 5
Рис. 72. Анизотропная дисторсия.
ном направлении. Действи-
Действительно, уравнение E.167) по-
показывает, что ^-компонента
смещения пропорциональна У-
координате точки предмета и
наоборот. Таким образом, само
смещение 'перпендикулярно
линии, соединяющей гауссову
точку с осью. Как результат,
будет иметь место скрученная
дисторсия (рис. 72); отдельные
линии прямоугольного предмета будут отображаться как S-об-
разные кривые. Направление скручивания определяется знаком
коэффициента А7. Его величина пропорциональна кубу расстоя-
расстояния от оптической оси до точки объекта. Таким образом, изоб-
изображением прямой линии, пересекающей оптическую ось в пер-
перпендикулярном направлении, будет кубическая парабола.
Коэффициент анизотропной дисторсии дается уравнением
E.74). Из сравнения уравнений E.73) и E.74) видно, что мож-
можно вычислить коэффициент А7, заменяя 2hg на g2 и 2g'h' на g'2
в выражении для А6. Тогда из уравнения E.166) получаем
5.2.6.3. Анизотропная кома. Наконец, оставим только коэф-
коэффициент А8. Из уравнений E.65) и E.66) видим, что
6X(zl)=A8[2X'o(XoY'o — X'oYo) - Yo(Xo'2+Yo'2)],
E.170)
6Y(zt) =Л8[2У'О(ХОУ'О — X'oYo) + XO(XO'2+YO'2)].
Из этого следует, что
[6X(zl)+2A8Yo(Xo'2+Yo'2)]2 +
+ [6Y(zi) — 2AsXo(Xo'2+Yo'2)Y =
= [Л8(Хо2+Уо2I/2(^о/2+Уо/2)]2 = /-2апсота. E.171)
Это уравнение окружности радиусом ran аота и центром в пе-
переменной точке с координатами
Xc=Xi — 2A8YO (Xo'2+ Yo'2),
E.172)
292
Теория аберраций
Можно видеть, что радиус окружности пропорционален тем же
величинам, что и в случае комы. Однако центр смещается не в
радиальном, а в азимутальном направлении от гауссовой точки
изображения на расстояние 2гаПсота-
Таким образом, для конуса, образованного лучами частиц,
вылетающих из точки объекта Хо, Yo, фигурой аберрации вновь
является ряд окружностей. Их центры расположены вдоль пря-
прямой линии, тянущейся от гауссовой точки в азимутальном на-
направлении. Круги ограничены двумя прямыми линиями с углом
60° между ними. Фигура аберрации выглядит подобно комете,
показанной на рис. 71, но с осью, перпендикулярной к линии,
связывающей гауссову точку изображения с оптической осью.
Это анизотропная кома.
Радиус наибольшего «руга дается
4o. E.173)
Он пропорционален расстоянию от точки предмета до оси и
квадрату угла аксептанса пучка. Самой яркой точкой фигуры
аберрации вновь является его вершина.
Коэффициент Л8 дается уравнением E.75). Единственным
различием между уравнениями E.74) и E.75) является замена
g2 на Л2 и g'2 на Л'2. Соответственно из уравнения E.169) по-
получим, что
{-2QmB [U (г)- UB]}-^(\2ma **£}_^ + В"(г) -
<5174>
Если одновременно присутствуют и кома, и анизотропная
кома, то из уравнений E.65) и E.66) имеем
[6X(zi)-2(AsXo-AeYo)(Xo'2+Yo'2)Y +
E.175)
Это уравнение круга с радиусом rComa sum и центром в точке с
переменными координатами
Xc = Xi+2(A,Xo-AsYo) (Xo/2 + Yo'2),
E.176)
Yc = Yi+2(A5Yo+A8Xo) {Xo'2+Yo'2).
Центр круга смещен теперь и в радиальном, и в азимутальном
направлениях от гауссовой точки изображения на расстояние
293
Глава 5
2rComasum. Для конуса из пучков частиц, покидающих точку
объекта, фигурой аберрации является ряд кругов, центры кото-
которых расположены вдоль прямой линии, тянущейся от гауссовой
точки, в направлении, определяемом коэффициентами Л5 и As.
Это очевидно из того факта, что и Хс—Xt, и Yc—У, линейно за-
зависят от (Xo'2 + Yo'2). Окружности ограничены двумя прямымн
линиями с углом 60° между ними. Радиус наибольшей окруж-
окружности дается
= (At* + Л82) '/2 (XO2 + YO2) 1/2 tg2
E.I77)
Очевидно, что уравнения E.160) и E.171), уравнения E.161) и
E.172) и уравнения E.162) и E.173) являются частными слу-
случаями уравнений E.175), E.176) и E.177) соответственно.
Рис. 73 Кома и анизотропная кома
Угол ■&, под которым ось «кометы» наклонена к прямой ли-
линии, соединяющей гауссову точку с осью, дается соотношением
tgb=(Yc — Y,)/(Xc — Xt)=Aa/As (если Уо = 0)
E.178)
(рис. 73), из которого очевидно, что если Л8 = 0 (кома), то Ф = 0
и ось направлена радиально, в то время как Л5 = 0 (анизотроп-
(анизотропная кома) дает ^ = п/2, а это означает, что ось кометы направ-
направлена азимутально. Выбор Уо = 0 не уменьшает общности этих
выводов. Это просто означает, что если радиальное направление
параллельно оси X, то кома направлена параллельно той же
оси и анизотропная кома направлена параллельно оси Y, кото-
которая теперь является азимутальным направлением. В этом слу-
случае Ф есть угол между осью X и осью кометы. В общем случае,
конечно, ■& — это угол между радиальным направлением и осью
кометы.
294
Теория аберраций
5.2.7. Об относительном вкладе различных
геометрических аберраций
Здесь мы закончим рассмотрение коэффициентов различных
геометрических аберраций. Прежде чем перейти к рассмотре-
рассмотрению хроматической аберрации, следует оценить относительный
вклад различных геометрических аберраций при разных ус-
условиях.
Было показано (уравнение E.79)), что радиус диска сфери-
сферической аберрации пропорционален tg3 40 и не зависит от распо-
расположения точки объекта. Уравнение E.177) показывает, что ра-
радиус наибольшего круга в фигурах аберрации комы и анизо-
анизотропной комы пропорционален rotg2^o, где г0 — расстояние от
точки объекта до оптической оси. Из уравнений E.149), E.153)
и E.165) следует, что эффекты астигматизма, кривизны поля и
анизотропного астигматизма пропорциональны ro2ig^0 Нако-
Наконец, как видно из уравнений E.157) и E 168), как дисторсия,
так и анизотропная дисторсия пропорциональны г03. Из этого
можно сделать следующие выводы:
1. Сферическая аберрация является наиболее важной гео-
геометрической аберрацией, так как она имеет место даже для
точек на оси и не может быть скорректирована другой аксиаль-
аксиально-симметричной линзой того же типа (см. разд. 5.2.1.3). С дру-
другой стороны, ее величина ие зависит от расположения точки
объекта, таким образом, она не увеличивается с расстоянием
от оси (что не так уж и важно для отклоняющих систем).
2. Кома и анизотропная кома важны для широких пучков,
но только относительно близко к оси.
3. Для больших расстояний от оси и относительно узких пуч-
пучков становятся очень важными астигматизм, кривизна поля и
анизотропный астигматизм. В дальнейшем будет показано, что
астигматизм обычно возникает также из-за отсутствия точной
осевой симметрии в реальных системах.
4. Дисторсия и анизотропная дисторсия доминируют при
больших расстояниях от оси; таким образом, они важны в от-
отклоняющих и проекционных системах. Они имеют место даже
для бесконечно узких пучков.
Особые свойства и относительная важность анизотропных
аберраций объяснены в разд. 5.2.6.
5.3. Хроматическая аберрация
Во введении к этой главе мы объяснили, почему энергети-
энергетический разброс частиц вызывает аберрацию даже в параксиаль-
параксиальном приближении. Главной причиной хроматической аберрации
является то, что на частицы с большими начальными энергиями
295
Глава 5
фокусирующее поле оказывает меньшее влияние, чем на части-
частицы с меньшими энергиями. Таким образом, если все частицы
покидают точку объекта под одним углом, то частицы с высо-
высокими энергиями образуют изображение на большем расстоянии
от предмета, чем частицы с «изкой энергией (рис. 74), и изоб-
изображение будет терять четкость как в случае сферической абер-
аберрации. К тому же вращение частиц с различными энергиями в
магнитном поле также будет различным.
Существует несколько причин энергетического разброса час-
частиц. Прежде всего никакой источник не может напускать моно-
монохроматический пучок частиц. Все начальные скорости различ-
различных частиц пучка отличаются, что соответствует различным
значениям Uo в распределении осевого потенциала. Этот вопрос
более детально будет проанализирован в разд. 5.6.8, но мы мо-
можем непосредственно видеть, что это обстоятельство особенно
вредно для пучков с низкой энергией, где разброс по энергиям
сравним со средней энергией пучка. Как будет видно из разд.
12.2, взаимодействия отдельных частиц в пучке вызывают до-
дополнительный разброс по энергиям (эффект Боэрша). Разброс
по энергиям имеет место также в просвечивающем электронном
микроскопе из-за энергетических потерь в образце.
Умеренная
энергия
Рис. 74. Хроматическая аберрация.
В разд. 4.3 было показано, что для нерелятивистских частиц
пропорциональное изменение всех потенциалов электрода не
меняет траекторию, если распределение магнитной индукции
одновременно изменяется пропорционально квадратному корню
из коэффициента подобия электростатического потенциала. Та-
Таким образом, низкочастотные нестабильности источника пита-
питания не вызывают большой проблемы для электростатических
линз. Однако влияние этих нестабильностей на магнитные лин-
линзы может быть довольно значительным. По мере изменения то-
токов возбуждения в катушке изменяется и распределение маг-
магнитной индукции, но так как уравнение D.40) квадратное от-
относительно этого распределения, то будет происходить явление
очень похожее на хроматическую аберрацию. Мы назовем его
магнитной хроматической аберрацией.
Как было обещано в разд. 5.1, для вычисления хроматиче-
хроматических аберраций будет использован метод характеристических
296
Теория аберраций
функций. Теперь параксиальная траектория возмущается ин-
инкрементом /С(С) параксиальной переменной функции КB), обус-
обусловленной ее производными по электростатическому потенциа-
потенциалу и магнитной индукции:
^B. E.179)
Инкремент /С(С) заменит /СD) в уравнении E.39), образуя
{ E.180)
Так как координаты вращающейся системы X и У зависят
как от магнитной индукции, так и от потенциала через уравне-
уравнения E.11) и E.20) и в E.179) проводится дифференцирование
по этим переменным, то следует начать с фиксированной сис-
системы координат и вводить вращающуюся систему координат
только после дифференцирования. Уравнения E.11) и E.12)
дают
= {—2Qmo/[U (z) — ип]
X{[U(z) - Uo]
E.181)
E.182)
Используя в этих выражениях вначале уравнения E.11),
E.16) — E.18) и E.20) и затем подставляя уравнения E.181)
и E.182) в уравнение E.179), получим
Uoy}4> \U" (z)/16-QB2 (z)/C2m0)] AU-
E.183)
Необходимо подставить сюда X(z), Y(z) и их производные
из уравнений E.43) и E.44), образовать интеграл E.180),
найти частные производные 5С* по Хо' и У</ и подставить их
в уравнения E.62) и E.63), где S* заменяется на 5с*. Это
опять требует некоторой работы, но к этому необходимо уже
привыкнуть. Принимая во внимание уравнения E.11) н E.67),
имеем
Глава 5
X (Xogh+X'oh2)[U"(z)/8 — QB2(z)/(l6m0)] +
+ {[U(z) - U0]*[U(zo) - U0]}-l'2[U(z) - Uo] X
X(Xog'h'+X'ohf*)/2+{-2Qm0[U(z) - U0]
XQYoB(z)/{4[U(z) - U0]}>AUdz+M l\{[U (z) — U0]X
{~2Qmo[U(z) — U0]}-v*QYo/2>ABdz, E.184)
- U0]3[U(zo) - Ua]}
X(Y&gh+Y'oh2)[U"(z)/8-QB2(z)/(l6m0)] +
+>{[U(z) ~ U0]*[U(Zo) - i/0]}-1/2[f/Br) - Uo] X
X (Yog'h'+Y'oh'*)l2- {—2Qmo[U(z) — U»])
XQX0B(z)/{4[U(z) — U0]})AUdz+M $<{[U(z) — U0]X
z
X[U(z0) ~U0]}-v*(Yogh+Y'oh2)\Q°\B(z)/Dm0) -
— {~2Qmo[U(z) — U0]}-V2QXo/2)\Bdz. E.185)
Рассмотрим вначале случай хроматической аберрации, вы-
вызванной только энергетическим разбросом. Тогда ДВ = 0 и урав-
уравнения E.184) и E.185) могут быть записаны в следующем виде:
E.186)
E.187)
где
J {[U{zo)-U0]/[U(z)-U0]y»x
го
w/( u"(z) Qg2(z) \
X\\8[U(Z)-UB] 16mo[U(z)-Uo]{
298
Теория аберраций
С3= - S {-2Qmo[U(z) - U0]}-"*[U(zo) - Uo] X
го
XQB(z)dz{4[U{z)—U0]}-1. E.190)
Заметим, что коэффициент Ci выражается в метрах, в то время
как два других коэффициента безразмерны.
Коэффициент Сг может быть записан различными способа-
способами, если использовать интегрирование по частям. Используя
уравнение E.113) н h(z0) = h(zi) =0, легко показать, что
Ч
{[U(z0)-Uoy[U(z)-UB]}^h'*dz =
г°
— J {W(z0)-Uv]/[U(z)-Uo]}^ {hh'-^V^dz^
X\\8ma[U(z)-U0] 4lU(z)-U0]fn U (г)- Uo
Используя это соотношение, из уравнения E.188) получим
- U0]/[U (г) - U9]} */* Л/г" rfz =
zi
(г)
Еще раз преобразуем этот коэффициент, снова проводя ин-
интегрирование по частям:
E.193)
299
Глава 5
Тогда из уравнения E.192) получим
X\lU(z)-U0\* mo[U(z)-
Видно, что коэффициент Ci никогда не может быть отрицатель-
отрицательным. Очевидно также, что величина С\ непосредственно связана
с функцией T(z) (уравнение D.51)) и, таким образом, с эффек-
эффективной длиной поля (см. уравнение D.164)). Аналогичное выра-
выражение может быть выведено также и для коэффициента Сч.
Рассмотрим теперь роль трех коэффициентов Си С2 и С3.
Вновь положим значения всех коэффициентов равными нулю,
«роме одного, рассматриваемого в настоящий момент.
5.3.1. Аксиальная хроматическая аберрация
Если только Ci — ненулевой коэффициент, то из уравнений
E.186) и E.187) получаем
6X(zt) = — MClX'oAU/[U(Zo) — Uо],
E.195)
6Y(Zi) =—MC1Y'oMJI[U(zo) — Uo].
Аналогичные выражения также следуют из уравнений E.186)
и E.187), если подставить X0=Yo = Q. Ci является единствен-
единственным коэффициентом хроматической аберрации, который оказы-
оказывает влияние, даже если объект расположен на оптической оси.
Поэтому он называется аксиальной хроматической аберрацией.
Поскольку уравнение E.195) не зависит от Хо и Уо, то эта абер-
аберрация одинакова для всех точек объекта. Для точки объекта
на оптической оси можно записать
V2I/2A£//[£/(zo) — t/o]. E.196)
(Следовало бы записать абсолютную величину М, но предпо-
предпочтительней воспользоваться этим обозначением, чтобы следо-
следовать той же схеме, что и для диска сферической аберрации.)
Если вновь рассмотреть конус частиц, которые покидают
точку объекта под углом f к оптической оси, определяемой
уравнением E.78), где ^0 — максимальное значение угла (поло-
(половинный угол аксептанса пучка), тогда уравнение E.196) дает
радиальное смещение для наиболее удаленной от центра тра-
траектории конуса частиц (радиус диска хроматической аберрации
300
Теория аберраций
в плоскости изображения) с общим разбросом по энергии AU0
в виде
6rci=MCcotg 4oMJ0/2[U (zo) — Uo] =M6rC0, E.197)
где
CC0=C, E.198)
есть коэффициент хроматической аберрации, связанный с объ-
объектом, и
6reo = 6rc,IM = Ccotgfo^U0/2[U{zo) — Uo] E.199)
есть радиус диска хроматической аберрации в плоскости объек-
объектов. Множитель 2 появляется в приведенных выше соотношени-
соотношениях, так как под AU0 подразумевается суммарный энергетиче-
энергетический разброс пучка, который есть разность между двумя пре-
предельными значениями энергии, в то время как в уравнениях
E.186) и E.187) AU — энергетический разброс одного конкрет-
конкретного луча, т. е. разность между энергией данной частицы и
средней энергией. Строго говоря, это также означает, что знак
коэффициента аберрации должен быть изменен, так как диф-
дифференцирование следует выполнить по Uo, который имеет отри-
отрицательный злак в выражении U (z)—Uo. Тем не менее истинное
определение суммарной энергии разброса предполагает, что в
этом случае знак произволен (см. замечание после уравнения
E.196)). В наших обозначениях 6rci является отрицательным
для положительных значений у0-
Следует заметить, что относительный энергетический разброс
AU0/[U(z0)—Uo\ является положительным числом, задаваемым
обычно как характеристический параметр источника. Очевидно,
что хроматическая аберрация тогда может быть уменьшена дву-
двумя различными путями: или уменьшением относительного энер-
энергетического разброса источника, или уменьшением коэффициен-
коэффициента аберрации линзы. Так как Ссо никогда не может изменить
знак (см. уравнение E.194)), важно компенсировать аксиаль-
аксиальную хроматическую аберрацию другим аксиально-симметрич-
аксиально-симметричным полем того же типа (см. разд. 5.2.1.3). Но аксиальная хро-
хроматическая аберрация очень строго ограничена рабочими ха-
характеристиками электронного и ионного зондов, потому что
1) даже лучшие источники имеют ненулевые разбросы по энер-
энергии, 2) всегда имеет место эффект Боэрша и 3) аксиальная
хроматическая аберрация имеет место даже «а оси. Таким об-
301
Глава 5
разом, чрезвычайно важно определить фокусирующие поля с
как можно более низкими коэффициентами хроматической абер-
аберрации. Пути достижения этого будут рассмотрены в гл. 9.
Радиус диска хроматической аберрации отличается от ра-
радиального смещения непараксиального луча и смещения пара-
параксиального луча в гауссовой плоскости изображения. Таким
образом, отображением точечного предмета будет не точка,
а диск радиусом |бгс,| с центром в гауссовой точке изображе-
изображения. Фигурой аберрации будет «руг радиуса |бгС(|, пропорцио-
пропорционального начальному наклону наиболее удаленного от центра
луча и относительному энергетическому разбросу.
Отметим различие между зависимостью третьего порядка
сферической аберрации от начального наклона наиболее уда-
удаленного от центра луча и зависимостью первого порядка акси-
аксиальной хроматической аберрации от той же величины. Это озна-
означает, что при низких значениях угла аксептанса действие
оптической системы ограничивается ее хроматической аберра-
аберрацией. При больших апертурах сферическая аберрация становит-
становится доминирующим ограничивающим фактором.
Физическим значением диска хроматической аберрации в
плоскости объекта, определяемого уравнения E.199), является
аберрационный объект конечных размеров, заменяющий иде-
идеальный точечный объект и усиленный идеальной линзой для
получения аберрационного изображения. Заменяя точечный объ-
объект этим диском, мы преобразуем аберрацию линзы в аберра-
аберрационный диск в плоскости объекта. Таким образом, если начи-
начинать от плоскости изображения и двигаться в обратном направ-
направлении к плоскости объекта, то сразу можно получить
аберрационный диск в плоскости объекта. Как и в случае сфе-
сферической аберрации, этот подход дает возможность рассматри-
рассматривать предельные случаи «улевого и бесконечного увеличений.
Используя уравнения D.61) и D.65), получим
1- = М>ССО [„ffilftj1'' Ч Y,-A£V{2 [U (г.) - (/.]} =
)-£/„]}, E.200)
где
является коэффициентом хроматической аберрации, связанным
с изображением. Заметим, что, для того чтобы сохранить сим-
симметрию уравнений E.199) и E.200), необходимо установить
связь разброса по энергии с потенциалом в пространстве изоб-
изображений в последующем выражении, что не всегда удобно.
302
Теория аберраций
Поэтому в пространстве нзображеиий иногда используют другой
коэффициент (Сс,*). Если переписать уравнение E.200) в виде
-6rci = C*cttgtiAUol{2[U(z,) — (/„]}, E.202)
тогда
Если продолжить движение назад от плоскости изображения,
то уравнения E.43) н E.44) должны быть заменены уравнения-
уравнениями E.84) и E.85) соответственно, с начальными условиями
E.87). Начиная с уравнения E.201), повторяя процедуру, из-
изложенную в разд. 5.2.1, и используя уравнения E.90) и E.96),
приходим к тому, что
u(zo)-U0\ -(П°> [u(zo)-U0\ ■
Используя обозначение Fc[h(z)], для подынтегрального выра-
выражения уравнения E.194) можно записать
Fc [h* (z) ] = {ho") 2FC [h(z)]=Fc [h B) ] / (Ы') \ E.205)
Если желательно вычислить коэффициенты аксиальной хро-
хроматической аберрации в прямом направлении, то уравнения
E.194) и E.198) могут быть записаны как
CC0=lFc[h{z)]dz, E.206)
го
которое дает с уравнением E.204), что
С« = №Г [u^ZulY'21 Fc \h (*)] dz. E.207)
го
Для того, чтобы вычислить коэффициенты аберрации в об-
обратном направлении, подставим уравнение E.205) в уравнение
E.207) и получим
SgHSr?.»-™*- <5-208'
Тогда уравнение E.204) дает
С со = (h'oT2 S Fe №* (z)] dz. E.209)
5.3.1.1. Нулевое и бесконечное увеличения. Рассмотрим эк-
экстремальные случаи нулевых и бесконечных увеличений тем же
303
Глава 5
способом, который использовался в разд. 5.2.1.1 для сфериче-
сферической аберрации. В случае нулевого увеличения будем двигаться
в прямом направлении, используя главный луч г2 (г) (рис. 66)
с точкой фокуса в пространстве изображений F2, являющейся
в данном случае изображением. Функция «обратной» аберра-
аберрации может быть переписана как
Fc[h*(z)] = [r'2(F2)]-*Fc[r2(z)]. E.210)
(Отметим, что F2 — осевая координата точки фокуса, в то вре-
время как Fc — аберрационная функция.) Подставляя это уравне-
уравнение вместе с zo = a и Zi = F2 в уравнение E.208), получим выра-
выражение для коэффициента хроматической аберрации, связанного
с изображением, при нулевом увеличении:
E-211)
Функция Fc[r2{z)] вычисляется в прямом направлении, и ин-
интегрирование начинается с конечной координаты z—a. Заметим,
что начальное смещение т2 (а) ие влияет на результат, так как
и числитель (подынтегральное выражение), и знаменатель про-
пропорциональны квадрату этой величины.
Уравнение E.201) дает бесконечный коэффициент хромати-
хроматической аберрации, связанный с предметом, при нулевом увели-
увеличении:
Ссо(м=о)^оо. E.212).
Диск хроматической аберрации имеет конечные размеры в
плоскости изображения, но бесконечно велик в плоскости
объекта.
В случае бесконечного увеличения используется обратное
направление. Воспользуемся главным лучом т\ (z) (рис. 67).
Теперь объектом является точка фокуса в пространстве объек-
объектов F\. Можно записать
Fc[h(z)] = [r',(Fl)]-2Fc[rl(z)]. E.213)
Подставляя это выражение совместно с zo=F\ и zt = b в урав-
уравнение E.206), получим коэффициент хроматической аберрации,
связанный с объектом, при бесконечном увеличении:
Се* = [г; (F,)]-» [gjfjl^]1/a | Fe [г, (г)]dz, E.214)
Функция Fc[ri(z)] вычисляется в обратном направлении и ин-
интегрирование заканчивается в конечной координате z=b. На-
Начальное смещение Г\{Ь) не влияет на результат.
304
Теория аберраций
Из уравнения E.201) для коэффициента хроматической,
аберрации, связанного с изображением, при бесконечном уве-
увеличении получим бесконечно большое значение
Сс1<в-»-оо. . E.215>
Диск хроматической аберрации конечен в плоскости объек-
объекта, но бесконечно велик в плоскости изображения.
Для любого конечного значения увеличения все четыре урав-
уравнения E.206)—E.209) одинаково справедливы.
Из уравнений E.212) и E.215) очевидно, что для малых
значений увеличения Ссо убывает с ростом абсолютной величи-
величины М, в то время как при больших |М| для Cct наблюдается
обратная зависимость. Обычно, как и в случае сферической
аберрации, эта тенденция сохраняется для всего диапазона из-
изменения М, тогда Ссо>Ссосо и См>Ссцм=о), но можно сконст-
сконструировать линзы с более сложной (и полезной) зависимостью
от увеличения.
5.3.1.2. Верхний предел аксиальной хроматической аберра-
аберрации. Нижние пределы хроматической аберрации будут обсуж-
обсуждаться в разд. 9.3.1 и 9.4.1. Можно также оценить максимальное
значение коэффициента аксиальной хроматической аберрации.
Выведем этот предел для электростатического и магнитного по-
полей отдельно.
Начнем с магнитных линз. В этом случае уравнения E.191),
E.192) и E.198) дают
Ссо = — ihh"dz = $ V2 dz, E.216)
го го
h(z)—это решение уравнения параксиальных лучей D.40)
для U(z) = const. Видно, что h"/h<0. Так как по определению
Л>0 между объектом и изображением, Л"<0 и можно заклю-
заключить, что А — монотонно убывающая функция z (известно, что
h'(zo) = l и h'(Zi)<0). Таким образом, h(z) должно иметь мак-
максимальное значение при некотором значении zm. Очевидно, что
0<Л'^1 для zo^z^zm и A'(z,-)<A'<0 для zm<z<zi. Таким об-
образом, можно записать
h (zi)
С„= I h'dh+
Нго)
E.217)
Зная, что h(zo)=h(Zi)=0, и принимая во внимание уравнение
E.94), получим
E.218)
305
Глава 5
где h(zm)—максимальное значение функции h(z). Оно может
быть довольно большим, особенно для высоких увеличений. Так
как М — отрицательное число, множитель в круглых скобках
делает предел еще выше. Этот коэффициент растет по мере то-
того, как абсолютная величина М убывает. Размеры пучка обыч-
обычно ограничены апертурой, радиус которой Rap определяется
соотношением
Rap = h(zm)tg*@. E.219)
В случае бесконечного увеличения для вычисления коэффи-
коэффициента хроматической аберрации необходимо использовать
уравнение E.214). Известно, что асимптотическое фокусное рас-
расстояние в пространстве объектов определяется уравнением
D.72). Тогда h(zm) заменяют на г\(Ь)/г\ (F\), которое прибли-
зизительно равно фокусному расстоянию f, и верхний предел
можно оценить как
Ссо «,//<!. E.220)
Отметим, что уравнение E.220) строго справедливо, только
если точки фокусов расположены за пределами линзы. В про-
противном случае уравнение D.72) обеспечивает только грубую
оценку. Отметим также, что, когда для вычисления коэффици-
коэффициентов хроматической аберрации используются уравнения
E.207) — E.209), множители, появляющиеся перед интегралами,
должны быть учтены в оценке верхних пределов даже для ко-
конечных увеличений.
Для электростатических линз ситуация не так проста, но все
же можно установить верхний предел для коэффициента акси-
аксиальной хроматической аберрации [9]. Начнем с уравнения
E.194) и перепишем его, используя уравнения D.47), D.50) и
D.51) и интегрируя по частям, в следующем виде:
= -2*$ {[U(zo) - U0]/[U(z) -
E.221)
Это выражение аналогично уравнению E.217). Так как а"/а
всегда отрицательно и о всегда положительно, а' — монотонно
убывающая функция г. Известно также, что a(z0) =a(zi) =0.
306
Теория аберраций
Таким образом, a(z) должна иметь максимальное значение
где-то между z0 и ги Очевидно, что величина, дифференциал
которой появляется в подынтегральном выражении уравнения
E.221), также имеет максимум в некоторой точке zm между zo
и Zi. Так как a' (zt) <о' (г) <о' (г0), можно записать, что
Соо=2 jV(z)d<a(z) {[U(Zo) — U0]l[U(z) — £/0]2}1/2> +
+ 2Z{o'(z)d<a(z){[U(Zo) -U0]/[U(z) - £/0]2}1/2><
гт
< 2а' (г„) <а (zm) {[U (z0) — U0]/[U (zm) — UQf) '/2 - a (z0) > —
-2o'(zi)io(zm){[U{zo) - U0]/[U(zm) - G0]2}1/2 -
-o(zt){[U{zo) - U0]/[U(zt) - f/0]2}1/2>. E.222)
Известно, что a(z0) =o(Zi) =0. Учитывая также уравнения
D.53), D.54) и E.94) и используя соотношения h(zm)<hmsx и
t/(zm)^£/min> где /imax— максимальное значение h (z) и Umin —
минимальное значение U{z) в интервале между объектом и
изображением, в конце концов получим
Ссо < 2о(z J {[£/(zo)- [/„]/[(/ (z J -£/.]«}!/« [a' (zo)-a' (Z/)] <
ется
E.223)
В случае бесконечного увеличения верхний предел оценива-
оценивая как
CcoJfi<2{[U(zo) — i/o]/[t/mm — f/0]}3/4, E.224)
где fi — фокусное расстояние в пространстве объектов.
Замечания, касающиеся магнитного случая, также справед-
справедливы и здесь. Как можно видеть из уравиений E.223) и E.224),
предельное значение коэффициента аксиальной хроматической
аберрации, связанного с объектом, увеличивается с ростом
абсолютной величины М, а отношение потенциала изображе-
изображение — объект становится меньше. Значения Cco/hmzx (для ко-
конечных значений М) и Cco°o/f\ (для бесконечного увеличения)
даны в табл. 4 для некоторых характеристических значений уве-
увеличений и отношения потенциала изображение — объект. Таб-
Таблица охватывает ускоряющие линзы с минимальным потенциа-
потенциалом в пространстве объектов, замедляющие линзы с минималь-
минимальным потенциалом в пространстве изображений и одиночные
лиизы с минимальным потенциалом с обеих сторон (средний
электрод имеет более высокую абсолютную величину потен-
потенциала).
307
Глава 5
Таблица 4
Верхние пределы коэффициента аксиальной хроматической аберрации
для электростатических линз, связанного с объектом и отиесеииого
к максимальному смещению hmax и фокусному расстоянию f\
в пространстве объектов для конечного и бесконечного увеличений М
соответственно
t/min=£/B,-) (за-
(замедляющие линзы)
£/mln=t/(Zo) =
=U(zi) (одиноч-
(одиночные лиизы)
Umin=U(zo) (ус-
(ускоряющие линзы)
C/(Z;) — С/0
</<*„>-</.
0,1
0,2
0,5
1,0
2,0
5,0
10,0
0.3
77,91
40,01
16,69
8,67
7,61
6,46
5,75
1.0
31,24
16,68
7,36
4,00
3,68
3,34
3,12
[Af I
2,0
21,24
11,68
5,36
3,00
2,84
2,67
2,56
4.0
16,24
9,18
4,36
2,50
2,42
2,33
2,28
СО
11,24
6,68
3,36
2,00
2,00
2,00
2,00
Как видно, хроматическая аберрация особенно сказывается
на замедляющих линзах даже при больших увеличениях. Для
одиночных линз зависимость коэффициента аберрации от уве-
увеличения аналогична зависимости в магнитных линзах (см.
уравнение E.218). Если абсолютная величина потенциала внут-
внутри одиночной линзы больше, чем в пространстве объектов и
изображений, то верхний предел ровно вдвое больше, чем для
магнитных линз. Когда абсолютная величина потенциала ниже
внутри одиночной лиизы, чем с обеих сторон, верхний предел
становится даже выше.
Однако это не обязательно означает, что хроматическая
аберрация электростатических линз должна всегда быть выше,
чем хроматическая аберрация магнитных линз. Существуют по
крайней мере два подтверждения этого:
1. Сравнение верхних пределов только обнаруживает тен-
тенденцию. С помощью тщательного конструирования коэффициент
аберрации может быть сделан значительно ниже, чем теорети-
теоретический верхний предел. Мы подходим к теоретическому преде-
пределу, только когда отношение потенциала максимум — минимум
становится очень близким к единице.
2. Самый нижний верхний предел для данного увеличения
появляется для сильно ускоряющих линз с Umin=U(z0). В слу-
случае бесконечного увеличения верхний предел такой же, как и
для одиночных линз, но для низких увеличений он может быть
еще ниже и даже ниже, чем для магнитных линз. (К сожалению,
308
Теория аберраций
степень lU отношения потенциалов требует большой величины
самого этого отношения, чтобы обеспечить существенное умень-
уменьшение верхнего предела.)
5.3.2. Хроматическая аберрация увеличения
Если только Сг — ненулевой коэффициент в уравнениях
<5.186) и E.187), то имеем
8X(zt) = — MC2Xo&.U/[U(zo) — Uo],
E.225)
8Y{zi)=— MC2YoAU/[U{zo) —£/„],
что имеет большое сходство со случаем дисторсии (уравнение
E.156)): аберрация не зависит ни от Хо', ни от Уо'; 8X(zt) про-
пропорционально Хо и 6УB() пропорционально Уо. Это означает
сдвиг в радиальном направлении. Однако изображение в этом
случае не стигматическое, потому что величина At/ меняется
в диапазоне от нуля до AU0/2. Таким образом, для данной
точки объекта точка изображения смещена вдоль радиальной
линии иа расстояние
bn=MC2(Xo*+Yo2)V2AU0/{2[U(zo) — Uo]}. E.226)
Так как сдвиг в радиальном направлении означает измене-
изменение увеличения, эта аберрация называется хроматической абер-
аберрацией увеличения.
5.3.3. Анизотропная хроматическая аберрация
Оставим теперь только коэффициент С3. После этого урав-
уравнения E.186) и E.187) дают
zt) =MCzYoAUI[U(zo) — Uo],
E.227)
) — Uo].
Эти выражения очень похожи на те, что мы имели в случае
анизотропной дисторсии (уравнение E.167)): аберрация не за-
зависит ни от Хо', ни от Yo', bX(Zi) пропорционально Yo, 6Y(zt)
пропорционально Хо. Это означает сдвиг в азимутальном на-
направлении. Изображение нестигматическое; для данной точки
предмета точка изображения смещена вдоль дуги на расстояние
) —Uo]}. E.228)
Так как коэффициент С3 отличается от нуля только при на-
наличии магнитных полей, эта аберрация называется анизотроп-
анизотропной хроматической аберрацией (см. разд. 5.2.6).
309
Глава 5
Уравнения E.21) и E.190) дают, что в чисто магнитных
полях
E.229)
т. е. коэффициент анизотропной хроматической аберрации ра-
равен половине поворота изображения. Следовательно, эта абер-
аберрация отсутствует в магнитных линзах, ие вызывающих враще-
вращения изображения.
5.3.4. Магнитная хроматическая аберрация
Рассмотрим теперь хроматическую аберрацию, вызванную
флуктуациями магнитной индукции. Для простоты предполо-
предположим, что U(z) =const (чисто магнитное поле). Тогда уравнения
E.184) и E.185) могут быть записаны в следующем виде:
E.230)
E.231)
где
QB*(z)h*
0)tei
dz, E.233)
C3m = S QB(г) [-2Qm0{U — Uo)n<\-U*dzl2. E.234)
zo
В уравнениях E.230) и E.231) Bmax — максимальное значение
аксиальной магнитной индукции и АВтзх — ее флуктуация.
Тогда
AB = B{z)ABmax/Bmax, E.235)
что учитывалось в уравнениях E.232)—E.234).
Из сравнения уравнений E.192) и E.232) для чисто магнит-
магнитных полей видно, что
&„==—2СЬ E.236)
таким образом, радиус диска суммарной аксиальной хромати-
хроматической аберрации для .магнитных полей может быть определен
как
310
Теория аберраций
8га= \М | С со tg -io{AU0/[2 (U — (/„) rei] — АВтях/Втах},
E.237)
где использованы уравнения E.197) и E.198) и учтено, что
АВтах обычно определяется как полная флуктуация максималь-
максимальной аксиальной индукции. Аналогичные выражения могут быть
записаны также для двух других коэффициентов хроматической
аберрации.
5.4. Асимптотические аберрации
Реальные коэффициенты геометрической и хроматической
аберраций определяются как определенные интегралы, взятые
между координатами реальных объекта и изображения. Выра-
Выражения, выведенные в предыдущих разделах этой главы, полно-
полностью основаны на лучах g(z) и h(z) с граничными условиями
уравнения E.42). Кроме того, по определению Л(г;)=0.
Однако известно, что если линза имеет физические границы,
то можно определить другой набор оптических характеристик.
В разд. 4.6 мы ввели асимптотические величины и будем исхо-
исходить из того, что читатель знаком с содержанием и обозначе-
обозначениями этого раздела (включая также и разд. 4.6.1). Поэтому
сразу же перейдем к последующему обсуждению.
Очевидно, что если существуют асимптотические величины
первого порядка, то также могут быть определены асимптотиче-
асимптотические аберрации. В действительности единственное различие
между ними и реальными аберрациями заключается в том, что
сейчас нас интересует поведение асимптот к удаленным лучам,
а не поведение самих удаленных лучей.
Асимптотическая аберрация — это расстояние между точкой,
в которой выходящая асимптота к удаленному лучу пересекает
асимптотическую плотность изображения, и точкой, в которой
выходящая асимптота к параксиальному лучу пересекает ту же
плоскость. Падающие асимптоты к удаленным лучам являются
теми же, что и для соответствующих параксиальных лучей.
Объект и изображение могут оба находиться в поле линзы.
Конечно, также можно определить асимптотическую аберрацию
в обратном порядке, начиная с плоскости изображения и опре-
определяя аберрацию в асимптотической плоскости объекта.
Соответственно характеристическая функция S* (уравнение
E.39)) теперь состоит из трех частей: одна — для падающей
асимптоты, другая — для главного луча внутри линзы и еще
одна — для выходящей асимптоты. Также очевидно, что если
главный луч ищется в виде
X(z)=XoG(z)+X'oH(z), E.238)
Y(z) = YoG(z)+Y'oH(z), E.239)
311
Глава 5
то начальные условия для лучей G(z) и Я (г) необходимо опре-
определить на входной плоскости линзы z=a, а не плоскости объ-
объекта. Имеем
G(a) = l, Н{а)=а-го\
E.240)
G'(a)=0, H'(a) = l,
где zo* — осевая координата асимптотической плоскости объек-
объекта. Эти начальные условия аналогичны начальным условиям,
задаваемым уравнением E.42) с тем отличием, что хотя на-
начальное значение Н определяется при z = a, очевидно, что оно
отлично от нуля. Уравнение E.45) заменяется на
Хо = X (а) — (а - zo*) X' (а), Х'о = Х'{а),
E.241)
Fo=F(a) — (a — Zo*)Y(a), Y'0=Y'(a).
Необходимо также помнить, что соотношение Гельмгольца —
Лагранжа D.65) необходимо заменить уравнением D.76) в
асимптотическом случае. Следовательно, уравнение E.67) не-
необходимо заменить на
GH'-HG'^{[U(a) - U0]J[U(z) - U0]}1'2. E.242)
Можно показать [148, 149], что с этими изменениями коэф-
коэффициенты геометрической и хроматической аберраций отлича-
отличаются от их реальных значений, только если
1) интегралы от плоскости объекта до плоскости изображе-
изображения заменяются интегралами вдоль поля линзы (от z = a до
г = Ь)\
2) постоянные, определенные в точках объекта и изображе-
изображения, заменяются на постоянные, определенные соответственно
при z — a и z = b;
3) лучи g и h заменяются на лучи G и Н соответственно.
Таким образом, все формулы, полученные в предыдущих раз-
разделах этой главы, можно использовать непосредственно при за-
завершении указанных преобразований. Следует быть особенно
внимательным к обратным и прямым выражениям, так же как
и к соотношениям между коэффициентами аберрации, связан-
связанными с объектом и изображением. Например, уравнения E.83),
E.105) и E.109) для сферической аберрации имеют теперь сле-
следующий вид:
Csi = CsoM**{[U(b) - С/„]/[С/(a) - U0]}V\ E.243)
С,/(м.-о) = — 4{-2Qmo[U(b) - f/0]}
312
Теория аберраций
X [Л F) ]-« S
а
CsooO=—4{—2Qm0[U(a) — £/0]}-1/2Х
! E.245)
Соответствующие уравнения E.201), E.211) и E.214) для ак-
аксиальной хроматической аберрации следует заменить на
С/о]/[С/(а) — UO]}3'2, E.246)
Сс/(м.-о) = {[С/F) - С/о]/[С/(а) - С/о]}VяX
JS№(z)]dz, E.247)
Ссо =о = [r'i(а)]-21Fc{n(z)]dz E.248)
соответственно. (Следовало бы записывать эти коэффициенты
со звездочкой, чтобы показать, что они являются асимптотиче-
асимптотическими коэффициентами. Тем не менее такое обозначение не яв-
является общепринятым и даже нет необходимости делать такое
различие, поскольку в большинстве случаев используются толь-
только асимптотические коэффициенты.)
С помощью интегрирования по частям можно получить мно-
множество разных видов коэффициентов асимптотической абер-
аберрации.
5.4.1. Зависимость коэффициентов
асимптотической аберрации от увеличения
Известно, что все коэффициенты реальной аберрации сильно
зависят от увеличения, так как увеличение оказывает непосред-
непосредственное влияние на положения объекта и изображения, кото-
которые появляются в начальных условиях и пределах интегралов
аберраций. Эта зависимость является достаточно сложной и в
общем случае для каждого значения увеличения интеграл абер-
аберрации следует вычислять отдельно.
В случае асимптотических аберраций пределы интегралов
аберраций являются фиксированными. Большинство интегралов
(кроме А7 и С3) по-прежнему зависят от увеличения, однако
через начальное условие E.240) для луча Я (г). Тем не менее
теперь ситуация намного проще. Это обусловлено тем [143], что
коэффициенты аберрации могут быть представлены как конеч-
313
Глава 5
ные полиномы величины, обратной увеличению. Покажем это
на примере сферической и хроматической аберраций.
Представим луч Я (г) как линейную комбинацию двух глав-
главных лучей n(z) и г2(г) (рис. 44 и 45) в виде уравнений D.55).
Сразу же отметим, что оба главных луча не зависят от положе-
положения объекта и изображения. Коэффициенты Ci и с2 выбираются
таким образом, чтобы уравнение D.55) удовлетворяло началь-
начальным условиям E.240). Таким образом, имеем
С, =
E.249)
c2=[(a-zo*)r\(a)-rl{a)]Jr2(a)r\(a) =
= ~rl(b)/[r\(a)r2(a)M*],
где при преобразовании с2 были использованы уравнение D.58)
и некоторые положения элементарной геометрии. Заметим, что
тот же результат может быть получен непосредственно из урав-
уравнений D.72), D.77), D.84) и D.86). Подставляя Ci и с2 в урав-
уравнение D.55), получим
Н(г)= [гг(г)-лр$$г,(г)]1г'г(а)- E-250)
Этот луч будет использоваться при выводе коэффициента абер-
аберрации в виде полиномов.
5.4.1.1. Полиномиальное выражение для коэффициента
асимптотической сферической аберрации. Можно начать с лю-
любой формы записи коэффициента сферической аберрации. Вы-
Выберем ее в виде уравнения E.121), которое для асимптотиче-
асимптотического случая может быть записано как
Cso= I [P(z)H* + Q(z)H3H'+R{z)H*H'2]dz, E.251)
51/'* (z) QB'*(z) , 3Q*B*(z)
241U (г)-{/„]* meltf(z)-tfe]+ 8m20 [U (г)- Uo]*
, 3QB (г) В' (г) U' (z) 35QB* (г) U'2 (z)
mo[U(z)-Uo]*
UU"{Z)
1
E.253)
R (z) = {[U (z) - Uty[U (a) - Ue]}4* x
mB[U (z)-Uo] - 2[U (z)-
(Следует отличать Q(z) от заряда Q.)
314
Теория аберраций
Подставим теперь уравнение E.250) и его производную в
уравнение E.251). После некоторых элементарных алгебраиче-
алгебраических преобразований получим коэффициент асимптотической
сферической аберрации в виде полинома четвертой степени от
величины, обратной асимптотическому увеличению:
Cso = Cso0 + Csol/M*
E.255)
где коэффициенты являются функциями распределений поля и
граничных условий и представляются в виде
C.oo=[ri'(a)]-*\[P(z)rl*+Q(z)rl>rl'+R(z)rl*rl'']dz,
E.256)
С- " ~ Ж |[4Р U *> + Q (Z) W> + ГК) +
? , E.257)
csoS=-
г) (гАП + ЛгА) +
2*)]dz, E.258)
, E.259)
Csot=
=\ '\{blA' [[P(z)rl + Q(z)rlr2 + R(z)rlr2*}dz. E.260)
Эти коэффициенты не зависят от положения объекта, следо-
следовательно, они представляют коэффициент сферической аберра-
аберрации в достаточно общем виде. Знание этих коэффициентов дает
полную информацию о коэффициенте сферической аберрации
для любого заданного увеличения М*. Вычисление является
тривиальным, так как увеличение появляется только в уравне-
уравнении E.255). Как известно, это неверно для случая коэффициен-
коэффициента реальной аберрации: обычно для каждого значения увеличе-
увеличения необходимо вычислять интеграл аберрации снова и снова.
Только в случае ньютоновских полей (см. разд. 4.6) можно ис-
использовать уравнение E.255) для вычисления коэффициента
реальной сферической аберрации.
315
Глава 5
Коэффициенты Csok (k=0, 1, 2, 3, 4) могут быть рассчитаны
не только из уравнений E.256)—E.260), но также из уравне-
уравнения E.251) для пяти различных значений увеличения. Подстав-
Подставляя Cso для каждого значения М* в уравнение E.255),получаем
систему пяти линейных алгебраических уравнений, из кото-
которой легко могут быть найдены коэффициенты. Однако исполь-
используемые увеличения должны подбираться достаточно аккуратно,
с тем чтобы избежать вычислительных неустойчивостей, появ-
появляющихся в случае, когда эти величины слишком близки друг
к другу. В общем случае следует предпочесть прямое решение
уравнений E.256) —E.260).
Уравнения E.243) и E.255) непосредственно дают коэффи-
коэффициент асимптотической сферической аберрации, связанной с
изображением, в виде
Csi={[U(b) - U0]/[U(a) -U0]y/2(Cso0M** +
+ CsolM*3 + Cso2M*2 + Cso3M* + Csoi). E.261)
Уравнения E.79) и E.255) дают радиус диска асимптотиче-
асимптотической сферической аберрации в плоскости изображения в виде
6г.,= {M*CSoo + CSol + Cso2fM* + Cso3/M*2 + Cso4lM*5)tgs ■Yo*.
E.262)
Это величина, которая должна быть настолько малой, насколь-
насколько это возможно, так как всегда желательно иметь малый раз-
размер пятна. Абсолютное значение величины в скобках стремится
к бесконечности как при нулевом, так и при бесконечном уве-
увеличениях. (Из разд. 5.2.1.1 известно, что для бесконечного уве-
увеличения диск сферической аберрации является бесконечно боль-
большим в плоскости изображения. Для нулевого увеличения он
имеет конечный размер, но в этом случае 1уо* = 0, так что рас-
расхождений нет.) Таким образом, он должен иметь минимальную
величину при некотором характерном значении увеличения. Это
следует также из исследований, приведенных в конце разд.
5.2.1.1: если М слишком мало, то коэффициент аберрации ста-
становится большим, а слишком большие увеличения непосредст-
непосредственно приводят к возрастанию радиуса диска. Оптимальное
увеличение является сложной функцией коэффициентов СЗОк,
так как первая производная функции в скобках дает уравнение
четвертого порядка для М*. Оно обычно лежит между —1 и
—10. Выбрав это оптимальное значение, можно использовать
данную линзу при минимально возможной сферической абер-
аберрации.
Из уравнений E.255) и E.261) сразу же следует, что
CSoo = Csoao, E.263)
316
Теория аберраций
- U0]J[U(b)
t^0). E.264)
Таким образом, эти два коэффициента непосредственно связа-
связаны с коэффициентами аберрации для бесконечного и нулевого
увеличений соответственно. Также очевидно, что уравнения
E.106) и E.110) верны и для асимптотических увеличений.
Уравнение E.263) можно также вывести из уравнений E.245),
E.251) и E.256), если соответствующим образом использовать
функцию Fs[ri(z)]. Для того чтобы получить уравнение E.264)
из соответствующих уравнений E.244), E.251) и E.260), необ-
необходимо также учесть уравнения D.72), D.73) и D.76).
Очевидно, что если все интегралы в уравнениях E.256) —
E.260) имеют положительные значения, то каждый член в урав-
уравнении E.255) положителен и значение Cs0 увеличивается по
мере того, как абсолютная величина М уменьшается. Теперь
уже ясно, что это совсем не обязательно, так как интегралы
могут быть отрицательными (даже если начать с уравнения
E.138)). Положительные значения интегралов являются доста-
достаточным условием для монотонного изменения коэффициента
аберрации, вызванного изменением увеличения.
Существует другая важная
особенность коэффициентов
асимптотической аберрации, о
которой следовало бы упомя-
упомянуть. Рассмотрим произволь-
произвольный осевой электростатиче-
электростатический потенциал или распреде-
распределение магнитной индукции
(сплошная кривая на рис. 75).
Бели теперь обратить это рас-
распределение (штриховая кривая
на том же рисунке), тогда, очевидно, все оптические параметры
также обратятся. Это означает, что величины исходного рас-
распределения в пространстве объектов будут эквивалентны соот-
соответствующим величинам в пространстве изображений обращен-
обращенного •распределения « наоборот. Увеличение леревернутой линзы
равно обратному увеличению исходной линзы. Фактически этот
случай был рассмотрен в разд. 5.2.1, когда анализировались
«прямой» и «обратный» методы вычисления коэффициентов
аберрации. Если для параметров леревернутой линзы использо-
использовать индекс «rev», то очевидно, что
Рис. 75. Перевернутое распределение
поля.
С so rev(l/M») —
Csi rev(l/M *) = (
E.265)
E.266)
317
Глава 5
Как следствие этих выражений коэффициент перевернутой лин-
линзы в пространстве объектов для бесконечного увеличения равен
коэффициенту первоначальной линзы в пространстве изображе-
изображений для нулевого увеличения и обратно.
Запишем теперь коэффициент сферической аберрации в про-
пространстве объектов для перевернутой линзы с увеличением
1/М*, используя уравнение E.255). Имеем
С so rev(l/M*) = Cso 0 rev + Cso i revM* + Cso 2 tevM*2 +
+ Сto з revM*3 + Cso 4 revM*4. E.267)
Сравнивая это выражение с уравнением E.261) и используя
уравнение E.265), можно видеть, что асимптотические коэффи-
коэффициенты перевернутой линзы связаны с коэффициентами исход-
исходной линзы посредством соотношения
— U0]/[U(a) —
(k=0, 1, 2, 3, 4), E.268)
где а и b — граничные координаты в пространстве объектов и в
пространстве изображений исходной линзы соответственно.
Это соотношение дает простой способ сравнения ускоряю-
ускоряющих и замедляющих электростатических линз. Очевидно, что
перевернутой по отношению к ускоряющей линзе является за-
замедляющая линза. Уравнение E.268) показывает для £/(&)>
>£/(а), что коэффициент сферической аберрации замедляющей
линзы обычно больше, чем тот же коэффициент ускоряющей
линзы. Кроме того, было показано (разд. 5.3.1.2), что хромати-
хроматическая аберрация замедляющих линз также является большой.
В свою очередь фокусное расстояние в пространстве объектов
замедляющей линзы равно фокусному расстоянию в простран-
пространстве изображения перевернутой линзы, но оно имеет большее
значение, чем фокусное расстояние ускоряющей линзы в прост-
пространстве объектов согласно уравнению D.76). (Таким образом,
коэффициенты добротности Cso/fi и Cco/fi (см. разд. 5.7.4) мо-
могут быть как лучше, так и хуже для замедляющих линз по
сравнению с ускоряющими).
Здесь необходимо сделать предостережение. Коэффициент
аберрации сильно зависит от увеличения. Для больших увели-
увеличений доминирующим членом в уравнении E.255) является Csoo;
для малых увеличений — Csoa- Если Cso4>Csoo, to Csoo rev>Csoo
и Cso4 rev может быть намного меньше, чем CSon> даже если
U(b)>U(а). Таким образом, коэффициент аберрации перевер-
перевернутой линзы больше, чем исходной линзы, только для больших
увеличений. С другой стороны, если Cs04<CSoo, то CSO4rev>CSo4
и Cso0 rev может быть много меньше, чем Cso0 Это означает, что
318
Теория аберраций
коэффициент сферической аберрации перевернутой линзы боль-
больше, чем исходной линзы, только для малых увеличений.
Также следует быть осторожным при определении перевер-
перевернутой линзы. Это предполагает полное обращение всего распре-
распределения потенциала, т. е. перестановку электродов и их напря-
напряжений. Перестановки только одних напряжений без изменения
положений электродов достаточно лишь в том случае, если рас-
расположение электродов симметрично относительно некоторой
средней плоскости.
Очевидно, что симметричная линза является специальным
случаем, означающим тот факт, что перевернутая линза совпа-
совпадает с исходной линзой. Тогда уравнение E.268) непосредст-
непосредственно дает
WoO==^so4, Csol = WO3. E.269)
Эти соотношения следуют также из симметрии уравнений
E.256) — E.260). Очевидно, для симметричной линзы CSOco =
= CSi(M=o), что согласуется с уравнениями E.263), E.264) и
E 269).
5.4.12. Полиномиальное выражение для коэффициента
асимптотической аксиальной хроматической аберрации. Урав-
Уравнение E.194) представляет собой простейший вид коэффициен-
коэффициента аксиальной хроматической аберрации, однако начнем с урав-
уравнения E.192), которое чаще используется на практике Для
асимптотического случая оно может быть записано в виде
С so = \[D (г) № + Е (г) HH'\ dz, E.270)
а
где
D(z) = {[U(a)-U0]/[U(z)-U0]}4*x
QBHz) \ ,, 27n
4[(У(г)-[/0] 8mo[£/(г)-£/„]( • W-"M
lu%JZlUo] • E-272)
Подставим уравнение E.250) и его производную в уравне-
ние E.270). Получим коэффициент асимптотической аксиальной
хроматической аберрации в виде полинома второй степени по
обратному асимптотическому увеличению:
С со = Ссо0 + CCOJM * + ССО2/М*2, E.273)
где коэффициенты зависят от распределения поля и граничных
условий
319
Глава 5
a
ft
+ E(z)rlr\]dz, E.274)
:<°l = , \t'< M» f t2D <z> r^ + E & (r^ + r'S*K dz> E-275)
r2 (a) in (a)\ j
r2r;]d2. E.276)
Как и в случае асимптотической сферической аберрации,
приведенные выше коэффициенты не зависят от положения
•объекта, таким образом, они представляют коэффициент акси-
аксиальной хроматической аберрации в общем виде. Знание этих
величин обеспечивает полную информацию о коэффициенте
асимптотической аксиальной хроматической аберрации для лю-
любого увеличения. Только в случае ньютоновских полей (см.
разд. 4.6) можно использовать уравнение E.273) для получения
коэффициента реальной хроматической аберрации.
Коэффициенты Ccok (&=0, 1, 2) могут быть вычислены не
только из уравнений E.274) — E.276), но также из расчета ин-
интеграла в уравнении E.270) для трех различных значений уве-
увеличения. Подставляя Ссо для каждого значения М* в уравнение
E.273), получим систему трех линейных алгебраических урав-
уравнений, из которых легко найти коэффициенты. Исходные значе-
значения увеличения тем не менее должны выбираться чрезвычайно
тщательно, с тем чтобы избежать вычислительных неустойчиво-
■стей, возникающих в случае, когда эти значения расположены
•близко друг от друга. В общем случае предпочтительно непо-
непосредственное вычисление интегралов в уравнениях E.274) —
E.276).
Коэффициент асимптотической аксиальной хроматической
аберрации, связанный с изображением, получаем из уравнений
E.246) и E.273) в следующем виде:
€cl={[U(b)—Uo]l[U(a)—Uo]}V*x
X (СсооМ*2 + CcoiM* + Ссо2). E.277)
Радиус диска асимптотической хроматической аберрации в
плоскости изображения задается уравнениями E.199) и E.273)
как
2lM*) X
Xtgto*AU0l{2[U(a)—U0]}. E.278)
Желательно минимизировать эту величину, с тем чтобы иметь
наименьший возможный размер пятна. Абсолютное значение
320
Теория аберраций
величины в круглых скобках стремится к бесконечности как
при нулевом, так и при бесконечном увеличении, таким обра-
образом, она минимальна при некотором характерном увеличении.
Это также следует из рассмотрения, приведенного в конце
разд. 5.3.1.1. Оптимальное увеличение в этом случае дается
простым выражением
E.279)
которое получается, если приравнять нулю первую производную
по М* функции в скобках. Его значение обычно близко к —1.
Выбрав оптимальное значение, можно работать с данной линзой
при наименьшей из возможных хроматической аберрации.
Из уравнений E.273) и E.277) следует, что
Ссоо = ССОоо, E.280)
- U0]/[U(b) — Uo]}3/2Cci(M*=o). E.281)
Таким образом, эти два коэффициента непосредственно свя-
связаны с коэффициентами аберрации для бесконечного и нулевого
увеличений соответственно. Уравнения E.212) и E.215) спра-
справедливы также для асимптотических увеличений. Уравнение
E.280) также может быть выведено из уравнений E.248),
E.270) и E.274). Для того чтобы вывести уравнение E.281) из
соответствующих уравнений E.247), E.270) и E.276), также
необходимо использовать уравнения D.72), D.73) и D.76).
Если все интегралы в уравнениях E.274) — E.276) положи-
положительны, то каждый член в уравнении E.273) положителен и
Сею увеличивается по мере уменьшения абсолютной величи-
величины М. Положительность интегралов является достаточным ус-
условием для монотонного изменения коэффициента аберрации с
увеличением.
Для перевернутой линзы, как и в случае сферической абер-
аберрации, имеем
С со rev(l/M*) = Ссцм*), E.282)
Cci rev(l/M») = Cco(M*). E.283)
Как следствие этих выражений коэффициент перевернутой лин-
линзы в пространстве объектов для бесконечного увеличения ра-
равен коэффициенту исходной линзы в пространстве изображений
для нулевого увеличения и обратно.
321
Глава 5
Если записать коэффициент хроматической аберрации для
перевернутой линзы в пространстве объектов с увеличением
\/М*, то, используя уравнение E.273), имеем
Ceo rev(l/M*) = Cco 0 rev + Cco I revAf* + CC0 2 ге\'Л1*2. E.284)
Сравнивая это выражение с уравнением E.277) и используя
уравнение E.282), можно видеть, что асимптотические коэффи-
коэффициенты перевернутой линзы связаны с коэффициентами исход-
исходной линзы следующим соотношением:
- U0]/[U(a) - £
(/2 = 0,1,2), E.285)
где а и Ь — координаты границ исходной линзы в пространстве
объектов и изображений соответственно.
Это соотношение обеспечивает простой способ сравнения
хроматической аберрации ускоряющих и замедляющих элект-
электростатических линз. Уравнение E.285) показывает, что в слу-
случае U(b) >f/(a)- коэффициент хроматической аберрации замед-
замедляющей линзы, как правило, больше, чем тот же коэффициент
для ускоряющей линзы. Это соответствует рассуждениям в
разд. 5.3.1.2 о более высоком верхнем пределе замедляющей
электростатической линзы. Тем не менее, как и в случае сфе-
сферической аберрации, это не исключает возможности существо-
существования замедляющей линзы с малой хроматической аберрацией
при заданном увеличении. Действительно, при больших увели-
увеличениях доминирующим членом в уравнении E.273) является
Ссоо', при малых увеличениях таковым является Ссо2. Если
ССо2^>Ссоо, то CCoorev3>Ccoo и Cco2rev может быть меньше, чем
Ссо2, даже в случае U(b)>U(a). Таким образом, коэффициент
аберрации перевернутой линзы больше того же коэффициента
исходной линзы только в случае больших увеличений. С дру-
другой СТОРОНЫ, еСЛИ Ссг^Ссоо, ТО CCo2rev3>CVo2 И Ccoorev МОЖеТ
быть меньше, чем Ссоо- Это означает, что коэффициент хрома-
хроматической аберрации перевернутой линзы больше, чем исходной
линзы, только в случае малых увеличений.
Напоминаем читателю снова, что перевернутая линза пред-
предполагает полное обращение всего распределения потенциала,
т. е. перестановку электродов и их напряжений. Перестановки
одних только напряжений без изменения положения электродов
достаточно только в том случае, когда расположение электро-
электродов симметрично по отношению к средней плоскости.
В специальном случае симметричных линз уравнение E.285)
дает
Ссо0 = Ссо2, M*0Pt = — 1. E.286)
322
Теория аберраций
Уравнение E.286) следует также из симметрии уравнений
E.274) — E.276). Очевидно, что для симметричной линзы Ссо«>=
= Cc,(m=o), что согласуется с уравнениями E.280), E.281) и
E.286).
Наконец, заметим, что аналогичные действия могут быть
применены для вычисления всех других коэффициентов асимп-
асимптотических аберраций. Все они могут быть выражены максимум
как полиномы третьей степени от обратного асимптотического
увеличения.
5.4.2. Аберрации тонких линз
В приближении тонкой линзы (разд. 4.9) не существует раз-
различия между асимптотическими и реальными параметрами; та-
таким образом, можно рассматривать аберрации тонкой линзы
как частные случаи асимпто-
асимптотических аберраций. Как и
раньше, будем рассматривать
только сферическую и акси-
аксиальную хроматическую абер-
аберрации, но используемые мето-
методы также можно легко рас-
распространить И на Другие виды Рис. 76. К вычислению аберраций
аберрации. Основная идея тонкой линзы,
элементарна: интегралы абер-
аберраций следует выразить таким образом, чтобы они содержали
только траектории, но не содержали их производных, тогда
можно рассматривать только незначительные изменения смеще-
смещения луча внутри линзы и не беспокоиться о резко изменяю-
изменяющихся углах наклона.
5.4.2.1. Сферическая аберрация. Коэффициент сферической
аберрации магнитных линз в виде E.135) —это как раз то, что
нам нужно. Полагая ft = p = const внутри линзы, где р — рас-
расстояние до объекта (рис. 76), и интегрируя по частям, получа-
получаем коэффициент сферической аберрации тонкой магнитной лин-
линзы в виде:
J^l I [ 3mo^-l)re, ~B>t B)] dZ- E-28?)
16mo(t/
Для электростатических линз можно вывести аналогичное
выражение, начиная с уравнения E.132). Существует семь про-
произвольных коэффициентов в электростатических членах этого
выражения, и можно записать семь уравнений, приравняв все
323
Глава 5
члены, содержащие h', нулю. В результате получим следующие
коэффициенты:
/г, = — 16, ki=— 8, £3 = /г4 = — 4,
E.288)
*в = 1, *7 = 0, Й8=—2.
Подставляя эти коэффициенты в уравнение E.132), опять пола-
полагая ft = /? = const внутри линзы и интегрируя по частям, полу-
получим коэффициент сферической аберрации для тонкой электро-
электростатической линзы:
ь
Cso = EpV64) J {[U (z)-UQ]/[U (a)-
Вводя обозначение Cso/p4 = 7 и используя уравнение D.77),
можно видеть, что в обоих случаях
=/,4/A — 4/М + 6/М2 — 4/М3 + 1/М4), E.290)
что эквивалентно полиномиальному выражению четвертой сте-
степени E.255). Из этого выражения следует, что в рассматривае-
рассматриваемом случае связь между коэффициентом сферической аберра-
аберрации и увеличением носит монотонный характер (см. обсужде-
обсуждение после уравнения E.281):
E.291)
Отметим также симметрию уравнения E.290). Таким обра-
образом, уравнение E.269) справедливо для любой тонкой линзы.
Необходимо понимать, что это приближение в действитель-
действительности не предполагает сосредоточения линзы в одной плоскос-
плоскости. Для такой бесконечно тонкой линзы, h' не является непре-
непрерывной функцией. Это приводит к тому, что h" ведет себя как
дельта-функция. Из уравнений D.49) и D.50) следует, что T(z)
также должна вести себя как дельта-функция. В интегралах
E.287) и E.289) есть члены, пропорциональные T2(z), но
дельта-функция не интегрируется в квадрате [150]. Это озна-
означает, что для бесконечно тонкой линзы коэффициент сфериче-
сферической аберрации является бесконечно большим, если фокусное
расстояние конечно. Чтобы обойти эту трудность, будем рас-
рассматривать реальные распределения поля и интегрировать их
по конечной длине линзы.
324
Теория аберраций
Фактический вид функции / зависит от линзы. Можно свя-
связать эту функцию с упрощенным решением уравнения паракси-
параксиальных лучей и выразить ее как комбинацию различных поле-
полевых интегралов и фокусного расстояния. Это легко может быть
сделано для магнитных линз [150], но такая же методика воз-
возможна и для электростатических линз. В итоге зависимость ко-
коэффициента аберрации от фокусного расстояния может ока-
оказаться более сложной, чем это следует из уравнения E.290).
5.4.2.2. Аксиальная хроматическая аберрация. Вначале вы-
выразим коэффициент аксиальной хроматической аберрации в ви-
виде E.194). Полагая опять h=p = const внутри линзы и исполь-
используя уравнение D.77), можно написать
Ссо=р2/=/,2A — l/Af)V,=ftV(l -2/M+l/M2), E.292)
где
X\{U(z)-U0\*
Уравнение E.292) эквивалентно полиномиальному выражению
второй степени E.273). Связь между коэффициентом хромати-
хроматической аберрации и увеличением в этом случае также носит мо-
монотонный характер:
Ссо1Ссооо= A — ММJ. E.294)
В силу симметрии уравнения E.292) уравнение E.286) спра-
справедливо для всех тонких линз.
Уравнение E.293) легко может быть связано с фокусным
расстоянием тонкой линзы. Для тонких магнитных линз урав-
уравнения D.51), D.77), D.117), E.292) и E.293) дают
MM) =f(l - \/М)\ E.295)
Коэффициент хроматической аберрации для тонких магнитных
линз зависит от магнитного поля только через фокусное рас-
расстояние. Сравнивая уравнение E.295) с E.218) и учитывая, что
в этом случае h(zm)=p, можно видеть, что коэффициент хрома-
хроматической аберрации тонких магнитных линз равен верхнему пре-
пределу хроматической аберрации. Это обстоятельство делает
весьма полезным приближение тонкой линзы в рассматривае-
рассматриваемом случае.
325
Глава 5
В случае тонких электростатических линз из уравнений
D.51), D.77), D.117), E.292) и E.293) получим, что
ССо = 2р25 {[С/(а) - U0]/[U(z) -
<2p{[U{a)-Uo]l[U(b)-U0]}V*X
X{[U(a) - U0]/[Umin—U0]y/2(l — l/M), E.296)
где f/min — минимальное значение потенциала. Сравнение с урав-
уравнением E.223) показывает, что верхний предел хроматической
аберрации тонкой линзы отличен от предела для толстой линзы
(пределы равны только для одиночных линз с Umm=U(a) =
= U(b)). Сравнение с данными табл. 4 показывает тем не менее,
что на практике верхний предел хроматической аберрации тон-
тонких линз, связанный с максимальным значением смещения (для
конечных увеличений) или с фокусным расстоянием в прост-
пространстве объектов (для бесконечных увеличений), значительно
меньше, чем для толстых линз. В любом случае между верх-
верхним пределом хроматической аберрации и фокусным расстоя-
расстоянием существует линейная зависимость.
5.5. Аберрации систем линз
В разд. 4.8.1 был введен матричный формализм для описа-
описания систем линз. Такой же подход удобен для расчета аберра-
аберраций систем линз через коэффициенты аберрации отдельных эле-
элементов системы. Окончательный вид матриц получается доста-
достаточно сложным. Причем в общем случае [151] выражение для
любого конкретного коэффициента аберрации системы линз со-
содержит не только соответствующие коэффициенты отдельных
линз, а может содержать весь набор их коэффициентов аберра-
аберраций. Единственным исключением являются аксиальные аберра-
аберрации, которые зависят только от аксиальных коэффициентов
аберраций отдельных линз. Тем не менее «смешивание» сфери-
сферической и аксиальной хроматической аберраций также не явля-
является простой задачей. Мы вернемся к этому вопросу в разд. 5.7.
Преимущества матричного формализма особенно очевидны
для асимптотических аберраций. В этом случае полиномиаль-
полиномиальные коэффициенты аберраций отдельных элементов дают всю
необходимую информацию для расчета аберраций системы.
Здесь требуется построение аберрационных матриц и их после-
последовательное умножение для цепочки элементов. Очень удобно
написать компьютерную программу, которая решала бы эту за-
задачу автоматически. Можно включить даже некоторые элемен-
элементы оптимизации путем циклического формирования матрицы с
последующим умножением для различных значений параметров
326
Теория аберраций
линзы [152]. Такой подход удобен для согласования различных
типов электронных и ионных оптических компонент, т. е. введе-
введение энергетических анализаторов в фокусирующую систему, так
как аберрационные матрицы могут быть построены для систем
с любым типом симметрии.
В дальнейшем для «сложения» сферической и аксиальной
хроматической аберраций будут выведены простые выражения
для систем, состоящих из двух линз. Результаты легко могут
быть обобщены на произвольное число линз.
5.5.1. Добавление сферической аберрации
Начнем с двухлинзовой системы, которая формирует проме-
промежуточное изображение между линзами (рис. 51, а). Для коэф-
коэффициента сферической аберрации первой линзы уравнение E.99)
дает
C/so=-4{-2Q/n0[t/B0) - £/0]}-1/2 lFs[h(z)]dz,
E.297)
где zm — координата промежуточного изображения и функция
Fs определяется уравнением E.97). Аналогично для коэффици-
коэффициента сферической аберрации второй линзы имеем
C"so=-4{-2Qma[U(zm) - ио]}~1'2]Fs[h(z)]dz.
zm
E.298)
Отметим, что h(z) для каждого из этих выражений дает от-
отдельный луч и начальные условия для этих лучей даются урав-
уравнением E.42). В частности, во втором выражении /t'(zm) = l-
Уравнение E.99) можно использовать без изменения для
вычисления коэффициента сферической аберрации Cso системы,
рассматривая ее как одну линзу. С другой стороны, интеграл,
появляющийся в уравнении E.99), можно рассматривать как
сумму двух интегралов: один, берущийся от zo до zm, другой —
от zm до Zi. Эти интегралы появляются соответственно в урав-
уравнениях E.297) и E.298). Таким образом, легко выразить коэф-
коэффициент аберрации составной линзы с помощью коэффициен-
коэффициентов аберрации ее компонент. Тем не менее следует помнить, что
для составной линзы h{z)—единственный луч и h'(zm)=h'm
может принимать любое отрицательное значение. Будем учиты-
учитывать это обстоятельство наряду с выражениями для угловых
увеличений составных линз
- UQ]/[U(zm) - Uo]}^/M', E.299)
327
Глава 5
G" = h't/h'm={[U(zm) - U0]f[U(z,) -~
E.300)
где G' и М' — соответственно угловое увеличение и увеличение
первой линзы, G" и М" — те же величины для второй линзы.
Приведенные выше соотношения следуют из уравнения D.65).
Очевидно, что полное угловое увеличение дается выражением
G = G'G", E.301)
а полное увеличение —
М=М'М". E.302)
Таким образом, коэффициент сферической аберрации системы,
связанный с объектом, может быть выражен как
Cso = C'so+{[[/(zo) - U0]/[U(zm) - £/0]}3/2C"So/M'4 =
= C/so+{[f/Bo) - UQ]/[U(Zi) - UQ]y*C"si/M\
E.303)
Первая часть этого выражения удобна тем, что содержит толь-
только коэффициенты, связанные с объектом, в то время как пре-
преимущество второй записи заключается в том, что здесь появля-
появляется суммарное увеличение. Отсюда, используя уравнение
E.83), можно получить коэффициент сферической аберрации
системы, связанный с изображением, в виде
E.304)
где С si и С" si — коэффициенты сферической аберрации первой
и второй линзы соответственно, причем оба связаны с изобра-
изображением.
Из уравнений E.79) и E.303) получим радиус диска сфери-
сферической аберрации в плоскости изображения:
вг„=Affirm,+ Sr,«, E.305)
где
6rSI1=M'C'sotg34o E.306)
есть радиус диска сферической аберрации первой линзы,
M"C"sotg3Tm E.307)
есть радиус диска сферической аберрации второй линзы и ут —
половинный угол аксептанса второй линзы. Из этого важного
соотношения следует, что радиус диска сферической аберрации
системы есть сумма радиуса диска сферической аберрации пер-
328
Теория аберраций
вой линзы, увеличенного второй линзой, и радиуса диска сфе-
сферической аберрации второй линзы.
Отметим, что если fo>0, то fm<0, бг3п<0, 6rs,-2>0 и из
уравнения E.305) следует положительное значение радиуса
диска для сложной системы.
Возводя в квадрат уравнение E.305) и учитывая знаки раз-
различных компонент, можно видеть, что
+ Frsi2J. E.308)
Важно отметить, что предположение об отсутствии корреляции
между аберрациями двух линз, которое приводит к квадрату
суммы аберрационных дисков [153], неверно и приводит к су-
существенному занижению размера аберрационного диска [154].
Следует помнить, что в уравнении E.303) коэффициенты
компонент системы C'so и C"so (или C"S() являются функциями
увеличений М' и М" соответственно. С другой стороны, увеличе-
увеличение М" зависит от расстояния между линзами. Таким образом,
коэффициент сферической аберрации составной линзы является
сложной функцией параметров системы. Это обстоятельство поз-
позволяет минимизировать суммарный коэффициент аберрации со-
соответствующим выбором этих параметров [155], хотя аберра-
аберрация сложной системы всегда больше, чем аберрации отдельных
компонент. Для тонких линз легко выразить уравнение E.303)
через фокусные расстояния и расстояния между компонентами
[156]. Практический пример сложной линзы с относительно ма-
малой сферической аберрацией — это система, состоящая из силь-
сильной линзы, формирующей мнимое изображение, и следующей
за ней слабой линзы [157].
Представляет интерес в качестве практического примера вы-
вычислить коэффициент аберрации системы, показанной на рис.
60. В этом случае М' бесконечно велико, а М" равно нулю. В со-
соответствии с этим только C'so и C"si являются конечными вели-
величинами, поэтому следует использовать вторую часть уравнения
E.303). Увеличение системы дается уравнением D.174). Имеем
CSO = C'SOOO— (f'ilfKC"si(M^o)/M. E.309)
Видно, что для данного суммарного увеличения М коэффи-
коэффициент сферической аберрации системы может быть сделан очень
близким к коэффициенту первой линзы для бесконечного увели-
увеличения, если выбрать первую линзу очень сильной по сравнению
со второй. Это полезный результат, так как коэффициент сфе-
сферической аберрации обычно имеет наименьшее значение для
бесконечных увеличений. Конечно, уравнение D.174) предпола-
предполагает, что в этом случае увеличение системы достигает больших
значений. Кроме того, так как второй член делится на М, этот
подход реально работает только для относительно больших уве-
329
Глава 5
личений. Как следствие можно пренебречь сферической аберра-
аберрацией второй линзы и наша задача состоит в том, чтобы выбрать
первую линзу с настолько малой сферической аберрацией при
бесконечном увеличении, насколько это возможно.
Легко обобщить полученный выше результат для последова-
последовательности следующих друг за другом линз, просто рассматривая
комбинацию пары линз как одну линзу и последовательно ис-
используя эту процедуру.
Наконец, отметим, что комбинации линз могут быть исполь-
использованы для коррекции и даже устранения неаксиальных гео-
геометрических аберраций [158, 159J.
5.5.2. Добавление аксиальной
хроматической аберрации
Рассмотрим теперь аксиальную хроматическую аберрацию
двухлинзовой системы с промежуточным изображением между
линзами (рис. 51, а). Коэффициент аберрации, связанный с объ-
объектом, определяется уравнением E.206). Для первой линзы
имеем
C'S0=lFc[h(z)]dz, E.310)
zo
где zm — координата промежуточного изображения, а функция
Fc является подынтегральным выражением в уравнении E.194).
Аналогично коэффициент аксиальной хроматической аберрации
второй линзы дается соотношением
C"co={[U(zm) - U0]f[U(zo) - иа]У" \lFc[h(z)]dz.
zm
E.311)
Заметим, что в этом выражении h'(zm) = 1.
Уравнение E.206) может быть использовано без изменения
для вычисления коэффициента аберрации Сс0 системы, если рас-
рассматривать ее как одну линзу. С другой стороны, интеграл, по-
появляющийся в уравнении E.206), может быть рассмотрен как
сумма двух интегралов: один, вычисляемый от zo до гт, а дру-
другой— от zm до 2,-. Эти интегралы появляются в уравнениях
E.310) и E.311) соответственно. Таким образом, можно выра-
выразить коэффициент аберрации составной линзы через коэффи-
коэффициенты аберрации ее компонентов, если учесть, что для состав-
составной линзы h(z) является единственным лучом и h'(zm)=h'm
может принимать любое отрицательное значение. Используя
уравнения E.299) — E.302), получаем коэффициент аксиальной
330
Теория аберраций
хроматической аберрации системы, связанный с объектом,
в следующем виде:
Cco = C'co+{[U(zo) — U0]/[U(zm) — £/0]}3/2С"со/М'2 =
,=С'со+{[С/(го) — U0]/[U(Zi) — U0]}V*C"ciIM2.
E.312)
Используя уравнение E.201), отсюда можно получить коэффи-
коэффициент хроматической аберрации системы, связанный с изобра-
изображением, в виде
CCI={[C/B,) - U0]/[U(zm) - UQ]}^C'ciM + C"ci,
E.313)
где С'ы и C"ci — коэффициенты хроматографической аберрации
первой и второй линзы соответственно, связанные с изображе-
изображением.
Уравнения E.197) и E.312) дают радиус диска хроматиче-
хроматической аберрации в плоскости изображения:
, E.314)
где
) - Uo]} E.315)
есть радиус диска хроматической аберрации первой линзы,
8rci2=M"C"cotgimAU0[{2[U(zm) - и0]} E.316)
есть радиус диска хроматической аберрации второй линзы и
fm—половинный угол аксептанса второй линзы. Таким обра-
образом, радиус диска хроматической аберрации системы является
суммой радиуса диска хроматической аберрации первой линзы.,
увеличенного второй линзой, и радиуса диска хроматической
аберрации второй линзы. Предположение об отсутствии корре-
корреляции между аберрациями двух линз, приводящее к квадрату
суммы радиусов аберрационных дисков, неверно и ведет к су-
существенной переоценке размера аберрационного диска.
Коэффициенты компонентов С'со и С"со (или С"ы) в уравне-
уравнении E.312) являются функциями увеличений М' и М" соответ-
соответственно. Увеличение М", с другой стороны, зависит от расстоя-
расстояния между двумя линзами. Таким образом, коэффициент хро-
хроматической аберрации составной линзы является сложной
функцией параметров системы. Аберрация сложной системы
всегда больше, чем аберрации отдельных компонент.
Заметим, что если fo>0, то fm<0, бгсп<0, бгСB>0 и урав-
уравнение E.314) дает положительное значение для радиуса диска
сложной системы.
331
Глава 5
Рассмотрим коэффициент хроматической аберрации дубле-
дублета, показанного на рис. 60. Так как в этом случае М' бесконечно
велико и М" равно нулю, только C'so и C"si являются конечны-
конечными величинами. Поэтому вторую часть уравнения E.312) необ-
необходимо использовать с увеличением системы, определяемым
уравнением D.174). В результате получим
С со = Ссох — М (/'i//) 3C"ci(M=0). E.317)
Вывод такой же, как и в случае сферической аберрации: если
выбрать первую линзу намного сильнее, чем вторая, то вкладом
второй линзы в хроматическую аберрацию можно пренебречь.
Однако существует различие, которое заключается в том, что
теперь второй член умножается на М, а не делится на него.
Таким образом, эта схема работает для относительно малых
увеличений (в соответствии с уравнением D.174) и тем, о чем
было сказано в конце разд. 4.5), что требует очень большого
отношения напряжений изображение — предмет, но, с другой
стороны, она имеет дополнительное преимущество вследствие
больших рабочих расстояний в пространстве изображений.
Процедура добавления хроматических аберраций может
быть легко обобщена для последовательности линз следующих
одна за другой.
5.6. Другие источники аберраций и коррекция
аберраций
Как было упомянуто во введении к этой главе, аберрации не
ограничиваются геометрическими и хроматическими ошибками
линз. Следует осознавать, что существуют другие независимые
источники дополнительных ошибок.
В разд. 5.2.1.3 также было упомянуто о том, что аберрации
можно компенсировать, используя дополнительные заряды, раз-
разрывы распределений поля, нестационарные поля илн другие ви-
виды симметрии, т. е. некоторые типы дополнительных источников
ошибки могут найти полезное применение для устранения не-
некоторых аберраций. Хотя этот подход обычно приводит к очень
сложным системам, все же сделаем краткий обзор всех упомя-
упомянутых источников.
5.6.1. Дифракция
Известно, что заряженные частицы обладают волновыми
свойствами и их дебройлевская длина волны дается уравнением
A.25). Подставляя импульс p = mv из уравнения B.90) и пред-
332
Теория аберраций
полагая, что частица расположена вблизи оптической оси, по-
получаем для длины волны
к (г) =h{—2Qmo[U(z) - t/0]rei}-1/2. E.318)
Заметим, что длина волны является функцией координаты z,
так как импульс меняется вместе с изменением релятивистского
потенциала. Для электронов подстановка фундаментальных кон-
констант дает
К (г) =12,251 [U(z) — t/0] rei | /2 [A]. E.319)
Для электронов с энергией 15 кэВ длина волны приблизитель-
приблизительно равна 0,1 А, но при более низких энергиях она становится
больше. Очевидно, что для ионов с той же энергией длина вол-
волны значительно меньше. Для Н+ она меньше в 1836,11/2 =
= 42,8 раза и гораздо меньше для более тяжелых ионов.
Как следствие волновой природы частиц возникает явление
дифракции, и если изображение точечного объекта формирует-
формируется идеальной линзой, то оно будет не точкой, а маленьким дис-
диском [диск Эйри), радиус которого дается следующим выраже-
выражением [16J:
4«, E.320)
где %t — длина волны вблизи изображения и f» — угол между
краевым лучом, формирующим изображение, и оптической осью.
Соотношение Аббе (см. замечания после уравнения D.65))
с учетом уравнения E.318) может быть записано как
Alsin^/sinfo={[t/Bo) — U0]rel/[U(Zi) — E/0]rel}1/2=WU
E.321)
где Ко — длина волны вблизи объекта. Далее, можно определить
радиус диска Эйри вблизи объекта
E.322)
так же как и в случае сферической и аксиальной хроматической
аберраций. Уравнение E.320) может быть переписано в более
удобном виде
i = 0,6M,o/sin fo. E.323)
Заметим, что 8гм отрицательно для положительных значений ^о,
как и в случае сферической и аксиальной хроматической абер-
аберраций.
Из уравнения E.323) явно следует, что дифракция может
приводить к очень жестким ограничениям разрешения электрон-
333
Глава 5
ного зонда, если половинный угол аксептанса мал. Действи-
Действительно, для электронов с энергией 15 кэВ и ч° = 1 мрад имеем
6rdo = 60 А, что является значительной величиной. Этим объяс-
объясняется тот факт, что дифракция является очень важным огра-
ограничивающим фактором разрешающей способности электронного
микроскопа. Определим разрешающую способность как радиус
диска Эйри в положении объекта: если расстояние между дву-
двумя точками меньше, чем 8гао, то их изображения нельзя отде-
отделить друг от друга из-за дифракции.
Отметим, что дифракция электронов не всегда является не-
негативным обстоятельством: она очень полезна как инструмент
для кристаллографических исследований.
Очевидно, что дифракция более важна для низкоэнергетич-
ных электронов и особенно для очень маленьких апертур пучка.
Для того чтобы увеличить ток зонда, обычно стараются исполь-
использовать настолько большие апертуры, насколько это возможно.
По мере увеличения апертуры дифракция становится все менее
и менее значительной, но в то же время сферическая аберра-
аберрация становится доминирующей. При малых энергиях и относи-
относительно малых апертурах обычно нельзя пренебрегать аксиаль-
аксиальной хроматической аберрацией, таким образом, дифракция не-
неотделима от этой аберрации. Конкуренция между различными
типами аберраций будет рассмотрена в разд. 5.7. Тем не менее
должно быть очевидным, что, так как дифракцию нельзя устра-
устранить или исправить, очень важно иметь линзы с минимально
возможными коэффициентами геометрической и хроматической
аберраций. Тщательно сконструированные линзы с незначи-
незначительными аберрациями позволяют работать при больших апер-
апертурах, для которых дифракционный диск пренебрежимо мал.
Наконец, хотелось бы отметить возможность использования
дифракции для уменьшения сферической аберрации. Идея за-
заключается в том, чтобы рассматривать суммарный аберрацион-
аберрационный диск, как диск Эйри, расширившийся из-за сферической
аберрации, вследствие чего некоторые компоненты волны при-
приходят к положению изображения не в фазе. Чистая дифракци-
дифракционная картина может быть затем восстановлена использовани-
использованием зонной пластинки [160].
5.6.2. Пространственный и поверхностный заряды
Гл. 12 посвящена проблемам, связанным с пространственным
зарядом. В основном существуют два типа проблем, которые
необходимо рассмотреть. Первая связана с распределенным за-
зарядом в пучке частиц, вторая — с взаимодействием отдельных
частиц между собой.
334
Теория аберраций
Распределенный заряд при фокусировке пучка в точку при-
приводит к появлению бесконечной электростатической силы оттал-
отталкивания. В результате точечное изображение точечного объекта
может быть образовано только тогда, когда первеанс пучка
(см. уравнение B.190)) пренебрежимо мал. Для любого конеч-
конечного тока пучка минимальный достижимый размер изображе-
изображения ограничивается пространственным зарядом. К счастью, как
будет видно в дальнейшем, при обычных токах пучка и энерги-
энергиях первеанс очень мал и влиянием распределенного пространст-
пространственного заряда, таким образом, можно пренебречь. Распреде-
Распределенный пространственный заряд может влиять на изображение
только для очень тяжелых ионов и/или при чрезвычайно низких
энергиях. В этих случаях удобно рассматривать размытие про-
пространственного заряда у изображения как добавку к диску сфе-
сферической аберрации.
Положение сильно ухудшается из-за взаимодействий от-
отдельных частиц между собой. Как известно, при этом происхо-
происходит дополнительное энергетическое уширение пучка {эффект
Боэрша). Тем не менее это энергетическое уширение может
быть рассмотрено просто как расширение (в некоторых случа-
случаях весьма существенное) энергетического диапазона вблизи ис-
источника частиц, приводящего к хроматической аберрации. Та-
Таким образом, с точки зрения исследования аберраций нет необ-
необходимости рассматривать эффект Боэрша отдельно.
Присутствие вторичных электронов и/или ионизированных
атомов, обусловленное неадекватными условиями вакуума,
в высшей степени нежелательно. Тем не менее их пространст-
пространственный заряд может служить для компенсации сферической и
хроматической аберраций электронных и ионных линз. Действи-
Действительно, отсутствие пространственного заряда является одним из
условий справедливости теоремы Шерцера (разд. 5.2.1.3). Сфе-
Сферическая аберрация возникает из-за того, что фокусирующая си-
сила слишком быстро увеличивается при удалении от оси. Если
можно реализовать распределение пространственного заряда,
создающее фокусирующую силу, которая тем больше по вели-
величине, чем ближе к оси расположена точка наблюдения (или
дефокусирующую силу, увеличивающуюся с расстоянием от
оси), то можно компенсировать сферическую аберрацию. Были
предприняты попытки использовать компенсацию пространст-
пространственным зарядом, но еще не предложено ни одного практически
приемлемого решения.
Другой источник ошибок заключается в присутствии пара-
паразитных зарядов на поверхностях изолирующих материалов
внутри оптической колонны. Их следует тщательно избегать, но
заряды, наведенные на проводниках, могут успешно использо-
использоваться для коррекции аберраций. Проводники могут быть вы-
335
Глава 5 __^^_
полнены в виде сетки [143] или фольги [161—164]. Они пред-
представляют собой разрывы в распределении потенциала. Малень-
Маленькие отверстия в сетке возмущают поле линзы, а фольга вызы-
вызывает рассеяние частиц. Поэтому этот подход достаточно трудно
реализовать на практике. Использование сверхпроводящих се-
сеток может оказаться более реальным решением [165].
Специальный случай коррекции аберрации, использующий
разрывы потенциала, заключается в применении областей с ну-
нулевым потенциалом (зеркало для частиц) [166].
5.6.3. Высокочастотные поля
Чтобы быть уверенным в надлежащем функционировании,
оптическую колонну необходимо экранировать от внешних
электрических полей. Даже магнитное поле Земли может при-
привести к значительным проблемам, если отсутствует соответству-
соответствующее экранирование. Тем не менее высокочастотные поля могут
обеспечить корректировку некоторых аберраций. Если соответ-
соответствующим образом выбрать фазу, то фокусирующую силу, дей-
действующую на частицы, находящиеся вдали от оси, можно осла-
ослабить, что необходимо для компенсации сферической аберрации.
Так как здесь рассматриваются чрезвычайно малые времен-
временные интервалы, необходимо использовать частоты мегагерцово-
го диапазона. В [165] содержится обзор исследований, приве-
приведенных в этом направлении.
5.6.4. Отсутствие аксиальной симметрии
Другой важный источник ошибок линзы заключается в не-
несовершенстве технологии. Невозможно сделать электроды или
наконечники полюсов полностью аксиально-симметричными.
Причиной этого являются неоднородности материала, так же
как и асимметрия, возникающая в процессе изготовления. Кро-
Кроме того, в многокомпонентных системах основной проблемой
может оказаться юстировка. В результате линза не сможет вос-
воспроизвести стигматическое изображение точечного объекта,
даже если он расположен на оси. Это легко видеть, рассматри-
рассматривая два параксиальных луча: один — в плоскости xz, другой —
в плоскости yz. Так как аксиальная симметрия отсутствует, два
луча образуют две разные точки изображения. Этот случай
вполне аналогичен случаю астигматизма (разд. 5.2.2). Поэтому
суммарную аберрацию называют аксиальным астигматизмом,
чтобы подчеркнуть тот факт, что она появляется даже для то-
точек предмета на оси.
336
Теория аберраций
Эта аберрация может быть исправлена специальным приспо-
приспособлением— стигматором. Как правило, это мультипольная лин-
линза, которая вносит такой же тип асимметрии (с противополож-
противоположным знаком), как и исходный источник аксиального астигма-
астигматизма. Варьируя возбуждения различных компонент поля муль-
типоля, можно компенсировать механические недостатки акси-
аксиально-симметричной системы.
Мультипольные линзы открывают совершенно новую область
фокусировки заряженных частиц. Более подробно они будут
рассмотрены в гл. 10. Здесь достаточно сказать, что они имеют
большее число функций, характеризующих поле, чем аксиаль-
аксиально-симметричные линзы (см. уравнение C.52)), а следователь-
следовательно, и больше возможностей для устранения аберраций. Это один
из многообещающих путей как для коррекции [147] аксиально-
симметричных линз, так и для создания систем, состоящих толь-
только из мультипольных линз. В дальнейшем будет показано, что
при помощи системы квадруполей можно получать стигматиче-
стигматические изображения для любой пары сопряженных точек вдоль
оптической оси, поэтому она может полностью заменить акси-
аксиально-симметричные фокусирующие элементы. Так как мульти-
поли используются также для отклонения пучка, они реально
могут вытеснить оптические колонны со всеми входящими в них
элементами.
В случае мультиполей проблема заключается в том, что из-
за большого числа электродов их механические дефекты и юс-
юстировка становятся основными факторами, ограничивающими
их функционирование. В настоящее время это единственная при-
причина их коммерческой несостоятельности. Есть твердая уверен-
уверенность, что в будущем мультипольная оптика займет место, кото-
которое она заслуживает. Современное состояние дел в этой облас-
области [167—169J внушает оптимизм.
Здесь хотелось бы подчеркнуть, что теория аберраций тре-
третьего порядка, представленная в этой главе, ограничивается
аксиально-симметричными полями. Аналогичная теория может
быть развита для полей мультиполей, включая отклоняющие
системы. Общая теория для любого типа симметрии [170], есте-
естественно, очень громоздка, но и очень полезна. В разд. 11.1.4 бу-
будет рассмотрен относительно простой, но всеобъемлющий способ
рассмотрения совместного действия всех аберраций, включая
аберрации отклонения. Необходимо также помнить, что для
очень широких пучков (и/или для полностью скомпенсирован-
скомпенсированных аберраций третьего порядка) следует учитывать аберрации
высших порядков [170а].
Глава 5
5.6.5. Другие методы коррекции
Существуют также и другие возможности для уменьшения
аберраций. Ниже будет представлен их краткий обзор.
5.6.5.1. Коаксиальные линзы. Некоторые приборы с аксиаль-
аксиально-симметричным пучком не могут быть описаны при помощи
параксиальных свойств. Например, можно расположить элект-
электроды вдоль оптической оси и использовать полый пучок, окру-
окружающий этот электрод [171]. Было показано [172J, что в та-
таких зональных системах могут возникать отрицательные значе-
значения коэффициентов сферической и аксиальной хроматической
аберраций.
5.6.5.2. Симметричные траектории. Если как электростатиче-
электростатический потенциал, так и распределения магнитной индукции сим-
симметричны по отношению к плоскости 2 = 0, то из уравнений
E.26) — E.31) следует, что функции а.. .1 также являются сим-
симметричными. Если, кроме того, увеличение равно —1, то реше-
решения уравнения параксиальных лучей h(z) и g(z) являются со-
соответственно симметричной и антисимметричной функциями по
отношению к той же плоскости. Из уравнений E.68) — E.75)
видно, что подынтегральные выражения у коэффициентов абер-
аберраций А4, А5 и Ае являются антисимметричными функциями 2;
таким образом, в этом случае исчезают дисторсия, кома и ани-
анизотропный астигматизм.
Если электростатический потенциал симметричен, а магнит-
магнитная индукция антисимметрична по отношению к плоскости 2 = 0,
то функции due становятся антисимметричными. Для единич-
единичного увеличения это условие дает нулевые значения для коэф-
коэффициентов Ац, А5, А7 и Л8: исчезают дисторсия, кома, анизо-
анизотропная дисторсия и анизотропная кома [16J.
5.6.5.3. Положение ограничивающей апертуры. Так как пучок
лучей, формирующий изображение, меняет свою геометрию в
зависимости от положения апертуры, то ее положение опреде-
определенно будет влиять на неаксиальные аберрации. Исследования
[16, 173] зависимости каждого коэффициента аберрации от по-
положения апертуры показывают, что соответствующим выбором
ее положения некоторые коэффициенты удается подавить.
Как будет показано в разд. 7.8.1 и 8.3.5, все изотропные не-
неаксиальные аберрации могут таким образом быть сведены к
нулю.
5.6.5.4. Цифровая обработка изображения. Использование
методов улучшения изображения с помощью современной элект-
338
Теория аберраций
роники, использующих цифровую или оптическую обработку
[41J, — хороший альтернативный путь для исправления аберра-
аберрации. Однако им можно пользоваться только в электронной мик-
микроскопии, а не в микропроизводстве или анализе поверхности,
где определяющим фактором является качество зонда заряжен-
заряженных частиц, а не получение изображения.
5.6.6. Синтез
По нашему мнению, окончательное решение трудной пробле-
проблемы уменьшения аберраций — это не стремление компенсировать
ее, а поиск таких оптических элементов, которые сами облада-
обладали бы минимальными аберрациями. Методы построения таких
оптических элементов доступны уже сейчас и будет представле-
представлены в гл. 9.
5.6.7. Об измерении аберраций
Теория аберраций требует сложных вычислений. Так как
сейчас компьютеры доступны для любой лаборатории, необхо-
необходимую вычислительную работу можно быстро выполнить, ис-
используя методы, описанные в следующей главе. Раньше боль-
большую часть работы приходилось выполнять экспериментально.
Конечно же, очень важно уметь оценивать реальные возможности
оптических элементов, рассчитанных численно. К сожалению,
объем этой книги не позволяет детально разобраться в этом во-
вопросе. Для ознакомления с различными экспериментальными
методами читатель отсылается к литературе [18—36]. Боль-
Большинство из них (тест Хартмана, метод светящегося круга, ме-
метод теней, метод разрезания, дифракционный метод, метод на-
наклона) были разработаны для измерения сферической аберра-
аберрации, но они также применимы для определения и других абер-
аберраций.
5.6.8. Яркость
Конечная цель любой зондоформирующей оптики — это сжа-
сжатие как можно большего тока на как можно меньшей площади.
Мы уже видели, что это очень трудная задача из-за большого
числа ограничивающих факторов, обсуждавшихся в этой главе.
Прежде чем перейти к дальнейшему рассмотрению, обсудим од-
одно из наиболее фундаментальных ограничений, присущее лю-
любым пучкам частиц.
Механизм формирования изображения или зонда основан на
том, что каждая точка объекта из-за разброса энергии частиц,
339
Глава 5
образующих пучок, является источником множества лучей. Раз-
Разброс энергии является причиной хроматической аберрации (см.
разд. 5.3). Рассмотрим теперь абсолютно идеальную систему
без аберраций и предположим, что эффектами дифракции и про-
пространственного заряда также можно пренебречь. Существует ли
в этом случае предельный ток, который все еще можно сфоку-
сфокусировать в пятно заданного размера? Можно ли произвольно
увеличивать плотность тока в точке падения?
Начнем с соотношения Аббе E.321), которое может быть за-
записано совместно с D.59) как
[U(Zi) — U0]reiri2 Sin2 tt= [U(Zo) — U0]reiro2 SHI2 fo.
E.324)
Начальные скорости частиц имеют максвелловское распре-
распределение. Соответственно плотность тока в поперечном сечении
пучка имеет гауссово распределение. Для упрощения вычисле-
вычислений реальный пучок можно заменить эквивалентным пучком с
постоянной плотностью тока, полный ток / которого равен то-
току в гауссовом пучке [174J. Тогда можно записать
I=nro40=nn2Ji, E.325)
где Jo и /,• — плотности тока у объекта и изображения соответ-
соответственно.
Теперь предположим, что объект сам является источником.
Кинетическая энергия у источника определяется B.32). С дру-
другой стороны, наиболее вероятное значение энергии в максвел-
ловском распределении дается выражением kT, где Т — темпе-
температура источника и £=--1,38-10-23 Дж/Д'= 1/11600 эВ/К — посто-
постоянная Больцмана. Тогда имеем
Uo = kT/Q + U(z0), E.326)
которое вместе с E.324) и E.325) дает
/,=/о{1 — Q[U(Zi) — U{zo)}lkT}sin2 'iilsin2 чо. E.327)
Если катод поддерживается при нулевом потенциале и началь-
начальные скорости распределены по всевозможным направлениям
так, что ^о = я/2, то E.327) упрощается до
// = Jo [ 1 — Q U (z,) IkT) sin2 v. E.328)
Это известная формула Лэнгмюра для максимальной плот-
плотности тока вблизи изображения, сформированного идеальной
системой. Аберрации могут уменьшить плотность тока, но нич-
ничто не может поднять ее выше этого значения [175].
Из E.328) очевидно, что можно повысить плотность тока,
используя источник с высокой испускающей способностью, по-
340
Теория аберраций
вышая напряжение на изображении U(г,) или увеличивая угол
*{i конуса частиц у изображения. Необходимо соблюдать осто-
осторожность в оценке роли температуры. В случае термоэмиссии
плотность тока у источника является экспоненциальной функци-
функцией его температуры, поэтому высокая температура означает вы-
высокую плотность тока. Очевидно, что угол f; нельзя сильно уве-
увеличить, так как это приведет к резкому увеличению аберраций
любой реальной системы. Напряжение на изображении также
ограничено практическими соображениями. Отсюда можно за-
заключить, что ограничение плотности тока — внутренне прису-
присущее свойство источника частиц. Ни одна фокусирующая систе-
система не поможет, если источник обладает ограниченной испускаю-
испускающей способностью.
Для нитевидного вольфрамового катода, работающего при
2900 К, имеем /о«5 А/см2. Катоды из гексаборида лантана
(LaB6) намного лучше: они работают при гораздо более низ-
низких температурах («1900 К) и обеспечивают плотность тока
эмиссии /==50 А/см2. При £/(г,) = 10 кВ и ч» = 5 мрад имеем
/t = 5 А/см2 для вольфрамового катода и /г = 76 А/см2 для като-
катода из LaB6. Вопрос о режимах работы источника будет обсуж-
обсуждаться в разд. 7.8.3.
Отметим, что в E.328) первым членом в квадратных скоб-
скобках можно пренебречь по сравнению со вторым для любого ре-
реального значения потенциала на изображении при работе с
очень низкими напряжениями.
Для характеристики работы источника необходимо рассмот-
рассмотреть плотность тока в единичном телесном угле, отнесенную к
абсолютной величине напряжения:
[А/(В-м*.ср)], E.329)
где Q — телесный угол, занимаемый конусом частиц. Он изме-
измеряется площадью поверхности сферы единичного радиуса, вы-
вырезаемой конусом с углом полураствора f.
Q=2jt(l— cosy) —* nf. E.330)
Величина {J называется удельной яркостью. Как следует из
E.324), E.325), E.329) и E.330), для малых углов и в отсутст-
отсутствие ограничений на апертуры удельная яркость является инва-
инвариантной для сопряженных точек оптической системы, свобод-
свободной от аберраций. Это очень важное утверждение следует из
общей теоремы Лиувилля [11J: плотность частиц в фазовом
пространстве при их движении в реальном пространстве со
временем не изменяется.
341
Глава 5
Важно отметить, что яркость, определяемая как плотность
тока в единичном телесном угле
—+ //(лиJ [А/(м2-ср)], E.331)
V->0
не является инвариантной, за исключением случая, когда по-
потенциал постоянен.
Очевидно, чтобы ограничить аберрации, необходим источник
с высокой яркостью: высокой плотностью тока в малом телес-
телесном угле. Из E.325) — E.330) легко вычислить удельную яр-
яркость. Для малых углов ^« имеем
P=//[n2r,-V|tf(zi)|], E.332)
или, используя E.328) и пренебрегая его первым членом,
$=Jo\Q\/nkT. E.333)»
Для приведенных выше примеров имеем {5 = 6,4 А/(В-см2-ср)
для вольфрамового катода и {5 = 97 А/(В-см2-ср) для катода из
LaB6.
Так как удельная яркость инвариантна, ни одна оптическая
система не может ее увеличить. Использованием фокусирующей
системы с малым увеличением можно уменьшить величину г,-,
но одновременно с той же скоростью увеличивается ^i\U(Zi) |1/2,
поэтому удельная яркость остается неизменной. Пространствен-
Пространственный заряд, и в особенности эффект Боэрша, способствует умень-
уменьшению яркости.
Формула Лагранжа E.328) пригодна для любых углов и
эквивалентна соотношению Аббе E.324). Из D.59) и E.325)
следует, что
E.334)
Но это соотношение нельзя использовать, если лрименяются
ограничивающие апертуры; следует иметь в виду, что вблизи
источника Yo не является малой величиной, поэтому соотноше-
соотношение, аналогичное E.332) и выраженное через параметры источ-
источника, записать нельзя.
Можно выразить радиус rGt гауссова изображения из
E.331) — E.332) как
E.335)
где bi — яркость на изображении. Отсюда очевидно, что для за-
заданного тока радиус гауссова изображения может приближать-
приближаться к нулю только в том случае, если яркость стремится к бес-
бесконечности. Естественно, это невозможно, так как яркость всег-
всегда конечна, и ее величина определяется источником. Таким
342
Теория аберраций
образом, невозможно получить сколь угодно малое пятно прос-
простым уменьшением размера источника, даже если оптическая
•система идеальна (аберрации, пространственный заряд и диф-
дифракция отсутствуют). Размер гауссова изображения определя-
определяется током, яркостью и половинным углом аксептанса пучка.
Для маленького пятна нужно использовать по возможности
большее напряжение изображения.
Понятие яркости крайне важно для источников конечных
размеров. Однако в источниках с собственной и полевой эмис-
эмиссией источник настолько мал, что гауссово изображение зани-
занимает очень малую часть конечного пятна (см. разд. 5.7.1).
В этом случае яркость может быть на 4 порядка выше, чем для
термоионных источников. Однако такую яркость трудно исполь-
использовать, так как плотность тока от очень маленького источника
•стремится к бесконечности. При этом считается, что пучок ис-
испускается прямым источником намного меньшим, чем сам нако-
наконечник катода с полевой эмиссией. Мнимый источник можно
рассматривать как точку с углом полураствора конуса fo- Ток
определяется через угловую яркость (или угловую плотность
тока или угловую интенсивность эмиссии) dl/dQ как
/ = nyldl/dQ = щЩ* п^ГЧ,0 dl/dQ. E.336)
и \zo) ио
Это выражение определяет половинный угол аксептанса, тре-
требуемый для заданного тока пучка. Угловая яркость приблизи-
приблизительно равна 1 мА/ср для термополевого источника эмиссии и
50 мА/ср для источника с полевой ионизацией. Для такого ис-
источника при Yo = 10 мрад имеем ток 15 нА.
5.7. Совместное действие аберраций разных видов
В разд. 5.5 рассматривалось добавление некоторых аберра-
аберраций для последовательности линз. Теперь интересно посмотреть,
как происходит перемешивание аберраций разных видов для
одной и той же линзы.
По существу смешение геометрических аберраций определя-
определяется уравнениями E.65) —E.66). Полная аберрация является их
векторной суммой. Но интереснее рассмотреть смешение абер-
аберраций, вызванных различными физическими причинами, как
это было описано в предыдущих разделах.
Как известно, роль аберраций состоит в увеличении изобра-
изображения без привлечения новых частиц. Это возможно только при
изменении распределения плотности тока в пучке. Поэтому
тщательное изучение аберраций должно основываться на ис-
исследовании распределения плотности тока. Было показано [176,
343
Глава 5
177], что влияния различных аксиальных аберраций (сфериче-
(сферической аберрации, хроматической аберрации, дифракции, тепло-
теплового распределения скоростей) на конечный размер зонда мож-
можно считать статистически независимыми друг от друга и имею-
имеющими некоррелированные гауссовы распределения плотности
тока. Как следствие этого приближения, чтобы получить ради-
радиус зонда, нужно сложить квадраты аберраций
r2i = r2Gi+ Frs,/4J + (8rciJ+ (Ым) \ E.337)
где радиус гауссова изображения (rG<) дисков сферической и
хроматической аберраций (8rsi и brci соответственно) и диска
Эйри Frdl) даются уравнениями E.335), E.79), E.197) и
E.320) соответственно. В качестве дополнительного члена сю-
сюда можно добавить квадрат полной аберрации отклонения. Та-
Таким образом, размер пятна зависит от тока в пучке, яркости,
коэффициентов аберрации линзы (которые в свою очередь за-
зависят от увеличения), потенциала на мишени и угла полурас-
полураствора y» конуса, образованного падающими частицами вблизи
мишени.
Оптимальную плоскость с минимальным размером пятна
можно определить геометрическими методами, только пренебре-
пренебрегая дифракцией. В противном случае необходимо учитывать эф-
эффекты волновой оптики. Чтобы добиться оптимального разре-
разрешения, необходимы методы, не связанные с фокусировкой.
Можно показать [178J, что оптимальная плоскость совпадает с
плоскостью гауссова изображения, когда хроматическая абер-
аберрация является доминирующей. Как известно из разд. 5.2.1.4,
оптимальная плоскость — это плоскость минимального рассея-
рассеяния, когда преобладает сферическая аберрация. Поэтому в со-
соответствии с E.146) 8rSi в E.337) делится на 4.
5.7.1. Пренебрежимо малые источники
Уравнение E.337) записано в предположении конечного ра-
радиуса источника. Если размер источника пренебрижимо мал,
как в случае источников с полевой эмиссией и автоионных ис-
источников, радиус гауссова изображения можно записать сразу
как
Гв1=Мго, E.338)
где го — мнимый размер источника, которым в большинстве слу-
случаев можно просто пренебречь. Угол ^ в соответствии с прос-
простым соотношением E.336) определяется током: чем больше
ток, тем больше становится угол ^г- Размер пятна однозначно
определяется уравнением E.337). Однако если считать задан-
344
Теория аберраций
ным размер пятна, то E.337) дает громоздкое выражение для
f г, которое в свою очередь определяет ток.
Эквивалентное значение постоянной плотности тока в пятне
определяется E.325) и E.336) — E.338). Это сложная функция
угла fi (или половинного угла аксептанса fo, который теперь
можно смело использовать — в этом случае он всегда мал), но
проще установить общее поведение этой функции [179J. Когда
fo очень мало, важны только дифракционные эффекты. В этом
случае плотность тока меняется пропорционально четвертой сте-
степени заданного половинного угла, т. е. стремится к нулю, когда
угол достигает нулевого значения. При умеренных углах, когда
и дифракцией, и сферической аберрацией можно пренебречь, ис-
используя E.197), получим, что хроматический член дает плот-
плотность тока, которая не зависит от угла аксептанса:
Л»^ <5-339>
Отсюда просто вычислить ток:
/chrom = nFr^J//chrom. E.340)
Даже при больших углах важен только сферический член и
плотность тока обратно пропорциональна четвертой степени по-
половинного угла аксептанса, т. е. быстро уменьшается с ростом
угла. Ток в этом случае вычисляется с помощью E.79), E.336)
и E.337). Имеем
er = л {AbrsiIMCso) '/41/dQ. E.341)
Отсюда следует, что максимальной плотности тока можно
достигнуть при такой взаимосвязи различных параметров, ког-
когда оптика хроматически ограничена. В этом режиме плотность
тока постоянна и может быть увеличена только либо использо-
использованием лучшего источника с большей угловой яркостью и мень-
меньшим энергетическим разбросом, либо применением фокусирую-
фокусирующей системы с низкой хроматической аберрацией. Так как плот-
плотность тока зависит от квадрата коэффициента хроматической
аберрации, то уменьшение этого коэффициента в 3 раза означа-
означало бы увеличение плотности тока на порядок.
5.7.2. Конечные источники
Для источников конечных размеров ситуация совершенно
другая. В этом случае ток определяется первым членом E.337).
Подставляя туда E.82), E.200), E.320) и E.335) и выражая
ток, получим
. E.342)
345
Глава 5
Если желательно получить эквивалентную постоянную плот-
плотность тока вблизи пятна, то при этом возникнут неприятности,
так как E.337) и E.342) определяются друг через друга. Ко-
Конечно, в качестве приближения можно вместо г,- в E.325) под-
подставить rGi, поскольку ток определяется через радиус гауссова
изображения.
Очевидно, что как для очень малых, так и очень больших
f,- пятно имеет очень большой радиус: в первом случае из-за
гауссова и дифракционного членов, во втором — из-за члена,
содержащего сферическую аберрацию. Очевидно, что существу-
существует оптимальный угол f<Opt, при котором радиус пятна минимален
для заданного тока. С другой стороны, при том же оптималь-
оптимальном угле ток будет максимальным для пятна заданного разме-
размера. Подставляя E.82), E.200), E.320) и E.335) в E.337) и
дифференцируя по ■уг, получим, что оптимальное значение угла
Y» определяется следующим соотношением [180J:
* 8 / /Гс» At/° I4
~ ЯСЬ ML 2 U(z,)-U0\
A"" 1'V E.343)
3,553k2ibiJI L2 U(Zi)—Un
Конечно же, это общее соотношение слишком сложно, поэто-
поэтому рассмотрим его частные случаи. Если дифракцией можно пре-
пренебречь, то уравнение становится ненамного проще. В случае
пренебрежения размерами источника в соответствии с E.335),
формально полагая / = 0, по существу получим случай, рас-
рассмотренный в предыдущем разделе. Отметим, что если пре-
пренебречь и дифракцией, и размерами источника, то уравнение
E.343) дает ■Y;oPt = 0, что очевидно, так как обе оставшиеся
аберрации растут с углом ^л Для важного частного случая от-
относительно малых углов, когда сферической аберрацией можно
пренебречь, формула совершенно непригодна, поскольку Cs,- по-
появляется в знаменателе (подробнее этот случай будет рассмот-
рассмотрен ниже). Поэтому, на практике E.343) можно использовать,
когда мы пренебрегаем хроматической аберрацией. Это воз-
возможно в высоковольтной электронной микроскопии. Поэтому
кратко обсудим этот случай.
5.7.2.1. Пренебрежение хроматической аберрацией. В этом
случае Сс* = 0 E.343) упрощается до
где
V opt (/=o) = 1,085 (UCsiY1* E.345)
346
Теория аберраций
является оптимальным углом в случае нулевого тока (размера-
(размерами источника пренебрегаем).
Подставляя E.82), E.320) и E.335) в E.337) и принимая
во внимание E.344) и E.345), получим минимально возмож-
возможный радиус пятна для заданного тока в виде
п min = r, min</=<o[l + // C,553Я(-2Ь() ]3'8, E.346)
где
П mm (/=o)=0№№/4Csiv* E.347)
есть минимальный радиус для нулевого тока, который в дей-
действительности является наименьшим возможным размером зон-
зонда для этого случая. Из этого уравнения следует, что для этого
частного случая коэффициент сферической аберрации оказыва-
оказывает очень слабое влияние на размер зонда: даже увеличение его
на порядок дало бы увеличение радиуса пятна в 1,78 раза.
Подставляя E.346) в E.344) и принимая во внимание
E.345) и E.347), получим
^oPt=Brinlin/Cs01/3, E.348)
которое вместе с E.342) дает максимальный ток для данного
размера пятна в виде
/тах = я26,[3Bг08/3/16СХ(-2/з — 0,36^2]. E.349)
Отметим, что тот же результат можно получить дифференциро-
дифференцированием E.342) по fj.
Интересно заметить, что E.82) и E.48) дают соотношение
6/W4 = rimin/2, E.350)
квадрат которого означает, что в плоскости наименьшего рас-
рассеяния сферический диск составляет только 25% конечного раз-
размера пятна.
Следующий интересный вывод можно сделать, сравнивая
E.345) и E.347) с E.320); имеем
Л min (/=0O' opt (/=0)==0,69А„«бГл-, E.351)
из чего следует, что дифракционная картина практически не
зависит от сферической аберрации.
Из сравнения E.341) и E.349) видно, что ток пропорциона-
пропорционален степени 2/3 радиуса зонда в случае источника пренебрежи-
пренебрежимо малых размеров, в то время как для источника конечных
размеров он пропорционален степени 8/3 той же величины. По-
Поэтому в малых зондах при использовании источников с полевой
эмиссией можно получить больший ток, чем от термоионных ис-
источников. Для больших зондов справедливо обратное. Естест-
347
Глава 5
венно, реальные характеристики зондов определяются характе-
характеристиками источника и фокусирующей системы. Так как ток за-
зависит от размера пятна и в свою очередь размер пятна зави-
зависит от угла fi, то для описания зондовой системы необходимо
знать обе зависимости.
Перейдем теперь к исследованию специального случая пре-
пренебрежимо малой дифракции, т. е. будем учитывать тепловые
скорости и сферическую аберрацию. Это возможно в случае, ес-
если размер пятна намного больше минимального, определяемого
E.347). Тогда из E.346) и E.347) следует
г, mm = 0t40Ce,v« (//&,) з/8> E.352)
E.344) и E.345) дают
t = 0,93Csr1/4 (I/b,) '/8, E.353)
и максимальный ток можно вычислить простой подстановкой
ki = 0 в E.349). Так как сферическая аберрация вносит только
25% в конечный размер пятна и единственным дополнительным
вкладом в этом случае является гауссово пятно, то можно про-
просто выбрать апертуру в соответствии с E.353), применяя для
гауссова пятна увеличение немного меньше значения, которое
бы обеспечивало желаемые размеры пятна, и работать в плос-
плоскости минимального рассеяния.
5.7.2.2. Пренебрежение сферической аберрацией. Как отмеча-
отмечалось выше, для важного случая относительно малых углов
E.343) применять нельзя, так как Csi появляется в знаменате-
знаменателе. Тем не менее дифференцирование E.337) или E.342) при-
приводит к выражению
V opt = V opt (/=o) A + I/3,553h2bi) v« E.354)
для оптимального угла, где теперь
Y/ opt (j.o> = 1 >095 \ CciAU0/\U(z,)-U0)} E.355)
есть оптимальный угол для нулевого значения тока (размера-
(размерами источника пренебрегаем).
Подставляя E.200), E.320) и E.335) в E.337) и учитывая
E.354) и E.355), получим минимально возможный радиус пят-
пятна для заданного тока в виде
П mm = п mm (/=о) [ 1 + //3,553^-26г] »/\ E.356)
где теперь
Лтт<,=о) = О,77{^Сс,-Л£/о/[£/(г,) — U0]}1/2 E.357)
есть наименьший возможный размер зонда.
348
Теория аберраций
Подставляя E.356) в E.354) и учитывая E.355) и E.357),
получим
V pt —
из которого, используя E.342), получим максимальный ток для
заданных размеров пятна в виде
-0.36A,?). E.359)
Сравнивая это уравнение с E.340), видим, что в случае пре-
пренебрежения размерами источника ток пропорционален квадрату
радиуса зонда, в то время как в случае источника конечных
размеров он пропорционален четвертой степени этой величины.
Поэтому заключение предыдущего раздела о превосходстве ис-
источников с полевой эмиссией для малых зондов применимо так-
также и в этом случае.
Уравнения E.200) и E.358) дают
(бгС(J=(ЛштJ/2, E.360)
это означает, что половину вклада в конечный размер пятна
вносит хроматический диск.
Из E.355) и E.357) имеем, что в этом случае
fi mln (l=0)"{i opt (/=0) = 0,84A,;. E.361)
Хроматическая аберрация несколько сильнее влияет на диф-
дифракционную картину, чем сферическая.
Если дифракцией пренебречь, т. е. если оставить только теп-
тепловые скорости и хроматическую аберрацию (размер пятна на-
намного больше минимального размера пятна, определяемого
E.357)), уравнения E.356) и E.357) дают
U mln = 0,56{CelДU0/[U (Zt) — t/o]} (I/bi) >/«. E.362)
Из E.354) и E.355) получим
= 0,80 (-^— -т- , E.363)
и максимальный ток можно вычислить простой подстановкой
А,, = 0в E.359).
Наконец в специальном случае, когда угол ^ настолько мал,
что можно пренебречь как хроматической, так и сферической
аберрацией, для вычисления размера пятна и тока можно даже
использовать E.337) и E.342) соответственно для любого за-
заданного угла ff-
349
Глава 5
5.7.3. Смешения аберраций в комбинации линз
С системой линз можно обращаться как с одной линзой.
Квадраты ее аберраций суммируются в соответствии с E.337),
где для системы из двух линз 6rS!- и 8rci теперь определяются
уравнениями E.305) и E.314) соответственно. Используя
E.338) для источников с полевой эмиссией, имеем
= М2гоЧ- (Мг,п + 8rsi2J/16 +
E.364)
где, как раньше, М — увеличение всей системы, а М" — увели-
увеличение второй линзы. Снова отметим (см. разд. 5.5), что нельзя
суммировать квадраты аберраций отдельных линз системы.
Суммирование квадратов аберраций различных линз широко
распространено в литературе, но тем не менее это не верно.
Формулу E.364) легко обобщить для системы, состоящей из
.любого количества линз.
5.7.4. Коэффициенты добротности
Проектируя фокусирующую систему, мы стремимся сделать
ее хорошей настолько, насколько это возможно. Но что же яв-
является основным критерием качества линзы? Будь она электро-
электростатической или магнитной (или их комбинацией)? Каким об-
образом можно сравнивать различные линзы?
К сожалению, это очень трудный вопрос. В самом деле, чис-
число геометрических и электрических или магнитных параметров,
линзовой конструкции, используемой на практике, может быть
весьма велико, а с другой стороны, различные приложения мо-
могут выдвигать сильно отличающиеся и даже противоречивые
требования. Например, в просвечивающих электронных микро-
микроскопах нужны линзы с очень большой оптической силой (ма-
(малым фокусным расстоянием), в то время как для зондофор-
мирующей системы требуется большее рабочее расстояние
(большое фокусное расстояние). Поэтому всегда необходимо
анализировать данную оптическую систему с точки зрения
конкретного применения.
Однако для всех приложений одно требование является об-
общим: максимально возможное уменьшение аберраций. По-ви-
По-видимому, абсолютным показателем добротности оптической си-
системы является размер аберрационного диска. В соответствии с
законами подобия, изложенными в разд. 2.8, размеры оптиче-
оптической системы можно менять произвольно: уменьшать или увели-
увеличивать. Тогда уместно поставить вопрос: как с учетом законов
350
Теория аберраций
подобия добиться наименьших размеров аберрационного диска?
К сожалению, уменьшение размеров неизбежно означает, что
расстояние между электродами и магнитными полюсами значи-
значительно уменьшится. Следовательно, поля станут сильнее, что в
свою очередь приведет к практическим трудностям, таким, как
электрический пробой и насыщение магнитных материалов.
В обычных условиях электроды не могут выдержать поле силь-
сильнее 15 кВ/мм, хотя в очень высоком вакууме некоторые спе-
специальные материалы могли бы выдержать и больше. Один этот
факт устанавливает практический предел миниатюризации раз-
размеров. Вдобавок, уменьшение размеров с использованием зако-
законов подобия ведет к настолько сильному уменьшению рабочих
расстояний, что они становятся совсем неприемлемыми.
Поэтому реально достижимый размер аберрационного диска
зависит от условий, определяемых экспериментом. Кроме того,
он сильно зависит от размеров источника, угла испускания, рас-
распределения энергии и увеличения (см. E.79), E.197) и E.337)).
Так как 6rSI- и 8rci соответственно пропорциональны |М|С80 и
|М|СС0 и обе эти величины имеют минимумы при вполне опре-
определенных увеличениях (см. разд. 5.4.1), то их можно использо-
использовать в качестве коэффициентов добротности. Они будут приме-
применяться в гл. 7 для численных расчетов электростатических линз,
но каждый раз необходимо устанавливать практически дости-
достижимые минимальные значения Cso и Ссо для данных размеров
зазора, возбуждения, рабочих расстояний и т. д. Этот способ
сравнения разных линз не получил широкого распространения,
поэтому необходимо найти более удовлетворительные коэффи-
коэффициенты добротности.
Трудности, связанные с использованием самого аберрацион-
аберрационного диска в качестве коэффициента добротности, ведут к ра-
разумному предположению: поскольку радиус диска имеет раз-
размерность длины, то он должен быть отнесен к другой величине,
имеющей ту же самую размерность. Тогда имеем безразмерный
коэффициент добротности. Вопрос в том, как выбрать эту вели-
величину. Можно предложить множество подходов. Аберрации
электростатических линз можно отнести к [U(z0)—U0]IU'max
или (f/max—U0)/U/max, где t/щах и U'max— максимальные абсо-
абсолютные величины электростатического потенциала и аксиаль-
аксиальной компоненты напряженности электростатического поля соот-
соответственно. Аналогично для магнитных линз таким же образом
Smax/B'max или, где можно, использовать диаметр окружности,
которую описывают частицы данной энергии в однородном маг-
магнитном поле с магнитной индукцией Втах [166]. Подобным же
образом могут быть использованы и другие величины (9, 44].
Очевидно, что минимальное значение коэффициентов абер-
аберрации должно ограничиваться наибольшим значением реализуе-
351
Глава 5
мого поля. Когда мы делим коэффициенты аберрации на выше-
вышеупомянутые величины, то конструируем коэффициент добротно-
добротности, который является величиной, определяемой коэффициента-
коэффициентами аберрации и максимальной напряженностью поля. Тогда,
пытаясь уменьшить величину коэффициента добротности, мы
фактически уменьшаем аберрации, поддерживая поле в разум-
разумных пределах.
Наконец, существуют еще три фактора, которые, однако,
должны учитываться при выборе коэффициента добротности
{202J. Первый состоит в том, что если мы хотим сравнивать
электростатические и магнитные линзы, то необходимы более
универсальные коэффициенты добротности, которые не зависе-
зависели бы от специфических характеристик электрического и маг-
магнитного полей. В качестве величины, к которой отнесены абер
рации, можно выбрать один из следующих параметров: физиче
екая длина фокусирующей системы, ее эффективная длина, оп-
определяемая, например, C.197), протяженность поля линзы (рас-
(расстояние (Ь—а) на рис. 46), рабочее расстояние в пространстве
объектов или изображений, фокусное расстояние в пространстве
объектов или изображений и т. д. Все они дают различную ин-
информацию о работе линз и позволяют проводить их сравнение.
Второй фактор состоит в том, что особенно трудно сравни-
сравнивать линзы разных типов, так как размеры аберрационных дис-
дисков сильно зависят от увеличения. Для того чтобы работать при
одинаковом увеличении, нужно использовать совершенно раз-
разные значения полей или отношений напряжения для различных
линз. Поэтому считается общепринятым сравнивать разные лин-
линзы при бесконечном увеличении.
Наконец, третий и, может быть, наиболее важный фактор —
следующий. Довольно давно было установлено [16], что для ис-
исчерпывающего сравнения коэффициентов аберрации различных
линз эти линзы должны быть оптически эквивалентны друг дру-
другу, т. е. иметь одну и ту же оптическую силу. Поэтому коэффи-
коэффициенты аберрации различных линз с одинаковой оптической си-
силой должны сравниваться при бесконечном увеличении для
одинаковых максимальных полей или отношений потенциалов.
Таким образом, коэффициент добротности, которому мы от-
отдаем предпочтение, является коэффициентом сферической и ак-
аксиальной хроматической аберраций в пространстве объектов,
вычисленный для бесконечного увеличения и отнесенный к фо-
фокусному расстоянию в пространстве объектов. Коэффициенты
добротности для различных линз должны сравниваться друг с
другом при одинаковых максимальных значениях полей или от-
отношений напряжений.
Для зондоформирующей оптики необходимы большие рабо-
рабочие расстояния, т. е. большие фокусные расстояния, поэтому
352
Теория' аберраций
низкие значения коэффициента добротности хороши не только
с точки зрения аберраций, но также с точки зрения рабочих
расстояний. Хотя во многих случаях приходится работать с
почти единичным увеличением и большие рабочие расстояния
требуются не всегда, мы уже договорились, что полноценное
сравнение можно проводить только для оптически эквивалент-
эквивалентных линз, поэтому вряд ли удастся отыскать лучшие общие ко-
коэффициенты добротности, чем Cso<x>/fi и CCOoolfi- Как станет ясно
в следующих главах, коэффициенты аксиальных аберраций с
увеличением фокусного расстояния обычно увеличиваются. По-
Поэтому поиск состоит в том, чтобы уменьшить два приведенных
выше коэффициента добротности и в то же время поддерживать
поля в разумных пределах. Конечно, для некоторых специаль-
специальных приложений, таких, например, как объективные линзы
электронного микроскопа, эти коэффициенты добротности не
самые удобные, так как, для того чтобы обеспечить большие
фокусные расстояния, линзы должны были бы иметь слишком
большую массу. В этом частном случае коэффициенты аберра-
аберрации могут быть отнесены к величинам, обсуждавшимся выше
(см. разд. 5.4.1).
Очевидно, для малых углов аксептанса более важен хрома-
хроматический коэффициент добротности, для больших углов аксеп-
аксептанса— сферический. Для окончательной оценки действия абер-
аберраций диски нужно сравнить при заданных рабочих расстояни-
расстояниях и увеличении. Хорошей практической альтернативой коэффи-
коэффициента добротности для зондоформирующей оптики является
r,/fi, где радиус зонда г,- вычисляется из E.337).
Заключение
В этой фундаментальной главе была дана простая, но полная
теория аберраций аксиально-симметричных фокусирующих си-
систем, включая геометрические аберрации третьего порядка, хро-
хроматическую аберрацию и другие источники ошибок. Вначале
был введен метод характеристических функций, который образу-
образует основу теории. Уравнения E.65) — E.67) определяют геомет-
геометрические аберрации третьего порядка. Значительное внимание
уделено сферической аберрации. Разный вид ее коэффициентов
дается формулами E.111), E.121) и E.132). Уравнения E.79)
и E.82) определяют диск сферической аберрации. Уравнение
E.83) связывает коэффициенты сферической аберрации, связан-
связанные с предметом и изображением соответственно. Теорема Шер-
цера дается уравнением E.138). Аберрации и их фигуры для
всех других семи геометрических аберраций также были опре-
определены. Аксиальный хроматический коэффициент аберрации да-
дается выражением E.192) или E.194). Уравнения E.197) и
353
Глава 5
E.200) определяют диск хроматической аберрации. Выражение
E.201) дает соотношение между аксиальными хроматическими
коэффициентами аберрации, связанными с объектом и изобра-
изображением соответственно. Случаи нулевого и бесконечного увели-
увеличений, так же как прямые и обратные методы вычисления ко-
коэффициентов аберрации, обсуждались для специальных случа-
случаев как сферической, так и аксиальной хроматической аберра-
аберрации. Следующими были рассмотрены асимптотические аберра-
аберрации. Уравнения E.255) и E.273) являются полиномиальными
выражениями для асимптотического сферического и хроматиче-
хроматического коэффициентов аберрации соответственно иа основе взаим-
взаимного увеличения. Аберрации тонких линз, а также их комбина-
комбинаций были обсуждены довольно подробно. Выражения E.305) и
E.314)—дополнительные формулы суммирования для диска
сферической и хроматической соответственно аберраций систе-
системы из двух линз. Были рассмотрены дифракция, пространствен-
пространственный заряд и другие дополнительные источники аберраций,
а также различные методы коррекции аберраций. Понятие яр-
яркости E.329) и E.331) было введено совместно с рассмотрени-
рассмотрением тока и его плотности. Одновременное действие различных
аберраций может быть выражено в виде E.337) для одной лин-
линзы и в виде E.364) для комбинации из двух линз. В конце об-
обсуждался вопрос о коэффициенте добротности.
Глава 6
ЧИСЛЕННЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ
ТРАЕКТОРИЙ ЛУЧЕЙ
И РАСЧЕТА АБЕРРАЦИЙ
После того как определены фокусирующие поля (см. гл. 3),
можно приступить к вычислению траекторий частиц в соответ-
соответствии с гл. 4 и затем рассчитать аберрационные коэффициенты
(гл. 5). Хотя вполне возможно получить решение общего урав-
уравнения световых лучей D.21) непосредственно с помощью чис-
численных методов, обычно ограничиваются рассмотрением парак-
параксиальных траекторий, которые также вполне пригодны для оп-
определения аберрации. Тогда достаточно узнать аксиальный по-
потенциал и распределение магнитной индукции, чтобы получить
полную информацию об оптических свойствах данной фокуси-
фокусирующей системы.
Как известно, асимптотические свойства первого порядка
электронных и ионных линз определяются кардинальными эле-
элементами. Для их определения достаточно знать два главных лу-
луча (разд. 4.6.1), т. е. проинтегрировать уравнение для паракси-
параксиальных лучей D.40) или D.50) для заданного распределения
поля и начальных условий. Хотя уравнение D.40) непосредст-
непосредственно определяет траекторию, для численных расчетов уравне-
уравнение D.50) обычно более предпочтительно, так как оно не со-
содержит вторую производную потенциала (см. разд. 3.3.5.1). За-
Заметим, что, если коэффициенты в уравнениях для определения
действительных лучей малы, начальные условия для получения
общего решения уравнения для параксиальных лучей могут
быть заданы произвольно, несмотря на то что уравнение спра-
справедливо только для малых смещений и углов.
Коэффициенты аберрации даются в виде определенных ин-
интегралов, которые в большинстве случаев необходимо вычис-
вычислить численными методами с достаточной точностью.
Теперь перейдем к практическим (в основном вычислитель-
вычислительным) методам расчета траекторий лучей и вычислениям коэф-
коэффициентов аберрации.
6.1. Аналитические модели
Аналитические решения имеют вполне определенные пре-
преимущества перед численными методами даже сейчас, в эпоху
изобилия вычислительных средств. Для этого существуют мно-
многочисленные причины:
355
Глава 6
1) прежде всего численные решения дают всегда более или
менее точное приближение, в то время как аналитические ре-
решения являются точными;
2) аналитические решения дают возможность более полно-
полного представления результатов и позволяют провести оценку
влияния различных параметров на решение;
3) их можно проверить с помощью обратной подстановки;
4) они расширяют границы анализа;
5) они позволяют устанавливать общие свойства и законо-
закономерности для данного класса полей;
6) они обеспечивают простые способы сравнения различных
численных методов;
7) они упрощают рассмотрение особых случаев.
При использовании аналитических методов существуют так-
также и проблемы:
1) как мы видели в гл. 3, аксиальные распределения полей в
реально используемых системах электродов и полюсов очень
редко могут быть выражены в аналитических функциях;
2) даже если известна точная конфигурация лучей, малове-
маловероятно, что можно было бы получить аналитические выражения
для коэффициентов аберрации.
Однако вследствие приведенных выше преимуществ хоте-
хотелось бы использовать любую возможность получить строгое ре-
решение. К счастью, для достаточно большого количества случаев
могут быть развиты аналитические модели, т. е. могут быть по-
получены математические функции, близкие к реальным распреде-
распределениям полей в некоторых классах электростатических и маг-
магнитных линз. Такие модели линз будут изучаться в последую-
последующих двух главах. Аналитические функции играют важную роль
также и в конструировании сложных линзовых систем (см.
гл.9).
Существует несколько общих методов отыскания классов
функций, которые делают возможным решение уравнения ,пля
параксиальных лучей в квадратурах [182—184J. Практически
они применяются для электростатических иммерсионных линз с
монотонным распределением потенциала и для коротких маг-
магнитных линз.
Частные решения возможны для достаточно большого коли-
количества случаев. Мы уже знаем решение для однородного поля.
Более сложные случаи включают параболические [16] и экспо-
экспоненциальные [173] распределения потенциала, линейные [185J
и эллиптические [186] магнитные поля, колоколообразную мо-
модель Глазера [16J, модель Гриве — Ленца [18, 187], модель
иммерсионной [188, 189] линзы, модель «одиночной» линзы
[190, 191] и некоторые другие модели, основанные на гипергео-
гипергеометрических функциях [193] и функциях Бесселя [192]. В не-
356
Численные методы (расчета траекторий лучей и аберраций
которых случаях (например, экспоненциальный потенциал, ко-
локолообразное магнитное поле) даже аберрационные коэффи-
коэффициенты могут быть выражены в квадратурах.
Мы будем широко использовать эти возможности в следую-
следующих главах. К сожалению, это не всегда возможно. В большин-
большинстве случаев нам нужно полагаться на численные методы для
определения как траекторий, так и аберрационных коэффициен-
коэффициентов.
6.2. Численный расчет траекторий лучей
Траектории частиц в общем случае полностью определяют-
определяются системой дифференциальных уравнений второго порядка
B.76) и B.77). В аксиально-симметричных полях траектории
определяются уравнениями D.12) и D.21). Так как теория фо-
фокусировки базируется на параксиальных лучах, нас в основном
интересуют решения уравнений для параксиальных лучей D.40)
или D.50). После определения траектории в меридиональной
плоскости ее вращение определяется уравнением D.32), кото-
которое является определенным интегралом.
Уравнения D.21), D.40), D.50) являются обыкновенными
дифференциальными уравнениями второго порядка вида
§- = /(?, У, У'), F-1)
где штрих означает дифференцирование по независимой пере-
переменной z, a f—произвольная функция трех переменных, опре-
определяемая конкретным видом дифференциального уравнения.
В нашем случае это зависит от того, какое используется урав-
уравнение, а также от распределений потенциала и магнитной ин-
индукции отображающих полей. Начальные условия даются в не-
некоторой точке г0> где
У(го)=Уо, y'(zo)=y'o- F.2)
Решение уравнения F.1) с начальными условиями F.2) назы-
называется задачей Коши.
Численное решение этой задачи представляет собой пошаго-
пошаговую процедуру. Мы начинаем из начальной точки го, в которой
величины у я у' заданы начальными условиями, и пытаемся оп-
определить величины у я у' в соседней точке Z\. Как только это
сделано, примем точку Z\ за начальную точку и процедуру по-
повторим. В произвольной точке z$ (/ = 0, 1, 2, ...) имеем
y(z,)=yh y'(zj)=y'j. F.3)
357
Глава 6
Положим теперь
h=Zj+i — Zj F.4)
для величины шага. Тогда можно записать разложение в ряд
Тейлора для у и у' в следующей точке в виде
±у}+!*у;+ ... +%уГ+ ■■■, F-5)
Очевидно, самое простое, что нужно сделать, — использовать
информацию, которую мы уже имеем в точке Zj, т. е. отбросить
члены у выше второго порядка в точке Zy В самом деле, из
уравнения F.1) имеем выражение
y"i=f(zi,yi-y'i), F-7)
которое может быть легко вычислено. Это метод Эйлера, кото-
который состоит в аппроксимации кривой последовательностью ли-
линейных отрезков. К сожалению, точность этого метода, исполь-
используемого в таком виде, неудовлетворительна. Для того чтобы по-
повысить точность, можно было бы использовать очень маленький
шаг h, что приводит к огромному количеству элементарных
вычислений. Это в свою очередь приводило бы к накоплению
ошибки округления (см. разд. 3.3.1.2) и к неустойчивости реше-
решения. Поэтому надо улучшить эту процедуру.
Есть много методов решения этой задачи. Они могут быть
разделены на две основные категории.
1. Одношаговые методы используют информацию о функции
f(z, у, у') внутри интервала, на котором ищется решение. Эти
методы требуют обычно вычисления значений функции не толь-
только в граничных точках интервала, но также и в точках, лежа-
лежащих внутри. Наиболее важный представитель этого класса ме-
методов — метод Рунге — Кутта (разд. 6.2.1).
2. Многошаговые методы используют информацию о функ-
функции в более чем одной точке сетки, и обычно они требуют ите-
итерации (см. разд. 6.2.2). Метод предиктора-корректора и метод
Нумерова — наиболее известные альтернативные методы этого
класса.
Следует помнить, что численное решение дифференциальных
уравнений является непростым делом. Проблемы устойчивости,
оценки ошибок и т. п. рассмотрены в соответствующей матема-
математической литературе [115, 194J. В рамках этой книги мы можем
представить только несколько простых практических методов.
Численные методы расчета траекторий лучей н аберраций
6.2.1. Метод Рунге — Кутта
Естественная идея повышения точности метода Эйлера мог-
могла бы заключаться в использовании большего числа членов
разложения в ряд Тейлора F.5) и F.6). Однако методы рядов
Тейлора высших порядков [195, 196] имеют малое практическое
значение, так как основаны на отыскании высших производных
функции / в заданных точках. Как известно, численное диффе-
дифференцирование является весьма неточной процедурой, особенно
если ее необходимо повторять много раз. Поэтому мы ищем
процедуру, которая была бы аналогична разложению в ряд Тей-
Тейлора до членов hp (где р называется порядком метода), но ко-
которая не требовала бы вычисления каких-либо производных
функции f(z, у, у'). Наиболее элегантная одношаговая процеду-
процедура, которая удовлетворяет этому требованию, — метод Рунге —
Кутта [194J. Ниже будет рассмотрен метод Рунге—Кутта чет-
четвертого порядка для решения дифференциального уравнения
второго порядка F.1).
Основная идея метода Рунге—Кутта состоит в том, чтобы
заменить производные высших порядков значениями функции
f(z, у, у') в промежуточных точках. Определим величины knk'
следующим образом:
F.8)
F.9)
это означает, что члены высших порядков в разложении в ряд
Тейлора заменены этими новыми величинами. Попытаемся оп-
определить их так, чтобы при подстановке в F.8) и F.9) их раз-
разложений в ряд Тейлора они бы совпадали с исходными разло-
разложениями в ряд Тейлора F.5) и F.6) соответственно до членов
четвертого порядка включительно.
Определим величины k и k'\
k = a\h + a2k2 + azkz + aAki, F.10)
Й' = Pt^i + Р2^2 + ^3^3+ ^4*4, F.11)
где вспомогательные величины k\, ..., k4 выражаются через
функцию f(z, у, у'), вычисленную при различных значениях ар-
аргументов, следующим образом:
F.12)
ka=(h*/2)f(z,+h/2, yi + hy'jV + hlA, y'j + kjh), F.13)
F.14)
F.15)
359
Глава 6
При этом отметим зависимость аргументов от самих вспомога-
вспомогательных величин.
Наша задача — определить восемь неизвестных коэффициен-
коэффициентов aq и р9 («7=1, 2, 3, 4) так, чтобы соответствующие разло-
разложения в ряд Тейлора совпадали друг с другом до четвертого
порядка включительно.
Сначала разложим величины ки ..., &4 в ряд Тейлора. Ко-
Коэффициент k\ уже представлен в требуемой форме, единствен-
единственное, что необходимо сделать, — переписать его в виде
£,=A2f,/2, F.16)
где индекс / означает, что соответствующая величина вычисля-
вычисляется в точке Zj.
Определение других коэффициентов намного сложнее. Необ-
Необходимо использовать уравнение C.302) для разложения в ряд
Тейлора функции трех переменных. Подставляя F.16) в F.13)
и учитывая члены до четвертой степени А включительно, полу-
получаем после некоторых элементарных преобразований
{ [/ - Г(~-)] / 8 ), F.17)
где
f'=df/dz=dfldz+y'dfldy+fdfldy', F.18)
f" = d*f/dz2 = d*f /dz*+fdf/ду+f'df/ду'+y'Wfldy* +
+ f2d2f/dy'2 + 2 (y'd2f/dzdy+fd*f/dzdy' + fy'd2f/dydy')
F.19)
являются соответственно первой и второй полными производ-
производными функции f по z.
Используя C.302) и подставляя F.16) и F.17) в F.14), по-
получаем первые члены разложения в ряд Тейлора следующего
коэффициента:
{ [ ($)]/} F.20)
Аналогично, подставляя F.20) в F.15) и используя C.302), по-
получаем соответствующие члены разложения в ряд Тейлора ко-
коэффициента ki в виде
h = (h2/2) (f, + hf'i + Щ"№. F.21)
Теперь можно сравнить F.5) и F.8) друг с другом, прини-
принимая во внимание F.7), F.10), F.16), F.17), F.20) и F.21).
Сначала сравним члены, содержащие h2fj, и получим
1. F.22)
360
Численные методы расчета траекторий лучей и аберраций
Следующий шаг состоит в сравнении членов, пропорциональных
h3f'j. В результате имеем
а2/2 + аз/2 + а4= 1/3. F.23)
Теперь сравним члены, пропорциональные h4f"j. Имеем
а2/4 + аз/4 + а4= 1/6. F.24)
Наконец, учитывая оставшиеся члены в F.17) и F.20), полу-
получаем
F.25)
Таким образом, имеется система четырех линейных алгебраиче-
алгебраических уравнений для четырех неизвестных. Ее решение имеет
вид
ai = a2=a3=l/3, a4 = 0. F.26)
Заменяя F.10) на F.11) и сравнивая таким же образом те-
теперь F.6) и F.9) друг с другом, можем записать следующие
четыре уравнения для четырех других неизвестных:
Pi + p2 + p3 + p4 = 2, F.27)
Ра/2+ р8/2 +04=1, F.28)
Р2/8 + Р3/8+04/2 = 1/3, F.29)
-Р2+Рз = 0. F.30)
Решение этой системы четырех линейных алгебраических урав-
уравнений есть
р, = р4=1/3, р2=Рз=2/3. F.31)
Подставляя теперь F.26) и F.31) в F.10) и F.11), соответ-
соответственно, получаем
F.32)
F.33)
что сразу дает окончательный результат при подстановке этих
выражений в F.8) и F.9) соответственно:
F.34)
F.35)
Это формулы Рунге — Кутта четвертого порядка для числен-
численного решения дифференциального уравнения второго порядка
F.1). Вспомогательные величины ku ..., &4 определяются урав-
уравнениями F.12) — F.15). Можно показать [194], что не только
члены, используемые в приведенном выше выводе, но также
361
Глава 6
члены, пропорциональные А4 при разложении в ряд Тейлора
y'i+i, совпадают друг с другом. (Доказательство последнего не-
несколько громоздко, потому что требует использования полной
третьей производной функции /.) Таким образом, разложения в
ряд Тейлора F.34) и F.35) совпадают с F.5) и F.6) соответ-
соответственно до членов четвертого порядка включительно.
Приведенные выше выражения достаточно просты и, конеч-
конечно, написать программу для вычисления траекторий лучей не
составляет труда. Однако следует обратить внимание на два
важных аспекта. Первая проблема — точность. При благоприят-
благоприятных условиях точность метода зависит только от величины ша-
шага h. Очевидно, что слишком большая величина h приведет к
ошибкам усечения, в то время как слишком маленькая величи-
величина h скажется в ошибках округления. Шаг должен быть выбран
так, чтобы отношение (k2—&з)/(&1—&г) оставалось малой вели-
величиной (максимум 0,02—0,03) вдоль всей траектории. Для расче-
расчета линзы обычно требуется 400—500 шагов.
Вторая проблема-—устойчивость, и она может стать причи-
причиной неприятностей. Решение называется устойчивым, если ма-
малая ошибка, возникающая где-либо во время выполнения вы-
вычислительной процедуры, не увеличивается неограниченно в
последующих вычислениях. Заметим, что устойчивость в общем
случае не зависит от величины шага h. К сожалению, метод
Рунге — Кутта может быть неустойчивым для некоторых диф-
дифференциальных уравнений. Поэтому необходимо соблюдать
осторожность всякий раз, когда распределение поля быстро ме-
меняется или когда функция в некотором смысле ведет себя
«плохо».
Заметим, что требование совпадения разложений в ряд Тей-
Тейлора до некоторого определенного порядка может быть обеспе-
обеспечено многими другими способами. Поэтому существуют различ-
различные формулы Рунге — Кутта, используемые разными автора-
авторами. Из-за способа, по которому они определяются, их точность
не может существенно отличаться друг от друга. Точность, од-
однако, может быть существенно повышена путем использования
методов Рунге—Кутта более высокого порядка.
Для читателя будет полезным упражнением доказать, что
формула Рунге — Кутта четвертого порядка для дифференци-
дифференциального уравнения первого порядка
dyldz=g(z,y) F.36)
есть
у 1+1 = у j -\-[ci + 2 (с2+ Сз) +Ci\jQ, F.37)
362
Численные методы расчета траекторий дучей и аберраций
где
F.38)
c2=hg (zj + /г/2, уi + с/2), F.39)
, у, + сг12), F.40)
, yi + сг). F.41)
Доказательство F.37) не так просто, как кажется. Несмотря
на то что g есть функция только двух переменных, мы должны
доказать, что члены четвертого порядка, соответствующие раз-
разложению в ряд Тейлора, действительно эквивалентны друг дру-
другу. Для этого требуется некоторое терпение.
6.2.2. Многошаговые методы
Хотя метод Рунге—Кутта в большинстве случаев вполне
пригоден для расчета траекторий лучей, он имеет определенный
недостаток: он не использует уже имеющуюся информацию о
траектории. Очевидно, что, если использовать эту информацию,
можно ожидать как улучшения скорости, так и повышения точ-
точности вычислительной процедуры. Это основная идея многоша-
многошаговых методов.
Лучше всего известен метод предиктора-корректора. Его схе-
схема достаточно проста. Вначале используется некоторый экстра-
поляционный метод для «предсказания» значения j/y+i по изве-
известным г/j, J/j_i и т. д. Затем оценивается эта величина и делает-
делается попытка «скорректировать» ее, чтобы получить наилучшую
аппроксимацию для yj+i. Если разность между скорректирован-
скорректированной и предсказанной величинами больше некоторого значения,
то делается следующая итерация.
Это приближение имеет ряд преимуществ. Так как всегда
используется предыдущая информация, функцию / надо оцени-
оценивать точно в узлах сетки, а не между ними. Точность и устой-
устойчивость вычислений могут быть проверены в каждой точке,
и возможен автоматический выбор длины шага, чтобы достичь
заданной точности. Этот метод обычно быстрее и более точен,
чем метод Рунге — Кутта. В последнем сообщении об этом ме-
методе [197] очень высокая точность достигнута минимизацией
ошибок округления.
Однако, как обычно, если есть преимущества, должны быть
и недостатки. Так как метод требует экстраполяции, основан-
основанной на некоторых полученных ранее значениях, вычисление са-
само по себе начаться не может: процедура должна как-то стар-
стартовать, обычно с помощью метода Рунге — Кутта. Кроме того,
363
Глава 6
если требуется изменить величину шага, следует снова выпол-
выполнить начальную процедуру. Таким образом, использование ме-
метода предиктора-корректора намного сложнее, чем использова-
использование метода Рунге — Кутта.
6.2.2.1. Метод Нумерова. Продемонстрируем очень простой
специальный многошаговый метод [198J, который может быть
использован для решения уравнения параксиальных лучей в
виде D.50). Начнем с уравнения C.386). В принятой системе
обозначений имеем
a(z+h)+a(z — h) — 2a(z)«/iV + /i4aIV/12. F.42)
Дифференцируя это выражение дважды по z и опуская члены,
содержащие h в степени, большей чем вторая, получим простое
выражение для четвертой производной а. Подставляя его об-
обратно в уравнение F.42) и учитывая D.50), получаем
a(z+h) — 2a(z)+a(z — h) +h2[T(z + h) a(z+h) +
+ \0T(z)e{z)+T(z — h)o(z — h)]l\2&0, F.43)
что эквивалентно
oy+i * [ A + A2 Tj-xl 12) oy-i — 2 A — 5h2 T,/12) at] X
, F.44)
где aj и Tj — значения функций a(z) и T(z) (уравнения D.47),
D.51)) соответственно, взятые вточкег^. Это простое рекуррент-
рекуррентное соотношение, при помощи которого можно вычислить все
последующие значения а на основе значений в предыдущих
точках. Вычислительная процедура быстрая, устойчивая и до-
достаточно точная, но требует независимой начальной процедуры.
Это метод Нумерова, который в литературе иногда называют
методом Фокса — Гудвина.
6.2.3. Дополнительные замечания о точности
Крайне важно контролировать точность вычислений. В до-
голнение к тому, что было сказано в разд. 3.3.1, следует отме-
отметить, что существуют несколько методов оценки точности чис-
численного расчета траекторий лучей.
Наиболее прямой и обычно используемый путь — изменять
размер шага h в относительно широком интервале, пока два
близких значения h не дадут приблизительно одинаковый ре-
результат. Таким образом, разность между величинами карди-
кардинальных элементов, полученная для каждого значения h, явля-
является хорошим приближением для абсолютной ошибки их вычис-
вычислений. Затем большее из двух значений h может быть использо-
использовано для дальнейших вычислений.
364
Численные методы расчета траекторий лучей и аберраций
Более точный метод состоит в том, чтобы использовать зна-
значения смещения и наклона луча в конце траектории в качестве
начальных условий и проделать вычисления в обратном поряд-
порядке. Для электростатических линз разность между конечными
значениями, полученная таким образом, и исходными началь-
начальными значениями определяет ошибку вычислений. Следует тем
не менее быть осторожным при рассмотрении магнитных линз.
Как следствие анизотропии электронного оптического показате-
показателя преломления (разд. 2.6) траектории в магнитных линзах в
общем случае необратимы. Проецирование траектории на вра-
вращающуюся меридиональную плоскость тем не менее по-преж-
по-прежнему пригодно для этих целей. Метод «назад — вперед» также
пригоден для аберрационных коэффициентов, отнесенных к объ-
объекту и изображению, с последующей проверкой соотношений
между этими коэффициентами.
Наконец, очень простой метод оценить ошибку — это посчи-
посчитать увеличение и угловое увеличение и затем, используя соот-
соотношение Лагранжа — Гельмгольца, проверить точность их зна-
значений. Высокая точность, которая может быть достигнута мето-
методом предиктора-корректора, предполагает новые возможности
для вычисления аберраций. Аберрационные коэффициенты мо-
могут быть определены классическим методом траекторий (см.
разд. 5.1), рассматривая небольшое число независимых лучей
через линзу [199], но их можно определить и с помощью подгон-
подгонки методом наименьших квадратов в конечных точках достаточ-
достаточно большого числа траекторий [ПО, 197J. Более того, так как
интегральные аберрационные коэффициенты дают только абер-
аберрации сопряженных точек предмета и изображения, а не произ-
произвольных точек траектории, альтернативный подход заключается
в том, чтобы развить метод для непосредственного определения
аберрационных фигур, используя большое число точно вычис-
вычисленных лучей. Этот подход требует решения основного уравне-
уравнения D.21), которое в свою очередь предполагает знание всего
поля, а не только его аксиального распределения. Проблема, та-
таким образом, переходит в проблему повышения точности расче-
расчета поля. Это наиболее серьезный источник ошибок, хотя про-
прогресс достигается также и в этом направлении (см. разд. 3.3).
Рассмотренный выше подход выглядит многообещающим, но
все еще находится в стадии развития. Поэтому мы будем ис-
использовать здесь классическое приближение для вычисления
аберрационных коэффициентов в виде определенных интегра-
интегралов. В следующем разделе будут рассмотрены численные мето-
методы их определения.
Глава 6
6.3. Численные методы для вычисления
аберрационных интегралов
Все коэффициенты геометрической и хроматической аберра-
аберрации были выражены в гл. 5 в форме определенных интегралов
в виде
А = \f[U{z), U'(z), U"(z), В {г), B'(z), В"(г),
а
h (z), h' (z), g (z), g' (г) ]dz = \f (z) dz, F.45)
где а и b — границы полей для асимптотического случая и ко-
координаты предмета и изображения соответственно для реально-
реального случая. Аналогично h(z) и g(z) —два независимых решения
уравнения параксиальных лучей с различными начальными
условиями для реального и асимптотического случаев. Уравне-
Уравнение F.45) является, таким образом, только формальным пред-
представлением аберрационных интегралов, как они записываются в
общем случае. Важно то, что сложная подынтегральная функ-
функция всегда является функцией только координаты z. Заметим,
что функция F{z) может даже
представлять подынтеграль-
подынтегральную функцию в виде комбина-
комбинации различных аберрационных
коэффициентов.
Аберрационные интегралы
могут быть выражены в квад-
квадратурах только в отдельных
F(z)
Рис. 77. Численное интегрирование.
случаях (такие примеры бу-
будут приведены в гл. 7 и 8). В
общем случае интегралы не-
необходимо вычислять численными методами. Так как опреде-
определенный интеграл равен площади под кривой F(z) (рис. 77),
проблема в основном сводится к проблеме интерполяции, пото-
потому что функция F(z) задается в виде дискретных величин в
N+1 точке в интервале а^г^б.
Будем использовать интерполяционную формулу Лагранжа
(уравнение C.390)), чтобы представить функцию F(z). Интег-
Интеграл от функции в пределах г} и zi+n можно выразить как
j F(z)dz=
zf+n
21 Li(z)F(zi)dz='
14
где
zi+n
= S U(z)dz {l=j,
F.46)
F.47)
366
Численные методы расчета траекторий лучей и аберраций
Li(z) определяется уравнением C.389) и п — порядок интерпо-
интерполяции, т. е. число точек, используемых для интерполяции (это
число в общем случае много меньше, чем полное число точек N,
в которых определена функция F).
Используя этот подход с различными значениями п, доволь-
довольно просто построить численные процедуры различной степени
точности. Рассмотрим простейшие алгоритмы.
6.3.1. Интегрирование методом трапеций
Использование линейной интерполяции эквивалентно замене
кривой, заданной функцией F(z), ломаной линией. Так как это
очень грубая .аппроксимация, она требует большого числа то-
точек для достижения приемлемой точности. Процедура, однако,
крайне простая и быстрая. Так как в этом случае я = 1, можно
использовать интерполяционную формулу C.391), с которой
уравнение F.46) дает
г/+1
S F(z)dz=h[F(zj)+F(zi+ly]J2, F.48)
ZJ
где размер шага h определяется уравнением F.4). Заметим, что
уравнение F.48) дает площадь трапеции, образованной при ли-
линейной интерполяции кривой (см. рис. 77). Затем интеграл для
всего интервала a^.z^.b находится как сумма веех трапеций
$F(z)dz*h{F{a)+2F(a+h)+2F(a+2h) + ...
...+2F[a+(N-l)h]+F(b)}/2, F.49)
которая может быть записана как
]F(z)dz = h{[F(a)+F(b)]/2 +
а
+NLF(a+ih)} ~(b — a)b?F"{z)l\2. F.50)
Это хорошо известная формула интегрирования методом трапе-
трапеций [115J. Остаточный член — это погрешность усечения, свя-
связанная с этим приближением. Конечно, F" (z) берется где-либо
в интервале a^z^b, но точное положение z не определено.
Однако формула позволяет определить верхнюю границу по-
погрешности усечения, если заменить F"(z) ее максимальным по
абсолютной величине значением на данном интервале. Оче-
Очевидно, для вогнутой кривой вторая производная отрицательна
и остаточный член, дающий ошибку, положителен, это означа-
367
Глава 6
ет, что аппроксимация трапециями приводит к заниженному
значению интеграла. Для выпуклой кривой справедливо проти-
противоположное.
Попытаемся в качестве простого примера определить чис-
численно интеграл
$dz/z = In 2 = 0,6931471806.
i
Так как в этом случае F"(z) —2/z3, ошибка усечения методом
трапеций должна лежать между /i2/6 и Л2/48. Выберем Л=0,1;
тогда ожидаемая ошибка должна быть в интервале между
2,08-10-4 и 1,67-Ю-3. Численный расчет дает 0,6937714032, т. е.
абсолютная ошибка есть 6,24-10~4.
6.3.2. Правило Симпсона
Для повышения точности будем использовать теперь квадра-
квадратичную интерполяцию. Это эквивалентно замене кривой F{z)
последовательностью парабол. Здесь имеем п — 2, поэтому бу-
будет использована интерполяционная формула C.392), что вмес-
вместе с уравнением F.46) дает
2Я-2
. F{z)dz = h[F(zj)+4F{zj+1)+F(zi+2)]l3. F.51)
Тогда интеграл по всему интервалу a^z^b аппроксимируется
следующей суммой:
. F(z)dz&h{F(a) +4F(a + h) + 2F(a + 2h) +4F(a+3h) + ...
... +2F[a+ (N — 2)h] +4F[a+(N —
F.52)
которую можно записать как
b N/2-l
$F{z)dz = h{F(a)+F(b)+2 Ц F(a + 2jh) +
a /=1
+ 4'LF[a+ B/ — l)A]}/3 — (b — a)h*F™ (z)/180.
F.53)
Это известное правило Симпсона [115J. Остаточный член — по-
погрешность усечения. Fiv(z) берется где-то на отрезке а^г^б,
но точное расположение этой точки не определено. Верхний
предел ошибки усечения может быть определен, если заменить
368
Численные методы расчета траекторий лучей и аберраций
F1V (z) ее максимальным по абсолютной величине значением на
данном интервале.
Заметим, что выражение F.53) справедливо в этом виде,
только когда N — четное число. Если N — нечетное, скорректи-
скорректированная формула должна быть использована на расширенном
интервале, что не очень удобно. Поэтому практически всегда
хорошо использовать четное число подынтервалов, т. е. опреде-
определить функцию в нечетном числе точек.
Для нашего простого примера F(z) = l/z (см. предыдущий
раздел) имеем /7lv(z)=24/25, и погрешность усечения в методе
Симпсона должна быть между Л4/7,5 и /i4/240. Выбрав /i = 0,lr
можно ожидать, что ошибка будет в интервале между 4,17-10
и 1,33-10~5. Численный расчет дает 0,6931502307, т. е. абсолют-
абсолютная ошибка есть 3,05-10~. Как видим, точность приблизитель-
приблизительно в 200 раз лучше, чем у метода трапеций. Конечно, повыше-
повышение точности зависит от подынтегральной функции и также от
размера шага, но вполне очевидно, что правило Симпсона име-
имеет определенные преимущества перед интегрированием методом
трапеций.
Интегрирование можно всегда представить как решение
дифференциального уравнения первого порядка. В самом деле,
если заменить g(z, у) на F(z) в уравнении F.36) и проинтегри-
проинтегрировать от z,- до z/+i, получим
yj+l = у, + I F (z) dz = yj + h [F (zj) + 4F (г, + /г/2) +
*' F.54)
где использовано F.51) со средней точкой внутри одного ин-
интервала вместо двух интервалов. Рассматривая уравнения
F.38) — F.41) применительно к функции одной переменной
F(z), мы сразу видим, что уравнение F.54) может быть сведе-
сведено к уравнению F.37). Поэтому правило Симпсона эквивалент-
эквивалентно формулам Рунге-—Кутта четвертого порядка.
6.3.3. Интегрирование методом Ромберга.
Гауссовы квадратуры
Есть много других методов вычисления определенных интег-
интегралов [115, 130]. Обычно подынтегральное выражение задано в
виде дискретных значений. Однако всегда можно представить
эти данные в интерполированном виде, например, используя ку-
кубический сплайн (см. разд. 3.3.5.4). Тогда точность численного
интегрирования может быть резко повышена. Упомянем здесь о
двух методах.
369
Глава 6
В первом методе (интегрирование методом Ромберга) фор-
формула трапеций используется как начальное приближение, потом
применяется процедура экстраполяции для повышения точно-
точности. Последовательные приближения вычисляются до тех пор,
пока не будет достигнута заданная точность. Величина шага вы-
выбирается автоматически, чтобы удовлетворить заданной точнос-
точности. Интегрирование методом Ромберга поэтому является итера-
итеративной процедурой, основанной на очень простой аппроксима-
аппроксимации. Детали можно найти в специальной литературе [115J.
Процедура требует очень малого объема памяти, поэтому мо-
может быть использована для программируемого калькулятора.
Метод гауссовых квадратур основан на теории ортогональ-
ортогональных функций. Идея состоит в том, чтобы разбить интервал ин-
интегрирования на неравномерные подынтервалы таким образом,
чтобы минимизировать ошибку. Это является особенно эффек-
эффективным, если разбиение используется между точками z:- и z3-+i.
Тогда размер шага становится меньше, что является дополни-
дополнительным преимуществом этого метода. Точность определяется
числом подынтервалов. Обычно используемая шеститочечная
формула [130]
F.55
t=i
j
очень точна, как можно видеть по пренебрежимо малому оста-
остаточному члену. Действительно, в большинстве случаев погреш-
погрешностью усечения можно пренебречь по сравнению с ошибкой
округления. В уравнении F.55) коэффициенты с,- и Wi задаются
в виде
ci = c2 = 0,4679139346 Wi = — а>2 = 0,2386191861
с3 = с4 = 0,3607615730 Ws=—w4 = 0,6612093865 F.56)
с5 = с6=0,1713244924 ш5 = —да6 = 0,9324695142
Для функции F(z) = l/z мы вычислили интеграл в интервале
l^z^2, используя шеститочечную гауссову квадратуру, т. е.
только 7 интервалов вместо десяти, как в двух предыдущих
разделах. Хотя был использован десятиразрядный калькулятор
с относительно высокой погрешностью округления, результат
составил 0,6931471799, что означает абсолютную погрешность
7-10~10. Преимущества метода очевидны.
Заключение
В этой короткой главе мы вкратце рассмотрели основные
численные методы для расчета траекторий лучей и вычисления
370
Численные методы расчета траекторий лучей и аберраций
аберрационных коэффициентов. Был продемонстрирован метод
Рунге — Кутта для решения обыкновенных дифференциальных
уравнений. Уравнения F.34) и F.35) с коэффициентами из
уравнений F.12) — F.15) представляют формулы Рунге —Кут-
—Кутта четвертого порядка для решения дифференциальных уравне-
уравнений второго порядка. Соответствующие выражения для решения
дифференциального уравнения первого порядка даются соотно-
соотношениями F.37) — F.41). Далее были кратко рассмотрены много-
многошаговые методы. Соотношение F.44) представляет формулу
Нумерова для решения уравнения параксиальных лучей в ви-
виде D.50). Аберрационные коэффициенты также могут быть по-
получены численно посредством метода трапеций F.50), правила
Симпсона F.53), итерационного метода Ромберга или через
гауссовы квадратуры F.55).
Глава 7
ЭЛЕКТРОСТАТИЧЕСКИЕ ЛИНЗЫ
7.1. Основные свойства и соотношения
Любая аксиально-симметричная система электродов образу-
образует электростатическую линзу (см. разд. 4.4). Характерной отли-
отличительной особенностью электростатической линзы в нереля-
нерелятивистском случае является независимость ее фокусирующих
свойств, а также аберраций от отношения заряда частицы к ее
массе и, следовательно, если в системе будут использоваться
ионы различных типов, то необходимо применять электростати-
электростатические линзы. Это свойство является следствием законов подо-
подобия, изложенных в разд. 2.8. Так как оптическую силу аксиаль-
аксиально-симметричных магнитных линз приблизительно можно счи-
считать пропорциональной отношению заряда частицы к ее массе
[см. уравнения D.51) и D.117)], это преимущество электроста-
электростатических линз особенно проявляется при работе с тяжелыми
ионами.
Далее заметим, что на свойства линзы оказывает влияние
только отношение потенциалов, и если необходимо совместить
траектории частиц противоположных знаков, то достаточно про-
просто поменять знаки всех потенциалов (включая и С/о) • Следова-
Следовательно, можно ограничиться вычислениями для электронов (т. е.
для потенциалов положительно заряженных электродов) и над-
надлежащим образом учитывать, что для положительных ионов по-
потенциалы электродов будут иметь ту же абсолютную величину,
но противоположный знак.
Еще одним специфическим свойством электростатических
линз является то, что они не только фокусируют, но, кроме то-
того, ускоряют или замедляют частицы. Исключение составляют
только одиночные линзы (см. разд. 7.4), в которых фокусиров-
фокусировка происходит без изменения энергии. Ускоряющие свойства
электростатических линз используются в электронных и ионных
источниках (см. разд. 7.8.3). Кроме того, электростатические
линзы могут быть использованы для анализа и разделения ча-
частиц по энергиям (линзовые фильтры).
Электростатические линзы обычно состоят из простых элект-
электродов (комбинации апертур и трубок), которые легко изгото-
изготовить и собрать. Единственными серьезными проблемами при
изготовлении являются необходимость учитывать электрический
пробой и накопление заряда на изолирующих поверхностях.
372
Электростатические линзы
В условиях рабочего вакуума электроды должны быть отделены
друг от друга настолько, чтобы максимальная напряженность
поля не превышала 15 кВ/мм.
Серьезной проблемой, связанной с электростатическими лин-
линзами, являются трудности при расчете их свойств из-за боль-
большого количества характеризующих их параметров. Число воз-
возможных комбинаций электродов неограниченно, и существует
огромное количество возможных наборов параметров, которые
обеспечивают линзы с различными свойствами. Даже свойства
простейших линз, состоящих из пары симметрично расположен-
расположенных апертур, зависят от большого числа параметров: отношения
электродных напряжений, размеров апертур, толщины электро-
электродов и расстояния между ними, а также от радиальных и про-
продольных размеров электродов. Последними часто пренебрегают,
но они крайне важны (см. ниже). Поэтому опубликовано чрез-
чрезвычайно мало точных расчетных данных, в основном только для
простейших конфигураций [44], и сравнивать свойства различ-
различных линз очень трудно. Обычно они публикуются в виде таб-
таблиц и графиков, где кардинальные элементы и коэффициенты
аберрации представлены как функции отношения напряжений
и геометрических параметров. Из-за большого числа этих пара-
параметров универсальные конструктивные кривые не рассчитыва-
рассчитываются. Конструирование электростатических линз обычно прово-
проводится методом проб и ошибок. Наилучший способ состоит в том,
чтобы накопить данные в памяти компьютера и составить про-
программу для их быстрого вызова и анализа. В гл. 9 будут описа-
описаны методы, которые позволяют синтезировать линзы с задан-
заданными свойствами.
Классификация электростатических линз дана в разд. 4.7.
Один из способов классификации линз определяется тем, явля-
являются ли линзы ограниченными или погруженными в поле. Гра-
Границы линзы обычно определяются двумя плоскостями z = a и
г = Ь, на которых поле линзы практически исчезает (разд. 4.6.1).
Исключением являются диафрагмы, поле которых не ограниче-
ограничено по крайней мере с одной стороны, и источники (катодные
линзы), у которых поле резко обрывается со стороны, обращен-
обращенной к объективу. Во всех других случаях электростатические
линзы можно рассматривать как ограниченные с обеих сторон.
Это означает, что ни на одной из них не должно быть электри-
электрического поля, т. е. наклон графика распределения потенциала
на обеих сторонах линзы должен стремиться к нулю. Безуслов-
Безусловно, линзы, подобные апертурным, не являются открытыми си-
системами, если только концы электродов не удлиняются в акси-
аксиальном направлении в виде дополнительных трубок, поддержи-
поддерживающих постоянное значение потенциала (см. рис. 23), или ес-
если следующий электрод оптической колонны удален не очень
373
Глава 7
далеко и имеет такое же значение потенциала, как и конечный
электрод линзы. Дополнительные трубки экранируют линзу от
контурного поля, возбуждаемого нулевым потенциалом на бес-
бесконечности в осевом направлении. Длина и диаметр этих трубок
являются двумя весьма важными параметрами, на которые час-
часто не обращают должного внимания, но которые могут оказы-
оказывать существенное влияние на работу линзы.
Радиальные расширения электродов открытых линз являют-
являются равнозначными параметрами, которыми иногда пренебрега-
пренебрегают. Рассмотрим снова апертурную линзу, изображенную на рис.
23. Ясно, что, если расстояние между электродами сравнимо с
их радиальными размерами, внешние поля, проникающие в ра-
радиальном направлении, будут существенно влиять на распреде-
распределение потенциала и, следовательно, на работу линзы. Как след-
следствие радиальные размеры электродов должны всегда вклю-
включаться в основные параметры линзы.
О Е
Рис. 78. Действие электростатической линзы (кривыми показаны некоторые из
эквипотенциальных линий).
Действие электростатической линзы может быть продемон-
продемонстрировано на примере простой линзы, состоящей из двух ци-
цилиндров, поле которой было рассмотрено в разд. 3.1.2.2. На рис.
78 изображена картина эквипотенциальных поверхностей такой
линзы. Кроме того, показан главный луч с векторами электро-
электростатического поля в двух точках для случая положительных по-
потенциалов электродов, причем V2>Vi. Как видно, в этом слу-
случае электроны ускоряются и фокусируются слева от линзы, тог-
тогда как справа от "линзы они дефокусируются. Так как электро-
электроны проводят больше времени в области с меньшим потенциа-
потенциалом, суммарным эффектом является фокусировка, как и ожида-
ожидалось в соответствии с основной теоремой электронной и ионной
оптики (разд. 4.4). Если Vz<Vi, то электроны замедляются и
фокусировка происходит с правой стороны, но теперь это уже
область с меньшим потенциалом. Для положительно заряжен-
заряженных частиц потенциалы электродов отрицательны и для ускоре-
ускорения должно выполняться соотношение Уг<^1- Тогда фокусиров-
фокусировка происходит с левой стороны, снова там, где скорость меньше.
Если Уг>1Л, то положительно заряженные частицы будут за-
374
Электростатические лиизы
медляться и действие фокусировки будет проявляться с правой
стороны (там, где скорость меньше). В основном те же эффек-
эффекты будут наблюдаться и в более сложных случаях с той только
разницей, что будет существовать более двух фокусирующих
или дефокусирующих областей. Если поле линзы ограничено с
обеих сторон, то суммарным эффектом всегда будет фокуси-
фокусировка.
Объект и его изображение обычно расположены вне поля,
следовательно, для расчетов (исключая диафрагмы и катодные
линзы) могут быть использованы асимптотические свойства оп-
оптических систем. Будем предполагать, что скорости не достига-
достигают релятивистских значений и что отсутствуют любые азиму-
азимутальные составляющие скоростей. Тогда траектории всегда пе-
пересекают оптическую ось и могут быть рассмотрены в меридио-
меридиональной плоскости гг. В этом случае можно использовать урав-
уравнение главных траекторий D.23). Тогда уравнение параксиаль-
параксиальных лучей D.40) примет вид
r'+
Так как в этом случае C=5(z)=0, то D.47) может быть пере-
переписано в виде
a(z) = r(z)\U(z)-U0\4* G.2)
и D.51) преобразуется к виду
G.3)
которое используется в уравнении параксиальных лучей в фор-
форме D.50) так же часто, как и в формулах тонкой линзы
D.117) —D.125).
Асимптотический коэффициент сферической аберрации для
объекта [уравнения E.251) — E.254)] может быть записан как
Uiz)~UoYl2
■
24[£/(z) — U a
~ 2[!/(»)-£.]' H*H'2 ) dZ< G'4)
где начальные условия для луча Н(г) определяются уравнени-
уравнением E.240).
375
Глава 7
Асимптотический осевой коэффициент хроматической абер-
аберрации для объекта (уравнения E.194) и E.270) — E.272)) в
свою очередь имеет вид
Г Г
U (a)-Uo 11/2 I U«(z)
Несмотря на трудности, описанные выше, мы сделаем по-
попытку дать систематический обзор существующих электроста-
электростатических линз и затем перейдем к исследованию их конкретных
типов.
7.2. Модели электростатических линз
Зачастую желательно оценить свойства линзы приближенно,
без проведения детального анализа. Это возможно, если имеет-
имеется простая математическая модель линзы, т. е. такое приближе-
приближение распределения осевого потенциала, которое достаточно близ-
близко к реальному и позволяет получить либо решение, близкое по
виду, либо приближение в простых выражениях. Существуют
два основных типа моделей линз: распределение потенциала ап-
аппроксимируется одной функцией для всей линзы (аналитичес-
(аналитическая модель) или же делится на ряд интервалов и распределе-
распределение на каждом интервале аппроксимируется элементарной
функцией (кусочные модели).
7.2.1. Аналитические модели
Аналитические модели имеют ряд преимуществ (см. разд.
6.1) и, следовательно, их использование всегда желательно. Так
как, к сожалению, не существует общей аналитической модели
для произвольной электростатической линзы, будем использо-
использовать их по ходу этой главы, каждый раз находя модель, которая
подходит для описания данного типа линз. Поэтому читатель
отсылается к соответствующим разд. 7.3.1.2, 7.4.1.3 и т. д.
7.2.2. Кусочно-линейная модель
Эта модель основана на приближении осевого распределения
потенциала линзы ломаной линией [9J, т. е. последовательно-
последовательностью интервалов, на которых поле однородно, но имеет разные
376
Электростатические лиизы
значения. Конечно, такое распределение не может быть реали-
реализовано на практике, но это здесь и не важно: мы просто ис-
используем это приближение как простейшую из возможных ма-
математических моделей для произвольного распределения элект-
электростатического потенциала. Эта модель напоминает интегриро-
интегрирование методом трапеций (см. разд. 6.3.1).
Траектория заряженной частицы внутри каждого интервала
представляет собой параболический сегмент. Эти сегменты оп-
определяются уравнением D.141). Наклон траектории дается
уравнением D.140). Если существуют интервалы, на которых
потенциал постоянен, то траектория на них будет прямолиней-
прямолинейна и описывается уравнением D.142). Естественно, мы должны
потребовать непрерывности как r(z), так и rr{z) на концах
каждого интервала. Этого легко добиться для r(z), но невоз-
невозможно для r'(z). Причиной являются разрывы первой произ-
производной потенциала в этих точках. Следовательно, вторая произ-
производная потенциала (которая считается равной нулю внутри каж-
каждого интервала) принимает бесконечно большие значения на
концах отрезков в случае, если считать переходную область 2Дг
между двумя интервалами бесконечно узкой. К счастью, та же
причина, которая приводит к «бесконечно большому» росту вто-
второй производной, ограничивает ее действие, но ведет к скачку
Аг' в наклоне траектории. Можно вычислить этот скачок, про-
проводя интегрирование уравнения параксиальных лучей G.1) по
области перехода в окрестности конца отрезка zh:
гь + Дг г^+Дг
Первой производной можно пренебречь по сравнению с очень
большой второй производной. Кроме того, в узкой переходной
области как r(z), так и U(z) могут рассматриваться как посто-
постоянные со значениями, которые они имеют на конце отрезка г*.
Тогда интегрирование дает
Этот скачок должен быть добавлен к наклону траектории в
каждой точке перехода любых двух интервалов. Таким образом,
вся траектория состоит из набора парабол с такими скачками
в каждом узле. Естественно, этот метод не является очень точ-
точным, но, как мы увидим в разд. 7.3.1.1, он может служить хо-
хорошим инструментом для быстрой оценки оптических свойств
электростатических линз.
377
Глава 7
7.2.3. Кусочно-квадратичная модель
Для аппроксимации осевого распределения потенциала на
каждом интервале будем использовать следующий вид квадра-
квадратичной функции:
Uk{z)=ak + bk{z — zk-1)+ck{z — zk-lJ G.8)
(по поводу нумерации узлов и интервалов см. рис. 41). В этом
случае электростатическое поле . внутри каждого интервала
представляется ломаной линией, а вторая производная потен-
потенциала— постоянной. Будем требовать непрерывности как U(z),
так и U'(г) в соответствии с уравнениями C.395) и C.396),
что в свою очередь приводит к следующим двум соотношениям
между коэффициентами:
G.9)
G.10)
где h = Zk+i—Zk — длина каждого интервала (k = l, 2, ..., п).
Так как первая производная непрерывна, в этой модели легко
удовлетворяются условия непрерывности как r(z), так и r'(z).
Однако вторая производная не является непрерывной.
Коэффициенты ан, bk и с*, различны для разных интервалов.
Так как имеется п интервалов, число коэффициентов Зл. Урав-
Уравнения G.9) и G.10) обеспечивают 2 (я—1) соотношений между
ними. Таким образом, имеем л+2 свободных коэффициента, ко-
которые могут быть использованы для построения кривой в я+1
узлах и, кроме того, для реализации одного из двух простых
граничных условий. Хотя эта модель гораздо лучше, чем линей-
линейная, можно видеть и ее слабости: обычно необходимо удовлет-
удовлетворить одному условию на каждой границе, а именно следует
обеспечить плавный переход в области, где поле отсутствует по
обеим сторонам линзы, требуя его обращения в нуль на обоих
концах. С помощью такой модели это достижимо только в не-
нескольких подходящих специальных случаях. Следующим недо-
недостатком является разрыв второй производной в каждом узле.
Распределение потенциала, задаваемое уравнением G.8)
может быть реализовано гиперболическими электродами. В са-
самом деле, подставляя уравнение G.8) и его вторую производ-
производную в систему C.20), получим уравнение гиперболы. Фиксируя
значение потенциала u(r, z), получим уравнение гиперболиче-
гиперболических эквипотенциалей. Можно исследовать оптические свойства
таких линз [200], но опять невозможно реализовать кусочно-
квадратичное распределение во всей его полноте из-за невоз-
невозможности суперпозиции различных систем гиперболических
электродов для каждого интервала. Однако к счастью, как и
прежде, нет необходимости в реализации и этой математиче-
378
Электростатические линзы
ской модели. Ее цель — служить аналитическим инструментом
для упрощенных вычислений.
Уравнение параксиальных лучей G.1) может быть строго
решено для распределения потенциала G.8) на каждом интер-
интервале [201]. Рассматривая для простоты положительный потен-
потенциал, вводя новую переменную
a»*(z) - if [Uk(z) - U0]-V4z G.11)
Ч-\
и подставляя уравнение G.8) и его производную в G.1), полу-
получим
£ 0. G.12)
Начальные условия при z=zk-i даются в виде
i) =/•*_! (zft_!), r'* (Zfc-i) =/•'*-! (Zft-0- G-13)
Для того чтобы удовлетворить условию непрерывности, началь-
начальные значения должны быть равны соответствующим конечным
значениям величин гиг' для предыдущего интервала. (Аргу-
(Аргументы этих конечных значений в дальнейшем будут опус-
опускаться.)
Решение уравнения G.12) зависит от знака коэффициента ск.
Из уравнений G.8) и C.38) можно видеть, что в этом случае
радиальные компоненты напряженности электростатического
поля выражаются просто как
Ег=скг. G.14)
Это значит, что при положительном г напряженность имеет тот
же знак, что и ск. Так как мы рассматриваем положительные
потенциалы, т. е. отрицательно заряженные частицы, положи-
положительное значение ск эквивалентно фокусирующему действию
в данном интервале, в то время как отрицательное ск соответ-
соответствует дефокусирующему действию. Если ск=0, имеем в этом
интервале однородное поле. Этот случай будет рассмотрен от-
отдельно. После того как частица пересекла ось, г становится
отрицательным, но тогда снова для фокусировки необходимо,
чтобы Ck было положительным. Рассмотрим, что будет происхо-
происходить в различных областях.
1. В первую очередь рассмотрим фокусирующие области,
где cft>0. Тогда решение уравнения G.12) для &-го интервала
при начальных условиях, заданных уравнением G.13), и обрат-
обратном преобразовании к начальным координатам запишется
в виде
rk {z)~rk-i cos a+2rV-i [ {ак — U0)/2ck] sin a, G.15)
379
Глава 7
r'k(z)=-(rk-1/2){2ck/[Uk(z) - f/0]}1/2sina+
— U0)I[Uk(z) -f/0]}1/2cosa, G.16)
где
a = 2-1/2in
2. Для дефокусирующих областей, в которых Сь<0, решени-
решением уравнения G.12) в первоначальных координатах для k-то
интервала при начальных условиях G.13) является
rk(z),=rk-lch^+2rfk-l[— (ak— i/0)/2c,]i/2shp, G.18)
r'k (z) = (rH/2) {- 2ck/[Uk (z) - t/o]}1/2 sh [i +
— U0)/[Uk (z) - J/0]}1/2chp, G.19)
где
^=2-i/2
— arcsin{[6*+2c*B — г*_1>] [6*« — 4c*(a* —
G.20)
3. Приведенные выше решения в простом специальном слу-
случае с* = 0 имеют особенности, но тем не менее решение уравне-
уравнения параксиальных лучей может быть получено без особых
трудностей. Если ЪкфЬ (область однородного поля), из уравне-
уравнений D.141) и D.140) имеем
r*(z)=r*-i— B/Vi/&*)X
— U0—{(ak — С/о) [a* — U0 + bk(z — z*_i)]}>.
G.21)
2.
G.22)
Отметим, что такие области с разными Ьк и b*+J не могут сле-
следовать одна за другой, потому что в этом случае пришлось бы
вернуться к кусочно-линейной модели с разрывными первыми
производными.
4. Если bk=Ck=O, имеем область, в которой поле отсутст-
отсутствует и траектория дается уравнением D.142).
Эта модель будет использоваться в разд. 9.5 для оптимиза-
оптимизации иммерсионных линз.
7.2.4. Сплайновая модель
Как мы видели в разд. 3.3.5.4, кубический сплайн является
наиболее гладкой из возможных интерполяционных функций.
Следовательно, совершенно естественно использовать ее как
380
Электростатические линзы
простую модель для представления громоздкого распределения
осевого потенциала. Как и прежде, распределение делится на п
интервалов (см. рис. 41). Оно представляется на k-u интервале
кубическим полиномом C.394), где и и q должны быть замене-
заменены осевым потенциалом U (z) и координатой z соответственно.
В этом случае U(z), V (z) и U" (z) являются непрерывными
функциями. Вторая производная распределения потенциала да-
дается ломаной линией, а третья производная постоянна внутри
каждого интервала. Непрерывность U(z), U'(z) и U" (z) в со-
соответствии с уравнениями C.395) — C.397) обеспечивается тре-
тремя соотношениями C.398) — C.400) между коэффициентами.
Коэффициенты Ak, Bk, Си и Dk различны для разных интер-
интервалов. Так как интервалов п, число коэффициентов 4л. Уравне-
Уравнения C.398)—C.400) обеспечивают 3(л—1) соотношений между
ними. Таким образом, имеется л+3 свободных коэффициента.
Они могут быть использованы для подгонки кривой в я-f-l уз-
узлах и, кроме того, для удовлетворения двух граничных усло-
условий. Это одна из сильных сторон сплайновой модели: легко
обеспечить плавный переход к областям, свободным от поля,
с обеих сторон линзы, удовлетворяя требованию нулевого поля
на обоих концах.
Отметим, что разрывность третьей производной и неопре-
неопределенность производных более высоких порядков не создает
никаких проблем, так как можно вычислить все оптические
свойства, включая и аберрации, используя только две первые
производные. Этот вопрос будет обсуждаться в разд. 9.8 и 9.9.2.
Аналитическое решение уравнения параксиальных лучей
для распределения потенциала в виде кубического полинома
неизвестно. Тем не менее сплайновая модель является крайне
удобной для значительного числа представлений различных
распределений потенциалов [202]. Она будет использована для
синтеза электронных линз в гл. 9.
7.3. Двухэлектродные иммерсионные линзы
Простейшая электростатическая линза состоит из двух
электродов, на которые поданы разные потенциалы. Если потен-
потенциалы различны по обе стороны линзы, то такая линза назы-
называется иммерсионной (см. разд. 4.7). (Легко сконструировать,
линзу с одинаковыми потенциалами, состоящую из двух
электродов (см. рис. 98). Такие линзы будут рассмотрены
в разд. 7.4.) Мы уже знакомы с двумя представителями этой
группы: двухцилиндровыми линзами (рис. 17) и двухапертур-
ными линзами (рис. 23). Нетрудно себе представить, что если
в качестве электродов использовать только цилиндры и апер-
апертуры различных размеров, то число всевозможных комбинаций-
381!
Глава 7
неограниченно велико. Так как, кроме того, электроды могут
иметь неограниченное разнообразие форм, то очевидно, что, да-
даже если имеются только два электрода, систематическое иссле-
исследование возможно только в том случае, если выделить наибо-
наиболее характерные параметры и изучить их влияние на оптиче-
оптические свойства различных линз.
Очевидно, что можно надеяться найти такие простые пара-
параметры только исходя из распределения осевого потенциала.
Огромное разнообразие таких параметров не способствует си-
систематическим исследованиям. Поэтому начнем с анализа рас-
распределения потенциала, а электродами займемся позже.
Распределение .осевого потенциала U(z) двухэлектродной
иммерсионной линзы имеет очень простую форму, показанную
на рис. 79. Это монотонная функция осевой координаты г,
асимптотически стремящаяся к потенциалам электродов Vi и Vi
по обе стороны линзы (z—a и z=b соответственно). Естествен-
Естественно, |У2|>|1Л| для ускоряющей линзы и |Vi|>|V2| для за-
Рис. 79. Распределение потенциала двухэлектродной иммерсионной линзы.
медляющей. Распределение потенциала не может содержать
областей с постоянным потенциалом, потому что для их поддер-
поддержания необходимы дополнительные электроды. Распределение
имеет одну точку перегиба гт, где осевая компонента поля до-
достигает своего максимального абсолютного значения |£/'|тах-
Координата этой точки может совпадать, а может и не совпа-
совпадать с геометрическим центром линзы. В этой связи мы можем
говорить о симметричных или асимметричных линзах. В пер-
первом случае линза геометрически симметрична относительно не-
некоторой средней плоскости, перпендикулярной оптической оси.
Очевидно, распределение потенциала может быть охаракте-
охарактеризовано следующими четырьмя параметрами:
1) протяженностью поля (Ь—а), где осевой потенциал за-
заметно отличается как от Vi, так и от Уг;
2) максимальной абсолютной величиной |£/'|тах градиента
осевого потенциала;
3) отношением электродных потенциалов (Уг—Uq)I(Vi—
4) степенью асимметрии, характеризуемой сдвигом zm отно-
относительно среднеарифметической координаты г= (а+Ь)/2.
382
Электростатические лиизы
Осмысленное сравнение различных линз должно основывать-
основываться на этих параметрах [202а, 202Ь]. Отметим, что удобнее
пользоваться безразмерными параметрами, следовательно, же-
желательно отнести определенные выше величины к некоторым
нормирующим множителям.
Кроме того, важно помнить, что протяженность поля (Ь—а)
определяется до некоторой степени произвольно (см. разд. 4.6).
Хорошо было бы иметь более объективный параметр. Такой
параметр удобно ввести в виде эффективной длины (см.
разд. 2.7.1, 3.1.3.2 и 4.10.2). Эффективная длина определяется
уравнением C.197), где функция Г (г) (уравнение G.3)) ис-
используется для F(z). Имеем
Lett = \T(z)dz/T(zm), G.23)-
а
где zm — теперь осевая координата максимума поля, но опреде-
определение эффективной длины совершенно произвольно, поэтому
некоторые могут отдавать предпочтение использованию осевой
координаты, где достигает максимума функция T(z). Это имеет
смысл, так как T(z) —функция, которая определяет оптические-
свойства. Ее максимум сдвинут в направлении меньшей абсо-
абсолютной величины потенциала в соответствии с тем, что это
область, которая обладает фокусирующим действием (см.
рис. 83). (Отметим, что для магнитной линзы функция T(z)
пропорциональна площади распределения магнитной индукции,,
поэтому ее максимум совпадает с максимумом абсолютной ве-
величины поля.) Однако, так как Tlz) в большинстве случаев —
функция усложненного вида, легче оценить ее при значении zmr
чем в точке ее максимума.
В любом случае важной количественной характеристикой
является интеграл функции Г (г). Он имеет прямое отношение-
к формулам тонкой линзы D.117) — D.125). Оптическая сила
тонкой линзы пропорциональна этой величине и через нее —
эффективной длине. Интеграл T(z) есть число, которое зависит
от геометрии линзы и отношения напряжений изображение —
объект (V2—Uo)l{V\—Uo). Максимальное значение поля зави-
зависит от тех же факторов, но, кроме того, от входной энергии
частиц (V\—Uо).
Эффективная длина может существенно отличаться для
различных линз даже с одинаковым максимальным полем. Она
совершенно по-разному зависит от физической длины фокуси-
фокусирующего элемента и протяженности поля (Ь—а). Меньшая эф-
эффективная длина при том же отношении напряжений означает
более высокую плотность поля.
К сожалению, полезность понятия эффективной длины огра-
ограничивается трудностью ее оценки. В большинстве случаев она
383
Глава 7
требует численного интегрирования, а результат справедлив на
уровне приближенной оценки фокусирующих свойств первого
порядка. Гораздо информативнее провести сложный расчет
хода лучей, включающий вычисление аберраций.
Для оценки максимального значения поля и его положения
необходимо знать точное распределение потенциала линзы. От-
Отношение потенциалов изображение — объект является числен-
численным параметром, обычно определяемым для данных целей как
область возможных значений. Эта область обычно находится
внутри интервала 1,2<(У2—U0)/(Vi—Uo)<90 для ускоряю-
ускоряющих линз и 0,01 •< (V2—Uo)/{Vi—Uo) <0,85 для замедляющих.
В проекторных линзах коэффициент напряжения обычно огра-
ограничивается электрическим пробоем и степенью пригодности
источников питания; следовательно, он должен быть ближе
к единице, чем в случае, когда линзы используются в качестве
источников.
7.3.1. Геометрически симметричные линзы
Начнем изучение с простейших линз, геометрически симмет-
симметричных относительно средней плоскости, перпендикулярной оп-
оптической оси. Это означает, что положение zm максимума поля
точно совпадает со средним арифметическим границ линзы а
и Ъ. Распределение ее потенциала имеет вид, задаваемый урав-
уравнением C.183), и антисимметрично относительно точки zm
(рис. 80).
Таким линзам уделяется много внимания в литературе, но
большинство опубликованных данных относится к тривиальным
конфигурациям электродов (двухцилиндровые трубки или слу-
случай двух апертур). Исключение составляют только полиноми-
полиномиальные линзы. Мы вернемся к ним в разд. 7.3.1.3—7.3.1.5, но
сначала попытаемся получить сведения на уровне первого по-
порядка о поведении двухэлектродных симметричных иммерсион-
иммерсионных линз на основе очень простой модели.
7.3.1.1. Линейная модель. Предположим, что потенциал по-
постоянен по обе стороны линзы и линейно растет внутри ее [16]
(рис. 80, кривая а). Это очень далеко от реальности, но, с дру-
другой стороны, эта модель настолько проста, что мы надеемся
получить некоторую информацию при очень малых затратах
труда.
Распределение потенциала дается как
(Vi>0 для г< —1/2
(У1 + У2)/2 + (У2-У1)г// для -//2<г<//2, G.24)
V2 > 0 для г > 1/2,
384
Электростатические линзы
-з
Рис. 80. Распределение потенциала симметричных двухэлектродяых иммер-
иммерсионных линз: а — линейная модель; б — аналитическая модель; в — двухци-
двухцилиндровая линза с нулевым зазором между электродами; г — кубическая по-
полиномиальная линза.
где l=b—а — протяженность поля гипотетической линзы, а по-
положительный потенциал выбран с целью дальнейшего упроще-
упрощения.
Будем рассматривать ход основного луча г2(г) (рис. 44)
с начальными условиями
г 2 (—1/2) = го, г'2 (—1/2 — Д z) = 0. G.25)
Применим процедуру, описанную в разд. 7.2.2 для кусочно-ли-
кусочно-линейной модели. Скачок наклона траектории на входе вычислим
из уравнения G.7). Получим
г'2(— //2 + Дг) =—ro(V2 — V,)/[4/(V, — £/„)]. G.26)
Смещение луча и его наклон вблизи внутренней стороны выход-
выходной поверхности линзы определяются уравнениями D.141) и
D.140) соответственно. Вместе с уравнением G.26) они дают
г2(//2) =го{3- [(У2 - l/0)/(Vi - t/0)]I/2>/2, G.27)
r'2(l/2 — Az)= — ro(V2~V1)/{4l[(Vi — U0)(V2— Uo)]^}.
G.28)
Окончательно получим наклон на внешней стороне выходной
поверхности линзы из уравнений G.7), G.27) и G.28):
— Vi)X
385
Глава 7
X [{V2 — Uo)- — (Vi — £/o)-1/2] [8l(V2 — f
G.29)
Теперь мы имеем всю необходимую информацию, чтобы вы-
вычислить асимптотические кардинальные элементы (здесь и да-
далее для упрощения звездочки будем опускать). Подставляя
уравнения G.25) и G.29) в D.73), получим фокусное расстоя-
расстояние в пространстве изображений
'//*= C/8) [1 - (V, - UO)/(V2-UO)]X
-f/oI/2-l}. G.30)
Вследствие симметрии системы можно получить фокусное рас-
расстояние в пространстве изображений путем простой перестанов-
перестановки V\ и V2. В самом деле, фокусное расстояние в пространстве
объектов равно фокусному расстоянию в пространстве изобра-
изображений перевернутой линзы. Следовательно, имеем
4h= C/8) [ (V2 - £/„)/(V, - Uo) - 1] X
X {1 - [(У, - U0)/(V2 - t/o)]}. G.31)
Эта величина дана как функция отношения потенциалов изо-
изображение— объект в табл. 5. Видно, что чем сильнее отноше-
отношение отличается от единицы, тем больше оптическая сила лин-
линзы. Кроме того, как следствие уравнения D.76) ясно, что оп-
оптическая сила замедляющей линзы в пространстве объектов
всегда меньше, чем оптическая сила ее перевернутого (уско-
(ускоряющего) двойника.
Положение фокуса в пространстве изображений получается
подстановкой уравнений G.27) и G.29) в D.71). В результате
получим
Положение фокуса в пространстве объектов может быть вы-
вычислено перестановкой потенциалов и соответствующим учетом
знака:
_р/1=1/2 I
11 3[(V
G.33)
Местоположение главной плоскости в пространстве изобра-
изображений определяется уравнениями D.73), G.30) и G.32):
п 4
/1 —fy,,) —IJ " ['-™>
Главная плоскость в пространстве объектов пересекает опти-
386
Электростатические лннзы
Таблица 5
Безразмерная оптическая сила линзы в пространстве объектов l/fi
как функция отношения потенциалов изображение — объект
(V2—U0)l(Vi—Uо) для различных симметричных двухэлектродных
иммерсионных линз
О| О
$
0,050
0,100
0,200
0,286
0,400
0,500
0,625
0,833
1,2"
1,6
2,0
2,5
3,5
5,0
10,0
20,0
Аналитиче-
Аналитическая модель
0,217
6,1931
0,1358
0,0967
0,0594
0,0372
0,0187
0,00298
0,00325
0,0237
0,0526
0,0937
0,1806
0,303
0,613
0,974
Двухцилиндровая
линза с нулевым
зазором
Приближе-
Приближение тонкой
линзы
0,465
0,343
0,208
0,1398
0,0823
0,0501
0,0245
0,00397
0,00435
0,0309
0,0709
0,1302
0,262
0,465
1,086
2,079
Численное
решение
0,385
0,308
0,1972
0,1353
0,0810
0,0496
0,0244
0,00398
0,00434
0,0308
0,0702
0,1280
0,253
0,441
0,971
1,724
Линейная
Приближе-
Приближение тонкой
линзы
1,600
0,854
6,401
0,245-
0,1342
0,0788
0,0375
0,00597
0,00654
0,0475
0,1115
0,212
0,458
0,897
2,701
7,157
модель
Аналитиче-
Аналитическое реше-
решение
1,237
0,730
0,371
0,233
0,1308
0,0777
0,0373
0,00597
0,00653
0,0471
0,1098
0,207
0,436
0,829
2,308
5,532
Кубическая
полиноми-
полиномиальная линза
0,629
0,444
0,259
0,1712
0,0998
0,0604
0,0294
0,00477
0,00520
0,0371
0,0854
0,1577
0,32!
0,578
1,408
2,778
ческую ось в точке Яь координата которой дается уравнения-
уравнениями D.72), G.31) и G.33):
И п =
G.35)
1—(/0)—1] '
Мы видим, что главные плоскости сдвинуты в сторону умень-
уменьшения потенциала и меняются местами, как и ожидалось,
(Я2 — #,)//=— 1/3. G.36)
Постоянное расстояние между ними является следствием про-
простоты модели. Уравнения G.34) и G.35) показывают, что сдвиг
растет по мере ослабления линзы (см. разд. 4.9).
Уравнения D.51) и G.24) позволяют вывести функцию
T(z), которая может быть записана в виде
т,,ч_ 3/16 дщ
(г—г*J '
где
G.38)
387
Глава 7
Отметим, что, если z растет от —оо до +оо, функция T(z)
имеет особенность при z=z*. Функция симметрична относитель-
относительно этой точки, которая, однако, всегда расположена за грани-
границами поля. Следовательно, только малая часть области опреде-
определения Т (z) играет роль в формировании изображенния. Из-за
чрезмерного упрощения модели (резкие начало и конец поля)
функция T(z) внутри области границ поля в общем случае от-
отличается от функции, изображенной на рис. 83.
Центр тяжести распределения поля дается уравнениями
D.125), G.37) и G.38):
J-1ГlnW*-и^У>-и°Ъ G-39>
В приближении тонкой линзы оптическая сила выводится
из уравнений D.117), D.118), G.37) и G.38) в следующем
виде:
(//Л)twn = C/16) [(V, - U0)/(V2 - f/o)]3/4X
X[(Va—U0)/(Vi — U0) — \]a, G.40)
(//Ь)шп= C/16) [(У. - U0)/(Vt - (/о)]5/4Х
X[(V2-Uo)/(V]-Uo)-\]2. G.41)
Очевидно, уравнения G.40) и G.41) также прямо следуют од-
одно из другого либо через уравнение D.76), либо простой пере-
перестановкой напряжений Vi и V2 вследствие симметрии системы.
Сравним оптическую силу линзы в пространстве объектов
в приближении тонкой линзы с оптической силой, заданной
уравнением G.31) в табл. 5. Видно, что приближение тонкой
линзы дает удовлетворительный результат (ошибка меньше
10%) в интервале отношения напряжений изображение — объ-
объект 0,2< (Vi—Uo)l(V\—£/0)<5. Формула тонкой линзы всегда
дает завышенную оценку оптической силы (см. разд. 4.9).
Можно вычислить все кардинальные элементы в приближе-
приближении тонкой линзы в соответствии с уравнениями D.120) —
D.124). Однако эти уравнения дают более сложные выражения,
чем соответствующие уравнения G.32)—G.36). Например, из
уравнений D.124), G.40) и G.41) имеем
(Н—Н\ 1
12 ""thin/*- 3[(V,Uo)/(Vit/o)l]
G.42)
Как видно, это выражение более реально для слабой линзы, чем
уравнение G.36), так как зависит от отношения напряжений
изображение —объект. Уравнение G.42) дает —7з, так же как
уравнение G.36), только для единичного значения отношения
388
Электростатические линзы
напряжений. Если увеличить отношение до 5, то расстояние
между главными плоскостями уменьшится на 18%.
Эта примитивная модель была рассмотрена, чтобы быстро
получить информацию о некоторых свойствах первого порядка
двухэлектродных симметричных иммерсионных линз. Мы ис-
используем эту модель для сравнения с реальными системами
(см. табл. 5 и заглавия соответствующих разделов).
7.3.1.2. Аналитическая модель. Распределение потенциала
двухэлектродной симметричной иммерсионной линзы всегда мо-
может быть записано в виде C.183). Так как в уравнении паракси-
параксиальных лучей G.1), так же как и в выражениях для коэффициен-
коэффициентов аберрации (уравнения G.4) и G.5)), присутствуют только
отношения первой и второй производных к распределению по-
потенциала, очевидно, что оптические свойства линзы зависят от
функции распределения ф(г) и отношения потенциалов изобра-
изображение— объект (Уг—Uo)/{Vi—Uo). Структура указанных урав-
уравнений показывает, что отношение потенциалов входит в них
в нелинейном виде, поэтому нужно всякий раз решать эти урав-
уравнения для каждого отношения потенциалов, за исключением
очень малых значений этого отношения, когда могут быть ис-
использованы формулы тонкой линзы, и очень больших значений,
когда некоторые уравнения могут быть упрощены. Можно ап-
аппроксимировать характеристические оптические величины сте-
степенными рядами отношения потенциалов [44], но результирую-
результирующее выражение также будет чрезмерно громоздким, а его точ-
точность будет зависеть от диапазона отношения напряжений.
Зависимость этих величин от отношения напряжений для реаль-
реальных линз будет исследована в соответствующих разделах чис-
численными методами.
К сожалению, уравнение параксиальных лучей может быть
строго решено только для некоторых специальных случаев
функции распределения cp(z). Рассмотрим его решение для рас-
распределения осевого потенциала
U(z)=*(Vi + V2)/2 + [(V2 - V,)/л]arctg (z/d), G.43)
где d— осевая координата точки, в которой потенциал на оси
точно равен половине между его средним значением и значе-
значением насыщения (рис. 80, кривая б). Сразу отметим, что это
распределение достигает насыщения довольно медленно. Как
показано ниже, в этом случае уравнение параксиальных лучей
D.50) может быть решено в строгом виде [203].
Прежде всего введем новые переменные у и г£> таким обра-
образом, чтобы
zjd = — ctgx|), G.44)
nt, G.45)
389
Глава 7
где о — зависимая переменная уравнения D.50). Тогда уравне-
уравнение G.43) может быть переписано в виде
Uto) = Vi+[(V2 — Vi)/n№. G.46)
Вводя обозначение
(V* — £/о)/( Vi — С/о) — 1,=х G.47)
и новую переменную
G.48)
уравнение D.50) после некоторых элементарных преобразова-
преобразований перепишем в виде
Введем еще одну новую переменную:
Ц=уГт- G.50)
Тогда уравнение G.49) преобразуется к виду
^ ^о, G1)
являющемуся уравнением Бесселя, решение которого есть
г] (I) = С/,/4 A) + C2/-i/4 A), G.52)
где Ci и С2 — постоянные, определяемые из начальных условий,
а /±1/4 — функция Бесселя первого рода порядка ±1/4. Отсюда,
используя уравнения G.2), G.45) — G.48) и G.50), получим два
независимых решения уравнения параксиальных лучей:
где нас не должны беспокоить постоянные коэффициенты, так
как они могут входить в постоянные интегрирования Ci и С2.
Отметим, что §>0 для ускоряющей линзы, однако для замед-
замедляющей линзы £<0. Следовательно, в последнем случае оба
решения являются мнимыми. Но мнимая единица также может
быть включена в постоянные интегрирования, где она исчезает,
так как будут использоваться только отношения двух решений.
В самом деле, подставив их в уравнение изображения D.58),
получим
hi a, (n/x+if,)//i/4 (я/х+гро) =
— /_1/4 (я/и + ф«) //-1/4 (я/х + фо), G.54)
что определяет соотношение между координатами объекта и
изображения. Увеличение дается формулой
390
Электростатические линзы
G.55)
Свойства функций Бесселя порядка ± 1/4 хорошо известны
и могут быть легко вычислены, но тем не менее большинство
преимуществ аналитической модели теряются из-за включения
численных процедур, следовательно, решение желательно упро-
упростить. Это возможно для больших | (малых к, т. е. слабых
линз), когда можно использовать соответствующие асимптоти-
асимптотические формулы для вычисления функций Бесселя:
1/2I2]-
G.56)
где
Р.F) «1 - Dv2 - 1) Dv2 - 9)/128£2, G.57)
G.58)
Если использовать эту аппроксимацию, то вычисление оптиче-
оптических свойств может быть выполнено в элементарных функциях,
но это потребует определенной работы. Для реальных очень
слабых линз можно удовлетвориться первыми членами Р*(%)
и Qv(§). Тогда после длительных, но элементарных преобразо-
преобразований получим приближенную формулу для оптической силы:
- U0) - I]2. G.59)
Следствием грубой аппроксимации, использованной при выводе
этого выражения, является 15%-ная ошибка даже для отноше-
отношения напряжений изображение —объект меньше 1,2, следова-
следовательно, им нельзя воспользоваться. Вместо этого значения, по-
полученные численно для асимптотической модели оптических
величин, будут сравниваться со значениями для реальных линз
и примитивной модели из предыдущего раздела в табл. 5 и на
рис. 81 и 82.
Как мы установили в разд. 5.7.4, коэффициенты добротно-
добротности, используемые в этой книге, в большинстве случаев опре-
определяются как CSooo/fi и Ccoea/fi, т.е. коэффициенты сферической
и хроматической аберрации, соответственно, вычисленные для
бесконечного увеличения, связанные с объектом и отнесенные
к фокусному расстоянию в пространстве объектов. Эти величи-
величины безразмерны и представлены как функции безразмерного
отношения напряжений изображение — объект (V2—Uo)l(V\—
Uo) на рис. 81 и 82 для коэффициентов сферической и хромати-
хроматической аберраций соответственно.
Единственная проблема состоит в выборе геометрических
параметров различных моделей и линз. До сих пор свободным
параметром линейной модели была длина /, а для аналитиче-
391
Глава 7
ской модели — длина d. Чтобы связать их друг с другом, а так-
также с реальными линзами, нужно установить определенный
принцип соответствия. Например, можно использовать опреде-
определение длины d и положить ее равной 1/4, или можно вычислить
эффективные длины обеих моделей и выбрать параметры таким
образом, чтобы эти длины оказались равными и т.д. Выберем
геометрические параметры так, чтобы максимальные абсолют-
абсолютные величины |f/'|max осевых компонент поля, отнесенных
к абсолютной величине разности потенциалов V2—Vu для всех
qZO,5 1,0 5 10 15 20
Рис. 81. Асимптотический коэффи-
коэффициент сферической аберрации для не-
неограниченного увеличения, связанный
с объектом и отнесенный к фокусно-
фокусному расстоянию в пространстве объек-
объектов для а — аналитической модели,
б — двухцилиндровой линзы с нуле-
нулевым зазором и в —кубической поли-
полиномиальной линзы. (Шкала по оси
абсцисс различна для ускоряющей
и замедляющей линз.)
0,2 0,5 1,0 5 Ю 15 20
Рис. 82. Асимптотический коэффици-
коэффициент хроматической аберрации для не-
неограниченного увеличения, связанный
с объектом и отнесенный к фокусно-
фокусному расстоянию в пространстве объек-
объектов для а — аналитической модели,
б — двухцилиндровой лиизы с нуле-
нулевым зазором ив — кубической поли-
полиномиальной линзы. (Шкала по оси
абсцисс различна для ускоряющей
и замедляющей линз.) Штриховой ли-
линией обозначен верхний предел хро-
хроматического коэффициента доброт-
добротности.
моделей и линз были одинаковы. Допустим, что этот выбор до
некоторой степени случаен, но, как известно, не существует уни-
универсального способа представления свойств электростатических
линз.
На рис. 80 был проиллюстрирован этот принцип путем изо-
изображения распределения осевого потенциала моделей и линз
так, чтобы все они имели одинаковый максимальный наклон
в геометрическом центре. Этот максимальный наклон постоянен
для линейной модели. Для аналитической модели из уравне-
уравнения G.43) имеем
G.60)
392
Электростатические линзы
Приравнивая эту величину наклону распределения потенциа-
потенциала G.43) для линейной модели, получим, что для сравнения
двух моделей нужно положить
d=l/n. G.61)
Эта величина используется, чтобы установить масштаб распре-
распределения потенциала G.43), а также для сравнения безразмер-
безразмерных фокусных расстояний l/fi в пространстве объектов
в табл. 5.
Оптическая сила этой модели существенно меньше, чем ли-
линейной. Этот результат не является неожиданным: плавно ме-
меняющееся поле имеет эффективную длину много больше, чем
ограниченная линейная модель.
Безразмерные коэффициенты добротности независимы от
выбора максимального наклона. Действительно, в соответствии
с уравнением G.60) максимальный наклон обратно пропорцио-
пропорционален коэффициенту подобия d. Изменяя этот множитель, мы
фактически меняем масштаб модели, благодаря чему безраз-
безразмерные параметры остаются неизменными (см. разд. 2.8).
На рис. 81 и 82 изображены коэффициенты добротности как
функции отношения напряжений изображение — объект. Коэф-
Коэффициент сферической аберрации тем больше, чем слабее линза.
Конечно, фокусное расстояние также увеличивается, но не так
быстро. В результате сферический коэффициент добротности
дает громадное увеличение по мере продвижения в область
слабых линз и становится меньше 10, только когда отношение
напряжений выше 10 или ниже 0,1 (рис. 81, кривая а). Коэф-
Коэффициент добротности незначительно улучшается для замедляю-
замедляющих линз по сравнению с ускоряющими.
Совершенно другая ситуация наблюдается для хроматиче-
хроматического коэффициента добротности (рис. 82, кривая а). Коэффи-
Коэффициент хроматической аберрации имеет верхний предел (см.
разд. 5.3.1.2), следовательно, он не может увеличиваться в той
же степени, что и коэффициент сферической аберрации. Тем не
менее для ускоряющей области хроматический коэффициент
добротности проявляет ту же тенденцию, что и сферический,
с тем отличием, что он растет, но только умеренно до тех пор,
пока не достигнет верхнего предела, равного 2 для очень сла-
слабых линз (см. табл. 4). Однако в замедляющей области верх-
верхний предел растет по мере усиления линзы и соответственно
растет действительное значение коэффициента добротности, но
оно никогда не становится больше 3 для диапазона отношения
напряжений, рассматриваемого здесь.
Следует подчеркнуть, что функция распределения крайне
медленно достигает насыщения. Следовательно, границы поля
находятся довольно далеко от центра линзы и необходимо.
393
Глава 7
большое число точек интегрирования для достижения приемле-
приемлемой точности. Ситуация тем хуже, чем сильнее линза. В диа-
диапазоне отношения напряжений 0,05< (V2—U0)/{Vi—U0)^20
оптическая сила все еще описывается уравнением D.76) при
относительной ошибке меньше 0,5%.
Тот факт, что в этой модели рассматриваются слабые поля,
обусловливает ее незначительное применение для практических
целей, но она может служить иллюстрацией для сравнения
с реальными линзами.
7.3.1.3. Двухцилиндровые линзы. Перейдем теперь к иссле-
исследованию реальных линз. Начнем с простейшей линзы, состоя-
состоящей из двух коаксиальных цилиндрических электродов одина-
одинаковых радиусов R, к которым приложены различные потенциа-
потенциалы Vi и Уч. соответственно и разделенных промежутком s (см.
рис. 17). Распределение потенциала такой линзы было рас-
рассмотрено в разд. 3.1.2.2. Мы знаем (табл. 2), что, если зазор
между двумя цилиндрами бесконечно мал, уравнение C.132)
дает очень хорошее приближение распределения потенциала
такой линзы. Следовательно, уравнение C.132) может служить
ее моделью. Для конечных, но малых значений зазора s урав-
уравнение C.131) еще применимо, но, если зазор сравним с радиу-
радиусом цилиндра, следует применять численные методы для на-
нахождения распределения потенциала.
Распределение потенциала антисимметрично относительно
плоскости z = zm = 0, на которой абсолютная величина наклона
имеет максимум. Этот максимум, вычисленный из уравне-
уравнения C.131), равен
|£/'|max=(l/s)|V2-Vi|th(«s/2tf) —> m | Va — Vi | /2/?,
s->0
G.62)
где и дается уравнением C.133). Максимальный наклон в слу-
случае, когда шириной зазора можно пренебречь, конечно, также
прямо следует из уравнения C.132). Приравнивая его постоян-
постоянному наклону для линейной модели распределения потенциала
(разд. 7.3.1.1), получим, что для сравнения двухцилиндровой
линзы с нулевым зазором и линейной модели следует исполь-
использовать
/ = 2#/ш. G.63)
Распределение потенциала, определяемое уравнением C.132)
вместе с этим максимальным наклоном показано на рис. 80
(кривая в). Величина /, даваемая формулой G.63), будет ис-
использована для вычисления безразмерного фокусного расстоя-
расстояния l/fi в пространстве объектов (см. табл. 5).
394
Электростатические линзы
-2
z/R
Рис. 83. Функция Т(г) для двухцилиндровой линзы с нулевым зазором при
(VI/)/(VI/M
Сразу же отметим, что это распределение характеризует го-
гораздо более сильные поля, чем распределение, используемое
в аналитической модели (разд. 7.3.1.2). Легко вычислить харак-
характеристическую функцию T(z) из уравнений G.3) и C.132).
В результате получим
Т(г) = C/16) Bй/#J[1 — (V, — Uo)I(V2 — £/o)]2X
X {1+ (V, — U0)/(V2 — U о) + [(Vi — U0)/{Vi — U0)]X
X exp (— 2az/R) + exp Baz/#) }. G.64)
Эта функция показана на рис. 83 для случая (У2—^o)/(Vi—
^о) =5. Видно, что она симметрична относительно некоторой
точки zM, где Т(г) максимально. Эта точка смещена в сторону
уменьшения потенциала. Ее координаты можно легко оценить
из уравнения G.64):
Zm№= (l/4a)ln[(Vi — Uo)/(V2 — Uo)]. G.65)
Это выражение показывает, что смещение кривой всегда отри-
отрицательно для ускоряющей линзы (гм<.гт) и положительно для
замедляющей (zM>zm) и, кроме того, тем больше, чем сильнее
линза. Максимальное значение функции T(z) дается формулой
Ттах = Т(гм) = C/16) Bа//?J th2 (tazM/R). G.66)
Максимальное значение растет с возбуждением и достигает
насыщения при очень высоких (или очень низких) отношениях
(V2-Uo)/(V1-Uo).
395
Глава 7 ^
Функцию T(z) легко строго проинтегрировать [204]. Так как
границы поля определить трудно, интегрирование ведется от
—оо до +оо. Тогда уравнения D.117) и D.118) вместе с
C.133) в приближении тонкой линзы дают
Rffi=0,495 [ (V2 - Uо) I(Vt - С/о) ]1/4 X
— U0)]-2\ G.67)
= 0,495[(V, - U0)/(V2 - f/0)]1/4X
X [(V2 - f/o)/(Fi — Uo) - I]-1} X
Xln[(V2 — f/o)/(V, — f/o)]— 2>. G.68)
Принимая во внимание уравнения G.63) и C.133), можно вы-
вычислить безразмерную величину l/fi для различных значений
отношения потенциалов изображение — объект. Результаты да-
даны в табл. 5. В этой таблице приведены также эти величины,
найденные численно. Они были получены численным решением
уравнения параксиальных лучей G.1) с распределением потен-
потенциала C.132). Как видно, формула тонкой линзы снова дает за-
завышенное значение оптической силы, но оно находится строго
в пределах 12% относительной погрешности в диапазоне
0,1^ (V2—U0)/(Vi—С/0)г£:10. Численно найденные значения
удовлетворяют уравнению D.76) при относительной погреш-
погрешности меньше 0,3%. Отметим также, что эти значения оптиче-
оптической силы лежат между значениями, полученными из линейной
и аналитической моделей. Это и ожидалось, так как поле этой
линзы является промежуточным между двумя этими моделями.
Пример двухцилиндровой линзы с пренебрежимо малым за-
зазором очень хорошо иллюстрирует тот факт, что физическая
толщина линзы не совпадает с оптическим понятием тонкой
линзы (разд. 4.9). В самом деле, из табл. 5 следует, что, если
отношение потенциалов изображение — объект лежит вне диа-
диапазона 0,1—10, приближение тонкой линзы неприменимо. При-
Причина состоит в том, что при сильном возбуждении поле глубоко
проникает внутрь цилиндров и линза становится толстой, хотя
зазор между цилиндрами по-прежнему пренебрежимо мал.
Основные свойства и сферическая аберрация симметричных
двухцилиндровых линз достаточно полно исследованы в литера-
литературе [36, 44, 66, 204—215]. Трудно поверить, но до недавнего
времени [215а] не было данных о хроматической аберрации.
Некоторые из опубликованных данных крайне неточны. Как
уже указывалось [66], результаты, полученные с помощью
уравнения C.131) для больших зазоров [36], имеют относи-
396
Электростатические линзы
тельную ошибку до 22% (см. обсуждение в разд. 3.1.2.2).
Мы попытаемся суммировать эти результаты в дальнейшем.
Прежде всего снова отметим замечательные особенности
свойств перевернутых линз. Как мы знаем, перевернутая линза
может быть получена из любой линзы перестановкой всех
электродов и их напряжений. Однако для геометрически сим-
симметричной линзы достаточно всего лишь перестановки электрод-
электродных напряжений, чтобы получить перевернутую линзу. Если
первоначальная линза является ускоряющей, то перевернутая
будет замедляющей с обратным отношением напряжений изо-
изображение— объект. Кроме того, очевидно, что величины, ха-
характеризующие линзу в пространстве объектов перевернутой
линзы, эквивалентны тем же величинам в пространстве изобра-
изображений первоначальной линзы и обратно. Следовательно, карди-
кардинальные элементы перевернутых симметричных линз ставятся
в соответствие тем же элементам первоначальных линз с по-
Рис. 84. Основные соотношения между главными элементами линзы и ее пе-
перевернутого аналога: а — первоначальная лииза, б — перевернутая линза.
мощью простых соотношений (рис. 84)
Fuev =—F2, /r2rev = —F\,
H\Tev = —H2, #2rev = —Hu G.69)
flrew = f2 f2rev = fl-
Для коэффициента аберрации соотношения E.265) — E.266) и
E.282) — E.283) остаются справедливыми. Следовательно, вооб-
вообще нет необходимости вычислять свойства симметричных за-
замедляющих линз: если известны свойства ускоряющих линз
в пространстве объектов и изображений, то всегда можно вы-
вычислить эти же свойства для замедляющих линз, используя
приведенные выше соотношения. (Прямые вычисления свойств
замедляющих линз имеют ценность для проверки результатов.)
Соответственно на всех последующих рисунках будут рассмат-
рассматриваться только ускоряющие линзы. Отметим, что здесь под
«симметричными» линзами мы понимаем линзы с геометриче-
геометрической симметрией. Так как потенциалы на электродах различны,
в действительности распределение потенциала антисимметрии-
397
Глава 7
но. Электростатические линзы могут быть полностью симмет-
симметричны только в том случае, если они имеют одинаковые потен-
потенциалы с обеих сторон (одиночные линзы).
Как видно на рис. 81, значение сферического коэффициента
добротности крайне велико для очень слабых линз. Причина
состоит в том, что, хотя фокусное расстояние быстро растет по
мере уменьшения олтической силы линзы, коэффициент сфери-
сферической аберрации растет еще быстрее. По этой причине линзы
с отношением напряжений изображение — объект меньше 2 ред-
редко применяются на практике и поэтому в дальнейшем рассмат-
рассматриваться не будут. С другой стороны, очень большие отношения
напряжений изображение — объект требуют мощных источников
и дорогого высоковольтного оборудования, имеющегося только
в специальных лабораториях. Хотя высокие отношения напряже-
напряжений необходимы, например, для замедления высокоэнергетиче-
высокоэнергетических пучков при анализе их энергии, а также для ускорения
частиц низких энергий, полученных в околопороговых процес-
процессах [210], оптические свойства меняются очень слабо с их ро-
ростом, поэтому нет необходимости рассматривать отношения на-
напряжений свыше 20. Еще одна причина, по которой мы стре-
стремимся к ограничению отношения напряжений, является нереля-
нерелятивистский подход, используемый в этой главе. Конечно, совсем
другое дело источники частиц, отношение напряжений дости-
достигает там громадных значений, но источники частиц не ограни-
ограничены областями, в которых поле отсутствует, поэтому они
должны рассматриваться отдельно.
На приведенных ниже рисунках даны кардинальные элемен-
элементы симметричных двухцилиндровых линз в пространстве объек-
объектов и изображений как функции отношения напряжений изоб-
изображение— объект (V2—UO)I(V\—Uо). Все величины выражены
в единицах радиуса цилиндров R. Кривые соответст-
соответствуют бесконечно тонким электродам. Были выбраны три значе-
значения зазоров s/R = Q,2, 1 и 2. Если зазор меньше 0,2R, то резуль-
результат остается практически неизменным: относительное различие
результатов для вычислений с нулевым зазором и вычислений
при s/R = Q,2 ни при каких обстоятельствах не превышает 3%.
С другой стороны, если зазор превышает диаметр цилиндров,
все более важную роль начинает играть проникновение внеш-
внешних полей, наводимых другими электродами через стенки ва-
вакуумной камеры. Этот нежелательный эффект может контро-
контролироваться дополнительным экранирующим электродом [212],
но тогда будет иметь место трехэлектродная иммерсионная
линза.
Влияние толщины электродов также было исследовано [44,
213]. Результаты показывают, что относительное различие меж-
между оптическими свойствами толстостенных линз и линз с беско-
398
Электростатические линзы
12 14 16 18 20
(V?-U0)/(V,-U0)
Рис. 85. Фокусные расстояния симметричных двухцилиндровых линз в прост-
пространстве объектов, отнесенные к радиусам нх цилиндров, как функции отно-
отношения напряжений изображение — объект (Vj— UQ)/(V\ — Uo). Квадраты —
s//?=0,2, крестики — s/R= 1, ромбы — s/R—2.
нечно тонкими стенками внутри данного интервала отношения
напряжений не превышает 20%, даже если толщина электро-
электродов равна их внутреннему радиусу. Этот факт может быть ис-
использован для эффективной защиты линзы (если зазор не очень
велик) от влияния внешних полей без существенного изменения
ее оптических свойств. Чтобы уменьшить число параметров,
будем рассматривать линзы с бесконечно тонкими электродами.
На рис. 85 и 86 показаны фокусные расстояния в простран-
пространстве объектов и изображений соответственно, как функции от-
отношения напряжений электродов. Как и ожидалось, фокусные
расстояния быстро уменьшаются с усилением возбуждения.
Для ускоряющих линз в соответствии с уравнением D.76) во
всех случаях f2>fi. Фокусное расстояние растет с увеличением
зазора в интервале s<2i? вначале медленно, а затем быстрее.
Влияние ширины зазора на фокусное расстояние уменьшается
по мере возрастания отношения напряжений.
На рис. 87 и 88 изображены положения главных плоскостей
соответственно в пространстве объектов и в пространстве изо-
изображений в зависимости от отношения электродных напряже-
напряжений. Видно, что обе главные плоскости сдвинуты в направлении
уменьшения потенциала и меняются местами. По мере сдвига
главных плоскостей растет и зазор. Как следует из разд. 4.9,
сдвиг становится очень большим для слабых линз. По мере воз-
возрастания силы линзы сдвиг быстро уменьшается вместе с отно-
отношением напряжений, если оно относительно мало. Для более
399
Глава 7
50 -
40 -
1
20 -
10 -
0 -
L
—I 1 i 1 r-
4 Б
S£=£=-;
—i—i—i—i—i—1~
8 10 12
—I 1
14
! r~
16
1 1
18 2
(V2-U0)/(V,-U0)
Рис. 86. Фокусные расстояния двухцилиндровых симметричных линз в прост-
пространстве изображений, отнесенные к радиусам цилиндров, в зависимости от
отношения напряжений изображение — объект (V2— Ua)/(V\ — Ua). Обозна-
Обозначения те же, что на рис. 85.
1 Г"
16 18 20
<V2'-U0)/(V.,-U0)
Рис. 87. Положения главных плоскостей симметричных двухцилиндровых линз
в пространстве объектов, отнесенные к радиусам цилиндров, в зависимости от
отношения напряжений изображение — объект (Vi~Uq)/(V\ — Uo). Обозна-
Обозначения те же, что на рис. 85.
400
Электростатические линзы
12 14 16 18 20
<v2-u0)/(vru0)
Рис. 88. Положения главных плоскостей симметричных двухцилиндровых линз
в пространстве изображений, отнесенные к радиусам цилиндров, в зависимо-
зависимости от отношения напряжений изображение — объект (V2~U0)/(Vi — U<>).
Обозначения те же, что на рис. 85.
16 18 20
(V2-Uo)/(V.|-Uo)
Рис. 89. Расстояние между главными плоскостями симметричной двухцилинд-
двухцилиндровой линзы, отнесенное к радиусу цилиндров, в зависимости от отношения
напряжений изображение — объект (V2-t/o)/(Vi-£/<>). Обозначения те же,
что иа рис. 85.
401
Глава 7
сильных линз зависимость от отношения напряжений становит-
становится очень слабой.
На рис. 89 изображена зависимость расстояния между глав-
главными плоскостями трех линз от отношения напряжений элект-
электродов. Расстояние увеличивается с ростом зазора и медленно
возрастает по мере увеличения отношения напряжений. Это то-
тоже не является неожиданностью, так как более высокое отно-
отношение напряжений означает увеличение толщины линзы.
Поскольку мы знаем кардинальные элементы, легко опре-
определить увеличение и положение изображения (объекта), если
известно положение объекта (изображения) (см. уравнение
D.77)). Для этого удобно воспользоваться графиками, на ко-
которых положение изображения дается как функция положения
объекта в виде семейства кри-
кривых для различных постоян-
постоянных увеличений и отношений
электродных потенциалов
[44]. Один из таких графи-
графиков, основанный на экспери-
экспериментальных результатах
[215J, изображен на рис. 90
для линзы с пренебрежимо
малым зазором. К сожалению,
вследствие самой природы
электростатических линз, об-
Рис. 90. Положение изображения Q суждавшейся выше, такие
в зависимости от положения объек- графики переполнят библио-
та Р для симметричной двухцилинд- теки, если мы попытаемся
ровой лиизы с пренебрежимо малым дать их для каждой МЫсЛИ-
зазором. Кривые соответствуют по- й линзы. Кроме ТОГО, непо-
непостоянным увеличениям и отношениям х^ '
напряжений изображение-объект, льзование таких графических
Как Р, так и Q измеряются от поло-
положения средней плоскости линзы [215].
представлений неизбежно
приводит к неточностям.
Одна из причин широкого
использования относительно небольшого числа простых линз,
несмотря на то что их качество с точки зрения аберраций ос-
оставляет желать лучшего, состоит в том, что данные о них су-
существуют в виде графиков и таблиц. Это отражает такое со-
состояние дел, когда компьютеры не были еще широко распрост-
распространены и инженерные работники полагались только на имею-
имеющиеся в их распоряжении данные. Но сейчас ситуация корен-
коренным образом изменилась, и есть возможность использовать
компьютеры для конструирования линз более высокого качест-
качества. Можно воспользоваться программой хода лучей и накопить
результаты вычислений такого рода в памяти компьютера.
Эти данные могут быть представлены в виде таблиц, таких, как
402
Электростатические линзы
Таблица
Зависимость положения объекта Р, увеличения М, коэффициента
сферической аберрации Cso, коэффициента хроматической аберрации Ссо
(оба связаны с объектом) и величии |Af|Go и [Af|Cro
от положения изображения Q для симметричной двухцилиндровой лиизы
с пренебрежимо малым зазором и (V2—U0)j{V\—t/o)=5a
Q/л
6,0
8,0
10,0
12,0
13,0
15,0
20,0
25,0
30,0
40,0
50,0
00
P/R
27,68
13,71
10,51
9,10
8,65
8,01
7,16
6,73
6,47
6,17
6,01
5,42
-M
0,15
0,41
0,67
0,94
1,07
1,33
1,98
2,63
3,28
4,58
5,88
со
CJR
40410
2337
791,4
437,8
355,9
260,7
164,3
127,4
108,5
89,4
80,0
52,6
\M\CJR
6061
958
530
412
381
347
325
335
356
409
470
оэ
cjr
134,9
31,96
18,41
13,59
12,22
10,41
8,19
7,18
6,60
5,96
5,62
4,50
\M\CJR
20,2
13,1
12,3
12,8
',3,1
13,8
16,2
18,9
21,6
27,3
33,0
00
а Положения объекта и изображения измеряются от средней плоскости линзы. Все
величины отнесены к радиусу цилиндров R.
табл. 6 и 7, где приведены положение объекта P/R, положение
изображения Q/R и увеличение М, а также коэффициенты сфе-
сферической Сво/Л и хроматической Cco/R аберраций для линз
с нулевым зазором при (V2—Uo)l(Vi—U0)=5 (положения объ-
объекта и изображения измеряются от средней плоскости линзы).
Как рис. 90, так и табл. 6 ясно показывают основные осо-
особенности всех линз: чем ближе объект к линзе, тем дальше от
нее изображение, и абсолютная величина М при этом растет
(см. уравнение D.77)). Чем сильнее линза, тем меньше Р и Q.
Интересно отметить, что телескопическую линзу (разд. 4.6.1)
можно сделать из двухцилиндровых симметричных линз с нуле-
нулевым зазором, но для этого потребуется отношение напряжений
свыше (v2—U0)/(Vl—£/о)=688О. У такой чрезвычайно сильной
линзы все ее действие сконцентрировано в пространстве объек-
объектов, где ее напряжение ниже.
Перейдем теперь к исследованию коэффициента сфериче-
сферической аберрации. На рис. 91, с изображена зависимость сфери-
сферического коэффициента добротности (коэффициент сферической
аберрации для неограниченного увеличения в пространстве
объектов, отнесенный к фокусному расстоянию линзы в прост-
пространстве объектов) от отношения напряжений на электродах.
Снова видим, что величина С$0со/^ очень велика для слабых
линз и резко уменьшается с увеличением силы линзы. Зависи-
Зависимость настолько сильна, что приходится показывать ее отдель-
отдельно для более высоких значений отношения напряжений
(рис. 91,6). С другой стороны, ширина зазора оказывает очень
403
Глава 7
Таблица 7
Зависимость положения изображения Q, увеличения М,
коэффициента сферической аберрации Cst и хроматической аберрации Сс,
(обе связаны с изображением) от положения объекта Р для симметричной
двухцилиндровой лиизы с пренебрежимо малым зазором
и (V2-Ua)!(Vi-Ua)=5=
P/R
7,0
8,0
9,0
10,0
12,0
15,0
20,0
25,0
30,0
40,0
50,0
оо
Q/R
21,54
I5J05
12,19
10,58
8,83
7,57
6,63
6,16
5,89
5,58
5,41
4,81
-М
2,18
1,33
0,96
0,75
0,52
0,36
0,24
0,18
0,14
0,10
0,08
0,00
CJR
37610
9130
3990
2290
ИЗО
624
374
284
239
195
173
112,1
CJR
414
206
137
104
74,0
55,4
43,2
37,8
34,7
31,4
29,7
24,1
а Положения объекта и изображения измеряются от средней плоскости линзы. Все
величины отнесены к радиусу цилиндров R.
слабое влияние на коэффициент добротности, хотя фокусное
расстояние зависит от него и приблизительно в такой же сте-
степени зависит и коэффициент аберрации. Видно, что в данном
интервале отношений напряжений лучшее значение, которое
можно достигнуть, есть CSOco/fi = 2, но для этого потребуется
наибольшее из возможных значений отношения напряжений
данного интервала. Для более достижимого на практике значе-
значения (У2—U0)/{V\ — Uo) =5 имеем CSOco/fi«15, что достаточно
велико.
Коэффициент сферической аберрации для нулевого увеличе-
увеличения, связанный с изображением и отнесенный к фокусному рас-
расстоянию в пространстве изображений, показан на рис. 92, а как
функция отношения электродных напряжений. Величина Cs,- 0//2
снова очень велика для слабых линз и резко уменьшается для
сильных линз. Эта зависимость показана отдельно на рис. 92,6
для более высоких значений отношения напряжений. Влияние
ширины зазора в этом случае выражено сильнее: чем больше
зазор, тем больше коэффициент аберрации. Так как CsiolU
представляет собой коэффициент добротности для замедляю-
замедляющих линз, видим, что, хотя сам по себе коэффициент сфериче-
сферической аберрации для них принимает намного более высокие зна-
значения, коэффициент добротности отчасти улучшается для ма-
малых зазоров, но ухудшается для больших. Для пренебрежимо
малых зазоров можно достигнуть Cso co/f i = 1,7 для наименьше-
наименьшего из возможных отношения напряжения в данном интервале.
Если (V2—£/0)/ (Vi—С/о) = 1 /5, то Cso co/f 1 = ИД что ненамного
404
Электростатические линзы
в
о
м
о
Я 200-
1О
16
18
2О
10
12
16 18 20
(v2-u0)/(vru0)
Рис. 91. Зависимость асимптотического коэффициента сферической аберрации
для бесконечного увеличения по отиошеиию к объекту и отнесенного к фокус-
фокусному расстоянию симметричной двухцилиндровой линзы в пространстве объек-
объекта от отношения электродных напряжений. Обозначения те же, что на рис. 85.
Кривые на рис. 91, а даны для всего интервала отношений напряжений, а кри-
кривые на рис. 91,6—только для (V2— U0)/(Vi — J/o)>4.
405
Глава 7
16 IB 2O
(v2-u0)/(vru0)
Рис. 92. Зависимость асимптотического коэффициента сферической аберрации
для нулевого увеличения по отношению к изображению и отнесенного к фо-
фокусному расстоянию симметричной двухцилиндровой линзы со стороны изобра-
изображения от отношения электродных напряжений. Обозначения те же, что на
рис. 85. Кривые на рис. 92, а даны для всего интервала отношения напряже-
напряжений, а кривые на рис. 92,6 —только для (V2-U0)/(Vi-U0)>4.
406
Электростатические линзы
отличается от значения для соответствующей ускоряющей линзы.
На рис. 81 (кривая б) также изображен сферический коэф-
коэффициент добротности. Сравнение показывает, что исследуемая
линза работает значительно лучше, чем аналитическая модель.
Однако, прежде чем перейти к общим выводам о преимущест-
преимуществах более сложных полей, нужно исследовать хроматический
коэффициент добротности. Наши вычисления показывают, что
хроматический коэффициент добротности приблизительно ра-
равен 2 для очень слабых линз и с увеличением силы линзы его
поведение становится таким же, как для аналитической моде-
модели: он уменьшается для ускоряющих линз и увеличивается для
замедляющих (см. рис. 82, кривая б). Однако для хроматиче-
хроматической аберрации более сильные поля этих линз являются причи-
причиной определенных недостатков; коэффициенты добротности
намного больше, чем для аналитической модели.
Приведенные кривые соответствуют только случаям беско-
бесконечного и нулевого увеличений. Коэффициенты аберрации силь-
сильно зависят от увеличения, но не надо их вычислять для каждо-
каждого его значения, если нас интересуют только асимптотические
коэффициенты. В этом случае следует вычислить пять коэффи-
коэффициентов для сферической аберрации и три — для хроматиче-
хроматической. Тогда можно воспользоваться полиномиальными выраже-
выражениями E.255) и E.273) для любого увеличения. Подходящие
коэффициенты даются уравнениями E.256) — E.260) и E.274) —
E.276). Можно воспользоваться пятью сферическими коэффи-
коэффициентами, заданными в табличной форме [44].
Зависимость коэффициентов аберрации в пространстве объ-
объектов от увеличения дана в табл. 6 для линзы с пренебрежимо
малым зазором и (V2—U0)l(Vi—U0)=5. Коэффициенты как
сферической, так и хроматической аберрации, связанные с объ-
объектом, сильно уменьшаются с ростом абсолютной величины М.
Уменьшение особенно заметно при малых \М\. Чем выше \М\,
тем медленнее достигают коэффициенты аберрации значений
для бесконечного увеличения. При М = —4 имеем Cs0/Cs0 ~ = 1,8
и CcolCco со = 1,4. Следовательно, наши коэффициенты доброт-
добротности дают приемлемую оценку аберраций даже при относи-
относительно низких увеличениях.
Коэффициенты абберации очень сильно зависят от отноше-
отношения напряжений на электродах. При фиксированном положении
объекта более сильная линза сокращает расстояния до изобра-
изображения и уменьшает |Л!|, что эквивалентно увеличению аберра-
аберраций. При фиксированном положении изображения чем больше
сила линзы, тем меньше расстояние до объекта, что эквивалент-
эквивалентно увеличению \М\ и уменьшению аберраций. При фиксирован-
фиксированном увеличении более сильная линза предполагает уменьшение
расстояния как до объекта, так и до изображения (см. рис. 90),
407
Глава 7
а аберрации при этом резко уменьшаются. В зависимости от
того, какая из переменных фиксирована, в итоге могут быть
сделаны разные выводы. Поэтому следует быть очень осторож-
осторожным при оценке иногда встречающихся в литературе . спорных
данных.
Коэффициент аберрации замедляющих линз при низких уве-
увеличениях много меньше, чем ускоряющих линз. Это следует как
из уравнений E.83) и E.265), так и из уравнений E.201) и
E.282). Для единичного увеличения имеем Csorev = [(^2—Uo)l
l(Vi — U0)]3'2CSO и Ccorev = [(^2-t/o)/(^i — U0)]3'2Cco, что
означает возрастание на порядок величины для (V2—Uo)/(Vi—
—1/0)=5. Для больших увеличений аберрации слабеют, и при
достижении бесконечного увеличения коэффициент сферической
аберрации падает до 2, а коэффициент хроматической аберра-
аберрации до 5. Даже этот незначительный рост замаскирован в коэф-
коэффициентах добротности, в которых коэффициенты аберраций
отнесены к большим фокусным расстояниям для замедляющих
линз. Это показывает, что с коэффициентами добротности необ-
необходимо обращаться очень аккуратно при работе с замедляющи-
замедляющими линзами.
Отметим, что простые выражения E.291) и E.294) не могут
быть использованы, так же как и табл. 6, вследствие сравни-
сравнительно большого отношения потенциалов. Для аберраций при-
приближение тонкой линзы справедливо только для очень слабых
линз.
Коэффициенты аберрации, связанные с изображением, для
такого же случая даны в табл. 7. При увеличении М—И) они
сильно уменьшаются (см. разд. 5.2.1.1 и 5.3.1.1). Уменьшение
особенно сильно при высоких увеличениях. При более низких
\М\ коэффициенты аберрации медленно достигают своих зна-
значений для нулевого увеличения. При М=—0,1 имеем Csi/CSio =
= 1,7 и CCi/Cci о = 1,3. Один из способов проверки точности вы-
вычислений заключается в использовании уравнений E.83) и
E.201) для сравнения коэффициентов аберрации в пространст-
пространстве объектов и в пространстве изображений. Как показывают
эти результаты, может быть достигнута вполне удовлетвори-
удовлетворительная точность.
Полный учет сферической аберрации симметричных двух-
двухцилиндровых линз для широкого диапазона увеличений можно
отыскать в литературе [44]. Так как радиусы дисков сфериче-
сферической и хроматической аберраций зависят соответственно от
MCso (уравнение E.79)) и МССО (уравнение E.197)), эти вели-
величины желательно знать для каждого конкретного увеличения
и отношения потенциалов на электродах (см. разд. 5.7.4). Как
мы видели в разд. 5.4.1.1, существует оптимальное значение
увеличения, которое минимизирует |Af|CS0 для данного отноше-
408
Электростатические линзы
ния электродных напряжений. Вычисления показывают, что для
этого случая оптимальное увеличение лежит в интервале меж-
между — 1 и —2 и его абсолютная величина медленно уменьшается
с ростом отношения напряжений. Минимальное значение
|M|CS0 очень сильно зависит от отношения напряжений: чем
больше (V2—U0)/{Vi—Uo), тем меньше диск сферической абер-
аберрации. В табл. 6 также дано \M\CSO/R- Его минимум наблю-
наблюдается при М = —1,98 и равен 325. В соответствии с уравне-
уравнением E.79), задавая значение половинного угла аксептанса
ао = 5мрад, имеем 6rsl//? = 4-10~5. При входной энергии частиц
10 кэВ во избежание пробоя следует выбрать зазор s=3 мм.
Следовательно, чтобы воспользоваться приближением малого
зазора, радиус цилиндров должен быть по крайней мере /? =
= 1 см. Тогда минимальный радиус пятна будет 400 нм. Если
задать половинный угол «0=1 мрад, то получим минимальный
радиус пятна всего лишь 3 нм. Радиус диска меняется относи-
относительно медленно вблизи его минимума. К сожалению, эта си-
ситуация выполняется не всегда.
Кроме того, в табл. 6 даны значения \M\CC0/R- Мы видим,
что минимальное значение достигается приблизительно при
M0Pt=—0,67 и равно 12,3. Из уравнений E.279) —E.281), ис-
используя коэффициенты хроматической аберрации для нулевого
и бесконечного увеличений, получим AfOpt = —0,69. Уравнение
E.197) дает для «о = 5 мрад и относительного разброса энер-
энергий AUo/i[U (a)—U0] = \0~4 радиус хроматического диска
6гс,У# = 3-10-6, откуда следует, что при )? = 1см радиус хрома-
хроматического диска равен 30 нм. Если ао = 1 мрад, радиус равен
6 нм. Радиус хроматического диска также слабо изменяется
вблизи его минимума.
Итак, при относительно широком пучке преимущественную
роль играет сферическая аберрация, тогда как в случае узкого
пучка важнее учет хроматической аберрации. Чем дальше два
минимума находятся друг от друга, тем лучше; следовательно,
всегда нужно использовать увеличение между этими двумя
оптимальными значениями ближе к тому, которое соответст-
соответствует доминирующему фактору, оптимизируя, таким образом,
размер пятна, задаваемого уравнением E.337).
Симметричная линза, состоящая из двух трубок, является
классическим примером фокусирующей системы, которой уделе-
уделено много внимания в основном из-за ее простоты. В следующем
разделе мы рассмотрим другую простую конфигурацию.
7.3.1.4. Двухапертурная линза. Эта линза также состоит из
двух электродов, разделенных расстоянием s, но теперь элект-
электродами служат плоские пластинки с круглыми отверстиями
радиуса R с приложенными к ним потенциалами V\ и Уг соот-
409
Глава 7
ветственно. Электроды расширяются в осевом направлении
в виде дополнительных трубок радиуса Rt, на которые поданы
те же потенциалы (рис. 23). Как отмечалось в разд. 7.1, радиус
и длина этих трубок наряду с радиальным расширением отвер-
отверстий являются важными параметрами линзы. Они необходимы
для защиты линзы от влияния внешних полей. В результате
эта простая двухэлектродная система становится довольно
сложной. Она имеет пять основных геометрических параметров:
R, s, Rt, длину трубок и радиальное расширение отверстий.
Фундаментальное различие между двухцилиндровой и этой
линзами состоит в том, что теперь R может принимать очень
малые значения. На первый взгляд это дает преимущество, за-
заключающееся в том, что малое отверстие в электроде не ока-
оказывает сильного влияния на распределение потенциала на очень
больших расстояниях от двух апертурных плоскостей; следова-
следовательно, с относительно малой погрешностью границами линзы
можно считать апертурные плоскости. (Как мы увидим
в разд. 7.3.1.5, даже этой относительно малой погрешностью
нельзя пренебречь.) В случае двухцилиндровой линзы это не-
невозможно, так как при очень малых радиусах влияние внешнего
поля будет очень большим даже при малом зазоре между
электродами.
В разд. 3.1.2.4 было рассмотрено распределение потенциала
двухапертурной линзы. Как мы знаем, точное решение возможг
но, но оно настолько сложное, что не позволяет избежать чис-
численных процедур. Даже упрощенная формула для распределе-
распределения осевого потенциала (уравнение C.184)) слишком сложна
для аналитического решения. Для приближенного аналитичес-
аналитического расчета применялась кусочно-квадратичная модель [216]
(разд. 7.2.3) в предположении, что поле линзы заключено меж-
между двумя диафрагмами. В другом подходе [217] между двумя
диафрагмами помещен средний «цилиндр» и предполагалось,
что потенциал линейно меняется вдоль этого цилиндра.
Наиболее полные данные [44] были получены для случая,
когда радиусы предохранительных трубок были Rt = 5R, а сами
трубки расширены внутрь области между электродами с зазо-
зазором 0,2 R между ними. Тогда нет необходимости в дальнейшем
радиальном расширении отверстий электродов, и линза стано-
становится закрытой системой, полностью защищенной от внешних
полей. Хотя эта система по существу является модифицирован-
модифицированной двухцилиндровой линзой, результаты показывают, что ее
наиболее существенными элементами все еще являются апер-
апертурные пластинки, так как они находятся ближе к оси, чем
защитные трубки. Данные получены для s/R=l и 2. Сравнение
с двухцилиндровыми линзами показывает, что сферический ко-
коэффициент добротности двухапертурной линзы хуже на 20—
410
Электростатические линзы
25%, но улучшается с увеличением отношения зазора к ра-
радиусу.
Специальный случай пренебрежимо малого зазора также
был исследован [218], но реальный интерес представляет как
раз обратная ситуация: пренебрежимо малый радиус позволяет
определить границы линзы более или менее точно. К сожале-
сожалению, данные для этого случая получены только для фиксиро-
фиксированного положения изображения [219] и объекта [220]. Так
как в случае пренебрежимо малого радиуса к важным геомет-
геометрическим параметрам относится только размер зазора s, все
оптические параметры могут быть выражены в единицах s.
С другой стороны, для двухцилиндровой линзы с пренебрежи-
пренебрежимо малым зазором важным геометрическим параметром явля-
является радиус R. Следовательно, при сравнении этих двух линз
появляются существенные трудности.
Идея линз с точно определенными границами очень прив-
привлекательна. Характеристические параметры таких линз могут
быть выражены в единицах физической длины линзы, которая
примерно совпадает с протяженностью поля. Такие линзы будут
рассмотрены в следующем разделе.
7.3.1.5. Полиномиальные линзы. Кривые бив распределения
потенциала на рис. 80 асимптотически стремятся к потенциа-
потенциалам электродов; следовательно, этим способом можно пользо-
пользоваться для субъективного определения границ поля. Кривая а
имеет резкие границы, но ей нельзя поставить в соответствие
никакое физическое поле. Как указывалось выше, желательно
четко определить его границы и затем, положив значение поля
на обоих концах линзы равным нулю, найти такое распределе-
распределение потенциала, которое имеет вид, показанный на рис. 80, но
достигает значений потенциалов на электродах в этих точках.
Такие функции потенциалов могут быть найдены в виде по-
полиномов. Линзы, которые имеют распределение осевого потен-
потенциала, описываемое такими функциями, будем называть поли-
полиномиальными линзами.
Простейшей функцией, удовлетворяющей нашим требова-
требованиям, является кубический полином. Следовательно, кубические
полиномиальные линзы [221]—это двухэлектродные симмет-
симметричные линзы, заслуживающие особого внимания.
Будем искать распределение осевого потенциала в виде ку-
кубического полинома
U(z)=A + Bz+Cz2+Dz3. G.70)
Имеем четыре неизвестных коэффициента. Они могут быть най-
найдены из четырех условий, которым необходимо удовлетворить:
на обоих концах поля (z=—L/2 и z=L/2, где L — общая длина
411
Глава 7
поля) первая производная потенциала должна обращаться
в нуль, а сам потенциал должен иметь значения V\ и V2 соот-
соответственно. В результате получим
U(z) = (V, + V8)/2 - (V2 - V,) [1/2 + 2(z/L - 1) (z/L+1/2J].
G.71)
Распределение потенциала антисимметрично вблизи плоскости
2=0, где абсолютная величина наклона имеет максимум, рав-
равный
\U'\max = U'@)l=l,5(V2-V1)/L. G.72)
Приравнивая эту величину постоянному наклону линейной мо-
модели (разд. 7.3.1.1), получим, что для сравнения этих моделей
необходимо использовать
l=L/l,5. G.73)
Эта величина используется в табл. 5 для вычисления безраз-
безразмерного фокусного расстояния в пространстве объектов l/fi.
Распределение потенциала, задаваемое уравнением G.71), по-
показано на рис. 80 кривой г с длиной, определяемой из уравне-
уравнения G.73). Мы видим, что из всех рассмотренных до сих пор
это реальное распределение с наибольшей плотностью поля.
Легко определить форму электродов, дающих осевое распре-
распределение потенциала G.71). Поскольку оно описывается кубиче-
кубической функцией, очевидно, что это распределение будет иметь
только три ненулевых производных. Следовательно, внеосевое
распределение потенциала C.20) может быть выражено доста-
достаточно просто. Вторая производная U(z) дается выражением
U"(z)=—12 (V2 — Vi) z/L3. G.74)
Распределение потенциала имеет точку перегиба при 2 = 0, где
поле имеет максимум. Подставляя уравнения G.71) и G.74)
в C.20) и полагая потенциал равным V в произвольной точке
с координатами гиг, получим уравнение эквипотенциальных
поверхностей:
(r/L)*=[2(z/I- I) (z/L+l/2J+ (V—Vi) (V2-
GJ5)
Если теперь подставить V= Vi, получим простое уравнение
для формы первого электрода. Аналогично, подставляя V=V2,
найдем форму второго электрода. Так как мы требуем, чтобы
осевой потенциал был равен Vt и V2 в точках входа и выхода
соответственно, эти эквипотенциальные линии будут касаться
оси в этих точках. Это также следует из формулы G.75). Для
412
Электростатические линзы
того чтобы сделать линзы проницаемыми для частиц, мы долж-
должны выбрать эквипотенциальные линии, слабо отличающиеся от
расчетных, так, чтобы при z=±L/2 они обеспечивали малые
отверстия. Такие электроды показаны на рис. 93 (сплошные
кривые). Поскольку распределение потенциала определено
только в интервале между г =—L/2 и z = L/2, за пределами лин-
линзы электроды должны быть продолжены как трубки с теми же
значениями потенциалов. При применении линзы в качестве
источника частиц электрод в пространстве объектов может за-
заканчиваться поверхностью, перпендикулярной к оптической оси
(см. рис. 127). Если отверстия малы, то потенциалы электродов
очень близки к их первоначальным значениям Vi и V2. Кроме
того, как было показано [219], изогнутые поверхности электро-
электродов могут быть заменены на
более простые структуры, в
которых каждый электрод
имеет всего лишь одну заост-
заостренную часть (штриховые
линии на рис. 93). Такое рас-
распределение осевого потенциа-
потенциала, а следовательно, и оптиче-
оптические свойства такой линзы
очень близки к свойствам иде-
идеальной кубической полиноми-
полиномиальной линзы.
Табл. 5 показывает, что
оптическая сила кубических
полиномиальных линз выше,
чем двухцилиндровых линз.
Это естественное следствие
большей плотности поля (рис. 80). Ее коэффициент добротнос-
добротности для бесконечного увеличения несколько хуже, чем для двух-
двухцилиндровой линзы (рис. 81 и 82).
Соотношения, связывающие положения объекта и изобра-
изображения с увеличением, так же как и зависимость коэффициентов
аберрации в пространстве объектов от увеличения, приведены
в табл. 8 для случая (V2—U0)l(Vi—Uo)=5. Количественно кар-
картина та же, что и для двухцилиндровой линзы (см. табл. 6-
и обсуждение в конце разд. 7.3.1.3). Минимальное значение
\M\CSo/L = l54 при М=—2,2. Минимальное значение \M\CCo/L =
= 4,6 при Mm—0,75. Используя коэффициент хроматической
аберрации для нулевого и бесконечного увеличений вместе-
с уравнениями E.279)—E.281), получим AfOpt=—0,70.
Довольно трудно сравнивать действие этой линзы с дейст-
действием двухцилиндровой линзы, поскольку в этом случае все ве-
величины отнесены к длине L, в то время как для двухцилиндро-
413
Рис. 93. Электроды кубической поли-
полиномиальной линзы (штриховые линии
показывают упрощенные электроды).
Глава 7
Таблица 8
Положение объекта Р, увеличение М, коэффициент сферической аберрации Cso,
коэффициент хроматической аберрации Ссо (оба связаны с объектом)
.и величины \М\Cso и |Л1|СС0 как функции положения изображения Q
для идеальной симметричной кубической полиномиальной линзы
при (W-I/o)/(Vi-I/.)=5-
Q/L
2,0
2,5
3,0
3,5
4,0
5,0
6,0
7,2
10,0
15,0-
20,0
27,3
00
P/L
8,65
5,02
3,92
3,39
3,08
2,72
2,53
2,39
2,21
2,08
2,02
1,97
1,86
-M
0,17
0,36
0,56
0,75
0,95
1,33
1,72
2,19
3,28
5,22
7,16
10,00
CD
CJL
18630
1886
647
341
222
128,2
91,7
70,4
49,7
37,5
32,8
29,5
22,2.
\M\CJL
3161
686
361
257
210
171,2
158,0
154,2
162,9
195,7
235
294
oo
CJL
42,96
13,98
8,32
6,10
4,96
3,81
3,24
2,86
2Л2
2,11
1,98
1,88
1,65
7.29
5,09
4,64
4,59
4,69
5,08
5,59
6,26
7,92
11,03
14,19
18,82
CO
а Положения объекта и изображения измеряются от средней плоскости линзы. Все
-величины отнесены к длине L.
вой линзы основным геометрическим параметром является ра-
радиус цилиндров R. Тем не менее мы можем сравнивать прибли-
приблизительно их действие, используя пример, данный в конце
разд. 7.3.1.3. Предположим снова, что входная энергия частиц
10 кэВ; следовательно, минимальное расстояние между элек-
электродами равно 3 мм. Используя упрощенную структуру элект-
электродов (штриховая линия на рис. 93), можно принять L=\ см.
Тогда все числа в табл. 6 и 8 можно прямо сравнивать друг
с другом. Используя уравнения E.79) и E.197) и предполагая
относительный разброс энергии 10~4, найдем минимальный ра-
радиус сферического диска 8rSi=l,3 нм для «о = 1 мрад и 6rsl=
= 193 нм для ао=5 мрад. Для минимальных хроматических
дисков имеем 6гс/=2,3 нм и бгС1= 11,5 нм. Так как два миниму-
минимума снова расположены довольно далеко друг от друга, общий
размер пятна необходимо оптимизировать выбором увеличения
между этими двумя оптимальными значениями.
Такое сравнение показывает, что кубическая полиномиаль-
яая линза по крайней мере в два раза лучше двухцилиндровой
линзы, что и объясняет ее популярность. Почему же в таком
случае ее коэффициент добротности уступает коэффициенту
добротности двухцилиндровых линз? Чтобы ответить на этот
вопрос, вспомним, какой смысл вкладывается в понятие коэф-
коэффициентов добротности: малая аберрация для фиксированной
оптической силы (см. разд. 5.7.4). Из табл. 5 следует, что опти-
оптическая сила полиномиальной линзы в 1,3 раза выше, чем
414
Электростатические линзы
двухцилиндровой линзы при (V2—Uo)l(Vi—f/o)=5, если срав-
сравнивать их на основе равенства полей в средней точке линзы.
Это равносильно предположению, что L—2,27R (см. уравнения
G.63) и G.73)). Однако в проводившемся выше сравнении ис-
использовалось R—L, что и является ответом на вопрос. Действи-
Действительно, это значит, что при таком сравнении оптическая сила
кубической полиномиальной линзы в три раза выше, чем двух-
двухцилиндровой. Поэтому если отнести аберрации к фокусному
расстоянию, то для полиномиальной линзы результат получится
хуже, чем для двухцилиндровой.
Кроме того, это обсуждение обещает пролить свет на зави-
зависимость свойств линзы от плотности поля. Большая плотность
поля обычно означает, что все величины, связанные с размера-
размерами линзы, включая фокусные расстояния и коэффициенты абер-
аберрации, становятся меньше. Но желательно, чтобы аберрации
уменьшались в большей степени, чем фокусные расстояния.
Только в этом случае можно говорить, что линза стала лучше
в полном смысле этого слова. Это желание отражено в выборе
коэффициента добротности.
Свойства кубической полиномиальной линзы хорошо иссле-
исследованы для фиксированных положений объекта и изображения.
Результаты показывают [219, 220, 222—224], что она превосхо-
превосходит двухапертурную линзу, которая является всего лишь дру-
другим типом симметричной двухэлектродной линзы и с которой
поэтому можно прямо сравнивать полиномиальную линзу.
В случае применения в качестве источника частиц, когда ци-
цилиндрического расширения со стороны объекта нет, это преиму-
преимущество проявляется особенно сильно. Хотя двухапертурные
линзы могут иметь очень маленькие отверстия, следует учиты-
учитывать, что отверстие в каждом электроде действует как линза
с оптической силой, определяемой разностью электрических по-
полей на обеих поверхностях отверстия (см. разд. 7.8.2). Так как
поле быстро изменяется вблизи обоих отверстий, аберрации
этих «линз» ухудшают качество изображения. Эту ситуацию
можно улучшить, удалив поля из области вблизи отверстий.
Это справедливо для полиномиальной линзы, которая имеет
«чистые» входные и выходные условия: электрическое поле при-
принимается равным нулю в непосредственной близости отверстия
по обе стороны, следовательно, отверстия в электродах не ска-
сказываются на оптических свойствах системы.
Кубическая полиномиальная линза не является единственно-
возможной, способной удовлетворить входные и выходные ус-
условия для распределения потенциала. Возможны также полино-
полиномиальные линзы более высоких степеней [220, 220а, 260]. Ко-
Коэффициенты при пятой, седьмой и т. п. степенях полинома обыч-
обычно выбираются так, чтобы первая производная и производные
415-
Глава 7
более высоких порядков обращались в нуль на каждом отвер-
отверстии электрода. Этот метод также можно использовать для
мультиэлектродных линз. Исследования показывают, что раз-
размеры пятна на образце обычно уменьшаются с увеличением
порядка используемой полиномиальной линзы. Однако в точ-
точках, лежащих вблизи оптической оси, электроды образуют
большие углы по отношению к ней. Следовательно, при увели-
увеличении степени полинома расстояние между электродами умень-
уменьшается, и в конце концов при увеличении степени полинома до
бесконечности полиномиальная линза вырождается в двухци-
двухцилиндровую линзу с нулевым зазором. Поэтому с ростом сте-
степени полинома увеличивается опасность электрического про-
пробоя. Эту опасность можно уменьшить использованием конусо-
конусообразных электродов, подобных изображенным на рис. 93 штри-
штриховой линией.
«Чистые» входные и выходные условия кубической полино-
полиномиальной линзы вместе с относительно хорошими свойствами
делают ее идеальной моделью для сравнения с другими линза-
линзами. Всегда следует стремиться сконструировать линзы с «чи-
«чистыми» граничными условиями, но работающие еще лучше, чем
кубическая полиномиальная линза.
7.3.2. Асимметричные линзы
Симметрия может быть ненужным ограничением для двух-
электродных иммерсионных линз. Действительно, положение
точки перегиба на распределении осевого потенциала и его ве-
величина в этой точке — две дополнительные степени свободы, ко-
которые могут быть использованы для поиска линз с лучшими
свойствами. Представим теперь краткий обзор имеющихся све-
сведений о свойствах асимметричных двухэлектродных линз.
7.3.2.1. Аналитические модели. Теоретическое исследование
таких линз может быть основано на аналитических моделях.
Желательна модель, которая описывает оптические свойства
в простых тригонометрических функциях. Как мы видели в
7.3.1.2, для симметричных двухэлектродных иммерсионных линз
такой модели не существует. Может быть, теперь нам повезет
'больше?
Эта идея заимствована из методов исследования магнитных
линз. В разд. 8.3.5 будет показано, что все оптические свойства
магнитных линз с колоколообразным распределением индукции
могут быть очень просто определены аналитически. Так как
в нерелятивистском случае уравнение D.51) имеет один элект-
электростатический и один магнитный член, то, естественно, предста-
представить распределение электростатического потенциала в таком
■416
Электростатические льязы
виде, при котором результирующая функция T(z) совпадает по
форме с колоколообразным магнитным полем [188]. Тогда все
вычисления станут похожими на вычисления в магнитном слу-
случае и будут возможны простые аналитические решения.
Начнем с кол околообразной функции T(z), симметричной от-
относительно плоскости 2 = 0. Из этого факта сразу же следует,
что распределение потенциала не будет антисимметрично отно-
относительно той же плоскости. Действительно, максимум функции
Т(z) всегда сдвинут в сторону уменьшения потенциала. Это оз-
означает, что в плоскости 2=0 потенциал не равен среднему двух
электродных напряжений. Следовательно, мы имеем модель
асимметричной линзы.
Приравнивая электростатическую часть уравнения D.51) его
магнитной части и подставляя колоколообразное распределение
индукции из уравнения (8.25), получим дифференциальное
уравнение для электростатического потенциала U(z), которое
легко проинтегрировать. Постоянные, появляющиеся в этом
уравнении, содержат параметры магнитного поля и отношение
заряда частицы к ее массе, но это не важно, так как в этой
точке нас интересует только структура распределения потен-
потенциала. Результат интегрирования есть
[/B)=/C1exp(/C2arctg2/6), G.76)
здесь б — параметр нормирования, а постоянные Ki и /G опре-
определяются из граничных условий на —сю и +оо, где значения
потенциала достигают напряжений на электродах Vi и V2-
Из этих условий имеем
Ki=(ViVa)l/2, K2=(\/n)\n(V2/Vl), G.77)
но здесь и начинаются трудности. Действительно, уравнение
Лапласа линейно по отношению к потенциалу, следовательно,
всегда можно записать распределение потенциала, создаваемого
системой п электродов с потенциалами 1/,- (£=1,2, ..., я),
в виде
U(z)=Zty(z)Vi, G.78)
где функции я|); зависят только от геометрических параметров
системы и не зависят от потенциалов электродов [16]. Соотно-
Соотношение C.183)—удобная форма записи этого уравнения для
любой двухэлектродной системы. Очевидно, если записать урав-
уравнение G.76) в таком виде, то функции ^i и г|J будут зависеть
от напряжений на электродах. Это означает, что распределение
потенциала не будет удовлетворять уравнению Лапласа и, сле-
следовательно, не может описывать никакого реального поля. Но
не может ли оно служить математической моделью? К сожале-
417
Глава 7
нию, ответ отрицателен. Точка перегиба функции, описываемой
уравнением G.76), имеет место при
z,-/6-(l/2n)ln(jyVi), G.79)
т. е. асимметрия линзы является функцией ее силы. Этого не
происходит, и, конечно, это не соответствует распределению ви-
вида C.183). Следовательно, нужно попытаться преобразовать
распределение потенциала к такому виду. Очевидно, это озна-
означает добавление постоянной в уравнение G.76), но, к сожале-
сожалению, столь незначительное изменение делает аналитическое рас-
рассмотрение невозможным. В результате приходится заключить,
что значение этой модели очень ограничено; поэтому в даль-
дальнейшем мы ее обсуждать не будем. Такая модель поля близка
к модели линзы, состоящей из диафрагмы и цилиндра (рис. 94).
Детали можно отыскать в литературе [188, 225].
Для описания этого типа
линз могут быть предложены
v2 другие аналитические моде-
модели [189, 226J, но обе они
страдают тем же недостат-
——»z кем: распределение потенциа-
потенциала представлено в виде, где
коэффициенты уравнения
G.78) зависят от напряжений
на электродах.
Рис. 94. Асимметричная линза, со- 7.3.2.2. Асимметричная
стоящая из цилиндра и диафрагмы. двухцилиндровая линза. Су-
Существует бесконечное множе-
множество способов изготовления асимметричных двухэлектродных
линз. Наиболее простая линза снова состоит из трубок и плос-
плоских диафрагм. Два коаксиальных цилиндра разных радиусов
Ri и R2 образуют асимметричную двухцилиндровую линзу. За-
Зазор s может быть отрицательным, если цилиндры частично пе-
перекрываются (рис. 95). Два плоских электрода с отверстиями
различных радиусов составляют асимметричную линзу из двух
диафрагм. Радиусы защитных трубок Rti и Rt2 в этом случае
также могут быть различны (рис. 96). Естественно, электроды
могут иметь коническую или любую другую форму.
Асимметричные двухцилиндровые линзы уже привлекали
внимание в литературе [36, 44, 206]. Электростатическое поле
такой линзы может быть рассчитано аналитически [227], если
предположить, что меньший цилиндр полубесконечной длины
помещен в бесконечно длинный больший цилиндр (s—>-—сю).
Обычно решение получается очень громоздкое, и оптические
свойства могут быть оценены только численно. Можно найти,
418
Электростатические линзы
что для фиксированного отношения потенциалов на электродах
оптическая сила уменьшается с увеличением /?г//?ь Уменьшение
становится пренебрежимо малым для больших значений (V2—
—U0)l(Vi—Uo). Сферические коэффициенты добротности даны
в табл. 9 как функции отношения напряжений и R2/R1. Можно
видеть, что оптимальные значения соответствуют симметрично-
симметричному случаю. Увеличение отношения радиусов (увеличение радиу-
радиуса высоковольтного электрода или уменьшение радиуса низко-
низковольтного) оказывает более неблагоприятное воздействие, чем
его уменьшение.
Таблица 9
Сферический коэффициент добротности Cso«,lfi как функция отношения
электродных напряжений (V2—U0)/(Vi—Uo) и асимметрии R2IR1
для двухцилиндровой линзы
12-и0
У i - Vo
4
5
6
8
10
12
14
16
18
20
0,5
27,89
16,06
10,86
6,50
4,65
3,66
3,06
2,64
2,35-
2,13
0,667-
27,02
15,52
10,55
6,35
4,56
3,58
3,00
2,62
2,36
2,18
1,0
26,57
15,41
10,53
6,32
4,51
3,56
2,97
2,60
2,34.
2,14
29,40
17,05
11,59
6,93
4,94
3,87
3,20
2,76
2,44
2,20
2,0
32,00
18,45
12,57
7,48
5,29
4,16
3,43
2,92
2,60
2,32
7.3.2.3. Гибридная линза. Исследование свойств кубической
полиномиальной линзы (разд. 7.3.1.5) при фиксированном поло-
положении изображения приводит к конструкции интересной сим-
Ri
Vi
s
R2
Щ
Рис. 95. Асимметричная двухцилиндро-
двухцилиндровая линза.
Рис. 96. Асимметричная линза из
двух диафрагм.
метричной линзы [219]. Если сместить антисимметричное рас-
распределение осевого потенциала .кубической полиномиальной
линзы в сторону изображения при заданном отношении элект-
419
Глава 7
родных потенциалов, то главные плоскости также сдвинутся
в сторону изображения. Следовательно, фиксированное поло-
положение изображения будет означать уменьшение расстояния
до него, т. е. уменьшение абсолютной величины М. Как следст-
следствие, для того чтобы обеспечить фиксированное увеличение,
асимметричная линза должна будет работать при более высо-
высоком отношении напряжений, что соответствует более низким
аберрациям.
Такой сдвиг в распределении потенциала может быть осу-
осуществлен приспособлением, изображенным на рис. 97. Оно на-
называется «гибридной линзой», так как электрод в пространстве
объекта заимствован из конической аппроксимации кубической
полиномиальной линзы (см. рис. 93, штриховые линии), в то
время как электрод в пространстве изображения есть просто
отверстие в пластине.
Как было показано [219], коэффициент сферической абер-
аберрации такой линзы приблизительно равен половине коэффи-
коэффициента кубической полиномиальной линзы для любого задан-
заданного увеличения при фиксированном положении изображения.
В случае когда хроматическая аберрация пренебрежимо мала,
минимальный диаметр зонда при заданном токе пропорциона-
пропорционален корню четвертой степени из Cso (см. уравнения E.346),
E.347)), следовательно, это уменьшение эквивалентно умень-
уменьшению диаметра зонда на 19%-
Как мы видели (разд. 7.3.1.5), двухапертурная линза хуже
полиномиальной из-за сильных полей вблизи отверстий. Такое
же отверстие в плоском электроде гибридной линзы дает очень
малые аберрации, так как, хотя поле вблизи него меняется бы-
быстро, на электрод подан высокий потенциал, следовательно,
члены, появляющиеся в выражении для коэффициентов абер-
аберрации, относительно малы. Этот факт можно продемонстриро-
продемонстрировать перестановкой электродов гибридной линзы. Если низкий
потенциал подать на плоский электрод с отвестием, то линза
будет работать значительно хуже.
Следует отметить, что проведенное сравнение было сделано
для фиксированного положения изображения и равных увели-
увеличений (так называемый случай фиксированного пучка в просве-
просвечивающей электронной микроскопии). Это означает, что раз-
различные линзы сравнивались при разных отношениях электрод-
электродных напряжений. Действительно, гибридная линза всегда рабо-
работает при более высоких отношениях напряжений, поэтому ее
аберрации ниже.
Подробные исследования свойств гибридной линзы можно
найти в литературе. Дано много расчетных кривых [228], кото-
которые показывают зависимость положения изображения и коэф-
420
Электростатические лиизы
фициента сферической аберрации от отношения напряжений,
толщины и угла раствора конуса первого электрода, увеличения
и расстояния между двумя электродами. Проблема состоит
в том, что все кривые вычислялись для фиксированного поло-
положения объекта. Кроме того, целью исследований было не толь-
только уменьшить сферическую аберрацию, но еще и получить ста-
стабильное положение изображения при меняющейся энергии
электронов. Следовательно, отношение потенциалов электродов
должно было выбираться выше 20, а положение объекта было
фиксировано в относительной близости к первому электроду.
Как следствие полученные данные относятся в основном к спе-
специфическому случаю высоковольтной электронной микроско-
микроскопии. Однако было найдено, что этот тип линз не подходит для
применения в качестве электронной пушки такого микроскопа
вследствие слабой защиты источника от электрического пробоя
[229]. Имеются данные [230] о зависимости аберраций от от-
отношения электродных напряжений для фиксированного положе-
положения изображения.
Рис. 97. Гибридная линза.
Рис. 98. Двухэлектродная однопо-
тенциальная лииза.
Итак, свойства асимметричных двухэлектродных иммерсион-
иммерсионных линз известны только для некоторых специальных случаев
и особых условий работы. Систематическое исследование требу-
требует более единообразного подхода, основанного на четырех па-
параметрах, выведенных в начале разд. 7.3 [202а].
7.4. Однопотенциальные линзы
Отличительной особенностью однопотенциальных (одиноч-
(одиночных) линз является то, что они имеют одинаковые постоянные
потенциалы как в пространстве объектов, так и в пространстве
изображений. Поэтому они используются только тогда, когда
требуется фокусировка при неизменной энергии пучка. Для фи-
физической реализации таких линз необходимо по крайней мере
421
Глава 7
два электрода (рис. 98). Большинство обычно используемых
однопотенциальных линз имеет по три электрода (рис. 99 и 100).
Распределение осевого потенциала двух- или трехэлектрод-
ной однопотенциальной линзы имеет типичную форму, показан-
показанную на рис. 101, с одним максимумом или минимумом в зави-
зависимости от того, выше или ниже потенциал среднего электрода,
чем потенциал крайних электродов. (Для простоты рассмот-
рассмотрим только положительный потенциал.) Функция распределе-
распределения асимптотически стремится к общему потенциалу крайних
электродов VV Отметим, что экстремальный потенциал f/ext
(£Лпах или Umin) не обязательно равен потенциалу Vz среднего
электрода. Действительно, всегда имеем £/max<V2 и Um\n>V<i,
а равенство — только для очень длинных средних электродов,
которые практически никогда не используются. Распределение
имеет две точки перегиба, где осевые компоненты электростати-
электростатического поля достигают экстремумов.
v3
v,
R,
v2
r
v3
rn
-cpr-'»-
Rt3
Рис. 99. Лииза, состоящая из трех
цилиндров.
Рис. 100. Линза, состоящая из трех
диафрагм.
Распределение потенциала не обязательно симметрично по
отношению к его экстремальной точке. Соответственно однопо-
тенциальные линзы могут быть симметричными или асиммет-
асимметричными. На рис. 99 и 100 показаны асимметричные линзы (от-
(отметим, что для однопотенциальных линз должно выполняться
соотношение VZ=V\). Так как однопотенциальная линза имеет
одинаковые потенциалы с обеих сторон, то геометрическая сим-
симметрия системы электродов относительно ее средней плоскости,
перпендикулярной к оптической оси, автоматически приводит
к общей симметрии распределения потенциала.
Отметим, что в общем случае однопотенциальная линза мо-
может иметь более трех электродов, следовательно, распределе-
распределение потенциала может быть гораздо более сложным, чем пока-
показанное на рис. 101. В общем его можно охарактеризовать сле-
следующими параметрами:
1) протяженностью поля (Ь—а), на которую распространя-
распространяется действие линзы;
422
Электростатические линзы
2) положением экстремальных точек распределения и вели-
величиной потенциала в этих точках, включая его- концевые зна-
значения;
3) положением точек перегиба распределения, а также по-
потенциалов в этих точках.
Эти параметры адекватно описывают любую электростати-
электростатическую линзу [202]. Для специального случая двухэлектродных
иммерсионных линз введены параметры, слегка отличающиеся
друг от друга (см. разд. 7.3). Фактически отношение электрод-
электродных потенциалов включено в п. 2; |£/'|тах и асимметрия опре-
определяются п. 3.
Рис. 101. Распределение осевого потенциала двух- или трехэлектродной одно-
потенциальной линзы.
Ниже ограничимся рассмотрением только двух- или трех-
электродных однопотенциальных линз. Распределение потенциа-
потенциала имеет типичную форму, показанную на рис. 101. Соответст-
Соответствующая функция Т(z) изображена на рис. 102. Очевидно, она
обращается в нуль при z=a и z=b и, кроме того, при z=zm,
где U (z) = Uexi. По обе стороны от этой точки существуют пики
с координатами a<CzMi<Czm и zm<zM2<b. Однако роль функ-
функции T(z), так же как и эффективной длины, ограничена по
причинам, изложенным в разд. 7.3.
По определению для однопотенциальных линз из уравнений
D.76), E.83) и E.201) получим, что
/i* = /2* = /*, G* = \IM\ Csi = M*CS0, Cci = M2CC0, G.80)
но положения главных плоскостей и фокусов в итоге могут быть
423
Глава 7
асимметричными. Отметим, что все эти выражения относятся
только к асимптотическим величинам. Для реальных величин
потенциалы с обеих сторон могут отличаться, если объект или
изображение локализованы внутри поля. Так как будут рас-
рассматриваться только асимптотические величины, звездочки бу-
будут опускаться.
-3
Рис. 102. Функция Т(г) для двух- или трехэлектродиой одиопотеициальной
линзы.
Однопотенциальные линзы подобны обычным стеклянным
линзам, используемым в геометрической оптике, так как они
также имеют одинаковые показатели преломления с обеих сто-
сторон. В остальном они, конечно, существенно отличаются. Суще-
Существуют два основных типа однопотенциальных линз в зависимо-
зависимости от того, выше или ниже потенциал среднего электрода по
сравнению с крайними. Свойства реальной линзы зависят от
большого числа геометрических параметров в той же мере, что
и от отношения электродных потенциалов.
Необходимо отметить, что термин «однопотенциальная лин-
линза» иногда используется буквально, т.е. «линза с одним потен-
потенциалом», что соответствует линзе, средний электрод которой
электрически связан с источником (К2=£/о).
7.4.1. Симметричные линзы
Начнем с наиболее простого случая линз, геометрически
симметричных относительно средней плоскости, перпендикуляр-
перпендикулярной к оптической оси. Например, на рис. 99 и 100 следует поло-
424
Электростатические линзы
жить Si = s2, Ri = R3 и Rti=Rt3- Это означает, что положение zm
экстремального потенциала точно совпадает со средним ариф-
арифметическим границ линзы а и Ь; поэтому удобно предположить,
что 2т = 0. Теперь распределение потенциала совершенно сим-
симметрично относительно средней плоскости и, следовательно,
совпадает с функцией T(z). Так как для симметричной линзы
перевернутая линза совпадает с первоначальной, из уравнения
G.69) получим, что теперь все кардинальные элементы распо-
расположены симметрично относительно главной плоскости. Отме-
Отметим, однако, что уравнение G.80) все еще имеет силу для соот-
соотношений между коэффициентами аберрации в пространстве
объектов и в пространстве изображений вследствие их зависи-
зависимости от увеличения. В этом случае уравнения E.265), E.266),
E.282) и E.283) должны быть отмечены особо.
-з
Рис. 103. Распределение потенциала симметричной однопотенциальной лиизы:
а — кусочно-лииейная моделв, б — аналитическая модель.
Давайте снова вначале исследуем очень простую модель,
чтобы иметь представление о свойствах первого порядка сим-
симметричных однопотенциальных линз.
7.4.1.1. Кусочно-линейная модель. Предположим, что потен-
потенциал постоянен по обе стороны линзы, а внутри меняется ли-
линейно, достигая своего экстремума при 2=0 (рис. 103, кри-
кривая а). Эта модель не очень близка к реальности, но по мень-
меньшей мере очень проста (см. разд. 7.3.1.1). Ее можно считать
грубым приближением распределения потенциала системы, со-
425
Глава 7
стоящей из трех плоских электродов с пренебрежимо малыми
отверстиями.
Распределение потенциала дается как
V1 при z-r: —Z/2,
tfexti -(U^-Vjzll при -//2<z-^0,
G81)
х при 2>//2,
где /=6—а — длина гипотетического поля линзы, а положи-
положительный потенциал выбран для дальнейшего упрощения.
Рассмотрим главный луч r2(z) (рис. 44) при начальных ус-
условиях уравнения G.25) и применим процедуру, описанную в
разд. 7.2.2. Скачок наклона траектории на входе вычисляется
из уравнения G.7):
r/2(—H2 + Az)= — ro{Uexi~Vi)/[2l(Vi—Uo)]. G.82)
Смещение луча и наклон слева от средней плоскости определя-
определяются из уравнений D.141) и D.140) соответственно. Вместе
с уравнением G.82) они дают
r2(O)=ro{3-[(f/ext-t/o)/(K1-f/o)]1/2}/2I G.83)
г'2(-Дг) =-ro(t/ext - 1/,)/{2/[(У1 - t/0) (t/ext - t/o)]1/2}-
G.84)
Теперь необходимо вычислить скачок наклона траектории на
средней плоскости, воспользовавшись уравнениями G.7), G.83)
и G.84). В результате получим
г'2(Дг) =г0(t/ext — Vx) [1,5(I/ext — £/о)-1/2 —
- (V1-t/o)-1/2][/(f/ext-t/oI/2]~1. G.85)
Следующим шагом является вычисление смещения траектории
и наклона на внутренней стороне выходной поверхности линзы
из уравнений D.141), D.140), G.83) и G.85). Получим
/■2 A/2) =го{4 - 3[ (t/ext — t/0)/(Vi - £Л>)]1/2/2 —
_3[AЛ-£/o)/(£/ext-£/<,)] 1/2/2}, G.86)
r'2(^/2 - AZ) =Го (t/ext - F,) [1,5 (t/ext - t/o)^2 -
- (V, - C/o)-I/2J[/(Vi - t/oI/2]. G.87)
Окончательно вычислим наклон на внешней стороне выходной
поверхности линзы, используя уравнения G.7), G.86) и G.87).
В результате имеем
г'2(Ц2 + Аг) =3 (Г о//) [(t/ext - t/0)/(F, - t/o) - 1] X
X {0,75 [ (F, - t/0)/(t/ext - t/o) ]'/2 +
+ 0,25[(t/ext-t/0)/(F,-t/0)]'/2-1}. G.88)
426
Электростатические линзы
Теперь есть вся необходимая информация, чтобы определить
асимптотические кардинальные элементы. Подставляя уравне-
уравнения G.25) и G.88) в уравнение D.73), получим оптическую
силу [11]:
llf = 0,75[ (t/ext - U0)l(Vi — U0) — 1] X
Х{4 —3[(Vi —C/0)/(C/ext— U0)Y" —
— C7o) ] 1/2>- G.89)
Эта величина изображена сплошной линией на рис. 104 как
функция отношения потенциалов (Uext—U0)/(Vi—Uo). Хотя эта
модель очень проста, она позволяет выявить свойства первого
2 4 6 8 10
(U..I -Uo)/(V< -Uo)
Рис. 104. Оптическая сила моделей одиопотенциальной лиизы, как функция
отношения потенциалов (Uext— Uo)/(V\ — Ua). Сплошная кривая соответствует
кусочио-линейной модели, штриховая — аналитической.
порядка однопотенциальных линз. По мере того как отношение
потенциалов все больше отличается от единицы, поведение оп-
оптической силы зависит от того, при более низком или более
высоком потенциале находится средний электрод по отноше-
отношению к крайним. Если абсолютная величина разности потен-
потенциалов \Uext—Vij фиксирована, то оптическая сила больше при
более низком потенциале на среднем электроде. Это вполне,
понятно, так как линза оказывает большее влияние на частицы
с низкой энергией, чем на частицы, ускоренные более высоким
потенциалом среднего электрода. В случае низкого потенциала
на среднем электроде оптическая сила монотонно растет с уве-
42Z-
Глава 7
личением разности потенциалов между электродами. Очевидно,
когда отношение потенциалов стремится к нулю, скорость час-
частиц также стремится к нулю и оптическая сила становится бес-
бесконечно большой. Дополнительное преимущество этого режима
состоит в том, что не требуются напряжения выше, чем V\. Од-
Однако, к сожалению, в этом случае аберрации обычно выше, чем
при высоком потенциале среднего электрода.
Если средний электрод имеет потенциал выше, чем крайние
электроды, то оптическая сила вначале растет с ростом отноше-
отношения потенциалов, достигает максимума 1,273 при (£/тах—Uo)/
I(V\—£/0) = 5,26, а затем монотонно уменьшается, достигая нуля
при (Umax—U0)/(Vi—Uo)=9 (телескопическая линза) и стано-
становится отрицательной. Если сравнивать рис. 104 и табл. 5, то
увидим, что оптическая сила однопотенциальных линз значи-
значительно выше, чем иммерсионных. Это и есть причина ее на пер-
первый взгляд странного поведения. Линза еще достаточно сильна
для частиц, пересекающих оптическую ось, но находящихся
в поле линзы. Следовательно, асимптотическое фокусное рас-
расстояние может быть любым. Отрицательная оптическая сила
соответствует случаю, когда траектории пересекают ось дважды
внутри линзы. Соответственно в этом случае главные плоскости
не меняются местами.
Положение точки фокуса в пространстве изображений полу-
получается подстановкой уравнений G.86) и G.88) в уравнение
D.71). Тогда местоположение главной плоскости в пространст-
пространстве изображений определяется уравнениями D.73) и G.89).
В результате имеем
Я2//=1/2-
2G 90)
f/)I1/2}
{3 —[(f/ext
Величина H2/l отрицательна, если (t/ext—U0)/(Vi—£/о)<9,
и главная плоскость в пространстве объектов расположена сим-
симметрично по другую сторону средней плоскости (#i =—Н2 = Н).
Величина Н2/1 изображена на рис. 105. Главные плоскости рас-
расположены ближе к центру, если потенциал среднего электрода
ниже. Вследствие симметрии теперь главные плоскости разде-
разделены промежутком
G.91)
который является функцией отношения напряжений. Длина про-
промежутка увеличивается с усилением возбуждения линзы.
Функция Т(z) легко может быть вычислена из уравнений
D.51) и G.81). Она симметрична относительно средней плос-
плоскости, но, так как модель не является непрерывной, она сильно
отличается от функции, показанной на рис. 102.
428
Электростатические линзы
В приближении тонкой линзы оптическая сила дается урав-
уравнениями D.117) или D.118). Вследствие симметрии будем ин-
интегрировать только по половине протяженности поля, а затем
результат удвоим:
1/2
2 S
/
1//шп=2 S T(z)dz= C/4/) X
X[(C/ext —
— С/о)— 1]2Х
,-С/о)]-1. G.92)
Формула такой линзы дает удовлетворительные результаты (от-
(относительная погрешность меньше 10%) только для интервала
отношения напряжений 0,3<(£/ext—U0)/{Vi—С/о)<2. Это очень
мало, если средний электрод имеет более высокий потенциал.
Естественно, она всегда дает завышенную оценку оптической
силы.
-20 -
-30
Рис. 105. Положение главной плоскости в пространстве изображений для ку-
кусочно-линейной модели однопотенциальмой линзы как функция отношения по-
потенциалов (Uexi-Ug)/(Vl-U0).
Вследствие симметрии центром тяжести линзы является
средняя плоскость. Следовательно, в приближении тонкой лин-
линзы уравнения D.122) и D.123) дают #i = #2 = 0, как и ожида-
ожидалось (см. разд. 4.9).
Мы получили некоторую информацию о свойствах первого
порядка однопотенциальных линз на основе этой простой моде-
модели. Теперь перейдем к рассмотрению более реалистических мо-
моделей.
42Э
Глава 7
7.4.1.2. Кусочно-квадратичная модель. Следующей степенью
усложнения является представление распределения потенциала
тремя гладко соединенными параболическими дугами. На осно-
основе этой модели уже развита [72] общая теория однопотенци-
альных линз. Были выведены точные формулы для фундамен-
фундаментальных оптических свойств таких линз на основе геометриче-
геометрических параметров. Было учтено влияние конечной толщины
электродов, отклонений от аксиальной симметрии и т.д. Влия-
Влияние положений точек перегиба распределения потенциала на
оптические свойства изучено еще не полностью. Эта модель яв-
является важным вкладом в теорию однопотенциальных линз, но
следует сознавать, что результаты требуют длительных вычис-
вычислений (оригинальная статья, описывающая эту модель, занима-
занимает 75 страниц) и не обладают достаточной точностью (см.
разд. 7.2.3). Мы отдаем предпочтение более простой модели
для грубого приближения и более точной для реального кон-
конструирования, поэтому эта модель здесь представлена не будет.
Интересующихся читателей отсылаем к литературе [36, 72].
7.4.1.3. Аналитическая модель. Рассмотрим колоколообраз-
ное распределение потенциала
(рис. 103, кривая б), где d — значение координаты на оси, в ко-
которой потенциал имеет среднее значение (Vi + £/ext)/2, называе-
называемое по этой причине полушириной поля. Можно связать d
и параметр линейной модели / произвольно, но удобно выбрать
d = l/4. G.94)
Тогда два распределения равны при z = d. Функция G.93) име-
имеет точку перегиба при z/d=±3~''2 и постепенно приближается
к Vi при z/d, стремящемся к ±оо. Для практических целей
можно считать поле линзы ограниченным в интервале а = — 10rf
и b=\Od, что дает погрешность меньше 1% для U(z)/Vu при
0<iUext/Vi<i2. Для Uext/Vi = 5 погрешность становится равной
4%, следовательно, при использовании этой модели для более
высоких значений отношений потенциалов возникают труд-
трудности.
Для этого случая уравнение параксиальных лучей G.1) мо-
может быть решено точно [190, 191, 231]. Сначала введем новые
переменные у и г|з так, чтобы
z/d=ctgq, G.95)
r=y{$)lsm$. G.96)
430
Электростатические линзы
((утметим сходство между этими соотношениями и уравнения-
уравнениями G.44) и G.45).) Тогда уравнение G.93) можно переписать
следующим образом:
U^)=Vl+{Utxt — Vi)sin»^. G.97)
Вводя новую переменную
G.98)
о
уравнение G.1) после некоторых преобразований можно за-
записать в виде
§ + оЛ/ = 0, G.99)
где
о>2 = 1+ (t/ext — Vi)/[2(V, - С/о)]. G.100)
Решение уравнения G.99) элементарно. Подставляя его
в уравнение G.96), получим
incoE;)/sin\|), G.101)
где С, и С2 — постоянные, которые должны определяться из
начальных условий, а £ определяется уравнением G.98), в кото-
которое, чтобы получить результат, подставим уравнения G.97)
и G.100):
?[( )^]% G.102)
о
Отметим, что со2—1>0, если Uext = Umax>Vu и ю2—КО, если
C/ext=C/mm<Ki.
Для соотношения между координатами объекта и изображе-
изображения г|зо и г|),п соответственно уравнение D.58) дает
U —£о = ля/(о. G.103)
Здесь /2 = 1, 2, ... — весь ряд, характеризующий порядковый но-
номер данного изображения в случае множества изображений.
Увеличение дается выражением
М = (— 1)" sin \|3o/sin г|з,„. G.104)
Так как нас интересуют асимптотические величины, рассмот-
рассмотрим ход главного луча n (z) (рис. 45). Он идет из бесконечно-
бесконечности (j|), = 0) на расстоянии г0 параллельно оси в плоскости изо-
изображений. Очевидно, чтобы на бесконечности величина остава-
оставалась конечной, следует положить в уравнении G.101) Ci = 0.
Воспользовавшись правилом Лопиталя, получим С2 = Го/со. Те-
Теперь можно рассмотреть уравнение D.68) для определения ме-
431
Глава 7
стоположения точки асимптотического фокуса в пространстве
объектов. В пределе из уравнений G.95) и G.96) получим
lim [ri(a) —ari ()];(|/|) yty (|
a->oo 1|)->л
G.105)
Подставляя это уравнение в уравнение D.68), положив
robj(z)=0 и проводя дифференцирование, получим координаты
точки асимптотического фокуса
F> = ~ d щ №у (л) = - &d cts К № ■ G-106>
Аналогично из уравнений D.72), G.95) и G.96) получим асим-
асимптотическое фокусное расстояние
/* = — cod/sin [со£ (я)]. G.107)
Положение главной плоскости дается уравнением D.72), как
Hi* = F1*+f1*.
Если средний электрод находится при более низком потен-
потенциале (£/ext = £Anin<l/i), то можно записать
ш» = 1 —#72, G.108)
где
йа=(У, —C/ext)/(Vi —tfo). G.109)
Тогда
%(n)=2K(k), G.110)
где K(k)—полный нормальный эллиптический интеграл перво-
первого рода, являющийся табличной функцией.
В этом случае найдем, что 2со/Ол. Если 2со/С<Зл/2, то
sin Bсо/С) <0 и ctgBco/C) >0, т.е. фокусное расстояние поло-
положительно и фокус в пространстве объектов расположен слева
от центра линзы. При 2со/С=Зя/2, что соответствует £ = 0,99, т.е.
(f/ext—Uo)/(Vi—f/o)=O,O2, фокус расположен в центре линзы
и фокусное расстояние достигает своего минимума. Увеличивая
силу линзы Bсо/С>Зя/2), добьемся того, что точка фокуса бу-
будет смещаться в пространство изображений и обратно, а фокус-
фокусное расстояние снова будет расти. При со/С=л (& = 0,999 т.е.
(Vext—U0)/(V1—(Jo) =0,002) реализуются телескопические ус-
условия (бесконечное фокусное расстояние), и в диапазоне
0<(f/ext—L'o)/(l/i—£Л>)<0,002 фокусное расстояние становит-
становится отрицательным. Как видим, поведение линзы обнаруживает
«микроструктуру» вблизи нулевого среднего потенциала. Такое
поведение было обнаружено у реальной линзы [232]. На рис.
104 штриховая линия, представляющая этот случай, очень
432
Электростатические линзы
близка к сплошной линии для линейной модели. Для преобра-
преобразования подобия было использовано уравнение G.94). Вслед-
Вследствие большого масштаба рисунка «микроструктура» не может
быть показана.
Если средний электрод имеет более высокий потенциал
Uext = Umax>Vu то можно записать
со2 = 1 + х2/2, G.111)
где
*2 = (t/ext —Vi)l(Vi — U 0) = — k\ G.112)
Тогда с помощью новой переменной %, определяемой соотноше-
соотношением
G.113)
легко показать, что
\ (л) =2 A + x2)-V2K[x A + х2)-'/2]. G.114)
В этом случае, как показывает анализ, фокусное расстояние
качественно ведет себя так же, как и для линейной модели, но
достигает минимума при гораздо более высоких значениях от-
отношения потенциалов (рис. 104, штриховая кривая). Соответ-
Соответственно для обычно применяемого диапазона отношения потен-
потенциалов (f/max—U0)l(Vi—£/о)<1О главные плоскости остаются
на небольшом удалении от центра линзы. В данном диапазоне
|#*|Д/<0,36, поэтому для таких линз может быть приемлемо
приближение тонкой линзы. (Положение главной плоскости не
может быть показано на рис. 105 вследствие его большого мас-
масштаба.)
Интегралы аберраций невозможно оценить прямо с по-
помощью приведенных выше аналитических решений, но все же,
работая с этими решениями, можно вычислить реальные гео-
геометрические коэффициенты хроматической аберрации [190,
191]. Полученные аналитические решения можно упростить
[231]. Результаты показывают, что для сильных линз и потен-
потенциала среднего электрода, близкого к нулю, можно добиться
достаточно малых реальных коэффициентов аберрации. Проб-
Проблема состоит в том, что объект должен находиться глубоко
внутри линзы, что не имеет практического смысла, поскольку
при этом поле линзы будет искажено.
Мы уже вычислили асимптотические коэффициенты доброт-
добротности для этой модели численным интегрированием. При более
низком потенциале среднего электрода наилучший сферический
коэффициент добротности может быть получен при (i/min—Uo)f
l(Vi—f/0) =0,06, он равен CSOco/f = 8,4. Хроматическая аберра-
аберрация для таких линз также высока (разд. 5.3.1.2). Действитель-
Действительно, в этом случае наилучшее значение хроматического коэффи-
433
Глава 7
циента добротности достигает теоретического верхнего преде-
предела СсоЛ = 2 При f/min«Vi.
Если потенциал среднего электрода выше, то ситуация ана-
аналогична случаю двухэлектродных иммерсионных линз: чем силь-
сильнее линза, тем меньше аберрации. Как отмечалось выше, наи-
наибольшее реальное значение для этой модели— (f/max—Uo)l
j(Vi—£/о)—5. В этом случае имеем CSOCo// = 5,6 и ССо~//=0,65.
Сравнивая эти значения с аналогичными значениями для сим-
симметричной двухцилиндровой линзы с тем же отношением потен-
потенциалов, получим, что параметры однопотенциальной линзы луч-
лучше по крайней мере в 2 раза (сферический коэффициент доб-
добротности в 2,7 раза, хроматический коэффициент добротности
в 2 раза меньше). Поскольку оптическая сила однопотенциаль-
ных линз приблизительно в 2 раза выше, чем для двухцилинд-
двухцилиндровых (см. рис. 104 и табл. 5), это означает, что, если отнести
коэффициенты аберрации к длине /, получим коэффициент сфе-
сферической аберрации в 5 раз, а коэффициент хроматической
аберрации в 4 раза меньше, чем для двухцилиндровой линзы.
Проблема, однако, состоит в том, что поле этой модели про-
простирается слишком далеко. Поэтому, когда мы попытаемся
использовать линзу, представленную нашей моделью для фор-
формирования изображения, увидим, что невозможно найти такие
условия, при которых объект или изображение не находились
бы внутри линзы. Ситуация иллюстрируется табл. 10, где
асимптотические положения объекта и изображения даются
вместе с коэффициентами аберраций для случая (Umax— U0)l
I(V\—С/о) =5, как функция увеличения. Общая тенденция та
же, что и для иммерсионной линзы: коэффициенты аберрации
сильно уменьшаются до их значений для бесконечного увеличе-
увеличения с ростом абсолютной величины М. Поскольку предполага-
предполагалось, что распределение потенциала сконцентрировано в интер-
интервале — 10<2/d<;10, из табл. 10 следует, что для низких уве-
увеличений изображение всегда будет внутри поля, а для более
высоких увеличений внутри поля будет объект. Это демонстри-
демонстрирует одну нз самых больших трудностей конструирования
электростатических линз для формирования зондирующего пуч-
пучка, где приемлемое рабочее расстояние должно обеспечиваться
по крайней мере с одной стороны линзы.
В табл 10 приведены также величины \M\Cs0/d и \M\CCojd.
Они достигают минимальных значений 251 и 12,3 соответствен-
соответственно при М — —3 и М = — 1. Кроме того, для положения минимума
|Af | Ссо уравнение E 286) даетЛГор1=—1.
Для того чтобы сравнить эти минимальные значения с при-
приведенными в табл. 6 и 8 для двухцилиндровой и кубической
полиномиальной линз соответственно, нужно отнести параметр
полуширины d к радиусу цилиндров R и к длине кубической
434
Электростатические линзы
Таблица 10
Положение объекта Р, увеличение М, коэффициент сферической
аберрации Cso, коэффициент хроматической аберрации Ссо
(оба связаны с объектом) и величины |Af|Cso и |М|ССО
как функции положения изображения Q для аналитической модели
симметричной однопотенциальной линзы при (Umsx—£/0)/( Vj—{У0)=5а
Qld
5,5
6,0
7,0
8,0
9,0
10,0
12,0
15,0
20,0
30,0
40,0
70,0
CD
P/d
37,35
24,12
15,44
12,14
10,40
9,32
8,06
7,10
6,33
5,71
5,45
5,13
4,77
-M
0,15
0,25
0,46
0,66
0,87
1,07
1,48
2,10
3,12
5,17
7,22
П.37
CO
CJd
93170
16160
2721
1043
564
366
207
125,3
80,5
54,1
45,1
36,0
27,3
\mc,0/d
13980
4040
1251
687
490
391
306
263
251
280
325
481
CO
Co/"*
185,0
76,9
31,5
19,45
14,29
11,51
8,66
6,75
5,42
4,45
4,07
3,64
3,18
1
тс. -г
27,7
19,22
14,47
12,84
12,43
12,32
12,82
14,18
16,91
23,0
29,4
48,7
аз
a Положения объекта и изображения измеряются от центра линзы Все величины
отнесены к полуширине d
полиномиальной линзы L. Это не очень легкая задача, но мож-
можно выразить d через параметры реальной однопотенциальной
линзы и затем осуществить сравнение способом, изложенным
в разд. 7.3.1.5. В качестве грубой оценки можно сказать, что
для трехэлектродной однопотенциальной линзы, состоящей из
трех трубок или диафрагм одинаковых радиусов н тонкого
среднего электрода, величина d приблизительно равна радиусу
отверстий или трубок. Теперь можно прямо сравнить результа-
результаты табл. 10 и табл. 6. Видно, что размеры дисков хроматиче-
хроматической аберрации приблизительно одинаковы в обоих случаях,
тогда как размеры дисков сферической аберрации несколько
меньше для однопотенциальных линз. При таком сравнении фо-
фокусное расстояние однопотенциальной линзы в 1,4 раза больше,
чем иммерсионной линзы, что несколько компенсирует более
высокий коэффициент добротности однопотенциальных линз.
Далее будем исследовать свойства реальных трехэлектрод-
ных однопотенциальных линз с большими плотностями полей,
чем в аналитической модели.
7.4.1.4. Трехцилиндровая линза. Начнем с очень простой
линзы, состоящей из трех коаксиальных цилиндрических элект-
электродов одинаковых радиусов Ri = R2=R3 = R, разделенных рав-
равными промежутками Si = s2 = s (рнс. 99). Два крайних электро-
электрода имеют одинаковые потенциалы (K3 = ^i)- Потенциал V2
центрального электрода может меняться от небольшого отри-
435
Глава 7
цательного значения, соответствующего Um\n = 0 (линза превра-
превращается в зеркало), до положительного значения, ограничивае-
ограничиваемого только практическими соображениями. Будем предпола-
предполагать, что толщина стенок электродов пренебрежимо мала, а дли-
длины 1\ и /3 достаточны, чтобы защитить линзу от воздействия
внешних полей в направлении оси. В этом случае линза имеет
только три параметра: отношение потенциалов (V2—U0)/(Vl—
—f/o), относительную длину центрального электрода UIR и от-
относительную ширину зазора s/R (четвертым параметром долж-
должно быть отношение радиусов крайних электродов к радиусу
центрального, но здесь оно предполагается равным единице).
Распределение потенциала такой линзы мало отличается от
распределения для аналитической модели, рассмотренной в пре-
предыдущем разделе, с тем только различием, что ее поле имеет
большую плотность, поэтому, возможно, придется рассматри-
рассматривать более высокие значения отношения потенциалов. Свойства
первого порядка и сферическая аберрация этой линзы описаны
в литературе [44, 67, 156, 233, 234]. Имеющиеся данные о ее
хроматической аберрации получены из предположения о линей-
линейном изменении потенциала между электродами [67], которое
является достаточно грубым приближением (разд. 3.1.2.2). Для
точного анализа следует полагаться на результаты численных
расчетов поля. В дальнейшем мы попытаемся суммировать
имеющиеся результаты.
На рис. 106—109 показаны кардинальные элементы и сфе-
сферическая аберрация симметричных трехцилиндровых линз как
функции отношения электродных напряжений для фиксирован-
фиксированной ширины зазора (sIR = 0,2) и двух различных относительных
длин центрального электрода (/2//? = 0,8 и 1,8). Зеркальный эф-
эффект для этих двух случаев наблюдается соответственно при
(V2—Uo)/(Vi—Uo) =—0,73 и —0,17. (Очевидно, что зеркальный
эффект имеет место при увеличении длины центрального элек-
электрода для наибольшего отрицательного значения отношения
напряжений. То же справедливо и при увеличении расстояния
между электродами.)
На рис. 106 изображено фокусное расстояние, отнесенное
к радиусу цилиндров. Как мы выяснили при изучении аналити-
аналитической модели (рис. 104), в окрестности значения напряжения,
при котором наблюдается зеркальный эффект, фокусное рас-
расстояние быстро изменяется. Пренебрегая этой переходной об-
областью, обладающей «микроструктурой», можно сказать, что
выше этой переходной области сила линзы очень велика и
уменьшается при дальнейшем увеличении отношения напряже-
напряжений. Фокусное расстояние стремится к бесконечности при при-
приближении отношения потенциалов к единице. Как только потен-
потенциал среднего электрода становится положительным по отно-
436
Электростатические линзы
шению к потенциалам крайних электродов, фокусное расстоя-
расстояние уменьшается с увеличением отношения напряжений и при
достаточно высоком отношении потенциалов ((V2—Uo)/(Vi—
-—f/0) = 14 и 9 соответственно для двух случаев, показанных на
рисунке) достигает своего минимума. Для (V2—U0)l(Vi—С/о)<
<7 фокусное расстояние уменьшается с увеличением длины
среднего электрода. При более высоких значениях отношения
потенциалов наблюдается обратная тенденция. Для малых от-
отношений напряжений увеличение расстояния между электрода-
электродами оказывает такое же воздействие на фокусное расстояние,
как и увеличение длины центрального электрода. Влияние ши-
ширины зазора максимально при минимальной длине центрального
электрода. Аналогично длина центрального электрода играет
наибольшую роль при минимальных размерах зазора [67].
На рис. 107 показана осевая координата главной плоскости
Н в пространстве объектов, отнесенная к радиусу R. Как мы
знаем, ее абсолютная величина равна абсолютной величине ко-
координаты главной плоскости в пространстве изображений: сле-
следовательно, расстояние между главными плоскостями в точно-
точности равно 2#. С увеличением силы линзы главные плоскости
удаляются от центральной. Их разделение тем сильнее, чем
длиннее центральный электрод. Для высоких значений отноше-
отношения напряжений Н может даже превышать f, этот факт озна-
означает, что фокусы движутся к противоположным сторонам
центральной плоскости. Мы уже встречались с инверсией точек
фокуса в аналитической модели в предыдущем разделе.
Это также может происходить и в других типах сильных
линз.
Коэффициент сферической аберрации при бесконечном уве-
увеличении для низких отношений напряжения качественно ведет
себя так же, как и для двухэлектродных линз: он достигает
высоких значений для слабых линз и резко уменьшается с уве-
увеличением силы линзы. Однако, как видно на рис. 108, Cso°o/R
достигает минимума при некотором высоком отношении напря-
напряжений и снова начинает расти от этого значения с увеличением
отношения напряжений. Интересно, что этот минимум находит-
находится в непосредственной близости от минимума фокусного рас-
расстояния (рис. 106). Действительно, для этих линз минимальные
значения равны CSOco/#=3,36 и 7,24 при значениях (Уг—Uo)l
I{V\—f/0) = 14 и 8 соответственно. Это очень хорошо иллюст-
иллюстрирует правильность выбора понятия коэффициента добротно-
добротности Csoco/f. Если сферическая аберрация меняется вместе с фо-
фокусным расстоянием и достигает минимума для наиболее силь-
сильных линз, тогда наша цель должна состоять в том, чтобы
выбрать такую систему электродов, для которой их отношение
минимально при данном отношении потенциалов.
437
Глава 7
-1
15 17 19
(V2-u0)/(v,-u0)
Рис. 106. Фокусное расстояние симметричной трехцилиндровой линзы, отне-
отнесенное к радиусу цилиндров, как функция отношения напряжения на электро-
электродах. Квадраты — 12/R = Q,8, крестики — 12/R=l,8 соответственно. Для обеих
кривых s/R = 0,2.
11
13
15 17 19
(V2-U0)/(V,-U0)
Рис. 107. Положение главной плоскости в пространстве объектов симметрич-
симметричной трехцилиндровой линзы, отнесенное к радиусу цилиндров, как функция
отношения напряжений на электродах. Параметры те же, что на рис. 106.
438
Электростатические линзы
Отметим, что в интересном на практике диапазоне отноше-
отношения напряжений минимум сферической аберрации выражен го-
гораздо сильнее для длинных средних электродов, чем для корот-
коротких. Соответственно при низких значениях отношения напря-
напряжений коэффициент сферической аберрации меньше для линз
с более длинным средним электродом, в то время как при высо-
высоких значениях наблюдается совершенно обратная тенденция.
Две эти кривые пересекаются при отношении напряжений, рав-
равном 8. Оказывается, для низких значений отношения напряже-
напряжений ширина зазора влияет на коэффициент сферической абер-
аберрации, так же как центральный электрод.
e
о
90-
80-
70*
60 -
50 -
40-
30-
20-
10 -
0 -
I
I
1
|
/
/
/
/
1 I
" и u— в о в '
-11 3 5 7 9 11 13 15 17 19
(v2-u0)/(v,-u0)
Рис. 108. Коэффициент сферической аберрации при бесконечном увеличении
для объекта, отнесенный к радиусу цилиндров симметричной трехцилиндровой
линзы, в зависимости от отношения напряжений на электродах. Параметры
те же, что на рис. 106.
На рис. 109 представлены коэффициенты добротности. Мы
видим, что характер их поведения очень похож на характер
поведения самих коэффициентов аберрации. Две кривые пересе-
пересекаются приблизительно при том же отношении напряжений, что
и кривые функции Csoca/R. Различие состоит только в том, что
коэффициент добротности не так резко увеличивается при вы-
высоких значениях отношения напряжений, в отличие от коэффи-
коэффициентов аберрации. Минимальные значения равны CSo~/f= 1,45
и 2,43 и достигаются точно в тех же точках, что и минимумы
Csoc»/R- По сравнению с двухэлектродными линзами это улуч-
улучшение, так как минимумы достигаются при более низких отно-
439
Глава 7
шениях напряжений. Сравнение будет более полезным, если
выбрать (У2—Uo)/(V\—f/0) =5. В этом случае предпочтительны
длинные линзы. Тогда имеем Cso°o/f = 3,78, но даже для самой
короткой линзы значение CSOco// = 8,31 намного меньше 15 для
двухцилиндровых лииз. Эти два значения близки к значе-
значению 5,6, полученному для аналитической модели в предыду-
предыдущем разделе.
Сравнивая сферический коэффициент добротности линз с вы-
высоким и низким потенциалом, найдем, что для последних самое
низкое значение достигается при отношениях напряжений, близ-
13
15 17 19
(V2-U0)/(V,-U0)
Рис. 109. Коэффициент сферической аберрации при бесконечном увеличении
для объекта, отнесенный к фокусному расстоянию симметричной трехцилинд-
ровой линзы, в зависимости от отношения напряжений на электродах. Пара-
Параметры те же, что на рис. 106.
ких к зеркальным, и равных 6,89 и 6,42 соответственно для двух
типов линз. Эти значения намного выше, чем минимальные зна-
значения для линз с высоким потенциалом, но они сравнимы при
(V2—U0)/(Vl—Uo)=5. Это важное соображение, так как линзы
с низким потенциалом имеют определенное преимущество, по-
поскольку не требуют дополнительных источников питания.
К сожалению, они обладают высокой хроматической аберра-
аберрацией.
Более высокую сферическую аберрацию линз с низким по-
потенциалом легко объяснить на основе рассмотренного в начале
этой главы принципа действия электростатических линз. Отри-
Отрицательно заряженные частицы всегда дефокусируются в обла-
440
Электростатические линзы
сти с более высоким потенциалом. Это означает, что траекто-
траектория отклоняется от оси перед входом в область центрального
электрода. В случае линз с высоким потенциалом справедливо
обратное.
Было показано [38], что, если отношение радиусов централь-
центрального и крайних электродов меняется, сферическая аберрация
минимальна для трубок одинаковых радиусов. Обычно сфери-
сферическая аберрация уменьшается с увеличением общей длины
линзы.
Коэффициент хроматической аберрации принимает очень
высокие значения, если центральный электрод имеет более низ-
низкий потенциал. Это является причиной того, почему линзы с вы-
высоким потенциалом имеют преимущество перед линзами с низ-
низким потенциалом. Приближенные вычисления показывают [67],
что для l2/R = s/R = 0,5 можно достигнуть Cco«>/f = 0fi3 для (Уг—
—U0)l(Vi—U0) = l0 и CcoJf = 0,95 для (V2—U0)/(V1—U0)=5.
Эти значения хуже примерно на 50% значений, полученных из
аналитической модели. Для низких отношений потенциалов
коэффициент хроматической аберрации вначале уменьшается
с ростом длины центрального электрода, достигает минимума
при некотором 12/R и затем увеличивается. При коротком цент-
центральном электроде коэффициент хроматической аберрации
уменьшается с ростом зазора. Однако для данного централь-
центрального электрода верно обратное.
Отметим, что зазор нельзя увеличивать выше некоторого
предела из-за проникновения внешних полей в радиальном на-
направлении. С другой стороны, если зазор очень мал по сравне-
сравнению с радиусами электродов и длиной центрального электрода,
то трехцилиндровая линза может анализироваться как система
из двух отдельных двухцилиндровых линз. Если, кроме того,
длина среднего электрода много больше его радиуса, то может
быть оправдано строгое применение аналитических выражений
для распределения осевого потенциала. Аналитические функции
также могут применяться для аппроксимации зависимости фо-
фокусирующих свойств и аберраций от параметров линзы [234].
В настоящее время в нашем распоряжении имеется пять
коэффициентов, необходимых для вычисления сферической
аберрации при конечном значении увеличений, заданных в таб-
табличной форме, и графики зависимости положения изображения
от положения объекта для разных отношений напряжений и
увеличений, а также графики MCS0 в зависимости от М для
разных значений отношения напряжений [44]. Сравнивая мини-
минимальные размеры пятна для отношения напряжений, равного 5,
с размерами пятна для двухцилиндровой линзы, найдем, что,
в то время как линза с коротким электродом ненамного лучше
своего двухцилиндрового аналога, линза с длинным средним
441
Глава 7
электродом дает (\М\CSO/R) mm ~ 100 приблизительно в три ра-
раза меньше, чем для двухцилиндровой линзы. Для линзы
с R=\ см это эквивалентно радиусам минимального размера
пятна 125 и 1 нм при половинном угле аксептанса 5 и 1 мрад
соответственно.
7.4.1.5. Трехапертурная линза. Симметричным однопотенци-
альным линзам, состоящим из трех электродов с круглыми от-
отверстиями (рис. 100 при Vi = V3, Яг = Яз, Rn = Rt3 = Rt, l\ — h
и Si = s2 = s), уделялось много внимания в литературе [36, 44,
72, 218, 231, 235]. Основная причина состоит в относительной
простоте, с которой упрощенную теорию, основанную на кусоч-
кусочно-квадратичной модели (разд. 7.4.1.2), можно применить
к этой линзе. Как мы видели в разд. 3.1.2.4, распределение по-
потенциала, создаваемое последовательностью круглых отверстий,
можно быстро оценить приближенным методом, основанным на
суперпозиции. Комбинация этого метода с кусочно-квадратич-
кусочно-квадратичной моделью [72] дала возможность очень подробно исследо-
исследовать свойства этих линз еще в то время, когда не были доступ-
доступны компьютеры. Позже стало возможным также применить
[231] к этой линзе аналитическую модель, описанную в
разд. 7.4.1.3.
Последние данные, основанные на численных расчетах поля
[44], получены для Ri = R2 = R, s/R=l и 2. В этих вычислениях
считалось, что Rt = 5R и экранирующие трубки находятся во
внутренней области между электродами с зазором длины 0,2 R.
Вычисления показывают, что, хотя эта линза имеет преимуще- ■
ства (более компактна и обладает большей плотностью поля),
ее свойства хуже, чем у трехцилиндровой линзы. Для (V2—
—Uo)l{V\—f/o)=5 сферические коэффициенты добротности рав-
равны CSOeo/f = 13,3 и 5,3 для s/R = l и 2 соответственно. В области
вблизи зеркального эффекта соответствующие коэффициенты
равны 7,0 в обоих случаях. Для конечных увеличений ситуация
еще хуже: минимальное значение \M\CSO/R даже для линз, об-
обладающих большей длиной, лишь немного меньше, чем для
двухцилиндровых линз.
Кроме того, еще имеются данные для других значений R2/Ri
и ширины зазора s [218, 235].
7.4.1.6. Другие типы симметричных линз. В литературе ис-
исследовалось множество других симметричных трехэлектродных
конфигураций [156, 236, 237]. Особого упоминания достойна
одна линза, которая привлекла много внимания [36, 72, 231,
232, 238—240]. Эта линза по существу является комбинацией
цилиндрической линзы и диафрагмы. Она состоит из двух пла-
пластин с одинаковыми круглыми отверстиями радиуса Ri и цн-
442
Электростатические линзы
линдрическим центральным электродом длины / и радиуса R2,
разделенных двумя одинаковыми зазорами ширины s каждый.
Экранирующие трубки радиуса Rt присоединены к каждой сто-
стороне электрода (рис. 110).
Эту линзу легко анализировать на основе кусочно-квадра-
кусочно-квадратичной [72] (разд. 7.4.1.2) и даже аналитической модели
(разд. 7.4.1.3), распространив ее на двойное колоколообразное
распределение потенциала [231]. Особое внимание уделялось
случаю [238, 239], когда средний электрод обладает более низ-
низким потенциалом. Представлены также экспериментальные дан-
данные [232, 240].
R,
s
R2
• 1-
r
V2
Rt
s
v3
Rt
—
Рис. 110. Цилиндрически-апертурная линза.
Тремя основными геометрическими параметрами этой лин-
линзы являются R2/R\, l и s. Суммируя основные результаты для
линзы с низким потенциалом, можно сказать следующее. При
данном отношении напряжений фокусное расстояние сначала
уменьшается с увеличением длины среднего электрода, как и в
случае трехцилиндровой линзы (рис. 106). Однако для элект-
электродов большей длины тенденция обратная: после прохождения
минимума фокусное расстояние увеличивается с ростом /. Рас-
Расстояние между главными плоскостями растет как с ростом /,
так и с ростом s. Коэффициент сферической аберрации для
бесконечного увеличения также достигает минимума при неко-
некотором оптимальном значении /, которое увеличивается с ростом
отношения напряжений. При этом оптимальном значении сфе-
сферическая аберрация почти не зависит от размеров зазора. Если
потенциал среднего электрода нулевой, наилучшее значение
сферического коэффициента добротности приблизительно рав-
равно 5. Минимум сферического коэффициента добротности дости-
достигается при том же самом отношении напряжений, при котором
сила линзы максимальна. Коэффициент хроматической аберра-
аберрации принимает минимальные значения при длинных централь-
443
Глава 7
ных электродах и больших зазорах и, конечно, его величина
всегда чересчур высока в режиме низких потенциалов.
Большое число возможных параметров снова обращает вни-
внимание на то, что исследовать однопотенциальные линзы необ-
необходимо на основе распределения осевого потенциала, а не кон-
конфигурации электродов [202Ь]. Однако в общем можно утверж-
утверждать, что симметричные однопотенциальные линзы имеют более
низкие аберрации, чем симметричные двухэлектродные иммер-
иммерсионные линзы. Если желательно и дальше улучшать свойства
линз, то нужно вернуться к асимметричным линзам.
7.4.2. Асимметричные линзы
Идея использования геометрически несимметричных однопо-
тенциальных линз основана на хорошо известном результате
световой оптики: при сильном увеличении сферическая аберра-
аберрация минимальна, если поверхность линзы с наибольшей кри-
кривизной обращена к объекту [18J. Очевидно, в электронной и
ионной оптике это соответствует ситуации, когда объект нахо-
находится со стороны максимального поля, т. е. линза и ее центр
сдвинуты в направлении максимального поля со стороны объ-
объекта. Такая асимметричная линза предложена давно [241] в
виде системы электродов, показанной на рис. 111 (Уз = У}).
Она работала в режиме более низкого потенциала среднего
электрода, и экспериментально было показано, что сферичес-
сферический коэффициент добротности такой линзы может достигать
Csox/f = 3,6, который выигрывает в сравнении с наилучшим'
значением 5, достижимым в этом режиме для симметричной
линзы, показанной на рис. ПО.
Число параметров этой линзы весьма велико. Очень важно
правильно выбрать ее геометрические размеры. При оптималь-
оптимальном расположении всех элементов [242] коэффициент доброт-
добротности можно уменьшить до 2,5. Хорошим представлением та-
такой линзы будет пара двухэлементных линз, причем более
сильная линза будет расположена ближе к объекту [155, 243].
Эта линза также исследовалась в режиме конечного увели-
увеличения [244, 245]. Особое внимание уделялось влиянию пара-
параметров S\/s2 и l/R2 (рис. 111) на коэффициент сферической
аберрации для М =—1 и М = —10. Позднее [246] для модифи-
модификации этой линзы было получено С5о0О// = 5,4 и Ccoao/f = 3,2
при ,^, = ^2 = ^3 = ^=1,5 мм, l = Si = s3 = 2R, s2=ll,3/?,
Rt = 6R, Vi = V3 и (V2—U0)/(Vl—U0)=0,2. Толщина первого и
третьего электродов одинакова и равна 2R/3.
Влияние различия в размерах зазоров S] и s2 на поведение
трехцилиндровой линзы (рис. 99) с одинаковыми радиусами
(R\ = R2 = R3 = R) и V2 = U0 исследовалось, исходя из предпо-
444
Электростатические линзы
ложения, что потенциал в зазорах меняется линейно [247].
Эти результаты представлены в виде таблиц для широкого
диапазона параметров Si/R, s2/R и 12/R, но, к сожалению, даны
только реальные коэффициенты аберрации.
Также была предложена линза, составленная из пары коак-
коаксиальных двухцилиндровых линз с разными диаметрами [155J
(рис. 112). Если зазор между двумя цилиндрами пренебрежи-
пренебрежимо мал, основными геометрическими параметрами такой линзы
являются отношение радиусов двух цилиндров R?/R] и рас-
расстояние / между линзами. Идея составной линзы работает, ес-
если l>2(Ri + R2). Было показано, что в режиме с более низким
потенциалом среднего электрода основной вклад в сферичес-
сферическую аберрацию дает ускоряющая компонента. Если R\<R2,
в пространстве объектов линза сильнее и коэффициент сфери-
сферической аберрации может быть уменьшен на 20% по сравнению
-I—
Рис. 111. Асимметричная однопотен-
циальная линза.
Рис. 112.
линз.
Пара двухцилиндровых
с однопотенциальной линзой с одинаковыми диаметрами ци-
цилиндров и пренебрежимо малым расстоянием между электро-
электродами.
Было также исследовано множество других асимметричных
конфигураций. В работе [245] на основе изучения трех раз-
различных линз с более высоким потенциалом на среднем элект-
электроде был сделан вывод, что для малых рабочих расстояний в
режиме конечного увеличения асимметричная структура имеет
наименьшую сферическую аберрацию, но если требуется боль-
большое рабочее расстояние, то предпочтительнее симметричная
линза, изображенная на рис. ПО, с толстым средним электро-
электродом и большими межэлектродными зазорами.
Очень интересное исследование [248] было посвящено изу-
изучению 16 различных асимметричных линзовых структур с более
низким потенциалом на средних электродах, которые применя-
применяются в источниках эмиссионного поля. Поскольку миниатюри-
миниатюризация линзы ограничена необходимостью поддерживать прием-
приемлемое рабочее расстояние между источником и первым элект-
445
Глава 7
родом линзы, то были найдены наименьшие коэффициенты сфе-
сферической и хроматической аберраций для бесконечного увели-
увеличения, отнесенные к этому рабочему расстоянию. Было пока-
показано, что коэффициент сферической аберрации, отнесенный к
рабочему расстоянию, имеет минимум при некотором отноше-
отношении потенциалов, характерном для каждой отдельной линзы.
Что касается геометрической формы линз, было установле-
установлено, что минимальный коэффициент сферической аберрации мо-
может быть уменьшен путем сильного уменьшения толщины пер-
первого электрода, расширением центрального электрода и суже-
сужением зазоров между электродами. Дальнейшее уменьшение
сферической аберрации возможно с помощью конического
центрального электрода. Наилучшая линза состоит из очень
тонкого плоского первого электрода, длинного конического
центрального электрода, вытянутого в сторону первого так,
что зазор очень мал (диаметр начального отверстия в четыре
раза больше, чем зазор между первыми двумя электродами),
с углом полураствора конуса 26,6° и коротким плоским третьим
электродом с большим отверстием (рис. 113). Зазор между
п
Рис. 113. Асимметричная линза с коническим центральным электродом.
первыми двумя электродами должен быть как можно короче,
чтобы обеспечить максимально возможное поле в пространст-
пространстве объектов. Положение и размер третьего электрода может
быть довольно произвольным: помещая его достаточно далеко
от центрального электрода, можно уменьшить сферическую
аберрацию на 10%- Отношение напряжений, которое обеспечи-
обеспечивает минимум сферической аберрации, не совпадает со значе-
значением, обеспечивающим минимум хроматической аберрации.
Для того, чтобы минимизировать совместное действие обеих
аберраций, необходима подгонка.
Эта линза имеет сферический коэффициент добротности
CSooo/f =1,3 и хроматический коэффициент добротности Cco<x,/f =
= 3,9. Как мы видели в этой главе, это пока лучший сферичес-
сферический коэффициент добротности. К сожалению, в этой работе со-
совершенно не учитывалось влияние отверстия в первом электро-
электроде. Это может привести к очень существенной ошибке, так как
поле достигает максимальных значений как раз в этом отверс-
отверстии. Как указывается в статье [248], открытие указанной апер-
446
Электростатические линзы
туры на 75% диаметра начального отверстия центрального
элемента увеличивает сферическую аберрацию на 30%. Однако
сравнение свойств этой линзы (рис. 111) с отверстием и без
отверстия показывает [246], что относительные ошибки в сфе-
сферическом и хроматическом коэффициентах добротности состав-
составляют соответственно 169 и 124%. Поэтому нужно быть очень
осторожным при оценке этих данных.
Заключение, которое можно сделать из изучения асиммет-
асимметричных однопотенциальных линз, состоит в том, что они дают
определенное уменьшение сферической аберрации. Их способ-
способность уменьшать хроматическую аберрацию изучена мало, так
как поведение этих линз исследовано не полностью для режи-
режима высокого потенциала.
Геометрическая асимметрия однопотенциальных линз явля-
является мостом к следующему классу линз, которые не обладают
электрической симметрией.
7.5. Трехэлектродные иммерсионные линзы
По определению линза, имеющая на обоих концах разные
значения постоянных потенциалов, является иммерсионной.
В этом определении число электродов не оговорено. Мы рас-
рассмотрели простейшие иммерсионные линзы с двумя электрода-
электродами в разд. 7.3. Теперь займемся более сложным случаем: клас-
классом трехэлектродных иммерсионных линз.
Причина, по которой мы решили прервать последователь-
последовательность иммерсионных линз, рассмотрев между ними однопотен-
циальные линзы, проста. Трехэлектродные однопотенциальные
линзы являются простейшим из возможных специальным слу-
случаем семейства трехэлектродных иммерсионных линз: единст-
единственное различие между ними состоит в том, равны или не рав-
равны потенциалы в пространстве объектов и изображений. Так,
например, линзы, показанные на рис. 99 и 100, становятся
иммерсионными, если положить Vi=^V3. Однопотенциальные
линзы всегда электрически симметричны, иммерсионные лин-
линзы — никогда. В конце последнего раздела мы ввели понятие
асимметричных однопотенциальных линз. Можно рассматри-
рассматривать трехэлектродную иммерсионную линзу как следующую
ступень усложнения, где вводится другая асимметрия путем
подачи на крайние электроды линзы разных напряжений. Кро-
Кроме того, это дает еще одну степень свободы в варьировании
свойств линзы.
Конечно, как и в двухэлектродном случае, трехэлектродные
иммерсионные линзы также могут быть геометрически симмет-
симметричными или асимметричными. Соответственно в этом смысле
можно различать симметричные и асимметричные линзы.
447
Глава 7
7.5.1. Геометрически симметричные линзы
Если линза геометрически симметрична относительно сред-
средней плоскости, перпендикулярной оптической оси, то мы имеем
•структуру электродов простых симметричных однопотенциаль-
ных линз, но с различными потенциалами на разных электро-
электродах. Действительно, если в распоряжении имеются три разных
напряжения, то с их помощью легче обеспечить симметрию
линзы, чем путем изменения ее геометрических размеров. В са-
самом деле, таким способом можно изменять степень асимметрии
простым изменением напряжения на одном из электродов сис-
системы. Поскольку теперь имеются три независимых напряжения,
т. е. два независимых отношения напряжений, в качестве элек-
электрических параметров, это дает большую свободу удовлетво-
удовлетворить нескольким требованиям одновременно.
В частности, становится возможным зафиксировать положе-
положение объекта и напряжение с его стороны и менять выходную
энергию частиц, в то время как положение изображения оста-
остается постоянным. Вследствие этого свойства трехэлектродные
иммерсионные линзы иногда называют изофокусирующими
[44J. Отметим, что этот термин первоначально относился к
линзам, у которых можно было произвольно изменять увеличе-
увеличение изображения. Изофокусирующий эффект достигается ис-
использованием одного отношения напряжений для контроля оп-
оптической силы линзы, в то время как другое отношение напря-
напряжений используется для изменения энергии на выходе. Если
напряжение на первом электроде фиксировано, то напряжение
на втором электроде становится функцией напряжения на
третьем. Эта функция зависит от требуемых положений объек-
объекта и изображения (см. разд. 7.5.1.1).
Отметим, что свойства перевернутых линз (переставлены
потенциалы первого и третьего электрода, в то время как по-
потенциал среднего электрода остается неизменным) снова мо-
могут быть исследованы на основе сказанного в разд. 7.3.1.3.
Кроме того, здесь можно прямо использовать уравнения G.69).
Теперь исследуем свойства некоторых симметричных трех-
электродных иммерсионных линз.
7.5.1.1. Трехцилиндровые линзы. Это такая же линза, как
и симметричная трехцилиндровая однопотенциальная линза
(разд. ТАЛА, рис. 99) с тем только отличием, что теперь на-
напряжения Vi и Уз неодинаковы. Существуют данные [44, 214,
249, 250] о свойствах первого порядка и сферической аберра-
аберрации этой линзы. Ее хроматическая аберрация исследуется ав-
авторами в настоящее время.
448
Электростатические линзы
На рисунках, приведенных ниже, будут даны кардинальные
элементы в пространстве объектов и изображений, как функ-
функции отношения потенциалов (V2—C/o)/(Vi—С/о) для (Уз—С/о)/
l(Vi—С/0)=2, 5, 10 и 20. Поскольку свойства замедляющих
линз могут быть прямо выведены из свойств ускоряющих линз,
нет необходимости вычислять их отдельно. Геометрическими па-
параметрами являются /2/i?=l,8 и s/R = 0,2. Они выбраны пото-
потому, что среди существующих данных соответствуют наилучшим
значениям сферического коэффициента добротности. Все вели-
величины отнесены к радиусу цилиндров R. Кривые соответствуют
бесконечно тонким электродам.
На рис. 114 и 115 даны фокусные расстояния в пространст-
пространстве объектов и изображений. Естественно, в любом случае для
ускоряющих линз f2>/i в соответствии с уравнением D.76).
При малых отношениях ускоряющих напряжений (V3—С/о)/
I(VX—С/о) линза ведет себя как однопотенциальная: фокусное
расстояние быстро растет по мере приближения (Уг—С/о)/
I(V\—Uо) к определенному значению, где достигает максиму-
максимума. Различие состоит в том, что теперь максимум имеет ко-
конечное значение и локализован при (V2—Uq)I(Vi—С/о)>1.
С ростом ускорения максимум сдвигается в сторону более вы-
высоких значений отношения напряжений и уменьшается. Фокус-
Фокусное расстояние имеет минимум, которого оно достигает при
достаточно высоком отношении напряжений. С ростом (Vz—
—U0)/(Vl—С/о) линза становится сильнее для всех значений
(V2—U0)/(V]—С/о), применяемых на практике. Действительно,
при высоких значениях (У3—Uo)/(V\—С/о) поведение лин-
линзы становится весьма похожим на поведение двухцилинд-
двухцилиндровой линзы с тем же отношением ускоряющих потенциа-
потенциалов.
Положения главных плоскостей в пространстве объектов и
изображений (рис. 116 и 117 соответственно) обнаруживают
очень интересное поведение. Общее правило состоит в том, что
главные плоскости меняются местами и обе сдвинуты в об-
область с более низким потенциалом. Если (V3—C/0)/(Vi—С/о)
мало, то совместное влияние однопотенциальной и иммерсион-
иммерсионной линзы приводит к весьма сложной кривой. Снова наблюда-
наблюдаются большие сдвиги для слабой линзы, затем они становятся
меньше и снова начинают расти при высоком возбуждении,
когда линза становится существенно однопотенциальной. Для
высоких значений (V3—C/0)/(Vi—С/о) кривые начинают отли-
отличаться при больших (У2—С/0)/AЛ—С/о), подобно тому как это
наблюдается для двухцилиндровых линз. Расстояние между
главными плоскостями показано на рис. 118.
Для конечных увеличений взаимное соотношение между
положениями объекта и изображения можно определить на
449
Глава 7
15 17 19
(v2-u0)/(v,-u0)
Рис. 114. Фокусное расстояние симметричной трехцилиндровой лиизы в про-
пространстве объектов (k/R8 /R02)
ф
р р рр р
(k/R=l,8, s/R=0,2), отиесеииое к радиусу цилиндров.
как функция отношения напряжений (К2— Uo)/( V\~ Uo) для (К3— Uo)/
UJ ( ) 1 (б 20 ()
фуц р ( o)/( o) C
— U0)=2 (квадраты), 5 (крестики), 10 (ромбы) и 20 (треугольники).
50 -
40 -
20 -
10 -
Рис. 115. Фокусное расстояние симметричной трехцилиндровой линзы в про-
пространстве изображений (I2/R=l,8, s/R = 0,2), отнесенное к радиусу цилиндров,
как функция отношения напряжений (V2— Uo)/(V\ — Uo) Обозначения те же,
что иа рис. 114.
450
Электростатические линзы
" -з-
-в
19 17 19
(V2-U0)/(V,-U0)
Рис. 116. Положение главной плоскости симметричной трехцилиндровой линзы
в пространстве объектов (/2//?=1,8, s/R=Q,2), отнесенное к радиусу цилинд-
цилиндров, как функция отношения иапряжений (Vi— Uo)/(Vi — Uq). Обозначения те
же, что на рис. 114.
-ю
-1
-i—г-
3
-I 1 1 Г
5 7
т—i—i—i—г
11 13
—i—I—i—i—r-
15 17 19
(v2-u0)/(v,-u0)
Рис. 117. Положение главной плоскости симметричной трехцилиндровой лии-
зы в пространстве изображений A2/R=l,8, s/R=0,2), отнесеииое к радиусу
цилиндров, как функция отношения напряжений (V2-U0)/(Vi-U0). Обозначе-
Обозначения те же, что на рис. 114.
451
Глава 7
основе семейства кривых для различных постоянных увеличе-
увеличения и отношения электродных потенциалов.
На рис. 119 показан коэффициент сферической аберрации
для объекта при бесконечном увеличении, отнесенный к фокус-
фокусному расстоянию (сферический коэффициент добротности) как
функция отношения потенциалов. Коэффициент добротности
для заданного отношения {V3—U0)l (Vi—U0) начинается с
высоких значений при отрицательном (Vj—U0)/(Vi—Uo).
С ростом (У2—U0)/(Vi—Uo) коэффициент добротности стано-
становится меньше, достигает минимума, затем резко возрастает,
15 17 19
(V2-U0)/(V,-U0)
Рис. \ 18. Расстояние между главными плоскостями симметричной трехцилинд-
ровой линзы A2/R=\,S, s/R=0,2), отнесенное к радиусу цилиндров, как функ-
функция отношения напряжений (V2—U0)/(Vi — U0). Обозначения те же, что на
рис. 114.
достигает максимума, после которого снова уменьшается, и до-
достигает второго слабо выраженного минимума и затем снова
растет. Чем больше (V3—U0)j(Vx—Uo), тем меньше сферичес-
сферическая аберрация. Если (V3~U0)l(Vl—U0)=20, то для (V2—
—U0)/(Vi—Uo) =—0,2 имеем CSOOc//i = l,39. Это реальное дости-
достижение, но, как обычно, надо свести отношение потенциалов к 5.
Тогда наилучшее значение есть CSOeo/f,=2,96 для (у3—£/„)/
/(У,—Uo) =5 и (V2—t/0)/(Vi—1/0) 0,1- Это значение сравни-
сравнимо с лучшим значением для однопотенциальнои линзы 3,78.
На рис. 120 показан коэффициент сферической аберрации
при нулевом увеличении, отнесенный к фокусному расстоянию,
как функция отношений электродных напряжений. CSio/f2 пред-
представляет собой сферический коэффициент добротности для за-
452
Электростатические линзы
3
о
о1
15 17 19
(V2-U0)/(V,-U0) .
Рис. 119. Коэффициент сферической аберрации для объекта при бесконечном
увеличении, отнесенный к фокусиому расстоииию симметричной трехцилиндро-
вой лиизы (/2/#=1,8, s/R=0,2), как функция отношения напряжений
(V2—U0)/(Vl — U0).-Обозначении те же, что на рис. 114.
7 9 11 13 15 17 19
(v2-u0)/(v,-u0)
Рнс. 120. Коэффициент сферической аберрации для изображения при нулевом
увеличении, отнесенный к фокусному расстоянию со стороны изображения сим-
симметричной трехцилиндровой лиизы (/.,/#= 1Д s/^ = 0,2), как функция отно-
отношения напряжений (V2-l/0)/(V,-y0). Обозначения те же, что на рис. 114.
45}
Глава 7
медляющих линз (уравнение E.265)). Характер этой кривой
такой же, как и для ускоряющих линз, но соответствующие
значения выше. В этом случае наилучшее значение С«о//2 =
= 1,48 для (Уз—!/„)/(Vi—1/0)=20 и (Va—I/o)/(V1—£/0) = 1,5.
Однако для отношений потенциалов ниже 5 результат намно-
намного хуже: лучшее значение Cs;0/f2 = 6,l для (Уз—U0)/(Vi—
-ио)=5и (V2—Uo)l(V1—U0)=0.
Для вычисления сферической аберрации в случае конечно-
конечного увеличения существует пять коэффициентов, представленных
в табличной форме вместе с графиками MCso от М для раз-
различных отношений напряжений [44]. Находим, что теперь ми-
минимальное значение (|Af|Cso/,/?)min = 14 при Af«—2 для (У3—
—U0)/(V1—U0)=5 и (У2—t/0)/(Vi—Uo)=— 0,1. Это в семь раз
лучше, чем для однопотенциальной линзы с тем же отношени-
отношением потенциалов изображения и объекта. Для линзы cR = 1 см
это означает, что минимальные радиусы пятен в плоскости изо-
изображения равны 18 и 0,14 нм при половинном угле аксептанса
5 и 1 мрад соответственно.
Это прекрасный результат, но как его сопоставить с тем
фактом, что сферический коэффициент добротности всего в
1,28 раза лучше, чем для однопотенциальных линз? Мы снова
имеем случай сравнения линз с разными фокусными расстоя-
расстояниями. В этом случае фокусное расстояние однопотенциальной
линзы в пространстве объектов равно 3,64 см. Та же величина
для иммерсионной линзы равна всего лишь 0,92 см, т. е. срав-
сравниваются две линзы, одна из которых в четыре раза сильнее
другой. Следовательно, преимущество в значительно меньшей
аберрации частично компенсируется более коротким рабочим
диапазоном. Но все же иммерсионная линза лучше однопотен-
однопотенциальной. Мы удостоверились, что асимметрия, введенная за
счет использования разных напряжений, дает реальные пре-
преимущества.
Другим преимуществом трехэлектродной иммерсионной
линзы является большая гибкость. Как мы теперь знаем, она
может работать как изофокусирующая линза, если менять по-
потенциал среднего электрода так, чтобы положения объекта и
изображения оставались неизменными, в то время как отноше-
отношение потенциалов изображения и объекта меняется. Как прави-
правило, существуют два значения У2 для каждого V3: одно обычно
выше, а другое ниже, чем напряжения на двух других элект-
электродах. Такая «кривая изофокусирующейлинзы» (У3—U0)/(Vi—
—Uq) в зависимости от (V2—Uo)/(V}—Uo) для фиксированной
пары положений объекта и изображения имеет форму замкну-
замкнутой петли [44]. Если линза работает при более высоком потен-
потенциале Уг, то изменению отношения потенциалов изображения и
объекта в широком интервале соответствуют всего лишь незна-
454
Электростатические линзы
чительные изменения увеличения. Если также желательно ме-
менять увеличение, то должны использоваться низкие значения
потенциала V2 [84J.
7.5.1.2. Другие типы геометрически симметричных линз.
Любая однопотенциальная линза может работать в качестве
иммерсионной при простом изменении выходного потенциала
V3. Одной из линз, для которой свойства первого порядка и
сферическая аберрация тщательно изучены [44, 251, 252J, яв-
является линза, состоящая из трех диафрагм (рис. 100). Хотя
она обладает большей плотностью поля, чем трехцилиндровая
линза, ее сферическая аберрация существенно выше.
Кроме того, можно сконструировать трехэлектродные поли-
полиномиальные линзы (см. разд. 7.3.1.5) [220, 253].
7.5.2. Асимметричные линзы
Удачное использование как геометрической, так и электри-
электрической асимметрий, естественно, приводит к идее использовать
их одновременно. Таким способом достигается наибольшее
усложнение трехэлектродных фокусирующих структур: асим-
асимметричные иммерсионные линзы. Такие линзы характеризуют-
характеризуются весьма большим числом параметров. Напомним, что полное
исследование их свойств возможно только на основе распреде-
распределений потенциалов. Параметры, выведенные в начале
разд. 7.4, должны адекватно описывать свойства этих линз.
Мы знаем только две таких полностью изученных линзы.
Первая — это асимметричная версия упрощенной трехэлект-
родной полиномиальной линзы, которая нашла применение в
тетроидной пушке [228J. Вторая — линза [246, 254J, показан-
показанная на рис. 111, но с изменяющимся потенциалом У3. Геомет-
Геометрические размеры были даны в разд. 7.4.2. Рассматривались
как конечное, так и бесконечное увеличение. В первом случае
положения объекта и изображения были фиксированы, варьи-
варьировалась конечная энергия пучка (изофокусирующая линза).
Сравнение работы этой линзы с работой гибридной линзы из
разд. 7.3.2.3 показало, что трехэлектродная линза обладает
лучшими характеристиками. Для (V3—U0)/{Vi—U0)=2 и
(У2—U0)/(Vi—£/о)=6,88 сферический коэффициент добротнос-
добротности равен Csoco/f 1 = 3, а хроматический коэффициент добротности
принимает значения вплоть до CCOoo/fi = 0,5. При увеличении
М = —3,45, половинном угле аксептанса 5 мрад и относитель-
относительном разбросе энергий 10~4 можно достигнуть вблизи гауссовой
плоскости изображения радиуса сферического пятна 32 нм и
хроматического пятна Т нм при размерах рабочей области в
455
Глава 7
пространстве объектов 6 мм и в пространстве изображений
25 мм. Из-за малого зазора между электродами была выбрана
входная энергия 5 кэВ. Отметим, что при такой низкой энергии
все размеры линзы в предыдущем примере должны быть
уменьшены в 2 раза. Тогда диск сферической аберрации трех-
цилиндровой иммерсионной линзы почти в четыре раза мень-
меньше, чем для этой линзы. Однако хроматическая аберрация этой
лиизы достаточно низка, что является определенным преиму-
преимуществом для зондоформирующей оптики.
На основе этих едва ли достаточных данных об асиммет-
асимметричных трехэлектродных иммерсионных линзах мы уже можем
сделать вывод, что они обещают хорошие перспективы в до-
дополнение к их гибкости, когда работают как изофокусирующие
линзы. В гл. 9 мы увидим, что такие линзы с очень малыми
аберрациями действительно могут быть сконструированы.
7.6. Многоэлектродные линзы
Когда одновременно требуется поддерживать постоянные
значения двух параметров линзы (например, положение изо-
изображения и увеличение), необходимы по крайней мере четыре
независимых напряжения, т. е. три переменных отношения на-
напряжений. Это приводит к электростатическим линзам с че-
четырьмя и более электродами. Очевидно, что большая гибкость
таких многоэлектродных линз обеспечивает дополнительную
свободу в поиске структур с более низкими полями и аберра-
аберрациями, хотя очень большое число параметров делает система-
систематизацию таких линз особенно трудной.
В принципе л-электродная линза может быть использована
для поддержания постоянных значений п—2 параметров. Сдер-
Сдерживает только то, что соотношение Гельмгольца — Лагранжа
(уравнение 4.76) между отношением потенциалов объекта и
изображения, линейным и угловым увеличением должно удов-
удовлетворяться для каждой сопряженной пары объект — изобра-
изображение: т. е. если одна из этих величин меняется, две другие
не могут оставаться постоянными [255].
Многоэлектродные линзы также могут быть симметричными
и асимметричными, как геометрически, так и электрически.
В основном они работают в режиме иммерсионных линз. Дан-
Данные существуют только для некоторых специальных систем.
Систематическое исследование возможно только на основе рас-
распределений потенциалов.
Перейдем теперь к краткому обзору существующих данных
о многоэлектродных линзах.
456
Электростатические линзы
7.6.1. Четырехэлектродные линзы
Простейшей четырехэлектродной линзой является геомет-
геометрически симметричная структура, состоящая из четырех ци-
цилиндров одинаковых диаметров, разделенных узкими зазорами
(четырехцилиндровая линза) [256]. Каждый из двух централь-
центральных цилиндров исследуемой линзы имел длину 0,8 R и ширина
всех зазоров равнялась 0,2 R, где R — радиус цилиндров. Было
установлено, что в режиме однопотенциальной линзы оптиче-
оптическая сила системы непрерывно возрастает при отклонении
(V3—Uo)l{Vi—Uo) от единицы. В режиме иммерсионной лин-
линзы оптическая сила растет с ростом (V4—£/0)/AЛ—Uo) и ста-
становится менее зависимой от величины (V3~Uo)/(Vi—Uo). Ко-
Коэффициент сферической аберрации дан только для нескольких,
отдельных значений увеличения. Кроме того, вычислены траек-
траектории в четырехцилиндровой линзе переменного радиуса [257J.
Для уменьшения хромати-
хроматической аберрации была пред-
предложена четырехэлектродная
асимметричная линза, сос-
состоящая из четырех диаф-
диафрагм [258]. Эта линза сос-
состоит из четырех плоских -
электродов с отверстиями.
Первый электрод расположен
на значительном расстоянии
Si2 от трех других и, кроме то-
того, радиус его отверстия R\ Рис 121. Четырехэлектродиая линза
больше, чем радиусы других с низкой хроматической аберрацией,
отверстий (рис. 121). Таким
образом, действие этой линзы между первыми двумя
электродами очень слабое, что неизбежно приводит к вы-
высокой сферической аберрации. Однако хроматические ко-
коэффициенты добротности достигают значений вплоть до ССо°°/
/fi = 0,44, но это обеспечивается тем, что (V4—U0)/{Vi—J70)=6,
(V2—U0)/(V4—U0) = l и (V3—Uo)/(V4—Uo) = l,8. Это означает,
что максимальное напряжение в 10 раз выше, чем входное.
Автор этой книги сконструировал асимметричную четырех-
электродную линзу [179, 259] с Csooa/fi = 2,08 и CcoJh=0,62.
Линза должна работать при максимальном отношении потен-
потенциалов объект — изображение, равном 7,5. Для того, чтобы до-
достигнуть больших значений рабочих областей (рабочая область
в пространстве объектов 8 мм, в пространстве изображений
25 мм), пришлось немного пожертвовать коэффициентом доб-
добротности: в окончательном варианте CSox,/fi = 2,5 и CCo<*>lf\ —0,7..
Для значения половинного угла аксептанса 5 мрад и относн,-
457
Глава 7
тельного разброса энергии 10~4 радиус диска сферической
аберрации равен 18 нм, а хроматической аберрации — 5 нм и
гауссовой плоскости изображения при М=—2,1. Прямое срав-
сравнение этой линзы с линзой, представленной в разд. 7.5.2, пока-
показывает, что достигнуто улучшение 44% в размерах сферическо-
сферического и 24% хроматического дисков аберраций при незначитель-
незначительном увеличении рабочей области в пространстве объектов.
Посредством некоторых геометрических изменений и повы-
повышением отношения максимального потенциала к потенциалу
объекта до 9 можно резко уменьшить сферическую аберрацию
этой линзы [260]. Такая система электродов показана на
рис. 122. В ней третий электрод находится внутри второго. Он
удерживается диском, приводящим к нарушению целостности
второго электрода. Отношения электродных потенциалов еле-
v4
Id
I
Рис. 122. Четырехэлектродная линза с низкими аберрациями (L
ность поля линзы) [260].
- протяжен-
дующие: (V2—£/0)/(V,—Uo) =— 0,75, (Уз-^о)/(^—UQ) =9 и
{Vt—£/0)/(Vi—f/0)=3. При этих значениях имеем CSOx,/fi =
=0,92 и Ccotx/fi = 0,55. Разность потенциалов достигает наи-
наибольшей величины между поддерживающим диском и внешним
цилиндром второго электрода, но эта граница находится очень
далеко от оси и ее можно эффективно изолировать. Зазор меж-
между вторым и третьим электродами 3,25 мм обеспечит надежный
режим работы для входных энергий свыше 5 кэВ. Этот пере-
пересчет означает, что протяженность поля линзы приблизительно
равна L = 6—а=35мм. Тогда CSOIx.=6,0mm и Ссою=3,6мм, что
является чрезвычайно низкими значениями. Для половинного
угла аксептанса 5 мрад и относительного разброса энергий 10~4
радиус диска сферической аберрации равен 7нм, а радиус диска
хроматической аберрации — 5 нм в гауссовой плоскости изоб-
изображения при М = —3,2. Конечно, чтобы получить этот резуль-
результат, пришлось принести в жертву часть рабочей области: те-
теперь рабочая область в пространстве объектов всего лишь
2,5 мм, а в пространстве изображений 8 мм.
458
Электростатические линзы
Это порождает очень важный вопрос, обычный при конст-
конструировании линз. Цель конструирования — удовлетворить
практическим требованиям. Нужно решить, что важнее: низкие
аберрации или большие рабочие области. Достаточно ли ма-
малы размеры источника, чтобы работать при относительно вы-
высоком увеличении, которое обеспечивает минимум |Af|Cso?
Если лимитирующим фактором являются аберрации, вопрос
заключается в том, какая из ошибок — хроматическая или
сферическая — преобладает. Требования к энергии определя-
определяют допустимое отношение максимального напряжения к напря-
напряжению объекта. Соответственно должен быть найден компро-
компромисс между этими противоречивыми характеристиками, причем
для каждого отдельного случая можно использовать различ-
различные коэффициенты добротности.
В нашем случае решение
принимается в пользу (У2—
—U0)/(Vi—и0). Зависимость
от этой величины сферических
и хроматических коэффициен-
коэффициентов добротности, так же как
и зависимость положения фо-
фокуса в пространстве объектов,
измеряемой относительно от-
отверстия в первом электроде,
показана на рис. 123 для
фиксированных отношений
(Уз—t/o)/(Vi—t/o)=9 и (V4—
-Uo)l(Vl-Uo)=3. Видно, ., .„ 0 05 1
что с увеличением отношения (v2-u0)/(v,-u0j
напряжений размеры рабочей Рис. 123. Зависимость аберраций и
области В пространстве объек- положения фокуса в пространстве
ТОВ резко возрастают что В °бъект°в Д-™ четырехэлектродной
„__ ' _ линзы, показанной на рис. 122, от
СВОЮ очередь приводит К отнош'ення потенциалов (V,-t/0)/
уменьшению увеличения. В /(V,-l/0) [260].
результате коэффициент сфе-
сферической аберрации медленно растет, а коэффициент хромати-
хроматической аберрации остается практически неизменным (рисунок
дан только для бесконечного увеличения). Хорошее компро-
компромиссное значение лежит вблизи (V2—Uo)f{V\—Uo) =— 0,3.
Интересно отметить, что полное удаление третьего электро-
электрода почти не меняет сферического коэффициента добротности,
но хроматический коэффициент добротности становится в три
раза хуже. Очевидное преимущество нашей системы состоит в
том, что удается добиться низких значений обеих аберраций
одновременно. Кроме того, четырехэлектродная система всегда
обладает большей гибкостью, чем трехэлектродная.
459
Глава 7
7.6.2. Линзы с пятью и более электродами
Сделаем обзор статей, которые посвящены реальным мно-
многоэлектродным линзам. Простейшей из таких конфигураций яв-
является пятицилиндровая линза, состоящая из пяти трубок
одинаковых диаметров, на которые поданы разные напряже-
напряжения [68, 261]. Число цилиндров может быть больше и их ди-
диаметр может меняться [262]. Электростатическая линза, состоя-
состоящая из пяти плоских электродов с отверстиями, была описана
уже давно [263J. Также было предложено уменьшение сфери-
сферической аберрации с помощью многоэлектродных систем [264,
265]. Однако данные, представленные в этих статьях, настоль-
настолько фрагментарны, что мы даже не будем пытаться их сумми-
суммировать. Необходимо осознать,- что в основном область электро-
электростатических многоэлектродных линз представляет широкое по-
поле для исследований.
Заслуживает внимания одно недавнее интересное усовер-
усовершенствование. Это понятие подвижной электростатической
линзы [255]. Основная идея заключается в использовании мно-
многоэлектродной системы в виде большого числа коротких коак-
коаксиальных колец, помещенных между двумя цилиндрами боль-
большей длины. Меняя соотношение напряжений между кольцами,
можно смоделировать линзу с переменной средней плоскостью.
Таким образом, линза, составленная из неподвижных элемен-
элементов, с помощью перераспределения электрического поля может
эффективно менять свою конфигурацию. Таким способом мож-
можно достигнуть большей гибкости действия линзы: при п неза-
независимых напряжений можно поддерживать постоянным п—1
свойство изображения против л—2 в случае изофокусирующей
линзы. Например, для трехцилиндровой линзы, смоделирован-
смоделированной этим способом, два свойства изображения можно поддер-
поддерживать постоянными при одновременном изменении остальных.
С помощью такой линзы можно выполнять следующие три ос-
основные операции: 1) менять увеличение при постоянных по-
положениях изображения и энергии (реальное изофокусирующее
действие), 2) обеспечивать постоянное положение изображений
двух объектов одновременно при изменении их общей энергии
[266] и 3) обеспечивать постоянное положение изображения
и увеличение при изменяющейся энергии. Этот подход также
можно использовать для синтеза электростатических линз (см.
разд. 9.10) [320 а, 320 Ь].
7.6.3. Сплайновые линзы
Мы уже рассматривали сплайновую модель электростати-
электростатических линз в разд. 7.2.4. Читатель, вероятно, отметил, что, хо-
хотя мы хорошо отзывались об этой модели, как удобной для
460
Электростатические линзы
значительного числа представлений различных распределений
потенциалов, мы еще ее не использовали. Причина состоит в
том, что в этой главе мы имели дело только со стандартными
линзами. Все эти линзы сконструированы на основе простых
конфигураций электродов, анализа их оптических свойств и
вывода соотношений между этими свойствами и параметрами
линзы.
На протяжении всей этой главы мы постоянно призывали
к другому подходу: конструировать электростатические линзы,
основываясь на распределении потенциала. В этом случае па-
параметры, выведенные в начале разд. 7.4, могут адекватно опи-
описать любую электростатическую линзу. Систематическое иссле~
дование электронных и ионных линз возможно с помощью из-
изменения этих основных параметров в процессе построения
сплайновой модели. Это можно сделать достаточно просто, сле-
следуя одной из двух основных стратегий [202]:
1) рассматривая класс сплайнов с фиксированным числом
интервалов,
2) аппроксимируя определенный класс распределений по-
потенциалов (например, распределения с одним максимумом и
двумя точками перегиба, которые соответствуют трехэлектрод-
ным линзам) сплайнами с переменным числом интервалов.
Таким образом, например, можно говорить о трехинтер-
вальных сплайновых линзах, которые подразумевают класс
двух-, трех- и четырехэлектродных линз, сконструированных из
трехинтервальных сплайновых функций. Точно так же, напри-
например, можно описать трехэлектродные однопотенциальные лин-
линзы, сконструированные из шестиинтервальных сплайновых
функций и т. д.
Этот подход также можно использовать для конструирова-
конструирования магнитных линз. Он составляет основу нашей процедуры
синтеза, которая будет описана в гл. 9 вместе с конкретными
примерами электростатических сплайновых линз (разд. 9.9.2).
7.7. Сравнение электростатических линз
разных типов
Попытаемся дать всесторонний обзор различных стандарт-
стандартных ограниченных электростатических линз. В литературе су-
существуют и другие обзоры [36, 84, 267]. Мы сделаем акцент
на набор исчерпывающих характеристик линзы, введенный
Хартингом и Ридом [44].
Как неоднократно отмечалось, сравнивать разные линзы
чрезвычайно трудно вследствие большого числа различных
требований и включенных в рассмотрение параметров. Тем не
461
Глава 7
Таблица It
Сравнение различных электростатических линз для уо=5 мрад,
=10-4 и входной энергии 5 кэВа
No
(^.,-t/0)/(K,-£/0)
/| , ММ
Сою f ММ
С* мм
С» 7,
CLoaa/J\
(\М\Съ„)т,п, мм
(|^1Со)шш ММ
<5г„ , нм
5г„ ^ нм
'i > НМ
(r,//,)xlO7
Ls, мм
с„/4
1
5
17
277
23
16
1,4
1620
62
200
20
54
32
1,91
146
12,1
2
5
6
111
8
19
1,4
770
23
97
8
26
43
0,83
134
9,6
3
5
18
69
14
3,8
0,77
470
49
58
15
21
11,6
2,17
31,8
6,5
4
5
4,6
14
14
3,0
3
61
37
8
10,9
11,1
24,1
5
7
10
30
5
3,0
0,5
*260
х 30
32
7
10,6
10,6
0,5
60
10
6
9
6,5
6,0
3,6
0,92
0,55
51
17,5
6,9
5>
0,33
18
10,8
7
5
14,5
14,9
10,8
1,03
0,76
173
39
46
10
15
10,6
1,67
8,9
6,5
а Параметры этих семи линз, так же как и значения переменных величии, даны
в тексте.
менее сведем все выводы, касающиеся ограниченных электро-
электростатических линз, в табл. 11, где суммированы основные особен-
особенности для следующих семи линз: 1) двухцилиндровая линза
с s/i?=0,2 и i? = 0,5 см; 2) кубическая полиномиальная линза
с L = 0,5cm; 3) трехцилиндровая однопотенциальная линза с
s//? = 0,2, i2/« = l,8 и # = 0,5 см [(V2—Uo)l(Vi—UQ)=b для
всех трех линз]; 4) точно такая же трехцилиндровая линза в
иммерсионном режиме с (V2—U0)/(Vi—Uo) =—0,1 и (V3—U0)l
/(V\—£/0)=5; 5) линза, изображенная на рис. Ill, с (V2—U0)l
/{Vi—U0)=7 и (Уз—U0)/(Vi—U0)=2; 6) линза, изображенная
на рис. 122, с (V2-U0)/(Vi-U0)=-0,75, {VZ-UO)I{VX-UO) =
= 9 и (У4—UQ)/(Vi—U0)=3, и последняя 7) сплайновая линза,
изображенная на рис. 152. Заданы следующие характеристи-
характеристики: {Vmax—Uo)/(Vl — Uo), fi, Csooo, Ccoco, Csooo/fl, Ccoco/fl,
(|M|CSo)min, (\M\Cco)min, 8rsi, 8rci, ri (вычислено из уравнения
E.337) без учета размеров источника и дифракции), r»/fi (аль-
(альтернативный коэффициент добротности, см. разд. 5.7.4), Lg ич
уравнения (9.34), CsOOB/Lg и CCooo/Lg. Все данные в таблице бы-
были вычислены для половинного угла аксептанса 5 мрад, отно-
относительного разброса энергий 10~4 и входной энергии 5 кэВ;
следовательно, все размеры первых четырех линз необходимо
уменьшить в 2 раза. Для этих линз 6rs; и бгс<- вычислялись при
таком увеличении, для которого |М|С*0 минимально. Для ос-
остальных трех линз было выбрано компромиссное значение уве-
увеличения между двумя минимумами. Читатель отсылается к бо-
462
Электростатические линзы
лее подробному обсуждению в соответствующие разделы, так
же как и к его конкретным требованиям, чтобы самому сде-
сделать вывод из этих данных.
7.8. Линзы, погруженные в поле
До сих пор мы рассматривали только электростатические
линзы, с обеих сторон связанные с областями постоянного по-
потенциала. Если это требование не выполняется, необходим со-
совершенно другой подход. Нельзя использовать асимптотические
свойства, а теоремы, выведенные в разд. 4.6.1, в этом случае
не верны. Однако такие линзы имеют важное практическое
значение по крайней мере в двух ситуациях. Первая — дейст-
действие произвольного отверстия в качестве линзы в области высо-
высокого поля (см. разд. 7.3.1.5) и вторая — в электронных и ион-
ионных источниках. Поэтому мы кратко рассмотрим такие линзы
в этом разделе.
7.8.1. Экспоненциальная модель
Первой из этих линз является линза, у которой аксиальное
распределение потенциала описывается формулой
[/(z) = £/@)exp(— z/a), G.115)
где а — коэффициент подобия. В зависимости от того, является
с положительным или отрицательным, оно представляет собой
координату z, при которой потенциал больше или меньше U(Q)
в 2,718 раза.
Распределение потенциала во всем пространстве сразу же
следует из уравнений C.20) или C.99):
«(r,z) = [/(O)exp(-2/a)/o(r/a), G.116)
где /о — функция Бесселя первого рода нулевого порядка. От-
Отсюда легко определить эквипотенциальные поверхности. С их
помощью можно заменить линзу, состоящую из трубки и за-
закрытой сферической крышки, этой моделью, которая фактичес-
фактически использовалась для вычисления оптических свойств такой
линзы [11]. Однако это не имеет большого значения по срав-
сравнению с тем фактом, что для этого распределения потенциалов
не только уравнение параксиальных лучей, но и интегралы
аберраций можно решить аналитически. Следовательно, эта
модель удобна для теоретического анализа определенного
класса электростатических линз, погруженных в поле.
463
Глава 7 ___^_
Решение уравнения параксиальных лучей G.1) для этого
распределения потенциалов элементарно:
r(z) =exp[z/4a] [r0 cosCl'2z/4a) —
— 3-1'Цго — 4ar/0)sinC1/2z/4a)], G.117)
где ro = r(O) и ro' = r'(O). Траектория является гармонической
функцией с экспоненциально изменяющейся амплитудой. Если
потенциал уменьшается (а>0), амплитуда увеличивается и
обратно.
Предположим, что координата объекта го = 0. Тогда коорди-
координаты последовательности изображений даются формулой
Zl = 4-3-^2nna, G.118)
где п — порядковый номер изображения. Отметим, что каждое
последующее изображение появляется при потенциале в 1415
раз выше или ниже, чем предыдущее. Это предполагает, что
экспоненциальная модель может описывать поля даже вблизи
источника.
Предполагалось [173J, что астигматизм такого поля можно
уничтожить выбором соответствующего положения ограничи-
ограничительной диафрагмы. Мы фактически показали [268], что все
не лежащие на оси изотропные аберрации этим способом мож-
можно свести к нулю. Действительно, после длительных вычисле-
вычислений можно получить все коэффициенты аберрации в точном
виде. Из уравнений E.42), E.121), E.194), E.69), E.72),
G.115), G.117) и G.118) имеем коэффициент сферической
аберрации, осевой коэффициент хроматической аберрации, ко-
коэффициент астигматизма и коэффициент комы соответственно:
Cs0=(9a/13)[expB-3-1/2jt) —1], G.119)
Ссо= (За/7) [ехрD-3-1/2я) — 1], G.120)
1)[ехрB.3-'/2я) — 1]/208а,
G.121)
[ехрB.3-'/2я) — 1]/52, G.122)
где
B = —ctgC1'azAl4a) G.123)
и za — осевая координата ограничительной диафрагмы. Отсюда
можно видеть, что при Za\cl=3,3329 кома исчезает. Аналогично
для za/ci, равного либо 2,8304, либо 3,8646, исчезает астигма-
астигматизм. Координаты ограничительной диафрагмы нет в выраже-
выражениях для коэффициентов сферической и хроматической абер-
аберраций, следовательно, их нельзя сделать нулевыми. Коэффи-
Коэффициент кривизны поля аналогичен коэффициенту астигматизма;
464
Электростатические линзы
коэффициент дисторсии содержит кубическое выражение по
В; следовательно, оба их можно сделать нулевыми соответст-
соответствующим выбором положения ограничительной диафрагмы.
Экспоненциальная модель может служить основой для бо-
более общих аналитических моделей, содержащих комбинацию
нескольких экспоненциальных полей.
7.8.2. Диафрагма с круглым отверстием
Одна из наиболее простых электростатических линз состо-
состоит из плоского электрода с круглым отверстием. На электрод
подан потенциал Vo и по крайней мере с одной стороны к нему
примыкает однородное электростатическое поле. Однородное
поле создается параллельными пластинками, находящимися
под разными потенциалами и расположенными на достаточном
расстоянии от пластинки с отверстием. Поле такой линзы было
вычислено в разд. 3.1.2.3. На рис. 21 и 22 показаны эквипо-
эквипотенциальные поверхности, создаваемые такой линзой.
Как мы видели в разд.
4.10.1.1, однородное поле фак-
фактически находится вне линзы.
Однако оно влияет на осевые
составляющие скорости час-
частиц, следовательно, в области
однородного поля траектории
частиц изменятся. Известно,
UU)
рис. 124. Распределение осевого по-
потенциала круглой диафрагмы.
что траектории в этой области
будут параболами, поэтому
их легко рассчитать и найти
реальные кардинальные элементы линзы.
Так как в этом случае теоремы разд. 4.6.1 не действитель-
действительны, главные плоскости не меняются местами, и, как мы очень
скоро увидим, легко сконструировать рассеивающую диафраг-
диафрагму с круглым отверстием. Чтобы показать это, рассмотрим ку-
кусочно-линейную модель из разд. 7.2.2. Предположим, что рас-
распределение потенциала задается двумя однородными полями
(рис. 124) в следующем виде:
( U@)~E,z для z<0,
и(г)~{ U@)-E2z для z>0, <7Л24>
где потенциал £/@) в центре отверстия определяется уравне-
уравнением C.176) через потенциал электрода Vo, радиус отверстия
R и однородные поля £, и Е2. При г=0 из уравнения G.7) по-
получим значение для скачка наклона
G.125)
465
Глава 7
Эта формула справедлива, если длина неоднородной области
вблизи отверстия мала. Тогда действие линзы сконцентрирова-
сконцентрировано вблизи z=0, как и в случае приближения тонкой линзы для
ограниченных линз. Параллельный пучок, идущий из прост-
пространства объектов [r'(—Az)=0j, получит радиальный «удар»,
определяемый уравнением G.125). Мы видим, что наклон,
вызванный отверстием, пропорционален разности двух одно-
однородных полей. Это является причиной того, почему даже при
очень маленьком отверстии действие линзы может быть весьма
сильным.
Знак наклона зависит от знака (Е2—£i). Соответственно
одиночное отверстие действует как собирающая или рассеиваю-
рассеивающая линза. Наклон r'(Az) определяет начальные условия для
параболической траектории в.однородном поле по правую сто-
сторону линзы. Пересечение этой траектории с осью определяет
реальную точку фокуса в пространстве изображений. Кроме
того, можно получить фиктивное «асимптотическое» фокусное
расстояние, предполагая, что главная плоскость совпадает с
плоскостью z=0, и пренебрегая однородным полем Е2. Тогда
для оптической силы имеем
= -г'(Az)/r@) = А{^-Щ\ • <7-126>
Мы должны учитывать тот факт, что эта формула дает хоро-
хорошее приближение даже в этом ограниченном смысле только
для слабой линзы, т. е. если f2*~>R- Если Е2 = 0, то f2* опреде-
определяет реальное (или асимптотическое) фокусное расстояние в
приближении слабой линзы. Естественно, оптическую силу
можно оценить точнее с помощью численного интегрирования
[9].
Практическое значение линзы из диафрагмы с круглым от-
отверстием состоит в том, что она появляется, как только мы
имеем дело с любым отверстием в конечных электродах элект-
электростатических линз, и в качестве составного элемента элект-
электронных и ионных источников.
7.8.3. Катодные линзы, электронные
и ионные источники
Диафрагма с круглым отверстием является простейшей
структурой для получения электронного пучка, если плоский
электрод, создающий электрическое поле слева от отверстия,
является катодом. В этом случае она называется катодной
466
Электростатические линзы
линзой (иммерсионным объективом). Электроны, покидающие
поверхность катода, ускоряются разностью потенциалов между
диафрагмой (анодом) и катодом. При таком расположении
Е\<0, |£2|-C|£i|, и, как следует из уравнения G.126), опти-
оптическая сила отрицательна, т. е. такая катодная линза всегда
дает расходящийся пучок электронов.
Ситуация может быть кардинально улучшена, если помес-
поместить вблизи катода еще одну диафрагму (электрод Венельта)
и подать на нее незначительное отрицательное напряжение
Vc по отношению к катоду (рис. 125). Этот контрольный элект-
электрод служит двум целям. Во-первых, он изменяет распределе-
распределение поля таким образом, что создается фокусирующее поле
вблизи поверхности катода, где электроны движутся относи-
относительно медленно, следовательно, это фокусирующее влияние
будет сильнее, чем дефокусирующее от отверстия анода. В ре-
результате будет формироваться сходящийся пучок. Во-вторых,
меняя напряжение Vc, можно контролировать ток пучка. В са-
самом деле, электроны, покидающие поверхность катода, имеют
максвелловское распределение скоростей. В соответствии с
уравнением E.326) наиболее вероятная энергия электронов
пропорциональна температуре катода, и при Г=2000 К она
приблизительно равна 0,2 эВ. Тогда, если Vc таково (напряже-
(напряжение отсечки), что вблизи оптической оси потенциал на эквипо-
эквипотенциальных поверхностях меньше —0,2 В, доля электронов,
проникающих туда, будет очень мала, и ток пучка практически
будет нулевым. Если теперь слегка повысить потенциал на
контрольном электроде, то все больше электронов будет прохо-
проходить через область его влияния, и ток пучка резко возрастет
вместе с радиальным расширением той части поверхности ка-
катода, на которой электроны могут его покинуть.
Так как разные электроны могут покидать одну и ту же
точку поверхности катода во всевозможных направлениях, их
траектории также будут различны, и они пересекут ось в раз-
разных точках (рис. 125). В результате изображение поверхности
катода будет сформировано после того, как электроны пучка
сформируют кроссовер, положение которого определяется тем,
где большинство электронов пересекут ось (рис. 126). Попереч-
Поперечное сечение этого кроссовера намного меньше, чем катода, но
вследствие упомянутого распределения начальных скоростей
оно никогда не может быть сведено к нулю. В некоторых зон-
доформирующих системах пытаются значительно уменьшить
размеры кроссовера. Различие между катодной линзой и элек-
электронной пушкой или ускоряющей линзой состоит только в том,
что в последних не ставят целью воспроизвести изображение
катода, а добиваются прохождения как можно большего тока
через как можно меньший кроссовер.
467
Глава 7
Так как теперь объект является частью линзы и поле лин-
линзы резко обрывается вблизи катода, в этом случае понятие
кардинальных элементов бесполезно. Кроме того, вследствие
очень больших начальных наклонов траекторий у поверхности
катода нельзя использовать формализм параксиальных лучей.
Вместо этого мы можем сделать предположение, что в непо-
непосредственной близости от катода поле однородно, следователь-
следовательно, траектории всегда представляют собой параболы. На неко-
некотором удалении от катода снова можно использовать уравне-
уравнение параксиальных лучей. Кроме того, ситуация осложняется
тем, что отрицательный пространственный заряд медленных
электронов на катоде создает дополнительный потенциальный
барьер, который в свою очередь ограничивает ток (см. гл. 12).
В результате строгое рассмотрение катодных линз и электрон-
электронных пушек является весьма сложной задачей, даже если ка-
катод имеет плоскую поверхность.
Катод
Рис. 125. Катодная линза.
Рис. 126. Кроссовер.
Однако в большинстве приборов катодная поверхность ис-
искривлена. В простейшем случае он имеет форму сферической
крышки, но в основном используются нитевидные и точечные
катоды. Анализировать такие источники электронов очень
трудно. Даже определение распределения поля — задача чрез-
чрезвычайно сложная вследствие большой напряженности поля
вблизи поверхности катода. Поэтому широко распространена
практика, когда предполагают, что все падение потенциала
происходит вблизи поверхности, и, следовательно, дальше час-
частицы движутся в области, свободной от поля, по прямолиней-
прямолинейным траекториям, исходящим из виртуального источника.
Цель конструирования любой пушки — совместить боль-
большую яркость и низкий разброс энергий. Тогда мы имеем четко
определенный пучок заряженных частиц с высокой плотностью
тока, распространяющийся в малом телесном угле. Следова-
Следовательно, желательно использовать катодные материалы с высо-
высокой плотностью тока на эмитирующей поверхности при малой
468
Электростатические линзы
ее площади. Яркость была рассмотрена в разд. 5.6.8; дополни-
дополнительные сведения о ней читатель может отыскать в литературе
[269J. Самое главное состоит в том, что удельная яркость,
определяемая из уравнения E.329), является инвариантной ве-
величиной: никакая фокусирующая система не может ее улуч-
улучшить. Следовательно, крайне важно иметь источники частиц
высокой яркости.
Следует признать, что общая теория электронной и ионной
оптики оказывает ограниченную помощь разработчикам пушек.
Причина состоит в неоднозначности ситуации, когда объект
является частью самой фокусирующей системы, а совместное
влияние распределения начальных скоростей и пространствен-
пространственного заряда делает фактически невозможным использование
большинства технических приемов, разработанных для обыч-
обычных фокусирующих элементов. Простая теория трехэлектрод-
ных электронных пушек была предложена уже давно [270] и
с тех пор ей было посвящено еще несколько работ, но и по
сей день не существует всесторонней теории или даже хорошо
разработанной методологии конструирования электронных и
ионных источников.
Число электрических и геометрических параметров, которые
влияют на свойства пушки, весьма велико, даже если катод
плоский и пушка имеет только три электрода. Наиболее важ-
важными параметрами являются положение и потенциал контроль-
контрольного электрода, его толщина и радиусы контрольного электро-
электрода и анода. В этом разделе мы рассмотрим только ненасыщен-
ненасыщенные пушки, в которых влиянием распределенного пространст-
пространственного заряда можно пренебречь. Пушки, используемые для
получения пучков с высокой интенсивностью, будут обсуждать-
обсуждаться в разд. 12.1.3.
В трехэлектродных (триодных) пушках изменение напря-
напряжения Vc контрольного электрода служит для фокусировки
пучка и контроля его тока одновременно. Поэтому трудно под-
поддерживать постоянное положение и размеры кроссовера при
изменении тока пучка. Эту трудность можно преодолеть, уве-
увеличив число электродов. Отличительной чертой тетродных и
пентодных пушек является независимость величин, характери-
характеризующих модуляции тока, от положения и размеров кроссовера.
Теорию и проектирование катодных пушек с плоским элект-
электродом и узкими пучками электронов, в основном применяю-
применяющихся в катодных трубках, можно найти в книге X. Мосса,
специально посвященной этой теме [271J.
В электронной микроскопии и зондоформирующих системах
в основном используются два типа эмиттеров. В связи с этим
мы можем различать пушки с термоионной и полевой эмисси-
эмиссией. Сделаем краткий обзор их свойств. Читатель может про-
469
Глава 7
смотреть материалы разд. 5.6.8 о яркости и 5.7.1, 5.7.2 о токе
источника, перед тем как перейти к дальнейшему.
7.8.3.1. Термоионные пушки. Эти пушки работают с термо-
термоионными эмиттерами. В основном используются два типа
эмиттеров: нитевидные вольфрамовые катоды и катоды из гек-
саборида лантана (LaBe).
В нитевидных вольфрамовых пушках вместо плоского ка-
катода стоит V-образная вольфрамовая проволока с прямым по-
подогревом, которая имеет маленькую эмитирующую площадку
на конце эмиттера. Типичная катодная проволока имеет диа-
диаметр —100 мкм и нагревается до ~2900 К. Катод может обес-
обеспечить плотность тока эмиссии приблизительно 5 А/см2, что
эквивалентно удельной яркости ~6А/(В-см2-ср) (см. разд.
5.6.8). Эти катоды обеспечивают однородную яркость в широ-
широком диапазоне направлений эмиссии, но их время жизни огра-
ограничено 10—50 ч. Они дают разброс энергии порядка 3 эВ.
Рабочие характеристики катода из гексаборана лантана на-
намного ниже, поэтому он может работать при более низких тем-
температурах A900 К), что удлиняет его время жизни (сотни или
даже тысячи часов). Такие катоды могут обеспечить плотность
тока эмиссии на порядок выше, чем нитевидные вольфрамовые
катоды, следовательно, их яркость может достигать 100 А/
/(В-см2-ср). Они имеют косвенный подогрев, и радиус их вер-
вершины очень мал A—10 мкм). Разброс энергии всего лишь око-
около 1 эВ. Единственным их недостатком является неоднородное
распределение яркости [272].
В термоионных пушках диаметр кроссовера около 10—
50 мкм, следовательно, чтобы получить маленькое пятно на
мишени, кроссовер необходимо уменьшить. Как мы знаем из
предыдущих разделов этой главы, сделать это нелегко, пото-
потому что при малых увеличениях аберрации обычно очень высо-
высоки. Поэтому уменьшение размеров кроссовера весьма жела-
желательно.
Распределение потенциала в электронных пушках со сфери-
сферическим или точечным катодами исследовалось в литературе
[273, 274] и на основе этого можно было бы установить усло-
условия эмиссии и отсечки. Однако из-за непропорциональности
размеров, включенных в рассмотрение, размеры сетки, исполь-
используемой в области катода, должны отличаться от их размеров
в других областях. Это весьма усложняет процесс итераций,
так как в этих условиях трудно обеспечить непрерывность.
Остроумный подход к этой проблеме предложен в [275] и со-
состоит в том, чтобы добавить тонкую заряженную проволоку,
точечный заряд и заряженный цилиндр к системе, взвешенной
таким образом, чтобы удовлетворялись граничные условия.
470
Электростатические лиизы
Влияние различных параметров на работу этой пушки изу-
изучалось с различных точек зрения [18, 38, 276—282J. Было
установлено, что при заданных пространственном расположе-
расположении контрольного электрода и температуре катода существует
оптимальный потенциал Vc, при котором наблюдается макси-
максимальная яркость. Плотность тока в области кроссовера зависит
от положения контрольного электрода. Само существование
кроссовера зависит от положения вершины катода по отноше-
отношению к контрольному электроду: он существует только тогда,
когда катод расположен на достаточном удалении позади кон-
контрольного электрода. Максимальная передача тока термоион-
термоионных пушек около 0,2%, большая часть тока теряется на элек-
электродах. Краткая сводка зависимости тока пушки, яркости и
других свойств от геометрических и физических параметров да-
дана Свифтом и Никсоном [276].
Вычисление аберраций катодных линз — задача весьма
сложная [9], поэтому обычно формой эмитирующей поверхно-
поверхности пренебрегают и считают, что аберрации пушки равны
аберрациям системы, формирующей пучок с виртуальным ис-
источником.
В большинстве электрон-
электронных пушек кроссовер форми-
формируется на небольшом удале-
удалении от катода. Однако можно
сконструировать пушки, фор-
формирующие кроссовер и на
большом расстоянии от като- , , , ,
A \ Вершина катода ' '
ТелефОКуСНЫе ПуШКИ) с полевой Линаа Мишень
[283]. Они обеспечивают бо- эмиссией
лее высокую передачу тока Рис. 127. Пушка с полевой эмиссией
за счет увеличения размеров
кроссовера.
7.8.3.2. Пушки с полевой эмиссией. В источниках с полевой
эмиссией используется очень острая холодная вершина, за ко-
которой следует электростатическая линза (рис. 127) [222].
Вблизи вершины возникает чрезвычайно высокое электроста-
электростатическое поле, следствием которого является относительно вы-
высокий A мА) ток эмиссии. Электроны как бы эмитируются из
очень маленького виртуального источника позади вершины.
Радиус виртуального источника пропорционален радиусу вер-
вершины и квадратному корню относительного разброса энергии
Для радиуса вершины 0,1 мкм и относительного разброса
энергии 10~4 радиус виртуального источника приблизительно
равен 1 нм. Из-за чрезвычайно малых размеров источника и
высокого тока эмиссии яркость такой пушки может быть в ты-
471
Глава 7
сячу раз выше, чем пушек из LaBe. Факторами, ограничиваю-
ограничивающими работу этой пушки, являются аберрации установленной
за вершиной линзы.
Эта пушка не формирует кроссовер; частицы покидают верши-
вершину в форме расходящегося пучка, который фокусируется лин-
линзой в маленькое пятнышко. Его размеры определяются увели-
увеличением и аберрациями этой линзы в соответствии с уравнением
E.337) (см. разд. 5.7.1). Для нормального функционирования
этой пушки необходим высокий вакуум (не ниже 10~9 торр).
Конструирование пушек с полевой эмиссией намного легче,
чем термоионных пушек. Из-за очень сильного электростати-
электростатического поля у вершины вблизи нее потенциал резко возраста-
возрастает и спадает на расстоянии порядка нескольких радиусов вер-
вершины. Дальше поле практически равно нулю. Если пушка
проектируется так, чтобы поле экранировалось отверстием в
первом электроде (см. разд. 7.3.1.5), то влиянием эмиттера
вообще можно пренебречь. В первом приближении можно
считать, что частицы появляются из области, в которой поле
отсутствует, тогда в этой пушке можно использовать любую
ограниченную линзу с нулевым полем на входе. На рис. 127
показана упрощенная кубическая полиномиальная линза с
единственной модификацией, состоящей в том, что электроды
ограничиваются плоскими поверхностями, перпендикулярными
оптической оси (область в пространстве объекта, в которой по-
поле отсутствует, обеспечивается упомянутым выше распределе-
распределением потенциала без введения дополнительных экранирующих
трубок). В соответствии с этим любая ограниченная электро-
электростатическая линза может быть использована как многоэлект-
многоэлектродная пушечная линза. За последнее время для источников
с полевой эмиссией успешно применялись многоэлектродные
пушечные линзы [228].
Более детальную информацию о пушках с полевой эмиссией
можно найти в литературе [124, 153, 224, 284—288J.
7.8.3.3. Ионные источники. Получение ионных пучков само
по себе является целой наукой. Объем этой книги не позволяет
раскрыть этот вопрос даже поверхностно. Мы ограничимся
простым перечислением основных типов ионных источников,
постоянно используемых на практике.
Электронно-ударная ионизация используется для получения
ионов при имплантации. Энергия ионизации обеспечивается за
счет электронов с высокой энергией. Механизмом ионизации
могут быть упругие столкновения, диссоциация частиц газа и
возбуждение.
Плазмотронные источники основаны на дуговом разряде
472
Электростатические линзы
при относительно высоком давлении. Электроны ускоряются
образующимся при этом процессе ионами газа.
В ионных источниках на жидком металле (электрогидроди-
(электрогидродинамических) электроны испускаются из конуса Тейлора жидко-
жидкого металла, выступающего из капилляра или с вершины ме-
металлического стержня, покрытого жидкой металлической плен-
пленкой. С помощью этих источников можно достигнуть высокой
яркости, но разброс энергий настолько высок (более 10 эВ),
что их практическая ценность ограничена из-за очень большой
хроматической аберрации.
По-видимому, наиболее многообещающими источниками в
настоящее время являются источники с полевой ионизацией.
Поле ионизации возникает, когда тонкий, острый металличес-
металлический наконечник имеет высокий потенциал в газообразной атмо-
атмосфере. Электроны будут туннелировать из атомов газа в ме-
металл, ионизируя газ внутри наконечника. По всей видимости,
ионы испускает виртуальный эмиттер, размеры которого много
меньше, чем размеры самого наконечника. Разброс энергии та-
таких источников весьма мал (~ 1 эВ).
За более детальной информацией о ионных источниках чи-
читатель отсылается к обзорным статьям [289, 290].
На этом мы заканчиваем главу об электростатических лин-
линзах. Дальнейшую информацию можно найти в гл. 9.
Заключение
Эта глава дает полный обзор свойств основных электроста-
электростатических линз. Мы начали с фундаментальных соотношений и
затем перешли к простым моделям линз. Ограниченные элект-
электростатические линзы были разделены на следующие четыре
основные группы: двухэлектродные иммерсионные, однопотен-
циальные, трехэлектродные иммерсионные и многоэлектродные.
В каждой группе были проанализированы различные конкрет-
конкретные конфигурации линз, которые затем сравнивались друг с
другом. Сравнение некоторых представителей каждой группы
дано в разд. 7.7. Последний раздел был посвящен линзам, по-
погруженным в поле, включая краткий обзор электронных и
ионных источников.
Глава 8
МАГНИТНЫЕ ЛИНЗЫ
8.1. Общие свойства и соотношения
Любое аксиально-симметричное поле, порожденное катуш-
катушками с током, содержащими или несодержащими ферромагнит-
ферромагнитные материалы, либо постоянными магнитами, является маг-
магнитной линзой (см. разд. 4.4 и 4.7). Как известно, характер-
характерной особенностью магнитных линз является то, что их оптиче-
оптические свойства зависят от отношения заряд — масса. Постоян-
Постоянные магнитные поля не могут ускорять заряженные частицы,
поэтому в отсутствие электростатических полей магнитные лин-
линзы оставляют энергию частиц неизменной.
Магнитные линзы обычно сложнее в изготовлении, чем
электростатические. Однако число определяющих параметров,
как правило, мало, и поэтому расчет свойств магнитных линз
намного проще, чем электростатических. Они также более под-
подробно рассмотрены в литературе вследствие исключительно
широкого применения в электронной микроскопии. К счастью,
имеется превосходная монография [50J, соответствующая со-
современному уровню теории магнитных линз. Поэтому в этой
главе мы можем ограничиться только рассмотрением их наи-
наиболее важных свойств. Магнитные линзы можно разделить на
две основные категории: длинные линзы с распределенными
полями и короткие линзы с сильно концентрированными поля-
полями. Следует отметить, что в длинных линзах трудно очертить
границы, и даже в случае коротких линз предмет или изобра-
изображение, либо оба вместе, могут находиться в области поля, по-
поэтому в этом случае важны реальные свойства линз.
Действие магнитных линз основано на силе Лоренца (урав-
(уравнение A.14)). Благодаря взаимодействию радиальной состав-
составляющей скорости частицы с продольной компонентой магнит-
магнитной индукции скорость приобретает азимутальную составляю-
составляющую, которая в свою очередь взаимодействует с продольной
компонентой, что приводит к радиальной фокусировке. Мы уже
сталкивались с этим эффектом в случае длинной магнитной
линзы в разд. 4.10.1.3. Радиальная компонента магнитной ин-
индукции взаимодействует с продольной и азимутальной состав-
составляющими скорости, вызывая появление новой азимутальной и
продольной составляющих соответственно. Присутствие указан-
474
Магнитные линзы
ной радиальной компоненты поля необходимо для фокусиров-
фокусировки пучка частиц, изначально параллельного оси.
Так как в этом случае все уравнения становятся пригодны-
пригодными для больших скоростей при простой замене потенциала на
релятивистский потенциал (уравнение B.89)), всегда легко
рассмотреть релятивистский случай, что особенно важно те-
теперь, потому что магнитные линзы в основном используются
для фокусировки электронов, для которых релятивистский пре-
предел составляет около 10 кэВ (см. разд. 2.2.1). С другой сторс-
ны, наличие азимутальной составляющей начальной скорости
или ненулевого поля в начальной точке приводит к необходи-
необходимости использования комплексных переменных для описания
траекторий в магнитных линзах. Поэтому общее уравнение
траекторий теперь принимает вид D.21), и траектория обычно
должна описываться во вращающейся меридиональной плос-
плоскости.
Уравнение параксиальных лучей D.40) или D.50) имеет
вид
где w(z)—комплексная величина, определенная через цилин-
цилиндрические координаты г и а уравнениями D.34) и D.35), элек-
электростатический потенциал U считается постоянным в области
линзы, a Tz — функция, определенная уравнением D.51) при
U = const. Можно использовать непосредственно вещественные
величины, но тогда уравнение D.31) приводит к нелинейному
дифференциальному уравнению:
g- = [Q/8mB (U-Uo) reI] [В2 (z) r-4CVQV], (8.2)
где С определяется уравнением D.26). Азимутальная коорди-
координата определяется уравнением D.27).
Так как функция T(z) пропорциональна квадрату функции
распределения магнитной индукции, изменение направления
тока в магнитных катушках не изменит расположение карди-
кардинальных элементов. Поворот изображения, однако, определяет-
определяется уравнением D.60), которое пропорционально интегралу
B{z), вычисленному между предметом и изображением. Поэто-
Поэтому, если меняется направление токов, направление вращения
тоже изменяется. Если интеграл от В(z) равен нулю, то вра-
вращение отсутствует. Как следствие можно легко сконструиро-
сконструировать магнитные линзы, не приводящие к повороту изображе-
изображения, на основе двух одинаковых коаксиальных катушек, по ко-
475
Глава 8
торым протекают одинаковые токи, но в противоположных на-
направлениях.
Реальные коэффициенты сферической аберрации и аксиаль-
аксиальной хроматической аберрации, связанные с предметом, вычис-
вычисляются из уравнений E.121) и E.194) соответственно при
U=const:
Cso=[4(£/— £/o)rei]-2?{[3Q2fi4(z)/8mo2 —
— Q{U— Uo)
(8.3)
= — [Q/8mo(U— £/o)re.] \B2(z)h2dz. (8.4)
Коэффициент сферической аберрации может быть вычислен
также из уравнения E.132) или в специальном случае из урав-
уравнения E.135).
Асимптотические аберрации даются аналогичными выраже-
выражениями, которые отличаются от этих только пределами интег-
интегрирования (а и Ь вместо zo и zi соответственно) и заменой лу-
луча h на луч Я (см. разд. 5.4). Также можно использовать по-
полиномиальные выражения E.255) — E.264) и E.273) — E.281).
[Заметим, что в указанных выражениях в этом случае Q(z) =
=£(г)=0.]
Концепция эффективной длины более обоснована в случае
магнитных линз, потому что функция T(z) в этом случае про-
пропорциональна квадрату функции распределения магнитной ин-
индукции, и поэтому они достигают максимума в одном и том же
месте. Эффективная длина определяется выражением G.23).
Используя выражение D.159), сразу приходим к соотношению
D.164) в том виде, как оно было использовано в разд. 4.10.2.
Магнитные линзы используются для формирования элект-
электронных зондов или для получения сильно увеличенных изобра-
изображений малых объектов. Их также можно использовать для
анализа по энергиям. Теперь рассмотрим различные типы маг-
магнитных линз. Так как длинные линзы — основа простых моде-
моделей магнитных линз, начнем с них.
8.2. Длинные линзы
Длинные магнитные линзы, как правило, представляют со-
собой аксиально-симметричные магнитные поля без четко очер-
очерченных границ. Поэтому они эквивалентны электростатическим
476
Магнитные линзы
линзам иммерсионного типа (разд. 7.8). Название «длинные
линзы» обусловлено тем, что поле внутри длинного соленоида
является простейшей реализацией этого класса линз. Длин-
Длинные линзы используются в некоторых бета-спектрометрах.
Другое интересное приложение будет представлено в разд.
(8.4.2.4). Двумя основными типами длинных линз являются
однородные магнитные поля и магнитные поля, линейно изме-
изменяющиеся вдоль оптической оси.
8.2.1. Однородные магнитные поля
Формирование изображения однородным магнитным полем,,
созданным длинным соленоидом или постоянным магнитом, об-
обсуждалось в разд. 2.7.2.1 и 4.10.1.3. Мы знаем, что такая линза
образует прямое (неперевернутое и неувеличенное) изображе-
изображение предмета, помещенного в поле. Единственная оставшаяся
проблема — рассчитать ее аберрации.
Подставляя уравнения D.150) и D.154) с го = 0 и го'=\ в-
(8.3) и (8.4), получаем сферический и аксиальный хроматичес-
хроматический коэффициенты аберрации:
(8.5)
где п — порядковый номер изображения, a ko определяется со-
соотношением D.146). Так как k0 пропорционально абсолютной
величине магнитной индукции, аберрации уменьшаются с уве-
увеличением поля. Этот результат аналогичен рассмотренному
нами случаю электростатической линзы. Аберрации возраста-
возрастают с увеличением порядкового номера изображения.
Уравнение (8.5) также может быть получено из простых,
соображений. Параксиальное приближение основано на пред-
предположении, что продольная составляющая скорости vOz равна
самой скорости v0. Если подставить
t)o* = foCosYo«a0(l — To2/2) (8.6)
сначала в B.142), а затем после элементарных тригонометри-
тригонометрических преобразований в E.79), то сразу придем к соотноше-
соотношению (8.5) для коэффициента сферической аберрации. Коэффи-
Коэффициент хроматической аберрации может быть получен, если вы-
выразить приращение скорости через приращение потенциала»,
а затем использовать выражение B.142) вместе с E.197).
8.2.2. Линейные магнитные поля
Пусть функция распределения магнитной индукции изменя-
изменяется линейно вдоль оси г:
(8.7)
477
Глава 8
где Во и Bi — постоянные. Подставляя это аксиальное распре-
распределение в C.45) — C.47), получаем компоненту магнитной ин-
индукции для произвольной точки пространства:
Вг = — Bir/2, Ва = 0, Bz=B0 + BlZ. (8.8)
Это так называемое пиковое магнитное поле.
Подставляя выражение (8.7) в уравнение параксиальных
лучей (8.1), получаем
d2w/dz2+(ko+klzJw = 0, (8.9)
где k0 дается уравнением D.146) и
к,2- QBi2/[8m0 (U — Uo) rei] >0. (8.10)
Начальные условия определяются уравнениями D.43) и
D.148).
Уравнение (8.9) имеет следующее точное решение [185]:
w(z) = (n/2k1)[k0(k0+k1z)/2y'2X
(8.11)
тде
Е=(Ао+*,2J/2*ь (8.12)
/р — функция Бесселя первого рода порядка р, ko>O, и знак
совпадает со знаком заряда частицы.
Можно просто определить отсюда функцию г (z), используя
выражение D.45); а (г) дается соотношениями D.34), D.46),
(8.7) и (8.10):
■a(z) —ao = arctg[Im(ay)/Re(ay)]±
±[ko(z — zo)+k1(z2 — Za2)/2, (8.13)
где положительный знак соответствует теперь отрицательно за-
заряженной частице, и обратно.
Если Во=&о = О, имеем
+ [r'o/,/4 (klZ2/2) + B*,) (го/я) X
ХГ2C/4)/_1/4(М2/2)]2}1/2, (8.14)
■а(г)-ао =
= arctg
г
го+ (г„/я) BкгI'2 Г2 C/4) /_1
±k1(z*-zl)/2, (8.15)
•478
Магнитные линзы
где Г — гамма-функция. Если в таком поле азимутальная сос-
составляющая начальной скорости равна нулю, то все частицы с
различными значениями г о и /V будут двигаться в одной мери-
меридиональной плоскости.
Однородное магнитное поле представляет другой специаль-
специальный случай, соответствующий Bi = &, = 0. Решение уравнения
параксиальных лучей (8.9) тогда дается выражениями D.150)
и D.151).
Оптические свойства первого порядка можно вывести и»
уравнения изображения D.58). Если объект расположен в точ-
точке 2о = 0 (что является приемлемым, так как величина Во мо-
может быть выбрана произвольно), то получаем координату
Zin «-го изображения и соответствующее увеличение Мп в виде
/,/4 (£)//-!/« (Cm) =/i/4(£o72£i) //_i/4 (ko*/2kl)=A = const, (8.16)
где
В случае Bo=ko=0 координата изображения определяется
выражением
и увеличение равно
Мп= (— 1)»2-1/2*11/4ГC/4J1„1/2/_1/4(А122г„/2). (8.20)
При больших значениях аргумента может быть использова-
использована асимптотическая формула G.56). Тогда положение изобра-
изображения и увеличение даются соотношениями
£m = arctg{ [Л cos я/8 — sin л/8]/[cos я/8 — A sin я/8]},
(8.21)
Мп=2Я-1'2 (— I)»(Л„7*1 + k0Zin) ~1/2 X
Xsin (n/8+Cta)//i/4 (Ao2/2*i) (8.22)
соответственно, где постоянная А определяется из (8.16).
Если Bo = ko=O, асимптотическая формула существенно уп-
упрощается
а, (8.23)
2. (8.24)
Мы вычислили различные электронные траектории в этом;
поле [185]. Например, на рис. 128 и 129 приведены соответст-
соответственно функции r(z) и а (г) при &о = О,2 см, &i = 0,l см~2, го =
= 1 см и ао = а'о = О для пяти различных значений параметра
/■</• Мы видим, что первые два изображения формируются при:
479
Глава 8
2а = 5,99 см и 2i2 = 9,24 см. Соответствующее увеличение есть
-Mi =0,578 и М2 = 0,489. Так формируется бесконечный набор
изображений. Каждое последующее изображение меньше, чем
предыдущее. Асимптотические формулы дают достаточно точ-
точные результаты, начиная с четвертого изображения.
Строгое решение для линейного поля будет использовано в
качестве модели магнитной линзы при синтезе новых магнит-
.ных линз (см. разд. 8.3.3. и 9.5).
1,0
0,8
I 0,6
0,4
0,2
о
\\
\
ч?
у
А
(■".
ч
\)
ч
~о,ю
-0,05
0,00
0,05
0,10
G 8 10 12. 14-
z, см
Рис. 128. Функция г (г) для различных значений га' в линейном магнитном по-
поле [185].
0,6
0,4
0,2
0,0
-0,2
/IJ
I.
У
иг
ill
1/r,
\
\\
\\\
'■■ V
ч
А
1
i
1!
Цп
III
i:L
f \
\\
у
I !
1 //
II
i
ii
Г
■\
\
Ц
1
'0
-0,10
-0,05-
D,DD
0,05
0,10
G 8 10 12
Z, CM
14
Рис. 129. Функция a(z) для различных значений г0' в линейном магнитном
поле [185].
480
Магнитные линзы
8.2.3. Длинные линзы с малой сферической
аберрацией
Если мы используем выражение E.135) для вычисления
коэффициента сферической аберрации, то увидим, что первые
два члена подынтегральной функции всегда положительны, а
знак третьего совпадает со знаком —ВВ". Так как в соответ-
соответствии с теоремой Шерцера Cso всегда положительно, можно
надеяться на уменьшение сферической аберрации, если значе-
значение интеграла по ВВ" предельно велико. Это эквивалентно
требованию, чтобы график функции распределения магнитной
индукции был всегда выгнут относительно оси, т. е. имел мини-
минимум для положительных или максимум для отрицательных зна-
значений распределения B(z). Магнитные поля с такими распре-
распределениями эквивалентны длинным линзам и могут быть сфор-
сформированы, например, соответствующим образом распределен-
распределенной неравномерной обмоткой длинного соленоида. Они дейст-
действительно, применялись для уменьшения сферической аберрации
в ^-спектрометрах [291J.
8.3. Модели магнитных линз
Подходы к моделированию линз были изложены в разд. 7.2.
В случае магнитных линз мы находимся в более выгодном по-
положении, чем в случае электростатических линз: существует
несколько хороших аналитических моделей для их описания.
Мы собираемся в деталях обсудить их, особенно колоколооб-
разную модель, но сначала кратко рассмотрим существующие
кусочно-аппроксимационные модели.
8.3.1. Прямоугольная модель
Простейшая возможная модель магнитной линзы представ-
представляет собой эквивалентный соленоид (см. разд. 3.1.4). Идея-за-
Идея-заключается в замене реальной линзы однородным полем конеч-
конечной протяженности, что, разумеется, практически нереализуе-
нереализуемо, но является весьма удобной математической моделью. Это
эквивалентно введению эффективной длины Ьец (см. разд.
4.10.2). Обычно Leif определяется таким образом, что эквива-
эквивалентный соленоид обеспечивает такую же оптическую силу,
какую имела бы рассматриваемая линза в приближении тон-
481
Глава 8
кой линзы (см. D.164)). Для того чтобы иметь одинаковую
оптическую силу, у полей с различной степенью концентрации
должны быть равны интегралы от В2 по оси вдоль поля. По-
Поэтому, если протяженность поля уменьшена в А раз, макси-
максимальная магнитная индукция должна быть умножена на А'".
Так как угол поворота изображения пропорционален интег-
интегралу от В, уменьшение эффективной длины ведет к уменьше-
уменьшению угла поворота изображения (два угла поворота изобра-
изображения относятся друг к другу, как корень квадратный из от-
отношения протяженностей полей). Таким образом, по мере того
как линза делается тоньше (ее поле становится более концент-
концентрированным, эффективная длина уменьшается), угол поворота
изображения, равномерно уменьшается при условии, что опти-
оптическая сила остается неизменной. Для бесконечно тонкой лин-
линзы угол поворота изображения равен нулю [9]. Другой пре-
предельный случай представляет однородное поле, которое явля-
является бесконечно протяженным. Мы видели в разд. 4.10.1.3, что
в этом случае угол поворота изображения равен л.
8.3.2. Модель со ступенчатой функцией
Аксиальное распределение магнитной индукции может быть
аппроксимировано кусочно-постоянным распределением, т. е.
последовательностью однородных полей различной напряжен-
напряженности. Распределение магнитной индукции разбивается на
некоторое количество сегментов, внутри каждого сегмента маг-
магнитная индукция считается постоянной. В пределах каждого
сегмента выражения D.150) и D.151) определяют функции
r(z) и a(z) соответственно. Хотя распределение магнитной ин-
индукции не является непрерывным, требование непрерывности
решения уравнения параксиальных лучей может быть легко
удовлетворено, так как w" остается конечным на стыках сег-
сегментов.
Эта модель не очень точна, но ее большое преимущество
заключается в крайней простоте, сочетаемой с гибкостью (она
может быть использована с любым распределением магнитной
индукции).
8.3.3. Кусочно-линейная модель
Точность аппроксимации может быть повышена с помощью
модели, базирующейся на замене реального распределения
магнитной индукции ломаной линией (набором линейных сег-
сегментов), как это было проделано в разд. 7.2.2 для распределе-
распределения электростатического потенциала. Так как траектория легко
482
Магнитные линзы
вычисляется внутри каждого линейного сегмента (см. разд.
8.2.2), полный анализ выбранной магнитной линзы может быть
выполнен с высокой точностью путем непрерывной сшивки по-
последовательных сегментов [292J. Эта модель была успешно
применена для синтеза магнитных линз [296].
8.3.4. Сплайновая модель
Следующее приближение заключается в использовании
квадратичной функции для аппроксимации распределения маг-
магнитной индукции на каждом сегменте, что эквивалентно кусоч-
кусочно-кубической аппроксимации магнитного скалярного потенци-
потенциала. Хотя в этом случае не существует аналитического реше-
решения уравнения параксиальных лучей, это приближение хорошо
подходит для моделирования магнитных линз (см. разд. 9.10).
8.3.5. Колоколообразная модель Глазера
Аксиальное распределение магнитной индукции в типичной
симметричной короткой магнитной линзе представляет собой
колоколообразную кривую, подобную изображенной на рис. 57
для однокатушечной линзы. На практике для концентрации
поля в малой области используются ферромагнитные материа-
материалы (см. рис. 27). Функция
B(z)=Bm3X/[l+(z/dJ], (8.25)
предложенная Глазером [16], хорошо аппроксимирует акси-
аксиальное распределение магнитной индукции такой линзы вблизи
насыщения (см. разд. 3.1.4). Хотя ненасыщенный режим более
желателен, детальное исследование свойств линзы, описывае-
описываемых этим распределением, остается крайне важным, потому
что оно позволяет получить не только точное решение уравне-
уравнения параксиальных лучей, но и аналитически вычислить коэф-
коэффициенты аберрации. Более того, как оказывается, формула
(8.25) описывает ньютоновское поле (см. разд. 4.6).
Функция распределения поля (8.25) показана на рис. 130
(кривая а). Здесь Бтах — максимальная величина функции
распределения магнитной индукции и d— ее полуширина;
Втах в основном зависит от уровня возбуждения; d определя-
определяется формой полюсных наконечников и степенью насыщения.
Ради простоты рассмотрим случай С = 0, т.е. когда лучи
берут начало либо на оси, либо в области за пределами поля,
с нулевой начальной азимутальной компонентой скорости (см.
уравнение D.26)). Тогда нет необходимости использовать ком-
483
Глава 8
плексную переменную w и оба уравнения (8.1) и (8.2) вместе
с (8.25) дают уравнение параксиальных лучей в виде
, сРг . ft2
[l + (z/dJ]2
r=0.
(8.26)
где величина k2 определена выражением D.159) через отноше-
отношение заряда к массе частицы, максимальную величину магнит-
магнитной индукции и релятивистский потенциал.
Введем новые переменные у и if, как в разд. 7.4.1.3, в ре-
результате имеем
z/d=ctgif, (8.27)
nif. (8.28)
Рис. 130. Модель Глазера (кривая а) и модель Гриве — Ленца (кривая б).
Теперь уравнение (8.26) может быть переписано в виде
г=0. (8.29)
Свойства линзы характеризуются безразмерным парамет-
параметром
a2=\+k2d2. (8.30)
Решение уравнения (8.29) элементарно. Возвращаясь к пе-
переменной г, можно записать
r/d= [С] cos coif+C2 sin coif]/sin if, (8.31)
где сохранена независимая переменная if для удобства по-
последующих вычислений. Постоянные интегрирования С\ и С2
484
Магнитные линзы
определяются из начальных условий. Заметим, что выражение
(8.31) формально похоже на G.101), где со дается соотношени-
соотношением G.100). Существенное различие между ними заключается
в том, что переменная if непосредственно связана с аксиаль-
аксиальной координатой z формулой (8.27), в то время как в случае
выражения G.101) переменная £ связана с г двумя формулами
G.95) и G.102), что значительно усложняет решение.
Подставляя два линейно-независимых решения (8.31) в
уравнение изображения D.58), получаем
to — 1р,-я=ля/и, (8.32)
где ipo и 1р,-я — координаты объекта и n-го изображения соот-
соответственно и п= 1, 2,... — порядковый номер изображения. За-
Заметим, что для Zm>zo имеем tyo>tyin благодаря соотношению
(8.27) (когда переменная z изменяется от —оо до +оо, соот-
соответствующие значения ip изменяются от я до 0). Очевидно, чем
сильнее поле, тем большее количество изображений может
быть сформировано. Так как максимальное значение левой
части выражения (8.32) равно я, максимальное число изобра-
изображений Лтах^со. Поэтому мы имеем одно изображение, если
k2d2<3, два изображения, если k2d2<8, три изображения, если
&2d2<15, и т. д. Увеличение дается выражением G.104).
Рассмотрим теперь главный луч rx(z) (см. рис. 45), чтобы
определить кардинальные элементы. Сначала обратим внима-
внимание на реальные величины. Очевидно, для рассматриваемого
луча Ci = 0 и C2 = r0/a>d, где го — расстояние от оси до парал-
параллельного ей луча, падающего в область поля из бесконечности.
Луч может пересечь ось несколько раз; соответственно в про-
пространстве объектов может образоваться п фокусов. Их коор-
координаты даются выражением
tyFln=nn/<>> или Fm = —F2n=dctgnn/<d. (8.33)
В самом деле, для этого луча ipo = ipF]n и г|зш = О. Тогда уравне-
уравнение (8.32) непосредственно дает (8.33). Координаты ^Fln соот-
соответствуют фокусам в пространстве объектов и поэтому равны
разности координат любой пары сопряженных точек, соответ-
соответствующих предмету и изображению. Соответственно для линз
с заданным параметром со количество фокусов равно количе-
количеству изображений при любом расположении объекта.
Мы можем вычислить п-е реальное фокусное расстояние из
простого соотношения
fn=fi«4*n = rolr'l(Fln). (8.34)
Дифференцируя выражение (8.31) по z, используя постоянные
интегрирования для луча rt(z) и подставляя координаты фо-
фокусов из (8.33), получаем
485
Глава 8
fn={— l)*-W/sinmt/<o. (8.35)
Эта важная формула показывает, что знак фокусного расстоя-
расстояния чередуется для последовательных значений, что естествен-
естественно, если помнить о многократных пересечениях оси лучом. Его
абсолютная величина всегда конечна для любого k2d2>0. Аб-
Абсолютное значение фокусного расстояния имеет минимум, рав-
равный d. Это имеет место для первого фокуса, когда со = 2, т. е.
k2d2 = 3. Тогда из уравнения (8.33) следует, что /ri« = —F2n = 0,
т. е. фокус находится в средней плоскости. Когда и>2, фокусы
инвертируются (как мы видели выше для некоторых сильных
электростатических линз), но оптическая сила уменьшается.
Если мы хотим, чтобы фокусное расстояние, соответствующее
второму фокусу, имело минимальное значение d, то должны
положить и = 4. Соответствующий фокус также расположен в
средней плоскости, это означает, что координата первого фо-
фокуса положительна, т. е. фокусы пересекаются.
Применяя уравнения D.72) и D.73) к реальным величи-
величинам и учитывая (8.33) и (8.35), получаем координаты главной
плоскости
. (8.36)
Для п= 1 имеем
Hi = — H2=dctgn/2a. (8.37)
Как видим, взаимное положение главных плоскостей ин-
инвертируется и расстояние между ними возрастает вместе с па-
параметром возбуждения k2d2. Для максимальной оптической
силы имеем Hi/d=l.
Кардинальные элементы d/f, Fi/d и Hi/d изображены в за-
зависимости от k2d2 на рис. 131 вместе с соответствующими
асимптотическими величинами (см. ниже).
Поворот изображения определяется уравнением D.60). Под-
Подставляя в него D.159), (8.25), (8.30) и (8.32), получаем
ain — ao = ±kd(y>in — i|)o) = +ляЫA +k2d2)~1'2. (8.38)
где верхний и нижний знаки относятся к положительно и от-
отрицательно заряженным частицам соответственно (k считается
положительным). Мы видим, что поворот изображения зависит
только от безразмерного параметра kd и не зависит от поло-
положения объекта. Для больших значений kd абсолютная величи-
величина угла поворота приближается к пп.
Уравнение (8.38) определяет физический смысл переменной
■ф. Это угловая координата, изменение которой между предме-
предметом и изображением прямо пропорционально повороту изобра-
изображения.
486
Магнитные линзы
Расстояние до объекта рп и расстояние до изображения qn
связаны с координатами объекта и изображения zo и zia выра-
выражениями:
qn — f2n = zin — F2n, pn — f\n=Fin — zo. (8.39)
Эти соотношения следуют из рис. 46, если использовать реаль-
реальные величины. Подставляя соответствующие значения для этих
величии, мы можем просто доказать, что формулы D.77) —
D.79) в этом случае пригодны для реальных величин. Это зна-
значит, что распределение магнитной индукции (8.25) представля-
представляет ньютоновское поле (см. разд. 4.6). Поэтому реальные кар-
Рис. 131. Реальные и асимптотические оптические силы, координаты фокусов
в пространстве объектов и расположение главных плоскостей как функции
безразмерного параметра возбуждения k2d2 для колоколообразиой модели.
Все величины отнесены к полуширине d. Реальные величины отнесены к пер-
первому фокусу.
динальные элементы не зависят от положения объекта и могут
служить для описания объективных свойств, так же как асимп-
асимптотические кардинальные элементы могут быть использованы
для описания проекционных свойств. Это одно из наиболее
важных свойств модели Глазера.
Теперь обсудим асимптотические свойства. Фокусное рас-
расстояние дается уравнением D.72), т. е. в (8.34) производная
rx(z) должна быть вычислена на —оо. Дифференцируя (8.31)
по z, используя соответствующие значения для постоянных ин-
интегрирования и подставляя в уравнение (8.34), получаем
/* = — cod/sin ясо.
(8.40)
487
Глава 8
Так как <в>1, sin(ro»)>0 и фокусное расстояние положитель-
положительно для малых возбуждений. С ростом со фокусное расстояние
осциллирует с возрастающей амплитудой между положитель-
положительными и отрицательными значениями. Его абсолютная величина
не может быть меньше d, так же как для реальных фокусных
расстояний. По определению в этом случае мы имеем только
одно фокусное расстояние, но траектория такая же, как и рань-
раньше, так что она может пересечь ось несколько раз. Бесконечное
фокусное расстояние (телескопическое условие) возникает вся-
всякий раз, когда и = и, т. е. для k2d2=3, 8, 15 и т. д.
Положение асимптотического фокуса можно вычислить,
следуя процедуре, аналогичной изложенной в разд. 7.4.1.3.
В результате
Л*,=— /У = — adctgna. (8.41)
Положение главной плоскости может быть вычислено из урав-
уравнения D.72); dff*, Fi*fd и H\*\d изображены в зависимости от
безразмерного параметра на рис. 131 вместе с реальными ве-
величинами.
Интегрируя уравнение D.60) от —оо до +оо, получаем
асимптотический угол поворота изображения в виде
(а, — а.о)* = +nkd, (8.42)
где выбор знака такой же, как в уравнении (8.38).
В приближении тонкой линзы уравнения D.117), D.159),
(8.1) и (8.25) дают
(8.43)
Мы приходим к такому же результату из уравнений (8.35) и
(8.40), используя первые члены соответствующего разложения
в ряд Тейлора. Интересно заметить, что для малых возбужде-
возбуждений реальная и асимптотическая оптические силы совпадают
друг с другом до членов третьего порядка разложения в ряд
Тейлора. Затем реальные значения становятся больше асимп-
асимптотических. Выражение для тонкой линзы является весьма гру-
грубым приближением. Оно зависит от k^d2 линейно, т. е. соответ-
соответствующая зависимость должна быть представлена прямой ли-
линией, касательной в начале системы координат к кривым,
представляющим реальную и асимптотическую оптические си-
силы на рис. 131. Естественно, это приводит к завышенным зна-
значениям. Относительная ошибка превышает 16% уже для k2d2 =
=0,2, что соответствует очень слабой линзе (типичное значение
для объективной линзы сильного электронного микроскопа
составляет около k2d2=2). Поэтому приближение тонкой линзы
может быть использовано только при крайне низких возбужде-
возбуждениях.
488
Магнитные линзы
Эффективная длина может быть введена в соответствии
с соотношением D.164). Подставляя в него (8.43), получаем
(8.44)
поэтому полуширина d — прямая мера степени концентрации
поля.
Теперь сосредоточимся на вычислении аберраций, начиная
с коэффициента сферической аберрации. Сначала необходимо
найти луч h(z), удовлетворяющий начальным условиям уравне-
уравнения E.42). Исходя из выполнения этих условий, используя
(8.31) и ее производную по z, определяем коэффициенты Ci и
С2. В результате
sini|)osini|). (8.45)
Распределение магнитной индукции (8.25) может быть записа-
записано с учетом (8.27):
В (z)=Bmax sin2 Ц. (8.46)
Дифференцируя это выражение дважды по z, подготовим всю
необходимую информацию для вычисления коэффициента сфе-
сферической аберрации. Подставляя эти выражения в E.135) и
используя уравнения D.159) и (8.30), получаем
- 3> Sln"
X sin4 [о (г|>—ф0)] dy. (8.47)
Преобразуем этот интеграл посредством некоторых тригоно-
тригонометрических соотношений и затем выполним интегрирование.
В результате [36]
♦/
[2 Dk?d2 — 3) sin2 яр + 7] sin4 [и (г|з — г|зо)] Л|з =
3A + кЩ (t,-- to)/2-(l + kWI'2 sin [2a ($i-%
+ A + k4*yi* sin [4co (ф,- - фо)]/8 + у\кЧг — 3) x
x{-C/16)sin2%+
—sin 2^ cos [2w (if, —
[A + kWyf/APcF] cos 2^/ sin [2ш (г|з,—ф0)]
+ sin 2% cos [4co (о|з,- — ipo)]/16 C + 4^2d2) —
" 8 (з"+ W) cos 2^' sin ^4@ (^ *
Для вычисления реального коэффициента необходимо про-
провести интегрирование от объекта до изображения. Координаты
489
Глава 8
изображения даются выражением (8.32). Подставляя это вы-
выражение для первого изображения {«=1) в (8.48), окончатель-
окончательно получаем
Cso/d= {nk2d*(l+k42)-w/4 —
— {4k2d2 — 3)/4 Dk2d2+3) sin [я A + k2d2) ~1'2] X
X cos [2i|>o — л A + k2d2) -1'2] }/sin4 yo, (8.49)
откуда можно вернуться к координате объекта го, используя
(8.27).
Так как случай реального изображения обычно соответству-
соответствует большому увеличению (объект очень близок к фокусу), важ-
важно знать коэффициент сферической аберрации, связанный с
объектом при бесконечно большом увеличении.
В этом случае tyo=tyF1, определяемому уравнением (8.33).
Подставляя соответствующую величину при п=\ в (8.49), по-
получаем
-3/2/4 —
— Dk2d2/3)/[8{4k2d2+3)]X
(8.50)
Зависимость этой величины от безразмерного параметра
возбуждения k2d2 показана на рис. 132 вместе с CCo°o/d. Для
очень малого параметра возбуждения уравнение (8.50) дает
CsoJd —► 2/n3k*d*, (8.51)
это означает, что для очень слабых линз коэффициент сфериче-
сферической аберрации крайне велик и значительно уменьшается с
ростом возбуждения. Мы уже сталкивались с аналогичной си-
ситуацией для электростатических линз. При очень больших
k2d% имеем
kd/6n, (8.52)
ка-*" во
т. е. коэффициент сферической аберрации медленно растет с
возбуждением. Поэтому он должен иметь минимум при некото-
некотором значении параметра возбуждения. Этот минимум составля-
составляет (CSOoo/rf)min = 0,252 и достигается при fe2d2~7, где зависи-
зависимость очень пологая (см. рис. 132). Поэтому можно получить
величину, близкую к минимуму, в широком интервале возбуж-
возбуждений. Однако для встречающихся на практике значений 1<
<&2d2<2 значение CSOx/d намного выше: оно изменяется меж-
между 0,736 и 0,370. Мы показали ранее, что минимальное фокус-
фокусное расстояние равно d и имеет место при k2d2 = 2>. В этом слу-
случае Csooo/d = CSo<x>/f=0,295, что мало по сравнению со случаем
490
Магнитные линзы
электростатических линз. (Заметим однако, что в электроста-
электростатическом случае мы имели дело только с асимптотическими ко-
коэффициентами.)
Сравнивая рис. 131 и рис. 132, видим, что как фокусное
расстояние, так и коэффициент сферической аберрации прояв-
проявляют одинаковые зависимости как функции параметра k2d2.
Это согласуется с утверждением, сделанным в разд. 5.7.4.
Фокусное расстояние определяется соотношением (8.35).
Поэтому мы получим выражение для Cso<x>/f, если просто заме-
заменим четвертую степень синуса на третью в выражении (8.50).
Тогда для очень малых параметров возбуждения имеем
CsoJf^z-I/*1**4, (8.53,
т. е. для очень слабых линз сферический коэффициент доброт-
добротности ведет себя так же, как и аберрационный коэффициент
Для очень больших k2d2 имеем постоянный предел
ccom/d
ю
который дает минимальное значение сферического коэффициен-
коэффициента добротности для данной модели.
Для аксиального распреде- 18
ления магнитной индукции '
(8.25) все геометрические
аберрационные коэффициенты '
могут быть вычислены в зам- с
кнутой форме. Можно пока- 02 ~_
зать аналитически [16], что °
все изотропные внеосевые Рис 132. Реальный сферический и ак-
аберрации могут быть устра- сиальный хроматический коэффициен-
нены подходящим расположе- ты аберраций для колоколообразиой
иием ограничивающей аперту- несешыеС™3по1^нрте™*™
ры. Асимптотические аберра- ции безразмерного параметра
ционные коэффициенты также
могут быть вычислены аналитически [293, 294]. Вслед-
Вследствие того что поле является ньютоновским, полиномиальные
выражения, аналогичные представленным в разд. 5.4.1, могут
быть записаны не только для асимптотических коэффициентов,
но и для реальных [295J.
Вычислим теперь реальный аксиальный коэффициент хро-
хроматической аберрации. Для этого воспользуемся выражением
E.194). Подставляя сюда D.159), (8.27), (8.30), (8.32), (8.45)
и (8.46) и интегрируя по координатам от объекта до изображе-
изображения, получаем следующий простой результат:
Ccold=nk2d2/[2(l + k2d2K'2 sin2 to]. (8.55)
491
Глава 8
Коэффициент хроматической аберрации, очевидно, имеет
минимум, когда т\>0 = л/2, т. е. го=0 (объект расположен в сред-
средней плоскости линзы) для любого фиксированного k2d2. Коэф-
Коэффициент ССо равен нулю как для нулевого, так и для бесконеч-
бесконечно большого значения параметра возбуждения. Он имеет мак-
максимум, когда k2d2 — 2. Максимум Ссо при го = 0 составляет
33/206
При бесконечном увеличении следует использовать собтно
шение (8.33). При этом имеем
Clfi— тг£>2Л2/ГО/1 с Ь%Н2\ 3/2 cin2.rr/n_i_fe2/-72\l/21 /С KR\
сооо/и. — Л«- и I |^ ^ 1 -р К и. J ' Sin Лу \ 1 ~г гс 61 ) ' I. IO.OD1
Зависимость этой величины от безразмерного параметра
возбуждения k2d2 показана на рис. 132 вместе с Cso<x>/d. Для
очень малых параметров возбуждения имеем
■2/nk2d2. (8.57)
Зависимость аналогична случаю сферической аберрации, одна-
однако изменения с ростом параметра возбуждения выражены не
так резко. Для очень больших k2d2 имеем
CC0Jd—^kdl2n, (8.58)
ка —> оо
что вновь аналогично зависимости для коэффициента сферичес-
сферической аберрации, хотя крутизна здесь выше. Минимум состав-
составляет (CCOCx>/d)min = 0,577 и достигается при k2d2^4 (см. рис. 132).
Для практически приемлемых значений l<&2d2<2, величина
Ccooo/d изменяется от 0,877 до 0,642. Для минимального фокус-
фокусного расстояния, которое равно d и достигается при k2d2 = 3,
имеем Ccooo/d =CCo°°/f = 0,589.
Так как фокусное расстояние определено выражением
(8.35), получаем выражение для Cco<x,/f, если просто заменим
вторую степень синуса на первую в соотношении (8.56). Тогда
для очень малых параметров возбуждения получаем постоян-
постоянный предел
С_//— 1, (8.59)
а для очень больших k2d2 — другой постоянный предел
что, очевидно, является минимальным значением хроматичес-
хроматического коэффициента добротности для этой модели. Верхний пре-
предел хроматической аберрации E.220) дает такое же значение,
как (8.59). Это также согласуется с утверждением, которое мы
сделали в разд. 5.4.2.2, что коэффициент хроматической абер-
492
Магнитные линзы
рации тонких магнитных линз равен верхнему пределу хрома-
хроматической аберрации.
Колоколообразная модель может быть также использована
для описания асимметричных линз. В этом случае можно счи-
считать, что распределение магнитной индукции состоит из двух
частей различной полуширины. Можно показать [16], что та-
такая асимметрия выгодна: коэффициенты как сферической, так
и хроматической аберрации уменьшаются, если полуширина в
пространстве объектов больше, чем в пространстве изображе-
изображений.
8.3.5.1. Обобщение колоколообразной модели. Можно обоб-
обобщить модель Глазера, используя аксиальное распределение
магнитной индукции [16]:
(8.61)
где m — любое число от нуля до бесконечности и I — пара-
параметр, имеющий размерность длины. Полуширина d связана с
этим параметром соотношением
d=l{2Um— II'2. (8.62)
Если /ге=0, уравнение (8.61) дает однородное поле и случай
соответствует колоколообразной модели (8.25). Поле одиноч-
одиночной петли с током C.255) соответствует параметрам пг = 3/2 и
1 = а. При ГП-+ОО получаем в пределе гауссово распределение
В (z) = Bmax exp [- (z/d) Чп 2]. (8.63)
Очевидно, гп>\ соответствует большей концентрации поля,
чем модель Глазера. Формула (8.63) дает распределение, близ-
близкое к случаю ненасыщенной линзы, но, к сожалению, при этом
уравнение параксиальных лучей нельзя точно проинтегриро-
проинтегрировать. В любом случае, даже если необходимы численные вы-
вычисления, уравнение (8.61) дает ценную модель для сравне-
сравнения магнитных линз с разной степенью концентрации поля.
8.3.6. Модель Гриве — Ленца
Для описания ненасыщенных линз было предложено [18,
187] аксиальное распределение магнитной индукции в виде
(8.64)
Это более концентрированное распределение, чем то, которое
дается функцией (8.25) (см. кривую б, рис. 130). Параметр б
соответствует аксиальному расстоянию от центра линзы, на
493
Глава 8
котором магнитная индукция уменьшается в ch 1 = 1,543 раза
по сравнению с Вщах.. Полуширина d равна
d = 6arcch 2 = 1,3176. (8.65)
Уравнение параксиальных лучей (8.2) может быть записано
с учетом D.159) и (8.64) для С = 0 в виде
d2r/dz2 + k2r/ch2z/8 = 0. (8.66)
Вводя новую переменную
ы=—thz/6, (8.67)
получаем отсюда, что
A — tP)<Pr/du2 — 2udr/du+k42r=0. (8.68)
Если теперь обозначить
£262=v(v+l), (8.69)
то решение уравнения (8.68) в исходных координатах есть
г (z) = C,PV [— th z/б + C2QV (— th г/6), (8.70)
где Pv и Qv — полиномы Лежандра 1-го и 2-го рода соответст-
соответственно. Оно имеет простое полиномиальное выражение, если
v — целое число. Если v можно записать в форме v=n-f'/2,
где п — целое число, то Рх и Qv могут быть выражены как пол-
полные эллиптические интегралы.
Траектории могут пересекать ось несколько раз, и соответ-
соответственно могут образоваться множественные изображения, как
в случае модели Глазера. В приближении тонкой линзы полу-
получаем из D.117), D.159), (8.1) и (8.64)
F//)шп = 2£262. (8.71)
Используя (8.65), это выражение можно переписать в виде
(rf/f)thin = l,519fc2d2. (8.72)
Сравнивая это уравнение с (8.43), видим, что оптическая сила
в приближении тонкой линзы несколько меньше, чем для мо-
модели Глазера. Эффективная длина дается D.164) и (8.72)
Letf = l,519rf. (8.73)
Реальные коэффициенты сферической и аксиальной хрома-
хроматической аберраций для этой модели в случае бесконечного
увеличения, связанные с объектом и отнесенные к параметру
6, представлены на рис. 133 как функции &262 [187]. Мы ви-
видим, что поведение кривых сходно с рис. 132 для модели Гла-
Глазера, численные значения, однако, различны. Например, если
£262 = 1 (k2d2=l,73), имеем CSOOc/rf^0,6 и CcoJci~0,8 против
494
Магнитные линзы
Рис. 133. Реальный сферический и ак-
аксиальный хроматический коэффициен-
коэффициенты аберраций для модели Гриве —
Ленца при бесконечном увеличении,
связанные с объектом и отнесенные
к параметру б, как функции безраз-
безразмерного параметра й^2 [187].
1000
100
10
1
0,1
0,01 0,1 1 10 100
0,4 и 0,7 соответственно для модели Глазера. Другое различие
в том, что для очень больших безразмерных параметров k282
как Csooo/б, так и Ссох/8 стремятся к постоянным значениям
('Д и '/2 соответственно).
8.3.7. Другие модели
Можно также решить уравнение параксиальных лучей в
замкнутой форме для некоторых других аксиальных распреде-
распределений магнитной индукции. Для экспоненциального распреде-
распределения
fiB)=Bmaxexp(— г/а) (8.74)
решение может быть выражено через функции Бесселя [16J.
Для эллиптического распределения
B(z)=Bmax[l-(z(q-lJy2 (8.75)
решение может быть записано через параболические цилиндри-
цилиндрические функции [186J. В вышеприведенных выражениях а и
q — постоянные с размерностью длины.
В случае гиперболического распределения, т. е. если его
можно записать в виде
B(z)/BmtiX=A/(z — D), (8.76)
где Л и D — постоянные, и точка z=D исключена, решение
есть [286]
r{z) = (г — £>)>/2{С, cos [(Л2 — 1/4) ln(l — z/D)] +
+ С2 sin[ (Л2 — 1/4) '/2 In A — z/D) ]}. (8.77)
n-е изображение имеет координату
zin=D{\ — ехр[ип(Л2 — 1/4)-'/2]}, (8.78)
(8.79)
495
а увеличение составляет
| М | = ехр [яп DЛ2 — 1) -1'2].
Глава 8
Строгое рассмотрение (включая аберрации) возможно в
случае специального класса распределений магнитной индук-
индукции, для которого уравнение параксиальных лучей может быть
решено через гипергеометрические функции [193]. Также воз-
возможно исследовать вопрос существования классов функций,
для которых решение уравнения параксиальных лучей может
быть дано в замкнутой форме.
8.4. Короткие линзы
8.4.1. Традиционные линзы
Короткие магнитные линзы—это аксиально-симметричные
магнитные поля, сконцентрированные в относительно коротком
интервале вдоль оси (в сравнении с радиальными размерами
возбуждающей катушки и/или магнитной системы). Простей-
Простейшая короткая магнитная линза состоит из одиночной петли с
током. Мы уже обсудили ее свойства в разд. 4.10.2.
Обсуждение колоколообразной модели Глазера показало,
что это распределение поля, медленно спадающее при больших
значениях аксиальной координаты z, не может дать фокусное
расстояние, меньшее чем полуширина поля d. Для достижения
более высокой оптической силы распределение магнитной ин-
индукции должно быть сильнее концентрировано. Тогда сила
линзы будет ограничивать траектории и обеспечит очень корот-
короткое фокусное расстояние, так как аксиальная протяженность
поля слишком мала, чтобы сформировать множественные изо-
изображения. Этого можно достичь использованием ненасыщен-
ненасыщенных магнитных материалов, которые концентрируют поле в за-
зазоре между полюсами (см. рис. 27). Как мы видели в разд.
3.1.4 для симметричных коротких линз, аксиальное распределе-
распределение магнитной индукции в основном зависит только от одного
параметра — отношения зазор —диаметр s/D. Чтобы избе-
избежать насыщения, полюсные наконечники обычно сужают
(рис. 28), и угол раствора конуса оптимизируется для каждого
заданного значения s/D, но при общем анализе мы вправе счи-
считать, что s/D — наиболее важный параметр. Это упрощает кон-
конструирование магнитных линз по сравнению с электростатичес-
электростатическими [297J.
Здесь мы предложим читателю вспомнить материал гл. 3,
особенно разд. 3.1.4 и 3.1.5. Оптические свойства магнитных
линз невозможно изучать без четкого представления их полей.
В разд. 8.3.5 мы установили, что свойства колоколообразной
модели зависят от безразмерного параметра kd. Для того что-
чтобы вычислить этот параметр для используемой на практике
линзы, мы должны знать величину BmSLXd, являющуюся функ-
496
Магнитные линзы
цией параметра линзы s/D и степени насыщения. Введя обоб-
обобщенную колоколообразную модель (разд. 8.3.5.1), мы предпола-
предполагаем, что аксиальное распределение магнитной индукции мо-
может быть представлено в виде (8.61), т. е. fimax — функция
возбуждения, а знаменатель является функцией только геомет-
геометрии линзы. Это справедливо только для далеких от насыщения.
линз, а для сильных линз вблизи насыщения все параметры
являются функциями возбуждения. (Единственное исключе-
исключение— если линза является «сильной» за счет использования
частиц с низкими энергиями. Тогда значения fimax могут быть
малы.)
Чтобы охарактеризовать различные виды линз, удобно ввес-
ввести безразмерный форм-фактор [16J
t=NI/Hmd, (8.80)
где N1 — число ампер-витков в катушке; d — полуширина акси-
аксиального распределения магнитной индукции и
Ят = Втах/ц0 (8.81)
есть интенсивность поля в се-
середине зазора. Зависимость
форм-фактора от параметра
s/D и степени насыщения
можно определить с помощью
измерений, либо численных , и, ■, -т^дт^,,, - •- ■
расчетов. Зависимость акси- ooos 1,5 2,5 з,5 2z/D
ального распределения маг-
магнитной индукции ОТ парамет- Рис. 134. Аксиальное распределение
pa s/D для ненасыщенных ко- магнитной индукции в ненасыщенных
ротких линз показана на рис. К0Р°Т™х ™нзах для различных зна-
,,. гоот /-л чении параметра s/D 183].
134 [83]. Очевидно, что для v v ' L .
заданного значения Втлх, чем
меньше s/D, тем сильнее сконцентрировано поле. Для очень
малых зазоров полуширина не стремится к нулю, но для боль-
больших зазоров полуширина является линейной функцией s/D.
Хотя число ампер-витков, необходимое для получения данного
fimax, также является функцией s/D и поэтому зависимость
форм-фактора от s/D несколько сложнее, оказывается [298J,
что форм-фактор все же монотонно уменьшается по мере роста
s/D. Для пренебрежимо малых значений s/D имеем £«2,3, для
s/D = 3 имеем £~2,0. Похоже поэтому, что чем больше сконцен-
сконцентрировано поле, тем больше форм-фактор. Однако в случае
насыщения по мере роста N1 величина Втях остается постоян-
постоянной, несмотря на рост d, и в результате форм-фактор возраста-
возрастает. Типичное значение форм-фактора выше 3. Это может быть
показано на примере обобщенной колоколообразной модели.
497
Глава 8
Из C.233), (8.61), (8.62) и (8.80) имеем после интегриро-
интегрирования
£=[я/B»"» — 1)]'/2Г(т — 1/2)/Г (т), (8.82)
где Г — гамма-функция. Подставляя т=\ и 3/г для модели
Глазера и одновитковой линзы соответственно, получаем £ = п
и £—2,61 соответственно. Переход к пределу m-м» дает £ =
= 2,13 для гауссова распределения. Отсюда ясно, что обобщен-
обобщенная колоколообразная модель может быть применена подгон-
подгонкой параметра т относительно форм-фактора для данной при-
применяемой на практике линзы. Однако, если форм-фактор мень-
меньше 2,13, такая подгонка невозможна.
Для модели Гриве — Ленца соотношения C.233), (8.64),
(8.65) и (8.80) дают форм-фактор 2,39, что очень близко к
случаю ненасыщенной линзы.
Так как реальные линзы не описываются ньютоновскими по-
полями, реальные кардинальные элементы не могут быть исполь-
использованы для определения свойств первого порядка при любом
увеличении. Значения реальных фокусных расстояний, однако,
представляют интерес, так как характеризуют оптическую силу
коротких магнитных линз. Реальные фокусные расстояния
симметричных ненасыщенных коротких линз представлены на
рис. 135 [83] как функции безразмерного параметра k2R2(R =
=D/2) для различных значений s/D. Как обычно, оптическая
сила увеличивается с ростом возбуждения. При малых возбуж-
возбуждениях фокусное расстояние увеличивается с уменьшением за-
зазора, но при умеренных значениях параметра возбуждения кри-
кривые сближаются, а при больших значениях возбуждения раз-
различие между фокусными расстояниями для различных значе-
значений s/D очень мало. При бесконечном возбуждении фокусное
расстояние достигает минимального значения около 0,2 D. Как
следует из рис. 134, если 0,2^s/D^2, то d/R изменяется в пре-
пределах от 0,65 до 2. Рис. 135 демонстрирует, что для k2R2=\
имеем f/R^\. Это означает, что f/d изменяется от 1,5 до 0,5 с
увеличением отношения зазор — диаметр. Соответствующие
значения для модели Глазера есть 2,1 и 1,1. Это существенный
выигрыш в оптической силе, особенно для больших зазоров,
когда форм-фактор наименьший.
Рис. 136 показывает соответствующие зависимости для
асимптотического фокусного расстояния. Для малых возбужде-
возбуждений реальные и асимптотические величины одинаковы, поэто-
поэтому в начале кривых фокусное расстояние резко уменьшается
с ростом возбуждения. При умеренных возбуждениях, однако,
асимптотическое фокусное расстояние достигает минимума,
после которого нарастает при дальнейшем увеличении возбуж-
возбуждения. Минимальное значение тем больше, чем больше зазор,
и достигается при наименьших возбуждениях. Если заново
498
Магнитные линзы
вычислить минимальные фокусные расстояния, чтобы отнести
их к полуширине d вместо R, то обнаружим, что соответствую-
соответствующие величины очень близки друг к другу в промежутке 1 и.
1,2, т. е. немного больше, чем для колоколообразной модели.
Они лежат в интервале l,06<&2d2<l,45. При больших возбуж-
возбуждениях характер зависимости резко меняется на обратный:
здесь наибольшая оптическая сила имеет место при наимень-
наименьших s/D.
Реальные коэффициенты сферической аберрации, связанные
с объектом при бесконечном увеличении и отнесенные к /?„
изображены на рис. 137 как функции параметра возбуждения
k2R2 для различных s/D. Для малых возбуждений сферическая
f/R
100
ю
1
0,1
-s/D = 0,2
-0,6
2,0
0,01 0,1 1 2 510
100 1000
Рис. 135. Реальные фокусные рас-
расстояния ненасыщенных коротких линз
в зависимости от параметра возбуж-
возбуждения kP-R2 для различных значений
s/D. Фокусное расстояние отнесено к
радиусу канала R = D/2 [83].
5 10
Рис. 136. Асимптотические фокусные
расстояния ненасыщенных коротких
линз в зависимости от параметра
возбуждения k2R2 для различных зна-
значений s/D. Фокусное расстояние от-
отнесено к радиусу канала R=D/2 [83].
аберрация велика. Она резко уменьшается с ростом возбужде-
возбуждения. Для больших зазоров аберрация намного ниже, чем для
малых. Кривые пересекаются приблизительно при k2R2 = 4. При
больших возбуждениях сферическая аберрация сильно умень-
уменьшается, особенно для малых зазоров. Сравнение с моделью
Глазера показывает, что теперь минимум отсутствует. Для
&2d2=l имеем 0,83<Csoao/d< 1,1 при 0,2<s/D<2. Соответству-
Соответствующее значение для модели Глазера Cso<x>/d = 0,736. Сферический
коэффициент добротности приближается к наилучшему значе-
значению (CSOoo/f)mln = 0,33 при бесконечном возбуждении. Это вдвое
больше соответствующего предельного значения 7в для модели
Глазера [формула (8.54I. Для k2d2=l имеем 0,73<Cso<x>/f<l,l
для данного интервала отношений зазор — диаметр.
Рис. 138 демонстрирует реальный аксиальный коэффициент
499
Глава 8 __
хроматической аберрации, связанный с объектом при бесконеч-
бесконечном увеличении и отнесенный к R, как функции параметра воз-
возбуждения k2R2 для различных значений s/D. Поведение этой
функции аналогично зависимости для сферической аберрации.
Для малых возбуждений хроматическая аберрация относитель-
относительно велика. Она резко уменьшается с ростом возбуждения. Для
больших зазоров аберрация ниже, чем для малых. Кривые пе-
пересекаются приблизительно при k2R2 = 2. Сравнение с моделью
Глазера опять показывает отсутствие минимума. Для k2d2=l
видим, что Ccoao/d изменяется между 0,86 и 0,8 для 0,2<s/D<
<2; для модели Глазера Cco<x,/d = 0,877. Хроматический коэф-
коэффициент добротности приближается к наилучшему значению
(CCOoo/f)min = 0,7 при бесконечном возбуждении. Это снова вы-
выше предельного значения, равного '/2 для модели Глазера
«"SOСО ' гл
1 2 510 100 1000
Рис, 137. Реальные сферические ко-
коэффициенты аберраций ненасыщен-
ненасыщенных коротких линз при бесконечном
увеличении, отнесенные к R=D/2,
как функции k2R2 для различных зна-
значений s/D [83].
oo
10
1
0.1
-coco
-
/R
2,0
!
-0,6
-
I Mi I mil I I
0,01 0,1
1 2 510 100 1000
Рис. 138. Реальные коэффициенты
хроматической аберрации ненасыщен-
ненасыщенных коротких линз при бесконечном
увеличении, отнесенные к R=D/2,
как функции k2R2 для различных зна-
значений s/D [83].
[формула (8.60)]. Для k2d2=l имеем Cco°c/f—0,76 на всем ин-
интервале отношений зазор — диаметр. Отметим сходство между
кривыми рис. 135 и рис. 138. В самом деле, при низких воз-
возбуждениях величина f/R почти такая же, как и Cco<x>/R в пол-
полном согласии с (8.59). Как мы видели, для более высоких воз-
возбуждений хроматический коэффициент добротности уменьшает-
уменьшается незначительно: фокусное расстояние и коэффициент хрома-
хроматической аберрации изменяются одинаковым образом.
Читатель может найти детальные графики и таблицы, опи-
описывающие свойства этих линз, в литературе [36, 50, 83, 84,
298—300]. Основной вывод из вышепроведенного обсуждения
заключается в том, что свойства традиционных коротких маг-
500
Магнитные линзы
нитных линз зависят от параметра s/D, конфигурации полюс-
полюсных наконечников и возбуждения. Их сферические аберрации
намного ниже, чем у традиционных электростатических линз.
Различие хроматических аберраций не так велико, но магнит-
магнитные линзы лучше и в этом отношении.
Можно представить оптические свойства первого порядка
и аберрации коротких магнитных линз для относительно низ-
низких возбуждений в виде универсальных кривых [84, 298, 301,
302]. Эта идея основана на введении соответствующим образом
выбранных масштабирующих множителей для параметров воз-
возбуждения и оптических свойств.
Действие данной линзы всегда зависит от способа примене-
применения. Поэтому сейчас самое время кратко обсудить наиболее
важные применения коротких магнитных линз. Существует не-
немало путаницы при классификации коротких линз на различ-
различные категории. В электронной микроскопии ситуация, однако,
ясна; магнитные линзы имеют три основных применения: как
конденсоры, объективы и проекционные линзы.
Конденсор — это линза, которая регулирует интенсивность
и расходимость пучка, освещающего объект.
Объективная линза должна давать высококачественное изо-
изображение объекта. Дифракция, а также сферическая и акси-
аксиальная хроматическая аберрация — наиболее важные факторы,
ограничивающие выполнение этой функции. Объективная линза
является наиболее важным элементом всего прибора: ее свой-
свойства в основном и определяют разрешение, которое в конечном
счете может быть достигнуто.
Назначение проекционной линзы — спроецировать с боль-
большим увеличением промежуточное изображение, сформирован-
сформированное объективной линзой, в конечную плоскость изображения
или перенести изображение в подходящую плоскость с единич-
единичным увеличением. Если объектив работает при большом увели-
увеличении, аксиальные аберрации проекционной линзы пренебрежи-
пренебрежимо малы благодаря соотношению Гельмгольца — Лагранжа
D.65). С другой стороны, так как для проекционной линзы в
качестве объектов могут использоваться сравнительно протя-
протяженные изображения, внеосевые аберрации играют важную
роль в их конструировании.
Путаница обычно связана с системами уменьшения разме-
размеров зонда. В увеличивающих системах образец глубоко погру-
погружен в магнитное поле объективной линзы, в то время как в
зондирующих устройствах он всегда располагается за предела-
пределами поля. Поэтому объективная линза зондирующего устройст-
устройства иногда называется проекционной линзой. Кроме того, ре-
реальные асимптотические свойства еще называют «объективны-
«объективными» и «проекционными» свойствами соответственно (см.
501
Глава 8
разд. 4.6). Поэтому следует быть очень внимательным в ис-
использовании рекомендаций из некоторых статей по конструи-
конструированию объективных и проекционных линз. Мы всегда долж-
должны рассматривать непосредственные требования для данного
применения.
«Оптимальные» конструкции для объективных и проекцион-
проекционных линз были рассмотрены несколькими авторами [84, 303—
305]. Однако следует понимать, что параметры возбуждения и
геометрия, при которых достигают минимума фокусные рас-
расстояния, сферическая и хроматическая аберрации, совершенно
различны. Поэтому «оптимальное» конструирование подразуме-
подразумевает некоторые дополнения к обычным практическим требова-
требованиям. Например, если коэффициенты аберраций нормированы
относительно минимально возможного асимптотического фокус-
фокусного расстояния, они имеют минимальное значение для каждого
фиксированного отношения s/D при определенном оптималь-
оптимальном возбуждении. Это минимальное значение уменьшается по
мере роста отношения s/D [84J. Поэтому в общем линзы с
высокими значениями s/D имеют относительно низкие аберра-
аберрации. Если, однако, рассмотреть сферическую аберрацию при
таких возбуждениях, когда хроматическая аберрация имеет
минимум, то увидим [300], что коэффициент сферической абер-
аберрации круто возрастает с увеличением отношения s/D. To
же самое происходит, если попытаться начать с мини-
минимума коэффициента сферической аберрации: для минимума
сферической аберрации коэффициент хроматической аберрации
приблизительно на 30% выше, чем наименьший достижимый.
Обе аберрации достигают своих минимумов при различных
значениях возбуждения, поэтому «оптимальная» геометрия
всегда должна пониматься в ограниченном смысле. Правиль-
Правильный выбор параметров возбуждения линзы и максимального
значения магнитной индукции более важен, чем выбор отно-
отношения s/D.
Факторы насыщения ферромагнитных материалов ограничи-
ограничивают возможные сочетания геометрии линзы и возбуждения.
Это ограничение определяет минимальные значения фокусного
расстояния и аберраций.
Хотелось бы отметить, что для достижения минимальной
сферической аберрации необходимо располагать образец вбли-
вблизи центра зазора. Это может быть использовано в однополевой
линзе типа объектив — конденсор, в которой первая половина
поля работает как конденсорная линза, в то время как вторая
половина действует как объектив [88].
До сих пор подробно обсуждались только симметричные
линзы с одним зазором. Короткие магнитные линзы, однако,
могут иметь совершенно асимметричные полюса [306, 309], и
502
Магнитные линзы
число зазоров, конечно, тоже не ограничено [310]. Так как на
максимальную магнитную индукцию асимметрия, вызванная,
например, различием внутренних диаметров полюсных нако-
наконечников, влияет слабо и свойства первого порядка в основ-
основном зависят от Втах, можно изменять форму полюсных нако-
наконечников без значительного влияния на фокусирующие свойст-
свойства. Такие асимметричные линзы можно использовать для уда-
удаления образцов из областей максимального поля. Линзы с дву-
двумя зазорами предназначены для устранения поворота изобра-
изображения.
Магнитные линзы с постоянными магнитами могут быть
также использованы для фокусировки пучков заряженных час-
частиц. Очевидно, преимущество заключается в отсутствии источ-
источников питания для обеспечения возбуждения. С другой сторо-
стороны, трудность регулировки фокусных расстояний является
здесь определенным недостатком.
Практическое проектирование магнитных линз — дело до-
довольно сложное из-за сложности расчета магнитных систем.
Интересующийся читатель может обратиться к исчерпывающей
работе Рикке [88] для более детального ознакомления. Допол-
Дополнительный материал может быть найден в обширной литера-
литературе [50, 84, 87, ПО, 123, 141, 297, 298]. Нам бы хотелось об-
обратить особое внимание читателя на библиографию приблизи-
приблизительно тысячи публикаций по свойствам магнитных линз, со-
составленную Хоуксом [50]. В ней приведено огромное количест-
количество работ, выполненных в этой области.
8.4.2. Нетрадиционные линзы
Прежде чем закончить эту главу, хотелось бы дать краткий
обзор некоторых недавних работ по магнитным линзам [94,
311].
8.4.2.1. Сверхпроводящие линзы. Современные электронные
микроскопы и аналитические приборы должны давать боль-
большой объем информации об объекте. Поэтому необходимо раз-
разместить относительно большое число устройств вблизи объек-
объективной линзы. Это требует уменьшения физических размеров
линзы. Поэтому необходимо уменьшить намагничивающую ка-
катушку, сохраняя число ампер-витков. Эта проблема может быть
решена использованием сверхпроводящих катушек [312, 313].
Размер магнитной катушки, а следовательно, и размеры маг-
магнитной системы таким образом могут быть сильно уменьшены.
В катушке может быть достигнута плотность тока 100 А/мм2.
За это мы платим тем, что проводники должны поддерживать-
поддерживаться при температуре жидкого гелия, хотя последние достиже-
503
Глава 8
ния в сверхпроводимости могут сделать это утверждение уста-
устаревшим. В результате действительные размеры всего устройст-
устройства не могут быть сильно уменьшены. К. тому же насыщение
препятствует уменьшению размеров линзы.
Однако существуют побочные эффекты, которые могут быть
с пользой применены к сверхпроводящим линзам [88]. Охлаж-
Охлажденные стенки вакуумной камеры значительно улучшают ваку-
вакуум и эффективно защищают от паразитных переменных магнит-
магнитных полей, возрастает защищенность образца от радиационно-
радиационного разрушения, сильно уменьшается термический дрейф образ-
образца и т. д. Поэтому практическое применение сверхпроводящих
линз имеет многообещающее будущее.
8.4.2.2. Уменьшение размера катушек другими способами.
Трудности практической реализации сверхпроводящих линз
стимулируют исследователей к поиску других способов умень-
уменьшения размеров возбуждающих катушек. Один из вариантов —■
повысить эффективность обычной охлаждающей системы. Та-
Таким образом может быть достигнута плотность тока 50 А/мм2.
Для повышения плотности компоновки и теплопроводности ка-
катушек была предложена обмотка, сделанная из тонкой медной
ленты. В этих экспериментах получены плотности токов до
200 А/мм2 [94].
8.4.2.3. Магнитные линзы без поворота изображения. Угол
поворота изображения в магнитной линзе дается выражением
D.60). Для случая поворота асимптотического изображения
можно подставить C.233), что дает
ш — ao = =FnoNI{-Q/[8m0(U- £/0)rei]}1/2, (8.83)
где отрицательный знак соответствует положительному заряду
частицы и обратно. Мы видим, что угол поворота асимптоти-
асимптотического изображения не зависит от распределения магнитного
поля.
Поворот изображения вносит значительные неудобства в
электронной микроскопии по двум причинам. Во-первых, вслед-
вследствие зависимости от тока, т. е. от оптической силы линзы,
угол поворота изображения будет изменяться в зависимости
от увеличения. Это делает затруднительной идентификацию
деталей изображения при больших увеличениях. Во-вторых, в
соответствии с E.229) анизотропный коэффициент хроматичес-
хроматической аберрации пропорционален углу поворота изображения.
Поэтому было бы хорошо, если бы поворота вообще не было.
Мы видели в разд. 8.1, что не вызывающая поворота изо-
изображения линза может быть легко сформирована двумя оди-
одинаковыми коаксиальными катушками с равными, но противо-
504
Магнитные линзы
положно направленными токами. Однако из-за конечного раз-
размера катушек практическая реализация таких линз была
затруднительной, пока не появились миниатюрные линзы. Маг-
Магнитная система такой линзы сделана из цельного куска желе-
железа, и система водяного охлаждения оптимизирована для обес-
обеспечения минимально возможных размеров [94]. Размер маг-
магнитной системы может быть также уменьшен использованием
специальных анизотропных магнитных материалов [313J.
8.4.2.4. Магнитные линзы, не содержащие железных частей.
Серьезный недостаток магнитных линз состоит в том, что
магнитная система занимает значительный объем. Было пока-
показано [314J, что миниатюрный соленоид диаметром всего две
трети диаметра полюсных наконечников (т. е. несколько мил-
миллиметров) и длиной несколько сантиметров может иметь такие
же свойства в первом порядке, как и значительно большая
обычная линза с железным кожухом. Очень высокие плотности
тока (80 А/мм2) могут быть достигнуты использованием поло-
полого, охлаждаемого водой проводника. Такие линзы представля-
представляют физическую реализацию модели эквивалентного соленоида
(см. разд. 3.1.4). Однако надо иметь в виду, что такие линзы
являются существенно длинными, и поэтому их сферическая
аберрация относительно велика.
Характеристики соленоидальной «мини-линзы» могут быть
улучшены созданием обмотки в форме широкого конуса [84].
В пределе коническая линза вырождается в плоскую линзу,
чье поле дается выражением C.271). Мы видели в разд. 3.1.5.6,
что плоская катушка всегда дает больший максимум магнит-
магнитной индукции, чем соленоид. Вдобавок ее поле сильнее скон-
сконцентрировано. Поэтому можно ожидать, что плоская линза
имеет очень хорошие оптические свойства. В самом деле, ее
фокусное расстояние может быть очень коротким, и коэффи-
коэффициент сферической аберрации очень малым. Кроме этого, в
этих линзах может быть достигнута плотность тока до
100 А/мм2. Действительно, плоские линзы с большим отноше-
отношением внутреннего и внешнего ди-
диаметров имеют более низкий коэф-
коэффициент сферической аберрации,
чем любые другие магнитные лин-
линзы [94].
8.4.2.5. Однополюсные линзы.
Если мы добавим к плоской линзе
железную пластину с отверстием
для прохождения частиц, то полу-
получим однополюсную магнитную Рнс. 139. Однополюсная лннза.
505
Глава 8
линзу. Поле такой линзы может быть описано экспоненциаль-
экспоненциальной моделью, рассмотренной в разд. 8.3.7. Однополюсная линза
может иметь практически любую форму обмотки (рис. 139).
Такие линзы по крайней мере так же эффективны, как обыч-
обычные линзы, при создании высоко концентрированных магнит-
магнитных полей. Они представляют многообещающее направление
будущего развития магнитных линз [94, 311].
Заключение
Эта глава представляет собой краткий обзор основных
свойств магнитных линз. Мы начали с главных соотношений и
затем сжато рассмотрели длинные линзы. Сравнительно под-
подробно описаны различные модели магнитных линз, причем
особое внимание уделено колоколообразной модели Глазера.
В некоторых деталях обсуждены короткие и различные нетра-
нетрадиционные линзы.
Глава 9
ОПТИМИЗАЦИЯ И СИНТЕЗ
ЭЛЕКТРОННЫХ И ИОННЫХ ЛИНЗ
С ПОМОЩЬЮ КОМПЬЮТЕРА
Желание иметь электронные и ионные оптические системы
с наперед заданными свойствами и столь малыми аберрация-
аберрациями, насколько это возможно, так же старо, как и сама элект-
электронная и ионная оптика. Как мы видели в предыдущих главах,
аберрации являются фундаментальными ограничениями при
создании любой лучевой оптики. Уменьшение аберраций осо-
особенно актуально для ионных пучков. Их необходимо фокуси-
фокусировать электростатическими линзами, которые должны обеспе-
обеспечивать независимость отклонения частиц от их отношения за-
заряда к массе. Как мы знаем, аберрации стандартных электро-
электростатических линз намного выше, чем у магнитных линз. Следо-
Следовательно, разрешающая способность ионных зондов всегда ог-
ограничивается аберрациями. Кроме того, уменьшение аберраций
магнитных линз также желательно для улучшения работы
электронных микроскопов, электронных зондовых приборов
и т. п.
Компенсировать аберрации можно, используя'дополнитель-
используя'дополнительные заряды, неоднородности поля, переменные поля или раз-
различные типы симметрии. Этот подход обсуждался в разд. 5.6.
Поскольку компенсация приводит к чрезмерному усложнению
систем, наш взгляд на эту проблему заключается в том, что
необходима не компенсация, а поиск таких оптических элемен-
элементов и систем, которые сами будут обеспечивать требуемые
свойства при минимальных аберрациях. Синтез таких систем и
является предметом настоящей главы.
Кроме того, так как множество областей применения требу-
требует различных конструкторских решений, недостаточно соста-
составить каталог свойств нескольких простых линз, но крайне не-
необходим общий метод конструирования. Процедуру синтеза,
представленную в разд. 9.10, можно рассматривать как реали-
реализацию такого метода.
9.1. Возможно ли устранение аберраций
в электронной и ионной оптике?
Теорема Шерцера (разд. 5.2.1.3) устанавливает, что ни
коэффициенты сферической, ни осевой хроматической аберра-
аберраций не могут быть отрицательными величинами. Но могут ли
507
Глава 9 _^____
они быть равными нулю? Об этом теорема не говорит ничего.
Этот вопрос подымается часто и вызывает много дискуссий.
Очевидно (см. разд. 5.7.4), что любая электронно-ионная
оптическая система всегда может быть уменьшена до сколь
угодно малых размеров. В соответствии с этим, если не за-
задаться практическими ограничениями, предел аберраций даже
самых плохих линз всегда равен нулю. Совсем другое дело
установить нижние пределы для нескольких безразмерных ко-
коэффициентов добротности или коэффициентов аберрации исхо-
исходя из соображений практической реализуемости.
Интересно, что по этому вопросу нет полного согласия. Не-
Некоторые советские ученые [315, 316] утверждают, что нижний
предел сферической аберрации всегда равен нулю. С другой
стороны, теоретическое рассмотрение этого вопроса на основе
методов вариационного исчисления определенно показало, что
ненулевой нижний предел существует как ' для сферической,
так и для осевой хроматической аберрации. Мы обратимся к
этим пределам в разд. 9.1.1 и 9.4.1.
Оставим пока теорию и попытаемся найти поля, при кото-
которых аберрации принимают нулевые значения, просто приравни-
приравнивая нулю подынтегральные выражения коэффициентов аберра-
аберрации или членов третьего порядка разложения траектории в
ряд Тейлора. Так как коэффициенты аберрации проще для
магнитных линз, сведем к ним наше рассмотрение. Приравни-
Приравнивая подынтегральное выражение уравнения E.135) к нулю,
получим простое дифференциальное уравнение для B(z). Ре-
Решение этого уравнения дает распределение магнитной индук-
индукции при нулевой сферической аберрации [317]. При этом, од-
однако, оказывается, что объект необходимо поместить в поле и
фокусирующее действие не может уменьшить наклон лучей бо-
более чем на 5%. Такая линза не обладает достаточной силой,
чтобы сформировать действительное изображение на приемле-
приемлемом расстоянии. Изображение практически всегда мнимое. Это
также было показано [318] для любой линзы, электростати-
электростатической или магнитной, которая имеет нулевую сферическую
аберрацию. Однако такая попытка позволила прийти к важ-
важному заключению, что магнитное поле, выпуклое в направле-
направлении оси, всегда дает относительно малую сферическую аберра-
аберрацию (см. разд. 8.2.3).
Можно попытаться найти более общий подход к этой проб-
проблеме. Повторим вывод уравнения параксиальных лучей D.31;,
данный в разд. 4.3, но теперь сохраним члены вплоть до треть-
третьего порядка малости. Для простоты предположим, что С=0,
т. е. будем учитывать только изотропные аберрации. Тогда по-
получим для магнитных линз следующее уравнение траектории
третьего порядка:
508
Оптимизация и синтез электронных и ионных линз
r" = {Ql[8mo(U - [/0)ге1]} {гВЦг) - г* В (z)B"(z)/2 -
— rVB (z) В' (z) + rr'2B2 (z) —
-С/о) rei]
Если пренебречь членами третьего порядка, получим уравне-
уравнение параксиальных лучей (8.2). Для того чтобы получить лин-
линзы, свободные от аберраций третьего порядка, мы должны по-
потребовать, чтобы сумма всех членов третьего порядка была
равна нулю. Разделив на r3B(z), используя уравнение (8.2) и
взяв полную производную, придем к [319]
-J-[r'5(z)/r+B'(z)/2]=0, (9.2)
решение которого есть
r'=[tf-B'(z)]r/2B(z), (9.3)
где К — произвольная постоянная. Дифференцируя это выраже-
выражение по г и используя снова уравнение (8.2), окончательно по-
получим следующее дифференциальное уравнение:
QB*(z)/[2mo(U — U0)rei]+2B(z)B"(z) —
— ЗВ'2 (г) + 4KB' (z) — К2 = 0. (9.4)
В этом уравнении нет ни г, ни его производных: его решение
сразу же дает такое распределение индукции, при котором
аберрации исчезают. Предполагая, что постоянная К — дейст-
действительная величина, можно решить это уравнение численно и
восстановить распределение, при котором исчезают аберрации.
В простейшем случае /С = 0. Тогда решением уравнения
(9.4) является гиперболическое распределение [319]
В (г) = [- 2/По (U - Uo) rei/Q] 1/2I (b-z), (9.5)
где b — произвольная постоянная. Подставляя это выражение-
в уравнение (8.2), мы получим
r"=-r/[4F-zJ], (9.6)
решением которого является
г=Сг(Ь-гу/*, (9.7)
где ci ■— произвольная постоянная. Уравнения (9.5) и (9.7) да-
дают
В{г)=Ыг\ (9.8)
что также следует из уравнения (9.3) (с2 — Другая произволь-
произвольная постоянная). Из этих выражений мы видим, что парал-
параллельный пучок лучей попадает в фокус на оси при z = b, где-
509-
Глава 9
индукция бесконечно велика. Естественно, на практике это ус-
условие нереализуемо.
Мы провели численные расчеты для различных значений по-
постоянной К. В результате мы всегда получали неимоверный
рост индукции с координатой z.
Таким образом, практический ответ на вопрос, поставлен-
поставленный в заглавие этого раздела, к сожалению, отрицателен. Хотя
теоретически и возможно записать математические выражения
для осевого распределения индукции, которые приводят к оп-
оптике без аберраций, но реализовать такие распределения прак-
практически невозможно. Следовательно, необходимо направить
усилия на уменьшение аберраций до их практически возмож-
возможных значений. Этот вывод в той же мере применим и для
электростатических линз. В то же время, однако, было бы ин-
интересно исследовать структуру уравнения (9.4) более подроб-
подробно. Мы предположили [268], что распределение поля, обеспе-
обеспечивающее минимум аберраций, должно удовлетворять некото-
некоторому специальному дифференциальному уравнению. Это неиз-
ъестное уравнение должно иметь вид, близкий к уравнению
(9.4).
9.1.1. Нижний предел осевой хроматической
аберрации магнитных линз
Для магнитных линз нижний предел осевой хроматической
аберрации можно установить элементарно [320]. Начнем с ко-
коэффициента аберрации вида E.216), который может быть пе-
переписан с помощью уравнений D.65) и E.42) в виде
1/М I 1/IMI
Ceo=—lhdh' = Shdh' + $hdh'. (9.9)
1 0 О
Уравнения D.159) и (8.2) дают
— h"lh = —h'dh'lhdh*ik\ (9.10)
тогда имеем
(kh + V)>0, (9.11)
an
решение которого есть
i (i_/i'2)i/2 для Л'>0,
kH>\(M-*-h'*yi* для А'<0. (9Л2)
Используя эти неравенства для уравнения (9.9) и выполнив
интегрирование, окончательно получим
£(Cco)mln=(n/4)(l+Af-2). (9.13)
:510
Оптимизация н синтез электронных и ионных лннз
Для бесконечного увеличения имеем просто п/4, что в точ-
точности равно половине величины для однородного магнитного
поля. Уравнение (9.13) соответствует уравнению (8.56) для
модели Глазера. Интересно отметить, что коэффициент хрома-
хроматической аберрации для этой модели весьма близок к нижнему
пределу. Для интервала 0,6<&2d2<2,5 относительное различие
не превышает 20%. Например, при Ы=\ имеем CCOoc/d=0,877
и уравнение (9.13) дает [CCo°c)min/d = п/4 = 0,785.
Это важный результат. Мы видим, что коэффициент осевой
хроматической аберрации имеет реальный предел (по край-
крайней мере, для магнитных линз), ниже которого его величина
не может быть уменьшена ни при каких обстоятельствах. Это
подтверждает наше предварительное заключение о необходи-
необходимости уменьшения аберраций до практически реализуемых ми-
минимальных величин.
9.2. Оптимизация: синтез против анализа
Неудача при попытке получить линзы, свободные от аберра-
аберраций, имеет далеко идущие последствия. Эта ситуация привела
Д. Габора к открытию голографии. Он отчаялся улучшить
разрешающую способность электронного микроскопа. И поско-
поскольку аберрации линз устранить нельзя, он стал думать об уст-
устранении самих линз. Результат хорошо известен.
Другие исследователи подошли к проблеме более консерва-
консервативно, пытаясь оптимизировать свойства электронных линз, т. е.
искать такие линзы, которые обеспечат требуемые свойства пер-
первого порядка с минимумом аберраций, без дополнительных
корректирующих элементов. Отметим, что это определение име-
имеет весьма общий характер. Фактически всякое качественное
конструирование есть процесс оптимизации (в большинстве
случаев он нацелен на минимизацию отношения затрат к вы-
выполненной работе).
Существуют два совершенно различных подхода к оптими-
оптимизации: анализ и синтез.
Метод анализа — это метод проб и ошибок. Конструктор
начинает с определенного набора заданных элементов (элект-
(электродов и полюсных наконечников) и пытается улучшить их ра-
работу, анализируя оптические свойства и варьируя геометричес-
геометрические размеры, так же как и электрические и магнитные пара-
параметры системы (т. е. возбуждение и расстояния между элемен-
элементами, иногда даже заменяя некоторые элементы другими), до
тех пор, пока система не начнет работать удовлетворительно.
Вследствие неограниченного числа возможных конфигураций
эта процедура чрезвычайно медленная и утомительная. Она
может дать быстрый и надежный результат, если удалось уга-
511
Глава 9
дать приемлемый вариант конструкции до начала работ. Ите-
Итерации могут быть автоматизированы с помощью, например,
сходящегося метода наименьших квадратов [96]. Гл. 7 и 8 по
существу посвящены только анализу. Это классический метод
конструирования электронных линз.
В этой главе будем обсуждать синтез. Оптимизация по-
посредством синтеза всегда была одной из наиболее престижных
целей электронной и ионной оптики. Этот подход основан на
том факте, что всякое поле, создающее изображение, его свой-
свойства первого порядка и аберрации всегда в итоге определяют-
определяются несколькими осевыми функциями (в случае осевой симмет-
симметрии— осевым потенциалом и распределением индукции). Толь--
ко эти распределения и их производные входят в уравнение
параксиальных лучей и в выражения для коэффициентов абер-
аберрации. Тогда вместо анализа огромного количества конфигу-
конфигураций и полюсных наконечников можно выбрать критерии, оп-
определяющие требуемую систему, в качестве начальных условий
и попытаться найти такое распределение поля, создающего
изображение, которое будет их реализовать. Конечной задачей
является синтез реальных конфигураций электродов и полюс-
полюсных наконечников, которые создают такое распределение поля.
Это задача повышенной сложности. Мы должны определить
неизвестные функции U(z), B(z) и r(z) так, чтобы они мини-
минимизировали несколько интегралов аберраций одновременно, и
в то же время эти функции должны удовлетворять дополни-
дополнительным требованиям. Одно из таких требований сформулиро-
сформулировано в виде дифференциального уравнения (уравнение парак-
параксиальных лучей).
Отметим, что иногда термин «синтез» используется как аль-
альтернатива так называемым «инверсным проблемам» электрон-
электронной оптики, т. е. поиску распределений поля, создающих задан-
заданные траектории [23J. Однако в большинстве практически ин-
интересных случаев мы интересуемся только конечными разме-
размерами пятна на мишени или общей формой пучка, но не от-
отдельными траекториями.
Рассмотрим простой пример идеальной квадрупольной лин-
линзы (разд. 3.1.3.3) в качестве иллюстрации различия между
подходами анализа и синтеза. Поскольку идеальный квадру-
поль состоит из четырех бесконечных гиперболических поверх-
поверхностей, но бесконечные поверхности на практике реализовать
невозможно, у нас есть два выхода. Аналитический подход со-
состоит в том, чтобы компенсировать недостающую часть гипер-
гиперболических поверхностей изменением формы остающихся элек-
электродов. Синтетический подход считает исходным идеальное
распределение поля и пытается воспроизвести его, выделяя
наиболее важные особенности квадруполя, т. е. существование
512
Оптимизация и синтез электронных и иоииых линз
двух взаимно перпендикулярных плоскостей симметрии. Тогда
легко получить решение: использовать множество простых
электродов, поддерживающих нужным образом выбранный по-
потенциал, вместо четырех электродов, форма которых подверг-
подверглась серьезным изменениям. (Этот многоэлектродный подход
также может быть использован для оптимизации конструкции
линз с осевой симметрией [320а, 320Ь].)
В следующих разделах мы предпримем атаку на проблему
уменьшения аберраций, используя метод синтеза.
9.3. Первые попытки синтеза
Уже в первое десятилетие электронной оптики многими ис-
исследователями предпринимались попытки синтеза электронных
линз с минимальными аберрациями. Начнем с краткого обзора
первых работ в этом направлении [9, 160, 321].
Эту работу начали с поиска тонких линз с минимальной
сферической аберрацией. Поскольку на тонкие линзы наклады-
накладываются очень серьезные ограничения, то эти результаты имеют
только исторический интерес.
Лучшее из найденных распределений потенциала для сла-
слабой однопотенциальной линзы есть
U(z) = Vi[l+Aexp(— Dz>)], (9.14)
где 1Л — постоянный потенциал с обеих сторон линзы, а Л и
D — постоянные, которые должны быть определены из несколь-
нескольких предварительно заданных величин, например, фокусного
расстояния и расстояния между главными плоскостями.
Наилучшее распределение для слабой иммерсионной линзы
дается выражением [323]
U'{z)=Aexp(— £>z2), (9.15)
а оптимальная тонкая магнитная линза определяется распре-
распределением Гаусса
£(z)=Bmaxexp(-D22). (9.16)
Кроме того, было показано [324], что тонкая магнитная линза,
имеющая острый пик вблизи центра, обладает очень малень-
маленькой сферической аберрацией. Как мы знаем, такая линза не
может быть реализована на практике.
Естественно, реальной проблемой является уменьшение
аберраций толстых линз. Было показано [325], что для мини-
минимизации сферической аберрации объект должен быть располо-
расположен вблизи максимума поля. Важность соответствующего ме-
метода для реконструкции электродов и подходящего выбора
коэффициентов добротности, с помощью которых можно про-
513
Глава 9
водить сравнение различных линз, была признана достаточно-
давно. Обычно требовалось, чтобы фокусные расстояния и
толщины сравниваемых линз были идентичны. Трудности в
определении толщины линзы приводили к разным результатам
при сравнении в зависимости от способа определения толщины
[236, 326].
Электростатические линзы с гиперболическими электродами
уже исследовались [160, 200] с целью уменьшения сферичес-
сферической аберрации, но первая реальная попытка синтеза толстых
линз была предпринята в 1952 г. Касьянковым [327]. Он вывел
систему нелинейных дифференциальных уравнений высокого
порядка, решение которой должно минимизировать некоторые
интегралы аберраций. К сожалению, как начальные условия,
так и практические методы численного решения этих уравнений
остаются неясными.
Первые попытки оптимизации не ограничивались осевой сим-
симметрией. В 1953 г. Берфут [328] вычислил формы электродов
очень сложной квадрупольно-октупольной линзы, для которой
корректируется сферическая аберрация.
9.4. Вариационное исчисление
Коэффициенты геометрической и хроматической аберраций
выражаются определенными интегралами вида
A=l'F(z)dz, (9.17)
где F(z)—весьма сложная функция координаты г, определен-
определенная на классе функций, таких, как распределение осевого по-
потенциала или индукции, их производных и двух линейно-неза-
линейно-независимых решений уравнения параксиальных лучей. Цель опти-
оптимизации — найти вид этих неизвестных функций, при котором
интеграл А был бы минимальным. Точно такая же цель стоит
и перед вариационным исчислением. Следовательно, вполне
естественно попытаться использовать эту область математики
для решения нашей проблемы.
Трудность заключается в том, что решение уравнения па-
параксиальных лучей зависит от тех же неизвестных распределе-
распределений яолей, что и само подынтегральное выражение; следо-
следовательно, этот интеграл является очень усложненным функцио-
функционалом. Все же эта проблема может быть решена с помощью
следующей процедуры.
Во-первых, определим множитель Лагранжа ц(г) так, что-
чтобы
=Or (9.18)
514
Оптимизация и синтез электроиных и ионных лииз
где б означает первую вариацию этого интеграла, a f(z) —
приравненное к нулю уравнение параксиальных лучей, т. е.
левую часть уравнения G.1) для электростатических полей и
для магнитных полей при С=0 [из уравнения (8.2)]. Отметим,
что по определению /(z)=0 для таких распределений полей и
траекторий, которые удовлетворяют уравнению параксиальных
лучей. Для реальных коэффициентов сферической и хромати-
хроматической аберраций можно записать
, h'(z), V(z), V'{z), V"{z)]. (9.20)
Тогда имеем
f(z)=f[h(z), h'{z), h"(z), V(z), V'(z), V"(z)]=0,
(9.21)
где h(z)—решение уравнения параксиальных лучей, определен-
определенное начальными условиями уравнения E.42), a V(z) равно
U(z) или В (z) для электростатического и магнитного полей со-
соответственно. Реальные выражения для магнитных полей су-
существенно проще, чем для электростатических.
Множитель Лагранжа является функцией z, так как требо-
требования, задаваемые видом f{z), должны удовлетворяться всег-
всегда. Теперь выполним вариацию подынтегрального выражения.
В результате получим
*o
где учитывалось соотношение
dfldh"~\. (9.23)
Интегрируя по частям с использованием формул
lydu'^yu' — ly'du, (9.24)
I ydu"=yu" — у V + J y"du, (9.25)
мы избавимся от вариаций h', h", V и V". Теперь, приравни-
приравнивая члены, содержащие bh и 8V, мы выведем дифференциаль-
дифференциальные уравнения
515
Глава 9
_|_ ц _12_ j =: 0 (9.26/
df \ d2 / й/7 df \ n /n O7V.
■"Ж?7" +^Г Ж^+М'-лТТЯГ =0 (Э.2/>
соответственно. Остатки, получившиеся от интегрирования по
частям, также должны быть приравнены к нулю:
dF , 3/ .
d f dF
(9.28)
Уравнения (9.21), (9.26) и (9.27) образуют систему трех
связанных дифференциальных уравнений высокого порядка,
которые определяют неизвестные функции V(z), h(z) и |х(г),
с граничными условиями, определяемыми ограничениями и
сформулированными с помощью уравнений (9.28). Поскольку
эти граничные условия могут быть заданы в разных (даже
заранее неизвестных) точках, то дифференциальные уравнения
обычно имеют весьма сложный вид и необходимы специальные
численные методы для их решения.
Уравнения (9.26) и (9.27) являются нелинейными уравнени-
уравнениями Эйлера — Лагранжа — Пуассона вариационного исчисле-
исчисления. Отметим их сходство с уравнением Эйлера E.4), которое
было выведено из общих вариационных принципов Ферма я
Гамильтона.
Для магнитных полей (V=B) коэффициент сферической
аберрации может быть записан в виде уравнения E.132) с про-
произвольными постоянными, выбранными таким образом, чтобы
выполнялось условие dF/dB" = 0. To же справедливо для коэф-
коэффициента осевой хроматической аберрации [уравнение E.194)].
Уравнения (8.1) и (9.19) дают
J>L-Tte\ df - <?5(г)А(г)
dh ~ K h dB 4m0 (U — t/0)rei'
Подставляя эти выражения в уравнения (9.26) — (9.28), полу-
получим
= 0, (9.30)
dF d f dF \ QB(z) . 0 (9Щ
dB dz\dB' J 4mo(U — Uo)iei ^ ' v '
516
Оптимизация и синтез электронных и ионных лииз
К счастью, в этом случае все эти дифференциальные уравне-
уравнения всего лишь второго порядка. Моузес [329] нашел эффек-
эффективный путь решения этой системы дифференциальных уравне-
уравнений при заданных ограничениях и конечных условиях, даже
если минимизироваться должна комбинация аберраций. Он
применил этот метод для определения распределений магнит-
магнитного поля с исчезающе малой комой и минимизированной сфе-
сферической аберрацией так же, как и для магнитных квадру-
польных систем с минимальной апертурой [330] и хроматиче-
хроматическими [331] аберрациями и для квадрупольно-октупольных
корректоров с минимальными полями [332]. Выведен [333]
ряд распределений магнитного поля с минимальной сферичес-
сферической аберрацией для случая, когда в пространстве объектов по-
поле отсутствует. Было найдено, что для круглых линз лучше
использовать асимметричные распределения полей, крутизна
которых выше в пространстве объектов, чем в пространстве
изображений.
Следующей проблемой является реконструкция реальных
полюсных наконечников, создающих эти оптимальные поля
(см. разд. 9.8). В работе Моузеса это было сделано в основ-
основном интуитивно.
Для электростатических линз ситуация менее благоприят-
благоприятна. Уравнения Эйлера — Лагранжа — Пуассона являются не-
нелинейными дифференциальными уравнениями четвертого по-
порядка с чрезвычайно сложными граничными условиями. Слож-
Сложность этих условий увеличивается с числом дополнительных
требований. Такие системы уравнений практически не подда-
поддаются численному решению. Для синтеза электронных и ионных
линз необходимо разрабатывать более простые методы.
Третнер [334] уменьшил число уравнений и производных с
помощью ряда преобразований. Такое упрощение возможно
для некоторых специальных случаев, но в общем его выпол-
выполнить очень трудно. Поэтому этот метод реально используется
только для поиска нижних пределов коэффициентов сферичес-
сферической и хроматической аберраций электростатических и магнит-
магнитных линз, однако вопрос о том, как достигнуть этих пределов,
остается открытым.
9.4.1. Нижние пределы коэффициентов
сферической и осевой хроматической аберраций
Установлены следующие пределы сферической и осевой хро-
хроматической аберраций [181, 334].
517
Глава 9
Для магнитных линз нижний предел коэффициента осевой
хроматической аберрации дается уравнением (9.13). Аналогич-
Аналогична для сферической аберрации имеем
(9.33)
где k — обратный диаметр витка, который частица описывает
в однородном магнитном поле с индукцией BmaK. Его можно
определить из уравнений B.143) и D.159).
Для модели Глазера коэффициент сферической аберрации
снова весьма близок к нижнему пределу, но только при силь-
сильном возбуждении. Для интервала 2<k2d2<4,5 относительное
различие не превышает 40%. Например, при k2d2 = 2 имеем
CSOco/d = 0,370 и уравнение (9.33) дает (Csox)min/d = 0,233. Для
плоской линзы (разд. 8.4.2.4) минимум коэффициента сфериче-
сферической аберрации очень близок к этому пределу. Это магнитная
линза с наименьшей из известных сферической аберрацией, но
ее хроматическая аберрация заметно выше, чем у линзы с же-
железными полюсными наконечниками [84]. Следовательно, мож-
можно сделать вывод, что не существует таких линз, которые пре-
превосходили бы все другие линзы по всем параметрам одновре-
одновременно.
Для электростатических линз минимальные значения отно-
относят к величине
Lg= [U(Zo) -Uo]/\ U'(z)\max (9.34)
(см.
Для
(ft.
разд. 5.7.4).
1С II \
y^solL-ig) min"
сферической
+
Имеем
= 0,23{1+М-4[(/Bо) — U0]/[U(zt) —
аберрации и
(Umax—U0)/[U(zo) — t/0]}-«/» +
2,8M-2{(f/max- t/o)/[t/(Z/) - f/o]}
f/o]}
76
(9.35)
(9.36)
для хроматической аберрации. Последнее соотношение явля-
является хорошим приближением, если отношение максимального
потенциала к потенциалу объекта не превышает 100.
Сравнение этих пределов с данными табл. 11 показывает,
как много сделано, чтобы подойти к теоретически возможному
минимальному значению коэффициентов аберрации для элект-
электростатических линз. Однако мы должны отметить, что эти
предельные значения были выведены для случая, когда объект
518
Оптимизация и синтез электронных и ионных линз
находится в зоне действия поля, а минимальные значения могут
быть получены только для нулевой отклоняющей способности
[334]. Третнер рекомендует асимметричное распределение при
сильном замедляющем поле позади плоскости объекта с после-
последующим ускоряющим полем. При этом максимум поля нахо-
находится вблизи объекта.
Уравнения (9.13) и (9.33) — (9.36) устанавливают соотно-
соотношения между минимальными значениями коэффициентов абер-
аберрации, с одной стороны, и геометрией линзы и возбуждением —
с другой. Очевидно, эти минимальные значения должны под-
поддерживаться максимально допустимыми полями. Вот почему
третнеровские коэффициенты добротности задуманы так, что-
чтобы минимизировалось произведение коэффициента аберрации
и максимума поля. Для большинства приложений в таком
применении есть очень много смысла, но, как мы видели в
разд. 5.7.4, универсальных коэффициентов добротности не су-
существует. В частности, они не несут никакой информации о
соотношении между коэффициентами аберрации и оптической
силой линзы. Поэтому в последующем изложении будут по-
прежнему использоваться предпочтительные коэффициен-
коэффициенты добротности для оптимизации линз, подразумевая, что
наши методы равно применимы для любых других коэффици-
коэффициентов добротности, включая третнеровские. Кроме того, мы
полагаем, что для поиска линз, которые ближе к этим преде-
пределам, чем остальные, необходимо выполнить дополнительные
исследования. Очевидно, наибольший интерес представляет
поиск линз, которые были бы как можно ближе к этим преде-
пределам как для сферической, так и для хроматической аберраций.
Интересно отметить, что предельные величины для электро-
электростатических и магнитных линз фактически весьма близки друг
к другу, особенно для сферической аберрации. По крайней ме-
мере это очевидно для правых сторон уравнений (9.33) и (9.35),
если мы рассматриваем однопотенциальные линзы. Правая
часть уравнения (9.36) имеет значение между 2 и 2,5 для прак-
практически используемых полей и бесконечного увеличения, что
всего в 2,5—3 раза выше, чем правая часть уравнения
(9.13). Теперь исследуем левые части этих уравнений. Абер-
Аберрации магнитных и электростатических линз отнесены к вели-
величинам l/k и Lg соответственно. Поскольку максимум электро-
электростатического поля находится вблизи | U'(z) |max=15 кВ/мм,
из уравнения (9.34) имеем
-Uo], (9.37)
причем необходимо подставлять значение потенциала в воль-
вольтах. Для того же значения потенциала уравнения B.145) и
D.159) дают
519.
Глава 9
1/Л=6,74- 10-«[(f/— f/0)rei]1/2/-Smax. (9.38)
Тогда очевидно, что левые части уравнений принимают одина-
одинаковые значения, если
)-£/о]1/2 = 99. (9.39)
Из этого соотношения следует, что, если Втах=1 Тл, предель-
предельный потенциал объекта равен 10 кВ. При более высоких значе-
значениях потенциала имеем (Lg)mln>lfk, т. е. при равенстве пра-
правых частей нижние пределы аберраций для электростатических
линз выше, чем для магнитных. Однако если потенциал в про-
пространстве объектов ниже, то справедливо обратное. В этом
случае пределы аберраций для электростатических линз могут
быть ниже, чем для магнитных. Следовательно, по крайней
мере в принципе, лучшие электростатические линзы должны
быть не хуже их лучших магнитных аналогов.
Тем не менее, как мы видели в предыдущих главах, стан-
стандартные электростатические линзы заметно уступали по каче-
качеству магнитным линзам [160] даже исходя из наших коэффи-
коэффициентов добротности. Поэтому широко распространено мнение,
что более низкое качество является их внутренне присущим
свойством. Важность электростатической оптики для фокусиро-
фокусирования ионных пучков и тот факт, что подавляющее большинст-
большинство работ об электростатических линзах посвящено только про-
простым двух- или трехэлектродным конфигурациям, привели к то-
тому, чтобы взяться за проект, нацеленный на улучшение элект-
электростатических линз [260]. Некоторые из полученных результа-
результатов будут изложены в разд. 9.10.1.
Заканчивая, мы должны отметить, что работа Третнера не
является бесспорной. Мы уже указали некоторые ограничения
выше. Кроме того, его результаты находятся в определенном
противоречии с результатами Касьянкова [316]. Этот факт
также вызвал определенную дискуссию [335, 336]. Тем не ме-
менее его работа интересна не только с теоретической точки зре-
зрения: до сих пор никто не смог предложить какую-либо лин-
линзу, характеристики которой выходили бы за его пределы. По-
Поэтому сам факт установления этих пределов является важным
вкладом в электронную и ионную оптику.
9.5. Динамическое программирование
Так как численные методы вариационного исчисления чрез-
чрезвычайно сложны для большинства практических приложений,
необходимо рассмотреть другие подходы. Первое предложение
основывалось на методах динамического программирования
[268, 337].
520
Оптимизация и синтез электронных и иоиных линз
Давайте снова сформулируем проблему. Мы хотим найти
распределение V(z), которое минимизирует интеграл аберра-
аберраций А (уравнение (9.17)), одновременно удовлетворяя диффе-
дифференциальному уравнению (9.21) и ограничениям, накладывае-
накладываемым практическими требованиями. Возможные распределения
образуют бесконечную систему, даже если длина распределе-
распределения и максимально допустимая сила поля ограничены.
Можно свести эту бесконечную систему к конечной, но
очень высокого порядка одним из множества различных спосо-
способов. К примеру, можно искать V(z) в виде полинома n-й сте-
степени или другой параметрической функции. В этом случае дш
должны определить коэффициенты полинома или параметра
такой функции. Этот подход очень прост и вполне реален
(разд. 9.7), но он не дает возможности рассмотреть значитель-
W/AW
м
3
2
1
О
-1
-г
-з
-м
Рис. 140. Вычислительная сетка для процедуры динамического программиро-
программирования.
ную часть существующих альтернатив. В самом деле, даже
если каждый коэффициент полинома может принимать только
т различных значений, возможное число вариаций составит
тп, которое астрономически велико для любой пары практиче-
практически используемых величин тип. Следовательно, необходимо
найти путь, позволяющий резко уменьшить число альтернатив,
без потери столь большого числа решений.
Рассмотрим прямоугольную вычислительную сетку, показан-
показанную на рис. 140. Она определяет область существования для
поиска функции распределения. Она ограничена максимально
допустимой напряженностью поля или ее производными. Ее раз-
С.
0
1:
1
/
/
2 " к -11
j.k-1
i.k
к "
N
521
Глава 9 ^___
меры в направлении оси задаются длиной L. Эта длина делит-
делится на N равных интервалов так, чтобы
Az=zk — zk-i = L/N=const, (9.40)
где k—l, 2,..., N — порядковый номер данного интервала.
Аппроксимируем неизвестное распределение V(z) или одну
из его производных прямой линией на каждом интервале. Обо-
Обозначим эту кусочно-линейную функцию W(z). Для магнитной
линзы можно предположить, что W(z)=B(z), что эквивалент-
эквивалентно кусочно-линейной модели разд. 8.3.3. Если желательно рез-
резко уменьшить объем вычислений, то можно использовать даже
модель со ступенчатой функцией из разд. 8.3.2, однако следует
помнить, что эта модель не является непрерывной, следователь-
следовательно, производную поля необходимо определять численно, как
разность значений функции в соседних интервалах. Для элек-
электростатических линз можно, например, положить W(z) =Ez(z),
но, как мы увидим в разд. 9.10, наиболее эффективный подход
заключается в использовании для кусочно-линейной функции
W(z) производной наивысшего порядка, которая появляется в
интеграле аберраций. Далее, предположим, что W(z) может
иметь только 2М+1 различных значений на границах интерва-
интервалов (рис. 140). Таким образом, задача сводится к поиску
NBM+l) точек пересечения вычислительной сетки, которые бу-
будут задавать линейные отрезки оптимизированной функции.
Уравнение параксиальных лучей (9.21) для каждого интер-
интервала может быть решено аналитически или численно. Непрерыв-
Непрерывность решения обеспечивается требованием, чтобы начальные
значения h и W для каждого интервала были бы равны их ко-
конечным значениям для предыдущего. Вклад каждого интерва-
интервала в интеграл аберраций можно найти численно одним из мето-
методов, выведенных в разд. 6.3.
Обозначим начальные и конечные значения функции W(z)
для &-го интервала, как
Wk(zk-l)=jAW, (9.41)
Wk(zk)=iAW (9.42)
соответственно, где AW—минимальное изменение функции
W(z) (рис. 140). Очевидно, решение уравнения параксиальных
лучей, так же как и вклад интеграла аберраций, будет зависеть
от фактических значений /, / и k.
До сих пор еще ничего не сделано для уменьшения астро-
астрономического числа BM+l)N+1 различных возможных распреде-
распределений. Для того чтобы найти эффективный путь поиска лучше-
лучшего решения, нужно свести многомерную задачу к одномерной-
многоэтапной процедуре решения, которая может решаться шаг
за шагом.
S22
Оптимизация и синтез электронных и ионных линз
Предположим, что мы нашли распределение W(z), для ко-
которого интеграл аберраций между начальной точкой с осевой
координатой k = 0 и произвольной точкой с координатами /,
k—1, минимален. Обозначим это промежуточное значение ин-
интеграла как G/(fe_i). Если Т7»,-*— вклад &-го интервала в интеграл
аберраций, тогда минимизированное значение G,* этого инте-
интеграла между той же начальной точкой и точкой с координата-
координатами г, k дается рекуррентным соотношением
G/*,= min[G/(fe_,) + .FGfe], (9.43)
где /—переменная величина для каждой заданной точки с ко-
координатами i, k. Процесс оптимизации направлен на то, чтобы
найти конкретное оптимальное значение /, для которого G,-*
минимально. Такая процедура дает как /0Pt(i, &), так и G,fe. Так
как мы начали с предположения, что оптимальное распределе-
распределение, приводящее к точке (j,k—1), известно, теперь необходима
найти остальную часть оптимального распределения.
Процедура поиска начинается с k=\ при начальном условии
Gjo — O, которое выражает простой факт, что вклад интервала,
находящегося вдали от объекта, в интеграл аберраций равен
нулю. Это совершенно справедливо для реальных коэффициен-
коэффициентов аберрации. Если рассматриваются асимптотические аберра-
аберрации, то поиск начинается с границы поля (z=a) при тех же на-,
чальных условиях. Следовательно, поиск в первом интервале сво-
сводится к сравнению различных величин Fiji. Начнем с решения
уравнения параксиальных лучей и вычисления вклада в инте-
интеграл аберраций для каждой пары величин t, /. Для каждого i
найдем соответствующее значение /opt, которое минимизирует
Fin, и запомним их вместе с конечными значениями h и А'. Про-
Проделав это для каждого из 2М+1 возможных i, получим 2М+1
данных для /ю opt, Gilt hn и h'n.
Теперь можно перейти ко второму интервалу и повторить
ту же процедуру, помня, что уравнение (9.43) больше не явля-
является тривиальным. Следует учесть, что теперь i для первого ин-
интервала становится / для второго. Следовательно, величины
Gji, необходимые для вычисления Gi2, равны величинам Gn
первого интервала. В результате имеется 2М+1 данных для
каждого набора }ц Opt, Gi2, hi2 и h'i2.
Будем продвигаться от интервала к интервалу по направле-
направлению к пространству изображений, используя (9.43) для опреде-
определения /((fe-i)opt и dk, до тех пор, пока не достигнем конца вычис-
вычислительной сетки (k = N). Теперь есть N массивов из 2М+\ ве-
величин каждый для //(fe-i)opt, Gik, hik и hrik, т. е. 2М+1 различных
оптимизированных функций Wi(z) с разными конечными значе-
523
Глава 9
ниями i вместе с соответствующими траекториями частиц. Каж-
Каждую функцию можно однозначно задать соответствующими оп-
оптимальными / для всех пар i и k. Выберем конкретное распре-
распределение среди многочисленных решений, которое в наилучшей
степени удовлетворяет данным практическим требованиям. На-
Например, если поле должно исчезать у границы в пространстве
изображений и W(z) означает само распределение поля, то,
очевидно, /=0 должно быть выбрано для конечной точки. Если
изображение может оказаться внутри поля, можно сделать
N переменной величиной и остановить вычисления на той паре
величин £ и k, где h=Q. Увеличение также можно сделать ве-
величиной, задаваемой предварительно. Поле не должно прояв-
проявлять вариаций, которые невозможно воспроизвести с достаточно
хорошим приближением при помощи полюсных наконечников и
электродов приемлемой формы и т. п.
Наиболее важные особенности этого метода следующие:
1. Нет необходимости угадывать результат. Алгоритм ищет
во всем пространстве задачи оптимальный путь без начальных
предположений.
2. Число действительно рассматриваемых распределений
сводится от {2M + \)N+l к ЛГBМ+1J.
3. Воспроизводится богатая картина оптимальных распреде-
распределений. Она содержит огромное число распределений, которые
можно рассматривать как решение подзадач начальной задачи
при разных начальных и конечных условиях.
4. В противоположность методам вариационного исчисления,
этот метод упрощается любыми дополнительными ограничения-
ограничениями, которые уменьшают число возможных выборов на конкрет-
конкретном этапе.
5. Этот метод может быть прямо применен к электростати-
электростатическим и магнитным линзам, а также и к системам линз с лю-
любой симметрией.
6. Вследствие дискретной природы метода необходимо уде-
уделять должное внимание правильному выбору размеров и числа
точек вычислительной сетки. Очень важно правильно выбрать
величины М, N и AzAW для получения как можно более пол-
полного диапазона возможных решений [296]. Требуется накопле-
накопление и умелое обращение с большими массивами данных.
7. Этот метод ориентирован на последующие узлы вычисли-
вычислительной сетки, а не на конечные узлы, неизвестные заранее.
Следствием этого может быть существование некоторых реше-
решений с меньшими аберрациями, чем найденные с помощью этого
алгоритма. Они могут быть предельными с точки зрения мате-
математики, однако это не означает, что метод недействителен.
В самом деле, этот метод дает эффективный простой путь по-
поиска с помощью системы, размеры которой можно контролиро-
524
Оптимизация и синтез электронных и ионных линз
вать из бесконечного числа возможных распределений. Экспе-
Эксперименты с вычислительными сетками малых размеров, где были
проанализированы все возможные распределения, показали
[338], что решения, найденные с помощью алгоритма динами-
динамического программирования, были или равны, или очень близки
к оптимальным.
Этот метод можно еще улучшить, если сделать несколько
следующих предположений [321, 338]:
1. Нацелить процедуру оптимизации на заданное конечное
условие, т. е. на выбор предшествующего узла для произволь-
произвольного узла вычислительной сетки таким образом, чтобы миними-
минимизировать коэффициент аберрации не в данном узле, но в зара-
заранее выбранной конечной точке с заданными характеристиками
(например, Я = 0 или h' = 0).
2. Сохранить первоначальный алгоритм, но сделать Az пе-
переменной величиной, чтобы обеспечивать плавное распределение
даже для сеток относительно малых размеров.
3. Заменить вычислительную сетку в плоскости Wz сеткой
в фазовой плоскости hh' параксиального луча. Влияние поля
должно аппроксимироваться импульсом дельта-функции в каж-
каждой узловой точке с последующим дрейфовым пространством.
Возможные значения поля должны выбираться таким образом,
чтобы импульсы и дрейфы всегда отображали узлы сами на
себя.
4. Избегать трудностей, связанных с дискретным характе-
характером метода, с помощью использования различных способов ди-
динамического программирования.
Метод динамического программирования успешно применял-
применялся к различным задачам электронной и ионной оптики. В слу-
случае магнитных линз использовалась кусочно-линейная модель
разд. 8.3.3 и W(z) определялась как
l/M], (9.44)
так, чтобы параметр
6=AWAz (9.45)
вычислительной сетки был безразмерен. Типичная диаграмма
решения показана на рис. 141 [296] для М=100, N = 20 и б =
= 0,005 (рассматриваются только положительные величины
W). Целый ряд распределений индукции минимизирует сфери-
сферическую аберрацию при различных начальных и конечных усло-
условиях. Выбирая конечную точку из практических соображений,
можно проследить решение обратно к начальной точке. Рас-
Рассмотрим, к примеру, простую диаграмму, показанную на
рис. 142, которая была вычислена для М = 20, N=10 и 6 = 0,1.
Этот случай дает представление о сетке умеренных размеров,
525
Глава 9
.1 S 10 15
~20 Д2
20
W/AW
Рис. 141. Диаграмма решения задачи поиска методам динамического про-
программирования распределения магнитной индукции с минимальной сфериче-
сферической аберрацией (М=100, jV=20, 6=0,005) [2,96].
Рис. 142. Диаграмма решения задачи поиска методом динамического програм-
программирования распределения магнитной индукции с минимальной сферической
аберрацией (М=20, N= 10, 6 = 0,1) [296].
но все еще со значительной областью определения. Практиче-
Практически интересные распределения индукции, взятые с этой диаграм-
диаграммы и отмеченные цифрами, показаны на рис. 143. Решения
№ 1,8, 17, 26 и 39 представляют длинные линзы с низкой сфе-
сферической аберрацией (разд. 8.2.3). Особенно интересно решение
№ 27, потому что оно представляет распределение с высоким
полем вблизи объекта, низким — вблизи изображения и реаль-
526
Оптимизация и синтез электронных и ионных линз
но очень низкой сферической аберрацией: &CSO = 0,396 при М =
=—5,32 (см. теоретические пределы, описываемые уравнением
(9.33)). Это соответствует конденсорному объективу, обсуждав-
обсуждавшемуся в разд. 8.4.1. Наш метод позволяет конструктору уста-
установить оптимальную скорость уменьшения этого поля [165]. Ре-
Решение № 27, кроме того, демонстрирует мощность метода в дру-
другом аспекте. Его сравнение с близко проходящей штриховой
кривой на этом рисунке, которая представляет гиперболическое
поле уравнения (8.76), показывает, что коэффициент сфериче-
сферической аберрации нашего решения на 47% меньше, чем коэффи-
коэффициент сферической аберрации гиперболического поля распреде-
распределения.
Рис. 143. Частное решение, представляющее практический интерес, взятое из
диаграммы на рис. 142 [296].
В случае электростатических линз [339—341] достаточно
выбрать кусочно-квадратичную модель разд. 7.2.3 и определить
W{z) как
W(z)=U'(z)/[U(zo) - Uo] [1/м], (9.46)
при этом б — снова безразмерная величина. Мы нашли мно-
множество интересных конфигураций, некоторые привычные, но
много и новых. Типичная диаграмма решения показана на
рис. 144 для М = 50, N=60 и 6 = 0,2. В эту диаграмму включено
большое количество распределений ускоряющих иммерсионных
линз, соответствующих различным начальным и конечным ус-
условиям. Все приемлемые решения начинаются и заканчиваются
полем, значения которого близки к нулю, и представляют двух-
двухцилиндровые линзы со вторым цилиндром, имеющим меньший
диаметр и более высокий потенциал по сравнению с первым при
фиксированном положении объекта.
Метод динамического программирования можно применить
для решения ряда проблем: оптимизации пучков высоких энер-
527
Глава 9
гий в ускорителях частиц, накопительных кольцах, системах
транспортировки пучка и т. п. [342]. Например, возбуждения
в длинном ряде квадруполей, используемых в сог/ласующих си-
системах накопительных колец, можно искать таким образом, что-
чтобы они минимизировали общую сумму бетатронных функций,
измеренных у средней плоскости каждого квадруполя, обеспе-
обеспечивая, таким образом, оптимальное согласование пучка
(разд. 10.4.5.1). Динамическое программирование можно при-
применять для уменьшения аберраций в системах Транспортировки
пучка, для минимизации нелинейных эффектов в корректирую-
корректирующих мультиполях и т. д.
Рис. 144. Диаграмма решения задачи поиска методом динамического програм-
программирования электростатической иммерсионной линзы с минимальной сфериче-
сферической аберрацией (Af=50, #=60, 6=0,2) [339].
Наконец, мы должны отметить, что распределения полей,
найденных методом динамического программирования, очень
редко пересекаются друг с другом (см. рис. 141—144). Их гра-
графики похожи на изоклины дифференциального уравнения, ко-
которое удовлетворяется оптимизированным распределением
поля. Как отмечалось в разд. 9.1, это неизвестное дифференци-
дифференциальное уравнение может быть связано с уравнением (9.4).
9.6. Метод оптимального контроля
Мы предложили другой очень эффективный метод для ре-
решения проблемы оптимизации [343J. Снова разделим отрезок
оси, на которой задано распределение, на N одинаковых интер-
интервалов и представим неизвестную функцию V(z) простым поли-
полиномиальным выражением в каждом интервале. Чем проще эти
выражения, тем быстрее и легче проходит эта процедура. По-
Потребуем непрерывности функции V(z) и ее производных низ-
528
Оптимизация и синтез электронных и ионных линз
шего порядка. Это требование связывает определенными соот-
соотношениями коэффициенты полиномов в соседних интервалах.
Зададим требование непрерывности таким образом, чтобы ко-
коэффициенты при членах наиболее высокого порядка оставались-
свободными. Тогда эта проблема сводится к проблеме поис-
поиска N коэффициентов, таких, чтобы результирующая функция
удовлетворяла уравнению параксиальных лучей (9.21) и прак-
практическим ограничениям, одновременно минимизируя интеграл
аберраций уравнения (9.17).
Начнем с произвольного набора свободных коэффициентов.
Уравнение параксиальных лучей решается с этими коэффици-
коэффициентами для каждого интервала, а соответствующий интеграл
аберраций оценивается численно. Естественно, с первой попыт-
попытки коэффициент аберрации будет слишком высок, а ограниче-
ограничения вряд ли будут выполнены. Далее введем штраф, отражаю-
отражающий нарушение ограничений на объективную функцию, постро-
построенную из интеграла аберраций. Эта сумма является функцией
мишени N коэффициентов, которую мы пытаемся минимизиро-
минимизировать. Таким образом, мы свели проблему к задаче минимизации-
функции.
Точно такая же проблема возникает в задачах оптимального-
контроля. Минимизация может быть выполнена с помощью лю-
любого из методов нелинейного программирования [344], напри-
например квазиньютоновским алгоритмом. Окончательный результат*
является набором новых коэффициентов, удовлетворяющих
уравнению параксиальных лучей совместно с заданными огра-
ограничениями и одновременно минимизирующих интеграл абер-
аберраций.
Недостатком этого метода по сравнению с методом динами-
динамического программирования является то, что с его помощью мож-
можно найти только локальный оптимум, следовательно, он требует
начального набора коэффициентов, который выбирает сам поль-
пользователь. С другой стороны, он обладает чрезвычайными быст-
быстротой и эффективностью. Почти всякая комбинация начальных:
данных сходится к приемлемому решению за 10—20 с счетного
времени на компьютере CDC Cyber 175 при N=\0. Увеличе-
Увеличение числа интервалов улучшает решения при незначительное
увеличении времени счета. Метод работает лучше всего при
N = 25—30. Дальнейшее увеличение числа интервалов пользы не
приносит, так как проблема усложняется настолько, что задача
сходится при значениях N^50.
Осевое распределение электростатического потенциала, по-
показанное на рис. 145, было получено с помощью этого метода.
Мы выбрали N=10 и ввели некоторые ограничения для потен-
потенциала и его производной по z. Это распределение соответствует
асимметричной трехэлектродной линзе с отношением потенциа-
529?
Глава 9
лов изображение — объект 0,72 и отношением максимального
потенциала к потенциалу объекта, равным 6. Объективная
функция была выбрана как CSo°o\U'\max/(Umax—£/р), т.е. как
коэффициент сферической аберрации, отнесенный к величине с
размерностью длины, подобной той, которая дается уравнением
(9.34). Это гарантирует, что в результирующем распределении
не будут существовать вариации неприемлемой величины. Дей-
Действительно, объективная функция не превышает 1,68 и распре-
распределение достаточно гладкое, чтобы его было легко реконструи-
реконструировать реальной системой электродов (рис. 146). Соответствую-
Соответствующая величина CSooo/Lg=l0, что'лучше, чем для любой стан-
U(z)-U0
U@)-U0
0,5
-*■ r/L
Рис. 145. Распределение электростатического потенциала с низкой сфериче-
сферической аберрацией, полученное методом оптимального контроля [343].
дартно сконструированной электростатической линзы (см.
табл. 11). Коэффициент добротности, которому мы отдаем пред-
предпочтение, равен Csooo//i = l,02, которая также находится вблизи
наилучших значений, достигаемых при таких низких отношени-
отношениях максимального потенциала к потенциалу объекта.
Известны еще два метода поиска локального оптимума для
электронных оптических систем [345, 346].
9.7. Аналитические функции
Наиболее легкий путь поиска распределений полей, обеспе-
обеспечивающих малые аберрации,— исследование аналитических
функций [260, 326, 347, 348]. Несколько аналитических моделей
линз были представлены в'гл. 7 и 8. Предполагалось [326],что
распределение потенциала, сформированное суммой экспонен-
экспоненциальных членов и имеющее серию пиков переменной аяплиту-
530
Оптимизация и синтез электронных и ионных линз
ды, может дать электростатические линзы с малыми сфериче-
сферическими аберрациями. С помощью компьютера легко запрограм-
запрограммировать поиск посредством различных вариаций параметризо-
параметризованных аналитических функций. Мы уже с успехом использова-
использовали этот метод [260] для систематического исследования ряда,
параметризованных аналитических функций различных классов
и нашли много интересных распределений потенциалов с отлич-
отличными свойствами. Они удовлетворяют практическим требова-
требованиям для зондовой оптики и имеют очень низкие сферическую
и хроматическую аберрации (Cso<x>/fi~l, CCo<x,/fi^0,5). На ос-
основе этих компьютерных экспериментов оказалось возможным
отказаться от утвердившегося мнения о внутренне присущем
превосходстве магнитных линз над электростатическими.
и@) 6,38UB) п72и(с)
-0,5 ■
Рис 146. Трехэлектродная электростатическая линза, реконструированная из
распределения осевого потенциала, изображенного на рис. 145 [352].
Одним из простейших классов параметризованных аналити-
аналитических функций является класс полиномов высших степеней,
коэффициенты которых — простые функции значений потенциа-
потенциала в заданных точках. Варьируя коэффициенты полинома седь-
седьмой степени, можно получить столь же хорошие результаты,,
как и при использовании более громоздких аналитических
функций. Ко всему прочему, реконструкция электродов или по-
полюсных наконечников не вызывает затруднений, так как в этом
случае число членов ряда C.20) конечно. Как мы увидим в сле-
следующем разделе, это чрезвычайно важное соображение. Одна-
Однако, как хорошо известно (см. раздел 3.3.5), при использовании
полиномов высших степеней возможны неожиданные флуктуа-
флуктуации. Эту трудность можно обойти, если использовать более
сложные методы, например полиномы Чебышева или кусочные
полиномиальные функции (см. разд. 9.9).
Простой подход, изложенный в этом разделе, весьма плодо-
плодотворен, поскольку не требует сложных математических методов,
531
Глава 9
однако способен обеспечить вполне приемлемые результаты.
■С его помощью можно получить отличные распределения по-
полей даже на персональном компьютере. Однако если кто-то же-
желает исследовать огромное разнообразие всех возможных рас-
распределений, то он должен воспользоваться методами, описан-
описанными в предыдущих разделах.
9.8. Реконструкция электродов и полюсных
наконечников по оптимизированному осевому
распределению поля
После того как найдено осевое распределение поля с нуж-
-ными оптическими свойствами, следующей задачей является
поиск таких конфигураций электродов и полюсных наконечни-
наконечников, которые бы создавали необходимое распределение. Так как
потенциал, созданный осесимметричной системой, в произволь-
произвольной точке пространства однозначно определяется его осевым
распределением, с теоретической точки зрения реконструкция
.электродов не составляет никакой проблемы.
Осесимметричный электростатический или магнитный ска-
скалярный потенциал можно вычислить по его осевому распреде-
распределению, используя расходящийся ряд C.20) или комплексный
интеграл C.112). Компоненты электрического поля и вектора
магнитной индукции определяются рядами C.38) —C.40) и
C.45) — C.47) соответственно. Комплексный интеграл может
-быть вычислен только для аналитических функций. Разложение
степенного ряда требует, чтобы осевое распределение задава-
задавалось как 2 (я—1) раз дифференцируемая функция координа-
координаты z, где п — число членов степенного ряда. К сожалению, для
лриемлемой сходимости необходимо весьма большое п. Еали
осевое распределение задано набором численных данных (что
является обычным при процедурах оптимизации, обсуждаемых
дальше) или даже если оно известно в виде громоздкой анали-
аналитической функции, то производные высших порядков необходи-
необходимо получать численными методами, которые дают большие по-
погрешности (см. разд. 3.3.5.1).
Если степенной ряд уравнения C.20) произвольно обрыва-
«тся при некотором я, результат может быть весьма ненадеж-
ненадежным. К примеру, раннее предположение Шерцера о распреде-
распределении потенциала для слабой однопотенциальной электростати-
электростатической линзы с минимальной сферической аберрацией (см.
уравнение (9 14)) было перенесено на участок эквипотенциаль-
эквипотенциальной поверхности с использованием только семи членов [326]',
поэтому полученный результат оказался действительным толь-
только для области, близкой к оси. Хотя радиус сходимости может
Оитимизация и синтез электронных и ионных линз
быть очень велик или даже бесконечен, в реальных вычислени-
вычислениях разложение в ряд может быть использовано практически
только в ограниченной области вокруг оси. Если осевое распре-
распределение известно с небольшой ошибкой, то ошибка возрастает
экспоненциально с радиальным расстоянием. Эта числовая не-
нестабильность делает использование разложения степенного ряда
для реконструкции электродов или полюсных наконечников
очень затруднительным [ПО, 348]. Ко всему прочему, даже
если мы достигнем успеха в реконструкции, результирующая
картина эквипотенциальных поверхностей обычно сильно услож-
усложнена и содержит полюсы и другие сингулярности; поэтому из-
изготовление электродов может оказаться невозможным.
Поскольку оптимизированное осевое распределение обычно
дается набором численных данных, они должны быть аппрокси-
аппроксимированы простыми, непрерывными, 2 (я—1) раз дифференци-
дифференцируемыми функциями, где п — большое число, определяемое тре-
требованиями заданной точности. Из-за указанных выше числен-
численных трудностей это очень сложная проблема. Поэтому вполне
понятно, почему некоторые исследователи выражают скепти-
скептицизм по поводу самой возможности решения проблемы синтеза
электронно-ионной оптики [ПО].
Существует несколько предположений о том, как преодо-
преодолеть эту трудность. Записывая распределение осевого потенциа-
потенциала как взвешенную сумму вкладов от системы электродов и
полюсных наконечников, можно с помощью матрицы обратного
преобразования или подгонки методом наименьших квадратов
установить геометрические формы, способные создавать желае-
желаемое осевое распределение ([349]. По существу это метод, обрат-
обратный методу зарядовой плотности (разд. 3.3.4), но практическо-
практического применения он не находит.
Другое предположение состоит в том, чтобы преобразовать
уравнение Лапласа в дифференциальное уравнение в частных
производных гиперболического типа, для которого потенциал в
произвольной точке пространства может быть выражен в виде
интеграла [350]. Решение первоначальной задачи также может
быть найдено в виде конечного ряда Фурье — Бесселя [351].
Однако эти методы на практике обычно не используются. Маг-
Магнитное поле без ферромагнитных материалов может быть лег-
легко реконструировано катушками с переменным числом вит-
витков [16].
Мы предложили [140] метод для замены осевого распреде-
распределения, заданного как последовательность дискретных данных,
непрерывными, 2(я—1) раз дифференцируемыми функциями с
минимальным интерполяционным шумом, использующим интер-
интерполяционные импульсы уравнения C.393). Применение этого
метода также не обходится без проблем.
533
Глава 9
Единственное исключение, где проблема реконструкции мо-
может быть решена тривиально, относится к полиномиальным
функциям (см. разд. 9.7). В этом случае степенной ряд уравне-
уравнения C.20) содержит вполне определенное число членов, так как
все производные высших порядков равны нулю. Тогда естест-
естественно применить полиномиальную интерполяцию к оптимизиро-
оптимизированной осевой функции, заданной в виде последовательности
дискретных данных. Однако это решение не является хорошим
из-за интерполяционного шума (см. разд. 3.3.5 и 9.7). Полиномы
можно использовать различными способами, которые, однако,
будут обсуждаться в следующем разделе.
Так как, по всей видимости, ничто не ведет в направлении
правильного решения проблемы реконструкции, мы должны
попытаться использовать тот факт, что сплайновая интерполя-
интерполяция (см. разд. 3.3.5.4) обеспечивает плавные кривые. Можно
достигнуть очень хорошей точности реконструкции при исполь-
использовании этого метода [260].
При аппроксимации численных данных гладкими кубиче-
кубическими сплайновыми кривыми все их производные выше 3-го по-
порядка внутри сплайновых интервалов будут равны нулю. Труд-
Трудность состоит в том, что 3-я производная не является непрерыв-
непрерывной, следовательно, 4-я производная становится бесконечной на
границах интервалов и последующие производные более высо-
высоких порядков могут быть представлены как производные ряда
дельта-функций. Строго говоря, степенной ряд уравнения
C.20) неприменим для осевых функций, имеющих нарушения
непрерывности производных высших порядков, потому что ре-
результирующая функция потенциала не будет непрерывной на
границах интервалов.
Попытаемся преодолеть эту трудность, просто проигнори-
проигнорировав эту функцию.
Процедура элементарна [352]. Предположим ad hoc, что
производные высших порядков на границах интервалов, кото-
которые нигде больше не появляются, в выражениях для фокуси-
фокусирующих свойств и аберраций третьего порядка также не влия-
влияют на распределение потенциала. Тогда мы можем использо-
использовать первые два члена уравнения C.20). Полагая значение по-
потенциала равным V в произвольной точке с координатами г
и z, помещенной в k-м интервале, получим уравнение эквипо-
эквипотенциальной поверхности в виде
r* = 4[Uk(z)-V]/Uk"(z), (9.47)
где Uk(z)—кубическая полиномиальная функция для k-то ин-
интервала (см. разд. 7.2.4). Как Uk(z), так и Uk"{z) имеют раз-
различные выражения для каждого интервала, но они обе явля-
являются непрерывными функциями на протяжении всей длины оп-
534
Оптимизация и синтез электронных и ионных линз
тической системы. Используя эту простую формулу, можно
реконструировать эквипотенциальные поверхности, а значит,
и электроды (полюсные наконечники), которые будут воспро-
воспроизводить те же функции U(z), U'(z) и U"(z) и, таким образом,
те же свойства первого и третьего порядка аберрации, как и
первоначальное теоретическое распределение, полученное мето-
методом оптимизации.
Сначала мы исследовали функцию U (г) и подсчитали чис-
число К ее точек перегиба. Очевидно, г достигает бесконечности
в каждой точке перегиба, где [/^" = 0, следовательно, число
электродов или полюсных наконечников равно Л'+l. Если зна-
значение второй производной отрицательно между двумя точками
перегиба или между точкой начала/конца и ближайшей точкой
перегиба, то нужно выбрать потенциал электрода несколько
выше, чем максимальный осевой потенциал в этом интервале.
Если вторая производная положительна, потенциал электрода
должен быть ниже, чем минимальный осевой потенциал.
Конечные размеры физической системы являются ограниче-
ограничением точности реконструкции, потому что электроды должны
быть обрезаны где-нибудь на конечном расстоянии от оси в
пределах максимального г и реалистических размеров, обычно
на расстоянии половины общей длины фокусирующего элемен-
элемента. Таким образом, часть материала электродов (полюсных на-
наконечников) не учитывается. С другой стороны, обрезание элек-
электродов имеет по крайней мере три преимущества:
1. Оно гарантирует некоторое минимальное расстояние меж-
между электродами, что предотвращает электрический пробой в слу-
случае электростатических линз.
2. Можно дополнительно упростить формы электродов в те-
течение этого процесса и заменить сложные искривленные грани-
границы легко изготовляемыми простыми правильными поверхно-
поверхностями.
3. Конечно, результирующая физическая система будет
иметь неограниченное число производных высших порядков,
следовательно, не будет проблем с математическими ограниче-
ограничениями метода или с аберрациями пятого порядка (см. обсуж-
обсуждение, приведенное ниже).
Что мы знаем о том, как работает этот метод? Аналитиче-
Аналитические процедуры для вычисления распределений электростати-
электростатических и магнитных полей, полученных при помощи реконст-
реконструированных конфигураций электродов и полюсных наконечни-
наконечников, так же как и программы хода лучей, используются для
упрощения форм электродов и для проверки того, создают ли
они реально распределение осевого поля и оптические свойства
достаточно близкие к первоначальным, полученным с помощью
алгоритма оптимизации. Эти аналитические процедуры также
535
Глава 9
используются для оценки точности метода. Мы нашли, что мак-
максимальное расхождение в осевом распределении, свойствах пер-
первого порядка и коэффициентах аберрации не превышает 10%*
(Влияние упрощения электродов на точность будет обсуждать-
обсуждаться ниже в разд. 9.10.1.) Это означает, что наш простой метод
реконструкции способен обеспечить практически реализуемую
фокусирующую систему с такой точностью.
Так как этот метод реконструкции устанавливает основные
элементы одного из методов синтеза (см. разд. 9.10), важно
остановиться и обсудить некоторые аспекты его реализации.
1. Физические величины никогда точно не измеряются и стро-
строгое совпадение — понятие для физики бессмысленное [353] (тем
более в практических задачах технического конструирования).
Поэтому предположения ad hoc обычно используются в физике
и технике. Хорошим результатом можно считать приближенную
реализацию заданного распределения осевого потенциала с по-
помощью реконструированной системы электродов. Это можно-
сделать с любой степенью точности с помощью бесконечного
числа различных пространственных распределений потенциа-
потенциалов, в которых сингулярности отсутствуют [351, 353]. Точно то-
тоже мы делаем в процедуре реконструкции. Пренебрегая влия-
влиянием нарушений непрерывности третьей производной сплайно-
вой функции и образуя относительно простые эквипотенциаль-
эквипотенциальные поверхности без полюсов и других сингулярностей, мы по
существу вводим аппроксимацию. Является ли она приемле-
приемлемой? На этот вопрос ответ может дать только практика. Чтобы
обеспечить «правильную» реконструкцию электродов, необходи-
необходимо всего лишь показать, что они воспроизводят описанное рас-
распределение потенциала с точностью, которая не оказывает су-
существенного влияния на положения кардинальных элементов и
коэффициенты аберрации. Вариациями функции пространствен-
пространственного потенциала, которые не оказывают существенного влияния
на оптические свойства, можно пренебречь [353а].
2. Нарушение непрерывности третьей производной и неопре-
неопределенность производных высших порядков в узлах сетки не
создают особенных проблем, потому что, когда выбраны окон-
окончательные упрощенные формы электродов, мы отклоняемся от
математически «неоправданного» распределения потенциала,
пренебрегая частями электродов и изменяя форму оставшихся
частей. Естественно, эта процедура вводит в распределение все
непрерывные производные более высоких порядков, но так как
они больше нигде не появляются, можно вычислить оптические
свойства, включая и аберрации, используя только две первые
производные. Сила этой процедуры реконструкции состоит в
том, что она способна найти положения и потенциалы электро-
электродов. Их действительная форма не оказывает существенного
536
Оптимизация и синтез электронных и ионных линз
влияния на оптические свойства. Хорошо известно [348], что
осевой потенциал и оптические свойства мало чувствительны к
относительно большим изменениям формы электродов. Это по-
положительное следствие отрицательной особенности, обсуждав-
обсуждавшейся выше, что ошибка растет экспоненциально с ростом рас-
расстояния от оси-. Эта особенность означает, что электроды раз-
разной формы могут давать вдоль оси приблизительно одинаковые
распределения. Следовательно, хотя ошибка аппроксимации с
удалением от оси, очевидно, увеличивается, это не является су-
существенной проблемой.
3. Приведенные выше аргументы можно применить также
и к проблеме аберраций высших порядков. Наш метод основан
на том факте, что аберрации третьего порядка всегда могут
быть выражены в виде интегралов, не зависящих от производ-
производных осевого потенциала или индукции, порядок которых выше
второго. Это, конечно, не относится к аберрациям пятого по-
порядка. Но, как и прежде, в первоначальном распределении про-
производные четвертого порядка почти везде равны нулю, следо-
следовательно, можно предположить, что неучтенное влияние высших
цроизводных в некоторых дискретных точках не вносит сущест-
существенного вклада в аберрации пятого порядка. Более того, после
упрощений фактической системы электродов получатся конеч-
конечные высшие производные, которые не могут давать сингулярно-
сингулярности в аберрациях пятого и более высоких порядков. Кроме
того, можно совсем избавиться от этой проблемы, используя
для реконструкции сплайны пятого порядка (см. разд. 9.9).
В этом случае используются три члена уравнения C.20), и фор-
форма электрода будет определяться уравнением
(z), (9.48)
где теперь Uk(z)— полиномиальная функция для k-ro интер-
интервала. В этом случае радиальные смещения достигают бесконеч-
бесконечности, где производные четвертого порядка осевого распреде-
распределения потенциала равны нулю, т. е. эти точки определяют гра-
границы электродов.
4. Все прямые численные методы вычисления поля по за-
заданной системе электродов или полюсных наконечников (см.
разд. 3.3) имеют ограниченную точность. Для методов конечных
разностей и конечных элементов мы должны задать потенциал
в каждой точке границы, где значение потенциала может быть
неизвестно. В случае метода плотности заряда аппроксимация
внутри областей сингулярности, так же как и предположение
о постоянстве зарядов по всем ограниченным поверхностям в
сильных полях, накладывает определенные ограничения. Как
хорошо известно, ршибки в вычислении оптических свойств
537
Глава 9
электростатических и магнитных линз почти всегда возникают
как следствие неточной оценки распределения полей. Эти не-
неточности делают практически невозможным получение правиль-
правильного представления о точности реконструкции.
5. Наконец, в случае сплайновых линз следующий важный
аспект заключается в том, что сплайн является не аппроксима-
аппроксимацией, а самой функцией, которую мы пытаемся реконструи-
реконструировать.
Как пример, трехэлектродная электростатическая линза,
реконструированная из оптимизированного осевого распределе-
распределения, изображенного на рис. 145, показана на рис. 146. Потен-
Потенциалы электродов выражены в единицах потенциала первого
электрода. Отметим, что отношение максимального потенциала
к потенциалу объекта для электродов несколько выше, чем для
осевого распределения. Максимальное расхождение между осе-
осевым потенциалом первоначальной функции и практически реа-
реализованной системы составляет 8,3% Umax- Сферический коэф-
коэффициент добротности CSOoo/fi = 0,95 лучше, чем для первона-
первоначальной функции, вследствие того, что она оптимизировалась
в соответствии с другой объективной функцией (см. разд. 9.6).
Хроматический коэффициент добротности равен CCOoo//i = 0,72.
9.9. Полиномиальные и сплаиновые линзы
9.9.1. Полиномиальные линзы
Мы видели в разд. 9.7, что, меняя коэффициенты полинома,
можно найти для линз очень хорошие поля. Эти коэффициенты
связаны простыми соотношениями с потенциалами в заданных
точках. Так как количество членов степенного ряда C.20)
в этом случае ограничено, точной реконструкции электродов
или полюсных наконечников можно достигнуть с помощью очень
простой процедуры (см. разд. 9.8).
Проблема заключается в том, что если полином использует-
используется для построения кривой, т. е. для аппроксимации некоторой
осевой функции, заданной в виде последовательности дискрет-
дискретных данных, то высокий интерполяционный шум, обсуждавший-
обсуждавшийся в разд. 3.3.5, может полностью нарушить первоначальное
распределение. Следовательно, полиномиальную интерполяцию
нельзя использовать в качестве практического рабочего инстру-
инструмента.
Существует, однако, очень эффективный способ использова-
использования отличных реконструкционных свойств простых полиномов.
Если мы не будем пытаться строить никакой кривой, но вместо
этого исследуем свойства полиномиальных полей, проблема ин-
интерполяционного шума сразу же исчезает. Таким образом, мож-
538
Оптимизация и синтез электронных и нежных линз
но взять несколько полиномиальных функций, менять их коэф-
коэффициенты и искать для таких наборов коэффициентов те функ-
функции, которые обеспечат наилучшие оптические свойства. Этим
способом были открыты электростатические полиномиальные
линзы (разд. 7.3.1.5). Среди них наилучшими из известных яв-
являются кубические полиномиальные линзы, следовательно, они
могут служить моделью для сравнения с другими полиномиаль-
полиномиальными и сплайновыми линзами. Если рассмотреть случай, когда
отношение потенциалов изображение — объект равно 5, то ко-
коэффициенты добротности равны CSOOo//i = 19,3 и Ceooo//i = 1,43
(см. рис. 81 и 82). В соответствующей обработке эти величины
могут быть использованы для сравнения.
Полиномы более высоких порядков могут быть успешно ис-
использованы для развития моделей линзовых полей, из которых
легко реконструировать электроды и полюсные наконечники.
Такие линзы были кратко обсуждены в разд. 7.3.1.5. Формула
реконструкции для полинома пятого порядка дается уравнени-
уравнением (9.48). Однако вследствие осциллирующей природы полино-
полиномов высших порядков этот подход, очевидно, ограничен. Хотя
мы и не собираемся проводить подгонку кривой, мы все же
должны избегать сильно флуктуирующих функций. Естествен-
Естественным путем является использование сплайновых функций для
представления осевого потенциала.
9.9.2. Сплайновые линзы
Модель сплайновой линзы была введена в разд. 7.2.4 и 8.3.4,
а понятие сплайновой линзы исчерпывающе обсуждено в
разд. 7.6.3. Основной замысел состоит в систематическом ис-
исследовании полей линзы на основе кубической сплайновой мо-
модели, которая является стандартным инструментом для варьи-
варьирования основных параметров осевых распределений различ-
различных классов линз. Кроме того, эта модель позволяет очень чет-
четко определить границы линзы, и есть простая и эффективная
процедура реконструкции реальных электродов или полюсных
наконечников, которые дают на оси сплайновые распределения
(см. разд. 9.8).
Как известно (разд. 3.3.5.4), кубический сплайн является
лучшим инструментом для замены дискретных данных гладкой
функцией. Сплайн представляет собой систему кубических по-
полиномов между каждой соседней парой узловых точек, обла-
обладающих тем свойством, что соседние полиномы соединяются
непрерывно при непрерывных первых и вторых производных.
Если разделить длину L распределения потенциала на N рав-
равных частей, то получим N+1 точки, в которых определены зна-
значения функции осевого потенциала U{z). Сплайн будет состо-
539
Глава 9
ять из N кубических выражений, по одному для каждого из
N интервалов, между последующими узлами. На k-м интерва-
интервале из уравнения C.394) для функции осевого потенциала
имеем
(9.49)
где zk-i — координата k-то интервала слева от точки (см.
рис. 41), a k=\, 2,..., N. Естественно, коэффициенты А к, Bkr
Ck и Dk различны для каждого интервала; следовательно, рас-
распределение потенциала и его производных имеет разные выра-
выражения для каждого из N интервалов. Чтобы обеспечить непре-
непрерывность сплайна, так же как и его первых и вторых производ-
производных, в каждом из N—1 узлов, уравнения C.398) — C.400)
должны удовлетворяться для этих коэффициентов, где б есть
то же, что и Дгв уравнении (9.40).
Оставшиеся N+3 свободных коэффициента могут быть ис-
использованы для построения некоторой кривой в N+1 точках и
для обеспечения нулевых наклонов на концах распределения
потенциалов, гарантируя таким образом плавный переход к об-
областям, в которых поле отсутствует с обеих сторон линзы, или
для удовлетворения любого другого граничного условия. У нас
есть два уравнения, чтобы удовлетворить условию нулевого на-
наклона:
Bi = 0, (9.50)
Я„+2С„6 + 3£„62 = 0. (9.51)
N+l коэффициент все еще остается свободным. Теперь, вме-
вместо того чтобы использовать эти коэффициенты для построения
некоторой кривой, будем варьировать их и искать такие наборы
коэффициентов, которые обеспечат наилучшие оптические свой-
свойства. Это сразу же облегчит проблему реконструкции, обсуж-
обсуждавшуюся в разд. 9.8. В самом деле, так как мы теперь не пы-
пытаемся строить никакой кривой, мы не аппроксимируем функцию
с бесконечным числом непрерывных и ограниченных производ-
производных высших порядков другой функцией только с тремя произ-
производными внутри интервалов, но неопределенными производны-
производными высших порядков на границах. Вместо этого исследуется сама
сплайновая функция. Конечно, все соображения, обсуждавшие-
обсуждавшиеся в разд. 9.8, все же справедливы, но по крайней мере теперь
осевая функция не является приближением. Поэтому, хотя оче-
очевидно, что аппроксимация заданной осевой функции 20-интер-
вальным сплайном намного лучше, чем двухинтервальным
сплайном, реконструкция двухинтервальной сплайновой линзы
осуществляется с той же точностью, что и 20-интервальной.
540
Оптимизация и синтез электронных и ионных линз
UU)-U0
U@)-U0
10
Нашей целью является систематическое исследование линз-
путем изменения основных параметров распределения потен-
потенциала в процессе конструирования сплайновой модели [202]
(см. разд. 7.6.3). Это может быть сделано в соответствии с од-
одной из двух основных стратегий:
1) рассматривая класс сплайнов с фиксированным числом,
интервалов,
2) аппроксимируя определенный класс распределений потен-
потенциала различными сплайнами.
Реальная задача конструирования сплайна является простой:
и устойчивой процедурой (см. разд. 3.3.5.4). Возможен не толь-
только кубический сплайн: также могут быть использованы сплай-
сплайны пятого и более высоких порядков.
Простейшая из возможных
сплайновых линз может быть
использована как «обычный де-
делитель». Если имеется только
один интервал, сплайн вырож-
вырождается в простую кубическую
полиномиальную функцию.
Это случай кубической поли-
полиномиальной линзы (разд.
7.3.1.5), которая может быть
названа сплайновой линзой с
тем же успехом, как прямая
линия — кривой. Ее коэффи-
коэффициенты добротности, приве-
приведенные в разд. 9.9.1, могут
быть использованы для срав-
сравнения различных сплайновых
линз.
Мы увидим в разд. 9.10,
что понятие сплайновых линз является мощным инструментом
для синтеза электронных и ионных линз. Оно может быть ис-
использовано как для электростатических, так и для магнитных,
линз. Как становится очевидным из разд. 9.9.2.1, множества
интересных распределений можно найти даже с помощью двух-
интервальных сплайнов. Очевидно, чтобы этот метод работал
в полную силу, необходимо использовать большее число интер-
интервалов для конструирования сплайнов. Мы нашли, что для кон-
конструирования линз с очень хорошими оптическими свойствами
обычно достаточно шестиинтервального сплайна. Например, ис-
исследование шестиинтервальных сплайнов привело нас [202] к
распределению потенциала, данного на рис. 147. Это распреде-
распределение имеет пять точек перегиба, следовательно, оно представ-
представляет шестиэлектродную линзу. Линза, реконструированная и»
О 0,5 1 •'«•
Рис. 147. Распределение потенциала
шестиэлектродной, шестиинтерваль-
ной электростатической сплайновой
линзы [260].
541
Глава 9
этого распределения, показана на рис. 148. Потенциалы элект-
электродов выражены в единицах потенциала первого электрода.
Коэффициенты добротности не превышают Cs<w°/fi = 0,58 и
Ccooo//i = 0,31. Точки фокусов находятся вне поля, обеспечивая,
таким образом, приемлемые рабочие расстояния.
9.9.2.1. Двухинтервальные онлайновые линзы. Как иллюст-
иллюстрацию понятия сплайновой линзы, рассмотрим простейшую не-
нетривиальную сплайновую линзу, которая определена на двух
интервалах [202]. В нашем распоряжении имеется восемь коэф-
коэффициентов, связанных между собой тремя непрерывными урав-
уравнениями: два уравнения для того, чтобы обеспечить нулевой
наклон на концах, и три уравнения для построения трех задан-
заданных значений потенциалов. Так как все оптические свойстваза-
r/L
0,3-
U(O)
0,3-
0,2-
У
3,4U<0)
0,2
0,4
0,8
г/L
Рис. 148. Шестиэлектродная электростатическая линза, реконструированная
*з распределения осевого потенциала, изображенного на рис. 147 [202].
висят от отношения потенциалов, достаточно в качестве единич-
,ного выбрать потенциал £/@) при г=0. Тогда реально имеются
два свободных параметра: потенциалы U(Lf2) и U(L) при z=
= 1/2 и z=L соответственно. Для сравнения с кубической поли-
полиномиальной линзой ограничим значения этих потенциалов ди-
диапазоном от 1/5 до 5. Конечно, можно выбрать два интервала,
длины которых являются переменными величинами, но тогда
пришлось бы вводить третий свободный параметр, который сде-
сделал бы модель эквивалентной трехинтервальному сплайну.
Наша цель в этом случае — продемонстрировать преимущества
модели, что можно сделать на простейшем примере.
542
Оптимизация и синтез электронных и ионных линз
Решение системы восьми алгебраических уравнений дает сле-
следующие значения коэффициентов:
Ci = [l2U(L/2) —9U@) — 3t/(L)]/L2,
£>i=2[5£/@) — 8U(L/2)+3U(L)]/L\ (9.52)
A2 = U(L/2),
C2«=6[t/@) —
D2=2[8U(L[2) —3U@)~5U(L)]fL3.
Эти коэффициенты обладают следующими свойствами:
1) Ai и А2— задаются значениями потенциалов в начальных
точках двух интервалов.
2) й| = 0в соответствии с уравнением (9.50).
3) В2 — значение градиента потенциала при z=L\2 (не за-
зависит от потенциала в этой точке). Отметим, что
U'(Lf2)[U(L)—U(Q)] = l,5L, как и для кубической полиноми-
полиномиальной линзы (см. уравнение G.72)).
Анализ уравнения (9.52) показывает, что распределение по-
потенциала имеет по крайней мере одну, максимум две точки
перегиба. В случае одной точки перегиба имеем двухэлектрод-
ную линзу, две точки перегиба соответствуют трехэлектродной
линзе. В каждом интервале может быть максимум одна точка
перегиба, но ее положение внутри интервала может быть вы-
выбрано произвольно. Если одна точка перегиба расположена точ-
точно посредине распределения, мы имеем дело со специальным
случаем симметричной кубической полиномиальной линзы.
Если имеются две точки и они расположены симметрично отно-
относительно средней плоскости распределения, то это соответству-
соответствует симметричной однопотенциальной линзе. В остальных случа-
случаях мы имеем широкий диапазон асимметричных иммерсионных,
или однопотенциальных линз.
Эти всевозможные случаи можно легко классифицировать,
исследуя распределение потенциала на выпуклость. Двумерная,
карта возможных комбинаций величин U(L/2) и U(L) делится
на шесть областей координатными осями и тремя прямыми ли-
линиями (рис. 149), уравнения которых следующие:
U(L)=4U(L/2)—3U(Q), (9.53)
U(L)=2U(L/2)-U@), (9.54)
U(L) = [4U(L!2)-U(Q)]/3. (9.55>
Эти линии соответствуют нулевой второй производной потен-
потенциала в точках z=0, z — L/2 и z—L соответственно. Распределе-
54*
Глава 9
щие потенциала вогнуто при z=0 ниже первой линии, при г =
= L/2 выше второй и z=L ниже третьей. Соответственно поло-
положения точек перегиба в этих шести областях меняются, как по-
показано на рис. 150. Если выбрать потенциалы U(L/2) и U(L)
таким образом, что окажемся точно на границе двух соседних
областей, одна из точек перегиба будет двигаться к соответст-
соответствующей узловой точке г=0, z=L/2 или z=L. Наиболее интерес-
интересный случай соответствует второй граничной линии, которая, как
мы уже указывали, соответствует симметричной кубической по-
полиномиальной линзе. Отметим, что все три линии проходят че-
U(U/2)/U@)
Рис. 149. Карта возможных двухинтервальных сплайновых линз. Три прямые
линии определяют границы между шестью областями А F. Они даются
уравнениями (9 53)—(9 55) соответственно. Кружок соответствует линзе с наи-
наилучшим хроматическим коэффициентом добротности в данной области [202].
рез точку, соответствующую тривиальному случаю £/@) =
= U(L/2)=U(L), когда распределение потенциала постоянно.
Также отметим, что теоретически мы должны иметь 23=8 раз-
различных областей на двумерной карте. Однако две из иих не
существуют, потому что кривая распределения не может быть
монотонно выпуклой или вогнутой вследствие требования ра-
равенства нулю производной на обеих концах.
Как пример, вычислим коэффициенты для симметричной од-
нопотенцйальной линзы. Подставляя £/(L) = £/@) в уравнение
{9.52), получим
i 2,
С, =-С,« 12 [С/A/2) - £/@)]/L2,
(9.56)
544
Оптимизация н синтез электронных и ионных линз
•з-
3
^*
N.
1,8
1,6;
1,4
1,2
1,0
0,8;
o,6:
0,4:
0,2
у
———^^
0,0 0,2 0,4 O,E
r 0 z
0,9-
0,8-
0,7-
0,6-
0,5-
0,4-
0,3-
0,2-
0,1-
0 0-
\
4
0,0 0,2 0,4 0,6
z/L
2,4
2,2
2,0-
1,8
1,6
1,4
12
1,0
0,8
0,6
0,4-
0,2
0.0-
^—
у
^y
у
a
Z)
Ы
0,8 1,0
4
^—
6
0
s
0,8 1,0
.
8
g
s
0,3
0,8
0,7
0,6
0,5-
0,4
0,3-
0,2
0,1
n n.
\
N.
N.
N.
0,0 0,2 0,4 0,6 0,8 1,0
3 5-
1
3,0
2,5
2,0-
1,5-
1,0-
0,5
0 0-
у
у
у
г
0,0 0,2 0 4 0,6 0,8 1,0
G Z/L
5-
4 ■
5-
2-
1 ■
0-
/ N.
/ \
/ \
/ \
у Ч
о,о о,г о,4 . о,б о,8 1,о 0,0 о,г
z/l
о,е о,8 1,0
Рис. 150. Осевые распределения потенциалов двухинтервальиых сплайновых
лииз. Каждая кривая представляет область иа рис. 149. Точки перегиба отме-
отмечены кружками [202].
£>1 = _£>2=16[f/@) — U(L/2)]/L\
Реконструированные электроды, создающие распределение
потенциала, данного на рис. 150, е, показаны на рис. 151.
Чтобы найти линзу с хорошим коэффициентом добротности
среди двухинтервальных сплайновых линз, мы должны искать
двумерные пространства рис. 149. Такой поиск был проведен
с целью найти линзы с наименьшими хроматическими коэффи-
коэффициентами добротности и дополнительным ограничением, чтобы
точка фокуса со стороны объекта находилась вне поля. Двумер-
Двумерная карта была разделена на 100X100 ячеек вычислительной
545
Глава 9
сетки и хроматический коэффициент добротности был вычислен
в каждом из 104 узлов. Наименьшее значение (CCOoo//i = 0,72)
было найдено в точке, отмеченной на рис. 149 [£/(L/2) =
= 5£/@), U(L) = 1,44£/@)]. Это соответствует трехэлектродной
линзе. Сравнение показывает, что этот коэффициент добротно-
добротности .в два раза лучше, чем для кубической полиномиальной
линзы. Отметим, что этот коэффициент лучше коэффициента
добротности кубической полиномиальной линзы и в ряде дру-
других случаев, соответствующих асимметричным двухэлектродньш
линзам.
r/L
0,6-
0,5-
0,4-
0,3-
0,2-
0,1 -
и(о)
5 4@)
1,33 U@)
0,2
0,6
0,8
Z/L
Рис. 151. Система электродов, воспроизводящих осевое распределение потен-
потенциала, показанное на рис. 150, е (потенциалы электродов выражены в единицах
потенциала первого электрода) [202].
9.10. Процедура синтеза
В предыдущих разделах этой главы мы обсуждали различ-
различные методы поиска осевого распределения поля, которое удов-
удовлетворяет заданным требованиям и имеет низкие аберрации.
В разд. 9.8 была детально исследована проблема реконструк-
реконструкции электродов и полюсных наконечников. Теперь мы в состоя-
состоянии сформулировать общий метод синтеза электронных и ион-
ионных оптических элементов с низкими аберрациями [354].
Обсуждавшиеся до сих пор процедуры оптимизации имеют
один общий недостаток: когда мы ищем оптимальное осевое
распределение, мы не учитываем проблемы, возникающие в тех
546
Оптимизация и синтез электронных и ионных линз
точках пространства, которые не лежат на оси. Процедура ре-
реконструкции полностью отделена от алгоритма оптимизации.
Это приводит к трудностям, обсуждавшимся в разд. 9.8. Если
мы хотим синтезировать линзы хорошо обоснованным и надеж-
надежным способом, то процесс реконструкции должен быть состав-
составной частью процедуры оптимизации, в противном случае от это-
этого необходимо полностью отказаться. Вместо аппроксимации
дискретной последовательности данных, характеризующей осе-
осевое распределение некоторой функции и позволяющей провести
более или менее точную реконструкцию, мы должны искать не-
неизвестное осевое распределение непосредственно в виде непре-
непрерывной функции, которую легко продолжить на точки простран-
пространства, не лежащие на оси, т. е. в виде полиномов, либо кубиче-
кубических сплайнов, либо сплайнов пятого порядка.
Как обсуждалось в разд. 9.9, когда применяется этот под-
подход, полиномиальные и сплайновые распределения не исполь-
используются для подгонки какой-либо кривой. Процедура оптимиза-
оптимизации прямо направлена на поиск таких наборов полиномиальных
или сплайновых коэффициентов, которые обеспечивают наилуч-
наилучшие оптические свойства. Это сразу же облегчает проблему
реконструкции, потому что не приходится аппроксимировать
никакой функции. Вместо этого мы пытаемся реконструировать
точно ту же функцию, которая является предметом нашего ис-
исследования, а именно саму полиномиальную или сплайновую
функцию. Естественно, обоснования процедуры реконструкции,
обсуждавшиеся в разд. 9.8, все еще имеют силу, но ко всему
прочему ситуация значительно проясняется.
Этот подход позволяет сочетать очевидные преимущества
как динамического программирования, так и процедуры опти-
оптимального контроля с легкостью и быстротой метода реконст-
реконструкции. В дальнейшем мы выведем алгоритм синтеза для слу-
случая кубических сплайнов, но подчеркнем, что метод работает
также с полиномами или сплайнами пятого порядка.
Распределение осевого электростатического или магнитного
скалярного потенциала представляется кусочной кубической
функцией, т. е. ищется решение в виде сплайновой линзы. Осе-
Осевая длина распределения L делится на N равных интервалов.
Неизвестное распределение U(z) ищется в виде уравнения
(9.49) для каждого интервала. Для обеспечения непрерывности
этой функции, ее первой и второй производных необходимо, что-
чтобы удовлетворялись уравнения C.398) — C.400).
Следующим этапом является формулировка ограничений
этой проблемы. Они всегда зависят от конкретных практиче-
практических требований, следовательно, для них невозможно дать об-
общий рецепт. Однако существует одно ограничение, общее для
всех проблем: рассматриваемые поля должны быть практиче-
547
Глава 9
ски реализуемыми. Следовательно, потенциал и его производ-
производные должны быть ограничены:
UkU(z)<U1u \U'{z)\<Ul', \U"{z)\<Ux", (9.57)
где Uj, Uи, U\ и U\" — a priori заданные числа. Если требует-
требуется, чтобы поле исчезало с обеих сторон распределения, то так-
также должны удовлетворяться уравнения (9.50) и (9.51). Обычно
так и происходит, но не всегда (например, для катодных линз).
Кроме того, можно потребовать, чтобы траектории частиц соби-
собирались к оси и при этом не пересекались внутри линзы, таким
образом обеспечивая определенное рабочее расстояние позади,
линзы. Это требование может быть сформулировано как
r(z)>p, г'(а)>0, (9.58)
где а — граница распределения со стороны объекта, а р — за-
заданное число. В зависимости от конкретных проблем также мо-
могут быть наложены другие ограничения.
Теперь выберем объективную функцию, с помощью которой
будет проводиться минимизация. Это ответственный момент,,
так как разные объективные функции могут привести к совер-
совершенно различным результатам. Конечно, вполне естественно,,
что объективная функция должна быть выбрана в соответствии
с реальными требованиями данной проблемы. Можно отнести
любой коэффициент аберрации к любому нормирующему фак-
фактору, например входной потенциал поделить на максимум поля
(уравнение (9.34)). Процедура оптимизации может быть наце-
нацелена на конечный размер пятна, генерируя линзы, способные
обеспечивать как можно более тонкий пучок при заданных огра-
ограничениях. Рабочее расстояние и другие свойства первого поряд-
порядка могут быть также включены в объективную функцию. Любые
коэффициенты добротности из обсуждавшихся в разд. 5.7.4, мо-
могут служить объективными функциями для синтеза.
В общем случае имеем слева N+1 свободных сплайновых
коэффициентов. Обычно используется один коэффициент для
того, чтобы отнести распределение потенциала к потенциалу
£/@) в начальной точке. Тогда A\ = U@) и число свободных ко-
коэффициентов сводится к N. Для заданного набора этих коэффи-
коэффициентов легко решить уравнение параксиальных лучей и оце-
оценить объективную функцию численно. Таким образом, проблема
поиска функции среди бесконечного числа различных возмож-
возможностей, такой, чтобы она удовлетворяла всем ограничениям,
включая уравнение параксиальных лучей, и одновременно ми-
минимизировала заданную объективную функцию, свелась к про-
проблеме поиска N сплайновых коэффициентов.
Это А/-мерная проблема оптимизации с ограничениями. Мож-
Можно решить ее, используя либо динамическое программирование,
548
Оптимизация и синтез электронных и ионных лииз
либо метод оптимального контроля, причем главным преиму-
преимуществом по сравнению с первоначальной версией этого метода
будет то, что оптимизированное распределение потенциала те-
теперь оценивается в виде непрерывной сплайновой функции вме-
вместо последовательности цифровых данных.
Если применяется метод динамического программирования,
мы должны использовать тот факт, что для сплайновой модели
вторая производная распределения осевого потенциала явля-
является линейной функцией координаты z внутри каждого интерва-
интервала. Из уравнения (9.49) имеем
Uk"(z)=2Ck + 6Dk(z — z*_,). (9.59)
Тогда полное распределение второй производной U"(z) дает-
дается последовательностью непрерывных линейных отрезков. Мож-
Можно упростить поиск, рассматривая вместо этих линейных отрез-
отрезков отрезки, соединяющие узлы вычислительной сетки, изобра-
изображенной на рис. 140. Таким образом, остается только 2М+1
различных дискретных значений второй производной на грани-
границах интервалов. Мы должны заменить W на U" в уравнениях
(9.41) и (9.42). Используя эти уравнения вместе с уравнением
(9.59), получим коэффициенты, выраженные через i и /:
2, (9.60)
Dk=(i — j)AU"l6Az, (9.61),
где
AU" = UX"№. (9.62)'
Этим iV-мерная задача сводится к одномерной многоэтапной
процедуре решения. Для данной пары величин i и / легко вы-
вычислить сплайновые коэффициенты, используя уравнения
C.398) —C.400) и (9.49) —(9.51). Оставшаяся часть процедуры
идентична процедуре, описанной в разд. 9.5.
Метод оптимального контроля также может быть модифици-
модифицирован, чтобы получить сплайновые функции для оптимизиро-
оптимизированного распределения потенциала в виде уравнения (9.49),
свободные коэффициенты которого определяются этим методом.
Если ограничения нарушаются, то к объективной функции до-
добавляется штраф в виде новой функции цели, которая миними-
минимизируется этим методом. Его детальное описание дано в разд. 9.6.
Методы динамического программирования и оптимального
контроля хорошо дополняют друг друга: первый обеспечивает
широкомасштабный поиск в дискретных областях, а второй об-
обладает высокой скоростью сходимости. Оба способны давать
549
Глава 9
вполне удовлетворительные результаты сами по себе, но про-
процедура синтеза может сочетать их, начиная с метода динами-
динамического программирования и улучшая результаты методом оп-
оптимального контроля.
После того как найдено оптимизированное распределение
осевого потенциала, реконструкция электродов или полюсных
наконечников становится чрезвычайно легкой. Всегда известно
не только распределение осевого потенциала, но и его непре-
непрерывная вторая производная. В нее не входит построение кри-
кривой, а только обобщение сплайновой функции на точки про-
пространства, не лежащие на оси, как обсуждалось в разд. 9.8 и
9.9. Результирующие электроды состоят не из цилиндров и дис-
дисков как стандартных деталей, но после соответствующих упро-
упрощений они становятся вполне приемлемыми. Поскольку поло-
положения и потенциалы электродов гораздо важнее, чем их форма,
искривленные границы всегда можно заменить легко изготов-
изготовляемыми прямыми поверхностями. Но даже относительно слож-
сложная система будет малой ценой за значительный выигрыш, ко-
который можно получать с помощью этого подхода. Стоимость
изготовления любого электрода или полюсного наконечника
всегда ничтожна по сравнению с общей стоимостью такого
сложного инструмента, как, например, установка для ионно-лу-
чевой литографии.
Описанный здесь метод является весьма мощным. Практиче-
Практические примеры его применения будут даны ниже. В первую оче-
очередь выделим некоторые его важные особенности.
1. Этот метод может применяться как к электростатическим,
так и магнитным линзам. Он может быть распространен на
фокусирующие и отклоняющие системы с любой симметрией и,
возможно, даже к синтезу целых оптических колонн.
2. Его можно использовать с произвольными объективными
функциями и любыми ограничениями в зависимости от практи-
практических требований.
3. Результирующие линзы всегда должны упрощаться и из-
изменяться с помощью стандартных аналитических методов вы-
вычисления поля и хода лучей.
Подход, альтернативный синтезу, основан на использовании
фиксированных многоэлектродных линз [320а, 320Ь]. В этом
случае меняются потенциалы на электродах. Они оптимизиру-
оптимизируются с помощью методов, подобных описанным выше. Главное
преимущество этого подхода заключается в том, что теперь нет
необходимости реконструировать электроды, поскольку они за-
заданы a priori.
Почти совсем не было работ по синтезу многокомпонент-
многокомпонентных систем и удалось получить единственный законченный ме-
метод, но «при сочетании изобретательности работающих в элект-
550
Оптимизация и синтез электронных и иоииых линз
ронной оптике и вычислительной технике несомненно будут по-
получены совершенно новые методы, о которых мы даже не мо-
можем здесь предположить» i[355J.
9.10.1. Приложение: нестандартные
электростатические линзы
Мы применили процедуру синтеза, обсуждавшуюся в
разд. 9.10, к конструированию нестандартных электростатиче-
электростатических линз с низкой сферической аберрацией. В качестве объек-
объективной функции был выбран коэффициент добротности CSOOo/fi,
а для минимизации использовался модифицированный метод
оптимального контроля. Первые результаты получились много-
многообещающими.
На рис. 152 показана пятиэлектродная однопотенциальная
0,74711@)
0,51- U(O) *| I O,78U(O)||1.°1U<0)
-0,1 О
-0,5 -
Рис. 152. Пятиэлектродная однопотенциальная линза, сконструированная мето-
методом синтеза [354].
линза с отношением максимального потенциала к потенциалу
электрода в пространстве объекта, равным 5 [354]. Ее сфери-
сферический коэффициент добротности равен 1,03, неоптимизирован-
ный хроматический коэффициент добротности равен 0,76. Огра-
Ограничениями, накладываемыми на линзу, были низкие значения
величины полей, при этом Cso<x,/Lg=8,9 и Cco«>/£g=6,5. Сравне-
Сравнение со стандартными электростатическими линзами приведено
в табл. 11, где она обозначена под № 7. Таблица говорит сама
за себя.
На рис. 153, чтобы проиллюстрировать процедуру конструи-
конструирования [321], показана схема четырехэлектродной электроста-
электростатической линзы с отношением максимального потенциала к по-
потенциалу объекта 5,43. Сначала создаются бесконечно длинные
электроды, части которых изображены на рисунке тонкими ли-
линиями. На следующем этапе электроды обрезаются до приемле-
551
Глава 9
мых размеров и обрезанные части отбрасываются, чтобы избе-
избежать пробоя (штриховая линия). Далее электроды спрямляют-
спрямляются. Окончательные спрямленные формы электродов изображе-
изображены жирными сплошными линиями.
Осевые распределения потенциала реконструированных вер-
версий были пересчитаны с помощью метода плотности зарядов;
затем были определены положения кардинальных элементов и
коэффициентов аберрации методом построения хода лучей и
численным интегрированием. Результаты показывают, что сфе-
сферический коэффициент добротности изменяется в течение трех
этапов процедуры реконструкции от 0,90 до 1,11, в то время как
хроматический коэффициент аберрации изменяется от 0,80 до
0,83. Итак, упрощение формы электродов не приводит к сущест-
существенному возрастанию аберраций. Кроме того, такая линза обес-
обеспечивает удобное рабочее расстояние в зондирующем режиме.
r/L
Ц0>
0,5 Н
5,43U@)
\ \
0,98U@)i 14,2511@)
6,5 -
Рис. 153. Четырехэлектродная электростатическая линза, сконструированная
методом синтеза. Формы электродов последовательно упрощаются до пло-
плоских поверхностей [321],
На рис. 154 изображено типичное распределение потенциала
для электростатической линзы с очень маленькой сферической
аберрацией [356]. Из-за математической сложности проблемы
очень трудно предсказать или даже объяснить, почему некото-
некоторое распределение дает низкие аберрации. Однако известно
£254], что сильное поле на входе линзы в общем должно умень-
уменьшать сферическую аберрацию. Распределение потенциала на
рис. 154 четко подтверждает это. Очень важная особенность
этого распределения состоит в том, что его минимум потенциа-
потенциала расположен в пространстве изображений, что является пре-
преимуществом при тестировании электронными и ионными пучка-
пучками и микроанализе частицами с низкой энергией. Из-за обычно
552
Оптимизация и синтез электронных и ионных линз
существующих сферических и хроматических аберраций замед-
замедляющих линз получение тонких пучков с низкой энергией со-
составляет большую проблему, особенно если максимально допу-
допустимый потенциал ограничен.
На рис. 155 показана трехэлектродная замедляющая линза,
реконструированная из распределения потенциала, изображен-
изображенного на рис. 154, и упрощенная спрямлением поверхностей.
Максимально необходимое напряжение на электродах всего
лишь в пять раз выше, чем потенциал электрода в пространстве
объектов. Выходная энергия частиц уменьшена до 22% входной
энергии. Сферический коэффициент добротности первоначально-
первоначального осевого распределения не превышает 0,28. После упрощения
он равен всего лишь 0,51 и даже хроматический коэффициент
добротности имеет приемлемое значение 1,33 для такого низ-
низкого выходного потенциала. При половинном угле аксептанса
5 мрад, фокусном расстоянии 51 мм и увеличении М=—3,3 ра-
радиус диска сферической аберрации равен всего лишь 6 нм.
На приведенных выше рисун-
ках размеры линз выражены че- u(o)"u°
рез длину L (расстояние между
точками оси, за которыми потен-
потенциалы практически постоянны с
обеих сторон линзы). Потенциа-
Потенциалы электродов отнесены к потен-
потенциалу первого электрода в про-
пространстве объекта, т. е. началь-
начальной энергии частиц. В этом слу-
случае минимальная длина L выби-
выбирается из требования, наклады-
ваемого на максимум электриче- £ ^\
ского ПОЛЯ, которая, чтобы избе-рис 154. Типичное осевое распределе-
Жать проооя, не должна превы-ние потенциала линзы с очень низкой'
шать определенного значения, сферической аберрацией {356].
Подобное требование для магнит-
магнитных линз состоит в том, чтобы избегать насыщения, Конечно,
еще можно использовать CSoco/Lg и CCOco/Lg как коэффициенты
добротности, где Le определяется уравнением (9.34). Тогда про-
процедура будет состоять в том, чтобы уменьшать аберрации, со-
сохраняя поля в допустимых пределах. Если же использовать ко-
коэффициенты добротности, которым мы отдаем предпочтение, то
ограничения, накладываемые на поля, необходимо ввести как
требования.
Обсуждавшиеся выше примеры не только подтверждают
эффективность процедуры синтеза, но также демонстрируют
возможности конструирования электростатических линз с очень
низкими аберрациями,
553
Глава 9
0,6
1,0
г/L
Рис. 155. Трехэлектродная электростатическая линза, реконструированная из
распределения осевого потенциала, изображенного иа рис. 154 [356].
9.11. Методы искусственного интеллекта
■Мы не можем завершить эту главу без краткого обсуждения
многообещающего нового подхода к конструированию электрон-
электронной и ионной оптики: использования методов искусственного
интеллекта.
В последние годы роль символьных вычислений в принятии
решений различного рода увеличивается. Появились программы,
способные по известным данным вывести правило без реального
проведения огромного количества численных расчетов. Экс-
Экспертные системы, имеющие встроенные знания в виде символи-
символически представленных фактов и правил, создаются с невероят-
невероятной скоростью.
Электронная и ионная оптика являются областью, где эти
новые подходы могут привести к значительным успехам.
Конструирование оптических элементов и систем основано
на знании простых фактов и правил. Начальными данными яв-
являются законы электронной и ионной оптики и информация о
существующих решениях. Ограничения задают допустимые зна-
значения этих параметров. Целью конструирования является до-
достижение заданных оптических свойств. Как мы знаем, это
можно сделать неограниченным количеством различных спосо-
способов. Процедура конструирования чрезвычайно сложна из-за
большого числа взаимно независимых переменных.
Оценка огромного количества опубликованных данных и
формулировка общих критериев конструирования могут быть
автоматизированы при помощи этих методов. Кроме того, ин-
554
Оптимизация и синтез электронных и иоииых лииз
тересно найти различные виды симметрии, приводящих к дан-
данному оптическому преобразованию.
Экспертная система для конструирования электронно-ион-
электронно-ионных линз может работать следующим образом. На первом этапе
должна быть установлена база данных, которая обеспечивает
эффективное представление, накопление и воспроизведение
больших количеств опубликованной информации. Дружески на-
настроенный к пользователю интерфейс позволит выбрать опре-
определенный набор или диапазон оптических свойств, а также и
коэффициент добротности. Пользователь может получить любую
новую конфигурацию электродов или модифицировать сущест-
существующую в соответствии с имеющимися требованиями. Система
автоматически выполнит расчет поля и ход лучей, определит
оптические свойства, добавит новую конфигурацию к базе дан-
данных и оценит ее на основе наиболее подходящего коэффициента
добротности. Как следующий этап развития, процедура синтеза
может быть введена в экспертную систему.
Заключение
Эта глава посвящена различным подходам к одной из наи-
наиболее престижных целей электронной и ионной оптики; синтезу
оптических систем с заранее заданными свойствами первого
порядка и минимальными аберрациями. Мы начали с обсужде-
обсуждения возможности существования безаберрационной оптики. Пос-
После короткого обсуждения первых попыток синтеза было пред-
представлено вариационное исчисление, как математически удовлет-
удовлетворительный, но скорее громоздкий подход к оптимизации линз.
Теоретические нижние пределы коэффициентов сферической и
хроматической аберраций даны в виде уравнений (9.13) и
(9.33) — (9.36). Динамическое программирование, метод опти-
оптимального контроля и подход с помощью аналитических функ-
функций являются альтернативами, которые могут быть использова-
использованы практически для оптимизации осевых распределений. Сле-
Следующей была представлена реконструкция электродов и полюс-
полюсных наконечников из оптимизированного набора осевых дан-
данных; затем обсуждались понятия полиномиальной и сплайновой
линз, на которых основан один из наших методов синтеза.
Он сочетает динамическое программирование и алгоритм опти-
оптимизации методом оптимального контроля с очень простой про-
процедурой реконструкции. Как пример применения процедуры
синтеза были описаны электростатические линзы высокого ка-
качества. Наконец, были представлены возможности метода ис-
искусственного интеллекта для конструирования электронно-ион-
электронно-ионной оптики.
Глава 10
МУЛЬТИПОЛЬНЫЕ ЛИНЗЫ
В гл. 4, 5, 7 и 8 были детально рассмотрены оптические
свойства осесимметричных полей. Как мы знаем, в приближе-
приближении первого порядка такие поля обладают свойством стигмати-
стигматической фокусировки, т. е. взаимно однозначного соответствия
между объектом и изображением. Это свойство абсолютно не-
необходимо для целей электронной микроскопии. Однако сущест-
существует много применений (например, ускорители заряженных час-
частиц, спектрометры, вакуумные трубки и в общем даже элект-
электронные и ионные зонды), где не требуется стигматическая фо-
фокусировка. Роль лучевой оптики для ускорителей частиц сво-
сводится к поддержанию пучка, анализу его параметров и достав-
доставке его к месту эксперимента. При этом формировать изображе-
изображение не нужно.
В таких случаях могут быть применены другие виды симмет-
симметрии, отличные от осевой. В некоторых случаях отступление от
осевой симметрии даже необходимо. К примеру, рассмотрим
снова ускоритель частиц высоких энеогий. Вследствие очень
высокой скорости частиц для фокусировки пучка осесимметрич-
ными линзами потребуются сильные поля. Поле осесимметрич-
ной линзы в основном направлено вдоль оси (этот факт приме-
применяется в параксиальном приближении) и поперечные фокуси-
фокусирующие компоненты относительно невелики. Если необходим
сильный фокусирующий эффект, то для этой цели намного луч-
лучше подходят квадруполи, поля которых почти перпендикулярны
оптической оси.
Другим приложением мультиполей является коррекция
аберраций. Мы видели в разд. 5.6.4, что аберрации осесиммет-
осесимметричных линз могут компенсироваться мультипольными полями.
Мультипольные стигматоры широко используются для коррек-
коррекции осевого астигматизма.
Система может состоять из одних мультиполей, образуя за-
законченную оптическую колонну. Как мы увидим в разд. 10.4,
система квадруполей может давать стигматические изображе-
изображения. Мультиполи используются также для отклонения пучка
(разд. 11.1.1). Предполагается, что такие оптические колонны
имеют более низкие аберрации, чем стандартные. Для того что-
чтобы практически реализовать такие системы, необходимо преодо-
556
Мультнпольные линзы
леть весьма значительные трудности, связанные с их слож-
-ностью.
Множество книг и монографий [22, 27, 29, 30, 35, 37, 62, 357,
•358] посвящено мультипольным линзам (в основном квадрупо-
лям). Ограниченный объем позволяет представить здесь только
лх основные особенности.
ЮЛ. Поля мультипольных линз
Мультипольные поля довольно подробно обсуждались в
разд. 3.1.1.3 и 3.1.3. Надеемся, что читатель изучит эти разделы,
прежде чем читать эту главу. Поскольку мультипольные поля
трехмерны, их разложения в ряд обычно содержат бесконечное
число функций даже в специальном случае N плоскостей сим-
симметрии, рассмотренном в разд. 3.1.1.3. Согласно обсуждению ком-
компонент высших гармоник в конце этого раздела, n-й член в урав-
уравнении C.52) для данного N можно всегда интерпретировать
жак вклад от идеального 2nN полюса. Следовательно, можно
изучать свойства квадруполей, октуполей, додекаполей и т. д.,
просто рассматривая разложение в ряд квадруполя. Это также
справедливо не только для симметричного случая, но и тогда,
когда мы имеем дело с N плоскостями антисимметрии. Единст-
Единственным недостатком этого подхода является то, что не все муль-
мультипольные линзы (например, гексаполи) будут включаться в
рассмотрение.
Рассмотрим тогда стандартную квадрупольную конфигура-
конфигурацию, показанную на рис. 11. Две перпендикулярные плоскости
(xz и yz) являются плоскостями симметрии для электростати-
электростатического поля и антисимметрии для магнитного. Больше ника-
;кой информации о знаках электрода и полюсного потенциала
•нам не понадобится.
Для симметричного распределения электростатического по-
потенциала можно непосредственно использовать уравнение
C.82). В нем U0(z) = U(z), U2(z), U4{z) и U6{z) — потенциалы
осесимметричной, квадрупольной, октупольной и додекаполь-
тюй компонент соответственно. Если к двум плоскостям сим-
симметрии добавить также две плоскости антисимметрии, распо-
расположенные под углом 45° к плоскостям симметрии, то октуполь-
ная составляющая будет отсутствовать (см. разд. 3.1.1.3). На-
Наличие осесимметричной компоненты говорит о том, что обычно
осевые (продольные) компоненты поля, создаваемые разными
электродами, не компенсируют друг друга вдоль оптической
оси. Это хорошо видно на продольном сечении квадруполя, по-
показанном на рис. 25. Очевидно, что в этом случае должно су-
существовать продольное поле. Если электроды имеют бесконеч-
.ную длину и возбуждены симметрично, то осесимметричной
557
Глава 10
компоненты не существует. С другой стороны, поскольку это
рассмотрение основано только на свойствах симметрии распре-
распределения потенциала, оно включает случай непроизвольного от-
отклонения от осевой смметрии (см. разд. 5.6.4), например, вслед-
вследствие эллиптичности апертуры.
Около оси можно пренебречь всеми членами, содержащими
степень поперечной координаты выше второй. Тогда уравнение
C.82) упрощается:
u(x,y,z)*U(z)—U"(z)(x2+y2)/4+U2(z)(x2 — у2).
A0.1)
Видно, что в этом случае распределение потенциала содер-
содержит только осесимметричные и квадрупольные члены. Это озна-
означает, что компоненты высших гармоник не оказывают влияния
на свойства мультипольных линз первого порядка.
В случае симметрично возбужденных и бесконечно длинных
идеальных квадруполеи единственным членом уравнения C.82)
будет тот, который содержит U2(z). Двумерное распределение
потенциала дается уравнением C.87), правая часть которого
совпадает с последним членом уравнения A0.1), если U2 по-
постоянно. Это означает, что для идеального квадруполя паракси-
параксиальное рассмотрение имеет силу во всем пространстве, ограни-
ограниченном электродами.
Уравнения A.13) и A.17) дают следующие выражения для
компонент электростатического поля вблизи оси:
Ex=[U"(z)/2-2U2(z)]x,
Ey=[U"(z)/2 + 2U2(z)]y, A0.2)
Поперечные компоненты линейно зависят от соответствую-
соответствующих координат. В отсутствие осесимметричной компоненты про-
продольная компонента поля находится в квадратичной зависимо-
зависимости от координат, следовательно, она гораздо меньше попереч-
поперечных компонент. Если зависимости от z нет (плоское поле), то
продольная компонента отсутствует. Поперечное поле вдоль оп-
оптической оси отсутствует, поэтому частицы, начавшие движение
по оси с нулевой поперечной компонентой начальной скорости,
будут продолжать движение по прямой.
Теперь необходимо вывести выражение для антисимметрич-
антисимметричного магнитного скалярного потенциала со. Напомним читате-
читателю, что уравнение C.82) было выведено для симметричного
случая, следовательно, здесь оно неприменимо. Начнем с обще-
общего уравнения C.27). Так как плоскости xz и yz—антисиммет-
yz—антисимметричны, изменение знака х или у должно изменить знак потен-
потенциала. Следовательно, необходимо устранить все члены, содер-
558
Мультипольные линзы
жащие четные степени х и у, из разложения в степенной ряд.
В результате получим:
<а {х, у, г) = 2Й2 (г) ху — Q (z) ху (х2+у2) /6 +
z)xy{x*—y>) + ..., A0.3)
где Q2(z) и Q^iz) —функции магнитных квадруполя и октуполя
■соответственно. Если в дополнение к двум антисимметричным
плоскостям существуют также две плоскости симметрии, распо-
расположенные под углом 45° к антисимметричным плоскостям, то
октупольная компонента будет отсутствовать. Такое располо-
расположение вполне обычно для магнитных квадруполей. В этом слу-
случае не существует осесимметричнои компоненты.
Вблизи оси можно пренебречь всеми членами, содержащи-
содержащими степени поперечных координат выше второй. Тогда в урав-
уравнении A0.3) остается только первый (квадрупольный) член.
Компоненты высших гармоник не оказывают влияния на свой-
свойства линзы первого порядка.
С помощью уравнений A.13) и A.22) получим следующие
выражения для компонент магнитной индукции вблизи оси:
z)y,
z)x, A0.4)
Снова поперечные компоненты линейно зависят от координат,
но в этом случае они взаимно перестановочны. Продольная
компонента квадратично зависит от координат, следовательно,
она гораздо меньше поперечных компонент. Если зависимость
от z совершенно отсутствует (плоское поле), то отсутствует и
продольная компонента, а следовательно, полей вдоль оптиче-
оптической оси не существует.
Квадрупольные функции U%(z) и £2гB) зависят от формы
электродов и полюсов соответственно, а также от их возбужде-
возбуждения. Они должны быть нормированы таким образом, чтобы со-
соответствующие потенциалы принимали заданные значения
вдоль поверхностей электродов и полюсов. Достаточно выра-
выразить коэффициенты в виде, подобном тому, который задан в
уравнении C.198) с некоторым характерным радиусом R, кото-
который определяется реальной конструкцией линзы. Например,
в случае вогнутых цилиндрических электродов и полюсов (см.
рис. 24) R является радиусом цилиндра. Эти коэффициенты ли-
линейно зависят от возбуждения. Для электростатической компо-
компоненты возбуждение является абсолютной величиной разности
между потенциалами электродов и средним осевым потенциа-
потенциалом. Для магнитной компоненты возбуждение выражается че-
через коэффициенты Q2 с помощью уравнения C.232).
559
Глава 10
Квадрупольные компоненты U2(z) и Q2{z) обычно являют-
являются весьма громоздкими функциями осевой координаты г. Мы
уже обсуждали эту проблему в разд. 3.1.3. Среди применяю-
применяющихся различных моделей наиболее популярны колоколообраз-
ная и прямоугольная. Простая конструкция идеальных мульти-
полей обсуждалась в разд. 3.1.3.3. Здесь можно предположить,
что обе квадрупольные функции зависят от z таким же обра-
образом, и эта зависимость может быть описана простой нормиро-
нормированной функцией формы k(z). Тогда можно записать
U2(z) = U2k(z), Q2(z)=Q2k(z), A0.5)
где U2 и £12—постоянные, выраженные через электродные или
полюсные потенциалы, а функция формы принимает вид колоко-
лообразной кривой или прямоугольника соответственно для
двух вышеуказанных моделей. В последнем случае удобно вос-
воспользоваться понятием эффективной длины, т. е. заменить ре-
реальную длину системы L величиной Leff, вычисленной из урав-
уравнения C.197). Для быстрой оценки может быть использована
эмпирическая формула [23]
U?, A0.6)
где R — характеристический радиус, указанный выше. Тогда
можно предположить, что k(z) = \ внутри области, определяе-
определяемой эффективной длиной, и k(z) = 0 вне ее.
10.2. Уравнения параксиальных лучей
Уравнения B.80) и B.81) являются общими уравнениями
траектории в декартовых координатах. Выражая скорости че-
через уравнение B.31), учитывая уравнения B.87), B.89) и
B.90), подставляя компоненты поля из уравнений A0.2) и
A0.4) и, наконец, пренебрегая членами, содержащими степени
х, у и х', у' выше первой, а также их комбинациями, получим
релятивистское уравнение параксиальных лучей для стандарт-
стандартной конфигурации в следующем виде:
зС - [2xUt (z)—xUm B)/2 - x'W (z)] x
x{\-Q[U(z)-Uo\!moc^{2[U(z)-Uo\tel}-1±
y
= - [2yU2 (z) + yU" (z)/2 + y'U' (z)] x
X {1 -Q [U (z) - Uoym^} {2 [U (z) - Uo] rel}
T
-*
560
Мультипольные лиизы
где верхние и нижние знаки последнего члена отвечают поло-
положительно и отрицательно заряженным частицам соответст-
соответственно.
Эти уравнения описывают проекции траекторий релятивист-
релятивистской заряженной частицы на плоскости xz и yz соответственно,
когда частица движется в поле квадруполя стандартной конфи-
конфигурации, изображенном на рис. 11. Они имеют замечательную
особенность: эти уравнения не только линейны и однородны для
переменных х и у, но и сами переменные независимы друг от
друга в этих двух уравнениях. В этом и состоит причина выбо-
выбора этой стандартной конфигурации. Легко видеть, что для лю-
любой другой конфигурации, например если немного усилить осе-
симметричное магнитное поле, уравнения не будут разделять-
разделяться, и будем иметь намного более сложный случай.
Отметим, что эти уравнения содержат только осесимметрич-
ные электростатические и магнитные функции квадрупольных
потенциалов. Компоненты высших гармоник не оказывают
влияния на параксиальные свойства. Функция [U(z)—f/0]rei
вычисляется подстановкой функций осевого потенциала U(z)
осесимметричной компоненты в уравнение B.89). В отсутствие
осесимм.етричных линз и любых осесимметричных компонент,
появляющихся из-за асимметрично возбужденных квадруполей,
U(z) постоянно и равно электростатическому потенциалу вдоль
оси (средняя энергия частицы выражена в электрон-вольтах),
и уравнения существенно упрощаются. Для специального слу-
случая, когда в системе нет квадруполей, оба уравнения в отсут-
отсутствие косых лучей (С=0) дают электростатические члены урав-
уравнения параксиальных лучей D.31), потому что в этом случае
каждая из плоскостей xz и yz может быть выбрана в качестве
меридиональной. В случае косых лучей уравнения в декартовых
координатах проще, чем в цилиндрических (см. разд. 4.10.1.2),
следовательно, нет необходимости рассматривать косые лучи
отдельно.
Для небольших скоростей релятивистский потенциал можно
заменить электростатическим и членом Q[U(z)—t/0]/(moc2)
можно пренебречь.
Если осесимметричная компонента отсутствует [U(z) = U=
= const], уравнения можно записать в гораздо более компакт-
компактной форме. Обозначим
q{z) =- U2(z) [I - Q (U - f/0)/(moc2)]/(f/ - f/0)reIT
+ [— 2Q/mo(U— f/obeiFWMz). A0.9)
Тогда уравнения A0.7) и A0.8) можно записать в виде
x" + q{z)x = 0, A0.10)
y"-q(z)y = 0 A0.11)
561
Глава 10
для двух проекций траектории. Отсюда видно, что для прямо-
прямоугольной модели, когда q(z) постоянно внутри поля квадрупо-
ля, решение одного из приведенных выше уравнений является
комбинацией гармонических функций, в то время как решение
другого — комбинацией двух гиперболических функций, завися-
зависящих от знака q. Следовательно, траектории частиц, распростра-
распространяющихся в плоскости xz, полностью отличаются от траектории
частиц, распространяющихся в плоскости yz. Фокусирующим
свойством обладает одна из двух ортогональных плоскостей,
а другая обладает дефокусирующим свойством. Если частица
попадает в случайную точку пространства, силы будут действо-
действовать так, чтобы оттолкнуть ее в направлении дефокусирующей
ллоскости и вырвать из фокусирующей. Подобная ситуация су-
существует, даже если q(z) является сложной функцией при ус-
условии, что знак ее не меняется. Если же знак q(z) меняется,
т. е. если мы имеем систему квадруполей, то можно одновре-
одновременно получить фокусирующее действие в обеих плоскостях.
Функция q(z) зависит от трехмерной формы электродов и
полюсов, а также от возбуждения. На практике, когда как объ-
объект, так и изображение помещены вне поля квадруполя и осо-
особенно в случае мультипольных систем, влиянием контурных
полей на концах отдельных элементов пренебречь нельзя.
Знак q(z) зависит от полярности электродов и полюсов. Рас-
Рассматривая уравнение A0.9), видим, что для положительно за-
заряженных частиц q(z) положительно (или отрицательно для от-
отрицательно заряженных частиц), если U2(z) положительно
и/или £2г(.г) отрицательно. Если, однако U2(z) отрицатель-
отрицательно и Q2(z) положительно, то qz{z) отрицательно для положи-
положительно заряженных частиц и положительно для отрицательно
заряженных частиц. Если обе функции имеют одинаковый знак
в комбинированной электростатической и магнитной системе, то
нужно сравнить два члена уравнения A0.9), и знак его больше-
большего члена будет определять знак q(z). Для положительного
q(z) плоскость xz является фокусирующей, для отрицательного
q(z) фокусирующей является плоскость yz. Оценивая направ-
направление силы Лоренца в различных точках плоскости (рис. 11),
видим, что рисунок соответствует случаю, когда q(z)<C0 для
положительно заряженной частицы.
Важно отметить, что стандартно ориентированные электро-
электростатические, магнитные и комбинированные квадрупольные лин-
линзы имеют сходные свойства. Эти свойства зависят только от
функции q(z), т. е. от формы и возбуждения электродов и/или
полюсов. Удобно предположить, что как U2(z), так и Q2{z)
одинаково зависят от координаты z (уравнение A0.5)). Тогда
U2 пропорционально электростатическому потенциалу V, прило-
приложенному к электродам и измеренному относительно осевого по-
562
Мультипольиые лиизы
тенциала, a Q2 пропорционально магнитному скалярному потен-
потенциалу со на полюсах (предполагается, что они имеют эквипо-
эквипотенциальные поверхности). U2 положительно, если электрод,пе-
электрод,пересекающий ось х, имеет положительный потенциал (на рис. 11,
следовательно, £/2<0). Аналогично для полярности магнитных
полюсов, показаннных на рис. 11, имеем Q2>0.
10.3. Формирование изображения
параксиальными лучами
Так как уравнения параксиальных лучей A0.10) и A0.11)
являются линейными однородными дифференциальными урав-
уравнениями второго порядка, общее решение каждого из них мо-
может быть записано в виде D.55), т. е. как комбинация двух
линейно-независимых частных решений. Пусть X\(z) и X2(z) —
частные решения уравнения A0.10), в то время как частными
решениями уравнения A0.11) являются yy(z) и #2B)• Рассмот-
Рассмотрим точки объекта с координатами х0, у0, z0- Применяя аргу-
аргументацию разд. 4.4 к обоим уравнениям A0.10) и A0.11), вы-
выведем общие решения в виде, эквивалентном уравнению D.57):
x(z) =хох2 {г) 1х2 (z0) +cx[xi (z) — xt (zo)x2(z)/x2 (z0)],
A0.12)
У (z)=yoy2{z)ly2 (zo)+cy[y1(z) —yi(zo)y2{z)ly2{zo)l A0.13)
где cx и cy — две различные произвольные постоянные, которые
определяют начальный наклон данной траектории.
Предположим, что существуют такие z = zxt, при которых
множитель при сх равен нулю. Тогда имеем
x2{zxi)/x2(z0) =*i (zxl)lxi (zo) =MX, A0.14)
но для этого конкретного значения z уравнение A0.12) упро-
упрощается до
x(zxi)~Mxxo, A0.15)
где Мх — увеличение в плоскости xz. Конечно, подстановка z=
= zXi в уравнение A0.13) не упрощает это уравнение: значе-
значение у для каждого су свое. Можно заключить, что линейное изо-
изображение точечного объекта формируется квадрупольной лин-
линзой. Это изображение параллельно оси у, а его расстояние от
оси z дается уравнением A0.15).
Предположим теперь, что мы имеем дело с такой системой
квадруполей, где существует z = zyi, при котором множитель
при су равен нулю. Тогда
y2(zyi)/y2{zo) =yi{zyi)/yi(z0) =МУ, A0.16)
563
Глава 10
и для z=zyi уравнение A0.13) упрощается до
y(zyi)=Myy0, A0.17)
тде Му — увеличение в плоскости yz. Подстановка z=zyl в
уравнение A0.12) не упрощает это уравнение: значение х для
каждого сх свое. Как следствие линейное изображение точки
•объекта формируется квадруполем. Изображение параллельно
оси х и его расстояние от оси z дается уравнением A0.17).
Как видим, два взаимно перпендикулярных линейных изо-
изображения точечного объекта формируются двумя различными
линейными увеличениями. Следовательно, фокусировка астигма-
тична (см. разд. 5.6.4). Если точка объекта находится на оси
(дго=г/о=0), то оба линейных изображения пересекают ось z.
Точечное изображение точечного объекта может быть сфор-
сформировано, если zXi = Zyi. Это условие может быть удовлетворено
для некоторого заданного положения объекта с помощью соот-
соответствующим образом выбранной системы квадруполей, но обыч-
обычно эти два увеличения остаются разными, следовательно, круг
в этой системе будет изображаться как эллипс. Обеспечить
стигматическую фокусировку при равенстве двух увеличений
для произвольного положения объекта — очень сложная, но все
же выполнимая задача (см. разд. 10.4).
Кардинальные элементы могут быть введены способом, ана-
аналогичным случаю осесимметричных линз. Однако в двух орто-
ортогональных плоскостях они обычно отличаются; следовательно,
их использование более сложно. Аналогично может быть ис-
использовано приближение тонкой линзы (см. разд. 10.4.2).
В заключение отметим, что рассмотрение, проведенное здесь,
действительно только для параксиального приближения. Если
используется более широкий пучок, теория первого порядка не-
неадекватна и необходимо принимать во внимание абберрации
(см. разд. 10.5).
10.4. Системы квадруполей
Как отмечалось в предыдущем разделе, для того чтобы
иметь действительное изображение в обеих ортогональных плос-
плоскостях, функция q(z) должна менять знак. Этого можно достиг-
достигнуть, если использовать сложное трехмерное расположение
электродов и полюсов. Однако существует гораздо более про-
простая альтернатива. Рассмотрим систему квадруполей, в которой
каждый повернут вокруг оптической оси z на 90° по отношению
к соседнему. Тогда имеем две альтернативные системы рассеи-
рассеивающих и собирающих линз в двух ортогональных плоско-
плоскостях xz и yz. Эта ситуация эквивалентна тому, что функция
q(z) меняет свой знак у каждого нового элемента. Линза, рассеи-
564
Мультипольиые линзы
вающая в плоскости xz, является собирающей в плоскости yz
ai обратно.
Системы осесимметричных линз были рассмотрены в
разд. 4.8. Мы установили, что понятие матрицы преобразования
(разд. 4.8.1) полезно для математического описания свойств
линзовых систем. Так как квадруполи почти всегда использу-
используются в комбинациях, очень удобно для их описания использо-
использовать матрицу преобразований, потому что матрица преобразо-
преобразования системы линз является просто произведением матриц
преобразований отдельных элементов.
10.4.1. Матрицы преобразований
Общее решение линейных и однородных дифференциальных
уравнений второго порядка A0.10) и A0.11) всегда может
быть записано в матричной форме
/ х (z) \ i х (г„) \
1 М - ' 1оМ A0.18)
(У(г) \ !У(г0)
где z0 — обычно начальное значение координаты z (в частно-
частности, это может быть координата объекта), a mz и пгу— матри-
матрицы преобразований в плоскостях xz и yz соответственно. Как мы
знаем из разд. 4.8.1, матрицы преобразований полностью опи-
описывают свойства данного оптического элемента. Так как теперь
эти свойства различны в двух ортогональных плоскостях, име-
имеем две матрицы преобразований вместо одной, как в случае
осесимметричных линз.
Рассмотрим прямоугольную модель при q(z)—q = const>0.
Это означает, что плоскость xz является плоскостью фокуси-
фокусировки, а плоскость yz — плоскостью рассеивания. Тогда частные
решения
xi B) = sin W2 {z — z0)], x2 (z) = cos [q1'2 (z — zo)],
A0.20)
yi (z) = sh[qV* (z -z0)], У2 (z) = chiqW (z - z0)]
должны быть подставлены в уравнения A0.12) и A0.13) вме-
вместе с
с*=<г'/2*'о. cy = q-^y'o, A0.21)
чтобы получить общее решение. Далее матрицы преобразова-
преобразований есть
563
Глава 10
(Ю.22)
ПОТОМУ ЧТО x(Zo)=Xo, X'{zo)=x'o, y(zo)=yo И y'{zo)=y'o.
Квадрупольные матрицы преобразований в плоскостях фокуси-
фокусировки и рассеивания обозначены mCOnv и т<цч соответственно.
Очевидно, соотношения тх = тСОпу и ту — тцч справедливы толь-
только потому, что мы выбрали q>0. При д<0 собирающая и рас-
рассеивающая плоскости меняются местами.
Обе матрицы имеют единичный определитель. Это справед-
справедливо, даже если q(z) является сложной функцией, вследствие
того что в уравнениях A0.10) и A0.11) полностью отсутствуют
первые производные рассматриваемых переменных. Отметим
различие во внешнем виде этих матриц преобразований и мат-
матриц, выраженных через асимптотические главные элементы осе-
симметричных линз в разд. 4.8.1. Естественно, все они пред-
представляют одни и те же свойства. Например, мы видели в
разд. 4.8.1, что определитель матрицы преобразований всегда
равен отношению фокусного расстояния объекта и фокусному
расстоянию изображения. Но два фокусных расстояния равны,
если линза имеет одинаковые осевые потенциалы с обеих сто-
сторон (см. уравнение D.76)), что полностью соответствует дан-
данному случаю (мы заменили осесимметричную компоненту по-
потенциала постоянным осевым потенциалом). Следовательно,
определители действительно должны быть равны единице.
Используя матрицы A0.22) и A0.23), легко определить оп-
оптические свойства любой системы квадрупольных линз простым
перемножением их матриц преобразований. Мы сделаем это для
некоторых специальных случаев в следующих разделах.
10.4.2. Представление с помощью тонких линз
Так как функция q(z) пропорциональна возбуждению и чем
длиннее линза, тем сильнее ее действие, очевидно, что опти-
оптическая сила квадрупольной линзы должна зависеть от
значения безразмерной величины qL2. Если \q\L2<^l, можно ис-
использовать приближение тонкой линзы (см. разд. 4.9). В этом
случае решение прямоугольной модели становится очень простым,
так как прямоугольники можно заменить сосредоточенными
тонкими зонами, в которых проявляется действие линзы. Части-
Частицы движутся вдоль прямых линий в дрейфовом пространстве
между тонкими линзами, где поле отсутствует. Хотя мы знаем,
что это очень грубая модель, будем использовать ее в дальней-
566
Мультипольные линзы
.шем, потому что это приближение позволяет сконцентрировать
внимание на основных физических свойствах. Отметим, однако,
что в реальной конструкторской работе приближение тонкой
.линзы должно всегда использоваться с большей осторожностью.
Как мы знаем из разд. 4.9.1, матрицу преобразований тол-
толстой линзы всегда можно разложить на комбинацию трех бо-
более простых матриц, представляющих либо а) два дрейфовых
пространства с тонкой линзой между ними, либо б) две тонкие
линзы с дрейфовым пространством между ними (см. рис. 54).
а) Для простоты предположим, что длины двух дрейфовых
пространств одинаковы: Ii=i2=l. По определению в этом слу-
случае /i = /2 = /- Тогда уравнение D.130) для матрицы преобразо-
преобразований maid системы из двух дрейфовых пространств и тонкой
линзы дает
Сравнивая эту матрицу с матрицей A0.22) для фокусирующей
плоскости и используя уравнение A0.20) при z—20 = L, найдем,
что две эти матрицы идентичны, если выбрать
^1/2sin(91/2L), A0.25)
tg(ql/2L/2) >L/2, A0.26)
где индекс conv означает, что приведенные выше величины от-
отнесены к фокусирующей плоскости.
Сравним теперь матрицу A0.24) с матрицей A0.23) для
рассеивающей плоскости. Две матрицы идентичны, если вы-
выбрать
1/fdiv ql'*&b(qV*L), A0.27)
A0.28)
где индекс div означает, что приведенные выше величины отне-
отнесены к рассеивающей плоскости.
Известно (см. разд. 4.9.1), что фокусное расстояние тонкой
линзы этой модели равно фокусному расстоянию первоначаль-
первоначальной толстой линзы. Из уравнений A0.25) и A0.27) очевидно,
что знаки фокусных расстояний в двух ортогональных плоско-
плоскостях различны (положительный в фокусирующей плоскости и
отрицательный в рассеивающей плоскости), а оптическая си-
сила выше в рассеивающей плоскости. Уравнения A0.26)
и A0.28) показывают, что /COnv>/div, т. е. главные плоскости
сдвинуты в разных направлениях от центральной плоскости
линзы.
567
Глава 10
Если первоначальная линза является тонкой, то можно за-
заменить тригонометрические функции их аргументами в урав-
уравнениях A0.25)—A0.28) и получим
(l/fconv)thin = — (l/fdiv)thin = <7£, A0.29)
(/conv)thin= (/div)thln = £/2, A0.30)
т. е. для тонкой квадрупольной линзы абсолютные величины
двух фокусных расстояний равны и главные плоскости совпада-
совпадают с центральной плоскостью линзы.
б) В случае второго представления пусть фокусные рас-
расстояния двух тонких линз будут /' и /" соответственно. Тогда
из уравнения D.133) для матрицы преобразований тш систе-
системы двух тонких линз и одного дрейфового пространства полу-
получим
l-d/f d
где / — фокусное расстояние составной линзы из уравнения
D.112).
При сравнении этой матрицы с матрицами A0.22) и A0.23)
сразу же видно, что соответствие возможно только тогда, когда
V—f"> т. е. две тонкие линзы должны быть идентичны. Тогда
находим, что для фокусирующей плоскости матрицы A0.22) и
A0.31) идентичны, если выбрать
l/rconv = ?1/2tg(r?'/2L/2), A0.32)
rfconv = <Г1/2 sin (qU*L)<L. A0.33)
Подставляя эти величины в уравнение D.112), естественно по-
получим фокусное расстояние составной линзы, задаваемое урав-
уравнением A0.25).
Теперь сравним матрицу A0.31) с матрицей A0.23) для рас-
рассеивающей плоскости. Две матрицы идентичны, если положить
l/fdiv=-<71/2th(<7'/2L/2), A0.34)
A0.35)
Если подставить эти величины в уравнение D.112), то получим
фокусное расстояние составной линзы, задаваемое уравнени-
уравнением A0.27).
Знаки этих фокусных расстояний в двух ортогональных плос-
плоскостях снова различны. Из уравнений A0.33) и A0.35) имеем
Если первоначальная линза является тонкой, можно заме-
заменить тригонометрические функции их аргументами в уравнени-
уравнениях A0.32) —A0.35); получим
568
Мультипольные линзы
(l/fconv)thln = —(l/fdlv)th!n = <7£/2, A0.36)
\^+"Conv/ thin ~~* l^*div/ thin ~~ *■*% ( JL vs»O / I
Если подставить эти величины в уравнение D.112) и прене-
пренебречь малыми членами, содержащими L3, то получим фокусное
расстояние составной линзы, задаваемое для приближения тон-
тонкой линзы уравнением A0.29).
10.4.3. Дублеты
Теперь рассмотрим систему двух квадруполей, повернутых
на 90° по отношению друг к другу вокруг оптической оси. Такая
система называется квадрупольным дублетом. Если мультипо-
ли, следующие друг за другом, повернуты так, что их осевые
функции изменяют знак у каждого нового элемента, то мы го-
говорим о мультипольных дублетах. В прямоугольной модели
квадрупольного дублета имеются два прямоугольника различ-
различной полярности, разделенных дрейфовым пространством. Если
два квадруполя в остальном идентичны друг другу, функция
q(z) антисимметрична по отношению к средней плоскости дрей-
дрейфового пространства. В этом случае мы говорим об антисим-
антисимметричном дублете (рис. 156,а).
Теперь исследуем свойства
антисимметричного дублета в
приближении тонкой линзы.
Очевидно, матрица преобразо-
преобразованной mm (уравнение 10.31)
будет соответствовать любому
дублету в приближении тон-
тонкой линзы. В соответствии с
уравнением A0.29) в специ-
специальном случае антисимметрич-
антисимметричного дублета f' = —f"=±f,
где f — положительная вели-
величина и верхний знак соответ-
соответствует плоскости, где первая
линза является фокусирую-
фокусирующей, а нижний — другой ор-
ортогональной плоскости. Тогда
составное фокусное расстоя-
расстояние равно f2/a">0, т. е. дублет
является фокусирующим в обе-
их плоскостях (отметим, что
теперь / означает абсолютную
величину фокусного расстоя-
расстояния отдельной компоненты), и
Рис. 156. Антисимметричный дублет:
а — функция q (г); б — траектория
в плоскости хг; в — траектория в пло-
плоскости уг.
569
Глава 10
уравнение A0.31) имеет вид
l^fd/f d
_rf//? l±d/f). (Ю.38).
Эта матрица описывает дублет в обеих ортогональных плоско-
плоскостях, если используются соответствующие знаки.
Очевидно, что результирующая составная линза больше не
является тонкой линзой (см. разд. 4.9.1). В этом частном случае
главные плоскости находятся далеко друг от друга. Но ясно,,
что в обеих ортогональных плоскостях мы имеем фокусирую-
фокусирующую линзу. Уравнение A0.38) показывает, что матричные ком-
компоненты Шц и /П22 могут быть равны только в тривиальном слу-
случае d/f=O, следовательно, антисимметричный дублет тонкой
линзы никогда не может представлять одиночную квадруполь-
ную линзу, которая оказывает дефокусирующй эффект в одной
из ортогональных плоскостей.
Этот результат не является для нас новым: мы видели в
разд. 4.8.2, что даже комбинация двух толстых линз с равными,
но противоположно направленными оптическими силами всег-
всегда дает суммарный фокусирующий эффект. Оказывается, что
частица всегда проходит через рассеивающую линзу ближе к
оси, чем через собирающую. Следовательно, влияние собираю-
собирающей линзы на изменение наклона траектории сильнее, чем рас-
рассеивающей линзы (рис. 156,6 и 156,в).
Теперь найдем связь между изображением и объектом, ис-
используя матрицу преобразований, составленную из матриц дрей-
дрейфового пространства в пространстве объектов длиной р, дубле-
дублета и дрейфового пространства в пространстве изображений
длиной q соответственно [29]. (Не путайте функцию q{z) и по-
положение изображения q.) Если т^тр и tndMtq— матрицы
дрейфового пространства в пространстве объектов и изображе-
изображений соответственно (см. уравнение D.96)), то имеем
т = mdritt ^doublet^drKt p = I q j j "^doublet I q j I»
где mdoubiet дается уравнением A0.38).
Из уравнения D.92) известно, что изображение формирует-
формируется, если элемент т^ этой матрицы имеет нулевое значение.
В результате вычислений получим
ml2 = p + q+d±(q — p)d/f — pqd/f2 = 0, A0.40)
где, как объяснялось выше, положительные и отрицательные
знаки соответствуют двум ортогональным плоскостям. Таким
образом, если фиксируется положение объекта, то точка изо-
изображения будет формироваться на расстоянии q, если уравне-
570
Мультипольные линзы
ние A0.40) одновременно удовлетворяется для обеих плоско-
плоскостей. Это требование дает
}2=P2(q+d)d/[(p + d) (p + q+d)] =
=q>(p+d)d/[(q+d) (p + q + d)], A0.41)
которое вследствие симметрии выражения может быть справед-
справедливо, только если q=p. В этом случае параметры f и d дублета
должны выбираться так, чтобы они удовлетворяли соотноше-
соотношению
f2=P2l(l + 2pld), A0.42)
из которого можно видеть, что параметры зависят от положе-
положения объекта р.
Теперь рассмотрим увеличение. В соответствии с уравнени-
уравнением D.92) увеличение определяется матричным элементом тц.
Из уравнений A0.38), A0.39) и A0.42) имеем
M = -{l + dlp±[{2+d/p)d/p]1/2}, A0.43)
откуда ясно, что увеличения в двух ортогональных плоскостях
будут разными для любого конечного dip. Очевидно, что абсо-
абсолютное значение увеличения больше в плоскости, где первая
линза является фокусирующей. В этой плоскости изображение
увеличено, в то время как в другой плоскости уменьшено. Про-
Произведение двух увеличений равно единице. Параметр d может
быть выбран на основе заданного увеличения в одной из орто-
ортогональных плоскостей. Тогда фокусное расстояние / определя-
определяется уравнением A0.42) для данного положения объекта р.
Чтобы получить более строгое решение, необходимо рассмот-
рассмотреть дублет толстых линз. Это может оказаться трудной зада-
задачей, если q(z) является сложной функцией. Очевидно, его
оптическая сила не может быть одинаковой в двух орто-
ортогональных плоскостях (см. уравнения A0.25) и A0.27)). Если
используется прямоугольная модель, то результат получается
качественно тот же, что и для тонких линз [23, 357]. Как и
прежде, точечное изображение точечного объекта может быть
сформировано, но увеличения в двух плоскостях различны, и
это требование может быть удовлетворено только для заданно-
заданного положения объекта. Если точечный объект движется, то два
изображения снова не совпадают и оба становятся линейными
(см. разд. 10.3).
Полное моделирование формирования осесимметричного
изображения теоретически возможно с помощью квадрупольно-
го дублета, но можно показать [62], что такой дублет всегда
будет давать рассеивающую линзу и, следовательно, не может
быть использован для получения реальных изображений реаль-
реальных объектов.
571
Глава 10
10.4.4. Триплеты
Следующей степенью усложнения является система трех
квадруполей, повернутых на 90° относительно каждого сосед-
соседнего вокруг оптической оси г. Такая система называется квадру-
польным триплетом. В прямоугольной модели мы теперь имеем
три прямоугольника чередующейся полярности, отделенные
друг от друга двумя дрейфовыми пространствами. Если два
внешних квадруполя идентичны друг другу и одинаково отде-
отделены от центрального дрейфовыми пространствами длины d
каждый, то функция q(z) симметрична относительно средней
плоскости центрального квадруполя. В этом случае мы имеем
симметричный триплет (рис. 157).
q(z)
И
Рис. 157. Симметричный триплет.
Если отдельные элементы симметричного триплета являют-
являются тонкими линзами, его матрица преобразования может быть
просто составлена из уравнений D.96) и D.129) в следующем
виде:
oyi d\n
iAo iA=i
'"triplet —
1
± i/U
где /out и /cent — фокусные расстояния внешней и центральной
линз соответственно. Верхний знак соответствует плоскости,
где центральная линза является фокусирующей.
Из этой матрицы могут быть выведены основные свойства
симметричного триплета. Оказывается, что симметричный три-
триплет, составленный из трех тонких линз, в большинстве случаев
все еще может рассматриваться как тонкая линза, поскольку
его главные плоскости близки к средней плоскости.
Наиболее важное свойство симметричного триплета состоит
в том, что он может обеспечить стигматическую фокусировку
с равными увеличениями в обеих ортогональных плоскостях.
Это делает возможным применение триплета в качестве элемен-
элемента для мультипольнои электронной микроскопии.
572
Мультипольные лиизы
10.4.5. Мультиплеты
Квадруплет (система четырех квадруполей) может обеспе-
обеспечить стигматическую фокусировку в широком интервале рас-
расстояний до объекта [23]. Большее число квадруполей, которые
могут следовать друг за другом с чередованием полярности,,
дают сильную фокусировку на большом расстоянии.
Периодическая последовательность квадруполей чередую-
чередующихся полярностей (чередующаяся градиентная фокусировка
[359]) используется в ускорителях частиц для трнспортировки
пучков на большие расстояния с ограничением до заданных
размеров в плоскости, перпендикулярной направлению его рас-
распространения. Если удовлетворяются определенные условия,,
результирующим эффектом такой системы является фокусиров-
фокусировка в обеих ортогональных плоскостях. Этот фокусирующий эф-
эффект, кроме того, может быть использован для компенсации
рассеивающего влияния собственного пространственного заря-
заряда пучка [360].
Рис. 158. Эллипс эмиттанса.
Матрица преобразований является эффективным инструмен-
инструментом для анализа свойств мультиплетов. Например, таким обра-
образом можно установить диапазон стабильности для параметров
системы, гарантирующих, что она будет выполнять свою задачу
даже при наличии малых возмущений.
10.4.5.1. Согласование пучка. Наконец, обсудим одно важ-
важное применение квадрупольных мультиплетов [357]. Подставим
частные решения x\{z) и X2(z) из уравнения A0.20) для фоку-
фокусирующей плоскости квадрупольной линзы в общее решение
x(z), даваемое уравнением A0.12). Принимая во внимание
уравнение A0.21), дифференцируя общее решение по z и до-
добавляя квадраты х и х', получим
х2 (z) +x'2 (z)/<7=xo2 + Xo/2/<7=const. A0.45)
Следовательно, траектория частицы в фазовой плоскости хх'',.
является эллипсом (рис. 158).
Для ускорителей частиц мы ие можем уделить много вни-
внимания отдельным траекториям в пучке. Следовательно, удобна
573-
Глава 10
рассмотреть хо и х'о как амплитуды, т. е. наибольшее возмож-
возможное смещение и наклон соответственно. Тогда наш эллипс бу-
будет представлять все частицы с произвольными фазами, но
ограниченные этими амплитудами. Следовательно, с помощью
фазовой плоскости хх' удобно описывать предельные свойства
пучка (даже если он не ламинарный) и те оптические систе-
системы, через которые он распространяется.
Будем называть эмиттансом пучка площадь, которую он за-
занимает в фазовой плоскости. Аналогично определим аксептанс
оптической системы как площадь ограничивающей фигуры в
фазовой плоскости. Очевидно, что фигуры аксептанса и эмит-
танса должны быть близки друг к другу насколько это возмож-
возможно, чтобы обеспечить наилучшую работу системы транспорти-
транспортировки пучка. Задача достижения этой цели называется согла-
согласованием.
В соответствии с теоремой Лиувилля (см. разд. 5.6.8) плот-
плотность частиц в фазовом пространстве не меняется со временем.
Как следствие эмиттанс пучка является инвариантом, т. е. пло-
площадь ограничивающей фигуры не меняется со временем. Ес-
Естественно, ее форма и ориентация могут изменяться, и фигура
эмиттанса может иметь весьма необычную форму.
Эллиптическая форма контура в фазовой плоскости являет-
■ся следствием того, что рассматривается движение частиц в
поле квадрупольной системы, т. е. под действием линейных сил
(см. уравнения A0.2) и A0.4)). Если пучок остается в линей-
линейных полях, эллиптическая форма сохранится, но ее ориентация
будет постоянно меняться. Нарушения контуров будут возни-
возникать как результат действия нелинейных сил, т. е. полей, кото-
которые не пропорциональны смещению, например поля мульти-
полей.
Как мы видели в разд. 5.6.8, удельная яркость также явля-
является инвариантом, и этот факт также является следствием тео-
теоремы Лиувилля. Следовательно, эмиттанс и яркость связаны
друг с другом.
Форму и ориентацию ограничивающего эллипса легко ме-
„нять с помощью простых линейных элементов. Влияние дрейфо-
дрейфового пространства состоит в том, что каждая точка эллипса сме-
смещена параллельно оси х на величину, пропорциональную на-
начальному отклонению частицы. Влияние тонкой квадрупольной
линзы состоит в том, что каждая точка эллипса смещена па-
параллельно оси х' на величину, пропорциональную начальному
положению координаты частицы. Естественно, площадь эллип-
эллипса остается неизменной.
На практике согласование достигается использованием ком-
комбинации дрейфовых пространств и толстых квадрупольных линз.
Эта процедура может быть весьма сложной [361].
574
Мультипольные линзы
10.5. Аберрации мультипольных линз
10.5.1. Геометрические аберрации
Уравнения параксиальных лучей A0.7) и A0.8) были выве-
выведены при условии, что членами высших порядков в распреде-
распределениях потенциала A0.1) и A0.3) можно пренебречь. Если
в этих выражениях оставить большее количество членов, то по-
получим более громоздкие уравнения траекторий. Тогда геомет-
геометрические аберрации квадрупольной линзы могут быть опреде-
определены как разность между более точными и параксиальными ре-
решениями. В зависимости от того, сколько членов рассматрива-
рассматривается, можно говорить об аберрациях третьего или пятого по-
порядков, как в случае осесимметричных линз (см. гл. 5).
Рассматривая геометрические аберрации третьего порядка
как малые возмущения параксиальных траекторий, замечаем,,
что аберрационные члены будут зависеть от различных факто-
факторов. Члены, обусловленные наклоном траектории, присутству-
присутствуют всегда и растут с возбуждением линзы. Дополнительные-
члены возникают из-за контурных полей, мультипольных ком-
компонент и изменений осевого электростатического потенциала.
Мультипольные аберрации можно разделить на те же классы,,
что и аберрации осесимметричных линз. Однако число коэффи-
коэффициентов аберрации больше вследствие более сложной природы
распределений полей. Определение этих коэффициентов абер-
аберрации различно в разных публикациях в зависимости от пред-
предположений, принимаемых в конкретных ситуациях [37, 362].
К примеру, астигматизм первого порядка квадрупольных си-
систем можно применить в ускорителях частиц, что в свою оче-
очередь требует отдельного рассмотрения для стигматических »
астигматических систем: в первом случае определение подоб-
подобно тому, которое используют для круглых линз, а во втором
отклонение оценивается из линейности изображения. Чтобы
в общем обеспечить единое представление электронно-ионных
оптических свойств мультипольных линз, [363], можно приме-
применить метод характеристических функций (разд. 5.1).
Вычисление коэффициентов аберрации начинают с того, что
устанавливают функции U(z), B(z), U2(z), U2(z), Ui(z), £24(z)
и т. д. Затем решают уравнения параксиальных лучей для не-
некоторых простых наборов начальных условий и подставляют
эти решения вместе с заданными функциями осевых потенциа-
потенциалов в коэффициенты аберраций, которые всегда можно выра-
выразить в виде определенных интегралов (см. разд. 11.1.4). Реаль-
Реальная оценка этих интегралов возможна с помощью численных
методов, выведенных в разд. 6.3. Реальные и асимптотические-
коэффициенты аберраций можно ввести в соответствии с прин-
575-
Глава 10
ципами, обсуждавшимися в разд. 5.4. Прямоугольная и колоко-
лообразная модели являются наиболеее часто используемыми
при определении коэффициентов аберраций для длинных и ко-
коротких мультиполей соответственно. (Отметим, что первая мо-
модель может обеспечить только грубое приближение; следова-
следовательно, для длинных линз имеет преимущество комбинация
этих двух моделей.)
Геометрические коэффициенты аберрации вычислены как
для реального [364, 365], так и для асимптотического случаев
[366, 367]. Исследовалась зависимость реальных аберраций от
возбуждения и положения объекта [368], и затем они сравни-
сравнивались для колоколообразной и реальной моделей [369]. Объ-
Объем не позволяет рассказать о ряде подробных работ, посвящен-
посвященных аберрациям квадрупольных систем [37, 165], но по край-
крайней мере следует обратить внимание на прекрасную работу ле-
ленинградской группы под руководством С. Я. Явора [35].
10.5.2. Коррекция аберраций с помощью
мультиполей
В разд. 5.6.4 мы обсудили один из наиболее многообещаю-
многообещающих способов компенсации аберраций осесимметричными лин-
линзами, а именно коррекцию мультипольными элементами. По-
Поскольку в уравнении C.82) первые квадрупольные, октуполь-
ные и додекапольные члены появляются в связи с членами вто-
второй, четвертой и шестой степеней поперечных координат, ясно,
что эти компоненты изначально ответственны за члены первого,
третьего и пятого порядков в уравнении траектории. Другими
-словами, идеальный квадруполь приводит к астигматической
фокусировке, идеальный октуполь ответствен за аберрации
третьего порядка, а идеальный додекаполь — за аберрации
пятого порядка. В случае реальных элементов появляются ком-
компоненты более высоких гармоник и ситуация усложняется. Ес-
Естественно, даже идеальный квадруполь имеет аберрации, но
приведенная выше классификация обеспечивает приемлемый
учет основных видов различных мультипольных компонент.
Теорема Шерцера (разд. 5.2.1.3) для мультиполей не спра-
справедлива. Следовательно, можно ожидать, что их аберрации при
различных обстоятельствах могут иметь разные знаки. Вслед-
Вследствие этого квадруполи, октуполи и додекаполи могут служить
"корректорами астигматизма, аберраций третьего и пятого по-
порядка соответственно.
Коррекция сферической аберрации осесимметричных линз
хорошо известна [147]. Аналогично можно корректировать
апертурные аберрации квадруполей, используя октупольную
-'576
Мультипольные линзы
линзу [160]. Возможна даже их физическая комбинация (см.
рис. 38,6).
Таким образом, по крайней мере в принципе, комбинация
квадрупольных систем с октуполями и додекаполями может
привести к безаберрационным оптическим колоннам. Линзы,
которые будут состоять из таких колонн, имеют весьма громозд-
громоздкую конструкцию [370]. Проблема правильной юстировки яв-
является основным фактором, сдерживающим их коммерческую
жизнеспособность в качестве альтернативы осесимметричным
системам. Последние работы в направлении использования гек-
сапольных линз для коррекции аберраций третьего порядка
[167—169] могут внести вклад в производство относительно про-
простых и безаберрационных электронно- и ионнооптических си-
систем.
10.5.3. Хроматическая аберрация
Введем хроматическую аберрацию мультипольных линз
аналогично тому, как для осесимметричных линз (см. разд. 5.3).
Как и прежде, коэффициенты хроматической аберрации могут
быть выведены с помощью метода характеристических функ-
функций. Однако здесь мы воспользуемся гораздо более простым
подходом.
Известно, что причиной осевой хроматической аберрации яв-
является уменьшение оптической силы линзы с увеличе-
увеличением энергии частиц. Очевидно, что если эту зависимость сде-
сделать обратной, то хроматическая аберрация изменит свой
знак. В случае нулевой зависимости хроматическая аберрация
исчезает. Как мы знаем, для осесимметричных линз такое не-
невозможно.
10.5.3.1. Ахроматические квадрупольные линзы. Исследуем
теперь, к чему приведет комбинация электростатической и маг-
магнитной квадрупольных линз [23]. Мы анализировали знак
функции q(z) в конце разд. 10.2. Известно, что если Uz(z) и
Q2(z) имеют одинаковые знаки, то электростатические и магнит-
магнитные силы действуют в противоположных направлениях, два
члена в уравнении A0.9) имеют разные знаки, а знак q(z) оп-
определяется большим членом. Однако для заданных осевых
функций эти члены являются функциями только энергии час-
частиц. В случае когда обе функции одинаково зависят от z (урав-
(уравнение A0.5)) и U2 и Q2 положительны, для положительно за-
заряженных частиц в уравнении A0.9) электростатический член
будет положительным, а магнитный — отрицательным (для от-
отрицательно заряженных частиц знаки меняются). Для малых
энергий первый член является доминирующим, тогда как для
577
Глава 10
больших энергий доминирующим становится второй член. Су-
Существует значение энергии, при котором два члена оди-
одинаковы; следовательно, результирующее значение q(z) равно-
нулю. В этом случае обе силы точно компенсируют друг друга
и действие линзы исчезает.
Поскольку абсолютная величина q(z) бесконечно велика при
нулевой энергии и стремится к нулю при бесконечно большой
энергии, но функция меняет знак где-то между ними, очевид-
очевидно, что она должна иметь экстремум при энергии, соответст-
соответствующей потенциалу £/=£/aChr, где система ахроматична. Условие
ахроматизма может быть записано как
dq/d(—QU)=0. A0.46)
Подставляя сюда выражение q(z) для нерелятивистского
случая из уравнения A0.9) и учитывая уравнение A0.5), най-
найдем, что для заданных величин U2 и Q2 значение U2 определя-
определяется выражением
2. A0.47)
(Для релятивистских частиц справедливо более сложное выра-
выражение.) Мы записали результат в таком виде, потому что обыч-
обычно значение UaChv задано, и мы хотим вычислить соотношение
между U2 и п2, которое обеспечивает ахроматичность системы
в окрестности этого конкретного значения потенциала.
Подставляя уравнение A0.47) обратно в нерелятивистское
уравнение A0.9), получим ^achr^), т. е. функцию q(z) для
ахроматического режима в следующем виде:
<7achr (Z).= U2k (z)/(£/achr — Uо) =— <7el (z) =
= =F {— Q/ [2m0 (Uachr — Uo) ]} 1/2^2й (г) = qmasn (г) /2,
A0.48)
т. е. в ахроматическом режиме функция q(z) равна ее электро-
электростатической части с отрицательным знаком или половине своей
магнитной части gwgn^). Следовательно, знак этой функции
определяется ее магнитной частью.
Из этого раздела следует важный вывод: комбинация элек-
электростатической и магнитной квадрупольных линз или система
таких линз может быть сделана ахроматической в некотором
интервале энергий. Это еще одна причина, позволяющая верить,
что безаберрационные оптические колонны на базе мультиполь-
ных линз действительно возможны.
578
Мультипольиые линзы
Заключение
В этой главе дан обзор наиболее важных свойств мульти-
польных линз. Поля мультипольных линз уже рассматривались
в гл. 3. Здесь анализируются поля стандартных квадрупольных
конфигураций, поскольку на их основе проводится соответст-
соответствующее рассмотрение квадруполей, октуполей и додекаполей.
Далее были выведены уравнения параксиальных лучей A0.7)
и A0.8) и проведено обсуждение формирования изображения
квадрупольными линзами. Обычно квадруполи формируют ли-
линейное изображение точечного объекта, но квадрупольные си-
системы способны к формированию стигматического изображе-
изображения. Применение матриц преобразований делает возможным
краткое обсуждение квадрупольных дуплетов, триплетов и
мультиплетов, включая понятие эмиттанса пучка. Наконец,
были рассмотрены аберрации мультипольных линз. Геометри-
Геометрические аберрации осесимметричных квадрупольных линз могут
быть компенсированы мультипольными элементами. Так как
комбинированные квадрупольные линзы могут быть сделаны
ахроматическими, можно построить безаберрационные оптиче-
оптические колонны, состоящие только из мультипольных элементов.
Глава 11
ОТКЛОНЕНИЕ ПУЧКОВ
Отклонение пучков частиц применяется в различных целях. Са-
Самый общий классический тип отклонения используется в катод-
но-лучевых трубках, установках литографии, сканирующих
электронных микроскопах и других аналитических приборах.
Его цель — сканирование пучка по поверхности. Главной осо-
особенностью этого типа отклонения является то, что неотклонен-
ный пучок имеет прямолинейную оптическую ось; следователь-
следовательно, анализ отклонения может быть основан на принципах, ис-
использованных в предыдущих главах.
Совершенно другой тип отклонения необходим в циклотро-
циклотронах, масс- и бета-спектрометрах, анализаторах энергии и т.д.
В этом случае отклонение используется либо для управления
пучками вдоль криволинейных траекторий, либо для разделе-
разделения частиц с различными энергиями и (или) массами. В обоих
случаях основная траектория пучка — кривая; пучок имеет кри-
криволинейную ось, которая требует специального рассмотрения.
В соответствии с приведенной выше классификацией будем
рассматривать два этих основных случая отдельно. Должно
быть ясно с самого начала, что для отклонения можно приме-
применить множество различных типов симметрии. Следовательно,
нужно ограничиться несколькими простыми случаями, особенно
теми, которые чаще всего встречаются на практике. Простейши-
Простейшими отклоняющими системами являются однородные электроста-
электростатические и магнитные поля. Они уже обсуждались в разд. 2.7.1.1
и 2.7.2.2 соответственно. К сожалению, чисто однородные поля
на практике реализовать невозможно вследствие присутствия
контурных полей на физических границах электродов или маг-
магнитных полюсов.
11.1. Отклонение для сканирования
Если наша цель — отклонение пучка заряженных частиц,
сфокусированного осесимметричными или квадрупольными по-
полями так, что оптической осью является прямая линия (ось де-
декартовой системы координат), то можно применить электроста-
электростатическое или магнитное отклонение. Для сканирования необхо-
необходимо отклонение в обоих ортогональных поперечных направле-
направлениях х и у.
580
Отклонение пучков
11.1.1. Электростатические отклоняющие поля
Начнем с электростатического поля, которое отклоняло бы
в направлении координаты х. Простейшим примером конфигура-
конфигурации электродов, с помощью которой получают такое поле, явля-
является плоско-параллельный конденсатор, показанный на рис. 5.
Плоскость yz является плоскостью антисимметрии; дополни-
дополнительно предположим, что плоскостью симметрии поля является
плоскость xz, хотя это требование не обязательно.
Поскольку это поле — дипольное, можно начать с общего
распределения мультипольного потенциала C.52) при ЛГ=1,
поскольку существует одна плоскость симметрии. Дополнитель-
Дополнительно, благодаря проведенному выше анализу симметрии разложе-
разложение распределения потенциала в ряд может содержать только
нечетные члены. Используя уравнения C.54), C.56), C.60),
C.62) и C.64), получим первые члены разложения в ряд C.52)
в виде
их (х, у, z)« £/, (z) * - [3 Uг (z) + £/," (г) /8] ху2 +
A1.1)
где индекс х означает, что распределение потенциала исполь-
используется для отклонения в направлении х. Функции U\(z) и
U3(z) определяют свойства отклонения. Они могут быть опре-
определены численно из реальной конфигурации электродов одним
из методов, представленных в разд. 3.3 [96]. Уравнение A1.1)
также прямо следует из общего уравнения C.28).
Дифференцируя уравнение A1.1) по х и у, видим, что пер-
первый член Ех равен Ui(z), т. е. ^-компонента электростатиче-
электростатического поля существует даже вдоль оптической оси, где #=0.
С другой стороны, компонента Еу вдоль оптической оси равна
нулю. Очевидно, такое расположение будет отклонять пучок с
прямолинейной осью в направлении х.
Теперь рассмотрим электростатическое поле, отклоняющее
в направлении у. Необходимо такое поле, для которого плос-
плоскость xz является плоскостью антисимметрии, а плоскость
yz— плоскостью симметрии.
В этом случае мы не можем воспользоваться разложением
потенциала мультиполя C.52), потому что он был выведен в
предположении, что плоскость xz является плоскостью симмет-
симметрии. Однако можно использовать общее выражение, задаваемое
уравнением C.28). Вследствие проведенного выше анализа
симметрии разложение распределения потенциала в ряд может
содержать только четные члены по х и нечетные по у. В ре-
результате получим первые члены разложения в виде
uy(x,y,z)*Wi{z)y+[3W3(z) - W(z)/8]*2t/-
(И-2)
581
Глава 11
где индекс у означает, что это распределение потенциала ис-
используется для отклонения в направлении у. Функции Wi(z)
и W3(z), которые определяют свойства отклонения, могут быть
определены из реального расположения электродов каким-либо
численным методом (см. разд. 3.3).
Дифференцируя уравнение A1.2) по х и у, видим, что пер-
первый член Еу равен Wi(z), т. е. «/-компонента электростатическо-
электростатического поля существует даже вдоль оптической оси z. Однако ком-
компонента поля Ех вдоль оптической оси равна нулю. Очевидно,
такое расположение будет отклонять пучок от прямолинейной
оси в направлении у.
Для сканирования пучка необходимо отклонение в обоих
направлениях. Суммарный отклоняющий потенциал и являет-
является суперпозицией их и иу:
и(х, у, z) =ux (х, у, z) +uy(x, у, z). A1.3)
Применяя уравнения A.13) и A.17) к уравнению A1.3) и
пренебрегая всеми членами, содержащими комбинации попе-
поперечных координат в степенях выше первой, получим следующие
приближенные выражения для компонент электростатического
поля:
Eyv-W^z), A1.4)
£«*-£/', (z)x-W\{z) у.
Эти выражения справедливы в окрестности оптической оси. Для
больших отклонений необходимо большее количество членов.
Отсюда можно четко видеть физический смысл функций U\(z)
и Wi(z). Для однородных полей как U\, так и W\ постоянны.
Функции U3(z) и W$(z) появляются только при больших откло-
отклонениях.
В катодно-лучевых трубках распределение потенциала
A1.3) обычно реализуется двумя парами параллельных плас-
пластин, разделенных и повернутых по отношению друг к другу
на 90° вокруг оптической оси. Однако удобнее использовать
свойство мультиполей, обсуждавшееся в разд. 3.1.3.3, заклю-
заключающееся в том, что большое число простых электродов, под-
поддерживающих соответствующие потенциалы, может быть ис-
использовано для получения любого мультипольного поля. В этом
частном случае удобно использовать восемь электродов, чтобы
получить два взаимно перпендикулярных дипольных поля при
одном достаточно простом расположении (рис. 159). Это так
называемый «октупольный дефлектор» [371], но он не являет-
является реальным октуполем, так как не имеет четырех плоскостей
симметрии.
582
Отклонение пучков
-vy-Pv
Рис. 159. Электростатический «окту-
польиый» дефлектор [371].
Такое расположение обла-
обладает несколькими преимущест-
преимуществами перед обычным двух-
электродным дефлектором:
1) оно более компактно,
2) имеет меньшие аберра-
аберрации,
3) может быть использова-
использовано одновременно как стигма-
тор или даже как квадруполь-
ная линза и октупольный кор-
корректор,
4) его поле легче вычис-
вычислить, чем поле двухэлементно-
двухэлементного дефлектора (см. разд. 3.1.3
и [22]).
Потенциалы электродов, необходимые для надлежащего
действия восьмиэлектродного дефлектора, даны на рис. 159. Че-
Через Vx и Vy обозначены потенциалы, используемые для откло-
отклонения в направлениях х и у соответственно. Результирующие
напряжения являются суперпозицией этих двух потенциалов,
взвешенных параметром р, который в итоге определяет распре-
распределение потенциала в плоскости ху @<р<1). Его величина
влияет на чувствительность отклонения и аберрации.
Преимуществами электростатического отклонения являются
высокая скорость отклонения, легкость изготовления и незави-
независимость от отношения заряда к массе частицы (см. разд. 2.7.1.1),
Возможность одновременного использования восьмиэлектродно-
восьмиэлектродного дефлектора для фокусировки и коррекции аберраций также
может считаться очень важным преимуществом. Его недостат-
недостатком является относительно низкая чувствительность отклоне-
отклонения. Если необходима более высокая чувствительность, то нуж-
нужно использовать магнитный дефлектор.
11.1.2. Магнитные отклоняющие поля
Обычно для сканирования используются два типа дефлек-
дефлекторов: седловая (рис. 160) и тороидальная (рис. 161) катушки.
В обоих случаях вблизи оптической оси токи отсутствуют, сле-
следовательно, в этой области можно использовать магнитный ска-
скалярный потенциал ш. При таком расположении, как показано
на рисунках, плоскость xz является плоскостью антисимметрии,
а плоскость yz — плоскостью симметрии для вектора плотности
тока J. Следовательно, в соответствии с уравнением A.4) и бла-
благодаря «вращательной» природе оператора «ротор» для векто-
вектора индукции В справедливо обратное. Действительно, для маг-
магнитного скалярного потенциала плоскость xz является плос-
583
Глава П
костью симметрии, а плоскость yz— плоскостью антисиммет-
антисимметрии. Как следствие уравнение A1.1) можно использовать для
(ах, но, естественно, Ui(z) и U3(z) должны быть заменены не-
некоторыми новыми функциями Qi(z) и Q3(z) соответственно.
Меняя плоскости симметрии и антисимметрии, придем к
функции магнитного скалярного потенциала (ау, задаваемой
уравнением A1.2), где W{(z) и W3(z) должны быть заменены
новыми функциями ai(z) и из(z) соответственно. Эти функции
можно определить из реального расположения отклоняющих
катушек одним из численных методов [96]. Суммарный потен-
потенциал является суперпозицией этих двух случаев и дается выра-
выражением
0) (Х, У, Z) =(йх (X, у, Z)+(Oy (X, у, Z). A1.5)
Используя уравнения A.13) и A.22) совместно с уравнения-
уравнениями A1.1), A1.2) и A1.5) и пренебрегая членами, содержащи-
t
1 у /
Рис. 160. Седловая катушка [96]. Рис. 161. Тороидальная катушка [96].
ми комбинации поперечных координат в степенях выше первой,
получим следующие приближенные выражения для компонент
вектора магнитной индукции:
Я</«— HoG)i(z), A1-6)
Вг«— no[Q'i(z)x+(a/l (г)у].
Эти выражения справедливы в окрестности оптической оси.
Для больших отклонений потребуется включить большее коли-
количество членов. Так как пучок распространяется в основном
вдоль оптической оси г, из уравнения A.14) следует, что ком-
компонента Вх отвечает за отклонение в. направлении у, а компо-
компонента Ву обеспечивает отклонение в направлении х.
11.1.3. Стигматическая фокусировка при малых
отклонениях
Покажем, что свойство стигматической фокусировки осесим-
метричных полей сохраняется в присутствии отклоняющих по-
полей, если отклонение недостаточно, чтобы нарушить паракси-
584
Отклонение пучков
альную природу пучка. Для простоты будет рассмотрен специ-
специальный случай чисто электростатических полей, но результаты
в равной мере справедливы также для магнитных полей.
Начиная с общих уравнений траектории B.80) и B.81) в де-
декартовых координатах, используя уравнения B.31), B.87),
B.89) и B.90), подставляя компоненты поля из уравнений
C.38), C.40) и A1.4) и пренебрегая всеми членами, содержа-
содержащими степени поперечных координат выше первой и их произ-
производными, получим две проекции релятивистской параксиальной
траектории в следующем виде:
x"+[x'U'(z)+xU"(z)/2]X
= U1{z){l-Q[U(z)-Uo]/(mQc^}{2[U(z)-Uo]rei}-i,
A1.7)
y"+[y'U'(z)+yU"(z)/2]X
X{1 - Q[U(z) - U0]/(mac*)} {2[U(z) - U0]rel}-> =
= Г,(е){1 -Q[U(z) - Uo)!(moc*)}{2[U(z) - UQ]rel}-K
A1.8)
Если отклонения нет [£A(z) — Wi(z) =0], оба уравнения дают
электростатическую часть уравнения параксиальных лучей D.31)
для осесимметричных полей и С=0, т. е. для случая, когда тра-
траектория лежит в одной из плоскостей xz или yz (см. обсуждение
в разд. 10.2). Общее решение этих уравнений с начальными ус-
условиями уравнения E.42) может быть записано в виде E.43) и
E.44), где координаты X и У можно заменить координатами х
и у соответственно, так как в случае чисто электростатических
полей нет необходимости введения вращающейся системы коор-
координат.
Единственное различие между уравнением D.31) и уравнени-
уравнениями A1.7) и A1.8) состоит в том, что уравнение D.31) однород-
однородно, тогда как каждое из двух других уравнений содержит член,
обусловленный присутствием отклоняющих функций U{ (z) и
Wi(z). Каждое из общих решений этих неоднородных уравнений
равно общему решению соответствующего однородного уравне-
уравнения плюс частное решение данного неоднородного уравнения.
Обозначим эти частные решения хряп(г) и #part(z). Они зависят
от функций f/i (г) и W\ (г) соответственно. Тогда общее решение
может быть записано как
x(z)=Xog(z)+X'0h(z)+xpatt(z), A1.9)
yog(z) +y'oh(z) +ypaTl(z). A1.10)
Так как по определению частное решение h (z) на изображе-
изображении равно нулю, если точечный объект расположен на оптиче-
585
Глава 11
ской оси (Хо=Уо = 0), тогда для изображения получим .
X(Zi)=Xpart(Zi), y(Zi)^ypart(Zi), (П-11)
т. е. мы по-прежнему имеем точечное изображение точечного
объекта, но оно больше не находится на оси, поскольку пучок
отклонен. Можно представить эту ситуацию, предполагая, что
прямолинейная ось пучка деформируется в искривленную, опре-
определяемую функциями xpart(z) и yPart(z). Так как эта ситуация
общая для всех лучей пучка, мы делаем заключение, что стиг-
стигматическая фокусировка сохраняется, когда к параксиальному
пучку прикладываются слабые отклоняющие поля. Кроме того,
так как уравнения A1.7) и A1.8) линейны и функции Ui(z) и
W\ (z) представляют поперечные компоненты поля, то малые
отклонения пропорциональны отклоняющим их полям. Таким об-
образом, мы можем предположить, что параксиальный пучок от-
отклоняется как целое и его фокусирующие свойства первого по-
порядка не нарушаются.
Если, однако, отклоняющее поле становится достаточно силь-
сильным, неоднородные члены уравнений A1.7) и A1.8) становятся
большими. Как следствие отдельные лучи пучка отклоняются от
оси настолько сильно, что параксиальное приближение ста-
становится недействительным. В результате появляются абер-
аберрации отклонения и сфокусированное пятно будет смазы-
смазываться по мере его отклонения от оси (см. разд. 11.1.4). Смеще-
Смещение пучка уже не будет пропорциональным отклоняющему полю.
Кроме того, отдельные лучи будут изменять свое положение по
отношению друг к другу, что в свою очередь приведет к появле-
появлению специального фокусирующего эффекта, обусловленного от-
отклонением.
Наконец, исследуем зависимость кривизны траектории от от-
отклонения [16]. Для этого предположим, что осесимметричные
поля не включены в рассмотрение [U (z) = £/ = const]. Тогда ле-
левые части уравнений A1.7) и A1.8) сводятся к х" и у" соот-
соответственно. Радиус кривизны р можно определить из уравнения
, A1.12)
где Еп — компонента вектора электростатического поля в на-
направлении нормали к траектории в данной точке. Используя
уравнения B.2), B.26), B.31), B.87) и B.90), получим
A1.13)
Сравнивая это уравнение с уравнениями A1.7) и A1.8), видим,
что х" и у" в этом случае представляют собой кривизну двух про-
586
Отклонение пучков
екций траектории в параксиальном приближении, что само по
себе очевидно, так как х'2 и у'2 в этом случае пренебрежимо
малы.
11.1.4. Аберрации отклонения
Если отклоняющие поля достаточно сильны, чтобы вызвать
значительное отклонение траектории от оси, то параксиальное
приближение недействительно и в дополнение к аберрациям фо-
фокусирующих элементов возникают аберрации отклонения: сфо-
сфокусированное пятно будет смазываться по мере его отклонения
от оси и смещение пучка уже не будет пропорционально откло-
отклоняющему полю.
Аберрации отклонения можно рассматривать аналогично
аберрациям осесимметричных линз (см. гл. 5). Однако вследст-
вследствие более сложных условий симметрии выражения для этих
коэффициентов аберрации более громоздкие, а также необходи-
необходимо большее число коэффициентов. В литературе дана исчерпы-
исчерпывающая информация о различных подходах к вычислению
аберраций отклонения магнитных [372, 373], электростатических
[374] и комбинированных [16, 51Ь] дефлекторов. Были опублико-
опубликованы выражения для аберраций при наложении магнитных
осесимметричных и отклоняющих полей [375], последние распро-
распространены на релятивистский случай комбинированных электро-
электростатических и магнитных фокусирующих и отклоняющих систем
[376].
В соответствии с методами, использованными для вычисле-
вычислений, разные подходы дают различные виды коэффициентов
аберрации. Аберрации сильно зависят от типа симметрии полей.
Для отклонения можно использовать множество разных видов
симметрии >и можно, по крайней мере в принципе, вычислить
аберрации для весьма общих случаев, включающих все различ-
различные виды осеоимметричных, мультипольных и других элементов.
Такое рассмотрение очень сложно [170], «о оно имеет по край-
крайней мере два существенных преимущества: 1) общее выражение
охватывает практически все возможные расположения элемен-
элементов как специальные случаи, 2) некоторые аберрации отдельных
элементов можно использовать для компенсации некоторых
аберраций, вызванных друлими элементами. Естественно, если
мы хотим работать с выражениями приемлемых размеров, то
должны пожертвовать общностью и рассматривать только прак-
практически важные комбинации разных видов симметрии. Напри-
Например, если есть желание разработать эффективный (метод для
синтеза электронных (ионных) оптических колонн, построенных
из мультипольных фокусирующих и отклоняющих элементов,
необходимо рассмотреть аберрации таких систем. В дальней-
587
Глава 11
шем мы опишем основные этапы вычисления, используя приме-
примеры таких расположений. Этот метод с таким же успехом можно
прямо использовать для других видов симметрии.
Рассмотрим комбинацию электростатических и магнитных
мультипольных линз « дефлекторов [377]. Для этого исполь-
используем метод характеристических функций, представленный в
разд. 5.1.
В первую очередь мы должны представить толя в виде элек-
электростатических скалярных и магнитных векторных потенциалов,
как это требуется уравнениями E.9) и E.10). Электростатиче-
Электростатический мультипольный потенциал дается уравнением C.82) для
стандартной конфигурации и содержит осесимметричные, 'Квад-
рупольные, октупольные и т. л. компоненты. Электростатический
отклоняющий потенциал представлен уравнением A1.3). Сум-
Суммарный электростатический потенциал u(x,y,z) вычисляется до-
добавлением мультипольного и отклоняющего потенциалов. Вклю-
Включая члены, содержащие степени поперечных координат вплоть
до четвертой, и используя уравнения A1.1) и A1.2), получим
и(х,у, г)»£/(z) + £/,(г)х+ Wi(г)у— U"(z) (х2+у2)/4+
+ U2(z) (х2-у2) - C/,"(z) (x* + xy>)/8- Wx"{z) (х2у+у>)/8 +
+ U3 (г) (х3 - Злгг/2) + W3 (г) Cx2y - г/3) +
(х2+г/2J/64 - U2"{z) (х*-у*)/12 +
. A1.14)
Для стандартной конфигурации магнитный мультипольный
(скалярный потенциал дается уравнением A0.3). Он содержит
квадрупольные и октупольные компоненты, если пренебречь
всеми членами, содержащими степени поперечных координат
выше четвертой. Магнитный отклоняющий потенциал определя-
определяется уравнением A1.5). Суммарный 'магнитный скалярный по-
потенциал (o(x,y,z) является суммой мультипольного и отклоняю-
отклоняющего потенциалов. Имеем
<о (х, у, z) «Q, (z)x+©i (z)y+2Q2(z)xy —
— их"(г) (*3 + a#2)/8-g>,"(z) (д»у+уЭ)/8-
— Q2"(z)xy(x2+y2)/6 + Q3(z) (x3 — 3xy*) +
+ а3(г)(Зх2у-уЗ)+4п1(г)ху(х2-у*). A1.15)
Теперь имеем обе комбинированные функции электростати-
электростатического и магнитного скалярного потенциалов. Однако для ме-
метода характеристических функций необходимы компоненты маг-
магнитного векторного потенциала Ах, Ау, Аг. В пространстве, сво-
свободном от токов, отношение векторного потенциала А к магнит-
магнитному скалярному потенциалу и дается уравнениями A.12) и
588
Отклонение пучков
A.22). Компоненты rot А и grad и определяются уравнения-
уравнениями A.6) и A.13) соответственно. Имеем
дАг/ду — дАу/dz = — цоды/дх,
дАх/дг — дАг1дх=—1юд(о1ду, A1.16)
дАу/дх — дАх/ду=— \iQde>ldz.
Магнитный векторный потенциал определяется с точностью до
градиента произвольной скалярной функции я|з, так как
rot grad i|) = 0 для любого \f- Выберем ^ так, чтобы
A1.17)
и предположим, что предмет Вг(х,у,z0) = 0. Тогда из уравнений
A1.16) и A1.17) имеем
— \io\ (д<й/ду)дг, A1.18)
1 (day/dx)dz. A1.19)
Если сперва положить i|>=const, то Аг=0 и получим выраже-
выражения для Ах и Ау дифференцированием уравнения A1.15) по у
и х и подстановкой частных производных в уравнения A1.18) и
A1.19) соответственно. Эти выражения будут содержать не-
несколько членов, которые можно проинтегрировать непосредст-
непосредственно, в то время как интегрирование других членов требует
специального знания осевых функций. Следовательно, удобно
выбрать функцию я|з таким образом, чтобы эти интегралы исчез-
исчезли [377]. (Для этого мы должны также предположить, что пер-
первые производные соответствующих осевых функций имели на
предмете нулевую величину.) Окончательно получим следующие
выражения для трех компонент магнитного векторного потен-
потенциала:
A1.20)
'1 (г) C*2+*/2)/8 + Q'2(z) (Sx2y+y*)/6],
A1.21)
(z)x — QiB)y+Q2(z) (x2 — y2) +
+ cos (z) (x3 - 3xy*) - Q3 (г) &х2у -y*) +
+ Q<(z)(x*-6xY+y*)]. (H-22)
Теперь мы готовы использовать уравнение E.10) для вычис-
вычисления вариационной функции К- Подставляя уравнения B.78),
B.90), A1.14) и A1.20) — A1.22), заменяя квадратные корни
589
Глава 11
их разложением в ряд Тейлора и сохраняя члены вплоть до чет-
четвертой степени комбинаций поперечных координат и их произ-
производных, найдем, что в нерелятивистском случае Кт все еще оп-
определяется уравнением E.11), но, естественно, КB) и Kw дают-
даются гораздо более громоздкими выражениями, чем электростати-
электростатические части уравнений E 12) и E.13). Подстановка члена КB>
в уравнение Эйлера E.4) дает уравнения параксиальных лучей
для комбинированных систем. Они содержат все члены нереля-
нерелятивистских уравнений A0.7) и A1.7), так же как и A0.8), и
A1.8), плюс дополнительный член, соответствующий функциям
магнитного отклоняющего потенциала иц и Qi.
Преобразование члена четвертой степени Kw вариационной
функции в соответствии с процедурой, описанной в разд. 5.1 —
5 3, — длительная и кропотливая работа. Даже если предполо-
предположить, что отклоняющая система управляется слабыми сигнала-
сигналами, сравнимыми с малыми величинами х, у, х' и у', так что чис-
число членов четвертой степени пренебрежимо мало [377], резуль-
результат появляется в виде «е менее чем 56 геометрических и шести
хроматических коэффициентов аберрации в форме определенных
интегралов. Однако их можно выразить через три основные
аберрационные функции, которые можно оценить, используя
различные комбинации параксиальных лучей.
Аберрации отклонений можно уменьшить соответствующим
подбором положений, размеров, углов вращения и силы деф-
дефлекторов [96]. Они могут быть полностью уничтожены (по край-
крайней мере в принципе) применением двух современных понятий.
Первое называется динамической коррекцией; второе — понятие
переменной оси линзы.
Идея динамической коррекции основывается на том, что
в сканирующей системе изображение формируется от точки
к точке [378, 379], следовательно, аберрации отклонения можно
корректировать простым применением соответствующих коррек-
корректирующих сигналов к отклоняющим токам
Понятие линзы ic переменной осью было впервые представле-
представлено в виде подвижной объективной линзы [380], распределение
осевой индукции которой выбиралось так, чтобы фокусирующие
элементы были как бы сдвинуты вбок, как если бы оптическая
ось была смещена Такое расположение может привести к исчез-
исчезновению некоторых аберраций отклонения, но его очень трудно
реализовать Однако идея подвижной объективной линзы была
применена на практике в модифицированном виде оптической
оси с электронным сдвигом, синхронизированной с отклоняю-
отклоняющим пучком Было продемонстрировано, что (результирующая
линза с переменной осью имеет желаемые свойства для лито-
литографических систем, электронный пучок которых управляется
сильным полем [381]
590
Отклонение пучков
Дополнительную информацию об общих свойствах сканиру-
сканирующих отклоняющих систем и их практических применениях
можно найти в литературе [272, 382—384].
11.2. Электростатические и магнитные призмы
Целью ускорителей частиц, масс- и бета^спектрометров и
•спектрографов, анализаторов энергии и т. д. является отклоне-
отклонение пучка частиц на большие углы с тем, чтобы оптическая ось
искривлялась Поскольку отклонение обычно зависит от энергии
и от отношения заряда к массе частицы, оно применимо для
разделения заряженных частиц в соответствии с их массами или
энергиями, как разложение света оптическими призмами. Для
этого можно использовать как электростатические, так и маг-
магнитные поля. Однако в случае больших отклонений оптическая
система действует не только как призма, но обладает также и
фокусирующим действием. Следовательно, электронно-ионная
оптическая призма соответствует сочетанию призмы и линзы.
Мы уже обсудили несколько простых примеров анализа масс
в разд 2 7.3.1. Для строгого исследования необходимо изучить
теорию движения частиц в системах с криволинейными осями.
Такая теория, разработанная Г. А. Гринбергом [385], построена
на описании траекторий, как функции их отклонений от так на-
называемой базовой траектории, которая может быть определена
как произвольная кривая в пространстве. Базовая траектория
является криволинейной осью пучка. С помощью этой теории
можно рассматривать оптические системы любой симметрии.
Кроме того, метод Гринберга дает возможность найти распреде-
распределение электростатического и(или) магнитного поля, которое
позволяет получить любую заранее заданную форму пучка.
В этом разделе мы уделим внимание только очень простым
специальным случаям. Ограничимся рассмотрением оптических
осей, представляющих собой окружность
11.2.1. Электростатические призмы
Простейшей электростатической призмой является плоско-
плоскопараллельный конденсатор (разд. 2 7 1). Его использование в
качестве анализатора скорости было обсуждено в разд. 2.7.1 2.
Было также установлено (разд. 2 7.1 1), что электростатическое
отклонение не зависит от отношения заряда к массе частицы,
поэтому для анализа масс его использовать нельзя Следова-
Следовательно, электростатическая призма является анализатором ско-
скорости (энергии). Она не может разделить частицы разных масс
с одинаковыми зарядом и энергией.
591
Глава 11
Электростатические призмы, базовой траекторией которых
является окружность, могут иметь форму цилиндрических, сфе-
сферических или тороидальных конденсаторов. Базовая траектория
задается эквипотенциальной поверхностью. В случае цилиндри-
цилиндрического конденсатора, поперечное сечение которого показано на
рис. 162, базовая траектория является окружностью радиуса р.
Предположим, что поле лризмы планарно, т. е. ие зависит от
координаты, перпендикулярной плоскости рисунка (см.
разд. 3.1.1.1). Другое предположение заключается в том, что
источник частиц помещен внутри конденсатора, т. е. потенциал
на базовой траекторий устанавливается таким образом, что он
соответствует начальной скорости частиц. На лрактике источник
обычно расположен вне конденсатора и используется только
его сектор для отклонения и фокусировки. В этом случае необ-
необходимо принимать во внимание контурные поля.
Рис. 162. Фокусировка в цилиндрическом конденсаторе.
Распределение потенциала и(г) внутри цилиндрического кон-
конденсатора легко определить, решив уравнение Лапласа A.21)
для планарного и осесимметричного случая (нет зависимости от
цилиндрических координат а и z) в отсутствие пространствен-
пространственного заряда. Граничные условия даются потенциалами Vi и Уг
на электродах радиусами R\ и R2 соответственно. В результате
имеем
u(r) = Vl+(V2 — V1)\n(r/R1)J\n(R2/Ri). A1.23)
Радиальные компоненты электростатического поля определяют-
определяются уравнениями A.13), A.17) и A1.23):
Er(r)=—(V2 — Vi)l[rln(R2IRi)]. (П.24)
Подставляя уравнение B.33) в уравнение A1.12), получим вы-
выражение для кривизны в нерелятивистском случае
1/р=£,(р)/[2«(р)]. A1.25)
592
Отклонение пучков
Отметим, что «ила, действующая на частицу, должна быть на-
направлена по оси цилиндрического конденсатора. Следовательно,
для положительно заряженных частиц м<0 и Ег<.0, тогда как
для отрицательно заряженных частиц как и, так и Ег>0.
Если требуется, чтобы базовая траектория была окружно-
окружностью радиуса р, то мы должны выбрать потенциалы электрода
так, чтобы для г=р электростатический потенциал и поле удов-
удовлетворяли уравнению A1.25). Подставляя г = р в уравнение
A1.24), видим, что это условие удовлетворяется, если
"(р)=— (V2— Vi)l[2\n(RilRi)]. A1.26)
Величина и(р) определяется начальной скоростью частиц на
выходе источника. Обычно Ri и R2 — заданные параметры. Раз-
Разность потенциалов V^—V\ должна быть выбрана так, чтобы
удовлетворялось уравнение A1.26). Тогда г = р — постоянный
радиус кривизны базовой траектории, т. е. окружность, и и(р)
должно удовлетворять A1.23). Требуемую разность потен-
потенциалов получим из уравнений A1.23) и A1.26) в виде
Vi = M(p)[l + 21n(p/fli)], У2 = ы(р)[1 + 21п(р/Да)]. A1.27)
Отсюда |Vi|>|«(p)| и |V2|<|«(p)|, что согласуется со зна-
знаком Ег, установленным выше.
Покажем теперь, что базовая траектория устойчива [386].
Рассмотрим малое отклонение из-за небольшого изменения на-
направления начальной скорости (см. рис. 162). Тогда можно вы-
выразить радиальную координату г как
г=рA + 8), A1.28)
где е — малая безразмерная величина. Из уравнения B.64)
имеем
r2daldt=const = p2a0, A1.29)
где ссо определяется начальной скоростью. Подставляя это вы-
выражение в уравнение B.63), получим
tPrfdfi — pWr3 — Q£,(r)/mo=0, A1.30)
откуда сразу же видно, что вдоль базовой траектории нет ника-
никаких изменений, потому что для г=р последние два члена в со-
соответствии с уравнением A1.12) исчезают.
Подставляя теперь уравнение A1.28) в A1.30), выражая
Ет(г) через Ег(р), используя разложения в ряд Тейлора для 1/г
и 1/г3, пренебрегая степенями е выше первой и принимая во
593
Глава 11
внимание уравнение A1.12), получим следующее дифференци-
дифференциальное уравнение для е:
= 0. A1.31)
Его решение запишется в виде
8 @ -sin [2'/2a0 (t — to) ] = sin [21/2 (a — ao) ], A1.32)
потому что в начальный момент времени to имеем s(to)=0
и в азимутальном направлении силы отсутствуют. Отсюда сле-
следует, что если
а, — ао = 2-'/2ля = «Х 127,28°, A1.33)
то 8( = 0, т. е. возмущенная траектория возвращается к базовой
окружности с азимутальной координатой а». Другими словами,
цилиндрический конденсатор фокусирует пучок на а,. В направ-
направлении, перпендикулярном к плоскости рисунка, не существует
никакой фокусировки; следовательно, изображением точки объ-
объекта является прямая линия.
Если поместить источник так, чтобы его азимутальная коор-
координата была ao, а координата продольной диафрагмы а(, то
можно измерить ток, который проходит через диафрагму, т. е.
число частиц с заданной энергией. Меняя потенциалы электро-
электродов и измеряя вариации тока, можно определить распределение
скорости частиц.
Преимущество сферического конденсатора по сравнению с
цилиндрическим состоит в том, что он обеспечивает фокусиров-
фокусировку во всех направлениях; следовательно, изображение в этом
случае стигматично.
Аберрации призм начинаются с величин второго порядка.
Для описания оптических свойств призмы очень полезен матрич-
матричный формализм. Читатель найдет исчерпывающую теоретиче-
теоретическую и практическую информацию об электростатических приз-
призмах в литературе [51Ь, 387].
11.2.2. Магнитные призмы
Простейшей магнитной призмой является однородное маг-
магнитное поле (разд. 2.7.2). Известно, что если частица входит
в поле перпендикулярно его направлению, то она будет двигать-
двигаться по окружности. Радиус такой круговой траектории опреде-
определяется уравнением B.137) н зависит как от энергии частицы,
так и от отношения ее заряда к массе Электростатические поля
имеют только энергетическую дисперсию, а магнитные поля об-
обладают как энергетической, так и массовой дисперсией, следо-
следовательно, их можно использовать как для энергетического ана-
анализа, так п для масс-спектрометрии.
594
Отклонение пупков
Мы уже рассмотрели один путь использования однородного
магнитного поля для отклонения частиц (разд. 2.7.2.2) и его
применение для массового анализа (разд. 2.7.3.1). Следующим
подходом является применение в качестве траектории полуок-
полуокружности. Такое устройство называется я-спектрометром
(рис. 163). Частицы с различными энергиями и (или) различны-
различными массами движутся по разным окружностям. Энергетический
или массовый спектр можно получить, двигая детектор вдоль
горизонтальной линии или меняя наяряженность магнитного
поля. Если, однако, рассмотреть траектории частиц с одинако-
одинаковыми массами и энергиями, но входящими в поле под углами,
различие которых пренебрежимо мало, то увидим, что все они
вернутся к горизонтальной линии приблизительно в одних точ-
точках. Хотя фокусировка несовершенна, мы, несомненно, имеем
кроссовер, по крайней мере, по азимутальной координате я,
который допускает некоторый конечный разброс угла а.
Рис 163 Принцип работы я-спектрометра.
Широкое применение получил другой вид магнитного спек-
спектрометра, основанный на магнитных секторных полях. Сектор-
Секторное поле — это область пространства, где магнитное поле пред-
предполагается плоским и однородным, тогда как вне этой области
оно предполагается равным нулю (рис. 164). Естественно, это
довольно грубое приближение: реально контурными полями пре-
пренебречь нельзя. Однако секторное поле можно использовать
в качестве модели, если магнитные полюсы достаточно близки
друг к другу.
Заряженные частицы движутся в секторном лоле по круго-
круговой траектории. Радиус кривизны дается уравнением B.137).
Вне сектора траектории являются прямыми линиями. Можно
показать [388], что секторное поле фокусирует пучок расходя-
расходящихся частиц так, что объект, вершина сектора га изображение
находятся на одной прямой (правило Барбера, см. рис. 164).
Дополнительная фокусировка в направлении, перпендикулярном
плоскости рисунка, обусловлена действием контурного поля.
Аберрации второго порядка магнитного секторного поля мож-
можно уменьшить соответствующим выбором криволинейных гра-
границ сектора.
38* 595
Глава 11
При некоторых применениях, например в ускорителях час-
частиц, дисперсия нежелательна Ахроматическое отклонение мо-
может быть выполнено с помощью комбинации нескольких сектор-
секторных полей.
Поскольку магнитные поля обладают как энергетической,
так и массовой дисперсией, а электростатические — только мас-
массовой, можно сочетать оба поля таким образом, чтобы общая
энергетическая дисперсия компенсировалась, в то время как
массовая дисперсия магнитного поля оставалась неизменной.
Как следствие может быть сконструирован масс-спектрометр
с двойной фокусировкой, обладающий свойством как угловой,
так и энергетической фокусировки: частицы, начинающие дви-
движение с разными начальными скоростями в разных направле-
направлениях, фокусируются «а одной линии.
Рнс 164 Фокусирующее действие магнитного секторного поля
Для отклонения и сепарации пучков частиц с помощью маг-
магнитных полей можно применить различные виды симметрии.
Использование матричного формализма для описания оптиче-
оптических свойств магнитных призм, так же как и других возможно-
возможностей для массового разделения, исчерпывающе представлено в
литературе [23, 51Ь, 388].
11.3. Новые виды симметрии — новые
возможности
В заключение этой главы хотелось бы обратить внимание
читателей на очень важную проблему. Мы видели, что отклоне-
отклонение можно осуществить множеством различных способов, ис-
используя различные виды симметрии. В гл. 10 было показано,
что осесимметричные системы можно заменить системами с
мультипольной симметрией. В разд. 3.1.1Л мы обсудили плос-
плоские поля. Мы видели, что разложение ib степенной ряд [уравне-
[уравнение C 36)] распределения потенциала симметричного плоского
поля имеет ту же структуру, что и распределение осесимметрич-
ного потенциала [уравнение C 20)]. Соответственно возможна
фокусировка симметричными плоскими полями с тем только
различием, что точка объекта будет изображаться прямой ли-
линией Интересные фокусирующие и отклоняющие свойства мож-
596
Отклонение пучков
ло получить суперпозицией электростатического и магнитного
полей, где общая средняя плоскость является плоскостью сим-
симметрии для электростатического и плоскостью антисимметрии
для магнитного полей [389, 390]. Изучались и некоторые дру-
другие возможности, но исследована только малая часть имеющих-
имеющихся видов симметрии.
/• ? * * г ? л-.
У У У
v\ /\ Лэ
С- 9 / \ / \ 25
10 ^ уч /ч 26
ЛЛЛ " У У У У Ll
XXX * VAVA»
XXX13 ХХХХ»
ууу 1Ч ww •,,
XXX «
Рис. 165. 31-полосовой орнамент в рельефе
Хорошо известно, что существует 230 конечных групп сим-
симметрии в трехмерном пространстве. Если ограничиться система-
системами с прямолинейными осями, то все еще останется 31 простран-
пространственная группа, содержащая трансляции в одном направлении.
Эти так называемые полосовые орнаменты в рельефе схемати-
схематически показаны на рис. 165 Маленькие стрелки, доказывающие
направление по или против часовой стрелки, показывают: на-
направлен ли в данной точке трехмерный орнамент к нам или от
нас соответственно Систематическое исследование 31 картинки
597
11
и применение новых свойств симметрии может привести к от-
открытию новой и, возможно, суперэлектронной и ионной оптиче-
оптических систем.
Заключение
В этой короткой главе было дано введение в системы откло-
отклонения пучка. Вначале было рассмотрено сканирующее отклоне-
отклонение. Были выведены выражения как для электростатических,
так и для магнитных отклоняющих полей. Было показано, что
стигматическая фокусировка поддерживается при малых откло-
отклонениях. Была выведена теория аберраций для комбинированных
электростатических и магнитных мультипольных линз и деф-
дефлекторов. Заключают главу краткий обзор электростатических
и магнитных призм и предложение исследовать необычные виды
симметрии.
Глава 12
ПУЧКИ ВЫСОКОЙ ИНТЕНСИВНОСТИ
Мы обсудили роль собственного пространственного заряда
пучка как источника аберраций в разд. 5.6.2. Известно, что про-
пространственный заряд может быть в двух основных видах: рас-
распределенный заряд и взаимодействие отдельных частиц. В этой
главе проблема распределенного пространственного заряда бу-
будет рассмотрена довольно подробно с последующим обсужде-
обсуждением эффекта Боэрша.
12.1. Оптика пространственного заряда
Положительный или отрицательный пространственный за-
заряд, распределенный в пучке частиц вследствие взаимодействия
их собственных зарядов, приводит к возникновению сил про-
пространственного заряда в самом пучке частиц. Эти силы в свою
очередь приводят к возникновению трех основных явлений:
1) уменьшению электростатического потенциала в простран-
пространстве, занимаемом пучком;
2) расширению пучка;
3) ограничению тока.
Вследствие неизбежности возникновения сил пространствен-
пространственного заряда невозможно получить стигматические изображения
даже с помощью параксиальных пучков, если только первеанс
[см. уравнение B.190)] не настолько мал, что влиянием про-
пространственного заряда можно пренебречь по сравнению со сфе-
сферической аберрацией. К счастью, это справедливо для большин-
большинства приложений, таких, как электронные микроскопы, установ-
установки литографии, аналитические измерительные приборы и т. д.
В самом деле, если ток пучка равен 1 мкА даже при напряже-
напряжениях вплоть до 1 кВ, уравнение B.190) дает первеанс, равный
всего лишь Р=3-10~п А/В3/2, что является очень малой вели-
величиной. Влиянием пространственного заряда в электронных пуч-
пучках можно пренебречь, если первеанс меньше 10~8 А/В3/2
В ионных пучках пространственный заряд играет более важную
роль. Для заданного ускоряющего напряжения увеличение мас-
массы ионов приводит к уменьшению скоростей, т. е увеличению
времени взаимодействия. Следовательно, при заданном первеан-
се эффекты пространственного заряда будут в (М0/т0I/2 раз
599
Глава 12
выше для ионов, чем для электронов, где Ма « т0 — массы по-
покоя ионов и электронов соответственно. Для протонов это озна-
означает увеличение в 42,8 раза, для тяжелых ионов увеличение еще
сильнее.
Обычное применение ионов не вызывает такого множества
проблем. В предыдущем примере масса иона должна быть рав-
равна 55 массам протона, чтобы вызвать такое же влияние прост-
пространственного заряда, как электронный лучок с первеансом
10~8 А/В3/2. Однако ситуация коренным образом меняется для
пучков с высоким значением тока частиц, имеющих такие при-
применения, как технология жестких электронных пучков (сварка,
резка, сверление и т. п.), вакуумная металлургия, микроволно-
микроволновые осцилляторы высокой мощности для преобразования посто-
постоянной энергии и усилительные трубки и т. д. В этих случаях
первеанс может быть на несколько порядков выше, чем в об-
обсуждавшихся до этого примерах. При этом мы не уделяем
должного внимания аберрациям, но появляется угроза самому
существованию пучка, если первеанс выше 10~6 А/В3/2 A мик-
ропервеанс). Появилась особая область электронной и ионной
оптики, посвященная этой проблеме. Это так называемая опти-
оптика пространственного заряда [42] и ее основной задачей яв-
является получение и поддержание длинного пучка заряженных
частиц с высокой плотностью тока, где эффектами простран-
пространственного заряда пренебречь нельзя.
В этой области было выполнено огромное количество работ.
По этому предмету существует множество книг и монографий
[11, 25, 28, 33, 40, 45, 391—394], включая и нашу [42], в кото-
которой читатель может найти 1851 ссылку.
Оптика пространственного заряда представляет очень слож-
сложную проблему. Для строгого описания пучка заряженных час-
частиц необходимо знать их распределение в пространственной фа-
фазе, т. е. функцию плотности пространственного заряда p(R) и
функцию распределения скорости v(R). Это требует одновре-
одновременного решения уравнений Максвелла и уравнений движения
всех частиц, которые, естественно, невозможно решить даже
в простейших случаях.
Даже если попытаться свести проблему к описанию пучка
как целого, мы встретим очень серьезные трудности. Все эффек-
эффекты пространственного заряда определяются распределением по-
потенциала «(R) внутри пучка. Для того чтобы определить это
распределение, мы должны решить уравнение Пуассона A.18),
которое требует знания распределения пространственного заря-
заряда p(R). В соответствии с уравнением B.189) в этом случае иам
необходимо знать распределение плотности тока J(R) и распре-
распределение скорости v(R). Оба они зависят от траекторий частиц
и, кроме того, v(R) зависит еще от неизвестного распределения
600
Пучки высокой интенсивности
потенциала «(R). Даже если предположить, что пучок ламинар-
ламинарный, и мы интересуемся только тем.и траекториями, которые оп-
определяют поверхность пучка, очевидно, что они зависят от элек-
электростатических и магнитных сил, действующих на частицы.
Если перейти к следующему этапу в этом направлении и пре-
пренебречь всеми внешними полями, мы все еще не будем знать,
как действуют силы пространственного заряда. Мы даже не бу-
будем точно знать, куда они направлены. Очевидно, необходимо
решить все уравнения одновременно, чтобы получить решение
этой очень трудной самосогласующейся задачи.
Кроме того, возникают некоторые другие сложности. Для
того чтобы определить точное распределение скоростей v(R),
необходимо учитывать распределение тепловых скоростей вбли-
вблизи источника частиц. К счастью, влияние тепловых скоростей
существенно только при очень низких напряжениях [11], по-
поэтому ими в большинстве случаев можно пренебречь. Следую-
Следующая проблема связана с собственным магнитным полем пучка.
Так как это поле определяется законом Био — Савара (уравне-
(уравнение C.249)), оно является суперпозицией элементарных сил,
которые всегда перпендикулярны данным траекториям элемен-
элементов тока (заряженных частиц). Следовательно, существование
этих сил делает задачу пространственного заряда трехмерной
даже в простейших случаях. (Для осесимметричного пучка соб-
собственное магнитное поле направлено тангенциально, что нару-
нарушает осевую симметрию.) Однако, к счастью, собственное маг-
магнитное поле пренебрежимо мало для нерелятивистских скоро-
скоростей частиц (см. разд. 12.1.1.2).
Анализ пучков с высокой плотностью частиц возможен толь-
только в том случае, если сделаны приближения. Обычно делают
следующие физические предположения [42]:
1. Пучок частиц ламинарный, и траектории частиц не пере-
пересекаются друг с другом. Это предположение автоматически ис-
исключает аберрации и эффекты, связанные с тепловыми скоро-
скоростями.
2. Распределение плотности тока и плотности пространст-
пространственного заряда часто считают неизменным во всем поперечном
сечении пучка и равным соответствующим величинам на оси
пучка. Это означает, что значения р и J резко падают до нуля
на границах пучка. Очевидно, это очень грубое приближение.
Даже предположение о гауссовом распределении в поперечном
сечении пучка является всего лишь приближением, поскольку на
распределение плотности тока оказывает влияние громоздкое
распределение потенциала внутри пучка.
3. Как следствие первых двух приближений пучок рассмат-
рассматривается как некая фаза с очень резкими границами. Поверх-
Поверхность пучка определяется семейством траекторий, и в большин-
601
Глава 12
стве случаев вычисляются только эти траектории. Этот подход
нельзя использовать вблизи источника, где напряжение очень
мало, и вблизи кроссовера, где очень высока плотность тока.
В этих областях пучок неламинарен и распределение плотности
тока весьма громоздко. Так как обычно эти области имеют важ-
лое значение, их необходимо рассматривать отдельно с большой
тщательностью.
4. Как волновыми свойствами, так и взаимодействием между
отдельными частицами (эффект Боэрша) обычно пренебрегают
при анализе пучков высокой интенсивности.
5. Наличие в пучке частиц противоположных знаков приво-
приводит как к частичной компенсации собственного пространствен-
пространственного заряда пучка, так и к появлению осцилляции в пучке. Пер-
Первое явление можно использовать как альтернативу для поддер-
поддержания пучков высокой интенсивности, второе имеет большое
значение в микроволновых приборах. Однако при анализе пуч-
пучка волнами пространственного заряда, влиянием высокочастот-
высокочастотных полей и другими явлениями, зависящими от времени, обыч-
обычно пренебрегают.
6. В большиистве приложений оптики пространственного за-
заряда считается, что частицы движутся со скоростями, во много
раз меньшими, чем скорость света. При высоких скоростях пер-
веанс настолько мал, что не учитывается. Следовательно, реля-
релятивистскими эффектами, включая собственное магнитное поле,
часто пренебрегают.
7. Обычно предполагается, что силы пространственного за-
заряда действуют в предопределенных направлениях, таким обра-
образом можно уменьшить размерность задачи.
Может показаться, что эти (и другие) предположения делают
задачу тривиальной, решение которой не имеет ничего общего
с реальностью. Но это совершенно не верно. Приближенные ре-
решения, основанные на этих предположениях, обычно достаточна
хороши, чтобы обеспечить приемлемые конструкторские реше-
решения в технической практике. Что же касается простоты, то каж-
каждый, кто попытается сконструировать электронную пушку или
фокусирующую систему для пучка с высокой интенсивностью,
сразу же оценит трудность задачи.
12.1.1. Силы пространственного заряда
12.1.1.1. Электростатические силы. Для того чтобы исследо-
исследовать природу сил пространственного заряда, рассмотрим про-
простейший случай бесконечно длинного дилиндрического пучка
заряженных частиц, движущегося в области, свободной от внеш-
внешних электростатических полей, но под влиянием очень сильного
магнитного поля, которое заставляет частицы двигаться вдоль
602
Пучки высокой интенсивном»
траектории, близкой к силовым линиям, параллельно оси пучка
[42]. Следовательно, мы предполагаем, что радиус поверхности,
ограничивающей пучок, ть = const. Далее предположим, что
плотность тока постоянна во всем поперечном сечении пучка и
равна /о. Таким образом, мы будем иметь дело с пучком одно-
однородного поперечного сечения.
Очевидно, в этом случае распределение плотности простран-
пространственного заряда p(R) будет зависеть только от распределения
потенциала «(R). В соответствии с уравнениями B.33), B.189)
и E.325) имеем
A2Л)
где общий ток пучка / должен выбираться соответственно зна-
знаку заряженной частицы.
Теперь мы сделаем следующее упрощение. Предположим,
что плотность пространственного заряда постоянна во всем по-
поперечном сечении пучка, т. е. «(R) =«=const. Это эквивалентно
первому шагу в методе последовательных приближений, когда
мы вначале предполагаем, что искомая величина равна некото-
некоторому априорно заданному значению. В этом случае предполо-
предположение состоит в том, что потенциал 1может меняться в левой
части уравнения Пуассона, но постоянен в правой части, т. е.
частицы движутся с постоянной скоростью, не ощущая ослаб-
ослабления потенциала, обусловленного пространственным зарядом.
Если первеанс пучка не слишком велик, это предположение при-
приводит к решению, весьма близкому к реальному, и дальнейших
итераций не требуется.
Тогда подставим уравнение A2.1) с «(R)=« = const в пра-
правую часть уравнения Пуассона A.21), учитывая осевую
симметрию и бесконечную длину пучка. В этом случае пробле-
проблема сводится к одномерной: потенциал является функцией толь-
только одной цилиндрической координаты г. Имеем
±.±(г*±\= I A2 2)
rdr\ dr J nrlso[-2Q(u-Uo)/m0]112' V
Отсюда, используя уравнения A.13) и A.17), с помощью ин-
интегрирования получим радиальное электростатическое поле про-
пространственного заряда внутри пучка в следующем виде:
потому что вдоль оси пучка поле должно быть равно нулю
вследствие его осевой симметрии. Мы видим, что поле простран-
пространственного заряда пропорционально смещению г, так же как
в первом члене уравнения C.38), который был использован при
603
Глава 12
выводе уравнения параксиальных лучей D.31). Отсюда можно
вывести важное заключение: предположение постоянной плот-
плотности пространственного заряда эквивалентно параксиальному
приближению.
Очевидно, что поле пространственного заряда пучка за его
пределами пропорционально 1/г, где имеет силу уравнение Лап-
Лапласа. Силы электростатического пространственного заряда да-
даются уравнениями A.14) и A2.3). На границах пучка имеем
F_,fra=-
эта величина всегда положительна: эта сила всегда действует,
как сила отталкивания.
Еще раз интегрируя уравнение A2.3), получим распределе-
распределение потенциала и (г) внутри пучка в следующем виде:
«(г) = «@) * — туг, A2.5)
где величина потенциала «@) вдоль оси определяется геомет-
геометрическими размерами площади постоянного внешнего потенциа-
потенциала. Так как для положительно заряженных частиц ток — вели-
величина положительная, а потенциал — отрицательная, для отри-
отрицательно заряженных частиц справедливо как раз противопо-
противоположное — абсолютная величина потенциала всегда наименьшая
вдоль оси пучка и наибольшая на его границах: следствием про-
пространственного заряда является ослабление потенциала. Общее
ослабление потенциала \и(гь)—и@)| зависит от тока пучка и
скорости частиц. Ослабление обычно составляет только несколь-
несколько процентов от потенциала ы; следовательно, первоначальное
предположение оправдывается. Однако, как мы увидим в
разд. 12.1.2, это небольшое ослабление связано с весьма сущест-
существенным расширением пучка.
Для очень больших значений тока такой упрощенный анализ
неадекватен. Решим уравнение Пуассона с распределением про-
пространственного заряда A2.1). Результат дает очень существен-
существенное ослабление потенциала [11]. С увеличением тока его абсо-
абсолютное значение на оси пучка уменьшается до тех пор, пока
не достигнет величины, составляющей 0,174 от потенциала во
внешней области. Максимально возможный ток, который может
проходить в этом пучке, определяется этим потенциалом. Мак-
Максимально достижимое значение первеанса равно 32,4 микропер-
веанса для электронов и 0,76 .микропервеанса для протонов.
Если попытаться увеличить значение проходящего тока, то не-
некоторые частицы под действием пространственного заряда по-
повернут обратно, и пучок разрушится.
604
Пучки высокой интенсивности
12.1.1.2. Магнитные силы. Исследуем теперь магнитные силы
пространственного заряда, действующие на частицу бесконечно
длинного цилиндрического пучка, обсуждавшегося" в предыду-
предыдущем разделе. В соответствии с законом Био — Савара магнит-
магнитная индукция, генерируемая прямолинейным током, дается
уравнением C.253). Она действует в азимутальном направлении
и вызывает магнитное отталкивание между токами, движущи-
движущимися параллельно друг другу в одном направлении. Это поле
разрушает осевую симметрию задачи. Предположим, что каж-
каждая частица движется в поле всего пучка, ток которого скон-
сконцентрирован вдоль его оси. Тогда радиальную силу Лоренца,
вызванную тангенциальным полем пространственного заряда и
осевой скоростью, легко вычислить из уравнений A.14) и
C.253). Ее величина равна
Fmagn(r)- HoQI[— 2Q(« — uo)/m0y/2/Bnr). A2.6)
Эта сила всегда отрицательна, т. е. она направлена к оси (сила
отталкивания).
Сложим электростатические и магнитные силы пространст-
пространственного заряда, действующие на частицу, находящуюся на гра-
границе (г=гь). Используя соотношения
е„цо=1/с2 A2.7)
и выражая силы через скорости частиц с помощью уравнения
B.33) (потому что в предыдущем .рассмотрении скорость была
выражена через потенциал в нерелятивистском приближении),
получим
т. е. релятивистски корректное выражение. Отсюда следует, что,
если частицы движутся со скоростью света, электростатическая
сила пространственного заряда компенсируется своим магнит-
магнитным аналогом. С другой стороны, для относительно малых ско-
скоростей магнитными силами пространственного заряда можно-
пренебречь. Следовательно, осевая симметрия системы сохра-
сохраняется.
12.1.2. Расширение пучка
Одним из наиболее важных следствий электростатических
сил пространственного заряда является расширение пучков вы-
высоких интенсивностей, если не приложены специальные уси-
усилия для поддержания поперечного сечения пучка в заданных
пределах. Исследуем эту проблему в параксиальном приближе-
приближении.
605-
Глава 12
Как мы видели, предположение постоянной плотности про-
пространственного заряда эквивалентно параксиальному приближе-
приближению в том смысле, что радиальная сила пространственного за-
заряда внутри пучка пропорциональна смещению г подобно ра-
радиальной электростатической силе в осесимметричной системе
электродов. Так как первый член уравнения C.38) есть
U"(z)r/2 и для p=const, поле пространственного заряда [урав-
[уравнение A2.3)] можно выразить как рг/Bе0). Очевидно, что влия-
влияние пространственного заряда можно учесть в уравнении парак-
параксиальных лучей D.31), если заменить U"(z) на f/"(z)+p/e°-
Предположение о постоянстве плотности пространственно-
пространственного заряда приемлемо для относительно низких первеансов. Для
Р=\,Ш микропервеанса ослабление потенциала внутри пучка
меньше 3%. Но диаметр первоначально коллимированного элек-
электронного пучка с таким первеансом удваивается после прохож-
прохождения пучком расстояния всего лишь в 4,5 раза больше, чем
его первоначальный диаметр. Следовательно, расширение пуч-
пучка — эффект, который нельзя игнорировать даже при сравни-
сравнительно малых интенсивностях, когда ослабление потенциала
пренебрежимо мало. (Первоначально коллимированный пучок
■с первеансом 10~8 А/В3/2 удвоит диаметр после прохождения
расстояния, в 63 раза большего его начального диаметра.) Это
важное наблюдение, так как оно предполагает, что в более
сложных случаях, когда пучок движется во внешнем электро-
электростатическом поле (см., например, периодическую электростати-
электростатическую фокусировку в разд. 12.1.4.2), обычно можно считать,
что внешний фокусирующий потенциал не зависит от простран-
пространственного заряда, т. е. он удовлетворяет уравнению Лапласа.
Пространственный заряд учитывается только как сила, дейст-
действующая на частицы, но его прямым влиянием на потенциал
обычно пренебрегают.
Рассмотрим осесимметричный пучок заряженных частиц,
движущихся в области пространства, свободной от внешних по-
полей (£ = 0, £/ = const). Предположим, что частицы не имеют ази-
азимутальных компонент их начальных скоростей (С=0) и
p = const. Заменяя U"(z) на р/ео в иерелятивистском варианте
уравнения параксиальных лучей D.31) и используя уравнение
A2.1) для траектории пограничной частицы в меридиональной
плоскости, получим
й*гь I /12 о}
I 12 о}
где гь теперь является переменной величиной. Правая часть
этого дифференциального уравнения положительна как для по-
положительно, так и для отрицательно заряженных частиц.
606
Пучки высокой интенсивности
Из этого уравнения сразу же следует, что пучок должен рас-
расширяться под влиянием сил пространственного заряда. Расши-
Расширение пропорционально первеансу пучка и корню квадратному
из массы частицы. Эффект расширения в 42,8 раза больше для
протонов, чем для электронов. Также очевидно, что при стрем-
стремлении гь к нулю вторая производная ть" стремится к бесконеч-
бесконечности, т. е. какой бы ни была начальная величина угла фо-
фокусировки, пограничные электроны никогда не пересекут ось.
Так как нелинейный член пространственного заряда всегда при-
присутствует в уравнении параксиальных лучей, точечное изобра-
изображение точечного объекта никогда не будет сформировано, если
только первеанс не равен нулю. Это и есть аберрации простран-
пространственного заряда, обсуждавшиеся в разд. 5.6.2.
Трудность проблемы пространственного заряда хорошо де-
демонстрируется тем фактом, что даже уравнение параксиальных
лучей A2.9), записанное для нерелятивистского пучка с по-
постоянной плотностью заряда, движущегося в области простран-
пространства, свободной от внешних сил, является нелинейным диффе-
дифференциальным уравнением. Решим его с начальными условиями,
заданными при 2=0 в виде г<,@)=го и г<,'(О)=Го'. Вводя без-
безразмерные переменные [11]
R(z)=rb(z)/ro, A2.10)
Z=i 77rY2z/r0, A2.10)
уравнение A2.9) можно переписать как
A2.11)
а начальные условия записать в виде
= 1, dR(O)/dZ=R'o. A2.12)
(Заметим, что теперь штрих означает дифференцирование
по Z.) В зависимости от знака Ro' пучок может быть первона-
первоначально сходящимся или расходящимся; /?</=0 соответствует
первоначально коллимированному пучку.
Умножая обе части уравнения A2.11) на dR и проводя ин-
интегрирование, получим
. A2.13)
Отсюда следует, что для первоначально сходящегося пучка
(Яо'<0)
-Я0'2). A2.14)
Интегрируя уравнение A2.13), используя при этом u=R' как
переменную интегрирования, получим решение в виде
607
Глава 12
R'
Z = 2 exp (—
exp (ы2) J«,
A2.15)
где R' определяется уравнением A2.13). Если пучок первона-
первоначально расходится или коллимирован, интегрирование произво-
производится от одной положительной величины до другой .положитель-
.положительной величины с большим значением. Если же имеется перво-
первоначально сходящийся пучок, то его поверхность можно разде-
разделить на две части, как показано на рис. 166. В области 0<Z<;
<Zm пучок все еще сходящийся, R'<0 и R<\. Следовательно,
необходимо провести интегрирование от одной отрицательной
величины до другой отрицательной величины с меньшим абсо-
-лютным значением. Минимальное поперечное сечение пучка до-
достигается при
A2.16)
После этого (Zm<Z) пучок начинает расходиться (R'>0) и
в уравнении A2.15) интеграл берется от отрицательной вели-
Рис. 166. Расширение первоначально сходящегося пучка.
"чины до положительной. Всю поверхность пучка можно описать
■выражением
*], A2.17)
где отрицательный и положительный знаки соответствуют схо-
сходящейся и расходящейся области соответственно, а функция
дается как
X
l*)du. A2.18)
Эта функция протабулирована для широкого диапазона х в ра-
работе [42].
'608
Пучки высокой интенсивности
Уравнение A2.17) показывает, что пучок симметричен в
продольном направлении по отношению к его минимальному
поперечному сечению. Профиль поверхности пучка можно вы-
вычислить для любых значений параметров, используя уравнения
A2.10) и A2.16) — A2.18). Если абсолютная величина безраз-
безразмерного начального наклона Яо' увеличивается, т. е. реальная
фокусировка пучка увеличивается и(или) первеанс уменьшает-
уменьшается, Rmin монотонно уменьшается, a Zm вначале увеличивается,
достигает максимума (Zmmax = l,08 при /?о' =—0,92), после ко-
которого уменьшается.
Естественно, параксиальное приближение можно использо-
использовать только для не очень больших значений первеанса. Даже
если Р имеет умеренное значение, приближение действительно,
только когда R относительно мало. Поскольку длинный пучок
расширяется сильнее, необходимо приложить некоторые усилия
для сохранения его поперечного сечения в разумных пределах
(см. разд. 12.1.4).
Максимальный ток, который можно пропустить через труб-
трубку радиуса г0 и длины L, можно вычислить, требуя, чтобы труб-
трубка была полностью заполнена пучком на выходе при условии,
что никаких потерь тока нет. Подставляя z=L и постоянные во
второе из уравнений A2.10), принимая 2mmax=l,08 и используя
продольную симметрию (Z=2Zm max), найдем, что для электронов
максимальный первеанс равен Pmax = l-54-10~4(r0/LJA/B3/'2
(для ионов Ртах гораздо меньше).
Ленточное [11], эллиптическое [395] и полое [396, 397]
расширение .пучков также было проанализировано. Проблема
расширения пучков в присутствии внешних полей будет обсуж-
обсуждаться в разд. 12.1.4.
12.1.3. Получение пучков высокой интенсивности
Разд. 7.8.3 был посвящен получению электронных и ионных
пучков низкой интенсивности. В пучках высокой интенсивности
ток ограничивается пространственным зарядом. Для того чтобы
получить максимальный ток, необходимо попытаться создать
поток частиц с ограниченным пространственным зарядом или
поток пространственного заряда между катодом и выведенным
электродом. • Следовательно, вначале мы должны изучить тео-
теорию потока пространственного заряда.
12.1.3.1. Поток пространственного заряда. Ограниченный за-
заряженный пространственный поток формируется в предположе-
предположении, что катод имеет неограниченную эмиссионную спо-
способность, но ток ограничивается облаком заряженных час-
частиц, формируемым у поверхности катода, так что нормаль-
609
Глава 12
ная компонента электростатического поля у этой поверхности
уменьшается до нуля. Траектории частиц в таком потоке опре-
определяются геометрическим расположением электродов. Обычно
в нашем распоряжении есть два электрода (диод), катод и вы-
выведенный электрод, и они образуют пару координатных поверх-
поверхностей ортогональной системы координат. Тогда траектории бу-
будут параллельны одной из координатных линий. В простейшем
случае прямолинейного потока пространственного заряда траек-
траекториями являются прямые линии и плотность тока постоянна
(вопреки наличию сил пространственного заряда) вследствие
высокой степени симметрии. Такой поток существует между дву-
двумя бесконечными параллельными плоскостями, между двумя
бесконечно длинными коаксиальными цилиндрами «ли между
двумя концентрическими сферами. Если поверхности открыты
и (или) их размеры конечны, то поток криволинеен. Проанали-
Проанализируем простейший случай прямолинейного потока пространст-
пространственного заряда между двумя бесконечными параллельными1
плоскостями более подробно.
Распределение потенциала в потоке определяется уравнением
Пуассона A.20) в декартовых координатах. Если предположить,
что каждая из двух бесконечных плоскостей перпендикулярна
оси z, то проблема становится одномерной: потенциал и зависит
только от координаты г. Тогда уравнения A-20) и B.189) дают
d2u/dz2 = — //[eoo(z)], A2.19)
где / = const и имеет знак заряда частицы, v(z) — абсолютная
величина скорости частицы. Плотность тока будет определяться
ограничивающим влиянием пространственного заряда.
Уравнение A2.19) можно решить точно, используя и2 (г) как
новую переменную. Она связана с потенциалом u(z) уравне-
уравнением B.33). Можно записать
vd2 (v2)/dz2 = 2JQ/eanio=const>0. A2.20)
Отсюда следует, что
d (dv2 V Tndv2 j /io oi\
[ 4^/8тУ A2.21)
и это выражение можно проинтегрировать непосредственно. Так
как v2 пропорционально потенциалу и (в соответствии с нашим
определением потока пространственного заряда) первая произ-
производная потенциала по z равна нулю вблизи поверхности катода
B=0), в результате получим
dv*/dz={8JQ[v(z) — u@)]/80m0}I/2. A2.22)
Это выражение легко проинтегрировать еще раз. Для простоты
предположим, что ы(О)=Ыо, т. е. частицы имеют нулевые на-
610
Пучки высокой интенсивности
чальные скорости у поверхности катода [и@)=0]. Тогда ре-
решением (будет
u2(z) = (9/Q/2e0/n0J/3z4/3. A2.23)
Поместим вторую плоскость на расстоянии d от катода и будем
считать ее потенциал равным У. Тогда уравнения B.33) и
A2.23) дают распределение потенциала в виде ,
и(г)— uo=(V— «0)(z/dL/3. A2.24)
Очевидно, что в отсутствие пространственного заряда распреде-
распределение потенциала должно быть линейным. Влияние простран-
пространственного заряда выражается степенной, с показателем 4/3, за-
зависимостью потенциала от координаты z.
Из уравнений B.33), A2.23) и A2.24) получим абсолютную
величину плотности тока в виде
)l/2-»oK/2 A2.25)
в соответствии с уравнением B.190). Это уравнение является
хорошо известным законом Чайлда — Ленгмюра [398]. Он оп-
определяет максимальную плотность тока, задаваемую простран-
пространственным зарядом. Зависимость ,в степени 3/2 справедлива для
всех типов потока, если градиент потенциала равен нулю вбли-
вблизи катода. Естественно, коэффициент, возникающий в уравне-
уравнении A2.25), который пропорционален максимальному первеан-
су, будет разным для разных геометрических расположений.
Таким образом, первеанс является геометрическим фактором.
12.1.3.2. Пушка Пирса. Получение пучка заряженных частиц
высокой интенсивности эквивалентно созданию потока про-
пространственного заряда катодом (или ионным источником) огра-
ограниченных размеров в a priori заданном пространстве. Рассмот-
Рассмотрим, к примеру, ситуацию, показанную на рис. 167. Имеется
плоский катод конечных размеров и необходимо получить
поток пространственного заряда между этим катодом и анодом,
помещенным на расстоянии d от катода и имеющим потен-
потенциал V. Проблема аналогична проблеме потока пространствен-
пространственного заряда между двумя бесконечными поверхностями с тем
основным отличием, что необходимо ограничить поперечные раз-
размеры потока до размеров, определяемых ограничениями, нало-
наложенными на пучок. Другими словами, необходимо убрать боль-
большую часть потока и оставить только малую его часть, которую
мы и назовем пучком.
Очевидно, мы затеяли хлопотное дело. Действительно, форма
•оставшегося потока пространственного заряда существенно из-
611
Глава 12
менится из-за отсутствия пространственного заряда вне пучка.
Мы уже видели в разд. 12.1.2, что пучок будет неизбежно рас-
расширяться. Для того чтобы поддерживать прямолинейный поток,
необходимо компенсировать влияние отброшенного пространст-
пространственного заряда.
Эта проблема была остроумно решена Пирсом [399], кото-
который предложил компенсировать отброшенный пространственный
заряд электрическим полем соответствующим образом выбран-
выбранных электродов. Таким способом можно получить пучок произ-
произвольной формы.
Условия течения пространственного заряда в пучке не изме-
изменятся, если будут удовлетворены два следующих требования:
67.5
Катод
Рис. 167. Пушка Пирса.
1) распределение потенциала внутри пучка должно опреде-
определяться распределением первоначального потока простран-
пространственного заряда;
2) в направлении, нормальном к прямолинейным траекто-
траекториям потока, не должно существовать никаких сил.
Эти два условия устанавливают граничные условия для ре-
решения уравнения Лапласа в области пространства за предела-
пределами пучка. Электроды пушки Пирса определяются этим реше-
решением. Таким образом, пушка Пирса состоит из катода и двух
электродов, формирующих пучок. Формы катода и этих элек-
электродов зависят от типа потока пространственного заряда, из
которого пучок формируется.
В качестве простого примера рассмотрим пушку Пирса для
получения цилиндрического пучка (см. рис. 167). Начнем с пря-
прямолинейного потока пространственного заряда между двумя
бесконечными параллельными поверхностями, обсуждавшимися
в разд. 12.1.3.1. Вырежем цилиндр радиусом гь из бесконечного
612
Пучки высокой интенсивности
потока и оставим его в качестве пучка. Для того чтобы опреде-
определить электрод, формирующий пучок, мы должны решить урав-
уравнение Лапласа в цилиндрических координатах (уравнение A.21)
при р = 0) для области пространства вне пучка {Г>гь). Вслед-
Вследствие осевой симметрии потенциал не зависит от координаты а.
Граничные условия определяются требованиями, перечисленны-
перечисленными выше. Распределение потенциала вдоль границы пучка дает-
дается уравнением A2.24). Второе условие выражается требова-
требованием, чтобы радиальная компонента электростатического поля
равнялась нулю вдоль той же границы.
Решение можно получить в виде бесконечного ряда [42].
Оказывается, что электрод с потенциалом катода совмещается
с катодом при угле 67,5° по отношению к границе пучка. Это
характеристический угол, который сохраняется для различных
конфигураций пучка.
Естественно, метод, выведенный выше, строго применим
только тогда, когда пучок движется между двумя заряженными
поверхностями. Выходом такой пушки является диафрагма, ко-
которая действует как линза (см. разд. 7.8.2). Следовательно,
после того как пучок покинет пушку, он расходится.
Если желательно получить на выходе пушки сходящийся или
коллимированный пучок, то необходимо использовать прямоли-
прямолинейный поток пространственного заряда между концентриче-
концентрическими сферическими поверхностями. Естественно, пучок после
прохождения пушки будет расширяться, следовательно, необ-
необходима дополнительная фокусировка (см. разд. 12.1.4).
Интересующийся читатель может найти подробную инфор-
информацию о конструировании электронных пушек для получения
параллельных и сходящихся цилиндрических, ленточных и по-
полых пучков в работе [42].
12.1.4. Поддержание пучков высокой
интенсивности
Вследствие действия сил пространственного заряда пучок
заряженных частиц высокой интенсивности неизбежно будет
расширяться, если не предприняты специальные меры для со-
сохранения его поперечного сечения. Поддержание пучков высо-
высокой интенсивности основано на компенсации сил пространствен-
пространственного заряда некоторыми другими силами, действующими в ос-
основном извне. Для этого существует множество практических
методов. Они делятся на две совершенно различные группы.
Одна основана на фокусировке однородных или квазиоднород-
квазиоднородных полей; другая ■— на принципе периодической фокусировки.
613
Глава 12
12.1.4.1. Фокусировка однородными магнитными полями.
В разд. 12.1.1 мы предположили, что поперечное сечение пучка
поддерживается очень сильным однородным магнитным полем.
Это поле действует на частицы таким образом, что они движут-
движутся очень близко к силовым линиям независимо от сил простран-
пространственного заряда. Исследуем эту ситуацию более подробно.
Рассмотрим нерелятивистский цилиндрический пучок, дви-
движущийся в сильном однородном магнитном поле, направленном
параллельно оси пучка. Если магнитное поле достаточно силь-
сильно, мы можем предположить, что радиальные силы пространст-
пространственного заряда компенсируются силой Лоренца, возникающей
из-за взаимодействия осевого магнитного поля В и азимуталь-
азимутальной компоненты скорости. Тогда смещение г приблизительно по-
постоянно, потенциал зависит только от г и уравнение B.63) мож-
можно записать совместно с уравнениями A.13) и A.17) как
(Q/m0) {du/dr — Bra) — ra = 0. A2.26)
Если источник помещен в магнитное поле и нет начальной
азимутальной компоненты скорости, то теорема Буша (урав-
(уравнение D.11)) вместе с уравнением B.135) дает
a = QB(ro2/r2—l)/2mo. A2.27)
Отметим, что г отличается от начального значения г0, хотя в
уравнении A2.26) мы считали ее вторую производную равной
нулю. Это опять эквивалентно первому шагу метода последова-
последовательных приближений, используемому в разд. 12.1.1.1. Подстав-
Подставляя уравнение A2.27) в уравнение A2.26), получим
du/dr=QB2r{r0*lr* — l)/4m0. A2.28)
Приравнивая это выражение к уравнению A2.3), взятому
с отрицательным знаком, получим
A2.29)
откуда очевидно, что r/r0 стремится к единице с увеличением В.
Другими словами, вопреки наличию сил пространственного за-
заряда, частицы все же следуют силовым линиям в сильном внеш-
внешнем магнитном поле.
Этот результат является хорошим приближением даже для
неоднородных магнитных полей [11]. Если |мы поместим пушку
Пирса, создающую сходящийся пучок, в магнитное поле, сило-
силовые линии которого следуют траекториям в непосредственной
близости от пушки, пучок будет сохранять форму в этой обла-
области и далее траектории будут приблизительно следовать сило-
силовым линиям. Если индукция увеличивается, пучок становится
уже. Следовательно, помещение пушки в магнитное поле, воз-
614
Пучки высокой интенсивности
растающее в осевом направлении, является хорошим практиче-
практическим способом улучшить сходимость пушки.
Существует другой метод поддержания пучков высокой ин-
интенсивности однородными магнитными полями. Предположим,
что катод полностью защищен от магнитного поля и скорость
не имеет начальной азимутальной компоненты. Тогда имеем
в уравнении D.9) фо = О и теорему Буша можно записать с по-
помощью уравнения D.5) для нерелятивистского случая как
а = — QB/2m0. A2.30)
Это выражение также справедливо для случая, когда источник
не защищен, но частицы испускаются из точечного источника
на оси (го = О).
Из уравнения A2.30) следует, что в этом случае угловая
скорость постоянна, т. е. весь пучок вращается вокруг оси как
одно целое. Центростремительная сила, вызывающая это вра-
вращение, уравновешивается радиальной силой пространственного
заряда. Этот способ называется фокусировкой Бриллюэна
[400].
Снова предполагая, что вторая производная г по времени
равна нулю, и подставляя уравнение A2.30) в уравнение
A2.26), получим
duldr+QB2r/4m0 = 0, A2.31)
в результате интегрирования которого имеем
u(r,z)=U{z) — QB2r2/8m0. A2.32).
Подставляя уравнение A2.31) в уравнение Пуассона A.21) и
учитывая симметрию и бесконечную длину пучка, найдем, что
плотность заряда является постоянной:
p = eoQ£2/2mo=const. A2.33)
Если снова пренебречь радиальной компонентой скорости
в сравнении с двумя другими компонентами, то уравнения
A.10), A.37), B.33), A2.30) и A2.32) дают, что осевая компо-
компонента скорости определяется только осевым потенциалом неза-
независимо от смещения г:
v2 =» {- 2Q[U @) - Uo] /m0}l'2. A2.34)
Если однородный внешний потенциал создается трубкой ра-
радиуса гь, потенциал которой и, то общий ток пучка выражается
с помощью уравнений B.189), A2.32), A2.33) и A2.34) как
[— 2Q (и — ио+ р)//п<,]1/2, A2.35)
где
A2.36)
615
Глава 12
Так как р и (и—и0) имеют противоположные знаки, очевид-
очевидно, что ток максимален при некотором оптимальном значении
параметра р. В результате имеем
poPt=— 2(м — во)/3, A2.37)
откуда индукция В, необходимая для ограничения максималь-
максимального тока в цилиндрическом пучке данного радиуса гь, может
быть определена с помощью уравнения A2.36). Подставляя
уравнение A2.37) в уравнение A2.35), получим максимальный
ток. Используя уравнение B.190), имеем максимальное значе-
значение первеанса
|2. A2.38)
Для электронов это выражение дает Ртах = 25,4 микропервеанса,
что несколько ниже, чем фокусировка с иммерсионным катодом.
Это и понятно, так как для фокусировки Бриллюэна определен-
определенно требуется более низкая индукция, чем в других случаях. Фо-
Фокусировка Бриллюэна кажется очень элегантным решением
проблемы преодоления расширения пространственного заряда
пучков высокой интенсивности. К сожалению, идеальную фоку-
фокусировку Бриллюэна реализовать невозможно. Она требует пол-
полной защиты катода от однородного магнитного поля, которая
означает, что распределение индукции предполагается ступен-
ступенчатой функцией, резко меняющейся от нуля до заданного
В = const. На практике фокусировка Бриллюэна может быть
реализована только приближенно. В результате получить пол-
полностью параллельный пучок невозможно.
Фокусировка пучков высокой интенсивности однородными
магнитными полями является прямым методом. Однако получе-
получение сильного однородного поля в относительно большом объеме
делает оборудование очень громоздким и трудным для эксплуа-
эксплуатации. Этот недостаток делает такой вид фокусировки неприем-
неприемлемым для многих применений.
12.1.4.2. Периодическая фокусировка. Естественной альтер-
альтернативой поддержанию пучка частиц высокой интенсивности яв-
является система периодически расположенных электростатиче-
электростатических или магнитных линз. Основная идея этого метода проде-
продемонстрирована на рис. 168. Каждая линза компенсирует влия-
влияние сил пространственного заряда в данной области. Поскольку
число линз, следующих друг за другом, велико, этим способом
можно поддерживать пучки значительной длины 1[11, 401].
Практически периодическую фокусирующую систему полу-
получают с помощью серии электродов с чередующимися более вы-
высокими in более низкими потенциалами или с помощью ряда
ферритовых колец. Распределение электростатического потен-
616
Пучки высокой интенсивности
циала или магнитной индукции таких систем непрерывно, сле-
следовательно, нельзя отделить действие отдельных линз друг от
друга. Вместо этого мы должны рассмотреть всю фокусирую-
фокусирующую систему как одну периодическую линзу.
Однако действие периодической линзы все же может быть
описано как суперпозиция ряда рассеивающих и собирающих
областей с результирующим фокусирующим эффектом. Фокуси-
Фокусирующий эффект необходимо выбирать таким образом, чтобы
в среднем он полностью компенсировал расширение пучка из-за
сил пространственного заряда. Если это требование выполняет-
выполняется, мы имеем случай оптимальной фокусировки, который, одна-
однако, не означает строгой компенсации сил пространственного за-
заряда вдоль всего пучка. Можно аппроксимировать только задан-
заданную конфигурацию пучка (например, строго цилиндрический
пучок), и границы пучка всегда имеют неровности.
Период неровностей при
оптимальной фокусировке при-
приблизительно равен периоду
фокусирующей системы. В слу-
случае неоптимальной фокусиров-
фокусировки баланс сил нарушается
и частицы отклоняются от
их равновесных траекторий.
Это отклонение приводит к
изменению плотности про-
пространственного заряда, как Рис. 168. Принцип периодической фо-
следствие электростатические кусировки.
силы, возникающие при этом,
будут отклонять частицы обратно к их равновесным траекто-
траекториям. В результате частицы будут осциллировать вокруг этих
траекторий, определяемых условием оптимальной фокусировки.
Мы показали [402], что период этих осцилляции соответствует
частоте плазмы.
Периодическая фокусировка цилиндрических [403, 404],
плоских [405—407], полых [408] и эллиптических пучков [360]
очень подробно рассмотрена в литературе. Читатель может най-
найти полный обзор как электростатической, так и магнитной фо-
фокусировки в работе [42].
Эксперимент с периодической электростатической фокуси-
фокусировкой показан на рис. 169 [409]. Электронный пучок длиной
22 см с первеансом 4-10~7 А/В3/2 был сфокусирован 33 электро-
электродами с чередующимися более низкими и более высокими потен-
потенциалами. Видно, что пучок легко проходит через отверстия
электродов, отдавая в конце свою энергию коллектору.
617
Глава 12
12.2. Эффект Боэрша
Взаимодействие отдельных частиц приводит к расширению
энергетического диапазона в пучке заряженных частиц. Это так
называемый эффект Боэрша [410], которому в последние годы
уделяют много внимания.. (В электронных накопительных коль-
кольцах он известен как эффект Тоушека.) Особенно сильно он про-
проявляется в районе кроссовера.
Основной механизм эффекта Боэрша — рассеяние частиц
пучка на самих себе. Поскольку число отдельных частиц огром-
огромно, то эффект весьма сложен. Результатом этих рассеяний явля-
является перераспределение энергии между поперечными и продоль-
продольными направлениями при рассмотрении в системе отсчета, свя-
связанной с пучком. Это можно трактовать как расширение
энергетического диапазона в лабораторной системе отсчета.
Рис. 169. Практическая реализация периодической электростатической фокуси-
фокусировки [409].
Теория эффекта Боэрша относительно проста в коллимиро-
ванных пучках. Проблемы начинаются при попытке исследова-
исследования кроссовера, где этот эффект проявляется наиболее сильно.
Множество упрощенных подходов дали противоречивые резуль-
результаты. Экспериментальная проверка этих результатов также за-
затруднительна, так как эффект сильно зависит от параметров ис-
источника и фокусирующей системы.
Если предположить, что расширение энергетического спектра
является результатом множества некоррелированных столкнове-
столкновений и перенос энергии однороден, то эффект Боэрша приводит
к гауссову распределению энергии. Предположение об однород-
однородности переноса энергии спорно даже в простом случае. При про-
618
Пучки высокой интенсивности
хождении частиц через кроссовер распределение энергии имеет
существенно негауссов вид.
Адекватное объяснение эффекта Боэрша должно основывать-
основываться на статистической теории [411]. Эффект можно рассматри-
рассматривать как обусловленный статистическими флуктуациями в про-
пространственном распределении частиц, который в свою очередь
приводит к изменению в энергетическом расширении. Эффекты
статистического взаимодействия можно оценить методами Мон-
Монте-Карло [412, 413].
Эффект Боэрша изучен еще не полностью. На распределения
скоростей в пучках заряженных частиц оказывает влияние мно-
множество геометрических факторов и распределений полей. Одна-
Однако имеются хорошие обзоры [411—414] существующих теорети-
теоретических и экспериментальных результатов. При практическом
конструировании эффект Боэрша должен приниматься во вни-
внимание как фактор, вносящий вклад в хроматическую аберрацию
(см. разд. 5.6.2).
Заключение
В последней главе мы суммировали наиболее важные эф-
эффекты пространственного заряда и вывели методы получения и
поддержания пучков заряженных частиц высокой интеноивно-
сти. Основные эффекты и предположения обсуждались впервые.
Электростатические и магнитные силы пространственного заря-
заряда даются уравнениями A2.4) и A2.6) соответственно. Расши-
Расширяющийся осесимметричный пучок определяется уравнением
A2.17), Закон прямолинейного течения пространственного за-
заряда дается уравнением A2.25). На его основе построена пуш-
пушка Пирса. Подробно рассмотрена фокусировка однородными
магнитными полями и периодическими системами. И наконец,
краткое обсуждение эффекта Боэрша заключает книгу.
ЛИТЕРАТУРА
1. Н. Busch. Ann. Phys. (Leipzig), 1926, 81, p. 974—993.
2. E. Bruche, 0. Scherzer. Geometrische Elektronenoptik, Berlin: Springer,
1934.
3. H. Busch, E. Bruche, eds. Beitrage zur Elektronenoptik, Leipzig: Barth,
1937.
4. /. G. Maloff, D. W, Epstein Electron Optics in Television, New York:
McGraw-Hill, 1938.
5. 0. Klemperer. Electron Optics, Cambridge: Cambridge University Press,
1939, 1953.
6. L. M. Myers. Electron Optics, Theoretical and Practical, London: Chapman
and Hall, 1939.
7. /. Picth. Einfiihrung in die Theorie der Elektronenoptik, Leipzig, 1939,
1957.
8. D.Gabor. The Electron Microscope, London: Hutton, 1945.
9. V. K. Zvorykin, G. A. Morton, E. G. Ramberg, J. Hillier, A. W. Vance.
Electron Optics and the Electron Microscope, New York: Wiley, 1945.
10. V. E. Cosslett. Introduction to Electron Optics, Oxford: Clarendon Press,
1946.
11. /. R. Pierce. Theory and Design of Electron Beams, Princeton: Van Nost-
rand, 1949, 1954.
12. L. de Broglie. Optique electronique et corpusculaire, Paris: Hermann, 1950.
13. L. Jacob. An Introduction to Electron Optics, London: Methuen, 1950.
14. A. A. Rusterholz. Elektronenoptik, Basel, 1950.
15. G. Dupouy. Elements d'optique electronique, Paris: Armand Colin, 1952.
16. №. Glaser. Grundlagen der Elektronenoptik, Wien: Springer, 1952. [Имеет-
[Имеется перевод: В. Глазер. Основы электронной оптики. — М.: ГИТТЛ, 1957.]
17. №. №. Harman, Fundamentals of Electronic Motion, New York, 1953.
18. P. Grivet. Optique electronique, Paris: Bordas, 1955, 1958.
19. F. Ollendorff, Elektronik des Einzelelektrons, West Berlin: Springer, 1955.
20. P. A. Sturrock. Static and Dynamic Electron Optics, Cambridge: Cambridge
University Press, 1955.
21. W, Glaser. Elektronen und Ionenoptik, in: Handbuch der Physik, West Ber-
Berlin: Springer, v. 33, pp. 123—395, 1956.
22. A. M. Страшкевич. Электронная оптика электростатических полей, не об-
обладающих осевой симметрией. — М.: Физматгиз, 1959.
23. В. М. Кельман, С. Я. Явор. Электронная оптика, Москва — Ленинград,
Издательство АН СССР, 1959 и 1963.
24. /. /. Tsukkerman. Electron Optics in Television, Oxford: Pergamon Press,
1961.
25. В. П. Тараненко. Электронные пушки. — Киев: Техника, 1964.
26. P. Grivet. Electron Optics, Oxford: Pergamon Press, 1965, 1972.
27. K. G. Steffen. High Energy Beam Optics, New York: Wiley, 1965.
620
Литература
28. И. В. АлямовсКий, Электронные пучки и электронные пушки, Советское
радио, Москва, Ь966.
29. А. Р. Banford. The Transport of Charged Particle Beams, London: Spon,
1966.
30. P. V. Hawkes. Quadrupole Optics, West Berlin: Springer, 1966.
31. A. M. Страшкевич. Электронная оптика электростатических систем, Энер-
Энергия, Москва — Ленинград, 1966.
32. A. Septier, ed. Focusing of Charged Particles I—II, New York: Academic,
1967.
33. P T. Kirstein, G. S Kino, W. E. Waters. Space Charge Flow, New York:
McGraw-Hill, 1967.
34. B. Paszkowski. Electron Optics, London: Iliffe Books, 1968.
35. С. Я. Явор. Фокусировка заряженных частиц квадрупольными линзами. —
М.: Атомиздат, 1968.
36. А. В. El-Kareh, I. С. I. El-Kareh. Electron Beams, Lenses and Optics I—II,
New York: Academic, 1970.
37. P. W. Hawkes. Quadrupoles in Electron Lens Design, New York, Academic,
1970.
38. 0. Klemperer, M. E. Barnett. Electron Optics, Cambridge: Cambridge Uni-
University Press, 1971.
39. P. W. Hawkes. Electron Optics and Electron Microscopy, London: Taylor
and Francis, 1972.
40. С. И. Молоковский, А. Д. Сушков. Интенсивные электронные и ионные
пучки. — Л.: Энергия, 1978.
41. P. W. Hawkes, ed. Image Processing Computer-Aided Design in Electron
Optics, London: Academic, 1973.
42. Gy. A. Nagy, M. Szilagyi. Introduction to the Theory of Space-Charged
Optics, New York: Halsted Press, 1974.
43. /. Dietrich. Superconducting Electron Optical Devices, New York: Plenum
Press, 1976.
44. E. Harting, F. H. Read. Electrostatic Lenses, Amsterdam: Elsevier, 1976.
45. J. D. Lawson. The Physics of Charged-Particle Beams, Oxford: Clarendon
Press, 1977.
46. В. П. Афанасьев, С. Я- Явор. Электростатические энергоанализаторы для
пучков заряженных частиц. — М.: Наука, 1978.
47. В. М. Кельман, С. П. Каретская, Л. В. Федулина, Е. М. Якушев. Электрон-
Электронно-оптические элементы призменных спектрометров заряженных частиц. —
Алма-Ата: Наука, 1979.
48. Л. А. Арцимович, С. Ю. Лукьянов. Движение заряженных частиц в элект-
электрических и магнитных полях. — М.: Мир, 1980.
49. A. Septier, ed. Applied Charged Particle Optics I—HI (Advances in Electro-
Electronics and Electron Physics, Suppl. 13A-C), New York: Academic, 1980—
1983.
50. P. W. Hawkes, ed. Magnetic Electron Lenses, West Berlin: Springer, 1982.
51. R. B. Miller. An Introduction to the Physics of Intense Charged Particle
Beams, New York: Plenum Press, 1982.
51a. J. J. Hren, F. A. Lenz, E. Munro, P. B. Sewell, eds. Electron Optical Sys-
Systems for Microscopy, Microanalysis and Microlitography, Scanning Electron
Microscopy, Inc., Illinois: AMF O'Hare, 1984.
ЫЪ.ХШеп Jiye. Aberration Theory in Electron and Ion Optics, Advances in
Electronics and Electron Physics, Suppl. 17, New York: Academic, 1986.
52. D. M. Cook. The Theory of the Electromagnetic Field, New Jersey: Prentice-
Hall, Englewood Cliff, 1975.
53. A. L. Fetter, J. D. Walecka, Theoretical Mechanics of Particles and Continue,
New York: McGraw-Hill, 1980.
54. M. Szilagyi. Appl. Phys. Lett., 1986, 49, No. 12, pp. 740—742.
621
Литература
55. В. М. Кельман, С. Я. Явор, А. Д. Дымников, Л. П. Овсянникова. — Изв.
АН СССР. сер. физика, 1963, 27, № 9, с. 1135—1138.
56. /. I. Thomson. Phil. Mag., 1910, 20, pp. 752—767.
57. F. W. Aston. Mass Spectra and Isotopes, London: E. Arnold, 1933.
58. W. Bleakney, I. A. Hippie. Phys. Rev., 1938, 53, pp. 521—529.
59. A. Stamatovic, G. J. Schulz. Rev. Sci. Instrum., 1968, 39, pp. 1752—1753.
60. W. Wien. Ann. Phys., 1902, 8, pp. 244—266.
61. M. Szilagyi. Optik, 1976, 46, pp. 211—218.
62. A. Septier, in: Advances in Electronics and Electron Physics, New York:
Academic, 1961, 14, pp. 85—205, 1961.
63. В. С Gregory, K. F. Sander. J. Electron. Control., 1962, 13, No. 2, pp. 123—
136.
64. M. Szilagyi. Optik, 1978, 50, No. 2, pp. 121—128.
65. S. Bertram. Proc. IRE, 1940, 28, pp. 418—420.
66. F. H. Read, A. Adams, J. R. Soto-Montiel. J. Phys. E: Sci. Instrum, 1971, 4,
pp. 625—632.
67. A. B. El-Kareh, M. A. Sturans. J. Appl. Phys., 1971, 42, No. 5, pp. 1870—
1876.
68. H. Ohiwa, R. J. Blackwell, B. M. Siegel. J. Vac. Sci. Technol., 1981, 19,
No. 4, pp. 1074—1076.
69. S. Gallai, M. Szilagyi. Periodica, Politech. Elect. Eng,, 1977, 21, No. 3,
pp. 243—247.
70. F. Ollendorff. Die Potentialfelder der Elektrotechnik, West Berlin: Springer,
1932.
71. N. N. Lebedev. Sov. Phys. Tech. Phys., 1957, 2, pp. 1943—1950.
72. E. Regenstreif, Ann. Radioelectricite, 1951, 6, No. 23, pp. 51—83; 6, No. 24,
pp. 114—155.
73. В. П. Афанасьев, С. Я. Явор. ЖТФ, 1973, 43, № 7, с. 1371—1380.
74. Л. А. Баранова, С. Я. Явор. ЖТФ, 1970, 40, № 8, с, 1767—1770.
75. A. Kiss, E. Koltay, L. P. Ovsyannikova, S. Ya. Yavor. Nucl. Instrum.
Methods., 1970, 78, No. 2, pp. 238—244.
76. T. Hayashi N. Sakudo. Rev. Sci. Instrum., 1968, 39, No. 7, pp. 958—961.
77. M.-Y. Bernard, Ann. Phys. (Paris), 1954, 9, No. 6, pp. 633—682.
78. /. E. Dayton, F. С Shoemaker, R. F. Mozley. Rev. Sci. Instrum., 1954, 25r
pp. 485—489.
79. G. E. Lee-Whiting, G. H. Keech. Calculation by conformal mapping of sha-
shapes of poles or electrodes for quadrupole lenses, Atomic Energy of Canada
Ltd., AECL-3253, Ontario: Chalk River, 1969.
80. R. Benaroya, W. J. Ramler. Nucl. Instrum. Methods, 1961, 10, pp. 113—
120.
81. E. Weber. Electromagnetic Fields, Theory and Applications, New York.:
Wiley, 1950.
82. F. Lenz. Z. Angew. Phys., 1950, 2, pp. 448—453.
83. G. Liebman, E. M. Grad. Proc. Phys. Soc, 1951, B64, pp. 956—971.
84. T. Mulvey, M. J. Wallington. Rep. Proc. Phys, 1973, 36, pp. 347—421.
85. T. Mulvey. Proc. Phys. Soc, 1953, B66, pp. 441—447.
86. H.-J. Hildebrandt, W. D. Riecke. Z. Angew. Phys. 1966, 20, No. 5, pp. 336—
342.
87. С Fed, P. Durandeau, см. [32], v. I, pp. 309—352.
88. W. D. Riecke, см. [50], pp. 163—357.
89. W. Kamminga. Optik, 1976, 45, pp. 39—54.
90. С. Я- Явор, М. Силадьи. ЖТФ, 1960, 30, № 8, с. 927—932.
91. М. Силадьи. ЖТФ, 1963, 33, № 5, с. 627—630.
92. Е. Durand. Electrostatique et Magnetostatique, Paris: Masson, 1953.
93. S. Ya Yavor, M. Szilagyi. Instrum. Exp. Techniques, 1961, 1, pp. 151—153.
94. T. Mulvey. см. [50], pp. 359—412.
95. E. Munro. J. Vac. Sci. Technol., 1975, 12, No. 6, pp. 1146—1150.
622
Литература
36. Е. Munro, H. С. Спи. Optik, 1982, 60D), pp. 371—390; 61A), pp. 1—16;
61B), pp. 121—145; 61C), pp. 213—236.
37. C. Germein. см. [32J, v. I, pp. 163—229.
98. /. С Francken. см. [32], v. I, pp. 101—162.
99. W. D. Ryan. IEEE Trans. Circuit. Theory., 1963, CT-10, pp. 385—391.
100. M. Szilagyi. см. [411, pp. 416—433.
101. /. R. Hechtel, J. A. Seeger. Proc. IRE, 1961, 49, pp. 933—940.
102. O. B. Belonozhko, I. S. Gaidukova, G. V. Deg-Shvarts, Instrum. Exp. Tech-
Techniques, 1967, No. 1, pp. 76—77.
103. T. Ya. Fishkova, M. Szilagyi, S. Ya. Yavor. Radio Eng. Electron. Phys., 1967,
12, pp. 1222—1224.
104. M. Szilagyi, E. V. Shpak, S. Ya. Yavor. Radio Eng. Electron. Phys., 1968,
13, pp. 159—160.
105. T. Ya. Fishkova, E. V. Shpak, M. Silagui, S. Ya. Yavor. Periodica Polytech.
Elect. Eng., 1968, 12, No. 3, pp. 301—306.
106. Л. П. Овсянникова, М. Снладьи. Periodica Polytech. Elect. Eng. 1974,
14A), 99—104.
107. Т. Я. Фишкова, М. Силадьи. ЖТФ, 1971, 16, № 1, с. 162—167.
108. M. Szilagyi, Zs. Kohalmi, B. Szekeres. Proceedings of the 8th International
Conference on Microwave and Optical Generation and Amplification, Amster-
Amsterdam: Kluwer-Deventer, 1970, pp. 20—26.
109. M. Bauer. J. Sci. Instrum., 1968, Ser. 2, 1, pp. 1081—1089.
110. E. Kasper. см. [50], pp. 57—118.
Ill N. K. Kang, I Orloff, L. W. Swanson, D. Tuggle. J. Vac. Sci. Technol., 1981,
19, No. 4, pp. 1077—1081.
112. P. A. Einstein. Proc. IEE, 1973, 120, No. 9, pp. 1048—1054.
113. E. Durand. Acad. Sci. Paris, 1957, 244, pp. 2355—2358.
114. S. Natali, D. DiChio, С E. Kuyatt. J Res. Natl. Bur. St. A. Phys. Chem.,
1972, 76A, No. 1, pp. 27—35.
115. R, L. Burden, J. D. Faires, A. C. Reynolds. Numerical Analysis, 2nd ed.
Boston: Prindle. Weber & Schmidt, 1981.
116. С Weber, см. [32], v. I, pp, 45—99.
117. R. Jurgens. Nucl Instrum. Methods, 1981, 187, pp. 263—265.
118. С. Н. Schaefer. Optik, 1983, 65, No. 4, pp. 347—359.
119. N. Franzen. см. .[51a], PP- 115—126.
120. G. E. Forsythe, W. R. Wasow. Finite-Difference Methods for Partial Duffe-
rential Equations, New York: Wiley, 1960.
121. P. Bonjour. см. [49], 1980, v. I, pp. 1—44.
122. О. С Zienkiewicz. The Finite Element Method in Engineering Science,
New-York: McGraw-Hill, 1971.
123. E. Munro. см. [411, PP- 284—323.
124. T. Mulvey. in: Electron Microscopy 1980, Proceedings of the 7th European
Congress on Electron Microscopy, v. 1, pp. 46—53, Seventh European Con-
Congress on Electron Microscopy Foundation, Leiden, 1980.
125. T. Mulvey, H. Nasr. Nucl. Instrum. Methods, 1981, 187, pp. 201—208.
126. B. Lencova, M. Lenc. Optik, 1984, 68, No. 1, pp. 37—60.
127. W. Kamminga J. Phys. D: Appl. Phys., 1975, 8, pp. 841—855.
128. M. V. K. Chari, P. P. Silvester, eds. Finite Elements in Electrical and Mag-
Magnetic Field Problems, Chichester: Wiley, 1980.
129. D. R. Cruise. J. Appl. Phys, 1963, 34, No. 12, pp. 3477—3479.
130. M. Abramowitz, I. A. Stegun, eds. Handbook of Mathematical Functions,
New York: Dover, 1972.
131. /. R. Mautz, R. F. Harrington. Proc. IEE, 1970, 117, No. 4, pp. 850—
852.
132. A. B. Birtles, В J. Mayo, A. W. Bennett. Proc. IEE, 1973, 120, No. 2,
pp. 213—220.
133. A. B. Birtles. Internat. J. Electron., 1972, 33, No. 6, pp. 649—657.
623
Литература
134. A. Renau, F. Н. Read, J. N. H. Brunt. J. Phys. E: Sci. Instrum., 1982, 15,
pp. 347—354.
135. B. Singer, M. Braun. IEEE Trans. Electron Devices, 1970, ВД-17, 10,
pp. 926—934.
136. H. A. van Hoof. J. Phys. E: Sci. Instrum., 1980, 13, pp. 1081—1089.
137. Y. Uchikawa, K. Gotoh, T. Ohye. Elect. Eng. Jpn., 1981, 101, No. 3, pp. 8—13.
137a. A. Takaoka, Y. Shin-Ya, K. Ura. Optik, 1985, 69, No. 4, pp. 166—171.
138. E. K. Kasper. см. [51a], pp. 63—73.
139. P. W. Hawkes. J. Phys. E: Sci. Instrum., 1981, 14, pp. 1353—1367.
140. M. Szilagyi. in: Electron Microscopy 1980, Proceedings of the 7th Euro-
European Congress on Electron Microscopy, v. 1, pp. 62—63, Seventh European
Congress on Electron Microscopy Foundation, Leiden, 1980.
141. P. W. Hawkes. см. [50], pp. 1—56.
142. O. Scherzer. Z. Phys., 1936, 101, pp. 593—603.
143. /. L. Verster. Philips Res. Rep., 1963, 18, No. 6, pp. 465—605.
144. О. И. Семан. Тр. Ин-та физики н астрономии АН ЭССР, 1955, № 2,
с. 3—49.
145. P. W. Hawkes. J. Microsc, 1967, 6, pp. 917—932.
146. P. W. Hawkes. Ultramicroscopy, 1977, 2, pp. 179—183.
147. O. Scherzer. Optik, 1947, 2, pp. 114—132.
148. F. Lenz. Optik, 1957, 14, No. 2, pp. 74—82.
149. P. W. Hawkes. Optik, 1968, 27, No. 5, pp. 287—304.
150. P. W. Hawkes. Optik, 1980, 56, No. 3, pp. 293—320.
151. P. W. Hawkes. Optik, 1970, 31, No. 6, pp. 592—599.
152. P. W. Hawkes. см. [41], pp. 230—248.
153. L. H. Veneklasen. Optik, 1972, 36, No. 4, pp. 410—433.
154. /. Orloff. Optik, 1983, 63, No. 4, pp. 369—372.
155. T. Saito, M. Kikuchi, O. J. Severs. J. Appl. Phys, 1979, 50, No. 10, pp. 6123—
6128.
156. G. Liebmann. Proc. Phys. Soc, 1949, B62, pp. 213—228.
157. L. Marton, K. Bol. J. Appl. Phys., 1947, 18, pp. 522—529.
158. /. Hillier. J. Appl. Phys., 1946, 17, No. 6, pp. 411—419.
159. H. Koops. J. Vac. Sci. Technol., 1973, 10, No. 6, pp. 909—912.
160. A. Septier. in Advances in Optical and Electron Microscopy R. Barer,
V. E. Cosslett, eds. v. I, pp. 204—274, New York: Academic, 1966.
161. E. Munro, N. D. Wittels. Optik, 1977, 47, No. 1, pp. 25—38.
162. T. Hanai, M. Hibino, S. Maruse. J. Electron Microsc, 1982, 31, No. 4,
pp. 360—367.
163. W. D. Meisburger, E. H. Jacobsen. Optik, 1982, 62, No. 4, pp. 359—366.
164. A. A. van Gorkutn. J. Vac. Sci. Technol., 1983, Bl, No 4, pp 1312—1315.
165. P. W. Hawkes. см. [49], 1980, v. 1, pp. 45—157.
166. E. Kasper. Optik, 1968—1969, 28, No. 1, pp. 54—64.
167. A. V. Crewe. Optik, 1982, 60, No. 3, pp. 271—281.
168. A. V. Crewe. Optik, 1984, 69, No. 1, pp. 24—29.
169. Xitnen Jiye, A. V. Crewe. Optik, 1985, 69, No. 4, pp. 141—146.
170. H. Rose, U. Petri. Optik, 1971, 33, pp. 151—165.
170a. Ai Kecong, M. Szilagyi. Optik, 1987.
171. D. Gabor. Nature, 1946, 158, p. 198.
172. /. P. van Merwe. J. Appl. Phys., 1981, 52, No. 2, pp. 589—592.
173. H. Voit. Z. Instrumentenkunde, 1939, 59, pp. 71—82.
174. D. R. Herriott, G. R. Brewer, in: Electron-Beam Technology in Microelectro-
Microelectronic Fabrication, New York: Academic, 1980, pp. 141—216.
175. D. B. Langmuir. Proc. IRE, 1937, 25, No. 8, pp. 977—991.
176. Л:. /. Harte. J. Vac. Sci. Technol., 1973, 10, No. 6, pp. 1098—1101.
177. W. Slowko. J. Vac. Sci. Technol., 1981, 19, No. 3, pp. 733—738.
178. H. P. Kuo, В. М. Siegel. Proceedigs of the 31st Annual EMSA Meeting,
1973, pp. 294—295.
624
Литература
179. М. Szilagyi, H. Paik, В. М. Siegel. in: Proceedings of the 10th International
Conference on Electron and Ion Beam Science and Technology, Monreal,
R. Bakish, ed., pp. 409—421. Electrochemical Society Proceedings v. 83-2»
New Jersey: Pennigton, 1983.
180. R. F. W. Pease, W. С Nixon. J. Sci. Instrum., 1965, 42, pp. 81—85.
181. W. Tretner. Optik, 1954, 11, No. 7, pp. 312—326; 1955, 12, No. 6, p. 293.
182. Г. А. Гринберг. ЖТФ, 1953, 23, № 11, с. 1904—1914.
183. Б. Э. Бонштедт. ЖТФ, 1955, 5, № 3, с. 541—543.
184. Н. Shimoyama. J. Electron Microsc, 1982, 31, No. 2, pp. 127—136.
185. M. Szilagyi. Periodica Polytech. Elect. Eng., 1969, 13, No. 3, pp. 221—
233.
186. M. Szilagyi, F. Blaschta. Optik, 1973, 37, No. 3, pp. 300—309.
187. F. Lenz. Ann. Phys. (Leipzig), 1951, 9, pp. 245—258.
188. R. G. E. Hutter. J. Appl. Phys., 1945, 16, pp. 678—699.
189. Л\ Kanaya, N. Baba. Optik, 1977, 47, No. 3, pp. 239—269.
190. W. Glaser, P. Schiske. Optik, 1954, 11, No. 9, 10, pp. 422—467.
191. W. Glaser, P. Schiske. Optik, 1955, 12, pp. 233—245.
192. P. I. Richards. Manual of Mathematical Physics, New York: Pergamon,.
1959.
193. Л\ Kanaya, N. Baba, S. Ono. Optik, 1976, 46, No. 2, pp. 125—148.
194. L. Collatz. The Numerical Treatment of Differential Equations, West Berlin:.
Springer, 1960.
195. G. Liebmann. Proc. Phys. Soc, 1949, B62, No. 12, pp. 753—772.
196. /. С E. Jennings, R. G. Pratt. Proc. Phys. Soc, 1955, 68, pp. 526—536.
197. E. Kasper. Optik, 1985, 69, No. 3, pp. 117—125.
198. J. С Burfoot. Brit. J. Appl. Phys, 1952, 3, pp. 22—24.
199. M. B. Heritage, см. [41], pp. 324—338.
200. R. Rudenberg. J. Franklin Inst., 1948, 246, pp. 311—339, 377—408.
201. A. Recknagel. Z. Phys., 1937, 104, pp. 381—394.
202. M. Szilagyi. J. Vac. Sci. Technol., 1987, A5, pp. 273—278.
202a. M. Szilagyi, J. Szep, E. Lugosi. IEEE Trans. Electron. Devices, 1987, ED-34,.
pt. 2, 8, pp. 1848—1858.
202b. M. Szilagyi, J. Szep. IEEE Trans. Electron. Devices, 1987, ED-34, pp. 2634—
2642.
203. W. Glaser, H. Robl. Z. Angew. Mat. Phys., 1951, 2, pp. 444—469.
204. L. S. Goddar. Proc. Cambridge Phil. Soc, 1946, 24, pp. 106—126.
205. F. Gray. Bell System Tech. J., 1939, 18, No. 1, pp. 1—31.
206. F. Firestein, J. Vine. Brit. J. Appl Phys, 1963, 14, pp. 449—455.
207. S. Natali, D. DiChio, E. Uva, C. E. Kuyatt. Rev. Sci. Instrum. 1972, 43„
No. 1, pp. 80—83.
208. С E. Kuyatt, S. Natali, D. DiChio. Rev. Sci. Instrum., 1972, 43, No. U
pp. 84—87.
9. R. J. ~
209. R. J. Romagnoli. Am. J. Phys., 1972, 40, pp. 401—403.
210. D. DiChio, S. Natali, С. Е. Kuyatt. Rev. Sci. Instrum., 1974, 45, pp. 559—
565.
211. D. DiChio, S. Natali, E. Kuyatt, Rev. Sci. Instrum. 1975, 46, No. U
pp. 71—76.
212. R. D. Cook, D. W. O. Heddle. J. Phys. E: Sci. Instrum, 1976, 9, pp. 279—
282.
213. T. Saito, O. J. Severs. J. Appl. Phys., 1979, 50, No. 5, pp. 3050—3056.
214. P. Bonjour. Rev. Phys. Appl., 1979, 14, pp. 533—540; 715—728.
215. Л:. Spangenberg, L. M. Field. Elec. Commun., 1943, 21, pp. 194—204.
215a. P. Vijayakumar, M. Szilagyi. Rev. Sci. Instrum., 1987, 58, No. 6, pp. 953—
957.
216. G. D. Archard. Brit. J. Appl. Phys, 1957. 8, pp. 127—130.
217. F. H. Read. J. Phys. E: Sci. Instrum., 1969, 2, pp. 165—169.
218. F. H. Read. J. Phys. E: Sci. Instrum., 1971, 4, pp. 562—566.
625
Литература
219. Е. Munro. in: Electron Microscopy 1972, Institute of Physics Conf, Series,
v. 14, pp. 22—23, London.
220. K. Kuroda, T. Suzuki. J. Appl. Phys., 1974, 45, pp. 1436—1441.
220a. A. Tonomura. Jpn. J. Appl. Phys., 1973, 12, No. 7, pp. 1065—1069.
221. /. W. Butler. Digital Computer techniques in Electron Microscopy. Pro-
Proceedings of the 6th International Congress on Electron Microscopy, Kyoto,
v. 1, pp. 191—192, Maruzen, Tokyo, 1966.
222. A. V. Crewe, D. N. Eggenberger, J. Wall, L. M. Welter. Rev. Sci. Instrum.,
1968, 39, No. 4, pp. 576—583.
523. A. V. Crewe, M. Isaacson, D. Johnson. Rev. Sci. Instrum., 1969, 40, No. 2,
pp. 241—246.
4. A. V. -
224. A. V. Crewe. in: Electron Microscopy in Materials Science, U. Valdre, ed.,
pp. 162—207, New York: Academic, 1971.
225. K. Kanaya, H. Yamazaki, T. Taoka, H. Fujita, M. Iwanaga, S. Shibata.
J. Electron Microsc, 1965, 14, No. 3, pp. 196—202.
226. K. Kanaya, H. Kawaktsu, T. Miya. J. Electron Microsc, 1972, 21, pp. 261 —
270.
227. H. H. Лебедев, И. П. Скальская. ЖТФ, 1960, 30, № 5, с. 472—479.
228. М. Denizart, S. Roques, F. Sonier, В. Jouffrey, J. Trinquier. Ultramicroscopy,
1981, 7, pp. 65—80.
529. M. Denizart, S. Roques, F. Sonier, B. Jouffrey. см. [51a], pp. 179—186.
230. M. M. El Gomati, M. Prufton, R. Browning. J. Phys. E: Sci. Instrum., 1985,
18, pp. 32—38.
231. K. Kanaya, H. Kawakatsu, H. Yamazaki, S. Sibata. J. Sci. Instrum., 1966,
43, pp. 416—429.
532. F. Heise, O. Rang. Optik, 1949, 5, No. 4, pp. 201—216.
233. A. Adams, F. H. Read. J. Phys., E: Sci. Instrum., 1972, 5, pp. 150—155.
234. T. Saito, O. J. Sovers. J. Appl. Phys., 1977, 48, No. 6, pp. 2306—2311.
235. F. H. Read. J. Phys. E: Sci. Instrum., 1969, 2, pp 679—684.
236. E. G. Ratnberg. J. Appl. Phys, 1942, 13, pp. 582—594.
237. H. Paik, G. N. Lewis, E. J. Kirkland, B. M. Siegel. J. Vac. Sci. Technol.,
1985, B3, No. 1, pp. 75—81.
238. G. D. Archard. Brit. J. Appl. Phys, 1956, 7, pp. 330—332.
239. /. Vine. Brit. J. Appl. Phys, 1960, 11, pp. 408—411.
240. G. F. Rempfer. J. Appl. Phys., 1985, 57, No. 7, pp. 2385—2401.
241. R. Seeliger. Optik, 1948, 4, pp. 258—262.
242. A. Septier. Aberration spherique de quelques lentilles electrostatiques a
symetrie de revolution pour des faisceaux de grande ouverture, CERN
Report No. 60-39, Geneva, 1960.
243. K. J. Hanszen. Optik, 1958, 15, No. 5, pp. 304—317.
244. G. V. Der-Shvarts, I. S. Makarova. Radio Eng. Electron. Phys., 1966, 11,
pp. 1581—1585.
5. G. V. ~ "
245. G. V. Der-Shvarts, I. S. Makarova. Radio Eng Electron. Phys., 1965, 14,
Nb. 2, pp. 330—332.
246. /. Orloff, L. W. Swanson. J. Appl. Phys., 1979, 50, No. 4, pp. 2494—
2501.
247. А. В .El-Kareh, M. A. Sturans. J. Appl Phys., 1971, 42, No. 12, pp. 4902—
4907.
548. 6. H. N. Riddle. J. Vac. Sci. Technol, 1978, 15, No. 3, pp. 857—860.
249. A. Adams, F. H. Read. J. Phys. E: Sci. Instrum., 1972, 5, pp. 156—160.
550. D. W. O. Heddle, N. Papadovassilakis, A. M. Yateem. J. Phys. E: Sci.
Instrum., 1982, 15, pp. 1210—1213.
251. R. E. Imhof, F. H. Read. J. Phys. E: Sci. Instrum., 1968, 1, pp. 859—860.
552. F. H. Read. J. Phys. E: Sci. Instrum, 1970, 3, pp. 127—131.
253. Л\ Kuroda, H. Ebisui, T. Suzuki. J. Appl. Phys., 1974, 45, pp. 2336—
2342.
€26
Литература
254. J. Orloff, L. W. Swason. Scanning El. Microscopy. 1979, 1979/1, 10,
pp. 39—44.
255. F. H. Read. J. Phys. E: Sci. Instrum., 1983, 16, pp. 636—642.
256. G. Martinez, M. Sancho, F. H. Read. J. Phys. E: Sci. Instrum., 1983, 16*
pp. 625—635.
257. E. Kisker. Rev. Sci. Instrum., 1982, 53, No. 1, pp. 114—116.
258. K. Kurihara. J. Vac. Sci. Technol., 1985, B3, No. 1, pp. 41—44.
259. B. M. Siegel, G. R. Hanson, M. Szilagyi, D. R. Thomas, R. J. BlackwelU
H. Paik. Proceedings of the SPIE (International Society for Optical Engi-
Engineering), v. 333, Submicron Lithography, P. D. Blais, ed., pp. 152—157,
Santa Clara, 1982.
260. M. Szilagyi. J. Vac. Sci. Technol., 1983, Bl, No. 4, pp. 1137—1140.
261. D. W. 0. Heddle, N. Papadovassilakis. J. Phys. E: Sci. Instrum., 1984, 17,
pp. 599—605.
262. /. Fink, E. Kisker. Rev. Sci. Instrum., 1980, 51, No. 7, pp. 918—920.
263. /. D. Cross, F. H. Read, E. A. Riddle. J. Sci. Instrum., 1967, 44, pp. 993—
996.
264. Л. Г. Гликман, В. М. Кельман, М. Ш. Нурманов. ЖТФ, 1973, 43, № 7,
с. 1358—1363.
265. Л. Г. Гликман, В. М. Кельман, М. Ш. Нурманов. ЖТФ, 1973, 43, № 11,
с. 2278—2280.
266. D. W. О. Heddle. J. Phys. E: Sci. Instrum., 1971, 4, pp. 981—983.
267. К. J. Hanszen, R. Lauer. см. [32], v. I, pp. 251—307.
268. M. Szilagyi. Reduction of Aberrations of Electron Optical Systems. Hunga-
Hungarian Academy of Sciences. Budapest, 1977.
269. С Lejeune, J. Aubert. см. [49], 1980, v. I, pp. 159—259.
270. R. R. Law. Proc. IRE, 1937, 25, No. 8, pp. 954—976.
271. H. Moss. Narrow Angle Electron Guns and Cathode Ray Tubes, Advances-
in Electronics and Electron Physics, L. Marton, ed., Suppl. 3, New York:
Academic, 1968.
272. E. Munro. см. [49], 1980, v. II, pp. 73—131.
273. /. Worster. Int. J. Electron., 1970, 28, No. 2, pp. 117—128.
274. W. Kamminga, J. C. Francken. Optik, 1971, 33, No. 4, pp. 375—398.
275. E. Kasper. Optik, 1979, 54, pp. 135—147.
276. D. W. Swift, W. С Nixon. Brit J. Appl. Phys., 1962, 13, pp. 288—293.
277. M. E. Haine, D. Under, см. [32], v. I, pp. 233—250.
278. Т. Е. Everhart. J. Appl. Phys., 1967, 38, No. 13, pp. 4944—4957.
279. W. Kamminga. см. [41], pp. 400—415.
280. /. C. Wiesner, Т. Е. Everhart. J. Appl. Phys., 1974, 44, pp. 2140—2148; 45,
pp. 2797—2798.
281. R. Lauer. in: Advances in Optical and Electron Microscopy R. Barer and
V. E. Cosslett, eds., v. 8, pp. 137—206, New York: Academic, 1982.
282. M. E. Haine, P. A. Einstein. Brit. J. Appl. Phys., 1952, 3, pp. 40—46.
283. К. Н. Steigerwald. Optik, 1949, 5, No. 8/9, pp. 469—478.
284. E. Kasper. in: Advances in Optical and Electron Microscopy R. Barer and
V. E. Cosslett, eds., v. 8, pp. 207—260, New York: Academic, 1982.
285. /. Orloff, L. W. Swanson. Optik, 1982, 61, No. 3, pp. 237—245.
286. N. K. Kang, D. Tuggle, L. W. Swanson. Optik, 1983, 63, No. 4, pp. 313—
331
287. L. W. Swanson. см. [51a], pp. 137—147.
288. /. Orloff. см. [51a], pp. 149—162.
289. A Septier. см. [321, v. II, pp. 123—159.
290. R. Levi-Setti. см. [49], 1980, v. I, pp. 261—320.
291. Л:. Siegbahn. Phil. Mag., 1946, 37, pp. 162—184.
292. M. Szilagyi. A new magnetic lens model, Proceedings of the 7th Interna-
International Congress on Electron Microscopy, v. 2, pp. 61—62, Grenoble, 1970.
293. P. W. Hawkes. Brit. J. Appl. Phys., 1968, 1, pp. 1549—1558.
62T
Литература
294. К. Капауа, Н. Kawakatsu, Y. Ishikawa. Bull. Electrotechnical Lab., Tokyo,
33, 1969, № 11, pp. 1233—1255.
295. P. W. Hawkes. Brit. J. Appl. Phys., 1968, 1, pp. 131—133.
296. M. Szilagyi. Optik, 1977, 49, No. 2, pp. 223—246.
297. T. Mulvey. см. [32], v. I, pp. 469—494.
298. F. Lam. см. [50], pp. 119—161.
299. W. Kamminga, J. L. Verster, J. С Francken. Optik, 1968—1969, 28, No. 5,
pp. 442—461.
,300. T. Mulvey, M. I. Wallington. J. Phys. E: Sci. Instrum., 1969, 2, pp. 466—
472,
:301. G. Liebmann. Proc. Phys. Soc, 1955, B68, pp. 737—745.
302. P. Durandeau, С Fert. Rev. Opt. Theor. Instrum., 1957, 36, 205—234.
303. G. Liebmann. Proc. Phys. Soc, 1951, B64, pp. 972—977.
304. G. Liebmann. Proc. Phys. Soc, 1952, B65, pp. 188—192.
305. W. D. Riecke [51a], pp. 1—14.
306. G. Liebmann. Proc. Phys. Soc, 1955, B68, pp. 682—685.
307. J. Dugas, P. Durandeau, С Fert. Rev. Opt. Theor. Instrum, 1961, 40,
pp. 277—305.
8. E. i
308. E. Munro, О. С Wells. Scanning Electron Microscopy, 1976/1, pp. 27—36,
1976.
309. K. Tsuno, T. Honda. Optik, 1983, 64, No. 4, pp. 367—378.
310. G. V. Der-Shvarts, V. P. Rachkov. Radio Eng. Electron. Phys., 1965, 10,
pp. 783—789.
311. T. Mulvey. см. [51a], pp. 15—27.
312. /. Dietrich. Superconducting Electron Optical Devices, New York: Plenum
Press, 1976.
313. /. L. Balladore, R. Murillo, J. Trinquier. см. [51a], pp. 29—35.
314. /. B. Le Poole. in: Proc. 3rd European Conf. Electron Microscopy, M. Titl-
bach, ed., Appendix, p. 6, Prague: Publishing House of the Czechslovak
Academy of Sciences, 1964.
315. О. И. Семан. МТФ, 1953, 24, No. 5, с 581—588.
316. П. П. Касьянков. ЖТФ. 25, No. 9, с. 1639—1648.
317. W. Glaser. Z. Phys., 1940, 116, pp. 19—33.
318. A. Recknagel. Z. Phys., 1940, 117, pp. 67—73.
319. A. V. Crewe. Ultramicroscopy, 1977, 2, pp. 281—284.
320. P. Schiske. Optik, 1956, 13, No. 11, pp. 502—505.
320a./. Szep, M. Szilagyi. IEEE Trans. Electron Devices, 1988.
320b. M. Szilagyi, J. Szep. J. Vac. Sci. Technol., 1988, 6, No. 3, pp. 953—957.
321. M. Szilagyi. см. [51a], pp. 75—84.
322. O. Scherzer. Z. Phys., 1936, 101, pp. 23—26.
323. R. Rebsch, W. Schneider. Z. Phys, 1937, 107, pp. 138—143.
324. W. Glaser. Z. Phys., 1938, 109, pp. 700—721.
325. R. Rebsch. Ann. Phys, 1938, 31, pp. 551—560.
326. G. N. Plass. J. Appl. Phys., 1942, 13, pp. 49—55, 524.
327. П. П. Касьянков. ЖТФ, 1952, 22, № I.e. 80—83.
328. /. С. Burfoot. Proc. Phys. Soc, 1953, B66, pp. 775—792.
329. R. W. Moses. [41], pp. 250—272.
330. R. W. Moses. Rev. Sci. Instrum, 1970, 41, No. 5, pp. 729—740.
331. R. W. Moses. Rev. Sci. Instrum, 1971, 42, No. 6, pp. 828—831.
332. R. W. Moses. Rev. Sci. Instrum, 1971, 42, No. 6, pp. 832—839.
333. H. Rose, R. W. Moses. Optik, 1973, 37, No. 3, pp. 316—336.
334. W. Tretner. Optik, 1959, 16, No. 3, pp. 155—184.
335. H. Griimm. Optik, 1956, 13, No. 2, pp. 92—93.
336. W. Tretner. Optik, 1956, 13, No. 11, pp. 516—519.
337. M. Szilagyi. Optik, 1977, 48, No. 2, pp. 215—224.
«628
Литература
338. A. Garren. M. Szilagyi, Computer implementation of electron optical opti-
optimization by dynamic programming, Lawrence Berkeley Laboratory Report
LBL-6175, Berkeley: University of California, 1977.
339. M. Szilagyi. Optik, 1978, 50, No. 1, 35—51.
340. M. Szilagyi. Proc. 9th Internat. Congress on Electron Microscopy, v. 1,
pp. 30—31, Toronto, 1978.
1. M. - -
341. M. Szilagyi. Applied Simulation and Modelling, pp, 41—44, Acta Press,
Anaheim, 1983.
342. M. Szilagyi. Particle Accelerators, 1981, 11, No. 4, pp. 213—217.
343. M. Szilagyi, S. J. Yakowitz, M. O. Duff. Appl. Phys. Lett., 1984, 44, No. 1,
pp. 7—9.
344. /. E. Dennis. Proc. IEEE, 1984, 72, No. 12, pp. 1765—1776.
345. /. P. van der Merwe. Appl. Phys. Lett., 1980, 36, No. 4, pp. 251—253.
346. M. Kodama. J. Phys. D: Appl. Phys., 1982, 15, pp. 965—974.
347. /. R. Ashley. Proc. IEEE, 1972, 60, No. 1, pp. 115—119.
348. A. Skollermo. Nucl. Instrum. Methods, 1976, 137, pp. 339—371.
349. P. W. Hawkes. Optik, 1973, 38, pp. 589—591.
350. K. J. Harker. J. Math. Phys., 1963, 4, pp. 993—997.
351. J. P. van der Merwe. J. Appl. Phys., 1979, 50, No. 8, pp. 5120—5126.
352. M. Szilagyi. Appl. Phys. Lett., 1984, 45, No. 5, pp. 499—501.
353. F. Berz. Phil. Mag., 1950, 41, pp. 209—220.
353a./. Szep, M. Szilagyi. J. Appl Phys., 1987, 62, No. 9, pp. 3539—3542.
354. M. Szilagyi. Proc. IEEE, 1985, 73, No. 3, pp. 412—418.
355. P. W. Hawkes. Computer-Aided Design in Electron Optics, 1973, 5, No. 4,
pp. 200—214.
356. M. Szitagyi. Appl. Phys. Lett., 1986, 49, No. 13, pp. 767—769.
357. E. Regenstreif. [32], I, pp. 353—410.
358. G. W. Grime, F. Watt. Beam Optics of Quadrupole Probe-Forming Systems,
Bristol (England): Adam Hilger, 1984.
359. E. D. Courant, M. S Livingston, H. S. Snyder. Phys. Rev., 1952, 88,
pp. 1190—1196.
360. M. Szilagyi. Proceedings of the 6th International Conference on Microwave
and Optical Generation and Amplification (MOGA), Cambridge, 1966, IEE
Conference Publications, 1967, v. 27, pp. 70—74.
361. M. Szilagyi. Design Considerations for low-beta straight sections at PETRA,
DESY Report M-81/19, Deutsches Elektronen-Synchrotron (DESY), Ham-
Hamburg, 1981.
362. P. W. Hawkes. см. [32], v. I, pp. 411—468.
363. P. W. Hawkes. Phil. Trans. R. Soc, 1965, A257, pp. 479—552.
364. M. Szilagyi, F. Blaschta, L. P. Ovsyannikova, S. Ya. Yavor. in: Electron
Microscopy 1972, Institute of Physics Conf. Series, v. 14, A. M. Glauert, ed.,
pp. 84—85, London, 1972.
365. M. Szilagyi, F. Blaschta, L. P. Ovsyannikova, S. Ya Yavor. Optik, 1973, 38,
No. 4, pp. 416—424.
366. P. W. Hawkes. Optik, 1967, 25, pp. 439—449.
367. P. W. Hawkes. Optik, 1967, 26, pp. 497—506.
368. F. Blaschta, M. Szilagyi. Optik, 1974, 39, No. 5, pp. 499—515.
369. M. Szilagyi, F. Blaschta, L. P. Ovsyannikova, S. Ya. Yavor. Optik, 1974, 39,
No. 4, pp 351—358.
370. H. Rose. Optik, 1971, 34, pp. 285—311.
371. /. Kelly, in: Advances in Electronics and Electron Physics, L. Marton, ed.,
1977, 43, pp. 43—138.
372. /. Haantjes, G. J. Lubben. Philips Res. Rep., 1957, 12, pp. 46—68; 1959, 14,
pp. 65—97.
373. A. Kaashoek. Philips Res. Rep. Suppl. 1968, 12, pp. 1—114.
374. С. С Т. Wang. IEEE Trans. Electron Devices, 1971, 18, No. 4, pp. 258—
274.
629
Литература
375. Е. Munro. Optik, 1974, 39, No. 4, pp. 450—466.
376. Li Yu, Ximen Ji-ye. Optik, 1982, 61, No. 3, pp. 315—332.
377. M. R. Smith, E. Munro. Optik, 1986, 74, No. 1, pp. 7—16.
378. A. V. Crewe, N. W. Parker. Optik, 1976, 46, No. 2, pp. 183—194.
379. Ximen Ji-ye, Li Yu. Optik, 1982, 62, No. 3, pp. 287—297.
380. H. Ohiwa, E. Goto, A. Ono. Electron. Commun. Jpn., 1971, 54B, No. 12^
pp. 44—51.
381. H. C. Pfeiffer, M. A. Sturans. см. [51a], pp. 109—114.
382. R. G. E. Hutter. in: Advances in Image Pickup and Display, B. Kazan, ed.,.
v. 1, pp. 163—224, New York: Academic, 1974.
383. E. F. Ritz. in: Advances in Electronics and Electron Physics, v. 59, pp. 299—
357, New York: Academic, 1979.
384. E. F. Ritz. см. [51a], pp. 97—108.
385. Г. А. Гринберг, Избранные вопросы математической теории электрических
и магнитных явлений. — Москва — Ленинград: Издательство АН СССР;
1948.
386. A. L. Hughes, V. Rojansky. Phys. Rev., 1929, 34, pp. 284—290.
387. H. Wollnik. см. [32], v. II, pp. 163—202.
388. H. A. Enge. см. [32], v. II, pp. 203—264.
389. С. Я. Явор, М. Силади. ЖТФ, 1964, т. 34, № 1, стр. 105—109.
390. М. Силади, С. Я. Явор. ЖТФ, 1965, т. 35, № 3, стр. 402—404.
391. R. Hutter. см. [32], v. II, pp. 3—22.
~~~ - - - "-2], v. II,
...... . 2], v. II,;...
394. /. D. Lawson. см. [49], v. Ill, pp. 1—48.
392. G. R. Brewer, см. [32], v. II, pp. 23—72.
393. G. R. Brewer, см. [32], v. II, pp. 73—121.
395. /. H. Bick. IEEE Trans. Electron Devices, 1965, ED-12, No. 7, pp. 408—
411.
396. M. Szilagyi. Tungsram Tech. Mitt., 1963, 10, pp. 438—443.
397. M. Szilagyi. Acta Phys. Hungarica. 1965, 18, No. 4, pp. 325—334.
398. /. Langmuir. Phys. Rev., 1913, 2, pp. 450—486.
399. /. R. Pierce. J. Appl. Phys., 1940, 11, pp. 548—554.
400. L. Brillouin. Phys. Rev, 1945, 67, pp. 260—266.
401. M. Szilagyi. Acta Phys. Hungarica, 1965, 18, No. 2, pp. 87—99.
402. M. Szilagyi. Proc. 5th Internat. Congress on Microwave Tubes, Paris: Du-
pon, 1965, pp. 339—341.
403. P. K. Tien. J. Appl. Phys, 1954, 25, No. 10, pp. 1281—1288.
404. M. Szitagyi. Radio Eng. Electron. Phys, 1966, 11, No. 5, pp. 751—757.
405. W. E. Waters. J. Appl. Phys., 1960, 31, No. 10, pp. 1814—1820.
406. M. Szilagyi. Tungsram Tech. Mitt, 1964, 14, pp. 614—622.
407. M. Szilagyi. Acta Phys. Hungarica, 1965, 18, No. 4, pp. 335—350.
408. K. K. N. Chang. Proc. IRE, 1957, 45, No. 11, pp. 1522—1527.
409. /. Fejes, M. Szitagyi. Tungsram Tech Mitt, 1973, No. 23, pp. 1002—1014.
410. H. Boersch. Z. Phys., 1954, 139, pp. 115—146.
411. H. Rose, R. Spehr. см. [49], 1983, III, pp. 475—530.
412. H. С Pfeiffer. Scanning Electron Microscopy, 1972, 1972/1, pp. 113—120.
413. G. H. Jansen, T. R. Groves, W. Stickel. J. Vac. Sci. Technol, 1985, B3,
No. 1, pp. 190—193.
414. B. Zimmerman, in Advances in Electronics and Electron Physics, L. Marton,
ed, v. 29, pp. 237—312, New York: Academic, 1970.
Предметный указатель
Аббе соотношение 195
Аберрация 51
— геометрическая 247
— коэффициент 255, 261
— релятивистская 250
— сферическая 265, 280, 323
— хроматическая 248, 300
Аберрации высших порядков 337
— отклонения 337
Аксептаис 574
Аксиально-симметричное поле 73, 149
Ампера закон циркуляции 116
Аналитическая модель 376
Асимптотический фокус 198
Астигматизм 283
— аксиальный 336
Био — Савара закон 121
Боэрша эффект 296, 335, 618
Бриллюэна фокусировка 615
Буша теорема 181
Векторный потенциал 12
Вина фильтр 59
Виртуальный источник 468
Возмущение 255
Вращения изображения уравнение
192
Гамильтона принцип 14
Гаусса закон 11
Гауса—Зейделя алгоритм 152
Гауссово приближение 19
Гауссовская диоптрика 156
Гауссовы квадратуры 370
Гексаполь 80
Гельмгольца — Лагранжа формула
195
Гистерезис 113
Главные лучи 201
Гривета — Ленца модель 493
Де Бройля длина волны 14
Декаполь 80
Диск минимального рассеяния 281
Дисперсии 596
Дисторсия 286, 287
— анизотропная 291
Дифракция 247, 333
Додекаполь 80
Дублет антисимметричный 569
— квадрупольный 569
— мультипольный 569
Зональные системы 338
Зонная пластика 334
Идеальный квадруполь 80
Интерполяционный импульс 174
Интерполяция 366
— квадратичная 368
— линейная 367
Ионное зеркало 210
Ионные источники 472
Кардинальные элементы 197
асимптотические 197, 198
реальные 197, 198
Кирхгофа закон 135
Кома 288
— анизотропная 293
Конформное отображение 111
Коши задача 357
Кривизна поля 285
Кроссовер 467
Кубический сплайн 174
Кусочно-квадратичная модель 378
Кусочно-линейная модель 376
Лагранжа интерполяция 172
— уравнение движения 16
Ламе коэффициенты 12
Лапласа уравнение 13
Линзовые фильтры 372
Линзы 209
— асимметричные 382
— бесконечно тонкие 324
— гибридные 419
— иммерсионные 210
— катодные 210
— коаксиальные 338
— магнитные 210
— мультипольные 337
■— одиоапертурные 210
— однопотенциальные 210
— полиномиальные 411
631
Предметный указатель
— сверхпроводящие 503
— симметричные 382
— с отрицательным фокусным рас-
расстоянием 220
— телескопические 209, 242
— тонкие 221
— электростатические 209, 210, 306
Лоренца сила 13, 56
Магнетрон 59
Магнитная линза 113
Магнитный резонанс 131
— спектрометр 595
Максвелла уравнения 11, 13
Масс-спектроскопия 52
Матрица переноса 212
Метод последовательных приближе-
приближений 223
Мопертюи принцип 17
Мультиплеты 573
Мультиполи длинные 102
— короткие 101
Мультипольное поле 74
планарное 79
Нумерова метод 358, 364
Ньютона поля 201
— формула 21
Обобщенный импульс 17
Октуполь 80
Ома закон 132
Оптическая сила 219
Параксиальных лучей уравнение 185
Первеаис 63, 335
Петцваля коэффициент 286
Пирса пушка 611
Планарные поля 70, 149
Погрешность абсолютная 141
— относительная 141
Поле круговой апертуры 93
— потенциальное 64
Предиктора-корректора метод 358, 363
Преломление 18
Приближение тонкой линзы 21, 388,
429
Пространственный заряд 248
Прямоугольная модель 103, 240
Пуассона уравнение 13
Разделение переменных 82
Разрешающая способность 334
Распределенный заряд 335
Резисторная сеть 135
Релаксации метод 153
Релятивистские эффекты 29
Ромберга метод 370
632
Рунге — Кутта метод 358
— — формула 361
Седловая точка 73
Симпсона правило 368
Синтеза метод 108
Скалярный потенциал 12
— — магнитный 14
Снелля формула 18, 40
Стигматическое изображение 192
Стигматор 337
Стокса теорема 14
Термоиониые пушки 170
Точечный эйконал 248
Триплет 572
Трохотрон 58
Увеличение 192
— асимптотическое 203
— бесконечное 198, 269, 304
— нулевое 198, 269, 304
— системы линз 243
— угловое 194
Узловые точки 20, 205
скрещивающиеся 207
Уравнение неразрывности 132
Фарадея закон 11
Ферма принцип 17, 248
Ферромагнитные материалы 115
Фокус 19
Форм-фактор 497
Характеристическая функция 248
Холла эффект 130
Циклоида 56
Циклотронная частота 50
Чайлда — Ленгмюра закон 611
Шерцера теорема 279
Шеститочечная формула 370
Эйлера — Лагранжа — Пуассона
уравнение 516
Эйлера — метод 358
— уравнения 249
Эйри диск 333
Электролитическая ванна 133
Электронное зеркало 210
Электронно-оптический показатель
преломления 40
Электронные пушкн 468
Эмиттанс 574
Эффективная длина 42, 103, 240, 383,
476
Оглавление
Предисловие к русскому изданию 5
Предисловие 7
ГЛАВА 1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 9
1.1. Введение 9
1.2. Электромагнитные поля 11
1.2.1. Уравнения Максвелла И
1.2.2. Статические поля 13
1.2.3. Теорема Стокса 14
1.3. Основы классической механики 14
1.3.1. Принцип Гамильтона; уравнения движения Лагранжа 14
1.3.2. Принцип Мопертюи 16
1.4. Краткий обзор геометрической оптики 17
1.4.1. Принцип Ферма; показатель преломления 17
1.4.2. Аксиально-симметричная линза 18
Заключение 21
ГЛАВА 2. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКОМ
И МАГНИТНОМ ПОЛЯХ 23
2.1. Лагранжиан 23
2.2. Сохранение энергии 25
2.2.1. Движение свободных частиц. Зависимость скорости от потенциала 26
2.3. Уравнения движения 29
2.4. Траекторные уравнения 34
2.5. Релятивистский потенциал 38
2.6. Электронно-оптический показатель преломления 39
2.7. Частицы в однородных полях 42
2.7.1. Плоский конденсатор 42
2.7.1.1. Отклонение частиц электростатическим полем 45
2.7.1.2. Простой анализатор скорости 46
2.7.2. Однородное магнитное поле 47
2.7.2.1. Длинные магнитные линзы 50
2.7.2.2. Отклонение частиц магнитным полем 51
2.7.3. Одновременное действие однородных электрического и магнитного
полей 52
2.7.3.1. Определение масс и другие приложения 58
2.8. Законы подобия 59
Заключение 63
ГЛАВА 3. ОПРЕДЕЛЕНИЕ ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЕЙ 64
3.1. Аналитические методы 65
3.1.1. Разложение потенциалов и полей в ряды 65
3.1.1.1. Пленарные поля 70
3.1.1.2. Аксиально-симметричное поле 72
3.1.1.3. Мультипольные поля 74
633
Оглавление
3.1.2. Аналитическое вычисление аксиально-симметричных потенциальных
полей 82
3.1.2.1. Разделение переменных 82
3.1.2.2. Трудности аналитических вычислений (электростатическое поле двух
цилиндров одного диаметра) 87
3.1.2.3. Поле круговой апертуры 93
3.1.2.4. Быстрое вычисление полей от двух и большего числа круговых апер-
апертур 98
3.1.3. Аналитическое вычисление мультипольиых полей 101
3.1.3.1. Короткие мультиполи 101
3.1.3.2. Длинные мультиполи 102
3.1.3.3. Идеальные мультиполи 106
3.1.3.4. Метод конформных преобразований ПО
3.1.4. О роли магнитных материалов 113
3.1.5. Аналитическое вычисление магнитных полей, индуцируемых тока-
мн 121
3.1.5.1. Закон Био — Савара 121
3.1.5.2. Поле прямолинейного проводника 123
3.1.5.3. Поле круговой петли 123
3.1.5.4. Поле тонкого соленоида 124
3.1.5.5. Поле многослойной катушки 125
3.1.5.6. Поле плоской катушки 127
3.2. Измерение полей и аналоговые методы 128
3.2.1. Измерение магнитных полей 129
3.2.1.1. Электромагнитная индукция 129
3.2.1.2. Эффект Холла 130
3.2.1.3. Пермаллоевые и висмутовые датчики 131
3.2.1.4. Магнитный резонанс 131
3.2.2. Аналоговые методы 132
3.2.2.1. Электролитическая ванна 132
3.2.2.2. Резисторная сеть 134
3.2.2.3. Другие аналоговые методы 140
3.3. Численные методы 141
3.3.1. Точность 141
3.3.1.1. Погрешности, связанные с природой задачи 142
3.3.1.2. Погрешности записи чисел в компьютере 143
3.3.1.3. Погрешности, обусловленные численными методами 145
3.3.2. Метод конечных разностей 145
3.3.2.1. Методы решения систем алгебраических уравнении 152
3.3.3. Метод конечных элементов 154
3.3.4. Метод зарядовой плотности (интегральный метод) 163-
3.3.5. Численное дифференцирование н интерполяция 170
3.3.5.1. Дифференцирование 170
3.3.5.2. Интерполяция Лагранжа 172
3.3.5.3. Интерполяционный импульс 174
3.3.5.4. Кубический сплайн 174
Заключение 177
ГЛАВА 4. ФОКУСИРОВКА В АКСИАЛЬНО-СИММЕТРИЧНЫХ ПОЛЯХ 179
4.1. Теорема Буша 179
4.2. Основное траекторное уравнение 181
4.3. Уравнение параксиальных лучей 184
4.4. Формирование изображения с помощью параксиальных лучей 190
4.5. Формула Гельмгольца—Лаграижа 194
4.6. Кардинальные элементы 196
4.6.1. Асимптотические кардинальные элементы 201
4.7. Электронные и ионные линзы 209
634
Оглавление
4.8. Системы лииз 211
4.8.1. Матрица переноса 211
■4.8.2. Система из двух толстых линз 214
4.9. Приближение тонкой линзы 221
4.9.1. Системы тонких линз 226
4.10. Примеры фокусирования параксиальных лучей 230
4.10.1. Параксиальные траектории в однородных полях 231
4.10.1.2. Скошенные лучи 234
4.10.1.3. Однородное магнитное поле 235
4.10.2. Одновитковая магнитная линза 238
4.10.3. Системы линз 242
4.10.3.1. Телескопическая система 242
4.10.3.2. Увеличение системы линз 243
Заключение 246
ГЛАВА 5. ТЕОРИЯ АБЕРРАЦИИ 247
5.1. Метод характеристических функций 248
5.2. Геометрические аберрации 257
5.2.1. Сферическая аберрация 264
5.2.1.1. Нулевое и бесконечное увеличение 269
5.2.1.2. Другие способы записи коэффициента сферической аберрации 272
5.2.1.3. Теорема ТЛерцера 279
5.2.1.4. Диск минимального рассеяния 280
5.2.2. Астигматизм 283
5.2.3. Кривизна поля 284
5.2.4. Дисторсия 286
5.2.5. Кома 287
5.2.6. Анизотропные аберрации 289
5.2.6.1. Анизотропный астигматизм 290
5.2.6.2. Анизотропная дисторсия 291
5.2.6.3. Анизотропная кома 292
5.2.7. Об относительном вкладе различных геометрических аберраций 295
5.3. Хроматическая аберрация 295
5.3.1. Аксиальная хроматическая аберрация 300
5.3.1.1. Нулевое и бесконечное увеличения 303
5.3.1.2. Верхний предел аксиальной хроматической аберрации 305
5.3.2. Хроматическая аберрация увеличения 309
5.3.3. Анизотропная хроматическая аберрация 309
5.3.4. Магнитная хроматическая аберрация 310
5.4. Асимптотические аберрации 311
5.4.1. Зависимость коэффициентов асимптотической аберрации от увеличе-
увеличения 313
5.4.1.1. Полиномиальное выражение для коэффициента асимптотической сфе-
сферической аберрации 314
5.4.1.2. Полиномиальное выражение для коэффициента асимптотической ак-
аксиальной хроматической аберрации 319
5.4.2. Аберрации тонких линз 323
5.4.2.1. Сферическая аберрация 323
5.4.2.2. Аксиальная хроматическая аберрация 325
5.5. Аберрации систем линз 326
5.5.1. Добавление сферической аберрации 327
5.5.2. Добавление аксиальной хроматической аберрации 330
5.6. Другие источники аберраций и коррекция аберраций 332
5.6.1. Дифракция 332
5.6.2. Пространственный и поверхностный заряды 334
5.6.3. Высокочастотные поля 336
5.6.4. Отсутствие аксиальной симметрии 336
635
Оглавление
5.6.5. Другие методы коррекции 338
5.6.5.1. Коаксиальные линзы 338
5.6.5.2. Симметричные траектории 338
5.6.5.3. Положение ограничивающей апертуры 338
5.6.5.4. Цифровая обработка изображения 338
5.6.6. Синтез 339
5.6.7. Об измерении аберраций 339
5.6.8. Яркость 339
5.7. Совместное действие аберраций разных видов 347
5.7.1. Пренебрежимо малые источники 344
5.7.2. Конечные источники 345
5.7.2.1. Пренебрежение хроматической аберрацией 346
5.7.2.2. Пренебрежение сферической аберрацией 348
5.7.3. Смешения аберраций в комбинации линз 350
5.7.4. Коэффициенты добротности 350
Заключение 353
ГЛАВА 6. ЧИСЛЕННЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ТРАЕКТОРИЙ ЛУ-
ЛУЧЕЙ И РАСЧЕТА АБЕРРАЦИИ 355
6.1. Аналитические модели 355
6.2. Численный расчет траекторий лучей 357
6.2.1. Метод Рунге — Кутта 359
6.2.2. Многошаговые методы 363
6.2.2.1. Метод Нумерова 364
6.2.3. Дополиительные замечания о точности 364
6.3. Численные методы для вычисления аберрационных интегралов 366
6.3.1. Интегрирование методом трапеций 367
6.3.2. Правило Симпсона 368
6.3.3. Интегрирование методом Ромберга. Гауссовы квадратуры 36&
Заключение 370
ГЛАВА 7. ЭЛЕКТРОСТАТИЧЕСКИЕ ЛИНЗЫ 372
7.1. Основные свойства и соотношения 372
7.2. Модели электростатических линз 376
7.2.1. Аналитические модели 376
7.2.2. Кусочно-линейная модель 376
7.2.3. Кусочно-квадратичная модель 378
7.2.4. Сплайновая модель 380
7.3. Двухэлектродные иммерсионные линзы 381
7.3.1. Геометрически симметричные линзы 384
7.3.1.1. Линейная модель 384
7.3.1.2. Аналитическая модель 389
7.3.1.3. Двухцилиндровые линзы 394
7.3.1.4. Двухапертурная линза 409
7.3.1.5. Полиномиальные линзы 411
7.3.2. Асимметричные линзы 416
7.3.2.1. Аналитические модели 416
7.3.2.2. Асимметричная двухцилиндровая лииэа 418
7.3.2.3. Гибридная линза 419
7.4. Однопотенциальиые линзы 421
7.4.1. Симметричные линзы 424
7.4.1.1. Кусочно-линейная модель 425
7.4.1.2. Кусочно-квадратичная модель 430
7.4.1.3. Аналитическая модель 430
7.4.1.4. Трехцилиндровая линза 435
7.4.1.5. Трехапертурная линза 442
636
Оглавление
7.4.1.6. Другие типы симметричных линз 442
7.4.2. Асимметричные линзы 444
7.5. Трехэлектродные иммерсионные линзы 447
7.5.1. Геометрически симметричные линзы 448
7.5.1.1. Трехцилиндровые линзы 448
7.5.1.2. Другие типы геометрически симметричных линз 455
7.5.2. Асимметричные линзы 455
7.6. Многоэлектродные линзы 456
7.6.1. Четырехэлектродные линзы 457
7.6.2. Линзы с пятью и более электродами 460
7.6.3. Сплайновые линзы 460
7.7. Сравнение электростатических линз разных типов 461
7.8. Линзы, погруженные в поле 463
7.8.1. Экспоненциальная модель 463
7.8.2. Диафрагма с круглым отверстием 465
7.8.3. Катодные линзы, электронные и ионные источники 466
7.8.3.1. Термоионные пушки 470
7.8.3.2. Пушки с полевой эмиссией 471
7.8.3.3. Ионные источники 472
Заключение 473
ГЛАВА 8. МАГНИТНЫЕ ЛИНЗЫ
8.1. Общие свойства и соотношения 474
8.2. Длинные линзы 476
8.2.1. Однородные магнитные поля 477
8.2.2. Линейные магнитные поля 477
8.2.3. Длинные линзы с малой сферической аберрацией 481
8.3. Модели магнитных линз 481
8.3.1. Прямоугольная модель 481
8.3.2. Модель со ступенчатой функцией 482
8.3.3. Кусочно-линейная модель 482
8.3.4. Сплайновая модель 483
8.3.5. Колоколообразная модель Глазера 483
8.3.5.1. Обобщение колоколообразной модели 493
8.3.6. Модель Гриве — Ленца 493
8.3.7. Другие модели 495
8.4. Короткие линзы 496
8.4.1. Традиционные линзы 496
8.4.2. Нетрадиционные лиизы 503
8.4.2.1. Сверхпроводящие линзы 503
8.4.2.2. Уменьшение размера катушек другими способами 504
8.4.2.3. Магнитные линзы без поворота изображения 504
8.4.2.4. Магнитные линзы, не содержащие железных частей 505
8.4.2.5. Однополюсные линзы 505
Заключение 506
ГЛАВА 9. ОПТИМИЗАЦИЯ И СИНТЕЗ ЭЛЕКТРОННЫХ И ИОННЫХ
ЛИНЗ С ПОМОЩЬЮ КОМПЬЮТЕРА 507
9.1. Возможно ли устранение аберраций в электронной и ионной оп-
оптике? 507
9.1.1. Нижний предел осевой хроматической аберрации магнитных линз 510
9.2. Оптимизация: синтез против анализа 511
9.3. Первые попытки синтеза 513
9.4. Вариационное исчисление 514
9.4.1. Нижние пределы коэффициентов сферической и осевой хроматиче-
хроматической аберраций 517
637-
Оглавление
9.5. Динамическое программирование 520
9.6. Метод оптимального контроля 528
9.7. Аналитические функции 530
9.8. Реконструкция электронов и полюсных наконечников по опт
роваиному осевому распределению поля 532
9.9. Полиномиальные и сплайновые линзы 538
9.9.1. Полиномиальные линзы 538
9.9.2. Сплайновые лиизы 539
9.9.2.1. Двухинтервальиые сплайновые линзы 542
9.10. Процедура синтеза 546
9.10.1. Приложение: нестандартные электростатические линзы 551
5.11. Методы искусственного интеллекта 554
Заключение 555
ТЛАВА 10. МУЛЬТИПОЛЬНЫЕ ЛИНЗЫ 556
10.1. Поля мультипольных линз 557
10.2. Уравнения параксиальных лучей 560
10.3. Формирование изображения параксиальными лучами 563
10.4. Системы квадруполей 564
10.4.1. Матрицы преобразований 565
10.4.2. Представление с помощью тонких линз 566
10.4.3. Дублеты 569
10.4.4. Триплеты 572
10.4.5. Мультиплеты 573
10.4.5.1. Согласование пучка 573
10.5. Аберрации мультипольных линз 575
10.5.1. Геометрические аберрации 575
10.5.2. Коррекция аберраций с помощью мультиполей 576
10.5.3. Хроматическая аберрация 577
10.5.3.1. Ахроматические квадрупольиые лиизы 577
Заключение 579
ГЛАВА П. ОТКЛОНЕНИЕ ПУЧКОВ 580
11.1. Отклонение для сканирования 580
11.1.1. Электростатические отклоняющие поля 581
11.1.2. Магнитные отклоняющие поля 583
11.1.3. Стигматическая фокусировка при малых отклонениях 584
11.1.4. Аберрации отклонения 587
11.2. Электростатические и магнитные призмы 591
11.2.1. Электростатические призмы 591
11.2.2. Магнитные призмы 594
11.3. Новые виды симметрии — новые возможности 596
Заключение 598
ГЛАВА 12. ПУЧКИ ВЫСОКОЙ ИНТЕНСИВНОСТИ 599
12.1. Оптика пространственного заряда 599
12.1.1. Силы пространственного заряда 602
12.1.1.1. Электростатические силы 602
12.1.1.2. Магнитные силы 605
12.1.2. Расширение пучка 605
12.1.3. Получение пучков высокой интенсивности 609
12.1.3.1. Поток пространственного заряда 609
12.1.3.2. Пушка Пирса 611
•12.1.4. Поддержание пучков высокой интенсивности 613
12.1.4.1. Фокусировка однородными магнитными полями 614
€38
Оглавление
12.1.4.2. Периодическая фокусирс
12.2. Эффект Боэрша 618
Заключение 619
Литература 620
Предметный указатель 631
Научное издание
Миклош Силадьи
Электронная и ионная оптика
Заведующий редакцией А. Н. Матвеев
Зам. зав. редакцией С. М. Жебровский
Ст. научный редактор М. Я. Рутковская
Художник А. Я. Коршунов
Художественный редактор В. И. Шаповалов
Технический редактор Л. П. Бирюкова
Корректор С. А. Денисова
ИБ № 7365
Сдано в набор 23.07.90. Подписано к печати 5.11.90. Формат 60Х90'А». Бумага кн.-жур-
кн.-журнальная. Печать высокая. Гарнитура Литературная. Объем 20 бум. л. Усл. печ. л. 40
Усл. кр.-отт. 40. Уч.-изд. л. 41. Изд. № 8/7666. Тираж 3400 экз. Зак. 433. Цена 4 р.
Издательство «Мир» В/О «Совэкспорткнига» Государственного комитета СССР по печати.
129820, ГСП, Москва, И-И0, 1-й Рижский пер., 2.
Московская типография № 11 Государственного комитета СССР по печати.
113105, Москва, Нагатинская ул., д. 1.