Текст
С. И.Березин
ТЕХНИКА ЭЛЕМЕНТАРНЫХ ВЫЧИСЛЕНИЙ
С. И. Березин
ТЕХНИКА ЭЛЕМЕНТАРНЫХ ВЫЧИСЛЕНИЙ
КРАТКОЕ ПРАКТИЧЕСКОЕ ПОСОБИЕ ДЛЯ САМООБУЧЕНИЯ
Издание второе, дополненное и переработанное
ЛЕНИНГРАД «МАШИНОСТРОЕНИЕ» ЛЕНИНГРАДСКОЕ ОТДЕЛЕНИЕ 1974
Б 48
БерезинС. И. Техника элементарных вычислений. Изд. 2-е, доп. и переработан. Л., «Машиностроение» (Ленингр. отд-ние), 1974. 136 с.
Книга дает краткие сведения о приближенных и сокращенных вычислениях, учит пользоваться конторскими счетами, вычислительными таблицами, логарифмической линейкой, ручными, полуавтоматическими и автоматическими вычислительными машинами (арифмометр «Феликс», вычислительные машины ВК-1, ВК-2, ВК-3).
Во 2-е издание книги (1-е изд. 1967 г.) дополнительно включены таблицы вычислений с дробными степенями, описание 11-шкальной логарифмической линейки, дисковых логарифмических линеек «Спутник». Введена новая глава, в которой приведено описание вычислительных машин ВК-1, ВК-2 и ВК-3 и методы работы на них.
Книга рассчитана на широкий круг читателей, пользующихся таблицами, простейшими счетными приборами и вычислительными машинами. Она может быть полезна студентам вузов, учащимся техникумов и средних школ.
Табл. 12. Ил. 28. Список.лит. 23 назв. -----------------
I I Г X J '
Рецензент канд. физ.-матем. наук В. Ф. Жевержеев
Редактор Т. А. Шамшина
Б
3314—313
038(01)—74
313—74
© Издательство «Машиностроение», 1974 г.
ПРЕДИСЛОВИЕ
В Постановлении ЦК КПСС «Об улучшении экономического образования трудящихся», опубликованном вгазете «Правда» 16/IX 1971 г., подчеркивается, что «на современном этапе коммунистического строительства ... неуклонно возрастают требования к экономическому образованию кадров, широких масс трудящихся», поэтому министерства и ведомства, партийные организации и руководители предприятий, объединений, совхозов и колхозов должны «принять меры к коренному улучшению экономического образования кадров, инженеров, техников, специалистов всех отраслей народного хозяйства, широких масс рабочих и колхозников».
Техника элементарных вычислений является той азбукой, из которой складывается понятие «экономическое образование». Отсутствие счетных навыков серьезно затруднит овладение вопросами экономики.
В самом деле, для того чтобы сделать какой-либо экономический расчет, проанализировать итоги хозяйственной деятельности цеха, бригады или звена, колхоза или совхоза, надо произвести целый ряд элементарных подсчетов, а планируя, составить несколько вариантов плана, чтобы затем выбрать оптимальный, наиболее экономически целесообразный, рентабельный
Предлагаемая книга представляет собой практическое руководство для самообучения, позволяющее читателю, имеющему образование в объеме 7—10 классов средней школы, самостоятельно, без посторонней помощи овладеть простейшими вычислительными навыками, научиться пользоваться конторскими счетами, таблицами, логарифмической линейкой, арифмометром и другими простейшими вычислительными машинами. С учетом этого пособие написано кратко, без лишних подробностей и сразу же ведет читателя к цели, показывая, как надо считать на счетах, логарифмической линейке, как пользоваться таблицами, учит работе на арифмометре и т. д. Наличие упражнений в каждой главе должно способствовать закреплению вычислительных навыков. * 1
Приводимая в конце книги литература позволит читателю в случае необходимости более глубоко и основательно познакомиться с теми или иными разделами техники вычислений.
Автор
1*
Глава I
ПРИЕМЫ СОКРАЩЕННЫХ ВЫЧИСЛЕНИЙ
В настоящей главе будут рассмотрены некоторые простейшие приемы, позволяющие в ряде случаев произвести действия сложения, вычитания, умножения и деления наиболее рациональным способом.
При этом следует помнить, что быстрота и точность вычислений при любой технике счета во многом зависят от того, насколько тщательно ведется оформление вычислительных работ на бумаге. Записывать числа следует четко, ясно. Все вычисления необходимо контролировать.
1. СЛОЖЕНИЕ
Способ последовательного поразрядного сложения. Применим способ поразрядного сложения для двузначных чисел.
Пример 1. Сложить двузначные числа: ,
32 , 28
16
123
Поразрядное сложение производится так!
32+ 8 = 40;
40+20= 60;
60+ 7 = 67;
67 + 40=107;
107+ 6=113;
113+10=123.
Таким образом, к первому слагаемому прибавляется второе слагаемое поразрядно: сначала 8 единиц 1-го разряда, затем 2 единицы 2-го разряда, т. е. 20. К полученной сумме аналогично прибавляется третье слагаемое и т. д.
Результаты промежуточных вычислений
32; 40; 60; 67; 107; 113; 123
можно запомнить либо записать на бумаге.
4
Сложение поразрядным способом можно применить и к трех-значным числам.
Пример 2. Сложить трехзначные числа:
428 +344
579
1351
К первому слагаемому прибавляется второе слагаемое поразрядно: сначала 4 единицы 1-го разряда, затем 4 единицы 2-го разряда, т. е. 40, далее 3 единицы 3-го разряда, т. е. 300. К полученной сумме аналогично прибавляется третье слагаемое. Результаты промежуточных вычислений таковы:
428; 432; 472; 772; 781; 851; 1351.
Сложение поразрядным способом можно производить и несколько иначе: сначала складывать все высшие разряды, затем следующие низшие и т. д.
В примере 1 складываем сначала 2-е разряды:
30 + 20--= 50;
50 + 40= 90;
90+ 10= 100.
Затем складываем 1-е разряды:
2 + 8=10; '
10 + 7 = 17;
17 + 6 = 23.
Далее складываем: 100 + 23 — 123.
Точно так же производится сложение в примере 2. Сначала складываем 3-и разряды:
400 + 300= 700;
700 + 500= 1200.
Затем складываем 2-е разряды:
20 + 40= 60;
60 + 70= 130.
Далее складываем 1-е разряды: 8+4+9—21. Итого 1200 + + 130+ 21 = 1351.
Упражнение. Выполнить сложение в уме двумя способами.
Результаты сверить:
1) 68 2) 74 3) 18 4) 81 5) 96
43 46 31 39 17
,57 +37 ,78 + 15 +83
+36 40 *86 77 44
72 58 33 24 78
12 48
5
Сложение методом столбцов. Требуется найти сумму следующих чисел:
64285 .12843 +17644
28679
21
23
22
21
10
123451
10
21
22
23
_____21
123451
находят сумму цифр каждого
При этом способе сложения столбца, начиная с последнего, и записывают ее отдельно. Причем каждая сумма, начиная со второй, записывается левее на один разряд по сравнению с предыдущей. Затем результаты суммируются поразрядно.
В качестве контроля рекомендуется проделать вычисления в обратном порядке, начиная с нахождения суммы цифр первого столбца и кончая последним. Результаты должны совпадать.
Упражнение. Сложить числа методом столбцов в прямом и об-
ратном порядке:
1) 52008 2) 127815 3) 66443 4) 462115
13922 24603 7148 83726
.64756 +38374 4-226752 ,13127 +25881 125318
75934 ' + 17005
17266 365616 5756 304241
9983 3859 66312 105706
Способ группировки по десяткам. Складывая несколько слагаемых, можно рационализировать вычисления, применяя так называемый способ группировки, облегчающий вычисления и позволяющий быстрее и точнее получить сумму.
Пример.
2 2 2 2 6“i +i 2"] 2 6 8-4 , 14-3-5-7“ 2-i 0 2 6-j 35 3 1 2 8-2 5~4-
69 3 5 6
Сложение ведем столбцами, начиная с единиц. Однако складываем не подряд 3 + 4 = 7; 7 + 7 = 14 и т. д., а сначала группируем слагаемые по десяткам. В столбце единиц можно сгруппировать цифры 3 и 7, 4 и 6, отмечая десятки, как показано. Производя сложение единиц, рассуждаем так: 1 десяток, второй десяток и 2 + 4=6 единиц, всего 26; 6 пишем, 2 в уме. Складывая-десятки, говорим; 2 + 8 = 10; 5 + 5 = 10; 2 + 1 = 3, в итоге 23, в уме 2, всего 25, 5 пишем, 2 в уме. Складывая сотни, считаем: десятков — 1 (7 + 3);
6
6 плюс 3 будет 9, 9 плюс 2 равняется И, в уме 2, всего получаем 23; 3 пишем, 2 в уме. Складывая столбик тысяч, замечаем, что 6 + 4 = 10 и 2 + 8 = 10, т. е. имеем 2 десятка, 2 + 5 = 7, 2 в уме, получаем 29; 9 пишем, 2 в уме. Складывая десятки Тысяч, получаем 1 + 3=4, в уме 2, всего 6. Таким образом, в итоге получим 69 356.
Упражнение. Сложить следующие числа, используя способ группировки по десяткам:
1) 4872 2) 36 128 3) 11071 4) 7247 5) 16 554
7634 48 816 1935 7853 95 575
+6436' +22 186 +15 165 .3568 ,24 716
3558 54 252 64 019 ^6601 ^53 133
2212 88 954 46 245 4755 16 327
------- 2192 85 652
Способ «круглого числа». Если одно из слагаемых близко к круглому числу, т. е. к числу, оканчивающемуся одним или несколькими нулями, то можно упростить сложение.
Пусть, например, требуется сложить 436 и 98. Второе слагаемое 98 близко к круглому числу 100 (меньше его на 2). Складывая 436 и 100, получаем 536, а отнимая 2, в итоге получаем 534.
Складывая 4867 и 402, сначала подсчитываем сумму 4867 + + 400 = 5267. Разницу 2 между вторым слагаемым и круглым числом (402 — 400 = 2) пока отбрасываем. Складывая 5267 и 2 (ранее отброшенную разницу), получаем 5269.
Если требуется сложить ряд близких" по величине слагаемых (например, при вычислении средней арифметической в статистических расчетах), то в этом случае также можно упростить вычисления.
Пример.
63 + 59 + 57 + 62 + 64 + 58 = 363.
В этом примере все слагаемые близки по величине к круглому числу 60. Представим слагаемые так: 63 = 60 + 3; 59 = 60 — 1; 57 = 60 — 3; 62 = 60 + 2; 64 = 60 + 4; 58 = 60 — 2. Сложим эти числа, оформив вычисления следующим образом:
+3 +2 +4 *
60 + 60 + 60 + 60 + 60 + 60 = 60 Хб + (3 + 2 + 4- 1 — 3 — 2)=!
—1—3 —2
= 360 + 3 = 363.
Упражнение. Сложить числа, применяя способ «круглого? числа: *
1) , 1248 2) ,54988 3) ,856
~г~ 203 312 '198
4) 42 5) 81 6) 74
37 80 68
39 78 71
,43 +83 +69
^40 79 67
41 77 73
38 82 70
44 -
Использование частных итогов. Когда слагаемых много, целесообразно производить сложение в несколько приемов, складывая
7
по четыре-пять чисел, общую сумму. Пример. а затем, суммируя частные итоги, получать 5 618
2 334 + 17 015 6 279' 8 186 39 432 24 147 5 683 +11445 4 919 6 347 52 541 5 556 . 13 702 + 9 865 14 532 43 655 135 628 135 628
Упражнение. Сложить следующие числа, используя частные итоги:
1) 324 547 2) 115 819 3) ' 76 716
147 003 26 556 123 547
28 218 127 331 177 336
46 675 184 584 28 515
+ 171313 21 392 114 649
33 886 +414 125 , 19 931
121 413 88 517 +124 773
72 955 139 426 51 916
4 136 66 529 5 819 146 491 22 774 158 412 317 003
45617
Заключительное упражнение. Решить примеры, применяя сложение методом столбцов и способы группировки по десяткам, круглого числа и использования частных итогов:
1) 72 428 13 681 2) 68 3) 328116 4) 308 5) 272 018
67 64 892 294 114 692
7 512 71 36 526 305 66 756
+48 345 5718 70 +69 104 243 99 584 297 . 299 ,128 824 "г 54 283
12 225 72 +271 938 +302’ 1 213
36 177 66 100 212 300 81 152
74 336 824 306 249 167
73 72 333 296
245 312 156 741 300
До тех пор, пока не сделана проверка вычисления, оно не может считаться законченным. Поэтому не следует забывать о проверке вычислений.
8
Для проверки сложения можно использовать два способа.
1. Сложение слагаемых в каком-либо другом порядке или каким-либо другим методом. Если суммы получатся равные, значит, сложение было произведено правильно.
2. Вычитание из суммы двух слагаемых одного из них. Если полученная разность равняется другому слагаемому, значит, сложение было произведено правильно. Например, складывая два числа, мы получили: 216+ 623 = 839. Вычитая из полученной суммы 839 первое слагаемое 216, получим второе слагаемое 623. Следовательно, сложение было сделано правильно.
2. ВЫЧИТАНИЕ
Вычитание при помощи дополнений. Решим пример: 63—37=26. Прибавляя к вычитаемому 3, получаем 40; одновременно прибавляя 3 к 63, получим 66. В результате: 66 — 40 = 26.
Иногда для получения «круглого» вычитаемого удобнее не прибавлять, а вычитать от уменьшаемого и вычитаемого одно и то же число. Так, если задано 114 — 62, то удобнее считать 112 — 60= 52.
Упражнение. Произвести вычитание при помощи дополнений:
+2 +2 4) 1524 — 627 =
1) 74мг-48 = 26; —3
2) 1426 - 122 = 5) 2286 - 359 = 1927;
3) 843 — 351= 6) 1768-564 =
В примере 1 округляем вычитаемое до 50, прибавив 2 единицы; одновременно увеличиваем на столько же единиц и уменьшаемое.
В примере 5 уменьшаем вычитаемое на 3 единицы и, произведя вычитание 2286 — 356, от полученной разности отнимаем еще 3 единицы.
Вычитание посредством сложения. При этом способе находим разность как слагаемое, для чего рассматриваем уменьшаемое как сумму, а вычитаемое — как одно из слагаемых.
Пример.
24 634
~~16 322
8 312
Производя вычитание посредством сложения, рассуждаем так: сколько надо прибавить единиц к 2 единицам вычитаемого, чтобы получить 4 единицы в уменьшаемом? Надо прибавить 2 единицы; эту цифру пишем в разность. Сколько надо прибавить к 2 десяткам, чтобы получить 3? Надо прибавить 1 десяток. Сколько надо прибавить к 3 сотням, чтобы получить 6? Очевидно, 3. Сколько надо прибавить к 16, чтобы получить 24? Надо прибавить 8. Разность 8312.
Чтобы убедиться в правильности вычитания, сложим вычитаемое и разность, которые в сумме должны дать уменьшаемое: 16 322 + + 8312 = 24 634.
Проверка показала, что вычитание произведено правильно, •так как сумма равна уменьшаемому.
Упражнение. Произвести вычитание посредством сложения:
1) 15 472 2) 38 958 3) 87 596 4) 49 914 5) 88 774
"12 321 "17 115 "43 321 "27 103 _ "62 491
9
Совместное сложение и вычитание. В том случае, когда некоторые числа должны быть сложены, а другие вычтены, решение задачи можно вести двояко:
' а) сначала сложить все числа, которые должны быть суммированы, а затем сложить числа, которые должны быть вычтены, и после этого вторую сумму вычесть из первой;
б) последовательно складывать и вычитать числа, стоящие в каждом столбце.
Следующий пример решен и тем и другим способом:
а) +28 678 б) +28 678
+ 11 244 +11 244
— 5 668 — 5 668
+ 14817 +14817
—21 996 —21 996
+54 739 27 075
—27 664
27 075
Для проверки вычитания можно использовать два способа.
1) Сложение. При этом уменьшаемое является суммой, а вычитаемое и разность — слагаемыми. Если вычитание сделано правильно, то, складывая вычитаемое и разность, получим уменьшаемое.
Пример Проверка
8536 ,3215
• - ~3215 '5321
5321 8536
Результат сложения равен уменьшаемому. Следовательно, вычитание произведено верно.
2) Вычитание. В этом случае, отнимая от уменьшаемого разность, мы должны получить вычитаемое.
Пример Проверка
6846 6846
"2323 "4523
4523 2323
Вычитая из уменьшаемого разность, мы получили вычитаемое. Значит, вычитание произведено верно.
3. УМНОЖЕНИЕ
При умножении многозначного числа на однозначный множитель умножение производим справа налево по обычному правилу, например 3254 X 6 — 19524.
Ниже рассматривается умножение многозначных чисел.
Выбор множителя. Перемножая два многозначных числа, множителем чаще всего берут то число, у которого меньше цифр. Например, при перемножении 84 на 1235 множителем следует взять 84:
4940
9880
103740
10
Однако в некоторых случаях возможны отступления от этого правила. Например, легче умножить 856 на 3163, чем, наоборот, 3163 на 856:
856 х3163
2568
, 5136
+ 856
2568
2707528
В числе 3163 цифра 3 повторяется дважды, кроме того, 6 кратно 3. Эти специфические особенности облегчают умножение.
Разбиение множителя на слагаемые. Иногда бывает полезно разбить множитель на несколько слагаемых, каждое из которых в два, три, четыре раза больше другого.
Пример. Пусть требуется умножить
488 X 155 (155 = 100 + 50 + 5).
Получаем:
488X 100 = 48 800
488 X 50 = 24 400 от предыдущего результата
488 X 5= 2 440 от предыдущего результата
75 640
Примеры:
1) 986 X 55 = 54 230 (55 = 50 + 5)^
2) 624 X 175 = 109 200 (175 = 100 + 50 + 25 или 200 — 25); 3) 6836 X 165 = 1 127 940 (165 = 100 + 50 + 10 + 5).
Умножение на 5; 50; 500; 0,05; 0,005. Так как 5 = ^, то для того чтобы умножить число на 5, можно сначала умножить его на 10, а затем разделить на 2.
Примеры.
1) 446x5 = -^- = 2230;
2) 268 X 5 =-^2-= 1340;
3) 5267 x 5 = -2^2. = 26 335.
Для того чтобы умножить число на 50 или 500, достаточно умножить его на 100 или 1000 соответственно, а затем разделить на 2. При умножении числа на 0,5 достаточно разделить его на 2. Для того чтобы умножить число на 0,05 или 0,005, достаточно уменьшить число в 10 или 100 раз, а затем разделить на 2.
11
Примеры.
1) 638х50=-^~ = 31 900;
2) 4672 X 500 = —-72 000 = 2 336 000;
3) 840x0,5 =^2- = 420;
4) 694X0,05 = J^1 = 34,7;
4? 46
5) 4246 х 0,005 = -^^- = 21,23.
Умножение на 25; 250; 0,25; 0,025. Так как 25 = то для 4
того чтобы умножить число на 25, можно сначала умножить его на 100, а затем разделить на 4.
Например:
88X25 = =2200.
4
Так как 250 = -^99.9- >т0 для того чтобы умножить число на 250, можно сначала умножить его на 1000, а затем разделить на 4. Например:
84 X 250=^^ = 21 000.
4
Так как 0,25 = то для того чтобы умножить число на 0,25, можно разделить его на 4. Например:
284
284 X 0,25 = ——- = 71.
Для того чтобы умножить число на 0,025, достаточно уменьшить его в 10 раз, а затем разделить на 4. Например:
8472 X 0,025 = =211,8.
4
Умножение двузначных чисел, у которых сумма единиц 1-го разряда равна 10, а число единиц 2-го разряда одинаково. Рассмотрим пример: 63 X 67 = 4221.
У данных сомножителей число десятков одинаково (6), а сумма единиц 1-го разряда 3 + 7 = 10. Результатом умножения является четырехзначное число, две последние цифры которого (21) получаются умножением 3 X 7 = 21. Две первые цифры результата получаются умножением числа десятков 6 на число, увеличенное по сравнению с числом десятков на единицу, т. е. на число 6 + 1 = 7: 6 X 7 = 42.
Вышеприведенное правило легко доказать алгебраически.
Пусть число десятков обоих сомножителей а\ число единиц первого сомножителя Ь} число единиц второго сомножителя с 12
(b + с = 10). Тогда первый сомножитель равен 10а + Ъ, второй равен 10а + с, а произведение примет вид (10а + Ь) (10а 4- с) ~ = 100а2 + Юас + lOab + Ьс = 100а2 + 10а (Ь + с) + Ьс = 100а2 + 4- 100а 4~ Ьс = 100а (а + 1) + Ьс.
Примеры.
1) 88 X 82 = 7216; 3) 14 X 16 = 224;
2) 76 X 74 = 5624; 4) 61 X 69 = 4209.
В примере 4 при перемножении единиц 1-го разряда сомножителей получается 1 X 9=9 — однозначное число. В этом случае в качестве двух последних цифр результата следует взять 09.
Умножение двузначных чисел, у которых число единиц 1-го разряда одинаково, а сумма десятков перемножаемых чисел равна 10. Решим пример: 87 X 27 = 2349.
У данных сомножителей число единиц 1-го разряда одинаково (7), а сумма десятков 8 4" 2 = 10. Результатом умножения явдяется четырехзначное число, две последние цифры которого получаются умножением 7 X 7 = 49. Две первые цифры результата получаются перемножением числа десятков сомножителей 8 X 2 = 16 и прибавлением к этому результату числа единиц одного из сомножителей, т. е. 16 4- 7 = 23.
Вышеприведенное правило легко доказать алгебраически.
Пусть число десятков первого сомножителя а, число десятков второго сомножителя b (а 4“ b = 10); число единиц первого и второго сомножителя с. Тогда первый сомножитель равен 10а 4“ с, второй равен 10b + с, а произведение примет вид (10а 4“ с) (10b 4-4- с) = ЮОаЬ 4- Юас + ЮЬс 4“ с2 = ЮОаЬ + Юс (а 4- Ь) + с2 = = ЮОаЬ 4- Ю0с + с2 = 100 (аЬ + с) 4- с\
Примеры.
1) 38 X 78 = 2964; 3) 65 X 45 = 2925;
2) 66 X 46 = 3036; 4) 82 X 22 = 1804.
Умножение с использованием формулы (а -{-b)(a — b)=z a2—b2. Используя формулу сокращенного умножения, можно ускорить перемножение двух чисел, если один сомножитель на несколько единиц меньше какого-то числа, а другой — на столько же единиц больше этого числа.
Пример. .
97 X 103 = 9991.
В данном примере 97 = 100 — 3, а 103 = 100 4" 3. Используя вышеприведенную формулу, можем записать:
(ЮО — 3) (100 4- 3) = ЮО2 — З2 = 10 000 — 9 = 9991.
Упражнение. Решить примеры с использованием формулы сокращенного умножения:
1) 12 X 18 = (15 — 3) (15 4- 3) = 225 — 9 = 216;
2) 95 X 105 = 9975;
3) 193 X 207 = 39951;
4) 9,8 X 10,2 = 99,96.
Умножение числа на 15. Чтобы умножить число на 15, можно увеличить его в 10 раз, затем прибавить к полученному числу его половину.
13
Примеры.
264 X 15 = 2640 + 1320 = 3960;
360 X 15 - 5400;
642 X 15 = 9630.
Для проверки умножения могут быть использованы два способа. 1. Умножение. Следует переставить сомножители и повторно их перемножить.
Пример Проверка 24!5 1341
х 1341 х2415
2415 6705
. 9660 ,1341 к
7245 ~*~5364
2415 2682
3238 515 3238 515
В обоих случаях получены одинаковые произведения. Следовательно, действие произведено правильно.
2. Деление. Один из сомножителей должен равняться произведению, деленному на другой сомножитель
Пример Проверка 975 14 300 _
X с! 9 ---------
_____275
? 14300
4. ДЕЛЕНИЕ
Иногда, в процессе вычислений, возникает необходимость, не производя действия деления, определить, делится ли одно число на другое без остатка, «нацело». При ответе на этот вопрос удобно пользоваться признаками делимости чисел. Напомним их.
Число делится на:
2 — если оно четное, причем нуль считается четной цифрой (например, числа 14 578 и 2140-делятся на 2, так как 8 и 0 — четные числа);
3 — если сумма цифр его делится на 3 (например, число 6339 делится на 3, так как сумма цифр егоб+3+3+9=21 делится на 3);
4 — если оно оканчивается двумя нулями или если число, образованное двумя его последними цифрами, делится на 4 (например, числа 6228 и 600 делятся на 4);
5 — если его последняя цифра 5 или оно оканчивается нулем (например, числа 2475 и 3560 делятся на 5);
6 — если оно четное и сумма его цифр делится на 3 (например, число 6432 делится на 6, так как оно четное и сумма его цифр 6 + 4 + + 3 + 2 = 15 делится на 3);
8 — если оно оканчивается тремя нулями или если число, образованное тремя его последними цифрами, делится на 8 (например,-числа 14 392, 36 400, 15 000 делятся на 8);
14
9 — если сумма его цифр делится на 9 (например, число 385 497 делится на 9, так как сумма его цифр 3+8+5+4+9+7=36 делится на 9);
10 — если оно оканчивается нулем (например, число 4820 делится на 10);
25 — если оно оканчивается двумя нулями или если число, образованное двумя его последними цифрами, делится на 25 (например, числа 8525, 1350, 12 100 делятся на 25);
125 — если оно оканчивается тремя нулями или если число, образованное тремя его последними цифрами, делится на 125 (например, числа 2375, 54 000 делятся на 125).
Деление на 5; 50; 500; 0,5; 0,05; 0,005. Так как 5 ~у, то
для того чтобы разделить число на 5, достаточно сначала умножить его на 2, а затем разделить на 10.
Примеры:
1) 234:5=^Ц^-=-^ = 46,8;
2) 832: 5=-8-32—-2- = = 166,4}
3) 23,102:5 = 23-’-^2 Х-2 = 46’2J-4-=4,6204.
Так как 50 = то для того чтобы разделить число на 50, достаточно сначала умножить его на 2, а затем разделить на 100. и 00/1 кл 234x2 468 .
Например, 234:50 = —^—=—=4,68.
Так как 500 = 1 то для того чтобы разделить число на 500,
достаточно сначала умножить его на 2, а затем разделить на 1000. и i-,ior> каа 1432X2 2864 о .
Например, 1432:500 = -w- = —= 2,864.
Чтобы разделить число на 0,5, достаточно умножить его на 2, а при делении на 0,05 или 0,005 после умножения числа на 2 следует увеличить число в первом случае в 10 раз, во втором случае — в 100 раз.
Примеры.
1) 8332 : 0,5 = 16 664;
2) 324 : 0,05 = 324 X 2 X 10 = 6480; .
3) 324 : 0,005 = 324 X 2 X 100 = 64 800.
Деление на 25; 250; 2,5; 0,25; 0,025; 0,0025. Так как 25 = ^р, то для того чтобы разделить число на 25, достаточно умножить его 1242 X 4 на 4, а затем разделить на 100. Например: '1242:25 =-— =
= —4968
100
15
Так как 250 = —-—} то для того чтобы разделить число на
250, достаточно умножить его на 4, а затем разделить на 1000. На-1940 у 4 4°68
1Ж:250—1ИГ-ТЙ»-4'И8-
Так как 2,5 = то для того чтобы разделить число на 2,5, достаточно умножить его на 4, а затем разделить на 10. Например, lte:,5__S£x±_4«_„,8.
Так как 0,25= то для того чтобы разделить число на 0,25, достаточно умножить его на 4.
При делении на 0,025 или 0,0025 после умножения числа на 4 увеличиваем. число в первом случае в 10 раз, во втором случае — в 100 раз.
Примеры.
1) 212 : 0,025 = 212 X 4 X 10 = 8480;
2) 212 : 0,0025 = 212 X 4 X 100 = 84 800;
3) 212 : 0,25= 212 X 4 = 848.
Деление чисел на 15. Рассмотрим следующие тождественные преобразования:
а 2а ( а\ 1Л Тб-зН^з?10-
Таким образом, для того чтобы разделить число на 15, достаточно отнять от числа одну его треть, а затем результат разделить на 10.
Например, 369 : 15 = (369 — 123) : 10 = 246 : 10 = 24,6.
Рассуждаем так: отнимаем одну треть от 3 (1) — остается 2; одну треть от 6 (2) — остается 4; одну треть от 9 (3) — остается 6. Получается 246. Это число делим на 10. Окончательно получаем 24,6.
Примеры.
1) 966 : 15 = 64,4; 3) 6945 : 15 = 463,0;
2) 6339 : 15 = 422,6; 4) 72 969 : 1,5 = 48 646;
5) 816 483 : 1,5 = 544 322.
В примере 3 от 6 отнимаем 2, от 9 — 3, от 45 — 15; остается 30. Полученную разность делим на 10. Окончательно получаем 463,0. В примере 5 от 81 отнимаем одну треть (27), от 6 — 2, от 48 — 16, от 3 — 1. Полученную разность на 10 не делим.
Для проверки правильности деления могут быть использованы следующие два способа.
1. Проверка деления умножением. Деление выполнено верно, если делимое есть произведение делителя на частное.
Пример Проверка
2352 : 28 = 84 84 X 28 = 2352
2. Проверка деления делением. Деление выполнено верно, если при делении делимого на частное получается делитель;
Пример Проверка
4956 : 42 = 118 4956 : 118 = 42
Глава II
ПРИБЛИЖЕННЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ
5. ТОЧНЫЕ И ПРИБЛИЖЕННЫЕ ЧИСЛА
В практической деятельности людей огромную роль играют всевозможные вычисления как с точными, так и особенно с приближенными числами.
Приближенным числом называется число, незначительно отличающееся от точного и заменяющее последнее в вычислениях. Приближенные числа появляются в результате, например,, измерений, взвешиваний, т. е. в результате обработки каких-то опытных данных. Арифметические действия с приближенными числами следует производить тоже приближенно, ограничиваясь той степенью точности, которая необходима в данной задаче. В практике вычислений установлено, что один лишний знак в числах в процессе умножения и деления на настольных малыхвычислительных машинах снижает производительность труда до 30%.
Выдающийся кораблестроитель и математик акад. А. Н. Крылов говорил, что «при производстве всяких численных вычислений надо руководствоваться правилом: точность вычислений должна соответствовать точности данных и той практической потребности, для которой вычисления производятся...».
«У корабельных инженеров, — писал он, — была привычка производить вычисления по весьма неудобным схемам с громадным числом (10—12) значащих цифр, из которых по самой сути дела могли быть верные лишь первые три, а все остальные были неверны и вместе с тем для практики не нужны».
А. Н. Крылов отмечал, что в прежнее время в проектах по кора- -блестроению до 9/10, а иногда до 34/35 вычислительной работы затрачивалось попусту на выписывание и исчисление лишних знаков. Со свойственной ему энергией и настойчивостью он внедрял культуру приближенных вычислений, прибегая в отдельных случаях даже к административным методам воздействия. Так, по его представле-' нию был уволен с работы главный корабельный инженер Севастопольского порта, не выполнивший указаний относительно техники вычислений. А. Н. Крылову принадлежат слова: «Помните, что каждая неверная цифра — это ошибка, всякая лишняя цифра — это пол-ошибки».
6. АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТИ ВЫЧИСЛЕНИЙ
Если мы захотим сосчитать число книг в своей библиотеке, то сможем сделать это точно, получив в результате подсчета, скажем, 143 названия. Другое дело, когда мы попытаемся измерить расстояние от дома до места работы. Измеряя это расстояние, например,-с помощью рулетки, мы при первом измерении можем получить, допустим, 459 м, при втором — 446 м, при третьем — 443 м, при четвертом — 452 м. Изучив результаты измерений, мы замечаем, что число сотен у всех чисел одинаково (4). Таким образом, число'4 у нас не вызывает сомнения. Числа десятков у вышеприведенных чисел не всегда совпадают, они сомнительны, а числа единиц все различны, следовательно, они неверны.
Таким образом, можно сделать вывод, что наши измерения дали лишь приближенное значение измеряемой величины. Чтобы определить более точно расстояние, найдем среднее арифметическое ре-459+446+443+452 1800
зультатов измерении: ----------— = 450 м.
Считая среднее арифметическое результатов измерений наиболее точным приближением к измеряемой величине, мы можем определить отклонения от него результатов отдельных измерений. Первое измерение больше среднего на 9 м (459—450), второе — меньше среднего на 4 м (450 — 446), третье — меньше среднего на 7 м (450 — 443) и, наконец, четвертое — больше среднего на 2 м (452 — 450).
Разность между истинным и приближенным значением какой-либо величины, взятая по абсолютной величине, называется абсолютной погрешностью. Она выражается именованным числом, в тех же единицах, какими произведено измерение (в нашем примере — в метрах).
Относительная погрешность — это отношение абсолютной погрешности к точному значению измеряемой величины. Относительная погрешность есть отвлеченное число. Иногда его умножают на 100 и тем самым выражают в процентах.
Для наглядности определение относительной погрешности сведем в таблицу:
№ измерения Результат измерения в м Среднее арифметическое результата измерения в м Абсолютная погрешность в м Относительная погрешность Относительная погрешность в %
1 459 450 9 9 450 = 0,0200 9x100 450 = 2,0
2 446 450 4 4 450 = 0,0089 4X100 450 = 0,9
3 443 450 7 7 450 = 0,0156 7x100 450 = 1,6
4 452 , 450 2 2 450 = 0,0045 2X100 450 = 0,5
18
Естественно считать, что чем меньше относительная погрешность, тем больше точность измерения. В нашем примере первое измерение, 459 м, имеющее процентную погрешность 2,0%, — самое неточное, а последнее, четвертое, 452 м, имеющее процентную погрешность лишь 0,5%, является наиболее точным.
Большое практическое значение имеет удобная запись приближенного числа. Для того чтобы по самому написанию числа судить о степени точности его, приняли за правило писать число так, чтобы все значащие цифры в нем, кроме последней, были верны, и только последняя цифра может быть сомнительной, но не более как на одну единицу. Например, если некоторая величина измеряется приближенным числом 3,48-106, то цифра 8 является сомнительной, но не более как на одну единицу.
7. ПРАВИЛО ОКРУГЛЕНИЯ ЧИСЕЛ
Округление по недостатку и избытку. В процессе вычислений мы встречаемся с многозначными числами — точными и приближенными. Иногда возникает необходимость округлить их, т. е. отбросить одну или несколько последних цифр.
Из начального курса арифметики известно, что если первая из отбрасываемых при округлении цифр равна 5 или более 5, то последнюю из оставляемых цифр увеличивают на одну единицу или, как говорят, «усиливают» ее. Если же первая отбрасываемая цифра менее 5, то последняя оставляемая цифра не меняется.
В зависимости от того, оставлена последняя цифра без изменения или увеличена, считают, что округление сделано по недостатку или по избытку. Числа можно округлять до целых, десятых, сотых, тысячных и т. д. долей; до десятков, сотен, тысяч и т. д. Например, территория СССР равна 22 402 200 км2 или приближенно 2,24-107 км2.
О приближенном числе, например 158,7, обычно говорят, что оно взято с точностью до 0,1 (одной десятой), либо с одним десятичным знаком, либо с погрешностью, не превышающей 0,1, т. е. погрешность числа меньше одной десятой.
Округляя число 0,682475 до тысячных, получим 0,682, до сотых — 0,68, до десятых — 0,7. В первом и во втором случаях округление сделано по недостатку, так как мы отбросили цифры менее 5, не увеличивая последней оставляемой цифры'. При округлении до десятых долей вместо 0,68 мы взяли 0,7, «усилив» цифру 6 на 1, т. е. сделали округление по избытку, так как отбрасываемая цифра 8 больше 5.
Рассмотрим ряд примеров последовательного округления некоторых постоянных с точностью до 0,01 (одной сотой):
л ^3,1415927;
л ^3,141593;
л ^3,14159;
л ^3,1416;
л ^3,142;
л 3,14;
/2=^1,4142136; /2=^1,414214; /2=%= 1,41421; /2^1,4142;
/2=^1,414;
/2«=1,415
/855Г=» 92,514864;
/8559"=® 92,51486;
/8559^ 92,5149;
/8559 ^92,515;
/8559’^92,52.
19
Как видим, во всех случаях округление произведено в соответствии с правилом: если при округлении отбрасываются цифры 0,1, 2, 3, 4, то последняя сохраняемая цифра не изменяется, а если первая из отбрасываемых цифр 5, 6, 7, 8, 9, то последняя сохраняемая цифра усиливается, увеличивается на одну единицу.
Различие понятий «десятичные знаки» и «значащие цифры». Десятичными знаками называются все цифры десятичной дроби, стоящие справа от запятой.' Под значащими .цифрами подразумеваются все цифры числа, кроме нулей, стоящих левее первой отличной от нуля цифры, и нулей, стоящих в конце числа, если они стоят взамен неизвестных или отбрЪшенных цифр. Например, число 392,48 имеет пять значащих цифр и только два десятичных знака. Число 0,0986 имеет три значащие цифры, но четыре десятичных знака. Число 473 916 имеет шесть значащих цифр и не имеет ни одного десятичного знака, так как это число целое. Округляя его до сотен, получим 473 900. В этом случае мы имеем только четыре значащие цифры, а нули, которыми мы заменили отброшенные цифры 1 и 6, в число значащих цифр не входят. Однако, поскольку 1 руб. = 100 коп., число 100 содержит три значащие цифры. Здесь нули поставлены не взамен неизвестных или отброшенных цифр, а показывают отсутствие единиц в некоторых разрядах, в данном случае — десятков и единиц. Действительно, в 1 руб. содержится ровно 100 коп., а разряды единиц и десятков равны нулю.
Для закрепления сказанного рассмотрим несколько примеров:
Число Количество десятичных знаков Количество значащих цифр
0,2 Один Одна
0,02 Два »
0,004 Три »
5,713 » Четыре
1;00009 Пять Шесть
8. СЛОЖЕНИЕ ПРИБЛИЖЕННЫХ ЧИСЕЛ
При сложении приближенных чисел следует помнить, что точность суммы не может быть выше точности слагаемых, входящих в нее. Следует учитывать столько десятичных знаков в написании приближенных чисел, сколько их в приближенном слагаемом с наименьшим'числом десятичных знаков.
Возможны два следующих случая:
1. Числа даны с одинаковой точностью, т. е. все слагаемые имеют одинаковое число десятичных знаков. В этом случае сложение приближенных чисел выполняется как обычно.
Напримеэ:
24,884
,17,163
5,421
11,965
59,433
20
в результате сохраняется столько десятичных знаков, сколько имеется их в каждом из приближенных слагаемых (т. е. три знака), с последующим округлением до заданной точности.
2. Точность слагаемых различна, т. е. они имеют неодинаковое число десятичных знаков.
Например, пусть требуется сложить приближенные числа: 114,8; 3,409; 0,6138; 26,58; 0,0005. Запишем их по обычным правилам столбиком и сложим:
114,8???
3,409?
+ 0,6138
26,58??
0,0005
145,4033 или 145,4
Однако так складывать не следует, потому что три последние цифры суммы (0; 3; 3) будут не точны и нет необходимости их выписывать.
В самом деле, десятитысячные доли имеются лишь в третьем и пятом слагаемых, но их нет в других. Тысячные доли имеются лишь у второго слагаемого и сотые — у четвертого, их нет у первого слагаемого, которое имеет лишь десятые доли. Поэтому следует отбросить у всех слагаемых цифры, стоящие правее десятых (сотые, тысячные и десятитысячные знаки), округлив их до десятых, и записать данные в следующей форме:
114,8
3,4
+ 0,6
26,6 ____0,0 145,4
В результате получили ту же сумму, сократив время на ее вычисление.
Пример 1, При составлении годового баланса по строительному тресту на 1/1 197... г. необходимо подсчитать общую стоимость основных средств, находящихся на строительных участках треста (в тыс. руб-)-
Исходные данные приводятся в следующей таблице:
№ строительного участка Стоимость основных средств по данным бухгалтерского учета в руб., коп. № строительного участка Стоимость основных средств по данным бухгалтерского учета в руб., коп.
1 488 173 — 08 6 821 719—’02
2 . 621 441-22 7 536 983—11
3 375 712-16 8 729 210-18
4 715 804-37 ' 9 1 098 277-01
5 554 067-17 10 695 421 — 42
Подсчитав с точностью до копейки, получаем в итоге 6 636 808р.
74 к., а округляя итог до требуемой точности, т. е. до тысяч, имеем 6637 тыс. руб.
21
Эту же сумму можно получить гораздо быстрее.
Для того чтобы сложить приближенно не более десяти слагаемых с заданной точностью, надо оставить в каждом из них на один знак больше, чем требуется получить в сумме с учетом заданной точности, округляя последнюю цифру каждого слагаемого. Если число слагаемых более десяти, — в каждом из них необходимо оставлять на два знака больше заданной точности.
Исходя из этого правила, мы можем записать наши слагаемые сокращенно в таком виде:
4882
6214
3757
7158
, 5541 + 8217
5370 ,7292 10983 6954
66368
Округляя последнюю щифру суммы до тысяч, мы получаем тот же результат: 6637 тыс. руб.
Пример 2. Определить общую стоимость товарных запасов на складах торга на 1/1 197... г. (в млн. руб.). Исходные данные приведены в следующей таблице:
№ склада Остаток товаров на 1/1 197... г. по данным -бухгалтерского учета в руб., коп. № склада Остаток товаров на 1/1 197.. г. по данным бухгалтерского учета в руб., коп. •
1 1 448 712-64 4 3 945 517-24
2 1 990 379 — 88 5 1 070 213-81
3 872 964-15 6 4 573 414—03
При точном подсчете получаем сумму 13 901 201 р. 75 к., а округляя с учетом заданной точности, — 14 млн. руб.
Поскольку у нас всего шесть слагаемых, то определить требуемую сумму с заданной точностью (до млн. руб.) можно, руководствуясь вышеприведенным правилом, т. е. оставляя на один знак больше заданной точности. В сумме получим:
14 '
20
+39
11 ’ 46
139^14 млн. руб., т. е. тот же результат.
Как видим, приближенное сложение, обеспечивая заданную точность, дает большую экономию времени и труда.
22
9. ВЫЧИТАНИЕ ПРИБЛИЖЕННЫХ ЧИСЕЛ
В процессе вычитания могут встретиться два случая.
1. Уменьшаемое и вычитаемое даны с одинаковой точностью.
Пример 1. Вычислить разность приближенных чисел 246,9876 и 181,3723 с точностью до 0,1.
При обычном вычитании запись выглядела бы так:
246,9876
"181,3723
65,6153
или при округлении с заданной точностью — 65,6.
Можно получить тот же результат быстрее, округлив уменьшаемое и вычитаемое' с точностью до 0,01. Тогда
246,99
"181,37
65,62
или при округлении с точностью до 0,1—65,6.
Пример 2. Вычислить разность чисел 5,88796420 и- 2,37248169 с точностью до 0,01.
Обычное вычитание дает:
5,88796420 "2,37248169
3,51548251
или при округлении с точностью до 0,01—3,52.
Производя вычисление с учетом правила вычитания приближенных чисел, имеем:
5,888 '
"2,372
3,516
или при округлении с заданной точностью до 0,01—3,52.
Как видим, тот же результат получен легче и быстрее.
2. Уменьшаемое и вычитаемое даны с различным числом десятичных знаков.
Пример. Вычислить с точностью до 0,1 разность чисел 8,78 и 2,3124.
Подписав, как обычно, вычитаемое под уменьшаемым и произведя вычитание, получим
8,78??
"2,3124
6,46?? или ^6,5.
Этот же результат может быть получен и в том случае, если мы отбросим тысячные и десятитысячные доли вычитаемого, которых •нет у уменьшаемого, и запишем наш пример так:
8,78
"2,31
6,47 6,5
23
10. УМНОЖЕНИЕ ПРИБЛИЖЕННЫХ ЧИСЕЛ
Прежде всего следует иметь в виду, что при умножении и делении приближенных чисел учитываются не десятичные знаки чисел', как при сложении и вычитании, а их значащие цифры.
Умножение двух приближенных чисел. При умножении двух приближенных чисел, имеющих одинаковое количество значащих цифр, в произведении следуетчсохранить столько значащих цифр, сколько их было в каждом сомножителе; если сомножители имеют неодинаковое число значащих цифр, то в произведении следует сохранить столько значащих цифр, сколько их имеется в сомножителе с наименьшим числом значащих цифр.
Пример 1. Сомножители имеют одинаковое число значащих цифр:
1293
+ 431 862
~ 9,1803 9,18.
Отбрасывая в полученном произведении справа две цифры (0 и 3), оставляем только три верных значащих цифры (9,18) по числу их в каждом сомножителе. Четвертая и пятая цифры сомнительны, и оставлять их в произведении не имеет смысла.
Пример 2. Сомножители имеют неодинаковое число значащих цифр:
.,0,1326
2 3,4
45084 или 0,45.
В соответствии с правилом в полученном произведении оставляем только две значащие цифры, т. е. столько, сколько имеется их в сомножителе с наименьшим числом значащих цифр (3,4).
Умножение на- точное число. В этом случае в приближенном числе оставляем на один десятичный знак больше, чем требуется в ответе, согласно заданной точности, и еще столько десятичных знаков, сколько имеется цифр в целой части точного сомножителя.
Пример. Вычислить произведение 4,8627567 X 16 с точностью до 0,1.
Перемножая как обычно, имеем
4,8627567
х________16
,291765402 +48627567
_ 77,8041072
или, округляя с заданной точностью, — 77,8.
24
На основании вышеприведенного правила запишем исходные данные в таком виде:
4,8628
_____16 . 291768 '48628
77,8048 или с округлением до 0,1—77,8.
Во множимом оставляем пять цифр, округляя по избытку последнюю цифру. Эти пять цифр оставлены из следующего расчета: три цифры (4,86) дает множимое после оставления в нем на один десятичный знак больше, чем требуется в ответе с заданной точностью; две последние (2 и ,8 с округлением) взятые по числу цифр в точном числе (16).
Умножение приближенных чисел с избытком значащих цифр. Если сомножители имеют большое число значащих цифр, превосходящее заданную точность, то в этом случае оставляем в каждом сомножителе на один десятичный знак больше, чем это требуется в ответе и полученное произведение округляем до заданной точности.
Например, требуется умножить 15,83185 на 5,34774 с точностью до 0,1. Округляем каждый сомножитель, оставляя на один, десятичный знак больше, чем это требуется в ответе:
7915 +4749 .
7915
84,6905 или ^84,7
11. ДЕЛЕНИЕ ПРИБЛИЖЕННЫХ ЧИСЕЛ
При делении двух приближенных чисел, имеющих одинаковое число значащих цифр, в частном следует сохранять столько значащих цифр, сколько их имеется в делимом и делителе; если же данные числа имеют неодинаковое число значащих цифр, то в частном следует сохранять столько значащих цифр, сколько их имеется в менее точном числе, причем менее точным считается число, имеющее меньше значащих цифр.
Пример 1. В делимом и делителе одинаковое число значащих цифр:
6612 1 1581
6324 | 4,1821^4,182
2880
1581
_12990
12648
3420
3162
2580
1581
999
25
В частном оставляем четыре значащие цифры, т. е. столько, сколько их имеется в делимом и делителе (по четыре).
Пример 2. Число значащих цифр в делимом и делителе различное:
64,02 I 14
~56 I 4,5 ^4,6
80 ~~~70
10
14
Так как остаток 10 больше то округляем частное и окончательно имеем 4,6.
Поскольку число значащих цифр в делимом и делителе различно (четыре и два), то в соответствии с правилом в частном сохраняем только две значащие цифры по числу их в делителе, который в данном примере имеет наименьшее число значащих цифр. Поэтому, получив в частном две значащие цифры, прекращаем деление; продолжая его, мы получили бы сомнительные цифры, а это не имеет смысла.
Пример 3. Разделить 75,6754598 на 2,4.
Сначала производим деление как обычно:
75,6754598 : 2,4 31,531441 32.
Тот же результат получим, округляя делимое до двух знаков (по числу цифр в делителе — менее точном числе):
_76 I 2,4
72 I 31 «а 32
40
~24
16
24 Округляем частное по избытку, так как остаток 16 больше —.
Еще раз обращаем внимание на то, что при сложении и вычитании с заданной точностью учитываются десятичные знаки, а при умножении и делении — значащие цифры чисел.
Глава III
КОНТОРСКИЕ СЧЕТЫ
12, НАЗНАЧЕНИЕ И УСТРОЙСТВО
вычислительную работу. Они
Рис. 1. Конторские счеты современного образца
Конторские счеты являются простейшим счетным прибором, позволяющим значительно ускорить используются главным образом для сложения, вычитания, реже — для умножения и деления. Точность и быстрота вычислений на счетах зависят лишь от практики. Навык в работе на счетах приобретается сравнительно легко и быстро.
Русские счеты изобретены около 500 лет назад. Более полутораста лет они известны во Франции, Германии и других странах Европы. Любопытно, что в Германии их называли русской счетной машиной.
Выдающийся русский математик XIX в., член Петербургской Академии наук, проф. В. Я. Буняковский,1 характеризуя роль русских счетов, утверждал, что «ни один из существующих арифметических снарядов и даже, вероятно, из тех которые со временем будут придуманы, не вытеснят из общего у нас употребления простых русских счетов. Усовершенствованные арифметические машины имеют на своей стороне неоспоримое преимущество перед счетами для производства сложных вычислений. Но они вообще менее удобны при простых выкладках, требуемых нуждами общежития».*
* О самосчетах и о новом их приложении. Приложение к XXVII тому Записок Академии наук, № 4, СПб, 1876.
27
Конторские счеты современного образца (рис. 1) состоят из деревянной рамы и закрепленных на ней проволок, на которых находится по 10 косточек, кроме 4-й проволоки снизу, на которой имеются 4 косточки.
Всего на счетах 13 проволок; назначение их следующее (считая снизу):
1-я — тысячные доли; 2-я — сотые доли; 8-я — тысячи; 9-я — десятки тысяч;
3-я — десятые доли; 10-я — сотни Тысяч;
4-я — четверти различных величин; 11-я — миллионы;
5-я — единицы; 12-я — десятки миллионов;
6-я — десятки; 7-я — сотни; 13-я — сотни миллионов.
Каждые' 10 косточек предыдущей проволоки равны 1 косточке последующей проволоки. Обычно 5 и 6-я косточки (средние) на каждой проволоке окрашены в темный цвет для того, чтобы ускорить откладывание косточек, облегчить «чтение» чисел. Иногда с этой же целью первые косточки на 8 и 11-й проволоках также окрашиваются в темный цвет, чтобы быстрее находить разряды — тысячи, миллионы и т. д. В иных случаях против этих проволок наклеивают на раму полоски бумаги или делают отметки краской. Если конторские счеты старого образца, т. е. имеют проволоки только для десятых и сотых долей числа, то в этом случае тысячам и миллионам соответствуют 7 и 10-я проволоки.
Важно выработать навык механически откладывать или сбрасывать необходимое количество косточек.
Получив на одной из проволок 10 косточек, мы должны заменить их 1 косточкой, лежащей на последующей проволоке — проволоке высшего разряда. Каждую косточку на любой проволоке, кроме той, на которой имеются 4 косточки, мы можем «разменять», заменив ее 10 косточками на ближайшей предыдущей проволоке — проволоке низшего разряда. Для этого сначала откладывают косточку высшего разряда, а затем лишь сбрасывают все косточки низшего (предыдущего) разряда. Для ускорения вычислений все нужные косточки надо стараться брать сразу, полностью, а не частями. Например, если мы хотим отложить на счетах число 5, то 5 косточек надо отложить сразу, а не по одной или, скажем, сначала 2, а потом<3. Выделенные темным цветом 5 и 6-я косточки позволяют отложить число одновременно, взяв 4 косточки светлые и 1 темную (5-ю).
При откладывании косточек нужно всякий раз смотреть на ту сторону счетов, где в данный момент число косточек на проволоке меньше. Это позволит быстрее определить остальное количество косточек на проволоке, вычитая меньшее число из десятка косточек, имеющихся на каждой проволоке.
Числа откладывают на счетах, начиная с высших разрядов. Косточки откладывают слегка согнутым средним и указательным пальцами, а сбрасывают — большим пальцем.
Если надо сбросить все число, стоящее на счетах, то это обычно делают ребром ладони правой руки или поднимают левый борт счетов — и все косточки прижимаются к правому борту, сбрасываются, и счеты приводятся в рабочее положение.
28
Косточки счетов должны легко передвигаться по проволоке не задевать косточек на соседних проволоках: это может привести к ошибкам в подсчетах. Чтобы косточки легко двигались, рекомендуется протереть проволоки графитом, полученным при чинке мягкого карандаша. Если косточки задевают соседние, надо выровнять проволоки.
Желая отложить на счетах какое-либо число, например 4623, поступаем следующим образом: на 8-й проволоке снизу (тысячи) откладываем 4 косточки, на 7-й (сотни) — 6, на 6-й (десятки) — 2 иг наконец, на 5 — 3 косточки, соответствующие 3 единицам.
В случае необходимости отложить на счетах дробное число, например 8,25, поступаем так: целую часть числа, цифру 8, откладываем на 5-й проволоке снизу, соответствующей единицам, а дробную — 0,25 — на 3 и 2-й проволоках, соответствующих десятым и сотым долям. 4-я проволока, имеющая всего 4 косточки, служит
12 3 4
для складывания четвертых долей единицы: —; —; —; — и одновременно является как бы заменителем запятой,отделяющей целую часть числа от дробной.
Упражнение. Отложить на счетах следующие числа: 6; 72; 128; 1280; 12,8; 4452; 60;. 720; 2200; 2210; 2002; 15 493; 999,9; 10,465; 523 770; 2,5; 133,4; 1175,6; 204,3; 1264,95; 0,003; 18 723; 256; 14 800,06; 48,14; 0,165; 445,4.
13. СЛОЖЕНИЕ
Сложение однозначных чисел. Сложение на конторских счетах начинается с единиц высшего разряда. Косточки откладываются справа налево, тогда как при вычитании, наоборот, они сбрасываются слева направо.
При сложении па счетах могут быть три случая: сумма слагаемых меньше 10, равна 10, больше 10.
Примеры.
1)34-4= 7;
2) 8 + 2 = 10;
3) 6 + 9= 15.
В примере 1, суммируя 3 и 4, откладываем сначала на 5-й проволоке снизу, (единицы) 3 косточки, затем 4, получаем 7.
В примере 2, суммируя 8 и 2, откладываем сначала на проволоке единиц 8 косточек, потом добавляем 2, получаем 10. Накопившиеся 10 косточек на проволоке единиц заменяем 1 косточкой высшего разряда на 6-й проволоке (десятки), сбрасывая 10 косточек на проволоке единиц.
В примере 3, суммируя 6 и 9, откладываем, сначала на 5-й проволоке снизу 6 косточек. Затем мы должны добавить 9 косточек. Но у нас на проволоке осталось всего 4 косточки. В этом случае мы откладываем 1 косточку высшего разряда, равную 10 косточкам предыдущего, и сбрасываем с проволоки, на которой отложено 6 косточек, 1 косточку (так как 10 — 9 = 1); в итоге получаем сумму 15.
Сложение на счетах проверяется последовательным вычитанием каждого слагаемого из полученной суммы.
Сложение многозначных чисел. Решим примеры.
Пример 1,
1234 + 3642 = 4876.
29
В этом случае поступаем следующим образом: движением руки справа налево откладываем на счетах, начиная с единиц, высшего разряда, первое слагаемое 1234. Затем в той же последовательности, т. е. начиная с единиц высшего разряда, откладываем второе слагаемое: к 1 косточке на 8-й проволоке (тысячи) прибавляем 3 косточки (3 тысячи второго слагаемого), к 2 косточкам на 7-й проволоке добавляем 6 косточек, к 3 косточкам на 6-й — 4 косточки и, наконец, к 4 косточкам на 5-й — 2 косточки. После произведенных действий получаем сумму 4876.
Пример 2.
873 + 605 = 1478.
Откладываем на счетах первое слагаемое 873. Затем прибавляем второе слагаемое: к 8 косточкам, соответствующим 8 сотням, нам надо прибавить 6 косточек, соответствующих 6 сотням. Но на этой проволоке осталось всего лишь 2 косточки. Поэтому откладываем 1 косточку на последующей проволоке, равную 10 косточкам на проволоке сотен, одновременно сбрасывая 4 косточки с проволоки, соответствующей сотням (так как 1(Х— 6=4), и получаем 14 сотен. Проволоку с 7 косточками оставляем без изменений, так как в другом слагаемом десятков нет (их число равно нулю). И, наконец, добавляя к 3 единицам первого слагаемого 5 единиц второго, получаем сумму 1478.
Пример 3.
9782 + 4576 = 14 358.
Откладываем на счетах первое слагаемое 9782. После этого прибавляем второе слагаемое, начиная с высшего разряда, для чего' к 9 косточкам добавляем 4 косточки. Так как на этой проволоке осталась всего 1 косточка, мы должны отложить 1 косточку на следующей проволоке, равную 10 косточкам проволоки, на которой имеется лишь одна свободная косточка, и сбросить 6 косточек (так как 10 — 4 = 6). Складывая цифры сотен 7 и 5, опять будем вынуждены положить сначала 1 косточку на проволоке тысяч (высшего разряда) и одновременно сбросить 5 косточек с проволоки сотен (так как 10 — 5 = 5). Суммируя цифры десятков 8 и 7, откладываем на проволоке сотен 1 косточку, и снимаем 3 косточки с проволоки десятков (так как 10 — 7 = 3). Складывая цифры единиц 2 и 6, добавляем к 2 косточкам на проволоке единиц еще 6 косточек. В итоге получаем сумму 14 358.
Упражнение, Проверить на счетах правильность подсчетов:
1) 142 + 328 = 470;
2) 348+ 1235= 1583;
3) 2446 + 3004 = 5450;
4) 1007 + 1786 = 2793;
5) 4129 + 8805 = 12 934;
6) 1876+ 234 = 2110;
7) 7217 + 8477 = 15 694;
'8 ) 641 + 11 200= 11 841;
9) 58 843 + 12 218 = 71 061;
10) 6666 + 347 = 7013;
11) 9124 + 4876= 14 000;
12) 3286 + 5004 = 8290;
13) 11 827 + 3453 + 1005 = 16 285;
30
14) 12 006 + 77 994 + 2100 = 92 100;
15) 6412 + 1715+ 9061 = 17 188;
16) 28 913 + 2215 + 112 = 31 240;
17) 9968 + 4563 = 14 531;
18) 128 + 217 = 345;
19) 6871 + 9599 + 47 = 16 517;
20) И 337 + 212 + 1041 = 12 590;
21) 15 р. 42 к. + 3 р. 16 к. = 18 р. 58 к.;
22) 23 кг 200 г + 4 кг 300 г = 27 кг 500 г;
23) 15 м 72 см + 12 м 5 см + 14 м 20 см = 41 м 97 см.
14. ВЫЧИТАНИЕ
Как уже было сказано, при вычитании косточки сбрасываются слева направо. Проверка правильности вычитания производится путем сложения.
Пример 1,
865 — 342 = 523.
Откладываем на счетах уменьшаемое 865. Затем приступаем к вычитанию, для чего последовательно, начиная с высших разрядов, движением руки слева направо сбрасываем соответствующее число косточек с каждой проволоки. От 8 косточек на проволоке сотен сбрасываем 3 косточки, отнимая 3 сотни; от 6 десятков отнимаем 4, сбрасывая 4 косточки, и, наконец, от 5 единиц-отнимаем'2, сбрасывая 2 косточки. В результате на счетах остается разность 523.
Пример 2.
438 — 249= 189.
Откладываем на счетах уменьшаемое 438. Затем последовательно, начиная с высших разрядов, производим вычитание: от 4 сотен отнимаем 2, сбрасывая 2 косточки; от 3 косточек, соответствующих 3 десяткам, мы должны отнять 4 косточки, соответствующие 4 десяткам. Но так как косточек на проволоке недостает, то отнимаем 1 сотню, сбрасывая косточку на проволоке высшего разряда, а на проволоку десятков прикладываем 6 косточек (так как 10 — 4 = 6) и приступаем к вычитанию 9 единиц. Но непосредственно сбросить 9 косточек с проволоки единиц нельзя: там имеется всего 8 косточек. В этом случае, сбрасывая один десяток, прикладываем 1 косточку на проволоке единиц (так как 10 — 9 = 1). В результате получаем разность 189.
Упражнение. Проверить на счетах правильность подсчетов:
1) 4815 — 3305 = 1510;
2) 5678 — 3340 = 2338;
3) 128 — 96 = 32;
4) 7002—2129 = 4873;
5) 83463 — 83122 = 341;
6) 984 — 343 = 641;
7) 4877—2354 = 2523;
8) 3365 — 2462 = 903;
9) 17846 — 13855= 3991;
10) 57 394 — 54 494 = 2900;
11) 15 466 — 13 872 = 1594;
12) 102 673 — 80 574 = 22 099;
31
13) 4956 — 3049 = 1907;
14) 7788 — 6984 = 804;
15) 96 078 — 92 275 = 3803;
16) 6897 — 4123 — 1442 = 1332;
17) 14 728 — 8102 — 26 — 2300 = 4300;
18) 87 р. 65 к. — 36 р. 35 к. = 51 р. 30 к.;
19) 1328 р. 16 к. — 728 р. 02 к. = 600 р. 14 к.;
20) 5000 р. — 100 р. — 575 р. — 25 р. = 4300 р.;
21) 1419 кг 700 г — 416 кг 900 г 1002 кг 800 г;
22) 3452 т — 2149 т = 1303 т;
23) 268 м — 40 м 60 см — 120 м 75 см = 106 м 65 см.
Напомним, что правильность сложения и вычитания проверяется обратными действиями: вычитанием и сложением.
Рекомендуем проверить правильность подсчетов обратным действием, чтобы убедиться в точности результатов. Следует иметь в виду, что пока не сделано проверки, вычисление нельзя считать законченным.
15. УМНОЖЕНИЕ
Умножение на конторских счетах не представляет больших трудностей, но требует достаточной практики, чтобы быстро получить верный результат.
Умножение на счетах можно производить двояко: либо непосредственно путем сложения, либо с помощью таблицы умножения.
Умножение на 10, 100, 1000 и т. д. При умножении числ^ на 10, 100, 1000 и т. д. откладываем множимое на счетах. Затем для умножения его на 10 переносим последовательно все косточки разрядом выше, на следующие проволоки. При умножении на 100 переносим косточки на 2 разряда выше, при умножении на 1000 — на 3 разряда выше и т. д.
Умножение на 0,1; 0,01; 0,001 и т. д. При умножении чисел на'0,1; 0,01; 0,001 и т. д. отложенные на счетах косточки переносятся разрядом ниже: в первом случае на 1 проволоку, во втором — на 2 и в третьем — на 3 проволоки и т. д.
Умножение на однозначные числа посредством сложения или вычитания. Для того чтобы умножить число на 2, откладываем его на счетах 2 раза.
При умножении числа на 3 откладываем число 3 раза.
При умножении числа на 4 сначала умножаем его на 2, затем полученное произведение удваиваем, прикладывая его еще раз.
> При умножении числа на 5 сначала умножаем его на 4, а затем прибавляем число еще один раз или умножаем его на 10 и полученное произведение делим на 2.
При умножении числа на 6 умножаем его сначала на 3, затем прикладываем полученное произведение еще раз.
Прй умножении числа на 7, 8 и 9 сначала умножаем его на 10, затем отнимаем число в первом случае 3 раза (10 — 7 = 3), во втором — 2 раза (10 — 8= 2) и, наконец, в третьем — 1 раз (10 — 9= 1).
Упражнение. Произвести на счетах умножение посредством сложения или вычитания:
1) 142 X 2 = 284;
2) 215 X 3 = 645;
3) 406 X 2 = 812;
4) 1521 X 3 = 4563;
5) 623 X 2 = 1246;
6) 623 X 3 = 1869;
32
7) 718 X 4 = 2872; И) 893 X 8 = 7144;
8) 718 X 5 = 3590; 12) 893 X 9 = 8037;
9) 845 X 6 = 5070; 13) 2488 X 9 = 22 392;
10) 845 X 7 = 5915; 14) 3512 X 8 = 28 096.
Умножение на однозначные числа с использованием таблицы умножения.. Рассмотрим два примера.
Пример 1.
214 X 3 = 642.
Откладываем на счетах множимое — 214. Затем, начиная с высшего разряда, каждую цифру множимого умножаем в уме на 3 (множитель). Одновременно сбрасываем косточки этой цифры с проволоки и заменяем их косточками произведения. Так, 2 X 3=6. Сбрасываем 2 косточки и вместо них откладываем произведение — 6 косточек. 1 X 3=3. Сбрасываем 1 косточку и взамен откладываем произведение 3. Далее, 4 X 3 = 12. Сбрасываем 4 косточки и, поскольку произведение двузначное число, откладываем 2 косточки на место сброшенных четырех, а 1 десяток прикладываем к имеющимся 3 десяткам и в результате получаем произведение 642.
Пример 2.
1845 X 8 = 14 760.
Откладываем на счетах множимое 1845 и начинаем тем же способом перемножение с высших разрядов каждой отдельной цифры множимого на 8. Так, 1X8=8. Сбрасываем единицу и вместо нее откладываем 8 косточек. 8 X 8 = 64. Сбрасываем 8 и, поскольку произведение — число двузначное, на место сброшенных 8 косточек откладываем 4 косточки, а 6 прибавляем к цифре последующего разряда — 8, получаем 14. Затем 4 X 8 = 32. Сбрасываем 4 косточки и на этой проволоке откладываем 2 косточки, а 3 прикладываем к цифре высшего разряда. 5 X 8 = 40. Сбрасываем 5 косточек с проволоки единиц и, поскольку произведение — число двузначное, прикладываем 4 к цифре на проволоке высшего разряда, оставляя свободной проволоку единиц (произведение оканчивается нулем). В результате получаем ответ 14 760.
Умножение на двузначные числа. При умножении чисел на 22, 33, 44 и т. д. сначала умножаем число на единицы, а затем к получен-’ ному результату прибавляем число, в 10 раз большее, перенося все косточки проволоками выше. Например, при умножении 81 на 22 сначала умножаем 81 на 2 и получаем 162. Затем к этому произведению прибавляем число 1620 (81 X 2 X 10) и получаем ответ 1782.
При умножении числа на 33 сначала умножаем его на 3, а затем к полученному произведению прибавляем число, которое в 16 раз больше этого произведения, и в результате получаем ответ. Например, умножая 28 на 33, сначала откладываем на счетах 28 и, как обычно, умножаем это число на 3 — получаем произведение 84. Затем прикладываем число, в 10 раз большее (84 X' 10), и получаем ответ 924.
Упражнение. Проверить на счетах тем и другим способом правильность подсчетов:
1) 112 X 2 = 224; 7) 343 X 4 = 1372;
2) 34,7 X 3 = 104,1; 8) 673 X 8 = 5384;
3) 22,81 X 2 = 45,62; 9) 228 X 2,2 = 501,6;
4) 53,3 X 0,02 = 1,066; 10) 535 X 6 = 3210;
5) 841 X 2 = 1682; 11) 76,7 X 44 = 3374,8;
6) 68 X 8 = 544; 12) 768 X 9 = 6912;
2 С. И. Березин
33
13) 8690 X 33 = 286 770;
14) 948 X 11 = 10 428;
15) 367 X 8,8 = 3229,6;
16) 642 X 55 = 35 310;
17) 1437 X 7 — 10 059;
18) 6,24 X 8 = 49,92;
19) 533 X 99 = 52 767;
20) 48,32 X £ = 289,92.
16. ДЕЛЕНИЕ
Деление на конторских счетах является наиболее трудоемкой операцией по сравнению со всеми другими видами вычислений.
Деление на 10, 100, 1000 и т. д. При делении чисел на 10, 100, 1000 и т. д. отложенные на счетах косточки переносим в первом случае 1 разрядом ниже (на 1 проволоку), во втором — на 2 разряда, в третьем — на 3 разряда ниже, например:
1340 : 10 = 134;
87 300 : 100 = 873;
68 000 : 1000 = 68.
Деление на 0,1; 0,01; 0,001 и т. д. При делении числа на 0,1; 0,01; 0,001 и т. д. отложенное на счетах делимое переносим на столько разрядов (проволок) выше, сколько нулей стоит перед единицей в делителе, включая и нуль целых, например:
942 : 0,1 = 9420 (на 1 проволоку);
87 : 0,01 = 8700 (на 2 проволоки); , 64 : 0,001 = 64 000 (на 3 проволоки).
Деление на однозначные числа с использованием таблицы умножения. Рассмотрим примеры.
Пример 1.
468 : 2 = 234.
Сначала откладываем на счетах делимое 468, а затем, начиная с низших разрядов, производим деление на 2, сбрасывая с каждой проволоки половину косточек. Так как 8:2=4, сбрасываем с проволоки единиц 4 косточки, оставляя на ней тоже 4 косточки; 6:2 = = 3 — сбрасываем 3 косточки с проволоки десятков, оставляя на ней также 3 косточки; 4:2=2 — сбрасываем 2 косточки с проволоки сотен, а 2 оставляем на ней; в результате получаем частное 234.
Пример 2,
1276 : 2 = 638.
Откладываем на счетах делимое 1276. Начиная с низших разрядов, производим деление; 6:2=3 — сбрасываем с проволоки единиц 3 косточки; 70 : 2 = 35 — сбрасываем с проволоки десятков 4 косточки, а 5 косточек прибавляем к единицам, к 3 косточкам, так как 40 — 35 = 5; 200 : 2 = 100 — сбрасываем 1 косточку из двух с проволоки сотен; наконец, 1000 : 2 = 500 — сбрасываем 1 косточку с проволоки тысяч и, прибавляя 5 косточек на проволоке сотен, получаем частное 638. Зная деление на 2, нетрудно разделить число на 4, 8, применяя последовательное деление сначала на 2, затем еще раз на 2, затем еще раз на 2 и т. д.
Деление на однозначные числа посредством вычитания. Результат, полученный в последнем примере, можно получить и другим способом — путем последовательного вычитания делителя из делимого. В этом случае, отложив на счетах делимое 1276, пальцем левой
34
руки отделяем, начиная с высшего разряда, наименьшее число цифр, в.которых содержится делитель 2, а затем начинаем отнимать делитель, отмечая каждое вычитание откладыванием косточки на самой верхней свободной проволоке. После 6 вычитаний косточек на проволоках этих цифр делимого уже не останется, а на верхней свободной проволоке будет 6 косточек — первая цифра результата. Теперь переходим к делению числа 7, также последовательно вычитая из него делитель 2. После трех вычитаний, каждое из'которых аналогично отмечается косточкой (теперь на второй сверху свободной проволоке), у нас остается единица. Присоединяя последнюю цифру 6, продолжаем деление — вычитание делителя. После 8 вычитаний, каждое из которых мы также отмечаем косточкой (уже на третьей свободной проволоке), на счетах не останется цифр делимого, а на верхних проволоках счетов читаем число 638. Это и есть частное от деления. Если число не делится без остатка, то деление продолжаем до тех пор, пока не получим ответ с необходимой точностью (до 0,1; 0,01 и т. д.).
Деление на двузначные числа. Решим примеры.
Пример 1.
768 : 24 = 32.
Откладываем на счетах делимое 768 и производим деление путем последовательного вычитания делителя. Каждое сбрасывание делителя отмечаем косточкой на самых верхних свободных проволоках. Пальцем левой руки отделяем две цифры высшего разряда 76, в которых содержится делитель 24, и начинаем его вычитание. После 3 сбрасываний косточек на этих разрядах остается 4. Теперь делим остальные цифры делимого, т. е. 48, на 24. После двукратного сбрасывания косточек на месте делимого цифр не остается (число делится без остатка), а частное, как это видно из отложенных косточёк на верхних свободных проволоках, равно 32.
Пример 2,
1157 : 48^24.
Откладываем на счетах делимое 1157. Затем тем же способом, начиная с высших разрядов, сбрасываем делитель 2 раза, получим в остатке 197, а на верхней свободной проволоке 2; продолжая делить остаток на 48 — сбрасывая делитель 4 раза и отметив 4 косточками на второй проволоке сверху, получим частное 24 и остаток 5, кото-748 \
рый отбрасываем, так как он меньше половины делителя I — I. Если нужно получить частное с точностью до 0,1, то в Этом случае продолжим деление, мысленно приписав нуль к остатку 5. Сбрасывая делитель 1 раз, получаем остаток 2, который отбрасываем, так как частное 24,1 вычислено *с требуемой точностью до 0,1. Если требуется большая точность, деление продолжается.
Деление на трехзначные числа. Рассмотрим пример;
28 896 : 672 = 43.
Откладываем на счетах делимое 28 896. Затем, отделив пальцем левой руки цифры, в которых содержится делитель (2889), сбрасываем делитель 672, отмечая косточкой, как и в предыдущих случаях, каждое сбрасывание делителя на первой верхней свободной прово-
2*
35
локе. Сбросив 4 раза, получаем в остатке 201. Присоединив остальные цифры делимого, делим 2016, сбрасывая делитель 672. Каждое сбрасывание делителя отмечаем косточкой на второй сверху свободной проволоке. После 3 сбрасываний косточек на месте делимого не осталось, число разделилось без остатка. На верхних проволоках читаем частное : 43. * '
Упражнение. 1. Проверить на счетах правильность подсчетов:
1) 88 : 22 = 4;
2) 1225 : 35 = 35;
3) 5412 : 12 = 451;
4) 4536 : 72 = 63;
5) 18 120 : 755 = 24;
6) 521,64 : 63 = 8,28; -
7) 23 124 : 246 = 94;
8) 1610 : 3,5 = 460;
9) 172,8 : 24 = 7,2;
10) 3939,6 : 46,9 = 84;
11) 215,36 : 673 = 0,32;
12) 2138,4 : 27 = 79,2;
13) 4712,5 : 725 = 6,5;
14) 27 289 : 535 — 51 (остаток 4);
15) 33 438 : 398 = 84 (остаток 6);
16) 13 670 : 157 = 87 (остаток 11);
17) 8435 : 337 = 25 (остаток 10);
18) 21 916 : 44 = 498 (остаток 4);
' 19) 16 469 : 43 = 383;
20) 9984 : 768 = 13.
Упражнение 2. Подсчитать по данным таблицы размер оборота магазинов Книготорга за IV квартал 197... г. (в руб. и коп.)
№ магазина Октябрь Ноябрь Декабрь Всего за квартал
1 9 001—15 89 72—24 9 600—05
2 12 999—04 12 700—16 13 150—71
3 21 000—28 20 015—42 21 888—06
4 8 500-17 7 900—47 8 800—64
5 Ю 500—40 11 300—30 13 992—91
Итого
Ответ: оборот магазинов Книготорга за IV квартал составил 190 322 руб.
Глава IV
ВЫЧИСЛИТЕЛЬНЫЕ ТАБЛИЦЫ
Вычислительные таблицы значительно облегчают всевозможные расчеты, повышают точность результата, позволяют экономить время и труд на производство различных вычислений. С помощью таблиц можно умножать, делить, возводить числа в квадрат и куб, извлекать квадратные и кубические корни, вычислять проценты и производить ряд других подсчетов.
Из имеющихся таблиц рассмотрим лишь пользующиеся наибольшей известностью: таблицы умножения двузначных чисел на двузначные числа; таблицы умножения О’Рурка; таблицы вычисления процентов, умножения и деления Л. Г. Асатиани; таблицы Барлоу квадратов, кубов, квадратных корней, кубических корней и обратных величин всех целых чисел от 1 до 15 000 и таблицы возведения в степень С. Д. Тишина и С. С. Тишина.
Обычно к каждой таблице предпосылаются краткие правила пользования. С ними надо предварительно подробно ознакомиться и разобрать приводимые автором примеры.
17. ТАБЛИЦЫ УМНОЖЕНИЯ ДВУЗНАЧНЫХ ЧИСЕЛ
НА ДВУЗНАЧНЫЕ ЧИСЛА
Описание таблиц. Эти таблицы небольшого объема, карманного формата неоднократно переиздавались издательством «Статистика». Таблицы содержат произведения однозначных и двузначных чисел на однозначные и двузначные. Всего 99 таблиц чисел от 2 до 99: каждое из них перемножается на 1—99.
Приводим извлечение из таблиц (табл. 1).
Мы видим, что на странице размещены две таблицы, которые озаглавлены числами, напечатанными жирным шрифтом, в данном случае — 72 и 73. Эти числа являются одним из сомножителей.
Вторые сомножители напечатаны жирным шрифтом в левых колонках, и рядом с ними в правых колонках находятся произведения данных сомножителей.
Умножение при помощи таблиц. Рассмотрим пример:
72 X 4 = 283,
37
Таблица 1
Извлечение из таблиц умножения двузначных чисел на двузначные числа
72 73
1 72 34 2448 67 4824 1 73 34 2482 67 4891
2 144 35 2520 68 4896 2 146 35 2555 68 4964
'3 216 36 2592 69 4968 3 219 36 2628 69 5037
4 288 37 2664 70 5040 4 292 37 2701 70 5110
5 360 38 2736 71 5112 5 365 38 2774 71 5183
6 432 39 2808 72 5184 6 438 39 2847 72 5256
7 504 40 2880 73 5256 7 511 40 2920 73 5329
8 576 41 2952 74 5328 8 584 41 2993 74 5402
9 648 42 3024 75 5400 9 657 42 3066 75 5475
10 720 43 3096 76 5472 10 730 43 3139 76 5548
11 792 44 3168 77 5544 11 803 44 3212 77 5621
12 864 45 3240 78 5616 12 876 45 3285 78 5694
13 936 46 3312 79 5688 13 949 46 3358 79 5767
14 1008 47 3384 80 5760 14 1022 47 3431 80 5840
15 1080 48 3456 81 5832 15 1095 48 3504 81 5913
16 1152 49 3528 82 5904 16 1168 49 3577 82 5986
17 1224 50 3600 83 5976 17 1241 50 3650 83 6059
18 1296 51 3672 84 6048 18 1314 51 3723 84 6132
19 1368 52 3744 85 6120 19 1387 52 3796 85 6205
20 1440 53 3816 86 6192 20 1460 53 3869 86 6278
21 1512 54 3888 87 6264 21 1533 54 3942 .87 6351
22 1584 55 3960 88 6336 22 1606 55 4015 88 6424
23 1656 56 4032 89 6408 23 1679 56 4088 89 6497
24 1728 57 4104 90 6480 24 1752 57 4161 90 6570
25 1800 58 4176 91 6552 25 1825 58 4234 91 6643
26 1872 59 4248 92 6624 26 1898 59 4307 92 6716
27 1944 60 4320 93 6696 27 1971 60 4380 93 6789
28 2016 61 4392 94 6768 28 2044 61 4453 94 6862
29 2088 62 4464 95 6840 29 2117 62 4526 95 6935
30 2160 63 4536 96 6912 30 2190 63 4599 96 7008
31 2232 64 4608 97 6984 31 2263 64 4672 97 7081
32 2304 65 4680 98 7056 32 2336 65 4745 98 7154
33 2376 66 4752 99 7128 33 2409 66 4818 99 .7227
38
в лейом столбце таблицы для числа 72 находим число 4, напечатанное жирным шрифтом, а в правом столбце рядом с числом 4 читаем искомое произведение 288.
Аналогично получим и следующие произведения:
72 X 52 = 3744;
73 X 96 = 7008.
Если нам необходимо перемножить 72 и 520, то к полученному произведению 72 X 52 = 3744 необходимо приписать нуль, т. е. увеличить произведение в 10 раз, и получим ответ 37 440; если будем умножать на 5200, то к полученному произведению нужно будет приписать два нуля и получим ответ 374 400. Если умножаем 72 на 5,2; 0,52; 0,052, то в полученном произведении 72 X 52 = 3744 отделяем соответственно: в первом случае — один знак справа, т. е. уменьшаем произведение в 10 раз (374,4), во втором — два знака (37,44) и в третьем — три знака (3,744).
С помощью этих таблиц и конторских счетов можно получать произведения не только двузначных чисел на двузначные, но и другие произведения.
Примеры.
1) 866 X 72 = 62 352;
2) 5365 X 72 = 386 280;
3) 905 518 х 72 = 65 197 296.
В примере 1 представим множимое 866 в виде суммы двух чисел: 860+ 6. Умножая 860 X 72, получаем 61 920; умножая 6 X 72, имеем 432. Сложив на счетах отдельные произведения, получим:
860x72 = 61920
6x72= 432 . '
866x72 = 62352
В примере 2 множимое 5365 представим в виде суммы двух чисел: 5300 + 65. Умножая 5300 X 72, получаем 381 600, умножая 65 X 72, имеем 4680. В окончательном виде ход перемножения запишем так:
' 5300x72 = 381600 65X72= 4680
5365X72 = 386280
В примере 3 представим множимое 905 518 в таком виде: 900 000+ + 5500 + 18. Умножая 900 000 X 72, имеем 64 800 000, умножая 5500 X 72, получаем 396 000 и, умножая 18 X 72, имеем 1296. Ход перемножения запишем в следующем виде и с помощью конторских счетов получим произведение:
900000X72 = 64800000 5500x72= 396000 18x 72= 1296
905518X72 = 65197296
Если бы мы умножали на 7,2, то в полученном произведении пришлось бы отделить 1 знак (6519729,6), а если на 0,0072, то четыре знака (6519,7296).
Деление при помощи таблиц. Эти таблицы могут быть использованы и для деления любых многозначных чисел на числа до 100.
39
Примеры:
n Q7OQ -73 __ 51*
2) 4206 : 72 = 58 (остаток 30);
3) 3352z: 73 = 45 (остаток 67).
В примере 1 (3723 : 73) смотрим таблицу для числа 73, соответствующего делителю, и ищем в таблице либо делимое, либо число менее делимого, но близкое к нему. В нашем случае имеется число 3723, точно соответствующее числу 51, напечатанному слева жирным шрифтом. Следовательно, 3723 делится без остатка на 73, и частное равно 51.
Нетрудно сообразить, что если бы потребовалось разделить 3723 : 730, то частное равнялось бы 5,1. Если 3723 : 7300, —то частное соответственно равно 0,51. Если же надо было бы разделить 3723 : 7,3, то в этом случае частное равнялось бы 510.
Во втором примере (4206 : 72) ищем в таблице, обозначенной числом 72.(делитель), делимое 4206. Точно такого делимого нет, берем наиболее близкое к нему меньшее число 4176, соответствующее частному 58, напечатанному слева жирным шрифтом. Вычитая 4176 от 4206, получаем остаток 30, который отбрасываем, так как он меньше /72\
половины делителя I -у I, и с точностью до единицы получаем частное 58.
В третьем примере (3352 : 73) ищем в таблице, озаглавленной числом 73 (делитель), делимое 3352. Поскольку точно такого числа нет, берем ближайшее число менее делимого — 3285, соответствующее частному 45, и получаем остаток 67, который более половины дели-/73\
теля а ПОЭТОМУ округляем частное с избытком и в результате получаем ответ с точностью до единицы: 46.
Если нужно получить ответ с заданной точностью (до 0,1; 0,01; 0,001), то продолжаем деление до получения требуемого знака точности .
С помощью этих таблиц можно находить процентное отношение любого числа к двузначному числу, определять квадраты и кубы чисел и производить еще ряд других вычислительных операций. Все эти действия легко осваиваются в процессе повседневной работы с таблицами.
Упражнение. На основании приведенных извлечений из таблиц умножения двузначных чисел на двузначные числа проверить правильность ответов:
1) 72x48 = 3456;
2)72x8,5 = 612,0;
3) 722 = 5184;
4) 7273 X 17=123 641J
5) 3888: 72 = 54;
6) 2592:0,72 = 3600;
7) 733 = 389 017;
8) 72x900 = 64 800;
9) 0,72x0,016 = 0,01152;
10) 7,3x6,2 = 45,26;
11) найти 45% от 720; ответ: 324;
12) определить процентное отношение 423,4 к 7300; ответ: 5,8%.
40
В примере 11 для нахождения 45% от 720 поступаем следующим образом: определяем, чему равен 1% от 720. Разделив 720 : 100, получаем, что 1% от числа 720 равен 7,2. Затем находим таблицу для числа 72, в средней колонке ищем число 45, обозначенное жирными цифрами, и рядом читаем число 3240. Но нам надо было умножить 7,2 на 45, т. е. число, в 10 раз меньшее, поэтому уменьшаем полученное произведение в 10 раз, отделяя запятой один знак, и окончательно имеет 324. Следовательно, 45% от 720 составляет 324.
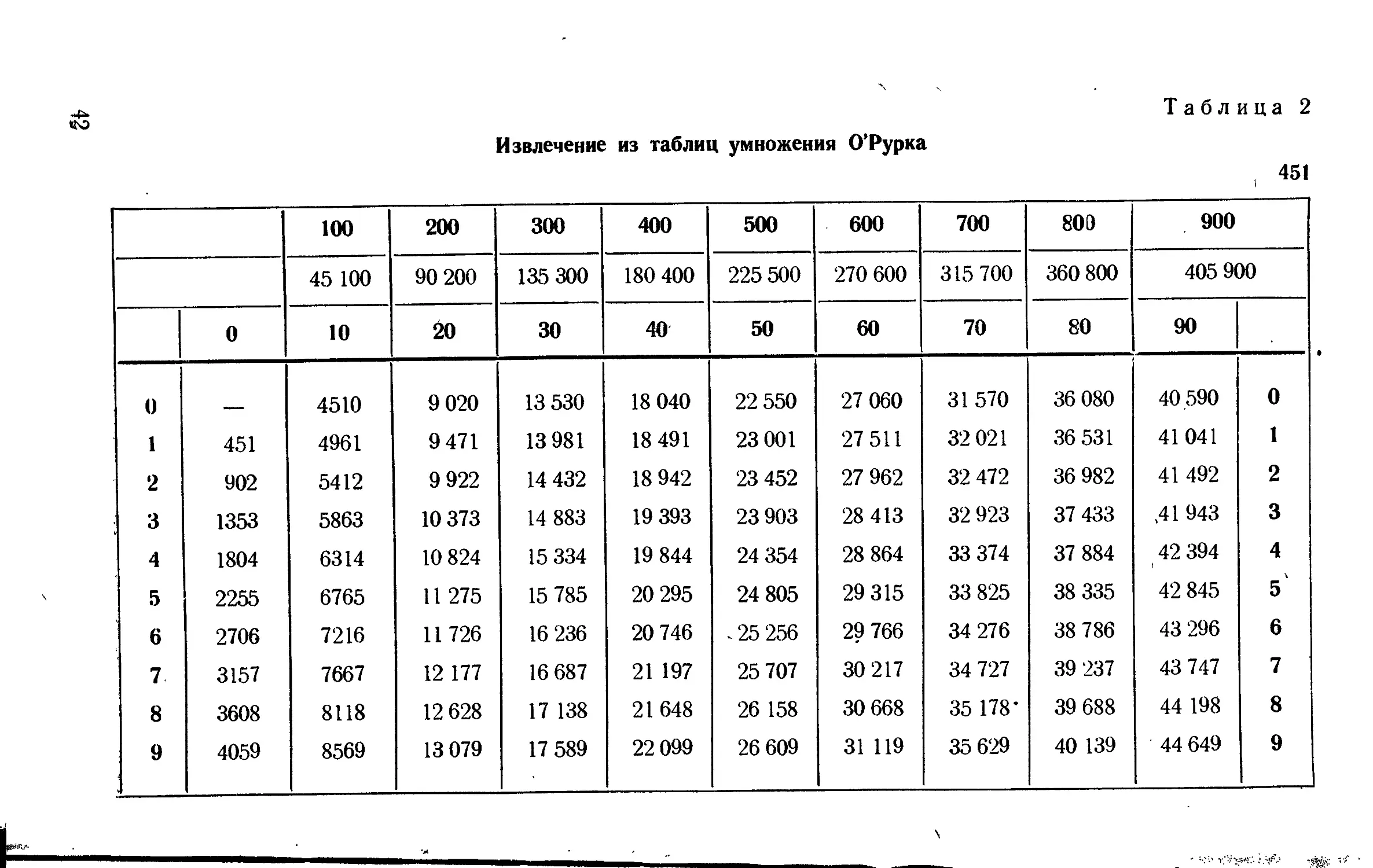
18. ТАБЛИЦЫ УМНОЖЕНИЯ О’РУРКА
Описание таблиц. В этих таблицах содержатся готовые произведения от умножения двузначных и трехзначных чисел — от 11 до 999 — на однозначные и двузначные числа — от 1, до 99. Таблицы состоят из 989 отдельных таблиМек, над каждой из которых помещен сомножитель (от 11 до 999), напечатанный жирным шрифтом. Второй сомножитель (от 1 до 99) состоит из двух слагаемых: десятков и единиц.
Числа десятков (0; 10; 20; 30; 40; 50; 60; 70; 80; 90) расположёны в третьей горизонтальной строке сверху и напечатаны жирным шрифтом. Единицы (0; 1; 2; 3; 4; 5; 6; 7; 8; 9), расположенные в крайних колонках таблички слева и справа, также напечатаны жирным шрифтом.
В двух верхних строках таблицы показано умножение на сотни трехзначного множителя.
Приводим в качестве примера две отдельные таблички, соответствующие числам 451 и 768 (табл. 2).
Умножение по таблицам на однозначные и двузначные числа. Решим примеры.
Пример /.
768 х 6 = 4608.
В табличке для числа 768, напечатанного жирным шрифтом в верхнем правом углу, это число является первым сомножителем. В колонке слева таблички находим цифру 6, соответствующую второму сомножителю, и в первой вертикальной графе, обозначенной 0 (так как число десятков во множителе равно, нулю), в строке против цифры 6 читаем произведение 4608.
Пример 2.
768 х 54 = 41 472.
В этом случае находим в табличке для числа 768 вертикальный столбец «50» и против цифры 4, взятой в колонке слева (справа), на пересечении строки со столбцом читаем произведение 41 472.
Умножение на трехзначные числа. Если потребовалось умножить 768 на 540, то к ранее найденному произведению надо приписать справа нуль, увеличив число в 10 раз.
Еще пример:
451 X 224 = 101 024.
Берем табличку для числа 451.
В том случае, когда множитель — трехзначное число, умножение ведем последовательно, представляя множитель как сумму сомножителей, В этом случае целесообразно комбинировать вычисления по таблицам с работой на конторских счетах.
41
Извлечение из таблиц умножения О'Рурка
Таблица 2
451
100 200 300 400 500 600 700 800 900
45 100 90 200 135 300 180 400 225 500 270 600 315 700 360 800 405 900
0 10 20 30 40 50 60 70 80 90
0 — 4510 9 020 13 530 18 040 22 550 27 060 31570 36 080 40 590 0
1 451 4961 9 471 13 981 18 491 23 001 27 511 32 021 36 531 41041 1
2 902 5412 9 922 14 432 18 942 23 452 27 962 32 472 36 982 41 492 2
3 1353 5863 10 373 14 883 19 393 23 903 28 413 32 923 37 433 .41 943 3
4 1804 6314 10 824 15 334 19 844 24 354 28 864 33 374 37 884 42 394 4
5 2255 6765 И 275 15 785 20 295 24 805 29 315 33 825 38 335 42 845 5
6 2706 7216 11726 16 236 20 746 . 25 256 29 766 34 276 38 786 43 296 6
7 3157 7667 12 177 16 687 21 197 25 707 30 217 34 727 39 237 43 747 7
8 3608 8118 12 628 17 138 21648 26 158 30 668 35 178’ 39 688 44 198 8
9 4059 8569 13 079 17 589 22 099 26 609 31 119 35 629 40 139 44 649 9
00
Продолжение табл. 2
768
100 200 300 400 500 600 700 800 900
76 800 153 600 230 400 307 200 384 400 460 800 537 600 614 400 691 200
0 10 20 30 40 50 60 70 80 90
0 — 7 680 15 360 23 040 30 720 38 400 46 080 53 760 61440 69 120 0
1 / 768 8 448 16 128 23 808 31488 39 168 46 848 54 528 62 208 69 888 1
2 1536 9 216 16 896 24 576 32 256 39 936 47 616 55 296 62 976 70 656 2
3 2304 9 984 17 664 25 344 33 024 40 704 48 384 56 064 63 744 71424 3'
4 3072 10 752 18 432 26 112 33 792 41472 49 152 56 832 64 512 72 192 4
5 3840 11520 19 200 26 880 34 560 42 240 49 920 57 600 65 280 72 960 5
6 4608 12 288 19 968 27 648 35 328 43 008 50 688 58 368 66 048 73 728 6
7 5376 13 056 20 736 28 416 36 096 43 776 51456 59 136 66 816 74 496 7
8 6144 13 824 21504 29 184 36 864 44 544 52 224 59 904 67 584 75 264 8
9 6912 14 592 22 272 29 952 37 632 45 312 52 992 60 672 68 352 76 032 9
Представим множитель в виде суммы двух чисел: 200+ 24. В табличке во второй строке сверху находим произведение 451 X X 200 = 90 200; в основной табличке находим произведение 451 X X 24 = 1Q 824. Сложив эти частные произведения на счетах, получаем: 451 X 224 = 90 200 + 10 824 = 101 024.
Умножение на многозначные числа. Решим пример:
451 X 3487 = 1 572 637.
Представим второй сомножитель, как и в предыдущем примере, в виде суммы двух слагаемых (3400 + 87). Производим умножение при помощи таблиц в такой последовательности:
451 X3400=1533 400
451 X 87= 39 237
451 X 3487 = 1 572 637
Эту сумму получаем на счетах.
Умножение с вычитанием частных произведений. Решим пример:
451 X 298 = 134 398.
В этом случае удобнее представить множитель 298 как разницу двух чисел (300 — 2). Умножение при помощи таблйц производим в такой последовательности:
451 X 300= 135 300
451 X 2 = 902
451 X298=134 398
Результат 451 X 298 находим вычитанием на счетах: 135 300 — — 902 = 134 398.
Деление на трехзначный делитель без остатка. Таблицы умножения могут быть использованы также и для деления, особенно в тех случаях, когда делитель не превышает трехзначного числа. Обычно при делении также пользуются конторскими счетами.'
Например:
24 576 : 768 = 32.
В этом случае находим табличку, соответствующую делителю, т. е. 768, и ищем в ней делимое — 24 576. Такое число находится на пересечении вертикального столбца «30» и строки «2», что соответствует 32. Итак, частное от деления 24 576 на 768 равно 32. Число делится без остатка.
Если бы потребовалось разделить число, в 10 раз большее, например 245 760 на 768, то частное соответственно составило бы 320, а при делении 245,76 — число, в 100 раз меньшее) на 768 частное равнялось бы 0,32.
Деление на трехзначное число с остатком. Решим пример:
28 954 : 451 = 64,2.
Находим табличку, соответствующую делителю 451, и в ней ищем делимое. Поскольку точно такого числа нет (что бывает очень часто), то берем имеющееся ближайшее к нему меньшее число 28 864, соответствующее частному 64, и определяем на счетах остаток (28 954 - 28 864 = 90).
44
785
100 200 300 400 500 700 800 900
78500 157000 235500 314 000 392500 549 500 628000 706500 '
0 10 20 30 40 г 50 ~ 70 80 90
0 — 7 850 15 700 23550 31400 39250 54950 62800 ^70 650 71435 0
1 785 8 635 16 485 24 335 32185 40 035 55 735 63585 1
2 1570 9 420 17270 ( 25 120 32970 40 820 56520 64370 72220 2
3 2355 10 205 18055 25905 33755 41605 57305 65155 73005 3
4 3140 10 990 18 840 26 690 34 540 42 390
5 3925 11775 19 625 27 475 35325 43175
6 4710 12 560 20 410 28260 36110 43 960 51810 59660 67510 75360 6
7 5495 13345 21195 29 045 36895 44 745 52 595 60445 68295 76145 7
8 6280 . 14 130 21980 29 830 37680 45530 53380 61230 69080 76930 8
9 7065 14 915 22 765 30 615 38 465 46315 54 465 62015 69 865 77 715 9
Рис. 2. Использование угольника при вычислениях по таблицам
Теперь ищем в табличке число 90 (остаток). В табличке есть число 902, которому соответствует частное 2. Но так как наш остаток — число, приблизительно в 10 раз меньшее, то, следовательно, частное от деления 90 : 451 будет равно 0,2 и ответ составит 64,2 (с точностью до 0,1).
Для того чтобы быстрее и точнее читать в табличках цифры, целесообразно вырезать из картона уголок. Накладывая его на таблицу, как показано на рис. 2, мы облегчаем нахождение произведения и избегаем ошибок, возможных при непосредственном чтении. Например, умножая 785 на 73 с помощью уголка, читаем произведение 57 305.
19. ТАБЛИЦЫ ВЫЧИСЛЕНИЯ ПРОЦЕНТОВ, УМНОЖЕНИЯ И ДЕЛЕНИЯ Л. Г. АСАТИАНИ
Описание таблиц. Эти таблицы предназначены для нахождения процентов (от 1 до 119) от трехзначных чисел (100 — 999), произведений трехзначных чисел на числа 1—119, частных от деления на трехзначные числа и процентных отношений к трехзначным числам.
Рассматривая приводимое ниже извлечение из этих таблиц -(табл. 3), замечаем, что наверху таблицы напечатаны жирным шрифтом три трехзначных числа. При умножении эти числа принимаются за множимое, при вычислении процентов — за базисное число, а при делении — за делитесь. Табличка для каждого трехзначного числа состоит из четырех граф, которые делятся по горизонтали на четыре части по 10 строк в каждой. Над каждой такой частью жирным шрифтом напечатаны десятки (10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ПО), а слева, в узкой графе, — единицы (1—9). Из этих чисел (1 —9 и 10— 110) составляются при умножении — множитель, дри вычислении процентов — Цисло процентов, при нахождении процентного отношения — само процентное отношение.
Умножение на двузначное число. Рассмотрим пример:
380 X 42 - 15 960.
Множимое 380 напечатано сверху таблицы жирным шрифтом. Множитель — число двузначное, содержащее 4 десятка и 2 единицы. Произведение читаем в графе под числом 40, в строке против числа 2. Не обращая внимания на точки, проставленные в числах произведений, читаем ответ: 15 960.
Нахождение процентов. Найти 15% от 3800. В табличке для числа 380 в графе под числом 10, в строке против числа 5 читаем ответ: 57.00. Но поскольку число 3800 вЛО раз больше табличного, то и результат надо увеличить в 10 раз, т. е. 15% от 3800 составит 570.
Найти 115% от 381. В табличке для числа 381 в графе под числом ПО, в строке пр’отив числа 5 читаем ответ: 438.15.
Умножение на четырехзначное число. Решим пример:
382 X 64,78 = 24745,96.
Представим множитель двумя числами (64 + 0,78) и произведем умножение по частям, с последующим сложением полученных произведений на счетах. Результаты умножения запишем так:
382 X 64 = 24 448;
382 X 0,78 = 297,96.
46
Следовательно, 382 X 64,78 = 24745,96. Отделяем столько десятичных знаков в произведении, сколько имеется их во множимом и множителе. В нашем примере отделяем два знака, учитывая, что в множителе два десятичных знака, а множимое — целое число.
Деление на трехзначное число. Рассмотрим пример:
22 098 : 381 = 58.
В этом случае находим табличку, соответствующую числу делителя 381, и ищем в ней делимое 22 098. Это число находим в колонке под числом 50 в строке 8. Следовательно, частное от деления равно 58 и число разделилось без остатка. Если в таблицах нет числа, точно соответствующего делимому, то, взяв несколько меньшее, определяем остаток и продолжаем деление до тех пор, пока не получим частное с заданной точностью.
Упражнение. Пользуясь извлечением из «Таблиц вычисления процентов, умножения и деления» Л. Г. Асатиани (табл. 3), проверить правильность ответов:
1) 382 X 21 = 8022;
2) 382 X 1,5= 573;
3) 9600 X 380 = 3-648 000;
4) 38,1 X 11,2 = 426,72;
5) 24320 : 380 = 64;
6) 388,62 : 38,1 = 10,2;
7) найти 85% от 3810; ответ 3238,5;
8) определить процентное отношение 2133,6 к 38 100; ответ 5,6%;
9) найти 67,7% от 3800; ответ 2573 (с точностью до 1);
10) определить процентное отношение 43 166 к 38 200; ответ 113%;
20. ТАБЛИЦЫ БАРЛОУ
Описание таблиц. Эти широко распространенные таблицы хорошо известны многим работникам вычислительных центров и счетных станций. Ими охотно пользуются и инженерно-технические работники при выполнении всевозможных вычислений.
Как видно из прилагаемого извлечения из таблиц (табл. 4), основное содержание их составляют таблицы квадратов, кубов, корней квадратных и кубических, а также обратных величин — для чисел п в интервале от 1 до 15 000, т. е. п2, п3, 10п, |/п,
1 и —.
п
Для всех чисел, начиная с п = 1000, даются значения величин КГбп. В некоторых столбцах этих таблиц первые цифры, общие для всего столбца, либо вынесены наверх, либо указаны и вверху и внизу. В последнем случае, начиная с числа со звездочкой слева и ниже, надо брать нижние цифры (см. графу Vn в табл. 4).
Определение квадратов и кубов, чисел. Найти квадраты и кубы чисел: 1252; 125,2; 12,52; 0,1252 и 0,001252.
* Находим в левой графе таблицы (табл. 4) соответствующее число и, а в столбцах и2 и п3 читаем ответы:
' 12522 = 1 567 504;
125,22 = 15675,04;
12,522 = 156,7504;
47
co
Таблица 3
Извлечение из таблиц вычисления процентов, умножения и деления Л. Г. Асатиани
380 381 382
— 40 80 — 40 80 — 40 80
152.00 304.00 152.40 304.80 152.80 305.60
1 3.80 155.80 307.80 1 3.81 156.21 308.61 1 3.82 156.62 309.42
2 7.60 159.60 311.60 2 7.62 160.02 ЗГ2.42 2 7.64 160.44 313.24
3 11.40 163.40 315.40 3 11.43 163.83 316.23 3 11.46 164.26 317.06
4 15.20 167.20 319.20 4 15.24 167.64 320.04 4 15.28 168.08 320.88
5 19.00 171.00 323.00 5 19.05 . 171.45 323.85 5 19.10 171.90 324.70
6 22.80 174.80 326.80 6 22.86 175.26 327.66 6 22.92 175.72 328.52
7 26.60 178.60 330.60 7 26.67 179.07 331.47 7 26.74 179.54 332.34
8 30.40 182.40 334.40 8 30.48 182.88 335.28 8 30.56 183.36 336.16
9 34.20 186.20 338.20 9 34.29 186.69 339.09 9 34.38 187.18 339.98
10 50 90 10 50 90 10 50 90
38.00 190.00 342.00 38.10 * 190.50 342.90 38.20 191.00 343.80
1 41.80 193.80 345.80 1 41.91 194.31 346.71 1 42.02 194.82 347.62
2 45.60 197.60 349.60 2 45.72 198.12 350.52 2 45.84 198.64 351.44
3 49.40 201.40 353.40 3 49.53 201.93 354.33 3 49.66 202.46 355.26
4 53.20 205.20 357.20 4 53.34 205.74 358.14 4 43.48 206.28 359.08
5 57.00 209.00 361.00 5 57.15 209.55 361.95 5 57.30 210.10 362.90
6 60.80 21280 364.80 6 60.96 213.36 365.76 6 61.12 213.92 366.72
7 64.60 216.60 368.60 7 64.77 217.17 369.57 7 64.94 217.74 370.54
8 68.40 220.40 372.40 8 68.58 220.98 373.38 8 68.76 221.56 374.36
9 72.20 224.20 376.20 9 72.39 224.79 377.19 9 72.58 225.38 378.18
Г/
20 60 100 20 60 100 20 60 100
76.00 228.00 380.00 76.20 228.60 381.00 76.40 229.20 382.00
1 , 79.80 231.80 383.80 1 80.01 232.41 384.81 1 80.22 233.02 385.82
2 83.60 235.60 387.60 2 83.82 236.22 388.62 2 84.04 236.84 389.64
3 87.40 239.40 391.40 3 87.63 240.03 392.43 3 87.86 240.66 393.46
4 91.20 243.20 395.20 4 91.44 243.84 396.24 4 91.68 244.48 397.28
5 95.00 247.00 399.00 5 95.25 247.65 400.05 5 95.50 248.30 401.10
6 98.80 250.80 402.80 6 99.06 251.46 403.86 6 99.32 252.12 404.92
7 102.60 254.60 406.60 7 102.87 255.27 407.67 7 103.14 255.94 408.75
8 106.40 258.40 410.40 8 106.68 259.08 411.48 8 106.96 259.76 412.56
9 110.20 262.20 414.20 9 110.49 262.89 415.29 9 110.78 263.58 416.38
30 70 НО 30 70 110 30 70 НО
114.00 266.00 418.00 114.30 266.70 419.10 114.60 267.40 420.20
1 117.80 269.80 421.80 1 118.11 270.51 422.91 1 118.42 271.22 424.02
2 121.60 273.60 425.60 2 121.92 274.32 426.72 2 122.24 275.04 427.84
3 125.40 277.40 429.40 3 125.73 278.13 430.53 3 126.06 278.86 431.66
4 129.20 281.20 433.20 4 129.54 281.94 434.34 4 129.88 282.68 435.48
5 133.00 285.00 437.00 5 133.35 285.75 438.15 5 133.73 286.50 439.30
6 136.80 288.80 440.80 6 137.16 289.56 441.96 6 137.52 290.32 443.12
7 140.60 292.60 444.60 7 140.97 293.37 445.77 7 141.34 294.14 446.94
8 144.40 296.40 448.40 8 144.78 297.18 449.58 8 145.16 297.96 450.76
9 148.20 . 300.20 452.20 9 148.59 300.99 453.39 9 148.98 301.78 454.58
3
Таблица 4
Извлечение из таблиц Барлоу
п п2 п3 /п V Юлг 3/— у п 1 п
1250 1251 1252 1253 1254 1 56 25 00 1 56 50 01 1 56 75 04 1 57 00 09 1 57 25 16 1 953 125 000 1 957 816 251 1 962 515 008 1 967 221 277 1 971 935 064 35-355339 369473 14139 383612 141М 397740 14128 411862 14122 14177 110+ Ь8°3 399 44712 L848 1П 44695 1.892 806 Л 44677 1.937 483 44658 1.982 141 44642 10- 772173 _ 2872 775045 2871 -777916 2868 780784 2868 783652 2865 0-000 80018100 6395 7993№ 6335 7987220 6374 7980846 „ „ 6364 7974482 6355
1255 1256 1257 1258 1259 1 57 50 25 1 57 75 36 1 58 00 49 1 58 25 64 1 58 50 81 1 976 656 375 1 981 385 216 1 986 121 593 ‘ 1 990 865 512 1 995 616 979 425979 440090 14111 454196 41Ю 463296 U1“ 482390 14094 14089 2.026 783 44623 2.071 406 „ 44605 2.116 011 44588 2.160 599 Л 44570 2.205 169 44553 786517 789381 2864 792244 2863 Z 797965 2~ 2858 7968127 6344 7961783 6334 7955449 7949126 6 7942812 6314 6304
17
Продолжение табл. 4
п п? п3 Vn /10л з/— у п 1 ' п
1260 1261 1262 1263 1264 1 58 76 00 1 59 01 21 1 59 26 44 1 59 51 69 1 59 76 96 2 000 376 000 2 005 142 581 2 009 916 728 2 014 698 447 2 019 487 744 496479 14083 510502 14077 524639 14072 538711 „ 14067 552778 14060 2.249 722 2.294 256 44 34 2.338 773 44517 44500 2.383 273 44482 2.427 755 л 44464^ 800823 «80 Ж7 2853 809388 2852 812240 2851 7936508 6294 7930214 6284 7923930 6274 7917656 _ „ „ 6264 7911392 6254
1265 1 60 02 25 2 024 284 625 566838 14056 2-472 219 44446 81509! 284д 7905138 6244
1295 1296 1297 1298 1299 1 67 70 25 1 67 96 16 1 68 22 09 1 68 48 04 1 68 74 01 2 171 747 375 2 176 782 336 2 181 825 073 2 186 875 592 2 191 933 899 986108 13892 *000000 13886 013886 13881 027767 13876 041643 13870 3’798 067 43929 3‘841 "6 43912 3'885 908 43895 3’929 803 43878 3.973 681 , - 43862 899919 2805 902724 2803 905527 2802 «32» 911180 2799 7722008 Л Л 5959 7716049 л Л 5949 7710100 5940 7704160 5931 7698220 5921
1300 1 69 00 00 2 197 000 000 055513 36- 4.017 543 110+ 913929 10- 7692308 о-ооо
0,1252й = 0,01567504; г
0,0012522 = 0,000001567504;
12523 = 1 962 515 008;
125,23 - 1962515,008;
12,523 = 1962,515008;
0,12523 = 0,001962515008;
0,0012523 = 0,000000001962515008.
Из приведенных примеров видно, что перенос запятой влево на один знак в числе п вызывает перенос запятой в ту же сторону на два знака в квадрате и на три знака — в кубе.
Извлечение квадратного корня. Рассмотрим примеры:
/1256; /Т2560.
Напомним, что прежде чем извлечь корень, подкоренное число следует разбивать на грани. Если извлекаем квадратный корень, то подкоренное число разбивается на грани по две цифры в каждой, если кубической — по три цифры. Если число целое, то разбиение на грани производится справа налево. Если число содержит десятичные доли, то разбиение на грани производится влево от запятой и вправо от запятой. Число знаков корня, стоящих налево от запятой, равно числу граней в целой части числа, если число больше единицы. Если число меньше единицы, но больше нуля, то при извлечении из него корня квадратного или кубического в результате получается 0 целых и столько нулей до первой значащей цифры, сколько чисто нулевых граней в дробной части числа.
Если левая крайняя грань подкоренного ^исла полная, т. е. содержит две цифры, значение квадратного корня читаем в столбце У п, а если эта грань неполная, то значение корня читаем в столбце
В приведенных примерах, разбивая подкоренное число на грани, имеем:____
/те — две грани, значение корня читаем в столбце К л, корень—двузначное число;
У 1'25'60—три грани, одна грань неполная, значение корня читаем в столбце У 10п, корень —трехзначное число.
В столбце Уп против числа п = 1256 читаем дробную часть корня: 440 090. Целая часть корня, равная 35 и общая для нескольких чисел, вынесена наверх. Следовательно,
У 12^56 = 35,440090.
Обращаем внимание на'то, что в таблицах целая часть корня отделена от дробной части не запятой, а точкой.
Для того чтобы вычислить значение корня У 1'25'60, находим сначала число в 10 раз меньшее п = 1256. В столбце для У10п этому числу соответствует 2,071406, а наверх вынесено 110+. Знак + указывает, что к найденному значению 2,071406 следует прибавить число ПО целых. Таким образом, окончательно получим:
К1'25'60 =110+ 2,071406 =112,071406.
52
Кстати заметим, что Значения квадратных корней непосредственно из таблиц могут быть получены с восемью-девятью значащими цифрами.
Рассмотрим следующие примеры:
1) /Т25Д 2) /0,01.255; 3) /1255; 4) /0,001255.
Разбиваем подкоренные числа на грани:
1) /Й253; 2) /0,01'25'5; 3) /ЙГбб; 4) /0,00'12'55.
В примере 1 левая крайняя грань, а в примере 2 первая грДнь после 0 целых — неполные, в них одна значащая цифра, поэтому при извлечении корня пользуемся столбцом V 10п и читаем ответы:
/Г25^ = 11,2026783; /0,01'25'5=0,112026783.
В примере 3 левая крайняя грань, а в примере 4 первая грань после чисто нулевой — полные, в них две значащие цифры, поэтому воспользуемся столбцом V п и прочтем ответы:
/Т2755 = 35,425979;
/0,00'12'55 = 0,035425979.
Извлечение кубического корня. Извлечем корень: . /1258; 2) /1 258 000; 3) /0,001258.
Находим в левом столбце число п = 1258, а в столбце3/ п читаем ответ;
1) /Р258= 10,795105;
2) /1'258'000 = 107,95105;
3) /0,001'258 = 0,10795105.
Нахождение обратных величин. Последний столбец приведенных таблиц Барлоу содержит значения обратных величин \ \ п / Пользуясь этими значениями, необходимо иметь в виду, что при переносе запятой в числе на один знак запятая в обратной величине этого числа должна быть тоже перенесена на один знак, но в противоположную сторону.
Например, при п= 1257 -^- = 0,0007955449; при л=1,257
— = 0,7955449; при «=0,001257 - =795,5449. п п
Пользование обратными величинами позволяет ускорить процесс деления на всех малых вычислительных машинах, который является наиболее трудоемким процессом по сравнению с умножением. Более подробно об этом см. в гл. VI.
Упражнение. На основании приведенных извлечений из таблиц Барлоу (табл. 4) проверить правильность ответов:
1) 12992 = 1 687 401;
2) 12643 = 2 019 487 744;
53
3) ^ = 0,0007993605;
4) |/12^54 = 3,5411862;
5) КТ25Л= 11,1982141;
6) 12543=1971935064;
7) К1297=36,013886;
8) К12640= 112,427755;
9) |/Т2бТ= 10,803680;
10) т^ = 0,0007722008.
21. ТАБЛИЦЫ ВОЗВЕДЕНИЯ В СТЕПЕНЬ
С. Д. ТИШИНА И С. С. ТИШИНА
Таблицы возведения в степень служат для Облегчения и ускорения наиболее трудоемкой части расчетов по формулам, содержащим степени с дробными и целыми показателями.
Подобные формулы встречаются при расчетах режимов резания, точности обработки на металлорежущих станках, расчетах деталей машин. Они применяются также в теплотехнике и во многих других отраслях техники.
Таблицы полезны инженерно-техническим работникам, преподавателям втузов, студентам высших технических учебных заведений и техникумов, а также всем занимающимся расчетами по формулам, содержащим степени с дробными и целыми показателями.
Все расчеты в таблицах произведены по семизначным логарифмам, что обеспечивает достаточную точность при вычислениях.
Описание таблиц. В 3-м издании таблиц даны числа (основания) от 0,0001 до 1000 и показатели степени от 0,01 до 2, 3 или 4 в зависимости от величины оснований.
Таблицы построены с такими интервалами:
Числа N Интервал г
0,0001—0,001 0,0001
0,001—0,01 0,001
0,01-1 0,01
1—10 0,1
10—1000 1,0
Показатель степени п Интервал
0,01—1,0 0,01
1,0—2,0 0,05
2,0—4,0 1,0
Отдельные дополнения и отклонения в построении таблиц оговариваются авторами во введении к таблицам.
Приводим извлечение из таблиц возведения в степень (табл. 5).
В верхнем внешнем углу страницы авторы указали диапазон чисел (оснований), помещенных на данной странице; показатели степени для каждой группы чисел (оснований) расположены в возрастающем порядке. Такое построение таблиц облегчает их использование.
54
Извлечение из таблиц возведения в степень С. Д. Тишина и С. С. Тишина
Таблица 5
1,1—5,0
N Показатели степени
0,64 0,65 0,66 0,67 0,68 0,69 0,70 0,71
1,1 1,0629 1,0639 1,0649 ‘ 1,0659 1,0670 1,0680 1,0690 1,0700
1,2 1,1238 1,1258 1,1279 1,1299 1,1320 1,1341 1,1361 1,1382
1,3 1,1828 1,1859 1,1891 1,1922 1,1953 1,1985 1,2016 1,2048
1,4 1,2403 1,2445 1,2487 1,2529 1,2571 1,2613 1,2656 1,2698
1,5 '1,2963 1,3015 1,3068 1,3121 1,3175 1,3228 1,3282 1,3336
1,6 1,3509 1,3573 1,3637 1,3701 1,3766 1,3831 1,3896 1,3961
1,7 1,4044 1,4119 1,4194 1,4269 1,4345 1,4421 1,4498 1,4575
1,8 1,4567 1,4653 1,4739 1,4826 1,4914 1,5002 1,5090 1,5179
1,9 1,5080 1,5177 1,5275 1,5373 1,5472 1,5572 1,5672 1,5773
2,0 1,5583 1,5692 1,5801 1,5911 1,6021 1,6133 1,6245 1,6358
2,1 1,6078 1,6197 1,6318 1,6439 1,6562 1,6685 1,6809 1,6935
2,2 1,6563 1,6695 1,6827 1,6960 1,7094 1,7229 1,7366 1,7503
2,3 1,7041 1,7184 1,7328 1,7473 1,7619 1,7766 1,7915 1,8065
2,4 1,7512 1,7666 1,7821 1,7978 1,8136 1,8296 < 1,8456 1,8619
2,5 1,7976 1,8141 1,8308 1,8477 1,8647 1,8818 1,8991 1,9166
2,6 1,8432 1,8609 1,8788 1,8968 1,9151 1,9334 1,9520 1,9707
2,7 1,8883 1,9072 1,9262 1,9454 1,9648 1,9845 2,0043 2,0243
е 1,8965 1,9155 1,9348 1,9542 1,9739 1,9937 2,0138 2,0340
2,8 1,9328 1,9528 1,9730 1,9934 2,0140 2,0349 2,0559 2,0772
2,9 • 1,9767 1,9978 2,0192 2,0408 2,0627 2,0848 2,1071 2,1296
3,0 2,0200 2,0423 2,0649 2,0877 2,1108 2,1341 2,1577 2,1815
Продолжение табл. 5
N Показатели степени
0,64 0,65 0,66 0,67 0,68 0,69 | 0,70 0,71
3,1 2,0629 2,0863 2,1101 2,1341 2,1584 2,1829 2,2078 2,2329
л 2,0805 2,1045 2,1287 2,1532 2,1780 2,2031 2,2285 2,2541
3,2 2,1052 2,1298 2,1548 2,1800 2,2055 2,2313 2,2574 2,2838
3,3 2,1471 2,1729 2,1990 2,2254 2,2521 2,2792 2,3064 2,3342
3,4 2,1885 2,2154 2,2427 2,2703 2,2983 2,3266 2,3552 2,3842
3,5 2,2295 2,2576 2,2860 2,3149 2,3440 2,3736 2,4035 2,4338
3,6 2,2700 2,2993 2,3289 2,3590 2,3894 2,4202 2,4514 2,4830
3,7 2,3102 2,3406 2,3714 2,4027 2,4343 2,4664 2,4989 2,5318
3,8 2,3500 2,3815 2,4136 2,4460 2,4789 2,5122 2,5459 2,5802
3,9 2,3894 2,4221 2,4553 2,4889 2,5230 2,5576 2,5927 2,6282
4,0 2,4284 2,4623 2,4967 2,5315 2,5669 2,6027 2,6390 2,6759
4,1 2,4671. 2,5021 2,5377 2,5737 2,6103 2,6474 2,6850 2,7232
4,2 2,5054 2,5416 2,5784 2,6156 2,6534 2,6918 2,7307 2,7702
4,3 2,5434 2,5808 2,6187 2,6572 2,6962 2,7359 2,7761 2,8168
4,4 2,5811 2,6197 2,6588 2,6984 2,7387- 2,7796 2,8211 2,8632
4,5 2,6185 2,6582 2,6985 2,7394 2,7809 2,8230 2,8658 2,9092
4,6 2,6556 2,6965 2,7379 2,7800 2,8228 2,8662 2,9103 2,9550
4,7 2,6924 2,7344 2,7771 2,8204 2,8644 2,9090 2,9544 3,0005
4,8 2,7289 2,7721 2,8159 2,8604 2,9057 2,9516 2,9983 3,0457
4,9 2,7652 2,8095 2,8545 2,9002 2,9467 2,9939 3,0418 3,0906
5,0 2,8012 ' 2,8466 2,8928 2,9397 2,9874 3,0359 3,0852 3,1352
Продолжение табл. 5
N Показатели степени
0,01 0,02 0,03 0,04 0,06 | 0,06 0,07 0,08
81 82 83 84 85 1,0449 1,0451 1,0452 1,0453 1,0454 1,0919 1,0921 1,0924 1,0927 1,0929 1,1409 1,1413 1,1418 1,1422 1,1426 1,1922 1,1928 1,1933 1,1939 1,1945 1,2457 1,2465 1,2472 1,2480 1,2487 1,3017 1,3027 1,3036 1,3045 1,3055 1,3602 1,3613 1,3625 1,3636 1,3648 1,4213 1,4227 1,4241 1,4254 1,4268
Показатели степени
0,64 0,65 0,66 0,67 | 0,68 0,69 0,70 | 0,71
81 82 83 84 85 16,6506 46,7819 16,9126 17,0427 17,1723 17,3986 17,5380 17,6767 17,8148 17,9524 18,1803 18,3281 18,4753 18,6219 18,7679 18,9970 19,1536 19,3100 19,4656 19,6205 19,8504 20,0167 20,1824 20,3474 20,5119 20,7422 20,9186 21,0942 21,2693 21,4437 21,6740 21,8610 22,0473 22,2329 22,4178 22,6477 22,8459 23,0433 23,2401 23,4362
N Показатели степени
1,80 1,85 1,90 1,95 2,0 3.0 1 4,0
81 82 83 84 85 2724,41 2785,26 . 2846,69 2908,73 2971,35 3393,89 3471,81 3550,54 3630,08 3710,44 4227,87 4327,59 4428,42 4530,34 4633,36 5266,79 5394,33 5523,35 5653,85 5785,85 6561 6724 6889 7056 7225 531 441 551 368 571 787 592 704 614 125 43 046 7?1 45 212 176 47 458 321 49 787 136 52 200 625
На каждой странице в графе, обозначенной буквой Л/, помещены числа (основания), возводимые в степень. В первой горизонтальной строке указаны показатели степени. На пересечении строки, показывающей основание степени, и столбца, указывающего показатель степени, читается результат возведения в степень.
Вычисление степеней с положительными показателями. Рассмотрим примеры:
1) 820,08 = 1,4227;
2) 840,б9 = 21,2693;
3) 811-90== 4227,87;
4) 852 =7225;
5) 834 =47458321;
6) е0,71 =2,0340 *;
7) л°’«4 =2,0805.
В примере 1 находим в таблице, в графе 2V, число 82 и в этой строке, в крайней правой графе показателя степени 0,08, читаем ответ 1,4227.
В примере 2 находим в таблице, в графе W, число 84 и в этой строке, в графе показателя степени 0,69, читаем ответ 21,2693.
В примере 6 находим в таблице, в графе W, число е и в этой строке, в крайней правой графе, соответствующей показателю степени 0,71, читаем ответ 2,0340.
В примере 7 находим в таблице, в графе Af, число лив этой строке, в первой левой графе с показателем степени 0,64, читаем ответ 2,0805.
Вычисление степеней с отрицательными показателями. Найдя ответы на приведенные примеры,, у которых показатель степени положителен, легко определить результаты в том случае, если показатель степени будет отрицателен.
Известно, что если х=82°’08= 1,4227, то #=82“°’08=g~^ =
Таким образом, получим:
“'‘"-«d?-0’000226'
85"8 ==^==0,0001385;
83-4 =474^321 =°-000000021?i
Л“0,64 =
23Й>-“Л г08б5 = 0’481‘
e“o.?i —
♦ Значение е и я даются в таблицах отдельной строкой.
58
Если в таблицах отсутствует необходимое основание а показатель степени имеется или, наоборот, отсутствует необходимый показатель степени п, а основание имеется, то в таких случаях для определения результата прибегают к методу линейной интерполяции, производя расчеты по формулам 1 и 2, приведенным авторами во введении к таблицам. Однако следует иметь в виду, что по мере возрастания основания и интервала в показателях степени метод линейной интерполяции дает существенную ошибку. Это положение иллюстрируется конкретными примерами.
Авторы показывают, как, пользуясь таблицами, можно возвести в степень числа, большие 1000, а также числа, у которых показатель степени задан в виде простой дроби, например:
'1 I
864 = 850;25 = 3,0364; 855 = 85°’«о = 5,9125.
Упражнение. Пользуясь приведенными извлечениями из «Таблиц возведения в степень», проверить правильность ответов:
1) 1,90,66= 1,5275; 5) 82ь*5 =3471,81;
2) е0,68 =1,9739; 6) л"<>’7 =0,464;
3) л0’71 =2,2541; 7) 84"°’65 = 0,0561;
4) е-0’6* =0,521; 8) 8Р’О5 =1,2457.
22. СОСТАВЛЕНИЕ ТАБЛИЦ ДЛЯ ПРАКТИЧЕСКИХ ЦЕЛЕЙ
х Систематически пользуясь таблицами, необходимо выработать навык и самим составлять таблицы в тех случаях, когда приходится вести какие-то однотипные' расчеты. При их составлении можно использовать таблицы Барлоу, О’Рурка, Асатиани и др. Широкое использование счетных таблиц значительно ускоряет процесс вычислений, повышает производительность труда работника, обеспечивает достоверность результатов вычислений. На практике часто приходится самостоятельно составлять простейшие вычислительные таблицы для однотипных вычислений. В этом случае надо особенно внимательно следить за правильностью ответов, внесенных в таблицу.
В качестве примера рассмотрим таблицу для вычисления стоимости хлопчатобумажной платяной ткани по 2 р. 16 к. за 1 м.
Количество метров Стоимость в руб. и коп. Количество метров Стоимость в руб. и коп.
1 2—16 6 12—96
2 4—32 7 15—12
3 6—48 < 8 17—28
4 8—64 9 19—44
5 10—80 10 21—60
Имея под руками такую таблицу, легко определить не только стоимость 5 или 8 м ткани, но и подсчитать стоимость отреза боль
59
шего метража, например 38 м. Для этого находим по таблице стоимость Зм — 6р. 48 к. и, увеличивая это число в 10 раз, получаем стоимость 30 м — 64 р. 80 к. Затем находим по таблице стоимость 8 м— 17 р. 28 к. Складывая стоимость отрезов в 30 м и 8 м: 64 р. 80 к. + 17 р. 28 к., получаем ответ 82 р. 08 к. Таким образом, 38 м ткани по 2 р. 16 к. за метр стоят 82 р. 08 к.
Можно составить' таблицу стоимости ткани для любого количества метров и сантиметров (с точностью до 10 см). Схематически она будет выглядеть так:
см м 0 10 20 30 40 50 60 70 80 90 см / / м
0 — -22 -43 -65 -86 1-08 1-30 1-51 1-73 1-94 0
1 2-16 2-38 2-59 2—81 3-02 3-24 3-46 3-67 3-89 4-10 1
2 4-32 2
3 6—48 3
4 8-64 4
5 10-80 5
6 12—96 6
7 15-12 7
8 17-28 8
9 19-44 9
10 21-60 10
С помощью этой таблицы нетрудно определить стоимость покупки в 1 м40см (3 р. 02 к.), 1 мбОсм (ЗрЛбк.), 1 м90 см (4 р. 10 к.), 15 м (32 р. 40 к.), 30 см (65 коп.).
Чтобы найти стоимость 1 м 40 см, в левой крайней графе находим цифру 1, а затем по этой строке ведем до графы для 40 см и на пересечении читаем результат 3 р. 02 к.
Рекомендуется с помощью «Таблиц умножения» О’Рурка самостоятельно запбл-нить таблицу до конца и v определить стоимость ткани: 5 м 60 см; 18 м 20 см; 9 м 50 см; 80 см; 60 см; 14 м 70 см; 6 м 40 см; 22 м 20 см; 3 м 90 см; 7 м 70 см.
Кроме приведенных форм можно использовать и другие, в зависимости от потребностей в подсчетах,
Глава V
СЧЕТНАЯ ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА
Логарифмическая линейка является доступным и портативным счетным прибором, позволяющим значительно сократить время и труд на всевозможные вычисления. Научиться быстро и точно работать на логарифмической линейке значительно легче, чем это многим кажется. Затратив несколько часов на изучение этой главы и решив все приведенные в ней примеры и задачи, изучающий линейку приобретает необходимые навыки в работе. Повседневное пользование линейкой позволит довольно скоро овладеть и техникой быстрого счета.
Лица, незнакомые с теорией логарифмов, могут пользоваться линейкой для умножения, деления, возведения чисел в квадрат и извлечения квадратного корня. Для этого им следует изучить п. 24—34 пособия, решив все приведенные примеры.
23. ПРИНЦИП УСТРОЙСТВА ЛОГАРИФМИЧЕСКОЙ ЛИНЕЙКИ
Если взять две обычные линейки, имеющие равномерные шкалы, то с их помощью можно производить действия сложения и вычитания. В этом легко убедиться, решив примеры: 2 + 4 = 6 и 8 — 3=5.
В первом случае, совместив шкалы линеек, как показано на рис. 3, найдем ответ: 6. Во втором, рассматривая положение шкал на рис. 4, читаем ответ: 5.
Однако использовать линейки для сложения и вычитания нецелесообразно. Этот прием оказывается очень полезным для умножения, деления, а также выполнения других операций над числами, если воспользоваться не обычными линейками с равномерными шкалами, а линейками с так называемыми логарифмическими шкалами.
Для построения логарифмической шкалы «нормальной» счетной линейки с длиной шкал 25 см воспользуемся следующим «уравнением логарифмической шкалы»:
а = т 1g а,
где а — метка штриха, поставленного на расстоянии а см от начала шкалы; т — «модуль» шкалы, равный ее длине, в нашем случае 25 см.
61
Рис. 3. Сложение при помощи двух линеек, имеющих равномерные шкалы
Разность 5 Вычитаемое 3
Рис. 4. Вычитание при помощи двух линеек, имеющих равномерные шкалы
Рис. 5. Построение логарифмической шкалы «нормальной» счетной линейки (с длиной шкал 25 см)
62
Умножая «модуль» шкалы (25) последовательно на 1g 1, 1g 2, lg 3, lg 4 и т. д., получаем длины отрезков (в см), соответствующие числам 1, 2, 3, 4_и т. д. (табл. 6).
Нанеся длины отрезков на линейку, получим логарифмическую шкалу (рис. 5).
Из курса математики средней школы известно, что для положительных чисел а и b и любого числа п #= О
1g (а£>) = lg а + 1g £>; lgy = lga—Ig6;
igan = n\ga; Igy^a =lga" =—,
т. e. логарифм произведения равен сумме логарифмов сомножителей, логарифм частного — разности логарифмов делимого и делителя, логарифм степени — логарифму основания, умноженному на показатель степени, и, наконец, логарифм корня — логарифму подкоренного числа, деленному на показатель степени корня.
Зная эти соотношения и используя логарифмическую шкалу, мы можем свести действие умножения к сложению логарифмов сомножителей, а действие деления — к вычитанию логарифма делителя из логарифма делимого и т. д.
Пример 1.
ab = с при a = 2 и 6 = 3. \
Таблица 6
Отрезки логарифмической шкалы, соответствующие числам от 1 до 10
Число а 1g а Длина шкалы в см Отрезок шкалы, соответствующий числу а, в см
1 0,0000 25 0
2 0,3010 25 7,53
3 0,4771 25 11,93
4 0,6021 25 15,05
5 0,6990 ‘ 25 17/48
6 0,7782 25 19,46
7 0,8451 25 21,13
8 0,9031 25 22,58
9 0,9542 25 23,86
10 1,0000 25 25,00
Логарифмируя обе части равенства, имеем lg а + lg b = 1g с. Взяв две линейки с логарифмическими шкалами и сделав установку, показанную на рис. 6, видим, что мы произвели сложение 1g 2 и lg 3, получив в результате 1g 6, т. е. произведение 2 на 3.
63
Пример 2.
— с яри а —8 и 6 = 4.
Логарифмируя обе части равенства, имеем lg cl — 1g b = 1g c.
Соответствующая установка показана на рис. 7, из которого видно,, что разность логарифмов делимого и делителя дает логарифм частного, которое в нашем примере равно 2.
24. ОПИСАНИЕ ЛОГАРИФМИЧЕСКОЙ ЛИНЕЙКИ
Счетную логарифмическую линейку составляют три части. * 1. Корпус линейки.
2. Движок, свободно передвигающийся в пазах корпуса линейки.
3. Бегунок, на стекле которого нанесена линия, называемая визирной линией (или волоском), служащая для облегчения чтения чисел на шкалах.
На лицевой стороне логарифмической линейки (рис. 8) обычно нанесено пять шкал (считая снизу вверх):
1) шкала мантисс логарифмов, расположенная внизу корпуса линейки;
2) шкала умножения, или основная шкала, расположенная частью на корпусе и частью на движке линейки;
3) обратная (красная) шкала, расположенная посередине движка и отличающаяся от основной только тем, что нанесена в обратном порядке, справа налево;
4) шкала квадратов, состоящая из двух совершенно одинаковых шкал (левой и правой), расположенная частью на движке в частью на корпусе линейки;
5) шкала кубов, расположенная вверху корпуса линейки, состоящая из' трех совершенно одинаковых шкал (левой, средней и правой).
На оборотной стороне движка (рис. 9) нанесены три шкалы тригонометрических величин (считая снизу вверх):
6) шкала тангенсов углов от 5°44' до 45°, обозначаемая tg;
7) шкала синусов и тангенсов малых углов от 0°34' до 5°44', обозначаемая буквами S и Т;
8) шкала синусов углов от 5°44' до 90°, обозначаемая sin.
По бокам логарифмической линейки нанесены сантиметровые деления и масштабная шкала.
На оборотной стороне корпуса линейки помещен ряд физических констант: коэффициенты линейного расширения, модули упругости и т. д., которые бывают необходимы при технических расчетах.
В продаже лмеются линейки со шкалами длиной 12,5; 25 и 50 см. Наиболее удобной считается линейка с длиной шкалы 25 см, поэтому все дальнейшие рассуждения будут вестись с расчетом на эту линейку.
От размера шкал зависит точность подсчетов: чем меньше длина шкалы линейки, тем меньше точность результата. Линейка с длиной шкалы 25 см, так называемая нормальная, при ее портативности обеспечивает результат вычислений с точностью до трех-четырех
64 - ’ S
оо
Делитель 4
S
СТ
к »
Рис. 7. Схема установки логарифмических шкал при делении
Шкала квадратов бегунок Шкала кудов
Рис. 6. Схема установки логарифмических шкал при умножении
Корпус линейки Обратная (красная) шкала
|||1ПГ|11П111П1Н111111|111нп||нТП|Н111япв11111а1«1|||л11ПМ1П1||||нн1111|||||1|п11Ини11Пй|||С1|111111иппииииш1и1П1иш11НЦН1П11
2
г
<!
30 ”.1.1 .1,15
Движок
Основная шкала
Визирная линия Шкала мантисс логарифмов (волосок)
Рис. 8. Лицевая сторона логарифмической линейки '
сл
знаков, вполне достаточный для большинства практических расчетов. Относительная точность подсчета на логарифмической линейке одинакова на всем протяжении шкалы.
При пользовании логарифмической линейкой необходимо помнить, что это счетный прибор, требующий осторожного обращения. Во избежание царапин, порчи шкал хранить линейку нужно в футляре, не ронять, не использовать в качестве обычной линейки, не класть ее в слишком сухое или слишком сырое место, так как это приведет к деформации шкал и понизит точность расчетов.
Шкала синусов (от 5°W до 90°)
Рис. 9. Оборотная сторона движка логарифмической линейки
Работать на линейке лучше с карандашом в руке, так как чернильные'пятна со шкал не удаляются. Загрязненные шкалы протирают кусочком ваты, смоченной в одеколоне или спирте. Нельзя протирать шкалы веществами, растворяющими целлулоид: ацетоном, амилацетатом, эфиром, уксусной кислотой и др.
В случае образования щели между движком и корпусом линейку следует отрегулировать: вынуть движок, снять бегунок, после чего корпус линейки обжать внутрь, в поперечном направлении, -вдоль всей линейки. Имеющиеся внутри линейки компенсационные пружины позволяют регулировать щель между движком и корпусом и ход движка линейки.
25. ЦЕНА ДЕЛЕНИЙ ОСНОВНОЙ ШКАЛЫ
Знание цены делений шкал является одним из важнейших условий в работе с логарифмической линейкой, обеспечивающих быстроту и точность подсчетов. Поэтому обращаем внимание изучающих на то, что цену делений 'шкал необходимо хорошо усвоить.
Перейдем к разбору цены делений основной шкалы.
Если мы внимательно рассмотрим основную шкалу, то увидим ряд отметок, нанесенных крупным шрифтом по всей длине шкалы: _ 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10; кроме того, в промежутке от 1 до 2 заметим ряд делений, обозначенных более мелким шрифтом: 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8 и 1,9. Деления в промежутке от 1 до 2 нанесены лишь потому, что это большой интервал, в котором легко можно прочитать числа, тогда как, например, в интервале от 8 до .9 или от 9 до 10 их было бы почти невозможно разобрать.
Рассматривая деления на основной шкале, замечаем, что они неодинаковы во всех интервалах. Так, интервал от 1 до 2 разделен на 10 крупных делений, причем каждое из этих делений разделено еще на 10 мелких. Интервалы от 2 до 3 и от 3 до 4 разделены каждый на 10 крупных делений, и затем каждое из этих делений разделено уже не на 10 мелких делений, как в первом случае, а всего лишь на 5.
66
Наконец, интервалы от 4 до 5 и все последующие разделены каждый на 10 крупных делений, а эти последние, в свою очередь, разделены уже не на 10, как в первом случае, и не на 5, как во втором, а всего лишь на 2.
Таким образом, цена мелких делений на основной шкале неодинакова и сводится к трем видам. Какова же цена мелких делений в каждом отдельном случае?
Для того чтобы уяснить это, предположим, что каждый интервал равен 100. Тогда в интервале от 1 до 2 мы имеем 10 крупных делений, из которых каждое разделено на 10 мелких, т. е. всего 100 деле-
ний, и, следовательно, каждое мелкое деление равно единице, так как 100 : 100 — 1. В интервалах от 2 до 3 и от 3 до 4 мы имеем цену делений, равную 2. Эти отрезки разделены на 10 крупных делений, а . каждое крупное — на 5 мелких, т. е. отрезок разделен всего на 50 делений, и, таким образом, цена деления будет равна 100 : 50 = 2. В интервале от 4 до 5 и во всех последующих цена каждого мелкого
деления равна 5. Полагая отрезок от 4 до 5 равным 100, замечаем, что он разделен на 10 крупных делений, а каждое крупное,, в свою очередь, разделено еще на 2, т. е. всего этот интервал разделен на 20 делений, а 100 : 20 = 5.
Итак, на основной шкале логарифмической линейки имеется три вида делений. Для лучшего запоминания цены делений отдельных участков основной шкалы сведем их в табл. 7.
Каждое пятое деление на
Таблица 7
Цена делений основной шкалы логарифмической линейки
Вид делений Интервал Цена деления
I 1—2 1
II 2—4 2
III 4-10 5
основной шкале отмечено более
длинной черточкой (это сделано для ускорения чтения чисел).
Точно такие же деления имеются и на обратной, или красной, шкале, и поэтому цена ее делений совпадает с ценой делений основной шкалы. Цена делений на шкалах квадратов и кубов одинакова. В интервале от 1 до 2 она равна 2, в интервале от 2 до 5—5 и, наконец, в интервале от 5 до 10 —- 10. В этом легко убедиться, рассуждая
аналогично тому, как мы это делали при определении цены деления основной шкалы.
Шкала мантисс логарифмов равномерна, и цена каждого' ее мелкого деления равна 2.
26. УСТАНОВКА И ЧТЕНИЕ ЧИСЕЛ НА ОСНОВНОЙ ШКАЛЕ
При установке и чтении чисел на логарифмической шкале не обращают внимания на запятую, если число дробное. Так, числа 0,11; 1,1; 11; ПО, 11 000 будут установлены в одном и том же месте шкалы.
На рис. 10 приведено несколько примеров установки и чтения чисел. По отметкам, показанным стрелками, мы видим, как нужно устанавливать числа на шкале. Для получения более точного результата в подсчетах нужно как можно тщательнее устанавливать числа на шкалах.
Очень важно научиться быстро и точно читать числа на шкале, поэтому начинающим необходимо больше практиковаться в установке и чтении чисел.
Ниже приведено несколько упражнений.
Установить волоском: 4; 6; 0,8; 0,05; 105; 17,5; 525; 9,1; 11 000; 2,5; 25; 1,03; 192; 16 400; 222; 202, 405; 450; 7950.
Если надо установить число, например 2230, то в этом случае в интервале от 2 до 3 берут два крупных деления — получают 2200, одно малое, равное 20, и половину следующего (устанавливают приблизительно), т. е. 10, и получают 2230.
Установить следующие числа: 423; 210; 3,11; 16,05; 503; 2,43; 0,451; 55,6.
Если число имеет более трех-четырех значащих цифр, в своем написании, например 18 607, то в этом случае устанавливают 18 600, отбрасывая цифру 7, так как ее на глаз не установить. Точно так же вместо 211 014,5 ставят 211 000, а 14,5 отбрасывают. Если же надо установить число 32 198, то в этом случае берут 32 200.
Установить следующие числа: 17,241; 20,002; 37614,2; 175,99; 926,14; 4050,3.
Для ускорения и точности в установке ряда постоянных величин их значения отмечены на шкалах линейки специальными символами. Эти символы, их значения и местоположения даются в табл. 8. Рекомендуется самим найти их на соответствующих шкалах.
Пользование специальными символами не представляет затруднений и легко усваивается в практической работе.
27. ПОРЯДОК ЧИСЕЛ
Для быстрого определения результата подсчета на логарифмической линейке необходимо усвоить понятие «порядок числа».
Порядком числа будем называть количество цифр в целой части этого числа, если оно больше или равное единице, и количество нулей между запятой и первой значащей цифрой, если число меныце единицы. В первом случае порядок чисел считается положительным, во втором—отрицательным (табл. 9).
Сравнивая порядок чисел с их характеристикой при логарифмировании,
68
Таблица 8
Некоторые специальные, обозначения на шкалах линейки
Специальные обозначения Значение Шкалы линейки
Л 3,14159 ОснЬвная и шкала квадратов
С |/ -^-=1,12838 Основная
Ci — = 3,56825 >
м —=0,31837 л Шкала квадратов
р' 360 - 60 2» -3437-’ Основная
р" зи.бо.бо _м6 265 2л
ру/ 10$ =636 620 Л >
Таблица 9
Порядок некоторых чисел
Числа больше единицы Числа меньше единицы
Число Порядок числа Число Порядок числа
2 +1 0,05 — 1
74 +2 0,0017 —2
1042 +4 0,0004 —3
128 614 +6 0,000003 —5
318 +3 0,01475 —1
61,7 +2 0,5 0
7 000 +4 0,000014 —4
4,8 4-1 0,16 0
28,6 4-2 0,0047 —2
351,64 +3 0,8649 0
1 001,9 +4 0,00125 —2
7,644 +1 0,514 0
864,172 4-3 0,0001 —3
69
Таблица 10
Сравнение порядка чисел с их характеристикой
Число Порядок числа ** Характеристика
6 + 1 0
72 +2 + 1
4814 4-4 +3
0,015 —1 —2
0,5 0 —1
замечаем, что он всегда больше характеристики на единицу (табл.-10). Более подробно характеристика логарифма чйсла будет рассматриваться в п. 37.
28. ПРОВЕРКА ЛИНЕЙКИ
Для обеспечения точности в работе с логарифмической линейкой полезно периодически производить ее проверку. В процессе проверки необходимо установить следующее.
.1. Лежит ли верхняя поверхность движка в одной плоскости с верхней поверхностью корпуса, нет ли перекоса.
2. Отмечает ли волосок бегунка начала и концы всех шкал при совмещении начального штриха основной шкалы на корпусе и движке линейки и совпадают ли черточки (риски) в вырезах оборотной стороны линейки с началом и концом тригонометрических шкал.
3. Достаточно ли легко и плавно передвигаются в пазах корпуса линейки движок и бегунок. Если они передвигаются с трудом, то можно несколько отогнуть рамку бегунка, а если очень легко, то подогнуть ее.
4. Правильность ответов при выборочных вычислениях, например: 22 = 4; 23 — 8; 1^25 = 5; у^64 = 4; 6:3= 2; мантисса 1g 3 равна 0,477; sin 30° = 0,5; tg 30° = 0,577 и т. д.
29. УМНОЖЕНИЕ
Правило умножения двух чисел. Для того чтобы перемножить два числа, поступают следующим образом: на корпусе линейки, на основной шкале, находят первый сомножитель, засекают его волоском, а затем подводят под волосок начало или конец движка, находят на основной шкале движка второй сомножитель, засекают его волоском и на основной шкале линейки на корпусе читают результат.
Пример 1.
2X4=8.
В данном случае поступают так: находят сначала на основной шкале корпуса линейки цифру 2, засекают ее волоском, под волосок подводят начало движка, выдвигая его вправо; затем на основной шкале движка находят цифру 4, засекают ее волоском и под волоском, на основной шкале линейки на корпусе, читают произведение: 8. Схема установки при умножении 2 на 4 показана на рис. 11,
70’
Пример 2.
4 X 8 = 32.
Находим на основной шкале корпуса линейки первый множитель 4, засекаем его волоском; затем подводим под волосок конец движка, выдвигая движок влево, находим на движке второй множитель 8, засекаем его волоском и под волоском на основной шкале корпуса линейки читаем произведение: 32.
В примере 1 при умножении 2 на 4 мы выдвигали движок вправо, в примере 2, при умножении 4 на 8, влево. Если бы при умножении
Первый сомножитель 2 Второй сомножитель Ч
Рис. И. Схема установки движка при умножении
4 на 8 мы выдвинули движок вправо, то второй множитель 8, взятый на движке, вышел бы за пределы корпуса линейки и мы не смогли бы прочитать результат.
Чтобы сократить число перебросок движка при производстве вычислений и тем самым ускорить подсчеты, у некоторых линеек на основной шкале и шкале квадратов слева и справа сделаны дополнения (рис. 12).
Рис. 12. Дополнительные отрезки шкал на основной шкале и шкале квадратов
На основной шкале слева дан дополнительный отрезок шкалы в интервале 8,85 — 10, а справа — отрезок в интервале 1 — 1,13. Так, при умножении 13 на 8 на линейке без дополнительных шкал мы делаем установку началом движка, выдвигаем его вправо и устанавливаем на 13. Второй множитель 8, взятый на движке, вышел за пределы основной шкалы на корпусе линейки, и для получения ответа необходимо сделать его переброску, установив против 13 не начало, а конец движка. После этого мы прочитаем ответ: 104. При наличии дополнительных шкал переброска исключается.
71
Сказанное относится и’ к дополнительным отрезкам шкалы квадратов (отрезок слева 7,8 — 10, отрезок справа 1 — 1,28). ~
Упражнение. Выполнить умножение двух чисел на линейке:
1) 25 X 3 = 75; 11) 145 X 2 = 290;
2) 8 X 9 = 72; 12) 1850 X 3 = 5550;
3) 6,5 X 6 = 39; 13) 175 X 0,12 = 21;
4) 0,4 X 0,5 = 0,2; 14) 725 X 6 = 4350;
5) 32 X 0,5 = 16; 15) 3,42 X 34,5 = 118;
6) 15 X 31 = 465; 16) 88,7 X 7,28 = 646;
7) 1,8 X 30= 54; 17) 52,6 X 0,331 = 17,41;
8) 22,5 X 2 = 45; 18) 40,5 X 49,5 = 2000;
9) 2-5 X 7 = 175; 19) 293 X 5,2 = 1524;
10) 16 X 1,6= 25,6; 20) 8,19 X 0,187 = 1,532.
Определение порядка произведения двух чисел. В приведенных выше примерах порядок произведения определяется легко. В тех же случаях, когда вычислить порядок произведения путем подсчета в уме затруднительно, можно воспользоваться специальным правилом для определения порядка произведения.
Например: 7700 X 0,02 = 154.
Произведя необходимую установку, читаем результат: цифры 1 — 5 — 4. Но сказать сразу, рассматривая положение волоска, каков будет этот результат— 15,4 или 154, или 1540и т. д. — нельзя, и для его определения потребуется или сделать подсчет в уме, или же воспользоваться следующим правилом.
При перемножении двух чисел порядок произведения равен сумме порядков сомножителей, если движок выдвигался влево, и сумме порядков сомножителей минус единица, если движок выдвигался вправо.
Обозначив порядок произведения через N, порядок множимого через и порядок множителя через п2, можем, пользуясь этим правилом, написать следующие формулы для порядка произведения двух чисел:
ч = «1 +
Л^пр ~h 1 •
Правилом знаков для определения порядка произведения следует пользоваться только в тех случаях, когда подсчет его действительно затруднителен; во всех прочих случаях нужно стараться получить ответ в уме путем грубой прикидки. Это значительно ускорит подсчеты. Рассмотрите с этой целью табл. 11.
Упражнение. Выполнить умножение двух чисел на линейке и определить порядок произведения:
1) 140 X 0,02 = 2,8;
2) 0,45 X 0,04 = 0,006;
3) 1550 X 0,02 = 31;
4) 0,04 X 0,03 = 0,0012;
5) 0,008 X 0,05 = 0,0004;
6) 75 X 0,06 = 4,5;
7) 550 X 0,3 = 165;
8) 2,4 X 1,6= 3,84;
9) 0,4 X 0,6 = 0,24;
10) 0,03 X 300 = 9;
11) 15,4 X л = 48,4;
12) 0,421 X 192,1 = 80,9;
13) 0,081 X 572 = 46,3;
14) 0,241 X 33,1 = 7,98;
15) 8,19 X 0,187= 1,532;
16) 3,49 X 0,0482 = 0,1682;
17) 3600 X 0,002 = 7,2;
18) 0,2 X 3,05= 0,61;
19) 2,75 X 285 = 784;
20) 4,38 X 0,0873 = 0,382.
72
Таблица И
Примеры определения порядка произведения грубой прикидкой
Действия Цифры ответа Грубая прикидка Ответ
12,2 X 40 5,87 X 0,9 739 X 9,8 220 : 20 5963 : 8,9 4,5 X 2,5 X 6,9, 83,3 X 1,72 3,96 ОО ОС ХГ Г- OJ III 1 1 00 СЧ СЧ г-н Г- г- со 1 1 1 1 1 1 1 Ю Г- —' со г- со 10X 40 = 400 6X1 =6 740 X 10 = 7400 200 : 20 = 10 6000 : 10=600 5x2 =1.0; 10X7 =70 -?-=20; 4 20X2 ==40 488 5,28' 7240 11 670 • 77,7 36,2
В примере 1 порядки сомножителей равны: /г1 = +3и/г2 = —1, движок при перемножении выдвигался вправо; следовательно, порядок произведения
/' tfnp = + 3+(-i)-i = +1.
Ответ: 2,8.
В примере 4 порядки сомножителей равны: пх = — 1 и п2 = — 1, движок при перемножении выдвигался влево; следовательно, порядок произведения
Ответ: 0,0012.
В примере 9 порядки сомножителей: их == 0 и я2 = 0, движок при перемножении выдвигался влево; следовательно, порядок произведения
Л^Л = 0 + 0 = 0.
Ответ: 0,24.
В примере 11 порядки сомножителей: пх = +2 и п2 = +1, движок при перемножении выдвигался вправо; следовательно, порядок произведения
ЛГпр = +2 + 1 - 1 = +2.
Ответ: 48,4.
В примере 20 порядки сомножителей: ях = 1 и я2 = —1, движок при перемножении выдвигался влево, следовательно, порядок произведения
Мл = + 1 + (-1) = 0.
Ответ: 0,382.
Умножение нескольких чисел. При перемножении трех и более сомножителей, например 2 Х'З X 4 X 6 = 144, поступаем следующим образом: сначала умножаем 2 на 3, получаем 6; затем рассматриваем 6 как новое число, которое необходимо умножить на 4,
73
т. е. засекаем 6 волоском, под волосок подводим конец движка, выдвигая его влево, находим на движке цифру 4 и засекаем волоском; в результате получаем 24. Затем 24 рассматриваем как новый множитель, который надо умножить на 6. Для этого под волосок, стоящий на 24, подводим еще раз конец движка, выдвигая его влево, находим на движке цифру 6, засекаем ее волоском и на основной шкале корпуса линейки читаем окончательный результат: 144.
‘ Разбор вышеприведенного примера приводит к выводу, что перемножение нескольких чисел ничем существенным не отличается от перемножения двух чисел. Перемножая ряд чисел, обычно не читают промежуточных результатов, так как это отнимает много времени.
Что касается нахождения порядка произведения, то в простых случаях его нужно определять путем прикидки в уме, а в'более сложных — пользуясь следующим правилом.
Порядок произведения нескольких сомножителей равен сумме порядков сомножителей минус столько единиц, сколько раз при перемножении движок выдвигался вправо (т. е. производилась установка числа началом движка).
Обозначив W — порядок произведения, nlt ..., nk — порядки сомножителей и а — число выдвижений движка вправо, получим следующую формулу для определения порядка произведения нескольких сомножителей:
N = пх + п2 + ... + п* — а.
Для облегчения подсчета порядка произведения каждый ход движка вправо отмечаем на бумаге каким-нибудь знаком — точкой, галочкой и т. д.
Разберем применение этой формулы на следующем примере:
0,4 X 20 X 0,5 X 0,06 X 2,5 = 0,6.
Порядки сомножителей соответственно равны: 0; +2; 0; —1; +-1; при перемножении движок выдвигался вправо два раза; следовательно, порядок произведения равен
#= 0+2+0+'(—1)+ 1-2= 0
и произведение равно 0,6.
Упражнение. Выполнить умножение нескольких чисел и определить порядок произведения:
1) 0,6 X 0,3 X 150 = 27;
2) 0,25 X 44 X 0,02 X 0,004 = 0,00088;
3) 45 X 12,5 X 0,003 X 0,2 = 0,338;
4) 5500 X 0,5 X 40 X 0,06 = 6600;
5) 0,3 X 0,002 X 0,04 X 0,4 X 25 = 0,00024;
6) 8,37 X 41,6 X 0,228 X л = 249;
7) 6,65 X 19,3 X 0,717 X 3,62 X 8,22 = 2740.
В примере 5 порядки сомножителей соответственно равны: 0; —2; —Г, 0; +2; движок выдвигался вправо два раза; следовательно, пор'ядок произведения
N = 0 + (-2) + (—1) + 0+ 2- 2= —3
и произведение равно 0,00024.
74
В примере 6 порядки сомножителей соответственно равны +1; +2; 0; +1; движок выдвигался вправо один раз; следовательно, порядок произведения
^=1 + 2+04-1 — 1 = +3
и произведение равно 249.
30. ДЕЛЕНИЕ
Правило деления двух чисел. Для того чтобы разделить с помощью логарифмической линейки одно число на другое, находят на основной шкале корпуса линейки делимое, засекают его волоском, затем под волосок подводят делитель, взятый на основной шкале движка, и частное читают на основной шкале корпуса линейки против начала или конца движка.
Пример 1.
а: 3=3.
Прежде всего находим на основной шкале корпуса линейки делимое — число 9 — и засекаем его волоском. Затем, выдвигая
Рис. 13. Схема установки движка при делении
движок вправо, подводим под волосок делитель, взятый на основной шкале движка, — число 3. Слева от бегунка, против начала движка, на основной шкале корпуса линейки читаем частное 3. Схема установки движка при делении на 3 дана на рис. 13.Z
Пример 2.
15 : 3 = 5.
Засекаем волоском на основной шкале корпуса линейки делимое — число 15. Затем, выдвигая движок влево, .подводим под волосок делитель, взятый на основной шкале движка, — число 3 — и справа от бегунка, против конца движка, на основной шкале линейки читаем частное 5.
Упражнение. Выполнить деление на линейке:
1) 1620 : 20 = 81;
2) 455 : 35 = 13;
3) 212 : 78,5 = 2,7;
4) 615 : 1,5 = 410;
5) 76,4 : 0,4-= 191;
6) 228 : 3 = 76.
75
Во всех приведенных примерах порядок частного определяется легко. В тех случаях, когда порядок частного вычислить путем подсчета в уме затруднительно, можно воспользоваться следующим правилом.
Определение порядка частного двух чисел. Порядок частного равен разности порядков делимого и делителя, если при делении движок выдвигался влево, и разности порядков делимого и делителя плюс единица, если движок, выдвигался вправо.
Обозначая через М порядок частного, через тх порядок делимого и через т2 порядок делителя, можем записать это правило в виде следующей формулы:
Мл = тх —
Мпр = /пх — /п2 + 1.
Как и при умножении, этим правилом следует пользоваться только в том случае, когда определение порядка частного действительно затруднено. Во всех других случаях нужно стараться получить ответ путем прикидки в уме — это позволит значительно ускорить подсчеты (см. табл. 11).
Упражнение. Выполнить деление на линейке и определить порядок частного:
1) 4,5 : 0,0225 = 200;
2) 0,275 : 0,5 = 0,55;
3) 0,016 : 0,8 = 0,02;
4) 0,0004 : 0,05 = 0,008;
5) 49,6 : 3250 = 0,01526;
6) 0,000372 : 0,00448 = 0,083.
В<примере 1 порядок делимого т1 = +1, порядок делителя т2 =—1, движок выдвигался вправо; следовательно, порядок частного
Жпр = +1 — (—1) + 1 = +3
и частное равно'200. -
В примере 4 порядок делимого тх = —3, порядок делителя т2 = —1, движок выдвигался влево; следовательно, порядок частного
2ИЛ == —3 — (—1) = -^-2
и частное равно 0,008.
В примере 5 порядок делимого тх = +2, порядок делителя /и2 == +4, движок выдвигался вправо; следовательно, порядок частного
Мпр= + 2-(+4)+ 1 = -1
и частное равно 0,01526.
В примере 6 порядок делимого т1 — —3, порядок делителя т2 = —2, движок выдвигался влево; следовательно, порядок частного
7ИД= —3 —(—2) = —1
и частное равно 0,083.
76
31. УМНОЖЕНИЕ И ДЕЛЕНИЕ НА ШКАЛЕ КВАДРАТОВ И С ПОМОЩЬЮ ОБРАТНОЙ ШКАЛЫ
Умножение и деление на шкале квадратов. В целях ускорения подсчетов иногда полезно производить умножение и деление на шкале квадратов и с помощью обратной, или красной, шкалы. Установка чисел при умножении и делении на шкале квадратов ничем не отличается от установки чисел на основной шкале. В связи с тем, что левая и правая шкала квадратов в два раза меньше основной шкалы, результат будет менее точен.
Умножение на шкале квадратов ускоряется тем, что не надо делать переброски движка. Цену делений шкалы квадратов рекомендуем установить самим. Умножение с помощью шкалы квадратов 2X3—6 показано на рис. 14.
В этом случае порядок произведения равен сумме порядков сомножителей, если произведение читается не на той шкале, на ко-
1?6
ig в
Шкала квадратов
Произведение 6 Произведение 6
2 3 k 5 6Л39Ю 20 30 40 50 fio708090100
И------* 1 I 1 ]Д-4 Ч I I ь 1 I |1| » ! I Т.
Ч 2^3 4 5 6 78910 40 5060708090100
Движок вправо
Первый Второй сомножитель 3 сомножитель %
Рис. 14. Схема установки движка при умножении на шкале
квадратов
торой взят первый сомножитель, и сумме порядков сомножителей минус единица, если произведение читается на той же шкале, на которой взят и первый сомножитель.
Порядок частного равен разности порядков делимого и делителя, если частное читается справа от делимого, и разности порядков делимого и делителя плюс единица, если частное читается слева от делимого.
Упражнение. Выполнить умножение и деление на шкале квадратов:
1) 2,45 X 55,7 = 136; 4) 63 : 3 = 21;
2) 45,9 X 7,68 = 353; 5) 4,3 ; 0,8 = 5,38.
3) 18,64 X 5 = 93,2;
В примере 1 ответ читается на правой шкале, тогда как первый сомножитель взят на левой. В этом случае порядок произведения равен сумме порядков сомножителей, т. е. +3. Ответ; 136.
- В примере 3 произведение читаем на левой шкале, т. е. на той же, на которой был взят первый сомножитель. Порядок произведения равен сумме порядков сомножителей минус единица, т. е. + 2 + 1 — .1 = +2. Ответ: 93,2.
В примере 4 частное читаем слева от делимого. В этом случае порядок частного равен разности порядков делимого и делителя плюс единица, т. е. + 2 — 1 + 1 = +2; таким образом, частное равно 21.
77
В примере 5 частное читаем справа от делимого. Порядок частного равен разности порядков делимого и делителя, т. е. + 1 — 0 = = +1. Ответ: 5,38.
Умножение при помощи обратной шкалы. Основная и обратная шкалы связаны обратной зависимостью, и для того чтобы перемножить два числа, нужно первое разделить на обратную величину второго.
Например: 25 X 3 = 25 : у = 75.
При умножении с помощью обратной шкалы поступаем следующим образом. Находим на основной шкале корпуса линейки делимое, например 25, и засекаем, его волоском. Затем отыскиваем на обратной шкале делитель — число 3 и, выдвигая движок влево, подводим его под волосок, а справа, против конца движка, на основной шкале читаем результат 75.
Умножение с помощью обратной шкалы 2 X 7 = 14 показано на рис. 15.
- Второй сомножитель 7
Красная шкала
10 9
1 ’ и
6
5
1.1 1.2 1.3
Основная шкало
< 15 1.6 1.? 1.8 1.9 сомножитель?
Произведение » движок вправо
Рис. 15. «Схема установки движка при умножении с помощью обратной шкалы
При умножении с помощью обратной шкалы порядок произведения равен сумме порядков сомножителей, если движок выдвигается вправо, и сумме порядков сомножителей минус единица, если движок выдвигается влево.
Упражнение. Выполнить умножение с помощью обратной шкалы:
1) 5,64X3,1 = 17,48;
. 2) 0,144X 17 = 2,45;
3) 38,2X5,9 = 225;-
4) 6,9x87 = 600;-
5) 0,0075X0,04 = 0,0003.
В примере 2 движок при перемножении выдвигается влево и поэтому порядок произведения равен сумме порядков сомножителей минус единица, т. е. 0+2 — 1 = +1. Ответ: 2,45..
В примере 5 при перемножении движок выдвигается вправо. В этом случае порядок произведения равен сумме порядков сомножителей, т. е. — 2 + (— 1) = “3, и ответ будет 0,0003.
Умножение посредством красных цифр. При помощй обратной шкалы одной установкой движка можно легко вычислить выражение вида а X b X с. Это вычисление называется умножением посредством красных цифр.
Например: 4,5 X 2 X 3,8 = 34,2.
78
В данном случае поступают так: находят на основной шкале корпуса линейки первый множитель 4,5 и засекают его волоском, затем под волосок подводят второй множитель 2, взятый на обратной шкале. После этого, не читая промежуточного результата, находят на основной шкале движка третий множитель 3,8, засекают его волоском и на основной шкале корпуса линейки читают результат 34,2.
Упражнение. Выполнить умножение с помощью красных цифр:
1) 5,6 X 2,5 X 0,3 = 4,2; 4) 12 X 0,4 X 5 = 24; 1
2) 32,2 X 4,5 X 2,7 = 392; 5) 35,2 X 9 X 0,25 = 79;
3) 44 X 1,5 X 3 = 198; 6) 2,5 X 30 X 0,22 = 16,5.
В примере 1 при перемножении с помощью обратной шкалы движок выдвигался вправо. 1Этвет: 4,2.
В примере 6 при перемножении движок выдвигался влево. В этом случае ответ: 16,5.
Для приобретения навыков в умножении и делении на шкале квадратов, а также в умножении с помощью обратной шкалы рекомендуется решить примеры, приведенные в п. 31 и 32. Отсутствие достаточных навыков замедляет темп работы, приводит к ошибкам.
32. КОМБИНИРОВАННЫЕ ДЕЙСТВИЯ УМНОЖЕНИЯ И ДЕЛЕНИЯ
Часто возникает необходимость произвести комбинированные действия умножения и деления.
Пример 1.
0,3X0,5X25
0,06X4,5 ’
Частное можно получить двояко:
1) путем деления 0,3 на 0,06 с последующим умйожением результата на 0,5, затем делением на 4,5 и, наконец, умножением на 25; схематично это можно выразить так:
2) путем перемножения отдельно сомножителей числителя • и отдельно сомножителей знаменателя с последующим делением числителя на знаменатель.
При использовании второго способа порядок частного определяется, как это делается обычно при делении двух чисел.
Первый способ позволяет несколько быстрее определить цифры частного; однако, как показывает практика, в этом случае тратится значительно больше времени на вычисление порядка частного. Во избежание ошибок рекомендуется прикидывать порядок частного в уме. В случае, когда в числителе дроби на один сомножитель больше, чем в знаменателе, можно воспользоваться следующим правилом для определения порядка частного.
79
Порядок частного равен разности между суммой порядков сомножителей в числителе и суммой порядков сомножителей в знаменателе плюс столько единиц, сколько было перебросок конечного штриха движка на место начального, и минус столько единиц, сколько было перебросок начального штриха движка на место конечного.
Пример 2.
20 X 40 X 50 X 18
30 X 90 X 85
В этом случае порядок частного подсчитывается следующим образом: сумма порядков сомножителей в числителе равна 8; сумма порядков сомножителей в знаменателе равна 6; одна переброска начального штриха движка на место конечного; следовательно, порядок частного равен 8 — 6 — 1 = 1. Ответ: 3,14.
Пример 3.
0,48 X 19,3 X 2,18
При подсчете перебросок движка не было; в этом случае порядок частного равен разности между суммами порядков сомножителей. в числителе и знаменателе, т. е.
= 0 + 2 + 1 — (+ 2 + 2) = —1.
Ответ: 0,033.
Упражнение. Выполнить комбинированные действия умножения и деления:
12X450 _
—40~=135,
15,5x8,7
5 -ZZ’
63,6 X 0,184 „о
0,3 ~39,
0,25X3X20X 1,6
0,75X5X8 -0,в;
1,1X2,4
109,2 X 0,0416 X 0,632 х 0,544 0,00726 X 14,32 X 0,649
15,86X0,00495X630
1,8,36 x 0,0274 x 5,6 -3в’Ь:
13,6X413X105X0,09
3,8x95x54x0,008 -JU’
17 X 37 X 47 X 20 „„
28 x 90 x 86 ,Л5’
0,064X0,052X3400
4900 X 0,00079X19
80
. 7,28 X 53,6 X 1,377
' 22,2x0,882 ’ !
12) ё4И<0 312 = 1’955;
o,Uo X и,
. 15,65 X 7,16
' 4,29 X 3,73 ’
14,55 X 9,04
14) 31,6 X 2,ЗЗ*-1,785’’
2,17X0,0983
15) 72,1X0,87 =°’°034-
Все ответы рекомендуется проверить путем грубой прикидки результата в уме. Это делается так.
В примере 3 запишем дробь, округляя цифры; подсчитав, получим
65Х б”_13ХЗ_„-
J_ 1 3
3
Ответ: результат — двузначное число.
В примере 9 запишем дробь, округляя числа; подсчитав, получим
20 X 40 X 50 X 20
30 x 90 x 90 ’
Ответ: целая часть результата — однозначное число.
В примере 11 дробь округленно запишем так: *
7x50x2 QQ
22x1
Ответ: целая часть результата — двузначное число.
В примере 12 запишем дробь, округляя числа. Получим частное
Ответ: целая часть результата — однозначное число.
33. ВОЗВЕДЕНИЕ В КВАДРАТ
Шкала квадратов, как и основная шкала, расположена на корпусе линейки и прилегающей к ней верхней стороне движка. Внимательно рассмотрев шкалу квадратов, заметим, что она состоит из двух совершенно одинаковых шкал, из которых одна называется левой, другая — правой. Левая шкала начинается с цифры 1 и кончается 10, правая начинается с 10 и кончается 100.
Мы не определяем здесь цены делений этих шкал, учитывая, что об этом уже говорилось раньше и изучающий логарифмическую линейку разобрался в них.
81
При возведении чисел в квадрат, куб, извлечении квадратного и кубического корней, а также при нахождении логарифмов чисел движком не пользуются и все вычисления проводятся лишь с помощью бегунка. Поэтому движок можно вынуть из линейки и все вычисления вести без него.
Правило возведения чисел в квадрат. Для того чтобы найти квадрат числа, необходимо отыскать это число на основной шкале, засечь его волоском и на шкале квадратов под волоском прочитать ( ответ.
Пример Л
2В = 4.
Находим на основной шкале число 2, засекаем его волоском. На шкале квадратов под волоском читаем квадрат числа: 4. Нахождение квадрата числа показано на рис. 16.
Пример 2.
72= 49.
На основной шкале находим число 7, засекаем его волоском. На шкале квадратов под волоском читаем ответ: 49.
Рис. 16. Схема установки волоска при возведе-
нии чисел в квадрат
Заметим, что в примере 1 мы читали ответ на левой шкале, а в примере 2 — на правой.
Определение порядка квадратов чисел. Для того чтобы определить порядок результата, т. е. число знаков в ответе, необходимо запомнить следующее правило.
Если квадрат числа читаем на левой шкале, то порядок квад-.рата равен удвоенному порядку возводимого в квадрат числа минус единица; если на правой, то порядок квадрата равен удвоенному порядку возводимого в квадрат числа.
Обозначая порядок квадрата через К, порядок числа, возводимого в квадрат, через и, запишем это правило в следующем виде:
шк == 1;
•^пр.шк=2/г.
Упражнение. Возвести числа в квадрат при помощи линейки:
1) 52 = 25; 6) 0,152 = 0,0225;
2) 252 = 625; 7) 0,042 = 0,0016;
3) 122 = 144; 8) 522 = 2704;
4) 602 = 3600; 9) 1802 = 32 400;
5) 2,32 = 5,29; 10) 3,12 = 9,61.
6
82
В примере 1 квадрат числа читаем на правой шкале.
Порядок числа 5 равен п ~ +1. Поскольку квадрат числа находится на правой шкале, то порядок квадрата
2л= 2(+1) = 2,
т. е. ответ — двузначное число 25.
В примере 6 квадрат числа находим на левой шкале. Порядок числа 0,15 равен п — 0. Следовательно, порядок квадрата
К = 2n — 1 = 2-0— 1 = — 1
и квадрат числа равен 0,0225.
В примере 9 порядок числа 180 равен я_= +3, квадрат числа читается на левой шкале. Следовательно, порядок квадрата
- 2п — 1- 2-3 — 1- +5
и квадрат числа равен 32 400.
При возведении числа в квадрат (в куб) полезно пользоваться табличкой, систематизирующей труд и облегчающей выработку навыков (табл. 12).
Т абл ица 12
Некоторые примеры определения порядка квадрата
Число Порядок числа Шкала квадратов Определение порядка квадрата Ответ
7 + 1 Правая 2п = 2х 1 = 2 49
2,57 + 1 Левая 2л—1 = 2х 1 — 1 = 1 6,6
190,5 +3 2п—1 — 2x3—1=5 36300
8 530 +4’ Правая 2п=2х4 = 8 72800000
85 300 +5 » 2я=‘2 х 5= 10 7280000000.,
0,07 -1 » 2п = 2х (—1) = -2 0,0049
0,007 —2 » 2л = 2х(—2) = —4 0,000049
0,7 0 » 2п==2х0 = 0 0,49
0,12 0 Левая 2п—1=2 X 0—1=—1 0,0144
0,06 — 1 Правая 2n==2 X (—1) = —2 0,0036
0,003 —2 Левая 2п— 1=2х(-2)—1=—5 0,000009
34. ИЗВЛЕЧЕНИЕ КВАДРАТНОГО КОРНЯ
Правило извлечения квадратного корня. Известно, что прежде чем извлечь квадратный корень, надо разбить подкоренное число на грани, по два знака в каждой. Если подкоренное число больше единицы, то разбиваем на грани целую часть числа справа налево, а если меньше единицы, то слева направо, считая *от запятой.
Для того чтобы извлечь квадратный корень, необходимо найти число на шкале квадратов, засечь его волоском и прочитать значение корня под волоском на основной шкале.
83
При извлечении квадратного корня движком также не пользуемся и все вычисления ведем только с помощью волоска на бегунке.
Поскольку шкала квадратов состоит из двух шкал, возникает вопрос, на какой шкале откладывать подкоренное число, на левой или правой.
Подкоренное число откладывается на левой шкале в том случае, если левая крайняя грань подкоренного числа неполная, т. е. имеет одну цифру, или если число однозначное, или если в числах, меньших единицы, в первой значащей грани одна цифра. В следующих примерах квадратные корни извлекаются по левой шкале:
V&25, /УбГ, Кб, Кб,00'04, Ко,00'00'09.
Если левая крайняя грань полная, т. е. состоит из двух цифр, или число двузначное, или если число меньше единицы и его первая значащая грань имеет две цифры, то подкоренное число откладывается на правой шкале.
Например:
Кзв, КЗБЧЮ, КоЖ, Ко,00'40, Ко,00'00'90.
Для наглядности приводим ряд примеров, показывающих, как определить, по какой из шкал надо извлекать квадратный корень: j/9,0—3 —в грани одна цифра, извлекаем по левой шкале; {/‘90 — 9,49 —в грани две цифры, извлекаем по правой шкале; К9'00 = 30 — по левой шкале;
К90'00,0 = 94,9 —по правой шкале;
V9'00'00,0 = 300 — по левой шкале;
КОД) =0,949 — по правой шкале;
КоЖ=о,з — по левой шкале;
1^0,00'90 = 0,0949 —по правой шкале;
Ко,00'09 = 0,03 —по левой шкале;
КО,00'00'90 = 0,00949 — по правой шкале;
К0,00'00'09 = 0,00.3 — по левой шкале.
Определение порядка квадратного корня. Порядок квадратного корня равен числу граней в целой части числа, если подкоренное число больше единицы, числу чисто нулевых граней со знаком минус, если подкоренное число меньше единицы.
Пример 1.
1/36 = 6.
Число 36 содержит одну грань, следовательно, целая 4асть корня будет однозначное число. Извлечение корня ведем по правой шкале, потому что в грани две цифры, грань полная. Извлечение квадратного корня из 36 показано на рис. 17.
Пример 2, ______
V49700 = 70.
84
В подкоренном числе содержатся две грани, следовательно, целая часть корня будет двузначным числом. Извлечение корня ведем по правой шкале.
Пример 3.
/Й44=12.
В подкоренном числе содержится также две грани, причем левая грань неполная. Ответ будет двузначным числом, а то обстоятельство, что одна грань неполная, для определения порядка корня значения не имеет. Извлечение корня ведем по левой шкале.
Пример 4.
/25'00'00 = 500.
В подкоренном числе три грани, следовательно, порядок корня равен трем. Извлечение корня ведем по правой шкале.
Рис. 17. Схема установки волоска при извлечении квадратного корня
Пример 5.
/0,00'04 = 0,02.
Порядок корня равен —1, так как подкоренное число имеет одну чисто нулевую грань. Извлечение корня ведем по левой шкале.
Пример 6.
/0,00'00'25 = 0,005.
Порядок корня равен —2, так как подкоренное число имеет две чисто нулевые грани. Извлечение корня ведем по правой шкале.
Упражнение. Извлечь квадратные корни на линейке:
1) /169=13; 6) V 0,000016 =0,004;
2) /6^9 =0,3; 7) у 0,0004 =0,02;
3) /0,0016 =0,04; 8) /0,0625=0,25?
4) /8100=90; 9) /0^64=0,8;
5) /490 000 = 700; Ю) J/qJ=0,632.
36. ВОЗВЕДЕНИЕ В КУБ
Шкала кубов расположена сверху корпуса линейки и состоит из трех равных шкал: левой, средней и правой.
Правило возведения в куб. Для того чтобы возвести число в куб, находят его на основной шкале линейки, засекают волоском и на шкале кубов под волоском читают ответ.
85
Пример
23 = 8.
Находим число 2 на основной шкале, засекаем его волоском; на левой шкале кубов читаем под волоском ответ: 8. Нахождение куба числа показано на рис. 18.
Пример 2.
43 = 64.
В этом случае куб числа читаем на средней шкале. Пример 3,
53 = 125.
В этом случае куб числа читаем на правой шкале.
Шкапа кубов
2
а3=8
If 12 1.3 1.4 1.5 1.6 1.7 1.8 1.9(?
3 4 5 6 7 ®9 1
Основная шкапа
а=2
Рис. 18. Схема установки волоска при возведении чисел в куб
Определение порядка кубов чисел. Для того чтобы быстро определить порядок результата, запомним следующее правило.
Если куб числа читаем по левой шкале, то порядок куба равен утроенному порядку возводимого в куб числа минус 2;' если по средней — утроенному порядку возводимого в куб числа минус 1, и, наконец, если куб числа находится по правой шкале, то порядок куба равен утроенному порядку возводимого в куб числа.
Обозначив порядок куба через L, а порядок возводимого в куб числа через п, можем записать это правило в следующем виде:
^л. ШК = ЗН 2, ^ср. шк = Зм U' ^пр.шк ” Зп.
Упражнение. Возвести числа в куб на линейке:
1) 33==27;
2) 63 = 216;
3) 153 = 3375;
4) 4003 = 64 000 000;
5) 0,73 = 0,343;
6) 0,2453 = 0,0147.
В примере 3 куб числа читаем по левой шкале. Порядок возводимого в куб числа п = +2; следовательно, порядок куба
Ал.шк = Зп-2 = 3(+2)-2=+4
и куб числа 15 равен четырехзначному числу 3375.
86
В примере 5 куб числа читаем по правой шкале. Порядок возводимого в куб числа п = 0; следовательно, порядок куба
^пр.шк Зя 3*0 0,
ответ: 0,343.
В примере 6 куб числа читаем по средней шкале. Порядок возводимого в куб числа п— 0; следовательно, порядок куба
^ср.шк == Зя — 1 = 3’0 — 1= 1
и куб числа равен 0,0147.
36. ИЗВЛЕЧЕНИЕ КУБИЧЕСКОГО КОРНЯ
Правило извлечения кубического корня. Прежде чем извлечь кубический корень, разбиваем подкоренное число на грани, по три знака в каждой. Если подкоренное число больше единицы, то разбиваем на грани целую часть числа справа налево; если число меньше единицы, разбиваем на грани слева направо, считая от запятой. При извлечении кубического корня движком также не пользуемся и все вычисления ведем только с помощью волоска бегунка.
Для того чтобы извлечь кубический корень, необходимо найти подкоренное число на шкале кубов, засечь его волоском и на основной шкале линейки под волоском прочитать значение корня.
Поскольку шкала кубов состоит из трех шкал, то так же, как и при извлечении квадратного корня, возникает вопрос, на какой из трех шкал следует откладывать подкоренное число.
Подкоренное число откладывается на лейой шкале, если его целая часть есть однозначное число или число меньше единицы с одной цифрой в левой крайней значащей грани.
Например:
Ув, VW5, Уо,000'001'2, 8/W.
Подкоренное число откладывается на средней шкале, если его целая часть есть двузначное число или в левой крайней значащей грани две цифры.
Например:
У84, УО/Пб, Уб8'921, s/0?027.
И, наконец, подкоренное число откладываем на правой шкале, если число трехзначное или левая крайняя значащая грань полная, т. е. имеет три цифры.
Например:
У125, У343'000, Уо,358, У0,000'593.
Определение порядка кубического корня. Порядок кубического корня равен чисду граней в целой части подкоренного числа, если подкоренное число больше единицы, и числу чисто нулевых граней со знаком минус, если подкоренное число меньше единицы.
Пример 1.
УГ728 = 12.
Так как подкоренное число содержит две грани, то порядок корня равен +2. Поскольку в левой крайней грани одна цифра,
87
то подкоренное число откладывается на левой шкале. Извлечение кубического корня из 1728 показано на рис. 19.
Пример 2. ____
VT25 = 5.
Так как подкоренное число содержит одну полную грань, то оно откладывается на правой шкале; порядок корня равен +1.
Пример 3.
V 68'921 =41.
Здесь подкоренное число содержит две грани, из которых крайняя левая грань неполная. Порядок корня 2, а то обстоятель-
ство, что одна грань неполная, в данном случае значения не имеет. Подкоренное число откладывается на средней шкале.
Пример 4.
/0/Й6=0,6.
В подкоренном числе нет чисто нулевых граней (число их равно нулю); следовательно, и порядок корня равен нулю. Подкоренное число откладывается на правой шкале, так как грань полная, содержит три цифры.
Пример 5.
/0,000'512 = 0,08.
В этом примере подкоренное число содержит одну чисто нулевую грань; следовательно, порядок корня равен — 1. Извлечение корня ведем по правой шкале, так как первая значащая грань полная, имеет три цифры.
Упражнение. Извлечь корни кубические на линейке:
1) /729=9; 6) /0^43=0,7;
2) /ТЗЗТ = 11; 7) /0,000031 =0,0314;
3) /27000 = 30; 8) /0,000008 = 0,02;
4) /125000 = 50; 9) /0,0715=0,415;
5) /55 = 3,8; 10) /0,00000262 = 0,0138.
88
ведем левой
грань,
В примере 3 подкоренное число содержит две грани, следовательно, порядок корня равен -f- 2 и корень — двузначное Извлечение кубического корня по средней шкале, так как в крайней грани две цифры.
В примерр 8 подкоренное число содержит одну чисто нулевую--------
следовательно, порядок корня равен — 1. Извлечение кубического корня ведем по левой шкале, так как в левой крайней значащей грани всего одна цифра.
37. ЛОГАРИФМЫ ЧИСЕЛ
Логарифмирование. Шкала мантисс логарифмов находится внизу корпуса линейки. Она равномерная. Цену ее делений мы уже определяли: она равна 2 (см. стр. 67).
Для того чтобы найти десятичный логарифм числа, находят это число на основной шкале линейки, засекают его волоском, а на шкале логарифмов читают мантиссу числа и приписывают спереди соответствующую характеристику.
Как известно, логарифм числа выражается обычно в виде десятичной дроби, причем целая часть дроби называется характеристикой, а дробная часть — мантиссой логарифма.
Характеристика логарифмов чисел, которые больше единицы, положительна и равна числу цифр в целой части числа минус единица, например:
1g 2000= 3,301, где 3 -— характеристика и 0,301 — мантисса логарифма. Характеристика равна 3, потому что число 2000 содержит 4 значащие цифры, а 4 - 1 = 3.
Характеристика логарифмов чисел меньших единицы отрицательна и содержит столько отрицательных единиц, сколько нулей стоит перед первой значащей цифрой числа, включая и нуль целых, например:
1g 0,0009 = 4,954,
1g 0,00324 = 3,510.
При вычислении логарифмов чисел, а также при нахождении числа по
число.
5:
&
1
его логарифму движком не пользуемся и вычисления ведем только с помощью волоска бегунка.
89
Например: вычислить 1g 6.
Находим на основной шкале число 6, засекаем его волоском и на шкале логарифмов, под волоском, читаем мантиссу: 0,778. Характеристика равна нулю. Следовательно, 1g 6 = 0,778.
Нахождение десятичных логарифмов чисел показано на рис. 20.
Упражнение. Вычислить на линейке десятичные логарифмы чисел:
1) 1g 6,62 == 0,821;
2) 1g 15= 1,176;
3) lg 0,47 = 1,672;
4) lg 300 = 2,477;
5) lg 7,15 = 0,854.
Напомним, что по шкале мантисс логарифмов находят десятичные мантиссы логарифмов. Для перехода от десятичных логарифмов к натуральным (основание которых е~ 2,7183) умножают десятичный логарифм на модуль перехода 2,3026 или делят на число 0,4343. Если надо перейти от натуральных логарифмов к десятичным, то умножают натуральный логарифм на 0,4343 или делят его на 2,3026. .
Упражнение. Вычислить на линейке натуральные логарифмы чисел:
1) In 0,21 = 2,3-1,322 = 2,3 (— 0,678) = — 1,56;
2) 10^5 = 2,3-0,699 = 1,63;
3) 1g 2 = 0,301; In 2 = 0,693;
4) lg 5,5 = 0,740; In 5,5 = 1,705.
Потенцирование. Для того чтобы найти число по его десятичному логарифму, находят на , шкале логарифмов мантиссу числа, засекают ее волоском, а на основной шкале, под волоском, читают само число, отделяя необходимое количество знаков в соответствии с характеристикой данного логарифма.
Например, требуется найти число, зная, что его десятичный логарифм равен 2,322.
Находим на шкале логарифмов мантиссу 0,322, засекаем ее волоском и на основной шкале под волоском читаем число 21. Характеристика 2. Следовательно, число, соответствующее логарифму 2,322, имеет три знака и равно 210.
Упражнение. Найти числа, зная их логарифмы:
1) lg W = 0,519; N = 3,3; 4) lg N = 0,838; N = 6,89;
2) lg N = 1,895; N = 78,6; 5) lg = 1,076; = 11,9;
3) lg N = 2,344; W = 221; 6) lg W = 1,534; W = 0,342.
Возведение чисел в любую степень и извлечение корней с любыми показателями. При помощи шкалы мантисс логарифмов производится возведением чисел в любую степень, а также извлечение корней. Напомним, что любой логарифм с отрицательной характеристикой и положительной мантиссой можно представить в виде отрицательной десятичной дроби. Для этого к положительной мантиссе прибавляют отрицательную единицу, а к отрицательной характеристике — положительную единицу, например:
+i-i
5,648 = 5,648=—4,352.
Это нужно иметь в виду, решая некоторые из приводимых ниже примеров.
90
Рассмотрим несколько примеров возведения чисел в степень. Пример 1.
х = 4,50,8.
Логарифмируя обе части равенства, получаем
1g х = 0,8 1g 4,5.
Находим на основной шкале линейки число 4,5 и засекаем его волоском. На шкале мантисс логарифмов под волоском читаем 1g 4,5 = 0,653. Умножая, как обычно, 0,8 X 0,653, имеем
1g х = 0,522.
Теперь, зная 1g х = 0,522, определяем х, для чего находим мантиссу 0,522 на шкале мантисс логарифмов, засекаем ее волоском и на основной шкале линейки под волоском чйтаем значение х = 3,32, так как характеристика логарифма равна нулю.
Пример 2.
х = 8,332,45
Логарифмируя, получаем
1g х = 2,45 1g 8,33
и тем же способом находим ответ: х = 180.
Упражнение. Возвести числа в степень:
1) х= з0’6; х= 1,932; 3) х = 6,43-2; х = 380;
2) х = 15,12-1; х= 300,6; 4) х= 0,8685’12; х= 0,484.
В примере 1, логарифмируя обе части равенства х=30,6, имеем
1g х = 0,6 1g 3.
Засекая на основной шкале линейки цифру 3, на шкале мантисс логарифмов читаем мантиссу 0,477 и в соответствии с характеристикой находим: 1g 3 = 0,477. Перемножая, получаем
1g х — 0,6-0,477 = 0,286.
Зная 1g х = 0,286, определяем х, для чего на шкале мантисс логарифмов находим мантиссу 0,286, засекаем ее волоском и на основной шкале читаем цифры 1—9—3—2. Поскольку характеристика логарифма 0,286 равна нулю, целая часть х есть однозначное число. Ответ: х= 1,932-.
В примере 4, логарифмируя обе части равенства х = 0,8685’12, имеем
1g х = 5,12 1g 0,868 = 5,12-1,939 = = 5,12 (— 0,061)= — 0,315 = 1,685.
Зная, что 1g х= 1,685, определяем х= 0,484.
Рассмотрим примеры извлечения корней.
Пример 1.
х = 5^243.
Логарифмируя, получаем
lg X = 11g 243.
О
91
Находим на основной шкале линейки 243 и, засекая волоском, читаем на шкале мантисс логарифмов под волоском мантиссу 0,386. Найдя 1g 243 == 2,386, делим его на 5, пользуясь для этого основной шкалой, и получаем 1g х = 0,477. Теперь определяем х, для чего находим на шкале мантисс логарифмов мантиссу 0,477, засекаем ее волоском и на основной шкале под волоском читаем значение х =3,00, так как характеристика логарифма равна нулю.
Пример 2.
х=/78 125.
Логарифмируя, получаем
lg х = у 1g 78 125;
4) х=уг6561=3;
5) х=в,2у/ТМ7 = 1,595.
тем же способом, что и в предыдущем примере, определяем х = 5.
Упражнение. Извлечь корни:
1) х=/128 = 2;
2) х= ^0,06432 =0,737;
3) х=а’/137 = 3,78;
В примере 5, логарифмируя обе части равенства, имеем
1 !gjM7=U66 = 0 204>
g 6,23 6,23 ’
Для определения х находим на шкале мантисс логарифмов мантиссу 0,204, засекаем ее волоском и на основной шкале под волоском читаем значение х. С учетом характеристики логарифма ответ будет х = 1,595,
38. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Тригонометрические шкалы и цена их делений. Как уже было сказано, тригонометрические шкалы нанесены на оборотной стороне движка. Верхняя шкала — шкала синусов углов от 5°44' до 90°,
Рис. 21. Вырезы на оборотной стороне логарифмической линейки для нахождения значений тригонометрических величин без перевертывания движка
средняя — шкала синусов и тангенсов малых углов от 0°34' до 5°44' и, наконец, нижняя — шкала тангенсов углов от 5°44( до 45°.
На оборотной стороне линейки имеются два выреза: слева и справа. В правом вырезе мы видим деления шкалы синусов (sin) и синусов и тангенсов малых углов (S и Т). В левом вырезе видны деления шкалы тангенсов (tg). В обоих вырезах сверху и снизу
92
на корпусе линейки нанесено по черточке. Это так называемые риски, заменяющие волосок и обеспечивающие более точную установку и чтение цифр на шкалах. На рис. 21 показаны эти вырезы на оборотной стороне линейки.
Для быстроты и точности подсчетов необходимо хорошо усвоить цену делений тригонометрических шкал.
Цена делений шкалы sin меняется резко. Так, на отрезке от 5°45' до 10° каждый градус разделен на 6 крупных делений, из которых каждое, в свою очередь, разделено еще на 2. Таким образом, цена деления каждого малого отрезка равна 1° : 12 = 60' : 12 = — 5', а более крупного — 10'.
Отрезки шкалы sin после 10° имеют цену делений:
10—20°.....................10'
20—40°.....................20'
40—60’.................... 30'
60—80°...................... 1° .
На отрезке 80—90° имеются три деления, соответствующие 82, 84 и 86°.
Шкала S и Т, содержащая углы от 0°34' до 5°44', имеет следующую цену делений:
0°34' —3’ ................. 1'
3° —5’ ................. 2'
5’-5’40'................ 5'
Шкала tg содержит углы от 5°44' до 45°. Цена ее делений следующая:
5’45' —20’................. 5'
20’-45’................... 10'
Напомним некоторые известные формулы тригонометрии, которые потребуются в процессе работы на линейке:
1 1,1
sin а =-----: cos а=------: tg а=-г—:
cosec а ’ sec а ctg а
cos а = sin (90° — а); ctg а == tg (90° — а).
Нахождение значений тригонометрических функций при помощи логарифмической линейки можно производить двумя способами: без перевертывания оборотной стороной (через вырезы, имеющиеся на обороте логарифмической линейки) и путем перевертывания движка оборотной стороной так, чтобы тригонометрические шкалы были на лицевой стороне линейки.
Нахождение значений синуса острого угла по шкале sin без перевертывания движка. Для того чтобы определить, например, значение sin 30°, находим на шкале синусов число 30, соответствующее 30°, и подводим его под черточку (риску) в правом вырезе корпуса линейки. После этого перевертываем линейку лицевой стороной и находим число на основной шкале движка, стоящее против конца основной шкалы корпуса линейки, — число 5.
Так как значения синусов углов, находящихся в пределах от 5°44' до 86°, имеют порядок 0, то sin 30° = 0,5. Левый конец движка
93
показывает на основной шкале число 2. Это — значение cosec 30° =2, 1
так как cosec а = .
sin а
Чтобы найти sin 63°30', перевернув линейку оборотной стороной, находим на шкале синусов 63°30'и подводим это деление под черточку на корпусе. Затем, перевернув линейку лицевой стороной, находим значение sin 63°30' на основной шкале движка против конца основной шкалы корпуса линейки: 8 9 5. Следовательно, sin 63°30' = 0,895. Нахождение sin 63°30' показано на рис. 22.
Sin 63°30'
Рис. 22. Установка движка логарифмической линейки при нахождении значений тригонометрических функций без перевертывания движка
Упражнение. Вычислить следующие значения тригонометрических функций:
1) sin 45° = 0,707; 7) sin 14°10' = 0,245;
2) sin 22° = 0,375; 8) sin 132° = 0,743;
3) sin 51° = 0,777; 9) sin 300° = — 0,866;
4) sin 9°30' = 0,165; 10) sin 202°30' = — 0,383;
5) sin 8°25' = 0,146; 11) cosec 27° = 2,2;
6) sin 80° = 0,985; 12) cosec 49° = 1,325.
_ В примере 8 нужно найти sin 132®. Известно, что sin 132® = — sin (180° — 48°) ~ sin 48°. Теперь, устанавливая шкалу синусов с пометкой 48° против черточки на корпусе в правом вырезе, перевертываем линейку лицевой стороной и читаем значение sin 48°, которое равно 0,743.
В примере 9 находим sin 300®. Зная, что sin 300° = == — sin (360°—300°) = — sin 60°, находим — sin 60°, который равен — 0,866.
Нахождение значения косинуса по его углу. Нахождение косинусов углов производится через синусы дополнительных углов.
Например: найти cos 35°.
По формулам преобразований тригонометрических функций имеем
cos 35° = sin (90° — 35°) = sin 55®.
Находим sin 55°; он равен 0,819.
94
Упражнение. Вычислить значения косинусов следующих углов.
1) cos 15° = 0,966;
2) cos 40°30' - 0,760;
3) cos 72°50' = 0,296;
4) cos 61° = 0,485;
5) cos 24° = 0,914;
6) cos 132° = — 0,669;
7) cos 147° = — 0,839;
8) cos 10°30' - 0,984;
9) cos 31°5' = 0,865;
10) cos 79°30' — 0,182.
В примере 6 cos 132° = —sin 42°. Находим значение sin 42° и берем его со знаком минус, учитывая, что косинусы углов второй четверти отрицательны. 1
Нахождение углов по значениям синусов и косинусов. Нахожде- _ ние угла по значению синуса производится так: на лицевой стороне " линейки находят значение синуса на основной шкале движка и устанавливают его против конца основной шкалы линейки, затем перевертывают линейку оборотной стороной и в правом вырезе против черточки на шкале синусов читают ответ.
Способ нахождения угла по значению косинуса дается ниже, в шестом и последующих примерах.
При определении угла по значению тригонометрической функции, что представляется, вообще говоря, задачей неоднозначной, мы получаем при помощи логарифмической линейки одно из возможных решений.
Упражнение. Найти угол по значениям синусов и косинусов:
1) 2) sin а = sin а = 0,309; 0,339; а = а = 18е*; 19°48';
3) sin а = 0,799; а = 53°;
4) sin а = — 0,242; а = 194°;
5) sin а = — 0,334; а =-= 199°30'
6) cos а = 0,588; а = 54°;
7) cos а = 0,225; а = 77°; '
8) cos а = 0,423; а = 65°;
9) cos а — 0,940; а = 20°;
Ю) cos а = 0,707; а = 45°.
В примере 1 мы устанавливаем значение sin а = 0,309 на основной шкале движка против конца основной шкалы линейки, затем перевертываем линейку оборотной стороной и в правом вырезе на шкале синусов против черточки читаем ответ: 18°.
В примере 6 сначала находим значение синуса угла и затем уже отыскиваем значение косинуса. Устанавливаем 0,588 на основной шкале движка против конца основной шкалы линейки, перевертываем линейку оборотной стороной и на шкале синусов против черточки читаем: 36°. Так как sin 36° — cos (90° — 36°), то а — 54°.
Нахождение значений тангенсов и котангенсов по их углам. Для того чтобы определить, например, значение tg 20°, находим на шкале тангенсов число 20 и подводим его, выдвигая движок влево, под черточку на корпусе линейки. Затем перевертываем линейку лицевой стороной и находим число на основной шкале движка, стоящее против начала основной шкалы линейки, — число 364; следовательно,
tg 20° = 0,364.
95
Так как ctg a = т0 конец движка одновременно показывает на основной шкале линейки значение котангенса угла 20°, которое равно 2,75.
Упражнение. Вычислить значения тангенсов и котангенсов
следующих углов:
1) tg 15° = 0,268; 4) tg 54° = 1,376;
2) tg 32° = 0-,625; 5) ctg 19° = 2,904;
3) tg 9°10' = 0,161; 6) ctg 61° = 0,554.
При отыскании значений тангенса и котангенса углов необходимо помнить, что до 45° значения тангенсов меньше единицы, а значения котангенсов больше единицы. Значения тангенсов углов от 45 до 90° больше единицы, а значения котангенсов меньше единицы.
В тех случаях, когда надо отыскать значение tg а при а > 45°, его определяют через котангенс дополнительного угла: tg а = = ctg (90° — а).
В примере 1, выдвигая движок влево, находим на шкале тангенсов деление, соответствующее 15°, подводим это деление под черточку на корпусе, перевертываем линейку лицевой стороной и на основной шкале движка, против начала основной шкалы, читаем число 268. Ответ: tg 15° = 0,268.
В примере 4 вместо tg 54° находим ctg 36°. На оборотной стороне линейки против черточки на левом вырезе устанавливаем шкалу тангенсов с делением 36°. Затем перевертываем линейку и читаем на основной шкале линейки, против конца движка, число 1376. Ответ: tg 54° = 1,376.
В примере 5, выдвигая движок влево, находим на шкале деление 19°, подводим его под черту на корпусе, перевертываем линейку лицевой стороной и против конца движка читаем на основной шкале линейки число 2904. Ответ: ctg 19° — 2,904.
В примере 6 значение ctg 61° находимч через tg 29°.
Нахождение углов по значениям тангенсов и котангенсов. Нахождение углов а по значениям tg а и ctg а ничем не отличается от нахождения углов по значениям sin а и cos а.
Например, требуется найти угол а при tg а = 0,466. Для этого на лицевой стороне линейки, против начала ее основной шкалы, устанавливаем На движке 466, затем перевертываем линейку оборотной стороной и в левом вырезе на шкале tg против черточки читаем ответ: а = 25°.
Упражнение. Найти угол по значениям тангенсов и котангенсов:
1) tga = 0,839; a = 40°;
2) tga = 0,259; a=14°30';
3) tga= 4,45; a= 77°20';
4) tga= 1,439; a = 55°12';
5) tga= 0,1530; a= 8°42';
6) ctga= 3,31; a= 16°48';
7) ctga= 0,6197; a= 58° 12'.
Нахождение значений синусов и тангенсов малых углов (до 5°44'). Вычисление значений синусов и тангенсов малых углов производят по средней шкале, используя вырез на правой стороне корпуса линейки, так же, как это делалось при определении значений синусов и тангенсов по шкалам sin и tg.
96
Порядок результата, найденного по шкале S и Т, равен — 1.
-Значения синусов и тангенсов малых углов совмещены на одной шкале, потому что до 5°44' эти значения различаются между собой лишь в четвертом и пятом знаках, что выходит за пределы точности логарифмической линейки, и поэтому практически их считают равными.
Упражнение, Вычислить значения тригонометрических функций:
1) sin 1°30' = 0,0262;
2) tg 2° 18' = 0,0402;
3) sin 0°42' = 0,0122;
4) tg а — 0,0734; а = 4°12';
5) sin а = 0,0542; а = 3°06\
Нахождение значений тригонометрических функций при движке, перевернутом оборотной стороной. Нахождение значений тригонометрических функций вторым способом производят так: вынимают движок из линейки, перевертывают его оборотной стороной и вставляют в корпус линейки, совмещая края шкал.
Sln230°~0,25
\$1п3ЗО°=О,125
\ \ Sin 30° Ту35° Sin 5'
\ \ । волосок ।
piiiiiiiiiiiiiiiiHiiniiiiiiiiiiiiiiiiiHiiiiiHUiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiTimiiiinmiiiiiiiiinniiiiiiiiiitiiiiiiiiiiiiHl
80. QO .tOO
[50 60'
К дц” ^-Оборотная
Sln30°-0J5/j5
lg Sin 30 ~ 1,699 Основная шкала корпуса линейки
Рис. 23. Схема нахождения значений тригонометрических функций при перевертывании движка
сторона движка
Чтобы найти значение тригонометрической функции, засекают волоском на соответствующей тригонометрической шкале требуемый угол и на основной шкале линейки под волоском читают значение соответствующей тригонометрической функции. Рекомендуем проделать это самостоятельно.
Нахождение значений синусов, тангенсов углов, а также синусов и тангенсов малых углов при перевернутом движке показано на рис. 23.
-С целью приобретения навыков в отыскании вторым способом значений тригонометрических функций по их углам, а также углов по значениям тригонометрических функций рекомендуем решить при перевернутом движке все приведенные выше примеры.
При перевернутом движке можно возводить в квадрат и куб значения тригонометрических функций, извлекать из них квадратные и кубические корни, находить их логарифмы и по логарифмам
4 С. И. Березин
97
5,46 sin 69° sin 12° А
sin2 67° : л = 0,27;
tg2 29° = 0,307;
4,46 sin 26°_9<
__1
тригонометрических функций определять значения самих функций, производить умножение и деление значений тригонометрических функций по обычным правилам.
Упражнение. Решить примеры:
1) 36,3 sin 47°= 26,5;
2) 6,09 sin 2°42' = 0,287;
3) 387 tg 4°45'= 32,2;
4) 8,69 ctg 25° = 18,6;
5) 8,63: sin 19е = 26,6;
10) sin3 4°30' = 0,000482;
11) л sin3 37° = 0,68;
12) 3,14 tg3 25°= 0,319;
13) sin 30° : sin 60° = 0,578;
14) sin 26° : tg 15°= 1,64.
В примере 1 конец перевернутого движка устанавливаем на первом сомножителе 36,3, взятом на основной шкале корпуса линейки. На шкале синусов находим угол 47°, засекаем его волоском и под волоском на основной шкале корпуса линейки читаем результат: 2—6—5. Порядок произведения подсчитываем, как обычно, при движке, выдвинутом влево: Мл~ + ^2- Порядок 36,3 равен + 2; порядок sin 47° равен 0; порядок произведения равен Ул = = 2 + 0 = + 2. Ответ: 26,5.
В примере 5 на основной шкале корпуса линейки засекаем волоском делимое 8,63. Под волосок подводим делитель sin 19°, взятый на перевернутом движке, и против начала движка на основной шкале корпуса линейки читаем ответ: 2—6—6. Порядок частного подсчитываем, используя формулу Л4пр = /пх — 1 = + 1 —
— 0 + 1 = + 2. Следовательно, ответ4: 26,6.
В примере 8 засекаем волоском на шкале тангенсов перевернутого движка tg 29° и под волоском на правой шкале квадратов читаем 3—0—7. Порядок квадрата по формуле: /Спр = 2п. Значение tg 29° меньше единицы, его порядок равен нулю. Следовательно, порядок квадрата
/£пр = 2п = 2-0 = 0;
ответ: tg2 29° == 0,307.
В примере 10 засекаем волоском на шкале S и Т перевернутого движка sin 4°30' и на шкале кубов читаем 4—8—2. Для определения порядка ответа воспользуемся уже известной нам формулой Lnp = Зп. В нашем примере порядок возводимого в куб числа равен — 1; следовательно, порядок куба равен Зп — 3 (—1) = —3. Ответ: sin3 4°30' = 0,000482.
В примере 14 засекаем волоском на перевернутом движке sin 26°, под волосок подводим tg 15° и против начала движка на основной шкале читаем цифры частного: 1—6—4. Определение порядка частного в данном случае не представляет трудностей. Он равен Л4пр = mx — т2 + 1 = 0 — 0+ 1 = + 1; следовательно, ответ: 1,64.
98
Вычисление десятичных логарифмов значений тригонометрических функций синуса и тангенса. Для того чтобы определить lg sin а или lg tg а, прежде всего находим значения sin а или tg а. Как известно, это можно сделать двояко: без перевертывания движка, через вырезы на оборотной стороне линейки, и с перевертыванием движка оборотной стороной.
В первом случае, найдя значение sin а, засекаем его волоском на основной шкале корпуса линейки, а на шкале мантисс логарифмов под волоском читаем мантиссу, устанавливая характеристику в зависимости от того, по какой шкале взят угол: если по шкале S и Т малых углов (до 5°44'), то характеристика равна 2, а если по шкале sin, то I.
Во втором случае, при перевернутом движке, засекая волоском а, одновременно под волоском на основной шкале читаем значение sin а, на шкале мантисс логарифмов — мантиссу lg sin а, на шкале квадратов — значение sin2 а и, наконец, на шкале кубов — значение sin3 а (рис. 23).
Упражнение, Найти логарифмы значений тригонометрических функций:
’ 1) lg sin 35° = 1,759; 4) lg tg 15°30' = 1,443;
2) lg sin 43°40' = 1,839; 5) lg tg 3°50' = 2,826;
3) lg sin 3°30z = 2,786; 6) lg tg 65°30' = 0,341.
39. ПРИМЕНЕНИЕ ЛОГАРИФМИЧЕСКОЙ ЛИНЕЙКИ В НЕКОТОРЫХ ПРАКТИЧЕСКИХ РАСЧЕТАХ
Вычисление площади круга по его диаметру и диаметра по площади круга. Площадь S круга выражается формулой
с nd* d2
S~ 4 “ 4 •
Л где d — диаметр круга.
Заменяя знаменатель дроби через С2, имеем:
Численное значение С = 1/ — = 1,128 нанесено на основной Г л
шкале как движка, так и корпуса линейки.
Диаметр окружности d данной площади S
d=cKs.
Пример 1. Определить площадь S круга при d = 12 см.
Для того чтобы найти площадь круга, засекаем волоском на основной шкале линейки число 12, делим это число на С = 1,128, для чего подводим под волосок особый значок С на основной шкале движка, и результат читаем на шкале квадратов линейки против^ начала движка.
В нашем примере
ЧЧЧ™)’— -
4*
99
Пример 2. Найти диаметр круга d, зная, что площадь круга S = 28,3 м2.
В этом случае устанавливаем начало движка против числа 28,3, взятого на правой шкале квадратов, находим особый значок С на основной шкале движка, засекаем его волоском и на основной шкале линейки читаем результат. В нашем примере
d=cKS=1.128 K28j = 6 см.
Линейка как таблица прямой и обратной пропорциональности. Если сдвинем движок линейки, например, вправо, и поставим начало движка против цифры 2, взятой на основной шкале корпуса линейки, то получим ряд прямой пропорциональности
1 1,5 2 3 4 5
-2 — 3—4 — 6 — 8 — 10 “ Т’ Я‘
В этом случае линейка может быть использована как таблица для перевода одних единиц в другие. Например, установив конец движка линейки против числа 80, взятого на основной шкале линейки, 100
получаем отношение что дает таблицу для перевода градусов оО
Цельсия (°C) в градусы Реомюра (°R) и обратно. Сделав такую установку, оставляя движок на месте, волоском бегунка можем засекать на движке любые значения шкалы °C и на шкале ^корпуса линейки читать соответствующие им значения шкалы °R, а засекая на шкале корпуса линейки значения °R, на шкале движка читать соответствующие им значения °C. Перевод некоторых значений градусов Цельсия в градусы Реомюра приведен ниже:
вС .......... 25 40 50 62,5 30 20 15 75 55
°R ....... . 20 32 40 50 24 16 12 60 44
Использование линейки для решения задач на пропорции.
Требуется найти х из уравнения
3 х
15“ 25*
Для того чтобы найти %, поступаем следующим образом: против числа 3, взятого на основной шкале корпуса линейкиг устанавливаем число 15 на основной шкале движка. Затем засекаем волоском на основной шкале движка число 25 и на основной шкале корпуса линейки под волоском читаем значение х = 5.
Упражнение, Решить задачи на пропорции:
- 1) = —; х=9;
2) зЗ=П: х=1;
3) | = х=2; •
4> Л2=ЗТ5=П)’ х=2,82; у=1,53;
100
~ tgl2°_tg28°
5) 30 “ х ’
При решении примеров 5 и 6 рекоменду.ется перевернуть движок тригонометрическими шкалами вверх.
Использование линейки для решения треугольников. Согласно теореме синусов, зависимость между сторонами треугольника и его углами выражается равенствами:
а _ b с sin А ~ sin В sin С*
где а,Ь, с — длины сторон треугольника; A, Bt С — противолежащие им углы.
Используя эту зависимость, можно находить неизвестные элементы треугольника.
Пример. Пусть, а—25 см, b = 35 см, А = 20°. Требуется «айти В, С, с.
Составляем пропорцию:
25 = 35 с sin 20° sin В ”” sin С ‘
Определяя неизвестные члены пропорции, получим:
sin В — 0,479;
В = 28°40';
С = 180° — (20° + 28°40') = 131°20';
с — 54,7 см.
Вычисление величин, связанных между собой обратно пропорциональной зависимостью. Рассмотрим следующий пример.
Пусть известно, что газ под давлением 8 атм занимает объем 1500 см3. Требуется вычислить, какой объем займет газ под давлением 6 атм; 4,5 атм; 2 атм и т. д.
Известно, что произведение давления газа на занимаемый им объем есть величина постоянная при данной температуре, т. е. pv = const, где р — давление; v — объем. Для различных значений давления и объема можно записать равенства:
Р1^1 = Р2^2 = Р&з = • ••
Таким образом,
8» 1500— 6*о2 = 4,5’.v3/= ...
Для нахождения неизвестных значений объема v2, v3 и т. д. воспользуемся обратной, или красной, шкалой логарифмической линейки. Для этого устанавливаем на основной шкале корпуса линейки число 1500, засекаем его волоском движка и подводим под-волосок число 8 на обратной шкале. Теперь любое число на основной шкале связано обратно-пропорциональной зависимостью с соответствующим числом на обратной шкале и произведение этих чисел есть величина постоянная.
101
Результаты вычислений приводятся ниже.
Давление р в атм............. 8 6 4,5 2 1,5
Объем v в см3 ............... 1500 2000 2660 6000 8000
Вычисление процентных отношений. Пусть сумма нескольких чисел равна 1600.
Требуется узнать, сколько процентов от общей суммы составляют числа 320, 480, 400 и т. д. Эта задача может быть решена с помощью логарифмической линейки.
Для этого установим начало движка против числа 1600 на основной шкале корпуса линейки. Получим соотношение или 100
, где число 100 на движке означает, что 1600 соответствует 100%. loUU
Теперь, не сдвигая движок с места, будем перемещать бегунок вдоль корпуса линейки. Под волоском бегунка на основной шкале движка и на основной шкале корпуса линейки можно одновременно прочитать количество процентов и число, которое ему соответствует.
Проценты некоторых чисел, входящих в сумму 1600, приведены ниже.
Числа % 4
320 20,0
480 30,0
400 25,0
192 12,0
208 13,0
1600 100,0
Упражнения,
1. На пяти курсах института обучается 7500 студентов, в том числе: на I курсе — 2000, на II — 1800, на III — 1650, на IV — 1200 и на V — 850. Определить состав студентов по курсам в %.
Ответ: на I курсе — 26,7%, на II — 24%, на III — 22%, на IV — 16% и на V — 11,3%.
2. По данным учебной части института, из общего числа студентов 9000 человек 48% занимается на дневном отделении, 20% — на вечернем и 32% — на заочном. Сколько студентов занимается на каждом из отделений?
Ответ: на дневном отделении занимается 4320 студентов, на вечернем — 1800 и на заочном — 2880. _____
Вычисление выражений вида c=Va2 + 62. В технических расчетах приходится часто складывать квадраты двух величин с последующим извлечением квадратного корня из суммы квадратов (например, нахождение гипотенузы по двум катетам).
Пример. Даны длины катетов а = 3 и b = 4. Найти длину гипотенузы с = а2 + Ь2.
102
Поступаем следующим образом: против числа а = 3 на основной шкале линейки ставим начало движка. Затем на основной шкале линейки засекаем волоском значение Ь= 4, читая на шкале квадратов движка 1,77. Прибавляя к 1,77 единицу, получаем 2,77. Теперь, засекая волоском 2,77 на шкале квадратов движка, на основной шкале под волоском читаем ответ: с = 5.
Этот пример можно решить и другим способом. Перевертываем движок оборотной стороной и вставляем его тригонометрическими шкалами вверх. Против большего из заданных чисел b = 4, взятого на основной шкале линейки, ставим конец движка и засекаем волоском на основной шкале линейки меньшее число а = 3, читая под волоском значение а = 36°50'. После этого подводим под волосок, выдвигая движок вправо, 36°50' на шкале sin и против конца движка читаем на основной шкале линейки ответ: 5.
Упражнение. Определить обоими способами с = |/#1 2 3 + Ь2 при следующих значениях а и Ь:
1) а = 3;
2) а = 4;
3) а = 5;
b = 5 6=7 6=7
(с = 5,84);
(с= 8,06); (с = 8,6).
Вычисление выражений вида с = УЬ2 — а2» В технических расчетах иногда приходится извлекать квадратный корень из разности квадратов. ______
Пример. Дано: а — 15; 6=25; найти с = У Ь2— а2.
Устанавливаем меньшее число а= 15 на основной шкале движка против начала шкалы корпуса линейки. Затем на основной шкале движка засекаем волоском большее число 6 = 25, читая под волоском на шкале квадратов корпуса линейки 2,76. Теперь, уменьшая это число на единицу, передвигая волосок влево, имеем 1,76, а под волоском на основной шкале движка читаем ответ: 20.
Этот пример можно решить и другим способом. Перевертываем движок оборотной стороной и вставляем его тригонометрическими шкалами вверх. Засекаем волоском на основной шкале корпуса линейки меньшее число а — 15, а конец движка устанавливаем против большего числа b = 25, взятого на основной шкале линейки, и читаем под волоском на шкале sin, против меньшего числа, значение а = 36°50'. Затем, передвигая волосок вправо, устанавливаем на шкале sin угол р = 90° — а (90° — 36°50' = 53° 10') и под волоском на основной шкале движка читаем ответ: 20.
Упражнение. Определить обоими способами с = У Ь2 — а2 при следующих значениях а и Ь:
1) а = 30;
2) а = 16;
3) а = 8
6= 45
6= 26
6= 15
(с = 33,5);
(с = 20,5);
(с = 12,7).
Комбинированные вычисления с использованием шкал квадратов и кубов. Вычисления на логарифмической линейке значительно ускоряются и упрощаются, если наряду с основной шкалой использовать и другие шкалы.
103
Упражнение. Выполнить
1) 82X2,5=160;
2) 2,52x21,5=134,4;
3) 202 . 16 = 25;
4) 17,62:42,3 = 7,32;
5) 32,1 КК5 = 122,3;
6) 19,3 /767 : л = 53,6;
комбинированные вычисления:
7) 2л 1^377 =38,6,
8) 11,7 /873: 3,24=10,36.
9) 5 /144: 2,9=20,7;
10) 2,21 //62: 3,79=1,255;
11) 0,875/427=3,06;
12) 17,52 /873 = 36. '
В примере 1 на основной шкале корпуса линейки засекаем волоском первый сомножитель 8, читаем на шкале квадратов: 64. Затем подводим под волосок конец шкалы квадратов движка, выдвигая движок влево; находим на шкале квадратов движка второй сомножитель 2,5, засекаем его волоском и на шкале квадратов корпуса читаем под волоском ответ: 160. Порядок произведения определяем прикидкой: 60 X 3 = 180; следовательно, ответ — трехзначное число.
Пример 2 решается аналогично.
В примере 3 находим квадрат числа и засекаем его волоском, затем подводим под волосок делитель, взятый на шкале квадратов движка, и против начала шкалы квадратов движка читаем на шкале квадратов корпуса ответ 25, порядок которого определяем путем прикидки в уме.
Пример 4 решается аналогично.
В примере 5 сначала извлекаем квадратный корень из 14,5 по правой шкале (подкоренное число имеет полную левую грань, в два знака) и на основной шкале читаем ответ: 3,8. Затем, подводя под волосок конец движка, находим на основной шкале движка второй сомножитель — число 32,1, засекаем его волоском и на основной шкале корпуса линейки читаем под волоском ответ: 122,3. Порядок ответа определяем путем прикидки в уме.
Примеры 6, 7, 8, 9, и 10 решаются аналогично.
В примере 11 извлекаем сначала корень кубический из 42,6 (извлечение производим по средней шкале, так как в левой грани две цифры), засекаем его волоском, затем, выдвигая движок влево, умножаем полученное значение корня на 0,875 и на основной шкале корпуса линейки читаем- рёзультат: 3,06.
Пример 12 решается аналогично.
ЛО. ДРУГИЕ ВИДЫ СЧЕТНЫХ ЛОГАРИФМИЧЕСКИХ ЛИНЕЕК
В последние годьгнаша промышленность выпустила ряд новых счетных логарифмических' линеек. К ним относятся следующие:
1. Счетная логарифмическая односторонняя линейка с 11 шкалами.
2. Счетная логарифмическая двусторонняя линейка с 19 шкалами.
3. Линейка гидротехника (В. Ф. Пояркова).
4. Дисковая счетная логарифмическая линейка «Спутник».
5. Круговая счетная логарифмическая линейка КЛ-1.
Умеющий пользоваться нормальной 10-шкальной счетной линейкой при желании без особого труда сумеет научиться считать на линейках других видов.
104
Здесь будут отмечены лишь их отличительные признаки и даны некоторые дополнительные указания к пользованию.
Счетная логарифмическая односторонняя линейка с 11 шкалами. Эта линейка имеет следующие отличительные черты.
1. В ней изъяты шкала мантисс логарифмов на корпусе и масштабная шкала на вертикальной кромке.
2. Вместо них дана шкала LLx, состоящая из двух частей: от 1,1 до е на вертикальной кромке и от е до 2ИО4 на корпусе. Эта шкала предназначается. для возведения чисел в любую степень (в том числе и дробную), извлечения корней и нахождения логарифмов (при любом основании).
3. На шкалах тригонометрических функций (на оборотной стороне движка) градусы разделены на десятые и сотые доли, а не на минуты и секунды, как у десятишкальной линейки. Это облегчает пересчет градусов в радианы и обр*атно, так как исключаются отдельный пересчет градусов, минут и секунд и суммирование результатов.
Особенно облегчается и упрощается расчет при пользовании шкалой S и Т (малых углов от 0ъ34,38' до 5°43,77'). Для этого следует перевернуть движок обратной стороной и совместить его с началом основной шкалы корпуса линейки. Засекая волоском угол в градусах на шкале малых углов, читаем на основной шкале значение угла в радианах.
Упражнение. Установить соответствие между углами в градусах и радианах:
1) 1,719° соответствует 0,03 рад;
2) 24° „ 0,419 рад;
3) 1,134 рад „ 65°;
4) 0,06 рад „ 3,44°.
В примере 1 перевертываем оборотной стороной и вставляем его вл линейку тригонометрическими шкалами вверх. Затем засекаем волоском бегунка на шкале S и Т малых углов число 1,719, соответствующее углу 1,719°, и на основной шкале корпуса линейки видим под волоском число 0,03. Это — число радиан, соответствующее углу 1,719°.
В примере 2 засекаем волоском на основной шкале корпуса линейки число 24, подводим под волосок число на основной шкале движка, отмеченное значком р (57,3), и против конца движка на основной шкале линейки читаем 419. Следовательно, 24° соответствуют 0,419 рад.
Счетная логарифмическая двусторонняя линейка с 19 шкалами. Большое число шкал на лицевой и оборотной стороне линейки делает ее очень удобной в обращении, позволяет ускорить подсчеты, исключает необходимость перевертывания движка. Перечень шкал, дается в кратком приложении к линейке.
На шкалах лицевой стороны линейки производятся умножение, деление, возведение в квадрат и куб, извлечение квадратных и кубических корней, нахождение значений тригонометрических функций.
На оборотной стороне линейки по степенным (показательным) шкалам производят вычисления любых степеней, корней и логариф-
1 мов, а по шкалам, сдвинутым на л, — определение числа пх или —.
б С. И. Березин
105
Шкала мантисс логарифмов позволяет находить мантиссы десятичных логарифмов.
Отметим еще одно положительное качество этой линейки — наличие на бегунке трех волосков (визирных линий).
Засекая на основной шкале средним волоском величину диаметра круга, на шкале квадратов под левым волоском читаем площадь круга. И наоборот, засекая на шкале квадратов средним волоском площадь круга, на основной шкале под правым волоском читаем величину диаметра.
Упражнение. Проверить правильность подсчетов:
S = 35,26; d = 6,7;
S = 12,57; d = 4,0;
S= 66,04; <2=9,17.
С помощью шкалы, сдвинутой на л, по сравнению с основной, можем быстро определить выражение пх. Для этого' на основной шкале засекаем волоском значение х, а на шкале, сдвинутой на л, под волоском читаем произведение лх. Например, Зл = 9,42. В этом случае засекаем на основной шкале множитель 3, а на шкале, сдвинутой на л, под волоском читаем ответ 9,42.
Упражнение. Проверить правильность подсчетов:
1) 6л = 18,8; 3) 0,76л = 2,38;
2) 8,6л = 27,0; 4) 0,5л = 1,57.
Линейка гидротехника (В. Ф. Пояркова). Линейка предназначена для гидравлических расчетов потока с равномерным режимом в трапецеидальных каналах, напорных и безнапорных трубах круглого сечения, лотках прямоугольного, параболического и полуциркульного сечения. Руководство к пользованию — на самой линейке.
Дисковая счетная логарифмическая линейка «Спутник» и круговая счетная логарифмическая линейка КЛ-1. Выпускаемая московским заводом «Калибр» дисковая счетная линейка является попыткой придать малой линейке с длиной шкал 12,5 см более портативную форму. Она предназначается для различных вычислений- по типу нормальной линейки. Круговая счетная логарифмическая линейка КЛ-1 очень портативна и позволяет производить умножение, деление, возведение чисел в квадрат и извлечение квадратного корня, вычислять значения тригонометрических функций и определять обратные величины.
Линейка КЛ-1 напоминает часы: она имеет два циферблата, заключенных в металлическую оправу с двумя головками.
Исчерпывающие указания к пользованию линейками «Спутник» и круговой счетной логарифмической линейкой КЛ-1 даются в брошюре Л. С. Хренова и Ю. В. Визирова «Логарифмическая линейка». В ней приводится описание линеек, рассматриваются способы их проверки, установка и чтение чисел на шкалах.
Подробно изложена техника вычислений на линейке «Спутник». Это — умножение и деление чйсел, возведение чисел в квадрат, в куб, извлечение квадратного и кубического корней, вычисление значений тригонометрических функций, отыскание обратных чисел, мантисс логарифмов, приемы комбинированного умножения и деления, вычислений с помощью шкалы обратных чисел.
106
Способы вычислений на круговой логарифмической линейке КЛ-1 показываются на примерах возведения чисел в квадрат и извлечения квадратного корня, вычисления выражений вида: 1 : г, 1 : х2 и 1 : J/G:, вычисления значений тригонометрических функций, умножения и деления чисел. Выполнение этих всех действий, кроме умножения и деления, на линейке КЛ-1 ничем не отличается от подобных действий на нормальной логарифмической линейке; умножение и деление чисел производятся несколько иначе.
Брошюра хорошо иллюстрирована как рисунками, так и примерами, позволяющими при необходимости без особого труда приобрести навыки в работе с этими линейками.
б*
107
Глава VI
АРИФМОМЕТР «ФЕЛИКС»
Арифмометр — наиболее простая настольная ручная вычисли-тельная машина, широко применяющаяся для малой механизации технических и хозяйственных расчетов.
Он используется главным образом для умножения и деления. С его помощью можно производить также сложение и вычитание, но при этих действиях нет преимуществ арифмометра перед конторскими счетами.
Арифмометр изобретен в 1874 г. русским инженером В. Т. Од-нером.
41. ОПИСАНИЕ АРИФМОМЕТРА
Арифмометр типа «Феликс» укреплен на подставке 8 и состоит из двух основных частей: неподвижной коробки-барабана 1 и подвижной каретки 13 (рис. 24). В основу устройства счетной части машины положен принцип колеса Однера — шайбы с переменным числом зубцов.
Барабан имеет девять установочных рычажков 2, при помощи которых можно установить девятизначное число. Номера рычажков показаны на барабане сверху и обозначены цифрами 9, 8, 7, 6, 5, 4, 5, 2, 1 (рис. 25). Для установки на барабане числа необходимо передвинуть в пазу рычажки по направлению к себе, установив их против соответствующих цифр. Если нам необходимо установить на барабане число, например 6583, то мы начнем это делать с цифр высшего разряда и рычажки 4, 5, 2 и 1 устанавливаем так, как это показано на рис. 25: рычажок 4 устанавливаем против цифры 6, рычажок’3 — против 5, рычажок 2 — против 8 и, наконец, рыча-жок 1 — против 3.
Подвижная каретка 13 (рис. 24) имеет два счётчика: левый — счетчик оборотов 10, правый — результатный (счетчик результатов) 7. Счетчик оборотов имеет восемь разрядов. В каждом окне счетчика видны нули. При повороте рукоятки от себя, по часовой стрелке, в счетчике оборотов появится белая единица, показывающая, что был сделан один оборот по часовой стрелке (например, при сложении и умножении). После поворота рукоятки на себя, против часовой стрелки, в окне счетчика оборотов появится красная единица, показывающая, что был сделан один оборот на себя
108
Рис. 24. Арифмометр «Феликс»:.
/ — барабан; 2 — установочные рычажки; 3 — движки-запятые; 4 —стрелки — указатели действий; 5 — рукоятка; 6 — гасительная ласточка (барашек) результатного счетчика; 7 — окна результатного счетчика; 8 — подставка; 9 — рычажок передвижения каретки; 10 — окна счетчика оборотов; 11 — гасительная ласточка (барашек) счетчика оборотов; 12 — стрелка — указатель разрядов счетчика оборотов; 13 — подвижная каретка; 14 — головка гасительной планки
109
(например, при вычитании и делении). Цифры со счетчика оборотов убираются при помощи гасительной ласточки И, которую надо повернуть от себя до характерного щелчка.
В правой части подвижной каретйи находится результатный счетчик 7, имеющий 13 окон, в каждом из которых видны нули. Движением рукоятки от себя, по часовой стрелке, цифры, установленные на барабане, переносят на результатный счетчик. Перенеся на счетчик число, необходимо обязательно проверить правильность установки числа на барабане. Результатный счетчик очищается и приводится в нулевое положение посредством гасительной ласточки 6, которую также надо повернуть от себя до характерного щелчка.
Стрелки — указатели действий 4 нанесены на барабане справа. Они показывают, что сложение и умножение производятся поворотом рукоятки от себя, по часовой стрелке, а вычитание и деление — поворотом ее в обратном направлении, т. е. к себе, против часовой стрелки.
Рукоятка 5 имеет штифт, который должен всегда находиться в гнезде кронщтейна, так как в противном случае нельзя будет ни установить число на барабане, ни передвинуть подвижную каретку, ни очистить счетчик — все будет застопорено. При повороте рукоятки ее надо несколько оттянуть вправо, чтобы вынуть штифт из гнезда кронштейна. Только после этого можно будет ее повернуть.
Рычажок передвижения каретки 9 позволяет перемещать ее влево .и вправо как на один разряд, так и на несколько разрядов сразу. При передвижении на один разряд вправо делают легкий удар по рычажку указательным пальцем левой руки в направлении слева направо, а при передвижении каретки на один разряд влево — легкий удар по рычажку большим пальцем левой руки. В случае необходимости перевести каретку на несколько разрядов поднимают рычажок, и после этого каретка свободно передвигается влево и вправо на любое число разрядов.
Головка гасительной планки 14 предназначена для очистки барабана. Отведя ее влево большим пальцем левой руки и повернув рукоятку на х/4 оборота по часовой стрелке, можно убрать все цифры, установленные на барабане, а установочные рычажки привести в нулевое положение.
Движки-запятые 3 счетчика оборотов, результатного счетчика и рычажков на барабане служат для отделения десятичных знаков и для разбивки числа на разряды.
Стрелка 12 (в последних выпусках точка) — указатель разрядов счетчика оборотов — нанесена с левой стороны на верхнем щитке над окнами счетчика оборотов и определяет положение каретки.
42. ПРОВЕРКА ИСПРАВНОСТИ
Проверка арифмометра должна производиться периодически. Рекомендуется ее делать всякий раз, когда приходится впервые работать на том или ином экземпляре машины.
Для проверки правильности работы механизма машины существует ряд способов. Приводим три способа проверки.
1. Устанавливаем на барабане слева направо число 012345679 и умножаем на 81. В результате должно получиться произведение, состоящее из девяток: 999 999 999. Поворачивая рукоятку арифмометра в обратном направлении, против часовой стрелки, убираем
ПО
со счетчика оборотов 8 десятков и единицу. После этого результат* ный счетчик и счетчик оборотов должны показывать нули.
2. Устанавливаем на барабане слева направо число 037037037 и умножаем его на числа, кратные трем. При умножении его на 3 должны получить 111 111 111, на 6-—222 222 222, на 9 — 333 333 333, на 12 — 444 444 444, на 15 — 555 555 555, на 18 — 666 666 666, на 21 — 777 777 777, на 24 - 888 8888 888, на 27 — 999 999 999.
Если сделать то же число оборотов рукоятки в обратном направлении, против часовой стрелки, счетчик оборотов и результатный счетчик должны показывать нули.
3. Устанавливаем на барабане слева направо число 123456789. Умножая его на 9, должны получить 1 111 111 101, на 18 — 2 222 222 202, на 27 — 3 333 333 303, на 36 — 4 444 444 404, на 45 — 5 555 555 505, на 54 — 6 666 666 606, на 63 — 7 777 777 707, на 72 — 8 888 888 808, на 81—9 999 9999 909.
При неисправности арифмометра указанные результаты не получатся. Произведения не. будут соответствовать приведенным числам либо, при поворотах рукоятки на себя, счетчик оборотов будет показывать нули, а в результатном счетчике останутся какие-либо цифры или наоборот.. В этом случае пользоваться арифмометром нельзя.
Следует отметить, что приведенные выше способы проверки арифмометра полностью не гарантируют его исправность. Иногда, правда очень редко, наблюдаются случаи, когда проверка не обнаруживает неисправность. Но это не исключает необходимости и целесообразности периодической проверки.
Перед тем как начать работу на арифмометре, надо привести его в исходное положение; поставить все установочные рычажки в нулевое положение, очистить счетчик оборотов и результатный счетчик, защелкнуть гасительные ласточки, вставить штифт рукоятки в углубление кронштейна, а каретку отвести в крайнее левое положение.
Во избежание поломки арифмометра нельзя вращать рукоятку, если каретка при передвижении остановилась между двумя разрядами: в этом случае не'будут вращаться ни рукоятка, ни ласточки. Если ласточки не защелкнуты, то весь механизм арифмометра будет также застопорен, а если штифт рукоятки не находится в углублении'кронштейна, то каретка двигаться не будет.
В процессе работы нельзя останавливать рукоятку арифмометра на неполном обороте. Обнаружив, что начали вращать рукоятку не в ту сторону, надо закончить начатый оборот и только после этого сделать исправительный, в обратном направлении. В противном случае в результате вычислений могут появиться ошибки.
43. СЛОЖЕНИЕ
Сложение и вычитание на арифмометре, как указывалось, обычно не производят. Поэтому об этих действиях будет сказано очень кратко и лишь с той целью, чтобы понять в дальнейшем действия умножения и деления. Умножение на арифмометре представляет собой последовательное сложение множимого, а деление — последовательное .вычитание делителя из делимого.
Сложение и умножение производится путем поворота рукоятки от себя, по часовой стрелке.
111
Пример.
1234 4- 641 = 1875.
Приведя арифмометр в исходное положение, устанавливаем на барабане справа с помощью рычажков 4, 3, 2 и 1 (рис. 25) первое слагаемое 1234 и путем поворота рукоятки от себя переносим его на результатный счетчик.
Каждый раз, перенеся установленное на барабане число на результатный счетчик, надо сверить его с числом, которое должно быть установлено, так как иногда из-за неправильной установки рычажка на барабане получаем вместо 1234 числа 1334 или 1233. Поэтому настоятельно рекомендуем во избежание ошибок в вычислениях очень внимательно устанавливать цифры на барабане и контролировать правильность установки числа. Единица в счетчике оборотов показывает, что был сделан один оборот рукоятки.
Затем очищаем барабан, убирая первое слагаемое при помощи головки гасительной планки. Для этого отводим ее большим пальцем левой руки и поворачиваем рукоятку арифмометра по часовой стрелке на г/4 оборота. После этого возвращаем рукоятку в исходное положение. В результате установленные на барабане цифры будут, убраны и рычажки придут в нулевое положение.
Затем, строго соблюдая разрядность, рычажками 5, 2 и 1 устанавливаем на барабане второе слагаемое 641. Сделав один оборот рукоятки по часовой стрелке, от себя, на результатном счетчике получаем сумму первого и второго слагаемых 1875. Счетчик оборотов показывает, что было произведено два оборота рукоятки по часовой стрелке. Если надо прибавить еще несколько слагаемых, то в этом случае снова очищаем барабан, устанавливаем на нем третье слагаемое. Затем путем поворота рукоятки от себя получаем на результатном счетчике сумму трех слагаемых и т. д.
Несколько сложнее обстоит дело в том случае, когда складываем десятичные дроби.
Пример.
124,5 + 63,712 + 8,66 = 196,872.
Рассматривая слагаемые, замечаем, что каждое из них имеет различное число десятичных знаков: первое — один, второе — три и третье — два. Припишем к первому слагаемому справа два нуля и к третьему слагаемому — один нуль, так чтобы количество цифр после запятой было одинаково в каждом слагаемом.
На барабане и в результатном счетчике отделим запятыми справа по три знака и только после этого начнем сложение, которое производится совершенно так же, как в предыдущем примере.
Сначала устанавливаем с помощью рычажков 6, 5, 4 и 3 первое слагаемое 124,500, переносим его путем поворота рукоятки по часовой стрелке, от себя, на барабан. Затем, сверив число на результатном счетчике с числом, установленным на барабане, очищаем барабан и устанавливаем с помощью рычажков 5, 4, 3, 2 и I второе слагаемое 63,712. Перенеся его на результатный счетчик, читаем 188,212. Наконец, еще раз очистив барабан, устанавливаем на нем рычажками 4, 3, 2 третье слагаемое — 8,660 и, перенеся его на результатный счетчик путем поворота рукоятки по часовой стрелке, читаем на. счетчике результатов окончательную сумму 196,872. Установленные запятые как на барабане, так и на резуль
112
татном счетчике позволили правильно определить в итоге число десятичных знаков. В счетчике оборотов стоит цифра 3 (белая), показывающая, что было сделано три оборота рукоятки по часовой стрелке.
Упражнение. Выполнить сложение на арифмометре:
1) 4856 + 1203 = 6059;
2) 133 + 1712 = 1845;
3) 15 724+ 3276= 19000;
4) 176445+128 515=304 960;
5) 56 877+ 3114 = 59 991;
6) 817+ 408+ 64+ 110 = = 1399;
7) 72,5 + 26,45 = 98,95;
8) 144,68+56,001+ 14,3 = 214,981;
9) 1026+ 17,05+ 38,44= 1081,49;
10) 672,4+ 25,6 + 100,62 = 798,62;
И) 14327,54 + 9631,002 =
= 23958,542;
12) 335,6 + 72,4 + 11,9 = 419,9.
44. ВЫЧИТАНИЕ
Вычитание и деление на арифмометре производятся путем поворота рукоятки к себе, против часовой стрелки.
Пример 1.
4857 — 1312 = 3545.
Прежде чем начать вычитание, приводим арифмометр в исходное положение и устанавливаем на барабане справа с помощью рычажков 4, 3, 2 и 1 уменьшаемое 4857. Поворотом рукоятки от себя, по часовой стрелке, переносим уменьшаемое на результатный счетчик, при этом обязательно проверяем правильность установленного на барабане числа. Затем очищаем барабан и» строго соблюдая разрядность, этими же рычажками устанавливаем вычитаемое 1312. После этого поворачиваем рукоятку один раз на себя, против часовой стрелки, и таким образом вычитаем 1312. В итоге на результатном счетчике читаем разность 3545.
Производя вычитание дробных чисел, надо, так же как и при сложении, приписать к уменьшаемому или вычитаемому такое количество нулей, чтобы количество цифр после запятой было одинаково.
Пример 2.
236,8 — 22,62 = 214,18.
В данном случае отделяем запятыми справа два десятичных знака как на барабане, так и на результатном счетчике. Затем устанавливаем на барабане с помощью рычажков 5, 4, 5, 2 уменьшаемое 236,8 и переносим его на результатный счетчик. Проверив правильность установки числа, очищаем барабан и с помощью рычажков 4, 3, 2 и 1 устанавливаем на нем вычитаемое 22,62. Поворотом рукоятки к себе, против часовой стрелки, производим вычитание. На результатном счетчике читаем разность 214,18.
Упражнение. Решить примеры:
1) 729 — 315 = 414;
2) 22 417 — 10 305= 12-112;
3) 9688 — 346 = 9342;
4) 844,16 — 214,03 = 630,13;
5) 1236,008 — 1002,2 = 233,808.
113
45. УМНОЖЕНИЕ
Правило умножения чисел на арифмометре. Для умножения приводим арифмометр в исходное положение, отодвинув каретку в крайнее левое положение, а затем на барабане, с правой стороны, устанавливаем один из сомножителей. Далее поворачиваем от себя рукоятку столько раз, сколько единиц в 1-м разряде второго сомножителя. Затем переводим каретку на один разряд вправо и делаем столько поворотов рукоятки от себя, сколько содержится десятков во 2-м разряде второго сомножителя, и т. д.
Пример 1.
125 X 3 = 375. #
Устанавливаем на барабане справа множимое 125. Затем поворачиваем рукоятку от себя, по часовой стрелке. После одного оборота рукоятки на результатном счетчике появится число 125, а на счетчике оборотов — единица, показывающая, что число на барабане (множимое) перенесено на результатный счетчик один раз. Повернув рукоятку еще раз, на*результатном счетчике читаем 250, а на счетчике оборотов — 2; повернув рукоятку еще один раз, на результатном счетчике читаем произведение 375, а на счетчике оборотов — множитель 3. Итак, 125 X 3 = 375.
Пример 2. Произведем умножение на двузначное число:
867 X 32 = 27 744.
В этом случае устанавливаем на барабане первый сомножитель 867 и ведем умножение как в примере 1. Получаем на результатном счетчике произведение 867 X 2 = 1734. После этого переводим каретку на один разряд вправо и трижды поворачиваем рукоятку от себя. В счетчике оборотов получаем множитель 32, а в результатном счетчике — произведение 27 744.
Упражнение. Выполнить умножение на арифмометре:
1) 563 X 42 = 23 646; 4) 1894 X 189 = 357 966;
2) 749 X 87 = 65 163; 5) 3690 X 108 = 398 520;
3) 822 X ИЗ = 92 886; 6) 753 X 66 = 49 698.
Выбор сомножителя для установки на барабан. Для экономии времени и сил при перемножении на арифмометре надо уметь рационализировать приемы вычислений.
Так, на барабан надо установить тот из сомножителей, в котором большее количество цифр и больше их сумма. Например, при умножении 64 767 на 112 на барабан устанавливается 64 767, а не 112. Если бы мы установили на барабане 112, то нам пришлось бы сделать 30 (6+ 4 4- 7 +6 + 7) оборотов рукоятки и четыре передвижения каретки вправо. Установив же на барабане 64 767, при умножении на 112 мы сделаем всего лишь четыре (1 + 1 + 2) оборота рукоятки и два передвижения каретки вправо и получим произведение 7 253 904.
Заметим, что умножение можно начать как с единиц 1-го разряда, так и с единиц последнего разряда множителя. В нашем примере можно было умножать множимое сначала на одну единицу 3-го разряда множителя, затем на одну единицу 2-го разряда, а потом на две единицы 1-го разряда. В этом случае перед началом
114
умножения каретку следует отвести вправо на несколько разрядов, так как в процессе умножения ее придется сдвигать влево.
Упражнение. Выполнить умножение наиболее рациональным способом:
1) 876 519 X 23 = 20 159 937; 4) 9878 X 234 = 2 311 452;
2) 9356 X 14 = 130 984; 5) 1214 X 798 = 968 772;
3) 38 176 X 201 = 7 673 376; 6) 4869 X 39 = 189 891.
Случай сомножителя, близкого к числу, изображаемому единицей с последующими нулями. Пусть требуется умножить 549 х 98 = = 53802.
Устанавливаем на барабане первый сомножитель 549 и умножаем его на 100. Затем переводим каретку на два деления влево и отнимаем разницу (100 — 98) X 549 ~ 2 X 549, для чего делаем два оборота рукоятки против часовой стрелки, на себя. На результатном счетчике читаем произведение 53 802, а на счетчике оборотов число 102, причем цифра 1 будет белая, а цифра 2 — красная. Это показывает, что мы сделали один оборот.рукоятки по часовой стрелке и два оборота против часовой стрелки вместо 17 (9 + 8) оборотов по часовой стрелке.
К этому способу прибегаем в тех случаях, когда умножаем на 6, 7, 8, 9. В первом случае умножаем на (10 — 4), во втором — на (10 — 3), в третьем — на (10 — 2) и, наконец, в последнем — на (10 — 1). Это дает некоторую экономию времени при вычислениях.
Упражнение. Выполнить умножение наиболее рациональным способом:
1) 1275 X 199 = 253 725; 4) 165 X 489 = 80 685; >
2) 4326 X 9997 = 43 247 022; 5) 988 X 694 = 685 672;
3) 598 X 3877 = 2 318 446; 6) 8923 X 399 = 3 560 277.
В примере 1 мы умножаем на 199 = (200 — 1), в примере 2 — на 9997 = (10000 — 3), в примере 3 — на 598 = (600 — 2), в примере 4 — на 489 = (500 — 11) и т. д.
Повторяющийся множитель. При умножении ряда чисел на один и тот же множитель, например: *
35 X 65 = 2275; 35 X 84 = 2940;
35 X 75 = 2625; 35 X 87 = 3045,
устанавливаем на барабане постоянный множитель 35 и, умножая его сначала на 65, получаем в результатном счетчике 2275. Затем при умножении 35 X 75 не сбрасываем цифр с барабана, счетчика оборотов и результатного счетчика, а только «доумножаем». Для этого добавляем один десяток, повернув рукоятку от себя по часовой стрелке. Получаем в результатном счетчике 2625, а на счетчике оборотов — 75. Для умножения 35 на 84 добавляем еще один десяток и, переведя каретку на одно деление влево, делаем оборот рукоятки на себя. Получаем в счетчике оборотов 84, а в результатном v счетчике — произведение 35 X 84 = 2940. Для последнего умножения (на 87) сделаем три оборота рукоятки от себя. Получаем в счетчике оборотов 87, а в результатном — произведение 35 X 87 = = 3045.
115
Упражнение. Решить примеры, используя «доумножение»:
1)‘ 242 X 48 = 116 166; 3) 694 X 226 = 156 844;
253 X 48 = 12 144; 794 X 226 = 179 444;
352 X 48 = 16 896; 1793 X 226 = 405 218;
552 X 48 = 26 496; 1790 X 226 = 404 540;
2) 1498 X 167 = 250 166; ’3792 X 226 = 856 992.
2499 X 167 = 447 333;
2497 X 167 = 416 999;
4397 X 167 = 734 299;
Способ одновременного умножения двух чисел на один и тот же множитель. Например, надо умножить 548 х 24 и 612 х 24. В этом случае набираем на барабане, начиная с 9-го разряда (рычажками 9, 8 и 7), число 548, а начиная с 3-го разряда (рычажками 3, 2 и 1) — число 612. Устанавливаем движок-запятую между 7 и 6-м разрядами результатного счетчика — и умножаем набранные числа на 24. В итоге, в счетчике оборотов читаем 24, а в результатном счетчике — два произведения: 13 152 и 14 688, которые отделены друг от друга запятой. Понятно, что небольшая емкость результатного счётчика ограничивает возможность применения этого способа.
Упражнение. Решить примеры:
1) 768 и 489 умножить на 14 (10 752 и 6846);
2) 338 и 705 умножить на 58 (19 604 й 40 890);
3) 675 и 914 умножить на 185 (124 875 и 169 090).
Получение суммы произведений. Для получения суммы произвел дений, например (24. X 15)+ (64 X 25)— 1960, устанавливаем справа на барабане число 24 и умножаем его на 15. На результатном счетчике читаем произведение: 360. Затем убираем со счетчика оборотов 15 и с барабана первый сомножитель 24. Оставляем на результатном счетчике произведение 360. После этого устанавливаем на барабане справа 64 и умножаем это число на 25. В итоге на результатном счетчике читаем искомую сумму 1960. На счетчике оборотов .будет стоять последний множитель 25.
Упражнение. Получить сумму произведений:
1) (251 X 390) + (117 X 85) = 107 835;
2) (2188 X 42) + (458 X 16) = 61 424;
3) (1872 X 22) + (1052 X 57) = 791 488.
Получение разностй произведений. Если нужно найти разность произведений, например (72 X 55) — (35 X 45) — 2385, то сначала умножаем 72 на 55 и получаем произведение 3960. Затем снимаем 55 со счетчика оборотов и очищаем барабан, оставляя на результатном счетчике произведение 3960. После этого устанавливаем на барабане число 45 и умножаем его на 35, поворачивая рукоятку к себе, против часовой стрелки, т. е. делая вычитание. В итоге получаем на счетчике оборотов множитель 35 (красными цифрами), а на результатном счетчике — искомую разность 2385.
Упражнение. Получить разность произведений:
1) (814 X 28) - (612 X 15) = 13 612;
2) -(912 X 57) — (320 X 42) = 38 544;
3) (654 X 31) - (157 X 102) = 4260.
116
Умножение нескольких сомножителей. В том случае, когда требуется перемножить несколько сомножителей, например 35 X 8 X X 45 X 12 = 151 200, сначала умножаем 35 X 8 и получаем 280. Затем очищаем барабан и устанавливаем на нем это первое произведение. Убирая цифры в обоих счетчиках, производим умножение 280 X 45. Получаем в результатном счетчике 12 600. Еще раз очищаем барабан и убираем цифры в обоих счетчиках. Устанавливаем на барабане второе произведение 12 600 и производим умножение на 12. После этого в результатном счетчике читаем окончательный ответ 151 200, а в счетчике оборотов — 12.
Упражнение. Решить примеры:
1) 75 X 32 X 15 = 36 000;
2) 12 X 25 X 64 = 19 200;
3) 82 X 21 X 45 X 23 = 1 782 270.
Определение порядка произведения. Если первая цифра произведения меньше первой цифры каждого из сомножителей, то порядок произведения равен сумме порядков сомножителей.
Пример 1.
598 X 76 = 45 448.
Поскольку первая цифра произведения (4) меньше первой цифры каждого из сомножителей (5 и 7), то порядок произведения равен' сумме порядков сомножителей: 3+2=5.
Если же первая цифра произведения больше первых цифр каждого из сомножителей, то порядок произведения равен сумме порядков сомножителей минус 1.
Пример 2.
316 X 26= 8216.
Так как первая цифра произведения (8) больше первой цифры каждого из сомножителей (3 и 2), то порядок произведения'будет равен сумме порядков сомножителей минус единица, т. е. 3 + 2 — — 1 = 4. Результат — четырехзначное число 8216.
46. ДЕЛЕНИЕ
Правило деления чисел на арифмометре. Прежде чем начать деление, приводим арифмометр в исходное положение.
Рассмотрим пример деления без остатка:
875 : 25 = 35.
Для деления на арифмометре отводим каретку вправо, устанавливая счетчик оборотов против движка-запятой с таким расчетом, чтобы можно было получить частное с необходимым числом знаков. В нашем примере устанавливаем стрелку — указатель разрядов против третьего окошечка счетчика оборотов. Затем на барабане слева, против одиннадцатого окошечка результатного счетчика, набираем (рычажками 9, 8 и 7) делимое 875. Поворотом рукоятки от себя переносим делимое на результатный счетчик.
Проверив правильность установки числа, очищаем барабан и убираем единицу со счетчика оборотов. После этого с помощью рычажков 9 и 8 устанавливаем на барабане делитель 25. Перед
117
тем как начать деление, надо посмотреть на первые цифры делимого и делителя и, если первая цифра делителя больше первой цифры делимого, то каретку отвести на один разряд влево. В нашем примере первая цифра делителя (2) меньше первой цифры делимого (8) и поэтому каретку отводить на один разряд влево не следует.
Затем можно начать деление, поворачивая рукоятку на себя до тех пор, пока делимое не разделится без остатка на делитель или не появятся девятки в результатном счетчике и одновременно не раздастся звонок, сигнализирующий, что производить деление на этом разряде дальше нельзя. В этом случае надо сделать так называемый исправительный оборот, повернув рукоятку обратно по часовой стрелке. Этот оборот также сопровождается звонком. После этого надо передвинуть каретку на одно деление влево и только тогда продолжать деление.
Если делимое делится без остатка, результатный счетчик будет показывать нули, а счетчик оборотов — частное (красными цифрами, за исключением белых 0 и 9).
В нашем примере после четырех оборотов рукоятки на себя, против часовой стрелки, на результатном счетчике появляются девятки и раздается звонок, сигнализирующий о том, что делить дальше нельзя. Сделав обратный исправительный оборот рукоятки и переведя каретку на один разряд влево, продолжаем деление. После шести оборотов на результатном счетчике опять появляются девятки и раздается звонок. Делаем обратный исправительный оборот и замечаем, что на результатном счетчике нули, а в счетчике оборотов частное 35 (красными цифрами). Итак, 875 делится на 25 без остатка, частное 35.
Деление с заданной точностью. Для того чтобы не производить лишней работы, следует предварительно установить, с какой точностью необходимо получить результат, прекращая деление по получении заданной точности.
Пример 1. Найти частное 698 : 88 с точностью до 0,1.
Устанавливаем слева на барабане с помощью рычажков 9, 8 и 7 делимое 698. Счетчик оборотов устанавливаем на четвертом разряде, передвинув каретку вправо так, чтобы четвертое справа окно оказалось против стрелки — указателя разрядов. После этого поворотом рукоятки от себя переносим делимое на результатный счетчик, не забывая сверить правильность установки числа. Затем очищаем барабан, убираем единицу со счетчика оборотов и в тех же разрядах рычажками 9 и 8 устанавливаем делитель 88. Замечая, что первая цифра делителя больше первой цифры делимого, отводим каретку на один разряд влево. Если мы этого не сделаем, то при первом же повороте рукоятки на себя раздастся звонок и на результатном счетчике появятся девятки, напоминающие, что надо отвести каретку на один разряд влево.
После этого начинаем деление, повертывая рукоятку на себя. При восьмом повороте рукоятки раздастся звонок, а в результатном счетчике появятся девятки, показывающие, что на этом разряде дальше делить нельзя. Сделав исправительный оборот, переводим каретку еще на один разряд влево и продолжаем деление. После 10 оборотов на себя раздается звонок и на результатном счетчике опять появляются девятки. Сделав исправительный оборот и переведя каретку еще на один разряд влево, продолжаем деление. После четырех поворотов рукоятки на себя раздается звонок. Сделав
118
снова исправительный оборот, Китаем на счетчике оборотов 793, а на результатном — 16 (остаток). Деление прекращаем, так как частное получено с заданной точностью до 0,1. Итак, 698 : 88 = 7,9 с округлением до 0,1.
Пример 2. Найти частное 7682 : 418 с точностью до 0,01.
Устанавливаем на барабане слева делимое. Поскольку нам надо получить ответ с точностью до 0,01, необходимо иметь в частном на одну цифру больше, т. е. пять знаков, с тем чтобы можно было сделать округление. Поэтому устанавливаем пятое справа окошечко счетчика оборотов против стрелки — указателя разрядов и переносим делимое на результатный счетчик. После этого очищаем барабан и убираем единицу со счетчика оборотов. Затем в этих же разрядах устанавливаем на барабане делитель и производим деление. В результате получаем на счетчике оборотов красными цифрами частное от деления 18,377 или с округлением до требуемой точности.— 18,36. На результатном счетчике видим остаток (414).
Определение порядка частного. Если первая цифра делимого меньше первой цифры делителя, то порядок частного равен разности порядков делимого и делителя. ,
Пример 1.
32 754 : 53 = 618.
В этом случае первая цифра делимого (3) меньше первой цифры делителя (5), поэтому порядок частного будет равен 5 — 2=3. Частное — трехзначное число 618.
Если первая цифра делимого больше первой значащей цифры делителя, то порядок частного равен разности порядков делимого и делителя плюс единица.
Пример 2.
8626 : 227 = 38.
Так как первая цифра делимого (8) больше первой цифры делителя (2), то порядок частного будет равен 4 — 3 + 1 = 2. Частное — двузначеное число 38.
Возможность установки делимого справа. Рассмотрим пример:
874 : 38 = 23.
Сначала устанавливаем делимое 874 на барабане слева при помощи рычажков 9, 8 и 7. Прикидываем возможное число знаков в ответе. Так как первая цифра делимого больше первой цифры делителя,. то порядок частного будет равен разности порядков делимого и делителя плюс единица, т. е. 3 — 2 + 1 = 2. Поэтому устанавливаем второе справа окошечко счетчика оборотов против стрелки указателя разрядов и ведем деление как обычно.
Как правило, делимое устанавливают на барабане слева в том случае, когда делимое число небольшое — до шести . значащих цифр.
Полученный результат (23) можно получить и в том случае, если мы установим делимое на барабане справа при помощи рычажков 3, 2 и 1. Отведя каретку на два разряда вправо, переносим делимое на результатный счетчик, очищаем барабан, убираем единицу со счетчика оборотов и устанавливаем делитель при помощи рычажков 3 и 2, Деление будет происходить так же, как и в первом случае.
119
Повторяющийся делитель. ~В этом случае деление целесообразно заменить более быстрым действием — умножением делимого на обратную величину делителя.
Примеры,
850 : 25 = 34;
700 : 25 = 28;
' 925 : 25 = "37;
1450 : 25 = 58;
1650 : 25 = 66.
Находим сначала обратную величину делителя 0,04, устанавливаем эту обратную величину 0,04 (постоянный множитель) на барабане и умножаем на него делимое 850. Произведение 34, полученное на результатном счетчике, равно частному отделения 850 : 25.
Следующее делимое 700 Меньше предыдущего на 150, т. е. на одну сотню и пять десятков. Поэтому, не производя нового умножения, мы только «доумножим», т. е. снимаем со счетчика оборотов одну сотню и 5 десятков и получим на счетчике оборотов второе делимое 700, а на результатном — 28.
Делимое 925 больше числа 700 на две сотни, два десятка и пять единиц. Не делая никаких новых установок, добавляем ко второму делимому эту разницу. Получаем на результатном счетчике 37 и т. д.
Как видим, процесс деления в этом случае действительно значительно ускоряется.
Таблица значений обратных величин для целых чисел от 2 до 10 000 дается в приложении к книге Л. С. Хренова «Малые вычислительные машины». Значения обратных величин всех целых чисел-от 2 до 15 000 приведены также и в таблицах Барлоу (графа — V \ п)
Упражнение, Проверить умножением на обратное число правильность ответов:
4680 : 72 = 65; 2304 : 72 = 32;
6696 : 72 = 93; 1872 : 72 = 26;
6408 : 72 = 89; 864 : 72 = 12;
4464 : 72 = 62; 5400 : 72 = 75.
Обратное число — = 0,0138889 вычисляем сами с помощью логарифмической линейки, вычислительных таблиц или арифмометра. Это число и будет нашим постоянным множителем, которое мы установим на барабане. На результатном счетчике отделяем семь знаков, установив движок-запятую между 7 и 8-м разрядами результатного счетчика (так как в постоянном множителе семь знаков после запятой). Умножаем 4680 на 0,0138889 и получаем в счетчике оборотов 4680 (первое делимое), а на результатном счетчике — частное 65.
Замечаем, что второе делимое 6696 больше первого на 2016 (6696 — 4680), т. е. на две тысячи, один десяток и шесть единиц. Чтобы не делать лишней работы, «доумножаем» — прибавляем к числу, имеющемуся на счетчике оборотов, эту разницу. Получаем в счетчике оборотов второе делимое 6696. На результатном счетчике 120
читаем 93 — частное от деления 6696 на 72. Аналогично переходим к третьему, четвертому делимому и т. д., соответственно получая частные: 89, 62, 32, 26, 12, 75.
При определении порядка обратного числа следует помнить, что если знаменатель дроби —целое число, то в обратном числе будет п
столько нулей до первой значащей цифры, включая и нуль целых, сколько имеется цифр в целой части числа. Например: -^- = 0,25; i-0'0* гаг»’”»8’ й-0’00952' пж-
= 0,0000893.
Если знаменатель меньше единицы, то порядок обратного числа будет иметь столько целых единиц, сколько имеется нулей в знаменателе'до первой значащей цифры, включая и нуль целых.
Например: ^ = 2,5; = 40; 0,0058 = 172,41 0,00007 =
= ,4285Л пиг38» оз-8’848-
Способ подбора делимого умножением. Деление заметно ускоряется, если производить его посредством умножения, путем подбора делимого.
Пример.
1885 : 29 = 65.
Переводим каретку в крайнее правое положение и устанавливаем справа на барабане делитель 29. Начинаем его умножать на 1, 2, 3 и 4 и т. д. до тех пор, пока первые цифры произведения не станут больше первых цифр делимого. Так, повернув рукоятку 7 раз по часовой стрелке, получаем 203 — первые цифры больше первых цифр делимого. Повернув рукоятку в обратном направлении, получаем 174, т. е. число, первые цифры которого меньше первых цифр делимого. :
Теперь, переведя каретку на один разряд влево, продолжим умножение, все время следя за результатным счетчиком. После пяти оборотов получаем на результатном счетчике 1885, т. е. наше делимое. На счетчике оборотов будет стоять частное — 65. Подобное положение означает, что число разделилось без остатка. Когда число не делится без остатка, прекращают деление, по получении требуемого числа знаков частного.
Упражнение. Проверить правильность ответов, используя способ подбора делимого умножением:
1) 21 228 : 870 = 24,4; 6) 6554: : 226 = 29;
2) 199,28 : 4,24 = 47; 7) 0,7843 : 341 = 0,0023;
3) 0.27468 : 0,509 = 0,54; 8) 0,07524 : 0,0418 = 1,8;
4) 0,045816 : 6,64 = 0,0069; 9) 0,007176 : 5,98 = 0,0012;
5) 0,0019916 : 0,00766 = 0,26; 10) 82 960 : 244 = 340.
Порядок частного в простых случаях можно определить прикидкой в уме,- а в более сложных следует применить вышеприведенные правила (см. стр. 119).
Глава VII
ДЕСЯТИКЛАВИШНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ ВК
47. ОБЩИЕ СВЕДЕНИЯ О МАШИНАХ ВК-1, ВК-2, ВК-3
Десятиклавишные вычислительные машины ВК-1, ВК-2 и ВК-3, выпускаемые нашей промышленностью, предназначены для выполнения четырех арифметических действий и являются усовершенствованными арифмометрами.
ВК-1 — ручная вычислительная машина;
ВК-2 — полуавтомат (все арифметические операции, кроме умножения, выполняются автоматически);
ВК-3 — полный автомат (все арифметические действия можно производить автоматически).
В основу устройства счетной части всех этих машин положен, как и в арифмометре, принцип колеса Однера — шайбы с переменным числом зубцов. Емкость счетчика оборотов и счетчика результатов такая же, как и у арифмометра: счетчик оборотов — 8-раз-рядный, счетчик результатов — 13-разрядный.
В отличие от арифмометра, у всех машин типа ВК передвигается установочный механизм, а счетчики результатов и оборотов остаются неподвижными. Счетчик оборотов снабжен механизмом передачи десятков, на нем нет красных цифр. Наличие 10 цифровых клавиш (вместо установочных рычажков арифмометра) позволяет производить установку чисел простым нажатием соответствующих клавиш. Это значительно ускоряет набор чисел на барабан и повышает производительность труда оператора.
Сравнительная производительность труда оператора на арифмометре «Феликс», вычислительных машинах ВК-1, ВК-2 и ВК-3 за один час работы с 4—5-значными числами приведена ниже. Производительность труда особенно повышается при работе так называемым слепым способом. При этом способе числа набирают пальцами левой руки, не глядя на клавиатуру; цифры нажимают в следующем порядке: мизинцем — цифра 1; безымянным—цифры 2, 3; средним — 4, 5, 0; указательным — 6, 7, 8, 9.
Этот способ может быть освоен сравнительно легко — все будет зависеть от тренировки.
Наличие окна контроля обеспечивает контроль правильности набора числа на барабан. Исходное положение установочного бара
122
бана — крайнее правое. Числа на клавиатуре набираются начиная с высших разрядов. При этом после каждого нажатия клавиши установочный барабан автоматически передвигается на один разряд влево.
Вычислительные машины Количество операций в час
Сложение | Умножение | Деление
Арифмометр «Феликс» 400—500 170—180 95-100
ВК-1 900—1000 310—330 190-210
ВК-2 1200-1300 370—400 320—350
вк-з 1200-1300 390—420 300—360
Для выработки навыков в работе на ВК-1, В К-2 и В К-3 рекомендуем выполнить все упражнения, приведенные в гл. Ill, IV и VI.
40. ОПИСАНИЕ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ ВК-1
Вычислительная десятиклавишная машина ВК-1 показана на рис. 26. Она имеет те же механизмы и приспособления, что и обычный арифмометр.
Цифровые клавиши 8 расположены в два ряда: в верхнем — клавиши с цифрами 2, 4, 5, 7 и 9, в нижнем — клавиши с цифрами 1, 3, 0, 6 и 8.
Набранное на клавиатуре 8 число видно в окне контроля установки числа 12, что позволяет контролировать правильность набора. Это число гасится нажатием рычага гашения 6.
Счетный механизм ВК-1 имеет 13-разрядный счетчик результатов 1 и 8-разрядный счетчик оборотов 3, которые очищаются от чисел (гасятся) нажатием на рычаги гашения 4 и 11,
Движки-запятые 2 позволяют отделить десятичные знаки, что облегчает чтение чисел на счетчиках результатов и оборотов и в окне контроля установки числа 12.
Транспортный механизм служит для перемещения установочного барабана относительно счетчиков. Исходное положение установочного барабана — крайнее правое. При нажатии на любую из цифровых клавиш 8 он автоматически передвигается на один разряд влево.
При нажатии клавиши поразрядного движения установленного числа вправо (9) или влево (10) установочный барабан передвигается на один разряд соответственно вправо или влево. Нажатие клавиши для отвода набранного на клавиатуре числа в крайнее левое положение 7 вызывает перемещение установочного барабана до отказа влево. Как увидим ниже, такое положение установочного барабана необходимо при делении. Если вести умножение начиная с низшего разряда множителя, то следует пользоваться клавишей поразрядного движения установленного числа влево 10; а если умножение начинается с высшего разряда множителя, то пользуются клавишей поразрядного движения установленного числа вправо 9. Клавишей 9 пользуются также при делении для поразрядного передвижения барабана, на котором установлен делитель.
123
Назначение рукоятки 5 то же, что и у арифмометра: она служит для приведения машины в действие.
Правила обращения с машиной ВК-1 примерно те же, что и с арифмометром. Если клавиши и рычаги застопорены, нужно проверить правильность положения рукоятки, штифт которой после ее поворота должен быть всегда в гнезде кронштейна. Рукоятку необходимо вращать всегда на полный оборот.
Рис. 26. Десятиклавишная вычислительная машина ВК-1:
/ — счетчик результатов; 2 — движки-запятые; 3 — счетчик оборотов; 4, 11 — рычаги гашения счетчика оборотов и счетчика результатов соответственно; 5 — рукоятка; 6 — рычаг гашения установленного числа на клавишах; 7 — клавиша для отвода набранного на клавиатуре числа в крайнее левое положение; 8 — цифровые клавиши (клавиатура); Р, 10 — клавиши поразрядного движения установленного числа вправо и влево соответственно; 12 — окно контроля установки числа.
Чтобы освободить правую руку оператора для записи результатов, рекомендуется нажимать клавиши поразрядного движения установленного числа вправо и влево, а также рычаг гашения счетчика результатов левой рукой.
Вращать рукоятку 5, нажимать рычаги гашения счетчика, оборотов и установленного числа на клавишах 4 и 6 следует правой рукой, причем рычаги гашения нужно нажимать одновременно указательным и большим пальцами в направлении рукоятки (это показано стрелками на корпусе машины).
Прежде чем приступить к вычислениям, необходимо все механизмы машины привести в исходное положение: рукоятку защелкнуть в кронштейне, счетчики результатов и оборотов погасить, установочный барабан должен находиться в крайнем правом положении.
124
49. СЛОЖЕНИЕ
Порядок сложения и вычитания на машине ВК-1 такой же, как и на арифмометре.
Пример. Найти сумму чисел:
1200 + 21,251 + 543,4 + 1046,1 = 2810,751.
Сначала движками-запятыми отделяем справа на счетчике результатов и в окнах контроля установленных чисел наибольшее количество десятичных знаков, имеющихся у слагаемых. В нашем примере наибольшее число их — три — у второго слагаемого. После этого, приведя машину в исходное положение, нажатием соответствующих клавиш 8 набираем первое слагаемое 1200,000 и поворотом рукоятки 5 по часовой стрелке передаем его на счетчик результатов 1. Затем нажатием на рычаг гашения 6 приводим клавиатуру в исходное положение; набираем второе слагаемое 21,251 и, перенеся его поворотом рукоятки по часовой стрелке, читаем в счетчике результатов сумму двух слагаемых 1221,251. Нажав рычаг гашения 6 и тем самым приведя клавиатуру в исходное положение, набираем третье слагаемое 543,400, делаем один поворот рукоятки по часовой стрелке и читаем в счетчике результатов сумму первых трех слагаемых 1764,651. Затем, еще раз приведя клавиатуру в исходное положение нажатием рычага гашения 6t набираем последнее слагаемое 1046,100 и, перенеся его в счетчик результатов, читаем окончательную сумму 2810,751. В счетчике оборотов 3 замечаем цифру 4, показывающую число слагаемых, т. е. число оборотов, рукоятки по часовой стрелке. Окончив вычисление, машину приводим в исходное положение.
50. ВЫЧИТАНИЕ
Вычитание на машине ВК-1 производится следующим образом. Набираем на клавиатуре уменьшаемое и поворотом рукоятки по часовой стрелке переводим его в результатный счетчик. Затем нажатием на рычаг 6 приводим клавиатуру в исходное состояние. Набираем на клавиатуре вычитаемое и поворотом рукоятки против часовой стрелки производим вычитание. В результатном счетчике получаем разность:
Пример. Найти разность:
364,66 — 212,4 = 152,26.
Сначала отделяем движками-запятыми 2 по два десятичных знака в счетчике результатов /ив окне контроля установки числа 12. Набрав на цифровых клавишах уменьшаемое 364,66, передаем его поворотом рукоятки 5 по часовой стрелке на счетчик результатов. Затем нажатием на рычаг гашения 6 приводим клавиатуру в исходное положение и набираем вычитаемое 212,40. Поворачивая рукоятку против часовой стрелки, производим вычитание. В счетчике результатов — разность 152,26. Закончив вычитание, машину приводим в исходное положение.
51. УМНОЖЕНИЕ
Пример. Найти произведение:
78 X 124 = 9672.
Набираем сначала на клавиатуре множимое 78, читая его в окне контроля установки числа. Затем переносим множимое на счетчик результатов, поворачивая рукоятку по часовой стрелке 4
125
раза — столько раз, сколько единиц в низшем разряде множителя. Переведя установочный барабан на один разряд вправо нажатием на клавишу 9, умножаем на следующий разряд множителя — 2; затем, переведя еще раз установочный барабан вправо на один разряд, умножаем на следующий разряд множителя — 1. После этого в счетчике результатов получаем произведение 9672, а в счетчике оборотов — множитель 124. В окне контроля набора читаем множимое 78.
Упражнение. Выполнить умножение:
1) 453 X 58 = 26 274; 4) 78,79 X 787,9 = 62078,641;
2) 87,6 X 3,7 = 324,12; 5) 268,96 X 164 = 44109,44;
3) 629 X 114 = 71 706; 6) 73,4 X 11,7 = 858,78.
52. ДЕЛЕНИЕ
Так же как и при умножении, при делении чисел на ВК-1 можно использовать все способы, применяемые при вычислениях на арифмометре.
Пример. Найти частное:
8256 : 192 = 43.
Сначала набираем на клавиатуре 8 делимое 8256 и нажатием на клавишу 7 отводим набранное число в крайнее левое положение. Затем поворотом рукоятки 5 по часовой стрелке переносим делимое в счетчик результатов. После этого, переведя барабан в исходное положение с помощью клавиши 9, набираем на клавиатуре делитель 192. Барабан вновь переводим в крайнее левое положение, нажимая на клавишу 7. Затем начинаем деление, вращая рукоятку против часовой стрелки, последовательно вычитая делитель из делимого до тех пор, пока не раздастся звонок. Делаем один исправительный оборот рукоятки в обратном направлении, по часовой стрелке, и переводим барабан на один разряд вправо, продолжая деление до получения в частном необходимого числа знаков. В нашем примере это будут два знака — частное 43, которое читаем в счетчике оборотов. Счетчик результатов будет показывать нули, что означает, что число разделилось нацело, без остатка.
Если число не делится нацело, без остатка, то счетчик результатов будет показывать остаток.
В случае, когда делимое и делитель дробные числа, сначала приводим их к целым числам.
Пример.
82,73 : 31,8 = 2,6 (остаток 5).
Увеличивая делимое и делитель в 100 раз, получаем 8273 : 3180 и дальше производим деление целых чисел, получив в счетчике оборотов частное 2,6, а в счетчике результатов 5 (остаток).
Порядок частного определяем либо путем прикидки в уме, либо используя вышеприведенное правило вычисления порядка частного (см. стр. 119).
Упражнение. Выполнить деление:
1) 7316 : 59 = 124; 4) 222,58 : 3,59 = 62;
2) 11 872 : 224 = 53; 5) 654,35 : 115 = 5,69;
3) 4989,6 : 8,4 = 594; 6) 43 428 : 660 = 65,8.
126
53. ОПИСАНИЕ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ ВК-2
Вычислительная десятиклавишная машина ВК-2 — полуавтомат. На ней можно производить четыре арифметических действия: деление, сложение и вычитание — автоматически, умножение — полуавтоматически. Наличие электропривода увеличивает скорость ведущих механизмов по сравнению с машинами с ручным приводом и освобождает правую руку работающего для записи. Надежность работы обеспечивается введением автоматической блокировки при работе основных механизмов машины. Машина работает при помощи электромотора переменного тока с напряжением в 127 или 220 В и производит не менее 4,8 об/с.
Вычислительная машина ВК-2 показана на рис. 27.
/J 12 11 10 9 о
Рис. 27. Полуавтоматическая десятиклавишная вычислительная машина ВК-2:
/ — счетчик результатов; 2 — движки-запятые; 3 — счетчик оборотов; 4 — сигнальный круг; 5, 12 — клавиши шагового перемещения каретки установочного барабана влево и вправо соответственно; 6 — клавиша гашения установленного числа на барабане (нулевая клавиша); 7 — стоп-рычаг; 8 — клавиши управления счетом (X, -г, +); 9 — клавиша освобождения каретки; 10 — цифровые клавиши (клавиатура); 11 — рычаг переключения; 13 — рычаг управления; 14, 15 — рычаги гашения счетчика оборотов и счетчика результатов соответственно; 16 — кнопка реверса; 17 -— окно установочного барабана
Назначение отдельных механизмов следующее.
Цифровые клавиши 10 служат для установки чисел на установочном барабане, который при наборе каждой цифры перемещается на один разряд влево.
Набранное число может быть' прочитано в окне установочного барабана 17.
Счетчик результатов 1 показывает: при сложении — сумму, при вычитании — разность, при умножении — произведение, при делении — остаток.
127
Счетчик оборотов 3 фиксирует количество оборотов установочного барабана, а именно: при сложении — число слагаемых, при умножении — множитель, при делении — частное.
Движки-запятые 2 служат для облегчения чтения чисел.
При помощи рычага управления 13, который может занимать одно из трех положений — левое, среднее или правое, вычислительная машина включается соответственно на действие умножения, сложения или вычитания; при правом положении рычага 13 и левом положении рычага переключения 11 можно производить также деление. Если же рычаг 11 находится в правом положении, то при среднем положении рычага 13 можно производить умножение.
Для поразрядного перемещения установочного барабана слева направо и справа налево служат соответственно клавиши 12 и 5. Быстрое перемещение установленного на барабане числа в левое крайнее положение происходит при нажатии клавиши 9.
Для гашения чисел, набранных на барабане, и освобождения цифровых клавиш 10, если до этого были произведены какие-либо действия, служит клавиша 6, а для гашения чисел на счетчиках результатов и оборотов — соответственно рычаги 15 и 14. Стоп-рычаг 7 предназначен для включения автоматического гашения вычитаемого числа и прекращения действия деления; для этого он должен быть опущен вниз до отказа.
Клавиши 8 служат для управления счетом: при сложении применяют клавиш + ,- вычитании и автоматическом делении 4-,' при умножении X. '
Сигнальный круг 4 указывает направление вращения счетных колес. Если.счетные колеса счетчика оборотов вращаются в одном направлении со счетными колесами счетчика результатов, то в сигнальном круге появляется черный цвет, а при вращении их в противоположном направлении — красный цвет.
Подготовку машины к работе производят следующим образом. При помощи вилки включают ее в штепсельную розетку и приводят в исходное положение. Затем, нажимая рычаги гашения 14 и 15, в окнах счетчика результатов 1 и счетчика оборотов 3 получают нули. Установочный барабан переводят в правое крайнее положение. В окне установочного барабана 17 нажатием клавиши гашения 6 устанавливают нули. В сигнальном круге 4 должен появиться черный цвет. Стоп-рычаг 7 должен находиться в верхнем положении.
После этого приступают к вычислениям. Набор числа на цифровой клавиатуре производят пальцами левой руки в том же порядке, что и при работе на ВК-1. Таким образом, правая рука освобождается для записи результатов вычислений.
54. СЛОЖЕНИЕ
При сложении рычаг управления 13 устанавливают в среднее положение. --
Пример 1.
15 412 + 2343+ 114 = 17 869.
Сложение производим следующим образом. При помощи клавиш 10 набираем последовательно слагаемые 15 412, 2343 и 114, нажимая после каждого набора клавишу + и 6. Правильность набора контролируем в окне установочного барабана 17,
128
Счетчик результатов Т покажет сумму 17 869, а счетчик оборотов 3 — число слагаемых 3.
Если необходимо сложить несколько десятичных дробей, то как и при сложении на ВК-1, приводим их к общему знаменателю (к одинаковому числу десятичных знаков набором цифры 0) и дальше ведем сложение так же, как в предыдущем примере.
Пример 2.
24,3 + 120,008 + 53,15= 197,458.
Приведя к общему знаменателю, имеем:
24,300 +120,008 53,150
197,458
Для облегчения чтения суммы полезно десятичные знаки отделять движком-запятой 2.
65. ВЫЧИТАНИЕ
При вычитании рычаг управления 13 ставят в правое положение.
Пример 1.
2864 — 1423 — 752 = 689.
Набираем уменьшаемое 2864 и нажимаем клавишу +. Затем последовательно набираем вычитаемое 1423 и 752, нажимая после каждого набора клавишу -ь. В счетчике результатов 1 читаем разность 689.
При вычитании десятичных дробей приводим их к общему знаменателю набором цифры 0 и дальше вычитание ведем так же, как и в примере 1.
Пример 2.
4485,1 — 311,06 — 1032,17 — 26 = 3115,87.
Приведя к общему знаменателю, получаем
4485,10 — 311,06 — 1032,17 — 26,00 = 3115,87.
В этом случае движком-запятой 2 отделяем два десятичных знака.
56. УМНОЖЕНИЕ
Умножение на ВК-2 можно производить так же, как и на ВК-1, \ начиная с низшего или высшего разряда множителя. Установочный барабан перемещается автоматически или вручную. Количество оборотов установочного барабана лучше подсчитывать на слух и по окончании умножения сверять с показанием счетчика оборотов. Для экономии времени рекомендуется устанавливать на барабан сомножитель, имеющий большее число знаков.
Пример 1.
683 X 76 = 51 908.
Умножение ведем без автоматического движения установочного барабана.
129
Устанавливаем рычаг управления 13 в среднее положение и набираем множимое 683. Затем, нажав клавишу X, держим ее опущенной до появления в счетчике оборотов числа единиц множителя 6, после чего освобождаем клавишу X и нажимаем клавишу шагового перемещения 5. Затем опять нажимаем клавишу X и держим ее опущенной до появления в счетчике оборотов числа десятков множителя 7, после этого освобождаем клавишу X. В счетчике резуль-v татов читаем произведение 51 908. Правильность установки сомножителей контролируем в окнах установочного барабана и счетчика оборотов. Если в счетчике оборотов получилось число, меньшее данного разряда, то нажатием клавиши X увеличиваем его, а если . число большее, то нажатием клавиши -г- уменьшаем его.
Пример 2.
539 X 146 = 78 694.
На этот раз умножение ведем с автоматическим перемещением установочного барабана влево.
Устанавливаем рычаг управления 13 в левое положение и набираем множимое 539. Затем, нажав клавишу X, держим ее опущенной до появления в счетчике оборотов 3 числа единиц множителя 6. Освобождаем клавишу X, после чего установочный барабан автоматически перемещается на один разряд влево. Затем производим те же операции при умножении на десятки и сотни множителя и в счетчике результатов читаем произведение 78 694. Если в счетчике оборотов одна из цифр окажется не соответствующей данному разряду множителя, то нажатием клавиши 12 возвращаем установочный барабан в данный разряд и исправляем ошибку, используя клавишу X или 4-.
Когда в множителе имеется цифра 0, то установочный барабан перемещаем до разряда со значащей цифрой нажатием клавиши 5.
Пример 3.
764 X 407 = 310 948.
Набрав множимое 764, нажимаем клавишу X до тех пор, пока в счетчике оборотов не появится цифра 7. Затем последовательно нажимаем клавишу 5 и клавишу X на время четырех оборотов, после чего освобождаем клавишу X и в счетчике результатов читаем произведение 310 948, а в счетчике оборотов — множитель 407.
При перемножении десятичных дробей число десятичных знаков в произведении определяем по известному арифметическому правилу: оно равно сумме десятичных знаков сомножителей.
Так, перемножая 6,79 X 3,5 = 23,765, получив в счетчике результатов 23765, отделяем три десятичных знака, так как в первом сомножителе два десятичных знака, а во втором — один, т. е. всего в сумме три,десятичных знака. Для того чтобы прочитать число без ошибки, можно перед началом умножения отделить указателем-запятой в счетчике результатов справа три знака.
67. ДЕЛЕНИЕ
В зависимости от требуемого в частном количестве знаков деление можем производить с установкой делимого в левых или правых разрядах счетчика результатов.
Пример 1.
1105,65 : 9,45= 117.
130
В этом случае деление производим в правых разрядах счетчика результатов.
Устанавливаем рычаг управления 13 в правое положение, набираем делимое 1105,65 и нажимаем клавишу +• Затем набираем делитель 9,45, нажатием клавиши 5 подводим высшие разряды делителя под высшие разряды делимого и нажимаем клавишу деления После остановки машины счетчик оборотов покажет частное 117. Число разделилось нацело, поэтому в счетчике результатов нули; если же число не делится нацело, то в счетчике результатов получим остаток от деления.
* Пример 2.
693,89 : 59,8.
В этом случае деление производим в левых разрядах счетчика результатов.
Устанавливаем рычаг управления 13 в правое положение, набираем делимое 693,89, нажимаем клавишу 9 и клавишу +• Затем набираем делитель 59,8. Нажатием клавиши 9 подводим высшие разряды делителя под высшие разряды делимого и нажимаем клавишу деления После остановки машины в счетчике оборотов читаем частное 11,6, а в счетчике результатов 21 (остаток). Порядок частного определяем либо прикидкой в уме, либо в соответствии с правилом вычисления порядка частного (см. стр. 119).
68. ОПИСАНИЕ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ ВК-3
Вычислительная машине ВК-3 является усовершенствованной моделью машины ВК-2. Она является полным автоматом и предназначена для выполнения четырех арифметических действий, причем х на ней, в отличие от вычислительной десятиклавишной машины ВК-2, можно производить автоматически не только деление, но и умножение. Эти действия выполняются на ВК-3 сокращенными способами и сопровождаются уменьшением числа ходов машины по сравнению с обычными способами, что достигается благодаря наличию специального пускового механизма.
Все ранее сказанное о машине ВК-2 относится и к ВК-3. Следует лишь отметить, что вычислительная десятиклавишная машина ВК-3 имеет значительно меньшее распространение, чем ВК-2.
Вычислительная машина ВК-3 показана на рис. 28.
В основу устройства счетной части машины положен принцип колеса Однера. Счетная часть в машине ВК-3 в основном такая же, как и в машине ВК-2.
Две дополнительные клавиши 11 и 14 предназначены для автоматического умножения. С помощью клавиши 14 набранное число передают на умножающий механизм. Затем на клавиатуре 10 набирают множитель, нажимают клавишу 11, и машина автоматически произведет умножение. При сложении используют клавишу +.
В тех же случаях, когда при выполнении сложения необходимо одновременно погасить показания счетчика оборотов, используем клавишу С.
59. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НА МАШИНЕ ВК-3
Перед началом вычисления машину приводим в исходное положение: гасим счетчики оборотов и результатов и установочный барабан, который приводим в крайнее правое положение.
131
Все арифметические действия, за исключением автоматического умножения, производим так же, как на машине ВК-2.
Рис. 28. Автоматическая десятиклавишная вычислитель-
ная машина ВК-3:
/ — счетчик результатов; 2 — окно установочного барабана;
3 — счетчик оборотов; 4 — сигнальный круг; 5 — клавиша гашения установленного числа на барабане; 6 — стоп-рычаг; 7, /3 — клавиши шагового перемещения каретки установочного \ барабана влево и вправо соответственно; 8 — клавиши управления счетом (С, 4-); 9 — клавиша освобождения каретки;
10 — цифровые клавиши (клавиатура); 11 — пусковая’клавиша автоматического умножения; 12 — рычаг управления; 14 — клавиша для передачи множимого в умножающий механизм; 15, 16 — рычаги гашения счетчика оборотов и счетчика результатов соответственно; 17 — кнопка реверса; 18 — движки-запятые
Автоматическое умножение на ВК-3 производим следующим образом.
Пример, Пусть требуется умножить
518 х 74 = 38 332.
Приведя машину в исходное положение, рычаг управления 12 отводим влево, кнопку реверса 17 устанавливаем в переднее положение, а стоп-рычаг 6 — в верхнее. После этого нажатием клавиш 10 набираем множитель 74 и, проверив его в окне 2, нажатием клавиши 14 передаем его в умножающий механизм. Затем нажатием клавиш 10 набираем множимое 518 и нажимаем клавишу 11, Машина автоматически выполнит умножение и остановится. Счетчик результатов покажет произведение 38 332.
ЗАКЛЮЧЕНИЕ
Описание в настоящем кратком пособии простейшие средства вычислительной техники позволяют осуществить только малую механиеацию вычислительных работ.
Перед многочисленной армией инженерных и управленческих работников нашей страны стоит задача полной механизации и автоматизации всех видов вычислительного труда и совершенствования на этой основе управления промышленностью. Эта задача решается применением электромеханических счетных машин, разных типов (клавишных и перфорационных) и, главным образом, электронных вычислительных машин (цифровых и аналоговых).
В сфере умственного труда электронная вычислительная техника осуществляет такой же коренной переворот, какой в прошлом совершили машины-орудия в сфере физического, мускульного труда человека.
Однако каковы бы ни были успехи электронной вычислительной техники, средства малой механизации вычислительных работ еще долгие годы не утратят свбего значения, и пользованию ими необходимо научить самые широкие круги читателей.
СПИСОК ЛИТЕРАТУРЫ
Асатиани Л. Г. Таблицы вычисления процентов, умножения и деления. М., Госстатиздат, 1954, 367с.
Берман Г. И. Приемы счета. М.—Л., Гостехиздат, 1950, 88 с.
Брадис В.М. Средства и способы элементарных вычислений. М., Учпедгиз, 1954, 230 с.
Брадис В. М. Четырехзначные математические таблицы. М., Просвещение, 1971, 95 с.
Исаков В., Лившиц Ф.-, Рожнов В. Финансовые вычисления. М., «Финансы», 1964, 244 с.
Карташян А. А. Дидактический материал для вычислений на логарифмической линейке. М., «Просвещение», 1964, 127 с.
Кобозев Н. Н. Логарифмическая линейка. М., «Высшая школа», 1971, 80 с.
Маслов П. П. Техника работы с цифрами. М., «Статистика», 1972, 134 с.
Мижов Д. С. Счетная логарифмическая линейка. Изд-во Томского университета, 1968, 66с.
Митропольский А. К. Краткие математические таблицы. М., «Наука», 1968, 95 с.
Назаров В. Г. Справочник по логарифмической линейке. М., Физматгиз, 1959, 47 с.
О’Р у р к. Таблицы умножения. М., «Статистика», 1969, 336 с.
Панов Д. Ю. Счетная линейка. М., «Наука», 1971, 168 с.
Румшисский Л. 3. Счетная линейка. М., «Наука», 1972, 64 с.
Таблицы Барлоу. М., «Мир», 1965, 258 с.
Таблицы умножения. М., «Статистика», 1971, 60 с.
Тишин С. Д., Тишин С. С., Таблицы возведения в степень. М., «Статистика», 1972, 400 с.
Хренов Л. С. Малые вычислительные машины. М., Физматгиз, 1963, 212 с..
Хренов Л. С., Визиров Ю. В. Логарифмическая линейка. М., «Высшая школа», 1968, 79 с.
Шир ок и х И. И. Логарифмическая линейка и ее применение. Томск, Кн. изд-во, 1964, 139 с.
Fricke Н. W. Der Rechenschieber. Leipzig, Fachbuchverlag, 1957, 190 S.
' Lehmann H. Der Rechenstab und seine Verwendung. Leipzig, Fachbuchverlag, 1964, 228 S.
19бб^§1ЦеГ Rechenvorteile. Leipzig, Verlagsqesellschaft,
ОГЛАВЛЕНИЕ
Предисловие............................................ 3
Глава I. Приемы сокращенных вычислений................. 4
1. Сложение.................................. —
2. Вычитание................................... 9
3. Умножение.................................. 10
4. Деление.................................... 14
Глава II. Приближенные числа и действия с ними ... .17
5. Точные и приближенные числа................. —
6. Абсолютная и относительная погрешности вычислений ......................................... 18
7. Правило округления чисел................... 19
8. Сложение приближенных чисел................ 20
9. Вычитание приближенных чисел............... 23
10. Умножение приближенных чисел............... 24
11. Деление приближенных чисел................. 25
Глава II Г. Конторские счеты......................... 27
12. Назначение и устройство...................... —
13. Сложение.................................... 29
14. Вычитание.................................. 31
15. Умножение................................... 32
16. Деление..................................... 34
Глава IV. Вычислительные таблицы........................ 37
17. Таблицы умножения двузначных чисел на двузначные числа........................................... —
18. Таблицы умножения О’Рурка ................... 41
19. Таблицы вычисления процентов, умножения и деления Л. Г. Асатиани................................. 46
20. Таблицы Барлоу............................ 47
21. Таблицы возведения в степень С. Д. Тишина и .
С. С. Тишина .................................. 54
22. Составление таблиц для практических целей ... 59
Глава V. Счетная логарифмическая линейка............ 61
23. Принцип устройства логарифмической линейки —
24. Описание логарифмической .линейки......... 64
25. Цена делений основной шкалы............... 66
26. Установка и чтение чисел на основной шкале ... 67
27. Порядок чисел............................. 68
28. Проверка линейки.......................... 70
29. Умножение.................................. —
30. Деление................................... 75
31. Умножение и деление на шкале квадратов и с помощью обратной шкалы........................... 77
32. Комбинированные действия умножения и деления 79
33. Возведение в квадрат.......................... 81
34. Извлечение квадратного корня.................. 83
35. Возведение в куб.............................. 85
36. Извлечение кубического корня.................. 87
37. Логарифмы чисел............................. 89
135
38. Тригонометрические функции.................. 92
39. Применение логарифмической линейки в некоторых практических расчетах ........................ 99
40. Другие виды счетных логарифмических линеек 104
Глава VI. Арифмометр «Феликс»....................108
41. Описание арифмометра....................... —
42. Проверка исправности.................... . 110
43. Сложение...............................111
44. Вычитание..............................113
45. Умножение..............................114
46. Деление................................... 117
Глава VII. Десятиклавишные вычислительные машины В К........................................... 122
47. Общие сведения о машинах ВК-1, ВК-2, ВК-3 ... —
48. Описание вычислительной машины ВК-1....123
49. Сложение...............................125
50. Вычитание.................................—
51. Умножение.........................л.......—
52. Деление................................126
53. Описание вычислительной машины ВК-2....127
54. Сложение............................... . 128
55. Вычитание.............................. . 129
56. Умножение.................................—
57. Деление .................................. 130
58. Описание вычислительной машины ВК-3.......131
59. Арифметические действия на машине ВК-3 . . . . —
Заключение........................................... 133
Список литературы...................................134
I Сергей Игнатьевич Березин | ТЕХНИКА ЭЛЕМЕНТАРНЫХ
ВЫЧИСЛЕНИЙ
Редактор издательства Т. С. Васильева Обложка художника В. У. Фонарева Технический редактор Т. П. Малашкина Корректор Л. И. Нефедова
Сдано в производство 20/VIII 1973 г. Подписано к печати 2/XI 1973 г. М-60022. Формат бумаги 84Х1О81/32. Бумага типографская № 3. Прив. печ. л. 7,14. Уч.-изд. л. 8,4. Тираж 70 000 экз. Зак. № 930. Цена 43 коп.
Ленинградское отделение издательства «МАШИНОСТРОЕНИЕ» 191065, Ленинград, ул. Дзержинского, 10
Ордена Трудового Красного Знамени Ленинградская типография № 1 «Печатный Двор» имени А. М. Горького Союзполиграфпрома при Государственном комитете Совета Министров СССР по делам издательств, полиграфии и книжной торговли, Ленинград, Гатчинская ул., 26
6Ш
ИЗДАТЕЛЬСТВО «МАШИНОСТРОЕНИЕ»