Автор: Михалев М.А.
Теги: движение жидкостей гидродинамика физика моделирование гидравлика гидравлические расчеты
ISBN: 978-5-7422-2190-6
Год: 2010
Текст
Федеральное агентство по образованию
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
М.А МИХАЛЕВ
ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ГИДРАВЛИЧЕСКИХ ЯВЛЕНИЙ
Учебное пособие
Санкт-Петербург
0
Издательство Политехнического университета
2010
Федеральное агентство по образованию
САН КТ- П ЕТЕРБУ Р ГСКИЙ ГОСУДАРСТВ ЕН Н Ы Й
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
М. А. МИХАЛЕВ
ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ГИДРАВЛИЧЕСКИХ ЯВЛЕНИЙ
Рекомендовано Учебно-методическим объединением
по университетскому политехническому образованию
в качестве учебного пособия для студентов
высших учебных заведений, обучающихся по направлению
подготовки «Техническая физика»
Санкт-Петербург
Издательство Политехнического университета
2010
УДК 532.5.072.12(075.8)
М69
Рецензенты:
Доктор физико-математических наук, профессор,
главный научный сотрудник отдела «Гидравлика сооружений
и техводоснабжение» ОАО «ВНИИГ им. Б. Е. Веденеева» В. И. Климович
Доктор физико-математических наук, профессор,
заведующий кафедрой «Гидроаэродинамика» СПбГПУ Е. М. Смирнов
Михалев М. А. Физическое моделирование гидравлических явлений :
учеб, пособие / М. А. Михалев. — СПб. : Изд-во Политехи, ун-та, 2010. —
443 с.
Излагаются основы физического моделирования гидравлических
явлений. Основное внимание уделяется методам построения критери-
альных уравнений - зависимости безразмерных чисел подобия, содер-
жащих искомые величины, от критериев подобия, представляющих
собой безразмерные комбинации физических констант и характерных
величин, заданных по условиям рассматриваемых задач. При недостаточ-
ности критериев подобия или при полном их отсутствии обосновыва-
ются два метода получения из чисел подобия критериев: метод ком-
бинаций чисел подобия и метод фрагментов. Инновационный подход к
проблеме физического моделирования позволяет по-новому оценить име-
ющиеся достижения и существенно расширить области применения
метода физического моделирования явлений в гидромеханике, гидравли-
ке, а также в смежных областях науки и техники.
Предназначено для студентов высших учебных заведений, обучаю-
щихся по направлениям: «Строительство», «Защита окружающей сре-
ды», «Электроэнергетика», «Природообустройство»; специальностям:
«Промышленное и гражданское строительство», «Гидротехническое стро-
ительство», «Городское строительство и хозяйство», «Инженерная защи-
та окружающей среды», «Нетрадиционные и возобновляемые источники
энергии», «Мелиорация, рекультивация и охрана земель». Пособие может
быть полезно для студентов, обучающихся по другим специальностям.
Печатается по решению редакционно-издательского совета Санкт-
Петербургского государственного политехнического университета.
© Михалев М. А., 2010
© Санкт-Петербургский государственный
ISBN 978-5-7422-2190-6 политехнический университет, 2010
Оглавление
1. Введение...........................................6
1.1. Основные понятия теории физического
моделирования....................................9
2. Основы теории подобия.............................17
3. Примеры использования метода подобия..............33
4. Основы метода размерностей........................59
4.1. Формула размерности........................62
4.2. Выбор основных единиц измерения............66
4.3. Пи-теорема (л-теорема).....................72
4.4. Комбинации чисел подобия...................80
4.5. Анализ комбинаций чисел подобия в области гидроме-
ханики..........................................91
5. Правила подготовки и проведения экспериментов....107
6. Другие методы, связанные ел- теоремой............124
6.1 Метод размерностей.........................124
6.2 . Метод линейных пропорциональностей.......129
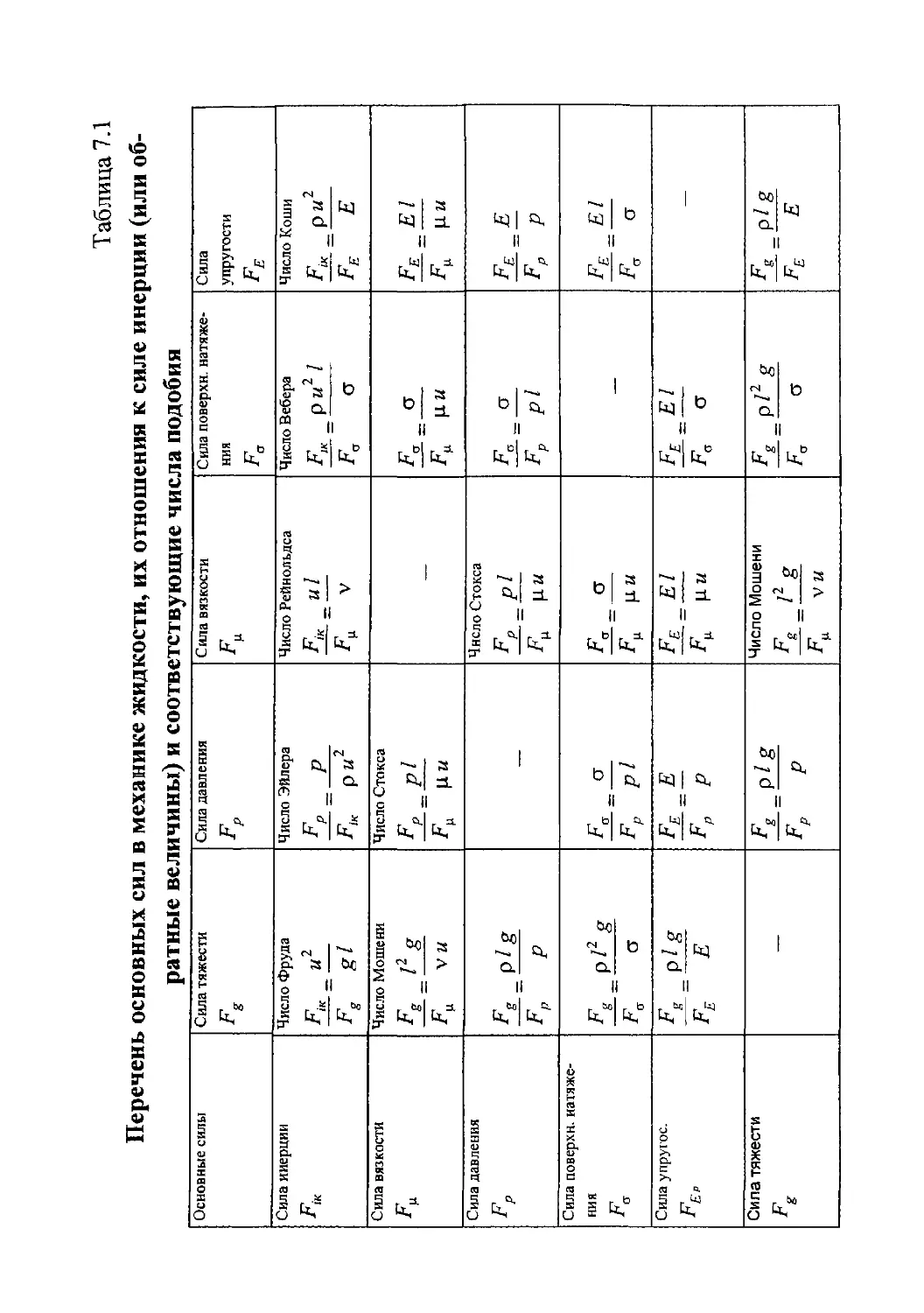
7. Метод соотношения сил Ньютона....................143
8. Роль интегральных соотношений в физическом
моделировании явлений...............................147
9. Индикаторы подобия - основа для установления связей
между коэффициентами подобия........................158
10. Моделирование явлений в жестком русле...........161
10.1. Моделирование равномерного движения
напорного потока...............................161
10.2. Моделирование равномерного движения
безнапорного потока............................180
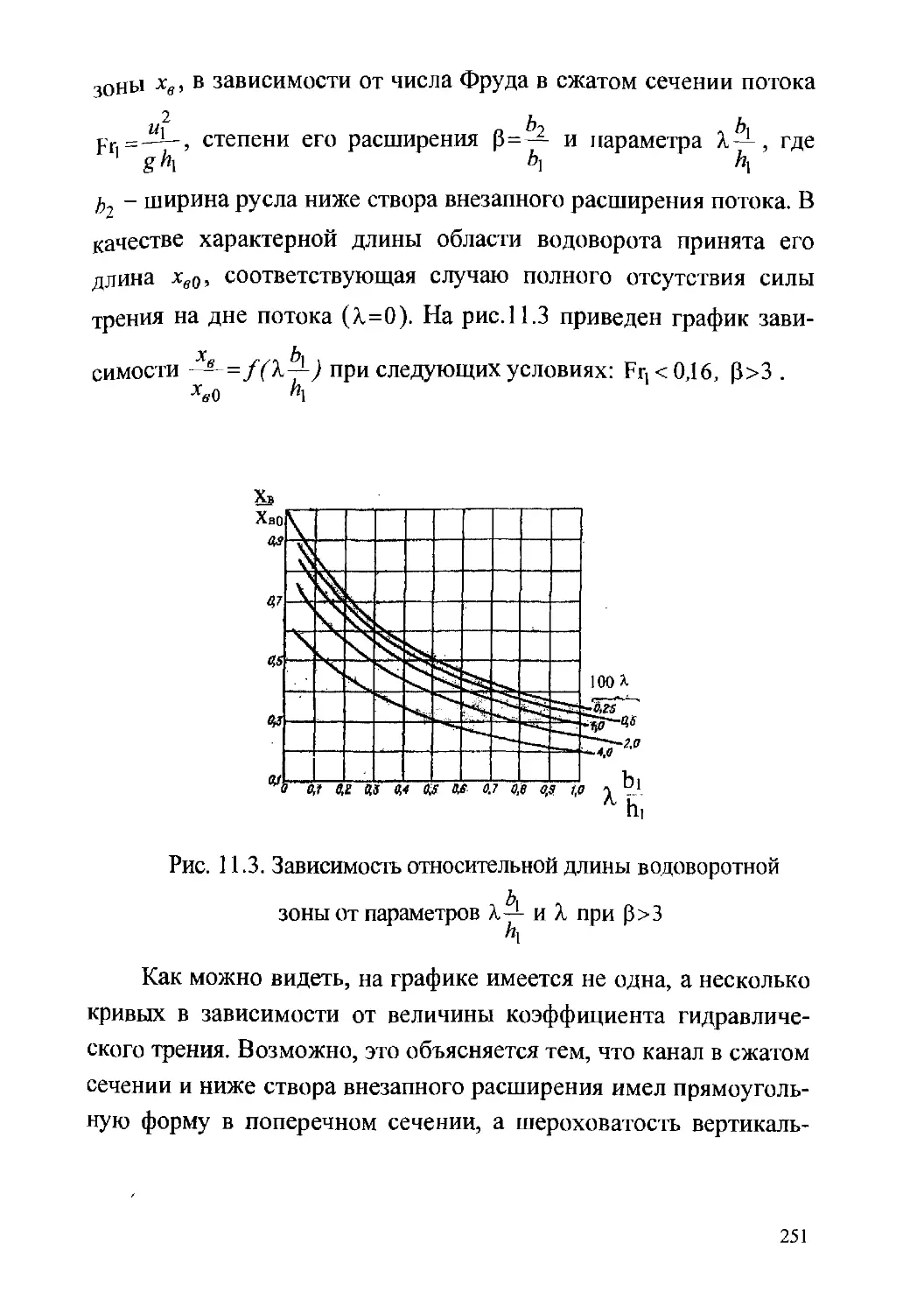
11. Приближенное моделирование потоков при равномерном
движении............................................201
з
11.1 .Приближенное моделирование потока в квадратичной
зоне сопротивления потоком в зоне гидравлически гладкого
русла............................................201
11.2. Приближенное моделирование потока в квадратичной
зоне сопротивления потоком в переходной зоне.....209
11.3. Приближенное моделирование потока в переходной
зоне потоком в той же зоне, или в зоне гидравлически глад-
кого русла.....................................227
11.4. Приближенное моделирование равномерного безна-
порного течения при разных линейных масштабных коэф-
фициентах глубин и плановых размерах потока......229
11.5. Приближенное моделирование равномерного безна-
порного течения при скорости потока на модели, не соот-
ветствующей правилу моделирования «по Фруду».....239
11.6. Моделирование гидравлических явлений в
водоемах и водотоках больших плановых размеров
и малых глубин...................................244
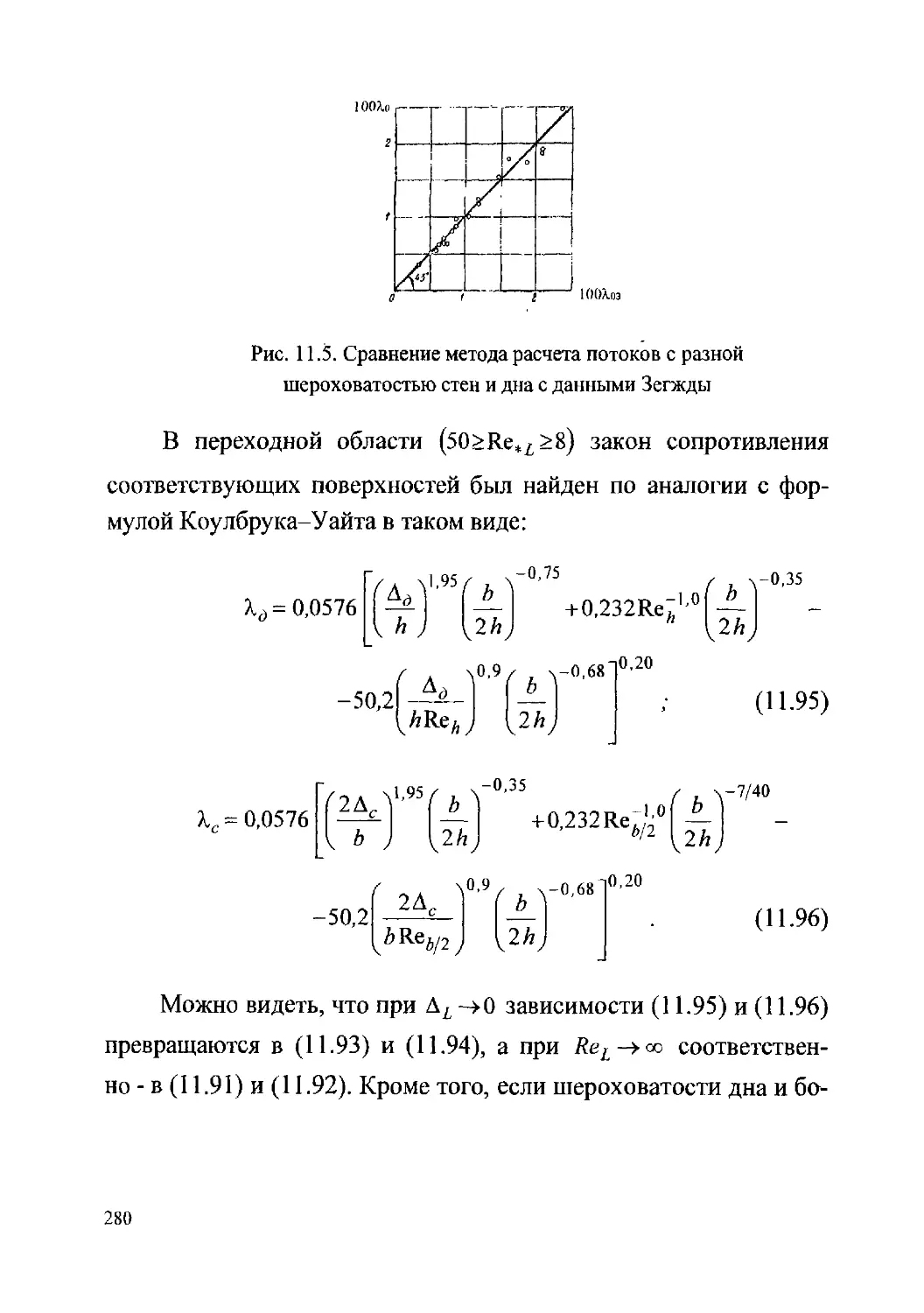
11.7. 0 моделировании безнапорных и напорных
потоков с неоднородной шероховатостью ложа......273
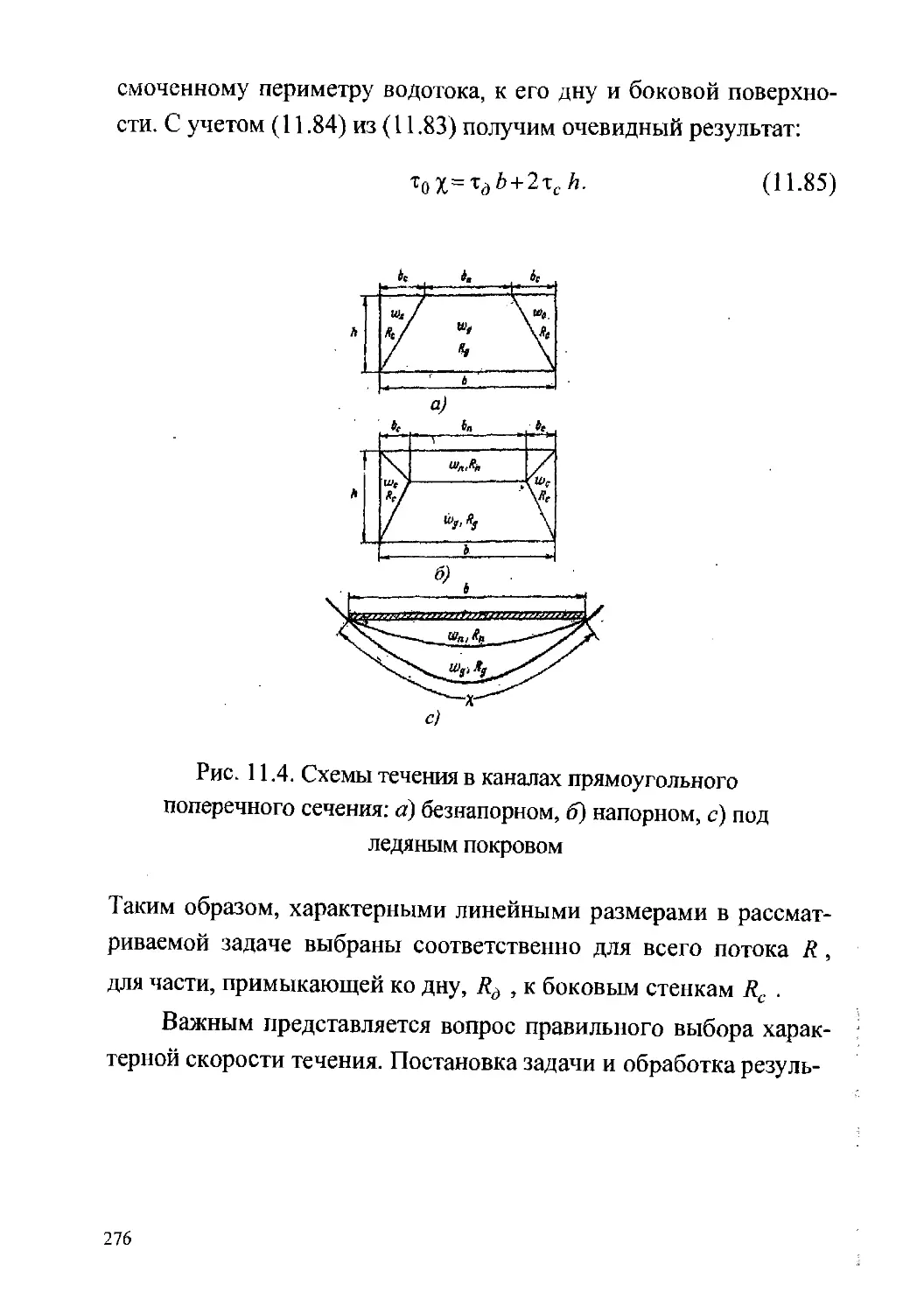
11.8. Движение воды в русле под ледяным покровом.292
11.9. Приближенное моделирование безнапорного
потока в натуре воздушным напорным потоком на
модели.........................................298
12. О возможности использования модели за пределами условий,
принятых в ее проекте.................................328
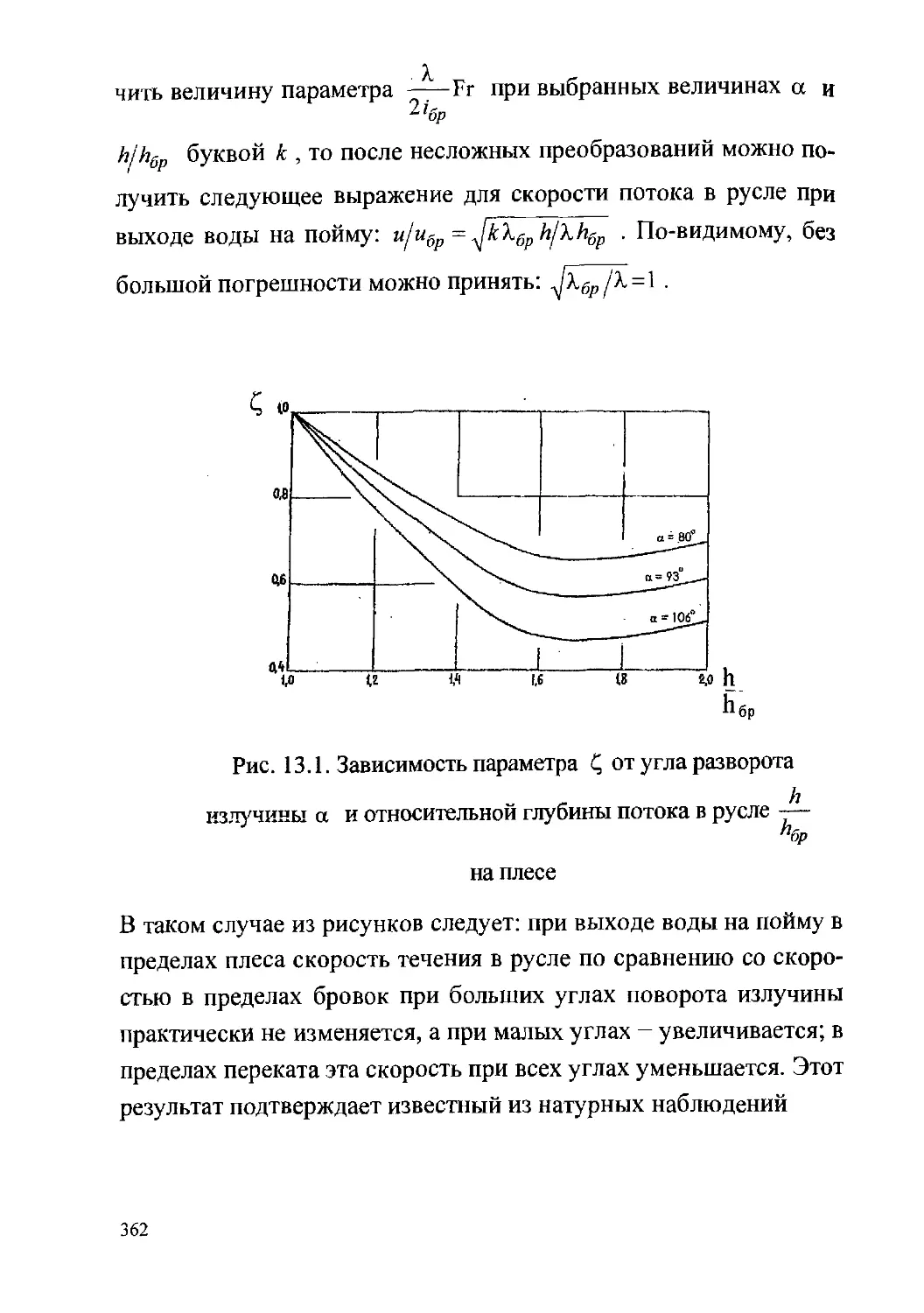
13. Моделирование неравномерного резкоизменяющегося движе-
ния безнапорных потоков...............................334
13.1. Моделирование неравномерного резкоизменяющегося
движения при сопряжении бьефов по типу поверхностного и
донного гидравлических прыжков.................334
4
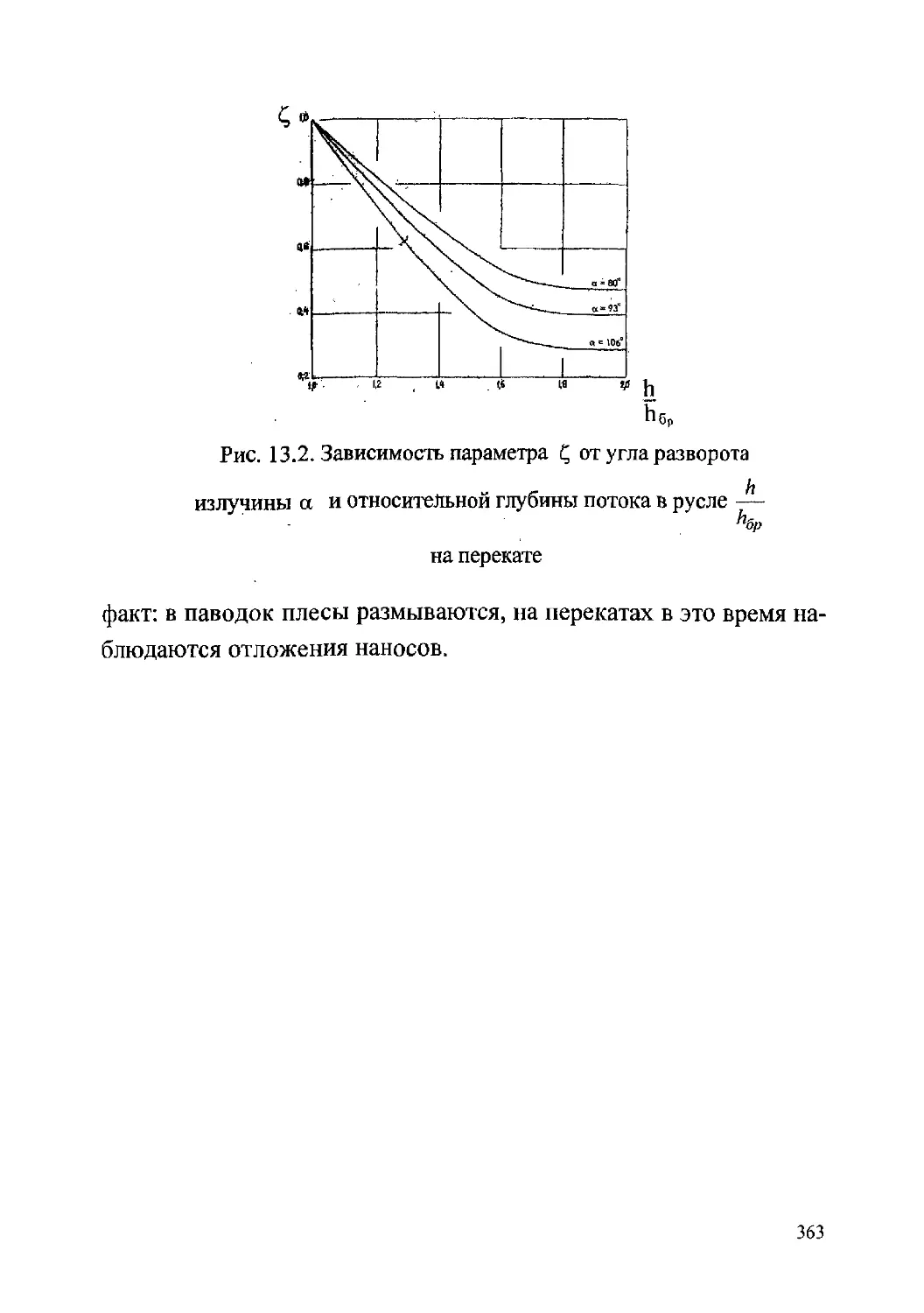
13.2. Моделирование неравномерного резкоизменяющегося
движения в случае взаимодействия руслового и пойменного
потоков.........................................354
14. Характерные величины. Метод фрагментов чисел
подобия.............................................364
15. Моделирование неустановившегося движения........371
15.1. Моделирование неустановившегося движения
воды в напорных трубопроводах и системах........371
15.1.1. Внезапное ускоренное движение жидкости
в жесткой трубе.............................371
15.1.2. Гидравлический удар в напорном
трубопроводе................................377
15.2. Моделирование неустановившегося движения
воды в открытых руслах...........................382
15.2.1. Моделирование явления прохождения в
реке волны паводка..........................382
15.2.2. Моделирование неустановившегося движения
воды в нижних бьефах насосных и гидроэлектрических
станций....................................400
16. Моделирование местных потерь напора и истечений через во-
досливы и отверстия.................................410
16.1. Моделирование местных потерь напора.......410
16.2. Моделирование истечений через водосливы....415
16.3. Моделирование истечений через большие
отверстия.......................................425
16.4. Моделирование истечений через малые отверстия...432
Оглавление..........................................435
5
1. ВВЕДЕНИЕ
Моделирование - исследование какого-либо явления путем
построения и изучения модели («заместителя», «схемы» или
«представителя») оригинала («прототипа», «натурного объекта»).
Моделирование - одна из основных категорий теории познания
(гносеологии, от греч. «гносис» — познание, «логос» - слово,
понятие, сущность). Это любой метод научного исследования:
теоретический или экспериментальный. Математическое модели-
рование - исследование явления на схеме оригинала («прототи-
па», «натурного объекта») с помощью математического описания
физических законов, действующих на схеме. Физическое моде-
лирование - исследование явления путем построения и изучение
физической модели оригинала («прототипа», «натурного объек-
та»), выполняемые на основе принципов теории подобия и раз-
мерностей.
Математические уравнения, описывающие физические за-
коны, представляют собой математические модели физических
явлений, так как эти уравнения описывают не реальные явления,
а их схематизацию - модель. Степень приближения модели к
действительности зависит от уровня развития науки и техники. В
ряде случаев решение практических задач сопряжено с непреодо-
лимыми математическими трудностями. Часто математическая
постановка задачи вообще отсутствует, так как исследуемое яв-
ление настолько сложно, что для него пока еще нет удовлетвори-
тельной схематизации. Тогда главную роль играют эксперимен-
тальные методы исследований.
Эти методы позволяют установить требования, которые
следует предъявлять к лабораторной модели и к проведению на
ней исследуемого процесса для того, чтобы результаты модели-
6
рования могли быть в дальнейшем использованы для практиче-
ских целей. Обработка данных лабораторных измерений и обоб-
щение их результатов в виде эмпирических формул также ведут-
ся в соответствии с методами подобия.
Как отмечает академик Л.И. Седов: «В настоящее время
грамотная постановка и обработка экспериментов немыслима без
учета вопросов подобия и размерностей» [50]. Эти методы ис-
пользуются также при теоретическом изучении явления как спо-
соб предсказания внутренней структуры переменных параметров,
входящих в выводимые из теории аналитические выражения, на
чем основано построение так называемых «автомодельных» ре-
шений.
Математическое моделирование находит все большее рас-
пространение в связи с широким применением вычислительной
техники. Там, где математическое моделирование затруднено или
вообще невозможно, находит применение физическое моделиро-
вание, например, математическая модель речного русла трудно
реализуется, в то время как физическую модель формы русла
создать довольно просто. Известно, что замкнутая система урав-
нений, описывающих турбулентное течение жидкости, отсутст-
вует, но если допустить, что такие уравнения одинаковы для мо-
дели и натуры, то можно сформулировать общие принципы мо-
делирования турбулентных течений жидкости.
Разумное сочетание физических и математических методов
моделирования - наиболее распространенный путь решения
практических задач. «Всякое изучение явлений природы начина-
ется с установления простейших опытных фактов, на основе ко-
торых можно формулировать законы, управляющие исследуемым
явлением, и записать их в виде некоторых математических соот-
ношений» [50].
7
Данная работа посвящена физическому моделированию яв-
лений. Если говорить об основе физического моделирова-
ния - методах подобия и размерностей, - то наиболее общими из
них являются последние. Теория подобия исходит из того, что
математические уравнения, описывающие изучаемый процесс,
известны; на основе анализа этих уравнений выносится суждение
об основных законах подобия. Теория размерностей, располагая
более совершенным математическим аппаратом, при формулиро-
вании этих законов обходится без математических уравнений.
При этом необходимо знать только параметры (в том числе физи-
ческие константы), влияющие на процесс. Однако в этом таится
большая опасность недоучета того или иного существенного
фактора, что повлечет за собой искажение и обесценивание ре-
зультатов экспериментального исследования.
Наконец, существует еще один путь отыскания законов по-
добия - это метод соотношения сил, действующих в системах
(«динамическое» подобие), который связывают с именем Ньюто-
на. Для его применения необходимо знать действующие силы и
Их размерности. Соотношения этих сил дают некоторые безраз-
мерные комбинации, играющие огромную роль в методах подо-
бия и размерностей, которые носят название чисел подобия. Ни-
же приводится описание всех трех методов.
Здесь следует дать некоторые рекомендации тем, кто наме-
рен самостоятельно изучать основы теории физического модели-
рования, а также преподавателям этой дисциплины. Дело в том,
что во многих технических направлениях и специальностях в об-
ласти строительства, водного хозяйства, экологических проблем
гидроэнергетики, гидротехники и гидромелиорации земель меха-
ника жидкости представлена, как правило, прикладной дисцип-
линой - гидравликой. Однако этих знаний явно недостаточно для
8
того, чтобы освоить метод подобия. С другой стороны, сущест-
вующие пробелы при изучении курса высшей математики в этих
направлениях и специальностях создают трудности с освоением
метода размерностей. В этих условиях остается единственная
возможность познания основ физического моделирования явле-
ний, которая связана с методом соотношения сил Ньютона. Но
все отмеченные методы теории физического моделирования не
существуют в полной изоляции друг от друга, поэтому для ос-
воения метода соотношения сил Ньютон потребуются знания ос-
новных положений методов теории подобия и размерностей. Так
из метода подобия это такие понятия, как подобие, характерная и
безразмерная величины. Из метода размерностей - это величины,
имеющие независимые размерности, л - теорема (формулировка
и выводы, опуская доказательство). В методах комбинаций чисел
подобия и фрагментов можно ограничиться только формулиров-
ками соответствующих теорем, сосредоточив основное внима-
ние на следствиях из этих теорем. Следуя указанным путем,
можно освоить объем знаний, необходимый для решения при-
кладных задач в области физического моделирования гидравли-
ческих явлений, прочно увязанный с методами физического мо-
делирования в целом.
1.1. Основные понятия теории физического
моделирования
Моделирование предполагает исследование свойств ориги-
нала посредством изучения свойств его модели, более удобной
для решения задачи исследования и находящейся с оригиналом в
определенном соотношении. Основная задача моделирования -
по результатам исследования модели дать заключение о характе-
9
ре протекания процессов в оригинале и о внутренних связях меду
параметрами, определяющими эти процессы. Моделирование
включает в себя построение модели, изучение ее и перенос полу-
ченных сведений на оригинал. Перенос сведений возможен толь-
ко при существовании взаимно однозначного соотношения меж-
ду оригиналом и моделью, которое называется подобием.
Под оригиналом понимается объект, свойства которого под-
лежат изучению методом моделирования. Понятие «оригинал»
имеет широкую интерпретацию: это естественные и искусствен-
ные объекты, различные явления и процессы, в них протекаю-
щие. Под явлением понимается совокупность процессов, характе-
ризующих функционирование объекта, проявляющихся в виде
изменения состояний и режимов работы.
Изменение состояния или режима работы в пространстве и
во времени определяется некоторыми показателями, которые на-
зываются параметрами. Следовательно, процесс понимается как
закономерное изменение в пространстве и во времени одних па-
раметров относительно группы других независимых параметров.
Пример из области гидротехники: объект - водосливная плотина,
явление - сопряжение бьефов; процесс - изменение второй со-
пряженной глубины гидравлического прыжка в плоских условиях
в зависимости от перепада уровней между верхним и нижним
бьефами и от удельного расхода воды на гребне водослива. В
строительном деле вместо слова «оригинал» чаще всего употреб-
ляется слово «натура».
Под моделью понимается вспомогательный объект, имею-
щий некоторые идентичные черты с оригиналом, отражающий
отдельные особенности поведения оригинала и служащий для
получения такой информации о нем, которую затруднительно
или вообще невозможно получить путем непосредственного изу-
10
чения оригинала. Например, на оригинале (в натуре), каким явля-
ется мостовая опора, практически невозможно изучить в явлении
местного размыва русла процесс изменения во времени глубины
воронки размыва при прохождении волны паводка. На модели
такая задача легко реализуется.
В общем случае понятие «модель» довольно широкое: это и
специально созданная экспериментальная установка, и символи-
ческое описание оригинала (чертеж, схема), и математическое
уравнение, и иной условный образ, который находится в опреде-
ленном соответствии с изучаемым объектом - оригиналом, а
именно: подобен ему.
Следует отметить особенность модели: она всегда конкрет-
на; для нее всегда имеется адекватная физическая реальность;
моделей самих по себе в отрыве от этой реальности не существу-
ет [9]. Основная задача модели - прогноз по результатам модели-
рования поведения оригинала в ситуациях, отличных от тех, на
основании которых была построена модель. Естественно, должны
быть установлены правила переноса этих результатов с модели
на натуру, в основе которых лежат законы перехода от парамет-
ров, характеризующих модель, к параметрам натуры.
Понятие «подобие» допускает широкое трактование. Наибо-
лее простое и понятное - это геометрическое подобие. В про-
стейшем случае речь идет о подобии многоугольников с одина-
ковым числом сторон, и в частности, для треугольников теорема
звучит так: треугольники подобны, если у них соответственные
углы равны, а сходственные стороны пропорциональны.
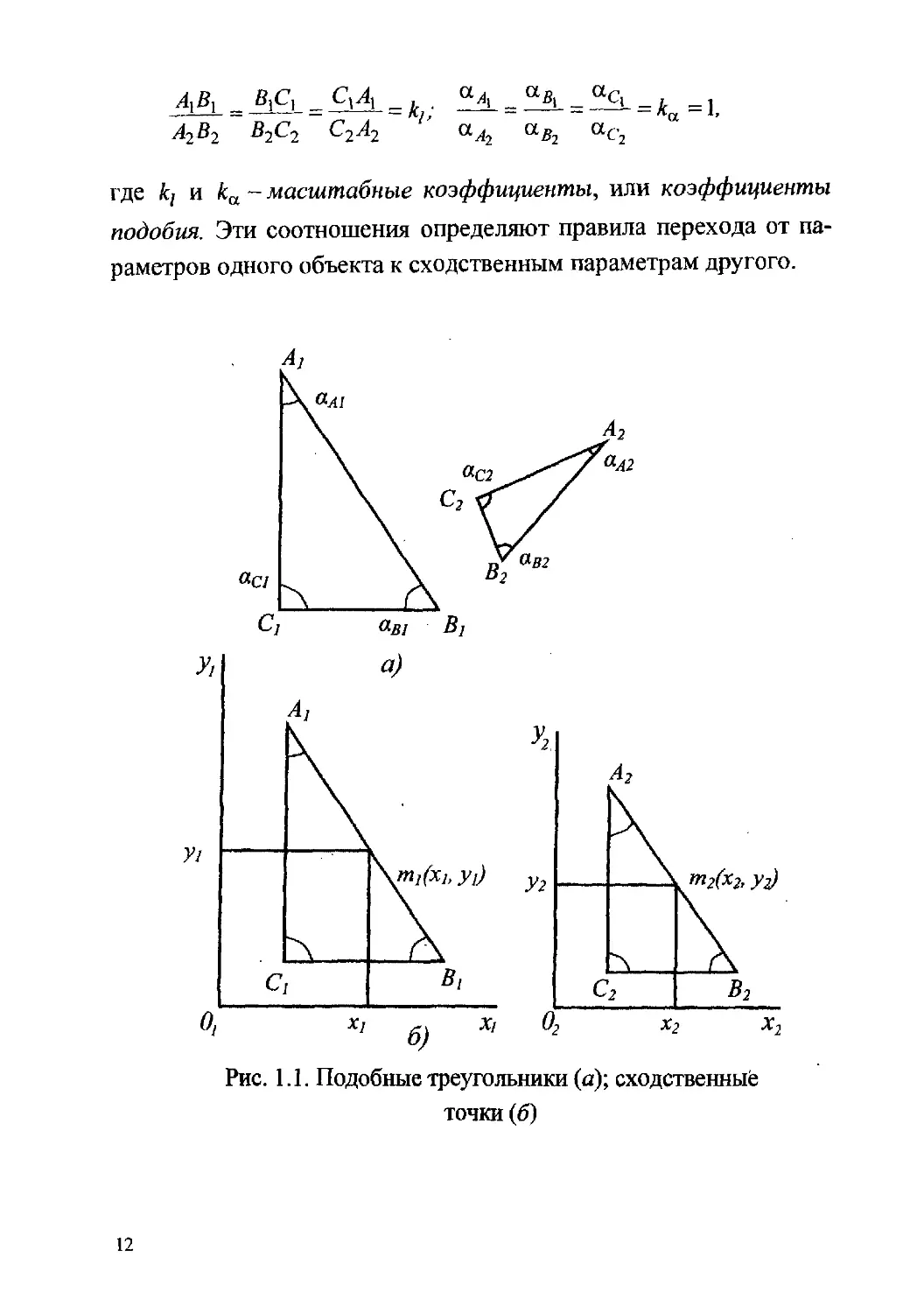
Рассмотрим два треугольника: (рис. 1.1 .а), обозначим соот-
ветственные вершины буквами А, В и С, а углы при вершинах-
буквой а с индексом. Тогда в соответствии с теоремой о подо-
бии можно записать:
п
ла ... gici с'4 k = ад| = ас» =ka -1
Л2В2 А^г А А 1 ал2 а^2 аС’2
где ki и ка - масштабные коэффициенты, или коэффициенты
подобия. Эти соотношения определяют правила перехода от па-
раметров одного объекта к сходственным параметрам другого.
Рис. 1.1. Подобные треугольники (а); сходственные
точки (б)
12
Заметим, что обычно линейный масштабный коэффициент назы-
вают просто «масштабом».
Понятие «сходственные точки» требует определенной ори-
ентации подобных треугольников в соответствующих плоскостях
(рис. 1.1.6). Рассмотрим в каждой из этих плоскостей свою сис-
тему декартовых координат: ^oj^i; х2о2-у2. Сходственными будут
точки, расположенные на контурных линиях соответствующих
треугольников, координаты которых удовлетворяют соотноше-
ниям:
2jlL-г • 21L- г • k - ь
~*у> кх — К.у,
xi2 У.2
где m^x^yj - сходственные точки, расположенные на контур-
ных линиях треугольников; кх и ку - масштабные коэффициен-
ты по направлению осей х и у.
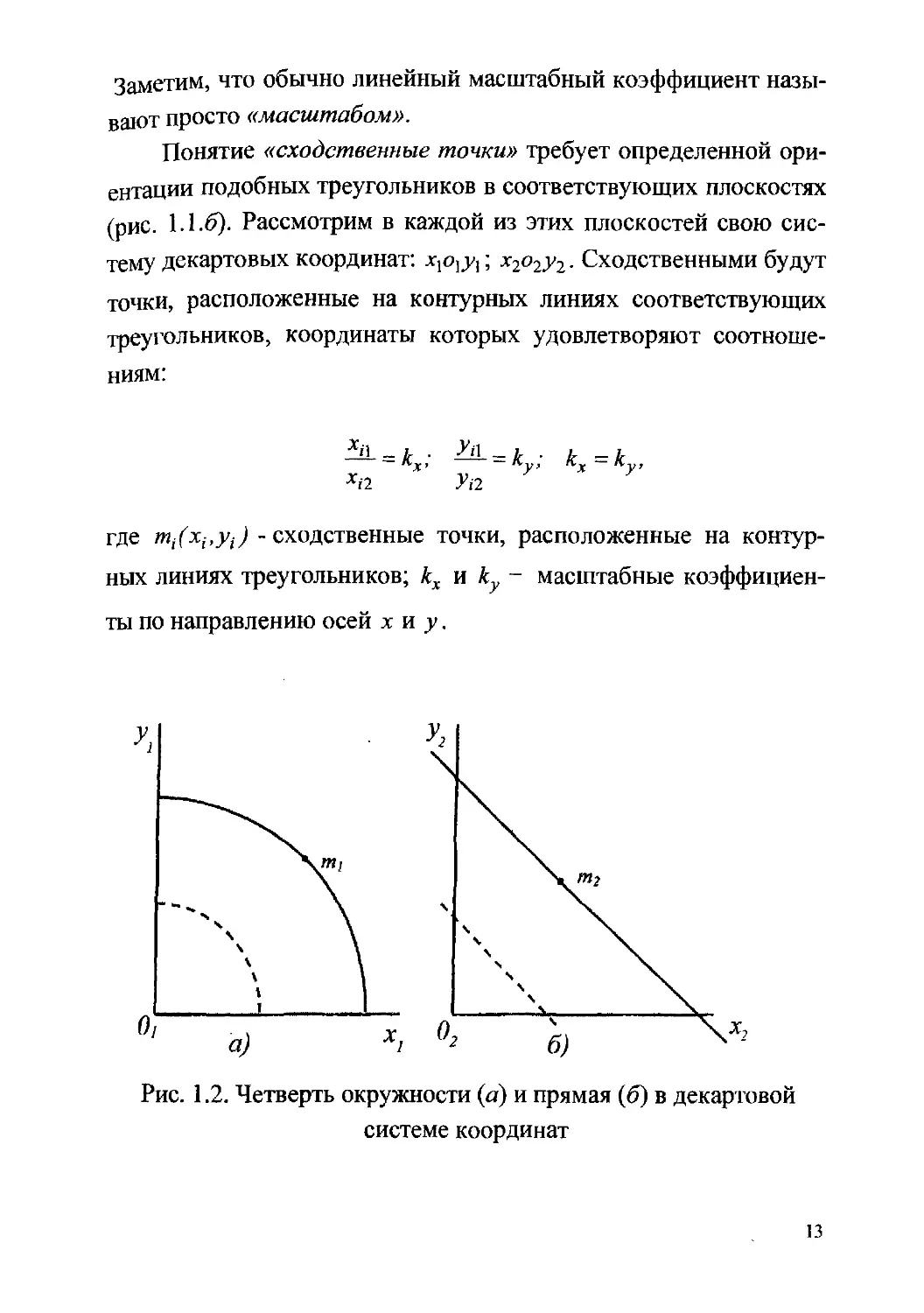
Рис. 1.2. Четверть окружности (а) и прямая (6) в декартовой
системе координат
13
Если речь идет о геометрическом подобии в трехмерном
пространстве, то подобие двух объектов означает, что координа-
ты всех пространственных точек первого объекта пропорцио-
нальны координатам сходственных пространственных точек вто-
рого объекта. В прямоугольной системе координат xyz имеем:
• XlL-k ^- = k к -к -к
*Х> ^Z’ Кх Ку Kz,
Уп zn
где - сходственные точки сопоставляемых объектов.
Кроме геометрического, существует еще аффинное подобие
(от лат. аффинис - родственный), при котором масштабные ко-
эффициенты по осям координат не равны друг другу. В этом слу-
чае сравниваемые геометрические фигуры и пространственные
объекты могут иметь различное начертание на плоскости и раз-
личные формы в пространстве. Например, можно говорить о
сходственных точках, расположенных на прямой линии (один
объект) и на дуге окружности (второй объект), на дуге окружно-
сти и на дуге эллипса и т.д. При аффинном подобии для коорди-
нат сходственных точек в прямоугольной системе xyz справед-
ливо соотношение
к у ^z'
Для перехода от одного объекта к другому приходится вво-
дить специальные, как правило, нелинейные преобразующие
функции, позволяющие каждой точке одного объекта найти соот-
ветствующую точку в другом. Рассмотрим пример аффинного
преобразования [9]. На рис. 1.2.а в декартовой системе координат
xjOjy] изображена четверть окружности, уравнение которой
х2 + у2 =24 . На рис. 1.2.6 в такой же системе координат х2о2у2
14
проведена прямая линия, уравнение которой х2 +у2-6 . Необхо-
димо найти преобразующие функции, позволяющие перейти от
точек, расположенных на прямой линии, к соответствующим
точкам на дуге окружности.
В общем случае задала эта не простая, но в данном варианте
преобразующие функции (они же масштабные коэффициенты)
легко находятся. Действительно, если положить
2 2
Х1 = Х2^х - х2 ~Г=’ У\ = У 2^ у = У2 ••
х]х2 у1У2
2 2
где кх = —г= * ку = , то дуга окружности и отрезок прямой
Чх2 уУ2
линии при условиях %] > 0; > 0; х2 > 0, у2 > 0 окажутся
аффинно-подобными. Каждой точке, расположенной на дуге ок-
ружности, можно сопоставить соответственную точку в пределах
упомянутого выше отрезка прямой, пользуясь простыми преобра-
зованиями: X! — 2-yfx^; Л = ^4у2 Как видим, преобразующие
функции (или масштабные коэффициенты) получаются нелиней-
ными и неравными друг другу. Заметим, что рассмотренная выше
окружность очерчена радиусом, равным 2д/б, из центра, совпа-
дающего с началом координат. Если провести окружность дру-
гим радиусом, то можно найти прямую, аффинно-подобную ей,
параллельную прямой, рассмотренной выше. Например, радиусу,
равному Тб, соответствует уравнение окружности xf + yf = 6 ,
уравнение аффинно-подобной прямой запишется так:
х2+>'2=3/2.
Таким образом, любой точке, находящейся внутри сектора,
ограниченного осями координат и дугой окружности (рис. 1.2.а),
можно найти соответственную точку внутри прямоугольного
15
треугольника, ограниченного осями координата и прямой линией
(рис. 1.2.6). Для пересчета одних координат в другие использу-
ются масштабные коэффициенты кх и ку. Можно найти уравне-
ние окружности и соответственное уравнение прямой, на кото-
рых будут находиться соответственные точки.
Существует также кинематическое и динамическое подобие
кинематических и динамических величин в сходственных про-
странственных и временных точках. Далее будут рассмотрены
соответствующие коэффициенты подобия. Кинематическое по-
добие возможно только в геометрически подобных системах; ди-
намическое подобие может иметь место только в том случае, если
реализовано и геометрическое, и кинематическое подобие [21].
16
2. ОСНОВЫ ТЕОРИИ ПОДОБИЯ
В теории подобия совокупность коэффициентов подобия
носит название множителей преобразования величин, применяе-
мых при сопоставлении и преобразовании сходственных пара-
метров моделируемых объектов.
Прежде всего, отметим, что физические величины, характе-
ризующие поведение оригинала, как правило, изменяются в про-
странстве и во времени. Между тем, множители преобразования
по своей сути величины постоянные. В связи с этим в теории по-
добия выделяют характерные величины, которые не зависят от
времени и координат. Но тогда можно утверждать, что коэффи-
циенты подобия служат для сопоставления и преобразования ха-
рактерных величин оригинала и модели. [37].
Выберем в одной области (скажем в оригинале) характерные
величины. Пусть это будут время, длина, масса, скорость, си-
ла и т. д. Характерные величины пометим чертой над буквенным
обозначением: Т\, Ц, Мх,щ, Fx. Проведем аналогичную операцию
в другой области (на модели): Т2, L2, М2, й2, F2. Найдем коэффи-
циенты подобия, которые будем обозначать буквой к с соответ-
ствующим подстрочным индексом:
Сформулируем условия подобия [22, 37]: два физических яв-
ления называются подобными, если величины, характеризующие
одно явление, могут быть получены из соответствующих вели-
чин другого, взятых в сходственных пространственно-
временных точках, простым умножением на коэффициенты по-
добия, одинаковые во всех точках. Иными словами, для любых
17
других не характерных величин (у них для отличия от характер-
ных нет черты сверху) должны выполнятся в случае подобия сле-
дующие условия:
Г)=^Г2, L] = fczL2, Мх-ктМ2, щ=кии2, F} = kFF2 и т. д.(2.2)
В соответствии с принципом Даламбера система сил, при-
ложенных к точке, включающая внешние и внутренние силы, а
также соответствующие силы инерции, находится в равновесии.
Следовательно, в задачах динамики уравнения движения состав-
ляются в форме уравнений равновесия статики. В соответствии с
этим принципом получается, что простые линейные преобразова-
ния типа (2.2), касающиеся сил, приложенных к сходственным
пространственно-временным точкам двух подобных систем:
F}=kFF2 (2.3)
в равной степени относится и к уравнениям движения. Отсюда
условия подобия двух физических явлений могут быть дополне-
ны такой формулировкой: явления считаются подобными, если
характеризующие их функции, определенные в сходственных
точках областей, могут быть получены одни из других с помо-
щью простого линейного преобразования типа (2.3).
Следует обратить внимание на фразу «сходственные про-
странственно-временные точки», входящую в определение по-
добия. Речь идет о признаках, которые выделяют группу явлений,
относящихся к некоторой частной задаче, ограниченной задан-
ными условиями. При математической постановке задачи эти
признаки однозначно определяют решение дифференциальных
уравнений. В теории подобия они получили наименование «усло-
вий однозначности» В состав этих условий входят следующие
характеристики изучаемого явления, подобие которых должно
18
быть обеспечено: геометрическая форма оригинала и модели;
граничные и начальные условия, физические свойства сред
(плотность, вязкость, наличие в водных объектах приме-
сей и т. п.). Следовательно, речь идет о тех случаях, когда сопос-
тавляемые явления с физической точки зрения принадлежат к од-
ному и тому же классу.
Возьмем теперь отношение какой-либо величины в ориги-
нале к этой же ранее выбранной характерной величине; с учетом
условий (2.1) и (2.2)получим:
7] ktT2 ^2 • j
=- = ~ idem.
Т{ к,Т2 т2
Следовательно, по аналогии можно записать:
^_«2 5_-^2итп
— —~ —~ _ f — — И Т > д»
Lt L2 М] М2 щ и2 F] F2
Таким образом, сравнимые безразмерные величины в сход-
ственных точках областей одинаковы (idem по латыни «то же са-
мое») Получается, что характерные величины играют роль «мас-
штабов», и два подобных явления в сходственных пространст-
венно-временных точках различаются между собой только мас-
штабами описывающих явление величин, в том числе и соответ-
ствующих уравнений.
Отсюда можно сделать вывод: если в дифференциальных
уравнениях движения перейти от обычных размерных величин к
безразмерным, которые получаются путем деления размерных
переменных на характерные величины, а затем сделать безраз-
мерными и сами уравнения, то полученные таким образом без-
размерные дифференциальные уравнения и соответствующие им
безразмерные граничные и начальные условия, а также условия
19
однозначности станут одинаковыми для обоих явлений. Рассмот-
рим теперь условия подобия двух изотермических потоков нью-
тоновских вязких несжимаемых жидкостей.
Как известно, ламинарное течение такой жидкости описыва-
ется уравнением Навье-Стокса [22]. Основная идея общего под-
хода к описанию турбулентного движения, выдвинутая Рей-
нольдсом, заключается в том, что, несмотря на всю хаотичность
этого движения, действительное (актуальное) движение описыва-
ется строго тем же уравнением Навье-Стокса.
Если обозначить оси координат через х, , где i пробегает
значения ; = 1, 2, 3, а также дополнительно ввести индекс j, про-
бегающий значения 1, 2, 3, то систему, состоящую из трех проек-
ций векторного уравнения Навье-Стокса на оси декартовой пря-
моугольной системы координат, можно представить в компакт-
ном виде:
—L+ >
dt f? J
.J^ = xl^ + W2u- j = 1,2,3; (2.4)
J dx p8x, 7
Здесь приняты обозначения: p - плотность среды, определяемая
как предел отношения массы малого объема среды к величине
объема при стремлении его к нулю (если вместо массы взять вес
малого объема, то получим удельный вес: y = gp), кроме то-
„2 “ хд,
ro,V =—- - оператор Лапласа, v - кинематический коэффици-
дх~
снт вязкости (величина p = vp называется динамическим коэф-
фициентом вязкости).
Уравнения (2.4) получаются путем применения закона из-
менения количества движения к элементарному объему сплош-
ной среды [22]. Принципиальное отличие уравнений динамики
сплошных сред от соответствующих уравнений для системы ма-
20
термальных точек состоит в том, что проекции векторов, стоящих
слева и справа в уравнениях (2.4), представляют соответственно
не произведения масс на ускорения и силы, как это следует из
второго закона Ньютона, а лишь плотности распределения всех
этих величин, т. е. величины, отнесенные к единице массы.
Следовательно, слева в уравнениях (2.4) стоят проекции
полного ускорения (отсюда эту систему иногда называют урав-
нениями в «ускорениях»). Как известно, ускорение есть полная
производная от вектора скорости по времени; в уравнениях (2.4)
проекции вектора скорости на оси координат х, обозначены w,,
следовательно, проекции вектора полного ускорения на те же
оси - —. Но и,- = f(t,xt), где t и х, - переменные Эйлера. В от-
dt
личие от метода Лагранжа, в котором величины являются пере-
менными координатами движущейся частицы жидкости, в методе
Эйлера - это координаты точек пространства, мимо которых в
данный момент времени проходят различные частицы жидкости.
По известному из математики правилу дифференцирования
сложной функции для проекции w, = f (t,xlrx2,x3) получим:
du, _ dUj duj dxy du, dx2 du, dx3 _
dt dt Эх, dt dx2 dt dx3 dt
du, du:
___Ln _i_____Ltt.
dx2 z dx3 J’
(2-5)
ди: ди: du= OU:
= —L+—-u, +—l-u2 +—Lu3,
dt dx3 2 J
dx} dx2 dx3 dx,
где u{ = ~, u2 = из = или ui ~ проекции векто-
ра скорости на оси координат х,.
Если ввести теперь индекс j=\, 2,3, то можно записать (2.5)
в компактной форме:
21
= .^L; j = 1,2,3. (2.6)
dt dt /=i J dxj
Первая составляющая ускорения в (2.6) называется локальной,
вторая - конвективной; первая является следствием нестацио-
нарности скоростного поля (изменения поля во времени); вто-
рая - следствием его неоднородности (поле изменяется от точки
к точке).
Обратимся к правым частям системы скалярных уравнений
(2.4), которые содержат проекции вектора сил на направления
осей координат, отнесенные, как было отмечено выше, к единице
массы, В динамике сплошной среды принято выделять два класса
действующих на частицы сил: объемные (или массовые) и по-
верхностные. Объемные силы действуют на элементы объема
(например, силы тяготения, электрического притяжения или от-
талкивания). К поверхностным относятся силы, которые дейст-
вуют на элементы поверхности (например, силы давления, внут-
реннего трения (вязкости) в среде).
Проекции вектора плотности распределения объемных сил
на оси прямоугольной системы координат обозначены в уравне-
ниях (2.4) X/. Если рассматривать движение в поле земного при-
тяжения, то из объемных сил на частицы среды действует только
сила тяжести. Пусть плоскость Х|0х2 - горизонтальна, а ось х3
направлена вертикально вниз, тогда 2q=X2 = 0> X3 = g, где
g - ускорение силы тяжести. Роль сил давления и внутреннего
трения отражена вторым и третьим членами в правой части урав-
нения (2.4).
Запишем уравнение (2.4) для оригинала, снабдив все вели-
чины, которые в него входят, соответствующей подстрочной
цифрой:
22
5»Д у
5“,i
uj\ ^~ = &~
Sxji
1 Ф1
Pi 5xn
+ ViV2M(|.
(2.7)
Для потока на модели это уравнение будет иметь вид
^+b/2^ = g2-J-^- + v2V2M,2.
а/2 Д 72 dxJ2 Р2 dxi2
(2.8)
Отсюда следует, что жидкости могут отличаться плотно-
стью и вязкостью (в оригинале и на модели жидкости ньютонов-
ские), на них могут действовать объемные силы разной интен-
сивности. Выберем для величин оригинала (для времени, длин
(координат точек), скоростей, давлений) некоторые характерные
для потока величины: Тх, Lx, И,, Рх (черту сверху опустим для уп-
рощения записи). Если обозначить штрихом безразмерные значе-
ния соответствующих величин, то должны быть справедливы со-
отношения:
= Txt', = Lxx'i, рх = Рхр, uiX = Ухи\ (2.9)
Поскольку безразмерные величины одинаковы для оригина-
ла и модели, подстрочную цифру опускаем. Произведем замену
величин в уравнении (2.7) в соответствии с соотношениями (2.9);
вспомним, что характерные величины не зависят от координат и
времени, поэтому их можно выносить из-под знаков дифферен-
циалов (и интегралов, кстати, тоже); получим:
Vx du’j Vx2 * , ди\ Рх др' v y 2 ,
~—7 + -L~21ui—r = g\----!----ui’
Tx dt Lx j=x 7 dxj pxLx dxx L2
(2.Ю)
Выберем на модели для соответствующих величин харак-
терные и произведем замену величин, входящих в уравнение
(2.8), по аналогии с соотношениями (2.9):
23
xi2=L2x'i’ Р2=Р2Р’ ui2 = P2u'i- (2Л1)
Выполним преобразование уравнения (2.8), используя соот-
ношения (2.11), и получим:
И2 ди\ Г2 Л , ди\ Р2 fy' v2T2 2 , zn
Т2 dt' L2 J а/, р2£2 дх\ L2
В уравнениях (2.10) и (2.12) безразмерные величины одина-
ковы для оригинала и модели, но сами уравнения имеют размер-
ность ускорения. Далее необходимо сделать безразмерными и
сами уравнения. С этой целью нужно выбрать какую-либо силу и
взять характерную для нее величину. Но при выбранных харак-
терных величинах, входящих в соотношения (2.9) и (2.11), такая
операция уже автоматически осуществилась для плотности рас-
пределения всех сил, входящих в уравнения (2.10) и (2.12). Рас-
смотрим, например, плотность распределения силы инерции, ее
конвективная составляющая, отнесенная к массе, представлена
вторыми членами в левых частях уравнений (2.10) и (2.12). Сле-
довательно, эти члены представляют собой конвективные состав-
ляющие ускорения в оригинале и на модели. Но тогда характер-
ная конвективная составляющая ускорения в оригинале равна
= V2/ьх, на модели - А2 =V2 /ь2.
Отнесем все величины, входящие в уравнения для оригина-
ла и модели, соответственно к А, и А2, тем самым и сами уравне-
ния сделаем безразмерными. Одновременно эта операция будет
означать, что плотности распределения всех сил, действующих в
оригинале и на модели, отнесены к плотности распределения ха-
рактерной силы инерции (нормированы по силе инерции). Таким
образом, на этой стадии реализуется так называемый «метод со-
отношения сил Ньютона», который также широко используется
24
при физическом моделировании; о нем речь пойдет далее. Заме-
тим, что ниже с тем, чтобы каждый раз не писать «плотность
распределения силы» будем для краткости слова «плотность рас-
пределения» опускать. Итак, имеем:
(2.13)
Ф, ае fa > Sx'j к,2 р.г; &; г,х,
= + (2.14)
V2T2 8t J dXj V2 p2^2 ^Xi ^2L2
Поскольку безразмерные уравнения (2.13) и (2.14) одинако-
вы для оригинала и модели, кроме того, они включают в себя
одинаковые безразмерные величины, то получается, что безраз-
мерные комбинации из характерных величин, содержащихся в
них, должны быть тоже одинаковыми:
_ ^2 . £1^1 _ _ ^*2 . V1 _ v2
KjF, V2T2' К,2 K22 ’ р.И2 р2К22’ KtL, V2L2' (2.15)
Эти комбинации называются “числами подобия”, каждому
из них присвоено имя ученого, известного своими работами в
этой области знаний:
L V2
— = Sh - число Струхала; — = Fr - число Фруда;
Р VL
—v = Ей - число Эйлера; — - Re - число Рейнольдса.
рЕ2 v
Таким образом, если два потока ньютоновской вязкой жид-
кости подобны, то для них справедливо условие:
Sh= idem, Ft = idem, Eu = idem, Re-idem. (2.16)
25
Этим доказывается, что данное условие является необходи-
мым. Доказательство достаточности условий подобия для любых
классов движения вязких несжимаемых жидкостей пока сопря-
жено с непреодолимыми трудностями. Существующие доказа-
тельства теоремы единственности решений уравнений Навье-
Стокса относятся к отдельным, наиболее простым видам движе-
ния.
Заметим, что из условий (2.15) можно получить следующие
выражения, которые вначале рассмотрим на примере числа Стру-
хала:
А.
-А или _A=i
V2T2 kukt
Далее найдем по аналогии для других чисел подобия:
ки _ ।_ ।. к1ки _ ।
klkg крки
(2.17)
где kg=~; кр=—; kv=~
gl Р2 V2
р
кр= — - коэффициенты подобия
Л
соответственно для объемных
сил, вязкости, плотности и давле-
ния.
Безразмерный степенный комплекс, составленный из коэф-
фициентов подобия, называется “индикатором подобия’’. Усло-
вия (2.16) и (2.17) составляют доказательство первой теоремы
подобия: если явления подобны, то числа подобия равны между
собой, а индикаторы подобия равны единице.
Обратимся вновь к зависимостям типа (2.3), из которых по-
лучим для подобных явлений соотношения:
26
b- = i = 4,; = VAI".! (2-18)
Lt2 Л/2 2 w2 M2
Видим, что в подобных явлениях отношения величин (не «харак-
терных») в сходственных пространственно-временных точках
равны соответствующему коэффициенту подобия, одинаковому
для всех точек. Такие отношения называются “симплексами" по-
добия. В связи с этим можно привести еще одно доказательство
первой теоремы подобия, которое обычно используют в учебной
литературе [16,21,41]. С этой целью воспользуемся соотноше-
ниями (2.1) или аналогичными (2.18) и введем новые:
6=^2/ xj\=klxj2’' uil=kuui2>' и]\=кииП;
Р\ = крР2- gl = kgg2> Pl = *рР2< V, = kvV2.
(2.19)
Произведем замену величин в уравнении (2.7) в соответствии с
этими соотношениями и получим:
Сравнивая уравнения (2.20) и (2.8), можно увидеть, что они
станут одинаковыми, если комбинации из масштабных коэффи-
циентов (в том числе и сами коэффициенты, например, kg) будут
равны друг другу:
ки _ kU _ кР _ куки
kt ki 8 kpki V
Если теперь все члены соотношения (2.21)
(2.21)
ки
разделить на —,
ki
то получим:
27
kl _ kgki _ kp _ ky _ ।
kukt k^ kpk-u k[ku
(2.22)
т. e. рассмотренные выше индикаторы подобия (2.17). К тому же
результату можно было прийти, разделив все члены уравнения
(2.20) на к„ /кг и приравняв единице комбинации из коэффициен-
тов подобия, которые получаются в этом случае в виде индикато-
ров подобия (2.17), (2.22).
Следует отметить, что второй путь доказательства первой
теоремы подобия менее предпочтителен, хотя он тоже правиль-
ный. Дело в том, что при этом теряется важное поня-
тие - “характерная величина”. Это понятие широко используется
при решении многих задач в области гидромеханики [22]. И хотя
во многих случаях нет никаких трудностей в выборе такой вели-
чины (чаще всего, как говорят, «она сама бросается в глаза»), в
других, например, в задачах нестационарного, неравномерного
движения, трудностей встречается немало, так как от правильно-
го выбора характерной величины зависит решение всей задачи.
Кроме того, если не использовать такое понятие, как “характер-
ная величина ” - не зависящая от координат и времени, - то в от-
дельных случаях можно получить абсурдные результаты.
Система уравнений, ньютоновской жидкости (2.4) не явля-
ется полной, так как не было учтено уравнение неразрывности,
которое является следствием закона сохранения массы; в ком-
пактной форме и для оригинала, и модели оно в предположении
несжимаемости жидкости имеет вид
f ^- = 0 и f ^- = 0.
i=i Sr(i /=1 dxi2
(2.23)
28
Произведем замену величин, входящих в первое уравнение
системы (2.23) в соответствии с соотношениями (2.19) и получим
^£^2=0. (2.24)
ki^dXil
Но в связи с тем, что отношение ku/kt не равно нулю, уравнения
неразрывности (2.23) в подобных явлениях имеют тождествен-
ный вид, не зависящий от выбора коэффициентов подобия.
Ранее был рассмотрен только один из возможных способов
приведения уравнений движения к безразмерному виду, который
обычно указывается во всех учебниках по моделированию
[9,21,22]. Он состоит в делении всех членов на комбинацию ха-
рактерных величин или масштабных коэффициентов при конвек-
тивной составляющей силы инерции (или в нормировании всех
сил по этой составляющей). Но в связи с тем, что уравнение дви-
жения содержит всего пять различных сил, можно осуществить
нормирование пятью разными способами и получить двадцать
комбинаций чисел или индикаторов подобия. Рассмотрим их на
примере комбинаций масштабных коэффициентов, вошедших в
соотношение (2.21). Результаты сведены в таблицу 2.1.
Естественно, что во второй строке таблицы указаны индика-
торы подобия, уже полученные ранее - это соотношения (2.22). В
остальных строчках, кроме них, появились новые индикаторы
подобия, из которых можно подучить комбинации уже известных
чисел подобия. Так, например, индикатору подобия в первой
строке ksktfku соответствует число подобия
g7’/p = gm/FK£ = Fr’lSh’1. В той же строке есть индикатор
kpkt/kpkiku, соответствующее ему число подобия
РТ/pLV = PTVjpLVV =EuSh4 . Далее идет индикатор ktkv/k} с
29
числом подобия Tv/I? = TvVfL2V = Re 'Sh ' . В третьей строке
указан индикатор подобия к /kt kpkg, ему соответствует число
Таблица 2.1
Индикаторы подобия при различных способах нормиро-
вания соотношения (2.21)
Норми- рующие комби- нации Комбинации коэффициентов подобия
ku/kt ku/kl kg kpM kvkJk2
kulkt 1 kukJkl kgkt/ku kPk,/kPkiku kvkt!ki
ки/к1 kl/kuk. 1 kgkllk2u kp/kpku kJkukt
kg ku/kgk, kU /kgkl 1 kp/k^kg kvkJkl kg
кР/кРк1 kpkuKl kpklkg/kp 1 kvkukp!klkp
подобия P/bpg = PV1!LpgV2 = EuFr . Кроме того, в той же строке
индикатору kukv/k2kg соответствует число подобия
vV/I?g = vVV/L?gV = FrRe“'. В четвертой строке есть новый ин-
дикатор kvkpku/kpkt с числом подобия ;
vpV/PT = vpVVjPTV = Eu”1 Re”1.
Появление новых чисел подобия объясняется иным методом
нормирования уравнения движения; они отражают другие соот- ;
ношения сил, входящих в это уравнение. Так, например, число j
подобия gT/V характеризует отношение силы тяжести к локаль-
ной составляющей силы инерции; число подобия
PjpLg - отношение силы давления к силе тяжести
30
vV/l^g ~ отношение силы вязкого трения также к силе тяжести
и т. д. И естественно, что новые числа подобия выражаются че-
рез уже известные, которым (так сложилось исторически) были
присвоены имена выдающихся ученых. Впрочем, некоторые но-
вые числа тоже носят имена ученых. Например, числу
PL/vpV = ReEu = St присвоено имя Стокса (иногда его называют
числом Лагранжа и обозначают La). Оно характеризует отноше-
ние силы давления к силе вязкого трения. В связи с тем, что ди-
намический коэффициент вязкости p = vp, можно записать:
St = P£/pL. Кроме того, число подобия, характеризующее отно-
шение силы тяжести к силе трения (выше приведена его обратная
величина), равное gl?/vV называют числом Мошени и обозна-
чают Mo, Mo = ReFr-1.
Из изложенного следует, что числа подобия можно пере-
множать, делить одно на другое, а далее будут показаны и другие
операции с их использованием, например, их можно возводить в
степень, извлекать из них корни, иными словами - создавать из
них различные комбинации. Эти операции с числами подобия
проводятся с целью создания необходимых условий для правиль-
ной организации физического моделирования явлений.
Среди чисел подобия (2.16) особо выделяют составленные
из характерных величин сравниваемых потоков и физических
констант среды, которые содержатся в постановке задачи об оп-
ределении движения, т. е. являются наперед заданными (как го-
ворят, они составляют условия однозначности). Такие числа по-
добия называются “критериями подобия”, они обусловливают
подобие двух сравниваемых явлений. Критериев подобия мень-
ше, чем чисел подобия, так как не все характерные величины мо-
гут быть наперед заданы.
31
Отметим, что при изложении данного вопроса здесь исполь-
зовалась терминология, принятая в [22]. В теории подобия суще-
ствует и иная терминология [42], в которой принятым терминам
“числа подобия” и “критерии подобия” соответствуют понятия:
“критерии подобия ”, “определяющие критерии подобия ” и “оп-
ределяемые критерии подобия ”.
Внутренняя связь между числами подобия устанавливается
в результате решения конкретной задачи, однако в гидромехани-
ке и в гидравлике известно множество примеров, когда вид дан-
ной связи устанавливался путем отыскания зависимости между
числами и критериями подобия с использованием эксперимен-
тальных данных. Покажем это в следующей главе на примерах из
области гидромеханики и гидравлики, в которых при физическом
моделировании использовались методы теории подобия.
32
3. ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ МЕТОДА
ПОДОБИЯ
Пусть в потоке вязкой несжимаемой жидкости с коэффици-
ентом кинематической вязкости v, плотностью р, движущейся с
постоянной скоростью находится закрепленный шар диамет-
ром d (рис. 3.1). Скорость задана на “бесконечно” большом уда-
лении от шара выше по течению; практически это означает, .что
речь идет о таком расстоянии, где влияние шара на поток пренеб-
режимо мало. Необходимо найти сопротивление шара набегаю-
щему на него потоку в предположении, что движение стационар-
но. Следовательно, число Струхала отсутствует.
Рис. 3.1. Схема обтекания закрепленного шара
В связи с тем, что числа Фруда тоже нет (шар либо свободно
висит на тонкой упругой нити, либо закреплен на тонкой упругой
подставке, как показано на рисунке), остаются два числа подо-
бия: Ей и Re. В данном случае число Рейнольдса Re = z<zW/v яв-
ляется критерием подобия, так как содержит заданные по усло-
вию задачи характерные величины: скорость и№, диаметр d и фи-
зическую константу v. Если предположить, что число Ей содер-
33
жит характерную неизвестную заранее величину, то оно будет
функцией числа Re. Следовательно, критериальное уравнение
должно быть записано в таком виде:
Eu = /(Re/ (3.1)
Далее необходимо пояснить, что в практических расчетах
обычно принимают в качестве числа Эйлера. Дело в том, что сила
сопротивления шара набегающему потоку жидкости W может
быть определена только после решения задачи об обтекании шара
с использованием метода математического моделирования явле-
ния. Она вычисляется суммированием по поверхности шара сил
давления потока на поверхность (сопротивление формы} и сил
трения жидкости о его поверхность (сопротивление трения}.
Другой путь решения задачи - физическое моделирование явле-
ния обтекания закрепленного шара потоком жидкости. При ана-
лизе подобного рода явлений всегда полезно использовать неко-
торые, заранее известные интегральные соотношения, вытекаю-
щие из условий движения или покоя тел. Такое условие реализу-
ется в процессе проведения опытов следующим образом. Под
действием набегающего потока шар отклоняется от положения
равновесия (см. рис.3.1, пунктир). Если с помощью дополнитель-
ных устройств (в самом простом случае это может быть тонкая
нить, закрепленная в центре лобовой части шара и переброшен-
ная через блок, к концу которой прикрепляются грузы разной
массы) привести шар в исходное состояние, то сила тяжести,
приложенная к грузу, будет равна силе сопротивления W. Таким
образом, в процессе проведения опытов сила сопротивления оп-
ределяется сравнительно просто.
С учетом сказанного запишем условие равновесия сил:
34
W=ApSp + TsSs,
(3-2)
где Sp и Ss - площади приложения сил соответственно давления
и трения, Ар -перепада давления, т4. - напряжение силы тре-
ния. Последние обычно связывают с кинетической энергией еди-
ницы объема сплошной среды:
т5=С2±рг£, (3.3)
где Ci и С2 - коэффициенты. Но площади приложения сил Sp и
Ss не являются характерными, обычно их заменяют площадью
миделевого сечения шара Sd=——, которая является величиной
характерной. При такой замене неизбежно появляются новые ко-
эффициенты: Sp=C”Sd, Ss = C2Sd . Принимая их и зависимости
(3.3) во внимание, произведем преобразования в (3.2) и введем
новые обозначения: Ср=С1'С1", СХ = С'2С2 . Назовем их коэффи-
циентами соответственно сопротивленя формы шара и сопротив-
ления трения. С учетом этих преобразований запишем уравнение
(3.2) в таком виде
(3-4)
Введем теперь для силы сопротивления следующее выраже-
ние:
W=^pu2mSd, (3.5)
35
в котором Cw - коэффициент сопротивленя шара. В таком слу-
чае вместо (3.4) получим
^W=<^p+<^T.
Как было об этом уже сказано выше, в процессе проведения
опытов сравнительно легко можно определить силу сопротивле-
ния плохо обтекаемого тела. Для того, чтобы найти силу давле-
ния потока на поверхность тела, необходимы, как правило, до-
полнительные довольно сложные исследования на специально
изготовленной для этой цели модели. Что касается силы трения,
то для ее определения нужны и специальное оборудование, и не-
простые методы проведения опытов. Если в процессе проведения
исследований были найдены силы сопротивления и давления, то
сила трения обычно находится как разность между ними.
Таким образом, в рассматриваемой задаче роль числа Эйле-
ра может взять на себя половина коэффициент сопротивленя ша-
ра Cw , поскольку отношение W!Sd имеет размерность перепада
давления [22]:
Тогда с учетом (3.6) критериальное уравнение (3.1) можно пред-
ставить в таком виде:
C^cpfReJ. (3.7)
Если в результате проведения опытов будет найдена вели-
чина коэффициента сопротивления, то сила сопротивления най-
дется из формулы (3.5).
Эксперименты полностью подтвердили зависимость (3.7). Ре-
зультаты опытов с шарами различных диаметров, помещенных в
36
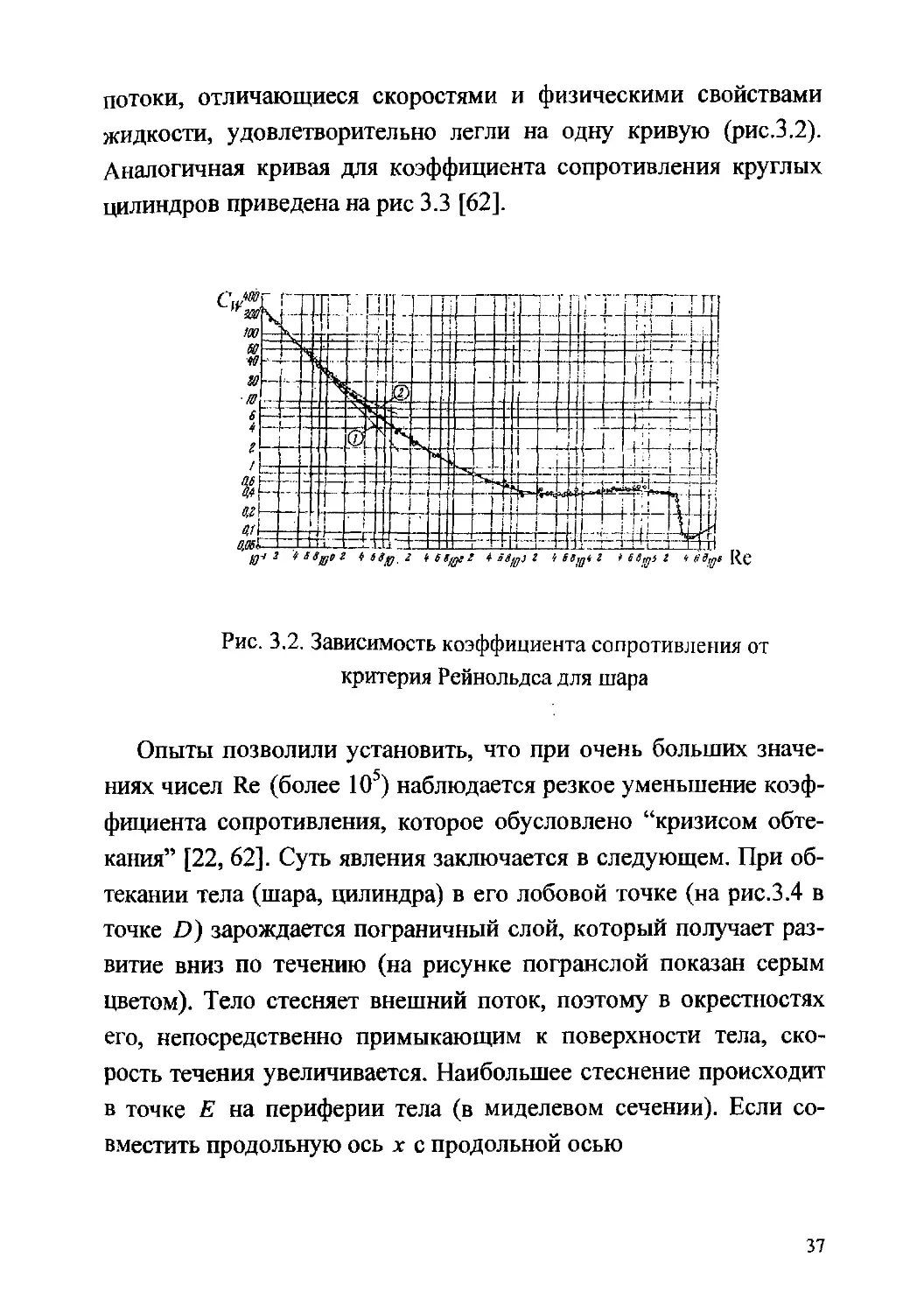
потоки, отличающиеся скоростями и физическими свойствами
жидкости, удовлетворительно легли на одну кривую (рис.3.2).
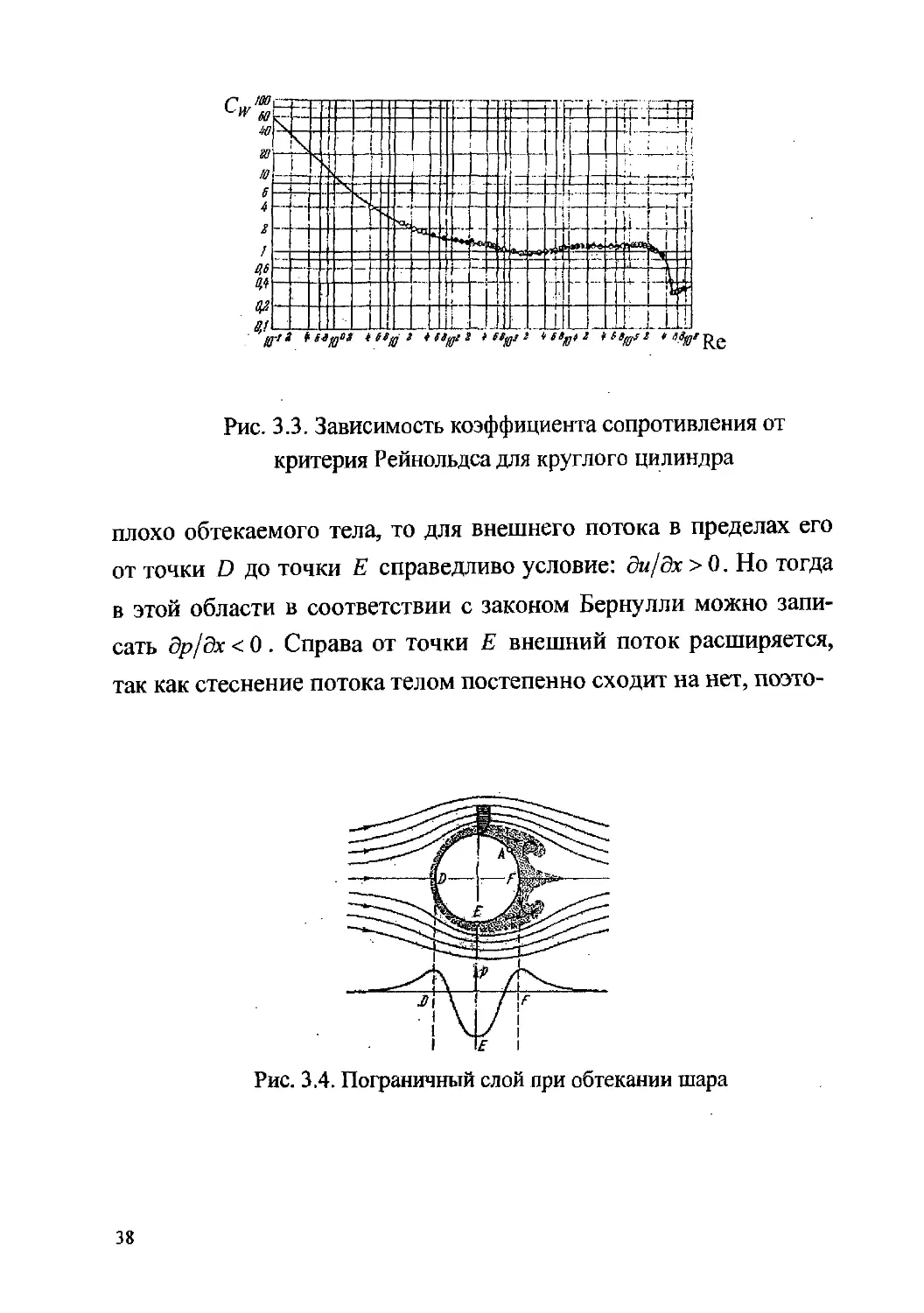
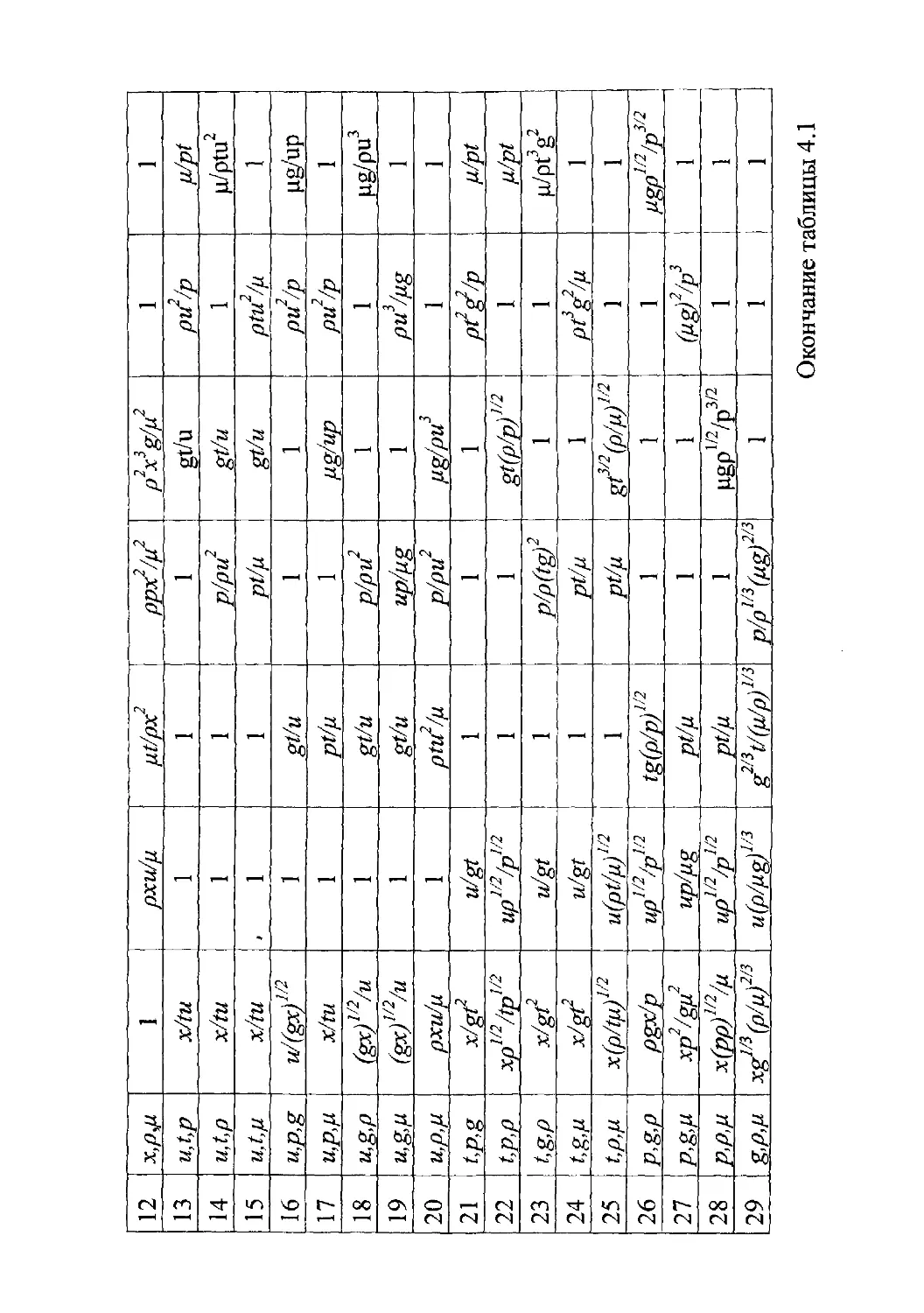
Аналогичная кривая для коэффициента сопротивления круглых
цилиндров приведена на рис 3.3 [62].
Рис. 3.2. Зависимость коэффициента сопротивления от
критерия Рейнольдса для шара
Опыты позволили установить, что при очень больших значе-
ниях чисел Re (более 105) наблюдается резкое уменьшение коэф-
фициента сопротивления, которое обусловлено “кризисом обте-
кания” [22, 62]. Суть явления заключается в следующем. При об-
текании тела (шара, цилиндра) в его лобовой точке (на рис.3.4 в
точке D) зарождается пограничный слой, который получает раз-
витие вниз по течению (на рисунке погранслой показан серым
цветом). Тело стесняет внешний поток, поэтому в окрестностях
его, непосредственно примыкающим к поверхности тела, ско-
рость течения увеличивается. Наибольшее стеснение происходит
в точке Е на периферии тела (в миделевом сечении). Если со-
вместить продольную ось х с продольной осью
37
Рис. 3.3. Зависимость коэффициента сопротивления от
критерия Рейнольдса для круглого цилиндра
плохо обтекаемого тела, то для внешнего потока в пределах его
от точки D до точки Е справедливо условие: ди/дх > 0. Но тогда
в этой области в соответствии с законом Бернулли можно запи-
сать др/дх < 0 . Справа от точки Е внешний поток расширяется,
так как стеснение потока телом постепенно сходит на нет, поэто-
Рис. 3.4. Пограничный слой при обтекании шара
38
му в этой области: ди/дх < 0, др)дх > 0 . Следовательно, потоку в
погранслое ниже точки Е приходится преодолевать не только
силу трения, но и силу увеличивающегося вниз по течению дав-
ления. Это приводит к тому, что в некоторой точке А погранич-
ный слой отрывается от поверхности тела. При малых числах
Рейнольдса здесь зарождаются и отрываются от поверхности тела
вихревые образования, которые сносятся вниз по течению (до-
рожка Кармана). При больших значениях числа Рейнольдса в
кормовой части плохо обтекаемого тела (в окрестности точки F)
образуется устойчивая вихревая область. В ней давление значи-
тельно понижается по сравнению с давлением во внешнем пото-
ке. Это понижение является причиной появления сопротивления
давления плохо обтекаемого тела (или сопротивленя формы).
При больших значениях чисел Рейнольдса ламинарный погра-
ничный слой, развивающийся на поверхности тел, переходит в
некоторой точке в турбулентный. Кризис сопротивления насту-
пает, когда точка перехода ламинарного пограничного слоя в
турбулентный расположена непосредственно перед точкой отры-
ва. Точка отрыва турбулентного пограничного слоя при том же
распределении скоростей во внешнем потоке всегда расположена
ниже по потоку, чем точка отрыва ламинарного слоя, что способ-
ствует улучшению обтекания тел. При прочих равных условиях
турбулентный поток обладает большей кинетической энергией,
чем ламинарный. Это объясняется большей наполненностью
эпюры распределения скорости в пределах пограничного слоя
при турбулентном режиме по сравнению с ламинарным. Обладая
большей кинетической энергией, турбулентный поток приобрета-
ет возможность, преодолевая силу сопротивления трения, пройти
вдоль поверхности тела до точки отрыва дополнительное рас-
39
стояние. Тем самым процесс обтекания шара и цилиндра улучша-
ется.
Известно точное решение задачи обтекания шара потоком
идеальной жидкости, в соответствии с которым сопротивление
шара потоку такой жидкости равно нулю («парадокс Даламбе-
ра»).
При моделировании явления обтекания шара и цилиндра
индикатор подобия, получающийся из критерия Re, рав-
ный kukl jkv, позволяет установить связь между масштабными ко-
эффициентами. В частности, если на модели используется жид-
кость тех же физических свойств, что и в натуре (kv =1), то
ки -к,х. Полезно заметить, что в промежутке 103 <Re<105 ко-
эффициент сопротивления Cw практически не зависит от вели-
чины критерия Re.
Область, в которой можно пренебречь влиянием одного из
критериев подобия, называется “автомодельной ” [21]. В кон-
кретном рассматриваемом случае взаимнооднозначное соответ-
ствие между моделью и натурой реализуется при обеспечении
только условий однозначности. В частности, при достижении по-
добия граничных условий для реализации соответствия доста-
точно только геометрического подобия модели и натуры. Имеет-
ся в виду то обстоятельство, что лабораторный стенд всегда ог-
раничен в своих размерах, поэтому необходимо выдерживать оп-
ределенные соотношения, которые вырабатываются практикой
моделирования, между размерами рабочей части лабораторной
установки и моделью изучаемого объекта, например, между раз-
мером рабочего участка аэродинамической трубы и размером
помещенного в нее тела. [58].
40
Понятие автомодельность широко используется в гидроме-
ханике [22] в тех случаях, когда появляется возможность описать
явление системой обыкновенных дифференциальных уравнений
вместо системы дифференциальных уравнений в частных произ-
водных. Возникает такая возможность тогда, когда в частных за-
дачах, вытекающих из общего решения рассматриваемой про-
блемы, могут отсутствовать некоторые характерные величины
(например, скорость течения, линейный размер и т. д.). Но тогда
в безразмерных дифференциальных уравнениях будут отсутство-
вать числа подобия, связанные с этими характерными величина-
ми. Следовательно, автомодельность можно трактовать как не-
зависимость рассматриваемого явления от этих чисел подобия.
Усложним задачу тем, что учтем нестационарные процессы
при обтекании тела и сжимаемость воздуха. Нестационарные
процессы могут протекать в двух формах: автоколебаний и вы-
нужденных колебаний тел в воздушном потоке. Автоколебания -
это вибрации струн в однородном потоке воздуха, например, те-
леграфных проводов в ветреную погоду. Колебания струн под
действием набегающего на них воздушного потока изучал чеш-
ский физик Струхал, который по высоте звука определял частоту
колебаний n-X/t, где t - период колебаний. Он впервые опреде-
лил, что безразмерный комплекс, равный d/tu^, в котором
d - диаметр струны, - скорость набегающего потока, сохра-
няет постоянное значение, приблизительно равное 0,2. Позднее
комплексу было присвоено имя числа Струхала. Этот вопрос был
более подробно изучен путем проведения исследований на физи-
ческой модели [22,62]. Если силу тяжести по-прежнему исклю-
чить из рассмотрения, то явление вполне определяется тремя
числами подобия: Re, Sh, Ей, роль последнего играет коэффици-
ент сопротивления Cw. Из трех чисел подобия одно является
41
критерием - это число Рейнольдса. Два других числа не являются
критериями, поскольку первое содержит заранее неизвестную ве-
личину - период колебаний, второе - неизвестный коэффициент
сопротивления. Таким образом, имеют место два критериальных
уравнения:
Sh = jYReJ и C^=<pfRe/
Опыты, результаты которых приведены на рис. 3.5 [22,62]
полностью подтверждают эти предположения. Во-первых, при
больших числах Рейнольдса имеется автомодельная область по
этому критерию, в которой число Sh постоянно и равно 0,21. Во-
вторых, если сравнить рис. 3.5 с рис. 3.3, то можно обнаружить,
что процесс автоколебаний практически не изменил величину ко-
эффициента сопротивления цилиндра в автомодельной области.
Рис. 3.5. Зависимость коэффициента сопротивления и числа
Струхала от критерия Рейнольдса для круглого цилиндра
Можно задачу сформулировать по-иному: будем искусст-
венно приводить тело, находящееся в том же потоке жидкости, в
колебательный режим с заданным периодом, но тогда число
Струхала станет критерием, и критериальное уравнение примет
вид:
Cw - yfRe, Sh).
42
Все изложенное относится к течению несжимаемой жидкости.
Для сжимаемой среды появится еще одно число подо-
бия - характерное число Маха (обозначается М), представляю-
щее собой отношение характерной скорости течения к характер-
ной скорости звука и3: М = их /и3, которое можно рассматривать
как меру сжимаемости среды [22,62]. При обтекании шарообраз-
ного тела потоком со сверхзвуковой скоростью (М > 1) к сопро-
тивлению формы и трения добавляется “волновое сопротивле-
ние”. В этом случае критериями являются числа Re и М; следо-
вательно,
Cw = F(Re, MJ,
что также хорошо подтверждается экспериментами (рис.3.6) [62].
Рис. 3.6. Зависимость коэффициента сопротивления от
критериев Маха и Рейнольдса
Кривая приблизительно совпадает с аналогичной кривой для не-
сжимаемой жидкости при условии М < 0,3. Следовательно, здесь
сжимаемость не оказывает существенного влияния на сопротив-
43
ление (автомодельная область по характерному числу Маха). В
связи с тем, что при нормальных условиях скорость распростра-
нения звуковых волн в воздухе приблизительно равна 330 м/с, то
дозвуковые течения реализуются при скорости движения воз-
душной среды <100 м/с. При числах М>0,8, наоборот, влияния
числа Re на сопротивление по сравнение с числом М практиче-
ски не обнаруживается (вновь автомодельная область по числу
Рейнольдса).
С тем, чтобы из общей силы сопротивления выделить силу
сопротивления давления (сопротивление формы), необходимо
изучить распределение давления по поверхности тела. Осуществ-
ляется это с помощью пьезометров; для этого шар (цилиндр) де-
лают полым внутри, а в стенках высверливают отверстия малого
диаметра. Типичная картина распределения давления по поверх-
ности круглого цилиндра приведена на рис. 3.7. Давление отне-
сено к кинетической энергии набегающего потока (к динамиче-
скому давлению: <?=рг/2/2). Там же пунктирной линией нанесено
распределение давления при обтекании круглого цилиндра пото-
ком идеальной жидкости.
Рис. 3.7. Распределение давления по поверхности шара
44
Сила сопротивления давления находится путем суммирова-
ния по поверхности тела давления, используя кривую его распре-
деления, приведенную на рис. 3.7. В случае идеальной жидкости
эта сила равна нулю. Вычитая силу сопротивления давления из
величины общей силы сопротивления, измеренной указанным
выше путем, находят силу сопротивления трения. Для определе-
ния силы волнового сопротивления применяются специальные
методы и приемы [58].
При обтекании тел потоком со свободной поверхностью об-
наруживается зависимость коэффициента сопротивления от кри-
терия Фруда. В этом случае этот критерий является аналогом
числа Маха в соответствии с газогидравлической аналогией, по-
зволяющей изучать сверхзвуковые обтекания тел газом путем на-
блюдения волн, образующихся на поверхности воды при обтека-
нии тел той же формы бурным потоком. Критерий Фруда можно
„ , с “2
представить в такой форме: Fr = -y, где ut- скорость распро-
wB
странения поверхностных волн на воде небольшой глубины (на
“мелкой воде”). Получается, что число Фруда является аналогом
числа Маха, возведенного в квадрат (в американской литературе
для полной аналогии в качестве числа Фруда принято Fr =—).
“в
Скорость распространения волн на мелкой воде определяется по
формуле Лагранжа: wB = -/gh. Отсюда следует принятое в отече-
W2
ственной литературе выражение для числа Фруда: Fr = —. В за-
gh
висимости от величины числа Фруда водные потоки делятся на
спокойные (Fr<l, и<ив) и бурные (Fr > 1, w>wB). Потоки от-
личаются по характеру обтекания ими тел, находящихся в воде.
45
При обтекании спокойным потоком преграды на его по-
верхности образуются волны, которые распространяются вверх
по течению (аналогичную картину можно наблюдать при паде-
нии тяжелого предмета в воду, образующиеся при этом волны
распространяются не только вниз по течению, но и вверх). На
рис. 3.8.а показана типичная картина обтекания спокойным пото-
ком преграды в виде мостовой опоры. Глубина и скорость потока
на большом удалении от опоры соответственно равны: h№ и и№.
Действие сил давления и трения порождает со стороны опоры
равное и противоположно направленное противодействие в виде
рассмотренной выше силы сопротивления, включающей в себя
обе силы.
При обтекании бурным потоком преграды на поверхности
потока образуется волна, которая сносится вниз по течению в ви-
де косого гидравлического прыжка. При движении судна на по-
верхности воды с большой скоростью в его носовой части на-
блюдается волна, которая, перемещаясь вместе с судном, образу-
ет на поверхности воды хорошо видимый след, имеющий в плане
форму клина. Аналогичный след в виде скачка уплотнения воз-
духа наблюдается при движении самолета со сверхзвуковой ско-
ростью. Только след на воде можно воочию наблюдать, в то вре-
мя как скачек уплотнения воспринимается наблюдателем как
ощущение взрыва в момент, когда волна уплотненного воздуха
достигает его органов слуха. На рис 3.8.6 показана типичная кар-
тина обтекания бурным потоком преграды в виде мостовой опо-
ры. Здесь у опоры возникает хорошо видимая волна на поверхно-
сти воды. При больших числах Фру да в кормовой части опоры I
давление может значительно отличаться от гидростатического;
вследствие образования здесь каверны. Но в этом случае опора
может испытывать слева полную величину волнового давления.
46
Практики и ученые, которые занимаются созданием и исследова-
ниями мостовых переходов, отмечают, что на равнинных реках
при разрушении мосты, как правило, опрокидываются вниз по
течению; на горных реках часто наблюдается опрокидывание
мостов навстречу потоку. Причиной разрушения может быть
подмыв мостовых опор (на рисунках схематично показаны во-
ронки размыва грунта у опор), а также воздействие на опоры
волнового сопротивления при больших числах Фруда, характер-
ных для горных рек.
В связи с тем, что поток имеет конечную глубину, критери-
альное уравнение должно содержать отношение h^jd, которое
входит в условия однозначности.
Следовательно, в общем виде уравнение связи между чис-
лами и критериями подобия будет иметь такой вид
//Eu, Re, Fr,/^/J) = 0.
В нем три критерия подобия (включая симплекс h^/d) и одно
число подобия - Ей.
Рис. 3.8. Обтекание мостовой опоры: а) спокойным,
б) бурным потоком
47
Есть все основания полагать, что и в этом случае, как об
этом было уже сказано выше, роль числа Эйлера играет половина
коэффициента сопротивления опоры. Но тогда можно записать
критериальное уравнение в таком виде:
Ей = = ф (Fr, Re, . (3.8)
На рис.3.9 приведены кривые, соответствующие зависимо-
сти (3.8), полученные по результатам экспериментов при посто-
янной величине числа Рейнольдса [25]. Можно отметить, что при
условии Fr < 0,1 коэффициент сопротивления не зависит от кри-
терия Фруда (автомодельная область по критерию Фруда). Таким
образом, аналогия чисел Фруда и Маха распространяется и на их
автомодельные области; в этих областях выполняется условие
M-VFr ~о,з.
Рис. 3.9. Зависимость коэффициента сопротивления
цилиндрической опоры от критерия Фруда и относительной
глубины потока
В разделе гидромеханики, описывающей движение судна,
вместо коэффициента сопротивления используют коэффициент
пропорциональности С}, так связанный с силой сопротивления:
48
Р7 = Qpg^3 • Выражая силу сопротивления через коэффициент со-
противления, найдем связь между коэффициентами Q и Cw
С, 1 = EuFrf—) .
2 I d ) \d )
Представим критериальное уравнение (3.8) в неявном виде
F(Eu, Fr, Re, /гда/d) = 0.
Заменим числа и критерии подобия их комбинациями в такой по-
следовательности:
F} (EuFr, Fr, *&,hjd) = 0; F2 [euF^/d)2, Fr, Re, hx jd\
Отсюда имеем: C( = F3 (Fr, Re, hrj'/d ).
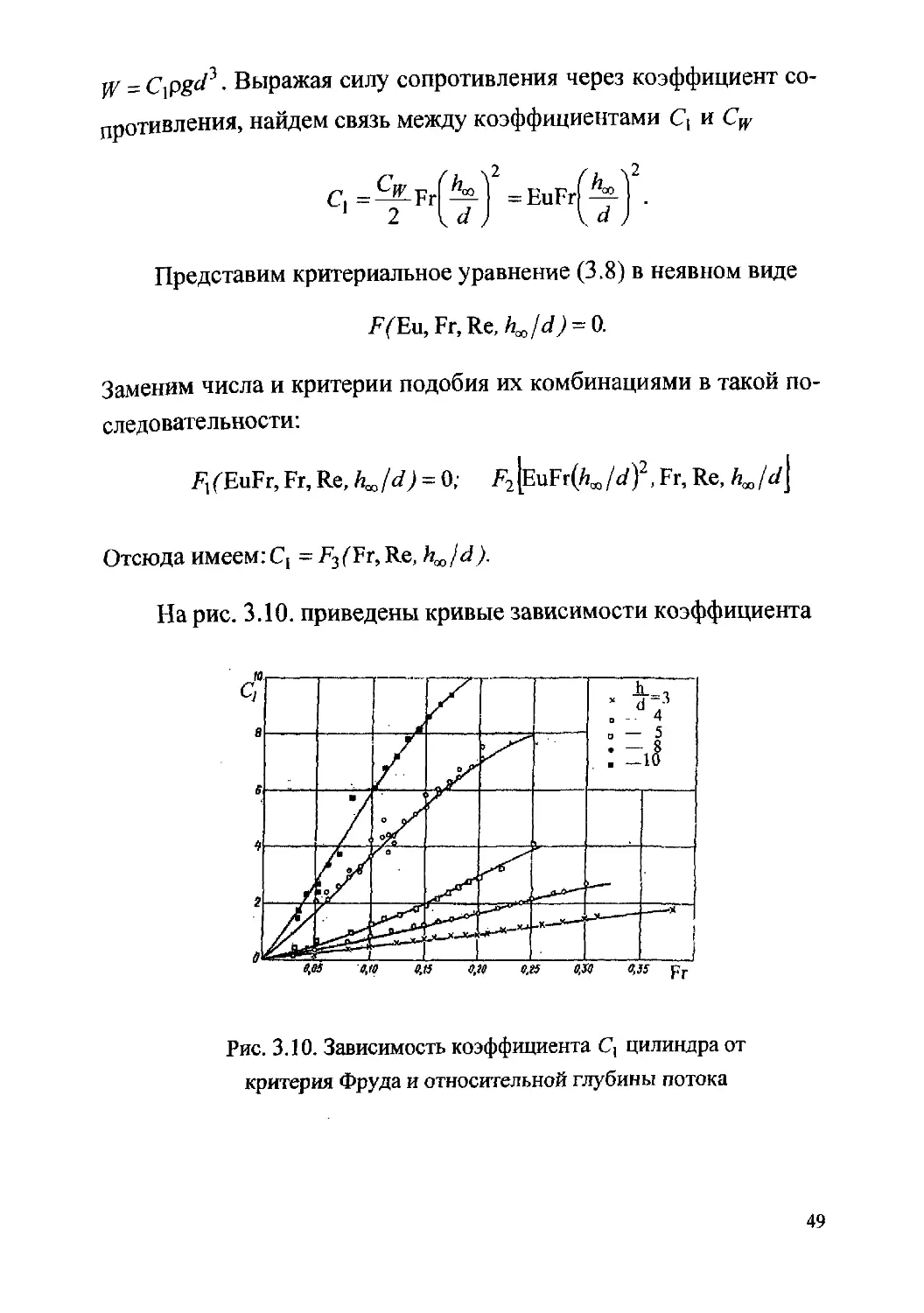
На рис. 3.10. приведены кривые зависимости коэффициента
Рис. 3.10. Зависимость коэффициента Q цилиндра от
критерия Фруда и относительной глубины потока
49
С] от числа Фруда и отношения h^jd , полученные по результа-
там экспериментов, проведенных в автомодельной области по
числу Рейнольдса [25]. Можно заметить, что связь коэффициента
Cj с определяющими явление критериями по сравнению с анало-
гичной связью коэффициента сопротивления Cw получается хо-
рошо выраженной при всех значениях критериев подобия. Недос-
татком этого графика является отсутствие на нем «видимой» об-
ласти, в которой явление автомодельно по критерию Фруда. Од-
нако не трудно догадаться, что эта область существует и нахо-
дится в начале графика (при Fr < 0,1), где зависимость коэффици-
ента Q от определяющих критериев линейна.
При моделировании обтекания тел сверхзвуковым потоком
сжимаемого газа или бурным потоком тяжелой несжимаемой
жидкости возникают определенные трудности, так как полное
подобие по всем критериям при испытании уменьшенной модели:
невозможно, ибо они противоречат друг другу. Так, например,;
уменьшая размеры модели, мы должны в соответствии с индика- }
тором подобия, следующим из условия Re = idem, увеличивать
скорость течения жидкости в модельной установке, что может,
привести к нарушению условия М = idem, или Fr = idem . На прак-
тике в этих случаях используют различные способы моделирова-1
ния: применяют иную жидкость, чем в натуре, подогревают ee,j
проводят эксперименты со сжатым воздухом и т. д. |
Если, например, на модели жидкость подогреть, то при ус-’
ловии Re = idem получим: |
я
ku=kvki\wniuM=uHktk~x =uHkt~ (3.9)|
v« , 1
50
Для воды при температуре tH -20°С, vH = 1,007 10 2см2/с . Если
на модели воду подогреть до tM = 35°С, vM = 0,727 Ю-2 см2/с , то
м « o,72uHkt. Иными словами, подогрев воды на модели позволя-
ет уменьшить скорость течения (в рассмотренном примере при-
близительно на 28% по сравнению со случаем, когда вода на мо-
дели имеет ту же температуру, что и в натуре).
В практике гидравлического моделирования различных
строительных объектов часто возникает необходимость исследо-
вать явления, происходящие при взаимодействии речного потока
с пойменным. В качестве примеров можно указать мостовые пе-
реходы через реки, участки трасс автомобильных и железных до-
рог, которые прокладываются вдоль берегов рек и т. п. Ширина
пойм равнинных рек колеблется от нескольких километров до де-
сятков километров. При ограниченных размерах площадей для
проведения такого рода исследований даже в крупных лаборато-
риях приходится задавать очень большие линейные масштабные
коэффициенты ki=lJlM. Если моделирование осуществлять по
критерию Фруда, то из соответствующего индикатора подобия,
равного kl/kgkj = 1, имеем: ки , если kg = 1 (явления в нату-
ре и на модели протекают в поле сил земного тяготения). Исполь-
зуем эти результаты для сравнения чисел Рейнольдса на модели
Re u и в натуре Re„, имея в виду, что при таком способе модели-
рования справедливы следующее соотношение между скоростя-
ми течения и линейными размерами: им =ulJ^kl, =l„lkt. По-
лучим, приняв kv = vH[vM -1 (на модели и в натуре используется
одна и та же жидкость):
Пр __ М М — И п
М
. -Re /р/2
51
Следовательно, число Рейнольдса в условиях модели может^
значительно уменьшиться по сравнению с натурой. Например,|
если kt =100, то число Рейнольдса на модели будет в тысячу раз|
меньше, чем в натуре, так что вместо автомодельной по числу
Рейнольдса области в натуре на модели можно оказаться в об л ас-;
ти, где явление существенно зависит от этого числа. j
Следует отметить также особенность речных потоков, кото-;
рая заключается в том, что глубина воды в русле реки на один-,
два порядка меньше его ширины, а по сравнению с поймой такое!
отличие может достигать нескольких порядков. При больших
значениях линейных масштабных коэффициентов глубина воды в
русле реки на модели может составлять несколько сантиметров, а
на пойме и того меньше. Производить измерения скоростей тече-
ния стандартными способами в таких условиях трудно, а иногда
вообще невозможно. Тогда принимают линейный масштабный!
коэффициент глубин потока kh отличным от соответствующего;
коэффициента плановых размеров потока kh так чтобы выполня-
лось условие kh <kt. Следовательно, здесь реализуется аффинное
подобие, о котором речь шла в главе 1. Особенности кинематиче-
ского подобия явлений в случае аффинного подобия будут рас-
смотрены ниже. Забегая вперед, нужно отметить, что возможно-
сти уменьшать масштабный линейный коэффициент kh по срав-
нению с kt ограничены. Между тем, на практике часто при моде-
лировании речных потоков коэффициент kh принимают во много
раз меньше kt (иногда на несколько порядков). Но тогда подвод-:
ные откосы дна в прибрежных частях русла и откосы речных
террас в пределах поймы на модели становятся почти вертикаль-!
ными. Ожидать кинематического подобия потока на такой моде-
ли натурному не приходится. В принципе аффинное подобие при
52
моделиРовании русловых потоков возможно, его обоснование и
ограничения будут обсуждены ниже.
Вернемся к обсуждаемой теме и отметим, что в практике
исследований русловых потоков на физических моделях широко
используется метод “моделирование безнапорных потоков на на-
порных моделях”. Иными словами, речь идет о моделировании
речного потока на модели, на которой вода заменяется воздухом,
а свободная поверхность водного потока - стеклом. Воздушный
поток под стеклом на модели имеет много общего с водным по-
током подо льдом. Особенности кинематического подобия таких
потоков будут также обсуждены ниже. Пока рассмотрим досто-
инства и недостатки моделирования водного потока воздушным
под стеклом, имитирующем свободную водную поверхность. За-
метим, прежде всего, что моделировать таким способом можно
только спокойные водные потоки, для которых справедливо ус-
ловие: Fr = w2/gA<0,l. У равнинных рек данное число Фруда на
порядок, а то и на два меньше указанного предела (например, у р.
Невы при средних значениях глубины потока и скорости течения
соответственно Юм и 1 м/с число Фруда равно 0,01). Воздуш-
ный поток на модели должен находиться в автомодельной облас-
ти по числу Маха: М < 0,3. Основное преимущество такого вида
моделирования заключается в том, что отпадает необходимость
учитывать критерий Фруда.
Посмотрим, какой должна быть скорость воздуха на модели
при условии Re = idem', с этой целью воспользуемся зависимо-
стями (3.9), в которых в качестве характерного линейного разме-
ра примем характерную глубину потока. Тогда вторую зависи-
мость в (3.9) можно записать в таком виде:
53
им ~~ UH^h
VH
(3.10)
При температуре /л<-20°С, ум = 15,0-10“2см2/с (воздух).
Если принять температуру воды такой же, как на модели, то
ум/ун «15,0 . Из-за того, что на модели применена жидкость бо-
лее вязкая, чем вода, ее скорость при прочих равных условиях
должна превышать скорость воды в условиях модели более чем
на порядок. Но тогда аэродинамическая модель не имеет никаких
преимуществ по сравнению с моделью гидравлической, посколь-
ку размеры модели с воздушным потоком получаются огромны-
ми. Например, если принять скорость воздуха на модели пре-
дельной по условию его несжимаемости, равной 100 м/с (на
практике обычно эта скорость не превышает 50-60м/с), то при
ин - 0,6м/с линейный масштабный коэффициент глубины потока
kh получается равным 10. Существенные преимущества получа-
ются только в том случае, если натурный поток находится в ав-
томодельной области по числам Маха и Рейнольдса, и число Re„
велико. Тогда на модели число Re u можно принять равным гра-
ничному значению, соответствующему началу автомодельной
области по числу Рейнольдса, так что Re^/Re,, < 1.
Рассмотрим этот случай подробнее. Допустим, что в усло-
виях модели число Рейнольдса принимается равным граничному
значению Re*(. Возьмем отношение числа Рейнольдса в натуре к
граничному значению на модели и выполним следующие преоб-
разования:
Re„ Re,. Re.. , kukh
RQ*M~RQ*HRQ*M~ Re kv
(3.11)
54
где Re* - граничное число Рейнольдса для натурного потока,
=ReH/Re* - масштабный коэффициент числа Рейнольдса. Ес-
ли принять равенство граничных чисел на модели Re*, и в натуре
Re*, то из этого следует: kRe = Re^/Re*,; кроме того,
ReH _ | (3 12)
Re^ kv
Далее запишем следующее соотношение:
Re„ кик^ /о i
К
которое, естественно не является индикатором подобия; соответ-
ствующие масштабные коэффициенты в зависимости (3.13) от-
мечены звездочками с тем, чтобы отличить их от масштабных ко-
эффициентов, входящих в индикатор подобия (3.12). Выражение
(3.13) можно сделать индикатором подобия, для этого нужно, как
это видно из зависимости (3.11), разделить его на масштабный
коэффициент kRe. Выполнив это, получим:
^v^Re
(3.14)
Наличие в зависимости (3.14) масштабного коэффициента числа
Рейнольдса избавляет от необходимости вводить новые обозна-
чения для скоростей течения и глубин потока, поэтому после
преобразований найдем:
и
м
к^м
kRe^n
- u»k*h
Re>.M
Re„v„
(3.15)
55
Если kRe =1, то зависимость (3.15) превращается в (3.10) (в этом
случае k*h = kfl).
Рассмотрим пример, в котором воспользуемся данными,
приведенными выше при обсуждении зависимости (3.10). Допус-
тим, что число Рейнольдса в натуре Re„=105. Обращаясь к
рис.3.3, находим величину граничного числа: Re* =103 (ниже ве-
личина граничного числа Рейнольдса для безнапорного потока
будет определяться расчетом). Принимаем скорость течения воды
в натуре равной 1,0м/с, воздуха на модели - 50,0м/с. Подставим
эти данные в зависимость (3.15), найдем: к% «300. Таким обра-
зом, открываются практически неограниченные возможности для
выбора линейного масштабного коэффициента глубины потока
при реализации этого способа приближенного моделирования
безнапорного потока в натуре воздушным напорным потоком на
модели.
Методика моделирования заключается в следующем. При
моделировании конкретного натурного объекта, исходя из произ-
водственных возможностей лаборатории, выбирают линейный
масштабный коэффициент кг. Далее, учитывая допустимую ве-
личину отличия одного линейного масштабного коэффициента от
другого (об этом речь пойдет ниже), находят величину коэффи-
циента kh. После изготовления модели проводят методические
исследования на ней, располагая стекло на таком уровне, при ко-
тором в натурных условиях производились измерения скоростей;
потока и был определен расход воды QH. Цель методических
опытов - найти скорость течения им и соответствующее ей числ»
Я
и h
Рейнольдса Re u - м м . Опыты проводят до тех пор, пока не бу-j
%
56
дет найдена такая скорость воздуха им, которой соответствует
uh
граничное число Рейнольдса Re*f = м м . Это нужно для того,
чтобы в основных опытах такой режим избегать, и проводить их
при условии им >и*м, особенно не заботясь о величине скорости
воздушного потока, лишь бы выполнялось это условие. Если оно
выполняется, то на модели производят измерение скорости воз-
душного потока, после чего методами гидрометрии определяют
расход воздушного потока QM. Далее находят масштабный коэф-
фициент расхода kQ = ktkhku и масштабный коэффициент скоро-
сти как отношение ки = kQ/khk[, в соответствии с которым про-
изводят пересчет скоростей течения, измеренных на модели, в
натурные условия.
Из сказанного выше следует, что использование автомо-
дельных областей приводит к хорошим возможностям при реали-
зации приближенного моделирования гидравлических явлений.
Отсюда возникает естественное желание применить этот способ к
случаю, когда безнапорный поток в натуре моделируется безна-
порным на модели, иными словами, на модели создается водный
поток. Обратимся к зависимости (3.13), учтем, что в ней в рас-
сматриваемом случае следует принять k*v = 1, получим:
Re„ . , *,*
~V = kRe = kukh.
(3-16)
Осуществим моделирование, исходя из условия Fr = idem, но в
этом случае имеем такую связь между масштабными коэффици-
ентами скорости и линейных размеров к*и = -/к^. Подставляя этот
результат в (3.16), найдем зависимость для определения линейно-
57
го масштабного коэффициента при таком способе моделирова-
ния:
Например, если принять kRe = 100, то k*h « 22.
Выше были рассмотрены примеры моделирования наиболее
простых течений вязкой жидкости. При решении конкретных за-
дач возможны такие случаи, когда среди чисел подобия не оказы-
вается ни одного критерия. Например, задача о свободном ста-
ционарном падении шара в жидкости представляется более
сложной, чем первая из рассмотренных ранее в качестве приме-
ров, ибо ни одно из трех чисел подобия: Eu, Fr и Re не может
быть критерием подобия, так как скорость падения шара (его
гидравлическая крупность) - величина, заранее неизвестная, вхо-
дит во все три числа. В этом случае составляют критерии подо-
бия, комбинируя числа подобия таким образом, чтобы исключить
величины, заранее неизвестные [22, 35, 37].
4. ОСНОВЫ МЕТОДА РАЗМЕРНОСТЕЙ
В практике исследований находят широкое применение
также методы теории размерностей. Они не используют в явном
виде дифференциальные уравнения и другие условия единствен-
ности их решения, но требуют достаточно глубокого понимания
сущности явлений, без чего нельзя правильно выбрать основную
систему физических параметров, описывающих явление, и ука-
зать, какие из них в данной конкретной задаче являются наперед
заданными, а какие - от них зависящими. Однако эти методы
весьма полезны в тех случаях, когда дифференциальные уравне-
ния, описывающие изучаемое явление, еще неизвестны, Они так-
же важны в трудных вопросах интегрирования дифференциаль-
ных уравнений гидродинамики для упрощения самого решения.
Анализ размерностей позволяет, не решая уравнений, опреде-
лить, будет ли задача автомодельной или нет, и тем самым
уменьшить число независимых переменных в уравнениях в част-
ных производных, сводя их к обыкновенным дифференциальным
уравнениям.
Измерить какую-то физическую величину означает срав-
нить ее с величиной того же рода, принятой в качестве эталона
или основы для сравнения. Результат сравнения и есть количест-
венная мера физической величины при условии, что сравнивае-
мые величины однородны; результат выражается числом с указа-
нием наименования эталонной единицы. Таким образом, можно
говорить о существовании величин, численные значения которых
зависят от системы единиц измерения; они называются размер-
ными. Величины, численное значение которых не зависит от сис-
темы единиц измерения, называются безразмерными.
59
Физические величины связаны между собой, поэтому, если
некоторые из них принять в качестве основных и установить для
них единицы измерения, то единицы измерения остальных вели-
чин, называемых производными, будут определенным образом
выражаться через единицы измерения основных величин. Прак-
тически в механических задачах достаточно установить единицы
измерения для трех величин, чтобы через них выразить единицы
измерения всех остальных.
Выражение производной единицы через основные называ-
ется размерностью. Зависимость единицы измерения производ-
ной величины от единиц измерения основных величин может
быть представлена в виде формулы, называемой формулой раз-
мерности. В международной системе (русская аббревиатура СИ)
в качестве основных приняты единицы измерения; длины (метр),
времени (секунда), массы (килограмм). Размерность основных ве-
личин обозначают соответственно: L, Т, М. Размерность произ-
водных величин принято обозначать символами этих величин,
взятыми в квадратные скобки. Например, размерность ускорения
а можно записать так: [a]-LT~2. Отсюда следует, что физиче-
ская величина будет размерной, если в ее размерности имеется
хотя бы одна из размерностей основных величин, возведенная в
степень, отличную от нуля.
Совокупность основных и производных единиц образует
систему единиц. Выбрав в системе единиц основные, определяют
производные единицы остальных физических величин, используя
функциональные зависимости между ними (определяющие соот-
ношения). Последние отражают какие-то физические законы. На-
пример, согласно второму закону Ньютона, сила, действующая на
тело, пропорциональна произведению его массы т на ускорение
а:
60
f = Cam,
(4-1)
где С - коэффициент пропорциональности.
Однако сам по себе физический закон однозначно не опре-
деляет вид функциональной зависимости. Действительно, если не
вводить никаких ограничений на выбор единиц измерения вели-
чин, входящих в уравнение (4.1), то коэффициент С будет раз-
мерной величиной. Пусть F размерность силы, А - ускорения,
М - массы, тогда получим размерность С:
\C\=FA~'M~X.
Но, если принять коэффициент С безразмерной постоянной
величиной, равной единице, то задавать произвольно размерность
силы станет невозможно, так как при выбранных основных еди-
ницах, например, в системе СИ {L,T и М) единица измерения
силы будет производной величиной, размерность которой одно-
значно определяется формулой
[f] = MLT~2, (4.2)
тем самым заметно упрощается, становится более определенной
зависимость (4.1).
В основе теории размерностей лежит принцип однородно-
сти (или гомогенности от греч. гомос - равный, генос - род) фи-
зических уравнений, впервые высказанный Ж. Фурье. Сущность
принципа заключается в утверждении, что размерности членов
любых физических уравнений одинаковы, т. е. они могут быть
выражены в одной и той же системе единиц измерения. При со-
блюдении этого условия уравнение остается справедливым при
любой избранной системе основных единиц измерения.
61
4.1. Формула размерности
Допустим, что имеется производная величина у, которая за-
висит от основных величин, где i = 1,2,3,..., к:
у = f(xvx2,x3,..., хк) (4.3)
Задача заключается в том, чтобы установить, как размерность
производной величины выражается через размерности основных
величин:
Ы = f(lxi Ж1 h 1- - ta 1) (4-4)
Иными словами - нужно найти вид функции /(x-J. Сделаем пе-
реход от одних значений основных единиц измерения к другим
(например, от сантиметров - к метрам, от граммов - к килограм-
мам и т. п.). Введем коэффициенты перехода от одной системы
основных единиц к другой, которые обозначим kt.
Следовательно, основная единица Х] изменится в раз и
станет равной ^Х]; х2 - в к2 раз и примет вид к2х2 и т. д. Есте-
ственно, что величина производной единицы тоже изменится и
станет равной куу, где ку - коэффициент перехода производ-
ной величины вследствие изменения системы основных еди-
ниц:
куУ = f(k\xv к2х2, к3х3.ккхк). (4.5)
В соответствии с принципом однородности вид физического
уравнения не меняется при переходе от одних значений принятой
системы единиц измерения к другой. Это означает, что функция,
62
(4.6)
x;- за-
(4.7)
связь
выражающая размерность любой физической величины через
размерность основных величин, должна удовлетворять условию:
f(kxxx,k2x2,k3x3,...,kkxk) =
= f(kx, к2, к3,..., kk)f(xx,x2, х3,..., хк),
где f(kx, к2, к3,..., кк) - функция (4.3), в которой величины
менены на к, . Отсюда, сравнивая (4.6) и (4.5), получим:
ky=f(kl,k2.k3,.-, кк).
Таким образом, при выполнении принципа однородности
между коэффициентами ку и кх легко устанавливается; далее это
будет показано на примере силы инерций.
Запишем уравнение (4.6) в компактной форме:
f(kixi) = f(kl)f(xl). (4.8)
Продифференцируем (4.8) по Лг ; учтем при этом, что f(xx) не за-
висит от к,, поэтому ~^х' = 0:
dkj
^(kjXj)] = d[f(kt)]
дкх дк, 1 ' ’
Произведем в соотношении (4.9) замену функции f(xt), ис-
пользуя зависимость (4.8); кроме того, умножив и разделив ле-
вую часть соотношения на d(kjxi), получим:
^\f(^iXj)Y(kixi) _ d[f(kj] f(kiX,)
dfkjXjdkf дкх f(kx)
Отсюда следует:
63
=d[f(kt)] 1
f(kixi)d(kixi) dk' /(kJ
Но на величины коэффициентов перехода от одной системы ос-
новных единиц к другой Л, никаких ограничений не накладыва-
лось, поэтому выражение (4.10) справедливо при любом kt. При-
нимаем = 1, тогда из (4.10) имеем:
f(xi)dxi
(4.11)
[с[/№, 1
I
где
= const. Разделим в (4.11) перемен-
ные и произведем интегрирование:
f(Xj)dXi xt
найдем
ln[/( xt >] = a/inx, + lnC;, (4.12)
где Ct - (p(kt) - постоянная. Отсюда имеем:
f(Xi) = x?‘Ci. (4.13)
Таким образом, если выполненные вычисления проделывать, по-
следовательно, принимая коэффициенты перехода равными
и т- Д-> то п0 аналогии с (4.13) получим:
f(xi) = Сх^х^х^...хакк. (4.14)
Возвращаясь к зависимости (4.4) в соответствии с (4.14)
имеем:
64
М=h]“' taF2taF’ -кF* •
(4-15)
Для коэффициента перехода производной величины от од-
ной системы основных единиц к другой, учитывая зависимость
(4.7), получим формулу:
ky=k^k^k^...k^. (4.16)
Таким образом, любая производная величина выражается
через основные в виде степенного одночлена, который называет-
ся формулой размерности. Следовательно, в международной сис-
теме формула размерности любой физической величины Q мо-
жет быть представлена в виде:
[g] = Z,aiTaW“3.
В этой системе единица измерения силы производная - эта сила,
действующая на массу в 1 кг и сообщающая ей ускорение в
1м/с2. Формула ее размерности приведена ранее (зависимость
(4.2)). Эта единица измерения силы называется ньютон и обозна-
чается буквой Н, Н = 1 кг • м/с2 .
Перейдем к другой системе основных единиц: выразим
массу в граммах (г), время - в секундах (с), длину - в санти-
метрах (см). Эта система используется в физике, ее аббревиа-
тура - СГС. В ней единица измерения силы называется дина,
обозначается дн: дн = 1 г см/с2 . Найдем коэффициент перехода
ky=kf, связывающий производную единицу измерения силы в
интернациональной системе. Вначале определим коэффициен-
ты перехода основных единиц системы СИ к системе СГС:
65
kL = 100, кт -1, км = 1000. В соответствии с зависимостью
(4.16), имея в виду формулу размерности (4.2), получим:
kf - kL к?2 км = 100 1000 = 105. Следовательно: 1Н = 105 дн.
Как известно, уравнения, описывающие физические явле-
ния, чаще всего имеют вид алгебраических сумм нескольких сла-
гаемых. В соответствии с принципом Фурье все члены уравнения
должны иметь одинаковую размерность. Если уравнение не
удовлетворяет принципу однородности, значит, оно ошибочно.
Вместе с тем есть и другой способ проверки правильности
составления уравнений, который также следует из принципа од-
нородности: уравнения остаются неизменными по форме при пе-
реходе от одной системы единиц к другой. Отсюда следует и та-
кое правило: если в уравнения входят трансцендентные функции,
то их аргументами могут быть только безразмерные величины.
Однако часто, в технической литературе, встречаются эмпи-
рические формулы, которые принципу однородности не удовле-
творяют. Такие зависимости не могут претендовать на широкое
обобщение; как правило, область их применения не выходит за
рамки тех условий, в которых они были получены. Например, ес-
ли они получены в лабораторных условиях, то говорить о воз-
можности их использования в натуре не приходится.
4.2. Выбор основных единиц измерения
В качестве основных величин можно выбрать любые, тогда
получится иная система единиц измерения, отличная от обще-
принятой СИ, в которой основными величинами являются масса
М, длина L и время Т . Выберем другие основные величин -
66
А, В, С. Это можно сделать только в том случае, если эти вели-
чины удовлетворяют двум условиям.
Во-первых, размерности [л], [#], [с] являются независимыми
функциями размерностей [Л/], [г] и [г]. Говорят, что они имеют
независимые размерности, удовлетворяющие следующему требо-
ванию: [Л] 5* [5]"[с]'” при любых п и т. Иными словами: величи-
ны имеют независимые размерности, если каждая из них не мо-
жет быть представлена в виде комбинации остальных.
Во-вторых, размерности [Л/], [1] и [Г] можно выразить един-
ственным образом через размерности [л], [я], [с], т. е. возможно
однозначное обратное преобразование. Для доказательства этих
условий представим размерности выбранных величин в виде
произведения размерностей основных величин, возведенных в
степени:
[Л] = [лф [Г]”2 [Г]аз; [5] = [М ]₽1 [Г]32 [if3; [с] - [лф [г]°2 ,
где а; , о; , (i = 1,2,3) - действительные числа. Эти выражения
прологарифмируем:
^[Л] = а^Лф a2lg[L]+ а3^[г],-
lg[5] = P1lg[M]+p2lg[L] + p3lg[n- (4.17)
^[С] = О1^[Л/]+ст2^[г] + ст3^[г].
Получили систему, состоящую из трех уравнений. Из курса
алгебры известно, что такая система имеет единственное реше-
ние, если определитель системы D, составленный из коэффици-
ентов уравнений (4.17), отличен от нуля:
67
а1 а2 а3
D - р| 02 Рз ф О-
(4.18)
СТ| ст2 ст3
Если определитель системы (4.17) не равен нулю, то эта система
называется определенной, она имеет решение, корни выражаются
формулами Крамера:
lgM = b. lg[z>b lg[7]=b (4.19)
где D/f = 1, 2,3) - определитель, получаемый из D заменой
столбца, составленного из коэффициентов при неизвестных
lg[A/], lg[l], lg[r], столбцам, составленным из свободных членов:
lg[^l lg[Z], lg[c]. Например:
1ёИ
1ё[^]
ig[c]
«2
P2
CT2
«3
Рз
o3
(4.20)
Получается, что при D Ф 0 размерности [Л/], [z] и [г] един-
ственным образом выражаются через размерности [л], [й] и [с]. В
то же время условие (4.18) свидетельствует о том, что размерно-
сти [л], и [С] независимы. Действительно, пусть имеет место
равенство:
И=[в]"[с]”,
тогда логарифмируя, получим:
IgM = «lg[s] + wlgfcj (4.21)
Произведем преобразования в (4.21) в соответствии с (4.17),
найдем:
68
a]lg[A/]+ oc2lg[z] + a3lg[7’] = («p, + wo, >lg[A/]+ («P2 + '™?2>1g[z-]+
+ fwp3+wo3;ig[rl
Отсюда, приравнивая коэффициенты при одинаковых членах,
найдем:
ОС, = «Р] +/п<5],
ос2 = «Р2 +^2’
ос3 = «р3 +wa3.
Обращаясь к определителю (4.18), видим, что в этом случае пер-
вая строка в нем является комбинацией второй и третьей строк,
но тогда определитель равен нулю, а это противоречит условию
(4.18).
Таким образом, условие (4.18) свидетельствует о том, что
величины А, В и С могут быть выбраны в качестве основных. Но
одновременно это условие будет использовано далее для выбора
среди множества величин, определяющих явление, таких, кото-
рые имеют независимые размерности. Заметим, что в общем слу-
чае полученный результат справедлив и при любом числе основ-
ных единиц измерения: если число их равно р, то количество ве-
личин, размерности которых исследуются на условие независи-
мости, также равно р; следовательно, порядок определителя
(4.18) равен р.
В качестве примера рассмотрим систему единиц, включаю-
щую силу F, длину I, время /, которые в системе МКГСС
(КГС - килограмм силы) приняты в качестве основных. Прежде
всего, убедимся в том, что выбранные величины имеют незави-
симые размерности. С этой целью выразим размерности этих ве-
личин через размерности основных в системе СИ:
69
ИЧИда]-2; [/] = М°№]°; НЧм]0№Г.
Составляем определитель из показателей степени основных еди-
ниц в системе СИ:
1 1 -2
О 1 О
О 0 1
= 1*0.
Определитель D можно разложить по элементам любой
строки или столбца, умножая их (эти элементы) на адъюнкты;
соответствующая идъюкта равна минору со знаком “+” или
Минор - определитель (/>-1)-го порядка, его образовали из D,
зачеркивая i - ю строку и j - й столбец; знак адъюнкты находится
из формулы (-1 /+Л Кроме того, определитель 2-го порядка рас-
крывается по правилу:
а11 а12
а2( а22
- а11а22 -а12а21-
Вычисляем определители D;:
lg[F] 1
D, = lg[/] 1
ig[d о
igk]
ig[']
igld
D2 =
-2
0 =lg[7?]-lg[/]+21g[z],'
1
-2
o =ig[4
i
i i igk]
D3 = О 1 lg[/]=lg[d
о o ig[d
1
О
О
И далее:
70
lg[M] = ^ = lg[F]-lg[/] + 21g[4-
ig[i]=^=ig[zl- igM=^=ig[d
Отсюда M= №[/]-•; [L]=[zJ- [Г] = И
Число основных единиц можно было бы увеличить, исполь-
зуя, например, в механических задачах не три единицы, а четыре.
Однако, как было показано ранее, в этом случае понадобилось бы
ввести дополнительную размерную константу. Если дополни-
тельно в число основных единиц ввести еще силу, то в формуле
Ньютона должна появиться постоянная С, размерность ее равна:
[с]-ЕЛ-1 Л/-1 = FM~'L~'T2,
где А - размерность ускорения [А] = LT~2; F - размерность силы.
Число основных единиц измерения можно также умень-
шить, но тогда некоторые размерные физические константы нуж-
но было бы превратить в постоянные. Например, исключим из
числа основных единиц массу, тогда останутся основными еди-
ницами только длина и время. В этом случае требуется найти
подходящий закон, из которого можно было бы определить зави-
симость массы от длины и времени. Таковым может быть закон
всемирного тяготения, согласно которому сила взаимного притя-
жения f материальных точек с массами mt и т2, находящимися
на расстоянии г друг от друга, равна:
где принято обозначение: G - гравитационная постоянная,
G = <6,6720 ± 0,0041) • 10”11 Нм2/кг2 .
71
Примем гравитационную постоянную безразмерной вели-
чиной, равной единице. Воспользуемся законом Ньютона для од-
ной из входящих в последнюю формулу масс, например, f - ат}.
Получим а = т2/г2, отсюда имеем: [те] = [«][/• ]2 = 1?Т~2.
В этой системе за единицу массы принимается масса тела, кото-
рая сообщает другому телу при расстоянии между центрами их
масс равном 1м, ускорение 1м/с2 . Размерность силы в этой сис-
теме единиц: [f]=L4T~4. Единица массы по сравнению с приня-
той в системе СИ выражалась бы очень большой величиной, что
создавало бы неоправданные неудобства при практическом ис-
пользовании этой системы единиц измерения.
Если принять скорость распространения света в вакууме
300000000 м/с) равной единице, то все скорости будут выра-
жаться в долях от скорости света и станут тоже величинами без-
размерными, а размерности длины и времени будут одинаковы-
ми. Известно, что в астрономии в качестве единицы звездных
расстояний принят световой год - путь, который свет проходит за
время, равное земному году(&9,46-1012км). Неудобства, связан-
ные с использованием этой системы единиц измерения в земных
условиях, очевидны.
4.3. Пи-теорема (л- теорема)
Рассмотрим уравнение связи между величинами, характери-
зующими явление, отражающее объективный физический закон.
В общем виде запишем его так:
Ф<Х1,Х2,Х3,.. ,,х„) = 0. (4.22)
72
Среди величин Xj(i = 1, 2,3,..., п) находится неизвестная размерная
величина. Предполагаем, что остальные (п -1) размерных вели-
чин заданы. Кроме того, уравнение (4.22) составлено правильно;
иными словами - оно удовлетворяет принципу однородности.
Следовательно, это уравнение, независимо от выбора единиц из-
мерения, всегда должно сохранить форму записи. Но в таком
случае уравнение можно привести к безразмерному виду, чему и
посвящается л-теорема.
Прежде всего, выберем из п величин kj с независимыми
размерностями: i = l, 2, 3,..., к, в их число искомая величина не
входит. Отразим это в уравнении связи (4.22):
..хп) = 0. (4.23)
Принимаем выбранные к величин в качестве основных, размер-
ности оставшихся производных (п-к) величин выразим через
размерности выбранных основных:
kt+i 1 = kF' kF2 -kF";
J
k]=k F1 kF2-kF"
Изменим единицы измерения основных величин в раз
(i =1,2,3,..., к) . Следовательно, новыми основными величинами
будут: кгх1г к2х2, к3х3,..., ккхк. В соответствии с этим произойдет
изменение и производных величин. Покажем это на примере пер-
вой производной величины хк+3, обозначив ее новое значение
4+1:
4+1 = [MiF'k^F2- = к“'к22... кккхк+].
73
Теперь запишем уравнение связи (4.23) в новой системе единиц
измерения:
f(klX},k2x2....ккхк к*1 к*2.....кккхм,
...klkxk+2,..., к?к°2....к°кх„) = 0.
В связи с тем, что на выбор величин к, никаких ограничений не
накладывалось, примем к{ = 1/xj, к2 = 1/х2кк = \/хк . В место
(4.25) при этом условии получим:
/ \
у 1Д...Д,------^*±1---------------------------------- =о. (4.26)
’ а1 а2 «3 ... Y<4 rPlrP2...rP* V°1 °2 ... /Ч v 7
к Л1 х2 Л3 хк Л1 х2 хк Л1 х2 хк J
Введем новые обозначения:
хп
ТТ - ХА:+1 _ хк+2 .. _
’ № •••!-“* ’ 2 vPlrP2 ...Л ’ ’ "~к га1га2...га-
Л1 Л2 хк Л1 х2 хк Л1 х2 хк
(4-27)
Произведем замену в (4.26) в соответствии с (4.27):
= (4.28)
Естественно, что писать в уравнениях (4.26) и (4.27) к еди-
ниц нет смысла, поэтому их обычно опускают. Если среди чисел
л имеется одно лт, содержащее искомую величину
xm,n>m>k + l, а остальные л- числа содержат величины х,, за-
данные по условию задачи, то уравнение (4.28) можно записать в
явном виде:
= "8. ~5;~—5Г = 7?(П1'712.---^я^Л (4.29)
XI Y* Z , , , y К
1 Л'у Л!
74
Рассматривая зависимости (4.24), можно отметить, что все
л- числа являются величинами безразмерными, следовательно,
их численное значение не изменяется при переходе к другой сис-
теме единиц измерения. Используя это свойство л - чисел, найдем
показатели степеней у основных единиц измерения из условия,
которое запишем для xt+1 члена уравнения связи (4.23):
_ _ „о. о о
— —л> лэ ...лд..
1 «2 Yak 1 L к
X] х2 ...хк
(4.30)
Выражая размерности всех величин, входящих в число л; через
размерности основных величин в системе СИ, собирая показате-
ли степеней при одинаковых основных величинах и приравнивая
их нулю, получим систему, состоящую из трех уравнений с тремя
неизвестными, которая легко разрешается относительно этих не-
известных.
Сравнивая уравнения (4.28) и (4.22), можно сделать сле-
дующие два заключения. Первоначальное уравнение связи вклю-
чало в себя размерные величины, полученное уравнение содер-
жит только безразмерные величины. Если в исходном уравнении
было п величин, то в полученном - (п-к), где к - число величин,
имеющих независимые размерности. В свою очередь последних
величин столько, сколько существует основных величин в приня-
той системе единиц измерения. Как известно, при решении задач
в механике таких единиц три, в частности, в СИ - это масса, дли-
на и время; следовательно, в общем случае в уравнение связи
(4.28) войдет (п - 3) п- чисел.
Естественно стремление получить такое уравнение связи, в
которое входило бы меньшее число безразмерных п - комплексов.
Казалось бы, достичь этого можно, увеличивая число величин,
имеющих независимые размерности, что равносильно увеличе-
75
нию в принятой системе единиц измерения числа основных еди-
ниц (скажем, с трех до четырех). Однако в действительности вы-
игрыш не получается, так как, введя новую основную единицу,
необходимо, как это было отмечено ранее, ввести дополнитель-
ную размерную физическую постоянную (о ней, в частности, шла
речь ранее, когда рассматривалось выражение для силы инер-
ции). Эту постоянную придется дополнительно включить в урав-
нение связи, а с нею в нем после преобразований получится до-
полнительное л - число. Таким образом, общее количество я- чи-
сел останется прежним, равным (п-3).
Обычно л - теорему (или теорему Букингэма) формулируют
так: всякое уравнение связи между размерными величинами, от-
ражающее объективный физический закон, может быть пред-
ставлено функциональной зависимостью между безразмерными
комплексами, число которых равно числу всех величин, сущест-
венных для данного процесса, за вычетом числа основных вели-
чин.
Практическое значение л- теоремы заключается, прежде
всего, в том, что с ее помощью можно существенно уменьшить
число рассматриваемых величин. В частности, если все входящие
в связь величины, кроме одной, имеют независимые размерности,
следовательно, « = Л + 1 (в механических задачах к = 3, п = 4), то
на основании л- теоремы эта связь полностью определяется с
точностью до постоянной. Действительно, в этом случае имеем
из (4.28):
У|/(Л1) = О;
(4-31)
(4.32)
76
где С - безразмерная постоянная (корень уравнения (4.31)) мо-
жет быть найдена экспериментально либо при решении задачи
математическим путем.
Рассмотрим два подобных явления и запишем соответст-
вующие уравнения связи между величинами Xt и х,, характери-
зующими эти явления:
^>(Хх,Х2, Х3,...,Х„)~0,
у(хх,х2,х3,...,х„) = 0.
(4.33)
Выберем из « величин в обоих явлениях по к с независимыми
размерностями, перепишем (4.33) в виде
^Хх,Х2,...,Хк,Хк+х,Хк+2,---,Хп) = Ь,
<$>(хх,х2,...,хк,хк+х,хк+2х„> = 0.
Исходя из л- теоремы, заменим уравнения связи (4.34)
уравнениями связи между п- числами; единицы опустим, полу-
чим:
'|/(П1,П2;П3)...,Пи J = 0, (4 35)
Ч/(Л1,л2,л3,..., пп_к) = 0.
где П, =
к+\
хк+\
Tti —
Yal y“2 Y°*
Л] л2 ...лк
ИТ. д.
В связи с тем, что явления подобны, величины Xt и х( бе-
рутся в сходственных пространственно-временных точках и
имеют одинаковые размерности. Кроме того, они получаются од-
но из другого простым умножением на коэффициенты подобия,
одинаковые во всех точках, т. е.: = ^;х; .
Произведем преобразование, числа П] используя это соот-
ношение:
77
п, =-----^±1---------^*±1----=-----A+j------п . (436)
tal^a2 Z-a* va'va2 Yak Z-al£a2 L-ak ‘
Л) a<2 **’ it ’л Л2 ""к л Л2 '"^k
Отсюда следует, что для выполнения условия П, = л, необходимо
потребовать, чтобы комбинация из коэффициентов подобия, со-
держащаяся в (4.36), была равна единице.
Выше в разделе 3, в котором речь шла о методах теории по-
добия, говорилось о числах подобия как о безразмерных комби-
нациях характерных величин. Безразмерные л- числа, по своей
структуре напоминающие числа подобия, представляют собой
комбинации не характерных величин, определяющих явление.
Покажем, что л - числа также являются числами подобия. С этой
целью воспользуемся основным положением теории подобия (см.
главу 3), в соответствии с которым отношение величин в рас-
сматриваемых подобных явлениях к своим характерным равно
соответствующим коэффициентам подобия, следователь-
но:^^ kjXj и Xj^kjXj, где черта над символом обозначает ха-
рактерную величину. Воспользуемся этими условиями для того,
чтобы выразить л - числа через характерные величины:
П _ -*ч+1__________K+i
1 ya| Ya2 Z-tt| £а2 ’
Я.] Я 2 ...Лк К] к2 ...нк
л _ *Аэ-1_______К+1
1 ral va2 ra* Z-alta2 Z-“*
Л1 л2 лк Л1 л2 Кк
Комбинации из величин, отмеченных сверху чертой, являются
числами подобия, а их отношения - индикаторами подобия (от-
метим соответствующие масштабные коэффициенты в индикато-
рах подобия чертой сверху). Найдем отношение л - чисел:
78
П) . Г хм
Л]
Y га' ?“2
*1 х2 ...хк
кк+\
Га1Га2
Л] л2 ...ик
(437)
Сравнивая (4.37) и (4.36), видим:
^к+\_______кк+1_____________ ।
talta2 как Га1Га2 как
ft] «2 Кк Л1 л2 'Ч
Следовательно, л- числа являются числами подобия, а их отно-
шения - индикаторами подобия.
Теперь можно сформулировать вторую теорему подобия,
которая по сути дела несколько перефразирует л- теорему Бу-
кингэма.
Вторая теорема подобия: всякое, уравнение связи между ве-
личинами, отражающее объективный физический закон, может
быть представлено функциональной зависимостью между чис-
лами подобия, полученными из величин, характеризующих явле-
ние.
Далее будет показано, что при достаточно большом количе-
стве входящих в уравнение связи (4.22) величин, характеризую-
щих явление, а также при больших возможностях получения из
них различных сочетаний величин, имеющих независимые раз-
мерности, количество чисел подобия (или л- чисел) может быть
значительным.
Исторически сложилось так, что некоторым числам подобия
были присвоены имена выдающихся ученых. Например, в гидро-
механике и гидравлике это числа: Струхала, Фруда, Эйлера, Рей-
нольдса; далее речь будет идти о числе Вебера. Назовем эти чис-
ла подобия фундаментальными [35, 37] и покажем, что другие
числа подобия, которые можно получить из уравнения связи, ис-
пользуя иные сочетания величин, имеющих независимые размер-
79
ности, однозначно связаны с фундаментальными, представляя
собой различные их комбинации.
4.4. Комбинации чисел подобия
В основе комбинирования чисел подобия лежат одна аксио-
ма и три теоремы. Под комбинацией понимается соединение двух
и более физических величин и констант, а также чисел подобия с
помощью простых арифметических действий перемножения и
деления. При этом каждая из комбинируемых физических вели-
чин (констант, каждое число подобия) может возводиться в сте-
пень, показатель степени - целое или дробное действительное
число.
Допустим, что из всех возможных сочетаний величин с не-
зависимыми размерностями выбрано одно, и в рамках теории
размерностей, используя выводы п- теоремы, получены соответ-
ствующие числа подобия, которые названы фундаментальными.
Аксиома. Фундаментальные числа подобия независимы; ни
одно из них нельзя получить из комбинации остальных чисел.
Первая теорема комбинаций чисел подобия. Числа подо-
бия, которые можно получить в рамках it- теоремы из величин,
входящих в уравнение связи, при выборе других величин с неза-
висимыми размерностями, являются комбинациями фундамен-
тальных.
Доказательство. Для того, чтобы не усложнять запись, бу-
дем считать, что число величин, имеющих независимые размер-
ности, равно трем. Теперь в уравнении связи (4.22) расположим
величины таким образом, чтобы первые три имели независимые
размерности и следующие за ними еще три также были величи-
нами с независимыми размерностями:
80
ф<Х[, Х2 > х3 > Х4 > х5 > х6> х7 ’ • • • > хп ) ~ 0-
(4.38)
Используя первую комбинацию величин с независимыми
размерностями, запишем уравнение между л-числами:
Х4___________Х5__________х6
“I “2 “3 ’ Г₽1 гРг гРз ’ rYl Л2 Лз ’
л2 j л2
"п
°2 °3
= 0,
Или
у(л4,л5,л6,...,л„.) = 0. (4.39)
Пусть числа п4,п5,п6,...,п„ будут фундаментальными. Те-
перь для следующей комбинации величин с независимыми раз-
мерностями запишем уравнение связи между новыми л- числа-
ми, которые в отличие от предыдущих будем отмечать штрихом:
Vi
х2
х7
х„
-У|______х2_______х3
V-S1 г^2 63 ’ 81 е2 83 ’ С| С2 -Лз ’ v-П 1у-ЛЗ ' ’ ’ „Ш1 “2 у.ш3
\^Л4 Л5 Л6 Л4 Л5 Л6 •А’Д Л5 Л6 Л4 л5 Л6 Л4 л5 л6
= 0;
(4.40)
Рассмотрим число, стоящее в (4.40) первым:
*1
1 8, 8, 83 •
х41х52х63
(4-41)
Далее выразим величины с новыми независимыми размерностя-
ми через старые, используя зависимости, имеющиеся в (4.39):
х4 = 7t4x“'x22x“3;
х5 = TtjXjP'x^Xj3 ;
Х6 = 7t6X]YlX22Xj3 .
(4.42)
81
Произведя подставки величин из (4.42) в (4.41), получим:
______________________5_______________________
L т“1 г“з ?' [тг rPlrP2r₽3p2L у71гУ2г7зР3 '
*^2 *^3 J 1Я5Л1 *^"3 J |**6*^1 л2 "^3 1
отсюда
л; =
S2 S3 OtjS] +P|52+Y|S3 а251+02б2+7253„а381+Рэ52+7333
R4 R5 Я6
\ **1 Л2 “j
(4.43)
В зависимости (4.43) слева стоит безразмерная величина,
справа - величины л4,л5,л6, тоже безразмерные. Следовательно,
выражение, стоящее в круглых скобках, тоже не имеет размерно-
сти. Но оно представляет собой комбинацию величин с незави-
симыми размерностями: х!,х2,х3, из них можно получить только
одно безразмерное число: единицу. А это значит:
l-aiS] -р]б2 -у]83 =0;
а2^1 _ Рг^2_ ?2^з = 0;
а381 -р3б2 - у383 = 0.
Тогда из (4.43) получаем
S =
1
S] 3?
Л4Ч Л6
(4.44)
Рассмотрим по аналогии новые и фундаментальные числа
подобия, связанные с величиной х„:
хп
®1 v®2 Y®3
Л4
(4-45)
82
Выразим теперь величину хп через старые величины с неза-
висимыми размерностями, используя зависимости, содержащиеся
в (4.39):
___ СТ) СТэ от
хп = V] х2 х3 •
Кроме того, с помощью формул (4.42) запишем (4.45) в виде
7Г„ =-----------------
Л4 ТГ5 7Г6
ГП1ГВ2„П3
Л2
“1Ш| +Р,ш2 +У|Ш3 а2ш, +р2<о2 +у2ш3 а Зсо, +Р3м2 +у3со3
кх1 х2 х3 7
4.46)
Учитывая, то выражение, стоящее в (4.46) в круглых скобках,
равно единице, получим
7t„ =------------------
Л4 7Г5 7Гб
(4-47)
Одновременно это означает, что должны выполняться условия:
tri -aj<»] -Р]Ю2 -у]®3 = 0;
О' 2 — OL 2 СО j Р 2 (Л 2 72^3 =
CTj Рз<й2 7з®3 ”
Теорема доказана: новые числа подобия являются комбинацией
фундаментальных чисел.
Следствие из первой теоремы комбинаций чисел подобия.
Любое число подобия, которое получено в рамках л - теоремы из
величин, входящих в уравнение связи, при различных сочетаниях
величин с независимыми размерностями, можно представить в
виде комбинации фундаментальных чисел подобия. Основываясь
на формулах (4.41), (4.44), (4.45), и (4.47), можно сформулировать
правило, позволяющее установить связь между любыми числами
подобия и фундаментальными числами. Получив выражение для
83
числа подобия лJ, нужно заменить входящие в него величины со-
ответствующими фундаментальными числами подобия (напри-
мер, величину х4 - числом л4, х5 - я5 ит. д. до х„ - л„). Вели-
чины с независимыми размерностями, которые использовались
для получения фундаментальных чисел подобия, заменяются
единицами (например, вместо х1, х2, х3 пишутся единицы).
Вторая теорема комбинаций чисел подобия. Пусть
X], х2, х3 ~ сочетание величин с независимыми размерностями,
которые использовались для получения фундаментальных чисел
подобия, при этом величина х3 входит в т фундаментальных чи-
сел. Заменим величину х3 такой х4, чтобы новое сочетание вели-
чин хр х2, х4 имело независимые размерности. Если использовать
это сочетание величин для получения новых чисел подобия, то
они с величиной х3 дадут фундаментальное число в какой-либо
степени и (т-\) комбинацию с ним других фундаментальных
чисел подобия, которые содержат величину х3. При этом
(п-к — т) чисел останутся фундаментальными. Если величина
х3 входит во все фундаментальные числа подобия, следователь-
но, т= п- к, то комбинаций будет (п-к-\).
Доказательство. Заменим сочетание величин с независмы-
ми размерностями хр х2, х3 на хр х2, х4. Допустим, что величины
хр х2, х4 также имеют независимые размерности. Запишем теперь
уравнение связи между it' - числами, используя это сочетание ве-
личин с независимыми размерностями:
F
*3 *5_____________х„
r«l r"2 "4 ’ »‘2 "Ц ’ >1 *2 *4 ’.........’ Z4
Л] Л2 Ад А| Л2 Ад Л| Л2 Ад Л| Ад
= 0. (4.48)
84
Прежде всего, следует обратить внимание на то, что все
числа подобия, кроме первого, не содержат величину х3. Рас-
смотрим это число подробнее:
тг' -
ТГ -----------------
"| "2 „«4
Л] л2 х4
(4.49)
Если в качестве величин с независимыми размерностями выбрать
хь х2, хз > то они с величиной х4 дадут такое число подобия:
тг4 —
х4
I, h h '
XI у л у J
I •/'‘3
(4.50)
Сравнивая числа подобия л' и тг4, можно заметить, что пер-
вое из них либо совпадает со вторым, либо является какой-либо
его степенью, а может быть числом, обратно пропорциональном
второму числу подобия. Рассмотрим далее следующее число по-
добия в уравнении (4.48):
х5
ТГ =--------------------,
'«I „т2 «'4
Aj Л2 Л 4
а также соответствующее число подобия л5, которое получится,
если выбрать в качестве величин с независимыми размерностями
•X]} Х2, Xj .
х5
YPl уР2 уРЗ
А| А^
85
Далее возьмем отношение числа п к числу л5, получим но-
вое число подобия:
v/’l „Р2 ГРЗ
/’ А । А A J
7С| — ---------.
1
А| А-*) А^
Это число можно преобразовать таким образом:
х3
7Т0 =-----2----.
" Y4\ v?2
aj а^ *^4
Сравнивая числа подобия nJ и л, видим, что речь идет об
одном и том же числе подобия, поэтому л0 = л . Таким образом,
любое число в уравнении (4.48), кроме первого, представляет со-
бой комбинацию первого числа с соответствующим числом по-
добия, которое найдется, если выбрать в качестве величин с неза-
висимыми размерностями хь х2, х3. Первое число получено с тем
же сочетанием величин с независимыми размерностями. При
этом любое число в уравнении (4.48), кроме первого, не содержит
величину х3. которую заменили на х4, но так, чтобы хь х2, х4 бы-
ло сочетанием величин с независимыми размерностями. Допус-
тим далее, что число л5 не зависит от величины х3, но тогда чис-
ло подобия л0 будет представлять комбинацию величин х],х2, х4
с независимыми размерностями, поэтому оно станет равным еди-
нице. Следовательно, фундаментальные числа подобия, не со-
держащие величину х3, при замене сочетания величин с незави-
симыми размерностями хьх2,х3 на Х|,х2,х4 остаются без изме-
нения. Тем самым вторая теорема комбинаций чисел подобия до-
казана.
86
Следствие из второй теоремы комбинаций чисел подобия.
Если при выбранной системе единиц с независимыми размерно-
стями, используя выводы л - теоремы, получены числа подобия,
среди которых имеются фундаментальные, то нефундаменталь-
ные числа подобия представляют собой комбинации с одним из
фундаментальных. Для того чтобы установить это фундамен-
тальное число, необходимо воспользоваться следствием из пер-
вой теоремы комбинаций чисел подобия.
Третья теорема комбинаций чисел подобия. Любые два
числа подобия, полученные в рамках теории размерностей при
выбранной системе величин с независимыми размерностями,
можно комбинировать таким образом, чтобы комбинация не со-
держала какую-либо величину, характеризующую явление, вхо-
дящую в оба числа подобия.
Доказательство. Выберем из уравнения связи между фун-
даментальными л - числами (4.28) любые два - л; и :
Заменим одно из чисел подобия, вошедшее в (4.51), комбинацией
с другим числом, но такой, чтобы в нее не вошла одна из величин
с независимыми размерностями, которые были использованы для
получения этих чисел подобия, пусть, например, это будет х3. Но
тогда необходимо одно из этих чисел подобия возвести в степень
п. Величина п определяется в зависимости от соотношения пока-
зателей степени г3 и j3. Если выполняется условие г3 > /3, то ве-
личина п найдется из зависимости:
/3-и/3=О. (4.52)
87
Разделим далее число л, на л", получим новое число подо-
бия
пк\ ~
xi
Л| Л2 л J
(4-53)
Такая запись обосновывается тем, что любое число подобия
представляет собой комбинацию величин и физических констант
с зависимыми размерностями, следовательно, вошедшие в число
подобия, определяемое формулой (4.53), величины х]гх2 и ху-
имеют независимые размерности. Этот вывод следует из резуль-
татов преобразований, в соответствии с которыми из числа подо-
бия л" была изъята величина х3.
Разделим теперь число л" на л;, получим такое число подо-
бия
пк2 -
Л1 Л2 xi
(4-54)
Следовательно, здесь на основании рассуждений, приведенных
выше, можно утверждать, что величины х1гх2 и ху имеют неза-
висимые размерности, кроме того, лЛ1 = 1/л^2 - Третья теорема до-
казана.
Следствие 1 из третьей теоремы комбинаций чисел подо-
бия: совсем не обязательно составлять комбинации всех без ис-
ключения фундаментальных чисел подобия, как это делается в
соответствии со второй теоремой; можно числа подобия комби-
нировать попарно. Тем самым создаются благоприятные возмож-
ности использовать в одном исследовании числа подобия, полу-
ченные при разном сочетании величин с независимыми размер-
88
ностями, не выходя, однако, за пределы всех чисел подобия, ко-
торые можно получить в рамках теории размерностей из уравне-
ния связи.
Следствие 2 из третьей теоремы комбинаций чисел подо-
бия: комбинация двух чисел подобия может заменить только од-
но из их, так как система чисел подобия должна обладать необ-
ходимой полнотой. Это означает, что любая система чисел подо-
бия в результате рекомбинаций должна дать систему фундамен-
тальных чисел подобия. Вопрос о том, какое из комбинирован-
ных чисел остается для участия в дальнейших преобразованиях,
определяется постановкой задачи исследований.
Обычно перед исследователем стоит цель: получить крите-
риальное уравнение - зависимость числа подобия, содержащего
искомую величину, от критериев подобия. Последние отличаются
от чисел подобия тем, что они составлены из характерных вели-
чин, которые, исходя из предварительных условий рассматривае-
мого вопроса, заранее заданы. В математической форме цель ис-
следований может быть записана в виде уравнения (4.29). Между
тем в задачах гидромеханики и гидравлики часто критериев по-
добия недостаточно, чтобы составить критериальное уравнение,
или их вообще нет. Тогда полезны комбинации чисел подобия, в
которые искомая величина не входит. Например, все фундамен-
тальные числа подобия содержат скорость течения. Но именно
скорость течения чаще всего по условиям решаемой задачи быва-
ет искомой. Следовательно, среди чисел подобия нет ни одного
критерия. Скорость течения входит в число величин с независи-
мыми размерностями, которые используются при получении
фундаментальных чисел подобия. Если заменить скорость тече-
ния другой величиной, входящей в уравнение связи, так, чтобы
новая система величин имела независимые размерности (напри-
89
мер, ускорением силы тяжести; коэффициентом кинематической,
или динамической вязкости и т д.), то все вновь полученные чис-
ла подобия, представляющие собой комбинации фундаменталь-
ных чисел, кроме одного, станут критериями. Но тогда можно со-
ставить критериальное уравнение.
Следует также иметь в виду основное положение, содержа-
щиеся в доказательстве л- теоремы: среди величин с независи-
мыми размерностями не должно быть таких, которые по условию
задачи являются искомыми. Конечно, в отдельных случаях мож-
но сразу получить критериальное уравнение. Правда, с одной
оговоркой: все оставшиеся величины, входящие в связь, по усло-
вию задачи являются заданными. Если это условие не выполняет-
ся, тогда необходима комбинация чисел подобия с целью полу-
чения критериев подобия. Кроме того, возникает вопрос, что
представляют собой новые числа подобия, какова их связь с из-
вестными числами подобия, названными здесь фундаментальны-
ми? Ответ на него содержится в доказанных выше теоремах о
комбинациях чисел подобия и вытекающих из них следствиях.
Отсутствие этих доказательств привело в настоящее время к то-
му, что в большинстве исследованиях, основанных на методах
физического моделирования явлений, не используется все много-
образие чисел подобия, которое можно получить в рамках л-
теоремы. Зачастую полученные эмпирические зависимости пред-
ставляются не в критериальной форме, что создает трудности при
их практическом использовании, в том числе для верификации
выводов, получаемых на основе математического моделирования
явлений.
90
4.5. Анализ комбинаций чисел подобия в области гидро-
механики
В качестве примера рассмотрим течение вязкой несжимае-
мой жидкости в предположении, что силы поверхностного натя-
жения не оказывают на него влияния. Течение характеризуется,
прежде всего, линейными размерами, которые определяют гра-
ницы области движения; в трехмерном пространственном движе-
нии таких размеров три, соответственно вдоль осей х, у и z.
Для простоты последующих выкладок будем считать ли-
нейные масштабы по всем трем направлениям одинаковыми, по-
этому рассмотрим только один линейный размер х. Кроме того,
явление характеризуется следующими кинематическими и дина-
мическими величинами: скоростью и, временем t, давлением р,
ускорением силы тяжести g. Свойства жидкости характеризуют
плотность р и динамический коэффициент вязкости ц.
Запишем уравнение связи (4.22) в виде.
<p(x,u,t, р, g, р, ц) = 0. (4.55)
Выберем из семи величин, входящих в связь, три с независимыми
размерностями. В качестве таковых возьмем те, которые обычно
используются с целью получения фундаментальных чисел подо-
бия: х, и, р. Прежде всего, проверим, действительно ли эти вели-
чины имеют независимые размерности. С этой целью запишем
формулы размерностей выбранных величин через размерности
основных величин в СИ, а затем из показателей степеней соста-
вим определитель и вычислим его значение
91
[x]=[m]°[z]1[t]°; о i
[р]=ИМ-3[г]°. 1 -з
о
-i = -i*o.
о
Определитель не равен нулю, следовательно, выбранные величи-
ны имеют независимые размерности.
Далее уравнение связи (4.55) представим в виде (4.26) и
(4.28):
\ х“'«“2р“3 хР|иР2рРз xY>„Y2pY3 XOlw°2pO3 J
1|/(Л], Л2, Л3, Л4)= 0.
Таким образом, вместо семи величин, входящих в связь, по-
лучены четыре it- числа в соответствии с формулой:
н-£ = 7- 3 = 4. В связи с тем, что все л - числа не имеют размер-
ностей, поступаем следующим образом. Выразим размерности
всех величин, входящих вл- числа, через размерности основных
величин в СИ и далее показатели степени при одинаковых раз-
мерностях приравняем нулю. Получим
t ________________[Т]1___________ [д/1° 1/1° 1'7’1° •
' Л“2р“з ’ [£]а'[ф[т]'“2[мр[£]~3“3 ~ ’
отсюда: а3 = 0; а]+а2-За3=0; 1 + а2=0.
Следовательно, а2 =-1, «! = 1, Л] = —= —, Sh - число Струха-
х Sh
ла. Следующее число:
л2 =
Р
хМ2р₽з
92
Давление в СИ имеет размерность [р] = н/м2 - кг/м с2.
МИИ2
[ср[£р[гр2[л/р[грРз
= [Л/]°[с]°[г]0.
1-03=0; -1- 0,-32+30з=О; -2 + 02 = О; 03 = 1; 02 = 2; 01=О.
Отсюда л2 = = Ей - число Эйлера.
pw2
Далее рассмотрим число:
7Г3 =-----------
хУ|нУ2рУз
№~2
[£]У| [Гр [Гр2 [Л/р [£рп
= [Л/]°[С]°[Г]0;
Уз =0; -2 + у2=0; 1-у,-у2 +Зу3 = 0; у2 = 2; У]=-1;
тт3 = = —; Fr - число Фруда.
и2 Fr
Следующее число:
Ц
ТСд — — .
хо'мО2раз
Динамическая вязкость в СИ имеет размерность:
[ц] = [р] [v] = кг/м • с; отсюда
-------МИИ_______________= [М ]0[£]0 [Г]°.
[£р [£р [Тр2 [Мр [LpO3 J J
1-сг3=0; — 1 — CTj -<У2 +Зо3 = 0; -1 + сг2 = 0; <т3=1; ст2 = 1; о, = 1;
л4 = -У- = — - —; Re - число Рейнольдса.
хир хи Re
Для определения сочетаний других величин, имеющих неза-
висимые размерности, составим полную матрицу размерностей,
количество строк которой соответствует общему числу величин в
уравнении связи, а количество столбцов - числу основных еди-
93
ниц измерения. Строки матрицы размерностей образуются из по-
казателей степени основных единиц измерения, через которые
выражаются размерности всех величин, входящих в связь. Далее
из элементов строк матрицы размерностей составляются все воз-
можные определители.
Размерности величин, входящих в уравнение связи (4.55), и
матрица размерностей имеют вид
[x]=[<]W 0 .
[Ф[<№]-’ 0 }
о о
-1
ЫФ/ВДи2 о 1
[Рнеш 1 ~3
1 1
о
-1
1
-2
-2
О
-1
Следовательно, матрица размерностей имеет размер 7x3, а
общее число определителей матрицы равно сочетанию из 7 по 3:
' 3!(7-3)!
Из 35 определителей матрицы размерностей, как показали
соответствующие проверки, 29 не равны нулю, следовательно, 29
сочетаний величин, входящих в связь, имеют независимые раз-
мерности. Им соответствует 29(7-3) = 29-4 = 116 тт- чисел. Как
было отмечено ранее, эти числа подобия являются либо различ-
ными комбинациями фундаментальных чисел, равных
iq = 1/Sh, л2 = Ей, тг3 = 1/Fr, л4 = 1/Re, либо совпадают с ними.
В таблице 4.1 приведен полный перечень 116 чисел подо-
бия, которые можно получить в рамках теории размерностей из
94
Таблица 4.1
Полный перечень чисел подобия в явлении - течение вязкой несжимаемой жидкости
№ Вели- ЧИНЫ с незави- СИМЫ- ми раз- мер- ностя- ми Величины
X и t _ p £ p
л~числа фундаментальные
Г 1 TCI 7t3 1 7C4
7t' -числа нефундаментальные
л. л2 7t3 л; Tt5 *6 7T’7
1 х,и,р 1 1 tu/x 1 gx/u pu/p up/xp
2 х,и,р 1 1 tu/x p/pu2 gx/u2 1 p/pxu
3 х,и,ц 1 1 tu/x xp/up gx/lP pxu/p 1
4 x,t,p 1 tu/x 1 1 gt2/x px2/t2p p/pt
5 X,t,p 1 tu/x 1 t2p/px2 gt2/x 1 pt/px2
6 x,t,p 1 tu/x 1 pt/p gfTx px2/pt 1
7 x,p,g 1 u/(gx)I/2 1 1 pgx/p p(g/x)1/2/p
8 X,p,p 1 u(p/p)1/2 t(p/p)1/2/x 1 pgx//7 1 p/x(pp)1/2
9 X,p,p 1 up/xp pt/p 1 2/ 2 gp /хр ppx2/p2 1
10 x,g,p 1 u/(gx)1/2 t(g/x)1/2 /?/pgx 1 1 / 3/2 !/2 p/px g
11 1 u/(gx)1/2 t/(g/x)1/2 p(x/gf2/p 1 3/2 1/2/ px g /p 1
12 x,p,/z 1 pxu/p pt/px2 2/ 2 ppx /p p2x3g/p2 1 1
13 U,t>P x/tu 1 1 1 gt/u pu/p p/pt
14 U,t,p x/tu 1 1 p/pu gt/a 1 ц/ptu2
15 u,t,p x/tu , 1 1 pt/p gt/u ptu/p 1
16 u,p,g u'/gx)1'2 1 gt/u 1 1 pu/p |lg/up
17 u,p,p x/tu 1 pt/p 1 pg/up pu/p 1
18 u,g,p (gx)I/2/u 1 gt/u p/pu 1 1 pg/pu3
19 U,g,p (gx)1/2/u 1 gt/u up/pg 1 pu3/pg 1
20 U,pp pxu/p 1 ptu2/p p/pu pg/pu 1 1
21 t,p,g x/gt2 u/gt 1 1 1 pt2g2/p p/pt
22 t’p’p xp1/2/tp1/2 1/2, 1/2 up /p 1 1 gt(p/p),/2 1 p/pt
23 t,g,p x/gt2 u/gt 1 p/p(tg)2 1 1 p/pt3g2
24 t,g,p x/gp u/gt 1 pt/p 1 pt3g2/p 1
25 t,p,p x(p/tp)i2 u(pt/p)122 1 pt/p .3/2 s / J/2 gt (P/P) 1 1
26 P,g>P pgx/p 1/2 / 1/2 up /p tg(p/p)1/2 1 1 1 pgp’V2
27 P>gP xp2/gp2 up/pg pt/p 1 1 (pg)2/p3 1
28 P>P.P x(pp)!/2/p ир1/2/рУ2 pt/p 1 n 1/2 л 3/2 Hgp T 1 1
29 g>P,P xg1/3(p/p)2/3 u(p/pg)I/3 2/Зл.// t \l/3 g t/(p/p) p/p1/3(pg)2/3 1 1 1
Окончание таблицы 4.1
уравнения связи (4.55), используя все сочетания величин, имею-
щих независимые размерности. Анализ этих данных позволяет
сделать некоторые предварительные выводы. Наибольшее коли-
чество, равное 35, в таблице составляют фундаментальные числа
подобия (в том числе те 4 из них, которые получены при исполь-
зовании величин с независимыми размерностями х, и, р, находя-
щиеся во второй строке таблицы 4.1). В сумму вошли не только
числа подобия, указанные во второй строке, но и их степени. Тем
самым можно отметить, что это обстоятельство в некоторой сте-
пени оправдывает выбор именно этих чисел подобия в качестве
фундаментальных. Кроме того, таблица содержит 16 различных
комбинаций фундаментальных чисел подобия, которые повторя-
ются в ней по нескольку раз (в таблице они отмечены обычным
шрифтом). Чаще других-12 раз - встречается число подобия
тт'7 = ц/pt, находящиеся в 4-ой строке таблицы (получено при ис-
пользовании величин с независимыми размерностямих,t,p). По
9 раз входят в таблицу числа подобия п'5 = gt2 /х (это число появ-
ляется в первый раз в той же 4-ой строке таблицы) и тг'5 = gt/u (в
первый раз число появляется в 13 строке, величины с независи-
мыми размерностями и, t, р ). Всего по три раза встречаются чис-
ла подобия л'7 =ир/хр (в таблице 1-я строка, величины с незави-
симыми размерностями х, и, р) и n'y-p/pPg2 (в таблице 23-я
строка, величины с независимыми размерностями t, g, р). Ос-
тальные числа подобия, отмеченные в таблице 4.1 обычным
шрифтом, входят в нее от 4-х до 6-ти раз (указана та строка, в ко-
торой они появляются впервые). Таким образом, из 116 чисел по-
добия только 20 не совпадают, из которых 4 являются фундамен-
тальными, а 16 - комбинациями фундаментальных, остальные 96
97
чисел подобия представляют собой различные степени фунда-
ментальных и нефундаментальных чисел подобия.
Покажем далее на примере чисел подобия, содержащихся в
таблице 4.1, справедливость основных положений, сформулиро-
ванных в теоремах о комбинации чисел подобия. Рассмотрим
вначале числа подобия, находящиеся в 1-ой строке таблицы. Пер-
вые три числа совпадают с фундаментальными или обратные им:
71'3=%!, %5 = тт3, тг'6 = 1/л2 • Нефундаментальное число п'у-ир/хр
расшифруем в соответствии с правилом, изложенным в следствии
к первой теореме комбинации чисел подобия. Величины х и и в
системе фундаментальных чисел подобия выбраны в качестве ве-
личин с независимыми размерностями, поэтому в выражении не-
фундаментального числа подобия л7 через комбинацию фунда-
ментальных чисел им соответствуют единицы. Из таблицы 4.1
следует, что величине ц соответствует фундаментальное число
тс4 = 1/Re , а величине р - тг2 = Ей, поэтому
л'7 - ир/хр - л4 /тт2 = 1/ReEu.
Проверим этот вывод:
1/ReEu = црм2 jpxup = ир/хр.
Как было отмечено ранее, произведение двух чисел подобия
Re и Ей называется числом Стокса, оно обозначается
St = ReEu = хр/up (его называют также числом Лагранжа и обо-
значают La).
В 4-ой строчке таблицы 4.1 находится число
7l's = gt2/x = 7Т37Г2 = 1/FrSh2.
Далее
98
7t'6 = рХ2Д2/2 = Л2 /л 2 =l/Sh2Eu.
И последнее число в той же строчке
л'7 = ух/ pt = л4/Л] л2 = Sh/ReEu = Sh/St.
В 10-ой строчке таблицы 2 есть такое число подобия
= t( g/*//2 = Я]^2 = 1/ShFr1'2.
Для подтверждения выводов, вытекающих из второй теоре-
мы комбинаций чисел подобия, рассмотрим 10-ю строчку табли-
цы 4.1, где в качестве величин с независимыми размерностями
выбраны х, g, р . Следовательно, в системе величин с независи-
мыми размерностями х, и, р, которые были использованы для по-
лучения фундаментальных чисел подобия, скорость и была заме-
нена ускорением силы тяжести g. Но тогда скорость и в системе
величин с независимыми размерностями х, g, р даст число Фруда,
или какую-либо его степень. Остальные числа подобия не будут
содержать скорость и и станут комбинациями соответствующих
фундаментальных чисел подобия с числом Фруда. Проверим эти
выводы.
Первое число подобия в этой строчке связано со скоростью
и: л2 = u/(gx)}'2 = Fr1/2. Запишем и расшифруем остальные числа
подобия. Следующее число Л3 = /g1/2/xl/2 = l/ShFr1/2 . Далее
л4 = p/pgx = EuFr . И, наконец, л7 = p/px3//2gl/2 = Fr’^/Re.
В третьей строчке таблицы 4.1 находятся числа подобия,
полученные с помощью системы величин с независимыми раз-
мерностями х, и, ц. Таким образом, эта система отличается от
аналогичной х, и, р, с помощью которой были получены фунда-
ментальные числа подобия, тем, что величину р заменили на ве-
99
личину ц. Но тогда величина р с системой величин с независи-
мыми размерностями х, и, ц даст число Рейнольдса, оно находит-
ся последним в рассматриваемой строке: л'6 = pxu/p = Re. Вели-
чина р входит еще в одно фундаментальное число подобия, ко-
торым является число Эйлера. Оно даст с числом Рейнольдса
следующую комбинацию: л'4 =xp/up = ReEu = St. Остальные
фундаментальные числа подобия, не содержащие величину р,
вошли в третью строку таблицы 4.1 без изменений:
Пз = tu/x = 1/Sh; п'5 = gxiu1 - 1/Fr.
Обратимся далее к выводам, относящимся к третьей теореме
подобия о попарной комбинации чисел подобия. Однако при
этом не имеются в виду любые произвольные комбинации, а
только такие, которые преследуют вполне определенную цель:
создать такое не фундаментальное число подобия, чтобы в нем
был исключен параметр, общий для двух фундаментальных чи-
сел, вошедших в комбинацию. Но такие комбинации уже были
приветны выше. Например, в 10-ой строчке таблицы 4.1 имеются
три комбинации фундаментальных чисел подобия, в которых от-
сутствует скорость течения:
tgX!1 / х^1 ~ 1/ShFr12; p/pgx = EuFr; p/px3'/2g1'/2 = Fr1/,2/Re.
Заметим, что отношение Re2/Fr = p2x3g/p2 =Ga называется
числом Г ал идея.
В 18-ой строчке таблицы 4.1 имеется число pg/pu3, а в 19-
ой-обратное ему pu3/pg = FrRe, в которых нет линейной вели-
чины. Корень кубический из произведения чисел Фруда и Рей-
нольдса называется числом Келегана:^/FrRe = Ke = ufp/pg)^3.
100
Можно сказать, что число Келегана есть безразмерная скорость
течения, a VGa = Re^/Fr1^3 =xg^3p2/3/p2 3 - безразмерная линей-
ная величина. В 29-ой строке таблицы 4.1 содержатся числа по-
добия, полученные при сочетании величин с независимыми раз-
мерностями g, р, ц, которые являются физическими константами.
Но тогда с оставшимися физическими величинами они дадут не-
фундаментальные числа подобия, представляющие собой эти ве-
личины в безразмерном виде. Так, два первых числа nj и л'2 яв-
ляются рассмотренными выше безразмерной линейной величи-
ной и безразмерной скоростью течения. Следующее число есть
безразмерное время: = /g2'/3/(p/p)1'/3 = Re1,/3/sh Fr2'/3. Наконец,
последнее число в этой строке представляет собой безразмерное
давление: л'4 = р/p^3(pg)2^ = Eu(FrRe)2,/3 =EuKe2
Таким образом, выполненный анализ свидетельствует о том,
что фундаментальные числа подобия можно комбинировать.
Важно отметить также следующее: если комбинации делать, пре-
следуя определенную цель, то обязательно придем к одному из
116 чисел подобия, которые можно получить из матрицы размер-
ностей, перебирая все возможные сочетания из величин, имею-
щих независимые размерности.
Можно, например, представить такую ситуацию, когда ли-
нейная величина (это, в частности, может быть глубина потока)
является величиной искомой, а она входит в три числа подобия из
четырех фундаментальных. Тогда в зависимости от решаемой за-
дачи можно предложить такие комбинации из фундаментальных
чисел подобия, которые не содержат линейный размер, и уже по
этому принципу в рассматриваемой задаче могут быть критерия-
ми подобия. Например, это может быть число подобия
л'з = gt/u = = 1/ShFr , которое впервые появилось в 13-ой
101
строчке таблицы 4.1. Не содержит линейный размер число Келе-
гана. В другой задаче неизвестной величиной может быть ско-
рость течения, тогда избавиться от неизвестной скорости течения
можно, введя в рассмотрение число Галилея, которое в зависимо-
сти от рассматриваемой задачи может играть роль критерия по-
добия. Приведенные выше комбинации фундаментальных чисел
подобия p/pgx-EuFr, а также t(gjx)}^ = l/ShFr1/2 не содержат
скорости течения.
Здесь уместно еще раз напомнить, что при доказательстве
л- теоремы было сформулировано следующее требование: среди
величин с независимыми размерностями не должно быть иско-
мой величины. Если ему следовать, то в отдельных частных слу-
чаях можно сразу получить критериальное уравнение. Один из
таких случаев был рассмотрен выше, когда в качестве величин с
независимыми размерностями были выбраны х, g, р. Они отли-
чаются от величин с независимыми размерностями х, и, р, кото-
рые использовались для получения фундаментальных чисел по-
добия тем, что скорость и была заменена ускорение силы тяже-
сти g . В результате такого выбора было получено число Фруда и
три комбинации этого числа с остальными фундаментальными
числами подобия. Если скорость является искомой величиной, а
остальные величины заданы, то в результате можно составить
критериальное уравнение в виде зависимости числа Фруда от
комбинаций чисел подобия, которые являются критериями подо-
бия. Но кроме ускорения силы тяжести, в данном случае имеется
еще три величины, каждая из которых совместно с величинами х,
и р образует сочетание величин с независимыми размерностями.
Это величины ^/?и ц. Но тогда можно получить 16 чисел подо-
бия, из которых 4 будут фундаментальными (либо какими-то сте-
пенями этих чисел), а из 12 комбинаций фундаментальных чисел
102
подобия 6 будут повторяться, в чем легко убедиться в результате
простого расчета.
Возьмем сочетание величин с независимыми размерностями
x,t, р, оно находится в 5-ой строчке таблицы. Видим, что первое
число подобия в ней обратно пропорционально числу Струхала:
п2 = zw/x = l/Sh . Следующее число: л'4 = t2plpx2 = Eu/sh2. И да-
лее: Л5 = gt2 j х = l/sh2Fr; тг'7 = щ/рх2 = 1/ShRe . Если скорость те-
чения по условию задачи является искомой величиной, то крите-
риальное уравнение в этом случае имеет вид:
Sh = f} (Tu/Sh2; Sh2Fr; ShRe),
или тоже самое в такой форме:
tujx = f2(t2р/рх2; gt2/х; \xt/рх2). (4-56)
Запишем аналогичные зависимости для сочетания величин с
независимыми размерностями х, g, р . Соответствующие комби-
нации чисел подобия были рассмотрены выше:
Fr = (p/ShFr1/2; EuFr; Fr1/2/Re),
или в такой форме:
/х'/2’ p/pgx>'^/px3/2g'/2) (4.57)
Рассмотрим далее сочетание величин с независимыми раз-
мерностями х, р, р , которые находятся в 8-ой строчке таблицы
4.1. Ему соответствует фундаментальное число подобия Эйлера и
комбинации остальных фундаментальных чисел подобия с ним:
л2 = up1/2/рУ2 = 1/Eu 1/2; л) = tp['2/р1/2х = Eul/2/Sh;л'5 = pgxjр = 1/EuFr
103
и, наконец, л) = цДр|'/2р1/2 = l/ReEu1/2 . Следовательно, можно
рассматривать следующие безразмерные уравнения связи:
Ей = ф/Еи1/2/8Ь; EuFr; Eu1/2 Re),
ир^/р^ = ф2 (tpnIр|/2х; pgx!p; ц/xp1/2p1/2 ). (4.58)
В 12-ой строке таблицы, где в качестве сочетания величин с
независимыми размерностями выбрано х, ц, р, имеем число Рей-
нольдса л'2 = xuj v = Re; кроме него, следующие сочетания с ним
остальных фундаментальных чисел подобия:
п'3 = ц//рх2 = 1/ShRe; л'4 = px2/pv = px2/v2p = EuRe2;
л'5 =x’gp2/p2 =Re2/Fr.
Таким образом, можно предложить следующие две формы записи
критериального уравнения:
Re = y/ShRe; EuRe2; Re2/Fr);
их/V = V|/2(ptfpx2; px2/v2p; x3gp2/p2). (4.59)
Следовательно, получили четыре критериальных уравнения,
каждое из которых представляет собой зависимость фундамен-
тального числа подобия от комбинаций остальных фундамен-
тальных чисел с ним. Всего комбинаций содержится в этих урав-
нениях 12, но из них оригинальных только 6, остальные 6 либо
повторяются, либо представляют собой оригинальные, возведен-
ные в какую-то степень. Оригинальные комбинации следующие:
ShRe, EuRe2, Re2/Fr, Eu2/sh, EuFr, ShFr.
Естественно, в этой ситуации возникает вопрос, какое из че-
тырех критериальных уравнений выбрать для нахождения его па-
104
раметров путем привлечения экспериментальных данных. По-
видимому, здесь следует согласиться с мнением [61]: если одно и
тоже явление можно описать с помощью нескольких уравнений
связи, то предпочтение следует отдать тому, у которого разброс
опытных точек относительно сглаживающей получается мини-
мальным.
В случаях, когда задача упрощается, поиск решения не-
сколько облегчается, однако, получить единственное критери-
альное уравнение можно только в самом простом явлении. Так,
если оно стационарное, то уравнение (4.56), связанное с числом
Струхала, отпадает, а в оставшихся трех критериальных уравне-
ниях исчезнут комбинации фундаментальных чисел подобия с
этим числом. При равномерном движении в поле сил земного
притяжения можно, используя уравнение этого вида движения в
качестве известного интегрального соотношения, найти явную
связь между числами подобия Фруда и Эйлера. Но тогда получа-
ется, что уравнения (4.57) и (4.58) дублируют друг друга, и оста-
ются только два критериальных уравнения:
Fr = Ф] (Eu Fr; Frl/2/Re) = 6(Tr1/2/Re). (4.60)
Re = y/EuRe2; Re2/Fr) = ^Re2/Fr). (4.61)
Легко заметить, что путем комбинации критерия подобия с чис-
лом подобия из первого уравнения можно получить второе и на-
оборот - из второго первое. Остается вопрос: какому из них от-
дать предпочтение?
Самый простой случай - это рассмотренное ранее стацио-
нарное обтекание закрепленного шара равномерным потоком не-
весомой жидкости (см. раздел 3). Здесь нет числа Фруда, поэтому
остаются два уравнения: (4.58) и (4.61), которые с учетом сказан-
105
ного предстанут в таком виде: Eu = ^(Eu'^Re) и Re = £(EuRe2J.
Но число Рейнольдса в поставленной задаче является критерием
подобия, поэтому остается только первое уравнение, которое, ис-
пользуя метод комбинаций чисел подобия, преобразуем так:
Eu = £(Eu]/2Re) = ^(Re). (4.62)
Но именно к такому критериальному уравнению пришли в разде-
ле 3, где этот случай был рассмотрен с позиций метода теории
подобия.
Рассмотрим еще одну задачу, о которой речь также шла в
разделе 3: обтекание опоры потоком тяжелой жидкости при усло-
вии, что движение на большом удалении от опоры стационарное
и равномерное. Если линейный размер опоры и скорость набе-
гающего потока заданы, то числа Рейнольдса и Фруда являются
критериями подобия. Но в таком случае из четырех полученных
выше критериальных уравнений представляет интерес только од-
но - (4.58), которое преобразуем путем комбинаций чисел и кри-
териев подобия, входящих в него, в следующее:
Eu = 0(EuFr;Eul,/2Re) = 01(Fr;Re). (4.63)
Как было отмечено ранее в разделе 3, в это уравнение долж-
на войти относительная глубина потока, что следует из условий
однозначности.
106
5. ПРАВИЛА ПОДГОТОВКИ И ПРОВЕДЕНИЯ
ЭКСПЕРИМЕНТОВ
Основные выводы, полученные в предыдущем разделе, по-
зволяют сформулировать перечень обязательных процедур, кото-
рые должны предшествовать проведению экспериментов. Эти
процедуры, перечисленные в указанной ниже последовательно-
сти, представляют в совокупности сводку правил подготовки к
проведению исследований на физической модели явления.
1) Постановка задачи исследований с подробным изложе-
нием ее цели, с указанием величин, определяющих явление,
выделения из них искомых величин, а также таких, которые
по условию задачи являются заданными.
2) Получение чисел подобия, определяющих явление.
3) Анализ чисел подобия для выявления критериев подобия.
4) Комбинация чисел подобия с целью получения критери-
ев, если последние отсутствуют или их количество недоста-
точно для записи критериального уравнения.
5) Использование интегральных соотношений для установ-
ления явных связей между числами и критериями подобия.
6) Составление критериальных уравнений в виде зависимо-
стей чисел подобия, содержащих искомую величину, от
критериев подобия.
Следует остановиться еще раз на пятом пункте. Речь идет об
условиях, которые характеризуют явление в целом, интегрально.
К ним относятся, например, равномерное движение жидкости или
тела в ней, условия равновесия сил, действующих в явлении
и т. п. Комбинируя числа подобия и вводя новые критерии, сле-
дует помнить о том, что новая совокупность чисел и критериев
должна быть такой, чтобы из нее всегда можно было получить
107
исходную фундаментальную совокупность чисел и критериев по-
добия. При этом необходимо учитывать наличие автомодельных
областей и результатов, обусловленных использованием инте-
гральных соотношений. Придерживаясь сформулированных пра-
вил, решим задачу о гидравлической крупности различных тел -
скорости их осаждения или всплытия в неподвижной жидкости.
Как было отмечено ранее, свободное осаждение или всплы-
тие тела в неподвижной жидкости с использованием методов
теории подобия представляется более сложным процессом по
сравнению с задачей, в которой тело закреплено и обтекается по-
током с заданной скоростью. Сложность состоит в том, что среди
чисел подобия нет ни одного критерия. Рассмотрим эту задачу
подробнее.
Если речь идет о речных наносах, то равномерное осажде-
ние их в неподвижной жидкости можно рассматривать как наи-
более простую форму движения. Кроме того, к понятию гидрав-
лической крупности приходится обращаться при определении
размеров частиц грунта, рассмотрении процессов осаждения и
всплытия частиц в жидкости, расчете различного рода отстойных
сооружений, определении транспортирующей способности пото-
ка, переносящего частицы во взвешенном состоянии, и т. п. Сле-
дует отметить, что методика изложения решения поставленной
задачи будет соответствовать той, которая принята в [20, 37].
Кроме того, различные аспекты проблемы осаждения и всплытия
частиц в жидкости можно найти в [8, 47, 56, 69].
Далее будем считать, что частицы имеют форму, близкую к
шарообразной, для частиц аллювия это предположение выполня-
ется (кроме гальки).
В связи с тем, что скорость осаждения является величиной
искомой, в разделе 4.5 были получены соответствующие крите-
108
риальные уравнения: (4.60) и (4.61). И хотя при получении этих
уравнений было использовано в общих словах интегральное со-
отношение, тем не менее, целесообразно рассмотреть его под-
робнее, учитывая, что осаждение частиц происходит в жидкой
среде, следовательно, они испытывают выталкивающую архиме-
дову силу. С этой целью составим уравнение равновесия сил,
действующих на частицу, осаждающуюся с постоянной скоро-
стью в неподвижной жидкости.
Первоначально частица падает ускоренно. Такое движение
будет наблюдаться до того момента, пока сила сопротивления
среды W не уравновесит силу тяжести G. С этого момента час-
тица начнет двигаться равномерно, а скорость ее падения (гид-
равлическая крупность) станет постоянной. Следовательно, при
падении частицы можно выделить три стадии ее движения: на-
чальный момент; ускоренное движение, равномерное движение.
Для различного рода расчетов практический интерес представля-
ет только третья стадия. Условие динамического равновесия для
равномерного падения может быть выражено равенством:
2
GrPySd =£<Р1-рЖ,
левая часть которого представляет силу сопротивления жидкости
падению рассматриваемой частицы, а правая-ее вес с учетом
архимедовой силы. Здесь Sd - площадь миделева сечения части-
цы; V - объем частицы; Cw - коэффициент сопротивления; со0 -
гидравлическая крупность; р, и р - плотность соответственно
материала частицы и воды. В связи с тем, что результаты прово-
димого здесь анализа будут сравниваться с точным решение, по-
лученным Г. Стоксом при малых числах Рейнольдса для тела,
имеющего форму шара, учтем это обстоятельство в приведенной
109
3
выше формуле. Объем частицы равен --------, а площадь миделева
6
nd2 , „
сечения---— , в которых d - характерный линеиныи размер
частицы. В таком случае из приведенной выше формулы следует
cw _2(Pi~P)gd
2 3 ро>о
(5.1)
В третьей главе было показано, что половина коэффициента
сопротивления равна числу Эйлера (формула (3.5)), поэтому
Eu = ^ = -^^^ = -^- = -Ri, (5.2)
2 3 pt£>o 3FrP 3
где FrD —-gd так называемое плотностное число Фруда,
/ Р
обратную величину называют числом Ричардсона, Ri = 1/Frp, ко-
торое характеризует отношение активной силы (в данном случае
это сила тяжести с учетом архимедовой силы) к силе инерции.
Отсюда следует, что в уравнения (4.60) и (4.61) вместо числа
Фруда должно войти плотностное число Фруда. Им на основании
условия равномерного падения частицы можно заменить число
Эйлера:
Frp = /(EuFrp; Frp1/2/Re) = <Frp1/2 /Re). (5.3)
Re = //EuRe2; Re2/Frp) = V1(Re2/Frp). (5.4)
В уравнения (5.3) и (5.4) вошла новая комбинация чисел по-
добия: Re2/Frp =
"pi -pW
ч Р J V2
——- Ga = Аг, которая называет-
Р J
по
Q rf5
ся числом Архимеда, где Ga= -~ -число Галилея,
v
- число Рейнольдса. Таким образом, вместо (5.3) и
v
(5.4) можно записать следующие критериальные уравнения:
Ргр=<рГАг); (5.5)
Re = (р/Аг). (5.6)
К аналогичному результату можно прийти, используя мето-
ды теории подобия. Математическую задачу об установлении
скоростей падения частиц в жидкости можно трактовать как за-
дачу о сопротивлении жидкости при движении в ней твердых тел.
Согласно принципу относительности механики, величина сопро-
тивления не зависит от того, движется ли равномерно тело в
жидкости или равномерный поток набегает на неподвижное тело.
Поэтому в математической постановке для описания явления об-
текания используются система уравнений движения вязкой жид-
кости.
При установившемся течении явление обтекания тел шаро-
образной формы имеются три числа подобия: Эйлера, Фруда и
Рейнольдса. Характерной скоростью и линейным размером явля-
ются гидравлическая крупность и диаметр частиц (чаще всего
подразумевается диаметр равнообъемного шара). Кроме того, из-
вестны плотности жидкости и материала частиц, соответственно
р и pi.
Поскольку во все упомянутые выше числа подобия входит
неизвестная величина гидравлической крупности, ни одно из них
не является критерием подобия. К этим числам подобия можно
in
добавить комплекс ——- , который представляет собой отно-
I Р J
шение веса, действующего на частицу, за вычетом архимедовой
силы, к архимедовой силе, и является критерием подобия. Этот
комплекс характеризует поведение твердых частиц в жидкой сре-
де. Если —- <0,т. е. Р| <р, частицы всплывают; при
k Р J
——- > 0, т. е. при р] >р частицы тонут.
I Р )
Далее следует воспользоваться интегральным соотношени-
ем, из которого следует, во-первых: число Фруда нужно заменить
плотностным числом Фруда, тем самым ввести в рассмотрение
комбинацию числа Фруда с комплексом ——- . Во-вторых,
I Р J
число Эйлера заменить плотностным числом Фруда. Но из этого
следует, что явление определяют только два числа подобия: Re и
Frp, среди которых нет критериев. В соответствии с вышеизло-
женным, для получения критерия подобия нужно из этих чисел
подобия составить безразмерный комплекс так, чтобы он не со-
держал неизвестную величину со0- Таким комплексом является
критерий Архимеда. Если заменить им плотностное число Фруда,
то получим критериальное уравнение (5.6), а если заменить число
Рейнольдса - критериальное уравнение (5.5). Вместо последнего
уравнения, используя приведенные выше соотношение (5.2),
можно получить такое:
Ri=<p2(Ar). (5.7)
Известно точное решение задачи обтекания шара, получен-
ное Г. Стоксом для предельного случая, в котором силы трения
112
значительно больше, чем силы инерции. Следовательно, такие
движения возникают при очень малых скоростях течения и чис-
лах Рейнольдса меньших единице (они получили название пол-
зущих) [62]. Полное сопротивление шара, одна треть которого
возникает вследствие разности давления в лобовой и в кормовой
точках шара, а две трети - вследствие сил трения, вычисляется по
известной формуле Стокса:
W = 3npvft)0 d. (5.8)
Воспользуемся для определения силы сопротивления зави-
симостью (3.7), получим
2
И^сЦр®^. (5.9)
Заменив в (5.9) W его значением из формулы (5.8), найдем
коэффициент сопротивления
24
Cw=^- (5.10)
Re
Сравнение формулы (5.10) с результатами измерений (см. на
рис 3.2 кривую 1) показывает, что она верна в области чисел Рей-
нольдса Re < 1.
Приравняем далее силу сопротивления, полученную в
результате теоретического решения Стокса (5.8), силе тяжести
7id3g(p1 -р)
Зпр vco0 d =-——
Отсюда получим формулу Стокса, по которой определяется
скорость осаждения в жидкости тяжелых частиц при условии
Reel
из
_ gd2 (р, - р)
со п ----------
0 18pv
(5.П)
Умножим в (5.11) левую и правую части на отношение —, в
v
результате получим
Аг
Re = —
18
(5-12)
Формула (5.12) соответствует критериальному уравнению
(5.6). Из нее после преобразований можно получить другую фор-
мулу, которая будет соответствовать критериальному уравнению
(5.5). Для этого нужно левую и правую части зависимости (5.12)
сначала возвести в квадрат, а затем разделить на плотностное
число Фруда, после преобразований найдем
Аг
Frn =----
р 324
(5-13)
Из формулы (5.13) с учетом (5.12) можно получить и такую
зависимость
— = 18.
F1P
(5.14)
Было предпринято несколько попыток улучшить решение
Стокса. Наиболее известная принадлежит К. Озеену, который
частично учел инерционные члены в уравнении Навье-Стокса.
Считается, что решение Озеена более или менее пригодно при
условии Re < 5 . Для коэффициента сопротивления оно дает фор-
мулу (см. на рис 3.2 кривую 2)
114
_ 24
~Re
fl + — Re \
I 16 J
Существует множество эмпирических формул, связываю-
щих величину коэффициента сопротивления с числом Рейнольд-
са, полученных путем подбора подходящих математических за-
висимостей для описания опытной кривой на рис. 3.2 при боль-
ших числах Рейнольдса. Достаточно подробный обзор этих фор-
мул сделан в [69].
Из эмпирических зависимостей, пригодных для определения
скорости осаждения тяжелых частиц в жидкости, наибольший
интерес представляет формула, приведенная в [47]
„ (£>nd Аг
Re = =------------кт
v 18 +0,61 Аг0,5
(5.15)
При малых числах Архимеда она превращается в формулу
Стокса в виде (5.12). Как показывают исследования, расчеты по
зависимости (5.15) хорошо согласуются с опытными данными в
переходной области, вплоть до нижней границы области квадра-
тичного сопротивления (для частиц кварца, осаждающихся в воде
при d = 0,1 см и температуре «20 °C, Аг = 1,62-104 ). В области
квадратичного сопротивления она дает систематические погреш-
ности в большую сторону.
Формула (5.15) соответствует критериальному уравнению
(5.6). Из нее после преобразований, которые были сделаны выше,
можно получить формулу, соответствующую критериальному
уравнению (5.5):
Р (18+ 0,61 Ar0'5 J2
(5-16)
115
Кроме того, по аналогии с зависимостью (5.14) найдем следую-
щую:
— = 18 +0,61 Аг0'5. (5.17)
FrP
Как показывают эксперименты, при осаждении достаточно
крупных частиц (частицы кварца в воде размером d > ОД см, при
температуре «20° С, Аг > 1,62 104 ) имеет место квадратичный
закон сопротивления, а гидравлическая крупность этих частиц
определяется из формулы:
®o=CKJEkz£gd, (5.18)
V Р
где Ск - постоянная. Умножив (5.18) на J/v, найдем зависимость
в форме критериального уравнения (5.6):
Re = С). Аг0,5. (5.19)
Ее можно преобразовать в формулу, соответствующую критери-
альному уравнению (5.5):
Frp=G2. (5.20)
Кроме того, разделив (5.19) на (5.20), получим
Обсуждаемые результаты исследований свидетельствуют о
некоторых преимуществах представления их в форме критери-
ального уравнения (5.5) по сравнению с критериальным уравне-
нием (5.6). В частности, это касается определении по опытным
пб
данным нижней границы области квадратичного сопротивленя. В
этой области плотностное число Фруда, как об этом свидетельст-
вует формула (5.20), постоянно и не зависит от критерия Архи-
меда. Здесь уместно провести аналогию с зависимостью коэффи-
циента сопротивления закрепленного шара от критерия Рей-
нольдса: в области квадратичного сопротивленя этот коэффици-
ент постоянен и не зависит от критерия Рейнольдса. Что касается
представления результатов измерений в форме критериального
уравнения (5.6), то здесь обнаружить область квадратичного со-
противления сложнее: ей соответствует та часть графика зависи-
мости числа Рейнольдса от критерия Архимеда, где число Рей-
нольдса пропорционально корню квадратному из критерия Ар-
химеда.
Необходимо далее остановиться на величине коэффициента
Ск. Обычно утверждается, что кривая зависимости коэффициен-
та сопротивления от числа Рейнольдса, приведенная на рис 3.2,
универсальна, поэтому отражает процесс осаждения в воде час-
тиц кварца. Пусть частица имеет форму шара, тогда, приравнивая
силу сопротивления силе тяжести частицы в воде, в соответствии
с зависимостью (5.1) имеем:
4
(5-22)
Подставляя в (5.22) значение плотностного числа Фруда из
(5.20), найдем
Из графика, приведенного на рис.3.2, следует, что в области
квадратичного сопротивления Cw = 0,4 , следовательно, Ск = 1,82 .
117
В тех случаях, когда частица по форме близка к шару, но, строго
говоря, не является шаром (такие тела называют шарообразны-
ми), в исходном уравнении динамического равновесия принима-
ют отношение объема частицы к площади миделевого сечения
равным VfS =kd, где коэффициент пропорциональности отра-
жает отличие формы частицы от шара. Если ввес ги коэффициент
пропорциональности в коэффициент сопротивления и обозначить
его СКц , то вместо зависимости (5.1) получим следующую
Gn=2/Frp. (5.24)
3
Сравнивая (5.24) и (5.22), находим: . Следова-
тельно, если в динамическом уравнении отношение объема шара
к площади миделевого сечения заменить величиной kd и ввести
величину к в коэффициент сопротивления, то последний будет в
полтора раза больше коэффициента сопротивления, полученного
при строгом выражении объема шара и площади окружности из-
вестными математическими зависимостями. Иными словами, ес-
ли Cw = 0,4, то CfVl = 0,6.
В связи с тем, что частицы естественных песчаных грунтов
имеют форму отличную от шара, обработку результатов измере-
ний, естественно, производят так, что получают коэффициент со-
противления в форме CWi . Между тем на основании опытов, от-
носящихся к песчаным грунтам в области квадратичного сопро-
тивления, обычно принимают СК «1,2 . Тогда из формулы (5.24) с
учетом (5.20) получим: Cwx =2/1,22 =1,4 . Таким образом, коэф-
фициент сопротивления частиц естественных песчаных грунтов в
области квадратичного сопротивления оказался почти в два с по-
ловиной раза больше аналогичного коэффициента для таких же
118
частиц, имеющих форму шара. Можно предположить, что такой
результат является ожидаемым.
Заметим, что приведенные зависимости относятся только к
“докризисному” падению тел в неподвижной жидкости (числа
Reel О5). Можно оценить крупность частиц, в скорости падения
которых в воде начнут проявляться «кризисные явления». С этой
целью в формулу для числа Рейнольдса необходимо подставить
скорость осаждения, используя зависимость (5.19), получим
1,2 Jf~ - I'jg J3/2
Re = . Принимая Re = 105 , найдем
V V
d «8см.
Как правило, для сравнения вновь полученных результатов с
уже имеющимися уравнения связи в критериальной форме не ис-
пользуется. В качестве примера можно рассмотреть “стеснен-
ное” падение частиц. Выше были получены зависимости, описы-
вающие движение в неподвижной жидкости одиночных частиц,
имеющих форму шара, вдали от стенок сосуда, в котором нахо-
дится жидкость. Теперь речь идет о движении множества таких
частиц, при котором важную роль играет их взаимодействие. Та-
кого рода исследования стесненного падения однородных твер-
дых тяжелых частиц в воде были выполнены в [56]. Их результа-
ты представлены на рис.5.1 в виде графика зависимости
Cw ~ /(Re,e) • Здесь £ = l-s - объемная доля жидкости в смеси,
s - объемная доля твердой фазы. Заметим, что для сферических
частиц величина е« 0,42 соответствует расстоянию между час-
тицами, равному одному диаметру. Если расстояние равно двум
диаметрам, то е » 0,92. Взаимодействие между частицами начи-
нается при объемной концентрации твердых частиц s >5 %.
119
Рис. 5.1. Зависимость коэффициента сопротивления частиц
при стесненном падении от числа Рейнольдса и объемной
доли жидкости в смеси
Получается, что в такой смеси частиц и воды происходят
два вида движения: падение частиц вниз и движение в промежут-
ках между частицами воды вверх. В промежутке между частица-
ми образуется “сжатое” водное сечение. Можно говорить о том,
что точка отрыва потока от тела перемещается в сторону лобовой
части (например, при е = 0,42 она находится в миделевом сече-
нии), поэтому, как это можно видеть на рисунке, сопротивление
увеличивается, следовательно, скорость падения уменьшается.
Можно привести соответствующие зависимости, отражающие
этот факт:
со = co0fl - 2s) и со = co0f 1 - s)2. (5.25)
Первая из них принадлежит В.Н. Гончарову, вторая - Ричардсону;
в них со0 и со скорость падения одиночной частицы и скорость
стесненного падения соответственно. По Гончарову получается,
что осаждение частиц прекращается при s = 0,5 , что не согласу-
ется с графиком, приведенным на рис.5.1.
120
С увеличением содержания мелких частиц происходит из-
менение свойств взвесенесущей жидкости, которая превращается
в однородную субстанцию, физические параметры которой отли-
чаются от параметров воды. В частности, можно привести фор-
мулу Эйнштейна (младшего), связывающую динамический ко-
эффициент вязкости ц5 такой жидкости (суспензии) с динами-
ческим коэффициентом вязкости ц воды
Hi =pfl + 2,5s_).
(5.26)
На рис.5.2 приведен график зависимости коэффициента со-
противления пузырьков воздуха в воде от числа Рейнольдса [56].
Пузырьки воздуха создавались с помощью специального устрой-
ства строго определенной формы, движение их в воде снималось
на кинопленку. В результате обработки данных киносъемки оп-
ределялись скорость всплытия пузырьков и их форма. Обнаруже-
но, что при условии Re < 400 пузырьки имеют сферическую фор-
му. Если Re <80, то коэффициент сопротивления пузырьков сов-
падает с коэффициентом сопротивления твердых сферических
частиц, осаждающихся в воде. В промежутке 400 < Re < 5000 пу-
зырьки имеют эллипсоидальную форму, при этом коэффициент
сопротивления в этой области резко увеличивается от минималь-
ного значения в ее начале до значения, во много раз превышаю-
щего коэффициент сопротивления твердой сферической частицы,
в конце области. Наконец, в промежутке 5-Ю3 < Reel О4 пузырь-
ки приобретают форму сфероидальной чаши, повернутой дном к
поверхности воды, коэффициент сопротивления их продолжает
увеличиваться и в этой области. Значительное уменьшение коэф-
фициента сопротивления при Re ® 400 связывают с тем, что по-
верхность раздела - вода-воздух - становится волнистой. Волни-
стая поверхность раздела препятствует образованию точек отры-
121
ва потока на ней, что является причиной улучшения обтекания
тела и уменьшения коэффициента сопротивления (кстати, малое
значение коэффициента сопротивления тела дельфина объясняют
способностью его кожи пронимать волнообразную форму при
больших скоростях перемещения животного в водной среде).
Рис. 5.2. Зависимость коэффициента сопротивления
пузырьков воздуха в воде от числа Рейнольдса
Увеличение уровня турбулентности потока (рис. 5.3) приводит к
тому, что кризис сопротивления наступает при числах Re<105:
чем выше уровень турбулентности внешнего потока, тем меньше
число Рейнольдса, при котором обнаруживаются кризисные яв-
ления [56, 69]. Но они наблюдаются только в области автомо-
дельной по числу Рейнольдса. При числах Re < 400 кризис сопро-
тивления не происходит при любом уровне турбулентности
внешнего потока. Таким образом, уменьшение величины числа
Рейнольдса, при котором наблюдается кризис сопротивления,
вследствие увеличения уровня турбулентности внешнего потока
имеет место только в том случае, если течение в следе за плохо
обтекаемым телом имеет турбулентный характер. Известно, что
при малых значениях числа Рейнольдса в следе происходит пере-
ход от ламинарного течения к вихревой дорожке Кармана (при
122
Re=i300); если число Рейнольдса увеличивать, то вихревые до-
рожки становятся нерегулярными, и течение в следе приобретает
турбулентный характер (при Re « 400) [62].
Рис. 5.3. Зависимость коэффициента сопротивления
шарообразных частиц от числа Рейнольдса при различном
уровне-турбулентности внешнего потока (1)
123
6. ДРУГИЕ МЕТОДЫ, СВЯЗАННЫЕ С
л-ТЕОРЕМОЙ
6.1. Метод размерностей
В практике моделирования находит применение метод раз-
мерностей, в основе которого лежит формула размерностей. В
сущности этот метод является разновидностью метода, основан-
ного на применении на практике выводов п -теоремы. Здесь так-
же предполагается, что связь между искомой величиной у и ве-
личинами х; , ее определяющими, удовлетворяет принципу одно-
родности.
Представим эту связь в виде формулы размерностей:
С а Ъ с е z
О 3^*2 *3*4..Хп
(6.1)
где Со - постоянная.
Прежде всего, покажем, что таким способом можно полу-
чить результаты, согласующиеся с выводами л- теоремы. Выбе-
рем среди величин х; три с независимыми размерностями. Пусть
это будут величины xhx2 и х3. Разделим искомую величину и
остальные величины на степенные комплексы, составленные из
величин с независимыми размерностями:
где р = п - 3, кроме того:
124
A = a-a + at + .... + <xp;
В = b - 0 + 0j + .... + 0p;
C = c-y + Y1 +.... +Yp.
(6.3)
В связи с тем, что размерности величин х; и у известны,
можно подобрать показатели степеней, обозначенные в зависи-
мостях (6.2) и (6.3) греческими буквами, так, чтобы комбинации
величин, вошедших в (6.2) в виде дробей, были безразмерными.
Это можно сделать, выражая размерности величин дробей через
размерности основных величин в СИ. Введем обозначения:
У . Хд
П~х?х^ху’ ха'х^хъ
71 =71 3 =--------£-----. 6.4)
р П J а Р у >
Ху
Получается, что в левой части зависимости (6.2) находится
безразмерная величина, в правой части - произведение безраз-
мерных величин. Но в таком случае показатели степеней у вели-
чин, имеющих независимые размерности, должны удовлетворять
условиям:
Л = 0; 5 = 0; С = 0. (6.5)
Следовательно,
71 = Д711,712,..-,7lJ, (6.6)
что согласуется с результатом, обусловленным п- теоремой. За-
метим, что число 7i позволяет найти показатели степени а, 0 и у.
Любое другое число устанавливает связь между показателями
степени, обозначенными буквами греческого алфавита (некото-
рые постоянные величины), с показателями степени, обозначен-
ными буквами латинского алфавита. Например, число тг( позво-
125
ляет не только определить показатели ab Pj и у1? но и установить
зависимость показателя степени “е” от этих постоянных и т. д.
Наконец, зависимости (6.5) после подстановки в них соответст-
вующих величин определяют связь между показателями степе-
ней, обозначенными буквами латинского алфавита. Естественно,
наиболее простой получается связь между величинами у и х,- при
п = 3. Тогда получим из формул (6.3) при условии(6.5):
а = a; b - Р; с - у.
Следовательно,
^ = C0x1“x2PxJ, (6.7)
что совпадает с формулой (4.32).
Чем больше величина п, тем сложнее использовать метод
размерностей и гораздо проще обращаться к выводам, обуслов-
ленным л-теоремой.
Согласно другому способу (обычно его связывают с именем
Рэлея), показатели степеней а, Ь, с,...., z в уравнении (6.1) опреде-
ляют, используя зависимости размерностей всех величин, входя-
щих в (6.1), от размерностей основных величин в СИ, напри-
мер: [у] = [л/]”’ [z]z [т], [х, ] = [z]Z| [гр и т. д. Из этого следу-
ет:
кШ [ту =
= [л/р1 [тр [тр [мУт2 [z.y/2 [гр... .[м]2т" [r]zt".
Отсюда, приравнивая показатели степеней в левой и в пра-
вой частях последней зависимости, получим три уравнения с п
неизвестными:
126
т - агп\ - bm2 zmn = О,
I - al} -bl2 -....-zl„ =0,
t-aty -bt2 -....-ztn = 0.
(6-8)
Если n > 3 , то, выбрав какие-либо три показателя степени,
можно установить из (6.8) связь их с остальными показателями.
Далее, комбинируя величины, придем к выражению (6.6), хотя
путь этот часто бывает сопряжен с преодолением больших труд-
ностей, так что преимущества непосредственного использования
л -теоремы в этом случае становятся очевидными. Если п = 3 , то
показатели степеней а, Ь и с находятся из трех уравнений (6.8);
тогда
Т - Cox^x2xj ,
что совпадает с (4.32) и (6.7).
Рассмотрим в качестве примера задачу об обтекании закре-
пленного шара. Сила сопротивления шара W является функцией
следующих величин: кинематической вязкости v и плотности
жидкости р, скорости набегающего потока на большом удалении
от шара ит и его диаметра d (характерный размер). Представим
связь между силой сопротивления W и указанными величинами в
виде формулы размерностей (6.1):
fr = Copau^dcve
(6-9)
Воспользуемся вначале первым из приведенных выше мето-
дов. Выберем в качестве величин с независимыми размерностя-
ми: р, um, d . Найдем параметры а, р, у , выражая размерности вы-
бранных величин и размерность силы сопротивления через раз-
127
мерности основных единиц в СИ, исходя из предположения, что
следующее отношение - величина безразмерная:
М№Г2
=[м]а[А]-3а[Лр[7’]-₽[1Г
= [A/]°[Z,]°[T]°.
Отсюда получим три уравнения:
1-а = 0; -2 + Р = 0; 1 + За-р-у = О.
Следовательно, а = 1; р = 2; у = 2.
Выполним аналогичные операции со следующим отношени-
ем:
__=______________[£]2е17']е______= [л/1°Гл]0Гг1°
ра‘г4М [М]“’[Л]’3"[Zp [7]-р> [Ар 1 J L J L J
Имеем: а]=0; 2e + 3aj-P]-yj =0; -e + p,=O. Отсюда
P,=e, y,=e.
Таким образом, получили следующие л-числа:
W ve 1
7С « « , 711 - _ ,
рг4<Г u^d2 Ree
В связи с тем, что площадь миделева сечения Sd~d2, а,
кроме того, постоянную можно внести в коэффициент сопротив-
ления Сцг = w/o,5pu^Sd , найдем: Cw = /(Re), что совпадает с
ранее полученным выводом (см. формулу (3.6) и объяснение к
ней).
Воспользуемся теперь вторым методом, выразим размерно-
сти всех величин, входящих в (6.9), через размерности основных
величин в СИ:
128
[Л/]1 [z]1 [г]2 = [M]a [z] 3" [Z]6 [Г]-b [Z]f [L\2e [Z ]-e.
Отсюда, приравнивая показатели степени при одинаковых
основных величинах, получим:
1 - а = 0; 1 + За - /> - с - 2е = 0; -2 + й + е = 0.
Следовательно: а = 1; b = 2 - е; с = 2 - е.
Подставив эти результаты в (6.9), найдем: W = Cf}pul~ed2~eve. От-
сюда приходим к следующему выражению
W 1
Не2
что полностью совпадает с предыдущими результатами
Теперь проверим соответствие полученных данных зависи-
мостям (6.3) при условиях (6.5), имеем:
а = 1, а = 1, «[=0, Ь = 2-е, р = 2, Р| =е,
с = 2-е, у = 2, Yi=e; подставляя эти результаты в (6.5), полу-
чим
Л = 1-1 = 0; В = 2-е-2 + е = 0; С = 2-е-2 + е = 0.
6.2. Метод линейных пропорциональностей
В конце 60-х годов прошлого столетия заграницей был
обоснован еще один метод, использующий основные положения
л-теоремы и непосредственно связанный с ней, названный «ме-
тодом синтеза», известный также под названием как «метод ли-
нейных пропорциональностей» [65]. Достаточно подробное из-
ложение метода читатель найдет в [61].
129
Сущность метода заключается в следующих основных по-
ложениях. Линейной пропорциональностью называется комбина-
ция двух или нескольких членов, входящих в уравнение связи,
имеющая размерность длины. Например, из двух величин скоро-
сти и и ускорения силы тяжести g можно составить линейную
пропорциональность и11g. В более сложных ситуациях прихо-
дится привлекать для составления таких пропорциональностей
большее число величин. При этом нужно иметь в виду следую-
щее обстоятельство. В уравнение связи не может входить вели-
чина с размерностью, содержащей такую основную единицу из-
мерения, которой нет в других величинах, входящих в это урав-
нение. Собственно, в этом и заключается принцип однородности
уравнений, описывающих явления. Например, в уравнение связи,
содержащем время t, скорость и, ускорение свободного падения
g, не может входить плотность р, так как в ее размерности име-
ется масса, которой нет в других величинах. Поэтому в такое
уравнение должна входить еще либо динамическая вязкость ц,
либо давление р. Кроме того, при составлении линейных про-
порциональностей одну из этих величин можно вообще не при-
нимать во внимание. Действительно, например, для того, чтобы
из произведения иц «удалить» массу, необходимо его разделить
на р. Аналогично из произведения нр масса «удаляется» путем
деления его на ц. При составлении линейных пропорционально-
стей рекомендуется не составлять их с плотностью р. Однако,
плотность привлекается в сочетаниях других величин в процессе
получения линейных пропорциональностей. Например, составим
линейную пропорциональность из величин g и ц. Вначале возь-
мем такую комбинацию этих величин, которая не будем содер-
жать время: [ц2/ g]= МН Далее разделим это сочетание на
130
р2, получим |p/p2g]= [у2/ g]= [Z.3j. Искомая линейная пропор-
циональность равна v2/3/g1, 3 . Если рассматривать сочетание и и
р, то линейной пропорциональностью будет выражение
ц /р и = v / и. Если в рассмотренных сочетаниях заменим ц на р
и рассмотрим сочетания g и р, а также и и р, то придем к тем же
самым линейным пропорциональностям.
Метод линейных пропорциональностей обладает целым ря-
дом неопределенностей. Прежде всего, не указано, в какой форме
следует рассматривать исходное сочетание двух величин: в фор-
ме их произведения, или в форме деления одной величины на
другую. От того какая форма сочетания была принята, зависит
вид линейной пропорциональности. Но существуют такие соче-
тания, которые можно представить только единственным обра-
зом. К ним относятся упомянутое выше сочетание величин ско-
рости и и ускорения силы тяжести g, а также - скорости и и
времени t, g и t. Кроме того, не ясно, какой из величин, размер-
ность которых содержит массу, отдавать предпочтение, если в
уравнение связи таких величин содержится более двух.
По-видимому, ответ на поставленные вопросы может быть
только один: из всех возможных сочетаний величин, участвую-
щих в процессе получения линейных пропорциональностей,
предпочтение следует отдавать тем, которые в последующих
преобразованиях дадут либо фундаментальные числа подобия,
либо простейшие комбинации этих чисел подобия (в лучшем
случае - не более двух, в крайнем - не более трех).
Далее допустим, что в уравнение связи входит п величин, из
которых имеют линейные размерности I величин. Таким обра-
зом, в процессе образования линейных пропорциональностей бу-
дут участвовать п-1 величин. В результате будет получено ко-
131
личество таких пропорциональностей, равное сочетанию из
N = п-1 по два: С* = 0,5(л-/-1)(и-/). С учетом величин, вхо-
дящих в уравнение связи и имеющих линейные размерности, об-
щее число линейных пропорциональностей будет равно
К = 0,5(и-/-1) (и-/)+/. (6.10)
Далее следовало бы доказать, что уравнение связи, содер-
жащее размерные величины, можно заменить уравнением связи,
содержащем линейные пропорциональности. На пути реализация
такого доказательства имеются большие трудности. Возможно,
что такое доказательство и не требуется, поскольку получены но-
вые величины, следуя определенному правилу, из величин, вхо-
дящих в уравнение связи. Вновь полученные величины имеют
независимые размерности, поскольку ни одна из них не может
быть получена путем комбинаций остальных, хотя все они имеют
одинаковые размерности. Но тогда в рамках теории размерностей
можно, выбрав какую-либо линейную пропорциональность, най-
ти отношения к ней остальных пропорциональностей. Известно,
что такие отношения величин, имеющих одинаковые размерно-
сти, называются симплексами подобия, в данном случае одновре-
менно они являются и числами подобия. Общее количество чисел
подобия, которое можно получить из линейных пропорциональ-
ностей, равно числу сочетаний из К по два
Z = C% = 0,5{[0,5(и-/-1)(п-1)+1 -1][0,5(л-/-1)(«-/)+/]}. (6.11)
В качестве косвенного доказательства правомерности заме-
ны исходного уравнения связи аналогичным уравнением, содер-
жащем линейные пропорциональности, может служить равенство
общего количества чисел подобия, которые можно получить из
первого и второго уравнений. Из исходного уравнения связи
132
можно получить в рамках п- теоремы все числа подобия, исполь-
зуя все возможные сочетания по три величин, имеющих незави-
симые размерности. Общее количество чисел подобия, которое
можно получить из линейных пропорциональностей, дает зави-
симость (6.11).
В качестве примера рассмотрим течение вязкой несжимае-
мой жидкости, полагая, как и ранее, что силы поверхностного на-
тяжения не оказывают на него влияние. Соответствующее урав-
нение связи приведено в разделе 4.5 (уравнение 4.55). Там же в
таблице 4.1 даны все числа подобия, которые можно получить,
руководствуясь выводами л- теоремы. Общее количество чисел
подобия равно 116.
Число членов в уравнении (4.55) - п = 7, один из них имеет
линейную размерность, тогда - I -1. Из зависимости (6.10) полу-
чаем общее число линейных пропорциональностей: Л? = 16, об-
щее количество чисел подобия найдем из зависимости (6.11):
Z = 120 . Разница объясняется тем, что не существует равенства
двух сочетаний из разного количества величин по разному числу
входящих в них элементов. В силу этого общее количество чисел
подобия, получаемое из линейных пропорциональностей, полу-
чается на четыре числа больше. Как показал выполненный в раз-
деле 4.5 анализ, среди 116 чисел подобия многие повторяются.
Можно утверждать, что таких повторов среди 120 чисел подобия
будет больше. В этом состоит косвенное доказательство право-
мерности замены уравнения связи, состоящего из размерных ве-
личин, определяющих явление, уравнением связи, включающем
линейные пропорциональности.
Далее возникает естественный вопрос, как ограничить коли-
чество чисел подобия? Если руководствоваться выводами п - тео-
ремы, то следует выбрать подходящие три величины с независи-
133
мыми размерностями и получить четыре числа подобия. В методе
линейных пропорциональностей нечто подобное достигается
следующими способами.
Прежде всего, выделяются величины с линейными размер-
ностями. Кроме того, при образовании линейных пропорцио-
нальностей не делают сочетаний величин, входящих в уравнение
связи, с одной из них, в размерность которой входит масса (со-
гласно методу рекомендуется не рассматривать сочетания с
плотностью, но, тем не менее, привлекать плотность там, где это
потребуется, для получения линейных пропорциональностей). Но
тогда зависимость (6.10) преобразуется и станет такой
К = 0,5(и-/-2)(л-/-1)+/. (6.12)
В частности, если вернуться к рассмотрению приведенного
выше примера, то получим следующее количество линейных
пропорциональностей: К = 11. Далее необходимо их проанализи-
ровать и исключить повторяющиеся пропорциональности, оста-
вив для дальнейшего анализа только одну. Забегая несколько
вперед, можно отметить, что среди одиннадцати линейных про-
порциональностей две повторяются, исключив одну из них, по-
лучим К -10 , в том числе сюда входит одна величина, которая в
уравнении связи имеет линейную размерность.
Далее рассматривают не все возможные отношения линей-
ных пропорциональностей друг к другу, а только одно, а именно:
только отношение к величине, которая до получения линейных
пропорциональностей имела линейную размерность. Тогда в рас-
сматриваемом случае будет получено К = 9 чисел подобия. До их
получения рекомендуется принимать во внимание такое количе-
ство линейных комбинаций, число которых на единицу меньше
общего количества величин, участвующих в образовании линей-
134
ных пропорциональностей. Следовательно, количество их в рас-
сматриваемом примере будет равно: п-l-\-1 = п-3 , что нахо-
дится в соответствии с основными положениями п- теоремы.
Иными словами, каждое уравнение связи, которое будет получе-
но из четырех линейных пропорциональности, будет содержать
только четыре числа подобия. До их получения рекомендуется
принимать во внимание только такие линейные пропорциональ-
ности, в которые входят все размерные величины, входящие в
уравнение связи. По нашему мнению, это надо делать после по-
лучения чисел подобия, представления их в соответствии с изло-
женными ранее методами в виде фундаментальных чисел подо-
бия и их комбинаций. Далее учитываются только такие четверки
чисел подобия, в которые входят все без исключения фундамен-
тальные числа.
Возвращаясь вновь к рассматриваемому примеру, найдем
общее количество уравнений связи, которое можно получить,
рассмотрев число сочетаний из девяти по четыре:^ =126. Коли-
чество уравнений получается просто огромным, практически это
означает, что нужно перебрать все возможные комбинации чисел
подобия. Если предположить, что в результате такого сложного
анализа будут отброшены повторы и комбинации, в которые не
входят все фундаментальные числа подобия, то все равно задача
получения единственного решения (или ограниченного числа
решений) представляется далекой от реализации. Отсюда следует
вывод: метод линейных пропорциональностей, как и формула
размерностей, могут быть использованы на практике при ограни-
ченном числе величин, входящем в уравнение связи. Ниже будет
это показано на некоторых примерах, а пока продолжим рассмот-
рение приведенного выше общего случая движения вязкой жид-
кости. Для этого найдем, следуя изложенным выше правилам,
135
линейные пропорциональности и соответствующие числа подо-
бия, используя уравнение (4.55). Для этого, прежде всего, выде-
лим величину с линейной размерностью и не станем составлять
линейные пропорциональности с плотностью. В результате полу-
чим следующее уравнение связи:
up и
J £
up
~ =0,
_ р J gpd
содержащее только линейные пропорциональности. Пропорцио-
нальности в квадратных скобках повторяются, поэтому одну из
них сократим. После деления на х получим следующее уравне-
ние связи, в которое входят числа подобия
— =0.
pgtv
Перейдем в последнем уравнении к фундаментальным чис-
лам подобия и их комбинациям
F{sh4, Eu 4Re4, Fr, ShEu1'2, SIC2Fr4, Re4 2Sh"12, EuFr, FrRe-lSh}= 0.
Можно заметить, что число Струхала встречается в послед-
нем уравнении чаще всего - пять раз, далее следует число Фру-
да - четыре раза, по три раза можно встретить в этом уравнении
числа Рейнольдса и Эйлера. Следовательно, среди возможных
комбинаций чисел подобия по четыре обязательно должны быть
такие, среди которых будет не полный набор фундаментальных
чисел подобия, поэтому далее они рассматриваться не будут. С
другой стороны, если в любую четверку чисел подобия, взятых из
последнего уравнения связи, входят все фундаментальные числа,
то путем комбинаций можно превратить их в четыре фундамен-
те
тальных числа подобия. Иными словами, любое полученное та-
ким путем уравнение связи можно превратить в обычное уравне-
ние, которое получается в рамках л - теоремы. Но справедливо и
обратное утверждение: безразмерное уравнение связи, получен-
ное в рамках л- теоремы, может быть превращено путем комби-
наций фундаментальных чисел подобия в любое уравнение связи,
определяемое методом линейных пропорциональностей. На этом
основании можно утверждать, что метод получения критериаль-
ных уравнений, в основе которого лежит л- теорема, является
фундаментальным. Другие методы, использующие теорию раз-
мерностей, могут рассматриваться в качестве вспомогательных, в
частности, при небольшом количестве величин, определяемых
явление. Покажем это на примерах использования метода линей-
ных пропорциональностей.
Обратимся вновь к задаче обтекания закрепленного шара
стационарным потоком вязкой жидкости (см. раздел 6.1). Запи-
шем уравнение связи
/(^,woo,v,p,rf)=0. (6.13)
Составим линейные пропорциональности, не учитывая величины
р nd.
( 1 /F w v J п
Ф—J—, --------, d =0.
V Р Р Цх> V и J
Получим из линейных пропорциональностей числа подобия
8f_k Д
d у Р р ию v d uxd)
Далее можно было, как рекомендует метод, составить три
уравнения, в каждом из которых войдет по два числа подобия.
137
Однако делать это не будем, а найдем вначале комбинации полу-
ченных чисел подобия. С этой целью возведем первое число в
квадрат и разделим на второе:
W рих v d _ v
р и2т d2 W umd’
(6-14)
но полученное число подобия (обратное числу Рейнольдса) име-
ется в последнем уравнении связи. Если оставить первое число (в
W
квадрате) и последнее, а также учесть, что —-—у « Cw , то при-
РС d2
дем к хорошо известному ранее не раз обсужденному результату:
ф(С[Г,Ке)=0.
Усложним задачу и рассмотрим движение тела в капельной
жидкости, или на ее поверхности. Первое относится к осаждению
тяжелых тел в жидкости под действием силы тяжести, второе
- движение транспортных средств под действием “движителей”.
При решении этих задач методом линейных пропорционально-
стей воспользуемся некоторыми полученными ранее результата-
ми. Введем в уравнение (6.13) дополнительно ускорение силы
тяжести g и плотность материала тела р,; обозначим скорость
движения и, характерный линейный размер - х. Получим урав-
нение связи в таком виде
f(W,u,g,v,pl,p,x)=Q. (6.15)
Учтем далее, что тела находятся в жидкости или на ее по-
верхности, поэтому нужно учесть Архимедову силу, а это дости-
гается умножением ускорения силы тяжести на отношение
(pi -р)/р • Введем обозначение g(p] - р)/р = gp , произведем соот-
ветствующие преобразования в уравнении (6.15)
138
и, gp.v.p, x)=0.
(6.16)
Составим линейные пропорциональности, а затем получим
числа подобия, в результате найдем из (6.16) такое безразмерное
уравнение связи
( W W W и2
v 2 2’ 3 ' ’
\ри х р gp X puvx gpx
Далее приступим к комбинациям чисел подобия, вошедших
в это уравнение. Комбинация первого и третьего чисел подобия
указана в зависимости (6.14), ее результат (величина, обратная
числу Рейнольдса) имеется в уравнение (6.17), на этом основании
из него можно убрать третий член, оставив в нем первый. Теперь
составим комбинацию из первого и второго членов уравнения
(6-17)
W PgPx3 gP х
р и2 х2 W и2
(6.18)
Результат (величина, обратная числу Фруда) также имеется
в уравнении (6.17), а это означает, что в нем можно оставить
только одно из двух первых чисел подобия. В зависимости от то-
го, какое из чисел подобия оставим, получим два различных
уравнения связи. Вначале оставим первое число и продолжим
анализ, рассмотрев комбинацию двух последних чисел подобия
(пятого и шестого), оставшихся в уравнении (6.17). С этой целью
возведем пятое число в квадрат и раздели на шестое
7 3
V gpX ^gpX
139
Отсюда следует, что шестое число в (6.17) также можно
опустить. Теперь запишем два безразмерных уравнения связи,
которые на основании выполненного анализа вполне адекватны
уравнению (6.17)
Обратимся вначале к первому уравнению и получим из него
критериальное уравнение для скорости осаждения тяжелых час-
тиц в капельной жидкости: и = <в0, х = d. Из сказанного в пре-
дыдущих разделах следует, что первый член в нем есть число
Эйлера Ей, которое с точностью до постоянной равно коэффици-
енту сопротивления Cw. Если частицы осаждаются под влиянием
силы тяжести (с учетом Архимедовой силы), то число Эйлера об-
ратно пропорционально плотностному числу Фруда (см. раздел
5). Тогда первый член можно опустить и получить такое уравне-
ние
f =0.
I v gPd)
Скорость осаждения в этой задаче - величина искомая, а
критерием в ней является комбинация числа подобия Рейнольдса
и плотностного Фруда - критерий Архимеда
gp П = 0
140
но этот результат был получен в разделе 5.
Допусти далее, что перемещение тела происходит с помо-
щью устройства, обеспечивающего движение - движителя. В
этой задаче скорость движения - величина заранее известная, по-
этому числа Фруда и Рейнольдса являются критериями. Важный
вопрос в ней - выбор характерной линейной величины. При фи-
зическом моделировании явлений, связанных с движением судов
в режиме плавания, в качестве такого размера принято принимать
корень кубический из объемного водоизмещения судна V, соот-
ветствующего статическому положению - Р|/3 [6]. В этом режи-
ме плавучесть судна равна архимедовой силе, поэтому в число
Фруда должно войти ускорение силы тяжести g. При движении
судна в режиме глиссирования (скольжения по поверхности во-
ды) архимедова сила практически становится равной нулю; пла-
вучесть судна определяется подъемной силой. В этом случае в
качестве характерного размера принимается ширина судна В.
Тогда, обозначив характерный размер буквой 1С, из первого урав-
нения в (6.19) найдем критериальное уравнение для коэффициен-
та сопротивления судна
что было доказано в разделе 3. В том же разделе обсуждался во-
прос о построении критериального уравнения для коэффициента
W W
сопротивления Q -------- =----, который вошел во второе
Р g 1С Р S V
уравнение системы (6.19). Критериальное уравнение для него бу-
дет таким
141
Q - flA
ll lc u2
V ’ gplc)
что также находится в полном соответствии с полученными в
разделе 3 результатами. Но, учитывая зависимость (6.18), в рас-
сматриваемом случае найдем связь между коэффициентами со-
противления:
С. =^Fr = Eu Fr.
1 2
Таким образом, при небольшом числе размерных величин,
входящих в уравнение связи, метод линейных пропорционально-
стей в сочетании с методом комбинаций чисел подобия может
дать неплохие результаты в поиске единственного критериально-
го уравнения или в доказательстве существования ограниченного
числа таких уравнений.
142
7. МЕТОД СООТНОШЕНИЯ СИЛ НЬЮТОНА
В качестве еще одного способа отыскания условий подобия
механических систем можно рассмотреть метод, предполагаю-
щий их динамическое подобие при обеспечении подобия условий
однозначности. В этом состоит сущность метода, основанного на
законе подобия Ньютона. Сначала необходимо составить список
сил, влияние которых в поставленной задаче наиболее сущест-
венно, и установить их размерности. Далее находят числа подо-
бия, представляющие собой отношения этих сил.
Следует отметить, что этот метод принципиально не отли-
чается от метода размерностей, так как величины сил определя-
ются параметрами, от которых зависит явление. С другой сторо-
ны, метод допускает существование уравнений, устанавливаю-
щих связь между силами, действующими в системе. Следова-
тельно, он ничем принципиально не отличается и от метода по-
добия. Однако метод имеет и существенный недостаток, который
заключается в том, что во многих физических процессах имеются
величины, не зависящие от сил (например, поток теплоты).
При применении метода Ньютона необходимо знать зави-
симость соответствующей силы от характерных величин и физи-
ческих констант в виде формулы размерностей и названия чисел
подобия, которые получаются как отношения сил; обычно эти
данные представляются в виде таблицы. Например, в таблице 7.1
сведены пять основных в механике жидкости сил и сила упруго-
сти, указаны их отношения и соответствующие числа подобия.
Приведем формулу размерностей силы инерции:
[^]=[рИИ[«Ь где а - ускорение, V - объем, р - плотность. Но
ускорение в жидкости состоит из локальной и конвективной со-
143
du ди du dl ди ди ~
ставляющих: а- — =-----1----= — + — и, здесь приняты ооо-
dt dt dl dt dt dl
значения: и - скорость, t - время, l - линейная величина. Отсю-
да формулу размерностей силы инерции получим в таком виде:
[^]=[р][И|МИ-1+[MJ2 И Но [е] = [/]3, тогда имеем:
to]=[p][/]3 [«][']-’
где Р1л = р Z3 и t~l, FlK = р и2 Z2 - соответственно локальная и кон-
вективная составляющие силы инерции. Возьмем отношение
F^/F^-l /7 и — Sh, получили число Струхала, которое в таблице
отсутствует; кроме того, в ней приведена только конвективная
составляющая силы инерции.
Рассмотрим далее формулу размерностей силы тяже-
сти: [Fg ]=[р]Ш и отношение FiK[Fg =и2/g I = Fr. Формула
размерности силы давления такова: [Fp] = [Др] [.у] = [р] [/]2, где Др
- перепад давления, у - площадь приложения силы давления.
Найдем отношение Fp/FlK = Др/р и2 = Ей.
Известно, что касательное напряжение, возникающее между
слоями движущейся жидкости вследствие ее вязкости, определя-
ется формулой Ньютона т = ц.ди/д I, в которой p = pv-
динамическая, a v - кинематическая вязкость жидкости. Отсюда
получив формулу размерностей силы вязкости
] = Ы М = Ы И2 = [ц] М И, найдем: FiK/Fp = р и Z/p = и l/v = Re.
Формула размерности силы поверхностного натяжения
[7?a] = [cr][z], в которой ст - коэффициент поверхностного натяже-
ния - [ст]=№Г’=№?2 , - позволяет найти число Вебера из
отношения FiKlFa = pw2z/cr = We.
144
Таблица 7.1
Перечень основных сил в механике жидкости, их отношения к силе инерции (или об-
ратные величины) и соответствующие числа подобия
Основные силы Сила тяжести Fg Сила давления FP Сила вязкости Сила поверхн. натяже- ния Fo Сила упругости 'fe
Сила инерции Число Фруда Fg si Число Эйлера FP _ Р FiK Р и2 Число Рейнольдса F* v Число Вебера F,K Р м2 / Лт СГ Число Коши FiK _pu2 fe e
Сила вязкости Число Моше ни vw Число Стокса FP _ Pl __ ^1^ II т |q s 1 4 Six II
Сила давления FP be гГ и ь, 1 ь. — Число Стокса ^р.= р£ F^ ^2- = — Fp pl Tll^ Ъ J |tn II Чз | t4
Сила поверхн. натяже- ния Fa О Q. II г Ьо| г Ь Ь. 1 Fp pl о| » II Г ь| г а ь, 11ч — 2| b II r 411 b ь, 1 b.
Сила упругое. <Х)| - рч 0.1 II г Ьс г ь, |ь. faq | сч il Г . Ч ь, 1 Ь, И И II q —
Сила тяжести Fg — аГ и . Ч . Ч ь, | 1ч Число Мошени у и 0^1^ II 73 Q Oq <x>| II г ч| r k, | k.
В таблице находится также число Коши, равное отношению
силы инерции к силе упругости, формула размерности которой
такова: Ы = 1Ф]2, где Е - модуль упругости,
[е] = [я] [l] 2 = [М] [е]-1 [г]~2. Отсюда имеем: FjKlFE=pu2 /е = Со.
Как следует из таблицы 7.1, некоторые из указанных в ней
комбинаций чисел подобия встречались ранее в таблице 2.1. И
это понятно, так как, используя различные методы нормирования
уравнений движения вязкой жидкости, получаем различные от-
ношения сил, действующих в явлении. Но в таблице 2.1 этот факт
не находит отражения в явном виде, в то время как в таблице 7.1
он очевиден.
В заключение изложенных выше разделов, в которых были
даны основные положения теории физического моделирования
явлений, сформулируем третью или обратную теорему подо-
бия-. необходимые и достаточные условия подобия сопоставляе-
мых явлений состоят в равенстве чисел подобия и пропорцио-
нальности сходственных параметров, входящих в условия одно-
значности. Доказательство третьей теоремы подобия сопряжено
с трудностями, связанными с тем, что, например, теорема един-
ственности решений уравнения Навье-Стокса, описывающая
движение вязких несжимаемых дикостей, доказана только для
отдельных наиболее простых видов движения.
146
8. РОЛЬ ИНТЕГРАЛЬНЫХ СООТНОШЕНИЙ В ФИ-
ЗИЧЕСКОМ МОДЕЛИРОВАНИИ ЯВЛЕНИЙ
Выше неоднократно подчеркивалась необходимость ис-
пользования при обсуждении задач физического моделирования
интегральных соотношений. В этом усматривалась двоякая поль-
за. Во-первых, найти с их помощью явные связи между числами
и критериями подобия такие, которые изначально заданы и не
нуждаются в опытной проверке. Во-вторых, уменьшить размер-
ность факторного пространства, что при организации физическо-
го моделирования представляется очень важным. В интегральных
соотношениях физические величины представлены либо в виде
средних в пределах какого-либо сечения, либо осредненных во
времени. Между тем в сформулированном выше условии подо-
бия речь идет о величинах, характеризующих одно явление, ко-
торые определенным образом связаны с величинами другого яв-
ления, взятых в сходственных пространственно-временных точ-
ках. Но характерными называются такие величины, которые не
зависят от координат и времени. Следовательно, выбранные над-
лежащем образом для величин, действующих в точке, характер-
ные величины будут играть роль характерных и для средних по
живому сечению и осредненных во времени величин. Действи-
тельно, пусть Y - средняя по площади Q величина у (или осред-
147
ненная во времени за период Q ), пусть К - характерная величина,
тогда
Y = — Jy dm = -L j Y у' dm' = Y Y'; y-Y y'; Y = Y Y'; K' = —7 JV dm',
где величины co штрихом - безразмерные. Но в таком случае ус-
ловие подобия следует дополнить словами: « а та же в сходствен-
ных пространственно- временных сечениях».
Интегральные соотношения представляют интерес еще и
потому, что они содержат условия на границах, которые в урав-
нениях движения отсутствуют. Но тогда комбинации чисел подо-
бия, входящие в безразмерные интегральные соотношения и до-
полнительные условия на границах, следует включать в состав
чисел подобия, вытекающих из безразмерных уравнений движе-
ния, и рассматривать их совместно. Впервые это положение было
реализовано в [21], затем получило дальнейшее развитие в [20],
появилось в последующих публикациях, посвященных рассмат-
риваемой проблеме [23, 24].
Как известно, одномерные уравнения неустановившегося
движения жидкости для напорного и безнапорного потоков
(уравнения Сен-Венана) получаются из уравнений неразрывности
и Бернулли для целого потока, в последнем учитываются инер-
ционный напор, обусловленный локальным ускорением, и потери
удельной энергии (напора) на участке между рассматриваемыми
сечениями потока на преодоление сопротивлений движению (на
148
преодоление трения). Последние выражаются теми же зависимо-
стями, что и в случае равномерного движения [5, 13, 63].
Уравнение одномерного неустановившегося движения воды
в напорном трубопроводе имеет вид:
дН , UdU \dU XU2 /О1Ч
-----= J =------+------+------, (8.1)
д х р g д х g dt D 2 g
где И и Jр - соответственно пьезометрический напор и уклон,
U - средняя скорость течения воды в трубе, диаметр которой ра-
вен D, х - продольная ось трубы, t - время, g - ускорение силы
тяжести, X - коэффициент гидравлического трения. Все члены
уравнения Бернулли имеют линейную размерность и в сумме
представляют собой полную энергию жидкости, отнесенную к
единице ее веса, которая называется полной удельной энергией
жидкости в сечении потока. Уравнение (8.1) представлено в без-
размерном виде, для того чтобы оно было пригодным для ис-
пользования в натуре и на модели, сделаем безразмерными вели-
чины, входящие в него. С этой целью введем характерные вели-
чины, которые вновь будем обозначать соответствующей буквой
с чертой сверху. В таком случае в натуре имеем
Нн = Нн Н', хн = L х’, tH = Т„ t', U„ = U„ U', D„ = LH L'.
Соответственно на модели:
149
ННН', x =L x', t=Tt', U=UMU', D =L L'.
В приведенных зависимостях величины со штрихом безразмер-
ные, одинаковые для модели и натуры, с буквой « н » относятся к
натуре, с «.и»-к модели. Используя эти зависимости, получим
из уравнения (8.1) два уравнения: одно для натуры, другое для
модели.
Нн д Н' r U2 U'dU' UH 1 5 U' U2 A. U'2 ,о . ч
----= Jn = ----------+ —------+ ~----------, (8.2а)
LH д х' р,‘ L„ g dx' Тн g dt' LH D' 2 g
= J __U_M2U'dU' t UM \dU' । U„2 A U'2
LM dx' p« LM g dx' TM g dt' LM D'2g'
Уравнения (8.2a) и (8.26) безразмерные, они содержат без-
размерные величины, следовательно, они пригодны для исполь-
зования на модели и в натуре. Но тогда будут одинаковыми без-
размерные комбинации из характерных величин, вошедшие в
if н
них. Рассмотрим их, начиная с первой = _.Л-, из которой най-
дем индикатор: khlkt=\, kh=HH/HM, kt=LHlLM . Поскольку
напор имеет линейную размерность, то отсюда следует ожидае-
мый результат: kh = kt . Кроме того, Jр„ =JPu- Опуская под-
строчные индексы, запишем одно число подобия и одну комби-
нацию чисел подобия, которые содержат два последних уравне-
но
ния: —= = Fr, —— = FrSh . Таким образом, в уравнения (8.1) и
gL gT
(8.2) в явном виде вошло число Фруда и комбинация этого числа
с числом Струхала. Ранее при анализе уравнения Навье-Стокса,
кроме этих чисел подобия, были получены числа Рейнольдса и
Эйлера. Для того, чтобы доказать их присутствие в интегральном
уравнении (8.1), необходимо рассмотреть последний член, во-
шедший в это уравнение. Судя по безразмерным уравнениям
(8.2), этот член содержит комбинацию из числа Фруда и коэффи-
циента гидравлического трения: ZFr. Отсюда возникает задача
установить, что представляет собой коэффициент гидравлическо-
го трения в общем контексте физического моделирования гид-
равлических явлений. О ее решении речь пойдет в следующих
разделах.
Пока запишем уравнение (8.1) для неравномерного и равно-
мерного режимов движения жидкости в трубе. В случае неравно-
мерного движения имеем
дН т UdU \U2 /ооч
—r~ = Jn=-------+------ (8.3)
д х р g д х Dig
В таком режиме необходимо решить вопрос о том, что выбрать в
качестве характерного линейного размера, поскольку течение
происходит в трубе переменного поперечного сечения.
В случае равномерного движения получим
151
хи2
----= — Fr
D2g 8
U2
Fr = —-, D = 4R.
gR
(8-4)
Зависимость (8.4) представляет собой формулу Шези, записан-
ную в безразмерном виде; в ней в качестве характерного линей-
ного размера выбран гидравлический радиус трубы, а в качестве
характерной скорости - средняя скорость потока.
Принимая во внимание числа подобия, полученные в ре-
зультате анализа уравнения Навье-Стокса, а также выявленные в
этом разделе в результате анализа уравнения Сен-Венана, запи-
шем в общем виде безразмерное уравнение связи для неустано-
вившегося движения жидкости в трубопроводе:
FI Sh, Fr, Re, Eu, Fr Sh, J — Fr | = 0 . (8.
I P 8 )
Видим, что уравнение (8.5) содержит избыточную инфор-
мацию о явлении, в частности, это касается чисел Фруда, Струха-
ла и их произведения, числа Эйлера и пьезометрического укло-
на и т. д. Но решение о том, что можно опустить, а что оставить
для дальнейшего анализа, зависит от конкретно поставленной за-
дачи.
Для установившегося неравномерного режима движения
жидкости в трубе вместо уравнения (8.5) будет справедливо сле-
дующее:
152
Fr,Re, Eu, J„, — Fr =0.
p 8 J
(8.6)
Если движение равномерное, то избыточную информацию в
(8.6) несут два последних члена, так как в соответствии с зависи-
мостью (8.4) один из них можно опустить, а какой конкретно-
будет зависеть от постановки задачи исследований.
В связи с обсуждаемой задачей о равномерном движении
жидкости возникает вопрос о фундаментальных числах подобия,
характеризующих это движение. Действительно, как это следует
из всего изложенного выше материала, фундаментальные числа
подобия представляют собой отношения сил, действующих в яв-
лении, к конвективной составляющей силы инерции. Но при рав-
номерном движении сила инерции и ее составляющие отсутст-
вуют. Обратимся к уравнению Навье-Стокса (2.4), в котором
приравняем левую часть нулю (считаем Xj = g), найдем
0 = g--1---/?+v V2 н- / = 1,2,3.
р6хг.
Выберем характерные величины для скорости течения, дав-
ления и линейного размера, превратим с их помощью размерные
величины в безразмерные, получим
0 = g-
Р др
р1.дх\
(8.7)
153
В зависимости от способа превращения уравнения (8.7) в
безразмерное (нормирования его) можно получить следующие
г Р <
три числа подобия: ---— (характеризует отношение силы давле-
v V
ния к силе тяжести), —— (характеризует отношение силы внут-
gP
. PL PL о „
реннего трения к силе тяжести), а также ---= = —— = St . 11о-
v р V [iV
следнее число выше было названо числом Стокса (или Лагран-
жа), оно характеризует отношение силы давления к силе внут-
реннего трения). Среди полученных чисел подобия, естественно,
не оказалось ни одного фундаментального. Обнаруженное проти-
воречие легко устраняется, если учесть некоторые особенности
предельного перехода от полных дифференциальных уравнений
Навье-Стокса к упрощенным уравнениям. Они заключаются в
том, что нельзя производить упрощения в дифференциальных
уравнениях. Например, для получения из уравнений Навье-
Стокса решений, соответствующих предельному случаю течений
с очень большим числом Рейнольдса, необходимо выполнить
предельный переход к исчезающей малой вязкости (ц->0) не в
самих дифференциальных уравнениях, а в их решениях [62,
с.75-81]. Действительно, если в дифференциальном уравнении
движения вязкой жидкости Навье-Стокса отбросить член, учиты-
вающий вязкость, то получим дифференциальное уравнение Эй-
лера идеальной жидкости. Отсюда следует, что при анализе явле-
154
ний с использованием методов теории подобия и размерностей
всегда нужно исходить из полных дифференциальных уравнений
и полного перечня величин, от которых явление зависит. Но то-
гда полученные выше из неполного дифференциального уравне-
ния равномерного движения числа подобия можно представить в
виде комбинации фундаментальных чисел подобия:
Р r r vV Fr
---= = Fr Eu , ——- = —
p g £ g F Re
= St = Eu Re.
v p V
Сказанное полностью
распространяется и на другой пре-
дельный случай течений при малых числах Рейнольдса, которые
называются ползущими движениями, когда в первом приближе-
нии можно полностью пренебречь инерционными членами по
сравнению с членами, зависящими от вязкости [62]. Например, в
[19] подчеркивается, что для вывода соотношений подобия в
уравнениях движения грунтовых вод инерционные члены сохра-
няют.
Обратимся далее к дифференциальному уравнению одно-
мерного неустановившегося движения в открытых руслах. Оно
отличается от уравнения (8.1) тем, что в него вместо пьезометри-
ческого уклона входит уклон J свободной поверхности водотока,
которая в этом случае является пьезометрической линией. Давле-
ние вдоль этой линии постоянно и равно атмосферному. В самой
жидкости давление существует, но оно имеет гравитационное
происхождение (весовое давление).
155
Если zd - отметка дна над плоскостью сравнения, а
z - отметка свободной поверхности, то z = zd + h , здесь
_ „ dzdzddh.dh
h - глубина потока. Отсюда J ------=------------= i----, где
д х д х д х д х
д zd ,,
i =------ - уклон дна водотока. С учетом этого можно записать
д х
дифференциальное уравнение одномерного неустановившегося
движения воды в открытом русле:
, . dh UdU 1 dU X0U2
д х g д х g dt R 2 g
(8.8)
где Xo - коэффициент гидравлического трения открытого потока,
R - его гидравлический радиус.
В случае неравномерного движения уравнение (8.8) перепи-
сывается так:
, . dh UdU л0 U2
J = i------+ ——.
д х g д х R 2 g
(8.9)
Если движение равномерное, то — = О, J = / , и (8.9) превраща-
ется в безразмерное уравнение Шези:
г - ^0 U2 ^0 г?
J = i = —— = - Fr.
R 2g 2
(8.10)
156
В общем виде безразмерное уравнение связи для одномер-
ного неустановившегося движения жидкости в открытых руслах
будет таким
Т (sh, Fr, Re, Eu, Fr Sh, J, Fr^j = 0. (8.11)
Отсюда получим уравнение связи для неравномерного устано-
вившегося движения
V ^Fr, Re, Eu, J, у Fr^j = 0, (8.12)
а также для равномерного движения
(р ^Fr, Re, Ей, г, у Frj = 0. (8.13)
Как и в случае движения жидкости в напорных трубопрово-
дах, уравнения (8.11-8.13) содержат избыточную информацию.
Одной из важных задач при организации исследований на физи-
ческих моделях является поиск зависимостей для коэффициентов
гидравлического трения от определяющих критериев.
157
9. ИНДИКАТОРЫ ПОДОБИЯ - ОСНОВА ДЛЯ
УСТАНОВЛЕНИЯ СВЯЗЕЙ МЕЖДУ
КОЭФФИЦИЕНТАМИ ПОДОБИЯ
Как было отмечено во введении, главная задача моделиро-
вания - прогноз поведения оригинала в ситуациях, отличных от
тех, на основе которых была построена модель. При этом должны
быть установлены правила переноса полученных на модели ре-
зультатов на оригинал, в соответствии с законами перехода от
параметров модели к параметрам оригинала. Для этой цели ис-
пользуются индикаторы подобия. Из условия равенства чисел
подобия оригинала и модели следует равенство единице индика-
торов подобия, представляющих собой комбинации масштабных
коэффициентов. Если выбрать какой-либо индикатор подобия в
качестве основы, то из него можно получить связь между мас-
штабными коэффициентами, входящими в него. Выше такие свя-
зи неоднократно использовались при организации моделирова-
ния, в котором основную роль играл один из критериев подобия.
Вместе с тем обращалось внимание на трудности, которые появ-
ляются в том случае, когда явление определяется не одним, а не-
сколькими критериями, а требования к организации моделирова-
ния противоречат друг другу. Наиболее показательным в этом
отношении является вывод о невозможности организовать точное
физическое моделирования явления, которое определяется двумя
критериями: Фруда и Рейнольдса. Однако осуществить прибли-
женное моделирование вполне возможно, например, используя на
модели жидкость иных физических свойств или проводя их при
иной температуре, чем в натурных условиях. Но наиболее при-
влекательным является метод приближенного моделирования,
когда используются автомодельные области, в пределах которых
158
явление слабо зависит от одного из критериев. Это делает воз-
можным принимать на модели значение этого критерия на грани-
це автомодельной области, отличным от его величины в натур-
ных условиях. Выше было показано, как при моделировании «по
Фруду», принимая в условиях модели «граничное число Рей-
нольдса», можно определить требуемое значение линейного
масштабного коэффициента. При этом его величина оказывается
вполне приемлемой для организации физического моделирования
в условиях ограниченных размеров лабораторного помещения. В
ряде случаев можно получить хорошие результаты, сочетая этот
вид моделирования с использование на модели жидкость иных
физических свойств, чем в натуре (например, моделирование
безнапорных водных потоков на напорных воздушных моделях).
Трудности многократно возрастают при физическом моде-
лировании двухфазных жидкостей, например, движения наносов
в водном потоке. В этом случае явления в каждой фазе характе-
ризуются своим набором критериев подобия, которые по харак-
теру влияния на явления могут отличаться друг от друга. Напри-
мер, взвесенесущий поток может относиться к области квадра-
тичного сопротивления, в то время как наносы по своим разме-
рам относятся к иным областям.
При моделировании явлений, происходящих в многофазных
потоках, полезно для проведения анализа условий моделирования
привлекать индикаторы подобия. В частности, такой анализ по-
зволяет в двухфазном потоке, каким является вода, переносимая
речные наносы, определить условия, при которых явления в не-
сущей жидкости и в переносимых ею наносах будут относиться к
одной и той же или к разным областям сопротивления. Можно
также установить, какими свойствами должны обладать несущая
жидкость и переносимый ею материал, если использование на
159
модели той же жидкости и того же песчаного материала, что и в
натуре, не может обеспечить подобия явлений. В первую очередь
это относится к явлениям, которые в натурных условиях проис-
ходят в мелкозернистых песках. Индикаторы подобия в этих ус-
ловиях позволяют установить, какими физическими свойствами
должны обладать участвующие в движении фазы для достижения
приближенного подобия явлений, протекающих в натуре и на
модели. Наконец, можно найти условия, при которых физическое
моделирование явлений в двухфазных потоках в том смысле, в
котором оно здесь обсуждается, станет невозможным. В качестве
альтернативы в этом случае следует рассмотреть организацию
серийных исследований на моделях разных линейных размеров, в
основу которых также положен анализ явления с помощью инди-
каторов подобия. В последующих разделах такой метод анализа
будет широко использоваться.
160
10. МОДЕЛИРОВАНИЕ ЯВЛЕНИЙ В ЖЕСТКОМ
РУСЛЕ
10.1. Моделирование равномерного движения напорного
потока.
Если движение равномерное, то перепад давления Др на
участке трубы длиной I уравновешивается сопротивлением тре-
ния. Отсюда, приравнивая силу давления (движущий перепад
давления) силе сопротивления трения [22], получим формулу
равномерного движения воды в трубе диаметром D:
71 D2
Ap^~ = x0TtDl, (10.1)
где т0 - напряжение трения на стенке трубы. Следовательно
* / о D
Др = тп —, R = —.
0 Я 4
Как отмечалось ранее, напряжение трения принято связы-
вать с кинетической энергией потока; тогда получим:
U2 I
Др = Хор^1 (10.2)
2 л
Но по традиции в гидромеханике и гидравлике вместо (10.2)
используется зависимость Дарси-Вейсбаха, которая условию рав-
номерного движения не соответствует:
U2 I
(103)
161
Сравнивая (10.2) и (10.3), находим связь между коэффици-
ентами гидравлического трения, входящими в эти зависимости:
X. = 4 Xq .
Обратимся далее к безразмерному уравнению связи (8.6),
соответствующему рассматриваемому виду движения, и опреде-
лим в нем число Эйлера, используя зависимость (10.3). Но преж-
де напомним, что в числа подобия должны входить характерные
величины, которые от времени и координат не зависят. Перепад
давления Др этому требованию не удовлетворяет, так как опре-
деляется на участке трубы произвольной длины /. Выберем в ка-
честве характерного линейного размера гидравлический радиус
трубы и определим характерный перепад давления Дрд на участ-
ке трубы с характерной длиною А. Тогда, учитывая линейную
пропорциональность рассматриваемых перепадов, найдем связь
между ними:
Др = ДрЛ (10.4)
Л
Запишем теперь число Эйлера, используя величину харак-
терного перепада давления в соответствии с (10.4) и выбрав в ка-
честве характерной среднюю скорость течения жидкости в трубе
Еи = ^Ц- = ^-. (10.5)
pU2 pU2 I
Теперь подставим в зависимость (10.5) величину перепада
давления, используя формулу (10.3), получим
Еи = |. (10.6)
162
Таким образом, число Эйлера равно одной восьмой коэффи-
циента гидравлического трения. Можно сказать, что с точностью
до постоянной роль числа Эйлера играет коэффициент гидравли-
ческого трения. В таком случае зависимость (8.4) следует пред-
ставить в таком виде:
- = , Fr7=—, gj=Jpg, (Ю.7)
8 Fr Fr7 gj R p
где Fr7 - преобразованное число Фруда, в котором ускорение си-
лы тяжести g заменено произведением Jp g. В таком виде оно
напоминает плотностное число Фруда
„С2 (prp'l пг л
Fr =----, g = ——- g . Обычно числа, обратные этим чис-
gP R Ip;
лам подобия Фруда, принято связывать с именем Ричардсона.
Они характеризуют отношение активной (движущей) силы к силе
инерции. Здесь уместна такая аналогия: допустим, движение
жидкости происходит не в напорном трубопроводе, а в открытом
русле, гидравлический радиус которого равен R, средняя ско-
рость течения U, дно имеет уклон J , движение равномерное,
поэтому свободная поверхность параллельна линии дна и являет-
ся пьезометрической линией. Но тогда произведение Jp g имеет
ясный физический смысл - оно характеризует отношение проек-
ции силы тяжести на ось потока к силе тяжести. Именно эта про-
екция является той активной (движущей) силой, которая приво-
дит жидкость в движение. Сказанное позволяет безразмерное
уравнение связи (8.6) для случая равномерного установившегося
движения в трубе записать в таком виде:
163
= 0.
(10.8)
В (10.8) в силу того, что движение установившееся равно-
мерное, последний член равен единице, поэтому для дальнейшего
анализа представим это уравнение так
/.(Frj.Re, Eu) = 0.
(Ю.9)
Заметим, что при анализе равномерного установившегося
движения жидкости в трубе возникают трудности, которые в пер-
вую очередь касаются входящего в безразмерное уравнение связи
числа Фруда. Обычно для их устранения трубу считают горизон-
тальной, тем самым число Фруда исключается из рассмотрения
[20, 22]. Однако полагаем, что эти трудности вполне преодолимы.
Это следует из постановки двух практических задач, анализ кото-
рых излагается ниже, поиска соответствующих критериальных
уравнений и получения экспериментальных зависимостей на их
базе.
Первую задачу сформулируем так: расход жидкости, гео-
метрические размеры трубы, в том числе высота выступов шеро-
ховатости ее внутренней поверхности и физические свойства
жидкости заданы; требуется определить перепад давления (или
падение пьезометрической линии) на участке трубы длиной I.
Следовательно, скорость течения по условию этой задачи задана.
Но тогда уравнение (10.9) содержит одно число подобия - Эйлера
и два критерия подобия - Фруда и Рейнольдса. В соответствии со
1 А.
сказанным выше имеем: — = Ей = - , поэтому критериальное
Fiy 8
уравнение для рассматриваемой задачи будет иметь такой вид:
X = <p(Re). (10.10)
164
Уравнение (10.10) следует дополнить условиями однознач-
ности, в них входят форма цилиндрической трубы, конфигурация
ее поперечного сечения, которую чаще всего характеризует гид-
равлический радиус, и высота выступов шероховатости А ее
внутренней поверхности. Однако не следует забывать, что ре-
зультаты исследований всегда имеют конкретный адрес: кон-
кретный цилиндрический трубопровод определенной конфигура-
ции поперечного сечения трубы (например, труба может быть в
поперечного сечения круглой, квадратной, треугольной и т. п.).
Это, в частности, означает, что каждую трубу нового поперечно-
го сечения или иной шероховатости ее внутренней поверхности
нужно исследовать заново, в том числе определять характерную
линейную величину ее поперечного сечения [22, 62].
С учетом этого запишем критериальное уравнение (10.10) в
окончательном виде
Л. = ф | Re, —, форма трубы |, г= — , (10.11)
V г ) 2
где г - радиус трубы (в гидромеханике принято абсолютную ше-
роховатость внутренней поверхности трубы относить к ее внут-
реннему радиусу).
Критериальное уравнение (10.11) позволяет наметить план
проведения экспериментов с целью определения в результате ис-
следований коэффициента гидравлического трения. Установив
его величину из графиков или соответствующих формул, можно
из (10.3) найти перепад давления на отрезке трубы длиной I и ве-
личину падения пьезометрической линии A hp по формуле:
Pg
, U2 I
Л-----,
2g D
(10.12)
165
а также пьезометрический уклон из зависимости
(10.13)
Сформулируем далее вторую задачу: в цилиндрической
трубе заданной геометрической формы известен перепад давле-
ния Др на длине трубы I; нужно определить расход воды и ско-
рость ее течения в трубе. Следовательно, в такой постановке за-
дачи среди чисел подобия в уравнении (10.9) нет ни одного кри-
терия. Для получения критерия подобия возьмем комбинацию
чисел Фруда и Рейнольдса и заменим ею число Рейнольдса, по-
лучим вместо (10.9)
V (Frj, АП, Eu) = 0, = (10.14)
Fr7 v2
где критерий Архимеда Агу аналогичен рассмотренному выше
fp> -
критерию того же названия, в котором отношение —- заме-
I Р J
нено пьезометрическим уклоном J. Отсюда, принимая во вни-
мание вышесказанное, получим вместо (10.11) следующее крите-
риальное уравнение
к = 0 | Агу, —, форма трубы |. (10.15)
( г J
Здесь уместно отметить, что в [22, с. 464-465] труба была
принята расположенной горизонтально, поэтому вместо уравне-
ния связи (10.9) исследовалось такое
/1(Re,Eu) = 0. (10.16)
166
Во втором расчетном случае при отсутствии критериев по-
добия было предложено в качестве критерия использовать сле-
дующую комбинацию из чисел подобия Эйлера и Рейнольдса
EuRe2. Но при этом связь числа Эйлера с коэффициентом гид-
равлического трения не была установлена, поэтому комбинацией
было заменено число Эйлера, а критериальное уравнение пред-
ставляло собой зависимость числа Рейнольдса от предложенного
критерия. Прежде, чем записать это уравнение, расшифруем
предложенный критерий, используя для числа Эйлера формулу
(10.5), имеем:
Eu Re2 = A = (10.17)
pU2l v2 р v2 Z
Теперь запишем упомянутое критериальное уравнение
Re = —= (10.18)
Экспериментальные данные, подтверждающие это критери-
альное уравнение, отсутствуют, но необходимости в их проведе-
нии нет. Докажем это, продолжив расшифровку критерия (10.17)
Э Др R3 &hn g R3 Jn g R3
^Лг, (10.19)
p V I Iv V
Таким образом, комбинация чисел подобия Эйлера и Рей-
нольдса также представляет собой найденный выше критерий
Архимеда, и критериальное уравнение (10.18) нужно записать в
таком виде (без записи условий однозначности)
Re = —= /(Аг7). (10.20)
v
167
Покажем далее, что предпочтение нужно отдать критери-
альному уравнению (10.15). С этой целью установим связь между
числами Рейнольдса и Архимеда. Возведем число Рейнольдса в
квадрат, а затем заменим скорость течения в соответствии с зави-
симостью (10.13) (формулой Шези), найдем
D 2 U2 R2 % Jpg В? 8
Re =----— =---;— = — Аг
v2 Л, v2 А,
(10.21)
Следовательно, имея в виду соотношения (10.6) и (10.7),
2 Re2
приходим к ожидаемому результату: Аг7 = Eu Re =---. Отсюда
Fry
можно сделать такой вывод: если получены графики, а также эм-
пирические формулы, соответствующие критериальному уравне-
нию (10.11), (а таких сегодня имеется достаточно большое коли-
чество), то эти графики и формулы могут быть с помощью зави-
симости (10.21) представлены в виде, отвечающем критериаль-
ному уравнению (10.15).
Вторая задача решается таким образом: при заданных пере-
паде давления на отрезке трубы известной длины, диаметре тру-
бы, размерах выступов шероховатости ее внутренней поверхно-
сти и параметрах, определяющих физические свойства жидкости,
из (10.15) находится коэффициент гидравлического трения. Далее
из формулы (10.3) определяется скорость течения и вычисляется
расход воды.
Следует отметить, что при наличии графиков и формул, со-
ответствующих критериальному уравнению (10.11), вторая зада-
ча сравнительно легко решается методом последовательного
приближения.
168
На рисунке (10.1) представлен график, полученный по ре-
зультатам исследований И. Никурадзе, выполненных в круглых
трубах, внутренние поверхности которых оклеивались однород-
ным песком с различными размерами зерен [22, 62]. На рисунке
по горизонтальной оси отложено число Рейнольдса, в котором в
качестве характерного размера выбран диаметр трубы
п U D
Rep =---, а в качестве характерного размера в относительной
v
шероховатости - радиус трубы r = D/2. Относительная шерохо-
ватость изменялась в широких пределах: от 1/15 до 1/1300. Таким
образом, постановка экспериментов и их обработка выполнялись
в соответствии с критериальным уравнением (10.11). На графике
выделяют две области, которые разделяет число Рейнольдса при-
близительно равное 2300. Если числа Рейнольдса меньше этого
граничного значения, то течение в трубе ламинарное, ему соот-
ветствует закон сопротивления Пуазейля, при котором коэффи-
циент гидравлического трения зависит только от числа Рейнольд-
са и обратно пропорционален ему
64
(10.22)
При больших значениях числа Рейнольдса вначале имеет
место промежуточная переходная область, а затем реализуется
область турбулентного режима течения. В ней три зоны, пределы
существования каждой определяет такое число Рейнольдса
г> А
Re„ =---, в котором щ - динамическая скорость потока
v
u2=^=-U2, (10.23)
Р 8
169
Тр - касательное напряжение на внутренней поверхности трубы.
Рис. 10,1. Зависимость коэффициента гидравлического
трения от критерия Рейнольдса и относительной
шероховатости по опытам в шероховатых трубах
Первая зона (ей на рисунке (10.1) соответствует нижняя
прямая) характеризует гидравлически гладкий режим без прояв-
ления шероховатости, при котором выступы элементов шерохо-
ватости лежат внутри ламинарного подслоя. В ней число Рей-
нольдса находится в пределах
0 < Re* < 5.
(10.24)
Известно [22, 62], что условной толщине ламинарного под-
слоя б соответствует следующее значение числа Рейнольдса
Re* =^<11,5.
v
Тогда условие( 10.24) можно записать еще и в таком виде
170
0<A<0,43S.
В этой зоне реализуется закон сопротивления Г. Блазиуса
0,3164
~ Re°,25 ’
(10.25)
Этот закон справедлив при Ren <105. Так называемый, уни-
версальный закон сопротивления Прандтля для гладких труб дает
прекрасное совпадение с опытными данными Никурадзе вплоть
до числа Рейнольдса 3,4-106, однако, выражается формулой, в
которую коэффициент гидравлического трения входит в неявном
виде
(10.26)
Никурадзе предложил пользоваться следующей явной зави-
симостью
X = 0,0032 +
0,221
Re0/37
(10.27)
Для зоны, в которой реализуется режим с полным проявле-
нием шероховатости (ее элементы выступают из ламинарного
подслоя), сопротивление в основном определяется их формой,
поэтому закон сопротивления получается квадратичным. Этой
зоне соответствует следующее условие:
Re* > 70,
(10.28)
которое можно записать в таком виде:
А > 6,15.
171
Закон сопротивления в этой зоне имеет вид
4= = 21g- + 1,74.
VI А
(10.29)
В переходной зоне, где выполняются условия
5 < Re. < 70;
0,43 < - < 6,1,
3
Колбрук и Уайт вывели для закона сопротивления следующую
формулу
4= = 1,74 - 21g
VI
Га 18,7
4- г=
(г Re^VXJ
(10.30)
При А -> 0 она переходит в формулу для гидравлически гладкой
трубы, а при условии Ren -> да - в формулу для вполне шерохо-
ватой трубы.
Выше неоднократно подчеркивалась важность использова-
ния в условиях приближенного моделирования явлений автомо-
дельных зон. В рассматриваемом случае подобная зона, в кото-
рой явление не зависит от числа Рейнольдса, характеризуется ус-
ловием (10.28). Получим из него величину граничного числа
Рейнольдса, используя формулу (10.23) между динамической и
средней скоростью потока.
г/. А _ pt U г А _ U D Д
v V 8 v г \ 8 2 v г
Отсюда, учитывая зависимость (10.29), находим
(U D\ 140 V8 г 396 г ( г V
~ =369 21g—-+1.74 -. (10.31)
I V )г VI А VIА I А )Д
172
Обратимся далее к решению второй сформулированной вы-
ше задачи: поиска зависимостей, соответствующих критериаль-
ному уравнению (10.15) для труб круглого поперечного сечения.
Следует отметить, что это было сделано в [3], однако, не имея
строгого обоснования такого подхода, автор произвел пересчет
опытных данных Никурадзе. В этом не было никакой необходи-
мости, так как задача заключалась в представлении эксперимен-
тальных формул, отвечающих критериальному уравнению
(10.11), в виде (10.15), используя преобразование (10.21). Сдела-
ем это.
В области ламинарного режима, где закон сопротивления
определяется зависимостью (10.22), получим
512
Х = —. (10.32)
Области ламинарного режима будет соответствовать сле-
дующее значение граничного числа Архимеда Aiy < 18400.
Для того чтобы при турбулентном режиме установить зону
существования гидравлически гладкого русла, найдем связь меж-
ду числом Рейнольдса Re* и критерием Архимеда Аг7
Re.2 = Л Л Re2 4 = 4 Ar, Н
8 v2 R2 8 R2
r=2R.
v2
Отсюда имеем
Аг7 = 0,25 Re2
(10.33)
С учетом (10.24) получим
173
2
0< Arj <6,25
г
A
(10.34)
Далее, используя зависимость (10.21), найдем связь между
числом Рейнольдса Ren и критерием Архимеда Лг7
ReD=4Re, Rep =16 Re2 = 128 Ar7/X. (10.35)
Обратимся теперь к формуле (10.25), которую возведем в
восьмую степень и произведем преобразования, используя зави-
симость (10.35)
х8 = (0,3164)8 = (0,3164)8 Л,
Re^ 128 Аг7
Отсюда имеем
(0,3164)8/7 0,1342
(1036)
С тем, чтобы определить пределы, в которых можно исполь-
зовать формулу (10.36), произведем подстановку коэффициента
гидравлического трения из нее в (10.35), получим
Rep = 128 Arj = 12SA г8/7 = 38 Дг8/7 j 0
и X 0,3142 J
Формула (10.36) - аналог зависимости Блазиу-
са - справедлива при условии ReD < 105; подставляя это значение
числа Рейнольдса в (10.37), найдем после преобразований
Arj < 2,926-106 . (10.38)
174
Покажем, что во второй задаче универсальный закон сопро-
тивления Прандтля в этой зоне оказался выраженным в явном
виде. Для поиска аналога закона (10.26) воспользуемся зависимо-
стью (10.35), из которой получим
Ren VX = 11,31 ^/ArJ
Подставляя этот результат в (10.26), найдем
= 2,0 lg(TA?;)+ 1,31.
у А
(10.39)
(10.40)
Используя зависимости (10.35) и (10.40), установим связь
между числом Рейнольдса и критерием Архимеда в неявном виде
ReD = 11,31 7Ai7 (2 Ig^ + 1,31).
Методом итераций, принимая Re/} =3,4-106, было получено
предельное значение критерия Архимеда, до которого закон со-
противления (10.40) остается справедливым, оно равно
Arj =8,5-1О8.
Обратимся далее к закону сопротивления Никурадзе (10.27)
и найдем его аналог во второй задаче. В ней этот закон выража-
ется формулой, в которую коэффициент гидравлического трения
входит в неявном виде. Для получения этой формулы воспользу-
емся зависимостью (10.35), из нее найдем
Подставив этот результат в формулу (10.27), придем к сле-
дующей зависимости
175
Х = 0,0032+ 0,1244
z ч 0.1185
Л
(10.41)
Поиск предельного значения критерия Архимеда, до кото-
рого формула (10.41) будет справедлива, затруднен, так как кри-
терий Архимеда в рассматриваемом случае зависит не только от
числа Рейнольдса, но и от коэффициента гидравлического тре-
ния, в чем легко убедиться. Но расчеты по формулам Прандтля и
Никурадзе дают практически совпадающие результаты, поэтому
можно предположить, что формула (10.41), как и (10.40), будет
справедлива до Aiy = 8,5 • 108.
Естественно, что в зоне квадратичного сопротивления во
второй задаче закон сопротивления не изменится и будет, как и в
первой задаче, выражаться формулой (10.26). Однако, необходи-
мо определить условия существования этой зоны, используя ана-
логичное условие (10.28) в первой задаче. Имея в виду эту цель,
воспользуемся зависимостью (10.33), получим, принимая во вни-
мание (10.28)
/ \2
Аг, >1225 -
Следовательно, граничное число Архимеда равно
/ \2
Аг, =1225 —
(10.41)
(10.42)
В переходной области, границы которой определяются ус-
ловием
/ \2 / -,2
6,25 - < Аг, < 1225 - ,
Ш Ia J
(10.43)
176
формула Коулбрука-Уайта (10.30) с учетом зависимости (10.39)
во второй задаче приобретает такой вид
1 =1,74-2 lg — +
VA, г
А 1,653
г ,/Агг
(10.44)
При А -> 0 она переходит в формулу для гидравлически гладкой
трубы, а при условии Аг7 -> оо - в формулу для вполне шерохова-
той трубы.
Покажем на примере, что все полученные выше зависимо-
сти, хорошо увязаны между собой. Допустим, нужно создать мо-
дель трубопровода для проведения испытаний в условиях равно-
мерного режима движения воды в нем. Натурный трубопровод
имеет такие характеристики: диаметр трубы D -1 м, относитель-
Г
ная гладкость внутренней поверхности — = 60, скорость течения
А
U = 1,5м/с, кинематическая вязкость воды v = 0,01 см2/с. Вначале
делаем предположение о том, что течение воды в трубопроводе
относится к зоне квадратичного сопротивления. По формуле
(10.29) находим величину коэффициента гидравлического тре-
ния: Х = -----------= = 0,0356 . Далее из формулы (10.23) опре-
(21g 60 + 1,74)2
деляем динамическую скорость потока
/0,0356 . ! , т „
и* = ------ 150 = 10,01 см/с . Теперь можно наити число Реи-
v 8
нольдса Re* = г = — —— 50 = 834,4 > 70 . Это означает,
v vr 0,01-60
что течение в трубе относится к режиму квадратичного сопро-
тивления, у которого критерий Рейнольдса равен
177
Ren = ^0 0^° =1’5-1°6 • Д^166 по формуле (10.31) находим гра-
ничное число Рейнольдса, соответствующее рассматриваемой за-
даче началу зоны квадратичного сопротивления
1<ел г = 369 (2 lg60 + 1,74) 60 = 0,117 • 106 . Принимаем на модели
число Рейнольдса равным граничному значению, находим мас-
штабный коэффициент числа Рейнольдса
Re„ Ren , к, к,. 1,5 . -
—~ = —— = kRe = ——- =-------= 12,79 . Моделирование будем
Re„ ReD<> kv 0,117
проводить при условии равенства критериев Фруда на модели и в
натуре. Но в таком случае, полагая, что натура и модель находят-
ся в поле земного тяготения, имеем такие соотношения между
масштабными коэффициентами:^ = 1, ки = , где kI,klt,kg -
масштабные коэффициенты соответственно линейный, скорости
и ускорения силы тяжести. Кроме того, считаем, что на модели и
в натуре используется одна и та же жидкость - вода, следова-
тельно, масштабный коэффициент вязкости kv -1 .Но тогда по-
лучим: kRe = Л/'2 - 12,79 . Отсюда линейный масштабный коэф-
фициент будет равен к{ - (12,79)2/3 =5,47 . Получается, что модель
может быть выполнена в масштабе одной пятой натуральной ве-
личины DM = 0,2 jw . Далее определим скорость течения и расход
воды в условиях модели: UM = UH/y/lq = \,5/4$ = 0,671 м/с ;
тг 0 22
QM = 0,671—— = 0,021 м3/с . Для определения уклона пьезомет-
рической линии воспользуемся зависимостью (10.13), из которой
следует, что при моделировании «по Фруду» уклоны этой линии
на модели и в натуре будут одинаковыми:
178
рн
= 0,0356
1,52
2-9,81-1
= 0,0041 . Расход воды в натуре равен
Jр м
0Н =1,5 ^ = 1,18 м3/с , масштабный коэффициент расхода воды
Icq = kj/2 . Проверим этот вывод: kQ = - 56 = к^2 = 53/2 = 56 .
Сформулируем задачу по-иному: заданы параметры трубо-
провода, вязкость жидкости и пьезометрический уклон, найти
скорость течения и расход воды в нем. Используем приведенные
в предыдущем примере данные и результаты. Прежде всего, оп-
ределим критерий Архимеда в натурных условиях
, 0,0041-981-(25)3 ° тт ~
Аг/н =------——— = 6,28-10* . Далее найдем из (10.42) гра-
ничное значение этого критерия Аг7г=1225 • (б0)2= 4,41-106 .
В связи с тем, что выполняется условие Аг//( > Аг7г, коэффици-
ент гидравлического трения определяем по формуле (10.29)
Х =------------г = 0,0356 . Теперь из формулы (10.13) можно
(2 1g 60 + 1,74)2
найти скорость течения воды в трубе
г г 10,0041 ~ Q ~ .
и = ’2 ‘9,ol -1 = 1,5 м/с . Будем, как и ранее, считать, что
моделирование явления реализуется «по Фруду», поэтому вы-
полняется условие JpH=Jрм . Принимаем на модели критерий
Архимеда равным граничному значению Аг/ и = Аг7., . Далее
возьмем отношение натурного значения критерия Архимеда к
модельному, получим соответствующий масштабный коэффици-
, Аг7„ 628 Л
ент кАг =-----=----= 142,4 . Учитывая сказанные выше сообра-
Аг/л 4,41
179
жения относительно масштабных коэффициентов ускорения и
вязкости, а также принимая масштабный коэффициент пьезомет-
рического уклона kj =JpHlJpM равным единице получим связь
между масштабным коэффициентом критерия Архимеда и ли-
нейным в таком виде kt = ^кАг = д/142,4 = 5,22 . Остальные расче-
ты совпадают с теми, которые были выполнены выше; основной
вывод состоит в том, что их результаты, полученные по двум ме-
тодам, отличающимся постановкой задачи и критериями подо-
бия, совпали.
10.2. Моделирование равномерного движения безнапор-
ного потока
При равномерном движении безнапорного открытого потока
активной (движущей) силой является составляющая силы тяже-
сти, параллельная оси русла, которая наклонена к горизонту под
некоторым весьма малым углом а (величина sin а ~ tg а ~ а на-
зывается уклоном дна i). На длине канала I образуется перепад
уровней свободной поверхности А А, свободная поверхность (как
об этом уже было указано ранее) является пьезометрической ли-
нией. Провидимому впервые А.П. Зегжда ввел по аналогии с пе-
репадом давлений в напорном потоке при равномерном режиме
движения на длине трубопровода I перепад давлений в открытом
безнапорном потоке на длине канала I на том основании, что
свободная поверхность является пьезометрической линией. В
разделе 10.1 рассматривалась аналогия между напорным потоком
и безнапорным, при этом напорный поток заменялся безнапор-
ным, у которого свободная поверхность совпадала с пьезометри-
ческой линией напорного потока, а скорость течения и геометри-
ческие параметры русла и трубы полностью совпадали. Аналогия
180
Зегжды предполагает наоборот замену безнапорного потока на-
порным, у которого пьезометрическая линия совпадает со сво-
бодной поверхностью безнапорного потока, а скорость течения и
геометрические параметры русла и трубы также полностью сов-
падают. Это позволило по образцу формулы (10.2) для перепада
давлений в напорном потоке получить соответствующую зависи-
мость для перепада давлений в открытом потоке, который в ука-
занном выше смысле аналогичен напорному потоку. Такая зави-
симость получается из условия равновесия отсека открытого по-
тока, длина которого равна I.
При равномерном движении безнапорного открытого потока
образующие поверхности дна параллельны свободной поверхно-
сти, в любом поперечном сечении площадь («живое сечение») <в,
средняя скорость U, смоченный периметр % и глубина потока
остаются неизменными. Приравнивая составляющую силы тяже-
сти (движущую силу) силе сопротивления трения, получим урав-
нение движения равномерного безнапорного открытого потока
pgco// = T0x/, (10.45)
где т0 - касательное напряжение, приложенное ко дну потока.
Отсюда найдем следующее выражение, аналогичное формуле
(10.2), приведенной в разделе 10.1,
pgAA = T0—, 7? = — , \h = li, (10.46)
R х
где R - гидравлический радиус потока. Будем, как и ранее, счи-
тать касательное напряжение пропорциональным кинетической
энергии потока, тогда из (10.46) следует
U2 I
pgAA = XopH_l. (10.47)
z К
181
В формуле (10.47) перепад уровней не является величиной
характерной, так как относится к нехарактерной длине водотока,
в качестве характерного выберем перепад уровней A hR на длине
потока, равной гидравлическому радиусу. Связь между ними,
учитывая ее линейный характер, определяет зависимость
А /г = A hR I/R . Подставляя этот результат в (10.47), получим
ц2
pgAAA=Xop —. (10.48)
Далее, используя уравнение (10.48) и характерные величи-
ны, запишем число Эйлера
Еи = Р^Л^ = Хо (10.49)
pH2 2
Таким образом, аналогия Зегжды позволяет для безнапорно-
го потока, у которого давление на свободной поверхности всюду
одинаковое и равное атмосферному, а давление гравитационной
природы внутри жидкости при равномерном режиме подчиняется
гидростатическому закону и в любом сечении тоже одинаковое,
ввести число Эйлера, роль которого играет половина коэффици-
ента гидравлического трения.
Теперь вместо зависимости (8.10) можно записать следую-
щую
= ~ = gi = ig. (10.50)
2 Fr Fr, g,. R
Следовательно, преобразованное число Фруда имеет ясный
физический смысл: оно характеризует отношение силы инерции к
проекции силы тяжести (движущей силы) на ось потока. Сказан-
182
ное позволяет безразмерное уравнение связи (8.13) для случая
равномерного движения безнапорного открытого потока записать
в такой форме
( 1 \
Ф Fr, Re, Eu, — Fr,- = 0.
I 2 ‘J
(10.51)
Но в соответствии с зависимостью (10.50), которая пред-
ставляет собой формулу Шези, записанную в безразмерном виде,
последний член в уравнении (10.51) равен единице, поэтому это
уравнение можно переписать в таком виде
ф (Fr;, Re, Еи)= 0. (10.53)
Далее, как это было сделано в случае движения воды в на-
порном трубопроводе, рассмотрим две задачи. Первую сформу-
лируем так: расход воды, геометрические параметры русла, в том
числе высота выступов шероховатости его дна и физические
свойства жидкости заданы; требуется определить перепад уровня
воды на участке водотока длиной /. Следовательно, скорость те-
чения по условию этой задачи задана. Но тогда уравнение (10.53)
содержит одно число подобия - Эйлера - и два критерия подо-
бия - Фруда и Рейнольдса. В соответствии со сказанным выше
имеем: — = Еи = —, поэтому критериальное уравнение для рас-
Ег; 2
сматриваемой задачи будет иметь такой вид:
= ф ( Re, форма русла j.
(10.54)
Критериальное уравнение (10.54) позволяет определить в
результате исследований коэффициент гидравлического трения,
затем найти перепад уровня воды на отрезке водотока длиной I
183
из следующей формулы, полученной в результате преобразова-
ния зависимости (10.47)
uLl
2gR
A h = Хо
(10.55)
Вторая задача формулируется так: в цилиндрическом безна-
порном открытом русле известен перепад уровней воды А Л на
длине водотока Z; нужно определить расход воды и скорость ее
течения. В такой постановке задачи среди чисел подобия в урав-
нении (10.53) нет ни одного критерия. Для получения критерия
подобия возьмем комбинацию чисел Фруда и Рейнольдса и заме-
ним ею число Рейнольдса, найдем
2 • 3
v(Fr;,Ar;,Eu) = 0, Аг/.=^- = ^. (10.56)
Fr;- v2
Отсюда, учитывая приведенные выше результаты, придем к
следующему критериальному уравнению
х0=е
Агг , —, форма русла
(10.57)
Далее из второй формулы в (10.56) найдем связь между кри-
териями Рейнольдса и Архимеда
Re2 = Ar- Fr- = = -2- Ат . (10.58)
' Ей Хо
Из сказанного следует такой вывод: если получены графики,
а также эмпирические формулы, соответствующие критериаль-
ному уравнению (10.54), то эти графики и формулы могут быть с
помощью зависимости (10.58) представлены в виде, отвечающем
критериальному уравнению (10.57),
184
Вторая задача решается таким образом: при заданных пере-
паде уровня воды на отрезке русла длиной I, гидравлическом ра-
диусе, размерах выступов шероховатости поверхности дна и па-
раметрах, определяющих физические свойства жидкости, из
(10.57) находится коэффициент гидравлического трения. Далее из
формулы (10.55) определяется скорость течения, затем вычисля-
ется расход воды.
Здесь, как это уже было сказано ранее, следует также отме-
тить, что при наличии графиков и формул, соответствующих
критериальному уравнению (10.64), вторая задача сравнительно
легко решается методом последовательного приближения.
На рисунке (10.2) представлены графики, полученные по ре-
зультатам исследований А.П. Зегжды, выполненных в открытых
безнапорных лотках прямоугольного поперечного сечения, внут-
ренняя поверхности которых оклеивались однородным песком с
различными размерами зерен [16, 21]. На рисунке по горизон-
тальной оси отложено число Рейнольдса, в котором в качестве
характерного размера выбран гидравлический радиус Re =--- .
v
К гидравлическому радиусу отнесена величина абсолютной ше-
роховатости дна водотока. Относительная шероховатость изме-
нялась в пределах от 1/5 до 1/80. Постановка экспериментов и их
обработка выполнялись в соответствии с критериальным уравне-
нием (10.54). На графике выделяют две области, которые разде-
ляет число Рейнольдса приблизительно равное 800. Если числа
Рейнольдса меньше этого граничного значения, то течение в рус-
ле ламинарное, ему соответствует закон сопротивления Пуазейля,
при котором коэффициент гидравлического трения зависит толь-
ко от числа Рейнольдса и обратно пропорционален ему
185
X
_ 16
Re
(10.59)
Рис. 10.2. Зависимость коэффициента гидравлического
трения от критерия Рейнольдса и относительной
шероховатости по опытам в открытом русле
В области турбулентного режима закон сопротивления оп-
ределяет, как и в напорном движении, число Рейнольдса
и, А
Re* =----, в котором ut - динамическая скорость потока нахо-
v
дится из формулы
м2=1о. = ^(7\ (!0.60)
Р 2
где т0 - касательное напряжение на поверхности дна водотока.
Для гидравлически гладкого режима без проявления шеро-
ховатости, при котором выступы элементов шероховатости лежат
внутри ламинарного подслоя, число Рейнольдса находится в пре-
делах
0<Re* <5.
(10.61)
186
В этой зоне получена формула, практически совпадающая с
зависимостью Прандтля, если учесть, что X = 4 Хо , ReD = 4 Re :
-7L = 4,01g(Re 7^)+ 2,0. (10.62)
По результатам исследований А.П. Зегжды формула (10.62) спра-
ведлива при Re <105.
Для зоны с полным проявлением шероховатости, в которой
ее элементы выступают из ламинарного подслоя, закон сопро-
тивления получается квадратичным. Этой зоне соответствует
следующее условие:
1g—^>1,65, Re, >44,7, (10.63)
v
которое можно записать в таком виде:
А > 3,89 5.
Закон сопротивления в этой зоне таков
_L = 41g- + 4,25. (10.64)
&
А.П. Зегжда отмечает следующее: для области квадратично-
го сопротивления преобразованная формула Никурадзе (10.39)
будет отличаться от (10.64) только постоянной, которая равна
4,68, а не 4,25,что сам автор объясняет погрешностями его опы-
тов.
В переходной зоне, где выполняются условия
5 < Re, < 44,7; 0,43 < - < 3,89 ,
187
Зегжда дал две формулы. Первой из них соответствует следую-
щий диапазон изменения числа Рейнольдса 5 < Re* <16, формула
имеет вид
1 л. R
—f= = 41g —h 5,75 .
(10.65)
В диапазоне изменения числа Рейнольдса
16 < Re * < 44,7 была предложена такая зависимость
1 Л w* А
' = 4 ig _ + 9 65 - 3,27 lg-----
Хо A v
(10.66)
Следует заметить, что в этом диапазоне изменения числа
Re* в рассматриваемой зоне не удалось найти единой зависимо-
сти типа формула Коулбрука и Уайта (10.30) в напорном потоке.
Кроме того, формула (10.65) не соответствует зоне, в которой ко-
эффициент гидравлического трения зависит не только от относи-
тельной шероховатости (или гладкости), но и от числа Рейнольд-
са. Для устранения этого несоответствия можно в диапазоне из-
менения числа Рейнольдса 5 < Re* <16 предложить следующую
зависимость
1
R
= 4 1g
+ 6,4-
0,5
lg^
v
(10.67)
В рассматриваемом случае автомодельная зона, в которой
явление не зависит от числа Рейнольдса, характеризуется услови-
ем (10.63); получим из него величину граничного числа Рей-
нольдса. Для этого, прежде всего, найдем связь между числами
Рейнольдса Re и Re*, используя зависимость (10.60) между ди-
188
намической и средней скоростью потока, а также (10.64) для ко-
эффициента гидравлического трения
= = (10.68)
v V 2 v R \ 2 S '
Отсюда, принимая Re, = Re*,, = 44,7 , получим значение Re,
/? /? I 7? \ р
Re, = Re, = 63,2 41g — + 4,25 -
' I A J А
(10.69)
Обратимся далее к решению второй задачи: поиска зависи-
мостей, соответствующих критериальному уравнению (10.57) для
безнапорного открытого потока, используя преобразование
(10.58).
В области ламинарного режима, где закон сопротивления
определяется зависимостью (10.59), получим
. _128
° Аг;-
(10.70)
Области ламинарного режима будет соответствовать следующее
значение граничного числа Архимеда Агг < 6400.
Далее найдем связь между числом Рейнольдса Re, и крите-
рием Архимеда Аг;. Из (10.68), принимая во внимание (10.58),
имеем
z \2 / \ 2 z \ 2
Re,2 = —Re2| —| = ArJ-| , Ar;=Re2|-| . (10.71)
2 (rJ ‘{rj ' (aJ
С учетом (10.61) получим пределы существования зоны
гидравлически гладкого русла
189
О < Ar < 25 -
IaJ
(10.72)
Во второй задаче аналог формулы Прандтля для открытого
безнапорного потока (10.62)с учетом зависимости (10.58) будет
таким
^L = 4,01g(/Ar;)+ 2,6.
(10.73)
С тем, чтобы определить область применимости формулы
(10.73), установим связь между числом Рейнольдса и критерием
Архимеда в неявном виде, используя зависимости (10.58) и
(10.73), получим
Re = 1,41 д/Ai; (4 IgyAi; + 2,б).
Отсюда методом последовательных приближений, прини-
мая Re = 105 , было найдено Аг; = 1,74 Ю7 .
В зоне квадратичного сопротивления во второй задаче закон
сопротивления не изменится и будет, как и в первой задаче, вы-
ражаться формулой (10.64). Необходимо найти условия сущест-
вования этой зоны, используя зависимость (10.63), относящуюся
к первой задаче. Воспользуемся с этой целью формулой (10.71),
получим при условии (10.63)
Аг, >1998 -
U)
Следовательно, граничное число Архимеда равно
/ D
Аг- =1998 -
V Ау
10.74)
(10.75)
190
В переходной зоне, границы которой определяются услови-
ем
25,0 - < Ап < 256,0 -
Ш IaJ
зависимость (10.67), учитывая (10.71), станет такой
1 л. R z- л
—т—- = 4 1g—h 6,4 -
А А
(10.76)
В той же зоне, ограниченной условием
/ р / п \2
256 - < Аг,- < 1998 - ,
IaJ ' ш
формула (10.66) превратится в следующую
1 /? (
_= = 41g - + 9,65 - 3,24 lg Ja7 - .
л/Ч А Ч Я?
(10.77)
Нужно отметить особенности постановки и решения первой
и второй задач в напорном и открытом безнапорном потоке. В
напорном трубопроводе геометрия потока определяется диамет-
ром трубы и шероховатостью внутренней поверхности, Кроме
того, в первой задаче скорость течения, во вто-
рой - пьезометрический уклон заданы. Обе задачи имеют единст-
венное решение. В безнапорном потоке в первой задаче расход
воды в русле задан, но если не задана геометрия потока, то задача
становится неопределенной, имеющей множество решений. При
заданной форме русла геометрия потока определяется положени-
ем уровня свободной поверхности над плоскостью сравнения.
Следовательно, уровень воды должен быть заданным. Во второй
191
задаче задан уклон дна водотока. Но при заданном уклоне дна за-
дача имеет бесчисленное множество решений, которые зависят от
величины гидравлического радиуса потока (от степени наполне-
ния русла водой). Иными словами, дополнительно здесь также
как и в первой задаче, нужно знать отметку уровня воды в задан-
ном сечении русла.
Как и в случае течения в напорном трубопроводе покажем
на примере, что все поученные выше зависимости, увязаны меж-
ду собой. Допустим нужно создать модель открытого русла для
проведения испытаний в условиях равномерного режима движе-
ния воды в нем. Натурный поток имеет такие характеристики:
скорость течения равна [7 = 1,0м/с, гидравлический радиус
7? = 10 м, относительная гладкость поверхности дна водотока
^ = 60, (параметры водотока близки к характеристикам основного
русла р. Невы в пределах городской черты), кинематическая вяз-
кость воды v = 0,01 см2/с. Вначале делаем предположение о том,
что течение воды в русле относится к зоне квадратичного сопро-
тивления. Исходя из этого, по формуле (10.64) находим в этом
случае величину коэффициента гидравлического трения:
Хо = 4 25)2 = О’ОО?7 ‘ И3 формулы (Ю-60) определяем ди-
/0,0077 1ЛП „
намическую скорость потока u,=-J—-------100 = 6,2 см/с. Далее
можно найти соответствующее число Рейнольдса
Re, = М+— 7? = ———1000 = 10333,3 > 44,7 . Это означает,
v vR 0,01-60
что течение в русле относится к режиму квадратичного сопро-
тивления, у которого критерий Рейнольдса равен
192
100 1000 1П7 д.
Re„=—--------= 10 . Теперь по формуле (10.69) находим гра-
0,01
ничное число Рейнольдса, соответствующее началу зоны квадра-
тичного сопротивления Rea = 63,2 (4 lg60 + 4,25) 60 = 43087 . При-
нимаем на модели число Рейнольдса равным граничному значе-
нию, находим масштабный коэффициент числа Рейнольдса
Д6». _ t = ^1 ки _ ДО— _ 232 j Моделирование будем
Re1( Rea Re kv 43087 K ?
проводить при условии равенства критериев Фруда на модели и в
натуре. Кроме того, на модели и в натуре жидкость одна и та же.
Имеем такие соотношения между масштабными коэффициента-
ми: kg = 1, kv = 1, кг1 = Jkj . Но тогда получим: kRe = к^2 = 232,1 .
Следовательно, линейный масштабный коэффициент будет ра-
вен к, - (232,l)2^3 = 37,8 . Выберем линейный масштабный коэф-
фициент к[ = 35 . Тогда гидравлический радиус потока на модели
равен RM = 0,286 м; скорость течения воды на модели будет рав-
на: U м=ин/ = 1,О/л/35 = 0,169 м/с .Но определить расход воды
на модели (да и в натуре) невозможно, так как нехватает еще од-
ного линейного размера (ширины русла, либо смоченного пери-
метра), или площади живого сечения. Пусть площадь живого се-
чения в натуре равна сон = 2100 м2, тогда расход воды в натурных
условиях равен QH = 2100м3/с . Найдем площадь живого сечения
(D„ СО,, 2100 , . 2
на модели из условия: сои=—0- = —*- =—— = 1,714 м , где
к/ 35
ка = к] - масштабный коэффициент площади живого сечения по-
тока. Отсюда расход воды на модели равен
QM = о)и UM = 1,714-0,169 = 0,29м3/с . Теперь можно найти мас-
штабный коэффициент расхода воды:
193
кп = — = —= 7241,4 = Х?/2 = 355'2 = 7247,1. Уклон дна водотока
в Q» 0-29 1
в соответствии
Х_°.«рг =
2 н
с зависимостью (10.50), будет
Ха м
FrH=FrA/- ^oH=^o.u - Найдем
равен
число
И *Л1
1
полу-
Фруда Fr„ =
= 0,01 = Fr = (0J69)— _ Q Отсюда
9,81-10 M 9,81-0,286
чим уклон дна: iH = iM = 2^277 0,01 = 38,5 -10“6 .
Сформулируем задачу по-иному: относительная шерохова-
тость, площадь живого сечения, гидравлический радиус русла,
вязкость жидкости и уклон дна заданы, нужно найти скорость те-
чения и расход воды в нем, а также выбрать линейный масштаб
модели для проведения на ней исследований при равномерном
движении воды в русле водотока. Как и в случае напорного пото-
ка, используем результаты, полученные при решении первой за-
дачи, для проверки соответствия приведенных формул:
/„ = 38,5-10 6, ®н= 2100 м2, /?,( = 10м, vH = 0,01 см2/с .
Прежде всего, определим критерий Архимеда в натурных
. 38,5-10"6-981 (1000)3 „„О1Лц тт
условиях Ат =-------------—= 3,78-10 . Далее найдем из
(0,01)2
(10.75) граничное значение этого критерия
Аг,-, = 1998 (бО)2 = 7,2 -106 .В связи с тем, что выполняется усло-
вие Аг/Н > Аг; г, коэффициент гидравлического трения определяем
по формуле (10.64) Хо= 0,0077 . Теперь, преобразовав зависи-
мость (10.50) в формулу Шези, можно найти скорость течения
2? 2-981 <
воды в русле реки: [7„ = — Ri = -----—10-38,5-10 6 =1,0 м/с .
V Xq у 0,0077
Будем, как и ранее, считать, что моделирование явления реализу-
194
ется «по Фруду», поэтому выполняется условие z„ = iM . Прини-
маем на модели критерий Архимеда равным граничному значе-
нию Аг/Л/ = Аг,г . Далее получим масштабный коэффициент кри-
терия Архимеда, взяв отношение натурного значения его к мо-
37 8
дельному, кАг =—— =——IO4 = 5,25-104 . Учитывая связь между
Аг,, 7,2
масштабным коэффициентом критерия Архимеда и линейным,
получим kt = l]kAr = ^5,25 - IO4 = 37,4 . Остальные расчеты совпа-
дают с выполненными выше; основной вывод состоит в том, что
их результаты, полученные по двум методам, отличающимся по-
становкой задачи и критериями подобия, совпали.
В [16,21] обращается внимание на две противоположные тен-
денции при организации физического моделирования гидравли-
ческих явлений. С одной стороны, существует естественное же-
лание иметь модельную установку небольших размеров (с боль-
шой величиной линейного масштабного коэффициента). Однако,
требование находится на модели в пределах зоны квадратичного
сопротивления, которое реализуется, если величины чисел Рей-
нольдса и Архимеда на модели выбирать не менее граничных,
определяемых формулами (10.69) и (10.75), как это следует из
рассмотренных выше примеров, приводит к сравнительно круп-
ным моделям (при ширине руса, приблизительно равной 210 м,
на модели русло должно иметь ширину около 6 м . С другой сто-
роны, если модель имеет малые размеры, то возникают трудности
с моделированием высоты выступов шероховатости. В рассмот-
ренном примере при относительной гладкости русла, равной
шестидесяти, высота выступов шероховатости в натуре равна
. 7? 1000 „
Ан = = 16,7 см . Отсюда высота выступов шероховато-
195
сти на модели должна быть Д1( = —^ = — = 0,48см , Такую ше-
роховатость можно создать путем наклеивания на дно водотока
однородного песка со средним размером частиц d0. Связь между
Д и d0 по опытам А.П. Зегжды приведена на рис. 10.3 В [16]
приводятся оценки для высоты выступов шероховатости бетон-
ной и ожелезненной бетонной поверхностей. Разница получилась
не слишком большой: у бетонной поверхности Д - 0,075 см , у
ожелезненной - Д = 0,065 см . Если планируется создать модель
русла из бетона, а по условиям моделирования высота выступов
шероховатости на модели получается меньше указанных вели-
чин, то прибегают к такому приближенному методу моделирова-
ния, при котором линейный масштаб глубин принимают отлич-
ным от линейного масштаба плановых размеров потока (модели-
рование с “искажением” линейных масштабов, по сути, речь идет
об аффинном подобии). Ниже будут приведены различные мето-
ды приближенного моделирования, направленные на уменьшение
размеров модели и преодоление трудностей, связанных при этом
с моделированием высоты выступов шероховатости.
Рис. 10.3. Зависимость к=f(d0)
1%
Возможна еще одна задача - третья - моделирование равно-
мерного режима безнапорного потока, в которой заранее неиз-
вестной является глубина потока. На практике она встречается
редко, но один пример можно привести. Речь идет о явлении, ко-
торое наблюдается при вступлении сильно насыщенного (мут-
ность более 10 кг/м3 ) мельчайшими наносами
(б/<0,001-0,002см ) речного потока в водохранилище, наполнен-
ное чистой водой [21]. Такой поток обладает свойствами жидко-
сти, плотность которой больше плотности воды. Войдя в водо-
хранилище, он опускается на дно и продолжает движение в сто-
рону плотины по его диу. Проще всего исследовать такой плот-
ностной поток в натурных условиях, измеряя скорость его дви-
жении по дну водохранилища. Подобного рода измерения явля-
ются наиболее доступными и в лабораторных условиях даже в
том случае, если они проводятся в лотках, где поток считается
плоским. Не вдаваясь в особенности такого плотностного течения
(плотность жидкости больше плотности воды, поток испытывает
сопротивление движению не только со стороны дна, но и со сто-
роны расположенного над ним слоя чистой воды и др.), рассмот-
рим задачу для потока чистой воды, в котором по каким-то при-
чинам не была измерена его глубина или ее невозможно было
измерить.
Обратимся к исходному уравнению (10.53). В нем нет ни
одного критерия подобия. Получим его, перемножая числа Фруда
и Рейнольдса, оставим комбинацию этих чисел в уравнении свя-
зи, заменив ею число Рейнольдса. В соответствии со сказанным
выше имеем: 1/Fr, =Eu = Х0/2, поэтому критериальное уравнение
для рассматриваемой задачи будет иметь такой вид:
197
Хо = N Ke , форма русла , Ке, = Fr,Re =-----, (10.78)
к R J giv
где Ke, - преобразованное число Келегана, в которое, кроме ха-
рактерной скорости потока и физических констант, входит уклон
дна водотока.
В области ламинарного режима движения закон сопротив-
ления определяет формула (10.59). В ней нужно число Рейнольд-
са заменить преобразованным числом Келегана. Связь между ни-
ми установим, воспользовавшись второй формулой в (10.78):
Re = = Ей Ке, = ^Ке,. (10.79)
Fr,- 2
Произведя замену числа Рейнольдса в (10.59) в соответствии
с формулой (10.79), получим после преобразований
/32
(Ю.80)
УКе,-
Как было отмечено выше, ламинарный режим существует в
области, в которой выполняется условие Re < 800 . Если заменить
число Рейнольдса, используя зависимость (10.79), а для коэффи-
циента гидравлического трения - формулу (10.80), то можно по-
лучить аналогичное условие существования области ламинарного
режима, определенное по числу Келегана: Ке, < 8•104.
В области турбулентной законы сопротивления определя-
ются пределами изменения числа Рейнольдса Re* = . Найдем
v
связь между этим числом и критерием Келегана. В процессе пре-
образований учтем связь между числом Рейнольдса и критерием
Келегана, определяемую зависимостью (10.79).
198
utA [ко Д д
Re* =---= л—Re —= — Ke,—.
v V 2 R I 2 J ‘ R
(10.81)
В зоне гидравлически гладкого русла пределы изменения
числа Re* определены условием (10.61), откуда можно устано-
вить пределы существования этой зоны, заменив число Re* кри-
терием Ке; согласно зависимости (10.81), получим:
п
0<Ке,<5-
Д
Г 2 Y/2
<Ло )
(10.82)
В этой зоне закон сопротивления определяется формулой Пран-
дтля (10.62), которую после преобразований можно дать в таком
виде с учетом (10.79)
1
лДо
= 41g
V/2
— Ке,-
I. 2 )
+ 2,6.
(10.83)
Зависимость (10.83) можно дать в более удобном для расче-
тов виде:
= 8,481g^J + 5,651g Ке,- + 3,68.
(10.84)
Исходная формула (10.62) справедлива при условии
Re <105 . Можно дать в неявном виде зависимость для определе-
ния аналогичного условия для критерия Келегана, используя
формулу (10.79):
105
8,481gl I + 5,651g Ке,- + 3,63
2
= Ке,.
199
при
условии
переходной зоне
/ \3/2
7? I 2 I
Се, <16 —— , учитывая зависимость (10.81),
А )
В
A J
формулу (10.67) можно представить в таком виде:
1 Л 1 , л
i= = 41g — + 6,4 -
Л
0,5
У/2 д'
Ке; —
) R
(10.85)
В той
/ \3/2
RI 2 '
16- —
А
первой рассмотренной выше задаче формула (10.66), ее можно
так преобразовать, принимая во внимание зависимость (10.81):
Л \3/2 л!
Ке,- .
2 J ‘ R
16-
же
< Ке, < 44,7 -
зоне
/ ~ Д/2
Я 2
— , которому соответствует в
А^А.О J
при
условии
~ = 41g - + 9,65 - 3,27 1g
Л,о А
(10.86)
В зоне квадратичного сопротивления сохраняется зависи-
мость (10.64). Величина преобразованного граничного числа Ке-
легана найдется из формулы:
/ Л \3/2
D ( 2
Ке(> > 44,7 - —
A^0J
D
1g- +1,06 .
A J
200
11. ПРИБЛИЖЕННОЕ МОДЕЛИРОВАНИЕ ПО-
ТОКОВ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ
11.1. Приближенное моделирование потока в квадратич-
ной зоне сопротивления потоком в зоне гидравлически глад-
кого русла
По-видимому, впервые в [16] был предложено моделировать
равномерное движение потоков, относящихся к зоне квадратич-
ного сопротивления, с помощью потоков, находящихся в зоне
гидравлически гладкого русла. Затем это предложение нашло от-
ражение в [21]. Смысл его заключается в следующем исходном
утверждении: если распределение скорости течения по живому
сечению у модельного потока, созданного в соответствии с этим
принципом, совпадет с распределением скорости у натурного по-
тока, то подобие этих потоков будет обеспечено. Средние скоро-
сти течения и геометрические параметры потоков, естественно,
предполагаются подобными. Таким образом, при таком способе
моделирования выдвигается требование обеспечить подобие не
только потоков в целом, но и подобие скоростей течения в сход-
ственных пространственных точках.
Для доказательства возможности такого метода приближен-
ного моделирования в [16, 21] сравнивались скорости течения в
сходственных точках двух потоков, один из которых относился к
зоне квадратичного сопротивления, другой - к зоне гидравличе-
ски гладкого русла. В настоящее время такое доказательство го-
раздо проще выполнить, если воспользоваться, так называемым
“универсальным законом распределения скорости течения в тур-
булентных потоках” [22, 62].
201
Как известно, в соответствии с феноменологической теори-
ей турбулентности Блазиуса-Прандтля-Кармана, касательные на-
пряжения турбулентного трения т выражаются следующей зави-
симостью [22, 62]
2 2
т = рк у
(11.1)
где к - постоянная Кармана (к = 0,38 т 0,42 ); у - расстояние, из-
меряемое по нормали к поверхности дна водотока, или к поверх-
ности трубы водовода; и - скорость течения в точке, располо-
женной на расстоянии у от дна, или внутренней стенки трубы
водовода. Далее рассматриваем слой потока на небольшом уда-
лении от поверхности, ограничивающей поток, в котором можно
принять т « т0, где т0 - касательное напряжение, приложенное к
этой поверхности. Но т0/р = м* , где и* - динамическая скорость
потока. В таком случае из (11.1) имеем
d и
и* =ку — .
d у
(И.2)
В (11.2) переменные разделились, после интегрирования по-
лучим
и 1 1
— = — In у + const,
и„ к
(11.3)
где константу интегрирования для гидравлически гладкого русла
определяют на уровне толщины ламинарного подслоя, а для рус-
ла с развитой шероховатостью - на уровне высоты бугорков ше-
роховатости. При этом для гидравлически гладкого русла распре-
деление скорости течения выражается зависимостью
202
_lL = lin!kZ + cl, (11.4)
И, К V
а для потока с развитой шероховатостью
- = -1п^ + С2, (11.5)
и* к А
где С, и С2 - постоянные. Строго говоря, зависимости (11.4) и
(11.5) справедливы на небольшом удалении от твердой поверхно-
сти, вдоль которой происходит течение жидкости (в пределах об-
ласти «генерирования» турбулентности). Однако, их распростра-
няют в напорном потоке до его оси, принимая у = г , а в безна-
порном - до свободной поверхности, где у = h ; здесь
г - внутренний радиус трубы, h - глубина потока; на этих уров-
нях в том и в другом потоках принимается и - итах . Подставляя
эти данные в зависимости (11.4) и (11.5), получим для открытого
безнапорного потока
^ = -1п^ + С, , (11.6)
W* К V
^ = 11п- + С2. (11.7)
к А
Если теперь из (11.6) вычесть (11.4), а из (11.7) - (11.5), то
получим одну и ту же зависимость, которая называется «универ-
сальным законом распределения скорости течения в турбулент-
ном потоке»
итах ~ ц 1 1п
И* К у
(П-8)
203
Аналогичный результат получается и в случае напорного
потока, для которого величину h в формуле (11.8) следует заме-
нить на г . Преобразуем зависимость (11.8), используя связь ме-
жду динамической и средней скоростью потока (10.60), придем к
следующей
и'^~" = (11.9)
U \ 2 к у
Рассмотрим два геометрически одинаковых потока, у кото-
рых средние скорости равны между собой, но один из них нахо-
дится в зоне квадратичного сопротивления, а другой в зоне гид-
равлически гладкого русла. Потребуем, чтобы коэффициенты
гидравлического трения у них были одинаковыми:
(Ло)КвС =(^о)гидгл- Тогда, учитывая универсальный характер рас-
пределения скорости в этих потоках, получим, что правые части
соответствующих зависимостей типа (11.9) у них одинаковы. Из
этого следует, что одинаковыми должны быть и левые части:
итах и j
U кв,с
Umax И j
U ) гид.гл
(11.10)
Таким образом, рассматриваемый здесь метод приближен-
ного моделирования потоков представляется вполне обоснован-
ным. В этой связи в [21] рекомендуется вместо постоянной 63,2 в
формуле (10.69) принимать 14,0 . В настоящей работе предлага-
ется в натурных условиях определять коэффициент гидравличе-
ского трения по формуле для зоны квадратичного сопротивле-
ния, после этого из формулы Прандтля для зоны гидравлически
гладкого русла находить число Рейнольдса и принимать его зна-
чение в качестве граничного. Но, прежде всего, необходимо ус-
тановить, при каких условиях возможен этот способ моделиро-
204
вания, так как при очень больших величинах выступов шерохо-
ватости гидравлически гладкий режим может отсутствовать. С
этой целью обратимся к соответствующим графикам, приведен-
ным на рисунках 10.1 и 10.2.
Из них следует, что в случае напорного потока такая воз-
можность может быть при условии г/Д > 45 , для безнапорного -
при 7?/Д > 30 . Если величины относительных гладкостей пото-
ков меньше указанных пределов, то приближенное моделирова-
ние возможно только с использованием граничного числа Рей-
нольдса, соответствующего началу зоны квадратичного сопро-
тивления.
Далее воспользуемся формулой Прандтля для зоны гидрав-
лически гладкого русла в открытом безнапорном потоке (10.62),
которую решим относительно числа Рейнольдса, а значение ко-
эффициента гидравлического трения, входящего в нее, примем
по формуле для зоны квадратичного сопротивления (10.64). Най-
денное таким образом число Рейнольдса будет граничным. Про-
изведя соответствующие преобразования, придем к следующей
формуле
7?ег = 3,651 41g ~ + 4,25 ] —. (11.11)
У А ) А
Сравнивая это число Рейнольдса с граничным, соответст-
вующем началу зоны квадратичного сопротивления (10.69), ви-
дим, что они существенно отличаются друг от друга, а именно:
граничное число Рейнольдса, найденное по формуле (11.11), в
17,3 раза меньше числа, определенного по формуле (10.69). Сле-
довательно, линейный масштабный коэффициент, полученный с
привлечением граничного числа Рейнольдса, соответствующего
зависимости (11.11), будет в (17,3)2/3 =6,7 раза больше масштаб-
205
ного коэффициента, определенного с использованием зависимо-
сти (10.69). Вместо к} =37,8 получим А) = 37,8-6,7 = 253,2 . Сле-
довательно, возможности создавать модели уменьшенных по
сравнению с натурой размеров существенно расширяются.
При решении этого вопроса в рамках второй задачи вос-
пользуемся преобразованной формулой Прандтля (10.73), кото-
рую решим относительно числа Архимеда, а коэффициент гид-
равлического трения, входящий в нее, примем по формуле для
зоны квадратичного сопротивления (10.64). Найденное таким
образом число Архимеда будет граничным. Произведя соответ-
ствующие преобразования, придем к следующей формуле
( 7? У
Аг,г=6,531^1 . (Н-12)
Сравнивая два значения граничных чисел Архимеда, опре-
деляемых по формулам (10.75) и (11.12), относящихся соответст-
венно к началу области квадратичного сопротивленя и гидравли-
чески гладкого русла, можно найти, что они отличаются друг от
друга в 306 раз. Отсюда можно установить, во сколько раз уве-
личится величина линейного масштабного коэффициента:
V306 = 6,7 , что полностью совпадает с полученным выше ре-
зультатом.
Обратимся теперь к движению жидкости в напорных водо-
водах и рассмотрим вопрос приближенного моделирования их с
заменой зоны квадратичного сопротивления, в которой поток на-
ходится в натурных условиях, зоной гидравлически гладкого
русла на модели. Здесь, как и в случае безнапорного потока,
удобно использовать для нахождения граничного значения числа
Рейнольдса формулу Прандтля (10.26), заменив в ней коэффици-
ент гидравлического трения согласно зависимости (10.29), спра-
206
ведливой для зоны квадратичного сопротивления. После преоб-
разований получим
ReDz = 18,62 (2 lg^ + 1,74^. (11.13)
Сравнивая формулы (10.31) и (11.13), найдем, во сколько
раз можно увеличить масштабный линейный коэффициент, ис-
пользуя на модели зону гидравлически гладкого русла вместо
( 396 А2/3
начала зоны квадратичного сопротивления: --- = 7,67 .
<18,62 J
Отсюда линейный масштабный коэффициент станет равным
к, = 5,47 7,67 = 42,0.
Выполним аналогичные расчеты, используя зависимости,
полученные во второй задаче. Выразим в аналоге закона сопро-
тивления Прандтля (10.40) коэффициент гидравлического трения
по формуле (10.29), соответствующей зоне квадратичного сопро-
тивления, после преобразований найдем
/ \2
ArJa=2,71^j . (11.14)
Определим, во сколько раз можно увеличить масштабный
линейный коэффициент, используя на модели зону гидравличе-
ски гладкого русла вместо начала зоны квадратичного сопротив-
11225
ления, сравнивая формулы (10.42) и (11.14): з/у^- = 7,67 . От-
сюда линейный масштабный коэффициент станет равным
^=5,47-7,67 = 42,0.
Таким образом, возможности изготовить модель весьма ма-
лых размеров по сравнению с натурой при обсуждаемом методе
моделирования существенно расширяются. Однако на этом пути
207
исследователя поджидают две опасности. Во-первых, с умень-
шением линейных размеров модели при моделировании «по
Фруду» в условиях модели уменьшаются скорости течения.
Нельзя допустить, чтобы скорость течения приблизилась к поро-
гу чувствительности измерительного прибора. В случае модели-
рования движения наносов (в том числе условий начала их тро-
гания, или первых подвижек) скорость течения на модели может
быть такой, при которой наносы останутся в покое. Во-вторых,
при малых глубинах на модели открытого потока и малых разме-
рах модели напорного водовода возникают трудности в проведе-
нии измерений. Кроме того, с уменьшением линейных размеров
модели соответственно должна уменьшиться высота выступов
абсолютной шероховатости, обеспечить которую не всегда воз-
можно. Выше было отмечено, что на модели, изготовленной из
бетона, минимальная высота выступов шероховатости равна
0,07-^0,06 см [16].
Отсюда, естественно, возникает задача увеличить, по воз-
можности, линейные масштабы модели (уменьшить линейный
масштабный коэффициент). Это означает, что при таком умень-
шении линейного масштабного коэффициента исследователь
должен возвратиться либо в начало зоны квадратичного сопро-
тивления, либо он неизбежно оказывается в пределах переходной
зоны. Если на рисунках 10.1 и 10.2 выбрать какую-либо кривую,
соответствующую определенному значению относительной
гладкости, совместить с ней в зоне квадратичного сопротивления
прямую, параллельную горизонтальной оси, а затем эту прямую
продлить до зоны гидравлически гладкого русла, то можно обна-
ружить, что прямая в переходной зоне пересекает кривые с раз-
ными значениями относительной гладкости. Особенно это хоро-
шо заметно на графиках (10.2) Никурадзе. Следовательно, при
208
постоянном значении коэффициента гидравлического трения с
уменьшением числа Рейнольдса в переходной зоне относитель-
ная гладкость уменьшается и наоборот: увеличивая число Рей-
нольдса в этой зоне, можно дойти до начала зоны квадратичного
сопротивления, которой соответствует величина выбранной
(максимальной) относительной гладкости. Эти наблюдения сви-
детельствуют о том, что зону квадратичного сопротивления в на-
турных условиях можно исследовать с помощью переходной зо-
ны в условиях модели, определяя по натурному значению коэф-
фициента гидравлического трения и выбранному числу Рей-
нольдса относительную гладкость и величину абсолютной шеро-
ховатости на модели.
11.2. Приближенное моделирование потока в квадратич-
ной зоне сопротивления потоком в переходной зоне
Суть метода заключается в следующем. Прежде всего, оп-
ределяем по натурным данным величину коэффициента гидрав-
лического трения. Затем подставляем его значение в зависимости
от решаемой задачи в соответствующую формулу, описываю-
щую закон сопротивления в переходной зоне. В этой зоне сопро-
тивление зависит от числа Рейнольдса и относительной шерохо-
ватости ограничивающих поток твердых поверхностей. Задача
намного проще решается, если в ней задаваться изначально чис-
лом Рейнольдса для модельного потока. Иными словами, начи-
нать расчет следует с назначения линейного масштабного коэф-
фициента. После этого в рамках первой и второй рассматривае-
мых задач из соответствующих формул определять величину от-
носительной гладкости.
209
Для безнапорного открытого потока в переходной зоне со-
противления в [16] предложено две формулы: (10.65), которая
справедлива при условии 5 < Re* <16, и (10.66), справедливую
при условии 16 < Re* <44,7. Вместо зависимости (10.65) можно
также применять предложенную нами (10.67). Ниже в этой зоне
для безнапорного открытого потока будут использоваться фор-
мулы (10.66) и (10.65), расчеты по последней из них получаются
намного проще, чем при использовании формулы (10.67).
Таким образом, для безнапорного открытого потока в пере-
ходной зоне после преобразований в соответствии с зависимо-
стью (10.68), связывающей числа Рейнольдса Re, и Re, получена
формула
~ = 7,27 1g- +10,14 - 3,27 1g Re). (11.15)
А.о А
Порядок расчетов таков: по натурным данным определяем
величину коэффициента гидравлического трения. Далее, исполь-
зуя формулу (10.69), находим граничное число Рейнольдса, соот-
ветствующее началу зоны квадратичного сопротивления. При-
нимаем граничное число Рейнольдса равным числу Рейнольдса
на модели и определяем при условии моделирования «по Фруду»
линейный масштабный коэффициент из формулы
ReH 7
—— = к
ReA7
(11.16)
Re
Теперь можно задаться, исходя главным образом из практи-
ческих соображений (к ним относятся: размеры лабораторной
установки, наличие и возможности измерительной техники
и т. п.), линейным масштабным коэффициентом, величина кото-
рого должна превышать значение, определенное по формуле
210
(11.16). Тем самым линейные размеры модели уменьшатся по
сравнению с теми, которые получаются при моделировании, ис-
пользуя начало зоны квадратичного сопротивления. Далее из той
же формулы (11.16) при назначенном таким образом коэффици-
енте к{ находим число Рейнольдса на модели Re „, а из зависи-
мости (11.15) - величину относительной гладкости модели
из нее - абсолютную величину выступов шероховатости в усло-
виях модели Ли . Для удобства расчетов преобразуем зависи-
мость (11.15) к такому виду:
IgOfl =^-1395 + 0,45Olg(Ti;ReJ. (11.17)
Остается проверить допустимость применения в расчетах фор-
мулы (11.15). Для этого нужно определить число Рейнольдса
Re*„, используя зависимость
Re*.«
(11.18)
и убедиться в том, что его величина находится в пределах:
16 < Ret„ < 44,7. Если это условие выполняется, то расчеты были
сделаны правильно, так как формула (11.15) справедлива в ука-
занном диапазоне изменения числа Рейнольдса. Но может ока-
заться, что величина числа Рейнольдса Re<M попала в пределы
5<Re* <16. Тогда расчет следует повторить, привлекая зависи-
мость (10.65), которая справедлива в этом диапазоне изменения
числа Рейнольдса. Из нее при заданном по натурным данным ко-
эффициенте гидравлического трения относительная гладкость
модели легко определяется
211
0.25 , ..
~ 1,44.
(H.19)
Обратимся далее к изложению рассматриваемой методики
приближенного моделирования открытого безнапорного потока
в рамках второй задачи. В переходной зоне, границы которой
определяются условием
/ р\2 ( R у!
25,0 - < Лг. < 256,0 - ,
IaJ IaJ
(11.20)
формула (10.65), относящаяся к этой зоне, и ее аналог (11.19) не
претерпят никаких изменений. В той же зоне, ограниченной ус-
ловием
/ d\2 f d\2
256 - < Аг,- < 1998 - ,
(И.21)
из формулы (10.77), относящейся к этой части переходной зоны,
можно получить следующую
4= = 7,27 1g ~ + 9,65 -3,241g (^А^), (11.22)
д/4-0 А
которую представим в виде, удобном для расчетов
lglTl =^-1.327 +0,4501g (7а^). (11.23)
Порядок расчетов во второй задаче в основном совпадает с
тем, который изложен выше в первой задаче. Вначале по натур-
ным данным определяем величину коэффициента гидравличе-
ского трения. Далее, используя формулу (10.75), находим гра-
ничное число Архимеда, соответствующее началу зоны квадра-
212
тичного сопротивления. Принимаем граничное число Архимеда
равным числу Архимеда на модели и определяем при условии
моделирования «по Фруду» линейный масштабный коэффициент
из формулы
.А.Г'
*/=3л& кАГ-~. (11-24)
( R'v
где Ar/Af =1998^—J .
Теперь можно задаться линейным масштабным коэффици-
ентом, величина которого должна превышать значение, опреде-
ленное по формуле (11.24). Из этой же формулы при выбранном
коэффициенте kt находим число Архимеда на модели Лгл<. Если
это число попадает в пределы, определяемые формулой (11.21),
то из зависимости (11.23) ищем величину относительной гладко-
сти модели — и абсолютную величину выступов шероховато-
сти в условиях модели . Если число Архимеда на модели по-
падает в пределы, определяемые формулой (11.20), то расчет ве-
дется по формуле (11.19).
Обратимся вновь к примеру, который был приведен в раз-
деле 10.2. Параметры потока в натуре: U = 1,0 м/с, Л = 10м,
R 7
— = 60, А.о =0,0077 , ReH =10 . Граничное число Рейнольдса,
соответствующее началу области квадратичного сопротивления
и принятое в качестве числа Рейнольдса на модели, составило
43087, при этом линейный масштабный коэффициент оказался
равным 37,8. Принимаем величину этого коэффициента равной
kt = 64 , теперь из формулы (11.16) находим число Рейнольдса на
213
модели
—=+ = 19532,2 . Далее в соответствии с (11.17)
643/2
имеем
-] =1^395+ o,4501g (Т0Д077-19531,2)= 1,633 (- | =43.
Д}м Д0077 7 Шл,
Отсюда получим RM = = 0,156 м, А м = = 0,36 см . Отме-
тим, что при выборе на модели числа Рейнольдса, соответст-
вующего началу области квадратичного сопротивления, и
Лу=35 были получены следующие результаты:
R = 0,286 м, А = — = 0,48 см.
м 60
Проверим правильность применения в расчетах формулы
(11.17). Прежде всего, найдем скорость течения воды на модели
UM = = 0,125 м/с . Найдем величину динамической ско-
рости, а также соответствующее число Рейнольдса
10,0077 „ 0,78-0,363
w,= 12,5 л----= 0,78 см/с, Re, =-----------= 28,3 . Таким об-
V 2 1 м 0,01
разом, число Re*„ находится в пределах 16 < Re,м <44,7, а это
значит, что формула (11.17) была использована правильно.
Для поиска решения в рамках второй задачи при тех усло-
виях, которые были приняты в первой задаче, имеем следующие
исходные данные: число Архимеда в натуре Лг,н =3,78-10" , его
граничное значение, соответствующее началу зоны квадратично-
го сопротивления Ari <? = 7,2-106 . С учетом этих данных мас-
штабный линейный коэффициент был принят равным к} = 35 .
Выбираем kt = 64 , находим число Архимеда на модели
214
Аг,-и
к.
3 78 -IO11
—-------— = 1,442-106 . Принимая во внимание этот
643
результата, из формулы (11.23)
= . и’ -1,327 + 0,4501g (у 1,442-106 =1,631.
А )м д/0,0077 ' ’
имеем:
Отсюда
= 43 , что полностью совпадает с результатами, получен-
ными при решении первой задачи. Проверим правильность ис-
пользования в условиях модели формулы (11.23), с этой целью
( \ ( R'? 1442-Ю6
найдем отношение (Аг1Л<).-1 — I = — = 780 . Таким обра-
зом, Ап и = 780 — , следовательно, число Архимеда на модели
находится в пределах, определяемых зависимостью (11.21), в ко-
торых справедлива формула (11.22), что и требовалось доказать.
Для напорного потока в переходной зоне закон сопротивле-
ния описывает зависимость Колбрука-Уайта (10.30). Была пред-
принята попытка использовать ее в расчетах в рамках обсуждае-
мого метода моделирования потоков, относящихся в натурных
условиях к зоне квадратичного сопротивления, потоками на мо-
дели, относящихся к переходной зоне. Однако она оказалась не-
удачной. Судя по всему, формула Колбрука-Уайта довольно хо-
рошо описывает закон сопротивления только по краям этой зо-
ны: у границы гидравлически гладкого русла и у противополож-
ной - квадратичного сопротивления. В центральной части полу-
чаются большие отклонения от опытных данных Никурадзе. Но
есть возможность преобразовать зависимость (10.68) Зегжды для
переходной зоны безнапорного потока в соответствующую для
потока напорного, используя связь между коэффициентами гид-
215
равлического трения этих потоков: X = 4 Хо. По нашему мнению,
вопрос требует дополнительного анализа, который приведен ни-
же.
Как было отмечено в начале этого раздела при обсуждении
зависимостей от (11.4) до (11.9), в качестве характерного линей-
ного размера в логарифмическом профиле скорости в напорном
потоке принят радиус трубы, в безнапорном - глубина потока.
Между тем, в [16] при обработке опытных данных в качестве ха-
рактерного размера был принят гидравлический радиус потока. В
связи с тем, что профиль скорости и закон сопротивления тесно
между собой увязаны [22, 62], это обстоятельство могло стать
причиной систематических погрешностей.
Обычно в гидромеханике по опытным данным строится
график зависимости В = /(Re*), где обозначено
—-2,51п —.
и* Д
(11.25)
В [16] по результатам измерений приведен график зависимости
A = ip(Re*), где
* 1 R
^ = -j=-41g —.
7ч д
(11.26)
Оба графика показаны на рис. 11.1 и 11.2. Найдем величину па-
раметра В при у = h в безнапорном потоке и у = г в напорном. В
том и в другом случае (на поверхности открытого безнапорного
потока и на оси напорного) выполняется условие и = итах. Но то-
гда для напорного потока можно записать
2?я = -2,5 In, (11.27)
и* Д
216
соответственно для безнапорного
ВБ =!W_2,5In-_ (11.28)
и* А
Рис. 11.1. Зависимость параметра В от числа Рейнольдса
В [20,22, 62] путем интегрирования универсального закона
распределения скорости течения в турбулентной зоне получена
связь между максимальной и средней скоростью течения для на-
порного
^ = — + 3,75 = J- + 3,75 (11.29)
и, и* V А
и для безнапорного потока
^ = — + 2,5 = —+ 2,5. (11.30)
и* и* у A q
Подставляя эти данные соответственно в зависимости (11.27) и
(11.28), найдем
+ 3,75-5,75 lg^, (П.31)
217
(11.32)
ВБ= .-- + 2,5-5,75 1g |.
V^o А
Из (11.31) после преобразований имеем
-^-21g- = -^--l,326, (11.33)
VX А 2,828
а из (11.32) соответственно
4="41ёТ = Г177-1768- О1-34)
А 1,414
Приведем зависимость (11.34) к виду (11.33), для чего разделим
левую и правую части в (11.34) на 2 .получим
~-21g- = -^--0,884. (11.35)
VI 6 А 2,828
Можно видеть, что зависимости (11.33) и (11.35) отличают-
ся одна от другой не только постоянными в правых частях, но и
тем, что слева в первой находится радиус трубы, а во второй -
глубина потока. При обработке опытных данных, как было от-
мечено выше, в [16] вместо глубины потока был взят гидравли-
ческий радиус. Но г = 2R, поэтому зависимости (11.33) и (11.35)
преобразуем следующим образом
4=-21g- = -^--0,724, (11.36)
Л А 2,828 V 7
* -21g- = -^-0,884. (11.37)
Vx А 2,828 7
Таким образом, если выбрать одинаковый характерный ли-
нейный размер, то правые части в двух последних зависимостях
218
станут отличаться друг от друга несущественно. Кроме того, бла-
годаря выбору в качестве характерного размера в безнапорном
потоке гидравлического радиуса удалось провести сравнение
двух потоков - напорного и безнапорного.
Приравнивая правые части формул (11.36) (11.37) друг дру-
гу, получим связь между параметрами ВБ и Вяв таком виде
Л£=5я+0,45. (11.38)
Небольшая разница в величинах параметров ВБ и Вн объ-
ясняется различиями в средних скоростях потока: в напорном по-
токе это средняя скорость течения по живому сечению, в безна-
порном - средняя скорость на вертикали.
По величине параметра Вн, приведенного на рис. 11.1, мож-
но с помощью зависимости (11.38) найти параметр ВБ. Но вели-
чина постоянной в формуле (11.38) не превышает естественный
разброс опытных точек, по которым были проведены сглажи-
вающие на рисунке, так что параметры ВБ и Вн практически
совпадают. Далее из зависимости (11.37) после ее преобразова-
ния при условии (11.26) можно найти связь параметра ВБ с пара-
метром А:
А = ^|-1,768. (11.39)
Результаты расчетов, выполненных по формуле (11.39) и
нанесенные на график 11.2, оказались в пределах разброса точек,
полученных в опытах А.П. Зегжды. Таким образом, преобразова-
ние формулы (10.66) в соответствующую для напорного потока
представляется вполне обоснованным также, как сделанные ра-
нее аналогичные преобразования в зонах гидравлически гладкого
219
русла и квадратичного сопротивления. Отсюда вместо (10.66)
имеем:
= 3,635 1g - + 5,453 -1,635 1g (VI Ren). (11.40)
v X Л
Формула останется справедливой в диапазоне изменения числа
Рейнольдса 16 < Re* <44,7 (следовательно, верхняя граница по
сравнению с верхней границей напорного потока уменьшилась).
В диапазоне изменения числа Рейнольдса 5 < Re* <16 справедли-
ва следующая зависимость (аналог формулы (10.65) для безна-
порного потока)
4= = 21g- + 3,477.
Vx д
(Н-41)
Рис. 11.2. Зависимость параметра А от числа Рейнольдса
Порядок расчетов остается прежним. Вначале по натурным
данным определяем величину коэффициента гидравлического
трения. Далее находим граничное число Рейнольдса, соответст- '
вующее началу зоны квадратичного сопротивления. С учетом \
изменения верхней границы, соответствующей началу этой зоны,
в формуле (10.31) произойдут изменения и она станет такой
220
Ren= 252,81 21g- + 1,74 j -
Ds 4 A ) A
(H-42)
Далее принимаем граничное число Рейнольдса равным чис-
лу Рейнольдса на модели и определяем при условии моделирова-
ния «по Фруду» линейный масштабный коэффициент из форму-
лы (11.16) Теперь можно задаться линейным масштабным коэф-
фициентом, величина которого должна превышать значение, оп-
ределенное по формуле (11.16). Потом из той же формулы
(11.16) при новом коэффициенте находим число Рейнольдса
на модели Re„, а из зависимостей (11.40), или (11.41) —
величины относительной гладкости и абсолютной шероховато-
сти в условиях модели. Для удобства расчетов преобразуем фор-
мулы (11.40) и (11.41) и дадим их в таком виде:
0,275
-1,50 + 0,45 lg(VlRenJ,
(11.43)
-7=-1,74.
VI
(11.44)
Проверку допустимости использования в расчетах этих
формул нужно осуществлять с помощью числа Рейнольдса Ret;K
(11.45)
величина которого должна находится в пределах: 16 < RetJM < 44,7
для формулы (11.43), либо в пределах 5 < RetJM < 16 для формулы
(11.44).
Рассмотрим далее методику приближенного моделирования
напорного потока в рамках второй задачи. Используя связь меж-
221
ду критерием Архимеда Aty и числом Рейнольдса Re* (10.33),
найдем границы подзон в переходной зоне и соответствующие
законы сопротивления. В первой из них, границы которой опре-
деляются условием
/ \2 / \2
6,25 - < Аг, < 64 - ,
(11.46)
остаются справедливыми формулы (11.41) и (11.44). Во второй,
ограниченной условием
/ \2 / х2
64 - < Аг, < 500 Г-
ш ш
(Н-47)
из формулы (11.40) можно получить, используя зависимость
(10.33), следующую
4= = 3,6351g- +
A А
3,73 -1,6351g (д/Аг?),
(11.48)
которую по аналогии с (11.43) можно представить в таком удоб-
ном для расчетов виде
0,275
-1,026+ 0,45 1g (./Агу).
(11.49)
Обратимся к примеру, который был приведен в разделе
10.1. Параметры потока в натуре:^/ = 1,5м/с, £> = 1,0м, — = 60,
А
X = 0,0356 ,
Re^ =1,5-106 . Граничное число Рей-
нольдса, соответствующее началу зоны квадратичного сопротив-
ления, найдем по формуле (11.42)
222
Ren, = 252,8 \ 2 lg- +1,74 | - = 252,8-5,3 60 = 80390.
A A ) A
Возьмем на модели число Рейнольдса равным граничному
значению, находим масштабный коэффициент числа Рейнольдса
Re 151О6
—= к- ------------= 18,66 . Следовательно, линейный масштаб-
Rena Re 80390
ный коэффициент будет равен kt = (18,6б)2,3 = 7,04 . Принимаем
величину этого коэффициента равной к; = 16 , тогда число Рей-
нольдса на модели станет равным Re Dм =
1,5-106
163/2
= 23437,5 . Да-
лее в соответствии с (11.43) имеем
। = 0,275 _ + Q П00356 23437,5)= 1,6, =39,8.
L /0,0356 7
Отсюда получим величины линейных параметров модели
1 312
£>= — = 0,0625м, г = 0,0312м, Л =—^ = 0,078 см.
"16 " 39,8
Проверим правильность применения формулы (11.43), с
этой целью найдем по зависимости (11.45) число Рейнольдса
Re*,,
=А*
>0,0356 23437,5
8 2-39,8
= 19,6 . Следовательно, число Рейнольдса
находится внутри диапазона 16 < Re* <44,7, использование в
расчетах формулы (11.43) было правильным.
Для поиска решения в рамках второй задачи имеем сле-
дующие исходные данные: коэффициент гидравлического трения
л =0,0356 , число Архимеда в натуре Аг/Н = 6,28-108 , его гра-
ничное значение, соответствующее началу зоны квадратичного
сопротивления (см условие (11.47)), равно
223
Аг7г = 500-3600 = 1,8-IO6 . Берем граничное число Архимеда рав-
ным числу Архимеда на модели и определяем при условии моде-
лирования «по Фруду» линейный масштабный коэффициент
кАг = ~ - = — = 348,9, к] = tfk^ = 7,04 . Принимаем величину
Аг/и 1,8
этого коэффициента равной £/=16 , тогда число Архимеда на
6,28 -108 „
модели станет равным Аг/и =-------— = 153320,3 . Далее вос-
16
пользуемся зависимостью (11.49) с тем, чтобы найти относи-
тельную гладкость в условиях модели
1g (- | = 0,275 -1,026 + 0.451g U'l53320.3)- 1,6, Д] =39,8.
Проверим правильность использования в условиях модели фор-
мулы (11.49), с этой целью найдем отношение
= 96,8 . Таким образом,
2
, следовательно, число Архимеда на модели на-
м
ходится в пределах, определяемых условием (11.47), в которых
справедлива формула (11.49). Это полностью совпадает с выпол-
ненными выше расчетами.
11.3. Приближенное моделирование потока в переходной
зоне сопротивления потоком в той же зоне, или в зоне гид-
равлически гладкого русла
Как правило, безнапорные открытые потоки в натурных ус-
ловиях относятся к зоне квадратичного сопротивления. Напор-
л 153320,3
" 39,82
Аг, „= 96.8К]
224
ные потоки чаще всего находятся в переходной зоне, за исклю-
чением рассмотренных в ранее приведенных примерах течений в
старых трубах, характеризующимися малыми значениями отно-
сительной гладкости. В реальных условиях новые трубы имеют
высокие значения относительной гладкости (малые величины
относительной шероховатости), поэтому течение жидкости в них
относится к переходной зоне сопротивления. Отсюда возникает
задача моделирования таких течений, реализация которой до по-
следнего времени была связана с огромными трудностями. По-
кажем, что в рамках обсуждаемых здесь методов приближенного
моделирования гидравлических явлений эти трудности вполне
преодолимы. По своей сути эти методы ничем не отличаются от
рассмотренных выше методов моделирования потоков, находя-
щихся в зоне квадратичного сопротивления, потоками, относя-
щимися к переходной зоне.
В натурных условиях в переходной зоне коэффициент гид-
равлического трения определяется зависимостями (11.40) в пер-
вой задаче и (11.48) - во второй. Для того чтобы в этом убедить-
ся, необходимо натурное число Рейнольдса (или Архимеда)
сравнить с граничным, соответствующим началу зоны квадра-
тичного сопротивления, которое определяется по формуле
(11.42) (граничное число Архимеда находится по формуле
(11.47) как верхнее значение). Далее в зависимости от того, какая
задача решается, находится коэффициент гидравлического тре-
ния натурного потока по формуле либо (11.40), либо (11.48). Те-
перь можно задаться линейным масштабным коэффициентом и
определить число Рейнольдса (или Архимеда) на модели, после
чего из зависимости (11.43) в первой задаче и (11.49) - во второй
найти относительную гладкость модели. При этом нужно убе-
диться в том, что формулы (11.40) и (11.48) в условиях модели
225
использовались правильно. С этой целью находится число Рей-
нольдса Re*w и если окажется, что оно попадает в диапазон
5 < ReM, <16, то расчеты нужно повторить, используя в них зави-
симости (11.41) и (11.44). Во второй задаче, если окажется, что
число Архимеда попало в диапазон, определяемый условием
(11.46), то расчеты нужно также повторить, используя в них те
же зависимости.
Обратимся к примеру, в котором будем рассматривать па-
раметры потока и трубы, неоднократно использовавшиеся в рас-
четах ранее, за исключением относительной гладкости внутрен-
ней поверхности трубы. Считаем, что труба новая, относитель-
ная гладкость ее внутренней поверхности равна 1000 . Число
Рейнольдса в натуре равно Re/J;( = 1,5 106 , граничное число Рей-
нольдса найдем по формуле (11.42),
ReDz = 252,8 (2 Igl ООО + 1,74)1000 = 1,96-106 . Таким образом число
Рейнольдса в натуре оказалось меньше его граничного значения,
соответствующего началу зоны квадратичного сопротивления.
Коэффициент гидравлического трения в натуре определим по
формуле (11.40), но в нее коэффициент гидравлического трения
входит в неявном виде и может быть найден методом итераций
А
= 3,635 1g 1000 + 5,453 -1,635 1g (-А 1,5 • 106). В
качестве первого
приближения лучше всего подойдет его значение в зоне квадра-
тичного сопротивления:
4= = 2 1g 1000+ 1,74 =7,74
Результат
расчетов: -j= = 7,7.
А. = 0,0168 . Принимаем величину линейного
масштабного коэффициента равной ^=10, тогда число Рей-
226
1 5-Ю6
нольдса на модели будет равным ReD = -—= 47434,2 . После
10'
этого из зависимости (11.43) находим относительную гладкость
модели
Igf-'l = °'275 -1,50+ 0,45lg(V0,017-47434)—2,3,1—) =212,3.
Л017 W,,
При этом нужно убедиться в том, что формула (11.40) была при-
менена правильно, для этого найдем число Рейнольдса Ret l<, ис-
/0,0168 47434,2 „
пользуя зависимость (11.45) Re**, =--------= 5,12 . Таким
V 8 2-212,3
образом число Рейнольдса находится в диапазоне 5 < Re* <16, в
котором нужно использовать зависимости (11.41) и (11.44). По
сути дела число Рейнольдса на модели находится на границе зо-
ны гидравлически гладкого русла. Такой способ моделирования
также возможен и был обсужден выше при обосновании метода
моделирования потоков, принадлежащих в натуре к зоне квадра-
тичного сопротивления, потоками на модели, относящимся к зо-
не гидравлически гладкого русла. Применяем формулу (11.44),
из которой находим:
(05 (г А
1g - = , ’ -1,74 = 2,118, - =131,2. Теперь по (11.45)
14 70,0168
0,0168 47434,2 ono тт
-------------= 8,28 . Число Рейнольдса нахо-
8 2-131,2
дится в условиях модели в нужном диапазоне его изменения. Ес-
ли
имеем: Re**, =
абсолютная высота выступов шероховатости в натуре
500 ппсп
=---= 0,050 см, то на модели она составляет
1000
= - 5°= 0,038 см.
131,2
227
Осуществим далее поиск решения в рамках второй задачи.
Определим вначале уклон пьезометрической линии, воспользу-
емся с этой целью зависимостью (10.13)
1 52
J „ = J „ =0,0167—------= 0,0019 . Число Архимеда в натуре
рн р м 2-981-1 г
л 0,0019-981 (25)3 1п8 „
равно ArjH =----(о о~у ~~—— = 2,94-10 . По условию (11.47) его
граничное значение, соответствующее началу зоны квадратично-
го сопротивления, равно Агл, = 500-106 =5 -108 . Натурное число
Архимеда меньше граничного значения, поэтому коэффициент
гидравлического трения найдем по формуле (11.48)
2,94 108 I = 7,7 . Величину ли-
нейного масштабного коэффициента принимаем такой же, как в
первой задаче kt =10 . Тогда число Архимеда на модели будет
294-Ю8 s
равным Ar/v| = — = 2,94-10 . Теперь из формулы (11.49)
. ( г\ 0,275
имеем 1g — - . -=-
ЧаА, л/0,0168
= 2,327.
отношение
Отсюда — = 212,3 , что полностью совпадает с расчетами, вы-
полненными в первой задаче. Проверим правильность использо-
вания в условиях модели формулы (11.48), с этой целью найдем
2 294-105
= —----х- = 6,52 . Таким образом,
м 212,32
/
I 7* i
Агу = 6,52 — , следовательно, число Архимеда находится в
диапазоне, определенном зависимостью (11,46), в котором рас-
четы следовало вести по формуле (11.44), они были выполнены
228
выше и дали такой результат:
= 131,2. То, что формула
(11.44) была использована правильно, подтверждает следующий
Jrf 2,94 1 05
расчет (Ai>J .• | J =17,1 , который говорит о том, что
число Архимеда находится в нужном диапазоне, определенном
зависимостью (11.46).
11.4. Приближенное моделирование равномерного без-
напорного течения при разных линейных масштабных коэф-
фициентах глубин и плановых размерах потока
В случае моделирования открытых безнапорных потоков
при равномерном режиме движения часто возникает такая ситуа-
ция, когда глубина воды на модели оказывается столь малой, что
проводить надежные исследования становится невозможным.
Это объясняется особенностями геометрии открытых потоков: в
них, как правило, ширина русла на порядок и более превышает
глубину потока. Вот тогда и возникает необходимость увеличить
глубину потока на модели по сравнению с той, которая получает-
ся, если линейные масштабные коэффициенты по всем трем на-
правлениям принимать одинаковыми. Но, прежде всего, нужно
решить некоторые принципиальные вопросы, непосредственно
связанные с необходимостью обеспечения геометрического, ки-
нематического и динамического подобия натурного и модельного
потоков. При обсуждении двух последних подобий потоков вы-
яснилось, что в качестве характерного линейного размера нужно
брать гидравлический радиус. В напорном потоке связь гидрав-
лического радиуса с линейными размерами потока очевидна, по-
этому линейный масштабный коэффициент гидравлического ра-
229
диуса одновременно является и масштабным коэффициентом
всех линейных размеров потока. В открытом безнапорном потоке
такая связь не очевидна, условия ее существования требуют дока-
зательства. Здесь следует подчеркнуть, что речь идет о равномер-
ном движении воды в русле реки, неравномерное движение в
первую очередь в широком сложном русле с выходом воды на
пойму пока не рассматривается. Оно обладает рядом особенно-
стей, которые требуют разработки специальных методов при-
ближенного моделирования.
Еще на один момент следует обратить внимание, а именно:
в [16] обсуждается возможность искажение модели во всех трех
направлениях. Во-первых, в этом нет необходимости, так как
плановые размеры модели чаще всего диктуются продольным
размером лабораторного стенда. В его пределах необходимо раз-
местить подходной участок модели от ее начала до створа, в ко-
тором проводятся исследования. Длина подходного участка
должна быть такой, чтобы изменения в потоке, вызванные на-
чальным створом модели, исчезли, и под влиянием геометрии
русла и его шероховатости в нем вновь сформировался поток,
существовавший до входного сечения. По данным [22, 62] длина
такого участка должна быть не менее ста глубин потока. В [16]
рекомендуется брать эту длину равной 25 - 50 глубин потока на
модели, такой же предлагается брать и длину участка от створа, в
котором проводятся исследования, до конца модели. В этом
смысле с поперечными размерами модели трудностей, как прави-
ло, не возникает. Следует также иметь в виду, что введение про-
дольного масштабного коэффициента, отличного от поперечного,
связано с изменение уклона дна модели по сравнению с натурой,
что создавало бы дополнительные трудности с организацией мо-
делирования. Во-вторых, (и это главное) ниже на примере моде-
230
пирования планового течения будет показано, что характерным
линейным размером для продольного направления потока явля-
ется характерный линейный размер потока в поперечном направ-
лении. Но тогда аффинное подобие таких потоков возможно
только в том случае, если линейные плановые масштабные коэф-
фициенты равны друг другу, и только линейный масштабный ко-
эффициент глубин потока с ними не совпадает.
Обычно русловые потоки и потоки в искусственных каналах
имеют трапецеидальную форму поперечного сечения или близ-
кую к ней. Для простоты доказательства будем рассматривать
безнапорные потоки в руслах, поперечное сечение которых имеет
форму трапеции. Возьмем отношение гидравлического радиуса
натурного потока к гидравлическому радиусу потока на модели,
найдем масштабный коэффициент гидравлического радиуса, ис-
пользуя известные зависимости гидравлики [13, 60, 63]
где обозначено: kh= — , Р = -, т = ctg <р, h и
b - соответственно глубина потока и ширина канала по дну,
Ф - угол наклона образующей откоса к горизонту,
т - коэффициент заложения откоса, подстрочные буквы “л/” и
“и” относят буквенное обозначение соответственно к модели и к
натуре. Пусть х - проекция образующей откоса в пределах глу-
бины наполнения канала на горизонтальную ось, которая совпа-
дает в сечении с дном канала, тогда т - - . Далее выполним не-
h
обходимые расчеты, в результате получим:
231
„ bu bM kb „ kb х„ хы kb kb „
-^- = ——=B„ —, = -^ = -~s =mM — . В них симво-
P" h„ hMkh ^Mkh H h„ hMkh Mkh
лом kb обозначен масштабный коэффициент продольных и по-
перечных линейных размеров. Допустим теперь, что модель вы-
полнена с одинаковыми линейными масштабными коэффициен-
тами (без искажения линейных размеров) kb-kh , но в этом слу-
чае получаем
= В, тн = тм=т, следовательно, kR = kh = kb . (11.51)
Вывод: если модель выполнена без искажения линейных разме-
ров, то масштабный коэффициент гидравлического радиуса сов-
падает с линейным масштабом модели.
Увеличим глубину воды на модели по сравнению с hM ,
полученной в условиях равенства всех линейных масштабных
коэффициентов, обозначим ее Н = nhv .В дальнейшем буквен-
ные обозначения без подстрочных символов будем относить ли-
бо к натуре, либо к модели, выполненной без искажения линей-
ных размеров. Буквенные обозначения с подстрочным символом
"Н" будем относить к модели. Но там, где это потребуется для
внесения большей ясности в преобразованиях, оставим прежние
обозначения. Прежде всего, выясним, что представляет собой
коэффициент п увеличения глубины потока на модели по срав-
нению с глубиной в неискаженном русле. Определим новый ли-
нейный масштабный коэффициент глубины потока
кн = = = n^kh (11.52)
Н nhM п п п кн
Отсюда следует, что параметр п равен отношению линей-
ного масштабного коэффициента, принятого без искажения ли-
нейных размеров модели, к новому масштабному коэффициенту
232
глубины потока. Из-за увеличения глубины потока на модели
произойдет увеличение угла наклона образующей откоса к гори-
зонту, следовательно, уменьшение коэффициента заложения от-
коса, который станет равным тн. Связь между коэффициентами
заложения откосов найдем из условия равенства ширин потока
поверху в обеих моделях, из которого следуют очевидные соот-
ношения:
I и т ткн
тн = = (11.53)
Н п кь
Существенным недостатком такого метода моделирования
является увеличение на модели крутизны откосов по сравнению
с натурой. Изучение на модели процессов, связанных с деформа-
цией под действием потока размываемых откосов, становится
невозможным. В том числе и решение задачи подбора в резуль-
тате модельных испытаний крупности камня для берегоукрепи-
тельных работ.
Определим гидравлический радиус на модели, на которой
глубину потока увеличили и приняли равной Н
RH=H—Р// + ™н =
+ 2 д/1 + «н Н nh" п
После преобразований придем к следующему выражению
Я"="------РГГ 2 <пя>
Гидравлический радиус в натуре равен
(П.55)
р + 2 -у 1 + ш
233
Берем отношение (11.55) к (11.54), получим новое значение
масштабного коэффициента гидравлического радиуса
kR =-^ = kH^ + 2^2 = kfl &п + 2 . (Ц.56)
Н RH р + 2 д/1+ «2 Р + 2 7>
Русла естественных рек в поперечном сечении имеют не-
правильную форму; их смоченный периметр можно найти по
чертежу с помощью курвиметра. Поперечное сечение искажен-
ного русла на модели так же можно изобразить на чертеже и
найти аналогичным образом его смоченный периметр. Следова-
тельно, предоставляется возможность определить масштабный
коэффициент смоченного периметра русла с учетом искажения
его размеров на модели. Найдем связь масштабного коэффици-
ента смоченного периметра с другими линейными масштабными
коэффициентами. Используем в этих расчетах параметры русла
трапецеидального поперечного сечения, вначале приведем
формулы для определения смоченного периметра в натуре и на
искаженной модели
%« = (р + 2 Ji + w2Хя =^(р + 27«2 + w2).
Далее находим
_ X» _ /, Р + 2 71 + т2
КИн - - Г'п • Т
Хя Р + 2 7«2+«2
(11.57)
Произведем замену дроби в (11.57), используя формулу (11.56),
получим
к -к кн
~ -7—
к1н
(11.58)
234
В связи с увеличением глубины потока на модели произой-
дет изменение уклона свободной поверхности. Найдем масштаб-
ный коэффициент уклона свободной поверхности. Пусть
перепад уровня воды в натуре в пределах длины русла 1Н; пере-
пад уровня на соответственной длине 1М на модели равен А Н.
Отсюда найдем масштабный коэффициент уклона поверхности
к
. Или,
кЬ
А,
принимая во внимание
(11.52), имеем: = — = -, iM = п iH . Но вместе с тем в условиях
модели необходимо сохранить режим равномерного движения,
поэтому равенства коэффициентов гидравлического трения и
преобразованных чисел Фруда в натуре и на модели, естествен-
но, сохраняются: кх =1, kFr. =1 . Из второго условия следует:
Fr! H = Рг! Л/ . Кроме связи уклона свободной поверхности в натуре
с уклоном на модели, в дальнейших преобразованиях с учетом
искажения глубины потока по сравнению с его плановыми раз-
R U2
мерами потребуются следующие: RM= —, U2M . Запишем
kR ку
преобразованное число Фруда на модели и найдем связь его с
_ iM пк?7 /„ nkjj „
аналогичным числом в натуре: Fr. м = Fr, „ .
J Г 1 М Т7- Zr Т?т- b tH
k# rrf/ kR
Но для обеспечения равномерного движения должно соблюдать-
ся условие: Fr, = Fri w . Отсюда следует kv = , — .
у п
При п = 1 получим кц - -у/к^, что соответствует условию строго-
го моделирования «по Фруду». Таким образом, режим течения на
модели сохраняется равномерным, но числа Фруда и Рейнольдса
235
будут больше, чем в натуре. Найдем связь между числами Фруда
6/2 к U2
на модели и в натуре: Fru =—*- = -£-—*~ = nFr„ . При этом
g к{] g R„
число Фруда на модели не должно превышать предельно допус-
тимого значения, приблизительно равного 0,1 . Наконец, полу-
чим
м
Re,.
м
аналогичную связь между числами Рейнольдса
»1/2
v к,; kR н k%2 '
Рассмотрим пример с потоком, параметры которого близки
к тем, которые были рассмотрены ранее в разделе 10.2:
R 7
17 = 1,0м/с, /? = 10м, — = 60, Хо=О,ОО77 , ReH = 107 , число
А
Фруда FrH = » 0,01 , уклон дна /„ = °'0^77 0,01 = 38,5 • 10 6 .
Rea = 43087 . Русло в натуре в поперечном разрезе имеет форму
близкую к трапеции с параметрами: hH = 11,5 м , р = 16,5, т = 2,5 ,
6 = 11,5-16,5 = 189,8 м, 5 = 189,8 + 5 11.5 = 247,Зм, где b и
В - ширина потока по дну и поверху. Площадь живого сечения и
расход воды равны: <в„ =11,52-19 = 2512,8 м2, QH = 2512,8 м3/с .
Допустим, что, исходя из производственных условий, модель
можно изготовить в масштабе Л/ =100 . В таком случае неиска-
женная модель будет обладать такими параметрами:
6^= 0,115 м, 6и=1,9м, Вм = 2,47 м, = 0,25 м2, С'Л, =0,1 м/с,
QM = 0,025 м3/с . Гидравлический радиус на неискаженной моде-
ли равен RM = 0,1 м , проверим это:
п Л11 с 16,54" 2,5 ~.
Ru = 0,115--------= 0,1 м .
16,5 + 2л/7Д5
236
Определим число Рейнольдса на неискаженной модели
Re
Л4
01 = 104 . По формуле (Н.11) находим число Рейнольд-
са на модели, соответствующее зоне гидравлически гладкого
русла (Re v )г гл = 3,65 (4 1g 60 + 4,25) 60 = 0,25 • 104 . Таким образом,
число Рейнольдса на модели находится в переходной зоне.
Увеличим глубину потока на модели в четыре раза, тогда
модель будет иметь следующие линейные масштабные коэффи-
циенты: кн =25, = kh = кь =100, п = 4 . Найдем величину
гидравлического радиуса на искаженной модели, используя за-
висимости (11.56)
= = 25 16.5 + 2 м 4.125 + 2 71 + (25/4)г
" RH 16,5 + 2 7^25 16.5 + 2 7^25
Отсюда имеем Rf, =----
" 29,6
= 0,338 м . Можно видеть, что гидравли-
ческий радиус на искаженной модели изменился не так, как из-
менилась в соответствии с новым масштабом глубина потока,
равная Н = 0,46 м . Находим скорость течения на модели
I 4
UM = 7 296 = 0368 м/с, а также площадь живого сечения, учтем
при этом, что коэффициент заложения откоса на модели изме-
ни 2,5 _ „ _
нился: тн = — = — = 0,625 , имеем
Н 4 4
+ тн Н} = 0,46(1,9 + 0,625 • 0,46) = 1,0 м2 . Отсюда рас-
ход воды на модели равен QM = 0,368 м3/с . Проверяем этот ре-
зультат, определив масштабный коэффициент расхода воды:
/г 1эа л
ko = kirkb'j~ = 25400-J— = 6800,8 . Получим
v У п V 4
237
2512,8
kQ 6800,8
= 0,369 м3/с . Проверим еще справедливость за-
висимости (11.58), с этой целью вначале из формулы (11.57) най-
дем масштабный коэффициент смоченного периметра, получим
, „ 16,5 + 2-71 + 6,25 , 252 тт п „
к =25---------------1 = 21,1, kR =---------= 29,6. Число Реи-
16,5 + 2 716 + 6,25 Rh 21,1
нольдса на искаженной модели оказалось равным:
„ 36,8-33,8 5 „
Re„ = — —— = 1,24-10 . Проверим этот результат:
107-2 , * п5 „
Re= Re„ = 1,24 -10 . Следовательно, выполняется
4/2 29,632
условие Re „ > Re, = 43087 , а это означает, что поток на модели
находится в зоне квадратичного сопротивления. Определим вы-
соту выступов шероховатости на искаженной модели
А и = = 0,57 см , число Фруда 1?ги = 0,01 • 4 = 0,04 и уклон
дна iM =n-i„ =4-38,5-Ю"6 = 1,54-10“4 .
Как видим, при таком способе моделирования достаточно
строго выполняются только два условия: равномерный режим те-
чения и равенство на модели и в натуре коэффициентов гидрав-
лического трения. Числа Рейнольдса и Фруда в условиях модели
отличаются от таковых в натуре, но находятся в соответствую-
щих автомодельных областях. Геометрическое подобие заменя-
ется аффинным. Но об аффинном подобии, строго говоря, можно
говорить только в том случае, если русло в натуре имеет прямо-
угольную форму. Представим себе, что русло в натуре имеет тре-
угольную форму, тогда на модели оно станет трапецеидальным.
Конечно, и в таком случае можно говорить об аффинном подо-
бии, однако, нет доказательства существования кинематического
подобия потоков в этих руслах. Фактически речь идет о необхо-
238
димости проведения серии исследований распределения скорости
течения в цилиндрических руслах при разных величинах гидрав-
лического радиуса. Цель исследований можно было сформулиро-
вать так: найти такое граничное значение гидравлического ра-
диуса, при котором потоки в рассматриваемых руслах можно
считать подобными. Тем самым определилась бы величина до-
пустимого искажения линейного масштаба глубин по сравнению
с линейными масштабами плановых размеров потока. Пока этот
вопрос остается открытым. Но здесь существует другой метод
приближенного моделирования открытых потоков, у которых
плановые размеры намного превышают их глубины. Используя
особенности таких потоков, можно на их основе обосновать для
больших акваторий такой метод приближенного аффинного по-
добия, при котором соблюдается равенство на модели и в натуре
чисел Фруда, Рейнольдса и величин коэффициентов гидравличе-
ского трения. Для больших рек, русла которых обладают этими
особенностями, можно рассмотреть метод приближенного моде-
лирования ограниченного круга практических задач. В том и в
другом случае в них решается вопрос о степени искажения ли-
нейного масштабного коэффициента глубин потока по сравнению
с плановыми линейными масштабными коэффициентами. Ниже
будут рассмотрены эти методы приближенного моделирования
открытых потоков.
11.5. Приближенное моделирование равномерного без-
напорного течения при скорости потока на модели, не соот-
ветствующей правилу моделирования «по Фруду»
При моделировании равномерного движения открыто-
го безнапорного потока часто возникает необходимость увели-
239
чить скорость течения на модели по сравнению со скоростью, со-
ответствующей правилу моделирования «по Фруду». Это, в част-
ности, может быть продиктовано требованием создать на модели
условия подобия процесса движения наносов, который наблюда-
ется в натуре, и т. п.
Обратимся к зависимости (10.50), соответствующей
равномерному движению воды в открытом безнапорном потоке.
Запишем ее в виде индикатора подобия
= }ikFr, >
где кк = —— - масштабный коэффициент коэффициента гид-
Fr;-
равлического трения, kFr = —- - масштабный коэффициент
' Fr.-
I м
преобразованного числа Фруда. Исходя из требования равенства
коэффициентов гидравлического трения в натуре и на модели,
имеем: k)fj = 1 , следовательно, kFr = 1 . Последнее равенство,
учитывая зависимость (10.50), представим в виде индикатора по-
добия
к2
О1-59)
ki kg kR
в котором ки, кг, kg, kR - масштабные коэффициенты соот-
ветственно скорости течения, уклона дна водотока (при равно-
мерном движении одновременно это и уклон его свободной по-
верхности), ускорения силы тяжести и линейного размера. При-
нимая масштабный коэффициент kg =1 , из зависимости (11.59)
получим
240
kt ku /kR
(11.60)
Если моделирование реализуется «по Фруду», то
ku=kR' к1=1' 1н=*М-
U2
Введем обозначение для числа Фруда на модели Fr„ = ——
gRM
в том случае, если это число соответствует условию FrH = Fr„ .
Допустим, что скорость течения на модели увеличили в п раз
„2 U2
(и > 1), тогда число Фруда на модели станет равным Fr(J =-— ,
я
о М
отсюда имеем Fr„ = п2 Frw . Как уже неоднократно отмечалось
выше, предельное значение числа Фруда, при котором поток
можно считать спокойным, не должно превышать 0,1 . Этим оп-
ределяется возможность увеличения скорости течения на модели.
Если моделирование осуществлялось в соответствии с ос-
новным правилом при соблюдении равенства чисел Фруда на мо-
дели и в натуре, то увеличение скорости течения на модели сверх
той, которая определяется этим правилом, повлечет за собой из-
менение режима течения на модели по сравнению с натурой.
Вместо равномерного режима течения в натуре на модели режим
течения будет неравномерный. Поддерживая постоянным уро-
вень воды в конце модели с помощью расположенных здесь ре-
гулирующих устройств, можно обнаружить выше по течению
подъем уровней воды по сравнению с теми, которым соответст-
вует равномерный режим течения. Существует такой способ при-
ближенного моделирования в этом случае: уровень воды в конце
модели понижают до тех пор, пока в створе наблюдений он не
станет равным уровню, соответствующему равномерному режи-
му. Но в целом течение воды на модели будет неравномерным:
241
выше по течению от створа, в котором проводятся исследования,
уровни воды будут выше, а ниже по течению ниже тех, которым
отвечает равномерный режим. Конечно, такой способ моделиро-
вания следует признать весьма приближенным.
Более подходящим в этом случае представляется такой ме-
тод моделирования, когда на стадии проектирования модели
предполагается увеличение скорости течения на ней. При этом
режим течения на модели сохраняется равномерным, но числа
Фруда и Рейнольдса будут больше, чем в натуре. Следовательно,
дну потока на модели нужно придать уклон больший, чем в нату-
ре. Таким образом, появляется масштабный коэффициент уклона
дна, отличный от единицы. Определим его, полагая, что требова-
ния равенства коэффициентов гидравлического трения и преоб-
разованных чисел Фруда в натуре и на модели, естественно, со-
храняются: k)Q = 1, kF = 1 . Из второго условия следует:
Fr;H = Fr(W . Рассмотрим преобразованное число Фруда в услови-
ем2
ях модели Fri w =-----— . Допустим, что скорость течения на
iM g
модели была увеличена в п раз, но это повлечет за собой увели-
чение числа Фруда на модели, которое станет равным Fr„ ; но то-
гда в соответствии с требованием kFr. = 1 уклон дна на модели
2 - 2 .
должен увеличиться в п раз и станет равным in м = п tM , где ук-
лон iM соответствует условию =iH .В таком случае масштаб-
ный коэффициент уклона дна станет равным
, ги 1 2 .
1г. — _Н— = _ 7 = М 7
. 7 ' П И ’
м и
Рассмотрим пример, который был приведен в конце
предыдущего раздела. Заданы такие параметры потока в натур-
242
ных условиях: (7н=1,0м/с, Лн=10м, ^ = 60, =0,0077,
7 1
Re„ = 10 , Re., =43087 , число Фруда Fr„ = 98| |0~0'01 ’ Уклон
дна iH = —-^7- 0,01 = 38,5 10 6 . При создании модели имели в ви-
ду следующие условия: iH = /и , Fr„ = Frw .
Русло в натуре в поперечном разрезе имеет форму близкую
к трапеции со следующими параметрами:
/г„=11,5м, Р = 16,5, от = 2,5, 6=189,8м, В=247,3м,
(о„ =2512,8 м2 , QH = 2512,8 м3/с . Линейный масштабный коэф-
фициент модели принят равным =100 , это определило основ-
ные параметры потока на модели:
hM =0,115м, Ьм= 1,9м, Вм= 2,47м, мл;= 0,25м2, UM = 0,1м/с,
QM = 0,025 м3 /с, RM= 0,1м и число Рейнольдса на модели
D 10-10 , п4 тт D “
Rew = QQi = 10 . Число Рейнольдса на модели находится в пе-
реходной зоне, поскольку его величина, соответствующая зоне
гидравлически гладкого русла, равна (Re =0,25-104 .
Увеличим скорость течения на модели в три раза: и = 3 .
Тогда скорость течения на модели станет равной U„ = 0,3м/с ,
число Фруда Fr„ = и2 FrH = 0,09 , число Рейнольдса
Re„ = 3ReJM = 3-104 , уклон дна in = п2 iH = 3,46-10 4 . Таким об-
разом, число Рейнольдса на модели находится в переходной об-
ласти. Далее в соответствии с (11.17) найдем величину относи-
тельной гладкости потока в связи с тем, что на модели произош-
ло увеличение числа Рейнольдса; имеем:
243
lg I -1 = .°---- - 1,395 + 0,450 1g (л/0,0077 30000)= 1,717,.
л/0,0077
| | =52,1. Отсюда получим АИЛ1 = = 0,19см.
522
На модели увеличатся скорость течения, числа Рейнольдса и
Фруда, но при сохранившихся линейных размерах режим потока
останется равномерным. Сохранится основное условие модели-
рования: ХОн =л0 „ , а изменившееся число Фруда не выйдет за
рамки автомодельной области. Проверим правильность приме-
нения в расчетах формулы (11.17). Определяем величину дина-
мической скорости потока и соответствующее число Рейнольдса:
1,86.0,192 35?
0,01
находится в пределах
формула (11.17) была исполь-
/0,0077 , ,
w+=30J—-— = 1,86 см/с, Re*„ =
Следовательно, число Retw
16 < Re,u < 44,7, а это значит, что
зована правильно.
11.6. Моделирование гидравлических явлений в водо-
емах и водотоках больших плановых размеров и малых глу-
бин
Как отмечалось ранее, перед исследователем часто возника-
ет необходимость изучить на физической модели явления в
больших по площади акваториях, например, в речных эстуариях,
в реках с широкими поймами, в морских заливах и т. п. Как пра-
вило, такие акватории характеризуются малыми глубинами воды
по сравнению с их плановыми размерами. Эта особенность таких
водоемов создает трудности при их моделировании. Даже в
крупных по занимаемой площади лабораториях при выбранном
линейном масштабном коэффициенте, определяемом размерами
244
лаборатории, глубины воды на модели получаются столь малы-
ми, что проведение исследований на них становится невозмож-
ным. Стремление увеличить глубину воды на модели, приняв для
нее линейный масштабный коэффициент, отличный от аналогич-
ных коэффициентов плановых размеров модели, представляется
вполне объяснимым. При этом, естественно, возникает вопрос:
каким должен быть масштабный линейный коэффициент глубин.
Иными словами: во сколько раз допустимо в условиях модели
увеличивать глубину потока по сравнению с натурой (во сколько
раз можно уменьшать линейный масштабный коэффициент глу-
бин потока по сравнению с линейными масштабными коэффици-
ентами плановых размеров модели). Этот вопрос рассматривался
в случае течение воды в широком русле без поймы. Однако ис-
черпывающий ответ на него не был получен в связи с существен-
ными искажениями формы русла в прибрежных областях потока.
Конечно, такие искажения неизбежны при любой степени отли-
чия упомянутых выше линейных масштабных коэффициентов.
Тем не менее, с выходом воды на пойму, особенно в случае подъ-
ема уровня воды на значительную величину, при котором глуби-
ны воды на пойме превышают глубину потока в русле реки в ме-
жень, влияние речных береговых откосов на общий характер те-
чений в период паводка невелико. В равной степени это относит-
ся и к явлениям, изучаемых в широких речных эстуариях и в
морских заливах, за исключением исследования процессов, свя-
занных с вдольбереговыми течениями.
Для анализа методов моделирования явлений в таких водо-
емах и водотоках воспользуемся уравнением Сен-Венана, запи-
санном в общей форме (уравнение «мелкой воды») [13]. При этом
будем пренебрегать влиянием ветра на свободной поверхности
воды, изменением атмосферного давления в пределах акватории,
245
нормальными вязкими и турбулентными напряжениями в попе-
речных сечениях потока, а также считать плотность воды посто-
янной. Тогда упомянутое уравнение можно записать в таком ви-
де, полагая, что площадь поперечного сечения потока и в общем
случае является функцией продольной координаты и времени:
g оз dt g и д х g и
которое при условии оз = const превращается в зависимость (8.8);
в (11.61) х - смоченный периметр, остальные обозначения сов-
падают с ранее приведенными, в том числе содержащимися в
уравнении (8.8). Как известно, в широком русле гидравлический
радиус практически совпадает с глубиной потока R ® h , а пло-
щадь живого сечения может быть определена по формуле:
(it&hb , где b - ширина потока. Введем эти данные в последний
член в правой части уравнения (11.61), перейдем от динамиче-
ской скорости к средней и представим это уравнение в таком ви-
де
1 d U и 1 dU2(o U2 х /11 z-nx
J =--------+------ +Х0---------—. (11.62)
g оз d t go dx 2g hb
Уравнение дано в безразмерном виде, сделаем безразмер-
ными содержащиеся в нем величины. С этой целью введем неко-
торые характерные из них в качестве масштабов. Пусть для глу-
бины потока это будет Н, для ширины и смоченного периметра -
В. Выберем характерную величину для продольной координаты
х. Как уже отмечалось ранее, в продольном направлении по са-
мому определению нет величины, которая отвечала бы требова-
ниям, предъявляемым к характерной величине, а именно: незави-
246
симость ее от координат и времени. Конечно, в некоторых случа-
ях без такого рода характерной величины не обойтись. Например,
при изучении явлений в пределах водобоя и рисбермы за водо-
сбросной плотиной в качестве характерной линейной величины
можно выбрать длину крепления русла. Но тогда явления следует
изучать только в пределах крепления. Кроме того, если в качестве
характерного линейного размера выбрана, например, ширина во-
досливного фронта, то длина крепления в конкретной рассматри-
ваемой задаче связана с этой характерной величиной простой ли-
нейной зависимостью, так что вполне можно обойтись только
одним характерным плановым линейным размером. В соответст-
вии со сказанным в качестве характерного линейного размера для
продольной координаты х следует выбрать характерную ширину
потока В. Следует отметить также трудности, которые обычно
возникают при решении задач неустановившегося и неравномер-
ного движения жидкости, связанные с необходимостью опреде-
ления силы сопротивления. Обычно в пределах расчетного участ-
ка ее принимают равной среднему арифметическому из величин,
найденных в контрольных створах, используя при этом формулы
равномерного режима движения. При решении плановых задач
чаще всего приходится сталкиваться с образованием в пределах
расчетной области водоворотных зон. Наиболее характерные
примеры: движение струи за гидроэлектростанцией или за рис-
бермой водосливной плотины в широком русле нижнего бьефа;
поток за мостовым переходом при стеснении части поймы под-
ходными дамбами, на гребне которых находится полотно дороги;
стоковое течение, возникающее в широком эстуарии при впаде-
нии в него реки и т. п. В таком случае возникает необходимость
выбора некоторой величины коэффициента гидравлического тре-
ния в качестве характерной, пусть это будет Л . Обозначим ха-
247
рактерную скорость V , характерное время Т , примем i » / , по-
лучим вместо (11.62) следующее уравнение, в котором величины
со штрихом безразмерные, кроме того, Х'о =
Л
У dU'а' У2 dU'2 (д' д V2 ,, U'2
----------+-------------+ Л----Хп---
gT(d' dt' g В (д' д х' gH 2h'
(11.63)
V2
Уравнение (11.63) содержит число Фруда - Fr =-, на ко-
gH
торое разделим все члены этого уравнения, в результате получим
где Sh = y^ - число Струхала. Умножим все члены последнего
уравнения в левой и в правой его частях на отношение линейных
g
масштабных коэффициентов —, получим
J B 'BdU'ri dU'2 (д' , В , U'2
-----= Sh---------+--------+ Л—Хп------.
Fr Н Н (д dt' (д' д х Н ° 2 h'
(11.65)
Если движение стационарное, то вместо (11.65) имеем:
J В dU'2 (д' д В y,U'2
-----= —----------+ Л—Хп---------.
Fr Н (д д х' Н ° 2 h'
(11.66)
В результате выполненных преобразований в полученное
безразмерное уравнение вошла следующая комбинация из харак-
терных линейных величин и характерного коэффициента гидрав-
. В „
лического трения Л— . Поскольку уравнение не имеет размерно-
248
сти и входящие в него члены тоже безразмерны, то эта комбина-
ция представляет собой новое число подобия, поэтому она оди-
накова для модели и натуры:
Л—~=Л—(11.67)
н и м ZJ v '
Нн “ м
Из нее можно получить индикатор подобия:
к
(11.68)
kh
в котором кх=^~ Произведем замену в (11.67) характерных ве-
Л„
м
личин отношением соответствующих величин к безразмерным,
. bH h' . bM h' „
получим: л0„ —-величины со штрихом
hH ^0 b
одинаковы для натур и модели, поскольку они не имеют размер-
ности, отсюда имеем:
чА=Х<ьЛ. (11.69)
«л "м
Однако, такая ситуация возможна только в том случае, если
линейные масштабные коэффициенты одинаковы: kb=kh , при
этом к} =1. Таким образом, в случае равенства линейных мас-
штабных коэффициентов условие (11.69) можно рассматривать
как само собой разумеющиеся. При физическом моделировании
подобных явлений оно сводится только к необходимости добить-
ся равенства коэффициентов гидравлического трения в натуре и
на модели. Если глубина воды на модели, входящая в правую
часть зависимости (11.69), недостаточна для проведения исследо-
ваний, то ее надо увеличить в п раз, так что она станет равной
249
nhM, и>1. Именно это обстоятельство и станет причиной появ-
ления линейного масштабного коэффициента глубин потока, от-
личного от линейного масштабного коэффициента его плановых
размеров: kh*kb . Параметр, находящийся в правой части зави-
симости (11.69), уменьшится в силу очевидного неравенства:
кОм—>кОм «>1 • Вместо зависимости (11.69) появится
h,. nh„
м м
(11.67) и соответствующий ей индикатор подобия (11.68).
Введем новое обозначение: nhM=hn . Тогда можно записать
следующее равенство
X
Ьм
О .и >
ППМ
Л Ь..
_м
“Л0л/7~-
hf,
(11.70)
Таким образом, при увеличении глубины потока на модели по
сравнению с глубиной, соответствующей равенству всех линей-
ных масштабных коэффициентов, появляется линейный мас-
штабный коэффициент глубин, отличающийся от линейных мас-
штабных коэффициентов плановых размеров потока. Одновре-
, Ь
менно происходит уменьшение на модели параметра кПм — по
К
сравнению с аналогичным параметром в натуре. Отсюда вытека-
ет задача исследовать, как указанный параметр влияет на харак-
теристики планового течения. Здесь можно сослаться на работу
[27], в которой рассматривается течение на участке внезапного
планового расширения безнапорного потока. В качестве харак-
терных величин приняты: глубина hx , ширина Ъх и скорость по-
тока в сжатом сечении щ; в этом сечении расчетом определялся
коэффициент гидравлического трения X. Целью исследований
было определение такой важной характеристики расширяющего-
ся в плане потока, какой является протяженность водоворотной
250
зоны хв, в зависимости от числа Фруда в сжатом сечении потока
2 Ь Ь
рг , степени его расширения р=— и параметра X—, где
1 gh\ ь\ \
- ширина русла ниже створа внезапного расширения потока. В
качестве характерной длины области водоворота принята его
длина хв$, соответствующая случаю полного отсутствия силы
трения на дне потока ( л=0). На рис.11.3 приведен график зави-
симости -^=/fX—) при следующих условиях: Б^сОДб, р>3 .
К
Рис. 11.3. Зависимость относительной длины водоворотной
зоны от параметров X— и X при р>3
h\
Как можно видеть, на графике имеется не одна, а несколько
кривых в зависимости от величины коэффициента гидравличе-
ского трения. Возможно, это объясняется тем, что канал в сжатом
сечении и ниже створа внезапного расширения имел прямоуголь-
ную форму в поперечном сечении, а шероховатость вертикаль-
251
них боковых стенок была пронята равной шероховатости дна.
Тем не менее, результаты экспериментов обнаруживают непо-
средственное влияние коэффициента гидравлического трения на
протяженность водоворотной зоны. Рассматривая рисунок, мож-
но сделать вывод о том, что при условии л—>1 относительная
h\
длина области водоворота практически не изменяется.
Иными словами, при этом условии имеется автомодельная
область по рассматриваемому параметру. Можно также сослаться
на [12,23,24], где приведены результаты многочисленных опы-
тов, подтверждающих этот вывод. Следовательно, условия при-
ближенного моделирования плановых течений будут зависеть от
величины параметра, равного произведению коэффициента гид-
равлического трения на отношение ширины потока к его глубине.
Вместе с тем можно сформулировать общие правила приближен-
ного аффинного моделирования плановых течений: рассматри-
ваемые течения считаются подобными только в том случае, если
обеспечено подобие длин водоворотных зон, так как только тогда
можно ожидать подобия распределения по ширине русла средних
на вертикалях скоростей течения. При этом следует подчеркнуть:
поскольку условие Хо н = Хо м не соблюдается, распределение
скоростей потока в точках на вертикалях модели не будет подоб-
ным натурному.
J в
Уравнение (11.66) содержит еще одно число подобия----,
Fr Н
к к
из которого следует такой индикатор подобия: - b = 1 , где
kh
J Fr
кj = , kFr = —- - масштабный
}Тг«
уклона свободной поверхности и числа Фруда соответственно.
коэффициент продольного
252
Далее необходимо выработать последующую стратегию модели-
рования. Допустим, выполняется условие кь - kh и kFr = 1 , тогда
kj = 1 , следовательно, продольные уклоны свободной поверхно-
сти в натуре и на модели совпадают. Положим
kb^kh, kb/kh>\ , тогда возможны два метода моделирования.
В первом условие— — = idem будет соблюдено, если принять
Fr Н
kFr=kb/kh>\ . Из этого следует FrH >Frw , но вместе с тем по-
лучим kj = 1 . Более предпочтителен второй метод, в котором
принимается естественный путь моделировании течений с учетом
силы тяжести, а именно: kFr = 1 . Но тогда из условия kj = kh/kb
получим: JM> JH . Таким образом, продольный уклон свободной
поверхности на модели будет больше, чем в натуре. Заметим, что
уклоны свободной поверхности на перечисленных выше объекта
моделировании невелики. Кроме того, протяженность участков
моделирования сравнительно небольшая, поэтому превышение
уровней воды на модели не будет заметно отличаться от натур-
ных. По сравнению с глубиной потока ими можно пренебречь и
считать, что этот факт не внесет заметных изменений в картину
течений. Результаты опытов подтверждают этот вывод.
Кроме образования водоворотных зон, течения в водотоках
и водоемах часто сопровождаются искривлением потока в плане.
Вопрос моделирования течений в искривленном русле достаточ-
но подробно рассматривается в [12,21, 23, 24] и в других публи-
кациях. В первую очередь речь идет о моделировании поперечно-
го уклона и о его влиянии на распределение продольных и попе-
речных скоростей течения. Как известно, величина поперечного
уклона Jr , если не учитывать турбулентное трение между
253
. и2
струями в плане, определяется из зависимости: Jr = — , в кото-
gf
рой г - радиус поворота. Умножим и разделим правую часть
этой формулы на глубину потока, выразим вошедшие в нее вели-
чины через характерные, получим после преобразований:
J.. В U'2 „
—----=---- . Здесь в качестве характерной величины для радиуса
Fr Н g г'
поворота принята В . Отсюда следует, что при условии Fr = idem
на модели произойдет увеличение не только продольного, но и
поперечного уклона. Степень влияния этого увеличения на ха-
рактер изменения продольных и поперечных скоростей на пово-
роте потока не очевидна. Во всяком случае, нельзя утверждать,
что она несущественна, и ею можно пренебречь, как влиянием
увеличения на модели продольного уклона на его кинематику.
Для обоснования подобного утверждения потребовалось привле-
чение опытных данных, которые приводятся в [12,23,24]. В
опытах изменялась величина коэффициента гидравлического
трения л0 при постоянной величине отношения b/h и, наобо-
рот, при постоянном отношении b/h изменялся коэффициент
Хо . Как оказалось, влияние этих параметров на кинематику по-
тока различно, но опытные данные обнаружили однозначную за-
висимость распределения скоростей течения и уклонов от пара-
метра Хо -
h
и автомодельность по нему. Обнаружено также
влияния на длину водоворотных зон непосредственно коэффици-
ента гидравлического трения. Но по сравнению с влиянием пара-
, Ь
метра л0 — оно не столь существенно, что находится в соответ-
h
ствии с выводами, изложенными в [27]. Однако не учитывать это
254
влияние или забывать о нем не приходится. Это можно доказать
на таком примере.
Допустим, что модель была запроектирована и прошла про-
верку при определенном уровне воды в пределах акватории (ему
соответствует заданный расход воды, ее глубина и скорость тече-
ния в характерном створе). В процессе исследований возникла
необходимость проведения их при другом уровне воды с иными
характеристиками потока (другим расходом, скоростью течения и
т.п.). Но в таком случае параметра Хо ~ изменится, его величина
h
станет отличаться от той, которая была принята в процессе про-
ектирования модели. С увеличением на модели глубины потока
параметр уменьшится, а с уменьшением, наоборот - увеличится.
Уменьшение числа Рейнольдса (скорости течения) в области гид-
равлически гладкого русла проводит к увеличению коэффициен-
та гидравлического трения, а увеличение числа Рейнольдса-к
уменьшению этого коэффициента. В области квадратичного со-
противления уменьшение относительной гладкости поверхно-
стей, ограничивающих поток, (увеличение относительной шеро-
ховатости) влечет за собой увеличение коэффициента гидравли-
ческого трения и наоборот: уменьшение шероховатости поверх-
ностей приводит к уменьшению этого коэффициента. Следова-
тельно, любое отступление от характеристик потока, заложенных
, b
в проект модели, связано с изменением параметра л0 — и требо-
h
ванием его корректировки в процессе проведения исследований.
Важно определить, в какую сторону произошли изменения и что
нужно сделать для того, чтобы исправить нарушение, если в этом
есть необходимость. Например, для того чтобы в области гидрав-
лически гладкого русла при увеличении глубины потока на моде-
255
X b
ли привести параметр
в соответствие, достаточно будет
уменьшить скорость потока. В области квадратичного сопротив-
ления необходимость такого рода корректировки повлечет за со-
бой такие более серьезные последствия, как увеличение шерохо-
ватости дна на модели. Но может иметь место и такой случай, ко-
гда коэффициент гидравлического трения на модели окажется в
иной области сопротивления, чем в натуре. Например, в натуре
область сопротивления - гидравлически гладкое русло, а на мо-
й
дели для приведения параметра л0 - в соответствие нужно,
h
чтобы коэффициент гидравлического трении относился к области
квадратичного сопротивления. Конечно, такую ситуацию нужно
по возможности избегать, учитывая влияние на явление самого
коэффициента гидравлического трения, причем последствия это-
го влияния практически невозможно предсказать. С тем, чтобы
уменьшить негативные последствия этого влияния, необходимо
проектировать модель так, чтобы изменения коэффициента гид-
равлического трения не выходили за пределы области сопротив-
ления в натуре. Альтернативой изложенного метода корректи-
X Ь
ровки параметра
может быть уменьшение глубины потока
на модели, что связано с изменением линейных масштабных ко-
эффициентов, иными словами - с созданием новой модели. Та-
ким образом, при проектировании модели необходимо рассмот-
реть различные варианты и в обсуждаемом смысле выбрать оп-
тимальный. Если на модели возникает необходимость проводить
опыты при глубинах потока меньших тех, при которых модель
бала запроектирована, то произойдет увеличение параметра
ь
h
. В некоторых случаях моделирования, как будет показано
256
ниже, корректировки этого параметра не потребуется. Более под-
робно вопросы моделирования в случае необходимости прово-
дить на модели исследования при разных уровнях потока и глу-
бинах рассмотрены в разделе 11.9.
Отметим, что в [23, 24] была предпринята попытка учесть
турбулентное трение между струями как при повороте потока в
плане, так и при внезапном его расширении. Однако однозначно-
го ответа на этот вопрос получено не было в силу того, что суще-
ствуют различные методы замыкания системы уравнений Рей-
нольдса. Опираясь в основном на опытные данные, авторы огра-
ничили круг плановых задач, моделирование которых по пара-
. Ъ ’ с-
метру л 0 - не вносит существенных ошибок в результаты ис-
h
следований. В основном это те задачи, которые были указаны
выше. Имея в виду эти данные и учитывая особенности плановых
течений, рассмотрим два случая их моделирования.
В первом случае выполняется условие:
^Он
^-<1, которое
характерно для потоков в руслах больших рек и в нижнем тече-
нии средних. Здесь приближенное моделирование плановых те-
чений реализуется в соответствии с зависимостью (11.67) и выте-
кающем из нее индикатором подобия (11.68). Если линейные
масштабные коэффициенты глубин и плановых размеров модели
разные: kh*kb , то из индикатора подобия в этом случае можно
найти масштабный коэффициент коэффициента гидравлического
трения:
Х кь
kh
(П.71)
257
Следовательно, уменьшая масштабный коэффициент глубин по-
тока (увеличивая глубину потока на модели по сравнению с глу-
биной, соответствующей равенству всех линейных масштабных
коэффициентов), необходимо в соответствии с принятой методи-
кой моделирования увеличивать на модели коэффициент гидрав-
лического трения по сравнению с натурой. Величина, на которую
необходимо умножить коэффициент гидравлического трения в
натуре, равна отношению линейного планового масштабного ко-
эффициента к линейному масштабному коэффициенту глубин
потока. Ясно, что возможности этого метод моделирования огра-
ничены. Покажем это на примере коэффициента гидравлического
трения, относящегося к области квадратичного сопротивления,
характерной для натурных потоков.
Прежде всего, введем некоторые дополнительные обозначе-
ния. В соответствии со сказанным выше глубину воды на модели
при равенстве всех линейных масштабных коэффициентов будем
обозначать hM, ширину, Ьм, абсолютную высоту выступов шеро-
ховатости дна Л.м , коэффициент гидравлического трения ХОл< .
Но так как kb=kh , то в этом случае не станем вводить новое обо-
значение для линейного масштабного коэффициента глубин по-
тока, а будем принимать его равным кь:
h b
^=кь, ~^=кь. (11.72)
hM Ьм
Если выполняется условие: kb^kh , то для ширины потока
на модели оставим прежнее обозначение Ьм, а глубину потока,
как это было принято выше, обозначим hn=nhM . Отсюда следу-
h h
ет: —=—— =кь , и с учетом первой формулы в (11.72) имеем:
258
(11.73)
В рассматриваемом случае обозначим высоту выступов шерохо-
ватости на модели Л,, , коэффициент гидравлического тре-
ния - Хо„.
Воспользуемся для натурного потока формулой квадратич-
ного закона сопротивления, в которой выполним следующие пре-
образования.
1 Л1 лиг
-j===41g-~-+4,25=41g——
д/^0и
(11.74)
Допустим, что первоначально предполагалось выполнить моде-
лирование с единым линейным масштабным коэффициентом так,
чтобы удовлетворить требованию: А.Он=А.Ол< . Но оказалось, что
глубина воды на модели hM недостаточна для проведения иссле-
дований, поэтому ее решено было увеличить в п раз: hn=nhM .
Тогда в соответствии с зависимостью (11.71) должно выполнять-
ся условие:
^"Ои _ _ kh
^-Оп кь
(11.75)
X
Используя преобразование (11.74), найдем отношение—-:
^Ол/
(5Z= К=—-------------_=—7—?-------------- (П.76)
Fo. Fa Я— М
д/Л0л< 7 -JA-Ом ч15 . ~Г л
I А» ) v I А.М kh Л„ J
Далее путем логарифмирования представим выражение в скобках
в знаменателе формулы (11.76) в виде суммы двух логарифмов
259
таким образ, чтобы первое слагаемое стало равным .----, учтем
также, что в соответствии со сказанным выше было принято ус-
ловие А.Он=А.Ол( , получим:
I
(11.77)
Зависимость (11.77) можно дать в удобном для расчетов виде,
учитывая при этом следующее соотношение кь &м=&н:
=^ехр
2,з(1-Ло;)
(11.78)
Из последней формулы находится высота выступов шерохо-
ватости Д„, что позволяет определить относительную гладкость
поверхности дна на модели: —. При больших величинах п мо-
Дл
жет оказаться, что высота выступов абсолютной шероховатости
становится соизмеримой с глубиной потока на модели. В таком
случае рекомендуется принять предельную величину относи-
тельной гладкости в условиях модели, равную 5,0 , которая была
в опытах А.П. Зегжды. Расчет повторяется, начиная с определе-
ния коэффициента гидравлического трения ХОи, после этого из
формулы (11.75) находится допустимое в рассматриваемых усло-
кь
виях отношение п=—.
260
Во втором случае выполняется условие: —>1, которое
hH
характерно для плановых течений в эстуариях рек, морских зали-
вах и т. п. Введем для условий модели допустимое значение па-
раметра, определяющего явление:
ь ।
~ Возьмем отноше-
ние параметра в натуре к его допустимому значению в условиях
модели:
°"
°" h
п h
=kj^
kh
(11.79)
Отсюда найдем
&0пЬлМд
(11.80)
Если принять (Х0„6Л(/Л„)^ =1, то вместо (11.80) получим:
д = ___
(11.81)
В этом методе моделирования, как и в предыдущем, пред-
ставляется важным обеспечить на модели ту же область сопро-
тивления, что и в натуре. Последняя устанавливается в результате
расчетов. В начале определяются число Рейнольдса и относи-
тельная гладкость поверхности дна. Затем, задаваясь областью
сопротивления, используя соответствующий закон, находится ко-
эффициент гидравлического трения Хо„ и динамическая ско-
рость потока в натуре: £/*„ =UH J, где UH - скорость течения
261
Ut„
в натуре. Далее по величине числа Рейнольдса Re*„ =----, в
V
котором Л„ - абсолютная высота выступов шероховатости в на-
туре, делают заключение о правильности использования закона
сопротивления. Если закон был использован неправильно, то
расчеты повторяют, внеся в них соответствующие коррективы.
Аналогичные расчеты на модели чаще всего приходится
выполнять методом последовательных приближений. По нашему
мнению, наиболее простой путь - начать их с определения коэф-
фициента кх, задаваясь величиной коэффициента гидравлическо-
го трения на модели Хо„. Здесь представляется важным попутно
решить одну важную задачу, с которой сталкивается исследова-
тель, используя метод физического моделирования явлений. Дело
в том, что абсолютная высота выступов шероховатости в услови-
ях модели имеет предел. Для некоторых видов материалов, ис-
пользуемых при изготовлении моделей, его величина найдена
опытным путем в частности в работах А.П. Зегжды и
А.Г. Аверкиева. При проектировании моделей исследователь час-
то наталкивается на практически непреодолимые трудности из-за
невозможности обеспечить на модели необходимую относитель-
ную шероховатость (или относительную гладкость). В обсуждае-
мом методе приближенного физического моделирования можно
заранее задаваться такой величиной коэффициента гидравличе-
ского трения в условиях модели, при которой эти трудности
сравнительно легко устраняются. Однако, как об этом было ска-
зано выше, при этом важно по возможности не выходить за пре-
делы области сопротивления, существующей в натуре. Если это
область квадратичного сопротивления, то на модели коэффици-
ент гидравлического трения не может превышать предельную ве-
262
личину, полученную в опытах А.П. Зегжды. Как показывают рас-
четы, величина отношения —— обычно не превышает 2^3.
^•Ои
Далее из формулы (11.80) или (11.81) находится линейный
масштабный коэффициент kh , глубина воды на модели: hn =— и
ки
при моделировании «по Фруду» - скорость течения на модели:
Un=-^= . Теперь можно найти число Рейнольдса на модели:
№
U h
Re„ =—~. Если течение в натуре относится к области гидрав-
v
лически гладкого русла или переходной, то и в условиях модели
следует использовать тот же самый закон сопротивления. Но в
него коэффициент гидравлического трения входит в неявном ви-
де, поэтому задача решается методом итераций. Коэффициент
гидравлического трения, полученный методом последовательных
приближений, сравнивается с принятым в начале расчетов. Если
они не совпадают, то итерации продолжаются. После их завер-
шения определяется динамическая скорость течения на модели и
соответствующее число Рейнольдса. Входящую в него высоту
выступов шероховатости дна можно определить, задаваясь пре-
дельной величиной числа Рейнольдса, соответствующей исполь-
зуемому закону сопротивления. На этом расчет заканчивается, в
результате которого все параметры течений в натуре и на модели
оказываются полностью увязанными между собой, в том числе и
выбранная величина линейного масштабного коэффициента пла-
новых размеров и полученная расчетом величина линейного
масштабного коэффициента глубин потока.
Если течение в натуре относится к области квадратичного
сопротивления, то на модели можно рекомендовать принимать
263
величину коэффициента гидравлического трения, соответствую-
щую предельному значению относительной гладкости, равной 5
(коэффициент гидравлического трения лОн «0,02 ). После опреде-
ления линейного масштабного коэффициента глубин воды на мо-
дели находится глубина потока и высота выступов шероховато-
сти. В обоих случаях необходима проверка на соответствие ис-
пользуемого закона сопротивления области, в которой этот закон
справедлив. Задача, естественно, сильно усложняется, если тече-
ние в натуре относится к переходной области сопротивления.
Следует иметь в виду, что в результате расчетов линейный
масштабный коэффициент глубин воды может оказаться числом,
неудобным в использовании (не кратным 2, 5, 10). Однако расче-
ты можно выполнить так, чтобы это неудобство устранить, имея
в виду два параметра, которые при решении задачи выбираются
произвольно - это линейный масштабный коэффициент kb и па-
раметр Величину последнего не обязательно при-
нимать равной единице, возможны отклонения от единицы в
большую сторону.
В заключение этого раздела необходимо сделать следующие
важные замечания. Первое касается выбора характерного створа,
в котором параметры потока должны быть известны. Наличие та-
кого створа обязательно и при математическом моделировании
гидромеханических явлений, так как из множества решений
только в этом случае можно выделить единственное. Например,
при решении задачи о гидравлическом прыжке, о внезапном рас-
ширении потока и т. п. параметры потока, как правило, задаются
в сжатом сечении. Часто возникает необходимость изучить тече-
ния в нижнем бьефе русловой ГЭС при пропуске паводковых во-
ды через водосбросную плотину. В этом случае в качестве «сжа-
264
того» принимается сечение, совпадающее с концом рисбермы во-
досбросов. Если модель не включает сами водосбросные соору-
жения, то при этом нужно позаботиться о том, чтобы сжатое се-
чение находилось на достаточном удалении от входного сечения
модели (на расстоянии не менее 50 глубин потока), само вход-
ное сечение должно быть оборудовано плавными переходными
устройствами.
Выбор характерного сечения в случае водоемов, обладаю-
щих большими плановыми размерами такими, как эстуарии, пру-
ды-охладители, водохранилища и т. п., часто затруднителен. Де-
ло в том, что поток входит в такие водоемы из устьев рек или из
водовыпусков промышленных и энергетических предприятий.
Плановые размеры устьевых участков рек и водовыпусков могут
на несколько порядков быть меньше плановых размеров соответ-
ствующего водоема. Потоки, выходя из устьев рек и водовыпус-
ков, создают в водоемах струйные течения. В [21] совершенно
справедливо в этой связи отмечается, что генерируемые в водо-
емах течения по своему характеру аналогичны явлениям, проис-
ходящим в различного рода промышленных устройствах, в кото-
рых происходит внезапное расширение входящего в них потока.
При этом происходят потери напора, вызванные «местными со-
противлениями». О них речь еще будет впереди, а пока ограни-
чимся следующим замечанием. При моделировании местных со-
противлений важно определить, при каких числах Рейнольдса в
условиях модели явление не будет зависеть от этого числа, так
как соблюсти равенство чисел Рейнольдса на модели и в натуре
чаще всего не удается. С этой целью на модели проводят серию
экспериментов, цель которых определить при прочих равных ус-
ловиях зависимость какого либо характерного параметра, опре-
деляющего явление, от числа Рейнольдса. В качестве такого па-
265
раметра могут быть «коэффициент местного сопротивления», ха-
рактерные размеры водоворотных зон и т. п. В [21] выполнен до-
вольно обширный обзор работ, в которых изучалась на моделях
зависимость относительных размеров длин водоворотных зон от
числа Рейнольдса Rec , определяемого по характеристикам пото-
ка во входном сечении. На основании анализа результатов этих
исследований было установлено, что при моделировании водных
потоков размеры длин водоворотных зон практически не изме-
няются при условии: Rec> 10000 . Проверка выполнения этого
условия обязательна в случае моделирования водоемов больших
плановых размеров и малых глубин. Однако оно не имеет непо-
средственного отношения к вопросу проектирования модели: вы-
бору линейных масштабных коэффициентов, высоты выступов
шероховатости, кинематических и других характеристик потока.
Для решения этих вопросов необходимо иметь в натуре харак-
терный створ, но как раз его чаще всего и нехватает. Естественно,
в первую очередь это касается вновь проектируемых сооружений
(например, прудов-охладителей воды электростанций). Но и мо-
делирование явлений в подобного рода действующих сооружени-
ях часто также сопряжено с трудностями из-за отсутствия харак-
терного створа. С аналогичной проблемой исследователь сталки-
вается при моделировании явлений в речных эстуариях и губах. В
качестве одного из немногих положительных в упомянутом
смысле примеров можно назвать имеющиеся по литературным
источникам данные о течении воды и шероховатости дна в пре-
делах баровой отмели реки Невы. Именно этот створ в рассмот-
ренном ниже примере расчетов модели Невской губы принят в
качестве характерного.
В случае физического моделирования явлений в действую-
щих сооружениях необходимы какие-либо данные натурных на-
266
блюдений и измерений. Чаще всего речь идет о размерах и очер-
тании водоворотных зон в пределах изучаемой акватории. Ли-
нейный плановый масштабный коэффициент назначается, исходя
из имеющихся производственных возможностей. Линейный мас-
штабный коэффициент глубин выбирается таким, чтобы можно
было с приемлемой точностью выполнять измерения на модель-
ной установке. По данным, приведенным в [12, 23, 24], диапазон
изменения отношения упомянутых линейных масштабных коэф-
фициентов велик: минимальное значение этого отношения равня-
ется двум-трем, максимальное достигает величины одного-двух
порядков. На изготовленной модели в [23, 24] предлагается сле-
дующий метод последовательного приближения соответствия ее
натуре и пригодности для проведения исследований. Вначале оп-
ределяются размеры и очертания водоворотных зон, соответст-
вующие тем, которые были измерены в натуре. Если они не сов-
падают, то на модели увеличивают шероховатость дна, следова-
тельно, увеличивают коэффициент гидравлического трения. Тем
. b „ _
самым увеличивают на модели параметр л— . Если есть необхо-
h
димость, то проводят дополнительные исследования в лотке, в
котором в плоских условиях определяют величину коэффициента
гидравлического трения. При этом геометрические (в том числе и
высота выступов шероховатости на дне) и кинематические пара-
метры потока в лотке совпадают с теми, которые имели место на
пространственной модели. Естественно, возможности такой
«подгонки модели под натуру» ограничены. В основном здесь
приходится полагаться на опыт и интуицию исследователя. В
большей степени это касается случаев, когда сооружения нахо-
дятся на стадии проектирования.
Рассмотрим примеры. Допустим, что надо изучить план те-
чений в нижнем бьефе русловой гидроэлектростанции. Ширина
267
потока в характерном створе равна 500м, средняя глубина во-
ды-Юм, коэффициент Шези С=50 , гидравлического тре-
ния - 0.0078 . Эти данные позволяют вычислить в натурных усло-
виях величину определяющего параметра:
Хо„—=0,0078^^ =0,39 <1, следовательно, изучаемое явление от-
10
носится к первому расчетному случаю. Выбираем линейный
масштабный коэффициент Аа=200. Но при таком линейном ко-
эффициенте глубина воды на модели будет равна всего 5см .
Увеличим глубину потока до 20см, п=4, kh=50 . Подставим
эти данные в формулу (11.78):
—=50ехр -
д„ L
мулу (11.74), найдем высоту выступов шероховатости в натуре:
2,3-0,5
0,353
=50схр[-3,258]=1,92 . Далее, используя фор-
2,83 - 1g
, 676,1=11,55“, Ан=-11,55'1000=17,1см.
А„ Д„ " 676,1
выступов шероховатости на модели с линейным
коэффициентом глубин kh =50 и линейным мас-
Высота
масштабным
штабным коэффициентом плановых размеров потока ^=200
171
должен быть равным А„=-^=8,9см . Отсюда получим относи-
Лл 20,0 ~ „
тельную гладкость потока на модели: “=—— = 2,25 . Проверим
величину коэффициента гидравлического трения в условиях, со-
ответствующих рассматриваемой задаче:
-=L==41gl 1,55-2,25=5,65, Хо„=О,О313, =°’О313 =4 _
7^7 0,0078 kh
Расчеты выполнены правильно, однако, они не приемлемы, так
268
как абсолютная высота выступов шероховатости равна почти по-
ловине глубины потока на модели. Кроме того, как об этом было
сказано выше, минимальная величина относительной гладкости в
опытах А.П. Зегжды была рана 5 . Принимая это значение отно-
сительной гладкости в качестве предельного, найдем коэффици-
ент гидравлического трения на модели и допустимую величину
масштабного линейного коэффициента глубины потока в услови-
ях рассматриваемой задачи:
-JL==41gl 1,55-5,0=7,0, Л0~0,02, --0-"=-0’°-= 2,5, Ь=80.
Хо„ 0,0078 kh
Получается, что в рассматриваемых конкретных условиях при-
ближенного моделирования планового течения масштабные ли-
нейные коэффициенты не могут отличаться друг от друга более
чем в два с половиной раза. Определяем глубину воды на модели:
, /г,, 1000 т _
пп=—=------=12,5см . 1еперь можно наити абсолютную высоту
kh 80
. h„ 12,5 _ , .,
выступов шероховатости: Д„=у^=у^-=2,5см . Пусть характер-
ная скорость течения в натуре UH равна 1,2 м/с, обозначим сред-
нюю скорость течения на модели с разными масштабными ли-
нейными коэффициентами U„ . При моделировании «по Фруду»
тг U 120 .
имеем: с/и=-^===-==13,4 см/с . Равенство чисел Фруда на мо-
обеспечено:
дели и в натуре
1 22 (и 4)2
Fr =— ---=0,0146, Fr =——=0,0146 . Определяем число
9,81-10 " 981-12,5
в - о 120-1000 , „ 7
Рейнольдса в натуре: Re„ =———=1,2-10 и в условиях моде-
ли: Re„ = 1,675-104 . Далее из формулы (10.69) находим
269
граничное число Рейнольдса на модели (7?л«/гп):
63,2 h„ 63,2-5 - з тт п ..
Re = , n = .-^=2,2-10 . Число Рейнольдса на модели
<02
больше граничного значения - поток на модели, как и в натуре,
относится к области квадратичного сопротивленя. Расход воды в
натуре равен: £л=6нЛн{7н = 500-10-1,2=6000м3/с . Найдем величи-
О 6*1 о6
ну расхода воды на модели: Qn -—^Ч==-----------42,0 л/с.
kbkh-Jkh 200-80-У80
Во втором примере рассмотрим модель Невской губы. Ши-
рина губы в натурных условиях приблизительно равна 15км ,
средняя глубина воды - 4,0 м, в качестве характерной скорости
принимаем скорость течения на Невском баре, приблизительно
равную 0,05 м/с; учтем, что баровые отмели сложены мелко- и
среднезернистыми песками [40]. В этих условиях найдем число
в-- о 5,0-400 _,п5 тт
Рейнольдса в натуре: ReH = - - — =2-10 . Допустим, что течение
воды в натурных условиях относится к области гидравлически
гладкого русла, в которой коэффициент гидравлического трения
определяется формулой (10.62): 2— = 4,0 lg(Re„ ^ХОн)+ 2,0 . Из
нее методом последовательного приближения было получено:
ХОл =0,003 . Убедимся в том, что формула была использована пра-
вильно, С этой целью найдем динамическую скорость потока:
тт 2'°" I о,ооз , и
J-y- = 5,0-J—-—«0,2 см/с. Допустим далее, что высота
выступов шероховатости в натуре определяется средним разме-
ром частиц грунта на баровой отмели: Дл«0,05см . Тогда дина-
мическое число Рейнольдса в натуре будет равным:
270
„ СЛНЛ„ 0,2-0,05 1П СА тт ,
Ret„ =-----=———=1,0<5,0 . Делаем вывод о том, что форму-
ла (10.62) была использована правильно. Во втором расчетном
случае должно соблюдаться условие:
Хо —>1. Проверим это:
0,003 ^^^=11,25 > 1. Отсюда следует, что условие выполняется.
4
Далее задаемся величиной коэффициента гидравлического
трения на модели: Хо„ =0,008, следовательно:
^=Т^=Ноп1=0’375’ Г1*2’7 • ПаРаметР прини-
мая 0,008 ЛОн пп)д
маем равным единице. Тогда из формулы (11.81) получим:
—\=в'375 =0,033 . Если выбрать А), =500, то
V-oA/M М,25
А/,=16,5. Отсюда найдем глубину воды на модели:
^_400_24,24см . При моделировании «по Фруду» скорость те-
16,5
чения на модели в пределах баровой отмели будет равна:
U„=-^== -у====1,23см/с . Теперь можно определить число Рей-
1 23-24 24
нольдса в условиях модели: Re„ = ' —=2981,8. Далее из
формулы (10.62) методом итерации находим коэффициент гид-
равлического трения на модели, который получился равным:
0,0077 , что не совпало с принятой величиной этого коэффициен-
та в начале расчетов, поэтому их нужно повторить, задавшись
новым значением этого коэффициента. В результате окончатель-
но пришли к следующим величинам:
ХОп =0,0076, к} = 0,395, kh =17,54, hn =22,8см, Un =1,19см/с,
271
Utn =0,1см/с, Ren =2721,7 . Формула (10.62) справедлива при ус-
t/*„A _
ловии: Re*„ =-----<5,0. Отсюда, принимая предельное значе-
V
ние этого числа, равном 5 , найдем максимальную высоту высту-
пов шероховатости, при которой режим течения в условиях мо-
дели, как и в натуре, будет относиться к области гидравлически
. 5,0-0,01 v
гладкого русла: А„<———<0,5см. Кроме того, имеем:
_ 0,0076 ~
ХОн ~ 0,003 ~
Из этого примера можно видеть, что линейный масштабный
коэффициент kh выражается величиной, неудобной при практи-
ческих расчетах. Положение можно улучшить, изменяя в нужную
сторону линейный масштабный коэффициент кь , а также прида-
вая параметру (А.о„bM/hn)^ различные значения, превышающие
единицу.
Определим расход воды на модели, предполагая, что расход
воды в Неве QH , равный 2500 м3/с , проходит в Невской губе при
уровне воды, соответствующем ординару, от которого измеря-
лись глубины воды на акватории. Найдем далее величину мас-
штабного коэффициента расхода воды:
kQ = kbkv kh=kb к%2 = 500-17,543/^2 =3,67-104 . Отсюда расход воды
О 2 5-106
на модели равен: Q„ =±*-=—----- = 68,1 л/с.
kQ 3,67-Ю4
Остается проверить в условиях модели величину числа Рей-
нольдса Rec , определяемого по характеристикам потока в усть-
евых участках рукавов дельты реки Невы. По данным, приведен-
ным в [40], расход воды в реке Q « 2500 м3/с , измеренный в рай-
272
оне пос. Новосаратовский, распределяется по рукавам в пределах
городской черты так, что большая его часть
(2«1500м3/с, В «260 м, Н «Юм, U «0,58 м/с) проходит в
русле Большой Невы. Отсюда получаем приблизительную вели-
чину числа Рейнольдса в устье Большой Невы в натурных усло-
виях: ReCK « 5, 9 • 106 . Теперь можно найти величину этого числа
на модели: Rec;M =B£CHfkh y[kh «8,1-IO4 >104 . Самая малая
часть (р«150м3/с, В «165 м, Я «6м, U «0,15 м/с) расхода
воды в реке проходит в пределах городской черты в русле Сред-
ней Невки. Отсюда находим число Рейнольдса:
ReCH «9,2-105, Rec „ «1, 2-104 >104 . Таким образом, числа
Рейнольдса в устьях рек дельты Невы, впадающих в Невскую гу-
бу, на модели превышают граничное значение. Если бы это усло-
вие не выполнялось, пришлось бы изменять плановый линейный
масштаб модели, и повторить все расчеты сначала.
Отметим, что в рассмотренных выше примерах фактически
решались вопросы проектирования моделей. В них не затраги-
вался важный момент проведения исследований на изготовлен-
ных моделях при уровнях и глубинах воды, отличных от тех, ко-
торые были выбраны при проектировании в качестве расчетных.
Подробнее об этом будет сказано в разделе 11.9.
11.7. О моделировании безнапорных и напорных потоков
с неоднородной шероховатостью ложа
Задача о сопротивлении русла с неоднородной шероховато-
стью смоченного периметра имеет большое практическое значе-
ние в связи с тем, что берега необлицованных искусственных ка-
налов часто приходится укреплять от волнений, из-за чего сопро-
273
тивление дна и берегов получаются различными. При исследова-
нии гидравлических явлений на моделях находят широкое рас-
пространение плоские остекленные лотки, в которых сопротив-
ление стеклянных боковых стенок может существенно отличать-
ся от сопротивления дна.
По-видимому, впервые задача рассматривалась в [72], когда
возникла необходимость определить динамическую скорость, от-
вечающую началу трогания частиц несвязного зернистого мате-
риала, и выбрать характерный линейный размер потока по ре-
зультатам исследований, проведенных в плоском остекленном
лотке. Позднее к этому вопросу возвратились в [68] при изучении
транспорта наносов и определении расхода воды, приходящегося
на «единицу ширины дна». В связи тем, что в [68] была исполь-
зована для определения коэффициента Шези формула Маннинга,
в [70] было предложено заменить ее зависимостями, полученны-
ми Никурадзе, отражающими законы сопротивления гладких и
шероховатых труб. В дальнейшем этот метод был применен в[73]
при изучении сопротивления дна при грядовом движении нано-
сов. Другие предложения и методы можно найти в работах
[17, 23,55,69,71].
Излагаемое в этом разделе решение задачи моделирования
безнапорных и напорных водотоков прямоугольного поперечного
сечения с разной шероховатостью внутренних поверхностей на
начальном этапе исходит из тех позиций, которые заложены в
метод, принятый в [70]. Основные положения этого решения ба-
зируется на методике расчета, изложенной в [29, 30]. Суть ее за-
ключается в том, что в площади живого сечения & = b h выделя-
ются частичные площади. В случае безнапорного потока две из
них примыкают к боковым стенкам канала a>c-Rch и одна ко
дну a>d=Rdb (рис. 11.4.а). При напорном течении в прямоуголь-
274
ном канале, имеющем, кроме дна, еще жесткую шероховатую
верхнюю поверхность (в дальнейшем просто поверхность) и
симметричные боковые стенки, в потоке выделяется еще пло-
щадь mn=Rnb , примыкающая к жесткой поверхности канала
(рис. 11.4.5). Здесь приняты такие обозначения: b -ширина ка-
нала; h - в безнапорном канале глубина его наполнения, в на-
порном высота канала; Rd, Rn, Rc - гидравлические радиусы час-
тей живого сечения потока, примыкающих соответственно к его
дну, поверхности и боковым стенкам.
Вначале рассмотрим течение в безнапорном канале. Если
боковые стенки имеют одинаковую шероховатость, то выполня-
ется равенство:
го=а>д+ 2ис. (11.82)
Далее сделаем допущение о том, что вдоль линий (условно
изображенных в виде отрезков прямых), разделяющих выделен-
ные площади, касательные напряжения отсутствуют. Но тогда,
если движение в целом равномерное, то оно будет таким же в ка-
ждом из выделенных отсеков жидкости. Обозначим гидравличе-
ский радиус всего сечения R , тогда с учетом (11.82) получим:
R_a_Rdb + 2Rch (Ц.83)
X b + 2h v
где х ~ смоченный периметр. Запишем условия равномерного
движения:
T0=pg/?z, xd=pgRdi, xc=pgRci, (11.84)
где i - уклон дна водотока; т0, тд, хс - среднее значение каса-
тельного напряжения трения, приложенного соответственно к
275
смоченному периметру водотока, к его дну и боковой поверхно-
сти. С учетом (11.84) из (11.83) получим очевидный результат:
(11.85)
'гоХ='Гдй + 2тсЛ-
Рис. 11.4. Схемы течения в каналах прямоугольного
поперечного сечения: «) безнапорном, б) напорном, с) под
ледяным покровом
Таким образом, характерными линейными размерами в рассмат-
риваемой задаче выбраны соответственно для всего потока R ,
для части, примыкающей ко дну, Rd , к боковым стенкам Rc .
Важным представляется вопрос правильного выбора харак-
терной скорости течения. Постановка задачи и обработка резуль-
276
татов экспериментов намного упрощается, если в качестве харак-
терной брать среднюю по живому сечению скорость течения U .
Принимая во внимание это допущение, имеем:
и2 и2 и2
тс=Хср^, (11.86)
где Х0АдДс “коэффициенты гидравлического трения соответ-
ственно для всего сечения, дна и боковой стенки. С учетом зави-
симостей (11.86) из (11.85) получим:
. Ь + 2 А.с h
Л Л —------------
0 b + 2h
(11.87)
Следовательно, задача может быть доведена до конца, если будут
найдены формулы для определения коэффициентов и Zc.
Для поиска этих зависимостей в [29, 30] были использованы
известные в гидромеханике результаты о сопротивлении движе-
нию плоских пластин [22,62]. Как известно, в этом случае в ка-
честве характерного линейного размера выбирается величина,
получившая гидромеханике название «толщины потери импуль-
са». Этот линейный размер зависит от характера распределения
скорости течения в поперечном сечении потока, которое в рас-
сматриваемом случае заранее не известно. Однако, «толщина по-
тери импульса» пропорциональна поперечному размеру погра-
ничного слоя. На участке развитого течения в канале величины,
характеризующие размеры пограничного слоя, равны глубине
потока h и его полуширине й/2 . Предполагалось, что зависимо-
сти, полученные в [22, 62] для определения сопротивления пло-
ских пластин, непосредственно использованы быть не могут, так
как в канале имеет место взаимное влияние на сопротивление дна
стенок канала и наоборот. Это влияние определяется относитель-
277
ной шириной канала b/lh . Оно учитывается введением в крите-
риальные уравнения для коэффициентов и относительной
ширины потока. При этом характерным линейным размером для
коэффициента является глубина потока h , а для Хс - его по-
луширина (боковые стенки симметрична относительно оси водо-
тока и имеют одинаковую шероховатость). В соответствии со
сказанным закон сопротивления в общем виде можно предста-
вить следующим критериальным уравнением:
^=/1^. Л •
£ 2л)
(11.88)
где в случае A.£=A.d, L=h, Re£=ReA =—, A£=Ad ; если
v
, то £=Z>/2, ReI-ReA/2=^, АЛ-АС.; Ad и
2 v
Ac - высота выступов шероховатости соответственно на дне и на
боковых стенках. Таким образом, общий вид критерильной зави-
симости в области квадратичного сопротивления должен быть
таким:
(11.89)
В области гидравлически гладкого русла:
Re£,—
2/г)
(11.90)
Переходной области соответствует критериальное уравнение
(11.88).
При отыскании критериальных связей (11.88)-(11.90) ис-
пользовались опытные данные А.П. Зегжды [16]. Связи устанав-
278
ливались в виде зависимостей степенного вида, как это принято
при определении законов сопротивления плоских пластин. Кри-
терием правильности выбора числовых коэффициентов являлось
хорошее совпадение величин л0 , определяемых зависимостями
(11.87)—(11.90), и соответствующими формулами
А.П. Зегжды ХОз . В опытах А.П. Зегжды отношение b/2h из-
менялось от 0,75 до 10. Результаты сравнения можно видеть на
рис. 11.5.
Для
< £
8<<150;
области квадратичного
сопротивления
Re*
>50
были найдены следующие со-
L -
V
отношения:
Хд = 0,0576
Хс= 0,0576
'_ь_} °''5
' ь Г0,39
<2
ь
2h
-0,07
(И-91)
(11.92)
Для области гидравлически гладкого русла
[105>Re£ >103; Re*£<8) соответственно:
/ х-0,070
=0,043 Re?0,20 —
h \2h)
/ х-0,035
Xc=0,043Re7,0'20 —
с b/2 \2h\
(11.93)
(11.94)
279
100А.О
Рис. 11.5. Сравнение метода расчета потоков с разной
шероховатостью стен и дна с данными Зегжды
В переходной области (50>Re*z>8) закон сопротивления
соответствующих поверхностей был найден по аналогии с фор-
мулой Коулбрука-Уайта в таком виде:
Хс = 0,0576
= 0,0576
(И-95)
~ . \1,95 / ,
2ДС ) | b
~b~I I 2/г
~0'35 / х—7/40
+ 0,232 Re/''° —
6/2 (2/г)
-50,2
Z>ReA/2
А0’9 / . ч-0,6810-20
b
2h
(11.96)
Можно видеть, что при Д£ ->0 зависимости (11.95) и (11.96)
превращаются в (11.93) и (11.94), а при Rei->co соответствен-
но - в (11.91) и (11.92). Кроме того, если шероховатости дна и бо-
280
ковых стенок одинаковы (Дс=Дд), то, обращаясь к формулам
(11.91) и (11.92), найдем:
ХС=^(6/2Й)-0'31. (11.97)
Аналогично из (11.93) и (11.94) получим:
Хс=ХДб/2й)~0''65. (11.98)
Таким образом, при одинаковом состоянии поверхности дна
и боковых стенок канала коэффициент гидравлического сопро-
тивления стенок равен аналогичному коэффициенту дна, умно-
женному на относительную ширину канала в степени, показатель
которой зависит от области сопротивления. При этом условии
дополнительно из зависимости (11.87), учитывая (11.97) и
(11.98), можно найти:
Хо -
1 + (А/2 А)/г
1+(/>/2/г)“! ’
(11.99)
где п =1,310 в области квадратичного сопротивления и п=1,165 в
области гидравлически гладкого русла.
Найденные зависимости были проверены на независимых
опытных данных, приведенных в [66, 67], и обнаружили хорошее
совпадение тех и других. В [66] отношение b/lh изменялось от
1,5 до 4,0; пределы изменения относительной гладкости: от 36 до
95. В [67] отношение b)2h изменялось от 0,84 до 2,43, относи-
тельная гладкость - от 66 до 284. Интересным также представля-
ется то, что часть опытов в [67] было выполнено в русле трапе-
цеидального поперечного сечения (заложение откосов т=1.1).
Расчеты по приведенным зависимостям обнаружили и в этом
случае хорошее совпадение с опытными данными, если в качест-
281
ве характерной полуширины потока принимать расстояние от
центра канала до середины откоса: (й0/2 Л)+лэт/2 , где Ьо - ширина
канала по дну.
Полученные результаты можно распространить на случай
напорного течения в прямоугольном канале с верхней поверхно-
стью, дном и симметричными боковыми стенками (рис. 11.46).
Допустим, что верхняя поверхность и дно имеют не одинаковую
«песочную» шероховатость, а боковые стенки - такую же, но
одинаковую шероховатость. В соответствии с рис. (11.46) име-
ем:
со=(й„+(й() + 2(йс . (11.100)
Дополним зависимости (11.84) еще одной:
tn=PgRni- (11.101)
Тогда вместо (11.84) найдем:
T]=pg7?]Z, xd=pgRdi, xn=pgRni, xc=pgRci, (11.102)
а вместо (11.85)получим:
Т1Х1 = (т()+т„)б + 2тс/г. (11.103)
Теперь из (11.100), учитывая (11.102), приходим к следующей:
7?1 =—+ \ (11.104)
X. 2(б + Л) 1 >
где Xi =2 (b+h) - смоченный периметр в напорном канале,
R{ - соответствующий гидравлический радиус.
Далее необходимо связать касательные напряжения трения,
приложенные к внутренним поверхностям канала, с характерной
282
скоростью потока. В [23, 51], где рассматривается плоское тече-
ние между двумя горизонтальными поверхностями с разной ше-
роховатостью, в качестве таковых принимаются средние скоро-
сти течения в каждой из выделенных в пределах живого сечения
площадей, одна из которых примыкает к поверхности, дру-
гая - ко дну канала. Однако при таком подходе поиск решения
задачи очень усложняется, так как все искомые параметры потока
зависят от этих заранее неизвестных скоростей. Это свидетельст-
вует о том, что упомянутые скорости не являются характерными.
В этой связи, как это было принято выше, в качестве характерной
скорости выберем среднюю скорость течения, относящуюся ко
всему сечению. В таком случае зависимости (11.86) дополним
еще такой:
U2
(11.105)
в которой - коэффициент гидравлического трения поверхно-
сти канала. Введем далее среднее значение касательного напря-
жения трения для всего сечения и обозначим его Т]:
. U1 v .
Tt=P^l—=Pg^z.
(11.106)
Тогда вместо зависимостей (11.86) можно записать следующие:
В них X] - коэффициент гидравлического трения всего сечения.
В таком случае из (11.104) получим:
283
_6(ХС+ХЙ)+2ЛХ
2(б + Л)
(11.108)
Теперь возникает не менее важный вопрос, а именно: с чем
сравнивать напорное течение. В [23], например, напорный поток
сравнивается с безнапорным, но таким, у которого ко дну прило-
жено напряжение трения, равное сумме напряжений, приложен-
ных ко дну и поверхности в плоском напорном потоке. Такое
сравнение не правомочно, поскольку потоки имеют разную ки-
нематическую структуру: у безнапорного потока максимум ско-
рости находится на его поверхности, у напорного потока внутри
его на расстоянии hn от поверхности, или h() от дна, так что вы-
полняется условие:
h=hn+h(). (11.109)
Если в качестве характерных линейных величин выбрать hn
и hd , то течения в напорном канале, примыкающие ко дну и к
поверхности, можно сравнивать с безнапорными потоками,
имеющими глубины соответственно hn и hd . При этом не будет
нарушен основной принцип построения критериальных уравне-
ний, в соответствии с которым параметры потока, содержащие
искомые величины, должны быть функциями параметров, в кото-
рые входят заданные величины. В такой постановке задачи вели-
чины hn и hd являются искомыми, но существуют связи между
ними и величинами, выбранными в рассматриваемой задаче в ка-
честве характерных. Наличие таких связей можно доказать путем
несложных расчетов.
На рис. 11.4.а и 11.4.6 условно выделена часть дна и поверх-
ности, равная Ьп , в пределах которой нет влияния боковых сте-
нок на распределение касательных напряжений по дну и поверх-
284
ности, в то время как в пределах частей, обозначенных на рисун-
ках Ьс , это влияние существенно. Тогда справедливы следующие
соотношения:
^d=Rdb=(b-bc)hd; an=Rnb=(b-bc)hn. (11.110)
Отсюда имеем:
Rn ьп
(11.111)
Обратимся далее к зависимостям (11.102), с учетом (11.107)
получим:
_ Rd _ Rn R _ Rc Г1 1 1121
Tj X] R\ ’ Т] Zq 7?! ’ Tj Zq 7?]
Принимая во внимание эти результаты, представим равенство
(11.111) в таком виде:
(11.113)
7?n h„ Хп
В соответствии со сказанным выше в области квадратичного
сопротивления (Re„£ >50)в случае зернистой шероховатости
вместо зависимости (11.91) следует предложить следующие две:
=0,0576
41
1м
(11.114)
b
2h.
Z х-0,39^ , ^-0,15
X = 0,0576 -М
1м
(11.115)
где Ал - высота выступов шероховатости на поверхности.
285
В области гидравлически гладкого русла (Re,/ <8) зависи-
мость (11.93) также заменяется двумя:
X(3=O,O43Re^0'20
( и \
и
>
z х-0,070
X,=0,043Re;«“H
\ Г1п /
(11.116)
(11.117)
Формулы (11.92) и (11.94) для коэффициента гидравлического
трения Хс остаются без изменения.
Найдем отношения коэффициентов гидравлического трения
в области квадратичного сопротивления и гидравлически гладко-
го русла:
при Re*z >50
0,13
при Re*/ <8
(11.118)
(11.119)
Если произвести подстановку величин из (11.118) и (11.119)
в (11.113), то получим:
h (А V'3'4 h
npHRe*z>50 ~= ~ ; npHRe*z<8 -^=1.(11.120)
hn IM К
Таким образом, в области гидравлически гладкого русла,
как и следовало ожидать, выполняется условие: hd=hn=hj2 . В
области квадратичного сопротивления отношение —, следова-
h„
286
Rd
тельно, и — зависят от отношения высоты выступов шерохова-
Rn
тости на дне канала к высоте выступов шероховатости на внут-
ренней верхней поверхности. И в том, и в другом случае отноше-
ния коэффициентов гидравлического трения и глубин от относи-
тельной ширины русла не зависят. Обычно по условию задачи
величины Ад и А„ должны быть заданы. Но тогда, используя
первую формулу в (11,120) и условие (11.109), можно найти ве-
личины hd и hc.
Обратимся далее к переходной области сопротивления, по-
лагая при этом, что в формуле (11.96) никаких изменений не про-
изойдет; а формулу (11.95) заменим следующими двумя:
0,0576
+ O,232Re;10
"И 035
(11.121)
= 0,0576
+O,232Re710
-50,2
х-0,35
/ 4 \°>9 Z , х-0,68
I Ъ
0,20
(11.122)
где Re^ =-^~, Re^ . Из формул (11.121) и (11.122) сле-
дует, что задача в этой области сопротивления может быть реше-
на методом последовательного приближения. Вначале задаются
287
одной из величин hd или hn , затем из формулы (11.109) находят
другую величину и их отношение, которое, исходя из зависимо-
сти (11.113), равно . Далее по формулам (11.121) и (11.122)
определяют коэффициенты кд и , а также их отношение, ко-
торое сравнивают с найденным выше, далее совершается проце-
дура в соответствии с методом последовательного приближения.
Изложенное выше позволяет определить средние значения
касательных напряжений трения, а также средние динамические
скорости потока в пределах дна и боковых стенок канала, в кото-
ром движется вода. Вопрос о распределении касательных напря-
жений по смоченному периметру каналов, различного попереч-
ного сечения, рассматривается в [4, 28, 36]. Однако найденные
экспериментальные зависимости базируются на ограниченном
числе экспериментальных данных и не могут претендовать на
обобщения; задача нуждается в дальнейших разработках.
Рассмотрим пример использования полученных результа-
тов. Пусть в канале прямоугольного поперечного сечения необ-
ходимо провести исследования, в ходе которых нужно опреде-
лить величину касательного напряжения на дне канала, или ди-
намическую скорость потока. Подобного рода задачи возникают,
например, при определении условий начала трогания под дейст-
вием набегающего потока частиц зернистого несвязного мате-
риала, уложенных на дно канала. Глубина потока /г=20,0см , ши-
рина канала b =100,0 см . Отсюда найдем величину гидравличе-
ского радиуса: Л=^-^^=14,28 см . Вначале рассмотрим случай,
когда дно и непрозрачные стенки лотка имеют одну и ту же зер-
нистую шероховатость, высота выступов которой соответствует
условию: Ad=Ac=0,2cM . Находим далее величину относительной
288
R
гладкости: —=71,4 . Далее определяем по формуле А.П. Зегжды
А
коэффициент гидравлического трения, полагая, что течение отно-
сится к области квадратичного сопротивления:
-i= = 4- 1g71,4+4,25; X=0,0074 . Допустим, что в канале создан
А
равномерный режим течения воды со скоростью С = 50см/с.
Отсюда найдем среднюю величину динамической скорости:
— = 50--Jo,0037=3,03 см/с . Для проверки правильности ис-
пользования закона сопротивления определим динамическое
п „ г. С, А 3,03-0,2 _
число Рейнольдса: Re* =---=-------=60,6>50,0 . Динамическое
v 0,01
число Рейнольдса находится в области квадратичного сопротив-
ления, к которой относится принятый закон сопротивления, сле-
довательно, расчеты были сделаны правильно.
Но касательные напряжения (или динамическая скорость
потока) распределены по дну и стенкам канала не равномерно.
Это следует из формул (11.91) и (11.92); вначале найдем входя-
щие
них
А_20,0
А - 0,2
=100,0,
А=^=250.0.
2А 0,2
h 50,0
2h ~ 20,0
величины:
Из формулы
(11.91) получим: 7^=0,0576(100,0) 0,39 (2,5) о15=О,ОО83. Соответ-
ственно из (11.92) имеем: А,с =0,0576(250,0)“0,39 (2,5) 0,07 =0,0063 .
Убедимся в том, что область сопротивленя соответствует исполь-
зованным формулам для расчета коэффициентов гидравлическо-
го трения. С этой целью определим соответствующие динамиче-
ские скорости потока и динамические числа Рейнольдса:
.------ С,., А 3 23-0 2
£7М= 50--/0,0042=3,23 см/с, Re^ = -^-=^^± = 64,6>50,0 .
v 0,01
289
Заметим, что этот расчет можно было не делать, результат его
ожидаем, так как выполняется условие Хд>Х. Далее имеем:
Utc = 50 -дД), 0031 = 2,80 см/с, Re*c=56>50. Проверим правиль-
ность вычисления коэффициентов гидравлического трения. В со-
ответствии с формулой (11.97) должно выполняться условие:
. Следовательно:
^^=(2,5) 0,31 =0,753. Находим
0,0083 v 7
0,0083 R
величину отношения 0074" ’*33 • ‘аким образом, среднее
значение касательного напряжения, приложенное ко дну канала,
более чем на 13% превышает среднее значение этого напряжения
в пределах всего смоченного периметра, определенное по форму-
ле А.П. Зегжды. Полезно также найти величину среднего значе-
ния коэффициента гидравлического трения, используя зависи-
.11в7. . 0,0083-100+2-0,0063-20 . „
мость (11.87): Ло=-------—-----------=0,0077 . Отсюда нахо-
0,0077 ,
дим отношение =1,055, которое свидетельствует о
том, что сравниваемые средние коэффициенты гидравлического
трения отличаются друг от друга на величину, немного превы-
шающую 5%.
Возьмем другой пример, в котором дно и стенки канала, по-
перечное сечение которого совпадает с рассмотренным выше, яв-
ляются гидравлически гладкими (например, стенки кана-
ла - зеркальное стекло, а дно - ожелезненная бетонная поверх-
ность). Определим вначале коэффициент гидравлического тре-
ния, используя формулу А.П. Зегжды (10.62). Находим число
Рейнольдса: Re=^-^=^^^=71400 . Далее из формулы (10.62)
методом итераций найдем коэффициент гидравлического трения
290
X : -4= = 4,0 lg(71400Tx)+2,0; X=0,00366. С тем, чтобы опреде-
лить коэффициенты гидравлического трения дна канала и его
стенок по формулам (11.93) и (11.94), найдем величины входя-
п ~ о 50-20 1п5
щих в них чисел Рейнольдса: Ке/г —=Ю , и
Re^2 = =2,5 • 105 . Далее можем установить коэффициенты
гидравлического трения дна: = 0,043(105)г°'20 (2.5)’0,07° =0,004 и
стенок канала: Хс =0,04з(2,5-Ю5) °’2° (2,5)-0,035 =0,0035. Для срав-
нения с коэффициентом гидравлического трения, найденного по
формуле А.П. Зегжды, определим величину соответствующего
коэффициента по формуле (11.87) для всего сечения:
0,00403-100+2-20-0,00347 v . .
Ло =---------—------------=0,00387. Коэффициенты от-
личаются друг от друга на величину, не превышающую 6% . По-
кажем, что расчеты были выполнены правильно. Докажем, преж-
де всего, что равенство (11.98) соблюдается:
-0,165
А,с ( Ъ 1 0,00347 /_ 0165 лог п с.
~= — =-------=(2,5) ’ =0,86 . Для того чтобы убедить-
~Кд \2hj 0,00403
ся в правильности использования формул (11.93) и (11.94), опре-
делим соответствующие динамические числа Рейнольдса. Затем,
принимая предельные значения этих чисел на границе области
гидравлически гладкого русла, установим допустимую величину
выступов шероховатости на этих поверхностях. Вначале находим
динамические скорости потока:
Utd =50-70,00403/2 =2,24см/с; Utc =50-70.00347/2 =2,08см/с .
Принимая предельную величину динамического числа Рейнольд-
са равной 8 , находим:
291
. 8-0,01 . 8-0,01 nnoo тт
Л„=—-—=0,036см; А,. =------=0,038см , Что касается ше-
д 2,24 2,08
роховатости стеклянной поверхности, то у зеркального стекла
она может быть на порядок меньше полученной. В то же время
нужно отметить, основываясь на результатах исследований
А.П, Зегжды, что высота выступов шероховатости ожелезненной
бетонной поверхности приблизительно равна 0,07 см.
Находим величину отношения Лэ/Х=1,10. Таким образом,
среднее значение касательного напряжения, приложенное ко дну
канала, на 10% превышает среднее значение этого напряжения в
пределах всего смоченного периметра, определенное по формуле
А.П. Зегжды.
11.8. Движение воды в русле под ледяным покровом
В качестве примера использования полученных в предыду-
щем разделе результатов рассмотрим течение воды под ледяным
покровом. Известно, что в естественных руслах нет ограничи-
вающих поток стенок, вместо них есть берега. Здесь вводятся та-
кие понятия, как смоченный периметр дна и нижней поверхности
льда (последний принимается равным ширине потока под ледя-
ным покровом b (рис. 11.4.с)). Разделим, как и ранее, площадь
живого сечения подо льдом на две: <в„ , примыкающую к ледя-
ному покрову, и - ко дну потока, так что выполняется усло-
вие:
со = ®„ + cod = Rnb + Rdx, (11.123)
292
где Rn,Rd “ соответствующие выделенным площадям гидравли-
ческие радиусы, % - смоченный периметр дна. Из (11.123) легко
получить
= (11.124)
Х2 Й + Х
где Хг = Ъ + х “ смоченный периметр дна и нижней поверхности
льда, Л2 - соответствующий гидравлический радиус. Если при-
R + R
нять А ~ х > то из (11.124) следует: R2 = .
В некоторых работах, например в [23] и др., вводится поня-
тие об эквивалентном касательном напряжении трения тэ , кото-
рое в открытом потоке, эквивалентном потоку подо льдом, при-
ложено только ко дну, так что выполняется условие:
ЪХ = \д + т„6, тэ=рХэу, (11.125)
где Хэ - соответствующий (эквивалентный) коэффициент гид-
равлического трения. Если воспользоваться формулами (11.86) и
(11.105), то из (11.123) и (11.125) получим:
R = - = Rd+R„-. (11.126)
XX X
Примем 6~х, тогда из (11.126) следует:
Лэ — , R ~ Rd + Rn .
Однако, как было отмечено ранее, такое сравнение не всегда до-
пустимо, так как в кинематическом отношении безнапорный и
напорный потоки отличаются друг от друга.
293
Имея это обстоятельство в виду, рассмотрим среднее значе-
ние касательного напряжения т0 по всему смоченному перимет-
ру. В таком случае будет справедливо условие:
E)X2='co(z’ + x) = W+V’- (11.127)
Примем далее следующие соотношения:
T0=pg^2/p, T„=pg«„/P, xd = pgRdip, (11.128)
где i - уклон пьезометрической линии в напорном потоке. Если
подставить (11.128) в (11.127), то придем к формуле (11.124). Ес-
ли же в (11.127) подставить значения касательных напряжений из
(11.86), то получим:
XO=^X + X”Z>. (11.129)
Х + й
При условии 6 ® х из (11.129) следует: Хо = . Кроме
того, из зависимостей (11.86) и (11.128) можно получить сле-
дующие соотношения:
Rn=R2^, Rd-R2^~, Rd-R„^. (11.130)
В связи с тем, что выше были изложены два метода расчета
потока подо льдом, полезно посмотреть, будут ли отличаться со-
ответствующие формулы для определения одних и тех же гид-
равлических параметров, например, средней скорости потока.
Если воспользоваться методом расчета, основанном на понятии
«эквивалентный коэффициент гидравлического трения», то фор-
294
мулу Шези можно записать в таком виде: и = — R gip . Подста-
Иэ
вим в нее значения Хэ и R , используя зависимость (11.126) при
условии b ® % , получим:
и = /^Т~8^' (Н.131)
По другому методу формула Шези имеет такой вид:
1~2 7~
и — —R2 gip Подставим в нее величины R2 и ?.о, используя
V
зависимости (11.124) и (11.129), при условии Ь « х вновь придем
к формуле (11.131). Таким образом, несмотря на различия в под-
ходах к решению задачи, расчетные зависимости для скорости
течения по обоим методам получаются одинаковыми.
Рассмотрим, как изменится пропускная способность речного
русла вследствие ледостава при следующих допущениях. Пусть
непосредственно перед ледоставом скорость течения воды в рус-
ле была и , гидравлический радиус R , коэффициент гидравличе-
ского трения X , уклон свободной поверхности при равномерном
режиме i , так что выполнялось условие:
giR = '>-~- (П.132)
Пусть после ледостава площадь живого сечения и уклон не
изменились. Естественно, такое явление могло произойти вслед-
ствие того, что одновременно с ледоставом уменьшился расход
воды, и скорость ее течения стала ил . Равномерному режиму под
ледяным покровом соответствует зависимость:
295
(11.133)
где R2 ~ R/2, ip = i, л0 - соответствующий коэффициент гид-
равлического трения. Если взять отношение (11.133) к (11.132),
то получим:
Ь-= Х
и \ 2 к0
(11.134)
Используем для коэффициента гидравлического трения Хо
формулу (11.129), в которой при условии 6 » % вынесем коэффи-
X
циент за скобки, в скобках заменим отношение — отноше-
нием — согласно зависимости (11.113), после этого произведем
преобразование в соответствии с первой формулой в (11.120), в
результате получим:
г г ?'314
—= 0,5 — 1+
(11.135)
Зависимость (11.135) относится к области квадратичного
сопротивления, поэтому в ней коэффициент гидравлического
трения в открытом русле Л определяется по формуле
А.П. Зегжды: = 41g — + 4,25.
На рис 11.6 приведены для этой области графики ЗаВИСИМО-
tt,,
сти отношения скоростей течения — от относительных ширины
русла и шероховатости поверхности дна для двух случаев: а) аб-
солютная шероховатость поверхности льда больше или равна аб-
296
солютной шероховатости поверхности дна; б) абсолютная шеро-
ховатость поверхности дна больше или равна абсолютной шеро-
ховатости поверхности льда.
Рис. 11.6. Кривые изменения скорости течения подо льдом
1 - blh=2,2 - blh=20
В [43] результаты расчетов по изложенной здесь методике
сравниваются с экспериментальными данными. Сравнение сви-
детельствует о том, что данные расчетов практически совпадают
с данными экспериментов. В [39] по результатам натурных на-
блюдений были выполнены расчеты, которые позволили опреде-
лить шероховатость нижней поверхности ледяного покрова при
ледоставе. Количественно было подтверждено предположение о
том, что в процессе ледостава шероховатость нижней поверхно-
сти льда изменяется во времени. На ранних этапах ледостава
вследствие образования торосов высота выступов шероховатости
наибольшая. С течением времени высота выступов уменьшается,
чему способствует рост толщины ледяного покрова и воздействие
воды, обладающей подо льдом положительной температурой.
Получены графики, позволяющие установить характер изменения
297
высоты выступов шероховатости нижней поверхности льда от
времени за период ледостава. Вместе с тем было показано, что
зависимости (11.114), (11.115), (11.121) и (11.122) пригодны для
использования в натурных условиях, если входящую в них по-
стоянную заменить элементарной функцией от относительной
шероховатости нижней поверхности льда. Однако в конце зимы,
когда высота выступов шероховатости нижней поверхности ле-
дяного покрова стремится к нулю, расчеты по предложенным за-
висимостям дают завышенные результаты по сравнению с расче-
тами по формулам (11.114), (11.115), (11.121) и (11.122). По-
видимому, это отклонение можно объяснить тем, что принятая
методика обработки натурных данных не учитывала таких явле-
ний в зимнюю пору в речном русле, как «донный лед», «берего-
вой припой» и т. п., которые могли существенно увеличить со-
противление дна, и оно автоматически оказалось включенным в
сопротивление нижней поверхности льда.
11.9. Приближенное моделирование безнапорного потока
в натуре воздушным напорным потоком на модели
Основные преимущества моделирования безнапорного по-
тока в натуре воздушным напорным потоком на модели были
рассмотрены в разделе 3. В первую очередь необходимость тако-
го метода моделирования возникает в том случае, когда исследу-
ются явления в реке совместно с поймой, в речных эстуари-
ях и т. п. Вместе с тем не исключается необходимость изучения
явлений в приземном слое атмосферы на воздушных напорных
моделях (к ним, например, относится ветровая эрозия почв). В
случае моделирования явлений в реках с широкими поймами и в
эстуариях рек плановые размеры воздушной модели можно су-
298
щественно уменьшить по сравнению с плановыми размерами
гидравлической модели того же объекта. Естественно, при этом
возникает вопрос, во сколько раз линейный масштабный коэф-
фициент плановых размеров будет отличаться от линейного мас-
штабного коэффициента глубин. Ветровая эрозия почв (дефля-
ция) наблюдается в приземном слое атмосферы, размеры которо-
го практически безграничны. При изучении этого явления на на-
порной воздушной модели необходимо выделить ту часть потока,
которую можно принять подобной потоку в натурных условиях.
Только после решения этого вопроса можно сформулировать
правила пересчета результатов исследований на модели в натуру.
Нужно отметить, что возможность моделирования безна-
порных потоков с помощью напорных следовала из работ
А.П. Зегжды. Именно он ввел и реализовал аналогию, в соответ-
ствии с которой безнапорные потоки стали рассматриваться как
напорные. Тем самым были созданы предпосылки для создания
единых законов сопротивления для напорных и безнапорных сис-
тем. Сегодня на пути такого единения стоит эмпирическая фор-
мула Дарси-Вейсбаха, не соответствующая закону равномерного
режима движения, но используемая по сложившейся в гидравли-
ке традиции для расчета движения жидкостей в напорных трубо-
проводах.
Обсуждение правил моделирования безнапорных открытых
потоков на напорных воздушных моделях началось в нашей
стране в середине прошлого века благодаря работам
А.Г. Аверкиева [1, 2]. Позднее этот метод моделирования посто-
янно совершенствовался, его основные положения можно найти
во многих публикациях, в том числе в [12, 21, 23, 24]. При этом
авторы подчеркивают, что вовсе не обязательно безнапорный
водный поток моделировать с помощью напорного воздушного.
299
Можно безнапорный водный поток моделировать с помощью на-
порного водного; процессы, происходящие в нижних слоях атмо-
сферы, - на напорной воздушной модели. В главе 3 упоминалось
о том, что движения тел со сверхзвуковой скоростью в воздухе
можно исследовать на водной модели в условиях бурного потока.
Моделирование безнапорного водного потока с помощью напор-
ного воздушного рассматривается главным образом как метод,
позволяющий существенно уменьшить плановые размеры моде-
ли. С этим исследователь неизбежно сталкивается, когда возни-
кает необходимость изучать явления в водных потоках больших
плановых размеров и малых глубин (в плановых задачах).
Уменьшить плановые размеры модели можно потому, что отпа-
дает необходимость реализовывать моделирование «по Фруду».
Такая возможность возникает только в том случае, если числа
Фруда в натуре малы (выше предельное значение числа Фруда
было принято равным 0,1 ). В этом случае свободную поверх-
ность в натуре можно приблизительно считать горизонтальной, а
на модели заменить ее горизонтально установленным стеклом.
Естественно, геометрические размеры русла на модели должны
быть афинно подобными геометрическим размерам русла в нату-
ре. На стадии калибровки модели стекло устанавливают на таком
уровне, при котором была получена путем измерений информа-
ция в натурных условиях в первую очередь о кинематических ха-
рактеристиках потока. Сказанное по сути дела затрагивает только
способы проектирования моделей и не касается вопросов прове-
дения исследований на изготовленных моделях при разных уров-
нях и глубинах потока. Как отмечалось выше в разделе 11.6, если
в процессе проведения исследований возникает необходимость
проведения их при других уровнях и глубинах потока, то чаще
всего это связано с дополнительными корректировкам парамет-
300
ров модели. Подробно эти вопросы рассматриваются в конце это-
го разделе на примере расчета воздушной напорной модели Нев-
ской губы и методики моделирования явлений на ней в условиях,
отличных от расчетных.
Остановимся на особенностях метода приближенного моде-
лирования открытых плановых потоков на напорных воздушных
моделях. Прежде всего, обратимся к интегральным соотношени-
ям с тем, чтобы получить числа подобия, характеризующие рас-
сматриваемое явление. Присвоим величинам в натуре подстроч-
ный символ "и", на модели - "м" . Запишем для натуры уравне-
ние мелкой воды (11.61):
1 dU„ 1 dU% Ц*н 1Н
g(aH dtH g(oH дхн g(nH ’
(11.136)
где JH - уклон свободной водной поверхности в натурных усло-
виях. Произведем в нем преобразования с целью перейти от раз-
мерных величин к безразмерным. В результате получим безраз-
мерное уравнение при стационарном движении (11.66):
ди'2<»’, л
FrnHn (о'дх' " Нн ° 2 h'
(11.137)
Запишем теперь аналогичное уравнение для воздушного по-
тока на напорной модели, полагая, что ./„ = 0 . Обозначим бук-
вой рм плотность воздуха на модели. Пусть \рм - перепад
давления, тогда уравнение при условии %м ® &м будет иметь та-
кой вид:
___1 1 dUMG)M 1 (Ц 138)
PMg дхм gm,, ct„ go)M дхм PMg(0M ’
301
где тОл( - среднее значение касательного напряжения, приложен-
ного ко дну и стеклянной поверхности воздушной модели. Заме-
тим, что в левой части уравнения (11.138) стоит уклон пьезомет-
рической линии напорного потока:
J »-----(11.139)
Но в таком случае уравнение (11.138) представим в таком виде:
J - 1 М ЮЛ| Вы Q | 140)
рм dtM gaM дхм g®M ’
Сравнивая уравнения (11.140) и (11.136), можно заметить,
что по структуре и количеству членов они совпадают. Но есть и
отличия: уклону свободной поверхности безнапорного водного
потока в натуре соответствует уклон пьезометрической линии
напорного воздушного потока; касательное напряжение трения (и
соответствующая динамическая скорость потока) приложено в
натуре к смоченному периметру открытого безнапорного русла.
Соответствующее напряжение на напорной воздушной модели
приложено и к смоченному периметру, и к поверхности стекла.
Принимая связь между динамической скоростью потока и сред-
ней на воздушной модели, как в безнапорном потоке, получим
(П-141)
где UM - средняя скорость напорного воздушного потока,
ХОл - коэффициент гидравлического трения, суммарно учиты-
вающий сопротивление смоченного периметра русла на модели и
поверхности стекла. В связи с тем, что напорная воздушная мо-
302
дель не пригодна для изучения нестационарных потоков, в даль-
нейшем будем рассматривать только установившееся движение
воздуха на ней.
Кроме введенных ранее характерных величин, на воздушной
модели есть необходимость использовать еще од-
ну - характерную величину пьезометрического уклона. Обозначая
ее JpM , получим: JpM=JpMJ'pM , где J'pM -нормированный
(дважды обезразмеренный) пьезометрический уклон. Аналогия
А.П. Зегжды позволяет рассматривать безнапорные потоки как
напорные, принимая в них свободную поверхность в качестве
пьезометрической линии. Но с другой стороны, напорные потоки
можно рассматривать как безнапорные, вводя в них число Фруда.
С учетом этих замечаний и зависимости (11.141), произведя в
(11.140) преобразования, аналогичные тем, которые были сдела-
ны при выводе уравнения (11.137) для безнапорного потока; по-
лучим для стационарного напорного:
Вм , _ д U'2 to' . Вм , U'2
Вгм Нм рм со' д х' м Нм 0 2 h'
(11.142)
Введем теперь характерную величину уклона свободной по-
верхности в натурном потоке. Обозначая ее JH , имеем:
. Произведем соответствующую замену в (11.137),
найдем для безнапорного потока:
J' = + Л Х'о —.
FrHHn to'ax' z h'
(11.143)
В связи с тем, что поток на модели аффинно подобен потоку
в натуре, величины со штрихом в безразмерных уравнениях
(11.142) и (11.143) одинаковы так же, как и сами эти уравнения.
303
Следовательно, одинаковы комбинации из характерных величин,
содержащиеся в уравнениях, - числа подобия. Они совпадают с
числами подобия в рассмотренной выше плановой задаче, в кото-
рой на модели был безнапорный водный поток. Но есть и некото-
рые не принципиальные отличия: в качестве характерного в на-
туре прият уклон свободной поверхности, в то время как на мо-
дели - уклон пьезометрической линии; характерная величина ко-
эффициента гидравлического трения в натуре относится к смо-
ченному периметру русла, а на модели учитывает смоченный пе-
риметр руса и поверхности стекла. Сопротивление на модели от-
личается от натурного, но этот факт также не имеет принципи-
ального значения. В обсуждаемом методе приближенного моде-
лирования изначально предполагается увеличивать на модели ко-
эффициент гидравлического трения по сравнению с натурой во
столько раз, во сколько линейный масштабный коэффициент ее
плановых размеров отличается от аналогичного коэффициента
глубин.
Однако наличие безразмерных величин, входящих в безраз-
мерные уравнения, и содержащихся в них чисел подобия являет-
ся необходимым, но недостаточным условием для реализации
физического моделировании явлений. Имеется целый круг задач,
решение которых в рамках обсуждаемого метода моделирования
невозможно (например, одной из них является поиск распределе-
ния скорости течения в точках на вертикали по данным измере-
ний на модели). Решение других задач обосновывается результа-
тами исследований методического характера. По сути дела, весь
изложенный выше материал может служить ярким подтвержде-
нием этих слов. Как и в случае моделирования плановой задачи
на моделях с водным потоком, здесь были проведены исследова-
ния, результаты которых сравнивались с данными натурных на-
304
блюдений и измерений на моделях с водным потоком.
[1,2,12,21, 23, 24]. Прежде всего, сравнивались длины водово-
ротных зон и распределение средних на вертикалях скоростей те-
чения в них. Основным источником сомнений было наличие
стекла на воздушной модели и зоны его влияние на распределе-
нии скорости течения, которое не совпадает с распределением
скорости в натуре вблизи свободной водной поверхности. Было
обнаружено, как уже отмечалось выше, влияние этих факторов
несущественно, если число Фруда в натуре не превышает вели-
чину 0,1 . Кроме того, необходимо было проверить, как влияет
наличие стекла на распределение скорости течения на повороте
потока. Здесь источником сомнений было наличие не одной об-
ласти поперечных течений, как в натурном потоке, а двух разно-
направленных: одной в зоне влияния стекла, другой - в зоне
влияния дна. По результатам этих работ авторы рекомендуют
проводить исследования безнапорных потоков на воздушных мо-
делях только в том случае, если Фруда в натуре не превышает ве-
личину 0.05 . Тем не менее, не выходя за рамки неизбежных
ошибок измерений, можно и в том, и в другом случае принимать
это число равным 0,1.
В [12] предлагается в этой связи следующий необычный ме-
тод моделирования. Подобной натурному потоку в створе счита-
ется только та часть воздушного потока, которая расположена
между дном и линией, соединяющей точки с максимальной ско-
ростью течения на вертикали. Однако поверхность, к различным
точкам которой приложена максимальная скорость течения в по-
токе, в отличие от свободной водной поверхности потока в нату-
ре не является плоскостью. В [23] отмечается, что в этих услови-
ях говорить о существовании какого-либо вида геометрического
подобия не приходится. Кроме того, поиск линии с максимальной
305
скоростью течения на вертикали, как это следует из раздела 11.8
и изложенного ниже материала, - дело далеко не простое.
Найдем, каким образом измеренные на модели уклон пьезо-
метрической линии и перепад давлений можно пересчитать в ук-
лон свободной поверхности и перепад уровней в натуре. С этой
целью вначале приравняем друг другу числа подобия, стоящие в
левых частях уравнений (11.142) и (11.143), получим:
/j]
Fr Н Fr Н 1 ’
Отсюда, переходя к индикатору подобия, имеем:
kj=klk~}, (11.145)
где kj = - масштабный коэффициент, позволяющий
Jрм Jрм
измеренный на модели пьезометрический уклон пересчитать в
уклон свободной поверхности в натуре.
Возможен также переход от уклона пьезометрической ли-
нии к соответствующему перепаду уровней. При этом следует
иметь в виду, что характерные перепады должны измеряться на
характерных длинах. Можно, например, в качестве характерной
длины выбрать характерную линейную величину В , связанную с
плановыми размерами потока. Тогда в натуре получим
-
(11.146)
где Azf -характерный перепад уровней воды на характерной
длине Вн . Далее в зависимости (11.139) выразим величины через
характерные и безразмерные; допустим, что падению пьезомет-
306
рической линии соответствует положительная величина ее пере-
пада; в результате придем к следующему выражению:
7 г
РМ РМ Р.м S дх'м Вы ^Х'м
где Az® -характерный перепад пьезометрической линии на ха-
рактерной длине модели Вм . Величины со штрихом, содержа-
щиеся в левой и правой частях зависимости (11.147), безразмер-
ные, одинаковые для модели и натуры (по сути дела, это уклон
пьезометрической линии, равный уклону свободной поверхно-
сти). Но тогда имеем:
(11-148)
Произведем подстановку зависимостей (11.146) и (11.148) в
(11.144), получим, переходя к индикаторам подобия:
(П-149)
где - масштабный коэффициент для перехода от перепада
пьезометрической линий на модели к перепаду уровней в натуре
на характерной длине В . Перепад уровней на длине LH нахо-
дится из зависимости:
(11.150)
Вн
Если характерные перепады уровней и пьезометрической
линии измерять на характерной длине Я , то по аналогии с
(11.149) получим
307
(11151)
Kb
где к н - масштабный коэффициент для перехода от перепада
пьезометрической линий на модели к перепаду уровней в натуре
на характерной длине И . Перепад уровней на длине Lu нахо-
дится из зависимости:
(11.152)
кь Нн
где A - характерный перепад пьезометрической линии на
характерной длине модели Нм .
Моделирование безнапорных потоков с помощью напорных
воздушных моделей может быть использовано не только для изу-
чения явлений в плановых задачах, в которых приходится линей-
ный масштабный коэффициент глубин потока принимать отлич-
ным от линейного масштабного коэффициента плановых разме-
ров, но и в случае равенства этих масштабных коэффициентов.
Это объясняется тем, что организовать такого рода моделирова-
ние намного проще, чем при использовании на модели безнапор-
ного водного потока. Действительно, модель с водным потоком
предполагает наличие водосберегательного бассейна, насосной
установки, напорного бака, площадки (или лотка) для размеще-
ния моделируемого объекта и соединительных трубопроводов, в
то время как для напорной воздушной модели нужны только вен-
тилятор, площадка для размещения моделируемого объекта и со-
единительные короба. Кроме того, как отмечалось выше, пре-
имущество такого моделирования состоит в том, что нет необхо-
димости требовать равенства на модели и в натуре чисел Фруда,
308
но только при условии, если в натуре число Фруда не превышает
величину 0,1.
Остановимся на этом методе моделирования подробнее. Ес-
ли модель геометрически подобна натуре (линейные масштабные
коэффициенты по всем трем направлениям одинаковы), то усло-
вие ).()- = idem
h
превращается в Хо = idem . Следовательно, зада-
ча сводится к тому, как в условиях модели добиться равенства
’ если в натуре коэффициент гидравлического грения
определяется только сопротивлением смоченного периметра рус-
ла, в то время как на модели, - суммарно учитывает сопротивле-
ние и смоченного периметра русла, и поверхности стекла.
Расчет модели начинается с выбора подходящего линейного
масштабного коэффициента кь . Принимаются во внимание про-
изводственные возможности, кроме того, в соответствии с
[2] - минимальная глубина потока на модели не может быть ме-
нее 1 -г 2 см . Существуют разные пути решения задачи, один из
возможных следующий. Задаемся средней скоростью воздушного
потока на модели UM . Здесь следует иметь в виду, что макси-
мальная скорость потока по условиям несжимаемости воздуха не
должна превышать « 50 з- 60 м/с . Однако производственные вен-
тиляторы, как правило, могут обеспечить в условиях модели ско-
рость не более 15 -е- 25 м/с . Находим среднюю глубину потока на
h
модели hu - — . Делаем предположение о том, что сопротивле-
кь
ние поверхности стекла и ложа модели относятся к области гид-
равлически гладкого руса. В этом случае hd = hn = hM/2 . Тогда в
соответствии с (11.117) находим:
309
= 0,043
UuhM
At At
2v „ j
At /
^-0,20 z х-0,07
Ьм
h,.
(11.153)
где bM - ширина модели в характерном створе,
vM - кинематический коэффициент вязкости воздуха. При усло-
вии b « х из зависимости (11.129), если произвести в ней замену
Хо на л0„ следует:
^-д ~ 2^-0 и ^-П '
(11.154)
где ХОн - коэффициент гидравлического трения в натурном по-
h X
токе. Теперь согласно (11.113) получим . Но
= hM , поэтому найдем:
hn =------— .
(11.155)
Подставляя это значение hn в формулу:
A.„=O,O43Re^0’20
z х-0,070
°м
. 2Л„ ,
(11.156)
найдем новую величину коэффициента и т. д., используя ме-
тод последовательных приближений, окончательно получим ве-
личины: , hn , hd . Далее нужно убедиться в том, что
формула (11.117) была использована правильно. С этой целью
найдем динамическую скорость в той части потока, которая при-
мыкает к стеклу U,Mn =UMJ~ , и соответствующее число Рей-
310
нольдса: Re,,(„ =------ , где А„ - высота выступов шерохова-
УМ
тости стекла. Остается определить высоту выступов шероховато-
сти поверхности дна модели Дй , полагая, что ей соответствует
квадратичный закон сопротивления. Для этого преобразуем фор-
мулу (11.114)
Хд -0,0576
/, V°’39< L Г0’15
— \ —I
(11.157)
и представим ее в таком, удобном для этих расчетов виде:
hd
К)
0,0576
Г L А0-15
Ъм
2,564
(11.158)
И вновь нужно убедиться в том, что формула (11.114) была ис-
пользована правильно. Для этого найдем динамическую скорость
в той части потока, которая примыкает к дну UtMd = UM , и
П ' ^*мд
соответствующее число Рейнольдса: Re*WfJ =--- .
Ум
Теперь нужно определить такое предельное значение скоро-
сти воздушного потока на модели Uмг , при котором число Рей-
нольдса в части потока, примыкающей ко дну, станет равным
граничному, соответствующему началу области квадратичного
сопротивления. Используя зависимость (10.69), получим:
D UMehd 63,2 hd „
Re = ------= —j=— . Отсюда имеем:
Ум M
311
(11.159)
Однако на этом расчеты не заканчиваются, так как с изме-
нением скорости течения изменяются все параметры воздушного
потока под стеклянной поверхностью. В дальнейших расчетах
необходимо определить величину суммарного коэффициента
гидравлического трения при новой скорости потока и найденной
выше величине высоты выступов шероховатости на дне.
Эти расчеты начинаются с использование формулы (11.156),
в которую подставляется скорость имг и определенная выше
глубина . В результате будет найдено новое значение коэффи-
циента гидравлического трения . Коэффициент гидравличе-
ского трения остается прежним. Далее определяем величину
отношения — и из формулы (11.155) - новую величину глубины
К
hn и т. д., используя метод последовательных приближений и за-
висимости (11.156) и (11.157), окончательно получим величины:
, hn , hd . Из формулы (11.129) при условии на-
ходим:
где ХОл( - средний коэффициент гидравлического трения моде-
ли, суммарно учитывающий сопротивление дна и стеклянной по-
верхности. Его нужно сравнить с натурным коэффициентом гид-
равлического трения и оценить ошибку.
Погрешности в величине суммарного коэффициента гид-
равлического трения неизбежны при изменении скорости воз-
312
душного потока и в большую сторону по сравнению с принятой в
начале расчетов. В этой связи полезно определить возможный
диапазон изменения скорости воздушного потока, в пределах ко-
торого погрешность величины коэффициента гидравлического
трения не будет превышать допустимого значения.
к
Туже задачу рассмотрим при условии kb*kh , — = п. Это
kh
означает, что глубина потока на модели по сравнению с натурой
увеличилась в п раз. В связи с тем, что в задаче выполняется ус-
ловие: кОи~<1, одновременно в п раз надо увеличить на моде-
ли
ли по сравнению с натурой коэффициент гидравлического тре-
ния. Отсюда зависимость (11.154) следует записать в таком виде:
А,д=2„10н-1и. (11.161)
Далее находим среднюю глубину потока на модели
h
Ил,= н- . Как и ранее, расчет начинаем с предположения о том,
что сопротивление поверхности стекла и ложа модели относятся
к области гидравлически гладкого руса. В этом случае
hd=hn- hM/2 . Тогда в соответствии с (11.153) находим коэффи-
циент А,и , а из (11.161)- Хд . Расчеты продолжаются методом
последовательных приближений с использованием формулы
(11.157). После их завершения из (11.158) находится величина
относительной шероховатости дна модели. При этом может ока-
заться, что коэффициент 'кд превышает предельное значение,
которое было в исследованиях А.П. Зегжды (« 0,02), а высота вы-
ступов шероховатости А6) будет соизмерима с глубиной hd , или
даже превышать ее. В таком случае в первом приближении нуж-
313
но определить величину допустимого искажения линейных мас-
штабных коэффициентов, используя следующее преобразование
формулы (1 1.161).
<0,02 + Х„
(11.162)
После этого все расчеты нужно повторить в том порядке, в
каком они были выполнены выше. В завершении их необходимо
установить диапазон изменения скорости потока на модели, в
пределах которого величина коэффициента гидравлического тре-
ния будет находиться в допустимых пределах. Из-за того, что ко-
эффициент кд и высота выступов шероховатости Лд могут по
условиям моделирования принять предельно большие значения,
скорость потока имг окажется небольшой по величине. При
этом число Рейнольдса, относящиеся к части потока, примыкаю-
щей к стеклянной поверхности ReMn , будет недопустимо малым.
В этом случае скорость движения потока на модели следует при-
нимать, исходя из условия, что это число Рейнольдса должно
превышать величину, соответствующую границе ламинарного
движения (по разным оценкам приблизительно равную 3000 ):
^„=-^•>3000.
ул<
(11.163)
Остановимся далее на методике моделирования явлений в
водоемах с малыми глубинами и очень большими плановыми
размерами на напорной воздушной модели, когда выполняется
условие: Zo„y->1. Как и в случае моделирования подобных яв-
лений на безнапорной модели (см. раздел 11.6), прежде всего,
314
выбирается линейный масштабный коэффициент кь . Далее не-
обходимо назначить масштабный коэффициент кК, задаваясь та-
кой величиной коэффициента гидравлического трения на модели
А,о
Хо„, чтобы отношение —- не превышало 2-3 . Вводится для
условий модели допустимое значение параметра, определяющего
явление:
I Ь”\
Onh
« / д
. Если оно выбирается равным единице, то из
зависимости (11.81) находится линейный масштабный коэффи-
к
циент глубины потока kh и отношение = п . Далее, как и в
двух рассмотренных выше случаях, выполняем следующие опе-
рации: задаемся средней скоростью воздушного потока UM, Ha-
д. ,
ходим среднюю глубину потока на модели лм = , , делаем пред-
ал
положение о том, что сопротивление поверхности стекла и ложа
модели относятся к области гидравлически гладкого руса. В этом
случае из (11.153) определяем коэффициент гидравлического
трения , а из (11.161) - . Расчеты продолжаются методом
последовательных приближений. Если в натуре поверхность дна
относится к области квадратичного сопротивления, то использу-
ется формула (11.157). После их завершения из (11.158) находит-
ся величина относительной шероховатости дна модели. По воз-
можности расчеты следует проводить так, чтобы сопротивление
на модели не выходило за пределы границ, в которых справедлив
закон сопротивления в натуре. Суждение о соответствии исполь-
зуемых формул своей области сопротивления делаются в зависи-
мости от величины динамического числа Рейнольдса. В случае
необходимости вносятся необходимые коррективы в параметры
315
потока на модели. Например, выше было показано, какой должна
быть при выбранной относительной высоте выступов шерохова-
тости скорость потока на модели, соответствующая границе ав-
томодельной области. Для других областей сопротивления с этой
целью можно использовать значения динамического числа Рей-
нольдса Rets на границах областей:
R (11164)
где в переходной области 50 > Re,, >5 ; на верхней границе гид-
равлически гладкого русла Re*., <5 ; &м ~ высота выступов
шероховатости, которая образуется при изготовлении модели
(например, по данным [2] для пластилина &м « 0,02 см ). Отсюда
получим:
В качестве нижней границе гидравлически гладкого русла
следует принимать условие (11.163), соответствующее границе
существования области ламинарного режима. Конечно, от этой
границы следует отодвинуться в сторону больших значений чис-
ла Рейнольдса.
В завершении исследований возникнет необходимость про-
извести пересчет измеренных на модели скоростей течения в на-
турные условия. Обычно при проектировании модели в качестве
исходной информации используется расход воды в натурных ус-
ловиях QH , измеренный в характерном створе. На модели в том
же створе при условии, что стеклянная поверхность находится на
уровне, при котором был найден расхода воды в натуре, произво-
316
дят измерения скоростей течения и методами гидрометрии нахо-
дят расход воздушного потока QM . Далее определяют масштаб-
ный коэффициент расхода воды:^ = QjQM Но kQ=kvkhkh,
отсюда имеем:
ку ~ кдкь kh , (11.166)
где ки ~ масштабный коэффициент скорости потока. В связи с
тем, что при проведении опытов устанавливать всякий раз один и
тот же режим работы вентиляторов практически невозможно,
приходится каждый раз определять величину масштабного коэф-
фициента скорости заново. Важно, чтобы во время проведения
очередного опыта режим работы вентиляторов был стационар-
ным. Следует также иметь в виду, что при проведении таких пе-
ресчетов неизбежны ошибки, связанные с отсутствием подобия
распределения скоростей течения потока на вертикалях в натуре
и на модели.
В качестве примеров обратимся к двум задачам, рассмот-
ренных в разделе 11.6. В первой изучался на модели с водным
потоком план течений в нижнем бьефе русловой гидроэлектро-
шанции. Ширина потока в характерном створе составляет 500м,
средняя глубина воды -10м, коэффициент гидравлического тре-
ния - 0.0078 , характерная скорость течения UH принята равной
1,2 м/с . Задаемся линейным масштабным коэффициентом плано-
вых размеров модели: ^=250 . Тогда глубина потока на модели
составит 4 см , ширина в характерном створе - 200 см . Скорость
воздушного потока принимаем равной 12 м/с . Подставим эти
данные в формулу (11.153), получим
317
/1200-4 Г'2"/200V'07
Z =0,043 -------- — =0,0047. Далее из формулы
" 2-0,15 ) I 4 )
(11.154) имеем: кд =2-0,0078-0,0047 = 0,0109 . Теперь согласно
(11.113) находим —=—=——- = 2,319 . Но hd+hn=hM , по-
v 7 hn 0,0047 д
h
этому hn = —— и 0,3Л,
j п 3319
. Подставляя это значение hn
в (11.156),
найдем новую величину коэффициента и т. д., используя ме-
тод последовательных приближений, придем к следующим ре-
зультатам: 7,„=О,ОО5, А,д=0,0106, Л„=О,32ЛИ, /^=0,68/^.
Найдем динамическую скорость, соответствующую части потока,
примыкающей к стеклу: U„M„ = UM = 12^0,0025 = 0,6 м/с .
Определим соответствующее число Рейнольдса:
„ 60-0,001 . .
Re,M„ =-------=--------= 0,4 , где высота выступов шерохова-
v„ 0,15
тости стекла Л(, принята равной 0,001см . Делаем вывод о том,
что формула (11.153) была использована правильно. Теперь из
зависимости (11.158) имеем:
hd
0,0106
0,0576
200 f Г*
2-0,68-4 I
= 0,052 . Отсюда получаем
высоту выступов шероховатости на дне модели:
Лд =0,052-0,68-40 = 0,14 см . Далее определяем динамическую
скорость потока UtMd = 12 д/0,0053 = 0,874 м/с и число
„ 87,4-0,141 „
Рейнольдса Re,wrt =--------=-----------= 82,2 . Делаем вывод о
vM 0,15
том, что формула (11.157) соответствует принятому в расчетах
318
закону сопротивления. Теперь из зависимости (11.159) найдем
скорость потока на границе области квадратичного сопротивле-
63,2 0,15 ,
ния: U,,, > --г-- --------- 653 см/с
мг д/0,0106 0,141 '
В дальнейших расчетах принимаем имг = 7м/с . Теперь об-
ратимся к формуле (11.156), из которой определим:
|’°’20|" 200 V01070
I I 2-0,32-4
=0,043
"700-0,32-4
. 0,15
= 0,00557 . Отсюда име-
ем; = °’0106 = 1,904 , hn = - 0,344/+, , hf. = 0,656/т, .
0,00557 " 2,904 м д
Далее реализуется процесс последовательных приближений
с использованием формул (11.156) и (11.157), найдено:
0,0055, Хд = 0,0107, A„=0,34^, ^=0,66^, ХОл, =0,0081.
„ ^“Ojm 0,0081 , ~
Следовательно-----=------= 1,038.
КОн 0,0078
Если задаться скоростью воздушного потока равной
20м/с , то, проведя подобные расчеты, можно получить:
XOw =0,0075 . Отсюда ^^ = ^^^ = 0,962 . Таким образом, если
А.Он 0,0078
скорость воздушного потока лежит в диапазоне от 7 м/с до
20 м/с , то ошибка величины коэффициента гидравлического
трения будет изменяться в нем от +3,8% до -3,8% . Это значит,
что параметр Хо „~ при скорости воздуха 7 м/с будет равен
1,038 , а при скорости 20 м/с - 0,962 , что допустимо.
Ту же задачу можно решить по иному. Допустим, что есть
необходимость уменьшить плановые размеры воздушной напор-
ной модели, так что линейный плановый масштабный коэффици-
319
ент следует принять равным кь = 400 . Но при таком масштабном
коэффициенте глубина потока на модели будет слишком малой,
к
поэтому выбираем kh = 100 . Отсюда — = 4 , тогда, учитывая
kh
условие Хо„—=0,39<1 , найдем коэффициент гидравлического
К
трения на модели: ХОл, = 4Х0н . Глубина потока на модели равна
10 см , ширина в характерном створе - 125 см . Скорость воздуш-
ного потока принимаем, как и ранее, равной 12 м/с . Подставим
эти данные в формулу (11.153), получим при условии
hd=hn=hj2 :
0,043 2 0iloJ =0,0043. Далее из формулы
(11.161) имеем: = 2-4-0,0078 - 0,0043 = 0,058 . Находим
hf. Z,, 0,058 ,, , Л,. ЛЛ„. г-,
—=—----------= 13,51 , и Л =—'- ~0,07Лм . Подставляя это
hn Хп 0,0043 " 14,51
значение hn в (11.156), найдем новую величину коэффициента
и т. д., используя метод последовательных приближений, при-
дем в конце-концов к следующим результатам:
Хп =0,0054, Хд =0,057, hn =0,087^ , hd = 0,913hM . Теперь
из зависимости (11.158) имеем: — =
hd
0,057 ( 125 \
0,05761^2-9,13 J
2,564
«2 .
Отсюда, как и следовало ожидать, при таком огромном коэффи-
циенте гидравлического трения дна результат получился абсурд-
ным: высота выступов шероховатости на дне модели в два раза
превышает глубину потока. Это свидетельствует о том, что вели-
чина искажения линейных масштабных коэффициента была при-
нята завышенной. Определим в первом приближении величину
320
допустимого искажения этих коэффициентов, используя формулу
(11.162): п <—Q Q078— = 1,63 . Следовательно, в рассматривае-
мой задаче линейный плановый масштабный коэффициент может
отличаться от линейного масштабного коэффициента глубин все-
го в 1,63 раза. Так, если выбрать kh = 250 , то най-
кь 400 1 ,
дем: — =-------=1,6 , что находится в соответствии с получен-
kf, 250
ным условием. Далее все расчеты нужно повторить заново при
новой глубине потока равной
=0,0054, Хд =0,0195, hn = 0,22Лг(,
« 0,2, \д = 0,62см, Ъ!,1г = 1,09 м/с,
hd
Используя условие (11.163), получим U
ил1г
4 см . Было найдено:
^=0,78^,
D 109-0,22'4
Re„ =-----------я 639
0,15
гмг >5,5 м/с .Принимаем:
= 6 м/с . Приведем результаты расчетов:
Хп =0,0062, Хд =0,0197, *„=0,24^, = 0,74/гм, Хо,( =0,0081,
0,0081 . ,
---=-------= 1,03 5 . Если принять UM = 20 м/с , то найдем:
T.QH 0,0078
мг
О At
=0,0050, =0,0195, //„=0,2^, ^ = 0,8^, XOjm = 0,0076,
0,0076 no_Q r
---=-------= 0,978 . Следовательно, если скорость воздушного
Xqh 0,0078
потока на модели будет находиться в диапазоне 6-20 м/с , то
ошибка величины коэффициента гидравлического трения будет
изменяться в нем от +3,5% до -2,2% . Это значит, что параметр
7.0л( — ПРИ скорости воздуха 6м/с будет равен 1,035 , а при
h,.
м
скорости 20м/с - 0,978 , что допустимо.
В разделе 11.6 в качестве примера рассмотрена модель Нев-
ской губы с водным потоком. Линейный плановый масштабный
321
коэффициент кь выбран равным 500 . Поставим задачу провести
исследования на напорной воздушной модели Невской губы, су-
щественно уменьшив ее плановые размеры, приняв, например,
коэффициент къ равным 2000 . Как показали ранее выполненные
расчеты, течение воды в натурных условиях относится к области
гидравлически гладкого русла с такими параметрами:
Re =2-105, Хп =0,003, 2lOh—=11,25, 6 =7,5м . Зададим ве-
hH
личину коэффициента гидравлического трения в условиях моде-
ли =0,0075, отсюда следует:
ку =—^ -о д - 2 5 - п _ Параметр X,
Хо„ 0,0075 Хо„ (
Ьи I
0л, т- при-
hn м
нимаем равным единице. Тогда из формулы (11.81) получим:
, к-,кь 0,4-2000 _ „ R
kh--r——\=-----------~ 70 . Находим глубину потока на моде-
11,25
, 400
ли: лл/=— =5,7см . Скорость воздушного
равной 12 м/с . Из формулы
4=O.O43^y”'2O^V007
" I О А К I I 5 Д
потока принимаем
(11.153) имеем:
2-0,15
= 0,0041 .
Теперь с учетом
(11.161) получим: Хд =2-2,5-0,003 -0,0041 = 0,0109 . Но если
стеклянная поверхность и дно модели относятся к области гид-
равлически гладкого русла, то в этом случае должны выполнять-
ся условия: Х() = , hd=hn= hM/2 . Отсюда можно найти в пер-
вом приближении предельную величину отношения коэффици-
ента гидравлического трения в условиях модели к аналогичному
коэффициенту в натуре: п = = 1,37, Лх=0,73 . Далее из
формулы (11.81) найдем новое значение линейного масштабного
322
коэффициента глубины потока и глубину потока на модели:
kh = 11 25—ssl30’ Ajm==130=^1CM ' ”асчеть1 продолжаются ме-
тодом последовательных приближений, в результате было полу-
чено: kh =120, л = 1,47, //„=3,3 см, = Kf) = 0,0044 . Далее по
формуле (11.164) определяем динамическое число Рейнольдса:
1200 JO, 0044/2 -0,02 с ~
Re^ =------—-----------— 7,5 . Следовательно, число Рейнольд-
са находится за пределами верхней границы гидравлически глад-
кого русла. Принимаем Re,_, = 5 , из формулы (11.165) определя-
ем скорость воздуха на модели, при которой сопротивление дви-
жению воздуха на модели будет соответствовать области гидрав-
лически гладкого русла: U„ 0,15-------------= 800см/с . Даль-
F М д/0-0044/2'0'02
нейшие расчеты проводятся при скорости воздуха на модели рав-
ной 8 м/с. Их результаты таковы: ЛА=112, /7 = 1,58,
hM = 3,6см, ХОл( =0,0047 . Определяем скорость воздуха на ниж-
ней границе гидравлически гладкого русла:
т. 3000-0,15 _
UM =---------= 125см/с. Если принять на нижнеи границе об-
3,6
ласти UM = 4м/с , то при h = 3,6см получим А.ом = 0,0054 . Таким
образом, произошло увеличение коэффициента гидравлического
трения на 15% , так что параметр ХОл1 стал равным 1,15.
h,.
м
В процессе проведения исследований на модели может воз-
никнуть необходимость изучить характер течений в Невской губе
непосредственно перед наводнением. Наводнением считается та-
кая ситуация, когда уровень воды в губе повышается на 1,6м над
ординаром. Условно будем считать, что глубина вода в пределах
323
акватории стала равной 5,6 м , на модели должна быть около
5 см .На верхней границе гидравлически гладкого русла при глу-
бине воздушного потока Ли=3,6см и скорости воздуха 8 м/с
А Ь,,
параметр Хо „ — был равен единице, а отношение
К» 0,0047 , „ r R
—— = Q q— = 1,57 . Если увеличить глубину потока на модели и
принять ее равной 5 см , то коэффициент гидравлического трения
на модели надо увеличить дополнительно в — = 1,4 раза. Следо-
т 3,6
вательно, коэффициент гидравлического трения на модели дол-
жен превышать натурный в 1,57-1,4 = 2,2 раза. Но тогда он вый-
дет за рамки гидравлически гладкого русла. В области гидравли-
чески гладкого русла коэффициент гидравлического трения уве-
личивается с уменьшением числа Рейнольдса и скорости потока.
Расчеты показывают, что даже при скорости воздуха равной
3 м/с достичь желаемого увеличения коэффициента гидравличе-
ского трения не удается. В создавшейся ситуации, как об этом
уже было сказано ранее, есть два альтернативных решения. Пер-
вое - увеличить линейный плановый масштабный коэффициент
(уменьшить размеры модели в плане), что приведет к увеличению
линейного масштабного коэффициента глубин (на модели глуби-
на потока уменьшится), тем самым может быть достигнут желае-
мый результат на вновь созданной модели. Конечно, это очень
дорогое решение. Альтернативой ему будет увеличение шерохо-
ватости на существующей модели, что приведет к увеличению
коэффициента гидравлического трения. Это, естественно, намно-
го более дешевое решение, но с ним связано появление дополни-
тельных погрешностей. Рассмотрим его подробнее, принимая
324
скорость воздушного потока равной 8 м/с , а глубину пото-
ка- 5см . Расчеты начинаем, используя формулу (11.153), име-
ем:
Хп = 0,043
800-5^1 °'2°<750Л °’07
0,3 J L 5 )
= 0,0045 . Теперь, используя
зависимость (11.161), приходим к результатам:
= 2-2,2-0,003 -0,0045 = 0,0088, h = 0,34/гм, /ь = 0,66/г
r I 2*1 С* -* yVf
Далее был реализован процесс итераций, по его завершению
найдено: hn = 0,36 hM , hd = 0,64 hM , X„=0,0047, T.d = 0,0085.
Относительную шероховатость поверхности дна на модели
определим из формулы (11.158):
hd
0,0085 Г 750 "I0,15
0,0576^2-0,64-5 )
2,564
= 0,05,
= 0,05-0,64-5 — 0,15 см.
По сравнению с абсолютной высотой выступов шероховатости
поверхности дна модели, изготовленной из пластилина
(» 0,02см), высоту выступов нужно увеличить в 7,5 раза. Прове-
ряем соответствие использованных зависимостей законам сопро-
тивленя:
D 800^0,0042,15 п 800^0,0024-0,001 л х
= —ой----------= 52 >50 ’ Re*n = —ois-----------= 0,26< 5 ’
800-0,36-5
0,15
= 9600 . Таким образом, закон сопротивления по-
верхности дна модели находится на границе области квадратич-
ного сопротивления, стеклянной поверхности - внутри области
гидравлически гладкого русла, что соответствует использован-
ным в расчетах зависимостям.
325
Можно предположить, что с увеличением скорости потока
на модели законы сопротивления сохранятся, поэтому, используя
их, придем при скорости 12 м/с к таким результатам:
hn =0,34/2,,, /гй = 0,66Лм, =0,0044, к() =0,0085. Отсюда
следует: 70„ =0,0064, —— = 0,967, Хо „ = 0,967 .
^0» '
Можно также утверждать, что с уменьшением скорости воз-
духа на модели сопротивление в части потока, примыкающей к
дну, станет относиться к переходной области. В этой связи воз-
никает необходимость использовать в расчетах для определения
коэффициента гидравлического трения соответствующую фор-
мулу (11.95). С целью уменьшения числа итераций начнем расче-
ты, используя параметры потока, полученные при его скорости
равной 8 м/с.
f400-0,36-5) °’20f 750 'I
0,043 ----------- --------------
0,15 ) ^2-0,36-5
= 0,0054,
ч195/ х-°'75
0,15 Г ( 750 | 0,23-0,15 { 750 '
0,64-5) 1^2-0,64-5 J +400-0,64-5^2-0,64-5^
-50,2
< 0,15-0,15
^0,64-5-400-0,64-5
750
2-0,64-5
-0,68~|0’20
= 0,0076,
hn = 0,42Ли, Ид = 0,58 л,, . Результаты процесса итераций:
Л„ = 0,4ЛЛ<, Ad=0,6A„, =0,0054, kf) =0,0078, ХОл1 = 1,0.
hM
400-0,4-5 400-^0,0039-0,15
ке„ =---------=5333 > 3000, Re*. =----------------« 25 .
0,15 0 0,15
326
Вывод: использованные в расчетах формулы соответствуют
своим законам сопротивления. Остается определить величины
чисел Рейнольдса Rec на модели в устьях рек, впадающих в Нев-
скую губу. В разделе 11.6 было сказано, что самая малая часть
расхода воды в Неве проходит в пределах городской черты в рус-
ле Средней Невки (g «150 м3/с, В ®165 м, Я ~ 6 м). Определим
число Рейнольдса в ее устье, полгая, что это число в устьях дру-
гих рек, будет превышать его. Прежде всего, найдем величину
масштабного коэффициента расхода потока. При скорости тече-
ния в приделах Невского бара, равной на модели 8 м/с, глубине
потока 3,6 см, ширине 7,5м определяем величину расхода возду-
ха qm =8-7,5-0,036 = 2,16м3/с . Отсюда имеем:
Найдем величину расхода воздуха в устье Средней Невки на мо-
6сЯи _ 15Qj,16 _ q |^мзус ПрИ ШИрИНе устья реки
дели: Qcum -
kQ
на модели
, 165 о_
— — 8,2 см 9
2()00
глубине потока
, 6 ,
^снм ~ ~ 5,3 СМ
тг &СНм
UcHm " h h
°СНм пСНм
скорость течения
в устье равна:
0 13
-----------~ 30м/с . Отсюда искомое число
0,082-0,053
Рейнольдса: Rec = 30q01| " ~1°5 >Ю4 . Необходимо на модели с
помощью простейших средств (например, решеток) добиться та-
кого распределения расходов по рукавам дельты реки, которое
наблюдается в натуре.
327
12. О ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ
МОДЕЛИ ЗА ПРЕДЕЛАМИ УСЛОВИЙ, ПРИНЯТЫХ
В ЕЕ ПРОЕКТЕ
В разделе 5 были изложены правила организации исследо-
ваний на физических моделях явлений на стадии, предшествую-
щей проведению самих экспериментов. В основном они касались
вопросов получения критериальных уравнений и в первую оче-
редь - при отсутствии среди чисел подобия критериев. Однако на
этом не заканчиваются трудности, связанные с реализацией фи-
зического моделирования явлений, поскольку при организации
исследований часто возникает такая ситуация, когда проводить
их приходится в условиях, отличающихся от принятых в проекте
модели. Например, в основу расчетов моделей участков рек или
гидротехнических сооружений, находящихся в них, обычно за-
кладываются сведения о геометрических, кинематических и ди-
намических характеристиках потока, которые были получены в
результате натурных измерений и наблюдений. Как правило, це-
лью исследований является получение этих характеристик в рас-
четных условиях. В этих условиях в соответствии с действующи-
ми нормативными документами гидрологические характеристика
потока назначаются с заданной вероятностью превышения в за-
висимости от класса сооружений. Последний определяется их на-
роднохозяйственным эффектом. Кроме расчетных, сооружения
дополнительно могут проверяться на работу в чрезвычайных ус-
ловиях эксплуатации. Таким образом, в основу расчетных и чрез-
вычайных условий эксплуатации сооружений положен вероятно-
стный прогноз появления гидрологических характеристик (рас-
ходов, уровней воды и т п.). Чаще всего целью исследований на
физической модели является изучение различных явлений в рус-
328
ле реки или непосредственно у сооружений в этих условиях экс-
плуатации. Если в качестве расчетной гидрологической характе-
ристики (или соответствующей чрезвычайным условиям эксплуа-
тации) берут расход воды в реке, то ему соответствует опреде-
ленный уровень воды, который может быть определен двумя
способами. По первому способу уровень так же, как и расход, на-
ходится в результате вероятностного прогноза. По второму - в
результате экстраполяции кривой связи расходов и уровней воды,
найденной методом сглаживания данных натурных наблюдений,
в область расчетных значений расходов воды в реке (или соот-
ветствующей чрезвычайным условиям эксплуатации). Если в на-
турных условиях расход и уровень воды в расчетных или чрезвы-
чайных условиях эксплуатации заданы, то числа Фруда и Рей-
нольдса в характерном створе известны. Следовательно, в этом
случае исследователь имеет дело с задачей, которая в разделе 10
названа первой. Но из-за того, что уровни воды находятся с из-
вестной долей неопределенности, цель исследований может быть
сформулирована так: определить, прежде всего, пропускную спо-
собность русла или расположенных в нем сооружений. В такой
постановке в задаче должен быть задан либо расход, либо уро-
вень воды в характерном створе. Но если задан расход воды, то
при отсутствии уровня (или глубины) потока с точки зрения ор-
ганизации физического моделирования задача становится неоп-
ределенной, так как в ней невозможно найти ни чисел, ни крите-
риев подобия. Если же задан уровень воды (или глубина потока),
то в этом случае исследователь имеет дело с задачей, которая в
разделе 10 названа второй. Она вполне определенна, поскольку в
ней можно вычислить числа и критерии Архимеда.
Далее необходимо проанализировать изменения на модели
при переходе от условий, при которых была рассчитана модель, к
329
новым условиям, продиктованным целью исследований. Модель
геометрически подобна натуре, кроме того, моделирование осу-
ществляется «по Фруду», поэтому равенство чисел Фруда в нату-
ре и на модели будет обеспечено. Обычно в натурных условиях с
увеличением глубины потока скорость течения в нем тоже увели-
чивается (увеличивается удельный расход потока), следователь-
но, число Рейнольдса увеличится и в натуре, и на модели. Как
правило, явления в натуре (речь идет о течениях в руслах рек) от-
носятся к области квадратичного сопротивления. Если в условиях
модели число Рейнольдса было принято на границе области
квадратичного сопротивления, то оно останется в этой области
(сдвинется в ней в сторону больших значений чисел Рейнольдса).
Из-за увеличения глубины потока произойдет уменьшение отно-
сительной шероховатости (увеличение относительной гладкости)
потока и на модели, и в натуре. По этой причине произойдет
уменьшение коэффициента гидравлического трения и там, и тут.
Таким образом, при увеличении глубины потока модель обладает
способностью «самонастраиваться» на нужный режим исследо-
ваний. Иная ситуация возникает в случае, когда возникает необ-
ходимость проводить исследования с меньшими расходами и
уровнями воды по сравнению с теми, на которые модель проек-
тировалась. Естественно, в этих условиях соблюдается равенство
относительной шероховатости в натуре и на модели, но из-за
уменьшения числа Рейнольдса на модели вместо границы облас-
ти квадратичного сопротивления явление может оказаться в об-
ласти переходной или гидравлически гладкого русла. Тем самым
будет нарушено равенство коэффициентов гидравлического тре-
ния. Можно предложить такой выход из создавшейся ситуации.
Если на стадии проектирования модели известно, что возникнет
необходимость проводить исследования при уровнях и расходах
330
воды меньших тех, на которые модель рассчитывалась, то вместо
числа Рейнольдса на границе области квадратичного сопротивле-
ния в расчетах модели следует принять большее значение этого
числа (сдвинуться «вглубь» этой области). Но сделать это надо
так, чтобы при моделировании явлений при уровнях и расходах
воды меньших расчетных не выходить за пределы этой области.
При таком методе моделирования, естественно, линейные мас-
штабные коэффициенты уменьшатся, что означает увеличение
размеров модели.
Из проведенного анализа следует важный вывод. Допустим,
что в основу расчетов модели положен такой метод приближен-
ного моделирования, при котором область сопротивления па мо-
дели не соответствует области сопротивления в натуре при со-
блюдении равенства коэффициентов гидравлического трения.
Например, вместо области квадратичного сопротивления, суще-
ствующей в натурных условиях, на модели принята переходная
область, или гидравлически гладкого русла (эти методы прибли-
женного моделирования изложены в разделе 11). Такая модель
пригодна для проведения исследований только в тех условиях,
которые были положены в основу ее проектирования. Любые от-
клонения от них влекут за собой нарушение основных принципов
физического моделирования явлений, а потому недопустимы.
Аналогичная картина наблюдается при моделировании яв-
лений в напорных трубопроводах с той разницей, что относи-
тельная шероховатость в этом случае остается всегда неизмен-
ной. Отклонения от расчетных условий происходят из-за того,
что скорость течения в трубопроводе может отличаться от той,
которая была принята в процессе проектирования модели, в ту
или в другую сторону. Если в расчетных условиях число Рей-
нольдса было выбрано на границе области квадратичного сопро-
331
тивленя, то при увеличении скорости течения, как и в случае без-
напорного потока, явление останется в той же области. Но сопро-
тивление в натурных трубопроводах чаще всего относится к пе-
реходной области, так что проводить исследования надо либо в
трубопроводах натурных размеров, либо, используя метод при-
ближенного моделирования, запроектировать модель так, чтобы
сопротивление относилось к области гидравлически гладкого
русла. Как об этом сказано выше, возможности такого способа
моделирования ограничены условиями, на которые модель была
рассчитана.
В [21] в этой связи предлагается такой приближенный спо-
соб проведения исследований, относящийся главным образом к
моделированию явлений в напорных трубопроводах. Рекоменду-
ется до проведения основных испытаний выполнить предвари-
тельные исследования методического характера. В них находится
зависимость в условиях модели любого явления (в том числе и
того, изучение которого предполагается выполнить) от числа
Рейнольдса. При этом диапазон изменения чисел Рейнольдса
должен быть достаточно большим, таким, чтобы в процессе ис-
следований была четко найдена область, в которой изучаемое яв-
ление (или связанное с ним, выбранное в качестве индикатора) не
зависит от числа Рейнольдса (автомодельная область). Основная
серия испытаний проводится при числах Рейнольдса, находящих-
ся в этой области.
Аналогичные трудности возникают при моделировании ус-
тановившегося неравномерного движения, в котором все пара-
метры потока неизменны во времени, но изменяются в зависимо-
сти от координат пространства, ограничивающего поток. Такого
рода трудности преодолеваются путем надлежащего выбора ха-
рактерного створа. Явления, происходящие за пределами этого
332
створа, увязываются с характеристиками потока в нем. Предпо-
лагается, что такая связь однозначна; во всяком случае, исследо-
вания в натурных условиях и на моделях ее не опровергают. В
речных системах установившееся движение воды, как правило,
(за редким исключением) неравномерное. Рассмотренные ранее
случаи (кроме плановой задачи) можно отнести к плавноизме-
няющемуся движению. Моделирование этого движения и равно-
мерного практически совпадают. Кроме этих двух видов, сущест-
вует еще и резкоизменяющиеся движение. Такой вид движения
наблюдается, например, при различных типах сопряжения бьефов
за водосбросами; в результате взаимодействия речного и поймен-
ного потоков при выходе воды из русла на пойму и т. п.
333
13. МОДЕЛИРОВАНИЕ НЕРАВНОМЕРНОГО
РЕЗКОИЗМЕНЯЮЩЕГОСЯ ДВИЖЕНИЯ БЕЗНА-
ПОРНЫХ ПОТОКОВ
13.1 Моделирование неравномерного резкоизменяюще-
гося движения при сопряжении бьефов по типу поверхност-
ного и донного гидравлических прыжков
Задача о сопряжении бьефов с помощью поверхностного и
донного гидравлических прыжков может служить хорошим при-
мером удачного сочетания методов физического и математиче-
ского моделирования этих явлений. Прежде всего, обратимся к
уравнению связи (8.12), относящемуся к неравномерному движе-
нию открытого потока.
у ^Fr, Re, Eu, у Fr^| = 0 , (13.1)
Последний член в нем заменим комбинацией его с уклоном сво-
бодной поверхности, оставив в связи уклон, получим уравнение в
таком виде:
\|/^Fr,Re,Eu,J,^-y^ = O. (13.2)
Полученная комбинация удобна в том смысле, что в случае
равномерного движения (J~i) она становится равной единице:
Xn Fr , „ г к-< кРг
—-—-1 . Получим из нее индикатор подобия: - =1 , где
2 . i h
kj - масштабный коэффициент уклона свободной поверхности
потока. При моделировании «по Фруду» kFr = 1, поэтому имеем
334
k^-kj . Следовательно, масштабный коэффициент уклона сво-
бодной поверхности равен масштабному коэффициенту коэффи-
циента гидравлического трения. Форма свободной поверхности
на модели будет подобна натурной при равенстве коэффициентов
гидравлического трения в натуре и на модели. В процессе иссле-
дований на модели может возникнуть необходимость проводить
их в условиях, отличных от расчетных (например, расчетным ус-
ловиям соответствует незатопленный донный гидравлический
прыжок, а исследовать нужно явления при различных степенях
его затопления). В соответствии со сказанным в предыдущем
разделе в этом случае равенство коэффициентов гидравлического
трения в натуре и на модели должно быть обеспечено. Кроме то-
го, возможны трудности с выбором линейного масштаба модели
из-за того, что предельно гладкая ожелезненная бетонная поверх-
ность имеет высоту выступов шероховатости приблизительно
равную 0,064-0,07 см.
Зависимость параметров гидравлического прыжка (высоты,
протяженности водоворотной области) от коэффициента гидрав-
лического трения доказана экспериментально [44,46, 59] и в ре-
зультате теоретического решения [32]. Однако это не всегда учи-
тывается при физическом моделировании сопряжения бьефов по
типу донного гидравлического прыжка. Следует иметь также в
виду еще один факт, на который долгое время не обращали вни-
мания при решении задачи о гидравлическом прыжке. Обычно
при теоретическом решении задачи используют закон изменения
количества движения, который применяют для отсека жидкости,
ограниченного двумя сечениями, одно из которых совпадает со
сжатым, другое выбирают па достаточно удаленном расстоянии
от него. В том и в другом створе распределение скорости по
плоскому живому сечении принимается равномерным. После
335
преобразований получают квадратное уравнение, из которого
следует формула «сопряженных глубин потока», приводимая во
всех учебниках по гидравлике. Обычно в качестве «первой со-
пряженной глубины» принимается глубина воды в сжатом сече-
нии. Число Фруда, входящее в формулу «сопряженных глубин»,
определяется по параметрам потока в сжатом сечении. Таким об-
разом, сжатое сечение является в задачах подобного рода харак-
терным сечением. В [27,45] показано, что осредненная кривая
поверхности в гидравлическом прыжке, представленная в без-
размерных координатах, зависит от отношения сопряженных
глубин потока и практически не зависит от числа Фруда. В рав-
ной степени это касается также величины среднего значения ук-
лона свободной поверхности в прыжке. На этом основании мож-
но утверждать, что относительная длина водоворотной зоны со-
вершенного донного гидравлического прыжка и отношение со-
пряженных глубин в основном определяют уклон осредненной
водной поверхности в нем. Таким образом, и отношение сопря-
женных глубин, и относительная длина водоворотной зоны в
гидравлическом прыжке должны быть в соответствии с зависи-
мостью (13.2) функциями числа Фруда и коэффициента гидрав-
лического трения. Исследования должны проводиться в области
автомодельной по числу Рейнольдса. Учитывая такой мощный
генератор дополнительной турбулизации потока, каким является
водоворот в прыжке, автомодельность имеет место при любых
числах Фруда, когда сопряжение бьефов происходит с образова-
нйем водоворотной зоны (Fr > 4) . Что касается числа Эйлера, то
оно в рассматриваемой задаче принимается равным коэффициен-
ту гидравлического трения, поскольку последний определяется
по1 формулам равномерного режима движения.
336
Между тем в процессе проведения лабораторных исследо-
ваний параметров гидравлического прыжка в условиях плоской
задачи было обнаружено, что глубина потока в конце водоворот-
ной зоны не равна второй сопряженной, определенной из квад-
ратного уравнения сопряженных глубин. Но в конце водоворот-
ной зоны корректив количества движения не может быть равным
единице. Отметим, что в пределах водоворотной зоны, учитывая
значительную неравномерность распределения скорости течения
по вертикали, корректив количества движения может принимать
значения, существенно превышающие единицу. Из уравнения
изменения количества движения следует, что с увеличением кор-
ректива количества движения глубина потока уменьшается. Та-
ким образом, в уравнение изменения количества движения необ-
ходимо ввести коррективы, учитывающие неравномерность рас-
пределения скорости течения в сжатом сечении и в сечении с со-
пряженной глубиной. Но тогда, как показано в [26, 27, 33], урав-
нение сопряженных глубин станет не квадратным, а кубическим:
>3 , / U
МА
где а - Л] A/2a1Fr1 + 1, а] и a6 - коррективы количества дви-
жения соответственно в сжатом сечении и в сечении со второй
м2
сопряженной глубиной, Fr, = —J— - число Фруда, отнесенное к
ghx
сжатому сечению, hx и их - глубина потока и скорость течения
в сжатом сечении, h6 - вторая сопряженная глубина. В конце
водоворотной зоны, где выполняется условие a6 = ag , там
h6=he ; если аб -> 1, то h6 -> h2 . Было сделано допущение о
том, что гидравлический прыжок является пристенной струей,
2Fna6=0, (13.3)
337
распространяющейся в ограниченном пространстве. Согласно
этому допущению в конце водоворотной зоны гидравлического
прыжка, где скорость течения на поверхности принимает нулевое
значение, ав = 1,56 . Если принять аб - а2 = а] = 1 , то уравнение
(13.3) превратится в квадратное
х 2
М + — - 2FF] -0.
hJ h.
Из него получают формулу сопряженных глубин
h2/hx = 0,5(71+ 8Fr( -1).
Следовательно, сопряженной глубине h2 соответствует
равномерное распределение скорости течения в сечениях с со-
пряженными глубинами и идеально гладкая поверхность водобоя
(Хо - 0) . Но при равномерном движении воды в русле реки кор-
ректив количества движения обычно лежит в пределах
а2 =1,02-5-1,05 . В таком случае для решения задачи должно ис-
пользоваться уравнение (13.3). Уравнение имеет действительные
корни, если его дискриминант меньше нуля. Анализ этого вопро-
са, проведенный в [27, 33], свидетельствует о том, что корни
уравнения действительны, если число Фруда равно четырем. При
числах Fr, < 4 наступает принципиально новое явление, полу-
чившее название прыжок-волна, в котором поверхностный водо-
ворот отсутствует. Решение уравнения (13.3), удовлетворяющее
поставленной задаче, найдется из формул
^ = “^^со/60°-7!’ С08ч/ = Зл/з a6Fq W . (13.4)
h\ а/3/z! < 3) \hx)
338
Таким образом, в случае донного незатопленного гидравли-
ческого прыжка уравнение связи может быть записано в таком
общем виде:
g = y(FriAo> аР “2), (13.5)
h х
где с = — , либо q = —; хв - длина водоворотной зоны прыж-
' А,
ка. Зависимость, определяющая кривую осредненной водной по-
верхности в совершенном гидравлическом прыжке, рассматривая
его как пристенную струю в ограниченном пространстве, полу-
чена в [26, 27, 33]:
А = - 2,о[А -1
А( hy (а - h)(a + hy) (Л|
(13.6)
Задача решается следующим образом. Вначале задаются коррек-
тивом количества движения, изменяя его в пределах
1<аб<1,56 . Тем самым, используя формулы (13.4), находят
глубины потока ниже водоворотной зоны, которые изменяются в
пределах h2> h6>he . Подставляя полученные величины глубин
потока в зависимость (13.6), находят длину водоворотной зоны
прыжка хв и длину участка ниже водоворота х2 в зависимости
от принятой величины корректива количества движения
аб < 1,56 . Далее, изменяя глубину потока в пределах водоворот-
ной зоны гидравлического прыжка от h} до he , из (13.6) находят
соответствующие расстояния от сжатого сечения. Если в этом
есть необходимость, то корректив количества движения в раз-
личных сечениях вальца может быть найден в результате реше-
ния трансцендентных уравнений (13.4).
339
Для определения числа Fq воспользуемся выражением, ха-
рактеризующим положение уровня воды в верхнем бьефе перед
подпорным сооружением относительно уровня поверхности го-
ризонтального водобоя (в учебниках по гидравлике разность этих
уровней обычно обозначают буквой Т )
T = h} +
oq w2
2^Ф?
(13.7)
в котором ср, - коэффициент скорости. При преобразовании за-
висимости (13.7) используются условие постоянства удельного
расхода воды q (задача плоская) и выражение для критической
глубины потока hk [26]:
<1 = Щ К ; hk = ^axq2lg . (13.8)
Результатом преобразований является следующее безразмерное
кубическое уравнение
1 Т hk
Л] J 2ср2 hk hx
(13-9)
Уравнение (13.9) имеет действительные корни, если его дискри-
минант меньше нуля, что равносильно выполнению следующего
условия:
3
(13.10)
Положительные корни уравнения (13.9) найдутся из формул
, РТ < т’ А1/2 ( \
пк ~ 2 \ 1 I ш ]
т=2анФ1Ьг cos 60 ±Т ;
Л1 V3 [hk) < 3)
cosip =
з
2\2{Т )
—. (13.11)
Ф1
340
Знаку минус в аргументе косинуса соответствует Т > hk > ; это
означает: течение в сжатом сечении бурное, следовательно, бье-
фы разделены плотиной, что как раз и является условием рас-
сматриваемой задачи. Знаку плюс соответствует Т > h} > hk ; те-
чение в сжатом сечении спокойное, следовательно, бьефы непо-
средственно сообщаются. Но тот и другой случай удовлетворяют
условию (13.10). График зависимости hxjhk = f{rjhk, <pj , по-
строенный при условии «1=1, приводится в учебниках гидрав-
лики.
Полученные результаты и выводы затрагивают течение во-
ды по поверхности водослива без учета сил трения. Кроме того,
как отмечается в [21], в высоких водосливных плотинах на неко-
тором расстоянии от гребня на дне потока зарождается турбу-
лентный пограничный слой, который растет вниз по течению и, в
конце концов, достигает свободной поверхности. Турбулизация
всей толщи струи воды, движущейся по водосливной поверхно-
сти, способствует интенсивному вовлечению воздуха в поток.
Образуется водо-воздушная смесь, параметры которой в сжатом
сечении (скорость течения, глубина потока, корректив количест-
ва движения) не совпадают с параметрами компактной, неаэри-
рованной струи. Кроме того, в сжатом сечении начинается валец
гидравлического прыжка, в котором движение воды носит пуль-
сирующий характер, что сопровождается защемлением воздуха и
дополнительном вовлечением его в поток. Естественно, на моде-
ли водосливной плотины, уменьшенной по сравнению с натурой
во много раз, пограничный слой не успевает развиться и захва-
тить всю толщу потока, поэтому аэрация потока происходит
только за счет защемления воздуха вальцом гидравлического
прыжка. В этой связи можно сказать, что аэрация потока в пол-
341
ной мере не моделируется. Видимо этим объясняется тот факт,
что в настоящее время не существует единого мнения о влиянии
аэрации потока на параметры гидравлического прыжка. В [21]
упоминаются также трудности воспроизводства на модели шеро-
ховатости водосливной поверхности, подобной натурной.
На основании изложенного можно записать критериальное
уравнение, связывающее глубину воды в сжатом сечении с опре-
деляющими параметрами
h (т А
тМ -Ло.Ф1.«1.е . (13.12)
hk \hk j
где 6 - относительное содержание воздуха в воде в сжатом се-
чении.
Из зависимости (13.7), используя формулы (13.8), получает-
Т
ся следующая связь отношения — с числом Фруда:
hk
Т l+Fnaj^tp, „
— =-----1 — . Тогда уравнение (13.12) можно дать в такой
hk л/Гг1 «1
форме
h
-^/(FrjAo^.aj.e). (13.13)
hk
Следует ввести также параметр 6 в уравнение (13.5) и предста-
вать его в виде
^ = /(Fr1A0,aI,a2,e). (13.14)
Здесь нужно особо остановиться на параметрах
ар а2, фр 6. Допустим, что при проведении опытов было
реализовано строгое моделирование явления перелива воды через
водосливную плотину. Но в таком случае упомянутые параметры
342
будут автоматически подобны натурным. Строго говоря, иначе и
нее может быть. Но исследователь, проводя опыты, целью кото-
рых является определение параметров гидравлического прыжка,
чаще всего вовсе не интересуется внутренней структурой тече-
ния. И ничего удивительного нет в том, что результаты исследо-
ваний у различных авторов не стыкуются, зачастую противоречат
друг другу. Сравнивать результаты исследований можно только в
том случае, если в процессе их проведения были дополнительно
получены сведения о параметрах cq, а2, ср,, 0.
Введем теперь параметр 0, включающий в себя и величины,
обозначенные выше символом <;, и отношение h{/hk . Дадим да-
лее уравнение связи в неявном виде:
F , Хо, ocp а2, <Pi, 6=0.
k hk J
(13.15)
В параметр 0 входят искомые величины. Но в соответствии со
сказанным выше параметры ар а2, Фр 6 являются тоже
искомыми. Среди оставшихся нет критериев. Умножим отноше-
ние T/hk на ар , получим критерий подобия в виде отношения
T/hk0 , где hko = Is ~ критическая глубина потока при
а] = 1, так что
^к ^ко
(13.16)
Параметр Хо также не является критерием, поскольку ха-
рактерный линейный размер заранее не известен. В качестве та-
кового можно принять критическую глубину потока hko . Такое
допущение не противоречит существующей в гидравлике тради-
ции принимать в качестве характерной в пределах выбранного
343
участка неравномерного движения жидкости среднюю глубину
потока. Можно утверждать, что критическая глубина hk0 отлича-
ется от средней в пределах водосливной грани плотины, но выби-
рать ее в качестве характерной вполне допустимо. Дадим теперь
критериальное уравнение в общем виде
Т
\hk<>
(13.17)
Перед исследователем может стоять такая зада-
ча - проверить принятое решение о сопряжении бьефов за водо-
сливной плотиной конкретного гидроузла. В такой задаче поло-
жение горизонтального дна в нижнем бьефе относительно уровня
воды в верхнем бьефе Т и удельный расход воды на водосливе
q заданы. В процессе проведения исследований необходимо пу-
тем измерений получить сведения обо всех параметрах, обозна-
ченных в уравнении (13.16) буквой £ :
Л] h6 Хв Л о
—, аь а2, 0 . Здесь возможны трудности с
hk h\ h\
оценкой содержания воздуха в сжатом сечении потока в натур-
ных условиях 6Н . В литературных источниках такие данные
встречаются редко. Не исключены затруднения при создании во-
досливной поверхности на модели, относительная шероховатость
которой должна быть равна натурной. Возможно, что моделиро-
вание можно будет осуществить только по одному из рассмот-
ренных выше приближенных методов. После того, как будут
найдены величины hx и ан из формулы (13.16) можно опреде-
лить критическую глубину потока hk . В свою очередь коэффи-
циент скорости вычисляется из уравнения (13.9), из него после
преобразований следует:
344
<Р1 =
(ММ3/2
72(m-i)'
(13.18)
Рассмотрим далее затопленный гидравлический прыжок,
который обычно получают, умножая вторую сопряженную глу-
бину потока h6 на коэффициент затопления: n3h6, п3>1 . Го-
воря о затопленном гидравлическом прыжке, приходится ограни-
чиваться случаем образования прыжка в нижнем бьефе при исте-
чении воды из-под затвора. Только в этом случае затопление
прыжка не влечет за собой существенное изменение параметров
потока в сжатом сечении. В случае сопряжения бьефов с помо-
щью водосливной плотины практического профиля процесс зато-
пление гидравлического прыжка сопровождается перемещением
сжатого сечения вверх по водосливной грани. В свою очередь это
связано с существенными изменениями параметров потока в сжа-
том сечении.
Обычно задача о затоплении гидравлического прыжка рас-
сматривается при некоторых идеальных условиях, а именно:
Хо = 0 . В этом случае вторая сопряженная глубина потока удов-
летворяет условию: h6 <h2 .В действительности идеальные ус-
ловия никогда не наблюдаются, поэтому вторая сопряженная все-
гда меньше h6 , и коэффициент затопления гидравлического
прыжка всегда несколько больше принятого значения.
Если затопить гидравлический прыжок в задаче о сопряже-
нии бьефов по типу истечения из-под затвора, то в сечении, сов-
падающем со сжатым (непосредственно у затвора со стороны
нижнего бьефа), глубина потока станет равной hm >hx .Ее можно
определить, решая совместно уравнения изменения количества
движения, составленные для соответственных отсеков жидкости,
параллельно для затопленного и незатопленного гидравлических
345
прыжков [45]. В связи с тем, что силы сопротивления в этой за-
даче не учитываются, единственным условием выбора соответст-
венных сечений, ограничивающих упомянутые отсеки, является
равенство в них коррективов а( и аб . При этих условиях было
найдено
_ L (fii Аб ~ ~ ^1 «б/А) /1 ]9)
Аб V {hxa6jh6 -1)«33
В этой задаче уравнение (13.3) и его решение (13.4) остают-
ся в силе, однако, в них параметр а следует заменить на ау, где
(13.20)
В соответствии с [27] в затопленном гидравлическом прыж-
ке можно выделить область, в пределах которой глубина воды
практически не изменяется и равна hm ; протяженность этой об-
ласти хт находится согласно зависимости
xm/hl=3fi(hm/hl-\y (13.21)
Во второй области, где глубина потока изменяется от hm до
he, осредненная свободная поверхность потока определяется из
формулы
— = 2,22—/и t ~ _ 2;of А _ М + Ы (13.22)
Л] (ai - h)(ai + hm) \
При моделировании затопленного донного гидравлического
прыжка в случае истечения из-под щита с хорошо скругленной
кромкой можно принять, что сжатое сечение совпадает с разме-
ром отверстия, образующегося при подъеме щита между его ни-
346
зом и поверхностью водосливного порога. В этом случае коррек-
тив oq можно принять равным единице. Кроме того, исключа-
ются потери энергии, связанные с движением струи воды по во-
досливной поверхности (<pj =1 ). Естественно, отсутствует аэра-
ция струи. Однако на практике чаще всего применяются плоские
щиты, низ которых не скруглен (с «острой кромкой»), поэтому
корректив а] и сжатое сечение следует оставить среди парамет-
ров, подлежащих изучению. Запишем теперь критериальное
уравнение (13.17) для донного затопленного прыжка в таком виде
Vhko
(13.23)
При этом параметр л0 характеризует гидравлическое трение
флютбета. В процессе проведения исследований необходимо пу-
тем измерений получить сведения обо всех параметрах, которые
обозначены в критериальном уравнении (13.23) буквой
s . ^1 ^б хв хт Г1 п
Ч ‘ У’ У’ ~Г' ~Г’ ~7Г’ “2 '
1 i 1
Затопленный донный гидравлический прыжок при сопряже-
нии бьефов с помощью водослива практического профиля рас-
смотрен в [11,38]. Отмечаются трудности, связанные с матема-
тическим описанием явления, так как сжатое сечение при затоп-
лении гидравлического прыжка перемещается вверх по течению
по водосливной грани. Положение сжатого сечения на водослив-
ной грани определяется при выбранном коэффициенте затопле-
ния глубиной потока hm , которую можно найти только экспери-
ментальным путем. Кроме того, на струю в месте сопряжения во-
дослива с плитой водобоя действует центробежная сила, что соз-
дает дополнительные трудности при использовании математиче-
ского аппарата. Принимая некоторые дополнительные допуще-
347
ния, удалось составить уравнение изменения количества движе-
ния для двух сечений, ограничивающих выделенный объем жид-
кости. Одно из них совпадает со сжатым сечением незатопленно-
го гидравлического прыжка, другое расположено в нижнем бьефе
за пределами водоворотной зоны прыжка. В результате была по-
лучена зависимость, позволяющая определить величину макси-
мальной скорости течения в различных сечениях гидравлическо-
го прыжка. Как и следовало ожидать, уменьшение максимальной
скорости в затопленном прыжке происходит более интенсивно,
чем в совершенном незатопленном. Таким образом, одинаковая
степень воздействия потока на незащищенное дно водотока будет
дметь место в затопленном прыжке на расстоянии от места со-
пряжения плотины с водобоем, существенно меньшем, чем в не-
затопленном прыжке. В соответствии с этим выводом длину кре-
пления при затоплении прыжка можно уменьшить по сравнению
с длиной крепления в случае совершенного гидравлического
прыжка.
В результате анализа, проведенного в [26,27,31,34], было
доказано, что донный затопленный гидравлический прыжок и
поверхностный прыжок (первый критический режим) описыва-
ются одними и теми же уравнениями. Это уравнение (13.3) и его
решение (13.4), но в них, как об этом уже было сказано ранее, па-
раметр а следует заменить параметром (13.20). В поверхно-
стном гидравлическом прыжке глубина потока = А] + ^7, где
d - высота уступа плотины, достаточная для образования этого
режима сопряжения бьефов. При этом вместо (13.21) будет спра-
ведлива следующая формула
xn?=3,0tZ. (13.24)
348
С учетом этих замечаний в остальном зависимость (13.22) остает-
ся без изменений.
Согласно [26,27], принимая во внимание данные экспери-
ментов, выполненных в [52], минимальная высота уступа, необ-
ходимая для образования поверхностного гидравлического
прыжка, находится из формул
djhx >0,l2Fr,, Fr, <30;
d/h{ > 0,5(72,4Fr, +1 -1), 250 > Fr, > 30. (13.25)
В водосливных плотинах с низовым уступом высота уступа
измеряется над дном нижнего бьефа, следовательно, сжатая глу-
бина потока образуется на уступе, поверхность которого в рас-
сматриваемой задаче принимается горизонтальной. Таким обра-
зом, параметр Т равен расстоянию от поверхности уступа до
уровня воды в верхнем бьефе плотины. В таком случае следует
ввести еще один параметр: То = Т + d. В [27] рассмотрены другие
критические режимы поверхностного прыжка и получены рас-
четные формулы для определения основных параметров этих ре-
жимов. Результаты расчетов по этим зависимостям полностью
соответствуют данным экспериментов, приведенных в [52-54].
В соответствии со сказанным при моделировании процесса
сопряжения бьефов с помощью водосливной плотины с низовым
уступом критериальное уравнение должно быть таким
(13.26)
"ко J
В (13.26) отсутствует еще один критерий, который по сути
дела играет роль коэффициента затопления гидравлического
прыжка п3. Для определения границ существования различных
режимов поверхностного гидравлического прыжка (второго кри-
349
тического, поверхностно-донного) в расчетные зависимости вво-
дятся дополнительные параметры. При проведении исследований
смену режимов можно наблюдать, изменяя глубину воды в ниж-
нем бьефе.
Как было отмечено выше, обсуждаемая здесь методика рас-
чета сопряжения бьефов с помощью донного и поверхностного
гидравлических прыжков справедлива в случае, когда водослив-
ная плотина уже запроектирована, и речь идет о проверке режима
сопряжения на модели. Иными словами параметры Т и зада-
ны. Если в процессе проведения исследований окажется, что их
надо изменить, то при заданном расчетном уровне воды в верх-
нем бьефе фактически это будет означать переход к сопряжению
бьефов с иными параметрами прыжков, поскольку отметка уров-
ня дна водобоя в нижнем бьефе тоже изменится. Дело в том, что
уровень воды в нижнем бьефе определяется по кривой связи рас-
ходов и уровней воды в зависимости от величины расчетного
расхода воды, поступающего сюда из верхнего бьефа. Следова-
тельно, при расчетной глубине воды в нижнем бьефе, соответст-
вующей тому или иному режиму сопряжения бьефов, уровень
дна в нижнем бьефе легко находится: достаточно из отметки
уровня воды вычесть глубину потока. Таким образом, если реша-
ется задача определения нужного режима сопряжения бьефов за
водосливной плотиной на стадии ее проектирования, то парамет-
ры Г и То являются искомыми. При такой постановке задачи в
ней заранее известны удельный расход q и перепад уровней во-
ды между верхним и нижним бьефами z. Но реализовать физиче-
ское моделирование в этом случае невозможно. Действительно,
каким образом можно выполнить модель водослива, если поло-
жение дна в нижнем бьефе не известно?
350
Можно задаться отметкой дна (параметры Т и То извест-
ны), но тогда задача сводится к ранее рассмотренной, решение
которой уже было найдено. Этот факт находит отражение и в ма-
тематической постановке задачи: поиск решения может быть
осуществлен только методом последовательного приближения.
Обратимся вначале к задаче сопряжения бьефов с помощью по-
верхностного гидравлического прыжка.
Из полученных ранее зависимостей останется (13.11), одна-
ко в ней в скобках под знаком косинуса нужно оставить знак ми-
нус. Формулы (13.25) преобразуются следующим образом:
То /Л, > 0,12 Fq +T/hx, Fq < 3 0;
Tjhi > 0,5(^/2,4Fq + 1 -1)+ T/hx, 250 > Fq > 30. (13.27)
Произойдут изменения и в зависимостях (13.4)
(\-3
. (13.28)
Й1)
Порядок расчета по формулам (13.11), (13.27), (13.28) за-
ключается в следующем. Задаемся величиной Т, определяем из
(13.11) hx , далее задаемся величиной То , так чтобы она удовле-
творяла зависимостям (13.27). Но так как T0-T = d, то можно
сказать, что на этом этапе выбирается высота уступа. Теперь
можно найти величину отношения T0/hj и сравнить ее с ре-
зультатами расчетов по формулам (13.28). Если принятое отно-
шение не совпадает с расчетным, то поиск продолжается методом
последовательного приближения, пока они не совпадут с прием-
лемой для дальнейших расчетов точностью. В связи с необходи-
351
мостью изменять высоту уступа в процессе итераций следует
указать верхнее предельное значение величины d , которое равно
— +1 = ~ г из 29)
h\ hx h}
При этом hm -> h6, если Ft, -> 0.
Таким образом, задача имеет множество решений, каждому
из которых соответствует принятое значение величины Т. Сле-
довательно, выбор нужных размеров плотины с уступом при за-
данных величинах удельного расхода и перепада уровней воды
между бьефами может быть выполнен на основе технико-
экономического сравнения вариантов. Однако здесь могут иметь
место соображения иного порядка. Например, наилучшей может
быть признана такая конструкция плотины (с такими размерами
Т nd), которой соответствует поверхностный режим сопряже-
ния бьефов в большом диапазоне изменения расходов воды,
сбрасываемых через плотину. С этой целью полезно на график
зависимости уровней от расходов воды в нижнем бьефе нанести
уровни воды, которым при различных значениях сбрасываемого
через плотину удельного расхода воды q соответствует поверх-
ностный режим сопряжения бьефов при выбранных величинах
Го и Т.
Вместо расчетов можно пользоваться графиками, приведен-
ными в [26, стр.221, рис. 3; стр. 224, рис. 6]. На первом (рис.З)
при «j = 1 дана зависимость К!К = !h> $\) На втором
(рис.6) совмещены два графика: T}hk =(p(z/hk,n3) и
hm!h\ = v(z/hk,n3).
Как было отмечено выше, глубину воды в затопленном гид-
равлическом прыжке определяют, умножая вторую сопряженную
352
глубину совершенного незатопленного гидравлического прыжка
на коэффициент затопления. Однако такая методика содержит
погрешность, так как глубина воды отсчитывается от расчетного
уровня воды в нижнем бьефе, поэтому при введении коэффици-
ента п3 изменяется величина Т, следовательно, и величина глу-
бины потока ; отсюда следует вывод о том, что коэффициент
затопления будет отличаться от принятого.
При заданных удельном расходе q и перепаде уровней во-
ды z для расчета донного гидравлического прыжка достаточны
зависимости (13.11), (13.3) и (13.22). Однако, в (13.3) величину а
следует заменить величиной а{ согласно формуле (13.20). Задача
решается следующим образом. Задаемся величиной Т , определя-
ем из (13.11) hx , затем w, и число Frj. Но в этой задаче Т = То ,
поэтому h6 = Т - z. Далее из (13.3) с учетом (13.20) можно найти
hm!h} ; после несложных преобразований имеем
+ 2Ft] —аб - 2Fr, at >1. (13.30)
\\hiJ h6
Теперь из (13.22) с учетом (13.21) определяем длину гидрав-
лического прыжка и строим кривую осредненной свободной по-
верхности воды в нем. В такой постановке задача имеет множе-
ство решений. С увеличением глубины h6 увеличиваются расчи-
стки в нижнем бьефе. С ними связано увеличение земляных (или
скальных) работ, но одновременно уменьшается дефицит осред-
ненного давления на плиту водобоя, от которого зависит толщина
этой плиты. Таким образом, если не учитывать роли пульсации
давления воды на плиту водобоя, то можно утверждать, что зада-
ча должна иметь оптимальное решение, которое можно найти пу-
тем технико-экономического сравнения вариантов.
353
Как было отмечено выше, чаще всего при гидравлическом
расчете гидротехнических сооружений задаются величиной зато-
пления гидравлического прыжка п3. В такой постановке задача
имеет единственное решение, но найти его можно методом по-
следовательного приближения. Порядок расчетов такой. При за-
данных величинах q и z назначаем величину Т, находим глу-
бину воды в нижнем бьефе, равную Т - z . По величине Т с уче-
том (13.16) из (13.11) определяем hx , следовательно - число
Фруда. Теперь из (13.4) можно найти вторую сопряженную глу-
бину воды в незатопленном гидравлическом прыжке h6 и коэф-
фициент затопления гидравлического прыжка п3 = ——- . При
h6
этом должно выполняться условие п3 > 1 . Если оно не выполня-
ется или нужна иная величина этого коэффициента, то задаются
другим значением величины Т , и расчеты проводят вновь. По их
завершении из формулы (13.30) находится глубина воды hm , ко-
торая должна быть больше глубины hx . Далее в соответствии со
сказанным выше можно определить длину гидравлического
прыжка и построить кривую осредненной свободной поверхности
воды в нем.
13.2 Моделирование неравномерного резкоизменяюще-
гося движения при взаимодействии руслового и пойменного
потоков
При выходе воды в паводок на пойму реки образуются два
взаимодействующих потока - русловой и пойменный. Необходи-
мость моделирования подобного рода явлений чаще всего возни-
кает при проектировании различных транспортных магистралей.
354
Трудности моделирования заключаются в необходимости осуще-
ствлять его одновременно для этих двух разных потоков. Для
пойменного потока равнинных рек характерны большая ширина
и малые глубины. Это типичное плановое течение, у которого па-
раметр, равный произведению коэффициента гидравлического
трения на относительную ширину потока, значительно больше
единицы. Как правило, в русловом потоке этот параметр меньше
единицы. Таким образом, возможность увеличения глубины по-
тока по сравнению с плановыми размерам модели («искажение»
линейных масштабных коэффициентов глубин и плановых раз-
меров потока) ограничена. Она определяется величиной предель-
ного отношения величины коэффициента гидравлического тре-
ния на модели к натурному значению этого коэффициента. Это
означает, что «искажение» может быть двух-трехкратным, не бо-
лее того. При таком способе моделирования указанный параметр
сохраняет свое значение для натурного и модельного руслового
потока. Для пойменного потока этот параметр на модели не равен
натурному, но находится в автомодельной области.
Имеются трудности и иного рода, связанные с определением
величины коэффициента гидравлического трении для пойменно-
го потока. Высота выступов шероховатости здесь может быть со-
измеримой с глубиной потока (например, кустарник) или превы-
шать его (стволы и частично подтопленные полыми водами кро-
ны деревьев). К сожалению, поиском законов сопротивления для
подобного вида «шероховатости» так, как это было сделано
А.П. Зегждой, пока никто серьезно не занимался. Выход из этой
ситуации один - стараться воссоздать на модели ландшафт (кус-
тарник, деревья, их взаимное расположение), который существу-
ет в натуре. Эта задача практически не выполнимая, поскольку
сведения об этом ландшафте, как правило, даются самые поверх-
355
ностные. Можно было бы подобрать на модели искусственную
шероховатость, адекватную натурной по степени воздействия на
поток. Однако заказчика на проведение моделирования чаще все-
го интересует работа сооружений в расчетных условиях, которые
либо не наблюдались, либо они были, но измерения параметров
потока не проводилось. Нужно отметить, что и в методическом
отношении с учетом необходимых требований приближенного
физического моделирования явление изучено слабо. Это объяс-
няется сложностью изготовления схематизированных моделей и
трудностями проведения исследований на них даже в случае при-
ближенного моделирования.
Рассмотрим схему явления. На перекате угол между векто-
рами скорости пойменного и руслового потоков может быть дос-
таточно большим. При взаимодействии двух потоков в зависимо-
сти от мощности пойменного вектор скорости руслового потока
поворачивается в сторону направления движения пойменного по-
тока. Конечно поток, находящийся в пределах ширины русла
выше отметки уровня воды в бровках, можно называть русловым
с большой долей условности. Вместо сопротивления ложа и бере-
гов русла здесь возникает сопротивление на границах взаимодей-
ствующих потоков турбулентной природы. Таких границ две: од-
на находится в том месте, где пойменный поток вступает в русло,
вторая-ниже по течению в месте выхода потока из русла на
пойму. Чем мощнее пойменный поток, тем больше отклоняется
вектор скорости условного руслового потока в сторону направле-
ния движения пойменного потока. При достижении некоторых
условий (большой скорости движения потока по пойме, больших
его расходах при высоких уровнях воды на пойме) условный ру-
словой поток прекращает свое существование, и образуется еди-
ный пойменный поток. Основываясь на этих рассуждениях, мож-
356
но сделать такой вывод. Допустим, что в русловом потоке в пре-
делах бровок назначен створ, в котором измерялись скорости те-
чения. Потом в этом створе проводились измерения составляю-
щих скорости течения в пределах ширины русла в условном по-
токе, нормальных к этому створу. Можно утверждать, что при
больших наполнениях водою поймы эта составляющая будет
стремиться к величине проекции скорости пойменного потока на
нормаль к створу.
На плесе в пределах вершины излучины направления русло-
вого и пойменного потоков мало отличаются друг от друга. Если
вогнутый берег «прижимной» (на плане речной долины линия ее
склона, ограничивающая пойму, совпадает с касательной в точке
вершины излучины) оба эти направления практически совпадают.
Здесь при малых уровнях воды на пойме скорость течения воды в
условном русловом потоке близка к средней из скоростей тече-
ния потока в русле и на пойме. При высоких уровнях воды ско-
рость течения в условном потоке приближается к скорости тече-
ния потока на пойме. Таким образом, на плесе и на перекате ско-
рости течения в условном русловом потоке при подъеме уровня
воды на пойме стремятся к вполне определенным пределам.
В качестве положительного примера можно привести ре-
зультаты исследований, изложенные в [48, 49]. Они проводились
на схематизированной модели участка реки с одним из типов ру-
слового процесса, который носит название ограниченное меанд-
рированием. Модель была изготовлена из бетона с последующем
ожелезнением поверхности. Искусственная шероховатость пой-
менных массивов создавалась с помощью крупнозернистого пес-
ка и гравия, которые закреплялись на поверхности бетона с по-
мощью цементного раствора. После проведения серии испытаний
такая шероховатость легко удалялась и заменялась в другой се-
357
рии шероховатостью с большей величиной выступов. На модели
склоны речной долины в пределах поймы были параллельными,
расстояние между ними в разных опытах оставалось неизмен-
ным. Изменялись относительная ширина меандрирующего русла
реки, его шероховатость и угол разворота излучины а (угол ме-
жду двумя направленными по течению векторами, которые яв-
ляются касательными к осевой линии русла в смежных точках ее
перегиба). Пойма вместе с руслом создавались с прямым уклоном
(имели наклон по направлению потока). При этом уклон руслово-
го потока в «бровках русла» (непосредственно перед выходом его
на пойму) принимался равным уклону трения (квазиравномерное
движение в русле) и уклону поймы. Перед началом опытов в из-
лучине намечались створы, в которых производились замеры
скоростей течения в русле до и после выходом воды на пойму в
пределах бровок. Определялась составляющая скорости течения,
нормальная створу ибр .
Кроме угла разворота излучины а и уклона всего поймен-
ного массива (он же и уклон в бровках, и уклон трения) i6 , в ка-
честве задаваемых параметров дополнительно использовалось
отношение Л/ h6p, где h и h6p -средняя глубина руслового по-
тока при входе воды на пойму и при наполнении основного русла
вровень с бровками соответственно. Необходимость соблюдения
равенства этих параметров на модели и в натуре непосредственно
вытекает из требования геометрического подобия русла, поймы и
водного потока. Коэффициенты гидравлического трения русла X
и поймы определялись по формулам Зегжды. Изучались спо-
койные русловые потоки, для которых число Фруда потока в
w2
бровках удовлетворяло условию: Fr6 =—— <1 . По результатам
gh6p
358
измерений определялось число Фруда для руслового потока при
выходе воды на пойму (с учетом условного потока), которое так-
w2
же удовлетворяло этому условию: Fr = — <1 . В соответствии с
gh
принятыми допущениями для руслового потока в бровках можно
X
записать следующее равенство: —Fr6/, = 1 . Помимо данных, по-
^бР
лученных на схематизированном русле меандрирующей реки, ав-
тор привел некоторые результаты исследований, выполненных в
аналогичных условиях на моделях рек Олекмы, Тунгуски, Нюк-
жи, Халхин-Гол, Воронеж в связи с проектированием на них мос-
товых переходов. Приводятся следующие пределы изменения ос-
новных параметров. Параметр X— изменялся от 0,1 до 0,68, где
h6P
, е: гт , В ~Ь
Ь -ширина русло в бровках. Параметр ------------ принимал
h~h6p
значения от 1,9 до 323, где В - ширина полосы меандрирования
(расстояние между склонами речной долины в пределах поймы).
На схематизированной модели меандрирующей реки угол а
принимал фиксированные значения: 80°, 93°, 106°. На моделях
упомянутых выше рек выбирались такие участки, в пределах ко-
торых этот угол был равен 90° . В связи с тем, что модели упомя-
нутых рек изготавливались с трехкратным искажением линейных
масштабных коэффициентов, искажение линейных масштабных
коэффициентов на схематизированной модели меандрирующего
русла реки принималось тем же самым.
Запишем в общем виде критериальное уравнение связи па-
раметров, определяющих явления в условном русловом потоке.
359
Воспользуемся критериальным уравнение (13.2), получим с уче-
том условий однозначности:
L п V Г ^Fr h 1 b 1 B~b \
v Fr,Re,Eu, J,-—,а,—A—A„-——
2 J »6P b6p b~ b6p J
= 0. (13.31)
Заметим, что уклон свободной поверхности в условном по-
токе при взаимодействии руслового и пойменного пото-
ков - величина не постоянная и трудно определяемая, поэтому в
качестве характерного был принят уклон потока в бровках i6p . С
учетом этого критериальное уравнение (13.31) перепишем в та-
ком виде:
Fr, Re, Eu, i$p
k
Л Fr h b В - b
--------, Ct,--------, A , A n----------------------
2 iftp hgp hfjp h — hgp ,
= 0. (13.32)
В процессе проведения исследований не удалось обнару-
жить влияния на условный русловой поток чисел Фруда, опреде-
ленных для этого потока и потока на пойме, а также и уклона
i6p . Возможно, это объясняется малым диапазоном изменения
уклона i6 и малыми значениями чисел Фруда, характерных для
спокойного потока. Числа Рейнольдса для руслового и пойменно-
го потоков находились в автомодельной области. Не было обна-
ружено влияния на явление коэффициентов гидравлического
трения (критерий Ей в двух последних уравнениях) и парамет-
ров, представляющих произведение коэффициента гидравличе-
ского трения на относительную ширину потока. На последнем
феномене следует остановиться особо. В связи с тем, что процесс
взаимодействия в основном проявляется на двух границах, отде-
ляющих пойменный поток от условного руслового, роль относи-
тельной ширины последнего не может быть заметной. Кроме то-
360
го, существенно изменить коэффициент гидравлического трения
в условиях модели X , как было отмечено ранее, невозможно. Эти
обстоятельства, по-видимому, достаточно убедительно объясня-
, Ь
ют отсутствие влияния на явление параметра л.—.
^бр
Предположим теперь такую ситуацию: пусть определенный
расход воды проходит по пойме с малой шероховатостью ее по-
верхности; допустим теперь, что тот же самый расход проходит
по той же пойме, шероховатость которой изменилась в большую
сторону (например, пойма сильно заросла кустарником). Но так
как сопротивление поймы увеличилось, то при том же расходе
воды должно в пределах рассматриваемого участка поймы про-
изойти повышение уровня воды. Из приведенных ниже графиков,
полученных по результатам исследований, следует, что при дос-
таточно больших затоплениях поймы повышение уровня воды не
оказывает влияние на процесс взаимодействия потоков. Если по-
гонный расход воды, приходящийся на единицу ширины пойм
одинаков, то процесс взаимодействия потоков в относительно
широкой и узкой пойме будет протекать одинаково. Так можно
Л , В-Ь
объяснить отсутствие влияния параметра ---------- на иссле-
h~h6P
дуемый процесс. Из этого вывода, однако, не следует, что про-
цессы на пойме не зависят ни от шероховатости ее поверхности,
ни от этого параметра.
На рис. 13.1. и 13.2. приведены кривые зависимости пара-
X
метра <^= ——Fr от угла разворота излучины а и относительной
^бР
глубины потока в русле h/h6p соответственно на плесе и на пе-
рекате. Характер изменения этих кривых в целом подтверждает
сделанные выше выводы. Если, следуя автору работы, обозна-
361
X v й
чить величину параметра ——Fr при выбранных величинах а и
h!h6p буквой к , то после несложных преобразований можно по-
лучить следующее выражение для скорости потока в русле при
выходе воды на пойму: = ^k'k6phl'kh6p . По-видимому, без
большой погрешности можно принять: Jk6p /Х = 1 .
Рис. 13.1. Зависимость параметра С, от угла разворота
- h
излучины а и относительной глубины потока в русле —
h6P
на плесе
В таком случае из рисунков следует: при выходе воды на пойму в
пределах плеса скорость течения в русле по сравнению со скоро-
стью в пределах бровок при больших углах поворота излучины
практически не изменяется, а при малых углах - увеличивается; в
пределах переката эта скорость при всех углах уменьшается. Этот
результат подтверждает известный из натурных наблюдений
362
Рис. 13.2. Зависимость параметра £ от угла разворота
излучины а и относительной глубины потока в русле —
h5p
на перекате
факт: в паводок плесы размываются, на перекатах в это время на-
блюдаются отложения наносов.
363
14. ХАРАКТЕРНЫЕ ВЕЛИЧИНЫ. МЕТОД
ФРАГМЕНТОВ ЧИСЕЛ ПОДОБИЯ
Все величины, определяющие явления, при использовании
методов физического моделирования условно можно разделить
на две группы: характерные и нехарактерные. Характерной на-
зывается такая величина, которая не зависит от координат и вре-
мени, нехарактерная - не обладает такими свойствами или одним
из них. Заметим, что в уравнения связи и в дифференциальные
уравнения, описывающие явления, входят нехарактерные вели-
чины. Понятие «характерная величина» появляется при изложе-
нии теории подобия. В этой теории оно является фундаменталь-
ным, так как без такого понятия этой теории не существовало бы.
Характерная величина играет здесь роль некоторого масштаба, в
котором измеряются и сравниваются физические величины,
имеющие одинаковые размерности. При соответствующем выбо-
ре характерных величин в условиях модели и натуры отношения
величин на модели и в натуре к своим характерным будут одина-
ковыми и безразмерными. Таким образом, характерная величина
должна не зависеть от координат и времени, а, кроме того, иметь
размерность соответствующей физической величины. Если пер-
вые два свойства характерной величины позволяют преобразо-
вать дифференциальные уравнения и привести их к безразмерно-
му виду, то третье - играет роль масштаба конкретной физиче-
ской величины. При этом нигде не говорится о том, что в качест-
ве характерной величины должно обязательно выбираться какое-
то значение конкретной величин, обладающее свойствами харак-
терной величины, хотя такая возможность не исключается.
Получаемые в методе размерностей я- числа, естественно,
состоят из величин нехарактерных. Но, заменяя в них нехарак-
364
терные величины произведением характерных на величины без-
размерные и имея в виду тот факт, что безразмерные величины
одинаковы для натуры и модели, легко доказать равенство л - чи-
сел и чисел подобия. Такое доказательство выше было сделано.
В предыдущих разделах термин «характерная величина»
упоминался довольно часто, чего нельзя сказать о его практиче-
ском использовании. Особой нужды останавливаться на ней бо-
лее подробно до сих пор не было, так как при равномерном дви-
жении многие физические величины соответствуют определению
характерной величины. Можно привести один пример, в котором
пришлось на этом вопросе остановиться особо. Так перепад дав-
ления А/j на произвольной длине водотока I не является харак-
терным, поскольку отнести такую длину к категории характерной
нельзя. Нужно было ввести в рассмотрение характерную длину, в
качестве которой был выбран гидравлический радиус потока.
При установившемся неравномерном движении большинст-
во величин, характеризующих явление, изменяются по длине по-
тока. Здесь в качестве характерных принимались параметры по-
тока в заданном створе (в начальном сечении). Если таковые от-
сутствовали, то выбирались значения соответствующих величин
в некоторых идеальных условиях. Например, длины водоворот-
ных зон сравнивались с длиной таких зон в идеальных условиях
(при отсутствии сил трения). Однако последнюю нужно прибли-
женно определить в методической серии опытов, изменяя в каж-
дой серии при прочих равных условиях шероховатость поверхно-
сти водотока. Затем, используя метод экстраполяции опытной
кривой, определить искомую величину при высоте выступов ше-
роховатости равной нулю. Конечно, можно воспользоваться ве-
личиной длины этой зоны, полученной в результате теоретиче-
ского решения.
365
Задача намного усложняется в случае неустановившегося
движения, в котором большинство параметров потока изменяют-
ся во времени (в том числе и в начальном сечении). Здесь вопрос
поиска характерных величин, играющих роль масштабов для
конкретных физических величин, среди которых нет характер-
ных, приобретает особую остроту.
Деление величин на характерные и нехарактерные происхо-
дит на стадии формулировки задачи исследований, ее постанов-
ки. В свою очередь характерные величины могут быть в соответ-
ствии с поставленной задачей исследований изначально задан-
ными (входящими в условия однозначности) и неизвестными
(искомыми, которые могут быть найдены в результате проведе-
ния моделирования). Такому делению характерных величин со-
ответствуют два важных понятия теории физического моделиро-
вания: критерии и числа подобия. Первые представляют собой
комбинации заданных характерных величин и физических кон-
стант, в комбинациях вторых содержится искомая характерная
величина. Цель исследований формулируется в виде критериаль-
ного уравнения - зависимости числа подобия от критериев подо-
бия. При отсутствии критериев ранее был предложен метод ком-
бинации чисел подобия с целью их получения. Такая комбинация
чисел подобия включает в себя заданные характерные величины.
Таким образом, при выборе характерных величин следует иметь
в виду необходимость получения среди них и заданных. Но тогда
вполне логично следующее заключение: при удачном выборе за-
данных характерных величин можно получить критерий подобия,
который полностью совпадет с таким же критерием, найденным в
результате комбинации чисел подобия. Следовательно, разумной
альтернативой метода комбинаций чисел подобия может стать
метод, в основе которого лежит поиск характерных величин в ка-
366
честве масштабов величин, определяющих явление. Кроме того,
создаются широкие возможности для нахождения характерных
величин, имеющих определенные размерности, что особенно
важно при решении трудных задач неустановившегося движения.
Назовем обсуждаемую операцию выбора характерных величин
методом фрагментов. Он базируется на двух леммах и одной
теореме.
Лемма 1. Если в числе подобия мысленно удалить величину
или физическую константу, содержащиеся в нем, то оставшаяся
часть числа подобия (назовем ее фрагментом числа подобия) бу-
дет характерной величиной, размерность которой совпадает с
размерностью удаленной величины или физической константы
соответственно. Это положение обоснованно основными свойст-
вами чисел подобия: они не имеют размерности и представляют
собой комбинации характерных величин.
Лемма 2. Если в числе подобия мысленно удалить величину
или физическую константу, содержащиеся в нем, а образовав-
шийся фрагмент числа подобия использовать для получения того
же самого числа подобия, то новое число подобия будет равно
единице.
Теорема. Если, выбрав число подобия, удалить из него ка-
кую-либо физическую величину или константу, а его фрагмент
использовать для замены тех же самых физических величин или
констант во всех рассматриваемых числах подобия, то вместо
выбранного числа получим единицу, а остальные числа подобия
превратятся в комбинации их с выбранным числом.
Доказательство. Согласно лемме 1 фрагмент числа подобия
состоит из характерных величин, поэтому является характерной
величиной, к тому же имеющей размерность удаленной величи-
ны. Согласно лемме 2, если в выбранном числе подобия удален-
367
ную величину или физическую константу заменить фрагментом
этого числа подобия, то получим число, равное единице. В ре-
зультате замены удаляемой величины в других числах подобия
образуются комплексы, которые являются числами подобия, так
как одна характерная величина в них (удаляемая) заменяется дру-
гой характерной (фрагментом выбранного числа подобия). Но
полученные комплексы не содержат удаляемую величину, вхо-
дящую в исходные числа подобия. Следовательно, операция за-
мены удаляемой величины в других числах подобия фрагментом
выбранного числа подобия полностью совпадает с методом ком-
бинации чисел подобия, в котором числа подобия объединяются
таким образом, что в их комбинацию не входит какая-либо вели-
чина или физическая константа. Теорема доказана.
На основании проведенных доказательств можно сформу-
лировать несколько следствий.
Следствие 1. Количество фрагментов числа подобия равно
количеству величин и физических констант, входящих в него.
Например, число Рейнольдса ---- имеет следующие три фраг-
v
мента: v/R (фрагмент имеет размерность скорости), UR (раз-
мерность кинематической вязкости), v/U (размерность линейной
величины). Число Рейнольдса в виде имеет четыре фраг-
Ц
мента: p/pR (размерность скорости), pUR (размерность дина-
мической вязкости), p/pU (размерность линейной величины),
pjUR (размерность плотности).
Следствие 2. Если физическую величину или константу со-
держат несколько чисел подобия, то число фрагментов, имеющих
размерность физической величины или константы, равно количе-
ству этих чисел подобия. Например, скорость течения входить во
368
все фундаментальные числа подобия. В зависимости от выбран-
ного числа можно найти следующие фрагменты чисел подобия.
Если выбрано число Рейнольдса, то в соответствии со сказанным
J72
выше это либо v/R , либо p/pR . Число Фруда — даст такой
gR
фрагмент, имеющий размерность скорости: JgR . Число Эйлера
. Число Струхала - R/Т.
Таким образом, имеются широкие возможности при поиске
характерных величин замены величин и физических констант
фрагментами чисел подобия, размерности которых совпадают.
Следствие 3. Если в конкретной системе чисел подобия (на-
пример, фундаментальной) удаляемая величина или константа
встречается п раз, то, выбрав фрагмент одного из этих чисел,
можно получить п -1 комбинацию выбранного числа подобия с
остальными числами подобия. Но система чисел подобия должна
всегда оставаться полной, поэтому выбранное число подобия
должно оставаться в уравнении связи. Таким образом, в уравне-
ние связи после проведения преобразований войдет п -1 комби-
нация чисел подобия и одно число подобия.
Рассмотрим пример, в котором покажем, как на практике
реализуется метод фрагментов. Выбираем систему фундамен-
тальных чисел подобия; в ней фрагментом числа Фруда JgR ,
имеющим размерность скорости, заменим скорость в остальных
и л
числах подобия. Берем число Рейнольдса --- , заменим в нем
v
скорость V фрагментом числа Фруда -jgR , получим комбини-
Л JgRR Re Г1
рованное число подобия -------= -= = VGa . Возьмем число
v VFr
369
„ R „ JR Sh
Струхала — , после аналогичной замены имеем: —j=— - ~у= .
UT JgT VFr
Преобразуем таким же образом число Эйлера , получим:
р?7
Ар АН т „ „ . -т
—— =------= 7^= EuFr , где АН -перепад пьезометрической
pgT? R
линии на характерной длине, равной гидравлическому радиусу,
Jp -ее уклон. Таким образом, в уравнение связи войдут сле-
дующие числа подобия: Fr, TGa, Sh/VFr, EuFr = Jp.
370
15. МОДЕЛИРОВАНИЕ НЕУСТАНОВИВШЕГО-
СЯ ДВИЖЕНИЯ
15.1. Моделирование неустановившегося движения воды
в напорных трубопроводах и системах
15.1.1. Внезапное ускоренное движение жидкости в жесткой тру-
бе
Как отмечается в [21], наиболее часто возникает необходи-
мость моделировать неустановившееся движение в задачах о
гидравлическом ударе в трубопроводах и в напорных системах с
уравнительными камерами и другими сооружениями. В качестве
примера рассмотрим результаты интересного исследования о
внезапном ускоренном движении жидкости в жесткой трубе, вы-
полненного в [18] и обсужденного в [23].
В [18] на опытной установке с напорным трубопроводом
изучалось возникновение движения жидкости из состояния по-
коя. Касательные напряжения трения на стенке трубопровода из-
мерялись термоанемометрическим методом. Опыты проводились
по следующей методике: при закрытом быстродействующем за-,
творе, расположенном в конце рабочего участка трубопровода, на
установке создавалось необходимое давление с помощью цен-
тробежного насоса. После этого затвор открывался по задаваемо-
му закону, и на рабочем участке трубопровода создавался уско-
ренный режим течения жидкости. Кроме касательных напряже-
ний, в опытах измерялись скорости течения и перепад давления в
пределах рабочей части трубопровода.
После открытия затвора в опытах было обнаружено уско-
ренное движение жидкости, при этом ускорение в течение опыта
371
оставалось практически постоянным, скорость движения жидко-
сти и касательные напряжения на стенке непрерывно плавно уве-
личивались. Но по истечении некоторого промежутка времен по-
сле начала опыта наблюдалось увеличение касательного напря-
жения скачком, в дальнейшем характер его изменения во времени
свидетельствовал о появлении ярко выраженной турбулентности.
Момент времени, при котором наблюдается турбулизация при-
стенного слоя, а затем всего потока, назван критическим. Ему со-
ответствует критическое число Рейнольдса, при достижении ко-
торого поток становится турбулентным. По результатам измере-
ний касательного напряжения и средней скорости течения был
вычислен изменяющийся во времени коэффициент гидравличе-
ского трения в период существования ламинарного режима тече-
ния. Именно эта часть исследований представляет интерес в рам-
ках обсуждаемой проблемы моделирования неустановившегося
движения.
Была предложена зависимость коэффициента гидравличе-
ского трения от определяющих параметров, которую можно так
записать:
Х = f(Re,R2/vt\ Rc = UR/v, 7?2/w = ShRe, Sh = R/Ut, t<tk, (15.1)
где R - гидравлический радиус трубы, U - средняя скорость
движения воды в ней, tk - критическое время, при достижении
которого поток становится турбулентным, t — текущее время.
Однако скорость течения и характер ее изменения во времени за-
ранее не известны, так что воспользоваться формулой практиче-
ски невозможно. Здесь число Рейнольдса не является критерием,
в то время как второй параметр в зависимости (15.1), равный
комбинации чисел Рейнольдса и Струхала, в которой отсутствует
скорость течения, есть критерий подобия. Отсюда следует, что
372
вместо числа Рейнольдса нужно найти критерий подобия. Отме-
тим, что по своей постановке задача совпадает с одной из рас-
смотренных ранее, в которой изначально, как и в обсуждаемой,
был задан перепад давления. В ней в качестве критерия было вы-
брано число Архимеда.
Неустановившееся движение в напорном трубопроводе опи-
сывается уравнением (8.1). Ранее было дано в общем виде без-
размерное уравнение связи для неустановившегося движения
жидкости в трубопроводе (8.5). Особенность обсуждаемых ис-
следований заключается в том, что они проводились в трубе по-
стоянного поперечного сечения, следовательно, конвективным
ускорением жидкости можно пренебречь вследствие его малости.
Но тогда вместо (8.1) можно записать следующее:
_^=,=1^ + АС. (15.2)
6 х р g dt D2 g
где Н и J - соответственно пьезометрический напор и уклон,
D - диаметр трубы. Если в этом уравнении выразить все входя-
щие в него величины через характерные и безразмерные, одина-
ковые для всех подобных явлений, то в результате получим:
т п ыди\ Ч и'2
Jn = FrSh--+ —Fr---, (15.3)
р dt' 8 D v 7
где Fr = U2/gR - число Фруда. Получается, что в уравнение от-
дельно не вошло число Фруда, но он появится в безразмерном
уравнении связи, принимая во внимание числа подобия, полу-
ченные в результате анализа уравнения Навье-Стокса. Так что
уравнение связи (8.5) не изменится. Прежде всего, составим в
нем комбинацию числа Фруда с последним параметром такую,
373
чтобы в последнем параметре остался только коэффициент гид-
равлического трения (постоянную в дальнейшем писать не бу-
дем). В связи оставим число Фруда и коэффициент гидравличе-
ского трения. Вместо (8.5) получим:
F(Sh,Fr,Re,Eu,FrSh, УрД)=0. (15.4)
Кроме пьезометрического уклона, в уравнении связи (15.4)
нет ни одного критерия, и в нем содержится избыточная инфор-
мация. Задачей последующих преобразований является поиск
критериев подобия и устранение избыточной информации. Пре-
жде всего, учтем, как это было сделано в конце предыдущего
раздела, что произведение числа Фруда на число Эйлера равно
пьзометрпческому уклону. Следовательно, число Эйлера обратно
пропорционально преобразованному числу Фруда, в котором ус-
корение силы тяжести заменено произведением его на пьезомет-
U2
рический уклон: Fry =------, gj-Jpg Если пьезометриче-
gj К
ский уклон ввести в число Фруда, тем самым заменим его преоб-
разованным числом Фруда, то из уравнения связи (15.4) можно
исключить число Эйлера, и это уравнение существенно упроща-
ется:
F(Sh,FrJ,Re,FrJShA) = O. (15.5)
Далее в (15.5) произведем замены, используя метод комби-
нации чисел подобия с целью получения критериев подобия.
Прежде всего, из чисел Sh и FiySh получим критерий FiySh2 ,
сохранив в уравнении связи число Sh . Далее из этого числа и
числа Рейнольдса получим критерий ShRe , в уравнении оставим
число Re . Числа Fry и Re заменим критерием Архимеда, со-
374
храним число Рейнольдса. Таким образом, вместо (15.5) придем к
следующему уравнению:
F (sh Re, Ar, Re, FrjSh2, x)= 0.
Для последующих преобразований полезно из критериев
Архимеда и FrjSh2 получить критерий Fr7Sh2Ar, в уравнении
связи оставим критерий Аг . В результате получим это уравнение
в таком виде:
F (shRe, Ar, Re, Fr7Sh2Ar, z) = 0. (15.6)
Вспомним теперь зависимость числа Рейнольдса от числа
Фруда и критерия Архимеда:
Re = 7F^A7. (15.7)
Воспользуемся далее методом фрагментов с тем, чтобы за-
менить в числах Рейнольдса и Фруда в (15.7) скорость потока со-
ответствующем фрагментом числа Струхала. В результате заме-
ны получим:
ShRe = jFr7Sh2Ar. (15.8)
В левой части этой зависимости получилась комбинация чи-
сел подобия Рейнольдса и Струхала, которая имеется в уравнении
связи (15.6). В правой части находится комбинация чисел подо-
бия Фруда и Струхала и критерия Архимеда, которая отличается
от той же комбинации в уравнении связи (15.6) показателем сте-
пени. Таким образом, в результате преобразований числа Рей-
нольдса в уравнении (15.6) пришли к одному и тому же крите-
рию, равному произведению числа Рейнольдса на число Струха-
ла. Отсюда окончательно уравнение связи станет таким:
375
F(ShRc, АгД) = О.
Его в критериальной форме можно записать в виде:
X = f (ShRe, Ar). (15.9)
В нем критерий ShRe = 7?2/v/ является характеристикой неста-
ционарное™ процесса. Критерий Ar = JpgR3 jу1, кроме физиче-
ских констант и характерного размера трубопровода, учитывает
величину задаваемого уклона пьезометрической линии.
При рассмотрении равномерного движения для установле-
ния связи между числами Рейнольдса и Архимеда была исполь-
зована зависимость (15.7). В ней модифицированное число Фруда
было заменено числом Эйлера. Последнее в этом случае с точно-
стью до постоянной равно коэффициенту гидравлического тре-
ния. Но тогда в существующих зависимостях для определения
коэффициента гидравлического трения, содержащих число Рей-
нольдса, стало возможным заменить число Рейнольдса числом
Архимеда. Тем самым, не производя новых расчетов, удалось по-
лучить зависимости для определения коэффициента гидравличе-
ского трения от числа Архимеда. В задаче неустановившегося
движения такая операция с уравнением (15.1) невозможна. Дей-
ствительно, замена в формуле (15.7) числа Фруда числом Эйлера
ничего не дает, поскольку в число Эйлера входит неизвестная по
условию задачи скорость течения. Если в числе Фруда заменить
скорость течения фрагментом числа Струхала, то получим крите-
рий подобия (15.8), который имеется в уравнении связи. Таким
образом, получить критериальное уравнение (15.9) в явном виде
можно только путем пересчета опытных данных заново.
376
15.1.2. Гидравлический удар в напорном трубопроводе
Рассмотрим теперь задачу о гидравлическом ударе в напор-
ном трубопроводе. В этой задаче к уравнению движения (8.1)
следует присоединить уравнение неразрывности, учитывающее
упругие свойства воды (модуль упругости Еж ) и стенок трубы
(модуль упругости Е ):
+ (15.10)
где с ~ скорость распространения ударной волны. Последняя
находится из формулы:
с= Еж/р
\1 + ОЕж/8Е’
(15.11)
в которой 3 - толщина стенки трубы, D - ее диаметр.
Обычно при решении задачи о гидравлическом ударе сопро-
тивлением трения пренебрегают. В таком случае, опуская член,
учитывающий конвективное ускорение, уравнение (8.1) можно
существенно упростить:
^ + 1^ = 0
dt р дх
(15.12)
Из уравнения (15.10) можно получить число подобия:
pR /
—5---- (в качестве характерной скорости принимается скорость
рс2ТУ
течения жидкости в трубе до закрытия задвижки и возникновения
гидравлического удара: V = и0 ). Следовательно, имеем:
377
—= EucSh , где Еис =-^- -число Эйлера, в которое в ка-
pc~TV ре2
честве характерной скорости входит скорость распространения
ударной волны. Приняв эту скорость в качестве характерной,
найдем время, за которое ударная волна пройдет характерное
расстояние, равное гидравлическому радиусу: Т -R/с .В таком
R с
случае имеем: Sh =----= — = М, где М - число Маха. Из урав-
и07’ и0
нения (15.12) можно получить число подобия: . Умножив и
рЯм0
разделив его на произведение c2w0 , получим:
рТ ЕисМ2
—— = — = EurM = EurSh .
pRuQ Sh
Ранее было дано в общем виде безразмерное уравнение свя-
зи для неустановившегося движения жидкости в трубопроводе
(8.5), которое для случая гидравлического удара запишем в таком
виде:
F (Sh, M, Euc, EucSh) = 0.
(15.13)
В зависимости от решаемой задачи из уравнения связи
(15.13) можно получить два критериальных уравнения. Если не-
обходимо найти повышение давления при мгновенном закрытии
задвижки, то критериальное уравнение будет таким:
Euc=/(M).
(15.14)
Если в результате исследований возникнет необходимость
установить зависимость изменения повышенного давления во
времени, то критериальное уравнение следует представить в та-
ком виде:
378
Euc = <p(Sh).
(15.15)
Например, для определения величины гидравлического уда-
ра при мгновенном закрытии задвижки существует формула Жу-
ковского-Аллиева:
р = рси0, (15.16)
из которой следует: Euc = 1/М , что соответствует уравнению
(15.14).
Известны трудности при организации математического и
физического моделирования гидравлического удара, связанные с
уменьшением скорости ударной волны в зависимости от давле-
ния, содержания в воде воздуха и твердых частиц, их плотности,
модулей упругости. К ним при физическом моделировании до-
бавляется необходимость уменьшения скорости ударной волны
на модели по сравнению с натурой, что следует из условия:
М = idem . В [63, с. 292] приводятся данные о зависимости скоро-
D Е
сти распространения ударной волны от параметра--— , а также
8 Е
£
о величине отношения —для воды и некоторых материалов, из
Е
которых изготавливаются трубы. Эти данные свидетельствуют о
том, что осуществить физическое моделирование явления гид-
равлического удара в стальной трубе, имеющей следующие за-
данные параметры:
(р А (D Р А
DH = 100см, 8Н = 1см, МЧ = 0,01, * = 1, с„ «1000м/с,
UX Е X
практически невозможно. Если выбрать, например, на модели в
качестве материала трубы оргстекло (Еж/Е = О,5-гО,8 ), то при
соблюдении геометрического подобия труб имеем в условиях
379
(Г) F А
модели: =50^80,
' ' м
«200м/с. Отсюда масштабный
коэффициент скорости будет равен 5, и при моделировании по
Фруду линейный масштабный коэффициент получается равным
25 . Следовательно, на модели труба из оргстекла должна иметь
размеры: £>Л/=4см, 8М = 0,04см. Конечно, будут трудности и
при изготовлении трубы с такими параметрами, и при проведе-
нии исследований на ней. При этом следует иметь в виду, что ма-
лейшие отклонения в геометрических размерах трубы влекут за
собой существенные изменения скорости распространения удар-
ной волны на модели. Можно попытаться увеличить размеры
трубы на модели, но для этого придется изготовить ее из другого
материала. В качестве такового можно принять, например, асбе-
стоцемент (ЕЖ]Е = 0,11). Тогда при соблюдении геометрического
подобия
труб имеем в условиях
модели:
f DEM.
---— =11,
с и «450м/с . Отсюда масштабный коэффициент
скорости будет «2,2, и при моделировании по Фруду линейный
масштабный коэффициент станет равным « 5 . Следовательно, на
модели труба из асбестоцемента должна иметь размеры:
DM - 20см, 8л1 = 0,2см. Асбестоцементные трубы таких размеров
(с такой толщиной стенок) изготовить невозможно.
В [21] при решении задачи о гидравлическом ударе вводит-
ся критерий Коши: Со = . Этот критерий был рассмотрен
£
выше в методе соотношения сил Ньютона; он равен отношению
конвективной силы инерции к силе упругости. Однако ничего
380
нового в решении задачи он не дает в силу существования оче-
Со
видного равенства: .
Е Со
Обратимся теперь к вопросу физического моделирования
неустановившегося движения в сложных напорных системах. К
ним, например, относятся напорные трубопроводы гидроэлектро-
станций с уравнительными резервуарами. В качестве исходного в
задаче следует рассматривать полное уравнение связи (8.5), либо
его преобразование в виде (15.4). В зависимости от постановки
задачи из них можно получить различные критериальные урав-
нения. Важно при этом соблюсти строгое геометрическое подо-
бие натурного и модельного объектов. Кроме того, явление на
модели должно относиться к области квадратичного сопротивле-
ния (или, по крайней мере, как этого требует метод приближен-
ного моделирования, - к границе этой области). Но этим не ис-
черпываются требования приближенного моделирования рас-
сматриваемого сложного объекта. Дело в том, что в объекте су-
ществуют узлы сопряжения различных элементов, обеспечиваю-
щих гидравлическое единство всей системы. Местные явления в
узлах сопряжения на модели из-за приближенного моделирова-
ния явлений могут отличаться от таковых в натуре. Например, в
[21] рекомендуется следующий метод приближенного физиче-
ского моделирования подобных систем. Как правило, модель по-
лучается весьма громоздкой из-за большой протяженности на-
порных трубопроводов, поэтому рекомендуется линейный мас-
штабный коэффициент длины трубопровода выбирать отличным
от алогичного коэффициента поперечного размера трубы
k
(kL>kD ). Далее по аналогии с индикатором подобия кх — = 1
381
к
вводится индикатор кх —- = 1 , соответствующий критерию ПОДО-
^Р
бия . Обоснование такому введению не приводится, скорее
оно продиктовано здравым смыслом: потери напора на длине
трубопровода на модели должны быть подобны потерям напора
на соответствующей длине трубопровода в натуре. Но достигает-
ся это путем существенного увеличения коэффициента гидравли-
ческого трения на модели по сравнению с натурой. Следователь-
но, поле скоростей на модели может претерпеть существенные
изменения по сравнению с натурой. Тем самым будет нарушено
подобие местных потерь напора в узлах сопряжения водопрово-
дящих элементов системы. Строго говоря, местные потери напо-
ра в этих узлах должны изучаться на специально создаваемых
физических моделях узлов. Цель исследований - определить па-
раметры модели, при достижении которых потери напора на мо-
дели станут подобными соответствующим потерям в натуре. Но
об этом речь пойдет в следующем разделе.
15.2. Моделирование неустановившегося движения воды
в открытых руслах
15.2.1. Моделирование явления прохождения в реке волны па-
водка
Проблема неустановившегося движения воды в открытых
руслах интересует практику главным образом с точки зрения мо-
делирования процесса прохождения в русле реки волны паводка.
В последнее время в этой области получило развитие математи-
ческих методов моделирования этого явления. Но, несмотря на
значительную стоимость изготовления физической модели реч-
382
ной системы, физическое моделирование явления прохождения
волны паводка в ней находит применение во многих гидравличе-
ских лабораториях мира [21]. Это можно объяснить несколькими
причинами. Физическая модель довольно подробно отображает
особенности речной системы: русла основной реки и ее притоков,
ландшафта речного бассейна и поймы. Из-за этого ее проще
адаптировать к реальным условиям прохождения в реке паводка.
Основные трудности в натурных условиях - определение шеро-
ховатости русла и поймы.
Что касается методики моделирования, то это типичная
плановая задача, которая была рассмотрена в разделе 11.6, где
приведено в безразмерном виде соответствующее интегральное
уравнение (11.65), содержащее безразмерные величины и числа
подобия. Вместе с тем следует обратиться к уравнению Навье-
Стокса (2.4) с тем, чтобы привести его к безразмерному виду при
условии, что линейные масштабные коэффициенты плановых
размеров модели не совпадают с линейным масштабным коэф-
фициентом глубин потока. Выберем декартову систему коорди-
нат, в которой ось z направим по вертикали вверх, продольную
ось х направим вниз по течению. При такой ориентации осей ко-
ординат ось у будет направлена поперек потока. Рассмотрим
проекцию уравнения на продольную ось х
диг дих дих дих 1 др
dt дх у ду dz р Эх
д2их д2их д2и
----- +---- +----
Эх2 ду2 dz2
(15.17)
Выразим далее размерные величины в виде произведения
безразмерных величин на характерные. В результате представим
уравнение (15.17) в таком виде:
383
К ди' V2 ( , ди'х , ди' 'l К2 , ди'
Т dt' В\ дх у ду') Н dz
vv( д2и' д2и' 'l v V д2и'
+ /?2| tlr'2 + ду'2 ) Н2 dz'2 '
\Рдр'
рВ дх’
(15.18)
Разделим все члены этого уравнения на У2/в , в результате по-
лучим:
ди' , ди' , ди' В , ди'
Shu—- + их—- + uv—- +— w,—i
B dt' дх' y ду' Н z dz'
п др
- - Ей'- +
дх'
1 с?2и(.
Res ^дх'2
д2и'х
ду'2
В2 д2и'х
Н2 dz'2 ’
(15.19)
где ShB =— и Res =— -числа Струхала и Рейнольдса соот-
VT v
ветственно, в которых в качестве характерного линейного разме-
ра принята ширина потока. Таким образом, кроме привычного
числа Эйлера, в уравнение (15.19) вошли числа Струхала и Рей-
нольдса, отличающиеся от обычных, рассмотренных выше, иным
характерным линейным размером, и отношение характерной ши-
рины потока к его характерной глубине в первой степени и в
квадрате. Наличие отношения В/Н позволяет от полученных чи-
сел Струхала и Рейнольдса перейти к обычным, если в этом есть
необходимость.
Среди чисел подобия не оказалось числа Фруда, но этот
факт вполне объясним, если учесть принятую ориентацию осей
прямоугольной декартовой системы координат. Однако, можно
доказать, что число Фруда здесь также присутствует. С этой це-
лью обратимся к близкой по постановке задаче о двухмерном
бурном потоке [10, 14], которая в своей исходной трактовке сов-
падает с задачей о двухмерном спокойном потоке [13,64]. Если
384
пренебречь составляющей ускорения на вертикальную ось, а
также проекциями на туже ось напряжений вязкой и турбулент-
ной природы, то в результате из проекции уравнения движения
на эту ось можно получить гидростатический закон распределе-
ния давления по глубине потока.
Р = Ра+Рё{^ +h-z),
(15.20)
где z0 - отметка дна водотока, h = z„ - z0 - глубина потока,
zn - отметка свободной поверхности воды, ра - атмосферное
давление на этой поверхности. Но в безнапорном потоке свобод-
ная поверхность является пьезометрической линией, поэтому
z„ - Нр - z0 + Л , здесь Н - пьезометрический напор. Разделим
(15.20) на р и вычислим частную производную по х, получим:
Эр
— = £
pox
<3z0 dh\ ( . Sh\ SH
“ + =£-'о+т- = g^~=~gJ. (15.21)
OX OX I OX J ox
Sz0 SH p
где z0 =--- уклон дна, J = —- уклон пьезометрической
дх Эх
линии.
Выразим в (15.21) размерные величины в виде произведения
безразмерных величин на характерные и представим это уравне-
ние в безразмерном виде:
ДР др' _ Н (Szq Sh' j _
pgB дх' В (Эх' дх'J
н( . В Sh'} НдН'
В\ пН дх') В дх'
(15.22)
здесь ДР -характерный перепад давления, J -характерный
пьезометрический уклон.
385
Вначале рассмотрим задачу, в которой характерные линей-
ные размеры по всем направлениям одинаковы и равны гидрав-
лическому радиусу потока: B = H = R . Вместо (15.22) в этом
случае имеем:
= + + (15.23)
pgR дх dx'J дх' J дх
Возьмем уравнение, содержащиеся в (15.23) в виде:
АР др' _дН’р
pgR дх дх’
(15.24)
из которого следует:
АР АРР2
= — /- = EuFtn = idem , Fr„ = —
pgR pV2gR
К2
gR’
(15.25)
где V - характерная скорость течения. Выберем теперь в (15.23)
другое уравнение:
pgR дх'
(15.26)
Из него имеем:
_^£= = EuFr^ = EuF /£/ Fr (15.27)
pgRJ J ю gRJ v 7
Принимая во внимание (15.25), получим:
J = idem,
(15.28)
где подстрочные буквы «н» и <ш» относят величину к натуре и
модели соответственно.
386
Поскольку безразмерные величины J' одинаковы на моде-
ли и в натуре, то, учитывая (15.28), имеем:
JII J м
(15.29)
где J - пьезометрический уклон, который при рассматриваемой
методике моделирования (В = Н = /?) оказался одинаковым на
модели и в натуре, впрочем, этот вывод был ожидаемым. Следо-
вательно, в (15.27) можно ввести поправки:
АР EuFifl . Г2 . ,
---=—r^EuFr/y = idem, FrftZ=——. (15.30)
PgRJ J gRJ
Возможен и другой путь, который уже был использован ра-
не, в частности, в конце параграфа 14. Он заключается в том, что
в (15.26) принимаем следующее условие:
PgR
(15.31)
Оно не противоречит общим принципам физического моде-
лирования явлений и делает идентичными в рассматриваемом
случае два уравнения, в одно из которых входят величины,
имеющие размерности, а в другое - величины безразмерные.
Особенность рассматриваемого случая состоит в том, что оба
уравнения содержат всего по два члена. Но условие (15.31) на-
кладывает определенное ограничение на моделирование. В дан-
ном случае его можно обнаружить, произведя в (15.31) следую-
щее преобразование:
А/-* . J
pgR R
(15.32)
387
в котором кН р - перепад пьезометрической высоты. Следова-
тельно, в качестве характерного уклона пьезометрической линии
нужно принимать отношение перепада пьезометрической высоты
к такому характерному линейному размеру, который равен гид-
равлическому радиусу потока. С учетом (15.25) имеем;
EuFrA =jR, ^«=EuFr^ =1. (15.33)
JR
Далее рассмотрим в той же последовательности задачу, в
которой характерный линейный размер глубины потока не сов-
падает с характерными линейными размерами потока в плане.
Возьмем вначале уравнение, содержащиеся в (15.22) в виде:
др gy ^//5^ 5р' дн'р
pgB дх' В дх' ’ pgH дх' дх'
Из него следует:
ДР ДРЕ2 г V2
----= —5-----= Eu FrH = idem , FrH =-
pgH pV2 gH " H gH
(15.34)
(15.35)
Сравнивая (15.34) и (15.24), можно обнаружить, что эти без-
размерные уравнения совпадают. Но есть и небольшая разница,
которая обнаруживается при сравнении зависимостей (15.35) и
(15.25): в первую в качестве характерного линейного размера
входит глубина потока, в то время как во вторую - его гидравли-
ческий радиус.
Выберем теперь в (15.22) другое уравнение:
кР др'_ -
pgB дх'
(15.36)
Из него имеем:
388
AP EuFrB „ V1 р Н
—d7 = —~ = EuFrBJ = idem, Fr^j =——= = Ргщ—. (15.37)
PgBJ J gBJ D
Отсюда можно записать (15.37) в таком виде:
АР ЕиРгя Н
----- - — = idem .
pgBJ J В
(15.38)
Но тогда, учитывая (15.35), получим:
П D D
J— = idem, =
Н Нн м Нм
к z^=l, kj=~,
kh kb
(15.39)
где кj = - масштабный коэффициент пьезометрического ук-
Jм
лона. Оказалось, что он равен отношению масштабного коэффи-
циента глубин к масштабному коэффициенту плановых размеров.
Этот результат представляется естественным.
Принимаем далее в (15.36) следующее условие:
АР
PgP
(15.40)
Но оно накладывает ограничение на моделирование, которое
можно обнаружить, произведя в (15.40) следующее преобразова-
ние:
ДР ^Нр =j
PgP В
(15.41)
Следовательно, в качестве характерного уклона пьезометри-
ческой линии нужно принимать отношение перепада пьезомет-
рической высоты к характерному линейному размеру, равному
ширине потока. Далее из(15.37) получим
389
АР
pgB
= Eu Frfi .
(15.42)
Сравнив (15.41) и (15.42), придем к следующему соотношению:
EuFrB = JB, l^ = EuFr5jfl=l. (15.43)
J в
Теперь преобразуем интегральное уравнение планового те-
чения (11.65) к виду, удобному для дальнейшего анализа.
JJ' 8U’u 8U'2 <£>' KB.,U'2
----= Sh»----------+ — -------- + Л—Л-о-------.
Frs ю' д t' со д х Н 2h'
(15.44)
Учитывая полученные результаты, которые вытекают из
уравнений (15.19) и (15.44), можно записать в общем виде сле-
дующее уравнение связи между числами подобия, определяю-
щими явлении неустановившегося движения воды в русле реки
при физическом моделировании в случае, когда масштабные ко-
эффициенты плановых размеров потока не совпадают с линей-
ным коэффициентом его глубин.
f -^,ShBjA^,Eu,Res
I FrB H
В В2 "
’н’ н2
= 0. (15.45)
Если в этом уравнении принять в числе подобия, которое
стоит первым в скобках, масштабный коэффициент уклона пье-
зометрической линии равным JB , то в соответствии с (15.43) это
число станет равным числу Эйлера. Тем самым из (15.45) число
Эйлера можно исключить. Кроме того, имея отношение линей-
ных характерных величин, можно всегда при необходимости воз-
вести его в квадрат. Таким образом, вместо уравнения связи
(15.45) придем к следующему:
390
—Й,811Й,А~ ,ReB
Frs B H B H
-о.
(15.46)
Естественно, методика моделирования полностью определя-
ется постановкой задачи исследований. В ней не ставится цель
изучить явление в деталях, нужно рассмотреть его в целом, а
именно - движение волны паводка в речной системе. Подобного
рода модели используются главным образом для того, чтобы об-
рисовать ситуацию в бассейне реки при прохождении паводка.
Задача распадается на две части. Первая - предсказать макси-
мальный уровень воды в конкретном створе. Это может быть
створ, расположенный в черте населенного пункта, мостового пе-
рехода, любого иного объекта народного хозяйства, затопление
которого связано с большими ущербами. Второе - предсказать
время прохождения пика паводка в этом створе, если известно
время прохождения паводка в другом створе, расположенном
выше по течению. Отсюда методика проектирования модели и
проведения на ней исследований должны быть подчинены реше-
нию этих задач. Кроме створов, где расположены важные для на-
родного хозяйства страны объекты, необходимо отметить те, в
которых в реку впадают притоки. Обозначим буквой I расстоя-
ние между двумя соседними створами, в которых находятся важ-
ные объекты, или расстояние от створа впадения в реку притока
до створа ближайшего объекта.
Коль скоро это плановая задача, то основной критерий по-
добия в ней - параметр А.- . Здесь необходим предварительный
h
детальный натурный анализ всей речной системы с целью оценки
пределов изменения этого критерия в области речного бассейна.
Следует заметить, что ширина поймы может на порядок и более
391
превышать ширину основного русла реки. При выходе воды на
пойму и больших ее затоплениях основной вклад в сопротивле-
ние движению воды вносит пойма. Следовательно, коэффициент
гидравлического трения достаточно определять по шероховато-
сти пойменного массива. Таким образом, ширину затопленной
паводковыми водами поймы нужно определять от одного корен-
ного берега до другого вместе с руслом реки, не учитывая от-
дельно ширину и шероховатость русла. Здесь имеются трудно-
сти, в первую очередь связанные с тем, что высота выступов ше-
роховатости может на пойме превышать глубину потока (кустар-
ник, стволы деревьев, растущие здесь). В настоящее время этот
вопрос не достаточно глубоко исследован.
В основе проектирования модели лежит паводковая ситуа-
ция, которая наблюдалась в бассейне реки и сопровождалась за-
топлением пойменных массивов на всем ее протяжении. Естест-
венно, уровни воды во всех интересующих практику створах реки
должны быть увязаны между собой. Далее между створами опре-
деляются средние значения ширины поймы и глубины воды. За-
тем дается предварительная грубая оценка относительной шеро-
ховатости поймы и коэффициента гидравлического трения. В ре-
зультате на всех, интересующих практику участках реки, опреде-
ляется в натурных условиях величина параметра | А.—| . Теперь
V h)„
можно приступить к выбору линейных масштабных коэффициен-
тов kb и kh . Задача эта не простая, учитывая многообразие эле-
ментов подстилающей поверхности и увеличение ширины поймы
вниз по течению реки. Линейные вертикальный и плановый мас-
штабные коэффициенты необходимо выбрать так, чтобы на всех
конкретных участках модели бассейна реки для определяющего
392
параметра выполнялось условие:
> 1. Но тогда надо знать
величину коэффициента гидравлического трения на модели. При
этом необходимо учесть, что в условиях натуры явление относит-
ся к области квадратичного сопротивления, которую необходимо
обеспечить и в условиях модели. В этой области явление не зави-
сит от числа Рейнольдса, которое можно в уравнении связи
(15.46) не учитывать. Однако нужно знать величину граничного
числа Рейнольдса, определяющую начало области квадратичного
сопротивления. В связи с тем, что число Рейнольдса не является в
рассматриваемой задаче критерием, принадлежность к этой об-
ласти на модели можно установить по величине граничного зна-
чения критерия Архимеда, задаваемого формулой (10.75) в раз-
деле 10.2. Но эта зависимость содержит число Архимеда в такой
форме:
Агд/ =
Re2
Fr,
igR3
(15.47)
где i - уклон дна русла реки, R - гидравлический радиус. Меж-
ду тем, используя в уравнении связи (15.46) два числа подобия,
содержащихся в нем, можно сделать комбинацию с целью полу-
чения числа Архимеда, в которую в качестве характерного разме-
ра войдет ширина поймы:
FrB v2
(15.48)
- ^*bj
Произведем в (15.48) преобразования таким образом, чтобы
число Архимеда с характерным линейным размером, равным ши-
рине поймы, было выражено через число Архимеда в виде
(15.47). Но в широкой пойме вместо гидравлического радиуса
393
R характерным вертикальным размером станет характерная глу-
бина потока Н (например, средняя в пределах поймы), а вместо
уклона русла реки i появится уклон всего пойменного массива
* Jr л & л /илах
Агву = в "% = -^Аг/Л — , Аг/Й = -^Ц-. (15.49)
Отсюда получим:
Аг/Л=^Аг " . (15.50)
'а В
Потребуем, чтобы число ArHj было равным величине гранично-
го значения критерия Архимеда, задаваемого формулой (10.75):
АгЯ|г
(15.51)
(Н\
где — ~ относительная гладкость поймы на модели,
Д„ - высота выступов шероховатости на пойме в условиях мо-
дели. Подставляя (15.51) в (15.50), находим относительную глад-
кость поймы при условии, что коэффициент гидравлического
трения поймы на модели лОл1 будет относиться к области квад-
ратичного сопротивленя:
-И
= 0,022— Ы^Аг
В \ JBB
(15.52)
Величину А.Ои найдем из формулы (10.64):
394
4- 4,25.
(15.53)
1
= 41g
Отметим, что условие — = idem
в рамках поставленной за-
дачи не приемлемо, так как, приняв его, получили бы: kb = kh .
Здесь следует обратиться к разделу 11, в котором рассматривался
вопрос моделирования плановых течений. Было отмечено, что
основным параметром, определяющем явление в плановом тече-
b г> ь
нии, является соотношение А- . Роль отношения - не велика и
h h
ею можно пренебречь в подобных задачах.
Далее, зная среднюю ширину поймы в пределах рассматри-
ваемых участков речной системы на модели Ьм и среднюю глу-
бину потока воды на пойме hM , определяем величины парамет-
ров А,,—~ на каждом участке. На правильно запроектированной
м
модели на всех участках должно выполняться условие > 1 .
h.,
В случае, если оно не выполняется, необходимо принять другое
значение отношения линейных масштабных коэффициентов и
начать процедуру проектирования модели заново. После того, как
проектирование модели будет закончено, останется подобрать
доступными средствами шероховатость поверхности поймы в
пределах каждого участка модели. О таких средствах речь идет,
например, в [7].
На созданной модели нужно воспроизвести ситуацию, кото-
рая была положена в основу проектирования. Здесь необходимы
сведения о гидрографах в замыкающих створах притоков. Если
на каких-либо участках результаты измерений не будут соответ-
ствовать натурным данным, то дальнейшую адаптацию модели
395
можно осуществить путем изменения в пределах этих участков
шероховатости поймы. В последующем по мере накопления на-
турных данных, получаемых при прохождении в реке паводков,
этот процесс можно продолжать.
Сказанное позволяет существенно уменьшить число пара-
метров, определяющих движение волны паводка как единого це-
лого в речной системе, и записать их в виде уравнения связи
(15.46):
= 0,
Ф ^vbj >
(15.54)
в которой число Агй/ определяется формулой (15.48). Модель,
запроектированная в соответствии с указанными параметрами,
пригодна для определения на ней разности уровней воды при
прохождении волны паводка между двумя створами, отстоящими
друг от друга на расстоянии I, а также времени, за которое пик
волны проходит это расстояние. Остается сформулировать пра-
вила пересчета этих результатов в натурные условия.
Что касается перепадов уровней воды, то они, естественно,
пересчитываются в натуру с масштабным коэффициентом kh .
Моделирование будем осуществлять «по Фруду». Имея в виду
эту цель, произведем вначале преобразование первого числа по-
добия в исходном уравнении связи (15.46): .
Frs и2 FrH Н
Если положить Fr/y = idem , то получим: Ау = —, что согласуется
с приведенным выше результатом и соответствует принятой ме-
тодике моделирования. Кроме того, в этом случае справедлива
следующая связь между линейным масштабным коэффициентом
396
глубин и масштабным коэффициентом скорости потока:
Теперь обратимся к числу Струхала и получим из условия
Sh в = idem
индикатор подобия:
kb
kukt
= 1 . Отсюда при условии
моделирования «по Фруду» найдем зависимость для определения
масштабного коэффициента времени: kt =
Однако, этот ре-
зультат справедлив для потока воды. Здесь же речь идет о пере-
мещении паводковой волны. Рассмотрим эту задачу подробнее.
Пусть ип - скорость перемещения пика паводковой волны,
a tn - время, за которое пик проходит расстояние, равное I . Так
как фронт волны распространяется вниз по течению (нисходящая
волна), то скорость ип находится из формулы [13]:
и„=соч-и, (15.55)
где и - скорость потока, с0 - скорость перемещения фронта
длинной волны. При неустановившемся движении в открытых
потоках она является аналогом скорости распространения воз-
мущений вдоль потока с при неустановившемся движении в на-
порных трубопроводах, которая находится из формулы (15.11).
Скорость с0 определяется по формуле Лагранжа:
= (15.56)
в ней h - глубина водоема.
Выберем для скоростей ип и с0 в качестве характерных
соответственно Vn и Со , возьмем для расстояния I в качестве
характерного размера величину В, для времени
397
t„ - характерное время Тп . Рассмотрим масштабный коэффици-
ент скорости перемещения пика паводковой волны:
кип
_ Сон + Vn
VnM CQm 4- VM
(15.57)
Выразим характерные величины, относящиеся к натуре, че-
рез соответствующие характерные величины, относящиеся к мо-
дели, и масштабные коэффициенты: Со„ = СОмкс, = VMku .
Имея их в виду, произведем замены в числителе зависимости
(15.57):
V С к + V к
к=^ = + 'Л /15 58)
UH т Г уч I Г х '
Упм Oh, + VM
При моделировании «по Фруду» имеем: ки = у[к^ . Но харак-
терная скорость перемещения длинной волны определяется через
характерную глубину по формуле Лагранжа: Со = ^gH. Отсюда
имеем: кс = —— = , " =Jkh . Подставляя эти результаты в за-
V I—
висимость (15.58), находим: кип = —— = ^jkh . Получается, что
^пм
масштабный коэффициент скорости перемещения пика паводко-
вой волны и масштабный коэффициент скорости потока выража-
ются через линейный масштабный коэффициент глубин одинако-
во. Этот результат не является неожиданным, если вспомнить,
что число Фруда равно отношению скорости потока к скорости
перемещения длинной волны.
Составим теперь из характерных величин Vn, Тп и В число
Струхала и потребуем, чтобы это число было одинаковым на мо-
398
дели и в натуре: Sh„ =----= idem . Такое требование является
вполне обоснованным, так как поток и перемещающееся в нем
длинная волна геометрически и кинематически подобны, но то-
гда в соответствии с гипотезой Ньютона отношение сил инерции
в них на модели и в натуре должно быть одинаковым. Исходя из
этого требования, получим соответствующий индикатор подобия:
= 1, где ktn = . Отсюда имеем: к1п = — = ~^= . Следо-
^un^tn к-un
вательно, время перемещения пика волны паводка, полученное на
модели, пересчитывается в натуру по тому же правилу, что и
время движения потока.
В заключении можно указать общее число параметров, оп-
ределяющих движение волны паводка как единого целого в реч-
ной системе, и записать их в виде уравнения связи, аналогичного
(15.54):
Ф ArSj ,Shs
D
,Sh„,A—
" Н
= 0.
В случае прогноза паводковой ситуации в бассейне реки мо-
дель должна быть приведенной в рабочее состояние. При этом
нужна оперативная информация о гидрографах в замыкающих
створах притоков. Модель должна иметь очень высокий уровень
автоматизации, позволяющей вносить оперативную информацию
об изменении расходов воды в замыкающих створах притоков,
уровнях воды в интересующих практику створах в бассейне реки
и времени прохождения пика паводковой волны этих створов.
399
15.2.2. Моделирование неустановившегося движения воды в
нижних бьефах насосных и гидроэлектрических станции
Характерная ситуация, когда нет необходимости прибегать
к искажению линейных масштабных коэффициентов на модели, с
которой сталкивается исследователь при изучении неустановив-
шегося движения, - это течения в отводящих каналах насосных и
гидроэлектрических станций, работающих в режиме попусков и
регулирования нагрузки в электрических сетях. Сюда следует от-
нести и специальную задачу - движение волны прорыва в ниж-
нем бьефе гидроузла, возникающей при разрушении плоти-
ны, - подробно рассмотренную в [23].
Обратимся к исходному уравнению, приведенному в разде-
ле 11.6, где дано в безразмерном виде интегральное уравнение
(11.64), содержащее безразмерные величины и числа подобия.
При равенстве линейных масштабных коэффициентов это урав-
нение превратится в следующее:
— = Sh
д U’2 со' U'2
R со' д t' + со' д х' + Л° 2 h'
д U' со'
(15.59)
в котором FrR = — - число Фруда, ShA = ~ число Струхала.
Воспользуемся так же безразмерной проекцией уравнения Навье-
Стокса на продольную ось координат (15.19), в которую входят
следующие числа подобия при равенстве всех линейных мае-
V R
штабных коэффициентов: число Рейнольдса Reft -— и число
v
Эйлера Ей . Кроме того, принимаем гидростатический закон рас-
пределения давления по глубине потока, а так же в качестве ха-
рактерного уклона пьезометрической линии JR - отношение пе-
400
репада пьезометрической высоты к характерному линейному
размеру, равному гидравлическому радиусу потока. В соответст-
вии с (15.33) имеем: ^r- = 1. В результате запишем критери-
Jr
альное уравнение в таком виде:
ч
w
Shft,A, ReA =0.
/
(15.60)
Далее используем следующее равенство, которое содержит
уравнение (15.23):
ДР др
pgR дх'
dll'}
+----
дх')
Из него, кроме ---= idem , имеем: Zo =idem, iOli =10м . Но в ре-
PgR
шаемой задаче А = 1, следовательно А.о„ = л()л/ . Теперь дадим
уравнение (15.60) в таком виде:
8ЬлД0Д0,Кел | = 0. (15.61)
lFr« )
При моделировании «по Фруду» имеем: FrA = idem , но тогда по-
лучается, что JR = —= idem . Выше было показано, что мас-
штабный коэффициент скорости перемещения фронта длинной
волны и масштабный коэффициент скорости потока, если моде-
лирование реализуется «по Фруду», выражаются через линейный
масштабный коэффициент одинаково. В таком случае, как об
этом было сказано ранее, масштабный коэффициент времени пе-
ремещения фронта длинной волны может быть получен из усло-
401
вия Sh/; - idem . Опираясь на требование геометрического подо-
бия, можно утверждать, что равенство уклонов дна натуры и мо-
дели будет соблюдено. Остается обеспечить равенство коэффи-
циентов гидравлического трения, учитывая при этом, что в на-
турных условиях поток находится в области квадратичного со-
противления. Следовательно, на модели число Рейнольдса долж-
но превышать граничное значение, определяемое формулой
(10.69). Но в эту формулу относительная гладкость дна входит в
неявном виде. Лучше использовать граничное значение числа
Архимеда, определяемое зависимостью (10.75). Для этого внача-
ле получим число Архимеда, совершив в (15.61) соответствую-
щую комбинацию, и заменим ею число Рейнольдса:
—= Агдj . Однако, в формулу (10.75) число Архи-
Fr« v2
меда входит в таком виде, который, используя принятые здесь
г- * Ф S к! г'
обозначения, можно представить так: Агд = ——z— . Связь меж-
v
ду рассматриваемыми двумя числами Архимеда легко устано-
вить: АгД; =Arft/ — . Принимая Arw =Аг/г и произведя преобра-
J R
зования в соответствии с (10.75), приходим к следующему выра-
жению:
^<0,022 Щагду. (15.62)
A \JR
Коэффициент гидравлического трения на модели определя-
ется по формуле (10.64), если в не подставить относительную
гладкость дна водотока, используя зависимость (15.62). При этом
движение воды на модели будет относиться, как и в натуре, к об-
ласти квадратичного сопротивления. Естественно, возникает во-
402
прос, что принимать в этой задаче в качестве характерного гид-
равлического радиуса.
На практике неустановившейся режим течения наблюдается
в отводящих каналах насосных и гидроэлектрических станций.
Он возникает при изменении подачи воды насосами потребите-
лям, а так же при работе ГЭС в режиме суточного регулирования
нагрузки. На волны, образующиеся в отводящих каналах в про-
цессе реализации подобных режимов, накладываются определен-
ные требования. Например, гребень волны не должен быть выше
бровки канала, волны не должны создавать помехи судоходству в
нижнем бьефе станции и т. п. В обычном режиме, который ус-
ловно можно считать равномерным, отводящий канал пропускает
расход воды Q . Волна возникает при внезапном изменении рас-
хода на величину Д£) . Модель должна быть оборудована устрой-
ством, позволяющем изменять расход воды либо мгновенно, либо
в соответствии с режимом работы регулирующего аппарата насо-
са или турбины. Таким образом, обычный режим является тем
фоном, на котором разворачиваются дальнейшие события. Он
определяет характерные величины, необходимые для решения
задачи. В частности, по кривой связи расходов и уровней воды по
расходу Q можно определить уровень воды в нижнем бьефе,
глубины, смоченный периметр, площадь живого сечения, гидрав-
лический радиус потока. После этого находится коэффициент
гидравлического трения, который выступает не только в роли ха-
рактерной величины, но и параметра, определяющего в какой-то
мере предысторию событий, их естественный фон. Коль скоро
обычный режим считается равномерным, то в зависимости
(15.62) можно принять: JR ~/0 .В окончательном виде уравнение
связи (15.61) будет таким:
403
V ShA, к0, z0, Aryy
= 0.
(15.63)
Рассмотрим теперь задачу физического моделирования вол-
ны, образующейся в нижнем бьефе при разрушении плотины.
Здесь возможны два случая. В первом разрушение произошло
при низком уровне воды в нижнем бьефе, и волна прорыва дви-
жется по незатопленной пойме («посуху»). Во втором разруше-
ние случилось во время прохождения в реке паводка, так что
пойма могла быть затоплена. При аварии плотина может быть
разрушена частично или полностью. В первом случае через обра-
зовавшийся в теле плотины проран вода станет изливаться в
нижний бьеф, уровень воды в водохранилище будет постепенно
понижаться. Наибольшие разрушения, скорее всего, произойдут в
нижнем бьефе вблизи плотины. Такое явление трудно поддается
моделированию из-за невозможности заранее установить разме-
ры прорана и их изменение во времени в процессе опорожнения
водохранилища. Во втором случае вниз по течению начнет дви-
гаться волна, высота которой в створе плотины практически бу-
дет равна перепаду уровней между бьефами. В этом случае
большие разрушения могут произойти не только в створе плоти-
ны, но и на всем протяжении реки, на котором волна прорыва бу-
дет уменьшаться в высоте («распластываться»). Именно этот слу-
чай будет рассмотрен ниже с точки зрения возможности его фи-
зического моделирования при условии, что излив происходит ли-
бо в «сухую», либо в затопленную пойму.
Прежде всего, следует обратить внимание на особенности
«волны посуху». Во-первых, она может не обладать свойствами
длинной волны на мелкой воде, так как при движении в узкой
пойме (особенно в узком каньоне горной реки) глубина воды мо-
жет не отличаться от ее ширины. Во-вторых, длинная волна рас-
404
пространяется в потоке воды малой глубины, в то время как вол-
на прорыва в рассматриваемом случае движется по сухой пойме.
Но если подходить к этим двум явлениям с позиций метода соот-
ношения сил Ньютона, то можно обнаружить, что силы, дейст-
вующие в них, одинаковы, следовательно, одинаковыми должны
быть и соотношения этих сил. В таком случае должны получить
одни и те же числа подобия. Вопрос заключается в том, что вы-
брать в качестве характерных величин, входящих в числа подо-
бия.
Движение волны прорыва, образующейся при разрушении
плотины, является одной из достаточно сложных задач, решае-
мой методом физического моделирования. Здесь многое зависит
от опыта и интуиции исследователя, а также от наличия соответ-
ствующего лабораторного оборудовании и средств для организа-
ции подобного рода исследований. В задаче с достаточной степе-
нью надежности заданны только две величины: высота волны в
створе плотины Но и уклон речной долины в нижнем бьефе
гидроузла in . К ним можно добавить высоту выступов шерохо-
ватости поймы Д„, которая оценивается в первом, достаточно
грубом приближении. В [23] делается допущение о том, что ве-
личина коэффициента гидравлического трения в натуре (пра-
вильнее было бы сказать - ее оценка) может быть найдена по
формуле, справедливой для области квадратичного сопротивле-
ния и равномерного режима движения воды, по величине отно-
шения — . Если выбран линейный масштаб модели, то анало-
гичный расчет следует выполнить для оценки величины коэффи-
циента гидравлического трения на модели. По нашему мнению,
как об этом было уже сказано выше, проще такой расчет сделать,
используя критерий Архимеда. Получим этот критерий, комби-
405
нируя числа Фруда, Рейнольдса и уклон речной долины, в ре-
зультате получим: Arш = Используя граничное значение
числа АгН; , задаваемое формулой (15.51), определим относи-
тельную гладкость поймы, необходимую для реализации на мо-
дели квадратичного закона сопротивления:
=0,022/Агя, .
В еличину А, Ол< найдем из формулы (15.53).
Коль скоро коэффициент гидравлического трения был най-
ден по аналогии из формулы, справедливой для равномерного
режима, то аналогию можно продолжить, полагая, что величина
АОи с точностью до постоянной равна числу Эйлера. Следова-
тельно, число Эйлера из уравнения связи можно исключить. В
связи с тем, что число Рейнольдса было заменено критерием Ар-
химеда, уравнение связи можно дать в таком виде:
С(Гг, Sh, Ао, i„, (15.64)
Аналогию с равномерным режимом можно продолжить и
дальше, используя известное безразмерное уравнение равномер-
но.м in ут
ного движения: ----= ~ . Далее, в качестве оценки характерной
2 Fr
скорости распространения волны посуху по аналогии принята
скорость, определяемая формулой Лагранжа для волны возмуще-
у 2
ния на мелкой воде: Ко = JgH0 . Но тогда число Фруда Fr = —*1-
становится равным единице, и из формулы равномерного режима
406
получаем, как об этом сказано в [23], «определяющий критерий»
в виде:
—(— = idem. (15.65)
Ч
Остается определить зависимость, по которой время про-
движения волны между двумя пунктами, измеренное на модели,
можно будет пересчитать в натуру. С этой целью вначале выби-
рается характерная длина в продольном направлении речной до-
лины. В качестве таковой принята приблизительная длина кривой
подпора в водохранилище: Zo = HQ/i„ . Волна пройдет это рас-
стояние, двигаясь с характерной скоростью Ко , за характерное
время:
Го =^- = —= (15.66)
ко in jgHo in Jg
При условии inH = inM получаем индикатор подобия:
= -Дц , где кн ~ ~ - масштабный коэффициент высоты
волны. Если составить теперь число Струхала в таком виде:
Sh = —— , то оно станет равным единице, а для пересчета време-
ни процесса в натуру используется формула (15.66). Заметим,
кстати, что можно было характерный продольный размер не вво-
дить в рассмотрение, а дать число Струхала в таком виде:
Sh# = . Но тогда, сохраняя условии моделирования преж-
де ?()
ними, принимая Sh/7 - idem , пришли бы для характерного времен
Го к выражению:
407
Но
П)
Но
(15.67)
которое отличается от (15.66) отсутствием в нем уклона i„ . Но
индикатор подобия остается прежним, поскольку при моделиро-
вании выполняется условие inH = inM , при соблюдении которого
зависимости (15.66) и (15.67) совпадают. Таким образом, мас-
штабный коэффициент времени перемещения волны прорыва
связан с линейным масштабным коэффициентом высоты волны
зависимостью, которая соответствует физическому моделирова-
нию «по Фруду» неустановившегося движения воды в открытых
руслах.
Проведенные на моделях исследования обнаружили, что
при резком сужении речной долины волна прорыва останавлива-
ется и может сохранять высокие уровни воды довольно продол-
жительное время. Это свидетельствует о том, что искажение ли-
нейных масштабов модели в подобного рода исследованиях не-
лОл/
допустимо. Кроме того, при условии----> 50 была найдена ав-
томодельная область по этому критерию.
Если уклон речной долины равен нулю, то задача о движе-
нии волны прорыва в сухом русле прямоугольного поперечного
сечения становится автомодельной при выборе в качестве харак-
терных следующих величин:
£0=н0Д0л v0=/gHQ, г0=-^
(15.68)
Здесь так же, как и в случае неравенства уклона речной долины
нулю, при условии А.о„ = А.Ол/ формула для определения харак-
408
терного времени Го в (15.68) превращается в (15.67). В случае
движения волны прорыва в русле, глубина воды в котором равна
Ло , в [23] утверждается, что единственным параметром задачи
является отношение Hq/Hq.
В заключении следует заметить, что большинство допуще-
ний, принятых в рассмотренной задаче, нуждаются в проверке в
натурных условиях. В первую очередь это касается формул, из
которых получаются масштабные коэффициенты времени
(15.66)-(15.68). Но для оценки в первом приближении последст-
вий разрушений водоудерживающих плотин, сопровождающихся
образованием волн прорыва, предложенная методика вполне
приемлема.
409
16. МОДЕЛИРОВАНИЕ МЕСТНЫХ ПОТЕРЬ
НАПОРА И ИСТЕЧЕНИЙ ЧЕРЕЗ ВОДОСЛИВЫ И
ОТВЕРСТИЯ
16.1. Моделирование местных потерь напора
Задача о местных потерях напора, как это ни покажется па-
радоксальным, в полном объеме с позиций методов физического
моделирования до сих пор не рассматривалась, хотя практически
все достижения в этой области были получены эксперименталь-
ным путем. Как правило, потери напора принимаются пропор-
циональными скоростному напору. В лучшем случае считается,
что коэффициент пропорциональности зависит от числа Рей-
нольдса. Рассмотрим эту задачу подробнее.
Предположим, что в трубопроводе имеются устройства, ко-
торые позволяют регулировать подачу воды, изменять направле-
ние ее течения, переходить от трубы одного поперечного сечения
к трубе с другим поперечным сечением и т. п. Такие устройства
являются источником повышенной турбулентности потока, в них
энергия осредненного движения переходит в энергию турбулент-
ных вихрей, которая в свою очередь переходит в тепловую энер-
гию (происходит диссипация - рассеяние - механической энер-
гии). При физическом моделировании в первую очередь должно
соблюдаться строгое геометрическое подобие этих устройств.
Описать с помощью математических методов процессы, проис-
ходящие в этих устройствах, чаще всего затруднительно. Полу-
чить числа подобия можно с помощью методов теории размерно-
стей. Но речь идет о течении ньютоновской жидкости, поэтому
набор величин, от которых зависит явление, вполне определен-
ный, так что в результате анализа размерностей получим извест-
но
ные числа подобия. Однако, чаще всего ни одной характерной
величины, кроме физических констант, в задаче не имеется. В
этой связи в качестве характерных величин принимаются пара-
метры потока вне пределов устройств, следовательно, в качестве
чисел подобия - те, которые характеризуют явления в трубопро-
воде.
При проведении испытаний исследователя не интересует то,
что происходит в устройстве, оно для него является «черным
ящиком». Но ему известны изменения в потоке до входа в «чер-
ный ящик» и после него. В частности, эти изменения проявляют-
ся в падении пьезометрической линии на участке трубопровода,
где расположено устройство. Перепад пьезометрической линии
ЛЯ и есть местная потеря напора, так как она сосредоточена на
сравнительно короткой длине усторойства по сравнению с дли-
ной трубопровода. Обычно в гидравлике принято этот перепад
связывать с характерным скоростным напором, и эта связь играет
здесь роль известного интегрального соотношения:
V2
(16.1)
2g
где V - характерная скорость течения жидкости в трубопроводе,
£, -коэффициент местной потери напора. Зависимость (16.1)
можно сделать безразмерной и представить в двух видах. Первый
получим, разделив левую и правую части на диаметр трубопро-
вода:
“=|FrD. (16.2)
411
к2
где Fro = — - число Фруда, в котором в качестве характерного
gD
размера выбран диаметр трубопровода. Отсюда из (16.2) найдем:
АН _
£>Frn ~ 2
(16.3)
Для получения второго безразмерного вида зависимости
(16.01) вначале умножим левую и правую ее части на плотность
жидкости р , а затем разделим на F2/g , в результате получим:
££^ = Д = ЕиЛ. (16.4)
pF2 pF2 2
где Ей = —- число Эйлера, в котором Ар - перепад давления
pF
на устройстве. Приравнивая формулы (16.3) и (16.4) друг другу,
имеем:
АН и
---= Еи = - .
£>Frn 2
(16.05)
Сравнивая (16.05) с соответствующими зависимостями, по-
лученными в условиях равномерного режима движения жидко-
сти, приходим к выводу, что коэффициенты местной потери на-
пора и гидравлического трения выражаются через числа подобия
одинаково. В рассматриваемом случае получается, что половина
коэффициента местной потери напора представляет собой и чис-
ло Эйлера, и комбинированное число, равное отношению относи-
тельной потери напора к числу Фруда. Таким образом, местные
потери напора в соответствии с (16.1) определяются по зависимо-
сти, которая совпадает с формулой для определения потерь напо-
ра по длине трубопровода. Это позволяет суммировать местные
412
потери напора с потерями по длине трубопровода. Аналогию
можно продолжить, если рассматривать оба явления с позиций
методов физического моделирования этих явлений. Оказывается,
что параметры, определяющие явления и связь между ними, по
своей сути совпадают.
Продолжая анализ, нужно сказать, что явление определяется
одним числом подобия (это может быть и коэффициент местной
потери напора, и число Эйлера, и комбинированное число, равное
отношению относительной потери напора к числу Фруда) и кри-
терием Рейнольдса, в который входят характерные величины, оп-
ределяющие течение в трубопроводе перед устройством, или по-
сле него. Безусловно, течение в трубопроводе оказывает влияние
на течение в устройстве. Доказательством тому служит извест-
ный факт: коэффициент местной потери напора зависит от того,
каков режима течения в трубопроводе - ламинарный или турбу-
лентный. Обычно устройство размещается в трубопроводе с рав-
номерным течением, параметры которого при известной скорости
течения определяет критериальное уравнение (10.11), связываю-
щее коэффициент гидравлического трения с числом Рейнольдса,
относительной шероховатостью внутренней поверхности трубо-
провода и формой трубы. Отсюда критериальное уравнение для
коэффициента местной потери напора можно представить в двух
видах:
Е, = ср f Re, —, форма трубы, параметры устройства |, (16.6)
у г J
^ = /(ReA, параметры устройства), (16.7)
гдег = £>/2, Re = PD/v . В уравнении (16.6) число Рейнольдса
выполняет две функции. В одной из них оно характеризует ре-
жим течения в трубопроводе. В другой выступает в качестве кри-
413
терия, от которого зависит коэффициент местной потери напора.
В уравнении (16.7) режим течения в трубопроводе «спрятан» в
коэффициенте гидравлического трения. Режим обнаруживается,
если для этого коэффициента использовать критериальное урав-
нение (10.11). Критерий Рейнольдса в (16.7) выполняет единст-
венную функцию: здесь он выступает как параметр, от которого
зависит коэффициент местной потери напора. При проведении
исследований нужно добиваться равенства коэффициентов гид-
равлического трения на модели и в натуре, изменяя в широких
пределах критерий Рейнольдса. Осуществить подобное модели-
рование очень трудно, здесь потребуется привлечение различных
методов приближенного моделирования, рассмотренных ранее в
предыдущих разделах. На практике могут встретиться такие слу-
чаи, когда исследовать приходится устройства в натуральную ве-
личину. Однако это не исключает необходимости поиска зависи-
мости коэффициента местной потери напора от критерия Рей-
нольдса. Параметрами устройства являются относительные раз-
меры величин, определяющие его геометрию (например, угол по-
ворота трубы в устройстве, изменяющем направление движения
потока; отношение площади сечения диафрагмы к площади сече-
ния трубы перед диафрагмой и отношение площадей сечения
труб перед диафрагмой и за нею; отношение площади сечения не
перекрытой простой задвижкой к площади сечения трубы; угол
поворота дискового затвора и т. п.).
В некоторых случаях местная потеря напора частично мо-
жет быть установлена теоретическим путем. Классическим при-
мером может служить задача Борда о потерях напора при резком
расширении трубы. В решении используются уравнения Бернул-
ли для двух сечений, выделенных в потоке, и уравнение измене-
ния количества движения, записанное для отсека жидкости, на-
414
холящегося между выделенными сечениями в трубе большего
размера. В результате получают формулу Борда [5, 13, 63]:
(16.8)
в которой ю| и ю2 ~ соответственно площадь сечения трубы ма-
лого и большого размеров (для труб круглого поперечного сече-
ния диаметры труб D{ и D2 ), И, _ характерная скорость тече-
ния в первой трубе. Формула Борда не учитывает потери напора в
водоворотных зонах, образующихся в месте расширения потока.
Такого рода потери описываются с помощью зависимости (16.1),
в которой коэффициент местной потери напора определяется
опытным путем (зависимость называется формулой Вейсбаха).
Обозначим эту часть потерь напора АН0 и, используя метод
сложения потерь напора, найдем общую местную потерю напора
при внезапном расширении потока [24]:
АН = \Нр + ДН0
И2
(16.9)
I ю2 JJ 2&
Из (16.9) получим формулу для определения коэффициента
местной потери напора
_ АН 1^ со^
2 DFrD 2^ ,
16.2. Моделирование истечений через водосливы
Задача об истечении через водосливы различного попереч-
ного сечения важна для практики. Поиски ее решение были нача-
ты еще в позапрошлом веке путем проведения исследований в
415
лабораторных условиях на моделях водосливов. Но в те времена
методы физического моделирования еще не были глубоко разра-
ботаны, поэтому результаты исследований интерпретировались
авторами, руководствуясь в основном здравым смыслом и интуи-
цией. Тем не менее, многие предложенные ими зависимости до
сих пор рекомендуются для практического использования без
должного критического переосмысления [63].
Решение задачи истечения через водослив с использованием
методов теории физического моделирования находим в [21]. За-
дача формулируется так: имеется водослив определенной геомет-
рической формы, известен расход воды Q , необходимо опреде-
лить напор на гребне водослива Н , при котором будет происхо-
дить перелив воды через гребень. В связи с тем, что движение
воды на подходе к водосливу установившееся неравномерное,
можно сразу сказать, что явление определяется тремя числами
подобия: Фруда, Рейнольдса и Эйлера. В [21] решение задачи
рассматривается с учетом только двух чисел подобия - Фруда и
Рейнольдса. При заданном расходе воды, высоте водослива р и
ширине водосливного фронта В в качестве характерной скоро-
сти течения можно взять среднюю скорость воды на подходе к
водосливу: К(| —j • Тогда число Фруда равно
г2 Л)2
Fr=~пг~\=—й о 6-10)
g(H + р) B2g(H + р)3
Оно не является критерием подобия, так как в нем не извес-
тен напор на гребне водослива, который находится в результате
проведения опытов. Вместе с тем, в гидравлике принята универ-
сальная формула для неподтопленного водослива в виде:
416
Q = mBj2gH^,
(16.H)
в которой т - коэффициент расхода.
Существует распространенное мнение, согласно которому
коэффициент расхода можно представить в виде произведения
различных коэффициентов, среди которых едва ли первое место
занимает «коэффициентом сжатия струи». Обычно в коэффици-
ент расхода дополнительно вводят параметр, учитывающий
влияние конструктивных особенностей водослива, которые вы-
зывают сжатие переливающейся струи уже в пределах гребня во-
дослива и называют его «коэффициентом сжатия струи». Либо
этот коэффициент непосредственно записывают в правую часть
формулы (16.11). С точки зрения методов физического модели-
рования сжатое сечение не имеет характерных величин. Для этих
методов характерными являются величины, определяющие пара-
метры потока на подходе к водосливу. Переливающаяся через
водослив струя должна формироваться прежде, чем она начнет
испытывать на себе влияние различных конструктивных элемен-
тов водослива (к ним, например, можно отнести наличие или от-
сутствие раздельных бычков, их плановое очертание, место рас-
положения в них пазов для затворов, форму напорной грани во-
дослива и т. п.). По сути дела, это влияние определяется геомет-
рическими параметрами водослива, которые на модели должны
быть строго подобными натурным. Следовательно, речь может
идти о местных потерях напора в упомянутых конструктивных
элементах водослива. Принимая этот путь исследований, навер-
ное, можно будет получить какие-то обобщающие зависимости
для «коэффициента сжатия струи», однако, потребуется проведе-
ние методических исследований на моделях различных водосли-
417
bob по единой методике, с обязательным соблюдением методов
физического моделирования.
Но существует и другой путь решения задачи - получить
связь между расходом воды и напором на гребне водослива, ис-
ходя из соображения размерностей [63], тогда приходят к форму-
ле водослива (16.11). При таком подходе можно сразу сказать:
коль скоро геометрия у водосливов разная, то следует ожидать,
что и коэффициенты расхода не будут у них совпадать. Задача
заключается в поиске зависимости коэффициента расхода кон-
кретного водослива от определяющих параметров в рамках тео-
рии физического моделирования явлений.
Прежде всего, покажем, что коэффициент т , входящий в
формулу (16.11), связан с двумя числами подобия Фруда и Рей-
нольдса. Вначале найдем связь его с числом Фруда, с этой целью
возведем левую и правую части формулы (16.11) в квадрат, ре-
шим ее относительно Fr , произведя соответствующие преобра-
зования с использованием формулы (16.10), в результате полу-
чим:
Fr = 2m2
Н
Н+Р;
(16.12)
Далее выразим коэффициент расхода через число Рейнольд-
са, которое запишем так:
Ке = 2=Д
v Bv
(16.13)
где q - удельный расход воды. Снова возведем левую и правую
части формулы (16.11) в квадрат, решим ее относительно Re2 ,
418
произведя преобразования с использованием формулы (16.13), в
результате получим:
Re2=2m2Gaw, (16.14)
где Ga н = - число Галилея. Интересным представляется
v2
тот факт, что число Фруда, не являясь критерием подобия (со-
держит напор на гребне водослива, который определяется в ре-
зультате проведения опытов), остается числом подобия и в том
случае, если найдена его связь с коэффициентом расхода, что
видно из формулы (16.12). Число Рейнольдса, будучи критерием
подобия (это видно из формулы (16.13), поскольку расход воды в
задаче задан), теряет свойства критерия, если выразить его через
коэффициент расхода, как это следует из формулы (16.14).
Далее сравним эти результаты с теми, которые предложены
в [21]. Здесь принято число Фруда вычислять по формуле:
rz2 /Э2
Frz= — = ——. (16.15)
gH B2(H + P)2gH
Выразим теперь число Fr£ через коэффициент расхода во-
дослива, используя формулу (16.15):
Fl7.
= 2т2
н У
н + Р)
(16.16)
Сравнивая зависимости (16.12) и (16.16), можно заметить,
что число Фруда Fr£ превышает число Fr в р раз, но этот
результат также получается при непосредственном сравнении
формул (16.15) и (16.10).
419
Из сказанного следует, что критерием подобия в рассматри-
ваемой задаче является число Рейнольдса в виде (16.13), а коэф-
фициент расхода водослива выступает как число подобия, связь
которого с числом Фруда может быть разной в зависимости от
того, какая формула используется для определения этого числа.
Остается установить, какую роль в рассматриваемой задаче игра-
ет число Эйлера.
Как об этом уже было ранее сказано, движение воды в пре-
делах водослива является резко неравномерным. Известно, что в
верхней части водосливной грани давление отличается от гидро-
статического. Водосливную поверхность приходится очерчивать
по некоторой кривой (кривая Кригера-Офицерова) для того, что-
бы на ней не возник вакуум. Но иногда с целью увеличения про-
пускной способности водослива водосливную грань специально
делают «вакуумной». Очертание нижней поверхности перели-
вающейся через стенку струи зависит от напора на гребне стенки.
Напор, при котором было выбрано безвакуумное очертание водо-
сливной поверхности Н, называется профилирующем. Водо-
сбросное сооружение в процессе эксплуатации может работать
при различных напорах. Если напор меньше профилирующего, то
водослив работает в безвакуумном режиме; если больше профи-
лирующего - режим работы водослива вакуумный. В этой связи
приходится вводить в формулу водослива дополнительный ко-
эффициент, зависящий от отношения напора на гребне водослива
к профилирующему напору, называемый коэффициентом полно-
ты напора. В [21, с.91-92] обсуждаются результаты исследования
струи на водосливной поверхности. Обнаружено, что в пределах
гребня водослива нет сечения, в котором давление по глубине
потока распределяется по гидростатическому закону.
420
Выберем в потоке два вертикальных сечения: одно в верх-
нем бьефе вдали от водослива 0-0, другое перед водосливом не-
посредственно у напорной грани 1-1, полагая, что в обоих сече-
ниях закон распределения давления по глубине потока гидроста-
тический. Запишем уравнение Бернулли для этих двух сечений,
пренебрегая потерями напора, выбрав в качестве плоскости срав-
нения горизонтальное дно водотока в верхнем бьефе.
г/2 н2
H + p + HL = H1+V
2g 1 2g
(16.17)
где Н] и их - соответственно глубина и скорость течения пото-
ка в сечении 1-1, так что здесь выполняется условие: q = Htu} .
Преобразуем (16.17) следующим образом:
(16.18)
Далее умножим левую и правую части зависимости (16.18)
на произведение gp , получим после преобразований:
АД к 1
—у = Ей = -
рЕ02 2
/ ,, \2
Н + р
ГнГ)
(16.19)
где АД = gpAH, - перепад давления на участке потока между
двумя сечениями 0-0 и 1-1, &НХ -соответствующий перепад
уровня воды. Формулу (16.18) можно преобразовать и таким об-
разом:
421
Сравнивая (16.19) и (16.20), приходим к зависимости:
Ей = 7----\,
(Я + p)Fr
(16.21)
характерной для неравномерного режима течения. Если для числа
Фруда использовать формулу (16.15), предложенную в [21], то
вместо (16.21) получим следующую зависимость:
р А//|
Ей =-----
//Fr£
(16.22)
в которой число Эйлера останется неизменным.
Выполненный анализ свидетельствует о том, что в рассмат-
риваемой задаче число Фруда не играет никакой роли и может
задаваться произвольно. Легко найти связь числа Фруда с коэф-
фициентом расхода водослива, которая зависит от того, какая
формула используется для этого числа. Но этот вывод в равной
степени относится и к числу Эйлера. Не только число Фруда, но и
число Эйлера не определяет рассматриваемое явление. Роль чис-
ла подобия выполняет в нем коэффициент расхода, роль критерия
подобия отводится числу Рейнольдса. Это хорошо подтверждают
опытные данные, приведенные на рис. 16.1. Здесь представлены
результаты лабораторных опытов, выполненных
А.Г. Аверкиевым для определения коэффициента расхода водо-
слива практического профиля [16,21]. Видно, что коэффициент
расхода зависит от критерия Рейнольдса и отношения профили-
рующего напора к напору на гребне водослива.
Приведенный график позволяет также определить предель-
ное значение числа Рейнольдса, при котором явление перестает
зависеть от этого критерия. Геометрические особенности водо-
422
Рис. 16.1. Зависимость коэффициента расхода от числа
Рейнольдса для водослива практического профиля
сливов отражаются в величине коэффициента расхода. Об этом
свидетельствуют рекомендации по выбору коэффициентов рас-
хода для водосливов различных конструктивных форм, приводи-
мые в научной и в учебной литературе [5, 13, 15, 60, 63]. К сожа-
лению, не во всех учебных пособиях приводятся значения пре-
дельных чисел Рейнольдса, при которых коэффициенты расхода
становятся независящим от этого числа, и на этом основании
считать их пригодными для применения в натурных условиях.
Такие сведения одновременно говорят о том, что в методическом
отношении исследования, на основании которых были получены
эти результаты, были проведены правильно. Кроме того (и это
представляется весьма важным), наличие указаний о величине
такого числа для различных водосливных устройств, позволяет
исследователю, моделирующему гидротехнические сооружения,
в составе которых имеются водосбросы, не проводить дополни-
тельных методических опытов по его определению.
В заключении сформулируем задачу по-иному: пусть в ней
изначально задан напор на гребне водослива, и нужно определить
величину расхода воды, поступающей через водослив в нижний
бьеф. В такой постановке в задаче нет критериев подобия, так как
423
в ней расход воды, входящий в числа подобия, заранее не извес-
тен. Найдем, как обычно, критерий подобия путем комбинации
чисел подобия. С этой целью разделим зависимость (16.14) на
(16.12), в результате получим критерий Галилея в таком виде:
Re2 (Н + р}3 g(H + р)3 .
Fr = "ОО = 72—=Ga(^)- (16-23)
Таким образом, роль числа подобия в этой задаче играет по-
прежнему коэффициент расхода водослива, в то время как число
Галилея является в ней критерием. Отсюда критериальное урав-
нение можно записать так:
™ = f(Ga{H+p)}. (16.24)
Однако, для получения зависимости (16.24) в явном виде или по-
лучения ее в виде графика нужно было бы произвести пересчет
всех опытных данных заново. Но в этом нет необходимости, если
обратить внимание на то, что в формуле (16.23) имеется еще одно
число подобия, а именно Gaн , которое также является критери-
ем подобия. Для его получения нет необходимости пересчиты-
вать заново опытные данные, достаточно, воспользовавшись гра-
фиком (16.1), найти величину этого критерия из формулы (16.14):
GaH =
Re2
2m2
(16.25)
Значения числа Рейнольдса и коэффициента расхода водо-
слива, входящие в формулу (16.25), непосредственно снимаются
с графика, приведенного на рис. 16.1. После этого можно постро-
ить график зависимости
т = ф(Оая).
424
16.3. Моделирование истечений через большие отверстия
Отверстия в стенке резервуара, через которые жидкость вы-
текает наружу, будем называть большими, если влиянием сил по-
верхностного натяжения на параметры образующейся при исте-
чении струи можно пренебречь. В следующем разделе будет дана
количественная оценка размерам таких отверстий и предложена
методика физического моделирования явления истечения жидко-
сти из малого отверстия. Здесь будем рассматривать большое от-
верстие и соответствующую методику его физического модели-
рования.
Следует отметить, что решение этой задачи было предложе-
но в [5, 15], причем в [5] приводятся результаты выполненных
исследований в лабораторных условиях и оригинальная методика
их обработки. Предполагается, что жидкость вытекает из замкну-
того резервуара наружу через отверстие в его стенке. Напор
Н (расстояние от центра отверстия до уровня жидкости в резер-
вуаре) и давление в резервуаре над уровнем жидкости р0 счи-
таются заданными и неизменными. В таком случае резервуар
должен иметь специальные устройства, позволяющие непрерыв-
но поддерживать в нем давление и уровень жидкости, компенси-
руя убыль ее из резервуара притоком в него в равном количестве.
Задачу, в которой задан напор, а расход жидкости неизвестен, на-
зовем первой. Дадим ее в той последовательности, в какой она
приводится в [5, 15].
Принимая плоскость сравнения проходящей через центр от-
верстия, составляем уравнение Бернулли для двух сечений: одно
совпадает со свободной поверхностью жидкости в резервуаре,
другое - со сжатым сечением вытекающей из отверстия струи.
425
2 2
// + £о = а +
pg Pg 2g 2g
(16.26)
где pi - давление вне резервуара (атмосферное, если истечение
происходит в атмосферу), щ - скорость в сжатом сечении,
- коэффициент, учитывающий местное сопротивление на
входе жидкости в отверстие. Решая (16.26) относительно скоро-
сти, получим:
(16.27)
Pg 7
где ф] = 1/д/1 + - коэффициент скорости. Если ©! - площадь
сжатого сечения, то можно записать формулу для расхода жидко-
сти:
0 = И]©1 =Ф1к>| 2g Н + Р-——
И Pg
Зададим теперь связь между площадью отверстия ®0 и
площадью сжатого сечения в таком виде: ©^©qb, в которой
е - коэффициент сжатия струи. Тогда придем к известной фор-
муле для определения расхода жидкости, истекающей из отвер-
стия в стенке резервуара
(? = ц©0 2g Н + ^—
(16.28)
где ц = Еф1 -коэффициент расхода отверстия. Из формулы
(16.28) следует, что в рамках поставленной задачи (если не пре-
следовать иные цели) явление полностью определяется только
одним параметром - коэффициентом расхода отверстия.
426
Далее обратимся непосредственно к [5] с тем, чтобы про-
следить, каким образом автор ставит задачу физического модели-
рования явления и предлагает осуществлять обработку результа-
тов выполненных им опытов. Прежде всего, вводится в рассмот-
рение скорость, играющая роль характерной. Фактически автор
пользуется рассмотренным выше методом фрагментов, выделив
из скорости истечения жидкости (16.27) фрагмент yj2gH , имею-
щий размерность скорости. Этот фрагмент используется для по-
лучения числа Фруда, в которое, кроме упомянутой скорости, в
качестве характерного линейного размера входит диаметр отвер-
стия dQ . Имеем
Fr;/ = = 2^ (16 29)
g^o do
Аналогичным образом получают число Рейнольдса
Re;/ = (16.30)
Далее безо всякого доказательства принимается, что коэффици-
ент расхода отверстия является функцией числа Рейнольдса Reя .
Заметим, что и в число Фруда Fr,, , и в число Рейнольдса Rew
входят заранее известные величины, поэтому они оба играют
роль критериев. Но тогда получается, что коэффициент расхода
отверстия одновременно является и функцией критерия Фруда.
Тем не менее, опытные данные были обработаны в соответствии
с зависимостью
P = /(Re„). (16.31)
Их результаты приведены на рис.16.2.
427
Рис. 16.2. Зависимость коэффициентов расхода, скорости и
сжатия струи от критерия Рейнольдса для отверстия в
стенке резервуара
Попробуем разобраться в методике моделирования, пред-
ложенной в [5]. Но прежде, для того чтобы избежать громоздких
записей, несколько упростим задачу. С этой целью положим:
р0 = pi (давление над свободной поверхностью в резервуаре и
вне его одинаково и равно атмосферному, иными словами, исте-
чение жидкости происходит из открытого резервуара). Такое
предположение не носит принципиальный характер, но сущест-
венно упрощает записи формул. В частности, вместо (16.28) име-
ем:
0 = циОл/21н. (16.32)
Найдем числа подобия в том случае, когда применяются
обычные методы теории физического моделирования (подобия,
размерностей или соотношения сил Ньютона). Запишем число
Фруда, используя характерные величины потока и отверстия, по-
лучим с учетом формулы (16.32)
Fr = ^-y = ц2^ = ц2рГя. (16.
®о£“О “О
428
Из зависимости (16.33) следует, что коэффициент расхода
отверстия однозначно связан с числом Фруда Fr (отношение
H/d0 по условию задачи задано), поэтому это число можно
вполне обоснованно заменить коэффициентом расхода. В равной
степени это относится и к числу Фруда Fr# , поскольку
Fr^^Fr/ц2. Следовательно, предложенное в [5] уравнение
(16.31) является вполне обоснованным и критериальным, о чем
свидетельствует приведенное доказательство. Запишем далее
число Рейнольдса в случае, когда применяются обычные методы
теории физического моделирования, используя скорость потока в
отверстии и характерный линейный размер отверстия, получим с
учетом формулы (16.32)
= (16.34)
®nv v
Из зависимости (16.34) следует, что число Рейнольдса Re
не является критерием, но оно однозначно связано с числом Яея,
в которое входят величины по условию задачи заданные.
Полезно попытаться получить критериальное уравнение в
рамках рассматриваемой задачи в том случае, когда используют-
ся обычные методы теории физического моделирования (подо-
бия, размерностей или соотношения сил Ньютона). Поскольку
числа подобия Re и Fr не являются критериями, то, комбини-
руя их, приходим к критерию:
Re2 _ P22gH<7o dQ _ э d0 _ gd§ _
Fr v2 p22H H 2H v2
(16.35)
где Gaj - критерий Галилея, в который в качестве характерного
линейного размера входит диаметр отверстия. Но критерий GaY/
429
не может однозначно определять коэффициент расхода отвер-
стия. Ясно, что для одного и того же отверстия коэффициент рас-
хода будет зависеть еще и от отношения — . В этом смысле кри-
терий Re# полностью отвечает поставленной задаче, поскольку
он учитывает и критерий Галилея, и упомянутое отношение. Это
можно видеть из следующей формулы, полученной непосредст-
венно из соотношений (16.35):
N “о
(16.36)
Сформулируем вторую задачу: задан расход жидкости Q,
вытекающей из отверстия в стенке резервуара, диаметром d0,
необходимо найти напор Н. Заметим, что в зависимости от вели-
чины разности давлений р0 - pt задача будет иметь множество
решений, при условии р0 = р{ решение будет единственным, его
и рассмотрим. В рамках методики, предложенной в [5], задача
может быть решена только методом последовательного прибли-
жения. Вначале задаются напором Н, определяют критерий Re#,
по графику на рис. 16.2 находят коэффициент расхода ц, после
этого из формулы (16.32) вычисляют расход жидкости и сравни-
вают его с заданным. Если расходы не совпадают, поиск решения
продолжается методом последовательного приближения.
Вместе с тем решение может быть найдено в таком виде,
при котором метод итераций окажется не нужным. Для этого по-
требуется составить критериальное уравнение. С этой целью,
прежде всего, запишем числа Фруда и Рейнольдса, соответст-
вующие сформулированной выше второй задаче:
430
Fr = —, Re = . Как видно, в такой записи оба числа яв-
Ио^О ®0v
ляются критериями подобия, и задача становится неопределен-
ной. Но если учесть формулу (16.32), то после подстановок эти
числа подобия преобразуются в следующие:
2 2Н nJlgHdQ
Fr - ц — , Re - ------ . В такой записи оба числа не
v
являются критериями подобия. Если оставить в уравнении связи
число Фруда в виде, полученном во второй записи, то следующее
преобразование свидетельствует о том, что число Фруда можно
заменить коэффициентом расхода отверстия:
d
ц2 = Fr—— = — . Оставим в уравнении связи число Рей-
277 (Од 2^77
нольдса в том виде, в котором оно было получено в первой запи-
си, тогда критериальное уравнение во второй задаче станет та-
ким:
P = /(Re). (16.37)
Решение задачи легко находится таким образом: по крите-
рию Re определяется коэффициент расхода отверстия, далее с
помощью формулы (16.32) - напор при условии, что расход жид-
Р2
кости задан: Н = —. Связь между критериями Re и Re,,
легко можно установить, используя следующее соотношение:
КсЛН = ^Д71=М!еи
®ov V
Таким образом, имея график зависимости (16.31), приведен-
ный на рис. 16.2, можно произвести пересчеты в соответствии с
431
формулой (16.38) и построить график зависимости (16.37). При
этом не нужно прибегать к пересчету всех опытных данных, дос-
таточно на рис. 16.2 по горизонтальной оси вместо величин Re#
отложить найденные величины Re.
Остается выяснить роль числа Эйлера в первой и во второй
задачах. Для ответа на этот вопрос можно было бы воспользо-
ваться уравнением Бернулли (16.26), однако, при этом потребу-
ются громоздкие преобразования. Выберем, как и ранее, плос-
кость сравнения совпадающей с центром отверстия, составим
уравнение Бернулли для двух сечений: одно совпадает со сво-
бодной поверхностью жидкости в резервуаре, другое совмещено
с плоскостью, в которой находится отверстие внутри резервуара.
Обозначим давление во втором сечении р2 , местными потерями
напора будем пренебрегать, получим:
2
Н + (16.38)
Pg Pg 2g
где и0 -скорость течения в отверстии. Введем обозначение:
АН = Н + ——— . Получим в результате известных преобразо-
pg
ваний:
АН АР . D А „ с «о Q2
^„Eu = —AP = pgAH, Fr = —= ——.
“ohr ри0 g«o f’oga'o
16.4. Моделирование истечений через малые отверстия
В [5] отмечено, что на величину коэффициента расхода при
истечении струи из малого отверстия в стенке резервуара влияет
432
поверхностное натяжение. На основании выполненных опытов
это было обнаружено в том случае, если диаметр круглого отвер-
стия равен или меньше Зсм . Такие отверстия названы малыми. В
таком случае явление должно зависеть от числа Вебера. Если
принять в качестве характерной скорости фрагмент, имеющий
размерность скорости, равный ^2gH, то число Вебера запишется
в таком виде: We# = , где о - коэффициент поверхност-
ст
ного натяжения (единица измерения Н/м, или дн/см ).
В первой задаче число Вебера является критерием, так как
напор Н по условию задачи является величиной заданной. Но
тогда в задаче имеется два критерия: Рейнольдса и Вебера, и кри-
териальное уравнение станет таким:
p = F(Re#, We#). (16.39)
График зависимости (16.39), полученный в результате обра-
ботки опытных данных автора и других исследователей, зани-
мавшихся истечением различных жидкостей через малые отвер-
стия в стенке резервуара, приведен в [5, рис.9.9, с. 180]. Опытные
данные вполне закономерно следуют этой зависимости.
Во второй задаче задан расход жидкости, вытекающий из
малого отверстия, нужно определить напор. Здесь в качестве кри-
терия выступают число Рейнольдса Re и число Вебера в еле-
Л д
дующем виде We = — Критериальное уравнение можно за-
®0о
писать так:
p = F(Re, We). (16.40)
433
Найдем связь между двумя рассмотренными здесь крите-
риями Вебера:
We = &А = = ц2 We^
®qO о
Таким образом, график зависимости (16.39) можно после
пересчетов критериев Рейнольдса и Вебера, используя данные,
приведенные в [5, рис.9.9, с.180], представить в виде графика за-
висимости (16.40).
434
Библиографический список
1. Аверкиев А.Г. Методика исследований безнапорных по-
токов на напорных моделях. - М.-Л.: Госэнергоиздат, 1957.
-35 с.
2. Аверкиев А.Г. Новый метод гидравлических модельных
исследований. // Известия ВНИИГ им. Б.Е. Веденеева. - Т.47.
- 1952.-С.3-20.
3. Айвазян О.В. Новый анализ аргументов равномерного
движения жидкости и его прикладные результаты. Материалы
научно-технической конференции: Проблемы гидравлики гидро-
технических сооружений и потоков в открытых руслах (ГТС-
2000). - СПб.: Издат. ВНИИГ им. Б.Е. Веденеева. - 2000. - С.58-
59.
4. Алибеков А.К., Михалев М.А. Условия начала трогания
несвязных грунтов. Сборник научных трудов: «Гидравлика ру-
словых потоков». - Калинин.: Издат. КИИ. - 1986. - С.8-14.
5. Альтшуль А.Д. Гидравлические сопротивления. -М.: Не-
дра, 1982. - 224 с.
6. Апухтин П.А., Войткунский Я.И. Сопротивление воды
движению судов. - М.-Л.: Машгиз, 1953. - 356 с.
7. Васильченко Г.В. Моделирование гидравлических сопро-
тивлений пойменным потокам равнинных рек. // Мелиорация и
водное хозяйство. - Вып. 50. - 1980. - С.68-75.
8. Великанов М.А. Динамика русловых потоков. -М.: Гос-
издат. технико-теорет. литерат., 1954. Том 1 - 323 с.,1955.
Том 2 - 323 с.
9. Веников В.А., Веников Г.В. Теория подобия и моделиро-
вания. - М.: Высш, шк., 1984. - С.3-197.
10. Высоцкий Л.И. Управление бурными потоками на водо-
сбросах. - М.: Энергоиздат., 1990. - С.41-45.
435
И. Ганкевич М.Я. Затопленный донный гидравлический
прыжок при сопряжении бьефов с помощью водослива практиче-
ского профиля. // Труды СПбГТУ-№ 475. Сборник научных
трудов: Энергетика, гидротехника. - СПб.: Издат.
СПбГТУ. - 1998. - С.102-110.
12. Гиляров Н.П. Моделирование речных потоков.-Л.:
Гидрометеоиздат., 1973. - 200 с.
13. Гиргидов А.Д. Техническая механика жидкости и газа.
- СПб.: Издат. СПбГТУ, 1999. - 395 с.
14. Емцев Б.Т. Двухмерные бурные потоки.-М.: Энергия,
1967.-С.7-30.
15. Емцев Б.Т, Техническая гидромеханика. -М.: Машино-
строение, 1987 - 439 с.
16. Зегжда А.П. Теория подобия и методика расчета гидро-
технических моделей. - Л.-М.: Госстройиздат., 1938. - 162 с.
17. Ибад-Заде Ю.А., Шеренков И.А. Новые данные о сопро-
тивлениях в открытых потоках. // Труды ин-та ВОДГЕО. - Вып
26.- 1970.-С.22-43.
18. Коппель Т.А., Лийв У.Р. Экспериментальное исследова-
ние возникновения движения жидкости в трубопроводах. // Изв.
АН СССР. МЖГ. - № 6. - 1977. - С.77-85.
19. Кочина П.Я., Кочина Н.Н. Гидромеханика подземных
вод и вопросы орошения. - М.: Физматлит.,1994. - С.25-28.
20. Кумина Т.Д., Михалев М.А. Инженерная гидрология:
Учеб, пособие. - Л.: Издат. ЛПИ, 1989. - 84 с.
21. Леви И.И. Моделирование гидравлических явле-
ний. - Л.: Энергия, 1967. - 235 с.
22. Лойцянский Л.Г. Механика жидкости и газа. - М.: Нау-
ка, 1973. - С.421-433, 612-694.
436
23. Лятхер В.М., Прудовский А.М. Гидравлическое модели-
рование. - М.: Энергоатомиздат., 1984. - 392 с.
24. Лятхер В.М., Прудовский А.М. Исследования открытых
потоков на напорных моделях. - М.: Энергия, 1971. - 288 с.
25. Марченко А.С. Сопротивление цилиндрических тел типа
опор при обтекании открытым водным потоком // Изв. ВНИИГ
им. Б.Е. Веденеева. - Т.108. - 1975. - С.48-54.
26. Михалев М.А. Гидравлический прыжок на гладком го-
ризонтальном дне в условиях плоской задачи. Материалы конфе-
ренций и совещаний по гидротехнике: Методы исследований и
гидравлических расчетов водосбросных гидротехнических со-
оружений. - Л.: Энергоатомиздат. Ленингр. отд-ние, 1985.
-С.219-226.
27. Михалев М.А. Гидравлический расчет потоков с водово-
ротом. - Л.: Энергия. Ленингр. отд-ние, 1971. - 184 с.
28. Михалев М.А. Дифференциальные уравнения и инте-
гральные соотношения движения вязкой тяжелой жидкости в от-
крытом русле. Сборник «Русловые процессы и методы их моде-
лирования». - Л.: Энергия, 1977. - С.30-38.
29. Михалев М.А. К вопросу о движении воды под ледяным
покровом. // Известия ВНИИГ им. Б.Е. Веденеева: Гидравлика
сооружений в эксплутационный и строительный периоды. - Т.
208. - 1988. - С.49-55.
30. Михалев М.А. К вопросу о сопротивлении открытых ру-
сел с неоднородной шероховатостью ложа. // Известия ВНИИГ
им. Б.Е. Веденеева: Сборник научных трудов. - Т.
145.- 1982.-С.100-105.
31. Михалев М.А. К расчету первого критического режима
поверхностного прыжка (плоская задача). // Гидротехническое
строительство. - № 11. - 1969. - С.49-51.
437
32. Михалев М.А. К теории донного гидравлического прыж-
ка на шероховатом водобое. // Известия ВНИИГ им.
Б.Е. Веденеева. - Т. 92. - 1970. - С.223-233.
33. Михалев М.А. К теории донного гидравлического прыж-
ка. И Известия ВНИИГ им. Б.Е. Веденеева. - Т. 78. - 1965.
-С.117-141.
34. Михалев М.А. К теории поверхностного гидравлическо-
го прыжка (1-й критический режим, плоская задача). // Известия
ВНИИГ им. Б.Е. Веденеева. - Т. 90. - 1969. - С.225-234.
35. Михалев М.А. Материалы по моделированию некоторых
видов движения вязкой жидкости. // Известия ВНИИГ им.
Б.Е. Веденеева. - Т.108. - 1975. - С.27-39.
36. Михалев М.А. О сопротивлении ложа и распределении
касательных напряжений в руслах различного поперечного сече-
ния. Межвузовский научный сборник: «Гидравлические исследо-
вания сооружений. Очистка жидкостей». - Саратов.: Издат. СПИ,
1981.-С.98-115.
37. Михалев М.А. Теория подобия и размерностей: Учеб,
пособие. - СПб.: Издат. СПбГТУ, 2001 - 68 с.
38. Михалев М.А., Ганкевич М.Я. Затопленный донный гид-
равлический прыжок при сопряжении бьефов с помощью водо-
слива практического профиля. // Известия ВНИИГ им.
Б.Е. Веденеева. - Т. 236. - 2000. - С.64-73.
39. Михалев М.А., Хапаева А.К., Янковский Н.Б. Гидравли-
ческие сопротивления русла с ледяным покровом и грядовым
рельефом дна. Сборник научных трудов: «Гидравлика русловых
и подземных потоков». - Тверь.: Издат. ТвеПИ, 1991. - С.49-54.
40. Нежиховский Р.А. Река Нева.-Л.: Гидрометеоиздат.,
1973.-192 с.
438
41. Орлов В.Т. Основы теории размерностей и подобия. Мо-
делирование гидравлических явлений: Учеб, пособие.-Л.: Из-
дат. ЛПИ, 1990. - 83 с.
42. Основы теории подобия и моделирования (терминоло-
гия). - М.: Наука, 1973. 21с.
43. Павлов С.Я., Хапаева А.К., Янковский Н.Б. Сопротивле-
ния потоку под ледяным покровом. Сборник научных трудов:
«Гидравлика сооружений». - Калинин.: Издат. КПИ, 1988.
- С.28-33.
44. Рахманов А.Н. О размерах гидравлического прыжка на
сильно шероховатом водобое. // Известия ВНИИГ им.
Б.Е. Веденеева. - Т. 73. - 1963. - С.45-59.
45. Рахманов А.Н. Очертание поверхностного водоворота и
транзитного потока и некоторые скоростные характеристики
донного гидравлического прыжка. // Известия ВНИИГ им.
Б.Е. Веденеева. - Т. 59. - 1958. - С.30-62.
46. Рахманов А.Н. Структура гидравлического прыжка на
сильно шероховатом водобое. // Известия ВНИИГ им.
Б.Е. Веденеева. - Т. 72. - 1963. - С.3-34.
47. Романов П.Г., Курочкина М.И. Гидромеханические про-
цессы химической технологии. - Л.: Химия, 1974. - С.107-133.
48. Саликов В.Г. Некоторые результаты экспериментальных
исследований взаимодействия руслового и пойменного потоков.
Труды IV Всесоюзного гидрологического съезда. - Л.: Гидроме-
теоиздат., 1976. - Т. II. - С.75-84.
49. Саликов В.Г. О русловом процессе на меандрирующих
реках в условиях выхода воды на пойму. Сборник научных тру-
дов: «Гидравлика сооружений и русловые процес-
сы». - Калинин.: Издат. КПИ, 1982. - С. 19-24.
439
50. Седов Л.И. Методы подобия и размерности в механике.
- М.: Наука, 1977. - С. 1-32.
51. Синотин В.И. О распределении скоростей в потоке при
наличии ледяного покрова. // Гидротехническое строительство.
-№2. - 1967.-С.29-31.
52. Складнее М.Ф. Граница поверхностно-донного режима
при сопряжении бьефов водопропускных сооружений, оканчи-
вающихся низовым уступом. И Известия ВНИИГ им.
Б.Е. Веденеева. - Т. 55. - 1956. - С.75-96.
53. Складнев М.Ф. О границах критических режимов по-
верхностного прыжка. И Известия ВНИИГ им. Б.Е. Ведене-
ева. - Т. 58. - 1958.-С.64-85.
54. Складнев М.Ф. О длине водоворотного участка поверх-
ностного и поверхностно-донного гидравлических прыжков.
// Известия ВНИИГ им. Б.Е. Веденеева. - Т. 55. - 1956. - С.176-
187.
55. Скребков Г.П. О проблеме гидравлического сопротивле-
ния призматических русел и путях ее решения. // Промышленная
теплотехника и гидравлика. Чебоксар. - Вып.4. - 1978. - С.3-46.
56. Coy С. Гидродинамика многофазных систем. Пер. с
англ. -М.: Мир, 1971. - С.29-59, 167-169, 201-209.
57. Теории подобия и размерностей. Моделирование /
П.М.Алабужев [и др.]. - М.: Высш, шк., 1968. - С.3-35.
58. Фабрикант Н.Я. Аэродинамика. - М.: Наука, 1964.
-814 с.
59. Хапаева А.К. Гидравлический прыжок на гладком и ше-
роховатом дне как пристенная струя. // Известия ВНИИГ им.
Б.Е. Веденеева. - Т. 92. - 1970. - С.234-245.
60. Чугаев Р.Р. Гидравлика. - Л.: Энегоиздат., Ленингр.
отдел., 1982. - 627 с.
440
61. Шарп Дж. Гидравлическое моделирование: Пер. с
англ. - М.: Мир, 1971. - 280 с.
62. Шлихтинг Г. Теория пограничного слоя. -М.: Наука,
1969.-737 с.
63. Штеренлихт Д.В. Гидравлика - М.: Энергоатомиздат,
1991. Кн. 1.-351 с., 1991. Кн. 2.-367 с.
64. Эббот М.Б. Гидравлика открытого потока. Вычисли-
тельная гидравлика. Пер. с англ. ~М.: Энергоатомиздат., 1983.
- С.34-53.
65. Barr D.I.H. A New Approach to Fully Graphical (Dimen-
sional) Solution of the Colebrook - White Function. - J. Inst. Water
Eng. and Scientists. № 1. 1978. pp. 19-30.
66. Blau E. Die Verteilung der Wandschubspannung in offenen
Gerinnen. - Schriftenreie “Wasser- und Grundbau”. Mitteilungen der
Forschugsanstalt fur Schiffahrt, Wasser- und Grundbau. Heft 29. Ber-
lin. 1971. ss. 5-188.
67. Bursali. Schubspannungmessung an der Sohle eines offenen
Kanals. - Proceedings of the XII Congress Intern. Assoc, for Hydr.
Research. Vol. 1. 1967. pp. 194-204.
68. Einstein H.A. Formulas for the transportation of Bed-
Load. - Transactions ASCE. Vol. 107. 1942. pp. 561-597.
69. Graf W.H. Hydraulics of Sediment Transport. McGraw-Hill
Book Company. New York. 1970. p. 513.
70. Johnson I.W. The importance of Side-Wall friction in bed-
load investigations. - Civil Engineering ASCE. Vol. 102. № 6. June.
1942. pp. 329-331.
71. Rajagopalan K.S. Boundary Sheer Distribution in Elliptical
and Cosine Curved Channel Sections. - Irrigation and Power. January.
1975. pp. 45-54.
441
72. Schields A. Anwendung der Ahnlichkeitmechanik und der
Turbulenzforschung auf die Geschiebebewegung. - Mitteilungen der
Preus. Versuchsanstalt fur Wasser- und Schiffbau. Heft 26. Berlin.
1936. s. 26.
73. Vanoni V.A. Li-San Hwang Relation between bed forms and
friction streams. - Pros, of ASCE. Journal of the Hydr. Division. Vol.
93. № HV3. May. 1967. pp. 121-144.
442
Михалев Михаил Андреевич
ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ГИДРАВЛИЧЕСКИХ ЯВЛЕНИЙ
Учебное пособие
Лицензия ЛР № 020593 от 07.08.97
Налоговая льгота — Общероссийский классификатор продукции
ОК 005-93, т. 2; 95 3005 — учебная литература
Подписано в печать 23.12.2008. Формат60x84/16. Печать цифровая.
Уел, печ. л. 27,75. Уч.-изд. л. 27,75, Тираж 100, Заказ 5965b.
Отпечатано с готового оригинал-макета, предоставленного автором,
в Цифровом типографском центре Издательства Политехнического
университета.
195251, Санкт-Петербург, Политехническая, 29.
Тел.: (812) 550-40-14
Тел./факс: (812) 297-57-76