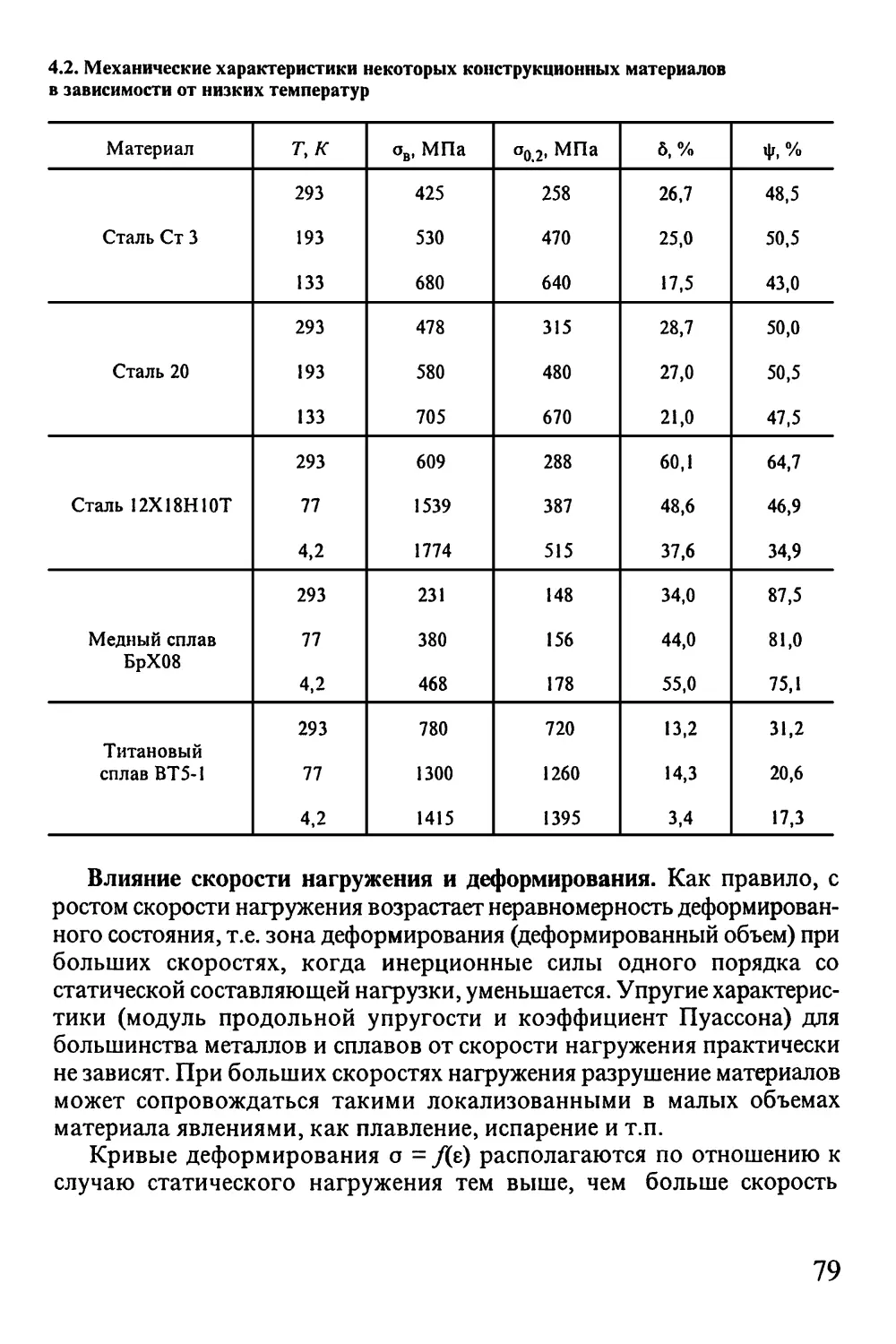
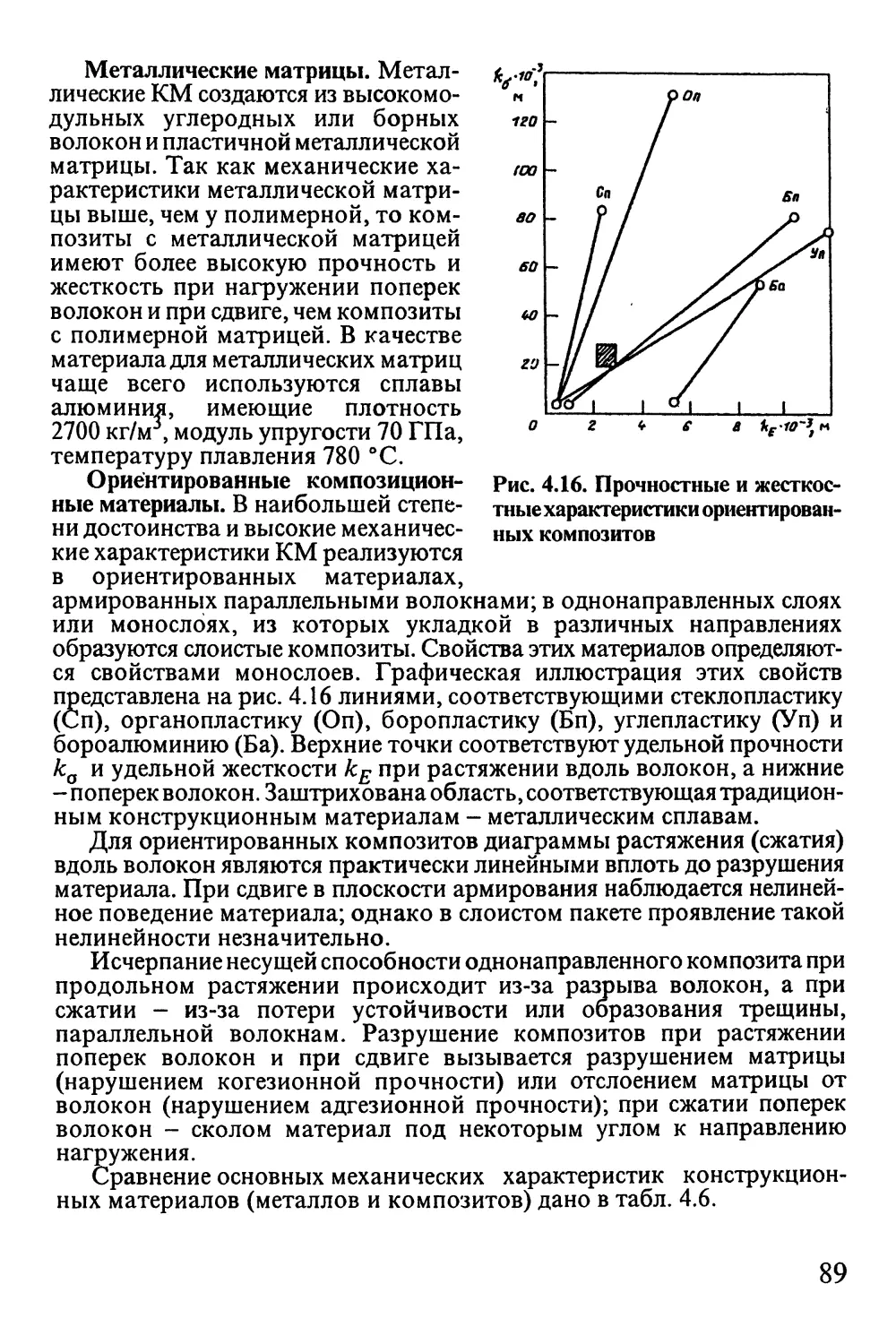
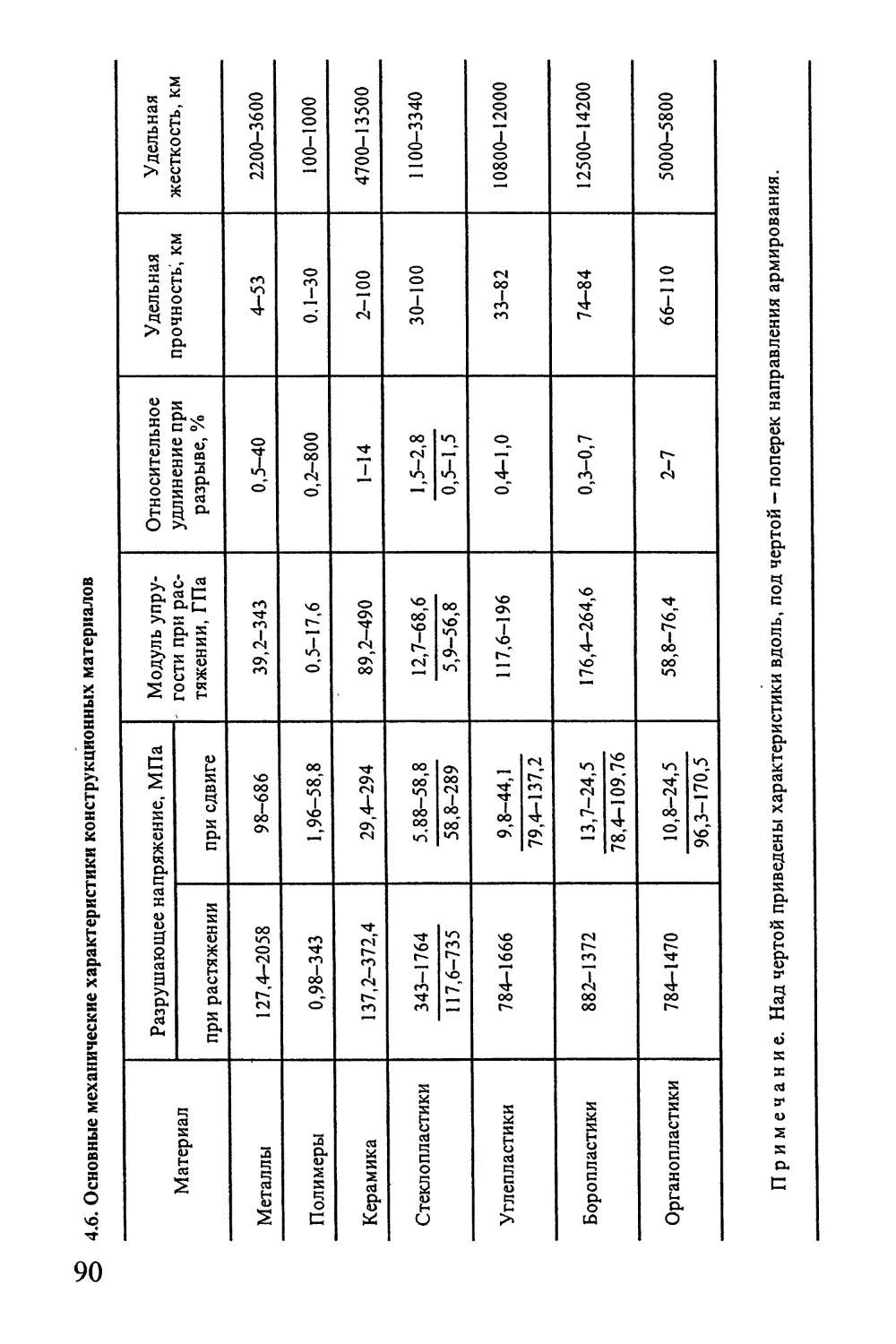
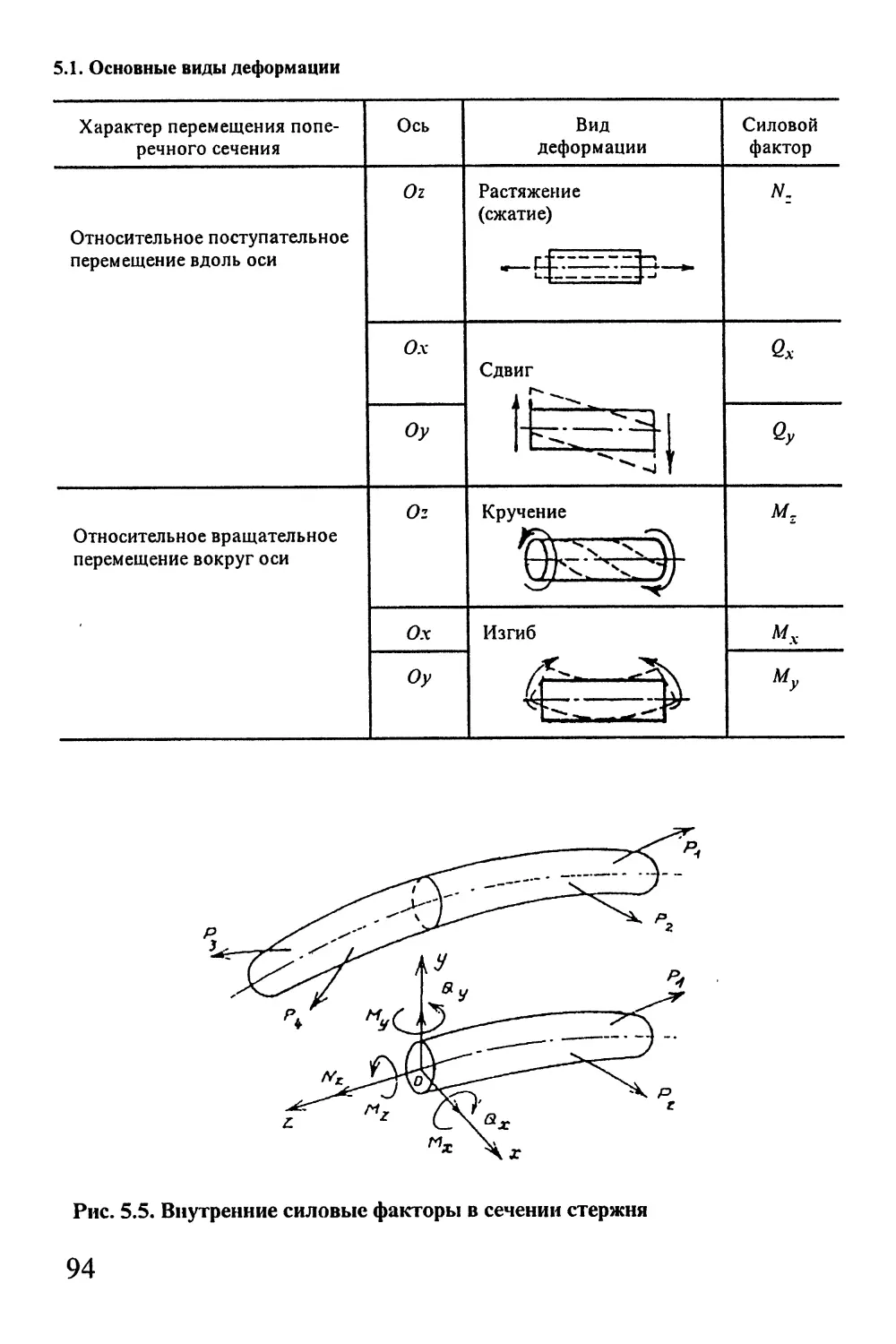
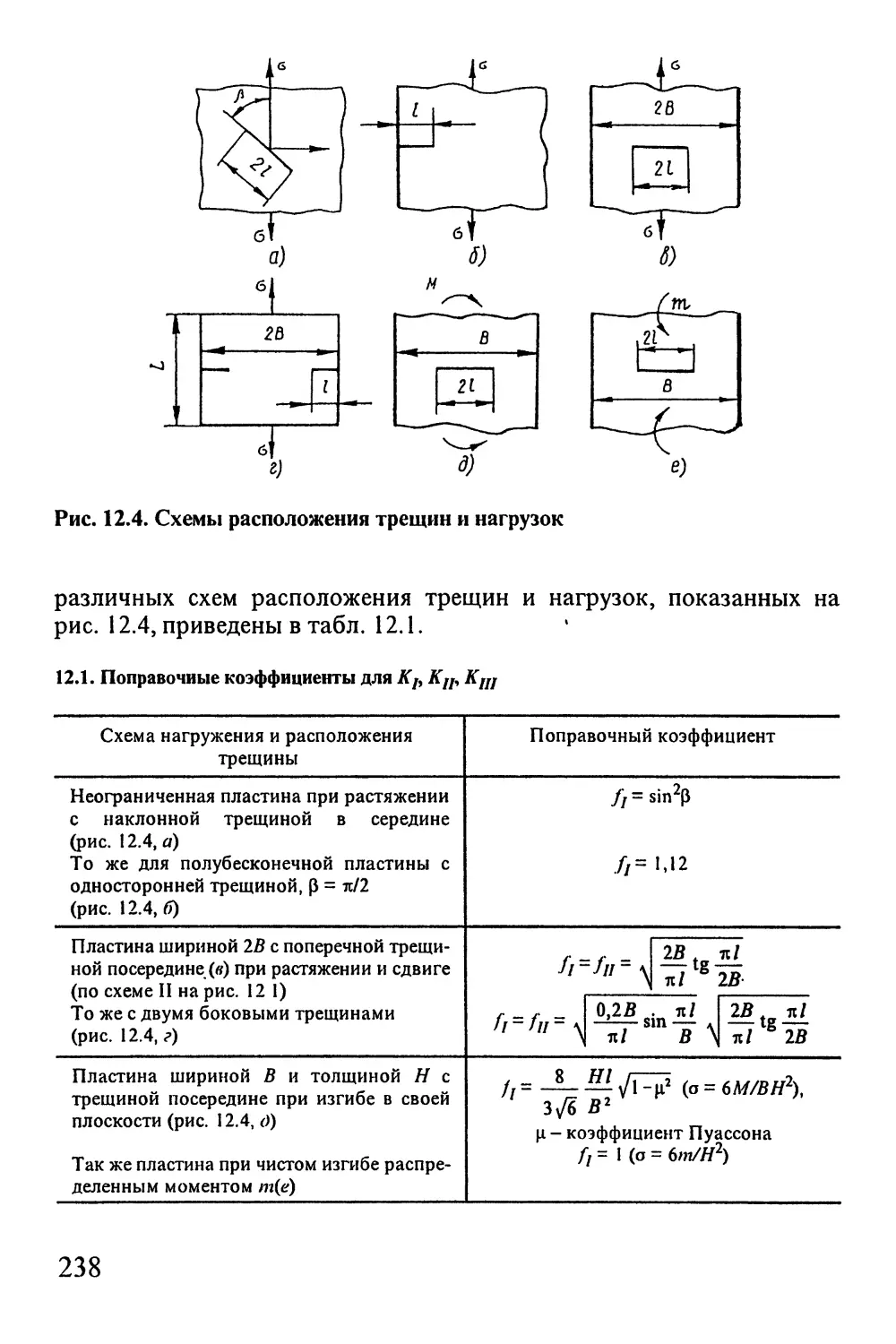
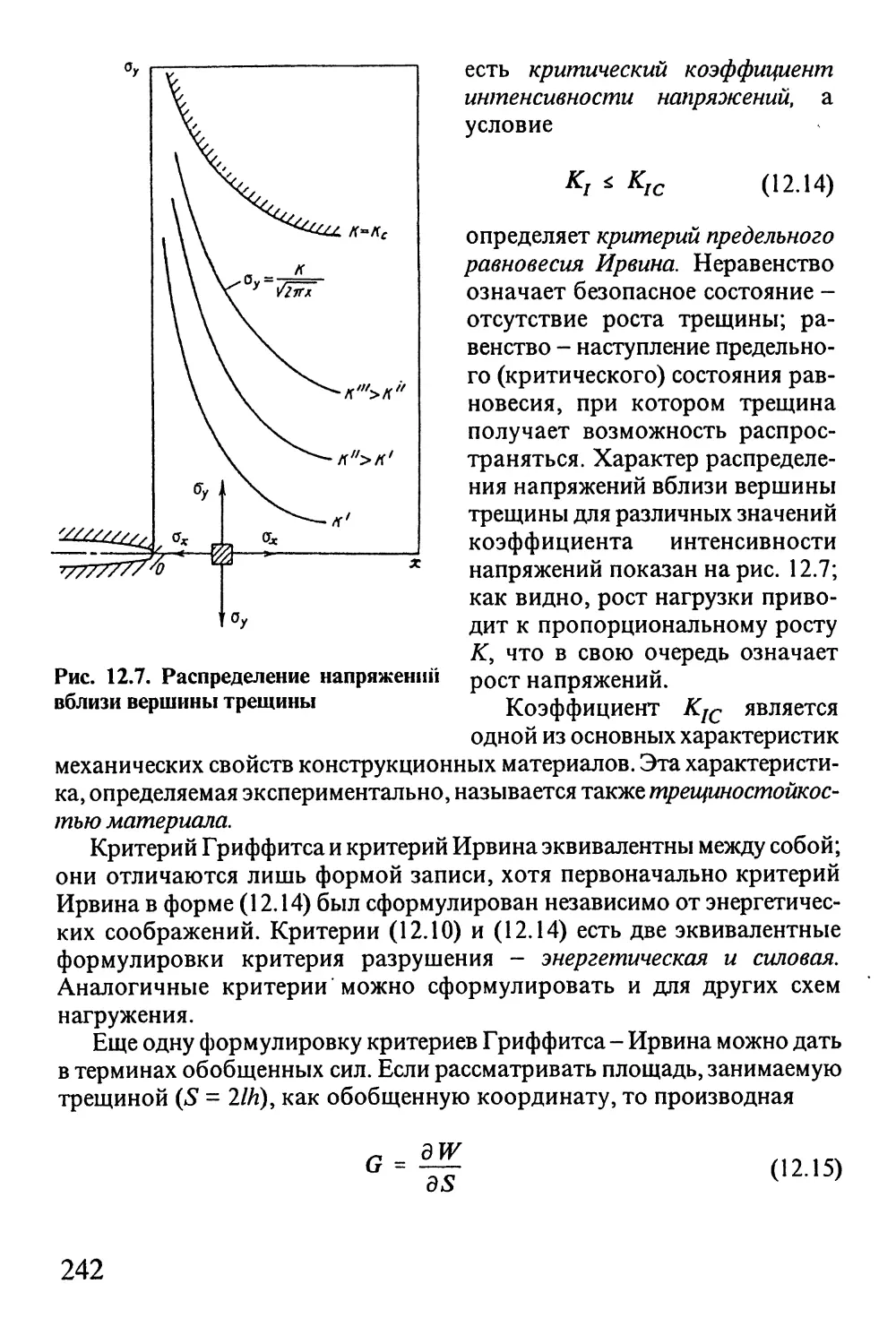
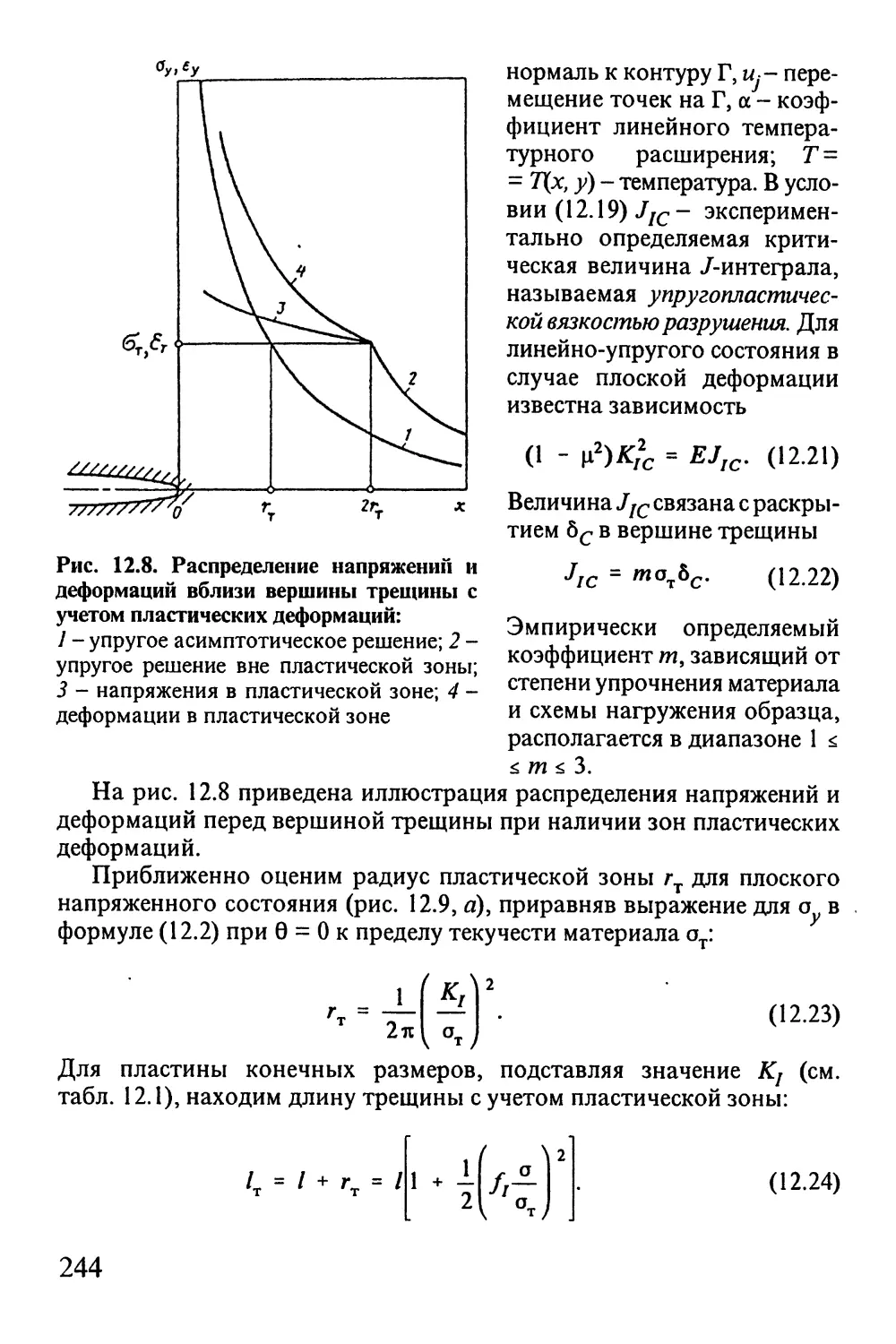
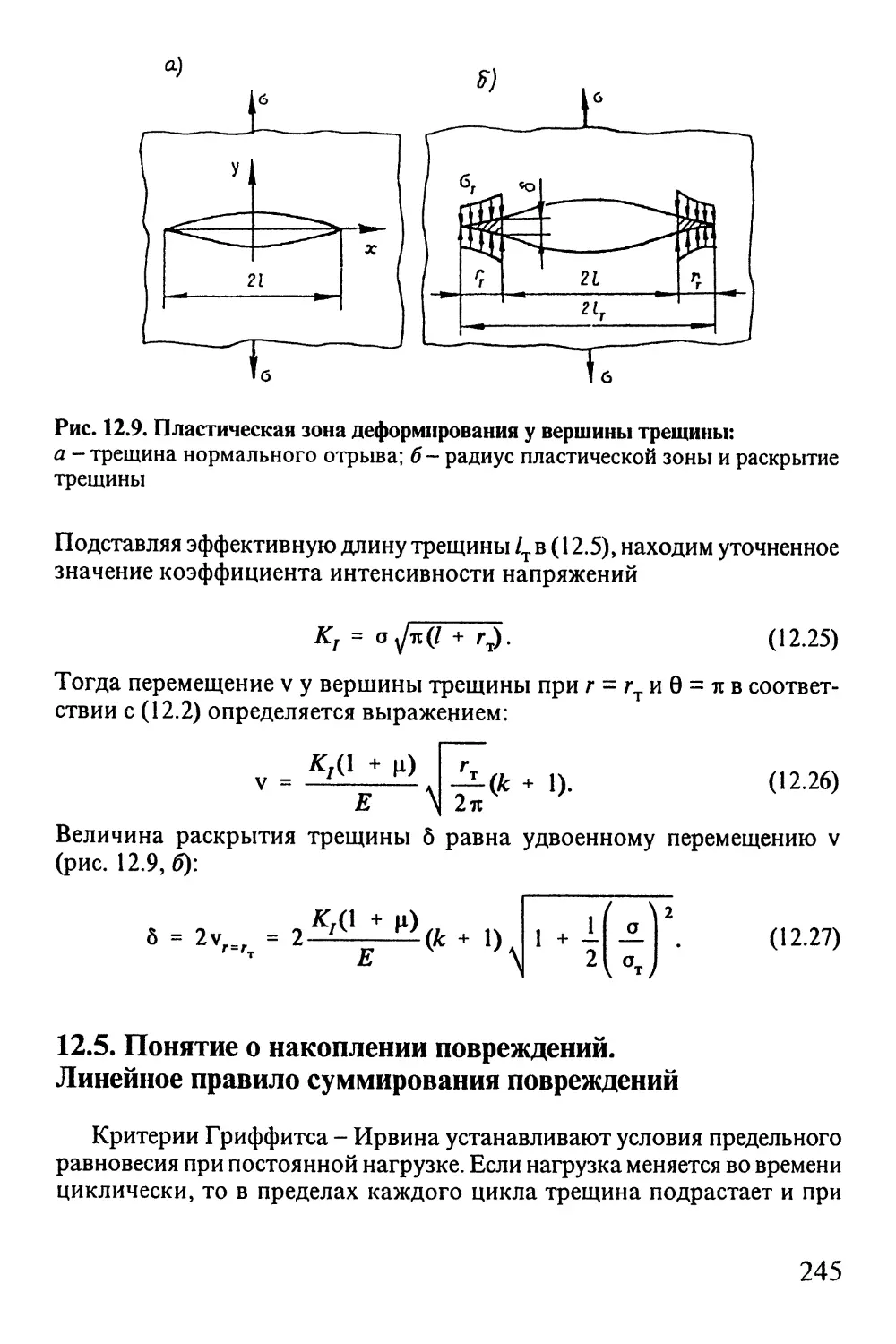
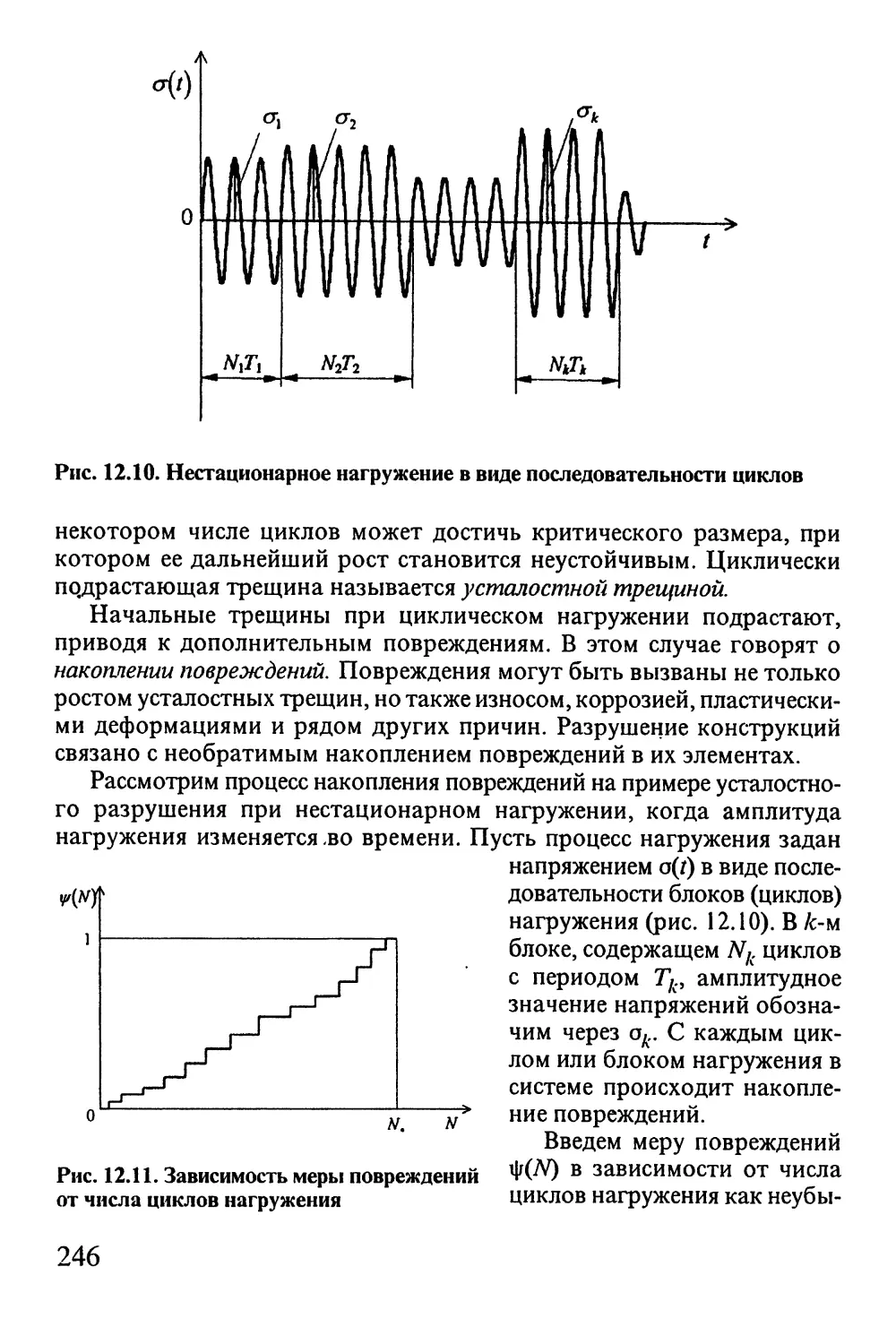
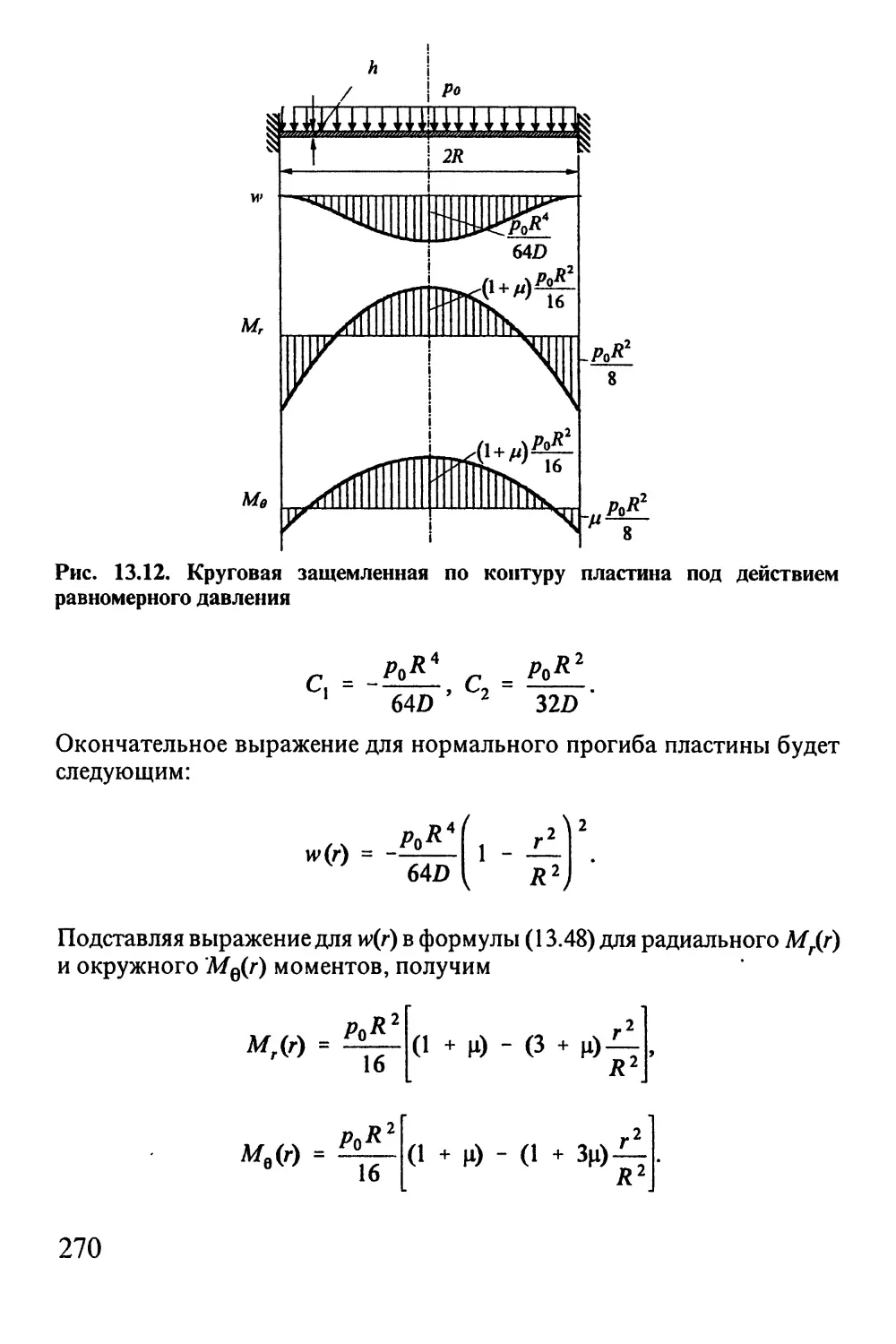
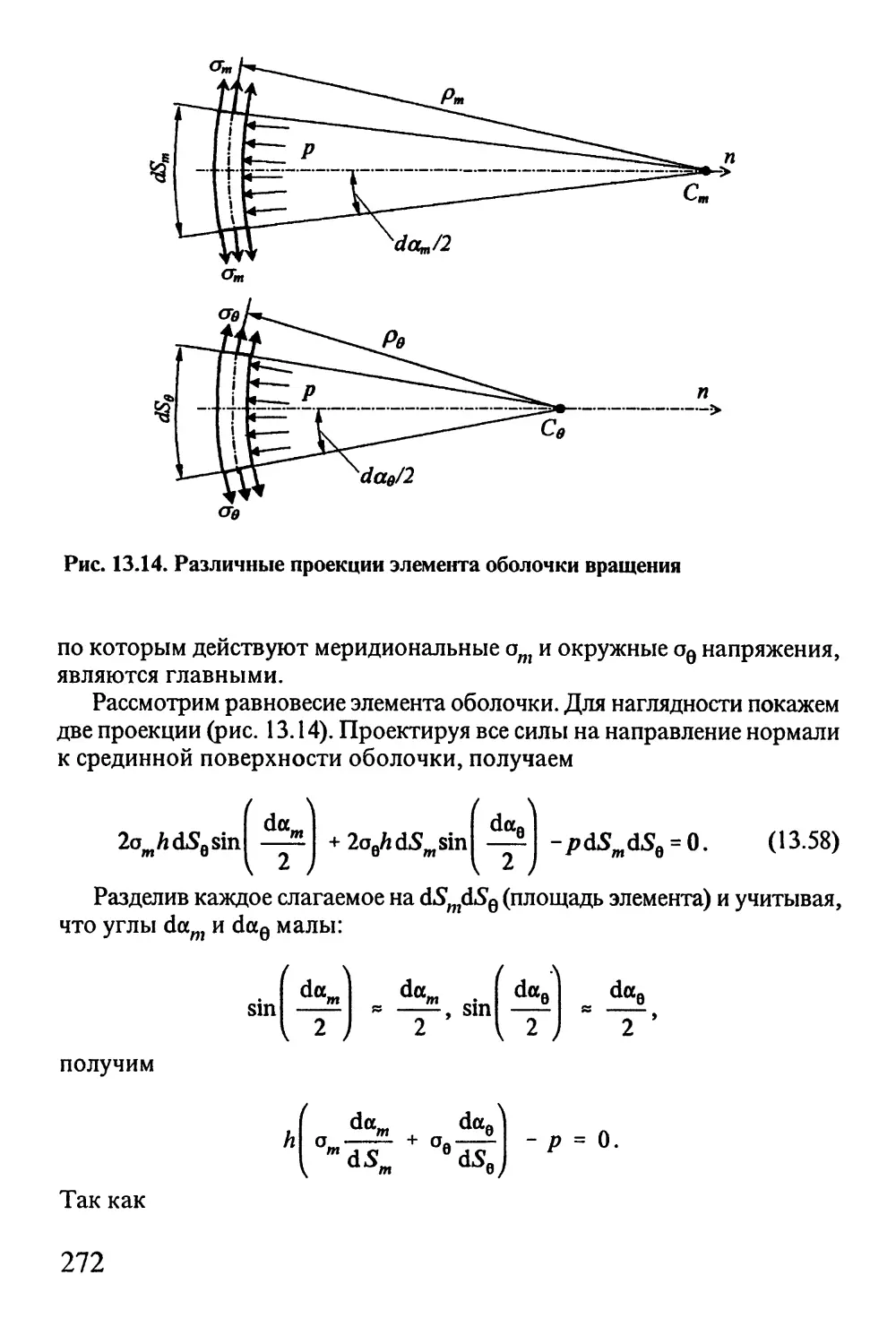
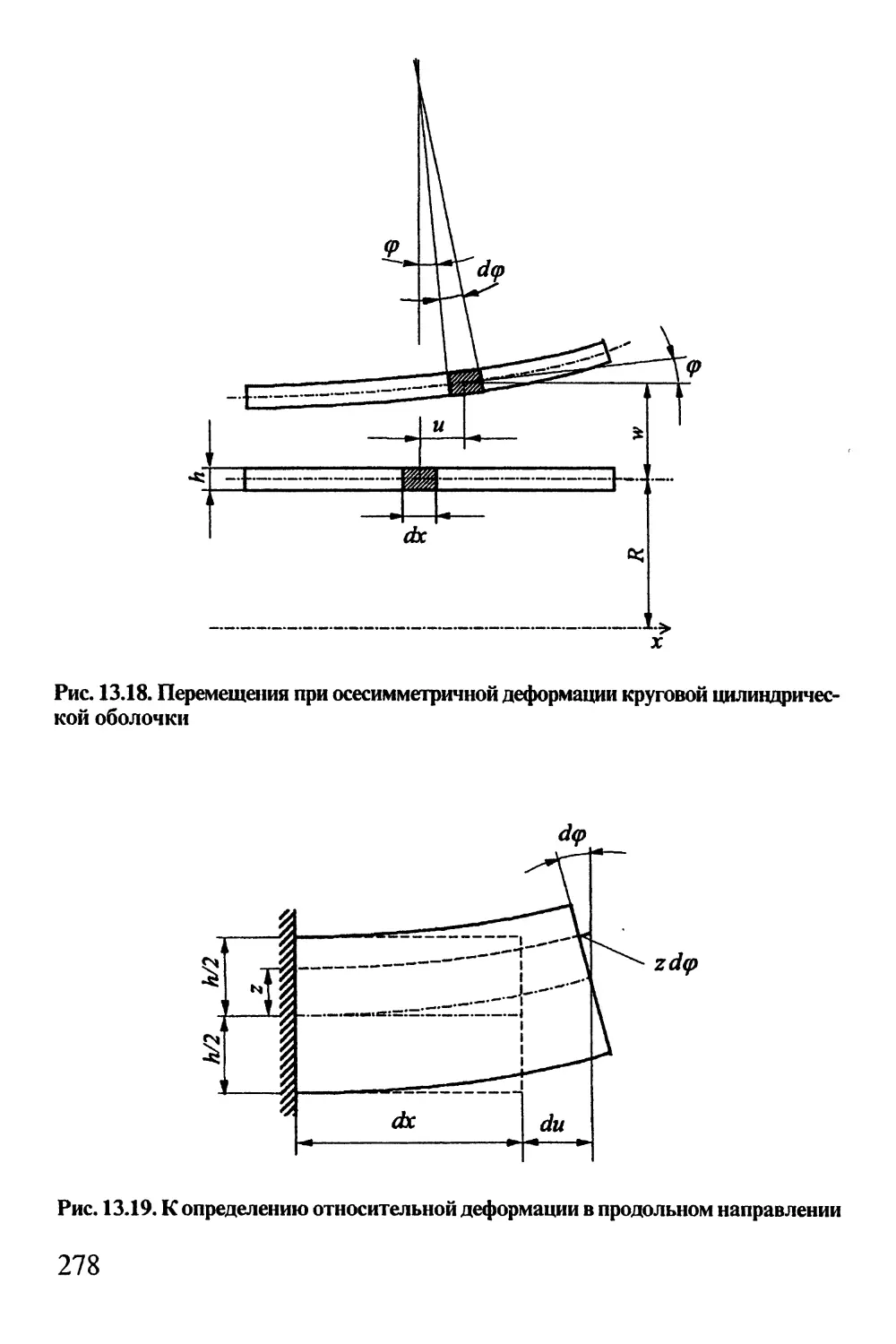
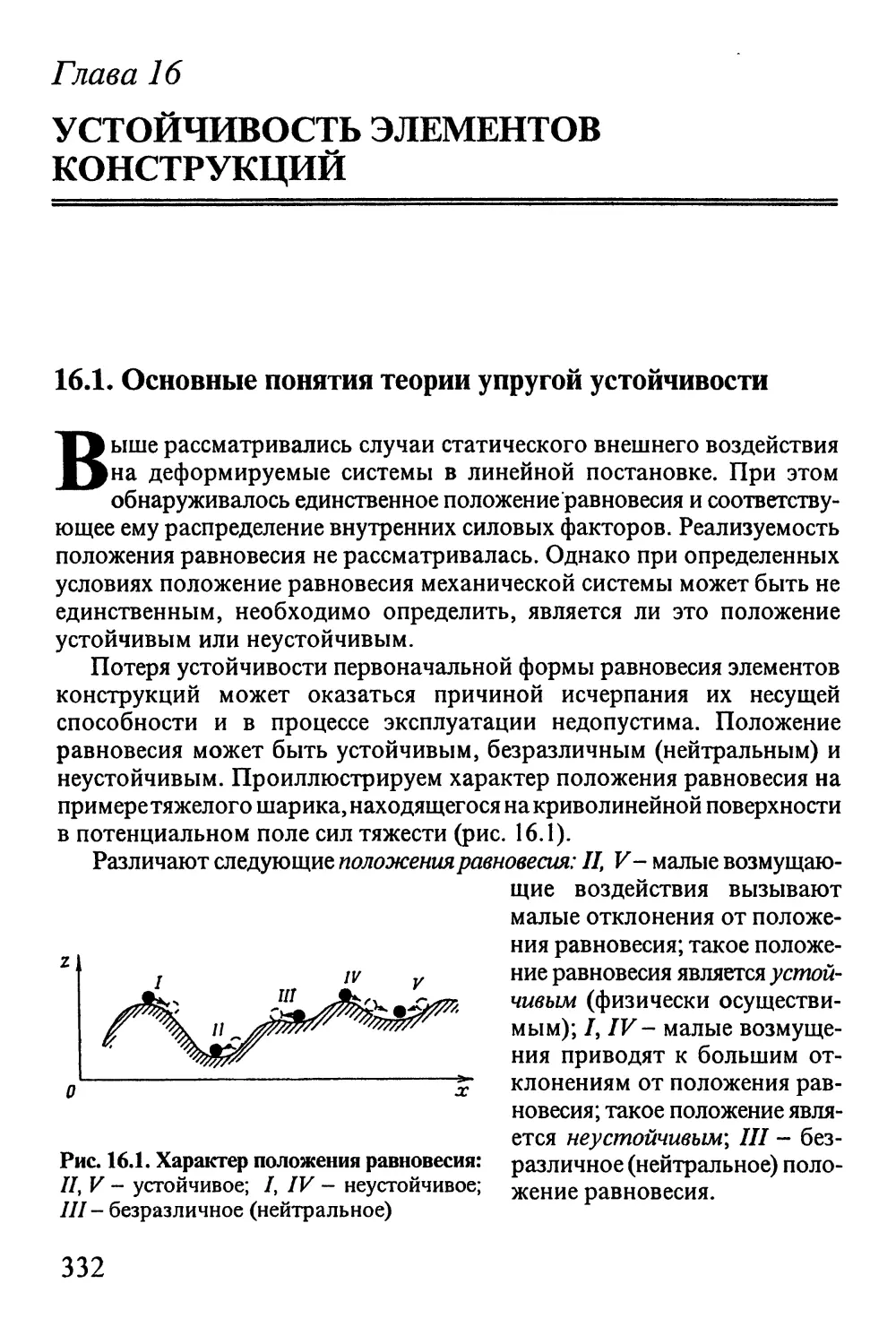
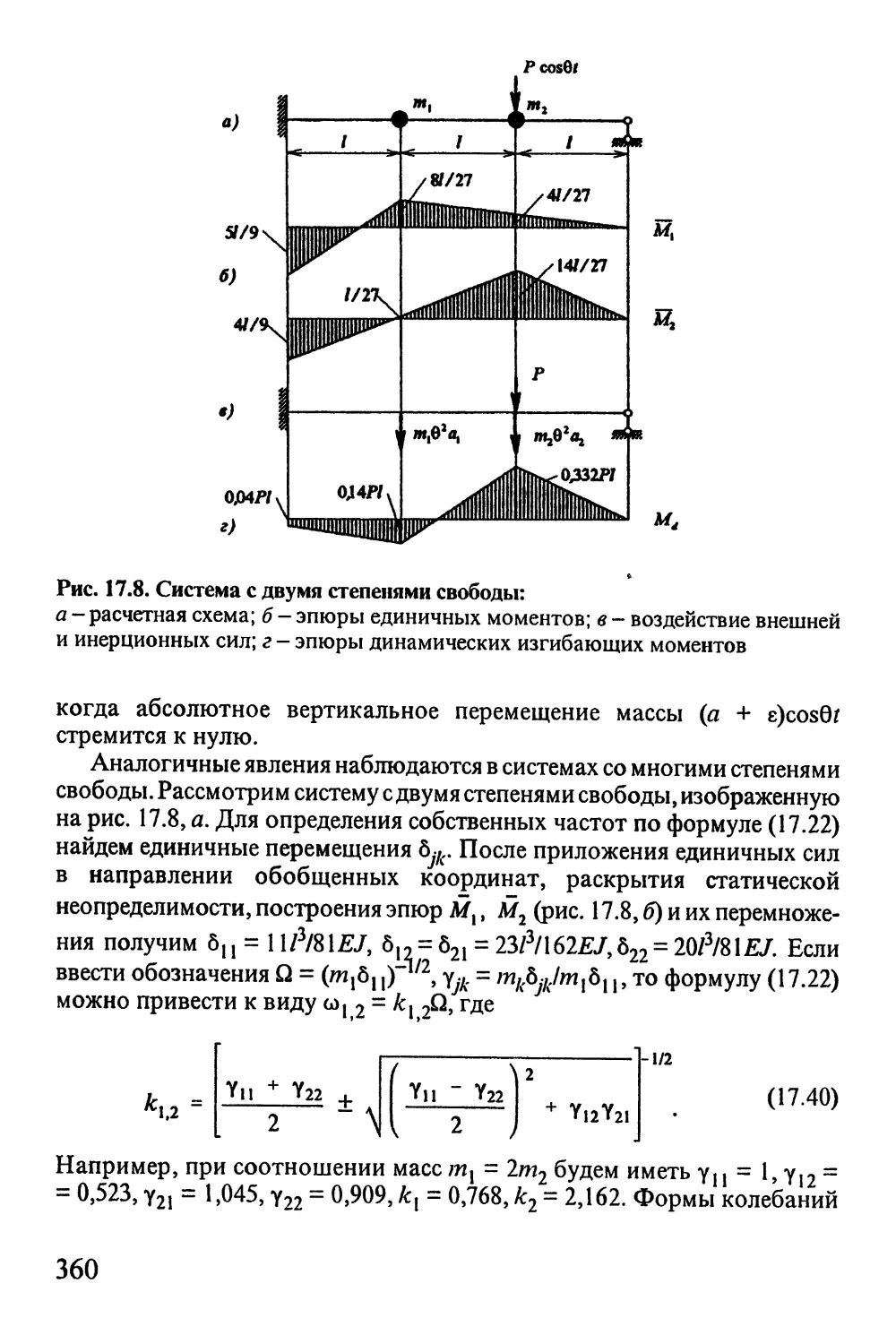
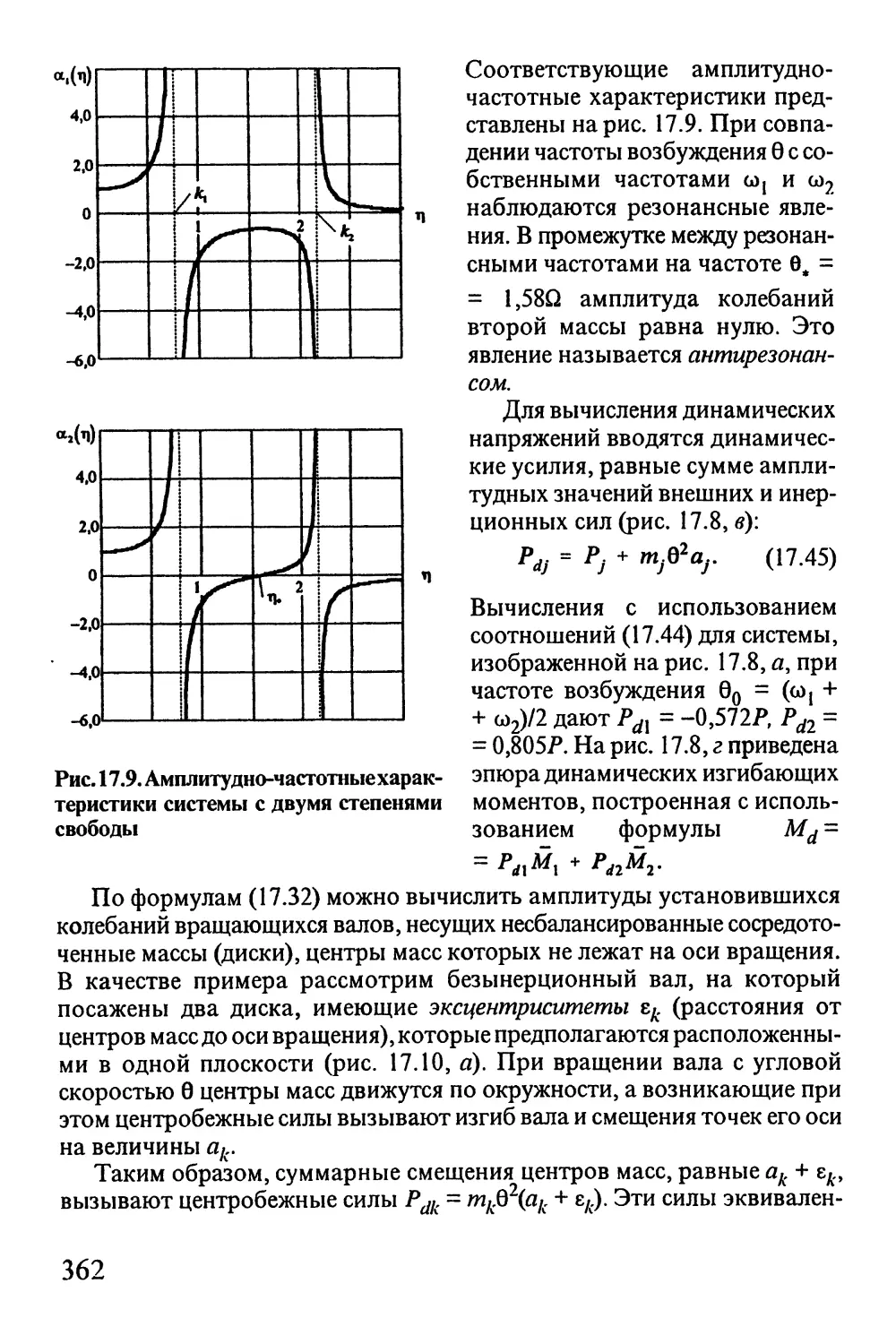
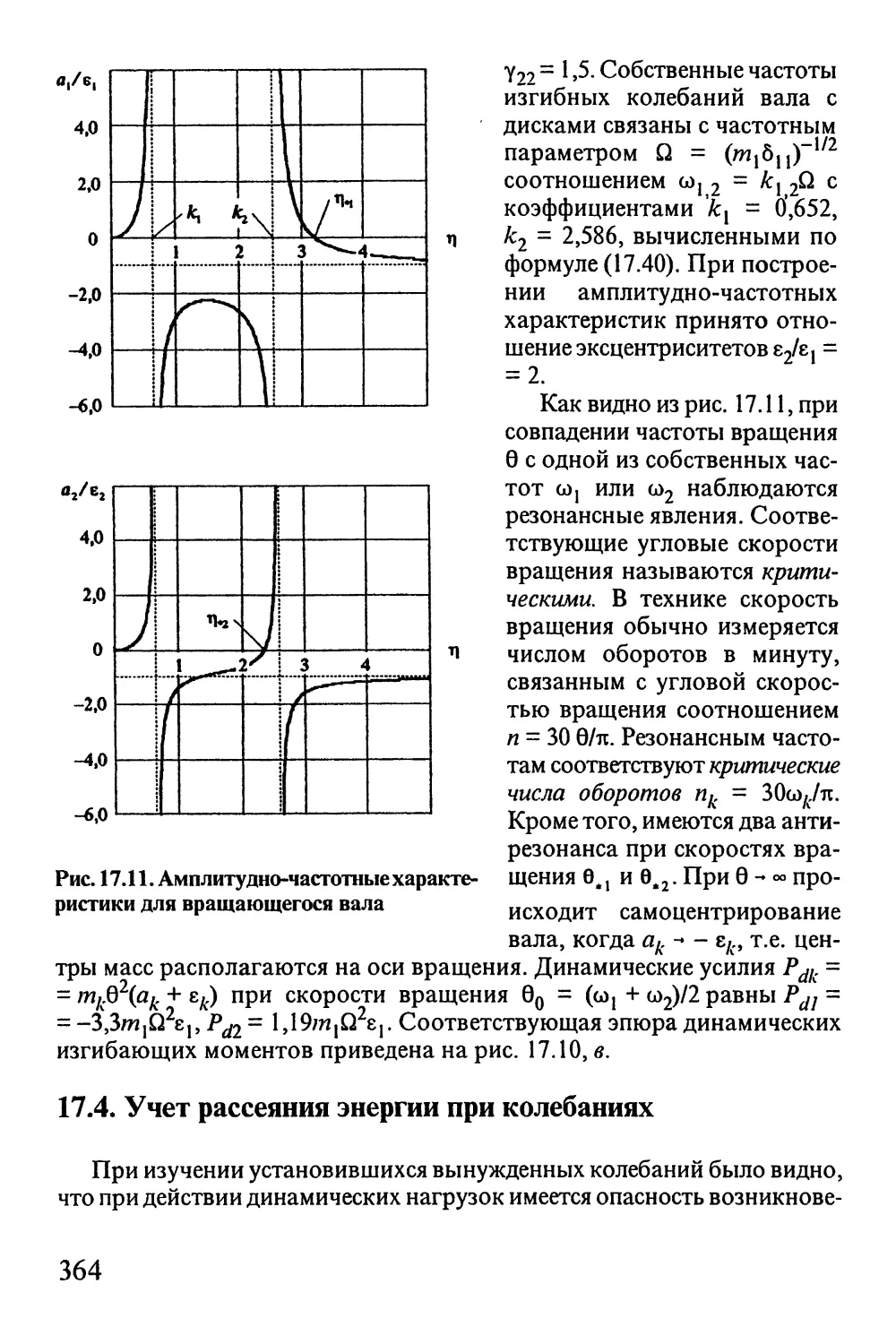
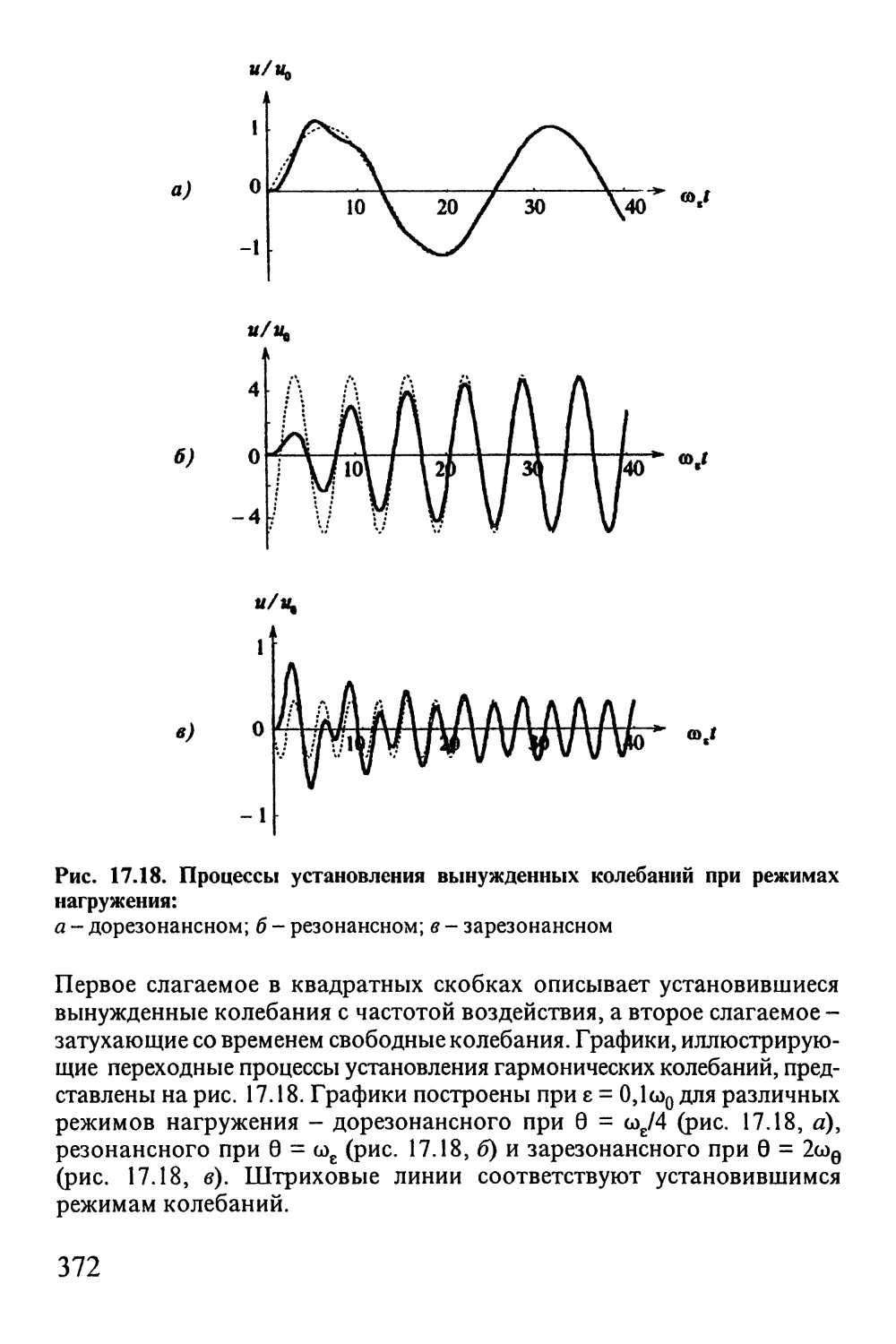
Автор: Окопный Ю.А. Радин В.П. Чирков В.П.
Теги: общее машиностроение технология машиностроения механика строительные конструкции теоретическая механика учебник для вузов издательство машиностроение
ISBN: 5-217-02974-9
Год: 2001
ДЛЯ ВУЗОВ
Ю.А. Окопный
В.П. Радин
В.П. Чирков
МЕХАНИКА
МАТЕРИАЛОВ
И КОНСТРУКЦИЙ
Допущено Министерством образования РФ
в качестве учебника для студентов
высших технических учебных заведений,
изучающих дисциплины
"Механика материалов и конструкций",
"Сопротивление материалов"
и родственные им дисциплины
МОСКВА
МАШИНОСТРОЕНИЕ •
2001
УДК 621.01(075.8)
ББК 22.21я73
0-51
Федеральная целевая программа книгоиздания России
Авторы: Ю.А. Окопный, В.П. Радин, В.П. Чирков
Рецензенты: В.В. Болотин, А.Г. Горшков,
В.Д. Потапов, В.А. Светлицкий, В.В. Харионовский
Механика материалов и конструкций: Учебник для вузов. -
0-51 М.: Машиностроение, 2001,-408 с.: ил.
Изложены современные методы расчета, обеспечивающие высокие
показатели механической надежности, долговечности и безопасности
инженерных конструкций, узлов и элементов оборудования.
Рассмотрены задачи прочности, устойчивости и колебаний стержней, элементы
теории пластин и оболочек, циклической и длительной прочности,
трещиностойкости.
Для студентов специальностей машиностроительного профиля,
инженерно-технических работников, занимающихся вопросами
обеспечения прочности в различных областях техники.
ISBN 5-217-02974-9 ББК 22.21я 73
© Издательство "Машиностроение", 2001
ОГЛАВЛЕНИЕ
Глава 1. ПРЕДМЕТ КУРСА "МЕХАНИКА МАТЕРИАЛОВ И
КОНСТРУКЦИЙ" 10
1.1. Введение 10
1.2. Модели и расчетные схемы конструкций 12
1.3. Основные гипотезы механики материалов
и конструкций 15
Глава 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НАДЕЖНОСТИ
КОНСТРУКЦИЙ 19
2.1. Общие сведения 19
2.2. Расчетные нагрузки и коэффициенты запаса 24
2.3. Расчеты по допускаемым нагрузкам и по
допускаемым напряжениям 27
Глава 3. ОСНОВЫ МЕХАНИКИ МАТЕРИАЛОВ 30
3.1. Понятие о напряжениях и деформациях 30
3.2. Напряженное состояние в точке. Тензор напряжений 32
3.3. Свойства тензора напряжений. Главные напряжения 34
3.4. Плоское напряженное состояние 40
3.5. Тензор деформаций 42
3.6. Упругость и пластичность. Закон Гука 45
3.7. Потенциальная энергия упругой деформации 52
3.8. Основы теории прочности 55
3.9. Критерии текучести и хрупкого разрушения 58
Глава 4. МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ 66
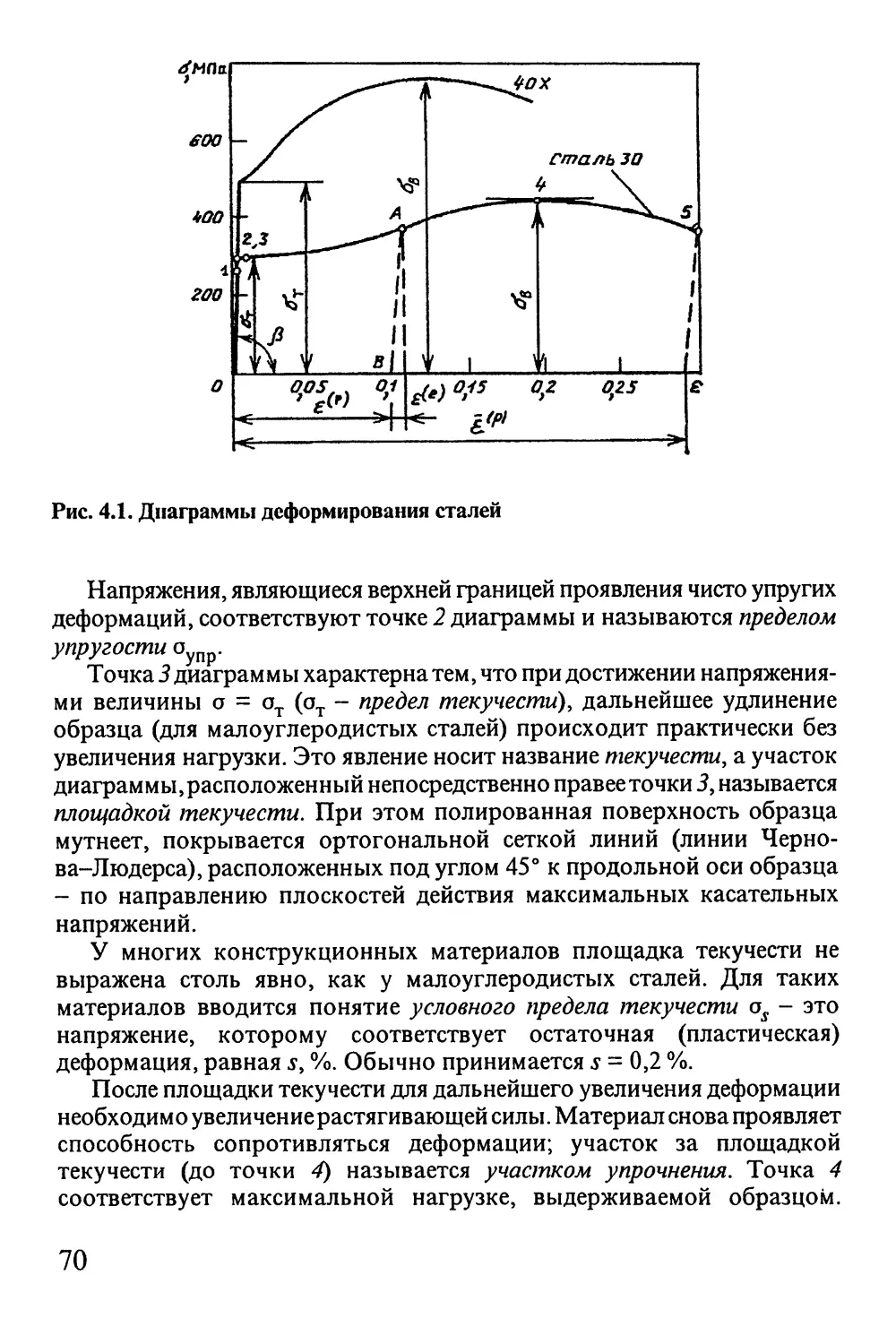
4.1. Механические состояния деформируемых тел 67
4.2. Диаграммы упругопластического деформирования
конструкционных материалов 69
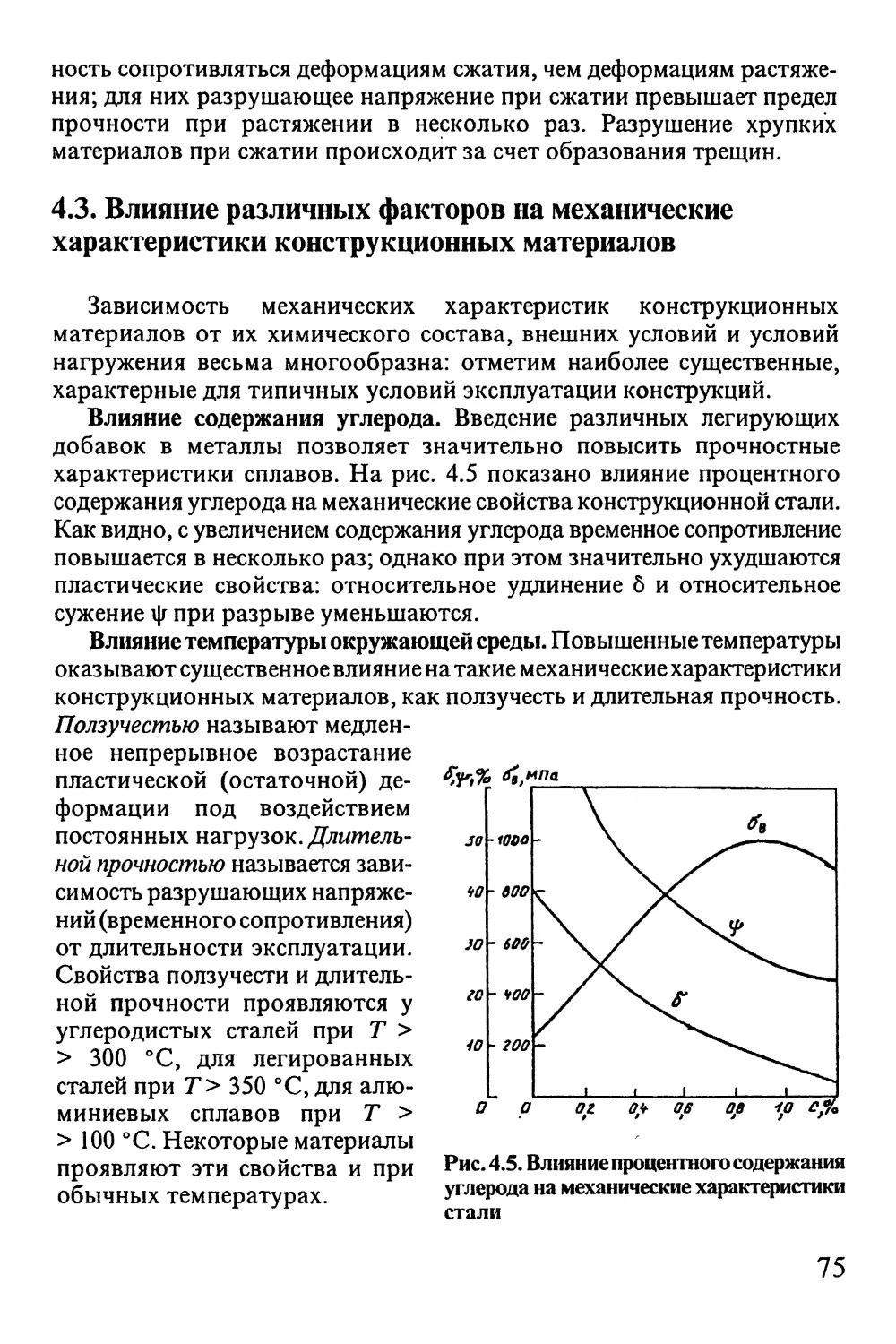
4.3. Влияние различных факторов на механические
характеристики конструкционных материалов 75
4.4. Композиционные материалы 83
Глава 5. РАСТЯЖЕНИЕ (СЖАТИЕ) ПРИЗМАТИЧЕСКИХ
СТЕРЖНЕЙ 91
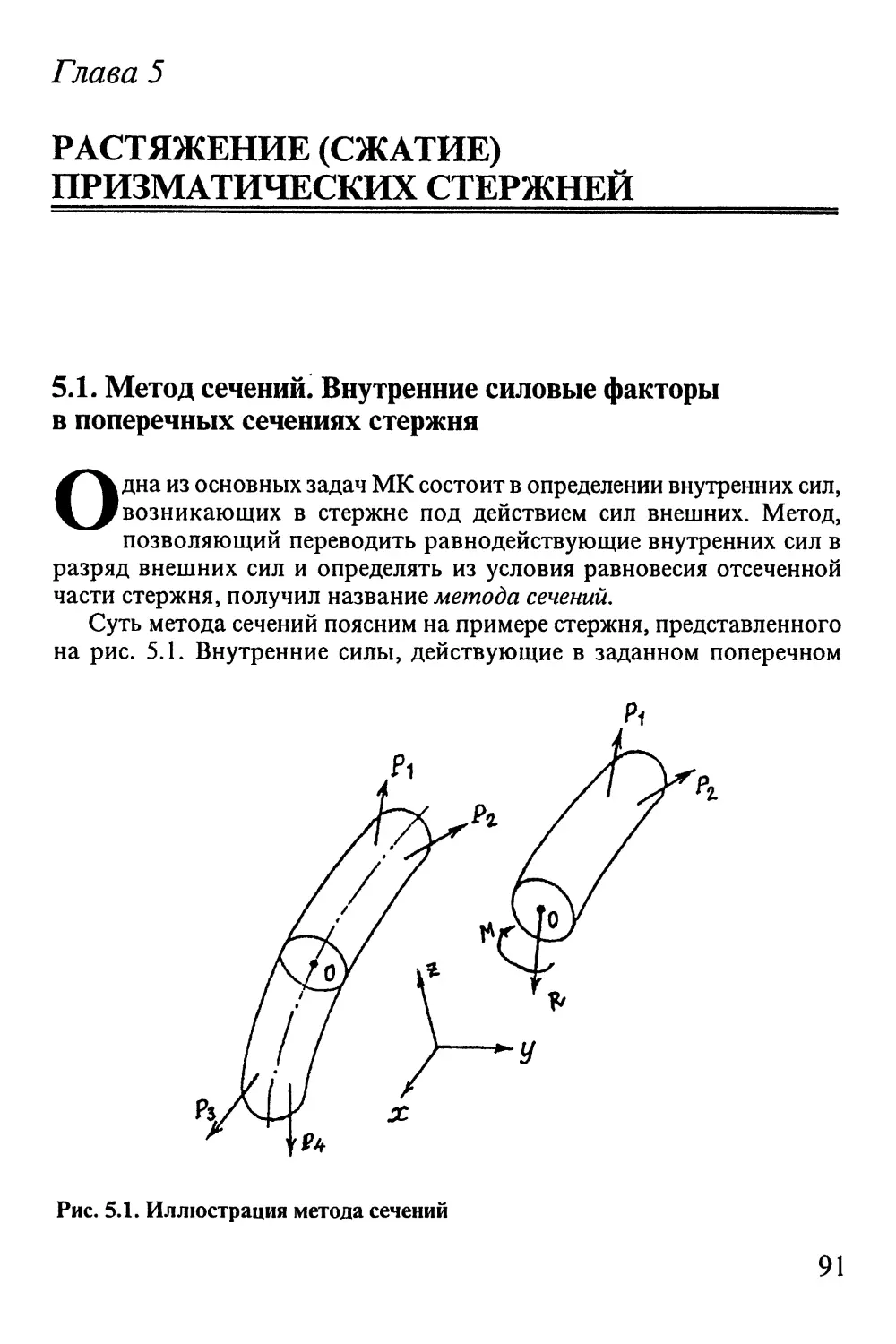
5.1. Метод сечений. Внутренние силовые факторы
в поперечных сечениях стержня 91
5.2. Представление внутренних силовых факторов
в интегральной форме 96
з
5.3. Напряжения при растяжении (сжатии) призматических
стержней. Расчет на прочность 96
5.4. Понятие о концентрации напряжений.
Принцип Сен-Венана 100
5.5. Определение деформаций и перемещений 102
5.6. Дифференциальное уравнение осевой деформации
прямолинейного стержня 104
5.7. Напряженное состояние при растяжении (сжатии) 106
5.8. Потенциальная энергия упругой деформации при
растяжении (сжатии) 107
5.9. Способы определения усилий в статически определимых
фермах 108
Глава 6. ИЗГИБ ПРИЗМАТИЧЕСКИХ СТЕРЖНЕЙ 112
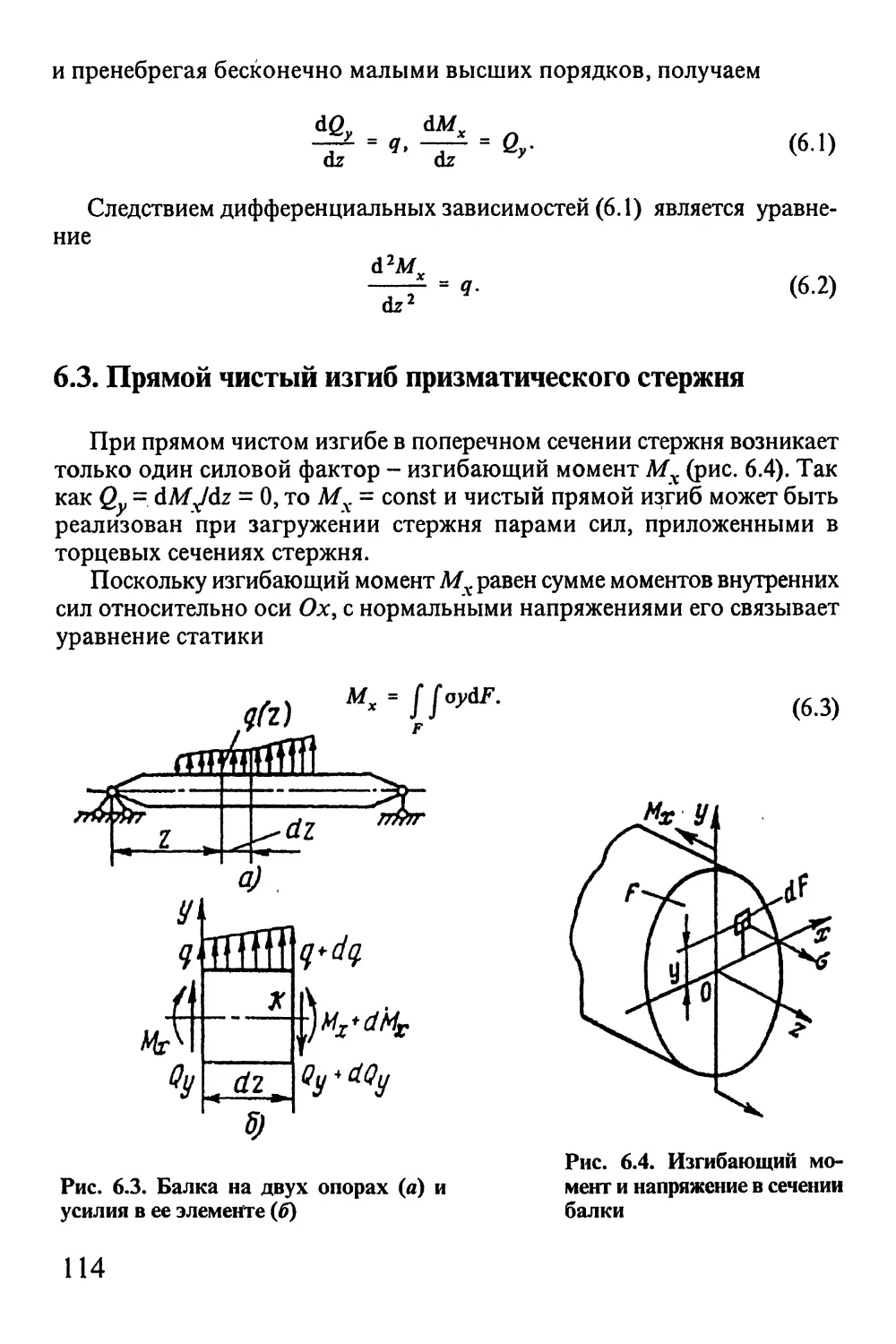
6.1. Классификация видов изгиба стержней 112
6.2. Дифференциальные зависимости между внутренними
силовыми факторами и внешней нагрузкой при прямом
поперечном изгибе 113
6.3. Прямой чистый изгиб призматического стержня 114
6.4. Прямой поперечный изгиб призматического стержня 120
6.5. Рациональные формы поперечных сечений при изгибе . ... 126
6.6. Понятие о составных балках 128
6.7. Дифференциальное уравнение прямого поперечного
изгиба призматического стержня 129
6.8. Применение метода начальных параметров для
интегрирования дифференциального уравнения
упругой кривой 133
6.9. Расчет балок, лежащих на упругом основании 136
Глава 7 КРУЧЕНИЕ СТЕРЖНЕЙ 140
7.1. Напряжения и деформации при кручении призматических
стержней кругового поперечного сечения 140
7.2. Расчет валов 145
7.3. Расчет цилиндрических винтовых пружин с малым
углом подъема витков 147
7.4. Кручение стержней некругового сечения 149
Глава 8. СЛОЖНЫЕ ВИДЫ ДЕФОРМАЦИЙ 152
8.1. Принцип независимости действия сил и границы его
применения 152
8.2. Косой изгиб призматического стержня 153
8.3. Сочетание косого изгиба и растяжения (сжатия)
призматического стержня 155
8.4. Сочетание изгиба и кручения призматического стержня .... 156
4
Глава 9. ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА
КОНСТРУКЦИЙ 159
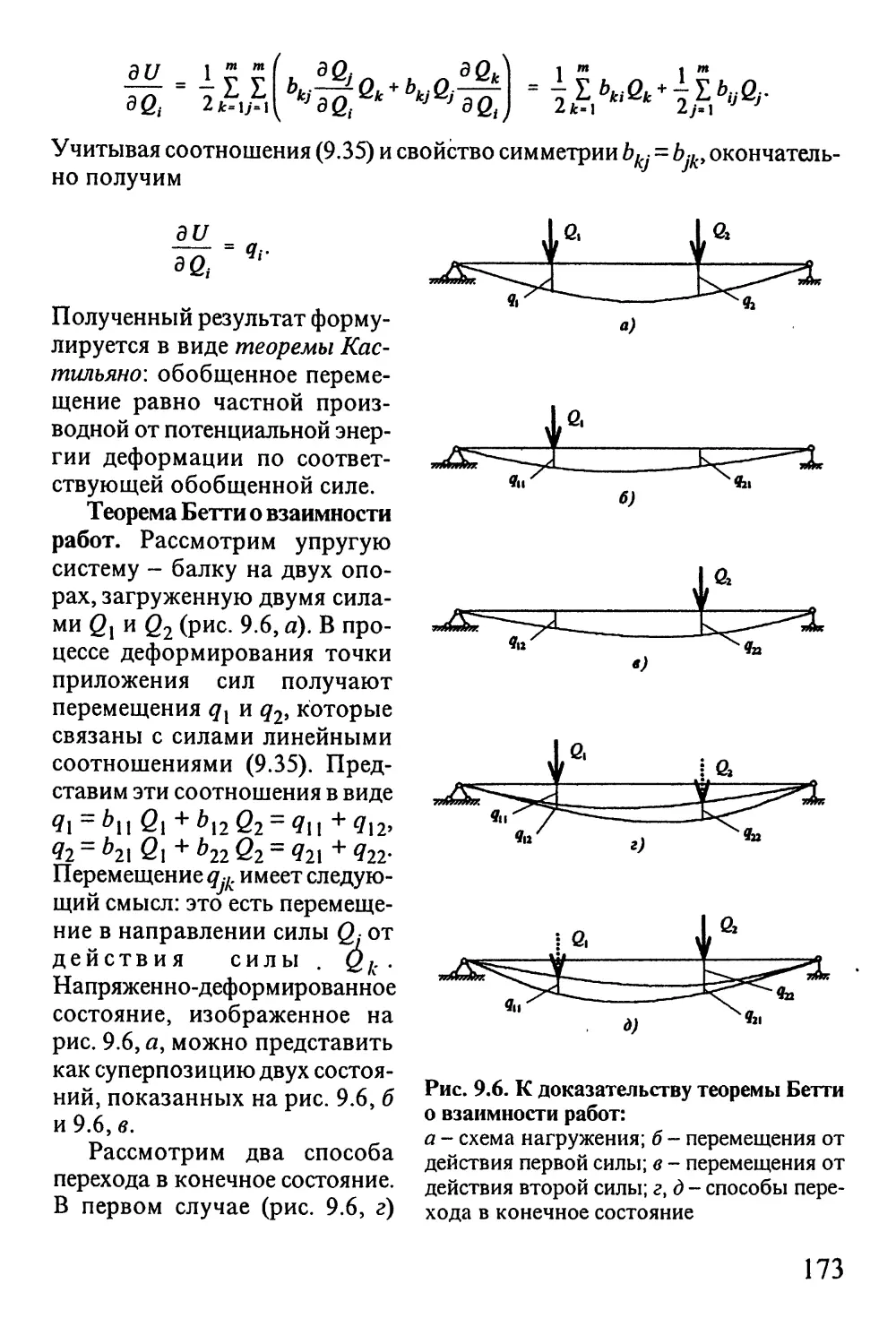
9.1. Виртуальная работа, обобщенные силы
и обобщенные перемещения 159
9.2. Потенциальная энергия упругой деформации 162
9.3. Принцип виртуальных перемещений. Вариационный
принцип Лагранжа 166
9.4. Энергетические теоремы 171
9.5. Определение перемещений. Формула
Максвелла - Мора 175
9.6. Вариационные методы Релея - Ритца и Бубнова -
Галеркина 180
9.7. Метод конечных элементов 182
Глава 10. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ 194
10.1. Классификация стержневых систем 194
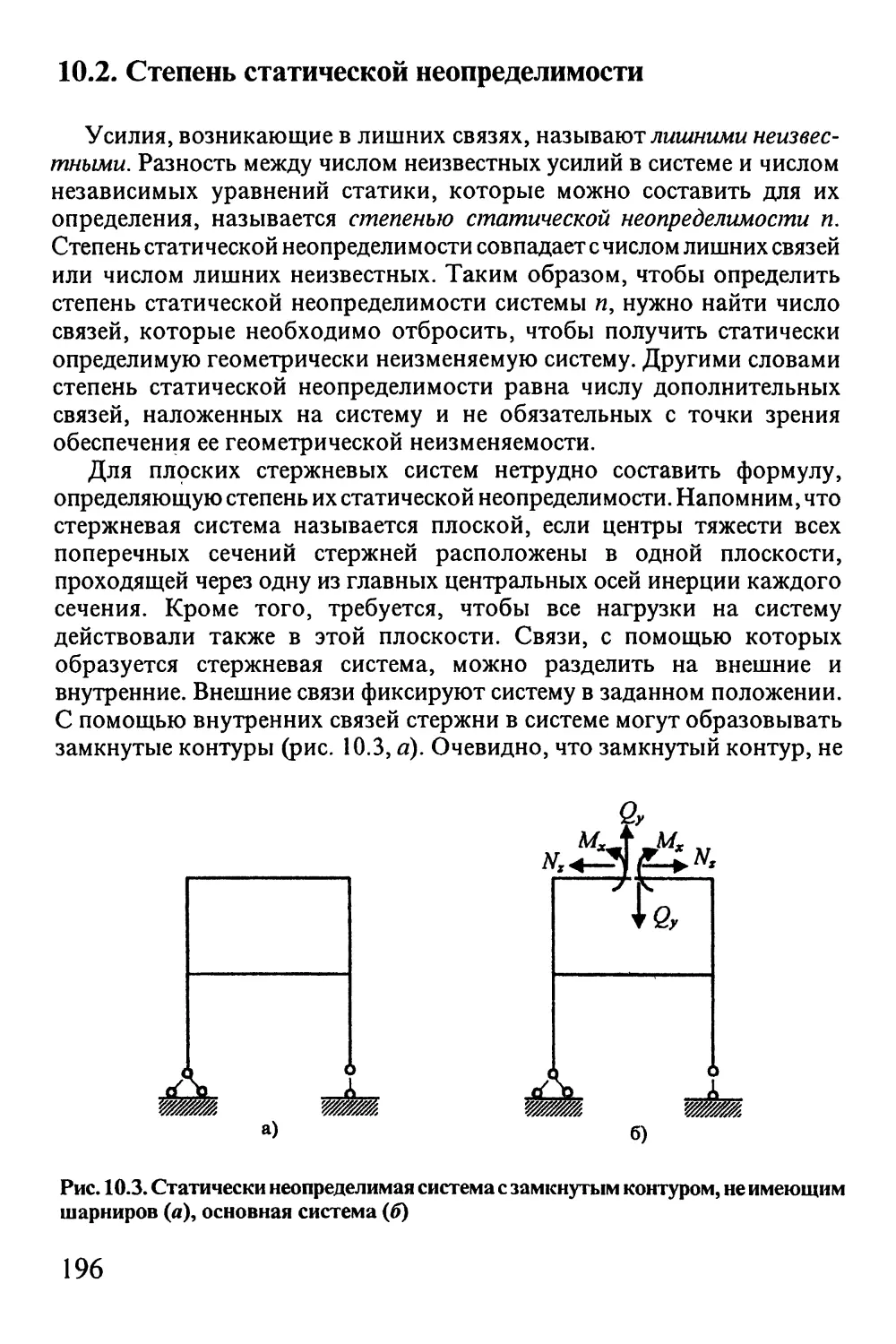
10.2. Степень статической неопределимости 196
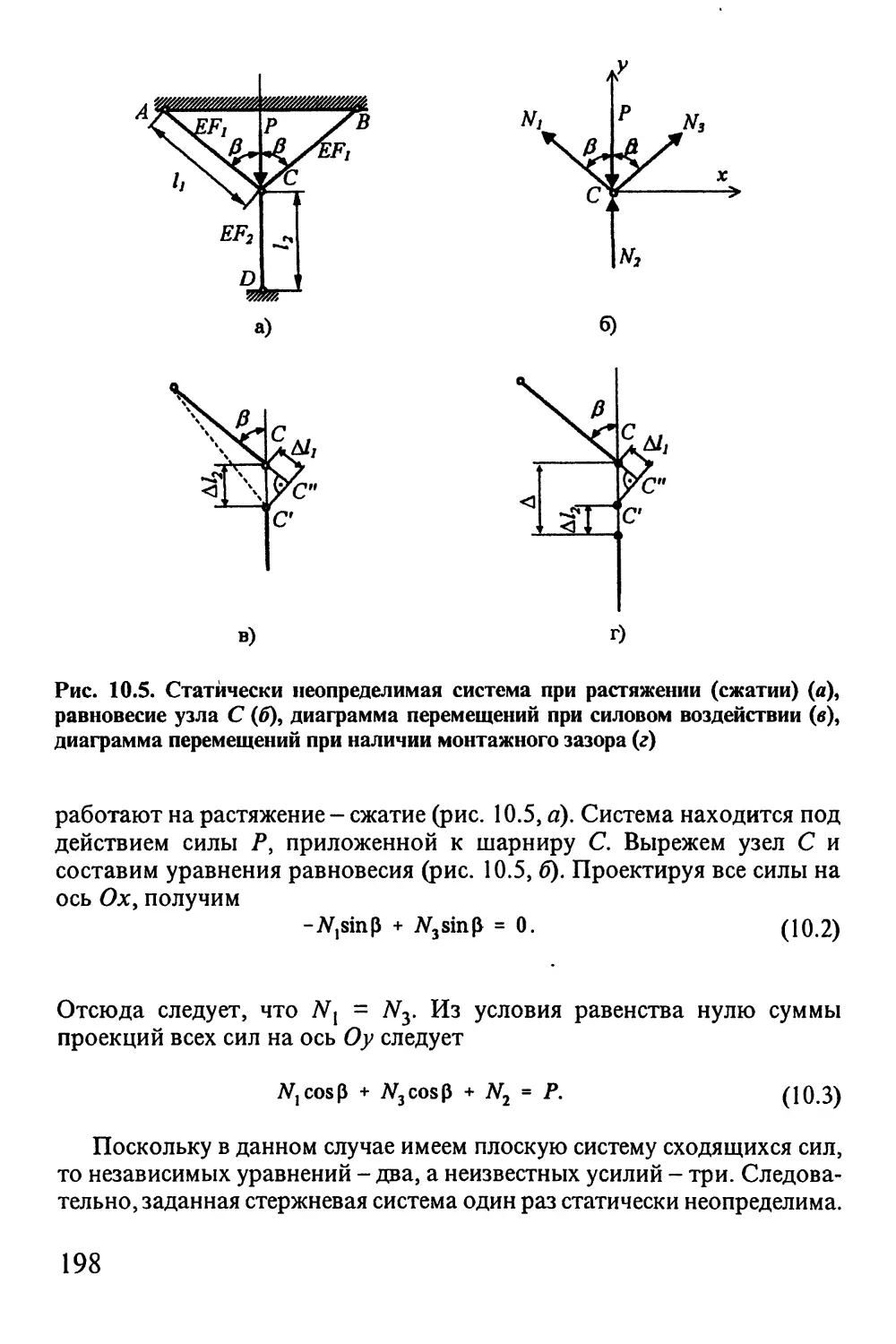
10.3. Особенности статически неопределимых систем 197
10.4. Канонические уравнения метода сил 200
10.5. Последовательность расчета статически
неопределимых систем по методу сил 206
10.6. Многопролетные неразрезные балки.
Уравнение трех моментов 210
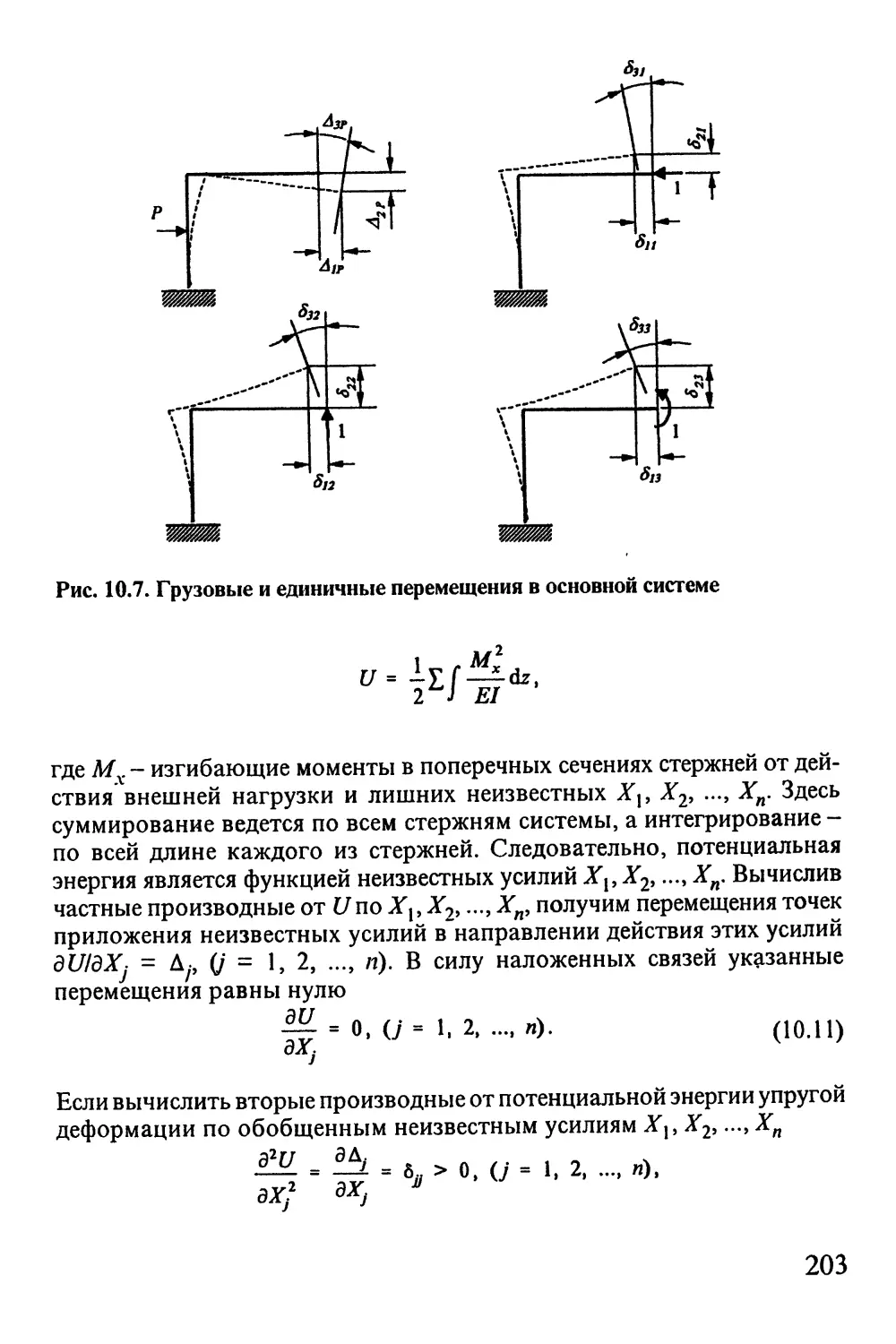
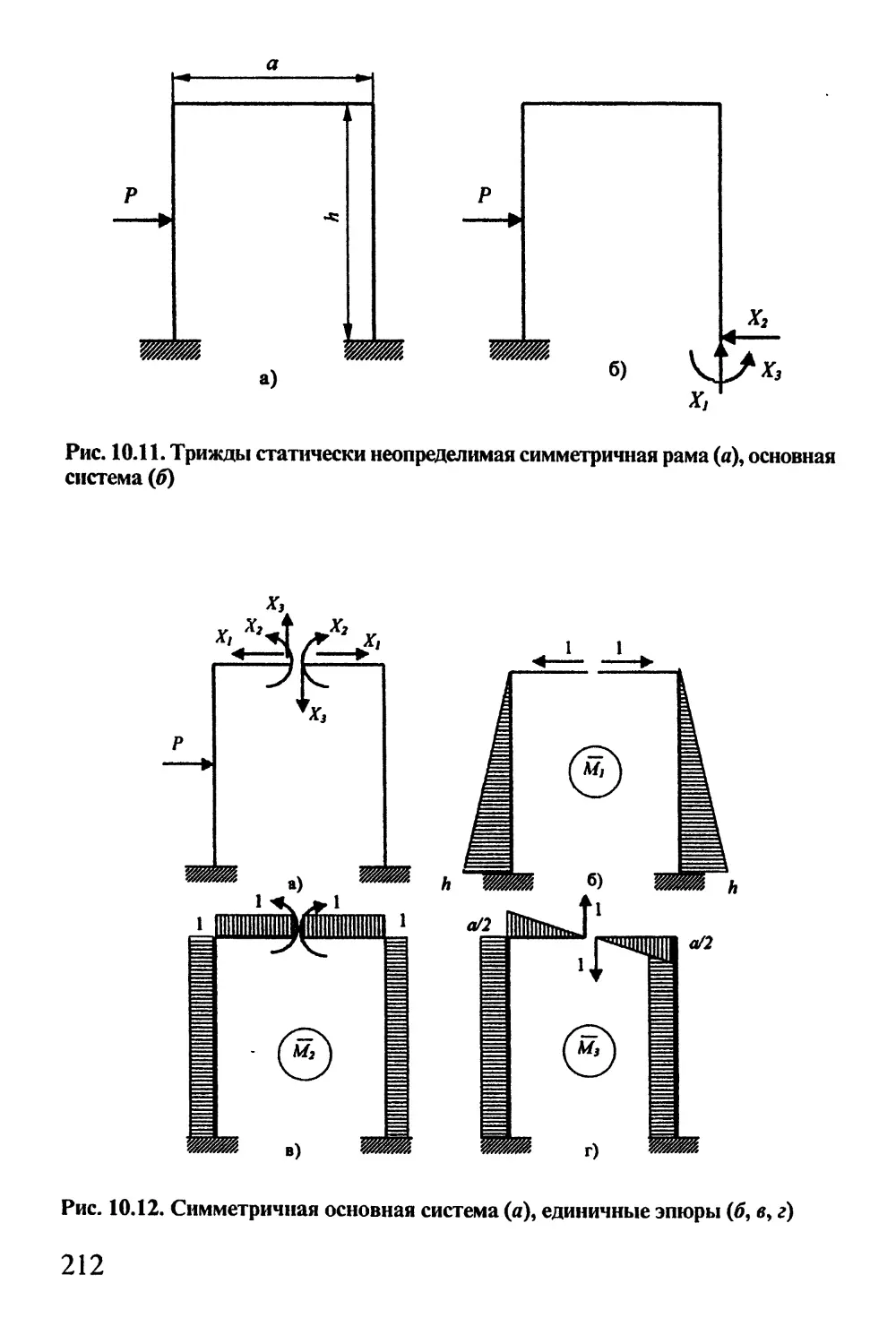
10.7. Использование симметрии статически
неопределимых систем 211
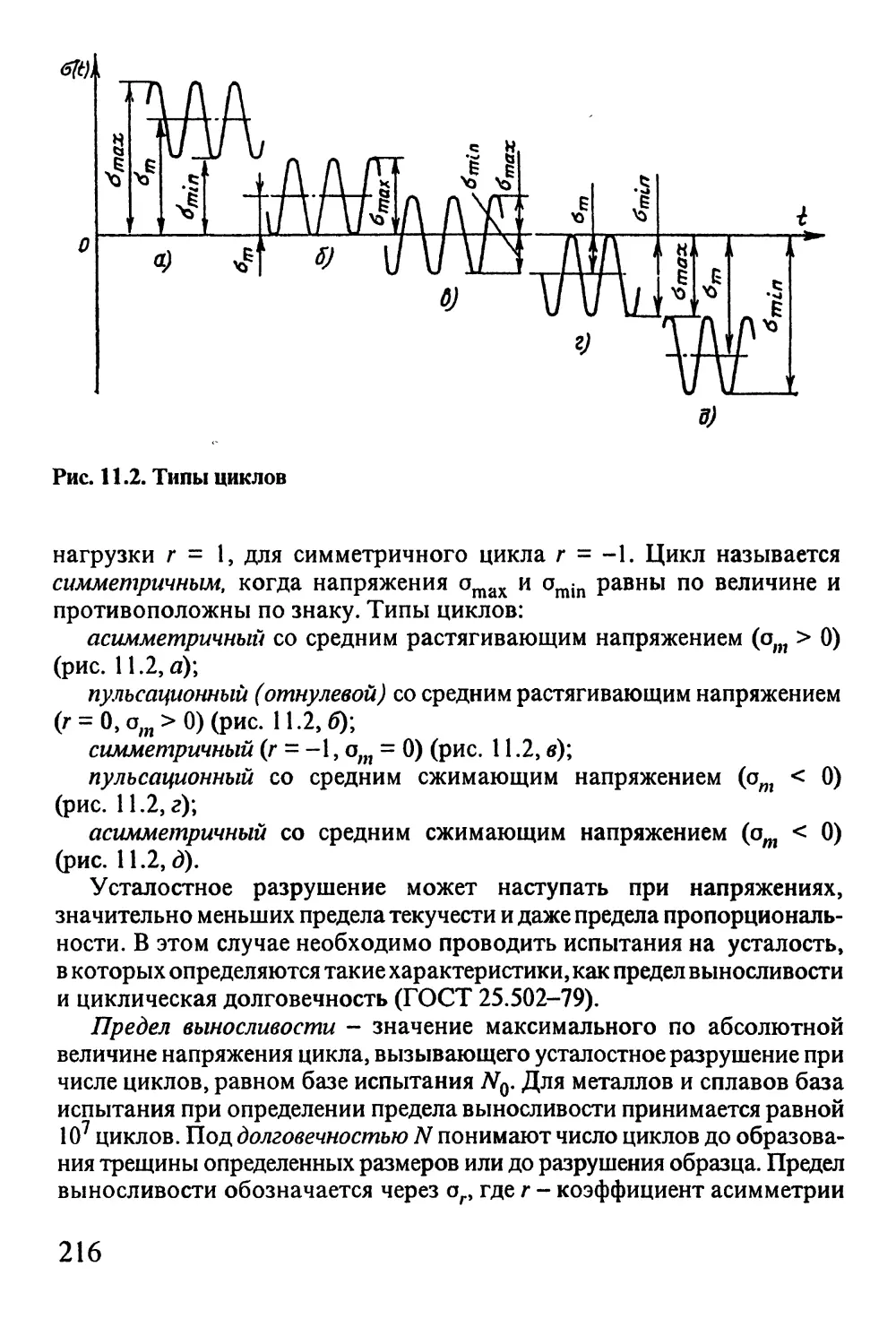
Глава 11. ПРОЧНОСТЬ ПРИ НАПРЯЖЕНИЯХ, ПЕРЕМЕННЫХ
ВО ВРЕМЕНИ 214
11.1. Механизм усталостного разрушения 214
11.2. Характеристики сопротивления усталости 215
11.3. Факторы, влияющие на сопротивление усталости 219
11.4. Прочность при регулярном многоцикловом
нагружении 223
11.5. Расчеты на прочность при малоцикловом
нагружении 226
Глава 12. ОСНОВЫ МЕХАНИКИ РАЗРУШЕНИЯ 234
12.1. Общие сведения о прочности конструкций
и механике разрушения 234
12.2. Напряжения и перемещения в окрестности трещин 235
12.3. Критерии хрупкого разрушения
Гриффитса - Ирвина 240
12.4. Критерии разрушения при наличии пластических
зон у трещин 243
12.5. Понятие о накоплении повреждений. Линейное
правило суммирования повреждений 245
5
Глава 13. ПЛАСТИНЫ И ОБОЛОЧКИ 249
13.1. Предпосылки теории изгиба пластин и оболочек 249
13.2. Изгиб пластин 250
13.3. Методы расчета прямоугольных пластин 258
13.4. Осесимметричный изгиб круговых и
кольцевых пластин 263
13.5. Безмоментная теория тонкостенных оболочек
вращения 271
13.6. Осесимметричная деформация круговых
цилиндрических оболочек 275
13.7. Краевой эффект в круговой цилиндрической
оболочке 285
Глава 14. ТОЛСТОСТЕННЫЕ ЦИЛИНДРЫ И
ВРАЩАЮЩИЕСЯ ДИСКИ 291
14.1. Осесимметричная деформация толстостенных
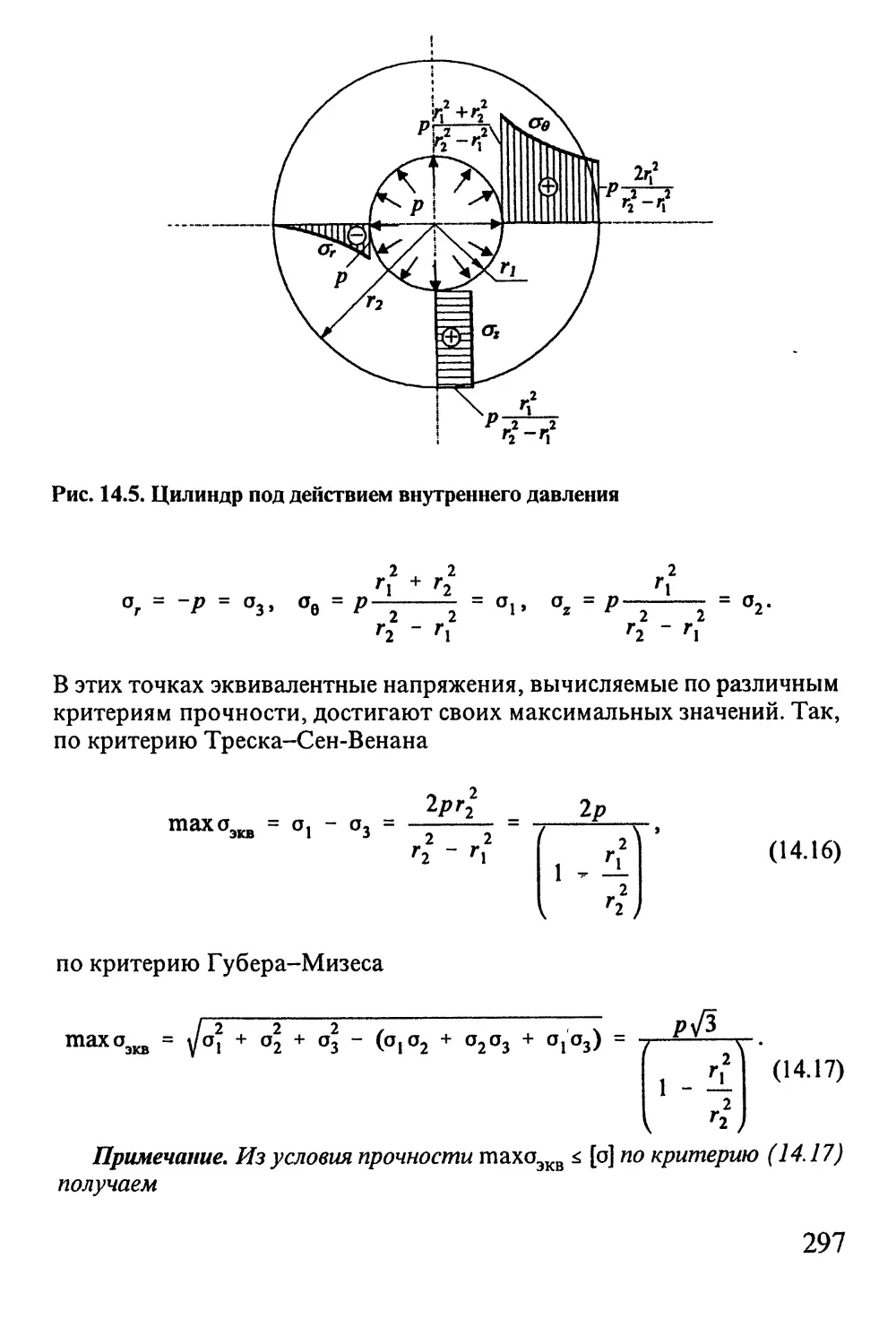
цилиндров. Задача Ламе 291
14.2. Составные цилиндры 299
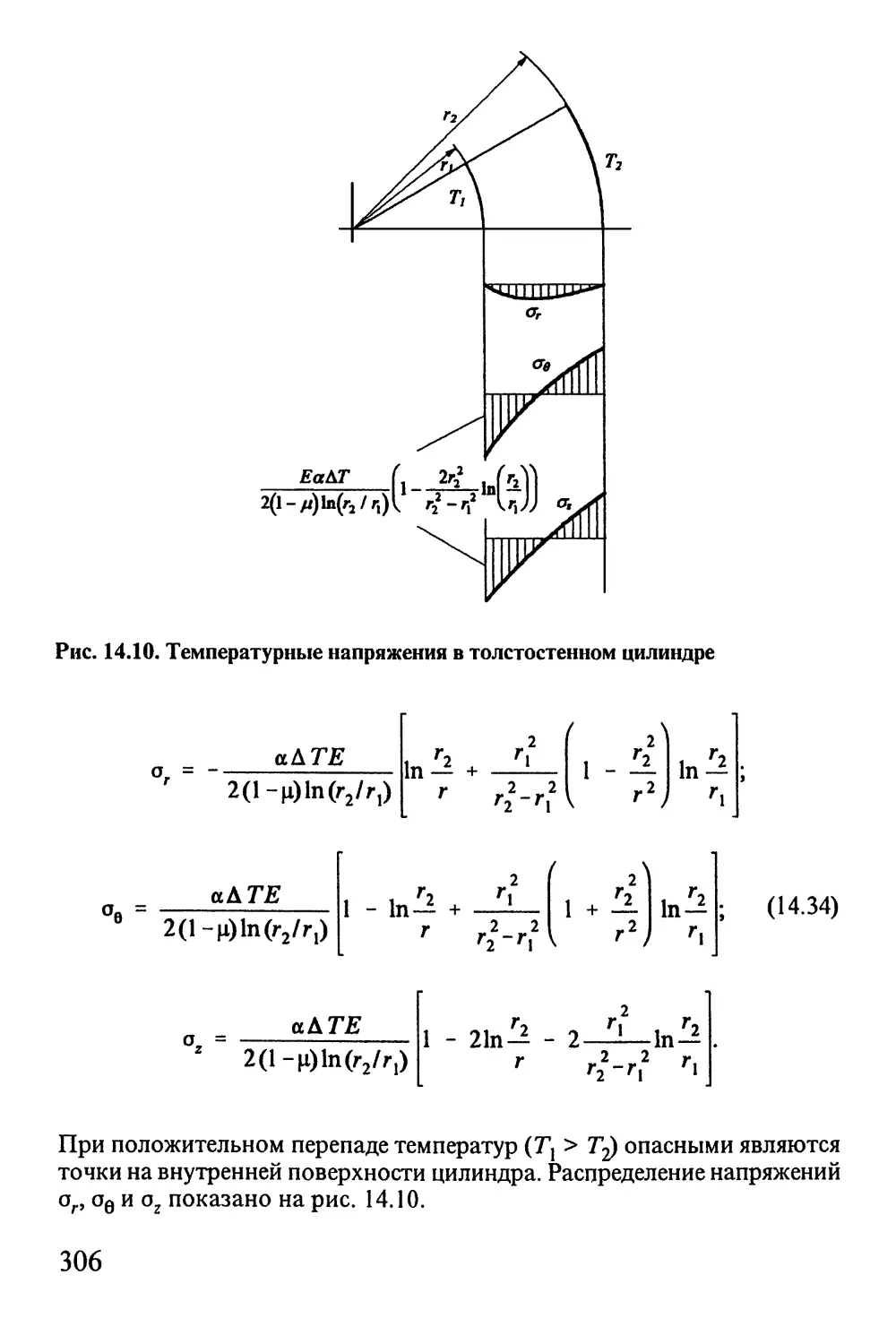
14.3. Температурные напряжения в толстостенных
цилиндрах 303
14.4. Вращающиеся диски 307
Глава 15. РАСЧЕТ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНОМУ
СОСТОЯНИЮ 311
15.1. Понятие о предельном состоянии конструкций.
Предельная нагрузка 311
15.2. Расчеты при растяжении (сжатии) 313
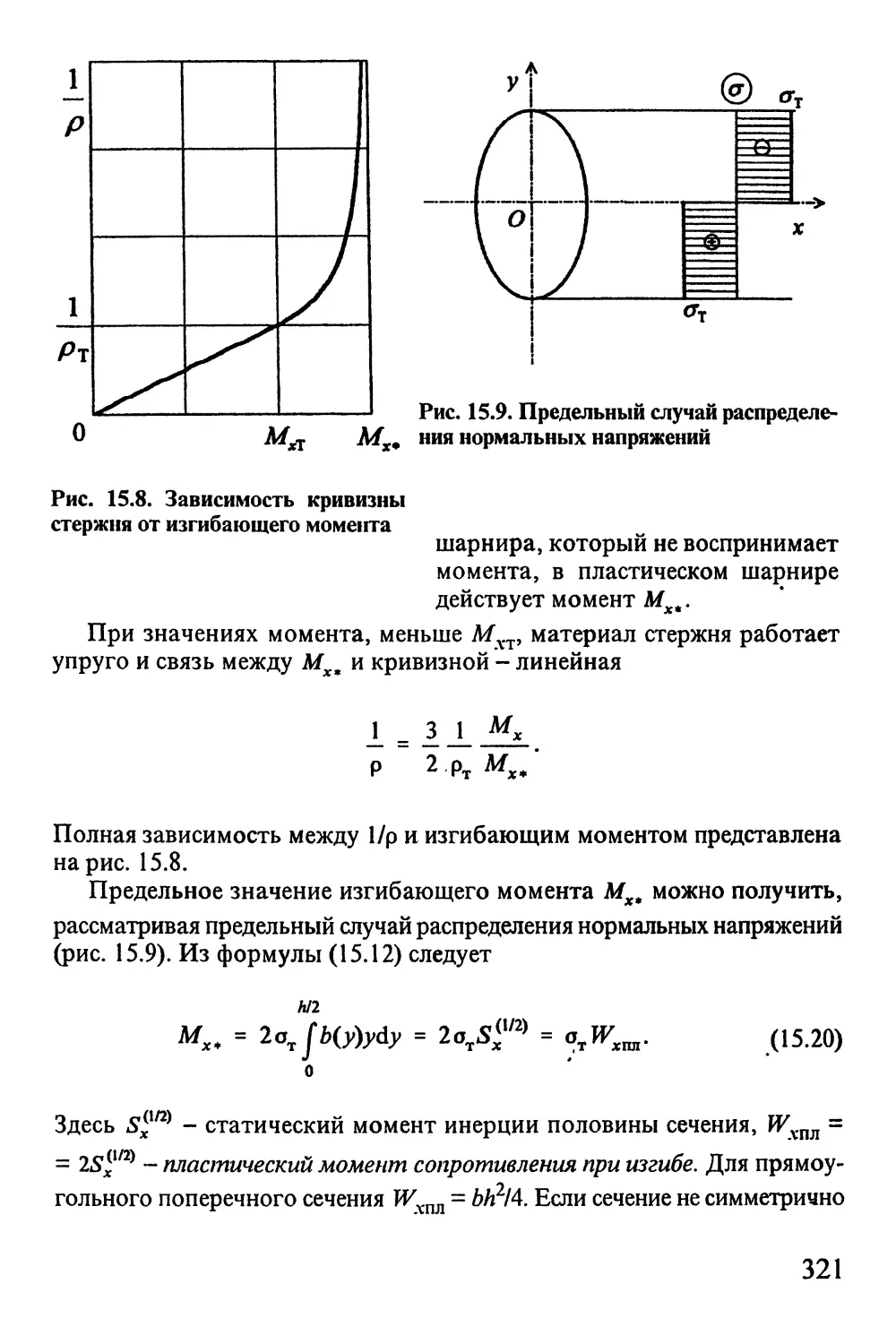
15.3. Упругопластический изгиб стержней 318
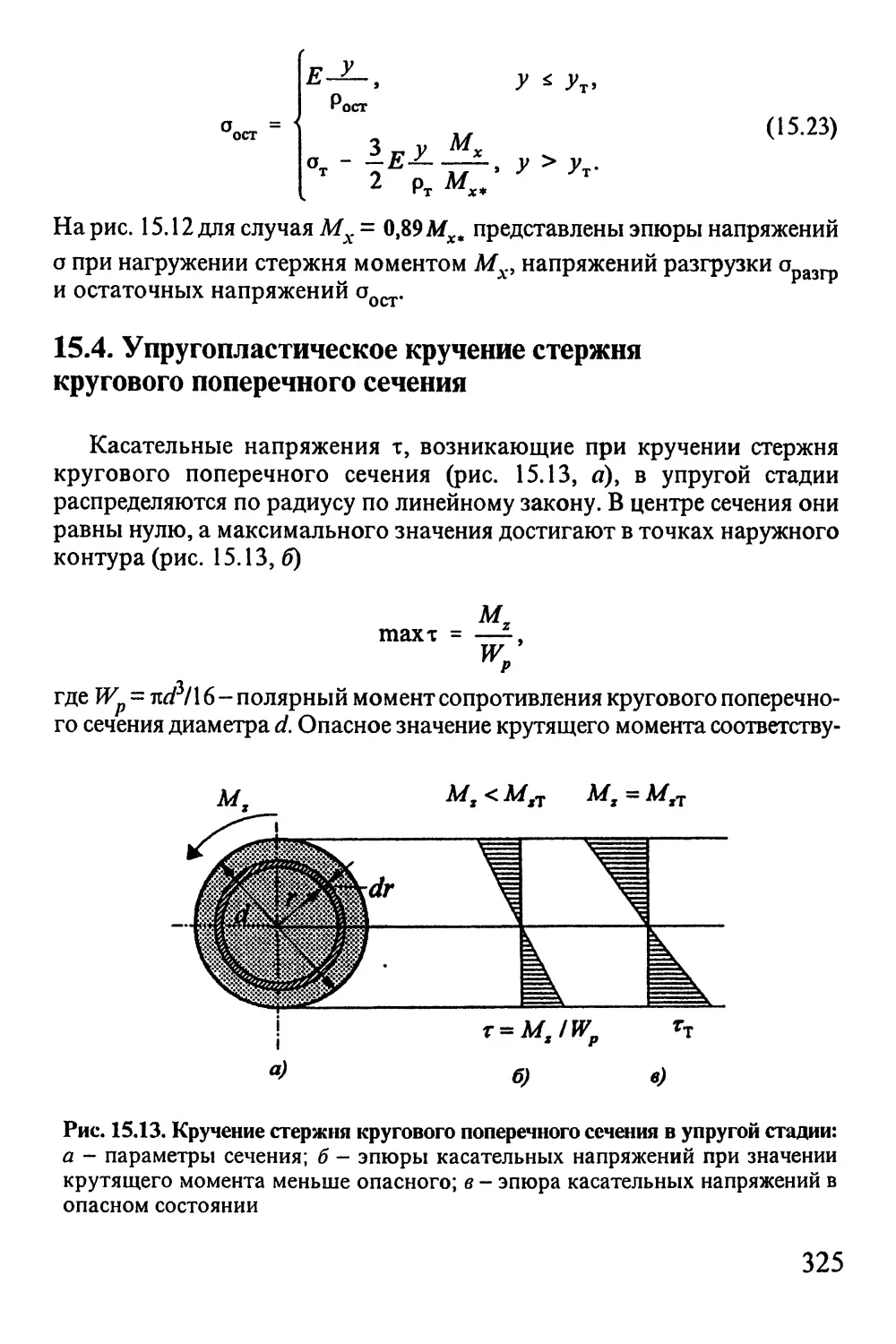
15.4. Упругопластическое кручение стержня
кругового поперечного сечения 325
15.5. Предельное состояние толстостенных труб 329
Глава 16. УСТОЙЧИВОСТЬ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ 332
16.1. Основные понятия теории упругой устойчивости 332
16.2. Устойчивость прямолинейного стержня при
продольном сжатии. Формула Эйлера 335
16.3. Расчеты на устойчивость за пределами упругости 341
16.4. Энергетический метод решения задач устойчивости 345
Глава 17. ДИНАМИКА СИСТЕМ С СОСРЕДОТОЧЕННЫМИ
ПАРАМЕТРАМИ 348
17.1. Основные понятия теории колебаний 348
17.2. Свободные колебания систем с конечным числом
степеней свободы 349
£
17.3. Установившиеся вынужденные колебания 356
17.4. Учет рассеяния энергии при колебаниях 364
Глава 18. ДИНАМИКА ЭЛЕМЕНТОВ КОНСТРУКЦИЙ 373
18.1. Уравнения колебаний систем с распределенными
параметрами 373
18.2. Свободные колебания стержней и пластин 377
18.3. Методы нахождения собственных частот
и форм колебаний 386
18.4. Вынужденные колебания 402
ЛИТЕРАТУРА 407
7
ПРЕДИСЛОВИЕ
В книге обобщен и систематизирован многолетний опыт
преподавания студентам различных специальностей МЭИ одной из основных
общеинженерных дисциплин - механики материалов и конструкций.
Эта дисциплина возникла как преемник сопротивления материалов, в
значительной мере сохранила содержательную часть этой традиционной
дисциплины, а также ее стиль, терминологию и методику изложения.
Вместе с тем, новая дисциплина отражает изменения, которые
инженерная деятельность получила в последние десятилетия, в частности из-за
появления новых конструкционных материалов, новых конструктивных
форм, повышенного внимания к надежности и безопасности технических
объектов и широкого использования современных численных методов
расчета конструкций.
Механика материалов и конструкций - комплексная дисциплина,
включающая элементы механики деформируемого твердого тела,
строительной механики, прикладной теории упругости, механики
разрушения, динамики и устойчивости конструкций. Видное место в этой
дисциплине принадлежит механическим свойствам конструкционных
материалов и вопросам конструкционной надежности.
Книга состоит из 18 глав. Первая глава носит вводный характер; в
ней дано представление об основных моделях и гипотезах механики
материалов и конструкций. Во второй главе изложены основы теории
надежности конструкций. Здесь дано современное представление о
выборе коэффициентов запаса прочности из
вероятностно-статистических соображений. В гл. 3 излагаются начала теории напряжений и
деформаций и основы теории прочности. Гл. 4 целиком посвящена
механическим свойствам конструкционных материалов. Наряду с
традиционными материалами рассмотрены высокоэффективные
композиционные материалы, получающие все большее распространение
в различных областях техники.
Гл. 5...8 в основной своей части следуют традиционному изложению,
принятому в курсах сопротивления материалов. Здесь последовательно
рассмотрены методы расчета стержней на растяжение, сжатие, изгиб,
кручение, а также на сочетание различных воздействий.
8
Гл. 9 посвящена вариационным методам расчета напряжений,
деформаций и перемещений в конструкциях сложной формы и (или)
структуры. Повышенное внимание к вариационным методам
обусловлено тем, что эти методы лежат в основе большинства современных
вычислительных методов расчета конструкций. Представление о
наиболее употребляемом методе - методе конечных элементов - дано в
конце главы. В гл. 10 изложены методы расчета статически
неопределяемых систем.
Вопросы конструкционной прочности, впервые затронутые во второй
главе, более подробно освещены в гл. 11 и 12. В первой из них изложены
инженерные методы расчета на долговечность при циклическом
нагружении, во второй приведены сведения из механики разрушения.
Этих сведений достаточно, чтобы выработать у студентов правильное
представление о требованиях к трещиностойкости конструкционных
материалов.
Гл. 13 и 14 содержат сведения из прикладной теории упругости. Одна
из глав посвящена расчету пластин и оболочек, другая - расчету
толстостенных цилиндров давления и вращающихся дисков.
Гл. 15 посвящена методам расчета конструкций по предельным
состояниям.
Элементы теории устойчивости конструкций приведены в гл. 16.
Книга завершается гл. 17 и 18, где достаточно обстоятельно
рассмотрены вопросы динамики систем с конечным числом степеней
свободы и систем с распределенными параметрами.
Авторы надеются, что книга окажется нужной как студентам, впервые
приступающим к изучению механики материалов и конструкций, так и
дипломированным специалистам в выборе конструкционных материалов
и оптимальных конструктивных форм, в обеспечении высоких
показателей надежности и безопасности напряженных конструкций и узлов,
создании эффективных и экономичных конструкций.
9
Глава 1
ПРЕДМЕТ КУРСА "МЕХАНИКА МАТЕРИАЛОВ
И КОНСТРУКЦИЙ"
1.1. Введение
Механика материалов и конструкций (ММК) - наука о расчетах
машин, конструкций и их элементов на прочность, жесткость
и устойчивость при гарантированной их долговечности. Под
прочностью будем понимать способность конструкции сопротивляться
действию внешних нагрузок и других воздействий (температуры,
смещению опорных устройств и т.п.) не разрушаясь. Если в процессе
нагружения изменение формы и размеров элементов конструкции
настолько незначительно, что не приводит к нарушению
эксплуатационных функций конструкции, считается, что конструкция обладает
необходимой жесткостью. Если малые внешние воздействия приводят
к малым и исчезающим после снятия воздействий отклонениям от
первоначального положения равновесия конструкции и ее элементов,
то такое состояние равновесия называется устойчивым. Срок, в течение
которого конструкция сохраняет заданные эксплуатационные функции,
называют ее долговечностью.
Расчет на прочность, жесткость и устойчивость служит обеспечению
механической надежности проектируемой конструкции и состоит из двух
этапов. На первом этапе вычисляются напряжения, деформации и
перемещения в элементах конструкций, подверженных действию внешних
нагрузок. Решению этой задачи служат методы механики материалов и
конструкций, строительной механики, теории упругости и т.п. Конечной
целью инженерного расчета на прочность является решение вопроса о
том, сможет ли конструкция достаточно надежно служить в течение
установленного срока. Второй этап расчета состоит либо в
сопоставлении вычисленных напряжений, деформаций и перемещений с некоторыми
нормативно допустимыми значениями, либо в сопоставлении расчетных
нагрузок с их предельными значениями. На этом этапе решается вопрос:
10
Jj
Общая
механика
Механика
z
Механика жидкости
и газа
Механика деформируемого
твердого тела
Механика сплошной среды
о 0>
5 о
I §
S ю
л °
о
(2
о
I
Механика материалов и конструкций
Рис. 1.1. Разделы механики
п
является ли конструкция достаточно надежной, долговечной и
экономичной.
Механика материалов и конструкций является втузовским курсом и
принадлежит к механике. ММК, являясь прикладным инженерным
курсом, включает в себя элементы различных разделов механики
деформируемого твердого тела (рис. 1.1). Выбор разделов и подробность
их изложения в курсе ММК зависят от программы и специализации, по
которой готовят инженеров.
В отличие от курса теоретической механики, где используется модель
абсолютно твердого тела, в ММК рассматривают конструкции, материал
которых описывается моделями деформируемого твердого тела, т.е. тела,
формы и размеры которого изменяются под действием приложенных
внешних нагрузок.
1.2. Модели и расчетные схемы конструкций
Модели прочностной надежности. Моделью называется совокупность
представлений, зависимостей, условий, ограничений, описывающих
процесс, явление. Пояпрочностнойнадежностью понимается отсутствие
отказов, связанных с разрушением или недопустимыми деформациями
элементов конструкций. Модель прочностной надежности включает в
себя модели материала, модели формы, модели нагружения и
разрушения.
Модели материала. В механике материалов и конструкций использует-
ся модель сплошного, однородного, деформируемого тела. Модель
сплошности позволяет рассматривать тело как непрерывную среду и
применять методы математического анализа. Модели материала должны
учитывать такие свойства, как упругость, пластичность и ползучесть,
а также учитывать изменение свойств конструкционных материалов от
внешних воздействий (температуры, скорости нагружения, интенсивности
радиационного облучения и т.д.).
Модели формы. Построение модели формы основано на схематизации
конструкции и ее элементов по геометрическим признакам. Стержень
(рис. 1.2, а) - тело, один из размеров которого (длина I) значительно
больше, чем размеры поперечного сечения. Стержень можно образовать
движением в пространстве плоской фигуры, центр тяжести которой
скользит вдоль некоторой кривой - оси стержня, а сама фигура остается
перпендикулярной к этой кривой и ее положения образуют совокупность
поперечных сечений стержня. Оболочка (рис. 1.2, 6) - тело, один из
размеров которого (толщина Л) мал по сравнению с двумя другими
габаритными размерами. Геометрическое место точек, равноудаленных
12
s) ')
О . в>
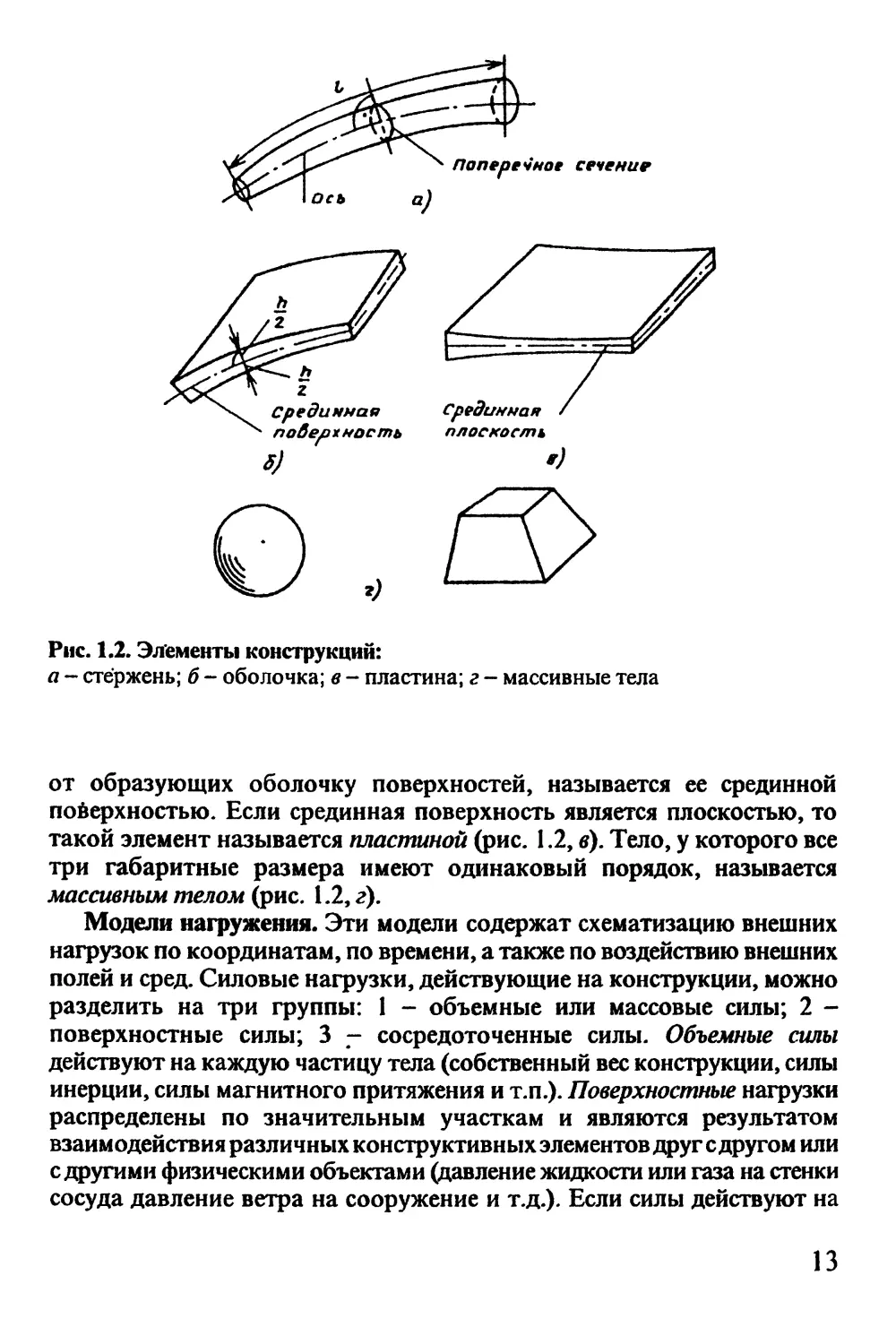
Рис. 1.2. Элементы конструкций:
а - стержень; б - оболочка; в - пластина; г - массивные тела
от образующих оболочку поверхностей, называется ее срединной
поверхностью. Если срединная поверхность является плоскостью, то
такой элемент называется пластиной (рис. 1.2, в). Тело, у которого все
три габаритные размера имеют одинаковый порядок, называется
массивным телом (рис. 1.2, г).
Модели нагружения. Эти модели содержат схематизацию внешних
нагрузок по координатам, по времени, а также по воздействию внешних
полей и сред. Силовые нагрузки, действующие на конструкции, можно
разделить на три группы: 1 - объемные или массовые силы; 2 -
поверхностные силы; 3 - сосредоточенные силы. Объемные силы
действуют на каждую частицу тела (собственный вес конструкции, силы
инерции, силы магнитного притяжения и т.п.). Поверхностные нагрузки
распределены по значительным участкам и являются результатом
взаимодействия различных конструктивных элементов друг с другом или
с другими физическими объектами (давление жидкости или газа на стенки
сосуда давление ветра на сооружение и т.д.). Если силы действуют на
13
небольшую поверхность конструкции, то они могут рассматриваться как
сосредоточенные нагрузки, считаемые условно приложенными в одной
точке. По характеру действия нагрузки можно разделить на статические
и динамические. Статические нагрузки возрастают до своей
номинальной величины и остаются постоянными во время эксплуатации
конструкции. Переменное или динамическое нагружение - нагружение,
изменяющееся во времени. Часто встречающимся видом переменного
нагружения являются циклические нагрузки, характеризующиеся
периодическим изменением величины и/или знака. Для многих
конструкций существенным является также воздействие температурного
поля. Изменение температуры элементов конструкции вызывает
температурные деформации. Если они не удовлетворяют уравнениям
совместности деформаций, то в элементах конструкции возникают
температурные напряжения, величина которых может оказаться
соизмеримой с напряжениями от внешних сил. Кроме того, изменение
температуры влияет на механические характеристики конструкционных
материалов. В некоторых случаях необходимо учитывать влияние
нейтронного облучения, электромагнитного поля, воздействие
коррозионных сред и т.п.
Модели разрушения. Эти модели представляют собой уравнения
(условия), связывающие параметры работоспособности состояния
элемента конструкции в момент разрушения с параметрами,
обеспечивающими прочность. Эти условия называют условиями (критериями)
прочности. Нарушение условий прочности соответствует переходу
конструкции или ее элементов в предельное состояние, при котором ее
дальнейшее применение но назначению недопустимо или
нецелесообразно. В зависимости от характера разрушения материала различают два
типа предельных состояний: хрупкое разрушение и появление
пластических деформаций (текучести). Различают четыре модели разрушения:
статическое разрушение, длительное статическое, малоцикловое,
усталостное (многоцикловое). При повышенных температурах
рассматривается длительная прочность. Сопротивление материала
зависит не только от величины действующего усилия, но и от
длительности воздействия.
Реальный объект и его расчетная схема. Расчет конструкций с учетом
многообразия механических характеристик материала и их изменения
вследствие взаимодействия с окружающей средой, отклонений от точных
геометрических размеров, изменчивости нагрузок и т.п. является либо
теоретически невозможным, либо практически неприемлемым по своей
сложности. Необходимо провести схематизацию конструкции,ютбросив
второстепенные факторы, не оказывающие существенного влияния на
достоверность и точность расчета. Расчетной схемой называется
U
1*
У/7 /// /// /// ///
/7777777777777777
В)
}
Рис. 1.3. Типы соединений и
опор:
А - шарнирный узел; В -
жесткий узел; С - абсолютно жес- Рис. 1.4. Давление колеса на рельс (я) и его
ткая заделка; Д - опора, со дер- схематизация (б)
жащая идеальные шарниры
упрощенная идеализированная схема, которая отражает наиболее
существенные особенности реального объекта, определяющие его поведение
под воздействием внешних нагрузок. Очевидно, что в зависимости от
поставленной задачи расчетная схема может видоизменяться.
В ММК особый интерес представляют стержневые системы
(расчетные схемы конструкций, составленные из стержней, соединенных
в узлах), расчетные схемы которых получают путем:
- идеализации очертания стержней (с прямолинейной или
криволинейной осью, с постоянным или переменным поперечным сечением
и т.д.);
- идеализации соединения стержней (идеальные шарниры, абсолютно
жесткие узлы и т.п., рис. 1.3);
- схематизации и идеализации опорных закреплений (рис. 1.3);
- схематизации нагрузок (сосредоточенные, распределенные вдоль
некоторых линий и т.п., рис. 1.3).
В качестве другого примера на рис. 1.4 показано, как рельс,
воспринимающий нагрузку Р от колеса через площадку контакта в
окрестности точки А, схематизируется стержнем, лежащим на упругом
основании и нагруженным сосредоточенной силой Р.
1.3. Основные гипотезы механики материалов и конструкций
Первые три гипотезы описывают свойства принимаемой модели
материала.
1. Гипотеза о сплошности материала: отвлекаясь от атомно-молекуляр-
ной, кристаллической и т.п. структуры, считаем материал сплошной
D5
а)
Рис. 1.5. Силы, действующие на деформируемое тело:
а - внешние силы; б - внутренние силы на элементарной площадке; в -
напряжения в точке
средой. Если материал - сплошная среда, то это означает, что внутренние
силы, возникающие как следствие действия внешних сил, и связанные
с ними деформации и перемещения являются непрерывными функциями
координат. Одно из следствий этой гипотезы - понятие о напряжении.
Одной из задач ММК является определение внутренних сил,
возникающих в результате приложения к деформируемому телу внешних сил
(нагрузок). Внутренние силы, действующие в некотором сечении
(рис. 1.5, а) и являющиеся результатом взаимодействия частей тела,
расположенных по разные стороны от сечения, непрерывно распределены
(как следствие гипотезы о сплошности) по сечению. Выделим в этом
сечении элементарную площадку AF. Равнодействующую сил,
приходящуюся на эту площадку, обозначим через АР (рис. 1.5, б). Тогда за меру
внутренних сил, действующих в данной точке сечения, следует принять
предел отношения
AF-0 AF
представляющий собой внутреннюю силу, приходящуюся на единицу
площади (или интенсивность внутренних сил в данной точке) и
называемую полным напряжением. Обычно полное напряжение принято
разлагать на две составляющие - по нормали к площадке и по
касательной к ней (как показано на рис. 1.5, в). Эти составляющие называют
нормальным напряжением а и касательным напряжением х. Полное,
нормальное и касательное напряжения связаны очевидным соотношением
16
01
5
1
Деформация
L^l
Рис. 1.6. Линейная диаграмма
деформирования
Рис. 1.7. Иллюстрация гипотезы о
малости перемещений
о2 + т2
а размерность напряжений определяется как отношение силы к площади,
т.е. dim/? = [сила/площадь]. Более строгие и полные представления о
напряжениях и деформациях даются в гл. 3.
2. Гипотеза об однородности и изотропности материала утверждает,
что свойства материала во всех точках одинаковы (однородность), а для
каждой точки одинаковы для всех направлений (изотропность),
3. Гипотеза о связи между напряжениями и деформациями. В данном
курсе ограничимся рассмотрением линейно-упругого материала, т.е.
материала, для которого связь между деформациями и напряжениями
(диаграмма деформирования) является линейной (рис. 1.6), а линия
нагружения и разгрузки совпадают. Данная зависимость между
напряжением и деформацией известна как закон Гука.
Таким образом, гипотезы 1...3 описывают модель сплошного,
однородного, изотропного и линейно-упругого материала.
4. Гипотеза о малости перемещений и деформаций предполагает, что
упругие деформации и связанные с ними перемещения элементов
конструкции малы по сравнению с их первоначальными размерами.
Например, упругое удлинение при растяжении стержня из
конструкционной малоуглеродистой стали не превышает 0,1 % его первоначальной
длины, т.е. метровый стержень упруго удлиняется не более чем на
миллиметр. Из этой гипотезы вытекает широко распространенный в
практике инженерных расчетов так называемый принщп неизменяемости
17
Рис. 1.9. Напряжения вдоль и
поперек волокон
Рис. 1.8. Иллюстрация гипотезы
плоских сечений первоначальных размеров при дефор-
мировании конструкций, который
иллюстрируется примером,
приведенным на рис. 1.7. Из этого
принципа следует, что при составлении уравнений равновесия, как и в курсе
теоретической механики, используется модель абсолютно твердого тела.
Как следствие гипотез о малости деформаций и линейной зависимости
между деформациями и усилиями при решении задач ММК применим
принцип суперпозиции (принцип независимости и сложения сил).
5. Гипотеза плоских сечений (гипотеза Д. Бернулли): поперечные
сечения, плоские и перпендикулярные к оси стержня до деформирования
остаются плоскими и перпендикулярными к искривленной оси стержня
и после деформирования (рис. 1.8).
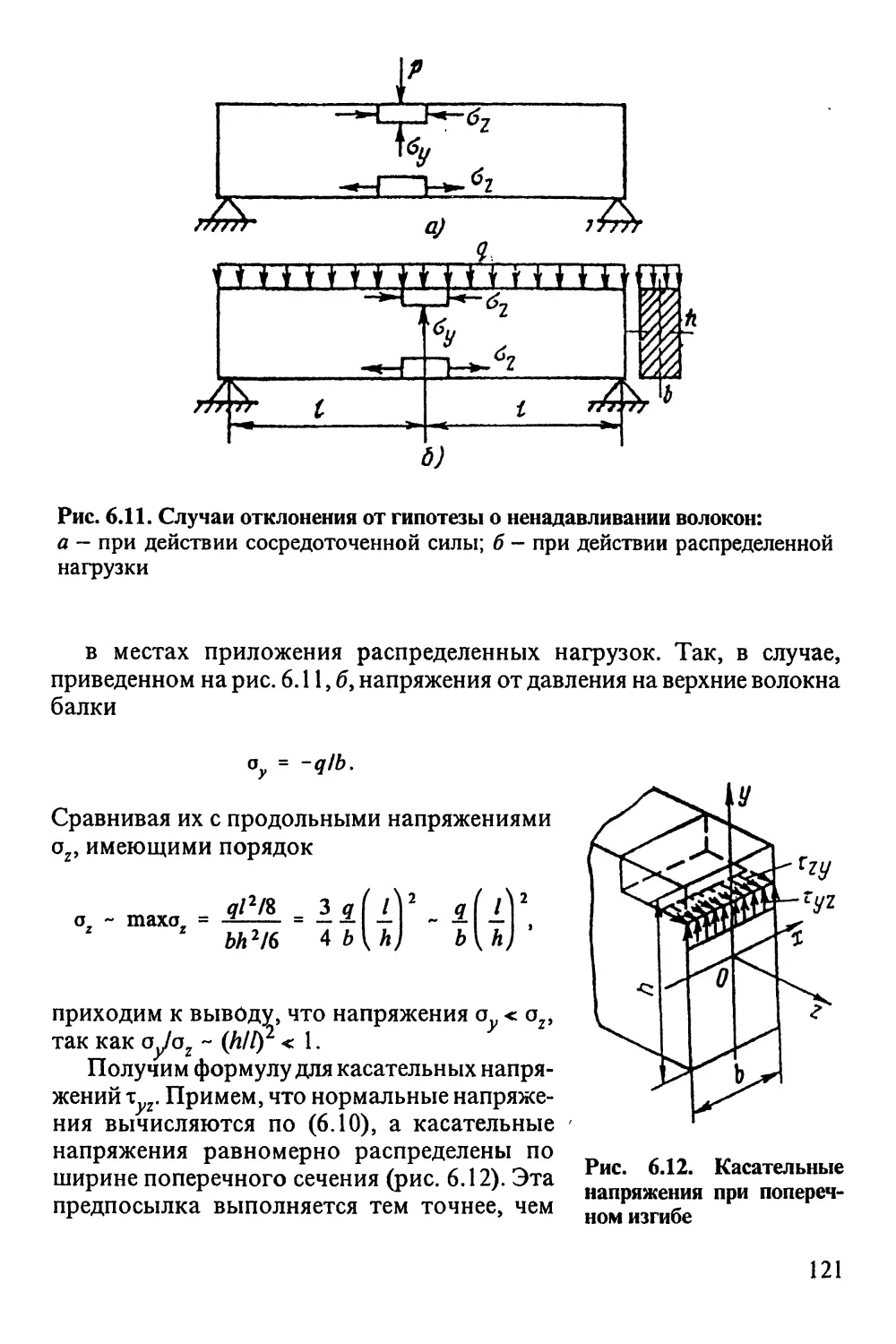
6. Гипотеза об отсутствии поперечного взаимодействия продольных
волокон принимает, что мысленно выделенные в стержне параллельно
его оси продольные волокна между собой не взаимодействуют (или, как
принято говорить, "не давят друг на друга"). Это означает, что
напряжения взаимодействия этих волокон пренебрежимо малы по
сравнению с рабочими напряжениями: ох < oz, о < oz (рис. 1.9).
Гипотезы 5,6 выполняются тем точнее, чем больше длина стержня
превышает размеры его поперечного сечения.
-F
F
'~t7~\p~W
18
Глава 2
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ
НАДЕЖНОСТИ КОНСТРУКЦИЙ
2.1. Общие сведения
Понятие надежности, а также методы прогнозирования, оценки,
нормирования и обеспечения надежности применяют к любым
сложным техническим объектам - машинам, конструкциям,
изделиям, сооружениям, системам и т.п.
Под надежностью технического объекта, согласно ГОСТ 27.002-89
"Надежность в технике. Основные понятия. Термины и определения",
понимают его свойство сохранять во времени способность выполнения
требуемых функций в заданных режимах и условиях применения.
Способность технического объекта выполнять требуемые функции
описывается совокупностью некоторых непосредственно измеряемых
параметров. В этом случае надежность можно трактовать как свойство
объекта сохранять во времени в установленных пределах значения этих
параметров. К таким параметрам относятся кинематические и
динамические характеристики объектов, показатели конструкционной прочности
деталей машин и их соединений, технологические параметры и т.д. С
течением времени значения этих параметров изменяются, что может
привести к достижению предельно допустимых значений параметров.
Теоретический анализ явлений, технологических процессов и
функционирования машин и конструкций основан на выборе физических
моделей или расчетных схем. Возможны два подхода к анализу:
детерминистический и стохастический (вероятностный). При
детерминистическом подходе все факторы, влияющие на поведение объекта,
считаются вполне определенными, неслучайными. Однако выводы,
основанные на детерминистических моделях, могут расходиться с
результатами опытных наблюдений за счет влияния разнообразных слабо
контролируемых и сложным образом взаимодействующих факторов.
Поэтому поведение реальных объектов в той или иной мере носит
№
неоднозначный, случайный характер. В отличие от детерминистического,
стохастический подход учитывает воздействия всего многообразия
случайных факторов и дает предсказания, содержащие вероятностные
оценки.
Особенностью реальных условий эксплуатации машин и конструкций
является случайный характер взаимодействия с окружающей средой. Это
проявляется в том, что мы не можем достоверно предвидеть все типы
внешних нагрузок и их интенсивности, которые могут встретиться в
процессе эксплуатации в течение всего срока службы. Кроме того,
источником неопределенности могут быть случайные свойства
материалов, которые наглядно проявляются при испытаниях,
обнаруживающих разброс экспериментальных данных. Еще один источник
неопределенности связан с разбросом геометрических параметров
конструкции: в принципе невозможно абсолютно точно выдержать
размеры конструкций, при их изготовлении допускаются некоторые
отклонения.
Методы и процедуры, связанные с обеспечением надежности
технического объекта в течение всего цикла его жизнедеятельности,
начиная от выработки технического задания и кончая списанием,
подлежат стандартизации. Методологическое значение стандартов и
нормативно-технических документов состоит в том, что они позволяют
регламентировать методы решения типовых задач анализа,
прогнозирования, оценивания и обеспечения надежности, отвечающие современному
научно-техническому уровню развития.
Надежность и ее составляющие. Надежность - это комплексное
свойство, в котором в зависимости от назначения и условий применения
в различной степени могут проявляться составные элементы надежности:
безотказность, долговечность, ремонтопригодность и сохраняемость.
Безотказностью называют свойство объекта непрерывно сохранять
работоспособное состояние в течение некоторого времени или
наработки. Под долговечностью понимают способность не достигать в течение
достаточно длительного времени предельного состояния, т.е. такого
состояния, при котором дальнейшее использование объекта по
назначению становится невозможным или нецелесообразным.
Ремонтопригодность - свойство объекта, заключающееся в приспособленности
к поддержанию и восстановлению работоспособного состояния путем
технического обслуживания и ремонта. Сохраняемость определяют как
свойство обеспечивать в заданных пределах способность объекта
выполнять требуемые функции в течение и после хранения и (или)
транспортирования.
Состояния технического объекта. Каждое состояние характеризуется
совокупностью значений параметров, а также качественных признаков.
20
Среди состояний следует различать исправное состояние, при котором
объект соответствует всем требованиям нормативно-технической
документации,работоспособное состояние, при котором объект способен
выполнять заданные функции в соответствии с установленными
требованиями, и предельное состояние, определение которого дано выше.
При этом переход объекта в предельное состояние влечет за собой
временное или окончательное прекращение эксплуатации.
Офазы. К понятиям отказа относят дефект, который характеризуется
несоответствием какому-либо из требований нормативно-технической
документации до начала эксплуатации, повреждение, влекущее
нарушение исправного состояния при сохранении работоспособного,
и собственно отказ как событие, заключающееся в нарушении
работоспособного состояния. Отказы могут быть полными или частичными,
независимыми или зависимыми, внезапными или постепенными,
устранимыми или неустранимыми, явными или скрытыми, устранимыми
или неустранимыми. К понятиям отказа относят также сбой-
самоустраняющийся отказ в виде кратковременной потери работоспособности,
конструктивный отказ, возникающий из-за ошибок проектирования и
конструирования, производственный отказ, причиной которого является
нарушение процесса изготовления или ремонта, эксплуатационный отказ,
обусловленный нарушением установленных правил эксплуатации,
приработочный отказ, характерный для начальной стадии эксплуатации
объекта, деградационный отказ, связанный со старением, изнашиванием,
коррозией и усталостью, и критический отказ, создающий угрозу для
жизни и здоровья людей, а также для окружающей среды. С понятием
критического отказа связаны такие термины, как безопасность, авария,
катастрофа, живучесть.
Временные понятия. Наработка - это продолжительность или объем
работы объекта. Она может измеряться в календарном времени (в часах,
годах и т.д.), в киловатт-часах, километрах пробега, числах циклов
нагружения и т.п. Долговечность объекта характеризуют его ресурс -
наработка до перехода в предельное состояние, срок службы -
календарная продолжительность эксплуатации до перехода в предельное
состояние, наработка до отказа, время безотказной работы. К
временным понятиям относятся также наработка между отказами, время
восстановления^ срок сохраняемости, средний ресурс, остаточный ресурс,
назначенный ресурс и т.д.
Показатели надежности - это количественные характеристики
одного или нескольких свойств, составляющих надежность. Общий
подход к расчетной оценке показателей надежности технических
объектов основан на трактовке отказа как результате взаимодействия
объекта с другими объектами и с окружающей средой.
21
Показатели безотказности.
Основной показатель безотказ-
л ности - вероятность
безотказной работы, вводится как
вероятность события, состоящего в
том, что в пределах заданной
наработки t не возникнет ни
одного отказа. Вероятностью
называется числовая характерис-
^> тика степени возможности на-
v2 ступления некоторого события
в определенных многократно
воспроизводимых условиях.
Вероятность события А можно
оценить на основе опытных
данных. Если проводится доста-
Рис. 2.1. Выброс случайного процесса из ТОЧно большое число опытов W,
допустимой области в которых событие^ появилось
NA раз, то в качестве оценки вероятности ¥(А) осуществления этого
события можно взять отношение NAIN. Вероятность как мера
возможности наступления события удовлетворяет условиям 0 < Р(А) <. 1, причем
значение Р(А) = 0 соответствует невозможному событию, а значение
Р(А) = 1 - достоверному событию.
Нормативные требования и условия эксплуатации накладывают
ограничения на совокупность параметров конструкции, которые могут
быть сформулированы как условия нахождения случайного вектора v(0,
компоненты которого отвечают за нормальное функционирование
объекта и характеризуют его качество, в заданной допустимой области
Q. Отказам и предельным состояниям соответствуют выходы (выбросы)
этого случайного вектора из допустимой области Q в пространстве
качества V, что проиллюстрировано на рис. 2.1 для случая трехмерного
пространства качества. При этом отказ интерпретируется как случайное
пересечение траекторией вектора качества v(f) предельной поверхности
Г, являющейся границей допустимой области Q. Вероятность безотказной
работы P(t) определяют как вероятность пребывания вектора качества
v(r) в допустимой области Q на отрезке времени [0, /]:
Р(0 = P(v(t) е Q; т е [0, /]}. (2.1)
ЗдесьР{} -вероятность события, заключенного в скобках,!-наработка
от начала эксплуатации до момента наступления этого события, t - время
или суммарная наработка.
22
В частном случае, когда способность объекта выполнять заданные
функции характеризуется одним скалярным параметром - v(r),
вероятность безотказной работы определяют как
Р(/) = РК(т) < v(t) < vjr); т е [0, /]},
где v, и v++ - нижнее и верхнее предельные значения этого параметра,
назначаемые из условий безотказного функционирования. В качестве
примера рассмотрим используемое в прочностных расчетах условие
прочности
о < а,, (2.2)
где о - некоторое приведенное (эквивалентное) напряжение, о, -
предельно допустимое значение этого напряжения. С позиций теории
надежности условие прочности (2.2) в вероятностной трактовке
записывается следующим образом:
Р{а < а,} = /\, (2.3)
где Рф - заданное достаточно высокое значение вероятности, называемое
нормативной вероятностью безотказной работы. В этом случае говорят,
что условие прочности (2.2) обеспечено с вероятностью /%.
Наряду с понятием вероятности безотказной работы используется
понятие вероятности отказа Q(t)y которая определяется как вероятность
того, что в течение заданной наработки, произойдет хотя бы один отказ.
Этот показатель связан с вероятностью безотказной работы
соотношением Q(t) = 1 - P(t). Для высоконадежных объектов вероятность
безотказной работы по отношению к критическим (аварийным,
катастрофическим) отказам должна быть весьма близка к единице, а вероятность отказа
- очень мала по сравнению с единицей. Для таких ситуаций вводится
показатель риска H(t) как вероятность наступления хотя бы одного
критического отказа на заданном отрезке времени. Типичные значения
допустимого риска, например в авиационных нормах, нормах
безопасности атомных энергетических установок составляют Нщ = 10 и
меньше, что соответствует нормативному значению вероятности
безаварийной работы Р„ = 0,999999 и выше.
Среди других показателей безотказности отметим частоту отказов
f{t) = dO(t)ldt и интенсивность отказов k(t) =f(t)IP(t), определяемую как
23
частоту отказов при условии, что до рассматриваемого момента времени
отказов не было.
Показатели долговечности. Гамма-процентный ресурс или гамма-
процентный срок службы t имеют смысл наработки или времени, в
течение которых вероятность безотказной работы будет не ниже значения
у/100, причем у измеряется в процентах. Эти показатели находятся из
решения уравнения P(t ) = у/100. Средний ресурс вычисляют через
вероятность безотказной работы следующим образом:
Г, = fP(t)dt.
2.2. Расчетные нагрузки и коэффициенты запаса
Условие прочности (2.2) записано в терминах напряжений, которые
вычисляются через внешние нагрузки, приложенные к конструкции.
Пусть нагрузки определены с точностью до одного параметра 5, а
приведенное напряжение о связано с этим параметром функциональной
зависимостью
o=fs(S). (2.4)
Тогда условие (2.2) можно переписать через внешние нагрузки как
S < R, (2.5)
где через R обозначено предельное значение параметра нагрузки, т.е.
такое ее значение, которое приводит к предельному состоянию
om=fR(R). (2.6)
Величина R, зависящая от свойств материала и условий нагружения,
называется несущей способностью или сопротивлением.
При заданном значении S отношение
» = f (2-7)
24
называется коэффициентом запаса. Он обозначает, во сколько раз нужно
увеличить нагрузку, чтобы достичь предельного состояния. Вместо
условия прочности (2.5) можно записать эквивалентное ему условие
п > 1. (2.8)
Если нагрузка и свойства материала являются случайными, то условия
прочности (2.5) и (2.8) теряют смысл; их нужно заменить вероятностными
соотношениями типа (2.3)
Р{5 < R) = Р„ (2.9)
или
РЫ > 1} = Р,. (2.10)
При этом коэффициент запаса (2.7) также будет случайным.
Практически расчет на прочность с учетом случайного характера
нагрузок и случайных свойств материала проводится следующим
образом. Вводится некоторое характерное значение нагрузки [5],
называемое допускаемым или нормативным, которое можно определить
из условия
P(S< [S]} = [PJ, (2.11)
где [Ps] - нормативное значение вероятности, называемое
обеспеченностью. Аналогичным образом определяется нормативное значение [R]
несущей способности
Р(Р > [R]) = [Рд]. (2.12)
Отношение
W - ^} (2.13)
называется нормативным коэффициентом запаса. Этот коэффициент
зависит от условий нагружения, от свойств материала, условий работы
конструкции, степени ее ответственности и ряда других факторов. Такой
коэффициент назначается исходя из многолетнего опыта эксплуатации
конструкций; для каждого типа конструкций он задается нормативно-
технической документацией.
25
В качестве нормативных значений [S] и [R] иногда берутся средние
значения соответствующих случайных параметров
<S> = -j-IS,,C«> = -|-I*;, (2.14)
Nj=\ J Nj=\ J
где S: и R - экспериментально полученные значения случайных
параметров в серии из N опытов. Однако в действующих нормах, в
частности строительных, нормативные значения не совпадают со
средними, а сдвинуты в сторону более опасных значений, что связано
со значительным разбросом экспериментальных данных около средних
значений. Для нагрузки принимается несколько большее значение, а для
несущей способности - меньшее
[5] = ks(S), [R] = kr(R). (2.15)
Коэффициенты ks > 1 и kr < 1 находятся из решения уравнений (2.11) и
(2.12). Таким образом, нормативный коэффициент запаса (2.13)
вычисляется через средние значения следующим образом:
(S) ks
С учетом случайного характера внешних нагрузок и сопротивлений
условие прочности (2.5) заменяется следующим расчетным
детерминистическим условием
S. < *♦• (2.16)
Здесь Sm - достаточно редко встречающееся в реальных условиях
эксплуатации высокое значение параметра нагрузки, Rm - также
достаточно редко встречающееся низкое значение несущей способности.
Эти значения называются расчетной нагрузкой и расчетным
сопротивлением. Они находятся из решения уравнений
FiS < SJ = i\, ¥{R > RJ = P„. (2.17)
В правой части соотношений (2.17) содержатся нормативные
значения вероятности, которые должны быть близки к единице (0,95;
0,99; 0,999;...).
26
Расчетные значения нагрузок и несущей способности можно выразить
через средние значения этих величин следующим образом:
S, = ks(S), R, = kR(R)t (2.18)
где коэффициенты ks > 1 ukR< 1 находятся из решения уравнений (2.17).
Расчетные значения связаны с соответствующими нормативными
значениями соотношениями
S, = kn[S\9 Rm = к0[К\. (2.19)
Коэффициент
К = VKs> (2.20)
называется коэффициентом перегрузки (больше единицы). Другой
коэффициент, учитывающий случайный характер несущей способности,
К = VK*> (2.21)
называется коэффициентом однородности (меньше единицы).
Условие прочности (2.16) можно заменить равенством
К
S, = —, (2.22)
т
где коэффициент т > 1 учитывает условия работы конструкции, степень
ее ответственности. С учетом обозначения (2.13) после подстановки (2.19)
и (2.22) для нормативного коэффициента запаса получим формулу,
учитывающую случайные свойства внешних нагрузок и несущей
способности, а также условия эксплуатации и степень ответственности
к
[п] = m " (2.23)
2.3. Расчеты по допускаемым нагрузкам и по допускаемым
напряжениям
Если пренебречь случайным разбросом прочностных свойств
материала конструкции, то расчетное и нормативное значения, а также
среднее значение несущей способности совпадают, R+ = [R] = (R) = Л,
27
а уравнение (2.13) позволяет получить выражение нормативной или
допускаемой нагрузки через нормативный коэффициент запаса
и = w <224>
При этом параметр несущей способности R связан с предельным
значением о„ напряжения функциональной зависимостью (2.6).
Если на заданную конструкцию действует фиксированная неслучайная
нагрузка S, то отношение (2.7)
»s = f (2.25)
определяет коэффициент запаса по нагрузке. При этом условие прочности
можно переписать следующим образом:
S < И. (2.26)
В терминах коэффициентов запаса с учетом формул (2.24) и (2.25) условие
прочности (2.26) примет вид
ns > [л]. (2.27)
Переход от нагрузок к вызываемым этими нагрузками напряжениями
производится по формулам типа (2.4). Отношение
па = — (2.28)
о
называется коэффициентом запаса по напряжениям. С учетом формул
(2.4), (2.6) и (2.5) можно получить связь между коэффициентами запаса
по нагрузкам и по напряжениям
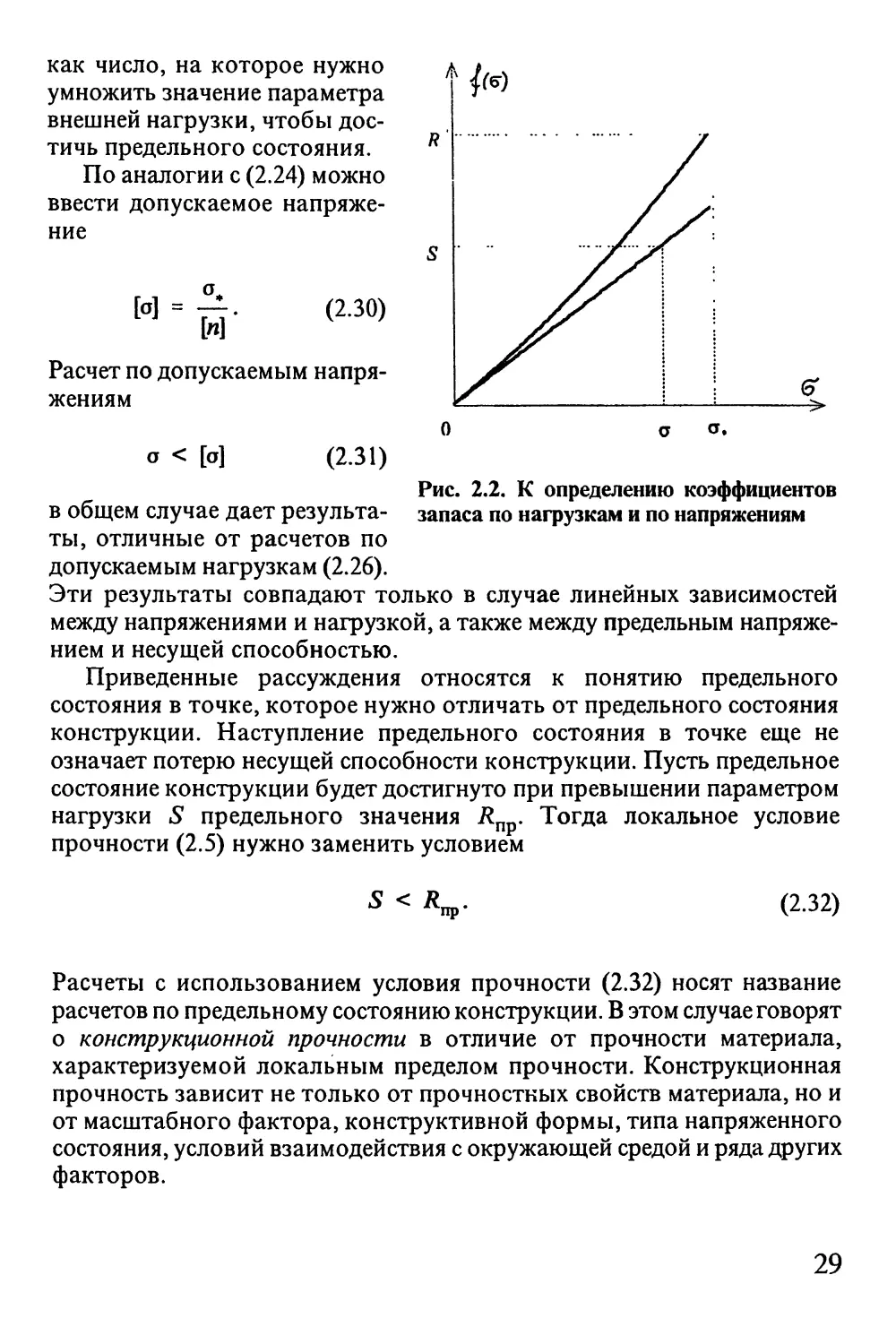
В общем случае коэффициенты запаса (2.25) и (2.28) не совпадают,
что видно на рис. 2.2. Равенство этих коэффициентов возможно только
в том случае, когда зависимости (2.4) и (2.6) линейны. При нелинейной
зависимости коэффициент запаса (2.28) теряет ясный физический смысл
28
как число, на которое нужно
умножить значение параметра
внешней нагрузки, чтобы
достичь предельного состояния.
По аналогии с (2.24) можно
ввести допускаемое
напряжение
[о] = £. (2.30)
Расчет по допускаемым
напряжениям
о < [о] (2.31)
в общем случае дает
результаты, отличные от расчетов по
допускаемым нагрузкам (2.26).
Эти результаты совпадают только в случае линейных зависимостей
между напряжениями и нагрузкой, а также между предельным
напряжением и несущей способностью.
Приведенные рассуждения относятся к понятию предельного
состояния в точке, которое нужно отличать от предельного состояния
конструкции. Наступление предельного состояния в точке еще не
означает потерю несущей способности конструкции. Пусть предельное
состояние конструкции будет достигнуто при превышении параметром
нагрузки S предельного значения Rn . Тогда локальное условие
прочности (2.5) нужно заменить условием
S < V (2.32)
Расчеты с использованием условия прочности (2.32) носят название
расчетов по предельному состоянию конструкции. В этом случае говорят
о конструкционной прочности в отличие от прочности материала,
характеризуемой локальным пределом прочности. Конструкционная
прочность зависит не только от прочностных свойств материала, но и
от масштабного фактора, конструктивной формы, типа напряженного
состояния, условий взаимодействия с окружающей средой и ряда других
факторов.
Рис. 2.2. К определению коэффициентов
запаса по нагрузкам и по напряжениям
29
Глава 3
ОСНОВЫ МЕХАНИКИ МАТЕРИАЛОВ
3.1. Понятие о напряжениях и деформациях
Внутренние силы, действующие в некотором сечении тела, можно
привести к главному вектору F и главному моменту G. В окрестности
точки М, принадлежащей сечению с единичным вектором нормали п,
выделим площадку A F. Главный вектор внутренних сил на площадке
обозначим через А Р (рис. 3.1). При уменьшении размеров A
Fуменьшается главный вектор и главный момент внутренних сил, при этом главный
момент уменьшается в большей степени. В пределе при A F-+ 0 получим
lim т£ = Ри* (зл>
AF-0 AF
Введенный таким образом вектор рп называется вектором напряжений
в точке. Вектор напряжений зависит не только от действующих на тело
внешних сил и координат точки М, но и от ориентации в пространстве
площадки F, определяемой вектором п. Совокупность всех векторов
напряжений в точке М для всевозможных направлений вектора п
определяет напряженное состояние в этой точке.
В общем случае направление вектора рп не совпадает с направлением
вектора п. Проекция вектора рп на направление вектора п называется
нормальным напряжением оп, а проекция на плоскость, проходящую через
точку М и ортогональную вектору п - касательным напряжением тп
(рис. 3.2). В международной системе единиц СИ напряжения измеряются
SJfec
Рис. 3.1. Главный вектор внутрен- Рис. 3.2. Вектор напряжений в точке
них сил на элементарной площадке п его проекции - нормальное и
касательное напряжения
30
Рис. 3.3. Вектор перемещений
в Паскалях: 1 Па = 1 Н/м2. При
действии внешних сил
происходит изменение объема тела и
его формы, т.е. тело
деформируется. При этом различают
начальное (недеформирован-
ное) и конечное
(деформированное) состояние тела.
Положение некоторой точки М не-
деформированного тела
(рис. 3.3) определим радиус-
вектором г (х, у, z). В
деформированном состоянии точка М
займет новое положение М',
определяемое
радиус-вектором г' (х, у, г). Вектор и = г' -
- г называется вектором перемещений точки М. Проекции вектора и на
координатные оси Ох, Оу, Oz определяют компоненты вектора
перемещений и(х, у, z), v(x, у, z), w(x, у, z), равные разности декартовых
координат точки тела после и до деформации.
Перемещение, при котором взаимное расположение точек тела не
меняется, не сопровождается деформациями; говорят, что тело
перемещается как жесткое целое (линейное перемещение в пространстве или
поворот относительно некоторой точки).
Деформации тела характеризуются изменением взаимного
расположения точек тела до и после деформации. Рассмотрим точку М и близкую
к ней точку N, расстояние между которыми в недеформированном
состоянии вдоль направления вектора s обозначим через A s (рис. 3.4).
В деформированном состоянии точки М и N переместятся в новое
положение (М' и N'), расстояние между которыми обозначим через A s'.
Предел отношения
lim
Ад - Aj
(3.2)
называется относительной линейной деформацией в точке М в
направлении вектора s. Компоненты s вдоль координатных осей Ох, Оу, Oz - ev,
8 и е2, соответственно, характеризуют изменение объема тела в процессе
деформирования.
Для описания деформаций, связанных с изменением формы тела,
рассмотрим точку М и две близкие к ней N и Р, расположенные в
недеформированном состоянии в направлении двух взаимно ортогональ-
31
Рис. 3.4. К определению линейной де- Рис. 3.5. К определению угловой
деформации формации
ных векторов s j и s2 (рис. 3.5). В деформированном состоянии положение
точек обозначим через М', N' и Р'. При А s{ - О, A s2 - 0 изменение угла
Yj2 между двумя ортогональными до деформации направлениями
называется угловой деформацией, которая складывается из двух углов at
ид2-
Если заданы три взаимно ортогональных вектора, направленных
вдоль координатных осей, то имеются три угловые деформации у , yxz
и у v которые вместе с линейными деформациями полностью определяют
деформированное состояние в точке.
3.2. Напряженное состояние в точке. Тензор напряжений
Вектор напряжений рп является физическим объектом, имеющим
длину, направление и точку приложения. В этом смысле он обладает
векторными свойствами. Однако этому объекту присущи некоторые
свойства, не характерные для векторов. В частности, величина и
направление вектора напряжений зависят от ориентации вектора п
нормали бесконечно малого элемента поверхности dF. Совокупность всех
возможных пар векторов (п, рп) в точке определяет напряженное
состояние в данной точке. Однако для полного описания напряженного
состояния в точке нет необходимости задавать бесконечное множество
направлений вектора п, достаточно определить векторы напряжений на
трех взаимно перпендикулярных элементарных площадках. Напряжения
на произвольно ориентированных площадках могут быть выражены
через три вектора напряжений.
Проведем через точку М три взаимно перпендикулярных плоскости
с векторами нормалей, направления которых совпадают с направлениями
координатных осей. Элементарные площадки образуем
дополнительными сечениями, параллельными исходным плоскостям и отстоящими от
32
о ~, п ~ Рис. 3.7. Компоненты тензора напря-
Рис. 3.6. Векторы напряжении на Y Y
г * WAUMM
элементарных площадках
жении
них на бесконечном малые расстояния dx, dy, dz. В результате в
окрестности точки М получим бесконечно малый параллелепипед, поверхность
которого образована элементарными площадками dFx = dy dz, dF = dx
dz, dFz = dx dy. Векторы напряжений рЛ., p , pz, действующие на
элементарных площадках, показаны на рис. З.о.
Разложим каждый вектор напряжений на составляющие вдоль
координатных осей (рис. 3.7). На каждой площадке действует одно
нормальное напряжение ох, о , oz, где индекс обозначает направление
вектора нормали к площадке, и дэа касательных напряжения т с двумя
индексами, из которых первый указывает направление действия
компоненты напряжения, второй - направление вектора нормали к
площадке.
Совокупность девяти компонент напряжений (по три на каждой из
трех взаимно перпендикулярных площадок) представляет собой
некоторый физический объект, называемый тензором напряжений в
точке. Тензор можно представить в виде матрицы, соответствующим
образом упорядочив девять компонент:
/ \
О X X
х ху xz
(3.3)
33
Для компонент тензора напряжений общепринятым является
следующее правило знаков: компонента считается положительной, если
на площадке с положительной внешней нормалью (т.е. направленной
вдоль одной из координатных осей) эта компонента направлена в
сторону положительного направления соответствующей оси. На рис. 3.7
все компоненты тензора напряжений изображены положительными. На
площадках с отрицательной внешней нормалью (грани параллелепипеда,
не видимые на рис. 3.6 и 3.7) положительная компонента направлена в
противоположном направлении. Напряжения на трех взаимно
ортогональных площадках с отрицательными направлениями нормалей также
характеризуют напряженное состояние в точке. Эти напряжения,
являющиеся компонентами тензора напряжений (3.3), определяются
аналогично напряжениям на площадках с положительной нормалью. Они
обозначаются теми же символами и имеют положительное направление,
обратное изображенному на рис. 3.7.
3.3. Свойства тензора напряжений. Главные напряжения
Тензор напряжений обладает свойством симметрии. Для
доказательства этого свойства рассмотрим элементарный параллелепипед с
действующими на его площадках компонентами тензора напряжений
(рис. 3.7). Так как тело находится в равновесии, следовательно, находится
в равновесии любая его часть, в том числе и элементарный объем.
Запишем одно из шести уравнений равновесия этого объема, а именно -
сумму моментов всех сил относительно Ох. Все силы, кроме двух, либо
не создают момента относительно оси Ох, либо взаимно уничтожаются.
Отличные от нуля моменты создают компоненты т (верхняя грань) и
т (правая грань):
-(zyzdxdy)dz + (xzydx dz)dy = 0.
После сокращения на элемент объема dK= dx dy dz получим
Хуг = V (3.4)
Аналогично, приравнивая к нулю сумму моментов всех сил
относительно осей Оу и Oz, получим еще два соотношения
Ххг = Tzx> Тху = Zyx* (3.5)
34
Условия симметрии (3.4) и
(3.5) тензора напряжений
называются также условиями
парности касательных
напряжений: касательные напряжения,
действующие по двум взаимно
перпендикулярным площадкам
в направлениях,
ортогональных ребру, образованному
пересечением этих площадок,
равны по величине. С учетом
этих свойств из девяти
компонент тензора напряжений
независимыми оказываются шесть
компонент.
Покажем теперь, что
компоненты тензора напряжений,
определенные для трех взаимно
перпендикулярных площадок,
полностью характеризуют напряженное состояние в точке, т.е. позволяют
вычислить компоненты вектора напряжений на площадках, произвольно
ориентированных относительно выбранной системы координат. Для
этого рассмотрим элементарный объем, образованный сечением
параллелепипеда, изображенного на рис. 3.7, плоскостью, пересекающей
координатные оси и имеющей единичный вектор нормали п с
компонентами пх, пу пг. На гранях полученного таким образом бесконечно малого
тетраэдра действуют напряжения, показанные на рис. 3.8. При этом
вектор напряжений рп на наклонной площадке разложен на
составляющие/7 v, ру pz вдоль координатных осей. Площади граней, ортогональных
координатным осям и вектору нормали, обозначим соответственно dFv,
dFyi dFz, dF. Эти площади связаны между собой соотношениями
Рис. 3.8. Напряжения на наклонной
элементарной площадке
dFx = dFnxi dFy = dFnyt dFz = dFn2
(3.6)
следующими из того, что грани, ортогональные координатным осям, есть
проекции наклонной площадки на соответствующую координатную
плоскость.
Проектируя силы, действующие на гранях элементарного тетраэдра,
на координатные оси, получим уравнения равновесия для
рассматриваемого объема. Например, проекции всех поверхностных сил на ось Ох
дают
35
p dF-o dF -x dF -x dF = 0.
^хш < xx xy у xz г '
С учетом соотношений (3.6) после сокращения на dF получим уравнение,
связывающее проекцию рх вектора напряжений с соответствующими
компонентами тензора напряжений. Объединяя это уравнение с двумя
аналогичными уравнениями, полученными проектированием сил на оси
Оу и Oz, приходим к следующим соотношениям:
р = о п +х п +х п .
гх wx'*x ху'*у *хг*г*
у ух'*х у у yz**z* К**-')
Pz = \хПх + \уПу + агПг*
носящим название формул Кохии. Эти формулы определяют вектор
напряжений на произвольно выбранной площадке с вектором п через
компоненты тензора напряжений.
Формулы (3.7) позволяют вычислить через компоненты тензора
напряжений полное напряжение
нормальное напряжение
°п = Pxnx+Pyny+Pznz (3.9)
и касательное напряжение (см. рис. 3.2):
Среди всех возможных направлений вектора нормали п существуют такие
направления, для которых вектор напряжений рп параллелен вектору п.
На соответствующих площадках действуют только нормальные
напряжения, а касательные напряжения отсутствуют. Такие площадки
называются главными, а нормальные напряжения на этих площадках
называются главными напряжениями. Пусть площадка с единичным
вектором нормали является главной. Условия коллинеарности векторов
рп и п есть условия пропорциональности их компонент:
36
Рх = ОЛх> Ру = °»у Рг = аПг'
С учетом формул Коши (3.7) получим систему линейных однородных
уравнений относительно неизвестных компонент пх, п , пг вектора
нормали к главной площадке
(а - а)п + х и +х п = О,
\ух "f*x *Ху"у хг *z v»
х п + (а - а)п +х п = 0,
ух х V v /"у vz г '
(3.11)
X Л +х п + (о ~ О^Л = 0.
Эта система уравнений имеет ненулевое решение, если определитель,
составленный из коэффициентов уравнений, обращается в нуль:
о - О X X
v ху xz
X О ~ О X
= 0.
(3.12)
Раскрывая определитель, приходим к кубическому уравнению
относительно главного напряжения о:
о3 - /,о2 + J2a - /3 = 0.
(3.13)
Здесь введены обозначения
"1 х у х*
°х
V
хху
°У
+
°х
хшх
\z
°z
+
°,
Хгу
ь\
°z
= °*°, + °X°Z + °уа2 ~ Ь1, + 4 + £) • (3-Й)
'»-
°*
X
ух
Т2ж
V
°,
х*>.
xxi
\г
°z
ш ax°y°z + 2 VX**V - о,£ - o,t*f - o2x^.
37
Уравнение (3.13) называется характеристическим уравнением для
тензора напряжений. Коэффициенты (3.14) этого уравнения называются
инвариантами тензора напряжений. Решение кубического уравнения
(3.13) имеет три вещественных корня Oj, о2, а3, которые обычно
упорядочиваются: ох > о2 ^ о3. Каждому значению о. (/ = 1, 2, 3)
соответствует вектор п7, характеризующий положение у-й главной
площадки, с компонентами п£,Пу, л/ . Для нахождения этих компонент
достаточно в уравнения (3.11) подставить найденное значение о- и решить
любые два из этих уравнений совместно с условием нормировки
{nifHnifHnif- 1. (3.15)
Главные напряжения обладают важным свойством по сравнению со
всеми другими площадками: нормальные напряжения на главных
площадках принимают экстремальные значения. Для доказательства
этого свойства достаточно исследовать на экстремум нормальное
напряжение (3.9) как функцию пх, п, пг при дополнительном ограничении
(3.15). Можно показать, что три главные площадки, соответствующие
главным напряжениям Oj, о2, а3, взаимно перпендикулярны или, что то
же самое, векторы п7 и п/с, соответствующие различным значениям^ и к -
ортогональны. Условие ортогональности имеет вид
nln? + и/л/ + л/лж* = О Ог * *) • (3.16)
Кубическое уравнение (3.12) можно переписать в виде
(о,-о)(о2-о)(о3-о) = 0.
Приводя это уравнение к виду (3.13), получим следующие выражения для
инвариантов (3.14) через главные напряжения:
Jx = Oj+02 + Оз, /2 = 0^2 + 0,03 + ^03, /3 = °1а2°3' (3.17)
Термин "инвариантность" обозначает независимость некоторой
величины от выбора системы координат.
Введем среднее (гидростатическое) напряжение по формуле
°о = (°* + <V°z)/3 = К + ^ + ОзУЗ. (3.18)
38
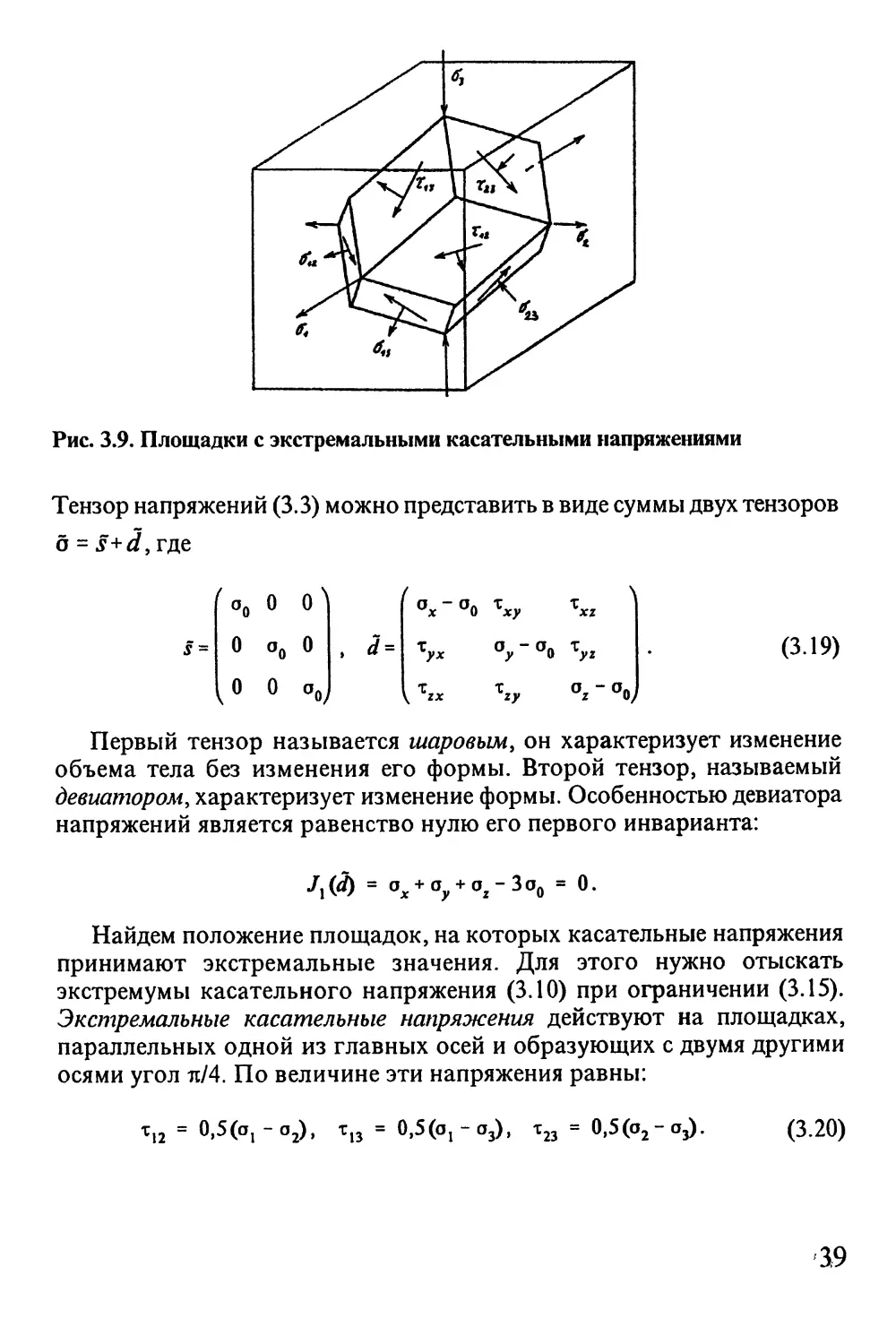
Рис. 3.9. Площадки с экстремальными касательными напряжениями
Тензор напряжений (3.3) можно представить в виде суммы двух тензоров
б = s + ^,где
(3.19)
Первый тензор называется шаровым, он характеризует изменение
объема тела без изменения его формы. Второй тензор, называемый
девиатором, характеризует изменение формы. Особенностью девиатора
напряжений является равенство нулю его первого инварианта:
/
0
1°
0
°о
0
°1
0
ао)
, i =
( \
°х"°0 хху Xxz
V °>~°° Ъг
^ Zzx Xzy az " °0J
J{(d)
a + о + о
x у z
3oft = 0.
Найдем положение площадок, на которых касательные напряжения
принимают экстремальные значения. Для этого нужно отыскать
экстремумы касательного напряжения (3.10) при ограничении (3.15).
Экстремальные касательные напряжения действуют на площадках,
параллельных одной из главных осей и образующих с двумя другими
осями угол л/4. По величине эти напряжения равны:
(^(с^-сд, т13 = 0,5(о,-о3), х23 = 0,5(о2-о3).
(3.20)
3,9
При этом на площадках с экстремальными касательными
напряжениями присутствуют нормальные напряжения, которые равны:
о12 = 0,5(^ + 02), о1? = (^(Oj+Oj), о23 = 0,5(о2 + Оз).
Фигура, которую образуют площадки с экстремальными касательными
напряжениями, изображена на рис. 3.9. Она принадлежит к классу
параллелоэдров и представляет собой 12-гранник с гранями в виде
ромбов, отношение диагоналей которых равно \Jl.
3.4. Плоское напряженное состояние
Рассмотрим важный для приложений случай плоского напряженного
состояния, реализуемого, например, в плоскости Oyz. Тензор напряжений
в этом случае имеет вид
'о О О
0 °, V
V 0 V °г ,
Геометрическая иллюстрация представлена на рис. 3.10. При этом
площадки х = const являются главными с соответствующими нулевыми
главными напряжениями. Инварианты (3.14) тензора напряжений равны:
J{ = оу + oz, J2 = oyoz - \yz, У3 = 0, а характеристическое уравнение (3.13)
принимает вид
Корни этого уравнения равны:
О, о
1.3
У г +
+ *«
(3.21)
Нумерация корней произведена для случая о,>0, о3<0.
Произвольная площадка характеризуется углом а на рис. 3.10, при
этом вектор п имеет компоненты: п = cos a, nz = sin а, пх = 0. Нормальное
и касательные напряжения (3.9) и (3.10) на наклонной площадке
выражаются через угол а следующим образом:
О = -L 1
а - а
-Z -cos2cc + х sin2a,
(3.22)
40
Рис. ЗЛО. Плоское напряженное состо- Рис- 3-11. Главные площадки и глав-
яние ные напряжения
■ £sin2a + т cos2a.
2 yz
(3.23)
Так как на главных площадках касательное напряжение отсутствует,
то, приравнивая к нулю выражение (3.23), получим уравнение для
определения угла а между нормалью п и осью Оу:
tg2a
2т
У*
(3.24)
Наименьший положительный корень уравнения (3.24) обозначим через
ctj. Так как tg(x) - периодическая функция с периодом тс, то имеем два
взаимно ортогональных направления, составляющих углы ctj и а2 = ах +
+ тс/2 с осью Оу. Эти направления соответствуют взаимно
перпендикулярным главным площадкам (рис. 3.11).
Если продифференцировать соотношение (3.22) по а и приравнять
производную к нулю, то придем к уравнению (3.24), что доказывает
экстремальность главных напряжений.
Для нахождения ориентации площадок с экстремальными
касательными напряжениями приравняем к нулю производную от выражения (3.23)
(o2-apcos2at-2^zsin2at = О,
откуда получим
tg2aT -
2т„
(3.25)
41
Сравнивая соотношения (3.24) и
(3.25), находим, что
tg2atg2ax = -1.
/»
* /КР /
*<
Это равенство возможно, если углы
2 а и 2 ат отличаются на угол тс/2.
Следовательно, направления площа
док с экстремальными касательными
напряжениями отличаются от направ
лений главных площадок на угол
и/4 (рис. 3.12).
Величины экстремальных каса Рис. 3.12. Главные площадки и
тельных напряжений получим после площадки с экстремальными каса-
подстановки (3.25) в соотношение тельными напряжениями
(3.23) с использованием формул
cos 2a =
1
sin 2 a
Jg2a_
V^l+tg22a V^l+tg22a
После некоторых преобразований получим
% « ^((a2-o,)/2)2 + T,V
(3.26)
Сравнивая это выражение с полученными ранее значениями главных
напряжений (3.21), выразим экстремальные касательные напряжения
через главные напряжения
т13 = 0,5(0,-03). (3.27)
Аналогичная подстановка в (3.22) приводит к выражению для
нормальных напряжений на площадках с ат:
°1з = °»5(°1 + аз)-
(3.28)
3.5. Тензор деформаций
Рассмотрим вначале случай плоской деформации (рис. 3.13). Пусть
плоский элемент MNPQ перемещается в пределах плоскости и деформи-
42
Рис. 3.13. Перемещения и деформации в плоскости
руется (изменяет форму и размеры). Координаты точек элемента до и
после деформации отмечены на рисунке.
По определению (3.2) относительная линейная деформация в точке
М в направлении оси Ох равна
т13 = 1/2 (о j -03).
(3.29)
Из рис. 3.13 следует
M'N' =
N
dx + i^dxl +
дх )
Учитывая, что MN = dx, получим
N
1+2
ix \дх) \дх)
1.
В случае малых деформаций, когда (dw/dx)«l, (dvldx)«\, можно
пренебречь квадратичными слагаемыми. С учетом приближенного
соотношения
у/\ +х« 1 +х/2,
43
справедливого при х« 1, окончательно для малой деформации получим
ди
х дх
Угловая деформация у определяется как сумма углов otj и а2 (см.
рис. 3.5 и 3.13). В случае малых деформаций
. дх дУ
а «tga = «_
- ди , дх
dx + —dx
дх
ди А
— ау
+Л дУ ди
d^dy *
Для угловой деформации у имеем
ху
ди L д\
Y—. = — +
*ху
ду дх
Проводя аналогичные выкладки в общем случае трехмерной
деформации, имеем девять соотношений:
ди dv _ dw
*х = to* *> = ду' *> = ~Ы'
ди д\ ди _,_ dw
Y- = Y- = ^+^- у»яу«ят,*^' <330>
= dw + dw
Уу1 ' Угу ~ dz ду'
связывающих линейные и угловые деформации с перемещениями. Эти
соотношения носят название соотношений Коши.
Три линейных и шесть угловых деформаций (3.30) образуют тензор
малых деформаций
44
гх М2уху 1/2YJ|
ШУух гу 1/2Т
[Шу2Х \/2yzy гг
(3.31)
Этот тензор полностью определяет деформированное состояние твердого
тела. Он обладает теми же свойствами, что и тензор напряжений.
Свойство симметрии непосредственно следует из определения угловых
деформаций. Главные значения и главные направления, а также
экстремальные значения угловых деформаций и соответствующие им
направления находятся теми же методами, что и для тензора напряжений.
Инварианты тензора деформаций определяются формулами,
аналогичными (3.14) и (3.17), причем первый инвариант тензора малых
деформаций имеет ясный физический смысл. Для его выяснения
рассмотрим элементарный объем, изображенный на рис. 3.6. До
деформации его объем равен dV0 = dx Ay dz. Если пренебречь
деформациями сдвига, которые изменяют форму, а не объем, то после деформации
ребра будут иметь размеры dx + — dx, dy+— dy, dz+ — dz (см.
дх dy dz
рис. 3.13), а его объем равен dV = (1 + ev) (1 + б^) (1 + ez) dx d^ dz.
Относительное изменение объема
dF-dFft
в =
dK0
в пределах малых деформаций составит
в -*, + V«,. (3.32)
что совпадает с определением первого инварианта. Очевидно, что
изменение объема есть физическая величина, не зависящая от выбора
системы координат.
Так же, как и тензор напряжений, тензор деформаций можно
разложить на шаровой тензор и девиатор по формулам типа (3.19). При
этом первый инвариант девиатора равен нулю, т.е. девиатор
характеризует деформацию тела без изменения его объема.
3,6. Упругость и пластичность. Закон Гука
Действие внешних сил на твердое тело приводит к возникновению
в точках его объема напряжений и деформаций. При этом напряженное
45
состояние в точке, связь между напряжениями на различных площадках,
проходящих через эту точку, определяются уравнениями статики и не
зависят от физических свойств материала. Деформированное состояние,
связь между перемещениями и деформациями устанавливаются с
привлечением геометрических или кинематических соображений и также
не зависят от свойств материала. Для того, чтобы установить связь между
напряжениями и деформациями, необходимо учитывать реальные
свойства материала и условия нагружения. Математические модели,
описывающие соотношения между напряжениями и деформациями,
разрабатываются на основе экспериментальных данных. Эти модели
должны с достаточной степенью точности отражать реальные свойства
материалов и условия нагружения.
Наиболее распространенными для конструкционных материалов
являются модели упругости и пластичности. Упругость - это свойство
тела изменять форму и размеры под действием внешних нагрузок и
восстанавливать исходную конфигурацию при снятии нагрузок.
Математически свойство упругости выражается в установлении взаимно
однозначной функциональной зависимости между компонентами тензора
напряжений и тензора деформаций. Свойство упругости отражает не
только свойства материалов, но и условия нагружения. Для большинства
конструкционных материалов свойство упругости проявляется при
умеренных значениях внешних сил, приводящих к малым деформациям,
и при малых скоростях нагружения, когда потери энергии за счет
температурных эффектов пренебрежимо малы. Материал называется
линейно-упругим, если компоненты тензора напряжений и тензора
деформаций связаны линейными соотношениями.
При высоких уровнях нагружения, когда в теле возникают
значительные деформации, материал частично теряет упругие свойства; при
разгрузке его первоначальные размеры и форма полностью не
восстанавливаются, а при полном снятии внешних нагрузок фиксируются
остаточные деформации. В этом случае зависимость между
напряжениями и деформациями перестает быть однозначной. Это свойство
материала называется пластичностью. Накапливаемые в процессе
пластического деформирования остаточные деформации называются
пластическими.
Высокий уровень нагружения может вызвать разрушение, т.е.
разделение тела на части. Твердые тела, выполненные из различных
материалов, разрушаются при разной величине деформации. Разрушение
носит хрупкий характер при малых деформациях и происходит, как
правило, без заметных пластических деформаций. Такое разрушение
характерно для чугуна, легированных сталей, бетона, стекла, керамики
и некоторых других конструкционных материалов. Для малоуглеродис-
46
тых сталей, цветных металлов, пластмасс характерен пластический тип
разрушения при наличии значительных остаточных деформаций. Однако
подразделение материалов по характеру разрушения на хрупкие и.
пластические весьма условно, оно обычно относится к некоторым
стандартным условиям эксплуатации. Один и тот же материал может
вести себя в зависимости от условий (температура, характер нагружения,
технология изготовления др.) как хрупкий или как пластичный.
Например, пластичные при нормальной температуре материалы
разрушаются как хрупкие при низких температурах. Поэтому правильнее
говорить не о хрупких и пластичных материалах, а о хрупком или
пластическом состоянии материала.
Пусть материал является линейно-упругим и изотропным. Рассмотрим
элементарный объем, находящийся в условиях одноосного напряженного
состояния (рис. 3.14), так что тензор напряжений имеет вид
ох 0 (^
0 0 0
\о о о;
При таком нагружении происходит увеличение размеров в направлении
оси Ох, характеризуемое линейной деформацией ex(ov), которая
пропорциональна величине напряжения
*>*) - °JE-
(3.33)
Соотношение (3.33) является математической записью закона Гука,
устанавливающего пропорциональную зависимость между напряжением
и соответствующей линейной
деформацией при одноосном
напряженном состоянии.
Коэффициент пропорциональности Е
называется модулем продольной
упругости или модулем Юнга. Он
имеет размерность напряжений.
Наряду с увеличением
размеров в направлении действия
напряжения ох происходит
уменьшение размеров в двух
ортогональных направлениях (рис. 3.14).
Соответствующие деформации
обозначим через гу(ох) и ez(ov),
Рис. 3.14. Одноосное напряженное
состояние
47
причем эти деформации отрицательны при положительных ох и
пропорциональны ех:
е,(°*) = -^>*)> Ez(°x) = -Р*Л°Х)- (3.34)
Коэффициент пропорциональности \i называется коэффициентом
Пуассона, который в силу изотропности материала одинаков для обоих
ортогональных направлений.
Соотношения, аналогичные (3.33) и (3.34), в случае одноосного
нагружения в направлении осей Оу, Oz напряжением о , oz
соответственно имеют вид
е/°Р = oyIEt гх(ау) = -\1гу(оу), г2(ру) = -\ity(ay)t (3.35)
Cz(°2> = °z,E> Cx(°z) = -Р*г(аг)> *>(°г) = ~Hc>z)- (3.36)
При одновременном действии напряжений по трем ортогональным осям,
когда отсутствуют касательные напряжения, для линейно-упругого
материала справедлив принцип суперпозиции (наложения решений):
*у = */<>*)+ *,(<>,)+ *,(°2)>
cz я cz(ox) + ez(op + e2(or).
С учетом формул (3.33)...(3.36) получим
е,= ^K-^(a, + °z)]. (3.37)
cz = ^К-^(°х + °Р]-
48
Касательные напряжения вызывают угловые деформации, причем при
малых деформациях они не влияют на изменение линейных размеров и,
следовательно, на линейные деформации. Поэтому (3.37) справедливы
также в случае произвольного напряженного состояния и выражают
так называемый обобщенный закон Гука.
Угловая деформация у обусловлена касательным напряжением х ,
деформации yxz и у - соответственно напряжениями xxz и х . Между
соответствующими касательными напряжениями и угловыми
деформациями для линейно-упругого изотропного тела существуют
пропорциональные зависимости
Уху ~ ~^Хху> Чхг ~ "7;Txz> 4yz ~ "Ti^yz* (3.38)
которые выражают закон Гука при сдвиге. Коэффициент
пропорциональности G называется модулем сдвига. Существенно, что нормальное
напряжение не влияет на угловые деформации, так как при этом
изменяются только линейные размеры отрезков, а не углы между ними
(рис. 3.14).
Линейная зависимость существует также между средним
напряжением (3.18), пропорциональным первому инварианту тензора напряжений,
и объемной деформацией (3.32), совпадающей с первым инвариантом
тензора деформаций:
в = о0/К. (3.39)
Соответствующий коэффициент пропорциональности К называется
объемным модулем упругости.
В формулы (3.33)...(3.39) входят упругие характеристики материала
Е9 ц, G и К, определяющие его упругие свойства. Однако эти
характеристики не являются независимыми. Для изотропного материала
независимыми упругими характеристиками являются две, в качестве которых
обычно выбираются модуль упругости Е и коэффициент Пуассона ц.
Чтобы выразить модуль сдвига G через £иц, рассмотрим плоскую
деформацию сдвига под действием касательных напряжений х (рис. 3.15).
Для упрощения выкладок используем квадратный элемент со стороной
а. По формулам (3.21) вычислим главные напряжения Oj = х, о3 = -х. Эти
напряжения, как следует из (3.24), действуют на площадках,
расположенных под углом тс/4 к исходным площадкам. Из рис. 3.15 найдем связь
49
Рис. 3.15. Плоская деформация сдвига
между линейной деформацией г{ в
направлении действия напряжения
Oj и угловой деформацией у.
Большая диагональ ромба,
характеризующая деформацию г1} равна
А'В' = y/(a + atgy)2 + a2.
Для малых деформаций tg у ~ у,
Y2«y« 1, \/1 +у - 1 + у/2. С
учетом этих соотношений
А В' = ау/2(\+у/2).
До деформации эта диагональ
имела размер АВ = a\Jl. Тогда
= А'В' -АВ = ду/2 (1ч- у/2) -а/Ё = у
Из обобщенного закона Гука (3.37) получим
откуда
Y = 2т(1 + ц)/£.
Сравнение полученной формулы с записью закона Гука при сдвиге (3.38)
дает
G = £/[2(1+ц)].
Сложим три соотношения упругости (3.37)
б = Б+Е+е = — (а + а + а ).
v °х ■> °z р v"х >» wz'*
(3.40)
(3.41)
С учетом обозначения (3.18) получим
50
в . 30 -2,)
Е °
Сравнивая это выражение с объемным законом Гука (3.39), приходим
к результату
ЛГ = £/[3(1-2*0]. (3.42)
Механические характеристики Е, \х, G и К находят после обработки
экспериментальных данных испытаний образцов на различные виды
нагрузок. Из физического смысла все эти характеристики не могут быть
отрицательными. Кроме того, из (3.42) следует, что коэффициент
Пуассона для изотропного материала не превышает значения 1/2. Таким
образом, получаем следующие ограничения для упругих постоянных
изотропного материала:
Я>0, G>0, К>0, 0*ц<; 1/2. (3.43)
Предельное значение ц - 1/2, как следует из (3.42), приводит к
предельному значению К - °°, что, согласно (3.39), соответствует несжимаемому
материалу (0-0 при о0 * 0).
В заключение выразим из соотношений упругости (3.37) напряжения
через деформации. Запишем первое из соотношений (3.37) в виде
ех = -|К(1+ц)-ц(ох + ^ + ог)].
С использованием равенства (3.41) будем иметь
е = —£о -—с—0,
Е х 1 -2ц
откуда
Е \iE а
сг = е + £ 6.
х l+|i х (1+|1)(1-2ц)
Аналогичные соотношения можно вывести для оу и ог В результате
получим
ах = 2Gex + A.6,
51
IGz + A.6,
(3.44)
a2 = 2Gzz + XQ.
Здесь использовано соотношение (3.40) для модуля сдвига. Кроме
того, введено обозначение
»Е
<l+|i)(l-2|i)
= K-2G/3.
(3.45)
В справедливости последнего равенства можно убедиться
непосредственной подстановкой G и К из (3.40) и (3.42).
3.7. Потенциальная энергия упругой деформации
Рассмотрим вначале элементарный объем dV = dx dy dz в условиях
одноосного напряженного состояния (рис. 3.16). На свободную
площадку действует сила oY dy dz. Эта сила совершает работу на перемещении
гх dx. При увеличении напряжения от нулевого уровня до значения ох
соответствующая деформация в силу закона Гука (3.33) также
увеличивается от нуля до значения ех, а работа пропорциональна заштрихованной
на рис. 3.17 площади: dA = dU= 0,5 ov гх d V. Если пренебречь
кинетической энергией и потерями, связанными с тепловыми, электромагнитными
и другими явлениями, то в силу закона сохранения энергии совершаемая
Л
dx
с d*(*+*x) ^
(fxdt/di
Рис. 3.16. Напряжение и деформация
при одноосном напряженном состоянии
Рис. 3.17. Линейная зависимость
напряжения от деформации
52
работа перейдет в потенциальную
энергию, накапливаемую в процессе
деформирования. Величина
^ df/
Ф = называется удельной по-
dV
тенциальной энергией деформации,
имеющей смысл потенциальной
энергии, накопленной в единице
объема тела. В случае одноосного
напряженного состояния
А
Ч\
1 \
у
Гдгу „ _j
—г > -*-
i *
/
/
/
< '
|tff*yrfy
"1
t/
/
/
Т<"
J _
y///////j>/s//////*>
и—^—-
f
Ф - 1/2 о е . (3.46) Рис. 3.18. Напряжения и деформации
при чистом сдвиге
При одновременном действии
напряжений ох, о и oz на главных площадках (т.е. при отсутствии
касательных напряжений) потенциальная энергия равна сумме работ,
совершаемых силами ох dy dz, о dx dz, oz dx dy на соответствующих
перемещениях гх dx, г dy, zz dz. Удельная потенциальная энергия равна
Ф = 1/2(охех + оЛ + оЛ).
(3.47)
В частном случае чистого сдвига в плоскости Оху, изображенном на
рис. 3.18, сила т dx dz совершает работу на перемещении уху dy.
Соответствующая этому случаю удельная потенциальная энергия
деформации равна
Ф = 1/2т у .
(3.48)
Подобные соотношения будут иметь место при сдвиге в других
плоскостях.
В общем случае напряженно-деформированного состояния будем
иметь
Ф = V2(axtx + oyzy + o2Bz + Txyyxy + xxzyxz + Tyzyyz).
(3.49)
Если деформации выразить через напряжения с помощью
соотношений упругости (3.37) и (3.38), то получим эквивалентную (3.49) форму
записи через компоненты тензора напряжений
Ф°= i[°' + °> + °* " Ш°х°у + °х°2 + °'°z)1 + 2G<X*> + Х*я + Х'г)' (350)
53
Выразив напряжения через деформации с использованием соотношений
(3.38) и (3.44), получим еще одну форму записи для Ф - через компоненты
тензора деформаций
Фе = G[z\ + г\ + г] + у^02+ W(Y^ - yL - Y^)]. (3.51)
Еще одну форму записи для удельной потенциальной энергии
деформации получим, разложив тензоры напряжений и деформаций на
шаровые тензоры и девиаторы по формулам типа (3.19). В результате
(3.49) можно привести к одной из форм
о т2
\
(3.52)
Ф = 1/2(а0в + ту) = 1/2(AT82 + Gy2) = 1/2
\ К G)
где использованы обозначения (3.18), (3.32), (3.40) и (3.42). Кроме того,
введены обозначения для т - интенсивности касательных напряжений
и y - интенсивности деформаций сдвига, которые выражаются через
вторые инварианты J2(da) и J2(dt) девиаторов тензора напряжений и
тензора деформаций следующим образом:
* = ЧЮ. Y2 = -4/2(4). (3.53)
Первые слагаемые в (3.52) соответствуют произведению шаровых
составляющих тензоров напряжений и деформаций, а вторые -
произведению девиаторных составляющих. Так как шаровой тензор
характеризует изменение объема, а девиатор - изменение формы, то
соотношения (3.52) можно интерпретировать как разложение удельной
потенциальной энергии на две составляющие Ф = Ф0 + Фф, где Ф0
соответствует изменению объема без изменения формы, а Фф -
изменению формы без изменения объема. Первая составляющая с учетом
(3.18) и (3.42) будет вычисляться через компоненты тензора напряжений
следующим образом:
Удельную потенциальную энергию изменения формы проще найти не
через интенсивность касательных напряжений, а как разность Ф - Ф0.
Вычитая (3.54) из (3.50), после преобразований получим
ФФ = "^[а* + Ь + °* " <°*°> + °*°«+ °у°*)] + ^(х*у + т« + т**>' (3.55)
54
3.8. Основы теории прочности
Под прочностью элементов конструкций понимается свойство
сопротивляться разрушению (разделению на части) или необратимому
изменению формы (пластическому деформированию) под действием
внешних нагрузок. Нарушение прочности соответствует переходу
конструкции или ее элементов в предельное состояние. Согласно ГОСТ
27.002-89 "Надежность в технике. Основные понятия. Термины и
определения" предельным состоянием называется такое состояние
конструкции, при котором ее дальнейшее применение по назначению
недопустимо или нецелесообразно. В зависимости от характера
разрушения материала различаются два типа предельных состояний:
хрупкое разрушение и появление пластических деформаций (текучести).
В простейшем случае одноосного напряженного состояния, когда на
одной из площадок действует нормальное напряжение о, условие
перехода в предельное состояние записывается в виде
о = о,, (3.56)
где о+ - предельное значение напряжения, соответствующее переходу
в предельное состояние. Так как напряжения определены в точке тела,
то условие (3.56) характеризует предельное состояние в определенной
точке конструкции, а не предельное состояние всей конструкции в целом.
Предельное состояние конструкции характеризуется выполнением
условия (3.56) для наиболее нагруженной точки в случае хрупкого
состояния материала. Для пластического состояния материала
предельное состояние конструкции означает выполнение условия (3.56) для
некоторой конечной области.
При сложном напряженном состоянии основная задача теории
прочности - найти такое соотношение между компонентами тензора
напряжений, когда в данной точке нагруженной конструкции наступит
предельное состояние. Это состояние можно представить в виде
уравнения
ф(^0/.°«.^т«'т7«> = °' (3-57)
которое в шестимерном пространстве (с учетом парности касательных
напряжений) представляет некоторую поверхность. Для более наглядной
иллюстрации перейдем к главным напряжениям, которые также
характеризуют напряженное состояние в точке. Уравнение (3.57),
записанное через главные напряжения
55
ЧФр°2»°з) = °» (3.58)
есть уравнение предельной поверхности
Г, соответствующей переходу в
предельное состояние (рис. 3.19). Эта
поверхность является границей области
Q, называемой областью допустимых
■>• состояний. Точка М(о{, о2, о3) в про-
&1 странстве главных напряжений
соответствует заданному напряженному
состоянию. Если эта точка находится
в области допустимых состояний
Рис. 3.19. Область допустимых
состояний и предельная повер- MeQ, (3.59)
хность в пространстве главных
напряжений то прочность обеспечена. Условие
(3.59) есть условие прочности. Выход
точки М из области Q через
поверхность Г означает переход в предельное состояние.
Предельное состояние есть состояние материала, из которого
изготовлена конструкция. Это состояние определяется свойствами
материала и регистрируется опытным путем, испытанием образцов или
деталей, выполненных из данного материала при различных типах
нагружения. В принципе можно провести большое число испытаний
образцов при различных видах напряженного состояния, зафиксировать
в каждом опыте факт наступления предельного состояния за счет
постепенного пропорционального увеличения компонент тензора
напряжений и экспериментально построить предельную поверхность.
Однако осуществление подобной серии экспериментов весьма сложно
технически и экономически нецелесообразно. Можно зафиксировать
наступление предельного состояния в сравнительно простых и доступных
опытах, например, при испытаниях призматических образцов на
растяжение или кручение. С точки зрения наступления предельного
состояния эти эксперименты будут эквивалентны экспериментам,
реализующим сложные виды напряженного состояния. Наиболее просто
осуществить испытания при одноосном напряженном состоянии, для
которого уравнение предельной поверхности (3.58) принимает вид (3.56).
С математической точки зрения переход от уравнения (3.58) к
эквивалентной форме записи (3.56) следующий. Запишем уравнение (3.58) в виде
Д°ро2>а3) = °.«
М г
56
Рис. 3.20. К определению эквивалентного напряжения
Если обозначить
°экв =Д°1.о2,Оз),.
то уравнение (3.58) можно привести к виду (3.56)
(3.60)
(3.61)
При этом величина о+ в правой части уравнения (3.61) имеет смысл
предельного напряжения при одноосном напряженном состоянии, а
°экв(°1> °2» °з) "" некотоРое напряжение, соответствующее одноосному
напряженному состоянию с точки зрения наступления предельного
состояния (рис. 3.20).
Переход от уравнения (3.58) к уравнению (3.61) эквивалентен
отображению области Q в трехмерном пространстве главных напряжений
в аналогичную область в одномерном пространстве (рис. 3.21). При
таком отображении область Q становится отрезком прямой, а предельная
поверхность стягивается в точку. Условие прочности (3.59) принимает
вид
<о
В силу отмеченных выше
принципиальных трудностей,
связанных с нахождением
предельной поверхности на основе
опытных данных, основной
задачей теории прочности ста-
М
т\/т
SI
~Г
**
(3.62)
*т
Рис. 3.21. Допустимая область в
одномерном пространстве
57
новится теоретическая аппроксимация этой поверхности путем принятия
некоторых гипотез о причине и характере наступления предельного
состояния. Осуществляется это следующим образом. Из физических
соображений, основанных на имеющихся опытных данных, выделяется
определяющий фактор, имеющий ясный физический смысл,
количественно выражаемый через компоненты тензора напряжений и ответственный
за наступление предельного состояния. Так как наступление предельного
состояния есть свойство материала, не зависящее от вида напряженного
состояния, то предельное значение выбранного фактора будет
одинаковым для сложного напряженного состояния и для эквивалентного ему
одноосного напряженного состояния. Таким образом устанавливается
теоретическим путем зависимость (3.60) между эквивалентным
напряжением и компонентами тензора напряжений при сложном напряженном
состоянии.
Выбор определяющего фактора, характеризующего наступление
предельного состояния, определяет критерий прочности. В зависимости
от выбора того или иного критерия прочности можно получить
различные аппроксимации предельной поверхности, отличающиеся
между собой и имеющие разные степени точности. Для проверки
выбранного критерия прочности и оценки связанной с этим выбором
точности проводятся доступные опыты в условиях сложного
напряженного состояния. Выбор критериев прочности определяется многими
факторами, главными из которых являются свойства материалов, в
частности прочностные свойства, определяющие характер предельного
состояния, - хрупкое разрушение или появление текучести.
3,9. Критерии текучести и хрупкого разрушения
Критерий текучести Треска - Сен-Венана (критерий наибольших
касательных напряжений). Многочисленные эксперименты над
образцами из пластического материала показывают, что причиной
перехода из упругого состояния в пластическое является сдвиг частиц
материала друг относительно друга по площадкам, на которых
действуют наибольшие касательные напряжения. ПЪэтому в качестве
критерия перехода в критическое состояние естественно выбрать
величину этих напряжений. Согласно этому критерию, предельное
состояние наступит тогда, когда наибольшее касательное напряжение
достигнет предельного значения т^, не зависящего от вида напряженного
состояния, а зависящего только от свойств материала.
58
Таким образом, условием наступления текучести является выполнение
условия
Хтах « Т* (3.63)
независимо от вида напряженного состояния. При выполнении условия
о{>о2>о^ наибольшее из экстремальных касательных напряжений (3.20)
равно
Тшах = (°1-°зУ2- (3.64)
Для эквивалентного одноосного напряжения состояния имеем
*хпах = °экв/2. (3.65)
Сравнивая предельные соотношения (3.61) и (3.63), с использованием
(3.65) получим связь предельного значения т, с предельным значением
о*, т.е.
Приравнивая выражения (3.64) и (3.65), получим функциональную
зависимость (3.60) по данному критерию
°экв я °Г°ъ- (3.66)
Предельная поверхность (3.61) в трехмерном пространстве главных
напряжений представляет собой боковую поверхность правильной
шестигранной призмы, ось которой образует одинаковые углы с
координатными осями. Такая призма называется призмой Кулона. Более
наглядно представление о предельной поверхности в случае плоского
напряженного состояния, задаваемого главными напряжениями ах и о
(oz = 0). Тогда сечение предельной поверхности - предельная линия,
которая строится следующим образом. В первом квадранте (ох>0, о>;>0)
при выполнении условия ох>о будем иметь ох = ох, о2 = о , о^ = о2 = 0,
аэкв = °\- Условие (3.61) дает уравнение ах = о^ отрезка АВ предельной
кривой на рис. 3.22. В этом же квадранте при ох<о получим о] = о , о2 =
=: ох, о3 = о2 = 0, что соответствует уравнению оу = о+ предельной кривой
(отрезок ВС). Во втором квадранте (ov<0, о >0) имеем Oj = о , о2 = о2 =
= 0, о3 = ох, оэкв = о - ох, а условие (3.61) приводит к уравнению о - ох =
59
= о^ отрезка CD. Аналогичным
образом строятся остальные
отрезки предельной кривой,
представляющей собой шестиугольник
Треска, изображенный на
рис. 3.22. Перемещая центр этого
шестиугольника вдоль прямой,
равнонаклоненной к
координатным осям Оох, Оо , Ooz, получим
предельную поверхность.
Критерий текучести Губера -
Мизеса. Недостатком критерия
Треска - Сен-Венана является то,
что он не учитывает среднее по
величине главное напряжение о2.
Было бы желательно выбрать в
качестве определяющего фактор,
зависящий от всех компонент тензора напряжений. Одним из таких
факторов является удельная потенциальная энергия деформации (3.50).
Эксперименты показывают, однако, что нагружение образцов из
пластичного материала, при котором меняется только объем без
изменения формы, не приводит к достижению предельного состояния
текучести. Причиной наступления текучести является искажение формы.
Соответствующий критерий формулируется следующим образом:
текучесть наступит при достижении удельной потенциальной энергией
изменения формы предельного значения Ф#, не зависящего от вида
напряженного состояния, а зависящего только от свойств материала.
Согласно этому критерию условие наступления текучести
записывается в виде
Рис. 3.22. Шестиугольник Треска и
эллипс Мизеса
ф *
(3.67)
Удельная потенциальная энергия изменения формы (3.55), выраженная
через главные напряжения, равна
ФФ = -^[°1+02+0з-(^02 + 010з + 02аз)]-
(3.68)
Это выражение путем элементарных преобразований может быть
приведено к виду
60
Фф - ~^h - of + (о, - o3)2 + (o2 - a3)2],
или с учетом (3.20) для экстремальных касательных напряжений
ф _ 2(1+Ц), 2 2 к
ф 32?—^12 2^'
Последняя формула подтверждает экспериментальные данные о
механизме наступления текучести за счет действия касательных
напряжений.
Для эквивалентного одноосного напряженного состояния
+ ±LEa2
1 3
Предельное значение Ф# равно:
ф* + 1в0«- (3.69)
ЪЕ
Сравнивая (3.68) и (3.69), получим
°экв = v°i + 02 + a3" (°| °2 + 0103 + 02°з)- (3.70)
В пространстве главных напряжений предельная поверхность
представляет собой боковую поверхность цилиндра, описанную по
отношению к призме Кулона в критерии Треска - Сен-Венана. В случае
плоского напряженного состояния с главными напряжениями ох, оу9 о2 =
= 0 по формулам (3.70) и (3.61) получим
о =\/о +0-00=0. (3.71)
"экв Vх У * У *
Это есть уравнение линии текучести, полученное сечением предельной
поверхности плоскостью oz = 0, в виде эллипса, описанного около
шестиугольника Треска (рис. 3.22). При этом максимальное расхождение
двух критериев составляет 13,4 %.
Рассмотрим частный случай плоского напряженного состояния, для
которого тензор напряжений имеет вид
61
(о х (Л
а = т О 0 .
(о 0 О J
Для этого случая выражение (3.21) представляют в виде
о, = 0,5о + ^о2/4 + т2, о2 = 0, о3 = 0,5о-^о2/4 + т2.
По критерию Треска - Сен-Венана (3.66) получим
оэкв = ^о2 + 4т2.
(3.72)
По критерию Губера - Мизеса
= V^TIt2.
(3.73)
Уравнение предельной поверхности (3.61) по этим критериям принимает
вид
\Jo2 + 4 т2 = о^, \/о2 + 3-и2 = о,.
(3.74)
Возводя в квадрат и разделив левую и правую части на о„, уравнения
(3.74) можно привести к виду
о2/д2 + т2/62 = 1.
Это есть уравнение эллипса с полуосями (о+, 0,5 о,,) для критерия
Треска- Сен-Венана и (о^, ojy/i)
- для критерия Губера - Мизеса.
Соответствующие кривые
текучести изображены на рис. 3.23.
Наибольшее расхождение при о = О
составляет 13,4%. Эксперименты,
проведенные для данного вида
напряженного состояния,
показывают лучшее согласование с
критерием Губера - Мизеса.
Критерий максимальных нор-
Рис. 3.23. Кривые текучести при плос- мальных напряжений. Для хрупко-
ком напряженном состоянии го состояния материала разруше-
* J
~\г о
Ч/я*
аь/24
J6*6
62
ние происходит путем отрыва
частиц материала. Другой
особенностью хрупкого материала
является его различная
сопротивляемость при действии
растягивающих и сжимающих напряжений,
т.е. хрупкие материалы лучше
работают на сжатие, чем на
растяжение. Простейший критерий
хрупкого разрушения
формулируется следующим образом:
разрушение наступит при достижении
максимальным нормальным
напряжением предельного значения
о+, характеризующего свойства
Рис. 3.24. Предельные поверхности при
хрупком разрушении
материала и не зависящего от вида
напряженного состояния. В силу
экстремальных свойств главных напряжений в качестве максимального
нормального напряжения выступает главное напряжение о1 (при
выполнении условия о{>о2>о^). По этому критерию
°«B°i- (3.75)
Для плоского напряженного состояния oY, о , о2 = 0 соответствующая
предельная линия показана на рис. 3.24 штриховой линией.
Родственным предыдущему критерию является критерий
максимальных линейных деформаций: разрушение наступит при достижении
максимальной линейной деформацией предельного значения с,,
характеризующего только свойства материала и не зависящего от вида
напряженного состояния. Линейные деформации находятся из закона
Гука (3.37). Экстремальные значения эти деформации принимают вдоль
главных направлений, среди которых максимальное значение равно
с, = [о, -ц(о2 + о3)]/£.
Приравнивая это значение соответствующей деформации при
эквивалентном одноосном напряженном состоянии
ci = a*JE>
получим
63
°зкв = О^Ц^ + Оз).
(3.76)
Сечение предельной поверхности для плоского напряженного состояния
показано на рис. 3.24 штрихпунктирной линией, построенной при ц =
= 0,3.
Приведенные критерии хрупкого разрушения экспериментально
подтверждаются для весьма хрупких материалов типа керамики,
кирпича, некоторых марок чугуна. Основным недостатком этих
критериев является то, что они не описывают разрушение при действии
сжимающих напряжений, при которых разрушение происходит не за счет
отрыва, а за счет сдвига. Свободным от этого недостатка является
критерий Мора, согласно которому разрушение происходит по
площадкам с экстремальными касательными напряжениями за счет
действия нормальных и касательных напряжений на этих площадках. На
площадке с максимальным касательным напряжением действуют
напряжения (3.27) и (3.28)
Ьз = (°1~°з)/2» °i3 = (°1 + °з)/2- (3.77)
Критерий Мора устанавливает связь между этими напряжениями в
предельном состоянии. На рис. 3.25 на плоскости параметров о13, т!3
показана предельная кривая, построенная теоретически и
подтвержденная данными экспериментов. Точка А на этой кривой соответствует
опытам на одноосное растяжение с предельным значением
разрушающего напряжения о+, точка С- сжатию с предельным значением
разрушающего напряжения о^, точка В - чистому сдвигу.
Рис. 3.25. К определению эквивалентного напряжения по критерию Мора
64
Если предельную кривую аппроксимировать прямой, проходящей
через точки А и С, то получим уравнение
т|3 = а + Ьоп. (3.78)
Константы а и b находятся из рассмотрения напряженного состояния в
точках А и С с использованием формул (3.77), (3.78):
1/2о, = a+U2boti 1/2о„ = а-№Ьо„.
Решая эти уравнения относительно а и Ь, находим
а = o.oJ(om + oJ,
Подставляя полученные константы в уравнение (3.78) с учетом формул
(3.77), запишем уравнение предельной кривой через главные напряжения
o,-<W°~ = <V (3,79)
Сравнивая уравнение (3.79) с соответствующим уравнением для
эквивалентного одноосного растяжения, имеем выражение для
эквивалентного напряжения по критерию Мора
°экв = °х-™°ъ> (3.80)
где введено обозначение
т = oJo„. (3.81)
Для случая плоского напряженного состояния ох, о , oz = 0 предельная
кривая (3.79) (прямая А С на рис. 3.25) на плоскости параметров (ov, о^)
имеет вид, показанный на рис. 3.24 сплошными линиями (т = 1/3).
Следует отметить, что критерий Мора хорошо согласуется с
экспериментальными данными как для хрупких, так и для пластичных
материалов. Для большинства пластичных материалов можно принять
о^ = о^. В этом случае результаты по критерию Мора и критерию
Треска - Сен-Венана совпадают (см. формулы (3.66) и (3.80) при т = 1,
а также рис. 3.22 и 3.24).
65
Глава 4
МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ
Механические характеристики определяются следующими
факторами:
• веществом, его структурой и свойствами;
• конструктивными особенностями элемента, т.е. размерами, формой,
наличием концентраторов, состоянием поверхности;
• условиями при нагружении: температурой, скоростью,
повторяемостью нагрузки и др.
Конструкционные материалы в процессе деформирования вплоть до
разрушения ведут себя по-разному. Пластичное поведение
характеризуется существенным изменением формы и размеров, при этом к моменту
разрушения развиваются значительные деформации, не исчезающие
после снятия нагрузки. Такие материалы называются пластичными. При
хрупком поведении разрушение наступает при весьма малых
деформациях, и материалы с такими свойствами называют хрупкими. Однако одни
и те же конструкционные материалы, находящиеся в различных условиях
деформирования, ведут себя по-разному: при одних условиях проявляют
себя как пластичные материалы, при других - как хрупкие. В связи с этим
основные макромеханические характеристики материалов - упругость,
пластичность, вязкость и др. - правильнее относить не к их свойствам,
а к состояниям материала.
Основные показатели механических характеристик материалов:
• показатели, определяемые без учета конструктивных особенностей
и условий эксплуатации изделия. Они определяются стандартными
лабораторными испытаниями образцов при нормальных (комнатных)
условиях и действии статических нагрузок;
• показатели конструкционной прочности материалов, которые
характеризуют их поведение в реальных условиях эксплуатации. К ним
относятся характеристики долговечности конструкции (усталостная
прочность, износоустойчивость, коррозионная стойкость) и надежности
материала в изделии (вязкость разрушения, энергия, поглощаемая при
распространении трещины, живучесть при циклическом нагружении и
т.п.);
66
4.1. Механические состояния деформируемых тел
В упругом состоянии деформации обратимы, и вся энергия,
затраченная на деформирование, при разгрузке возвращается (диссипация энергии
отсутствует). Для любого твердого тела процесс деформирования
начинается с упругой деформации. Изотропное тело имеет две константы
упругости - модуль упругости Е и коэффициент Пуассона ц. Для
анизотропных тел число упругих констант в общем случае равно 21. Из
основных констант упругости можно получить их производные- модуль
сдвига G (3.40), модуль объемной деформации (3.42) и постоянную Ламе
#(3.45).
Вязкое сопротивление - в некотором смысле противоположно
упругому - работа внешних сил, уравновешенных силами вязкого
сопротивления, полностью рассеивается в виде теплоты. Вязкое
сопротивление определяется величиной касательной силы, необходимой
для поддержания ламинарного скольжения слоев, или течения с
определенной скоростью. Таким образом, вязкость можно определить
как сопротивление течению.
Представление о вязкоупругой деформации дает поведение моделей,
сочетающих свойства вязкости и упругости в такой последовательности:
при нагружении тела в нем возникает мгновенная упругая деформация,
подчиняющаяся закону Гука; далее при том же максимальном
напряжении наблюдается вязкая деформация, подчиняющаяся закону Ньютона.
Наиболее распространенными в теории линейной вязкоупругости
являются реологические модели Максвелла и Фойгта, дающие связь
между напряжениями и деформациями и скоростями их изменения:
дг 1 да а хж
— = + — - модель Максвелла,
dt Е dt ц
о = Ее + ц— - модель Фойгта,
dt
где ц - коэффициент вязкости.
Пластическое состояние характеризуется наличием остаточных
деформаций, фиксируемых после снятия внешних нагрузок. Объем тела
при пластической деформации не изменяется: условие постоянства
объема записывается в виде 0 = ех + е + ez = 0 (эксперименты
показывают, что изменение объема не превышает 0,5 %).
67
В случае, когда все напряжения изменяются пропорционально одной
из составляющих, в процессе пластической деформации направления
главных деформаций совпадают с направлениями главных нормальных
напряжений, направления максимальных сдвигов - с направлениями
максимальных касательных напряжений, а главные направления
девиатора напряжений - с главными направлениями девиатора
деформаций.
Одной из распространенных моделей поведения материала при
упругопластических деформациях является модель пластичности,
основанная на деформационной теории Генки-Ильюшина, описываемая
уравнениями:
ty ~ £ = ^~Е у "
hi
Здесь
e = —(ev + ev + с,) - средняя деформация,
о = —(ox + ay + oz) - среднее напряжение,
ф - безразмерный коэффициент, называемый параметром пластичности
(с точностью до множителя он совпадает с интенсивностью касательных
напряжений). При ф = 1 эта модель описывает поведение упругого
материала.
Высокоэластическое состояние наиболее характерно для полимеров;
особенностями этого состояния являются большая изменяемость формы
и деформирование без изменения объема. Для материалов, находящихся
68
в высокоэластическом состоянии, наблюдается существенная зависимость
их свойств от длительности и скорости нагружения, температуры и т.д.
Состояние разрушения- состояние, при котором за счет интенсивного
развития трещин в материале тела начинается нарушение его сплошности
и непрерывности. Физический процесс разрушения материала
представляется в виде двух основных стадий - стадии рассеянных разрушений
(зарождение и развитие микроскопических трещин) и стадии развития
магистральной трещины. Очаги зарождения микротрещин распределены
по всему объему материала, находящегося в однородном напряженном
состоянии, достаточно равномерно. Относительная длительность первой
и второй стадии разрушения зависит от свойств материала, характера
напряженного состояния и условий нагружения.
4.2. Диаграммы упругопластического деформирования
конструкционных материалов
Основным опытом для определения механических характеристик
конструкционных материалов является опыт на растяжение
призматического образца центрально приложенной силой, направленной по
продольной оси; при этом в средней части образца реализуется
однородное напряженное состояние. Форма, размеры образца и методика
проведения испытаний определяются соответствующими стандартами,
например ГОСТ 1497-84. По результатам испытаний строится
зависимость о =/(е) между напряжениями о = PIF и деформациями е = Л///,
которая называется диаграммой деформирования. Опыты на растяжение
образцов выявляют некоторые общие свойства конструкционных
материалов - свойства упругости и пластичности. На рис. 4.1 показаны
типичные кривые деформирования при растяжении образцов сталей 30
и40Х.
Если напряжения не превышают предела пропорциональности опц
(точка 1 на диаграмме) и зависимость между напряжениями и
деформациями линейна, то она описывается законом Гука о = Ее, где Е - модуль
продольной упругости материала. Размерность модуля упругости - Н/м
(Паскаль). Значение модуля упругости Е на кривой деформирования о =
=/(е) численно равно тангенсу угла наклона линейного участка: Е = tgp.
Таким образом, величину Е можно рассматривать как характеристику
упругого сопротивления или как характеристику интенсивности
нарастания напряжения с увеличением деформации. Физический смысл
коэффициента Е определяется как напряжение, необходимое для
увеличения длины образца в два раза. Такое толкование довольно
искусственно, поскольку величина упругого удлинения у большинства
твердых тел редко достигает даже 1 %.
69
Рис. 4.1. Диаграммы деформирования сталей
Напряжения, являющиеся верхней границей проявления чисто упругих
деформаций, соответствуют точке 2 диаграммы и называются пределом
упругости оупр.
Точка 3 диаграммы характерна тем, что при достижении
напряжениями величины о = ат (ат - предел текучести), дальнейшее удлинение
образца (для малоуглеродистых сталей) происходит практически без
увеличения нагрузки. Это явление носит название текучести, а участок
диаграммы, расположенный непосредственно правее точки 3, называется
площадкой текучести. При этом полированная поверхность образца
мутнеет, покрывается ортогональной сеткой линий (линии Черно-
ва-Людерса), расположенных под углом 45° к продольной оси образца
- по направлению плоскостей действия максимальных касательных
напряжений.
У многих конструкционных материалов площадка текучести не
выражена столь явно, как у малоуглеродистых сталей. Для таких
материалов вводится понятие условного предела текучести os - это
напряжение, которому соответствует остаточная (пластическая)
деформация, равная s, %. Обычно принимается s = 0,2 %.
После площадки текучести для дальнейшего увеличения деформации
необходимо увеличениерастягивающей силы. Материал снова проявляет
способность сопротивляться деформации; участок за площадкой
текучести (до точки 4) называется участком упрочнения. Точка 4
соответствует максимальной нагрузке, выдерживаемой образцом.
70
Соответствующее
напряжение называется временным
сопротивлением ов (или
пределом прочности опч).
Дальнейшая деформация
образца происходит без
увеличения или даже с
уменьшением нагрузки вплоть до
разрушения (точка 5). Точке 4
на диаграмме соответствует
начало локального
уменьшения размеров
поперечного сечения образца, где, в
основном,
сосредоточивается вся последующая
пластическая деформация.
Диаграмма, приведенная
на рис. 4.1, является
диаграммой условных напряжений, условность состоит в том, что все силы
относились к F0 - первоначальной площади поперечного сечения
образца; в действительности же при растяжении площадь поперечного
сечения образца уменьшается. Если учитывать текущее значение площади
поперечного сечения при определении напряжений, то получим
диаграмму истинных напряжений (рис. 4.2).
Если в некоторый момент нагружения (точка А на рис. 4.1) прекратить
нагружение и снять нагрузку, то разгрузка образца пойдет по линии АВ,
параллельной линейному участку диаграммы 0-1. При этом полная
деформация в точке А равна:
/Г,НПа\
1000 \
800
бОО
too
zoo
О
*ох
/Т
I IV?
/к
*
'Ул
~т
rvT
IV?
{
^^Л
^^^Стпаль SO
ft!-
Л № ♦ rtf i i
V
оь се 08
ft»
i
\
f
J f-
•*•£
Рис. 4.2. Диаграмма истинных напряжений
= М
+ £'
<Р)
(4.1)
где е^ - о/Е - упругая деформация, е^ - пластическая (остаточная
деформация). Соотношение (4.1) справедливо для любой точки
диаграммы.
После того как материал испытал воздействие осевого усилия одного
знака (например, растяжение) в области пластических деформаций (о >
> от), сопротивляемость этого материала пластической деформации при
действии сил другого знака (сжатие) понижается. Это явление носит
название эффекта Баушингера.
При растяжении образца происходит не только увеличение его длины,
но и уменьшение размеров поперечного сечения, т.е. в упругой области
деформация в поперечном направлении е' = -це, е - деформация в
71
продольном направлении, ц- коэффициент Пуассона. Для изотропных
материалов значения коэффициента Пуассона находятся в пределах
О < \i < 0,5.
Для сталей различных марок Е = 195...206 ГПа, G = 79...89 ГПа, ц =
= 0,23...0,31, для сплавов алюминия Е = 69...71 ГПа, G = 26...27 ГПа,
ц = 0,30...0,33.
Механические свойства некоторых материалов даны в табл. 4.1.
4.1. Механические свойства некоторых материалов
Материал
Сталь СтЗ
Сталь 15
Сталь 45
Сталь ЗОХГСА
Чугун СЧ15-32
Медь прутковая
Дюралюмин Д16
Дельта-древесина
Текстолит
£, ГПа
200
200
200
200
150
ПО
75
20
30
от, МПа
240/240
210/210
340/340
950/950
-
250/250
240/240
-
75/115
ов, МПа
450/-
350/-
610/-
1200/-
150/640
320/-
420/-
250/160
| 127/168
6,%
26
28
24
13
0,6
15
18
-
1,5
*.%
50
55
45
50
-
45
-
-
-
Примечание. В знаменателе указана соответствующая характеристика при
сжатии.
Характеристиками пластичности материала являются относительное
удлинение и относительное сужение при разрыве:
6 = JLlJL юо %, (4.2)
*- -^—-^\00%t (4.3)
где /0, FQ-длина рабочей части образца и площадь поперечного сечения
до деформации, /к - длина рабочей части образца после разрыва, FK -
72
конечная площадь поперечного сечения в шейке образца после разрыва.
По величине относительного удлинения при разрыве проводится
разделение состояния материалов на пластическое и хрупкое. Материалы;
имеющие к моменту разрушения достаточно большие значения 6(6 >
> 10 %), относят к пластическим материалам', к хрупким относят
материалы с относительным удлинением 6 < 3 %.
Оценка пластических свойств материала может быть проведена по
такой характеристике, как ударная вязкость -
КС = AIF, (4.4)
где А - работа, затрачиваемая на ударное разрушение образца, Дж (или
Нм), jF- площадь поперечного сечения образца в месте концентратора,
м2 (или см2).
Работа А деформации при разрушении образца может быть
определена по диаграмме растяжения о =Де). Так, если первоначальная
длина образца /0, то работа деформации, совершаемая силой Р на
перемещении и,
«<*
А = fP(u)du, (4.5)
о
где ик - перемещение в момент, предшествующий разрушению. Тогда по
зависимости о = (P/F0) =/(е) и г = ull0, находим
«Л
А0 = F0l0 f f(e)dz = F0l0A,t (4.6)
о
"Л
где А{ = Г/(е)с1е - площадь диаграммы деформирования (работа
о
деформации на единицу объема материала). Для сталей КС = 50...
100 Н-м/см2. Материалы с ударной вязкостью КС < 30 Н-м/см2 относят
к числу хрупких.
Диаграммы растяжения о =/(е) других распространенных материалов
приведены на рис. 4.3. Некоторые пластичные материалы (например
титан) в районе площадки текучести обнаруживают особенность,
73
оуппа[
бОо\
«СО
200
r^^~—~ ~~~ ' ' ■—— .^ / итан
Дюралю мин
L^*- ■—-
Г ———
^~~~-~0~~~~~^
1 1 1 1
.— -т
медь
Алюминий
005 Of1Q Of1S 010 025 OJQ £
Рис. 4.3. Диаграммы деформирования конструкционных материалов
называемую "зубом текучести", для таких материалов вводится понятие
верхнего и нижнего предела текучести (о*, о").
Экспериментальное изучение свойств материалов при сжатии
проводится на коротких образцах с тем, чтобы исключить возможность
искривления образца. Для пластичных материалов характер диаграммы
о -Дг) при сжатии примерно до возникновения текучести такой же, как
и при растяжении. На рис. 4.4 показаны диаграммы растяжения и сжатия
для хрупкого материала (серый
чугун) и сжатия для пластичного
(сталь 30). В процессе
деформации образец укорачивается; при
этом размеры поперечного
сечения увеличиваются. Из-за трения
между опорными плитами
нагружающего устройства и
торцевыми поверхностями образца
он принимает бочкообразную
форму. Для ряда пластичных
материалов обнаружить
напряжение, аналогичное временному
сопротивлению при растяжении,
не удается, так как образец
сплющивается.
Хрупкие материалы
проявляют значительно лучшую способ-
>мпа|
600
бОО
400
200
-
- /
Г
уг чугун серый v
уг (сжатие) Я
SСталь 30
Чугун серый
(растяжение)
.. 1. - I I
О10
015
ого
Рис. 4.4. Диаграммы деформирования
чугуна и стали
74
ность сопротивляться деформациям сжатия, чем деформациям
растяжения; для них разрушающее напряжение при сжатии превышает предел
прочности при растяжении в несколько раз. Разрушение хрупких
материалов при сжатии происходит за счет образования трещин.
4,3. Влияние различных факторов на механические
характеристики конструкционных материалов
Зависимость механических характеристик конструкционных
материалов от их химического состава, внешних условий и условий
нагружения весьма многообразна: отметим наиболее существенные,
характерные для типичных условий эксплуатации конструкций.
Влияние содержания углерода. Введение различных легирующих
добавок в металлы позволяет значительно повысить прочностные
характеристики сплавов. На рис. 4.5 показано влияние процентного
содержания углерода на механические свойства конструкционной стали.
Как видно, с увеличением содержания углерода временное сопротивление
повышается в несколько раз; однако при этом значительно ухудшаются
пластические свойства: относительное удлинение б и относительное
сужение \|г при разрыве уменьшаются.
Влияние температуры окружающей среды. Повышенные температуры
оказывают существенное влияние на такие механические характеристики
конструкционных материалов, как ползучесть и длительная прочность.
Ползучестью называют
медленное непрерывное возрастание
пластической (остаточной)
деформации под воздействием
постоянных нагрузок.
Длительной прочностью называется
зависимость разрушающих
напряжений (временного сопротивления)
от длительности эксплуатации.
Свойства ползучести и
длительной прочности проявляются у
углеродистых сталей при Т >
> 300 °С, для легированных
сталей при Т> 350 °С, для
алюминиевых сплавов при Т >
> 100 °С. Некоторые материалы
проявляют эти свойства и при
обычных температурах.
$Г*% *в,"п*
ьюсо
щ
J о
го
40
V 200
Рис. 4.5. Влияние процентного содержания
углерода на механические характеристики
стали
75
МПа |
soo
5О0
ЧОО
JO0
zoo
100
—*
\
""ПА I
- —'г
I
\ V
ХГ—ч\ \
I 1 _^_j
Рис. 4.6. Влияние температуры на
характеристики прочности сталей
200
*ЮО
600 Г°С
Рис. 4.7. Зависимости
относительного сужения от температуры
Мерой оценки ползучести материала
является предел ползучести -
напряжение, при котором пластическая
деформация за определенный промежуток времени достигает заданной
величины. В некоторых случаях сопротивление ползучести оценивается
величиной скорости деформации по прошествии заданного времени. При
обозначении предела ползучести указывается величина деформации,
время и температура испытаний. Например, для жаропрочного сплава
ХН77ТЮР при температуре 700 °С за время 100 ч и деформации
ползучести 0,2 % предел ползучести составляет 400 МПа: о0 уюоОЩ =
= 400 МПа.
Ползучесть сопровождается релаксацией напряжений -
самопроизвольным уменьшением напряжений с течением времени при неизменной
деформации. Скорость релаксации напряжений возрастает при
повышении температуры. Мерой скорости релаксации служит время
релаксации - промежуток времени, в течение которого напряжение
уменьшается по сравнению с начальным значением в е = 2,718 раза.
Прочность материала при повышенных температурах оценивается
пределом длительной прочности - напряжением, при котором материал
разрушается не ранее заданного времени. При обозначении предела
длительной прочности указывается продолжительность нагружения и
температура испытания. Так, для сплава ХН77ТЮР при температуре
700 °С и времени 1000 ч предел длительной прочности составляет
адл юоо(7М)= 330 МПа. При кратковременных испытаниях для этого же
сплава при температуре 700 °С пределы прочности и текучести
соответственно равны: ов = 830 МПа, о0 2 = 560 МПа.
Влияние повышенных температур на характеристики прочности и
пластичности можно проследить на рис. 4.6 и 4.7, где представлены
76
осредненные результаты
экспериментов для: 1 - углеродистой
стали, содержащей 0,15 % углерода;
2 - 0,40 % углерода, 3 - хромистой
стали. Прочность углеродистых
сталей с повышением температуры
до 650...700 °С снижается почти в
10 раз. Наиболее резкое снижение
ов наблюдается для алюминиевых
сплавов. Наибольшими
значениями ов при высоких температурах
обладают литые жаропрочные
сплавы, содержащие 70...80 %
никеля. Снижение пределов
текучести от с повышением
температуры происходит примерно так же,
как и снижение ов. Для
углеродистых сталей характерным является
ухудшение пластических свойств
(охрупчивание) при температурах около 300 °С (кривая 2 на рис. 4.7).
Влияние температур на упругие свойства. Температурный коэффи-
1 dr „ .,
циент линейного расширения а = и температурный коэффициент
г dT
1 АЕ - .
модуля упругости г\ = связаны между собой соотношением
&
*0
09
г
V
°7
Об
OS
t
ом
-
-
-
1
*\ ^2
1 1
s^
\ч*
«V N.
1 1 1
О 100 200 JOO *tOQ 500 °С
Рис. 4.8. Зависимости модуля упругости
от температуры
r\ + am = 0, или (х\/а) = -т = const,
где г и т - постоянные, характеризующие параметры кристаллической
решетки. На рис. 4.8 приведена зависимость безразмерного модуля
упругости Е1Е0 некоторых конструкционных материалов от температуры
(Е0 - модуль упругости материала при обычной температуре): / -
коррозионно-стойкая сталь, 2 - алюминиевые сплавы, 3 - углеродистые
стали, 4 - титановые сплавы.
Для сталей с повышением температуры испытаний с 25 до 450 °С
модули упругости Е и G уменьшаются на 20...40 %, при этом, начиная
с 300...400 °С, наблюдается расхождение между значениями модулей,
определенными при статических и динамических испытаниях.
Изменение модулей упругости при малых колебаниях температуры
(от-50 до +50 °С) незначительно и им обычно пренебрегают.
77
Влияние низких
температур. При охлаждении
степень изменения
механических свойств
конструкционных материалов
зависит от их природы и
структурного состояния,
режима нагружения и
уровня рабочих
температур. Основными
факторами, определяющими
характер изменения их
механических свойств,
являются низкотемпературное
упрочнение и охрупчива-
ние. В общем случае
увеличение прочности
материалов за счет
низкотемпературного упрочнения нейтрализуется их охрупчиванием,
вызывающим существенное снижение разрушающих напряжений. При выборе
материалов для криогенной техники нужно находить компромиссный
вариант с учетом их упрочнения и способностью сохранять необходимую
пластичность. К материалам, удовлетворяющим этим требованиям,
относятся высоконикелевые и алюминиевые сплавы, титан и сплавы на
его основе. Алюминиевые и медные сплавы, стали с высоким
содержанием никеля характеризуются достаточно высокой вязкостью разрушения.
При пониженных температурах их прочность увеличивается, изменяется
характер деформационного упрочнения и может возрастать
пластичность. На рис. 4.9 для сплава Амг5 представлены типичные зависимости
характеристик прочности (ов, о0 *) пластичности (б, ф) и трещиностойкос-
ти (J1C, К{С) при криогенных температурах; здесь 71С - упругопластичес-
кая вязкость разрушения, К{С - критический коэффициент интенсивности
напряжений. Модуль упругости при понижении температуры для этого
сплава меняется следующим образом: при Т = 293 К модуль Е =
= 66,4 ГПа, при Т = 173 К - 67,4 ГПа и при Т = 77 К - 70,3 ГПа. Для
некоторых других конструкционных материалов зависимости
механических характеристик от низких температур представлены в табл. 4.2.
Рис. 4.9. Влияние низких температур на
характеристики прочности, пластичности и трещино-
стойкости
78
4.2. Механические характеристики некоторых конструкционных материалов
в зависимости от низких температур
Материал
Сталь Ст 3
Сталь 20
Сталь 12X18H10T
Медный сплав
БрХ08
Титановый
сплав BT5-1
Т,К
293
193
133
293
193
133
293
77
4,2
293
77
4,2
293
77
4,2
ов, МПа
425
530
680
478
580
705
609
1539
1774
231
380
468
780
1300
1415
о0 2, МПа
258
470
640
315
480
670
288
387
515
148
156
178
720
1260
1395
6,%
26,7
25,0
17,5
28,7
27,0
21,0
60,1
48,6
37,6
34,0
44,0
55,0
13,2
14,3
3,4
ф,%
48,5
50,5
43,0
50,0
50,5
47,5
64,7
46,9
34,9
87,5
81,0
75,1
31,2
20,6
17,3
Влияние скорости нагружения и деформирования. Как правило, с
ростом скорости нагружения возрастает неравномерность
деформированного состояния, т.е. зона деформирования (деформированный объем) при
больших скоростях, когда инерционные силы одного порядка со
статической составляющей нагрузки, уменьшается. Упругие
характеристики (модуль продольной упругости и коэффициент Пуассона) для
большинства металлов и сплавов от скорости нагружения практически
не зависят. При больших скоростях нагружения разрушение материалов
может сопровождаться такими локализованными в малых объемах
материала явлениями, как плавление, испарение и т.п.
Кривые деформирования о =/(е) располагаются по отношению к
случаю статического нагружения тем выше, чем больше скорость
79
*«*>&.
*АЪ
~ол
чт
Рис. 4.10. Влияние скорости деформирования и температуры на временное
сопротивление:
а - алюминиевых сплавов; б - малоуглеродистых сталей
деформирования. Влияние скорости деформирования е на временное
сопротивление ов для алюминиевых сплавов и малоуглеродистых сталей
показано соответственно на рис. 4.10. Увеличение скорости
деформирования ухудшает пластические характеристики материала.
Влияние высоких давлений. Высокие гидростатические давления,
накладываемые на поля напряжений, оказывают влияние на некоторые
характеристики конструкционных материалов. Так, для сталей, предел
текучести от (о0 £ и временное сопротивление ов до давлений 3103 МПа
возрастают пропорционально действующему давлению. При этом
наибольшая линейная деформация остается неизменной, а локальная
деформация в зоне разрыва растягиваемого образца существенно
возрастает с увеличением давления. Модуль сдвига материалов с
увеличением давления возрастает, однако это возрастание не превышает
нескольких процентов. Улучшение пластических свойств материалов с
увеличением давления объясняется "самозалечиванием" разрывов,
микротрещин за счет сжимающих напряжений.
Влияние радиационных эффектов (облучения). При взаимодействии
ионизирующего излучения с конструкционными материалами
происходят существенные изменения их механических характеристик,
вызываемые радиационными повреждениями. Степень радиационных
повреждений определяется количеством поглощенной материалом энергии, а
80
10 F, И\сц*
Рис. 4.11. Влияние облучения на
условный предел текучести
нп а
SOD
чоо
zoo
\
\ „
VV
_ \ ^ —
\\?
L !_.._
1"
ь^
с -ч
1 —-^
.1.. 1 , . . .
600 гмсп/с
Рис. 4.12. Влияние температуры на
характеристики прочности
облученной и необлученной стали
также скоростью ее передачи. Наиболее существенное воздействие на
конструкционные материалы оказывает нейтронное излучение. Мерой
измерения энергии излучения служит флюенс нейтронов F(нейтрон/см2).
Основным результатом воздействия быстрых нейтронов на металлы
является образование точечных дефектов решетки - вакансий и
внедренных или промежуточных атомов; это основной механизм
образования радиационных повреждений в сплавах и металлах.
Влияние облучения на механические характеристики материалов
определяется как режимами самого облучения, так и температурой
испытаний, скоростью нагружения, химическим составом сплава и др.
В режимах облучения различают величину флюенса, энергетический
спектр, температуру облучения и среду, в которой происходит облучение.
При облучении повышается предел прочности ов и условный предел
текучести о0 2. Данное явление называется радиационным упрочнением.
Радиационному упрочнению подвержены все металлы и сплавы,
применяемые в реакторостроении, на рис. 4.11 приведены зависимости
условного предела текучести о0 2 от флюенса быстрых нейтронов для:
У-никеля, 2-коррозионно-стойкой стали 304,3 -коррозионно-стойкой
стали 316, 4- меди, 5- сплавов алюминия.
Диаграммы растяжения для облученных образцов всегда
располагаются выше диаграмм для образцов, не подвергавшихся облучению.
Площадь диаграммы, характеризующая работу деформирования, для
облученных образцов значительно меньше; это объясняется, несмотря
на повышение пределов текучести и временного сопротивления,
81
JOO
£00
Рис. 4.13. Зависимость изменения
объема от температуры
существенным сокращением
способности материала к
пластическому деформированию.
Характеристики
кратковременной прочности зависят от
температуры, при которой
проводятся испытания облученных
образцов. На рис. 4.12
иллюстрируется влияние температуры
испытания на ов и от облученной 1 и не-
облученной 2 стали. С
увеличением температуры различие между
характеристиками прочности
облученных и необлученных
образцов уменьшается вплоть до
полного исчезновения.
Другим опасным результатом
нейтронного воздействия является
радиационное распухание, под которым понимается увеличение объема
и уменьшение плотности неделящихся материалов в результате их
облучения большими флюенсами нейтронов F= (4...8)-10 2 нейтрон/см2
при температурах облучения 270...560 °С. Радиационное распухание было
обнаружено в экспериментах по облучению коррозионно-стойких сталей,
никеля и его сплавов, алюминия, молибдена, ванадия и других металлов.
Данное явление объясняется процессами зарождения и роста скоплений
радиационных повреждений. Эффект радиационного распухания во
многом определяет ресурс работы деталей и узлов активных зон и
экономичность реакторов на быстрых нейтронах. Очевидно, что
развитие пористости при распухании заметно ухудшает механические
свойства конструкционных материалов.
Основными параметрами, определяющими степень распухания,
являются температура, флюенс нейтронов, химический состав материала
и характер его обработки. Распухание происходит в интервале
температур (0,22...0,55) Гпл, т.е. в температурном диапазоне, характерном
для рабочих режимов реакторов на быстрых нейтронах. В частности, для
сталей (рис. 4.13) распухание наблюдается при температурах 300...670 °С.
Зависимость изменения объема от температуры имеет колоколообразный
характер; максимум изменения объема наблюдается при температуре
около 510 °С. Кривые 1...4 на рис. 4.13 построены для флюенса нейтронов
F= 71022, 5-10 , 31022 и МО22 нейтрон/см2 соответственно.
Одним из путей уменьшения радиационного распухания, например
для хромоникелевых сталей, служит их предварительное холодное
деформирование.
82
4.4. Композиционные материалы
Основные понятия. Классификация композиционных материалов
(КМ). Композиционными называются материалы, обладающие
совокупностью следующих признаков:
не встречаются в природе, поскольку целенаправленно созданы
человеком;
состоят из двух или более компонентов, различающихся по своему
химическому составу;
имеют свойства, отличающиеся от свойств компонентов;
неоднородны в микромасштабе и однородны в макромасштабе;
состав,форма,распределениеотдельныхкомпонентов
"спроектированы" заранее.
Компонент, распределенный непрерывно во всем объеме КМ,
называется матрицей; прерывистый, разъединенный в объеме
композиции - арматурой или армирующим элементом. Роль матрицы заключается
в придании изделию требуемой формы и созданию монолитного
материала, в обеспечении несущей способности композиции
перераспределением усилий на армирующие элементы - волокна. К волокнам,
используемым в качестве арматуры КМ, предъявляются достаточно
жесткие требования: небольшая плотность, высокая прочность в
интервале рабочих температур, технологичность, высокая химическая
стойкость, нетоксичность при изготовлении и эксплуатации и другие.
Для армирования применяют "усы" (нитевидные монокристаллы),
имеющие диаметр от долей микрометра до нескольких микрометров и
длину от долей миллиметра до нескольких сантиметров, металлическую
проволоку (сталь, вольфрам, молибден), органические и неорганические
волокна (углеродные, борные, стеклянные, карбидокремниевые,
кварцевые).
В зависимости от геометрии армирующих элементов, их взаимного
расположения КМ бывают изотропными или анизотропными. К
макроскопически изотропным КМ относятся дисперсно-упрочненные
сплавы и хаотично армированные КМ; к анизотропным КМ -
материалы, в которых волокна ориентированы в определенных направлениях.
Хаотично армированные КМ упрочняются короткими элементами
игольчатой формы (отрезками волокон или "усами"), ориентированными
в объеме случайным образом. В этом случае КМ является
квазиизотропным, т.е. анизотропным в микрообъемах и изотропным в объеме всей
композиции.
Классификация КМ может быть проведена по следующим основным
признакам:
83
- материалу матрицы и армирующих элементов;
- геометрии компонентов;
- структуре и расположению компонентов;
- методу получения.
Название КМ дается, как правило, по названию материала матрицы:
с металлической матрицей - называются металлическими КМ, с
полимерной - ПКМ, с неорганической - неорганическими КМ. Название
полимерных КМ состоит из двух частей: в первой указывается материал
волокна, во второй - "пластик" или "волокнит". В соответствии с
геометрией армирующих элементов (порошки, гранулы, волокна,
пластины) КМ подразделяются на порошковые (гранулированные),
волокнистые и пластинчатые. По структуре и расположению
компонентов КМ разделяются на группы с каркасной, матричной, сложной и
комбинированной структурой. В соответствии с классификацией по
методам получения подразделяются на КМ, получаемые жидко- и
твердофазными методами, методами осаждения - напыления и
комбинированными методами.
При определении механических характеристик анизотропных КМ
требуется получить большее число упругих и прочностных
характеристик, чем при определении характеристик традиционных
конструкционных материалов. Например, для определения девяти упругих постоянных
ортотропного КМ необходимо испытать на растяжение (сжатие) шесть
типов образцов. Для анизотропных КМ величины механических
характеристик должны быть указаны в соответствии с направлением.
Армирующие элементы композиционных материалов. Металлические
волокна. Для армирования КМ применяют проволоку из сталей (У8А,
12Х18Н10Т, 09Х18Н10Т, 09Х13Н13М2), вольфрама (ВА, ВР-20),
молибдена (ВМ-2, ВМ-3), бериллия, титана (ВТ1-0, ОТ-4), ниобия и др.
Наиболее распространенной является проволока диаметром 20... 1500 мкм
из коррозионно-стойких сталей, имеющих большую теплостойкость и
поверхность, слабо взаимодействующую с материалом матрицы.
Применяется в виде тканных сеток различного типа плетения.
Волокна бора, карбида кремния, "борсика". Благодаря высокой
прочности, жесткости, малой плотности волокна бора, карбида кремния
и "борсика" (B|SiC) широко применяются для упрочнения матриц на
основе легких металлов (алюминий, магний, титан и их сплавы). Волокна
бора и карбида кремния получают осаждением из газовой среды на
нагретую до высоких температур поверхность вольфрамовой проволоки;
диаметр волокон 90...200 мкм. Волокна из бора имеют предел прочности
при растяжении порядка 2...4 ГПа, модуль упругости 370...430 ГПа,
плотность 2500...2700 кг/м3, они хорошо совмещаются как с полимерной,
так и с металлической матрицей.
84
Углеродные волокна. Углеродные волокна обладают по ряду
показателей уникальными механическими и физико-химическими
свойствами и по удельным показателям превосходят все жаростойкие
волокна ка = (9...20) 104 м, кЕ = (4....32) 10° м. Удельная прочность ка =
= ов/у, ов - временное сопротивление, у = pg- удельный вес. Удельная
прочность измеряется в единицах длины и имеет простой физический
смысл - равна длине волокна, разрушающегося под действием
собственного веса. Аналогично вводится удельный модуль упругости (удельная
жесткость) kE = Ely. Механические характеристики некоторых
высокомодульных углеродных волокон приведены в табл. 4.3.
4.3. Механические характеристики некоторых высокомодульных углеродных волокон
Марка
волокна
ВМН-3
ВЭН-210
Кулон
£, ГПа
250
343
400-600
ов.Ю2,
МПа 1
14,3
14,7
20,0
Марка
волокна
|ЛУ-4
|Урал-24
|Элур
£,ГПа
250
150-200
150
<Vl°2.
МПа
30,1-35,0
17-20
20,0
Углеродные волокнистые материалы имеют также и высокие
характеристики теплостойкости; в инертной среде основные
механические характеристики практически не изменяются до температуры 1500 °С.
Волокна из углерода имеют отрицательный температурный коэффициент
линейного расширения, что в совокупности с соответствующим
положительным коэффициентом материала матрицы позволяет создавать
материалы для конструкций, сохраняющих свои размеры при
температурных воздействиях.
Стеклянные волокна сочетают сравнительно малую плотность с
высокими теплостойкостью, химической стойкостью и прочностью.
Предел прочности полученных вытягиванием стеклянных волокон
составляет 2...6 ГПа, модуль упругости 50... 130 ГПа, плотность
2500...2600 кг/м3. Стеклянные волокна с неповрежденной поверхностью
имеют предел прочности 5...6 ГПа. Для промышленных волокон
(алюмоборосиликатные диаметром 6-10 м) предел прочности составляет
2...2,5 ГПа, модуль упругости - 73 ГПа.
Теоретическая прочность стекла, по оценкам А. Гриффитса,
составляет -14 ГПа, а для образцов диаметром МО"3 м прочность почти
в 100 раз меньше. Это объясняется наличием поверхностных дефектов
- поверхностных трещин. Значительное повышение предела прочности
(почти на порядок) происходит при травлении образцов кислотой, при
85
котором происходит сглаживание
поверхности. При уменьшении
диаметра волокна предел
прочности резко увеличивается;
экстраполяция экспериментальных данных
дает для предела прочности
величину ~11 ГПа, что близко к
теоретическому пределу.
Стеклянные волокна имеют
низкую стойкость к
многократному изгибу и истиранию, которая
может быть существенно
повышена пропиткой смолами, лаками.
Склеивание волокон в нить
увеличивает ее прочность на 20...25 %,
а пропитка лаками-на 80... 100%.
Волокна используются в качестве
армирующего элемента КМ в виде
отдельных волокон разного
диаметра, нитей и жгутов различной
толщины, лент и тканей
разнообразного плетения (рис. 4.14).
Стекловолокнистые
наполнители характеризуются плотностью
упаковки волокон и их взаимным
расположением.
Линейная плотность нитей
оценивается в тексах (текс
представляет собой массу (в граммах)
нити длиной 1000 м). Еще одна важная характеристика нитей и жгутов
-разрывная нагрузка, определяющая среднюю прочность и допускаемые
усилия. При этом средняя прочность волокон не может быть
использована для оценки прочности армированных стеклопластиков, так как
благодаря полимерной матрице коэффициент использования прочности
волокон повышается. Для однонаправленных материалов отмеченное
повышение прочности волокна в композиции составляет 170...900 %.
Промышленностью производятся стеклянные нити с числом сложений
от 2 до 48 и линейной плотностью от 12,5 до 286 текс. Наиболее часто
при намотке используются нити линейной плотности 100 и 50 текс. Этот
вид наполнителя технологически удобен для изготовления
крупногабаритных деталей сложной конфигурации.
Рис. 4.14. Типы плетений стеклянных
волокон
86
4S00
i200\-
Прочность композитов
существенно зависит от
объемного содержания наполнителя.
На рис. 4.15 приведена
зависимость разрушающего
напряжения ор при растяжении
стеклопластика от объемного
содержания VH волокнистого
наполнителя: 1 - напыление, 2,
3, 5 - пропитка под давлением
(2 - растяжение в поперечном
направлении, 3 - транс-
версально-изотропный
материал, 5 - растяжение в
продольном направлении), 4, 6-
прессование (4 - растяжение в
поперечном направлении,
6-растяжение в продольном
направлении), 7- спиральная намотка,
8 - протяжка, 9 - стекложгут.
Представленные
зависимости иллюстрируют взаимосвязь
свойств исходных компонентов
со свойствами композиции.
Высокомодульные органические волокна получают формированием
через фильеры из концентрированных растворов полимеров. В
зависимости от состава полимера и метода формирования получают
органические волокна, имеющие плотность 1410...1450 кг/м3, предел
прочности при растяжении 1,8...3,0 ГПа, модуль упругости 70... 130 ГПа.
Волокна сохраняют первоначальные характеристики до температуры
180 °С. Криогенные температуры охрупчивания волокон не вызывают.
Матрицы композиционных материалов. Армирующие элементы
композиции соединяются изотропной полимерной или металлической
матрицей, которая обеспечивает монолитность материала, фиксирует
форму изделия, способствует совместной работе волокон,
перераспределяет нагрузку при разрушении части волокон. Материал матрицы
определяет уровень рабочих температур композита, характеризует
устойчивость материала к воздействию внешней среды, химическую
стойкость. Некоторые физико-механические характеристики полимерных
термореактивных матриц приведены в табл. 4.4.
vHtv.(o6)
Рис. 4.15. Зависимость разрушающего
напряжения стеклопластика от объемного
содержания наполнителя
87
4.4. Физико-механические характеристики полимерных термореактивных матриц
Материал
матриц
Полиэфирные
Фенолформаль-
дегидные
Эпоксидные
Кремний -
органические
Полиамидные
Предел
прочности,
МПа,
растяжение (сжатие)
30-70
(80-150)
40-70
(100-125)
35-100
(90-160)
25-50
(60-100)
90-95
(250-280)
Модуль
упругости, ГПа
2,8-3,8
7-11
2,4-4,2
6,8-10
3,2-5,0
Плотность
р-10"3,
кг/м3
1,2-1,35
1,2-1,3
1,2-1,3
1,35-1,40
1,41-1,43
стойкость,
°С
50-80
140-180
130-150
250-280
250-320
Относительное
удлинение б, %
1,0-5,0
0,4-0,5
2-9
0,3-0,5
1-2,5
Объемная
усадка,
%
5-10
15-25
1-5
15-20
3-20
Термореактивные полимерные матрицы (связующие) образуются из
смолы, отвердителя, катализатора или инициатора отверждения и
растворителя, который вводится для понижения вязкости и улучшения
пропитки системы армирующих элементов.
Термопластичные полимерные матрицы при нагревании
расплавляются, а при последующем охлаждении - затвердевают, не теряя своих
первоначальных свойств. Их недостатком, как конструкционного
материала, является ярко проявляемая зависимость механических свойств
от температуры. Физико-механические характеристики полимерных
термопластичных матриц приведены в табл. 4.5.
4.5. Физико-механические характеристики полимерных термопластичных матриц
Материал
матрицы
Нейлон-6,6
Полифени-
ленсульфид
Сополимер
этилена
Полисульфон
Полиэфир
термопластичный
Предел
прочности
при
растяжении, МПа
83
77
45
72
56
Модуль
упругости, ГПа
2,8
4,2
1,4
2,7
2,5
Плотность
Р-Ю"3»
кг/м3
1,14
1,34
1,7
1,24
1,32
стойкость, °С
65
135
74
174
68
Относительное
удлинение 6, %
10
3-4
150
50-100
10
88
м
no
too
во
60
to
го
-
- J
-jl
Ca 1
_J I
OOn
"1
Bn
Уу/*A
J 1
Рис. 4.16. Прочностные и жесткос-
тные характеристики
ориентированных композитов
Металлические матрицы. Метал- * .
лические КМ создаются из
высокомодульных углеродных или борных
волокон и пластичной металлической
матрицы. Так как механические
характеристики металлической
матрицы выше, чем у полимерной, то
композиты с металлической матрицей
имеют более высокую прочность и
жесткость при нагружении поперек
волокон и при сдвиге, чем композиты
с полимерной матрицей. В качестве
материала для металлических матриц
чаще всего используются сплавы
алюминия, имеющие плотность
2700 кг/м3, модуль упругости 70 ГПа,
температуру плавления 780 °С.
Ориентированные
композиционные материалы. В наибольшей
степени достоинства и высокие
механические характеристики КМ реализуются
в ориентированных материалах,
армированных параллельными волокнами; в однонаправленных слоях
или монослоях, из которых укладкой в различных направлениях
образуются слоистые композиты. Свойства этих материалов
определяются свойствами монослоев. Графическая иллюстрация этих свойств
представлена на рис. 4.16 линиями, соответствующими стеклопластику
(Сп), органопластику (Оп), боропластику (Бп), углепластику (Уп) и
бороалюминию (Ба). Верхние точки соответствуют удельной прочности
ка и удельной жесткости кЕ при растяжении вдоль волокон, а нижние
- поперек волокон. Заштрихована область, соответствующая
традиционным конструкционным материалам - металлическим сплавам.
Для ориентированных композитов диаграммы растяжения (сжатия)
вдоль волокон являются практически линейными вплоть до разрушения
материала. При сдвиге в плоскости армирования наблюдается
нелинейное поведение материала; однако в слоистом пакете проявление такой
нелинейности незначительно.
Исчерпание несущей способности однонаправленного композита при
продольном растяжении происходит из-за разрыва волокон, а при
сжатии - из-за потери устойчивости или образования трещины,
параллельной волокнам. Разрушение композитов при растяжении
поперек волокон и при сдвиге вызывается разрушением матрицы
(нарушением когезионной прочности) или отслоением матрицы от
волокон (нарушением адгезионной прочности); при сжатии поперек
волокон - сколом материал под некоторым углом к направлению
нагружения.
Сравнение основных механических характеристик
конструкционных материалов (металлов и композитов) дано в табл. 4.6.
89
О 4.6. Основные механические характеристики конструкционных материалов
Материал
Металлы
Полимеры
Керамика
Стеклопластики
Углепластики
Боропластики
Органопластики
Разрушающее напряжение, МПа
при растяжении
127,4-2058
0,98-343
137,2-372,4
343-1764
117,6-735
784-1666
882-1372
784-1470
при сдвиге
98-686
1,96-58,8
29,4-294
5,88-58,8
58,8-289
9,8-44,1
79,4-137,2
13,7-24,5
78,4-109,76
10,8-24,5
96,3-170,5
Модуль упру-
- гости при
растяжении, ГПа
39,2-343
0,5-17,6
89,2-490
12,7-68,6
5,9-56,8
117,6-196
176,4-264,6
58,8-76,4
Относительное
удлинение при
разрыве, %
0,5-40
0,2-800
1-14
1,5-2,8
0,5-1,5
0,4-1,0
0,3-0,7
2-7
Удельная
прочность', км
4-53
0,1-30
2-100
30-100
33-82
74-84
66-110
Удельная
жесткость, км
2200-3600
100-1000
4700-13500
1100-3340
10800-12000
12500-14200
5000-5800
Примечание. Над чертой приведены характеристики вдоль, под чертой - поперек направления армирования.
Глава 5
РАСТЯЖЕНИЕ (СЖАТИЕ)
ПРИЗМАТИЧЕСКИХ СТЕРЖНЕЙ
5.1. Метод сечений. Внутренние силовые факторы
в поперечных сечениях стержня
Одна из основных задач МК состоит в определении внутренних сил,
возникающих в стержне под действием сил внешних. Метод,
позволяющий переводить равнодействующие внутренних сил в
разряд внешних сил и определять из условия равновесия отсеченной
части стержня, получил название лгешядя сечений.
Суть метода сечений поясним на примере стержня, представленного
на рис. 5.1. Внутренние силы, действующие в заданном поперечном
Pi
Рис. 5.1. Иллюстрация метода сечений
91
(
Рис. 5.2. Местная система координат Рис. 5.3. Проекции главного вектора
и главного момента
сечении, являются результатом взаимодействия частей стержня,
разделенных этим сечением. Мысленно отсекая и исключая из
рассмотрения одну из частей, заменяем действие этой части на оставшуюся силами,
распределенными по сечению. Эти силы могут быть отнесены в разряд
внешних сил, а их равнодействующие определяются из уравнений
равновесия статики, составленных для этой части стержня. Заменяя эти
силы их равнодействующими - главным вектором R и главным моментом
М (за точку приведения принят центр тяжести поперечного сечения -
точка О), шесть их скалярных составляющих определим из шести
уравнений равновесия статики указанной части стержня:
$> = 0, 5> = 0, £z = О,
$Х = 0, 5>у = О, £т2 = 0.
Технически удобнее систему координат, относительно которой
составляются уравнения равновесия, связать с поперечным сечением, в
котором эти силы определяются (рис. 5.2). Начало координат помещаем
в центре тяжести поперечного сечения, ось Oz направим по касательной
к оси стержня в сторону от сечения, оси Ох и Оу поместим в плоскости
поперечного сечения.
Разложим главный вектор R и главный момент М по осям этой
системы координат на шесть скалярных составляющих (рис. 5.3) и
назовем эти составляющие внутренними силовыми факторами,
действующими в данном поперечном сечении. Внутренние силовые факторы
имеют вполне определенный физический смысл; они связаны с отдельны-
ми видами деформаций:
92
Рис. 5.4. Линейные и угловые
перемещения сечения
являются также и определениями
Nz - продольная сила,
определяемая через сумму проекций
внутренних сил, действующих в
данном поперечном сечении, на ось
Oz\
Qx и 2 - поперечные силы
(суммы проекций внутренних сил на
оси Ох и Оу соответственно);
Мх и м - изгибающие
моменты (суммы моментов внутренних
сил относительно осей Ох и О,,);
Мг - крутящий момент (сумма
моментов внутренних сил
относительно оси Oz).
Приведенные формулировки
внутренних силовых факторов.
Каждый внутренний силовой фактор связан с одним из видов
деформаций стержня. Используя гипотезу плоских сечений (гипотезу
Бернулли), поперечное сечение стержня можно рассматривать как
абсолютно жесткую пластинку (рис. 5.4). Деформации стержня
определяются разностью ее положений до и после приложения внешних
нагрузок и, следовательно, могут быть выражены через параметры ее
перемещения. Для абсолютно твердого тела таких параметров шесть -
три линейных и три угловых. Линейные перемещения - и, v, w вдоль осей
Ох, Оу, Oz соответственно и cpY, уу и cpz - угловые перемещения
относительно указанных осей. Каждый из этих параметров связан с одним из
видов деформации стержня и с соответствующим этому виду деформации
внутренним силовым фактором (табл. 5.1).
Поскольку внутренние силы возникают в стержне в результате
действия внешних сил (нагрузок), внутренние силовые факторы
однозначно выражаются через внешние силы. Определим их для стержня
(рис. 5.5), воспользовавшись методом сечений. Отбрасывая левую часть
стержня, определим внутренние силовые факторы из уравнений
равновесия для его правой части.
Если спроектировать все силы, действующие на правую часть стержня,
на ось Oz, то из шести силовых факторов в это уравнение равновесия
статики войдет лишь один - продольная сила Nz:
прав прав
93
5.1. Основные виды деформации
Характер перемещения
поперечного сечения
Ось
Вид
деформации
Силовой
фактор
Ог
Относительное поступательное
перемещение вдоль оси
Растяжение
(сжатие)
Ох
Сдвиг
Оу
less
QX
Oz
Относительное вращательное
перемещение вокруг оси
Кручение
Ох
Изгиб
Оу
I Т те** \
М.
Рис. 5.5. Внутренние силовые факторы в сечении стержня
94
Отсюда
внеш
Nz = - Е г.
прав
(5.1)
Этот же результат, но с обратным знаком получим, рассматривая
равновесие левой части стержня. Действительно, из условия равновесия
для всего стержня следует:
внсшн внешн внешн внешн внешн
£ z = О, £ г + £2 = 0, Е г = - Е г,
прав лев прав лев
тогда с учетом (5.1) получаем:
N.
внешн внешн
Е *- Е *
прав лев
I *
(5.2)
Аналогично могут быть получены выражения для других внутренних
силовых факторов; с учетом (5.2) имеем:
N. =
М. =
отс
н
Е т;
■ Q* =
, мх =
Е*
отс
нешн
Е т.
, е,=
.к
внешн
Е у
отс
| внешн
(5.3)
Соотношения (5.3) дают правило вычисления внутренних силовых
факторов. Согласно этому правилу, например, продольная сила Nz
численно равна сумме проекций на ось Oz внешних сил, действующих на
отсеченную (левую или правую) часть стержня, а крутящий момент Мг
численно равен сумме моментов относительно оси Oz тех же внешних сил.
Аналогично вычисляются и другие внутренние силовые факторы.
Отметим, что выражение "численно равен" здесь имеет двоякий смысл.
Во-первых, оно означает, что значения этих силовых факторов
вычисляются по модулю, а правила знаков для них будут даны ниже, при
изучении отдельных видов деформации. Во-вторых, оно подчеркивает,
что формулировки, вытекающие из соотношений (5.3), не являются
определениями внутренних силовых факторов, а дают лишь способ их
вычисления.
95
5.2, Представление внутренних силовых факторов
в интегральной форме
Независимо от характера распределения
внутренних сил по поперечному сечению
они всегда приводятся к стандартной
системе силовых факторов Qx, Q , Nv Мх,
Ъхъ-угЯ Л/ , Mv алгебраические величины которых
зависят от места расположения
поперечного сечения, т.е. от продольной координаты
Z.
Компоненты тензора напряжений oz, tvz
и т , действующие по площадке AF в
произвольной точке поперечного сечения
с координатами (хуу), показаны на рис. 5.6,
Рис. 5.6. Напряжения на эле- тогда.
ментарной площадке
Qx ' [*„&. Qy ' faiF. *, = f°iF.
F F F
Mx - foydF> My = foxdF, Mz = f(x„x-Tay)dF.
(5.4)
Выражения (5.4) представляют внутренние силовые факторы в
интегральной форме.
5.3. Напряжения при растяжении (сжатии)
призматических стержней. Расчет на прочность
Переходя к изучению основных видов деформации стержней,
ограничимся рассмотрением стержней постоянного поперечного сечения
с прямолинейной осью, т.е. призматических стержней. Начнем с
рассмотрения деформации растяжения (сжатия).
Под растяжением (сжатием) понимают такой вид деформации
стержня, при котором в его поперечных сечениях возникает лишь один
внутренний силовой фактор -продольная сила Nr Поскольку продольная
сила численно равна сумме проекций на ось стержня всех внешних сил,
приложенных к одной из отсеченных частей (для прямолинейного
стержня она совпадает в каждом сечении с осью Oz), то растяжение
(сжатие) имеет место в том случае, когда все внешние силы, действующие
по одну сторону от данного поперечного сечения, сводятся к
96
Рис. 5.7. Внешние и внутренние силы при растяжении (сжатии)
равнодействующей, направленной вдоль оси стержня (рис. 5.7). Одна и
та же продольная сила Nz при действии на различные части стержня
(левую или правую) имеет противоположные направления. Знак Nz
зависит от характера вызываемой ею деформации. Продольная сила
считается положительной, если вызывает растяжение элемента
(рис. 5.8, а), и она отрицательна, если вызывает сжатие (рис. 5.8, б).
Будем предполагать, что выполняется гипотеза плоских сечений и
гипотеза об отсутствии поперечного взаимодействия продольных
волокон (см. гл. 1); таким образом, деформация растяжения сводится к
одноосному напряженному состоянию и в поперечных сечениях стержня
возникают лишь нормальные напряжения ог (см. рис. 5.6), индекс г у
которых опускаем.
Тогда продольная сила Nz в поперечном сечении площадью F,
очевидно, будет равна
N2 = fodF.
F
(5.5)
Соотношение (5.5) является уравнением
связывающим продольную силу Nz и
нормальное напряжение о, которое в общем
случае является функцией координат х и у
и поэтому не может быть найдено из одного
лишь уравнения статики (5.5). Таким
образом, задача определения напряжений даже
в самом простейшем случае
деформирования стержня (растяжение или сжатие)
оказывается статически неопределимой.
Необходимое для решения этой задачи
дополнительное уравнение вытекает из
гипотезы плоских сечений. Поскольку
равновесия статики,
/Yz>0
^Hz>0
/vz<o
—^
а)
I
Н7<0
I)
Рис. 5.8. Правило знаков для
продольной силы
97
поперечные сечения, оставаясь плоскими и перпендикулярными к оси
стержня, в процессе деформирования лишь поступательно перемещаются
вдоль оси (что приводит к одинаковому удлинению всех продольных
волокон), то приходим к уравнению г = const, из которого ввиду
однозначности связи о и 8 (для линейно-упругого материала это - закон
Гука: о = Ег) вытекает, что напряжения о = const.
Тогда из (5.5) следует, что Nz = о^или
( • - у- (5.6)
Таким образом, при растяжении (сжатии) призматического стержня
нормальные напряжения равномерно распределены по поперечному
сечению, а касательные напряжения в сечениях отсутствуют, что является
следствием гипотезы плоских сечений. Указанное, несмотря на казалось
бы очевидность и простоту (5.6), является фундаментальным результатом,
справедливым, строго говоря, лишь для призматического стержня.
Условие прочности при растяжении (сжатии) призматического стержня
из пластического материала (т.е. материала, одинаково работающего
на растяжение и на сжатие) будет иметь вид:
К
о « -^ * М. (5.7)
где [о] - допускаемое напряжение. Напряжение о в условии (5.7)
подставляется по модулю, так как знаки в этом случае роли не играют.
Для стержней из хрупких материалов, неодинаково сопротивляющихся
растяжению и сжатию, знак напряжения имеет принципиальное значение,
и условие прочности необходимо формулировать отдельно для
растяжения и сжатия
о = _£ * [о 1,
(5.8)
lacl = -=- * [°вЬ
где о и ос - напряжения растяжения и сжатия, а [ор] и [oj -
соответствующие допускаемые напряжения.
В практике инженерных расчетов, исходя из условия прочности,
решаются три основные задачи механики материалов и конструкций. В
98
применении к случаю растяжения (сжатия) призматического стержня эти
задачи формулируются следующим образом.
Проверка прочности (поверочныйрасчет). Этот расчет проводится,
если нагрузка (в нашем случае ее представляет Nz), сечение стержня F и
его материал [о] заданы.
Необходимо убедиться, что выполняется условие прочности
К
о - -j£ * [а].
Поверочный расчет заключается в том, что определяется фактический
коэффициент запаса прочности п и сравнивается с нормативным
коэффициентом запаса [п]:
°* a*F
п = — = -— * [и],
о Nz
где о+ - предельное (или опасное) напряжение, т.е. напряжение,
вызывающее отказ элемента конструкции (напомним, что, например, для
стержня из пластического материала это предел текучести от или
условный предел текучести о0 2).
Подбор сечения (проектный расчет). В этом расчете по заданной
нагрузке (Nz) определяются размеры поперечного сечения стержня (F)
из заданного материала ([о] дано). Минимальное значение F получим,
если в условии прочности (5.7) принять знак равенства:
и "Й-
м
Определение допускаемой нагрузки, т.е. максимального значения
нагрузки, которое допускает данный элемент конструкции (F и [о]
заданы) при выполнении условий прочности (5.7):
[N2] = [o]F.
Деформации элементов конструкции (е = А///) не должны превышать
некоторой допускаемой (нормативной) величины. При растяжении
(сжатии) это требование удовлетворяется, если выполняется условие
жесткости
А/ * [А/],
99
где [А/] -допускаемое значение удлинения. Условие жесткости позволяет
решать три типа задачи, аналогичных расчетам на прочность.
5.4. Понятие о концентрации напряжений.
Принцип Сен-Венана
Даже для призматического стержня равномерное распределение
напряжений по поперечному сечению не всегда имеет место. Так,
отклонения от равномерного распределения напряжений наблюдаются
в окрестности сечений, содержащих вырезы, выточки, отверстия,
трещины, в местах резкого изменения поперечного сечения, а также в
местах приложения сосредоточенных сил и т.п. Неравномерное
распределение напряжений в указанных местах является следствием
искажения плоскостей поперечных сечений или их депланации.
Концентрация напряжений - локальное увеличение напряжений
в элементах конструкций, обусловленное резкими переходами в
поперечных сечениях, наличием отверстий, вырезов, канавок, трещин
и т.п. Источники концентрации напряжений получили название
концентраторов напряжений. Графики распределения напряжений в
растягиваемой полосе, ослабленной отверстием, показаны на рис. 5.9, а\
ослабленной полукруглыми вырезами - на рис. 5.9, б.
Степень концентрации напряжений оценивается коэффициентом
концентрации
а = <W4> (5.9)
где omax- максимальное
напряжение в месте концентрации, он -
номинальное напряжение,
определяемое с учетом площади
ослабленного концентратором сечения.
Коэффициент а, вычисляемый по
формуле (5.9), называется
теоретическим коэффициентом
концентрации.
В действительности
коэффициент концентрации реальных
элементов конструкции -
эффективный коэффициент концентрации /с,
определяемый экспериментально,
оказывается меньше теоретическо-
Рис. 5.9. Концентрация напряжений в
полосе, ослабленной:
а - отверстием; б - вырезами
100
d
1.8
1,0
02 0,4 Qff «5 r/rf
У///,<// У////Л W/"'
ж
V
Цпк
*=£
£f\p
ш
к
f
Рис. 5.10. Зависимость коэффициента концен- n _,, „
TY Рис. 5.11. Иллюстрация принци-
трации от параметра г паСен-Венана
го (а > к). Зависимость теоретического коэффициента концентрации для
растягиваемой полосы от параметров различных типов концентраторов
приведена на рис. 5.10.
При (rid) - 0 для концентратора типа I a « 2, а для типа II - a =3.
Концентрация напряжений особенно опасна для материалов,
находящихся в хрупком состоянии; в пластическом состоянии
концентрация напряжений менее опасна, поскольку при напряжениях о z от
происходит перераспределение напряжений.
Однако, как показали эксперименты и точные решения методами
теории упругости, местные отклонения от равномерного распределения
напряжений, вызванные концентраторами, достаточно быстро затухают
по мере удаления от сечения с концентратором, и на расстояниях порядка
ширины сечения распределение напряжений можно считать практически
равномерным. Отмеченное свойство является частным случаем широко
используемого практически во всех разделах механики деформируемого
твердого тела принципа Сен-Венана.
Принцип Сен-Венана формулируется следующим образом: если тело
подвергается действию нагрузки, приложенной к небольшой области,
то напряжения в теле существенно зависят и от величин составляющих
силы и момента, статически эквивалентных нагрузке, и от закона
распределения последней лишь в небольшой части тела, примыкающей
к месту приложения нагрузки. Вне этой части тела напряжения
практически зависят от величин составляющих силы и момента,
статически эквивалентных нагрузке, и не зависят от закона ее
распределения (рис. 5.11).
101
5.5. Определение деформаций и перемещений
Определим упругие деформации стержня, показанного на рис. 5.12,
предполагая, что изменение его длины при растяжении А/, называемое
абсолютной продольной деформацией или удлинением, мало по сравнению
с его первоначальной длиной / (А/ < < /). Тогда относительная
продольная деформация будет равна
А/
(5.10)
Учитывая, что согласно закону Гука для одноосного растяжения
(сжатия)
г
(5.11)
где Е- модуль продольной упругости материала стержня, а нормальные
напряжения определяются по формуле (5.6): о = NJF (в нашем случае
Nz = Р), для абсолютной деформации получаем
А/
EF'
(5.12)
Произведение EFпринято называть жесткостью поперечного сечения
стержня при растяжении (сжатии), так как удлинение обратно
пропорционально EF.
Как показывают эксперименты, при растяжении стержня размеры его
поперечного сечения уменьшаются (рис. 5.12), а при сжатии -
увеличиваются. Это явление получило название эффекта Пуассона.
По аналогии с продольной деформацией изменение размеров
поперечного сечения АЬ (на рис. 5.12
А6 < 0) будем называть абсолютной
поперечной деформацией, а г' = ШЬ -
относительной поперечной
деформацией. Относительные продольная и
поперечная деформации, имеющие
противоположные знаки, связаны
между собой коэффициентом ji,
являющимся константой материала и
называемым коэффициентом попе- Рис 5.12. Продольная и поперечная
деформации стержня
А
/
/
\ \
\
гг.—
1 1
Л ь
V
\t J
р
-fc
At
'^.
102
л—
А
1^
ii
ш
Pf
1 Li
'i^l^- J*
III
Шшш
■^i ■ "^
ill
Ш
imral
PT
... Lf}
"*» W^
ПЖ
шшш
illlllllll
p*
^.
Ну
. 6
Рис. 5.13. Ступенчатый стержень
речной деформации или коэффициентом Пуассона:
Как известно (см. гл. 3), для изотропного материала 0 й ц <, 1/25.13)
Формула (5.12) для удлинения стержня А/ применима только в случае,
когда по длине стержня ни жесткость поперечного сечения, ни
продольная сила не меняются (EF = const, Nz = const). Удлинение стержня со
ступенчатым изменением EFn Nz (рис. 5.13) может быть определено как
сумма удлинений отдельных ступеней:
А/- £^
*-1 (EF)k
1°Л
*=i
(5.14)
(индекс к у модуля продольной упругости означает, что участки стержня
могут быть изготовлены из различных материалов). В случае, когда Nz
и EF меняются по длине стержня / непрерывно, обобщая формулу (5.14),
получаем
А/
/
Nzdz
EF
(5.15)
С упругими продольными деформациями стержня при растяжении
(сжатии) связаны продольные перемещения его сечений. На рис. 5.14
приведены три случая определения таких перемещений, откуда видно,
что перемещения поперечных сечений численно равны удлинениям
заштрихованных частей стержня:
103
1
ч
Ж
И 1
а)
\ • I
Рис. 5.14. Абсолютные
перемещения:
а - торцевого сечения; б -
промежуточного сечения; в -
взаимное перемещение сечений
перемещение свободного торцевого
сечения 1-1 при неподвижном другом
торцевом сечении (рис. 5.14, а) численно
равно удлинению стержня;
перемещение промежуточного
сечения 2-2 (рис. 5.14, б) численно равно
удлинению части стержня, заключенной
между данным сечением и сечением
неподвижным;
взаимное перемещение сечений 3-3 и
4-4 (рис. 5.14, в) численно равно
удлинению части стержня, заключенной между
этими сечениями.
5*6. Дифференциальное уравнение осевой деформации
прямолинейного стержня
Выделим элемент стержня dz двумя поперечными сечениями
(рис. 5.15). В результате осевой деформации первоначальная длина
элемента dz изменится на величину Adz = Ezdz. Согласно рис. 5.15 эта
величина может быть найдена как разность перемещений его торцев
(краев)
Adz
dz.
Приравнивая эти выражения,
получаем
z,dz = —dz
dz
или
е, =
du
dz'
(5.16)
Используя закон Гука о = Ег и
формулу для напряжений при
одноосном растяжении о = NJF, получаем Рис- 5Л5- Перемещения элемента
стержня
104
dz ef'
(5.17)
Интенсивность распределенной нагрузки qz и продольное усилие Nz
связаны дифференциальной зависимостью
Чг в
"d7
(5.18)
Получим систему уравнений относительно Nz и и. Исключим Nz из
(5.17) и (5.18):
&2и _ d
dz2 dz
l^J £F dz
или
dz dz2
(5.19)
(5.20)
Учитывая (5.18), получаем дифференциальное уравнение осевой
деформации прямолинейного стержня относительно перемещений u(z):
d2u , Чг
dz2 ~ EF'
(5.21)
Решение этого уравнения в случае одного участка, где функции Nz(z)
и u(z) сохраняют свой вид, получаем интегрированием (5.21) дважды:
«Ь'Ы!*
о V о
dz + C{z + С2
(5.22)
Постоянные интегрирования С{ и С2 имеют ясный механический
смысл:
El
EF
EF '
(5.23)
lz=0
"1,-0 = «0 = C2«
Здесь и0и N0-~ перемещение вдоль оси и продольная сила в поперечном
105
сечении, проходящем через начало координат. Величины и0 и N0
называются начальными параметрами.
Учитывая (5.23), для N и u(z) получаем
*о . 1
u(z) = u* + jfz + jfI\ !qdz
\ о
<Ь,
(5.24)
N2 = N0 + jqdz.
5.7. Напряженное состояние при растяжении (сжатии)
Напряженное состояние при растяжении стержня является одноосным
(рис. 5.16, а). Поскольку на поперечных и продольных площадках
касательные напряжения не возникают, то эти площадки являются
главными. Причем в случае растяжения о{ = о > 0, о2 = а3 = 0, а в случае
сжатия о, = о2 = 0, а о3 = о < 0.
Напряжения на площадках, наклоненных к оси стержня под углом ">
а, определяются по формулам для упрощенного плоского напряженного
состояния (см. гл. 3):
ocos2a, т = 0,5asin2a.
(5.25)
Площадки с экстремальными касательными напряжениями т13
(рис. 5.16, б), как известно, наклонены по отношению к исходным под
углами р = ±45° (это следует и из формулы для xj и равны т13 = о/2.
б -*-CH»"tf
а)
—э»-
6~*
*' 2 <Л~ 2
Рис. 5.16. Напряженное состояние стержня при растяжении:
а - на исходных площадках; б - на площадках с экстремальными касательными
напряжениями
106
Именно с действием экстремальных т связывается появление на
боковой поверхности образца из малоуглеродистой стали,
испытываемого на растяжение, линий скольжения, ориентированных под углом р =
= ±45° к оси образца. На площадках с экстремальными т действуют и
нормальные напряжения, равные oI3 = о/2.
5.8. Потенциальная энергия упругой деформации
при растяжении (сжатии)
При нагружении упругого тела внешние силы совершают работу А,
которая переходит в потенциальную энергию упругой деформации U и
является полностью обратимой: A-U. Это выполняется в том случае,
когда внешние силы прикладываются квазистатически (с бесконечно
малой скоростью) и когда можно пренебречь диссипацией энергии в
материале тела и в окружающую среду.
Для стержня, растягиваемого в пределах упругих деформаций силой
Р на величину А/ (рис. 5.12) при Nz = const и EF = const,
Л " \PkMk.
где Pk и Alk - текущие значения силы и удлинения. Учитывая (5.12),
получаем
А - 1 —
2 EF'
Так как А = U, то для потенциальной энергии упругой деформации
имеем
1 Р21
U = -—.
2 EF
В общем случае
2 J EF
о
Потенциальная энергия упругой деформации всегда положительна.
При ее вычислении принцип независимости действия сил (принцип
суперпозиции) неприменим, так как U и Nz связаны нелинейной
зависимостью.
107
Энергия, накапливаемая в единице объема и = U/V, где V~ FI- объем
стержня, определяет удельную потенциальную энергию упругой
деформации. Для случая EF = const и Nz = const:
2 2
5.9. Способы определения усилий
в статически определимых фермах
Фермой называется шарнирно-стержневая система, составленная из
прямолинейных стержней, соединенных в узлах полными идеальными
шарнирами, т.е. шарнирами, возле которых обращаются в нуль
изгибающие моменты во всех соединяемых стержнях (рис. 5.17, а).
Каждый стержень фермы начинается и заканчивается шарниром. Ферма
-это расчетная схема стержневой конструкции, получаемая
схематизацией и идеализацией ее элементов. В качестве примера на рис. 5.17, б
приведена конструкция сварного узла А, схематизируемого в расчетной
схеме идеальным шарниром.
В конструкциях ферменного типа стержневые элементы работают
только на растяжение (сжатие), это объясняется тем, что фермы
нагружаются сосредоточенными силами, приложенными в узлах. На
рис. 5.17, а показана ферма балочного типа (она имеет опоры как у
статически определимой однопролетной балки и выполняет примерно
те же функции, что и балка, перекрывающая пролет длиной I) с
параллельными поясами, соединенными стержнями решетки в виде
раскосов.
Для определения усилий в стержнях ферм используется метод
сечений,применительно к стержневым системам, получивший название
Рис. 5.17. Ферма:
а - расчетная схема; б - сварной узел
108
V *
"> С Ni
<3
L P,
*t\N^
Рис. 5.18. Иллюстрация способа вырезания узлов
статического метода. Он состоит в том, что от системы отсекается
некоторая часть, а попадающие в сечение усилия определяются
условиями равновесия отсеченной части. Статический метод для расчета
ферм реализуется следующими способами.
Способ вырезания узлов заключается в последовательном вырезании
и рассмотрении равновесия узлов фермы (рис. 5.18). Рекомендуется
начинать эту операцию с узла, где сходится не более двух стержней
(например, узел А). Поскольку имеем систему сил, сходящихся в одной
точке, то для каждого узла можно составить два независимых уравнения
равновесия в виде суммы проекций всех сил на какие-либо две оси, в
качестве которых целесообразно выбирать нормали к осям стержней (оси
пх и я2). Отметим, что если двухстержневой узел не загружен (например,
узел Z)), то усилия в нем равны нулю (на рис. 5.18 нулевые стержни
зачеркнуты).
Следующим вырезается узел, в котором могут сходиться и более двух
стержней (например, узел С), но неизвестных (ранее не определенных)
усилий в нем должно быть не более двух (в узле С это Иъ и ^4, а ранее
определенное усилие N2 заключено в кружок). Усилия #3 и N4
определяются из двух уравнений равновесия для узла С.
Обратим внимание на случай, когда в узле фермы сходятся три
стержня, два из которых лежит на одной прямой (узлы Е и L); усилия в
этих двух стержнях при отсутствии в узле внешней нагрузки равны по
величине и по знаку, а усилие в третьем стержне равно нулю (узел Е).
Способ вырезания узлов является универсальным, позволяющим
определять усилия во всех стержнях статически определимой фермы.
Недостаток этого способа заключается в том, что последующие усилия
выражаются через ранее определенные; это приводит к накоплению
вычислительной погрешности. Кроме того, если необходимо знать усилия
лишь в отдельных стержнях фермы, то приходится определять усилия
и в других стержнях, через которые выражаются искомые усилия.
109
Рис. 5.19. Иллюстрация способа моментной точки
Способ моментной точки позволяет выражать усилия в стержнях через
внешнюю нагрузку без промежуточных операций. Он применим для тех
случаев, когда, отсекая часть фермы, удается провести сечение, в которое
попадает не более трех стержней /Тогда усилие в одном из этих стержней
определяется из суммы моментов сил, приложенных к отсеченной части,
относительно точки, где пересекаются оси двух других стержней. Такая
точка кп получила название моментной точки для определения усилия
N„
Например, усилие Nx в ферме (рис. 5.19) определяется из уравнения
внешн L* к\
г тк1 = О, JV, + Е тк1 = О, JV, = --Н22 .
прав прав Г|
На рис. 5.19 показаны моментные точки к2 и къ (а также тг и г3),
необходимые для определения усилий N2 и N3.
Однако в случае, если два стержня из трех, попадающих в сечение,
параллельны, то моментная точка для третьего стержня находится в
бесконечности (рис. 5.20). Способ моментной точки в этом случае
неприменим и приходится обращаться к способу проекций.
О И
Рис. 5.20. Иллюстрация способа проекций
по
Рис. 5.21. Иллюстрация способа совместных сечений
Способ проекций заключается в том, что для отсеченной части
составляется уравнение равновесия в виде суммы проекций всех сил на
ось, перпендикулярную к параллельным стержням. Например, для
консольной фермы с параллельными поясами (рис. 5.20) усилие N^
определим из уравнения £ V = 0:
лев
-N,cos<p - Р = 0, N] = -Р/сощ.
Способ совместных сечений применяется в случае, когда для выделения
части фермы не удается провести сечение, проходящее через три стержня.
Например, для определения усилия N^ в ферме (рис. 5.21) удается
отделить правую часть фермы сечением 1-1, проходящим через четыре
стержня. Тогда в уравнение
£ К= 0, tfjcoscp - N2 + £ К= 0
прав прав
войдет второе неизвестное усилие N2, которое находим, отделяя сечением
2-2 верхнюю часть фермы, из уравнения равновесия:
внешн
верхи верхи
111
Глава 6
ИЗГИБ ПРИЗМАТИЧЕСКИХ СТЕРЖНЕЙ
6.1. Классификация видов изгиба стержня
Под изгибом понимается такой вид нагружения, при котором в
поперечных сечениях стержня возникают изгибающие моменты
Мх или М или оба одновременно. Деформации изгиба
вызываются внешними силами, пересекающими ось стержня и перпендикулярными
к ней. Стержень, работающий на изгиб, обычно называют балкой.
Устраним неопределенность выбора положения осей Ох и Оу системы
координат, связанной с поперечным сечением стержня. Примем, что оси
ОхиОу- главные центральные оси инерции поперечного сечения стержня.
Плоскости, проведенные через ось стержня Oz и главные центральные
оси инерции сечения Ох или Оу, называются главными плоскостями
инерции стержня. На рис. 6.1 такие плоскости выделены штриховкой.
Если все внешние силы, вызывающие изгиб балки, лежат в одной из
главных плоскостей инерции, например, как в случаях, представленных
на рис. 6.1, а, б, то изгиб называется прямым. В случае, когда это условие
не выполняется, изгиб называется косым (рис. 6.1, в).
Q) В) в/
Рис. 6.1. Виды изгиба:
а, б - прямой; в - косой
112
Кроме изгибающих моментов в поперечных сечениях балки при
изгибе могут возникать поперечные силы Qx и (или) Q . Так, при прямом
изгибе балки, показанном на рис. 6.1, д, в поперечных сечениях
возникают изгибающий момент Мх и поперечная сила Q , а в случае,
показанном на рис. 6.1, б - М и Qx. В поперечных сечениях балки,
работающей на косой изгиб (рис. 6Л, в), возникают MY, А/ , Q и Qr
Если поперечные силы Qx и (или) Qy в сечениях балки не возникают,
изгиб называется чистым. В противном случае (при Qx ф О и (или) б *
* 0) изгиб называется поперечным.
6.2. Дифференциальные зависимости между
внутренними силовыми факторами и внешней
нагрузкой при прямом поперечном изгибе
М?>0
Мх>0
Quy0
Введем правило знаков для изгибающего момента и поперечной силы
(рис. 6.2). Изгибающий момент считается положительным, если вызывает
сжатие верхних волокон балки;
поперечная сила
положительная, если стремится повернуть
элемент балки по часовой
стрелке.
Исследуем связь
изгибающего момента Мх9 поперечной
силы Q и распределенной
нагрузки интенсивностью q на
примере балки, показанной на
рис. 6.3, я, для чего составим
уравнения равновесия элемента
балки (рис. 6.3, б). При этом
будем считать, что
интенсивность распределенной нагрузки
q(z) на бесконечно малом
отрезке dz может быть
аппроксимирована линейной функцией. Тогда, записывая уравнения равновесия
элемента
^
Мх<0
"х
<0
О)
б)
Рис. 6.2. Правило знаков:
а - для изгибающего момента; б - для
поперечной силы
J> = 0, Qy + qdz + Uldgdz - (Qy + dQJ = 0,
JX = 0, Mx + Qydz + 4dz(dz/2) + U2dqdzV3dz - (Mx + dMx) « 0
113
и пренебрегая бесконечно малыми высших порядков, получаем
(к
(6.1)
Следствием дифференциальных зависимостей (6.1) является
уравнение
ах
(к2
?•
(6.2)
6.3. Прямой чистый изгиб призматического стержня
При прямом чистом изгибе в поперечном сечении стержня возникает
только один силовой фактор - изгибающий момент Мх (рис. 6.4). Так
как Q = dMJdz = 0, то Мх = const и чистый прямой изгиб может быть
реализован при загружении стержня парами сил, приложенными в
торцевых сечениях стержня.
Поскольку изгибающий момент Мх равен сумме моментов внутренних
сил относительно оси Ох, с нормальными напряжениями его связывает
уравнение статики
/7&ЬЯ7
qfz)
Мх = f foy&F.
F
■dz
a)
4
Mr
0
*
реши*
di
Ф
Qy*UQy
Рис. 6.3. Балка на двух опорах (а) и
усилия в ее элементе (б)
£*Л
(6.3)
Рис. 6.4. Изгибающий
момент и напряжение в сечении
балки
114
Сформулируем предпосылки
теории чистого прямого изгиба
призматического стержня. Для
этого проанализируем
деформации модели стержня из
низкомодульного материала, на боковой
поверхности которого нанесена
сетка продольных и поперечных Рис 6 5 деформирование сечений стер-
рисок (рис. 6.5). жня при ЧИСТом изгибе
Поскольку поперечные риски
при изгибе стержня парами сил,
приложенными в торцевых сечениях, остаются прямыми и
перпендикулярными к искривленным продольным рискам, выполняется гипотеза
плоских сечений, которая, как показывает решение этой задачи методами
теории упругости, перестает быть гипотезой, становясь точным фактом
- законом плоских сечений. Изменение расстояний между продольными
рисками свидетельствует о справедливости гипотезы о ненадавливании
продольных волокон (ох = о = 0).
Ортогональность продольных и поперечных рисок перед
деформированием и после него указывает на отсутствие сдвигов, касательных
напряжений в поперечных и продольных сечениях стержня,
Таким образом, чистый прямой изгиб призматического стержня
сводится к одноосному растяжению или сжатию продольных волокон
напряжениями о (индекс z в дальнейшем опускаем). При этом часть
волокон находится в зоне растяжения (нижние волокна на рис. 6.5), а
другая часть - в зоне сжатия (верхние волокна).
Эти зоны разделены нейтральным слоем (п-п), не меняющим своей
длины, напряжения в котором равны нулю.
Учитывая сформулированные выше предпосылки и полагая, что
материал стержня линейно-упругий (о = Ее), выведем формулы для
кривизны нейтрального слоя 1/р (р - радиус кривизны) и нормальных
напряжений о. Предварительно отметим, что постоянство поперечного
сечения призматического стержня и изгибающего момента (Мх = const)
обеспечивает постоянство радиуса кривизны нейтрального слоя по длине
стержня (рис. 6.6, я), нейтральный слой (п-п) описывается дугой
окружности.
Рассмотрим призматический стержень в условиях прямого чистого
изгиба (рис. 6.6, а) с поперечным сечением, симметричным относительно
вертикальной оси Оу. Это условие не отразится на конечном результате
(чтобы прямой изгиб был возможен, необходимо совпадение оси Оу с
главной осью инерции поперечного сечения, которая и является осью
симметрии). Ось Ох поместим на нейтральном слое, положение которого
заранее неизвестно.
й
Е=аЫ§\)
115
Рис. 6.6. Радиус кривизны (а) и деформирование продольного волокна (6) при
чистом изгибе
Рассмотрим вырезанный из стержня элемент длиной dz (рис. 6.6, б).
Поскольку интерес представляют деформации элемента, определяемые
относительным смещением его точек, одно из торцевых сечений элемента
(левое сечение на рис. 6.6, 6) можно условно считать неподвижным.
Ввиду малости d(p считаем, что точки поперечного сечения при
повороте на этот угол перемещаются не по дугам, а по соответствующим
касательным.
Вычислим относительную деформацию продольного волокна АВ,
отстоящего от нейтрального слоя на у:
г = ВВХ/АВ = BBxIOOv
Из подобия треугольников СООх и ОхВВх следует, что
ВВ1/001 = ОхВ1СО = у /р.
Продольная деформация г оказалась линейной функцией расстояния
от нейтрального слоя, что является прямым следствием закона плоских
сечений:
е = у 1р. (6.4)
Тогда нормальное напряжение, растягивающее волокно АВ, на
основании закона Гука будет равно
о - Е?-. (6.5)
Р
116
Формула (6.5) неудобна для практического использования, так как
содержит две неизвестные: кривизну нейтрального слоя 1/р и положение
нейтральной оси Ох, от которой отсчитывается координата у. Для
определения этих неизвестных воспользуемся уравнениями равновесия
статики. Первое выражает требование равенства нулю продольной силы
»- ■//•
tf-°- (6.6)
Подставляя в это уравнение выражение (6.5)
V F
и учитывая, что (Е/р) * О, получаем
[fydF-0.
(6.7)
Интеграл в левой части уравнения (6.7) представляет статический
момент поперечного сечения стержня относительно нейтральной оси Ох,
который может быть равным нулю только относительно центральной
оси. Поэтому нейтральная ось Ох проходит через центр тяжести
поперечного сечения.
Второе уравнение равновесия статики (6.3) связывает нормальные
напряжения с изгибающим моментом (который легко может быть
выражен через внешние силы и поэтому считается заданной величиной).
Подставляя в уравнение (6.3) выражение для напряжений (6.5)
f//^ = M, (6.8)
и учитывая, что Г fy2dF = Jx, где Jx - главный центральный момент
F
инерции относительно оси Ох, для кривизны нейтрального слоя получаем
формулу
1/р - MXIEJX. (6.9)
Кривизна нейтрального слоя 1/р является мерой деформации стержня
при прямом чистом изгибе. Согласно (6.9) 1/р тем меньше, чем больше
117
max &
Рис. 6.7. Эпюра нормальных
напряжений при изгибе
величина EJxi называемая
жесткостью поперечного сечения при изгибе
(по аналогии с жесткостью
поперечного сечения при растяжении EF).
Подставляя (6.9) в (6.5), получаем
формулу Ш. Кулона для нормальных
напряжений в виде
Mv
-у.
(6.10)
Для согласования знаков изгибающего момента Мх и нормальных
напряжений о в правой части формулы (6.10) ставится знак минус, так
как при Мх > 0 нормальные напряжения о при у > 0 оказываются
сжимающими. Однако в практических расчетах удобнее, не
придерживаясь формального привила знаков, определять напряжения по модулю,
а знак ставить по смыслу.
Нормальные напряжения при чистом изгибе призматического стержня
являются линейной функцией координаты у и достигают наибольших
значений в волокнах, наиболее удаленных от нейтральной оси (рис. 6.7),
т.е.
тах|а| = -^утах = =
J 1у
wv
Геометрическая характеристика Wx = JxJym2iX, имеющая размерность м3,
- момент сопротивления при изгибе, вводится для поперечных сечений,
симметричных относительно Ох. Поскольку при заданном Мх
напряжения тахо тем меньше, чем больше Wx, момент сопротивления является
геометрической характеристикой прочности поперечного сечения при
изгибе.
Приведем примеры
вычисления моментов сопротивления
для простейших форм
поперечных сечений, показанных на
рис. 6.8. Для прямоугольного
поперечного сечения
(рис. 6.8, а) имеем Jx = Ыгг1\2,
= bh 16. Аналогично для круга
_ , Л _ (рис. 6.8, б)получаем WY =
Рис. 6.8. Формы поперечного сечения: = ^з/32 (где j = ^/64, у* =
а - прямоугольное; б - круговое; в - коль- ,,«>, л 'тах
„м/л = «/2), а для кругового кольце-
цевое
118
вого сечения (рис. 6.8, в), у которого
получаем
Wx = —(1 - р4).
32
Отметим, что момент сопротивления свойством аддитивности не
обладает.
Итак, максимальные нормальные напряжения в сечении с
изгибающим моментом Мх определяются по формуле
тах|о| = MXIWX. (6.11)
Этой формулой удобно пользоваться при расчете балок из
пластичного материала в упругой области, одинаково работающего на растяжение
и сжатие. Поскольку знак напряжения в этом случае не имеет значения,
напряжения вычисляются по модулю, и условие прочности при изгибе
балки в форме призматического стержня получает вид
max|o| = m*xMxIWx й [о], (6.12)
где maxMv - максимальный изгибающий момент; [о] - допускаемое
напряжение на простое растяжение (сжатие).
При расчете балок из хрупких материалов следует различать
наибольшие растягивающие тахо и наибольшие сжимающие тах|ос|
напряжения (рис. 6.9), которые также определяются по модулю непосред-
1
!И
f 1
) §
i
'Л i
///л
тахб(
У max \
г Утпх
та
г
^
х6р
Рис. 6.9. Наибольшие растягивающие и сжимающие напряжения при изгибе
119
ственно по (6.10) и сравниваются с допускаемыми напряжениями на
растяжение [о ] и сжатие [oj. Условие прочности в этом случае будет
иметь вид
М
max°p = -f-Ух
-*-"w * [ор];
тах|ос| = ^1 * [о.].
(6.13)
(6.14)
6.4. Прямой поперечный изгиб призматического стержня
При прямом поперечном изгибе в сечениях стержня возникает
изгибающий момент Мх и поперечная сила Q (рис. 6.10), которые
связаны с нормальными о и касательными т z напряжениями:
Мх = ffoyuF, Qy = ff^dF.
Выведенная в случае чистого изгиба стержня формула (6.10) для
прямого поперечного изгиба неприменима, поскольку из-за сдвигов,
вызываемых касательными напряжениями т , происходит депланация
поперечных сечений (отклонение от закона плоских сечений). Однако
для балок с высотой поперечного сечения
СМ)<1(рис. 6.11) погрешность для (6.10)
невелика и эту формулу применяют для
определения нормальных напряжений
поперечного изгиба как приближенную.
При выводе формулы (6.10)
использовалась гипотеза об отсутствии поперечного
взаимодействия продольных волокон. При
поперечном изгибе наблюдаются
отклонения от этой гипотезы:
в местах приложения сосредоточенных
сил (см. рис. 6.11, а). Под сосредоточенной
силой напряжения поперечного
взаимодействия могут быть достаточно велики и
во много раз превышать продольные
напряжения oz, убывая при этом в соответствии с
принципом Сен-Венана по мере удаления от
точки приложения силы;
Рис. 6.10. Внутренние
силовые факторы и напряжения
при поперечном изгибе
120
ttHttHtutniHi
777ТТГ
д)
^4v*
Рис. 6.11. Случаи отклонения от гипотезы о ненадавливании волокон:
а - при действии сосредоточенной силы; б - при действии распределенной
нагрузки
в местах приложения распределенных нагрузок. Так, в случае,
приведенном на рис. 6.11,6, напряжения от давления на верхние волокна
балки
-qlb.
Сравнивая их с продольными напряжениями
о2, имеющими порядок
2 bh2/6 4*Ы b\h)'
maxo.
приходим к выводу, что напряжения о < о2,
так как a^oz ~ (Л//)2 < 1 •
Получим формулу для касательных
напряжений т . Примем, что нормальные
напряжения вычисляются по (6.10), а касательные
напряжения равномерно распределены по
ширине поперечного сечения (рис. 6.12). Эта
предпосылка выполняется тем точнее, чем
Рис. 6.12. Касательные
напряжения при
поперечном изгибе
121
л
гпг
di
Lt^^
ч
Mr.
Рис. 6.13. Выделение элемента балки
уже поперечное сечение стержня. Точное решение задачи для
прямоугольного поперечного сечения показывает, что отклонение от
равномерного распределения т зависит от отношения сторон bih. При bih = 1 оно
составляет 12,6 %, при bih = 0,5 - только 3,3 %.
Непосредственное определение напряжений т затруднительно,
поэтому находим равные им (вследствие закона парности) касательные
напряжения т , возникающие на продольной площадке с координатой
у элемента длиной dz, вырезанного из балки (рис. 6.13). Сам элемент
показан на рис. 6.14.
От этого элемента продольным сечением, отстоящим от нейтрального
слоя на у, отсекаем верхнюю часть, заменяя действие отброшенной
6*d6
Рис. 6.14. Внуренние силовые факторы и напряжения в элементе балки
122
нижней части касательными напряжениями т (индекс zy в дальнейшем
опускаем), равнодействующая которых (рис. 6.15)
dT = xbdz.
Согласно второй предпосылке т = const по ширине элемента Ь.
Нормальные напряжения о и о + do, действующие на торцевых
площадках элемента, также заменим равнодействующими:
„Л/ Л/ и
К + <^с = //<* + «Ь)^
Л/ +dAT
Согласно первой предпосылке, нормальные напряжения определяются
по (6.10), a S" - статический момент отсеченной части площади
поперечного сечения о> относительно оси Ох.
Рассмотрим условие равновесия элемента (рис. 6.15), составив для него
уравнение статики £z = 0,
После несложных преобразований, учитывая, что
dM
<k
Gy,
получаем формулу для касательных
напряжений при прямом поперечном изгибе
призматического стержня
ел"
'А
(6.15)
%*<Mfc,
Рис. 6.15. Усилия в отсечен-
которая называется формулой Журавского. ной части элемента
123
В этой формуле Ъ - ширина
сечения в том месте, где определяются
касательные напряжения,, а
статический момент, подставляемый в (6.15),
может быть вычислен как для
верхней, так и для нижней части
(статические моменты этих частей сечения
относительно его центральной оси Ох
отличаются только знаком, так как
статический момент всего сечения
равен нулю).
В качестве примера применения
формулы Журавского построим
эпюру касательных напряжений для
прямоугольного поперечного сечения балки (рис. 6.16). Учитывая, что
для этого сечения
Рис. 6.16. Эпюра касательных
напряжений
4H[i(H]
8
h2
J =М3/12,
получаем
QX 3Qy
J.b
IF
h2
где F= bh - площадь прямоугольника.
Как видно из формулы, касательные напряжения по высоте сечения
меняются по закону квадратической параболы, достигая максимума на
нейтральной оси:
тахт
2F '
Сделаем несколько замечаний, касающихся расчетов на прочность
при прямом поперечном изгибе. В отличие от простых видов
деформации, когда в поперечных сечениях стержня возникает лишь один силовой
фактор, к которым относятся и растяжение (сжатие), и чистый изгиб,
прямой поперечный изгиб должен быть отнесен к сложным видам
деформации.
В поперечных сечениях стержня при поперечном изгибе возникают
два силовых фактора: изгибающий момент Мх и поперечная сила Qy
124
тахб
(рис. 6.17), напряженное
состояние является
упрощенным плоским, при
котором в окрестности
произвольно выбранных точек
поперечного сечения
действуют нормальные о и
касательные т напряжения.
Поэтому условие прочности
для таких точек должно
быть сформулировано на
основе какого-либо
критерия прочности (см. гл. 3).
Учитывая, что наибольшие нормальные напряжения возникают в
крайних волокнах, в которых касательные напряжения отсутствуют
(рис. 6.17), а наибольшие касательные напряжения во многих случаях
имеют место в нейтральном слое, где нормальные напряжения равны
нулю, условия прочности формулируются отдельно по нормальным и
касательным напряжениям:
Рис. 6.17. Напряженное состояние при
поперечном изгибе
тахо <. [о]; тахх <. [х].
Покажем, что доминирующим в расчетах на прочность балки при
поперечном изгибе является расчет по нормальным напряжениям. Для
этого оценим порядок тахо и тахт на примере консольной балки,
показанной на рис. 6.18:
тахо
тахМх
Л3'
тах-с -
F
Р_
А*'
т
Р1|ЩЩР1101ШШ^^
Иг
Рис. 6.18. Консольная балка
125
так как maxMx ~ PI, Qy~ P,F~ h2, Wx ~ A3.
Тогда
тахт _ P/h2
max о рцнъ
= hll « 1,
откуда тахт < maxo.
Поскольку [т]/[о] ~ 0,5, то определяющим в этом случае будет расчет
по нормальным напряжениям и условие прочности, например, для балки
из пластического материала, работающей на прямой изгиб, как и в случае
чистого изгиба будет иметь вид (6.12):
тахМ.
1 ИГ
6.5. Рациональные формы поперечных сечений при изгибе
Наиболее рациональным является сечение, обладающее минимальной
площадью при заданной нагрузке (изгибающем моменте) на балку. В этом
случае расход материала на изготовление балки будет минимальным.
Для получения балки минимальной материалоемкости нужно
стремиться к тому, чтобы по возможности наибольший объем материала
работал при напряжениях, равных допускаемым или близким к ним.
Прежде всего рациональное сечение балки при изгибе должно
удовлетворять условию равнопрочности ее растянутой и сжатой зон.
Иными словами, необходимо, чтобы наибольшие напряжения растяжения
тахОр и наибольшие напряжения сжатия тахас одновременно достигали
допускаемых напряжений [о ] и [oj. Поэтому для балки из пластичного
материала, одинаково работающего на растяжение и сжатие ([о ] = [о J =
= [о]), условие равнопрочности выполняется для сечений, симметричных
относительно нейтральной оси. К таким сечениям относится, например,
прямоугольное (рис. 6.19, а), при котором обеспечено условие
тахор = тах|ос|.
Однако в этом случае материал, равномерно распределенный по
высоте сечения, плохо используется в зоне нейтральной оси.
Чтобы получить более рациональное сечение, необходимо возможно
большую часть материала переместить в зоны, максимально удаленные
от нейтральной оси. Таким "образом, приходим к рациональному для
126
а) б) в)
Рис. 6.19. Рациональные формы поперечных сечений при изгибе для пластичных
материалов:
a - прямоугольное; б - симметричный двутавр; в - коробчатое
пластичного материала сечению в форме симметричного двутавра
(рис. 6.19, 6), у которого большая часть материала сосредоточена на
полках (горизонтальных массивных листах), соединенных стенкой
(вертикальным листом), толщина которой 6 назначается из условия
прочности стенки по касательным напряжениям, а также из соображений
ее устойчивости.
К двутавровому сечению близко по критерию рациональности так
называемое коробчатое сечение (рис. 6.19, в) и двутавры с параллельными
гранями полок (широкополочные двутавры и тавры).
Рассуждая аналогично, приходим к выводу, что для балок из хрупкого
материала наиболее рациональным будет сечение в форме
несимметричного двутавра, удовлетворяющего условию равнопрочности на
растяжение и сжатие (рис. 6.20):
у (с> [в.] '
/max L с
которое вытекает из требования
тахар ^ Щ
тахос [ос]'
Идея рациональности
поперечного сечения стержней при изгибе
реализована в стандартных
тонкостенных профилях, получаемых
тах<*с
тахбр
Рис. 6.20. Несимметричный двутавр
127
чш&
V й
а)
YVTTTTk
б)
Vfrrrh
в)
/TZZZZb
ЧПШЕ&
Рис. 6.21. Стандартные прокатные профили:
a - двутавр; б - швеллер; в - неравнобокий
уголок; г - равнобокий уголок
Рис. 6.22. Замкнутые
сварные профили
методами горячего прессования или прокатки из легированных
конструкционных углеродистых сталей, а также алюминиевых сплавов,
получивших распространение в строительстве, машиностроении,
авиационном машиностроении.
Широко распространены профили, показанные на рис. 6.21. Реже
встречаются тавр, таврошвеллер, зетовый профиль и др. Употребляются
также холодногнутые замкнутые сварные профили (рис. 6.22).
Поскольку по соображениям технологии сортамент стандартных
профилей по размерам ограничен (например, наибольший прокатный
двутавр имеет высоту 550 мм), то для больших пролетов приходится
применять составные (сварные или клепаные) балки.
6.6. Понятие о составных балках
Работу составных балок проиллюстрируем на простом примере
трехслойной балки прямоугольного поперечного сечения (рис. 6.23). Если
слои между собой не связаны и силы трения между ними отсутствуют,
то каждый из них деформируется как отдельная балка, имеющая свой
нейтральный слой (рис. 6.23, а).
Нагрузка между этими балками распределяется пропорционально их
жесткостям при изгибе (в данном примере поровну). Это означает, что
моменты инерции и сопротивления трех независимо друг от друга
деформирующихся балок должны быть просуммированы:
12
4 х 6
Ml
2
128
Рис. 6.23. Составные балки:
а - трехслойная балка; б - монолитная балка
Если балки скрепить (сваркой, болтами или другим способом), то с
точностью до пренебрежения податливостью наложенных связей сечение
балки будет работать как монолитное с моментами инерции и
сопротивления, равными
jx . Ш. = 2.25b/,- W, - « = l,Sbh\
12 * 6
Как видно, при переходе к монолитному сечению жесткость балки
позрастает в 9 раз, а прочность - в 3 раза.
В инженерной практике наиболее распространены сварные
двутавровые балки.
6.7. Дифференциальное уравнение прямого поперечного изгиба
призматического стержня
Мерой деформации призматического стержня при прямом чистом
изгибе является кривизна нейтрального слоя, определяемая по (6.9).
Можно показать, что с достаточной для инженерных расчетов точностью
этой формулой можно пользоваться и в случае прямого поперечного
изгиба стержня.
Для практических целей кроме кривизны 1/р необходимо определять
вертикальные перемещения центров тяжести отдельных поперечных
сечений - прогибы балки v, а иногда углы поворота этих сечений ф
129
У>
0',
У
\
1
г
^у—-.
■* —— - . 4I+-«W-
"^^^
-£,
iC \'
р
Z
^^ \
(рис. 6.24). Согласно гипотезе
плоских сечений, угол
поворота сечения <р равен углу
наклона касательной к изогнутой
оси балки, который ввиду
малости
Ф
tg<p = —.
Рис. 6.24. Прогибы и углы поворота сечений
призматического стержня
Составим уравнение для
функции прогиба v = v(z) по
известному закону изменения
ее кривизны.
В прямоугольных декартовых координатах
d2v
(к2
f dvV
[dzj
(6.16)
В инженерной практике применяются достаточно жесткие балки, для
которых наибольший прогиб/мал по сравнению с длиной (/7/«1), а
первая производная от прогиба имеет порядок
&z I'
Следовательно, величиной (dv/dz)2« 1, стоящей в знаменателе (6.16),
можно пренебречь, и выражение для кривизны упрощается:
l/p«d2v/dz2.
(6.17)
Тогда подставив (6.17) в (6.9), условившись, что ось Оу направлена вверх,
и согласовав знаки 1/р и MY, приходим к приближенному
дифференциальному уравнению прямого изгиба балки
d2v
dz2
MJEJxt
(6.18)
130
известному также как дифференциальное уравнение упругой кривой.
Если учесть точное выражение для кривизны по формуле (6.16), то
уравнение упругой кривой
d2v
dz2
1 +
№
3/2
(6.19)
является нелинейным дифференциальным уравнением. Поэтому линейное
дифференциальное уравнение (6.18), описывающее малые прогибы балки,
иногда называют линеаризованным уравнением упругой кривой.
Решаем уравнение путем двукратного почленного интегрирования.
При первом интегрировании получаем выражение
dv
dz
= f_JLdz + C,
J EJ
(6.20)
которое с учетом ф « tg ф = dv/ dz дает также закон изменения углов
поворота поперечных сечений по длине балки.
Повторным интегрированием получаем функцию прогиба
МУ
v(z) = fdzf—-dz + Cz + D
(6.21)
Постоянные интегрирования С и D должны быть найдены из
граничных условий.
Во всех приведенных выше уравнениях функция изгибающего момента
Мх (z) предполагалась известной, что возможно лишь для статически
определимых балок. Простейшие варианты статически определимых
балок и соответствующие граничные условия показаны на рис. 6.25.
**
-41
т
| a \ L* К ^
vfoho M\ =0
xg
v(0)*0
vfU'O
a)
6)
\Z'0
Рис. 6.25. Статически определимые балки:
о - шарнирно-опертая; б - консольная
131
Условия, накладываемые на прогиб и угол поворота сечения,
получили название кинематических граничных условий. Как видно, для
шарнирно опертой балки требуется, чтобы прогиб на опорах v(0) = v(/) =
= 0, а для консольной балки прогиб и угол поворота сечения в заделке
v(o) = i*fi>
dz
= 0.
lz*0
Дифференциальное уравнение в форме (6.18) неприменимо для расчета
статически неопределимых балок, так как содержит неизвестный
изгибающий момент Мх, появившийся в результате двукратного
интегрирования уравнения четвертого порядка:
d4v а
и" тт- <6-22>
В уравнении (6.22) нагрузка q известна, поэтому его можно получить из
(6.18), учитывая, что
d2A/
dz2
При интегрировании (6.22) необходимо задать четыре граничных
условия (по два на каждом конце балки), в том числе так называемые
силовые граничные условия - условия, накладываемые на силовые
величины (изгибающий момент и поперечную силу), которые
выражаются через производные от прогиба. Из (6.18) следует, что
К - BJx¥l, (6.23)
dz
а с учетом дифференциального соотношения Q = dMxldz
dz
Qy - Ч77. (6.24)
Вернемся к интегрированию уравнения второго порядка. Если имеется
несколько участков, для которых правая часть уравнения (6.18)/(z) =
= MXJEJX содержитразные аналитические выражения, то интегрирование
усложняется.
На рис. 6.26 приведена эпюра Мх> содержащая п участков. Для
каждого участка независимое интегрирование дает по две константы,
132
а при п участках требуется
определить Ъг постоянных.
Добавим к двум граничным
условиям на опорах 2 (п - 1)
условия непрерывности и
гладкости упругой кривой на
границе смежных участков,
заключающиеся в равенстве прогибов
v и углов поворота сечений
dv/dz на этих границах:
уЦ-0) = v(ay + 0),
У\
ттф^Ъ
я
лнгг
fui
m
ап±
^рт
Рис. 6.26. Эпюра изгибающего момента,
имеющая несколько участков
dv
dz
dv
dz
(/= 1,2....,и-1).
(6.25)
Тогда получим In граничных условий, необходимых для нахождения
постоянных интегрирования.
6.8. Применение метода начальных параметров для
интегрирования дифференциального уравнения упругой кривой
Трудности при определении функции прогиба v(z) для нескольких
участков интегрирования, связанные с определением постоянных
интегрирования, в значительной степени преодолимы при условии, что
решение дифференциального уравнения (6.18) можно представить в виде,
когда постоянные интегрирования имеют ясный физический смысл.
Такую возможность представляет метод начальных параметров Коши.
Разложим функцию прогиба v(z) на первом участке интегрирования
в степенной ряд Маклорена:
v(z) = aQ + axz + a2z2 +агг*+....
Отметим, что ряд сходится, если функция и все ее производные на
заданном интервале непрерывны. Дифференцируя ряд почленно
dv(z)
dz
tfj + 2a2z + 3a3z2 + ...
и полагая z = О, получаем
133
dv
a, = — .
1 dz|0
Аналогично для остальных коэффициентов ряда
1 d"v
1 d2v
7 ал
1 d2v
2! dz2'
n\ dz1
Тогда выражение для функции прогиба получает вид
v(z) = v(0)
dv
dz
z + d2v
1! dz2
z + d v
2! dz3
z3 t d4v
3! + dz4
4!
(6.26)
Коэффициентами ряда являются значения функции v(z) и ее производных,
определенные при z= 0. Физический смысл этих коэффициентов очевиден:
v(0) - прогиб сечения в начале координат, (dv/dz) 10 * ф(0) - угол
поворота этого сечения.
Из формулы (6.23) следует, что
а из (6.24)
d2v
«и
d3v
dz3
d4v
dz4
Л/х(0)
, EJ*
_ е/о)
EJ
о *
1 _ яФ)
i EJX-
Из уравнения (6.22) получаем
С учетом приведенных соотношений выражение для прогиба v(z)
принимает вид
v(z) = У(0) + Фо^ +
M0z2
со Z
4о z4
1! EJ 2! EJ 3! EJ 4!
(6.27)
Величины, отмеченные индексом "0" и вычисленные в начале
координат, - начальные параметры задачи. Выражение (6.27) записано для случая
134
q=q0- const. Если интенсивность распределенной нагрузки q изменяется
по линейному закону q = q0+ q0z, то в (6.27) добавляется слагаемое
Чо z5
EJX 5!
Функцию углов поворота сечений <p(z) получаем, дифференцируя
зависимость (6.27),
Ф(г) = ф0 +
Л/,
о z Qo z2 Яо гъ
EJX 1! EJX 2! EJX 3!
Решение в форме (6.27) справедливо только для первого участка 0 <.
<; z < ах и становится неприемлемым при переходе ко второму, так как
функция v(z) или ее производные на границе участков могут иметь скачки
(рис. 6.27).
Решение на втором участке (al<z<a2) будем искать в виде
v2(z) = v1(z) + Av(z-fll),
где Av = v2 - Vj (рис. 6.27) - линейная комбинация (разность) решений
дифференциального уравнения (6.18).
По методу начальных параметров
Av(z-a,) = Av(flj) +Аф^,)
(z-д,) Шх{ах)(2-ах?
1!
EJ
X
\4
2!
+ bQy{ax){z-axy tLq{ax)(z-axy ^
EJ 3! + £/v 4!
О af а2 *
Рис. 6.27. Скачки функции прогибов и ее производных на границах участков
135
Принимаем за начальные параметры скачки Av, Дер, ДМХ, AQ A q.
Рассуждая аналогично, построим решения для третьего, четвертого
и всех последующих участков. Например, для и-го участка
v„00 = v(0) + <po—+—-— + —- + —- +
Y° 1! EJX 2! EJX 3! EJX 4!
""' "~l (z - a) «-> AM (a) (z - a)2
+ E Av(ay) + E АФ(Л)1—ii + £ *v^ / + (6>28)
y-i y-i 1! y-i ^/x 2! v '
+ У Ag,(*y) (^ - a/ + у Agfry) fr - a)4 +
+ уГ, Д/х 3! +ум jj/x 4!
Возможны случаи, когда часть начальных параметров неизвестна и
определяется из граничных условий на правой или промежуточных
опорах балки. Например, для балки, показанной на рис. 6.25, а, известны
все начальные параметры (v0 = О, М0 =; О, Q0 = q 111, q0 = -q) кроме одного
Ф0, который определим, используя граничное условие на правой опоре
v(/) = 0.
6.9. Расчет балок, лежащих на упругом основании
Рассмотрим балки, лежащие на линейно-упругом основании, так
называемого винклерова типа. Такая модель была предложена немецким
инженером Э. Винклером. Она обладает следующими свойствами:
1. Реакция основания пропорциональна перемещению v,
совпадающему с прогибом связанной с основанием балки, и имеет противоположное
направление (рис. 6.28):
r(z) = -cv(z)t (6.29)
где с - коэффициент упругости
основания, называемый также
коэффициентом отпора, Н/м2.
Реакция основания является
погонной нагрузкой (как и q),
распределенной вдоль оси балки. Введенный
указанным образом коэффициент
отпора с учитывает не только
свойства основания, но и ширину балки Ъ
(рис. 6.29). Поэтому часто вводят
коэффициент отпора с0, представляю-
I
77Г,
jL
EJ
//) /// /// М М /// /// /// М М М
Н *- Ч \rftj
Рис. 6.28. Балка на упругом
основании
136
щий собой давление, необходимое для
погружения в основание на единицу длины,
и связанный с коэффициентом с
соотношением:
с0Ь.
У1
р°^-шт *
чм >» )ШШ(£^
Рис. 6.29. Коэффициент
упругости основания с учетом
ширины балки
2. Связь между балкой и основанием
является двусторонней (рис. 6.30), ее можно
представить как бесконечный набор не
связанных между собой пружин.
У ряда оснований из бетона,
уплотненного грунта, резины и других материалов прогибы в различных точках
основания оказывают взаимное влияние (рис. 6.31), хотя в ряде случаев
(рыхлый грунт, песок) оно пренебрежимо мало.
Ограничимся рассмотрением малых прогибов балки с постоянной
жесткостью поперечного сечения при изгибе EJ = const, лежащей на
упругом основании с постоянным коэффициентом отпора с = const и
загруженной распределенной нагрузкой с интенсивностью q(z) (рис. 6.28).
Для описания малых прогибов такой балки используем линеаризованное
дифференциальное уравнение упругой кривой в форме (6.22), в которое
внешняя нагрузка должна быть подставлена с учетом реакции основания:
d4v
EJ— = q-cv.
dz*
Перенося с v в левую часть и вводя обозначение 4/с4 = clEJ, после
преобразований приходим к дифференциальному уравнению изгиба балки
на упругом основании винклерова типа:
d4v
dz4
+ 4A:4v
JL
EJ'
(6.30)
Рис. 6.30. Двухсторонняя связь балки и Рис. 6.31. Взаимное влияние прогибов в
основания различных точках балки
137
Решение этого уравнения складывается из общего интеграла v0
однородного уравнения
—l + 4£4v0 = 0 (6.31)
dz4
и частного интервала v^ неоднородного уравнения (6.30).
Общий интеграл уравнения (6.31) получим, осуществляя подстановку
у = Ataz, приводящую к характеристическому уравнению
а4 + 4А;4 = 0,
из которого определяются характеристические показатели а как четыре
корня этого уравнения:
а12М = ±у/±Ш = ±(1±0*.
Тогда решение (6.30) примет вид
v(z) = ^j^^' + ^e-^^^ + ^^'^ + ^^'^' + v.W» (6.32)
где А1,А2,АзнА4- постоянные интегрирования, подлежащие
определению из граничных условий.
Частный интеграл неоднородного уравнения (6.30) определяется
видом правой части. Например, если q(z) - полином не старше третьей
степени, то
d4v,
* 0;
dz4
v, = q(z)/4kAEJ = q(z)/c. (6.33)
Если q = const, то v+ = qlc дает величину погружения в основание
балки как жесткого целого.
Преобразуем решение (6.32), делая подстановку по формуле Эйлера,
Q±ikz = cosfcztisinkz.
После преобразований получаем
138
v (z) s Cj t'kz sin к z + С\ t~kz cos к z +
+ C3e^zsin/:z + C4e*zcosfcz + v„(z).
Другую форму решения получим, переходя посредством подстановки в
(6.34) e±/cz = ch kz ± sh kz к гиперболическим функциям:
v(z) = D^hkzsinkz + D2shkzcoskz +
(6.35)
+ D^chkzsmkz + /)4chA:zcosA:z+ v#(z).
Решение в форме (6.35) удобно при расчете сравнительно коротких
балок. Для расчета длинных балок предпочтительнее решение в форме
(6.34). Поясним это на примере бесконечно длинной балки. Устремляя
аргумент z к бесконечности, обратим внимание, что
lime~*z = 0, lime*2 = ~.
Это показывает, что наличие в выражении (6.34) третьего и четвертого
слагаемых противоречит требованию ограниченности прогибов балки на
бесконечности. Такое противоречие устраняется при условии, что С3 =
= С4 = 0, и тогда для бесконечно длинной балки выражение (6.34)
принимает вид
v(z) = e'^CjSinfcz+C^cosfoO + v^z). (6.36)
Выясним, какая балка может считаться достаточно длинной для того,
чтобы при ее расчете можно было использовать выражение (6.36).
Преобразуем аргумент kz, введя длину полуволны синусоиды Л, к виду:
kz - zTikt (6.37)
где
X = Tilk = ъу/ШШ. (6.38)
При A z = Я аргумент kz изменяется на п (поэтому Л и названа длиной
полуволны синусоиды). При этом прогиб уменьшается в е* * 23 раза.
Таким образом, балка длиной / > X считается достаточно длинной, чтобы
ее прогибы описывались выражением (6.36).
139
Глава 7
КРУЧЕНИЕ СТЕРЖНЕЙ
7.1. Напряжения и деформации при кручении призматических
стержней кругового поперечного сечения
ТП^учением называется такой вид деформаций, при котором в
J\^ поперечном сечении стержня возникает лишь один силовой
фактор - крутящий момент Мг. Крутящий момент по определению
равен сумме моментов внутренних сил относительно продольной оси
стержня Oz. Нормальные силы, параллельные оси Oz, вклада в крутящий
момент не вносят. С силами, лежащими в плоскости поперечного сечения
стержня (интенсивность этих сил - касательные напряжения тХ2 и т 2),
момент Mz связывает вытекающее из его определения уравнение
равновесия статики (рис. 7.1):
Мч
//<■
V*
■т v)dF.
(7.1)
Условимся считать Мг положительным, если со стороны отброшенной
части стержня видим его направленным против часовой стрелки
(рис. 7.2). Это правило
проиллюстрировано на рис. 7.1 и зависимостью (7.1), где
крутящий момент Мг принят
положительным. Численно крутящий момент
равен сумме моментов внешних сил,
приложенных к отсеченной части
стержня, относительно оси Oz.
Рис. 7.1. Кручение
призматического стержня кругового
поперечного сечения
Рис. 7.2. Правило знаков для крутящего
момента
140
$а|
«я
*!| .
SI 1
—J
.е
Рис. 7.3. Изменение ортогональной сетки на
поверхности упругого стержня при кручении
Рассмотрим кручение
призматических стержней
кругового поперечного сечения.
Исследование деформаций упругого
стержня с нанесенной на его
поверхности ортогональной
сеткой рисок (рис. 7.3)
позволяет сформулировать следующие
предпосылки теории кручения
этого стержня:
1) поперечные сечения
остаются плоскими (выполняется гипотеза Бернулли);
2) расстояния между поперечными сечениями не изменяются,
следовательно, ez = 0;
3) контуры поперечных сечений и их радиусы не деформируются. Это
означает, что поперечные сечения ведут себя как жесткие круговые
пластинки, поворачивающиеся при деформировании относительно оси
стержня Oz. Отсюда следует, что любые деформации в плоскости
пластинки равны нулю, в том числе гх = г = 0;
4) материал стержня подчиняется закону Гука. Учитывая, что гх = е =
= е2 = 0, из обобщенного закона Гука в форме (3.44) получаем ах = о =
= oz = 0. Это означает, что в поперечных сечениях стержня возникают
лишь касательные напряжения т, а согласно закону парности касательных
напряжений, равные им напряжения действуют и в сопряженных
продольных сечениях. Следовательно, напряженное состояние стержня -
чистый сдвиг.
Выведем формулу для касательных напряжений при кручении
призматического стержня кругового поперечного сечения. Как показано
на рис. 7.4, поворот правого торцевого сечения относительно
неподвижного левого на угол q> (назовем его углом закручивания стержня)
вызывает поворот продольных волокон на угол у (угол сдвига, поскольку
на величину у искажаются углы
ортогональной сетки продольных
и поперечных рисок модели,
представленной на рис. 7.3).
Двумя смежными сечениями
вырежем элемент стержня
(рис. 7.4) длиной dz и, поскольку
нас интересуют деформации
элемента, левое сечение его будем
считать неподвижным (рис. 7.5). Рпс 7Л Деформации упругого стержня
При повороте правого сечения на при кручении
§§рг
. z Л \*dz *ТМг
141
угол dip в соответствии с
гипотезой о недеформируемости
радиусов, правый конец
волокна А В (отстоящий от оси
элемента на величину полярного
радиуса р) будет перемещаться
по дуге ВВХ, вызывая поворот
волокна на угол сдвига
Y = ВВХIAB =
pdg>
dz *
(7.2)
Рис. 7.5. Угол сдвига и угол закручивания
элемента стержня
Обратим внимание на то,
что в соответствии с рис. 7.5 и
7.6, а сдвиг у и связанное с ним касательное напряжение т
перпендикулярны к радиусу р. Определим т, воспользовавшись законом Гука для
чистого сдвига и учитывая (7.2),
т = Gy = Gp
d<p
dz'
(7.3)
где d<p/dz - погонный угол закручивания стержня, который остается пока
неизвестным. Для его нахождения обратимся к условию статики (7.1),
записав его в более удобной для данного случая форме (рис. 7.6, а),
Мг = Г fxpcLF.
(7.4)
Подставляя (7.3) в (7.4) и
учитывая, что
Я»3
dF = J
полярный момент инерции
поперечного сечения (//; =
= тс йГ/32 для круга диаметром
d)9 получаем
dg>
dz
GJn
(7.5)
Рис. 7.6. Касательные напряжения при
кручении:
а - на элементарной площадке; б -
распределение по сечению
142
Подставляя выражение (7.5) в (7.3), получаем формулу для
касательных напряжений при кручении призматического стержня кругового
поперечного сечения
Мг
* - -f*- (7.6)
jp
Из (7.2) и (7.6) следует, что сдвиги и касательные напряжения
пропорциональны расстоянию от оси стержня. Обратим внимание на
структурную аналогию формулы (7.6) с (6.10) для нормальных
напряжений чистого изгиба.
Мерой деформации стержня при кручении является погонный угол
закручивания стержня, определяемый по (7.5). Поскольку величина GJ *
стоит в знаменателе формулы и при заданной нагрузке (Mz через нее
выражается) d(p/dz тем меньше, чем больше GJp, последнюю называют
жесткостью поперечного сечения при кручении.
Пользуясь (7.5) для определения угла закручивания элемента длиной
dz
МТ
dtp = —— <te,
GJ,
найдем полный угол закручивания стержня длиной /:
' M,dz
J GJ
О Р
(7.7)
В случае, если по длине стержня М2 и GJV постоянны, то получаем
(7.8)
р
МЛ
GJp
а если эти величины кусочно-постоянны, то
*-i \GJPh
Отметим, что формулы (7.7), (7.8) и (7.9) по структуре аналогичны
формулам (5.12), (5.15) и (5.14) для деформаций при растяжении стержня.
Как видно из (7.6) и рис. 7.6, наибольшие касательные напряжения
возникают у внешней поверхности стержня, т.е. при pmax = dll\
143
/пах г
Рис. 7.7. Касательные
напряжения при
кручении стержня
кольцевого поперечного
сечения
М,
2Jp/d
Ml
(7.10)
где W -момент сопротивления при кручении или
полярный момент сопротивления',
Wn = nd*/\6.
(7.11)
Полярный момент сопротивления / , стоящий
в знаменателе формулы (7.10) для максимальных
касательных напряжений, очевидно, является
геометрической характеристикой сечения, а
условие прочности стержня при кручении
принимает вид
М„,
Wm
■*М,
(7.12)
где [т] - допускаемое напряжение на кручение.
Как показали эксперименты и точное решение этой задачи в теории
упругости, все гипотезы, сформулированные ранее для стержня со
сплошным круговым сечением, остаются справедливыми и для стержня
кольцевого поперечного сечения (рис. 7.7). Поэтому все выведенные ранее
формулы пригодны для расчета стержня кольцевого сечения с той лишь
разницей, что полярный момент инерции определяется как разность
моментов инерции кругов с диаметром D и d\
J = 7iZ>4/32-tc^4/32 = -^(l-p*),
p 32
(7.13)
где p = dlD\ момент сопротивления
^ = Vp«- yo,5z> = ^|Vp4).
(7.14)
Учитывая линейный характер изменения касательных напряжений
по радиусу и связанное с этим лучшее использование материала,
кольцевое сечение следует признать наиболее рациональным при
кручении стержня. Коэффициент использования материала тем выше,
чем меньше относительная толщина трубы.
Например, сравним массу и максимальные касательные напряжения
для стержней кругового и кольцевого поперечного сечения, имеющих
144
IM Kpy- Jc -w/A
Пусть U HQIf-r^. ( )
Цевого \V '^T \Jm7
n'n a) L
6)
одинаковый внешний радиус г, М
нагруженных одинаковым кру- ""
тящим моментом М2.
внутренний радиус кольцевого
поперечного сечения гх = 0,6 г. В "* д\
этом случае максимальные каса- ДО
тельные напряжения для кольце- — *
вого поперечного сечения
возрастают по сравнению с
напряжениями для кругового сечения
на 15 %, а масса снижается на
Как отмечено ранее, напря- Р"с; 7.8. Характер разрушения при круче-
НИИ*
женное состояние при кручении а _ с образ0ванием продольных трещин;
стержня чистый сдвиг, являю- б - по траектории главного напряжения
щийся частным случаем
плоского напряженного состояния (см.
гл. 3). На площадках, совпадающих с плоскостью поперечного сечения,
и на парных им площадках продольных сечений возникают экстремаль-
тах ,
ные касательные напряжения Tmin, а главные напряжения Oj 3 = ±т
действуют на площадках, наклоненных к оси стержня под углами ±45°;
главное напряжение о2 = 0. {
Особенности напряженного состояния при кручении нашли отражение
в характере разрушения стержней. Так, разрушение стержня из дерева,
плохо работающего на скалывание вдоль волокон, происходит от
продольных трещин (рис. 7.8, а), из хрупкого материала (например,
чугуна) - по винтовой линии, наклоненной к образующим под углом 45°,
т.е. по траектории главного напряжения о3 (рис. 7.8, б).
7.2. Расчет валов
Расчет вала на прочность и жесткость. Пусть известна мощность W
(кВт), предаваемая вращающимся с заданной частотой п (мин ) валом
от источника мощности (например, двигателя) к ее потребителю
(например, станку), а момент Г, передаваемый валом, требуется найти,
так как его значение необходимо для расчета вала.
Если частота вращения вала п и соответствующая ей угловая скорость
а) (с"1) постоянны, а Ф - угол поворота вала в данный момент времени
/, то работа вращательного движения
Л = ГФ.
145
Тогда передаваемая валом мощность
dA _ ТдФ
dt " dt
W= ?± = ^ = Го>. (7.15)
Отсюда
Г= И7<о = 30/71 (W/ и), (7.16)
где учтено, что о> = тс л/30.
Если мощность подается на вал через ведущий шкив, а раздается
потребителям через несколько ведомых шкивов, то по формуле (7.16)
определяются моменты на шкивах, а затем строится эпюра крутящих
моментов. Расчет вала на прочность и жесткость ведется, очевидно, по
™г max*
Определение диаметра вала из условия прочности. Условие прочности
при кручении вала имеет вид (7.12), где допускаемые напряжения [т]
принимаются пониженными по сравнению с допускаемыми
напряжениями обычного статического расчета в связи с необходимостью учета
наличия концентраторов напряжений (например, шпоночных канавок),
переменного характера нагрузки и наличия наряду с кручением и изгиба
вала.
Требуемое значение W = тс ^з/1б получаем из условия (7.12), принимая
в нем знак равенства
К = А#1ИМ1/И. (7.17)
откуда получаем формулу для определения диаметра вала кругового
сечения
з
d =
i^zmax (718)
Определение диаметра вала из условия жесткости. Условие жесткости
состоит в наложении ограничения на погонный угол закручивания вала
0 = d<p/dz, так как недостаточно жесткие валы не обеспечивают
устойчивой передачи мощности и подвержены вибрациям:
°«-^*М- (7.19)
Тогда, учитывая, что J = тс ^/32, для диаметра вала из условия
жесткости имеем
146
32Мгтя>
г таз
\ nG[Q]
(7.20)
Для вала кольцевого поперечного сечения J и W вычисляются по (7.13)
и (7.14).
Потенциальная энергия упругой деформации при кручении.
Предполагая, что работа, совершаемая моментом М2 на угловом перемещении dtp,
полностью переходит в потенциальную энергию упругой деформации,
получаем,что
2J GJ
о р
В случае, если на участке длиной / выполняется условие Мг = const,
GJ = const, справедливо
U
\Щ1
2 GJ '
При вычислении потенциальной энергии упругой деформации
принцип независимости действия сил (принцип суперпозиции)
неприменим.
7.3. Расчет цилиндрических винтовых пружин с малым углом
подъема витков
Еще одной областью применения теории кручения стержней является
расчет пружин, навитых из проволоки кругового поперечного сечения.
Теория призматического
стержня к расчету пружин
применима лишь приближенно, так как
последние являются стержнями
с криволинейной осью.
Будем рассматривать
пружины, навитые на цилиндрические
оправки с малым шагом витков
(рис. 7.9), т.е. угол наклона
витков а настолько мал (а < 8... 10°),
что можно принять sin а ~ 0,
cos а * 1, а поперечные сечения
пружин лежащими в
диаметральных плоскостях. Так, ниж- рис ? 9 Внутренние силовые факт0ры в
няя часть пружины, показан- ЦИЛИНдрцЧеских винтовых пружинах
147
'* /MZZ2P1)
mctxt.
*P
Рис. 7.10. Распределение
касательных напряжений среза
и кручения в сечениях витков
пружины
Тогда
ной на рис. 7.9, отсечена диаметральной
плоскостью Q, совпадающей с плоскостью
чертежа. В поперечных сечениях витков
такой пружины возникают лишь поперечная
сила Q = Ри крутящий момент Mz = PD/2
и, следовательно, витки пружины работают
на срез и кручение. Как видно из рис. 7.10,
опасной точкой является внутренняя точка
к контура сечения витка, в которой
складываются напряжения кручения, приближенно
определяемые по (7.10):
крхпах
Mi
%PD
и наибольшие напряжения среза, которые
определим по приближенной формуле,
считая, что т по сечению распределены
равномерно
\?»QyIF=APInd\
т + т
кртах wcp
Tid* { 2D
(7.21)
Иногда наибольшие напряжения среза определяют по более точной
формуле Журавского (6.15). Опуская выкладки, по этой формуле
получаем
т = 4/30 IF =
\6Р
3nd2
Однако учитывая, что для пружин, применяемых в технике d«D
(обычно d/D = 1/5... 1/12), вторым слагаемым в (7.21), учитывающим
влияние поперечной силы, пренебрегают, считая, что витки пружины
работают лишь на кручение. Тогда условие прочности для пружины
запишем в виде
ЪРР
nd>
*М-
(7.22)
148
Пружины изготовляются из специальных сортов стали с высоким
пределом пропорциональности, для которых [о] = 400...600 МПа.
Определим перемещение точки приложения силы Р, называемое
осадкой пружины X, для чего приравниваем работу силы Р при
квазистатическом нагружении пружины А = 0,5 Р X потенциальной энергии
упругой деформации пружины U. Учитывая только энергию деформации
кручения, получим
U = 0,5Мгф.
С использованием зависимости (7.8), в которой / = nDn - длина
проволоки пружины, п - число витков, а также учитывая, что Мг~Р D/2,
/ = п d*/32, будем иметь
17= AP2D*nlGd*.
Тогда из условия А = U,
0,5РА. = 4P2D*n/Gd\
получаем формулу для осадки пружины
А. = *PD*n/Gd4. (7.23)
Для практических расчетов эту формулу удобнее представить в виде
X = Р/с,
где с - жесткость пружины, равная силе, которую нужно приложить
к пружине, чтобы вызвать осадку, равную единице;
с = Gd*l{%D*n).
7.4. Кручение стержней некругового сечения
Как следует из опыта с моделью стержня из податливого материала
с нанесенной на его поверхность ортогональной сеткой рисок (рис. 7.11),
при кручении стержней некругового сечения (в нашем случае -
прямоугольного) имеет место депланация сечений, и теория кручения
стержня Кулона, основанная на гипотезе плоских сечений, становится
неприменимой.
149
Рис. 7.12. Распределение касательных
Рис. 7.11. Депланация поперечных „аПряжений при кручении стержня
сечений при кручении стержня некруго- прямоугольного поперечного сечения
вого поперечного сечения
Решение таких задач получено в теории упругости; на рис. 7.12
приведены эпюры касательных напряжений для стержня прямоугольного
сечения. Как видно, максимальные напряжения возникают в точках,
лежащих посередине длинной стороны прямоугольника, т.е. в наиболее
близких к центру кручения точках контура, а не в наиболее удаленных -
угловых точках, как это следует из теории Кулона (в угловых точках т =
= 0 согласно закону о парности касательных напряжений).
Решение этой задачи дается в удобной для практических расчетов
форме:
Мг _ Мг1 .
wk h
где Wu = а Ъ с - момент сопротивления при кручении этого сечения; Jk =
= р b г - его крутильная характеристика, числовые коэффициенты а, р,
у, зависящие от отношения сторон прямоугольника Ыс. В табл. 7.1
приведены выборочные значения этих коэффициентов.
Как видно, для вытянутых прямоугольников значение коэффициентов
аир приближается к 1/3.
150
7.1. Коэффициенты для расчета прямоугольных сечений на кручение
Ыс
а
Р
У
1
0,21
0,14
1,00
1,5
0,23
0,20
0,86
2
0,25
0,23
0,79
3
0,27
0,26
0,75
6
0,30
0,30
0,74
10
0,31
0,31
| 0,74
ос
1/3
1/3
0,74
151
Глава 8
СЛОЖНЫЕ ВИДЫ ДЕФОРМАЦИЙ
8.1. Принцип независимости действия сил
и границы его применения
Вид деформации является сложным, когда в поперечном сечении
стержня возникают два и более силовых факторов. Сложный вид
деформации можно рассматривать как сумму простых видов
(растяжение, изгиб, кручение), если применим принцип независимости
действия сил - частный случай принципа суперпозиции (наложения),
применяемый в механике деформируемого твердого тела.
Напомним формулировку принципа независимости действия сил:
напряжение (деформация) от группы сил равно сумме напряжений
(деформаций) от каждой силы в отдельности. Принцип справедлив, если
функция и аргумент связаны
линейной зависимостью, В задачах
механики материалов и конструкций он
становится неприменим, если:
• напряжения в какой-либо части
конструкции от одной из сил или
группы сил превышают предел
пропорциональности опц;
• деформации или перемещения
становятся настолько большими, что
нарушается линейная зависимость
между ними и нагрузкой.
Например, дифференциальное
уравнение изгиба стержня (6.19)
является нелинейным (см. гл. 6) и
вытекающая из него зависимость
прогиба/от нагрузки Р для консоль-
Рис. 8.1. Изгибные деформации: ной балки, изображенной на
а - консольная балка; б - зависи- рис. 8.1, а, также является нелинейной
мость прогиба от нагрузки
152
(рис. 8.1,6). Однако если прогибы балки невелики (f< < I) настолько, что
(dv/dz)~ < < 1 (так как dv/dz -///), то дифференциальное уравнение изгиба
можно с достаточной степенью точности считать линейным (как видно
из рис. 8.1, б, начальный участок зависимости/(/V, описываемый этим
уравнением, также является линейным).
8.2. Косой изгиб призматического стержня
Косой изгиб имеет место, когда силы, его вызывающие, не лежат в
одной из главных плоскостей инерции. Однако если разложить внешние
силы по главным осям инерции Ох и Оу, то получим две системы сил ?j Y,
Plx,..., Рпх и Р1у, Р2у,..., Рпу9 каждая из которых вызывает прямой изгиб
с изгибающими моментами соответственно М и Мх (рис. 8.2). Применяя
принцип независимости действия сил, нормальные напряжения о
(рис. 8.3) определим как алгебраическую сумму напряжений от Мх и Му\
Мх Mv
J х J у
Прогибы стержня есть геометрическая сумма прогибов от прямых
изгибов (рис. 8.2):
/-l//?+/?-
Рис. 8.2. Косой изгиб призматического стержня
153
Рис. 8.3. Нормальные напряжения при косом
изгибе
Таким образом, расчет на косой изгиб
с применением принципа независимости
действия сил сводится к расчету на два
прямых изгиба с последующим
алгебраическим суммированием напряжений и
геометрическим суммированием
прогибов.
В случае поперечных сечений,
имеющих две оси симметрии и выступающие
угловые точки (рис. 8.4) с равными по
модулю и максимальными
одноименными координатами 1*41 ~хв~хс~ \xd\ =
= хтах и У а = У в = \Ус\ = \Ув\ = >W> напряжения в этих точках
3A.B,C.D - j Ут*х~ j *max - w - уу '
(8.2)
Слагаемые в формуле (8.2) рекомендуется определять по модулю, а знаки
ставить по смыслу. Например, на рис. 8.5 верхний ряд знаков "+" и "-"
соответствует напряжениям от Мх, а нижний ряд - от М', и напряжения
в этих точках
W
у
W..
Ml-
w '
у
My
w'
ш
OV
ш
D
W* шч
m ХЛ \ хл
В
Щ ЩЩ
1°
в
Рис. 8.4. Поперечные сечения, имеющие две оси симметрии и выступающие
угловые точки
154
Условие прочности для балок из
пластического материала с указанным
типом сечений запишется в виде
тахо
Wy
(8.3)
В остальных случаях для определения
тахо (или maxcL, и тах|ос| для хрупкого
материала) необходимо по общей
формуле (8.1) проверить напряжения во всех
подозрительных точках.
Есть и другой путы положив в (8.1)
о = 0, получим уравнение нейтральной
линии. Так как напряжения в точках
поперечного сечения будут
пропорциональны расстояниям от нейтральной
линии, то таха будут возникать в наиболее удаленных от нее точках
Рис. 8.5. Определение знаков
нормальных напряжений в
угловых точках
8.3. Сочетание косого изгиба и растяжения (сжатия)
призматического стержня
Рис. 8.6. Внецентренное
приложение внешней
нагрузки
Этот случай отличается от предыдущего
тем, что добавляется продольная сила Nz.
Нормальные напряжения определяются
формулой
N2 Мх Му
а напряжения в угловых точках сечении,
показанных на рис. 8.4,
N„ М
"A.B.C.D
+ м.
w. w„
(8.5)
В частном случае внецентренного
приложения продольной силы Р (рис. 8.6) Nz = Р,
Мх = -Рур, Му = -Рхр9 и формулы для
напряжений принимают вид
155
о = — +
F
*У,
Рхп
-х;
(8.6)
A.B.C.D р цг
РУп Рхп
(8.7)
8.4. Сочетание изгиба и кручения
призматического стержня
Исследуем этот вид деформации стержня на примере расчета вала
кругового (кольцевого) поперечного сечения на совместное действие
изгиба и кручения (рис 8.7).
Примем следующий порядок расчета.
1. Разлагаем все внешние силы на составляющие по осям Ох и Оу:
2х>
Л«> И Л>» *2у> '"» *j
2. Строим эпюры изгибающих моментов М и Мх от этих групп сил.
У кругового и кольцевого поперечного сечений все центральные оси
главные, поэтому косого изгиба у
вала вообще не может быть,
следовательно, нет смысла в каждом сечении
находить два изгибающих момента
Мх и М , а целесообразно их
заменить результирующим (суммарным)
изгибающим моментом (рис. 8.8)
Рис. 8.7. Совместное действие изгиба
и кручения
Рис. 8.8. Результирующий
изгибающий момент
156
^„зг - М2 + М)%
который вызывает прямой изгиб в
плоскости его действия относительно
нейтральной оси п-п,
перпендикулярной к вектору Мтг Эпюра
суммарного момента имеет пространственное
очертание и поэтому неудобна для
построения и анализа. Поскольку все
направления у кругового сечения с
точки зрения прочности
равноправны, то обычно эпюру Мизг
спрямляют, помещая все ординаты в одну
(например, вертикальную) плоскость.
Обратим внимание на то, что
центральный участок этой эпюры
является нелинейным.
3. Строим эпюру крутящего
момента Mv
Наибольшие напряжения изгиба
возникают в точках к и /с', наиболее
удаленных от нейтральной оси
(рис. 8.9),
М...
W.„
Рис. 8.9. Нормальные и касательные
напряжения при совместном
действии изгиба и кручения: а -
распределение по сечению; б -
напряженное состояние
где Wmr - момент сопротивления при изгибе.
В этих точках имеют место и наибольшие касательные напряжения
кручения
w,
где W - момент сопротивления при кручении.
Как следует из рис. 8.9, напряженное состояние является упрощенным
плоским (сочетание одноосного растяжения и чистого сдвига). Если вал
выполнен из пластического материала, оценка его прочности должна
быть произведена по одному из критериев текучести, например, по
критерию Треска-Сен-Венана (3.72) имеем
оэкв = у/*Г& = JW^IW^y + A{MJWf?
157
Учитывая, что W = 2Wmr9 для эквивалентных напряжений получаем
_ J м1 + м] _ мя
wm
w.„
где Мэкв = у Мтг + Mz - эквивалентный момент, с введением которого
задача расчета вала на совместное действие изгиба и кручения сводится
к расчету на эквивалентный изгиб.
Аналогично для Мэкв по критерию Губера - Мизеса (3.73) получаем
Л^экв - № + 3/Шжа.
Тогда условие прочности для вала из пластичного материала будет
иметь вид
Мш
W...
* М-
(8.8)
Для стержня из хрупкого материала условие прочности следует
записать в виде
^ * К],
ЦТ L PJ'
(8.9)
где Мэкв должен быть записан применительно к одному из критериев
хрупкого разрушения. Например, по критерию Мора (3.80) для
упрощенного плоского напряженного
состояния
Рис. 8.10. Сочетание изгиба,
растяжения и кручения
ч«-
1
лм + 1+т
"* ИЗГ /ч
{м,
ИЗГ + Mz*
где m = [op]/[oc].
Для выявления опасной точки при
сочетании изгиба, растяжения и кручения
стержня прямоугольного поперечного сечения
(рис. 8.10) должны быть сравнены
напряжения косого изгиба с растяжением в точке А
с эквивалентными напряжениями в точках
В и С.
158
Глава 9
ВАРИАЦИОННЫЕ МЕТОДЫ
РАСЧЕТА КОНСТРУКЦИЙ
9.1. Виртуальная работа, обобщенные силы
и обобщенные перемещения
Рассмотрим упругое тело, находящееся в равновесии под действием
внешних сил Fj, F2,...» ¥п и закрепленное в отдельных точках путем
наложения связей - ограничений на перемещения (рис. 9.1).
Приложенные силы вызывают деформирование - перемещения точек
тела. Например, точка А/, приложения силы F- переместится в точку М!
(рис. 9.2). Соответствующий вектор перемещений обозначим иу. В
деформированном состоянии тело также находится в равновесии. Такое
состояние называется истинным состоянием. Очертание тела после
деформации в истинном состоянии изображено на рис. 9.1 штриховой
линией.
Наряду с истинным состоянием рассмотрим также смежное состояние,
которое отличается от истинного малыми перемещениями, совместимыми
с наложенными связями. Такие перемещения называются возможными
или виртуальными перемещениями.
На рис. 9.2 показан вектор 6и-
виртуального перемещения точки
приложения силы Fy- из истинного
состояния М! в смежное
состояние М.".
По определению работа силы
Fy на перемещении би^ точки ее
приложения равна скалярному
произведению вектора этой силы
на вектор соответствующего пере- Рис 9.1. Деформирование упругого тела
мещения под действием внешних сил
159
bAj = Fy.6uy
(9.1)
M
M'
МЧ
8u,
или произведению величины
(модуля) Fj этой силы на проекцию
buF вектора виртуального
перемещения 6u;. на направление
действия силы
И - FJ6UF/
(9.2)
Рис. 9.2. Перемещение и виртуальное
перемещение
Введенная таким образом работа
силы на виртуальном
перемещении называется виртуальной
работой. Суммарная работа всех
внешних сил на соответствующих виртуальных перемещениях
6А
1^\
7 = 1 '
(9.3)
есть виртуальная работа внешних сил.
Положение точек тела в деформированном состоянии можно
определить не только векторами перемещений и-, но и некоторыми
параметрами qx,qly..., qnji функционально связанными с перемещениями:
U; = »у(0р 02» •"» О» С/ = 1» 2> .... Л).
(9.4)
Введенные таким образом параметры qk называются обобщенными
перемещениями. Это могут быть перемещения, углы поворота, а также
некоторые величины, не имеющие ясного геометрического или
физического представления.
Виртуальные перемещения би или их проекции buF вычисляются
через вариации обобщенных перемещений bqk по правилам, аналогичным
правилам дифференцирования сложных функций (9.4):
бы.
*=i oqk
(9.5)
Если подставить выражение (9.5) в формулу (9.3) для виртуальной
работы
160
7-1 Ar= 1 Э^
и привести полученную формулу к форме, по структуре схожей с (9.3),
путем обозначения
то получим
б*= 1^—5. <*- 1, 2 т),
j-\ dqk
*-i
(9.6)
(9.7)
Величины, вводимые по формуле (9.6), называются обобщенными
силами. Выражение (9.7) позволяет дать следующее определение
обобщенных сил: обобщенными силами называются коэффициенты при
вариациях обобщенных перемещений в выражении для виртуальной
работы внешних сил. Размерность обобщенной силы равна размерности
работы, деленной на размерность соответствующего обобщенного
перемещения.
В механике конструкций обычно задаются обобщенные силы как
сосредоточенные силы, моменты, распределенные нагрузки и т.д., а
обобщенные перемещения выбираются в соответствии с формулой (9.7).
Поясним сказанное на примере консольной балки, загруженной системой
внешних сил, приводящихся к равномерно распределенной нагрузке,
сосредоточенной силе и моменту (рис. 9.3). Функция прогиба v(z)
полностью определяет положение изогнутой оси балки. На рис. 9.3
показано также виртуальное перемещение 6v(z), близкое к истинному
Рис. 9.3. Обобщенные силы и обобщенные перемещения для консольной балки
161
и не противоречащее наложенным связям: перемещение и угол поворота
в заделке на левом торце равны нулю. Сила Р совершает работу на
перемещении vp = v(/j), момент М - на угловом перемещении (рм =
= dv(z)/dz|z=/. Сила qdz совершает работу на перемещении v(z), а
'о
распределенная нагрузка совершает работу q fv(z)dz. Обобщенным
о
силам Ql = Р, б2= ^» бз = Ч соответствует выражение для виртуальной
работы ЪА = РЪ\р + МЪум + #6v , откуда можно определить обобщенные
перемещения: qx = vP - перемещение точки приложения силы Р, <у2 = Ф^
- угол поворота сечения, в котором приложен сосредоточенный момент
'о
М, Чз = у/д= fv(z)cb - площадь, заключенная между недеформирован-
о
ной осью балки и ее изогнутой осью на участке приложения
распределенной нагрузки.
9.2. Потенциальная энергия упругой деформации
Для линейных упругих систем обобщенные силы и обобщенные
перемещения пропорциональны внешним нагрузкам и перемещениям.
Кроме того, нагрузки и вызванные этими нагрузками перемещения
связаны линейными соотношениями, следовательно, обобщенные силы
и обобщенные перемещения также линейно связаны между собой
е*« ickjqr (9.8)
7 = 1
При возрастании величины обобщенной силы от нуля до конечного
значения Qk соответствующее этой силе обобщенное перемещение
возрастает пропорционально от нуля до конечного значения qk (рис. 9.4).
Элементарнаяработа, совершаемая обобщенной силой Q в
промежуточном состоянии на перемещении dqk, с точностью до бесконечно малых
первого порядка равна dAk = Qdqk. Эта работа отмечена на рис. 9.4
двойной штриховкой. После интегрирования по всей заштрихованной
области получим выражение для работы, совершаемой обобщенной
силой Qk на соответствующем этой силе обобщенном перемещении: Ак =
= Qkqk/2. Суммарная работа всех обобщенных сил равна
Л = 4 I G*fc. (9.9)
2 *=i
162
Если пренебречь потерями,
связанными с тепловыми и
другими эффектами,
кинетической энергией при
медленном (квазистатическом) нагру-
жении, то работа внешних сил
целиком затрачивается на
сообщение системе
потенциальной энергии упругой
деформации: A-U. Таким образом, для
потенциальной энергии
упругой деформации получим
формулу
Рис. 9.4. Работа обобщенной силы на
обобщенном перемещении
U = \l Qk4k>
2 к=\
(9.10)
являющейся содержанием теоремы Клапейрона: потенциальная энергия.
упругой деформации линейной системы равна полусумме произведений
значений обобщенных сил на значения обобщенных перемещений.
В третьей главе потенциальная энергия упругой деформации была
определена как
U
Я/ФИК,
(9.11)
где удельная потенциальная энергия упругой деформации Ф выражается
через компоненты тензоров напряжений и деформаций по формулам
(3.49)-(3.52). Выразим потенциальную энергию U через внутренние
силовые факторы, возникающие в стержневых системах при различных
видах деформации.
Рассмотрим вначале сочетание чистого изгиба с растяжением, когда
в поперечных сечениях действуют внутренние силовые факторы Nv Мх,
Му и реализуется одноосное напряженное состояние, причем напряжение
о = oz вычисляется по формуле (8.4)
F
М„
М.,
(9.12)
Удельная потенциальная энергия деформации в соответствии с формулой
(3.50) равна Ф = 1/2о2/£. Формула (9.11) для потенциальной энергии
после подстановки (9.12) приводится к виду
163
и-яШ
n; m:
м
1-х2
2
2 *__xy-
FJ„
NMV MMV .
- 2-4^* - 2—^—Lxy dV.
FJ„
J J
x у
(9.13)
Внутренние силовые факторы Nz(z)9 Mx(z)9 My(z) являются функциями
продольной координаты z. В общем случае для стержня переменного
сечения его геометрические характеристики F(z), Jx(z), J (z) также
являются функциями z. Поэтому интегрирование по объему в формуле
(9.13) можно свести к последовательному интегрированию по площади
поперечного сечения и по длине стержня. Например, первый интеграл
в (9.13) вычисляется как
1 N2
1 ust,iy-
2Е
_1_
2Е
/
Nfo
F2(:
нн
6z = ±'A.
2Е{ F(z)
При вычислении последующих интегралов используем обозначения
Sx-[[ydF, Sy = j[xdF, Jx = jfy2dF, Jy-jfx'dF, Jxy = jjxydF.
Так как координаты в формуле (9.12) отсчитываются относительно
главных центральных осей, то в этих осях Sx = О, S
последние три слагаемых в (9.13) исчезают. В результате получим
О, Jxy = 0 и
Л1 EF(z\ 11 EJ (z) 21 -
2{EF(z)
2{EJx(z)
l{EJJz)
(9.14)
Если ввести обозначения dv(z) = Nz(z)dzlEF(z), dq>v(z) = Mx(z)dz/EJx(z),
M (z)dz/EJ (z), имеющие смысл обобщенных перемещений, на
которых внутренние силовые факторы совершают элементарную работу,
то формулу (9.14) можно представить в виде
ФруЮ
U- I J4(z)dv(z) +1 JMx(z)d%(z) + ±fMy(z)d<fy(z), (9.15)
0 0 о
откуда следует, что потенциальная энергия упругой деформации равна
работе внутренних силовых факторов на соответствующих обобщенных
перемещениях.
164
При поперечном изгибе в плоскости Оуг помимо нормальных
напряжений возникают касательные напряжения т = и вычисляемые
по формуле Журавского (6.15)
*0> z)
Qy&Sx(y)
b(y)Jx(z)
Энергию, идущую на деформацию сдвига, вычислим с использованием
формул (9.11), (3.50) и формулы Журавского:
^ = Ы
Qy(z)
j?v У
Ьг(у)
dF
6z.
Эту формулу с использованием обозначения
*,«
можно привести к виду
г*
я
) F
S&)
dF
и,
Q,
J2x(z)V Ь*{у)
Ц a'gf(2)
(9.16)
(9.17)
где безразмерный коэффициент к (z) учитывает неравномерность
распределения касательных напряжений по сечению. В соответствии с
формулой (9.16) этот коэффициент зависит от формы поперечного
сечения и является его геометрической характеристикой. Например, для
стержня прямоугольного поперечного сечения с размерами сторон b и
h, для которого F= bh, Jx = ЫгЧХ!, Sx(y) = b(h2/4-y)I2, после вычисления
интеграла в формуле (9.16) получим к = 1,2.
При поперечном изгибе в плоскости Oxz по аналогии с формулой
(9.17) получим
ип
i/*.«
GF(z)
dz.
(9.18)
При кручении стержня в поперечных сечениях возникает крутящий
момент Mz(z), который совершает элементарную работу на обобщенном
перемещении d(pz(z) = Mz(z)dzlGJk(z)y где GJk(z) - жесткость поперечного
сечения при кручении. По аналогии с формулой (9.14) получим
Ul
мт
2 J GJk(z)
(9.19)
165
Объединяя формулы (9.14), (9.17)...(9.19), в общем случае деформации
стержня при наличии всех внутренних силовых факторов получим
U
1 N2
t^-dz
J EF
-dz
К
GF
UZ
I yGF
EJ„
(9.20)
Оценим слагаемые в формуле (9.20). При сочетании изгиба с
растяжением, когда продольная сила и изгибающие моменты имеют
порядок Nz ~ Р, Мх - Му ~ PI, энергия растяжения UN и энергия изгиба
2/3/
UM имеют порядок UN - P~l/Ehz, UM - Р flEhr. Здесь учтено, что F ~ h
где h - характерный размер поперечного сечения. При этом
Л~Л
ь2,/2
отношение UNIUM ~ h II" < < 1, и первым слагаемым в формуле (9.20)
можно пренебречь по сравнению со вторым и третьим слагаемыми. Иная
ситуация имеет место при внецентренном растяжении, когда Nz - Р, Мх ~
- М - Ph, при этом слагаемые UN и UM имеют одинаковый порядок и
энергией растяжения пренебрегать нельзя. При поперечном изгибе
энергия сдвига (9.17) и (9.18) с учетом того, что Q~ P,G~ Е,к~ 1, имеет
порядок Uq ~ Р l/Eh . Так как отношение Uq/Um ~ Л2//2 < < 1, то вкладом
энергии деформации сдвига можно пренебречь по сравнению с энергией
изгиба. При М2 ~ Мх - М энергия деформации кручения (9.19) имеет
тот же порядок, что и энергия деформации изгиба.
С учетом проведенных оценок в формуле (9.20) можно отбросить
четвертое и пятое слагаемые, соответствующие учету деформаций сдвига
от действия поперечных сил, и представить эту формулу в виде
U
.^2
' М)
J EF 1 EJ 1
м:
i
м
EJy J GJk
(9.21)
9.3. Принцип виртуальных перемещений.
Вариационный принцип Лагранжа
Принцип виртуальных перемещений является одним из общих
принципов механики. Применительно к упругим системам этот принцип
формулируется следующим образом: для того чтобы данная упругая
система находилась в состоянии равновесия, необходимо и достаточно,
166
чтобы виртуальная работа внешних сил была равна вариации
потенциальной энергии упругой деформации, т.е.
ЬА = bU. (9.22)
Виртуальная работа внешних обобщенных сил находится по формуле
(9.7), а потенциальная энергия упругой деформации вычисляется по
формуле (9.11), которая применительно к стержневым системам
принимает вид (9.20). Следует отметить, что в выражении (9.7) для
виртуальной работы внешние силы и соответствующие им обобщенные
силы заданы и не варьируются, а переход в смежные состояния
осуществляется путем варьирования обобщенных перемещений (см.
рис. 9.4).
Если внешние силы потенциальные, то существует некоторая функция
П {потенциал внешних сил) такая, что обобщенные силы находятся через
эту функцию следующим образом: Qk = -dTUdqk. В этом случае
ЬА = £ Qkbqk = - Е |%, = -6П,
к = \ fc=i oqk
и принцип виртуальных перемещений (9.22) можно записать в виде 6((/+
+ П) = 0. Величина
Э = U + П (9.23)
называется полной потенциальной энергией системы. Вариационный
принцип
ЬЭ = 0 (9.24)
носит имя вариационного принципа Лагранжа. Он формулируется
следующим образом: в состоянии равновесия полная потенциальная
энергия системы принимает стационарное значение по сравнению со
всеми смежными состояниями. Можно показать, что полная
потенциальная энергия в состоянии равновесия принимает минимальное значение.
Потенциал внешних сил выражается через обобщенные силы и
обобщенные перемещения следующим образом:
П » - Е Qkqk. (9.25)
167
л
ы
Рис. 9.5. Истинное и смежное состояния для изгибаемого участка балки
Для линейной упругой системы П = -1А, что видно из сравнения формул
(9.9) и (9.25).
Покажем эквивалентность вариационного принципа Лагранжа и
уравнений равновесия на примере изгиба балки. Рассмотрим участок
балки длиной / при действии распределенной нагрузки q(z). Пусть в
сечении z = О задана внешняя поперечная сила Р и сосредоточенный
изгибающий момент М, а в сечении z = / зафиксированы перемещение
v(/) = V/ и угол поворота ф(/) = ф7 (рис. 9.5). В результате деформирования
изогнутая ось балки примет положение, описываемое функцией прогиба
v(z). Штриховой линией на рис. 9.5 показано смежное состояние, которое
характеризуется виртуальными перемещениями 6v(z) и 6q>(z), причем
6v(/) = 0 и бф(/) = 0, так как в этом сечении наложены ограничения (связи)
на перемещение и угол поворота.
Пренебрегая вкладом энергии деформации сдвига, представим
потенциальную энергию деформации (9.20) в виде
U
1
EJV
dz
dz.
Здесь учтено, что изгибающий момент связан с прогибом и углом
поворота следующим образом:
Mx(z) = EJX¥?& = ЫхШ.
(9.26)
Потенциал внешних сил равен
П = -fq(z)v(z)dz - Pv(0) - Л/«р(0).
168
Полная потенциальная энергия (9.23) для данного примера определяется
выражением
Э » I |£/1*е&Г<ь - fq(z)v(z)dz - Pv(0) - Л/Ф(0).
(9.27)
При вычислении вариации функционала (9.27) будем учитывать, что
смежное состояние определяется только варьированием перемещений,
в данном примере - прогиба v(z) и угла поворота cp(z) = dv(z)/dz. Внешние
силы и вызванные этими силами внутренние силовые факторы Mx(z) и
Qy(z) при этом не варьируются. С учетом сказанного вариация
функционала полной потенциальной энергии равна
6Э = |Мх(г)б[-^] dz - fq(z)6v(z)dz - РЬ\(0) - М6Ф(0). (9.28)
о ^ ' о
Здесь использовано соотношение (9.26) и правило вычисления вариации,
аналогичное вычислению производной от сложной функции: 6(d(p/dz)2 =
= 2(d(p/dz)6(d(p/dz).
Операции варьирования 6() и дифференцирования d()/dz
переставимы, поэтому 6(d(p/dz) = d(6cp)/dz. С учетом известной формулы wdv/dz =
= d(wv)/dz - vdw/dz первое слагаемое в (9.28) можно преобразовать
следующим образом:
) * dz
■/
d(Mx6q>) Шх
dz
dz
бф
iz-iMjwwA
[-Ж£Ь
Проводя далее аналогичные преобразования, вместо последнего
интеграла пЬлучим
j><^«d(6v)d,,
J dz dz
dz
^6v
d2M
dz3
-6v
dz = [e/z)6v(z)]
f -6vdz.
J dz2
169
Здесь использована дифференциальная зависимость между поперечной
силой и изгибающим моментом Q = dM^Jdz. Учитывая, что 6v(/) = О,
бф(/) = 0, в итоге приходим к выражению для вариации полной энергии
63 =
■/!
d2Mx(z)
dz2
- q(z)
6v(z)dz -
(9.29)
- [Mx(0) + М]6Ф(0) + [(2/0) - P]6v(0).
Согласно вариационному принципу Лагранжа (9.24) выражение (9.29)
нужно приравнять к нулю. Так как вариации 6v(z), 6v(0) и 6ф(0)
произвольные, то выполнение условия (9.24) возможно только тогда,
когда множители при этих вариациях обращаются в нуль. Этот результат
является содержанием основной леммы вариационного исчисления. На
основании этой леммы получим
d2Mx(z)
dz2
= $(*).
(9.30)
(2,(0) = J\ А£хф) = -M.
(9.31)
Уравнение (9.30) справедливо при любых значениях z на отрезке [0,
/]. Это есть уравнение равновесия, полученное из условия равновесия
элементарного объема Fdz. Множители при виртуальных перемещениях
6v(0) и бф(0) во внеинтегральных слагаемых в формуле (9.29) дают
статические граничные условия (9.31). Эти условия, полученные из
вариационного принципа, называются естественными граничными
условиями. Кинематические граничные условия v(/) = v7 и ф(/) = ф,
выполняются автоматически, они следуют из определения виртуальных
перемещений как малых возможных перемещений, совместимых со
связями.
Учитывая зависимость (9.26), уравнение (9.30) можно переписать в
виде
d2
dz2
EJx(z)
d2v(z)
dz2
= g«.
(9.32)
170
9.4. Энергетические теоремы
Теорема Лагранжа. Потенциальную энергию упругой деформации для1
упругой системы можно вычислить через обобщенные силы и
обобщенные перемещения по формуле Клапейрона (9.10). Учитывая связь между
обобщенными силами и обобщенными перемещениями (9.8),
потенциальную энергию можно представить в виде функционала от обобщенных
перемещений £%,, q2,••> #m). Вариация этого функционала вычисляется
через виртуальные перемещения по формуле
ьи
k=\dqk
На основании принципа виртуальных перемещений (9.22) с
использованием формулы (9.7) получим
ш д г г nt т
Е ^-ьЧк = £ Qkbqk, £
эи
[д4к
-Qk
bqk = 0,
откуда в силу основной леммы вариационного исчисления
£* = ТТ- (9.33)
эи
dqk
Формула (9.41) является содержанием теоремы Лагранжа:
обобщенная сила равна частной производной от потенциальной энергии
деформации по соответствующему этой силе обобщенному перемещению.
Для линейной упругой системы обобщенные силы и обобщенные
перемещения связаны линейными соотношениями (9.8), а потенциальная
энергия U является квадратичным функционалом от обобщенных
перемещений
Z k=\j=\
Вычислим частную производную от этого функционала
dU _ 1 у у
dqt 2jt=i;=i
dqj dqk
Частные производные dqld #( равны единице приу = i и равны нулю при
171
j * i, поэтому
dU 1 " 1 "
dq. 2k=\ 2;=i J
С использованием формул (9.8) и (9.33) будем иметь
1 т 1
2jk=i 2
откуда Q. = £ Сд..^. Сравнивая полученную формулу с формулой (9.8),
к=\
т
переписанной в виде Q.= Y, cikqki получим, что коэффициенты,
к=\
связывающие обобщенные силы и обобщенные перемещения,
удовлетворяют условию
ckj = Ък- (9.34)
Теорема Кастильяно. Если рассматривать соотношения (9.8) как
систему линейных уравнений относительно обобщенных перемещений,
то решение этой системы уравнений имеет вид
т
%-lbkjQp (9.35)
причем коэффициенты Ьк-являются элементами матрицы [Ьк], обратной
по отношению к матрице [ск], составленной из коэффициентов С/ •. Так
как квадратная матрица [скл симметрична [ее элементы удовлетворяют
условиям (9.34)], то обратная матрица также симметрична, т.е.
выполняются условия bkj - bjh.
С учетом соотношений (9.35) и формулы Клапейрона (9.10)
потенциальную энергию деформации можно представить в виде квадратичного
функционала от обобщенных сил
Частная производная от этого функционала равна
172
BU _ 1 * £1 , dQ. L „dQk\ _ 1 " L л . 1
dQ. 2k=\j=\\ JdQ. dQt) 2*-i 2;=i
Учитывая соотношения (9.35) и свойство симметрии bk: = Ь:к>
окончательно получим
Яг
Полученный результат
формулируется в виде теоремы Кас-
тильяно: обобщенное
перемещение равно частной
производной от потенциальной
энергии деформации по
соответствующей обобщенной силе.
Теорема Бетти о взаимности
работ. Рассмотрим упругую
систему - балку на двух
опорах, загруженную двумя
силами Q{ и Q2 (рис. 9.6, я). В
процессе деформирования точки
приложения сил получают
перемещения q{ и q2, которые
связаны с силами линейными
соотношениями (9.35).
Представим эти соотношения в виде
Ч\-Ьи Q\+b]2Q2 = qu + ql2,
Я2 = b2\ Q\ + 622 Ql = #21 + #22-
Перемещение q-k имеет
следующий смысл: это есть
перемещение в направлении силы Q от
действия силы . Qk .
Напряженно-деформированное
состояние, изображенное на
рис. 9.6, я, можно представить
как суперпозицию двух
состояний, показанных на рис. 9.6, б
и 9.6, е.
Рассмотрим два способа
перехода в конечное состояние.
В первом случае (рис. 9.6, г)
^=^
е,
6)
Рис. 9.6. К доказательству теоремы Бетти
о взаимности работ:
а - схема нагружения; б - перемещения от
действия первой силы; в - перемещения от
действия второй силы; г, д - способы
перехода в конечное состояние
173
приложим вначале силу Ql9 которая на перемещении #и совершает
работу Qx qx j/2. Затем, оставляя постоянной силу Q{i приложим силу Q2,
которая на перемещении q22 совершает работу Q2 q2<jl, при этом
приложенная ранее сила Qx совершает на перемещении <7|2
дополнительную работу Qx qn. Суммарная работа, равная потенциальной энергии
упругой деформации, в данном случае находится по формуле
и\ = б^ц/2 + Qxqn + Q2q2J2. (9.36)
Во втором случае, показанном на рис. 9.6, д, сначала прикладывается
сила Qb а затем Qv Суммируя работу от действия каждой силы,
аналогично предыдущему случаю получим
U2 = Q2q22/2 + Q2q2X + Qxqnl2. (9.37)
В линейной системе потенциальная энергия упругой деформации не
зависит от последовательности приложения нагрузок, а определяется
лишь конечным состоянием. Поэтому потенциальная энергия,
накопленная при первом и втором вариантах нагружения, одинакова и равна
потенциальной энергии при одновременном приложении сил. Из
сравнения выражений (9.36) и (9.37) следует
6i*i2= Qibv (9.38)
Полученная зависимость является содержанием теоремы Бетти о
взаимности работ: работа сил первого состояния на соответствующих
им перемещениях второго состояния равна работе сил второго состояния
на соответствующих им перемещениях первого состояния.
Теорема Бетти остается в силе, если размерности Q{kQ2 различны,
т.е. <2j и Q2 имеют смысл обобщенных сил (рис. 9.7).
Перепишем соотношение (9.38) в виде
i ■ t (9ЭД
Величина б12 = 4\^Qi имеет смысл обобщенного перемещения в
направлении обобщенной силы Qx от действия единичной силы Q2 = 1.
Аналогичный смысл имеет величина 621. Из соотношения (9.39) как
следствие теоремы Бетти формулируется теорема Максвелла о взаимное-
ти перемещений: обобщенное перемещение точки приложения первой
обобщенной силы по ее направлению от действия второй единичной силы
174
Рис. 9.8. Иллюстрация теоремы о
взаимности перемещений
j ^&
*-====^^^3-^^^———— равно обобщенному перемещению
^ яа точки приложения второй
обобщенной силы по ее направлению
Рис. 9.7. Перемещения от действия силы от действия первой единичной
и момента силы. Математически запись этой
теоремы выглядит следующим
образом:
6i2 = 62i- (9.40)
В частном случае, когда обобщенные силы имеют одинаковую
размерность и равны между собой, то из выражений (9.38)...(9.40) следует
#12 = ^12 = #21 = ^21- В этом случае можно дать другую формулировку
теоремы о взаимности перемещений: перемещение точки 1 под действием
силы Q, приложенной в точке 2, равно перемещению точки 2 под
действием той же силы, приложенной в точке 1. Иллюстрация этой
формулировки теоремы приведена на рис. 9.8.
9.5. Определение перемещений. Формула Максвелла - Мора
Рассмотрим упругое тело под действием внешних нагрузок, которые
сводятся к системе обобщенных сил Q{9 Q2, ..., Qm. Напряженно-
деформированное состояние тела будем обозначать символом 1. Пусть
в этом состоянии в точке М нужно определить обобщенное перемещение
q0{ в некотором направлении. На рис. 9.9, а показано линейное
перемещение, хотя это может быть угол поворота, взаимное сближение
двух точек, взаимный угол поворота и т.д. Первый индекс обобщенного
перемещения #oi обозначает направление перемещения, второй -
причину, вызвавшую это перемещение, в данном случае - напряженно-
деформированное состояние 1.
175
©
м
а)
б)
Наряду с исходным состоянием 1
рассмотрим вспомогательное
состояние 0, вызванное действием
дополнительной обобщенной силы <20,
которая приложена в точке М в
направлении искомого перемещения q0]
(рис. 9.9, б).
На основании теоремы Бетти о
взаимности работ работа силы <20 на
перемещении q0{ равна сумме работ
обобщенных сил Qk (к = 1,2,..., т)
первого (исходного) состояния на
соответствующих им обобщенных
перемещениях qkQ во
вспомогательном состоянии (на перемещениях в
направлении действия сил Qk от силы
Go):
fiotfoi = I Qklkn- (9.41)
Рис. 9.9.
Напряженно-деформированные состояния упругого тела:
а - исходное; б - вспомогательное
Формула (9.41) является
обобщением формулы (9.38), записанной для
случая, когда в каждом состоянии
действует по одной силе. Если ввести
обозначение б/с0 = qk01QQ так, что qk0 - 6к0 Q0, то после сокращения на
Qo из формулы (9.41) получим
Ям = Е бАо-
*=i
(9.42)
Коэффициенты б/с0 имеют смысл обобщенных перемещений, вызванных
единичной силой Q0 = 1.
Применительно к стержневым системам роль обобщенных сил играют
внутренние силовые факторы, совершающие работу на соответствующих
обобщенных перемещениях. По аналогии с формулой (9.15) вместо (9.42)
будем иметь
о о
/ /
♦ jMy{z)u%u(z) + fMt(z)d%0(z).
(9.43)
176
Здесь, как и в формуле (9.21), отброшены слагаемые, учитывающие
работу поперечных сил. В формуле (9.43) через v0 (z), q>x0 (z), ф^0 (z) и <pz0 (z)
обозначены обобщенные перемещения, соответствующие внутренним
силовым факторам, которые вызваны действием единичной силы Q0 = 1.
Дифференциалы этих перемещений вычисляются следующим образом:
dv0. №9 d^0. Ы±ш d= . £s*L, афг0 - *«£L.
0 EF *х0 EJX *у0 EJy ™ <?/*
Функции Nz0(z), Mx0(z)9 MyQ(z), Mz0(z) имеют смысл внутренних
силовых факторов, вычисленных во вспомогательном состоянии от
действия единичной силы QQ = 1. В итоге формула (9.43) примет вид
г NzNz0 г М М 0 М М 0 г М М 0
о о х о у о *
Полученная формула (9.44) для определения перемещений в упругих
стержневых системах носит имя формулы Максвелла - Мора.
Последовательность определения перемещений по формуле (9.44)
складывается из следующих этапов. Сначала находятся внутренние
силовые факторы от действия заданных внешних сил. Затем к системе,
освобожденной от внешних нагрузок, прикладывается единичная
безразмерная обобщенная сила Q0 = 1 в том сечении, в котором нужно
найти перемещение; в направлении искомого перемещения, и находятся
внутренние силовые факторы от действия этой единичной силы. На
последнем этапе вычисляются интегралы в формуле (9.44), которые
называются интегралами Максвелла - Мора.
При использовании формул Максвелла - Мора нужно иметь в виду,
что перемещения и силы здесь понимаются в обобщенном смысле.
Например, если для стержневой системы, изображенной на рис. 9.10, а,
требуется найти вертикальное перемещение сечения К, то в этом сечении
в направлении этого перемещения прикладывается единичная сила
(рис. 9.10, б). Для нахождения угла поворота некоторого сечения в этом
сечении в направлении искомого угла прикладывается единичный момент
(рис. 9.10, в). Для нахождения взаимного смещения двух сечений в этих
сечениях прикладываются две единичные силы, как показано на
рис. 9.10, г, и т.д.
177
~QT к г^м
а)
б)
Яь,
Щ^
*)
Рис. 9.10. Определение перемещений в стержневой системе (а):
б - линейного; в - углового; г - взаимного
Основная трудность практического применения формулы (9.44)
состоит в вычислении интегралов Максвелла - Мора. Для упрощения
вычислений можно воспользоваться способом Верещагина, который
состоите следующем. Рассмотрим один из интегралов в (9.44), например,
1 Mx(z)Mx0(z) й=
EJV
(9.45)
Разобьем отрезок [0,1\ на п отрезков, в пределах которых жесткость EJX
постоянна, а изгибающий момент Mx0(z) от действия единичной
обобщенной силы есть линейная функция: MxQ(z) = m+kz. На одном
из этих отрезков [а, Ь] вычисления сводятся к нахождению интеграла
JMx(z)Mx0(z)dz = [Mx(z)(m + kz)dz = т f Mx(z)dz + k jzMx(z)dz.
178
Интеграл с*) = fMx(z)dz равен
мЛ
заштрихованной на рис. 9.11
площади, а интеграл о
ъ
S^- fzMx(z)dz есть статичес- л\
кии момент площади со
относительно оси О - О' на рис. 9.11.
Известно, что статический момент
площади относительно заданной
оси равен произведению площади Рис. 9.11. Способ Верещагина перемно-
на расстояние от ее центра тяжес- жения эпюр
ти до оси: S(,
zc а). Тогда
fMx(z)Mx0(z)dz = ww + Цо = o)(w + kz^ = (от^,
(9.46)
где r) = m + kzc = Mx0(zc) (рис. 9.11).
Формула (9.46) представляет собой способ Верещагина - способ
перемножения эпюр на отрезке [а, Ь]: интеграл от произведения двух
функций, одна из которых линейная, равен произведению площади под
произвольной функцией Mx(z) на ординату линейной функции MxQ(z)
под центром тяжести Mx(z).
Интеграл (9.45) равен сумме интегралов, каждый из которых
вычисляется по правилу (9.46):
1 Mx(z)Mxb(z) ^ в - <*л
EJ„
С*/А
(9.47)
где а)/с, г|А, и (EJx)k - значения площадей, ординат и жесткостей на й>м
участке разбиения отрезка [0, /]. Таким о(5разом, вычисление интеграла
Максвелла - Мора по правилу Верещагина сводится к вычислению
площадей и ординат геометрических фигур.
Правило Верещагина справедливо при ограничениях, следующих из
его вывода:
- в пределах участка жесткость постоянна;
- одна из эпюр линейная;
179
- произвольная функция Mx(z) в пределах участка не должна менять
знак.
Аналогичным образом правило Верещагина применяется для
вычисления остальных интегралов в формуле (9.44).
9.6. Вариационные методы Релея - Ритца и Бубнова -
Галеркина
Эти методы основаны на вариационных принципах и относятся к
классу так называемых прямых методов. Рассмотрим сущность методов
на примере задачи об изгибе балок. Будем исходить из вариационного
принципа Лагранжа (9.24). Полную потенциальную энергию деформации
(9.27) запишем в следующем виде:
Э = I [EJ\
d2v(z)
dz2
dz + II[v(z)], (9.48)
где потенциал внешних сил П [v(z)] является линейным функционалом
от v(z).
Будем искать приближенное решение в виде ряда
v(*) = ickwk(?)t (9.49)
где wk(z) - некоторая система заранее выбранных базисных функций,
удовлетворяющих кинематическим граничным условиям (ограничениям
на перемещения и углы поворота в соответствии с наложенными
связями); ^-неопределенные коэффициенты, подлежащие определению.
Если подставить ряд (9.49) в функционал (9.48), то после вычисления
интегралов получим, что полная потенциальная энергия будет зависеть
от неизвестных коэффициентов: Э = Э(с{, с2,..., с„), причем эта
зависимость будет представлять собой неоднородную квадратичную форму
Э^ЕЕу^Е^- (950)
При вычислении вариации ЬЭ неопределенные коэффициенты ск
выступают в качестве варьируемых параметров, и вариационное
п
уравнение принимает вид 6Э= £ (33/3^)6^=0, откуда в силу
произвольности вариаций Ьск приходим к системе уравнений
180
|^ = 0, {к = 1,2,...,и) (9>51)
для нахождения неизвестных коэффициентов ряда (9.49). Учитывая (9.50),
получим, что система уравнений (9.51) представляет собой систему
линейных уравнений
ZakjCj + bki (*= 1,2,...,и). (9.52)
7-1
Изложенный метод называется методом Релея -Ритца.
Для иллюстрации метода Бубнова -Галеркина рассмотрим вариацию
полной потенциальной энергии в форме (9.29). В первом слагаемом
подынтегральное выражение при вариации б v(z) есть не что иное, как
уравнение равновесия, а внеинтегральные члены определяют статические
и кинематические граничные условия. Перепишем формулу (9.29) в виде
ЬЭ = fL[v(z)]6v(z)dz + L0[v(z)]6v(z)
(9.53)
Оператор L [v(z)], соответствующий уравнению равновесия, согласно
(9.32) имеет вид
L[v(z)] = -£L
dzz
\EJx(z)^^-
dz2
q(z).
Второе слагаемое в (9.53) в операторной форме описывает
внеинтегральные слагаемые в (9.29), соответствующие статическим и кинематическим
граничным условиям.
В методе Бубнова - Галеркина приближенное решение ищется в виде
ряда, аналогичного (9.49). Отличие состоит в выборе базисных функций
wk(z). В методе Бубнова - Галеркина эти функции должны удовлетворять
всем граничным условиям - не только кинематическим, как в методе
Релея - Ритца, но и статическим.
После подстановки ряда (9.49) в функционал (9.53) убеждаемся, что
внеинтегральные слагаемые исчезают, так как функции wk(z) удовлетво-
п
ряютвсем граничным условиям. Учитывая, что бv(z) = £ wk(z)bck, из
вариационного уравнения б Э = 0 в силу произвольности вариаций б ск
приходим к системе уравнений для определения неизвестных коэффици-
181
ентов ск\
i
fL[v(z)]wk(z)dz = Ot (Л-1,2 я). (9.54)
о
Эти уравнения после подстановки ряда (9.49) и интегрирования
приводятся к системе линейных уравнений, по виду совпадающей с (9.52),
естественно, с другими коэффициентами ак: и Ьк. Уравнения (9.54)
называются условиями ортогональности базисных функций wk(z) к
оператору L [v(z)].
9.7. Метод конечных элементов
Метод конечных элементов - один из прямых методов на базе
вариационных принципов. Метод основан на дискретизации системы
с последующим решением на ЭВМ. Существует большое количество
модификаций метода, различающихся способом разбиения на конечные
элементы и использованием различных вариационных принципов.
Основные соотношения метода конечных элементов записываются в
компактной матричной форме.
Рассмотрим основные этапы решения задач механики конструкций
методом конечных элементов1. На первом этапе конструкция разбивается
на конечные элементы простой формы, производится нумерация
элементов и узлов - точек, в которых конечные элементы
взаимодействуют между собой. В качестве неизвестных выбираются перемещения
узлов.
На втором этапе перемещения в каждом конечном элементе
аппроксимируются простыми функциями (чаще всего полиномами) и
выражаются через неизвестные перемещения узлов. Через узловые
перемещения выражаются также деформации и напряжения. Рассмотрим
/с-й конечный элемент, имеющий т узлов, каждый из которых содержит
г неизвестных перемещений. Тогда конечный элемент будет иметь s =
= т,х г узловых перемещений, которые образуют .у-мерный вектор
узловых перемещений fk (матрица - столбец). Вектор перемещений в
конечном элементе обозначим ик. Связь векторов ик и f/v, в матричной
форме имеет вид
и* - НЛ. (9.55)
где матрица НА,, называемая матрицей формы, составлена из элементов,
являющихся функциями от координат точек внутри конечного элемента.
Матрица Нк является аналогом базисных функций wk(z) в методе Релея -
Ритца, а вектор fk - аналог неизвестных коэффициентов ск, с той
182
разницей, что ряд типа (9.49) аппроксимирует перемещение во всей
конструкции, а соотношение (9.55) - в конечном элементе.
Деформации в конечном элементе представляются в виде вектора,
деформаций е/с, составленного из компонент тензора деформаций. Связь
деформаций с перемещениями дается соотношениями Коши (3.30). В
матричной форме эта связь имеет вид
Ч = *Ч> (9.56)
где матрица Р составлена из операторов дифференцирования д/дх, д1ду9
dldz. Подстановка (9.55) в (9.56) дает связь вектора деформаций с
вектором узловых перемещений
Ч = РНЛ = V* (9.57)
Матрица Вк = РН/; в случае аппроксимации перемещений линейными
функциями координат имеет элементы в виде констант.
Напряжения связаны с деформациями законом Гука, который в
трехмерном случае имеет вид (3.37), (3.38). Представляя компоненты
тензора напряжений в виде вектора напряжений ок, получим матричную
форму записи закона Гука
°* - ЪЧ> (9.58)
где матрица упругости D составлена из элементов, зависящих от упругих
постоянных Е, p., G. Вектор напряжений связан с вектором узловых
перемещений матричным соотношением
°* - 1>ВЛ, (9.59)
следующим из (9.57) и (9.58).
Третий этап состоит в применении одного из вариационных
принципов, например, принципа Лагранжа (9.24). Потенциальная
энергия упругой деформации f/складывается из потенциальных энергий
деформации элементов. Выражение для потенциальной энергии (9.11)
в /:-м конечном элементе можно представить в матричной форме
Uk = \H№a*dV' (9.60)
у.
где индекс "т" обозначает операцию транспонирования матрицы (замена
183
строк на столбцы): Для вектора гк операция г\ переводит матрицу-
столбец в матрицу- строку. Интегрирование в формуле (9.60) проводится
по объему, занимаемому А>м элементом. Учитывая, что г\ = (Rk fk)T =
= f^B^, формулу (9.60) с учетом (9.59) можно записать в виде
Uk = \ffffTkBlDJikfkdV.
2 г.
Так как вектор fk составлен из неизвестных коэффициентов, то этот
вектор можно вынести за знаки интегрирования
ик - in
Матрица
///BlDBtdK
h-
vk
называется матрицей жесткости конечного элемента. Если перемещения
ик - линейные функции координат, то Кк = B^DB^ Vk, где Vk - объем
А:-го элемента. С учетом (9.61) потенциальная энергия деформации
конечного элемента выражается через вектор узловых перемещений
Uk = \Ъ*к*к. (9.62)
Суммируя потенциальную энергию по всем к = 1,2,..., Оконечным
N
элементам, получим U= £ f^K^.f^/2. Это выражение можно привести
к форме U = fт К f/2, где f - вектор узловых перемещений для всей
системы.' Матрица К, элементы которой составлены из элементов матриц
КА. путем суммирования по общим узлам, принадлежащим соседним
конечным элементам, называется матрицей жесткости конструкции или
глобальной матрицей жесткости.
Аналогичным образом определяется потенциал внешних сил. Этот
потенциал выражается через узловые перемещения следующим образом:
184
П = -FQ,
(9.63)
где Q - вектор внешних нагрузок, приведенных к узлам конечных
элементов. Этот вектор для А>го конечного элемента вычисляется
следующим образом:
Qk-l[[*Ur*V+I№4s*S, 964
vk sk
где q v - вектор внешних сил, распределенных по объему Vk конечного
элемента, a qs - вектор поверхностных сил. Глобальный вектор
внешних нагрузок Q формируется из векторов Qk по тем же правилам,
что и матрица жесткости.
Полная потенциальная энергии складывается из потенциальной
энергии упругой деформации и потенциала внешних сил
3 = ifTKf-fTe. (9.65)
Этот функционал является неоднородной квадратичной формой
неизвестных коэффициентов/j,/2, .-.,/д/, из которых составлен вектор
узловых перемещений. Вычисляя вариацию функционала (9.65) 6 Э =
м
= £ (дЭ/д/)Ь/. и приравнивая эту вариацию к нулю, на основании
основной леммы вариационного исчисления приходим к линейной
системе уравнений относительно неизвестных коэффициентов - узловых
перемещений. В матричной форме эти уравнения имеют вид
Kf = Q. (9.66)
На последнем этапе проводится решение полученной системы
уравнений с использованием ЭВМ, находятся перемещения, деформации
и напряжения по формулам (9.55), (9.57), (9.59).
Покажем, как реализуются приведенные выше основные соотношения
(9.55)...(9.66) метода конечных элементов применительно к стержневым
системам. Рассмотрим прямолинейный стержневой элемент постоянного
поперечного сечения длиной /, находящийся в условиях растяжения,
изгиба и кручения. Этот конечный элемент имеет два узла и 12 узловых
перемещений (которые также называются степенями свободы): по три
перемещения на каждом торце и по три угла поворота. Локальная
185
Рис. 9.12. Стержневой конечный элемент
система координат, узловые перемещения, их нумерация и
положительные направления показаны на рис. 9.12.
В рамках теории деформирования стержней, основанной на гипотезе
плоских сечений, связь между четырехмерным вектором перемещений
и(х) в стержневом элементе, компонентами которого являются
перемещения и(х), v(x), w(x) в направлении координатных осей Ох, Оу, Oz и угол
поворота ф(х) относительно оси Ох, и узловыми перемещениями дается
формулами:
ы(х) = 1
f)/,*^' iw-h-TU+T/if
(9.67)
v<*)«
X2 X3
1-3— + 2—
I2 I3)
A+l*-2y+^U+
+ |3^-2^|/8-|^-^
/ I2)
/12.
w(x)
1 -3—+ 2— /1
I2 /3 ,УЗ
+ 1^-2^Ц
x-2±-+2L
/ /2j
/s +
/ /2J
186
В матричной форме эти соотношения записываются в виде (9.55), где
матрица формы Н(х) размерностью (4х 12), связывающая четырехмерный
вектор перемещений и(х) в стержневом элементе и двенадцатимерный
вектор узловых перемещений f, в соответствии с (9.67) имеет следующие
ненулевые элементы: Я1 j = Я44 = 1 - х//, Я17 = Я4 ,0 = х//, Я22 = #31 = 1 -
~Зх2//2 + 2х3//3,Я26 = -Я35 = х-2х2// + х3//2?,Я28 = Яз9 = Зх1//2~
- 2х3 / /3, Я3 j 1 = -Я2 12 = х211 ~х3 / /2. Остальные элементы равны нулю.
Элементы Яд. матрицы формы имеют смысл перемещений точек стержня
в направлении у-й составляющей вектора перемещений от действия
единичного перемещения в направлении узлового перемещения fk при
условии, что остальные узловые перемещения равны нулю.
Потенциальная энергия упругой деформации стержневого элемента
находится по формуле (9.21). Если в этой формуле в соответствии с
принятой на рис. 9.12 системой координат выразить внутренние силовые
факторы через перемещения Nx = EFdu I Эх, М - EJZI d2w /Эх2, Mz =
= EJ d2v I Эх2, Mx = GJk Эф / Эх, то вместо (9.21) получим
U
;/!
\EF\
ди
дх
+ EJ
Э2У
(, дх2
+ EJ
d2w
дх2
+ G/,
Ш:
dx. (9.68)
Подставляя выражения (9.67) в формулу (9.68), после приведения
последней к квадратичной форме от вектора узловых перемещений (9.62)
получим следующие выражения для ненулевых элементов матрицы
жесткости:
к)к ~ /
= fEF
dx dx
dx, (jtk = 1,7);
*W
Ь " /
GJU
dHAi dK
& -dx, Qtk » 4,10);
dx dx
EJt, P- ^dx, (/.A: = 3,5,9,11);
(9.69)
dx2 dx2
' d2Я2/d2Я2.
Kjk = JEJ2—-A —^dx, </.*
о
dx2 dx2
2,6,8,12).
187
Остальные элементы матрицы жесткости равны нулю. После вычисления
интегралов в (9.69) получим выражение (9.70) для матрицы жесткости
прямолинейного стержневого элемента.
Для вычисления вектора узловых усилий в конечном элементе
дополним вектор перемещений и(х) углами поворота х=:^и^/Эл:иг|| =
= д vId х относительно осей Оу и Oz соответственно. Тогда соотношения
(9.67) дополнятся следующими:
SL о
\2liJ,
0
\2EJ}
I3
О
0
0
GJk
Симметрично
о
о
AEJy
I
О
0
0
О
AEJ.
EF
I
0
О
о
о
о
EF
О
12EJ:
0
0
6EJt
1г
0
\2EJ:
/3
0
0
\2EJy
"~Т~
0
6EJy
~Т~
0
0
0
\2EJV
У
/3
0
0
0
1
0
0
0
0
0
GJk
I
0
0
6£/,
/а
0
2EJy
I
0
0
0
6EJy
~F~
0
4EJ¥
У
1
0
6EJ:
-jr
0
0
0
2EJZ
__
0
6EJm
"Y
0
0
0
4/Г./,
/
(9.70)
(9.71)
Расширенный шестимерный вектор перемещений и'(х) и вектор
узловых перемещений связаны соотношением типа (9.55) посредством
расширенной матрицы форм Н' размерностью (6x12). Эта матрица по
сравнению с матрицей Н дополнена двумя строками с элементами
-#;3=я;9=-яб2=я68=б(х//2-х2//3),
188
-#55 = #66=1-4х// + 3х2//2 , #5>11 = -#6>12 = 2x//-3x2//2 .
Остальные элементы в этих строках равны нулю.
Если вектор внешней нагрузки q(x) составлен из распределенных
вдоль оси стержня нагрузок q^x), qy(x), qz(x) и распределенных моментов
тх(х), ту(х), mz(x), то вектор узловых усилий находится по формуле
(9.64), которая для стержневого конечного элемента принимает вид
Q = |H'T(*)q(*)dx.
(9.72)
Например, равномерно распределенная нагрузка q , действующая в
направлении оси Оу9 сводится к узловым усилиям Q2 = q fH22(x)dx =
о
/ /
о о
/
= qy[HV2(x)dx = -qyl2/\2.
О
Если кроме распределенных нагрузок в некотором сечении х = jc0
приложены сосредоточенные силы Рх, P. Pz и сосредоточенные моменты
Мх, М, Mv образующие вектор Р(х0), то в формуле (9.72) нужно
добавить слагаемое Q0 = Н т (xQ) Р(х0). Если вектор сосредоточенных
нагрузок приложен в одном из узловых сечений, то приведения этих
[р(0)|
нагрузок к узлам не требуется. В этом случае Q0 = |
, если х0 = 0, и
О
, если х0 = /. Здесь символом 0 обозначен шестимерный вектор
с нулевыми элементами.
В частном случае плоской стержневой системы стержни будут
испытывать деформации растяжения и изгиба, при этом каждый узел
стержневых элементов будет иметь по три степени свободы: два
перемещения и угол поворота. Например, при деформировании в
плоскости Оху отличными от нуля будут узловые перемещения/|,/2,/6,
/7, /8, /12, остальные узловые перемещения равны нулю. Матрица
жесткости может быть получена из (9.70) вычеркиванием строк и
189
столбцов, соответствующих нулевым компонентам вектора узловых
перемещений:
К =
EF
I
\2EJ 6EJ
/3
6EJ
I2
4EJ
I
EF
I
EF
I
О
EF
I
\2EJ 6EJ
/3
6EJ,
I2
2EJ,
\2EJ, 6EJ
О
/3
6EJ2
~1Г
I2
2EJZ
I
О
О
/2
\2EJ2
/3
6EJZ
"I2"
I
6EJ.
I2
4EJ2
I
(9.73)
Если учитывать только изгибные деформации, то отличными от нуля
будут узловые перемещения /2»Л>Л> А2- Удалением в (9.73) первой и
четвертой строки и соответствующих столбцов получим матрицу
-жесткости стержневого элемента, работающего на изгиб в одной
плоскости
К =
EJ.
12 6/ -12 6/
6/ 4/2 -6/ 2/2
-12 -6/ 12 -6/
6/ 2/2 -6/ 4/2
(9.74)
Проиллюстрируем процедуру применения метода конечных элементов
на простом примере изгиба плоской рамы постоянной изгибной
жесткостью EJ, изображенной на рис. 9.13, а. Разобьем данную систему
на три стержневых элемента, как показано на рис. 9.13, б. Из граничных
условий и условия нерастяжимости оси следует, что узловые перемещения
Л =/б =Л ~fi ~Н =/\г = 0 • Отличными от нуля узловыми
перемещениями будут перемещение/8 =/2 = v2 и угол поворота/12 =
_,г(2)
(2) _ лз) _
/б = ф2 второго узла, а также угол поворота /12 -fs Фз третьего
190
а)
б)
•)
Рис. 9.13. Применение метода конечных элементов к расчету рамы:
а - схема нагружения; б- разбиение на конечные элементы; в - эпюра поперечной
силы; г - эпюра изгибающего момента
узла. Эти перемещения образуют трехмерный вектор узловых
перемещений f. Первый стержневой элемент имеет две степени свободы v2 и ф2,
второй элемент - три степени свободы v2, ф2 и ф3, третий элемент - одну
степень свободы ф3. Матрицы жесткости элементов получим из (9.74)
вычеркиванием строк и столбцов, соответствующих нулевым узловым
перемещениям:
191
к<"> =
12EJ 6EJ
I
А2
6EJ \EJ
it '■
, к<2> =
6EJ
6EJ
6EJ
ll
4EJ
2EJ
h
6EJ
ll
2EJ
1г
4EJ
к
, К» =
AEj]
. h j
После суммирования элементов матриц жесткости, соответствующих
совпадающим узловым перемещениям Кп = АГЦ + АГЦ , К12 = К1Х =
= К§ + ^(22), К22 = A:2(2} + #2(2}, #зз = К1ъ + *п} > получим глобальную
матрицу жесткости
К =
\2EJ + 12Jg/
А3
6E£+6EJ
6EJ
6EJ+6El
I1 I2
М '2
4E£+4EJ
1EJ
6EJ
ll
2EJ
4EJ + 4EJ
Вектор узловых усилий Q = [-Р О 0]т содержит заданную силу Р,
сосредоточенную во втором узле и действующую в направлении,
противоположном узловому перемещению/j = v2.
Уравнение равновесия (9.66) для заданной системы принимает вид
24 0 6а 1
0 8я2 2а2\
6а 2а2 6а2\
к
Ф2
[фз
=
-р
0
0
EJ
Здесь учтено, что 1Х = /2 = я, /3 = 2я. Решая эту систему уравнений,
11 Раъ Ра1 Ра1
получим v2 = -— ——, Ф2 = -——, Фз =- -rz-=rr • По формулам (9.67)
находим перемещения для каждого из стержневых элементов в локальной
192
системе координат: v^(x) = (Зх2la2- 2х3 Iя3) v2- (х2 Iа -х3 Iа1) ф2,
x€[0...a]'ivV\x) = (\-3x2/a2 + 2x3la3)\2 + (x-2x1la + x3/a2\(p2-
- (х2 I а - х3 / а2) <р3, х е [0 ... л]; v(3)(x) = (х - х2 / а + х3 / Аа1) q>3,
х в [0... 2я]. Для нахождения внутренних силовых факторов
воспользуемся формулами М(х) = £7 d2 v(x) / d х2, Q(x) = EJ d* v(x) / d x3.
Эпюры поперечной силы и изгибающего момента представлены на
рис. 9.13, в, г.
193
Глава 10
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ
СИСТЕМЫ
10.1. Классификация стержневых систем
При расчетах на прочность и жесткость реальных конструкций в
качестве расчетных схем часто используются стержни и
стержневые системы: балки, рамы, фермы и т.д. С точки зрения механики
материалов и конструкций представляет интерес классификация
стержневых систем по кинематическим и статическим признакам. По
кинематическим признакам стержневые системы подразделяются на
следующие группы:
1. Геометрически изменяемые системы (механизмы). Как правило,
такие системы не могут воспринимать силовую нагрузку
произвольного направления. Перемещения в таких системах возможны
без деформаций стержней (см., например, рис. 10.1).
2. Геометрически неизменяемые системы. Перемещения в таких
системах происходят лишь вследствие деформирования материала,
из которого изготовлены элементы системы. Именно такие
системы выступают в качестве расчетных схем при проведении
прочностных расчетов реальных конструкций.
3. Мгновенно изменяемые системы Эти системы ведут себя как
механизмы при бесконечно малых перемещениях. Однако при
конечных перемещениях их поведение аналогично геометрически
неизменяемым системам. На рис. 10.2 приведены примеры
Рис. 10.1. Кинематически изменяемые системы (механизмы)
194
а)
Рис. 10.2. Мгновенно изменяемые системы
мгновенно изменяемых систем, допускающих бесконечно малые
перемещения, совместимые со связями. Шарнирно-стержневая
система (рис. 10.2, а), у которой три шарнира лежат на одной
прямой, допускает бесконечно малое перемещение шарнира А в
вертикальном направлении и поворот стержней на бесконечно
малые углы. Если направления опорных стержней пересекаются
в одной точке О (рис. 10.2, 6), то в этом случае также допускается
бесконечно малый поворот бруса АВ вокруг этой точки.
По статическим признакам стержневые системы принято делить на
две группы:
1. Статически определимые системы Все реакции опор и все усилия
в элементах этих систем могут быть определены только из
уравнений равновесия. Удаление хотя бы одной связи в статически
определимой системе превращает ее в геометрически изменяемую.
2. Статически неопределимые системы. Все реакции и/или усилия в
таких системах не могут быть определены только из уравнений
статики.
Статически неопределимые системы имеют место в том случае, когда
число связей, наложенных на систему, превышает минимальное число
связей, необходимых для обеспечения геометрической неизменяемости.
В этом случае говорят, что на систему наложены так называемые лишние
связи.
Термин лишние связи является условным и отражает лишь тот факт,
что число связей в системе превышает число независимых уравнений
равновесия, которые могут быть составлены для определения всех усилий
в системе. Наличие таких связей в большинстве несущих конструкций
обусловлено необходимостью обеспечения требуемых условий прочности
и жесткости.
О
/К 8ф
//////////////////////////////
б)
195
10.2. Степень статической неопределимости
Усилия, возникающие в лишних связях, называют лишними
неизвестными. Разность между числом неизвестных усилий в системе и числом
независимых уравнений статики, которые можно составить для их
определения, называется степенью статической неопределимости п.
Степень статической неопределимости совпадает с числом лишних связей
или числом лишних неизвестных. Таким образом, чтобы определить
степень статической неопределимости системы л, нужно найти число
связей, которые необходимо отбросить, чтобы получить статически
определимую геометрически неизменяемую систему. Другими словами
степень статической неопределимости равна числу дополнительных
связей, наложенных на систему и не обязательных с точки зрения
обеспечения ее геометрической неизменяемости.
Для плоских стержневых систем нетрудно составить формулу,
определяющую степень их статической неопределимости. Напомним, что
стержневая система называется плоской, если центры тяжести всех
поперечных сечений стержней расположены в одной плоскости,
проходящей через одну из главных центральных осей инерции каждого
сечения. Кроме того, требуется, чтобы все нагрузки на систему
действовали также в этой плоскости. Связи, с помощью которых
образуется стержневая система, можно разделить на внешние и
внутренние. Внешние связи фиксируют систему в заданном положении.
С помощью внутренних связей стержни в системе могут образовывать
замкнутые контуры (рис. 10.3, а). Очевидно, что замкнутый контур, не
а)
Рис. 10.3. Статически неопределимая система с замкнутым контуром, не имеющим
шарниров (я), основная система (б)
196
содержащий шарниров, в плоской
системе трижды статически
неопределим. Чтобы превратить такой контур
в статически определимый, можно,
например, сделать сечение одного из
его элементов (рис. 10.3, б). При этом
устраняются три связи на взаимные
линейные и угловое перемещения.
Реакциями этих связей являются
м м продольная Nz и поперечная Q силы
'ШШЯЬ 'ШшРл и изгибающий момент Мх,
действующие в этом сечении.
Рис. 10.4. Пример пять раз статичес- Включение в состав плоской
стерки неопределимой системы жневой системы шарнира,
соединяющего два стержня, уменьшает степень
статической неопределимости на
единицу. Такие шарниры называются простыми. Шарнир, с помощью
которого соединяются три стержня, снижает степень статической
неопределимости на два. И вообще, если в некотором шарнире
соединяются т стержней, то снижение статической неопределимости
будет равно т - 1. В этом случае говорят, что шарнир имеет кратность
/77-1. Итак, если включить в рассмотрение системы опорные стержни,
то степень статической неопределимости п плоской стержневой системы
может быть определена по формуле
и = ЗА: - j, (10.1)
где к - число замкнутых контуров, s - число простых шарниров,
вычисленное с учетом их кратности. В качестве примера рассмотрим
плоскую стержневую систему, изображенную на рис. 10.4. Эта система
имеет пять замкнутых контуров, т.е. к = 5 (они отмечены римскими
цифрами), четыре простых шарнира и три двукратных, т.е. s = 10. Таким
образом, для рассматриваемой системы по формуле (10.1) получим
п = 3-5 - 10 = 5.
10.3. Особенности статически неопределимых систем
В отличие от статически определимых систем статически
неопределимые системы обладают рядом характерных особенностей. Рассмотрим
простейшую статически неопределимую систему, стержни которой
197
а)
ATj \F Л/,
ы2
б)
в)
Рис. 10.5. Статически неопределимая система при растяжении (сжатии) (а),
равновесие узла С (£), диаграмма перемещений при силовом воздействии (в),
диаграмма перемещений при наличии монтажного зазора (г)
работают на растяжение - сжатие (рис. 10.5, а). Система находится под
действием силы Р, приложенной к шарниру С. Вырежем узел С и
составим уравнения равновесия (рис. 10.5, б). Проектируя все силы на
ось Ох, получим
-NjSinp + N3sinp = 0. (10.2)
Отсюда следует, что N{ = Ny Из условия равенства нулю суммы
проекций всех сил на ось Оу следует
N,cosp + 7V3C0SP + N2 = P.
(10.3)
Поскольку в данном случае имеем плоскую систему сходящихся сил,
то независимых уравнений - два, а неизвестных усилий - три.
Следовательно, заданная стержневая система один раз статически неопределима.
198
Составим уравнение совместности деформаций (рис. 10.5, в). При
нагружении системы шарнир С перемещается по вертикали на величину
СС'. Очевидно, что длина этого отрезка совпадает с укорочением
стержня CD. Из точки С" опустим перпендикуляр на продолжение оси
стержня АС. Ввиду малости деформаций стержней по сравнению с их
длиной отрезок СС" будет практически совпадать с удлинением стержня
АС. Тогда из геометрических соображений следует уравнение
совместности деформаций
А/, = A/2cosp (Ю.4)
или
= cos р.
EFX EF2
Решение системы уравнений (10.2), (10.3) и (10.4) дает выражения для
усилий в стержнях А С, ВС и DC
N = N = ^cosp N я Р х я Щ'1гш
1 3 l + 2A.cos2p' 2 l+2A.cos2p' ^#/i
Здесь через Л обозначено отношение жесткостей стержней. Если Л > > 1,
т.е. жесткость стержней АС и БС значительно больше, чем жесткость
стержня DC, то вся нагрузка практически воспринимается верхними
стержнями, а нижний стержень не нагружен. Противоположная картина
наблюдается при Я - 0.
Теперь рассмотрим случай температурного нагружения системы.
Пусть температура стержней А С и ВС, имеющих одинаковые
температурные коэффициенты линейного расширения а, увеличивается на А Г. Тогда
для определения возникающих при этом сжимающих усилий в стержнях
имеем уравнения равновесия
//,sinp - NjSinp = 0, -Njcosp - W3cosp + ЛГ2 = 0, (Ю.5)
и такое же, как и в предыдущем варианте силового нагружения,
уравнение совместности деформаций (10.4), где А/, должно учитывать
температурную деформацию, т.е.
N.L
А/. = аД77. - —12.
1 * EFX
199
После вычислений для температурных усилий в стержнях получим
aATEF. 2aA7EF,cosp
#1 = N* = —» ^2 = l "•
l+2Xcos2p l + 2A.cos2p
Пусть вследствие неточности изготовления стержень DC оказался
короче, чем /2, на некоторую малую величину Д. Тогда после сборки в
стержнях системы возникнут усилия, для определения которых имеем
уравнения равновесия (10.5), а уравнение совместности деформаций в
данном случае следует записать в виде
1 - I а - 22
EF2
cos р.
EFX
Таким образом, для монтажных усилий в стержнях системы получим
N = м cosp A£^i N а 2cos2p Д^^1
3 1 + 2Axos2p lx 1 + 2A.cos2p lx
Рассмотренные выше примеры позволяют сделать выводы о
некоторых особенностях статически неопределимых систем, а именно:
1. Величина усилий в статически неопределимой системе,
возникающих в результате воздействия внешних нагрузок, существенно
зависит от распределения жесткостей; если элементы системы
изготовлены из различных материалов, то распределение усилий
зависит также от модулей упругости этих материалов.
2. Температурные воздействия, как правило, приводят к
возникновению усилий в статически неопределимых системах.
3. Неточности изготовления элементов (в частности стержней),
смещения опор также приводят к возникновению усилий после
монтажа системы.
Существуют различные методы расчета статически неопределимых
систем: метод сил, метод перемещений, смешанный или комбинированный
метод. Широкое распространение в последние годы получил метод
конечных элементов.
10.4. Канонические уравнения метода сил
Метод сил является одним из основных и наиболее распространенным
методом расчета статически неопределимых систем. Название метода
связано с тем, что в его систему уравнений в качестве неизвестных входят
200
усилия - реакции внешних и внутренних связей стержневой системы.
Основная идея метода сил заключается в том, что исходную статически
неопределимую систему путем отбрасывания лишних связей превращают
в статически определимую геометрически неизменяемую систему.
Полученная таким образом система называется основной системой.
Вместо отброшенных связей к основной системе прикладываются
обобщенные силы, называемые лишними неизвестными А",, Хь..., Хп.
Число неизвестных равно степени статической неопределимости системы
п. Значения A'j, Х2,..., Хп определяются из условия того, что основная
система под действием внешних нагрузок и неизвестных усилий
деформируется так же, как и исходная статически неопределимая. Это
означает, что все перемещения в основной системе, в том числе и
перемещения в направлении лишних неизвестных, должны совпадать с
соответствующими перемещениями исходной системы. В силу опорных
закреплений или условий непрерывности обобщенные перемещения в
направлении неизвестных усилий равны нулю. Таким образом, получаем
условия для определения лишних неизвестных, называемые уравнениями
совместности деформаций или уравнениями метода сил
А. = *2 - .« = Ал - 0. (Ю.6)
Применяя принцип суперпозиции, справедливый для линейно-упругих
систем, представим обобщенные перемещения А,, (/ = U 2, ..., п) в
направлении у-й неизвестной Х- в уравнениях (10.6) в виде суммы
перемещений Д.^ от лишних неизвестных Хк (к = 1,2,..., п) и
перемещений Ljp от внешней нагрузки
А, = £ AJX + Ljpt (j = 1, 2, .... /,). (10.7)
Перемещения Д .^ являются линейными функциями неизвестных усилий
Хк. В связи с этим их можно представить в виде
V* = V**' U« * ■ 1. 2» .». и). (10.8)
Здесь 6к - так называемые единичные перемещения, которые имеют смысл
перемещений в направлении действия лишней неизвестной Xj от
единичной обобщенной силы, приложенной к основной системе вместо
неизвестной Хк. Обобщенные перемещения от внешней нагрузки А/7>
201
а) б)
Рис. 10.6. Трижды статически неопределимая система (а), основная система (б)
называются грузовыми перемещениями. С учетом (10.7) и (10.8)
окончательный вид уравнений метода сил (10.6) будет следующим:
E*;A+.V = °. О-.1.2,..., л). (10.9)
На рис. 10,6, а в качестве примера представлена трижды статически
неопределимая система. В качестве основной может быть принята
система, изображенная на рис. 10.6, б. Система уравнений для
определения лишних неизвестных X{i Х2, Xj в Данном случае будет иметь вид:
621ХХ + Ь21Хг + 623ЛГ3 + А2Р = 0, (Ю.10)
63i*i + ьъгхг + 6зз*з + азр = °-
Физический смысл коэффициентов системы уравнений (10.10) ясен из
рис. 10.7.
Уравнения (10.9) представляют собой неоднородную систему
линейных алгебраических уравнений, порядок которой равен степени
статической неопределимости системы. Эти уравнения получили
название канонических уравнений метода сил, так как их вид не зависит
от особенностей системы и от вида деформаций, которые испытывают
стержни статически неопределимых систем при нагружении.
Системе канонических уравнений можно дать энергетическое
толкование. Составим выражение для потенциальной энергии упругой
деформации основной системы
202
~~7
\.Su
---'"К
#
^
Рис. 10.7. Грузовые и единичные перемещения в основной системе
2^J EI
где Мх - изгибающие моменты в поперечных сечениях стержней от
действия внешней нагрузки и лишних неизвестных Хх, Х2, ..., Хп. Здесь
суммирование ведется по всем стержням системы, а интегрирование -
по всей длине каждого из стержней. Следовательно, потенциальная
энергия является функцией неизвестных усилий Хи Х2,...» Хп, Вычислив
частные производные от £/по Хх, Х2,..., Хп, получим перемещения точек
приложения неизвестных усилий в направлении действия этих усилий
dU/dXj = А;., С/ = 1,2, ..., /?). В силу наложенных связей указанные
перемещения равны нулю
1, 2, .... л).
эи Л ,.
— = о, о
эх.
(10.11)
Если вычислить вторые производные от потенциальной энергии упругой
деформации по обобщенным неизвестным усилиям Xl9 Хь ..., Хп
вх? эх-
203
то на основании свойств диагональных элементов матрицы единичных
перемещений приходим к выводу, что условия (10.11) эквивалентны
каноническим уравнениям метода сил и соответствуют минимуму
потенциальной энергии системы (вариационный принцип Лагранжа).
Единичные 6/v, и грузовые перемещения Д^ удобно определять
энергетическими методами, например, методом Максвелла-Мора. Если
учитываются только изгибные деформации стержней в плоской
статически неопределимой системе, то формулы Максвелла-Мора
запишутся в виде
^ г М.М. п МРМ.
** = Е/-^<Ь> Д„ = Zf-Z-lta, (Ю.12)
X X
где Mj - изгибающий момент в основной системе от действия единичной
силы, приложенной в направлении действия неизвестной Х-, МР -
изгибающий момент в основной системе от действия внешней нагрузки,
Е1Х- изгибная жесткость стержней. Суммирование проводится по всем
стержням системы. В более общем случае, когда кроме деформаций
изгиба учитываются деформации растяжения (сжатия) и сдвига,
единичные и грузовые перемещения могут быть вычислены по формулам:
jP ^J EIX ^J EF ^J yGF
(10.13)
где Njt Qj - продольная и поперечная силы при единичном воздействии,
NP, QP - продольная и поперечная силы при действии на основную
систему внешней нагрузки, EF, GF - жесткости поперечных сечений
стержней при растяжении и сдвиге, у - коэффициент, учитывающий
форму поперечного сечения. При расчете статически йеопределимых
ферм, стержни в которых работают только на растяжение (сжатие),
единичные и грузовые перемещения определяются вторыми членами
формул (10.13).
При расчете статически неопределимых систем при температурном
воздействии вид канонических уравнений метода сил сохраняется.
Единичные перемещения 6jk имеют те же значения, что и при расчете на
силовое воздействие. Вместо грузовых перемещений вычисляются
температурные перемещения А/Т в основной системе по направлению
204
лишних неизвестных усилий. Если принять линейный закон
распределения температуры по высоте h поперечного сечения стержней, то
температурные перемещения А т можно определить по формуле
V = Za^jp-fMjdz + ZalilllfNjdz,
где Г|, Т2 - приращения температуры верхнего и нижнего волокон
стержней системы.
Если в направлении какой-либо неизвестной, например Х-, имеется
монтажный зазор А -, то в правой части соответствующего уравнения
метода сил нужно вместо нуля поставить значение величины зазора.
Таким образом, для определения единичных и грузовых перемещений
необходимо составить аналитические выражения для моментов Мр МР
и вычислить интегралы (10.12). В случае прямолинейных стержней с
кусочно-постоянной жесткостью при вычислении интегралов возможно
применение графоаналитического метода Верещагина.
Система канонических уравнений метода сил характеризуется
матрицей единичных перемещений (матрицей податливостей),
элементами которой являются единичные перемещения
б11 612 - 61«
621 *22 " Н (10.14)
Матрица единичных перемещений обладает рядом важных свойств,
которые учитываются при решении системы уравнений (10.9).
Диагональные элементы матрицы 6^. представляют собой перемещения в
направлении лишней неизвестной X: от единичного воздействия, приложенного
вместо X:. Они получили название главных перемещений. Диагональные
элементы матрицы (10.14) всегда положительны
б.. = f-^— > 0.
м J EI
Очевидно, что побочные перемещения (недиагональные элементы матрицы
6jkJ * к) могут иметь любой знак и в частном случае могут быть равными
нулю. Кроме того, матрица [6д,] является симметричной, т.е. 6к = 6kj. Этот
[«*] =
205
факт есть содержание теоремы Максвелла о взаимности перемещений,
являющейся следствием энергетической теоремы Бетти. Матрица
единичных перемещений является положительно определенной, а ее
определитель det[6J и все главные миноры положительны.
Положительная определенность матрицы [6г] обусловлена тем, что через ее элементы
вычисляется квадратичная форма - потенциальная энергия упругой
деформации f/^основной системы, загруженной лишними неизвестными
10.5. Последовательность расчета статически
неопределимых систем по методу сил
Определение неизвестных усилий в статически неопределимой системе
(раскрытие статической неопределимости) можно разбить на следующие
этапы.
Выбор основной системы. Для одной и той же статически
неопределимой системы можно составить различные варианты основных систем
(например, рис. 10.8, где для статически неопределимой системы,
рассмотренной ранее, приведены еще четыре варианта основных систем).
Рис. 10.8. Варианты основных систем
206
За лишние неизвестные при этом могут быть приняты как внутренние
силовые факторы в некоторых сечениях, так и реакции опор. Все
варианты основных систем должны удовлетворять обязательным
требованиям. Основная система должна быть статически определимой,
т.е. связей должно быть отброшено не меньше, чем статическая
неопределимость заданной системы. Основная система должна быть
геометрически неизменяемой, т.е. связей должно бытьртброшено не
больше, чем статическая неопределимость л. При выборе рабочего
варианта основной системы руководствуются также соображениями
простоты расчетов, включая вычисление единичных и грузовых
перемещений, решение системы канонических уравнений метода сил и
т.д. Некоторые рекомендации будут изложены ниже.
Построение единичных и грузовых эпюр. Для выбранной основной
системы строятся аналитические выражения или эпюры внутренних
силовых факторов, которые используются при определении единичных
и грузовых перемещений. На рис. 10.9 представлены такие эпюры для
системы, изображенной на рис. 10.6.
Вычисление коэффициентов канонических уравнений метода сил. Здесь,
как уже отмечалось, возможно применение различных методов
вычисления интегралов в выражениях (10.12) или (10.13), в том числе и
графоаналитического метода. Отметим,<что,в системах, состоящих из
прямолинейных стержней, всегда выполняется одно из условий
применимости графоаналитического метода. А именно, эпюры моментов
от действия единичных нагрузок для таких систем являются линейными.
Рис. 10.9. Грузовая и единичные эпюры
207
Вычисления коэффициентов уравнений метода сил (10.10) для
рассматриваемой системы (см. рис. 10.6) с использованием грузовой и
единичных эпюр (рис. 10.9) дают
\р ~
*п
5 Ра3 д _ _Ра3 д _ 1 Ра2
6 Е1х' v Е1х' ър 2 Е1х
8 а3 . 32 а3 . л а
= 1~еТх' *»~TWs' " ~ЁТХ'
а* в „а2 , 8 , а2
S12 = 521 = 4"^р S13 = 531 = 2~£f' 5» = 632 = 6 £/
X
Решение системы канонических уравнений метода сил. Для любых
правильно выбранных основных систем уравнения (10.9) всегда имеют
единственное решение Хх> Х2,..., Хп. Это следует из свойств матрицы
коэффициентов (10.14), в качестве которой выступает матрица единичных
перемещений.
В результате решения уравнений (10.10) для лишних неизвестных Хх>
Хь Хъ статически неопределимой системы (см. рис. 10.6) получим
X. = -!!/>, Х2 = - — Р, Хъ = — Ра.
1 32 2 32 3 16
Здесь знак минус для Х2 означает, что истинное направление этой
реакции противоположно первоначально выбранному.
Построение эпюр внутренних силовых факторов. После того как
вычислены значения лишних неизвестных Х^, Х2, ..., Хп, могут быть
определены внутренние силовые факторы в любых сечениях стержней
системы и построены их эпюры. Например, эпюру изгибающих моментов
Мх в статически неопределимой системе можно построить следующим
образом. Построим эпюры изгибающих моментов от каждого из
найденных усилий Х{, Х2, ..., Хп, Для этого можно использовать
построенные ранее единичные эпюры Му Просуммировав по
характерным точкам ординаты эпюр от действия всех сил Xj с ординатами
грузовой эпюры, т.е.
мх = мр + i м,х,,
7-1
208
получим окончательную эпюру Мх для заданной статически
неопределимой системы. Другой способ построения эпюры Мх заключается просто
в применении обычного метода сечений к основной системе, загруженной 1
внешними силами и силами ХХ>Х2,..., Хп.
Эпюра изгибающего момента Мх для рассматриваемого примера
статически неопределимой системы имеет вид, представленный на
рис. 9.13, см. гл. 9. Напомним, что эта эпюра построена с использованием
метода конечных элементов, который в случае сосредоточенных нагрузок
и при использовании кубической аппроксимации изгибных перемещений
дает точный результат.
Деформационная проверка. Если после раскрытия статической
неопределимости требуется определить перемещение какого-либо сечения
А^ с использованием интеграла Максвелла-Мора
^ гМхМКл
А* = E/-^dz, (10.15)
то, казалось бы, возникает необходимость вторичного раскрытия
статической неопределимости. Причем эту процедуру нужно провести
при действии уже не внешней заданной нагрузки, а единичной силы,
приложенной в том сечении, перемещение которого нас интересует.
Однако это единичное воздействие можно приложить к основной
системе, построить соответствующую эпюру Мк и, вычислив интегралы
в формуле (10.15), определить А^. Это возможно в силу того, что, как уже
отмечалось при формулировке содержания метода сил, основная система
под действием внешней нагрузки и сил Х{, Хъ..., Хп деформируется так
же, как исходная статически неопределимая система. Таким способом
можно определить любые перемещения в основной системе, в том числе
и перемещения в направлении лишних неизвестных. Поскольку эти
перемещения должны равняться нулю в силу наложенных связей, то
деформационная проверка и заключается в проверке равенства нулю
перемещений А • в основной системе, т.е.
М М
Л, = Zf-fr1** - 0, U = 1. 2, ... и).
X
Деформационная проверка контролирует правильность расчета
статически неопределимой системы от этапа определения единичных и
грузовых перемещений до построения окончательной эпюры
изгибающего момента Мх. Она проверяет также правильность решения системы
канонических уравнений метода сил, но не дает указаний о корректности
209
выбора основной системы и правильности построения для этой системы
единичных и грузовых эпюр.
10.6, Многопролетные неразрезные балки.
Уравнение трех моментов
Неразрезными называются балки, лежащие более чем на двух опорах
и не имеющие промежуточных шарниров. Такие балки нашли широкое
применение в различных конструкциях и относятся к классу статически
неопределимых систем. Если балка имеет п + 2 опоры, то система
является п раз статически неопределимой. Один из вариантов основной
системы - балка, полученная путем отбрасывания промежуточных опор.
Их действие заменяется неизвестными реакциями Х{, Х2, ..., Хп,
приложенными к основной системе. Уравнения (10.6) в этом случае будут
выражать условия равенства нулю прогибов в точках крепления
промежуточных опор. Однако такой способ расчета является
нерациональным. Значительно меньше вычислений будет при другом выборе
основной системы^ полученной путём врезания шарниров над всеми
промежуточными опорами (рис. 10.10). Лишними неизвестными в этом
.tnfll^^
Рис. 10.10. Неразрезная многопролетная балка
210
случае будут изгибающие моменты в опорных сечениях балки. Основная
система представляет собой ряд шарнирно опертых балок, нагруженных
заданной нагрузкой и неизвестными изгибающими моментами Хх, Х2,
..., Хп, приложенными в сечениях, где поставлены дополнительные
шарниры. При таком выборе основной системы действие заданной
нагрузки распространяется только на пролет, в котором она приложена.
В силу особенности эпюр единичных моментов, которая заключается в
том, что Мк отличен от нуля только в двух прилегающих к /с-й опоре
пролетах (рис. 10.10), матрица единичных перемещений будет трехдиаго-
нальной. В каждое каноническое уравнение входит не более трех
неизвестных Хк_{, Хк, Xk+V Поэтому А:-е уравнение метода сил носит
название уравнения трех моментов
Ьк,к-\Хк-\ + bktkXk + Ьк,к+\Хк+\ + \? = °
(к = 1, 2, .... и; Х0 = Хп+1 = 0).
Физический смысл уравнения трех моментов заключается в том, что
взаимный угол поворота крайних сечений соседних пролетов должен
равняться нулю.
10.7. Использование симметрии статически
неопределимых систем
Симметричной называется такая система, у которой не только ее
геометрическая схема и/или схема нагружения имеет ось симметрии, но
и жесткости симметрично расположенных элементов равны друг другу.
Использование симметрии статически неопределимых систем позволяет
значительно упростить их расчет. Рассмотрим три раза статически
неопределимую симметричную раму (рис. 10.11, а). При ее расчете с
помощью основной системы (рис. 10.111, б), не учитывающей симметрию,
необходимо составить и решить систему трех канонически^ уравнений
с тремя неизвестными (10.10).3десь все единичные перемещения отличны
от нуля. Если при расчете рассматриваемой рамы в качестве основной
принять систему, изображенную на рис. 10.12, а, то эпюры Л/, и М2 от
симметричных единичных воздействий будут симметричными
(рис. 10.12, б, в), а эпюра Мъ от кососимметричного единичного
воздействия - антисимметричной (рис. 10.12, г). Результат умножения
симметричной эпюры на антисимметричную равен нулю. Следовательно,
211
а)
ш б) vi>*
Рис. 10.11. Трижды статически неопределимая симметричная рама (а), основная
система (б)
1 а/2
Ш ( *4
в) ш%ж тиж Г)
Рис. 10.12. Симметричная основная система (а), единичные эпюры (б, в, г)
212
для рассматриваемой рамы часть побочных перемещений равна нулю
613 = б31 = 523 = б32 = °>
а система канонических уравнений (10.10) распадается на две
независимые системы уравнений
«и*| + ьпхг + А./> - °.
ЬпХг + ЬпХ2 + А2? = О,
Ь33Х3 * ДЗР = 0.
Первая из этих систем содержит два симметричных неизвестных усилия
(продольную силу и изгибающий момент Хи JSf2) и состоит из двух
уравнений, а третье уравнение определяет кососимметричное
неизвестное усилие - поперечную силу А"3.
Дальнейшие упрощения при использовании симметричных основных
систем возникают, если внешняя нагрузка симметричная или кососиммет-
ричная. Так, в случае симметричной нагрузки эпюра грузовых
изгибающих моментов будет симметричной. Это значит, что грузовые
перемещения, соответствующие кососимметричным неизвестным, и, следовательно,
сами эти неизвестные будут равны нулю. И наоборот, в случае кососим-
метричной нагрузки симметричные неизвестные усилия будут равны
нулю.
213
Глава 11
ПРОЧНОСТЬ ПРИ НАПРЯЖЕНИЯХ,
ПЕРЕМЕННЫХ ВО ВРЕМЕНИ
11.1. Механизм усталостного разрушения
Элементы конструкций и деталей машин, подвергающихся действию
усилий, переменных во времени и повторяющихся большое число
. раз, разрушаются внезапно, без заметных остаточных деформаций
при амплитудных значениях напряжений, меньших ов (или даже от). При
этом разрушение происходит не сразу. На основании этого существовала
гипотеза, что металл "устает", изменяет свою структуру, из пластического
состояния переходит в хрупкое; отсюда появился термин - "усталостное"
разрушение.
В действительности при переменных напряжениях принципиальных
изменений в структуре материала не наблюдается, происходит процесс
постепенного накопления повреждений, который приводит к
образованию микроскопических трещин. Длина трещин увеличивается, они
объединяются, образуя первую макротрещину (протяженностью порядка
0,1...0,5 мм). Трещина, являясь концентратором напряжений, развивается
и ослабляет сечение, что приводит к внезапному разрушению. Процесс
постепенного накопления
повреждений под действием переменных во
времени напряжений, приводящий к
образованию трещин, их развитию и
разрушению материала, называется
усталостным разрушением
(усталостью).
Усталостные изломы имеют
следующие характерные участки (рис. 11.1):
1 - фокус излома и очаг разрушения;
2 - вторичные ступени и рубцы; 3 -
усталостные линии; 4 - зона
ускоренного развития излома; 5 - зона излома.
Рис. 11.1. Характерные участки фокУс излома " малая локальная зона,
усталостных изломов близкая к точке, в которой формирует-
ся начальная макроскопическая трещина усталости и откуда начинается
ее развитие; фокус излома располагается в достаточно тонком
поверхностном слое материала в местах концентрации напряжений или
сосредоточенных дефектов. Очаг разрушения- малая зона, прилегающая к фокусу
излома; соответствует начальной макроскопической трещине усталости.
В зоне развивающейся трещины усталости наблюдаются характерные
усталостные линии, волнообразно расходящиеся от очага разрушения.
Форма усталостных линий зависит от конфигурации детали и характера
ее нагружения. Если происходит зарождение нескольких трещин из
разных фокусов, то при их последующем слиянии на поверхности излома
образуются ступеньки и рубцы. Участок ускоренного развития излома
является переходной зоной между участком собственно усталостного
развития магистральной трещины и зоны долома; образуется
непосредственно перед разрушением. В зоне долома наблюдаются характерные
признаки макрохрупкого разрушения материала.
После образования зародыша трещины ее развитие определяется
характером распределения напряжений. Если возникновение трещины
вызывается главным образом касательными напряжениями, то ее
развитие происходит под действием нормальных напряжений.
11.2. Характеристики сопротивления усталости
Тжсмотримрегулярноенагружение-натружеше, характеризующееся
периодическим законом изменения нагрузок или напряжений с одним
максимумом и одним минимумом в течение одного периода при
постоянстве параметров цикла напряжений за все время испытаний или
эксплуатации. Циклом напряжений называется совокупность
последовательных значений переменных напряжений за один период процесса их
изменения. Цикл напряжений характеризуется следующими величинами:
• максимальным (наибольшим по алгебраической величине)
напряжением цикла отах (ттах);
• минимальным (наименьшим по алгебраической величине)
напряжением цикла omin (xmin).
Среднее напряжение цикла ат и амплитуда цикла оа определяются по
формулам:
„ _ (gmax + qmin) „ _ (°max," amin)
Коэффициентом асимметрии цикла г называют отношение
минимального напряжения цикла к максимальному: г - omin/omax. Для постоянной
215
бГОА
Рис. 11.2. Типы циклов
нагрузки г = 1, для симметричного цикла г = -1. Цикл называется
симметричным, когда напряжения отах и omin равны по величине и
противоположны по знаку. Типы циклов:
асимметричный со средним растягивающим напряжением (ош > 0)
(рис. 11.2, а);
пулъсационныи (отнулевой) со средним растягивающим напряжением
(/• = 0, от>0) (рис. 11.2,6);
симметричный (г = -1, ош = 0) (рис. 11.2, в);
пулъсационныи со средним сжимающим напряжением (ow < 0)
(рис. 11.2, г);
асимметричный со средним сжимающим напряжением (от < 0)
(рис. 11.2,д).
Усталостное разрушение может наступать при напряжениях,
значительно меньших предела текучести и даже предела
пропорциональности. В этом случае необходимо проводить испытания на усталость,
в которых определяются такие характеристики, как предел выносливости
и циклическая долговечность (ГОСТ 25.502-79).
Предел выносливости - значение максимального по абсолютной
величине напряжения цикла, вызывающего усталостное разрушение при
числе циклов, равном базе испытания NQ. Для металлов и сплавов база
испытания при определении предела выносливости принимается равной
107 циклов. Под долговечностью N понимают число циклов до
образования трещины определенных размеров или до разрушения образца. Предел
выносливости обозначается через ог, где г - коэффициент асимметрии
216
*таЛ
Л,
I
-4--
Рис. 11.3. Кривая усталости (кривая Вёлера)
цикла. Например: о_{ - предел
выносливости при
симметричном цикле, о0 - при пуль-
сационном (отнулевом).
Усталостная микротрещина
возникает в малом
субмикроскопическом объеме материала
и ее возникновение зависит от
распределения
микроскопических и субмикроскопических
дефектов. Их распределение по
объему материала следует
законам распределения
случайных величин. Существенное
влияние оказывает и технологический фактор - таким образом можно
говорить о статистической природе явления усталости, что объясняет
большой разброс экспериментальных результатов.
Кривая усталости (кривая Вёлера) в координатах (omax, N ),
полученная из опытов при симметричном цикле напряжений, приведена
на рис. 11.3, где отах - максимальное напряжение цикла, N - число
циклов нагружения до разрушения. У черных металлов (сталь, чугун) при
нормальных температурах кривая усталости имеет горизонтальную
асимптоту (кривая 1), соответствующую физическому пределу
выносливости o_j. Для цветных металлов и сталей при повышенных температурах
и в коррозионных средах достигнуть физического предела выносливости
не удается (кривая 2). Здесь показаны некоторые характеристики
усталости: условный предел усталости oaN, ограничиваемый заданным
числом циклов нагружения ЛГ; долговечность N0 при заданном значении
напряжения.
При высоких уровнях напряжения, когда разрушение сопровождается
заметными пластическими деформациями, имеет место так называемая
малоцикловая усталость (10 < N < 106); при более низких уровнях
циклических напряжений (N >. 106) усталость называется многоцикловой.
Зависимость оа = /(ош) для предельных циклов (приводящих к
усталостному разрушению при данной базе испытаний) называется
диаграммой предельных амплитуд напряжений (рис. 11.4). Луч, выходящий
из начала координат этой диаграммы, является геометрическим местом
точек, характеризующих циклы с одинаковой асимметрией (при
постоянном р постоянным остается коэффициент асимметрии г); такие
циклы называются подобными. В пределах области, ограниченной кривой
ABC, не наблюдается усталостного разрушения при заданном числе
циклов N <; N0. Предел выносливости любого асимметричного цикла
217
1
«а
А
т
0
If
|< tfr >| rffl
|^ Z_! 1 а»
c
<*m
может принимать значения в
интервале о_{ <ог< ов. Если
предел выносливости по
величине близок к временному
сопротивлению ов, то он
может быть выше предела
текучести материала от. В этом
случае уже во время первого
цикла изменения напряжений
появляются пластические
деформации. Для исключения
возможности их появления
необходимо поставить
условие отах < оТ. В дополнение к
Рис. 11.4. Диаграмма предельных амплитуд
напряжений
кривой предельных амплитуд
на рис. 11.4 проведена
вспомогательная прямая EF, отсекающая на координатных осях отрезки,
равные пределу текучести. Рассмотрим характерные области L..4. В
области 1 не наблюдается пластических деформаций и усталостного
разрушения. В области 2 имеет место усталостное разрушение при N <
< N0, происходящее в пределах упругих деформаций. В области 3 уже во
время первого цикла нагружения появляются пластические деформации,
однако усталостного разрушения при N < NQ не происходит. В области
4 усталостное разрушение сопровождается пластическими деформациями,
Существуют различные схематизации зависимости оа =/(от) области
безопасных значений напряжений оа и от (область 1).
Приведем наиболее распространенные из них.
• Формула Серенсена - Кинасошвили:
- *ИМ, ♦ = (2а_, - о0)/о(
о>
(11.1)
где о0 - предел выносливости для пульсационного цикла; ф -
коэффициент влияния асимметрии цикла на предельную амплитуду. Для
углеродистых сталей ф = 0,1 ...0,2, для легированных сталей и сплавов ф = 0,15...0,32.
При кручении обычно принимается фт = 0,5фа.
• Формула Хейвуда:
°а = a-i0 " а*/°в)
ф + ±-51(2 + ат/ав)(1 -Ф)
, (р = о_,/ав, (Ц.2)
где ов - временное сопротивление.
• Формула Биргера:
218
= а.,(1
>„)
1/2
(И.З)
Для материалов с высоким относительно ов пределом выносливости
o_j и отношением oJob ъ 0,8 предпочтительнее использовать формулы
(11.2) и (11.3). При onJoB > 0,3 уравнение (11.1) дает завышенные значения
предельных амплитуд (в расчетах это идет в запас прочности).
11.3. Факторы, влияющие на сопротивление усталости
В расчетах на прочность при напряжениях, переменных во времени,
используют характеристики сопротивления усталости материала,
полученные из эксперимента при симметричном цикле изменения
напряжений на стандартных образцах с круговым или прямоугольным
поперечным сечением. Для деталей значение предела выносливости о_1д,
как правило, в 2-6 раз меньше предела выносливости o_j гладких
полированных лабораторных образцов из такого же материала. Эта
разница количественно оценивается коэффициентом снижения предела
выносливости ЛГ, который учитывает влияние основных факторов на
сопротивление усталости:
К =
(11.4)
-U
По ГОСТу 25.504-82 К определен для:
• растяжения - сжатия и изгиба
л: =
к
1
К
do
к>
Fa
KVKA
(П.5)
• кручения
(п.6)
Основными факторами, влияющими на сопротивление усталости,
являются:
• концентрация напряжений (К0, КТ)\
• масштабный фактор, т.е. влияние абсолютных размеров детали
(KdoKdx)>
• качество обработки поверхности (KFa, KFx);
• технологические методы поверхностного упрочнения деталей (Kv)\
219
• технологическая анизотропия материала (Л:А);
• эксплуатационные факторы (температура, коррозия, частота
нагружения, облучение и др.).
Влияние концентрации напряжений. Концентрацией напряжений
называют увеличение напряжений в местах резкого изменения очертания
и размеров детали по сравнению с номинальными. Уровень
концентрации напряжений определяется теоретическим коэффициентом
концентрации ct0 = omax/aHOM, где оном - номинальное напряжение. Как правило,
К0 < а0 и КТ < ат, что отражает явление так называемой неполной
чувствительности материала к концентрации напряжений.
Коэффициенты Ка, Кх и aa, ат связаны между собой эмпирическими зависимостями:
К = 1 + q(aa - 1), Кх = 1 + д(ах - 1),
(И.7)
где q - коэффициент чувствительности материала к концентрации
напряжений, зависящий от свойств материала и типа концентратора. На
рис. 11.5 приведена зависимость коэффициента q для растягиваемой
стальной пластинки с двумя выточками от радиуса выточки р и от
отношения предела текучести от к пределу прочности ов.
Для цветных металлов и аустенитных сталей q « 1 (они
малочувствительны к концентраторам напряжений). Чугун практически
нечувствителен к внешним концентраторам (q ~ 0). Чувствительность сталей к
надрезу увеличивается с увеличением их прочности. Величина q не
является константой материала, она уменьшается с увеличением уровня
напряжений из-за
возрастающего влияния пластических
деформаций. В приближенных
расчетах принимают: для
литых материалов q = 0,1...0,2;
для малоуглеродистых и
жаропрочных сплавов q =
= 0,2...0,4; для алюминиевых
сплавов q = 0,3...0,5; для
легированных сталей q = 0,6...0,8;
для титановых сплавов q =
= 0,8...0,9.
Влияние абсолютных
размеров детали. С увеличением
диаметра гладких образцов их
пределы выносливости
снижаются. Это объясняется
влиянием металлургического, техно-
0,8
0,6
о,ь
о,г
0,8^^~~~~~
[ / /Уо& .
Г/ // У^5
Y- i i
г-»
J L 1
О 12 3 15 J),mh
Рис. 11.5. Зависимость коэффициента
чувствительности материала от радиуса
выточки растягиваемой пластины
220
логического и статистического факторов. Выносливость материалов с
увеличением размеров образцов или деталей существенно уменьшается
при испытании гладких образцов на изгиб и кручение и мало зависит
от размеров при растяжении и сжатии. Выносливость надрезанных
образцов падает с увеличением размеров при любом виде деформации.
Эффективный коэффициент концентрации Ка (Кт) зависит не только
от q и а0 (ат), но и от градиента напряжений по сечению, т.е. изменение
диаметра образца существенно влияет на предел выносливости, если при
этом меняется градиент напряжений. Влияние размеров на К0 (Кх) при
неравномерном распределении напряжений по сечению является
следствием локализации зон максимальных напряжений по сечению
образца.
Влияние металлургического фактора заключается в ухудшении
механических свойств металла с ростом размеров заготовки, оно
учитывается коэффициентом Kda = Kv Для легированных сталей:
Кх = 1 - 0,21g(rf/rf0), d * 150 мм;
Кх = 0,74, d > 150 мм,
где d0 = 7,5 мм - диаметр гладкого лабораторного образца; d- диаметр
рассчитываемой детали. Для углеродистых сталей принимается Кх = 1.
Технологический фактор обусловлен упрочнением материала и
остаточными напряжениями, появляющимися в результате его
механической обработки. Разработаны специальные приемы, позволяющие
существенно снизить влияние этого фактора.
Статистический масштабный фактор характеризуется
коэффициентами Kda и Kdx\ в ГОСТе 25.504-82 рекомендуется принимать Kda = Kdx =
= Кь где
Г1 — (1 — o?J/cL,)0,771g(</4) d * 150 мм,
\o^]lo_x d > 150 мм.
Здесь величина o?J - предел выносливости при растяжении (сжатии). При
отсутствии экспериментальных данных рекомендуется принимать
o?J/oM = 0,8. Статистический масштабный фактор обусловлен наличием
микротрещин, неоднородностей, имеющих случайный характер
возникновения и распределения по объему материала.
В местах напрессовки деталей на валы или оси возникает
концентрация напряжений и коррозия трения, так называемая фреттинг-коррозия,
221
которая приводит к резкому снижению предела выносливости в 3-6 раз
и оценивается коэффициентом Ка> зависящим от типа соединения
(посадки), размеров вала и предела прочности ов материала. Причинами
столь резкого снижения пределов выносливости деталей в зонах контакта
являются концентрация напряжений у края контакта и физико-
химические процессы (фреттинг-процессы), протекающие на стыке двух
сопрягаемых деталей при малых взаимных циклических смещениях.
Механические процессы износа при фреттинге сопровождаются
химическими процессами взаимодействия поверхностных слоев и
отделившихся частиц износа с окружающей средой. Кроме того, в местах
контакта происходят процессы электроэрозионного разрушения.
Влияние качества обработки поверхности. Механическая обработка
оставляет на поверхности детали неровности, являющиеся
концентраторами напряжений, что заметно снижает сопротивление усталости. Кроме
того, при обработке резанием поверхность упрочняется и возникают
остаточные напряжения. Суммарное влияние этих факторов на величину
пределов выносливости оценивается коэффициентами KFo и KFx в
зависимости от предела прочности ов и показателя шероховатости Rz:
KF = 1 - 0,221gfo
V 20
KFx = 0,575^о + 0,425.
При низком качестве обработки поверхности предел выносливости
деталей из легированных сталей может снижаться на 50 % и более.
Влияние технологических методов поверхностного упрочнения. К
методам поверхностного упрочнения относятся:
• поверхностное пластическое деформирование (обдувка дробью,
обкатка роликами, алмазное выглаживание);
• химико-термические методы (цементация, азотирование,
цианирование);
• поверхностная закалка с нагревом токами высокой частоты;
• лучевые методы (лазерная обработка, ионная имплантация,
обработка электронным лучом).
Перечисленные методы позволяют повышать предел выносливости
в 2-3 раза; эффективность этих методов оценивается коэффициентом Ку.
Причинами увеличения пределавыносливости методами поверхностного
упрочнения являются остаточные сжимающие напряжения в
поверхностном слое и повышение прочности материала при его поверхностной
обработке.
222
Влияние технологической анизотропии материала. Коэффициент
анизотропии КА, приведенный в табл. 11.1, учитывают, если первое
главное напряжение о{ при изгибе и растяжении (сжатии) направлено
перпендикулярно к направлению прокатки материала. При деформациях
кручения анизотропия материала не учитывается.
11.1. Влияние технологической анизотропии материала на выносливость
Предел прочности материала ов, МПа
ибОО
600...900
900... 1200
>1200
Значения коэффициента анизотропии
0,90
0,86
0,83
0,80
11.4. Прочность при регулярном многоцикловом нагружении
Линейное напряженное состояние. При определении запасов прочности
элементов конструкций и деталей машин, находящихся под действием
переменных во времени напряжений, используют коэффициенты запаса
прочности по напряжениям и по долговечности. Коэффициент запаса
прочности по напряжениям па = аш/ал, где о, - предельное разрушающее
напряжение; оа- амплитуда цикла. Коэффициент запаса по
долговечности (числу циклов) nN = NJN, где N9 > 10 - число циклов до разрушения
(циклическая долговечность); N- эксплуатационное число циклов. Для
линейного напряженного состояния при симметричном цикле
напряжений из предельной диаграммы усталости (см. рис. 11.4) следует, что
а„ = о_jд. Предел выносливости детали о_jд определяют с учетом всех
факторов, снижающих его, по сравнению с пределом выносливости
лабораторных образцов:
где К вычисляется по формуле (11.5) или (11.6). Так как коэффициент К
определяется в зависимости от размеров детали и заранее неизвестен, то
расчет на прочность носит поверочный характер: сначала задают
223
размеры поперечного сечения детали или приближенно их оценивают,
затем вычисляют коэффициент запаса прочности п0 и проверяют
выполнение условия прочности:
п = -^ = * [п]. (\\ \Х)
а а
Здесь [л] - нормативный коэффициент запаса прочности.
При асимметричном цикле нагружения коэффициент запаса
прочности вычисляют по формуле
(11.14)
Ко + il/a
а т "п
где ф определяется по (11.1). Запас прочности, оцениваемый
соотношением (11.14), называется запасом усталостной прочности по подобному
циклу.
При асимметричных циклах нагружения наступление предельного
состояния может быть связано с появлением пластических деформаций
(области 3 и 4 на рис. 11.4). В этом случае кроме коэффициента па
необходимо определить коэффициент запаса прочности по текучести:
(11.15)
+ сг
из коэффициентов nQ и пх выбирается наименьший.
При расчетах на кручение (чистый сдвиг) проверочный расчет на
прочность (вычисление коэффициента запаса ит) проводится
аналогично.
Сложное напряженное состояние. Рассмотрим упрощенное плоское
напряженное состояние (рис. 11.6), возникающее, например, в стержне
при совместном действии изгиба и кручения или растяжения (сжатия) и
кручения. Предположим, что напряжения о и т меняются по
симметричному циклу синхронно и синфазно (т.е. с одинаковой частотой и фазой),
как показано на рисунке. Условие наступления предельного состояния
записываем, как и для статического нагружения, используя один из
критериев прочности. Например, по критерию максимальных
касательных напряжений для эквивалентной амплитуды нормальных напряжений
при разрушении имеем:
-Я,
, + 4<р = а.]д1 (11.16)
224
6Xi
б \\ II б
Рис. 11.6. Изменение нормальных и касательных напряжений во времени
где оа и т - предельные значения амплитуд нормальных и касательных
напряжении по усталостному разрушению.
Лучшее приближение к опытным данным дает уточненный критерий
максимальных касательных напряжений:
К
р + YVp = °-1д>
Y = о.|я/т-1я-
(11.17)
В случае пропорционального нагружения, когда о = иоа, т = ита>
коэффициент запаса прочности при одновременном действии
нормальных и касательных напряжений находится по формуле
-1д
/
2 , 2
°а + У\
(11.18)
Если ввести коэффициенты запаса прочности отдельно по нормальным
па = о_1д/оа и касательным ит = т_|д/та напряжениям, то общий
коэффициент запаса прочности определяется формулой Гафа-Полпарда:
1
1
1
(11.19)
ИЛИ
п =
ф
225
В общем случае (объемное напряженное состояние) при синхронном
и синфазном изменении напряжений для вычисления амплитуды
эквивалентного симметричного цикла используют критерий Губе-
ра-Мизеса. Коэффициент запаса прочности вычисляется по формуле
" у „ , -=' (11.20)
^/1/2[(а1а - о2а)2 + (а2а - а3а)2 + <аи - а3а)2]
где о1а, о2а, о3а - амплитудные значения напряжений на главных
площадках. Формулы (И. 16)...(11.20) обобщаются также на случай
асимметричных циклов и несинхронного и несинфазного изменения
напряжений.
11.5. Расчеты на прочность при малоцикловом нагружении
Характеристики сопротивления малоцикловой усталости. При
многоцикловом усталостном разрушении, рассмотренном в предыдущих
параграфах, деформации материала являются упругими. Разрушение
происходит в местах концентрации напряжений (как результат развития
трещины) и носит характер хрупкого разрушения - без заметных
пластических деформаций. Другим видом усталости является малоцикло-
ваяусталость. Разрушение от малоцикловой усталости - это разрушение
в условиях повторного упругопластического деформирования с числом
циклов до разрушения, меньшем 105.
Характер разрушения при малоцикловой усталости зависит от
способности материала к накоплению пластических деформаций при
циклическом деформировании. Циклически стабильными называются
материалы, остаточные деформации в которых не меняются во всех
циклах. Для циклически разупрочняющихся материалов характерны
увеличение остаточных деформаций и рост суммарной пластической
деформации. Если остаточная деформация уменьшается от цикла к циклу,
а суммарная пластическая деформация стремится к некоторому
предельному значению, то такой материал называется циклически
упрочняющимся.
226
Рис. 11.7. Петли гистерезиса:
а - мягкое нагружение; б - жесткое нагружение
Процесс упругопластического деформирования при малоцикловом
нагружении исследуется путем построения петель гистерезиса в
координатах напряжение - деформация. Схематическое представление
таких петель показано на рис. 11.7, где цифрами отмечены номера циклов
нагружения. Мягкое нагружение - циклическое нагружение, при котором
в процессе испытания средние и амплитудные значения циклических
напряжений сохраняют свои
исходные значения. При
жестком нагружении остаются
постоянными средние и
амплитудные значения циклических
деформаций.
Связь между напряжениями
и деформациями при
циклическом нагружении за пределами
упругости выражают
диаграммы упругопластического де-
формирования. На рис. 11.8
приведена диаграмма для
первого симметричного по
напряжениям цикла. По оси абсцисс
отложено полное удлинение е,
по оси ординат - напряжение
а. Напряжения и деформация в Рис п 8 Диаграмма упругопластического
исходном нулевом полуцикле деформирования для первого симметричного
на участке ОА обозначены сГ> по напряжениям цикла
227
и е®\ После достижения напряжения о^ и удлинения е^ происходит
изменение знака нагрузки - начинается разгрузка. Напряжение при
разгрузке уменьшаются в пределах упругости на величину о^ + от'
(где ат' - предел текучести после разгрузки). При дальнейшем нагружении
сжатием в точке С достигается напряжение о^ = </ ' (в силу симметрии
цикла нагружения). Участок кривой деформирования ABC характеризует
первый полуцикл. В точке D первый цикл заканчивается. При
малоцикловой усталости длительность нагружения исчисляют в полуциклах (к =
= N12). Величина BD = б^ - деформация пластического гистерезиса в
первом полуцикле, определяемая как разность пластических деформаций
в нулевом (растяжение) и в первом полуциклах (сжатие). Поэтому
величина б*1* - это размах (удвоенная амплитуда), б*1) = 2е®, где еа -
амплитуда пластической деформации. Пластическая деформация
удлинения, накопления в нулевом полуцикле ОВ, может быть больше DB,
и их разность OD = ен(1) - односторонне накопленная пластическая
деформация за первый цикл. Новый, второй цикл, начинается в точке
D, и он в целом будет смещен по отношению к первому циклу по оси
абсцисс на величину ен(1).
Предел текучести после разгрузки из точки А меньше исходного
предела текучести (о*0 < о*0)). Снижение предела текучести при
реверсивном (изменяющемся по знаку) нагружении называется эффектом
Баушиигера.
Причиной изменения пределов упругости, пропорциональности и
условного предела текучести при реверсивном нагружении являются
остаточные ориентированные микронапряжения, возникающие в
предшествующей пластической деформации; они способствуют более
раннему возникновению пластической деформации при повторной
нагрузке другого знака.
Для описания свойств диаграммы циклического деформирования
используются оси координат с началом в точке разгрузки А для первого
полуцикла, в точке С- для второго полуцикла и т.д. Напряжения в этих
координатах обозначают через s, деформации через е. Относительные
напряжения и деформации вводятся следующим образом: о = oloT, е =
= е/ет, s = s/oT, с = е/ет, где отиет- предел текучести и соответствующее
ему значение деформации в нулевом полуцикле.
Соотношение
228
5<» = о*» - 2,
связывающее предел текучести при реверсивном нагружении с уровнем
предшествующего напряжения, где о*0 - предел текучести в первом
полу цикле, было предложено Мазингом. Для первого полуцикла
нагружения справедлив принцип Мазинга:
J= 2Де/2), (11.21)
где функция Де/2) соответствует функции/^) в исходном нагружении.
В относительных координатах уравнение (11.21) для области упругой
деформации имеет вид г{к) = sik), а для области упругопластической
деформации - e(fc) = sik) + г^. В первом приближении t^k) * 6(*\ т.е.
пластическая составляющая деформации приданном уровне напряжений
равна ширине петли гистерезиса, которая образовалась бы после
разгрузки от этого уровня напряжений. Уменьшение ширины петли
характеризует повышение сопротивления циклическим пластическим
деформациям, т.е. циклическое упрочнение, а увеличение ширины петли -
уменьшение этого сопротивления, т.е. циклическое разупрочнение.
Эксперименты показывают, что 6(fc) может быть задана в виде:
• для упрочняющихся материалов
1{к) = 6(1)/ЛГа; (11.22)
• для разупрочняющихся материалов
Ь{к) = 6(,)ехр[Р(* - 1)], (П.23)
где К- число полуциклов нагружения; аир- коэффициенты, зависящие
от свойств материала; 6(1) - ширина петли гистерезиса в первом
полуцикле. Ширина петли 6(1) связана с величиной исходной деформации
6(,) = А(е^ - 1), (П.24)
где ё(0) определяется по уравнению исходной кривой деформации
нулевого полуцикла; А - постоянная материала. Уравнения (11.22)...
(11.24) отражают полуцикловую трансформацию диаграммы деформиро-
229
вания. Предельные изменения
обобщенной диаграммы в
процессе циклического нагруже-
ния могут быть представлены
в соответствии со схемой,
приведенной на рис. 11.9.
Материалы, упрочняющиеся при
циклическом нагружении,
переходят в состояние, когда
зависимость между напряжениями и
деформациями становится
близкой к линейной (прямая
ОАВ). Диаграмма разупрочня-
ющихся материалов
приближается к диаграмме идеальной
пластичности (линия О АС).
Закономерности
малоциклового разрушения. В
зависимости от характера и значений
накопленных односторонних
деформаций различают квазистатическое, усталостное и смешанное
малоцикловые разрушения. Накопление односторонней деформации у
циклически анизотропных материалов приводит при мягком нагружении
к разрушению с образованием шейки без образования трещины. Такое
разрушение, называемое квазистатическим, возникает, когда
односторонне накопленная пластическая деформация достигает располагаемой
пластичности материала: е^ = zf. Располагаемая пластичность материала
определяется как
$пц
0
- /j"^ Т *я0в
[ Ч е
Рис. 11.9. Диаграмма деформирования в
процессе циклического нагружения
zf = In-
1
1 -Фв
, или zf
ln-
1
1 -ф
(11.25)
где фв и \|/ - коэффициенты уменьшения поперечного сечения,
соответствующие достижению предела прочности или разрыву образца.
• Усттостноемтоцикловоеразрушение-фъзфуштшЪеь выраженно-
<*)
:<*>
го накопления односторонних деформаций. При этом е1' или г{
составляют не более 0,1 от деформаций при статическом разрыве.
• Смешанное малоцикловое разрушение - разрушение, при котором
значения односторонне накопленных деформаций приблизительно равны
If * (0,1-0,9)8,-.
230
Как было установлено (Мэнсон -Коффин), малоцикловая прочность
при жестком нагружении определяется с помощью характеристик
пластичности статического разрушения. Зависимость долговечности N,
от величины пластической деформации в цикле нагружения г имеет вид
eP*/M' = c/4ln7-4;' (Ц-26)
где т - показатель пластичности, может быть принят в первом
приближении в пределах 0,4...0,6.
Если при малоцикловом жестком нагружении прочность коррелирует-
ся в основном с характеристиками пластичности материала при
однократном разрушении, то в условиях мягкого нагружения основное
влияние оказывают статические прочностные свойства. Уравнение
кривой усталости при мягком нагружении приближенно представляется
в следующем виде:
oN- = obN:, (11.27)
где v = lg(oB/o_1)/lg(iV0 WB); NBn Na - число циклов до разрушения
соответственно на уровнях пределов прочности и усталости материала.
Для ряда конструкционных материалов в первом приближении можно
принять значения для NB и Na соответственно 10 и 106.
Деформационно-кинетические критерии малоцикловой прочности.
Деформационно-кинетические критерии малоцикловой прочности
основаны на суммировании усталостных и квазистатических
повреждений. Осуществляется линейное суммирование повреждений, вызванных
циклическими и односторонне накопленными деформациями.
Доля усталостного повреждения
a rdN
/CUV
Ж'
i "л
где N— число циклов нагружения; N*- число циклов, определяемое при
заданной в цикле деформации по кривой усталости в условиях жесткого
нагружения; Nj- число циклов до разрушения (появления трещины).
231
Доля квазистатического повреждения
й - Г Ле
J 8,
О /
где е- односторонне накопленная в процессе статического и
циклического нагружения деформация; е^- односторонне накопленная деформация
к моменту разрушения; е^- располагаемая пластичность.
Предельное состояние по условиям малоциклового разрушения
наступает при
<*/♦<*.
1 /» о /
Условия прочности по критериям усталостного и квазистатического
разрушения
1 /' о /
Расчетная долговечность, вычисленная по критериям (11.28) и (11.29),
как правило, больше фактической. Для точной оценки накопленного
усталостного повреждения следует использовать параметры
фактической кривой усталости, полученной с учетом температурных и
временных особенностей.
Коэффициенты запаса при малоцикловом нагружении. Несущую
способность элементов конструкций при малоцикловом нагружении
определяют либо по предельным, соответствующим образованию
трещин, местным деформациям (напряжениям) для числа циклов, равных
эксплуатационным, либо по предельным числам циклов для деформаций
(напряжений) от эксплуатационных нагрузок. Предельные состояния по
образованию трещин могут создаваться в зонах концентрации
напряжений - от силовых и температурных нагрузок, вне зон
концентрации - от действия местных температурных напряжений.
Коэффициент запаса прочности по местным деформациям еа
(напряжениям оа) для заданного режима нагружения вычисляют по
формуле
пе = e*lel\ па = aj<^t
232
где е* (о*) - разрушающие амплитуды местных деформаций
(напряжений), устанавливаемые для эксплуатационного числа циклов N = N3 й
< 105; el (<£) - амплитуда местных деформаций (напряжений) в наиболее
нагруженной при эксплуатации зоне рассчитываемого на прочность
конструктивного элемента.
При заданных эксплуатационных уровнях деформаций (напряжений)
определяют коэффициент запаса по долговечности
nN = N/N\ (11.30)
где N - разрушающее число циклов (N <, 10 ); N3 - эксплуатационное
число циклов нагружения.
233
Глава 12
ОСНОВЫ МЕХАНИКИ РАЗРУШЕНИЯ
12.1. Общие сведения о прочности конструкций
и механике разрушения
Любая конструкция или элементы конструкции при определенных
условиях могут разрушаться, т.е. разделяться на части. Возможно
частичное и полное разрушение тела. В зависимости от свойств
материала конструкции, условий нагружения, температурных и других
условий окружающей среды различают хрупкое и вязкое (пластическое)
разрушение. Однако эти виды разрушения могут проявляться
одновременно или последовательно, начинаясь, например, с хрупкого и переходя
затем в пластическое.
Хрупкое разрушение происходит за счет возникновения и
распространения трещин, которые развиваются из незначительных дефектов и
микроскопических трещин до магистральных трещин критического
размера, что является причиной разрушения. При хрупком разрушении
скорость распространения трещины составляет 0,2...0,5 скорости
распространения звука, а излом имеет кристаллический вид.
Различают также квазихрупкое разрушение, которое происходит с
образованием пластической зоны перед фронтом трещины.
Вязкое разрушение происходит после существенной пластической
деформации, охватывающей весь (или значительный) объем тела и
является результатом исчерпания способности материала сопротивляться
пластическим деформациям. Скорость распространения трещины в этом
случае невелика (порядка 0,05 скорости звука), а излом имеет
волокнистый вид.
Особо следует выделить постепенное развитие трещины при
повторно-переменном циклическом нагружении; такому усталостному
разрушению предшествует накопление в материале конструкции
необратимых повреждений.
Особую значимость для практических приложений имеет хрупкое
разрушение, обусловленное быстрым распространением трещин при
средних по величине напряжениях, не превышающих предел текучести
234
материала и поэтому кажущихся безопасными. Кроме того, с точки
зрения прочности существенным является не только факт возникновения
трещины, но м темп ее роста (скорость распространения трещины).
Механика разрушения как составная часть механики деформируемого
твердого тела изучает законы разделения твердых тел на части под
действием нагрузок, исследует напряжения в окрестности трещин, изучает
условия развития трещин и их влияние на прочность конструкции.
12.2. Напряжения и перемещения в окрестности трещин
Основным понятием механики разрушения является трещина, которая
определяется как разрыв сплошности материала. Различают три
простейших типа деформации берегов трещины при действии различных
внешних нагрузок (рис. 12.1). При деформации растяжения по схеме /
образуется трещина нормального отрыва, когда поверхности трещины
смещаются (расходятся) в перпендикулярном направлении. При
деформации сдвига по схеме //образуется трещина поперечного сдвига,
при котором поверхности трещины смещаются поперек ее передней
кромки. При деформировании по схеме /// возникают трещины
продольного сдвига, при котором поверхности трещины смещаются вдоль
ее передней кромки.
Составляющие поля напряжений Ojk (J, k = х, у) у вершины трещины
(рис. 12.2) могут быть представлены формулой
Рис. 12.1. Типы деформации трещины:
/-нормального отрыва; //-поперечного сдвига; ///- продольного сдвига
235
Рис. 12.2. Поле напряжений у вершины трещины
У
шиш.
miuuh
где К - коэффициент интенсивности
напряжений у вершины трещины (его
размерность - Нм"3/2); г и 0 -
полярные координаты с полюсом в вершине
трещины и в плоскости,
перпендикулярной к кромке трещины; fk -
некоторая функция угла 6.
Обозначение коэффициента
интенсивности напряжений К производится
в зависимости от типа деформации
трещин: Kh КП, Кш.
Наибольший практический интерес
представляет трещина нормального
отрыва. Так, для узкой трещины
длиной 11 в тонкой пластине, которая
растягивается в направлении,
ортогональном трещине (рис. 12.3),
напряжения и перемещения, полученные методами теории упругости,
вычисляются по формулам:
тнтжигггггптн
Рис. 12.3. Трещина нормального
отрыва в тонкой пластине
*/ е. -
cos —I 1
2
y/lizr
. 0 . 30
sm — sin —
2 2
°y =
Kj e
——
cosy/I^ 2
. 9 . 36
+ sm — sin —
2 2
236
Кг I е
. б 30
sm — cos —
2 2 2
и =
*/(! + ц)
N
cos —I к - 1 + 2sin2 —
1% 2\ 2
(12.2)
К/0 + и)
N
— sin- fc + 1 - 2cos2-|;
2и 21 2 '
Здесь
1 + Ц
Kj^oyfrd (12.3)
- коэффициент интенсивности напряжений, который связан с
напряжением оу предельным соотношением
Kj = lim sJbCr о (г, 0),
в~0
(12.4)
откуда вытекает его физический смысл.
Как видно из формул, интенсивность поля напряжений в окрестности
вершины трещины в линейной постановке характеризуется единственным
параметром KIt являющимся функцией вида внешнего нагружения,
геометрии пластины и размеров трещины.
Формулы, аналогичные (12.3), получены и для других схем
нагружения:
Kj = о\/я7, КП = Tyfnl, Кш = xyfid.
(12.5)
Для трещин другого расположения или пластин ограниченных
размеров коэффициенты интенсивности напряжений записываются в виде
Kj = /гоу/тГ19 Кп = fHxy/ni9 Кш = fjj^yfid,
где fj,/ц, fjjj - поправочные коэффициенты, выражения которых для
237
Рис. 12.4. Схемы расположения трещин и нагрузок
различных схем расположения трещин и нагрузок, показанных на
рис. 12.4, приведены в табл. 12.1.
12.1. Поправочные коэффициенты для К1у Кп, Кш
Схема нагружения и расположения
трещины
Неограниченная пластина при растяжении
с наклонной трещиной в середине
(рис. 12.4, а)
То же для полубесконечной пластины с
односторонней трещиной, (3 = тс/2
(рис. 12.4, 6)
Пластина шириной 2В с поперечной
трещиной посередине («) при растяжении и сдвиге
(по схеме II на рис. 12 1)
То же с двумя боковыми трещинами
(рис. 12.4, г)
Пластина шириной В и толщиной Я с
трещиной посередине при изгибе в своей
плоскости (рис. 12.4, 0)
Так же пластина при чистом изгибе
распределенным моментом т{ё)
Поправочный коэффициент
//=sin2p
//=1,12
// =
U = ///= ^
=///~ \
я/ 25
0,2В .*/
' Sin—~ А
те/ В Л
i*tg^
я/ 2В
// = — — v^y (о = ш/вн\
1 3v/6 Я2
ц. - коэффициент Пуассона
fj = 1 (о = 6т/Я2)
238
а)
i
Ъ
би 6* <
Щ: . 57 6л
к
3
2
1
0
« /±71 ,\
~\ -*-
\
\
- ч
-*»< ч\
117 -* \
- ч\ А
rf-*rP
То
Н№
1ПЛ
ост
инь
i
/
/
. 0\
-М
-\ «*—
\
\
л\
Г-+-6..
h6'
г
Толстые
пластины
Рис. 12.5. Области пластических деформаций:
а - плоское напряженное состояние (тонкие пластины); б - плоская деформация
(толстые пластины)
Как видно из формул (12.2), напряжения вблизи вершины трещины
весьма велики и при г - 0 стремятся к бесконечности как величина Г .
Однако с учетом пластических свойств материала у вершины трещины
образуется зона пластических деформаций на участке 0 й г й г . На
рис. 12.5, а показана область пластической деформации для случая
плоского напряженного состояния (тонкие пластины), а на рис. 12.5, б —
для случая плоской деформации (толстые пластины). Используя критерий
текучести Треска-Сен-Венана, находим:
_ (1 - 2ц)
2я
,* К
2яа?
(12.6)
Принимая коэффициент Пуассона ц = 0,3, получим, что (г,*/гр = 9, т.е.
при плоской деформации протяженность зоны пластической деформации
перед вершиной трещины почти на порядок меньше, чем при плоском
напряженном состоянии. Деформацию можно считать плоской
практически по всей длине трещины, если выполнены условия:
А > 2,5
к;
i >
к?
где h - толщина пластины.
239
12.3. Критерии хрупкого разрушения Гриффитса-Ирвина
Хрупкое разрушение конструкции при наличии начальных трещин
происходит за счет интенсивного развития трещин. Приложенная
внешняя нагрузка к конструкции с трещиной, имеющей начальную длину
2/, приводит к увеличению размеров трещин. При умеренных
напряжениях трещина увеличивается медленно. При достижении некоторого
критического значения 2/, (происходит быстрое, неустойчивое развитие)
трещина может привести к разрушению конструкции.
Потенциальная энергия упругой деформации в пластине с трещиной
и без трещины различна, так как на образование трещины затрачивается
определенная работа. Эта работа как разность потенциальных энергий
системы без трещины и с трещиной для случая нагружения, показанного
на рис. 12.3, равна
W = no2l2h/E.
Кроме того, для образования трещины нужно затратить
определенную работу на преодоление сил взаимодействия слоев. Обозначим через
у работу, которую необходимо затратить на образование единицы новой
поверхности. Величина у, являющаяся характеристикой трещиностойкос-
ти материала, называется поверхностной энергией разрушения. Суммарная
площадь берегов трещины равна 4/А, поэтому работа на ее образование
равна
Г = 4у/А. (12.7)
При росте трещины на величину 6/ высвобождается энергия
&W = Жы = 1*ЛА5/ (128)
Если эта энергия больше или равна дополнительной работе, затраченной
на продвижение трещины
6Г = |^6/ = 4уЛ6/, (12.9)
то рост трещины будет неустойчивым. Условие предельного равновесия
трещины имеет вид
240
6W = 6Г.
(12.10)
Критерий предельного рановесия (12.10) есть критерий Гриффитса,
согласно которому после подстановки (12.8) и (12.9) определяем
критическое напряжение при заданной начальной длине трещины
о. =
2Еу
(12.11)
Формула (12.11) (формула Гриффитса) получена для плоского
напряженного состояния; она определяет напряжения, при которых происходит
самопроизвольный, без совершения дополнительной работы внешними
силами, рост трещины. При заданной нагрузке о из формулы (12.11)
получим критический начальный размер трещины
= lEl
по2
L
(12.12)
который может привести к ее неустойчивому росту.
На рис. 12.6 приведена графическая иллюстрация зависимости
критического напряжения от длины трещины; штриховой линией отмечен
докритический рост трещины. Кривая a2Jt = const называется кривой
критического разрушения. В области ниже этой кривой рост трещины
энергетически невозможен. Однако, если трещина подросла (за счет
циклических нагрузок или за счет коррозии) и ее параметры
соответствуют кривой o\lm = const, трещина становится неустойчивой. Малые
возмущения приводят к выделению энергии деформации, большей, чем
требуется на работу разрушения, происходит самопроизвольное
движение трещины, которое носит динамический характер.
Запишем соотношение (12.11) через
коэффициент интенсивности
напряжений
к,
Величина
o^yftd = j2Ey.
c^L^const
re
JlE^
(12.13)
Рис. 12.6. Зависимость критического
напряжения от длины трещины
241
есть критический коэффициент
интенсивности напряжений, а
условие
*/**j
/С
(12.14)
определяет критерий предельного
равновесия Ирвина. Неравенство
означает безопасное состояние -
отсутствие роста трещины;
равенство - наступление
предельного (критического) состояния
равновесия, при котором трещина
получает возможность
распространяться. Характер
распределения напряжений вблизи вершины
трещины для различных значений
коэффициента интенсивности
напряжений показан на рис. 12.7;
как видно, рост нагрузки
приводит к пропорциональному росту
К, что в свою очередь означает
рост напряжений.
Коэффициент К1С является
одной из основных характеристик
механических свойств конструкционных материалов. Эта
характеристика, определяемая экспериментально, называется также трещиностойкос-
тью материала.
Критерий Гриффитса и критерий Ирвина эквивалентны между собой;
они отличаются лишь формой записи, хотя первоначально критерий
Ирвина в форме (12.14) был сформулирован независимо от
энергетических соображений. Критерии (12.10) и (12.14) есть две эквивалентные
формулировки критерия разрушения - энергетическая и силовая.
Аналогичные критерии можно сформулировать и для других схем
нагружения.
Еще одну формулировку критериев Гриффитса - Ирвина можно дать
в терминах обобщенных сил. Если рассматривать площадь, занимаемую
трещиной (S = 2lh), как обобщенную координату, то производная
Рис. 12.7. Распределение напряжений
вблизи вершины трещины
G
as
(12.15)
242
по формуле Лагранжа (9.33) имеет смысл обобщенной силы, затраченной
на продвижение трещины. По (12.8) находим, что
Е
или с учетом обозначения (12.3)
К1
G = -L. (12.16)
Е
В предельном состоянии условие (12.14) принимает вид
G = GICi (12.17)
где критическое значение обобщенной силы Grc, называемое вязкостью
разрушения, равно:
GIC = & - 2у. (12.18)
12.4. Критерии разрушения при наличии пластических зон
у трещин
При относительно высоких уровнях приложенных нагрузок и
достаточной пластичности материала в сечении с трещиной возникают
зоны пластической деформации, соизмеримые с остаточным сечением
детали. В этих случаях модели линейной механики разрушения
неприменимы.
Известно несколько критериев, применяемых в нелинейной механике
разрушения. Наибольшее распространение получил энергетический
критерий в виде
/ * JIC, (12.19)
в котором инвариантный энергетический интеграл / ("джи - интеграл")
может быть вычислен по формуле
/ \
I ды I v дт*
/ = Л Wdy - оуй(-^ ds + feotfetf—dxdy. (12.20)
J I дх ) ^ дх
г ч ' А
Здесь Г - контур интегрирования, окружающий вершину трещины, А -
область внутри контура Г; W - плотность энергии деформации, п( -
243
Оу,6у
нормаль к контуру Г, и-
перемещение точек на Г, а -
коэффициент линейного
температурного расширения; Г =
= Т\х, у) - температура. В
условии (12.19)//с~
экспериментально определяемая
критическая величина /-интеграла,
называемая упругопластичес-
кой вязкостью разрушения. Для
линейно-упругого состояния в
случае плоской деформации
известна зависимость
(1 - ii2)K?c = EJIC. (12.21)
Величина JIC связана с
раскрытием бс в вершине трещины
Рис. 12.8. Распределение напряжений и
деформаций вблизи вершины трещины с
учетом пластических деформаций:
1 - упругое асимптотическое решение; 2 -
упругое решение вне пластической зоны;
3 - напряжения в пластической зоне; 4 -
деформации в пластической зоне
Jrc = maT6c.
(12.22)
Эмпирически определяемый
коэффициент т, зависящий от
степени упрочнения материала
и схемы нагружения образца,
располагается в диапазоне 1 <
< т z 3.
На рис. 12.8 приведена иллюстрация распределения напряжений и
деформаций перед вершиной трещины при наличии зон пластических
деформаций.
Приближенно оценим радиус пластической зоны гТ для плоского
напряженного состояния (рис. 12.9, а), приравняв выражение для о в
формуле (12.2) при 0 = 0 к пределу текучести материала от:
(12.23)
Для пластины конечных размеров, подставляя значение Kj (см.
табл. 12.1), находим длину трещины с учетом пластической зоны:
/=/ + /■=/
(12.24)
244
/
s.
й
г,
«о
^
>-J
, -.
1 --
21
«г
^—J
Й
«"г
\
Рис. 12.9. Пластическая зона деформирования у вершины трещины:
а - трещина нормального отрыва; б - радиус пластической зоны и раскрытие
трещины
Подставляя эффективную длину трещины /т в (12.5), находим уточненное
значение коэффициента интенсивности напряжений
Я/ = Oy/n(f + гт).
(12.25)
Тогда перемещение v у вершины трещины при /• = гти0 = тгв
соответствии с (12.2) определяется выражением:
v =
NS***
(12.26)
Величина раскрытия трещины б равна удвоенному перемещению v
(рис. 12.9,6):
б = 2v
a:,(i + ц)
2-£ —(к + 1)
N
i + i
2
V°t/
(12.27)
12.5. Понятие о накоплении повреждений.
Линейное правило суммирования повреждений
Критерии Гриффитса - Ирвина устанавливают условия предельного
равновесия при постоянной нагрузке. Если нагрузка меняется во времени
циклически, то в пределах каждого цикла трещина подрастает и при
245
Рис. 12.10. Нестационарное нагружение в виде последовательности циклов
некотором числе циклов может достичь критического размера, при
котором ее дальнейший рост становится неустойчивым. Циклически
подрастающая трещина называется усталостной трещиной.
Начальные трещины при циклическом нагружении подрастают,
приводя к дополнительным повреждениям. В этом случае говорят о
накоплении повреждений. Повреждения могут быть вызваны не только
ростом усталостных трещин, но также износом, коррозией,
пластическими деформациями и рядом других причин. Разрушение конструкций
связано с необратимым накоплением повреждений в их элементах.
Рассмотрим процесс накопления повреждений на примере
усталостного разрушения при нестационарном нагружении, когда амплитуда
нагружения изменяется .во времени. Пусть процесс нагружения задан
напряжением o(t) в виде после-
K*0t
Рис. 12.11. Зависимость меры повреждений
от числа циклов нагружения
довательности блоков (циклов)
нагружения (рис. 12.10). В /с-м
блоке, содержащем Nk циклов
с периодом Тк, амплитудное
значение напряжений
обозначим через ок. С каждым
циклом или блоком нагружения в
системе происходит
накопление повреждений.
Введем меру повреждений
\|/(N) в зависимости от числа
циклов нагружения как неубы-
246
вающую функцию, принимающую значение i|j(0) = 0 в начале нагружения,
ф(ЛО = 1 при предельном значении N, числа циклов, соответствующем
усталостному разрушению (рис. 12.11). Введем также меру повреждений
фА,, вносимых /ом блоком нагружения.
Эту меру можно определить следующим образом:
Ф* = Nk/N*(°k). (12.28)
Здесь Nm(ok) - число циклов до разрушения при напряжении ок.
В простейшем случае процесс накопления повреждений можно
описать на основе линейного правила суммирования повреждений:
повреждения, вызванные циклами напряжений с амплитудой о-, не
зависят от состояния конструкции и последовательности загружения,
а суммируются с повреждениями от предыдущих циклов:
4>(Л0 = Е*у = EttTV (19.29)
Тогда условие усталостного разрушения принимает вид
Ф(Ю = t тгут = L (12.30)
где fc, - номер блока нагружения, на котором произошло разрушение.
Из условия (12.30) находится критическое число циклов
N. = t Ny
Линейное правило суммирования повреждений (12.29) применимо
также к общему случаю нагружения, реализация которого изображена
на рис. 12.12. В этом случае процесс нагружения разбивается на
интервалы с амплитудными напряжениями о,, о2,..., оп. Роль блоков
нагружения в формуле (12.30) играет число циклов Nj к моменту
разрушения, для которых амплитуда попадает в интервал о...
В заключение рассмотрим применение (12.29) к случайному процессу
нагружения. Процесс нагружения на рис. 12.12 можно считать одной из
возможных реализаций случайного процесса o(t). Подобная ситуация
характерна для реальных условий эксплуатации конструкций. Число
циклов нагружения N достаточно велико, оно исчисляется сотнями тысяч.
При больших N отношение числа циклов N: с амплитудой о- к общему
247
Рис. 12.12. Изменение напряжений при нагружении в виде случайного процесса
числу циклов определяет вероятность попадания амплитудного значения
напряжений в интервал о:
P(cj) = N/N.
Мера повреждения (12.29) для случайного процесса нагружения
принимает вид
У»1 N,(Pj)
а условие разрушения (12.30) определяет предельное число циклов
N. =
{j-iN.i°j)
248
Глава 13
ПЛАСТИНЫ И ОБОЛОЧКИ
13.1. Предпосылки теории изгиба пластин и оболочек
Напомним, что оболочкой называется тело, ограниченное двумя
поверхностями, расстояние между которыми (толщина А) мало по
сравнению с остальными размерами. Геометрическое место точек,
равноотстоящих от ограничивающих оболочку поверхностей, называется
срединной поверхностью. Пластина - частный случай оболочки, у
которой срединная поверхность есть плоскость. Отрезок прямой
единичной длины, перпендикулярный к срединной поверхности,
называется нормальным элементом или просто нормалью.
Классическая теория пластин и оболочек построена на системе
гипотез, аналогичных гипотезам в теории изгиба стержней, а именно:
- материал считается сплошным, однородным и изотропным;
- материал является линейно упругим;
- перемещения малы по сравнению с характерными размерами, а
деформации малы по сравнению с единицей.
Такую же роль, как гипотеза Бернулли в теории стержней, в теории
пластин и оболочек играет гипотеза Кирхгофа-Лява, гласящая: нормаль
остается нормалью и после деформации, т.е. нормальный элемент
остается прямолинейным и перпендикулярным к срединной поверхности,
а также не меняет своей длины.
Аналогично гипотезе о ненадавливании волокон вводится гипотеза
о ненадавливании слоев: слои, параллельные срединной поверхности,
не давят друг на друга.
Выберем систему координат, связанную со срединной поверхностью
оболочки, т.е. начало координат расположим на срединной поверхности,
оси Ох и Оу направим по касательной, а ось Oz - по нормали к
срединной поверхности. Тогда напряжения oz в соответствии с гипотезой
о нанадавливании слоев равны нулю. Кроме того, из гипотезы
Кирхгофа-Лява следует, что деформации yvz и у отсутствуют, так как при
наличии сдвигов относительно срединной поверхности нормальный до
деформации элемент не остался бы нормальным к срединной поверхности
249
и получил бы искривление. Отсюда следует, что напряжения xxz = х -
= 0. Следовательно, напряженное состояние в точках пластины или
оболочки является плоским, а обобщенный закон Гука примет вид:
Е
е- = -(°*-^°,)> *, еу-у
(а„-Ц°,), Чху = ^Г-
(13.1)
Разрешая эти соотношения относительно напряжений, получим
F Е
°- = "(е* + НО. о, = -<** + №х), *„ = Gy
i-ц2
У" У 1_Ц2 >
ху
ху
(13.2)
13.2. Изгиб пластин
Рассмотрим пластину, имеющую постоянную толщину h и находящу
юся под действием распределенной нагрузки р(х, у), нормальной к
срединной плоскости. В рамках гипотезы о малости перемещений
пренебрежем растяжением срединной плоскости, сдвигами и кручением
в этой плоскости, т.е. внутренними силовыми факторами Nx, Ny, N и
Nyx, Mz. Для определения остальных внутренних силовых факторов
воспользуемся методом сечений. Проведем два сечения вертикальными
плоскостями, ортогональными к осям Ох и Оу на расстоянии х и у от
начала координат (рис. 13.1). В сечении х = const вдоль оси Оу действуют
распределенные (т.е. отнесенные к единице длины) внутренние силовые
факторы: Qx - поперечная сила, Мх - изгибающий момент, Мух -
крутящий момент.
Аналогично в сечении у - const
действуют внутренние
силовые факторы Q , М и
Мх . Размерность
поперечных сил - Н/м, размерность
моментов - Н-м/м. На
рис. 13.1 показаны
положительные направления для
всех внутренних силовых
факторов. Если какой-либо
силовой фактор действует
в другом направлении, то
он считается отрицатель-
Рис. 13.1. Внутренние силовые факторы в ным.
сечениях пластины
250
dMxv
M„+—^dy
Mv+ *-dx
Рис. 13.2. Равновесие бесконечно малого элемента пластины
Двумя плоскостями, параллельным указанным выше и отстоящими
от них на расстоянии dx и dy, выделим элемент пластины (рис. 13.2).
Внутренние силовые факторы в сечениях х + dx = const и у + dy = const
по сравнению с силовыми факторами в исходных сечениях получат
бесконечно малые приращения, показанные на рисунке.
Учитывая, что внутренние силовые факторы распределены вдоль оси
Ох и Оуу а распределенная нагрузка р по площади элемента dxdy,
запишем уравнение равновесия в виде суммы проекций всех сил,
действующих на элемент, на ось Or.
QAy
' 9Q N
* дх
dy + Qydx
Qy
By
dy
dx+pdxdy = 0,
откуда после преобразований и сокращения на dxdy получаем первое
уравнение равновесия
£6, + £6j-
дх ду
(13.3)
Сумма моментов всех сил относительно оси 0'у\ параллельной оси Оу,
приводит к уравнению
251
МАу
Мх + ?-Ах
дх
Ау + МхуАх
дМг„
Л/„. + &Ау
Qx + ^Ax\Aydx
дх )
(
д<2
ду
ху ду
Ах +
Ах
Ах
- б,** у -pdxAy^ = 0.
В этом уравнении бесконечно малые первого порядка уничтожаются.
Пренебрегая бесконечно малыми высших порядков, получаем:
дх
дМ
ху
ду
= б,
(13.4)
Аналогично, записав сумму моментов всех сил относительно оси О'х',
получим уравнение
дМ
ух
дМ
дх
ду
У _
(13.5)
ди dv
——. g г: ■ у =
дх' у ду' Тд*
dv + ди
дх ду
Уравнения равновесия (13.3)...(13.5) содержат шесть неизвестных -
внутренние силовые факторы Qx, Q , Мх, М' М , М . Таким образом,
задача об изгибе пластин является статически неопределимой, и
уравнения равновесия нужно дополнить соотношениями, получаемыми
из анализа деформированного состояния элемента.
Деформации гу, гу, у связаны с перемещениями соотношениями
Коши:
Д** Дл/ Я\7 %11
(13.6)
Так как г2 = 0, что следует из условия нерастяжимости нормали по
гипотезе Кирхгофа-Лява, то из соотношения Коши ez = dwldz = 0 -
нормальное перемещение не зависит от координаты z и совпадает в
любой точке с нормальным перемещением w(x,y) (прогибом) срединной
плоскости.
Рассмотрим сечение пластины вертикальной плоскостью у = const в
недеформированном и деформированном состояниях (рис. 13.3). Точки
на срединной плоскости в процессе деформирования получили
вертикальное перемещение w(x, у). Точка А, отстоящая от срединной
плоскости на расстоянии z, переместится вверх на ту же величину, а
нормаль, проходящая через точку А, повернется на некоторый угол фх.
252
В соответствии с гипотезой
Кирхгофа-Лява нормаль
остается перпендикулярной к
деформированной срединной
поверхности, т.е. касательная
к срединной поверхности с
осью Ох также составит угол
cpY. Так как tgcpA. = dw/dx, а
деформации и перемещения
малы, то фл. * tg(pY = dw/dx. Точка
А получит перемещение в
направлении оси Ох, равное
-zm
-z-
dw
дх
Рис. 13.3. Перемещения в пластине при
изгибе
Объединив полученный результат с результатом анализа деформаций
в плоскости х = const, имеем:
и = -z-
, dw
дх''
V =
, dw
ду'
(13.7)
Подстановка (13.7) в соотношения Коши (13.6) приводит к зависимостям
компонент тензора деформаций от прогиба w(x, у), т.е.:
ev =
,d2w
дх2''
гу =
td2w
ду2
~ d2W
Уху дхду
(13.8)
Соотношения (13.8) дополняют уравнения равновесия до полной
системы уравнений. Путем введения обозначений
К =
d2w
дх2*
d2w .
ду2
•lz
d2w
дхду
соотношения (13.8).можно привести к виду
-zk % е = -zk . Y
х* у лп,у9 \ху
-Izk
ху
(13.9)
(13.10)
Под величинами кх и /: в случае малых деформаций понимают кривизну
сечений у = const и х = const деформированной срединной поверхности;
кху = кух = dcp}Jdx = д(рх/ду характеризуют закручивание поверхности.
Подставив выражения (13.8) для деформаций в соотношения
упругости (13.2), с учетом зависимости G = £/[2(1 + ц)], получим
253
Ez
d2W d2w
dx2 dy2
\
Ez
1-ц2
\
d2w d2W
dy2 dx2)
Ez d2w
(13.11)
ХУ 1 + |! дхЭу
В сечении x = const напряжение ox, действующее в точке А на
расстоянии z от срединной плоскости, создает момент (рис. 13.4)
dMxdy = -oxdydz-z.
Знак минус введен для согласования правил знаков моментов и
напряжений. Сократив на dy и проинтегрировав по толщине пластины,
имеем
Л/2
Мх = " / °xzdz-
-Л/2
Аналогично получим формулы для моментов М , М и М .
Окончательно выражения для внутренних силовых факторов через напряжения
имеют вид:
Л/2
Л/2
Mv
| oxzdz, Му = - | oyzdz,
-Л/2
-Л/2
Л/2
(13.12)
Mv
МУХ = " / Xxyzdz-
-Л/2
Равенство М - Мух следует из закона парности касательных
напряжений т = т ".
Подставляя (13.11) в (13.12) и
учитывая, что прогиб w(x,y) не
зависит от z, после
интегрирования по толщине пластины
получаем выражения для моментов
через прогиб:
Рис. 13.4. К определению
изгибающего момента
254
Л/ = D
d2w d2W i.
—- + Ц—- , M
\ дх2 ду2) У
Mxy = Myx = Z)(l - ц)
d2w d2w
{ ду2 dx2)
32w
дхду
Здесь
D = Eh3/[\2(\ - Ц2)]
(13.13)
(13.14)
- числовая характеристика, называемая цилиндрической жесткостью.
В обозначениях (13.9) выражения (13.13) имеют вид:
Л/
B{kx + yJcy), Му = D(lcy + \ikx), Мху = D(\-\i)kxy. (13.15)
Уравнения равновесия (13.4) и (13.5) позволяют с использованием
(13.13) выразить через прогиб поперечные силы. После элементарных
преобразований получим
Q = Z)A(Aw), Qy = D±(Aw).
дх у ду
В формулах (13.16) использовано обозначение
Aw
•2 ду у
дх'
(13.16)
(13.17)
для оператора Лапласа от функции w(x, у).
Подстановка (13.16) в оставшееся уравнение равновесия (13.3)
приводит к разрешающему уравнению изгиба пластин постоянной
толщины
DAAw =р.
(13.18)
Это уравнение называется уравнением Жермен-Лагранжа.
Повторенный, дважды оператор Лапласа АА называется .бигармоническим
оператором. Его развернутая запись имеет вид:
АА
Э4
а4
+ 2-
дх4 дх2ду2
JL
дх4
(13.19)
Решение уравнения в частных производных четвертого порядка
должно удовлетворять граничным (краевым) условиям, причем в каждой
точке контура, ограничивающего срединную плоскость пластины,
должно быть задано по два краевых условия. Рассмотрим типичные
255
*;
б)
*)
Рис. 13.5. Типичные краевые условия:
а - жесткое защемление; б - шарнирное опирание; в - свободный край
краевые условия для кромки х = О прямоугольной пластины. В случае
жестокого защемления (заделки) (рис. 13.5, а) должны быть наложены
ограничения на прогиб и угол поворота нормали:
„(О, у) = 0; ^ЬЛ
дх
= 0.
(13.20)
х=0
При шарнирном опирании, схематически изображенном на рис. 13.5, б
двойной линией, краевые условия имеют вид:
w(0, у) = 0, Мхф, у) = 0.
(13.21)
Используя первую формулу (13.13) и учитывая, что и>(0, у) не меняется
вдоль координаты у и, следовательно, все производные, в том числе и
вторая, от w(0, у) по у тождественно равны нулю, т.е. d2wldy2 = 0 при
х = 0, условия (13.21) можно переписать в виде
„(0, у) = 0; ^ЬЛ
дх'
= 0.
(13.22)
Ьс=0
На свободной кромке х = 0 (рис. 13.5, в) должны обращаться в нуль
три силовых фактора
Мх(0, у) = 0, бх(0, у) = 0, Мухф, у) = 0.
Однако, как показал Кирхгоф, два последних условия не являются
независимыми, они объединяются в одно
q: = qx
эм
ух _
ду
= о.
(13.23)
256
Действительно, если момент
М представить в виде пары
сил, то на границе двух
близких отрезков длиной dy,
показанных на рис. 13.6, будет
действовать неуравновешенная
сила дМуу1ду, которая вместе с
поперечной силой Qx образует
силу Q*, называемую
обобщенной кирхгофовой силой. Таким
образом, краевые условия на
свободной кромке я= 0 имеют Рис- ^ „К определению обобщенной
кирхгофовой силы
вид: r т
М ГО, у) = D
дх2 дУ2)
= 0,
х=0
е;<о, у) = Df-
ох
*» + (2 - $*»
дх2 ду2\
х=0
(13.24)
Комбинации краевых условий типа (13.20), (13.22), (13.24) на всем
контуре вместе с уравнением (13.18) определяют краевую задачу об
изгибе пластин.
Сравнение (13.11) и (13.13) дает следующие зависимости напряжений
через моменты:
12М.
о = --
ГГ*' °у
\2MV 12Л/
и* ху аз
(13.25)
Из этих формул видно, что наибольших значений напряжения достигают
в слоях у поверхностей пластины при z = ±Л/2:
, , 6\МХ\ , , 6|М1
max|oJ = -£-, тах|о \ = -£-, тах|тхд„
Л2 Л2 А
6\Мху\
. (13.26)
Вычислим потенциальную энергию упругой деформации U для случая
плоского напряженно-деформированного состояния
257
U = |///(°А + °А + Vv)dfr-
Подставив сюда выражения (13.8) и (13.11) для деформаций и
напряжений, после интегрирования по координате г получим
1
" - \№>
d2w d2w
дх2 а-2
5
ду2)
Э2и>
Эх2
Э2и> + Э2и>
,2 а„2
+ 2(1 - |1)
d2w
дхду
I J
ду1
dxdy,
дх1)
d2w
ду2
(13.27)
где интегрирование проводится по площади Q срединной плоскости
пластины. С учетом (13.9) и (13.13) выражение (13.27) можно привести
к виду:
U = \[[(Ккх + Муку + 2Mxykxy)dxdy.
(13.28)
Запишем еще две эквивалентные формы записи выражения (13.27):
U - {fjD
(Aw)2 + 2(1-ц)
d2W ]2 d2W d2W
d*dy, (13.29)
\Д дхду) дх2 ду2) \
U = \lIDkk* + kyf + 2° " т* " WK^- (13.30)
13.3. Методы расчета прямоугольных пластин
Рассмотрим прямоугольную в плане пластину постоянной толщины
с размерами срединной плоскости: а - вдоль координаты х, Ь - вдоль
координаты у. Точное решение w(x, у) дифференциального уравнения
в частных производных (13.18) с заданными краевыми условиями в
общем случае получить невозможно. Оно известно только для двух
частных случаев:
1) пластина шарнирно оперта по всем кромкам (рис. 13.7, а);
2) пластина шарнирно оперта по двум противоположным кромкам,
а две другие кромки имеют произвольные условия (на рис. 13.7, б для
определенности приведен случай, когда кромки у = 0 и у = Ъ защемлены).
258
л .
У
c?l 1
»Q
f 1
•C5 1
f
o\
У
a
щ *"
x'
X
a)
6)
Рис. 13.7. Частные случаи закрепления прямоугольной пластины:
а - пластина шарнирно оперта по всем кромкам; б - две противоположные
кромки шарнирно оперты, другие защемлены
Решение Навье дифференциального уравнения (13.18) для первого
случая (см. рис. 13.7, а) представляется в виде двойного
тригонометрического ряда (ряда Фурье):
(13.31)
(13.32)
»(*.*>« Е Е/„Н= Н?
m = ln = l \ а ) \ о
rjxefmn - неизвестные коэффициенты, а базисные функции
nw(*,>0 = sin(=)sin(^
подобраны так, чтобы каждая удовлетворяла краевым условиям, которые
в соответствии с (13.22) имеют вид:
w = ^ = 0, (х = 0, a); w = -^ = 0, (у = О, Ь).
дх2 ду2
В виде аналогичного ряда представляется и заданная внешняя
нагрузка
Р(х> У) = Е Е Л™Н ^^ sin ^5Z
(13.33)
Коэффициенты Фурье этого ряда находятся по известным формулам
259
0 0 \ / \ /
Подставляя ряды (13.31) и (13.33) в уравнение (13.18) и приравнивая
коэффициенты при базисных функциях, получаем выражения для/ШЛ:
J т\
Dn4(m2la2 + n2/bY
Решение Навье имеет вид
Нх,у)= I £ /Г°\ 5т[=)8шЫ, '(,3.34)
m = in = i Dn\m2 + а2/!2)2 \ я / \ * /
где через а = я/й обозначено отношение сторон.
Для решения второй задачи (рис. 13.7,6) воспользуемся решением Леей
в виде одинарного тригонометрического ряда
Нх,у)= E/M(y)sin|^E|, (13.35)
m = l V а I
в котором базисные функции удовлетворяют краевым условиям
w = —- = 0, (х = 0, а),
дх2
а коэффициенты/w0;) есть функции от у. Внешняя нагрузка
представляется в виде аналогичного ряда
Р(х,У)= Ел.(У)в4—] (13.36)
с коэффициентами Фурье
Р„(У) = |//>(x^)sin( ^i] d*. (13.37)
о \ а /
Подстановка рядов (13.35) и (13.36) в уравнение (13.18) дает систему
обыкновенных дифференциальных уравнений для функций/тО), т.е.
260
—T - 2—r—- + ——fm —, (m - 1,2,...). (13.38)
Решение/т(у) уравнений равно сумме общего решения соответствующего
однородного уравнения и частного решения /шт(у) неоднородного
уравнения. Это решение имеет вид
Ш = (С1т+ С2ту)сЪ^ + (С3т+ САту)*Ь™У +/,»• (13.39)
а а
Постоянные интегрирования С!ш, С^, СЪт, С4т находятся из граничных
условий при у = 0иу = Ь,а частное решение определяется правой частью
уравнения (13.38).
В качестве примера рассмотрим пластину, защемленную по кромкам
у = О, Ъ (рис. 13.7, б), находящуюся под действием равномерно
распределенной нагрузки р(х, у) =р0. Коэффициенты (13.37) при этом равны:
, т = 1, 3, 5, ...,
О, т = 2, 4, ...,
а частное решение, удовлетворяющее уравнению (13.38), имеет вид
ЛтО) = —ГТ~"' т = *> 3' 5'-
m5it5Z)
При постоянной нагрузке прогиб и>(.х, >>) есть симметричная функция
относительно оси О'х' (см. рис. 13.7, б). В системе координат х\ у' =
= у-Ы2в решении (13.39) нужно отбросить антисимметричные члены
ychQnnyla) и sh(tmzy/a):
/>') = Clmch=: + C4m/sh^4 i^. (13.40)
Для нахождения постоянных интегрирования С1ш и С4ш используем
граничные условия
w = ?W = 0 [ = ±Ь
ду' V 2
261
откуда после подстановки ряда (13.35) с учетом (13.40) получим систему
уравнений для определения постоянных интегрирования:
C,ch™b + Cbshmnb --^о
2а т2 2а m5%sD
с mnshnmb + С Л««* + Ьтк^тпЬ] = Q
а 1а \ 2а 2 а 2а )
Окончательное выражение для прогиба w(x, у) имеет вид:
w(x,y) = ——- I -—х
Я5£> m = l,3.... m5
, + P„(?-iW,,*bft,(y " 0 " (shP» + P«chPM)chPM(f - 1)
PM + chPmshp,
/и г-/и
Здесь введены обозначения Рш = тпЫ2а, х = 2л7й, у = 2у/6 и произведен
переход к исходной системе координат.
При произвольных краевых условиях применяют приближенные
методы, наиболее эффективные из которых основаны на вариационных
принципах (см. гл. 9).
Метод Релея—Ритца применительно к задаче об изгибе пластин
заключается в следующем. Решение для нормального прогиба w(x9 у)
представляется в виде ряда
w(*, у) = Е ckwk(x, у), (13.41)
к = \
в котором базисные функции wk(x, у) удовлетворяют кинематическим
граничным условиям, а ^-неопределенные коэффициенты. Подстановка
ряда (13.41) в выражение для потенциальной энергии упругой
деформации (13.29) и для потенциала внешних сил
П = ~ffp(x> У)п(х, y)dxdy
после вычисления интегралов дает зависимость полной энергии системы
Э = U + П от коэффициентов ск. Уравнения
262
|^ = 0, (fc = 1, 2, ..., п)
дск
приводят к системе линейных уравнений относительно искомых
коэффициентов ск.
В методе Бубиова-Галеркина решение также ищется в виде ряда
(13.41), но здесь базисные функции wk(x, у) должны удовлетворять и
кинематическим, и статическим краевым условиям. Введем оператор
L[w(x9 у)] = DAAu> - /?,
соответствующий уравнению равновесия (13.18). Условия
ортогональности базисных функций wk(x, у) к оператору L[w(x, у)]
и
L
о
I ctwk(x* У)
к=\
wk(x9 y)dxdy = О
приводит к системе линейных уравнении относительно неизвестных
коэффициентов с1с
13.4. Осесимметричный изгиб круговых
и кольцевых пластин
Для круговых или кольцевых пластин целесообразно перейти от
декартовых координат х, у на срединной плоскости к полярной системе
координат /*, 0 (рис. 13.8). Этот переход осуществляется при помощи
взаимно однозначного преобразования координат
х = rcosO, у = rsinO, г = \]х2 + у2, 0 = arctg—.
X
В полярной системе координат справедливы все соотношения,
выведенные в декартовых координатах. В частности, уравнение равновесия
(13.18) инвариантно относительно преобразования координат, т.е. его
вид остается неизменным. Оператор Лапласа в полярной системе
координат запишется как
д = 4 + 1^ + Л4« 03.42)
дг2 г дг г2 Э02
где первое слагаемое определяет кривизну кг деформированной
263
срединной поверхности в радиальном направлении г, а два последующих
- кривизну к0 в окружном направлении:
_ d2w(r, 0) _ 1 dw(r, 0) 1 d2w(r, 0)
дг>
дг
эе2
(13.43)
Применяя дважды оператор Лапласа (13.42) к функции н>(/*, 0), запишем
уравнения равновесия (13.18) в полярной системе координат
D
дг2
1±
г дг
г2 эе2
aV
+ !*£♦
дг2 г дг
р. (13.44)
1 dhvl
г2 эе2)
При этом внешняя нагрузка р(г, 0) также задается в полярной системе
координат.
Осесимметричный изгиб круговых и кольцевых пластин имеет место
в том случае, когда внешняя нагрузка р(г, 0) и граничные условия не
зависят от окружной координаты 0. В этом случае прогиб также является
функцией только координаты г, а соотношения (13.42)...(13.44) не
содержат производных по окружной координате
D\
AL
dr2
.El
dr2
IА
г dr'
LA
г dr
_ d2w(r)
dr2
dhv
dr2
r dr
. 1 dw(r)
' r dr
= P(r).
(13.45)
Рис. 13.8. Полярная система
координат для кольцевой пластины
Чтобы показать внутренние
силовые факторы, возникающие при
осесимметричной деформации
круговых и кольцевых пластин, проведем
через точку А на срединной
плоскости два сечения: плоскостью 0 = const
и цилиндрической поверхностью г ==
= const. Еще два сечения 0 + d0 =
= const и г + dr = const определяют
элементарный объем, показанный на
рис. 13.9. В сечении г - const
действуют поперечная сила Qr и изгибающий
момент в радиальном направлении
Мг В сечении 0 = const действует
изгибающий момент в окружном
264
Рис. 13.9. Бесконечно малый элемент пластины и внутренние силовые факторы
направлении Ме. Аналогичные силовые факторы действуют в двух
других, не видимых на рисунке, сечениях. Остальные силовые факторы
бе> ^гв и ^вг в слУчае осесимметричной деформации отсутствуют.
Размерность силовых факторов такая же, как и в декартовых
координатах.
Формулы (13.15), (13.16) в полярных координатах при
осесимметричной деформации записываются так:
I dr2 г dr
Ме = Я(ке + цкг) = D
/ \
I ^ + м ^W
г dr dr2)
(13.46)
а. Bib. „. в£
d2w 1 dw
dr2 r dr
Напряжения of и oe определяются через изгибающие моменты Мг и
Ме по формулам (13.25) и (13.26) с точностью до обозначений.
Уравнение (13.45) легко проинтегрировать. Для этого представим
оператор Лапласа в виде
А =
dr2
LA
г dr
г dr\ dr)
(13.47)
265
Тогда уравнение изгиба (13.45) можно переписать следующим образом:
(13.48)
г dr { dr[r dr\ dr)\) D
Пусть p(r) =/>0,т.е. пластина находится под действием распределенной
нагрузки постоянной интенсивности. Умножая левую и правую части
(13.48) на г и интегрируя, получим
dr
г drI dr
2D
+ А
После деления наг и вторичного интегрирования приходим к уравнению
1А г—
г drT dr
РоГ_
AD
+ Л,1пг + Л2.
Еще раз умножаем на г и интегрируем. С учетом того, что
/Vlnrdr = —lnr - —,
J 2 4
получаем уравнение первого порядка, т.е.
dr 16D Ч 2 4 J 2 2 3
Его решение находим в результате деления на г и интегрирования
•4 А,гг .2
V г
w{r) = ^— +
642)
•(lnr - 1) + Л2— + Л31пг + АА.
Переобозначив константы интегрирования А4 = Сх,Аг-Ах =4С2,Аг =
= СрА{/4 = С4, окончательно получим
w(r) = С, + C2r2 + Cjlnr + C4r2lnr +
Por
6AD
(13.49)
Решение w0(r) = С, + C2r + C3lnr + C4r2lnr есть общее решение
однородного уравнения, а
266
Mr
Po
tttttmtmi
I
rQr
. r .
5 "Ф
Qr *Qr
a)
Po
б;
Рис. 13.10. Равновесие центральной части пластины:
а - сосредоточенная сила в центре отсутствует; б - в центре действует
сосредоточенная сила
и>Дг)
64Z)
(13.50)
имеет смысл частного решения уравнения (13.48) для случая р0 = const.
В общем случае произвольной нагрузки р(г) частное решение находится
путем четырехкратного последовательного интегрирования
"*(г)" £/7 {/r[/7(/rp(r)dr)dr]dr}d" (115,)
Постоянные интегрирования в решении (13.49) определяются из
граничных условий при г = г1 и /*= г2, причем на каждой кромке должны
удовлетворяться два условия. Особенностью сплошных круговых
пластин, для которых г, = 0, является неограниченное возрастание
решения (13.49) при г - 0, связанное с особенностью функции lnr при г -
- 0. В окрестности г = 0 функция lnr ведет себя как г . Следовательно,
из условия ограниченности перемещения при г - 0 следует положить
С3 = 0. Дополнительное условие получим из анализа поведения
поперечной силы в окрестности точки г = 0. Подставив (13.49) в третью
формулу (13.46), получим
4ЯС, ^
QM) = L + тт-
2
(13.52)
Рассмотрим сечение пластины цилиндрической поверхностью г = const
(рис. 13.10, я). Из условия равновесия элемента получим
р0пг2 - Qr2nr = 0.
(13.53)
Сравнивая (13.52) и (13.53), получим, что С4 = 0. Если в центре пластины
приложена сосредоточенная сила Р (рис. 13.10, б), то уравнение
равновесия (13.53) примет вид
267
Рис. 13.11. Кольцевая пластина с различными участками интегрирования
р0пг2 + Р - Qr2nr = 0.
Подставляя сюда выражение (13.52), имеем С4 = PI%%D. Таким образом,
для сплошной круговой пластины решение для нормального прогиба
будет следующим:
w(r) = С, + С2г7
Рг2
8тг/)
lnr + w^(r).
(13.54)
Для кольцевых пластин решение удобнее искать в форме функции от
безразмерного радиуса р = r//*j или р = rlr2:
и>(р) = С, + С2р2 + С31пр + С4р21пр + и>Др).
(13.55)
При этом упрощается процедура нахождения постоянных
интегрирования из граничных условий.
Если на кольцевую или круговую пластину действуют различные
нагрузки или она имеет различную жесткость на отдельных участках,
то решение ищется раздельно на каждом из участков. Постоянные
интегрирования находятся из граничных условий и дополнительных
условий, соответствующих условиям стыковки решений на границах
участков. Например, для кольцевой пластины, шарнирно опертой по
радиусу г2, нагруженной во внутренней области 1 распределенной
нагрузкой р0, а по внешнему контуру 2 нагрузкой q (рис. 13.11), решение
ищется в виде:
268
wx(f) = Cx + C7
/ \2
\Г2)
+ C3ln—+ C4
/ \
\r2j
ln72'Pii5ArGlr-r^
w2(r) + АХ+АЛЦ + Аг\п±- + A4U- ln-^, (r e [r2, r3]).
Восемь постоянных интегрирования Cx - C4 и Л j - A4 находятся из
четырех граничных условий:
Л/,{,)(п) = 0, ег(,)(г.) = 0, А/Г(2)(гз) = 0, б,(2)0з) = О
!,%> = О, Л/«
и четырех условий стыковки решений при г = г2:
w,(r2) = 0, w2(r2) = 0J
dw,(r)
dr
dw2(r)
dr
. A/^frj) = M?\r]>.
В качестве простейшего примера рассмотрим сплошную защемленную
по контуру пластину, находящуюся под действием равномерно
распределенной нагрузки (рис. 13.12). В данном случае С3 = С4 = 0, и
решение для нормального прогиба ищем в виде:
w(r) = С, + С2г2 -
2 РоГ
64Z)
(13.56)
Граничные условия формулируем для г = R, где прогиб и угол
поворота нормали должны обращаться в нуль:
W(R) = dwOO
dr
= 0.
(13.57)
r = R
Подстановка решения (13.56) в граничные условия (13.57) дает систему
уравнений для определения постоянных интегрирования С( и С2:
С, + С,Д:
PqR4
64D
= 0,
2rR - ^£! = 0.
16D
Решая эту систему, получим
269
Рис. 13.12. Круговая защемленная по контуру пластина под действием
равномерного давления
А,*4 г P0R2
640
322)
Окончательное выражение для нормального прогиба пластины будет
следующим:
w(r) = -
P0R4
64D
1 -
R<
Подставляя выражение для w(r) в формулы (13.48) для радиального Мг(г)
и окружного MQ(r) моментов, получим
М,(г) =
p0R:
16
(1 + ц) - (3 + ц)-Ц
R2
Ма(г)
Ро*'
16
(1 + (1) - (1 + Зц)-^-
Л2
270
Эпюры нормального прогиба и изгибающих моментов представлены
на рис. 13.12. Из эпюр следует, что опасные точки в пластине находятся
при г = R, где максимальные эквивалентные напряжения тахоэкв,
вычисленные по критерию Треска-Сбн-Венана, определяются
выражением:
6|М,| 3A)«2
тахаэм = тахо, = — = -_.
13.5. Безмоментная теория тонкостенных оболочек вращения
Рассмотрим оболочки, срединная поверхность которых является
поверхностью вращения, т.е. поверхностью, полученной путем вращения
некоторой плоской кривой вокруг неподвижной оси. Примем, что
нагрузка, действующая на оболочку, является осесимметричной. Для
тонкостенных оболочек при выполнении гипотез, сформулированных
в § 13.1, задача определения напряжений становится одномерной. Теория
оболочек, построенная на предположении, что напряжения равномерно
распределены по ее толщине и, следовательно, изгибающие моменты в
ее сечениях равны нулю, называется безмомеитной.
Двумя парами меридиональных сечений плоскостями, проходящими
через ось вращения, и нормальных конических сечений, составляющих
с меридианом в данной точке прямой угол, выделим из оболочки
толщиной h элемент с размерами dSm и dSQ (рис. 13.13). Здесь Ст - центр
кривизны меридиана в данной точке; рт = FCm - радиус кривизны
меридиана срединной поверхности; ре = FCQ - радиус кривизны
нормального сечения; р - давление, вызываемое внешней нагрузкой.
Выделенный элемент не испытывает сдвигов и, следовательно, площадки,
Рис. 13.13. Бесконечно малый элемент оболочки вращения
271
Рис. 13.14. Различные проекции элемента оболочки вращения
по которым действуют меридиональные от и окружные ое напряжения,
являются главными.
Рассмотрим равновесие элемента оболочки. Для наглядности покажем
две проекции (рис. 13.14). Проектируя все силы на направление нормали
к срединной поверхности оболочки, получаем
2сг AdSAsin
dot
2 )
+ 2ae/idSmsin
dccft
/>dSmdSe = 0
(13.58)
Разделив каждое слагаемое на dSmdSQ (площадь элемента) и учитывая,
что углы daw и dae малы:
sin
da„
2;
da„
sin
dcu
2
получим
(dam dafl
mdS„ edSft
/7 = 0.
Так как
272
d«e
dSa
то окончательно уравнение
равновесия запишем в виде
Рт Ре h '
(13.59)
которое называется уравнением
Лапласа.
Уравнение (13.59) содержит
две неизвестные величины: от и
Oq. Таким образом, для
нахождения напряжений необходимо
составить дополнительно еще
одно уравнение равновесия. Для
этого, используя метод сечений, рассмотрим равновесие части оболочки,
выделенной коническим сечением (рис. 13.15). Проектируя все силы на
ось Oz, получим
Рис. 13.15. Равновесие отсеченной части
оболочки вращения
olnrhcosa - Р = 0.
Здесь Р- равнодействующая внешних сил, приложенных к
рассматриваемой части оболочки, включая опорные реакции; а - угол между
направлением действия меридиональных напряжений от и осью Oz; г -
текущее значение радиуса срединной поверхности оболочки. Из этого
уравнения для меридиональных напряжений от получаем
о_ =
27irftcosa
(13.60)
В частном случае сферической оболочки, у которой рт = р0 = R, где
R - радиус срединной поверхности, нагруженной газовым давлением р,
в силу центральной симметрии напряжения от и ое равны и тогда
непосредственно из (13.59) следует:
о» = ол
pR
2h
(13.61)
Для цилиндрических и конических оболочек, у которых радиус кривизны
в меридиональном направлении pw - °°, уравнение (13.59) определяет
273
окружные напряжения ое
ае = ^. (13.62)
Если у конических оболочек радиус кривизны в окружном направлении
ре есть функция координаты z, то у цилиндрической оболочки ре = R,
т.е. равен радиусу ее срединной поверхности. Тогда вместо (13.62) можно
записать
ае = ^ ■ (13.63)
Вычисление равнодействующих внешних сил при:
а) газовом давлении р^. Для этого проводим нормальное коническое
сечение и используем "принцип отвердения", т.е. газ остается в
отсеченной части оболочки и давление со стороны отброшенной части действует
по перпендикуляру к плоскости сечения. Из суммы проекций на ось Ог
всех сил, действующих на отсеченную часть оболочки, для
равнодействующей Р имеем
Р = Рх + р0ш2.
Здесь Рх - собственный вес отсеченной части оболочки. Величиной Р,
для тонкостенных оболочек обычно пренебрегают;
б) гидростатическое давление. Если оболочка заполнена жидкостью
с плотностью р, то для равнодействующей Р имеем
Р = Рх + pgHnr2 + pgV,
гдеg- ускорение свободного падения, Н- уровень жидкости (расстояние
от свободной поверхности жидкости до рассматриваемого сечения),
V- объем жидкости в отсеченной части оболочки;
в) совместное действие гидростатического и газового давлений. В этом
случае равнодействующая внешних сил определяется как комбинация
предыдущих результатов:
Р = р\ + (Ро + PgH)™2 + pgV. (13.64)
Особенности применения критериев прочности к расчету
тонкостенных оболочек вращения. Для безмоментных оболочек напряженное
состояние можно рассматривать как плоское. Действительно, напряжения
274
в направлении нормали к срединной поверхности оболочки оп имеют
порядок давления р, а из уравнения Лапласа следует, что напряжения от
и ое имеют порядок pRIh, где R - характерный радиус срединной
поверхности. Учитывая, что в безмоментной теории рассматриваются
тонкостенные оболочки, для которых hIR < < 1, имеем: о > >
°/1И
oQ > > оп. Тогда, например, в случае растягивающих напряжений от и
ое по критерию текучести Треска-Сен-Венана для оэкв имеем:
\°т ПРИ °т > °в>
|ав при ое > от.
13.6, Осесимметричная деформация круговых
цилиндрических оболочек
Рассмотрим круговую цилиндрическую оболочку толщиной h и
радиусом срединной поверхности R (рис. 13.16). Положение точек
оболочки на срединной поверхности будем определять координатой х
вдоль образующей и криволинейной координатой у = Rd в окружном
направлении; координата z направлена по нормали к срединной
поверхности.
Пусть оболочка находится в условиях осесимметричного нагружения
нормальным давлением р(х) и стационарного температурного поля 7\х,
г). Кроме того, в продольном направлении на оболочку действует
растягивающее усилие Nx = const.
В случае осесимметричного закрепления оболочки при указанном
выше нагружении все
внутренние силовые факторы зависят
только от координаты х.
Напряженное состояние оболочки
описывается тензором
напряжений
о О
х
О о, О
и задача определения
напряженно-деформированного
состояния является осесиммет-
ричной и одномерной.
Рис. 13.16. Круговая цилиндрическая
оболочка
275
Рис. 13.17. Равновесие бесконечно малого элемента круговой цилиндрической
оболочки
Вывод уравнений равновесия. Рассмотрим равновесие элемента
оболочки размерами chr, dy = Rd0, выделенного в окрестности некоторой
точки (рис. 13.17). На рисунке показаны положительные направления
внутренних силовых факторов и введены обозначения: Nv - продольное
усилие, N - окружное усилие, Мх - изгибающий момент в направлении
координаты х, М- изгибающий момент в направлении координаты у,
Q - поперечная сила. Все внутренние силовые факторы являются
погонными, т.е. отнесенными к единице длины.
Из первого уравнения равновесия для элемента, а именно суммы
проекций всех сил на ось Ох
-Nxdy + (Nx + dNJdy = О,
получаем
dNx = 0, (13.65)
т.е. при действии только нормальной нагрузки продольное усилие Nx =
= const не меняется по длине и определяется условиями закрепления
оболочки или нагружения на ее краях. Проектируя все силы на
направление нормали к срединной поверхности, получаем:
pdxdy + Qdy - (Q + dQ)dy - 2^dxsin —1=0.
276
Учитывая, что sin(d6/2) = ~ d0/2 = dy/2Rt приходим к уравнению
f^-P- 03.66)
dx R
Третье уравнение равновесия получим, используя равенство нулю
моментов всех сил, действующих на элемент, относительно линии КК':
Mxdy - (Мх + dMJdy + Qdxdy +pdxdy— - 2Nydx—sm— = 0.
Отбрасывая слагаемые более высокого порядка малости, получим
dA/
djc
6. (13.67)
Остальные уравнения статики обращаются в тождества. Поскольку
уравнения (13.65)...(13.67) содержат неизвестные силовые факторы Nx,
Ny9 Q, Мх и, кроме того, на рассматриваемый элемент действует не
вошедший в уравнения изгибающий момент М , то задача их
определения является статически неопределимой. Для раскрытия статической
неопределимости необходимо рассмотреть деформации оболочки.
Обозначим через w(x) - перемещения точек срединной поверхности
оболочки по оси z (нормальный прогиб); и(х) - перемещения точек
срединной поверхности оболочки по оси х\ ф(х) = dvtVdx- угол поворота
нормали к срединной поверхности (рис. 13.18). Тогда относительная
деформация продольного волокна, отстоящего от срединной поверхности
на расстоянии z (рис. 13.19) определится по формуле
= du^dq» ш ди _ zdq, щ 41 _ d|W
dx dx dx dx dx2 K
Аналогично определим относительную деформацию в окружном
направлении (рис. 13.20)
(R + w)dQ - RAQ = w_
RdQ R
«> = «в = v ;7Q = T- (13.69)
Связь между внутренними силовыми факторами и перемещениями.
Запишем обобщенный закон Гука с учетом температурных деформаций
(соотношения Дюамеля-Неймана):
277
Рис. 13.18. Перемещения при осесимметричной деформации круговой
цилиндрической оболочки
Рис. 13.19. К определению относительной деформации в продольном направлении
278
Рис. 13.20. К определению относительной деформации в окружном направлении
*х = £(°* " ^°у) + aTi Zy = \{°у " ЦОх> + аТ* (13'70)
где а - температурный коэффициент линейного расширения материала
оболочки. В формулах (13.70) принято, что о2 = 0, т.е. используется
гипотеза о ненадавливаемости слоев. Обратные по отношению к (13.70)
соотношения с учетом (13.68) и (13.69) имеют вид:
1 -р
К + Це, " 0 + И)«Л
Е
\du d2w , w ,. ^ ,Л rn
— - z + ц— - (1 + u)aT\
1 - n2[dx dx2 R '
E
1 -ц:
[e„ + цех - (1 + ц)аГ] =
2l У
R dx dx2
(13.71)
279
Рис. 13.21. Нормальные напряжения в сечениях оболочки
Рассмотрим интегральное представление внутренних силовых факторов
(рис. 13.21):
А/2
А/2
А/2
А/2
Nx = | oxdz, А^ = | oyiz, Мх = - | o^zdz, М, = - | o^zdz. (13.72)
-А/2
-А/2
-А/2
-А/2
Подставляя в (13.72) выражения для напряжений в виде (13.71), после
интегрирования получим:
N =
Eh
IV
£ ♦ "i - <' ♦ **
#.,
Eh
л dx
(13.73)
М =Д
dV-
dx3
+ (1 + \i)kT\
;My = D
Ц1^ + (1 + ^
(be2
где £> - цилиндрическая жесткость, e^, кт- обобщенные температурные
деформации - линейная температурная деформация срединной
поверхности и температурная кривизна образующей, определяемые
формулами:
1 *° 12 т
гТ = JL | «rdz, fcr = — | «7zdz. (13.74)
-Л/2
-A/2
280
В выражения (13.73) для Nx и N входит величина duldx = е0 (деформация
срединной поверхности), обусловленная условиями закрепления на краях
оболочки. Исключим величину е0 из этих выражений, выразив N через
N-
1-Ц
w
(l-^-O+tOO-tOe,
«Skl^-e,
Тогда
N..
Eh\ * - г,
pNx.
(13.75)
Поперечная сила также может быть выражена через нормальный прогиб,
если в (13.67) подставить Мх из (13.73):
е =
dx
D
dx3 <Ьс
(13.76)
Уравнения равновесия цилиндрической оболочки в перемещениях.
Подставим выражения для N (13.75) и Q (13.76) в уравнение равновесия
(13.66)
D
[dx4
Вводя обозначение
fd1-)
4кА
Eh = 12(1 - ц2)
DR2 R2h2
(13.77)
окончательно получим
/
d4vt> At 4 1
dx4 Л
ц-
R
d2k
+ 4А:4Дег - (1 + \i) £.
dx2
(13.78)
Уравнение (13.78) является уравнением равновесия круговой цилиндрической
оболочки, находящейся под действием осесимметричнои внешней
нагрузки и осесимметричного температурного поля.
Интегрирование дифференциального уравнения осесимметричнои
деформации круговой цилиндрической оболочки. Решение уравнения
(13.78) имеет вид:
281
w(x) = w0(x) + wm = w0(x) + wv + w„ + w^, (13.79)
где w0(x) - общее решение однородного уравнения; wwp - частное решение
неоднородного уравнения, определяемое внешними силовыми
нагрузками; так, если р(х) - полином не старше третьей степени, то
•' Eh
( \
R2 Nx\
(13.80)
н>,е - частное решение, соответствующее линейным температурным
деформациям гтсрединной поверхности:
w- = *вг; (13.81)
w,k - частное решение, соответствующее изгибным температурным
деформациям:
В случае, если ктне зависит от координаты х или зависит от нее линейно,
частное решение wtk = 0. Общее решение w0(x) однородного уравнения
запишем в виде
w0(x) = C^T^coskx + C2tkxsinkx + Csckxcoskx + C^sinkx, (13.83)
где к определяется из (13.77):
к = VHZmS. (13.84)
щ
Выясним физический смысл частного решения w + w,t. Для этого
определим напряжения в оболочке, используя безмоментную теорию:
°Л1= N-Jk OQ-pRlh. Для деформации ее в окружном направлении имеем
282
Найдем прогиб w оболочки:
Лег= Ш
т Eh
Nx\ п
. D R\ pR Nx\
Сравнивая полученное выражение для w с (13.80) и (13.81), видим, что
частное решение w.p + w#e есть прогиб оболочки, определяемый по
безмоментной теории.
Окончательно для решения уравнения осесимметричной деформации
круговой цилиндрической оболочки получаем в виде
w(x) = Cxc~kxcoskx + C2cTkxsmkx + C^coskx +
(13.85)
+ C4e**sinfcK + w„p + w^ + w,k.
Постоянные интегрирования C{, C2, C3, C4, входящие в решение (13.85),
определяются из граничных условий. Приведем типичные граничные
условия:
шарнирное опирание -
w = 0, -^ = -(1 + ц)£г; (13.86)
dx2
жесткое закрепление -
w = 0, -^ = 0; (13.87)
ах
свободный край, загруженный моментом т и поперечной нагрузкой q,
распределенными по торцу оболочки -
^--0+и)*г+»^.-С ♦,»£♦£ (13.88)
dx2 D dx3 а* D
свободный незагруженный край -
^ = -(1+тТ9^---(1+»А: (1з.89)
dx2 dx3 dx
Выразим напряжения через внутренние силовые факторы. В формуле
для напряжений ох выделим члены, определяющие продольное усилие
Nx и изгибающий момент Мх
283
1 Eh
12
h 1 V
Eh*
CDC /J
Л3 12(1 -ц2)
d2w
dx2
(1+H)fc,
£z
(1 + ц)е7
1-ц2
(1+ц)*7
£
1-ц2
■(1+ц)«Г.
Учитывая выражения (13.73) для Nx и Мх через перемещения, для
напряжений ov в случае произвольного закона распределения
температуры по толщине оболочки получим
N.
12М,
о„ =
xz + -^—(tT + zkT - аТ).
h hl 1-Ц
Аналогично может быть получена формула для напряжений о :
(13.90)
Ny
о = —-
у h
12М„
-z +
-(ег + zkT - а.Т).
(13.91)
А3 1-Ц
Если закон распределения температуры по толщине оболочки
линейный, т.е.
Г(х,г) = Т0(х) + АГ(х)±,
где Г0(л:) - приращения температуры точек срединной поверхности
оболочки, а АГ(х) = Т(х, Ы2) - Т(х, -И/2) - перепад температуры по
толщине, то температурные деформации определятся по формулам:
гт = — [ aTdz = аГ0, кт = — f aTzdz = .
Л4 АМ/2 А
Выражения, заключенные в круглые скобки, в формулах для напряжений
(13.90) и (13.91), будут равны нулю, так как
гт + zkT = аГ0 + аДГ- = аТ(х, z).
284
В этом случае напряжения ох и оу меняются по толщине оболочки по
линейному закону
Nx \2МХ Nv 12М
х h h3 У h h3 К '
и достигают наибольших по модулю значений у ее поверхностей при
г = ±Л/2:
min * h h2 min ' A A2 ( '
13.7. Краевой эффект в круговой цилиндрической оболочке
Во многих случаях напряженное состояние в оболочке может быть
разделено на основное (безмоментное) состояние и краевой эффект.
Рассмотрим круговую цилиндрическую оболочку, защемленную по
краям, нагруженную внутренним нормальным давлением р(х) и
находящуюся в стационарном температурном поле 1\х, z). Осесимметрич-
ные деформации оболочки описываются уравнением (13.78). Вблизи
краев х = 0, х = / оболочка работает преимущественно на изгиб
(рис. 13.22). Влияние краев оболочки на напряженное состояние в средней
ее части, которое близко к безмоментному, мало.
Местный изгиб, возникающий в результате закрепления краев
нагруженной оболочки, резкого изменения ее размеров и формы, а также
в областях приложения сосредоточенных нагрузок, называется краевым
эффектом.
А
Z
1
1
у/а
\
?|
*ш
3—
1
г
1
' 'V ' ■ .>"
«я
/
а».
I-
1'
Рис. 13.22. Круговая цилиндрическая оболочка, защемленная по краям
285
Определение постоянных интегрирования С{...С4 в решении (13.85)
при использовании концепции краевого эффекта упрощается. Для
тонкостенных оболочек с hIR < < 1 в связи с быстрым изменением
функций е±/сл "изгибные" члены в решении (13.85) (Cl3e±kxcoskx,
С2 4е sin/cx) дают существенный вклад в w(x) только в зоне краевого
эффекта, протяженность которой оценивается величиной Я = ти//:, где
X - длина полуволны краевого эффекта. При изменении х от 0 до Я
функция е"Ал уменьшается в е* « 23 раза.
Оценим длину полуволны краевого эффекта. Определяя волновое
число к формулой (13.84) и принимая ц = 0,3, получим
* " I " 77^= ~~ 2'45^' (13.94)
* l/3(l - ц2)
Например, для оболочки толщиной h = 0,1 R формула (13.94) дает Я «
~ 0,8#. Таким образом, если длина цилиндрической оболочки
удовлетворяет условию / > 2Я, то оболочку в окрестности края х = 0 можно
рассматривать как полубесконечную, а в решении (13.85) для w(x)
положить С3 = 0, С4 = 0 из условия ограниченности решения при х - «.
Тогда вблизи края х = 0 для л: > 0 решение, основанное на концепции
краевого эффекта, имеет вид
w(x) = C,e~**cosAa: + C2eTkxsmkx + w + w,e + и>^. (13.95)
Здесь постоянные интегрирования Cj и С2 определяются из граничных
условий при х = 0.
Рассмотрим ряд простейших примеров. Пусть круговая
цилиндрическая оболочка толщиной h и радиусом срединной поверхности R
находится под действием внутреннего давления интенсивностью р0
(рис. 13.22). Примем, что Nx = 0. Построим решение типа краевого
эффекта в окрестности защемленного края оболочки. Постоянные Сх и
С2 в решении
d R*
w(x) = C.e^cosfcx + C,e~**sinfcx: + ——
определим из граничных условий (13.87). Для этого сначала вычислим
первую производную от w(x):
— = -кекх[(Сх - CJcoskx + (С, + Q an Лис].
286
Несложные вычисления дают
с, ■ с, -- -**:.
! 2 Eh
Таким образом, выражение для нормального прогиба вблизи края х =
= 0 будет иметь следующий вид:
w(x) = [1 - e~**(cosfoc + sinkx)].
Eh
Используя выражения (13.73), (13.75) и (13.76), для внутренних
силовых факторов получим
Ny(x) = p0R[\ - e*fcx(cosfcx + sin/cx)];
Mx(x) = 2k2D-
Q(x)
tP0R2
Eh
4k3D
■e'^icoskx - sin
Eh
^coskx'y
ikx)\
My(x) = iiMx{x).
В зависимости от безразмерной координаты кх эпюры нормального
прогиба и>, окружного усилия N , изгибающего момента в направлении
образующей Мх и поперечной силы Q представлены на рис. 13.23. Здесь
значению длины краевого эффекта А соответствует кх = я. Из эпюр
следует, что вне зоны краевого эффекта, т.е. при х > X или кх > к,
нормальный прогиб w(x) и окружное усилие N (х) практически равны
значениям, определяемым по безмоментной теории w(x) « pQR2IEh,
N (х) * p0R. Изгибные внутренние силовые факторы MY, М = \iMx и Q
достигают наибольших по модулю значений при х = 0, а при х > X
пренебрежимо малы. Для сечения х = 0 вычислим наибольшие изгибные
напряжения
6МХ ^з PoR
maxcr = = v .
л2 /TV h
287
nil n
Рис. 13.23. Эпюры нормального прогиба и внутренних силовых факторов в зоне
краевого эффекта
Отношение наибольших изгибных напряжений тахох к кольцевым
напряжениям оу = pQR/h, вычисленным по безмоментной теории,
составляет ^3/(1 - ц2). Для \х = 0,3 это отношение равно 1,82.
Теперь рассмотрим случай температурного нагружения цилиндричес
кой оболочки, защемленной на одном конце (х = 0). Пусть Т(х, z) = Г0,
т.е. оболочка равномерно нагрета на температуру Г0. Температурные
деформации (13.74) в этом случае соответственно равны ет = aTQ, кт =
= 0. Согласно (13.95) решение ищем в виде
w(x) = Cje^cosA:^ + C2tkxkx + eTR.
288
Рис. 13.24. Эпюры окружного усилия в цилиндрической оболочке при равномерном
нагреве
Таким образом, решение для нормального прогиба w(x), изгибающих
моментов Мх(х), М (х) и поперечной силы Q(x) в данном случае будет
совпадать с предыдущим примером, если заменить безмоментный прогиб
p0R2IEh от давления на безмоментный прогиб от температуры eTR. Для
окружного усилия N (х) из (13.75) следует
Ny(x) = -aT^Eht^icoskx + sinfcx).
Эпюра для N (х) представлена на рис. 13.24. В сечении х = 0 при г = -Л/2
возникают следующие напряжения:
у/ЗаТ0Е
аТ0Е\
^Ц
/Г
и2;
(13.96)
Если оболочка защемлена на обоих концах и равномерно нагрета на
температуру Г0, то в ней дополнительно возникает сжимающее усилие
Nx = -aT0Eh и безмрментное решение определится как
и>
и>
W.
= (1 + \i)*T0R.
Дальнейшее решение проводится аналогично предыдущим случаям.
Пусть температура срединной поверхности оболочки не изменяется,
т.е. Т0 = 0, а по толщине имеет место линейный закон изменения
температуры 7%х, z) = bTilh. Тогда гт = 0, кт = аАГ/Л. Безмоментные
решения для прогиба (13.80)...(13.82) w.p = w,e = w.k = 0 и, следовательно,
289
w(x) = 0. Все внутренние силовые факторы равны нулю, кроме
изгибающих моментов Мх и М' , которые в соответствии с (13.73) равны
мх-му- ы> + №т - D{X 7)аАГ-
В точках на поверхностях оболочки при z = ±Ы2 возникнут напряжения,
определяемые величиной
max max . аЬТЕ
min * min у 2(1 - ц)
290
Глава 14
ТОЛСТОСТЕННЫЕ ЦИЛИНДРЫ
И ВРАЩАЮЩИЕСЯ ДИСКИ
14.1. Осесимметричная деформация толстостенных
цилиндров. Задача Ламе
Многие элементы конструкций и детали машин при расчете на
прочность могут быть схематизированы в виде толстостенных
осесимметричных тел цилиндрической формы. Сюда можно
отнести некоторые типы трубопроводов, сосуды высокого давления,
диски паровых и газовых турбин, валы и втулки при наличии прессовых
посадок и т.д. Нагружение также часто является осесимметричным:
газовое или гидростатическое давление, осесимметричноетемпературное
поле, центробежные силы инерции, нагрузки от прессовых посадок. В
указанных случаях имеет место задача о расчете на прочность
толстостенных цилиндров или дисков при осесимметричном нагружении.
Рассмотрим тела вращения, нагруженные силами, симметричными
относительно оси тела. Будем использовать цилиндрическую систему
координат г, 0, z. При совмещении оси Ог с осью тела вращения
напряжения, деформации перемещения тела в силу геометрической
симметрии и симметрии нагрузки от угла 0 зависеть не будут.
Осесимметричная задача, в которой напряжения и деформации не
зависят от координат z и 0 и, следовательно, являются функциями только
координаты г, называется плоской осесимметричной задачей теории
упругости. При решении этой задачи применяем обычные гипотезы
механики материалов и конструкций (материал сплошной, однородный,
изотропный и линейно упругий; деформации малы). Специальных
гипотез о характере распределения напряжений и деформаций принимать
не будем.
Рассмотрим открытый толстостенный цилиндр (рис. 14.1, а),
находящийся под действием внутреннего давления рх и внешнего
давлениярг. Выделим элементарный участок длиной dz в этом цилиндре
(рис. 14.1, б). Поверхности диска, ограниченные сечениями т -т и п -л,
291
тп
а)
б)
Рис. 14.1. Открытый толстостенный цилиндр:
а - геометрические параметры и схема нагружения; б - выделение бесконечно
малого элемента
свободны от напряжений, т.е. о2 = 0, хп = 0, x6z = 0. Так как толщина
диска мала, а напряжения меняются непрерывно, то можно считать, что
во всех точках поперечных сечений диска напряжения oz, xrv xQz
пренебрежимо малы. Таким образом, в точках диска имеет место плоское
напряженное состояние. Давления/?! ир2 приводят к возникновению в
каждой точке диска окружных (кольцевых) напряжений ое и радиальных
напряжений ог Напряжения ог и ое, действующие на элемент ABCD,
расположенный на расстоянии г
<Jr+dcrr
Рис. 14.2. Перемещения и напряжения в
толстостенном цилиндре
от центра диска, показаны на
рис. 14.1, б и 14.2. Элемент A BCD
получен двумя концентрическими
цилиндрическими поверхностями,
находящимися друг от друга на
расстоянии dr, и двумя
радиальными сечениями, образующими
между собой угол d0. В силу
осевой симметрии деформированного
состояния диска на площадках, по
которым действуют напряжения ог
и о0, касательные напряжения
отсутствуют. Поэтому ог и о0
являются главными напряжениями.
Составим уравнение
равновесия для элемента ABCD. Суммиро-
292
вание всех сил действующих на элемент в радиальном направлении,
приводит к уравнению
(or + dar)(r + dr)d6dz - orrd6dz - 2o0drdzsin| — = 0. (14.1)
Принимая для малых углов sin(d0/2) ~ d0/2 и пренебрегая бесконечно
малыми более высокого порядка, получаем уравнение равновесия в
напряжениях
dor о„ - ой
—^ + -Z - = 0. (14.2)
dr г
Остальные уравнения равновесия для элемента обращаются в тождества.
Уравнение (14.2) содержит две неизвестных функции ог(г) и oe(r).
Следовательно, задача является статически неопределимой и для ее
решения необходимо обратиться к рассмотрению деформаций.
Деформации в радиальном и окружном направлениях. Обозначим
перемещения точек диска в радиальном направлении через и(г) (рис. 14.2).
Примем, что и(г) положительно, если перемещение направлено от центра
диска. Относительная линейная деформация в радиальном направлении
определяется следующим образом:
А'В' - АВ Аи /tA^
с'= —Ж~ - Тт* (143)
а в окружном направлении -
A'D' -AD и
~ = = —.
6 AD г
(14.4)
Если исключить из (14.3) и (14.4) перемещение м(г), то получим уравнение
совместности деформаций
A(v) - ег = 0. (14.5)
йг
Уравнение равновесия в перемещениях. Исключим из уравнения (14.2)
напряжения ог и ое. Для этого в формулы обобщенного закона Гука для
плоского напряженного состояния
293
1
;0>, + Цее), ов
1 -ц;
(ее + И*>)
(14.6)
вместо деформаций гг и ее подставим их выражения через перемещение
(14.3) и (14.4). Тогда получим
о. = — + ц—
1 - jiHdr г)
о. =
1
.21 г dr
(14.7)
Подставляя напряжения ог и ое в виде (14.7) в (14.2), получаем линейное
дифференциальное уравнение второго порядка относительно
перемещения и(г) Сравнение равновесия в перемещениях):
d2u + j_ dw
dr2 +
г dr
= 0,
(14.8)
которое можно переписать в виде, удобном для интегрирования
0. (14.9)
_d_
dr
1 d , ч
-—(иг)
г dr
Решение уравнения (14.9)
и(г) = Схг +
(14.10)
содержит две постоянные интегрирования Сх и С2, которые определяются
из граничных условий
°г(г\) = ~Р\> °Лгт> = ~Рг-
(14.11)
Условия (14.11) представляют собой уравнения равновесия для
элементарных объемов у внутренней и внешней поверхностей диска
соответственно.
После подстановки найденных из граничных условий постоянных Сх
и С2 в решение (14.10) и выражения (14.7) для радиального перемещения
и(г) и для напряжений ог, о6 получаем
2 2
и(г) = { ~ УРхГ' ~ РгТг г + { + * ^ ~ ^ Г2 ! ,
£
(14.12)
Г> - г.
294
Рис. 14.3. Плоская деформация толстое- Рис-14-4- Обобщенная плоская дефор-
тенного цилиндра мация толстостенного цилиндра
°„»Ф¥'*4^Ц- (14|3)
г2 -г, г2 - гх г
Формулы (14.12) и (14.13) называются формулами Ламе (1795-1871). Они
получены для случая плоского напряженного состояния, которое,
например, реализуется в открытом цилиндре (рис. 14.1, а). Здесь
продольные напряжения oz равны нулю, а для деформаций е2 из
обобщенного закона Гука имеем
2 2
1 г t 41 2\i Р\г\ - Рггг
Л Г2 ~ Г\
т.е. все сечения цилиндра после деформации остаются плоскими.
Если условия нагружения и закрепления цилиндра таковы, что
продольная деформация равна нулю е2 = О (рис. 14.3), то приходим к
задаче, называемой плоской деформацией. Напряжения ог и ое также
определяются формулами Ламе, а продольные напряжения из закона
Гука
2 2
°z = *ФГ + ое) = l/xT\ ~ ft/2 = const.
г22 - г,2
Здесь поперечные сечения цилиндра также остаются плоскими.
При наличии продольных усилий в цилиндрических телах,
приводящих ко. = const * 0 и г2 = const * О, говорят об обобщенной плоской
деформации К такой задаче приводит расчет закрытого цилиндра
(рис. 14.4). Предположим, что напряжения о2 одинаковы для всех сечений,
295
достаточно удаленных от краев цилиндра. Уравнение равновесия для
отсеченной части
ъ(г% - r?)oz + ът\рг - пг?рх = О
приводит к формуле
2 2
Pi Г г - руГу
°* = 2 2 = С0Ш1, <,4Л4>
г2 - г,
Таким образом, для закрытого цилиндра oz * 0 и напряженное состояние
является объемным.
Вычисляя деформацию е2 в продольном направлении
*, - > - Ц<о, ♦ ае)] = » - 2И ^ - *'» . сооЛг
Г2 Г\
убеждаемся, что сечения остаются плоскими, но цилиндр в осевом
направлении получает удлинение (укорочение). Напряжения ог и ое
вычисляются по формуле (14.13) и наличие напряжения о2 не оказывает
влияния на их величину.
Напряженное состояние в тонких дисках, где под напряжениями ог
и Oq понимают их значения, осредненные по толщине диска, называется
обобщенным плоским напряженным состоянием. При этом oz « 0.
При определении радиальных перемещений и{г) для случаев плоской
деформации и обобщенной плоской деформации необходимо учесть
влияние ог В силу соотношений
«(/•) = J4(r)dr, е, = f £И fl - ji-^
О
делаем вывод, что в данных случаях напряженного состояния к первой
формуле Ламе (14.12) нужно добавить член -\ю2г/Е.
Цилиндр под действием внутреннего давления. В этом случае/?! = Р>
р2 = 0 по формулам (14.13), (14.14) для напряжений ог, ое и oz имеем:
2
г
°ГР
г\
,2
r22-r,2v 'V
°в=/>-
г
1+-
г.
\
г2
2
Распределение напряжений по радиусу цилиндра приведено на рис. 14.5.
Опасные точки находятся на внутренней поверхности цилиндра, где
296
Рис. 14.5. Цилиндр под действием внутреннего давления
°г = -Р = °3» °в = Р~
Г, + Г,
= а1> °z =Р —
= 00.
В этих точках эквивалентные напряжения, вычисляемые по различным
критериям прочности, достигают своих максимальных значений. Так,
по критерию Треска-Сен-Венана
таХОэкв = °i " °з =
2рг2
2/7
1^
2
(14.16)
по критерию Губера-Мизеса
max
°экв = \j°l + °2 + °3 " (°Ia2 + °2°3 + °1°з) = 7"^
VS
j _ rf | 04.17)
Примечание, Из условия прочности тахоэкв й [о] по критерию (14.17)
получаем
297
Рис. 14.6. Цилиндр под действием внешнего давления
1
1 - еЛ
[о]
Отсюда следует, что при р = [о]1 у/3 отношение г21гх обращается в
бесконечность, а прир > [о]1у/3 эквивалентное напряжение во внутренних
точках цилиндра будет больше допускаемого напряжения при сколь угодно
большой толщине стенки. Если давление превысит величину рТ = o^lyfb, mo
во внутренних точках возникает пластическая деформация. Этот факт
не означает, однако, что при больших давлениях обеспечить прочность
цилиндра вообще невозможно. Предельное состояние для цилиндра
наступает тогда, когда пластические деформации распространяются на
всю толщину стенки.
Цилиндр под действием внешнего давления. В этом* случае рх = 09р2 =
=р и для напряжений ог, ое и oz имеем:
°г~Р-
Ъ-г.
°в = ~Р-
1+-
(14.18)
Соответствующие эпюры приведены на рис. 14.6. Опасными, как и в
298
предыдущем случае, являются внутренние точки цилиндра. При
уменьшении внутреннего диаметра цилиндра (г{ - 0) окружные
напряжения на наружной поверхности стремятся к величине -/?, на
внутренней поверхности - к величине -2р.
Примечание. Для сплошного цилиндра, нагруженного внешним
давлением, окружные напряжения одинаковы и равны -р. Таким образом,
вблизи малого центрального отверстия окружные напряжения
возрастают вдвое, что является следствием концентрации напряжений.
Если внешнее и внутреннее давления в цилиндре одинаковы (P\-ptPi-
=р), то ог = -р, ое = -/?, oz = -/?, т.е. все напряжения равны между собой
и не зависят ни от текущего радиуса г, ни от отношения радиусов гх1гг.
Тонкостенный цилиндрический сосуд под внутренним давлением. Пусть
толщина 6 стенки цилиндра мала, так что 6 « г{, тогда из (14.13) и
(14.14) для напряжений ог ое и oz следует:
°е = />т> °ж = PTZ* °r<Ti) = ~Р> °гЫ = 0. (14.19)
о /о
Формулы (14.19) называются формулами Мариотта. Из них следует, что
окружные напряжения о0 вдвое больше осевых напряжений oz, а
радиальные напряжения ог малы по сравнению с ое, так как oJo$ ~ б/г.
Формулами Мариотта можно пользоваться при Ыг < 0,1; погрешность
при вычислении эквивалентного напряжения не превышает 5 %.
Приведем без вывода формулы для напряжений ог и ов в
толстостенном сферическом сосуде, нагруженном внутренним/?, и внешним
давлением р2
„ - Р\г\ ~ Рггг , _ч ri3r2 1 /1/|от
°г ; — - (Pi ~ Pi— J з- (1420>
'2 ~ Т\ Г2 ~ Г1 Г
« -3 м -3 ,3*3
°e ; — + (Pi ~ Рт>-г JT3- (14.21)
r2 - г, тг - rx 2r
14.2. Составные цилиндры
Как отмечалось выше, увеличение толщины стенки цилиндра не может
во всех случаях обеспечить необходимую прочность конструкции. В
условиях высоких давлений применяются составные цилиндры,
соединяемые прессовой или горячей посадкой.
299
Найдем напряжения,
возникающие при посадке
одного цилиндра на другой
с натягом А (рис. 14.7), где
г j и /*2 + А/2 - радиусы
внутреннего цилиндра, г2 и гъ -
радиусы наружного
цилиндра, / - длина цилиндров.
Пусть цилиндры
изготовлены из различных
материалов (Ev Ц| иЕ2, \i2- модули
упругости и коэффициенты
Пуассона внутреннего и наружного цилиндров соответственно).
Если длины соединяемых цилиндров одинаковы, то контактное
давление/^, равномерно распределено по посадочной поверхности и его
определяют из уравнения совместности деформаций. Сумма абсолютных
значений перемещений обоих цилиндров в радиальном направлении,
вызванных контактным давлением, равна разности радиусов посадочных
поверхностей до их соединения:
Рис. 14.7. Параметры составного цилиндра
l"ll + \ul\ = Т-
(14.22)
Воспользовавшись (14.15), подставив в них р = рк, г{ - г2, г2 - гъ и
положив г = г2, найдем для наружного цилиндра напряжения на
посадочной поверхности:
°г = ~Рк> °е = /V
а, = 0.
Величину радиальных перемещений и2 = еег2 точек на внутренней
поверхности внешнего цилиндра можно вычислить с использованием
обобщенного закона Гука:
и2 = тг(ао " ft>°,)
Е2
РкГ2
2 2
>Ч + г,
V гъ -г.
Н
Аналогично, обозначив/? ~ рк и положив /* = г2в формуле (14.18), для
внутреннего цилиндра найдем напряжения
300
-Рк'
-Рк-
:. °г = О
и радиальное перемещение
_ '2
(°в ~ h°f)
Ркгг
*i
+ h
Подставляя выражения для ы, и и2 в уравнение совместности деформаций
(14.22), для контактного давления/^, получаем
А
Рк = т~
\Г2
h
1
2 . 2
'з + Г2
2 2
V Г3 Г2
1*2
(14.23)
Для частного случая, когда внутренний и внешний цилиндры
изготовлены из одинакового материала (Е{ = Е2 = Е, ц, = ц2 = Ц). формула (14.23)
упрощается и принимает вид:
Рк =
М
2г,
2 2 2 2
^2 + ^1 + ^3 + Г2
Го ~ Г,
(14.24)
Таким образом, в результате посадки с натягом одного цилиндра на
другой внутренний цилиндр оказался нагружен внешним давлением рк,
а наружный - таким же по величине внутренним давлением рк. Если
такой составной цилиндр нагрузить внутренним рабочим давлением, то
он будет деформироваться как единое целое и напряжения в нем
определяются по формулам (14.15). Эти напряжения должны быть
алгебраически просуммированы с напряжениями, вызванными
контактным давлением/?^. Во внутренних, наиболее нагруженных точках,
напряжения ое от рабочего давления и давления/?А, имеют разные знаки,
поэтому суммарные напряжения снижаются и составной цилиндр может
выдержать большее внутреннее давление, чем сплошной с теми же
геометрическими параметрами.
Для составного цилиндра может быть сформулирована задача
оптимального проектирования. Пусть заданы: внутренний радиус
внутреннего цилиндра гх, внутреннее (рабочее) давлениер, допускаемые
напряжения [о] и модуль продольной упругости Е. Требуется определить
внешний радиус составного цилиндра г3, радиус контактной поверхности
301
Рис. 14.8. Напряжения в составном цилиндре от контактного давления
Рис. 14.9. Напряжения в составном цилиндре от контактного давления и
рабочей нагрузки
г2 и натяг А. В качестве условий оптимальности могут быть приняты
следующие:
о^=о®, тахоэкв = [°], ^ = 0, (14.25)
т.е. равнопрочность внутреннего и внешнего цилиндров, равенство
максимальных эквивалентных напряжений допускаемым и условие
минимальности эквивалентных напряжений по величине радиуса
контактной поверхности. Реализация условий (14.25) дает формулы
Гадолина
302
Проиллюстрируем применение формул Гадолина. Пусть гх = 0,05 м,
р = 50 МПа, £ = 200 ГПа и [о] = 150 МПа. Тогда вычисления по
формулам (14.26) дают: г2 = 0,075 м, г2 = 0,0612 м, А = 3,06-10"5 м. При
известном натяге А по формуле (14.24) вычислим величину контактного
давления рк = 5 МПа. Эпюры напряжений ог и ое представлены на
рис. 14.8. Суммарные напряжения от рабочего давления/? и контактного
давления рк иллюстрирует рис. 14.9, где штриховой линией показаны
также напряжения в сплошном цилиндре с толщиной стенки г3 - гх. Из
рисунка следует, что при одинаковых весовых показателях максимальные
эквивалентные напряжения в составном цилиндре (150 МПа) оказались
существенно меньше, чем в сплошном (180 МПа).
14.3. Температурные напряжения в толстостенных цилиндрах
При наличии неравномерного по толщине температурного поля в
цилиндре возникают температурные напряжения. Предположим, что
температурное поле Т(г) является осесимметричным и стационарным
(температура во времени постоянна).
Формулы обобщенного закона Гука с учетом температурного
расширения имеют вид:
г, = —К - \x(oQ + oz)] + ссГ,
= ^К - ц(ог + ог)] + аТ, (14.27)
cz = \.К ~ ^К + °е)1 + аТ = с01181-
Деформация е2 в продольном направлении постоянна для открытого и
закрытого цилиндров. Радиальные ог и окружные ое напряжения
удовлетворяют уравнению равновесия (14.2), а деформации ег и г0
выражаются через радиальные перемещения и(г) по формулам (14.3) и
(14.4) соответственно. Используя формулы (14.2)...(14.4) и выражения для
напряжений через деформации, обратные (14.27), получим уравнения
303
равновесия в перемещениях с учетом температурного поля Т(г)\
U L 1Л14> _ U _ 1 "г
dr7
г dr
1 +»adT(r)
1 - ц dr
Решение этого уравнения имеет вид
м(г) = С,/- + С21 + ±\-±-± ГaT(p)pdp,
г г 1 - u J
(14.28)
(14.29)
где постоянные интегрирования Сх и С2 находятся из граничных условий
на внутренней и наружной поверхности цилиндра:
°Г(Г\) = °> °Лгг) = °>
т.е. предполагается, что поверхности цилиндра свободны от напряжений.
Кроме того, для определения неизвестной деформации г2 в продольном
направлении будем считать, что расширение цилиндра в продольном
направлении не стеснено. Тогда для любого сечения продольное усилие
N2 равно нулю:
2л 'г
N.
z= [ [ojdrdQ = О,
О г,
откуда после подстановки о2, определяемого формулой (14.27), находится
деформация ez. Вычисления, аналогичные проведенным в § 14.1, дают для
напряжений аг, о6 и о2 следующие формулы:
l-|i
г2-л2
.i/7Xp)pdp + TrlJL/rWrdr
г. * *> >\ »■
О, =
1-Ц
г2+г2
iL /T(p)pdp + _L JL fr(r)rdr - «Г(г)
; (14.30)
304
1-ц
2а
2 2
fT(r)rdr - аГ(г)
Рассмотрим некоторые частные случаи.
Линейный закон изменения температуры по толщине стенки цилиндра.
В этом случае
Т(г) = Г, - АГ-
г - г,
(14.31)
где ДГ = Т1 - Т2, Т1 и Т2 - температура на внутренней и наружной
поверхности цилиндра соответственно. Вычисления с использованием
выражений (14.30) для напряжений ог, ое, ог дают следующие формулы:
аДГ£
3(1-ц)(г2-г,)
г -
,\{
1 - li-
3 3
2 2
V'2-'l /J
a ATE
3(1-ц)(г2-г,)
2r +
1 -
'л/
Г2 4
2 2
(14.32)
a ATE
3(\-ii)(r2-ri)
Ъг - 2-
з з
2 2
Логарифмический закон изменения температуры по толщине стенки
цилиндра. Изменение температуры Т\г) по толщине стенки цилиндра в
форме
Т(г) = Г, - АГ
ln(r/r,)
In (r2/r,)
(14.33)
представляет собой решение задачи теплопроводности при стационарном
тепловом режиме. В этом случае напряжения вычисляются по формулам:
305
Еа&Т
2(1-л)Цг2/г,)
Ьж~^аШ «
Рис. 14.10. Температурные напряжения в толстостенном цилиндре
а ATE
2(1-ц)1п(г2/г,)
1п^ +
2 _2
ln-2-
а ATE
2(1-ц)1п(г2/г.)
1 - ln-i +
2 2
1+^
Г2
г,
(14.34)
а ATE
2(1-ц)1п(г2/г.)
1 - 21n-?- - 2-
-ln-
r22-r,2 '.
При положительном перепаде температур (Тх > Т^ опасными являются
точки на внутренней поверхности цилиндра. Распределение напряжений
<зг, ое и oz показано на рис. 14.10.
306
Примечание. Формулы (14.32), (14.34) справедливы для сечений,
удаленных от краев цилиндра на расстояние порядка наружного радиуса
и более. В случае тонкого диска ог-0, а для ог и ов формулы (14.32) и
(14.34) остаются справедливыми.
При одновременном нагружении цилиндра внутренним и внешним
давлением (задача Ламе) и неравномерном нагреве для вычисления
суммарных напряжений используется принцип суперпозиции.
Для высоких значений температур Тх и Т2 (но при небольших
перепадах) в формулы (14.32) и (14.34) следует подставить значения Е
и ju, соответствующие средней температуре стенки цилиндра.
14.4. Вращающиеся диски
Рассмотрим тонкий, вращающийся с угловой скоростью о> = const
диск,имеющий плоскость симметрии. Центробежныесилы, действующие
на диск, симметричны относительно оси вращения, а напряженное
состояние в точках диска двухосное; радиальные и окружные напряжения
постоянны по толщине диска. Осевое напряжение ввиду малости
толщины диска oz « 0.
Для получения уравнения равновесия элемента диска в уравнении
(14.1) необходимо учесть инерционную центробежную силу dP =
= pG)2/-2dzdrd0, где р - плотность материала, pdzrdrdO = dm - масса
элемента, or/- = ап - нормальное ускорение. Тогда уравнение равновесия
в напряжениях для вращающегося диска примет вид:
do, о„
+
dr г
-р<о2г. (14.35)
После использования закона Гука (14.6) и соотношений для
деформаций (14.3) и (14.4), оно приводится к дифференциальному
уравнению второго порядка относительного радиального перемещения
м(г), т.е.
d2u ]^ dw и_ 1 - ц2
г2
dr2 г dr г2 Е
Общий интеграл этого уравнения имеет вид
.2
pw2r. (14.36)
и(г) = Схг + С2- - t.po>V, (14.37)
'' 2r %Е
307
где Cj и С2- постоянные интегрирования.
Для радиальных ог и окружных о0 напряжений по формулам закона
Гука получим
1 -и2
1 -ц*
С,(1 + и) - (1 - ц)-
С,(1 + й) + (1 - ц)-
(3 + ^) g Г •
(14.38)
(1 + Зц)^-Г\
Рассмотрим два случая.
Диск без отверстия. В этом случае из условия ограниченности решения
при г - 0 следует положить С2 = 0, а вторую постоянную определим из
условия ог(г2) = 0:
с _ Р0>2 2(3 + Ц)(1 - |Х)
. - -—Гл — .
8
Тогда для диска без отверстия имеем
Е
О
°е = ^(3 + Ц)
2 _ 1 -И ЗЦ,2
3 + ц
(14.39)
Опасные точки находятся при г = 0, где
2 2
parr,
оЛ = *-—i-(3 + ц).
■'е
8
Эпюры напряжений, вычисленных по формулам (14.39), представлены
на рис. 14.11.
Диск с отверстием. Здесь постоянные интегрирования определяются
из граничных условий: аг(гх) = 0, ог(/*9) = 0. Для перемещений и(г),
вызванных инерционными силами, получаем:
и(г)
1-Ц2 2
—£-ро/
8£
2 2
3 + Ц, 2 ^ 2ч _,_ З + Ll г\ г2 3
|>ц * 2 1-м г
(14.40)
308
pm2R2
О-/*)
Рис. 14.11. Напряжения в сплошном диске от центробежных сил
а для радиальных ог и окружных о0 напряжении соответственно:
( \
о, - £^(з + ц)
2 2
Г, Г
1 '2 _ г2
°е = £2-<3 + ц)
2 2
1 г2 з + ц ;
(14.41)
На рис. 14.12 представлены эпюры напряжений во вращающемся диске.
Из эпюр следует, что опасные точки расположены при г = г,, где
наибольшего значения достигают окружные напряжения
Если вращающийся диск нагружен в точках г = гх и г - г2 давлениями
/?, и/?9, то к инерционным напряжениям (14.41) необходимо добавить
напряжения от давлений/?j ир2, вычисленные по формулам Ламе (14.13).
Практический интерес представляет задача о расчете на прочность
вращающегося диска, посаженного на вал с натягом А (рис. 14.13). При
вращении за счет деформаций диска под действием инерционных сил
309
!=-И>-/0*п?<»+/')]
Рис. 14.13. Диск, посаженный на вал с
натягом
начальный натяг А уменьшается и
может быть определен согласно
выражению
Рис. 14.12. Напряжения в диске с
отверстием от центробежных сил
А - 2uJr{) - 2w2(r.),
Wj(rj) - перемещение точек вала, а
и2(г\) - перемещения точек диска при г = г{. Значение частоты вращения,
при которой натяг AQ = 0 и, следовательно, контактное давление между
валом и диском обращается в нуль, называется освобождающей частотой
вращения соосв. Если диск посажен на сплошной вал с натягом А, а
характеристики материалов диска и вала р, Е, \х одинаковы, то
освобождающая частота вращения определяется по формуле
2ЕД
\ (3 + \i)prxr:
1'2
310
Глава 15
РАСЧЕТ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНОМУ
СОСТОЯНИЮ
15.1. Понятие о предельном состоянии конструкций.
Предельная нагрузка
В гл. 2 с общих позиций были обсуждены два подхода к расчетам на
прочность конструкций: расчет на прочность по допускаемым
напряжениям и расчет на прочность по допускаемым нагрузкам.
Расчеты на прочность по допускаемым напряжениям основаны на
понятии предельного состояния в точке. Под предельным состоянием
здесь понимается такое состояние, при котором наступила текучесть (для
пластичных материалов) или разрушение (для хрупких материалов) хотя
бы в одной точке. Расчеты по допускаемым напряжениям обеспечивают
прочностную надежность конструкций, но во многих случаях приводят
к необоснованному завышению весовых показателей. Такая ситуация,
например, наблюдается для конструкций из пластичных материалов при
неравномерном распределении напряжений (при изгибе, кручении), в
статически неопределимых системах. Появление местных пластических
деформаций и даже переход в пластическое состояние одного или
нескольких элементов во многих случаях не приводят к отказу
конструкции в целом.
Расчет на прочность по допускаемым нагрузкам основывается на
понятии предельного состояния конструкции. Предельным состоянием
конструкции называется такое ее состояние, при котором она теряет
способность сопротивляться внешним нагрузкам или перестает
удовлетворять необходимым эксплуатационным требованиям. Расчеты
на прочность по допускаемым нагрузкам иногда называют: расчеты по
предельному состоянию, расчеты по несущей способности или расчеты
по разрушающим нагрузкам. Различают три вида предельных состояний
конструкций:
- первое предельное состояние - по несущей способности (прочности,
устойчивости и при переменных напряжениях по выносливости);
311
- второе предельное состояние - по развитию чрезмерных
деформаций;
- третье предельное состояние - по образованию или раскрытию
трещин.
В дальнейшем ограничимся рассмотрением конструкций,
выполненных из пластичных материалов. В расчетах по допускаемым напряжениям
исходят из условия прочности вида
о
тахо <, [о] = —-, (15.1)
М
где, напомним, тахо - максимальное эквивалентное напряжение, [о] -
допускаемое напряжение, от - предел текучести, [п] - нормативный
коэффициент запаса прочности. Величина нагрузки [Р]9 при которой
напряжение в опасной точке конструкции равно допускаемому значению
[о], называется допускаемой нагрузкой, а нагрузка Рт, при которой
напряжение в этой точке равно пределу текучести, - опасной нагрузкой.
В расчетах по предельному состоянию центральным понятием
является предельная нагрузка Р., при которой конструкция переходит в
предельное состояние (полностью исчерпывает несущую способность).
Предельную нагрузку, деленную на нормативный коэффициент запаса
прочности [п], назовем предельно допускаемой нагрузкой и обозначим [Р]Л
Условие прочности записывается в виде
Р * PI- (15.3)
В большинстве случаев предельно допускаемая нагрузка [Р\0 больше
допускаемой нагрузки [Р]9 вычисленной с тем же нормативным
коэффициентом запаса, в некоторых случаях равна ей, т.е.
[Р1 * [Р\. (15.4)
При расчетах по предельному состоянию значение нормативного
коэффициента запаса прочности устанавливается, как правило, таким,
чтобы напряжения во всех точках конструкции для предельно
допускаемой нагрузки были меньше предела текучести. Расчеты по предельному
состоянию широко применяются при проектировании строительных
312
конструкций. Все большее
распространение такие расчеты получают
и в машиностроении, поскольку
позволяют вскрыть возможные
резервы прочности, уменьшить
массу конструкций.
Для облегчения определения
предельных нагрузок, а эта
процедура связана с упругопластичес-
ким анализом конструкций,
действительные диаграммы
деформирования материала заменяют
упрощенными, условными диаграммами.
Наиболее популярной
схематизацией зависимостей о - е или т - у для
пластичных материалов является
диаграмма Прандтля (рис. 15.1).
Материал, деформирование
которого характеризуется диаграммой Прандтля, называется идеальным
упругопластическим. При нагружении такого материала связь между
напряжениями и деформациями может быть описана следующим
образом:
""
0
^
/
£у,
7".
1
Рис. 15.1. Диаграмма деформирования
идеального упругропластического
материала
\Ее9 е й 8Т, \Gy, у <; ут,
(растяжение); т = \ (сдвиг). (15.5)
е > ет,
Yt>»
Диаграмма Прандтля основана на предположении, что предел
пропорциональности и предел текучести материала совпадают, а
площадка текучести имеет неограниченную протяженность (рис. 15.1).
При разгрузке материал ведет себя как упругий. Модули упругости, а
также и пределы текучести при растяжении и сжатии одинаковые.
15.2. Расчеты при растяжении (сжатии)
При растяжении (сжатии) напряжения равномерно распределяются
по площади поперечного сечения. В связи с этим предельное состояние
стержня, изготовленного из идеального упругопластического материала,
наступает тогда, когда продольное усилие в нем достигает величины o^F,
где через F обозначена площадь поперечного сечения. Рассмотрим
статически определимую систему, схема которой представлена на
313
м
a f Ь
N*
-XJL,
В
Рис. 15.2. Статически определимая
система при растяжении (сжатии)
-9-
-+-
i
i
<'.
Рис. 15.3. Предельное состояние
статически определимой системы
при растяжении (сжатии)
рис. 15.2. Здесь жесткий брус А В удерживается двумя вертикально
расположенными стержнями, площади поперечного сечения F которых
одинаковы. Линейные размеры а и b определяют координаты точки
приложения нагрузки Р. Применяя метод сечений, несложно получить
выражения для продольных сил, возникающих в стержнях:
Nt
а + b
>N2
а + b
(15.6)
Пусть а < b. Тогда из (15.6) следует, что N{ > N2. При возрастании Р
текучесть наступает в первом стержне, т.е. Nx = oTF. Значение нагрузки
Р. = oF
а + b
(15.7)
соответствует переходу конструкции в предельное состояние: брус ЛЯ
будет поворачиваться вокруг точки В, т.е. система превращается в
механизм, и конструкция не в состоянии сопротивляться внешней
нагрузке (рис. 15.3). В данном случае опасная Рт и предельная Р.
нагрузки совпадают, а расчеты на прочность по допускаемым
напряжениям и по предельному состоянию дают одинаковые результаты. Такая
ситуация сохраняется для всех статически определимых систем, стержни
314
Nt
a
A
+P
M
F
a
В
N,
<xTF
ЛГ,
В
N3
С
X
-A/,
Рис. 15.5. Опасное состояние
статически неопределимой
системы
которых работают на растяже-
НИР ^P^lfЯТИР^
Рис. 15.4. Работа статически неопределимой ^ ''
системы в упругой стадии ТепеРь рассмотрим стати
чески неопределимую систему
(рис. 15.4). В упругой стадии
усилия в стержнях конструкции определяются из двух уравнений
равновесия (для рассматриваемой системы независимых уравнений
равновесия можно составить только два) и дополнительного уравнения
совместности деформаций, которое составляется из условия отсутствия
изгибных деформаций бруса ABC:
А/, - Д/9 АЛ - AL
1) Ща + гЩа = 0\ 2) Nxa-N3a = Pa\ 3) —i ^ = —? ^. (15.8)
а а
Выражая в третьем уравнении удлинения стержней через усилия и решая
систему (15.8), получим
N. = -Р, N2 = i-P, ЛГ, = -Ip.
1 6 2 3 3 6
При возрастании силы Р текучесть впервые наступит в стержне 1. Из
условия
"i
получим значение опасной нагрузки
5 Р
6 F
315
^т = |°т^ (15.9)
При таком значении силы Р стержни 2 и 5 работают в упругой стадии.
Напряжения в них соответственно равны: о2 = 20^5, а3 = -0^5.
Следовательно, возможно дальнейшее увеличение силы Р. Система
становится уже статически определимой, так как N^ = от/г(рис. 15.5).
Поэтому из уравнений равновесия получим
N2 = 2(Р - от/0, N3 = -(Р - oTF).
Отсюда следует, что при возрастании силы Р следующим в состояние
текучести перейдет стержень 2. Из условия oTF = 2(Р - OjP) получим
величину предельной нагрузки
Л = |°т^. (15.10)
Нагрузку больше этого значения конструкция выдержать не может.
Сравним результаты расчетов по допускаемым напряжениям и по
предельному состоянию. Примем некоторое значение нормативного
коэффициента запаса прочности [л]. Тогда из условия (15.1) с учетом
(15.9) получим величину допускаемой нагрузки [Р]:
и-|тг
5 [п]
Из расчета по предельному состоянию предельно допускаемое значение
нагрузки [Р]„ будет равно (15.2), (15.10):
3 °tF
2 [и]
При одном и том же нормативном коэффициенте запаса прочности
предельно допускаемая нагрузка [Р]т больше допускаемой [Р] в 1,25 раза.
В качестве еще одного примера рассмотрим брус с жестко
закрепленными концами и находящийся под действием продольной силы Р. Схема
нагружения и параметры бруса представлены на рис. 15.6, а. Сравним
результаты вычисления допускаемых нагрузок из расчетов на прочность
по допускаемым нагрузкам и по предельному состоянию. При работе
бруса в упругой стадии необходимо раскрыть статическую неопредели-
316
мость. Например, если в качестве
основной системы принять брус с
отброшенной нижней опорой, заменив ее
действие реакцией X, то уравнение для
определения этой реакции будет
следующим:
IL
EF
XI
2EF
Ш
EF
Отсюда X = 2Р/5, и максимальные
напряжения возникают на верхнем
участке бруса. Условие прочности по
допускаемым напряжением примет вид
Ъ Р °т
тахо = * [о] = —-.
5 F [п]
Отсюда получаем допускаемое
значение нагрузки
mkm
i | i
1'-
k 1 1 !
I и
F
i III
[ p
* 1 III
lyl
Jll
i |
■» I i
т 1
mmm.
1 x
aTF
arF
2F
6)
a)
[P] =
1?£
3 [n] "
Рис. 15.6. Статически
неопределимый ступенчатый брус:
а - упругая стадия работы; б -
предельное состояние
Опасное состояние системы
соответствует достижению наибольшими
напряжениями, возникающими выше
точки приложения силы, предела
текучести. Для перехода системы в
предельное состояние необходимо, чтобы предела текучести достигли
напряжения и в сечениях бруса ниже точки приложения силы Р. В этом случае
рассмотрение равновесия участка бруса в окрестности точки приложения
силы (рис. 15.6, б) дает предельную нагрузку, равную Р, = lo^F.
Предельно допускаемая нагрузка будет равна [Р]т = laxity]. Таким
образом, для данной системы имеем [Р]л = 1,2[Р].
Статически неопределимые системы имеют резерв прочностной
надежности. Допускаемые нагрузки, полученные из расчета по
предельному состоянию, всегда выше, чем допускаемые нагрузки,
вычисленные из расчета по допускаемым напряжениям.
317
15.3. Упругопластический изгиб стержней
Рассмотрим чистый изгиб стержня, поперечное сечение которого
имеет две оси симметрии (рис. 15.7, а). Считаем, что выполняется
гипотеза плоских сечений (гипотеза Бернулли), согласно которой
относительные деформации волокон 8 распределяются по высоте
поперечного сечения по линейному закону
У
3
р
(15.11)
где у - координата волокна в системе хОу, связанной с главными
центральными осями поперечного сечения, 1/р - кривизна изогнутой оси
стержня, р - радиус кривизны. По определению изгибающий момент Мх
связан с нормальными напряжениями о соотношением
мх = - / °уКуНу-
-Л/2
(15.12)
Здесь А - высота поперечного сечения, Ь(у) - ширина сечения на уровне
у. Если связь между напряжениями и деформациями была бы линейной
о = Ег, то из выражений (15.11) и (15.12) следуют обычные формулы
изгиба стержня:
а)
б)
Рис. 15.7. Упругопластический изгиб стержня:
а - поперечное сечение с двумя осями симметрии; б - упругая зона и зоны
текучести
318
1 мх л/ ш. ,
- = -=f, о = ~~ГУ> Jx = / У2ЬШУ, (15.13)
р х * -ыг
где Jx - осевой момент инерции поперечного сечения относительно оси
Ох.
Наибольшие нормальные напряжения возникают в наиболее
удаленных от нейтральной линии точках поперечного сечения и
определяются как
Мх
тахо = —±, (15.14)
X
где Wx = UJh - момент сопротивления поперечного сечения при изгибе.
Если элемент конструкции работает на изгиб, то при расчетах на
прочность по допускаемым напряжениям в условие (15.1) подставляются
тахо, определяемые формулой (15.14). В этом случае за опасное
принимается состояние элемента, соответствующее достижению
наибольшими нормальными напряжениями предела текучести от.
Опасное значение момента при этом равно Мхт = oTWx. Однако при
таком значении изгибающего момента несущая способность стержневого
элемента не исчерпывается и он сохраняет способность воспринимать
внешнюю нагрузку.
При дальнейшем увеличении изгибающего момента пластическое
состояние материала распространяется внутрь сечения по направлению
к нейтральной оси. В поперечном сечении образуются зоны текучести
в верхней и нижней части, а в окрестности нейтрального слоя остается
упругая зона, где напряжения меньше от (рис. 15.7, б). Границам
указанных зон соответствует значение координаты ут9 которое при
соблюдении гипотезы Бернулли (15.11) можно определить из условия
Здесь и далее знаки напряжений, деформаций и моментов выбираются
по смыслу.
Формула (15.12), определяющая изгибающий момент Mv, справедлива
при любом законе распределения нормальных напряжений по высоте
поперечного сечения. Используем ее для случая упругопластического
деформирования материала стержня. Учтем, что рассматриваемое
поперечное сечение имеет две оси симметрии
319
Л/2
Ут
Л/2
Мх = 2fob(y)ydy = 2[ob(y)ydy + 2oTfb(y)ydy. (15.16)
Ут
В упругой зоне 0 <, у < ут справедлив закон Гука: о = Ег = Еу/р. Тогда
выражение (15.16) можно переписать в виде
М = 2
.*
Л/2
-fb(y)y2dy + orfb(y)y&y
= 2
£Л
V Р
. (15.17)
Здесь 7 - осевой момент инерции половины упругой зоны
относительно нейтральной оси, Sxnn - статический момент инерции верхней зоны
текучести.
Пусть поперечное сечение имеет форму прямоугольника шириной Ъ =
= const и высотой h. В этом случае вместо (15.17) можно записать
М = lb
ЕУт_ + ?1
Lp 3 2
hi
4
(15.18)
Учитывая, что координата границы упругой зоны ут связана с кривизной
соотношением (15.15), и разрешая формулу (15.18) относительно 1/р,
получим связь между кривизной и изгибающим моментом при упруго-
пластическом изгибе стержня
J_±
ft Рт
1
-1/2
(15.19)
Формула (15.19) справедлива при Мх •*. Mxr = a^bh /6. Кривизна 1/рт
соответствует появлению текучести в крайних волокнах поперечного
сечения и определяется следующим образом:
_1_
Рт
1^1
h Е'
Кривизна 1/р -» ~ при Мх - Мх, - aTbh /4, а ут - 0. Это означает, что
пластическая зона распространяется на все поперечное сечение и в
стержне образуется так называемый пластический шарнир. Момент Мх,
является предельным моментом для стержня. В отличие от идеального
320
МхТ МХФ ния нормальных напряжений
Рис. 15.8. Зависимость кривизны
стержня от изгибающего момента
шарнира, который не воспринимает
момента, в пластическом шарнире
действует момент Мхл.
При значениях момента, меньше MYT, материал стержня работает
упруго и связь между МХ0 и кривизной - линейная
I = 3 1 мх
Р 2 Рт Мх*
Полная зависимость между 1/р и изгибающим моментом представлена
на рис. 15.8.
Предельное значение изгибающего момента МХ0 можно получить,
рассматривая предельный случай распределения нормальных напряжений
(рис. 15.9). Из формулы (15.12) следует
ыг
Мх. = 2orfb(y)ydy = 2aTSi,/2) = arWxna. (15.20)
о
Здесь Sxn) - статический момент инерции половины сечения, Wxnn =
= 2Sxn) - пластический момент сопротивления при изгибе. Для
прямоугольного поперечного сечения Wxnn = bh2/4. Если сечение не симметрично
321
я
шжшшшшшш
тшк мх9 мхт mm
Рис. 15.10. Статически определимая система при изгибе
относительно оси Ох, то нетрудно показать, что
W
Six) + 5
(2)
(15.21)
где Sx\ S® - статические моменты соответственно верхней и нижней
частей поперечного сечения относительно нейтральной оси. Продольная
сила при изгибе равна нулю. Поэтому площадь сжатой зоны сечения
равна площади растянутой зоны. Нейтральная ось в сечении,
совпадающем с пластическим шарниром, делит это сечение на две равновеликие
части. Поэтому при несимметричном поперечном сечении нейтральная
ось не проходит через центр тяжести сечения.
Изложенные элементы теории упругопластического изгиба часто
используются не только для случая чистого изгиба, но и для поперечного,
т.е. когда кроме моментов в поперечных сечениях стержней возникают
перерезывающие силы. В последнем случае влиянием сдвигов обычно
пренебрегают.
Рассмотрим пример определения допускаемых нагрузок при изгибе,
исходя из расчетов по допускаемым напряжениям и по предельному
состоянию. Пусть шарнирно опертая по концам балка находится под
действием равномерно распределенной нагрузки интенсивностью q
(рис. 15.10). Из эпюры изгибающего момента следует, что опасное
322
сечение находится в середине балки, причем maxMY = #/2/8. Условие
прочности при расчете по допускаемым напряжениям дает
™v„ - maxM* < °т . ы * 8 °т w
шаха = й —; \д\ = W„.
W, М /2 [и] *
Расчет на прочность по предельным нагрузкам приводит к следующему
результату:
тахМ. й
М„
<Л„Л
;М-"?м
8 °rw
XIUT
[п] [п]
Таким образом, отношение предельно допускаемой нагрузки [q]t к [q]
равно отношению пластического момента сопротивления WxunK й^т.е.
w
ЯГ
Для прямоугольного поперечного сечения это отношение составляет 1,5.
Мы рассмотрели статически определимую систему, переход которой
в предельное состояние связан с образованием одного пластического
шарнира (рис. 15.10). Для статически неопределимых систем переход в
предельное состояние происходит с образованием п + 1 пластических
шарниров, где п - степень статической неопределимости. На рис. 15.11
представлена один раз статически неопределимая система. Механизм
разрушения такой системы определяется двумя пластическими
шарнирами, образующимися в сечениях с наибольшими значениями изгибающих
моментов. Отличие результатов
расчетов на прочность с
использованием различных подходов для
статически неопределимых систем
значительно большее, чем для
статически определимых.
Как отмечалось выше, если
изгибающий момент превышает
опасное значение, определяемое
величиной MYT = oTWx, то в
поперечном сечении стержня
появляются зоны текучести. При снятии
нагрузки в статически определи- рис. 15.11. Предельное состояние стати-
мых стержнях изгибающие момен- чески неопределимой системы при
изгибе
323
ты во всех сечениях будут равны нулю. Несмотря на это, нормальные
напряжения в сечениях, в которых имела место текучесть материала, не
исчезнут, а образуют так называемые остаточные напряжения. Построим
эпюру остаточных напряжений оост для случая стержня с прямоугольным
поперечным сечением. Разгрузка равносильна приложению поля упругих
напряжений, обратных по знаку первоначальным:
М
разгр
*У = Ж
гразгр
Изменение кривизны 1/рразгр при разгрузке происходит упруго:
"разгр
Ebh3
Определим остаточную кривизну 1/рост после разгрузки:
1
Рост
"разгр
Рт
J_
i-
м.
А/,
-ш
3 мх
**/
2 М.
(15.22)
Остаточные напряжения оост будут иметь кососимметричную эпюру и
для у г О определяются выражениями
от изо-т У^з
Рис. 15.12. Пример определения остаточных напряжений при упругопластическом
изгибе
324
IeJL
uv
у * yT
> У > Ут
(15.23)
2 pT Mx,
На рис. 15.12 для случая Mx = 0,89 Мхм представлены эпюры напряжений
о при нагружении стержня моментом Мх, напряжений разгрузки о
и остаточных напряжений оост.
15.4. Упругопластическое кручение стержня
кругового поперечного сечения
Касательные напряжения т, возникающие при кручении стержня
кругового поперечного сечения (рис. 15.13, я), в упругой стадии
распределяются по радиусу по линейному закону. В центре сечения они
равны нулю, а максимального значения достигают в точках наружного
контура (рис. 15.13,6)
тахт =
Mi
-*rAl
где W = nd /16 - полярный момент сопротивления кругового
поперечного сечения диаметра d. Опасное значение крутящего момента соответству-
Мж<МжТ Мг=М9-
Рис. 15.13. Кручение стержня кругового поперечного сечения в упругой стадии:
а - параметры сечения; б - эпюры касательных напряжений при значении
крутящего момента меньше опасного; в - эпюра касательных напряжений в
опасном состоянии
325
м,>м,
К = м,.
Рис. 15.14. Упругопластическое кручение стержня кругового поперечного сечения:
а - упругая и пластическая зоны; б - предельное состояние
ет достижению максимальных касательных напряжении тахт предела
текучести при сдвиге тт, т.е. MZT -\Wp = ттти/3/16 (рис. 15.13, в). Если
стержень выполнен из идеального упругопластического материала,
следующего диаграмме Прандтля, то при возрастании крутящего
момента напряжения, равные пределу текучести тт, возникают уже в
некоторой кольцевой области поперечного сечения (рис. 15.14, а). Как
и при изгибе назовем эту область зоной текучести. Внутри этой области
напряжения ниже предела текучести и материал находится в упругом
состоянии. Исчерпанию несущей способности стержня соответствует
предельное значение крутящего момента М2Ш, при котором зона
текучести распространяется на все поперечное сечение, а касательные
напряжения во всех точках равны тт (рис. 15.14, б).
По аналогии с изгибом упругопластического стержня получим
зависимость между относительным углом закручивания поперечного
сечения 0 и крутящим моментом Мг Пусть гт - радиус окружности -
границы между зоной текучести и упругой зоной (рис. 15.14, а). Тогда,
учитывая связь между углом сдвига у в точке с координатой г и
относительным углом закручивания 0: у = г0, и закон Гука при сдвиге
т = Су, имеем
т
Mz = f-zrdF= 2п Nr2dr = 2и
d/2
\
G fyr 2dr + тт fr 2dr
(15.24)
После вычисления интегралов в выражении (15.24) получим
326
%jf lid1 1 7CT4
12 T 6 (G6)3
(15.25)
Разрешая соотношение (15.25) относительно угла закручивания 0,
получим
1вА
4 ТМ..
А/2 <; MZT,
2 т
М„
\ -1/3
(15.26)
V
М.
. ^2 > м„>
Z*/
где 0Т = Ix^Gd- относительный угол закручивания, соответствующий
опасному значению крутящего момента MZT, М2. - предельное значение
крутящего момента
НА **Ъ
z* т 12
(15.27)
при котором относительный угол закручивания 6 - ~. Величину
предельного крутящего момента можно получить проще, сразу
рассмотрев случай равенства касательных напряжений во всех точках
поперечного сечения тт (рис. 15.14, б):
<иг
nd3
A#„*2*/V2*- V*|--*
W .
т 'рил
(15.28)
Здесь введен пластический момент сопротивления при кручении стержня
кругового поперечного сучения W_пл = та/3/12.
Сравнивая условие прочности при расчетах по допускаемым
напряжениям
Mz тт
тахт = —- <. —
Wp [п]
и условие прочности при расчетах по предельному состоянию
м7 * —z-
z [л]
т W
И
327
2w/3
Рис. 15.15. Статически неопределимая система при кручении:
а - расчетная схема; б - эпюра крутящего момента в упругой стадии; в -
равновесие элемента бруса; г - эпюра крутящего момента в предельном
состоянии
приходим к выводу, что при одинаковых коэффициентах запаса
прочности расчет по предельному состоянию статически определимых
систем дает допускаемое значение нагрузки в W IW = 4/3 ~ 1,33 раза
больше, чем при расчетах по допускаемым напряжениям. Для статически
неопределимых систем это отличие может быть значительно большим.
Рассмотрим простейшую статически неопределимую систему при
кручении (рис. 15.15, а). Несложно установить, что для упругой стадии
работы стержня эпюра крутящих моментов имеет вид, представленный
на рис. 15.15, б. Расчет по допускаемым напряжениям дает допускаемое
значение приложенного к брусу момента [m]j
2т
3W„
W
[т] = IjlZjl,
1 2 [п]
При увеличении момента т в состояние текучести сначала перейдет
левый участок бруса, а правый участок в это время будет работать
упруго. Предельному состоянию системы соответствует переход в
состояние текучести обоих участков. Тогда из условия равновесия
328
(рис. 15.15, в) предельное значение момента тл равно 2М2. = 2xTW .
Эпюра крутящего момента по длине стержня для этого случая
представлена на рис. 15.15, г. Допускаемое значение момента [т]2 из расчета по
предельному состоянию будет равно
2т W
[т] = т '**.
2 W
Отношение допускаемых значений моментов,рассчитанных различными
способами, составляет
М* . 2'2'^пя . JUS я 1§78>
К з-и; 9
15,5. Предельное состояние толстостенных труб ^
Пусть толстостенная труба, изготовленная из идеального упругоплас-
тического материала, находится под действием внутреннего давления
р (рис. 15.16, а). При осесимметричной деформации трубы по
соответствующим площадкам возникают радиальные ог, окружные ое и в случае
плоской или обобщенной плоской деформации осевые напряжения oz.
Эти напряжения являются главными. Если в осевом направлении к трубе
не прикладываются дополнительные нагрузки, то в качестве первого
главного напряжения Oj выступает ое, в качестве второго главного
напряжения о2 - ог и, наконец, напряжения ог будут третьим главным
напряжением о3.
В упругой стадии опасные точки находятся на внутренней
поверхности трубы при г = г |, где
2 2
°i = °е = РГ\* \ °з = °г = -/>• (15.29)
Давление, при котором впервые появится текучесть в опасных точках,
определим с использованием критерия Треска-Сен-Венана, согласно
которому тахаэкв = о{ - о3. Тогда условие наступления текучести
запишется в виде
тахоэкв = ов - ог = р— = оТ. (15.30)
Г2 " Г\
329
а)
Из (15.30) следует формула для
опасного значения внутреннего давления
-О " Р2),
(15.31)
где введено обозначение р = гх1гг.
При величинах давления, больше
рт, пластическая зона в стенке трубы
распространяется от гх к г2. В
предельном состоянии текучесть имеет
место по всей толщине стенки трубы,
т.е. при всех гх йг й г0
°i - аз = ае(г) " °ЛГ) = °т- (15.32)
Для определения предельного
значения нагрузки рл воспользуемся
уравнением равновесия осесимметричной
задачи теории упругости
da, + о^
Ar г
0,
Рис. 15.16. Предельное состояние которое Д™ оДг) и oQ(r), удовлетворя-
трубы:
а - схема нагружения; б -
зависимость опасного давления, предель-
ющих условию текучести (15.32),
можно переписать в виде
(15.33)
ного давления и их отношения от
параметра р
Интеграл этого уравнения
or(r) = от1пг + С,
dr
г
(15.34)
содержит неизвестную константу Сх и, кроме того, неизвестным пока
является давление рш, приводящее трубу в предельное состояние. Для
определения указанных величин воспользуемся граничными условиями
при г = г j и г = г2, которые при заданном нагружении имеют вид
330
°r(ri) = -Р*> °г(гг) = °-
Подставляя сюда решение (15.34), получим
р. = o.lnCp"1). (15.35)
На рис. 15.16, б представлены зависимости опасного значения
давления/?1/от( 15.31), предельного давления pJaT (15.35) и их отношения pjpr
от параметра р, определяющего соотношение между внутренним и
внешним радиусами трубы (0 < р < 1). При Р - 0, что соответствует трубе
с большой толщиной стенки, рт - 0,72, а рч неограниченно возрастает.
При всех значениях р предельное давление больше опасного. Если р -
- 1, что соответствует уменьшению толщины стенки трубы, рт и р.
стремятся к нулю, а их отношение pJpT стремится к единице, т.е. для
тонкостенной трубы результаты расчетов на прочность по предельному
состоянию и по допускаемым напряжениям практически совпадают.
331
Глава 16
УСТОЙЧИВОСТЬ ЭЛЕМЕНТОВ
КОНСТРУКЦИЙ
16.1. Основные понятия теории упругой устойчивости
Выше рассматривались случаи статического внешнего воздействия
на деформируемые системы в линейной постановке. При этом
обнаруживалось единственное положение равновесия и
соответствующее ему распределение внутренних силовых факторов. Реализуемость
положения равновесия не рассматривалась. Однако при определенных
условиях положение равновесия механической системы может быть не
единственным, необходимо определить, является ли это положение
устойчивым или неустойчивым.
Потеря устойчивости первоначальной формы равновесия элементов
конструкций может оказаться причиной исчерпания их несущей
способности и в процессе эксплуатации недопустима. Положение
равновесия может быть устойчивым, безразличным (нейтральным) и
неустойчивым. Проиллюстрируем характер положения равновесия на
примере тяжелого шарика, находящегося на криволинейной поверхности
в потенциальном поле сил тяжести (рис. 16.1).
Различают следующие положения равновесия: II, V- малые
возмущающие воздействия вызывают
малые отклонения от
положения равновесия; такое
положение равновесия является
устойчивым (физически
осуществимым); /, IV- малые
возмущения приводят к большим
отклонениям от положения
равновесия; такое положение
является неустойчивым; III - без-
Рис. 16.1. Характер положения равновесия: различное (нейтральное) поло-
//, V - устойчивое; /, IV - неустойчивое; жение равновесия.
III - безразличное (нейтральное)
%я&»
332
Рис. 16.2. Устойчивость положения J °J
равновесия системы в однородном поле
сил тяготения: Рис. 16.3. Устойчивость положения
а - устойчивое; б - неустойчивое равновесия деформируемой системы:
а - центральное сжатие стержня; б -
бифуркационная кривая
На основании этого примера можно нестрого определить условие
устойчивости форм равновесия системы как свойство системы мало
отклоняться от положения равновесия под действием малых возмущений.
Другое определение условия устойчивости дается теоремой Лагранжа
-Дирихле: необходимым и достаточным условием устойчивости форм
равновесия систем, находящихся под действием потенциальных сил,
является достижение потенциальной энергией в этом положении
изолированного минимума.
Частным случаем этой теоремы является принцип Торичелли,
установленный эмпирически. Система, находящаяся в однородном поле
сил тяготения, стремится принять такую конфигурацию, при которой
ее центр масс (точка Q будет занимать наинизшее положение (рис. 16.2).
В данном примере устойчивым является положение, которому соответ
ствует минимальное значение потенциальной энергии (рис. 16.2, а),
неустойчивым - положение, в котором потенциальная энергия принимает
максимальное значение (рис. 16.2,6).
Равновесное состояние деформируемой системы также может быть
устойчивым, неустойчивым и безразличным. Так, при центральном
сжатии стержня с прямолинейной осью монотонно возрастающей силой
с фиксированной линией действия (рис. 16.3, а) характерны следующие
ситуации: Р< РШ,Р- Р,иР> Рш9 где Р. - критическое значение внешней
нагрузки.
333
Если Р < Pt9 то при снятии
малых поперечных возмущений
продольная ось стержня стремится
вернуться к исходному
прямолинейному положению равновесия.
При Р= Рш возможно
множество форм равновесия -
прямолинейная и близкие к ней мало
деформированные, что
соответствует безразличному положению
равновесия. При этом исходная
прямолинейная форма равновесия
стержня перестает быть устойчи-
Рис. 16.4. Потеря устойчивости плоской вой. Нагрузка Р= Р,, при которой
формы изгиба прямолинейная форма равновесия
перестает быть устойчивой,
называется критической.
При Р > Р. прямолинейное положение оси стержня статически
возможно, но неустойчиво. При малых поперечных возмущениях
продольная ось стержня получает необратимые поперечные перемещения,
устойчивой является искривленная форма равновесия. Эти равновесные
положения, которые можно получить только при рассмотрении задачи
в нелинейной постановке, иллюстрируются на рис. 16.3, б. Точка Р- Рл,
в которой происходит разветвление форм равновесия, называется точкой
бифуркации. Рассмотренное на этом примере явление наблюдается и при
других видах деформаций стержней, пластин и оболочек. Например,
изгиб тонкостенных стержней в плоскости наибольшей жесткости при
Р > Рт может сопровождаться потерей устойчивости плоской формы
изгиба, т.е. изгибом в плоскости наименьшей жесткости и кручением
стержня (рис. 16.4).
В приведенных примерах характерным является несоответствие
формы, которую принимает стержень после потери устойчивости,
приложенным силам. Действительно, в первом примере продольное
усилие вызывает сжатие стержня, а его продольная ось при потере
устойчивости искривляется как при изгибе. Нарушение устойчивости
рассмотренного типа получило название потери устойчивости первого
рода. Другим типом потери устойчивости первоначальной формы
равновесия является потеря устойчивости с переходом к несмежной
форме равновесия. Примером такого типа потери устойчивости может
служить поведение пологой оболочки под действием силы Р (рис. 16.5, а).
334
а)
Рис. 16.5. Потеря устойчивости с переходном к несмежной форме равновесия:
а - потеря устойчивости второго рода; б- верхняя и нижняя критические силы
При достижении силой Р критического значения Р„ происходит
мгновенное прощелкивание оболочки - выпуклость ее при этом будет
направлена в сторону, противоположную первоначальному
направлению. Состояние оболочки до прощелкивания при Р = Р0 является
неустойчивым - малые возмущения приводят к изменению форм
равновесия. После прощелкивания (штриховая линия на рис. 16.5, а)
оболочка принимает устойчивую форму равновесия. Такой тип потери
устойчивости носит название потери устойчивости второго рода: форма
потери устойчивости соответствует характеру приложенных сил. Если
после перехода системы в новое устойчивое положение равновесия
уменьшать силу Р, то при Р = Рпм происходит прощелкивание в обратном
направлении. Силы Рт и Ртт называются соответственно верхней и
нижней критической силами (рис. 16.5, б).
16.2. Устойчивость прямолинейного стержня
при продольном сжатии. Формула Эйлера
Найдем условия, при которых решение дифференциального уравнения
изгиба стержня под действием продольного усилия Р не является
единственно возможным, т.е. условия, при которых наряду с прямолинейной
формой равновесия возможно существование смежных искривленных
форм равновесия. Рассмотрим шарнирно опертый стрежень, находящийся
в состоянии безразличного равновесия в отклоненном от первоначальной
прямолинейной формы равновесия положении (рис. 16.6).
Запишем дифференциальное уравнение равновесия в предположении,
о v < < /, (dv/dz)1 < < 1,
что
335
Рис. 16.6. Центральное сжатие шарнирно опертого стержня
d2v _ Мх
dz2 " EJ'
(16.1)
Данное уравнение является линеаризированным уравнением изгиба (см.
гл. 6); Кроме того, предположим, что ось ненагруженного стержня
прямолинейна, внешние нагрузки и реакции опор вплоть до момента
потери устойчивости действуют вдоль этой оси. В этом случае
изгибающий момент в сечении с координатой z равен
Мх = M(z) = -Pw(z)
и уравнение (16.1) принимает вид:
dz2 EJX
0.
Вводя обозначение
fc2 =
EJ.
для уравнения (16.1) получаем
d2v
dz2
+ k2v = 0.
(16.2)
(16-3)-
Для шарнирно опертого стержня при z = 0 и z = / краевые условия
записываются в виде
v(0) = 0, v(0 = 0. (16.4)
Вопрос об устойчивости прямолинейной формы равновесия сжатого
стержня сводится к отысканию наименьшего собственного значения для
дифференциального уравнения (16.3) при линейных однородных краевых
336
условиях (16.4). Особенностью краевой задачи (16.3), (16.4) является
возможность получения нетривиальных решений только при некоторых
определенных значениях параметра нагрузки, являющихся
собственными значениями краевой задачи и имеющих смысл критических
параметров, соответствующих разветвлению форм равновесия.
Спектр собственных значений и соответствующих ему собственных
функций краевой задачи имеет следующие свойства: все собственные
значения положительны; собственным значениям соответствуют
ортогональные собственные функции, каждая из которых представляет
собой форму равновесия (устойчивую или неустойчивую). 1
Тривиальное решение v(z) s 0 краевой задачи соответствует
прямолинейной форме равновесия стержня. Найдем нетривиальные
решения. Решение уравнения (16.3) имеет вид
v(z) = C^sinfcz + C2cosfcz, (16.5)
где Cj и С2 - постоянные интегрирования, определяемые из краевых
условий (16.4):
С2 = 0, CjSinfc/ = 0.
Так как Сх * 0 (С{ = 0 соответствует тривиальному решению), то
получаем характеристическое уравнение
sink! = 0,
откуда следует, что
kl = mi, (п = 1,2, ...)
и, учитывая обозначение к2 = P/EJX, для силы Р получаем
(Л n2n2EJv
р£ —tt-^(w = 1'2—)- (166)
Формула (16.6) носит название формулы Эйлера.
Корни уравнения sin/:/ = 0 дают те значения силы ?, при которых
существуют формы равновесия стержня с искривленной осью. Если Р =
= PJ£, то форма изогнутой оси стержня с точностью до масштаба
(постоянной Cj), описывается функцией
vn(z) = sin(nnz/l) (п = 1, 2,...); (16.7)
графическая иллюстрация (16.7) приведена на рис. 16.7.
337
п^З n-1 n-1
Рис. 16.7. Формы потери устойчивости шарнирно опертого стержня
Формула Эйлера (16.6) позволяет найти те значения силы Р, для
которых существуют нетривиальные решения уравнения (16.3); эти
значения силы называются критическими. Физический смысл (реальный)
имеет первая критическая сила Р*' (л = 1):
кр
/> = тс2
EJ
(16.8)
Под критической силой понимают силу, при которой прямолинейная
форма равновесия стержня перестает быть устойчивой, т.е. если Р - Р^
(л = 1, 2,...), то возможны смежные искривленные формы равновесия
стержня.
Формулы, полученные выше, не позволяют получить криволинейные
формы равновесия для Р > Р , так как они выведены из
дифференциального уравнения (16.1), которое является приближенным
(линеаризированным). Точное уравнение изгиба записывается в виде
d2v
dz2
1 +
dv
dz
3/2
EJ„
(16.9)
Когда P > PK , прогибы v(z) достигают таких значений, что пренебрегать
величиной (dv/dz)2 по сравнению с единицей нельзя. Оценивая решение
нелинейной задачи, приведем некоторые результаты. Если сила Р
незначительно превышает критическое значение, то максимальный
прогиб/= v(//2) можно определить по приближенной формуле
338
/ =
2/2/
JPJT3
(16.10)
где Рэ = ti2EJxJ12 - критическая сила,
определяемая по формуле Эйлера.
Например, если Р = 1,05РЭ, т.е.
превышает критическое значение силы на
5%, то по формуле (16.10) получаем
/ = 0,2/ - прогибы составляют 20 %
длины стержня.
При Р = Рк обнаруживается
увеличение податливости стержня в от
ношении поперечного изгиба -
стержень как бы теряет изгибную
жесткость. Это объясняется наличием
близких статически возможных форм
равновесия стержня. Если рассмотреть
зависимость потенциальной энергии U
упругой деформации стержня от
величины силы Р {рис. 16.8), можно сделать
следующие выводы:
- при Р < Р наблюдается единственное состояние равновесия,
соответствующее прямолинейной форме равновесия;
- при Р > Р^ заданному значению силы Р соответствуют, по крайней
мере, два состояния равновесия (на рис. 16.8 - состояние А и В).
В реальных системах реализуется лишь одно из возможных состояний,
а именно, соответствующее меньшей потенциальной энергии системы
(состояние В).
Зависимость критической силы от условий закрепления стержня.
Обобщенная формула Эйлера. Определяя критическую силу для сжатых
стержней при различных условиях закрепления (различных краевых
условиях), приходим к другим вариантам формулы Эйлера, которые
можно обобщить, вводя приведенную длину стержня /0 = ц/:
Рис. 16.8. Множественность
состояний равновесия при Р > J*
кр
(ц/)2
(16.11)
Формула (16.11) называется обобщенной формулой Эйлера. Здесь ц -
коэффициент приведения длины, показывающий, как следует изменить
длину шарнирно опертого стержня, чтобы критическая сила для него
равнялась критической силе стержня длиной / при рассматриваемых
условиях закрепления стержня. Коэффициент ц есть число, показываю-
339
1
If
4
tx~
p
J
/
1
\
\
-fi
-
sfffr/r
1
\
I
1
1
P
//7/7 !
2
P
;
/
i
\
\
4j-
-
///// !
0.7
/>
I!
1
\
\
ь
Jtt-1
0.5
.''I
A
4
/
/7^7 *
1
p
1 s
1 g
rfforr
0,3 J
Рис. 16.9. Коэффициент приведения длины ц для различных случаев закрепления
сжатых стержней
щее, во сколько раз длина полуволны синусоиды, которую можно
полностью или частично уложить на оси искривленного стержня, больше
его фактической длины. Это объясняется тем, что поведение участка
стержня между точками перегиба изогнутой оси такое же, как и стержня,
шарнирно опертого по концам; поэтому вместо фактической длины
стержня в (16.11) подставляется величина /0 = \il. Значения коэффициента
приведения длины \х для различных случаев закрепления концов стержня
приведены на рис. 16.9.
Границы применимости формулы Эйлера. Формула Эйлера (16.8) или
(16.11) применима, когда материал стержня подчиняется закону Гука,
так как была получена как решение краевой задачи для
дифференциального уравнения изгиба стержня в форме (16.1). Однако возможна
ситуация, когда критическая сила, определяемая по формуле Эйлера,
вызываете стержне напряжения, превышающие предел
пропорциональности а,
П1Г
Определим границы применимости формулы Эйлера:
* э W
Критические напряжения ок , соответствующие силе Р = Рко, равны:
% =
кр
.a = lt2
кр>
£/„
п2Е
г*'
(16.12)
F (ц/)2/г
где А = ц/Я- гибкость стержня i = (JIF)1'2- радиус инерции поперечного
сечения стержня. Предельным является случай, когда ок = апц. Отсюда
следует, что формула Эйлера справедлива для стержней, у которых
340
Л » А„, где А, - предельная гибкость, являющаяся константой
материала стержня
К = *УЩ^. (16.13)
Например, для малоуглеродистых сталей, имеющих Е = 200 ГПа,
опц = = 200 МПа, для предельной гибкости получаем значение А, «
100.
Из (16.12) видно, что если коэффициент приведения длины ц
при изгибе в разных плоскостях одинаков, то расчет следует вести
по минимальному моменту инерции поперечного сечения. В других
случаях расчет необходимо вести по большей гибкости.
16.3. Расчеты на устойчивость за пределами упругости
Наиболее надежным способом определения критической силы в
упругопластической области деформирования материала является
эксперимент. Таким способом для различных материалов получено
большое число результатов, позволяющих определить зависимость ок =
= окр(А) в области А < А„, где формула Эйлера неприменима. Известны
различные аналитические аппроксимации экспериментальных
результатов, однако из-за большого разброса экспериментальных точек при
А <, А, аппроксимация в виде прямой линии, предложенная Ф.С.
Ясинским, представляется наиболее простой и целесообразной. Формула
Ясинского имеет вид:
% = а - bk> (16.14)
где а и Ъ - константы, которые определяются из условий стыковки
линейного участка (16.14) с гиперболой Эйлера при А = А., где окр =
= п2Е/Х2 = опц и с прямой о=:оТ при А = А0. Для малых значений гибкости
А(А < А0, где А0 = 40 - Для распространенных конструкционных сталей)
расчет на устойчивость не проводится; критические напряжения
определяются пределом текучести или пределом прочности на сжатие
для хрупких материалов. Из этих условий для а и Ь получаем:
а = °пц + ЬК> Ъ = (от - атЖК ~ *о)- (16.15)
Полный график зависимости критических напряжений о от гибкости
А = \xl/i показан на рис. 16.10.
341
"кр.
300
200
°кр " °т
/
V
1 1
N
\
\
^Х0
orKPs=fl-
\ °ч>
*прсд
кХ
Х2
Для того чтобы избежать
резких переломов на графике ок =
а (Л), в точках X = Я0 и X = А.,,
используется эмпирическая
формула Джонсона, описывающая
изменение ovn в неупругой области по
параболическому закону
% = °о
аХ2
$о
100
150
Рис. 16.10. Зависимость критических
напряжений от гибкости стержня
где константы о0 и а подбираются
из условия непрерывности и
гладкости в точках сопряжения.
Практические расчеты на
устойчивость. В практических
расчетах на устойчивость часто
пользуются так называемым коэффициентом снижения допускаемых
напряжений.
Запишем условие устойчивости для сжатого стержня
° = j * [а]у
(16.16)
где [о]у = окр/[и]у допускаемое напряжение при расчетах на устойчивость,
[л] - нормативный коэффициент запаса устойчивости. Напряжение [о]
всегда меньше соответствующего допускаемого напряжения в расчетах
на прочность при сжатии:
[о] = Или [о]с = —.
и и
Нормативный коэффициент запаса устойчивости должен быть больше
нормативного коэффициента запаса прочности; для конструкционных
сталей этот коэффициент назначается в зависимости от гибкости в
пределах 1,8...3,0; для различных марок чугуна - в пределах 5,0...5,5
(меньшим его значениям соответствуют большие гибкости). Допускаемые
напряжения при расчетах на устойчивость свяжем с допускаемыми
напряжениями при расчетах на прочность:
К
кр т
My °г М
м= % и_^ = ф[о1,
от Му М
342
где
ф= %^ = ф(Л)< 1.
Получили, что [о]у = ф(Я)[о] и условие устойчивости записывается в виде
а = ^ * ф(Я)[а]. (16.17)
.г
Коэффициент ф для данного материала зависит только от величины
гибкости Я; этот коэффициент называется коэффициентом снижения
допускаемых напряжений или коэффициентом продольного изгиба.
Значения коэффициента ф в зависимости от гибкости Я для различных
материалов приведены в табл. 16.1.
16.1. Значения коэффициента <р
Гибкость
0
10
20
30
40
50
60
70
80
90
100
Сталь
Ст2, СтЗ,
Ст4
1,00
0,99
0,96
0,94
0,92
0,89
0,86
0,81
0,75
0,69
1 0,60
Ст5
1,00
0,98
0,96
0,93
0,89
0,85
0,80
0,74
1 0,67
0,59
0,50
15ГФ,
10Г2С1,
15ХСРД
1,00
0,98
0,95
0,92
0,89
0,-84
0,78
0,71
0,63
0,54
1 0,46
юхснд
1,00
0,98
0,95
0,92
0,88,
0,82
0,77
0,68
0,59
0,50
1 °>43
Чугун
СЧ 15-32,
СЧ 12-28,
СЧ 18-36,
СЧ 21-40
1,00
0,97
0,91
0,81
0,69
0,57
0,44
0,34
0,26
0,20
1 0,16
СЧ 24-44^
СЧ 28-48
1,00
0,95
0,87
0,75 "
0,60
0,43
0,32
0,23
0,18
0,14
0,12
Дерево
J,00
0,99
0,97
0,93
0,87
0,80
0,71
0,61
0,48
0,38
1 0,31
343
Гибкость
А,
ПО
120
130
140
150
160
170
180
190
200
210
220
Сталь
Ст2, СтЗ.
Ст4
0,52
0,45
0,40
0,36
0,32
0,29
0,26
0,23
0,21
0,19
0.17
[ 0,16
Ст5
0,43
0,37
0,32
0,28
0,25
0,23
0,21
0,19
0,17
0,15
0,14
0,13
15ГФ,
10Г2С1,
15ХСРД
0,39
0,33
0,29
0,25
0,23
0,21
0,19
0,17
0,15
0,13
0,12
0,11
10ХСНД
0,36
0,31
0,27
0,23
0,20
0,18
0,16
0,14
0,12
0,11
0,10
0,09
Чугун
СЧ 15-32,
СЧ 12-28,
СЧ 18-36,
СЧ 21-40
-
-
-
-
-
-
-
1
-
-
-
-
СЧ 24-44,
СЧ 28-48 !
-
-
-
- .
-
-
-
-
-
-
-
1
Дерево
0,26
0,22
0,18
0,16
0,14
0,12
0,11
0,10
0,09
0,08
-
-
Проверочный расчет сжатых стержней. Последовательность
проверочного расчета сжатых стержней на устойчивость заключается
в следующем:
по заданным размерам поперечного сечения и условиям закрепления
стержня определяется величина гибкости Ятах;
по найденной величине Лтах для материала стержня в табл. 16.1
находится коэффициент снижения допускаемых напряжений <р(А);
проверяется выполнение условия устойчивости (16.17).
Проектный расчет. В расчетные формулы о = PIF <, <р(А)[о] и F >
> Р/ф(Л)[о] входят две неизвестные величины: F и ф(А), поэтому при
подборе размеров поперечного сечения используется метод
последовательных приближений, в котором варьируется величина (р. Обычно в
качестве первого приближения принимается значение (pj = 0,5...0,6 и по
формуле
344
на к-м шаге определяют размеры, поперечного сечения. Для найденного
значения Fk находят соответствующее ему Хк и по табл. 16.1 значение фЛ';
следующее приближение будет
Ф**1 = °-5(Ф* + Ф*')- (16.18)
При о й [о] или допускаемой малой перегрузке расчет прекращается.
Рациональные формы поперечных сечений сжатых стержней.
Рациональными являются те сечения, которые имеют наибольший
момент инерции поперечного сечения при заданной площади, будучи
равноустойчивыми относительно обеих главных осей инерции. Условие
равноустойчивости: Хх = Я . Если условия закрепления в обеих плоскостях
одинаковы (\ix = ц ), то из условия равноустойчивости следует, что
Jx = / . Этому соответствует кольцевое поперечное сечение с
минимальной толщиной стенки. На практике толщину стенки назначают из
условия локальной (местной) устойчивости. Рациональными сечениями
являются также коробчатые сечения, которые могут быть составлены
из стандартных прокатных профилей.
Для стержней большой гибкости (А > д..), когда о < опц,
нецелесообразно применять конструкционные материалы с повышенными
прочностными характеристиками, так как модуль упругости материала
Е - единственная механическая характеристика, определяющая
сопротивление стержня потере устойчивости, для большинства
конструкционных сталей практически одинакова.
16.4. Энергетический метод решения задач устойчивости
Согласно вариационному принципу Лагранжа, состояние равновесия
консервативной механической системы'устойчиво тогда и только тогда,
когда ее полная потенциальная энергия минимальна. Необходимое
условие минимума полной энергии системы Э записывается в виде
вариационного уравнения Лагранжа (гл. 9)
53 = 6(17 + Л) = 6(С/ - А) = 0, (16.19)
которое является условием стационарности (6Э = 0) полной
потенциальной энергии механической системы в состоянии равновесия. В уравнении
345
(16.19): U- потенциальная энергия упругой деформации, П - потенциал
внешних сил, А - работа внешних сил. Об устойчивости равновесного
положения можно судить по знаку второй вариации б2Э от полной
энергии. Если исходное положение устойчиво, то вторая вариация
положительна:
б2Э > 0. (16.20)
Если
б2Э < 0, (16.21)
то рассматриваемая равновесная форма будет неустойчивой.
Безразличному равновесию (критическому состоянию) соответствует
62Э = 0. (16.22)
Энергетический метод служит основой для различных приближенных
методов решения задач устойчивости. Пусть форма прогиба при потере
устойчивости приближенно может быть представлена в виде ряда
v(z) =/lVl(z) +/2v2(z) + - +/„vn(*) = ifkvk. (16.23)
где vA.(z) - функции, удовлетворяющие кинематическим граничным
условиям, т.е. условиям, налагаемым на прогибы и углы поворота,/А,
- некоторые параметры. В этом случае вариацию полной энергии можно
представить как сумму вариаций, соответствующих возможным
изменениям параметров fk:
*э= 1^6/, 06.24)
и из условия стационарности 6Э = 0 следует, что
Е^*Л = 0. (16.25)
*«! dfk
Так как вариации bfk являются независимыми, то равенство (16.25) будет
иметь место, если каждый из множителей при bfk будет равен нулю:
346
дЭ = 0 ээ
э/, " ' э/2
о,
о.
(16.26)
Равенства (16.26) представляют собой систему я линейных однородных
алгебраических уравнений относительно^, в коэффициенты при которых
входит нагрузка Р. Из условия существования нетривиального решения
этой системы получаем характеристическое уравнение, наименьший
корень которого приближенно соответствует первой критической силе.
Этот метод носит название метода Ритца.
В случае, если функция v(z) задается с точностью до одного
неопределенного параметра/j : v =f\V\, представляющего собой масштаб v(z),
получаем простейший вариант метода Ритца - метод Релея.
Так, для однопролетного стержня, сжатого силой Р, выражения для
U и А имеют вид:
U
1
/
EJ
d2v
dz:
dz, А =
'J
dv
dz
dz,
(16.27)
и из условия (16.26) для критической силы Рк получаем
о
d^v
dz3
dz/
/
dv
dz
кр'
dz.
(16.28)
Согласно теореме Релея, значение Р , полученное по формуле (16.28),
всегда выше истинного значения критической силы Рк при условии, что
функция v(z) удовлетворяет всем кинематическим граничным условиям.
347
Глава 17
ДИНАМИКА СИСТЕМ
С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
17.1. Основные понятия теории колебаний
При динамическом воздействии внешних нагрузок элементы
конструкций испытывают переменные во времени изменения
напряженно-деформированного состояния, при этом отдельные точки
конструкции совершают движение по некоторому закону. Движение
называется колебательным, если скорость движения многократно меняет
знак. Колебания называются периодическими, если движение повторяется
через равные промежутки времени, наименьший из которых называется
периодом колебаний. Периодические колебания называются
гармоническими, если движение описывается тригонометрическими функциями.
Рассмотрим движение некоторой точки конструкции, которое
определяется скалярной функцией времени u(t). При гармонических
колебаниях эту функцию зададим в виде (рис. 17.1)
u(t) = asm((A>t + ф).
с sin<p
Рис. 17.1. Параметры гармонических
колебаний
(17.1)
Наибольшее значение
функции (17.1), равное а,
называется амтитудой колебаний.
Параметр а), имеющий
размерность с~\ называется
угловой частотой.
Безразмерная величина (р,
определяющая значение функции при
i = 0, имеет смысл начальной
фазы колебаний, а аргумент
функции ш + <р называется
фазой колебаний.
Функция (17.1) является
периодической функцией с
348
периодом 2тг: sin(cor + ф) = sin(o>/ + ф + 2ir) = sin[o)(f + 2nlu) + ф] = sin[o)(f +
+ 7) + ф], откуда получим выражение, связывающее угловую частоту о>
с периодом колебаний Т:
2п
<*~- (17.2)
В технике обычно пользуются другой характеристикой частоты,
измеряемой в герцах (Гц) и имеющей смысл числа циклов колебаний в
секунду:
у. 1 (О
Скорость движения при гармонических колебаниях v(f) = du(t)ldt =
= G)tfcos(cof + ф) и ускорение w(t) = d2u(t)ldt2 = ~o)2asin(o)/ + ф) также
описываются гармоническими функциями с той же частотой и фазой, с
амплитудами соответственно соя и о>2я.
При изучении колебательных процессов в элементах конструкций,
которые рассматриваются как механические системы, вводится понятие
числа степеней свободы, под которым понимается количество
независимых параметров, называемых обобщенными координатами, достаточных
для описания конфигурации системы в любой момент времени.
Нахождение числа степеней свободы связано с идеализацией реальной
механической системы и с выбором расчетной схемы. Реальные системы
имеют распределенную массу, и для полного описания поведения такой
системы в любой момент времени нужно знать движение каждой точки
системы, т.е.распределенные системы являются системами с бесконечным
числом степеней свободы. Если заменить распределенную массу конечным
числом сосредоточенных масс, получим систему с конечным числом
степеней свободы, для описания динамического поведения которой
достаточно ввести конечное число обобщенных координат.
17.2. Свободные колебания систем с конечным
числом степеней свободы
Колебания называются свободными (собственными), если они
происходят при отсутствии внешних воздействий и без поступления
энергии извне. Они совершаются за счет первоначально накопленной
энергии путем задания перемещений и скоростей в начальный момент
времени и поддерживаются благодаря наличию внутренних упругих сил.
349
Изучим свободные
колебания механической системы с п
степенями свободы на примере
плоских изгибных колебаний
балки длиной /, имеющей из-
гибную жесткость EJ и
несущей п сосредоточенных масс
(рис. 17.2, а). Будем считать
балку безынерционной, точнее,
пренебрегаем массой балки по
сравнению с
сосредоточенными массами. В качестве
обобщенных координат примем
вертикальные перемещения
масс u{t).
Для вывода уравнений
колебаний воспользуемся
принципом Даламбера: состояние движения механической системы можно
рассматривать как состояние равновесия, если к действующим внешним
силам, внутренним силам и реакциям фязей добавить фиктивные
(даламберовы) силы инерции. При свободн&х колебаниях внешние силы
отсутствуют, а силы инерции, направленное против движения и равные
произведению массы на ускорение, для рассматриваемого примера равны
Рис. 17.2. Изгибные колебания балки с
сосредоточенными массами:
а - перемещения от действия сил инерции;
б - единичные перемещения
h = "тк
&t2
(к = 1, 2, ,.., л).
(17.4)
Если в точке присоединения сосредоточенной массы тк приложить
единичную безразмерную силу в направлении обобщенной координаты
uk(t)9 то массы получат единичные перемещения 61/с, б2/с, ..., 6пк
(рис. 17.2, б), которые можно вычислить по формуле Максвелла-Мора
uJk
i
MjMkdz
Ш
(17.5)
через изгибающие моменты Mj(z\ Mk(z) от действия единичных сил.
От действия /с-й силы инерции (17.4) в направленииу-й обобщенной
координаты получим перемещение
350
bjkh = ~mk-
d_4
dt2
»jk-
Воспользовавшись принципом независимости действия сил для линейных
систем, согласно которому перемещение в какой-либо точке равно сумме
перемещений от действия всех сил, находим
Uj(t) = £
к=\
т.
d4(0
dt2
Jjh>
откуда получим систему однородных обыкновенных дифференциальных
уравнений второго порядка, описывающих свободные колебания в
линейной системе с п степенями свободы
d4«
Е тк *—bJk + Uj(t) = О, 0= 1, 2, ..., л).
fc-i dt2
(17.6)
Систему уравнений (17.6) можно записать в более компактной
матричной форме
FAu(/) + u(0 - 0,
(17.7)
где введен вектор и(0, составленный из обобщенных координат Wj(0,
w2(0> •••> ип(0- Матрица А, называемая инерционной, есть диагональная
матрица с элементами ш1? т2> ..., тп, расположенными по главной
диагонали. Матрица F с элементами бд называется матрицей единичных
перемещений или матрицей податливостей. В правой части введен вектор
0 той же размерности, что и вектор u(r), составленный из нулей. Умножая
слева на матрицу С = F"*1, уравнению (17.7) можно придать вид
Att(0 + Cu(0 = 0.
(17.8)
Матрица С с элементами С:к называется матрицей упругих коэффициентов
или матрицей жесткости. В развернутой форме записи матричное
уравнение (17.8) эквивалентно системе уравнений
т,
d2u(i) п
—ГТ^ + 1 cjkuk(t) = 0, </ - 1, 2, ..., л).
dt2 k=\
(17.9)
Будем искать решение системы уравнений (17.6) или (17.9) в классе
гармонических функций типа (17.1)
351
Uj(t) = ajSinfot + ф)
(17.10)
с амплитудами д., частотой со и начальной фазой ф. Подставим решение
(17.10) в уравнение (17.6)
<*2 L mkbjkak + aj< = °> (/ = 1» 2, ..., п).
А:=1
(17.11)
Полученная система линейных однородных алгебраических уравнений
относительно амплитуд ау имеет нетривиальное (ненулевое) решение, если
определитель, составленный из коэффициентов уравнений, равен нулю:
- (й1т1Ьи
-со2т,б21
-co2m2612
1 - co2m-
"^Ai
2V22
-co2m26„2
-<*2тпЬ\п
-<*2тпъгп
1 - co2m„
0.
(17.12)
Уравнение (17.12) называется частотным или характеристическим
уравнением. Раскрывая определитель, получим полином и-й степени
относительно со2, имеющий п корней <о2, g>2, ..., <д>2. Положительные
значения со,, со2,..., сол называются собственными частотами системы.
Таким образом, механическая система с п степенями свободы имеет
п собственных частот. Упорядоченная совокупность собственных частот
со, <. со, <. ... £ со
(17.13)
образует спектр собственных частот. Все собственные частоты
действительны и положительны, что следует из симметрии и
положительной определенности матриц А и F.
Каждой собственной частоте со соответствуют амплитуды
колебаний а^\ а^\ ..., а®. Совокупность этих амплитуд называется /?-й
собственной формой колебаний. Совокупность всех собственных частот
и соответствующих им собственных форм образует спектр собственных
колебаний.
Собственные формы колебаний находятся из системы уравнений
(17.11) после подстановки со = оу
»
,(р)
-«; i ** v* + «г = о, о* = 1,2,..., и).
fc=l J
(17.14)
352
Так как определитель
коэффициентов этой системы
равен нулю, то она является
линейно зависимой. В случае,
когда а) - простой (не
кратный) корень
характеристического уравнения (17.12),
после отбрасывания одного
из уравнений (17.14),
например последнего, получим
(/2-1) независимых
уравнений, которые можно решить
с точностью до какой-либо
амплитуды, скажем а^,
выразив все остальные амплитуды через нее.
Собственные формы колебаний обладают следующим свойством:
собственные формы, соответствующие различным собственным частотам,
ортогональны. Условие ортогональности собственных форм записывается
следующим образом:
Рис. 17.3. Консольный стержень с
сосредоточенной массой:
а - расчетная схема; б - эпюра единичного
момента
£ т^а® = О, (р *q).
(17.15)
Физический смысл условия ортогональности заключается в том, что
суммарная работа сил инерции, соответствующих одной форме
колебаний, совершаемая на перемещениях, соответствующих другой
форме колебаний, равна нулю.
В качестве примера рассмотрим систему с одной степенью свободы
в виде консольного стержня с сосредоточенной массой, изображенного
на рис. 17.3, а. Уравнение колебаний (17.6) принимает вид
т
ьи^Ш + м(0 = о,
dr2
(17.16)
где единичное перемещение вычисляется через единичный момент
Mx(z) (рис. 17.3, 6) по формуле Максвелла-Мора (17.5):
J El
Ju
I3
3EJ'
353
б)
Если ввести обозначение
1
<оЛ
тб,
S
т
(17.17)
Рис. 17.4. Консольный стержень с двумя
сосредоточенными массами:
а - расчетная схема; б - эпюры единичных
моментов; в - собственные формы
колебаний
где с = 1/6,, = ЪЕМЪ есть
жесткость системы (усилие,
которое нужно приложить в
направлении обобщенной
координаты u(t)9 чтобы получить
единичное перемещение в этом
направлении), то уравнение
(17.16) можно переписать в
виде
0(0 + о>о«(0 = 0. (17.18)
После подстановки решения
(17.10) в уравнение (17.16)
приходим к уравнению
относительно амплитуды
(1 - и>2тЬп)а = 0.
(17.19)
Частотное уравнение (17.12) принимает вид 1 - о> тЬп = 0, откуда
получим выражение для собственной частоты со, = у]\1тЪи. Из сравнения
этого выражения с формулой (17.17) видно, что параметр о>0 имеет смысл
собственной частоты системы с одной степенью свободы. Из уравнения
(17.19) при (0 = 0), следует, что собственная форма а^ может принимать
любое значение. Это значение определяется начальным смещением, за
счет которого осуществляются свободные колебания.
Для второго примера возьмем систему с двумя степенями свободы,
изображенную на рис. 17.4, а. Элементы матрицы единичных
перемещений вычислим по формулам Максвелла-Мора (17.5) после перемножения
по правилу Верещагина эпюр изгибающих моментов от действия
единичных сил (рис. 17.4,6):
»., =
/3
•42
6,, =
5/3
3EJ' 1Z " 6EJ
Уравнения (17.11) принимают вид:
^22
8/3
3EJ'
(17.20)
354
(1 - ко2т16и)а1 - <o2m2&X2a2 = 0;
-cD2m,e2lfl, + (1 - a>2m2622)a2 = 0.
Частотное уравнение (17.12), записанное для п = 2,
(17.21)
1 - (а2т,бп -(о2т2б12
1 - (D2/W06-
-еЛи,821
2 "22
0
после раскрытия определителя и решения биквадратного уравнения
приводит к значениям собственных частот, которые после некоторых
преобразований можно привести к виду
1
N
тхЬхх + т2622
2 -N
т,6п - т2522
(17.22)
)
+ т,т2612
Формулу (17.22) можно переписать следующим образом:
(о12 = kl2yJEJImxls,
(17.23)
где безразмерные коэффициенты к{9 к2 зависят от соотношений между
массами тх,т2и единичными перемещениями бд. Для рассматриваемого
примера при тх ~т2 = т эти коэффициенты равны кх = 0,584, к2 = 3,884.
Для нахождения р-и собственной формы подставим значение со в
уравнения (17.21). Отбросив второе уравнение, выразим амплитуду а^
через амплитуду а®:
»
ах .
co^w2612
(17.24)
С использованием обозначений (17.20) и (17.23) получим
м _ * - У'з
5m2kp/6mi
»
355
При Wj = т2 формы колебаний определяются соотношениями
я2(1) = 3,12а/0, д2(2) = -0,32л/2>. Подстановкой этих соотношений в (17.15)
при р = \, q = 2 убеждаемся в ортогональности собственных форм.
Графическая иллюстрация форм колебаний показана на рис. 17.4, в.
17.3. Установившиеся вынужденные колебания
Пусть в системе с п степенями свободы, например, изображенной на
рис. 17.2, я, в направлении обобщенных координат uk(t) действуют
переменные внешние силы Pk(t), образующие и-мерный вектор Р(*).
Согласно принципу Даламбера в точке присоединения массы тк
действует активная внешняя сила Pk(t) и даламберова сила инерции
-mkd2uk(t)ldt2. Тогда на основе принципа независимости действия сил
найдем перемещения
fc-1
dWfl
dt2
fy*>
откуда приходим к системе уравнении
d4(0
*— К ч >у in, j -> ' *-*
Е Щ—ГТ-bjk + "/<> = I РкЩк> 0* = U 2, ..., /1), (17.25)
описывающих вынужденные колебания в линейной системе с п степенями
свободы. В матричной форме, аналогичной (17.7), эта система уравнений
принимает вид
FAu(0 + u(0 = FP(*). (17.26)
Другие формы уравнений вынужденных колебаний запишем по аналогии
с (17.8) и (17.9):
Au(0 + Cu(0 = Р(0, (17.27)
d2u(t) п
mj J— + £ cjkuk(i) = P(t), 0' = 1, 2, ..., л). (17.28)
dt2 *=i
Пусть внешние силы Pk(t) изменяются по гармоническому закону
Pk(t) = ^cos0r (17.29)
356
с амплитудами Рк и одинаковой частотой 0. Решение уравнений (17.25)
будем искать в классе гармонических функций, описывающих
установившиеся колебания с частотой вынуждающих сил:
Uj(t) = flj.cosOf.
(17.30)
Для нахождения амплитуд я. подставим (17.30) в уравнения (17.25). В
результате приходим к системе линейных алгебраических уравнений
относительно амплитуд колебаний
"в2 I mk6Jkak + а, = £ Pk6jk, </ = 1, 2, ..., и). (17.31)
Решение системы уравнений (17.31) можно получить различными
способами, например, по формулам Крамера
D(Q)
_ "/
(17.32)
где D(0) - определитель, составленный из коэффициентов при я;- в
уравнениях (17.31):
/>(0) =
1 - в2ш|в|| -02m2si2 - -в2*».»!.
-в2»»,^, 1 - 62т2б22 ...
-е^б,
л!
вч*2„
-62т26й2 ... 1 - 62т„6п
(17.33)
Определитель /^{0) в числителе (17.32) получен из определителя (17.33)
путем заменыу'-го столбца столбцом, образованным правыми частями
уравнений (17.31).
Из сравнения (17.33) с (17.12) видно, что при совпадении частоты
вынужденных колебаний 0 с одной из собственных частот о>р
определитель (17.33) обращается в нуль, при этом амплитуды (17.32)
неограниченно возрастают. Это явление называется резонансом, а частоты 0 = ыр —
резонансными частотами. Графики зависимостей ajdd) называются
амплитудно-частотными характеристиками системы.
357
Рассмотрим более подробно
систему с одной степенью
свободы. Для этой системы уравнения
(17.31)
-0 т{Ьиа{
следует
принимают
вид
+ ах = Р,6И, откуда
01 =
Л»п
е2т,бп
(17.34)
в/©,
Рис. 17.5. Зависимость коэффициента
динамичности от частоты силового
возбуждения
следующем виде:
Учитывая, что тх6п = 1/wf, где
со j - собственная частота, и вводя
обозначение для параметра а0 =
= Р\Ьп, имеющего смысл
статического перемещения от действия
амплитудного значения внешней
силы, запишем формулу (17.34) в
1 - 62/со2
Отношение
*(в>»
к (в)1
II-*
2
СО»
1-1
(17.35)
(17.36)
называется коэффициентом динамического усиления или коэффициентом
динамичности. График зависимости k(Q) показан на рис. 17.5.
Динамические напряжения вызываются как действием внешней силы
Pj(0, так и силой инерции -т^и^Ш2. Амплитудное значение
суммарной силы Pd = Р{ + mlQ2al называется динамической силой. С
учетом (17.34) получим
'r'i + ™i02-
Л*и
Л
1 - mxQ2bu 1 - т1в26п l - e2/<of (1?*3?)
Из сравнения формул (17.36) и (17.37) для системы с одной степенью
свободы следует |Р^(б)| = Р{к(д)9 т.е. коэффициент динамичности имеет
смысл коэффициента усиления внешней нагрузки.
358
№j/^P=meh
Рис. 17.6. Действие центробежной силы на консольный стержень
Рассмотрим важный для технических приложений случай, когда
сосредоточенная масса т присоединена с эксцентриситетом 8 к упругой
балке и вращается с угловой скоростью 0 вокруг точки О (рис. 17.6). При
этом возникает центробежная сила Р = mQ е. Вертикальная проекция
этой силы P(t) = m02ecos0f вызывает изгибные колебания балки.
Уравнение колебаний в данном случае имеет вид
md U®6U + u(t) = m02e5ucos0f.
At1
Решение этого уравнения в классе гармонических функций u(t) = acosQt
имеет амплитуду
m026ne
1 - m026,
которую с учетом mbx х = 1/<о2 можно представить в форме
02/o>f
1 - 02/o>i
(17.38)
Коэффициент динамичности в этом
случае вводится как
02/со
(17.39)
8 |1 - 02/о>?|
График зависимости (17.39) представлен
на рис. 17.7. При 0 = g>j система
находится в резонансном режиме. При 0 - «, как
следует из формулы (17.38), амплитуда
а - -е. Этому соответствует наблюдаемое
на практике явление самоцентрирования,
е/ю,
Рис. 17.7. Зависимость
коэффициента динамичности от частоты
при действии центробежной силы
359
PcosQt
1>»г
ОД32Р/
M,
ц
к
Рис. 17.8. Система с двумя степенями свободы:
а - расчетная схема; б - эпюры единичных моментов; в - воздействие внешней
и инерционных сил; г - эпюры динамических изгибающих моментов
когда абсолютное вертикальное перемещение массы (а + 8)cos0r
стремится к нулю.
Аналогичные явления наблюдаются в системах со многими степенями
свободы. Рассмотрим систему с двумя степенями свободы, изображенную
на рис. 17.8, а. Для определения собственных частот по формуле (17.22)
найдем единичные перемещения 6^. После приложения единичных сил
в направлении обобщенных координат, раскрытия статической
неопределимости, построения эпюр Мх, М2 (рис. 17.8, б) и их
перемножения получим 6п = 11/3/81£/, 612 = 621 = 23/3/162£/,622 = 20/3/81£/. Если
ввести обозначенияQ = (Wj6,{)А/\yJk = mkbjklmxbu,4o формулу (17.22)
можно привести к виду a>j 2 = kx 9Q, где
*1Д =
Til + Y22
N
ид
Yu Y22
+ Y12Y2i
(17.40)
Например, при соотношении масс от, = 1т2 будем иметь Yn = 1, Y12 =
= 0,523, Y2! = 1,045, у22 = 0,909, *, = 0,768, к2 = 2,162. Формы колебаний
360
связаны соотношением (17.24), которое в принятых обозначениях можно
представить в виде
(р) * ~ ^р (р)
аг = f-fli • (17.41)
У\2кр
Для данного примера д20)/д2(,) = 1,33, а^1ах{2) = -1,504, при этом условие
ортогональности (17.15), которое для п = 2, можно записать в виде
т2 а? а»
—-— — + 1=0, П7 42)
выполняется.
Амплитуды вынужденных колебаний находятся из уравнений (17.31),
которые для рассматриваемого примера принимают вид
(1 - Q2mxbu)ax - 62w2S12a2 = Рб12 = а01,
(17.43)
-Ь2тхЬ1Хах + (1 - е2т2622)а2 = Р622 = д02,
где через я07- = Рб 2 обозначены статические перемещения от действия
амплитудного значения внешней силы. С учетом обозначений для Q и
у-к после введения безразмерной частоты r\ = 0/Q уравнения (17.43) можно
переписать следующим образом:
(1 - х\2)а{ - г\2упа2 = д01,
-Л2У21«1 + 0 " Л2Уи)*2 = ai
4)2*
Решение этих уравнений по формулам Крамера (17.32) относительно
безразмерных амплитуд ау- = afa^ имеет вид
1 - ц2у22 + t\2yna01/a{
1о\
(1 - Л2)(1 " n2Y22> - n4Y12Y2.'
1 - Л2 + Л2У2|до|/д02
(1 - г|2)0 ~ П2У22> - П4У,2У21
(17.44)
361
4,0
2,01
-2,0
-4,0
-6.0'
1
ГЧ
и
i/P
iL
~ii
1
Л
У-J
ч
-6,01
Рис. 17.9. Амплитудно-частотные
характеристики системы с двумя степенями
свободы
Соответствующие амплитудно-
частотные характеристики
представлены на рис. 17.9. При
совпадении частоты возбуждения 0 с
собственными частотами a)j и g>?
наблюдаются резонансные
явления. В промежутке между
резонансными частотами на частоте 8, =
= 1,58Q амплитуда колебаний
второй массы равна нулю. Это
явление называется
антирезонансом.
Для вычисления динамических
напряжений вводятся
динамические усилия, равные сумме
амплитудных значений внешних и
инерционных сил (рис. 17.8, в):
pj
mjQ2aj.
(17.45)
Вычисления с использованием
соотношений (17.44) для системы,
изображенной на рис. 17.8, а, при
частоте возбуждения 0О = (g)j +
+ о)2)/2 дают Pdl = -0,572Р, Pdl =
= 0,805Р. На рис. 17.8, г приведена
эпюра динамических изгибающих
моментов, построенная с
использованием формулы
Md =
= рЛ1м{
рлгмг.
По формулам (17.32) можно вычислить амплитуды установившихся
колебаний вращающихся валов, несущих несбалансированные
сосредоточенные массы (диски), центры масс которых не лежат на оси вращения.
В качестве примера рассмотрим безынерционный вал, на который
посажены два диска, имеющие эксцентриситеты гк (расстояния от
центров масс до оси вращения), которые предполагаются
расположенными в одной плоскости (рис. 17.10, а). При вращении вала с угловой
скоростью 0 центры масс движутся по окружности, а возникающие при
этом центробежные силы вызывают изгиб вала и смещения точек его оси
на величины ак.
Таким образом, суммарные смещения центров масс, равные ак + еА.,
вызывают центробежные силы Pdk = mkQ2(ak + гк). Эти силы эквивален-
362
тны амплитудным значениям динамических усилий (17.45) при силовом
возбуждении колебаний, причем роль внешних нагрузок играют силы
Рк = ткд2ек. Вместо уравнений (17.31) будем иметь
-в2 I mk6Jkak + о, = в2 £ ткекЬ.к9 </ = 1, 2, ..., и). (17.46)
Решение системы уравнений (17.46), полученное по формулам (17.32),
при п = 2 имеет вид
Л20 - q2y22)vi + Л4У12У2
(1 - л2) 0 - Л2У22) - VY|2Y2i'
Л2(1 - ti2)v2 +
VY21V,
(17.47)
«;
(1 - ti2)(l - г|2у22) - T)4Y,2Y2,
Здесь введены те же обозначения для безразмерной частоты г| и для
параметров yjk, что и в формулах (17.44). Кроме того, введены
обозначения V, = Ej + Yi282> v2 = Y218l + Y2282-
Амплитудно-частотные характеристики, построенные по формулам
(17.47) для вала,
изображенного на рис. 17.10, д,
приведены на рис. 17.11.
При вычислении
единичных перемещений
использовались эпюры
изгибающих моментов
от действия единичных
сил (рис. 17.10, б), при
этом опорные
подшипники рассматривались
как шарнирные опоры.
Единичные
перемещения равны
б)
б,,-622-
= 4P/9EJ, 612 = 621 =
= 7/3/18£/.При
соотношении масс дисков т? =
= 1,5т, коэффициенты
yjk принимаю!
следующие значения: уц = 1,
Y12=l53125,Y2i=0,875,
*;
A^/i^rfe,/
Рис. 17.10. Вынужденные колебания вращающегося
вала с дисками:
а - расчетная схема; б - эпюры единичных
моментов; в - эпюра динамических изгибающих
моментов
363
\J\\K '
1 i ! :
i/H
ML
i
ii
4
[ I
\l
1
—1
I
V*
аЬ?
1
\ J
Y22 = 1 >5. Собственные частоты
изгибных колебаний вала с
дисками связаны с частотным
у-1/2
0)j 2 = ^i 2Й С
'*, = 6,652,
параметром Q = (т16и)
соотношением
коэффициентами
к2 = 2,586, вычисленными по
формуле (17.40). При
построении амплитудно-частотных
характеристик принято
отношение эксцентриситетов г71г1 =
= 2.
Как видно из рис. 17.11, при
совпадении частоты вращения
0 с одной из собственных
частот (»>! или о)2 наблюдаются
резонансные явления.
Соответствующие угловые скорости
вращения называются
критическими. В технике скорость
вращения обычно измеряется
числом оборотов в минуту,
связанным с угловой
скоростью вращения соотношением
п = 30 в/я. Резонансным
частотам соответствуют критические
числа оборотов пк = ЗОсодУя.
Кроме того, имеются два
антирезонанса при скоростях
вращения 6М и е#2. При в - *
происходит самоцентрирование
вала, когда ак - - гк, т.е.
центры масс располагаются на оси вращения. Динамические усилия Pdk =
= ткв\ак + гк) при скорости вращения 60 = (о^ + а)2)/2 равны Pd) =
= -3,3JW|Q28j, Pd2 = l,19#W|Q2ej. Соответствующая эпюра динамических
изгибающих моментов приведена на рис. 17.10, в.
НА. Учет рассеяния энергии при колебаниях
Г
""У
1 _2'
\ 1
: I
|
| 3 4 1
*Т . ."■" —*"
if 1
il 1
Рис. 17.11. Амплитудно-частотные
характеристики для вращающегося вала
При изучении установившихся вынужденных колебаний было видно,
что при действии динамических нагрузок имеется опасность возникнове-
364
Рис. 17.12. Система с одной степенью
свободы с демпфером
ния резонансных режимов,
которые сопровождаются
неограниченным возрастанием
амплитуды колебаний и,
следовательно, напряжений. Однако
в реальных конструкциях и
машинах наблюдаемые
резонансные явления
сопровождаются хотя и значительными, но
конечными амплитудами. Это
связано с тем, что в
резонансных режимах происходит
интенсивное рассеяние
(диссипация) энергии, вызывающее нагрев, акустическое излучение и другие
необратимые явления. В приведенных выше примерах эти явления не
учитывались.
Рассмотрим простейший вариант учета диссипации энергии за счет
сил вязкого трения, пропорциональных скорости движения. Такие силы
возникают, например, в гидравлическом амортизаторе (демпфере),
схематическое изображение которого показчно на рис. 17.12. В
соответствии с принципом Даламбера на массу т действует внешняя сила Р(0>
даламберова сила инерции -md2u(t)ldt2 и реактивная сила вязкого
сопротивления -bdu(t)ldt, пропорциональная скорости и, как и сила
инерции, направленная против движения. Коэффициент
пропорциональности b называется коэффициентом вязкого трения.
При действии единичной силы масса т получит перемещение 5j j, а
при совместном действии внешней, инерционной и реактивной сил это
перемещение будет равно u(t) = [P(t) - md2u{t)ldt2 - bdu(t)ldt]bn, откуда
получим уравнение вынужденных колебаний диссипативной системы с
одной степенью свободы
т ^ + Ъ—^
6И + и(0 = Р(0*ц- (17.48)
dt2 dt
Разделим обе части этого уравнения на mbx j и обозначим 2е = Ь/т,
о>о = 1/тб| |. Тогда уравнение (17.48) можно записать в виде
iMo + 2ed«(o + ы2м(0 = т. (17.49)
dt2 dt т
Параметр (а>0 совпадает с собственной частотой системы без диссипации,
365
а параметр е, имеющий размерность частоты, называется коэффициентом
()ел^«0м/>о<?анш.Вводятсятакжебезразмерныехарактеристикидемпфиро-
вания у = е/с*)0 - относительное демпфирование и х = 2я8/о>0 -
логарифмический декремент колебаний.
Уравнение (17.49) при P(t) = 0 описывает свободные колебания в
системе с диссипацией, происходящие за счет начальных условий м(0) и
v(0) = du(t)/dt\ t-0. Общее решение этого уравнения имеет вид
м(0 = е
H(0)coso)e/ * "<°>е + v(0> sincoe/
(17.50)
Здесь (i)c = yju>l - £2 - собственная частота с поправкой на диссипацию.
При 8 = 0 свободные колебания имеют периодический характер
(рис. 17.13, а), а при 8 > 0 они затухают во времени, причем если 8 < а>0,
то затухания будут сопровождаться колебаниями (рис. 17.13, б)\ при 8 >
> (о0 затухание будет монотонным, не колебательным (рис. 17.13, в).
Значение коэффициента демпфирования 8 = о>0, которое соответствует
переходу от колебательного процесса затухания колебаний к
монотонному, называется критическим демпфированием. При 8 < о)0
логарифмический декремент колебаний х = 2718/о>0 можно интерпретировать как
натуральный логарифм отношения двух следующих друг за другом
максимальных значений: х = \n(aklak+l) (рис. 17.13, б).
При гармонической внешней силе P(t) = PcosQt решение уравнения
(17.49), описывающее установившиеся колебания, будем искать в классе
гармонических функций с частотой возбуждающей силы:
u(t) = acos(8/ - ф).
(17.51)
Рис. 17.13. Свободные колебания системы с одной степенью свободы:
а - периодические при отсутствии демпфирования; б - затухающие при
докритическом демпфировании; в - монотонно затухающие при закритическом
демпфировании
366
Другая форма записи решения (17.51) имеет вид
u(t) = C,cos0r + C2sin0/,
(17.5.2)
где константы Cj и С2 связаны с амплитудой а и фазовым углом ф
соотношениями
.53)
Сх = acoscp, С2 = дэтф, а = уС2 + С22, ф = arctg(C2/C,).(17
После подстановки (17.52) в уравнение (17.49) и приравнивания
коэффициентов при cos0f и sinBf получим систему уравнений
(со2 - О2) С, + 2е0С2 = Р1т\
-286С, + (со2 - 02)С2 = О,
откуда находим константы Сх и С2:
с, =
«о - е2
(о)„ - в2)2 + 4е262 т
£■ с
2е0
(со2 - 02)1 + 4е202 т
(17.54)
Переходя к решению в форме (17.51), с учетом соотношений (17.53) для
амплитуды и фазового угла получим выражения
а =
^(1 - 02/<о£)2 + (280/со2)2
:, ф = arctg
2е0
02
(17.55)
Здесь учтено, что отношение Р1(ти>0) = Рбп = я0 есть статическое
перемещение.
Величина к(д) = a(Q)laQ имеет смысл коэффициента динамичности
*№> =
1 -
02
LV
<о<
'о/
-1/2
2е0
соЛ
/ J
(17.56)
Амплитудно-частотная характеристика (17.56) и фазочастотная
характеристика представлены на рис. 17.14 и 17.15 при различных
значениях коэффициента демпфирования. Штриховые линии на этих
367
п лплл 4 Рис. 17.15. Фазо-частотные характерис-
Рис. 17.14. Амплитудно-частотные v v
J ~ тики
характеристики диссипативнои
системы с одной степенью свободы
рисунках соответствуют системе без диссипации. При наличии
демпфирования амплитуды установившихся колебаний остаются
конечными во всем частотном диапазоне, смягчаются резонансные
явления, исчезают антирезонансы.
Для диссипативных систем с конечным числом степеней свободы
уравнения колебаний в матричной форме имеют вид
Ай(0 + Вй + Си(0 = Р(0, (17.57)
где использованы обозначения уравнений (17.27) и введена матрица
коэффициентов вязкого трения В. Решение уравнений (17.57) при
установившихся колебаниях, когда внешние силы изменяются по закону
Р(Г) = Pcos0r, ищется в виде u(t) = Ujcos0f + u2sin0f. Подставляя это
выражение в (17.57) и приравнивая коэффициенты при одинаковых
гармониках, получим уравнения относительно векторов Uj и и2:
(С - 82A)u, + 8Bu2 = Р;
-ЭВи, + (С - 02А)и2 = О,
решение которых в матричной форме имеет вид:
и, = В"1(С - 02А)[(С - в2А)В",(С - 02А) + ^В]"1?;
368
u2 = e[(c - е2А)В-Чс - e2A) + e^r1?.
Это решение совпадает с (17.54) при п = 1.
Более эффективным является представление решения уравнений в виде
разложения по собственным формам колебаний а}к):
(17.58)
ФункцииУ)с(г) называются главными координатами. В матричной форме
разложение (17.58) имеет вид
u(0 = Vf«,
(17.59)
где V - матрица собственных форм, составленная по столбцам из форм
колебаний af*:
V =
Л0> „(2)
»
»
(О (2) (и)
а а ... л
л и и
Подставим разложение (17.59) в уравнение (17.57) и умножим слева
на матрицу (AV)""1 = V^A .
V'A-'AVfCO + V"!A-!BVf(0 + V^A-'CVfW = \~lArlP(t).
Заметим, что Е = V'A^AV есть единичная матрица, диагональные
элементы которой равны единице, недиагональные - нулю, а матрица
Q2 = V"1 A^CV есть диагональная матрица с элементами о? на главной
диагонали, равными квадратам собственных частот системы без
диссипации. Матрица V"1 A~'BV при В = 2вА также будет диагональной
с элементами 2е на главной диагонали. В результате приходим к
разделяющейся системе уравнений относительно главных координат
Л(1) + 2е/Л(/) + <4fkQ) = <4ЛЛ*)> (* = U 2, ..., л), (17.60)
369
где введено обозначение/0/,(/) для компонентов вектора f0(r) = V~*CTlP(t).
Решение каждого из уравнений (17.60), описывающего колебания
системы с одной степенью свободы, для случая периодического
возбуждения P(r) = Pcos0/ в классе установившихся движений дается
формулами (17.51) и (17.55), которые принимают вид
Л(0 =Acos(0/ - Фл); (17.61)
/о* <„ 2е0
Л = , Ф* = arctg
TZ~7i' (17.62)
^(1 - в2/а£)2 + (2е0/со*)2 <*1 - 6:
Здесь/0/с- компоненты вектора f0 = V'CT1?, имеющего смысл вектора
статических перемещений, приведенного к главным координатам.
Решение в исходных обобщенных координатах дается соотношениями
(17.58) или (17.59).
На рис. 17.16 в качестве примера приведены амплитудно-частотные
характеристики для системы, изображенной на рис. 17.8, а. Графики
построены при значении коэффициента демпфирования £ = 0,1Q.
Соответствующие графики при 8 = 0 показаны на рис. 17.9.
Если внешняя нагрузка во времени изменяется произвольным
образом, то колебательный процесс носит неустановившийся характер.
Такой же тип колебательного процесса наблюдается и при периодической
нагрузке на начальном этапе, пока происходит процесс установления
колебаний. Проиллюстрируем сказанное на примере диссипативной
системы с одной степенью свободы, колебания которой при
произвольной нагрузке описывается уравнением (17.49). Общее решение u(i) этого
уравнения складывается из общего решения u0(t) однородного уравнения
и частного решения мДг) неоднородного. Общее решение при начальных
условиях м(0) и v(0) = diY(r)/d/|r=0 дается формулой (17.50). Частное
решение можно получить с использованием интеграла Дюамеля
uSt) = — ГP(T)e-E<'->sincoc(* - т)(1т. (17.63)
e о
Пусть в начальный момент времени / = 0 начинает действовать
постоянная сила Р. Решение при нулевых начальных условиях,
полученное после вычисления интеграла (17.63), имеет вид
370
г
Л/
А
Л
«i/^i
V
&
,^/Ца
d
л
>\
^aJ
10 20 30 40 50
0 0,5 1,0 1,5 2,0 2,5 6/Q
Рис. 17.16. Амплитудно-частотные рис. п.17. Переходный колебательный
характеристики диссипативной систе- процесс при ступенчатом нагружении
мы с двумя степенями свободы
м(0 = и0
1 - е-
COSO)e/ + Sin(Def
0>„
где и0 = Р/woq - статическое смещение. График, иллюстрирующий
переходный колебательный процесс выхода на постоянный режим,
показан на рис. 17.17, построенном при е = 0,1о>0.
Рассмотрим процесс установления вынужденных колебаний из
состояния покоя под воздействием гармонической нагрузки P(t) =
= Psin0/, приложенной в момент времени / = 0. Реакция системы на это
воздействие дается формулой
и(0 =
J(l - 02/о$2 + (2е0/^)2
,-с/6
sin(0/ + ф) + е~ы—sin(a>e* + ф
Здесь использованы принятые ранее обозначения, кроме того, введены
фазовые углы
Ф = arctg ■
2е0
(*>Л
е2
-, ф = arctg
2ебУ
02 - со* + 2е2
371
I
a) 0
-1
4
6) 0
-4
и/ц
1
*; о
Рис. 17.18. Процессы установления вынужденных колебаний при режимах
нагружения:
а - дорезонансном; б - резонансном; в - зарезонансном
Первое слагаемое в квадратных скобках описывает установившиеся
вынужденные колебания с частотой воздействия, а второе слагаемое -
затухающие со временем свободные колебания. Графики,
иллюстрирующие переходные процессы установления гармонических колебаний,
представлены на рис. 17.18. Графики построены при е = 0,1со0 для различных
режимов нагружения - дорезонансного при 0 = соЕ/4 (рис. 17.18, а),
резонансного при 0 = о>е (рис. 17.18, б) и зарезонансного при 0 = 2о)0
(рис. 17.18, в). Штриховые линии соответствуют установившимся
режимам колебаний.
«М
Go »■'
см
372
Глава 18
ДИНАМИКА ЭЛЕМЕНТОВ КОНСТРУКЦИЙ
18Л. Уравнения колебаний систем
с распределенными параметрами
Упругие системы с распределенными массой и жесткостью (стержни,
пластины, оболочки, упругие тела) обладают бесконечным числом
степеней свободы. В отличие от систем с сосредоточенными
параметрами (с конечным числом степеней свободы), колебания которых
можно описать системой обыкновенных дифференциальных уравнений,
динамическое поведение распределенных систем описывается
дифференциальными уравнениями в частных производных. Особенностью
распределенных систем является необходимость при решении задач
динамики, кроме начальных условий, задать краевые условия.
Для получения уравнений колебаний распределенных систем с
использованием принципа Даламбера нужно рассмотреть уравнения
равновесия, добавив в них фиктивные силы инерции. Например, при
продольной деформации стержня на его элементарный объем действуют
внутренние и внешние силы, показанные на рис. 18.1, где q(z, t) - внешняя
нагрузка, приходящаяся на единицу длины стержня, Nz(z, t) - внутренний
силовой фактор (продольная сила). На продольном перемещении
w(z, t) даламберова сила инерции элементарного объема Fdz равна / =
-с"»
о
I
~*ц.
XT dN.j
/N-+n?dz
z
Рис. 18.1. Силы, действующие на элементарный объем стержня
373
= -pFdzd2w/dt2, где p - плотность материала, F- площадь поперечного
сечения. Проектируя все силы на ось Oz9
8N
N+ —-dz
dz
- Nz + qdz - pFdz — = 0,
dt2
2,,,/эЛ.
получим уравнениеdNJdz + q~ pFd w/dt = 0. Из закона Гука о = NJF =
= Ег = Edwidz следует Nz = EFdw/dz. Таким образом, приходим к
уравнению продольных колебаний стержня
dz
EF(z)
dw(zt t)
dz
dt2
При t = 0 должны выполняться начальные условия
dw(zt t) 1
w(zt 0) = uQ(z),
dt
ve«.
(18.1)
(18.2)
18.1. Типы краевых условий для продольных колебаний стержней
Тип закрепления
Схема
Краевое условие
Заделка
4
¥-
и'(0, о = о
Свободный край
¥~
EF М*. t)
dz
Сосредоточенная
сила
Р
I 7
О
EF М*. 0
dz
= Р
Упругое закрепле-
1 с
§лллЕ
7—-
= сн>(0, 0
Сосредоточенная
масса
A/f
?—
£F
О
8w(z, 0
dz
э/2
374
Кроме того, уравнение (18.1) нужно дополнить краевыми условиями,
причем на каждом из торцов стержня z = 0, z = / ставится по одному
условию, тип которого в зависимости от условий закрепления или
условий нагружения выбирается по табл. 18.1, где эти условия приведены
для одного из краев z = 0.
Аналогичным образом выводится уравнение крутильных колебаний
стержня. Для этого вместо продольного перемещения w(z, t) нужно
рассматривать угол поворота cp(z, /)> вместо жесткости при растяжении
EF- жесткость при кручении GJk, вместо погонной массы р^и погонной
нагрузки q(z, t) - погонный момент инерции рУ и погонный крутящий
момент ji(z, t):
2_
dz
GJk(z)
a<p(z, t)
dz
p dt2
(18.3)
Начальные и краевые условия формулируются по аналогии с (18.2) и
табл. 18.1.
Уравнение статического равновесия при изгибе стержня имеет вид
(9.32)
dz2
EJx(z)
d2v(z)
dz2
= q(?)-
При рассмотрении динамических процессов к распределенной по оси
стержня нагрузке #(z, 0 следует добавить соответствующую силу инерции
-pFd2vldt2, в результате получим уравнение изгибных колебаний
dz2
\EJx(z)
d2\(zt t)
dz2
9F
d2v(z, t)
dt1
q{2% t).
(18.4)
Это уравнение решается при начальных условиях типа (18.2). Кроме того,
должны быть сформулированы краевые условия (по два на каждом конце
стержня), основные типы которых для z = 0 приведены в табл. 18.2.
375
18.2. Типы краевых условий для изгибных колебаний стержней
Тип закрепления
Схема
Краевое условие
Заделка
°Щ
^—.
v = 0,iv=0
dz
Скользящая
заделка
Yf/л.
О
¥—.
dz[ хыг)
: 0,^=0
dz
Свободный край
О
I 7 -
9*1 'dz1 dz1
Загруженный край
М
v>
о
¥-
dz[ "dz1 xBz2
Сосредоточенный
груз
m.ll
?-
*lEJ&\=m&.
dz{ xbv
EJ^L^lJ^
dz2 dzdt2
Шарнирное опира-
ние
О
7-
v = 0, EJ ^- = 0
dz2
Упругое
закрепление
О
J-+
dz2)
= c,v, £/ —=0
1 xdz2
У//?////,
4 = b%EJ*L = c*L
xdz2 2dz
О
Уравнение изгибных колебаний пластины постоянной толщины h
можно получить из уравнения статического равновесия (13.18), добавив
в это уравнение распределенную по поверхности пластины инерционную
нагрузку -phd2w/dt2:
376
DAAw(xt у, t) + рЛ^*'^ О в р(х> ^ /)в (18 5)
dt1
Наряду с начальными условиями на каждом краю пластины нужно
поставить по два условия, аналогичных приведенным в табл. 18.2
краевым условиям для стержней.
18.2. Свободные колебания стержней и пластин
Продольные колебания стержней. Для стержня с постоянными
жесткостными и массовыми характеристиками EF- const и pF= const
уравнение свободных продольных колебаний, полученное из (18.1) при
q = О, можно привести к виду
1 d2w(zt i) _ d2w(zt t) , Q
где параметр с0 = \/£/р имеет смысл скорости распространения
продольных волн в стержне.
Решение уравнения (18.6) ищется методом разделения переменных с
функцией времени из класса гармонических функций (17.1) с частотой
а) и начальной фазой (р0
w(zt t) = PT(z)sin(cDf + <р0). (18.7)
Амплитуда W(z), определяющая форму колебаний, является функцией
продольной координаты г. Эта функция удовлетворяет уравнению,
которое можно получить подстановкой (18.7) в (18.6):
dz2
В отличие от алгебраических уравнений (17.11) для систем с конечным
числом степеней свободы, в системе с распределенными параметрами
пришли к дифференциальному уравнению для амплитуд колебаний.
Если ввести обозначение р = со/с0 = (л>у/р/Е,то приходим к
однородному обыкновенному дифференциальному уравнению второго порядка
^Ш. + pW{z) = 0. (18.8)
dz2
377
2*
Н—Зя/2
— х
%/г
ю
15
Рис. 18.2. Зависимость собственных
частот продольных колебаний стержня от
жесткости опоры
&ь А Общее решение уравнения (18.8)
имеет вид
W(z) = Cjcospz + C2sinpz. (18.9)
Решение (18.9) должно
удовлетворять краевым условиям при
z = 0 и z = I (см. табл. 18.1),
которые приводят к системе
однородных линейных уравнений для
определения постоянных С{ и
С2. Из условия существования
нетривиального решения этой
системы (равенство нулю
определителя) следует уравнение
частот. Например, для
защемленного по обоим торцам
стержня из краевых условий W(0) =
= 0 и W(l) = 0 получим Сх = О,
C2sinp/ = 0, откуда приходим к
частотному уравнению sinK = 0, имеющего корни кк = pAi = кп9 (к= 1,2,
...). Здесь введен безразмерный частотный параметр кк = <*>к1/с0.
Собственные формы колебаний определяются при о) = о>А, с точностью
до постоянного множителя: Wk(z) = sin(/:7iz//).
Для стержня, защемленного на левом торце и упруго закрепленного
на правом с помощью пружины жесткостью с, краевые условия имеют
вид W(0) = 0, EFAW{z)IAz\z-l + cW{t) = 0. Первое из этих условий дает
С{ = 0, а второе приводит к частотному уравнению (cl/EF)tgK + к = 0.
Зависимость первых трех корней этого уравнения от безразмерного
параметра с = cl/EF, характеризующего отношение жесткостей пружины
и стержня, показаны на рис. 18.2. С ростом жесткости пружины
собственные частоты увеличиваются. В предельном случае с - °°
частотное уравнение переходит в уравнение sinK = 0 для защемленного
с обоих торцов стержня, а при с -* 0 - в уравнение cosk = 'Ф'для
консольного стержня, имеющего корни к/с = (2к - 1)тг/2, (к = 1,2,...).
Собственные частоты и формы колебаний вычисляются через к/с
следующим образом: со/с = (кк/1)^Е/р, Wk(z) = s\n(Kkz/l).
Крутильные колебания стержней. Уравнение (18.3) при ц = 0
описывает свободные крутильные колебания. Для стержня постоянного
сечения путем введения параметра сх = JGJk/pJ , имеющего смысл
378
скорости распространения крутильных волн, это уравнение можно *
привести к виду, аналогичному (18.6), ii
,гд2ф, г) _ д2ф, О
dz2
dt2
= 0.
Применение метода разделения переменных приводит к уравнению для
амплитуды колебаний i
d23>(z)
dz2
+ pfO(z) = 0,
ae
с точностью до частотного параметра Pj = g)/cj = u>\/pJJGJki
совпадающему с уравнением (18.8) для продольных колебаний. Общее решение
этого уравнения O(z) = CjCosPjZ + C2sinp,z содержит две константы,
которые после подстановки решения в краевые условия образуют систему^
линейных однородных уравнений. Условие существования нетривиШйо-5
го решения этой системы приводит к частотному уравнению. ^f iUi<i'
Для примера определим собственные частоты и формы вала, свободно
вращающегося в подшипниках и несущего на торце z = /диск, имеющий
массовый момент инерции /0. Краевые условия записываются в виде
G//cd<P(z)/dz|z=0 = 0, G//cdO(z)/dz|2=/ = /0о)2Ф(/). Из первого условия
следует, что постоянная С2 = 0. Подстановка решения O(z) = C^co'sPjZ'
во второе условие дает частотное уравнение G/^sinPj/ + /0g)2cosP,/ =
= 0. Это уравнение после
введения обозначений для
безразмерного частотного параметра
к = Pj/ = co//cj и отношения
инерционных характеристик
диска и вала а = I0l(pJpl)
приводится к следующему: tgK +
+ ак = 0.
Графики зависимости
первых трех собственных частот
от параметра а приведены на
рис. 18.3. Как видно из
графиков, с увеличением массового
момента инерции диска
собственные частоты уменьша-
ются. В предельном случае ос - рис жз 3авИсиМосгь собственных частот
- 0 получим вал со свободны- крутильных колебаний вала с диском от
ми торцами, имеющий частот- массового момента инерции диска
к
8
6
4
2
(
L.
)
/*Ъ
^
i ;
' 2
——Т
г :
S*i
i < * •
\ А
f
-iii^-I
\ С
Х**ч,фъ
у-Ьк/1
^г*
•2ii^aO/*
—-э%/1
>*W2l
* , .• >*i '
379
ное уравнение simc = 0 с корнями кА, = /ся, (к = 1,2, ...). В другом
предельном случае а - °° приходим к частотному уравнению cosk = 0 для
консольного стержня, имеющего корни кА, = (2к - 1)тс/2, (к = 1,2, ...).
Собственные частоты и собственные формы связаны с безразмерным
частотным параметром к/с следующим образом: соА, = (Kk/l)JGJk/pJ'
uk(z) = cos(k^/(). Для вала кругового поперечного сечения, для которого
Jk = Jpib>k=(Kk/l)y/Gfc.
Изгибные колебания стержней. Свободные изгибные колебания
стержня постоянного поперечного сечения описываются уравнением
(18.4) при # = 0:
EJ ^ИьЛ + рР^ЬЛ . о.
х dz< dt2
Подстановка v(z, /) = K(z)sin(cof + ф) приводит к обыкновенному
дифференциальному уравнению
EJxd*V® - 9F<*2V(z) = 0,
dzA
которое после введения частотного параметра
Р4 - jf»2 (18.10)
приводится к стандартному виду
*^М - p<K(z) = 0. (18.11)
Общее решение этого уравнения ищется в виде V{z) = Се*2, где С -
произвольная постоянная, А - характеристический показатель.
Подстановка в уравнение (18.11) дает характеристическое уравнение Я4 -
- р4 = 0, корнями которого являются А| = р, Я2 = -р, А3 = i'P, Я4 = -/В.
Действительным корням соответствуют экспоненциальные функции e*z
и e~Pz, их полусумма и полуразность образуют гиперболические функции
chpz и shpz. Чисто мнимым корням соответствуют тригонометрические
функции cospz и sinpz. Таким образом, имеем четыре функции, которые
образуют общее решение уравнения (18.11):
380
Рис. 18.4. Свободные колебания консольного стержня
V(z) = Cjcospz + C2sinpz + C3chpz + C4shpz.
(18.12)
Постоянные Ck находятся из граничных условий (см. табл. 18.2).
Рассмотрим свободные колебания консольного стержня,
изображенного на рис. 18.4. Граничные условия для амплитуды формулируются
следующим образом:
К(0) = 0,
&V(z)
dz
= 0, M(l) = EJ
d2V(z)
2*0
dz2
= 0,
z=l
6,(0 = ^
d3F(z)
dz3
= 0.
\x-l
Подстановка в эти условия решения (18.12) приводит к системе уравнений
относительно неизвестных постоянных:
С} + С3 = 0;
С2 + С4 = 0;
-CjCosp/ - C2sinp/ + C2chp/ + C4shp/ = 0;
CjSinp/ - C2cosp/ + C3shp/ + C4chp/ = 0.
Вводя безразмерный частотный параметр
X = Р/ = /
p/fa2
N EJ*
(18.13)
381
и исключая постоянные С3 и С4 с помощью первых двух уравнений,
получим систему уравнений:
Ct(cosx + chx) + C2(sinx + shx) = 0;
CjCsinx ~ shx) " C2(cosx + chx) = 0.
(18.14)
Эта система линейных однородных алгебраических уравнений,
аналогичная системе уравнений (17.11) для амплитуд колебаний в системе
с конечным числом степеней свободы, имеет нетривиальное решение в
том случае, когда определитель, составленный из коэффициентов
уравнений, равен нулю:
cosx + chx sinX + shx
sinx - shx -(cosx + chx)
= 0.
(18.15)
Параметр x, как видно из формул (18.10) и (18.13), зависит от частоты
со. Следовательно, уравнение (18.15), аналогичное уравнению (17.12) для
системы с конечным числом степеней свободы, имеет смысл частотного
уравнения. Раскрывая определитель в (18.15), с учетом соотношений
cos2x + sin2x = 1, ch2x - sh2x = 1 получим трансцендентное частотное
уравнение
cosx chx = -1.
(18.16)
Уравнение (18.16) имеет счетное бесконечное множество корней %{i
Х2, .. (рис. 18.5). Первые два корня равны Xi = 1,875, %2 = 4,694.
Последующие корни, как видно из рис. 18.5, достаточно точно
удовлетворяют уравнению cosx = 0, т.е. Х/с = (к - 1/2)тг, (/с = 3,4,...). По формуле
(18.13) найдем собственные частоты изгибных колебаний стержня
2
9F
(18.17)
через безразмерные коэффициенты х^, зависящие от условий закрепления
стержня.
Для нахождения собственных форм колебаний вернемся к
общему решению (18.12). Для консольного стержня С3 = -Cj, С4 = -С2.
382
Рис. 18.5. Корни частотного
уравнения (18.16)
Отбрасывая второе из
уравнений (18.14), из первого
выразим постоянную С2 через Сх:
с = _ cosx + chx с
2 sinx + shx *
Таким образом, форма
колебаний определяется с точностью до произвольной постоянной Сх. Полагая
С| = 1, для к-й собственной частоты получим соответствующую ей
собственную форму
Vk(z) = cospkz - chp^ - k(sm%z - shp^), (18.18)
smxfc + shx*
где в соответствии с (18.13) $к = %к\1. Первые три собственные формы
колебаний консольного стержня показаны на рис. 18.6. Аналогичным
образом находятся собственные частоты и формы колебаний при других
типах граничных условий, некоторые из которых приведены в табл. 18.3.
Собственные формы колебаний удовлетворяют условиям
ортогональности. В системах с конечным числом степеней свободы эти условия
имеют вид (17.15). Для стержневых систем условия ортогональности
изгибных собственных форм записываются так:
/
jpFVj(z)Vk(z)dz « 0, </ * к). (18.19)
о
Собственные формы изгибных
колебаний стержней постоянного
поперечного сечения ^.(z), удов-
Рис. 18.6. Собственные формы
колебаний консольного стержня
383
18.3. Собственные частоты и формы изгибных колебаний стержней
Условия закрепления
я*
а
Щ
1
1
*
1
i 1
Й&? я?&
ЯР
I
1
^
^
Уравнение
частот
sinx = 0
cosxchx = 1
cosxchx = -1
tgx-thX = 0
Корни уравнения
Номер
1
2
к
1
2
к
1
2
/v
1
2
/с
Значения
7С
2тс
А'тс
4,730
7,859
тг(2Л: + 1)/2
1,875
4,694
л(2/с-1)/2
3,927
7,069
%(4к + 1)/4
Форма
колебаний
sinpfcZ
К|Л(2)
^•(2)
УЖ)
Vlk(z) = cosfc - chp*z - °0SXfc " C]*Xk(sinVk2 - shp*z)
VyM)= co%z - chhz - -r125—^Фпр*г - shp^z)
V3k(z) = cosp/cz - chp^z - -^ --2£(sinp/cz - shpA.z)
sinxt
cosxt
sinxt
cosx,
- shx*
+ chxk
+ shX*
- chx*
sinx* + shx^
летворяющие краевым условиям и условиям ортогональности (18.19),
называются балочными функциями.
Изгибные колебания пластин. Свободные колебания пластин
описываются уравнением (18.5) при/? = 0. Представив решение этого
уравнения в форме w(x, у, i) = W(x, >>)sin(G>f + <р), получим
384
AAW(x, у)
ph
D
<*2\¥(х, y) = 0.
(18.20)
Точное решение уравнения (18.20) при произвольных краевых
условиях получить не удается. В частном случае прямоугольной
пластины, шарнирно опертой по всем кромкам (см. рис. 13.7, а), формы
колебаний можно представить в виде
rniy
WJx% у) = sin^±sin^, (m, п = 1, 2, ...,),
(18.21)
удовлетворяющем всем граничным условиям
W{X, у) -. *"Ь у) = о
дх2
\х = 0, а
, W(Xt у) = М(*. У) т о
ду2
1^ = 0, ь
Параметры т и п имеют смысл чисел полуволн, укладывающихся в
направлении осей Ох и Оу соответственно. Подстановка (18.21) в
уравнение (18.20) приводит к следующим значениям собственных частот
т2п2 п2ъ2
N Ph'
(18.22)
Рассмотрим еще один случай, когда удается получить точное решение
задачи об определении собственных частот и форм изгибных колебаний
прямоугольных пластин. Пусть по двум противоположным кромкам,
например, х = 0 и х = а реализуются условия шарнирного опирания, а
по другим кромкам краевые условия произвольны. Тогда формы
колебаний можно представить в виде произведения двух функций
тих
WJx. у) = sin^^Ow(y), (m = 1, 2 ),
(18.23)
первая из которых удовлетворяет условиям шарнирного опирания.
Подстановка (18.23) в уравнение (18.20) приводит к обыкновенному
дифференциальному уравнению относительно функций Фт(у)'
• / •
dyA
Ay1
Ph..
ы2 Ф» = 0.
(18.24)
Общее решение уравнения (18.24), выраженное через тригонометрические
и гиперболические функции, при каждом значении т содержит четыре
385
константы Clm, C2m, C3m, С4ш. Подстановка решения в краевые условия
при у = 0 и при у-Ъ приводит к системе линейных уравнений
относительно констант. Уравнение частот получается в виде равенства нулю
определителя, составленного из коэффициентов при Скт. Например, для
пластины, защемленной по кромкам у = 0 и у = Ь, на которых
выполняются краевые условия Фт(0) = Фт(Ь) = d<&Jdy\y=0 = dOJdy^ = О,
общее решение имеет вид
Pi.
NN d
р/мо2 _ m2n2
^2m
2^2
NN л
p/i(o2 m27t
Частотное уравнение
1
0
cosplmb
0
Pi.
sinp1(l/>
1
0
chP2«*
0
P2«
Shp2m*
"PlmsinPl«^ PlmC°Splw6 P2>P2^ P2«chP2^
= 0
после раскрытия определителя приводится к виду
2cosplm*chp2w*
Pirn
Pirn
P2m
Plmj
sinpiwfcshp2wt& = 2.
18.3. Методы нахождения собственных частот
и форм колебаний
Метод начальных параметров. Этот метод для стержневых систем
относится к точным методам определения собственных частот и форм
колебаний, существенно сокращая процедуру нахождения частотного
уравнения.
Общее решение (18.12) уравнения изгибных колебаний (18.11) не
является единственным. Это решение может быть также представлено
в виде линейной комбинации функций, входящих в (18.12). В качестве
таких функций удобно использовать функции Крылова
386
S{(Pz) = (chpz + cosPz)/2,
S2(pz) = (shpz + sinp2)/2,
(18.25)
S3(pz) = (chpz - cospz)/2,
S4($z) = (shpz - sinpz)/2.
Функции Крылова образуют так называемую фундаментальную
систему Коши, обладающую тем свойством, что матрица Коши,
составленная из этих функций и их производных по pz при z = О, является
единичной. Это позволяет в качестве произвольных постоянных в
решении V(z) = C{S$z) + C2S2(№) + С3Я3фг) + C4S,4(pz) использовать
начальные параметры - значения функции V(z) и ее производных при
z = 0:
F(z) = vACte) + ^52(pz) + *^3(Pz) + ^ W- (18.26)
Р р2 р3
где v0 = F(0), Фо = dF(z)/dz|z=0, ф0 = dV(z)/dz2|2=0> % = dV(z)/dz3|z=0.
Используя соотношения между функциями Крылова и их производными
1 dS2(pz) 1 d2S3(pz) i d3S4(Pz)
Л,фг) = - -
S2Qz)
S3(pz)
P dz p2 dz2 p3 dz3
1 dS3(pz) i d2S4(Pz) = i d3S,(pz)
P dz p2 dz2 p3 dz3
1 dS4(pt) = l d2S,(Pz) = i d352(Pz)
P dz p2 dz2 p3 dz3
(18.27)
1 <LS,(pz) i d2S2(pz) i d353(Pz)
•i4(PZ) = — -
P dz p2 dz2 p3 dz
нетрудно получить выражения для производных от V(z), которые
содержатся в краевых условиях
387
SAQz) =
1 dSx(pz) i d2S2(Pz) i й%ф2)
dz
dz2
dz'
d2V(z)
dz2
v0p2S3(pz) + <p0PS4(Pz) + ♦Дфг) + -^2(pz);
(18.28)
^M = v0p352(Pz) + cp0p2S3(pz) + Ф0Р54(Р2) + Vi<M-
dz*
Для стержней, имеющих промежуточные опоры и сосредоточенные
массы, решение для каждого участка zk е [1^\9 У, (к = 1, 2, ..., л)
записывается в виде (18.26) с учетом условий сопряжения решений при
переходе от одного участка к другому. На первом участке z{ е [0,1{] две
константы находятся из краевых условий при zx = 0. Из условий
сопряжения все константы на последующих участках выражаются через
оставшиеся константы первого участка. Подстановка в краевые условия
при zn = 1п на последнем участке дает однородную линейную систему
уравнений относительно оставшихся констант, из условия существования
нетривиального решения которой следует уравнение частот.
Продемонстрируем процедуру применения метода начальных
параметров на примере изображенного на рис. 18.7 стержня постоянного
сечения, имеющего в сечении z = / упругую опору и несущего в этом
сечении сосредоточенную массу. Решение Vfe) на первом участке z е [0,
/], удовлетворяющее условиям Kj(0) = v0 = 0, dK|(z)/dz|2=0 = (р0 = 0 в
соответствии с (18.26) принимает вид
V{(z) = -^S3(Pz) + -7*4<М-
Р2 Р3
(18.29)
При переходе от первого участка ко второму нужно учесть скачок
сосредоточенной силы
AG(0 = m«?Vx{l) - cVx{l),
(18.30)
Рис. 18.7. Стержень с сосредоточенной массой и упругой опорой
388
Д0(О = /Ш02К,(/) - cF,(/), (18.30)
вызванной силой инерции массы т и реакцией в промежуточной опоре.
Этот скачок эквивалентен разрыву третьей производной Д0(/) = &Q(l)IEJx
и выполняет роль начального параметра для второго участка. Таким
образом, решение на втором участке z е [/, 2/]
F2(z) = Vx(z) * ^@-SA[p(z - 01
Р3
с учетом (18.29) и (18.30) принимает вид
W) = Ц*ъ®*) + V4(P*)+ ть)2"ск,(/)54[р(г - /)].
Р2 р3 JST^P3
Выразив из (18.29) значение Vx{t) через начальные параметры F,(/) =
= ф053(р/УР2 + ^о54(РО/Р3. получим
F2(z) = ^\s3®z) + ^-(пт2 - c)S4[p(z - /)] +
Р2 [ Р3^,
(18.31)
+ -^к(рг) + ^^(««2 " <0SJP(* " 01 •
Подстановка (18.31) в граничные условия V2(2l) = 0, d2F2(z)/dz2|z=2/ = 0
с учетом соотношений (18.27) между функциями Крылова приводит к
системе уравнений относительно параметров i|/0 и 60
[Х353(2Х) ♦ (тх4-г)53(х)54С0]рф0 +
+ [%3SA(2X) + (т%4 ~ ^)^4(Х)]»0 = °.
[Х35,(2Х) + (тх4 - ^ЗДЗДРФо *
+ ЕхЧСх) + (тх4 " ?)ЗДЗД«о = 0.
(18.32)
Здесь использованы обозначения для безразмерных параметров частоты
7Г - Л/3/
X = р/, массы m = m/pF/ и жесткости с = cr/EJx. Условие существования
ненулевого решения системы уравнений (18.32) приводит к частотному
уравнению
389
ЬЗДх) + (тх4 ~ ^S,(x)S4(x)][x3S2(2x) + (тХА - £)ЗДЗД] -
(18.33)
- \х% <2х>+ (™х4 - ^ЗДЗДНхЗДх)+ (^х4 - Z)SA2(x)] = о.
Трансцендентное уравнение (18.33) имеет бесконечное счетное
множество корней. Наименьшие три корня, полученные численным решением
уравнения (18.33) при т = 1, с = 6, равны Xi = 1,792, х2 = 3,463, %з =
= 4,695. Собственные частоты ььк находятся через значения Xk по формуле
(18.17). Собственные формы колебаний определяются решениями (18.29)
и (18.31) на каждом из участков при о> = ык. При этом одну из констант,
например й0, нужно выразить через другую с использованием любого
из уравнений (18.32). Первые три формы колебаний V^k\z), определенные
с точностью до произвольной константы i|i0, приведены на рис. 18.8.
В тех случаях, когда точное решение задачи о нахождении
собственных частот и форм колебаний не существует или оно становится
довольно громоздким, целесообразно применять приближенные и
численные методы, основанные на вариационных принципах или на
методах дискретизации. Чаще всего эти методы применяются для
приближенной оценки одной или нескольких низших собственных частот
распределенной системы.
Метод непосредственной дискретизации. Простейшим способом
дискретизации распределенной системы является разбиение всего объема
V, занимаемого упругим телом, на ряд объемов Vk и сосредоточение
каждой массы pVk в одной или нескольких точках. Так, при
динамическом расчете стержневых систем стержни разбивают на участки длиной
1к и площадью поперечного сечения Fk, а массу каждого участка pFklk
сосредотачивают либо посередине участка, либо разносят по его концам.
Некоторые примеры дискретизации шарнирно опертой балки
постоянного поперечного
сечения приведены на рис. 18.9. Если
всю массу т = рЛ сосредоточить
посередине пролета (рис. 18.9, я),
то получим дискретную систему
с одной степенью свободы,
собственная частота которой
находится по формуле (17.17): а) =
= 1/^т6п, где 6П = /3/48£/.
Таким образом, приходим к
приближенному значению низ-
Рис. 18.8. Собственные формы колебаний шей собственной частоты со, =
для стержня на рис. 18.7
390
а)
1/2
т
г
1/2
б)
т/2 т/2
>|<
■ - //з ,L //з
//3
тЯЯЯ»
т/4
в)
т/2
t
т/4
1/2 1/2
< э4< ^
т/6 «/3 w/З ж/6
г)
1
//з //з
he ^т^ >■
//3
-С »н
Рис. 18.9. Примеры дискретизации балки при помощи сосредоточенных масс:
а - одной; б - двух; в - трех; г - четырех
у которое отличается от точного значения для балки
тс2 y/EJ/pF/l2 на 30 %. Если всю массу сосредоточить в двух точках на
расстоянии //3 друг от друга и от опор (рис. 18.9, б), то приходим к
системе с двумя степенями свободы, собственные частоты которой
вычисляются по формуле (17.22). Для низшей собственной частоты
получим приближенную оценку о, = 8,05 \jEJIpFll2, которая отличается
от точного значения на 18,5 %.
Лучшего приближения можно добиться, разбив стержень на два
(рис. 18.9, в) или на три (рис. 18.9, г) участка, сосредоточив массы на
концах участков. В первом из этих случаев имеем систему с одной
степенью свободы, собственная частота которой отличается от первой
собственной частоты балки на 0,7 %. В последнем случае система с двумя
степенями свободы имеет низшую собственную частоту o)j =
, отличающуюся от точного значения на 0,1 %.
Метод Релея. Для консервативных систем, т.е. систем без диссипации
энергии, полная энергия при отсутствии внешних сил складывается из
391
потенциальной энергии упругой деформации U и кинетической энергии
движения частиц Т. Применительно к стержневым системам
потенциальная энергия изгибных деформаций равна
и-\[Ч
d2v(zt t)
dz2
dz.
(18.34)
Для элементарного объема Fdz кинетическая энергия пропорциональна
квадрату скорости
dT = ipFdz
dv(z, t)
dt
После интегрирования по всей длине стержня находим
Tmi!n
dv(z, t)
dt
dz.
(18.35)
В процессе колебаний полная энергия системы остается постоянной:
Э = U+ Т= const. Записывая перемещение в виде v(z, /) = F(z)sin(a>/ + ф),
получим
2 J *
d2V(z)
dz7
dz •
(18.36)
♦ "2cos>' + «P> ]pFV\z)Az = const.
Из последнего выражения видно, что в момент времени, когда
потенциальная энергия принимает максимальное значение, кинетическая энергия
минимальна, и наоборот. Приравнивая максимальные значения
потенциальной и кинетической энергии, получим
г!"-
d2V(z)
dz2
dz = HL j?FV2(z)dzt
откуда следует
392
/
ял
.,2 = О
\d2V(z)\
dz2
dz
(18.37)
CpFy2(z)dz
Если в формулу (18.37), называемую формулой Релея, подставить
точное выражение для собственной формы Vk(z)> то получим точное
значение собственной частоты соА.. Обычно формулу Релея применяют
для приближенного нахождения собственной частоты, чаще всего
низшей, подставляя в нее приближенное выражение для предполагаемой
формы колебаний. Например, если для консольного стержня (см.
рис. 18.4) взять аппроксимирующую функцию V{(z) = Az2,
удовлетворяющую кинематическим краевым условиям, то вычисление интегралов в
(18.37) приводит к результату o>j = 4,472 JEJJpFIl2, отличающемуся
на 27 % от точного значения (18.17), в котором Xi = 3,516. Если же взять
аппроксимацию в виде полинома четвертой степени Vx(z) = A(z4 - 4z3/ +
+ 6z2/2), то погрешность формулы (18.37) составит 2,5 %. Заметим, что
формула Релея (18.37) дает завышенное значение собственной частоты.
Если в систему введена дополнительная жесткость или присоединена
сосредоточенная масса, как показано на рис. 18.7, то в формуле Релея
нужно учесть их вклад в потенциальную и кинетическую энергию. В
пружине жесткостью с накапливается потенциальная энергия cv2(/, t)/2,
а сосредоточенная масса т добавляет кинетическую энергию
m[dv(/, t)ldt]2/2. Тогда формула Релея применительно к системе на рис. 18.7
примет вид
2/
d2V(z)
dz'
dz + cV2(l)
(18.38)
fpFV2(z)dz + mV2(l)
откуда видно, что введение дополнительной жесткости повышает, а
введение дополнительной массы понижает собственную частоту.
Оценим низшую собственную частоту для стержня на рис. 18.7,
задавшись аппроксимацией формы колебаний Vx(z) = A(z4-5rl + 6z /),
удовлетворяющей краевым условиям при z = 0 и z = 2/. Вычисления
по формуле (18.38) при с = 6EJx/i3, т = рЛ дают значение g)j =
393
= 3,182 JEJJpF/l2, которое отличается от точного значения низшей
собственной частоты, полученного выше методом начальных
параметров, на 0,9 %.
Применительно к изгибным колебаниям прямоугольных пластин
формула Релея записывается в виде
№•£'*«-*
d2w\2_ d2w d2w
[дхду) дх2 ду2
>dxdy
ffphW2(xt y)dxdy
Для круговых или кольцевых пластин при осесимметричной деформации
имеем
i°
л2 = Il_
d2W + 1 dW
\ dr2 г dr
2(1-ц)
1 dW d2W
г dr dr2
rdr
fphW2(r)rdr
Метод Ритца. Приближенное решение для собственной формы
колебаний ищется в виде разложения
*=1
(18.39)
по полной системе базисных функций ф/с, каждая из которых
удовлетворяет, по крайней мере, кинематическим краевым условиям.
Неопределенные коэффициенты fk находятся из условия экстремума функционала
Э0 = U0 - о2Г0>
(18.40)
где U0 - максимальное во времени значение потенциальной энергии,
ы2Т0 - максимальное во времени значение кинетической энергии при
гармонических колебаниях с частотой о>.
В результате подстановки ряда (18.39) в (18.40) получим квадратичную
форму относительно коэффициентов^},. Условие экстремума
функционала (18.40)
394
_• = 0, (* e 1. 2, ..., п) (18.41)
приводит к системе линейных однородных алгебраических уравнений
относительно коэффициентов fk
Е {с.к - *\)fk = 0, (/ = 1. 2, .... и). (18.42)
Условие существования нетривиального решения системы уравнений
(18.42) дает уравнение частот, а собственные формы находятся из
уравнений (18.42) при со = <х>к, где со/с - корни частотного уравнения, и
разложения (18.39).
Применительно к стержневым системам разложение (18.39) принимает
п
вид V(z) = £ fktyk(z). Функционалы £/0 и Т0 в (18.40) формируются как
А:=1
коэффициенты при тригонометрических функциях в выражении (18.36)
для полной энергии системы. В результате для функционала (18.40)
получим
i'
-• - i!EJ-
d2V(z)
&z
2
dz - i£ tpFV\z)Az. (18.43)
2 о
После подстановки ряда (18.39) в (18.43) получим квадратичную форму
Э0 = \ Ц (cjk - JajJfjA (18.44)
с коэффициентами
1 ' d2\|r GO d4.(z) 1 '
Условия экстремума (18.41) функционала (18.44) приводят к системе
уравнений (18.42), которая имеет ненулевое решение, если определитель,
составленный из коэффициентов три/к, равен нулю:
dct(cJk - (*2ajk) = 0. (18.46)
395
Заметим, что если в разложении (18.39) сохранить только один член ряда,
то решение частотного уравнения (18.46) будет тождественно совпадать
с формулой Релея (18.37).
МетодБубнова-Галеркина. В методеБубнова-Галеркина
приближенное решение для форм колебаний ищется в виде разложения (18.39). В
отличие от метода Ритца базисные функции $к должны удовлетворять
всем краевым условиям - не только кинематическим, но и статическим.
Коэффициенты в (18.39) определяются из условия ортогональности
результата подстановки ряда в уравнение колебаний по отношению ко
всем базисным функциям.
Поясним сказанное на примере свободных колебаний стержня
постоянного поперечного сечения, собственные формы колебаний
которого описываются уравнением
EJX&*V® - pFu2V(z) = 0.
dz4
(18.47)
После подстановки ряда (18.39) уравнение (18.47) примет вид
EJ
dz4
Л = о.
(18.48)
Условие ортогональности к базисным функциям, которое применительно
к уравнению (18.48) записывается в виде
I
*=1
!^/J^^*/r)dz-p^f4«*y«dz
Л=0, (/=1,2 я),
приводит к системе линейных однородных уравнении относительно
неизвестных коэффициентов
Е ®jk ~ "Ч*)Л = 0, (f = 1, 2, .... п\
(18.49)
где введены обозначения, аналогичные (18.45):
Р,* = EJxf*jtod*k®uzt aJk = pFjijtoibW*.
о d* о
Процедура получения частотного уравнения аналогична изложенной
выше для метода Ритца.
396
Метод конечных элементов. Основы метода конечных элементов и
его применение к задачам статического расчета изложены в гл. 9. В
задачах динамики дополнительно к потенциальной энергии упругой
деформации конечного элемента (9.60) составляется выражение для
кинетической энергии
где рк - объемная плотность материала в пределах конечного элемента.
Выражая вектор перемещений и/с через вектор узловых перемещений fk
при помощи соотношения (9.55), перепишем выражение для кинетической
энергии в виде
1 dfk
тк в
* 2 d/
///P*W -^.
df
Если ввести обозначение для матрицы
Mk-[ffptfflkAr. (1850)
называемой матрицей инерции конечного элемента, то для кинетической
энергии конечного элемента получим выражение
Суммируя кинетическую энергию (18.51) по всем конечным элементам,
получим выражение для кинетической энергии всей системы
2 df d/
Глобальная матрица инерции М формируется по тем же правилам, что
397
и матрица жесткости. Применение одного из вариационных принципов
приводит к системе уравнений относительно неизвестных параметров -
узловых перемещений. В матричной форме эти уравнения имеют
вид
М— + Kf = Q.
d/
(18.52)
Для стержневого конечного элемента (см. рис. 9.12) кинетическая
энергия вычисляется как
Подставляя выражения для перемещений (9.67) в (18.53) и приводя
выражение для кинетической энергии к виду (18.51), получим выражения
для элементов матрицы инерции
/
Mjk = j9FHXj(x)Hlk(x)dxt а к = 1,7);
!Jk = f9FH2j(x)H2k(x)dxt а к = 2, 6, 8, 12);
MiV =
Mjk - f9FHy(x)H3k(x)dxt а * - 3, 5, 9, И);
Mjk = f9JpHAj(x)H4k(x)dxt а к = 4, 10).
Здесь функции форм имеют тот же смысл, что и в формулах (9.69).
Остальные элементы матрицы инерции равны нулю. После вычисления
интегралов получим выражение для матрицы инерции прямолинейного
стержневого элемента
398
М=рИ
о
13
35
О
О
О
3/-'
о
]|
"гТо"
о
105
г
11,
210
О
О
О
'/»
105
Симметрично
О
9_
70
О
О
13
420
О
13
35
О
9_
70
О
.Л,
420
О
]3
35
О
О
О
it,
6F
О
О
О
О
О
•',
3/-'
о
ii/
420
О
140
О
U_
210
О
1
105
/2
О
13
420
О
О
О
1
I2
140
О
210
О
О
О
-L/«
105
(18.54)
Если учитывать только изгибные деформации, например, в плоскости
Оху, то отличными от нуля будут узловые перемещения/2,/6,/8,/12,
остальные узловые перемещения равны нулю. Матрица инерции может
быть получена из (18.54) вычеркиванием строк и столбцов,
соответствующих нулевым компонентам вектора узловых перемещений:
М
420
156
22/
54
22/
4/2
13/
54
13/
156
-13/
-З/2
-22/
-13/ -З/2 -22/ 4/2
(18.55)
Проиллюстрируем процедуру применения метода конечных элементов
к проблеме нахождения собственных частот и форм изгибных колебаний
стержня, изображенного на рис. 18.7. Разобьем данную систему на два
стержневых элемента, стыкующихся в узловом сечении z = /. Из
граничных условии следует, что узловые перемещения^ =у6 -/8 -
= 0. Отличными от нуля узловыми перемещениями будут перемещение
399
/8 =/2 = v2 и угол поворота/12' =/6 = Ф2 ВТ0Р0Г0 узла, а также угол
поворота /f2 = ф3 третьего узла. Эти перемещения образуют трехмерный
вектор узловых перемещений f. С учетом краевых условий первый
стержневой элемент имеет две степени свободы v2 и ф2, а второй
элемент-три степени свободы v2, ф2 и ф3. Матрицы жесткости и инерции
стержневых элементов получим из (9.74) и (18.55) вычеркиванием строк
и столбцов, соответствующих нулевым узловым перемещениям:
К0) =
К<2> =
EJ„
/3
12 -61
-6/ 4/2
12 6/ 6/]
6/
6/
4/2 2/2
2/2 4/2J
1 мо) = £^
J 420
г
420
156 -22/
[-22/ 4/2
i
156 22/ —13/1
22/ 4/2 -
-13/ -3/2
-з/2
4/2.
Чтобы получить глобальные матрицы жесткости и инерции,
просуммируем элементы матриц, соответствующих совпадающим
узловым перемещениям. Кроме того, учтем сосредоточенную массу т
и жесткость промежуточной опоры с во втором узле. В результате
получим следующие выражения для глобальных матриц жесткости и
инерции:
/3
24+с 0 6/
0 8/2 г/2
6/ 2/2 4/2
, М =
420
312+420 in
0
-13/
0
g/2
-3/2
-13/
-3/2
4/2
Здесь использованы обозначения т = mlpFl и с = cl IEJX для
безразмерных параметров сосредоточенной массы и жесткости опоры.
Свободные колебания описываются уравнением М? + Kf = О,
полученным из (18.52) при Q = 0. Представляя решение в виде f(r) =
= wsin(co/ + ф), получим матричное уравнение для амплитуд свободных
колебаний
(К - q2m)w = 0.
(18.56)
400
Условие существования нетривиального решения уравнения (18.56)
det(K - о)2М) = 0 есть частотное уравнение. Численное решение этого
уравнения при с - 6, in = 1 дает следующие значения трех собственных
частот: ик = xl y/EJJpF/l2, х] = 3,22, xl = 13,88, xl = 36,36.
Решение системы уравнений (18.56) при со = ык определяет собствен-
(к) (£)// № (к)
ные векторы vr ' с компонентами v^ //, <р2 , Ф3 :
*0>в
" 0,456
0,229
1-0,860
, w<2> =
0,031
-0,615
0,788
, w<3> =
-0,017]
-0,554
-0,832!
Для нахождения собственных форм используются выражения (9.67),
связывающие перемещения в конечных элементах с узловыми
перемещениями:
Vf>{z)
3£i-2^|v» +
I I2
I /*j
,„<*>
fF, ze[0.../];
V?<j>-
1-3-L + 2J-
l2 /3
..(*),
z\ z\
z,-2—+—
/ /*;
<pf+
2 3
fufi.
I ' I1)
J®
q^-x-Zefl).../].
Построенные по этим формулам собственные формы колебаний близки
к изображенным на рис. 18.8 формам, полученным методом начальных
параметров.
Сравнение полученных методом конечных элементов собственных
частот с точными значениями, найденными выше методом начальных
параметров, показывает, что метод конечных элементов дает хорошую
оценку для низшей собственной частоты с погрешностью около 0,3 %.
Однако погрешность для последующих собственных частот возрастает,
достигая 15,7 % для второй частоты и 64,4 % для третьей. Лучшего
результата можно добиться, увеличивая число конечных элементов. Если
исходную систему разбить на четыре конечных элемента, имеющих семь
степеней свободы, то первые три собственные частоты могут быть
401
определены с достаточно высокой точностью (погрешность составляет
0,02 %, 0,55 % и 1,4 % соответственно для первой, второй и третьей
собственных частот).
18.4. Вынужденные колебания
Уравнения колебаний, полученные в п. 18.1, можно записать в
операторной форме
А д2и(х; ° + Сн(х, /) = <7(х, 0, (18.57)
где А и С - инерционный и упругий операторы, м(х, /) - обобщенное
перемещение как функция координат и времени. Конкретный вид
операторов А и С для стержней и пластин можно получить из
сопоставления (18.57) с (18.1), (18.3)...(18.5).
Если внешняя нагрузка изменяется по гармоническому закону
q(x> t) = e(x)sin(0f + Ф) (18.58)
с частотой 0 и амплитудой Q(x), то при вынужденных колебаниях
устанавливается периодический режим с той же частотой
м(х, 0 = £/(x)sin(6* + Ф). (18.59)
Подстановка (18.58) и (18.59) в (18.57) приводит к операторному
уравнению для амплитуды колебаний
(С- Q2A)U(x) = Q(x), (18.60)
которое решается с привлечением соответствующих краевых условий.
Применительно к изгибным колебаниям стержней постоянного
сечения операторы А и С, как это следует из сравнения (18.4) и (18.57),
имеют вид А = pF, С = EJxd*/dz4. Уравнение (18.60) относительно
амплитуды колебаний V(z) принимает вид
EJx^p? ~ Р™2^*) = *о«- (18.61)
Q.Z
Решение уравнения (18.61) складывается из общего решения однородного
уравнения и частного решения. В случае q0 = const это решение имеет вид
402
Viz) = C,sinpz + C2cospz + CjShp* + C4chpz -
%
PEJX
Здесь введено обозначение p = JpFQ2/EJx. Постоянные Ck находятся
из краевых условий. Например, для шарнирно опертой балки с краевыми
условиями V(0) = V(l) = 0, d2V(z)/dz2\z-0 l = 0 после определения
постоянных приходим к следующему выражению:
К(*)=-
Яо
2&EJ
1-
COSY . Л 1
^ smx
-chx
shx
shpz + cospz+chp^-2
(18.62)
где % = p/. Нетрудно заметить, что при % = %к = А:тг, (/: = 1,3,...) выражение
(18.62) не определено. Это соответствует совпадению частоты
возбуждения 0 с собственными частотами системы соЛ, т.е. резонансным явлениям.
При четных значениях к резонансных явлений не наблюдается вследствие
того, что соответствующие этим частотам несимметричные формы
колебаний при симметричной относительно сечения z - 111 нагрузке не
возбуждаются. Зависимость амплитуды колебаний в некотором сечении
z = z0 от частоты возбуждения аналогична амплитудно-частотным
зависимостям в системах с конечным числом степеней свободы, что видно
из сравнения рис. 18.10, построенного для безразмерной амплитуды V -
= VEJJq^ в сечении z = //2, и рис. 17.9.
Решения, аналогичные (18.62), можно получить для других типов
нагрузок и краевых условий.
Если найдены собственные частоты о>А, и собственные формы
колебаний Uk(z)9ro эффективным способом исследования вынужденных
колебаний является разложение решения уравнения (18.57) по формам
колебаний:
"(х, I) = Z UkWk(f). (18.63)
*=i
Функции времени/^(0>
называемые главными координатами, 0 05
удовлетворяют уравнениям
VA^Wi
Рис. 18.10. Зависимость амплиту- -ОД5!
ды колебаний шарнирно опертой
балки от частоты возбуждения -0,1
В
id.
k*>
ю
403
Л« + <■>*/*« = fc(0. (* - 1. 2, ...),
(18.64)
которые можно получить после подстановки разложения (18.63) в
уравнение (18.57) и применения процедуры метода Бубнова-Галеркина.
Поясним сказанное на примере изгибных колебаний стержня
постоянного поперечного сечения, которые описываются уравнением
Э^О + ЭЧф, о ж q(z
аг4 dt1
(18.65)
Подстановка в это уравнение ряда (18.63), переписанного в виде
v(z, 0 = £ У^)Щ.
(18.66)
приводит к уравнению
/■1
d4Kf(z)
A2fj(f)
dt'
= <7(*. о.
Проведем ортогонализацию этого уравнения по отношению к
собственным формам колебаний, т.е. умножим обе части уравнения на Vk(z) и
проинтегрируем по длине стержня:
7-1
' Я4
dAV(z\
d2fj(t)
+ 9FfVj(z)Vk(z)dz-^
{ dt
= fq(Zit)Vk(z)dz.
Использование условий ортогональности собственных форм по
кинетической энергии (18.19) и по потенциальной энергии
'/. dAVs(z)
CEJX J— Vk(z)dz = 0 при у + к,
{ dz4
а также выражений для собственных частот
404
'fEJx^-VkWz
2 0 dZ
* / '
fpFVfa)d*
0
следующих из формулы Релея (18.37), приводит к уравнениям (18.64)
относительно главных координат, в которых обобщенные силы вводятся
следующим образом:
fq(z, t)Vk(z)dz
?*(') = —, (18.67)
f9FVt(z)dz
о
Решение уравнений (18.64) в классе установившихся гармонических
движенийу^(г) = FA,sin(cor + ф) дает следующие выражения для амплитуд
обобщенных координат через амплитуды обобщенных сил Fk = QjJ((^k -
- б2). Окончательно для амплитуды вынужденных колебаний с
использованием разложения (18.66) получим формулу
т = £ &Щ. (18 68)
Амплитудные значения обобщенных сил Qk определяются через
амплитуду внешней нагрузки q0(z) по формуле (18.67).
Для шарнирно опертой балки собственные частоты и формы
колебаний приведены в табл. 18.3: g>a, = k2n2JEJxlpFH29 Vk(z) =
= sin(knzll). Учитывая, что
' hl/кп, к = 1, 3, ... ' ,
{sin(knz/l)dz = \ , f sin2(fctiz//)dz = //2,
i I 0, k'2, 4, ... J
по формуле (18.67) при #0 = const найдем амплитуды обобщенных сил
■{
4q0/pFkn, к = 1, 3, ...
0, к = 2, 4, ...'
405
а по формуле (18.68) амплитуду вынужденных колебаний
т'-^Л-1^Г^- (18.69)
Ряд (18.69) сходится довольно быстро, вычисления приводят к тому же
результату, что и непосредственное решение по формуле (18.62). Так,
безразмерная амплитуда V в сечении z = 112 при 0 = а>|/2, вычисленная
по формуле (18.62), равна 0,01738, а по формуле (18.69) в одночленном
приближении - 0,01743, в двучленном приближении - 0,01737.
Весьма эффективным методом исследования вынужденных колебаний
сложных механических систем является метод конечных элементов,
численная реализация которого осуществляется с помощью
универсальных программных комплексов, осуществляющих автоматическое
разбиение на конечные элементы, формирование глобальных матриц
жесткости и инерции, вектора узловых усилий, вычисление собственных
частот и форм колебаний, численное интегрирование уравнений
вынужденных колебаний (18.52).
Учет диссипации энергии при исследовании вынужденных колебаний
проводится введением в операторное соотношение (18.57) диссипативно-
го оператора. Этот оператор вводится различными способами.
Например, при использовании модели внешнего трения операторное
соотношение (18.57) записывается в виде
л Э2и(х, Л »Эм(х, /) „ / л /л
А Ц^ + В—^_£ + с«(х, 0 = q(x, 0,
dt2 &
где диссипативный оператор В принимается пропорциональным
инерционному оператору: В = 2еА. В модели внутреннего трения вместо
упругого оператора С берется вязкоупругий оператор вида С(1 + r|d/df).
В методе конечных элементов учет диссипации энергии проводится
введением в уравнение (18.52) матрицы демпфирования В:
МА!1 + Bil + кг = q.
dt2 dt
Матрица демпфирования берется пропорциональной инерционной
матрице В = 2еМ при использовании модели внешнего трения, или
пропорциональной матрице жесткости В = г)К для модели внутреннего
трения. Используется также комбинированная модель трения, согласно
которой В = 2еМ + т]К.
406
ЛИТЕРАТУРА
1. Александров А.В., Потапов В.Д. Основы теории упругости и пластичности.
М.: Высшая школа, 1990. 400 с.
2. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление
материалов. М.: Высшая школа, 2000. 560 с.
3. Благонадежин В.Л., Окопный Ю.А., Чирков В.П. Механика материалов
и конструкций. М.: Изд-во МЭИ, 1994. 312 с.
4. Биргер И.А., Мавлютов P.P. Сопротивление материалов. М.: Наука, 1986.
560 с.
5. Болотин В.В. Ресурс машин и конструкций. М.: Машиностроение, 1990.
448 с.
6. Вибрации в технике. Справочник в 6 т. Т. 1. Колебания линейных систем /
Под ред. В.В. Болотина. М.: Машиностроение, 2-е изд., 1999. 504 с.
7. Дарков А.В., Шпиро Г.С. Сопротивление материалов. М.: Высшая школа,
1989.624 с.
8. Композиционные материалы. Справочник / Под общ. ред. В.В. Васильева,
Ю.М. Тарнопольского. М.: Машиностроение, 1990. 512 с.
9. Конструкционные материалы. Справочник / Под общ. ред. Б.Н. Арзама-
сова. М.: Машиностроение, 1990. 688 с.
10. Минин Л.С, Окопный Ю.А., Радин В.П., Хроматов В.Е. Сборник задач
по механике материалов и конструкций. М.: Изд-во МЭИ, 1998. 304 с.
11. Нормы расчета на прочность оборудования и трубопроводов атомных
энергетических установок. Энергоатомиздат, 1989. 529 с.
12. Работнов Ю.Н. Механика деформируемого твердого тела. М.: Наука, 1988.
712с.
13. Сопротивление материалов / Под ред. Г.С. Писаренко. Киев: Вища школа,
1986.775 с.
14. Сборник задач по сопротивлению материалов / Под ред. А.С. Вольмира.
М.: Наука, 1984.408 с. N
15. Светлицкий В.А. Задачи и примеры по теории колебаний. М.: Изд-во
МГТУ им. Н.Э. Баумана. Часть 1, 1994. 308 с. Часть 2, 1998. 264 с.
16. Феодосьев В.И. Сопротивление материалов. М.: Изд-во МГТУ им.
Н.Э.Баумана, 1999.592 с.
17. Филин А.П. Прикладная механика твердого деформируемого тела. В 3
томах. М.: Наука. Т. 1, 1975. 832 с. Т. 2, 1978. 616 с. Т. 3, 1981. 480 с.
407
Учебное издание
Юрий Афанасьевич ОКОПНЫЙ,
Владимир Павлович РАДИН, Виктор Петрович ЧИРКОВ
Механика материалов и конструкций
Лицензия ЛР № 080003 от 12.09.96
Редактор С. М. Макеева
Художественный редактор Т.Н. Голицына
Корректоры Л.Е. Сонюшкина, Л. И. Сажина
Технические редакторы Т.И. Андреева, С.А. Жиркина
Сдано в набор 09.10.00 Подписано в печать 01.02.01 Формат 60x88/16.
Бумага офсетная. Печать офсетная. Гарнитура Тайме.
Усл. печ. л. 24,99. Усл. кр.-отт. 24,99. Уч.-изд. л. 20,04.
Тираж 1000 экз. Заказ 29 т
Издательство "Машиностроение", 107076, Москва, Стромынский пер., 4.
Отпечатано в типографии НИИ "Геодезия", г. Красноармейск Московской обл.