И. Г. КАПЛАН
СИММЕТРИЯ
МНОГОЭЛЕКТРОННЫХ
СИСТЕМ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1969

530.3
К 20
УДК 539.1
Симметрия многоэлектронных систем, К а п л а н И. Г.,
«Наука», Глав. ред. физ.-мат. лит-ры, 1969 г.
Книга посвящена применению методов теории групп к квантово-
механическим расчетам атомов и молекул. Первая часть содержит
последовательное изложение математического аппарата теории
групп. Отдельные главы отведены группам перестановок, группам
линейных преобразований, тензорным представлениям и неприводи-
неприводимым тензорным операторам. Во второй части изложено применение
теоретико-групповых методов к различным задачам квантовой ме-
механики. Основное внимание уделяется вопросам классификации и
расчету молекулярных состояний. Подробно изложен метод генеало-
генеалогических коэффициентов, позволяющий выразить матричные эле-
элементы многоэлектронной задачи через одноэлектронные и двухэлек-
тронные матричные элементы. Описывается применение этого метода
к атомным и молекулярным системам. Приложение содержит боль-
большое количество таблиц, удобных для проведения конкретных кван-
товомеханических расчетов.
Книга рассчитана на научных работников — физиков и химиков,
желающих овладеть методами теории групп и использовать их в
своих исследованиях. Она может быть также полезна студентам
и аспирантам, специализирующимся в области теоретической физики
и квантовой химии.
Табл. 58, рис. 22, библ. 96 назв.
97-68

ОГЛАВЛЕНИЕ
Предисловие 8
ЧАСТЬ ПЕРВАЯ
МАТЕМАТИЧЕСКИЙ АППАРАТ
Глава I. Основные понятия и теоремы теории групп ... 13
§ I. Свойства групповых операций 13
1-1. Групповые постулаты 13
-2 Примеры групп . 14
-3. Изоморфизм и гомоморфизм 17
-4. Прямое произведение групп 18
-5. Подгруппы; смежные классы 19
-6. Классы сопряженных элементов 20
-7. Инвариантная группа, фактор-группа ...... 21
§ 2. Представления групп 22
1-8. Определение 22
1-9. Векторные пространства ; . 24
-10 Приводимость представления 27
-11. Свойства неприводимых представлений 29
-12. Характеры . . .... 10
-13. Вычисление характеров неприводимых представле-
представлений 32
-14. Разложение приводимого представления 34
-15 Прямое произведение представлений 36
1-16. Коэффициенты Клебша — Гордана ....;.. 39
1-17. Регулярное представление 41
1-18. Построение базисных функций неприводимых пред-
представлений . 42
Глава II. Группа перестановок 47
§ 1. Общие сведения , ... 47
2-1. Операции с перестановками .47
2-2. Классы . . 49
2-3. Схемы Юнга и неприводимые представления ... 50

4 ОГЛАВЛЕНИЕ
§ 2. Стандартное ортогональное представление Юнга — Яманути 52
2-4. Таблицы Юнга 62
2-5 Нахождение явного вида матриц стандартного пред-
представления 55
2-6. Сопряженное представление 59
2-7. Построение антисимметричной функции из базисных
функций сопряженных представлений 61
2-8. Операторы Юнга 62
2-9. Построение базисных функций стандартного пред-
представления из произведений N ортогональных фуйк-
ций 64
§ 3. Нестандартное представление 68
2-Ю. Определение 68
2-11. Трансформационная матрица 71
2-12, Некоторые обобщения 76
2-13. Операторы Юнга в нестандартном представлении . . 78
Глава III. Группы линейных преобразований 82
§ 1. Непрерывные группы 82
3-1. Определение. Специфика непрерывных групп ... 82
3-2. Примеры линейных групп 85
3-3. Инфинитезимальные операторы 87
§ 2. Группа трехмерных вращений 90
3-4. Операции вращения и операторы углового момента 90
3-5. Неприводимые представления 92
3-6. Приведение прямого произведения двух неприводи-
неприводимых представлений 96
3-7. Приведение прямого произведения k неприводимых
представлений, Зл/-символы 98
§ 3. Точечные группы . 103
3-8. Элементы симметрии и операции симметрии . . .103
3-9. Классификация точечных групп 106
Глава IV. Тензорные представления и тензорные операторы 117
§ I. Взаимосвязь линейных групп и групп перестановок . 117
4-1. Построение тензорного представления 117
4 2. Разбиение тензорного представления на неприводи-
неприводимые части 118

ОГЛАВЛЕНИЕ б
4-3. Формулы для характеров симметризованных степе-
степеней представлений 124
4-4. Теорема Литтлвуда 128
4-5, Редукция #2j+i-> #з 131
§ 2. Неприводимые тензорные операторы 136
4-6. Определение . . 136
4-7. Теорема Вигнера — Эккарта 140
4-8. Матричные элементы сферических тензоров . . 142
ЧАСТЬ ВТОРАЯ
СИММЕТРИЯ И КВАНТОВОМЕХАНИЧЕСКИЙ РАСЧЕТ
Глава V. Основы применения теории групп в квантовой ме-
механике . . .... 149
5-1. Симметрия уравнения Шредингера и классификация
состояний . . 149
5-2. Законы сохранения 153
5-3. Теория возмущений 156
5-4. Вариационный метод 161
5-5, Правила отбора 164
Глава VI. Классификация состояний 170
§ JL Электроны в центральном поле 170
6-1. Эквивалентные электроны. LS-связь 170
6-2. Дополнительные квантовые числа. Число старшин-
старшинства 177
6-3. Эквивалентные электроны, //-связь 179
6-4. Конфигурация из нескольких групп эквивалентных
электронов 182
§ 2. Связь молекулярных термов с ядерным спином .... 184
6-5. Классификация молекулярных термов и суммарный
ядерный спин 184
6-6. Нахождение ядерных статистических весов коорди-
координатных состояний 191
6-7. Статистические веса вращательных уровней и мо-
молекулярные спин-модификации 194
6-8. Переход от вращательной статистической суммы
к интегралу состояний. Число симметрии .... 203
? 3. Классификация состояний в приближенных квантовохими-
ческих расчетах 204
6-9. Метод взаимодействия конфигураций и квазидиаго-
нализация секулярного уравнения 204
6-10. Способ нахождения возможных мультиплетов при
расчетах по методу валентных схем 208

5 ОГЛАВЛЕНИЕ
6-11. Нахождение возможных мультиплетов при полном
учете взаимодействия конфигураций кольца из шести
s-орбиталей 219
Глава VII. Метод генеалогических коэффициентов . . . .228
§ 1. Эквивалентные электроны 228
7-1. Определение генеалогических коэффициентов . . . 228
7-2. Вычисление матричных элементов симметричных
операторов 236
§ 2. Конфигурация из нескольких групп эквивалентных электро-
электронов. Состояние с произвольной перестановочной симметрией 242
7-3. Одна оболочка 242
7-4. Конфигурация из двух оболочек 250
7-5. Произвольная многооболочечная конфигурация . 260
7-6. Формулы для матричных элементов не зависящих
от спина симметричных операторов 263
§ 3 Векторно несвязанные состояния 267
7-7. Конфигурация из однократно заполненных орбиталей 267
7-8 Произвольное заполнение орбиталей 270
Глава VIII. Расчет электронных состояний молекулярных си-
систем . . . . 273
§ 1. Молекула водорода. Учет конфигурационного взаимодей-
взаимодействия 273
8-1. Метод валентных схем 273
8-2. Метод молекулярных орбиталей 278
8-3. Ортогонализованные атомные орбитали 280
§ 2 Вычисление энергетической матрицы для произвольных мо-
молекулярных систем . . 282
8-4. Матричные элементы операторов F и G 282
8-5. Выражение для матричных элементов гамильто-
гамильтониана 291
8-6. Взаимодействие двух подсистем в состояниях с за-
заданными спинами 303
§ 3 Симметричные системы 312
8-7. Построение базисных функций группы симметрии
молекулы в методе молекулярных орбиталей . . 312
8-8 Методика расчета в приближении метода валентных
схем .... 318
8-9. Расчет молекулы Нз при учете взаимодействия всех
конфигураций с ls-орбиталями 332

ОГЛАВЛЕНИЕ 7
Приложение 1. Таблицы характеров точечных групп 338
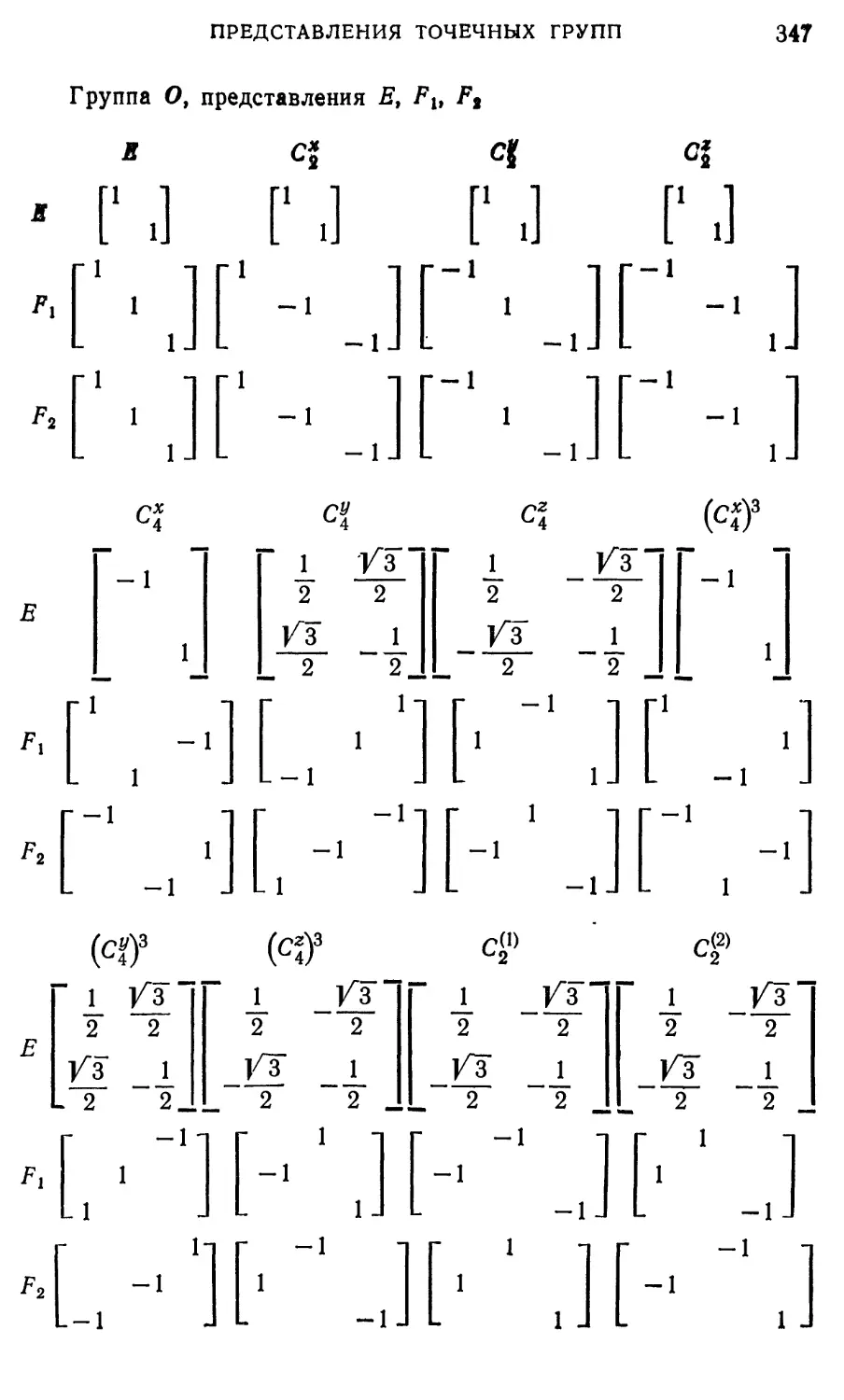
Приложение 2. Матрицы ортогональных неприводимых пред-
представлений точечных групп 344
Приложение 3. Таблицы редукции представлений t/^/il на ГРУП"
пе /?з 349
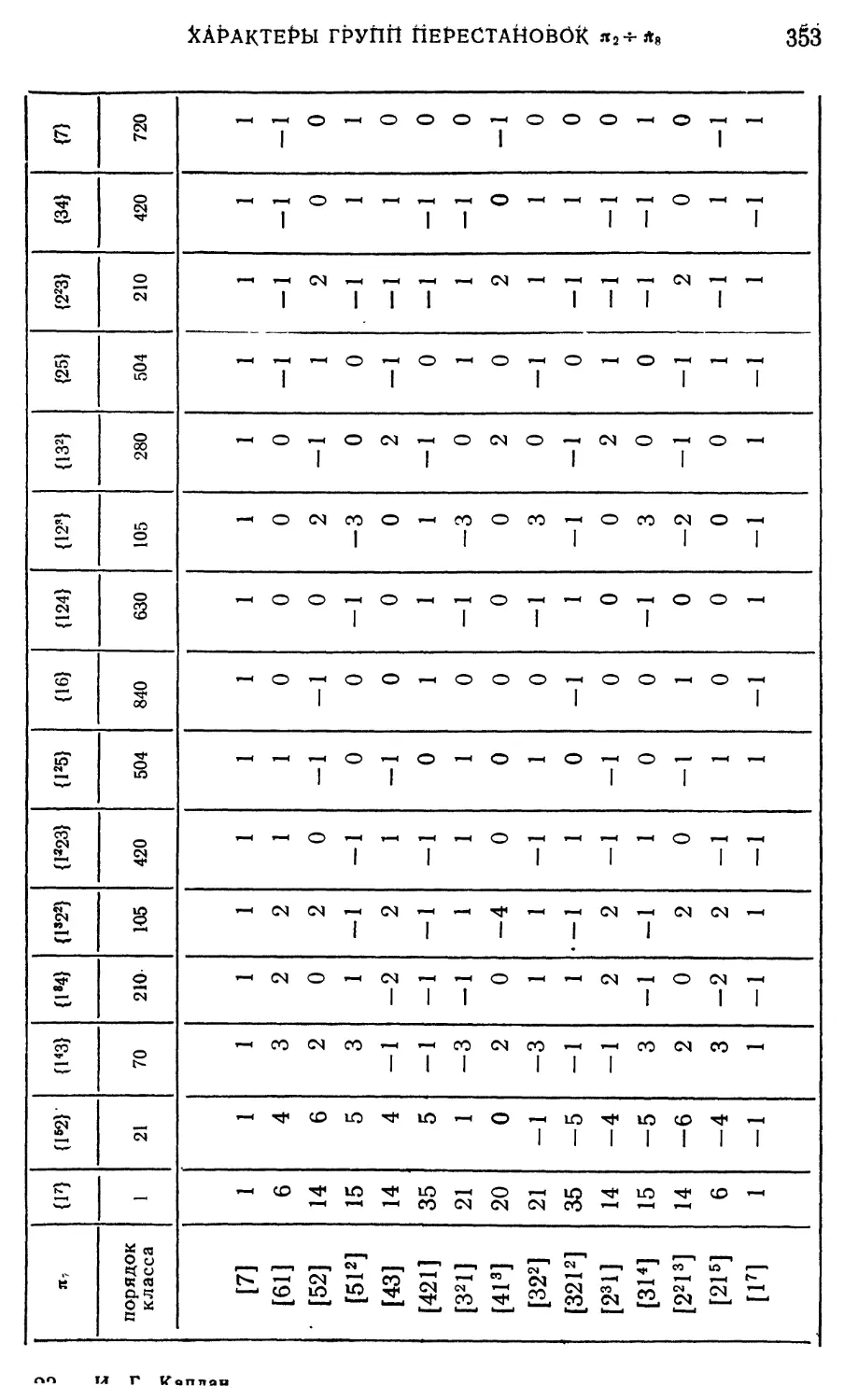
Приложение 4. Таблицы характеров групп перестановок
Jt2-f-jt8 352
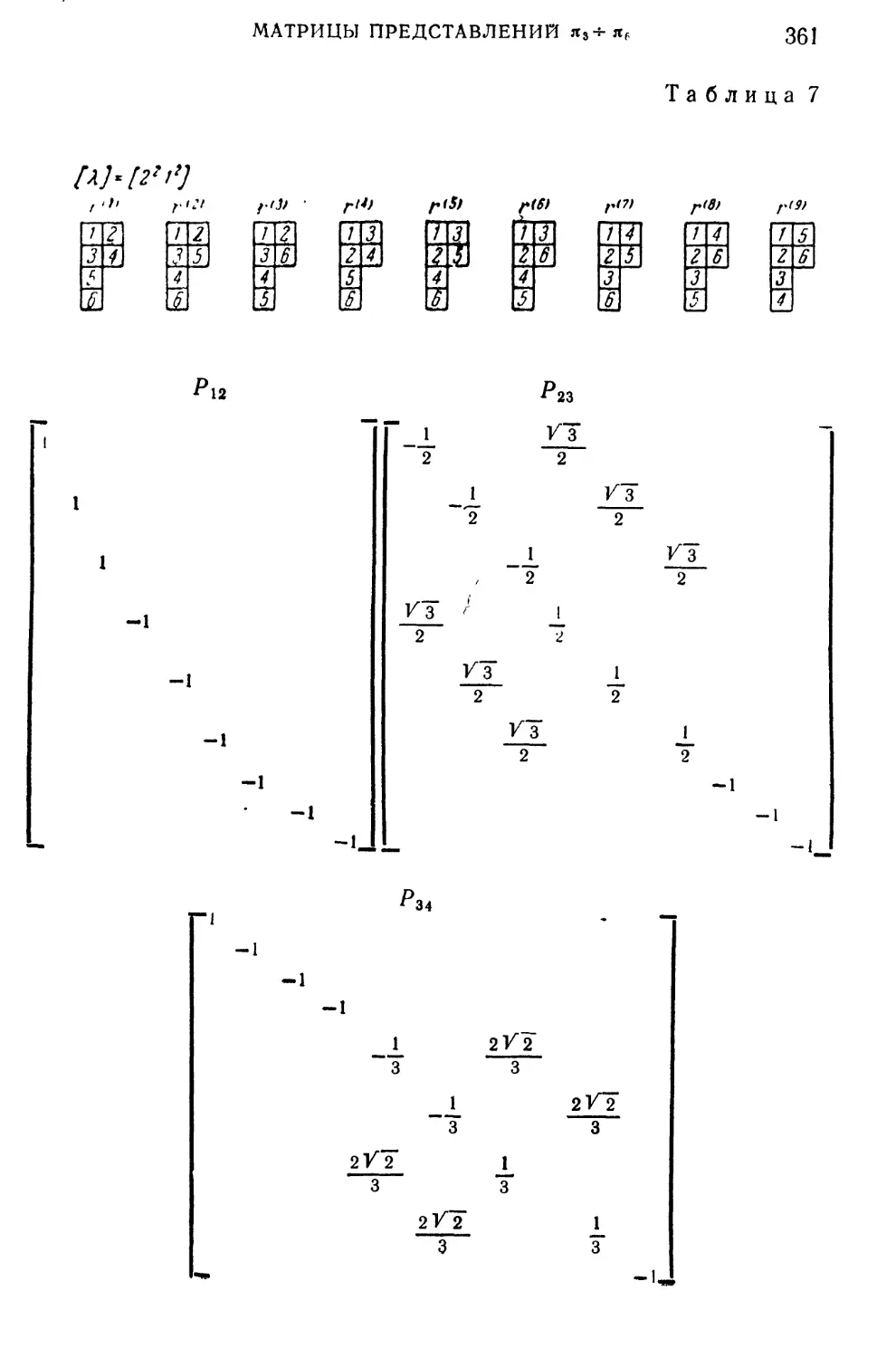
Приложение 5. Матрицы ортогональных неприводимых пред-
представлений групп перестановок я3 -?- яб . . . . 355
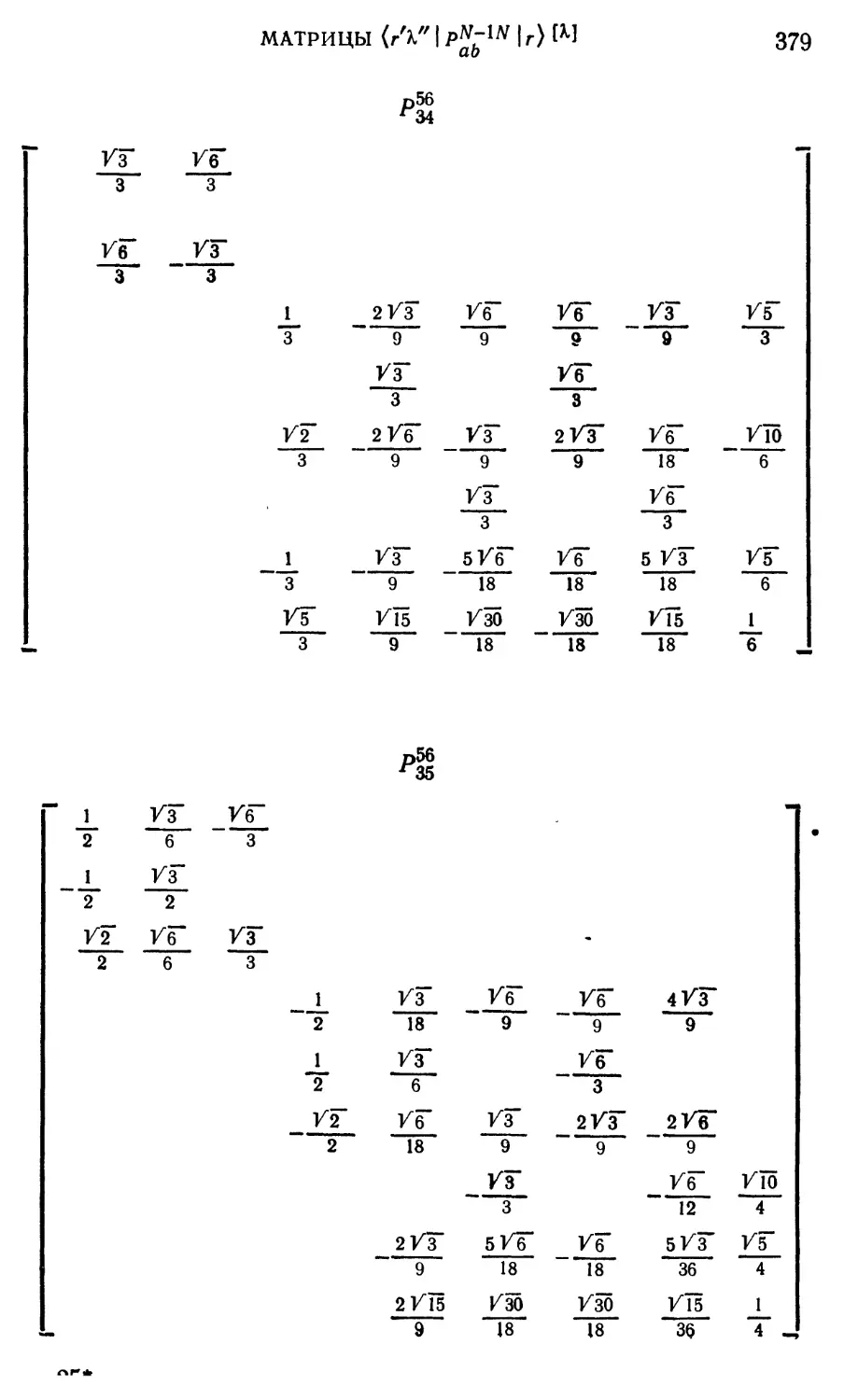
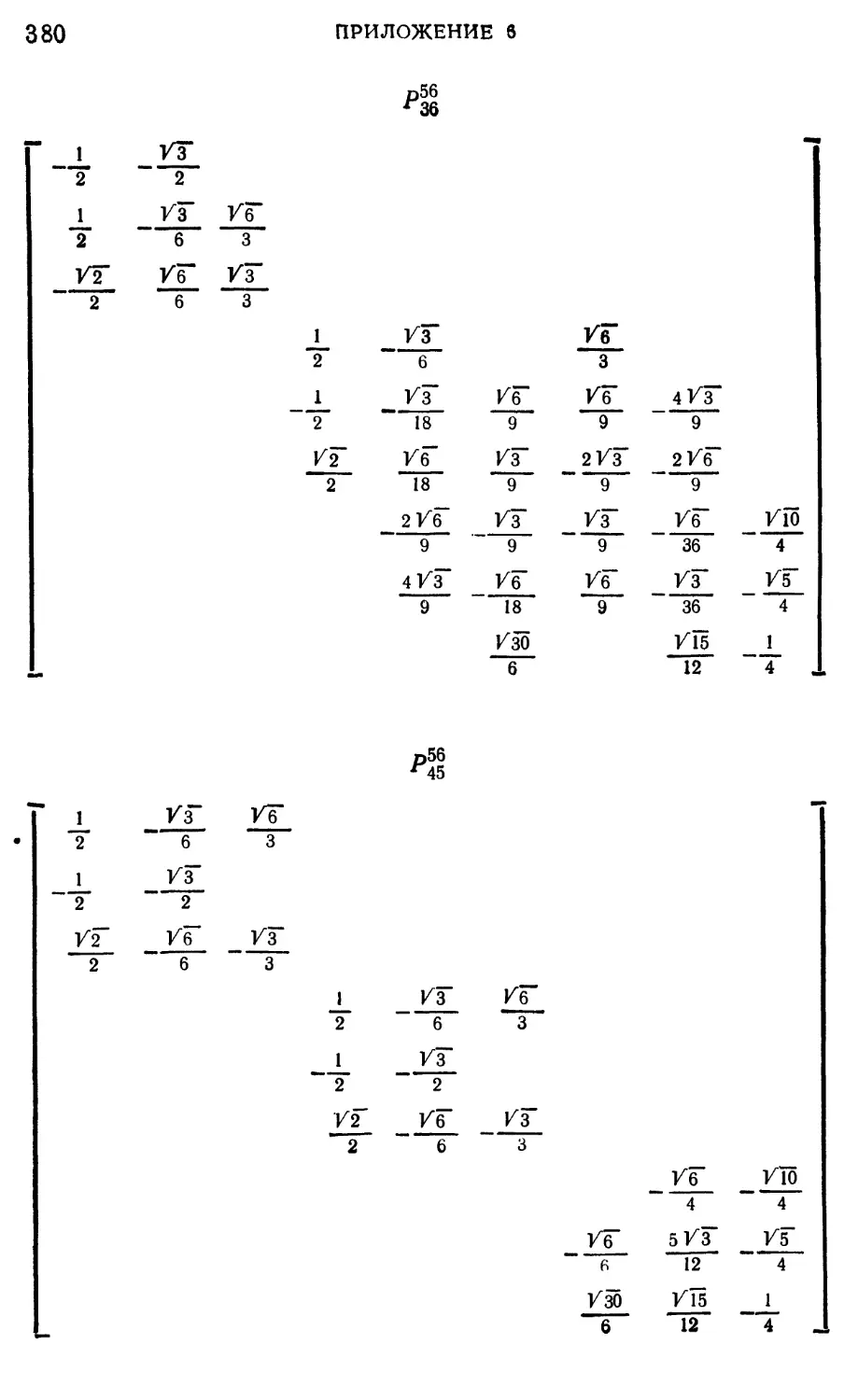
Приложение 6. Таблицы матриц (г'к" | Р^1 N | г)[К] для W»=3 -f- 6 367
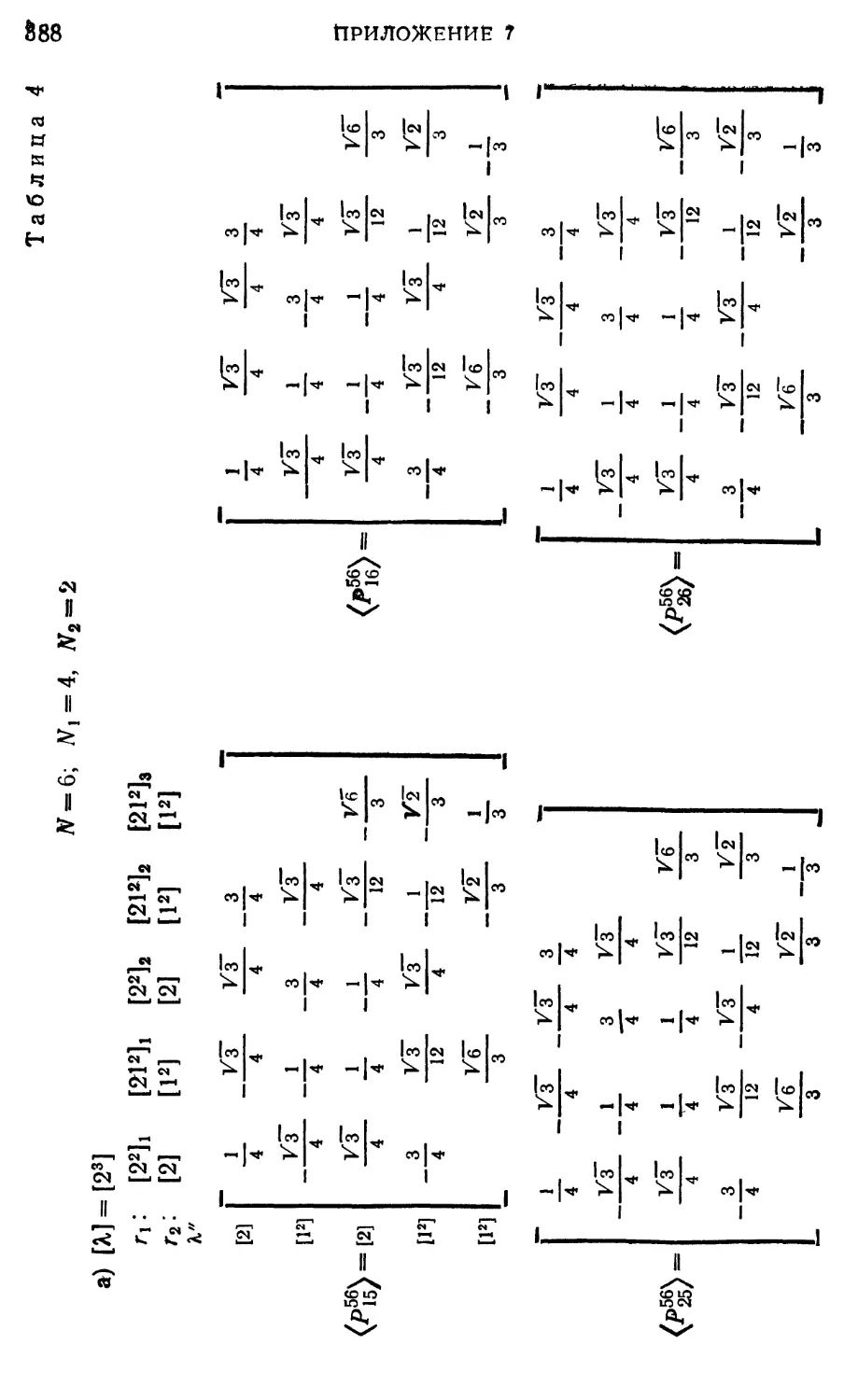
Приложение 7. Таблицы матриц ( (г'/2) Я V | Р%~1 N\rxr^
для #=3~6 384
Литература Ф 405

ПРЕДИСЛОВИЕ
В настоящее время при решении большого круга фи-
физических и химических проблем широко применяются
методы теории групп. Привлечение теории групп дает
возможность качественно выяснить ряд свойств рас-
рассматриваемых систем, не прибегая к количественному
решению задачи, а также существенно облегчает сам
расчет. В основе применения абстрактного аппарата тео-
теории групп к конкретным вопросам строения вещества
лежат свойства симметрии исследуемых объектов. Эту
симметрию в случае атомно-молекулярных систем мож-
можно разделить на два типа: а) симметрию относительно
пространственных преобразований; б) симметрию отно-
относительно перестановок тождественных частиц. Оба типа
симметрии вытекают из свойств уравнения Шредингера
для многочастичных систем.
Процесс проникновения методов теории групп в кван-
квантовую механику может быть условно разделен на три
этапа. Начальный этап A927—1930 гг.) характеризует-
характеризуется быстрым внедрением теоретико-групповых методов
в формирующуюся в эти годы квантовую механику.
В первую очередь здесь следует отметить основопола-
основополагающие работы Вигнера, а также Бете, Вейля, Ван-
дер-Вардена.
Однако непривычный математический аппарат и воз-
возможность получения многих результатов прямым вычис-
вычислением без привлечения теории групп способствовали
появлению у ряда физиков отрицательного отношения
к теоретико-групповым методам. В литературе того пе-
периода даже появилось выражение «групповая чума».
После опубликования Слейтером в 1929 г. детерминант-
ного метода расчета многоэлектронных систем интерес
к теории групп временно угасает (исключение состав-
составляют область молекулярных колебаний и некоторые во-

ПРЕДИСЛОВИЕ 9
просы теории твердого тела). Простота и наглядность
детерминантного метода способствовали использованию
его при решении целого ряда задач теории атома, мо-
молекулы и твердого тела. Попытки применения метода
детерминантов к расчетам сложных электронных конфи-
конфигураций упирались, однако, в практически непреодоли-
непреодолимые расчетные трудности.
Третий этап, характеризующийся широким использо-
использованием методов теории групп в квантовомеханических
исследованиях, связан с появлением серии классических
статей Рака A942—1949 гг.). Рака развил новые ме-
методы расчета, основанные на генеалогическом построе-
построении волновой функции. Для классификации состояний
и построения волновых функций оказалось удобным ис-
использовать ранее не применявшиеся в физике группы
непрерывных преобразований из числа так называемых
групп Ли. Работы Рака в области атомной спектроско-
спектроскопии и последовавшие за ними работы Яна, Эдмондса
и др. в области оболочечной теории ядра послужили
основой для применения групп непрерывных преобразо-
преобразований и групп перестановок в других областях физики,
а также и химии. Ярким примером, иллюстрирующим
эффективность методов теории групп в решении слож-
сложных физических проблем, являются недавние успехи в
области систематики элементарных частиц.
Настоящая книга посвящена применению методов
теории групп к квантовомеханическим расчетам много-
многоэлектронных систем. В ней полностью опущены вопросы
применения теории групп к твердому телу. Изложение
последних потребовало бы специальной монографии.
Основное место в книге отведено применению теоретико-
групповых1 методов к классификации и расчету молеку-
молекулярных состояний. Подробно излагается метод генеало-
генеалогических коэффициентов, получивший широкое распро-
распространение в атомной и ядерной спектроскопии. Этот
метод развит в настоящей монографии применительно к
молекулярным системам. Для случая взаимодействий,
не связанных со спином, в гл. VII, VIII детально раз-
разработана методика расчета с координатными волновыми
функциями и показана полезность применения подобной
методики для решения задач квантовой химии. Книга

10 ПРЕДИСЛОВИЕ
снабжена большим количеством таблиц, удобных при
проведении конкретных квантовомеханических расчетов.
Для чтения книги не требуется предварительного
знания теории групп (но предполагается, что читатель
знаком с основами квантовой механики). Математиче-
Математический аппарат теории групп излагается в первой части
книги. Автор ориентируется при этом на читателя, ин-
интересующегося практическим использованием методов
теории групп в квантовомеханических расчетах. Значи-
Значительно подробнее, чем это принято в большинстве руко-
руководств для физиков, излагается аппарат группы переста-
перестановок, поскольку последний является основным рабочим
инструментом в случае расчетов с координатными вол-
волновыми функциями.
Мне приятно выразить благодарность А. С. Компа-
нейцу за моральную поддержку и полезные советы в
процессе написания книги. Благодарю Е. Д. Трифонова,
прочитавшего книгу в рукописи и сделавшего ряд цен-
ценных замечаний, а также мою жену Л. В. Попову за
неоценимую помощь в редактировании и оформлении
рукописи.

ЧАСТЬ ПЕРВАЯ
МАТЕМАТИЧЕСКИЙ
АППАРАТ
Без знания дробей
никто не может
признаваться
сведущим в арифметике
ЦИЦЕРОН

ГЛАВА I
ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
ТЕОРИИ ГРУПП
§ 1. Свойства групповых операций
1-1. Групповые постулаты. Группой G называется
совокупность элементов Л, В, ..., удовлетворяющих сле-
следующим четырем условиям.
1. Определен «закон умножения» элементов, т. е. за-
задано правило, согласно которому каждой паре элемен-
элементов Р, Q ставится в соответствие некоторый элемент /?,
содержащийся в этой же совокупности. Элемент R на-
называется произведением элементов Р и Q и записывает-
записывается в виде
A.1)
2. Произведение сомножителей ассоциативно:
, A.2)
т. е. для однозначного задания произведения достаточно
задать порядок сомножителей.
3. Среди элементов группы имеется единичный эле-
элемент ?, обладающий свойством
EQ = QE = Q A.3)
для любого Q, принадлежащего группе (условие при-
принадлежности элемента Q группе О символически обо-
обозначается следующим образом: Q^O).
4. Для каждого элемента Q^O существует обратный
элемент Q^gC, удовлетворяющий равенству
= E. A.4)
Элемент обратный произведению элементов, равен
l {p-\ A.5)

14 ОСНОЁЫ ТЕОРИИ ГРУПП ГЛ. I
в чем легко убедиться, умножив PQ на Q-{P-{ и вос-
воспользовавшись правилом ассоциативности.
Произведение элементов группы в общем случае не-
некоммутативно, т. е.
PQ?=QP.
Если для всех элементов группы выполняется равенство
PQ = QP, то группа называется абелевой. Частным слу-
случаем абелевых групп являются циклические группы, все
элементы которых могут быть получены путем последо-
последовательного возведения в степень одного элемента, т. е.
п элементов циклической группы могут быть представ-
представлены следующим образом:
Л, А\ Л3, ..., Ап^Е. A.6)
Для элементов группы справедлива следующая тео-
теорема: если Ga пробегает все элементы группы О, а
Go — некоторый фиксированный элемент группы О, то
произведение G0Ga (или GaG0) также пробегает все эле-
элементы группы и притом по одному разу.
Действительно, любой элемент группы Gb может быть
получен умножением справа Go на Ga = GolGb- При
этом среди произведений G0Ga не может быть повто-
повторяющихся, так как если GoGa=GoGb, то, умножая это
равенство на Go1 слева, получаем Ga = Gb, следователь-
следовательно, для разных Ga все G0Ga разные.
Из доказанной теоремы следует свойство инвариант-
инвариантности суммы по всем элементам группы для произволь-
произвольной функции, определенной на элементах группы:
Sf(Gfl)=2/(G0Gfl)=S/(G,). A.7)
Ga Ga Gb
1-2. Примеры групп. 1. Простейшим примером груп-
группы является совокупность рациональных чисел (исклю-
(исключая нуль) по отношению к операции умножения. Умно-
Умножение чисел по определению ассоциативно, единичным
элементом является единица, каждое число имеет об-
обратное.
2. Совокупность всех векторов трехмерного прост-
пространства образует группу по отношению к операции ело-

$ 1 СВОЙСТВА ГРУППОВЫХ ОПЕРАЦИЙ 15
жения. Умножение элементов группы сводится в дан-
данном случае к сложению векторов. Операция сложения
векторов обладает свойством ассоциативности. Единич-
Единичным элементом является вектор нулевой длины. Взаим-
Взаимно обратными элементами группы являются равные по
величине и противоположно 'направленные векторы.
3. В качестве более сложного примера рассмотрим
перестановки N объектов. Пронумеруем объекты це-
целыми числами от 1 до N. Как известно, из N чисел мо-
можно составить N1 различных перестановок, которые мо-
можно изобразить с помощью символа
12 3 ... N
it
i
где ik обозначает то число, которое в результате пере-
перестановки занимает место числа k. Произведение двух
перестановок Р2Р\ также является перестановкой, дей-
действие которой эквивалентно последовательному действию
сначала перестановки Рь потом Р2- Каждой перестанов-
перестановке A.8) можно сопоставить обратную перестановку
h h • • • (/v ^
2 3 ... NJ' (L9)
Последовательное действие прямой и обратной переста-
перестановок оставляет объекты на своих местах, т. е. является
тождественной перестановкой, обозначим ее /.
Таким образом, N1 перестановок N объектов состав-
составляют группу, называемую группой перестановок, либо
симметрической группой, будем обозначать ее я#. Эле-
Элементы группы перестановок удобно разбивать на про-
произведение циклов. Циклом называется перестановка, ко-
которую можно записать в виде *)
з ц • • • h lk+i • • • *
где ik+i .. • In обозначают числа, которые в результате
перестановки остаются на своих местах. Так, шесть
элементов группы яз могут быть представлены как
*) В гл. II для цикла употребляется т^кже обозначение

16
ОСНОВЫ ТЕОРИИ ГРУПП
ГЛ. I
циклические перестановки
Рис. 1.1
4. Другим примером группы является совокупность
пространственных преобразований равностороннего тре-
треугольника, при которых он совмещается сам с собой.
Такие преобразования
называются операция-
операциями симметрии (несим-
(несимметричные тела не мо-
могут быть совмещены
сами с собой ни при
каких преобразовани-
преобразованиях, кроме тождествен-
тождественного). Существует
шесть различных неэк-
неэквивалентных операций
симметрии равносто-
равностороннего треугольника.
В качестве этих шести операций могут быть выбраны
следующие (рис. 1.1):
Е — тождественная операция, оставляющая треуголь-
треугольник неизменным;
Сз, Сз—повороты по часовой стрелке на 120° и 240°
вокруг оси, перпендикулярной плоскости треугольника
и проходящей через его центр тяжести;
о^\ о®\ о® — отражения в плоскостях, перпендику-
перпендикулярных плоскости треугольника и проходящих через его
медианы.
Все остальные операции симметрии эквивалентны од-
одной из вышеперечисленных. Например, повороты на 180°
вокруг осей, проходящих через медианы, эквивалентны
отражениям gv.
Найдем все возможные попарные произведения из
приведенных выше шести операций симметрии равно-
равностороннего треугольника и представим результаты в
виде таблицы (табл. 1.1). Операция, применяющаяся
к треугольнику первой, помещена в верхней строке таб-
таблицы. Как видно из таблицы, последовательное приме-
применение любых двух операций эквивалентно операции из
этого же набора. Для каждой операции Q имеется

СВОЙСТВА ГРУППОВЫХ ОПЕРАЦИЙ
17
обратная операция Q~\ приводящая к тождественному
преобразованию Е. Пользуясь таблицей, легко прове-
проверить, что выполняется правило ассоциативности. Следо-
Следовательно, операции симметрии треугольника образуют
группу, ее принято обозначать C3v. Группа С3г/принад-
С3г/принадлежит к так называемым точечным группам (см. § 3
гл. III).
Таблица 1.1
Таблица умножения группы C3V
Е
С3
с\
of
of
of
Е
Е
С3
с\
of
of
of
сз
С3
с§
Е
of
of
of
г2
сз
Г2
сз
Е
Сз
of
of
of
<v
of
of
of
E
Сз
С2
сз
<2)
of
of
of
cl
E
c3
aC)
of
of
of
c3
c2
E
1-3. Изоморфизм и гомоморфизм. Группа может со-
содержать как конечное число элементов, так и бесконеч-
бесконечное. В зависимости от этого группы делят на конечные
и бесконечные. Количество элементов группы называют
ее порядком. Две группы одинакового порядка О и (У
называются изоморфными, если между их элементами
можно установить взаимно однозначное соответствие,
при котором выполняется условие, что если элементу
Леб соответствует /1'е С7, а элементу Bg О соот-
соответствует B'^l G\ то элементу С=АВ соответствует эле-
элемент С' — А'В''. Изоморфные группы тождественны с точ-
точки зрения их абстрактных групповых свойств, хотя кон-
конкретный смысл их элементов может быть совершенно
различен.
Примером изоморфных групп являются приведенные
в предыдущем разделе точечная группа C3v и группа
перестановок Яз. Действительно, каждой операции

18
ОСНОВЫ ТЕОРИИ ГРУПП
ГЛе
симметрии треугольника можно сопоставить соответст-
соответствующую перестановку номеров вершин. В результате по-
получаем взаимно однозначное соответствие между эле-
элементами групп C3v и я3.
JT3
Е
I
С3
^132
Г2
^123
Pi3
о?
Pi»
of
Pl2
Приведенный пример является частным случаем бо-
более общего положения (теорема Кейли):
любая конечная группа порядка п изоморфна под-
подгруппе группы перестановок яп-
Если каждому элементу А группы G соответствует
элемент А' группы О\ причем из АВ = С следует А'ВГ =
= С, то группы называются гомоморфными. В отличие
от изоморфизма гомоморфизм не требует взаимной од-
однозначности элементов групп, один элемент группы G'
может соответствовать нескольким элементам группы О.
1-4. Прямое произведение групп. Пусть две конечные
группы Ох и G2 не содержат общих элементов, кроме
единичного. Обозначим их порядок gi и §2 соответствен-
соответственно. Если элементы группы О\ коммутируют с элемен-
элементами группы (?2, то, составив все возможные произве-
произведения элементов этих групп, мы получим совокупность
g\g2 элементов, также образующую группу. Действи-
Действительно, в силу условия коммутативности произведение
двух элементов полученной совокупности представляет
элемент, принадлежащий к этой же совокупности:
АгА2 • ВХВ<2 = АгВг • А2В2 = СХС2.
Очевидно выполнение и других групповых постулатов.
Полученную группу называют прямым произведением
групп Cj и С2 и обозначают Ох X G2.
Простейшим примером коммутирующих групп яв-
являются группы перестановок, элементы которых дейст-
действуют на разные совокупности предметов. Составим, на-
например, прямое произведение двух групп перестановок
яг- Пусть перестановки первой группы действуют на

§ 1 СВОЙСТВА ГРУППОВЫХ ОПЕРАЦИЙ 1ф
числа 1, 2, а перестановки второй группы — на числа 3,4.
Прямое произведение групп я2 X Щ будет содержать
четыре элемента:
щ х щ: /, р12, Р34> Л2 • Л*. A.12)
1-5. Подгруппы; смежные классы. Если из группы G
можно выделить некоторую совокупность элементов //,
образующую группу, при том же определении закона
умножения, то Н называется подгруппой группы G.
Всякая группа имеет тривиальную подгруппу, состоя-
состоящую из одного единичного элемента группы. В дальней-
дальнейшем, говоря о подгруппе, мы будем подразумевать не-
нетривиальную подгруппу.
Пусть элемент G\ входит в конечную группу G, но
не принадлежит к ее подгруппе //, состоящей из h эле-
элементов. Умножим (например, слева) все элементы Я
на G\. Мы получим некоторую совокупность h элементов,
которую обозначим G\H. Ни один элемент из G\H не
принадлежит к //. В противном случае для некоторых
элементов На, НЪ^Н мы имели бы равенство G\Ha = Hb
или G\ = HbHa\ т. е. G\ efl, что противоречит исходному
условию. Возьмем теперь некоторый элемент G2^G, не
принадлежащий // и GXH, w образуем совокупность
G2H. Аналогичным образом можно показать, что G\H и
G2H не имеют общих элементов. Если //, GXH и G2H не
исчерпывают всех элементов группы, то составляем G3//
и т. д., пока все элементы группы G не будут разбиты
на т совокупностей:
Я, G,//, G2#, ..., Gm^H. A.13)
Следовательно, порядок группы g — mh. В результате
приходим к теореме, называемой теоремой Лагранжа:
порядок подгруппы конечной группы является де-
делителем порядка группы.
Из теоремы Лагранжа вытекает очевидно следствие:
группа, порядок которой является простым числом, не
имеет подгрупп.
Разбиение элементов группы на совокупности A.13)
однозначно определяется заданием подгруппы //, так
как любой элемент совокупности G&// может играть

so основы теории групп гл. i
роль Gk. Действительно, пусть Gk = GkHa, где На —
произвольный элемент подгруппы И. Совокупность эле-
элементов GkH" = GkHaH'== GkH. Последнее равенство сле-
следует из теоремы раздела 1-1.
Совокупности A.13) называются левыми смежными
классами по подгруппе Н. Аналогично определяются
правые смежные классы. Число смежных классов под-
подгруппы называется индексом подгруппы. За исключе-
исключением самой Н ни один из смежных классов GkH не
образует подгруппу, так как не содержит единичного
элемента.
В качестве примера рассмотрим совокупность пере-
перестановок /, Р\2 группы я3 (см. A.11)). Эта совокупность
образует подгруппу, обозначаемую яг. Индекс подгруп-
подгруппы m = g/h = 6/2 = 3. Следовательно, имеется три смеж-
смежных класса. Ниже приведены левые смежные классы по
подгруппе я2:
/
: р
13,
1-6. Классы сопряженных элементов. Два элемента
А и В называются сопряженными, если A = QBQ~\ где
Q — элемент той же группы. Если два элемента А и В
сопряжены с третьим элементом С, то они также сопря-
сопряжены друг с другом. Действительно, из A = QCQ~\ B =
= RCR-1 следует C=Q-M1Q, откуда B = RQ~lAQR-l =
= (/?Q)^(/?Q~1). Поэтому элементы группы разби-
разбиваются на совокупности сопряженных друг с другом
элементов. Такие совокупности называются классами
группы. Класс определяется заданием одного своего эле-
элемента, так как, задав элемент Л, мы получим все осталь-
остальные элементы, составляя произведения GbAGb~\ где
Gb пробегает все элементы группы (при этом некоторые
элементы класса могут повторяться). С помощью таб-
таблицы умножения группы CZv нетрудно убедиться, что
ее шесть элементов разбиваются на три класса: Е;
Г Г2 „ JV гг<2) ггC)
С3, Сз и av , av , av .
Приведем без доказательства также следующие свой-
свойства классов.

4 1 СВОЙСТВА ГРУППОВЫХ ОПЕРАЦИЙ 21
1. Единичный элемент является сам по себе классом.
2. Все классы, кроме единичного, не являются под-
подгруппами, поскольку не содержат единичного элемента.
3. Каждый элемент абелевой группы является классом.
4. Количество элементов в классе является делите-
делителем порядка группы.
1-7. Инвариантная группа, фактор-группа. Рассмот-
Рассмотрим совокупность элементов
GQHaGo\ A.14)
где Go — некоторый фиксированный элемент группы G,
На пробегает все элементы подгруппы Я. Легко прове-
проверить, что произведения A.14) удовлетворяют всем четы-
четырем групповым постулатам и образуют, следовательно,
подгруппу группы G. Эта подгруппа называется подоб-
подобной подгруппе Я. Если при любом выборе элемента Go
подобная подгруппа совпадает с Я, т. е. для любого
G0HGil=H, A.15)
то подгруппа Я называется инвариантной. Из A.15)
следует
A.16)
т. е. левые смежные классы по инвариантной подгруппе
совпадают с правыми смежными классами.
Пусть инвариантная подгруппа Я имеет индекс т.
Составим m смежных классов Я, например, левых:
Я, О,Я, О2Я, ..., О^Я. A.17)
Найдем произведение двух смежных классов совокуп-
совокупности A.17):
G1H^G2H=G,(HG2)H = (GlG2)H. A.18)
Мы воспользовались равенством A.16) и тем обстоя-
обстоятельством, что произведение группы на саму себя снова
даст эту же группу. Таким образом, произведение двух
смежных классов из совокупности A.17) дает другой
смежный класс из этой же совокупности. Далее, каж-
каждому смежному классу GkH можно сопоставить

ОСНОВЫ ТЕОРИИ ГРУПП
ГЛ. t
обратный смежный класс GI //, причем их произведе-
произведение равно инвариантной подгруппе //, Следовательно,
т смежных классов A.17) можно рассматривать как
элементы некоторой группы, в которой роль единичного
элемента играет сама инвариантная подгруппа. Эта
группа, порядок которой равен индексу подгруппы //,
называется фактор-группой по инвариантной подгруппе
Н и обозначается О/М. Группа, не имеющая инвари-
инвариантной подгруппы, называется простой.
Пример. Группа С3г, имеет подгруппу С3, состоя-
состоящую из трех элементов Е, С3 и С\. Пользуясь табли-
таблицей умножения группы (см. табл. 1.1), нетрудно убе-
убедиться, что эта подгруппа является инвариантной. Ин-
Индекс подгруппы С3 равен 2, следовательно, имеется два
смежных класса:
С3 \ Е, С3, С3;
а С ' аA> аB) аC)
образующих фактор-группу второго порядка С3г//С3.
Роль единичного элемента играет подгруппа С3. Таб-
Таблица умножения фактор-группы имеет следующий вид:
с,
ovC3
с3
avC3
ovC3
с3
§ 2. Представления групп
1-8. Определение. Группа квадратных матриц, гомо-
гомоморфная данной группе, называется ее представлением.
Число строк или столбцов матриц представления назы-
называется размерностью представления.
Как следует из определения, каждому элементу груп-
группы Q может быть сопоставлена матрица T(Q), причем
произведению элементов группы QP = R соответствует
произведение матриц
A.19)

§ 2 ПРЕДСТАВЛЕНИЯ ГРУПП 23
Перемножение матриц в левой части равенства A.19)
осуществляется по обычным формулам матричной ал-
алгебры*). Если все матрицы представления различны,
представление изоморфно группе; такое представление
называется точным.
Матрицы представления могут быть получены путем
подбора либо другим способом так, чтобы они удовлет-
удовлетворяли таблице умножения группы. Однако в физиче-
физических приложениях представления возникают при нахож-
нахождении результата действия элементов группы на функ-
функции координат. Применяемые в физике группы являются
либо группами линейных пространственных преобразо-
преобразований, либо группами перестановок координат частиц.
Действие их элементов на функцию координат порож-
порождает набор новых функций, линейно преобразующихся
друг через друга при воздействии элементов группы.
Рассмотрим этот процесс несколько подробнее.
Пусть г|H — функция координат, определяемая в кон-
конфигурационном пространстве системы**). Действие на
\f>o элемента группы Q^Q переводит г|H в некоторую дру-
другую функцию, обозначим ее \|)q=Q\|H. Если Q пробегает
все элементы группы, то получим g функций, однако не-
некоторые из них могут оказаться линейно зависимыми.
Пусть число линейно независимых функций г|)г- равно
/ (f^S)- Под действием элементов группы функции \|)*
будут преобразовываться только друг через друга, так
как в силу свойств группы (см. теорему раздела 1-1)
никакие другие функции не могут войти в этот набор.
Итак, имеем
f
Q^=2r^(Q)^ A.20)
Коэффициенты Tik(Q) образуют квадратную матрицу
порядка /. Из определения матрицы F(Q) следует, что
*) Матричный элемент произведения матриц
Г/л (QP) = 2 Ти (Q) Т1к (Р).
/
**) Для системы N электронов размерность конфигурационного
пространства равна AN. Каждый электрон описывается тремя про-
пространственными и одной спиновой координатами.

24 ОСНОВЫ ТЕОРИИ ГРУПП ГЛ. I
при действии элемента группы Q на функцию ^ послед-
последняя преобразуется по &-му столбцу матрицы F(Q). Каж-
Каждому элементу группы Q соответствует своя матрица
T(Q). Произведению двух элементов QP соответствует
матрица, являющаяся произведением матриц T(Q) и
Г(Р), так как
= 2 B Ги (Q) Г„ (Р)) ^ = S [Г
Следовательно, матрицы F(Q) образуют f-мерное пред-
представление группы О. Набор f функций г|}г-, на котором
определены матрицы F(Q), называется базисом пред-
представления.
1-9. Векторные пространства. Векторное пространст-
пространство п измерений состоит из множества векторов х, кото-
которые получают, образуя все возможные комбинации из п
линейно независимых базисных векторов ег-:
x=2j**e,. A.21)
? = 1
Х\ называется компонентной вектора х вдоль направления
ег-, Х{ может быть комплексной величиной, векторное
пространство является в этом случае комплексным.
При линейном преобразовании от одной системы ба-
базисных векторов к другой компоненты вектора в старой
системе координат линейно преобразуются через компо-
компоненты в новой системе. Если
е;=2ад, A.22)
ТО ИЗ
следует
Если вектор х изображать в виде одностолбцовой мат-
матрицы X из его компонент, а матрицу преобразования

I 2 ПРЕДСТАВЛЕНИЯ ГРУПП 25
,(.1.22) обозначить через S, то равенство A.23) может
быть записано как
X = SX', A.24)
.откуда
X' = S~lX9 A.25)
где S — матрица обратного преобразования.
Вместо преобразования базисных векторов можно
-осуществить преобразование векторного пространства,
лри котором каждому вектору х сопоставляется вектору,
равный
у = Лх. A.26)
А можно рассматривать как оператор, переводящий век-
вектор х в вектор у. Аналитическим выражением опера-
оператора А является я-мерная матрица, связывающая ком-
компоненты векторов:
У/-2 <*«**, A.27)
или в матричной записи
К = ЛХ. A.28)
Пусть векторы у и х связаны между собой соотно-
соотношением A.28). Совершим преобразование базисных век-
векторов A.22). В новой системе координат
Y' = A'X'. ' A.29)
Найдем связь между Аг и А. Для этого перейдем в ста-
старую систему координат, совершим в ней преобразова-
преобразование A.28) и вернемся в новую систему координат:
или
Y/^S~lASX'. A.30)
Сравнивая A.29) и A.30), получаем
A' = S~lAS. A.31)

26 ОСНОВЫ ТЕОРИИ ГРУПП ГЛ. I
Комплексное векторное пространство называется уни-
унитарным, если квадрат длины вектора равен сумме квад-
квадратов модулей его компонент
|х|2=2|*/|2. A.32)
Из A.32) следует, что базисные векторы унитарного
пространства образуют ортонормированный набор
(е,е;) = б,;, A.33)
Скалярное произведение двух векторов в унитарном про-
пространстве равно
2^,. A.34)
Унитарным преобразованием называется линейное пре-
преобразование, не меняющее скалярного произведения век-
векторов. Из определения унитарного преобразования сле-
следует
S<^ = S^. = S^X4'- A-35)
Равенство A.35) удовлетворяется при выполнении условия
?*!**«-V A36)
Так как по определению обратной матрицы
2^„ = 6Ы, A.37)
то из сравнения A.36) и A.37) следует, что s"! = s*ik,
что символически может быть записано в виде *)
S~l = S* *" A.38)
или
SS* = S*S = I. A.38а)
Матрицы, удовлетворяющие условиям A.38) или A.38а),
называются унитарными. Из A.38а) следует, что, по-
*) 5 обозначает матрицу, транспонированную относительно мат-
матрицы S, их матричные элементы связаны условием s.k = ski.

§2 ПРЕДСТАВЛЕНИЯ ГРУПП 27
мимо A.36), для матричных элементов унитарных мат-
матриц справедливы также соотношения
|4% = V A.36а)
Для вещественных матриц вместо A.38а) имеем
SS = SS = I. A.39)
Матрицы, удовлетворяющие условиям A.39), называ-
называются ортогональными. Их матричные элементы удов-
удовлетворяют условиям ортогональности:
2л
к
1-10. Приводимость представления, f базисных функ-
функций представления Г (см. раздел 1-8) можно рассмат-
рассматривать как базисные векторы в n-мерном векторном
пространстве, обозначим его Ш. Говорят, что простран-
пространство §Я преобразуется по представлению Г. Согласно
A.20) действие операций Q группы О на базисный век-
вектор -фи порождает вектор Qtyk, также принадлежащий
31. Поскольку любой вектор векторного пространства
может быть выражен в виде линейной комбинации ба-
базисных векторов, то действие операций группы перево-
переводит каждый вектор пространства SW в другой вектор,
также принадлежащий 91. Следовательно, простран-
пространство §Я инвариантно относительно преобразований груп-
группы О.
При линейном преобразовании базисных векторов
г|>;=25(.Л A.41)
матрицы представления Г переходят, согласно A.31), в
матрицы
/T A.42)

ОСНОВЫ ТЕОРИИ ГРУПП
ГЛ. I
Представления, связанные между собой соотношением
A.42), называются эквивалентными. Очевидно, что су-
существует бесконечное множество эквивалентных пред-
представлений. Преобразование представления к любому
эквивалентному называется подобным преобразова-
преобразованием.
Если существует подобное преобразование, приводя-
приводящее все матрицы представления Г к квазидиагональной
форме
г' = s~]rs
i
A.43)
то представление Г называется приводимым. В резуль-
результате подобного преобразования оно разлагается на т
представлений меньшей размерности, что записывается
так:
A.44)
Приводимость представления означает, что с помощью
линейного преобразования базисных векторов простран-
пространство Ш разбивается на инвариантные подпространства
$Ц(а\ преобразующиеся по представлениям Г<а). Опера-
Операции группы О преобразуют векторы каждого подпро-
подпространства только друг через друга, не смешивая их с
векторами других подпространств.
Если не существует преобразования, приводящего
матрицы представления к квазидиагональной форме
A.43), то представление называется неприводимым. От-
Отметим, что неприводимое представление группы являет-
является, очевидно, и представлением ее подгруппы. Однако
по отношению к подгруппе это представление может
оказаться приводимым и распасться при приведении на
неприводимые представления подгруппы. Подобный про-
процесс называется редукцией на подгруппе.

§ 2
ПРЕДСТАВЛЕНИЯ ГРУПП
Примером приводимого представления группы C3z,
является следующий набор матриц:
1 О О
О 1 О
О 0 1
1 00
О 0 1
О 1 О
0 0 1
1 О О
О 1 О
О 0 1
0 1 О
1 О О
г(с!) =
Г (or®)»
О
О
1
О
1
О
1
О
О
1
О
О
О
1
О
О
О
1
A.45)
Легко проверить непосредственным перемножением,
что матрицы A.45) удовлетворяют таблице умножения
группы (см. табл. 1.1). С помощью преобразования
A.43) это представление может быть разбито на два
неприводимых представления: одномерное и двухмер-
двухмерное. В следующих разделах будут приведены способы
нахождения возможных неприводимых представлений,
входящих в чразложение A.44).
1-11. Свойства неприводимых представлений. Приве-
Приведем без доказательства следующие важные свойства
неприводимых представлений конечных групп*).
1. Число неэквивалентных неприводимых представ-
представлений группы равняется числу классов в группе.
2. Сумма квадратов размерностей неэквивалентных
неприводимых представлений группы равна ее порядку,
т. е. справедливо равенство
f2 j_ f2 4- 4- f2 = а
A.46)
где fa обозначает размерность os-го неприводимого пред-
представления. Из A.46) следует, что у абелевых групп все
неприводимые представления одномерны, поскольку чи-
число неприводимых представлений равняется числу эле-
элементов группы.
3. Размерность неприводимых представлений конеч-
конечной группы является делителем ее порядка.
*) Доказательство этих свойств можно найти в курсах по теории
групп, например, в [1—4].

30 ОСНОВЫ ТЕОРИИ ГРУПП ГЛ. I
4. Для матричных элементов неприводимых пред-
представлений справедливы следующие соотношения ортого-
ортогональности:
f aifAAm. A.47)
A.48)
В A.47) суммирование проводится по всем g элемен-
элементам группы. В A.48) суммируются все f\ членов мат-
матрицы Г<а)G?) для каждого из неприводимых представле-
представлений Па>. В соответствии с равенством A.46) общее ко-
количество членов в сумме A.48) равно порядку группы g.
1-12. Характеры. Пусть матрицы Г<°>(/?) образуют
представление группы О. Сумма диагональных элемен-
элементов матрицы Г(а>G?) называется характером операции R
в представлении Г<а) и обозначается rta)(R):
Х(а)(Я)=2Г??(#). A.49)
Каждое представление характеризуется набором g ха-
характеров.
Характеры эквивалентных представлений совпадают.
Действительно, согласно правилам перемножения матриц,
2
iJ,m
2 B
I, m\ i
Ты (R) - 2 б,п/Ггт (/?) = 2 Гтт G?).
Um m
Задание представлений наборами характеров не разли-
различает эквивалентные представления. Это очень удобно,
поскольку для физических приложений существенны
именно неэквивалентные представления. Задание харак-
характеров представлений позволяет различить неэквивалент-
неэквивалентные представления.
Так как элементы группы, принадлежащие к одному
классу, связаны между собой соотношением, аналогич-
аналогичным A.42), их характеры также должны совпадать.

§ 2 ПРЕДСТАВЛЕНИЯ ГРУПП 31
Следовательно, класс может быть охарактеризован за-
заданием характера одного из своих элементов. А число
различных характеров представления равно числу клас-
классов группы.
Характеры неприводимых представлений удовлетво-
удовлетворяют следующему соотношению ортогональности:
Соотношение A.50) получается из A.47), если прирав-
приравнять в последнем i = k и 1 = т и просуммировать обе ча-
части равенства по k, т.
Поскольку характеры элементов, принадлежащих к
одному классу, одинаковы, соотношение A.50) можно
переписать в виде
|ад(а)(СГ5С(Р)(С) = ^> A.51)
где сумма берется по всем классам С группы, а gc обо-
обозначает количество элементов в классе С
Если Уgcjg%{a)o6o3Y{2i4\[ihaCai то, поскольку количе-
количество классов равно количеству неприводимых представ-
представлений, величины аСа образуют квадратную матрицу.
Соотношение ортогональности A.51) совпадает для ве-
величин аСа с условием унитарности по первому индексу
A.36). Следовательно, матрица jaCa|| унитарна, и для
ее матричных элементов справедливо также условие
унитарности A.36а). Отсюда получаем второе соотноше-
соотношение ортогональности для характеров неприводимых
представлений:
Х(а) (Q = -? 6Cick. A.52)
Среди неприводимых представлений группы всегда
имеется одномерное представление, осуществляемое ба-
базисной функцией, инвариантной по отношению ко всем
операциям группы. Все характеры такого представления

32 основы теории групп гл. i
равны единице, само представление обычно называют
единичным и обозначают А\.
1-13. Вычисление характеров неприводимых пред-
представлений. В следующем разделе будет показано, что
для нахождения разложения приводимого представле-
представления на неприводимые достаточно знания характеров
представлений. Приводимое представление задается
либо непосредственно своими матрицами (в этом случае
нахождение характеров тривиально), либо задаются его
базисные функции. В последнем случае для нахождения
характера определяют результат действия операций
группы на базисные функции и суммируют диагональ-
диагональные элементы. Для неприводимых представлений суще-
существует ряд способов вычисления характеров, основан-
основанных на свойствах конкретных групп и не требующих
знания базисных функций неприводимых представлений
(см., например, [3, 4]). Мы приведем здесь способ нахо-
нахождения характеров неприводимых представлений про-
произвольной конечной группы, требующий знания только
таблицы умножения группы.
Пусть элементы Rj^CJf Rk^Ck, где CJf Ck — два
произвольных класса группы Q. Совокупность всех воз-
возможных произведений RjRk обозначим CjCk. Эта сово-
совокупность может включать элементы, принадлежащие к
различным классам группы. Можно показать, что про-
произведение классов коммутативно и что элементы одного
класса встречаются в нем одинаковое число раз. По-
Последнее обстоятельство позволяет представить произве-
произведение классов в виде некоторого разложения по классам
группы:
С/С4 -ад-g^C,. A.53)
Коэффициенты cljk находятся из таблицы умножения
группы. Сопоставление каждому классу соответствую-
соответствующих матриц неприводимого представления приводит к
соотношениям (см. [4], стр. 136)
*^) 2 c\kglt(C^ A.54)

§ 2 ПРЕДСТАВЛЕНИЯ ГРУПП 33
где gj, gh — количество элементов в классах Cj и Ck.
Соотношение A.54) справедливо для любого неприводи-
неприводимого представления группы. Поскольку размерность не-
неприводимого представления равна характеру единичного
класса Си из равенства A.46) следует дополнительное
соотношение
а=1
A.55)
Для групп небольшого порядка уравнение A.55) при
данных г и g может быть единственным образом удо-
удовлетворено целочисленными значениями %((X)(Ci)- Урав-
Уравнений A.54) и A.55) достаточно для нахождения харак-
характеров всех неприводимых представлений группы. Полу-
Полученные значения характеров должны удовлетворять
соотношениям ортогональности A.51) и A.52).
В качестве примера найдем характеры неприводи-
неприводимых представлений группы Свь, таблица умножения ко-
которой приведена выше (см. табл. 1.1). Группа С3г, имеет
три класса и, следовательно, три неприводимых пред-
представления, характеры которых мы должны найти. Про-
Пронумеруем классы группы:
Сг:Е;
Сг .' Сз, Сз;
откуда
?i=l, ?2 = 2, ?з = 3.-
Из таблицы умножения группы находим
Сз^з = 3Ct + ЗС2,
^2^з == 2С3.
Следовательно, уравнения A.54) имеют вид
A54а)
I 6x(C2)x(C3)-6X(C1)x(Q.
i;V. 3 И. Г. Каплан

34
ОСНОВЫ ТЕОРИИ ГРУПП
ГЛ, I
Уравнение A.66)
[%A) (Сг)]*+
имеет единственное решение
[Х<з> (Q]2
Таблица 1.2
Характеры неприводимых
представлений точечной
группы Czv
A.55а)
Подставляя в A.54а) поочередно %(С1)=1 и X(Q)==S2,
решаем получившиеся системы уравнений. Решения, не
удовлетворяющие соотношениям ортогональности A.51)
и A.52), отбрасываем. В результате получаем харак-
характеры всех трех неприводимых представлений, которые
мы свели в табл. 1.2*).
Вместо символа класса мы
поставили один из его эле-
элементов, поскольку характе-
характеры для всех элементов
класса одинаковы. Цифра
перед обозначением харак-
характера класса в верхней стро-
строке таблицы указывает на ко-
количество элементов в классе.
1-14. Разложение приво-
приводимого представления. Пусть
задано некоторое приводи-
приводимое представление Г. Со-
Согласно определению приводимого представления всегда
существует унитарное преобразование, приводящее его
к квазидиагональной форме A.43). Допустим, что даль-
дальнейшее приведение невозможно, т. е. представления Г<а\
входящие в разложение A.44), являются неприводимы-
неприводимыми. Одно и то же неприводимое представление может
встречаться в разложении приводимого представления
несколько раз. Поэтому в общем случае
•р . ^ti />C)pC) /1 сс\
I — ^j а 1 , vi.оо;
Р
5СA)
5СB)
5СC)
Е
1
1
2
2Сз
1
1
-1
3%
1
-1
0
*) Для обозначения неприводимых представлений точечных
групп обычно используется специальная символика. В Приложении 1
таблицы характеров точечных групп даны в обозначениях Шенфли-
са, принятых, например, в книге [5].

§2
ПРЕДСТАВЛЕНИЯ ГРУПП
35
где а(Р) обозначает количество раз, которое содержится
представление Г<Р> в разложении представления Г. Так
как подобное преобразование не меняет характеров
представления, то характеры представления Г равны
^(г> ^ __ ^ а<3)%C) (#). A.57)
Р
Умножим A.46) на х(а)(#)* и просуммируем по всем
элементам группы. В силу соотношений ортогонально-
ортогональности A.50) получим
* " (#)•. A.58)
Для приложений это соотношение удобно переписать в
следующем виде:
* ~ (С)*. A.59)
Если характеры представлений известны, формула
A.59) позволяет легко найти неприводимые представле-
представления, содержащиеся в разложении данного приводимого
представления.
Определим, например, неприводимые представления
группы CZvi содержащиеся в разложении представления
A.45). Характеры этого представления равны
х(Г)
Е
3
2С3
0
3cv
1
Взяв характеры неприводимых представлений группы
Czv из табл. 1.2, по формуле A.59) находим
Следовательно, представление A.45) распадается на два
неприводимых представления: одномерное Г^> и двух-
двухмерное Г<3)»

36
ОСНОВЫ ТЕОРИИ ГРУПП
ГЛ, 1
1-15. Прямое произведение представлений. Рассмот-
Рассмотрим два неприводимых представления Г(а) и Г<Р> груп-
группы О, определенные на наборах базисных функций
г|)<«> (/=1, 2, ..., /а) и i|f> (k= 1, 2,..., fe), соответ-
соответственно. Если составить все возможные произведения
ф^фСр), то получим базис /^-мерного представления
группы. Это представление называется прямым произве-
произведением представлений Г(а) и Г^ и обозначается Г^ХГ^.
Матричные элементы прямого произведения представле-
представлений являются произведениями матричных элементов
представлений Г(а) и Г®к
2 С
/, т
-во)
а характеры равны произведению характеров перемно-
перемножаемых представлений:
Матрица Пах&>(/?)* с матричными элементами из
A.60) называется прямым произведением матриц
Г(а)(/?) и №(J?) *). В отличие от обычного произведе-
произведения квадратных матриц, когда порядок результирую-
результирующей матрицы равен порядку матриц-сомножителей, по-
порядок матрицы, являющейся прямым произведением
двух матриц, равен произведению порядков перемно-
перемножаемых матриц. Прямое произведение двух матриц мо-
может быть представлено в «ящичной» форме. Например,
для матриц второго порядка
АХВ
а21В j а12В
пллЪ>
11*21
«11*12 «12*11 «12*12
«11*22 «12*21 «12*22
«21*11 «21*12 «22*11 «22*12
«21*21 «21*22 «22*21 «22*22
A.62)
Очевидно, что АВФВА, но они могут быть сведены
друг к другу соответствующей перестановкой строк и
столбцов. Поэтому характеры прямого произведения не
*) В литературе употребляется также эквивалентный термин —
кронекеровское произведение матриц.

ПРЕДСТАВЛЕНИЯ ГРУПП
37
зависят от порядка перемножения представлений. По-
Последнее следует также из формулы A.61).
Если оба перемножаемых представления совпадают,
то
X(axa)(/?) = [xw(/?)]2. A.63)
Так, характеры прямого произведения представлений
j43)rC) группы C3v (см. табл. 1.2) равны
[*C)(Я)]2
Е
4
2С3
1
3aw
0
Это представление приводимо. Разложение его на не-
неприводимые части, осуществляемое по формуле A.59),
содержит по одному разу все неприводимые представ-
представления группы Czv, т. е.
р(з) х Г<3) = ГA) + ГB) + Г<3>. A.64)
Если в прямом произведении Г<а>ХГ<а) базисы пред-
представлений Па) совпадают, то базис прямого произведе-
произведения симметричен относительно перестановки базисов-со-
базисов-сомножителей. Такое прямое произведение называется
симметрическим произведением представления самого
на себя и обозначается [Г<а)]2. Его размерность меньше
/2 и равна /а(/а + 1)/2, характеры симметрического про-
произведения не равны произведению характеров A.63),
а определяются формулой, являющейся частным слу-
случаем более общей формулы D.18)
Например, характеры симметрического произведе-
произведения [Г<3>]2 группы C3v равны
hc<3)]2(tf)
Е
3
2С3
0
3aw
1

88 ОСНОВЫ ТЕОРИИ ГРУПП ГЛ. I
Разлагая это представление на неприводимые части,
получаем
A.66)
Прямое произведение неприводимых представлений
всегда приводимо (исключение составляет случай, ко-
когда одно из перемножаемых представлений одномерно).
Разложение прямого произведения на неприводимые
представления
Г(а) X Г(Р) = 2 а(т)Г(т) A.67)
т
принято называть рядом Клебша — Гордана. Коэффи-
Коэффициенты разложения определяются общей формулой
A.58)
я(т) = т 2%{а х Р) {R) %(х) {R)*=12%{а) {R) %ф) {R) %{x) {RT-
R R
A.68)
Найдем условие присутствия в разложении A.67)
единичного представления А\. Характеры единичного
представления %(i4i)(#)=l для всех операций группы.
В силу соотношений ортогональности A.50) получаем
"ш = j 2 Х(а) (R) Х(Р) (Я) = бра., A.69)
R
где Г(а) обозначает представление, матричные элементы
которого комплексно сопряжены матричным элементам
представления ПЧ Такие представления называются
комплексно сопряженными. Следовательно, единичное
представление содержится в разложении прямого про-
произведения неприводимых представлений тогда и только
тогда, если перемножаемые представления являются
комплексно сопряженными. В случае вещественных пред-
представлений единичное представление содержится лишь в
прямом произведении неприводимого представления на
самого себя.
Аналогично прямому произведению двух неприводи-
неприводимых представлений группы, можно определить прямое
произведение произвольного числа неприводимых пред-
представлений. Характеры такого прямого произведения бу-

§ U ПРЕДСТАВЛЕНИЯ ГРУПП 39
дут равны произведению характеров перемножаемых
представлений:
х(а X 3 X ... X а» (Д) в х(а) (#) %ф) (#) . _ %«о) (Ry ц jq)
Рассматриваемые выше прямые произведения пред-
представлений относились к одной и той же группе. Если
Gj X G2 является прямым произведением групп (см.
раздел 1-4), а неприводимые представления T{a)^Gv
ГйбС2, то прямое произведение представлений Г^Х
ХГ^ является неприводимым представлением группы
G1X G2. Аналогично выводу формулы A.61) можно по-
показать, что элементу R = R\R2 группы Ог X О2 соответ-
соответствует характер
X@Xp)(tf) = X(a)(#i)x(p)(#2). A.71)
Различные неприводимые представления группы Gx X G2
определяются различными попарными комбинациями
неприводимых представлений групп О1 и G2.
1-16. Коэффициенты Клебша — Гордана. Разложение
A.67) прямого произведения представлений на непри-
неприводимые части осуществляется с помощью линейного
преобразования от базисных функций <ф^а)<ф|р) к наборам
базисных функций г|^т), не смешивающихся друг с дру-
другом под действием элементов группы:
ф| ( РА | axt). A.72)
i, к
Индекс а различает представления т в случае их повто-
повторения в разложении A.67). Коэффициенты (a/, §k\ax?)
называются коэффициентами Клебша — Гордана. По-
Поскольку базисные функции обычно выбирают ортонор-
мированными, коэффициенты Клебша — Гордана обра-
образуют унитарную матрицу *), обозначим ее Сарт. Эта
*) Базисные функции \|)Jats относящиеся к различным непри-
неприводимым представлениям, автоматически ортогональны друг другу
(см. раздел 1-18). В случае наличия в разложении A.67) повторяю-
повторяющихся неприводимых представлений их базисы всегда можно орто-
гонализовать.

40
ОСНОВЫ ТЕОРИИ ГРУПП
ГЛ. I
матрица осуществляет приведение прямого произведе-
произведения. Согласно A.43)
Г<т.) !
|Г(Т2):
. A.73)
Строки матрицы Са$х нумеруются индексами /, k, сово-
совокупность которых пробегает faf$ значений, а столбцы —
индексами а, т, t. Для большинства встречающихся в
физических приложениях групп унитарная матрица ко-
коэффициентов Клебша — Гордана может быть выбрана
вещественной, для ее матричных элементов справедливы
соотношения ортогональности A.40):
axt) (ш, рй | axt) =
| art) (а/, р/г | axt) ==
A.74)
В случае ортогональных преобразований обратная
матрица равна транспонированной. Поэтому преобразо-
преобразованием, обратным A.72), будет
= 2 ^at) (axt\ai,
a,i,t
или б матричной форме
2
а, х
A.75)
A.76)
Соотношение A.76) эквивалентно равенству для мат-
матричных элементов
а,х
(ш,
A.77)
Умножим A.77) на Г|^0?) и просуммируем по всем
элементам группы. В тех случаях, когда представление
Г(То) входит один раз в разложение A.67) и, следова-
следовательно, сумма по ах в A.77) содержит только один член

§ 2 ПРЕДСТАВЛЕНИЯ ГРУПП 41
с то, соотношения ортогональности A.47) приводят к ра-
равенству
<ш, $k | Vo> <Vo | of, рй> = -^
A.78)
Равенство A.78) может быть использовано для вычис-
вычисления коэффициентов Клебша — Гордана, если матрич-
матричные элементы неприводимых представлений группы из-
известны. При наличии в разложении A.67) повторяю-
повторяющихся неприводимых представлений коэффициенты
Клебша — Гордана определены с точностью до унитар-
унитарного преобразования. Этот случай исследован в работе
Костер а [6].
Как следует из определения коэффициентов Клеб-
Клебша — Гордана,
для всех Т<х\ не входящих в разложение прямого про-
произведения Г<а)ХГ(Р).
1-17. Регулярное представление. Пусть г|?о — некото-
некоторая функция координат, не обладающая свойствами
симметрии по отношению к операциям группы О. Дей-
Действие на яро g элементов группы О породит g линейно
независимых функций
¦* = **<>• A.79)
Под действием операций группы функции яря переходят
друг в друга, так как
Q** = QR% = Р$о=Ър. A.80)
Следовательно, функции A.79) образуют базис ^-мер-
^-мерного представления группы О. Такое представление на-
называется регулярным. Согласно A.80) матрицы регу-
регулярного представления, за исключением матрицы тожде-
тождественного преобразования ?", имеют нулевые диагональ-
диагональные элементы. Тождественное преобразование всегда
осуществляется диагональной единичной матрицей. От1
сюда следует, что характеры регулярного представления
равны
О для ИФЕ. A.81)

42 основы теории групп гл. i
Подставляя A.81) в A.59) и учитывая, что для любого
представления х(а)(^)=/а» находим
т. е. каждое неприводимое представление содержится в
разложении регулярного представления число раз, рав-
равное своей размерности.
Запишем выражение A.57) для характера приводи-
приводимого представления через входящие в него неприводи-
неприводимые представления для случая R = E:
Если приводимое представление является регулярным,
т0 /г ~8> а а(р) = /з- В результате приходим к соотно-
соотношению
2/| = g. A.82)
Мы доказали тем самым применявшееся уже нами ра-
ранее свойство: сумма квадратов размерностей всех не-
неприводимых представлений группы равна ее порядку.
Отметим, что для построения регулярного представ-
представления не обязательно использование базисных функций
A.79). В качестве базиса представления могут высту-
выступать сами элементы группы. Знание таблицы умноже-
умножения группы достаточно для написания матриц регуляр-
регулярного представления.
1-18. Построение базисных функций неприводимых
представлений. Рассмотренное в предыдущем разделе
регулярное представление определено на базисе из g
линейно независимых функций tyR A.79). Разложение
регулярного представления на неприводимые части со-
содержит все неприводимые представления группы. Пока-
Покажем, что это разложение осуществляется составлением
следующих линейных комбинаций базисных функций г|)Д:
¦8?" 7 2 ^ <*>*¦«• d-83)

§ 2 ПРЕДСТАВЛЕНИЯ ГРУПП 43
где Г^(^)—матричный элемент матрицы неприводимо-
неприводимого представления Г<а>, отвечающей операции R\ сумми-
суммирование проводится по всем g операциям группы.
Подействуем на функцию A.83) произвольной опе-
операцией группы Q:
? г W* «** ? 2 г (Q"'p)^ A -84)
Мы обозначили операцию Q7? через Р и использовали
свойство инвариантности суммирования по группе A.7).
Представим, далее, матричный элемент произведения
через произведения матричных элементов и воспользу-
воспользуемся свойством унитарных матриц A.38):
г» (q-1p)* = 2 И? (q-1)* it? (Pf = 2 И? (Q) it? (pf-
A.85)
Подставляя A.85) в A.84), окончательно получаем
<SC<. A.86)
Следовательно, функции -ф^ преобразуются по г-му
столбцу неприводимого представления Г(а), а совокуп-
совокупность /а функций tyfg с фиксированным вторым индек-
индексом образует базис неприводимого представления Па>.
Всего, соответственно числу различных индексов /г, мо-
можно образовать fa независимых базисов. Это естествен-
естественно, поскольку в разложение регулярного представления
каждое неприводимое представление входит столько
раз, какова его размерность.
Из вида формулы A.83) следует, что для получения
базисной функции представления Т^ достаточно подей-
подействовать оператором
^^(RU A.87)
на некоторую произвольную функцию яро. Для каждого
неприводимого представления таких операторов имеется
/2. Они образуют fa наборов, различающихся вторым

44 ОСНОВЫ ТЕОРИИ ГРУПП ГЛ. t
индексом. Каждый из этих наборов может быть исполь-
использован для получения базисных функций неприводимого
представления. В следующих главах будут приведены
примеры использования операторов A.87) для постро-
построения базисных функций.
Если функция -фо обладает определенными свойства-
свойствами симметрии по отношению к операциям группы О, то
результат действия на нее оператора г$ в некоторых
случаях может привести к нулю. Найдем результат дей-
действия оператора е$ на функцию A.83):
ii V ГЙ? (l?\*
Мы воспользовались равенством A.86) и соотношения-
соотношениями ортогональности A.47). Следовательно, действие е$
на базисную функцию неприводимого представления
дает либо нуль, либо другую базисную функцию этого
же неприводимого представления. При i = k действие
оператора в$> на базисную функцию ^ дает снова эту
же функцию. Операторы, обладающие такими свойства-
свойствами, называются операторами проектирования. Для них
справедливо операторное равенство
*!?*№-*}?• A.89)
Любую произвольную функцию -ф можно предста-
представить в виде суммы функций, преобразующихся по не-
неприводимым представлениям группы, причем
*=S«{?- A.90)
Суммирование по а в A.90) проводится по всем непри-
неприводимым представлениям группы, суммирование по / —
по всем независимым базисам представления Па> (f=l,
2,..., /а). Функции tyf) даются формулой A.83) с / = ?.
Для доказательства справедливости A.90) подставим
в него выражение для ф{^ из A.83) и воспользуемся

§ ? ПРЕДСТАВЛЕНИЯ ГРУПП 45
определением характера A.49). В результате получим*)
Сумма по а с учетом соотношения ортогональности
A.52) равна
2 faX(a) (Я) = 2 %{а) (Е) Х{а) (R) = gbB* A.92)
a a
Подставляя A.92) в A.91), получаем тождество \|)=г|),
что и доказывает справедливость исходного равенства.
Пусть функция ¦фМ преобразуется по i'-му столбцу
представления Г<а>, индекс k характеризует способ кон-
конструкции функций данного базиса (в частном случае
функция -ф^ может быть построена по A.83), хотя это
отнюдь не обязательно для справедливости приведен-
приведенного ниже доказательства). Докажем, что функции, пре-
преобразующиеся по различным неприводимым представ-
представлениям либо по различным столбцам одного неприво-
неприводимого представления, ортогональны друг другу, причем
А (a; k, n) для кфп,
, дл, *.,.
A.93)
где A (a; k, n) определяется выбором базисов k и п и не
зависит от i, т.
Для доказательства воспользуемся * тем обстоятель-
обстоятельством, что интеграл, взятый по всему пространству, ин-
инвариантен по отношению к любому преобразованию ко-
координат. Поэтому интеграл A.93) не изменится, если на
подынтегральную функцию подействовать некоторой
операцией группы:
= R J
(Я)'
A.94)
*) Так как ф0 — произвольная функция, мы в качестве г|H мо-
можем взять функцию г|).

46 основы теории групп гл. t
Просуммируем равенство A.94) по всем операциям
группы. Интеграл слева просто умножится на порядок
группы. К выражению справа применим соотношение
ортогональности A.47). В результате получим
Сумма по \x в A.95) не зависит от /, т. При k = n
вследствие ортонормированности базисных функций она
равна fa. Обозначив при k Ф п
приходим к равенству A.93).
Таким образом, произвольная функция г|э может быть
разложена на наборе ортогональных функций tyffl.
Функции tyff могут наглядно рассматриваться как ком-
компоненты вектора -ф в пространстве базисных векторов
неприводимых представлений группы. Проекционный
оператор е^ проектирует вектор г|э на направление (а/),
т. е. выделяет компоненту вектора -ф вдоль этого направ-
направления. Если вектор \f> не имеет компоненты вдоль дан-
данного направления, то, естественно, результат действия
ejy на \|) дает нуль. Геометрическая интерпретация дей-
действия оператора е^ на \f> несколько сложнее. Его мо-
можно рассматривать как проектирование на направление
(а/) предварительно повернутого вектора -ф. Поворот
совершается таким образом, чтобы компонента ^ при-
приняла направление (а/). Поэтому действие е^ на -ф рав-
равно нулю в том случае, если -ф не имеет компоненты
вдоль направления (ак)ш

ГЛАВА II
ГРУППА ПЕРЕСТАНОВОК
§ 1. Общие сведения
2-1. Операции с перестановками. Рассмотрим пере-
перестановки N целых чисел 1, 2,..., N. Всего существует
N\ таких перестановок. Каждая из этих перестановок,
обозначаемая
/1 2 3 ... ЛЛ
P-L : , ; К B.0
\h h h • • • 1n/
может быть представлена в виде произведения комму-
коммутирующих циклов A.10). Для этого нужно в качестве
первых двух элементов цикла поставить числа 1 и i\.
1 Затем поставить число, в которое переходит 1и и т. д.,
пока мы не дойдем до числа, переходящего в 1. Далее
проделать аналогичную процедуру с оставшимися эле-
элементами. Например,
1 2 3 4 б 6\
2 4 5 13 6)-A24)Cб)F). B.2)
По определению цикл инвариантен относительно цикли-
циклической перестановки его элементов:
(Wa ... ik) - (Уз • • • Ш = (is • • • hhhl B.3)
Количество элементов в цикле называется его длиной.
Из определения цикла следует, что если возвести его
в степень, равную его длине, то получим тождественную
перестановку:
(/А-..'*)*-/. B.4)
Из B.4) следует, что
(V2... W1-^... W*- B.6)

48 ГРУППА ПЕРЕСТАНОВОК ГЛ. II
Цикл из двух элементов принято называть транспозицией:
(iiti-W1- B-6)
При операциях с перестановками полезно пользо-
пользоваться следующими правилами.
1. Произведение QPQ~l, где Q, Р — произвольные
перестановки, является перестановкой, которую можно
получить, подействовав перестановкой Q на Р (в том
смысле, в каком перестановка действует на аргументы
функции). Например,
A 3) C5) A 3) = A 5),
A 2 3) B 3) A 2 3)-] = A 3).
2. Если циклы перемножаемых перестановок не со-
содержат общих элементов, то их произведение не зависит
от порядка сомножителей.
3. Если два цикла имеют общий элемент, то их мо-
можно соединить в один, предварительно поставив общий
элемент в конце одного и начале другого цикла, т. е.
(ik ... lm)(mn ... q) = (ik ... Imn ... q). B.7)
Например,
A245) C 46) = E 124) D63) = E 124 6 3).
4. Если при перемножении циклов в результирую-
результирующем цикле окагкется несколько общих элементов, то по-
полезно разбить его на циклы типа
(ik ... lmi)ss(k ... lm). B.8)
Произвольный цикл всегда можно представить в виде
произведения транспозиций. Такое представление неод-
неоднозначно. Так, например,
A23 ... А>) =
= B 1)B&)B&-1)...B 3)=... B.9)
При этом, однако, числа транспозиций, осуществляю-
осуществляющих данную перестановку, всегда будут иметь одинако-
одинаковую четность. В зависимости от четности числа транс-
транспозиций, осуществляющих перестановку, последние де-
делятся на четные и нечетные.

$ 1 ОБЩИЕ СВЕДЕНИЯ 49
Нетрудно показать, что любую перестановку можно
.представить как произведение транспозиций вида
(i—И), где i—1, i— два последовательных числа. На-
Например,
B 4 5) = B 4) D 5) = B 3) C 4) B 3) D 5).
Это обстоятельство играет важную роль при нахожде-
нахождении явного вида матриц представлений группы пере-
перестановок.
2-2. Классы. В.§ 1 гл. I было показано, что ЛП пере-
перестановок N объектов удовлетворяют четырем групповым
постулатам и, следовательно, образуют группу, которую
мы обозначили символом ztN. Входящие в группу nN
четные перестановки сами по себе образуют группу, на-
называемую знакопеременной и являющуюся подгруппой
группы 7tN. Помимо этого, группа ftjv обладает еще N—1
очевидными подгруппами, это stN_l9 itN_2, ..., яг.
Согласно определению класса все перестановки, свя-
связанные между собой соотношением Pi = QPjQ~l, где
Q — любая перестановка группы jtN, принадлежат к од-
одному и тому же классу. Поскольку перестановки QPjQ~l
получаются действием перестановки Q на Ру (см. раз-
раздел 2-1), циклическая структура перестановок Рг и Pj
одинакова, т. е. количество циклов и их длины совпа-
совпадают. Перестановки Pt и Pj различаются лишь элемен-
элементами в циклах. Следовательно, каждый класс группы
jtjv характеризуется определенным разбиением N эле-
элементов на циклы. Число различных классов определяет-
определяется количеством различных разбиений числа N на целые
неотрицательные слагаемые, т. е. равно числу различ-
различных целочисленных решений (включая нуль) уравнения
Iv! + 2v2+ ... +NvN = N. B.10)
Наборы чисел vi, v2,..., vNi удовлетворяющие уравне-
уравнению B.10), однозначно определяют классы я^, будем
обозначать классы символом \lVl 2Vg ... mV/w}, где v^
равно количеству циклов длиной /г, входящих в переста-
перестановки класса. Класс {1^} соответствует тождественной
перестановке. Так, шесть перестановок группы щ

50 ГРУППА ПЕРЕСТАНОВОК ГЛ. II
разбиваются на три класса:
{12} :
{3} :A2 3), A3 2).
Группа я4 содержит пять классов: {I4}, {122}, {22}, {1 3}, {4}.
Получим формулу, связывающую количество эле-
элементов в классе с его циклической структурой. Пусть.
{lVl 2Vj2 ... mVm) — произвольный класс группы nN. Рас-
Расположим N чисел внутри циклов в натуральном поряд-
порядке и подействуем на выбранную таким образом исход-
исходную перестановку всеми АЛ перестановками группы,
оставляя скобки на местах. Поскольку порядок циклов
несуществен, очевидно, что vi! V2!... vm! перестановок
будут совпадать. К одинаковым перестановкам приве-
приведут также циклические перестановки внутри каждого
цикла, таких перестановок для одного цикла длиной k
будет k штук, а всего их будет 2V* 3vs ... raV В ре-
результате получаем, что порядок класса будет равен
N\ /о ii\
« <2Л1>
Например, класс {122} группы пА имеет 4!/B!2)=6 эле-
элементов, класс {13} — 4!/3 = 8 элементов.
2-3. Схемы Юнга и неприводимые представления.
Так как число неэквивалентных неприводимых пред-
представлений группы равно числу классов, то неэквива-
неэквивалентные неприводимые представления группы nN, так
же как и классы, определяются различными разбиени-
разбиениями числа N на целые неотрицательные слагаемые.
Каждое неприводимое представление характеризуется
одним из таких разбиений. Эти разбиения располагают
обычно в порядке убывания слагаемых ЛДО:
яо> + *»+...+ я(т) - N, ХA) > ЯB) > ... > Xм. B.12)
Отдельные XW в B.12) могут совпадать. Очевидно, что
m не может превышать N. B.12) можно рассматривать

6БЩИЕ СВЕДЕНИЕ
81
как уравнение для нахождения возможных разбиений
числа М на целые слагаемые, в этом смысле оно полно-
полностью эквивалентно уравнению B.10). Наглядным изо-
изображением разбиений B.12) являются так называемые
схемы Юнга, в которых каждому числу Х& сопостав-
сопоставляется строка с числом клеток, равным №\ Будем
обозначать в дальнейшем схемы Юнга символом
[А,]=[АЯ> V2)... A/w)]. Наличие нескольким одинаковых по
величине строк Я,<г*> для сокращения записи будет отме-
отмечаться в виде степени при одной из №\
Например,
Очевидно, что из двух клеток можно составить толь-
только две схемы Юнга:
п
[2] [1*1
B.13)
В случае группы яз можно составить три схемы Юнга
из трех клеток:
ЕР §'
?Щ
[31 [21] //'/
B.14)
Группа Jt4 обладает пятью схемами Юнга:
B.15)
М
1311 [2г] [21г1

52 ГРУППА ПЕРЕСТАНОВОК ГЛ П
Каждая схема Юнга из N клеток однозначно соот-
соответствует определенному неприводимому представлению
группы jtjv, поэтому неприводимые представления
группы jtjy принято нумеровать символом соответствую-
соответствующих им схем Юнга [А,] и обозначать Г^ либо просто [к].
Как будет показано ниже, задание схемы Юнга опреде-
определяет перестановочную симметрию базисных функций
неприводимого представления, т. е. их поведение по от-
отношению к действию операторов перестановки аргу-
аргументов.
§ 2. Стандартное ортогональное представление
Юнга—Яманути
2-4. Таблицы Юнга. Неприводимое представление
Т[к] группы ям при переходе к ее подгруппе jtjv-i в об-
общем случае становится приводимым и может быть раз-
разложено на неприводимые представления Г^'1 группы
jtiv_i (редукция на подгруппе). Представления Пг], на
которые распадается представление Г[Ч определяются
всеми возможными схемами Юнга из N—1 клеток, ко-
которые могут быть получены из исходной схемы Юнга
отнятием одной клетки [7]. Например, неприводимое
представление группы Я5, характеризуемое схемой Юнга
П2Ч], распадается на неприводимые представления Г122!
и H2l2J группы я4:
fz2i] [г2] [21*]
В свою очередь при переходе от группы jtjv-i к ее под-
подгруппе Jtjv-2 представления F^'J аналогично распадаются
на* неприводимые представления Г^ группы я^-2 и т. д,
вплоть до группы п\.
Из fx базисных функций представления IW можно
составить такие линейные комбинации, что определен-
определенные на них матрицы неприводимого представления ПЧ
отвечающие перестановкам подгрупп я^.1э ;%_2, ... и

§ 2 СТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ ЮНГА-ЯМАНУТЙ 53
образующие представления этих подгрупп, будут сразу
иметь приведенную форму. Выбранные таким образом
базисные функции представления Т[Х] будут одновремен-
одновременно являться базисными функциями представлений Т[К'\
ПЯ'Ч ... при переходе к подгруппам я^-ь rtjv-2> ... Каж-
Каждая базисная функция может быть однозначно охарак-
охарактеризована последовательностью неприводимых пред-
представлений, по которым она преобразуется при переходе
от группы jtiv к ее подгруппам. Такой способ выбора
базисных функций наглядно может быть записан сле-
следующим образом. Каждой базисной функции сопостав-
сопоставляется схема Юнга Г^ с помещенными в ее клетках це-
целыми числами от 1 до N. Числа располагаются таким
образом, чтобы при отбрасывании клетки с числом N
получалась схема Юнга Т[к'\ характеризующая неприво-
неприводимое представление, по которому преобразуется базис-
базисная функция при переходе к группе tin-u при последую-
последующем отбрасывании клетки с числом N—1—схема Юнга
Г^"] и т. д., пока мы не дойдем до схемы Юнга с одной
клеткой. Очевидно, что возможны только такие разме-
размещения чисел в схеме Юнга, чтобы при чтении их слева
направо по строкам и сверху вниз по столбцам они
были расположены в возрастающем порядке (в против-
противном случае на некотором этапе приведения появятся не-
неразрешенные схемы Юнга). Схему Юнга с таким по-
порядком размещения чисел в ней будем называть стан-
стандартной таблицей Юнга. N чисел можно разместить в
клетках схемы Юнга N1 способами, так что всего воз-
возможны N1 различных таблиц Юнга. Говоря в дальней-
дальнейшем о таблицах Юнга, мы будем подразумевать
только стандартные таблицы, число которых всегда
меньше ЛП.
Таким образом, каждой базисной функции неприво-
неприводимого представления Т[Х] может быть сопоставлена таб-
таблица Юнга, а размерность неприводимого представле-
представления определяется числом стандартных таблиц Юнга,
т. е. числом способов размещения N чисел в схеме Юнга
так, чтобы они располагались в возрастающем порядке
слева направо по строкам и сверху вниз по столбцам.
Например, для представления ПХ1 = П281 группы я6
можно выписать пять стандартных таблиц Юнга

§4 . Группа перестаноёок
(пронумеруем их символом г<2')).
1
3
5
2
4
6
ГB)
1
3
4
2
5
6
Г<3)
1
2
5
3
4
6
Г D)
1
2
4
3
5
Ь
1
2
3
4
5
6
ГЛ. И
B.16)
г® : [221]
Пять базисных функций, соответствующих таблицам
Юнга B.16), однозначно характеризуются следующи-
следующими последовательностями представлений групп я5>
Jt4, jt3, Щ:
B.17)
Условимся располагать таблицы Юнга по степени от-
отклонения последовательности чисел от натурального
ряда (если читать по строкам, двигаясь сверху вниз) и
в этом же порядке нумеровать базисные функции. Вна-
Вначале располагаем таблицы Юнга, у которых число 2
находится в первой строке, затем — таблицы Юнга с
числом 2 во второй строке. Среди совокупности таблиц
Юнга, имеющих число 2 в одинаковых строках, впе-
впереди помещаем те, у которых число 3 находится в пер-
первой строке, затем те, у которых число 3 находится во
второй строке, и т. д. Аналогично поступаем по отноше-
отношению к последующим числам*). Первой всегда будет
стоять таблица Юнга, в которой числа образуют нату-
натуральный ряд. Будем называть ее фундаментальной. По-
Поскольку каждая базисная функция задается своей таб-
таблицей Юнга, строки и столбцы неприводимого представ-
*) Нетрудно убедиться, что порядок
Юнга B.16) соответствует этому правилу.
расположения таблиц

§ 2 СТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ ЮНГА-ЯМАНУТИ 55
ления, по которому преобразуются базисные функции,
могут быть пронумерованы таблицами Юнга.
В тех случаях, когда нас интересует только размер-
размерность неприводимого представления группы перестано-
перестановок ял, выписывание всех возможных таблиц Юнга для
больших N становится нерациональным. Размерность
неприводимого представления может быть вычислена по
следующей формуле [3, 7]:
B.18)
где №*>— длина строки i, a m — количество строк в схе-
схеме Юнга [к]. Для представления П23] формула B.18)
дает значение fx=5, в полном соответствии с числом
таблиц Юнга. Действительно, подставляя в B.18) зна-
значения №*) и т, получаем /*i = 4, /г2 = 3, /г3 = 2, откуда
/х=F!2)/D! 3! 2!) =5.
2-5. Нахождение явного вида матриц стандартного
представления. Изложенный в предыдущем разделе спо-
способ выбора базисных функций неприводимых представ-
представлений группы jtiv автоматически приводит к ортогональ-
ортогональному набору функций. Это связано с тем, что базисные
функции характеризуются различными последователь-
последовательностями неприводимых представлений, по которым они
преобразуются при переходе от группы я^ к ее под-
подгруппам. Если базисные функции выбирать также и
нормированными, то для однозначного определения ма-
матриц полученного таким образом ортогонального пред-
представления необходимо задать только фазы матричных
элементов. Для этого достаточно задать матрицу транс-
транспозиции Pi-\u поскольку все остальные перестановки
группы могут быть выражены в виде произведения
транспозиций типа P;-i *. Юнг [7] и Яманути [8] пока-
показали, что это представление может быть выбрано веще-
вещественным, и дали простые правила составления матриц
транспозиций Рг_1 г-. Согласно их результатам матрица
ГМ{Р{~ц) имеет следующие не равные нулю элементы:
a) rJ.^(Pt_i t)= 1, если в таблице Юнга г числа /, i—1
находятся б одной строке;

56
ГРУППА ПЕРЕСТАНОВОК
ГЛ. II
б) Г^](Р/_и) = — 1, если в таблице Юнга г числа i,
i—1 находятся в одном столбце.
г t
в)
d
d ' "
если таблицы Юнга г и t отличаются только перестанов-
перестановкой чисел /—1, /, причем в г строка с числом /—1 рас-
расположена выше строки с числом /. Через d обозначено
аксиальное расстояние между /—1 и /, определяемое
как число вертикальных и горизонтальных шагов, кото-
которые нужно совершить в таблице Юнга, двигаясь от i—1
к i. Так, в таблице Юнга И4> из B.16) с123 = 2, d34 = 3.
Выпишем, например, матрицу перестановки Р2з для
неприводимого представления П23], таблицы Юнга кото-
которого приведены в B.16) (пустые места означают нули).
гA) гB) гC) гD) гE)
r(D
ГB)
ГD)
ГE)
Определенное nq этим правилам представление при-
принято называть стандартным ортогональным представле-
1
2
п
2
1
2
/3
2
КЗ
2
1
2
/з
2
1

§ 2 СТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ ЮНГА-ЯМАНУТИ 57
нием Юнга — Яманути либо просто стандартным пред-
представлением. Для его матричных элементов справедливы
следующие соотношения ортогональности.
1. Соотношения, вытекающие из ортогональности
представления (см. A.40):
?] (Р) г?] (Р) = б/и. B.19)
2. Соотношения ортогональности, справедливые для
любых конечных групп (частный случай соотношений
A.47), A.48)):
^ f *. B.20)
B.21)
Способ построения матриц стандартного представ-
представления группы itN обеспечивает редуцированную форму
матриц, относящихся к подгруппам лм^и :%_2, ..., л2.
Это означает, что если, например, перестановка Pi при-
принадлежит к группе Jtjv-2, то
T%4Pi)-\\№(Pi), B.22)
где г", t" — таблицы Юнга, получаемые из таблиц г и t
отнятием клеток с числами N—1, N. Если при таком
изъятии получаются разные схемы Юнга [к"], то матрич-
матричный элемент B.22) равен нулю.
Матрицы перестановок чисел fti + 1, fti + 2,..., N диа-
гональны по таблицам Юнга п\ первых чисел. Если обо-
обозначить их символом гь то таблица Юнга г может быть
записана в виде r=(np2), где р2 обозначает часть таб-
таблицы Юнга г с числами tti + 1,..., N. При этом матрич-
матричные элементы одинаковы для всех п, относящихся к
данной схеме Юнга из П\ клеток, т. е.
B-23)

58 ГРУППА ПЕРЕСТАНОВОК ГЛ. И
где Р2 обозначает некоторую перестановку чисел
/ii + l,..., N. В Приложении 4 приведены матрицы ряда
неприводимых представлений групп nN. Нетрудно убе-
убедиться в том, что приведенные там представления удо-
удовлетворяют соотношениям B.19) — B.23).
В качестве простейшего примера рассмотрим стан-
стандартные неприводимые представления группы jt3. Груп-
Группа Яз имеет три неприводимых представления, схемы
Юнга которых приведены выше (см. B.14)).
Представления П3] и П1'1 одномерные, так как каждо-
каждому из них отвечает только одна таблица Юнга. Это —
таблицы
В соответствии с правилами Юнга — Яманути базисная
функция представления П31 не меняет знака при пере-
перестановках и осуществляет симметричное представление
группы яз. Это, очевидно, единичное представление, все
характеры которого равны единице. Базисная функция
представления F[13J меняет знак при нечетных переста-
перестановках и не меняет знака при четных перестановках.
Такая функция называется антисимметричной, а поро-
порождаемое ею одномерное представление антисимметрич-
антисимметричным. Его характеры равны (—1)р, где р — четность пе-
перестановки (р равно 0 для четных и 1 для нечетных
перестановок). Отметим, что и в общем случае группы
nN схеме Юнга [N] всегда отвечает одномерное симме-
симметричное представление, а схеме Юнга [1^] — одномерное
антисимметричное представление.
Представление Г[21] имеет две стандартные таблицы
Юнга:
dtt-* B.24)
Следовательно, размерность представления равна двум.

СТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ ЮНГА-ЯМАНУТИ
59
Таблицы Юнга B.24) нумеруют строки и столбцы ма-
матриц этого представления.
[Я] = [21]
[1
[
= /
1
2
/3
2
/
"I
lj
5l2^23^i2
2~
1
2
Pn
Г1
[ -
яш = я
1
2
j/3
_ 2"
"I
lj
Я23
1
2
/3
2
12p23 p132==
1
2
1
n
2
/3""
2
1
2 _
Я723
Кз "
2
1
2
B.
25)
2-6. Сопряженное представление. Каждому стандарт-
стандартному представлению Г^ может быть сопоставлено со-
сопряженное (или ассоциированное) представление Г^ той
же размерности, матрицы Т&ЦР) которого отличаются
от матриц стандартного представления Т[кЦР) множи-
множителем (—1)р, где р — четность перестановки Р.
Простейшим примером сопряженных представлений
являются определенные в предыдущем разделе симме-
симметричное и антисимметричное представления. Первому из
Них отвечает схема Юнга [N], второму — [lN]. Схема
Юнга [1^] получается из [N] заменой строки на столбец.
Оказывается, что и в общем случае для представления,
характеризуемого схемой Юнга [А,], сопряженное пред-
представление будет характеризоваться так называемой ду-
дуальной схемой Юнга [А,], получающейся из [к] заменой
|трок столбцами. Строки и столбцы сопряженного пред-
представления нумеруются таблицами Юнга г, отвечающими
рхеме Юнга [X]. Каждой таблице Юнга № будет соот-
соответствовать таблица Юнга г^\ получаемая из № заме-
рой строк столбцами. Поскольку таблицы Юнга г рас-
располагаются по степени отклонения чисел от натурального

60
ГРУППА ПЕРЕСТАНОВОК
ГЛ, И
порядка, порядок расположения таблицы Юнга г будет
обратным. Например,
ГC)
ШЧ*'2]
Г<2>
При таком порядке расположения таблиц Юнга г
правила составления матриц ГЙ(Р*-ц) те же, что и для
T[K](Pi~\i), за исключением недиагональных элементов
Щ](Р1-и)> которые для таблиц Юнга г, ?, отличаю-
отличающихся только перестановкой чисел I—1, i, равны
Г$ (Л-i t) = - /1-1/d2. B.26)
Знак минус перед корнем в B.26) введен для выполне-
выполнения условия
Так, представление, сопряженное представлению [21]
(см. B.25)), характеризуется той же схемой Юнга [21].
Однако порядок расположения таблиц Юнга г будет
уже другой:
Согласно правилам составления матриц транспозиций
стандартного представления, при учете B.26) получаем
Г ,]•
2
B.27)

§ 2 СТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ ЮНГА-ЯМАНУТИ 61
Сравнение матриц B.27) с аналогичными матрицами
стандартного представления Г[21] (см. B.25)) показы-
показывает, что они отличаются на множитель —1. Остальные
матрицы представления Г1213 получаются перемножением
матриц B.27) и, следовательно, будут отличаться от
матриц представления П211 множителем (—1)р.
2-7. Построение антисимметричной функции из ба-
базисных функций сопряженных представлений. Рассмот-
Рассмотрим прямое произведение Г[ "l] x Г' 2] двух неприводимых
представлений группы nN. При соответствующем выборе
линейных комбинаций базисных функций произойдет
распад прямого произведения на неприводимые части.
Определим условия появления при этом приведении ан-
антисимметричного представления. Характеры антисимме-
антисимметричного представления равны (—1)*>. Подставляя их
в формулу A.58) и используя соотношения ортогональ-
ортогональности A.50), находим
-^. B.28)
Следовательно, антисимметричное представление появ-
появляется в разложении Г[ i] х Г1 2* только один раз и
лишь в том случае, если [^2] = [Xi]. Другими словами,
если представления Г^1 и Пя-'] не являются сопряжен-
сопряженными, то из произведений базисных функций -ф^'Н^
невозможно образовать антисимметричную линейную
комбинацию. Если же Г^1 и Г^ сопряжены, то из про-
произведений их базисных функций можно образовать
одну и только одну антисимметричную функцию. Лег-
Легко проверить, что такой антисимметричной функцией
будет
^^S B.29)

62 ГРУППА ПЕРЕСТАНОВОК ГЛ. II
где суммирование _проводится по всем /\ таблицам Юнга,
а множитель ^Vfx введен для нормировки. Подейству-
Подействуем на функцию B.29) произвольной перестановкой Р:
где сумма по г, согласно B.19), равна 6tu- В результате
получаем
что и доказывает справедливость равенства B.29).
2-8. Операторы Юнга. В гл. I было показано, что для
любой конечной группы набор базисных функций не-
неприводимого представления может быть получен дей-
действием операторов A.87) на некоторую произвольную
функцию. Операторы A.87), определенные на стандарт-
стандартном ортогональном представлении Юнга — Яманути, бу-
будем называть операторами Юнга и обозначать©^1. Нор-
Нормализованный оператор Юнга имеет бледующий вид:
. B.30)
Сумма по Р пробегает все N\ перестановок группы я#.
Оператор со^] отличается от е(™ отсутствием знака ком-
комплексно сопряженного у матричного элемента (посколь-
(поскольку матрицы представления Г^ действительны) и множи-
множителем перед суммой. Множитель выбран таким образом,
чтобы действие оператора ю^ на произведение N орто-
ортогональных функций фа(/) давало нормированную функ-
функцию (см. следующий раздел).
Для каждого представления Т[1] можно образовать
ft операторов <й[г]\ а всего для группы nN существует ЛП
операторов, поскольку
1-ЛП.

§ й СТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ ЮНГА-ЯМАНУТИ 63
Согласно B.20), B.21) величины УШ\ Г#](Р) обра-
образуют ортогональную матрицу размерности N1. Поэтому
B.30) можно рассматривать как ортогональное преоб-
преобразование от ЛП операторов перестановок Р к ЛП опе-
операторам ®$\ Обратным преобразованием будет
(lkV B-31)
Г, t
Из равенства A.88) может быть получено выражение
для произведения двух операторов Юнга, если сделать
подстановку ej.^ = У7л/ЛП c&U1. R результате получим
«М-^А* B-32)
Представив Р в виде суммы B.31) и воспользовавшись
соотношением B.32), находим
PcD^=2r^(P)coLV, B.33)
и
т. е. друг через друга под действием перестановок пре-
преобразуются только операторы с фиксированным вторым
индексом. Из B.33) следует, что набор /\ операторов
Юнга (о^ с фиксированным вторым индексом образует
базис представления ПЧ Следовательно, операторы
ЬРнга (o^J можно рассматривать в качестве базисных
векторов неприводимого представления ПЧ
Если в B.33) изменить порядок действия операто-
операторов, то результат уже будет иной. С помощью равенств
B.31), B.32) находим
со^]Р=2ГЙ](Р)(о^. B.34)
и
Рассмотрим несколько примеров на составление опе-
операторов Юнга. Группа я2 имеет два одномерных пред-
представления, каждому из которых отвечает один опера-
оператор Юнга. Это
L B.35)
B.36)

64 ГРУППА ПЕРЕСТАНОВОК ГЛ. П
Оператор B.35) является оператором симметризации,
а оператор B.36)—антисимметризации. Аналогично со-
составляются операторы Юнга одномерных представлений
П31 и П131 группы я3:
0[3] e уъA + ?12+р™+Лз+Рт+Рт)' B-37)
1 - Pl2 - Р23 - р18 + Рт + Рт). B.38)
Размерность представления П211 равна двум. Следо-
Следовательно, в этом случае можно составить четыре неза-
независимых оператора Юнга. Взяв матричные элементы
стандартного представления из B.25), по формуле B.30)
находим следующие четыре оператора:
B + 2Р12 - ^23 - Лз - Л2з - Рт)>
B.39)
)
2-9. Построение базисных функций стандартного пред-
представления из произведений N ортогональных функций.
Рассмотрим набор N ортонормированных функций фа(/)
(i в аргументе функции обозначает совокупность пере-
переменных, от которых зависит функция <ра):
juab. B.40)
Составим функцию Фо, являющуюся произведением N
функций фа:
..флг(Л0. B.41)
Из Фо можно образовать ЛП различных функций двумя
способами: либо переставляя номера аргументов, остав-
оставляя номера функций на местах, либо переставляя но-
номера функций при неизменном порядке номеров аргу-
аргументов. Перестановки, действующие на номера функций,

$ 2 СТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ ЮНГА-ЯМАНУТИ 65
в отличие от перестановок, действующих на номера ар-
аргументов, будем обозначать чертой сверху символа пе-
перестановки. Нетрудно убедиться, что между этими дву-
двумя типами перестановок существует простая связь.
А именно,
РФО-Р-1ФО. B.42)
Поскольку перестановки Р и Р действуют на разные
объекты, они коммутируют:
РРФО = РРФО. B.43)
Совокупность перестановок Р и Р образуют две комму-
коммутирующие группы л:^ и nN.
Подействуем на Фо перестановками номеров аргу-
аргументов. Мы получим N1 взаимно ортогональных функ-
функций:
фр в рфо = ф1 Aг) ф2 (у ... ф„ (/„). B.44)
Ортогональность функций ФР следует из условий B.40).
Функции ФР образуют базис регулярного представления
группы jijv (см. раздел 1-17).
Линейные комбинации функций ФР, образующие ба-
базис стандартного ортогонального представления, нахо-
находятся действием оператора Юнга B.30) на функцию Фо:
(^) 2 Г'^ (Р) ФР. B.45)
Р
Согласно B.33)
РФ[$ и 2 гЩ;1 (Р) Ф^]. - B.46)
U
Следовательно, под действием перестановок аргументов
друг через друга преобразуются функции Ф^] с фикси-
фиксированным вторым индексом (в соответствии с общим
правилом A.86)). Таблица Юнга г, соответствующая
первому индексу, нумерует базисные функции представ-
представления ПЧ Она характеризует симметрию функции Ф$3
по отношению к перестановкам аргументов. Таблица
Юнга /, соответствующая второму индексу, нумерует
различные базисы представления ЛЧ Она характеризует
симметрию функции Ф^1 по отношению к перестановкам
5 И. Г, Каплан

66 группа перестановок гл. и
номеров функций сра. Для доказательства последнего
утверждения подействуем на функцию B.45) переста-
перестановкой Р. В силу равенств B.43) и B.42)
" '
Фо. B.47)
Выражая операторы в правой части равенства B.47)
согласно соотношению B.34), окончательно получаем
РФ?]=2Г$(Р)Ф?]. B.48)
и
Следовательно, под действием перестановок номеров
функций фа друг через друга преобразуются функции
Ф^] с фиксированным первым индексом.
Таким образом, из N1 функций B.44) можно соста-
составить N\ линейно независимых функций B.45), которые
мы обозначили Ф$]. Если каждой функции Ф^] сопоста-
сопоставить точку на плоскости, то эти N\ точек разбиваются
на квадраты, каждый из которых характеризуется опре-
определенной схемой Юнга [к] и содержит f\ точек. Строки
квадратов нумеруются таблицей Юнга г, столбцы — таб-
таблицей Юнга t. Функции, отвечающие точкам, располо-
расположенным в одном столбце квадрата, преобразуются друг
через друга под действием перестановок аргументов.
Функции, отвечающие точкам, расположенным в одной
строке квадрата, преобразуются друг через друга под
действием перестановок номеров фа.
Например, для N = 4 4! функций Фг^ разбиваются на
пять квадратов, в соответствии с пятью схемами Юнга
B.15):
S-e.
[4] [31] [2»] [21*] [И]
Перестановки номеров (ра
В разделе 1-18 было показано, что для любой ко-
конечной группы базисные функции, преобразующиеся по

§ 2 СТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ ЮНГА-ЯМАНУТИ 67
различным столбцам одного неприводимого представ-
представления, ортогональны друг другу. Однако базисные функ-
функции, преобразующиеся по одному столбцу, но принад-
принадлежащие к различным базисам, уже не ортогональны
друг другу, см. A.93). Функции Ф^1 удовлетворяют бо-
более сильному соотношению ортогональности, чем соот-
соотношение A.93), они ортогональны по всем своим индек-
индексам, т. е.
= 6^6rw6*s. B.49)
Дополнительное по сравнению с A.93) условие ортого-
ортогональности по вторым индексам следует из того обстоя-
обстоятельства, что при фиксированных первых индексах функ-
функции Ф^] и Ф^ принадлежат к одному базису группы
перестановок nN.
Равенство B.49) может быть получено и непосред-
непосредственно, если для Ф^1 взять его выражение B.45) и вос-
воспользоваться ортогональностью функций ФР и соотноше-
соотношением ортогональности B.20). Действительно,
J фй^ф^1 dv=Цт! S Г^] (р)г"* (Q) Г ф*ф<*dV=
p,Q J
р
Допустим, что в B.41) т функций фа совпадают, т. е.
фо = ф1A)... <p1(m)<p2(m + 1)... <Ptf-m+i(Л0- B-50)
Количество независимых функций Ф$\ которые можно
образовать, действуя fl операторами Юнга со^] на функ-
функцию B.50), меньше fl, так как некоторые из Ф$] ста-
становятся линейно зависимыми, а часть функций обра-
обращается в нуль. Это объясняется тем, что функция B.50)
симметрична относительно перестановок аргументов ме-
между т функциями фь Осуществляются лишь такие таб-
таблицы Юнга, в которых первые т чисел расположены в

68 ГРУППА ПЕРЕСТАНОВОК ГЛ. II
одной строке (рис. 2.1). Поэтому в возможные схемы
Юнга [к] всегда вложена схема Юнга из одной строки
с т клетками. Так как общее количество клеток в схеме
Юнга [к] равно N, последняя не может иметь столбец
с длиной, превышающей Л/"—т+\ клеток.
Например, в случае
фо = Ф1A)ф1B)ф1C)ф2D)ф3E)
возможны следующие схемы Юнга груп-
группы Я5:
М = [5], [41], [32],
Рис 2 1
* Схемы Юнга [22 1], [2 I3], [15] не осуще-
осуществляются.
Полученный выше результат не связан с разбиением
Фо на произведение функций фа и может быть сформу-
сформулирован более общо:
если имеется функция от N переменных, среди ко-
которых т переменных одинаковы, а остальные N— т
переменных различны, то осуществляются только
такие типы перестановочной симметрии, схемы
Юнга которых имеют хотя бы одну строку с ко«
личеством клеток не менее т и не имеют столб-
столбцов с количеством клеток, большим N—m+l.
§ 3. Нестандартное представление
2-10. Определение. Если вместо N\ перестановок груп-
группы jtjvограничиться щ\ перестановками чисел 1,2, ...,nb
то стандартное представление Г^ распадается на непри-
неприводимые представления Г^1 группы яП1- Однако при рас-
рассмотрении n2l перестановок чисел п{ + 1у л4 + 2, ...,
n\ + n2=N распада представления Г^ на неприводимые
представления Г^2] группы пП2 в общем случае не про*
изойдет. Это связано с тем, что в таблицах Юнга, ха«
растеризующих симметрию базисных функций представ-
представления Г[Ч последние числа, как правило, не образуют
схемы Юнга. На рис. 2.2 заштрихованы клетки с п2 по-
последними числами. Как видно из рисунка, заштрихо-
заштрихованные клетки не образуют схемы Юнга.
В ряде задач квантовой механики удобно опериро-
оперировать с базисными функциями представления ПЧ харак-

§ 3 НЕСТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ 69
теризующимися определенной перестановочной симмет-
симметрией по отношению к перестановкам как первых П\ чи-
чисел, так и последующих п2 чисел (ni + n2=N). Такие ба-
базисные функции образуют базис представления, рас-
распадающегося на неприводимые части при пере-
переходе от группы nN к ее подгруппе яп,ХЯ/22, яв-
являющейся прямым произведением групп яП1 и яЯ2.
В отличие от стандартного представления, реду-
редуцированного на подгруппах я^-ь я^_2,..., Яг, Ц
представления, редуцированные на иной сово- Ш
купности подгрупп, будем называть нестандарт-
нестандартными*). Каждое нестандартное представление Рис-2-2-
задается совокупностью подгрупп, на кото-
которых оно редуцировано. В следующем разделе будет при-
приведен способ нахождения матриц нестандартного пред-
представления через матрицы стандартного представления.
Возможные неприводимые представления "" * ~"
на которые распадается представление Пл' при редукции
на подгруппе пПх X яя?, определяются из разложения
IWi S а (МЛ) Г[К] X ПЧ B.51)
которое можно найти либо по таблице характеров, пом-
помня, чтп хяпяктепы ппеягтяилрния FM V ГМ оппетте.
ня, что характеры представления Гм X Г^ определяют-
определяются формулой A.71), либо с помощью теоремы Литтлвуда
(раздел 4-4). Вместо таблицы Юнга для N чисел ба-
базисные функции будут характеризоваться таблицей
Юнга первых rt\ чисел и таблицей Юнга последующих
Пч чисел.
Например, представление П2'3 при редукции на под-
подгруппе л;3 X я3 распадается на следующие неприводи-
неприводимые представления:
Базисные функции вместо таблиц Юнга B.16) будут
нумероваться следующими парами таблиц Юнга из трех
клеток:
[21Ы21],, [21],[21]2, [21]2[21]х, [21]2[21]2, [I3] [13]. B.52)
*) Понятие о нестандартных представлениях было впервые вве-
введено в работе Эллиота, Хоупа, Яна [9] и исследоваио в общем слу-
случае автором [10, 11].

70 ГРУППА ПЕРЕСТАНОВОК ГЛ. II
В B.52) мы обозначили таблицу Юнга № символом со-
соответствующей схемы Юнга с индексом i в нижнем пра-
правом углу. В соответствии с ковенцией, принятой в раз-
разделе 2-4, нумерация таблиц Юнга ведется по степени
отклонения чисел в них от натурального ряда. Для одно-
одномерных представлений вместо таблицы Юнга берется
соответствующая схема Юнга без индекса.
Стандартное представление соответствует последова-
последовательной симметризации N чисел. Для полной характе-
характеристики симметрии базисной функции стандартного
представления требуется задание N — 2 промежуточных
схем Юнга, что эквивалентно заданию таблицы Юнга
N чисел, поскольку промежуточные схемы Юнга опре-
определяются последовательным отщеплением от таблицы
Юнга клеток с числами N, N—1, ... В общем случае
может быть задано представление, соответствующее сим-
симметризации N чисел, предварительно разбитых на k
групп, каждая со своей схемой симметрии. Это отвечает
представлению, редуцированному на подгруппе
B.53)
Для полной характеристики симметрии базисной функ-
функции такого представления, помимо задания таблицы
Юнга для каждой группы ял/, требуется еще задание
k — 2 промежуточных схем Юнга, а также порядка сим:
метризации k групп в общую схему Юнга [к]. Базисные
функции нестандартных представлений будем нумеро-
нумеровать символом (г)А, где А обозначает тип редукции на
подгруппах. Для стандартного представления роль (г)А
играет таблица Юнга г.
В качестве примера рассмотрим нестандартное пред-
представление Г[28], редуцированное на подгруппе
я2 X л2 X я2.
Его базисные функции характеризуются заданием трех
таблиц Юнга из двух клеток *) и одной промежуточной
*) В данном случае таблицы Юнга однозначно соответствуют
схемам Юнга.

§3
НЕСТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ
71
схемы Юнга из четырех клеток. Возможны два способа
симметризации:
а) (я2 X я2) X я2, б) я2 X (я2 X я2). B.64)
Базисные функции представлений, симметризованных по
способам а и б B.54), будут связаны между собой ли-
линейным преобразованием. Допустим, что мы избрали
способ симметризации а. Вместо последовательности
промежуточных схем Юнга B.17) базисные функции
представления будут характеризоваться следующими на-
наборами:
(Г<У
(r<V
(г<5>/
[Я,]
[2]
[2]
[Р]
[I2]
[12]
[Я2]
[2]
[12]
[2]
И2]
[I2]
[22]
[212]
[212]
[22]
[212]
[*а]
[2]
[12]
[12]
[2]
[12]
B.55)
2-11. Трансформационная матрица. Для нахождения
явного вида матриц нестандартного представления най-
найдем линейное преобразование, связывающее базисные
функции стандартного и нестандартного представлений.
Коэффициенты этого преобразования образуют матри-
матрицу, которую мы будем называть трансформационной
матрицей. Базисные функции нестандартного представ-
представления нумеруются символом (г)А, конкретный вид ко-
которого может быть довольно громоздким (см., напри-
например, B.55)). Поэтому для обозначения базисных функ-
функций и матричных элементов удобно использовать сим-
символику Дирака. А именно:
Трансформационная матрица определяется соотноше-
соотношением
I [Ц (г)А) = 21 [Ч г) {г \(г)А)'м. B.57)

72 ГРУППА ПЕРЕСТАНОВОК ГЛ. II
Суммирование в B.57) проводится по всем стандартным
таблицам Юнга представления ПЧ
Потребуем, чтобы трансформационная матрица была
ортогональной, т. е. чтобы ее матричные элементы удов-
удовлетворяли условиям ортогональности:
Ортогональность трансформационной матрицы обеспе-
обеспечивает ортогональность нестандартного представления,
поскольку матрицы стандартного представления ортого-
ортогональны.
Если трансформационная матрица известна, то мат-
матрицы нестандартного представления находятся через
матрицы стандартного представления по формуле A.31).
Учитывая, что для ортогональных матриц обратная мат-
матрица равна транспонированной, получаем согласно
A.31)
<(r)A\P\(t)A)W = 2 <(r)»w (r\P\tf] <<|@лГ. B.59)
Г, t
Получим выражения для матричных элементов тран-
трансформационной матрицы, связывающей базисные функ-
функции стандартного представления с базисными функциями
представления, редуцированного на подгруппе яП1Х яП2
(ni + n2 = N). Так как первые п\ чисел в базисных
функциях стандартного представления уже имеют опре-
определенную симметрию, нам необходимо симметризовать
последние п2 чисел. Для этого подействуем оператором
Юнга со^ группы перестановок чисел /ii+l, #i + 2, ...,
ni + n2 на какую-либо из базисных функций стандартно-
стандартного представления (назовем ее пробной). Таблицы Юнга
стандартного представления Г^ будем обозначать в виде
(гф2), где гх — стандартная таблица Юнга первых пх
чисел, р2 — совокупность оставшихся клеток с числами
rti + l, ..., П1 + П2, в общем случае не образующая таб-
таблицу Юнга. В получившейся базисной функции |pjrir2)
симметрия первых П\ чисел останется такой же, как в

§ 3 НЕСТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ 73
исходной пробной функции, симметрия последних п2 чи-
чисел будет характеризоваться таблицей Юнга г2:
IW г/2) = <ЧЯ | W (г,Р2)> = с 2<г21Р21 /2f'! Р21 [Я,] (г,р2)) =
I [*¦] (Г1Р2)>.
2
P2 P2
Следовательно, новые базисные функции выражаются
через старые с помощью линейного преобразования
I [Я.] rxr2) = S | [X] (rlP2)> ((rlP2)\rir2f\ B.60)
Р2
матрица которого выражается через известные матрич-
матричные элементы стандартного представления *)
((/-1Р2)кл/М =.с S <ra|Pa|/2>IXil <(A-iP2)|/52I(r1p2)>[M. B.61)
Суммирование в B.60) проводится по всем таблицам
Юнга (прг), первые П\ чисел в которых составляют таб-
таблицу гх\ Р2 —перестановки чисел ^ + 1, ..., пх + п2'> с —
нормировочная константа, определяемая из условия
КклТ^- B.62)
Р2
Матрицы представления, по которому преобразуются
функции B.60), не зависят от выбора t2 и рг, последние
определяют только конструкцию базисных функций не-
нестандартного представления. Трансформационные мат-
матрицы зависят от t2 и р2, при этом матрицы, происходя-
происходящие от пробных функций с разными рг, различаются
только по фазе. Для определенности условимся в каче-
качестве (гфг) выбирать таблицу Юнга с натуральным по-
порядком расположения чисел щ+1,..., ni + n2i если чи-
читать последовательно по строкам, а в качестве /2 —фун-
—фундаментальную таблицу Юнга представления [к2] (если
действие ©^ на пробную функцию дает нуль, то в каче-
качестве t2 берем следующую за фундаментальной таблицу).
Строки трансформационной матрицы нумеруются
таблицами Юнга (rip2), столбцы — таблицами Юнга гх
*) Другой способ вычисления трансформационной матрицы,
основанный на рекуррентных соотношениях, приведен в работе [12].

74
ГРУППА ПЕРЕСТАНОВОК
ГЛ. II
и г2. Имеет место диагональность по гь Следовательно,
трансформационная матрица разбивается на блоки.
Блоки, имеющие гь относящиеся к одной схеме Юнга из
пг клеток, одинаковы в силу соотношения B.23). Поэто-
Поэтому в обозначении трансформационной матрицы вместо
гх можно поставить символ соответствующей схемы Юн-
Юнга [к{\:
2)f\ B.63)
Матричные элементы B.63) не равны нулю лишь для
таких [ki] и [к2]у которые входят в разложение B:51).
Если в разложении B.51) некоторые а(МДг)>1, необ-
необходима дальнейшая идентификация функций B.60). Это
достигается заданием второго индекса t2i определяемого
оператором Юнга а>[гк/2- Функции КЭДпМ^)), различаю-
различающиеся только /2, уже не будут ортогональны друг другу
и, следовательно, не будет ортогональной трансформа-
трансформационная матрица. В этом случае необходимо ортогона-
лизовать матрицу (см. [11]).
Приведем вид трансформационной матрицы, осу-
осуществляющей переход от базиса B.16) к базису B.52).
Матрицы, необходимые для расчета по формуле B.61),
берем из табл. 1 и 6 Приложения 5, недостающие мат-
матрицы Г[28](Р2) находим перемножением матриц транспо-
транспозиций. После проведения нормировки по формуле B.62)
получаем следующую ортогональную матрицу:
г,: [21], [21], [21]2 [21]2 [Р]
г2:[21], [21]2 [21], [21]2 [13]
{г\гхг2Г = г
г B)
[23] _ „C)
rw
гE)_
. B.64)

§3
НЕСТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ
75
В соответствии с B.63) трансформационная матрица
разбилась на блоки. Блоки, относящиеся к [>^il = [21], со-
совпадают.
В случае редукции на подгруппе л^_2 X я2 матрич-
матричные элементы B.61) выражаются в явном виде через ак-
аксиальное расстояние между числами N—1 и N. Для это-
этого надо в B.61) подставить выражение для матрицы
транспозиции ((r^l^V-i wl^ife)I*1» приведенное на
стр. 56. Трансформационная матрица содержит либо
единицы, либо блоки вида
v>
[2]
[I2]
U
d+l
Ы
B.65)
где d—аксиальное расстояние между числами N—1 и
N в таблицах Юнга (^pQ, (rftZ)- Обе таблицы Юнга
различаются только перестановкой чисел N— 1 и N, при-
причем в таблице (r^) JV—1 расположено выше N.
Например, трансформационная матрица перехода от
стандартного представления Г[212}, таблицы Юнга кото-
которого приведены на стр. 60, к представлению П21'1, ре-
редуцированному на подгруппе я2 X я2, имеет следующий
вид:
: [2]
M • [I2]
r(l)
[212] B)
r
rC)
"" l
[i2]
[2]
Уз
3
Кб"
3
[I2]
[I2]
—
Кб
3
Кз"
3
Найдем явный вид матриц представления П2Ч реду-
редуцированного на подгруппе ttiXJt2. Таблицы Юнга

76
группа перестановок
ГЛ. II
стандартного представления приведены ранее (см. B.24)),
d23=2. Согласно B.65)
[*d: [2] [I2]
,[21].
r(D
г B)
Матрицы нестандартного представления находим
формуле B.59). Вместо матриц B.25) получаем
[Я] = [21]
по
23
[',)¦
13
1
2
2
^123
1
2
2
2
1
2
П
[
2
1
2
1
2
/3
2
I
1 I'
^132
Vs
2
1
2
Ргз нестандартного
подгруппе Щ X Щ,
B.66)
J_
2 2
X JL
^2 2
Как и следовало ожидать, матрица
представления, редуцированного на
совпала с матрицей Р\2 стандартного представления, ре-
редуцированного на подгруппе я2 X пх.
2-12. Некоторые обобщения. В предыдущем разделе
мы рассмотрели способ нахождения матрицы преобра-
преобразования от стандартного базиса к базису представления,
редуцированного на подгруппе ля, X ^rt2. Матрица преоб-
преобразования к представлению с более сложным типом ре-
редукции всегда может быть выражена через произведе-
произведения трансформационных матриц B.61). Например, ба-
базисную функцию представления с типом редукции
(лЯ1 X пП2) X пп, B.67)
находим последовательным действием двух операторов
Юнга ©и? и ©[У на пробную функцию стандартного
j?

§ 8 НЕСТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ 77
представления. Оператор ©^ определен на группе пере-
перестановок чисел fti + 1, пх + 2, ..., tti+n2; оператор ©J.^1 —
на группе перестановок чисел П\ + п2+1, пх + п2 + 2, ...,
ni + n2 + nz=N. Промежуточная схема Юнга для чисел
от 1 до п\+п2задана симметрией пробной функции стан-
стандартного представления. Таблицу Юнга г можно раз-
разбить на три части, каждая из которых относится к чис-
числам одной из групп яГ/ из B.67). Запишем ее в виде
г=(г1р2рз) = (г12рз), г\2 соответствует схеме Юнга [к\2\-
В результате получаем, что
I [A] (rxr2) XX2rz) = 231 [*] (г1РЛ>з)> {(гхрм)\М Я12г3)[М, B.68)
где трансформационная матрица равна произведению
двух более простых, вычисляемых по формуле B.61):
. B.69)
Представление с типом редукции
*й1 X (яП2 X пПь)
находится последовательно. Вначале осуществляется ре-
редукция яй1 X ^rtJ+rt3, затем — пП2 X л;^. В результате по-
получаем
W4 2 j* [М. B.70)
Трансформационная матрица, связывающая базисы
двух нестандартных представлений, может быть выра-
выражена в виде произведения матриц преобразования к
стандартному базису:
((r)A\(r)B) = %((r)A\r)(r\(r)*). B.71)
г
В ряде приложений находит применение «косое»
представление, матрицы которого определяются на двух
наборах базисных функций, каждый со своим типом ре-
редукции [10, 11]. Матричные элементы такого представ-
представления
((r)A\P\(t)B)[k] B.72)
появляются, например, в качестве коэффициентов

78 ГРУППА ПЕРЕСТАНОВОК ГЛ. И
разложения результата действия перестановки Р на
функции с типом редукции В по функциям с типом ре-
редукции А:
Р\Ш)В) 2 I m(r)A)((r)A\P\(t)*f \ B.73)
(г)А
Трансформационная матрица B.71) является частным
случаем матрицы B.72) при Р=1. Очевидным обобще-
обобщением формулы B.59) будет
(()\)(\\)(\(rf]. B.74)
Г, t
2-13. Операторы Юнга в нестандартном представле-
представлении. Аналогично определению оператора Юнга в стан-
стандартном представлении B.36) в нестандартном пред-
представлении
^(Ж^А\№ш- <2-7б>
Входящие в B.75) матричные элементы нестандартного
представления находятся по формуле B.59) через из-
известные матрицы стандартного представления и транс-
трансформационные матрицы. Оператор B.75) может быть
выражен через стандартные операторы Юнга подгрупп,
на которых редуцировано представление ПЧ и матрицы
нестандартного представления.
Рассмотрим представление ПЧ редуцированное на
подгруппе ял, X л:„2 (щ + п2 = N). Получим соотношение,
связывающее операторы Юнга этого представления с
операторами Юнга стандартных представлений групп
яЛ1 и я„2.
Предварительно заметим, что любую перестановку
Р группы jtjv можно представить в виде произведения
P = Q-Pl-P2, B.76)
где Pi e яй1, P2^nnv a Q принадлежит к одному из
смежных классов по подгруппе яЛ1 X яп? (см. раздел
1-5). Например, подгруппа я2хя2 группы я4 содержит
четыре элемента. Индекс подгруппы равен шести. Сле-
Следовательно, 24 перестановки группы лч могут быть раз-
разбиты на шесть смежных классов. Первый смежный класс

§ 3 НЕСТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ 79
составляет сама подгруппа Я2ХЯ2. Перестановки по-
последующих смежных классов находятся умножением
элементов подгруппы на перестановки, не входящие в
подгруппу. При этом разбиение на смежные классы опре-
определяется заданием подгруппы и не зависит от выбора
перестановок-сомножителей. Ниже приведены левые
смежные классы по подгруппе я? X я2, обозначенной
буквой //.
И • Л ^12» ^34» Р\2 ' ^34»
Р13 • И ' Pj3, ^123> * 131» ^1234*»
^23 * Н '- ^23» ^132» ^231» ^1342» (С) „„,
р И • Р Р Р Р (*"**)
*14 * ll * ^14» *124> ^143' ^1243)
Р24 * Н • ^24» ^142» ^243» ^1432»
^13 * ^24 * " • ^13 * ^24» -«1423» ^1324» ^14 * ^23*
Оператор Юнга в представлении с редукцией яЯ1 X яПа
имеет следующий вид:
Представим Р в виде произведения B.76). Матричный
элемент в B.78) равен
Mi, «2 01, fa
B.79)
Так как выбранное нами представление имеет приведен-
приведенную форму по отношению к перестановкам группы
яЯ1 X я«2, а следовательно, и по отношению к перестанов-
перестановкам групп я„, и яП2, то
Далее, подставляем равенства B.79) и B.80) в B.78).
Учитывая определение оператора Юнга для стандартного

80 ГРУППА ПЕРЕСТАНОВОК ГЛ. Н
представления B.30), окончательно получаем [13]
Выбор Q в B.81) неоднозначен. В качестве Q может
быть выбрана любая совокупность N\l(ti\\n2\) переста-
перестановок, по одной из каждого смежного класса. Суммиро-
Суммирование по ии и2 проводится по всем стандартным табли-
таблицам Юнга представлений T[h] и ПИ возможные пары
[к\]9 [Ад] определяются из разложения B.51).
В разделе 2-8 было показано, что операторы Юнга
coj.^ могут рассматриваться как базисные векторы не-
неприводимого представления ПЧ Проведенное там дока-
доказательство не связано со способом редукции представ-
представления на подгруппах и справедливо поэтому для любо-
любого нестандартного представления. В связи с этим B.81)
можно рассматривать как соотношение для базисных
функций и переписать в виде
h nx\n2\ V/2
2 2
Функция B.82) преобразуется по нестандартному пред-
представлению группы Ял-, редуцированному на подгруппе
яЯ1 X л;Л2. Преобразуем формулу B.82) так, чтобы волно-
волновая функция принадлежала представлению ПХ] с произ-
произвольным типом редукции на подгруппах. Для этого
умножим левую и правую части равенства B.82) на мат-
матричный элемент {г\Г2\(г)А)№ трансформационной мат-
матрицы и просуммируем по гь г2. Предварительно пред-
представим матричный элемент из правой части B.82) в
виде
w S k \ B.83)

§ 3 НЕСТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ 81
По определению трансформационной матрицы
S IM'V-2><ri'-2l('-L>W = |[A]('f1>- B.84)
ri.r2
Воспользовавшись, далее, соотношением ортогонально-
ортогональности, аналогичным B.58), окончательно получаем
/ j /j \\Г) l^ I lliU>2/ V I L^lJ Мл/ N^J ^2/* \^«OO/
«1, «2 Q
В частном случае [^] = [1^] формула B.85) переходит
в известную формулу, связывающую антисимметричные
функции двух подсистем (см. (8.8) в [14]):
- О" Q^in'?ini], B.86)
где q — четность перестановки Q.
Необходимым условием нормированности функций
B.85), B.86) является ортогональность базисных функ-
функций, входящих в сумму по Q, для различных Q.

ГЛАВА III
ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ
§ 1. Непрерывные группы
3-1. Определение. Специфика непрерывных групп.
В предыдущих главах рассматривались дискретные
группы, т. е. группы, элементы которых образуют диск-
дискретные множества. Дискретное множество элементов
всегда можно пронумеровать целыми положительными
числами. Существует большой класс групп, элементы
которых образуют непрерывные множества. Каждый
элемент характеризуется набором параметров, которые
могут изменяться непрерывным образом. Такие группы
называются непрерывными группами.
Например, совокупность преобразований
2, C.1)
в которых параметры аи а2 могут принимать любое зна-
значение на числовой оси (от —оо до +оо), образует двух-
параметрическую непрерывную группу. Любое, даже
бесконечно малое, изменение параметров аь а2 приводит
к новому элементу группы.
Формально каждому элементу Ga дискретной груп-
группы мы также можем сопоставить значения некоторого
параметра а. Параметр произведения элементов Gc =
— GaGb равен с. Таблица умножения группы задает нам
дискретную функцию
с-ф(а, 6), C.2)
ставящую в соответствие значениям параметра а, Ь зна-
значение параметра произведения с. Все элементы дискрет-
дискретной группы могут, таким образом, быть описаны зада-
заданием одного параметра, который принимает g дискрет-
дискретных значений. Для непрерывных групп функция C.2)
является непрерывной функцией своих аргументов, а ко-

§ 1 НЕПРЕРЫВНЫЕ ГРУППЫ 83
личество параметров, характеризующих элемент группы,
может быть любым, в том числе и бесконечным.
В дальнейшем будем рассматривать группы линей-
линейных преобразований /г-мерного векторного пространства,
характеризующиеся заданием конечного числа парамет-
параметров. Эти группы являются частным случаем групп Ли.
r-параметрической группой Ли называется группа пре-
преобразований
**в/*(*р ..., *я; ар ..., аг)э /= 1, 2, ..., п, C.3)
для которой функция C.3) является аналитической
функцией параметров ар.
Последовательное применение двух преобразований
4 = /,(*р ..., хп; av ..., аг),
<-/,«.....<; »!..... К)
эквивалентно третьему преобразованию
параметры которого являются функциями параметров
первых двух преобразований:
Ск = Ък(<*и •••» arJ 6i, ...» br), Л = 1Э ..., г. C.4)
Преобразования C.3) обязаны удовлетворять также и
трем остальным групповым постулатам.
Так, для двухпараметрической группы C.1) соотно-
соотношения C.4) имеют следующий вид:
c1 = blav c2=: bla2 + b2* C.5)
Единичный элемент этой группы характеризуется значе-
значениями параметров: ai = l, a2 = 0. Поскольку по определе-
определению обратного элемента последовательное применение
прямого и обратного преобразований должно дать то-
тождественное преобразование (ci=l, C2 = 0), то из соотно-
соотношений C.5) находим следующую связь между парамет-
параметрами прямого и обратного преобразований:
ai = l/ai, «2=—аг/ai.
Основные понятия и теоремы, установленные в гл. I
для дискретных групп, непосредственно обобщаются и

84 ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ. Ill
на непрерывные группы. Теряют смысл лишь те утверж-
утверждения, в основе которых лежит конечность порядка
группы (например, утверждение о том, что размерности
неприводимых представлений группы являются делите-
делителем ее порядка). Без изменений переносятся на непре-
непрерывные группы понятия подгрупп, классов сопряженных
элементов, приводимости представления и т. п. Посколь-
Поскольку имеется непрерывное множество элементов группы,
каждое неприводимое представление содержит непре-
непрерывное множество матриц. Число неэквивалентных не-
неприводимых представлений бесконечно, но они состав-
составляют дискретный ряд, причем размерности всех непри-
неприводимых представлений конечны, т. е. число функций
базиса, преобразующихся друг через друга под дейст-
действием операций группы, является конечным*).
Суммирование по элементам группы для непрерыв-
непрерывных групп заменяется интегрированием по области
изменения параметров. Элемент объема при интегриро-
интегрировании выбирается таким образом, чтобы результат инте-
интегрирования произвольной непрерывной функции пара-
параметров группы был бы инвариантен относительно
любого преобразования группы. Такое интегрирование
называется инвариантным. Математически требование
инвариантности интеграла по параметрам группы запи-
записывается следующим образом:
C.6)
где операции группы R и Q являются функциями пара-
параметров, а интеграл берется по всей области изменения
параметров группы. Равенство C.6) является естествен-
естественным обобщением на непрерывные группы доказанного
в разделе 1-1 соотношения A.7).
*) Последнее справедливо только для так называемых ком-
компактных непрерывных групп [15], к числу которых относятся прак-
практически все применяющиеся в физических приложениях непрерывные
группы (исключение составляет группа Лоренца). Для некомпакт-
некомпактных групп не может быть сформулировано также условие инва-
инвариантного интегрирования C.6), поскольку интеграл по области
изменения параметров таких групп расходится.

§ 1 НЕПРЕРЫВНЫЕ ГРУППЫ 86
Замена суммирования в A.47) и A.50) на инвари-
инвариантное интегрирование приводит к следующей форме
соотношений ортогональности для непрерывных групп:
J rg (*)* Г? (R) dxR - MiA« ? J Л*. C.7)
R a R
J X(a) (*Г Х(Р) (*) Л* - 6ap J ЛЛ. C.7a)
J J
Я R
Формула A.58) переходит в
a« - -т1- J Х(Г)(/?)х(а) (Rrdx* C.8)
R
3-2. Примеры линейных групп. Рассмотрим векторное
пространство п измерений. Подвергнем его линейному
преобразованию с матрицей ||а^||. Каждый вектор про-
пространства х преобразуется в новый вектор х' с компо-
компонентами
*;=2а,Л. C.9)
Линейное преобразование называется собственным, ес-
если определитель матрицы преобразования не равен ну-
нулю. Совокупность собственных линейных преобразова-
преобразований /г-мерного пространства образует -группу, которую
называют общей линейной группой и обозначают QLn *).
Действительно, произведение линейных преобразований
является также линейным преобразованием, матрица
которого находится перемножением матриц преобразо-
преобразований-сомножителей. Так как определитель преобразо-
преобразования не равен нулю, для каждого преобразования А
существует обратное преобразование Л*1, причем после-
последовательное применение прямого и обратного преобра-
преобразований приводит к тождественному преобразованию.
Наконец, выполняется правило ассоциативности.
*) Обозначение GLn соответствует начальным буквам англий-
английского названия группы general linear group.

86 ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ. ГИ
Поскольку каждое линейное преобразование задает-
задается своей матрицей, эти матрицы осуществляют я-мерное
представление группы GLn. Матрицы преобразований
являются, вообще говоря, комплексными, поэтому для
характеристики преобразования необходимо задать 2/г2
действительных параметров.
Если линейные преобразования ограничить унитар-
унитарными, то получим группу унитарных преобразований п-
мерного пространства, обозначаемую символом Un. Для
матричных элементов преобразования выполняются ус-
условия унитарности
2аХ-в„. C.10)
Из C.10) вытекают п2 уравнений, связывающих 2п2 па-
параметров*). Количество независимых параметров рав-
равно я2. Следовательно, каждый элемент унитарной группы
характеризуется заданием ^действительных параметров.
Унитарные преобразования с детерминантом, равным
единице, образуют группу унитарных унимодулярных
преобразований, обозначаемую SUn (в связи с другим
названием этой группы — специальная унитарная груп-
группа). Дополнительно к условиям C.10) на матричные
элементы преобразований группы SUn накладывается
также условие равенства детерминанта преобразования
единице. Поэтому каждое преобразование группы SUn
характеризуется заданием п2—1 действительных пара-
параметров.
Совокупность вещественных унитарных преобразова-
преобразований, т. е. ортогональные преобразования, образуют под-
подгруппу унитарной группы, называемую ортогональной
группой Оп. Условия ортогональности (см. A.40)) дают
п + п(п—1)/2 уравнений, связывающих п2 параметров
матрицы. Следовательно, элементы ортогональной груп-
группы характеризуются заданием п(п—1)/2 параметров.
Так как детерминант транспонированной матрицы ра-
равен детерминанту исходной, то из соотношения A.39)
следует, что квадрат детерминанта ортогонального пре-
*) При * = & имеется п уравнений для модулей матричных эле-
элементов, при 1Фк имеется п(п— 1)/2 уравнений для действительной
и столько же для мнимой части матричных элементов.

§ I НЕПРЕРЫВНЫЕ ГРУППЫ 87
образования равен 1, а сам детерминант может прини-
принимать только два значения: ±1. Ортогональное преобра-
преобразование с детерминантом, равным 1, соответствует вра-
вращению пространства вокруг начала координат. Ортого-
Ортогональное преобразование с детерминантом —1 является
комбинацией вращения и инверсии пространства отно-
относительно начала координат.
Если ограничиться ортогональными преобразованиями
с детерминантом, равным 1, то получим группу вра-
вращений п-мерного пространства Rn. При п = 3 Rn пере-
переходит в группу вращений трехмерного пространства
/?з, получившую широкое применение в физике.
Всякая подгруппа ортогональной группы называется
точечной группой. Группа вращений /?3 относится к не-
непрерывным точечным группам. В теории молекул и кри-
кристаллов получили применение конечные точечные груп-
группы, элементы которых состоят из комбинаций поворотов
на определенные углы и отражений в плоскости. Клас-
Классификация точечных групп приводится в § 3 этой главы.
Если описанные выше группы линейных преобразо-
преобразований расположить в порядке вложения их друг в дру-
друга, то получим следующую схему:
3-3. Инфинитезимальные операторы. Любое конечное
преобразование непрерывной группы может быть пред-
представлено в виде последовательности бесконечно малых
преобразований. В теории групп Ли [15,16] доказывается,
что задание бесконечно малых преобразований одно-
однозначно определяет конечное преобразование, причем
через матрицы неприводимого представления группы,
отвечающие бесконечно малым преобразованиям, выра-
выражаются все матрицы неприводимого представления. Дру-
Другими словами, непрерывная группа полностью характе-
характеризуется ее бесконечно малыми преобразованиями.
Перепишем преобразование C.3), обозначив для ком-
компактности совокупность г параметров ар буквой а, а со-
совокупность п координат Xi буквой х:
xi-fiix.a). C.3а)

88 ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ, III
Можно записать другое эквивалентное выражение для
х\, являющееся тождественной операцией:
*; = М*'; о). (
Бесконечно малое изменение x-t вместо дифференциро-
дифференцирования выражения C.3а) может быть получено введе-
введением бесконечно малого параметра в C.36):
x\ + dx\^ft(xf\ 6a). C.11)
Разложив правую часть C.11) в ряд Маклорена и огра-
ограничиваясь членами первого порядка малости, получаем
Обозначим
[*^о_М*>. (злз)
Задание в д-мерном пространстве г векторов C.13)опре-
C.13)определяет бесконечно малое изменение положения любой
точки пространства, поскольку
г
xt + dxt = xt+ 2 W/PUNap. C.14)
p=i
Найдем изменение произвольной функции F(x) при
бесконечно малом изменении х:
п п г
dF (x) = %-щ dxt = J] |^ ^ и[р(хNар =
^i> C.15)
/ P=l
где через /р обозначен оператор

§ 1 НЕПРЕРЫВНЫЕ ГРУППЫ 89
Операторы /р называются инфинитезимальными опера-
операторами группы. Их количество равно числу параметров
группы. Согласно C.15) бесконечно малое изменение
функции F(x) производится действием на функцию ли-
линейной комбинации инфинитезимальных операторов. Мо-
Можно показать [2, 16], что результат коммутации двух
инфинитезимальных операторов всегда выражается ли-
линейно через инфинитезимальные операторы группы:
г
/р/а — /а/р^[/р/а] == 2и ?рсмт» ("•*')
т=1
Коэффициенты с*а называются структурными констан-
константами группы.
В качестве примера рассмотрим группу вращений в
трехмерном пространстве. Согласно классификации пре-
предыдущего раздела группа /?3 относится к группам орто-
ортогональных преобразований с детерминантом преобразо-
преобразования, равным 1. Количество независимых параметров
равно п(п—1)/2 = 3. В качестве параметров могутбыть
выбраны углы Эйлера, либо координаты вектора, на-
направленного по оси вращения и равного по длине углу
поворота. Очевидно, что задание такого вектора одно-
однозначно определяет поворот.
Обозначим декартовы координаты точки в трехмер-
трехмерном пространстве через х, у, г. Рассмотрим преобразо-
преобразование с изменением одного параметра, например пово-
поворот на угол ах вокруг оси х. Соотношения C.3) имеют
в этом случае следующий вид:
х' = х,
у1' = у cos ах — г sin a*, C.18)
zr = у sin ax + z qos ax.
По формуле C.13) находим*)
«jrjf-O, uyx~-z, uzx = y. C.19)
Следовательно,
*) В C.19) и ниже координаты и параметры преобразования
обозначены одинаково.

00 ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ. Ш
Аналогичным образом получим два других инфините-
зимальных оператора:
'у ~~ Z дх Х дг *
<3'21)
Непосредственное вычисление показывает, что опера-
операторы C.20), C.21) удовлетворяют следующим соотно-
соотношениям коммутации:
[/ЛЬ-'*> [W=-Ix, [/ЛН-V C.22)
§ 2. Группа трехмерных вращений
3-4. Операции вращения и операторы углового мо-
момента. В предыдущем разделе было показано, что изме-
изменение функции координат при бесконечно малом пово-
повороте определяется инфинитезимальными операторами
C.20), C.21). Так, при бесконечно малом повороте во-
вокруг оси хр на угол бес
. C.23)
В квантовой механике изменение волновой функции при
бесконечно малых поворотах выражают через операторы
орбитального углового момента J [б]. Оператор J яв-
является векторной величиной, его три компоненты /р свя-
связаны с инфинитезимальными операторами /р простым
соотношением *):
/Р=-//р. C.24)
Соотношения коммутации для /р вытекают из C.22):
[JJy] = Uz, [JyJz] = Ux, [J,Jx] = iJg. C.25)
В общем случае операторы углового момента J в
квантовой механике определяются как операторы, ком-
*) Собственные значения оператора /р даются в единицах
fi=/i/2jt, где h — постоянная Планка. Умножение оператора /р на I
делает его эрмитовым, для матрицы /р выполняются условия эрми-
товости:

§ 2 ГРУППА ТРЕХМЕРНЫХ ВРАЩЕНИЙ 91
поненты которых подчиняются перестановочным соотно-
соотношениям C.25). Этому определению удовлетворяют так-
также и операторы спинового углового момента, компо-
компоненты которых нельзя представить в виде C.20), C.21).
Покажем, что операторы углового момента опреде-
определяют изменение функции координат и при любом конеч-
конечном повороте. Согласно C.23) и C.24) при бесконечно
малом повороте вокруг оси хр на угол бос производная
функция F(x) получит приращение
dF(x) = l6aJpF(x). C.26)
Функция F(x) переходит при этом в функцию
F'(x) = (l+ibaJQ)F(x). C.27)
Поворот на конечный угол а может быть выполнен как k
последовательных поворотов на угол a/k. Если k доста-
достаточно большое число, то для каждого из поворотов спра-
справедливо соотношение C.27). Функция F(x) при пово-
повороте на угол а переходит в функцию
F' (х) = lim A+ /-i iX F (x) - eiaJ<>F (x). C.28)
В случае поворота вокруг оси, направленной по произ-
произвольному единичному вектору п, очевидно обобщение
формулы C.28):
F'(x) = eia^F(x). C.29)
Из C.29) следует, что
Rna = eia(nJ) ^ C.30)
можно рассматривать как оператор конечного поворота
вокруг оси п на угол ос. При нахождении результата дей-
действия оператора C.30) на функцию координат его необ-
необходимо представить в виде степенного ряда и найти ре-
результат действия каждого члена ряда на функцию.
Вращение на угол а вокруг оси п может быть преоб-
преобразовано во вращение на тот же угол вокруг другой
оси п'. Для этого надо с помощью вращения R совме-
совместить ось п с осью п', выполнить вращение на угол а
и, наконец, вернуть ось п в ее первоначальное положе-
положение с помощью вращения Z?, т. е.
Rn,a = R~lRn',aR. C.31)

92 ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ. III
Следовательно, все вращения на один угол принадле-
принадлежат к одному классу группы /?3. Если для задания опе-
операции вращения необходимо задать ось вращения и
угол вращения, то классы группы /?3 характеризуются
только величиной угла вращения.
3-5. Неприводимые представления*). Знание комму-
коммутационных соотношений, которым удовлетворяют инфи-
нитезимальные операторы непрерывной группы, оказы-
оказывается достаточным для нахождения всех неприводимых
представлений группы. Инфинитезимальными операто-
операторами группы трехмерных вращений являются операторы
углового момента, удовлетворяющие коммутационным
соотношениям C.25). Для нахождения возможных не-
неприводимых представлений задается система собствен-
собственных функций одного из операторов /р, например /2. На
эти собственные функции накладывается требование,
чтобы они являлись одновременно собственными функ-
функциями и для оператора квадрата углового момента
J2 = j2x + Jl + Jl C.32)
Этому требованию всегда можно удовлетворить, так как
операторы Jz и Р коммутируют**). Поэтому собствен-
собственные функции -ф^ характеризуются двумя индексами,
определяемыми собственными значениями операторов Р
и /2. Далее, с помощью соотношений коммутации C.25)
находят результат действия операторов Jx, Jy и Р на
функции ф^. При этом оказывается, что [5, 17]
C*33)
*) Подробные сведения о представлениях группы трехмерных
вращений читатель может найти в [17—19].
**) Напомним, что коммутативность операторов является необ-
необходимым и достаточным условием существования у них общей си-
системы базисных функций [5].

§ 2 ГРУППА ТРЕХМЕРНЫХ ВРАЩЕНИЙ 93
где число j может принимать только целые и полуцелые
значения, а т при заданном / принимает 2/+1 значений,
лежащих в пределах \т\ «</:
m = /, /-1, ..., -/. C.34)
Из равенств C.33) следует, что функции i|)W с фиксиро-
фиксированными у преобразуются друг через друга при беско-
бесконечно малых поворотах. Поскольку оператор конечного
поворота, согласно C.30), выражается через оператор
углового момента, то функции ^ будут преобразовы-
преобразовываться друг через друга и при конечных поворотах, т. е.
«...¦ffi-I^.Ka)*». C-35)
где коэффициенты Dm>m(Rn,a) образуют матрицу, соот-
соответствующую повороту на угол а вокруг оси п. Следо-
Следовательно, 2/+1 функций -ф^ образуют базис 2/+1-мер-
2/+1-мерного представления группы вращений /?3. Можно по-
показать, что это представление, обозначаемое обычно D^\
является неприводимым [17]. Его матричные элементы
удовлетворяют соотношению ортогональности, являюще-
являющемуся частным случаем соотношения C.7). Элемент объ-
объема для группы /?3 может быть выбран в виде произ-
произведения d%R = dud(py где dQ — элемент телесного угла
для направления оси поворота, а dq> — дифференциал
угла поворота:
В результате вместо C.7) получаем
D% (#)* nWv (R) dxR = -^j Ьи>Ьтт\»>. C.36)
J
Явный вид матриц представления ?№>(а, р, у), выражен-
выраженных через углы Эйлера a, p и у» был получен Вигне-
ром [18].
Нетрудно найти характер класса, отвечающего пово-
повороту на угол ос. Так как классы группы /?3 характери-
характеризуются только углом поворота и не зависят от

94 ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ. III
направления оси вращения, то выберем ось вращения
вдоль оси г. Оператор поворота C.30) примет вид
#*ав*'а/*. C.37)
Для нахождения результата действия оператора C.37)
на функцию ifjj разлагаем экспоненту в ряд и учиты-
учитываем, что
т. е. в каждом члене ряда оператор заменяется на его
собственное значение. Поэтому окончательно получаем
ц а\|)(/) = eima"tyV\ C.38)
Следовательно, матрица преобразования /?2>а диагональ-
на, а ее характер для представления ?№') равен
/
х(/)(а)= '
Разделив числитель и знаменатель в C.39) на eial2> по-
получим более удобное для вычислений выражение:
Из формулы C.40) следует, что
Следовательно, повороты на одинаковый угол, но в про-
противоположных направлениях принадлежат к одному
классу, т. е. класс характеризуется абсолютной величи-
величиной угла поворота.
Совокупность поворотов вокруг заданной оси обра*
зует группу двухмерных вращений /?2. Группа /?2 яв-
является абелевой, все ее неприводимые представления
одномерны. Из равенства C.38) следует, что 2/+1 ба-
базисных функций неприводимого представления DW груп-
группы /?3 принадлежат к различным неприводимым пред-
представлениям группы /?2, характеризуемым заданием чис-
числа т.

§ 2 ГРУППА ТРЕХМЕРНЫХ ВРАЩЕНИЙ 95
В случае полуцелых / и, следовательно, полуцелых т
базисная функция -ф^, согласно C.38), меняет знак при
повороте на 2я. Тождественное преобразование отвечает
повороту на 4я. В результате каждому повороту /?п,а
соответствуют две матрицы D^(Rn,a), отличающиеся
знаком. Для получения однозначных представлений вво-
вводят так называемую двойную группу трехмерных вра-
вращений [20], в которой поворот на угол 2я считается эле-
элементом, отличным от тождественного. Повороты на углы
а (а-^2я) и 2я + а считаются разными элементами, в
результате чего объем двойной группы удваивается по
сравнению с объемом обычной группы У?3.
Вид базисных функций ф^ в случае целых / = / мо-
может быть найден непосредственным решением системы
уравнений, которую образуют первые два равенства в
C.33). Предварительно надо подставить вместо Я, Jz
их выражения в сферических координатах. Решением
получившихся уравнений являются хорошо известные в
теории уравнений математической физики сферические
функции У;ш(9, ф). Можно показать [17], что матричные
элементы представлений DM с целым / пропорциональ-
пропорциональны сферическим функциям, а именно
/>&«>, р, YHt-
где а, р и у — углы Эйлера. В связи с этим матричные
элементы Dm>m(u<> P> у) называют обобщенными сфериче-
сферическими функциями /-го порядка.
Таким образом, неприводимые представления груп-
группы трехмерных вращений характеризуются числом /, ко-
которое может быть только целым либо полуцелым. Раз-
Размерность неприводимого представления D<# равна 2/+1.
Базисные функции a|)j? характеризуются двумя индек-
индексами, индекс / указывает на принадлежность к неприво-
неприводимому представлению Z)(j), индекс т нумерует базисные
функции внутри одного неприводимого представления.
С другой стороны, функции -ф^ являются собствен-
собственными функциями операторов квадрата углового момента

96 ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ. III
и его проекции на ось г. В связи с этим индексы /, т
получают дополнительную интерпретацию. Индекс/опре-
Индекс/определяет собственное значение квадрата углового момента,
равное/(/+1), а т — проекцию момента на ось г*).
3-6. Приведение прямого произведения двух непри-
неприводимых представлений. Составим прямое произведение
двух неприводимых представлений Diil) X D(/2). Получив-
Получившееся представление имеет размерность B/i + l) B/2+1)
и является приводимым. Его базис образуют произве-
произведения базисных функций представлений-сомножителей
Ф^Фот?- Так как каждая из функций -ф^ является соб-
собственной функцией оператора /г-2, то, как нетрудно убе-
убедиться, их произведение является собственной функцией
оператора Jz^Jlz + J,z C.41)
с собственным значением
т = т1 + т2. C.42)
Однако произведения ф^'Ч^ не являются собственны-
собственными функциями оператора Я. Составляя из них линейные
комбинации, являющиеся собственными функциями опе-
оператора Я, мы совершим разбиение прямого произведе-
произведения на неприводимые представления DU\ Для нахожде-
нахождения возможных неприводимых представлений DU\
входящих в разложение исходного представления, выпи-
выписывают, руководствуясь правиломC.42), B/i + l) B/2+1)
собственных значений проекции углового момента. Да-
Далее выделяют из полученного набора значений т сово-
совокупностей 2/+1 значений вида C.34), отвечающих не-
неприводимым представлениям D^K В результате полу-
получают искомое разложение**)
D(/t) х D</>> = D</i+b> + D(/i+/ri) + _ C.43)
*) Принято говорить, что значение вектора углового момента J
равно /, подразумевая под этим, что максимальное значение проекции
момента равно /.
**) Разбиение прямого произведения C.43) на неприводимые
части эквивалентно нахождению возможных значений вектора угло-
углового момента /, получающегося при сложении векторов угловых мо-
моментов, отвечающих представлениям-сомножителям. Поэтому в кван-
товомеханических приложениях разложение C.43) называют прави-
правилом сложения угловых моментов.

§ 2 ГРУППА ТРЕХМЕРНЫХ ВРАЩЕНИЙ 97
Каждое неприводимое представление D(J) входит в раз-
разложение C.43) один раз, при этом значения / лежат в
интервале |/, ~/а 1</</х+ /а. C-44)
/i + /2 + / — целое число.
Если построить треугольник, периметр которого являет-
является целым числом, а стороны равны /ь /2, /, то соотноше-
соотношения для его сторон будут совпадать с C.44). Условия
C.44) называют условиями треугольника с целым пери-
периметром и обозначают A(/i/2/)-
Линейное преобразование от базисных функций пря-
прямого произведения к базисным функциям неприводимых
представлений, входящих в разложение C.43), осуще-
осуществляется с помощью матрицы коэффициентов Клеб-
ша — Гордана (см. раздел 1-16):
*«'" S «?</>.- i2m2\jm). C.45)
т.\, т2
Коэффициенты Клебша — Гордана (j\ffiu j2m2\jm) не
равны нулю лишь при выполнении условий C.42), C.44).
Суммирование по т2 в C.45) является формальным, по-
поскольку т2 = га— гп\. Согласно A.74) коэффициенты
(]\ти J2tn2\jm) удовлетворяют соотношениям ортого-
ортогональности:
-SOVp i2m2\jm){j{m'v \2^^
2 (/>!, /2m21 im) {jxmv j2m21I'm*) = 6/7,6ww,.
ttl\, mi
Различные формы явных выражений коэффициентов
Клебша — Гордана через входящие в них параметры
/ь /2, /> гпи т2 приведены в [21,22], там же можно найти
ссылки на имеющиеся таблицы. Из явных выражений
для коэффициентов Клебша — Гордана можно получить
следующие соотношения:
(-l)MH<Ji-ml9 j2-m2\j-m)9 C.47a)
(-l)ll+h4(j2m2, hm^lm), C.476)
0-im1,/~m|y2-m2>. C.47b)

98 ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ. III
В случае сложения двух одинаковых угловых моментов
в равный нулю результирующий момент коэффициенты
Клебша — Гордана различаются только по фазе и равны
</«, / - т 100) - (- l)hm T/JLr . C.48)
Заметим, что при построении функции C.45) важен по-
порядок связываемых функций. В случае одинаковых угло-
угловых моментов /i = /2 = / функция C.45) при перестановке
местами -ф^ и г|)^ , в силу соотношения C.476), изме-
изменяется на фазовый множитель
C.49)
Вместо коэффициентов Клебша — Гордана часто
пользуются более симметричными коэффициентами, на-
называемыми 3/-символами. 3/-символы записываются в
виде двухрядной матрицы
/i /2 /з
, т1 т2 тъ
Они связаны с коэффициентами Клебша — Гордана сле-
следующим соотношением:
//2/ТГ(^ '2 М. C.50)
З/'-символы инвариантны относительно любой четной пе-
перестановки своих столбцов и умножаются на (— i)/l+/2+/»
при любой нечетной перестановке.
3-7. Приведение прямого произведения k неприводи-
неприводимых представлений, Злу-символы. В случае прямого про-
произведения k неприводимых представлений
D('i)XD(/a)X ... XDV*> C.51)
разбиение его на неприводимые части осуществляется
последовательным приведением прямых произведений
пар неприводимых представлений. Такое приведение мо-
может осуществляться несколькими различными способа-
способами. В тех случаях, когда не требуется конкретизация,

§ 2 ГРУППА ТРЕХМЕРНЫХ ВРАЩЕНИИ 99
способ приведения будем обозначать заглавными ла-
латинскими буквами Л, В, ... Так, для k = 3 имеется два
различных способа приведения:
а) вначале приводится прямое произведение первых
двух представлений Difx) X Z)(/a), затем приводятся пря-
прямые произведения полученных при этом представлений
D(/l2) на оставшееся представление ?>(/з).
б) вначале приводится прямое произведение послед-
последних двух представлений D(/a) X D{h\ затем уже приво-
приводятся прямые произведения D{h) на полученные в резуль-
результате первого приведения представления /)(/2з).
Порядок приведения удобно обозначать, заключая
приводимые представления в скобки. Рассмотренные
выше два способа приведения могут быть записаны в
виде
a) (Z)(/l) X D(h)) X D(h\ б) Dih) X (Z)(/?) X Dih)). C.52)
Матрица, осуществляющая приведение прямого про-
произведения C.51), является обобщением матрицы коэф-
коэффициентов Клебша — Гордана. Поскольку процесс при-
приведения состоит из последовательного приведения пар
представлений, коэффициенты линейного преобразова-
преобразования от базисных функций исходного прямого произве-
произведения к базисным функциям ф^ результирующих не-
неприводимых представлений будут выражаться через про-
произведения соответствующих коэффициентов Клебша —
Гордана. В процессе приведения появятся k — 2 проме-
промежуточных неприводимых представлений Z^M, поэтому
базисные функции г|э<Я будут характеризоваться k — 2
дополнительными квантовыми числами /пр. Эти числа
можно рассматривать как собственные значения k — 2
промежуточных операторов углового момента /Пр, появ-
появляющихся при векторном сложении k угловых моментов
Ji, «b. • • •» h. Представления DV\ получающиеся в ре-
результате приведения прямого произведения C.51), не
зависят от способа приведения. Однако вид базисных
функций ф^ зависит от способа приведения, так как от
этого зависят наборы коэффициентов Клебша — Горда-
Гордана, выражающих ^ через базисные функции прямого

100 ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ. III
произведения C.51). Базисные функции, получающиеся
при разных способах приведения прямого произведения,
в квантовой механике принято называть функциями со-
состояний с различными способами связи угловых момен-
моментов. Способ связи угловых моментов будем обозначать,
так же как и способ приведения, буквами Л, В, ..., а
базисную функцию представления DW со способом свя-
связи угловых моментов А —
€»((/. — ШиЛ (з.вз)
где (/пр)А обозначает набор k — 2 значений промежуточ-
промежуточных угловых моментов, получаемых при данном способе
связи угловых моментов Ji, J2, ..., J*.
Наборы базисных функций представления ?№') с раз-
различными способами связи угловых моментов преобра-
преобразуются друг через друга с помощью некоторого унитар-
унитарного преобразования
^^((.^(п/ХСп/КиТ C.54)
(^пр)
Коэффициенты этого преобразования не должны зави-
зависеть от номера базисной функции, т. е. от числа /л, и
равны, в силу ортогональности базисных функций, ин-
интегралу по конфигурационному пространству
- J *ff ((/. • •' h) (U7 €> ((/, • • • h) (/и/) dV. C.55)
Матрицу преобразования C.54) будем называть транс-
трансформационной матрицей группы трехмерных вращений.
Очевидно, что трансформационная матрица диагональ-
на по /. Найдем ее явный вид для случая связи трех
моментов.
В соответствии с двумя способами приведения пря-
прямого произведения C.52) возможны два способа связи
угловых моментов. Базисные функции, отвечающие этим

§ 2 ГРУППА ТРЕХМЕРНЫХ ВРАЩЕНИЙ Ю1
способам связи, находятся последовательным примене-
применением формулы C.45):
Ш\, Wo,
/72з» ^12
C.56)
Аналогично
#1з, /7J23
C.57)
Трансформационную матрицу, связывающую базисные
функции C.56) и C.57), находим по формуле C.55).
Используя ортонормированность функций ty™ и веще-
вещественность коэффициентов Клебша — Гордана, получаем
((/i/2) /12/31 h (/Уз) /2з>(/) - 2 (Ami, /2m21 /12/n12> X
/»1, /»2, /И3,
/Wi2, /»23
X 0*12^12. /3^3 I /"*> (/2^2» кЩ\Ь^23>{1гЩ* /23^23 I M>.
C.58)
Матричные элементы C.58) не зависят от m^ и являются
функцией шести переменных. Они связаны с так назы-
называемыми коэффициентами Рака W *) следующим соот-
соотношением:
= УB/12+0B/23+1) W(/1/2//3; /12/23). C.59)
Аналогичным образом может быть показано, что и
при изменении порядка связываемых моментов элементы
*) Эти коэффициенты были введены Рака в его ставших те-
теперь классическими работах [23, 61], посвященных расчету сложных
атомных спектров.

102 ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ. III
трансформационной матрицы могут быть выражены че-
через коэффициенты Рака. Так, в случае перестановки мо-
моментов /2 и /з имеет место соотношение [61]
<0Ч/2) /12/3 I (/l/з) /l3/2>(/> =
= УB/12+ 1)B/13+ 1) ^(/12/3/2/13; /7i). C.60)
Из C.58) следует, что коэффициенты W(j\j2jjz\ /12/23)
не равны нулю лишь при выполнении четырех условий
треугольника:
л (/1/2/12)» л (/2/3/23), A (/12/3/), А (/i/
Часто вместо коэффициентов Рака употребляют бо-
более симметричные выражения, называемые 6/-символа-
ми и записываемые в виде двухрядной матрицы
C.61)
б/'-символы инвариантны относительно любой переста-
перестановки их столбцов и перестановки верхних и нижних
аргументов в любой паре столбцов. Для коэффициентов
Рака это соответствует следующим соотношениям сим-
симметрии:
W(abcd\ ef)=W(badc, ef)=W(cdab\ ef)=W(acbd\ ef) =
e (- l)e+f-a-dW(ebcf] ad) = (- \)e+i-b~c W(aefd\ be). C.62)
В случае равенства нулю одного из аргументов коэффи-
коэффициенты Рака приобретают простой вид. Так,
W(abcd; е0)= (-У 6аЛа C.63)
Коэффициенты Рака и связанные с ними 6/-символы на-
нашли широкое применение при решении целого ряда фи-
физических задач [19, 21, 24—26]. В настоящее время из-
изданы таблицы коэффициентов Рака и 6/-символов, охва-
охватывающие довольно широкую область изменения их
аргументов (см., например, [27,28]).
6/-символы появляются при связывании трех угло-
угловых моментов. В задачах с четырьмя угловыми момен-
моментами появляются 9/-символы [29], выражающиеся в виде

§ 3 ТОЧЕЧНЫЕ ГРУППЫ ЮЗ
суммы произведений трех 6/-символов. В общем случае
связывания м+1 угловых моментов трансформационная
матрица выражается через Зм/-символы (подробнее от-
относительно Зм/-символов см. [22]).
§ 3. Точечные группы
3-8. Элементы симметрии и операции симметрии. Со-
Согласно классификации групп линейных преобразований
векторного пространства (раздел 3-2) всякая подгруппа
группы ортогональных преобразований называется то-
точечной. Следовательно, к точечным группам относится
и рассмотренная в предыдущем параграфе группа вра-
вращений в трехмерном пространстве. Название «точечные»
эти группы получили потому, что входящие в них пре-
преобразования оставляют неподвижной по крайней мере
одну точку пространства (начало координат). Действи-
Действительно, все ортогональные преобразования сводятся к
комбинации двух типов преобразований — вращения и
отражения относительно плоскости, проходящей через
начало координат. Точка пространства, соответствующая
началу координат, остается при этом неподвижной.
Говорят, что тело обладает симметрией некоторой то-»
чечной группы, если под действием преобразований этой
группы оно совмещается само с собой. Преобразования
точечной группы совпадают в этом случае с преобразо-
преобразованиями симметрии тела. Необходимым условием, что-
чтобы тело было симметричным, является наличие у него
осей и плоскостей, преобразования относительно кото-
которых совмещают тело само с собой. Подобные оси и пло-
плоскости принято называть элементами симметрии. Каждый
элемент симметрии порождает соответствующие преоб-»
разования симметрии, которые называют обычно опера-
операциями симметрии.
Если при повороте вокруг некоторой оси на угол 2я
тело совмещается само с собой п раз, то ось называется
осью симметрии п-го порядка и обозначается Сп
(рис. 3.1,а). Наименьший угол поворота, при котором
происходит совмещение, равен в этом случае 2я/м. Опе-
Операцию такого поворота обозначают, так же как и ось
поворота, символом Сп. Последовательность k поворотов

104
ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ
ГЛ. Ill
на угол 2я/л, т. е. поворот на угол 2nk/ny обозна-
обозначают С*. Очевидно, что операция Сп, проведенная /г раз,
эквивалентна тождественному преобразованию. Послед-
Последнее принято обозначать символом ?, т. е.
Другим возможным элементом симметрии является пло-
плоскость симметрии, а соответствующей операцией сим-
симметрии — отражение тела в этой плоскости. Изображен-
Изображенный на рис. 3.1, а равносторонний треугольник с хвости-
хвостиками у вершин не имеет иных плоскостей симметрии,
а)
Рис. 3.1.
кроме тривиальной — плоскость треугольника. Очевидно,
что гантель симметрична относительно отражения в пло-
плоскости, перпендикулярной перемычке и проходящей че-
через ее середину (рис. 3.1,6). Плоскость симметрии обо-
обозначается символом о. При этом плоскость, перпендику-
перпендикулярную оси Сп, обозначают с^, плоскость, проходящую
через ось Сп, обозначают ov (либо а^, см. ниже). Такое
же обозначение принято и для соответствующих опера-
операций симметрии. Очевидно, что
Может случиться, что совмещение тела с самим собой
происходит только при последовательном применении
двух операций симметрии: поворота на угол 2я/м и от-
отражения в плоскости, перпендикулярной оси поворота.

§ 3 ТОЧЕЧНЫЕ ГРУППЫ 105
Такая операция симметрии называется зеркально-пово-
зеркально-поворотной и обозначается символом Sn. Ось поворота в
этом случае называют зеркально-поворотной осью п-го
порядка и также обозначают Sn. Последовательность
выполнения операций поворота и отражения несуще-
несущественна:
= Cneh. C.64)
На рис. 3.1, в изображена конфигурация из двух скреп-
скрепленных гантелей, повернутых на угол 90° друг к другу.
Такая конфигурация обладает зеркально-поворотной
осью четвертого порядка.
Зеркально-поворотная ось является новым элементом
симметрии лишь в случае четного п. При п нечетном из
C.64) следует, что
®hy C.65)
т. е. имеются независимые ось симметрии 2т + 1-го по-
порядка и перпендикулярная к ней плоскость симметрии.
Отметим, что при п четном зеркально-поворотная ось
Sn одновременно является осью поворота Сп/2.
Зеркально-поворотная ось второго порядка эквива-
эквивалентна наличию у тела центра симметрии, расположен-
расположенного в точке пересечения оси S2 с плоскостью Oh. Опера-
Операция S2 является операцией инверсии относительно цент-
центра симметрии и обозначается символом /:
C.66)
Операции симметрии обычно не коммутативны. Ис-
Исключение составляют только следующие операции:
а) повороты вокруг одной оси;
б) повороты на угол я вокруг взаимно перпендику-
перпендикулярных осей (результат эквивалентен повороту на
угол я вокруг оси, перпендикулярной первым двум);
в) поворот и отражение в плоскости, перпендикуляр-
перпендикулярной оси поворота (см. C.64));

106 ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ. III
г) отражения во взаимно перпендикулярных плоско-
плоскостях (результирующая операция эквивалентна повороту
на угол я вокруг оси, проходящей через линию пересече-
пересечения плоскостей).
Из а) и в) следует, что операция инверсии коммути-
коммутирует с любой операцией симметрии.
Совокупность операций симметрии для данного тела
образует его точечную группу симметрии. В следующем
разделе мы рассмотрим точечные группы симметрии мо-
молекул. Принадлежность молекулы к той или иной точеч-
точечной группе определяется элементами симметрии, кото-
которыми она обладает. Поэтому и классификацию точечных
групп удобно проводить, исходя из тех элементов сим-
симметрии, которые порождают операции данной группы.
При разбиении операций группы на классы полезно ру-
руководствоваться следующими правилами, доказатель-
доказательство которых аналогично доказательству соотношения
C.31).
1. Два поворота на одинаковый угол вокруг
разных осей относятся к одному классу, если в числе
операций группы есть преобразование, совмещающее
обе оси.
2. Два поворота вокруг одной оси на одинаковый
угол, но в противоположных направлениях относятся к
одному классу, если в числе операций группы есть опе-
операция поворота, меняющего направление оси на обрат-
обратное, либо операция отражения в плоскости, проходящей
через ось (в этом случае ось называется двусторон-
двусторонней).
3. Два отражения в разных плоскостях принадлежат
к одному классу, если среди операций группы имеется
преобразование, переводящее одну плоскость в дру-
другую.
3-9. Классификация точечных групп. Существует не-
несколько систем обозначений точечных групп. Мы будем
придерживаться обозначений Шенфлиса, принятых, в
частности, в [5, 30]. Классификацию начнем с простей-
простейших точечных групп, переходя от них к группам с до-
дополнительными элементами симметрии. В заключение
рассмотрим непрерывные точечные группы, выделив сре-
среди них те, которыми могут обладать молекулы,

§ 3 ТОЧЕЧНЫЕ ГРУППЫ 107
I. Дискретные аксиальные точечные
группы
Принадлежащие к ним точечные группы содержат
только одну ось симметрии, порядок которой выше вто-
второго *).
Группы Сп. Имеется один элемент симметрии —ось
симметрии ft-го порядка. Группа состоит из п операций,
являющихся вращениями на углы 2nk/n вокруг оси
симметрии. Все операции группы коммутативны, т. е.
группа абелева. Следовательно, каждая операция груп-
группы составляет класс, а неприводимые представления од-
одномерны.
Необходимым условием принадлежности молекулы к
группе Сп является отсутствие у нее плоскостей сим-
симметрии. В качестве примера можно привести дихлорза-
мещенную молекулу аллена (рис. 3.2,а). Молекула
Н2С—ССЬ будет обладать группой симметрии С2, а
молекула Н3С—СС13 — группой С3, если концевые груп-
группы атомов слегка развернуть по отношению друг к дру-
другу (равновесные конфигурации обеих молекул обладают
более высокой симметрией).
Группы S2n. Имеется одна зеркально-поворотная
ось S2n. Группа абелева и состоит из 2п зеркально-пово-
зеркально-поворотных операций S2«. Как показано в предыдущем раз-
разделе, зеркально-поворотная ось может быть только чет-
четного порядка, при нечетном порядке она сводится к
обычной оси симметрии нечетного порядка и перпенди-
перпендикулярной к ней плоскости симметрии. Операция S2 яв-
является операцией инверсии, поэтому группа 52 состоит
из двух элементов: Е и / — и часто обозначается сим-
символом Ct. Примером молекулы, обладающей группой
симметрии S29 может служить транс-форма молекулы
ClBrHC—СНВгС! (рис. 3.2,6).
Группы Cnh. Имеется ось симметрии м-го порядка и
перпендикулярная к ней плоскость симметрии вн.
*) В обозначениях точечных групп Сл, Dn и т. д. индекс п
обозначает порядок главной оси симметрии. Эти обозначения не
следует смешивать с обозначениями линейных гр\пп GLn, Un и т. д^
где индекс п обозначает размерность векторного пространства, в
котором заданы группы.

108
ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ
Аксиальные точечные группы
а) С2
Вр
ж) С,
/Н С /N °° /ti С
V,
^ун
Рис. ЗА

§ 3 ТОЧЕЧНЫЕ ГРУППЫ 109
Группа Cnh содержит 2п операций: п поворотов Скп и п
зеркально-поворотных операций CknOh. Все операции
группы коммутативны, следовательно, имеется 2п клас-
классов. Группа C\h содержит всего два элемента: Е и с^,
эту группу обозначают обычно Cs. Очевидно, что груп-
группа tnh может быть представлена как прямое произве-
произведение группы Сп на С5, т. е. Cnh = Сп X Cs. Все груп-
группы C2mh имеют центр симметрии. Примерами молекул,
относящихся к группе С2л, являются плоские транс-
трансизомеры молекул С2Н2С12 (рис. 3.2, в) и СбН2С12Вг2.
Группы Cnv. Имеется ось симметрии я-го порядка и
п плоскостей симметрии, проходящих через ось. Группа
Cnv содержит 2п операций: п поворотов Сп и п отра-
отражений gv. Операции отражений и повороты не коммути-
коммутируют друг с другом. Благодаря наличию проходящих че-
через ось плоскостей ov, ось является двусторонней, т. е.
повороты Сп и С~п относятся к одному классу. Все п
отражений относятся к одному классу лишь в случае
нечетного п, при п-=2т операции отражения разбивают-
разбиваются на два класса по т элементов в каждом, так как по-
повороты вокруг оси совмещают друг с другом лишь че-
чередующиеся плоскости, соседние плоскости не могут
быть совмещены.
Существует много молекул, относящихся к точечным
группам Cnv. Так, к группе C2v относятся: Н2О, H2S,
SO2, NO2, цис-изомер С2Н2С12 (рис. 3.2,г), Н2СО и др.
К группе Czv относятся: NH3, PC13, СН3С1 и др.
Группы Dn. Имеется ось симметрии п-го порядка и
п перпендикулярных к ней осей симметрии второго по-
порядка, пересекающихся под углом я/n. Группа содер-
содержит 2п операций: п поворотов С„ вокруг вертикальной
оси и п поворотов на угол я вокруг горизонтальных
осей, обозначаемых обычно посредством ?/2. Разбиение
операций группы на классы производится так же,
как в группе Cnv (группы Dn и Cnv являются изо-
изоморфными). Группа D2 имеет три взаимно перпен-
перпендикулярные оси второго порядка и обозначается
буквой V.
Молекулы, равновесная конфигурация которых ха-
характеризуется осями симметрии группы Dn, обладают

ПО ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ, III
обычно еще плоскостями симметрии и принадлежат по-
поэтому к точечным группам с более высокой симметрией,
чем Dn%
Группы Dnh. К системе осей группы Dn добавляет-
добавляется горизонтальная плоскость симметрии, проходящая
через п осей U2. Это приводит к появлению проходящих
через ось Сп п вертикальных плоскостей симметрии.
Группа содержит 4п операций: к 2п операциям группы
Dn добавляется п отражений gv и п зеркально-пово-
зеркально-поворотных операций Cknoh. Dnu может быть представлена
как прямое произведение Dn X CSi поскольку отражение
Он коммутирует со всеми операциями группы Dn.
Примером молекулы, обладающей группой D2h, мо-
может служить равновесная конфигурация молекулы эти-
этилена (рис. 3.2, д). Группой D3h обладают все плоские
симметричные молекулы типа ХУз, например BF3, a
также циклопропан, цис-изомер этана, 1-, 3-, 5-трихлор-
бензол, С6Н3С13 и др. Молекула бензола характеризует-
характеризуется симметрией группы D6h.
Группы Dnd. К системе осей группы Dn добавляет-
добавляется п плоскостей симметрии, проходящих через ось С„
и делящих пополам угол между двумя соседними осями
второго порядка. Группа содержит 4п операций: 2п опе-
операций группы Dn, n отражений ва и п зеркально-пово-
зеркально-поворотных операций а^^Л. Зеркально-поворотные операции
OdU2 эквивалентны повороту вокруг оси Сп и отражению
в перпендикулярной к ней плоскости. Ось Сп превра-
превращается, следовательно, в зеркально-поворотную ось
вдвое большего порядка S2n- При нечетном п D2m+X d =
= D2m+l X С,.
Примером молекулы, имеющей группу симметрии
D2(i, является молекула аллена, плоскости СН2 групп
которой взаимно перпендикулярны (рис. 3.2, е); к груп-
группе Dzd относится транс-изомер этана (угол между СН3-
группами составляет 60°).
II. Кубические точечные группы
Точечные группы этого типа имеют несколько осей
симметрии, порядок которых выше второго.

§3
ТОЧЕЧНЫЕ ГРУППЫ
111
Группа Т. Если к трем осям группы D2^*V доба-
добавить четыре наклонные оси третьего порядка, повороты
вокруг которых переводят оси второго порядка друг в
друга, то получим систему осей тетраэдра. Ее удобно
изобразить, проводя оси третьего порядка вдоль четырех
Кубические точечные группы
в) О
пространственных диагоналей куба, а оси второго по-
порядка через центры противоположных граней (рис. 3.3, а).
Операции поворота вокруг этих осей образуют группу,
обозначаемую символом Т. Группа Т содержит 12 опе-
операций, распадающихся на четыре класса: ?, три пово-
поворота С2, четыре поворота С3 и четыре поворота С\.
Равновесных конфигураций молекул, обладающих
симметрией точечной группы Т, не существует. Если
в молекуле тетраметилметана С(СН3L, принадлежа-
принадлежащей к группе с боле$ высокой симметрией Т& слегка

112 ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ. III
повернуть метиловые группы, то получившаяся неравно-
неравновесная конфигурация будет обладать симметрией Т.
Группа Td. К системе осей группы Т добавляется
шесть плоскостей симметрии, каждая из которых про-
проходит через две оси третьего порядка и одну ось
второго. Оси второго порядка одновременно являются
зеркально-поворотными осями четвертого порядка. 24 опе-
операции группы распадаются на пять классов: восемь по-
поворотов Сз, Сз, шесть отражений crd, шесть зеркально-
поворотных операций S4, S4, три поворота C2=S4.
К группе Td относятся все молекулы, имеющие
симметрию тетраэдра: СН4 (рис. 3.3,6), ССЦ, Р4 и др.
Группа Тн. К системе осей группы Т добавляется
центр симметрии. При этом автоматически появляются
три взаимно перпендикулярные плоскости, каждая из
которых проходит через две оси второго порядка. Оче-
Очевидно, что Th— Tx Ct. Точечная симметрия Ть по-ви-
по-видимому, не осуществляется в качестве группы симмет-
симметрии молекулы.
Группа О. Элементами симметрии этой группы яв-
являются оси симметрии куба: три оси четвертого поряд-
порядка, четыре оси третьего порядка (рис. 3.3,в). 24 опера-
операции группы распадаются на пять классов: ?, восемь по-
поворотов Сз, Сз, шесть поворотов С4, С4, три поворота С4
вокруг осей четвертого порядка и шесть поворотов Сг
вокруг осей второго порядка.
Молекулы, обладающие системой осей группы О,
как правило, имеют еще и плоскости симметрии и от-
относятся поэтому к группе с более высокой симмет-
симметрией Oh.
Группа Oh. Элементами симметрии группы являют-
являются все элементы симметрии куба либо правильного ок-
октаэдра. К осям симметрии группы О добавляется шесть
плоскостей симметрии сг^, проходящих через противопо-
противоположные ребра куба, и три плоскости симметрии crv, про-
проходящие через центр куба и параллельные его граням.
Оси С3 становятся при этом зеркально-поворотными
осями S6. Группа Oh содержит центр симметрии и мо-
может быть представлена как прямое произведение: Oh =
*= О XCt. 48 операций группы разбиваются на десять

§3 ТОЧЕЧНЫЕ ГРУППЫ ИЗ
классов, которые получаются из классов группы О при
нахождении прямого произведения О X С,.
Примерами молекул, обладающих точечной симмет-
симметрией Ohy являются молекулы OsFs (рис. 3.3,г), SPa
(рис. 3.3, (Э), UF6.
На этом исчерпываются конечные точечные группы,
которыми могут обладать молекулы, рассматриваемые
как жесткие конструкции. Если расположить рассмо-
рассмотренные выше группы в порядке добавления новых
элементов симметрии, то получим следующую схему:
с
п
\ / \ / \ \
S2n Cnh Cnv Dnh Dnd Th Td Oh.
III. Непрерывные точечные группы
Если в дискретных аксиальных точечных группах
устремить порядок оси Сп к бесконечности, то получим
непрерывные аксиальные точечные группы С^, С^, С^,
А»> Ах>/г (группа Daad не может быть определена). Все
эти непрерывные группы /являются подгруппами груп-
группы ортогональных преобразований в трехмерном про-
пространстве О3. Группы С^, С^, D^ не осуществляются
в качестве групп симметрии молекулы и мы их рассмат-
рассматривать не будем.
Группа Оъ. Преобразования группы являются ком-
комбинациями вращений вокруг любой оси, проходящей че-
через начало координат, и инверсии. Группа О3 может
быть представлена как прямое произведение группы
трехмерных вращений на группу Ct: 03 = /?3ХС/.
Классы группы О3 могут быть получены из классов
группы /?3. Помимо двух классов по одному элементу
в каждом, Е и /, группа О3 содержит еще два непре-
непрерывных множества классов с непрерывным множеством
элементов в каждом классе. Это — повороты на угол с
абсолютной величиной |ф| и комбинация поворотов с
инверсией. Группа О3 является точечной группой сим-
симметрии атома.
Группа Coot?. Имеются ось симметрии Со и непре-
непрерывное множество проходящих через ось плоскостей

114 ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ. III
av. Группа содержит непрерывное множество классов,
содержащих по две операции поворота в каждом, С(ф)
и С(—ф), и один класс отражений, состоящий из непре-
непрерывного множества операций отражения ov.
Симметрией группы С«>и обладают все линейные
молекулы, несимметричные относительно своей середи-
середины. Например, HD, NO, N20, HCN (см. рис. 3.2,ас).
Группа Dooh- К элементам симметрии группы Сооо
добавляется центр симметрии. Это приводит к появле-
появлению плоскости симметрии ah и непрерывного множества
осей второго порядка U2. Группа Дх>л может быть пред-
представлена как прямое произведение Д^д = Coov X Ch
Классы группы Д^ непосредственно получаются из
КЛаССОВ ГруППЫ Coot,.
Группой Dooh обладают все линейные молекулы, сим-
симметричные относительно своей середины. К их числу
относятся все двухатомные молекулы с одинаковыми
ядрами, молекулы С2Н2 (см. рис. 3.2, з), C2N2, С02,
С3О2 и др.
Таблицы характеров точечных групп приведены в
Приложении 1. В Приложении 2 приведены матрицы не-
неприводимых представлений важнейших точечных групп.
IV. Группы симметрии нежестких
молекул
Рассмотренные выше точечные группы состоят из со-
совокупностей операций вращения и отражения молекулы
как целого. Молекула представляется в виде жесткой
конфигурации атомов, закрепленных в положениях рав-
равновесия (равновесная конфигурация). Между тем в ряде
случаев молекула может иметь несколько равновесных
конфигураций, отвечающих одинаковой энергии и раз-
разделенных конечным потенциальным барьером. Переход
молекулы из одной конфигурации в другую не меняет
ее энергии. Появляются новые элементы симметрии, рас-
расширяющие исходную точечную группу. Группы симмет-
симметрии таких «нежестких» молекул были исследованы Лон-
ге-Хиггинсом [311, см. также работу Альтмана [92].
Простейшим примером является молекула аммиака
NH§, точечная группа симметрии C3v. Атом азота мо*

ТОЧЕЧНЫЕ ГРУППЫ
115
жет находиться либо над плоскостью, в которой распо-
расположены три атома водорода, либо под ней (рис. 3.4,а).
Экспериментально доказано существование переходов
атома азота из одного положения в другое. К операциям
симметрии группы С31) добавляются отражения в пло-
плоскости сгд, общее количество операций симметрии удваи-
удваивается. В результате в задачах, где учитываются пере-
переходы NH3 из одной конфигурации в другую, молекула
Группы симметрии нежестких молекул
z
2 г
W 4ф
б)
Рис. 3.4.
должна характеризоваться точечной группой симмет-
симметрии Dzh.
Другие примеры можно найти среди молекул с внут-
внутренним вращением, когда одна часть молекулы может
разворачиваться относительно другой на большие углы.
Обычно это имеет место для метильных групп СН3, со-
соединенных с оставшейся частью молекулы одинарной
а-связью. Например, в молекуле этана две группы СН3
могут поворачиваться вокруг связи С—С. Имеются три
равновесные конфигурации, соответствующие углам
разворота одной группы СН3 относительно другой: 60°,
180° и 300° (рис. 3.4,6). Эти конфигурации отличаются
лишь перестановками атомов Н. Переход из одной кон-
конфигурации в другую эквивалентен следующим переста-
перестановкам атомов Н одной из метильных групп: /, Р123,
Р\32. В результате группа симметрии молекулы этана

Пб ГРУППЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ГЛ. Ш
Оъа (либо Вш для цис-изомера), содержащая 12 эле-
элементов, при учете внутреннего вращения расширяется
до группы симметрии из 12*3 = 36 элементов.
Наличие у молекулы нескольких частей с внутренним
вращением приводит к резкому увеличению порядка
группы симметрии. Так, в молекуле триметилбора
В(СН3)з (рис. 3.4, в) имеет место внутреннее вращение
всех трех метальных групп. Точечная симметрия карка-
каркаса из атомов бора и углерода — Dzh. К каждой из две-
двенадцати операций симметрии группы Dsh добавляется
3*3 «3 = 27 возможных ориентации метильных групп.
Порядок получившейся группы оказывается равным
12-27 = 324.
Отметим, что согласно теореме Кейли (раздел 1-3)
все конечные группы симметрии нежестких молекул дол-
должны быть изоморфны соответствующим подгруппам
групп перестановок ядер.

ГЛАВА IV
ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ
И ТЕНЗОРНЫЕ ОПЕРАТОРЫ
§ I. Взаимосвязь линейных групп и групп перестановок
4-1. Построение тензорного представления. Пусть за-
задан набор п ортонормированных функций гр^. Набор
функций г|J- можно рассматривать как вектор в п-мер-
ном векторном пространстве. При унитарном преобра-
преобразовании пространства V вектор с компонентами -фг- пе-
переходит в новый вектор с компонентами
ф; = 2и****. D.1)
Составим произведение двух векторов и применим к
каждому из них преобразование D.1). Компоненты про-
произведения преобразуются при этом по следующему за-
закону:
ч>М= 2!«аЛАК
«1, «2
Матрица преобразования D.2) является прямым про-
произведением матриц преобразования D.1). п2 величин
•ф^ образуют тензор второго ранга, определенный в
n-мерном векторном пространстве. Обозначим компо-
компоненты этого тензора Ttxi2. Аналогично можно образовать
тензор N-го ранга, определяемый как набор nN компо-
компонент
преобразующихся при преобразованиях векторного про-
пространства D.1) по закону
Гп , = 2 tit у и, k ... и, и Tk у у . D.4)

118 ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ. IV
Следовательно, преобразование n-мерного пространства
U индуцирует преобразование
UN(U)=UXUX ... XU D.5)
п^-мерного пространства тензоров N-ro ранга. Матрицы,
соответствующие преобразованию TlN(U), образуют тен-
тензорное представление N-ro ранга унитарной группы
Un. Это представление является прямым произведени-
произведением N n-мерных представлений группы Un и согласно
результатам раздела 1-15 должно быть приводимым.
Если ввести аргументы, от которых зависят функции
%, то тензор D.3) может быть записан как функция от
этих аргументов:
Г,А... ,„0,2 N) = ^ A)^ B)... bN № D.6)
где числа 1,2, ..., N нумеруют совокупности аргумен-
аргументов фуНКЦИЙ 1|)г- *).
4-2. Разбиение тензорного представления на неприво-
неприводимые части. Из вида преобразования D.4) следует,
что если подействовать на тензор D.6) некоторой пере-
перестановкой его индексов Р, то полученный новый тензор
будет иметь тот же закон преобразования, что и исход-
исходный. Покажем это на примере тензора второго ранга:
{WtJ - Ки - 2 «,,*«,,*/«¦ - Л "<•*."«.V**- DJ>
Следовательно, операции перестановки индексов и уни-
унитарных преобразований коммутируют. Если мы соста-
составим из тензоров комбинации, обладающие определенны-
определенными свойствами симметрии относительно перестановок
индексов, то тензоры, входящие в каждую из комбина-
комбинаций, будут преобразовываться при унитарных преобра-
преобразованиях только друг через друга. Такие комбинации
могут быть получены действием операторов Юнга B.30)
*) Выражение D.6) совпадает с выражением для волновой
функции системы N невзаимодействующих частиц, если через i|),(A)
обозначить волновую функцию &-й частицы в состоянии, характе*
ризуемом набором квантовых чисел / (см. гл. VI),

§ 1 ЛИНЕЙНЫЕ ГРУППЫ И ГРУППЫ ПЕРЕСТАНОВОК Ц9
на номера аргументов в тензоре D.6). В образованных
таким образом тензорах
«№^...,„0. 2,....АО D.8)
символ t характеризует симметрию относительно пере-
перестановки индексов, а символ г — симметрию относитель-
относительно перестановок аргументов (см. раздел 2-9). Если по-
подействовать на D.8) унитарным преобразованием D.5),
то в силу существования соотношения коммутации
nN{UW$-«WUN(U) D.9)
получим
ло-
...^1 ^ <4Л0>
4>S
1 N
Следовательно, тензоры вида D.8) с фиксированными
[к], г, t и текущими индексами /ь i%..., In преобразу-
преобразуются при унитарных преобразованиях друг через друга.
Однако не все из них независимы. Количество незави-
независимых симметризованных тензоров определяет размер-
размерность неприводимого представления унитарной группы
Unt характеризуемого схемой симметрии [к]. Обозначим
это представление Un\ а его размерность дк(п). Из спо-
способа получения базиса представления C/L1 может быть
получено и правило нахождения его размерности.
Прежде всего отметим, что могут осуществляться
только такие представления и?\ схема Юнга которых
состоит из столбцов с длиной, не превышающей п. Это
связано с тем, что среди N индексов тензора Tit {
не может быть более п разных (см. раздел 2-9, п со*
ответствует в обозначениях этого раздела величине
N—m+l). Для данной схемы Юнга [к] существует f\
операторов ©$1 Симметрия тензора D.8) относительно
перестановки аргументов характеризуется таблицей
Юнга г. Задав г, мы получим совокупность тензоров,
преобразующихся друг через друга при унитарных

120 ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ. IV
преобразованиях. Всего таких совокупностей, различаю-
различающихся таблицей Юнга г, будет fx. Из тензоров каждой
совокупности может быть построен базис неприводимого
представления Un\ При этом следует иметь в виду, что
тензоры, полученные действием операторов ©^ с фикси-
фиксированным г0 на компоненты Tit t , различающиеся
только перестановками индексов, будут линейно зави-
зависимы. Действительно, пусть
Тогда в силу соотношений B.43) и B.48)
«to,... tN=да»,... iN=зд.г?л... tN
Следовательно, для нахождения размерности неприво-
неприводимого представления Uln ] может быть предложена сле-
следующая процедура. Вначале выделяем все компоненты
тензора, которые не преобразуются друг через друга
при перестановках индексов. Затем действуем на них по-
поочередно f% операторами ©^ с фиксированным первым
индексом. Действие операторов Юнга на часть компо-
компонент даст нулевой результат. Размерность неприводи-
неприводимого представления Ь%{п) определится количеством не
равных нулю симметризованных тензоров. Ниже мы
приведем примеры использования этой процедуры.
Таким образом, неприводимые представления уни-
унитарной группы Un, входящие в разложение тензорного
представления N-ro ранга, характеризуются схемами
Юнга из N клеток с числом клеток в столбце не более
п. Каждое неприводимое представление унитарной груп-
группы со схемой симметрии [К] входит в разложение число
раз, равное размерности неприводимого представления
группы перестановок, характеризуемого той же схемой
симметрии [к]*). nN базисных функций в результате
*) Эти результаты были впервые получены Вейлем [32]. Здесь
дан несколько иной вывод, отличающийся от оригинального исполь-
использованием операторов Ю^

§ 1 ЛИНЕЙНЫЕ ГРУППЫ И ГРУППЫ ПЕРЕСТАНОВОК 121
приведения тензорного представления можно располо-
расположить на плоскости в виде ряда прямоугольников, каж-
каждый из которых характеризуется определенной схемой
Юнга [К] и содержит f%6\(n) функций. Функции, нахо-
находящиеся в одной строке прямоугольника, преобразуются
друг через друга при унитарных преобразованиях, а
функции, находящиеся в одном столбце, — при переста-
перестановках номеров аргументов. Очевидно, что
Простейшим примером является разбиение на непри-
неприводимые части тензорного представления второго ранга
в пространстве двух измерений. Из четырех компонент
можно составить три симметричные комбинации со[2
и одну антисимметричную со11 ч^:
В качестве более сложного примера рассмотрим тен-
тензорное представление третьего ранга, определенное в
трехмерном пространстве. 27 компонент тензора третьего
ранга могут быть разбиты на три типа: а) все индексы
тензора одинаковы; б) два одинаковых индекса; в) все
индексы разные. Выпишем их, расположив в одном
столбце компоненты, преобразующиеся друг через друга
при перестановках:
а) Тххх Тууу Tzzz б) Тхху Txxz Туух Tyyz Tzzx Tzzy в) Txyz
ТХух ?xzx Tyxy Tyzy Tzxz Tzyz TyXZ
Туxx Tzxx T xyy TZyy Txzz TyZZ TXZy
T
1 yzx
D.12)

122 ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ. IV
Разрешены все три возможные схемы Юнга из трех кле-
клеток: [31, [21] и [I3]. Следовательно, в разложение тензор-
тензорного представления войдут три неэквивалентных
неприводимых представления. Определим их раз-
размерности.
Для [Я]=[3] имеется один оператор Юнга со^. Неза-
Независимые линейные комбинации могут быть найдены дей-
действием co[3J на компоненты, расположенные в первой
строке D.12). Всего получим 10 таких комбинаций. Сле-
Следовательно, б[з] C)= 10.
Для [Л,] = [21] имеется четыре оператора Юнга со^;
их явный вид выписан на стр. 64. Операторы Юнга с
различным индексом г дают тензоры, принадлежащие
к различным базисам неприводимого представления
унитарной группы. Независимые тензоры, принадлежа-
принадлежащие к одному базису, находятся действием операторов
©I2/1, co[|1] на компоненты первой строки D.12). Действие
со^ на компоненты первого типа дает нуль (см. раздел
2-9). Шесть независимых базисных функций мы полу-
получим, подействовав со^11 на шесть компонент первой
строки второго прямоугольника в D.12) (действие со^
на эти компоненты дает нуль, так как они симметричны по
первым двух индексам). Еще две базисные функции мы
найдем, подействовав со^13 и со[|1] на Txyz. Следователь-
Следовательно, размерность представления 6[2i]C) = 8. Всего в иско-
искомое разложение войдет два таких представления,
ПОСКОЛЬКУ/[21] = 2.
Наконец, антисимметричный тензор может быть об-
образован только одним способом. Для этого нужно опе-
оператором антисимметризации со[18] подействовать на ком-
компоненту с тремя разными индексами, например на Txyz.
Следовательно, размерность б[Р] C)= 1.
Итак, 27-мерное пространство тензора третьего ран-
ранга может быть разложено на следующие неприводимые
подпространства: одно десятимерное, два восьмимерных
и одно одномерное. Сопоставив каждой базисной функ-
функции неприводимых подпространств точку на плоскости,
получим три прямоугольника. Функции, отвечающие
строкам прямоугольника, преобразуются друг через дру-

§ 1 ЛИНЕЙНЫЕ ГРУППЫ И ГРУППЫ ПЕРЕСТАНОВОК 123
га при унитарных преобразованиях, функции, отвечаю-
отвечающие столбцам, — при перестановках аргументов:
к
та <d
[8] [21] (!•]
Унитарные преобразования
Может быть получена и общая формула, связываю-
связывающая размерность неприводимого представления унитар-
унитарной группы Un с параметрами характеризующей его
схемы Юнга [к]. А именно [3, 4]:
n-i, D.13)
где iy / пробегают значения от 1 до м, №*> обозначает ко-
количество клеток в i'-й строке схемы Юнга. Для схемы
Юнга с т строками, начиная с /=m+l, W*> в формуле
для /ii надо приравнять нулю.
В случае симметричного представления [Я] = [ЛГ| фор-
формула D.13) принимает вид
^ж-;- DЛ4>
в случае антисимметричного [A,]=[1N] —
6W
Выражение D.14) совпадает с формулой для числа спо-
способов распределения N частиц но п одночастичным со-
состояниям в статистике Бозе — Эйнштейна, а выражение
D.15) —с аналогичной величиной в статистике Ферми —
Дирака. Это совпадение не случайно. Оно объясняется
тем, что полная волновая функция, характеризующая
состояние системы N частиц, должна быть симметрич-
симметричной относительно перестановок частиц в случае

124 ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ. IV
статистики Бозе — Эйнштейна и антисимметричной — в
случае статистики Ферми —Дирака.
4-3. Формулы для характеров симметризованных сте-
степеней представлений. В предыдущем разделе было пока-
показано, что симметризация заданного в n-мерном вектор-
векторном пространстве тензора N-ro ранга с помощью опе-
операторов Юнга со^ приводит к разбиению исходного
м^-мерного тензорного представления на неприводимые
части. Характеры %[l](U) получающихся неприводимых
представлений U[n] могут быть выражены через харак-
характеры %(U) векторного n-мерного представления группы
Un. Приведем это соотношение без доказательства (ср.
[33], §25):
A
(и2)... xv
D.16)
где суммирование проводится по всем классам Cv груп-
группы перестановок я^, класс Cv содержит gc переста-
перестановок, имеющих одинаковую циклическую структуру,
включающую vi единичных циклов, v2 транспозиций, ...,
vm циклов длиной т. %[K](CV) — характер неприводимого
представления П^ группы jtjv, отвечающей классу Cv.
В случае произвольной группы G тензорному пред-
представлению раздела 4-1 может быть сопоставлено прямое
произведение N представлений Г группы G, являющееся
N-й степенью представления Г:
Г^ = ГхГх ... ХГ. D.17)
Симметризация базисных функций представления D.17)
по схемам Юнга из N клеток приводит к распаду его
на представления меньшей размерности, называемые
симметризованными степенями представления Г. В при-
приложениях наиболее часто встречается представление с
симметричным базисом, отвечающее [А,] = [ЛГ|. Оно назы-
называется симметрической N-степенью представления Г и
обозначается [Г]^. К такому представлению принадлежат,
например, волновые функции так называемых обертон-

§ 1 ЛИНЕЙНЫЕ ГРУППЫ И ГРУППЫ ПЕРЕСТАНОВОК 126
ны$ колебательных состояний [77], возникающих в мо-
молекуле при многоквантовых инфракрасных переходах.
Формула для характеров [T\N, обозначаемых [хРЧ#), где
R— произвольная операция группы G, получается как
частный случай формулы D.16) при [А,] = [ЛГ|:
Ы"(*> - аГГ^с jf'WxM*2)... хЧ*"). D.18)
Взяв циклическую структуру классов Cv и значения
gc из таблиц характеров групп щ, я3, я4 (Приложе-
(Приложение 4), получаем следующие формулы:
D-19)
При больших ./V вычисление характеров по формуле
D.18) становится очень громоздким. Существуют более
компактные формулы, позволяющие легко находить
ЬсРЧЯ) ПРИ любом N. Вид формул зависит от размерно-
размерности исходного представления Г.
Для одномерных представлений
поэтому из формулы D.18) следует очень простой ре-
результат:
[Jd"(*)-x"(*). D.20)
Формулы для двух- и трехмерных представлений были
получены А. С. Компанейцем [51]. Рассмотрим вывод
этих формул на примере двухмерных представлений.
Обозначим базисные функции представления Г бук-
буквами х9 у. Их можно рассматривать как компоненты
двухмерного вектора. При любом преобразовании R то-
точечной группы О Rx, Ry преобразуются через х% у

126 ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ4 IV
с помощью ортогональной матрицы, которая может быть
интерпретирована как матрица поворота или отражения
пространства ху. Повороту на угол ад отвечает матрица
Г cos ар — sin ар Л
• D.21)
[sin ад cos ад J v '
с суммой диагональных элементов, равной 2 cos aR. При-
Приравнивая характер операции R %(R) = 2cosaR, получаем
значение угла поворота aR. Подчеркнем, что если декар-
декартовы координаты ху у не преобразуются по данному пред-
представлению, этот поворот не имеет ничего общего с фак-
фактическим преобразованием симметрии.
Отражению в двухмерном пространстве отвечает мат-
матрица
Г-,]
D.22)
с равным нулю характером. Для того чтобы выяснить,
является ли данная операция R отражением в простран-
пространстве ху, либо поворотом на угол ад=л/2, характер ко-
которого также равен нулю, достаточно рассмотреть %(/?2).
Если %(R2)=2, то данное преобразование является
отражением, если %(R2)=—2, то поворотом.
Симметрическое произведение двухмерного представ-
представления N раз само на себя есть представление с базисом
из N+1 величин
Л xN~ly, ..., yN. D.23)
Очевидно, что характер операции отражения, опреде-
определяющейся матрицей D.22), равен
[%)N(R)=l + (~l)N • D.24)
Для нахождения характера операции /?, отвечающей по-
повороту, удобно перейти к сферическим компонентам двух-
двухмерного вектора, x±iy. Базис D.23) заменяется на
{х + iy)\ (х + iyf'1 (x - /у), ...Ах- iyf. D.26)

§ 1 ЛИНЕЙНЫЕ ГРУППЫ И ГРУППЫ ПЕРЕСТАНОВОК 127
Матрица поворота D.21) в сферическом базисе диаго-
нальна и равна
[V0*
Диагональной будет и матрица поворота, определенная
на базисе D.25). Сумма ее диагональных элементов со-
составляет геометрическую прогрессию
откуда следует, что
^§^ D.26,
Для трехмерных представлений аналогичным образом
могут быть получены следующие формулы [51]: для опе-
операции R, эквивалентной повороту в пространстве xyz,
sin г—В- sin5
[хТО) = - 5—^—; D.27)
sin a^ sin -^-
для операции /?, эквивалентной преобразованию в про-
пространстве xyz, содержащему отражение,
( + )
sin , Z- sin
[%}N (R) = г-1 , aR = aR+n. D.28)
Если координаты х> у, z не преобразуются по дан-
данному трехмерному представлению, то вид преобразова-
преобразования в пространстве xyz, соответствующего операции R,
определяется операцией R' изоморфной группы, в кото-
которой координаты ху у, z преобразуются по данному пред-
представлению. Подобное сопоставление применимо и для
двухмерных представлений. Его удобно осуществлять с
помощью таблиц характеров точечных групп (см. При-
Приложение 1).
Приведем в качестве примера характеры некоторых
симметрических степеней представления Е группы Сгу.

128
ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ
ГЛ. IV
В данном случае обозначения элементов группы соот-
соответствуют аналогичным операциям в пространстве ху.
Характеры симметрических степеней легко вычисляются
по формулам D.24) и D.26):
aR
%(R)
[%V(R)
lxV(R)
[%V(R)
E
0
2
5
8
10
2Л/3
-1
-1
-1
1
0
1
0
0
При расчетах по формулам D.26) — D.28) следует
считать, что
sin тл
sin я
= (— 1) т,
sin 2mn
-= m.
4-4. Теорема Литтлвуда. Литтлвудом [34] была дока-
доказана теорема, позволяющая определить, какие неприво-
неприводимые представления IW группы jtjv можно образовать
из прямого произведения неприводимых представлений
П*"] и Г^2] групп яя, и Jtrt2 {n\ + ti2 = N)> т. е. при расши-
расширении подгруппы яЯ1 X Лп2 до группы nN. Такой процесс
в отличие от обычного прямого произведения называется
внешним произведением и обозначается ®. Пользуясь
теоремой Литтлвуда, легко найти разложение внешнего
произведения на неприводимые части:
= 2 а
2, Я) ТЫ.
D.29>
Поскольку симметризованный по схеме Юнга [Я] тензор
N-ro ранга может одновременно служить как базисом
группы перестановок, так и базисом группы унитарных
преобразований Un (см. предыдущий раздел), то тео-
теорема Литтлвуда может быть применена и при нахож-
нахождении возможных неприводимых представлений f/[^J»
входящих в разложение прямого произведения
X
- 2 а (Яр К Я) U[P.
А.
D.30)

§ 1
ЛИНЕЙНЫЕ ГРУППЫ И ГРУППЫ ПЕРЕСТАНОВОК
129
Сумма по [Я] в правой части D.30) включает только те
схемы Юнга из D.29), длина столбцов в которых не
превышает п. Это ограничение автоматически отпадает
при п > N.
Прежде чем сформулировать теорему Литтлвуда,
введем понятие решеточных перестановок (lattice per-
permutation). Решеточными перестановками выражения
х^х^х^ • • • называют перестановки элементов хи #2, *з» • •.,
приводящие к выражениям, среди любых m первых чле-
членов которых Х\ встречается число раз не меньшее, чем
Х2\ аналогично Х2 встречается число раз не меньшее, чем
*з, и т- Д-
Например, можно выписать шесть решеточных пере-
перестановок выражения х\х2хъ:
12 3* 12 13* 1231*
Приведем формулировку теоремы:
для нахождения возможных схем Юнга, кото-
которые можно построить из схем Юнга [A,i] s= [A^f*. • •]
и [Я2] = [^2!L2) ...], нужно к схеме Юнга [A,i] по-
последовательно прибавить всеми возможными спо-
способами Я^ клеток с индексами а, X® клеток с
индексами р и т. д. так, чтобы в образуемых схе-
схемах Юнга [к] прибавленные индексы удовлетворяли
двум условиям: а) не должно быть двух одина-
одинаковых индексов в одном столбце; б) если прочесть
все прибавленные индексы справа налево последо-
последовательно по строкам, то получим решеточные пе-
перестановки выражения Л р*2 ...
Примеры
1. [I3]® [12]
9 И. Г. Каплан
U
I
+
a

130
ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ. IV
т. е.
[13]®[12]=М221]
2. [21] ® [21]
вр
w
а\я\
1*1*1 +
ОС
ОС
а
И
Собирая подобные члены, получаем
ОС
ОС
/з
ОС
ОС
Разложение D.30) должно совпадать для любого
я>АЛ Это обстоятельство может быть использовано в
качестве критерия правильности при проверке разложе-
разложения по теореме Литтлвуда. А именно: должно выпол-
выполняться условие
2 . D.31)
Размерности представлений 6%(п) вычисляются по фор-
формуле D.13). Проверим выполнение условия D.31) для
первого примера. По формуле D.13) находим
[X]
h E)
[I3]
10
[I2]
10
[24]
75
[21»]
24
[Iе]
1
что дает, в полном соответствии с D.31),
10.10 = 75 + 24+1.
Равенство D.31) удовлетворяется и при больших п.
Действительно, для п = 7 получаем
35-21=490+224 + 21.

§ 1 ЛИНЕЙНЫЕ ГРУППЫ И ГРУППЫ ПЕРЕСТАНОВОК 131
В тех случаях, когда требуется определить возмож-
возможные представления П^ХПН на которые распадается
представление Г^ при редукции на подгруппе лП{ X яЯ2,
можно также воспользоваться теоремой Литтлвуда. Для
этого нужно применить теорему Литтлвуда к каждому
возможному члену разложения *)
=?= 2 а (Я, V Л2)Г^хГМ D.32)
и отбросить те члены, которые не дают данные [X]. При
небольших П2 этот путь решения оказывается короче,
чем разложение по таблице характеров групп jcjv и
и лП1 X пП2.
Например, пусть требуется найти представления, воз-
возникающие при редукции Г[Х] = П321 на подгруппе язХяг.
В качестве [к\] могут быть только схемы Юнга [3] и [21],
так как [I3] не вписывается в [32]. Искомое разложение
имеет вид
[32] = [3] X [2] + [2 1] X [2] + [21] X [I2].
Представление Г[3]ХГ[131 не войдет в разложение, так
как, согласно теореме Литтлвуда, схема Юнга [32] не мо-
может быть построена из схем Юнга [3] и [I2].
4-5. Редукция ?/2у+1->/?з. Рассмотрим 2/+1 функ-
функций ф^, образующих базис неприводимого представле-
представления DW группы трехмерных вращений /?3. При враще-
вращениях функции базиса преобразуются, друг через друга:
tn
Набор 2/+1 функций ф^> можно рассматривать как
вектор в 2/+1-мерном пространстве. Каждое вращение
в трехмерном пространстве порождает, таким образом,
некоторое унитарное преобразование в 2/+1-мерном про-
пространстве, осуществляемое матрицами представления /Ж
*) Как следует из теоремы Фробениуса (см. стр. 188) коэффи-
коэффициенты a(i, Х\, h) из D.32) равны коэффициентам а(ки А*, ^) из
D.29).

132 ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ. IV
Группа таких преобразований является подгруппой
группы всех унитарных преобразований Un.
Произведение функций
^^•••^ D-34)
при вращениях трехмерного пространства преобразует-
преобразуется по столбцу mim2... mN прямого произведения пред-
представлений
Входящие в его разложение неприводимые представле-
представления DW находятся последовательным применением раз-
разложения C.43). С другой стороны, при унитарных пре-
преобразованиях произведение D.34) преобразуется по тен-
тензорному представлению N-ro ранга группы U2j+\. Вхо-
Входящие в его разложение неприводимые представления
u\fl\ характеризуются схемами Юнга из N клеток с дли-
длиной столбца, не превышающей 2/+1 клеток (см. раз-
раздел 4-2). Так как группа /?3 является подгруппой группы
02j+i» то неприводимые представления U^f+i при ограни-
ограничении операциями группы /?з в общем случае становятся
приводимыми и распадаются на неприводимые пред-
представления Z)<J). При классификации состояний системы
N тождественных частиц часто бывает важно знать, ка-
какие D<J> входят в разложение
rjl"J • ^0 («О Г\\^) / Л О F? \
^2/+1 ==^J а V . D.00)
/
Для нахождения разложения D.35) используем рекур-
рекуррентный метод, предложенный Яном [35].
Предварительно учтем, что одномерное представле-
представление f/|}+1 ^ должно соответствовать представлению
поскольку отличные от нуля компоненты тензора
Л л 2/+11
Til J должны иметь все индексы тг- разные и от-
т{ ... т2у+1
вечают, следовательно, моменту / = 0. Можно показать,

§ 1
ЛИНЕЙНЫЕ ГРУППЫ И ГРУППЫ ПЕРЕСТАНОВОК
133
что, с точки зрения разложения D.35), являются экви-
эквивалентными представления I/^+i со схемами Юнга
:
D.3ба)
Г:
2J+1\
L
J^\ =
D.366)
В основе соотношений D.36) лежит то обстоятельство,
что схема Юнга, все столбцы которой имеют длину
2/+1, отвечает угловому моменту /==0. Значения /, со-
соответствующие двум схемам Юнга, из которых состоит
прямоугольник в D.366), должны быть одинаковы,
иначе при векторном сложении не получился бы / = 0.
Рассмотрим метод нахождения разложения D.35) на
примере группы G3 (/ = 1). Представление [1] осущест-
осуществляется тремя функциями -ф^, -ф^, $% преобразующи-
преобразующимися при вращениях по неприводимому представлению
DV\ Следовательно,
t/1J^DA).
D.37)
Для jV = 2 в разложение тензорного представления
входят два неприводимых представления: ?Д21 и U{P,
а в разложение прямого произведения D^XD^ входят
три неприводимых представления: DV\ D^ и D<°>. Для
нахождения соответствия между ними используем свой-
свойства симметрии базисной функции ^(/A)/B)) пред-
представления D<J> по отношению к перестановке порядка
сложения моментов /(*"). Согласно C.49) при такой пе-
перестановке функция умножается на (— 1J/W = (— IO
(в случае целых /), т. е. она симметрична при четных /

134 ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ. IV
и антисимметрична при нечетных /. Поскольку базис-
базисные функции представления U[?] симметричны относи-
относительно перестановок индексов, а базисные функции
представления U[P — антисимметричны, получаем
t/f=DB) + Z)@), uP-Da\ D.38)
Далее исходим из разложений D.38). Образуем из
схемы Юнга [2] возможные схемы Юнга из трех клеток.
Отвечающие этим схемам Юнга представления D& на-
находим по правилу треугольника C.44). Аналогично по-
поступаем со схемой Юнга [I2]:
СП ® ? = ГГП +
(?>B) X /Я X D{{) = D{3) +.D{2) + 2DA),
D.39)
В результате получаем два уравнения:
Учитывая, что представлению f/з*3может отвечать толь-
только D(°\ из уравнения D.40) находим искомые разложе-
разложения:
D«> + d{\ U[2l] = D{2) + D(\ Um = D{0). D.41)

$ 1 ЛИНЕЙНЫЕ ГРУППЫ И ГРУППЫ ПЕРЕСТАНОВОК
Для N=4 аналогично D.39) имеем
ГГП ® ? = Mill +
136
D.42)
Согласно D.36) представление f/з221 имеет такую же
/-структуру, как и представление U[?\ а представление
з21'1—такую же как и U[P.
'— такую же, как и
находим
Учитывая это, из D.42)
-D{l
D.43)
Аналогичным образом можно найти /-структуру любого
представления f/^+i. Необходимо только иметь в виду,
что при полуцелых / представлению U$+\ отвечают не-
нечетные /, а представлению U^Jli — четные /. В Приложе-
Приложении 3 приведены результаты редукции ряда представ-
представлений U[2fll ДЛЯ /= 1-5-3.
Неприводимые представления группы ?/2у+1 остаются
неприводимыми при переходе к ее подгруппе SU2j+l [4].
При этом, однако, некоторые из неприводимых пред-
представлений могут стать эквивалентными. Оказывается, что
условие эквивалентности неприводимых представлений

136 ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ. 1\
группы SU2j+\ совпадает с условиями D.36). Результа-
Результаты редукции неприводимых представлений группы
SU2j+\ на неприводимые представления группы /?3, есте-
естественно, совпадают с аналогичными результатами ре-
редукции ?/2/+1->/?3. Однако в случае группы SU2j+] имеет
место однозначное соответствие между различными не-
неприводимыми представлениями этой группы и их
/-структурой.
В случае группы унитарных преобразований в двух-
двухмерном пространстве редукция U2—>Rz не приводит к
распаду представлений и[ \ Это связано с тем, что
группа /?3 изоморфна группе SU2. Между неприводи-
неприводимыми представлениями этих групп существует взаимно
однозначное соответствие*), в чем нетрудно убедиться,
проделав вышеописанную процедуру последовательного
прибавления клеток к схемам Юнга. Сх^мы Юнга пред-
представлений щ не могут иметь более двух клеток в
столбце, т. е. состоят из двух строк. Угловой момент /,
соответствующий схеме Юнга [к], связан с длиной строк
АЯ> и А/2) следующим соотношением:
/ = ^-(ЯA)-ЯB>). D.44)
Так, согласно D.44)
§ 2. Неприводимые тензорные операторы
4-6. Определение. В предыдущем параграфе было по-
показано, что nN компонент тензора /V-ro ранга под дей-
действием унитарных преобразований n-мерного простран-
пространства преобразуются по приводимому представлению, ко-
которое распадается на неприводимые при симметризации
тензора по схемам Юнга. Симметризованные таким об-
образом тензоры являются неприводимыми по отношению
к операциям унитарной группы Un, т. е. компоненты
*) Это обстоятельство имеет большое значение для классифи-
классификации состояний систем частиц со спинами 1/2, так как позволяет
каждому значению суммарного спина S сопоставить некоторую
схему Юнга (см. гл. VI).

§ 2 НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ 137
симметризованного тензора преобразуются при унитар-
унитарных операциях только друг через друга. Однако по от-
отношению к операциям группы трехмерных вращений /?3
эти тензоры, вообще говоря, не являются неприводимы-
неприводимыми. Например, из шести компонент симметричного тен-
тензора второго ранга, преобразующегося по неприводи-
неприводимому представлению U[i\ можно образовать, согласно
D.38), один скаляр (неприводимое представление D<0>)
и пять линейных комбинаций, преобразующихся по не-
неприводимому представлению D^\
В общем случае неприводимым тензором группы ли-
линейных преобразований называется совокупность fa ве-
величин Г|а), преобразующихся при операциях группы по
неприводимому представлению Га) этой группы:
1а). D.45)
Из определения D.45) следует, что любой набор ба-
базисных функций, на котором задано неприводимое пред-
представление, может рассматриваться как неприводимый
тензор. Так, примером неприводимого тензора, принад-
принадлежащего к представлению DW группы /?3, является на-
набор, 27+1 сферических функций У/М@, ф)*). Декартовы
компоненты произвольного вектора А образуют тензор
первого ранга. Однако закон преобразования их при
трехмерных вращениях более сложен^ чем в случае сфе-
сферических компонент
Л Л А {А tiA)
образующих неприводимый тензор представления
Поэтому при вычислении матричных элементов вектор-
векторных величин с базисными функциями группы /?3 удобно
пользоваться сферическими компонентами векторов.
Для обычных (декартовых) тензоров TN (N обозна-
обозначает ранг тензора) определены три типа операций.
*) Неприводимые тензоры группы /?3 называют сферическими
тензорами.

138 ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ. IV
1. Сложение тензоров одинакового ранга
Vn-Tb+иП. D.46)
2. Умножение тензоров
т/E) тB)т/C) (л .7ч
Viklmn= UkVlmn, D.47)
приводящее к тензору, ранг которого равен сумме ран-
рангов тензоров-сомножителей.
3. Свертка по паре индексов, приводящая к пониже-
понижению ранга тензора,
lf-24. D.48)
к
Для тензора четного ранга N/2 последовательных свер-
сверток приводят к скаляру, например:
Г@)=2 4 D.49)
U к
Скалярное произведение двух тензоров определяется
как свертка по всем индексам:
y«-2lflVB. D.49а)
U к
В случае неприводимых тензоров операция сложения
аналогична сложению декартовых тензоров:
VT-Tf+Uf. D.50)
Вместо операции умножения и свертки для неприводи-
неприводимых тензоров определяется следующая операция:
УР> ~ 2 2ft/? (а/, р*|тО, D.61)
I, к
в результате которой получается тензор, преобразую-
преобразующийся по неприводимому представлению Г(т), входящему
в разложение прямого произведения Г(а) х Г(Р). Коэффи-
Коэффициенты в формуле D.51) являются коэффициентами
Клебша — Гордана (см. раздел 1-16).
Тензор, принадлежащий к единичному представле-
представлению группы, является скаляром по отношению к опера-
диям данной группы. Согласно A.69) необходимым и
достаточным условием появления единичного представ-

§ 2 НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ 139
ления в разложении прямого произведения двух пред-
представлений является их комплексная сопряженность. Сле-
Следовательно, из произведения неприводимых тензоров,
принадлежащих различным представлениям, нельзя об-
образовать скаляра. В случае группы /?3 скаляр характе-
характеризуется значением углового момента / = 0 и строится
из сферических тензоров с одинаковыми /. Подставляя
в D.51) значения коэффициентов Клебша — Гордана из
C.48), получаем следующий скаляр из сферических,
тензоров:
?^% D-52)
Выражение D.52) без множителя перед суммой принято
называть скалярным произведением сферических тен-
тензоров и обозначать
(г(/)[/(/)) = 2(-l)mrS??/i2». D.53)
т
Для /=1 оно совпадает с обычным скалярным произ-
произведением двух векторов, выраженным в сферических
координатах.
При вычислении матричных элементов операторов
важно знать, по каким неприводимым чредставлениям
преобразуются сомножители в подынтегральной функ-
функции. Это дает, например, возможность сразу выделить
все не равные нулю матричные элементы и получить
теоретико-групповые правила отбора (см. гл. V). По-
Поэтому удобно оператор в матричном элементе представ-
представлять в виде суммы операторов, преобразующихся по
определенным неприводимым представлениям группы.
Неприводимый тензорный оператор определяется (ана-
(аналогично неприводимому тензору) как совокупность fa
величин ТТ] с законом преобразования*)
D.54)
*) Под действием операций группы неприводимые тензорные
операторы преобразуются так же, как неприводимые тензоры. Раз-
Различие в написании формул D.54) и D.45) объясняется тем, что
операторы в старом и новом базисах связаны между собой соот-
соотношением A.31),

140 ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ. IV
Использование неприводимых тензорных операторов
существенно облегчает расчет матричных элементов, так
как позволяет применить целый ряд полезных соотно-
соотношений, полученных Вигнером и Рака (см. [18, 24—26]).
В основе всех этих соотношений лежит теорема Вигне-
ра — Эккарта.
4-7. Теорема Вигнера — Эккарта. Рассмотрим мат-
матричный элемент неприводимого тензорного оператора 71Т)
<a/|7iT)|pfe>, D.55)
определенный на функциях, преобразующихся по непри-
неприводимым представлениям Г(а), Г , принадлежащим той
же группе, что и представление Г(т). Исследуем транс-
трансформационные свойства функции, получающейся в ре-
результате действия оператора Г?т) на функцию tyf\ по
отношению к операциям группы:
Следовательно, функция 7^T)i|)Jp преобразуется по пря-
прямому произведению Г(т) X ГA3) и может быть представ-
представлена с помощью коэффициентов Клебша — Гордана в
виде разложения по базисным функциям неприводимых
представлений группы (см. A.75)):
с, Р)(а|лт|т*, pfe), D.56)
а, \х, т
где индекс а различает повторяющиеся неприводимые
представления, символы т, р в аргументе функции Ф
указывают, что ее вид зависит от базисных функций
прямого произведения. Подставим D.56) в D.55):
(Ш | 71Т) | Pfe) = 2 (aixm | xti pfe) J ф<а>*ф<а|1> (Tp) dV. D.57)
a, |li, m
Согласно условию ортогональности для базисных функ-

§ 2 НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ 141
ций неприводимых представлений A.93)
J bJSimAa (а, т, р), D.58)
где величина Лв(а, т, р) определяется видом функций
^*а) и ®та) (Т> Р) и не зависит от f, /п. Подставляя D.58)
в D.57), получаем аналитическое выражение теоремы
Вигнера — Эккарта *):
(ai | T{tx) | pfe> = 2 (ao/1 т*, pfe) Ла (a, т, р). D.59)
Из соотношения D.59) следует, что зависимость мат-
матричного элемента от номеров столбцов неприводимых
представлений, по которым преобразуются сомножите-
сомножители, целиком содержится в коэффициентах Клебша —
Гордана. Наличие коэффициентов Клебша — Гордана
позволяет сразу получить условия обращения матрич-
матричного элемента в нуль. А именно:
матричный элемент D.59) обращается в нуль во
всех случаях, когда разложение прямого произве-
произведения Г<*)хГ<Э> на неприводимые части не содержит
представления Г<4
Различные по своей физической природе системы мо-
могут обладать одинаковой симметрией. Матричные эле-
элементы, входящие в квантовомеханические расчеты та-
таких систем, различаются для каждой из них только фак-
фактором Ла, коэффициенты Клебша — Гордана для них
одинаковы. Следовательно, теорема Вигнера — Эккарта
позволяет «отделить» свойства симметрии исследуемой
системы от ее физической природы.
Обычно употребляемые в квантовой механике опе-
операторы симметричны по всем частицам, т. е. преобразу-
преобразуются по единичному представлению T[N] группы пере-
перестановок (см. гл. II). Так как Г[АП х Г^-Г1*1, сумма по
а в D.49) в данном случае сводится к одному члену.
В результате теорема Вигнера — Эккарта принимает
*) Эта теорема была доказана Вигнером [39] и Эккартом [36]
для группы трехмерных вращений. Впоследствии Костер [6] моди-
модифицировал ее на случай произвольных конечных групп, придав ей
вид D.59).

142 ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ. IV
следующую форму:
Тт | [AJ гх> - <[AJ г21 [N], [AJ гх) ([А,] || T[N] || [XJ> -
D.60)
где двойная черта в матричном элементе обозначает его
независимость от таблиц Юнга гу нумерующих базис-
базисные функции. Равенство D.60) лежит в основе извест-
известного квантовомеханического правила отбора, согласно
которому возмущение, описываемое симметричным
оператором, индуцирует в системе переходы только
между состояниями с одинаковой перестановочной сим-
симметрией.
4-8. Матричные элементы сферических тензоров.
В случае группы /?3 в разложении прямого произведе-
произведения на неприводимые части не содержится повторяю-
повторяющихся представлений (см. формулу C.43)). Сумма поя
в D.59) сводится к одному члену
Цт\Т&> |/'m') = (/m|x?, j'm')A{U к, /')• D.61)
Вместо величин Л(/, х, /') обычно вводят так называе-
называемые приведенные матричные элементы, (j\\T (/'), свя-
связанные с Л(/, х, /') соотношением
А (/, х, Л -
Это приводит к следующим двум эквивалентным записям
теоремы Вигнера —Эккарта:
{jm | Tf \j'm') - (- 1)'+х-'' {%1*к:[тГ) (J ЦТ» Ю =
I
-!т I ^^/il^ll/). D.63)
Поскольку приведенный матричный элемент не за^
висит от значения проекций углового момента m, k, m\
достаточно найти простейший, с точки зрения вычисле-
вычисления, матричный элемент (jm \ T^ \ j'm') и определить
(J || Г(х) ||/') из формулы D.63). Вычислим, например, при-

§ 2 НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ 143
веденный матричный элемент оператора углового мо-
момента J. Сферические компоненты вектора углового мо-
момента
/ / J (J±U)
образуют неприводимый сферический тензор первого
ранга. Так как г|)^ являются собственными функциями
оператора /z, то
(Jm | Jz | \'т!) = bubmntm. D.64)
С другой стороны, Jz зэ To\ следовательно, согласно
D.63)
h(J I ^) D.66)
D 66)
Входящий в D.65) 3/-символ равен [5]
- m 0 m) VTQTTTWTW '
Сравнивая D.64) и D.65), получаем
(/II /lift - б/Г У/(/+1)B/+1). D.67)
Для скалярного оператора имеет место равенство
D-68)
| Г» |/'т'> = |^. (/1| Г» ||/>.
Найдем матричный элемент скалярного произведения
сферических тензоров. Согласно D.53)
'>. D.69)
Л /",т"
Применим теорему Вигнера — Эккарта к каждому из
матричных элементов в правой части равенства D.69).

144 ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ. IV
В результате получим следующее выражение:
f V2j+i {~l)
X 2 (- l)ft (/w I **. /""О (Г™" I к - *, /'«')• D-70)
ft, m"
Согласно C.47а), C.47b)
(j"m"\%-k, \'m') =
(fiJyVm'l^. /V>. D.71)
Подставим D.71) в D.70) и просуммируем произведе-
произведения коэффициентов Клебша — Гор дана с помощью со-
соотношений ортогональности C.46). Окончательно полу-
получаем
-1 )м" а ||г(х) || и <г II f^(x) ii г>. D.72)
Так как скалярное произведение тензоров есть тензор
нулевого ранга, сравнение равенств D.68) и D.72) при-
приводит к следующей формуле для приведенного матрич-
матричного элемента скалярного произведения:
D.73)
Суммирование в D.73) проводится по всем /"', удовле-
удовлетворяющим правилу треугольника A(/x/#//).
В формулах D.72), D.73) операторы Г<х) и ?/(х) дей-
действуют на координаты всей системы. Пусть рассматри-
рассматриваемая система состоит из двух подсистем, характери-
характеризующихся угловыми моментами /i и /г; оператор Г(х)
действует на координаты первой подсистемы, а ?/(х) — на
координаты второй подсистемы. Приведем без доказа-
доказательства несколько полезных для приложений формул
[21, 22].

§ 2 НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ 145
Приведенный матричный элемент скалярного произ-
произведения операторов, действующих на разные подсисте-
подсистемы, равен
D.74)
Для оператора, действующего на координаты только
одной подсистемы, справедливы равенства:
\, ^
D.75)
D.76)
В случае скалярного оператора формулы D.75), D.76)
приобретают простой вид. Из C.61) и C.63) следует,
что
I а Ь i
\d с OJ
D.77)
Подставляя в D.75), D.76) вместо 6/-символа его зна-
значение D.77), получаем
(ш\\ т*\гт=*/,/*/,/?//- AйтI/2</.»т@)
|/> D.79)
Соответствующие равенства для полных матричных эле-
элементов легко находятся из соотношений D.78), D.79)

146 ТЕНЗОРНЫЕ ПРЕДСТАВЛЕНИЯ И ОПЕРАТОРЫ ГЛ. IV
для приведенных матричных элементов-, если восполь-
воспользоваться равенством D.68). В результате приходим к
довольно очевидным равенствам:
(hhim | Г»\r//mf) = V,ViVm-'ft I Г@) | /,>. D.80)
{Шт\ ^|Ш'т') = б/1/;б/2/;б//бтт.</2| f/@)|/2). D.81)
Матричные элементы, стоящие в правых частях равенств
D.80) и D.81), не зависят от проекций угловых момен-
моментов. Эти матричные элементы не следует путать с при-
приведенными матричными элементами, поскольку они свя-
связаны с последними соотношением D.68).

ЧАСТЬ ВТОРАЯ
СИММЕТРИЯ И
КВАНТОВОМЕХАНИЧЕСКИИ
РАСЧЕТ
Хорошая теория сложных систем
должна представлять собой
лишь хорошую «карикатуру» на эти системы,
утрирующую те свойства их,
которые являются наиболее типическими,
и умышленно игнорирующую все остальные —
несущественные свойства
Я. Я. ФРЕНКЕЛЬ

ГЛАВА V
ОСНОВЫ ПРИМЕНЕНИЯ ТЕОРИИ ГРУПП
В КВАНТОВОЙ МЕХАНИКЕ
5-1. Симметрия уравнения Шредингера и классифи-
классификация состояний. Применение теории групп в квантовой
механике основано на свойстве инвариантности уравне-
уравнения Шредингера по отношению к преобразованиям ряда
групп. Уравнение Шредингера для изолированной кван-
товомеханической системы частиц инвариантно относи-
относительно преобразований следующих групп:
а) группы перемещений системы в пространстве как
целого;
б) группы ортогональных преобразований О3, состоя-
состоящей из поворотов системы как целого вокруг любой оси,
проходящей через центр тяжести системы, выбранной за
начало координат, и инверсии относительно начала коор-
координат;
в) группы перестановок тождественных частиц.
Если система помещена во внешнее силовое поле, то
уравнение Шредингера, описывающее движение систе-
системы, инвариантно относительно: а) группы симметрии
потенциального поля, в котором движутся частицы;
б) группы перестановок тождественных частиц.
При разделении электронного и ядерного движений
(приближение Борна — Оппенгеймера [37, 38]) движе-
движение электронов можно рассматривать происходящим во
внешнем поле, создаваемом равновесной конфигурацией
неподвижных ядер. Потенциальное поле в этом случае
обладает симметрией точечной группы молекулы.
Пусть стационарное уравнение Шредингера для си-
системы частиц
SV$(x) = E$(x) E.1)
инвариантно относительно преобразований R некоторой
группы G. Это означает, что гамильтониан &6 не ме-
меняет своего вида при преобразованиях группы О.

ISO ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ ГЛ. V
ty(x) обозначает стационарную волновую функцию си-
системы в состоянии с энергией ?, х — совокупность коор-
координат частиц (в том числе и спиновых). Подействуем
на обе части уравнения Шредингера операцией J?g6.
Согласно условию гамильтониан $в инвариантен отно-
относительно операций группы О. Поэтому уравнение E.1)
перейдет в
. F.2)
Из F.2) следует, что функция R^{x) также является
решением уравнения Шредингера при собственном зна-
значении ?"*). Может представиться два случая.
1. Уровень Е не вырожден. Тогда
= cty(x). E.3)
Из требования нормированности волновых функций сле-
следует, что |с|2=1.
2. Уровень Е f-кратно вырожден, т. е. имеется / ли-
линейно независимых волновых функций tyi(x)y являю-
являющихся решениями уравнения E.1) при данном собствен-
собственном значении Е. Поскольку функция R^i{x) также яв-
является решением уравнения E.1) при собственном
значении ?, она должна выражаться в виде линейной
комбинации f независимых функций г|)г-(л:), т. е.
f
~ 2 Г
для любой операции R^O. Следовательно, система соб-
собственных функций tyi(x) образует f-мерное представле-
представление группы G.
Таким образом, из свойств симметрии уравнения
Шредингера следует, что волновые функции, принадле-
принадлежащие к одному уровню энергии, преобразуются по
представлению группы симметрии уравнения. В общем
случае это представление является приводимым и мо-
может быть разбито на неприводимые части подобным
преобразованием. Волновые функции при этом разбива-
*) Этот результат, являющийся основополагающим для всех
применений теории групп в квантовой механике, был получен впер-
впервые в работе Вигнера [39] и иногда называется теоремой Вигнера.

ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ 151
ются на неприводимые наборы. Все волновые функции,
относящиеся к одному набору, принадлежат к одному
уровню энергии. Возможное совпадение значений энер-
энергии для разных наборов, не обусловленное симметрией
уравнения Шредингера, называется случайны^ выро-
вырождением. Например, в случае системы частиц, помещен-
помещенных в магнитное поле, два уровня энергии, сответствую-
щих разным неприводимым представлениям, при не-
некотором значении магнитного поля могут совпасть.
Следовательно, при этом значении магнитного поля
имеет место случайное вырождение.
Следует выделить случайное вырождение, возникаю-
возникающее вследствие приближенного решения задачи. Напри-
Например, в уже упоминавшемся приближении Борна — Оп-
пенгеймера, применяющемся при квантовомеханических
исследованиях свойств молекул и твердых тел, движе-
движение электронов рассматривается в потенциальном поле
неподвижных ядер. При определенных конфигурациях
ядер различные электронные термы могут пересекаться,
т. е. имеет место случайное вырождение. Задача нахо-
нахождения энергии электронных термов решается прибли-
приближенно. При решении этой задачи по методу теории воз-
возмущений в нулевом приближении пренебрегают взаимо-
взаимодействием между электронами. Решения получившегося
приближенного уравнения Шредингера должны так же,
как и для точного нерелятивистского уравнения, класси-
классифицироваться по неприводимым представлениям группы
перестановок электронов. Однако волновые функции ну-
нулевого приближения, преобразующиеся по различным
неприводимым представлениям группы перестановок,
описывают состояния, обладающие одинаковой энергией.
Причиной этого дополнительного вырождения является
распад в данном приближении уравнения Шредингера
для системы электронов на уравнения Шредингера для
отдельных электронов.
Наличие такого случайного вырождения обычно все-
всегда может быть выделено. Как правило, вырождение
уровней энергии, отвечающих решениям точного урав-
уравнения Шредингера, обусловлено его симметрией. По-
Поэтому собственные функции каждого уровня энергии

152 ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ ГЛ. V
образуют неприводимое представление группы симмет-
симметрии уравнения, размерность этого представления опре-
определяет кратность вырождения данного уровня. В резуль-
результате, не решая уравнения Шредингера, можно сразу
определить возможные кратности вырождения энерге-
энергетических уровней и законы преобразования волновых
функций при операциях группы симметрии системы.
Рассмотрим, например, молекулу Н2О. Равновесная
конфигурация ядер обладает точечной группой симмет-
симметрии C2v. Уровни энергии системы молекулярных элек-
электронов при равновесной конфигурации ядер классифи-
классифицируются по неприводимым представлениям группы
C2v. Группа C2v является абелевой, все ее неприводи-
неприводимые представления одномерны. Отсюда мы сразу заклю-
заключаем, что в системе не может быть вырожденных уров-
уровней (если только нет случайного вырождения). Волно-
Волновые функции системы могут быть разбиты на четыре
типа, в соответствии с четырьмя неприводимыми пред-
представлениями группы C2zr
При точечной симметрии С3г, (молекулы NH3, CH3CI
и др.) возможны два типа невырожденных состояний
и один тип двукратно вырожденных состояний. Другие
типы состояний в системе не осуществляются. Напри-
Например, нет трехкратно вырожденных уровней.
Интересный пример, с точки зрения классификации
состояний, представляет задача о нерелятивистском дви-
движении электрона в кулоновом поле (атом Н, ион Не+
и др.). Уравнение Шредингера для этой задачи инва-
инвариантно относительно преобразований группы О3- По-
Последняя является прямым произведением /?3 X Ct. Ко-
Координатные волновые функции электрона классифици-
классифицируются по 21+ 1 -мерным неприводимым представлениям
группы /?3 (задаются значение орбитального момента
электрона / и его проекция т на ось г) и по одномер-
одномерным неприводимым представлениям группы Ct (задает-
(задается четность состояния). Следовало бы ожидать, что
уровни энергии электрона должны быть вырождены
только по т, причем кратность вырождения должна
быть равна 2/+1, где / = 0, 1, 2, ... Однако решение
уравнения Шредингера показывает, что состояния элек-
электрона, помимо квантовых чисел / и т, характеризуются

ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ 153
главным квантовым числом /г, причем уровни энергии
нумеруются только числом п. Все состояния с одинако-
одинаковыми я, но различными / принадлежат к одному уровню
энергии; кратность вырождения последнего равна п2.
Оказалось, что это вырождение отнюдь не является
случайным. Как показал Фок [40] (см. также [41]),
в импульсном представлении уравнение Шредингера
для движения электрона в кулоновом поле инвариантно
относительно преобразований групп четырехмерных
вращений /?4, подгруппой которой является группа /?3.
Уровни энергии должны классифицироваться по непри-
неприводимым представлениям группы /?4. Естественно, что
неприводимые представления DQ\ на которые распада-
распадаются классифицирующие энергетические уровни непри-
неприводимые представления группы /?4 при редукции /?4 ->
->/?3, относятся все к одному энергетическому уровню.
Следует заметить, что при отсутствии магнитного
поля гамильтониан является действительной величиной,
поэтому комплексно сопряженные функции должны от-
относиться к одному и тому же уровню энергии. Действи-
Действительно, г|)*(л:) удовлетворяет уравнению E.1) при том
же собственном значении, что и ty(x):
SVV(x) = Etf(x). E.1a)
Поэтому комплексно сопряженные неприводимые пред-
представления должны относиться к одному уровню энергии,
т. е. при классификации состояний их можно рассмат-
рассматривать как одно представление с удвоенной размер-
размерностью. Из молекулярных точечных групп комплексно
сопряженными представлениями обладают только ак-
аксиальные точечные группы Сп.
5-2. Законы сохранения. Уравнение E.2) можно за-
записать в виде
30R$(x) = R30$(x), E.5)
рткуда следует, что
&€R = R3V, E.6)
т. е. из условия инвариантности гамильтониана относи-
относительно преобразования R следует равенство нулю их

.154 ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКИ ГЛ. V
коммутатора
В квантовой механике доказывается (см., например,
[5]), что необходимым условием сохранения физической
величины, отвечающей эрмитову оператору Г, является
равенство нулю коммутатора
В таких случаях говорят, что имеет место закон сохра-
сохранения.
Так как любая операция группы симметрии уравне-
уравнения Шредингера коммутирует с гамильтонианом, то
каждому элементу группы соответствует некоторый за-
закон сохранения. В случае непрерывных групп имеется
даже непрерывное множество законов сохранения. Для
выделения независимых законов сохранения в случае
непрерывных групп*) можно воспользоваться следую-
следующей общей теоремой [33]:
если уравнение Шредингера инвариантно относи-
относительно преобразований некоторой г-па-раметриче-
ской группы Ли, то каждый из г инфинитезималь-
ных операторов соответствует сохраняющейся фи-
физической величине, причем любой закон сохране-
сохранения, связанный с симметрией Относительно преобра-
преобразований данной группы Ли, является следствием г
законов сохранения, связанных с инфинитезималь-
ными операторами группы.
В качестве примера рассмотрим систему N частиц
в однородном внешнем поле. Потенциальная энергия та-
такой системы не изменится, если совершить параллель-
параллельный перенос системы в пространстве. Следовательно,
гамильтониан системы инвариантен относительно груп-
группы параллельных переносов. Эта группа является трех-
параметрической группой Ли. Найдем вид ее инфините-
зимальных операторов.
Преобразования группы заданы в ЗМ-мерном конфи-
конфигурационном пространстве системы, образуемом УУтрой-
*) Нахождение независимых законов сохранения в случае ко-
конечных групп рассмотрено Соколовым и Широковским [42].

ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ 155
ками координат XiyiZi каждой частицы. Каждая опера-
операция характеризуется заданием трех параметров, в каче-
качестве которых могут быть выбраны три декартовы
компоненты вектора переноса а. В результате операции
группы радиус-вектор каждой частицы системы полу-
получает одинаковое приращение на вектор а:
г; = ^ + а. F.7)
По формуле C.13) находим
E.8)
Uy.x = Uzi% = UXjy = UZjy = Ux.z = UyiZ = 0.
Подставляя E.8) в определение инфинитезимальных
операторов C.16), получаем
Инфинитезимальные операторы E.9) пропорциональны
операторам проекций импульса системы:
Рх=- ШХУ Ру = - ihly, P2=- ihl2. E.10)
Следовательно, в однородном поле имеют место законы
сохранения трех проекций импульса системы или, как
следствие этого, закон сохранения вектора импульса си-
стемы.
Если система помещена в центрально-симметричное
поле, то уравнение Шредингера инвариантно относи-
относительно вращений в трехмерном пространстве. Инфините-
зимальными операторами группы /?3 являются, с точ-
точностью до постоянной, операторы компонент углового
момента C.24). Поэтому в центрально-симметричном
поле имеют место законы сохранения компонент угло-
углового момента системы. Естественно, что сохраняется и
вектор углового момента.
В отсутствие поля (изолированная система) в силу
однородности и изотропности пространства выполняют-
выполняются как закон сохранения вектора импульса, так и закон
сохранения вектора углового момента. В случае внеш-
внешних полей, обладающих симметрией дискретных точечных

156 ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ ГЛ. V
групп, также может быть выделен независимый набор
сохраняющихся величин. Так, в потенциальном поле ку-
кубической симметрии сохраняется некоторая функция
компонент углового момента [42].
5-3. Теория возмущений. Рассмотрим физическую си-
систему, гамильтониан 3&0 которой инвариантен относи-
относительно операций группы GQ. Решения уравнения Шре-
дингера
Q/V qW =jC\p V & . 1 1 ^
преобразуются по неприводимым представлениям груп-
группы Go. Если эту систему поместить во внешнее стацио-
стационарное поле с потенциалом У, инвариантным относи-
относительно преобразований группы Gb то состояния систе-
системы будут описываться решениями уравнения
CV0+V)ty = Ety F.12)
и классифицироваться по неприводимым представле-
представлениям группы симметрии уравнения E.12), обозначим ее
G. Группа О является «пересечением» групп О0 и Gx
и определяется общими элементами симметрии, кото-
которыми обладают группы О0 и Gx. Выделим два случая.
1. Группа (?! шире О0 либо совпадает с ней. Группа
симметрии уравнения E.12) в этом случае останется
той же, что и у уравнения E.11). Состояния системы
будут классифицироваться, так же как и до наложения
поля У, по неприводимым представлениям группы О0.
2. Группа Gi является подгруппой группы GQ. Сим-
Симметрия уравнения E.12) совпадает с симметрией поля
V*). Новые уровни системы классифицируются по не-
неприводимым представлениям группы Ог. Значения раз-
размерностей неприводимых представлений подгруппы все-
всегда меньше или равны соответствующим значениям для
группы (редукция на подгруппе). Поэтому кратность
вырождения уровней энергии при наложении поля V в
этом случае уменьшается.
*) Очевидно, что если к выражению, обладающему симметрией
некоторой группы, добавить выражение, обладающее симметрией ее
подгруппы, то сумма будет обладать симметрией подгруппы. Так,
можно полностью «испортить» симметрию функции, добавив ,к
функции несимметричный член.

ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ 157
Если V можно рассматривать как малую поправку
к уже действующему в системе полю, то решение урав-
уравнения E.12) может быть получено методами теории
возмущений [5, 30]. Решение ищется в виде разложения
по некоторому малому параметру. Пусть уровень ?(°)
невозмущенной задачи f-кратно вырожден, обозначим
принадлежащие ему волновые функции у$\ v= I, 2,..., f.
В первом приближении теории возмущений поправки
?<*) к энергии ?(°) находятся как решения секулярного
уравнения
'и ... Vlt
••• V2f
= 0, E.13)
Vn
где матричные элементы оператора V определены на
волновых функциях невозмущенной задачи:
E.14)
Условием применимости теории возмущений является
малость расщепления уровня 2?(°) по сравнению с раз-
разностью уровней невозмущенной задачи.
Возникает вопрос, на сколько уровней расщепляется
первоначально вырожденный уровень при наложении
возмущений различной симметрии. Прежде чем отве-
ответить на этот вопрос, покажем, что имеет место следую-
следующая теорема:
если оператор Л°> инвариантен относительно пре-
преобразований группы G, то матричный элемент опе-
оператора, определенный на базисных функциях, при-
принадлежащих к различным неприводимым пред-
представлениям группы О, диагоналей по отношению к
неприводимым представлениям и номерам базис-
базисных функций и не зависит от номеров базисных
функций, т. е.
где а различает базисы эквивалентных неприводи-
неприводимых представлений ™"Л

158 ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ ГЛ. V
Доказательство немедленно следует из теоремы Виг-
нера — Эккарта D.59), если учесть, что оператор, инва-
инвариантный относительно преобразований группы, при-
принадлежит к ее единичному представлению А{. Так как
для любого представления Г
то сумма по а в D.59) сводится к одному члену, а ко-
коэффициент Клебша — Гордана равен
(Ы\Аи аТ> = ваа-6«'. E.16)
Пусть симметрия возмущения V шире либо та же,
что и симметрия $@0. Оператор V инвариантен относи-
относительно преобразований группы б0. В силу теоремы
E.15) недиагональные матричные элементы секулярного
уравнения E.13) обратятся в нуль, а диагональные эле-
элементы будут все одинаковы. Поэтому уравнение E.13)
имеет один f-кратный корень, его значение определит
сдвиг уровня ?(°). Расщепления в данном случае не про-
произойдет.
Картина, однако, может измениться, если имеет ме-
место случайное вырождение (например, вырождение, свя-
связанное с распадом уравнения Шредингера для N-элек-
тронной системы при пренебрежении взаимодействием
электронов (см. раздел 5-1)). В этом случае представ-
представление Г, образуемое f функциями г|^0), содержит т не-
неприводимых представлений ГФ>:
т
Г=2Г(Р), E.17)
отвечающих одинаковой энергии вследствие случайного
вырождения. Возмущение может снять случайное вы-
вырождение. Предварительно из f функций я|><°> нужно со-
ставить базисные функции неприводимых представлений
Г<Р). Если в разложении E.17) нет кратных неприводи-
неприводимых представлений, то согласно E.15) секулярное урав-
уравнение диагонализуется, причем диагональные матричные
элементы, относящиеся к одному неприводимому пред-
представлению, совпадут. Если же какое-либо неприводимое
представление, например Г(а), входит несколько раз, то
не равны нулю недиагональные матричные элементы

ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ
159
для функций, преобразующихся по одному и тому же
столбцу представления Г<а>. Необходимо решать секуляр-
ное уравнение, порядок которого равен кратности вхо-
вхождения Г<а) в E.17). В обоих случаях, уровень ?<0) рас-
расщепится не более чем на т уровней. Это естественно,
так как по условию возмущение не понизило симметрии,
следовательно, вырождение, обусловленное симметрией
гамильтониана, должно сохраниться.
Рассмотрим теперь случай, когда группа симметрии
возмущения является подгруппой группы симметрии О0
невозмущенного гамильтониана. Оператор V инвариан-
инвариантен относительно преобразований группы Gx cz On. Не-
Неприводимое представление группы по отношению к ее
подгруппе может оказаться приводимым и распасться
на неприводимые представления подгруппы. В этом слу-
случае имеет место расщепление уровня Е(°\ Матричные
элементы будут по-прежнему подчиняться теореме E.15),
если из функций^.0* построить базисные функции непри-
неприводимых представлений группы О\. С помощью таблицы
характеров можно, не прибегая к решению секулярного
уравнения, определить возможное расщепление перво-
первоначально вырожденного уровня, происходящее в резуль-
результате наложения возмущения.
Пусть, например, гамильтониан о%?0 симметричен от-
относительно операций группы Td. Исследуем поведение
трехкратно вырожденного уровня, соответствующего не-
неприводимому представлению Fu при наложении возму-
возмущающего поля с симметрией D2. Выпишем ту часть таб-
таблицы характеров группы Td, которая соответствует опе-
операциям группы D2:
Е
3
-1
С2
-1
Взяв характеры неприводимых представлений группы D2
из Приложения 1, по формуле A.59) находим
„(Si)
1.

160 ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ ГЛ. V
Первоначально трехкратно вырожденный уровень F\
расщепляется на три невырожденных уровня, отвечаю-
отвечающих неприводимым представлениям Ви В2 и В3 груп-
n?i D2. В данном примере возмущение полностью сни-
снимает вырождение.
В качестве другого примера рассмотрим расщепле-
расщепление уровней энергии системы с центрально-симметрич-
центрально-симметричным гамильтонианом при наложении возмущающего
поля октаэдрической симметрии (точечная группа О).
Уровни энергии невозмущенной задачи классифициру-
классифицируются по неприводимым представлениям ZX>> группы /?3-
Уровни энергии возмущенной системы должны класси-
классифицироваться по неприводимым представлениям груп-
группы О, по отношению к которым представления D® яв-
являются приводимыми (за исключением начальных зна-
значений /). Для нахождения^неприводимых представлений
группы О, содержащихся в представлении DU\ харак-
характеры представления D^\ соответствующие операциям
группы О, определяем по формуле C.40). Так, для /=2
E.18)
Подставляя углы а, соответствующие операциям поворо-
поворотов Сг, Сз и С4, получаем приводимое представление
группы О с характерами:
sin
sin
5
~2 a
a
~2
5СB) (а)
Е
5
8С3
-1
6С2
1
6С4
-1
1
Оно распадается на следующие неприводимые пред-
представления:
Следовательно, пятикратно вырожденный уровень с
| = 2 в октаэдрическом поле распадается на двукратно-
и трехкратно вырожденные уровни. В табл. 5.1 приве-

Применение теории групп k квантовой механике 161
дены разложения представлений D^ для нескольких це^
лых значений /.
5-4. Вариационный метод. Как известно, уравнение
Шредингера может быть получено из вариационного
принципа:
= 0. E.19)
В другой формулировке вариационного принципа энер-
энергия Е является множителем Табли а 51
Лагранжа в задаче об ус-
условном экстремуме: Редукция #3 -> О
при
ВИИ
6 J o|)*#i|) dV = 0 E.20)
дополнительном усло-
E.21)
1
2
3
4
5
6
Г"
E + F2
В случае многоэлектронной
системы вариационная функ-
функция г|) обычно ищется в виде линейной комбинации проб-
пробных функций \|?v [38, 43]:
п
^=2<Vi|V E-22)
Функции \J)V должны по возможности лучше соответство-
соответствовать специфике рассматриваемой задачи. Если подста-
подставить E.22) в E.20) и проварьировать коэффициенты cv
при условии E.21), то получим систему уравнений для
определения cv. Эта система имеет не равные нулю ре-
решения при значениях энергии ?, удовлетворяющих се-
кулярному уравнению:
Q/V 22 —
= 0. E.23)
И И. Г. Каплан

162 ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ ГЛ. V
Наличие в E.23) интегралов неортогональности
связано с тем, что пробные функции не всегда являются
ортонормированным набором. Наименьший корень дает
энергию низшего состояния, остальные корни — энергию
более высоких состояний, причем приближение для
них обычно оказывается худшим, чем для низшего со-
состояния.
Интересно отметить, что если при формулировке тео-
теории возмущений вместо возмущения V взять гамильто-
гамильтониан е%? = ей?0+У и считать для общности функции г|^0)
неортонормированными, то модифицированное таким
образом секулярное уравнение E.13) совпадает с урав-
уравнением E.23). Формально, следовательно, вариацион-
вариационный метод совпадает с методом теории возмущений для
вырожденных состояний. Различие этих методов заклю-
заключается в том, что в теории возмущений для вырожден-
вырожденных состояний функции a|^0) принадлежат в нулевом
приближении к одному уровню энергии, в случае вариа-
вариационного метода этого ограничения нет, функции \J)V в
E.22) могут быть любыми.
Расчеты по вариационному методу дают тем более
хорошие результаты, чем больше функций входит в сум-
сумму E.22). Это приводит к секулярным уравнениям боль-
больших порядков, решение которых затруднительно даже
при применении электронно-счетных машин. Например,
задача нахождения уровней энергии системы шести ато-
атомов водорода при учете всех возможных конфигураций,
которые можно построить из шести ls-орбиталей, сво-
сводится к решению секулярного уравнения 924-го порядка
(см. раздел 6-11). Его решение возможно только при
предварительной квазидиагонализации, что достигается
составлением из исходных пробных функций линейных
комбинаций, преобразующихся по неприводимым пред-
представлениям группы симметрии гамильтониана. Такое по-
построение в некоторых случаях может приводить к пол-
полной диагонализации секулярного уравнения. Рассмот-
Рассмотрим эту процедуру подробнее.

ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ 163
Пусть гамильтониан задачи инвариантен относитель-
относительно операций группы G. Разобьем п пробных функций,
входящих в разложение вариационной функции E.22),
на отдельные наборы, функции внутри которых преобра-
преобразуются только друг через друга под действием операций
группы О. Каждый из таких наборов образует пред-
представление группы G. Эти представления, очевидно, не
могут быть шире, чем регулярное, следовательно, в раз-
разложении их на неприводимые части каждое неприводи-
неприводимое представление Г<а> входит число раз не большее,
чем его размерность fa. Построение базисных функций
неприводимых представлений удобно проводить с по-
помощью операторов е^ (см. раздел 1-18). Набор fa
функций {
с фиксированным индексом k образует базис неприво-
неприводимого представления Г<а>. Независимые базисы разли-
различаются индексом k. В тех случаях, когда представление
Г<а) входит в разложение приводимого представления fa
раз, индекс к пробегает все возможные fa значений.
Если же кратность вхождения неприводимого представ-
представления a<a>< fa, то для построения a<a> независимых бази-
базисов представления Г<а> выбираются любые a<a) наборов
операторов е^ с фиксированным вторым индексом. В ка-
качестве i|?v в E.24) может быть выбрана любая из функций
данной совокупности. Если действие оператора effi на i|)
дает нуль, то выбирается следующая функция совокупно-
совокупности, и т. д., пока не получится отличный от нуля результат.
После того как совершено линейное преобразование
от функций i|)v к функциям a|)(^, согласно теореме E.15)
должно произойти значительное упрощение секулярного
уравнения. Диагональные члены, относящиеся к одному
неприводимому представлению, станут равны. Все не-
недиагональные члены обратятся в нуль, за исключением
матричных элементов с базисными функциями, преобра-
преобразующимися по одному и тому же столбцу эквивалент-
эквивалентных неприводимых представлений, т. е. матричных эле-
элементов вида
(^\т\Щ). E.25)
11*

164 ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ ГЛ. V
Интегралы неортогональности также обращаются все в
нуль, за исключением
Следовательно, исходное секулярное уравнение распа-
распадается на секулярные уравнения, относящиеся к крат-
кратным неприводимым представлениям. Порядок секуляр-
ного уравнения, соответствующего неприводимому пред-
представлению Г<а\ равен суммарной кратности вхождения
представления Г<а) в разложение всех приводимых пред-
представлений, образуемых исходным набором функций t|v
Если каждое неприводимое представление появляется
один раз, то имеет место полная диагонализация. При-
Примеры применения вышеописанной методики приведены
в разделах 6-11, 8-8.
5-5. Правила отбора. В предыдущих двух разделах
было показано, что нахождение уровней энергии систе-
системы методом теории возмущений либо вариационным ме-
методом требует вычисления матричных элементов скаляр-
скалярного оператора, принадлежащего к единичному пред-
представлению группы симметрии уравнения Шредингера.
В ряде задач система разбивается на две взаимодейст-
взаимодействующие подсистемы, например, взаимодействие атомов
и молекул с полем фотонов, спин-орбитальное взаимо-
взаимодействие и т. д. При нахождении вероятностей перехода
подсистемы из одного состояния в другое требуется
вычислять матричные элементы от тензорных операто-
операторов. Применение теоремы Вигнера — Эккарта позволяет
существенно упростить вычисление таких матричных
элементов (см. разделы 4-7, 4-8). Более того, теорема
Вигнера— Эккарта дает возможность определить, какие
матричные элементы обращаются в нуль, не прибегая
к их вычислению. Соответствующие правила называются
правилами отбора и могут быть сформулированы сле-
следующим образом:
необходимым условием неравенства нулю матрич-
матричного элемента
{Ы\Т\рй> = J i|><a>Ti|>f dV, E.27)

ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ 165
в котором компоненты тензора Т преобразуются по
представлению Г<т) некоторой группы, а функции
^/a) и ^Т — соответственно по представлениям Г<а>
иГ(Р)той же группы, является наличие в разложении
прямого произведения Г^ХГ^ представления Г<а).
Представление Г<т> обычно является приводимым и
при нахождении правил отбора его удобно предвари-
предварительно разложить на неприводимые представления, осу-
осуществив разложение
Г(г> = 2а(т)Г(т>. E>28)
X
Подынтегральная функция в E.27) принадлежит к
базису представления, являющегося прямым произвел
дением
Г(а)* X Г(Г) х Г(Р). E.29)
Если в прямом произведении IWXF^ содержится Г<а\
то в прямом произведении E.29) обязательно содер-
содержится единичное представление (см. раздел 1-15). В ре-
результате приходим к еще одной формулировке правил
отбора:
необходимым условием неравенства нулю матрич-
матричного элемента E.27) является наличие в разложе-
разложении прямого произведения E.29) единичного пред-
представления.
Рассмотрим несколько примеров на применение пра-
правил отбора. Пусть оператор Т является скаляром по
отношению к операциям группы G. Правила отбора
для этого случая фактически уже были даны в разделе
5-3 (соотношение E.15)). С точки зрения вероятности
квантовых переходов их можно сформулировать следую-
следующим образом:
скалярный оператор индуцирует переходы только
между состояниями с одинаковым типом симмет-
симметрии, т. е. между состояниями, преобразующимися
по эквивалентным неприводимым представлениям;
переходы между состояниями с различным типом
симметрии запрещены.
Вероятность излучательных переходов в дипольном
приближении пропорциональна квадрату матричного

166 ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ ГЛ. V
элемента вектора дипольного момента, который в слу-
случае электрического излучения является полярным век-
вектором, а в случае магнитного — аксиальным вектором *).
Найдем правила отбора для точечной группы D2d. Три
компоненты вектора дипольного момента образуют по
отношению к операциям группы D2d приводимое пред-
представление. Для электрического дипольного момента это
представление распадается на неприводимые представ-
представления В2 и Е. В таблице характеров группы D2d (При-
(Приложение 1) указаны неприводимые представления, по
которым преобразуются компоненты полярного вектора.
Компонента z принадлежит к представлению ?2, ком-
компоненты #, у образуют базис для представления Е. Для
нахождения разрешенных переходов необходимо найти
разложения прямых произведений (В2 + Е)Х Т$\ где Г(Р)
пробегает все неприводимые представления группы D2d.
По формулам A.59), A.61) находим
В2ХВХ = А2, ЕХВг = ?, E.30)
B2XB2^=AU ?Xfi2 = ?,
В2ХЕ = ?, Е X Е = Ах + А2 + Вх + В2.
Из E.30) следует, что для электрического дипольного
излучения, поляризованного по оси 2, разрешены пере-
переходы
Ах*г+Въ А2++Ви ?<->?, E.31)
для излучения, поляризованного в плоскости ху,
Аг, Аъ Ви 52^->?. E.32)
Остальные переходы запрещены.
Согласно таблице характеров группы D2d (см. При-
Приложение 1) г-компонента аксиального вектора принад-
принадлежит к неприводимому представлению Л2, а х-, у-ком-
поненты — к представлению Е. Поэтому правила отбора
*) Обычный, или полярный, вектор меняет знак при инверсии и
остается неизменным при отражении Gv в плоскости, проходящей
через вектор. Аксиальный вектор остается неизменным при инверсии,
но меняет знак при отражении ov Примером аксиального вектора
является векторное произведение двух полярных векторов.

ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ 167
для магнитного дипольного излучения в случае излуче-
излучения, поляризованного в плоскости ху, будут совпадать
с правилами отбора E.32). Для магнитного излучения,
поляризованного по оси г, правила отбора будут уже
отличаться от E.31), аналогичная процедура приводит
к следующим разрешенным в этом случае переходам:
А1++А2, В1<->В2у Е<-+Е. E.33)
Для электрических квадрупольных переходов опера-
оператором в матричном элементе перехода является сфери-
сферический тензор второго ранга. Его пять компонент пре-
преобразуются по представлению DW группы /?3. В случае
переходов между состояниями с симметрией непри-
неприводимых представлений группы /?3 правила отбора сле-
следуют из условия треугольника А(/2/') (см. C.44)).
В случае дискретных точечных групп необходимо раз-
разложить тензор Т№ на неприводимые тензоры соответ-
соответствующей точечной группы, т. е. практически провести
редукцию представления D& на точечной группе. На-
Например, для группы О, согласно табл. 5.1, D{2) = Е + F2.
Далее находим разложение прямых произведений пред-
представлений Е и F2 со всеми неприводимыми представле-
представлениями группы О. В результате получаем следующие
разрешенные переходы:
Е++Аи Л2, ?; Л«-*42. ?, Fu F2\ F2^AU ?, Fu F2.
E.34)
Аналогично находятся правила отбора в случае 2'-
польного излучения любого порядка. -Вначале осуще-
осуществляется разложение представления ДО на неприводи-
неприводимые представления данной точечной группы, после чего
применяется обычная процедура.
При нахождении правил отбора для диагональных
матричных элементов следует учесть, что в случае дей-
действительных волновых функций их произведение в диа-
диагональном матричном элементе образует базис не для
прямого произведения представлений, а для симметри-
симметрического произведения представления самого на себя (см.
раздел 1-15). Эта ситуация осуществляется при от-
отсутствии магнитного поля, когда все волновые функции
могут быть выбраны действительными, так же как и

168 ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ ГЛ. V
представления, по которым они преобразуются. Усло-
Условием неравенства диагонального матричного элемента
нулю является наличие в разложении симметрического
произведения [Г(а)]2 одного из неприводимых представ-
представлений, по которым преобразуется оператор.
Например, в случае группы D2d оператор электри-
электрического дипольного момента принадлежит к представле-
представлению В2 + Е. По формуле A.65) находим характеры сим-
симметрических произведений всех неприводимых представ-
представлений. Разложение их на неприводимые части имеет
следующий вид:
Ш2 - А» [Л2]2 = Аи [Bxf = Аи [S2]2 = Аъ
[Е]2 = А1 + В] + В2.
Поскольку за исключением [Е]2 ни одно из симметриче-
симметрических произведений не содержит представлений ?2, Е,
единственным неисчезающим диагональным матричным
элементом будет матричный элемент с базисными функ-
функциями представления Е.
Молекулярные полосы поглощения в инфракрасной
области спектра обнаруживают, помимо основных ли-
линий, менее интенсивные линии, называемые обертонами
и возникающие вследствие поглощения N квантов основ-
основной частоты. Правила отбора для обертонов такие же,
как и для обычных дипольных переходов. Необходимо
только помнить, что представление, к которому принад-
принадлежат волновые функции конечного состояния, является
симметрической N-й степенью представления, по кото-
которому преобразуется соответствующая нормальная коор-
координата [5]. В разделе 4-3 приведены формулы, позво-
позволяющие легко найти характеры симметрических N-x сте-
степеней представлений при любых значениях N.
Описанная выше процедура нахождения правил от-
отбора соответствует расчетам вероятностей переходов
квантовомеханической системы из состояния 1 в состоя-
состояние 2 в первом приближении теории возмущений, по-
поскольку в этом приближении вероятность перехода про-
пропорциональна квадрату модуля матричного элемента
оператора перехода (обозначим этот матричный эле-
элемент через V12). Может случиться, что для рассматри-
рассматриваемого перехода Vi2 = 0. Во втором приближении тео-

ПРИМЕНЕНИЕ ТЕОРИИ ГРУПП В КВАНТОВОЙ МЕХАНИКЕ 169
рии возмущений квантовый переход рассматривается
происходящим через промежуточные состояния. Этот
случай реализуется, например, в спектрах комбинацион-
комбинационного рассеяния [77]. Вероятность перехода пропорцио-
пропорциональна квадрату модуля суммы по промежуточным со-
состояниям v [5]:
IiV^VJ^-Ej. E.35)
V
Для того чтобы произведения матричных элементов в
E.35) не обращались в нуль, необходимо, чтобы выпол-
выполнялись правила отбора для матричных элементов V\v и
Vv2. Обозначим представления, к которым принадлежат
волновые функции состояний 1, 2 и v, через ГA), Г<2) и
F<v) соответственно, а представление, по которому преоб-
преобразуется оператор в матричных элементах, — через Г<т).
Матричные элементы FV2 не равны нулю лишь для таких
Т<у\ которые содержатся в прямом произведении Г(Т>Х
ХП2). Матричные же элементы Vlv не равны нулю, если
в прямом произведении Г<г> X F<v) содержится представ-
представление ГО). Объединяя эти два условия, получаем, что
необходимым условием неравенства нулю выражения
E.35) является наличие в разложении прямого произ-
произведения г(г) х г(г) х гB) E 36)
представления Г*1).
Этот результат естественно обобщается на п-е при-
приближение теории возмущений. А именно:
необходимым условием разрешения в п-ы прибли-
приближении теории возмущений квантового перехода ме-
между состояниями 1 и 2 является наличие в разло-
разложении прямого произведения
(Г(П х Г*" X ... X Г<г>) х Г<2> E.37)
п
представления Г*1).
Например, дипольный переход (Г^еее/Х1)) в централь-
центральном поле между состояниями, характеризующимися зна-
значениями угловых моментов / и J + k, разрешен только
в k-u приближении теории возмущений, поскольку пред-
представление DW появляется в разложении прямых произ-
произведений, содержащих не менее k представлений W

ГЛАВА VI
КЛАССИФИКАЦИЯ СОСТОЯНИИ
§ 1. Электроны в центральном поле
6-1. Эквивалентные электроны. LS-связь. Известно,
что уравнение Шредингера для многочастичных систем
не допускает точного решения в конечном виде. Возмож-
Возможным способом решения было бы численное табулирова-
табулирование, однако такая таблица даже при очень грубом шаге
табулирования должна быть колоссальных размеров.
Хартри [44] приводит такой пример. Если при табули-
табулировании волновой функции стационарного состояния ато-
атома Fe B6 электронов) ограничиться только десятью зна-
значениями каждой переменной, то составление таблицы
потребовало бы вычисления 1078 значений волновой
функции. Это число превышает общее количество всех
атомов в солнечной системе. Приведенный" пример по-
показывает, что при расчетах многочастичных задач не
только желательно, но совершенно необходимо пользо-
пользоваться приближениями.
При квантовомеханических расчетах многоэлектрон-
Hbfx систем наиболее широко используется так называе-
называемое одночастичное приближение, когда каждый элек-
электрон рассматривается как находящийся в стационарном
состоянии в поле ядер и остальных электронов. Для
атома это поле с хорошей степенью точности можно счи-
считать центрально-симметричным и классифицировать од-
ноэлектронные состояния по неприводимым представле-
представлениям группы 03- Помимо четности, состояние каждого
электрона характеризуется четверкой квантовых чисел
п, U т, а, где п — главное квантовое число, /—-орби-
/—-орбитальный угловой момент, т — его проекция на ось г,
а —проекция спина электрона на ось г. Каждый из элек-
электронов атома обладает своей четверкой квантовых чи-

§ 1
ЭЛЕКТРОНЫ В ЦЕНТРАЛЬНОМ ПОЛЕ
171
сел. Обычно при нахождении уровней энергии атомов с
небольшим атомным весом релятивистскими взаимодей-
взаимодействиями пренебрегают (их учитывают потом в виде воз-
возмущения). В результате спиновые и орбитальные со-
состояния системы электронов рассматриваются незави-
независимо. Это приближение называют случаем Рассель —
Саундерса, или LS-связью.
В приближении LS-связи полный спин электронов 5
и полный орбитальный момент L сохраняются; их зна-
значения характеризуют энергети- .
ческие уровни системы. Каждый
уровень характеризуется также 4
конфигурацией одноэлектронных
состояний, из которых он возни- 3
кает. Для задания электронной
конфигурации достаточно задать
главное квантовое число п и ор-
орбитальный момент / каждого
электрона. Электроны с одинако-
одинаковыми пи/ называются эквива-
эквивалентными. Совокупность эквива-
эквивалентных электронов данного типа
образует оболочку. Так как в со-
соответствии с принципом Паули каждый электрон должен
характеризоваться различным набором квантовых чи-
чисел я, /, т, сг, оболочка (nl)N может содержать не более
2B/-И) электронов*). Оболочка, все состояния кото-
которой заполнены, называется замкнутой.
Полный орбитальный и спиновый моменты получают-
получаются в результате векторного сложения моментов отдель-
отдельных электронов. Сложение угловых моментов, когда чис-
число их невелико, удобно представить в виде диаграммы.
На рис. 6.1 приведена диаграмма для 1=1. Цифры в
кружках указывают число раз, которое встречается
данное значение суммарного момента L в системе N
2 3
Рис. 6.1.
4 N
*) Приведенная выше формулировка принципа Паули вытекает
из более общей формулировки, согласно которой осуществляются
только такие состояния многоэлектронной системы, полная волновая
функция которых антисимметрична относительно перестановок элекг-
ронов.

172 классификация состояний гл. vi
электронов *). Обозначим это число aLN. Поскольку чис-
число состояний в системе N угловых моментов не изме-
изменяется при их векторном сложении,
На примере диаграммы рис. 6.1 легко проверить выпол-
выполнение этого равенства. Так, для Л/ = 4 имеем
ЬЗ + 6.3 + 6.5 + 3.7+1 -9 = 81.
Однако aLN отнюдь не равны числу различных энер-
энергетических уровней конфигурации (nl)N с данным зна-
значением L. Дело в том, что часть состояний с одинако-
одинаковыми L отличается друг от друга только перестановкой
электронов. В силу тождественности электронов такие
состояния должны обладать одинаковой энергией (так
называемое перестановочное вырождение). Другая часть
состояний запрещена, так как не удовлетворяет требо-
требованиям принципа Паули. Истинное число энергетических
уровней в системе эквивалентных электронов изящно
определяется с помощью теоретико-группового рассмот-
рассмотрения.
В нулевом приближении по взаимодействию электро-
электронов координатная волновая функция электронной конфи-
конфигурации (nl)N составляется из произведений N одноэлек-
тронных функций, которые принято называть орбиталями:
<Qnlmx A) <JW2 B) ... 4>nimN (N), F.1)
где число i в аргументе орбитали обозначает совокуп-
совокупность координат /-го электрона. Всего можно образовать
B/+1)^ таких произведений, принадлежащих в отсут-
отсутствие взаимодействия между электронами к одному уров-
уровню энергии. Орбитали cpn/?n, различающиеся значением,
числа т, можно рассматривать как базисные векторы!
2/Н- 1-мерного векторного пространства. При унитарных
преобразованиях этого пространства произведения F.1)
преобразуются по тензорному закону и образуют базис
*) Фактически такая диаграмма соответствует разложению пря1-
мого произведения N неприводимых представлений DW группы /?
на неприводимые представления ?XL>

§1
ЭЛЕКТРОНЫ В ЦЕНТРАЛЬНОМ ПОЛЕ
173
B1+ 1)^-мерного тензорного представления группы ?/2ж-
Разбиение его на неприводимые части разобрано нами в
разделе 4-2. Из результатов этого раздела следует, что
каждое неприводимое представление Uy+i входит в раз-
разложение тензорного представления число раз, равное
размерности /\ неприводимого представления группы пе-
перестановок, характеризуемого той же схемой Юнга [Я],
причем число клеток в столбце схемы Юнга не превы-
превышает 2/+1. Это означает, что всегда существует линей-
линейное преобразование, переводящее исходные B/+!)^
функций F.1) в наборы функций, каждый из которых
характеризуется определенной схемой Юнга из N кле-
клеток с длиной столбца, не превышающей 2/+1, и содер-
содержит /х,6х,B/Н-1) функций, где 6хB/+1)-—размерность
представления Щнх- Функции каждого набора можно
расположить на плоскости в виде прямоугольника
Функции, находящиеся в одной строке этого прямо-
прямоугольника, преобразуются по неприводимому предста-
представлению U21+1. Функции, находящиеся в одном столбце
прямоугольника, преобразуются по неприводимому пред-
представлению ГМ группы jtjv и нумеруются таблицами
Юнга г.
Например, для 1=1, N=4 (конфигурация р4) 81 функ-
функция разбивается на четыре набора соответственно: [к]=
= [4], [31], [22], [212] ([Я] = [14] не осуществляется). По фор-
формулам B.18) и D.13) находим размерности:
[X]
МЗ)
h
[4]
15
1
[31]
15
3
[22]
6
2
[212]
со со

174 КЛАССИФИКАЦИЯ СОСТОЯНИЙ ГЛ. VI
Легко проверить, что S /я*л = 81. Изображая каждую
А*
функцию точкой на плоскости, получаем диаграмму,
аналогичную приведенной в разделе 4-2 для случая /=1,
N = 3:
[4] [31] [22] [212
Унитарные преобразования
Полная волновая функция, описывающая состояния
электронов, должна быть антисимметрична относительно
перестановок электронов. В приближении LS-связи пол-
полная волновая функция 4я может быть представлена
в виде линейной комбинации произведений координат-
координатной волновой функции Ф на спиновую волновую функ-
функцию Q. Применение математического аппарата группы
перестановок позволяет легко выписать искомую линей-
линейную комбинацию. Как доказано в разделе 2-7, для по-
построения антисимметричной функции из бинарных про-
произведений функции-сомножители должны принадлежать
к сопряженным представлениям группы jtjv- Согласно
B.29)
I JMJ (8.2)
V h r
Каждый электрон обладает спиновым угловым момен-
моментом, равным 1/2. Симметризация спиновой функции на
схеме Юнга [к] автоматически приводит к тому, что
функции О;*1, различающиеся значениями проекций спи-
спиновых моментов, преобразуются по неприводимым пред-
представлениям U[k] группы унитарных преобразований U2.
Неприводимые представления Ul2K] характеризуются схе-
схемами Юнга, содержащими не более двух строк. По-
Поскольку схемы Юнга [X] и [К] дуальны друг другу, коор-

§ 1 ЭЛЕКТРОНЫ В ЦЕНТРАЛЬНОМ ПОЛЕ 175
динатные схемы Юнга [X] не могут содержать более двух
столбцов.
В рассмотренной выше конфигурации электронов
осуществляются только орбитальные состояния, соот-
соответствующие на диаграмме прямоугольникам с [Я] = [22]
и [212]. Далее, следует учесть, что функции, расположен-
расположенные в одном столбце прямоугольника, входят в одну ан-
антисимметричную комбинацию F.2), поэтому каждый
столбец отвечает одному физическому состоянию. Число
физически различных орбитальных состояний опреде-
определяется числом столбцов, т. е. равной ^B/+ 1). Всего
имеем б[22] C) + б[212] C) = 9 разрешенных орбитальных
состояний.
Для того чтобы определить значения полного орби-
орбитального момента L, соответствующие разрешенным
представлениям U21+1, нужно проделать редукцию U3->
->/?3; неприводимые представления f/2t+i распадутся при
этом на неприводимые представления DW группы /?3.
Этот процесс подробно описан в разделе 4-5. Для кон-
конфигурации р4 разложение дается соотношениями D.43).
Из них вытекает, что координатные представления от-
отвечают следующим значениям L:
Мкоорд: [22] [212] ,R «.
L = 2,0 L = l F'd)
Им соответствуют ассоциированные представления спи-
спиновых волновых функций, однозначно связанные со зна-
значением полного спина
Мсш»: И [31]
5 = 0 5 = 1
Следовательно, конфигурация четырех эквивалентных
электронов р4 может обладать следующими разрешен-
разрешенными мультиплетами *JS+1L: *S, 3Я, {D. Аналогичными
*) Атомные термы с различным значением полного орбитального
момента L принято обозначать заглавными буквами латинского
алфавита L = 0 12 3 4 5 6 7..
SPDFGHIK
Обозначение S для L = 0 не следует путать с обозначением полгюго
спина системы 5.

176 КЛАССИФИКАЦИЯ СОСТОЯНИЙ ГЛ. VI
мультиплетами обладает также конфигурация р2, яв-
являющаяся дополнением конфигурации р4 до замкнутой
оболочки. Этот результат следует из соотношений экви-
эквивалентности D.36).
Таким образом, для нахождения разрешенных муль-
типлетов конфигурации эквивалентных электронов (nl)N
может быть предложена следующая общая процедура.
Вначале выписываются все разрешенные координатные
схемы Юнга из N клеток, состоящие из двух столбцов
с длиной столбца, не превышающей 2/+1. Каждой ко-
координатной схеме Юнга сопоставляется дуальная ей спи-
спиновая схема Юнга. Разрешенные значения L находятся
в результате редукции ?/?/+1->/?з (практически берут-
берутся из таблиц Приложения 3), мультиплетности выписы-
выписываются, исходя из вида спиновых схем Юнга. Схемати-
Схематически вышеописанная процедура может быть представ-
представлена следующим образом*):
S& с/?1
I . F.4)
Простейшим примером является двухэлектронная
конфигурация (nlJ. Согласно результатам раздела 4-5,
в разложение представления U2i+\ могут входить пред-
представления Z)(L) только с четным значением момента L,
а в разложение U[li+\ — представления D^ с нечетным
значением L. Поскольку спиновым представлениям СД
отвечает 5 = 0, a U[?] — S=ly то применение схемы F.4)
позволяет сделать общее заключение: в случае конфи-
конфигурации электронов (nlJ термы с четным значением L
синглетны, а термы с нечетным значением L триплетны.
*) В случае эквивалентных электронов уже существуют таблицы
разрешенных мультиплетов, найденные другим способом, не требую-
требующим привлечения теории групп [5]. Приведенный здесь теоретико-
групповой способ нагляднее общепринятого, к тому же он позволяет
провести более детальную классификацию в случае повторяющихся
термов. Данный способ представляет и методический интерес, по-
поскольку в ряде более сложных случаев, например при нахождении
разрешенных молекулярных мультиплетов (см. раздел. 6-5), может
Оыть применена сходная методика.

§ 1 ЭЛЕКТРОНЫ В ЦЕНТРАЛЬНОМ ПОЛЕ 177
В качестве другого примера использования методики
F.4) определим разрешенные мультиплеты конфигура-
конфигурации d3. Результаты рассмотрения удобно свести в таб-
таблицу (значения L в первом столбце табл. 6.1 взяты из
табл. 4 Приложения 3).
Таблица 6.1
Разрешенные термы конфигурации d3
Мультиплеты
[21] L=l, 22, 3, 4, 5
[I3] L-l, 3
21] S=l/2
3] S = 3/2
2P, B?>J, *F, 2G, 2H
4P, 4F
6-2. Дополнительные квантовые числа. Число стар-
старшинства. Так как каждому представлению [/^ отве-
отвечает одно представление D(s\ а между координатной и
спиновой схемами Юнга в силу принципа Паули суще-
существует взаимно однозначное соответствие, задание коор-
координатной схемы Юнга [X] эквивалентно заданию значе-
значения полного спина 5. Вместо квантовых чисел L и S
атомные термы могут, следовательно, нумероваться кван-
квантовыми числами L и [X]*). Сопоставление каждому тер-
терму схемы Юнга [к] и орбитального момента L эквива-
эквивалентно классификации орбитальных состояний по не-
неприводимым представлениям групп U2i+l и /?3. Задание
проекции М орбитального момента н~а ось z означает
дополнительную классификацию орбитальных состояний
по неприводимым представлениям группы двухмерных
вращений /?2.
Для конфигурации pN подобная классификация од-
однозначно определяет состояние. Однако в случае конфи-
конфигураций dN и fN одной схеме симметрии [к] может со-
соответствовать несколько одинаковых значений L. Так,
для конфигурации ds два состояния с L = 2 обла-
обладают одинаковой перестановочной симметрией [Я] = [21]
*) Напомним, что, поскольку мы не учитываем релятивистские
взаимодействия электронов, каждый терм вырожден BS+1) BL +
+ 1) раз.

178 классификация состоянии гл. vi
(см. табл. 6.1). Для различения кратных термов удобно
ввести дополнительные квантовые числа *). Естественно
было бы использовать для этой цели неприводимые
представления некоторой подгруппы группы #2/+ь со-
содержащей группу /?3 в качестве своей подгруппы. Рака
[45] показал, что такой дополнительной группой являет-
является группа вращений в 21 + 1-мерном пространстве /?2/+i.
Координатные волновые функции конфигурации в этом
случае строятся таким образом, чтобы они одновремен-
одновременно были базисными функциями неприводимых представ-
представлений следующей цепочки групп:
U2l+l zd R2l+l zd /?3 => /?2. F.5)
Согласно определению группы /?2/+i ее операции
оставляют инвариантным скалярное произведение двух
векторов, заданных в 21 + 1-мерном пространстве. Един-
Единственным скалярным произведением, инвариантным как
по отношению к операциям группы #2/+ь так и группы
/?з, является волновая функция конфигурации /2 в со-
состоянии с L = 0 (см. D.52)):
F-6)
Система двух электронов с L = 0 должна обязательно
обладать и значением 5 = 0 (см. стр. 176). О таких элек-
электронах говорят как о замкнутой паре. Если к конфигу-
конфигурации lN~2 добавить замкнутую пару, то, в силу инва-
инвариантности F.6) по отношению к операциям группы
Rti+u образовавшаяся конфигурация 1N~212AS) будет
обладать теми же неприводимыми представлениями
группы /?2ж, что и конфигурация lN~2. Это обстоятель-
обстоятельство позволяет каждое неприводимое представление
группы /?2/+i характеризовать тем минимальным чис-
числом электронов v конфигурации /и, при котором это
представление впервые появляется. Очевидно, что и термы
со значениями L, соответствующими L-структуре непри-
*) Как правило, такие дополнительные квантовые числа не яв-
являются «хорошими», т. е. матрица гамильтониана недиагональна по
этим числам. Примером взаимодействий, при которых вводимое
ниже число старшинства является хорошим квантовым числом, мо-
могут служить короткодействующие силы, в частности б-силы [64].

§ I ЭЛЕКТРОНЫ 6 ЦЕНТРАЛЬНОМ ПОЛЕ 179
водимого представления группы /?2/+ь отвечающего
данному v, появляются впервые в конфигурации 1°. По-
Поэтому каждый терм можно характеризовать дополни-
дополнительным квантовым числом v. Число v называют числом
старшинства (seniority number). Оно пишется обычно в
левом нижнем углу обозначения мультиплета: 2S+lvL. Так,
два 2D терма конфигурации d3 различаются значениями
числа старшинства и записываются 2\D и \D.
Таким образом, кратные мультиплеты классифици-
классифицируются по значениям числа старшинства и, показываю-
показывающего, в какой конфигурации данный терм появляется
впервые. Наличие в конфигурации lN состояния [X]vL
означает, что в данном состоянии имеется {N — v)/2
замкнутых пар. Подчеркнем, что матрица гамильтониана
многоэлектронной системы недиагональна по числу v.
Это объясняется тем, что в общем случае гамильтониан
не инвариантен относительно операций группы /?гж-
Тем не менее такая классификация значительно упро-
упрощает построение волновых функций кратных термов и
вычисление матричных элементов (см. [25]).
Набор квантовых чисел [к], и, L однозначно харак-
характеризует термы конфигурации dN. Для конфигурации
fN такая классификация оказывается недостаточной, по-
появляются кратные термы, обладающие одинаковыми на-
наборами [Я], у, L. Однако в случае f-оболочки, и только
в этом случае, в цепочку групп F.5) может быть добав-
добавлена еще одна группа, являющаяся группой ортогональ-
ортогональных преобразований семимерного пространства, остав-
оставляющих инвариантной трилинейную антисимметричную
форму [25, 45]. Эту группу принято обозначать G2. В ре-
результате, однозначная классификация состояний конфи-
конфигураций fN осуществляется с помощью неприводимых
представлений расширенной цепочки групп
U7 ZD /?7 => О2 => /?3-ZD /?2. F.7)
6-3. Эквивалентные электроны, уу-связь. В тяжелых
атомах уже в нулевом приближении теории возмуще-
возмущений необходимо учитывать спин-орбитальное взаимо-
взаимодействие. Одноэлектронные уровни энергии характери-
характеризуются значениями полного углового момента электро-
электрона /, получающегося в результате сложения векторов
12*

180 КЛАССИФИКАЦИЯ СОСТОЯНИЙ ГЛ, Vt
орбитального и спинового угловых моментов
j = 1 + s. F.8)
Так как 5=1/2, то при данном / / принимает два значе-
значения: /±1/2. Волновые функции, описывающие состояние
одного электрона, являются в данном случае базисом
неприводимых представлений DW группы /?3, появляю-
появляющихся в разложении прямого произведения D^X/)A/2).
Согласно общей формуле C.45)
2 F-9)
Энергетические термы УУ-электронной системы харак-
характеризуются суммарным угловым моментом /, получае-
получаемым в результате векторного сложения угловых момен-
моментов / отдельных электронов. Такая схема построения энер-
энергетических термов называется схемой //-связи. В схеме
//-связи эквивалентными являются электроны с одина-
одинаковыми значениями п и /. Очевидно, что конфигурация
эквивалентных электронов (nj)N, в силу требования
принципа Паули, не может содержать более 2/+1 элек-
электронов.
Полная волновая функция конфигурации (nj)N в
нулевом приближении по взаимодействию электронов
строится из произведений одноэлектронных орбиталей
F.9)
B) ... $nj*N(N). F.10)
В отличие от случая LS-связи, когда из произведений
F.1) строилась координатная волновая функция Фг >
обладающая перестановочной симметрией схемы Юнга
[К], в случае //-связи из произведений F.10) строится
полная волновая функция, чья перестановочная симмет-
симметрия ограничена только антисимметричным представле-
представлением [X]=[F].
В конфигурации (nj)N разрешены только те значения
полного углового момента /, при которых функция свя-
связанных моментов антисимметрична. Для конфигурации
(я/J из соотношения C.49) следует, что
F.11)

ЭЛЕКТРОНЫ В ЦЕНТРАЛЬНОМ ПОЛЕ
181
так как (—lJj = — 1. Следовательно, / может принимать
только четные значения. В случае произвольной кон-
конфигурации (nj)N разрешенные значения / находятся из
разложения
I/I^-2fl(y)D(y). F.12)
Процедура нахождения подобных разложений описана в
разделе 4-5. В табл. 6.2 приведены разрешенные значе-
значения / для конфигураций (nj)N с /=1/2 -*• 7/2. Приведены
только конфигурации, отвечающие заполнению /-оболо-
/-оболочек не более чем наполовину, так как значения / для
конфигураций (nj)N H(njf!+l~N совпадают.
Таблица 6.2
Разрешенные значения полного углового момента J
конфигурации j
/
1/2
3/2
5/2
7/2
N
1
1
2
1
2
3
1
2
3
4
/
1/2
3/2
0, 2
5/2
0, 2, 4
3/2, 5/2, 9/2
7/2
0, 2, 4, 6
3/2, 5/2, 7/2, 9/2, 11/2, 15/2
0, 22, 42, 5, 6, 8
Для конфигурации G/2L, как следует из табл. 6.2,
термы с 7 = 2 и 4 повторяются два раза. В этом случае,
так же как и при LS-связи, повторяющиеся термы мож-
можно различать числом старшинства v. Кратные термы
конфигурации G/2L делятся на термы с v = 2, получае-
получаемые из соответствующих термов конфигурации G/2J, и
термы с v = 4, впервые появляющиеся в конфигурации
G/2) \

182 КЛАССИФИКАЦИЯ СОСТОЯНИЙ ГЛ. VI
6-4. Конфигурация из нескольких групп эквивалент-
эквивалентных электронов. Рассмотрим вначале конфигурацию двух
неэквивалентных электронов П\1\П212 в схеме LS-связи.
Принцип Паули не накладывает в данном случае ника-
никаких ограничений на возможные значения полного орби-
орбитального момента L и спина S системы. Требование ан-
антисимметричности полной волновой функции может быть
выполнено при любых наборах значений L и S. Это ста-
становится очевидным, если вспомнить, что одноэлектрон-
ные орбитали в центральном поле являются произведе-
произведениями радиальных волновых ,функций Rni(f) на угло-
угловые функции Yim(Q, ф) [5]:
<fnlm(r, 9, ф) -/?ft/(Г) У//я (в, ф). F.13)
В случае эквивалентных электронов радиальные волно-
волновые функции для всех электронов одинаковы. Антисим-
Антисимметричность полной волновой функции достигается со-
составлением соответствующих комбинаций произведений
координатных волновых функций на спиновые; радиаль-
радиальная часть таких комбинаций всегда симметрична от-
относительно перестановок электронов. Это накладывает
ограничения на возможные значения L и S. В случае не-
неэквивалентных электронов радиальные волновые функ-
функции электронов разные. Антисимметричность полной
волновой функции всегда может быть достигнута за счет
антисимметризации радиальных волновых функций.
Следовательно, в системе неэквивалентных электро-
нов осуществляются все возможные значения L и S, ко-
которые могут быть получены в результате векторного
сложения орбитального и спинового моментов отдель-
отдельных электронов.
Конфигурации с числом неэквивалентных электронов
/V>3 характеризуются большим количеством кратных
термов. Для различения кратных термов в качестве до-
дополнительных квантовых чисел могут быть использованы
квантовые числа тех термов конфигурации с числом
электронов N—1, из которых данный терм происходит.
В таких случаях говорят о задании генеалогии терма.
Например, термы конфигурации трех неэквивалент-
неэквивалентных р-электронов npripn"p удобно характеризовать

§ 1 ЭЛЕКТРОНЫ В ЦЕНТРАЛЬНОМ ПОЛЕ 183
заданием термов конфигурации прп'р:
(прп'р): lSn"p, 2Р;
(прп'р): *Sn"p, 2Р, 4Р;
(прп'р): lPn"p, 2SPD\
(прп'р): гРп"р, 2SPD, 4SPD\
(прп'р): lDn"p, 2PDF\
{прп'р): *Dn"py 2PDF, 4PDF.
Так, терм 2Р встречается в данной конфигурации шесть
раз, однако каждый из этих шести термов имеет различ-
различную генеалогию по отношению к конфигурации прп'р.
Всего в конфигурации осуществляется 21 терм, что со-
составляет SBS+ 1)BL + 1) = 216 состояний. Естественно,
что разрешены все Bs+lKB/+ 1K = 216 состояний кон-
конфигурации прп'рп"р. Для трех эквивалентных р-элек-
тронов разрешено всего три терма: !S, !D, 3P или 20
состояний.
Очевидно обобщение на общий случай конфигурации
из нескольких групп эквивалентных электронов *):
/да ... ГкК F.14)
В приближении LS-связи каждая оболочка 1паа характе-
характеризуется заданием схемы Юнга [ка] (однозначно свя-
связанной со значением спина оболочки. 5а), орбитального
момента La и дополнительных квантовых чисел, обозна-
обозначим их аа. Орбитальные состояния всей конфигурации
характеризуются заданием общей схемы симметрии [AJ,
суммарного орбитального момента L и его проекции М.
Кроме того, для однозначной классификации орбиталь-
орбитальных состояний необходимо задать k — 2 промежуточных
орбитальных моментов Lnp (см. раздел 3-7) и k — 2 про-
промежуточных схем Юнга [Хщ>] (см. раздел 2-10), а также
способ связи оболочек, обозначим его А. Задание пол-
полной схемы симметрии орбитального состояния [к] экви-
эквивалентно заданию полного спина системы S. При этом
*) В обозначении конфигурации главные квантовые числа оболо-
оболочек опущены.

184 классификация состояний гл. vi
каждому орбитальному состоянию системы соответ-
соответствуют 25+1 спиновых состояний.
В результате энергетические термы конфигурации
F.14) характеризуются следующим набором квантовые
чисел:
iVN»^ .... «*М«А. [KP]A(LJA> Мш- FЛ5)
При заданных La возможные значения полного орби-
орбитального момента L и набор k—2 промежуточных орби-
орбитальных моментов, обозначенный нами (Lnp)A, опре-
определяются правилами векторного сложения k угловых
моментов. Возможные схемы Юнга [к] и набор k — 2
промежуточных схем [Япр]А определяются либо последо-
последовательным применением теоремы Литтлвуда (см. раз-
раздел 4-4) к внешнему произведению
[AjelAJ® ... ®[А*] F.16)
(при условии, что получаемые при этом схемы Юнга не
содержат более двух столбцов), либо правилами век-
векторного сложения k угловых моментов Sa (ввиду одно-
однозначного соответствия [Xa]«->Sa).
В случае //-связи состояния конфигурации из k групп
эквивалентных электронов характеризуются значениями
полного углового момента / и k — 2 промежуточных
угловых моментов /пр, определяемых правилами вектор-
векторного сложения угловых моментов Ja отдельных оболочек.
Разрешенные значения /а находятся из табл. 6.2.
§ 2. Связь молекулярных термов с ядерным спином
6-5. Классификация молекулярных термов и суммар-
суммарный ядерный спин. Ядерный спин при незначительности
непосредственного влияния на величину молекулярных
термов (сверхтонкое взаимодействие) оказывает суще-
существенное косвенное влияние на разрешенные типы сим-
симметрии термов. При пренебрежении сверхтонкими вза-
взаимодействиями полная волновая функция молекулы мо-
может быть представлена в виде линейной комбинации
произведений координатной волновой функции Ф(х, X)
(х обозначает координаты электронов, X — координаты

§ 2 МОЛЕКУЛЯРНЫЕ ТЕРМЫ И ЯДЕРНЫЙ СПИН 185
ядер) на спиновую функцию ядер Q((?i), где а* обозна-
обозначает спиновые координаты ядер. В отношении переста-
перестановочной симметрии полной волновой функции строго
выполняется так называемый принцип запрета, который
может быть сформулирован следующим образом:
в природе осуществляются только такие состояния
системы тождественных частиц со спином /, полная
волновая функция которых при перестановке лю-
любой пары частиц умножается на (—\J\ т. е. сим-
симметрична при целых значениях / (статистика Бозе)
и антисимметрична при полуцелых / (статистика
Ферми).
Принцип запрета налагает определенную взаимо-
взаимосвязь между перестановочными симметриями коорди-
координатной и спиновой функций, взятых по отдельности. По-
Построение полной волновой функции, антисимметричной
по отношению к перестановкам тождественных ядер, про-
производится аналогично построению полной волновой
функции электронов в системе LS-связи (см. F.2)):
F.17)
где перестановочные симметрии координатной и спино-
спиновой функций характеризуются взаимно дуальными схе-
схемами Юнга из /V клеток.
Для построения симметричной полной волновой
функции координатная и спиновая функции должны об-
обладать одинаковой перестановочной симметрией отно-
относительно координат ядер:
iV- X)Ql"\a{). F.18)
Спиновая волновая функция Q[r ] для системы тож-
тождественных ядер со спином i преобразуется по непри-
неприводимому представлению ?/2*+i группы унитарных пре-
преобразований в 2/+1-мерном векторном пространстве
спинов. Поэтому спиновая схема Юнга [к] не может
иметь более 2/+1 строк (см. раздел 4-2). Это сразу на-
накладывает ограничения на вид координатной схемы Юнга.
В случае целого i она также не может иметь более

186 классификация состояний гл. vi
2/+1 строк, в случае полуцелого i — более 2/+1 столб-
столбцов.
Для ядер со спином /=1/2 значения суммарного спи-
спина / однозначно связаны с видом схемы Юнга, опреде-
определяющей перестановочную симметрию спиновой волновой
функции. Для ядер с произвольным спином i такая од-
однозначность нарушается (ситуация аналогичная сложе-
сложению орбитальных моментов эквивалентных электронов).
Возможные значения суммарного спина / определяются
из разложения
& - 2 «Р/Л F.19)
метод нахождения которого приведен в разделе 4-5 (см.
также Приложение 3).
При нахождении координатной волновой функции
молекулы обычно используют ряд приближений. Вслед-
Вследствие большой разницы в массах скорости движения
электронов значительно превышают скорости движения
ядер, поэтому движение электронов можно рассмат-
рассматривать происходящим в потенциальном поле, создавае-
создаваемом неподвижными ядрами. Электронная волновая функ-
функция и энергетические термы Е(Х) получаются при этом
зависящими от положения ядер X как от параметров.
Далее, учитывается движение ядер в поле с потенци-
потенциальной энергией Е(Х). В этом приближении, называе-
называемом приближением Борна — Оппенгеймера, координат-
координатная волновая функция молекулы может быть представ-
представлена как произведение электронной волновой функции
на ядерную волновую функцию*):
Ф(х, Х) = Ф9Л(*. Х)Фи(Х). F.20)
X в аргументе функции F.20) обозначает совокупность
Ъп координат ядер, отвечающих Ъп степеням свободы
системы п ядер. Из этих Зп степеней свободы три со-
соответствуют поступательному движению молекулы как
целого и могут быть исключены переходом в систему ко-
координат, связанную с центром инерции молекулы. Три
степени свободы соответствуют вращению молекулы как
*) Приближение F.20) часто называют адиабатическим при-
приближением (относительно критериев его применимости см. [46], § 116).

§ 2 МОЛЕКУЛЯРНЫЕ ТЕРМЫ И ЯДЕРНЫЙ СПИН 187
жесткого тела*). Оставшиеся Зп — 6 степеней свободы
связаны с колебательным движением ядер друг относи-
относительно друга. В качестве координат колебательного дви-
движения обычно выбирают так называемые нормальные
координаты, приводящие выражение для энергии малых
колебаний к сумме квадратов [5, 46]. При предположе-
предположении, что относительные смещения ядер от положений
равновесия невелики, электронная волновая функция
может быть взята при равновесной конфигурации ядер.
Координатная волновая функция молекулы F.20) пред-
представляется в виде произведения волновых функций каж-
каждого типа движения:
Ф(*. Х) = Ф9Л(х, Х°)Фкол(<Э)Фвр(#), F.21)
где х — координаты электронов, Х° — координаты равно-
равновесной конфигурации ядер, Q —нормальные колебатель-
колебательные координаты и Ф — совокупность трех углов Эйлера,
определяющих ориентацию молекулы в пространстве.
Приближение F.21) предполагает, что ядра совер-
совершают малые колебания около положений равновесия,
отвечающих равновесной конфигурации молекулы. По-
Потенциальная энергия системы ядер в этом приближении
инвариантна лишь относительно тех перестановок тож-
тождественных ядер, которые соответствуют вращениям или
отражениям равновесной конфигурации ядер. Электрон-
Электронные и колебательные уровни энергии классифицируются
по неприводимым представлениям Г(а) точечной группы
симметрии молекулы, а волновые функции являются
базисными функциями представлений* ПЧ Так как в об-
общем случае не все перестановки тождественных ядер
осуществляются при операциях точечной группы, то по-
последняя изоморфна подгруппе группы перестановок тож-
тождественных ядер nN. Для построения базисных функций
представлений группы перестановок из базисных функ-
функций ее точечной подгруппы необходимо исходить из
N\fg равновесных конфигураций ядер, отличающихся
друг от друга перестановками тождественных ядер, не реа-
реализуемых при операциях точечной симметрии (g обозна-
*) Для линейных молекул вращение вокруг оси молекулы не
имеет смысла, поскольку момент инерции молекулы относительно
этой оси считается равным нулю. Поэтому в случае линейных моле-
молекул имеется Зя—5 независимых колебательных степеней свободы.

188 КЛАССИФИКАЦИЯ СОСТОЯНИЙ ГЛ. V!
чает в данном случае порядок точечной группы). Это по-
построение осуществляется действием соответствующих опе-
операторов Юнга на базисные функции представлений Г<а>.
Возникает вопрос: какие представления Т[Ч можно
построить на базисе представления Г(а) при расширении
точечной подгруппы до лолной группы перестановок.
Ответ на этот вопрос дает теорема взаимности Фробе-
ниуса*):
приводимое представление Г группы G, которое
можно построить на базисе неприводимого пред-
представления Г<Л) подгруппы//е G, содержит каждое
неприводимое представление Г(я) группы G столько
же раз, сколько раз в разложении представления
П#) при редукции 0->Н содержится представле-
представление Г<4
Следовательно, количество независимых базисов пред-
представления Г[Ч которые могут быть построены из базиса
представления Г<а), дается коэффициентами разложения
тп[А»] • ^у! ((Х)тр'(Х) /л qq\
а
Коэффициенты а%] находятся по формуле A.59) с по-
помощью таблиц характеров точечной группы и группы
перестановок. Предварительно необходимо каждой опе-
операции точечной группы сопоставить соответствующую
перестановку ядер.
Связь между перестановочными симметриями коор-
координатной и спиновой функций зависит от статистики
ядер (см. соотношения F.17), F.18)). Наличие такой
связи и учет разложений F.22) и F.19) позволяют каж-
каждому типу точечной симметрии Г<а) сопоставить возможные
значения суммарного ядерного спина /. Схематически ме-
метод нахождения разрешенных ядерных молекулярных
мультиплетов [47] может быть представлен следующим
образом:
а) Статистика Бозе б) Статистика Ферми
|| II F.23)
1 <—> U 1 •*—>• U
*) Доказательство теоремы см. в [41], стр. 224.

МОЛЕКУЛЯРНЫЕ ТЕРМЫ И ЯДЕРНЫЙ СПИН
189
Классы Tj
Классы я4
Е
{V}
с3
{13}
с.
И22)
st
{4}
Рассмотрим несколько примеров.
1. Молекула метана С12Н4*), /(С12)=0, /(Н) = 1/2;
точечная группа симметрии Td изоморфна группе л4.
Между классами этих групп существует взаимно одно-
однозначное соответствие, а именно:
F.24)
Взаимно однозначное соответствие должно быть и между
неприводимыми представлениями. Сравнивая таблицы
характеров, находим:
F.25)
Для /=1/2 осуществляются спиновые схемы Юнга
Мсшш: [4], [31], [22],
1:2, 1, 0.
Им соответствуют координатные схемы Юнга
Мкоорд: [I4], [212], [22]
или согласно F.25) неприводимые представления
В результате получаем следующие разрешенные муль-
типлеты:
Неприводимые пред-
представления Та
Неприводимые пред-
представления я4
[4]
А2
Е
[2Ц
Ft
[212]
Fa
[31]
2. Дейтерозамещенный метан C12D4, /(D) = l. Точеч-
Точечная группа такая же, как и у метана СН4. Ядра подчи-
подчиняются статистике Бозе. Выпишем возможные спино-
спиновые схемы Юнга вместе со значениями суммарного
*) Верхний индекс у символа химического элемента обозначает,
к какому изотопу относится ядро. Ядра различных изотопов могут
обладать разными спинами.

190
КЛАССИФИКАЦИЯ СОСТОЯНИЙ
ГЛ. VI
ядерного спина, взяв последние из табл. 2 Приложе-
Приложения 3,
[4W [4], [31], [22], [212];
/ : 4, 2, 0; 3, 2, 1; 2, 0; 1.
Координатные схемы Юнга совпадают со спиновыми.
Учитывая соответствие между неприводимыми представ-
представлениями F.25), получаем следующие разрешенные муль-
типлеты:
*AXEF2,
lAxE.
F.27)
' 3. Молекула этилена С2 Н4, точечная группа сим-
симметрии D2h. Так же как и в случае метана, возможные
спиновые схемы Юнга
Mew W, [31], [24,
/ : 2, 1, 0.
Им соответствуют дуальные координатные схемы Юнга
[Я]кооРД:[14], [212], [22].
Однако группа я4 шире точечной группы D2ju содер-
содержащей 8 операций. В табл. 6.3 приведены соответствие
между классами этих групп, а также характеры непри-
неприводимых представлений Г[Ч отвечающих операциям то-
точечной группы (ось С2 выбрана по связи С = С, ось С2
перпендикулярна плоскости молекулы).
Таблица 6.3
Характеры неприводимых представлений группы я4,
соответствующие операциям группы D2h
Классы D2h
Классы я4
Х[1']
зс12'2'
Е
{I4}
1
3
2
С2
{22}
1
-1
2
су
{22}
1
-1
2
cz
{22}
1
-1
2
I
{22}
1
1
2
V
{22}
1
1
2
°хг
{22}
1
-1
2
°ху
{I4}
1
3
2

§ 2 МОЛЕКУЛЯРНЫЕ ТЕРМЫ И ЯДЕРНЫЙ СПИН 191
Разложения представлений Г^ на неприводимые пред-
представления группы D2h имеют следующий вид:
Таким образом, для молекулы этилена осуществляются
следующие ядерные мультиплеты:
5Л 3d d d \д /o\ (a ъц\
fig, LJ^gD2iilJ2,iiy ^g\^/' yJ.Ao)
6-6. Нахождение ядерных статистических весов коор-
координатных состояний. В предыдущем разделе было по-
показано, как методы теории групп позволяют находить
разрешенные типы координатной симметрии и соот-
соответствующие им значения суммарного ядерного спина.
В нулевом приближении по взаимодействию ядерных
спинов все ядерные мультиплеты с данным типом сим-
симметрии координатной волновой функции относятся к од-
одному уровню энергии. Кратность вырождения энергети-
энергетического уровня Г<а) по отношению к спиновым состоя-
состояниям ядер называют ядерным статистическим весом
уровня; обозначим его p^j.
Если молекула состоит из ядер со спином i=0 и
одной группы тождественных ядер с не равным нулю
спином, то ядерный статистический вес терма Па> равен
сумме всех его мультиплетностей, умноженных на крат-
кратность каждого мультиплета; обозначим ее а$+[, т. е.
Р^а) = 2 а<а>+1 B/ + 1). F.30)
Формула F.30) позволяет легко подсчитать ядерные
статистические веса термов, если их мультиплетности
известны. Выпишем, например, ядерные статистические
веса разрешенных термов молекул, рассмотренных в пре-
предыдущем разделе, проставляя значение р^а) в виде мно-
множителя перед обозначением терма:
С12Н4: 5Л2, 1?, 3/^;
C12D4: 9Л1? 6?, 3FU 15F2; F.31)
QT—I • 7/1 Q D QD OD
2 Г14. / Л», OJD^gy OIj2ui 3™2um

192 классификация состояний гл. vi
При наличии в молекуле, помимо тождественных ядер
со спином f, также различных одиночных ядер с ia=t=0
статистические веса, получаемые от учета тождествен-
тождественных ядер, необходимо умножить на число спиновых со-
состояний одиночных ядер; обозначим его у. Если прону-
пронумеровать одиночные ядра индексом а, то
Y = IIB/a + l). F.32)
а
Полное число спиновых состояний молекулы равно
Ряд = Y 2 Р<а>/„ = B/ + 1)" П B1а + 1), F.33)
а а
гДе Ряад учитывает только вклад тождественных ядер,
fa — размерность неприводимого представления Г<4
Ядерные статистические веса термов могут быть най-
найдены и без предварительного определения разрешенных
значений суммарного ядерного спина [5, 48—50]. Изла-
Излагаемый ниже метод исходит из схемы F.23), но не тре-
требует осуществления разложения F.19).
Рассмотрим молекулу, состоящую из группы тожде-
тождественных ядер со спином i и одиночных ядер, число спи-
спиновых состояний которых равно у (см. F.32)). Для си-
системы тождественных ядер может быть построено
Bi+l)N различных спиновых функций. Эти Bi+l)N
функций, так же как в случае конфигурации эквива-
эквивалентных электронов lN (см. раздел 6-1), линейным пре-
преобразованием могут быть разбиты на неприводимые на-
наборы функций. Каждый такой набор характеризуется
определенной схемой Юнга [к] из N клеток с длиной
столбца, не превышающей 2i + l, и содержит fK8xBi+l)
функций. Эти функции можно расположить в виде пря-
прямоугольной матрицы
Спиновые функции, находящиеся в одном столбце, об-
образуют базис неприводимого представления Г^ группы

§ 2 МОЛЕКУЛЯРНЫЕ ТЕРМЫ И ЯДЕРНЫЙ СПИН 193
перестановок и при составлении полной волновой функ-
функции по формулам F.17), F.18) войдут в одну линейную
комбинацию. Число различных полных волновых функ-
функций, которые можно составить для координатного со-
состояния П^ равно 6^B/+1) в случае симметричной пол-
полной волновой функции и 8%Bi+l)—в случае антисим-
антисимметричной*). Очевидно, что
fixB/+l)=SaL7)B/+l), F.34)
/
где а^ определяется разложением F.19). В то же вре-
время 6хB/+1) может быть вычислено независимо по фор-
формуле D.13).
Количество координатных состояний Г*Ч которые мо-
могут быть построены из координатных состояний с точеч-
точечной симметрией Г<а>, равно, согласно теореме Фробениу-
са, коэффициентам а^ разложения F.22). В результате
приходим к следующим формулам для ядерного ста-
статистического веса р^:
а) Статистика Бозе б) Статистика Ферми
Pjg = Y S <\B1 + 1) pg) = v 2 ajj%B/ + !)¦ F.35)
Л» А»
Изложенный метод особенно прост для молекул, то-
точечная группа симметрии которых изоморфна группе пе-
перестановок тождественных ядер. В этом случае сумма
по X в формулах F.35) пропадает, коэффициенты afk)
равны 1 либо 0. В более сложных случаях, например
для молекул, состоящих из нескольких групп тождест-
тождественных ядер, ядерные статистические веса проще нахо-
находить, осуществляя разложение представления, образуе-
образуемого спинами ядер при операциях точечной группы, не-
непосредственно на неприводимые представления точечной
группы (см. [5], § 105).
*) Отметим, что, поскольку все /^ координатных волновых функ-
функций, принадлежащих базису представления Г* \ при построении пол-
полной волновой функции входят в одну линейную комбинацию, они
описывают одно физическое состояние.
13 И. Г. Канлан

194 классификация состояний гл. vi
6-7. Статистические веса вращательных уровней и
молекулярные спин-модификации. Развитые в разделах
6-5 и 6-6 методы позволяют при заданных разрешенных
типах симметрии полной координатной функции F.21)
определить возможные типы симметрии координатных
функций отдельных видов движения. Рассмотрим, на-
например, вращательное движение молекулы, находящей-
находящейся в основных электронном и колебательном состоя-
состояниях. Для большинства молекул электронная волновая
функция основного состояния полностью симметрична,
т. е. принадлежит к единичному представлению точеч-
точечной группы симметрии молекулы. Волновая функция
низшего колебательного состояния также принадлежит
к единичному представлению. Следовательно, в данном
случае симметрия координатной волновой функции F.21)
относительно преобразований точечной группы совпа-
совпадает с симметрией вращательной волновой функции.
Определение разрешенных вращательных термов и
их ядерных статистических весов наиболее просто для
двухатомных молекул. Точечная группа симметрии двух-
двухатомных молекул с одинаковыми ядрамиZ)^ = COOVX Ct.
Неприводимые представления группы Ct характеризуют
поведение координатной функции F.21) относительно
инверсии. Поскольку практически для всех молекул в
основном состоянии Фэл при инверсии не меняется, а
Фкол для двухатомных молекул всегда полностью сим-
симметрична, то операции группы Сг-, затрагивают только
Фвр. Поведение вращательных функций при операциях
инверсии определяется множителем (—1)к, где К обо-
обозначает орбитальный момент количества движения мо-
молекулы. (Вращательные уровни энергии связаны со зна-
значением К простым соотношением
в* = -5Г *(*+!), F.36)
где /0 — момент инерции молекулы.) Симметричные от-
относительно инверсии состояния Ag осуществляются при
четных значениях К> антисимметричные относительно ин-
инверсии состояния Аи осуществляются при нечетных зна-
значениях К. Операция инверсии соответствует переста-
перестановке ядер молекулы, поэтому группа Ct изоморфна

МОЛЕКУЛЯРНЫЕ ТЕРМЫ И ЯДЕРНЫЙ СПИН
195
группе перестановок Я2. Между неприводимыми пред-
представлениями этих групп существует взаимно однознач-
однозначное соответствие
Ci
К
[2]
четные
[Р]
Аи
нечетные
После того как установлена взаимосвязь между пере-
перестановочной симметрией координатной волновой функ-
функции и вращательными состояниями, ядерные статисти-
статистические веса вращательных уровней легко находятся по
правилам предыдущего раздела.
Найдем ядерные статистические веса вращательных
уровней молекул Н2 и D2. Для наглядности обе моле-
молекулы рассмотрим параллельно.
а) Н2(/=1/2, статистика Ферми)
Лкпин •
/ :
-]кооРд:
К :
Ряд •'
б) D2
[
1, 3,
(/= 1
Men,
/
^jKOOp
к
Pan
[2]
1
[I2]
5,
1
0,
[I2
0
[2
2,
3
, статистика
•
;
:0
[21
0, 2
[2]
, 2,
6
4
1,
1
]
4, ...
Бозе)
[I2]
1
[I2]
3, 5
3
В связи со слабостью взаимодействия ядерных спи-
спинов с электронами переходы между состояниями с раз-
различной симметрией ядерных спиновых функций крайне
маловероятны. Поэтому молекулы, находящиеся в со-
состояниях с различной симметрией [Х]СПИн, ведут себя
13*

196 классификация состояний гл. vi
практически как различные модификации вещества, ко-
которые принято называть спин-модификациями. Двух-
Двухатомные молекулы, находящиеся в состояниях с боль-
большим ядерным статистическим весом, называют орто-
модификациями, а находящиеся в состояниях с мень-
меньшим весом—парамодификациями. Для Н2 Рорто/рпара =
= 3:1, ДЛЯ D2 Рорто/рпара = 2 : 1.
Как показано выше, состояния с четными и нечет-
нечетными значениями вращательного момента К осуществ-
осуществляются с разными ядерными статистическими весами.
Для молекул, ядра которых не обладают спином, неко-
некоторые значения К могут быть вообще запрещены.
Рассмотрим, например, молекулу о26- Ядра изотопа
кислорода О16 имеют 1 = 0 и подчиняются статистике
Бозе. Следовательно, координатная волновая функция,
совпадающая в данном случае с полной, может быть
только симметричной относительно перестановок ядер,
т. е. принадлежит неприводимому представлению П21
Основное электронное состояние молекулы кислорода,
обозначаемое 32~, симметрично относительно инверсии
и меняет знак при отражениях ov в плоскости, проходя-
проходящей через молекулярную ось. Так как для двухатомных
молекул инверсия эквивалентна перестановке ядер, то
электронная волновая функция основного состояния мо-
молекулы О2 симметрична относительно перестановки ядер.
Отсюда следует, что и вращательная волновая функция
должна быть симметрична относительно перестановки
ядер. Последнее осуществляется только при четных зна-
значениях /С Следовательно, для молекулы О26 в основном
электронном состоянии нечетные значения вращатель-
вращательного момента запрещены.
В состоянии теплового равновесия вращательная ста-
статистическая сумма гомоядерных молекул с не равным
нулю спином ядер должна складываться из враща-
вращательных сумм для орто- и парамодификаций, умно-
умноженных на соответствующие ядерные статистические
веса:
Н2: ZBp = 3ZX + Z2,
П • 7 - 47 i fi7
LJ- ^вр — oL\ -f- oZ2,

§ 2 МОЛЕКУЛЯРНЫЕ ТЕРМЫ И ЯДЕРНЫЙ СПИН 197
где*)
Z2= 2 (
К=0, 2, 4, ..•
Однако тепловое равновесие в смеси двух модификаций
устанавливается очень долго. Поэтому в отсутствие спе-
специальных катализаторов имеющиеся смеси модифика-
модификаций обычно неравновесны.
Многоатомные молекулы также могут находиться в
различных спин-модификациях, практически не смеши-
смешивающихся друг с другом. Для этого необходимо, чтобы
состояния с различной симметрией спиновой волновой
функции относились к энергетическим уровням, интер-
интервалы между которыми велики по сравнению с энергией
взаимодействия ядерных спинов. В противном случае
внутримолекулярное взаимодействие ядерных спинов с
электронным движением приводит к смешению спин-
модификаций. Спин-модификации многоатомных моле-
молекул классифицируются по неприводимым представле-
представлениям точечной группы вращения молекулы.
При нахождении вращательных уровней энергии мно-
многоатомной молекулы, рассматриваемой как жесткий ро-
ротатор, различают три случая.
1. Асимметричный волчок — все три главных момента
инерции молекулы различны. Молекулы такого типа
либо вообще не имеют осей симметрии, либо обладают
осями симметрии второго порядка.
2. Симметричный волчок — два главных момента
инерции одинаковы. Это имеет место для всех молекул,
обладающих одной осью симметрии, порядок которой
выше второго.
3. Шаровой волчок — все три главных момента инер-
инерции совпадают, К этому классу относятся молекулы, об-
обладающие симметрией одной из кубических точечных
групп.
*) В суммах F.38) для Н2 и D2 величина момента инерции /0,
входящего в выражение для энергии &к} различна.

198
КЛАССИФИКАЦИЯ СОСТОЯНИЙ
ГЛ. VI
Для асимметричного волчка каждому значению угло-
углового момента J соответствует 27+1 невырожденных
уровней энергии*). Гамильтониан, отвечающий враще-
вращению тела произвольной формы, инвариантен относи-
относительно операций точечной группы D2. Поэтому уровни
энергии асимметричного волчка можно классифициро-
классифицировать по неприводимым представлениям этой группы. Как
показывает непосредственный подсчет, для каждого /
имеется следующее распределение уровней данного типа
симметрии [5]:
F.39)
Примером молекулы типа асимметричного волчка
является молекула этилена С22Н4. Молекула имеет центр
симметрии, поэтому ее точечная симметрия D2h. Раз-
Разрешенные типы симметрии и ядерные статистические
веса полной координатной функции найдены в преды-
предыдущем разделе (см. F.31)). Если в соответствии с при-
принятой терминологией четные относительно инверсии со-
состояния называть положительными и обозначать знаком
плюс, а нечетные — отрицательными и обозначать зна-
знаком минус, то вращательные уровни этилена классифи-
классифицируются следующим образом:
(+) И
7А, ЗВ^ ЗВ2, ЗВ3- F.40)
Каждое из неприводимых представлений F.40) отве-
отвечает определенному энергетическому уровню. Всего, в
соответствии с четырьмя неприводимыми представле-
Четные /
Нечетные /
А
//2+1
(/-0/2
//2
(/+0/2
*) Здесь и ниже, говоря о вырождении вращательных уровней,
мы имеем в виду вырождение, связанное с различными направлени-
направлениями углового момента относительно молекулы. Помимо этого, всегда
существует 2/+1-кратное вырождение по направлениям углового
момента относительно неподвижной системы координат.

f 2 МОЛЕКУЛЯРНЫЕ ТЕРМЫ И ЯДЕРНЫЙ СПИН 199
ниями группы D2h, молекула этилена может находиться
в четырех спин-модификациях, ядерные статистические
веса которых находятся в отношении 7:3:3:3.
В случае молекул типа симметричного и шарового
волчков имеет место вырождение вращательных уров-
уровней*). Представление, образуемое вращательными вол-
волновыми функциями, принадлежащими к одному уровню
энергии, может быть приводимо по отношению к опера-
операциям точечной группы симметрии молекулы. В этом слу-
случае ядерный статистический вес вращательного уровня
будет равен сумме ядерных статистических весов непри-
неприводимых представлений точечной группы, входящих в
разложение исходного приводимого представления. Для
нахождения вращательной статистической суммы необ-
необходимо еще учесть вырождение, связанное с инверсией
молекулы, т. е. просуммировать по положительным и
отрицательным уровням.
Рассмотрим эту процедуру на примере молекулы типа
шарового волчка, например, С12Н4, группа симметрии
Td. Вращательные уровни шарового волчка вырождены
по 27+1 направлениям момента / относительно моле-
молекулы. Ядерные статистические веса координатных со-
состояний молекулы С12Н4 найдены в разделе 6-6. Разре-
Разрешено три типа термов: 5Л2, 3-Fj, IE. Группа Та наряду
с поворотами содержит операции отражения ad. Поведе-
Поведение вращательных функций может быть определено толь-
только по отношению к поворотам вокруг осей. Однако за-
задание поведения вращательной функции по отношению
к повороту С2 вокруг оси, перпендикулярной плоскости
симметрии, определяет поведение полной координатной
функции относительно отражения ва, если ее поведение
относительно инверсии / задано, так как
od = IC2. F.41)
Если плоскости симметрии группы Td заменить перпен-
перпендикулярными им осями второго порядка, то получим
группу О, изоморфную Td. Разложение неприводимых
представлений DW при редукции /?3->О приведено в
*) См. примечание на стр. 198.

200
КЛАССИФИКАЦИЯ СОСТОЯНИЙ
ГЛ. VI
табл. 5.1. Соответствие между типами симметрии вра-
вращательной функции и полной координатной функции
определяем по таблицам характеров групп Td и О с уче-
учетом соотношения F.41) *). Результаты рассмотрения
удобно представить в виде табл. 6.4.
Таблица 6.4
Классификация вращательных состояний
молекулы метана
Значения
/
0
1
2
3
4
Типы симметрии
вращательных состояний
Ах
Fx
Е, F2
А2, Fu F2
Ль Е, Fu F2
Типы симметрии и ядерные
статистические веса полной
координатной функции
(+)
\Е
5Л2, З/7!
l?, SF{
<-)
5Л2
IE, 3F{
5Л2, 1?, 3F,
Как видно из табл. 6.4, возможность инверсии при-
приводит к удвоению только вращательных состояний типа
Е. Вращательные состояния с симметрией А\ и F2 отве-
отвечают отрицательным координатным функциям с сим-
симметрией А2 и F\ соответственно.
При справедливости классификации энергетических
состояний метана по неприводимым представлениям то-
точечной группы Td метан существует в виде трех раз-
различных спин-модификаций. Каждая спин-модификация
характеризуется своей вращательной статистической сум-
суммой. Для нахождения статистического веса координат-
координатного состояния с симметрией Па) необходимо учесть, что
принадлежащие к нему fa координатных функций при
*) Поскольку группа Td не содержит центра симметрии, построе-
построение из базисных функций ее неприводимых представлений собствен-
собственных функций оператора инверсии производится непосредственным
действием соответствующих операторов проектирования, а именно

§ 2 МОЛЕКУЛЯРНЫЕ ТЕРМЫ И ЯДЕРНЫЙ СПИН 201
составлении полной волновой функции войдут в сочета-
сочетании со спиновыми функциями в одну линейную комби-
комбинацию. Поэтому каждое неприводимое представление Г<а>
при нахождении статистического веса учитывается как
одно состояние. Далее, следует учесть еще 2/+1-крат-
2/+1-кратное вырождение по направлениям углового момента в
пространстве. В результате вращательная статистиче-
статистическая сумма отдельной спин-модификации может быть
представлена следующей формулой:
Zg - Pg S Of+ + af) B/ + l)e-*(<*lT9 F.42)
где af)+ — кратность вхождения положительного коор-
координатного состояния с симметрией Г<а) в приводимое
представление, образуемое 2/+1 вращательными функ*
циями, р<2—ядерный статистический вес состояния Г<а>,
е(уа) — энергия вращательного уровня шарового волчка,
дополнительный значок а в энергии учитывает возмож-
возможность расщепления вращательного уровня с данным J
в кристаллическом поле симметрии Td.
Типы симметрии и ядерные статистические веса ко-
координатных состояний метана, осуществляющиеся при
начальных значениях /, приведены в табл. 6.4. Подстав-
Подставляя приведенные там значения в формулу F.42), полу-
получаем вращательные статистические суммы для каждой
из трех спин-модификаций метана:
...), F.43)
В газообразном метане вращательные уровни класси-
классифицируются только по значению углового момента /.
Вследствие того, что, начиная с / > 2, имеет место вы-
вырождение по неприводимым представлениям точечной
группы, внутримолекулярные спиновые взаимодействия
должны эффективно смешивать спин-модификации [76].
В состоянии теплового равновесия
ZBp = S Zjg = 5 + 9e"El/r + 2&е?т + 77e~e'IT + 177е^/т +...
* F.44)

202
КЛАССИФИКАЦИЯ СОСТОЯНИЙ
ГЛ. VI
Интересно отметить, что небольшое искажение рав-
равновесной конфигурации симметричной молекулы, почти
не меняющее энергию, приводит к скачкообразному из-
изменению вращательной статистической суммы. Это свя-
связано с увеличением статистических весов вращательных
уровней при понижении симметрии молекулы. Пусть, на-
например, в результате искажения конфигурации метан
становится асимметричным волчком с точечной симмет-
симметрией D2h Вращательные уровни энергии молекулы бу-
будут теперь классифицироваться по неприводимым пред-
представлениям группы Ьъ соответствие их значениям уг-
углового момента / приведено выше, см. F.39). Ядерные
статистические веса в данном случае такие же, как и у
этилена (см. F.40)). Выпишем результаты редукции
RZ->D2 для начальных значений /.
J
0
1
2
3
4
1АХ
1
2
1
3
35,
1
1
2
2
ЗВ2
1
1
2
2
зв
1
1
2
2
Вращательная статистическая сумма при пренебреже-
пренебрежении расщеплением уровня энергии с данным / (искаже-
(искажение шарового волчка мало) приобретает следующий вид:
ZBp = 7
F.45)
Значение ZBp, вычисленной по формуле F.45), долж-
должно значительно превышать ZBp из формулы F.44). Сле-
Следовательно, в точке изменения симметрии молекулы
имеет место скачок вращательной статистической суммы.
Причиной такого скачка является уменьшение незави-
независимых вращательных состояний при переходе к более
симметричной молекулярной конфигурации. Этот эффект
имеет место и в классической статистике (см. следую-
следующий раздел).

§ 2] МОЛЕКУЛЯРНЫЕ ТЕРМЫ И ЯДЕРНЫЙ СПИН 203
6-8. Переход от вращательной статистической суммы
к интегралу состояний. Число симметрии. Совершим
предельный переход от квантовой вращательной суммы
к классическому интегралу состояний для молекулы
типа шарового волчка. Равновесная по спин-модифика-
спин-модификациям вращательная статистическая сумма для моле-
молекулы с симметрией Td дается выражением F.42), про-
просуммированным по а (вращательные уровни энергии
считаем зависящими только от /),
F.46)
При высоких температурах, когда T^&j, основной вклад
в сумму F.46) дают члены с большими /. Однако при
больших значениях углового момента вращение квази-
классично, что позволяет заменить сумму по / соответ-
соответствующим интегралом. Далее, можно приравнять af)+
и af) , так как при больших / представление D<J) содер-
содержит наборы регулярных представлений, так что поло-
положительные и отрицательные термы встречаются одина-
одинаковое число раз. Найдем вид af} при больших /. Со-
Согласно A.58)
S F.47)
где R пробегает g операций точечной группы. Если груп-
группу Td заменить изоморфной ей группой О, то все опе-
операции R будут эквивалентны вращениям вокруг осей
симметрии, характеры которых зависят только от угла
поворота а и даются формулой C.40). Для всех опера-
операций, кроме тождественной ?, %(J)(/?) порядка единицы,
для тождественной операции %^ЦЕ) = 2/+1. Следова-
Следовательно, при /->оо основной вклад в сумму F.47) дает
операция Е, откуда следует, что
*&ooe-jB/+l). F.48)

204 КЛАССИФИКАЦИЯ СОСТОЯНИЙ ГЛ. VI
В результате статистическая сумма F.46) переходит в
()
где a=g/2 равно количеству различных поворотов моле-
молекулы вокруг осей симметрии, совмещающих ее саму с
собой. Это число называют числом симметрии молекулы.
Ряд является полным числом ядерных спиновых состоя-
состояний (см. F.33)). Интегрирование по / в F.49) приводит
к классическому значению интеграла вращательных со-
состояний
^/0rf2. F.50)
Таким образом, при высоких температурах враща-
вращательная статистическая сумма переходит в классический
интеграл вращательных состояний, умноженный на число
ядерных спиновых состояний и деленный на число сим-
симметрии молекулы. В проведенном выводе число симмет-
симметрии о естественным образом вошло в классическое вы-
выражение F.49). Число симметрии было введено Эрен-
фестом и Тркалом [52] еще до создания квантовой меха-
механики. Для того чтобы каждое физическое состояние
учитывалось один раз, функция состояний, получаемая
при интегрировании по всем значениям углов поворота,
делилась на число физически неразличимых ориентации
молекулы в пространстве.
Из классического приближения F.49), так же как и
при квантовомеханическом рассмотрении, следует, что
при изменении симметрии молекулы, сопровождающемся
изменением числа симметрии а, вращательная функция
состояний претерпевает скачок.
§ 3. Классификация состояний в приближенных
квантовохимических расчетах
6-9. Метод взаимодействия конфигураций и квазиди-
агонализация секулярного уравнения. Как известно, при-
природа химической связи была объяснена только после со*
здания квантовой механики и введения понятия спина

§ 3 КЛАССИФИКАЦИЯ В КВАНТОВОХИМЙЧЁСКИХ РАСЧЕТАХ 205
электрона. Между тем непосредственного участия в об-
образовании молекул спины электронов не принимают;
взаимодействия, обусловливающие химическую связь,
имеют чисто электростатическую природу. Зависимость
энергии системы электронов от значения их полного
спина S происходит вследствие существования корре-
корреляции между относительным расположением электронов
в пространстве и направлениями их спинов. При пре-
пренебрежении спиновыми взаимодействиями полная вол-
волновая функция системы N электронов согласно F.2) вы-
выражается в виде суммы произведений координатной вол-
волновой функции Ф[г ] на спиновую Й~Х], симметризован-
ных по взаимно дуальным схемам Юнга. Уровни энер-
энергии системы взаимодействующих электронов характери-
характеризуются перестановочной симметрией [к] координатной
волновой функции. Так как спиновые схемы Юнга [к]
однозначно связаны со значением спина S, то каждому
уровню энергии можно приписать определенное значе-
значение полного спина. Все свойства рассматриваемых си-
систем, не связанные со спиновыми взаимодействиями;
вполне определяются заданием координатной волновой
функции электронов Ф^1.
Обычно при квантовомеханических расчетах исходят
из одночастичного приближения. Задается конфигура-
конфигурация из k одноэлектронных координатных орбиталей фа,
на которых определенным образом размещены N элек-
электронов,
Ф>2 ... Ф^, 2 na = N. F.51)
На каждой орбитали, в соответствии с принципом Пау-
Паули, может находиться не более двух электронов, т. е.
na<<2, &>Af/2. При па = 2 наборы квантовых чисел элек-
электронов, сидящих на а-й орбитали, различаются значе-
значениями проекций спинов; говорят, что спины таких элек-
электронов спарены. Одноэлектронные орбитали должны
быть решениями уравнений Хартри — Фока. В тех слу-
случаях, когда такие решения неизвестны, в качестве фа
берутся либо орбитали, локализованные на отдельных
атомах (метод валентных схем), либо молекулярные

206 КЛАССИФИКАЦИЯ СОСТОЯНИЙ ГЛ. VI
орбитали в виде линейной комбинации атомных орбита-
лей (метод МОЛКАО).
Количество конфигураций из k орбиталей, среди ко-
которых га орбиталей двукратно заполнены, а N — 2га —
заполнены однократно, очевидно, равно числу способов
выбора га орбиталей из k (число сочетаний из k по га),
умноженному на число способов распределения остав-
оставшихся N — 2га электронов среди k— га орбиталей, т. е.
равно
n(k, га, АО = \\кт о = мм—о м iu , mi- F.52)
v ' ' \m)\N—2m] m\ (N — 2m)! (k + m — N)\ v 7
Для каждой конфигурации может быть построено
2N-2m различных антисимметричных волновых функций,
поскольку каждый из N — 2га неспаренных электронов
может иметь два различных значения проекций спина.
Общее количество состояний для набора k орбиталей с
N электронами определится суммированием по всем воз-
возможным конфигурациям произведения числа состояний
для одной конфигурации на количество конфигураций
данного типа *):
E(N/2) EWI2)
n(k,N)- ^N2m S t
(
F.53)
Вместо суммирования выражения F.53) число состоя-
состояний может быть найдено непосредственно из следующих
простых соображений. Если орбитали фа приписать опре-
определенное значение проекции спина электрона, то полу-
получим так называемую спин-орбиталь, на которой может
находиться не более одного электрона. Число способов,
которым можно разместить N электронов среди 2k спин-
орбиталей, равно числу сочетаний из 2k no N, т. е.
F.54)
Суммирование по га в формуле F.53) приводит к ре-
результату, эквивалентному формуле F.54) [53].
*) E(N/2) обозначает целую часть числа Nj2<

§ 3 КЛАССИФИКАЦИЯ В КВАНТОВОХИМИЧЕСКИХ РАСЧЕТАХ 207
В нулевом приближении по взаимодействию электро-
электронов волновая функция системы строится в виде линей-
ной комбинации I I антисимметричных функций, со-
составляемых из произведений орбиталей фа на соответ-
соответствующие спиновые функции. Коэффициенты такой ли-
линейной комбинации находятся минимизацией энергии си-
системы (см. раздел 5-4). Вариационный метод, учитываю-
учитывающий различные возможные конфигурации одноэлектрон-
одноэлектронных орбиталей, называют методом взаимодействия кон-
конфигураций. В этом приближении не может быть выде-
выделена определенная конфигурация одноэлектроиных орби-
орбиталей, которой обладает рассматриваемая система. По-
Поэтому метод взаимодействия конфигураций является
улучшением одночастичного приближения. Использова-
Использование достаточно большого количества конфигураций при-
приводит часто к очень хорошему согласию с эксперимен-
экспериментом [38].
При учете всех конфигураций, возникающих из вы-
выбранного набора одноэлектронных орбиталей, порядок
получающегося секулярного уравнения очень велик даже
для небольших систем. Так, для четырех электронов и
четырех орбиталей имеем n(k, N) = 8!/4! 4! = 70 состоя-
состояний. Однако в рассматриваемом приближении разделе-
разделения полной волновой функции на координатную и спино-
спиновую возможна квазидиагонализация секулярного урав-
уравнения. Поскольку гамильтониан молекулы инвариантен
относительно перестановок электронов, при построении
волновых функций состояний по формуле F.2) секуляр-
ное уравнение распадается на блоки, каждому из кото-
которых отвечает определенное неприводимое представление
Пя] координатной волновой функции. Координатная схе-
схема Юнга [к] однозначно связана со значением полного
спина S системы электронов, поэтому каждому спину S
будет соответствовать свое секулярное уравнение с раз-
размерностью, равной числу способов, которыми можно осу-
осуществить в системе данное значение S.
Для симметричных молекул возможна дальнейшая
квазидиагонализация секулярного уравнения. Для этого
надо из волновых функций, отвечающих данному спи-
спину ?, достроить базисные функции, принадлежащие к

208 КЛАССИФИКАЦИЯ СОСТОЯНИЙ ГЛ. VI
неприводимым представлениям точечной группы сим-
симметрии молекулы. Согласно теореме E.15) диагональ-
диагональные члены энергетической матрицы, относящиеся к од-
одному неприводимому представлению, будут одинаковы,
а все недиагональные члены обратятся в нуль, за ис-
исключением матричных элементов с базисными функ-
функциями, преобразующимися по одному и тому же столб-
столбцу эквивалентных неприводимых представлений.
Состояния системы N электронов с точечной симмет-
симметрией Па) и полным спином электронов S будем назы-
называть электронными молекулярными мультиплетами и
обозначать 28+1ГН Если из исходных ( N ] функций со-
составить линейные комбинации, являющиеся собствен-
собственными функциями мультиплетов, то первоначальное секу-
лярное уравнение распадется на отдельные секулярные
уравнения, каждое из которых соответствует некоторому
мультиплету 2s+!rK Порядок получающихся секулярных
уравнений равен кратности вхождения данного мульти-
плета в разложение представления, образуемого исход-
исходным набором базисных функций.
При полном учете всех конфигураций расчеты по
методу валентных схем и методу молекулярных орбита-
лей эквивалентны [38]. Это связано с тем, что переход от
одноэлектронных орбиталей метода валентных схем к
молекулярным орбиталям метода МОЛКАО связан с
линейным преобразованием функций базиса секулярного
уравнения, корни же секулярного уравнения не зависят
от выбора линейной комбинации базисных функций.
Естественно, что одинакова и мультиплетная структура,
получаемая при расчете по обоим методам.
Представляет интерес, прежде чем проводить непо-
непосредственный расчет, определить возможные мульти-
плеты и максимальный порядок секулярных уравнений,
с которыми мы встретимся при решении задачи. В сле-
следующем разделе излагается способ нахождения возмож-
возможных мультиплетов и их кратностей при расчетах по ме-
методу валентных схем.
6-10. Способ нахождения возможных мультиплетов
при расчетах по методу валентных схем [54]. Ограни-
Ограничимся случаем, когда н# каждом атоме задана одна

§ 3 КЛАССИФИКАЦИЯ В КВАНТОВОХИМИЧЕСКИХ РАСЧЕТАХ 209
невырожденная одноэлектронная орбиталь, а число ва-
валентных электронов равно числу орбиталей*). В этом
случае конфигурации нейтральных атомов отвечает одно-
однократное заполнение орбиталей. Взаимодействие валент-
валентных электронов нейтральной конфигурации атомов при-
приводит к образованию так называемой ковалентнои хими-
химической связи. Если один или несколько электронов пере-
переходят со «своих» орбиталей на орбитали соседних атомов,
то образуется ионная конфигурация атомов, ответствен-
ответственная за так называемую ионную химическую связь. В ре-
реальных молекулах вклад в химическую связь дают как
ковалентные, так и ионные конфигурации. Расчет элек-
электронных состояний молекулы будет тем точнее, чем бо-
более полно проведен учет взаимодействия конфигураций.
I. Ковалентные структуры
Ковалентнои структурой в рассматриваемом случае
называют конфигурацию однократно заполненных орби-
орбиталей, характеризуемую определенным способом сложе-
сложения спинов отдельных электронов в полный спин S.
Обычно существует несколько независимых способов
сложения электронных спинов, приводящих к данному
значению полного спина S. Количество таких способов
и определяет число независимых ковалентных структур
со спином S, которые можно построить из N валентных
электронов; обозначим это число n(N,S).
В квантовой химии при нахождении независимых ко-
ковалентных структур пользуются так -называемым пра-
правилом Румера [30, 55, 56]. Согласно этому правилу обо-
обозначения орбиталей с валентными электронами распо-
располагают по окружности, после чего всеми возможными
способами соединяют их попарно валентными штрихами
так, чтобы ни одна пара валентных штрихов не пересе-
пересекалась. Валентный штрих, соединяющий две орбитали,
означает, что спины находящихся на них электронов
спарены.
*) Этот случай реализуется в расчетах я-электронных систем
сопряженных и ароматических углеводородов, а также в задачах
взаимодействия s-электронов (см. раздел 6-11), общий случай разо-
разобран в работе [94].
J4 И. Г.

210 КЛАССИФИКАЦИЯ СОСТОЯНИЙ ГЛ. VI
Например, для четырех орбиталей имеем две незави-
независимые ковалентные структуры cS = 0:
F.55)
>3
II
Для построения волновых функций ковалентных
структур обычно составляют определенные линейные
комбинации детерминантов из спин-орбиталей, отвечаю-
отвечающие заданным способам связи спинов электронов [30,
56]. Применение аппарата группы перестановок позво-
позволяет записать полную волновую функцию системы элек-
электронов через произведения соответствующим образом
симметризованных координатной и спиновой волновых
функций, что дает возможность иного подхода к описа-
описанию ковалентных структур. В основе его лежит исполь-
использование координатных волновых функций. Такой подход
был развит независимо в работах автора [57] и Матсена
[58]*). Разработанная нами методика [87] применима к
конфигурациям с произвольным заполнением орбиталей
и позволяет проводить компактное вычисление матрич-
матричных элементов гамильтониана с помощью техники генеа-
генеалогических коэффициентов (см. гл. VII, VIII).
В нулевом приближении координатная волновая
функция системы валентных электронов записывается
как произведение N одноэлектронных орбиталей фа,
каждая из которых локализована на определенном
атоме,
F.56)
Нейтральной конфигурации атомов отвечает однократ-
однократное заполнение орбиталей, т. е. все фа в F.56) разные.
Будем предполагать, что они образуют ортонормирован-
ный набор. Построение базисных функций неприводи-
неприводимых представлений Г[^ группы перестановок ztN осуще-
*) Впервые координатные волновые функции в молекулярных
расчетах были применены Котани и Сига [93].

§3 КЛАССИФИКАЦИЯ В КВАНТОВОХИМИЧЕСКИХ РАСЧЕТАХ 211
ствляется действием на функцию F.56) операторов
Юнга ©^ (см. раздел 2-9). Получающиеся при этом
f\ функций Ф]?] разбиваются на f% наборов, нумеруемых
индексом /. Каждый набор состоит из fx функций Ф^1
с фиксированным индексом /, составляющих базис не-
неприводимого представления ПЧ При этом все функции,
принадлежащие к одному базису, соответствуют одному
физическому состоянию, так как входят в одну анти-
антисимметричную комбинацию при составлении полной вол-
волновой функции:
Ч^ = 2Ф!ЗД]. F.57)
г
При данной схеме симметрии [к] различные состояния
нумеруются индексом /, который характеризует симмет-
симметрию функции F.57) относительно перестановок орбита-
лей. Следовательно, число различных состояний с пере-
перестановочной симметрией [к] равно размерности /х
неприводимого представления Г[Ч Это и есть число не-
независимых ковалентных структур со спином S, поскольку
функции F.57) описывают конфигурацию нейтральных
атомов в состоянии с определенным значением спина S.
Выразим /\ через число валентных электронов N и
значение спина S. Для этого учтем, что размерности
представлений Т[1] и Г[Я] одинаковы. Согласно D.44)
F.58)
с другой стороны,
#:=ЯA)+ХB). F.59)
Соотношения F.58), F.59) позволяют выразить длины
строк спиновой схемы Юнга через два параметра N и S:
Х<о = JL + S, № = ~ - 5. F.60)
Подставляя эти значения в формулу для размерности
неприводимого представления B.18), получаем искомое
выражение:
14*

212 КЛАССИФИКАЦИЯ СОСТОЯНИЙ tJ\. V!
Для N=A, S = 0 формула F.61), в соответствии с F.55),
дает /гD,0) =2.
В расчетах нижних электронных состояний молекулы
бензола часто учитываются только шесть я-электронов
бензольного кольца. Количество ковалентных структур
с S=0 должно быть равно пF,0)=5. При выписывании
независимых ковалентных структур по правилу Румера
этими пятью структурами являются известные в орга-
органической химии две структуры Кекуле и три структуры
Дьюара [56]. Количество ковалентных структур с S = l
равно я F, 1) = 9; аналогично находится число независи-
независимых ковалентных структур с большей мультиплетно-
стью.
Волновые функции ковалентных структур являются
линейными комбинациями функций F.57). Поскольку
корни секулярного уравнения инвариантны относительно
линейного преобразования функций базиса, расчеты с
функциями F.57) полностью эквивалентны расчетам с
функциями ковалентных структур. В то же время ис-
использование при расчетах координатных волновых функ-
функций Фп ] позволяет значительно упростить и системати-
систематизировать вычисление матричных элементов (см.
гл. VIII).
Если почему-либо требуется выписать конкретный
вид функции структур, то координатные волновые функ-
функции, соответствующие ковалентным структурам, легко вы-
выражаются через координатные функции Ф^1. Для этого
следует учесть, что симметрия координатных волновых
функций Ф$] относительно перестановок орбиталей
определяется заданием таблиц Юнга / стандартного
представления группы перестановок. Координатные вол-
волновые функции ковалентных структур, очевидно, дол-
должны быть симметричны относительно перестановок
атомных орбиталей, электроны которых спарены, поэто-
поэтому они, как правило, принадлежат к нестандартному
представлению группы перестановок. Переход от базис-
базисных функций стандартного представления к базисным
функциям нестандартного представления совершается с
помощью соответствующих наборов операторов Юнга и
описан в § 3 гл. II.

§ 3 КЛАССИФИКАЦИЯ В КВАНТОЁОХИМЙЧЕСКИХ РАСЧЁТАХ 213
Так, для Л/ = 4 и [А,] = [22] имеем две стандартные таб-
таблицы Юнга:
F.62)
7
3
Z
4
1
Z
3
4
, по своему построению симметрична относительно
перестановок орбиталей Р\2 и Р34 (в отличие от пере-
перестановок номеров электронов, перестановки номеров ор-
орбиталей, в соответствии с конвенцией раздела 2-9, от-
отличаем чертой над символом перестановки). Следова-
Следовательно,
Ф1=ФЙ?. F.63)
Для получения функции, симметричной относительно пе-
перестановок Ри и Р2з, подействуем на Ф^1 операторами
симметризации
Фп = c(l+ Pm)A + Л>з)ФЙ?> F.64)
где с — нормировочный множитель. Последовательное
применение формулы B.48) с матричными элементами
транспозиций, взятыми из табл. 2 Приложения 5, при-
приводит к следующей нормированной координатной функ-
функции для структуры II:
4 й?*?? F-65)
В случае симметричных молекул появляется допол-
дополнительное вырождение, связанное с симметрией моле-
молекулярного потенциального поля, в котором рассматри-
рассматривается движение электронов. Все fa состояний, принад-
принадлежащих к одному неприводимому представлению Г<а)
точечной группы симметрии молекулы, относятся к од-
одному уровню энергии. Для нахождения возможных не-
неприводимых представлений Г^, которые осуществляют-
осуществляются при данной перестановочной симметрии Г^, восполь-
воспользуемся тем обстоятельством, что дискретная точечная
группа симметрии молекулы изоморфна подгруппе груп-
группы перестановок орбиталей. Действительно, любую

214 КЛАССИФИКАЦИЯ СОСТОЯНИЙ ГЛ. VI
операцию точечной группы можно представить как неко-
некоторую перестановку орбиталей,таккак каждая орбиталь
локализована на определенном атоме. При переходе от
полной группы перестановок к ее точечной подгруппе
представление Г^ распадется на неприводимые пред-
представления Г<а), находимые с помощью разложения по
таблицам характеров. Каждому Г<а) отвечает значение
спина S, ^однозначно связанное с перестановочной сим-
симметрией [к] спиновой волновой функции.
Таким образом, методика нахождения возможных
электронных мультиплетов в случае ковалентных струк-
структур аналогична методике нахождения ядерных молеку-
молекулярных мультиплетов F.236) и может быть представле-
представлена в виде следующей схемы:
\ F.66)
Примеры применения методики F.66) даны в следую-
следующем разделе.
В основе методики F.66) лежит предположение, что
заданные на атомах орбитали принадлежат к одному
типу и остаются инвариантными при действии операций
точечной группы, поэтому любая операция точечной
группы эквивалентна перестановке орбиталей. Это и об-
обусловливает связь между перестановочной симметрией
координатной волновой функции и ее точечной симмет-
симметрией. В случае задания на атомах орбиталей разного
типа процедура нахождения разрешенных мультиплетов
несколько усложняется. Задача нахождения разрешен-
разрешенных молекулярных мультиплетов из произвольных атом-
атомных термов впервые рассмотрена в работе Котани [63].
Рассмотрение этой же задачи при учете перестановочной
симметрии координатной волновой функции и возможно-
возможности смешивания различных конфигураций проведено в
работе [94].
Действие операции точечной группы R на конфигу-
конфигурацию вырожденных локализованных орбиталей, отве-
отвечающих определенным значениям углового момента /,
сводится к последовательности двух операций; переста-

§ 3 К^ССИФИКАЦИЯ В КВАНТОВОХИМИЧЕСКИХ РАСЧЕТАХ 215
новке орбиталей Р и операции точечной симметрии в
пространстве каждой орбитали. Перестановка Р всегда
может быть разбита на циклы, следовательно, и атомы
разбиваются на отдельные совокупности, не преобра-
преобразующиеся друг через друга при действии операции R.
Характер не будет равен нулю лишь в том случае, если
атомы внутри совокупности находятся в одинаковом со-
состоянии. Можно показать, что для состояния с переста-
перестановочной симметрией [А,]_характер операции /?, соответ-
соответствующей перестановке Р, составленной из циклов дли-
длиной пи n2l .. \, ftfc, равен [94]
xw (/?)=х[М (Р) x(/l) (Я*1) х(/г) (Я • • • i{lk) (Rn») т (/?), F.67)
где x(R) обозначает число конфигураций, остающихся
инвариантными при действии операции R. Часть угло-
угловых моментов ji в формуле F.67) может совпадать.
В случае однотипных невырожденных орбиталей, когда
применима методика F.66), формула F.67) переходит в
F.67а)
II. Ионные структуры
Так же как в случае ковалентных структур, число
учитываемых орбиталей считаем равным числу взаимо-
взаимодействующих электронов. Рассматриваем однотипные
невырожденные орбитали. Ионной конфигурации атомов
будет отвечать электронная конфигурация, содержащая
дважды заполненные орбитали. Согласно формуле
F.52) количество ионных конфигураций, содержа-
содержащих т двукратно заполненных орбиталей и, соответ-
соответственно, N—2т однократно заполненных орбиталей,
равно
n(N,m, A0-(w|J(;'_2m)r F-68)
Ионной структурой назовем ионную конфигурацию,
характеризуемую определенным способом сложения не-
спаренных спинов в полный спин S. Каждая дважды за-
заполненная орбиталь ф^ имеет координатную схему

216
КЛАССИФИКАЦИЯ СОСТОЯНИЙ
«• ГЛ. VI
Юнга [2]. При порядке расположения орбиталей ионной
конфигурации
ф?ф22 • • • q&qwi • • • Ъ-ш (е-69)
координатная волновая функция дважды заполненных
орбиталей характеризуется, очевидно, следующей схе-
схемой Юнга из 2т клеток:
соответствующей спину S = 0. Схемы Юнга [2] для каж-
каждой орбитали единственным образом связываются в схе-
схему Юнга [2т], поэтому для дважды заполнен-
заполненных орбиталей имеется только одно состояние.
. . . Число независимых состояний со спином S
LLU конфигурации F.69) равно размерности пред-
представления, характеризуемого схемой Юнга для
однократно заполненных орбиталей. Эта схе-
схема Юнга, обозначим ее [А/2т)], определяется
отнятием т верхних строк из общей схемы
Юнга [к]. На рис. 6.2 [А/2т>] заштрихована.
Рис. 6.2. Схема Юнга [А/2т>] отвечает состоянию со зна-
значением полного спина S, получаемого при век-
векторном сложении N—2т неспаренных спинов. Согласно
F.61) количество независимых состояний в этом случае
равно
n(N-2m, S)**f,
щ
1
1
ш
Общее количество ионных структур вида F.69) со
спином S равно
n(N, m, S) =
(m\Y(N-2m)\
F.71)

§ 3 КЛАССИФИКАЦИЯ В КВАНТОБОХИМЙЧЕСКИХ РАСЧЕТАХ 217
Для несимметричных молекул квазидиагонализация
секулярного уравнения может быть проведена только
по значению полного спина S. Порядок получающихся
секулярных уравнений равен количеству состояний с
данным значением S, происходящих от всех возможных
ионных конфигураций F.69) и от ковалентной конфигу-
конфигурации (т = 0), т. е. определяется суммированием выра-
выражения F.71) по всем т, при которых осуществляется
данное S. В результате суммирования (см. [53]) полу-
получаем следующее выражение:
E(N/2-S)
V /at о\ 2S+1 / N+l \ N+l г ,кт оч12
F.72)
где n(N,S) определяется соотношениемF.61), E(N/2—5)
— целая часть числа N/2 — S.
В случае симметричных молекул составление из
функций структур базисных функций неприводимых
представлений Г<а> точечной группы симметрии молеку-
молекулы позволяет провести дальнейшее понижение порядка
секулярных уравнений. Нахождение возможных Г<а>,
входящих в разложение приводимого представления то-
точечной группы, образуемого ионными структурами, лег-
легко осуществляется, если известны его характеры. Рас-
Рассмотрим процесс нахождения характеров такого пред-
представления.
Прежде всего ионные конфигурации необходимо раз-
разбить на отдельные наборы, состоящие из конфигураций,
преобразующихся друг через друга при действии опера-
операций точечной группы О. Для этого каждая ионная кон-
конфигурация отождествляется с равновесной конфигура-
конфигурацией молекулы содержащей соответствующее количество
положительно и отрицательно заряженных атомов, после
чего удобно руководствоваться следующими правилами,
1. Если ионная конфигурация не имеет элементов
симметрии, то действие на нее всех g операций симмет-
симметрии точечной группы молекулы приводит к g различным
конфигурациям, образующим регулярное представление.
2. Если существует некоторая подгруппа И (обо-
(обозначим ее порядок h) точечной группы молекулы,

218 классификация состояний гл. vi
относительно которой данная ионная конфигурация инва-
инвариантна, то представление, порождаемое данной конфи-
конфигурацией, уже регулярного и имеет размерность g/h.
Для доказательства последнего утверждения разо-
разобьем все элементы группы О на левые смежные клас-
классы относительно подгруппы Н'.Н, RXH, R2H, ...,
RmH (m = g/h, см. раздел 1-5). Очевидно, что действие
на рассматриваемую ионную конфигурацию операций,
входящих в один смежный класс, эквивалентно. По-
Поскольку всего имеется g/h смеж-
смежных классов, то число разных
конфигураций, порождаемых кон-
конфигурацией с группой симмет-
симметрии //, равно g/h.
Рассмотрим в качестве приме-
Рис- б-3' ра гипотетическую молекулу из
четырех атомов, обладающую
симметрией группы D4 (g = 8). Согласно формуле F.68)
имеется 4!/2! = 12 конфигураций с одной парой ионов.
Эти 12 конфигураций могут быть разбиты на два несме-
шивающихся при операциях точечной группы набора
(рис. 6.3). Конфигурация / не имеет элементов симмет-
симметрии, следовательно, набор / включает 8 конфигураций.
Конфигурация 2 инвариантна относительно операций
группы Н с элементами Е и U2. Следовательно, набор 2
содержит 8/2 = 4 конфигураций.
Из данной ионной конфигурации можно составить
/.em) (см. F.70)) ионных структур со спином S. Эти
fkBm) ионных структур преобразуются по неприводимо-
неприводимого2^
му представлению 11Л J группы перестановок орбита*
лей с неспаренными спинами nN-2m- Одновременно они
составляют базис в общем случае приводимого пред-
представления подгруппы группы Ялг-2т, изоморфной точеч-
ной группе симметрии молекулы. Характеры этого пред-
hBm)l/m *
ставления х I") находятся из таблицы характеров
1lK J при сопоставлении каждой операции Н точеч-
точечной группы соответствующей перестановки Р орбиталей
с неспаренными спинами. Поскольку представление то-
точечной группы, образуемое ионными структурами, не

§ 3 КЛАССИФИКАЦИЯ В КВАНТОВОХИМИЧЕСКИХ РАСЧЕТАХ 219
зависит от выбора ионной конфигурации из набора пре-
преобразующихся друг через друга конфигураций, то спра-
справедлива следующая теорема*):
характеры представления точечной группы, обра-
образуемого ионными структурами со спином S, по-
построенными из набора преобразующихся друг через
друга конфигураций, равны характерам х "* ЧР)>
умноженным на число ионных конфигураций
данного набора, остающихся неизменными при дей-
действии операции /? = Р.
После того как для каждого из наборов конфигура-
конфигураций найдены характеры приводимых представлений, об-
образуемых ионными структурами, разложение их на не-
неприводимые части даст все возможные мультиплеты
25+1Г(а), которые можно построить на ионных структу-
структурах. Порядок секулярного уравнения, соответствующего
мультиплету 2S+Ir((Z), будет равен сумме кратностей вхо-
вхождения его в разложение приводимых представлений
образуемых как ионными, так и ковалентными струк-
структурами.
В следующем разделе приведено применение описан-
описанной методики к нахождению возможных мультиплетов
кольца из шести атомов Н.
6-11. Нахождение возможных мультиплетов при пол-
полном учете взаимодействия конфигураций кольца из ше-
шести 5-орбиталей. Рассмотрим шесть атомов водорода,
расположенных в вершинах правильного'шестиугольни-
правильного'шестиугольника. Допустим, что требуется найти энергию взаимодей-
взаимодействия такой системы при учете всех возможных кон-
конфигураций, которые можно построить из атомных s-op-
биталей. Порядок исходного секулярного уравнения для
данной вариационной задачи согласно F.54) должен
A2\
1 = 924. Рассматриваемая система обладает
точечной симметрией группы D6h. Поскольку ls-орбитали
*) Напомним, что рассматривается случай задания на атомах
невырожденных однотипных орбиталей. Общий случай см. в ра-
работе [94].

220 классификация состояний гл. vi
симметричны относительно отражения в плоскости
кольца, достаточно ограничиться симметрией точечной
группы D& Составление собственных функций мульти-
плетов позволяет разбить исходное секулярное уравне-
уравнение 924-го порядка на секулярные уравнения гораздо
меньшего порядка.
Такого рода модельная задача была решена Мэти-
сом [60] и подробно обсуждается в книге Слейтера [38].
Приведенный там метод нахождения мультиплетов
основан на распределении между атомами спинов элек-
электронов всеми возможными способами. Каждому рас-
распределению ставится в соответствие детерминантная
функция. Далее ищется результат действия на эти де-
терминантные функции всех операций точечной группы.
Найденные таким способом представления отвечают оп-
определенным значениям проекции полного спина Ms.
Представления, отвечающие определённым значениям
полного спина S, находятся вычитанием друг из друга
представлений с разными Ms. Подобный метод доста-
достаточно громоздок уже для сравнительно простой задачи
нахождения 14 мультиплетов, возникающих от ковалент-
ных структур (см. [38], стр. 462—469). Метод, изложен-
изложенный в предыдущем разделе, позволяет без особого труда
найти все 268 мультиплетов, возникающих в данной ва-
вариационной задаче. Рассмотрим процесс нахождения
этих мультиплетов последовательно.
I. Ковалентные структуры
Электронная конфигурация отвечает однократному
заполнению орбиталей. Поскольку количество орбиталей
равно числу электронов, имеется только одна конфигу-
конфигурация такого типа. Возможные спиновые схемы Юнга:
[Я]СПиН: [6] [51] [42] [З2]
S : 3 2 1 О FJ3)
Им соответствуют координатные схемы Юнга:
[I6] [214] [2212] [23] F.74)
Количество независимых ковалентных структур, отве-
отвечающих данному значению S, определяется размер-

§ 3 КЛАССИФИКАЦИЯ В КВАНТОВОХИМИЧЕСКИХ РАСЧЕТАХ 221
Значение S
Количество
структур
3
1
2
5
1
9
0
5
ностью неприводимого представления Г^ (см. F.61)) и
равно
F.75)
Группа D6 изоморфна подгруппе группы перестано-
перестановок тс6. В табл. 6.5 приведено соответствие между клас-
классами этих групп, а также характеры неприводимых
представлений Т^\ отвечающие операциям точечной
группы.
Та блица 6.5
Характеры неприводимых представлений группы яб,
соответствующие операциям группы D6
Классы Dr
Классы яв
xt21<1
Е
{Iе}
1
5
9
5
с2
{24
-1
1
-3
3
2С,
{З2}
1
-1
0
2
2С-
{6}
1
1
0
0
ги2
{23}
-1
1
— 3
3
ги2
{ 1222 }
1
1
1
1
Разложения этих представлений на неприводимые
представления группы D6 имеют следующий вид:
Г[1в] = В Г[214] = Л +Е +Е
Г12ЧЧ = А2 + 2Вг + 2Ег + Е2У Г[23] = 2Аг + В2 + Е2.
F.76)
Следовательно, из 20 возможных ковалентных структур
(см. F.75)) может быть построено 14 мультиплетов:
7В19 *АгЕгЕ2, 3А2ВгB)ЕгB)Е29
F.77)
(цифра в скобках после мультиплета указывает на его
кратность).

222
классификация состояний
ГЛ. VI
Рис. 6.4.
II. Ионные конфигурации Н4Н+Н~
Всего имеется согласно F.68) 30 конфигураций тако-
такого вида. Они разбиваются на три набора конфигураций,
не смешивающихся под действием операций точечной
группы (рис. 6.4). Конфигура-
Конфигурации типа 1 и 2 не имеют эле-
элементов симметрии и образуют
регулярные наборы по 12 кон-
конфигураций в каждом. Конфи-
Конфигурации типа 3 инвариантны
относительно поворота Г72 (обо-
(обозначения осей симметрии приведены на рис. 6.5), следо-
следовательно, _их группа симметрии состоит из двух элемен-
элементов: Е и U2- Набор конфигурации 3 уже регулярного и
содержит согласно приведенному на
стр. 218 правилу g/h = 6 конфигу-
конфигураций. .
Для каждой из конфигураций
вышеперечисленных наборов может
быть построено /ЛB) ионных струк-
структур со спином S (см. F.70)). Пере-
Перестановочная симметрия спиновых
волновых функций неспаренных
электронов характеризуется тремя
[Щ:
[4] [31] [22]
2 1 0
Рис. 6.5.
схемами Юнга
F.78)
Им соответствуют координатные схемы Юнга
[А<2>]: [I4] [212] [22]
/,B): 1 3 2
F.79)
Характеры представлений точечной группы, образуе-
образуемых ионными структурами, находим по правилам, дан-
данным в п. II раздела 6-10. Для представлений, образуе-
образуемых регулярными наборами, характеры всех операций,
кроме тождественной Е, равны нулю. Характер опера-

§3 КЛАССИФИКАЦИЯ В КВАНТОВОХИМИЧЕСКИХ РАСЧЕТАХ 223
ции Е равен размерности представления, т. е. у}х *(Е) =
= 12/ B). Для представлений, образуемых набором 3, не
а
равен нулю также характер операции ?/2. Действие лю-
любой из трех операций П2 оставляет инвариантными две
конфигурации из набора 3. Согласно теореме, приведен-
приведенной на стр. 219, для представлений, образуемых ионны-
ионными структурами набора 3, %\l (U2)= 2%^ J(P). P обо-
обозначает перестановку четырех орбиталей с_неспаренны-
ми спинами, соответствующую операции Щ. В данном
случае Р принадлежит к классу {22} группы яА.
В табл. 6.6 приведены характеры представлений, обра-
образуемых наборами 1 и 3 (представления, образуемые на-
наборами 1 и 2 эквивалентны). Разложение этих представ-
представлений на неприводимые представления группы D6 дает
нам 120 мультиплетов, порождаемых конфигурациями
вида Н4Н+Н". Они сведены в общую табл. 6.7.
III. Ионные конфигурации Н2(Н+J(Н-J
Конфигураций такого вида имеется 6!/B!K = 90. Они
распадаются на 11 несмешивающихся под дейстзием
операций точечной груп-
группы наборов. На рис. 6.6
изображено по одной кон-
конфигурации из каждого на-
набора. Поскольку имеется
всего два неспаренных
спина, то возможны толь-
только триплетные и синглет-
ные состояния, отвечаю-
отвечающие координатным схе-
схемам Юнга [А,<4)] = [12] и [2]
соответственно. В обоих Рис б б
случаях /D) = 1, следова-
следовательно, размерности представлений, образуемых ион-
ионными структурами, совпадают с размерностью пред-
представлений, образуемых наборами ионных конфигура-
конфигураций.

224
КЛАССИФИКАЦИЯ СОСТОЯНИЙ
[ГЛ. VI
Конфигурации 4, 5, 8 и // образуют регулярные на-
наборы. Так как /[2] =/[12] = 1, то соответствующие ионные
структуры образуют регулярные представления. В раз-
разложение регулярного представления каждое неприводи-
неприводимое представление входит число раз, равное своей раз-
размерности. Следовательно, из каждого перечисленного
набора могут быть образованы 16 мультиплетов:
3'lAlA2BlB2El{2)E2B). F.80)
Конфигурации наборов 6, 7 и 13 имеют ось симмет-
симметрии U2 (обозначения осей симметрии см. на рис. 6.5).
Таблица 6.6
Характеры неэквивалентных представлений,
образуемых ионными структурами
хГ1
xl21'1
х!22'
хГ1
Хз2'2'
х[?]
хГ1
хР
хт
х\121
„[2]
xii21
у[2]
Xl5
Е
12
36
24
6
18
12
6
6
6
6
6
6
6
6
2
С
0
0
0
0
0
0
0
0
0
0
-6
6
0
0
0
2С3
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2
2С6
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
зи2
0
0
0
0
0
0
-2
2
0
0
0
0
0
0
0
зи2
0
0
0
2
-2
4
0
0
-2
2
0
0
2
2
2

§ 3 КЛАССИФИКАЦИЯ В КВАНТОВОХИМИЧЕСКИХ РАСЧЕТАХ 225
Они образуют эквивалентные шестимерные представле-
представления. Характер операции С/2 равен 2%^ J(P)=±2, верх-
верхний знак для [кЩ=2, нижний —для [I2].
Таблица 6.7
Кратности мультиплетов, порождаемых различными наборами
конфигураций, в задаче о взаимодействии кольца из шести
атомов Н
Ко
Ki
К2
К3
К,
Аб
*7
Кь
к,
Кю
Ки
Ка
Кц
J"
А 15
к„
Полная
крат-
кратность
муль-
типле-
та
7вх
1
1
М»
1
1
1
1
4
м2
1
1
2
1
1
1
3
*в2
1
1
2
1
2
2
1
6
5Е2
1
2
2
1
6
м,
3
3
1
1
1
1
1
1
12
м2
1
J
1
1
18
2
3
3
1
1
1
1
1
1
1
1
1
1
18
Зя2
J
15
3?i
2
6
6
3
2
2
1
1
2
1
1
2
2
1
1
33
ЬЕ2
1
6
6
3
2
2
1
1
2
1
1
2
1
1
30
м»
(
(
(
(
]
]
]
]
2
2
2
2
[
1
22
А2
2
2
1
1
1
1
1
1
10
хвх
2
2
2
1
1
1
1
1
-1
1
1
1
1
16
хв2
1
2
2
1
1
1
1
1
1
1
1
13
1Ег
4
4
2
2
2
1
1
2
1
1
2
1
1
2
1
27
1
4
4
2
2
2
1
1
2
1
1
2
2
1
1
2
1
30
Группа симметрии конфигураций типа 12 состоит из
элементов Е и С2. Операция С2 оставляет инвариантными
все шесть конфигураций набора 12. Поэтому %^ J(C2) =
= ± 6 в зависимости от [W4)].
Конфигурации наборов 9, /0 и /4 имеют ось симмет-
симметрии ?72 и также образуют шестимерные представления.
Однако характеры представлений, образуемых ионными
15 И. Г. Каплан

226 классификация состояний гл. vi
структурами наборов 9, 10 и набора 14, различны^ Это
объясняется тем, что для наборов 9 и 10 операция U2 со-
соответствует перестановке орбиталей с неспаренными спи-
спинами, в результате же действия операции Г72 на конфигу-
конфигурации набора 14 атомы с неспаренными спинами останут-
останутся на своих местах, поскольку ось J72 проходит через них.
Характеры неэквивалентных представлений приведены в
табл. 6.6. Всего конфигурации вида Н2(Н+J(Н-J поро-
порождают 120 мультиплетов (см. табл. 6.7).
IV. Ионные конфигурации (Н+K(Н"K
Можно образовать 6!/C!J = 20 конфигураций такого
вида, распадающихся на три набора (рис. 6.7). По-
Поскольку все спины спарены, возможны только синглет-
ные состояния.
Конфигурации набора 15 инвариантны относительно
группы Н с элементами Е, Сз, С3, 3?/2. Следовательно,
они образуют двухмерное
представление, его характе-
характеры приведены в табл. 6.6.
Набор 16 является регуляр-
регулярным. Характеры представ-
рис 6.7. ления, образуемого набо-
набором 17, совпадают с харак-
характерами %921 из табл. 6.6. Разложение приводимых
представлений, порождаемых конфигурациями вида
(Н+K(Н")з, приводит к 14 мультиплетам.
В табл. 6.7 приведены кратности всех мультиплетов,
которые можно построить при полном учете конфигура-
конфигураций й системе шести s-орбиталей. Ко обозначает кова-
лентную конфигурацию, К\ + Кп — ионные конфигура-
конфигурации, изображенные на рис. 6.4, 6.6, 6.7. Нижняя строка
таблицы дает полную кратность каждого мультиплета,
равную порядку секулярного уравнения, отвечающего
данному мультиплету. Исходное секулярное уравнение
924-го порядка распадается на 19 секулярных уравне-
уравнений. Максимальный порядок секулярного уравнения ра-
равен 33. Решение этих уравнений приводит к 268 энерге-
энергетическим уровням, часть которых вырождена. Это вы-

§ 3 КЛАССИФИКАЦИЯ В КВАНТОВОХИМИЧЕСКИХ РАСЧЕТАХ 227
рождение обусловлено точечной симметрией задачи и
может быть снято только при искажении кольца. Как
показали расчеты, проведенные Мэтисом [60], низший
энергетический уровень системы имеет симметрию ХА\.
Кривая потенциальной энергии для этого состояния
имеет минимум, т. е. при некотором равновесном рассто-
расстоянии энергия кольца из шести атомов Н ниже энергии
этих же атомов, разведенных на бесконечность. Однако
энергия кольца выше энергии трех молекул Нг, рассчи-
рассчитанных эквивалентным методом. Следовательно, подоб-
подобное кольцо должно самопроизвольно распасться на три
молекулы Н2, что согласуется с экспериментальными
данными.

ГЛАВА VII
МЕТОД ГЕНЕАЛОГИЧЕСКИХ
КОЭФФИЦИЕНТОВ
§ 1. Эквивалентные электроны
7-1. Определение генеалогических коэффициентов.
Полная волновая функция системы электронов, поме-
помещенных в центральное поле, должна удовлетворять двум
условиям: а) быть антисимметричной относительно пе-
перестановок электронов; б) быть собственной функцией
операторов квадрата углового момента Р и его г-компо-
ненты Jz. Если имеет место LS-связь, то «правильные»
функции нулевого приближения теории возмущений дол-
должны быть,собственными функциями двух пар операто-
операторов L2, Lz и S2, Sz, где L и S обозначают орбитальный
и спиновый угловые моменты системы электронов.
В одноэлектронном приближении антисимметризация
полной волновой функции легко может быть достигнута
построением ее в виде линейной комбинации детерми-
детерминантов [62]. Каждый такой детерминант отвечает опре-
определенному значению проекции орбитального момента
системы электронов ML и проекции спинового момента
MSy но не является собственной функцией операторов
L2 и S2. Расчет, следовательно, проводится в схеме
moMLMs и в случае кратных термов требует дополни-
дополнительного преобразования к схеме LSMSML. Коэффици-
Коэффициенты линейной комбинации детерминантов в исходной
вариационной функции определяются из требования ми-
минимума средней энергии системы.
Детерминантный метод расчета энергии электроста-
электростатического взаимодействия электронов был развит Слей-
тером в 1929 г. в его классической работе [62] и приме-
применен в дальнейшем к расчету атомных термов ряда про-
простых электронных конфигураций [14]. В течение ряда лет
(до появления работ Рака [23, 61]) детерминантный ме-
метод оставался основным методом расчета атомных тер-

§ 1 ЭКВИВАЛЕНТНЫЕ ЭЛЕКТРОНЫ 229
мов. Однако попытки применения его к сложным элек-
электронным конфигурациям упирались в целый ряд рас-
расчетных трудностей, связанных, в частности, с громозд-
громоздкостью нахождения матричных элементов секулярного
уравнения. Существенным недостатком детерминантного
метода является также отсутствие аналитических фор-
формул для вычисления матричных элехментов, что не по-
позволяет получить рекуррентные соотношения, сводящие
Af-электронную задачу к задаче с меньшим числом
электронов.
Другой возможный путь построения волновой функ-
функции заключается в предварительном составлении соб-
собственной функции связанных угловых моментов и по-
последующей антисимметризации полученной функции.
Например, при /'/-связи для конфигурации трех неэкви-
неэквивалентных электронов с угловыми моментами /ь /2, /з
последовательное связывание угловых моментов Д- при-
приводит к волновой функции
¦ [(/i(l)/2B))/i2/sC); /Af], G.1)
вид которой дается выражением C.56). Функция G.1)
не удовлетворяет принципу Паули, поскольку не являет-
является антисимметричной. Для антисимметризации получен-
полученной функции подействуем на нее оператором Юнга ©[р1-
В результате получим нормированную антисимметрич-
антисимметричную функцию
о^1* K/i A) /2 B)) Л2/3 О); /М] =
{*[(/(l)/B))//3C); /Af]-
-*[(/i B)/2A))/12/зC); /Af]-*[(/1(l)/2C))/12/3B); /Af]-
- * [(/! C) /2 B)) /ia/3 A); /Af ] +1|) [^ B)/2 C)) /12/3 A); /Af ] +
12/3B); /Af]}. G.2)
Однако, если электроны эквивалентны, т. е. /1 = /2 =
=/з=/ (при этом предполагается, что радиальные вол-
волновые функции электронов также одинаковы), то функ-
функции, входящие в сумму G.2), перестанут быть ортого-
ортогональными друг другу, часть из них вообще совпадет.
Функция G.2) уже не будет нормированной.

230 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ, VII
Действительно, согласно C.49) действие перестанов-
перестановки Р\2 на функцию связанных моментов при / полуцелом
равно
/4); /Af], G.3)
т. е. функция в G.3) антисимметрична только при чет-
четных значениях суммарного момента. Следовательно, вы-
выражение G.2) при нечетных значениях /12 обращается
в нуль, а при четных переходит в ненормированную
сумму трех слагаемых
*[(/(!)/B))/'/C); /Af] —
- ¦ [(/ A) / C)) J'j B); JM] + о|> [(/ B) / C)) /'/ A); /Af]. G.4)
Очевидно, что функции, входящие в сумму G.4), неор-
неортогональны друг другу, поскольку они являются функ-
функциями с различным порядком связи угловых моментов
и связаны поэтому друг с другом посредством транс-
трансформационной матрицы группы /?3 (см. раздел 3-6).
Однако именно это обстоятельство позволяет предста-
представить их как линейную комбинацию взаимно ортогональ-
ортогональных функций. Для этого вспомним, что функции
¦ К/A)УB))///C);/А1] и г|)[(/A)/B))/7C); JM] G.5)
при У Ф У ортогональны друг другу. Последние две
функции в G.4) могут быть разложены по функциям
G.5) с помощью трансформационной матрицы, порядок
связи моментов / в которой отмечаем номерами аргу-
аргументов у моментов, поскольку все ]\ одинаковы,
¦ К/ A) / О)) /'/ B); /А*] - S ¦ К/ A) / B)) /7 C); JM] X
X ((/ A) / B)) /'/ C) | (/ A) / C)) У] B)f\ G.6)
Входящие в G.6) элементы трансформационной матри-
матрицы даются формулой C.60)
Ш AOB)) /'/
= VB/'+l)B7/ + l) W (J'jjl'; Jj) G.7)
(в обозначении коэффициента Рака индексы 1, 2, 3 опу-
опущены) .

§ 1 ЭКВИВАЛЕНТНЫЕ ЭЛЕКТРОНЫ 231
Аналогично
¦ И/B)/C)O7A); /М] - S * К/ A) / B)) /7 C); JM]x
X <(/A) / B)) У\ C) | (/ B) / C)) Fj(l))u\ G.8)
Функция в левой части равенства G.8) отличается от
аналогичной в равенстве G.6) перестановкой электро-
электронов Р\2. Поэтому разложение G.8) получится из разло-
разложения G.6), если подействовать на последнее переста-
перестановкой Р\2- При этом функция в сумме G.6) умножится
на (—1)/+1. Следовательно, трансформационная матри-
матрица разложения G.8) равна матрице разложения G.6),
умноженной на (—1)/+1,
<(/ A) / B)) У] C) | (/ B)/C)O7/A)>(/) =
= (-1)/+1/B/'+ 1)B7/+1)Г(///77/; //). G.9)
Таким образом, нормированную антисимметричную
волновую функцию трех эквивалентных электронов с
учетом равенств G.6) — G.9) можно записать в следую-
следующем виде:
четн
-2УB//+1)B//+1I17(////7/; //)Ь(/2/', /C); /М), G.10)
где а обозначает дополнительные квантовые числа, не-
необходимые для характеристики состояния с данным зна-
значением /, если оно встречается несколько раз в конфи-
конфигурации /3; Cjjjj — нормировочный множитель.
Формально разложение G.10) может быть записано
следующим образом:
2 ', /C); JM)<fJ', /; /|}/%/). G.11)
Явный вид коэффициентов этой линейной комбинации
дается разложением G.10), из которого, в частности,
следует независимость их от числа М,
', /; Л} №) =
= ClTy \ЬЛ. - 2 УB/' + 1) BГ +l)W (ГЦ]'\ Л)} • G.12)

232 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
В тех случаях, когда антисимметричное состояние сдан-
сданным значением / встречается в конфигурации /3 один
раз (для /^7/2 это всегда имеет место, см. табл. 6.2),
для вычисления коэффициентов G.12) можно исходить
из любого^ четного значения /', находящегося в интер-
интервале 0</'<2/.
Разложение G.11) означает, что волновая функция
данного состояния трех электронов может быть пред-
представлена как линейная суперпозиция волновых функций,
отвечающих разрешенным состояниям двух электронов,
характеризующимся значением углового момента Г.
Квадраты модуля коэффициентов этой линейной ком-
комбинации выражают долю участия состояния рГ в обра-
образовании искомого состояния /За/. Поэтому коэффициен-
коэффициенты G.12) называются генеалогическими коэффициен-
коэффициентами (coefficients of fractional parentage).
Генеалогические коэффициенты G.12) могут рас-
рассматриваться как элементы трансформационной мат-
матрицы, осуществляющей преобразование от функций
связанных моментов, антисимметричных только по отно-
отношению к первым двум электронам, к полностью анти-
антисимметричным функциям. Эта матрица является прямо-
прямоугольной, так как число разрешенных принципом Пау-
Паули состояний конфигурации /2 в общем случае не равно
числу состояний конфигурации /3. Поэтому для отличия
от квадратных унитарных матриц в обозначение генеа-
генеалогических коэффициентов введена фигурная скобка. Ге-
Генеалогические коэффициенты, так же как и трансфор-
трансформационные матрицы группы /?3, являются действитель-
действительными величинами.
В случае конфигурации jN генеалогические коэффи-
коэффициенты определяются аналогично G.11)
K/W /(АО;
а', /'
G.13)
Функции, входящие в сумму G.13), отвечают состоя-
состояниям, антисимметричным по перестановкам электронов,
конфигурации jN~K Сумма по а'/' пробегает все анти-
антисимметричные состояния конфигурации jN~l. Генеало-
Генеалогические коэффициенты, отвечающие кратным термам,

§ 1 ЭКВИВАЛЕНТНЫЕ ЭЛЕКТРОНЫ 233
должны обеспечивать ортогональность волновых функ-
функций, что удовлетворяется при выполнении условия орто-
ортогональности
2 {j /; |}/></"-V/', /; J\}j"aJ) = 6aa. G.14)
а', /'
В формуле записи G.14) учтена вещественность генеа-
генеалогических коэффициентов. Волновые функции с раз-
разными / автоматически ортогональны друг другу по по-
построению, поэтому эта ортогональность не накладывает
дополнительных условий на генеалогические коэффи-
коэффициенты.
Антисимметричная функция конфигурации jN всегда
может быть представлена в виде конечного ряда G.13).
Это следует из того обстоятельства, что функции
-фО'^^а'/', /(Л/); JM) образуют полный набор функций,
антисимметричных относительно перестановок первых
N—1 электронов. Поэтому любая функция, обладаю-
обладающая этим свойством, а следовательно, и функция, анти-
антисимметричная относительно всех N электронов, может
быть разложена по базисным функциям этого набора.
Для вычисления генеалогических коэффициентов кон-
конфигурации с числом электронов Л/>3 можно воспользо-
воспользоваться рекуррентным соотношением [64]
N(]"-WJ', /; 1\I»[а'ПГ>{1»-1а'Г', /; J \} j"[a'J')J) =
= бай,б -.-(tf-1) 2 (-l)r+1'+r+IW(rjjJ; /VOX
j j a//^ j/t
X</w-2a"/", /; Г IW^-W/O </*-V'/", /; 7' D/^aV7)- G.15)
Квадратные скобки в правой части генеалогических ко-
коэффициентов означают, что функция ip(jN[a/J/]I) полу-
получена антисимметризацией функции я|з(/^-1а///,/(Л/); JM).
В случае кратных термов возникает трудность в выде-
выделении независимых функций (подробности см. в [64]).
Изложенный выше способ нахождения генеалогиче-
генеалогических коэффициентов, в основе которого лежит сравне-
сравнение результатов непосредственной антисимметризации
волновой функции с ее записью с помощью генеалогиче-
генеалогических коэффициентов, был предложен для случая //-связи
в работах Шварца и де-Шалита [65] и Редмонда [66].

234 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
Он может быть использован и в схеме LS-связи. Однако
для случая LS-связи генеалогические коэффициенты были
найдены ранее в работах Рака [61, 45]. В своих работах,
послуживших основой для последующего широкого при-
применения генеалогического метода в атомной и ядерной
спектроскопии, Рака развил и усовершенствовал идею
генеалогического построения электронных состояний, со-
содержавшуюся в забытой работе Бэчера и Гудсмита [67].
Сущность метода, примененного Рака для нахождения
генеалогических коэффициентов р- и d-оболочек, заклю-
заключается в следующем.
Волновая функция конфигурации /2, описывающая
состояние с квантовыми числами SLMSML, строится с
помощью коэффициентов векторного сложения
X (-<*!, ±o2\SMs). G.16)
По построению она уже обладает определенной пере-
перестановочной симметрией. При перестановке электронов
согласно соотношению C.49), примененному отдельно к
орбитальному и спиновому моментам, функция G.16)
умножается на
/ __ * 42/+1-L-S
Следовательно, антисимметричное состояние характери-
характеризуется четным значением L + S. Добавление третьего
электрона приводит к функции
'I', /C); SLMSML) =
- 2 S
$t (J3
X (L'M'L, lm3\LML)(S'M's, j-or3| SMS)9 G.17)
в общем случае антисимметричной только по отноше-
отношению к перестановкам первых двух электронов.

§ 1 ЭКВИВАЛЕНТНЫЕ ЭЛЕКТРОНЫ 235
Функция, антисимметричная относительно всех пере-
перестановок, строится в виде линейной комбинации функ«
ций G.17)*)
- S ¦(/2S/Z/f /C); SL)(l2S'L'y /; SL \}l2aSL). G.18)
s\ и
Входящие в формулу G.18) генеалогические коэффи-
коэффициенты имеют тот же физический смысл, что и коэффи-
коэффициенты линейной комбинации G.11). Сумма по S'U про-
пробегает только разрешенные термы конфигурации /2. Из-
Изменив способ связи угловых моментов, получим
'L'9 /C);
, (U)S"L"; SL)(ly (U)S"L"\ SL\PS'L'9 I) SL).
S", L"
G.19)
Входящая в G.19) трансформационная матрица являет-
является произведением трансформационных матриц для орби-
орбитального и спинового моментов и равна согласно C.59)
"I"; SL \12S'L\ I;
X W (j 1 S J; S'S")
Сумма по S", L" в G.19) содержит все осуществ-
осуществляющиеся при векторном сложении пары значений S",
L", среди них есть и такие, для которых S"+L" равно
нечетному числу. Поэтому, если подставить разложение
G.19) в формулу G.18), требование антисимметрично-
антисимметричности функции G.18) выполняется только при обращении
в нуль коэффициентов при -ф(/, {ll)S"L"\ SL) для всех
S"+L'\ равных нечетному числу. Это приводит
•) Для сокращения записи несущественные для последующего
вывода квантовые числа Ма и ML опускаются.

236 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
к следующей системе уравнений для генеалогических
коэффициентов:
2 </, W)S"L"; SL \PS'U, l\ SL) X
X {PS'L', Z; SL \}l3aSL) = 0 (S" + L" нечетное). G.21)
Число независимых решений этой системы при фикси-
фиксированных SL дает число разрешенных термов данного
типа в конфигурации /3. Если оно превышает единицу,
термы различаются дополнительным квантовым чис-
числом а.
Аналогичным образом может быть получена система
уравнений для генеалогических коэффициентов конфигу-
конфигурации lN, если генеалогические коэффициенты конфигу-
конфигурации lN~l известны [61]:
{, ()"U"\ SL |(S"L", l)S'U, l\ SL)X
X </A'-Y's"L", /; S'L' |) P-WS'L*) X
X (lN-xaS'L\ l\ SL |) lNaSL) = 0 G.22)
(S'" + L'" нечетное).
Трансформационная матрица определяется подобно
G.20). Получающиеся системы уравнений позволяют
сравнительно легко найти генеалогические коэффициен-
коэффициенты для конфигураций pN и dN. Они были затабулиро-
ваны Рака [61]. В случае конфигурации fN появляется
большое количество кратных термов. Для этого случая
Рака был разработан теоретико-групповой способ, осно-
основанный на факторизации генеалогических коэффициен-
коэффициентов при классификации состояний по неприводимым
представлениям соответствующих непрерывных групп
(подробнее см. [45, 25])*).
7-2. Вычисление матричных элементов симметричных
операторов. В физических приложениях часто требуется
вычислять матричные элементы операторов, симметрич-
*) Таблицы генеалогических коэффициентов для всех разрешен-
разрешенных термов р- и d-оболочек и термов максимальной мультиплетно-
сти ряда конфигураций fN приведены также в книге Собельмана
[26].

§ 1 ЭКВИВАЛЕНТНЫЕ ЭЛЕКТРОНЫ 237
ных относительно всех электронов рассматриваемой си-
системы. Такие операторы могут быть разбиты на два
типа:
F=2f< и G=2 gik. G.23)
i l i<k
Оператор F является суммой одноэлектронных опера-
операторов fiy каждый из которых действует на координаты
только одного электрона. Примером операторов типа F
могут служить операторы взаимодействия рассматривае-
рассматриваемой системы электронов с внешним полем либо взаимо-
взаимодействия электронов с ядрами. Оператор G является
суммой двухэлектронных операторов gih. Примером
такого оператора является энергия электростатического
взаимодействия электронов.
Особенностью генеалогического разложения G.13)
либо G.18) является то, что исходная функция, анти-
антисимметричная по всем электронам, разлагается на на-
наборе функций, в которых последний электрон выделен
и характеризуется определенными квантовыми числами.
Это обстоятельство позволяет выразить матричные эле-
элементы операторов F и G в многоэлектронной задаче че-
через одноэлектронные и двухэлектронные матричные эле-
элементы и генеалогические коэффициенты. Более того, ока-
оказывается, что для вычисления матричных элементов не
требуется знания конкретного вида волновой функции,
достаточно знать соответствующие генеалогические ко-
коэффициенты. Излагаемый ниже вывод формул для мат-
матричных элементов проведен для случая //-связи. Все фор-
формулы останутся справедливыми и для LS-связи, необхо-
необходимо только в этом случае заменить в них момент / на
/, а / — на L, S.
Поскольку в состояниях, описываемых антисиммет-
антисимметричными функциями, все электроны равноправны, мат-
матричные элементы всех операторов fi одинаковы. Поэтому
может быть взят какой-либо один оператор, например
оператор fNy действующий на координаты последнего
электрона:
(jNaJM | F | jNaJM) = N (jNaJM \ fN \ jNaJM). G.24)

238 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
Подставим в матричный элемент G.24) волновую функ-
функцию конфигурации в виде разложения G.13):
(jNaJM\F\jNa7M)~
- N 2 2 <jN-W. /; / 1} jNaJ) (/"-W, /; 71} j»aT) X
X^-V/', /(JV); /Allfol/^a'/', /(#); /M). G.25)
Входящий в G.25) матричный элемент оператора In
легко вычисляется с помощью аппарата неприводимых
тензорных операторов. Пусть, например, оператор fN яв-
является k-й компонентой неприводимого сферического
тензора ранга х, обозначим его fk}(N). Согласно тео-
теореме Вигнера — Эккарта D.63)
; JM\fN\p-la'T'9 j(
— M k M)
G.26)
Оператор f^(N) в приведенном матричном элементе дей-
действует только на координаты N-то электрона. Для него
справедливо соотношение D.76), в котором роль второй
подсистемы играет N~& электрон:
<//, /(АО; /1/(хЧло!а'7', у(А0;7>
G.27)
Подставляя G.26), G.27) в G.25), получаем оконча-
окончательное выражение для матричного элемента тензорного

§ 1 ЭКВИВАЛЕНТНЫЕ ЭЛЕКТРОНЫ 239
N
2
N
оператора F™ = 2 f?(t). А именно,
х 2К-Г(
X </"" V/', /; / |} /%/> </"-V/', /; Л } /"а7>. G.28)
Необходимым условием неравенства матричного элемен-
элемента G.28) нулю является выполнение условий треуголь-
треугольника Д(/х/) и Д(/и/).
В случае скалярного оператора формула G.28) при-
приобретает очень простой вид. Для этого нужно подста-
подставить в G.28) вместо 6/-символа его значение из D.77),
а вместо 3/-символа значение
<7-29)
Заменяя, далее, приведенный матричный элемент опе-
оператора f(°> по формуле D.68) и используя соотношения
ортогональности для генеалогических коэффициентов
G.14), окончательно получаем
(faJM | F@) I falM) = б^б^Ы (jm \ f@) | /m>. G.30)
Рассмотрим вычисление матричных элементов ска-
скалярного оператора G. Матричные элементы скалярного
оператора диагональны по / и не зависят от М (см.
D.68)), поэтому значение М в обозначении матричного
элемента будем опускать. Получим рекуррентную фор-
формулу, выражающую матричные элементы оператора G
через матричные элементы оператора
N-1

240 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
действующего только на координаты первых N—1 элек-
электронов. Вследствие неразличимости электронов матрич-
матричные элементы операторов gih не зависят от номеров
электронов /, k. Оператор G содержит N(N—1)/2 чле-
членов, а оператор G'— (N—1)(А/ — 2)/2, поэтому
(jNaJ\ G |№> = ^ {j»aJ\G'\j«&J). G.31)
Подставим в G.31) выражение для волновой функции
G.13)
{jNaJ\G jNaJ) =
a'Jf u'7'
X<JN~W7', /; J\}j"aJ)X
x (j"-w, jm JI G'\i»-w, j№ />.
Оператор Gr не действует на координаты Л/-го электро-
электрона. Для скалярного оператора, действующего только на
первую подсистему, справедливо соотношение D.80).
Окончательно получаем
</"а/1 G | №> = л^г S <Р V/', /; / |} /%/) X
X (/^"'aV7, /; / |} /^fi/> <jN-la'J' \ G' \ j^a'J'). G.32)
Матричный элемент оператора G можно выразить
также через двухэлектронные матричные элементы. Для
этого необходимо ввести генеалогические коэффициенты,
соответствующие отщеплению от конфигурации jN сразу
двух электронов. Они определяются разложением
^/2a77, j2(N-l, N)J"\ JM)X
X (/"-V/', рГ; /|}/%/>, G.33)
волновые функции в правой части которого антисиммет^
ричны относительно перестановок первых N—2 элек-
электронов и относительно перестановки N—1-го и N-ro
электронов. Суммирование в G.33) проводится по всем
разрешенным термам конфигураций jN~2 и /2.

§ Г ЭКВИВАЛЕНТНЫЕ ЭЛЕКТРОНЫ 241
Генеалогические коэффициенты разложения G.33)не-
G.33)нетрудно выразить через генеалогические коэффициенты,
отвечающие отщеплению одного электрона. Для этого
в выражении G.13) отщепим из конфигурации jN~l один
электрон с помощью генеалогических коэффициентов
этой конфигурации (предварительно в выражении G.13)
переобозначим а'/' на а7/7)
аИ/"а/М)= 2 2 ^(/"-V/', j(N-l))T9 j(N)\ JM)X
а', 7' <*'. Г
X <pV/', /; Г |} iN-'a'F) (JN-WP, /; /1} /%/). G.34)
Изменим способ связи угловых моментов, связав j(N—1)
и/(АО,
= 2
21 (/^а'/', /2 (yv - 1, N) /"; /M) (/' (/7) /" | {J'i) ?/
G.35)
Трансформационная матрица связывает два различных
способа сложения трех моментов /', /, /, поэтому она,
аналогично C.59), выражается через коэффициенты
Рака
</'(//)/"|(/'/)/7)(/) = VB/"+l)B/4-l)W(J'jJi; J'J").
G.36)
Подставив G.35) в G.34), получаем искомую формулу
Q ) X
xu'dnnwnri)' G.37)
С помощью разложения G.33) матричные элементы
скалярного оператора легко могут быть выражены через
двухэлектронные матричные элементы. Для этого за-
заменим оператор О на оператор gN-\ Ni действующий
только на координаты N— 1-го и N-ro электронов:
Га/1 О | /"а/> = N{N-l) </"«/1 g^ N | j»aJ). G.38)
И. Г. Каплан

242 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
Подставим в G.38) разложение G.33). В силу ортого-
ортогональности базисных функций конфигурации jN~2 и ска-
лярности оператора g^-i n получаем
а', /', /"
X (jX-W, ?J"; J |} j»aJ) </2/" | gAM N | f/">• G.39)
Относительно метода расчета матричных элементов
электростатического взаимодействия двухэлектронных
конфигураций см. [25, 26].
С ростом числа электронов в конфигурации jN рас-
расчет по формуле G.39) становится весьма громоздким.
Существует другой путь расчета, основанный на выра-
выражении оператора взаимодействия через сумму скаляр-
скалярных произведений тензорных операторов. Задача в этом
случае сводится к вычислению матричных элементов от
операторов типа F. Подобная методика была разрабо-
разработана Рака [61] (см. также [25, 26]).
§ 2. Конфигурация из нескольких групп
эквивалентных электронов. Состояние с произвольной
перестановочной симметрией
7-3. Одна оболочка. В предыдущем параграфе рас-
рассматривались генеалогические коэффициенты антисим-
антисимметричных состояний конфигурации эквивалентных
электронов. При построении полной волновой функции
системы электронов цз произведений координатной вол-
волновой функции на спиновую (формула F.2)) переста-
перестановочная симметрия каждой из этих функций опреде-
определяется взаимно дуальными схемами Юнга. Если опера-
оператор рассматриваемого взаимодействия действует только
на пространственные либо только на спиновые коор-
координаты, то для описания взаимодействия достаточно
задать конкретный вид только координатной либо спи-
спиновой волновой функции. Матричные элементы в этом
случае удобно вычислять, осуществив предварительно
генеалогическое разложение, связывающее состояние N
электронов с перестановочной симметрией схемы Юнга

§ 2 КОНФИГУРАЦИЯ ЭКВИВАЛЕНТНЫХ ЭЛЕКТРОНОВ 243
[А,] с состоянием, в котором N—1 (или N — 2) электро-
электронов характеризуются перестановочной симметрией [V].
В настоящем параграфе будут получены формулы
для генеалогических коэффициентов произвольной кон-
конфигурации из нескольких групп эквивалентных электро-
электронов в состоянии с перестановочной симметрией [К]. Угло-
Угловой момент электрона обозначается /\ это может быть
либо орбитальный момент /, либо спиновый момент s.
При //-связи представление волновой функции в виде
F.2) неправомочно. Но формулы для этого случая будут
частным случаем полученных ниже, если положить в
них [Я] = [1^]. Рассмотрение начнем с одной группы
эквивалентных электронов.
Предварительно напомним, что независимые базис-
базисные функции, принадлежащие к неприводимому пред-
представлению ГМ группы перестановок Лдг, нумеруются та-
таблицами Юнга г (см. раздел 2-4). Задание таблицы Юнга
г соответствует одновременному заданию N— 2 непри-
неприводимых представлений Г[ , Г[ , ..., к которым при-
принадлежит данная базисная функция при переходе к
группам Jtjv-i, nN-2, ... В частности, перестановочная
симметрия функции Ф^1 относительно перестановок пер-
первых N—1 чисел характеризуется схемой Юнга [А/], по-
получаемой при отнятии из таблицы Юнга г клетки с чис-
числом N.
Генеалогические коэффициенты определяются как
матричные элементы ортогонального преобразования:
Ф (jN [X] raJM) - 2 Ф (/"-1 [X] г' а77, / (N); JM) X
а',/'
X (/"-1 [Л'] а'/', /; / |} jN [l] а/). G.40)
Они не зависят от таблиц Юнга и проекций углового
момента. Обратное преобразование имеет следующий
вид:
Ф 0#ЛМ М rV/7, / (Л0;
("[]\*[X']a'J\ /; /). G.41)
Сумма в G.41) включает все разрешенные схемы Юнга
из N клеток, которые получаются при добавлении одной
16*

244 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
клетки к схеме Юнга [А/]. Из соотношений G.40) и G.41)
следует, что генеалогические коэффициенты образуют
прямоугольную матрицу, строки которой нумеруются
значениями углового момента а7/7, осуществляющимися
при заданных [А/] и /, а столбцы — возможными схемами
Юнга [Я], которые могут быть получены из данной схемы
Юнга [X] добавлением одной клетки.
Базисные функции разложения G.40) обладают пе-
перестановочной симметрией [А/]г' относительно перестано-
перестановок первых N—1 электронов. Необходимо так выбрать
генеалогические коэффициенты, чтобы функция G.40)
вела себя соответствующим образом и при перестанов-
перестановках ЛЛ-го электрона с остальными А/— 1. Поскольку лю-
любая перестановка может быть записана как произведе-
произведение транспозиций типа Рг г_ь а по отношению к транс-
транспозициям Р12, P23, ..., Pn-2 n-\ функция G.40) уже
имеет правильные трансформационные свойства, доста-
достаточно задать ее поведение по отношению к транспози-
транспозиции Pjv-i n- На этом основан излагаемый ниже метод
нахождения генеалогических коэффициентов, развитый
в работах Яна [68, 69].
Запишем базисную функцию разложения G.40) с
помощью генеалогических коэффициентов конфигура-
конфигурации jN~l:
j[] /(-1))/', /(Л0; ш)х
а", /"
X </"-2 [Я"] а'7", /; Г \} jN~l [X] а7/7). G.42)
Действие перестановки PN-w на функцию связанных мо-
моментов, стоящую в правой части равенства G.42), при-
приводит к функции с другим способом связи угловых мо-
моментов /", /, /:
PN-tNVW^lWrW, /0V-1))/', /(Л0; т =
= 2 Ф ((/"-2 [Я"] г"а'7", / (Л0 O', / (Л^ - 1); JM) X
у
X ((/"/(Л0)T'j(N-l)\ (J"j(N-l)) J'j{N))(l). G.43)
Трансформационная матрица в G.43) выражается ана-

§ 2 КОНФИГУРАЦИЯ ЭКВИВАЛЕНТНЫХ ЭЛЕКТРОНОВ 245
логично G.7) через коэффициенты Рака:
<('"/(АО) Г'}(N-l)\ (Г/(N-1)) У\(N))U) =
= VB7'+l)BJ'+l) WA'ЦТ\ Л"). G.44)
Из G.43) следует, что матрица оператора PN-in в пред-
представлении функций связанных моментов, симметризован-
ных только по отношению первых N — 2 электронов, со-
совпадает с трансформационной матрицей G.44). Введем
для нее обозначение
П (АЛ —1)| (П (N - 1)) Г\ (N))U). G.45)
Генеалогические коэффициенты разложения G.42)
можно рассматривать как элементы трансформационной
матрицы, осуществляющей преобразование от функций
связанных моментов, симметризованных относительно
перестановок первых N — 2 электронов, к функциям, сим-
метризованным относительно перестановок первых 7V— 1
электронов. Поэтому матрица оператора Pn-\n в пред-
представлении функций G.42) может быгь выражена через
матрицу G.45) по стандартной формуле матричного ис-
исчисления (см. A.31)):
</"-' [Я'] г'а'Г, / (АО; / I Ры-ш I /""' [Щ r'a'F, j (N); J) =
= 2 (/*"' [Щ «Т {| jN~2 [X"] а"/", /; /') X
а", У"
X </"/'/1 PN.1N | J"J7J) (j»~2 [K'\ a"/", /; У |} j"~l WWT).
G.46)
При записи G.46) учтена ортогональность матрицы опе-
оператора Pjv-i n относительно квантовых чисел конфигу-
конфигурации jN~2.
Генеалогические коэффициенты разложения G.40) осу-
осуществляют преобразование от функций с определенной
перестановочной симметрией только первых N—1 элек-
электронов к базисным функциям неприводимого представле-
представления Г^ полной группы перестановок я#. Потребуем, что-
чтобы это представление совпадало со стандартным орто-
ортогональным представлением Юнга —Яманути. Матрица

246
МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ
ГЛ. VII
оператора Pn-i n должна в этом случае совпадать с
матрицей стандартного представления T[X1(Pn-i n), на-
находимой по правилам, данным в разделе 2-5. Аналогично
формуле G.46) получаем
(jN [X] raJ | PN_lN | f [Ц raj) » Г^1 (pN_lN) =
= 22 (lN [Я] a/ {| /лг-i [X>] a'J', j; J) X
a',/' u,j,
X О'* [ЛП rW, / (Л^); /1 Р„-ш | y^1 [Л1 r7^?, / (JV); /) X
X O'"" №1 a7/7, /; / |} jN Щ a/). G.47)
Соотношения G.47) позволяют найти генеалогический
коэффициент конфигурации jN, если генеалогические ко-
коэффициенты конфигурации jN~l известны. Такой рекур-
рекуррентный способ осуществляется начиная с конфигура-
конфигурации /3, поскольку генеалогические коэффициенты конфи-
конфигурации /2 равны единице.
В качестве примера рассмотрим процесс нахождения
генеалогических коэффициентов конфигурации pz в со-
состоянии с квантовыми числами [Я]=[21], /=1. Генеало-
Генеалогические коэффициенты конфигурации р2 равны 1, по-
поэтому матрица G.46) совпадает с матрицей G.45).
В данном случае генеалогические коэффициенты легко
находятся из сравнения результата действия переста-
перестановки Р2з на G.40) (при учете G.43)) с результатом
действия перестановки Я2з на базисные функции стан-
стандартного представления.
Матрицы стандартного представления П21! приведены
в разделе 2-5. Обозначим таблицы Юнга № номером у
схемы Юнга [21]. Матрица оператора Р2$ равна
J21L [21J2
2 2
V3
т. е.
G.48)

§ 2 КОНФИГУРАЦИЯ ЭКВИВАЛЕНТНЫХ ЭЛЕКТРОНОВ 247
Конфигурация р2 обладает тремя разрешенными состоя-
состояниями: [2] 5, D и [I2] Р. Поскольку таблице Юнга [21]t
отвечает схема Юнга [А/] = [2], а [21]2 —[А/] = [12], то со-
состояние [21]iP происходит от двух состояний конфигу-
конфигурации р2 (обозначим сокращенно генеалогические коэф-
коэффициенты этих состояний через х и у), а состояние
[21]2Р— от одного состояния конфигурации р2 (генеало-
(генеалогический коэффициент равен единице).
2]S, p; Р) +
+ yd)(p2[2]Dyp; Р), G.49)
]Р, р; Р).
Подействуем на функцию Ф(рг[21]\Р) перестановкой
Р2з. Появляющаяся при этом трансформационная мат-
матрица согласно G.43), G.44) выражается через коэффи-
коэффициенты Рака. Необходимые для ее вычисления коэф-
коэффициенты Рака равны
IF@110; ll)«IFA110; 11) = 1FB11O; 11) =
-IF@112; llH-g"»
№A112; ll)=--i, IFB112; H)*-^-.
В результате находим, что
J]St p; Р) +
Сравнивая коэффициенты при одинаковых членах в
выражениях G.50) и G.48) (в G.48) необходимо пред-
предварительно подставить равенства G.49)), получаем си-
систему уравнений для нахождения х, у:
х j-

248
МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ
ГЛ. VII
откуда следует, что
-2.
х з >
V*
или
/г, Р)-
Таким способом Ян вычислил генеалогические коэф-
коэффициенты состояний нуклонов для конфигураций pN[€>9]
и dN[68]. В табл. 7.1 приведены генеалогические коэф-
коэффициенты для атомной /^-конфигурации. При пользо-
пользовании таблицей следует помнить, что в одну линейную
комбинацию входят только генеалогические коэффи-
коэффициенты с одинаковой схемой Юнга конфигурации pN~K
В табл. 7.1 эти коэффициенты отделены вертикальной
чертой.
Таблица 7.1
Генеалогические коэффициенты ( pN [к] L { | р^ [К] //, р; L)
Р2
Р3
[Я'1
и
[X]
[21]
[13]
L:
Р
п
S
S
2/3
[2]
D
-/5/3
1
Р
1
1
1
''V
[22] 5
D
[212]Р
[21]
Р D
-1/2 /3/2
/3/8" /5/8"
[I3]
S
1
PMV,
[24] Р
S Z?
/Т/6" /5/6"
[2J.]
1
Вычисление генеалогических коэффициентов с по-
помощью соотношений G.47) значительно упрощается при
предварительной факторизации генеалогических коэф-

§ 2 КОНФИГУРАЦИЯ ЭКВИВАЛЕНТНЫХ ЭЛЕКТРОНОВ 24с/
фициентов на основе теоретико-групповой классифика-
классификации состояний [70]. Используя построение волновых
функций с помощью операторов Юнга а>[^, Хассит [71]
получил соотношение, непосредственно выражающее ге-
генеалогические коэффициенты разложения G.40) через
генеалогические коэффициенты конфигурации jN~l и
коэффициенты Рака. В частном случае антисимметрич-
антисимметричных состояний формула Хассита переходит в соотноше-
соотношение, аналогичное G.15).
Для вычисления матричных элементов операторов
типа G (см. G.23)) удобно волновую функцию конфи-
конфигурации jN представить в виде генеалогического разло-
разложения по волновым функциям векторно связанных кон-
конфигураций jN~2 и р. Появляющиеся при этом генеало-
генеалогические коэффициенты определяются равенством
= 2 Ф О^ [К] r'a'/', /2 (N - 1, N) [к"] /"; JM) X
а', У, 1"
X (jN-2 [Я'] а'/', /2 [Я"] /", / |} /" [Я] а/>. G.51)
Они могут быть выражены через генеалогические коэф-
коэффициенты отщепления одной частицы. Для этого к вол-
волновой функции конфигурации jN, характеризующейся
таблицей Юнга г, применим дважды разложение G.40)
и свяжем отщепленные угловые моменты между собой:
<D(jN[X\raJM) =
= 2 2 Ф (jN~2 [Я7] г'а'Г, /2 (N - 1, NO"; JM) X
а'.'' а', 7', 7"
X (/"-2 [Щ а'У, /; Г \} ]^ [Я7] а'7'> X
X О'^1 М й'Л /; / I> 1N Wа/> </'(/'/V"I W)/^. G.52)
Суммирование по 7" в G.52) включает как четные, так
и нечетные значения, т. е. в G.52) входят как симмет-
симметричные, так и антисимметричные состояния электронов
N—1 и N. С помощью трансформационной матрицы
группы перестановок функция G.52) может быть

250 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
представлена в виде линейной комбинации функций
G.51):
Ф (/" [Я] raJM) = 2 Ф (/" [Ц r'r"aJM) (r'r" \ r)[K]. G.53)
г"
Входящая в G.53) трансформационная матрица диаго-
нальна по схеме Юнга \к'\ первых N — 2 электронов и
не зависит от таблицы Юнга г'. Она может быть запи-
записана в виде
где [%*] обозначает схему Юнга первых N— 1 электронов,
а г" обозначено как [Я"] ввиду однозначного соответ-
соответствия между ними. Вид такой матрицы приведен в гл. II
(см. B.65)).
Разлагая функции в правой части G.53) по формуле
G.51) и сравнивая с разложением G.52), получаем иско-
искомое соотношение
)[М </"-2 [Щ а'/', /2 [Я"] /"; J |} jN [Ц а/) =
= 2 </"-2 [Л'] а'/', /; 7' |} /"-1 [Я'] а'77) X
X О'^1 [*1 № /; / I /W W а/) </' (/7) Г | (/7) /7>(/). G.54)
С помощью формулы G.54) в работе [9] найдены ге-
генеалогические коэффициенты (pN~2, p2\}pN) для всех воз-
возможных состояний нуклонной оболочки. В табл. 7.2 при-
приведены генеалогические коэффициенты для разрешенных
состояний конфигураций эквивалентных р-электронов.
Генеалогические коэффициенты, входящие в разные ли-
нейные комбинации, разделены вертикальной чертой.
L" однозначно определяет [%"], однако для удобства мы
приводим значения как [Я7/], так и L".
7-4. Конфигурация из двух оболочек. Рассмотрим
конфигурацию из двух групп эквивалентных электронов,
находящихся в состоянии с перестановочной симметрией
схемы Юнга [к] и полным угловым моментом /. Каждая
группа электронов в свою очередь обладает определен-
определенной перестановочной симметрией [ка] и угловым момен-
моментом /а- Построение волновой функции конфигурации,
отвечающей значениям углового момента / и его проек-

КОНФИГУРАЦИЯ ЭКВИВАЛЕНТНЫХ ЭЛЕКТРОНОВ
251
ции М, осуществляется с помощью коэффициентов Клеб-
ша — Гордана:
- 2 Ф(/"' ft] ГЛ/^ФЙГ [М Г2«2^2) X
All, Ш]
X(/iAflf J2M2\JM). G.55)
Функция G.55) обладает определенной перестановочной
симметрией относительно перестановок первых П\ элек-
электронов и последующих щ электронов. Для симметризации
Таблица 7.2
Генеалогические коэффициенты
(pN Щ L {| /А [V] I', р* [V] L"; L)
UL"
[21] Р
И3]5
[1], [2]
PS PD
-2/3 /5/3
1
[1], [I2]
РР
1
-1
1
L'L"
p4[X] L:
[22]S
D
[212]P
[2]
SSDS
2
3
1
3
, [2]
SD DD
~~3~
i VT
3 3
[2], [I2]
SP DP
К 6 К 6
[I2],
PS
[2]
PD
/I
[i2], [i2]
pp
-i
-b
— 1
p3 [^], p2 [V7]
L7 L"
[221]P
[21], [2]
PS PD DD
-VT/Q VbftA T^5/8
[21], [I2]
PP DP
[i3], [i2]
SP
l

252 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
ее по схеме Юнга из П\ + п2 клеток воспользуемся фор-
формулой B.85):
ф O'i1 [К] Vi> /22 [К] <h?
м\
у ,( )А | ,[К]
X Ф (j? [\] 'A/pV [К] r&J2i Ш). G.56)
В качестве Q в G.56) может быть взята любая совокуп-
совокупность N\/ni\ri2\ перестановок по одной из каждого смеж-
смежного класса относительно подгруппы яЯ1 X лП2. Мы будем
брать перестановки, сохраняющие возрастающий поря-
порядок номеров электронов внутри каждой оболочки. В ре-
результате перестановки Q N-Pi электрон либо остается на
месте, либо занимает место электрона п\. Все N\/ni\n2\
функций разложения G.56) ортогональны друг другу
в силу ортогональности одноэлектронных функций с раз-
разными /а. Это обусловливает нормированность функций
G.56).
Для вычисления матричных элементов операторов F
и G G.23) волновую функцию G.56) удобно предста-
представить в виде разложения по волновым функциям, сим-
метризованным только по отношению к первым N—1
или Af — 2 электронам. Коэффициенты такого разложе-
разложения будем, так же как в случае одной группы эквива-
эквивалентных электронов, называть генеалогическими.
а) Генеалогические коэффициенты типа (N—1, 1\}N)
формально определяются разложением:
гТ, h(N); J
/', /,; /1} JT [Я,] a,/lf /2 [Л2] a2/2; [Я] /)
2
[X'} r'f, Ja№ JM)(A? [\] a,/,, fiT
/, }2i JI} 17 [K] a,/,, # [Я2] a2/2; [A] /). G.57)

§ 2 КОНФИГУРАЦИЯ ЭКВИВАЛЕНТНЫХ ЭЛЕКТРОНОВ 25,,
Суммирование по [%'Y отсутствует, поскольку задание
таблицы Юнга г однозначно определяет перестановоч-
перестановочную симметрию первых N—\ электронов, т. е. [А/] и г'.
Для нахождения явного вида коэффициентов разло-
разложения G.57) будем исходить из выражения G.56). На-
Нашей задачей является преобразование его к виду G.57).
В качестве (г)л в G.56) выбираем стандартную таблицу
Юнга г.
Разобьем сумму по Q в G.56) на две суммы. В пер-
первую сумму включим все перестановки Qb переводящие
N-ft электрон на место электрона п\. Из нее мы получим
вид коэффициентов (%Х~ХГ2\ /, I} /7722)- Во вторую сумму
войдут оставшиеся перестановки Q2, в результате дей-
действия которых N-й электрон останется на своем месте.
Эта сумма определит нам коэффициенты (/^/g2, /2|} /"'/г')-
Очевидно, что число перестановок в каждой сумме равно
G.58)
п (Q) = п (Q0 + п (Q2) = №1пх\ п2\
Рассмотрим первую сумму. Перестановки Q\ мож-
можно представить в виде произведения Q (N — 1) P\N\ где
P\N) = Pn N-i ...П1 переводит N на место пь a Q(N— 1)
на координаты Af-ro электрона не действует, т. е.
Q(N—lj^Jtjv-i. После действия перестановки P\N) на
функцию в G.56) имеем
21 = С2 2 (r\Q(N-l)P\N)\rir2)wQ(N-l)X
r,,r2 Q(N-l)
X ^(JT N rPiJv /? [К] Wr Ш\ 12 ...
... я1-Шл1п1 + 1 ... iV-1), G.59)
fx nil/nil'^ /7fim
Расположение номеров электронов в аргументе функции
Ф7 в G.59) соответствует их распределению между обо-
оболочками. Отщепим Af-й электрон из оболочки /^ с по-
помощью однооболочечных генеалогических коэффициен-
коэффициентов и изменим способ связи угловых моментов так,

254 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ« VII
чтобы угловой момент оставшихся П\—1 электронов пер-
первой оболочки был векторно связан с угловым моментом
/2 второй оболочки,
ф' - , 2 , ф ((/?•-' [К] '№> I? [К] 'М) Л /, № Щ х
х аг1 [К] *'Л iv A 11 /?• Ы V.) х
х<(/;/2)/7, к/;/,)/,//'. G.61)
Представим матричный элемент оператора Q(N—l)PiN)
в G.59) в виде произведения сомножителей, выбрав
симметрию промежуточного состояния, отвечающую
нестандартному представлению с типом редукции
К)
fl'r'X G.62)
Так как Q(N—1)ел:^~ь то, поскольку представления,
на которых определен матричный элементQ(N — 1),уже
имеют приведенную форму относительно перестановок
группы 7tN-\ (ср. B.22)), справедливо равенство
Докажем далее, что матрица Р\т в G.62) диаго-
нальна по таблицам Юнга первых П\ — 1 чисел и по-
последующих ti2 чисел. Для этого учтем, что в результате
действия перестановки Р\т на базисную функцию
ЦЭДпгг) получается функция, номера аргументов в ко*
торой разбиты на такие же подгруппы, как и в функции
([Я](г{г2)Х'1), т. е. матричный элемент перестановки Р<ло
может быть записан в следующем виде:
J Ф*[Ц A2 --. fti-1, пгпг + 1 ...N-l N) X
ХФО2 -¦ ^1-1 Nn^ + l ... N-l)dV. G.64)

§ 2 КОНФИГУРАЦИЯ ЭКВИВАЛЕНТНЫХ ЭЛЕКТРОНОВ 255
В качестве оператора в G.64) можно рассматривать еди-
единицу. С точки зрения группы перестановок это — непри-
неприводимый тензорный оператор, преобразующийся по еди-
единичному представлению. Поэтому к каждой из выделен-
выделенных групп чисел в G.64) мы можем применить теорему
Вигнера — Эккарта в форме D.60), откуда следует, что
;;22
G.65)
Следовательно, матричный элемент G.65) диагоналей
по схемам Юнга [А{], [Я2] и не зависит от таблиц Юнга.
С учетом G.63) и G.65) равенство G.62) переходит в
(г' | Q (N - 1) | r\r2f] <(А;А2) А'1 | /><"> | (А{1) \%2f\ G.66)
Подставим G.61) и G.66) в G.59), заменив сумму по rt,
Гч на эквивалентное суммирование по r{Aj, r2. Так как
аналогично G.56)
{r'\Q{N -\)\r[r2f'] Q{N
/<r
h-
h
то Ei примет окончательно следующий вид:
Sl=i"K-ir| S ?
xj aj, /J, /
A'] rV, /, (yV); /M) (/«¦-' [Я;] o;/J, /,; /, |} /»• [A,] a,/,) X
x <(/;/2) л, | да /л>(/) <(W я'11 p<№ | (Mi) ал)*1.
G.68)

256 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ - ГЛ. VII
Сравнение этой суммы с первой половиной разложения
G.57) дает нам искомое выражение для генеалогиче-
генеалогического коэффициента:
«2/2;
Ух'
х (№)/'/,!(/;/,)/./^'((WA'i iPHft1) *A>14- G.69)
Преобразуя аналогичным образом 22, содержащую
суммирование по Q2, получим выражение для генеало-
генеалогических коэффициентов отщепления электрона из вто-
второй оболочки. Поскольку по определению перестановки
Q2 не действуют на координаты Af-ro электрона, вместо
матрицы p\N) в выражение для генеалогического коэф-
коэффициента войдет соответствующая трансформационная
матрица группы перестановок. Окончательное выраже-
выражение имеет следующий вид:
X] г, /2;
х
X <(/,/Э ^/21Л та ^2>(/) <(А.^ Я/11 Я, (А21) Я2)[Х1. G.70)
Выражения для генеалогических коэффициентов G.69),
G.70) диагональны относительно квантовых чисел обо-
оболочек, из которых не отщепляется электрон; входящие
в них трансформационные матрицы повторйют способ
связи в обеих частях генеалогического коэффициента.

§ 2 КОНФИГУРАЦИЯ ЭКВИВАЛЕНТНЫХ ЭЛЕКТРОНОВ 257
б) Генеалогические коэффициенты Tuna{N — 2,2|}jV).
Определяются как коэффициенты разложения *)
-2 2,Ф((/?'-2[Я.;]а;/;, /2"'[А2]а2/2)[Я']г'Л
«1-
«1-
r2[^]a^, /2»>[А2]а2/2)-
/', /? [А"] /Г; /1} /?' [\] а,/,, /»> [\] а2/2; [Я] /)
2 2,
2
2,
2« 72
\\ [Г] /? /1} /у- [Л,] al/1, /? [Я2] а2/2;
, ф ((/г1
-L N)[k"]J", JM) X
/^ [Г] Г; /1} /?' [Я,] а/р Й» [Я2] а2/2; [X] /). G.71)
Выбор базисной функции представления, редуцированно-
редуцированного на подгруппе nN-2Xn2i соответствует заданию пере*
становочной симметрии первых N — 2 'электронов и по-
последних двух, поэтому сумма по [\']г' и [Х'Т отсутствует.
Для получения явного вида генеалогических коэффи-
коэффициентов исходим из выражения волновой функции G.56),
в котором в качестве (г)Л выбираем г'г'\ где г' — табли*
ца Юнга первых N—2 электронов, г" — таблица Юнга
последних двух электронов, отвечающая только двум
возможностям [Я//]=[2] и [^7/]=[12]. Сумму по Q разобьем
*) Условимся, так же как и при предыдущем выводе, кванто-
квантовые числа конфигурации, оставшейся после отщепления электронов,
обозначать штрихом. Квантовые числа, характеризующие состояния
двух отщепленных электронов, будем обозначать двумя штрихами.
17 И. Г. Каплан

258 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ, VII
на четыре суммы 2* согласно делению перестановок по
их действию на координаты 7V—1-го и N-то электронов.
Qj — перестановки, переводящие электроны N—l,N
на место щ — 1, пг
Q2 » » электрон N — 1
на место пх
Q3 » » электрон N
на место щ
Q4 —перестановки, оставляющие электроны N—l,N
на своих местах.
Первая сумма, соответствующим образом преобразован-
преобразованная, определит коэффициенты (У/11/, /?|} /f1/"')- Из чет-
четвертой суммы получаются выражения для коэффициен-
коэффициентов (У?1/?2"» l\\) /?7*22)• Для нахождения вида коэффици-
коэффициентов (/f1/?2» /1/21} /?722) необходимо объединить вто-
вторую и третью суммы.
Подробный вывод выражения для перечисленных
выше трех типов генеалогических коэффициентов дается
в работе [72]. Приведем конечные формулы:
/г; /, |! /г м «,/,> <(ед /'/г | (/;/п
X ((Я(Л2) Я'Я" | Р\~Ш I (Я1 1Х1
', /1 [Г] /"; /1} /». [Я,] а,/,, /». [Я2] а2/2; [Я] /) =
/ / , VI,
%%* «з(«2— 1) | / .„2_2 гл,1 ,у/ -2
fvfK N(N-l) J V2 NVz'W
«2/2> <(/,/2) /v2' 1 /, да) /2>(/ x
w- GJ3)

§ 2 КОНФИГУРАЦИЯ ЭКВИВАЛЕНТНЫХ ЭЛЕКТРОНОВ 259
М /', /,/2 [Г] Г; /1} /»' [Я,] а,/,, # [Я2] а2/2; [Я] /)
1 9
а,/,) (Й-1 [^] а^, /2; /21} #¦ [А,] а2/2) X
X <(ЭД Л'Г | Р^-1) | (Ц1) Лр (^1) Я2)[М, G.74)
где Pi —перестановка, переводящая электроны N—1
и N в первую оболочку, p[N~l) — перестановка, переводя-
переводящая N—1-й электрон в первую оболочку. В результате
действия обеих перестановок сохраняется возрастающий
порядок номеров электронов внутри каждой оболочки.
Нетрудно показать, что
pN-lN^l РМ-2...пг-М-Ш-3...П1 (°РИ  НвЧвТНОМ),
I PNN-2...nlPN-W-*...nl-l (ПРИ П* ЧеТНОм),
Р\Ы~1) = Рм-ш-2...П1. G.75)
Входящие в выражения G.72), G.73) трансформаци-
трансформационные матрицы группы /?3 выражаются через коэффи-
коэффициенты Рака либо через 6/-символы. Трансформацион-
Трансформационная матрица группы /?3, входящая в G.74), связывает
функции с различными способами сложения четырех
угловых моментов и выражается поэтому через 9/-симво-
лы. Матрицы группы jtjv, входящие в G.72) — G.74), вы-
вычисляются по способу, изложенному в § 3 гл. II. В ра-
работе [73] приведены матрицы группы перестановок, необ-
необходимые, для вычисления генеалогических коэффициен-
коэффициентов G.72) —G.74) систем с общим числом электронов
N = 3 + 6. В этой работе затабулированы матрицы, охва-
охватывающие более широкий класс перестановочной симмет-
симметрии, осуществляющейся для нуклонных состояний *).
*) Хори [12] получил выражения для генеалогических коэффи-
коэффициентов двухоболочечной конфигурации типа (N — га, m\}N). Для
т«=1 и 2 они переходят в формулы G.69)—G.70) и G.72) —G.74)
соответственно.
17*

260 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
7-5. Произвольная многооболочечная конфигурация.
Рассмотрим конфигурацию из k групп эквивалентных
электронов. Обозначим ее буквой /(,
*##...#; S«0 = iV. G-76)
Числа заполнения па могут быть любыми в пределах от
1 до 2/а+1. Каждая оболочка характеризуется зада-
заданием квантовых чисел [Яа]аа/а, а вся конфигурация— за-
заданием общей схемы симметрии [X], суммарного углового
момента / и его проекции М. Для полного описания со-
состояния необходимо дополнительно задать k—2 проме-
промежуточных угловых моментов /при4 — 2 промежуточных
схем Юнга [Япр], а также способ связи оболочек, обозна-
обозначим его буквой А (см. раздел 6-4). Полный набор кван-
квантовых чисел, характеризующих конфигурацию G.76),
обозначим сокращенно
p[k]aJM,
где р обозначает набор k схем Юнга {ка} и k—2 проме-
промежуточных схем Юнга, аналогичный смысл по отношению
к угловым моментам имеет обозначение а.
Генеалогические коэффициенты конфигурации G.76)
определяются как коэффициенты разложений, являю-
являющихся обобщением соответствующих разложений для
двухоболочечной конфигурации G.57) и G.71).
a) <#-1,
Ф (/Ср [Ц raJM) = 2 2 ф (Кар' W] г'о!У, }а (N); JM) X
X (КаР' [Щ а'/', /V, / |} Кр [Ц а/>. G.77)
б) (N-2,2\}N)
а=»1 р\ а', /',
X (/Св»р' [Я'] а'/', ы» [Я /"; /1} Кр [Ч а/>. G.78)

§ 2 КОНФИГУРАЦИЯ ЭКВИВАЛЕНТНЫХ ЭЛЕКТРОНОВ 261
Суммирование в G.77), G.78) проводится только по
тем схемам симметрии и угловым моментам в р' и а',
которые затрагиваются в результате отщепления элек-
электронов. По [Я/] и [%"] суммирование не проводится, по-
поскольку последние задаются таблицами Юнга г', г". Каь
обозначает конфигурацию К, у которой один электрон
отщеплен из оболочки /"", а другой — из оболочки /?*;
аналогичный смысл имеют обозначения Каа и Ка-
Вывод выражений для генеалогических коэффициен-
коэффициентов разложений G.77), G.78) аналогичен выводу для
конфигурации из двух оболочек, но более громоздок.
Приведем результаты [72]:
a) (N-1, 1|Щ
{IJ^] C /.: '. I } Га" [К] «Л) X
x <(/,.../;... Jfna | (/,... (J'ja) /.... /ft)T x
x «v.. ^ • • • 4)"' vi I Пт I (*i... D04 • • • V>T-
G.79)
6) (N-2, 2\}N)
- M /Г; /J} 1У [K] «./a) x
<(/,,../.... //' /v: i (/,... (jX) ja... h)Af}
G.80)

262
МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
аьр' W] а'/', иь [Г] /"; / |} *р \Ц а/) =
* k K 2nanb \
... (я.; i) к ... (x; i) \ ... д
{rja)ja...
. G.81)
Все перестановки в формулах G.79) — G.81) сохраняют
возрастающий порядок номеров электронов внутри обо-
оболочек. Р{а] переводит N-й электрон на место последне-
последнего электрона в оболочке ]паа, номер этого электрона обо-
значим
lN
—^Пс', PaalN переводит электроны jV—1 и
N в оболочку jnaa\ PNal N переводит электрон N—1 в обо-
оболочку ]'1а, а электрон N — в оболочку \пъь (а < Ь). Эти пе-
перестановки следующим образом выражаются через
циклы:
DN-\N __
* aa —
pNa;w
NN-2...ma-W-lN-Z...ma
(N ~
~ Ша)
NN-2... mb-\mb-2 ... maN-\N-Z ...mb
(для {N — mb) нечетного),
N-2 ... mhr N-lN-3 ... mh-\mb-2 ... ma
(для (N — mb) четного).
G.82)
Матрицы перестановок, входящие в выражения ге-
генеалогических коэффициентов G.79) — G.81), вычис-
вычисляются через матрицы стандартного представления и
трансформационные матрицы группы перестановок по

§2 КОНФИГУРАЦИЯ ЭКВИВАЛЕНТНЫХ ЭЛЕКТРОНОВ 263
правилам, данным в § 3 гл. II. Трансформационные мат-*
рицы группы /?з выражаются через 3/г/-символы (см.
раздел 3-7).
В случае однократно заполненных оболочек (все
тга=1) выражения для генеалогических коэффициентов
G.79) — G.81) совпадают с формулами, полученными
Яном [74]. Для антисимметричных состояний [Х] = [1^]
выражения G.79) — G.81) переходят в соответствующие
формулы работы Левинсона [75], так как для однораз-
одноразмерных представлений матрицы перестановок равны ±1.
7-6. Формулы для матричных элементов не завися-
зависящих от спина симметричных операторов. Рассмотрим
произвольную конфигурацию G.76) в состоянии с LS-
связью. При LS-связи в качестве угловых моментов }а
нужно брать орбитальные моменты электронов /а. Анти-
Антисимметричная полная волновая функция, аналогично
F.2), строится из произведений координатной волновой
функции на спиновую, симметризованных каждая по
взаимно дуальным схемам Юнга,
aLM) = ^= 2 Ф (/Ср [Ц raLM) Q (s" [Ц г). G.83)
В случае, когда операторы не зависят от спиновых
переменных, для вычисления матричных элементов до-
достаточно знания только координатной волновой функ-
функции. Получим формулы для матричных элементов опе-
операторов F и G (см. G.23)), предполагая их не завися-
зависящими от спиновых координат.
а) Оператор F. Ввиду тождественности электронов
оператор F в матричном элементе можно заменить на
NfN, где оператор fN действует только на N-и электрон.
Так как оператор In не зависит от спиновых координат,
то, учитывая ортонормированность спиновых волновых
функций, получаем
(К9[Л]aLM\F\Kp [Я] aLM) -
" N -E S <**[Я] raLM I'" I *P W ГаШ)> G.84)
г
Разложим координатную волновую функцию согласно
формуле G.77). Суммирование по г в G.84) эквивалентно

264 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ, VII
суммированию по [А/]г', где [А/] пробегает все воз-
возможные схемы Юнга, получаемые из [К] отнятием одной
клетки. Учитывая ортогональность базисных функций
разложения G.77) и независимость генеалогических ко-
коэффициентов от таблиц Юнга г', получаем следующую
формулу:
</Ср [Ц aLM\F\Kp [Я] aLM) «
а-1 р', А,' а', V
X <А:ар'[Л']а7/, /в(Ю; LM|fw|7CaP'[^]a'L', la(N); LM) X
</СаР'[V] о!U, la,L\} Kp [Ц aL). G.85)
Для не равных нулю недиагональных по конфигура-
конфигурации матричных элементов аналогичным образом полу-
получаем
</Ср[Я] aLM\F\Kap [Ц alM) =
p', A,' a', Z/
X </Ce(/[V]a'L', Ia(N)\ LM\fN\Kap'[Щa'L', Ш); LM)X
X (KapT [X] a'L'9 lb\ L\)Kbap [Ц aL>, G.86)
где /(^обозначает конфигурацию, получаемую из К при
удалении одного электрона из оболочки 1паа и добавле-
добавлении его к оболочке 1пъь (оболочка 1пьь может и не вхо-
входить-в конфигурацию К, т. е. п& = 0).
Матричные элементы оператора fw в G.85), G.86)
вычисляются с помощью техники тензорных операторов
(ср. раздел 7-2).
б) Оператор G. Полную волновую функцию записы-
записываем аналогично G.83), выбрав вместо стандартного
представления представление, редуцированное на под-
подгруппе я>м-2 X я2:
G.87)
* 'К А.', г',

§ 2 КОНФИГУРАЦИЯ ЭКВИВАЛЕНТНЫХ ЭЛЕКТРОНОВ 265
Суммирование по V, г', А," в G.87) эквивалентно сум-
суммированию по всем таблицам Юнга г представления
ПЧ [V] пробегает все схемы Юнга, получаемые из [к]
отнятием двух клеток, [X"] может быть только двух ти-
типов—[2] и[12].
Оператор G считаем скаляром, следовательно, его
матричные элементы должны быть диагональны по угло-
угловым моментам и не зависеть от их проекций. Замена G
N(N-1)
на ——^—- gtf-itf и учет ортонормированности спиновых
волновых функций приводят к следующему выражению
для матричного элемента:
"^ 2
Далее, подставляем в правую часть G.88) разложение
координатной волновой функции G.78). Оператор gN-\ jv
действует только на координаты N—1-го и N-ro элек-
электронов. Поскольку в базисных функциях разложения
G.78) электроны N—1, N отщеплены, то учет скаляр-
ности оператора gN-iN (см. соотношение D.81)) и неза-
независимости генеалогических коэффициентов от таблиц
Юнга г' приводит к искомой формуле
</Ср [Я] aZ. | G | /Ср [Я] aL> =
X (КаьР'Мa'L', "tjbW\L"\ L\}K9[4O.L) X
X {Kab9r W\ off, tjb [X"\ L"; L\}Kp [Ц aL). G.89)
Входящие в G.89) генеалогические коэффициенты при
а = Ь находятся по формуле G.80), при афЬ — по фор-
формуле G.81); g{ab}ab(L") обозначает двухэлектронный
матричный элемент оператора g,
b iL") = ('A I*-"] L" I g I /A [* L")- G-90)
Недиагональные по конфигурации матричные эле-
элементы не исчезают только для конфигураций,

266 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
различающихся не более чем на две орбитали. Анало-
Аналогично ранее введенному обозначению Ка обозначим
через Kat конфигурацию, получаемую из конфигура-
конфигурации К при переходе двух электронов соответственно из
оболочек 1паа и 1пьъ в оболочки 1псс и lndd. Разлагая ко-
координатную волновую функцию по формуле G.78) и
учитывая ортогональность базисных функций разложе-
разложения, приходим к следующим формулам для недиаго-
недиагональных по конфигурации матричных элементов скаляр-
скалярного оператора:
(Kp[4aL\G\Kbap[k]aL) =
_N(N-l) 1 у у у f [n „~
X (KacP'MoT/, Tj,W\L"\ L\}Kp[ЦaL) X
X {KacP' W off, lblc [%"] L"; L\}Kp [Ц aL). G.91)
k
p', А/, Г d',L',L"
X </Саг,р' [Я'] a'Z/, /e/ft [Я"] L"; L |} Kp № aL) X
X (KabPf W a'U, lcld [k"] L"\ L |} K%p [k] aL). G.92)
Если воспользоваться свойством коэффициентов
Клебша — Гордана C.476), то нетрудно показать, что
двухэлектронный матричный элемент, входящий в G.91),
G.92), равен
,Г т7.™ G.93,
(для [Г]
где gab,cd(L") обозначает матричный элемент, взятый
на несимметризованных функциях связанных моментов,
отвечающих одинаковому порядку связи электронов с
обеих сторон матричного элемента, т. е.
g \1C(N - \)l4(N)f°\ G.94)

§ 3 ВЕКТОРНО НЕСВЯЗАННЫЕ СОСТОЯНИЯ 26?
Способы вычисления матричного элемента G.94) в слу-
случае электростатического взаимодействия электронов по-
подробно изложены в руководствах [25, 26].
§ 3. Векторно несвязанные состояния
7-7. Конфигурация из однократно заполненных орби-
орбиталей. Для системы электронов, помещенных в поле про-
произвольной симметрии, вектор углового момента пере-
перестает быть хорошим квантовым числом. Теряет смысл
и понятие сложения угловых моментов. Координатное
состояние каждого электрона описывается заданием од-
ноэлектронной орбитали фа@- Обозначим через К про-
произвольную конфигурацию k одноэлектронных орбиталей
К: Ф>2*...Ф?; 2лв = Л. G.95)
а-1
Конфигурацию, получаемую из К отнятием орбитали
фа, будем обозначать Ка\ аналогичный смысл имеет обо-
обозначение Каъ- Пусть орбитали в G.95) не вырождены
и образуют ортонормированный набор. В соответствии
с принципом Паули на каждой орбитали может нахо-
находиться не более двух электронов, т. е. паК2*).
Рассмотрим случай однократного заполнения орби-
орбиталей. Нормированная координатная функция, описываю-
описывающая состояние с перестановочной симметрией схемы
Юнга [Д в данном случае может быть построена непо-
непосредственным действием операторов со^1 на несимметри-
зованное произведение одноэлектронных орбиталей:
Ф^1 (К) = 4*1 Фо (К) = (-{ft]12 2 Г^1 (Р) РФ0 (Ю, G.96)
р
где Р пробегает все N1 перестановок группы я#, аФ0(/С)
обозначает произведение орбиталей
G.97)
Таблица Юнга г характеризует симметрию функции
G.96) относительно перестановок координат электронов,
*) Генеалогические коэффициенты для векторно несвязанных
состояний нуклонов рассмотрены в [95].

268 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
таблица Юнга/ — симметрию относительно перестановок
орбиталей. Всего можно построить fx различных со-
состояний с перестановочной симметрией [X]. Они разли-
различаются видом таблицы Юнга /, задание которой эвива-
лентно заданию N—2 промежуточных схем Юнга групп
jtiv-ь л:#_2, ..., я2. Следовательно, роль символа р из
раздела 7-5, обозначающего набор k схем Юнга [ка] и
k—2 промежуточных схем Юнга, играет в данном слу-
случае таблица Юнга t.
Генеалогические коэффициенты конфигурации одно-
однократно заполненных орбиталей формально определяют-
определяются разложениями:
a) <tf-l, 1\}N)
ф^1 (К) - 2 2 ф?! {/д Фа (Ю (ка м ^, Фа |} к [Ц t).
а=\ и'
G.98)
б) (N-2, 2\}N)
X </Caft [X']«', ФлФ, [Г] |} К [X] t). G.99)
Суммирование по и' проводится по всем таблицам Юнга
представления Г[Х'\ Выбор в G.99) представления, ре-
редуцированного на подгруппе ji]\r-2XJt2, соответствует
заданию схем Юнга [А/] и [X"], поэтому суммирование
по ним не проводится.
Выражения для коэффициентов разложения G.98),
G.99) могут быть получены из общих формул раздела
7-5, если отбросить в последних все множители, относя-
относящиеся к сложению угловых моментов. Для лучшего уяс-
уяснения специфики рассматриваемого случая получим яв-
явный вид генеалогических коэффициентов, преобразовав
соответствующим образом выражение G.96).
Для нахождения вида генеалогических коэффициен-
коэффициентов (N— 1,1|}jV) разобьем совокупность N\ перестано-
перестановок в G.96) на jV групп по месту, на которое они пере-
переводят ЛЛй электрон. Каждая из таких групп содержит
(N—1)! перестановок, которые всегда можно предста-
представить в виде произведений Q(N—\)P{a\ где переста-

§ 3 ВЕКТОРНО НЕСВЯЗАННЫЕ СОСТОЯНИЯ 269
новка Р{а] переводит Л/-й электрон на орбиталь фа, a
перестановки Q(N—\) на координаты N-го электрона
не действуют, т. е. Q(N— l)^nN-h В качестве Р{а] не
обязательно, как в G.82), брать перестановку Pnn-\-<i>
сохраняющую возрастающий порядок номеров электро-
электронов (не считая N-ro), может быть взята и простая транс*
позиция PaN.
Учитывая свойства стандартного представления, мат-
матричный элемент перестановки Р = Q (N — 1) Pf] можно
представить в виде
= 2 (rf I Q (N - 1) | и')М («'11PTI t)m. G.100)
Поскольку
G.101)
подстановка G.100), G.101) в равенство G.96) позволяет
записать его в виде разложения G.98):
фМ (К) = /? ^)* 2 2 («'1 | Р« | ^Ф^(Ка) Фа (АО.
а"' "' G.102)
Сравнение G.102) с G.98) дает нам явный вид генеало-
генеалогических коэффициентов
{ка[я']и', <ра\жтt) = (^7if («'iI^wI*)m- G-103)
Для нахождения вида генеалогических коэффициен-
коэффициентов типа (N—2,2 |}N) исходим из функции G.96), в ко-
которой вместо таблицы Юнга г заданы таблица Юнга
первых N—2 электронов тг и таблица Юнга последних
двух электронов г". Перестановки Р могут быть разбиты

270 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
на (N— 1) N совокупностей по месту, на которое они
переводят электроны N—1 и N. Каждая такая со-
совокупность содержит (N—2)! перестановок. Несложные
преобразования [59] приводят к следующему выражению
для генеалогических коэффициентов:
В качестве Раь может быть взята любая перестановка,
переводящая электрон N—1 на орбиталь фа, а электрон
N — на орбиталь щ. В частности, можно выбрать Раь N =
= PaN-iPbN- Входящая в G.104) матрица РаьШ вы-
выражается через соответствующую матрицу стандартно-
стандартного представления, если последнюю умножить слева на
трансформационную матрицу (и'к"\и'р2)[к\ содержащую
либо единицы, либо блоки вида B.65). В Приложении
6 приведены таблицы матриц \г'к"\Раь \t/ для всех
разрешенных схем Юнга [к] конфигураций с числом
электронов от 3 до 6.
7-8. Произвольное заполнение орбиталей. В общем
случае конфигурации G.95) па может принимать два
значения: 1 и 2. Каждая двукратно заполненная орби-
орбиталь характеризуется схемой Юнга из двух клеток [2].
Набор схем Юнга двукратно заполненных орбиталей и
необходимых для однозначной характеристики состоя-
состояния промежуточных схем Юнга будем обозначать сим-
символом р. Так как представления, характеризующие
электроны, находящиеся на одной орбитали, одномерны,
количество независимых наборов р, относящихся к за-
заданной [AJ, равно размерности f% неприводимого пред-
представления РЧ Однако не все такие наборы осуществ-
осуществляются, поскольку заполненные орбитали не могут иметь
[Х] = [12]. Количество независимых состояний определяется
формулой F.70).
Генеалогические коэффициенты конфигурации G.95)
являются частным случаем генеалогических коэффици-
коэффициентов, определенных в разделе 7-5. Различие между
ними заключается в отсутствии в рассматриваемых

§ 3 ВЕКТОРНО НЕСВЯЗАННЫЕ СОСТОЯНИЯ 271
состояниях векторной связи. Вместо G.77), G.78) имеем
следующие разложения:
а) <#-1, 1\}N)
Ф(/Ср[Я]г) =
2 %(аР№)уа(Ю(ар'[П <Ра \)КрЩ). G.105)
а=1 Р'
б) (N-2,2\}N)
Ф (/Ср [Ц г'г") = 2' 2 Ф (tfaaP' [X'] гО Фа (N - 1) Фа (JV) X
а р'
+ 2 2 ф (/^р' [я'] го ф (ФаФб [Г] | iv -1, jv) х
а<& р'
X <*«*!/ [Я,'], ФаФ, [Г] | } /Ср [Я]). G.106)
Сумма по р' берется по всем независимым наборам кон-
конфигурации, оставшейся после отщепления электронов.
Первое слагаемое в формуле G.106) присутствует толь-
только в разложении функций с г"=[2]. Штрих у суммы по
а означает, что она берется только по двукратно запол-
заполненным орбиталям.
Выражения для коэффициентов разложения G.105),
G.106) получаются из формул G.79) — G.81), если
учесть, что в данном случае отсутствует векторная
связь, и все па-^2. В результате получаем
а) C/V-l, 1\}N)
{Кар'1П Ф.|}/Ср[Я]) = {|7^}1/2<р/^1|Р^)|рП G.107)
б) <iV-2,

272 МЕТОД ГЕНЕАЛОГИЧЕСКИХ КОЭФФИЦИЕНТОВ ГЛ. VII
Входящие в G.107) — G.109) матрицы определены на
функциях, принадлежащих к представлениям с различ-
различными типами редукции на подгруппах. Они находятся
через матрицы стандартного представления с помощью
соотношения B.74). Вид перестановок в матричных эле-
элементах G.107) — G.109) дается в общем случае форму-
формулой G.82).
В следующей главе с помощью генеалогических раз-
разложений G.105), G.106) будут получены формулы для
матричных элементов, не зависящих от спина операто-
операторов F и G в случае произвольных молекулярных систем.

ГЛАВА VIII
РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИИ
МОЛЕКУЛЯРНЫХ СИСТЕМ
§ 1. Молекула водорода.
Учет конфигурационного взаимодействия
8-1. Метод валентных схем. Молекула водорода была
впервые рассчитана Гайтлером и Лондоном в 1927 г.
[78]. Эта работа явилась основополагающей для постро-
построения теории химической связи. Метод Гайтлера — Лон-
Лондона (или, как его принято называть в квантовой хи-
химии, метод валентных схем) был применен в дальней-
дальнейшем к расчету целого ряда более сложных молекул.
В первоначальном расчете Гайтлер и Лондон исхо-
исходили из ковалентной конфигурации молекулы Н2, взяв
в качестве исходного набора базисных функций две ls-
орбитали атома водорода. Этого оказалось достаточным,
чтобы качественно объяснить природу химической свя-
связи в молекуле Н2. В данном разделе мы покажем, как
проводится расчет молекулы Н2 с учетом всех конфигу-
конфигураций, возникающих из ls-орбиталей. Этот расчет, так
же как и все последующие расчеты в этой главе, бу-
будет проводиться без использования спиновых волновых
функций.
В § 3 гл. VI уже говорилось, что все свойства моле-
молекул, не связанные со спиновыми взаимодействиями, мо-
могут быть описаны заданием только координатных вол-
волновых функций, обладающих перестановочной симмет-
симметрией соответствующих схем Юнга. Эта перестановочная
симметрия несет в себе как бы «память» о спине. Ме-
Методика расчета с координатными волновыми функциями
является более последовательной и наглядной, чем опе-
оперирование со спиновыми функциями в задачах, где опе-
операторы взаимодействия спина не содержат.
Обозначим ls-орбитали атомов Н в молекуле Н2 че-
через фа и фь. Для конфигурации нейтральных атомов

274 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
могут быть построены две ковалентные структуры: син-
глетная и триплетная. Отвечающие им координатные
волновые функции находятся действием операторов
Юнга о)[2] и со112] на произведение орбиталей сраA)фьB).
Учитывая неортогональность орбиталей, получаем сле-
следующие нормированные комбинации:
к (8.1)
(8.2)
где р обозначает интеграл перекрывания,
(8.3)
(в записи (8.3) учтено, что ls-орбитали являются дей-
действительными функциями).
Молекула Нг принадлежит к точечной группе A»ft.
Ее электронные состояния должны классифицироваться
по неприводимым представлениям этой группы и, в
частности, характеризоваться определенной симметрией
по отношению к инверсии относительно центра инерции
молекулы. По своему построению функция (8.1) яв-
является четной по отношению к инверсии, а функция
(8.2)—нечетной. Поскольку они составлены из ls-орби-
талей, состояние, описываемое функцией (8.1), обозна-
обозначается J2g*), а состояние, описываемое функцией
(8.2), —32„.
Электронная часть гамильтониана молекулы может
быть представлена в виде суммы трех слагаемых:
2), (8.4)
*) Состояния молекул, принадлежащих к точечным группам
D<x>h* А»о» принято классифицировать по величине проекции пол-
полного орбитального момента электронов на молекулярную ось. В за-
зависимости от величины проекции М термы обозначаются заглавны-
заглавными греческими буквами:
М: О 1 2

§ 1
УЧЕТ КОНФИГУРАЦИОННОГО ВЗАИМОДЕЙСТВИЯ
275
где &6а(\) и &вьB) — гамильтонианы изолированных
атомов, а W(l, 2)—оператор взаимодействия атомов
Н. В атомных единицах
(8-5)
Обозначения расстояний, входящих в выражения (8.5),
приведены на рис. 8.1.
При учете только ковалент-
ной конфигурации задача сво-
сводится к решению секулярного
уравнения второго порядка. Вол-
новые функции (8.1) и .(8.2) при-
принадлежат к различным мульти-
плетам. Следовательно, секуляр- а {
ное уравнение не имеет недиаго-
нальных элементов. Энергия мо-
моРис 8 j
9
лекулы в состояниях (8.1), (8.2) определяется диагональ-
диагональными матричными элементами гамильтониана (8.4)*):
(8.6)
f^ (8.7)
где ?i5(H) энергия атома Н в ls-состоянии,
Q = J Ф|A)Ф|B) ^(Ь 2)rfl/, (8.8)
(8.9)
Q называют кулоновским интегралом. Он представляет
собой энергию электростатического взаимодействия двух
атомов водорода. А называют обменным интегралом.
Связанную с ним энергию называют обменной энергией.
Обменная энергия не имеет классического аналога. Она
*) При выводе выражений (8.6), (8.7) следует учесть, что
<Фв1еИ?Лф*>-?и(Н)р (см. [38]).

276 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ„ VIII
возникает вследствие того, что каждый электрон, как
это следует из вида функций (8.1), (8.2), может с рав-
равной вероятностью находиться в состояниях фа и фь. При
этом в случае симметричной координатной функции
(состояние ]Hg) вероятность найти электроны близко
расположенными велика, в случае антисимметричной
(состояние 12,и)—мала. Это обусловливает зависимость
энергии системы электронов от их полного спина. Под-
Подчеркнем, что обменная
энергия является частью
обычной энергии электро-
электростатического взаимодей-
взаимодействия, связанной с кван-
товомеханической корре-
корреляцией в распределении
электронной плотности.
—^ тЯаь>а™& В Работе Гайтлера —
"ЗчГ7« Лондона [78] был вычис-
& Р'* лен кулоновский интеграл
Рис. 8.2. и проведена приближен-
приближенная оценка обменного ин-
интеграла. Точное значение обменного интеграла было
дано Сугиурой [79]. Значение интегралов Q и А при раз-
различных расстояниях между атомами Н затабулиро-
ваны в книге Слейтера [38]. На рис. 8.2 изображены
энергии состояний lHg и 3SW как функции расстояния
Яаь между атомами Н. Энергия отсчитывается в рид-
бергах (Ry). При бесконечном разведении атомов энер-
энергия равна 2?"is(H) или — 2Ry. Кривая, отвечающая синг-
летному состоянию, имеет минимум и соответствует ос-
основному состоянию молекул водорода. Она качественно
согласуется с экспериментальной кривой, но распола-
располагается заметно выше. Получаемая при этом расчете энер-*
гия связи составляет 3,14 эв, что на 1,61 эв меньше экс-
экспериментального значения. Основную часть энергии свя-
связи составляет обменная энергия. Доля кулоновского
интеграла в точке минимума потенциальной кривой
меньше 5%, с увеличением расстояния между ядрами
она несколько повышается, но нигде не превышает 15%*).
*) В других молекулах вклад кулоновской энергии в общую
энергию связи может быть значительно больше [91].

§ 1 УЧЕТ КОНФИГУРАЦИОННОГО ВЗАИМОДЕЙСТВИЯ 277
Учтем теперь ионные конфигурации. Всего из двух
ls-орбиталей можно построить две ионные конфигура-
конфигурации: ф^ и ф|. Обе конфигурации соответствуют синглет-
ному состоянию. Для построения функций, обладающих
определенной симметрией по отношению к инверсии
молекулы, необходимо взять линейные комбинации ко-
координатных функций ионных конфигураций. Они имеют
следующий вид:
к , (8.10)
. (8.11)
При учете взаимодействия ковалентной и ионных
конфигураций наряду с функциями (8.10), (8.11) учи-
учитываются функции (8.1), (8.2). Переобозначим послед-
последние: ФД^езФ121 и ФC2Ц) = Ф[12] Всего имеем четыре
исходные вариационные функции:
Фг(Ъ,)9 Ф2(ЧЕ,), Ф(ЩЯ), Ф(*2И). (8.12)
Энергии состояний !SW и 32U определяются диаго-
диагональными матричными элементами гамильтониана. Для
32М выражение диагонального матричного элемента
дается соотношением (8.7). Энергия состояния JEU мо-
может быть записана в виде
Ж1*.)--^. - (8-13)
где матричные элементы
, (8.14)
Р = <Ф*Ф* I Зв | Ф,ф,) = <ФвФ> | &в | ф,Фа). (8.15)
Энергия состояний с симметрией !ЕЯ находится в ре-
результате решения секулярного уравнения второго па-
рядка, определенного на функциях Ф^1^) и Фг^Е^).
Эти функции не ортогональны друг другу. Интеграл не-
неортогональности равен
т^г. (8.16)

278
РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ
ГЛ. VIII
В дополнение к обозначениям (8.14), (8.15) обозначим
матричные элементы
(8.17)
= 6. (8.18)
В результате секулярное уравнение примет следующий
-Е
F-рЯ)
TTV
= 0.
Значения интегралов, необходимых для расчета матрич-
матричных элементов а, р, v и б, приведены в книге Слейте-
ра [38].
На рис. 8.3 изображены энергии термов Н2, получен-
полученных с учетом конфигурационного взаимодействия. Энер-
Энергия триплетного терма
32W такая же, как в ме-
методе Гайтлера—Лондона.
Появляются новый синг-
летный терм 12и и два
терма l2ig. Понижение
энергии основного состоя-
состояния вследствие учета ион-
НЫХ СТРУКТУР незначи-
тельно. Для энергии свя-
связи получается значение
3,21 эв [80]. Для лучшего
согласия с экспериментом
необходимо ввести в волновые функции дополнительные
вариационные параметры, а также слагаемые, явно за-
зависящие от расстояния между электронами. Подробное
обсуждение этих вопросов содержится в [38, 56].
8-2. Метод молекулярных орбиталей. Метод молеку-
молекулярных орбиталей был предложен Гундом [81] одновре-
одновременно с методом Гайтлера — Лондона. В дальнейшем
был развит ряд усовершенствований метода молекуляр-
молекулярных орбиталей, включающих процедуру самосогласова-
самосогласования [82, 83]. В основе большинства вариантов метода
молекулярных орбиталей лежит представление молеку-
Рис. 8.3.

§ 1 УЧЕТ КОНФИГУРАЦИОННОГО ВЗАИМОДЕЙСТВИЯ 279
лярной орбитали в виде линейной комбинации атомных
орбиталей, коэффициенты в которой определяются из
требования минимума энергии системы. Для симметрич-
симметричных молекул коэффициенты таких линейных комбинаций
обычно могут быть найдены из требования принадлеж-
принадлежности молекулярных орбиталей к базису неприводимых
представлений группы симметрии молекулы.
Из атомных ls-орбиталей для молекулы Н2 можно
построить две молекулярные орбитали: четную по отно-
отношению к инверсии (og) и нечетную—(аи):
Энергия одноэлектронной конфигурации с орбиталью
og ниже энергии конфигурации с орбиталью ои. Основ-
Основному состоянию молекулы Н2 должна отвечать конфи-
конфигурация o2g. Координатная волновая функция конфигу-
конфигурации og описывает состояние lI>g. Она представляется
через атомные орбитали в следующем виде:
12)
(8.20)
Расчет энергии основного состояния с волновой функ-
функцией (8.20) приводит к значению энергии связи 2,681 эв
[84], что гораздо хуже, чем значение 3,14 эв, получаемое
с ковалентной структурой Гайтлера — Лондона. Это
объясняется тем, что ионные и ковалентные структуры
входят в функцию (8.20) с одинаковым весом. Для бо-
более точного расчета, помимо конфигурации о2, необхо-
необходимо учесть и другие конфигурации, которые могут да-
давать вклад в основное состояние.
Из двух молекулярных орбиталей могут быть обра-
образованы три конфигурации:
Первые две конфигурации отвечают синглетному состоя-
состоянию. Электроны последней конфигурации могут нахо-
находиться как в синглетном, так и в триплетном состояниях.
Координатные волновые функции этих состояний

280 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
находятся действием операторов &№ и со[121 на произведе-
произведение молекулярных орбиталей og(l)ouB). Координат-
Координатная функция конфигурации a2g приведена выше (8.20).
Остальные три координатные функции имеют следую-
следующий вид:
(8.22)
Сравнивая эти функции с волновыми функциями,
получаемыми в методе валентных схем, мы видим, что
они линейно связаны друг с другом. А именно,
фмо W. %)=Vijttw [Ф|С w+ф'с ('2*)]•
[Ф2ВС(%)-Ф?С(Х)], (8.23)
Поскольку корни секулярного уравнения инвариантны
по отношению к линейному преобразованию функций
базиса, расчет электронных состояний молекулы водо-
водорода методом молекулярных орбиталей при учете взаи-
взаимодействия конфигураций должен быть полностью экви-
эквивалентен разобранному в предыдущем разделе расчету
методом валентных схем. Последний результат может
быть сформулирован более общо:
при одинаковом атомном базисе и полном учете
взаимодействия конфигураций расчеты по методу
валентных схем и методу молекулярных орбиталей
полностью эквивалентны.
8-3. Ортогонализованные атомные орбитали. В слу-
случае многоэлектронных систем неортогональность одно

§ 1 УЧЕТ КОНФИГУРАЦИОННОГО ВЗАИМОДЕЙСТВИЯ 281
электронных орбиталей значительно усложняет вычис-
вычисление матричных элементов гамильтониана. В свое вре-
время Ванье [85] показал, как в случае кристалла могут
быть построены ортогональные комбинации атомных
орбиталей, локализованные в определенных узлах ре-
решетки. Аналогичная процедура может быть применена
и для молекулярных систем *) [38]. Рассмотрим ее на
простейшем примере молекулы Нг.
Исходим из молекулярных орбиталей (8.19). Нетруд-
Нетрудно показать, что эти орбитали ортогональны друг другу.
Составим из них симметричную и антисимметричную
комбинации:
1 <8-24) _
^2 Рис. 8.4.
Орбитали (8.24) также ор-
ортогональны друг другу, но в отличие от орбиталей (8.19)
они локализованы. Чтобы показать это, подставим в
(8.24) выражения (8.19). В результате получим
(8.25)
где
(8.26)
Орбиталь ф^ преимущественно локализована у ядра а,
ф? —у ядра Ь\ их вид приведен на рис. 8.4.
*) Функции Ванье строятся из ортонормированного набора де-
локализованных молекулярных орбиталей, в качестве которых выби-
выбирают обычно функции Блоха [38]. Метод построения ортогональных
локализованных орбиталей из атомных орбиталей развит в работе
Лёвдина [89].

282 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
Из орбиталей (8.25) можно составить функцию, ана-
аналогичную координатной функции основного состояния
Н2 в методе Гайтлера — Лондона:
Ф (^) = ~ [фО A) <pg B) + <pg A) <р? B)]. (8.27)
Расчет среднего значения гамильтониана в состоянии,
описываемом функцией (8.27), приводит к энергетиче-
энергетической кривой, не имеющей минимума и расположенной
выше аналогичной кривой для состояния 32U [86].
Этот результат не является удивительным, если
учесть, что в методе Гайтлера — Лондона основной
вклад в химическую связь дает обменная энергия, опре-
определяющаяся степенью перекрывания орбиталей. Орби-
Орбитали же (8.25) построены так, чтобы их перекрывание
равнялось нулю. Включение в расчет взаимодействия
всех конфигураций, которые можно построить на орби-
талях (8.25), приводит к тем же результатам, что и рас-
расчеты с неортогональными орбиталями фа и щ. Послед-
Последнее объясняется тем, что координатные волновые функ-
функции, построенные из орбиталей (8.25), так же как и в
методе молекулярных орбиталей, являются линейными
комбинациями координатных функций раздела 8-1.
§ 2. Вычисление энергетической матрицы
для произвольных молекулярных систем
8-4. Матричные элементы операторов F и О. Рас-
Рассмотрим произвольную конфигурацию К из k одно-
электронных орбиталей, на которых размещены N элек-
электронов,
k
IS. ~Jl\~Jl<> r-^b ^S^ *л AT /Q OQ\
J\. ф, ф2 • • • фь > J-J ^k = " • \p.ZO)
В соответствии с принципом Паули числа заполнения
па-*С2. Предполагаем, что орбитали фа образуют орто-
нормированный набор. В качестве фа могут быть выбра-
выбраны молекулярные орбитали либо ортогонализованные
атомные орбитали.
При пренебрежении спин-орбитальными взаимодей-
взаимодействиями состояния системы N электронов классифици-

§ 2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 283
руются неприводимыми представлениями Г^ группы
перестановок nN (см. § 3 гл. VI). Количество независи-
независимых состояний с перестановочной симметрией [А,], кото-
которые можно построить для данной конфигурации, опреде-
определяется формулой F.70). Координатные волновые функ-
функции таких состояний характеризуются способом кон-
конструкции из одноэлектронных орбиталей и различаются
символом р, обозначающим набор схем Юнга двукратно
заполненных орбиталей и k—2 промежуточных схем
Юнга. Антисимметричная полная волновая функция
строится из произведений координатной волновой функ-
функции на спиновую, симметризованных каждая по взаимно
дуальным схемам Юнга,
<' (/С) = ^7=- S ф# (Ю Ф (sN). (8.29)
В координатной волновой функции, входящей в (8.29),
р характеризует симметрию функции относительно пе-
перестановок орбиталей, г — относительно перестановок
номеров электронов. Спиновая функция описывает со-
состояние со значением полного спина S, определяемым
соотношением F.58). Значение проекции спина Ms в
функции (8.29) не задано, так как для дальнейшего это
несущественно.
Выражение полной волновой функции в виде (8.29)
будет использовано нами для нахождения матричных
элементов, не зависящих от спина симметричных опера-
операторов F и G (см. G.23)). При этом не потребуется зна-
знания конкретного вида спиновой функции Q, так как, в
силу независимости операторов от спиновых переменных
и ортонормированности спиновых функций, все спиновые
функции исчезнут в процессе вычисления матричных
элементов.
а) Оператор F. Ввиду тождественности электронов
и симметричности оператора F его можно заменить в
матричном элементе на NfNy где оператор fN действует
только на N-й электрон. Так как оператор fN не зависит
от спиновых координат, а спиновые функции, входящие
в сумму (8.29), пронормированы, матричный элемент
F\W(iq) (8.30)

284 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ, VIII
СВОДИТСЯ К
SW^ (8.31)
Матричные элементы, входящие в (8.31), легко вы-
вычисляются, если провести разложение координатных вол-
волновых функций с помощью равенства G.105) с коэффи-
коэффициентами G.107). Подставим разложение G.105) в
(8.31) и заменим сумму по г эквивалентной ей суммой
по \к'\г'. Выражение (8.31) перейдет в
2 2 Z
_ fx, N
а, Ъ р', (? Х\ г'
X <Ф. | fH | %) (Р'Я'11 /W | Р)[М (р^'11 Pf | Р>[М. (8.32)
Из способа конструкции функций Ф%^(Ка) следует, что
Вследствие ортогональности матриц перестановок
2 <Р'Я'11PW |p)W (p'X'l | />W I pf1 = бд. (8.34)
Подставляя (8.33) —(8.34) в (8.32) и учитывая, что
сумма по г' сводится к умножению на /^,, окончательно
получаем простой результат
(Кр | F | Кр>!М = б(-..? яа (Фа | /1 Фа). (8.35)
Из формулы (8.35) следует, что величина диагональных
по конфигурации матричных элементов оператора F не
зависит от перестановочной симметрии состояния, а сле-
следовательно, и от значения суммарного спина.
Матричные элементы оператора F, взятые между
различными конфигурациями, не равны нулю лишь для
конфигураций, отличающихся не более чем на одну ор-
биталь. Обозначим через Ка конфигурацию, получае-
получаемую из К при переходе электрона с орбитали <р0 на но-
новую орбиталь щ:
<:ф>2...ф;;'-Ч •••«>?. (8.36)

§ 2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 285
Проделав выкладки, аналогичные выводу формулы
(8.35), приходим к следующей формуле:
fab. (8.37)
Наличие б - в (8.37) означает, что в неравных нулю мат-
матричных элементах орбитали в конфигурации Ка должны
быть симметризованы так же, как и в конфигурации К;
fab обозначает одноэлектронный матричный элемент;
(8.38)
При выводе формулы (8.37) предполагалось, что поря-
порядок общих орбиталей в конфигурации К и Ка одина-
одинаков, причем орбиталь щ должна следовать за <ра. Пусть
Ка — РКа>
где Р — перестановка орбиталей__конфигурации (8.36),
приводящая ее к конфигурации Ка. Согласно соотноше-
соотношениям B.47), B.48)
ф? {р<) - я® (К)-S Г1] (р) ф[$ СО (8.39)
р
Подставляя в правую часть матричного элемента
выражение (8.39) и применяя к каждому, члену суммы
по р формулу (8.37), получаем более общую формулу:
a^^ab. (8.37а)
Пусть требуется вычислить матричный элемент
где К: **
В данном случае Къа '- ФЬФСФ^ и Кьа = РтКъа- Из табл. 1
Приложения 5 следует, что r[12211(Pi32)= — У*3/2. Поэтому,
согласно формуле (837а)
Приложения 5 следует, чт
согласно формуле (8.37а),
<ФаФ,Ф^@ I F

286 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
Формула (8.37а), так же как и формула (8.37), вы-
выведена при условии, что орбиталь ф& не содержится в
конфигурации /С, т. е. Пь = 0. Если Яь=1, то орбиталь щ
становится двукратно заполненной и конфигурация Ка
не сводится к виду (8.36). Формула для матричного эле-
элемента в этом случае получается, аналогично (8.35), раз-
разложением координатных волновых функций с помощью
генеалогических коэффициентов. Приводя порядок ор-
орбиталей в конфигурации, оставшейся в правой части
матричного элемента после отщепления орбитали щу к
порядку орбиталей в конфигурации Ка, окончательно
получаем
р', Р', Ь'
X (р'Я'1 | PW | р)Ш (р'Я'11 рш) | рум. (8.376)
Перестановки Р^ и Р^ переводят ЛЛй электрон на
орбитали фа и ф& конфигураций К и Кьа соответственно,
при сохранении возрастающего порядка номеров элек-
электронов на остальных орбиталях (см. G.75)). Рг приводит
порядок орбиталей в конфигурации Ка к порядку орби-
орбиталей в конфигурации Ка.
Диапазон применения формулы (8.376) шире, чем
(8.37а); Пь может равняться как 0, так и 1. Так, напри-
например, матричный элемент с К '- Ф^ФЙ» Кьа • ф^Фа необходи-
необходимо вычислять по формуле (8.376), так_как (8.37а) в дан-
данном случае неприменима. Имеем Ка: фьфа, Ка'.ЦаЩ,
откуда Р' = Р\2 и, следовательно, Г^-] (р') = ± бр,-, (плюс
для [V] = [2], минус для [V] = [l2]). В данном случаеР^ =
= РГ = Р2з. Взяв матрицу (VI |Р2з1Л[21] из табл. 1 При-
Приложения 5, по формуле (8.376) находим
i ab'
Оператор G. При построении полной волновой функ-
функции вместо стандартного представления выбираем пред-
представление, редуцированное на подгруппе ям-2Хя2. Сум-
Суммирование по г заменяется эквивалентным ему суммиро-

§ 2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 28?
ванием по г', X', г" (г" однозначно связано с X"):
Ввиду тождественности электронов или, что то же
самое, антисимметричности полной волновой функции,
оператор G в матричном элементе можно заменить на
N(N~\)
2— ?лг-ш> гДе &n-in — оператор взаимодействия
N-ro и N— 1-го электронов. Так как оператор G по ус-
условию не зависит от спиновых координат, а спиновые вол-
волновые функции ортонормированы, имеет место равенство
G | Кр)[Х] = DXIWI G
Т ТГ S W p WI О IФЙ- р (Ю>. (8-40)
К к К — в общем случае две различные конфигурации.
Подставим в матричные элементы правой части равен-
равенства (8.40) разложение координатных волновых функций
G.106) с генеалогическими коэффициентами G.108),
G.109). Это приводит к выражению, являющемуся ис-
исходным ^ля получения более компактных формул:
</Ср | G J /Ср>[А-] =
" S S S -k V* I2! I Я'1* I P>W <P^ [2] IPVNI p>W X
ьЪ
а с <dr\ X' p7,
X Й
+ S S S S^A'[2]|PiSr"'|p>IXI<pY[2]|Pew-"'|p>IXlx
a < 6 с r',X' P', 7
c<d

288 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
Входящие в (8.41) двухэлектронные матричные элементы
равны:
&ab, cd Sab, cd ~" Sab, dc J _ дЛЯ И//1 _. Г j2l
^ (8.42)
ry[2] = a
&aa, bb &aa, bby
где
(8.43)
Интеграл gabtab называют кулоновским, a gab,ba-"обмен-
gab,ba-"обменным *). Обозначим их более кратко:
gab. ab e Oflft, gflfe, fea e Ря*. (8.44)
При а == Ь может быть определен только кулоновский
интеграл ааа.
Рассмотрим диагональные по конфигурациям матрич-
матричные элементы, К = К. В силу ортогональности одноэлек-
тронных орбиталей ненулевой вклад в (8.41) дают толь-
только первая сумма при а = Ь и четвертая при с = а, d = 6,
так как
Согласно определениям (8.42) и (8.44), в сумму (8.41)
войдут только кулоновские и обменные интегралы. Учи-
Учитывая ортогональность матриц нестандартного предста-
представления и независимость членов суммы от г\ получаем
следующую компактную формулу [87]:
</Ср|
|Ч S С ^). . (8.45)
*) Отметим, что, в отличие от определенных на неортогональ-
неортогональных орбиталях кулоновском и обменном интегралах (8.8), (8.9),
содержащих в качестве оператора сумму одноэлектронного и двух-
электронного операторов, в интегралы (8.44) входит только двух-
электронный оператор.

§ 2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 289
где штрих у суммы по а означает, что суммирование про-
проводится только по двукратно заполненным орбиталям, а
коэффициенты Npfb находятся перемножением столбцов р
и р матрицы Г ](PabW) нестандартного представления и
равны
2 (ir(pM\pa;\pf(Pix\pa;\Pf.
Р', ^', А."
(8.46)
Перестановка Раь переводит электрон N— 1 на орбиталь
фа, а электрон N — на орбиталь щ при сохранении воз-
возрастающего порядка номеров остальных электронов,
к равна нулю для всех строк с [Я"] = [2] и равна единице
для строк с [Х"] = [12]. В Приложении 6 затабулированы
матрицы Г[Х](РаьШ)для всех разрешенных симметрии си-
систем с числом электронов /V = 3-r-6.
Недиагональные по конфигурации матричные эле-
элементы не равны нулю лишь для конфигураций, отли-
отличающихся не более чем на две орбитали. Подставляя в
(8.41) выражения для двухэлектронных матричных эле-
элементов (8.42) и учитывая соотношения ортогональности
для координатных функций конфигураций, оставшихся
после отщепления двух орбиталей, получаем следующие
формулы:
a abgaa ab + V^JbN%,bbgab, bb+
V%(nb+l)c Ъ ь nc(NZ, cbgca. cb + N? cbgca, bc), (8.47)
Ъ
(KP\G\K%pf] = УЦпс+\){nd+ \)Nfa cdgaa cd, (8.48a)
(Kp\G\ Кс:ьрТ] = V^Jh C, Jab.cc (8.486)
,ec (8.48b)

290 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
В приведенных выше формулах Kat обозначает конфигу-
конфигурацию, получаемую из конфигурации К при переходе
двух электронов, соответственно, с орбитали фа на фс и с
орбитали фь на щ\ па> пъ, пС1 па обозначают везде числа
заполнения в конфигурации К. Подчеркнем, что порядок
расположения индексов отвечает порядку расположения
орбиталей в конфигурациях; так, если орбиталь фс рас-
расположена за орбиталью фа, но впереди орбитали фь, то в
(8.47) надо писать (С, ^ л + #?. ,*?«. fte> Коэффи-
циенты перед двухэлектронными матричными ^лемента-
ми находятся перемножением столбцов р и р соответ-
соответствующих матриц нестандартного представления группы
перестановок. А именно:
a = S <pV [2] IРГ1ЛГI p> ' <pV [2] I P&IW I pI ', (8.49)
p'. v
.«*- 2 <pVr|/>2»1Ar|p>lXI<pYr|pS-IAf|p>IM, (8.60a)
p', A/, X"
p', V, A,"
(8.506)
Параметр х и перестановки Р" Р^"ш имеют тот же
смысл, что и в (8.46), PNa~XN переводит электроны N — 1,
/V на двукратно заполненную орбиталь фа. В Приложе-
Приложениях 6, 7 затабулированы матрицы, необходимые для
расчета коэффициентов (8.49) — (8.50) для конфигураций
различного типа с числом электронов Л/ = 3-*-6. Примеры
использования формул (8.47) — (8.50) см. в следующих
разделах, например в 8-9.
Выведенные выше формулы справедливы при усло-
условии, что слева и справа в матричных элементах конфи-
конфигурации имеют одинаковый порядок общих орбиталей,
что позволяет использовать соотношения ортогонально-
ортогональности для координатных функций, оставшихся N—2
электронов. В противном случае в выражении (8.41) не-
необходимо привести конфигурации, оставшиеся после от-
отщепления N—1-го и Л/-го электронов, к одинаковому

§ 2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 291
порядку орбиталей. Это осуществляется с помощью со-
соотношения, аналогичного (8.39). Так, если
Kab == * Aflfc»
ТО
) = 2 Щ} (РО Ф%! (Каь), (8.51)
р'
где rL,J, (p') принадлежит к нестандартному представле-
представлению группы я^-2, тип редукции которого определяется
способом связи орбиталей конфигурации Каъ- Получаю-
Получающиеся в этом случае формулы для недиагональных по
конфигурациям матричных элементов совпадают с фор-
формулами (8.47)—(8.48), однако с несколько более слож-
сложными, чем в (8.49) — (8.50), выражениями для вычисле-
вычисления коэффициентов:
_
Р', Р'
p', p' Xflk"
/\ \[) /l /I j г ab I J-v \P Л Л I *cd I P/ > \O,D?j
g^ 2(D
р', р' X', X»
х <р WI рйг1" I p)[XI (p Ya" | Рй"w I p)!M.
Пример расчета по формулам (8.52) см. на стр. 331.
8-5. Выражение для матричных элементов гамиль-
гамильтониана. Электронную часть гамильтониана молекулы
всегда можно представить в виде суммы симметричных
операторов F и G:
#?-F+G-S//+Sfir,y. (8.53)
В атомных единицах

292 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
где/?*с — расстояние между/-м электроном и ядрос с с за-
зарядом Zc; гц — расстояние между /-м и /-м электронами.
В предыдущем разделе нами получены формулы для
матричных элементов операторов F и G в случае произ-
произвольной конфигурации орбиталей. В настоящем разделе
мы исследуем выражения для матричных элементов га-
гамильтониана, рассмотрев последовательно различные
типы конфигураций. Предварительно заметим, что если
в качестве f взять одноэлектронный оператор из (8.54),
то диагональный матричный элемент (8.38) дает энергию
электрона, описываемого' координатной волновой функ-
функцией фа, в поле молекулярного остова, обозначим ее еа:
(8-55)
I. Конфигурация однократно заполнен-
заполненных орбиталей.
Обозначим ее К\
Кх: Ф1Ф2 • • • Флг- (8.56)
Вместо символа р различные физические состояния ну-
нумеруются в этом случае таблицами Юнга г, задание ко-
которых эквивалентно заданию N — 2 промежуточных схем
Юнга групп Я/у-!, Яд,_2, ... Количество состояний кон-
конфигурации, обладающей перестановочной симметрией
схемы Юнга [Я], равно размерности неприводимого пред-
представления Г[Х1 группы nN.
С помощью формул (8.35) и (8.45) для матричных
элементов F и G (с числами заполнения па = пь=1) вы-
выпишем выражения для матричных элементов гамильто-
гамильтониана (8.53). Для диагональных по конфигурации ма-
матричных элементов имеем
N
(Кгг | № | &г)ш = бгг 2 efl + S (brraab + N^abl (8.57)
а=1 a<b
Матричный элемент, диагональный по г, складывается
из двух частей: энергии изолированных электронов в
поле молекулярного остова и среднего значения энер-
энергии взаимодействия электронов между собой. Кулонов-

§ 2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 293
ские интегралы входят только в диагональные матрич-
матричные элементы. Зависимость от перестановочной симмет-
симметрии системы (и, следовательно, от спина) заключена
только в коэффициентах при обменных интегралах.
Недиагональные по конфигурации матричные эле-
элементы определяются с помощью формул (8.37), (8.47),
(8.48) с па=1 и равны*)
. ЬЬ
2 « сьёса, сь + К, сьёса. Ьс)>
сфа,Ъ
- /(»с+1)К+1) (Кь. саёаъ, еа + К. саёаь, ас)- (8-59)
Числа заполнения в соотношениях (8.58), (8.59) рав-
равны 1 или 0 (последнее, если электрон переходит на не-
незаполненную орбиталь). Входящие в них коэффициенты
даются формулами (8.49), (8.50), в которых вместо сим-
символов р нужно поставить таблицы Юнга. В Приложе-
Приложении 6 приведены матрицы {r'x"\P%blN\r) для всех воз-
возможных симметрии систем с общим числом электронов
от трех до шести. Расчет по формулам (8.46), (8.50) сво-
сводится к перемножению соответствующих столбцов матриц.
В качестве примера рассмотрим конфигурацию из че-
четырех однократно заполненных орбитадей в состоянии
со спином S = 0. Перестановочная симметрия координат-
координатных состояний задается схемой Юнга [Х] = [22]. Всего мо-
можно составить две независимые координатные функции,
симметрия которых определяется таблицами Юнга
1
3
Z
4
1
2
3
4
*) Порядок расположения индексов в формуле (8.58), так же
как и в (8.47), соответствует порядку расположения орбиталей в
конфигурациях, т. е. в Afca, съ индекс с может располагаться и за
индексами а, Ь.

294 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ4 VIII
Поскольку функции, имеющие симметрию различных
таблиц Юнга, ортогональны, секулярное уравнение при-
примет вид
вхх — Е &6Х2
_
или
± | у^ _ ^J + 4 1 ^12 р.
Взяв матрицы (|Patl) из табл. 2 Приложения 6, по
формулам (8.57), (8.46) находим
а + 2и ttflft "*" ^12 + Рз4 ~" Y (Pi3 + Рн + Ргз + Р24Х
а<Ь
а а<Ъ
ОЦ/) G%O __- ( ft J ft | Q Q \
v/t>i2 = Q/t>2\ — —p— V — P13 r P14 "Г Р23 — H24/>
откуда
± /Bр12 + 2р34 ~ Раз - Pi4 - Р23J + 3 (р14 + Рзз - Pi3 - ft*)-
Если обозначить (см. [30], стр. 327)
Q = 2 efl + 2 aflft, P12 + Рз4 = a,
a<b (8.61)
то получим известную формулу Лондона — Эйринга [30]
Е = Q ± /a2 + p2+ Y2-ap~aY-PY. (8.62)
II. Конфигурация двукратно заполнен-
заполненных орбиталей.
Обозначим такую конфигурацию Ко
Ко- Ф^.-.Ф^. (8.63)

/
2
1
г
§ 2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 295
Каждая двукратно заполненная орбиталь соответствует
спаренным спинам и характеризуется схемой Юнга [2].
При заданном порядке связи орбиталей т схем Юнга
[2] единственным образом связываются в общую схему
симметрии [X] = [2W]. Осуществляется только одно состоя-
состояние, симметрия которого относительно перестановок ор-
орбиталей характеризуется таблицей Юнга Го:
(8.64)
Матричные элементы оператора F не зависят от сим-
симметрии волновой функции. В матричных элементах опе-
оператора G (8.45) зависимость от симметрии состояния
содержится только в коэффициентах при обменных инте-
интегралах. Поскольку в таблицу Юнга (8.64) все орбитали
конфигурации Ко входят эквивалентно, коэффициенты
Nffi = Nab должны быть одинаковы для всех пар а, Ъ
и не зависеть от числа орбиталей. Элементарный расчет
по формуле (8.46) с матричными элементами
(/*'Я"| Р3а\ | /*0)I22j, взятыми из табл. 2 Приложения 6, дает
значение А^1 = —1/2. Это значение сохранится и в слу-
случае произвольного т.
Подставляя в формулы (8.35), (8.45) па= пъ = 2,
Na2™] = — 1/2, приходим к следующему простому резуль-
результату:
<*о I #? I КоI2 = 2 Bеа + ааа) + 2 2 Baaft - ft*). (8.65)
а а< Ь
Первый член в (8.65) определяет энергию системы при
отсутствии взаимодействия между электронами, распо-
расположенными на разных орбиталях. Энергия этого взаимо-
взаимодействия дается вторым членом. Как следует из (8.65),
энергия взаимодействия пар электронов, расположенных
на разных орбиталях, равна разности удвоенного куло-
новского интеграла и обменного, умноженной на два.

296 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
III. П р о и з в о л ь н а я конфигурация.
Любую конфигурацию невырожденных орбиталей
всегда можно представить как совокупность двух выше
рассмотренных конфигураций. Расположим орбитали
конфигурации К так, чтобы сначала шли двукратно за-
заполненные орбитали, потом — однократно заполненные.
Тогда конфигурация К может быть записана как
*-W,:qto...qtolwI...qW (8-66)
Перестановочная симметрия конфигурации (8.66) ха-
характеризуется таблицами Юнга г, состоящими из посто-
постоянной таблицы Юнга г0 двукратно заполненных орбита-
лей и таблицы Юнга г\ однократно заполненных орбита-
лей. Очевидно, что число таблиц Юнга г, нумерующих
независимые состояния конфигурации (8.66), характе-
характеризующиеся схемой Юнга [X], равно числу различных
таблиц Юнга п, т. е. равно размерности неприводимого
представления со схемой Юнга [Х<2т)] (см. рис. 6.2).
Условимся орбитали конфигурации Ко обозначать
буквами а, Ь, а орбитали конфигурации К\ — буквами
с, d. Матричный элемент гамильтониана, так же как в
предыдущих случаях, находится с помощью формул
(8.35) и (8.45). В нем можно выделить члены, опреде-
определенные только на орбиталях конфигурации /Со или
только на орбиталях конфигурации К\, и «интерферен-
«интерференционные» члены, отвечающие взаимодействию конфигу-
конфигураций. Рассмотрим сначала члены, определенные на
орбиталях конфигурации К\.
В общей формуле (8.45) с K=KoKi коэффициенты
при обменных интегралах конфигурации К\ содержат
перестановки, затрагивающие электроны, находящиеся
на орбиталях с cpm+i по флг-т, и определяются соотноше-
соотношением (8.46), содержащим матрицы представления, реду-
редуцированного На ПОДГруППе Л2тХЛлг-2т,
г,, ».,.
(8-67)

§ 2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 297
Перестановки PcdW действуют только на последние
N— 2т электронов. Преобразование матриц,, входящих
в (8.67), к приведенной форме по отношению к переста-
перестановкам последних N — 2т чисел приводит (8.67) к виду
Nr?-r*^Nr?= / 2 „(-If X
x'i« r'v к"
\Л2т)Л Г7 B/ггI
что совпадает с коэффициентами, определенными на
ГЛ2тI
представлении Г1 \ Поскольку коэффициенты при
кулоновских интегралах равны всегда 6^,, из (8.68) сле-
следует вывод, что в состоянии с конфигурацией К = КоК)
часть матричного элемента гамильтониана, определен-
определенная на орбиталях конфигурации /Ci, имеет тот же вид,
что и для изолированной конфигурации К\.
Аналогичным образом приходим к выводу, что для
части матричного элемента гамильтониана, определен-
определенной на орбиталях конфигурации /Со, справедливо выра-
выражение (8.65), выведенное для изолированной конфигу-
конфигурации Ко. Последнее следует хотя бы из того, что мы
всегда можем поменять местами конфигурации К\ и /Со,
представив /С в виде К\Ко-
Рассмотрим теперь члены, отвечающие взаимодейст-
взаимодействию конфигураций Ко и К\. Они имеют следующий вид:
< К/у, | &€ | Kror^ = 2 S FГ,,«ас + NZU Г°%сУ (8-69)
Все таблицы Юнга конфигурации встроятся одинаково:
к таблице г0 снизу приставляется таблица г\. Следо-
Следовательно, в общей схеме Юнга [К] орбитали конфигу-
конфигурации /Со связываются с орбиталями конфигурации К\
единственным образом, независимо от вида Г\ и [К].
Можно ожидать, что коэффициенты Nrfcu ГоП не должны
зависеть от [Х\ и г\ и являются одинаковыми для всех
пар а, с. Это подтверждается расчетом по формуле
(8.46) для различных типов симметрии. Во всех случаях
получается одинаковый результат, а именно:
N%ur*x = -\bri?x. (8.70)

298 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
Отсюда следует, что часть матричного элемента гамиль-
гамильтониана, отвечающая взаимодействию конфигурации Ко
с конфигурацией К\, не зависит от перестановочной сим-
симметрии состояния и равна
(K4l | т 1 kv,>w = вг
Подчеркнем, что выражение (8.71) не совпадает с мат-
матричным элементом энергии взаимодействия изолирован-
изолированных электронных систем с конфигурациями Ко и К\. Так,
оно не содержит одноэлектронных интегралов, отвечаю-
отвечающих взаимодействию электронов одной системы с ядра-
ядрами другой. Это объясняется тем, что электроны конфи-
конфигурации К не могут быть разделены на принадлежащие
конфигурациям Ко и Ки поскольку они входят в одну
антисимметричную функцию.
Для среднего значения гамильтониана конфигурации
электронов (8.66) в состоянии с перестановочной сим-
симметрией Щ получаем следующее выражение:
= 2 Bеа + О +22 Bаай - рай) + 2
а а<Ь с
S Baac - p J, (8.72)
1 ^ a, ft^m, m+l^c,
Входящий в (8.72) кулоновский интеграл ааа определен
только для двукратно заполненных орбиталей.
Недиагональные матричные элементы гамильтониана
содержат только обменные интегралы конфигурации К\
и равны
(KVl | т | Кг^ = | N[%d. . (8.73)
с<. а
Следовательно, секулярное уравнение для произволь-
произвольной конфигурации К сводится к секулярному уравнению
для конфигурации однократно заполненных орбиталей
К\, обладающей симметрией ХРт)]. Обозначим корни се-
кулярного уравнения конфигурации К\ через Ei(K\, 5),

§ 1 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 299
где S обозначает суммарный спин состояния и однозначно
определяется видом [Х<2т)]. Полная энергия конфигу-
конфигурации К в состоянии со спином S складывается из трех
частей: энергии конфигурации /Ci Ei(K\,S), энергии кон-
конфигурации /Со и энергии взаимодействия конфигураций
Ко и Кх
+ 2 S Baflft - (W + S Baac ~ fc*)- (8.74)
a,
Зависимость от спина системы содержится только в соб-
собственной энергии Ei(Ku S) конфигурации К\. Матрицы,
приведенные в Приложении 6, позволяют легко выпи-
выписать секулярное уравнение конфигурации Кх при нали-<
чии в ней до шести орбиталей.
kBm)l
Если представление Г одномерно, решать секу-
секулярное уравнение не надо. Энергия конфигурации дается
ормулой (8.72). Это осуществляется в двух случаях:
Bт)] = [1дгт] и [ЛBт)] = [2]. Коэффициенты Ncd перед
обменными интегралами равны
ОД—1. ЯЗ-1- (8-75)
Недиагональные по конфигурации матричные эле-
элементы гамильтониана находятся с помощью формул
(8.37), (8.47), (8.48). Удобно в каждой из конфигураций
выделить общие двукратно заполненные орбитали. То-
Тогда коэффициенты при двухэлектронных матричных эле«
ментах, определенные на оставшихся орбиталях, будут
\к{2т)]
вычисляться с помощью матриц представления Г1
где т — число общих двукратно заполненных орбита-
лей. Часть суммы по с в (8.47), отвечающая общим дву-
двукратно заполненным орбиталям, будет выражаться ана-
аналогично равенству (8.71)
|Ко(KrfJot - Vna(nb+l) SBgeat eb - gea, be\
e
(8.76)

300 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
где е пробегает все двукратно заполненные орбитали
конфигурации /Co-
/Coil р и м е р ы.
1. Конфигурация
Кг: Ф^Ф32Ф4Ф5-
Найдем энергию конфигурации /Ci в состоянии со спи-
спином 5=1. Спину 5=1 отвечает координатная схема
Юнга [Я] = [2312]. Схема Юнга однократно заполненных
орбиталей [М6>] = [12]. Представление Г[12] одномерно, по-
поэтому энергия находится из формулы (8.72) с N[cJ =
Е (Къ S = 1) = 2 Bеа + ааа) + 2 2 Bаа6 - fW +
а=1 а<Ь
5 3 5
+ 2 е, + (а45 - р45) +22 Bаас - рас).
4 1 4
2. Конфигурация
Состоянию конфигурации Ки с 5=2 отвечает коорди-
координатная схема Юнга [2214]. Схема Юнга однократно за-
заполненных орбиталей [М4)] = [14]. Имеем невырожденный
случай. Энергия состояния, так же как и в предыдущем
примере, определяется формулой (8.72) с М$ = —1
2
Е (Ки, S = 2) = 2 Bаа + ааа) + 2 Bа12 - р12) +
+ 2 ес + 2 Kd - Рй) +22 Bаа, - рас).
<:=3 c<d a=*\ с=3
В состоянии со спином 5=1 [Х] = [2М2], [W4)] = [2 12].
Энергия однократно заполненных орбиталей опреде-
определяется решением секулярного уравнения третьего по-
порядка. Его матричные элементы находятся по формуле
(8.57) с коэффициентами, определяемыми формулой

§ 2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 301
(8.46). С помощью приведенных в табл. 2 Приложения
6 матриц (г'Х" \Р%\гу2{2] получаем
б
c<d
(р46 - Рзб + Зр45 - Зр35), (8.77)
Обозначим решения секулярного уравнения с матрич-
матричными элементами (8.77) Ei(K\,S=\), индекс / пробе-
пробегает три значения. Уровни энергии конфигурации Кп
определяются добавлением постоянного члена к Е{(Къ
5 = 1). Согласно формуле (8.74)
Et (/Си, S = 1) = Et (Кх, S - 1) + 2 Bга + ааа) +
а=1
2 6
+ 2 Bа12 - р12) +22 &аас - $ас)- (8.78)
13
В состоянии со спином 5 = 0 [Я]=[24], [W4)] = [22]. Име-
Имеются два уровня энергии, определяемые формулой, ана-
аналогичной формуле (8.78). Уровни энергии однократно
заполненных орбиталей Ei(K\, 5 = 0) даются формулой
(8.62), матричные элементы в которой вычисляются с
ОрбитаЛЯМИ фз, ф4, ф5 И ф6.
3. Получим выражение для матричного элемента га-
гамильтониана, учитывающего взаимодействие конфигура-
конфигураций /Со (8.63) и (Ко)д. Новую орбиталь щ помещаем

302 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
рядом с фа, перестановка Р%~ш совпадает в этом случае
с РаЬШ> и из равенства (8.49) следует, что ЛС,а&=1.
Подставляя в (8.37) и (8.47) яо = 2, Пь = 0 и учитывая
(8.76), получаем
, ab + ^Рёеа.еЬ ~ ёеа,Ье)} - (8.79)
4. Рассмотрим матричный элемент с конфигурациями
К: Ф? ... ФЛФ* и /CJ: Ф? ... Ф2тФаФс. (8.80)
Коэффициенты на двухэлектронных матричных элемен-
элементах, определенных на однократно заполненных орбита-
лях, находятся с помощью представлений группы яг-
Осуществляются два типа состояний: синглетное с
[Я] = [2т+1] и триплетное с [Я] = [2т12]. Используя соотно-
соотношения (8.37), (8.47) и (8.76), получаем
(К | W | Kcbf] - fbc + gabf ac ± gab, ca + S Bgeb>ec - g#b J.
(8.81)
Знак плюс для [Я]=[2т+1], знак минус для [Я] = [2т12].
5. Вычислим еще в качестве примера матричный эле-
элемент
((Ko)ba\^\(Ko)dcf\ (8.82)
заданный на конфигурациях, отличающихся на две ор-
битали. Если обозначить конфигурацию Ко без орбита-
лей ф2ф2 через К'0\то конфигурации, входящие в (8.82),
могут быть записаны как
и *0>2фЛг (8-83)
Конфигурации (8.83) составлены таким образом, что по-
порядок общих орбиталей в них одинаков. Поэтому при
вычислении матричных элементов гамильтониана можно
пользоваться формулами для коэффициентов (8.50). Из

§ 2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 303
формул (8.50) и (8.48) следует, что матричный элемент
(8.82) эквивалентен матричному элементу
1ф^)и<2т~4I- (8-84)
Если обозначить конфигурацию в левой части мат-
матричного элемента (8.84) через/С,то конфигурация справа
запишется как Кы- Матричный элемент дается фор-
формулами (8.48), (8.50) с соответственно переобозначен-
переобозначенными индексами. Рассмотрим вначале синглетное состо-
состояние [А,Bт-4)]=[22]. Символы р и р в формулах (8.50)
соответствуют в данном случае таблице Юнга-[22]1. Взяв
матричные элементы (r'X" | P|J | гA))[22] из табл. 2 Прило-
Приложения 6, находим
<ФаФ6Ф2с I & | ф^ф/21 = 28ьв, ad - gbc> da. (8.85)
Триплетному состоянию отвечает [A,Bm~4)]=[212]. Пере-
Перестановочная симметрия конфигурации справа характе-
характеризуется таблицей Юнга [212]ь конфигурация слева сим-
метризована по нестандартному представлению с типом
редукции я2 X я2, ей отвечает р:[12] [2]. Необходимые
для вычисления по формуле (8.50) матричные элементы
берем из первого столбца матрицы (г'Х" | РЦ | r)[212J (см.
табл. 2 Приложения 6) и из второго столбца матрицы
(%"k"\P^\rxr^m2](см. табл.2 Приложения?). В резуль-
результате получаем
<ФаФ6Ф? I & I Ф&ф/''1 = - ёъс, аа- (8-86>
8-6. Взаимодействие двух подсистем в состояниях с
заданными спинами. Рассмотрим систему электронов,
состоящую из двух подсистем с числом электронов N\
и N2 соответственно. Пусть каждая подсистема находит-
находится в состоянии с определенным значением суммарного
спина 5г. Полный спин системы 5 определяется прави-
правилами векторного сложения спинов S\ и S2. В основе та-
такого способа связи, когда вначале связываются спины
электронов внутри каждой подсистемы, а затем уже по-
полученные суммарные спины связываются между собой,
может лежать, например, пространственное разделение

304 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
подсистем (среднее расстояние между подсистемами су-
существенно больше межэлектронных расстояний внутри
каждой из них).
При пренебрежении в гамильтониане членами, содер-
содержащими спин, все свойства системы адекватно описыва-
описываются заданием координатной волновой функции, обла-
обладающей перестановочной симметрией соответствующей
схемы Юнга [к]. Каждая подсистема характеризуется
своей координатной функцией
<D%W (8.87)
где Кг обозначает конфигурацию орбиталей /-й подси-
подсистемы, п — таблица Юнга, характеризующая симметрию
функции (8.87) относительно перестановок координат
электронов, символ р; характеризует симметрию относи-
относительно перестановок орбиталей.
Правильная координатная волновая функция си-
системы в нулевом приближении строится из произведений
функций (8.87) и должна обладать перестановочной
симметрией схемы Юнга [к]. Согласно формуле B.85)
с (г)А = г такая функция может быть записана в виде
J
(8.88)
Вычисление матричных элементов гамильтониана в
состоянии с координатной волновой функцией (8.88) мо-
может быть проведено с помощью генеалогического разло-
разложения функции. Вместо выписывания такого разложе-
разложения воспользуемся результатами предыдущих разделов.
В разделе 8-5 было показано, что для произвольной
конфигурации, состоящей из конфигурации дважды за-
заполненных орбиталей Ко, и конфигурации однократно
заполненных орбиталей К\ (см. (8.66)) матричные эле-
элементы гамильтониана выражаются в виде суммы мат-
матричных элементов, вычисленных для изолированных
конфигураций Ко и Ки и члена, отвечающего взаимодей-
взаимодействию конфигураций. Этот результат должен быть спра-

§ 2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 305
ведлив и в случае двух произвольных конфигураций К\
и К2.
Обозначим орбитали конфигурации К\ буквами а, Ь,
орбитали конфигурации Къ-^с, d. Матричный элемент
гамильтониана разбивается на сумму трех слагаемых:
где
? = 6р,р, ? («А + « J Д
(8.90)
? ?(«А + асс) + е2 ncnd(Ьр-*ы + NfdVcd),
(8.91)
,рА,раас
Индекс а пробегает все орбитали конфигурации К1у
индекс с —все орбитали конфигурации /Сг- Следует
помнить, что ааа и асс определены только для двукратно
заполненных орбиталей. Npat\ NQcf2 в (8.90), (8.91) даются
формулой (8.46), в которой в качестве УУ надо брать А/^
и Af2 соответственно. Для N^f2'Plp2 справедливо следую-
следующее выражение, непосредственно вытекающее из фор-
формулы (8.46):
д^р2, рй = 2 2 (-D"((р'У2) v^ |р»;™|Plp2)[M х
X((Py2)kT\P^\-9lp2f\ (8.93)
Сумма в (8.93) соответствует перемножению столбцов
pip2 и р!р2 матрицы (\РасШ\) с дополнительным умно-
умножением каждого произведения на ±1, в зависимости
от [к"]. РасШ обозначает перестановку, переводя-
переводящую электрон N— 1 на орбиталь фо конфигурации /Сь а
электрон// — на орбиталь фс конфигурации /С2. Матрицы
20 И. Г. Каплан

306 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ4 VIII
(\РасШ\) заданы на наборах базисных функций, при-
принадлежащих к представлениям с различным типом ре-
редукции на подгруппах, причем символы pi и рг харак-
характеризуют симметрию конфигураций К\ и /С2, символы
р[ и Pg — симметрию тех же конфигураций без одной
орбитали каждая.
При вычислении матричных элементов (8.90), (8.91)
конфигураций К\ и /С2 следует иметь в виду, что в каж-
каждой конфигурации удобно выделить двукратно заполнен-
заполненные орбитали, так как для каждой конфигурации мат-
матричный элемент, отвечающий взаимодействию электро-
электронов двукратно заполненных орбиталей с однократно
заполненными, не зависит от перестановочной симмет-
симметрии состояния и дается формулой (8.71). Очевидно, что
такой же формулой выражается и матричный элемент
взаимодействия двукратно заполненных орбиталей од-
одной конфигурации с однократно заполненными орбита-
лями другой. Поэтому фактически задача вычисления
выражения (8.92) сводится к вычислению матричного
элемента между однократно заполненными орбиталями
конфигураций К\ и /С2.
Пусть индекс а нумерует двукратно заполненные ор-
орбитали конфигурации Ки Ъ — однократно заполненные;
аналогично для конфигурации К2 с нумерует двукратно
заполненные орбитали, d — однократно заполненные. То-
Тогда выражение (8.92) для диагональных матричных эле-
элементов может быть представлено в следующем виде:
KL р,р, = 2 2 B«ас - Р J + 2 Baad - (J J +
а, с а, а
+ 2 Ba6c - fy + S (ам + й™ r'%d), (8.94)
о, с о, а
где г{ и Г2 — таблицы Юнга однократно заполненных
орбиталей конфигураций К\ и /С2.
Для недиагонального матричного элемента
(8.9Б)
Коэффициенты перед обменными интегралами, опреде-

§ 2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 307
ленными на однократно заполненных орбиталях, равны
X ((г/2) VX" | Р&» | f Ir2)^Bm)l, (8.96)
где перестановки РыШ определены только на однократ-
однократно заполненных орбиталях, N означает в данном случае
общее число однократно заполненных орбиталей конфи-
конфигураций К\ и /С2, [№тЦ — характеризующая их схема
Юнга, т — общее число двукратно заполненных орбита-
лей конфигураций К\ и К2- Матрицы (|Ры*1) для систем
с N=3^6 приведены в Приложении 7.
Полная энергия системы в состоянии с координатной
функцией (8.88) определяется решением секулярного
уравнения с матричными элементами, находимыми по
формулам (8.89) — (8.96). Порядок секулярного уравне-
уравнения равен произведению чисел вырождения подсистем.
Определим энергию взаимодействия подсистем как раз-
разность полной энергии системы и суммарной энергии изо-
изолированных подсистем. В случае, когда состояния под-
подсистем не вырождены, энергия взаимодействия электро-
электронов подсистем дается непосредственно формулой (8.94).
Если все орбитали одной из подсистем двукратно запол-
заполнены, то выражение (8.94) для энергии взаимодействия
существенно упрощается. Пусть первая подсистема имеет
только двукратно заполненные орбитали, т. е. характери-
характеризуется конфигурацией Ко (см. (8.63)). Это означает, что
в (8.94) нужно отбросить все члены, содержащие сум-
суммирование по Ь. В результате приходим к важному вы-
выводу, что энергия взаимодействия электронов подсисте-
подсистемы с конфигурацией Ко с электронами произвольной
подсистемы не зависит от перестановочной симметрии
(или от значения спина) последней и равна*)
?вз (KOSX = 0, K2S2; S2) = 22 Bаа, - р J + 2 Bcw - pfld),
а, с atd
(8.97)
*) В полную энергию взаимодействия подсистем входит также
не зависящий от перестановочной симметрии состояний член, вклю-
включающий интегралы взаимодействия электронов одной подсистемы с
ядрами другой. Он включен в еа (см. (8.55)).
20*

808 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
где а нумеруют орбитали конфигурации /Со, с — двукрат-
двукратно заполненные орбитали конфигурации /С2, d — одно-
однократно заполненные орбитали конфигурации /С2.
Все предыдущие формулы справедливы при условии
ортогональности одноэлектронных орбиталей обеих под-
подсистем. В случае взаимодействия двух молекул условие
ортогональности одноэлектронных орбиталей уже не со-
соблюдается: орбитали, принадлежащие к разным моле-
молекулам, перекрываются. Нетрудно показать, что получен-
полученные выше формулы верны с точностью до членов, про-
пропорциональных интегралам перекрывания (ср. [88, 89]).
При расстояниях между молекулами, больших вну-
внутримолекулярных расстояний (а именно при таких рас-
расстояниях взаимодействующие молекулы можно рас-
рассматривать как обособленные подсистемы), интегралы
перекрывания много меньше единицы и энергия взаи-
взаимодействия электронов молекул с удовлетворительной
точностью дается формулами (8.94) и (8.97). Следова-
Следовательно, при пренебрежении интегралами перекрывания
энергия взаимодействия молекулы, находящейся в основ-
основном синглетном состоянии, с молекулой, находящейся в
произвольном возбужденном электронном состоянии, со-
согласно формуле (8.97), не зависит от мультиплетности
возбужденного состояния.
Если не учитывать обмен электронами между подси-
подсистемами и волновую функцию системы брать в виде
простого произведения волновых функций подсистем, то
выражение для энергии взаимодействия не должно за-
зависеть от значений спинов подсистем. Энергия взаимо-
взаимодействия электронов определяется только через кулонов-
ские интегралы и равна
?вз(КЛ, K2S2) = S naticaac, (8.98)
а, с
где К\ и /G— две произвольные конфигурации электрон-
электронных орбиталей, а пробегает все орбитали конфигурации
Ки с — все орбитали конфигурации Кг.
Этот результат становится физически более нагляд-
наглядным, если учесть, что потенциал электростатического
поля, создаваемого в некоторой точке пространства R
квантовомеханической системой зарядов, не зависит от

§ 2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 309
спина системы. Последнее следует из того обстоятель-
обстоятельства, что оператор потенциала
относится к классу одноэлектронных операторов типа F.
Согласно формуле (8.35)
V (R) = (Kp\V (R) | Kpf] = 2 "а (ф« | J^bfl | Фа) , (8-99)
т. е. среднее значение потенциала в точке R не зависит
от перестановочной симметрии координатной волновой
функции системы зарядов и, следовательно, не зависит
от спина системы. Энергия взаимодействия двух си-
систем зарядов при отсутствии обмена равна среднему
значению потенциала, создаваемого одной системой, ус-
усредненного в свою очередь по волновым функциям дру-
другой системы, т. е. равна среднему значению оператора
2 eV (R;), где / нумерует электроны второй системы. По-
Подобный оператор также относится к операторам типа F,
что и обусловливает независимость энергии взаимодей-
взаимодействия от перестановочной симметрии состояний.
Примеры.
1. Взаимодействие подсистем, одна из которых со-
содержит только двукратно заполненные орбитали,
tff. cpftl [^] = [22] S=0,
/t2: ФзФ4 M=[l2] 5=1.
Энергия взаимодействия дается вторым членом в фор-
формуле (8.97)
5, = 0; К29 S2=l; S=1)=S 2 Baai
l
2. Взаимодействие двух подсистем с однократно за-
заполненными орбиталями
Кх: ф1ф2ф3 M = [l3] Sx = ^,
К2: Ф4Ф5Ф6 [^] = [13] 52 = |,

310 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
в состоянии с [Я] = [23], S = 0. Энергия взаимодействия
дается последним членом в формуле (8.94). Коэффици-
Коэффициенты ШтлтЩ находятся по формуле (8.96) и опре-
определяются последним столбцом матриц (|р|д|)[2'] из
табл. 4 Приложения 7. В результате получаем
3. Взаимодействие подсистем
*,: Ф?Ф22Ф3Ф4
К2:
в состоянии с [Я]=[2314], S = 2. Энергия взаимодействия
определяется формулой (8.94). Коэффициенты перед об-
обменными интегралами, определенными на однократно
заполненных орбиталях, даются формулой (8.75) и рав-
равны N[l2 = — 1» откуда
2 2 Bаа5 - ра5) +22 Bаа, -
а=1 а-1 d-6
4 4 7
22 (ам -
Ь3 d6
4. Система, состоящая из двух подсистем, одна из ко-
которых находится в вырожденном состоянии,
Кг: ФхФгФз М-[21] S^i,
W = [l2] S2-l.
Состояние первой подсистемы дважды вырождено в со-
соответствии с размерностью представления Г[211 Энергия
системы в состоянии с [Я] = [221], S= 1/2 определяется ре-
решением секулярного уравнения второго порядка. Энерге-

§2 ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОЙ МАТРИЦЫ 311
тическая матрица, согласно формуле (8.89), имеет сле-
следующий вид:
Lт
Матричные элементы для конфигураций К\ и /С2 да-
даются формулой (8.57), коэффициенты перед обменными
интегралами в которой находятся по формуле (8.46).
С помощью матриц (г'Л"| Pfb I r)[2l] из Приложения 6
получаем
з
a <b
3
ab-$l2 + \$lZ + $2z\ (8Л00)
a< b
Для конфигурации /С2
Поскольку конфигурации К\ и /С2 содержат только од-
однократно заполненные орбитали, диагональные матрич-
матричные элементы взаимодействия конфигураций даются по-
последним членом формулы (8.94), недиагональные —по-
—последним членом формулы (8.95). Коэффициенты перед
обменными интегралами находим по формуле (8.96) с
помощью матриц (|Р^|)[221] из табл. 3 Приложения 7
3 5
aad ~ у (Pl4 + Pl5 + P24 + P25 — Рз4 — Рзб)>
6 = 1 d-4
3 5
abd+~Q (Pl4 + Pl5 + P24 ~ P25 — 5P34 — 5Рзб)>
1d4 _
, [21],[I2! ^ ^1«2ОТ. [21].[12J = -3- (Pl4 + Pl5 - 024 ~ Ргб)'

312 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
§ 3. Симметричные системы
8-7. Построение базисных функций группы симмет-
симметрии молекулы в методе молекулярных орбиталей. В слу-
случае симметричных молекул гамильтониан системы инва-
инвариантен относительно пространственных преобразований
точечной группы симметрии молекулы. Выбор вариаци-
вариационных функций в виде базисных функций неприводимых
представлений точечной группы позволяет существенно
понизить порядок секулярного уравнения. Согласно ре-
результатам раздела 5-4 исходное секулярное уравнение
распадается в этом случае на секулярные уравнения,
относящиеся к эквивалентным неприводимым представ-
представлениям точечной группы. Порядок секулярного уравне-
уравнения, соответствующего неприводимому представлению
Па), равен кратности вхождения представления Г<а) в
разложение приводимого представления, образуемого
исходным набором вариационных функций. Если каждое
неприводимое представление появляется в разложении
один раз, то имеет место полная диагонализация секу-
секулярного уравнения.
При нахождении одноэлектронных молекулярных ор-
орбиталей в виде линейной комбинации атомных орбита-
лей (метод МОЛКАО) требуется решать секулярное
уравнение, порядок которого равен числу учитываемых
атомных орбиталей. Построение базисных функций не-
неприводимых представлений точечной группы симметрии
молекулы для каждого из наборов преобразующихся
друг через друга орбиталей легко осуществляется с
помощью операторов проектирования е^ (см. раз-
раздел 1-18)*). Для этого оператором z{fk действуют на про-
произвольно выбранную' из данного набора орбиталь. Если
действие на нее оператора е($ дает нуль, то выбирается
следующая орбиталь и т. д., пока не получится отличный
от нуля результат. В тех случаях, когда исходные атом-
атомные орбитали ортонормированы и образуют регулярный
*) Альтернативный метод построения симметризованных моле-
молекулярных орбиталей с помощью приводящей матрицы см. в ра-
работе [96].

§3
СИММЕТРИЧНЫЕ СИСТЕМЫ
313
набор, нормированные базисные функции получаются
действием нормализованных операторов
(8.101)
<ра
Рис. 8.5.
на любую орбиталь набора. В остальных случаях полу-
полученные базисные функции надо нормировать.
В качестве примера рассмотрим симметричную си-
систему четырех идентичных ато-
атомов, на каждом из которых й\
задана орбиталь одного типа
(рис. 8.5). Данная конфигура-
конфигурация атомов инвариантна отно-
относительно операций точечной -
группы D4. Набор четырех ор-
биталей фа, фь, фс, ф^ образует
базис приводимого представ-
представления группы D4. Выпишем ха-
характеры этого представления,
учитывая, что последние рав-
равны числу орбиталей, остающихся инвариантными при
действии операций группы:
(8.102)
Разложение представления (8.102) на неприводимые
части осуществляется с помощью таблицы характеров
группы DA по стандартной процедуре A.59) и имеет
следующий вид:
(8.103)
Е
4
С2
0
2С4
0
2U2
0 ,
2U2
2
Поскольку каждое неприводимое представление входит
в разложение (8.103) один раз, исходное секулярное
уравнение при взятии симметризованных вариационных
функций распадается на три уравнения первого порядка.
Двукратный корень секулярного уравнения, отвечающий

314
РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ
ГЛ. VIII
дважды вырожденному представлению, не зависит от
того, с какой из базисных функций он вычисляется.
Построение базисных функций неприводимых пред-
представлений, входящих в разложение (8.103), осущест-
осуществляем действием соответствующих операторов (8.101) на
орбиталь фа. Для удобства выпишем орбитали, в кото-
которые переходит qpa под действием восьми операций груп-
группы D4:
RVa
Е
Фа
Ф*
с2
С3
Ф*
up
ф*
uf
Ус
up
Фа
Uf
Ф</
Для построения базисных функций одномерных пред-
представлений достаточно таблиц характеров. Базисные
функции двухмерного представления находим с по-
помощью матриц представления Е группы DA (Приложе-
(Приложение 2), использовав набор двух операторов ef, и eg.
В результате получаем следующие нормированные
функции:
 (Фа
Ус + <Pdh
=  (Фа - Ф^ - Ус + <Pd)>
(8.104)
Многоэлектронная координатная волновая функция в
методе МО строится из произведения молекулярных ор*
биталей. В состоянии с определенным значением пол-
полного спина координатная волновая функция симметрич-
симметричной молекулы должна удовлетворять двум условиям (см.
раздел 6-9): а) принадлежать к базису неприводимого
представления Г™ группы перестановок электронов лп;
б) принадлежать к базису неприводимого представле-
представления Г<а) точечной группы симметрии молекулы.

§ 3 СИММЕТРИЧНЫЕ СИСТЕМЫ 315
В разделе 8-5 приведены формулы для матричных
элементов гальмитониана произвольной электронной си-
системы, определенных на координатных волновых функ-
функциях с заданной перестановочной симметрией Фгр3(/()>
где индекс р характеризует симметрию функции относи-
относительно перестановок орбиталей, г — относительно пере-
перестановок электронов; возможные схемы Юнга [к] опре-
определяются видом электронной конфигурации /С. Поэтому
при построении функции, одновременно обладающей тре-
требуемой точечной и перестановочной симметриями, же-
желательно исходить из функций Фгр3(/(), уже имеющих со-
соответствующую перестановочную симметрию. Требуемая
симметрия относительно операций точечной группы до-
достигается действием операторов е§? на функции ФМ (/<").
Поскольку операции пространственных преобразований
точечной группы и операции перестановок координат
электронов коммутируют, действие е($ на Ф%](К) может
быть заменено действием ей? на несимметризованное
по перестановкам произведение молекулярных орбита-
лей с последующей симметризацией по перестановкам.
Отметим, что действие операции точечной группы на про-
произведение функций определяется как последовательное
применение этой операции к каждому сомножителю,
т. е.
Если часть молекулярных орбиталей принадлежит к од-
одному базису неприводимого представления, т. е. орбитали
переходят друг в друга при операциях точечной груп-
группы, то полученные в результате действия операторов ell
базисные функции представления Г(а) могут обладать
также и определенной перестановочной симметрией, что
следует учитывать при последующей симметризации
функций по перестановкам*). Если все молекулярные
*) Построение базисных функций неприводимых представлений
точечной группы из бинарных произведений функций, преобразую-
преобразующихся по прямому произведению группы, может быть осуществлено
также с помощью коэффициентов Клебша — Гордана (см. раз-
раздел 1-16). В работе [90] для всех точечных групп приведены так на-
называемые V-коэффициенты, пропорциональные коэффициентам Клеб-
Клебша т— Гордана.

316 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
орбитали принадлежат к различным неприводимым пред-
представлениям, то полученные базисные функции представ-
представления Г(а> будут состоять из произведений молекулярных
орбиталей, не переходящих друг в друга при переста-
перестановках координат электронов. Каждый член таких ли-
линейных комбинаций следует далее симметризовать по
перестановкам. Последнее проводится как формальная
операция замены произведений молекулярных орбита-
лей возможными для данной конфигурации симметри-
зованными функциями Фгр, что позволяет использовать
при вычислении матричных элементов гамильтониана со-
соотношения раздела 8-5.
Проиллюстрируем вышеизложенное на примере си-
системы четырех электронов, заполняющих определенные
формулами (8.104) молекулярные орбитали оА> и вЕ.
Предварительно обозначим для краткости
а* = а0, af = g{ , cf = а2. (8.105)
Из орбиталей (8.105) может быть образовано три элек-
электронных конфигурации:
offi, ago|, o*pxor (8.106)
Произведение орбиталей cro(l)aoB) полностью симме-
симметрично, поэтому координатные функции, отвечающие
конфигурациям (8.106), образуют базис для прямого
произведения ЕхЕ. Разложение его на неприводимые
части имеет следующий вид:
Е X Е = Аг + А2 + Вх + В2. (8.107)
Следовательно, из произведения орбиталей конфигура-
конфигураций (8.106) могут быть построены базисные функции
четырех одномерных представлений. Это построение осу-
осуществляем с помощью операторов проектирования одно-
одномерных представлений е<а\ для записи которых доста-
достаточно знания таблицы характеров. Предварительно вы-
выпишем результаты действия операций группы D4 на
орбитали о\ и аг, воспользовавшись определением базис-
базисной функции неприводимого представления (см. A.20))

§3
СИММЕТРИЧНЫЕ СИСТЕМЫ
317
и матрицами представления Е группы ZL, приведен-
приведенными в Приложении 2:
Ro2
Е
02
с2
-02
-02
02
-0!
-*%
-0,
?У<2)
02
<*!
и?
-02
— CFl
02
В результате получаем следующие четыре ортонор-
мированные функции, принадлежащие к базисам одно-
одномерных неприводимых представлений группы D4:
J=
^ C)а1D) + а2C)а2D)],
C)a2D)-
(8.108)
Фв* = J= <т0 A) с0 B) [а, C) а, D) - а2 C) а2 D)].
Функции (8.108) обладают определенной симметрией
относительно перестановок первых двух электронов
([A,i] = [2]) и последних двух. В данном случае это одно-
однозначно определяет возможную полную схему Юнга [А],
а следовательно, и значение полного спина 5. Из вида
функций (8.108) следует, что осуществляются три синг-
летных состояния: 1Аи ]В]} 1В2 — и одно триплетное со-
состояние 3Л2, с координатными волновыми функциями
.109)
Поскольку матричные элементы гамильтониана не за-
зависят от таблицы Юнга г, характеризующей симметрию
2( O.C7J2]),

318 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
функции относительно перестановок координат электро-
электронов (при выводе формул раздела 8-4 проводится сум-
суммирование по всем г), значения таблицы Юнга г в обо-
обозначениях функций (8.109) опущены. В аргументах
функций указана только симметрия относительно пере-
перестановок однократно заполненных орбиталей, для каж-
каждой из двукратно заполненных орбиталей возможен
только один тип симметрии [А] = [2].
Энергия системы в состояниях с координатными вол-
волновыми функциями (8.109) определяется средним значе-
значением гамильтониана в этих состояниях. Диагональные
по конфигурации матричные элементы находятся по фор-
формуле (8.72) с учетом (8.75), недиагональные—по фор-
формуле (8.48в) с N^a ^=1, так как перестановки Р% =*
= Р|4=1. Учитывая, что g\\} 22 = Pi2, окончательно по-
получаем
J («и + «22) + 2 (a01 + a02) - (Poi + ft») + Pi2>
+ 2" (an + a22) + 2 (a01 + a02) - (pOi + Ы - Pi2> (8.110)
E (lBx) = 2e0 + гг + e2 + сц» + 2 (a01 + a02) +
+ a12 "" (Poi + P02) + Pl2>
E CЛ2) = 2e0 + гх + e2 + a00 + 2 (a01 + a02) +
+ a12 — (Poi + fW "" Pl2>
где все интегралы определены на молекулярных орби-
талях (8.105).
8-8. Методика расчета в приближении метода валент-
валентных схем. В методе валентных схем одноэлектронные
орйитали локализованы на определенных атомах си-
системы. В простейшем варианте метода в качестве таких
орбиталей берутся атомные орбитали, а интегралами пе-
перекрывания пренебрегают. При более точных расчетах
используются ортогональные наборы локализованных
орбиталей типа функций Ванье [38, 85], либо функций
Лёвдина [89].

§ S СИММЕТРИЧНЫЕ СИСТЕМЫ 319
Многоэлектронная координатная волновая функция
строится из произведений одноэлектронных орбиталеи и
для симметричных молекул при пренебрежении спин-
орбитальными взаимодействиями должна так же, как и
в методе молекулярных орбиталеи, удовлетворять двум
требованиям: а) принадлежать к базису неприводимого
Представления Пя] группы перестановок электронов;
б) принадлежать к базису неприводимого представле-
представления Па) точечной группы симметрии молекулы.
Под действием операций точечной группы электрон-
электронные орбитали, первоначально локализованные на одних
ft'
Vi <?"' ti" <pi'
Рис. 8.6.
ядрах, локализуются на других. В результате каждой
операции R точечной группы можно сопоставить опреде-
определенную перестановку Р индексов орбиталеи.
Пусть в вершинах правильного треугольника заданы
электронные орбитали трех разных типов, различаемых
количеством штрихов (рис. 8.6). Результат действия
операции С3 (поворот по часовой стрелке на угол 2я/3)
равен
Следовательно, действие операции С3 на_ электронные
орбитали эквивалентно перестановке ядер Раъс- Действие
этой же операции на ядра эквивалентно обратной пере-
перестановке расЬ = Р~1Ьс. В случае задания на атомах невы-
невырожденных орбиталеи одного типа симметризация коор-
координатной волновой функции относительно перестановок
координат электронов автоматически приводит и к опре-
определенной симметрии относительно перестановок индексов

320 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
орбиталей (ср. раздел 2-9), а следовательно, и относи-
относительно операций точечной симметрии*).
Это обстоятельство обязательно надо учитывать при
построении функций, принадлежащих одновременно к
базисам представлений Г^ и Г<а). Рассмотрим процесс
построения таких функций для ковалентных и ионных
структур в случае, когда количество взаимодействующих
электронов равно числу одноэлектронных орбиталей,
причем на каждом атоме задана орбит^ль одного типа.
I. Ковалентные структуры
В рассматриваемом случае ковалентные структуры
соответствуют однократному заполнению обриталей и
относятся все к одной электронной конфигурации вида
(8.56). Координатная волновая функция, отвечающая
определенному значению полного спина S, находится
действием оператора Юнга со^] на несимметризованное
произведение орбиталей (см. раздел 2-9). В получаю-
получающихся функциях Ф^ таблица Юнга г характеризует
симметрию относительно перестановок координат элек-
электронов, таблица Юнга t — относительно перестановок
орбиталей. Следовательно, функции Ф^ образуют ба-
базис для неприводимых представлений двух коммутирую-
коммутирующих групп: группы перестановок координат электронов
jtiv и группы перестановок орбиталей vcN. Так как в об-
общем случае часть перестановок орбиталей при опера-
операциях дискретной точечной группы не осуществляется, то
*) Такая ситуация имеет место только при задании на каждом
атоме одинаковых невырожденных орбиталей. В случае задания на
атомах орбиталей разного типа перестановки координат электронов
не будут связаны с перестановками орбиталей. Действительно, если
для орбиталей одного типа
Рц<9а (О Ф* B) = Ф« B) Щ (D^PabVa (О Ф* B),
то для орбиталей разного типа <р' и ф"
Р12< W < B) = Ф;B) ф" МФРаьЧа @ % B)-

§ 3 СИММЕТРИЧНЫЕ СИСТЕМЫ 321
последняя изоморфна подгруппе группы nN. Неприводи-
Неприводимые представления Г(а>, на которые распадается пред-
представление ТЩ при переходе от полной группы переста-
перестановок орбиталей к ее точечной подгруппе, даются раз-
разложением
"ptM « XT' (ft)"p(oi) /о i i 1 \
А =: ZA ЯК 1 > ^O.lllj
а
находимым с помощью таблиц характеров. Разложение
(8.111) позволяет определить возможные мультиплеты,
которые можно построить из функций ковалентных
структур (см. F.66)).
Построение собственных функций проводится еле-»
дующим образом. Исходим из набора f% функций Ф^»
принадлежащих к одному базису представления Г^1
группы nN. Базисные функции, принадлежащие одновре-
одновременно к представлениям Г^ и Т^а\ находим действием
операторов е^ (см. (8.101)) на произвольную пробную
функцию Ф^о данного набора. Если результат такого
действия равен нулю, берется другая функция набора
и т. д. е(Д> берутся только для тех представлений Г<а\
которые входят в разложение (8.111).
В операторах е^ операции точечной группы R заме-
заменяем соответствующими перестановками орбиталей Р.
С помощью соотношения B.48) находим искомые ли-
линейные комбинации:
Ф$ ([Я] го) - с 2 Г$ (R)* РФ%1« с 2 2 Г$ (/?)* If 0] (Р) Ф$
R R t
ИЛИ
"~ "' (8.112)
(8.113)
где множитель с находится из условия нормировки
функции (8.112). Матрицы неприводимых представле-
представлений точечных групп приведены в Приложении 2. Мат-
Матрицы перестановок F, соответствующих операциям
21 И. Г. Каплан

322 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ, VIII
точечных групп, могут быть вычислены с помощью мат-
матриц транспозиций Г^(Рг-_1,^), находимых по правилам,
изложенным в разделе 2-5. В Приложении 5 приведены
полностью матрицы неприводимых представлений групп
Яз и Я4 и матрицы транспозиций для неприводимых пред-
представлений ГруПП Л?5 И Яб.
После того как коэффициенты аД,* сосчитаны, вы*
числение матричных элементов гамильтониана в со-
состояниях с функциями (8.112) сводится к применению
формул раздела 8-5.
Рассмотрим в качестве примера ковалентную конфи-
конфигурацию шести я-электронов молекулы СбН6 в состоя-
состоянии со спином 5 = 0. Количество независимых ковалент-
ных структур со спином 5 = 0 определяется размерно-
размерностью неприводимого представления Г[2 J (см. раздел
6-10) и равно f[23]=5. Точечная группа симметрии моле-
молекулы бензола D6h. Так как все одноэлектронные орби-
тали ведут себя одинаково по отношению к отражению
в плоскости кольца, то вместо Dqh достаточно рассмат-
рассматривать группу DQ. Согласно F.76) разложение (8.111)
имеет в данном случае следующий вид:
rm±?Ai+B2 + E2. (8.114)
Линейные комбинации функций Ф^1, преобразующиеся
по неприводимым представлениям (8.114),_находим по
формулам (8.112)—(8.113). Матрицы Т[^(Р) приведены
в табл. 9 Приложения 5,матрицы T$(R) для одномер-
одномерных представлений берем из таблиц характеров При-
Приложения 1, для двухмерного представления ?2"~из
Приложения 2. Независимые ортогональные функции
флл\) и фАА2) получаем, беря последовательно в качестве
пробных функций Ф?5! и Ф[?2 (значение г0 несуще-
несущественно). Фв? получаем, взяв пробную функцию Ф^)-
Базисные функции представления Е2 находим с помощью
операторов ef» и eff, взяв в качестве пробной функ-
функции Ф^] (действие ей на Ф^1 и Ф[?2 дает нуль). В ре-
результате приходим к следующим линейным комби-

§ 3 СИММЕТРИЧНЫЕ СИСТЕМЫ 323
нациям:
Фх (Мх) = -jL= (БФ, + "УЗФ2 + /ЗФз + ЗФ4),
Ф2 (МО = у= (/6Ф2 + /6Ф3 - 2 /2Ф4 + 5Ф5),
L- (ЗФ, - /ЗФ2 - /ЗФ3 - ЗФ4), (8.115)
где Ф^ обозначает у
Матричные элементы гамильтониана с функциями
ФСдаются формулой (8.57). Входящие в эту формулу
коэффициенты перед обменными интегралами вычисляем
по формуле (8.46) с помощью матриц (г'А | РЪаь \г) из
табл. 4 Приложения 6. Благодаря симметрии бензоль-
бензольного кольца для обменных интегралов (так же как и для
кулоновских) справедливы следующие равенства, запи-
записанные для последовательно пронумерованных атомов
кольца:
Pl2 ~ 023 — Р34 = f*45 = Рбб в Pl6»
Pl3 = Р24 = Р35 = Р46 = Pl5 = Р26» (8.116)
Pl4 = Р25 = Рзб-
Матричные элементы гамильтониана с учетом равенств
(8.116) приведены в табл. 8.1, где Q обозначает
2 % + 2 <w
а а<Ь
Использование в качестве вариационных функций
функций (8.115) приводит к распаду исходного секуляр-
ного уравнения на два уравнения первого порядка и
одно — второго. Из уравнений первого порядка получаем
значения энергий уровней с симметрией В2 и Е2 (уро-
(уровень *?2 двукратно вырожден):
=Q-ahAt ?A?2)=Q-2p12~p14. (8.117)

324 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ, VIII
Таблица 8.1
Таблица матричных элементов гамильтониана
я-электронов молекулы бензола
для состояний со спином 5 = 0
<«„-« +
&6 = 0 —
<^33 = Q-
^>44 sb Q —
C^?55 я Q ~
vu 14 == &V 4
Jut/5 Jut/7
C?6 35 — (УF 5С
C%?45 = <&&$<
3 3
ft Qft R
~2" P12 ^Pi3 2"Pl4
ilft 2_p3_±p14
Ap12-p3_lp
7 R 1 A 3 ft
"g"Pl2~ "Pl3"""Pl4
10 ft 2
=s-2"Pi2-Pi3+ *Pu
~ ("o"Pl2 ~" Pl3+"n" Pl4J
,=/6(-ipI2-lp13 + -ipI4)

§ 3 СИММЕТРИЧНЫЕ СИСТЕМЫ 325
Значения энергий двух уровней с симметрией А\ нахо-
находятся из решения секулярного уравнения второго по-
порядка с матричными элементами
Q + -g- Р12 ~ -g" Р13 — 5" &4>
Q-f P12~|Pi3 + t- Рн, (8.118)
Если в формулах (8.117) и (8.118) оставить обменные
интегралы только между соседними атомами, то полу-
полученные значения энергий совпадут с энергиями элек-
электронных состояний молекулы С6Н6, приведенными в кни-
книге Эйринга и др. [30], стр. 334.
В случае, когда точечная группа симметрии изо-
изоморфна группе перестановок, распада секулярных урав-
уравнений, отвечающих заданным значениям спина 5, не
происходит, но имеет место вырождение термов. Рас-
Рассмотрим, например, систему четырех электронов в тет-
раэдрическом поле. Точечная группа Td содержит
24 элемента и является изоморфной группе перестано-
перестановок Jt4-
Между неприводимыми представлениями этих групп
существует взаимно однозначное соответствие (см.
F.25)). Это позволяет сразу выписать разрешенные
мультиплеты, поскольку каждому значению спина S од-
однозначно отвечает неприводимое представление точеч-
точечной группы. Разрешены термы
5Л2, *FU гЕ. (8.119)
В соответствии с размерностями неприводимых пред-
представлений не вырожден только квинтетный терм, три-
плетный терм трижды вырожден, синглетный — дважды.
Электроны, находящиеся в вершинах тетраэдра, рас-
расположены на равных расстояниях друг от друга. Следо-
Следовательно, все кулоновские и, соответственно, обменные
интегралы одинаковы:
«а* = а, р^ = Р (для а, 6=1, 2, 3, 4). (8.120)
Терму ЪА2 отвечает антисимметричная координатная

326 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛл VIII
волновая функция, принадлежащая к представлению
Г[14]. Его энергия находится по формуле (8.57), в кото*
рой Nab== — 1 для всех а, Ь. Учитывая (8.120), получаем
= 4e + 6a-6p. (8.121)
Термам 3fi и 1Е отвечают координатные волновые функ-
функции с перестановочной симметрией [Я] = [212] и [22] соот-
соответственно. Матричные элементы для состояний с такой
перестановочной симметрией найдены нами в разделе
8-5 (формулы (8.60) и (8.77); в формулах (8.77) необ-
необходимо сдвинуть нумерацию орбиталей на две единицы).
Согласно соотношениям E.15) все диагональные матрич-
матричные элементы гамильтониана для представлений Па>
должны совпадать, а недиагональные элементы равны
нулю. Подстановка в (8.60) и (8.77) равенств (8.120)
показывает, что это действительно так. Для энергий
термов получаем
= 4е + 6а - 2р, Е (гЕ) = 4е + 6а. (8.122)
П. Ионные структуры
Если ковалентным структурам в рассматриваемом
случае может быть сопоставлена только одна электрон-
электронная конфигурация, то ионным структурам обычно отве-
отвечает относительно большое число различных электрон-
электронных конфигураций. Это число дается формулой F.68).
Для построения координатных функций, являющихся
одновременно базисными функциями представлений Г^
и Г<4 необходимо разбить ионные конфигурации на от-
отдельные наборы, конфигурации внутри которых перехо-
переходят друг в друга при операциях точечной группы сим-
симметрии молекулы. Далее, для каждой конфигурации
составляются координатные волновые функции Ф[р](/С),
в обозначении которых символ р характеризует симмет-
симметрию функции относительно перестановок орбиталей и в
значительной степени определяется электронной конфи-
конфигурацией К\ /- — таблица Юнга, характеризующая сим-
симметрию функции относительно перестановок координат
электронов, вид ее для нас несуществен, поскольку мат-
матричные элементы гамильтониана не зависят от г. Элек-

§ 3 СИММЕТРИЧНЫЕ СИСТЕМЫ 32?
тронную конфигурацию удобно представить в виде сово-
совокупности двух конфигураций Ко и К\ (см. (8.66)). Сим-
метризованная по перестановкам координатная волновая
функция в этом случае может быть записана как
ф№(Кгог\), где таблица Юнга г0 характеризует симмет-
симметрию относительно перестановок орбиталей конфигура-
конфигурации /Со, таблица Юнга г — относительно перестановок
орбиталей конфигурации К\. Значение спина опреде-
определяется перестановочной симметрией конфигурации К\,
схему Юнга которой обозначим, как и в предыдущих
разделах, [А/2™)] (т обозначает число двукратно запол-
заполненных орбиталей и равно числу пар ионов данной мо-
молекулярной конфигурации). Линейные комбинации
фуцкций ф№(КгоГ\), преобразующиеся по неприводи-
неприводимым представлениям точечной группы, находим для
каждого набора действием операторов е^ на произ-
произвольную функцию набора. Не равный нулю результат
будет лишь для тех е^\ которые соответствуют пред-
представлениям Г<а), входящим в разложение приводимого
представления точечной группы, образуемого данным на-
набором ионных структур. Способ нахождения характеров
таких представлений изложен в п. II раздела 6-10.
Пусть рассматриваемые ионные конфигурации обра-
образуют регулярный набор. Такой набор содержит g кон-
конфигураций, где g—-порядок точечной группы. Обозна-
Обозначим произвольную конфигурацию набора, называемую
в дальнейшем порождающей конфигурацией, через /С,
все остальные конфигурации Kr получают из порождаю-
порождающей действием на нее операций группы R. Собственные
функции молекулярных мультиплетов легко находятся
действием операторов (8.101) на функцию 0№(КгоГ\) и
равны
Ф$ № гол) = (-^I/2 2 Гй (/?)*Ф[М (Кягоп). (8.123)
В следующем разделе разобран пример на составление
функций (8.123).
Несколько более сложно построение собственных
функций молекулярных мультиплетов в случае ионных
конфигураций, обладающих элементами симметрии.

328 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
Базисные функции неприводимых представлений строят-
строятся в этом случае следующим образом.
Вначале выписываются элементы подгруппы //, от-
относительно которых выбранная порождающая конфигу-
конфигурация инвариантна. Все элементы точечной группы О
разбиваются на левые смежные классы относительно
подгруппы Н. В результате каждый элемент точечной
группы может быть представлен в виде произведения
RaQ, где Q обозначает операции точечной группы, оста-
оставляющие порождающую конфигурацию инвариантной,
т. е. Qe/У. Число различных конфигураций, входящих
в набор, равно числу операций /?а, т. е. равно g/h. Далее
учитываем, что действие операции Q сводится к пере-
перестановке однократно заполненных орбиталей, обозначим
такую перестановку Q. Согласно B.48)
? (8.124)
В результате находим
egow(Wi)-
2 2 ГЙ? (RaQ)m r[rfm)] (Q)Ф[К] (KRror{) (8.125)
RQ
ИЛИ
S 2
^ Л ail r, (Ra) Ф1М (KR/ori), (8.126)
где коэффициенты в линейной комбинации (8.126) равны
множитель с находится из условия нормировки функции
(8.126).
Рассмотрим в качестве примера построение собствен-
собственных функций мультиплетов, возникающих при учете че-
четырех конфигураций с одной парой ионов, типа изобра-
изображенной на рис. 8.7. Точечная группа симметрии равно-
равновесной конфигурации ядер — D4. Изображенная на
рис. 8.7 электронная конфигурация инвариантна отно-
относительно операций подгруппы группы /54> состоящей из

§3
СИММЕТРИЧНЫЕ СИСТЕМЫ
329
двух элементов Q: E u U^K Представим все элементы
группы Z?4 B виде произведения /?aQ*).'
RaQ
R
Е
Е
В?
с.
с,
?/<»
с2
с,
Of
с3
г3
и?
Имеется четыре независимых ионных конфигурации:
(8.128)
Возможны два типа спиновых состояний, соответ-
соответствующие значениям полного спина 5 = 0 и S = l. Рас-
Рассмотрим состояние со спином S=l; ему отвечает коор-
координатная волновая функция, симметризованная по схе-
схеме Юнга [Х] = [212]. Схема Юнга однократно заполненных
<
Рис. 8.7.
орбиталей [^2>] = [12]. Согласно теореме п. II раздела 6-10
характеры представления, образуемого координатными
*) Этот процесс эквивалентен разбиению группы 0 4 на смежные
классы относительно подгруппы из двух элементов: Е и U^- Опе-
Операции точечной группы рассматриваем действующими на координаты
электронов при фиксированных ядрах. Все повороты производятся
по часовой стрелке.

330
РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ
ГЛ. VIII
функциями конфигураций (8.128) в состоянии с
= [212], равны
Е
4
С2
0
2С4
0
2U2
0
2U2
-2
(8.129)
Разложение его на неприводимые части имеет следую-
следующий вид:
Т = А2 + В1+Е. (8.130)
Базисные функции неприводимых представлений (8.130)
находим по формулам (8.126) — (8.127), учитывая, что
Матричные элементы ^fk(RaQ) берем из Приложений 1
и 2. Базисные функции двухмерного представления Е
строятся с помощью пары операторов ef2 и е|2 (действие
efj и efj на Ф[212К#[2][12])дает нуль). В результате по-
получаем следующие нормированные комбинации:
(8.131)
где введены для краткости обозначения
сЛ2] [I2]). Ф4 = Ф[2|21
(8.132)

§ 3 СИММЕТРИЧНЫЕ СИСТЕМЫ 331
Исходное секулярное уравнение четвертого порядка
линейным преобразованием разбивается на четыре
уравнения первого порядка, два из которых, относя-
относящихся к представлению Е, совпадают. Матричные эле-
элементы гамильтониана, диагональные по конфигурациям
(8.128), легко находятся по формуле (8.72). Недиаго-
Недиагональные по конфигурациям матричные элементы опре-
определяются формулами (8.48), поскольку конфигурации
(8.128) различаются друг от друга на две орбитали. Так,
с точностью до порядка орбиталей
°4
s"dd
В данном случае конфигурации, остающиеся после от-
отщепления двух орбиталей, имеют схемы Юнга [А/] = [2]
или [I2], поэтому в формулах (8.52) 2 ~*А'р' 2- Входя-
р', р' р/
щие в (8.52) матричные элементы берем из табл. 2.
Приложения 6. Например, в случае матричного эле-
элемента между конфигурациями К и Кс, коэффициенты
N[al)XM [2] [1'] находятся перемножением первых столбцов
матриц перестановок Р\\ и РЦ с дополнительным умно-
умножением на r[A/1(Pi2) = ± 1 в зависимости от [V] (вид [К']
определяется из таблиц Юнга представления П212]). Это
приводит к
#?«-< К[2] [12]| ев \Kct[2] [I2] >'21'' -gab, a. (8.133)
Для матричного элемента между конфигурациями К и
Кс7 коэффициенты #L2i!d!i!21lI2] определяются квадратом
первого столбца матрицы перестановки P3\t, умножен-
умноженным на Т[Х ] (Р12). Матричный элемент дается формулой
(8.48в)
^13=<^[2][12]1^1^сЛ2][12]У2^^ gaa.dd. (8.134)
В силу симметрии задачи для одноэлектронных куло-
новских и обменных интегралов соблюдаются следующие

332 расчет электронных состояний гл. viii
равенства:
®аа = ®ЪЬ = ®сс e ^dd e а0»
е* = efe = е, = sd - е, рлЬ - рл, = p,d - рм - Рх, (8.135)
«arf = «^ = «2»
Легко усмотреть, что
^л, rfrf - gcc ьь = Рг- (8.136)
Обозначим, далее,
Учет равенств (8.135) — (8.137) приводит к следующим
выражениям для матричных элементов гамильтониана,
определенных на функциях (8.132):
^12 - ^23 - ^?34 - ^?14 - Y, (8.138)
ей?13 = ^?24 ~ — Рг-
В результате для энергии триплетных ионных состоя-
состояний, характеризующихся координатными волновыми
функциями (8.131), получаем следующие выражения:
Е CЛ2) = 4е + а0 + 4а, + а2 - 2рх - 2р2 + 2Y,
4е + а0 + 4а, + а2 - 2р, - 2р2 - 2Y, (8.139)
4е + а0 + 4а, + О2 - 2р,.
8-9. Расчет молекулы Н3 при учете взаимодействия
всех конфигураций с ls-орбиталями. Применим метд-
дику расчета, развитую в предыдущем разделе, к нахо-
нахождению энергии симметричной треугольной системы из
трех атомов Н, предполагая, что на каждом атоме за-
задана одна ls-орбиталь. В качестве одноэлектронных
орбиталей выбираем ортонормированный набор грех ло-
локализованных орбиталей фа, фь, фс, строя их из атомных
ls-орбиталей по методу Ванье (см. [38], гл. 9, § 5).
Имеется единственная ковалентная конфигурация
/Со: Фвф*Фс (8Л40)

§ 3 СИММЕТРИЧНЫЕ СИСТЕМЫ 333
Спину S = 3/2 отвечает одно состояние с координатной
волновой функцией Ф(Ко [I3]). Спину S = l/2 отвечают
два состояния с координатными волновыми функциями
Ф(Ко[21]\) и Ф(/Со[21Ь). Точечная группа симметрии
равновесной конфигурации ядер— Ds. Группа Dz изо-
изоморфна группе перестановок я3- Из сравнения таблиц
характеров следует, что между неприводимыми предста-
представлениями этих групп существует следующее взаимно
однозначное соответствие:
[13] [21W [3]г. (8.141)
Отсюда вытекает, что при учете только ковалентной кон-
конфигурации осуществляются два терма: Мг и 2Е. Терму
М2 отвечает координатная волновая функция
(8.142)
Среднее значение гамильтониана в состоянии с волно-
волновой функцией (8.142) находим по формуле (8.57), в ко-
которой все коэффициенты Nab=—1-
Е (М2) - (Ко I & | К0)т - 3 (в + а - Р). (8.143)
При записи выражения (8.143) учтено, что, поскольку
все орбитали одинаковы, из симметрии ядерной конфи-
конфигурации следует
еа == Ч = ес = 8>
ъаь = ъас = аЬс = а, (8.144)
Рай = Рае = he == Р-
Терм 2Е дважды вырожден, соответствующие ему коор-
координатные волновые функции обозначим
( 5)
Матричные элементы гамильтониана в состояниях с вол-
волновыми функциями (8.145) даются формулой (8.57), ко-
коэффициенты перед обменными интегралами в которой
вычисляются по формуле (8.46). Учитывая равенства
(8.144), с помощью матриц табл. 1 Приложения 6 на-
находим
(8.146)

334
РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ
ГЛ. VIII
Учтем теперь ионные конфигурации. В данном слу-
случае ионные конфигурации не обладают элементами то-
точечной симметрии и образуют поэтому регулярные на-
наборы. Все конфигурации этого набора получаются из
одной действием на нее элементов группы. А именно:
с3
с
Поскольку спины электронов, находящихся на дву-
двукратно заполненных орбиталях, спарены, разрешены
только дублетные термы. Обозначим для краткости
(8Л47)
Разложение регулярного представления содержит все
неприводимые представления группы. Искомые коорди-
координатные функции мультиплетов, построенных на ионных
конфигурациях, легко находятся по формуле (8.123).
Матричные элементы ^fk(R) берем из Приложений 1
и 2:
(8.148)
- Ф4 - Ф5 " Фб)>
,_1ф,_1ф,\ (8.149)
Ф3 - Ф5

S 3 СИММЕТРИЧНЫЕ СИСТЕМЫ 335
Ф12B?) = 1 (- ф2 + ф3- Ф5 + Ф6),
|-1ф2-|ф3-Ф4+ (8.150)
Фигурными скобками в (8.149), (8.150) отмечены коор-
координатные функции, описывающие вырожденные энерге-
энергетические состояния.
Таким образом, учет ионных конфигураций приводит
к появлению двух дополнительных дублетных термов 2Е
и по одному дублетному терму 2А\ и 2Л2. Для нахожде-
нахождения их энергий необходимо предварительно найти мат-
матричные элементы гамильтониана, определенные на функ-
функциях (8.147).
Диагональные по конфигурациям матричные элемен-
элементы вычисляем по формуле (8.72). Обозначив в дополне-
дополнение к обозначениям (8.144)
находим ««« = «** = «. = «о> (8.151)
^п = 3е + ао + 2а-р, /=1, 2 6. (8.152)
Недиагональные по конфигурациям матричные эле-
элементы находим по формулам (8.37), (8.47), (8.48). Мат-
Матричные элементы перестановок, необходимые для вычис-
вычисления коэффициентов (8.49), (8.50), берем из первого
столбца соответствующих матриц табл. 1 Приложения 6.
Так, матричные элементы е%?12 и &6ХЬ находятся по фор-
формулам (8.48а) и (8.48в) соответственно:
-?ЬЬ ac^-4l< (»-163)
8ьь. со -Р. (8-154)
матричный элемент &}н — по формулам (8.376) и
(8.47), а матричный элемент #г?15 — по формулам (8.37)
и (8.47):
~fba- {Sba, aa + Sbb, ab) S ~ (f + 2Y2). (8-155)
1^1ф26Фс) =
- foe + Чьа, be ~ gba, cb = f + 2Y3 ~ Yl- (8-156)

336 РАСЧЕТ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ГЛ. VIII
Нетрудно проверить, что в силу симметрии задачи
все остальные матричные элементы равны одному из
матричных элементов (8.153) — (8.156). А именно:
&6п — 0^13 = 0^23 = ^45 — ^46 == ^56 ~ ~~ Yb
2Y3-Y.. ( '
S^l6 = ^25 = ^34 = Р-
Термы 2А\ и 2А2 встречаются по одному разу. Их энер-
энергия дается средним значением гамильтониана в состоя-
состояниях с координатными функциями (8.148). Выпишем
выражения для энергий этих термов, учтя соотношения
(8.157):
Е BАХ) = Зе + <х0 + 2а - 3yi - 2у2 + 2у3, (8.158)
Е BА2) = Зе + а0 + 2а - 2р - Yi + 2у2 - 2уз- (8.159)
Учет взаимодействия койалентных и ионных конфи-
конфигураций приводит к появлению трех дублетных термов
2Е. Их энергия дается корнями секулярного уравнения
третьей степени. Для записи секулярного уравнения не-
необходимо выбрать по одной функции из наборов (8.145),
(8.149) и (8.150). Выберем следующую тройку базисных
функций:
Ф10B?), ФпB?), Ф12B?). (8.160)
Для нахождения недиагональных матричных элементов
между функциями ковалентных и ионных структур не-
необходимо, помимо матричных элементов (8.157), знать
матричные элементы между функциями (8.147) и
(8.145). С помощью формул (8.37а) и (8.47) находим
(/ - \ у, + Y2 + Уз) > (8.161)
^06 = -Ц- (/ + Yi + Ъ + Уз).

§ 3 СИММЕТРИЧНЫЕ СИСТЕМЫ 337
В результате получаем следующие выражения для
матричных элементов секулярного уравнения:
 Yi-2y2-Y3.
Ф10)= (8.162)
l/ + Yl-yY2-TY3),
(Ф10 Ш\ Ф,2> = (Ф121 & |Фю>= -1i
В проведенном выше расчете максимально использо-
использованы свойства симметрии рассматриваемой системы.
Для получения численных результатов необходимо, да-
далее, вычислить молекулярные интегралы, входящие в
выражения (8.143), (8.158) и (8.162).

Приложение 1
ТАБЛИЦЫ ХАРАКТЕРОВ ТОЧЕЧНЫХ ГРУПП
В приводимых ниже таблицах каждый класс характеризуется
одним принадлежащим ему элементом. Числа перед символами эле-
элементов группы в верхних строках таблицы указывают количество
элементов в классе. Обозначения операций точечных групп приве-
приведены в разделе 3-8. Приняты следующие обозначения неприводи-
неприводимых представлений. Одномерные неприводимые представления обо-
обозначаются буквами Л, В, двухмерные — буквой ?, трехмерные —
буквой F. Функции базисов представления А симметричны относи-
относительно поворотов вокруг главной оси симметрии п-то порядка, функ-
функции базисов представлений В антисимметричны. А\ везде обозначает
полностью симметричное (единичное) представление. Представле-
Представления, различающиеся поведением базисных функций относительно
поворотов вокруг осей симметрии с порядком, меньшим п, либо
относительно отражений ev, Od, отличаются индексом внизу сим-
символа представления. Представления с различной симметрией базис-
базисных функций относительно отражения в плоскости Он, отличаются
количеством штрихов. Наконец, индексы gnu указывают на сим-
симметрию базисных функций относительно инверсии.
Координаты х, у, z у символов представления указывают не-
неприводимые представления, по которым преобразуются соответ-
соответствующие компоненты полярного вектора. Аналогично обозначения
Rx, Ry, Rz указывают неприводимые представления, по которым
преобразуются компоненты аксиального вектора.
Ag \Rxi
Att {x,
A#, Kz)
У,г)
c,
А {г,
°{rx;
Rz}
y\
Ry)
c.
A
A"
л*. 4
1
1
j
с,
а
1
-1
Сз
А {г, Rz}
е1х-у\
\Rx, Ryi
Е С, С|
1 1 1
( 1 е е2 (е=е21й/3)
U е2 е

ТАБЛИЦЫ ХАРАКТЕРОВ ТОЧЕЧНЫХ ГРУПП
339
Au
Bg
Ba
{Rz)
{z)
{Rx, Ry)
{x,y)
С
A
A
В
B
IV
1 {*}
2{Rz)
2 {». Rx)
i {*, Ry)
Dt
A
Bt
B3
Bs
{*.
{у,
Rz)
Rx)
Ry)
E
E
E
1
1
1
1
c,
qZ
1
1
-1
-1
1
-1
-1
1
/
<*v
C2
1
-1
1
-1
Ai[z)
A i О \
/Л.2 X^Zi
pJ x9 у \
\Rx, Ryi
A\
A2{z
E\
% Rz)
x,y\
x,Ryi
E
E
1
1
2
2C3
2C3
1
1
-1
3av
su2
1
-1
0
A
В
E
{2, Rz)
( Y 11 Л
A{RZ)
B{z}
e\ x> y \
XRx.Ryi
E C4
E S4
1 1
1 -1
I 1 /
I 1 -/
C2
C2
1
1
-1
-1
сз
sl
1
-1
i
с
A
ч:
E2
,Ryi
E
1
f 1
t 1
[ 1
t 1
1
?
?2
?3
c2
1
?2
?3
?
1
?3
?2
?
?4
c\
1
?3
?2
22*

340
ПРИЛОЖЕНИЕ 1
A
В
E\
E2
[*, Rz)
j*> У \
Ux, Ry)
E
1
1
f 1
( 1
( 1
I 1
Ce
1
-1
?2
— ?
?
-?2
Сз
1
1
— ?
?2
?2
— ?
С
1
-1
1
1
~1
-1
Г2
C3
1
1
?2
— ?
— ?
?2
cl
1
-1
_? (е = е2я//6)
?2
-?2
?
c4,
Ai
A2
Bi
B2
{Rz
)
у \
Ry\
D
A
A
В
в
E
4
i
2 {^,
2
ix,
\Rx
Rz
У
• Rt
}
D2d
Ax
A2 {Rz}
Bx
B2{z)
E\Rx,R
}
E
E
E
1
1
1
1
2
C2
c2
c2
1
1
1
1
-2
2C4
2C4
254
1
1
-1
-1
0
2av
2U2
2U2
1
-1
1
-1
0
2av
2U2
2ad
1
-1
-1
1
0
Ax{z)
At {Rz)
El\Xff д }
Et.
Ax
A2{z,
Ex\X'
E2
Rz)
y \
E
E
1
1
2
2
2C5
2C5
1
1
2 cos a
2 cos 2a
2C\
2C§
1
1
2 cos 2a
2 cos 4a
ъщ
l
-l
0

ТАБЛИЦЫ ХАРАКТЕРОВ ТОЧЕЧНЫХ ГРУПП
341
CO CO CO CO
^ fc <N *.
СМ
со
О
сч
««
tq
ее
сч
О
сч
«о
•«г
t»
(М
I I
I
СЧ <М
X
3
X
с?
II
V — S (N
Q?
Q?
^ Ч"

842
ПРИЛОЖЕНИЕ 1
A
E
T
> У> * \
E
1
( 1
t 1
3
3C2
1
1
1
-1
4C3
1
e
e2
0
4C|
1
e2 (е==/Ш73)
e
0
0
At
A,
E
F.
\x,
\Rx
У,г )
, Ry, RzS
Ta
At
A3
E
FARj
Ftix,
r> Ryf Rz)
y,z)
E
E
1
1
2
3
3
8C3
8C3
1
1
-1
0
0
3C2
3C2
1
1
2
-i
— 1
6C2
1
-1
0
-1
1
6C4
654
1
0
1
-1
At Ы)
A2 {Rz)
41,%,}
E,
Em
E
1
1
2
2
2
2Сф
1
1
2С08ф
2 cos 2ф
2 cos тф
о*
1
-1
0
0
0

ТАБЛИЦЫ ХАРАКТЕРОВ ТОЧЕЧНЫХ ГРУПП
343
Dooh
Alg
A2g{R<
Аш {z}
E2g
г)
r, Ry)
У)
Е
1
1
1
1
2
2
2
2
2Сф
1
1
1
1
2cosq>
2coscp
2 cos 2ф
2 cos 2ф
1
1
-1
-1
0
0
0
0
/
1
-1
1
-1
2
-2
2
-2
2/Сф
1
-1
1
-1
2coscp
—2coscp
2os2q)
-2cos29
IU2
1
-1
i
1
0
0
0
0
Отметим, что при разложении представления на неприводимые
представления групп CooV и Dooh следует иметь в виду, что сумми-
суммирование по операциям Е и I проводить не нужно, поскольку эти
операции учитываются при интегрировании по ф от 0 до 2л. Харак-
Характеры точечных групп, неприведенных выше, легко выписываются в
силу наличия соотношений

Приложение 2
МАТРИЦЫ ОРТОГОНАЛЬНЫХ НЕПРИВОДИМЫХ
ПРЕДСТАВЛЕНИЙ ТОЧЕЧНЫХ ГРУПП
Для нахождения матриц неприводимых представлений точечных
групп достаточно знать матрицы представлений для групп, состоя-
состоящих из операций чистых вращений. Все остальные точечные группы
либо изоморфны точечным группам чистых вращений, либо могут
быть выражены в виде прямого произведения таких групп на груп-
группы Cs и С*. Ниже приводятся матрицы двухмерных и трехмер-
трехмерных ортогональных неприводимых представлений групп Dn (n = 3 ч-
-4-6), Т и Q. Операции симметрии этих групп могут быть найдены
г
а
Ум
?\
1
4
и
2
а
7
ьУ
S)D6
3 а
е> в
из рис. П. 1. Ось г для групп Dn совпадает с главной осью симметрии
Сп и направлена перпендикулярно плоскости рисунка. Вращение
везде производится в направлении часовой стрелки. С?— вращение

ПРЕДСТАВЛЕНИЯ ТОЧЕЧНЫХ ГРУПП
345
вокруг оси rt-ro порядка, совпадающей с осью X, С^ — вращение
вокруг оси третьего порядка, проходящей через вершину а, Со-
Совращение вокруг оси второго порядка, проходящей через точки k,
лежащие на серединах противоположных ребер куба. Пустые места
в матрицах означают нули.
Группа ?>з, представление Е
FT Г2
Ц~~ 1 уз'
2
1
1
Vf
2
2 _
Vf
1 _
2
7 _
,3)
У5Ш
Т
1
Группа Z>4, представление
Я С4
uf
uf
[-.-][, ']['-Л J
Группа Z>5, представления EY и
cos a sin а
— sin а cos а
cos 2а sin 2а
;1 Г cos 2а sin 2а"| Tcos 2а - sin 2а1 Tcos а - sin а!
;] L- sin 2а cos2aj [sin 2а cos 2а J Lsina cos a I
И cos 2а sin 2а"] Г
-sin 2а cos2aj [
cos 4a sin 4a
sin 2a cos2aj [-sin 4a cos 4a.
и
"cos 4a -sin 4a
sin 4a cos 4a
it
cos 2a —sin 2al
sin 2a cos 2a J
— cos a —sin a]
[ —
-
sin a cos a J
[cos 2a sin 2a
uf
—cos 2a sin2al
sin 2a cos 2a]
cos 4a -sin4al
uf
v\
E)
2 [sin 2a - cos 2aJ [~ sin4a-cos4aj
- cos 2a - sin 2al Г-cos a sin a"
sin 2a cos 2a J [ sin a cos a
cos 4a sin 4a ] f cos 2a - sin 2a"j
1
1 f" 1 f *~ cos 2a ~ sin 2a] Г
J L U L-sin 2a cos 2a J [
[1 1 rcos4a sin 4a 1 Г со;
-lj Lsin 4a - cos 4aJ [-sin2a-cos2aj

346 ПРИЛОЖЕНИЕ
Группа Z>6, представления Е{ и Е2
и
^з
 ~
2 _,
1 УЗ
2 2
Уз_ _J_
L 2 2 J
(О rrB)
I
2 2
/3 1
1 Уз
2 2
УЗ _1_
2 2
1 УЗ
2 2
L 2 2
УЗ 1
2 2 J
-1
2
J
2
Уз
.. 2
- !
~
Уз
. 2
2
!
~T J
Уз '
2
1
2" .
-1
1
U2
~~2 Г
XL I
2 2
~T" 
2 2
1 ^3
2 2
У? j^
2 2
-1
2
УЗ
2
Уз
2
-1
-1
2
Уз
2
2 2
H I
2 2
2 2
Группа Г, представление Z7
[¦¦г
(c?J
L ¦ -IK. IL
C3
-1
1
с*
¦]["'
U2
(СзЬJ
-1
-
Ll
'¦][¦. ¦][."'-][-..¦]

ПРЕДСТАВЛЕНИЯ ТОЧЕЧНЫХ ГРУПП
Группа О, представления Е, Flt Ft
в ci cjf с\
347
¦ Г J Г,] Г,] Г J
-['¦.И1-..]["¦.,И-.]
•Г ¦.]['-..]["'¦-,]["'-.]
-1
1
1
2
Кз
_ 2
Кз
2
1
2_
И _1
2 2
-1
-[", -1L. ¦ "][¦
'Г ..¦][,-"'][-
.it1 _. ¦]
(off
Г®
1
2
Кз
- 2
Кз"""
2
1
о
1
2
Кз"
2
КЗ"
2
1
2 _
1
2
KJ
_ 2~
Кз"
2"
1
2
1
2
Кз"
2
Кз"
2
1
2
[.¦][-,][-..][¦..]
Г !1 Г "! 1Г х 1 Г ~1 1
L-i JL —1J L lJL I J

348
ПРИЛОЖЕНИЕ 2
с<4> cf
1
2
KIT
_ 2
Кз
2
1
2
1
2
Vz
_ 2
К"з "
2
1
2
-1
1
-1
1
¦i, - к. - г., -и, ¦]
4 ¦¦][„¦"] [',¦]['-,-]
1
2
Кз
_ 2
Кз~~
2
1
2 _
1
2
КЗ
_ 2
Кз"
2
1
2 _
1
2
2
Кз "
2
1
2 _
1
2
2
Кз""
2
1
2 .
•¦K,1[, [¦.'][.."¦¦]
'¦[¦ -."][. ¦¦ -¦][¦. ¦] [_. "¦ ¦]
(Cff
1
2
2
2
1
2
1
2
KF
_ 2
2
1
2 _
1
coj to
_ 2
2
1
2
1
2
кг
2
К*з"~
2
1
2 _
-L' -][-.,'] [,' ¦] 1-, -
-[..' -][-., 1 [,' ¦] [-,

Приложение 3
ТАБЛИЦЫ РЕДУКЦИИ ПРЕДСТАВЛЕНИЙ
НА ГРУППЕ Яз
Ниже приводятся результаты редукции представлений Е4/+Р
описывающих состояние системы с числом частиц #=1-ь4. При
большем числе частиц результаты редукции могут быть найдены по
методу, изложенному в разделе 4-4.
Таблица 1
У-1/2
N
1
2
3
4
[1]
[2]
П2]=[0]
[3]
[21]-[1]
[4]
[31]» [2]
[22] = [0]
1/2
г
3/2
1/2
2
1
0
6». B)
2"
4
2
б
3
1

360
ПРИЛОЖЕНИЕ 3
Таблица 2
N
1
2
3
4
[1]
[2]
[121
[3]
[21]
[13]-[0]
[4]
[31]
[22] ^[2]
[212]^[12]
/
1
0,2
1
1,3
1,2
0
0,2,4
1,2,3
0,2
1
3
CD CO
10
8
1
15
15
6
3
Таблица 3
/=3/2
N
1
2
3
4
[X]
[1]
[2]
[I2]
[3]
[21]
[13]-[1]
[4]
[31]
[22]
[212]
[14]^[0]
/
3/2
1,3
0,2
3/2, 5/2, 9/2
1/2, 3/2, 5/2, 7/2
3/2
0, 2, 3, 4, 6
12,2,32,4,5
0,22,4
1,2,3
0
6Я,D)
4
10
6
20
20
4
35
45
20
15
1

РЕДУКЦИЯ ПРЕДСТАВЛЕНИЙ U[y]+l НА ГРУППЕ #3 351
У-2
Таблица 4
N
1
2
3
4
[M
[1]
2]
I2
[3]
[2i:
[i3]^
[4]
[3i:
[22
[21
[I4]-
]
121
]
2]
[1]
2
0,2,4
1,3
0, 2,3, 4,6
1,22,3,4,5
1,3
0, 22, 42, 5, 6, 8
12,22,33,42, 52,6,7
o2,22,3,42,6
12,2,32,4,5
2
«A. E)
5
15
10
35
40
10
70
105
50
45
5
/=5/2
Таблица 5
N
1
2
3
4
W | / |
[1]
[2]
I2)
[3]
ЧУ]
,lt]
[22]
[212]
П4] = [12]
5/2
5,3, 1
4,2,0
3/2,5/2,7/2,9/2,11/2,15/2
1/2,3/2, E/2J, G/2J, 9/2, 11/2, 13/2
3/2, 5/2, 9/2
0, 22, 3, 42, 5, б2, 7, 8, 10
13,22,34,43,54,62,72,8,9
О2, 23, 3, 43, 5, б2, 8
12,22,33,42,52,6,7
4,2,0
6
21
15
56
70
20
126
210
105
105
15
7 = 3
Таблица 6
In
г
1
2
3
4
[Л]
[1]
[2]
I2]
[3]
[21]
[V]
[4]
[31]
[22]
[212]
[И]-[13]
з 1
0,2,4,6
1,3,5
1,32,4,5,6,7,9
1,22,32, 42,52,6,7,8
0, 2, 3, 4, 6
О2, 22,3, 43,5, б3, 7, 82, 9, 10, 12
13,23,35,44,55,64, 74,82,92,10, 11
О2, 24, 3, 44, 52, б3, 7,82, 10
13,22,34, 43, 54, б2, 72, 8,9
0, 2, 3, 4, 6
7
28
21
84
112
35
210
378
196
210
35

П р и лож ение 4
ТАБЛИЦЫ ХАРАКТЕРОВ ГРУПП ПЕРЕСТАНОВОК
Я2-*-Яв
«2
порядок
класса
[2]
[12]
О2}
1
1
1
{2}
1
1
-1
«з
порядок
класса
[3]
[21]
[13]
{I8}
1
1
2
1
{12}
3
1
0
-1
{3}
2
1
-1
1
поря-
порядок
класса
[4]
[31]
[22]
[212]
[I4]
О4)
1
1
3
2
3
1
И22]
6
1
1
0
-1
-1
{13}
8
1
0
-1
0
1
{22}
6
1
-L
2
-1
1
{4}
3
1
-1
0
1
-1
порядок
класса
[5
41
32
31
221
213
[I5
{I8}
1
1
4
5
6
5
4
1
{1«2>
10
1
2
1
0
1
-2
-1
02з}
20
(
)
{14}
30
1
0
-1
0
1
0
-1
{122}
15
1
0
1
2
1
0
1
{23}
20
1
-1
1
0
-1
1
-1
{5}
24
1
-1
0
1
0
-1
1
¦«.
порядок
класса
[6]
51]
42]
412]
[З2]
т]
[313]
[23]
[2212]
[214]
[I6]
{Iе}
1
1
5
9
10
5
16
10
5
9
5
1
{1*2}
15
1
3
3
2
1
0
2
-1
-3
-3
-1
03з}
40
1
2
0
1
-1
-2
1
-1
0
2
1
024}
90
1
1
-1
0
-1
0
0
1
1
{1222}
45
1
1
1
-2
1
0
-2
1
1
1
1
{123}
120
1
0
0
-1
1
0
1
-1
0
0
-1
{15}
144
1
0
-1
0
0
1
0
0
-1
0
1
{24}
90
1
—1
1
0
-1
0
0
-1
1
-1
1
{23)
15
1
-1
3
-2
-3
0
2
3
~3
1
-1
{З2}
40
1
-1
0
1
2
-2
1
2
0
1
1
{6}
120
1
-1
0
1
0
0
-1
0
0
1
-1

ХАРАКТЕРЫ rpyflit ПЕРЕСТАНОВОК
3§3
s
I
I
{25}
CO
h
{124}
{16}
I
|
I
I
со"
1
К
720
420
210
504
280
105
630
840
504
420
210
-
орядок
класса
с
~ 7
i
i
~ 7
—i О
—* о
~ о
—| О
- <М
- <м
—1 СО
^ CD
Е s
о
7
см
о
7
7
(М
о
(М
CD
с7
1
о
о
со
1
7
о
о
1
7
—
со
ю
ю
3
о
1
7
о
о
о
7
<М
1
7
9
о
1
1
о
7
о
1
7
7
7
о
1
о
со
7
о
—
7
со
1
—'
со
7
о
«
о
о
о
о
7
о
(М
о
о
см
о
7
о
со
7
о
—
—
со
1
7
я
со
о
1
о
7
7
7
о
7
7
ю
1
8
<N
о
I
1
о
о
о
7
1
(М
(М
7
7
2
[US
т
о
о
со
7
о
о
7
7
со
ю
1
ю
со
о
7
7
о
7
(М
о
см
CD
1
со
7
1
-
о
о
о
о
—
1
см
°\
со
1
CD
to
7
7
7
—
—
7
—•
7

3S4
ПРИЛОЖЕНИЕ 4
ч — О — О О — С
I I
> — о о — о — —
I I
II
II
I
II
II
~7
i
~7
~7
"^ СО
1
—•о
— о
7
1
7
1
О СО СО (М
1
О ОО —1
О 1—• СЧ О
оо со со
1 1
—•о о
1
ооо
оо
1
7
о
сч coco о
1
7 1
— ооо
1 1
1
7
7
СО "^
1
о •—«
1
о •—
~ 1
7
7
7
7
>^© О — ©г-н
I I I
II
II
.OO—•© —<© —<© —'OO—i©—'O—i©—i © ©-^
III I I
II
I I I I
s
II
II
II
I I
.(NO—.(M—i© —i© —<
III
—i ©—i© —<(M—i ©
III
II
II
I I I I
II
0
I I I I
III I I I I
СООООЮ
77 17 1
О с[с
в
'hNO'h00^10^OC0O(NC0O^10<*00^ON'H
<N (M (M CO CO —1 t^ Ю CT> rf< Ю t^ —• CO CO <N (M (M
'^1Го7^1ч с*7"'—1 ^ "СЯ i—i см -1 oT (N-и-1 Г1-< Г1
^ CD CO Ю CS Ю —CO ^ СЧ ?0 ^ СЧ ^СЧ ^ COJ^

Приложение Ь
МАТРИЦЫ ОРТОГОНАЛЬНЫХ НЕПРИВОДИМЫХ
ПРЕДСТАВЛЕНИЙ ГРУПП ПЕРЕСТАНОВОК Я3-^яб
Ниже приведены матрицы стандартного ортогонального пред-
представления Юнга — Яманути, правила нахождения которого даны в
разделе 2-5. Строки и столбцы матриц нумеруются таблицами Юнга,
расположенными в порядке отклонения последовательности чисел в
них от натурального ряда (если читать по строкам, двигаясь сверху
вниз).
Матрицы одномерных представлений не приводятся, так как их
можно найти из таблиц характеров (Приложение 4). Приведены
полностью матрицы неприводимых представлений групп я3 и я4
Во всех остальных случаях даются только матрицы транспозиций
Г^(Я<_ь<). Согласно теореме раздела 2-1 матрицы остальных пере-
перестановок всегда могут быть представлены в виде произведения
матриц типа Т^ (Pi-i, i)- В табл. 9 приведены матрицы Г^ (Р)
подгруппы группы яб, изоморфной точечной группе D6. Пустые ме-
места в матрицах означают нули.
Таблица 1
1
~1
КЗ
2
Кз
2
1
2 .
1
2
Уг
2
Уз '
2
1
2 .
_ 1
~2
Кз
2
Уз'
2
1
2.
1
2
Уз
. 2
Уз
2
1
2

356
ЙРИЛОЖЕНЙЁ
/XH2'J
Таблица 2
1
3
г
4
i
2
3
4
[' -J Г,] Г.] Г ,
Та б лица 3
Pl2
-1
1

Уз
2
/>23
Уз
2
J_
2
2VT
2/2

МАТРИЦЫ ПРЕДСТАВЛЕНИЙ я3-*-лг
357
1
2
Уз
2
I
1
2
loo
2
1
2
Уз
б
Ito
1
_ 3
— 1
T
Уз
б
Уб
.- 3
Pis
loo
2
1
2
>1B2
loo
2
1
2
Pl43
Уз
2
1
6
V2
3
Pl243
too
2
1
6
У2
3
24 и.
—
P24
1 Уз
2 6
УЗ 5
6 6
Уб У2
3 3
P234
Уб "
3
У2
3
1 Уз Уб "
2 6 3
Уз 1 У2
2 6 3
2У2
3 "
Pl24
2У
3
1
3
"" 1 Уз
2 6
г Уз 5
б 6
Уб У2
3 3
Pl324
2У2
3
1
3
Уз
"Г
УЗ 2
з "з"
Уб У2
3 3
Pl423
Уз
3
У? 2
3 3
Уб VI
_~~3~ 3~
vi
со
УЗ 2
X" "з
Уб VI
_ я з
Г. Каплан
-
1
2
Уз
б
Уб
Уб"
3
У2
3
1
3 _
Уб "
3
У2
3
1
3 .
Уб""
3
V~2
3
1
3 _
Уб"""
3
УТ
1
з _
3
¦
-
-
1
2
Уз
6
Уб
3
р
Ри
Уз
6
5
~6
V2
3
243
loo
2
Уб -
3
У2
3
1
3 _
~-
1 2У2
"б"
V2
Уз
3
Уб
3
1
2
Ico
2
— 1
VI
3
Уб
3
3
рН2
Уз
б
5
6
V2
3
Pl342
Уз
6
1
б
2У2
3
Р12-Р34
!
3
2 У1
3
Уз
3
2
3
УТ
3
1
3 _
1
2
Уз
2
Уб"
3
У2
3
1
со|
"¦ 1
с
Уз
Уб"
3
У2
3
1
3 _
¦
г
1
2
__Уз
6
Уб
2У7
3
3
|to
3
V?
3
1
' ~Т~ ~"з .
3
Pl23
1
2
Уз
2
Р.34
Уз
6
1
6
2У2
3
Pi 234
• со
6
1
6
2У2
3
Pl432
Уз
2
1
6
toi
3
Уз "
2
1
2
1
\ б"
3
У2
3
1
3 .
Уб -
3
У2
3
1
з _
2V2
3
1
jco

358
ПРИЛОЖЕНИЕ 5
Таблица 4
рA)
Лг
3\4
5]
гB)
1\2
3\5
А
гC)
1\3
А
рD)
1
2
4
3
5
гE)
/\4
2\5
-1
-1
1
2
/з~
2
1
2
2
^23
/з
2
1
2
•
/з
2
1
2
-1
-1
1
3
2}/!
3
2/2
3
Г 1
3
1
2
V*
2
уз
2
1
2
1
2
/з"
2
/3
2
1
2
-1

МАТРИЦЫ ПРЕДСТАВЛЕНИЙ яг
359
Таблица 5
рB)
-1
-UL
1 У
2 2
2 2
-1
-U
¦-1
2J/2"
3
3
-1
2
4
УТъ
. 4
VTb
1
1

360
ПРИЛОЖЕНИЕ 5
Таблица б
/
3
5
2
4
6
Г B)
1
3
4
2
5
6
гC)
1
2
5
3
4
6
Г D)
1
Z
4
3
5
6
Г<5)
1
2
3
4
5
6
-1
-1
/з
/3 J_
2 2
2 2
__ i
-1
1
LO|
2/2
3
2/2
3
1
3 _
2
CO|
2
2
1
2
1
2
/3"
/3
2
1
2 2
-1
'56
__ 1

МАТРИЦЫ ПРЕДСТАВЛЕНИЙ я3ч-я6 361
Таблица 7
/
3
4
6,
1
2
5
3
4
г
i
4
I
61
3
6
г
3
I
1
rl9>
1
z
3
4
5
В
-1
-1
-1
-1
1
~2
VJ
2
1
2
г
VT
2
1
2
VI
2
VT
2
1
1
VT
2
1
2
VI
2
J_
2
34
2^2"
3
2VT
3
J
3
2^2"
3
3
1
3
3
1
3
-1
-u.

ПРИЛОЖЕНИЕ 3
I

2
± HI
2 2
2 2
-1
-1
-1 JCDL
~4 4
vw 1
4 4
2K2
3
1
3
2^2"
3
" 2^2
3
1
3
-1.

МАТРИЦЫ ПРЕДСТАВЛЕНИЙ
Г (О
г B)
у-D)
363
Таблица 8
г E)
-1
-1
тшт 1
45
-1
-1
1
4
У15
-L
-1
-1
5
5 ^

564
ПРИЛОЖЕНИЕ 5
Таблица 9
Матрицы представления Г^ для подгруппы группы я6, изо-
изоморфной точечной группе De
= ?> ^14 ^25 •/36 = ^2
1
1
4
Ico
4
4
3
4
VS
4
3
4
1
4
Уз
4
^3
4
1
4
3
4
Кз
4
3
4
/з
4
Кз"
4
1
4
135*
з
_2
3
/2
_ 3
Vs
3 _
^654321 —
4 4
"Т" "Т
Уз 1
12
12
1
12
3
VL
3

МАТРИЦЫ ПРЕДСТАВЛЕНИЙ яа
365
1
4
КЗ
4
Кз"
4
3
4
VW
4
1
4
3
4
Кз
4
' 123456 — ^6
4
1
4
1
4
п
12
Кб
3 _
4
Кз"
12
Кз"
4
1
12
Кз"
3
Кб
3
Кз
3
2
3
К2
3
3
К2
3
1
3
VT
"з _
¦ =г/B)
уз в
о
К2
3 J
4
4
4
4
Т
Кз"
4
?
4
Т
Кз"
4
Кз;

ПРИЛОЖЕНИЕ 5
1
4
Ico
4
Кз
4
3
4
Кз
4
3
4
1
4
Ico
4
4
1
4
1
4
Кз"
12
Кб"
3
4
Кз"
4
Ico
12
1
12
4
4
Я.
3
?1
Кз"
4
1
4
1
4
V*
12
со
Кз"
4
1
4
3
4
кг
4
3
4
КзГ
12
Кз"
4
1
12
К2"
3
Кб"
3
К2"
3
1
3

Приложение 6
ТАБЛИЦЫ МАТРИЦ (r'k" \ P*[flN \ г )
' ДЛЯ ЛГ =
Приводимые ниже матрицы используются при вычислении
матричных элементов гамильтониана многоэлектронной системы (см.
раздел 8-5). Строки матриц определены на наборах базисных функ-
функций, имеющих определенную симметрию относительно перестановок
ДО—1-го и ДО-го электронов. Такие матрицы связаны с матрицами
стандартного представления следующей формулой:
(га-1 рГ " I rf] - 2 {г'к" | f f. (г | p»;lN I rf]. (u.i)
Входящая в формулу (П. 1) трансформационная матрица перехода
от стандартного представления к представлению, редуцированному
на подгруппе я^_2 ХЯ2> находилась по методу, изложенному в
разделе 2-11 (см. B.65)). Необходимые матрицы стандартного пред-
представления вычислялись с помощью матриц транспозиций Приложе-
Приложения 5.
PablN означает перестановку, переводящую электрон ДО—1
на орбиталь фа, а электрон ДО на орбиталь фь~. При этом предпола-
предполагается, что в результате действия перестановки сохраняется возра-
возрастающий порядок номеров электронов на орбиталях конфигурации
Каь, получаемой из конфигурации К при отщеплении орбиталей фа
и фь. Выражения таких перестановок в общем виде даются форму-
формулами G.82). Для случая однократного заполнения орбиталей требо-
требование сохранения возрастающего порядка номеров электронов вну-
внутри конфигурации Каь не является обязательным, возможен и иной
выбор перестановок PablN.
Строки матриц нумеруются таблицами Юнга г' ДО — 2 первых
электронов и схемами Юнга [У] ДО— 1-го и ДО-го электронов. Столб-
Столбцы нумеруются полными таблицами Юнга г. Все таблицы Юнга
расположены в порядке отклонения чисел в них от натурального
ряда. Для каждой таблицы приведены только нумерующие строки
схемы Юнга [к."]. Пустые места в матрицах означают нули.

368
ПРИЛОЖЕНИЕ 6
Таблица 1
[Я]-[21], 5=1/2
К"
12]
[I2]
а) [Я] = [22],
р23
М2
р23
МЗ
р23
*23
Уз
2
/Г
2
Таблица 2
б) [Я]-
УГ
з
1
2
VT
2
2
!
7 _
1
2
VT
2
vT
2
1
2
р34
^24
2
[2]
W
УГ УТ
з _
р34
МЗ
УГ
б
УГ
2
УТ _УТ
— 2 6
3
Уз
з _
2
VT
2
3
6
/г
2
р34
^24
2
~Т"" з
Кб" УТ
6 3
1 УТ
'1 2
2 6 3
/2" /б" УТ
 6 3 _,
УГ УГ
з з
з ^

МАТРИЦЫ <Л" | рЛМЛГ |Г> [К]
369
Таблица 3
^ —5
а) [Л] = [221], 5=1/2
г>45
"к"
[2]
12]
[I2]
1
1
2
1
2
VT
2
1
2
1
" 2
УГ
2
1
1
2
1
2
Ico
3
ico
Б
1
2
1
2
VT
3
Ico
6
КГ
3
3
p45
M4
YT
2
Ico
6
Ico
6
p45
VT
2
Уз
h
Уе
G
Ico
ooj
2
3
/2"
3
VT
2
УГ
6
~T
to,
6
VT
6
Ico
2
1
3
to,
6
00 |
VT
T~
1
3" .
-
VT
3
to,
3 -
1
3 _
-
VT
3
vr
3
!
1" -
1
2
"
VT
T "
¦- !
4
УГ
4
3
4
-
1
2
1
2
to,
2
1
2
1
2
Ico
ooj
IcO
T
УГ
4
1
4
1
4
УГ
12
VT
"T
I
~2
1
2
УГ
3
ico
6
ico
2
Ico
6
Ico
6
p45
VT
4
3
4
J_
4
Ico
4
YT
2
УГ
6
Ico
6
VT
~T
VT
2
"з"
to.
6
3
4
VT
4
VT
12
1
12
VI
3
VT
2
VT
l
3
VT
6
VT
3
to.
3
l
"з
Уе
3
У2
3
1
3
Ico
ooj
VT
jco
1
3

370
ПРИЛОЖЕНИЕ 6
р45
I
4
Ico
4
VT
4
3
4
VT
4
1
7
!
Ico
12
VT
3
Ico
4
3
4
!
~T
VT
4
3
4
Ico
4
Ico
12
1
12
VT
loo
—
VT
3
VT
3
1
-l
/з"
3
/6"
3
VT
3
2
3
VT
§
/6~
3
VT
3
i
/3
2
1
2
1
2
~2~
VT
6
1
6
2/Г
3
/6"
3
/F
3
1
3 _
1
2
/3"
2
2
1
2
1
2
VT
—F"
/3
2
1
2
6) [A,] =
A."
rt 21
[1 J
[I2]
[2]
[12]
VT
3
l
3
~ :
VT
3
Pf2
VT
3
VT
6
/To
6
/30
e
Кб"
6 .
l
2
VT
6
1
2
K15
6
p45
^13
/3~"
6
1
6
VT
2
VT
6
/6~
3
VT
6
/10
6
/3
6
VT
6

МАТРИЦЫ (Л*I
371
D45
1
2
VT
6
1
2
VT5
6
V3
2
1
6
VT
6
VT
6
VT
6
3~~
VlO
6
V30
6
VT
6 _
1
2
VT
- 6
1
2
Vl5
6
V3
2
1
6
VF
6
V5~
2V2
3
XL
VTo
12
VlO
4
VT
4 ,
D45
23
24
1
2
СЛЭ,
6
1
2
KT5
V3
6
1
6
СЛЭ,
2
vr
6
VT
3
to,
6
VlO
6
V3
6
Ve
6
p45
*25
2
VT
6
1
2
V15
6 *
V3
2
1
6
vr
6
ел,
6
2V2"
1
CO
VT
12
VlO
12
Vf
4
Ve
4
2
6
1
2
VT5
6
1
-
vr
2
1
6
vr
6
VT
6
1
¦3
VT -
3
VT
3
VT
6
VT
3
VTo
6
p45
M4
VT
6
VT
3
Vlo
6
V30
6
VT
6
V30
6
VT
6 •
'
p45
•35
VT
3
VT
3
2/2
3
/6"
12
/To
""IF
VlO
4
VT
4
p45
KT V10
4 4
Vlo VT
4 4 ,

372
ПРИЛОЖЕНИЕ б
Таблица 4
а) [Я]-[2>], 5 = 0
р56
М2
[2]
[2]
[I2]
[I2]
p56
-
1
1
1
2
K2~
2
1
VT
3
Кб"
3
1

l
2
КГ
3
Кб"
6
vt
3
oojto
К2"
3
р56
М4
VT
-
-
VT
6
Кб"
6
-
VT
2
VT
6
1
3
кг
6
vT
3
VT
3
~3
-
1
2
1
2
кГ
2
~~3~
"Т
1
3
1
4
КГ
4
~Т~
3

1
2
1
2
~3~
Кб"
6
VT
4
1
4
1
4
VT
12
~Г~
VT
2
VT
6
_
р56
~4~
3
4
1
4
VT
4
VT
6
) Г
2
7
6
3
4
VT
4
кг
12
1
12
VT
3
) б
3
V2~
3
_ 1
3
Кб"
3
VT
3
- 1
3
p56
*24
1
~2
1
2
КГ
2
2
vt
3
vT
6
VT
2
КГ
6
Кб"
6
VT
6
кг
2
1
3
VT
6
Кб"
3
VT
3
1
3 -
1
~2
1
2
VT
- 2
1
2
1
2
КГ
3
VT
2
КГ
6
кг
2
кг
6
1
3
кг
6
Кб
3
Кг
3
1
3

МАТРИЦЫ (Л
L>>\
373
p56
^26
\
4
~4~
vr
4
3
4
vr
4
1
4
1
4
vr
12
"~з~
4
3
4
1
4
vr
4
3
4
vr
4
vr
12
1
12
VF
3
Ve
3
V2
3
T
4
vr
4
vr
4
3
4
vr
4
1
4
1
4
vr
12
Ve~
3
V3
4
3
4
1
4
VF
4
3
7
vr
4
VF
12
1
12
VF
3
Ve
3
>2
3
1
3
p56
vr
3
Ve"
3
VF
3
2
3
VF
3
Ve
3
VF
3
l

2
VF
2
VF
2
1
2
p56
^35
1
2
VF
2
vr
6
1
6
2VF
3
3
V2
3
1
3
1
2
Ico
2
VF
2
1
2
1
2
VF
2
6
J
~6
2VF
3
Ve"
3
VF
3
l
3 -
1
VF
2
VF
F~
l
2
__ 1
2
VF
2
V3
2
1


J74
1
2
VT
2
1
т
Кз
4
Кз
3
4
ПРИЛОЖЕНИЕ 1
р5б
Мб
Ico
2
1
2
1
2
Ico
2
VT
4
1
4
1
12
Кб"
Г"
VT
2
1
2
-1 .
р56
Мб
Ico
4
3
4
1
1
VT
4
1
1
—
3
4
Ico
4
VT
12
I
12
VT
p56
*¦
1
1 .
-
VT
3
VT
3
1
3 _
б) [Ц
m
12]
[I2)
[12]
[2]
[I2]
[2]
[121
[I2]
= [2212], s-
l
l
3
1
K2~
3
1
1
3
VT
3
1
3
K2~
3
2КГ
9
2КГ
9
VT
9
VTb
9
p56
M2
3
1
3
Кб"
9
VT
9
5КГ
18
Кзо
18
VT
3
2
3
VF
9
2VT
9
VT
18
Кзо
18
2
3
K2"
3
VT
9
vr
18
5КГ
18
VTb
18
VT
3
/To
6
vr
6
1
6"

матрицы (Л" I рлг-ш | r) W 375
1
2
кг
6
VT
6
6
6
VT
6
1
3
1
2
VJ
3
l
6
VT
6
VT
6
КГ
6
кг"
6
1
6
1
2
5K2~
•12
Kio
12
VT
2
1
6
VJ
6
1
6
OS Q,,
6
VJ
6
VT
9
VT
2
VT
9
кг
18
V15
18
K2
6
1
6
кг
18
Ico
18
VT
2
5 КГ
36
Кзо
36
VJ
3
2
3
VT
9
2 КГ
9
VT
18
Кзо
18
2
3
K2~
3
кг
9
VT
18
5 КГ
18
Kl5
18
Vb
3
VI
6
K5
6
1
6
1
2
VT
6
кг
6
VT
6
КГ5
6
КЗ
6
VT
6
1
3
1
2
Кг"
3
1
6
VT
6
VT
6
VT
6
кг"
6
1
6
1
2
5 K2~
12
12"
Ico
2
1
6
VJ
6
1
6
VT
6
1
2
_кг"
2
VT
9
кг
6
кг
9
VT
18
KI5
18
K2
2
1
2
кг
18
Ico
18
VT
6
5 КГ
36
Кзо
36
VT
9
VT
3
2 КГ
9
VT
18
Кзо
18
VT
9
кг
18
VT
3
5 КГ
18
К 15
18
кг
3
Kio
6
кг
6
1
*6~

376 ПРИЛОЖЕНИЕ
г>56
15
1
4
1
4
УТ
4
УТ
4
УТ
4
Ito
4
Кз
12
УТ
4
УТ
12
1
12
1
4
УТ
12
1
3
кг
3
Кб
6
УТ
6
УТ
6
1
6
1
2
5 КГ
12
Кш
12
УТ
4
УТ
4
VT
4
1
4
1
4
кг
4
1
4
3
4
УТ
4
УТ
36
КГ
12
кг
36
УТ
9
KI5
9
УТ
2
1
2
УТ
18
УТ
18
УТ
6 ..
5 КГ
36
Кзо
36
УТ
9
УТ
3
2 КГ
9
УТ
18
Кзо
18
4 КГ
9
2 КГ
9
Ito
12
5 КГ
36
УТъ
3fi
Кш
4
УТ
4
1
4
1
I
1
4
УТ
4
УТ
4
\Т
4
УТ
4
Кз
4
УТ
12
кг
12
1
4
1
1*
УТ
12
УТ
3
2
3
ItO
6
УТ
6
кг
6
1
6
1
6
УТ
12
УТо
4
4
YT
4
Ito
4
!
~т
1
4
УТ
4
3
4
!
~4~
КГ
4
КГ
12
УТ
36
КГ
36
_КГ
9
2 КГ
9
УТ
2
х
Ico
18
КГ
18
УТ
18
УТ
36
Кзо
12
Ito
3
VT
9
2 КГ
9
УТ
9
УТ
9
4КЗ
9
2 КГ
9
УТ
36
КГ
33
КТб
12
У\0
4
КГ
4
!

МАТРИЦЫ (rV | pN-W | r) [X]
ab
1
2
VT
6
6
VT
6
VTb
6
VT
6
КГ
6
1
УТ
3
1
6
КГ
6
VT
6
КГ
6
VT
6
1
6
1
2
5КГ
12
KlO
12
VT
2
1
~6
6
1
6
VT
6
1
6
VT
6
VT
9
VT
2
vt
9
VT
18
KT5
18
K2
6
1
6
VT
18
VT
18
vt
2
5КГ
36
Кзо
36
УТ
3
oo|to
9
2 КГ
9
VT
18
Кзо
18
со, to
УТ
3
УТ
9
кг
18
5VT
18
КТ5
18
КГ
3
KlO
6
кг
6
1
6
1

Ico
6
VT
6
VT
s
Kl5
6
25 И.
VT
6
VT
6
1
3
1
2
to,
3
1
6
6
Г. Каплан
CO
6
VT
6
VT
6
1
6
1
2
5КГ
12
KlO
12
VT
2
1
6
VT
6
1
6
КГ
6
1
2
VT
2
Ico
9
VT
6
кг
9
VT
18
Kl5
18
K2
2
-1
кг
18
КГ
18
vt
6
5КГ
36
Кзо
36
-
VT
9
КГ
3
2КГ
9
КГ
18
V30
18
Ico
9
VT
18
VT
3
5 VT
18
KT5
18
КГ
3
KTo
6
КГ
6
1
6

ПРИЛОЖЕНИЕ в
1
4
1
4
to,
4
vt
4
со,
4
VT
4
CO,
12
CO,
4
VT
12
1
12
1
4
to,
12
1
3
vr
3
VT
6
CO,
6
VT
6
1
6
1
2
5 VT
12
KTo
12
VT
4
Ico
4
Ito
4
1
4
1
4
VT
4
1
4
3
4
VT
4
VT
36
CO,
12
VT
36
9
K15
9
VT
2
1
2
VT
18
CO,
18
CO,
6
5 VT
36
Кзо
36
vr
9
3
2 VT
9
VT
18
Кзо
18
'?
9
2КГ
9
Ito
12
5КГ
36
KTB
36
KlO
4
VT
4
1
4
p
26
1
4
J_
4
vt
4
vT
4
Ico
4
Ito
4
КЗ
4
VT
12
vt
12
1
4
1
12
VT
12
to.
3
001 tO
VT
6
CO,
6
VT
6
1
6
1
6
VT
12
KTo
4
Кз
4
VT
4
VT
4
1
4
1
4
to,
4
3
~ 4
1_
4
VT
4
Ico
12
VT
36
vt
36
VT
9
2КГ
9
K2"
2
1
2
Кб"
18
VT
18
Ico
18
vt
36
Кзо
12
VT
3
VT
9
2КГ
9
VT
9
vT
9
4K3
9
2 КГ
9
VT
36
VT
36
KT5
12
KTo
4
4~
1
4

матрицы (Л" | pw-ш | r) [X] 379
d56
УТ
3
УГ
3
УГ
3
/Г
3
1
3
/Г
3
1
3
/5"
3
2/3
9
/Г
3
2/б"
9
/Г
9
/15
9
УГ
9
/Г
9
/Г
3
5/б"
18
/30
18
УГ
9
УГ
3
2VT
9
/6"
18
/30
18
/3"
9
УГ
18
УГ
3
5 /3*
18
УТъ
18
Уъ
3
/То
6
/5"
6
1
6
35
1
2
1
т
/2*
2
/Г
6
/г
2
/6"
6
/6"
3
/Г
3
1
2
1
2
/Г
2
/Г
18
/Г
6
/б"
18
2/Г
9
2/15
9
/6"
9
/Г
9
/3"
Jeo
5/6
18
/30
18
/6"
9
/6"
3
2/Г
9
/6"
18
/30
18
4/Г
9
2/в"
9
/6"
12
5/3"
36
/Т5
36
/I
4
/5
4
1
4

380 приложение б
1
2
1
2
УТ
2
VT
2
УГ
" 6
УГ
6
УГ
3
УГ
-1
1
т
1
2
2
6
18
УГ
18
2КГ
9
4 КГ
9
vr
9
vr
9
УГ
9
кг
18
Кзо
6
УГ
3
vr
9
2 КГ
9
кг
9
УГ
9
4КЗ
9
2 КГ
9
УГ
36
кг
36
KI5
12
KlO
4
КГ
4
1
4
Г45
1
2
1
2
КГ
2
КГ
- 6
со,
2
КГ
6
кг
3
со,
3
1
2
1
~ 2
КГ
2
со.
6
УГ
2
КГ
6
vr
3
3
УГ
6
Кзо
6
_КГ
4
5 КГ
12
К15
12
KlO
4
КГ
4
1
4

МАТРИЦЫ<Л"|Р^лг1г)[М
381
в)
[I2]
w
№
[2]
JL
" 2
-i
2
/Г
УТ
2
/Г
6
УТ
6
/6"
3
/3"
/3"
3
/6"
3
VT
12
/3"
12
/15
4
4
4 .
УТ УТ
з з
/б" /з"
" Г
3
з
3
Уз УТ
з з
/6" VT
-3 з
1 _
УТ
3
i
'3
/2"
6
КГ
2
214],
F
/б"
3
/2"
6
1
6
1
S-2
56
/30
6
У\ъ
30
/15
1o~
з/ю
10
/To
10 .
1
2
/з"
б"
УТ
12
1
2"
VT
4
/3
"б"
1
6
/2"
12
со,
2
V2
~
рЪо
^13
/б"
3
УТ
6
1
6
1
2
/30
6
/15
30
/15
"""То"
3/1С
10
КТо
10

382
ПРИЛОЖЕНИЕ б
121
121,
l«5|_ |O| V
CO
«I -12
I I
12
vh
I I
I- -,- Isl- -i
| ,
121
§1- S|:
12
-Jo*
I
I
I I I

МАТРИЦЫ (r'l" I Р%-Щ г) 14
383
l»l'
SI- Si
gh 21
i
?1- -I
I
Sh S
IS I
Us
«I
I3U 121
i i i
I I
1СЧ
coco ^
Iй U I21
-12 '^j- -I
SI- Sh
SI» SN

П р и лож ение 7
ТАБЛИЦЫ МАТРИЦ
ДЛЯ #
Л л]
Ниже приведены матрицы, необходимые для расчета энергии
взаимодействия двух подсистем по формулам раздела 8-6. Эти
матрицы вычислялись с помощью трансформационных матриц пере-
перехода от стандартного представления к нестандартным представле-
представлениям, индуцируемым наборами базисных функций в левой и правой
частях матричного элемента. Согласно общей формуле B.59)
ч-ш |
lXI
Я'%" | r>lXI <
| rf> <г | rf
f2
(П. 2)
Трансформационные матрицы вычислялись по методу, изложенному
в разделе 2-11, там же приведены примеры нахождения таких
матриц (см. B.64)). Перестановки P^XN переводят электрон N—1
на орбиталь фа первой подсистемы, а электрон N — на орбиталь фс
второй подсистемы, при условии сохранения возрастающего порядка
номеров первых N — 2 электронов.
Таблицы Юнга, нумерующие строки и столбцы матриц, везде
расположены в порядке отклонения чисел в них от натурального
ряда (см. Приложение 5). Пустые места в матрицах означают нули.
Таблица 1
[2]
[I2]
[Я]
р
JV = 3;
= [21]
[2]
1
2
VI
2
Nl
[I2
УГ
2
1
2
/р23\ _
V 23/ ~
УГ
2
VI
2
*2 „

МАТРИЦЫ {(г'/2) W | P^-
Таблица 2
a)
[22]
o:
r»:
[2]
[2]
[1
[1
2]
2]
Я"
[2] J. Л
1 J I 2 2 '
2 2
 Г
VT 1
1
2
2
2
2
2
1
2
2
~2
6) [M - [21«J
r,: [2] [1«J
r2: [I2! [2]
[I2
[I2]
2

V2
2
[I2]
[I2]
V2
2
V2
2
2
2
— ICM
VT
2
1
2
-1cm
VT
2
1
2
1
2
2
1
2
1
2
2
VT
2
/2"
2
/2
2
2

386
со
Я
S
ПРИЛОЖЕНИЕ 7
1 I"
fch -.-
feh -i
l l
I I I
<N CN CN '
-i- 'd<
^ ^
(I
i i
-,

f 45\
V 34/ =
6) m-
/3"
2
-
[213]
МАТРИЦЫ <
VT
2
1
2
1
/T
6
/б"
"з"
/Г
6
5
б"
/2~
3
-
VT
Г"
/2"
3
l
/к»
-¦" 1
/ 45\
V 35/=
2
VT
2
3 _ _
2)w
/Г
2
1
7
l
2
/T
6
VT
3
/Г
6
5
6
VT
3
3
/6
3
/2
col
1
3
[21]! [21]2 [I3] [I3]
[I2] [I2] [2] [I2]
[l2l
s
12]
H2]

VT
6
1
"T
/15
6
/3
6
/Г /5"
з з
/15
6
 6 6
VT
2
6 6
I _VT
 6
/15 VT
6 6
VT
з
^_
2
/IS
6
vr
3
/ТВ
6 «
» =
1
з
/T
3
/5"
3
VT
з
/ТВ
6
6 «
-1
1
1
VT
6
1
2
/15
6
1
2
/Г
6
1

/ТВ
6
-|co
VT
3
6~"
VT
2
i VT
6 3 ^
VT i
6 2
/Г /IB
6 6
_vT
l /Г
6 3
/Г i
6 2
/5~ /15
6 6
VT
3
1
2
/IB
6
/5"
3
/IB
6
1
"б" ^
•
VT
3
/ТВ
6
1
6 _
VT
3
/IB
6
i
6 _

888
к
Приложение ?
1 r
..
h fch -
i«
i
i i
fch -h -i
-2 ^
Ico
I
leo
~k ^
I I I
*M со
II
-1*
i
i i i
CO
jl
?i
II
M
?L
5Г
?i
M
[21
<N
?i
M
M
r—i
?i
<N
?1
1
со
Ico
leo
|
с
1
\« |co
1
?2
1 1
^*
CO
•* —
1 j
1
Ico
1* ^
1
i
CO
-
leo
?2
Ico
?2
CO
i
•ч CO
со
1
Ico
CO
1
IT"
ч
1
CO
Ico
u
leo
eo
Ico
Ico
CO
I* -
^ l«
leo
CO
CO
CO
?2 l«
CO
]

МАТРИЦЫ
389
,|cs 2r
i
ii
юсо
I I
I I
-I*
-I- 4
I
II
I I
-J

390
ПРИЛОЖЕНИЕ 7
fc
I
-Iе
!^|co i«|s
I
I r
i i i
I I
I.
- a Я~ -h
CO
CO
CO
I(N
is
со
^ _
1
IcO
I I I
wr -•
СЧ (CO
I
sr s-, tr
-I"
i h
i i
со
I I
e

МАТРИЦЫ
391
I I
-Jo,
i i
feh
l«*

392
в)[Л] = [2212]
n:
r2:
Г121
I* J
[2]
Г121
I» J
Г121
U J
)= [2]
Г» 21
11 J
Г01
Г121
I* J
[I2]
-
1
1
1
1
[22]
[I2]
— l
4
1
4
/2
4
VT
4
/3
4
_/6
4
-
1
i"
l
4
/r
4
CO,
4
VT
4
Кб"
4
i [214,
[2]
1
4
1
4
; _vf
4
12
¦ VT
12
" /6"
12
_V?
6
vr
6
/15
6
1
4
I
T ~~
VT
4
12
Ico
12
(.
12
vr
6
vr
6
/ТВ
6
ПРИЛОЖЕНИЕ 7
[212]
[I2]
to,
4
to)
4
/6"
12
vr
12
Ico
6
Ve"
4
V§o
12
VF
4
vr
4
ve-
it ¦
Ve"
12
vr
6
vr
4
V30
12
i [22]2
[I2]
CO,
4
vr
4
V6~
4
1
4
!
4
Ico
4
vr
4
Ve"
4
1

I
T
V2"
4
[212]
[2]
4
4
Ico
4
!
IF
l
12
1
to,
12
to,
6
1
6
VT
6
Ico
4
VT
4
Ve"
4
I
IT
1
12
VT
' 12
to,
6
1
"б
VT
6
2 [212b
[i2]
4
4
VT
12
to,
IF
1
"б
to.
4
VTo
12
Ico
4
-YL
4
/F
" 12
VT
12
__ 1
to,
4
/To
" 12
[212]3
[2]
VT
H
to,
3
2
3
1
6
VT
12
/Го
12
/F
3
VT
3
2
co|
1
6
to)
1
12
/To
12
[212]
[I2]
2
3
2
3
VF
12
1
4
vr
12
2
(со
2
3
to,
12
1
4
vr
12
з[14]
[I2]
VTo
4
vr
4
_1_
4
_/To
4
vr
4
J^
4

МАТРИЦЫ (fc\rQ АЛ" | Р%~Ш | rx r2y^l 393
1
4
I
7
/2~
4
CO,
4
CO,
4
Ico
4
4
1
4
to,
4
VT
12
CO,
12
VT
12
Ico
1
6
VT
6
/ТВ
6
/2
~7~
VT
4
_/б"
12
Ico
12
VT
6
Ico
4
/30
12
/3
4
/T
4
/б"
~7~
i
~7
l
4
to,
4
_/?
4
VT
Ico
4
1
12
1
IT
VT
12
VT
6~
1
6
VT
6
4
/6~
7"
/F
12
to,
12
I
~~~6
to,
4
/To
12
to,
3
to,
3
2
3
!
T
to,
12
/To
12
2
3
2
"з
/2"
12
1
4
/5"
12
/10
4
/Г
4
1
4
1
7
I
7
to,
4
4
Ico
4
Ico
4
1
4
1
4
VT
4
CO,
12
Ico
12
Ico
12
Ico
6
Ico
6
/15
6
/2
4~
/T
4
Ico
12
VT
12
Ico
6
-YL
4
/30
12
VT
4
vT
4
Ico
4
1
7
l
4
to,
4
/3
4
Ico
4
Ico
4
1
12
1
12
VT
12
to,
6
1
6
VT
6
/6
4
Ico
4
VT
IT
VT
12
1
6
VT
4
/To
12
to,
3
VT
3
2
3
1
6
to,
12
/10
12
2
3
2
to,
12
1
\
VT
12
VI
4
/5
4
1
4

394
ПРИЛОЖЕНИЕ 7
2
1
VT
2
1
2
VT
2
VT
2
VT
2
1
2
2
1
6
1
6
VT
6
3~
l
3
кг
3
VT
6
(Г
1
3
VT
2
Kio
6
3
_VT
3
2
3
1
6
VT
12
Klo
12
1

T
VT
"IT
1
4
""IT
Klo
"T
"T
1
4
1
2
1
2
vT
2
1
2
1
2
VT
2
КГ
2
K2"
2
1
2
1
~2
VT
~~T
1
~6
1
6
КГ
6
VT
3
1
3
КГ
"T"
VT
6
VT
6
1
3
K2"
2
КГо
a
VT
3
K2"
3
~3
1
6
VT
12
Klo
IT
2
3
2
"T
VT
12
1
~ 4
СЛ,
"ТГ
Kio
4
КГ
4
1


1
2
1
2
ГТ
2
МАТРИЦЫ
1
2
1
2
/Г
2
/2"
2
VT
2
395
1
2
*2
VT
Т
1
2
1
2
/2~
2
/2
2
VT
2
1
2
/Г
4
/То
4
/т
4
3
4
/Г
4
/10
4
VT
4
1
4
1
т
1
2
/Г
2
1
2
_ 1
2
/2~
2
/2
2
/2"
2
2
1
2
2~
1
7
1
2
/Г
2
/2
2
2
2
/То
4
VT
4
3
4
VT
4
/10
4
VT
4
1
4
26*

396
ПРИЛОЖЕНИЕ 7
то
И
К
03
со
II
а?
со
Jeo \r# ко
I I
i "Г ~V "i
I I
|
I I
IcO <N I I ItO U
Vf t«k Vr
I ' I
I I
II
?! til I I I
I I I
I
-|<N
i I i I i I i I i I
^ rJ^ J00 r** v I"* J5° w [who Iе0 «
^_ ^_ >| w|^ rtu rtu >| V| V| >-|
coo

матрицы
397
I
Мо\ \ъ
q« fe|-
fch
«Г
-i* -Г
i i
fch

398
ПРИЛОЖЕНИЕ 7
1
I I
I I
.,. i:h -»Li
. ?
-I<N V
| |
I |
i
i^ I-
i
Li- -
i i
V
<N
CO '—'
<N
i—i CO
1—I у—• CO
т....
1
1
s: •
s
fef-
i
fch
CD
<N
CO
1
|
i
s:
7
i
i i
leo
l«
-fch
.t|.
1
1
1

МАТРИЦЫ ((r[r% X V |
-I
J<© CO («CO
I I
I I
399
I
fch И- fc|- fch
i i
-и feh
i<oU i«L i<n|
i i
I
fch
Is
1-Й
fch
hejco f«o|co M|<n
m

400
ПРИЛОЖЕНИЕ 7
в) [Я] = [2*12]
г,: [21], [21], [21], [21], [21], [21], [I3] [13] [I3]
г»: [21], [21], [I3] [21], [21], [I3] [21], [21], [I3]
[I2]
[2]
[I
[I
[2]
[I2
1
J
1
J
1
J
]
¦1
]
1
4
1
~
VT
4
/т
12
1
4
/F
4
/F
4
/Гб
(
1
._
1
4
/F
со,
12
1
~
VT
4
to,
4
/15
~~6~
/3"
4
/з"
""IF
/Т
12
1
12
Ico
4
Ico
4
/т
12
/т
/3
4
/Т
12
Ico
12
!
тт
/т
4
/т
4
/т
12
/т
6
/т
6
/т
6
/F
з"
/т
6
/Г
4
/10
12
/б"
~~6~
со,
6
/F
~Г
/Т
6
/б"
~т
/То
12
/з
Т
/Т
4~~
Ico
4
!
IF
/Т
12
/т
12
Ico
12
/Г.
6
/т
4
/3"
4
Ico
4
1
"TF
со,
12
/6"
12
/б"
12
/т
6
3
4
!
~Т
/F
4
со,
36
1
4
/F
4
/F
12
/15
3
4
1
4
/F
4
/Т
36
1
4
/F
4
/F
12
/Г5
" 18
/F
2
!
Т"
/т
<г
1
т
/F
4
/30
36
/F
2
1
F
/Т
9
"~Т
/F
4
/зо
36
/F
3
/Т
со,
6
/т
6
/т
4
/ш
12
/F
3
/Т
6
/т
6
/т
6
/т
4
/То
12
/Т
9~~
/F
2
!
т
т
_/F
4
/зЗ
36
/Т
9
2
1
2
!
"б"
/F
4
/зо
3,6
/30
9
/Т
3
Ico
9
/30
9
/Т
"Г
VT
9-

МАТРИЦЫ ((r'f'A Я/Я/' I pN-W I r Г\Щ 401
2 2
-IX _ЮГ L У*
6 6 2 2
_VT VT _VT _^_
6 6 2 2
L ?i ?GE _?? 2V? Кзо
6 3 18 9 9 ~
2 6 3
ЮЕ _ЮГ _ЮЕ
2 6 3
_КГ КГ КГ i_ j_ _V?
6 6 6 6 3 3
КГ VT KT
4 4 2
^l Ю5 -10! -H? Ii? _I±
3 12 9 36 18 9 .
1
4
!
"T
КГ
со,
12
1
4
КГ
4
КГ
4
KT5
6
кг
4
VT
12
Кб"
IF
l
12
со,
4
кг
4
кг
12
КГ
6
Кё"
6
VT
to,
3
VT
6
vw
4
KTo
12
VT
4
КГ
4
vr
~
1
12
со,
12
VT
ПГ
VT
12
VT
6
3
4
1
4
KF
4
КГ
36
i
to,
4
K2"
12
КГ5
18
KF
2
1
2
Vr
9
1
6
VT
4
Кзо
36
VT
3
кг
6
Кз"
6
Ico
6
VT
4
КГо
12
VT
9
Кг"
T
l
2
1
6
K2~
4
Кзо
36
КГо
9
~T
Кб
9

402
1
4
1
4
VT
4
vr
12
T
VT
4
VT
4
/15-
/Г
4
/Г
12
IF
1
"" 12
VT
4
/Г
4
"IF
/5"
ПРИЛОЖЕНИЕ 7
vr
6
/Г
6
/F
3
_yr
~~ 6
/Г
4
/lo
/Г
4
/r
4
~T"
12"
/Г
12
VT
12
vr
~ 12
VT
" 4
!
4
/F
4
36"
1
4
VT
4
/F
12
/IB
VT
2
1
2
VT
9
1
6
/F
4
/30
VT
3
б"
/T
6
vr
6
VT
4
12
9
VT
2
1
2
1
6
/F
4
/30
/30
9
VT
3
vr
18
36
12
36
9 _
1
2
1
2
;T
/Г
6
VT
"¦ 6
1
6
/6"
6
/Г
3
6
vr
6
VT
3
VT
3
4"
/To
12
/F
2
/Г
6
2
VT
2
/F
18
/F
6
/15
9
/F
2
1
T
/Г
9
1
6
VT
4
/30
36
vr
3
/Г
3
2/Г
9
I
3
VT
2
/30
"" 18
/a
9
~3~
VT
9 .

МАТРИЦЫ {(r\r? IV | Р^ГlN I r, г,) M 403
1
2
1
2
VT
2
/Г
2
VT
6
/б~
6
/6-
3
vr
3
l
6
vr
6
IT
6
IT
6
vr
18
1
2
VT
2
/Г
6
2 IT
9
1
3
VT
2
VT
3
IT
6
IT
6
IT
6
IT
4
vr
9
2
1
2
_ 1
6
IT
4
/30
9
vr
3
V? _V]E /зо /То _/зо
3 9 18 12 36
VT
2
/Г /б~
VT
2
VT
6
IT
3
1
6
/зГ
6
/б"
6
/б-
6
/г
18
1
2
/Г
2
VT
2lT
9
1
3
VT
2
/г
3
IT
6
/г
6
iT
6
4
/6"
9
VT
2
I
2
i
6
vT
4
/30
9
vr
3
/5" /15 /30 V\o /зо IT
3 9 18 12 36 9 ,

404
-1
VT
3
VT
3
VT
3
VT
3
ПРИЛОЖЕНИЕ 7
VT
3
vr
3
VT
9
VT
3
2/15
9
2/Г
9
1
T
/Г
2
/зо
18
/б"
3
VT
3
2/6"
9
1
3
VT
2
/30
18
/30
9
"~3~
/Г
9

ЛИТЕРАТУРА
1. Р. Бауэр, Введение в теорию групп, 1937.
2. В. И. Смирнов, Курс высшей математики, Гостехиздат, 1957§
т. III, ч. 1.
3. Ф. Д. М у р н а г а н, Теория представлений групп, ИЛ, 1950.
4. М. X а м е р м е ш, Теория групп и ее применение к физическим
проблемам, «Мир», 1966.
5. Л. Д. Ландау, Е. М. Л и ф ш и ц, Квантовая механика, Физ-
матгиз, 1963.
6. G. F. Koster, Phys. Rev. 109, 227 A958).
7. D. E. Rutherford, Substitutional Analysis, Edinburgh, 1947.
8. T. Yamanouchi, Proc. Phys.-Math. Soc. Japan 19, 436 A937).
9. J. P. Elliott, J. Hope, H. A. J a h n, Phil. Trans. Roy. Soc.
A246, 241 A953).
10. И. Г. Каплан, ЖЭТФ 41, 560 A961).
11. И. Г. Каплан, Канд. диссерт., ИХФ АН СССР, 1962.
12. Н. Horie, J. Phys. Soc. Japan 19, 1783 A964).
13. H. A. J ah n, Phys. Rev. 96, 989 A954).
14. E. Кондон, Г. Шорт л и, Теория атомных спектров, ИЛ, 1949.
15. Л. С. П о н т р я г и н, Непрерывные группы, Гостехиздат, 1954.
16. G. R а с a h, Group Theory and Spectroscopy, Princeton, 1951.
17. И. М. Гельфанд, Р. А. Минлос, З. Я. Шапиро, Пред-
Представления группы вращений и группы Лоренца, Физматгиз,
1958.
18. Е. Вигнер, Теория групп, ИЛ, 1961.
19. М. Е. Rose, Elementary Theory of Angular Momentum, N. Y.,
1957.
20. H. А. В ethe, Ann. Physik 3, 133 A929). '
21. A. Edmonds, Angular Momentum in Quantum Mechanics, Prin-
Princeton, 1957 (А. Эдмондс, В сб. «Деформация атомных ядер»,
ИЛ, 1958).
22. А. П. Ю ц и с, И. Б. Л е в и н с о н, В. В. В а н а г а с, Матема-
Математический аппарат теории момента количества движения, Виль-
Вильнюс, 1960; А. П. Юцис, А. А. Б а н д з а й т и с, Теория мо-
момента количества движения в квантовой механике, Вильнюс, 1965.
23 G. Racah, Phys. Rev. 62, 438 A942).
24. U. F a n о, G. R а с a h, Irreducible Tensorial Sets, N. Y., 1959.
25. B. R. J u d d, Operator Techniques in Atomic Spectroscopy, N. Y.,
1963.
26. И. И. С о б е л ь м а н, Введение в теорию атомных спектров,
Физматгиз, 1963.
27. М. R о t е п b e r g, R. В i v i n s, N. Metropolis, J. K. Woo-
ten, The 3j- and 6j-Symbols, L.; 1959,

406 ЛИТЕРАТУРА
28. Т. I s h i d z u, Tables of the . Racah Coefficients, Tokyo, 1960;
А. Ф. Никифоров, В. Б. Уваров, Ю. Л. Левитан, Та-
Таблицы коэффициентов Рака, Изд. ВЦ АН СССР, 1962.
29. Е. W i g n e г, On Matrices Which Reduce the Kxonecker Products
of Representations of Simply Reducible Groups, Princeton, 1951.
30. Г. Э й р и н г, Д. Уолтер, Д. К и м б а л л, Квантовая химия,
ИЛ, 1948.
31. К. С. Longuet-Higgins, Mol. Phys. 6, 445 A963).
32. Г. В е й л ь, Классические группы, ИЛ, 1947.
33. Г. Я. Любарский, Теория групп и ее применение в физике,
Физматгиз, 1958.
34. D. E. L i 111 е w о о d, The Theory of Group Characters and Mat-
Matrix Representations of Group, Oxford, 1950.
35. H. A. Jahn, Proc. Roy. Soc. A201, 516 A950).
36. С Eckart, Revs Mod. Phys. 2, 305 A930).
37. M. Born, J. R. Oppenheimer, Ann. Phys. 84, 457 A927).
38. Дж. Слэтер, Электронная структура молекул, «Мир», 1965.
39. Е. Wigner, Zs. f. Physik 43, 624 A927).
40. В. А. Фок, Изв. АН СССР (сер. физ.) 2, 169 A935);
V. A. Foek, Zs. f. Physik 98, 145 A935).
41. М. П. Петрашень, Е. Д. Трифонов, Применения теории
групп в квантовой механике, «Наука», 1967.
42. А. В. Соколов, В. П. Широковский, УФН 60, 617 A956).
43. П. Г о м б а ш, Проблема многих частиц в квантовой механике,
N ИЛ, 1953.
44. Д. X а р т р и, Расчеты атомных структур, ИЛ, 1960.
45. G. Racah, Phys. Rev. 75, 1352 A949)\
46. А. С. Давыдов, Квантовая механика, Физматгиз, 1963.
47. И. Г. К а план, ЖЭТФ 37, 1050 A959).
48. Е. В. Wilson, J. Chem. Phys. 3, 276 A935).
49. И. Н. Го дне в, ЖФХ 19, 637 A945).
50. Е. Д. Трифонов, ДАН СССР 129, 74 A959).
51. А. С. Компанеец, ЖЭТФ 10, 1175 A940).
52. Р. Е г е n f e s t, V. Т г k a 1, Proc. Sect. Sci. Amsterdam 23, 162
A921).
53. G. J. Mulder, Mol. Phys. 10, 479 A966).
54. И. Г. Каплан, ЖЭТФ 51, 169 A966).
55. Г. Г. Гельман, Квантовая химия, ОНТИ, 1937.
56. У. К о з м а н, Введение в квантовую химию, ИЛ, 1960.
57. И. Г. Каплан, Литовский физический сборник 3, 227 A963);
Теор. и эксп. химия 1, 608 A965).
58. F. A. Mat sen, Advances in Quantum Chemistry 1, 60 A964);
J. Phys. Chem. 68, 3282 A964).
59. И. Г. Каплан, Теор. и эксп. химия 1, 619 A965).
60. L. F. Mattheiss, Phys. Rev. 123, 1209 A961).
61. G. Racah, Phys. Rev. 63, 367 A943).
62. J. С Slater, Phys. Rev. 34, 1293 A929); Quantum Theory o!
Atomic Structure, N. Y., I960, vol. I.
63. M. Kotani, Proc. Phys.-Math. Soc. Japan 19, 460 A937).
64. A d e Shalit, I. Talmi, Nuclear Shell Theory, N. Y., 1963.
65. C. Schwartz, A. de Shalit, Phys. Rev. 94, 1257 A954).

ЛИТЕРАТУРА 407
66. P. J. Re dmond, Proc. Roy. Soc. A222, 84 A954).
67. S. Goudsmit, R. F. Bacher, Phys. Rev. 46, 948 A934).
68. H. A. Jahn, Proc. Roy. Soc. A205, 192 A951).
69. H. A. Jahn, H. van W i e r i n g e n, Proc. Roy. Soc. A209, 502
A951).
70. A. R. Edmonds, В. Н. Flowers, Proc. Roy. Soc. A214, 515
A952).
71. A. Hassitt, Proc. Roy. Soc. A229, 110 A955).
72. И. Г. Каплан, ЖЭТФ 41, 790 A961).
73. И. Г. Каплан, Таблицы трансформационных матриц группы
перестановок, входящих в координатные генеалогические коэф-
коэффициенты, 1962 (ротапринт).
74. Н. A. Jahn, Phys. Rev. 96, 989 A954).
75. И. Б. Л ев и неон, Труды АН Лит. ССР, сер. Б, 4, 17 A957).
76. R. Cure, J. К a s р е г, К. Р i t z е г, К. S a t b i a n a n d a n, J.
Chem. Phys. 44, 4636 A966).
77. Г. Г е р ц б е р г, Колебательные и вращательные спектры много-
многоатомных молекул, ИЛ, 1949.
78. W. Heitler, F. London, Zs. f. Physik 44, 455 A927).
79. Y. S u g i u r a, Zs. f. Physik 45, 484 A927).
80. S. Weinbaum, J. Chem. Phys. 1, 593 A933).
81. F. Hund, Zs. f. Physik 40, 742 A927); 42, 93 A927).
82. С. С. J. Root ha an, Revs Mod. Phys. 23, 69 A951); 32, 179
A960).
83. P. J. Parr, Quantum Theory of Molecular Electronic Structure,
N. Y., 1964.
84. С A. Coulson, Trans. Far. Soc. 33, 1479 A937).
85. G. Wannier, Phys. Rev. 52, 191 A937).
86. J. С Slater, J. Chem. Phys. 19, 220 A951).
87. И. Г. Каплан, Т^ор. и эксп. химия 3, 150 A967).
88. J. H. V a n V 1 e с k, Phys. Rev. 49, 232 A936).
89. P. O. Lowdin, J. Chem. Phys. 18, 365 A950).
90. J. S. Griffith, The Irreducible Tensor Method for Molecular
Symmetry Groups, L., 1962.
91. S. Frag a, R. Mul liken, Revs Mod. Phys. 32, 254 A960).
92. S. L. Altmann, Proc. Roy. Soc, 298, 184 A967).
93. M. Kotani, M. S i g a, Proc. Phys.-Math. Soc. Japan 19, 471
A937).
94. И. Г. Каплан, О. Б. Родимова, ЖЭТФ 55, 1881 A968).
95. В. Г. Неуда чин, Ю. Ф. Смирнов, ЖЭТФ 36, 186 A959).
96. А. Б. Болотин, И. Б. Л е в и н с о н, Труды АН Лит. ССР,
сер. Б, 3,21 A960),