Ряды - Власова Е.А.

Автор: Власова Е.А.
Теги: анализ математический анализ функциональный анализ математика ряды
ISBN: 5-7038-2884-8
Год: 2000
Похожие
Сборник задач по математическому анализу. Том 2. Интегралы. Ряды
Ряды
Высшая математика. Том 3. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного
Текст
                    МАТЕМАТИКА
В ТЕХНИЧЕСКОМ УНИВЕРСИТЕТЕ
Е.А. Власова
Издательство МГТУ имени Н.Э. Баумана

Математика в техническом
университете
Выпуск IX
Серил удостоена
Премии Правительства
Российской Федерации
в области науки и техники
за 2003 год

Комплекс учебников из 21 выпуска
Под редакцией B.C. Зарубина и А.П. Крищенко
I. Введение в анализ
П. Дифференциальное исчисление функций
одного переменного
III. Аналитическая геометрия
IV Линейная алгебра
V Дифференциальное исчисление функций
многих переменных
VI. Интегральное исчисление функций
одного переменного
VII. Кратные и криволинейные интегралы.
Элементы теории поля
VIII. Дифференциальные уравнения
IX. Ряды
X. Теория функций комплексного переменного
XI. Интегральные преобразования
и операционное исчисление
XII. Дифференциальные уравнения
математической физики
XIII. Приближенные методы математической физики
XIV Методы оптимизации
XV Вариационное исчисление и оптимальное управление
XVI. Теория вероятностей
XVII. Математическая статистика
XVIII. Случайные процессы
XIX. Дискретная математика
XX. Исследование операций
XXI. Математическое моделирование в технике

Е.А. Власова
РЯДЫ
Под редакцией
д-ра техн. наук, профессора B.C. Зарубина
и д-ра физ.-мат. наук, профессора А.П. Крищенко
Издание третье, исправленное
Рекомендовано Министерством образования
Российской Федерации
в качестве учебника для студентов
высших технических учебных заведений
Москва
Издательство МГТУ имени Н.Э. Баумана
2006

УДК 517.5.52(075.8)
ББК 22.16
В58
Рецензенты: чл.-корр. РАН Е.И. Моисеев, проф. В.И. Богачев
Власова Б.А.
В58 Ряды: Учеб. для вузов / Под ред. B.C. Зарубина, А.П. Кри-
щенко. - 3-е изд., исправл. - М.: Изд-во МГТУ им. Н.Э.
Баумана, 2006. - 616 с. (Сер. Математика в техническом
университете; Вып. IX).
ISBN 5-7038-2884-8 (Вып. IX)
ISBN 5-7038-2484-2
Книга является девятым выпуском комплекса учебников
„Математика в техническом университете" и знакомит читателя с основными
понятиями теории числовых и функциональных рядов. В книге
представлены степенные ряды, ряды Тейлора, тригонометрические ряды Фурье и
их приложения, а также интегралы Фурье. Изложена теория рядов в
банаховых и гильбертовых пространствах, и в объеме, необходимом для ее
изучения, рассмотрены вопросы функционального анализа, теории меры и
интеграла Лебега. Теоретический материал сопровождается подробно
разобранными примерами, рисунками и большим количеством задач разного
уровня сложности.
Содержание учебника соответствует курсу лекций, который автор
читает в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов. Учебник может быть
полезен преподавателям и аспирантам.
Ил. 55. Библиогр. 44 назв.
УДК 517.5.52(075.8)
ББК 22.16
© Е.А. Власова, 2000;
2006, с изменениями
© Московский государственный
технический университет
им. Н.Э. Баумана, 2000;
2006, с изменениями
ISBN 5-7038-2884-8 (Вып. IX) © Издательство МГТУ
ISBN 5-7038-2484-2 <; < им НЭ- Баумана, 2000;
<PpD 2006, с изменениями

ПРЕДИСЛОВИЕ
Предлагаемая читателю книга является девятым выпуском
комплекса учебников п Математика в техническом
университете". В учебнике систематически изложен курс теории рядов —
важный раздел математического анализа, широко
применяемый в различного рода исследованиях и вычислениях как в
самой математике, так и во многих ее приложениях. Под
общим термином „ряд" объединены определенные
математические конструкции, применяемые к элементам совершенно
различной природы: действительным и комплексным числам,
действительным и комплексным функциям, элементам
произвольных нормированных пространств.
В главе 1 рассмотрены простейшие примеры рядов —
числовые ряды. Функциональные ряды, в том числе степенные ряды,
ряды Тейлора, тригонометрические ряды Фурье и их
приложения, представлены в главах 2 и 3. В главе 4 изложена теория
интеграла Фурье — важного обобщения тригонометрического
ряда Фурье. Главы 5-7 знакомят читателя с теорией рядов
в нормированных пространствах. В этих же главах в связи с
потребностями теории в необходимом объеме развиты теория
меры и интеграл Лебега.
Содержание учебника логически разбито на две части.
Первая часть (главы 1-4) относится к основному курсу высшей
математики, традиционно излагаемому студентам технических
вузов. Материал второй части учебника (главы 5-7) входит в
программы повышенного уровня подготовки и предназначен
для студентов технических университетов, обучающихся по
специальности „Прикладная математика".
Изучение курса теории рядов требует от читателя
определенного уровня подготовки. Предполагается, что читатель
владеет материалом первых восьми выпусков комплекса
учебников „Математика в техническом университете". В тексте

ПРЕДИСЛОВИЕ
книги имеются ссылки на другие выпуски комплекса
учебников. Такой ссылкой служит номер выпуска. Например, [1-7.5]
означает ссылку на пятый параграф седьмой главы в первом
выпуске. Ссылки без римских цифр относятся только к
этому, девятому, выпуску. Так, (см. 1.2) отсылает читателя ко
второму параграфу первой главы, а (см. Д.3.1) — к первому
дополнению третьей главы этой книги. Ссылки в тексте на
номера формул и рисунков набраны обычным шрифтом
(например, (2.1) — первая формула в главе 2, рис. 1.5 — пятый
рисунок в главе 1).
Большинство используемых обозначений помещено в
перечне основных обозначений. В нем наряду с их краткой
расшифровкой указаны глава и параграф, в которых можно найти
их более подробное объяснение. Кроме того, приведены
таблицы с написанием и русским произношением букв латинского и
греческого алфавитов.
В конце книги помещены список рекомендуемой литературы
и предметный указатель, в котором расположены в
алфавитном порядке (по существительному в именительном падеже)
все выделенные в тексте полужирным курсивом термины с
указанием страницы, где они строго определены или описаны.
Выделение термина светлым курсивом означает, что в данном
параграфе он отнесен к ключевым словам и читателю
должно быть известно значение этого термина. Читатель может
уточнить это значение, найдя при помощи предметного
указателя необходимую страницу, на которой используемый термин
определен или описал. Если термин введен в другом выпуске,
то дана ссылка на этот выпуск (например, I означает ссылку
на первый выпуск, 1-217 — на страницу 217 первого выпуска),
а также указана курсивом страница предлагаемой книги, на
которой имеются некоторые пояснения, относящиеся к этому
термину.
Глава 2 учебника написана совместно с Г.В. Гришиной.
Большую помощь в подготовке издания учебника автору
оказали научные редакторы B.C. Зарубин и А.П. Крищенко, а также

А.Н. Канатников и Ю.И. Малов. Всем им автор выражает
глубокую благодарность.
Перед чтением книги в целях самоконтроля предлагается
выполнить приведенные ниже задания. В тексте заданий
прямым полужирным шрифтом выделены термины, значение
которых должно быть известно читателю, а в конце каждого
задания указана ссылка на номер выпуска, в котором можно
найти соответствующие разъяснения.
Задания для самопроверки
1. Найдите точные верхнюю и нижнюю грани
множества (0,1]. [I]
2. Для всякого п £ N вычислите точную верхнюю и
точную нижнюю грани функции хп на отрезке [0,1]. Докажите,
что sup х2/(1 — х) = +оо и inf х2/(1 — х) = — оо. [I]
[) €(12]
3. Докажите, что счетное объединение счетных
множеств является счетным множеством. Какие множества
имеют мощность континуума? [I]
4. Докажите, что абсолютная величина (модуль)
действительного или комплексного числа обладает
следующим свойством: \х + у\ ^ \х\ + \у\. [I]
5. Приведите примеры различных промежутков
числовой прямой: конечных и бесконечных интервала и
полуинтервала, отрезка. Какие точки являются граничными,
внутренними для промежутка (0,1]? [I]
6. В чем отличие проколотой окрестности точки от
окрестности точки? [I]
7. Найдите действительную, мнимую части и
модуль комплексного числа z = (3 — г)/(4 + Зг). Изобразите
на комплексной плоскости множество комплексных чисел,
удовлетворяющих неравенству \z — 1 + г| < 1. Является ли это
множество точек открытым (замкнутым)? Укажите его
границу. [I]

8 ПРЕДИСЛОВИЕ
8. Какие функции называют периодическими? [I]
9. Докажите, пользуясь методом математической
индукции, что для любого натурального числа п справедливо
равенство 1 +q + ~- + qn~l = (1 -gn)/(l -g), q^l. [I]
10. Выпишите первые пять членов числовой
последовательности {ап}™=1 с общим членом ап = (1 + l/n)n
Докажите, что последовательность {ап}^=1 является
возрастающей и ограниченной. [I]
11. Сформулируйте и запишите в символическом виде
определения конечного и бесконечного пределов числовой
последовательности. Какие последовательности
называют сходящимися, расходящимися? Перечислите свойства
сходящихся последовательностей. [I]
12. Для числовой последовательности {ап}^=1 докажите
справедливость утверждения: liman = 0 <*=$► lim |an| = 0. [I]
n—юо n—юо
13. Сформулируйте признак Вейерштрасса
сходимости ограниченной монотонной последовательности. [I]
14. Докажите утверждение: если числовая
последовательность {хп}™=1 сходится к числу Ь, то любая ее
подпоследовательность также сходится к числу Ь. [I]
15. Запишите выражение для первого замечательного
предела. [I]
16. Используя второй замечательный предел, вычисли-
5n [I]
17. Сформулируйте и запишите определения (по Коши)
двустороннего и односторонних (левого и правого)
пределов действительной функции действительного
переменного в точке а Е К. [I]
18. Сформулируйте теоремы об эквивалентных
бесконечно больших и бесконечно малых функциях
(последовательностях). [I]
19. Докажите, что функция х^, /3 > 0, является бесконечно
большой более высокого порядка роста по сравнению с
функцией 1паж, а > 0, при х -> +оо. [I]

20. Докажите, что функция х^, /3 > 0, является бесконечно
большой более низкого порядка роста по сравнению с
функцией ах, а > 1, при х -> 4-оо. [I]
21. Каковы свойства непрерывных функций в точке,
на отрезке? [I]
22. Является ли точка х = 0 точкой разрыва первого
рода функции у = \х\/х? [I]
23. Найдите производную n-го порядка функции у =
= \п(1 + х). [II]
24. Что понимают под левой и правой производными
функции в точке? [II]
25. Является ли функция у = х2 непрерывно
дифференцируемой на отрезке [0,1]? [II]
26. Докажите, что производная нечетной
дифференцируемой функции является четной функцией. [I], [И]
27. Запишите формулы Тейлора и Маклорена с
остаточным членом в форме: а) Пеано; б) Лагранжа. [II]
28. Сформулируйте достаточные условия убывания
(возрастания) дифференцируемой функции. [II]
29. Приведите необходимые и достаточные условия
существования экстремума дифференцируемой
функции. [И]
30. Является ли функция у = \пх строго выпуклой
вверх в области определения? Постройте ее график. [II]
31. Найдите первообразную функции sin5x. [VI]
32. Сформулируйте свойства определенного
интеграла. Запишите формулу Ньютона — Лейбница вычисления
определенного интеграла. Является ли функция cosx
интегрируемой на отрезке [0, тг]? [VI]
33. Используя правило интегрирования по частям,
тг/5
вычислите интеграл / (х2 + 2х + 3) cosbxdx. [VI]

10 ПРЕДИСЛОВИЕ
34. Вычислите производную интеграла с переменным
х
верхним пределом f cos2tdt. [VI]
о
35. Укажите, при каких значениях параметра р Е R несоб-
+dx
ственный интеграл / — сходится. [VI]
1 хР
36. Исследуйте на абсолютную и условную сходимость
несобственные интегралы от функций x~1sinx и x~3cosa: по
промежутку [1, +оо). [VI]
37. Каковы свойства собственных и несобственных
интегралов, зависящих от параметра? При каких условиях
такие интегралы можно дифференцировать и
интегрировать по параметру? [VI]
38. Выясните, является ли несобственный интеграл
+оо
f x~2cos\xdx сходящимся равномерно по параметру А
1
на множестве R. [VI]
39. Напишите общее решение дифференциального
уравнения ху1 = 2у. Найдите особые точки этого уравнения.
Найдите решение задачи Коти: ху1 = 2у, у(1) = 1. [VIII]
40. Назовите методы интегрирования обыкновенных
дифференциальных уравнений второго порядка,
разрешенных относительно старшей производной. [VIII]
41. Укажите какой-нибудь базис в линейном
пространстве многочленов степени не выше п с обычными операциями
сложения и умножения на числа. Какова размерность этого
линейного пространства? Является ли система многочленов
pi = l + 2t2 - 3t3, P2 = 3t - 7t2, рз = 2 +13 линейно
независимой? Какова размерность линейной оболочки этой
системы? Докажите, что многочлен 3t — 3t2 — 7t3 является линейной
комбинацией многочленов pi, рг» Рз- [IV]
42. Приведите примеры конечномерных и
бесконечномерных евклидовых пространств. [IV]
43. Запишите неравенство Коши — Буняковского. [IV]

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Л и ► — начало и окончание доказательства
# — окончание примера или замечания
a Е -А, А Э а — элемент а принадлежит множеству А
(множество А содержит элемент а) 1-1.1
а £ А — элемент а не принадлежит множеству А 1-1.1
А = {х: ...} — множество А состоит из элементов я,
обладающих свойством, указанным после двоеточия 1-1.1
А = 0 — множество А пусто 1-1.1
А С В, В D А — множество А включено в множество В (В
включает А) 1-1.2
А С 5, В D А — множество А включено в множество В или
совпадает с ним 1-1.2
N — множество натуральных чисел 1-1.3
Z — множество целых чисел 1-1.3
Q — множество рациональных чисел 1-1.3
М — множество действительных чисел 1-1.3
С — множество комплексных чисел 1-4.3
F — множество R или С в утверждениях, где
рассматриваются параллельно действительный и комплексный
случаи 5.3
[а, Ь] — отрезок с концами в точках а и b I-1.3
(а, Ь) — интервал с концами в точках а и b I-1.3
[а, Ь), (а, Ь] — полуинтервалы с концами в точках а и b I-1.3
М — абсолютное значение числа х 1-1.3

12 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
+оо, —оо — бесконечные точки расширенной (пополненной)
числовой прямой 1-1.3
оо — объединение бесконечных точек +оо и —сю 1-1.3
(—оо, +оо), (—оо, а), (Ь,+оо) — бесконечные интервалы
1-1.3
(—оо, а], [Ь, +оо) — бесконечные полуинтервалы 1-1.3
Аи В — объединение множеств А и В 1-1.4
АПВ — пересечение множеств А и В 1-1.4
А\В — разность множеств А и В 1-1.4
оо оо
U Еп, Р| Еп — счетное объединение и счетное пересечение
71=1 n=1 множеств Еп 7.1
U Еп — счетное или конечное объединение множеств Еп
(п) 7.1
А => В — из высказывания А следует В 1-1.5
А <==> В — высказывания А и В равносильны 1-1.5
Зх: — существует такое ж, что 1-1.5
3\х: — существует единственное ж, такое, что 1-1.5
Ух — для любого х 1-1.5
У = f(x) — переменное у — функция переменного х 1-2.1
f(a) = f(x) — значение функции f(x) в точке а 1-2.1
х—а
.6
f(x)\ — разность значений функции f(x) в точках Ь и а VI
\а
f~l — функция, обратная к функции / 1-2.3
до f — композиция функций /ид 1-2.4
М(х\ у) — точка М плоскости с координатами х (абсцисса) и
у (ордината) 1-2.5
X х У — произведение (декартово) множеств X и У 1-2.5
W1 — произведение (декартово) п множеств
действительных чисел 1-2.5

п
13
^ ак — сумма п слагаемых ai, ..., a^, ..., ап 1-2.6
k=i
п
Y\ a>k — произведение п сомножителей oi, a*, an
к=1 1-2.6
п! — произведение всех натуральных чисел от 1 до п
включительно 1-2.6
к = 1, п — число к принимает последовательно целые значения
от 1 до п включительно 1-2.6
Ат — матрица, транспонированная к А III
supX, sup a: — точная верхняя грань множества X 1-2.7
тех
inf X, inf x — точная нижняя грань множества X 1-2.7
тех
sgna: — функция знака числа х 1-3.2
[х] — целая часть числа х 1-3.2
г — мнимая единица (г2 = — 1) 1-4.3
Re z — действительная часть комплексного числа z I-4.3
Imz — мнимая часть комплексного числа z I-4.3
~z — число, комплексно сопряженное числу z I-4.3
р{х,у) — расстояние между точками х и у метрического
пространства 1-5.1
р(х,М) — расстояние от элемента х гильбертова
пространства до подмножества М 6.2
sup f(x) — точная верхняя грань функции f(x) на множестве
хех X 1-5.7
inf f(x) — точная нижняя грань функции f(x) на множестве
хеХ X 1-5.7
max/(ж), min/(a;) — наибольшее и наименьшее значения функ-
%€Х х£Х
ции f(x) на множестве X 5.1, 6.1

14 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
{#n}> {xn}%Li — бесконечная последовательность элементов хп
1-6.2, 1.1
lim{o:n}, lim хп — предел последовательности {хп} элементов
71—>ОО
нормированного пространства 5.1
х —> а — переменное х стремится к точке а 1-7.1
lim f(x) — предел функции f(x) в точке а (при х -> а) 1-7.1
x-ta
/(а + 0), /(а-0) — пределы функции f(x) в точке а справа
(х -f а + 0) и слева (х -> а - 0) 1-7.2
${х) = о(д(х)), х -> а — функция f(x) более высокого порядка
малости по сравнению с функцией д(х) при х -> а
1-10.1
f(x)~g(x), х —> а — функции f(x) и д{х) являются
эквивалентными при х -> а 1-10.2
у7(ж), у\ dy/dx — производная функции у = f(x) II
Д(а + 0), /i(o — 0) — обобщенные правая и левая
производные функции /(ж) в точке а 3.3
//7(а) и frrr(a) — значения производных второго и третьего
порядков функции f(x) в точке а II
/(п)(а) — значение производной n-го порядка (n-й
производной) функции f(x) в точке а II
f^n'(x), -7—^f(x) — производная n-го порядка (п-я производ-
(XX
ная) функции f(x) II
fx(xiy)i ^(Ж»У) — частная производная функции /(ж,у) по
переменному х V
/ f(x)dx — неопределенный интеграл от функции f(x) VI
ь ь
ix)dx, f f(x)dx — определенный интеграл (Римана) от
а
функции f(x) по отрезку [а, 6] VI, 7.1

15
+оо
V.p. / f(x)dx — главное значение несобственного интеграла
~°° от функции f(x) по числовой прямой 4.4
ь
(L)J f(x)dx — интеграл Лебега от функции f(x) по отрезку
[а,Ь] 7.1
(L)J f(x)dx, f f(x)dx — интеграл Лебега от функции f(x) по
Е Е
множеству Е 7.1
оо
^ an, an G E (an G С), — действительный (комплексный) чис-
71=1 ловой ряд 1.1
оо
S fn{x) — функциональный ряд 2.1
оо
]Г) a;n, xn G L — ряд из элементов нормированного простран-
71=1 стваЬ 5.5
ип(х) —> и(х), хЕХ — функциональная последовательность
{ип(х)} сходится к функции и(х) поточечно на
множестве X 2.1
ип(х) =^и(х) — функциональная последовательность {ип(х)}
сходится равномерно на множестве X к функции
и{х) 2.2
ип(х) ^z^u(x) — функциональная последовательность {ип(х)}
не является равномерно сходящейся на множестве X
к функции и(х) 2.2
(х> У) — скалярное произведение элементов х и у евклидова
или гильбертова пространства 3.1, 6.1
11Ж11> II^IU — норма элемента х нормированного пространства
L 3.1, 5.1
оо
/ ~ Yl fk*Pk — РЯД справа является рядом Фурье элемента /
k~l по ортонормированной системе {^А:} в евклидовом
пространстве 3.1

16 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Ео[а,Ь] — евклидово пространство кусочно непрерывных на
отрезке [а, Ь] функций 3.1, 6.1
■F[/](^)> F~l[f]W — прямое и обратное преобразования
Фурье функции f(x) 4.5
FC[/](A), Fs[f](X) — косинус- и синус-преобразования Фурье
функции f(x) 4.6
C[a,b] — нормированное пространство непрерывных на
отрезке [а, Ь] функций 5.1
Со[а,Ь] — нормированное пространство многочленов,
определенных на отрезке [а, Ь] 5.2
m — нормированное пространство ограниченных
числовых последовательностей 5.1
^р, р ^ 1, — нормированное пространство числовых последова-
оо
тельностей {хп}, таких, что ^ \хп\р < +оо 5.1
п=1
А — замыкание множества А 5.4
<Q> — линейная оболочка системы Q 5.6
^2 — гильбертово пространство числовых последователь-
оо
ностей {а;п}, таких, что ^ \хп\2 < +оо 6.1
п=1
х JL у — ортогональные элементы гильбертова пространства
6.3
z A. L — элемент z ортогонален подмножеству L гильбертова
пространства 6.3
L1- — ортогональное дополнение к подпространству L
гильбертова пространства 6.3
L 0 L1- — ортогональная сумма подпространств L и L1
гильбертова пространства 6.3
— конечная сумма или ряд элементов ап 7.1
(п)

17
тЕ, m(E) — мера Лебега множества Е 7.1
га* £7, тп*Е — внешняя и внутренняя меры множества Е 7.1
L\[a,b] — банахово простралство функций, суммируемых на
отрезке [а, Ь] 7.1
1/2[а,Ь] — гильбертово пространство суммируемых с
квадратом на отрезке [а, Ь] функций 7.2
Z/2([л,Ь],V9) — гильбертово пространство суммируемых с
квадратом и весом ip на отрезке [а, Ь] функций 7.5

18
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Буквы латинского алфавита
Начертание
А а
В Ъ
С с
D d
Е е
F f
G g
Н h
I i
J J
К k
L 1
M m
A a
В b
С с
D d
E e
F f
G g
H h
I i
J j
К к
L I
M m

Произношение
a
бэ
цэ
ДЭ
e
эф
же
аш
и
йот
ка
эль
эм
Начертание
N п
О о
Р Р
Qq
R г
S s
Т t
U u
V v
W w
X х
Yy
Z z
N п
О о
Р Р
Qq
R г
S s
Т t
U и
V v
W w
X х
Y у
Z z

Произношение
эн
о
пэ
ку
эр
эс
тэ
у
вэ
дубль-вэ
икс
игрек
зэт
Представлен наиболее употребительный (но не
единственный) вариалт произношения (в частности, вместо „йот" иногда
говорят „жи").
Буквы греческого алфавита

Начертание
А а
в р
Г 7
A S
Е е
z С
Н v
С с/ "

Произношение
альфа
бета
гамма
дельта
эпсилон
дзета
эта
тэта

Начертание
I ь
К к
Л А
М \1
N и
S £
О о
П 7Г

Произношение
йота
каппа
ламбда
ми
ни
кси
омикрон
пи

Начертание
Р Р
Е а
Т г
Г v
Ф ip
х х
ф ф

Произношение
ро
сигма
тау
ипсилон
фи
хи
пси
омега
Наряду с указанным произношением также говорят
„лямбда", „мю" и „ню".

1. ЧИСЛОВЫЕ РЯДЫ
Эта глава посвящена классической теории бесконечных
сумм чисел, или числовых рядов. Понятие бесконечных сумм
фактически было известно ученым Древней Греции (Евдокс,
Евклид, Архимед). Нахождение бесконечных сумм являлось
составной частью так называемого метода исчерпывания,
широко используемого древнегреческими учеными для
нахождения площадей фигур, объемов тел, длин кривых и т.д. Так,
например, Архимед для вычисления площади
параболического сегмента (т.е. фигуры, ограниченной прямой и параболой)
нашел сумму бесконечной геометрической прогрессии со
знаменателем 1/4. Ряд, как самостоятельное понятие, математики
стали использовать в XVII в. И. Ньютон и Г. Лейбниц
применяли ряды для решения алгебраических и дифференциальных
уравнений. Теория рядов в XVIII-XIX вв. развивалась в
работах Я. и И. Бернулли, Б. Тейлора, К. Маклорена, Л. Эйлера,
Ж. Даламбера, Ж. Лагранжа и др. Строгая теория рядов была
создана в XIX в. на основе понятия предела в трудах К. Гаусса,
Б. Больцано, О. Коши, П. Дирихле, Н. Абеля, К. Вейерштрасса,
Б. Римана и др.
1.1. Основные определения
Определение 1.1. Всякое выражение
а>1 + о>2 + о>з + • • • + О"п + • • • (1-1)
представляющее собой последовательность действительных или
комплексных чисел oi, a2, ап, соединенных знаками
плюс, называют числовым рядом (или рядом). При этом
члены последовательности {an}^=i называют членами ряда

20 1. ЧИСЛОВЫЕ РЯДЫ
(1.1), а общий член ап последовательности {an}™=i — общим
членом ряда (1.1).
Отметим, что для ряда важен порядок суммирования его
членов: изменив порядок суммирования членов ряда (т.е.
изменив числовую последовательность, по которой строится ряд),
мы получим другой ряд.
Для обозначения ряда а\ + a<i + аз +... + ап + ... применяют
оо
следующую краткую форму записи: ^ ап-
п=1
Обычно члены ряда нумеруют начиная с единицы (как
в определении ряда (1.1)). Однако иногда бывает удобно
начинать нумерацию членов ряда с нуля. В этом случае ряд
имеет вид
оо
^an = ao + ai+a2 + ... + an + ... (1.2)
п=0
Более того, члены ряда можно нумеровать начиная с любого
номера. Так, при всех к Е N выражения вида
п=к
наряду с выражениями (1.1) и (1.2), также называют рядами.
Числовой ряд, членами которого являются
действительные (комплексные) числа, называют действительным
(комплексным) числовым рядом.
оо
Пример 1.1. Выпишем первые четыре члена ряда ^ ап по
п=1
известному общему члену ряда ап = (5п +1)/(п2+ 2). Первый
член ряда а\ найдем, подставив в формулу общего члена ряда
число п = 1, т.е.
5п +
5 1 + 1_ 6
~ 12 .о " Ч ~
n=l i +^ о

1.1. Основные определения
21
Второй член ряда ач, находим, подставляя в формулу
определяющую ап, число п = 2, т.е.
Q>2 =
5п
п=2
5-2 + 1
22 + 2
11
6
Аналогично получаем
5га
5га +
п=3
5-3 + 1 _ 16
32 + 2 ~ 11'
raJ
п=4
5-4+1
42 + 2
Таким образом, имеем
21
18
16
7
6'
П=1
П=1
Пример 1.2. Подберем один из возможных вариантов
формулы общего члена ряда
2 4
8
п=1
по указанным первым его членам. Итак, имеем
01 = 5'
°2 = 8'
6
8
Нетрудно заметить, что числители написанных выше дробей,
являются первыми четными числами: 2, 4, 6, 8.
Естественно предположить, что числителем дроби, равной п- ^у члену
рассматриваемого ряда, будет n-е по счету четное число, т.е.
число 2п. Знаменатели же дробей 2/5, 4/8, 6/11, 8/14 таковы,
нто каждый последующий больше предыдущего на три
единицы, т.е. являются первыми четырьмя членами арифметической

22 1. ЧИСЛОВЫЕ РЯДЫ
прогрессии с разностью, равной 3, и первым членом, равным 5.
Тогда га-й член данной прогрессии можно вычислить по
формуле 5 + 3(га - 1) (bn = b\+ d(n - 1), d = 3, bi = 5). Таким образом,
общий член рассматриваемого ряда можно вычислять,
например, по формуле
N
поскольку все указанные начальные члены ряда вычисляются
по этой формуле.
Отметим, что по начальным членам ряда общий член ряда
нельзя определить однозначно. Поэтому, вообще говоря, можно
привести и другие формулы общего члена ряда, при которых
начальными членами ряда будут те же числа 2/5, 4/8, 6/11 и
8/14. Ряд в целом при этом будет уже другим. #
Числовой ряд определен нами как чисто формальное
выражение вида (1.1) или (1.2), содержащее бесконечное число
знаков сложения. Однако сложение бесконечного набора
чисел не является элементарной арифметической операцией.. Этой
операции необходимо придать строгий математический смысл.
Понятие суммы ряда можно определять многими способами,
однако наиболее естественным является способ определения
суммы ряда как предела последовательности сумм первых п
его членов. Перейдем к точным определениям.
71
Определение 1.2. Для всякого п Е N сумму Sn = ^2 а& пер-
оо А;=1
вых п членов ряда ^ ап называют п-и частичной суммой
71=1
этого числового ряда.
оо
Таким образом, с любым числовым рядом ^2 ап связана
71=1
числовая последовательность {Sn}n^=l его частичных сумм.
Определение 1.3. Числовой (действительный или ком-
оо
плексный) ряд ^ ап называют сходящимся, если существует
71=1

1.1. Основные определения 23
конечный предел S последовательности {Sn}n<Ll его частичных
сумм. При этом число S называют суммой числового ряда
оо оо
52 ап И ПИШуТ 52 ап = S.
Т1=1 71=1
Таким образом, по определению
оо
Ean = S Ф=Ф* lim Sn = S. S Ф оо.
71-ЮО
71=1
Если числовой ряд является сходящимся и его сумма равна 5,
то говорят также, что имеет место сходимость числового
ряда к числу S.
оо
Замечание 1.1. Введенная выше запись 52 ап — & Для
ОО 71=1
обозначения того факта, что суммой ряда 52 ап является число
71=1 ОО
5, соответствует тому, что одним и тем же выражением 52 ап
71=1
обозначается как сам ряд, так и его сумма (если этот ряд
оо
сходится). Что обозначает выражение 52 ап (РЯД или сумму
71=1
ряда), обычно ясно из контекста.
Пример 1.3. Для числового ряда
111 \_
+ 2 + 4 + 8+'"+2"+'" =
71=1
частичные суммы имеют вид
Для всякого n E N значение jSn равно сумме первых п членов
геометрической прогрессии с первым членом, равным 1, и
знаменателем, равным 1/2. Учитывая, что сумма п первых членов

24 1. ЧИСЛОВЫЕ РЯДЫ
геометрической прогрессии с первым членом Ь\ и знаменателем
q вычисляется по формуле Sn = b\(qn — l)/(g — 1), имеем:
_(l/2")-l _ Л 1\ 1
(1/2) - 1 ~
При п —> оо существует предел последовательности частичных
сумм Sn, а именно:
im Sn = lim (2 - —^-г ) = 2.
lim
71—ЮО
В силу определения 1.3 рассматриваемый ряд является
сходящимся, и его сумма равна числу 2 — пределу
последовательности частичных сумм этого ряда при п —> оо. Таким образом,
можем записать
71=1
Определение 1.4. Числовой (действительный или ком-
оо
плексный) ряд ^ ап называют расходящимся, если последо-
71=1
вательность его частичных сумм {Sn}^=l не имеет конечного
предела при п -> оо, т.е. либо этот предел не существует, либо
он равен бесконечности.
Для расходящихся рядов понятие суммы ряда не определено
(эти ряды не имеют суммы). Если числовой ряд является
расходящимся, то говорят также, что имеет место расходимость
этого числового ряда.
Отметим, что определения 1.3 и 1.4 указывают на тесную
связь между теорией числовых рядов и теорией числовых
последовательностей. Действительно, в соответствии с
определениями сходимость (расходимость) числовых рядов эквивалентна
сходимости (расходимости) числовых последовательностей их

1.1. Основные определения 25
частичных сумм. С другой стороны, сходимость
(расходимость) всякой числовой последовательности эквивалентна
сходимости (расходимости) некоторого числового ряда.
Действительно, каждой последовательности {sn} можно однозначно
оо
поставить в соответствие некоторый ряд ]Г) а^, последователь-
к=\
ностью частичных сумм которого является последовательность
оо
{sn}. Таким рядом является, очевидно, ряд s\ + ^2 (s^ — s^-i) с
к=2
членами а\ = si, а>2 = $2 — si, ..., а^ = Sk — Sfc-i, ..., для которого
имеем
71
Sn = Y2ak = 51 + (52 - 5i) + + (Sn - Sn-i) = 5n, П E N.
A:=l
Таким образом, любой результат, полученный в теории рядов,
можно сформулировать на языке теории последовательностей,
и наоборот.
Уточним понятия сходимости и суммы для комплексных
числовых рядов.
оо
Теорема 1.1. Комплексный числовой ряд ^2 ап сходится к
71=1
комплексному числу S = А + гВ, А, В € R, тогда и только тогда,
оо оо
когда сходятся действительные ряды ]^ Rean и ^2 Iman, а их
71=1 71=1
суммы равны числам А и В соответственно.
оо
< Рассмотрим комплексный ряд £) an. Для всякого п £ N
обозначим n=1
an = Rean GR, (3n = Iman G R.
oo oo
Пусть комплексный ряд ^2 an = ^2 (an + i/3n) сходится,
причем n=1 n=1
oo
an = S = A + iB, A,BgR.
71=1

26 1. ЧИСЛОВЫЕ РЯДЫ
Частичные суммы данного ряда имеют вид
к=\ к=1 к=1 к=1
оо
где Ап — п-я частичная сумма действительного ряда ^2 R-ean =
71=1
00
5^ an, а Вп — п-я частичная сумма действительного ряда
71=1
00 ОО
£ Iman = £ А»-
71=1 71=1
Напомним, что, согласно определению предела
последовательности комплексных чисел [X], комплексное число S =
= А + гВ является пределом комплексной последовательности
{Sn}n<>=l = {Ап + гВп}£=1, если для любого положительного
числа е найдется номер iV, зависящий от е и такой, что для любого
номера п> N верно неравенство
\Sn-S\ = \An + iBn-A-iB\ = y/(An-A)* + (В„-В)2 < е.
Отсюда следует, что для любого номера п> N выполняются
неравенства
\Ап-А\<е, \Вп-В\<е.
Значит, действительные последовательности {Ап}^! и {Вп}п<>=1
сходятся к действительным числам А = Re 5 и В = Im S соот-
ОО ОО 00 ОО
ветственно. Поэтому ряды ^ Rean = J2 ап и Е ^man = Л fin
П=1 71=1 71=1 71=1
сходятся, причем
71=1 71=1
ИЛИ
ОО ОО ОО
71=1 71=1 71=1 71=1

1.1. Основные определения 27
оо
Докажем обратное утверждение. Пусть ряды ^ Rean =
оо оо оо п=1
^an и J] Iman = ^/Зп с действительными членами схо-
П=1 71=1 71=1
дятся к числам А и В соответственно. В этом случае последо-
71 П
вательности {Ап-А} и {Вп-В}, где Ап = £ «п, #п = Е An
*=1 *=1
являются бесконечно малыми последовательностями. Отсюда
в силу неравенства
\Sn-(A + iB)\ = \(An-A)+i(Bn-B)\ =
последовательность {\Sn - (А + iB)\}, где Sn = J2 (an + ipn) =
= An + iBn, также является бесконечно малой
последовательностью. Это означает, что последовательность {Sn} сходится к
комплексному числу A + iB, и, следовательно,
71=1 71=1 71=1
Таким образом, сходимость ряда с комплексными членами
эквивалентна одновременной сходимости двух рядов с
действительными членами, т.е. ряда, составленного из действительных
частей членов исходного ряда, и ряда, составленного из
мнимых частей этого ряда. Поэтому теория числовых комплексных
рядов естественным образом сводится к изучению числовых
действительных рядов.
В теории числовых рядов решают две основные задачи:
исследуют ряд на сходимость, т.е. выясняют, сходится ряд или
расходится, и вычисляют сумму сходящегося ряда. Для
решения первой задачи используют различные признаки сходимости
и расходимости рядов (см. 1.2-1.9). Вторая задача, вообще
говоря, является более сложной, поскольку общие приемы
вычисления сумм рядов существуют лишь для некоторых видов

28 1. ЧИСЛОВЫЕ РЯДЫ
рядов. Поэтому в тех случаях, когда точное значение суммы
ряда найти не удается, ограничиваются приближенными
вычислениями.
Пример 1.4. Исследуем на сходимость и (в случае
сходимости) найдем сумму геометрического ряда
оо
71=1
Используя формулу для вычисления суммы п первых членов
геометрической прогрессии, получаем
га, q=l.
Вычислим lim Sn при различных значениях q.
п—юо
При \q\ ф 1 имеем
hm = hm
l-q n->ooVl-
поскольку
lim qn =
n->oo
n = f 0, |g| < 1;
\oo, |g|>l.
При 9 = 1, очевидно, получим
lim Sn = lim n = oo.
n—юо n—>oo
Наконец, при 9 = — 1 рассматриваемый ряд принимает вид
п=1

1.1. Основные определения
29
Последовательность частичных сумм данного ряда следующая:
Si = 1, S2 = 1 - 1 = О, S3 = 1 - 1 + 1 = 1,
т.е.
= o, кек
Поскольку две подпоследовательности {S2k-i}<kLi и {S
последовательности {Sn}™=l имеют различные пределы:
lim
fc-»oo
fc-юо
= О,
то предел последовательности Sn частичных сумм рассматри-
оо
ваемого ряда при п —> оо не существует и ряд ^ (—1)п~1 рас-
п=1
ходится.
Таким образом, исходный ряд сходится при \q\ < 1 и
расходится при \q\ ^ 1, причем верно следующее равенство.
Пример 1.5. Найдем сумму ряда
Последовательность {S1,,
вид
n"
1
Учитывая, что
частичных сумм этого ряда имеет
1 1
п(п +
п п +
-, n€N,

30 1. ЧИСЛОВЫЕ РЯДЫ
получаем
„ . 1111 1 1
2 2 3 3 п п + 1 * n + :
Отсюда имеем
lim Sn = lim (1 ) = 1.
n—foo n—>оо\ fl+l/
Следовательно,
Пример 1.6. Найдем сумму ряда
Рассмотрим n-ю частичную сумму данного ряда
11 1
71 1-2-3 2-3-4 n(n + l)(n+ 2)"
Разложим общий член ряда на простейшие дроби методом
неопределенных коэффициентов [VI]:
1 А В С
= - + 7 +
n(n + l)(n + 2) n п+1 п + 2
Приравнивая числители дробей, имеем
1 = А{п + 1)(п + 2) + 5п(п + 2) + Сп{п + 1).

1.2. Необходимый признак сходимости рядов 31
Подставляя в левую и правую части данного тождества
значения п = 0, п = -1, п = -2, получаем:
п = 0: \ = 2А => А = 1/2;
п = -1: 1 = -В =» В = -1;
п = -2: 1 = -2С(-1) =» С =1/2.
Следовательно,
1 i+2
2п п + 1 2(п + 2)
2\n n + 1/ 2\n + l n + 2
Отсюда (см. пример 1.5)
ini i ini i
s = iyVl 1_Л_iyV_t L_
n 2£-~'\k fc + 1/ 2^\A: + 1 fc + 2
ik=l fc=l
1
2\ n + 1/ 242 n
Поэтому имеем
1 1 1 1 \ 1
Л
4 2(n + 2)/ 4
Таким образом,
_ 1
~4'
1.2. Необходимый признак сходимости рядов
Сформулируем простейшее необходимое условие
сходимости числового ряда, которое называют необходимым
признаком сходимости ряда.

32 1. ЧИСЛОВЫЕ РЯДЫ
Теорема 1.2 (необходимый признак сходимости рл-
оо
да). Если ряд 53 ак сходится, то lim а* = 0.
jfe=l *"►«>
оо
М Поскольку ряд 53 аА; сходится, то существует предел после-
А;=1
довательности частичных сумм этого ряда, т.е. lim 5* = 5, где
А;-юо
А;
д^А: ^ $3 ап« Тогда, используя арифметические свойства сходя-
п=1
щихся последовательностей [1-6.4], получаем
lim а*= lim(S/b-Sfc_i)= lim S* - lim Sk-i=S-S = 0. ►
A;—)>oo A;—)>oo A;—)>oo A
Покажем теперь, что условие lim ak = 0 не является доста-
к-юо
оо
точным для сходимости ряда 53 аА;- Рассмотрим, например,
оо А;=1
РЯД 53 1/v^- Д-^^ этого ряда необходимый признак сходимо-
к=1
сти выполнен: lim a* = lim l/\/fc = 0. Покажем, однако, что
оо А;—юо А;—>оо
рл(? 5Z 1/>/^ расходится. Для последовательности частичных
сумм 5П = 53 1/v^fc этого ряда справедлива следующая оценка:
Jb=l
V 2
поскольку l/\/fc ^ l/\/^ для любого Л < п. Следовательно,
согласно теореме о предельном переходе в неравенстве [1-6.4],
имеем
lim Sn ^ lim \fn — +оо,
> п>оо
п—>оо
т.е. lim Sn = +оо, и ряд 53 l/>/fc расходится.
Итак, стремление к нулю общего члена ряда является
необходимым, но не достаточным условием сходимости рядов. Это

1.2. Необходимый признак сходимости рядов 33
означает, что если необходимый признак сходимости ряда не
выполнен, т.е. предел lim а* не существует или lim а* ф О, то
qq А;—юо А;—юо
ряд ^2 &к расходится. Если же необходимый признак выпол-
А;=1
нен, т.е. lim a* = 0, то по одному только этому условию ничего
*->оо оо
определенного о сходимости ряда сказать нельзя — ряд ^ ak
может как сходиться, так и расходиться.
Пример 1.7. Исследуем на сходимость ряд
2п1 1 3 5
п=1
Проверим, выполняется ли необходимый признак сходимости
ряда:
,. 2п-1 2 /л
hm an = hm = - ^ 0.
п—)>оо n—>oo oTl + 2 О
Необходимый признак сходимости ряда не выполняется, и,
следовательно, этот ряд расходится.
Пример 1.8. Выясним, сходится ли ряд Дирихле
п=1
Для этого ряда необходимый признак не выполняется при р ^ 0,
и, следовательно, ряд расходится. Если же р > 0, то lim l/np =
п—юо
= 0, и необходимый признак выполнен. Но о сходимости ряда
пока нельзя сделать никаких выводов — он может сходиться, а
может и расходиться. Окончательный ответ мы дадим далее,
после изучения достаточных признаков сходимости рядов.
Пример 1.9. Докажем, что ряд
оо
п=1 п=1

34 1. ЧИСЛОВЫЕ РЯДЫ
расходится. Для этого проверим выполнение необходимого
признака сходимости ряда:
.. .. /2п2 — 3\™2 Г неопределенность 1
hm ап = hm —5—- = 1ОО =
п-^оо п^оо\2п2 + 1/ L типа 1°° J
-4 \^Ч^\2^+Т
(При вычислении предела мы воспользовались вторым
замечательным пределом lim (l +j) =e [1-7.7] и тем, что верно
/ \ lim yn
равенство lim (хп)Уп = ( lim xn J71-"00 в случае, когда его пра-
вая часть имеет смысл.) Таким образом, ряд ^ а>п расходится.
1.3. Свойства сходящихся рядов
Рассмотрим произвольный {действительный или
комплексов
ный) числовой ряд Yl ak-
k=i
оо
Определение 1.5. Числовой ряд X) аь полученный из
оо k=n+l
ряда YI ак путем отбрасывания первых п его членов, называют
к=1 оо
п-м остатком ряда ^2 а* и его сумму (при условии, что этот
А;=1
остаток сходится) обозначают Rni
• • • + ап+1 + • • •
k=n+l
Приведем несколько простейших утверждений,
относящихся к сходящимся рядам.

1.3. Свойства сходящихся рядов 35
оо
Свойство 1.1. Если ряд ^ а& сходится, то сходится и
А;=1
любой из его остатков. Обратно, если сходится хотя бы один
из остатков ряда, то сходится и сам ряд. При этом для всех
п £ N справедливо равенство
а*> или s=sn+Rn'
к=1 к=\ к=п+1
<4 Пусть п Е N произвольное число. Очевидно, что га-ю частпич-
оо
ную сумму п-го остатка ^2 ак (обозначим ее Rn.m) можно
к=п+\
представить в виде
= Sn+m — Sn,
оо
где 5n, 5n_j-m — частичные суммы ряда ^ а^. Следовательно,
к=1
Sn+m = Sn + Rntm, ТПеК (1.3)
оо
Пусть ряд ^2 пк сходится, т.е. при любых п G N существует
А;=1
предел при m -> оо в левой части равенства (1.3). Тогда для
всех п G N существует предел при га —> оо и в правой части
этого равенства, т.е. все остатки ряда сходятся, причем
lim Sn+m = Sn+ lim Дп>т, или S = Sn + Rn.
т-юо т-юо
оо
Пусть, наоборот, хотя бы один из остатков ряда ^ ак
к=\
сходится, т.е. хотя бы при одном п G N существует предел
при гп —> оо в правой части равенства (1.3). Тогда существует
предел при га —> оо в левой части этого равенства, и, значит,
оо
РЯД Y1 ак сходится, причем
А;=1
lim Sn+m = Sn + lim Дп,т, или S = Sn + Rn. ►
т—юо т—>оо

36 1. ЧИСЛОВЫЕ РЯДЫ
оо
Следствие 1.1. Все остатки Yl ak, п = О,1, 2,... ряда
оо к=п+1
^2 аь сходятся и расходятся одновременно, т.е. если сходится
А;=1
хотя бы один остаток, то сходятся и все остальные остатки
(в том числе и сам ряд), а если хотя бы один из остатков
расходится, то расходятся и все остальные остатки (в том числе
и сам ряд).
оо
Свойство 1.2. Если ряд ^2 а* сходится, то последователь-
А;=1
ность {Rn}™=i сумм его n-х остатков стремится к нулю при
п —> оо:
lim Rn = 0.
п—юо
оо
М Если ряд ^2 а/с сходится, то в силу свойства 1.1 для всех п Е N
А;=1 оо
верно равенство Rn = S — 5П, где S — сумма ряда ^ а^, т.е.
А;=1
lim Sn = S. Отсюда
п—>оо
lim Rn = lim (S - Sn) = 5 - lim Sn = S - S = 0. ►
п—юо п—юо п—юо
oo
Свойство 1.3. Если в ряде ^ ак отбросить конечное число
А;=1
членов или заменить конечное число членов другими, то это не
отразится на его сходимости или расходимости.
М Остатки первоначального и измененного рядов с номерами,
превышающими номера отброшенных или замененных членов,
совпадают, следовательно, сходятся или расходятся
одновременно. Тогда из свойства 1.1 и следствия 1.1 вытекает, что
одновременно сходятся или расходятся первоначальный и
измененный ряды. ►
Свойство 1.4. Отбрасывание членов, равных нулю (с
сохранением порядка оставшихся членов), не влияет на
сходимость или расходимость ряда, а в случае сходимости не
изменяет сумму ряда. #

1.3. Свойства сходящихся рядов 37
оо
Если A G К (А Е С) — некоторое число, то ряд ^ (Xa>k)
оо jfe=l
называют произведением ряда J2 ак на число А.
*=1
оо
Свойство 1.5. Если ряд ^ ак сходится и имеет сумму S,
оо А;=1
то ряд ^2 Хак, А Е К (A G С), также сходится и имеет сумму AS:
к=1
к=1 к=1
п ~ п п
4 Пусть Sn = ]Г) ак, тогда Sn= Y, \ak = \J2 ak = ASn. Поэто-
к=1 к=1 к=1
му в силу арифметических свойств сходящихся
последовательностей [1-6.4] имеем
оо оо
Е\ак = lim Sn = lim XSn = A lim Sn = XS = ХУ^ак. ►
n—>oo n—>oo n—>oo ^—'
fc=l ib=l
Ряд вида
k=l
членами которого являются суммы ск = ак + Ък членов рядов
оо оо
Z) ак и ^ Ък с одинаковыми номерами, называют суммой
*=1 ib=l
оо оо оо
рлдов ^2 ак и ^2 Ьк. Говорят также, что ряд ^ (аА; + Ьк)
к=1 к=1 к=1
оо оо
получен почленным суммированием рядов ^2 ак и ^ Ь^.
к=1 к=1
оо оо
Свойство 1.6. Если ряды ^2 ак и ^2 Ьк сходятся и имеют
А;=1 А;=1
оо
суммы Аи В соответственно, то ряд ^ (ак + Ьк) также сходит-
А;=1

38 1. ЧИСЛОВЫЕ РЯДЫ
ся и его сумма равна А + В:
к=1 к=1 к=1
п п
Пусть Ап = £ <>>к и Вп = ]Г) h, n G N. Тогда
к=1 к=1
к=1 к=1 к=1
и в силу арифметических свойств сходящихся
последовательностей [1-6.4] получаем
+ ^) = lim Sn = lim (An + Bn) =
nteo п-юо
"" оо оо
= lim An + lim Bn = A + В =
n—юо n—юо
fc=l ife=l
Часто возникает необходимость „снять скобки" в почленной
оо оо оо
сумме 53 (ак + Ьк) рядов 53 ак и S Ьл- Однако просто убрать
к=1 к=1 к=1
оо
скобки в ряде 53 (ак + Ьк), не задумываясь о сходимости рядов
А;=1
оо оо оо
S ак, ^2 Ьк и 53 (ак + Ьк), нельзя, поскольку ряд
А;=1 А;=1 к=1
к=1
и соответствующий ряд без скобок
ai + bi + a2 + Ь2 + ... + ак + Ьк + ...
являются, вообще говоря, различными рядами. Общим членом
первого ряда является величина ск = ак + Ьк, а общим членом

1.3. Свойства сходящихся рядов 39
второго ряда — величина dk, равная u(fc+i)/2» если к нечетно, и
равная bjt/2, если к четно. Поэтому в общем случае сходимость
первого ряда не гарантирует даже сходимости второго ряда,
не говоря уже о равенстве их сумм. Например,
к=1
в то время как ряд без скобок
1-1 + 1-1 + ... + 1-1 + ...
оо
расходится (см. пример 1.4). Тем не менее, если ряды ^ ак и
оо jfe=l
^2 Ьк сходятся, скобки в их сумме снимать можно.
А:=1
оо оо
Свойство 1.7. Если ряды ^ ак и Z) Ък сходятся, то в их
jfe=l k=l
почленной сумме можно снять скобки:
k=i
< Рассмотрим ряды ах+0 + а2 + 0 + аз + 0+ + ак + 0 +
оо оо
И0 +6i+0 + b2 + 0 + 63+ +0 + 6*+ РЯДЫ X) °>к И X) Ьк
к=1 к=1
получены из этих рядов путем отбрасывания нулей. Поэтому в
соответствии со свойством 1.4 ряды с нулями сходятся и имеют
место равенства
к=1
оо
0 + 6i + 0 + Ь2 + 0 + 63 + • • • + 0 + Ьк +... = J3 Ьк.
к=1

40 1. ЧИСЛОВЫЕ РЯДЫ
Сложив почленно ряды в левых и правых частях этих равенств,
в силу свойства 1.6 получим
к=1
ИЛИ
оо
аг + bi + a2 + Ь2 + ... + ак + Ьк +... = ^(а* + Ък). ►
к=\
Свойство 1.8. Если каждый член ак сходящегося ряда
оо
5^ ак не превышает соответствующий член Ьк сходящегося
А;=1 оо оо
ряда ^2 Ък, то сумма ряда ^ ак не превышает сумму ряда
А;=1 к=1
оо оо оо
X) Ьк, Т.е. X) ак ^ Е Ьк-
к=1 к=1 к=1
п п
М Действительно, если ак < Ь^, к G N, то Ап = ^ ак < ^ Ь^ =
А;=1 А:=1
= Bn, n G N. Переходя в этом неравенстве к пределу при п -» оо,
получаем требуемое утверждение. ►
В частности, отсюда следует, что если ап ^ 0, п G N, то
оо
п=1
Теорема 1.3 (критерий Коши сходимости числового
оо
ряда). Числовой ряд ^ afc сходится тогда и только тогда,
k=i
когда для любого е > 0 найдется такой номер iV, зависящий от
£, что для всех п^ N и для любого натурального т выполняется
неравенство
п+т
^2 пк = \ап+1 + 0>п+2 + - • • + 0>п+т\ <£,
к=п+1

1.3. Свойства сходящихся рядов 41
т.е.
\/е>0 3N(e) 4n>N{e) VmGN:
K+l + an+2 + - • • + 0>п+тп\ < £•
4 Утверждение этой теоремы следует непосредственно из
критерия Коши сходимости числовых последовательностей [1-6.5].
В данном случае этот критерий необходимо применить к
последовательности {Sn} частичных сумм рассматриваемого ряда:
сходится <$=>- {Sn}%L\ сходится
3N(e)EN 4n>N{e) VmGN: \Sn+m-Sn\<e.
Остается заметить, что
S S + an+2 + .
Построив отрицание критерия Коши сходимости рядов,
оо
получим критерий расходимости рядов: числовой ряд ^ а*
к=1
расходится тогда и только тогда, когда найдется такое е > О,
что для всякого номера N найдутся номер п^ N и натуральное
число т такие, что выполняется неравенство
п+т
]Г ак = |an+i
или
Зе > 0 ViV е N Зп > JV
Пример 1.10. С помощью критерия Коши докажем, что
оо
гармонический ряд ^ 1/п расходится.
п=1

42 1. ЧИСЛОВЫЕ РЯДЫ
Покажем, что для данного ряда выполняется утверждение:
Эе>0 ViVeN 3n^N 3meN: — + — + ... + —— >e.
п+1 п+2 п+т
Пусть е = 1/2, и для любого натурального N положим п = N,
т = п. Тогда
1 1 1
п+1 п+2 п+т
1 1 1
п+1 п+2 2п
J_ 1 1 1 _ 1 _
^2^ + 2^ + '" + 2^"П'2^"2"£-
Следовательно, гармонический ряд расходится.
1.4. Знакоположительные
ряды. Признаки сравнения
В этом и следующих трех параграфах рассмотрим ряды
оо
^2 ак, все члены которых неотрицательны: а^ ^ 0, к Е N. Та-
к=1
кие ряды называют знакоположительными (или рядами
с неотрицательными членами). Для знакоположительных
рядов приведем достаточные условия (признаки),
обеспечивающие их сходимость или расходимость. Заметим, что можно
отдельно рассматривать знакоотрицательные ряды (или
ряды с неположительными членами), однако равенство
A:=l k=l
позволяет свести анализ знакоотрицательных рядов к анализу
знакоположительных. Поэтому далее будем изучать только
знакоположительные ряды.
Последовательность {Sn}^=l частичных сумм знакоположи-
оо
тельного ряда ]Г) а* не убывает, так как
А:=1
-Sn = an+i ^ 0, п е N.

1.4. Знакоположительные ряды. Признаки сравнения 43
Поэтому, согласно признаку Вейерштрасса [1-6.5],
последовательность {Sn} имеет конечный предел (и, следовательно, ряд
оо
Y, o>k сходится) тогда и только тогда, когда последователь-
*=i
ность {Sn} ограничена сверху, т.е. когда найдется такое число
М > 0, что Sn < M, n G N. При этом для обозначения
сходимости знакоположительного ряда используют запись
к=1
оо
Заметим, что если знакоположительный ряд ^ а& расхо-
к=1
дится, то lim Sn = +оэ. Действительно, в силу сказанного
п—>оо
выше расходимость знакоположительного ряда эквивалентна
тому, что неубывающая последовательность {Sn} частичных
сумм этого ряда не ограничена сверху. Отсюда вытекает
сходимость последовательности {Sn} к +оо [1-6.7]. С другой
стороны, из равенства lim Sn = +00 автоматически следует
п-юо
расходимость ряда. Таким образом, для
знакоположительного ряда (а* ^ 0, к € N) имеем
Edk расходится <=> lim Sn = +00.
n-юо
к=\
Поэтому часто для обозначения расходимости
знакоположительного ряда используют запись
А:=1
(такая запись одновременно указывает непосредственно на
расходимость ряда и на причину расходимости — бесконечность
суммы).

44 1. ЧИСЛОВЫЕ РЯДЫ
Теорема 1.4 (признак сравнения). Пусть для
знакоположительных рядов
оо
Q>h* dk ^ 0, k Е N: (1.4)
А;=1
оо
Х^Ь*> h>0> fceN, (1.5)
k=l
и некоторого натурального числа N при всех к > N
выполняется неравенство ак ^ Ьк. Тогда:
а) если сходится ряд (1.5), то сходится и ряд (1.4);
б) если расходится ряд (1.4), то расходится и ряд (1.5).
< Поскольку изменение конечного числа членов не влияет на
сходимость и расходимость рядов (см. свойство 1.3), то можно
считать, что
О < ак < Ък, keN
(для этого достаточно заменить первые N членов ряда (1.4)
нулями). Отсюда следует, что
Ап^Вп, neN, (1.6)
п п
где Ап = £ а*, Вп = £ Ьк.
к=1 к=1
Пусть ряд (1.5) сходится. Тогда существует конечный
предел последовательности {2?п}, и, следовательно,
последовательность {Вп} ограничена. В силу соотношения (1.6) числовая
последовательность {Ап} также ограничена. Согласно признаку
Вейерштрасса [1-6.5], существует конечный предел
последовательности {Ап} (т.е. сходится ряд (1.4)), причем
оо оо
lim An < lim 2?n, или У^а* ^
п-юо п-юо ^—'
к=1 к=1

1.4. Знакоположительные ряды. Признаки сравнения 45
Пусть теперь ряд (1.4) расходится. Тогда lim An = +оо, и
п-*оо
последовательность {Ап} не ограничена сверху. Отсюда в силу
соотношения (1.6) следует неограниченность
последовательности {#п}, что для знакоположительных рядов эквивалентно
оо
равенству lim Bn = +оо. Значит, ряд У" 6* расходится. ►
Пример 1.11. Исследуем на сходимость
знакоположительный ряд
'Inn'
п=2
Поскольку для любого натурального числа n ^ 2 верно
неравенство
1 ^
Inn п'
то в силу признака сравнения из расходимости гармонического
оо оо
ряда Y1 1/п (см- пример 1.10) следует, что ряд Yl l/lnn также
п=1 п=2
расходится.
Пример 1.12. Выясним, сходится ли знакоположительный
ряд ^
1
Воспользуемся признаком сравнения. Для любого натурального
числа п справедливо неравенство
поскольку значение логарифма 1п(п + 1) растет с увеличением
оо
номера п. Так как геометрический ряд £) (1/2)П сходится (см.
п=1
оо
пример 1.4), то в силу свойства 1.5 ряд ^ 1/(2п1п2) также
п=1

46 1. ЧИСЛОВЫЕ РЯДЫ
сходится. Отсюда, согласно признаку сравнения (см. теорему
1.4), сходится и ряд
00
У"
Пример 1.13. Применим признак сравнения для
исследования на сходимость ряда
п=2
Из неравенств ln^n ^ln^2 и па< п, верных при п = 2, 3,
вытекает, что справедливо и следующее неравенство:
In'n In'2
nQ п
1 п = 2, 3,
оо
Так как гармонический ряд J2 1/п расходится (см. пример
71=1
оо
1.10), то расходится и ряд ^ (1п^2)/п (см. свойство 1.5).
71=1
В силу признака сравнения приходим к следующему
заключению.
расходится при а ^ 1, /3 ^ 0.
Теорема 1.5 (предельный признак сравнения). Бели
оо оо
для знакоположительных рядов J2 ak и S fyfe c ненулевыми
А;=1 А:=1
членами (а^ > 0, 6* > 0, fc E N) справедливо соотношение
lim ^- = С, 0 < С < оо,
Aj-юо Ok
то эти ряды либо оба сходятся, либо оба расходятся.

1.4. Знакоположительные ряды. Признаки сравнения 47
В соответствии с условиями теоремы имеем
lim^ = C, lim^ = -^, 0<С<оо.
k-юо 0k k-юо CLk С
Поскольку последовательности {а*/Ь*}£5^, (WaA:}/£=Ar
сходятся, то они ограничены. Поэтому найдутся такие
положительные числа М и L, что
0<^^М, 0 < — ^ L, А; е N.
Следовательно, для любых натуральных чисел к верны
неравенства
ак < МЪк, Ьк < Lak.
Используя свойство 1.5 рядов и признак сравнения, заключаем,
оо оо
что ряды J2 ак и ^2 Ьк либо одновременно оба сходятся, либо
А:=1 А:=1
одновременно оба расходятся. ►
Отметим, что предельный признак сравнения применим не
только для рядов с ненулевыми членами, но и для
произвольных знакоположительных рядов. Для этого необходимо лишь
предварительно отбросить все члены, равные нулю (при этом,
согласно свойству 1.4, сходимость или расходимость рядов не
нарушится).
Следствие 1.2. Если знакоположительные
последовательности {ак} и {Ьк} с ненулевыми членами (ак > 0, Ък > 0, к G N)
являются эквивалентными бесконечно малыми, т.е.
у = х>
0к
то ряды ^2 ак и ]С Ьк сходятся и расходятся одновременно.
A:=l jfc=l

48 1. ЧИСЛОВЫЕ РЯДЫ
Пример 1.14. Исследуем на сходимость
знакоположительный ряд
1 1
<v , .„ Зп + 71 — In 71
71=1
Сравним этот ряд с геометрическим рядом Yl 1/371, Ьп = 1/Зп.
п=1
Найдем предел отношения общих членов этих двух рядов. Для
этого воспользуемся следующими соотношениями сравнения
скоростей роста основных элементарных функций:
lim -^=0, /3>0, aeR; (1.7)
lim — =0, a>l, fieR. (1.8)
Учитывая (1.7) и (1.8), а также арифметические свойства
сходящихся последовательностей, получаем
а Зп 1
lim -^ = lim ;— = lim * = 1.
n-юо bn n->oo Зп+П— mn 71-юо \л- Л lnn n
Отсюда, согласно предельному признаку сравнения, исследуе-
оо
мый ряд Y1 ап сходится, поскольку сходится геометрический
71 = 1
с»
ряд ^2 Ьп (см. пример 1.4, q = 1/3 < 1).
71=1
Пример 1.15. Выясним, сходится ли знакоположительный
РЯД
Поскольку имеют место следующие эквивалентности
бесконечно больших последовательностей:
7п2 + пу/п + 1 ~ 7п2, \/9п6 + 5п5 + 2 ~ V^ = Зп3,

1.4. Знакоположительные ряды. Признаки сравнения 49
ТО
72ftil 7п2
В соответствии с предельным признаком сравнения исследуе-
оо
мый ряд X) an расходится, так как расходится гармонический
71=1
ОО
ряд £ 1/п.
Пример 1.16. Исследуем на сходимость знакоположитель-
оо
ный ряд ^2 an с общим членом
п=1
Найдем такую бесконечно малую последовательность,
эквивалентную последовательности {an}, для которой исследование
на сходимость соответствующего ряда является элементарным.
Согласно (1.7) и (1.8), имеем
,. "3 л 1. 1 л ,. 1п2(п + 1) л
lim — = 0, lim — = 0, lim —Ц L = 0.
п—>^оо еп п—>оо еп п—>оо 4П
Кроме того, lim (sinn/4n) = 0, так как последовательность
п-юо
{sinn/4n} представляет собой произведение бесконечно малой
последовательности {1/4п} и ограниченной последовательности
{sinn} [I-6.7]. Отсюда в силу свойств эквивалентных
бесконечно больших и бесконечно малых последовательностей [1-6]
получаем
4n+ln2(n +
4» " U/ П
ОО
Так как геометрический ряд ^ (е/4) (см. пример 1.4,
п=1
q — е/4 < 1) сходится, то, согласно предельному признаку срав-
оо
нения, ряд ^2 an также сходится.
п=1

50
1. ЧИСЛОВЫЕ РЯДЫ .
1.5. Интегральный признак сходимости Коши
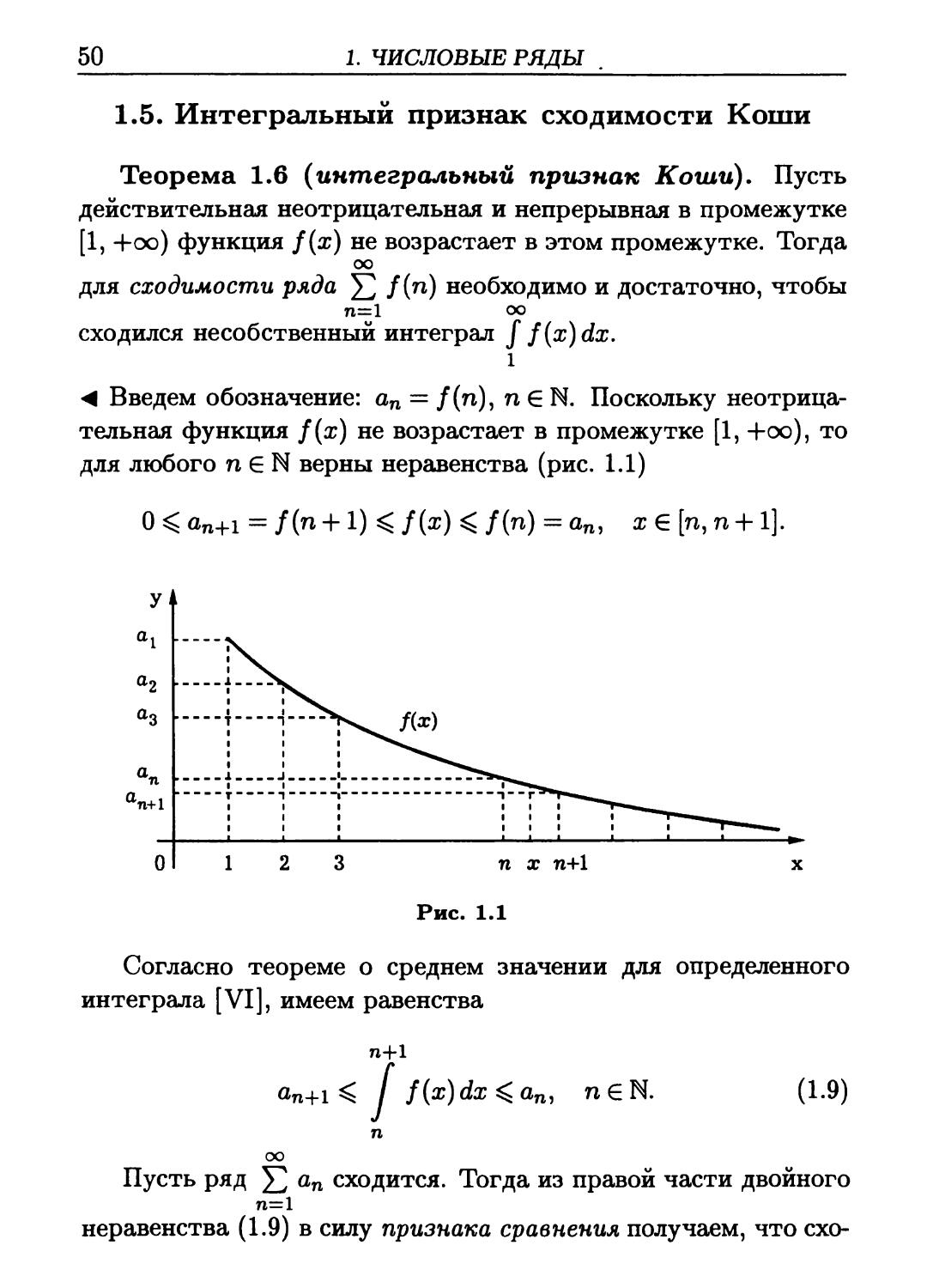
Теорема 1.6 (интегральный признак Коши), Пусть
действительная неотрицательная и непрерывная в промежутке
[1, +оо) функция f(x) не возрастает в этом промежутке. Тогда
оо
для сходимости ряда £) /(^) необходимо и достаточно, чтобы
71=1 ОО
сходился несобственный интеграл f f(x)dx.
l
^ Введем обозначение: ап = /(n), n Е N. Поскольку
неотрицательная функция f(x) не возрастает в промежутке [1, +оо), то
для любого п Е N верны неравенства (рис. 1.1)
0 ^ ап+1 = /(п + 1) < f(x) ^ f(n) = ап, х Е [n, n + 1].
Согласно теореме о среднем значении для определенного
интеграла [VI], имеем равенства
п+1
f(x)dx
(1.9)
Пусть ряд ^ ап сходится. Тогда из правой части двойного
71=1
неравенства (1.9) в силу признака сравнения получаем, что схо-

1.5. Интегральный признак сходимости Коши 51
оо п+1
дится и знакоположительный ряд ^ f f(x)dx. Это означает,
п=1 п
что последовательность
k п+1 *+1
»=1п 1
сходится и, следовательно, ограничена, т.е. найдется положи-
тельное число М, для которого f f(x)dx ^ M, k Е N. Функция
t 1
F(t) = f f(x)dx не убывает в промежутке [1,+оо), поскольку
1
подынтегральная функция является неотрицательной в этом
промежутке. Докажем, что функция F(t) ограничена в [1, +оо).
Действительно, для любого действительного числа t ^ 1
найдется натуральное число к > £, и, значит,
Таким образом, функция F(t) не убывает и ограничена
в промежутке [1, +оо). Следовательно, согласно признаку
Вейерштрасса для монотонной функции [1-7.4], существует
конечный предел функции F(t) при t -> +oo. Это и означает,
что несобственный интеграл сходится:
оо t
ff(x)dx= lim [f(x)dx= lim F(t).
Обратно, пусть теперь сходится интеграл f f(x)dx. Тогда
сходится и ряд
оо
У4 f f(x)dx= lim У" [ f{x)dx= lim [ f(x)dx= [f{x)dx.
n~1 n n=1 n 11

52 1. ЧИСЛОВЫЕ РЯДЫ
Используя левую часть двойного неравенства (1.9), в
соответствии с признаком сравнения получаем сходимость ряда
оо оо оо
1С ап+1 — 1С ап- Отсюда следует, что и ряд $^ ап также схо-
п=1 п-2 п=1
ДИТСЯ. ►
Отметим, что если функция f(x) удовлетворяет условиям
теоремы 1.6 в промежутке [га, +оо), то для сходимости ряда
оо
С f{n) необходимо и достаточно, чтобы сходился несобствен-
п-тп оо
ный интеграл f f(x)dx.
m
Пример 1.17. Исследуем на сходимость ряды:
ОО 1 ОО 4
а)
Так как функции х, lnx, 1п2х в промежутке [2,+оо)
положительны, непрерывны и возрастают, то функции l/(xlnx)
и l/(xln2x) в этом промежутке положительны, непрерывны и
убывают. Следовательно, функции l/(xlnx) и l/(xln2x) в
промежутке [2, +оо) удовлетворяют условиям теоремы 1.6.
Согласно определению несобственного интеграла от ограниченной
непрерывной функции по бесконечному промежутку [VI], имеем:
оо Я Я
dlnx
а) ■ ■ ■
. [ dx Г dx [
) / —— = hm / —— = hm I
J Xlnx R-++oo J xlnx Я-^+ооУ
2
2 2 2
= lim (lnlnR - Inln2) = +оо;
Я Я
Г dx Г dx [dlnx
о) / 9 = hm / ту— = hm / 9 =
J x\nzx я-^-нооу x\rrx я-^+ооУ ln^x

1.5. Интегральный признак сходимости Коши 53
Поскольку в случае (а) несобственный интеграл f dx/(xlnx)
2
расходится, то в силу интегрального признака Коши расхо-
оо
дится и ряд Y1 1/(га In га). В случае (б) несобственный интеграл
оо п=2
f dx/(x\n2x) сходится, следовательно, в силу интегрального
2 оо
признака Коши ряд Y1 1/(га In га) также сходится.
п=2
Пример 1Л8. Исследуем на сходимость ряд Дирихле
Если р ^ 0, то lim 1/гар = lim п~р ф 0, т.е. не выполнен
п—^оо п—^оо оо
необходимый признак сходимости ряда, и ряд ^Г, 1/пр
расходится. n=1
При р > 0 можно использовать интегральный признак Коши,
поскольку функция f(x) = 1/хр в промежутке [1, +оо)
удовлетворяет условиям теоремы 1.6, и ап = 1/пр = /(п). Исследуем
оо
на сходимость несобственный интеграл / l/xpdx.
1
Если р ф 1, то
R
оо R
/ — dx= lim / — = lim ( — J
xp я-^+ооУ xp я-^+оо \ -p + 1 /
l l
Если p = 1, то
оо R
— = lim / — = lim InR = +oo.
x я-и-ооу x я-++оо

54 1. ЧИСЛОВЫЕ РЯДЫ
Таким образом, несобственный интеграл
оо
/ete J сходится при р > 1;
хР \ расходится при р < 1.
Согласно теореме 1.6, получаем следующее утверждение.
~ и ^^ * Г сходится прир>1;
Ряд Дирихле > — —> < ^ Л
^—' пР 1 расходится при р < 1.
n=l v
Пример 1Л9. Исследуем на сходимость ряд
п=2
Отметим, что при р = 1 и р = 2 сходимость данного ряда была
проверена в примере 1.17. Выясним в общем случае, при каких
значениях параметра р данный ряд сходится, а при каких —
расходится.
Так как последовательность {ln~pn}n=2 при р ^ 0 не
убывает, то имеем
_1_ = ЬГРп ^ hr^ n = 2,3,...
(при р = 0 неравенство обращается в равенство). Поскольку
с»
гармонический ряд ^ 1/га расходится (см. пример 1.10), в силу
71=1 ОО
свойства 1.5 расходится и ряд 5^(1п~р2)/п. Следовательно,
71=2
согласно признаку сравнения, при р ^ 0 расходится и ряд
n=2
При р>0 функция 1/(х\прх) в промежутке [2,+оо)
непрерывна, положительна и убывает (функции х и lnpx, p > 0,
непрерывны, положительны и возрастают в [2, +оо)). Таким

1.5. Интегральный признак сходимости Копт 55
оо
образом, исследовать на сходимость ряд ^Г, l/(n\npn) прир > О
п=2
можно с помощью интегрального признака Коши. Выясним,
оо
сходится ли несобственный интеграл J l/(xlnpx)dx. Согласно
2
определению несобственного интеграла от ограниченной
непрерывной функции по бесконечному промежутку [VI], имеем
R R
dlnx
[ dx Г dx [
/ , р = lim / , р = bm /
J Х\ПРХ R-++ooJ x\liPX R-l+ooJ
\прх'
2
Используя замену переменных в определенном интеграле [VI],
получаем
.. f dlnx г 1 Г du
hm / —— = \u = lnx = hm / — =
->+ooy lnpx L J я->+оо J up
2
oo
- [*a
In 2
oo
j сходится при р > 1;
\ расходится при р < 1
In 2
(см. аналогичный интеграл в примере 1.18). Следовательно,
оо
/
dx ( сходится при р > 1;
xlnpx \ расходится при р ^ 1,
2
и в силу интегрального признака Коши для положительных
оо
значений р имеем расходимость ряда £ l/(nlnpn) при 0 <р ^ 1
п=2
и сходимость при р > 1.
Итак, учитывая доказанную расходимость ряда при р ^ О,
получаем следующее утверждение.
1 Г сходится при р > 1;
_ nlnpn \ расходится при р ^ 1.

56 1. ЧИСЛОВЫЕ РЯДЫ
При исследовании рядов на сходимость часто используют
оо
признаки сравнения с рядами Дирихле ^ 1/пр и геометри-
71=1
с»
ческими рядами ]Г] Яп- Рассмотрим далее несколько таких
71=1
примеров.
Предварительно отметим, что при решении задач на
исследование сходимости рядов с использованием предельного
признака сравнения необходимо иметь в виду следующие основные
соотношения эквивалентности бесконечно малых функций
(последовательностей) [1-10.2]. А именно, если ип — бесконечно
малая функция (последовательность), т.е. lim un = 0, то при
71—КХ>
п -> оо верны соотношения:
smun ~ и
arcsinwn '
tgun ~ ur
arctgtxn -
1 — costzn
715
„±
aUn - 1 ~ (\na)un,
ln(l + txn)-wn;
(l + Wn)a-l^aWr
a>0, a^ 1;
, a > 0, а ф ]
Кроме того, для бесконечно малых функций
(последовательностей) имеет место следующее утверждение [1-10.2]:
«71 ~ Рп, п -> оо
где о(/9п) — функция (последовательность), являющаяся при
п -> оо бесконечно малой более высокого порядка малости по
сравнению с функцией (последовательностью) (Зп.
Пример 1.20. Исследуем на сходимость
знакоположительный ряд
п + In2 n + arctg n2

1.5. Интегральный признак сходимости Копт 57
Рассмотрим общий член данного ряда. Числитель
Inf 1 + sin -) + e1/n - cos -
V га/ n
есть бесконечно малая последовательность. Сравним числитель
с бесконечно малой 1/га при га -» оо. Имеем следующие
соотношения:
/ . 1\ .1 / . 1\ 1 /1\
In 1 + sin— J = sin— + o sin— = — + o[ — , ra -> oo;
ei/n - cos i = (e1/71 - l) + (l - cos i) =
1 /1\ 1 / 1\ 1 /1\
n \nJ 2n2 \n2/ n \n/
lnfl + sin-) +e1/n-cos- = -+o(-) +
V n/ n n \n/
1 /1\ 2 /1\ 2
H ho - =-+o - ~-, n
n \n/ n \n/ n
oo.
Знаменатель га + In2ra + arctgra2 общего члена исследуемого ряда
есть сумма бесконечно больших функций га, In2 га и
ограниченной функции arctgra2 (0 < arctgra2 < тг/2, га Е N), причем из (1.7)
следует, что функция га является бесконечно большой более
высокого порядка, чем функция In2 га. Таким образом, согласно
теоремам об эквивалентных бесконечно больших функциях
(последовательностях) [1-10.4], имеем
га + In2ra + arctgra2 ~ га, га -> оо.
Следовательно,
1 1
—, га-»оо.
га + In ra + arctg га2 га
Окончательно получаем
га + In2га + arctgra2 га га га
2
- = —z, га-»оо.

58 1. ЧИСЛОВЫЕ РЯДЫ
оо
Так как ряд ^ 1/п2 сходится (это ряд Дирихле с параметром
71=1
р = 2 > 1), то в силу предельного признака сравнения сходится
и исходный ряд.
Пример 1.21. Исследуем на сходимость
знакоположительный ряд
^ р>0.
п=2
Если q ^ 0, то для всех п > 3 верно неравенство ln9n/ra1+p ^
^ 1/п1+р, так как Inn > 1 при п > 3. Поскольку ряд Дирихле
оо
£) 1/п1+р при р > 0 сходится, то в силу признака сравнения
71=1 ОО
сходится и ряд J2 In9 n/nl+p при всех g ^ 0 и р > 0.
п=2
Если q > 0, то, согласно равенству (1.7), имеем
1пп Л
hm —72=°' Р>0-
Сходящаяся последовательность {in9n/np/2} ограничена, т.е.
можно найти такое положительное число М, что
^м 23
Следовательно,
с»
Поскольку ряд Дирихле ^ 1/п1+р/2, р > 0, сходится, то, соглас-
71=1
но признаку сравнения, будет сходиться и ряд
71=2

1.5. Интегральный признак сходимости Копт 59
Итак, верно следующее утверждение.
сходится при q е R, р > 0.
Пример 1.22. Докажем расходимость
знакоположительного ряда
71=2
Из (1.7) следует равенство
lim -—— = +00, /9<1,
►+00 \npn
которое по определению предела эквивалентно утверждению:
Ve>0 3M(e)eN Vn>M(e):
Пусть e = 1. Тогда для всех номеров п, больших некоторого
натурального числа М, зависящего от /3 и р, будет справедливо
неравенство
1 1 п1-^
n iP '
Следовательно,
С»
Отсюда в силу расходимости гармонического ряда £) 1/п (см.
п=1
пример 1.10) и признака сравнения следует расходимость ряда
п=2
Итак, приходим к следующему утверждению.

60 1. ЧИСЛОВЫЕ РЯДЫ
Пример 1.23. Докажем сходимость знакоположительного
ряда
Из равенства (1.8) следует, что при любых р Е R и q > 1 верно
соотношение lim np/(y/q) = 0. Сходящаяся последовательность
п-юо v v '
{np/[y/q) } ограничена, т.е. можно найти такое положительное
число М, что
пр
Следовательно,
с»
с» оо
Геометрический ряд ^ l/(y/q) = ^ {l/y/q) при g > 1 схо-
п=1 п=1
дится (см. пример 1.4), поскольку при этом 0 < l/y/q < 1.
Таким образом, согласно признаку сравнения, приходим к
следующему утверждению.
Ряд 2^ — сходится при р е R, q > 1.
1.6. Признак Даламбера
Важным признаком сходимости знакоположительных
числовых рядов является следующий признак.
Теорема 1.7 (предельный признак Даламбера). Пусть
для числового ряда с положительными членами
an, an>0, nGN, (1.10)
n=l

1.6. Признак Даламбера 61
существует предел (конечный или бесконечный)
последовательности отношений an+i/an общего члена ряда an+i к
предыдущему члену ап:
г an+i ^ п
lim = q, q^O.
n-юо an
Тогда справедливы следующие утверждения:
а) если q < 1, то ряд (1.10) сходящийся;
б) если q > 1 или q = +оо, то ряд (1.10) расходящийся.
<4 а. Пусть lim an+i/an = g < 1. Для числа г = (q+ l)/2 верно
и—юо
неравенство g < г < 1. Поэтому lim (an+i/an — г) = q — г < 0.
Из свойств сходящихся последовательностей [1-6.4] вытекает,
что
3n0eN Vn^n0: ^±i^r<l. (1.11)
Учитывая (1.11), для любого натурального числа к имеем
Qno+1 ^„ anp+2 ^ м Qno-|-A; ^ м
^ Т, ^ Г, ^ г.
Следовательно,
ano
Отсюда получаем, что ano+k ^ anorA;> ^ ^ N.
Если п — произвольное натуральное число, для которого
п ^ по, то, полагая к = п — по, получаем неравенство
пп ^ rnor '
Это неравенство позволяет применить признак сравнения для
доказательства сходимости ряда (1.10). Действительно, в силу
условия 0 < г < 1 геометрический ряд
с»
г =
jno rno—l
п—\ п=1

62 1. ЧИСЛОВЫЕ РЯДЫ
сходится. Таким образом, согласно признаку сравнения, ряд
(1.10) также сходится.
б. Пусть lim an+i/an = q, причем q > 1 или q = +оо. Если
п—юо
q ф +оо, то положим г = (q + 1)/2, а если q = +oo, то в
качестве г возьмем любое число, большее единицы. Тогда 1 < г < q и
lim (an+i/an — r)=s, где s = q — r>0 при q ф +оо или 5 = +oo
n—foo
при q = +oo. Из свойств последовательностей, имеющих
положительный предел (конечный или бесконечный) [1-6] получаем
3n0eN Vn^n0: ^2±1>г>1. (1.12)
Тогда
О < апо < ano+i < ano+2 < < an0+k <
Следовательно, предел последовательности {ап} не может быть
меньше числа апо > 0. Таким образом, не выполняется
необходимый признак сходимости ряда, и ряд (1.10) расходится. ►
Замечание 1,2. Теорема 1.7 не охватывает случай, когда
lim
n-юо ап
с»
Здесь ничего определенного о сходимости ряда ^ ап, ап > О,
п=1
заранее сказать нельзя (невозможно воспользоваться
предельным признаком Даламбера). Для выяснения вопроса о
сходимости такого ряда требуется дополнительное исследование.
с»
Например, для расходящегося гармонического ряда ]Г) 1/п пре-
п=1
дел последовательности отношений an+i/an равен единице:
1 1т an+l т Л
an+i = ——г, an = - ==> hm = lim —— = 1.
п +1 п п-+оо ап п-+оо п + 1

1.6. Признак Даламбера 63
Однако для сходящегося ряда Yl Vn2 (это РЯД Дирихле с
п=1
показателем степени р = 2 > 1) соответствующий предел
последовательности отношений an+i/an также равен единице:
1 1 ,. an+i ,. п2
= a = =* lim = llm = l
Замечание 1.3. Анализируя доказательство теоремы 1.7,
замечаем, что выводы о сходимости и расходимости ряда (1.10)
были сделаны из условий (1.11) и (1.12). Это позволяет
сформулировать более общий по сравнению с предельным признаком
Даламбера достаточный признак сходимости
знакоположительных рядов, который обычно называют признаком Долам-
бера:
1) если существует такое число q G (0,1), что для любого
натурального числа п ^ по верно неравенство an+i/an ^ g, то
ряд (1.10) сходится;
2) если для любого натурального числа п ^ по верно
неравенство an+i/an^l, то ряд (1.10) расходится.
Пример 1,24, Исследуем на сходимость ряд с
положительными членами
Используя предельный признак Даламбера, видим, что
исходный ряд сходится:
ап =
2-5-8-...-(3n-l)-(3n + 2) Зп + 2
a
r an+i 3n + 2 3^n
lim —— = lim = - < 1.
an П-+ОО 5n +1 5

64 1. ЧИСЛОВЫЕ РЯДЫ
Пример 1.25. Исследуем на сходимость ряд с
положительными членами
f (Зп)!
n=l
Напомним, что по определению п! = 1 • 2 • 3 •... • п. Применим
предельный признак Даламбера:
(Зп)!
ап =
(п!)343п>
(3(п+1))1 _ (Зп + 3)!
_ (Зп)!(3п + 1)(3п + 2)(3п+3) _ оп(3п+1)(3п+2)(3п+3)
(п!)3(п+1)343"-64 ~ 64(п+1)3
.. an+i .. (Зп + 1)(3п + 2)(3п + 3) 27п3 27
lim = lim — г"5 = lim „л Q = — < 1.
П-+00 ап п->оо 64(п + 1)'3 П-ЮОО47Т3 64
В силу теоремы 1.7 заключаем, что исследуемый ряд сходится.
Пример 1.26. Исследуем на сходимость
знакоположительный ряд
ОО
n=l
Очевидно, что при а = 0 ряд сходится. Пусть а > 0. Тогда
получаем ряд с положительными членами, для анализа которого
воспользуемся предельным признаком Даламбера. Имеем
п\ап
а>п = ——,
пп
(n + l)!an+1nn _ апп / п у_ а
' {п + 1)п{п + 1)п\ап " (n + l)n "aVn + l/ ~Л+Г\П"

1.6. Признак Даламбера 65
Известно, что lim (l + 1/n) = е (второй замечательный
п-юо4 '
предел [1-6.6]). Учитывая это, получаем
lim = hm
п-юо an п-юо
Тогда из теоремы 1.7 следует, что если а < е, то исходный ряд
сходится; если же а > е, то ряд расходится.
Если a = е, то lim an+\/an = 1 и предельным признаком
п—юо
Даламбера нельзя воспользоваться. Исследуем этот случай
отдельно. Известно, что последовательность |(1 + 1/п)п}
монотонно возрастает [1-6.6]. Следовательно,
(1 + - ) < е, n e N.
V п/
Поэтому при a = e имеем
Согласно признаку Даламбера (см. замечание 1.3), исходный
ряд при a = e расходится.
Итак, приходим к следующему утверждению.
п\ап Г сходится при 0 < а < е,
пп \ расходится при а ^ е.
Из примеров 1.24-1.26 ясно, что предельный признак
Даламбера особенно эффективно можно применять для
исследования на сходимость рядов с общим членом, представимым в
виде дроби, числитель и знаменатель которой являются
произведениями п первых членов некоторых последовательностей.

66 1. ЧИСЛОВЫЕ РЯДЫ
1.7. Радикальный признак Коши
Важным признаком сходимости знакоположительных
рядов является предельный радикальный признак Коши.
Теорема 1.8 (предельный радикальный признак
Косо
ши). Пусть для знакоположительного ряда ]Г) ап, ап > 0, п Е N,
п=1
существует (конечный или бесконечный) предел
lim ^a^ = q.
n-юо
Тогда справедливы следующие утверждения:
оо
а) если q < 1, то ряд ]Г] ап сходящийся]
п=1 с»
б) если q > 1 или q = +оо, то ряд ^2 ап расходящийся.
< а. Пусть lim tf/a^ = q < 1. Число г = (q + l)/2 удовлетворяет
п—юо
неравенству ^ < г < 1. Поэтому lim (v/a^ — г) = q — г < 0. Из
п—>с»
свойств сходящихся последовательностей [1-6.4] следует, что
г<1. (1.13)
00
Отсюда ап < гп для любого п ^ по- Геометрический ряд ^ ^п
п=1
сходится, так как 0 < г < 1. Поэтому, согласно признаку
с»
сравнения, ряд ]Г] an также сходится.
п=1
б. Пусть lim v/a^ = о, причем a > 1 или 5 = +оо. Если
n->oo v
q ф +оо, то положим r = (q + 1)/2, а если ^ = +оо, то в качестве
г возьмем любое число, большее единицы. Тогда 1 < г < q и
lim ( q/a^ — г) = 5, где s = q — г > 0 при g 7^ +°°» или s = +00
(
при g = +00.
В силу свойств последовательностей, имеющих
положительный предел (конечный или бесконечный) [1-6], заключаем, что
T>\. (1.14)

1.7. Радикальный признак Копт 67
Поэтому
an > 1, n ^ no => lim an ^ 1
П—ЮО
при условии, что этот предел существует. Таким образом,
в любом случае (существует предел последовательности an
или нет) не выполнен необходимый признак сходимости ряда.
оо
Следовательно, ряд ]Р ап расходится. ►
п=1
Замечание 1.4. Так же как и в случае предельного
признака Даламбера, если
lim \/a^= 1,
п-юо
то предельный радикальный признак Коши использовать не-
оо
льзя, т.е. ряд ]П an, an ^ 0, может оказаться как сходящимся,
п=1
с»
так и расходящимся. Рассмотрим, например, ряды ]Р 1/п и
п=1
00
X) 1/п2. Первый ряд — гармонический, он расходится; вто-
п=1
рой — рл^ Дирихле с параметром р = 2, он сходится. Однако
для этих рядов
lim r/= 1, Um Д
п->оо у п lim ^/n п-^с» у п
у 2
При решении задач с использованием предельного
радикального признака Коши полезно помнить, что
lim \/n" = l, абШ
п—>оо
Действительно,
lim V^= lim па/п = lim elnna/n =
71>
П—>СХ) П—ЮО
а inn lim
= lim е п =
п->оо

68 1. ЧИСЛОВЫЕ РЯДЫ
Замечание 1,5. Анализируя доказательство теоремы 1.8,
замечаем, что выводы о сходимости и расходимости знакопо-
оо
ложительного ряда ^ ап были сделаны из (1.13) и (1.14), что
71=1
позволяет сформулировать более общий по сравнению с
предельным радикальным признаком Коши достаточный признак
сходимости знакоположительных рядов, который обычно
называют радикальным признаком Коихи:
1) если найдется число g < 1, такое, что для всех п, начиная
с некоторого номера по, выполняется неравенство tfa^ < g, то
с»
ряд Yj an сходится;
п=1
2) если же для любого п ^ щ выполняется неравенство
оо
q/a^ ^ 1, то ряд £ ап расходится.
71=1
Пример 1.27. Исследуем на сходимость с помощью
предельного радикального признака Коши знакоположительный
РЯД
71=1
Вычислим
)o
= - < 1.
, _. у
Следовательно, исследуемый ряд сходится.
Пример 1.28. Исследуем на сходимость с помощью
предельного радикального признака Коши знакоположительный
ряд

1.7. Радикальный признак Копт 69
Найдем
lim >/a^= lim \/( -) = lim
n
Таким образом, исследуемый ряд сходится. #
Из примеров 1.27-1.28 ясно, что радикальный признак Ко-
ши удобно использовать для исследования на сходимость рядов,
общие члены которых в качестве сомножителей содержат п-е
степени выражений, зависящих от п.
При анализе сходимости рядов часто бывает полезна также
следующая асимптотическая формула Стирлинга*:
(77, \ п .
— J ч/2тгп, п—юо.
В частности, из формулы Стирлинга следует, что
n! ~ —, п —> оо.
е
В приведенных выше формулах функции в левых и правых
частях являются эквивалентными бесконечно большими
функциями натурального аргумента (последовательностями).
Пример 1.29, Исследуем на сходимость
знакоположительный ряд
*См.: Никольский СМ., т. 1.

70 1. ЧИСЛОВЫЕ РЯДЫ
Используя эквивалентность \/п\ ~ п/е, п —> оо, вычисляем
,. ^! ,. п/е
= hm ^_ = hm ' ^ = +оо,
поскольку
lim - = +00, lim n1/^ = lim eln"1/VS = A ^ = e° = 1.
n—>c» e n—too n—foo
Согласно предельному радикальному признаку Коши,
исследуемый ряд расходится.
1.8. Абсолютная и условная сходимости
В отличие от знакопостоянных (знакоположительных и зна-
коотрицательных) рядов произвольные действительные ряды,
членами которых являются числа разных знаков, называют
знакопеременными рядами, В этом параграфе рассмотрим
произвольные (знакопеременные) действительные ряды и ряды
с комплексными членами. Отметим, что все утверждения,
приведенные в 1,2 и 1.3 (необходимый признак сходимости ряда,
свойства 1.1-1.8, критерий Коши сходимости числового ряда),
справедливы как для действительных, так и для комплексных
рядов.
Определение 1,6. Действительный (комплексный) ряд
с»
J2an, aneR(aneC), (1.15)
п=1
называют абсолютно сходящимся, если сходится
действительный ряд
f>n| (1-16)
п=1
из абсолютных значений (модулей) членов ряда (1.15).

1.8. Абсолютная и условная сходимости 71
Если числовой ряд является абсолютно сходящимся, то
говорят также, что имеет место абсолютная сходимость
этого числового ряда.
оо
Заметим, если Е ап — комплексный ряд, т.е. ап = ап
где а„, /Зп Е R, n E N, то \ап\ = у/^ТЩ и
n=l n=l
оо оо
Теорема 1.9. Комплексный ряд Е an = E (an +i>Pn) яв-
п=1 п=1
ляется абсолютно сходящимся тогда и только тогда, когда
оо
абсолютно сходящимися являются действительные ряды У^ ап
^ а п=1
п=1
оо
^ Пусть ряд Y1 ап сходится абсолютно. Поскольку для любого
натурального числа п верны неравенства
ОО
то в силу признака сравнения из сходимости ряда У\ \ап\
°° °° п=1
следует сходимость рядов X) \ап\ и ]£ 1А»1-
п=1 п=1 оо оо
Пусть теперь сходятся абсолютно ряды Y1 ап и Z) А»-
Поскольку n=1 n=1
то
оо оо
Поэтому из сходимости рядов Y1 \ап\ и Y1 \0п\ в соответствии
п=1 п=\
со свойством 1.6 и признаком сравнения следует сходимость

72 1. ЧИСЛОВЫЕ РЯДЫ
Теорема 1.10. Всякий (действительный или комплексный)
абсолютно сходящийся ряд сходится.
А Пусть ряд (1.15) сходится абсолютно, т.е. сходится ряд
(1.16). Применив к ряду (1.16) критерий Коши сходимости
ряда, получим утверждение
п+т
Ve>0 3N(e)eN Vn>N{e) VmGN: ^2\ak\<e. (1.17)
k=n
Поскольку
п+т
к=п
п+т
к=п
(в частности, для комплексных чисел это неравенство
вытекает из неравенства треугольника [1-4.3]), то из (1.17) следует
утверждение критерия Коши сходимости для ряда (1.15).
Значит, ряд (1.15) сходится. ►
Согласно данной теореме, анализ рядов на сходимость
целесообразно начинать с их анализа на абсолютную сходимость.
Причем, поскольку исследование рядов на абсолютную
сходимость связано с изучением сходимости знакоположительных
рядов (рядов из модулей их членов), признаками абсолютной
сходимости действительных или комплексных рядов являются
признаки сходимости знакоположительных рядов, изложенные
в предыдущих параграфах.
В соответствии с теоремой 1.10 любой абсолютно
сходящийся ряд сходится. Однако условие, что ряд не является
абсолютно сходящимся, не означает, что этот ряд расходится.
Определение 1.7. Действительный или комплексный ряд
оо
X) ап называют условно сходящимся, если он сходится, но
п=1 оо
не является абсолютно сходящимся, т.е. если Y1 ап сходится, а
ряд £ \ап\ расходится.
п=\

1.8. Абсолютная и условная сходимости 73
Если числовой ряд является условно сходящимся, то говорят
также, что имеет место условная сходимость этого
числового ряда.
Замечание 1.6. Согласно теореме 1.9, комплексный ряд
оо
^2 а>п не является абсолютно сходящимся тогда и только тогда,
п=1
когда не является абсолютно сходящимся хотя бы один из рядов
оо оо
^2 ап или X) Рп, где ап = Rean, /3n = Iman, n G N. Таким
п=1 п=1
образом, в силу определения 1.7 и теоремы 1.1 комплексный
оо
ряд Y1 ап является условно сходящимся тогда и только тогда,
п=1 оо оо
когда оба действительных ряда ^ ап и Y1 Рп сходятся и хотя
П=1 71=1
бы один из этих рядов сходится условно.
Пример 1.30. Рассмотрим действительный ряд
n
Ряд из модулей членов этого ряда является гармоническим
рядом и потому расходится. Таким образом, исходный ряд не
является абсолютно сходящимся. Тем не менее ряд сходится.
Для непосредственного доказательства сходимости и
вычисления суммы данного ряда воспользуемся формулой Маклорена
для функции 1п(1 + х), х G [0,1]:
-
п
где остаточный член в форме Лагранжа для функции f(x)
= ln(l + х) имеет вид

74 1. ЧИСЛОВЫЕ РЯДЫ
Отметим,
Переходя
получаем
При х
где Sn —
что при 0 < х < 1
1
Rn(x)\ . ,
п+1
хп+1
(1 + 0Х)'
»+1
. 1
"п+Г
к пределу при п -> оо в последнем неравенстве [1-6.4],
Ymx]iRn{x)\=% ж €[0,1].
= 1
п-я
1 1 (-1)п+1
2 ' 3 '■ ' п '
частичная сумма ряда
Кп{1) n + Rn( ),
оо
(—l)n+1/n. Поскольку
lim |Дп(1)| = 0 и, значит, lim Rn(l) = 0, то lim Sn = In2.
П->ОО П-ЮО П-ЮО
Следовательно,
1 П
и, в частности, рассматриваемый ряд сходится. Наконец,
поскольку он не является абсолютно сходящимся, исследуемый
ряд является условно сходящимся.
Замечание 1.7. Обратим особое внимание на удобство
использования признаков Даламбера и Коти для исследования
ряда на абсолютную сходимость.
Действительно, если при использовании признака
Даламбера или радикального признака Коши (см. замечания 1.3 и 1.5)
для исследования ряда (1.16) на сходимость оказалось, что
или
\ап\
т.е. ряд (1.16) расходится, то будет расходиться и ряд (1.15). В
этом случае не вьгаолняется необходимый признак сходимости
как для ряда (1.16), так и для ряда (1.15), поскольку
lim ап = 0 <=> lim \ап\ = 0.
п—юо п—юо

1.8. Абсолютная и условная сходимости 75
Если при исследовании ряда (1.15) на абсолютную
сходимость с помощью предельного признаки Даламбера или
предельного признака Коши получили, что
цт fe*i > 1 или lim VkJ > 1,
n-юо \ап\ п-юо '
то ряд (1.16) будет расходящимся вследствие невыполнения
необходимого признака сходимости (см. доказательства теорем
1.7 и 1.8). В этом случае в силу тех же соображений, которые
изложены выше, будет расходиться и ряд (1.15).
Пример 1.31. Исследуем на сходимость ряд
П=1
Исследуем этот ряд на абсолютную сходимость. Для выяснения
сходимости ряда
ть(Зг—1)п/Ьп
воспользуемся предельным
тг=1
признаком Даламбера. Обозначая ап =п(3г—1)П/ЬП, получаем
п|3г-11п
Следовательно,
,. K+i| r (n + l)10(n+1)/2bn л/10 .. п + 1 VT0
lim ——— = lim — jz— = —— lim = ——.
n->oo \an\ n->oo Ъп^1П • 10ntz 0 n->oo n 0
oo
Таким образом, если y/lO/b < 1, т.е. b > \/lO, то ряд j^ \an\
n=l
сходится и, следовательно, исходный ряд сходится абсолютно.
00
Если же \/Ш/Ь > 1, т.е. b < \/lO, то ряд ^ \ап\ расходится и,
тг=1
следовательно, исходный ряд не является абсолютно
сходящимся. Более того, исходный ряд в этом случае расходится в силу
невыполнения необходимого признака сходимости ряда.

76 1. ЧИСЛОВЫЕ РЯДЫ
При Ь = УГО предельный признак Даламбера использовать
нельзя. В этом случае \ап\ = п, и поскольку \ап\ = п не
стремится к нулю при п -» +оо, то не выполняется необходимый
оо оо
признак сходимости как для ряда J2 \ап\, так и для ряда £) ап.
п=\ п=1
Следовательно, в этом случае исходный ряд не является
абсолютно сходящимся и не является сходящимся. #
Рассмотрим теперь некоторые свойства абсолютно и
условно сходящихся рядов.
Теорема 1.11 (теорема о перестановке членов аб-
оо
солютно сходящегося ряда). Если ряд Y1 ап сходится
оо п=1 оо
абсолютно, то любой ряд Y1 Ьп, полученный из ряда Y1 ап пе-
п=1 п=1
ресталовкой (изменением порядка суммирования) его членов,
тоже абсолютно сходится. Более того, он имеет ту же сумму,
оо оо
что и исходный ряд: X] Ьп = Y1 ап-
п=1 п=1
оо оо
<4 Пусть ряд Y1 ап сходится абсолютно и 5Z ап = 5 и, кроме
п—\ оо п=\ оо
того, произвольный ряд Y^ Ъп получен из исходного ряда Y1 ап
п=1 п=1
путем некоторой перестановки его членов. Это означает, что
члены бесконечной суммы (ряда) а\ + а^ +... + ап +... сначала
некоторым образом переставили, получив ряд аП1 + аП2 + ... +
+ аПк + ..., в котором на первом месте в бесконечной сумме
стоит некоторый член аП1, на втором месте — некоторый член
аП2 и т.д., а затем члены ряда переобозначили следующим
образом: Ь\ = аП1, &2 = аП2, Ьь = anfc> В результате такой
операции никакой член исходного ряда не теряется, не
повторяется, он просто, быть может, перемещается на какое-то другое
место в бесконечной сумме. Разумеется, в преобразованном
ряде не появляются никакие новые, посторонние члены, не
являющиеся членами исходного ряда.

1.8. Абсолютная и условная сходимости
77
Необходимо доказать, что ряд J2 Ьп сходится и имеет ту
п=1
оо
же сумму S. Поскольку ряд ^ \ап\ сходится, то для этого ряда
п=1
выполняется утверждение критерия Копш, т.е.
п+тп
Ve>0 3iVi(e)GN
VmeN:
^. (1.18)
Так как Yl an = S, то, согласно определению суммы ряда,
имеем n=1
3N2(e)eN Vn>N2(e):
(1.19)
Если iVo = max{JVi,JV2}, TO из (1.18) и (1.19) следует, что
п+т п
/ ; \ак\ < о и I / ;ак "" S < —, n > iVo, m G N.
A;=n A;=l
Зафиксируем какой-нибудь номер щ > iVo, тогда
по
~ и
A;=no
(1.20)
k=l
n
Рассмотрим частичные суммы Sn = ^ Ьд?- Выберем нату-
к=1 N
ральное число N так, чтобы в сумму Sn = Y1 ^к входили в
к=1
качестве слагаемых все члены ai, 0,2, ..., апо. Если п> JV, то
сумма iSn также будет содержать все члены oi, аг» • • • ? аПо. Оце-
ним разность
k=l
— 5 при n > JV, используя (1.20):
По По
no
A;=l

78 1. ЧИСЛОВЫЕ РЯДЫ
Докажем, что первое слагаемое также меньше е/2. Сумма
П 710
53 Ьк содержит сумму 53 ак и еще п—щ слагаемых, каждое из
fc=l A;=l
которых (согласно условию теоремы) есть член ак с некоторым
номером к > по, т.е.
п по
к=1 к=1
где к{ > по, г = 1, п—по. Пусть число m G N таково, что щ + т =
= max{fci, fc2,..., fcn-no}- Тогда
п—по по+т
что в силу (1.20) меньше е/2. Отсюда
: б, п > N,
к=1
п
что доказывает равенство lim ^T,bk = S. Следовательно, ряд
оо
J2 Ьк сходится и его сумма равна S.
к=1 оо
Покажем, что ряд ^ Ьк сходится абсолютно, т.е. сходится
оо к=1
РЯД 53 1^А;|- Из доказанного выше следует, что ряд, полученный
к=1
из знакоположительного сходящегося ряда (он автоматически
является абсолютно сходящимся) путем перестановки его
членов, также сходится и эти ряды имеют одинаковые суммы.
оо
Поскольку знакоположительный ряд 53 1аА;| сходится, а ряд
оо fc=l оо
53 |&fc|, очевидно, может быть получен из ряда 53 1аА;| путем пе-
fc=l оо А;=1
рестановки его членов, то ряд 53 \^к\ тоже сходится (их суммы
к=1 оо
при этом равны). Следовательно, ряд 53 Ьк сходится
абсолютно. ► к=1

1.8. Абсолютная и условная сходимости 79
Для условно сходящихся рядов теорема 1.11, вообще говоря,
неверна. Вернемся к примеру 1.30. Известно, что
ОО /
i n
n=l
После перестановки членов ряда и их группировки получаем
/ 1 1__2
\2А:-1 4Л-2 4к
ОО
2Ч 2
п=1
Группировка членов ряда по три в данном случае не влияет на
его сходимость, так как общий член ряда стремится к нулю.
Итак, в результате перестановки членов рассматриваемого
ряда сумма уменьшилась вдвое. Этот результат, несмотря
на то что кажется парадоксальным, совершенно не случаен.
Более того, применяя различные перестановки членов условно
сходящегося ряда, можно получить любую сумму.
Теорема 1.12 (теорема Римана). Пусть действитель-
оо
ный ряд Y1 ап сходится условно. Тогда для любого действи-
п=1
тельного числа S можно надлежащей перестановкой членов
ОО ОО
ряда Y1 ап получить условно сходящийся ряд ^2 Ъп, сумма ко-
торого равна S. #
Доказательство теоремы приведено в Д. 1.1.
Отметим, что теорема Римана верна и в том случае, когда
S равно +оо или —оо. Можно так переставить члены условно
сходящегося ряда, что последовательность частичных сумм
полученного ряда будет иметь предел, равный +оо или —оо.

80 1. ЧИСЛОВЫЕ РЯДЫ
1.9. Знакочередующиеся ряды
Определение 1.8. Действительный ряд, у которого
любые два соседних члена имеют противоположные знаки,
называют знакочередующимся рядом.
Знакочередующийся ряд можно представить в виде
n = ai - а2 + а3 - ап > 0, nGN,
n=l
если первый член ряда положителен, или в виде
оо
(-\)пап = -ах + а2 - а3 + ... ап > 0, п Е N,
п=1
оо
если первый член ряда отрицателен. Ряды £3 (—l)n+1an и
ОО 71=1
^ (—l)nan являются сходящимися или расходящимися одновре-
п=1
менно, поскольку первый ряд есть произведение второго на
число —1. Поэтому в дальнейшем будем рассматривать только
оо
знакочередующиеся ряды вида ^ (—1)п+1ап, ап > 0.
Для знакочередующихся рядов верен следующий
достаточный признак сходимости.
Теорема 1.13 {признак Лейбница). Пусть знакочереду-
оо
ющийся ряд ^2 (—l)71"1"1^ an > 0, nGN, удовлетворяет усло-
п=1
виям:
2) lim an = 0.
n-юо
Тогда этот знакочередующийся ряд сходится.
< Рассмотрим частичную сумму ряда с номером 2п. Ее можно
представить в виде
ai ~ a2 + аз - а4 + • • • + a2n-i - а>2п =

1.9. Знакочередующиеся ряды 81
Поскольку {п2к-\ — Q>2k) ^ 0 для всех к 6 N, то £2n ^ 0. Кроме
того, S271 — S2(n-i) = Cb2n-i ~ a>2n ^ 0, n € N, и последовательность
{S2n}%Li является неубывающей. Представляя частичную
сумму S2n иначе, получаем, что последовательность {S2n}^L\
ограничена сверху числом а\:
04 + ... + a2n-i - а>2п =
= а1 - («2 - «з) - (О4 - аб) - - («2п-2 - O2n-l) ~ а2п
поскольку {п2к-2 — a2k-i) ^ 0 для всех fc = 2, 3,..., п. В силу
признака Вейерштрасса о сходимости монотонной ограниченной
последовательности [1-6.5] последовательность {S2n}n=i cxo"
дится. Пусть lim S2n = S. Поскольку 52П+1 = ^2п + в2п+ь т0
п—>оо
lim 52n+i = Hm 52n + lim a2n+i =5 + 0 = 5.
n—>oo n—юо n—>oo
В силу определения предела имеем
Iim52n = 5 ^=> Ve>0 3Ni = Ni (e) G N
n->oo
Vn>iV1(e):
lim S2n+i = S *=> Ve > 0 3iV2 = JV2(e) € N
»oo
n-»oo
Пусть N = max{2iVi, 2ЛГ2 + 1}. Если т> N — четное число, то
т = 2п, где п> N\. Поэтому |5т — S\ = |52П — S\ < e.
Аналогично рассматривается случай нечетного т> N. Таким образом,
оо
lim 5m = 5, ряд У2 (—1)п+1ап сходится и имеет сумму 5. ►
п->0° п=1
оо
Следствие 1.3. Если знакочередующийся ряд ^С(~1)п+1ап>
71=1
о>п > 0, п G N, удовлетворяет условиям признака Лейбница, то
его сумма 5 удовлетворяет неравенству 0 < 5 < а\.
Ч В ходе доказательства признака Лейбница было показано,
что последовательность частичных сумм ^гп}0^ является

82 1. ЧИСЛОВЫЕ РЯДЫ
неубывающей и ограничена снизу нулем, а сверху — числом
а\\ 0 < S2n ^ oi« Переходя в этом неравенстве к пределу,
получаем, что предел последовательности {S2n)°°-V равный
5 и совпадающий с суммой ряда, удовлетворяет неравенству
оо
Следствие 1.4. Если знакочередующийся ряд ^{—1)п*1ап,
п=1
ап > О, п Е N, удовлетворяет условиям признака Лейбница,
оо
то модуль суммы всякого его остатка Rn= ]Г) (—
оценивается сверху числом an+i: k=n+i
\Rn\^an+u neK (1.21)
< Если ряд X) (~l)n+lan удовлетворяет условиям признака
71=1
Лейбница, то и любой его остаток с четным номером i?2n =
= ]Г) (—l)fc+1afc удовлетворяет условиям признака Лейбница.
В силу следствия 1.3 имеем оценку для суммы остатка с
номером 2п: 0 < i?2n ^ а2п+ъ и' слеДовательно» |^2п| ^ «2п+ь
оо оо
Ряд (—1) ]Г) (—l)fc+1a^= X) (—l)fcafc, противоположный ос-
fc=2n fc=2n
татку с нечетным номером, также удовлетворяет условиям
признака Лейбница. В силу следствия 1.3 имеем 0 < — i?2n-i ^
^ a2n> и, следовательно, \R2n-i\ ^ а2п- Таким образом, для
любого номера п справедлива формула (1.21). ►
Вернемся к произвольным знакопеременным рядам.
Учитывая соотношения между сходимостью, условной сходимостью
и абсолютной сходимостью рядов (см. 1.8), отметим, что при
исследовании знакопеременных рядов на сходимость следует
придерживаться следующего плана.
1. Исследовать ряд на абсолютную сходимость. Если ряд
оо
^2 \ап\ сходится, то исследование завершается, поскольку в
71=1 ОО
этом случае ряд ^ ап сходится (абсолютно) (см. теорему 1.10).
71=1

1.9. Знакочередующиеся ряды 83
оо
Если ряд ]Г) \ап\ расходится вследствие невыполнения необ-
га=1
ходимого признака сходимости числового ряда ( lim \an\ т^О),
оо чп->оо 7
то lim ап/0и ряд ]Г) ап расходится, а исследование заверша-
ется.
оо
Если ряд X) |ап| расходится, но необходимый признак схо-
п=1
димости выполнен ( lim \ап\ = 0), то переходим к п. 2.
2. Исследовать ряд на условную сходимость. Если при этом
ряд является знакочередующимся, то при условии монотонного
стремления к нулю последовательности {\ап\} можно
использовать признак Лейбница.
Пример 1.32. Исследуем на сходимость
знакочередующиеся ряды:
71=1 V 71 = 1
71=1 71 = 1
а. Проверим сначала, сходится ли ряд абсолютно. Для этого
составим ряд из модулей его членов:
(_1)п-и
71=1
Этот ряд, как ряд Дирихле с параметром р = 1/2 < 1,
расходится (см. пример 1.18). Итак, исследуемый ряд не является
абсолютно сходящимся. Но |(—1)п+1/у/п\ -> О при п -» оо, и
необходимый признак сходимости ряда выполнен. Исследуем ряд
оо
на условную сходимость. Данный ряд имеет вид X) (~ 1)п4*1ати
71=1
где ап = 1/у/п, т.е. является знакочередующимся, причем
последовательность {l/i/n}^ монотонно стремится к нулю. Уело-

84 1. ЧИСЛОВЫЕ РЯДЫ
вия признака Лейбница выполнены. Согласно теореме 1.13,
оо
ряд 2 (—1)п+1/л/™ сходится. Таким образом, исследуемый ряд
га=1
является условно сходящимся.
б. Выясним, сходится ли ряд абсолютно. Составим ряд из
модулей его членов:
оо
оо , о
Е, г\п'п
1 ~
1
Этот ряд расходится (см. пример 1.13), поэтому исследуемый
ряд не является абсолютно сходяпщмся. Выясним, имеет ли
место условная сходимость. Докажем, что для некоторого
остатка исследуемого ряда вьшолняются условия признака Лейбница.
Ряд имеет вид
71=1 71=1
значит, он является знакочередующимся, причем lim an =
71—ЮО
= lim In2 п/п = 0. Покажем, что при некотором выборе нату-
71-ЮО
рального числа по последовательность {In2 n/n}£°_no будет не-
возрастающей. Для этого рассмотрим функцию (р(х) = 1п2х/х,
х ^ 1, и вычислим ее производную:
,, ч 21nz(l/s)z-ln2z 21nz-ln2z lnz(2~lnz)
*{х) = ^ = —^— = —?—
Видно, что <р'(х) < 0 при х > е2. Поэтому функция ip(x)
убывает в промежутке (е2, +оо) [II], а также убывает
последовательность {ln2n/n}£°_no, начинающаяся с номера по = 8 > е2.
оо
Согласно признаку Лейбница, ряд Yl (—I)11"*1 In2 п/п сходится,
п=8
оо
и, следовательно, сходится ряд Yl (—I)71"1 In2 п/п. Итак, иссле-
71=1
дуемый ряд сходится условно.

1.10. Умножение рядов 8 5
в. Исследуем ряд на абсолютную сходимость:
71=1
п=1
Проверим, выполняется ли необходимый признак сходимости
ряда:
hm I 1 = hm -, ттп = lim "7 тпг = ~ т1 0.
п-^оо \ п + 1 / п-»оо / п+ 1 \ ^°°[1 I I ] в
Необходимый признак сходимости ряда не выполнен, поэтому
ряды JIGHhrи SS~^расходятся-
г. Исследуем ряд на абсолютную сходимость. Рассмотрим
ряд, составленный из модулей его членов:
n=l
Воспользуемся радикальным признаком сходимости Коши:
=Q L
Следовательно, ряд 2^ ( ] сходится, и, значит, исследуе-
ОО о
мый ряд У2 (— -)п также сходится, причем абсолютно.
n=l 2n+1
1.10. Умножение рядов
В 1.3 для рядов были введены арифметические операции
сложения рядов и умножения ряда на число. Определим
операцию умножения ряда на ряд.

86 1. ЧИСЛОВЫЕ РЯДЫ
оо оо
Рассмотрим два произвольных числовых ряда Y1 ап и ^2 Ьп.
га=1 га=1
Составим бесконечную таблицу (матрицу), элементами
которой являются всевозможные произведения ambk членов этих
рядов (рис. 1.2).
0464
Рис. 1.2
Элементы таблицы можно различными способами
занумеровать, представив таким образом таблицу в виде некоторой
последовательности {vn}£Li- Например, нумерацию можно
начать с верхнего левого угла и далее продолжить по диагоналям,
как показано стрелками на рис. 1.2:
Занумеровав элементы таблицы (см. рис. 1.2) каким-либо
способом (не обязательно продемонстрированным выше), получим
некоторую числовую последовательность {vn}^Ll, любой член
которой является произведением некоторых членов ат и Ьк ря-

1.10. Умножение рядов 8 7
оо оо
дов ^ ап и Y1 Ьп- В соответствии с этой последовательностью
п=1 71=1
оо оо
{t>n}£Li составим ряд Yl vn- Всякий числовой ряд X) vn, по-
71=1 71=1
лученный таким способом, называют произведением рядов
оо
п=1 п=1
Сходимость и сумма произведения рядов, вообще говоря,
зависят от последовательности {уп}™=1, т.е. от способа
нумерации элементов таблицы (см. рис. 1.2). Однако если какое-либо
оо оо
произведение рядов ^) ап и ^ Ьп является абсолютно сходя-
71=1 71=1
гцимся рядом и имеет сумму 5, то, согласно теореме 1.11, и
оо оо
любое другое произведение рядов £) ап и ^ 6П, использующее
71=1 71=1
иную нумерацию слагаемых аш6^, абсолютно сходится и имеет
ту же сумму 5.
оо оо
Теорема 1.14 (теорема Коши). Если ряды ]Г) ап и ^ 6П
71=1 71=1
сходятся абсолютно и имеют суммы А и В соответственно, то
любое произведение этих рядов сходится абсолютно и имеет
сумму АВ.
оо оо оо
< Пусть Yl vn — произведение рядов ^ ап и ^ Ьп. Для
71=1 71=1 71=1
любого натурального числа N рассмотрим первые N членов
этого ряда: vi = amibkl, v2 = am2bk2, ..., vN = аШдгhN. Полагая
N* =max{mi, ...,mN, fci,..., kN}, получаем
n=l
oo oo
Согласно условию теоремы, ряды ^ \ат\ и ^ |&аг| сходятся, i,
m=l k=l
значит, последовательности их частичных сумм ограничены.
Учитывая неравенство (1.22), видим, что последовательность

88
1. ЧИСЛОВЫЕ РЯДЫ
частичных сумм знакоположительного ряда X) \vn\ ограниче-
га=1
на, и, следовательно, ряд сходится (см. 1.4). Таким образом,
оо оо оо
произведение Yl vn рядов ^) ап и ]Г) Ъп является абсолютно
п—\ га=1 п=1
сходящимся рядом. Обозначим его сумму S.
оо
В силу теоремы 1.11 любое другое произведение рядов ^ а>п
ОО 71=1
и J2 Ьп также будет абсолютно сходящимся к числу 5 рядом.
71=1 оо оо
Рассмотрим произведение рядов J]an и ]Г) 6П,
составлений 71=1
ное следующим образом. Располагая всевозможные
произведения ambk в бесконечной таблице, занумеруем их, начиная с
произведения а\Ь\^ в соответствии с указанными в таблице
направлениями стрелок (рис. 1.3). В результате такой нумерации
элементов таблицы получаем следующее произведение рядов
оо оо
71=1 71=1
ОО
(I-23)
71=1
1 I
CLlbl 1 O1&2
' \
Q,2,0\ •+— Q>2^2
CLqO\ •*— CI3O2 "
Qi^O\ -+— Q4Q2 -»
0164
I
0/2^4
CI3D4
Рис. 1.3

1.10. Умножение рядов 8 9
Составим из этого ряда новый ряд, расставив скобки в ряде
(1.23) следующим образом:
+ ^263 + «зЬз + ^362 + ash) + ... (1.24)
(порядок членов исходного ряда при этом не изменяется).
Очевидно, что общий член Sn последовательности частичных сумм
ряда (1.24) равен произведению (ai+a2+...+an) (61+62+.-.+Ьп)-
Кроме того, последовательность {Sn} является подпоследова-
оо
тельностью частичных сумм сходящегося к числу S ряда ^2 vn
га=1
и, следовательно, также сходится к S: lim Sn = 5. Однако,
оо оо п—юо
поскольку ряды X) ап и Z) Ьп имеют суммы, равные А и В
п=\ п=1
соответственно, имеем
lim (ai + п2 + ... + ап) = A, lim (61 + 62 + ... + Ьп) = В.
п-юо п-юо
Следовательно,
5 = lim Sn = lim (ai + a2 + ... + an)(&i + 62 + •.• + bn) =
n>oo n>oo
= lim (ai + a2 + ... + an) lim (61 + 62 + • • • + bn) = AB. ►
n->oo n-too
00 00
Если ряды Yl an и Yl Ъп не являются абсолютно сходящи-
n=l n=l
мися, то сходимость и сумма произведения этих рядов зависят
от способа нумерации членов ambk^ составляющих это
произведение. На практике часто используют правило умножения
рядов, которое заключается в том, что составляют ряд,
членами которого являются суммы элементов таблицы на рис. 1.2,
расположенных по ее диагоналям:
n=l

90 1. ЧИСЛОВЫЕ РЯДЫ
оо
Построенный таким образом ряд J2 °п с общим членом Сп =
71=1
= а\Ъп + a2bn-i + + °>nb\ называют произведением рядов
оо оо
J2 ап и Z) &n e форме Коши. Для произведения рядов в
71=1 П=1
форме Коши справедлива следующая теорема.
Теорема 1.15 (теорема Мертенса)*. Если из двух схо-
оо оо
дящихся рядов Y1 ап и Y1 Ьп хотя бы один сходится абсолютно,
71=1 71=1
то их произведение в форме Коши сходится и имеет сумму,
равную произведению сумм этих рядов. #
оо l
Пример 1.33. Рассмотрим произведение рядов ^ _1 и
оо / i)n-l n=l
^2 в форме Коши. Первый ряд знакоположительный
71=1 П
и имеет сумму, равную 2 (см. пример 1.3). Второй ряд условно
сходится, и его сумма равна In 2 (см. пример 1.30). Согласно
теореме Мертенса, произведение этих рядов в форме Коши
сходится и имеет сумму 2 In 2:
fc2"-fc =21n2-
71=1 fc=l
1.11. Оценки сумм рядов
Часто, когда вычислить точную сумму ряда не
представляется возможным, ограничиваются приближенным значением
этой суммы. Для приближенного вычисления суммы S произ-
оо
вольного ряда Y2 Ь^ с заданной точностью 6 > О находят его
к=\
частичную сумму Sn с таким номером п, для которого модуль
*См.: Ильин В.А., Садовничий Б.Л., Сендов Бл.Х.

1.11. Оценки сумм рядов 91
суммы n-го остатка ряда не превышает заданной точности:
оо
k=l
где п е N таково, что \S - Sn\ = \Rn\ < S. Для экономии
вычислений номер п при этом стараются выбрать минимально
возможным.
Наиболее просто оцениваются суммы знакочередующихся ря-
оо
Зое. В самом деле, если знакочередующийся ряд ^ (—1)п+1ап,
п=Х
ап > 0, удовлетворяет условиям признака Лейбница, то,
согласно следствию 1.4, абсолютная погрешность суммы ряда,
вычисленной приближенно с помощью некоторой n-й частичной
суммы этого ряда, не превышает модуля первого отброшенного
члена ряда:
Поэтому для обеспечения заданной точности S оценки S « Sn
достаточно найти такой номер п, что an+i < 5.
Пример 1.34. Докажем, что ряд
п=1
сходится, и вычислим приближенное значение его суммы с
точностью до 0,01.
Данный ряд сходится абсолютно, поскольку сходится ряд
оо оо
^2 \ап\ = ^2 1/(п3+1) из модулей его членов. Это следует из
п=1 п=1
предельного признака сравнения, в котором в качестве ряда
оо
сравнения нужно взять сходящийся ряд Дирихле ^ 1/п.
п=1
Вычислим теперь сумму исходного ряда с заданной
точностью. Для этого необходимо найти такой наименьший номер

92 1. ЧИСЛОВЫЕ РЯДЫ
оо
n E N, при котором для исследуемого ряда £ (—1)п/(п3+1) бу-
п=1
дет выполняться неравенство
\S-Sn\< 0,01,
ОО
где S = £ (-1)*/(*3+1), Sn = £ (-1)*/(А;3+1). Поскольку
исследуемый ряд является знакочередующимся и удовлетворяет
условиям признака Лейбница (1/(п3+1) стремится к нулю при
п -> оо, монотонно убывая), то
Следовательно, достаточно найти минимальное число п Е N, для
которого выполняется неравенство
(п + 1)3 + 1 '
Преобразуем это неравенство: (п + I)3 + 1 > 100, п + 1 > s/99,
п > v^99 — 1 = 3,62... В результате находим, что п = 4. Таким
образом,
п=1
С ТОЧНОСТЬЮ ДО 0,01. #
Если сходящийся ряд не удовлетворяет условиям признака
Лейбница, то модуль суммы Rn его n-го остатка, вообще
говоря, уже нельзя оценивать по формуле (1.21). Для оценки
\Rn\ при этом используют другие приемы. Например, если ряд
знакоположительный, то его остаток оценивают сверху рядом,
сумму которого можно вычислить.

1.11. Оценки сумм рядов 93
Пример 1.35. Оценим погрешность, возникающую при
замене суммы ряда
ОО -
суммой его первых п членов. Вычислим сумму ряда с
точностью до 0,001.
Рассмотрим сумму Е^ остатка с номером п:
ОО -
= V -
5*fc!(2fc
+ 5"+2(n + 2)!(2n + 5) + 5n+3(n + 3)!(2n + 7)+"'"
2n + 3
+ 5(n + 2)(2n + 5) +
2n + 3
, ,
5"+1(n+l)!(2n+3)V fr{ 5fc(n + 2)... (n+fc+1) (2(n+fc)+3)
Поскольку
2"+3 ^ I ^ 1 ,,.
2(n+fc) + 3 ' (n + 2)(n + 3)...(n
то имеем оценку
1
)•
5n+10
5n+10
5Л+Нп+1)!(2п+3) 5n+9
(см. пример 1.4, значение суммы геометрического ряда при
g = l/(5n + 10)).

94 1. ЧИСЛОВЫЕ РЯДЫ
Используя полученную оценку, определяем, сколько членов
ряда необходимо просуммировать, чтобы обеспечить заданную
точность:
0 Л
20
Следовательно, для достижения заданной точности достаточно
просуммировать три члена ряда (п = 2), что дает
Дополнение 1.1. Доказательство теоремы
Римана об условно сходящихся рядах
оо
Докажем теорему 1.12 (теорему Римана). Пусть ^2 ап —
п=1
условно сходящийся ряд. Рассмотрим последовательность
неотрицательных членов ряда (перенумеруем эти члены, не
нарушая их естественного порядка следования, и обозначим
полученную последовательность {щ}^) и последовательность
модулей отрицательных его членов (их также перенумеруем, не
нарушая их естественного порядка следования, и обозначим
полученную последовательность {^ШО- Покажем, что обе
эти последовательности бесконечны. Действительно, обе
последовательности одновременно конечными, очевидно, быть не
могут. Если только одна последовательность, например после-
оо
довательность неотрицательных членов ряда 5Z ап> оказалась
71=1

Д. 1.1. Доказательство теоремы Римана 95
конечной, то, отбрасывая все первые члены этого ряда вплоть
до последнего неотрицательного, получаем знакопостоянный
(знакоотприцательный) ряд, который сходится и расходится
одновременно с исходным рядом (см. свойства рядов в 1.3), т.е.
является условно сходящимся рядом. Но знакопостоянный ряд
не может быть условно сходящимся, если он сходится, то
только абсолютно. Значит, последовательность неотрицательных
оо
членов условно сходящегося ряда Y1 ап не может быть конеч-
п=1
ной. Аналогично можно доказать, что и последовательность
оо
отрицательных членов условно сходящегося ряда Y1 ап не
может быть конечной. n=1
Составим теперь из последовательностей {м*}^ и {^}°2.1
оо оо
два знакоположительных ряда: ]П щ и ]П vi. Поскольку исход-
оо г=1 г=1
ный ряд Y^ai сходится, то, согласно необходимому признаку
г=1
сходимости числового ряда, выполняется равенство lim щ =
i—юо
= lim \п{\ = 0. Так как {uj}0^ и {^г}^1 являются подпосле-
i>oo
довательностями {К!}0^, то
lim щ = 0 и lim Vi = 0. (1.25)
i—юо г—>оо
оо
Докажем, что оба этих ряда расходятся, т.е. X) иг = +°° и
оо г=1
J2 Щ = +оо. Обозначим частичные суммы п-го порядка пер-
г=1
вого ряда через С/п, второго ряда через Vn. Тогда, если
п оо
Sn= Y2ai — п~я частичная сумма исходного ряда ]^а$, то,
i=i i=i
очевидно, Sn = Uk — Vm, где к — число неотрицательных
членов в сумме i5n, am — число отрицательных членов в сумме
Sn, т + к = п. Числа кит зависят от п и, увеличиваясь
вместе с п, стремятся к бесконечности в силу доказанной выше
бесконечности последовательностей {u;}?^ и {vi}^.

96 1. ЧИСЛОВЫЕ РЯДЫ
оо оо
Если оба ряда J2ui и ^2vi сходятся, то сходится и ряд
ОО 1=1 1=1
^2 |^г|5 поскольку его n-я частичная сумма равна 5 *=[/& + Vm
(см. обозначения выше) и, следовательно,
оо оо оо
Е\(ц\ = lim 5* = lim Uk + lim Vm = У^щ + V4 < +oo,
п-юо k-too m-юо <*—' <*—'
г=1 г=1 г=1
oo
что противоречит условной сходимости ряда ^2 аг-
г=1
оо
Если сходится один из рядов, например ряд J2 uii a ДРУГ°й
оо г=1
ряд расходится, т.е. Ylvi = +°°> то имеет место равенство
г=1
оо оо оо
Еп{ = lim Sn = lim [//fe — lim Vm = /^ге» — /и» = —oo,
n—>oo fc—>oo m—>oo ^—' ^—'
г=1 i=l i=l
oo
что противоречит условию сходимости ряда ]Р щ. Если сходит-
оо оо г=1
ся ряд ^ Щ, а ряд X) ^г расходится, то аналогично имеет место
г=1 оо г=1
равенство ^2 аг = +оо, которое также противоречит условию
г=1 оо
сходимости ряда Ylai-
г=1
оо оо
Итак, оба ряда расходятся: ^2щ = +оо и ^2 vi = +°°-
г=1 г=1
Отсюда, в частности, следует, что и все остатки этих рядов
также расходятся (их суммы равны +оо).
Пусть задано произвольное число S G К. Для
доказательства теоремы Римана необходимо провести такую перестанов-
оо
ку членов ряда ^ сц, при которой получится ряд с суммой 5.
г=1
Покажем, как это сделать. Поскольку неубывающая
последовательность Uk стремится к 4-оо при к —> оо, то найдется такой

Д. 1.1. Доказательство теоремы Римала 97
номер &i, что
г=1 г=1
(если к\ = 1, то первое неравенство отсутствует).
Аналогично для возрастающей последовательности Vm, которая также
стремится к 4-оо при га —> оо, найдется такой номер rai, что
TTli — l k\ TTli к\
г=1 г=1 г=1 г=1
(если rai = 1, то первое неравенство отсутствует), что
эквивалентно неравенствам
к\ mi — I к\ mi
г=1 г=1 г=1 i=l
Далее аналогично выбираем номер &2 > fci, такой, что
A;i mi /С2 —1 fci mi ^2
i=l i=l i=ki + l i=l i=l
(если fc2 = fci + 1, то первое неравенство отсутствует). Выбор
А:
возможен, поскольку ^2 щ —> +оо при к —> оо. Аналогично,
m i=ki + l
так как ]Р ^ —>• 4-оо при га —^ оо, можно выбрать такой
1=7711 + 1
номер ГП2, что
к\ 7711 &2 7712 — 1
г=1 г=1
к\ ТП\ к2 ТП2
(если m2 = mi -f 1, то первое неравенство отсутствует).

98 1. ЧИСЛОВЫЕ РЯДЫ
Продолжая далее таким же образом, последовательно
выбираем номера к\ < &2 < • • • < h < ... и rai < 7712 < ... < пц < ... При
оо оо
этом, поскольку ряды ]П V{ и ]П щ расходятся, процесс выбора
г=1 г=1
не может прерваться, и мы получаем бесконечные
последовательности {ki} и {тгц}.
Согласно выбору последовательностей {ki} и {га/}, для всех
I Е N и всех к, таких, что ki + 1 ^ к < fcj+i, выполняются
неравенства
к\ пц пц к
г=1 г=1 г
fci mi
г=1 г=1
(если fc/+i = fc/ +1, то первое неравенство отсутствует), а для
всех / Е N и всех т, таких, что пц +1 ^ га < raj+i, выполняются
неравенства
к\
г=1
г=1
mi
i=ki+l
i=raj+l
mi+1
г=1 г=1
(если ra/+i = га/ + 1, то первое неравенство отсутствует).
оо
Учитывая, что каждый член исходного ряда ^2 ап совпада-
п=1
ет либо с некоторым членом щ, либо с некоторым членом — Vj,
рассмотрим следующую перестановку членов исходного ряда:
Ьг = ^1 + ''' + Uki - vl ~ • • • - Vmi + Ukl+l
г=1

Д. 1.1. Доказательство теоремы Римана
99
Докажем, что сумма полученного ряда равна S. Разобьем
множество натуральных чисел N на следующие отрезки:
, mi+fc2-l],
В зависимости от того, в какой из этих отрезков попадает
натуральное число N (а для вычисления предела достаточно
рассматривать только большие значения ЛГ), частичная сумма
N
J2 Ь{ полученного ряда с номером N принимает различный вид,
и, следовательно, по-разному оценивается расстояние от нее до
числа S. N
График зависимости частичных сумм 5дг = Yl h этого ряда
от номера N представлен на рис. 1.4. г=1
l
.ш/ 1
Т 1
V
1 2
m,
Рис. 1.4
m2
т3
N
Номер N может принадлежать для некоторого I E N отрезку
вида [mi+hi, пц+ki+i—1]. Если при этом окажется, что N =
= mi + k, где kt + 1 ^ к ^ к1+г - 1, то (см. (1.26))
N
mi
г=1

100
1. ЧИСЛОВЫЕ РЯДЫ
Тогда в соответствии с (1.27)
N N
к\ 7711
4=1 i=l
(fci mi
г=1 г=1
77l[ —1
77l[ —1
J2 Vi)+vm
Если N = т/ + Л/, / Е N, то последняя сумма в (1.28) отсутствует,
и, следуя приведенным выше рассуждениям, получаем, что и в
этом случае верна та же оценка. Таким образом,
N
(1.29)
Номер ЛГ, кроме того, может принадлежать также отрезку вида
[fcf+i+mj, fcj+i+raj+i-1] для некоторого I G N. Аналогично, если
при этом N = fcf+i + m, где ггц +1 ^ га ^ raj+i — 1, то частичная
сумма ряда имеет следующий вид (см. (1.29)):
N
к\
тп\
(1.30)
г=пц + 1

Д. 1.1. Доказательство теоремы Римала
101
С учетом (1.26) имеем
N N
г=1
ттц
г=1
i=kt+l
Л\
V
О
Если N = fcj+i+mp I E N, то последняя сумма в (1.30)
отсутствует, и полученное неравенство снова выполняется.
Следовательно, при N = ki+i + m, ттц < m < mj+i — 1, I G N, справедливо
соотношение
N
IS
Ьг-S
(1.31)
Наконец, поскольку
получаем
Это означает, что
oo и mi -> oo при Z -> oo, то из (1.25)
lim wfc = lim vmi = 0.
Тогда из (1.29) и (1.31) следует, что
N
Ьг - 5
1=1
г=1
vmi < е, TV e
с, N б
-l], Z > /i;

102 1. ЧИСЛОВЫЕ РЯДЫ
Положим iVo = max{mj1+i+fcj1+i, fcj2+2+mJ2+i}- Тогда
1=1
N 00
и поэтому lim Y]bn = S. Таким образом, У] Ьп = £, что и
Ч1 п1
требовалось доказать. ►
Дополнение 1.2. Признаки
сходимости Дирихле и Абеля
Приведем несколько достаточных признаков сходимости
оо
знакопеременных рядов вида ^ unVn- Предварительно дока-
п=1
жем важное тождество, широко используемое в теории рядов и
называемое преобразованием Абеля.
Лемма 1.1. Пусть {и^}^=1 и {v^^Li — произвольные
числовые последовательности, и Sk = Щ + u<i +... + зд, k E N, 5о = 0.
Тогда для любых натуральных рид, таких, что q > p, имеем
SqVq ~ Sp-lVp.
k=p k=p
Поскольку щ = Sk — Sk-i при всех к G N, то
я я я я
2
к=р к=р к=р к=р
В последней сумме заменим индекс к суммирования на I = к — 1:
1 = к-1 =* к = 1 + 1
к=р =* 1=р-1
k = q =» l = q-lj i=p—i
9-1 g-l
= [ z = л ] = 2^ ^^+1 = 2^ «Sjfc^+i + Sp-iVp.
k=p-l k=p

Д. 1.2. Признаки сходимости рядов 103
Таким образом,
k=p k=p k=p
q-1
= ^ Sk(Vk ~ Vk+l) + SQVQ - Sp-lVp- ►
k=p
Теорема 1.16 (признак Абеля — Дирихле). Пусть
оо
для ряда Yl ukVk c действительными членами выполняются
к=\
условия:
1) последовательность {vk)™=i является невозрастающей,
т.е. vk ^ fcN
2) lim vk = 0;
к—>оо оо
3) последовательность {Sn} частичных сумм ряда ^
ограничена, т.е. существует такое число М, что k=l
\Sn\ =
п
м, п е
оо
Тогда ряд ^2 ukVk сходится.
к=1
оо
<< Доказательство сходимости ряда Yl ukvk проведем с помо-
к=1
щью критерия Коши сходимости числового ряда. Для этого
выберем произвольное число е > 0. Поскольку lim vk = 0, то
для выбранного е > 0 найдется такой номер N(e) € N, что
где М — константа из условия 3 теоремы. Выберем
произвольные п> N(e) итЕМи применим преобразование Абеля к
n-fm
сумме Y2 икук (в лемме 1.1 в этом случае p = n + l, g =

104 1. ЧИСЛОВЫЕ РЯДЫ
к оо
= X] ui — частичные суммы ряда ^ щ):
1=1 1=1
п+т n-fm—1
к=п+1 k=n+l
Отсюда, учитывая, что Vk ^ Vk+i и ^к ^ 0 для всех к £ N
(второе неравенство следует из условия, что Vk монотонно
стремится к нулю при к —> оо), а также что частичные суммы
Sk ограничены по модулю константой М (условие 3 теоремы),
для всех п > N(e) и т Е N получаем
n-fm
n-fm—1
n-fm—1
5Z I^K^ " v*+l) + \Sn+m\vn+m + \Sn\vn+l
k=n+l
n-fm-1 ^ £
k=n+l
= M(vn+i - vn+m) + у < Mvn+i + — < M— + у = е.
oo
Таким образом, для ряда £) ик^к выполнено условие критерия
к=1
Коши сходимости рядов. Следовательно, он сходится. ►
Отметим здесь, что признак Лейбница (см. теорему 1.13)
является следствием только что доказанной теоремы. Действи-
оо
тельно, знакочередующийся ряд ]C("~l)fcvb удовлетворяющий
k=l
условиям признака Лейбница (vk монотонно стремится к нулю
при к —> оо), удовлетворяет также и условиям признака
Абеля — Дирихле, если положить щ = (—l)fc.

Д. 1.2. Признаки сходимости рядов 105
оо
Теорема 1.17 (признак Абеля). Если ряд JZ ик схо-
к=1
дится, а действительная числовая последовательность {vk}^L\
оо
монотонна и ограничена, то ряд ^ щу^ сходится.
оо
<4 Во-первых, поскольку ряд Yl ик сходится, то последователь-
к=1
п
ность его частичных сумм Sn = J2 ик ограничена:
к=1
п
3M>0 VnGN: |5n| = ^зд ^ М. (1.32)
к=1
Во-вторых, согласно теореме Вейерштрасса [1-6.5],
монотонная и ограниченная последовательность действительных чисел
{vfc}^ сходится, т.е. существует предел lim Vk = v, где v — не-
к—>оо
которое конечное действительное число. Тогда, согласно
критерию Коши сходимости числовой последовательности [1-6.5],
имеем
Ve>0 3Ni(e)(EN Vn>Ni(e) Mm e N:
g^:, (1.33)
oo
где M — константа из (1.32). Пусть сумма ряда ^ щ равна
п к=1
S, т.е. lim Sn = 5, где Sn = У) щ. Тогда, учитывая, что
lim vn = v, получаем lim Snvn = Sv. По определению предела
п->оо п->оо
последовательности это означает, что
Ve>0 3N2{e)£N Vn>N2(e): \Snvn - Sv\ < |
и, в частности,
Vn>iV2(e) VmGN: |5n+TO«n+m - 5«| < |. (1-34)

106 1. ЧИСЛОВЫЕ РЯДЫ
Кроме того, lim Snvn+i = Sv, что эквивалентно утверждению
п—>оо
Ve>0 3iV3(e)€N Vn>JV3(e): \Snvn+1 -Sv\ < |. (1.35)
Взяв Nq — max{iVi, ЛГ2, N3}, получим, что для всех п > No и
для всех m € N выполняются все неравенства (1.33) —(1.35).
Кроме того, в силу монотонности последовательности {v^} все
ненулевые разности Vk — Vfc+i, к Е N, имеют один и тот же знак,
следовательно,
n-fm—I n-fm—1
\vk-vk+1\=
Тогда, используя преобразование Абеля и учитывая данное
равенство и неравенства (1.32) —(1.35), для всех п > No и для
всех га Е N получаем
n-fm n+m—1
/ J ЩУк = 2_^ SkiVk—Vk+^+Sn+mVn+m—Sv+Sv—SnVn+i
k=n+l I
n-fm—1
00
Условие критерия Коши сходимости ряда JZ wfcvfc выполнено,
поэтому ряд сходится. ►
Пример 1.36. Докажем, что если невозрастающая
последовательность {an}n*Li стремится к нулю, то ряд
n=l
сходится при любом aGK.

Д. 1.2. Признаки сходимости рядов 107
Если а = 2тгга, га Е Z, то sin27rran = 0 при всех п £ N, и ряд
сходится.
Пусть а ^ 2тгга, га Е Z. Докажем, что частичные суммы ряда
оо п
^2 sinfca ограничены в совокупности. Пусть Sn = £) sinfca.
k=i k=i
Тогда
sin — • Sn = sin — sina + sin — sin2a + ... + sin — sinna =
A Zt £ Zt
1 / a 3a\ 1 / 3a 5a
^sTj +-(
(2n-l)a
а (2п+1)а\ _ . (п + 1)а . па
Итак,
. а _ (п + 1)а . па
sin-.5n = sin—^—sinT.
Отсюда, учитывая, что а ф 2тгга, га Е N, и, следовательно,
sin(a/2) ф О, получаем
. (n + l)a . па
sin sin — i
с 2 2 I с i ^
sm-
. a
ЯП-
Таким образом, для любой невозрастающей
последовательности {an}, являющейся бесконечно малой при п —> оо, и любом
оо
a G Е ряд ^2 ап sinna удовлетворяет условиям признака Абе-
п=1
ля — Дирихле и потому сходится. #
Иногда для исследования знакопеременных рядов на
сходимость применяют признаки Абеля — Дирихле и Абеля не
раздельно, а в комбинации.

108 1. ЧИСЛОВЫЕ РЯДЫ
Пример 1.37. Исследуем на сходимость ряд
Е°° sin па
n=1^^arctgn-
оо
Из примера 1.36 следует, что ряд £) sm™* сходится при лю-
n=i vn
бом а £ М, поскольку последовательность 1/у/п не возрастает и
является бесконечно малой. Возрастающая последовательность
{arctgn}^! стремится к тг/2 при п -> оо. Следовательно, в силу
признака Абеля исследуемый ряд сходится при любом aER.
Вопросы и задачи
1.1. Напипште одну из возможных формул n-го члена ряда
по указанным первым его членам:
з 4 | | 1 1 2. 1_ 2_
в) 3-3 + 3-3 + 3-3 + ...
1.2. Напишите 4-5 первых членов ряда по известной
формуле для общего члена ап:
Зп-2 ^ 2 + (-1)п
1.3. Докажите следующие равенства:
.22 2 1
а)5 + 2^ + - + ^ + - = 2;
. , 1 1 1 (-1)"
5_1\ /_5__ (-l)71"1^ _ 169
1
+ + | 1 , Л-
3-4 4-5 (п + 2)(п + 3) 3'

Вопросы и задачи 109
1
00 1 1 °° 1
1i
ж > м п . ^ = -; к
j4n + 4n3 6' К) 2-s Збп2 + 12п-35 ~ 21'
п=1 п=1
71=1 Х ' 71=2
ОО - ОО
и) > — — = 1; м) > sin-—cos-—=-sin2.
y^n!(n + 2) ' ^ Z^ 2n 2n 2
1.4. Докажите расходимость следующих рядов:
°° лп . л ОО ОО
71=1 71=1
1.5. Пользуясь критерием Коши, докажите расходимость
следующих рядов:
^ 1 11111111
П=1
1.6. Докажите, что если сходятся действительные ряды
оо оо оо оо
Е ап и Е ьп> то сходятся ряды X) КМ и X) (ап + Ьп)2.
П=1 П=1 П=1 71=1
1.7. Пользуясь признаками сравнения, исследуйте на
сходимость ряды:
f-l ч v* 51п3(7п+1) + у/1п(8п2+5)
3n+2+ln10(n2)
22n г)

ПО 1. ЧИСЛОВЫЕ РЯДЫ
1.8. Используя интегральный признак Коши, исследуйте на
сходимость знакоположительные ряды:
ОО ОО , ОО _^Л7 ОО -
n=l
oo
1.9. Исследуйте на сходимость данные знакоположительные
ряды, используя признаки сравнения:
^sin5n ^ arctgn + V^
n=l
oo
г)
n=l n=l
2П ^ 1
П+21пп v^
n=l n=l n=l
,f 1 .5 ~//1+пч5 \ ~. 2п +
^^ (() ^ 4пз+5п+3-
n=l v v п=1 х ' n=l
1.10. Исследуйте ряды на сходимость с помощью признака
Даламбера:
42"(n!)3 ^ (2п + 3)!
; Oj^ ; В
Z^ (3n)! ; Oj^(3n + 4)3"; В) ^ 1-8-27-...-П3 ;
^; е)£ (»+2)!
n=1-v->-/ n=1 vv n=0
OO ,/o 4, OO
nl(2n)! .

Вопросы и задачи 111
1.11. Исследуйте на сходимость ряды с помощью
радикального признака Коши:
Ъп у ^ ^
J
*) Е (^зJ {-rJ б) Е (гпп) в) Е
l l l
n=l n=l n=l
ОО п On OO
1.12. Исследуйте ряды на абсолютную сходимость.
Установите, какие из указанных рядов расходятся в связи с
невыполнением необходимого признака сходимости:
V 3п \п ^ п\еп . тгп ^
т; в)
71=1 71=1 71=1
г)
;
П=1 ' 71=1 ^ "' П=1
ОО
ж)
1.13. Исследуйте на абсолютную и условную сходимость
следующие ряды:
' б^Е n(n
(2 + 1/„)
n=l v ' ' п=1
71=1 71=1
*) £(-i)
71=2

112 1. ЧИСЛОВЫЕ РЯДЫ
1.14. Установите сходимость рядов и вычислите их суммы
с точностью до 0,01:
n=l n=l n—\
1.15. Докажите, что если последовательность {an}(^L.l
монотонно стремится к нулю при п -> оо, то при любом а ^ 2тгт,
оо
т Е Z, ряд 53 On cos па сходится.
п=1
1.16. Исследуйте на сходимость ряд
ОО . -
Е sin па 1
л lnln(n + 2)C°Sn'
п=1
1.17. Исследуйте на сходимость ряды:
1 1п
п=1
оо оо
1.18. Докажите, что ряд ^ UkVk сходится, если ряд ^ 1
оо Л=1 А;=1
сходится, а ряд ^ (^ — Vk+i) сходится абсолютно.
1.19. Вычислите с точностью до 0,001 суммы рядов:
п=1 п=1 п=1
1.20. Оцените погрешность, возникающую при замене сум-
оо
мы ряда Y1 ап суммой первых пяти его членов, если:
71=1
а) «п = 4-т; б) а„ = Ь

Вопросы и задачи 113
1.21. Определите, при каких значениях параметра a G Ж
сходятся следующие ряды:
111111
а)1 2" + 3 ¥ + 5~¥ + 7~-";
1__}_ J_ JL 1_
) + За 2Q + 5а + 7а 4а +'"
1.22. Определите, при каких значениях параметра a G Ж не
выполняется необходимый признак сходимости ряда
1.23. Определите, при каких положительных значениях
действительного параметра Ъ сходится ряд
1.24. Определите, при каких положительных значениях
оо
параметра a G Ж сходится ряд Y1 ап> если задан общий член
71=1
ряда:
г) arcsin-11—-——: д) 1 —cos—.
1.25. Определите, при каких значениях параметров a G Ж и
/? G R сходится ряд
1.26. Исследуйте на сходимость в зависимости от значений
параметров a G Ж и Ь G Ж ряд
(7n + 4)Q6n
71=1 V '

114 1. ЧИСЛОВЫЕ РЯДЫ
1.27. Определите, при каких значениях параметра р G
сходится ряд
00 5-....(3n + 5)
1.28. Определите, при каких значениях параметра a Е IR,
а ^ 0, сходится ряд
1.29. Определите, при каких значениях параметра а €
сходится ряд
3n + 51n13n
1.30. Определите, при каких значениях параметра q G
ряд 5Jtg— сходится: а) абсолютно; б) условно.
п=1

2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
В этой главе рассмотрены ряды и последовательности,
членами которых являются действительные или комплексные
функции, определенные на множестве X действительных или
комплексных чисел. Изучены некоторые функциональные
свойства (непрерывность, дифференцируемость, интегрируемость)
сумм таких рядов, возможность и методы разложения функций
в ряды из степенных функций.
2.1. Сходимость функциональных
последовательностей и рядов
Пусть U = (u(x)}, х Е X, — некоторое множество
действительных или комплексных функций м(х), определенных на
множестве XcR (XcC). Тогда последовательность элементов
множества U, т.е. всякое отображение множества
натуральных чисел N в множество £/, при котором каждому номеру п Е N
ставится в соответствие некоторая функция ип(х) Е С/,
называют функциональной последовательностью (или
последовательностью функций) и обозначают
}™=1, хеХ, или щ{х), и2{х), ип{х), хеХ.
Множество X при этом называют областью определения
функциональной последовательности {^(ж)}^, а
функции ип(х) EU — членами (элементами) функциональной
последовательности {un(x)}^Ll.
При фиксированном xq E X всякой функциональной
последовательности {^п(ж)}^=1? х ЕХ, соответствует числовая
(действительная или комплексная) последовательность {un(xo)}^Li,
элементами которой являются значения ип(хо) функций ип(х)
в точке жо-

116 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Определение 2.1. Заданную на множестве X С R {X С С)
функциональную последовательность {ип(х)}™=1
называют сходящейся в точке xq E X, если сходится числовая
последовательность {un(xo)}%Ll. В противном случае,
функциональную последовательность {ип(х)}^=1 называют
расходящейся в точке xq.
Если последовательность {un(x)}^=l1 xEl, сходится в
каждой точке некоторого множества Mel, то эту
функциональную последовательность называют сходящейся на
множестве М. Множество Xq С X всех точек х G X, в
которых последовательность {ип(х)}^=1, определенная на X,
сходится, называют областью сходимости
функциональной последовательности {iXnfaOKJLi-
Если функциональная последовательность {ип(х)}™=1
сходится на множестве МсХ, то всякой точке х е М можно
поставить в соответствие предел числовой последовательности
значений функций ип(х) в этой точке. Таким образом, если
последовательность {ип(х)}™=1 сходится на множестве М, то на
М определена некоторая функция
и(х) = lim un(x), x G M,
п—>оо
которую называют предельной функцией
последовательности {ип(х)}™=1 на множестве М. В этом случае говорят, что
функциональная последовательность {ип(х)}(^>=1
является сходящейся поточечно к функции и(х) на множестве М
или что имеет место поточечная сходимость
функциональной последовательности {^п(х)}^_1 на множестве М
к функции и (ж), и при этом используют следующие
обозначения:
ип(х) ->и(х), х€М.
В соответствии с определением предела числовой
последовательности [1-6.3] можно сформулировать эквивалентное опре-

2.1. Сходимость функциональных последовательностей и рядов 117
деление поточечной сходимости функциональной
последовательности {un(x)}^L1 к функции и(х) на множестве М:
3N{x,e)eN Vra>iV(z,e): \un{x)-u{x)\<e. (2.1)
Заметим, что номер N(x,e) зависит и от элемента х G X, и от
числа е > 0.
В дальнейшем, если из контекста ясно, о какой области
определения X идет речь, функциональные последовательности
{ип(х)}™=1, х G X, будем обозначать {un(x)}.
Пример 2.1. Рассмотрим функциональную
последовательность {un(x)}, определенную на множестве X = [0,1]
следующим образом:
un{x) = -, n EN, zG[0,1].
Покажем, что эта последовательность сходится во всей области
определения X = [0,1], и ее предельной функцией является
функция и(х) = 0. Действительно,
х 1
lim un(x) = lim — = х lim — = х • 0 = 0, х G X = [0, 1]
n-Юо п->оо 71 п->оо 71
(множитель х, не зависящий от га, вынесен за знак предела).
Пример 2.2. Рассмотрим последовательность функций
un(x) = xn, га G N, определенных на множестве X = Ш. Для всех
х G (—1,1] получаем
г / ч г п /0, же (-1,1);
lim un(x) = lim xn = < / ,
n—юо n—юо ^ 1, X = 1,
а при x ^ — 1 и x > 1 последовательность {хп} не имеет
предела. Таким образом, областью сходимости функциональной
последовательности {х71} является множество Хо = (—1,1], на
котором эта последовательность сходится поточечно к
функции и(х), равной нулю во всех точках ж G (—1,1) и равной
единице в точке х = 1.

118 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Определение 2.2. Пусть на множестве X С R (X С С)
определена последовательность действительных или
комплексных функций /i(#), /2(^)1 •••> /п(я)> Выражение вида
*) = /i(s) + /2(z)+ ... + /„(*) + ..., (2.2)
71 = 1
в котором члены последовательности {/п(я)} соединены
знаками плюс, называют функциональным рядом, определенным
на множестве X, а функции /i(x), /2(2:), • •, /n(s)> — чле-
нами этого функционального ряда.
При фиксированном хо G X всякому функциональному ряду
оо
Х^ /n(z) соответствует числовой (действительный или гсол«-
п=1 оо
плексный) ряд ^2 /п(^о)? ^лекал«гл которого являются значения
71 = 1
/n(zo) функций fn(x) в точке х0.
Определение 2.3. Функциональный ряд (2.2) называют
сходящимся в точке xq E X, если сходится числовой ряд
71=1
из значений его членов в этой точке. В противном
случае функциональный ряд (2.2) называют расходящимся в
точке xq G X.
Если функциональный ряд (2.2) сходится в каждой точке
некоторого множества МсХ, то говорят, что
функциональный ряд (2.2) является сходящимся (поточечно) на
множестве М или что имеет место поточечная сходимость
функционального ряда (2.2) на множестве М. Множество
Xq С X всех точек х из X, в которых ряд (2.2), определенный
на множестве X, сходится, называют областью сходимости
функционального ряда (2.2).

2.1. Сходимость функциональных последовательностей и рядов 119
По аналогии с числовыми рядами для всякого функциональ-
оо
ного ряда Yl fn{x)i х Е X, можно построить
последовательна
ность {Sn(x)}<^Ll функций вида
х), хеХ, п = 1,2,
Функцию 5п(х), х Е X, называют га-й частичной суммой
оо
функционального ряда J2 /п(я), х е X. Таким образом,
71=1
каждому функциональному ряду соответствует
функциональная последовательность его частичных сумм. Верно и
обратное утверждение: каждой функциональной последовательности
{5п(х)}^=1, х е X, можно поставить в соответствие функцио-
оо
нальный ряд Yl fn{x), х Е X, последовательностью частичных
71=1
сумм которого является функциональная последовательность
{sn(x)}^=l. Действительно, полагая /i(z) = s\(x) и fn{x) =
= sn(x)-sn-i(x), n = 2, 3,..., получаем Sn{x) = sn(x), n G N.
Указанное соответствие между функциональными рядами и
последовательностями позволяет любое утверждение,
справедливое для функциональных последовательностей,
сформулировать в терминах теории функциональных рядов, и наоборот. В
частности, определение 2.3 можно сформулировать следующим
образом: функциональный ряд (2.2) сходится в точке хо G X
тогда и только тогда, когда в точке xq сходится функциональная
последовательность {Sn(x)} его частичных сумм, и ряд (2.2)
расходится в точке xq в том и только том случае, если в этой
точке расходится функциональная последовательность {Sn(x)}
его частичных сумм.
Определение 2.4. Если функциональный ряд (2.2)
сходится на множестве X, т.е.
УхеХ 3 ton Sn(x)=S(x),
71—ЮО

120 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
то определенную таким образом предельную функцию S(x)
называют суммой функционального ряда (2.2) на
множестве X и пишут
оо
fn(x) = s(x), xex.
71=1
Определение 2.5. Для всякого п Е N функциональный ряд
Z) fkix)i х € -X"? называют га-м остатком функционалъ-
к=п+1 оо
ного ряда £] Л(я), я Е X.
к=1
оо
Поскольку сходимость функционального ряда ^ fkix) на
к=1
множестве X означает сходимость в каждой точке xq Е X чи-
оо
елового ряда ^ Л(яо)> то в силу свойств 1.1 и 1.2 функцио-
оо
нальный ряд Yl fkix) сходится на множестве X тогда и только
к=1
тогда, когда в каждой точке хеХ сходится (к некоторому чи-
оо
слу Rn(x)) всякий п-й остаток ^ Д(х) этого ряда. При этом
к=п+1
имеет место равенство
, nGN, x EX, (2.3)
оо
где S(x) = ]Г) fk(x) — сумма функционального ряда; Sn(x) =
п к=1
= J2 fkix) — га-я частичная сумма этого ряда. Кроме того,
J2
к=1 ^
если функциональный ряд ^ fk(x) сходится на множестве X,
k=i
то
ton Дп(ж)=0, хЕХ (2.4)
п—>оо
Как известно, для числовых рядов (см. теорему 1.3) имеет
место критерий Коши сходимости числового ряда. Для
сходимости функциональных рядов используют следующий
критерий.

2.1. Сходимость функциональных последовательностей и рядов 121
Теорема 2.1 (критерий Коши сходимости функцио-
оо
нального ряда). Функциональный ряд ]Г) Д(х) сходится на
А;=1
множестве X тогда и только тогда, когда для любых х е X и
е > О найдется натуральное число N(x,e), зависящее от х и £,
такое, что для всех п > N(x,e) и р G N выполняется неравенство
п+р
\Sn+p(x)-Sn(x)\ = \
оо
Определение 2.6. Функциональный ряд ]Г) /п(я) назы-
п=1
вают абсолютно сходящимся на множестве X, если на
оо
множестве X сходится функциональный ряд Y1 |/п(#)| из мо~
дулей его членов. n=l
Согласно теореме 1.10, абсолютно сходящийся на множестве
X функциональный ряд сходится на этом множестве.
Обратное утверждение, вообще говоря, неверно. Функциональный
ряд, сходящийся условно в каждой точке множества У,
называют условно сходящимся на множестве Y
Функциональный ряд обычно начинают изучать с
исследования его на сходимость, которое сводится к определению
области сходимости этого ряда. При этом можно использовать
известные свойства числовых рядов и признаки их
сходимости (см. 1). В результате такого исследования, как правило,
оказывается, что в одних точках области сходимости
функциональный ряд сходится абсолютно, а в других — условно.
Поэтому для функциональных рядов в области сходимости
выделяют области абсолютной и условной сходимости.
Другой и, как правило, более сложной задачей теории
функциональных рядов является нахождение суммы
функционального ряда. Приведем некоторые примеры функциональных
рядов.

122 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Пример 2.3. Рассмотрим ряд Дирихле
со г
как функциональный ряд. Областью сходимости ряда Дирихле
является полуось 1 < х < оо (заметим, что это область
абсолютной сходимости). При х ^ 1 ряд Дирихле расходится. В самом
деле, для х Е (0, 1] это было показано в примере 1.18. Если же
х ^ 0, то не выполнен необходимый признак сходимости ряда
(см. теорему 1.2), и, следовательно, ряд Дирихле при х < 0
расходится.
Пример 2.4. Исследуем на сходимость функциональный
ряд
00 ( Л\п
оо
Так как ряд Дирихле ]Р 1/пх сходится при х > 1, то в этой
п=1 оо
области функциональный ряд ]Г (—1)п/пх сходится абсолют-
п=1 оо
но. В фиксированной точке х Е (0,1] числовой ряд ]Г (—1)п/пх
п=\
сходится условно по признаку Лейбница (см. теорему 1.13).
Наконец, при х < 0 общий член /п(#) = (—1)пп~х ряда не стремится
к нулю при п -> оо (не выполнен необходимый признак
сходимости ряда), и, следовательно, ряд расходится.
Итак, исследуемый функциональный ряд сходится при х > О,
причем при х > 1 сходится абсолютно, а при 0 < х ^ 1
условно.
Пример 2.5. Исследуем на сходимость функциональный
РЯД
00
Ш Jb» Us ^ V/.
п=1

2.1. Сходимость функциональных последовательностей и рядов 123
При фиксированном х > 0 он представляет собой
геометрический ряд с параметром q = lnx (см. пример 1.4). Следовательно,
он сходится, причем абсолютно, при \q\ < 1, т.е. при |1пх| < 1,
и расходится при |lnx| ^ 1. Таким образом, областью
сходимости (причем, абсолютной) исследуемого функционального ряда
является интервал (1/е, е), в котором имеем
1 — lnx
n=l
В остальных точках области определения рассматриваемый
функциональный ряд расходится.
Пример 2.6. Исследуем на сходимость функциональный
РЯД
оо
Так как для всякого х Е К верно неравенство
cosnx 1
3/2'
п
а ряд Дирихле ]Г) п~ъ'2 сходится (см. примеры 1.18 и 2.3), то,
п=1
согласно признаку сравнения (см. теорему 1.4), исходный ряд
сходится абсолютно в любой точке х G К. #
При исследовании функциональных рядов на сходимость
наиболее часто используют предельные признаки Даламбера и
Коши абсолютной сходимости числовых рядов. Действительно,
если для функционального ряда (2.2) в его области определения
X существует один из пределов
lim
n-юо
ш
= (р{х) или

124 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
то область абсолютной сходимости функционального ряда (2.2)
содержит все точки, в которых выполняется неравенство <р(х) <
< 1 или неравенство ф(х) < 1 соответственно. В тех точках
х € X, в которых выполняется неравенство (р(х) > 1 или
неравенство ф(х) > 1, функциональный ряд (2.2) расходится (см.
замечание 1.7). Чтобы установить сходимость или расходимость
функционального ряда в точках, удовлетворяющих условию
<р(х) = 1 или ф(х) = 1, необходимо провести дополнительное
исследование (в таких точках ряд может как сходиться абсолютно
или условно, так и расходиться). Проиллюстрируем сказанное
следующими примерами.
Пример 2.7. Рассмотрим функциональный ряд
(хф-\.
JnVx + 1/
n=l
Исследуем этот ряд на абсолютную сходимость, используя
предельный признак Даламбера:
1ЯГ-1
lim ' ,7;\ ' = lim-
n-+oo \Jn\X)\ n-teo П + 1 I X +
IX-1
\X+1
Решим неравенство \(х — 1)/(х + 1)|<1, выполняя следующие
эквивалентные его преобразования:
\х - 1| < \х + 1|; (х - I)2 < (х + I)2; х > 0.
Таким образом, неравенство |(х — 1)/{х + 1)| > 1 равносильно
неравенству я < 0. Значит, исследуемый функциональный ряд
сходится абсолютно при х > 0 и расходится при х < 0. Если
оо
х = 0, то получаем знакочередующийся ряд ^ (—1)п/п, сходя-
71=1
щийся условно в соответствии с признаком Лейбница.
Итак, рассматриваемый функциональный ряд сходится
абсолютно при х > 0 и условно при х = 0, а при х < 0 ряд
расходится.

2.1. Сходимость функциональных последовательностей и рядов 125
Пример 2.8. Найдем область сходимости
функционального ряда
ie"x, хек.
71=1
При любом значении х Е R данный ряд является
знакоположительным числовым рядом, поскольку fn(x) = пепх > О для всех
xeR. Воспользуемся предельным признаком Коши. Поскольку
lim y/nenx = ех, рассматриваемый функциональный ряд схо-
71—ЮО
дится при ех < 1, т.е. при х < О, и расходится при ех > 1, т.е.
при х > 0. В точке я = 0 функциональный ряд принимает вид
00
5]пи, очевидно, расходится.
71=1
Таким образом, исследуемый функциональный ряд сходится
при х < 0 и расходится при х ^ 0.
Пример 2.9. Исследуем на абсолютную сходимость
функциональный комплексный ряд
71=1
Используя предельный признак Коши, получаем
lim
71—ЮО
z + n
п l v
= - lim
3 71—ЮО
n
Следовательно, функциональный ряд сходится абсолютно при
всех z G С.
Пример 2.10. Исследуем на абсолютную сходимость
функциональный комплексный ряд

126
2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Для этого воспользуемся предельным признаком Даламбера.
Пусть fn(z) = l/{n(z + l)n), n G N. Тогда имеем
lim
n—юо
/»(*)
= lim
71—ЮО
lim
n
Решая неравенство l/\z + 1| < 1, заключаем, что
функциональный ряд сходится абсолютно при \z + 1| > 1, т.е. вне
замкнутого круга радиуса 1 с центром в точке —1. При \z + 1| <
< 1, т.е. в открытом круге радиуса 1 с центром в точке — 1,
функциональный ряд расходится. Рассмотрим точки,
принадлежащие окружности \z + 1| = 1. В любой такой точке ряд
оо
J2 l/(n(z + 1)п) не является абсолютно сходящимся, посколь-
п=1
ку ряд, составленный из модулей его членов, имеет вид
E
71=1
т.е. является гармоническим (расходящимся) рядом.
Следовательно, областью абсолютной сходимости функционального
оо
ряда Yl l/(n(z + 1)п) является множество комплексных чисел z,
71 = 1
удовлетворяющих неравенству \z + 1| > 1.
Отметим, что среди точек границы этой области
(окружности \z +1| = 1 в комплексной плоскости С) есть такие, в которых
данный функциональный ряд расходится, например z = 0:
1
z=0
71=1
n
(ряд расходится, так как является гармоническим рядом), и
есть точки, в которых данный ряд сходится (условно), напри-

2.2. Равномерная сходимость функциональных рядов 127
мер z = —2:
ОО Л 00 1 00 / -Чи
Vn(^ + l) z=2/ П(1) П
71 = 1 Ч ' 71=1 V ' 71=1
(ряд сходится в соответствии с признаком Лейбница).
2.2. Равномерная сходимость функциональных
последовательностей и рядов
Используя понятие поточечной сходимости
функциональных последовательностей и рядов на множестве, нельзя
развить в полной мере теорию функциональных
последовательностей и рядов, поскольку при поточечном предельном переходе
не сохраняется даже непрерывность функций, не говоря уже
о дифференцируемости. Примером может служить
функциональная последовательность {ип(х)} с общим членом ип{х) = хп,
х е [О, 1]. Ее предельная функция
г / ч / ч /О, х Е[0,1);
71-ЮО ^ 1, X = 1,
является разрывной на [0,1], хотя все функции ип(х)
непрерывны на [0,1].
Пусть функциональная последовательность {ип(х)}
сходится на множестве X к функции и(х), т.е. в каждой точке х € X
числовая последовательность {ип(х)} сходится к пределу и(х).
Согласно (2.1), это означает, что для каждого х Е X и
произвольного числа е > 0 найдется такой номер N(x,e), что для
любого п > N(x,e) верно неравенство |wn(x) — u(x)\ < s. Можно
показать, что достаточным условием непрерывности предела
последовательности непрерывных функций является
существование номера N(e), общего для всех xGl, т.е. такого, что при
п > N(e) неравенство |wn(a;) — u(x)\ < e выполняется для всех
х е X. Очевидно, что для обеспечения выполнения
указанного условия в качестве N(e) необходимо выбирать наибольший

128 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
из номеров N(x,e), где х £ X. Если множество X состоит из
бесконечного числа точек, то такой наибольший номер может
существовать, а может и не существовать. Приведем
соответствующие примеры.
Рассмотрим функциональную последовательность {ип(х)},
определенную на множестве X = [О,1] следующим образом:
(см. пример 2.1). Предельной функцией этой
последовательности на множестве X является функция и(х) = 0. Для каждой
точки х Е [0,1] и любого числа е > 0 выберем номер ЛГ(х,£),
используя формулу N(x,e) = [х/е] ([х/е] — целая часть
числа х/е). Тогда для любого натурального числа п, такого,
что п ^ N(x,e) + 1 = [х/е] + 1 > х/е, справедливо неравенство
х/п < £, или |wn(x) — и(х)\ < е. Отметим, что выбранный номер
N(x,e) +1 является наименьшим среди всех номеров, начиная
с которых выполняется неравенство \ип(х) — и(х)\ < е. Если
положить N(e) = max [х/е] = [1/е], то для любого п ^ N(e) +1 ^
*€[0,1]
^ N(x,e) + 1 > х/е неравенство х/п < £, или \ип(х) — и(х)\ < £,
будет выполняться одновременно для всех х € [0,1]. Итак, для
данной последовательности удалось подобрать номер N = [1/е],
зависящий только от е и общий для всех точек множества X.
Рассмотрим теперь ту же функциональную
последовательность {ип(х)}, ип(х) = х/п, п е N, но определенную на
множестве X = [0, +оо). Для каждого фиксированного х G [0, +оо)
имеем lim (х/п) = х lim (1/n) = 0, т.е. предельная функция сно-
п-юо п-юо
ва является нулевой: и(х) = 0, х G [0, +оо). Как и в предыдущем
случае, для любых е > 0 и х Е [0, +оо) положим N(x,e) = [х/е].
Тогда для любого п > N(x,e) верно неравенство \ип(х)—и(х)\ <
< е. Однако для всякого е > 0 подобрать номер N(e), общий
для всех точек х G [0, +оо), уже нельзя. Действительно, если бы
для некоторого числа 0 < е < 1 нашелся такой номер N(e), что
при всех п > N(e) неравенство \ип(х) — и(х)\ < £, или х/п < б,

2.2. Равномерная сходимость функциональных рядов 129
выполнялось бы для всех х Е [0, +оо) одновременно, то это
неравенство выполнялось бы и для х = п > N(e): {х/п) \х=п = 1 < е.
Однако полученное неравенство е > 1 противоречит
первоначальному неравенству 0 < е < 1. Таким образом, для данной
последовательности нельзя подобрать номер N(e), зависящий
только от е и общий для всех точек множества X.
Определение 2.7. Функциональную
последовательность {ип(х)} называют равномерно сходящейся к
функции и(х) на множестве X, если для любого е > О найдется такой
номер N(e) Е N, что для всех п > N(e) и х G X выполняется
неравенство
\ип(х)-и(х)\ <е.
В этом случае функцию и(х) называют равномерным
пределом функциональной последовательности {ип(х)} на
множестве X, а также говорят, что сходимость
функциональной последовательности {ип(х)} является
равномерной на множестве X.
Равномерную на множестве X сходимость
последовательности {ип(х)} к функции и(х) обозначают следующим образом:
ип(х) =^u(x), n—> оо, или ип(х)
X
Соответственно, запись ип(х) =?±£ и(х) означает, что последо-
вательность {ип(х)} не является равномерно сходящейся на
множестве X к функции и(х).
Поточечная сходимость функциональной
последовательности — более широкое понятие по сравнению с понятием
равномерной сходимости. А именно, непосредственно из определения
равномерной сходимости следует, что если функциональная
последовательность {ип(х)} сходится к функции и(х) равномерно
на множестве X, то эта последовательность сходится к и(х) и
поточечно на X:
(ип(х)

130 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Обратное утверждение, вообще говоря, неверно: наличие
поточечной сходимости функциональной последовательности на
множестве X не гарантирует ее равномерную сходимость на
этом множестве. Бели функциональная последовательность
{ип(х)} сходится к функции и(х) поточечно на множестве X, но
не является равномерно сходящейся на этом множестве, то
говорят, что функциональная последовательность {ип(х)}
сходится к и(х) неравномерно на множестве X или что
имеет место неравномерная сходимость
функциональной последовательности {ип(х)} к функции и(х) на
множестве X,
Понятие равномерной сходимости на множестве
наглядно иллюстрируется геометрически. Пусть х G X = [а, Ь] С R,
ип(х) Е Е, п е N, и ип(х) =tu(x). Построим графики функций
х
у = и(х) — е и у = и(х) + £, где и(х) = lim ип(х), х € X. Тогда
п—юо
из равномерной на X = [а, 6] сходимости последовательности
{пп(х)} к функции и(ж) следует, что для всякого достаточно
большого номера п и всех х G [а, Ь]
„п,_, будут верны неравенства w(x)— б <
4+6 Ч ^ < un(ж) < u(z) +б. Другими
словами, это означает, что, начиная
с некоторого номера N(e),
графики всех функций un(x), n ^ N(e),
"^ будут расположены в „£-трубке",
окружающей график функции и(х)
Рис' 2Л (рис. 2.1).
Теорема 2.2. Для последовательности функций {ип(х)}
и функции п(х), определеных на множестве X, справедливо
следующее утверждение:
ип(х) =tu(x) Ф=Ф- lim sup|un(x) — и(х)\ = 0.
<4 Пусть последовательность {ип(х)} сходится равномерно на
множестве X к функции и(х). Тогда, согласно определению 2.7,

2.2. Равномерная сходимость функциональных рядов 131
получаем
Ve>0 3N{e)eN 4n>N{e) VxGX: \un{x)-u{x)\<e. (2.5)
Отсюда следует, что при всяком п > N(e) функция ctn(x) =
= \v>n(x) — w(x)| ограничена на множестве X. Поэтому для
всякого п > N(e) существует конечная точная верхняя грань
an = supan(z) = sup \un(x) - u(x)\.
xex xex
Используя свойство точной верхней грани и соотношение (2.5),
имеем
0<an = sup\un(x) - u(x)\ <£, п> N(e),
ex*
откуда и следует, что lim ап = lim sup|wn(x) — u(x)\ = 0.
n->oo n"^°°xG^
Пусть теперь an = sup \un(x) — u(x)\ -> 0 при n -> oo. Тогда
xex
Ve>0 3N(e)eN 4n>N(e): an<e. (2.6)
Согласно свойству точной верхней грани, для всех х € X верно
неравенство \un(x) — u(x)\ < sup |wn(x) — u(x)\ = an. С учетом
xex
этого из (2.6) следует, что
\un{x)-u{x)\ <an <e, n>N(e)y xeX,
что и означает в силу определения 2.7 равномерную на
множестве X сходимость последовательности {ип(х)} к функции
и(х). ►
Пример 2.11. Рассмотрим функциональную
последовательность {#n}£Li, определенную на X = [0,1). Для любой
точки х £ X имеем lim хп = 0, т.е. данная последовательность
п-юо
на множестве X = [0,1) сходится поточечно к нулевой функции.

132 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Покажем, что эта сходимость является равномерной на
любом отрезке [0, д], 0 < q < 1. Имеем:
sup \xn\ = gn, n e N, lim sup \xn\ = lim qn = 0.
[] n^°°[] n>°°
Согласно теореме 2.2, получаем xn =t0 при 0 < q < 1.
Теперь покажем, что сходимость последовательности {хп}
к функции и(х) = 0 на всем множестве X = [0,1) не является
равномерной. Действительно,
sup \хп\ = 1, n e N, lim sup |xn| = 1^0.
xG[0,l) n>oo[
В силу теоремы 2.2 имеем хп ^t 0. #
Перейдем к изучению функциональных рядов.
оо
Определение 2.8. Функциональный ряд Y1 /п(^) на-
п=1
зывают равномерно сходящимся на множестве X, если
функциональная последовательность {Sn(x)} частичных сумм
этого ряда сходится равномерно на множестве X:
Sn(x)=*S(x).
В этом случае также говорят, что имеет место равномерная
оо
сходимость функционального ряда ^ /п(я) на множе-
п=1
стве X.
оо
Если функциональный ряд £) /п(#) сходится на множестве
п=1
X, но не является равномерно сходящимся на этом множестве,
оо
то говорят, что функциональный ряд £) fn(x) сходится
п=1
неравномерно на множестве X или что имеет место
неравномерная сходимость функционального ряда на
множестве X.

2.2. Равномерная сходимость функциональных рядов 133
Теорема 2.3. Если последовательность {Sn(x)} частичных
00
сумм функционального ряда ^2 fn{x) сходится равномерно на
п=1
множестве X к некоторой функции S(x), то функция S(x)
является суммой этого функционального ряда на множестве X.
<4 Так как Sn{x) =£JSr(x), то последовательность {Sn(x)} cxo-
л.
дится к функции S(x) поточечно на X, Это означает, что ряд
оо оо
J2 /п(#) сходится на множестве X и £ /n(#) = S(x), x £ X. ►
п=1 п=1
Из поточечной сходимости функционального ряда на
множестве следует поточечная сходимость к нулю на этом
множестве последовательности сумм остатков этого ряда (см. (2.4)).
Для равномерной сходимости функционального ряда на
множестве имеет место аналогичное свойство.
оо
Теорема 2.4. Функциональный ряд J2 /п(#) сходится
п=1
равномерно на множестве X тогда и только тогда, когда
каждый его остаток сходится на X, и последовательность
сумм этих остатков {Д^х)}0^ равномерно на множестве X
сходится к нулю (Rnfe) =£0).
л.
оо
< Во-первых, функциональный ряд ^ /п(#) сходится (поточеч-
п=1
но) на множестве X тогда и только тогда, когда на X сходятся
оо
все его остатки Y1 Д(х)> п € N (см. 2.1). При этом для
k=n+l
всех п € N выполняется равенство Rn(x)=S(x)—Sn(x)1 xeX, где
5(х), Sn(x) и Rn(x) — сумма ряда, п-я частичная сумма ряда и
сумма n-го остатка ряда соответственно (см. (2.3)).
Во-вторых, используя теорему 2.2, получаем
Sn(x)=^S{x) <=* lim sup \Sn(x)-S(x)\ =0
X n*oo
lim sup\Rn{x)\=0

134 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
оо
Поскольку равномерная сходимость ряда ^2 /п(#) н& множе-
п=1
стве X равносильна равномерной сходимости
последовательности {Sn(x)} частичных сумм этого ряда на множестве X, то
теорема доказана. ►
Пример 2.12. Рассмотрим геометрический функциональ-
оо
ный ряд ^2 #п1> который сходится на множестве |х| < 1 и
п=1
имеет сумму (см. пример 1.4)
= -±-, хб(-1,1).
1 X
п=1
Покажем, что этот ряд сходится на X = (—1,1)
неравномерно. При х £ (—1,1) имеем:
При любом п G N функция |Дп(я)| не ограничена на X = (—1,1),
поскольку
хп
х
lim \Rn(x)\= lim =+оо.
no1 v л x^iolx
Следовательно, sup |i?n(x)| = +oo для всех n G N и, значит,
xG(-l,l)
lim supl-Rnfx)! Ф 0. Согласно теореме 2.2, Rn(x)^t0, а в силу
n^°°GXl оо ^
GX оо
теоремы 2.4 и сам ряд Y1 хП~1 сходится на X = (—1,1) также
п=1
неравномерно.
Заметим, что последовательность {^(х)} не является
равномерно сходящейся к тождественно равной нулю функции и

2.2. Равномерная сходимость функциональных рядов
135
в любом промежутке (—1,6], — 1 < 6 < 1. Действительно, для
всякого фиксированного п £ N имеем
sup \Rn(x)\ = sup
(]
lim f^- = -,
x-f-i+ol — x 2
Следовательно, lim sup |Дп(я)| 7^0. Согласно теореме 2.2,
n>°°(]
0, а в силу теоремы 2.4 и сам ряд ^ хп 1 сходится
(-1»6) п=1
на (—1,6], —1 <6< 1, также неравномерно.
Факт отсутствия равномерной сходимости
функциональной последовательности {Rn(x)} к тождественно равной нулю
функции в промежутках (—1,1) и (—1,6], —1 < 6 < 1, можно
проиллюстрировать геометрически: из рис. 2.2 ясно, что при
е < 1/2 графики функций y = Rn(x)=xn/(l — x) не лежат
целиком в е-окрестности („е-трубке") графика предельной функции
У = 0.
(п четное)
Рис. 2.2
(п нечетное)
Пример 2.13. Рассмотрим функциональный ряд
хеш

136 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
В соответствии с признаком Лейбница (см. теорему 1.13), этот
ряд сходится в каждой точке х е X = R. В силу следствия 1.4
имеем следующую оценку суммы остатка этого
знакочередующегося при каждом хеШ ряда:
Следовательно, в силу свойства точной верхней грани
Щгь + 2)
пе
Поскольку lim l/ln(n + 2) =0, то и lim sup|i?7l(x)| = 0. Это
означает, что последовательность сумм остатков
функционального ряда равномерно на X = К сходится к тождественно
равной нулю функции (Д71(х)=^0). Таким образом, исход-
ный функциональный ряд сходится равномерно во всей области
определения X = R. #
Необходимым признаком поточечной сходимости
функционального ряда является поточечная сходимость к нулю общего
члена этого ряда. Для равномерной сходимости имеет место
аналогичное свойство.
Теорема 2.5 (необходимый признак равномерной схо-
оо
димости функционального ряда). Если ряд ^ /п(#) схо-
п=1
дится равномерно на множестве X, то последовательность его
членов {/п(#)} равномерно сходится на множестве X к нулю:
/п(я?)=*0, п->оо.
< Согласно определению 2.8 равномерной сходимости
функционального ряда, имеем
3N(e)eN Vn > N(e) ЧхеХ: \Sn(x) - S(x)\ < |,

2.2. Равномерная сходимость функциональных рядов, 137
где Sn(x) и S(x) — частичная сумма и сумма функционального
ряда соответственно. Но тогда для всех п > N(e) и всех х Е X
получаем
< \Sn+1(x) - S(x)\ + \Sn(x) - S(x)\ < | + | = е-
Следовательно, fn(x)=z0. ►
Если для функционального ряда на множестве X не
выполнен необходимый признак равномерной сходимости, то этот
функциональный ряд не является равномерно сходящимся на X.
00
Пример 2.14. Рассмотрим функциональный ряд ^2 хп~1.
„ n=1
В примере 2.12 показано, что этот геометрический ряд при
\х\ < 1 сходится, но неравномерно. Последнее можно доказать
и с помощью необходимого признака равномерной сходимости.
Действительно, для общего члена /п(#) = хп~1 этого ряда
имеем sup |/n(#)| = sup \хп\ = 1, п £ N. Отсюда следует, что
()
lim sup |/п(я)| = 1^0, и, значит, fn(x) =^ 0. Необходи-
n>oo(_M) (-1,1)
мыи признак равномерной сходимости функционального ряда
на X = (—1,1) не выполняется, следовательно, исходный ряд не
является равномерно сходящимся в интервале (—1,1). #
Сформулируем простой для проверки достаточный признак
равномерной сходимости функциональных рядов. Для этого
введем следующие понятия.
оо
Определение 2.9. Числовой ряд Yl an c неотрицательны-
п=1
ми членами ап ^ 0, п £ N, называют мажорирующим рядом
или числовой мажорантой на множестве X для функцио-
оо
нального ряда ]Г /п(х), х £ X, если для всех х £ X справедливы
п=1
неравенства

138 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Теорема 2.6 (признак Вейерштрасса равномерной
сходимости функционального ряда). Бели функциональ-
00
ный ряд ^2 fn(x) имеет на множестве X сходящуюся числовую
п=1
мажоранту, то этот ряд сходится на множестве X равномерно
и абсолютно.
оо
< Пусть числовой ряд 5Z ап, ап ^ 0, п £ N, является мажори-
п=1 оо
рующим для функционального ряда ^ /п(#) на множестве X.
п=1
оо
Тогда в силу признака сравнения ряд ^Г, |/п(#)| сходится на
оо п=1
множестве X, т.е. ряд ]Г fn(x) сходится на X абсолютно.
П=1 00
Из абсолютной сходимости ряда ^ /п(#) на множестве X
п=1
оо
следует, что на X сходится сам ряд J^ /n(#) и каждый его п-й
оо п=1
остаток: Rn{x) = ^1 Д(ж), х G X, n E N. Кроме того, в силу
А;=п-Н оо
сходимости знакоположительного ряда Y1 ап последователь-
п=1
ность сумм его остатков стремится к нулю при п —> оо, т.е.
Выберем произвольное е > 0. Тогда для любого номера n > N(e)
и любого натурального числа р имеем
п+р
E
k=n+l
2> хеХ-
к=п+1 к=п+1
В случае произвольных фиксированных х Е X и п > N(e) в
неравенстве |/n+i(x) + ... + /п+р(х)| < е/2 перейдем к пределу

2.2. Равномерная сходимость функциональных рядов 139
при р -> оо. При этом для любых га > N(e) и х £ X получим
оо
где N(e) зависит только от € и не зависит от х £ X. Следо-
оо
вательно, Rn{x) =^0, га -> оо, и функциональный ряд ^ /п(^)
^ п=1
сходится на множестве X равномерно (см. теорему 2.4). ►
Пример 2.15. Докажем, что функциональный ряд
Е°° cosnx
п2
n=l
сходится равномерно на всей числовой прямой R.
Действительно, для всех х G R и п £ N справедливо неравен-
cosnx 1 _ . _ оо 1
ство Ту— ^ —«. Поскольку ряд Дирихле, \^ —~ сходится, то,
согласно признаку Веиерштрасса, данный функциональный ряд
сходится на всей числовой прямой равномерно и абсолютно. #
Итак, функциональный ряд со сходящейся числовой
мажорантой сходится равномерно и абсолютно. Причем из хода
доказательства признака Веиерштрасса ясно, что при этом ряд
оо
2 1/п(#)| сходится на X также равномерно. Однако условие
п=0
существования сходящейся числовой мажоранты для
функционального ряда является только достаточным условием для его
равномерной и абсолютной сходимости, но не является
необходимым условием. Понятия абсолютной и равномерной
сходимости, вообще говоря, не связаны между собой. Так, равномерная
сходимость ряда на множестве X может иметь место и без
абсолютной сходимости на этом множестве. Кроме того, может
оо
оказаться, что ряд Y1 /п(^) сходится абсолютно и равномер-
п=1

140
2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
но на множестве
а ряд ^ |/п(#)| — неравномерно на этом
п=1
множестве. Приведем соответствующие примеры.
Пример 2.16. Рассмотрим функциональный ряд
zeC.
Для любых фиксированных z € С имеем
1
n+\z\
—, n->oo.
п
00
Так как гармонический ряд ^ 1/га расходится, то в соответ-
п=1
ствии с предельным признаком сравнения ряд из модулей членов
исходного ряда расходится на всей комплексной плоскости С.
00
Однако сам функциональный ряд ^ (—l)n/(n + \z\2) cxo-
п=1
дится на всей комплексной плоскости С, поскольку при всех
z E С удовлетворяет признаку Лейбница. Действительно, этот
ряд является знакочередующимся, и для любого z e С
последовательность модулей его членов |(—l)n/(n + |z|2)| = l/(n + \z\2)
монотонно стремится к нулю при п -> оо. Таким образом,
областью сходимости данного функционального ряда является вся
комплексная плоскость С.
Покажем, что данный ряд сходится на множестве С
равномерно. Согласно следствию 1.4 об оценке остатка ряда,
удовлетворяющего условиям признака Лейбница, имеем
(-1)"
к=п+1
Следовательно, О
N
1
1
С.
1/(га + 1) для всех п € N. По-
скольку lira l/(n + 1) = 0, то и lim sup|i?n(2)| =0. В силу
П—>ОО П-ЮО ZQ£

2.2. Равномерная сходимость функциональных рядов 141
теоремы 2.2 получаем Rn(z)=t0 и, значит, функциональный
оо С
ряд 53 (—l)n/(n + \z\2) сходится равномерно на множестве С
п=1
(см. теорему 2.4).
Итак, рассматриваемый функциональный ряд сходится
равномерно на всей комплексной плоскости, но при этом не
является сходящимся абсолютно ни в одной ее точке.
Пример 2.17. Докажем, что на R функциональный ряд
оо
53 (—1)пх2/(1 + х2)п сходится равномерно, а функциональный
п=1
оо
ряд 53 х2/(1 + х2)п, составленный из модулей членов первого
п=1
ряда, сходится при каждом х Е R, но неравномерно на М.
оо
В самом деле, при каждом х ЕШ ряд 5^ (—1)пя /(1 + х2)п
п=1
удовлетворяет признаку Лейбница, так как является
знакочередующимся, и последовательность модулей его членов
!/»(*)! =
(1+Х2)п
X2
Х2)
2)п
монотонно стремится к нулю при п —> оо для каждого х Е R. В
силу следствия 1.4 об оценке остатка ряда, удовлетворяющего
признаку Лейбница, имеем для любого действительного х ф О
х2 х2
1> (n + l)x2 п + 1
(здесь мы воспользовались формулой бинома Ньютона для
представления выражения (1 + х2)п+1 в виде суммы). Кроме
того, очевидно, что для любого п Е N имеет место следующее
равенство: Rn{0) = 0. Таким образом,
eR' neN'

142 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Отсюда, как и в примере 2.16, заключаем, что Rn(x) =ZO.
ОО JH
Следовательно, ряд JZ (—1)пя /(1 + ж2)п сходится равномерно
п=1«
на всей числовой прямой R.
Рассмотрим функциональный ряд, составленный из модулей
членов исходного ряда:
оо
Этот ряд при х ф О является геометрическим с параметром
q = 1/(1 +ж2) (см. пример 1.4). Поскольку q = 1/(1 +ж2) Е (0,1)
при всех х Е R, х ф 0, то этот ряд сходится при всех х Е R\ {0}.
оо оо
При х = 0 имеем £ я2/(1 + х2)п = £0 = 0. Таким образом,
п=1 п=1
оо
исходный функциональный ряд £ (—1)паг/(1+ аг)п сходится
п=1
абсолютно в каждой точке х Е R.
оо
Докажем, что сходимость ряда £ x /(1 + х )п на множе-
п=1
стве R не является равномерной. Обозначим n-й остаток этого
ряда Яп(ж). Очевидно, что Rn{0) = 0. При х ф 0 имеем
9 9 9
аг аг аг
+ х2)п+1
X2
/ 1
V + 1 + х
+ {1 + х2)2
X2 1
1 _J_ (1+X2)n
1+Х2
(см. пример 1.4). Отсюда для всякого номера п Е N получаем
= lim L
Шп()

2.2. Равномерная сходимость функциональных рядов 143
и, следовательно, lim sup|i2n(a;)| = 1^0. Согласно теореме
2.2, это означает, что Rn(x)^^0, т.е. последовательность
{Rn{x)} остатков ряда сходится к нулю на множестве* R
неравномерно. Тогда из теоремы 2.4 следует, что и ряд
* /(1 + х )п сходится на R неравномерно.
оо
п=1
Замечание 2.1. Из равномерной сходимости
функционального ряда на множестве X следует его равномерная сходимость
оо
на любом множестве Y С X, Действительно, если ряд Yl fk(x)
k=i
сходится к функции f(x) равномерно на множестве X, то для
любого е > 0 найдется такой номер N(e) E N, что при всех
п
п > N(e) выполняется неравенство Yl fk{x) — f{x) <е для лю~
к=\
бого х Е X. Но тогда это неравенство будет справедливо и для
оо
любого х € Y С X. И, значит, ряд X) fk{x) равномерно схо-
Ь=1
дится на Y С X. Обратное утверждение неверно. Существуют
ряды, сходящиеся, например, равномерно на любом отрезке, но
неравномерно на всей числовой прямой.
оо
Пример 2.18. Покажем, что функциональный ряд Yl zn/n'
n=l
сходится равномерно на любом отрезке [а, Ь]сКи
неравномерно на всей прямой R.
Рассмотрим произвольный отрезок [а, Ь] С Ш и положим
оо
q = max{|a|, \b\} > 0. Тогда числовой ряд £ qn/n\ является
п=1 оо
мажорантой для исходного функционального ряда Y1 яп/п'
п=1
оо
на отрезке [а, Ь]. Знакоположительный числовой ряд
сходится при q > 0 в силу предельного признака Даламбера,
п=1
*Из доказательства ясно, что {Rn(x)} будет сходиться неравномерно на
любом подмножестве R, содержащем некоторую окрестность точки х = 0.

144 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
поскольку
Пт ( q — ) = lim —^--=0<1, q > 0.
Следовательно, согласно признаку Вейерштрасса равномерной
оо
сходимости (см. теорему 2.6), ряд ^2 хп/п\ сходится равно-
п=1
мерно на любом отрезке [а, Ь] С R.
оо
Поскольку ряд ^2 хп/п\ сходится на любом отрезке [а, Ь] С
п=1
С R, то он сходится и на всей числовой прямой R. Покажем, что
эта сходимость на R не является равномерной. Действительно,
lim |/n(z)| = Ит |^n/^!| = +°o №* всякого п Е N. Поэтому
x—>oo x—>oo
при каждом фиксированном n E N функция |/п(я)| является
неограниченной на R, следовательно,
()| пеК
Отсюда lim sup|/n(x)| ^0. В соответствии с теоремой 2.2
n^°°xeR
/п(ж) = хп/п\ ^z±^0, т.е. не выполняется необходимый признак
равномерной сходимости функционального ряда (см. теорему
2.5). Поэтому исходный ряд сходится на R неравномерно. #
Признак Вейерштрасса равномерной сходимости
функциональных рядов очень прост, но для его применения необходим
сходящийся числовой ряд, мажорирующий данный
функциональный ряд. Непосредственно „увидеть" такой ряд не всегда
удается. Очевидно, что наилучшей числовой мажорантой для
оо
функционального ряда Yl fn{x) на множестве X является чи-
оо п=1
еловой ряд J2 SUP 1/п(ж)|> требующий умения находить точные
п=\хех
верхние грани функции на множестве. Одним из способов
нахождения (или оценки) точной верхней грани модуля общего
члена функционального ряда является исследование его на
экстремум. Проиллюстрируем это на примере.

2.2. Равномерная сходимость функциональных рядов 145
Пример 2.19. Исследуем на равномерную сходимость на
оо 4 2
множестве R. функциональный ряд Y1 хе~п х
п=1
Попробуем подыскать для этого ряда мажорирующий
числовой ряд на R. Найдем максимум на множестве R
дифференцируемой на R функции |/п(я)| = |ж|е~п х при фиксированном
значении п £ N. Так как |/п(#)| является четной функцией, то
ограничимся изучением ее только при х ^ 0. Если х ^ 0, то
|/n(#)| = fn(x) = хе~п х , поэтому при всех х ^ 0
\fn(x)\' = (xe"^2)/ = e-^2(l-2nV) =
Отсюда следует, что |/п(я)|' > 0 в интервале (0, у/2/(2п2)) и
\fn{x)\r <0 в интервале (\/2/(2п2), +оо). Поэтому функция
|/п(я)| в интервале (0, у/2/(2п2)) возрастает, а в интервале
(\/2/(2п2), +оо) убывает. Таким образом, точка х = у/2/(2п2)
является точкой локального максимума функции |/п(я)| в ин~
тервале (0,+оо) [II]. Поскольку |/п(0)| =0, что меньше
значения |/n(z)| B точке х = \/2/(2п2), то в этой точке функция
|/п(ж)| достигает наибольшего значения в промежутке [0, +оо),
которое и является ее наибольшим значением на всей оси R
вследствие четности функции |/п(ж)|. Следовательно, для
любого х G R справедливо неравенство
оо
Итак, ряд Дирихле £ 1/п2 является мажорирующим числовым
п=1
рядом для исходного функционального ряда на всей прямой R.
Поскольку он сходится, то в силу признака Вейерштрасса (см.
теорему 2.6) исходный функциональный ряд сходится
равномерно на всей числовой прямой R. #

146 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Сформулируем критерий равномерной сходимости
функционального ряда.
Теорема 2.7 (критерий Коши равномерной сходимос-
оо
ти функционального ряда). Функциональный ряд Х)/п(ж)
п=1
является равномерно сходящимся на множестве X тогда и
только тогда, когда для любого числа е > О найдется номер N(e) Е N,
зависящий только от е, такой, что для любых п > N(e), p Е N и
х Е X выполняется неравенство
\Sn+p(x) - Sn(x)\ = |/n+1(x) +... + fn+p(x)\ < e. (2.7)
OO
<4 Необходимость. Пусть функциональный ряд ^2 fn(x)
n=l
сходится равномерно на множестве X. Тогда Rn{x) =£0, где
Rn{x) — сумма n-го остатка этого ряда. Это означает, что
для любого е > 0 найдется такой номер N(e) G N, что для всех
п > N(e) и всех х Е X справедлива оценка: |Дп(х)| < е. Если
S(x) и Sn(x) — сумма и п-я частичная сумма рассматриваемого
ряда соответственно, то Rn{x) = S(x) — Sn(x), nE N. Поэтому
для любого п > iV(e), любого р Е N и всех хЕ X имеем
что соответствует (2.7).
оо
Достаточность. Пусть для ряда Y1 /п(^) выполня-
п=1
ется неравенство (2.7). Из этого неравенства в силу
критерия Коши сходимости функционального ряда (см. теорему 2.1)
оо
следует, что ряд ^2 fn{x) сходится на множестве X к неко-
п=1
торой сумме S(x), х Е X. Следовательно, lim Sn(x) = S(x),
п—>оо
х Е X, и, в частности, для всякого п Е N справедливо равенство

2.2. Равномерная сходимость функциональных рядов 147
lim Sn+P(x) = S(x), х Е X. Поэтому, переходя в неравенстве
р—>оо
(2.7), т.е. в неравенстве \Sn+p(x) - Sn(x)\ < е, к пределу при
р -* оо, получаем
Vn>JV(e) Vx€X: |Я„(х)| = |S(x) -5„(х)| < е,
т.е. Дп(ж)=£0. А это означает равномерную сходимость
ОО
функционального ряда Y2 /п(ж) на X. ►
п=1
Замечание 2.2. Как известно, из поточечной сходимости
00
функционального ряда j^ |/n(z)| на множестве X следует по-
п=1 оо
точечная сходимость на X и функционального ряда Yl fn{x)-
n=l
Аналогичное свойство верно и для равномерной сходимости: ес-
оо
ли функциональный ряд £) |/п(^)| сходится на X равномерно,
п=1
оо
то и функциональный ряд Y1 /п(^) также сходится на X равно-
п=1
мерно. Действительно, выберем произвольное е > 0. Тогда из
критерия Коши равномерной сходимости для функционально-
оо
го ряда X) |/п(я)| следует, что найдется такой номер N(e) E N,
п=1
что для всех п > N(e), pGNhiGX выполняется неравенство
| + • • • + \fn+P(x)\ < e.
Отсюда для произвольных п > iV(e), р Е N и х Е X получаем
|/n+l(*) + ..- +fn+p{x)\ < |/n+l(«)| + .-. + |/n+p(*)| < С,
т.е. выполняется утверждение критерия Коши равномерной
оо
сходимости и для функционального ряда Yl fn{x)- Следова-
оо п=1
тельно, функциональный ряд Y1 /п(^) равномерно сходится на
71=1
множестве X,

148 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
2.3. Свойства равномерно сходящихся рядов
оо
Теорема 2.8. Если оба функциональных ряда Y1 /п(я) и
оо п=1
Y1 9п(х) сходятся равномерно на множестве X, то всякая их
п=1
линейная комбинация
ж)), а,/?ЕЕ (a, fie С), (2.8)
n=l
также является равномерно сходящимся на множестве X рядом.
При этом для сумм рядов верно равенство
оо оо оо
х 1 Gt in IX J ™i IDCln IX) I — GL 7 in IXJ ™i /5 j Gn l«С J« X с ./*. • I ^ • У J
n=l n=l n=l
oo oo
^ Поскольку функциональные ряды Yl /n(^) и 5^ ffn(^) сходят-
n=l n=l
ел (пото'че'чпо) на множестве X, то, согласно свойствам 1.5 и
1.6, при любых а,/? € R (а,/?ЕС) функциональный ряд (2.8)
сходится в каждой точке х € X, причем его сумма связана с
суммами исходных рядов формулой (2.9). Докажем, что ряд
(2.8) сходится равномерно на множестве X. Если а = fi = 0, то
это утверждение очевидно. Пусть теперь \а\ + \fi\ ф 0. Так кале
оо оо
ряды ]Г) fn(x) и Y1 9п{х) равномерно сходятся на X, то в си-
п=1 п=1
лу критерия Коши равномерной сходимости функционального
ряда (см. теорему 2.7) для любого е > 0 найдется такой номер
N(e) € N, что для любых п > N(e), р £ N и х Е X одновременно
выполняются следующие неравенства:

2.3. Свойства равномерно сходящихся рядов 149
Отсюда для всех п > N(e), р Е N и х Е X получим
v , р
И
■fc=l
|а|е__ |/?|е _
/Q| "• I III /O| )
т.е. для функционального ряда (2.8) выполняется условие
критерия Копш равномерной сходимости функционального ряда на
множестве X. Следовательно, этот ряд сходится равномерно на
множестве X. ►
Рассмотрим некоторые свойства функциональных рядов,
членами которых являются непрерывные действительные
функции, определенные в промежутке (конечном или бесконечном)
IcR.
Теорема 2.9 (теорема о предельном переходе для
функциональных рядов). Пусть функции /n(z), n € N,
определены в интервале (а, Ь) и имеют в некоторой точке хо Е (а, Ь)
конечные пределы lim fn(x) = аЛ, п Е N. Тогда, если функцио-
оо
нальный ряд Yl fn(x) сходится равномерно в интервале (а, Ь),
п=1
то справедливы утверждения:
оо
а) числовой ряд Y1 ап сходится;
п=1
б) lim § fn(x) = f an, или lim 2 fn(x) = E Um fn{x).
^►^ x^x x>xo
oo
^ Из равномерной сходимости функционального ряда Y1 /п(^)?
п=0
согласно критерию Коши, следует, что для любого е > 0
существует такой номер N(e) E N, что для всех п > iV(e), р Е N и
х Е (a, b) выполняется неравенство
п+р

150 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Переходя в данном неравенстве к пределу при х ->• xq [I-7.4],
получаем
п+р
£ ак <|<е, n>N(e), peN,
оо
т.е. для ряда ]Г) ап выполнено условие критерия Коши сходи-
п=1
мости числового ряда (см. теорему 1.3), и, следовательно, он
сходится.
Обозначим
n=l Jfc=l n=l
Тогда для любого n € N
\A-An\. (2.10)
ОО
Из равномерной сходимости функционального ряда J2 /п(^) и
оо п=1
из сходимости числового ряда ^ ап следует, что для любого
п=1
б: > 0 найдется такой номер N(e) E N, что для всех п > N(e) и
х Е (а, Ь) одновременно верны неравенства
\S(x)-Sn(x)\<~ и \А-Ап\<6-. (2.11)
Поскольку lim Sn(x) = Лп для любого п Е N, можно указать
X—►Хо
такое 5 = tf(e,n) > 0, что для всех х Е (а, Ь), удовлетворяющих
условию 0 < \х — хо\ < 5, выполняется неравенство
\Sn(x)-An\<£~. (2.12)

2.3. Свойства равномерно сходящихся рядов 151
Выберем произвольное е > 0. Подберем номер N(e), который
необходим для выполнения неравенств (2.11) при п > N(e) и
х € (а, Ь). Выберем произвольный номер п > N(e), укажем число
£(£) = J(e,n), которое требуется для выполнения неравенства
(2.12) при всех х G (а, Ь), таких, что 0 < \х - хо\ < 6(е). Тогда
для этих значений х будут выполняться неравенства (2.11) и
(2.12). Следовательно, используя (2.10), получаем
№)-4<f + f + f =с> *€(а,Ь), 0<\х-х0\<6{е).
Это означает, что lim S(x) = Л, или
71=1 71=1 71=1
Замечание 2.3. Отметим, что теорема справедлива и
в том случае, если интервал (а, 6) заменить произвольным
промежутком X, а пределы — односторонними пределами
слева или справа.
Теорема 2.10 (теорема о непрерывности суммы
равномерно сходящегося ряда). Если функциональный ряд
ОО
Z] /п(я) сходится равномерно в промежутке 1сКи все его
п=1
члены fn(x) являются непрерывными на X функциями, то
ОО
сумма S(x) функционального ряда ^2 /п(я) также непрерывна
71=1
наХ.
< Пусть хо — произвольная фиксированная точка промежутка
^СЕ. Поскольку функции /п(я) непрерывны в точке жо, то
^т /п(я) = /п(яо) (если хо — граничная точка промежутка
-X", то предел следует понимать как односторонний). Тогда,
согласно теореме 2.9 (см. замечание 2.3), имеем
„Ы = S(x0),
Д/n()
71=1 71=1 П=1

152 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
что и означает непрерывность функции S(x) в точке х$.
Поскольку xq является произвольной точкой промежутка X,
функция S(x) непрерывна в промежутке X. ►
Замечание 2.4. Условие равномерной сходимости
функционального ряда является достаточным для непрерывности
суммы ряда из непрерывных функций, но не является
необходимым, т.е. сходящийся к непрерывной функции функциональный
ряд с непрерывными членами не обязательно должен быть
равномерно сходящимся.
Пример 2.20. Функциональный ряд
"-*"-1), are (0,1),
n=l
с непрерывными членами имеет сумму S(x) = 0, непрерывную
в интервале (0,1), но не является в этом интервале равномерно
сходящимся.
Действительно, для каждого х Е (0,1) последовательность
{«Sn(a;)}, Sn(x) = жп, частичных сумм функционального ряда
стремится к нулю при п —> оо. Однако
sup |5п(ж)| = 1, neN, и lim sup \Sn(x)\ = 1 ф 0.
«€(0,1) п^°°
Таким образом, согласно теореме 2.2, имеем Sn(x) =^£ 0, и, зна-
(0,1)
чит, исходный ряд сходится к тождественно нулевой функции
неравномерно в (0,1). #
В силу взаимно однозначного соответствия между
функциональными рядами и последовательностями (см. 2.1) теорему
2.10 можно переформулировать следующим образом.
Теорема 2.11. Пусть функциональная последовательность
{Sn{x)} сходится равномерно в промежутке IcRk функции

2.3. Свойства равномерно сходящихся рядов 153
S(x), и пусть функции Sn(x), n Е N, непрерывны на X. Тогда
предельная функция S(x) также непрерывна на X:
lim S(x) = S(xo)i xo G X,
X—IXq
lim lim Sn(x) = lim lim Sn(x), xo G X.
xtxontoo n->oox->xo
ИЛИ
Теорема 2.12 (теорема о почленном интегрирова-
00
нии ряда). Пусть ряд ^ /п(^), составленный из непрерывных
на отрезке [а, Ь] функций /п(ж), сходится равномерно на [а, Ь] и
имеет сумму S(x). Тогда функция S(x) интегрируема на [а, Ь],
и для произвольных с,х€ [а, Ь] верно равенство
X
f
{
XX
s(t)dt= /(Е/»(«))Л = Е / Ut)dt. (2.13)
с "=1
^ Согласно теореме 2.10 о непрерывности суммы равномерно
сходящегося на отрезке [а, Ь] функционального ряда,
составленного из непрерывных на [а, Ь] членов, S(x) является
непрерывной функцией на [а, Ь], следовательно, интегрируемой на
любом отрезке [с, х] С [а, Ь] (в том числе и на любом отрезке
[я» с] с [а, 6], где х < с) [VI]. Рассмотрим функциональный ряд
00 X X
Yl J fn{t) dt и функцию F(x) = / S(t) dt, определенные на отрез-
*=1 с с
п х
ке [а, Ь]. Обозначим Fn(x) = X) / fk(t)dt. Использовав свойства
к=1с
°пределенного интеграла [VI], получим
п *
fk(t)dt= / 5]/fc(t)dt= / Sn(t)dt,

154 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
где Sn(t) = J2 /fcW> * € [°> Ь]. Поскольку функциональный ряд
/п(*) сходится к функции S(t) равномерно на отрезке [а, 6],
оо
п=1
то Sn(t) =zS(t), пли lim sup \S(t) - Sn(t)\ = О (см. теорему
[а,6] n->°°te[M
2.2). Используя свойства определенного интеграла [VI], для
всех п Е N получаем
(К sup \F(x)-Fn(x)\= sup \[s{t)dt- [sn(t)dt =
x€[a,b] xe[a,b] \J J
x x
= sup f(S(t)-Sn{t))dt < sup \f\S(t)-Sn(t)\dt <
xe[a,b] J xe[a,b]\J
с с
< sup (\x-c\ sup |5(t)-5n(«)|) <(6-a) sup |5(t)-5n(t)|.
Отсюда в силу того, что lim sup \S(t) — Sn(t)\ =0, справед-
n^°°te[aM
ливо равенство lim sup \F(x) — Fn(x)\ =0. А это означает,
что Fn(x) ==^ F(x), и, следовательно, функциональный ряд
оо х Ml
S Jfn(t)dt равномерно на отрезке [а, Ь] сходится к функции
п=1 с х
F{x) = fS{t)dt. ►
С
В случае использования равенства (2.13) говорят о почлен-
00
ном интегрировании функционального ряда J2 /п(^)-
п=1
Замечание 2.5. В ходе доказательства теоремы 2.12 было
00
установлено, что если функциональный ряд ^ /п(я) из непре-
п=1
рывных функций сходится равномерно на [а, Ь] к функции S(x),
оо х
то при любом с G [а, Ь] функциональный ряд j^ / /n(£) dt сходит-
X 71=1 С
ся равномерно на [а, Ь] к функции / S(t)dt.
с

2.3. Свойства равномерно сходящихся рядов 155
Теорема 2.13 (теорема о почленном
дифференцировании рлда). Пусть /п(я), п € N, — непрерывно
дифференцируемые на отрезке [а, Ь] функции; функциональный ряд
00
2 fn(x)> составленный из производных этих функций, сходит-
п=1 ^ оо
ся равномерно на [а, &]; функциональный ряд ^ /п(я) сходится
п=1
при некотором xq е [а, Ь]. Тогда справедливы следующие
утверждения:
оо
1) РЯД XI /п(#) сходится равномерно на [а, 6];
п=1 оо
2) сумма S(x) = Yl /n(^) этого ряда — непрерывно диффе-
71=1
ренцируемая на [а, Ь] функция;
3) верно равенство
Л(*)» ж е 1°> ч- (2Л4)
п=1
оо
< Функциональный ряд J2 fn(x) из непрерывных функций
п=1
fn(x)i n ^ N, равномерно сходится на отрезке [а, 6], следователь-
оо
но, согласно теореме 2.10, его сумма s(x}= J2 fh(x) является
71=1
непрерывной на отрезке [а, Ь] функцией. В силу теоремы 2.12
для точки xq (см. условие теоремы) и любого х G [а, Ь] имеем
fs(t)dt = f; [&(t)dt = f^{fn(x) - /„(xo)), (2.15)
xo n=1xo n=l
причем последний ряд сходится равномерно на всем отрезке
[а, Ь]. Но по условию теоремы также сходится и числовой ряд
оо
^2 /п (#())• Заметим, что этот числовой ряд можно рассма-
п=1
тривать как функциональный ряд, члены которого являются
постоянными на [а, Ь] функциями, вследствие чего он является

156 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
равномерно сходящимся на отрезке [а, Ь]. Тогда сумма
функциональных рядов
оо
71=1 71=1 71=1
также является равномерно сходящимся на отрезке [а, 6]
функциональным рядом (см. теорему 2.8). При этом его сумма S(x)
00 00
равна S(x) = £ fn(x) = £ (/п(я) - /п(яо)) + S(x0). Следова-
п=1 п=1
тельно, равенство (2.15) можно переписать так:
/
оо
s(t)dt = J]/nW -YlfnM = S(x) - S{x0), x e [a, b].
n=1 n=1
X
Поскольку функция / s(t) dt является дифференцируемой на от-
резке [а, Ь] (как интеграл с переменным верхним пределом от
непрерывной функции [VI]), то и функция S(x)
дифференцируема на [а, Ь], причем
8(х) = (js(t)dt\ = {S(x) - S(x0))' = S'(x), x e [a, b].
Отсюда следует, что, во-первых, сумма S(x) является
непрерывно дифференцируемой на [а, Ь] функцией, поскольку s(x)
непрерывна на [а, Ь], и, во-вторых, верно равенство
ti(x), хе[а,Ь]. ►
П=1
При использовании равенства (2.14) говорят о почленном
оо
дифференцировании функционального ряда ]Г) /п(я)-
п=1

2.4. Комплексные степенные ряды 157
2.4. Комплексные степенные ряды
Определение 2.10. Комплексным степенным рядом
(или рядом по степеням z — z$) называют функциональный
ряд
00
п=0
членами которого являются комплексные многочлены fn{z) =
= Cn(z — zo)n от комплексного переменного z = х + гу G С. При
этом комплексные числа cn = an+ibn, n = 0,1, 2,..., называют
коэффициентами этого степенного ряда, а точку zq =
= xq + гуо G С — центром степенного ряда.
Всякий степенной ряд определен на всей комплексной
плоскости С и сходится, по крайней мере, в своем центре, т.е. в
точке z = zo E С. Таким образом, область сходимости всякого
степенного ряда является непустым множеством — она всегда
содержит центр ряда.
оо
Заметим, что если в степенном ряде £) Cn(z — zo)n с цен-
п=0
тром в точке zo сделать замену переменного w = z — zo, то
00
получим степенной ряд £) CnWn, w G С, с центром в нуле. По-
п=0
этому в дальнейшем, не ограничивая общности рассуждений,
можно рассматривать только ряды с центром в нуле — ряды
оо
вида Y1 Сп**1! * € С При этом все факты, доказанные для сте-
71=0
пенных рядов с центром в нуле без всяких затруднений можно
перенести на степенные ряды с центром в произвольной точке
Теорема 2.14 (теорема Абеля). Пусть степенной ряд
оо
^2 CnZn сходится в некоторой точке z = z$ G С, z$ ф 0. Тогда он
п=о
сходится абсолютно в каждой точке открытого круга \z\ < \zq\

158 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
комплексной плоскости и сходится равномерно в любом
замкнутом круге \z\ ^ г, где г < \zo\.
00
Если степенной ряд ^ CnZn расходится в некоторой точке
п=0
z\ Е С, то он расходится во всех точках zGC, для которых
И > l*il-
оо
< Пусть степенной ряд J2 °пгП сходится в точке zq ф 0. В
71=0
силу необходимого признака сходимости числового ряда (см.
теорему 1.2) \cuZq | -» 0 при п ->■ оо. Значит, последовательность
{IcnZol} является ограниченной [1-6.4], т.е. найдется такое
число М > О, что для любых п Е N выполняется неравенство
\cnZQ | ^ М. Пусть произвольное число zGC таково, что \z\ <
<\zo\. 1огда
\CnZn\ =
\ZQ
оо
При всех \z\ < \zq\ ряд J2 M\z/zo\n является геометрическим
п=0
рядом с параметром q = \z/zo\ < 1 и потому сходится. Согласно
оо
признаку сравнения (см. теорему 1.4), ряд J^ \cnZn\ также схо-
71=0
дится. Таким образом, в открытом круге \z\ < \zo\ комплексной
оо
плоскости С ряд 5Z °пхП сходится абсолютно.
71=0
Рассмотрим произвольный замкнутый круг \z\ ^ г, где 0 <
< г < |zo|. Для всех точек этого замкнутого круга верны
неравенства
-■ - / г \п
< W
оо
Следовательно, ряд ^ CnZn имеет сходящуюся числовую мажо-
71=0
ранту — геометрический ряд
00

2.4. Комплексные степенные ряды 159
и в силу признака Вейерштпрасса равномерной сходимости
функционального ряда (см. теорему 2.6) сходится равномерно
(и абсолютно) в замкнутом круге \z\ ^ г.
00
Наконец, пусть степенной ряд £) CnZn расходится в некото-
п=0
рой точке z\ Е С. Тогда этот ряд расходится во всех точках
z E С, для которых \z\ > \z\\. Предположим, что это не так, т.е.
существует некоторая точка z<i Е С, удовлетворяющая условию
00
\z<i\ > \z\\ и такая, что в этой точке ряд J2 CnZn сходится. Но
п=0
тогда, согласно доказанному выше, ряд будет сходиться и в
точке z\, что противоречит условию теоремы. Следовательно,
оо
предположение неверно, и степенной ряд J2 °пгП расходится во
п=0
всех точках z Е С, удовлетворяющих условию \z\ > \z\\. ►
оо
Итак, всякий степенной ряд J2 сп*п сходится как минимум
п=0
в одной точке комплексной плоскости — в центре ряда zq = 0.
Кроме того, характер сходимости степенного ряда в различных
точках комплексной плоскости С определяется доказанной
выше теоремой 2.14. Однако, основываясь на теореме 2.14, можно
доказать и более общую теорему об области сходимости
степенного ряда.
оо
Теорема 2.15. Для всякого степенного ряда ^ CnZn cy-
п=0
ществует действительное число* Я, 0 ^ R ^ +оо, такое, что
справедливы следующие утверждения:
1) при всех zGC, для которых \z\ < Д, степенной ряд
сходится, причем абсолютно;
2) в любом замкнутом круге \z\ ^ г, где г < Я, степенной
ряд сходится абсолютно и равномерно;
3) при всех z G С, для которых \z\ > Д, ряд расходится.
* Строго говоря, число R является точкой (возможно, бесконечной
точкой) расширенной полупрямой [0, +оо] [1-1.3].

160 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
оо
<4 Всякий ряд Yl °nzU сходится либо только в одной точке
п=0
комплексной плоскости — в центре ряда zo = 0, либо на всей
комплексной плоскости С, либо более чем в одной точке, но не
на всей комплексной плоскости. Рассмотрим каждый из трех
вариантов.
00
а. Пусть ряд Yl °nzn сходится только в одной точке ком-
плексной плоскости — в центре ряда zq = 0. Тогда условиям
теоремы удовлетворяет число R = 0: первое и второе утверждения
тривиальны, а третье утверждение верно по предположению.
оо
б. Пусть ряд 5Z Сп*" сходится на всей комплексной плос-
п=0
кости С. Положим R = +оо и докажем, что заданное таким
образом значение R удовлетворяет условиям теоремы. Можно
считать, что третье утверждение теоремы, выполняется, так
как точек z, удовлетворяющих условию \z\ > R просто нет.
Докажем первое утверждение. Пусть z G С — произвольная точка.
Выберем такую точку zo, что |zo| > \z\. Поскольку ряд в точке
zq сходится (он сходится на всей комплексной плоскости), то в
соответствии с теоремой 2.14 этот ряд сходится абсолютно и в
оо
точке z, т.е. степенной ряд ^2 CnZn абсолютно сходится в любой
п=0
точке комплексной плоскости. Наконец, в силу той же теоремы
2.14 ряд сходится равномерно в любом замкнутом круге \z\ ^ г
(г — любое положительное число). Итак, второе утверждение
теоремы также выполняется.
оо
в. Пусть ряд Y1 Сп**1 сходится более чем в одной точке ком-
п=0
плексной плоскости, но не на всей плоскости. Тогда существует
хотя бы одна точка z\ G С, в которой ряд сходится, причем
z\ ф 0, и существует хотя бы одна точка z<i G С, в которой ряд
расходится. Рассмотрим множество М значений х = \z\ для
оо
тех точек z G С, в которых ряд J2 cnzTl сходится. Поскольку
п=0
всякий степенной ряд сходится в своем центре, в данном слу-

2.4. Комплексные степенные ряды 161
чае в точке zo = 0, то число х = О принадлежит множеству М
и, следовательно, множество М не пусто. Так как ряд
расходится в некоторой точке ;&2, то, согласно теореме 2.14, он
расходится при всех 2ЕС, таких, что \z\ > l^l-
Следовательно, множество М является подмножеством отрезка [0, \z2\\ и
потому ограничено.
Для ограниченного непустого множества М существует его
точная верхняя грань supM < +00 [1-2.7]. Положим Л = supM
и докажем, что число Л обладает нужными свойствами. Во-
первых, R > О, так как \z\ | Е М и в соответствии с определением
точной верхней грани R ^ \z\\ > 0. Далее, докажем, что если
оо
\z\ < Л, то ряд ]П CnZn сходится, причем абсолютно. Итак,
п=0
пусть z — произвольное комплексное число, для которого
\z\ = х < R. Согласно определению точной верхней грани и ее
свойствам [1-2.7], имеем
Ve>0 3x0eM: R^xo>supM-e = R-e.
В частности, если е = R — \z\ = R — х > 0, то найдется такая
точка хо Е М, что выполняется неравенство х < хо ^ Я. Так
оо
как хо Е М, то жо = |^о|, где точка zo E С такова, что ]П CuZq
п=0
оо
сходится. Согласно теореме 2.14, в точке z ряд ]Р ^z71 также
п=0
сходится, причем абсолютно, поскольку |я|=ж<жо = |зй|.
Покажем, что в любом замкнутом круге \z\ ^ г, где г < Л,
оо
степенной ряд ]П CnZn сходится равномерно, т.е. докажем вто-
п=0
рое утверждение теоремы. Пусть 0 < г < R. Поскольку ряд
оо
Y^ CnZn сходится в открытом круге \z\ < Л, то он сходится и
71=0
в кольце г < \z\ < Л. Пусть точка zq принадлежит указанному
кольцу. Тогда г < |zo| и степенной ряд сходится в точке z$. В
оо
силу теоремы 2.14 степенной ряд ]П CnZn сходится равномерно
п=0
(и абсолютно) в замкнутом круге \z\ ^ г.

162 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Наконец, докажем третье утверждение теоремы. Если \z\ >
> R = supM, то действительное число х = \z\ не принадлежит
множеству М. А в силу определения множества М это означа-
оо
ет, что в точке z ряд JZ Сп**1 расходится. ►
п=о
Из приведенного доказательства вытекает следующее. Если
оо
степенной ряд J2 CnZn сходится только в одной точке zq = О,
п=о
то R = 0. Если ряд сходится более чем в одной точке из
С, но не на всей комплексной плоскости, то 0 < R < +оо,
Наконец, если ряд сходится на всей комплексной плоскости
С, то R = +оо. Для каждого степенного ряда число R в
теореме 2.15 определяется однозначно. Это число называют
оо
радиусом сходимости степенного ряда ^ CnZn, а открытый
п=0
круг \z\ < R в комплексной плоскости с центром в нуле и
радиусом R — кругом сходимости этого ряда.
Если радиус сходимости равен нулю (R = 0), то круг
сходимости пуст (однако область сходимости при этом не является
пустой — степенной ряд сходится в своем центре zq = 0), а если
R = +оо, то кругом сходимости является вся комплексная плос-
оо
кость С. Если же радиус сходимости степенного ряда ^ CnZn
является конечным положительным числом (0 < R < +оо), то
этот ряд сходится, причем абсолютно, в открытом круге \z\ < R
и расходится при \z\ > R.
Отметим, что в теореме 2.15 ничего не говорится о
поведении степенного ряда на границе круга сходимости, т.е. в таких
точках z E С, что \z\ = R. В этих точках ряд может как
сходиться, так и расходиться, поэтому необходимо
дополнительное исследование. Таким образом, область сходимости любого
оо
степенного ряда Yl °nzn c центром в нуле представляет собой
п=0
объединение его круга сходимости (открытого круга \z\ < R с
центром в точке zq = 0 и радиусом Л, равным радиусу сходи-

2.4. Комплексные степенные ряды
163
Область
абсолютной
и равномерной
сходимости
Отдельные точки
сходимости на границе
круга сходимости
Рис. 2.3
Область
расходимости
мости ряда) и некоторого
множества (возможно,
пустого) точек комплексной сходимости
плоскости, принадлежащих
границе круга сходимости
\z\ = R. Точками расходи-
оо
мости ряда ^2 CnZn
ЯВЛЯЛО
ются все остальные точки
комплексной плоскости С
(рис. 2.3).
Кроме того, нетрудно
увидеть, что если
степенной ряд сходится
абсолютно в какой-либо точке z\,
лежащей на границе
круга сходимости (\z\| = Я), то
ряд сходится абсолютно на всей границе \z\ = R этого круга.
Действительно, для всякой точки z, лежащей на границе круга
сходимости, имеем равенство \z\ = R = \z\\. Следовательно, ряд
оо оо
2 \°п\ \z|п> составленный из модулей степенного ряда ^2 CnZn,
п=0 п=0
будет одинаковым для всех точек границы круга сходимости и
оо
будет совпадать со сходящимся рядом ^ \сп\ \zi\n.
Обратимся теперь к вопросу о том, как определить радиус
сходимости конкретного степенного ряда. Поскольку внутри
оо
своего круга сходимости всякий степенной ряд ]Г) CnZn cxo-
71=0
ОО
дится абсолютно, то в этом круге ряд из модулей ^ \cnZn\
сходится, и к нему применимы признаки сходимости
знакоположительных числовых рядов.
Предположим, что существует конечный или бесконечный
предел lim \cn+\lcn\ — А. Рассмотрим произвольное фиксиро-
п—>оо

1642. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
оо
ванное г/Ои применим к ряду ^ \cnzn\ предельный признак
п=0
Даламбера. Вычислим следующий предел:
lim ™1" , ' = \z\ lim
00
Из предельного признака Даламбера следует, что ряд ^
п=0
сходится при A|z| < 1 и расходится при A|z| > 1. Следовательно,
00
если 0 < А < +оо, то ряд ^2 °nZn сходится абсолютно при всех
п=0
z E С, удовлетворяющих неравенству
, . 1 1 г
= lim
п->оо
lim
п->оо| сп
и расходится при всех z E С, удовлетворяющих неравенству
Это означает, что радиус сходимости степенного ряда R =
= 1/А = lim \cn/cn+i\. Если А = 0, то ряд сходится абсолютно
п—>оо
при всех z Е С, и, значит, Л = +оо = lim \cnlcn+\\- Если же
п—>оо
А = +оо, то ряд расходится всюду, кроме одной точки z = 0, и,
следовательно, Д = 0= lim Icn/cn+i].
п—>оо оо
Итак, радиус сходимости степенного ряда £^ CnZ71 можно
п=0
определить, используя формулу
R= lim
п—>оо
(2.16)
если предел справа существует.
Предположим, что существует конечный или бесконечный
предел lim iV|cn| = А. Рассмотрим произвольное фиксирован-
п—>оо
00
ное z E С и применим к ряду ]П \cnZn\ предельный признак
п=0

2.4. Комплексные степенные ряды 165
Коши. Для этого вычислим следующий предел:
zn\ = \z\ lim
n->oo
оо
Согласно предельному признаку Коши, ряд J2 lcn^n| сходится
п=0
при X\z\ < 1 и расходится при A|z| > 1. Таким образом, если
оо
О < А < +оо, то ряд ^2 cnzn сходится абсолютно при
п=0
. . 1 1
|*1<д =
и расходится при
М>|-^
A lim
п—>оо
Это означает, что радиус сходимости степенного ряда R =
= 1/А = 1/( lim ^/Icnl). Если А = 0, то ряд сходится
абсо(
лютно на всей комплексной плоскости, и, значит, R = +оо =
= 1/( lim ^/Ic^l). При А = +оо ряд всюду, кроме нуля, расхо-
п—>оо
дится, и, следовательно, R = 0 = 1/( lim ij/|cn|).
оо
Таким образом, радиус сходимости степенного ряда ]П
п=0
можно вычислить, используя формулу
Д= ,. ^^-т, (2-17)
если предел справа существует.
Если пределы lim |cn/cn+i| и lim у/\с^\ для степенного ря-
оо п—>оо п->оо
Да £ Сп^п не существуют (как, например, для рядов только
71=0
с четными или нечетными степенями z), то формулы (2.16)

166
2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
и (2.17) применять нельзя. Однако непосредственное
использование предельных признаков Даламбера и Копта для рядов
оо
^|сп2:п| часто позволяет определить радиус круга сходимо-
п=0
сти.
Рассмотрим несколько примеров исследования степенных
рядов на сходимость.
Пример 2.21. Найдем область сходимости степенного ряда
n=l
Используя формулу (2.16) для нахождения радиуса сходимости,
получаем
R= lim
n—>oo
■ lim
П—ЮО
= lim
/гГ—Т —«|
= lim
- 1 + 1
1
-.
2
На границе круга сходимости, т.е. при \z\ = 1/2, данный ряд
расходится, так как последовательность |cnZn| не стремится к
нулю при п -> оо. Действительно,
= 2пу/п -1 + 1— = л/п->оо.
Итак, ряд сходится абсолютно при \z\ < 1/2 и расходится при
\z\ ^ 1/2.
Пример 2.22. Найдем область сходимости степенного ряд
V2. (2.18)
71=1

2.4. Комплексные степенные ряды 167
Согласно свойству 1.4, этот ряд можно рассматривать как
оо
степенной, если представить его в виде ^ CkZk, где с* = 5* при
к = п2, п Е N, и с*; = 0 при всех остальных А;. Таким образом,
получаем, что бесконечное число коэффициентов с^ этого ряда
равны нулю, и поэтому применение формул (2.16) и (2.17) для
вычисления радиуса сходимости этого ряда в данном случае
невозможно. Однако если ряд (2.18) рассматривать не как
степенной, а как обычный функциональный ряд, то к ряду
из модулей этого ряда вполне можно применить предельные
признаки Даламбера и Коши. Применим предельный признак
Коши:
lim ?/|5nV2|= lim |5z|n
n->oo V n-юо
При \z\ < 1/5 последний предел равен нулю (меньше единицы),
и, значит, ряд абсолютно сходится, а при \z\ > 1/5 предел равен
+оо (больше единицы), и, значит, ряд расходится.
Следовательно, радиус сходимости R = 1/5. На границе
круга сходимости ряд расходится, так как при \z\ = 1/5 все члены
ряда по модулю равны единице, и не выполняется необходимый
признак сходимости ряда.
Пример 2.23. Найдем область сходимости степенного ряда
п=0
Согласно формуле (2.16), имеем
п! 1
R = lim — = lim = 0.
( + l)! + l
Следовательно, ряд сходится только в одной точке z = 0.
Пример 2.24. Найдем область сходимости степенного ряда
оо
П /
п=1

168
2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Центром данного ряда является точка zq = г. После замены
оо
w = z — г получаем ряд J^ (w/n)n с центром в нуле. Используя
п=1
формулу (2.17), находим радиус сходимости ряда
lim Z
n->oo
= lim n = +00.
Таким образом, ряд Y1 (w/n)n сходится в любой точке ком-
п=\ оо
плексной плоскости С, следовательно, и ряд Yl(z~i)n/nTl cx°-
п=1
дится всюду на комплексной плоскости С.
Пример 2.25. Исследуем на сходимость степенной ряд
fi=l
п2п
с центром в точке zq = 1 — г. После замены tu = z — zq =
оо
= z — 1 + i получаем ряд ]П wn/(n2n) с центром в нуле. Для
п=1
него, применяя формулу (2.16), находим радиус сходимости
Точка
условной
сходимости
Точка
Точка
условной
сходимости
Круг
абсолютной
сходимости
Рис. 2.4
Д=Шп("+1>2"+'=2.
n->oo n2n
Отсюда получаем, что ряд
оо
X) wn/(n2n) сходится абсо-
п=1
лютно в круге \w\ < 2, и,
значит, ряд f2{z-l + i)n/{n2n)
расходи- сходится абсолютно в круге
мости |г - 1 + i| < 2 радиуса 2 с
центром в zo = 1 — г (рис. 2.4).
Выясним, сходится ли ряд
абсолютно на всей границе

2.4. Комплексные степенные ряды 169
круга сходимости, т.е. в точках комплексной плоскости,
удовлетворяющих условию \z — 1 + i\ = 2. Для всех таких точек ряд,
составленный из модулей членов исходного ряда, имеет вид
00 ПП °° 1
У
n2 n
n=l n=l
Полученный ряд является гармоническим (см. пример 1.10) и,
следовательно, расходится. Поэтому на границе круга
сходимости исследуемый степенной ряд не является абсолютно
сходящимся. Однако среди точек этой границы могут быть
точки, где ряд расходится, и точки, где ряд сходится
условно. Выясним, сходится ли ряд в конкретных точках z\ = 3 — г,
Z2 = — 1 — ги;гз = 1 + г, лежащих на границе круга сходимости.
При z = z\ = 3 — г имеем гармонический ряд
f n2n ^
п=1 п=1
Следовательно, в точке z\ исходный ряд расходится.
Пусть z = Z2 = —1 — i. Тогда имеем ряд
П2 „2 ^ п '
п=1 п=1 п=1
который сходится условно в соответствии с признаком
Лейбница (см. теорему 1.13). Точка z*i — точка условной сходимости
исходного ряда.
Пусть теперь z = z$ = 1 + г. Тогда ряд принимает вид
п2п ^ п2п ^ п'
п=1 п=1 п=1
Поскольку i2k = (—I)*5, г2*5"1 = г(—I)*""1, A; E N, и действитель-
оо оо
ные ряды J2 (-l)k/2k, X) (-1) /(2*~ х) являются условно
fc=i k=i

170 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
сходящимися вследствие признака Лейбница, то в силу свойств
1.5-1.7 имеем
2k-l j2k. _^_
;—7 + ттг) =
, .- ь — ^ _... _ 2к-1
п=1 к=1 к=1 к=1
Таким образом, согласно замечанию 1.6, комплексный ряд
оо
^2 in/n является условно сходящимся. Следовательно, точка
п=1
£з — точка условной сходимости исходного ряда.
2.5. Действительные степенные ряды
В этом параграфе рассмотрены действительные
степенные ряды, т.е. ряды вида
п=0
где х ЕIR, a центр ряда xq и коэффициенты ряда ап — заданные
действительные числа.
Рассмотрим этот же ряд (с теми же коэффициентами и с
тем же центром), но не от действительного переменного ж,
а от комплексного переменного z (такую операцию называют
выходом в комплексную плоскость):
{-x0)n, zeC.
n=0
Как показано в 2.4, этот комплексный степенной ряд имеет
некоторый радиус сходимости Д, 0 ^ R ^ +оо, т.е. абсолютно
сходится внутри открытого круга Kr = {z Е С: \z — хо\ < R} в
комплексной плоскости (R > 0) и расходится вне замкнутого
круга ~K^={z ЕС: |*-жо| ^ Д} (при |*-жо| > Л, Л < +оо).
Поскольку множество действительных чисел R является подмно-

2.5. Действительные степенные ряды 171
жеством (действительной осью) комплексной плоскости С, то
оо
исходный ряд ]Р ап(х — хо)п от действительного переменного
71=0
z = xGKcC абсолютно сходится в интервале (xq — Д, xq + R) С
С Kr (т.е. при \х — xq\ < Д, R > 0) и расходится вне отрезка
[so - Л, жо + Д] (т.е. при |х - хо| > Д, Д < +оо).
Таким образом, для всякого действительного степенного
оо
ряда ^2 ап(х — хо)п существует единственное число Д, 0 ^
71=0
^ Д ^ 4-оо, такое, что этот ряд сходится, причем абсолютно,
на интервале (xq — Д, xq + R) С К и расходится вне отрезка
оо
[xq — Д, хо 4- Д]. При этом, если Д = 0, то ряд ]П ап(х — хо)п
71=0
сходится в единственной точке xq = 0, а при Д = 4-оо областью
сходимости ряда является вся числовая прямая R.
оо
Радиус сходимости Д, 0 ^ Д ^ 4-оо, ряда ^ ап(г—хо)п от
п=0
комплексного переменного z E С называют радиусом схо-
оо
димости действительного степенного ряда ]П an(x —xo)n, a
71=0
интервал (xq — Д, хо 4- Д) С R — мнтервололс сжодилюспш
этого ряда.
Не ограничивая общности рассуждений и получаемых
результатов, далее будем рассматривать в основном только дей-
оо
ствительные степенные ряды ^ апхп с центром в нуле (хо = 0).
п=0
Поскольку множество действительных чисел является
подмножеством комплексных чисел, то сформулированная ниже
теорема является следствием теоремы 2.15 о комплексных
степенных рядах.
Теорема 2.16. Пусть Д — радиус сходимости действи-
оо
тельного степенного ряда ^ апхп. Тогда этот ряд сходится
п=0
равномерно и абсолютно на любом отрезке [—г, г], целиком
лежащем в интервале сходимости: [—г, г] С (—Д, Д). #

172 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Следствие 2.1. Сумма всякого действительного степенно-
оо
го ряда ^2 а-п.хп является непрерьганои функцией в интервале
71=0
сходимости (—Д, Д).
<4 Рассмотрим произвольный отрезок [—г, г] С (—Д, Д). Соглас-
оо
но теореме 2.16, ряд ]П апхп на отрезке [—г, г] сходится равно-
71=0
мерно. Так как степенные функции /п(#) = апхп непрерывны,
то в силу теоремы 2.10 о непрерывности суммы равномерно схо-
оо
дящегося ряда с непрерывными членами сумма ряда ^2 а>пхп
п=0
является непрерывной на отрезке [—г, г]. Поскольку отрезок
[—г, г] С (—Д, Д) произволен, то сумма ряда непрерывна в
любой точке интервала (—Д, Д). ►
Теорема 2.17. Радиусы сходимости действительных
степенных рядов
a) 5>nzn, б)
71=0 71=0 П=1
равны.
<4 Обозначим через Дх, Д2 и Дз радиусы сходимости рядов (а),
(б) и (в) соответственно и заметим, что
|ап*П+ '\х\\апхп\^х2\аппхп-\ п Е N, x E R.
Из этих неравенств и признака сравнения (см. теорему 1.4)
следует, что сходимость ряда (в) в некоторой точке xq E Ш
обусловливает сходимость в этой точке ряда (а). А из сходимости
ряда (а) следует сходимость ряда (б). Это означает, что
Дз < Ri < Д2. (2.20)
Докажем, что Д2 < Дз, те- что из сходимости ряда (б)
следует сходимость ряда (в). Пусть xq ф 0 и xq Е (—

2.5. Действительные степенные ряды
173
т.е. в точке хо ряд (б) сходится. Покажем, что в точке хо ряд
(в) также сходится. Поскольку |хо| < Лг> то найдется такое
г > 0, что |хо| < г < #2- Запишем модуль общего члена ряда (в)
в точке хо в виде
n(n + l)
anr
n+l
\x0
п+1
В соответствии с необходимым признаком сходимости ряда из
сходимости ряда (б) в точке х = г (эта точка принадлежит
интервалу сходимости, поскольку 0 < г < R2) следует, что
общий член ряда (б) стремится к нулю:
\апг
п+1
lim .
71->ОО| 71+ 1
= 0.
В частности, последовательность {|(a7lrrl"hl)/(n +1)|}
ограничена, т.е. существует такое число М > 0, что верно неравенство
апГ
n+1
пе
Пусть q = |#о/Ч- Отметим, что 0 < q < 1, поскольку |хо| < г.
Тогда
4
х0
Обозначая через Сп правую часть последнего неравенства,
получаем
lim
= hm
n->cx>
n + 2)Mqn+2x20
n
= lim
= Я < 1-
Следовательно, в силу предельного признака Даламбера знако-
срав-
Итак,
положительный ряд ]Р Сп сходится. Согласно признаку срав-
71=0 ОО
кенг^л (см. теорему 1.4), сходится и ряд ]П |папХо~ |
71=1
ряд (в) в точке хо сходится, причем абсолютно. Это означает,

174 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
что Дг < Дз- И, наконец, учитывая (2.20), получаем требуемое
равенство: R\ = Д2 = Д3. ►
Следствие 2.2. Ряды (а), (б), (в) из (2.19) сходятся
равномерно на любом отрезке [—г, г], целиком содержащемся
в их общем интервале сходимости (—Д, Д). #
Заметим, что членами ряда (б) из (2.19) являются
интегралы на отрезке [0, х] от членов ряда (а) из (2.19):
/a xn+l
ппХ п + 1 ' п = 0'1'2'-"
о
Членами же ряда (в) являются производные членов ряда (а):
Так как ряды (а), (б) и (в) имеют один и тот же интервал
сходимости (—Д, R) и равномерно сходятся на любом отрезке [—г, г],
г Е (0, Д), то из теорем 2.12 и 2.13 следует, что любой
степенной ряд на всем его интервале сходимости можно почленно
интегрировать и дифференцировать. Поскольку при
почленном интегрировании и дифференцировании степенных рядов
получены степенные ряды с теми же интервалами сходимости,
то к ним можно применить теорему 2.17. Следовательно,
операции дифференцирования и интегрирования степенного ряда
внутри интервала сходимости можно повторять сколь угодно
много раз, получая при этом степенные ряды с теми же
интервалами сходимости. Сформулируем сказанное в виде теорем.
Функцию /(ж), определенную в некоторой окрестности
точки гго, называют бесконечно дифференцируемой в этой
точке, если в ней она имеет производные любого порядка.
Функция f(x) бесконечно дифференцируема в интервале, если
она бесконечно дифференцируема в каждой точке этого
интервала.

2.5. Действительные степенные ряды
175
Теорема 2.18. Для всякого действительного степенного
оо
ряда ]П апхп с суммой S(x) и радиусом сходимости R справед-
71=0
ливо равенство
п=0
n=0
причем радиус сходимости ряда справа также равен R.
Теорема 2.19. Сумма S(x) действительного степенного
оо
ряда ^2 ап%п с радиусом сходимости R является бесконечно
71=0
дифференцируемой в интервале (—Д, R) функцией, причем
имеет место равенство
x
(-Д, R),
n=\
где радиус сходимости ряда справа также равен R. #
Дифференцирование и интегрирование часто применяют
для нахождения сумм степенных рядов.
Пример 2.26. Найдем сумму степенного ряда
х3 х5 х7 (-I)»"1*2"-1
5() + + + LL +
Применим к ряду ^2
ламбера: n=1
1-U271-1
2п-1
2п-1
предельный признак Да-
lira
п-юо
2(n + l)-
- lim
Согласно предельному признаку Даламбера, этот ряд сходится
(а исходный ряд сходится абсолютно) при х2 < 1 и расходится

176 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
при х2 > 1. Следовательно, (—1,1) — это интервал сходимости
исходного ряда.
Рассмотрим ряд, полученный из данного ряда почленным
дифференцированием в интервале (—1,1):
На основании теоремы 2.19 полученный ряд сходится в
интервале (—1,1) к функции S'(x). Заметим, что члены последнего
ряда образуют геометрическую прогрессию со знаменателем
(—х2), и поэтому сумма этого ряда может быть легко найдена
(см. пример 1.4):
71=0
Тогда при х Е (—1,1)
dx
= arctgx + C.
Постоянную С найдем из очевидного условия 5(0) = 0 (при х = 0
все члены исходного ряда равны нулю). Следовательно, С=0 и
S(x) = arctgz, x e (—1,1).
Рассмотрим точки, принадлежащие концам интервала
сходимости: х = 1 и х = — 1. При х = 1 исследуемый ряд имеет
оо
вид ^2{—1)п~1/(2п — 1). Этот ряд сходится в силу признака
71=1
Лейбница (см. теорему 1.13). Его сумма подсчитана в 3.11:
71=1
При х = — 1 имеем ряд
2n -1 4
4 6V ;

2.6. Ряд Тейлора 177
Таким образом, при всех х € [—1,1]
х3 х5
3 5 ' 2n-l
а при х ф [—1,1] этот ряд расходится. #
Примеры вычисления сумм рядов с помощью почленного
дифференцирования и интегрирования рассмотрены также в
2.7, 2.8.
2.6. Ряд Тейлора
В этом параграфе рассмотрены действительные функции
действительного переменного и функциональные ряды, членами
которых являются степенные функции действительного
переменного.
Определение 2.11. Пусть функция f(x) задана в
некоторой окрестности точки хо и имеет в этой точке производные
любого порядка. Тогда степенной ряд
£;
п=0
I6
называют рядом Тейлора функции f(x) в точке xq.
При xq = 0 ряд Тейлора называют рядом Маклорена.
Возникают следующие вопросы: каков интервал
сходимости ряда Тейлора функции f(x) в точке xq? сходится ли он к
функции /(х), и если да, то существует ли другой степенной
ряд, сумма которого на этом интервале совпадает с /(я)?
Определение 2.12. Действительную функцию f(x)
действительного переменного называют аналитической в
точке xq, если она определена в некоторой окрестности точки

178 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
xq и ее можно представить в этой окрестности некоторым
сходящимся степенным рядом:
00
f(x) = Sпп^х ~~ Х°)П' х е (х°" е'х° +£)'е > °-
71=0
Такое представление аналитической функции называют ее
разложением в степенной ряд в окрестности точки хо-
Следующая теорема показывает, что разложение
аналитической функции в степенной ряд единственно и этим рядом
является ее ряд Тейлора.
Теорема 2.20. Если в некоторой окрестности точки xq для
функции f(x) справедливо разложение
оо
/(*) = ^2ап(х -хо)п, хе(х0-е, х0 + е),е> О,
п=0
то функция f(x) бесконечно дифференцируема в этой
окрестности и
4 Пусть f(x) = Y1 о>п(х — хо)п — некоторое разложение функ-
71=0
ции f(x) в степенной ряд в окрестности (xq — е, xq + e) точки xq
и R — радиус сходимости этого ряда. Тогда (хо — е, xq + e) С
С (xq — Д, хо -f -R), и следовательно, Д > 0. Согласно свойствам
действительных степенных рядов (см. теорему 2.19), этот ряд
можно почленно дифференцировать в интервале сходимости
(хо — Д, хо + R) любое число раз. Поэтому для любого числа
х G (хо — £, хо + е) имеем
оо
/(»>(*) = Y^k(k-l)...(k-n+l)ak{x-x0)k-n, n = 0,1,2,...

2.6. Ряд Тейлора 179
Полагая в этих равенствах х = хо, получаем
/Ы = а„, f'(xo) = au f"(xo) = 2la2, f
Следовательно,
что и требовалось доказать. ►
Таким образом, аналитическую в точке xq функцию можно
определить как функцию, которая в некоторой окрестности
точки xq является суммой своего ряда Тейлора.
Теорема 2.20 утверждает, что всякая аналитическая в точке
xq функция бесконечно дифференцируема в некоторой
окрестности этой точки. Однако не всякая бесконечно
дифференцируемая в окрестности точки функция является аналитической
в этой точке, т.е. сумма ряда Тейлора бесконечно
дифференцируемой в окрестности точки xq функции может не совпадать с
ней ни в какой окрестности точки xq. Это иллюстрирует
следующий пример.
Пример 2.27 (пример Кохии). Рассмотрим функцию
Эта функция бесконечно дифференцируема в любой точке
х ф 0. Докажем, что эта функция бесконечно
дифференцируема и в точке xq = 0. При х ф 0 производные функции К(х)
вычисляются по формулам
Применяя метод математической индукции, нетрудно
показать, что производная функции К(х) произвольного порядка п
имеет вид

180 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
где Рп(1/х) — некоторый многочлен относительно 1/х, т.е.
К^п\х) представляет собой линейную комбинацию слагаемых
вида
^е"1/*2 0 < т < mn,
х
где тп — степень многочлена Рп(1/х). Делая замену t = 1/х2,
убеждаемся в том, что
lim
0
1 -1/х2
= hm
x->0 Xm
Следовательно, для всех п = 0,1, 2,...
^Цх) = lim Рп (-V1/*2 =0.
0 \Х
Используя (2.21), с помощью метода математической индукции
докажем, что функция К(х) в точке хо = 0 бесконечно
дифференцируема и что для всех п = 0,1, 2,...
if(n)(0) = 0. (2.22)
Действительно, при п = 0 это равенсто верно, поскольку по
условию If (0) = 0. Верно это равенство и при п = 1, так как
JT (0) = ,im *<">-f» . и- ЗЙ - Шп ^ = 0.
х->0 X — 0 х->0 X х->0 X
Предположим, что равенство (2.22) имеет место для всех
натуральных п ^ fc, fe € N. Докажем, что равенство (2.22) имеет
место и для п = fc -f 1:
х->0 X — 0 х->0
х->0

2.6. Ряд Тейлора. 181
где Q(\/x) — многочлен от 1/х степени, на единицу большей
степени многочлена Р&(1/х). При этом последний предел
равен нулю, поскольку (2.21) верно не только для многочленов
Рп(1/х), но и вообще для всех многочленов Q(l/x) от 1/х.
Следовательно, функция К(х) имеет в точке хо = 0 все
производные, и для всех п = 0,1, 2,... выполняется равенство (2.22).
Покажем, что функция К(х) не является аналитической
в точке хо = 0, т.е. ни в какой окрестности точки xq = О
она не является суммой своего ряда Тейлора (см. теорему
2.20). Действительно, в силу (2.22) все члены ряда Тейлора
функции К(х) в любой окрестности точки xq = 0 тождественно
равны нулю. Следовательно, сумма ряда Тейлора в этой
окрестности также равна нулю и, значит, не совпадает с
функцией К(х). Таким образом, рассматриваемая функция
К(х) бесконечно дифференцируема на множестве R, но не
является аналитической в точке xq = 0. #
Этот пример показывает также, что различные бесконечно
дифференцируемые функции могут иметь один и тот же ряд
Тейлора. Действительно, функция К(х) из примера Коши и
не совпадающая с ней ни в одной точке, кроме xq = 0, нулевая
функция д(х) = 0 имеют один и тот же ряд Тейлора в точке
оо
жо = 0, у которого все коэффициенты нулевые: ^ 0 • хп. От-
п=0
метим, что этот ряд сходится на всей числовой прямой R, т.е.
его радиус сходимости бесконечен. Кроме того, существуют
бесконечно дифференцируемые в любой точке х € Ш функции,
ряды Тейлора которых имеют нулевой радиус сходимости (см.
задачу 2.17).
Найдем условия, при которых бесконечно
дифференцируемую функцию можно представить своим рядом Тейлора. Из
курса математического анализа известно, что если функция
f(x) бесконечно дифференцируема в окрестности (хо — г, хо + г)
точки х = хо, то для нее в этой окрестности справедлива фор-

182 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
мула Тейлора
^k , n = 0,1,2,... (2.23)
к=0
где Rn(x) — остаточный член формулы Тейлора. Заметим,
что остаточный член можно представить, например, в форме
Лагранжа:
) ^
(П+ 1)!
Теорема 2.21. Пусть функция /(х) бесконечно
дифференцируема в интервале (хо — г, хо + г). Тогда ее ряд Тейлора
оо f(n)(x }
^2 -—j-^- ix ~~ хо)п сходится в интервале (хо — г, хо + г) к функ-
п=0 п'
ции /(х) в том и только в том случае, когда остаточный член
Rn{x) формулы Тейлора (2.23) для любого х Е (хо — г, хо + г)
стремится к нулю при п -> оо.
< Очевидно, что формулу Тейлора (2.23) для бесконечно
дифференцируемой в интервале (хо — г, хо +г) функции /(х) при
любом п € N можно записать в виде
S(x) = Sn{x) + Дп(х), х € (х0 - г, х0 + г), (2.24)
где Sn(x) — n-я частичная сумма ряда Тейлора функции /(х)
в точке Хо-
Тогда, если функцию /(х) в интервале (хо — г, хо +г) можно
представить своим рядом Тейлора, то для всех точек из этого
интервала lim 5п(х) = /(х). Из (2.24) следует, что Яп(х) =
п—юо
= /(х) - 5п(х), поэтому
lim Rn(x) = lim (/(х) - 5n(x)) =0, х € (х0 - г, х0 + г).
п—»оо п—»оо
Обратно, пусть для остаточного члена формулы Тейлора
(2.23) при всех х € (хо — г, хо + г) справедливо соотношение

2.6. Ряд Тейлора 183
lim Rn(x) = 0. Поскольку опять же из (2.24) следует равенство
п->оо
) f{)R(), то
f{x) - Rn{x)) = /(х), х€ (хо-г, хо + г),
т.е. ряд Тейлора функции /(х) в интервале (х0 - г, хо + г)
сходится, причем к самой функции /(х). ►
Следующая теорема формулирует достаточное условие
того, что функцию f(x) можно представить своим рядом Тейлора.
Теорема 2.22. Пусть функция f(x) бесконечно
дифференцируема в интервале (хо — г, хо + г) и ее производные в этом
интервале ограничены в совокупности, т.е. существует такое
М > 0, что
|/^(х)|<М, z€(xo-r,xo
Тогда в интервале (хо — г, хо + г) функцию /(х) можно
представить своим рядом Тейлора в точке хо, т.е.
л=0
Ч Возьмем произвольную точку х £ (хо — г, xq + г) и оценим
остаточный член Rn(x) формулы Тейлора (2.23), записав его в
форме Лагранжа:
\Rn(x)\ =
(п + 1)!
(п + 1)!
Здесь £ — некоторая точка, лежащая между хо и х. Так
оо
как ряд ]П гп+1/(п + 1)\ сходится при любом г > 0 (см. при-
п=0
мер 2.18), то в силу необходимого признака сходимости ряда
имеем lim rn+l/(n+ 1)! =0. Поэтому, переходя к пределу при
п—юо
и -> оо в полученном выше неравенстве, получаем равенство
lim |Дп(я)1 =0. Следовательно, lim Ял (я) = 0. Отсюда, со-
П-+ОО П-^ОО
гласно теореме 2.21, получаем утверждение теоремы. ►

184 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
2.7. Разложение элементарных
функций в ряд Тейлора
Сначала найдем разложения некоторых основных
элементарных функций в ряд Маклорена.
1. Разложение в ряд Маклорена функции f(x) = ex.
Поскольку
/(")(*) = (е*)Н = е*, n€N, x G (-оо, +оо),
то /(п)(0) = 1 при всех п Е N. Поэтому ряд Маклорена функции
оо
ех имеет вид Y1 хп/п\ Покажем, что этот ряд сходится к самой
п=0
функции ех на всей числовой прямой. Рассмотрим для этого в
формуле Маклорена для функции f(x) = ex остаточный член в
форме Лагранжа
Х
Учитывая, что £ = tfrr, 0 < # < 1, и, следовательно, е^ < e'x',
получаем оценку
Поскольку lim |x|n+1/(n + 1)! = 0 для всех х € R (это предел
П—>ОО QQ
общего члена сходящегося ряда ^ |х|п+1/(п + 1)' — см- пример
2.18), то n=1
lim Rn(x) =0, хе (-оо, +оо),
п—►оо
оо
и, следовательно, ряд 52 хп/п\ сходится к функции ех на всей
числовой прямой EL n=0

2.7. Разложение элементарных функций в ряд Тейлора 185
Итак, для функции /(х) = ех справедливо следующее
разложение.
2. Разложение в ряд Маклорена функции f(x) = sinx.
Функция f(x) = sinx бесконечно дифференцируема на всей
числовой прямой, причем п-я производная функции /(х)
вычисляется по формуле [II]
Поэтому при х = 0 имеем
п = 2k;
i n-2*-l nGR
Таким образом, ряд Маклорена функции /(х) = sinx имеет вид
оо
Y^ (—I)n~1x2n~1/(2n—1)! Поскольку функция /(х) = sinx беско-
п=1
нечно дифференцируема и 1/^(^)1 < 1 ПРИ всех х € (~°°) +о°)>
т.е. все производные ограничены в совокупности, то в силу
теоремы 2.22 данный ряд Маклорена сходится к функции
/(х) = sinx на всей числовой прямой R.
Итак, для функции /(х) = sinx имеет место следующее
разложение.

186 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
3. Разложение в ряд Маклорена функции f(x) = cos ж.
Как и для функции f(x) = sinx, можно получить разложение
в ряд Маклорена и определить интервал его сходимости для
функции f(x) = cosx. Однако можно поступить проще —
почленно продифференцировать ряд Маклорена (степенной ряд с
радиусом сходимости R = +oo) для функции sinx (см. теорему
2.19):
тХ2п-2=У ^г+гх'
Причем, это равенство верно во всем интервале сходимости
исходного ряда, т.е. на всей числовой прямой.
Итак, для функции f(x) =cosx верно следующее
разложение.
ллп /у% _
СОЬ X -
оо
п=0
f—1)п гг2
/оМ 91
(-1)'
2п!
X4
А\
г
-х2п + ... хе (-оо, +оо).
4. Разложение в ряд Маклорена функции f(x) =
= (1 + ж)а, а е R. Если а = 0, то /(х) = 1 и разложение в ряд
с»
Маклорена тривиально: /(х) = 1 = 1 + ^ 0 • xn, a; E К.
71=1
Если а = n € N, то разложение в ряд Маклорена можно
получить, используя формулу бинома Ньютона:

2.7. Разложение элементарных функции в ряд Тейлора
187
Наконец, если а ^ N и а ф О, то легко заметить, что п-я
производная степенной функции f(x) для всех х Е (—оо, +оо),
х Ф — 1, имеет вид
n Е
(В точке х = — 1 п-я производная /(х) не существует, если
п> а). Найдем значения производных функции f(x) при х = 0:
/(п>(0) = a(a- 1)... (a- (n-1)), n E N.
Следовательно, ряд Маклорена функции (1 + х)а при a ^ N и
а/0 имеет вид
Заметим, что ряд Маклорена функции (1 + х)а для a = 0
и a G N является частным случаем этого ряда, поскольку при
a = 0 все коэффициенты этого ряда равны нулю, а при a E N
эти коэффициенты равны нулю, начиная с номера п = а + 1.
Итак, пусть а £ N и a ^ 0. Найдем радиус сходимости
полученного ряда Маклорена функции f(x) — (1 + x)Q, используя
формулу (2.16). Полагая
/n,Q —
a(a-l)...(a-(n-
it.
71
получаем
я- 1;™ \jnjct _
:= lim
= lim
n->oo
a(a-l)... (a-n+l)(n+l)!
a(a-l)... (a-n+l)(a-(n+l-l))n!
= lim
П-ЮО
n+1
a—n
= 1.

188
2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Таким образом, ряд Маклорена функции (1 + х)а при \х\ < 1
абсолютно сходится, а при |х| > 1 расходится.
Покажем теперь, что в интервале |х| < 1 полученный ряд
Маклорена функции (1+х)а сходится к самой функции (1+х)а.
Для этого запишем остаточный член Rn(x) формулы
Тейлора для этой функции в интегральной форме (см. Д.2.1):
/ "I \ / \
п\
X
f{x-t)n(l + t)a-(n+lUt =
a(a — 1)... (a — n)
n\
— t\n
1
)n{l+t)*-ldt.
\)
Для фиксированного х из интервала (—1,1) рассмотрим
функцию
&(<) =
x-t
Г+7
t-X , X + l
-i}-
Графики функции qx(t) (а это гиперболы) для отрицательных
значений параметра х Е (—1, 0] и для положительных значений
параметра х Е [0,1) изображены на рис. 2.5.
Рис. 2.5

2.7. Разложение элементарных функций в ряд Тейлора
189
При любом х Е (—1,1) функция qx(t) убывает по
переменному t в интервале (—1,1). В частности, убывает она и на отрезке
[О, х] С (—1,1) (или [ж, 0] при х < 0). Следовательно, если х Е
е [0,1), то для всех t Е [0, х] верно неравенство 0 = qx{x) < qx(t) <
^ <7z(0) = я, и, значит, |дх(*)| ^ \х\- Если же х Е (—1, 0], то для
всех t Е [х, 0] верно неравенство 0 = qx{x) ^ qx{t) ^ qx{0) = х, т.е.
0 ^ — qx(t) ^ —х, и, значит, |^х(01 ^ \х\- Таким образом, при
всех значениях х Е (—1,1) верно неравенство
\qx(t)\^\xl te[0,x].
Используя это неравенство, получаем
|Д»(*)1 =
a(a — l)...(a — п)
п\
a(a — 1)...(а — п)
П!
п!
а
П!
Так как при |х| < 1 сомножитель /n,a-ixn представляет собой
общий член сходящегося ряда Маклорена функции (1 + х)а~1 то
/n а-1 хп = 0, ж Е (—1,1). Переходя к пределу при п -> оо в
неравенстве
0<\Rn(x)\<\fn>a-l(x)\\(l+x)a-l\,
согласно теореме о „зажатой" последовательности [1-6.5], для
любой фиксированной точки х Е (—1,1) получаем lim \Rn(x)\ =
n—too
= 0. Следовательно, lim Rn(x) =0 при любом х Е (—1,1), и в

190 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
интервале (—1,1) ряд Маклорена степенной функции (1 + х)а
сходится к ней самой.
Таким образом, для степенной функции (1 + х)а с
показателем а £ {NU {0}} справедливо следующее разложение.
a ~а(а_
n-l
a(a-l) 2
1 ax 2!
I)...(a-n4
, o(o-l).
-1) n
..(a —n + 1) n
n! X '■"'
Ряд Р'аклорена функции (l + x)Q обычно называют
биномиальным рядом.
В точках х = ±1 биномиальный ряд при различных
значениях показателя а может быть как сходящимся, так и
расходящимся. Можно доказать, что в точке х = — 1 биномиальный
ряд сходится при a > 0, а в точке х = 1 — при а > —1.
Найдем разложение в ряд Маклорена функции f(x) = l/(l+x).
Это разложение может быть получено как частный случай
разложения степенной функции (1 + х)а с показателем а = — 1.
-iyV> + ..., я €(-1,1).
Как видим, полученный ряд является геометрическим рядом с
параметром q = — ж. Он сходится только в интервале (—1,1), а
при |х| ^ 1 — расходится.
5. Разложение в ряд Маклорена функции f(x) =
= 1п(1 + ж). Разложение функции 1п(1 + х) можно получить,
интегрируя почленно ряд Маклорена функции f(x) = 1/(1 + х)

2.7. Разложение элементарных функции в ряд Тейлора 191
(см. теорему 2.18):
{ 4=0
n=0"0 n=C
n=0
В точке rr = —1 данная формула неверна (в этой точке и сама
функция ln(l + rr) не определена, и ряд расходится, поскольку
является гармоническим). В точке же х = 1 полученная
формула справедлива. Действительно, функция f(x) = ln(l + х) в
этой точке определена и равна In2, а ряд Маклорена при х = 1
представляет собой сходящийся в силу признака Лейбница ряд
с той же суммой (см. пример 1.30):
п
Таким образом, для функции 1п(1 + х) верно следующее
разложение.
~(_l)n+l
n=l "
Xn X2 X3
n
Полученные пять разложений основных элементарных
функций в ряд Маклорена часто называют стандартными
разложениями.
Обратимся теперь к вопросу о способах разложения
произвольных элементарных функций в степенные ряды. Для
разложения элементарной функции в ряд Тейлора применяют два

192 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
метода. Первый основан на непосредственном разложении
функции в ряд Тейлора. Вычисляя производные всех порядков
функции f(x) в точке xq, формально составляют ряд Тейлора,
затем находят его область сходимости и выясняют, в каких
точках из области сходимости ряд сходится к данной функции.
Примеры использования этого метода — пять стандартных
разложений, полученных выше.
Отметим, что непосредственное разложение часто
приводит к трудновыполнимым громоздким вычислениям. Основная
трудность — получение формулы общего члена ряда. Как
правило, это вообще невозможно. В таких случаях ограничиваются
вычислением нескольких начальных членов ряда.
Второй метод базируется на использовании стандартных
разложений. Рассмотрим некоторые варианты этого метода.
А. Замена переменного. Если f(x) = g(axf3)1 a G R, /3 G N,
с»
а д(и) — функция с известным разложением д(и) = Y1
к=о
и G U С R, то
f(x)=g(axP)=g(u)
и=ах" к=о к=о
Полученное разложение функции f(x) справедливо для всех
х G R, таких, что ах^ G U.
Например, для нахождения разложения функции е~(х-1)
по степеням (х — 1), т.е. в ряд Тейлора в окрестности точки
х = 1, воспользуемся известным разложением в ряд Маклорена
функции е*, сделав в нем замену переменного t = — (х — I)2.
Тогда для всех х 6 (—сю, +оо) получим
л\п(„_ 1\2п
п!
Поскольку разложение в степенной ряд единственно и
совпадает с рядом Тейлора (см. теорему 2.20), данное разложение

2.7. Разложение элементарных функции в ряд Тейлора 193
является разложением функции е"^""1) в ряд Тейлора в точке
х = 1.
Б. Арифметрические операции над рядами. Этот
способ основан на том, что если имеются два степенных ря-
оо с»
да ^2 апхп и Y1 Ьпхп с радиусами сходимости i?i и Й25 т0
п=0 п=0
в интервале (—Я, R) с радиусом R = min{Ri,R2} эти два
ряда можно складывать, вычитать и умножать на числа. Ряд
оо
5^ (аап + (ЗЬп)хп с произвольными а, /3 Е Ш будет сходиться
п=0
в интервале (—Я, Л), R = min{-Ri, Я2}» причем для всех х из
этого интервала будет выполняться равенство otfi(x)+/3f2(x) =
£ (аап + 13Ьп)хп, где fx(x) = £ anxn, а /2(х) = £ Ъпхп. По-
п=0 п=0 п=0
оо
кажем, что если R\ ф Й2» то ряд ]Г (аап + /ЗЬп)хп при |х| > R
п=0
расходится. Действительно, при R < \х\ ^ тах{Дх,R2} один из
с» оо
рядов Y1 апХп или Y1 Ьпхп будет сходиться, а другой — расхо-
п=0 п=0
диться. Следовательно, на этом множестве будет расходиться
оо
и РЯД ]С (аап + Pbn)xn (a^O, (3 ф 0). Согласно теореме 2.15,
п=0
оо
ряд ^2 (аап + РЪп)хп будет расходиться при всех я, таких, что
п=0
И>д.
Таким образом, если Y^ anxn — ряд Маклорена функции
п=0
оо
fi{x) в интервале (—-Ri, -Ri) и ]Г Ьпхп — ряд Маклорена функ-
п=0
ции f2(x) в интервале (—-Й2>-Й2)> то при всех а,/? € R ряд
оо
2 (аап + /ЗЬп)хп — это ряд Маклорена функции afi(x)+/3f2(x)
п=о
в интервале (—Я, R), R = min{i?i, #2}-
Проиллюстрируем этот способ следующим примером.
Найдем разложение в ряд Маклорена функции sin(x + 2). Для этого
представим ее в виде sin(x + 2) = sinx cos 2 + cos x sin2. Зная раз-

194 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
ложения функций sin я и cos я в ряд Маклорена на всей прямой
R, получаем искомое разложение функции sin (ж+ 2):
n=0 v '"' n=0
где
п\
sin2, n = 2k]
11 = 0,1,2,
cos2, n = :
n!
В. Интегрирование и дифференцирование рядов.
Способы с использованием интегрирования и диффернциро-
вания рядов основаны на теоремах 2.18 и 2.19 и уже были
продемонстрированы при разложении в ряд Маклорена
функций 1п(1 + х) и cos ж. Приведем еще один пример. Разложим в
ряд Маклорена функцию arcctgx. Для этого сначала разложим
в ряд Маклорена производную этой функции:
(arcctgz)' = -±г = " Е(-1)П*2П = Е(-1)"+1*2п, * 6 (-1,1).
i+X n=0 п=0
Здесь использовано стандартное разложение
1№ У €(-1,1),
п=0
в ряд Маклорена степенной функции (1 + у) *, в котором
сделана замена переменного у = ж2. Проинтегрировав теперь
почленно полученный степенной ряд Yl (—1)п+1я2п на отрезке
п=0

2.7. Разложение элементарных функций в ряд Тейлора
195
[О, х], х € (—1,1) (см. теорему 2.18), получим
arcctgs- £= /т^КсН = У2(-1)п+1 [t*ndt =
= Е(~1ПЖГ+1. «€(-1,1).
n=0
2n
Отметим, что в силу теоремы 2.18 интервалом сходимости
полученного степенного ряда является интервал (—1,1). На
концах интервала сходимости, т.е. в точках х = ±1, ряд
сходится к значениям функции arcctgx в этих точках, поскольку
]Г (—1)п/(2п + 1) = тг/4 (см. 3.11). Следовательно, областью
п=0
сходимости полученного ряда является отрезок [—1,1].
Итак, имеет место следующее разложение.
Приведем еще несколько примеров разложения функции в
ряды Тейлора.
Пример 2.28. Найдем первые четыре члена разложения
функции tgn; в ряд Тейлора в точке х = тг/4. Для этого
вычислим
= 2;
= 4;
4 / cos2 x
2sina;
„/7ГЧ _ ZS1I1X
\ 4 / cos3 x
j/ttn _
V4/ =
x + 3sin2xcos2x)
COS6X
= 16.

196 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Подставив полученные значения производных в формулу
получим представление
Используя методы теории функций комплексного переменного
[X], можно показать, что это представление имеет место для
всех точек интервала (0,7г/2).
Пример 2.29. Разложим в ряд по степеням х — 2 функцию
и определим интервал, в котором верно это разложение.
Преобразуем функцию к виду, удобному для использования
стандартного разложения в ряд Маклорена степенной функции
1
-2(1+§<-*))
-1/3 ,
о
о
где у = -(х — 2). Используя стандартное разложение в
биномиальный ряд степенной функции (1 + у)а с показателем а = —1/3,

2.7. Разложение элементарных функции в ряд Тейлора 197
получаем
1 1 ^(-1Г-1-4-7-...-(Зп-2)3"
v/2 ^^ 3"n! 2«l ;
Использованное выше разложение функции (1 + у)"1'3 в
биномиальный ряд справедливо для — 1 < у < 1, а следовательно,
и для х, удовлетворяющих неравенствам
Найденный интервал и является интервалом сходимости
полученного ряда Тейлора для функции /(я).
Пример 2.30. Разложим в ряд Маклорена функцию
и определим интервал сходимости этого ряда к функции f(x).
Разложим f(x) на сумму простейших дробей [VI]:
f(x)_- * = 2 i 1
J \*' l~ i 1 \(~ _ о^ 1(т — 91 <Ut -I- 1 V
С»
Поскольку 1/(1 -q) = £} qn при |g| < 1 (см. пример 1.4), по-
п=0
лученные дроби необходимо представить в виде, удооном для

198 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
применения этой формулы:
J №) ~о ~Гл ITToT "' *> '
3(1 -ж/2) 3 1- (-х)
п=0
Используя формулу (2.16), получаем, что радиус сходимости
с» с»
ряда ]Г) хп/2п равен 2, а радиус сходимости ряда X) (—1)пхп
п=0 п=0
равен 1. Тогда радиус сходимости ряда Маклорена для
функции /(ж), являющегося линейной комбинацией этих рядов,
равен R = min{l,2} = 1, т.е. полученное разложение имеет место
при хе (-1, 1).
Пример 2.31. Разложим в ряд Маклорена функцию
X
f(x) = Erf(z) = /V'2 Л, хеШ,
о
отличающуюся от так называемого интеграла вероятности
2 х
(или интеграла ошибок) erf (х) = -7=fe l dt только
нормировочным коэффициентом. Воспользуемся разложением
подынтегральной функции в ряд Маклорена и почленно
проинтегрируем этот ряд (см. теорему 2.18):
п!
—'- dt =
Поскольку используемое в данном случае разложение функции
е~1 справедливо при всех t E (—оо, +оо), то и полученное
разложение имеет место при всех х G (—оо, +оо) (см. теорему 2.18).

2.8. Применение рядов в приближенных вычислениях 199
2.8. Применение рядов
в приближенных вычислениях
Если функция f(x) является аналитической в точке xq, т.е.
в некоторой окрестности точки гго представима степенным
рядом
f
п=0
то в качестве приближенного значения функции f(x) в точке х
из окрестности точки xq можно взять частичную сумму этого
ряда:
Естественно, что при этом, чем меньше п, тем проще
аппроксимирующая функция Sn(x), но больше, вообще говоря,
погрешность такого приближения. Поскольку f(x) = Sn(x) + Rn{x),
при каждом фиксированном п точность приближения f(x) w
« Sn(x) оценивается суммой остатка ряда
\f(x)-Sn(x)\ =
k=n+l
Поэтому при заданной погрешности S > 0 число слагаемых в
частичной сумме Sn(x) необходимо выбирать так, чтобы оно
было наименьшим среди таких п, для которых выполняется
оценка
Оценивать сумму остатка ряда можно различными
способами. Можно использовать представления остаточного члена
формулы Тейлора в форме Лагранжа, Коши [II] или в
интегральной (см. Д.2.1). Можно, кроме того, строить для ряда
числовую мажоранту, сумму которой несложно вычислить. В
отдельных случаях можно применять признак Лейбница, если

200 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
ряд в интересующих нас точках является знакочередующимся.
Если степенной ряд в некоторой точке х удовлетворяет
признаку Лейбница, то справедлива оценка (см. следствие 1.4)
\Rn(x)\ < |an+1(x - xo)n+11 = K+i| \
\х -
Пример 2.32. Выясним, сколько членов разложенья функ-
ОО
ции ех в степенной ряд ех = Y1 хп/п\ необходимо взять, чтобы
п=0
погрешность S вычисления числа е (т.е. значения функции ех в
точке х = 1) в соответствии с формулой
2! (п-1)!
не превышала 10~4.
Аппроксимирующим выражением для числа е здесь является
значение частичной суммы Sn-i(l) ряда Маклорена функции
ех в точке х = 1. Поэтому для оценки погрешности данного
приближения необходимо оценить сумму i^-^l) остатка с
номером п — 1 ряда Маклорена функции ех при х = 1 (см. 2.7):
—
ni
Суммируя справа геометрический ряд с параметром q = l/(n+l)
(см. пример 1.4), получаем

2.8. Применение рядов в приближенных вычислениях 201
Таким образом, погрешность 6 приближенного вычисления
числа е по указанной формуле равна сумме iin_i(l) остатка
ряда Маклорена функции ех в точке х = 1 и удовлетворяет
неравенствам
п + 1
0<6<
п\п
-4
Для выполнения неравенства 8 ^ 10 достаточно найти
натуральное число п, для которого —}— ^ 10~4. Минимальным
из таких чисел является п = 8, поскольку
п\п
8 8 ' >ш-,
п=7
п\п
7-7! 7-5040 4410
9 9
ч-4
8 • 8 • 5040 8 • 40320 32000
п=8
и числовая последовательность < ^— > = \ (1 + - ) —-> убывает,
I n!n J L \ nj ту. )
как произведение убывающих последовательностей.
Итак, для вычисления числа е с заданной погрешностью
достаточно взять сумму первых восьми слагаемых разложения
оо
е = ^2 1/п!, т.е.
п=0
Пример 2.33. Вычислим sin9° с точностью до 10~4.
Перейдем от градусной меры к радианной: 9° = тг/20. Используя
разложение функции sin ж в ряд Маклорена, при х = тг/20 имеем
равенство
sm9 =Бш- =
Этот ряд удовлетворяет признаку Лейбница, поэтому
абсолютное значение суммы его остатка можно оценить модулем

202
2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
первого из отбрасываемых членов (см. следствие 1.4).
Следовательно, полагая
-""20
получаем погрешность
п-\ ,
6 =
7Г\2*+1
для которой верна оценка
2п+1
Г 1 / 7Г \2п+И
Так как последовательность < jt -гу ( — J > убывает с
ростом п и
к
к
0~4
к Ш > °'0006 >10"4' к Q < °'0000008 < 10~4'
то можно ограничиться первыми двумя слагаемыми:
Пример 2.34. Вычислим уЮ с точностью до 0,001.
Преобразовав исходное число к виду

2.8. Применение рядов в приближенных вычислениях 203
воспользуемся разложением степенной функции (1 + ж)1/3 в
точке ж = 1/4 Е (—1,1) в биномиальный ряд:
/1ч
3! \4
1/3(1/3 -1)(1/3-2)(1/3-
4!
1/3(1/3-1)... (1/3-п + 1
■"+ п!
_ Л 1 1 2 2-5 2-5-8
V +3'4 2!-32-42 + 3!-33-43 4! • З4 ■ 4
-■)■
2-5-8-...-(3n-4) (
= 2 + 0,1666...-0,0138...+0,0019...-0,0003... + ...
Этот биномиальный ряд удовлетворяет признаку Лейбница.
Поэтому абсолютная величина суммы остатка этого ряда,
равная погрешности 6 оценки суммы ряда его частичной суммой,
не превышает модуль первого из отбрасываемых членов (см.
следствие 1.4). Как видно, первым членом этого ряда, по
модулю не превышающим 0,001, является пятый член.
Следовательно, для достижения заданной точности можно ограничиться
суммой первых четырех членов ряда. Таким образом,
v/10 = 2 + 0,1666...-0,0138...+
+ 0,0019... «2,155, <К 0,001. #
В случае приближенного вычисления с помощью рядов
следует иметь в виду, что всякое число можно представить рядом
не единственным способом. Поэтому из всех возможных
представлений следует выбирать ряд, имеющий наибольшую ско-

204 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
рость сходимости, т.е. ряд требующий суммирования меньшего
числа своих членов для достижения заданной точности оценки
суммы.
Например, для вычисления значения In2 можно
использовать ряд Маклорена функции 1п(1 + х) в точке х = 1:
| () + ... (2.25)
Для вычисления In 2 с точностью до 10~3 придется суммировать
не менее 103 членов ряда, что никак нельзя признать удачным
способом вычисления, особенно при ручном расчете.
Число In 2 можно представить также в виде суммы другого,
быстро сходящегося ряда. Сделать это можно, например,
следующим образом. Рассмотрим сначала ряд Маклорена для
р
функции 1пг~з~ ПРИ х ^ (~~
- х) =
1-х
_ (-1)п+1жп
~ п
1 п 1 п
n=l n=l
Пусть 1 +1 = (1 + x)/(l - ж), т.е. х = t/(2 +1). Тогда
предыдущее разложение можно переписать следующим образом:
причем это разложение верно при всех — 1 < £/(2 +1) < 1, т.е.

2.8. Применение рядов в приближенных вычислениях 205
Подставляя в (2.26) значение t = 1, получаем новое
представление числа In 2 в виде суммы ряда:
(1 1/1\3 1 /1\2"-1 \
з + з(з) + " + *ггт(з) +->
Этот ряд является уже быстро сходящимся. Действительно,
сумму Rn остатка этого ряда можно оценить следующим
образом:
..v2n+l I /l\2n+3
0<Rn
(1 /l
2^т(з
2n+l
2 /1\2п+1 1 _ 2 /1\2"+19
+ lV3/ 1/1\2 ~ 2п + 1\3/ 8
т.е. сумма остатка быстро убывает с увеличением номера п.
Бели Sn — частичная сумма ряда (2.27), то погрешность
S приближения In 2 « 5П, равная сумме Rn остатка этого
ряда, удовлетворяет соотношению 0 < S = i?n ^ гп, п = 0,1,2,...
Поскольку
Д2 ^ г2, г2 = 4 в зз = gio > °'0018 > °'ОО15
Гз =
для вычисления In 2 с точностью до 0,001 достаточно взять
сумму первых трех ненулевых членов ряда (2.27):
1п2 « 2(\ + -^з + -г^) « 0,6667 + 0,0247 + 0,0016 « 0,693.

206
2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Напомним, что при вычислении значения In 2 с помощью ряда
(2.25) для обеспечения той же точности требовалось
суммировать тысячу членов ряда.
Аналогично нетрудно показать, что ряд (2.26) является
быстро сходящимся не только при t = 1, но и при любом t Е (0,1].
Это позволяет использовать ряд (2.26) для эффективного
вычисления (т.е. обеспечения заданной точности при суммировании
небольшого числа первых членов ряда), например, значения
1п(п-Ь 1), если уже известно значение Inn. Действительно,
1п(п
-Y n e N,
где 0 < 1/n ^ 1, и поэтому значение ln(l + 1/n) можно
эффективно вычислить с помощью ряда (2.26).
Степенные ряды часто используются также для
приближенного вычисления определенных интегралов.
Пример 2.35. Вычислим с точностью до 10~4
определенный интеграл
dx.
2
Первообразная подынтегральной функции е~х не выражается
явно через элементарные функции, поэтому для оценки этого
интеграла поступим следующим образом. Разложим
подынтегральную функцию в ряд Маклорена в интервале (—оо, +оо)
(см. 2.7) и почленно проинтегрируем этот степенной ряд (см.
теорему 2.18):
(_1)»яДп+1
1
0
3
i
0
+
X
5-
5
2!
= х ——
_ 1
3
(2n+l)n!
1
(-1)"
5-2!

2.8. Применение рядов в приближенных вычислениях 207
Пусть Snn Rn — n-я частичная сумма и сумма n-го остатка
этого ряда соответственно. Тогда погрешность приближения
1 _ 2
Je x dx « Sn равна 6 = \Rn\. Полученный для интеграла
о
ряд является знакочередующимся и удовлетворяет признаку
Лейбница. Следовательно, для суммы Rn остатка этого ряда
справедливо соотношение (см. следствие 1.4)
S = \Rn\< X *
(2(n + l) + l)(n+l)! (2п + 3)(п + 1)Г
Проведя вычисления, получаем
№|< >1°-'
Таким образом, заданная точность оценки /е~х dx « Sn
о
будет обеспечена, если вычислить сумму первых семи членов
полученного ряда (п = 6):
1 S<10~'- *
Рассмотрим еще одну задачу, в которой применение
рядов Тейлора позволяет быстро получить решение. Это
задача вычисления производной f^n\xo) некоторой функции f(x)
в точке хо G R при условии, что ряд Тейлора функции f(x) в
окрестности точки хо известен. Действительно, если f(x) =
00
= S ап{х — £о)п — вычисленный каким-то образом ряд Тейло-
п=0
ра функции f(x) в окрестности точки х = жо, то

208 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
следовательно, f(n'(xo) = п\ап, где ап — коэффициент при
члене (х — хо)п ряда Тейлора функции /(ж).
Пример 2.36. Найдем значение /(25)(0) для функции
0, х = 0.
Покажем, что в точке хо = 0 существуют производные любого
порядка. Действительно, используя разложение синуса (см. 2.7)
и замену м = ж3/3, при х ф 0 получаем
(_1)п-1ж6п-5
А так как /(0) = 0, то это разложение верно при всех х G R.
Согласно теореме 2.20, функция f(x) бесконечно
дифференцируема в точке хо = 0, и полученный степенной ряд является ее
рядом Тейлора. Поскольку коэффициент абП-5 при члене х6п~5
в ряде Тейлора функции f(x) определяется формулой
имеем
(-i)5-1
O25 = O6-5-5 =
(2-5-1)!32-5"1 9!-39'
Следовательно,
Заметим, что из полученного выше разложения функции
f(x) в ряд Тейлора следует, что все ее производные порядка,
отличного от 6п — 5, п G N, в точке х = 0 равны нулю.

2.9. Интегрирование дифференциальных уравнении 209
2.9. Интегрирование обыкновенных
дифференциальных уравнений
с помощью рядов
В том случае, если обыкновенное дифференциальное
уравнение проинтегрировать в квадратурах (т.е. выразить решение
уравнения через элементарные функции или интегралы от них)
не удается или принципиально невозможно, можно представить
решение этого уравнения в виде степенного ряда. В этом
параграфе разобраны основные приемы представления решения
с помощью степенного ряда на примере обыкновенных
дифференциальных уравнений второго порядка.
Рассмотрим обыкновенное дифференциальное уравнение
второго порядка, разрешенное относительно старшей производной
[VIII]
y" = F(x,y,y'), (2.28)
а также уравнение более общего вида
p(x)y" = F1(x,y,y'). (2.29)
Уравнение (2.29) принципиально отличается от (2.28) тем, что
оно может иметь особые точки, абсцисса xq которых
удовлетворяет уравнению р(жо) = 0. В окрестности таких точек
уравнение (2.29) нельзя разрешить относительно старшей
производной у" и свести к виду (2.28). В окрестности
остальных (неособых) точек уравнение (2.29) можно привести к виду
(2.28).
Если функция F(x,j/,j/') из правой части (2.28) в некоторой
окрестности точки Р(жо, Уо> У\) €■ К3 удовлетворяет
определенным условиям гладкости* по совокупности независимых
переменных х, у и у', то можно показать, что существует решение
(общее или частное) уравнения (2.28), и это решение является
*См.: Карташев Л.Я., Рождественский Б.Л.

210 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
действительной аналитической функцией в некоторой
окрестности точки хо, т.е. его можно представить в этой окрестности
в виде степенного ряда
(2.30)
п=0
Для этого необходимо, по крайней мере, существование в
некоторой окрестности точки Р(жо, 2/о> 2/1) всех частных
производных функции F(rr,y,y') любого порядка по всем переменным.
Если точка Р(жо, 2/(Ь 2/1) является неособой для уравнения
(2.29), т.е. p(xq) ф 0, то при тех же ограничениях на функцию
Fi(x,y,2/), и при условии аналитичности функции р(х) в
некоторой окрестности точки жо, существует решение у = у(х)
(общее или частное) уравнения (2.29), и это решение является
в этой окрестности действительной аналитической функцией,
т.е. его можно представить рядом (2.30).
Если же р(хо) = 0, то в указанных условиях в окрестности
точки Р(жо, уо, 2/i) может существовать решение в виде
обобщенного степенного ряда
-xo)'\ (2.31)
п=0 п=0
где 7 — некоторое (не обязательно целое и положительное)
действительное число. (Таких решений может быть, вообще
говоря, несколько.)
Ниже описаны два конкретных метода нахождения решений
уравнений (2.28) и (2.29) в виде степенного ряда и в виде
обобщенного степенного ряда.
Метод последовательных дифференцирований. Этот
метод проиллюстрируем на задаче Коши
(2.32)

2.9. Интегрирование дифференциальных уравнений 211
где функция F(x, у, у') такова, что решение у = у(х) этой задачи
в некоторой окрестности точки яо существует, единственно
и является аналитической функцией (в частности, функция
F(x,y,y') в некоторой области DcR3, содержащей точку
Р(хо)Уо,у\), имеет все частные производные любого порядка
по всем переменным я, у и у').
Тогда решение у = у(х) можно представить в этой
окрестности своим рядом Тейлора
^о) (233)
п!
Чтобы явно найти это решение, достаточно вычислить
значения всех производных у^{хо) функции у(х) в точке xq. В
соответствии с начальными условиями имеем
а используя дифференциальное уравнение у" = F(x,y,y'),
находим
у"(а?о) = F{xo,y{xo),y'{xo)) = F(a?o,yo, Vi)-
Далее, продифференцировав уравнение у" = F(x,y,y;) по
переменному я, получим
откуда при х =
где у'(хо) = Уь а у"(яо) — вычисленное выше значение.
Продолжая процесс дифференцирования уравнения у" = F(x,y,y'),

212 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
последовательно находим все производные функции у (я),
выраженные через частные производные функции F(x,y,y') и
производные функции у(х) меньших порядков. Подставляя в
ряд Тейлора (2.33) значения полученных производных в точке
xq, получаем полностью определенный степенной ряд Тейлора
функции у = у(х).
Наконец, остается найти интервал (xq — R,xq + R)
сходимости полученного ряда и выяснить, при каких значениях х из
этого интервала сумма полученного ряда (2.33) является
решением задачи (2.32).
Полученное решение задачи Коши, разумеется,
существенно зависит от начальных условий, т.е. у(х) = у(#,у(ьУ1)- Если
числа уо и у\ в задаче Коши (2.32) рассматривать как
произвольные постоянные С\ и Сг, то полученная описанным выше
способом функция у = у{х,уо,у\) = y(x,Ci,C2) будет общим
решением дифференциального уравнения (2.28).
Этот способ можно применять и для решения
дифференциального уравнения любого порядка, разрешенного
относительно старшей производной:
Не следует, однако, переоценивать возможности данного
метода интегрирования дифференциальных уравнений.
Теоретически здесь никаких проблем не возникает, однако на
практике они могут появиться. Дело в том, что для нахождения
всех производных необходимо получить функциональную или
рекуррентную зависимость производной у^п\хо) от своего
порядка п. Однако реально выявить такую зависимость удается
не всегда. В этом случае нельзя определить весь ряд,
задающий решение дифференциального уравнения. Будет известна
только часть степенного ряда, которая определяет не точное
решение задачи, а приближенное. Однако в инженерных
задачах, когда вполне достаточно найти приближенное значение,

2.9. Интегрирование дифференциальных уравнении 213
этот метод является эффективным способом решения задачи
Коши.
Пример 2.37. Найдем пять членов разложения в ряд
Маклорена решения задачи Коши
У' = хуу',
У(О) = 1,
У(0) = 1.
Решение у(х) данной задачи имеет разложение
Вычислим значения производных у^п^(0), п = О,1, 2,
Используя начальные условия, получаем
у(0) = 1, i/(0) = 1.
Подставляя эти значения в уравнение у11 = хуу1, находим
у"(О)=О-у(О)-у'(О)=О.
Дифференцируя уравнение у11 = хуу1 по х и учитывая при этом,
что у и у' являются функциями от х, находим
и, следовательно, у'"(0) = 1.
Далее дифференцируем уравнение уш = уу' + х(у')2 + хуу":
» + (у')2 + 2жу'у» + уу» + Ху'у"
= 2(у')2 "

214 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Подставляя сюда х = 0 и известные значения у(0) — 1, у'(0) =
= 1, у"(0) = 0, у'"(0) = 1, получаем у^{0) = 2. Затем находим
у<5> = 4у'у" + 2у'у" + 2уу'" + Ъу'у" +
+ Му")2 + з*уУ"+уу'"+ху'у'"+хуу{4) =
= 9У'у" + Зуу'" + Му")2 + zxy'y'"+ху'у'"+*уу(4\
откуда у(5)(0) = 3.
Таким образом, искомое разложение решения задачи Коши
имеет вид
/ ч , х* 2а;4 Зх5
У(Х) = 1 + Х + - + —+ — + ... #
Метод неопределенных коэффициентов. Этод метод
проиллюстрируем на примере нахождения частного решения
уравнения (2.29), т.е. при решении следующей задачи Коши:
(2-34)
где функция F\(x,y,y') удовлетворяет тем же условиям, что
и функция F(x,y,y') в задаче (2.32), а р(х) — действительная
аналитическая функция в некоторой окрестности точки xq.
Метод заключается в том, что решение задачи ищут в виде
обычного степенного ряда (2.30) (или обобщенного степенного
ряда (2.31), если xq является нулем функции р{х)) с
неопределенными коэффициентами. Чтобы найти неопределенные
коэффициенты, нужно:
1) дважды продифференцировав ряд (2.30) или ряд (2.31) с
неизвестными коэффициентами, найти разложения в степенной
(или обобщенный степенной) ряд для производных у'{х) и у"(я),

2.9. Интегрирование дифференциальных уравнений 215
а также найти разложение в степенной ряд аналитической
функции р(я);
2) подставить полученные для у(я), у'(х), у"(х) разложения
с неопределенными коэффициентами и разложение р(х) в
уравнение р{х)у" = i*i(x,y,y');
3) представить получившееся при этом выражение Fi(rE,y,y')
в виде степенного ряда (это возможно, если функция F\(x1y1yt):
как функция от трех независимых переменных я, у и у',
удовлетворяет определенным условиям гладкости, о которых
говорилось выше);
4) из полученного равенства степенных рядов,
приравнивая коэффициенты при равных степенях х — яо, получить
рекуррентные уравнения; из этих уравнений найти
коэффициенты ап;
5) если решение ищется в виде обобщенного степенного
ряда (2.31), то сначала, приравнивая коэффициенты при
наименьшей степени х — хо, найти значение (или несколько значений)
неизвестного параметра 7; после этого для каждого
найденного значения 7 определить неизвестные коэффициенты ап, как
описано выше;
6) полученные ряды необходимо исследовать на сходимость;
в области своей сходимости ряды являются решениями задачи
Коши (2.34).
Как правило, этот метод применяют при решении линейных
дифференциальных уравнений
Po(x)y"+Pi(x)y'+p2(x)y = f(x) (2.35)
с аналитическими коэффициентами ро{х), Pi{x), P2(x) и
аналитической же правой частью /(я).
Приведем без доказательства две теоремы.
Теорема 2.23. Пусть в уравнении (2.35) коэффициенты
Ро(ж), Р\{х), Р2{х) и правая часть f(x) являются
действительными аналитическими функциями в окрестности точки хо,

причем po(so) Ф 0. Тогда в некоторой окрестности точки
решение задачи Коши
Ро{х)у" +Pi{x)y' +р2{х)у = f{x),
у'{хо)=У1
существует, единственно и его можно представить в виде
степенного ряда
п=0
с некоторыми коэффициентами onGK. #
Отметим, что при выполнении условий теоремы 2.23 общее
решение уравнения (2.35) также можно представить в виде
степенного ряда и найти по правилам, изложенным выше, если
положить у(хо) = Ci, у'(хо) = Сг, где Ci, C<i — произвольные
постоянные.
Прежде чем сформулировать вторую теорему, напомним,
что точка xq является нулем кратности s Е N аналитической
в окрестности точки хо функции р{х), если в этой окрестности
функцию р(х) можно представить в виде
p{x) = {x-xo)sq{x),
где q(x) — также аналитическая функция в окрестности точки
хо и q{xo) ф 0.
Теорема 2.24. Пусть функцииро{х), р\{х) ир2{х) являются
действительными аналитическими функциями в окрестности
точки хо и точка xq является нулем кратности 5 функции ро{х).
Пусть, кроме того, точка хо является нулем кратности не менее
5 — 1 функции р\ (х) (при 5 > 1) и нулем кратности не менее 5 — 2
функции Р2{х) (при 5 > 2). Тогда существует по крайней мере
одно нетривиальное решение уравнения
Ро (*) У* + Pi (х) У1 + Р2 {х)у = 0, (2.36)

2.9. Интегрирование дифференциальных уравнений 217
которое можно представить в виде обобщенного степенного
ряда
(2.37)
71=0 71=0
где по ф 0, а 7 — некоторое действительное число, не
обязательно целое или положительное. #
Руководствуясь теоремой 2.24, для линейного однородного
дифференциального уравнения (2.36) всегда можно найти
нетривиальное частное решение у\(х) вида (2.37), определенное
в некоторой окрестности (возможно проколотой или
односторонней) точки xq при р{хо) = 0. Как известно [VIII], общим
решением уравнения (2.36) является совокупность всех
линейных комбинаций двух линейно независимых частных решений.
Второе решение У2{х), линейно независимое с у\{х), в
некоторых случаях также можно представить в виде (2.37) или в
виде произведения обобщенного степенного ряда и функции
Отметим, что теорема 2.24 не гарантирует существования
какого-либо нетривиального решения всякой задачи Коши
Po{x)y"+Pi{x)y'+p2{x)y = O,
= уо,
в виде обобщенного степенного ряда, поскольку, например,
может не существовать ни одного решения вида (2.37) уравнения
(2.36), определенного в точке хо (например, в случае, когда
7<0).
Пример 2.38. Найдем решение задачи Коши

218 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
в виде суммы ряда и определим область сходимости
полученного решения.
Поскольку коэффициенты ро(х) = 1, р\(х) = 0 и р2{х) = х
уравнения у" + ху = 0 являются аналитическими функциями
и значение функции ро{х) в точке хо = 0 отлично от нуля,
то на основании теоремы 2.23 решение этой задачи можно
представить в виде обычного степенного ряда с центром в
нуле:
оо
у(х) = ^апхп (2.38)
п=0
Из начальных условий следует, что
ао=1/(О)=О, ai = y'(0) = l.
Учитывая (2.38), представляем функции ху(х) и уп{х) в виде
степенных рядов:
ОО ОО г -| ОО
v^4 n v^4 n+i замена \-^ и
п=0 п=0 L J Jfe=l
у"(х) = (f^anxA = f>nzn)" = f)n(n -
=0 ' 71=0 71=2
[замена 1 v^/i м/» -.ч к
fc=l
Подставляя эти разложения в уравнение у" + ху = 0,
получаем равенство
ОО
су Л- \ I (1с -I- 0\ (к -\- ]\ П 4-/7 I Т П

2.9. Интегрирование дифференциальных уравнении 219
выполняющееся в некоторой окрестности точки хо = 0. Это
равенство верно только в случае, когда а2 и все коэффициенты
при членах хк равны нулю:
а2 = 0; (к + 2){к + l)afc+2 + а*_1 =0, к € N.
Осуществляя замену п = к — 1, а также учитывая полученные
ранее значения для ао и ах, получаем систему
ап ' , (2-39)
Отсюда следует, что ао = 0, аз = 0, ае = 0 и т. д., т.е. азп = 0,
п = 0,1, 2,..., а также а2 = 0, а^ = 0, ag = 0 и т. д., т.е. азп+2 = 0,
п = 0,1, 2,... Подсчитаем, используя рекуррентную формулу
(2.39), первые несколько коэффициентов азп+i с номерами
1,4,7,
п = 0: ai = 1;
Л1 1
п = 1: а4 = —
4-3 3.4'
п = 3:
7-6 (3-4)(6-7)'
a-j 1
10-9 (3-4)(6-7)(9-10)'
Эти вычисления позволяют сделать предположение, что для
любого натурального п верна формула
(-1Г
(3-4) (6-7) (Зп(Зп + 1))'
Докажем истинность этой формулы методом математической
индукции. При п — 1, 2 и 3 формула верна. Предположим,

220 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
что она имеет место и для п = га, и покажем, что тогда она
справедлива и для п = т +1. Используя рекуррентную формулу
(2.39), имеем
fl3m+1
~ аЗт+4 = -
(Зт + 4)(3т + 3)
(-1Г -1
(3 • 4) (6 • 7) (Зт(3т + 1)) (Зт + 3) (Зт + 4)
~~ (3 • 4) (6 • 7) (Зт(3т + 1)) (3(т+1) (3(т+1) + 1))'
что и требовалось доказать. Следовательно, формула (2.40)
верна при всех п Е N.
Итак, решением задачи Копш является (в области своей
сходимости) ряд
Найдем область сходимости полученного ряда, пользуясь
предельным признаком Даламбера и формулой (2.39). Для всех
х е (—оо, +оо)
= lim
71—ЮО
хг
lim
71—ЮО
(Зп + 4)(3п + 3)
Таким образом, ряд сходится (и является решением задачи
Коши) на всей числовой прямой.
Пример 2.39. Решим задачу Коши
(х2 - \)у" - 2ху' + 2у = 21п(1 + гг) + ;
1 + х
,У(О)=О, i/(0) = 1.
Коэффициенты ро{х) = х2 — 1, pi(x) = —2х, рг(^) = 2 и
правая часть f(x) = 21n(l + х) + (1 — Зх)/(1 + х) дифференциального

2.9. Интегрирование дифференциальных уравнений 221
уравнения этой задачи являются аналитическими функциями
в окрестности точки хо = 0, причем значение функции ро(х)
в точке хо = 0 отлично от нуля (ро(О) = — 1 ф 0). Поэтому на
основании теоремы 2.23 решение этой задачи можно предста-
оо
вить в виде степенного ряда с центром в нуле: у(х) = ]П
п=0
Согласно теореме 2.19, в области сходимости этого ряда
1 и y"(x) = JTcnn(n-l)xn-2.
п=1 п=2
Функция 1п(1 + х) имеет следующий ряд Маклорена:
п=1
Разложим в ряд Маклорена функцию (1 — Згг)/(1 + х):
1 — Згг _ 4 — 3(1 + ж) _ 4 _
1 + х 1 + х 1 + х
-1)п4хп, are (-1,1). (2.41)
п=0 п=1
Подставив полученные разложения в дифференциальное
уравнение задачи Коши, получим равенство
оо с» оо
(X2 -1)2Сп"(" " i)*""2 - 2ЖЕCn"1""1 + 2E
п=2 п=1 п=0
оо „ оо
1
n=l n=l
верное в некоторой окрестности точки xq = 0.

222 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Умножим ряды в левой части равенства на
соответствующие коэффициенты, а ряды в правой части сложим:
ОО
п~2
(п - \)хп~2 -
71=2 71=2 71=1
71=0 71=1
Сделаем во втором ряде левой части равенства замену
переменного к = п — 2, чтобы его общий член содержал степень хп:
71=2 fc=0
71=0
Теперь, возвращаясь к исходному равенству, получаем
n=2 n=0
71=1 71=0 71=1
Наконец, в рядах равенства выделим члены с номерами п = 0
и п = 1, а преобразованные таким образом ряды сложим:
2(со -с2)-
71=2
71=2

2.9. Интегрирование дифференциальных уравнении 223
Поскольку последнее равенство верно в некоторой
окрестности точки хо = 0, то остается приравнять коэффициенты при
одинаковых степенях в левой и правой частях:
х°: 2(со-с2) = 1;
х1: -без = -2;
хп:
п > 2.
ОО
Используя начальные условия для функции у = у(х) = Y2
71=0
находим со = у{0) = 0, с\ = у'(0) = 1. Из равенств, полученных
выше, имеем с2 = —1/2 и сз = 1/3, а при n ^ 2
^ n(n+l)(n
Из полученной рекуррентной формулы найдем несколько
первых коэффициентов помимо уже известных: с\ = —1/4, с$ =
= 1/5, Итак,
11 11
С0 =0, С\ = 1, С2 = --, Сз = -, С4 = --, С5 = -,
Судя по вычисленным значениям, можно предположить, что
общая формула для определения коэффициентов Сп имеет вид
(2.42)
п
Докажем методом математической индукции, что данная
формула действительно верна. Для номеров п = 1, 2, 3, 4 и 5
формула (2.42) справедлива. Пусть она верна при некотором

224 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
п = т. Докажем ее истинность для номера п = т + 2. Для
этого в рекуррентную формулу для Ст+2 подставим значение
1
(m + l)(m + 2) m
m(m
"" m(m + l)(m + 2) "" m + 2 ~" m + 2
Значит, формула (2.42) справедлива и для п = т + 2. Так как
формула (2.42) верна для п = 1, она истинна для всех нечетных
п G N. А поскольку формула (2.42) верна также и для п = 2,
то из доказанного следует, что она истинна для всех четных
п G N. Таким образом, формула (2.42) справедлива для всех
натуральных п.
Итак, решение поставленной задачи Коши можно
представить в окрестности нуля следующим степенным рядом:
n=l
Заметим, что этот ряд представляет собой ряд Маклорена
функции 1п(1 + х) (см. 2.7), причем областью сходимости этого
ряда является полуинтервал (—1,1].
Подставляя в исходное дифференциальное уравнение
функцию у = 1п(1 + я), окончательно убеждаемся, что она
действительно является решением данной задачи Коши, причем на всем
интервале х G (—1, +оо).
Замечание 2.6. Пример 2.39 показывает, что решение
дифференциального уравнения, найденное с помощью рядов,
является, вообще говоря, решением этого уравнения только

2.9. Интегрирование дифференциальных уравнении 225
в некоторой окрестности точки #о, но не является решением
этого уравнения в максимально возможной области изменения
переменого х.
Пример 2.40. Найдем решение дифференциального
уравнения
^ 0 (2.43)
в промежутке [0, +оо) с начальными условиями у(0) = 0 и
у'(0) = 0 в виде обобщенного степенного ряда.
Коэффициентыро{х) = я, р\(х) = —3/2 и Р2(х) = я уравнения
(2.43) являются аналитическими функциями на множестве М, а
точка xq = 0 является нулем функции ро{х) порядка 5 = 1.
Значит, уравнение (2.43) в окрестности точки хо = 0 удовлетворяет
условиям теоремы 2.24 и имеет по крайней мере одно
нетривиальное решение уравнения (2.43), которое можно представить
в виде обобщенного степенного ряда
71=0 71=0
Заметим, что, поскольку в данной задаче требуется
найти решение, проходящее через точку х = 0, необходимо, чтобы
7^0. При этом, если 7 — целое или рациональное число с
<Х)
нечетным знаменателем, то функция у(х) = х1 Yl an%n опреде-
71=0
(X)
лена во всей области сходимости степенного ряда Y1 ап^Пч в
71=0
противном случае — только в неотрицательных точках этой
области (х ^ 0).
(X)
Поскольку степенной ряд ]Г) апхп можно почленно диффе-
71=0
ренцироватпъ в интервале сходимости, то, применяя правило
Дифференцирования произведения, во всей области
определения решения у(я), за исключением точки х = 0 при ^ < 1 и,

226 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
возможно, граничных точек, имеем
оо . оо оо
п=0 п=0 п=0
оо оо
i1 + Y,'yanxn+'f-1 + ^ Е0"
71=1 П=1
71=1 71=0
ОО
Отметим, что если ряд у(х) = ^ anxnJrl продифференциро-
71=0
вать почленно, то получится ряд, который был найден выше
для у'(х). Поэтому обобщенные степенные ряды, как и
обычные степенные ряды, в области сходимости (за исключением,
возможно, точки х = 0 и граничных точек) можно почленно
дифференцировать.
Таким образом, почленно дифференцируя обобщенный
степенной ряд для функции у'(я), во всей области определения
решения у{х), за исключением точки х = 0 при 7 < 2 и,
возможно, граничных точек, имеем
оо
71=0
Подставив полученные ряды для у(х), у'(х) и уп(х) в
дифференциальное уравнение (2.43), получим равенство, которое
выполняется в некоторой окрестности нуля (возможно,
проколотой окрестности или правой полуокрестности):
71=0
ОО л ОО
~~ ■ . - — = 0 (2 44)
оо «
-^■^(if + ^anX
71=0
оо
71+7-1+Е
71=0

2.9. Интегрировалие дифференциальных уравнении 227
Заметим, что
71=0 71=0
71=0
71=2
5
[замена ]
= [fc=n-2J =
f + 2) (7 + к - l
k=Q
Поэтому, возвращаясь к равенству (2.44), имеем
Приравняем нулю коэффициенты при всех степенях х:
(245)
Учитьшая, что ao Ф 0, из первого уравнения получаем либо
7 = 5/2, либо 7 = 0. Если у = 0, то из начального условия у(0) = 0
следует, что ao = 0, а этого быть не может.

228 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Итак, пусть 7 = 5/2 и по ф 0. Заметим, что при 7 == 5/2
(X)
функция у(я) = я5'2 J^ ап#п удовлетворяет начальным услови-
71=0
ям у(0) = 0 и j/;(0) = 0 при любых значениях коэффициентов ап.
Поэтому эти начальные условия никак не влияют на
определение коэффициентов an.
Далее, из второго уравнения системы (2.45) делаем вывод,
что а\ = 0. Используя третье уравнение, получаем
рекуррентную формулу
* = 012
Так как а\ = 0, то аз = 0 и а$ = 0 и т.д., т.е. а& = 0 для всех
нечетных номеров к = 2п + 1, п = 0,1, 2,...
Если же А; — четное число, т.е. к = 2n, n = 0,1, 2,..., то
271+2 (2n + 2)(2n + 9/2) (n+l)(4n + 9)"
Вычислим значения первых нескольких коэффициентов
°2 = ~~9~; °4 = ~213 = 2I-913'
&6 CLQ
п*
°6 3-17 3I-9-13-17' п* 4-21 4! • 9 -13 -17 - 21 '
По нгшденным значениям строим формулу
истинность которой докажем методом математической
индукции. Для начальных значений п от 1 до 4 эта формула
справедлива (показано выше). Предположим, что она справедлива
при п = т, и докажем, что она верна и при п = т + 1. Для

2.9. Интегрирование дифференциальных уравнении 229
этого достаточно в рекуррентную формулу (2.46) подставить
выражение для а2Ш из (2.47):
«2<m+l) " «2m+2 - "(„,+1)(4m + 9)
(т + 1)(4т + 9) т! -9-13-17-... • (4т+ 5)
=
(т + 1)! • 9 • 13 ■ 17 • (4т + 5) ■ (4(т+1) + 5)'
Таким образом, искомое решение имеет вид
где С = по ф О — произвольная константа.
Чтобы найти область сходимости степенного ряда,
воспользуемся, учитывая рекуррентную формулу (2.46), предельным
признаком Даламбера. Получим, что
lim
П—ЮО
2(n+l)+2
2n+2
= я2 lim ■; ttt: ^7 = 0 < 1
П—f(X)
(n + l)(4n + 9)
при всех x G (—oo,+oo). Так как множитель я5/2 определен
при х ^ 0, то полученный обобщенный степенной ряд (2.48)
определен и является решением рассматриваемой задачи Коши
при всех х^Ои произвольной константе С = ао ф 0.
Итак, дифференциальное уравнение (2.43) имеет
бесконечное множество решений, удовлетворяющих начальным
условиям у(0) = 0 и уг(0) = 0, которое описывается формулой (2.48).
Все эти решения определены при х ^ 0 и отличаются лишь
множителем С = ао ф 0, который может принимать произвольное

230 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
значение. Отметим, что при С = 0 формула (2.48) дает нулевую
функцию у(х) = 0, которая также является решением
поставленной задачи Коши.
Обратим внимание на то, что начальное условие у'(0) = 0
нашей задачи Коши никак не влияет на полученные решения.
Дело в том, что в соответствии с видом дифференциального
уравнения (2.43) всякое его решение, имеющее в точке х = 0
значение у(0) = 0, всегда имеет значение производной у'(0) = 0.
В частности, дифференциальное уравнение (2.43) с начальными
условиями у(0) = 0 и у'(0) = 1 не имеет решения.
Дополнение 2.1. Остаточный член
формулы Тейлора в интегральной форме
Теорема 2.25. Пусть функция f(x) имеет в некоторой
окрестности точки гго непрерывную производную (п + 1)-го
порядка. Тогда для любого х из указанной окрестности точки
хо имеет место формула Тейлора
с остаточным членом Rn(x) в интегральной форме:
хо
Ч Пусть точка х принадлежит указанной в условии теоремы
окрестности. Поскольку все производные до (п + 1)-го
порядка включительно непрерывны на отрезке [гго, я], то, согласно
формуле Ньютона — Лейбница, имеем
X X
f(x)-f(xo) = If'(t)dt = -1f'(t)d(x-t).
xq xq

Д.2.1. Остаточный член в интегральной форме
231
Используя правило интегрирования по частям, получаем
X
f(x)-f(xo) = -Jf(t)d(x-t) =
хо
X
= -f'(t)(x-t)X + f(x-t)f"(t)dt =
хо J
Хо
X
= f'(xo)(x-xo) + J(x-t)f"(t)dt.
Хо
Снова применяя правило интегрирования по частям,
находим
х
f(x)-f(x0) = f'(xo)(x-xo) -\ff"(t)d(x-t)2 =
ХО
X
= f'(xo)(x-xo)-h"(t)(x-t)2 X + 4(x-t)2f"(t)dt =
2 хо 2 J
хо
X
+ \j{x - t)2f'"(t)dt
= f'(xo)(x - хо) + \f"{xo){x -
и т.д. Применяя интегрирование по частям в n-й раз,
окончательно получаем
f(x) - f(x0) = f'(xo)(x -
2!
(x - хо)2 +...
А это и есть утверждение теоремы. ►

232 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Вопросы и задачи
2.1. Найдите области сходимости заданных
функциональных рядов. Исследуйте ряды на абсолютную сходимость:
оо
fcrn/r- f\
)
71=1 71=1 71=1
71=1 71=1 V ' 71=1 71=1
оо ^ °°
1
71=1 71=1 V 7 71=1 V 7
2.2. Найдите область абсолютной сходимости
функционального ряда
00 -
Сходится ли данный ряд в точках z = 0 и z = 1 — г?
2.3. Докажите равномерную сходимость следующих
функциональных рядов в заданных промежутках:
71=1 71=1
71=2 71=1
ж)
пх =
71=1 71=1
ОО . „ , ОО
х-ч sm па;п +cos па; /л ч ч v^ e

Вопросы и задачи 233
и) Ё^з^е^' (-
71=1
к) 2^ ^г ' I°> +о°); н)
71=1
2.4. Докажите, что если члены равномерно сходящегося на
с»
множестве X функционального ряда ^ /п(#) умножить на од-
71=1
ну и ту же ограниченную на X функцию <р{х), то равномерная
сходимость ряда не нарушится.
2.5. Найдите круг сходимости следующих степенных рядов:
оо
2.6. Найдите круг сходимости степенного ряда при
произвольном значении параметра а. Выясните, сходится ли ряд в
точках si, Z2> 23> Z4 при указанных значениях c*i и с*2
параметра а. Если ряд сходится, то уточните, как — абсолютно или
условно. Нарисуйте круг сходимости. Выполните эти задания
для следующих рядов:
а) > -^— v /у м =_/— ai=5, a2 =

234 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
2.7. Найдите области сходимости следующих
действительных степенных рядов:
00 О71 71 00 /. n\Tl^ OO К
Е о Е^-; ■> Е£
71=1 V -'"
2.8. Укажите области сходимости следующих
функциональных рядов и найдите их суммы:
^71+1 *
71=1 71=0
2.9. Разложите по степеням х следующие функции и
укажите интервалы, в которых эти разложения справедливы (если
функция не определена при х = 0, то доопределите ее по
непрерывности):
()
д)жсо8а;2; е) arctga;; ж) a;2arctga;; з) a;2arcsina;; и) cos(a;3—3);
ч ^5 4 1/ /^—7\ \ 2 ч ?sin2t _
к) / ; л) ln(a;+v# +1); м) arccosx ; н) / а;
V1 + х2 J t
X
о) / rchtdt] п)
о
2.10. Разложите в ряд по степеням x — xq следующие
функции и укажите интервал сходимости полученного разложения:
а) 1п(5х + 3), х0 = 1; б) 1пж, х0 = 1; в) ,х + ы2х5)' Х° = 2)
т)у/2х, жо = 2; д) sin-,a;o = -; e) arcsin(-2x2 -4a;-2), xq = -1.

Вопросы и задачи 235
2.11. Найдите первые четыре члена разложения в ряд
Тейлора в окрестности точки хо для следующих функций:
a) tga;, х0 = 1; б) tgx, х0 = -; в) /1 + д.2)3» х° = 1;
О
2.12. Используя значения радиусов сходимости рядов
Тейлора основных элементарных функций, укажите интервалы
сходимости разложений в ряд Тейлора в окрестности точки xq
следующих функций:
а) 1п(5 + За;2), х0 = 0; б) —?—, х0 = -2; в) е5*42, х0 = 0;
ж + 5
2.13. Применяя различные приемы, найдите суммы
следующих функциональных рядов:
s2n+1
-l) x2n+1
2-4-...-2n
n=l
2.14. Вычислите указанные значения с заданной
точностью е:
а) ^=, e = 10"3; б) coslO0, е = 1(Г4; в) sinl, е = КГ5;
г) JL, е = Ю-3; д) arcsini, е = 10"3; е) ^250, е = 10~3;
ж) 1пЗ, £ = 10~4; з) arctg-, е = 10"3.

236 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
2.15. Вычислите интегралы с точностью до 10~3:
2 11/3 2
ч Г sina; f . 2 . \ f dx ч /* ех _
а) / — <*я; б) у sina;2cto; в) у Тп=р; Г^ / Т ;
0 0 0 1
0,1 1/2 1/2
/ех — 1 /* / /* 1 — cos ж
dx; е) / vl + a;3da;; ж) / ^—dx.
оо о
2.16. Для заданных функций найдите значения
производных порядка п в точке х = 0, пользуясь разложениями этих
функций в ряд Маклорена, которые получены с помощью
разложений основных элементарных функций:
Х2
а) х2>/Т+~х, п = 5; б) a;6arctgx, п = 12,13; в) j, n = 10;
1 + а;4
2.17. Докажите, что функция f(x) = ^ e~n cos их является
71=1
бесконечно дифференцируемой на числовой прямой R. Найдите
разложение этой функции в ряд Маклорена и покажите, что
радиус сходимости полученного ряда равен нулю.
2.18. Применяя метод последовательных
дифференцирований, найдите указанное число ненулевых членов разложения в
степенной ряд решений следующих дифференциальных
уравнений при указанных начальных условиях:
а) у" = х2 + у2, у(0) = 0, j/'(0) = 1 (четыре члена);
, У(О) = 4, у'(0) = -2 (пять членов);
1-х2
в) у' = hi, y(0) = 1 (пять членов);
У
г) уп = eysiny\ у(тг) = 1, у'(тг) = тг/2 (пять членов);
Д) У(4) =ху + у'х2, у(0) = у'(0) =у"(0) = у'"(0) = 1 (семь членов).

Вопросы и задачи 237
2.19. Найдите в виде степенного ряда решение уравнения
у" — ху = 0, удовлетворяющее начальным условиям:
а) у(0) = 1, i/(0) = 0; б) у(0) = 0, у'(0) = 1.
2.20. С помощью степенных рядов проинтегрируйте
следующие дифференциальные уравнения при заданных начальных
условиях:
а)у" + яу' + у = 1, у(0)=0, 1/(0) =0;
6)(l-arV-*y = 0, У(0)=0, i/(0) = 1;
в) (1 - х2)у" - Ъху' - 4у = 0, у(0) = 1, i/(0) = 0.
2.21. Решите задачи Коши:
{у" + Аху' + у = 4a;cosa; — 9а;2 — 5х — 2,
у(0)=0,
1/(0) = 0;
{(ж2 - 3)у" - 2ху' + 2у = (5 -ж2)со8а? + 2xsina;,
»(0) = 1,
1/(0) =0.
2.22. Найдите частные решения следующих
дифференциальных уравнений в окрестностях их особых точек:
2у = 0, у(0) = 1, у'(0)=0;
= О, у(0) = 1, |/(0)=0;
= 0, у(0) = 1, у'(0)=0.

3. РЯДЫ ФУРЬЕ
Примерно с середины XVIII в. Д. Бернулли, Ж. Даламбер,
Ж. Лагранж и Л. Эйлер, изучавшие некоторые проблемы
математической физики, оказались вовлеченными в дискуссию по
поводу возможности представления „произвольной" 2тг-перио-
дической функции в виде суммы тригонометрического ряда
оо
ао/2+ ^2 (akcoskx + bksinkx). В начале XIX в. работы фран-
k=l
цузского математика Ж.Б. Фурье открыли новую эпоху в
развитии теории тригонометрических рядов. Фурье мог
представить в виде суммы тригонометрического ряда (в настоящее
время называемого рядом Фурье) любую функцию, которую
ему в то время могли предложить. В его книге
„Аналитическая теория тепла", вышедшей в 1822 г., содержится много
частных примеров таких представлений и их применения.
Попытки Фурье доказать, что любую функцию можно разложить
в тригонометрический ряд, привели к углубленному
исследованию понятия функции и проблемы представимости функций
тригонометрическими рядами такими учеными, как Дирихле,
Лобачевский, Риман и др. Дальнейшее изучение рядов Фурье
способствовало развитию теории интегрирования, послужило
одной из предпосылок для создания ряда современных
математических дисциплин, таких, как дифференциальные уравнения
с частными производными, теория функций действительного
переменного, функциональный анализ.
3.1. Ортонормированные системы и ряды Фурье
В этой главе много внимания уделено бесконечномерным
евклидовым пространствам. Напомним, что евклидовым
пространством называют линейное пространство L, в котором

3.1. Ортонормнрованные системы и ряды Фурье 239
задано скалярное умножение, т.е. отображение /: L x L —> R,
ставящее в соответствие упорядоченной паре элементов
линейного пространства L число и удовлетворяющее аксиомам
скалярного умножения:
1) (&! У) = (У, x),x,yeL;
2) (я + у, z) = (x, z) + (y, z), x,y,zeL;
3) (Arc, у) = А (я;, у), я, у 6 L, А 6 R;
4) (ж, а;) ^ 0, причем (х, а;) = 0 лишь в случае, когда х = 0.
Линейное (евклидово) пространство бесконечномерное, если
в нем можно выбрать любое количество линейно независимых
элементов.
Линейное пространство образует множество всех кусочно
непрерывных на отрезке [а, 6] функций, т.е. функций,
непрерывных всюду на отрезке [а, 6] за исключением конечного числа
точек, в которых эти функции имеют разрывы первого рода.
При этом под сложением элементов линейного пространства и
умножением элемента на число понимаются обычные операдии
сложения функций и умножения функции на число. Нулевым
элементом в этом линейном пространстве является функция,
тождественно равная нулю на отрезке [а, 6], т.е. равенство / = 0
в этом линейном пространстве означает, что f(x) = 0 на [а, 6].
Отметим, что произведение любых двух функций / и g из
рассматриваемого линейного пространства является кусочно
непрерывной и, следовательно, интегрируемой на отрезке [а, 6]
функцией. Значит, в этом линейном пространстве определено
отображение, которое любым двум функциям / и g ставит в
соответствие действительное число (/, д):
(3.1)
Легко проверить, что данное отображение удовлетворяет
первым трем аксиомам скалярного умножения. Однако последняя

240 3. РЯДЫ ФУРЬЕ
аксиома (четвертая) не выполняется. Действительно,
ь
(/,/)= ff2(x)dx = 0
для любой функции /(ж), равной нулю на [а, 6] всюду, кроме
некоторого конечного числа точек. Такая функция кусочно
непрерывна на [а, 6], но не является нулевым элементом линейного
пространства, так как она не равна тождественно нулю на всем
отрезке [а, 6]. Чтобы обеспечить выполнение четвертой
аксиомы скалярного умножения для введенного отображения (/, #),
условимся рассматривать только те кусочно непрерывные на
отрезке [а, 6] функции /(ж), значения которых в каждой
внутренней точке их разрыва х\ равны полусумме правого и левого
пределов в этой точке:
а значения на концах отрезка [а, 6] одинаковы и равны
полусумме односторонних пределов функции в этих точках:
Докажем, что для суженного линейного пространства
кусочно непрерывных функций введенное отображение (/, д)
удовлетворяет четвертой аксиоме скалярного умножения.
ь
Пусть (/, /) = / /2(#) dx = 0 и точка xq Е (а, 6) — произволь-
а
ная точка непрерывности функции /, в которой /(я?о) Ф 0.
Тогда /2(я) ^ 0 на [а, 6], /2(я) непрерывна в точке хо и /2(яо) > 0.
Согласно свойствам определенного интеграла [VI], заключаем,
что
ь
f2(x)dx>0,
/■

3.1. Ортонормированные системы и ряды Фурье 241
что противоречит предположениям. Следовательно, в любой
точке х непрерывности функции / выполняется равенство
/(х) = 0.
Пусть теперь xq E (а, 6) — точка разрыва функции f(x).
Поскольку точек разрыва у функции конечное число, то для любой
точки разрыва хо найдется такая ее проколотая окрестность, в
которой функция f(x) будет непрерывна и, значит, равна нулю.
Поэтому
/(*0-0)= Ит /(х)=0, /(*о+О)= lim
х^х0 х-кго+О
поскольку f(x) = О в точках непрерывности. Отсюда, согласно
условию (3.2), имеем равенство /(xq) = 0. Аналогично для точек
а и 6 найдутся интервалы (а, ао) и (&о, 6), в которых функция
/ непрерывна. Следовательно, /(а+0) = 0 и /(6—0) = 0. В силу
условия (3.3) получаем /(а) = /(6) = 0. Таким образом, f(x) = 0,
х е [а, 6].
Итак, линейное пространство всех кусочно непрерывных на
отрезке [а, 6] функций, удовлетворяющих условиям (3.2), (3.3),
является евклидовым пространством со скалярным
произведением (3.1). Это евклидово пространство будем обозначать
через Eo[a,b].
В каждом евклидовом пространстве Е можно ввести
евклидову норму по формуле
В случае евклидова пространства Eo[a,b] норма элемента /
определяется следующим образом:
(3.4)
Два элемента f и g евклидова пространства называют
ортогональными, если (/, д) = 0.
Пусть в евклидовом пространстве Е задана некоторая
бесконечная последовательность элементов ^ъ ^2» •••? 'Фпч ••• Эту

242
3. РЯДЫ ФУРЬЕ
последовательность называют ортонормированной
системой, если для любых натуральных г и j, г ф j,
10,
ь j ~\l, <=i,
т.е. элементы этой последовательности попарно ортогональны
и все имеют единичную норму.
Пример ЗЛ. Ортонормированной системой в евклидовом
пространстве Ео[—тг,тг] является тригонометрическая
система:
1 cosz sinz
cos nz sin nz
>/5F '
(3.5)
Легко проверить, что все функции тригонометрической
системы попарно ортогональны и норма каждой из этих функций
равна единице.
Действительно, первая функция тригонометрической
системы ортогональна каждой из последующих, поскольку для
любого n Е N имеем
ТГ
1 cosnz . 1
— 7Г
7Г
л/2тг
1 sin nx
ах =
sin nx
iirn
= 0;
—7Г
7Г
-cosnz
inn
= 0.
cosnx cosmx
Попарно ортогональны и функции
■у /I y 7|
поскольку
тг тг
/cosnz cosmz I f / х \
—т= -=-dx = — I I cos(n+m)z + cos(n—mjzlaz =
у тг утг 2тг J \ /
, пфт,
sin(n + m)z
2тг(п + m)
sin(n — m)z
2тг(п — m)
= 0.

3.1. Ортонормированные системы и ряды Фурье 243
тт , sinnx sinmx
Далее, попарно ортогональны функции вида —т="~> —7=""»
фт, так как
7Г 7Г
/sinnx sinrax I /* / \
—т= т=~ «х = тг~ / ( cosfn — га)х — cosfn + m)x ) ax = 0.
— 7Г
Ортогональны также и функции вида —^=-, —-=-, n,m E N,
поскольку
cosnx sinmx ,
(это интеграл от нечетной функции по симметричному
относительно нуля интервалу).
Вычислим нормы функций тригонометрической системы
/ 1 Y
(3.5). Для первой функции имеем f (-=\ dx = 1. Для
_тг ^ л/27г/
остальных функций получаем
Л
7Г
1 /*„ ^ , . 1 / sin2nx>
— 7Г —7Г
7Г 7Г
Л
—7Г —7Г
где n G N — произвольное число. #
Рассмотрим произвольное бесконечномерное евклидово
пространство Е, в котором задана произвольная ортонормирован-
ная система {Vto}jbLi> и произвольный элемент /.
Определение 3.1. Назовем рядом Фурье элемента / G Е
по ортонормированной системе {'Фк^-х РЯД (формально
записанную бесконечную сумму) вида
f>V>b (3-6)
*=1

244 3. РЯДЫ ФУРЬЕ
fk — коэффициенты Фурье, определяемые равенством
кек (3.7)
оо
Чтобы подчеркнуть, что ряд ]Г) Дф^ является не просто
fc=i
произвольным рядом по ортонормированной системе
{V*fc}jfc?=i> a именно рядом Фурье элемента /, будем использовать
запись
Для ряда Фурье (3.6) элемента / определим n-ю частичную
сумму
(3.8)
k=\
Говорят, что ряд (3.6) сходится по норме к некоторому
элементу g Е Е, если \\Sn — g\\ -> 0 при п -> оо.
Рассмотрим всевозможные линейные комбинации
(3.9)
k=i
для ортонормированной системы ф\^ яр2^ Фп с
произвольными коэффициентами с* G IR, А; = 1, п. Выясним, при каких
коэффициентах с& эта линейная комбинация наиболее близка к
данной функции, т.е. норма разности имеет наименьшее
значение.
Теорема 3.1. Пусть {^*}£=1 — ортонормированная
система евклидова пространства Е и / G Е. Тогда
|||

3.1. Ортонормировалные системы и ряды Фурье 245
п
где Sn = ]Г) /fcV>fc — п'я частичная сумма ряда Фурье элемента
к=\
f по ортонормированной системе {^*}£=1-
4 Учитывая ортонормированность системы, равенство (3.7) и
свойства скалярного умножения, имеем
к=1 4=1
к=1 к=1 к=1 к=1
k=l k=l k=l
n
Отсюда следует, что минимальным значением
является значение k=l
2_
к=1 "к=1
которое достигается при с^ = Д, А; = 1, п. ►
Итак, из всех линейных комбинаций вида (3.9) п-я
частичная сумма ряда Фурье осуществляет наилучшее приближение
элемента / в смысле нормы, порождаемой скалярным
умножением евклидова пространства Е.
Следствие 3.1. Для любого элемента / G Е и любой
ортонормированной в Е системы {фк^-х верно неравенство
||
к=1 к=1
при всех n G N и ci, C2,..., Сп G R.

246 3. РЯДЫ ФУРЬЕ
Следствие 3.2. Для любого элемента / G Е и любой
ортонормированной в Е системы {^}^=1 при всех п G N верно
равенство
k=l к=1
Д, к G N, — коэффициенты Фурье элемента / по
ортонормированной системе {'фк}^^
Теорема 3.2. Для любого элемента / G Е и любой орто-
оо
нормированной в Е системы {^k}^\ ряд X) fk> составленный
к=1
из квадратов коэффициентов Фурье элемента /, сходится. При
этом справедливо следующее неравенство Бесселл:
(3.12)
к=1
п
<4 Из равенства (3.11) следует, что ||/||2— Yl fk ^ 0 Для всех
n G N. Следовательно, все частичные суммы знакоположи-
оо
тельного ряда ^ /^ ограничены одним и тем же числом ||/||2 и
*=1
оо п
/^ сходится (см. 1.4). Переходя в неравенстве ^ /^ ^
=i fc=i
2 к пределу при п ->- оо, получаем неравенство Бесселя. ►
В евклидовом пространстве J5o[—тг,тг] построим ряд Фурье
по тригонометрической системе (3.5) для некоторой функции
/ G Ео[—7г,тг]. Этот ряд, согласно (3.6), (3.7) и (3.1), имеет
следующий вид:
k=l
г 1 \^/~ coskx ?sinkx\ /о _ч
Л + Пл+Л) ("3)

3.1. Ортонормированные системы и ряды Фурье
247
где
— ТГ
ТГ
/
/
J
1 /
= -т= / f{x)coskxdx, keN;
/к J
1
-7=
V тг
— ТГ
ТГ
, A; G N.
Ряд (3.13) называют тригонометрическим рядом Фурье.
Неравенство Бесселя для любой функции f € Ео[—тг,тг]
принимает следующий вид:
тг
/■
Отметим, что наиболее употребительной является другая
форма записи тригонометрического ряда Фурье:
оо
(3.14)
k=i
где коэффициенты ao, a^ и 6* определяются формулами:
— ТГ
~ ТГ
; = —т= = — / f(x)coskxdx, к е
у ТГ ТГ J
—тг
^ тг
= —р: = — / /(z)sinfarete, A; G
\/тг тг у
—тг
(3.15)

248 3. РЯДЫ ФУРЬЕ
Неравенство Бесселя в этом случае принимает вид
(3.16)
Замечание 3.1. Из формулы (3.16) следует, что для любой
функции / из евклидова пространства Eq[—тг,тг]
коэффициенты ak и bk ее ряда Фурье по тригонометрической системе (3.5)
стремятся к нулю при А; —> оо (необходимый признак
сходимости ряда в неравенстве (3.16) слева).
Для любого натурального А; имеет место тождество
ak cos kx + bk sin kx =
sinfcx) = Akcos(kx — у?*),
где Ak = л/а| + 6^, a <pk, 0 ^ ipk < 2тг, — величина, однозначно
определяемая из уравнений
Следовательно, ряд (3.14) можно записать также в виде
функционального ряда
/(*)~f+i>
члены Akcos(kx — ifk) которого называют гармоническими
колебаниями (или гармониками). При этом Ak называют

3.1. Ортонормированные системы и ряды Фурье 249
амплитудой колебания, к — циклической (круговой)
частотой, aapk — начальной фазой колебания. Равенство
оо
f(x) = у + ^Akcos(kx - ipk),
k=l
если оно имеет место, называют разложением функции f(x)
в сумму гармонических колебаний (гармоник).
Для произвольного бесконечномерного евклидова
пространства Е введем понятия и сформулируем ряд теорем, с ними
связанных.
Определение 3.2. В бесконечномерном евклидовом
пространстве Е ортонормированную систему {фк}™=1
называют замкнутой, если для любого элемента / G Е и для
любого числа е > О существуют такой номер п G N и такие числа
С1,С2, ...,Сп GR, ЧТО
fc=l
Другими словами, замкнутость ортонормированной
системы {^}^=1 в евклидовом пространстве Е означает, что всякий
элемент из Е можно сколь угодно точно (по норме евклидова
пространства Е) приблизить конечными линейными
комбинациями из элементов системы {^}^=1-
Теорема 3.3. Если ортонормированная система {V*fc}jb=i
замкнута в Е, то для любого элемента / G Е верно равенство
Парсеваля:
Ел2 = и/и2 (зл?)
к=1
^ Пусть / G Е и е — произвольное положительное число.
Поскольку {^}^=1 — замкнутая система, то найдутся n G N
n 2
и ci, с2,..., Си G R, такие, что || X) скФк - f\\ < e- Отсюда,

250 3. РЯДЫ ФУРЬЕ
п
учитывая неравенство (3.10), заключаем, что ||/||2 — ]Г) j\ < e,
или II/H < Х)/*+е- Тогда, используя неравенство Бесселя
к=1
(3.12), получаем
оо оо
к=1 к=1
Поскольку е > 0 произвольно, то, переходя в последнем нера-
оо
венстве к пределу при е —> +0, получаем Yj fk = ll/ll2- ^
к=1
Определение 3.3. В бесконечномерном евклидовом
пространстве Е ортонормированную систему {^}^1
называют полной, если единственным элементом в Е, ортогональным
всем элементам фк этой системы, является нулевой элемент.
Таким образом, свойство полноты ортонормированной
системы {V>fc}jfcLi означает, что верно утверждение
Теорема 3.4. Любая замкнутая ортонормированная
система {V^jfcLi бесконечномерного евклидова пространства Е
является полной.
М Пусть {^*}^1 — замкнутая ортонормированная система в
евклидовом пространстве Е и для элемента / G Е выполняются
равенства (/, ipk) = О, к G N. Тогда, согласно (3.7), все
коэффициенты Фурье элемента / равны нулю, т.е. Д = 0, к G N.
Поскольку система {^fc}^! замкнута, то выполняется равен-
оо
ство Парсеваля (3.17) и ||/||2 = 5^/^ = 0. Отсюда вытекает,
к=1
что / = 0 и, следовательно, система {^k}^=i является полной. ►
Теорема 3.5. Если ортонормированная система {ф^^х в
евклидовом пространстве Е полна (а тем более замкнута), то

3.1. Ортопормировавные системы и ряды Фурье 251
любые элементы / и j в £, имеющие одинаковые ряды Фурье
по этой системе, совпадают: / = д.
<4 Допустим, что элементы /ид имеют один и тот же ряд
Фурье по полной ортонормированной системе {V*A;}jfcLi:
и 9
к=\ к=\
где ск = (/, фк) = {9, Фк),ке N. Тогда
т.е. элемент / — д ортогонален всем элементам ф^ к G N. Так
как {фк)^-\ — полная ортонормированная система, то / — д = О
и/ = 0. ►
Вернемся к евклидову пространству Ео[—тг,тг] и выясним,
является ли тригонометрическая система (3.5) замкнутой.
Отметим, что выражение вида
Т(х) = oto + } (otkcoskx + PkSinkx), \otn\+\/3n\ > 0»
k=i
обычно называют тригонометрическим полиномом, а
параметр п в этом выражении — порядком
тригонометрического полинома. Говорят, что действительную функцию
f{x), определенную на отрезке [а, 6], можно равномерно
приблизить тригонометрическими полиномами на указанном отрезке,
если для любого числа е > 0 найдется такой
тригонометрический полином Т(х), что
\f(x)-T(x)\<e, хе[а,Ь].
Легко видеть, что данное определение равномерного
приближения функции / тригонометрическими полиномами
эквивалентно существованию последовательности тригонометрических

252
3. РЯДЫ ФУРЬЕ
полиномов {Тт(х)}^=1, равномерно сходящейся на [а, Ь] к
функции /:
Tm(x)=*f(x).
[а,Ь]
Теперь сформулируем теорему, с помощью которой
доказывается замкнутость тригонометрической системы.
Теорема 3.6 (теорема Вейерштрасса). Если функция
f(x) непрерывна на отрезке [—тг, тг] и удовлетворяет условию
/(тг) = /(—тг), то эту функцию можно равномерно на отрезке
[—7г, тг] приблизить тригонометрическими полиномами.
Теорема 3.7. Тригонометрическая система (3.5) замкнута,
т.е. для любой функции / Е £?о[—тг,тг] и для любого числа е > О
существует такой тригонометрический полином Т(х), что
\
J\f(x)-T(x)\
dx<e.
<4 Теорема 3.7 в общем случае доказана в 7.6. Здесь приведем
доказательство в случае непрерывной функции /. Поскольку
/ Е Eq[—7г,тг], то /(—тг) = /(тг). Согласно теореме 3.6, для
произвольного числа е > 0 найдется тригонометрический полином
Г(х), такой, что
^ хЕ[-7г,тг].
Используя свойства определенного интеграла [VI], получаем
\
J\f(x)-T(x)f
dx<
\
Ле \2 Г7*
—= dx = \ — 2тг = е.
у/7ж1 V 2тг

3.2. Комплексная форма записи ряда Фурье 253
Из теорем 3.7 и 3.4 следует, что тригонометрическая
система полна в Ео[—7г,тг], и в силу теоремы 3.3 имеет место
равенство Парсеваля:
(3.18)
где ао, ak, bk — коэффициенты тригонометрического ряда
Фурье функции / е ЕЬ[—7г,7г] (см. формулы (3.14) и (3.15)).
Если две функции / и g из евклидова пространства Ео[—тг,7г]
имеют одинаковые тригонометрические ряды Фурье, то,
согласно теореме 3.5, эти функции как элементы евклидова
пространства Ео[—7Г,тг] равны, т.е. для любого х Е [—тг, тг]
выполняется равенство f(x) = g{x).
Заметим в заключение, что поскольку определенный
интеграл не зависит от значений функции в конечном числе точек,
то равенство Парсеваля (3.18) верно не только для функций из
евклидова пространства Ео[—п,п], но и для произвольных
кусочно непрерывных на отрезке [—тг, тг] функций (не обязательно
удовлетворяющих условиям (3.2) и (3.3)).
3.2. Комплексная форма записи
тригонометрического ряда Фурье
Общим тригонометрическим рядом называют
функциональный ряд вида
оо
— + ^(afccosfc£ + bfcsinfcr), (3.19)
k=i
где х Е R, а {afc}j£_o> {^}ь=1 — произвольные
последовательности комплексных (действительных) чисел.
Если функциональный ряд (3.19) сходится к какой-либо
функции S(x) на всей числовой оси, то предельная функция

254
3. РЯДЫ ФУРЬЕ
S(x) является периодической с периодом 2тг (возможно, с
меньшим периодом), поскольку такой период имеют все члены
ряда (3.19).
Согласно формулам Эйлера, для любого к Е N имеем
= ак
е%кх _|_ e-ikx
\-Ьк
= \{ак - ibk)eik* + l(ak+ ibk)e~ikx = cke
~ikx = ckeikx
где
^ ^ fcEN, (3.20)
a i — мнимая единица. Наоборот, если ск и с-к — произвольные
комплексные числа, то для любого к Е N
ckeikx+c-ke-ikx =
= ck(coskx + i sinfcx) + c-k(cos(—kx) + г sin(—kx)) =
= (ck + c-k) cos kx + i(ck- c-k) sinfcx = ak cos fcx + 6* sinfcx,
где
ak=ck + c-k, bk = i{ck-c-k). (3.21)
Докажем эквивалентность формул (3.20) и (3.21):
{ак = ск+с-к, ^_^ (ак = ск+с-к,
Ьк = г (cfc-c_fc); \ibk = -cfc+c_fc;
Если в дополнение к формулам (3.20) обозначить со = ао/2, то
наряду с формой (3.19) любой тригонометрический ряд

3.2. Комплексная форма записи ряда Фурье 255
может быть записан в комплексной форме:
оо
— + ^(afc cos kx + bk sin kx) =
oo
= О) + Yl{CkeikX + c-ke~ikx) = c0 + (cieix + c_ie~ix) +...
k=i
-..., (3.22)
где коэффициенты ak и bk общего тригонометрического ряда
связаны с коэффициентами ск и с-к тригонометрического ряда
в комплексной форме с помощью формул (3.20) и (3.21).
Поскольку
к=1
к=п
= lim ( со + У^(ckeikx + c-ke~ikx) ) = lim У^ ckeikx,
к=1 ' к=-п
тригонометрический ряд в комплексной форме (3.22) можно
записать в виде следующего функционального ряда, бесконечного
в обе стороны:
ОО т k—OQ
Jkx . Л . „-ikx\ __ V^ Л. Лкх
ckeikx + c-ke~ikx) = ^5 ckeikx, (3.23)
ifc=-oo
причем сумму ряда справа понимают только в смысле суммы
функционального ряда слева.
Ряд Фурье произвольной функции f(x) G Ео[—п,п],
являющийся тригонометрическим рядом, можно представить и в
комплексной форме. Коэффициенты этого ряда в комплексной
форме записи (3.23) можно вычислить непосредственно, минуя
нахождение ak и bk по формулам (3.15). Используя соотношения

256 3. РЯДЫ ФУРЬЕ
(3.20) и (3.15), для любого натурального к находим
7Г
Cfc =-(afc-ibfc) = — / f(x)(coskx-ismkx)dx =
—7Г
7Г 7Г
/"/()((*)i(te))d^ [ f()~ikx
;г //(ic)(coe(*a:)+t8in(te))dx=^- [ f(x)e~ikxdx;
2тг у 2тг у
—7Г
_ifc = -(afc+ibfc) = — / /(x
—7Г
7Г
JL
Кроме того, со = ao/2 = (1/(2тг)) / f(x)dx. Следовательно, для
—7Г
любого целого числа А; справедлива формула
, kEZ. (3.24)
Ряд (3.23) с коэффициентами (3.24) называют рядом
Фурье в комплексной форме функции f(x) и используют запись
+ ОО
/(х)~ У" ckeikx
к=-оо
3,3, Ряды Фурье по тригонометрической системе
Пусть f(x) — произвольная действительная функция,
интегрируемая на отрезке [—тг,тг]. Ряд Фурье (3.14) функции
f(x) по тригонометрической системе (3.5) с
коэффициентами, вычисляемыми по формулам (3.15), можно рассматривать

3.3. Ряды Фурье по тригонометрической системе 257
как функциональный ряд, заданный на отрезке [—тг, тг]. Изучим
ряды Фурье с точки зрения их поточечной сходимости.
Несмотря на то что ряд Фурье и строится по функции /(ж),
но априори нет оснований считать, что этот функциональный
ряд в какой-то точке х Е [—тг, тг] будет сходиться, и тем более,
что он будет сходиться к значению f{x). Однако в
математической физике и ряде других разделов математики важную
роль играет вопрос об условиях, при выполнении которых
тригонометрический ряд Фурье функции f(x) сходится в точке х
отрезка [—тг, тг] именно к значению f{x). Еще в конце прошлого
века было известно, что существуют непрерывные на отрезке
[—тг, тг] функции, удовлетворяющие условию /(—тг) = /(тг),
тригонометрические ряды Фурье которых расходятся в наперед
заданной точке отрезка [—тг, тг] (или даже расходятся на
бесконечном множестве точек отрезка [—тг, тг]).
Таким образом, даже непрерывность функции f(x) на
отрезке [—тг, тг] без дополнительных условий не обеспечивает
равномерную сходимость (часто используемое свойство
функциональных рядов) тригонометрического ряда Фурье этой
функции на указанном отрезке, более того, сходимость этого ряда
в наперед заданной точке данного отрезка.
Анализ поточечной сходимости рядов Фурье по
тригонометрической системе начнем со следующей теоремы.
Теорема 3.8. Пусть тригонометрический ряд
оо
— + V^ (an cos пх + Ьп sin пх) (3.25)
2 п=1
сходится равномерно на отрезке [—тг, тг] к некоторой функции
f{x). Тогда этот ряд является рядом Фурье функции f(x) по
тригонометрической системе (3.5).
< Из теоремы о непрерывности суммы равномерно
сходящегося функционального ряда с непрерывными слагаемыми (см.
теорему 2.10) следует, что функция f(x) непрерывна на [—тг, тг],

258 3. РЯДЫ ФУРЬЕ
кроме того, /(—тг) = /(яг). Значит, она принадлежит евклидову
пространству #о[-тг,тг] и может быть разложена в ряд Фурье
по тригонометрической системе (3.5). Найдем коэффициенты
Фурье этого разложения. Поскольку, согласно условию
теоремы,
оо
/(я) = у + ^T{ancosnx + bnsinnx), х G [-тг, тг],
п=1
то для всех k G N имеем равенства
/ (х) cos кх = — cos kx +
, (3.26)
n=l
f(x) sin fcx = — sin kx +
). (3.27)
n=l
Докажем, что ряды справа сходятся равномерно на
отрезке [-тг, тг]. Так как ряд (3.25) сходится на [-тг, тг] равномерно,
то, согласно критерию Коши равномерной сходимости
функционального ряда (см. теорему 2.7), для любого е > 0 найдется
такое N(e) G N, что для любых т > iV(e), p G N и х G [—тг, тг]
выполняется неравенство
(x)-Sm(x)\ =
т+р
fan cos пх + Ъп sinnz)
п=т+1
<£,
где 5т+р(х) и 5т(ж) — частичные суммы ряда (3.25).
Обозначим Sm(x) и Sm+p(x) частичные суммы с номерами т и т+р
ряда (3.26), а Sm(x) и Sm+P{x) — соответствующие частичные

3.3. Ряды Фурье по тригонометрической системе 259
суммы ряда (3.27). Поскольку для любых k Е N и х Е [—тг, тг]
верны оценки |cosfcx| ^1 и |sinfcx| ^ 1, для всех х Е [—тг, тг] имеем
тп+р
\Sm+p{x) — Sm(x)\= У^
n=m+l
m+p
coskx 2Z (ancosnx"*"^nsinnx)
и аналогично
\Sm+p(x) - Sm{x)\ < е, хе [-тг, тг].
Отсюда, согласно критерию Коши равномерной сходимости
функционального ряда, ряды, стоящие в правых частях
равенств (3.26) и (3.27), сходятся равномерно на отрезке [—тг, тг].
Следовательно, на отрезке [—тг, тг] их можно почленно
интегрировать (см. теорему 2.12). Проинтегрируем обе части равенств
(3.26) и (3.27) на отрезке [-тг, тг]:
тг тг
/ f(x) coskxdx = — / coskxdx +
—тг —тг
~ / } } X
+ 2JI an / cosna;cos&жda;+ 6n / sinna;cosfca;da; I,
ТГ ТГ
/ f(x) sinkxdx = — / sinkxdx +
^{ J и , ul ■ ■ и Л
2_j\ an / cosnxsinkxdx + bn / sinnxsinkxdx 1.
i \ j j /
—тг —тг
00 *

260 3. РЯДЫ ФУРЬЕ
Учитывая, что тригонометрическая система является орто-
нормированной, т.е. при всех fc, n Е NU {0}, кфп,
/I 7Г
/ cosnx coskxdx = 0, / sinnx coskxdx = 0,
-7Г -7Г
7Г
/ sinnx sinkxdx = 0,
— 7Г
а при всех A; G N
7Г 7Г
/" 2, j /" ■ 2, j
/ cos kxdx= I sm kxdx = ж,
J J
— 7Г —7Г
приходим к формулам
7Г 7Г
/ f(x) coskxdx = тга^, / f(x) sinkxdx = тгЬ^.
— 7Г —7Г
Аналогично, проинтегрировав на отрезке [—тг, тг] равномерно
7Г
сходящийся ряд (3.25), получим J f(x)dx = ttuq.
Таким образом, все коэффициенты а^ и Ь^
тригонометрического ряда (3.25) совпадают с соответствующими
коэффициентами Фурье разложения функции f(x) по тригонометрической
системе (3.5) (см. формулы (3.15)). Следовательно, согласно
теореме 3.5, ряд (3.25) является рядом Фурье функции f(x) по
тригонометрической системе (3.5). ►
В следующей теореме приведены достаточные условия
равномерной сходимости общих тригонометрических рядов.
Теорема 3.9 (теорема о равномерной сходимости
тригонометрического ряда). Если для последователь-

3.3. Ряды Фурье по тригонометрической системе 261
оо
ностей коэффициентов {ап}£10 и {Ьп}™=1 ряд £ (KI + \ьп\)
п=\
сходится, то тригонометрический ряд
оо
— + ^ (an cos nx + bn sin nx)
71=1
сходится абсолютно и равномерно на всей числовой прямой.
< Для любого действительного х выполняется неравенство
|ancosnx + bnsinnx| ^ |an||cosnx| + |bn||sinnx| ^ \ап\ + \bn\.
оо
Следовательно, ряд |ао|/2 + ^ (|ап| + |ЬП|) является мажори-
п=\
оо
рующим для рядов ао/2 + J^ (ancosnx + bnsinnx) и |ао|/2+
n=l
оо
+ ]П (|ancosnx| + |bnsinnx|). Согласно признаку Вейерштрасса
равномерной сходимости функционального ряда (см. теорему
2.6), эти ряды сходятся абсолютно и равномерно на Ш. ►
Используя результаты теоремы 3.8, непосредственно
получаем следствие теоремы 3.9.
Следствие 3.3. Если для некоторых последовательностей
оо
коэффициентов {ап}™=0 и {Ьп}™=1 ряд £(lan| + |bn|) сходит-
п=1
оо
ся, то тригонометрический ряд ao/2+ ^ (ancosnx-f bnsinnx)
71=1
является рядом Фурье своей суммы на отрезке [—тг, тг].
Замечание 3.2. Из условий теоремы 3.9 также следует,
что ряд
^ + Y,{Kcosnx\ + \bnsmnx\) (3.28)
71=1
сходится равномерно на всей числовой прямой.

262 3. РЯДЫ ФУРЬЕ
Выясним условия, которым должна удовлетворять функция
/(ж), чтобы ее ряд Фурье по тригонометрической системе
сходился к ней. Ниже приведено несколько достаточных признаков
сходимости тригонометрических рядов Фурье, содержащих
такие условия.
Прежде всего покажем, что любую частичную сумму
ряда Фурье всякой кусочно непрерывной (на самом деле любой
интегрируемой) на отрезке [—тг, тг] функции можно
представить в виде некоторого интегрального выражения. Для этого
введем следующую функцию, которую будем называть ядром
Дирихле:
Dn(x) = - +cosx + cos2x + ... + cosnx. (3.29)
Для всех х ф 2тг7П, т E Z, ядро Дирихле можно записать в виде
sin(n-f -)х
Вп(х)= : . хГ , (3.30)
2sin-
так как
п
X X д» д»
— Dn(x) = sin-
Л —1
Отметим, что
-)x-sin(fc--)xj =sin(n+-)z.
7Г
- f Dn(x)dx = l. (3.31)
тг J
— 7Г
7Г
Это следует из равенства / cos(nx)dx = 0, верного для всех
—7Г
п € N, и определения (3.29) ядра Дирихле.

3.3. Ряды Фурье по тригонометрической системе 263
Лемма 3.1. Для любой 27г-периодической и кусочно
непрерывной на отрезке [—я*, тг] функции f(x) частичную сумму
п
Sn{x) = тг + У [QkCoskx + bksinkx) (3.32)
ее тригонометрического ряда Фурье в форме (3.14) можно
представить следующим образом:
7Г
Sn(x) = ^ f(f{x+u) + f(x-u))Dn{u)du, xeR. (3.33)
А Подставляя в формулу (3.32) выражения для а* и 6* из
формул Фурье (3.15), находим
7Г
k=l
7Г 7Г
- / /(*) cos(kt)dt) cosfcxH- ( - / f(t) sin{kt)dt) sinkx
ttJ ) \nj )
—7Г — 7Г
= — / /(<)(- + У^ (cos fct cos А;ж + sin kt sin А;ж)) dt =
_^г Л —1

264 3. РЯДЫ ФУРЬЕ
(сделаем замену переменных: u = t — ж, t = x + u, dt = du,
пределы интегрирования можно не менять, так как подынтегральная
функция периодическая, а замена линейная)
-du =
2sini
0
= - / f(u + x) ) . V du+- / f(u + x) \ . V du =
к J 2sin- nj 2sin-
0 2 -7Г 2
(сделаем замену переменных во втором интеграле и = —у, у =
= —u, du = — dy, затем переобозначим переменное у вновь на и)
2sin|
Сформулируем еще одну вспомогательную теорему,
доказательство которой приведено в Д.3.1.
Теорема 3.10 (лемма Римана). Бели функция f(x)
кусочно непрерывна на отрезке [а, 6], то
lim [ f(x)cos(£x)dx= lim f f{x) sin{£x)dx = 0. # (3.34)
■-►oo у f-^ooy
6
f-юо
a a
Для формулировки основной теоремы введем следующие
понятия. Обобщенной левой производной функции f(x)
в точке хо называют значение предела
lim
если такой существует, и обозначают его fr_{xQ—0).
Аналогично обобщенной правой производной функции /(ж) в точке

3.3. Ряды Фурье по тригонометрической системе 265
называют значение предела
f{xQ+h)-f(xQ+O)
если такой существует, и обозначают его /+(хо+О). Напомним,
что /(хо-О) = lim f{xo-e) и /(хо+О) = lim f{xo+e). Если
функция /(х) дифференцируема в точке хо, то обе обобщенные
производные существуют и равны производной /'(хо), т.е.
Теорема 3.11. Пусть функция /(х) удовлетворяет
следующим условиям:
1) /(х) определена при всех х Е Ш и имеет период 2тг;
2) /(х) кусочно непрерывна на отрезке [—тг, тг];
3) в любой точке х Е Е существуют конечные обобщенные
правая и левая производные.
Тогда тригонометрический ряд Фурье функции /(х)
сходится в любой точке х Е Ш и имеет в этой точке сумму, равную
(/(х+0) + /(х-0))/2.
^ Составим для функции /(х), удовлетворяющей условиям
теоремы 3.11, тригонометрический ряд Фурье в форме (3.14):
оо
f(x) ~ "1Г + У^ (Qfe cos ^x + bfc sin fcx),
где ajt, bjt — коэффициенты Фурье функции /(х). В силу
леммы 3.1 частичную сумму ^(х) (3.32) ряда Фурье функции /(х)
можно представить в виде (3.33). Из условия 2 теоремы 3.11
следует, что в любой точке х Е R существуют односторонние
пределы /(х+0) и /(х—0) функции /(х). Используя
соотношение (3.31), запишем:
А*+0) + /(х-С
_ 1 Г/(х+0) + /(х-0) sin(n+l)u^
тгу 2 sin^

266 3. РЯДЫ ФУРЬЕ
Введя обозначение Rn{x) = Sn(x) - (f(x + 0) + f{x - 0))/2, из
равенств (3.33) и (3.35) будем иметь
Rn(x) =
о
sin(n + -)tt
/(s-O))J
2
f(x+u)-f(x+O) и \_._{_ , 1
о
1 ff
1 }(f(x-u)-f(x-0) и \ . / l\
- / :L-^ п )sin(n+-)udu =
тгУ V u 2sin^y V 2/
7Г
= - / 9i{u,x) sin[n + -judu+ - / д2{щ
Согласно условию теоремы, функция /(ж) является кусочно
непрерывной в любом конечном промежутке из R и в каждой
точке iGl существуют обобщенные левая и правая
производные функции/(х). Кроме того, lim u = 1. Следовательно,
обе введенные выше функции
/(х+ц)/(х+0) ц
31 (и,х) =
2sin|'
и
как функции переменного и при фиксированном переменном
#, удовлетворяют условиям теоремы 3.10 (являются кусочно

3.3. Ряды Фурье по тригонометрической системе 267
непрерывными). Поэтому с учетом леммы Римана имеем
7Г
= Ит - / (gi{u,x)+g2{u,x)) sm(n+-)udu =
n—►oo 7Г у \ / \ Z/
(Параметр £ здесь соответствует величине п + 1/2,
стремящейся к бесконечности при п -> оо.) ►
Таким образом, если для функции /(ж) выполняются
условия теоремы 3.11, то в каждой точке, где она непрерывна,
ее тригонометрический ряд Фурье сходится к значению
самой функции в этой точке (поскольку в этих точках f(x) =
= (/(х+0) + f(x—0))/2), а в каждой ее точке разрыва
тригонометрический ряд Фурье сходится к среднему арифметическому
значений пределов этой функции в точке слева и справа.
Если функцию f(x) выбрать из евклидова пространства Eq[—тг,7г]
(периодически продолжив с периодом 2тг на всю числовую
прямую), то при выполнении условий теоремы 3.11
тригонометрический ряд Фурье функции f(x) будет сходиться к этой
функции в каждой точке х Е R.
Отметим два очевидных следствия теоремы 3.11. Первое из
них относится к кусочно дифференцируемым на конечном
отрезке [а, Ь] функциям, т.е. к таким функциям, для которых
отрезок [а, Ь] можно разбить на конечное число частичных
промежутков, внутри которых функция дифференцируема, на
концах имеет предельные значения и обобщенные левую и
правую производные соответственно.
Следствие 3.4. Если функция / определена на R, имеет
период 2тг, кусочно дифференцируема на отрезке [—тг, тг], то ее
ряд Фурье сходится в каждой точке х Е Е и его сумма равна
(

268 3. РЯДЫ ФУРЬЕ
Следствие 3.5. Если 2тг-периодическая функция всюду
дифференцируема на R, то ее тригонометрический ряд Фурье
всюду на R сходится к функции /(х).
Замечание 3.3. Если функция / удовлетворяет условиям
1 и 2 теоремы 3.11 и в некоторой точке х Е [—тг, тг]
существуют конечные обобщенные левая и правая производные (не
обязательно в любой точке х Е IR, как в условии 3), то
тригонометрический ряд Фурье сходится в этой точке и имеет
сумму (/(х+0) + /(х—0))/2. Это ясно из доказательства
теоремы 3.11, в которой свойства функции /(х), обозначенные в
условии 3, использованы только применительно к конкретной
точке х, в которой исследуется сходимость ряда Фурье. На
самом деле имеет место так называемый принцип локализации
Римана: сходимость или расходимость в точке х G R
тригонометрического ряда Фурье функции /(х) зависит только от
поведения этой функции в любой малой окрестности этой
точки х. Действительно, поскольку частичная сумма ряда Фурье
функции /(х) имеет вид (3.33), то
5(х)= lim Sn(x) = lim - [(f(x+u) + f(x-u))-
n—►oo тг—►oo ТГ J V /
1 ?/ xsinfn + ijti
= lim - / (f(x+u) + f{x-u)) I . l> du +
n^oonj \ / 2sin-
0 2
1 /7 vsinfn + iju
lim - / (/(д?+ц) + /(д?-ц)) V . и du =
j Vy 4 2sin|
1 \f xSinfn+Mu
= lim - / (f(x+u) + f(x-u)) ) . I1 da.
n^oonj \ J 2sin-
0 2
Здесь S — произвольное положительное число, а предел в
предпоследней строке равен нулю на основании теоремы 3.10,
так как подынтегральная функция кусочно непрерывна на
отрезке [5, тг] в силу кусочной непрерывности функции /(х).

3.3. Ряды Фурье по тригонометрической системе 269
Кроме того, последний предел зависит только от значения
функции /(х) в J-окрестности точки х, а 8 произвольное
положительное число. #
Сформулируем еще один достаточный признак сходимости
тригонометрических рядов Фурье (подробнее см. Д.3.2).
Функцию /(х) называют кусочно монотонной на
отрезке [а, Ь], если существует конечное число точек а = хо < х\ < ...
< хп = Ь, таких, что в интервалах (xj_i, Xj), j = 1, п, функция
f(x) монотонна (не убывает или не возрастает).
Теорема 3.12 (признак Дирихле). Пусть функция /(х),
определенная на R, удовлетворяет условиям:
1) имеет период 2тг;
2) кусочно непрерывна на отрезке [—тг, тг];
3) кусочно монотонна на отрезке [—тг, тг].
Тогда тригонометрический ряд Фурье функции f(x)
сходится в любой точке х Е Ш и имеет в этой точке сумму, равную
(/(*+0) + /(*-0))/2. #
Признак Дирихле называют также теоремой Дирихле.
Условия 2 и 3 теоремы 3.12, накладываемые на функцию /(х),
часто называют условиями Дирихле и говорят, что функция
f(x) удовлетворяет условиям Дирихле. Условие 3 признака
Дирихле иногда заменяют требованием конечности числа
локальных экстремумов на отрезке [—тг, тг], что для кусочно
непрерывной функции эквивалентно условию 3. Действительно, если
функция f(x) кусочно непрерывна на отрезке [—тг, тг] и имеет
на этом отрезке конечное число точек локального
экстремума, то на отрезке [—тг, тг] можно указать конечное число точек
—тг = xq <х\ < < хп = тг, таких, что в интервалах (ху-ь xj)i
j = 1, п, функция /(х) ограничена, непрерывна и монотонна,
причем на отрезке [—тг, тг] функция /(х) имеет разрывы только
первого рода,что означает кусочную непрерывность и
кусочную монотонность функции /(х) на отрезке [—тг, тг]. С другой
стороны, очевидно, что если функция кусочно монотонна на
отрезке [—тг, тг], то она на этом отрезке имеет конечное число
точек локального экстремума.

270 3. РЯДЫ ФУРЬЕ
3.4. О порядке малости коэффициентов Фурье
Как показано в 3.1, для функций f(x) из евклидова
пространства Ео[—п,п] их коэффициенты Фурье ап и Ъп (см.
формулы (3.15)) по тригонометрической системе (3.5) стремятся
к нулю при п —У оо.
Оказывается, что скорость сходимости коэффициентов
Фурье к нулю (т.е. порядок их малости) зависит от степени
гладкости (дифференцируемое™) разлагаемой в
тригонометрический ряд Фурье функции.
Говорят, что функция f(x) имеет на отрезке [а, Ь]
кусочно непрерывную производную*, если существует конечное
число точек а = хо <х\ < <хп = Ь, таких, что в интервалах
(xj-i, Xj), j = 1, п, существует и непрерывна производная /;(х),
а в самих точках Xj существуют конечные односторонние
пределы lim ff(x) и lim ff(x). Будем говорить, что функция
f(x) имеет на отрезке [а, Ь] кусочно непрерывную производную
порядка п ^ 1, если функция /^"^(х) (функция f(x) при п = 1)
имеет на отрезке [а, Ь] кусочно непрерывную производную.
Теорема 3.13. Если функция f(x) непрерывна на отрезке
[—тг, тг], удовлетворяет условию /(—тг) = /(тг) и имеет на [—тг, тг]
кусочно непрерывную производную, то тригонометрический
ряд Фурье функции f(x) сходится равномерно на отрезке
[—тг, тг] к самой функции /(х). Более того, ряд, составленный
из модулей членов тригонометрического ряда Фурье функции
/(ж), также сходится равномерно на отрезке [—тг, тг].
М Пусть функция f(x) непрерывна на [—тг, тг], удовлетворяет
условию /(—тг) = /(тг), а ее рядом Фурье является ряд
оо
— + \^ {ak cos кх + bk sin kx). (3.36)
* Отметим, что условие существования кусочно непрерывной
производной сильнее, чем условие кусочной дифференцируемости: если выполняется
первое условие, то выполняется и второе. Однако кусочно
дифференцируемая функция может и не иметь кусочно непрерывной производной.

3.4. О порядке малости коэффициентов Фурье 271
Докажем, что сходится числовой ряд
Ы. (3.37)
Согласно условию теоремы, производная fr(x) существует
всюду на отрезке [—7г, 7г] за исключением конечного числа
точек —7г = хо < xi < < хп = 7г, причем в каждом интервале
(xj-i, Xj), j = 1, п, функция f'(x) непрерывна, а в точках Xj
существуют односторонние пределы этой функции. Доопределим
функцию /'(х) в точках xj произвольным образом (тогда
получим кусочно непрерывную на [—7г, 7г] функцию) ц рассмотрим ее
тригонометрический ряд Фурье ао/2+ ^ (a^
Используя формулы (3.15), коэффициенты Фурье а* и /3*
функции /'(х) при А; Е N можно вычислить следующим образом:
Xj
Л Г 1 Г
= — / ff(x) cos kxdx = — V^ / f'(x) cos kxdx =
-7Г •?-1Х>_1
1 n Xf 1 n \XJ
= —У*4 / cosfcxd/(x) = -Y^/(x)cosA;xГ +
ju я ^ А; Г
+ —У / /(x)sinfcxdx = — //(x)sinfcxdx =
7rf-f у тгу
If 1 v--< f
= — f(x)sinkxdx =— ) / /'(x)sinfcxdx =
7Г У 7T£-J У
—тг ' 3:j-i
ln 7 in
= —^ / sinfcxd/(x) = — 2^/(x)sinfcx —
fcA 7 fc }
} I f(x)coskxdx = / f (x) cos kxdx = —
7rf-f У тгУ

272 3. РЯДЫ ФУРЬЕ
(здесь использованы правило интегрирования по частям и
условие /(—7г) = /(я")). Следовательно, при всех А; Е N
и доказательство сходимости ряда (3.37) сводится к доказа-
оо
тельству сходимости ряда ]П (|а*|/А; + |/
*=1
Используя неравенство
получаем
с» оо оо
2 L
Поскольку ряды Y1 1/^2> 1С aL 1С /^1 сходятся (последние два
*=1 А:=1 А:=1
в силу равенства Парсеваля (3.18) для /'(х)), то и ряд (3.37)
также сходится:
Итак, ряд (3.37) сходится. Следовательно, согласно теореме
3.9, тригонометрический ряд Фурье (3.36) и ряд
I I

3.4. О порядке малости коэффициентов Фурье 273
сходятся равномерно на R и, кроме того, ряд (3.36) является
тригонометрическим рядом Фурье своей суммы (см.
теорему 3.8). Обозначим сумму ряда (3.36) через 5(х). Функция
S(x) непрерывна на [—7г, тг] как сумма равномерно сходящегося
функционального ряда с непрерывными слагаемыми (см.
теорему 2.10). Кроме того, S(x) является периодической функцией
с периодом 27Г, поскольку таковыми являются все члены
тригонометрического ряда Фурье (3.36), и, значит, S(—тг) = £(тг).
Отсюда следует, что функция S(x) принадлежит евклидову
пространству Eq[—7г,7г]. Непрерывная функция f(x) с
условием /(—тг) = /(тг) также принадлежит евклидову пространству
1?о[—я",я"]. Так как тригонометрические ряды Фурье функций
f(x) и S(x) совпадают, то в силу полноты
тригонометрической системы в евклидовом пространстве Ео[—тг,7г] из теоремы
3.5 следует, что и сами функции f(x) и S(x) совпадают, и,
значит, тригонометрический ряд Фурье (3.36) функции f(x)
сходится на [—7Г, тг] к самой функции f(x). ►
Замечание 3.4. В ходе доказательства теоремы 3.13 для
функции f(x) и ее производной ff(x) были получены формулы
A: EN, (3.38)
где аь и Ьк — коэффициенты Фурье функции /(х), а а*
и /3k — коэффициенты Фурье функции ff(x) (функция f(x)
удовлетворяет условиям теоремы 3.13).
Теорема 3.14. Пусть функция f(x) имеет на отрезке
[—тг, тг] непрерывные производные до порядка т включительно
и кусочно непрерывную производную порядка т + 1, причем
выполняются условия:
/(-*) = /(*). /'(-*) = /'("), /(т)(-7г) = /(т>(7г). (3.39)
Тогда сходится ряд

274 3. РЯДЫ ФУРЬЕ
где a,k и bk — коэффициенты тригонометрического ряда Фурье
функции /(х).
М Доопределим функцию /(ш+1)(х) в точках разрыва
произвольным образом. Тогда /(т+1)(х) будет кусочно непрерывной
на отрезке [—тг, тг], а все функции /^(х), А; = 1, т, будут
непрерывны на [—7г, 7г]. Для каждой из этих функций выполняются
условия теоремы 3.13. Следовательно, можно использовать
формулы (3.38). Обозначим через ajj, , /?£ , 5 = 1,га+1,
коэффициенты тригонометрического ряда Фурье функций f(s\x).
Тогда в соответствии с формулами (3.38) получим
(m+l) __ , Am) __ .2>-l) __
КР ~К а " • •
(m+i^m+i m нечетное;
а£ ' = крь ' = — к ак
-с
Аналогично
m нечетное;
k(_l)(m+2)/2fcm+lafcj m четное.
Следовательно, |4т+1)| + |^го+1)| = кт+1 (\ак\ + \Ьк\) и
laim+1)| 1/з1т+1)|
кт(\ак\ + \Ьк\) = ' * + |К* '.
/С /С
Как и в доказательстве теоремы 3.13, устанавливаем, что
ряд £ (|^Ш 1/^ + 1/5^ \/к) сходится. Следовательно, схо-
*=1 с»
дится и ряд Y1 А;т(|а*| + \bk\)- ►
Используя равенство |aj.m+1)| + |^ш+1)| = кт+1(\ак\ + |6fc|) и
свойство стремления к нулю коэффициентов Фурье a^.m и
(Згк } при А; -> оо, получаем следующее утверждение о порядке
малости коэффициентов Фурье.

3.5. Дифференцирование и интегрирование рядов Фурье 275
Следствие 3.6. Если функция f(x) удовлетворяет
условиям теоремы 3.14, то ее коэффициенты Фурье по
тригонометрической системе (3.5) удовлетворяют соотношениям:
■ оо.
3.5. Дифференцирование и интегрирование
тригонометрических рядов Фурье
С условиями гладкости (дифференцируемости) разлагаемой
в тригонометрический ряд Фурье функции (и, значит, с
условиями малости ее коэффициентов Фурье) непосредственно
связана такая важная задача, как почленное дифференцирование
тригонометрического ряда Фурье.
Теорема 3.15. Пусть функция f(x) удовлетворяет
условиям теоремы 3.14. Тогда тригонометрический ряд Фурье
функции f(x) можно га раз почленно дифференцировать на
отрезке [—7Г, тг], т.е. для любых х Е [—тг, 7г]
/(*) (х) = J2 (а* cos(5) kx + bk sin(s) kx), s = 07^,
k=l
где а£ и Ь^ — коэффициенты Фурье функции f(x).
< Для каждого s = 0, т рассмотрим ряды:
5) кх + Ьк sin(5) кх) =
к=\
= J2 к3 (ак cos (fcx + у) + bib sin(fcx + у) J.
Здесь использованы тригонометрические формулы
sin(">(:r) = sin(x + у), cos^(x) = cos(x + у), п е N.

276 3. РЯДЫ ФУРЬЕ
Все эти ряды на всем отрезке [—7г, тг] мажорируются
сходящимся рядом (3.40) (см. теорему 3.14). Поэтому, согласно признаку
Вейерштрасса равномерной сходимости функционального
ряда (см. теорему 2.6), каждый из этих рядов (при всех s = 0, га)
сходится равномерно на отрезке [—7г, тг]. Это означает, что все
эти ряды (и их суммы) удовлетворяют условиям теоремы 2.13
о почленном дифференцировании функционального ряда.
Применяя эту теорему поочередно ко всем рядам (для 5 = 0, га—1),
получаем, что исходный тригонометрический ряд Фурье
функции f(x) можно га раз почленно дифференцировать, причем
каждый раз сумма полученного ряда будет совпадать с
производной функции f(x) соответствующего порядка (в силу
теоремы 3.11 сумма исходного тригонометрического ряда Фурье
функции f(x) на [—тг, тг] равна самой функции f(x)). ►
Изучим возможность почленного интегрирования
тригонометрических рядов Фурье кусочно непрерывных функций. Мы
допускаем, что тригонометрический ряд Фурье функции f(x)
может расходиться в некоторых точках отрезка [—тг, тг], а в
точках сходимости его сумма может отличаться от f(x).
Теорема 3.16. Для любой кусочно непрерывной на отрезке
[—тг, тг] функции f(x) ее тригонометрический ряд Фурье
с»
f(x) ~ "7Г + У^ ian cos пх + Ьп sinnx)
п=1
можно почленно интегрировать на любом промежутке [а, Ь] из
этого отрезка:
f(x)dx = — x +22(-bn—— + an—— ) [а,Ь]с[-тг,тг].
1 a n=l la
n=l
Рассмотрим функцию
x
F(x)=Jf(t)dt, Х6[-7Г,7Г],

3.5. Дифференцирование и интегрирование рядов Фурье 277
которая является непрерывной на отрезке [—7г, 7г] и
дифференцируемой в каждой точке непрерывности функции f(x) [VI].
Производная функции F(x) за исключением, быть может,
конечного числа точек существует и совпадает с кусочно
непрерывной функцией f(x). Кусочно непрерывную производную
будет иметь и непрерывная на отрезке [—тг, 7г] функция
Функция Ф(х) удовлетворяет условию Ф(7г) = Ф(—7г), поскольку
Ф(тг) - Ф(-тг) = F(tt) - F(-tt) - тга0 =
7Г — 7Г 7Г
= If(t)dt- ff(t)dt-7rao= ff(t)dt-naQ = 0.
0 0 -тг
Таким образом, функция Ф(х) удовлетворяет условиям
теоремы 3.13. На основании этой теоремы тригонометрический
ряд Фурье функции Ф(х) сходится к Ф(х) равномерно на
отрезке [—7Г, 7Г]:
А °°
F(x) - -£х = Ф(х) = —- + y2(Ancosnx + Bnsmnx), хЕ[-тг,тг].
2 2 ^-^
71=1
Кроме того, для коэффициентов Фурье Ап и Вп функции Ф(х)
и коэффициентов Фурье ап и Ьп функции f(x) имеют место
соотношения (см. замечание 3.4):
п = А вп = ^, пек
п п
Следовательно,
»=1 " "

/
cosnx sinnz
1 п
о n=l
И, наконец, получаем равенство
ь
/■
' , cosnx sinnx> '
правая часть которого является, как нетрудно видеть,
результатом почленного интегрирования тригонометрического ряда
Фурье функции /(х). ►
3.6. Разложение функций в тригонометрические
ряды Фурье на отрезке [—тг, тг]
В 3.3 описаны условия, при которых функцию,
определенную на всей числовой прямой М, можно разложить в сходящийся
тригонометрический ряд Фурье. Рассмотрим функцию /(х),
определенную и интегрируемую только на отрезке [—7г, 7г], и
поставим задачу ее разложения в тригонометрический ряд
Фурье. Естественно, что функция f(x) должна удовлетворять на
этом отрезке некоторым дополнительным условиям. Каким?
Ответ на этот вопрос дают следующие две теоремы, первая из
которых является следствием теоремы 3.11, а вторая —
следствием теоремы 3.12.
Теорема 3.17. Пусть функция f(x) определена на отрезке
[—тг, 7г] и удовлетворяет условиям:
1) f(x) кусочно непрерывна на отрезке [—тг, тг];
2) в любой точке х Е (—тг, тг) существуют конечные
обобщенные правая и левая производные, в точке х = — тг существует
конечная обобщенная правая производная, а в точке х = тг —
конечная обобщенная левая производная.

3.6. Разложение функции в ряды Фурье на отрезке [—тг, тг] 279
Тогда тригонометрический ряд Фурье функции f(x)
сходится в любой точке х Е [—7г, тг] и для него справедливо
равенство
= S(x) =
n=l
xE (-тг, тг);
X = ±7Г.
2
В частности, если х Е (—тг, тг) — точка непрерывности функции
/(я), то 5(х) = /(х).
«* Изменим, если необходимо, значения функции /(х) на
концах отрезка [—тг, тг] так, чтобы они совпали, т.е. вместо /(х)
рассмотрим функцию
~ _ Г/0&), хЕ(-тг,тг);
1 С, х = ±тг,
где С — произвольная числовая константа. Функцию /(х)
можно периодически продолжить на всю числовую прямую Е.
Изменение функции /(х) в двух точках отрезка [—тг, тг] не
влияет на значения интегралов (3.15), через которые выражаются
ее коэффициенты Фурье. Следовательно, тригонометрические
ряды Фурье функций /(х) и /(х) совпадают. Функция /(х)
удовлетворяет всем условиям теоремы 3.11. Поэтому ее
тригонометрический ряд Фурье сходится всюду на Е (в том числе и
на отрезке [—тг, тг]), а сумма этого ряда во всех точках х Е Е
равна (/(х+0) + /(х—0))/2. Поскольку тригонометрические ряды
Фурье функций /(х) и /(х) совпадают, а на интервале (—тг, тг)
и сами функции /(х) и /(х) совпадают, то утверждение
теоремы для всех внутренних точек отрезка [—тг, тг] доказано. На
концах отрезка [—тг, тг] в силу периодичности функции /(х)
имеем /(тг+О) = /(-тг+О) = /(-тг+О), /(-тг-О) = /(тг-О) = /(тг-О),
откуда получаем утверждение теоремы и для точек х = —тг,

280 3. РЯДЫ ФУРЬЕ
Теорема 3.18 (признак Дирихле). Пусть функция f(x)
определена на отрезке [—тг, тг] и удовлетворяет условиям:
1) кусочно непрерывна на отрезке [—тг, тг];
2) кусочно монотонна на отрезке [—тг, тг].
Тогда тригонометрический ряд Фурье функции f(x)
сходится в любой точке х Е [—тг, тг] и для него справедливо
равенство
оо
— + \^ (an cos пх + Ьп sin nx) = S(x) =
2 n=i
/(-тг+О) + /(тг-О)
В частности, если х Е (—тг, тг) — точка непрерывности функции
/(я), то 5(х) = /(*).
< Доказательство теоремы аналогично доказательству
теоремы 3.17, но основано на том, что периодически продолженная
функция f(x) будет удовлетворять условиям теоремы 3.12. ►
Как и теоремы 3.11, 3.12, теоремы 3.17 и 3.18 не связаны
никаким отношением следствия (см. Д.3.2).
Пусть функция f(x) определена на отрезке [—тг, тг] и
удовлетворяет условиям теоремы 3.17 или 3.18. Сумма S(x) ее
тригонометрического ряда Фурье (3.14), в отличие от самой
функции /(х), определена уже не только на отрезке [—тг, тг],
но и на всем множестве действительных чисел R, причем
периодична с периодом 2тг. Согласно теоремам 3.17 и 3.18, в
тех точках интервала (—тг, тг), в которых функция f(x)
непрерывна, сумма S(x) совпадает со значением /(х), а в тех
точках интервала (—тг, тг), в которых функция f(x) разрывна,
сумма S(x) равна (/(х+0) + f(x—0))/2. И, наконец, на
концах отрезка 5(-тг) = 5(тг) = (/(-тг+О) + /(тг—0))/2. Для того
чтобы построить график функции S(x) во всей области
определения М, необходимо на отрезке [—тг, тг] построить график

3.6. Разложение функции в ряды Фурье на отрезке [—тг, тг] 281
функции /(ж), заменив значения функции f(x) в точках
разрыва х Е (—тг, тг), если они есть, соответствующими значениями
(f(x+O) + f(x—0))/2, а значения функции на концах отрезка
[-тг, тг] — значением (/(—тг+О) + /(тг—0))/2, и продолжить
полученный график периодически на всю числовую прямую с
периодом 2тг.
Заметим, что если функция f(x) определена на отрезке
[-тг, тг] и на некотором множестве вне этого отрезка (например,
на всем множестве Ш), но не является периодической с периодом
2тг, то вне отрезка [—тг, тг] она будет отличаться от суммы
своего тригонометрического ряда Фурье. Действительно, при
формировании тригонометрического ряда Фурье (3.14) значения
функции f(x) вне отрезка [—тг, тг] не используются и, значит,
не влияют на сумму 5(ж), которая вне отрезка [—тг, тг]
является простым периодическим продолжением своих значений на
отрезке [—тг, тг]. Таким образом, периодическая с периодом 2тг
функция 5(ж), являющаяся суммой тригонометрического ряда
Фурье функции /(ж), будет описывать функцию f(x) вне
отрезка [—тг, тг] тогда и только тогда, когда сама функция f(x)
является периодической с периодом 2тг.
Пример 3.2. Разложим функцию f(x) = ж, заданную на
отрезке [—тг, тг], в тригонометрический ряд Фурье.
Вычислим коэффициенты Фурье этой функции (см. (3.15)):
а0
1 [ а 1х2
= — xdx = — —
тг У тг 2
= 0,
—ТГ
ТГ
1 Г j l ( sinnxi* if \
an = — / xcosnxdx = — х / smnxdx I = 0,
тгу тг\п1-7гпУ /
-7Г -ТГ
, If. . 1 / cosnx * If , \
bn = — / xsmnxdx = — —x + — / cosnxax I =
ТГУ ТГ\ П -тг П J )
—тг —тг
= --cosmr = (-l)n+1-, n e N.
n n

282
3. РЯДЫ ФУРЬЕ
Отсюда следует, что тригонометрический ряд Фурье функции
f(x) = ж, заданной на отрезке [-тг, тг], имеет вид
00
n=l
1. .
n
/1 1 (-l)n+1
= 2(sinx— -sin2x+ -sin3x — ...H si
\ 2 3 n
sinnrc
Так как функция f(x) = x непрерывна и дифференцируема в
интервале (—тг, тг), а на концах отрезка [—тг, тг] имеет
соответственно левую и правую производные, то она удовлетворяет
условиям теоремы 3.17. Поскольку функция f(x) = x
непрерывна на (—тг, тг), то в силу теоремы 3.17 сумма S(x) ее
тригонометрического ряда Фурье в интервале (—тг, тг) совпадает с
f(x): S(x) = f(x) = ж, х G (—тг, тг). На концах же отрезка [—тг, тг]
имеем 5(-тг) = 5(тг) = (/(-тг+О) + /(тг-0))/2 = (-тг + тг)/2 = 0.
Наконец, учитывая 2тг-периодичность функции 5(ж), получаем
-л
S(x) =
О я х (Запись
-я
числа
д. | -ТГ
О,
]
обозначает целую часть
Рис. 3.1
, т.е. наибольшее целое, не пре-
восходящее это число.) Графики функций
f(x) и S(x) представлены на рис. 3.1 и 3.2.
•-Зя
\-л
\л
/ i
Рис. 3.2

3.6. Разложение функций в ряды Фурье на отрезке [—тг, тг] 283
-л -
S8(x) л
Л X -i
-л -
О л х
S20(x)
я х -л
я
-я
Я X -Л
-я
О я х
Рис. 3.3

284
3. РЯДЫ ФУРЬЕ
Заметим, что если продолжить функцию f(x) = xc отрезка
[—тг, тг] на всю числовую прямую по той же формуле f(x) = х,
то вне отрезка [—тг, тг] сумма S(x) уже не будет представлять
собой функцию f(x) (будет от нее существенно отличаться).
Для геометрической иллюстрации свойства сходимости по-
следовательности {Sn(x)}, Sn{x) = 2 £ l(-l)k+l/k) sinfcx, ча-
стичных сумм ряда Фурье функции f(x)=x на рис. 3.3
представлены графики частичных сумм у = Sn(x), x Е [—тг, тг], с
номерами п = 1, 2, 3, 8, 20 и 100. Рис. 3.3 наглядно
показывает, что во всех внутренних точках отрезка [—тг, тг] (точках
непрерывности функции f(x) = х) последовательность {Sn(x)}
сходится к функции f(x) = ж, а на концах отрезка такой
сходимости нет.
Пример 3.3. Разложим функцию
—1, — тг ^ х ^ — тг/3;
f{x) = { 0, -тг/3 < х < тг/2;
1, тг/2 ^ х ^ тг,
л
-я
л х
Рис. 3.4
заданную на отрезке [—тг, тг], в
тригонометрический ряд Фурье.
График функции f(x) приведен
на рис. 3.4. Функция f(x)
является кусочно постоянной и
удовлетворяет всем условиям
теоремы 3.17.
Вычисляя для данной
функции коэффициенты Фурье
3 2 тг
ао = - (-l)dx+- / 0 • dx + - / dx =
тг У тг У тг У
2 „ 1
-3+0+-
1
'6'
тг
3
тг
2

3.6. Разложение функции в ряды Фурье на отрезке [—тг, тг] 285
тг
3
ТГ
2
ап = — (—l)cosnxdx + — / 0-cosnxdx+ — cosnxdx =
тг
3
7Г
2
smnx
1 / sin7
ТГ \ 71
sinnx
тг
3
-тг П
7Г
2
(sms
1 f 1 ( 1 /*
= — / (—l)sinnxdx-\— / O-sinnxdx + — sinnxdx =
к J к J n J
7Г
3
7Г
2
Я" \ 1 / П7Г л/ ^чп П7Г\
fj = ^(cosT-2(-1) +cost)'
получаем, что тригонометрическим рядом Фурье функции f(x)
является следующий ряд:
1
П=1
+ (cos ^ + 2(-l)n+1 + cos ^) sinnx J.
J
J
График суммы ряда Фурье S(x) изображен на рис. 3.5.
1л
Ьл
О Е
2
-1
Рис. 3.5
я

286 3. РЯДЫ ФУРЬЕ
3.7. Сдвиг отрезка разложения
До сих пор мы изучали множество кусочно непрерывных
функций, определенных на отрезке [—тг, тг], евклидово
пространство Ео[—тг,тг] и ортонормированную систему в этом
евклидовом пространстве:
11 1 . 1 1 .
cosnx,
Рассмотрим теперь евклидово пространство Ео[а,Ь] функций,
определенных на сдвинутом отрезке [а, Ь], Ь — а = 2тг.
Приведенная выше система функций будет ортонормированной и в этом
евклидовом пространстве, так как интеграл от периодической
функции р(х) с периодом Т по отрезку длиной Т не изменяется,
когда отрезок интегрирования сдвигается вдоль числовой оси.
Другими словами, если <р(х) = <р(х + Т) для всех х G R, то для
любых 7, A G R
7+Т А+Т Т/2
/ tp(x)dx= I (p(x)dx= / ip(x)dx. (3.41)
7 Л -Г/2
Действительно, для любого 7 £ R
7+Т О Т 7+Т
/ (р(х) dx = (p(x) dx+ ip(x) dx+ I cp(x) dx =
7 7 О Г
0 T
<p(x-T)d{x-T)= [j
0 T
7 T
r /• /• /•
= — / v^v*^) ^ "t" / ¥?(*r) ^*£ "b / ¥4^0 du ^ / ip(x) dx.
J J J J
0 0 0 0
Положив в этом равенстве 7 = Л и 7 = —Т/2, получим равенство
(3.41).

3.7. Сдвиг отрезка разложения 287
Поскольку функции sinnrr и cosnrr периодические с
периодом Т = 2тг, то в силу соотношения (3.41) рассматриваемая
тригонометрическая система (3.5) будет ортонормированной
в любом евклидовом пространстве Ео[а,Ь], Ь — а = 2тг, или,
другими словами, будет ортонормированной системой функций на
любом отрезке [а, а + 2тг], являющемся сдвигом отрезка [—тг, тг].
Если функция f(x) определена на всей числовой прямой
Ш и является периодической с периодом 2тг, то соотношение
(3.41) позволяет вычислить коэффициенты Фурье ее ряда Фурье
по полной ортонормированной (тригонометрической) системе
(3.5) на отрезке [а, а + 2тг] с помощью значений функции f(x)
на отрезке [—тг, тг]:
оо
f(x) ~ — + ^(afccosfcx + 6fcsinfcx), x G [а, а + 2тг],
где
а+2тг 7Г
пк = — / f(x)coskxdx = — I f(x)coskxdx, k = 0,1, 2,...,
тг у тг J
а — тг
а+2тг тг
1 /* 1 /
Ьк = — / f(x)smkxdx=—f(x)sinkxdx, fc = l,2,...
тг У тг У
а — тг
Впрочем, иногда удобно, наоборот, определять
коэффициенты тригонометрического ряда Фурье (2тг)-периодической
функции f(x) с помощью ее значения на каком-либо отрезке
[а, а + 2тг]:
а+2тг
1 Г
ак = — / f(x)coskxdx, fc = 0,1,2,...
тг У
а
а+2тг
Ь/Ь = — / /(x)sinfcxrfx, fc = 1, 2,...
тг У
(3.42)

288 3. РЯДЫ ФУРЬЕ
Пример 3.4. Найдем разложение в ряд Фурье на отрезке
[—тг, тг] функции, определенной следующим образом:
\
0<Ж<ТГ.
Продолжим функцию /(ж) на всю числовую прямую до
периодической (с периодом 2тг) функции /(ж). Тогда разложения
функций /(ж) и /(ж) в тригонометрический ряд Фурье на
отрезке [—тг, тг] будут совпадать. В интервале (0, 2тг] функция /(ж)
совпадает с функцией ж. Поскольку аналитическое выражение
функции /(ж) на отрезке [0, 2тг] более простое (/(ж) = ж), чем
выражение этой функции на отрезке [—тг, тг] (/(ж) = /(ж)), то
для вычисления коэффициентов Фурье функции /(ж) (и,
значит, функции /(ж)) удобнее использовать значения функции на
отрезке [0, 2тг] и формулы (3.42). При этом значение функции
/(ж) в единственной точке разрыва ж = 0 на ее разложение в
ряд Фурье никак не влияет. В результате получаем:
-5FT. = 2*'
-7Г О
7Г
1 f ~ I f
ап = — f(x)cosnxdx = — / s
тг У тгу
гж 1 f
/ sinnxdx I = О,
0 П{ I
If— 1 f
= — / f(x)sinnxdx = — / :
я" У тгу
1 / sinni
= - ж
тг \ n
2тг
27Г 2*
9-п- 27Г \
совпж 2п 1 f \ 2
+• — / совпжаж = —.
nj п
о /

3.7. Сдвиг отрезка разложения
289
Таким образом, функция f(x) на отрезке [—тг, тг] имеет
следующий ряд Фурье:
f(x) ~ S(x) = тг - 2 (sinx + - sin 2x + ... + - sinnx + ...].
\ 2 п /
Наконец, так как функция f(x)
удовлетворяет условиям теоремы 3.15, то
7Г, X •— U,
а вне отрезка [—тг, тг] функция S(x)
продолжается периодически.
Графики функций /(ж), /(ж) и 5(ж)
представлены на рис. 3.6-3.8
соответственно.
У)
2л
• л
-л 0
У=/(х)
Л X
Рис. 3.6
А
"" V
-2л
У/
0
У=7(х)
А <
2л х
Рис. 3.7
' V
-2л
У-
2л
/ л*
0
y=S(x)
А * .•••
2л х
Рис. 3.8

290 3. РЯДЫ ФУРЬЕ
3.8. Разложение функций в тригонометрические
ряды Фурье на отрезке [-/, I]
Теорию тригонометрических рядов Фурье
2тг-периодических функций и функций, определенных на отрезке [—тг, тг], с
помощью линейного отображения (замены переменного)
У = тх (-l^x^l <*=> -тг ^ у ^ тг)
можно перенести на случай произвольных 2/-периодических
функций и функций, определенных на произвольном отрезке
[—/, /]. Действительно, при замене переменного х = yl/n
функция f(x) становится функцией <р(у) = /(у'/71")» т-е-
2тг-периодической, если f(x) была 2/-периодической, или определенной на
отрезке [—тг, тг], если f(x) была определена на отрезке [—f, /].
Рассмотрим тригонометрический ряд Фурье функции <р(у) =
= /Ы/тг) на отрезке [—тг, тг]:
оо
n=l
7Г
вп = - / <р(у) cosnydy, n = 0,1,2,
— 7Г
7Г
Ьп = - <р{у) sinnydy, n = 1, 2,
Выполняя обратную замену переменного у = ттх/l в
тригонометрическом ряде Фурье и заменяя функцию (р(тгх/1) функцией
/(ж), заключаем, что 2/-периодической функции f(x)
соответствует ряд Фурье вида
оо
+ ^) (3.43)
n=l

3.8. Разложение функции в ряды Фурье на отрезке [—1,1] 291
В формулах для коэффициентов Фурье ап и Ьп также можно
перейти от функции (р(у) к функции f(x):
= - /(—)
ТГ J \ ТГ /
1 Г птгп*
= -y/(z)cos — dx, n = 0,l,2, (3.44)
= - I f[ — )s
±J1^x, n=l,2,... (3.45)
-/
Этот же ряд можно получить иначе: рассмотреть евклидово
пространство Eq[—1,1] и полную ортпонормированную систему
функций
1 1 тгх 1 . тгх
fCOS——, —т= sin——,
л/2/
1 птга; 1 . птггг
C0S sn
(3<46)
в нем (с помощью замены у = пх/1 доказательство полноты
и ортонормированности этой системы в Eq[—IJ] сводится к
доказательству полноты и ортонормированности системы (3.5)
Поскольку между 2тг-периодическими функциями
(функциями, определенными на отрезке [—тг, тг]) и 2/-периодическими
функциями (функциями, определенными на отрезке [—/, /])
существует взаимно однозначное соответствие, задаваемое
строго монотонной, сколь угодно раз дифференцируемой линейной
заменой переменных у = тгх//, то все изложенные выше
факты теории тригонометрических рядов Фурье вида (3.14) можно

292 3. РЯДЫ ФУРЬЕ
перенести на тригонометрические ряды Фурье вида (3.43). В
частности, для тригонометрических рядов Фурье вида (3.43)
2/-периодических функций и функций, определенных на
отрезке [—/,/], верны соответствующие аналоги всех теорем и
утверждений из 3.3-3.7 относительно тригонометрических
рядов Фурье вида (3.14) 2тг-периодических функций и функций,
определенных на отрезке [—тг, тг]. Эти аналоги теорем и
утверждений получаются простой заменой условия 2тг-периодично-
сти условием 2/-периодичности, отрезка [—тг, тг] — отрезком
[—^ ']> условий функции в точках —тг и тг — условиями функции
в точках — I и I, и, наконец, заменой тригонометрического ряда
Фурье (3.14) тригонометрическим рядом Фурье (3.43).
В частности, если таким образом изменить содержание 3.7,
то получим теорию тригонометрических рядов Фурье на
произвольном отрезке [а, Ь]. В самом деле, произвольный
отрезок [а, Ь] можно рассматривать как сдвиг отрезка [—/,/], где
/ = (Ь — а)/2. А поскольку функции sm(nirx/l) и cos(rnrx/l)
являются 2/-периодическими, то в силу соотношения (3.41)
тригонометрическая система (3.46) является ортонормированной
системой не только на отрезке [—/,/], но и на любом
сдвинутом отрезке [а, а + 21]. Следовательно, для функции f(x) можно
построить тригонометрический ряд Фурье вида (3.43) на
произвольном отрезке [а, Ь] = [а, а + 21], где / = (Ь — а)/2. Кроме
того, если функция f(x) определена на всей числовой прямой
R и является 2/-периодической, то в силу того же соотношения
(3.41) ее коэффициенты Фурье по тригонометрической
системе (3.46) на сдвинутом отрезке [а, а + 21] можно определить с
помощью значений функции f(x) на отрезке [—/, /]:
1 /* La
= j I f{x)cos-^-dx, fc = 0,1,2,...;
~\ (3-47)
Л
У/(ф^Жг, к = 1,2,3,...
-i

3.8. Разложение функции в ряды Фурье на отрезке [-/, I] 293
Если функция f(x) определена только на отрезке [а, Ь] =
= [а, а + 2/], I = (Ь- а)/2, то коэффициенты ее ряда Фурье
(3.43) по тригонометрической системе (3.46) можно получить
с помощью интегралов на этом отрезке, а также на отрезке
[—/,/], предварительно продолжив эту функцию периодически
с периодом 2/ на всю числовую прямую R. Для такого
продолжения требуется, чтобы выполнялось условие /(a) = f(b). Если
функция f(x) не удовлетворяет этому условию, то ее следует
переопределить в точках а и b = a + 2/, положив f(a) = f(b) = С,
где С — произвольная константа. Интегралы в (3.47) при
таком переопределении не изменяются, значит, не изменяется и
ряд Фурье (3.43) функции /(х).
Итак, если 2/-периодическая функция f(x) удовлетворяет
условиям аналогов теорем 3.11 или 3.12, то ее
тригонометрический ряд Фурье (3.43) будет сходиться в каждой точке х Е Ш к
значению (/(х+0) +/(х—0))/2. Если же функция f(x)
определена только на отрезке [а, Ь] = [а, а + 2/] и удовлетворяет
на нем условиям аналогов теорем 3.17 или 3.18, то ее ряд
Фурье (3.43) будет сходиться в каждой точке х £ [а, Ь],
причем во всех внутренних точках этого отрезка — к значению
(/(х+0) + f{x—0))/2, а на его концах х = а и х = Ь — к
значению (/(—а+0) + /(6—0))/2. Сумма S(x) тригонометрического
ряда Фурье (3.43) функции, определенной только на отрезке
[a,b] = [a, a + 2J], так же как и сумма ряда Фурье 2/-периодиче-
ской функции, определенной на R, определена на всей числовой
прямой Ш и является 2/-периодической. Ее график на Ш
является периодическим продолжением графика S(x) на отрезке
В заключение отметим, что комплексная форма
тригонометрического ряда Фурье (3.43) в данном случае имеет вид
k^±?° ik1x 1 f _.knx
f(x)~ 2-*, Cke% l ' Ck = 2/ / f^e г l dx'
k=-oo i

294
3. РЯДЫ ФУРЬЕ
Пример 3.5. Найдем разложение в ряд Фурье функции
/(х), заданной на отрезке [—2, 2], где
/(*) =
-2 -1 О
1
Рис. 3.9
График функции f(x) изображен на
рис. 3.9. Функция f(x) является
кусочно непрерывной на отрезке [—2, 2],
дифференцируемой в каждой точке
интервала (—2,2), за исключением
точек —1 и 1, в которых, однако,
существуют обобщенные левые и
правые производные. Кроме того, в
точке х = —2 существует правая
производная, а в х = 2 — левая
производная.
Таким образом, функция f(x) на отрезке [—2, 2]
удовлетворяет условиям аналога теоремы 3.17, следовательно, ее ряд
Фурье (3.43) в любой точке х Е (—2, 2), х ф — 1 (это точки
непрерывности функции f(x)) будет сходиться к значению функции
/(х), во внутренней точке разрыва х = — 1 будет сходиться к
значению (/(-1+0) + /(-1-0))/2 = (0 + 1)/2 = 1/2, а на
концах х = -2 и z = 2 — к значению (/(-2+0) + /(2-0))/2 =
= (0 + 4)/2 = 2.
По формулам (3.44) вычисляем коэффициенты Фурье а^ в
разложении функции f{x). Первый коэффициент вычисляется
достаточно просто:
-2
-1
13

3.8. Разложение функции в ряды Фурье на отрезке [-1,1] 295
Для вычисления остальных коэффициентов а& нужно дважды
применить интегрирование по частям:
1
-2
1 2
птгх , 1 Г птгх .
\ — dx = -J COS —dx +
-1
У*
о ПТГХ
cos —г— ах =
1 . П7ГХ
= — sin - Л
ПТГ 2
-1
ar . птгх
+ —sin—-
птг 2
2 2 /• .
I X S1
I птг У
. птгх ,
xsin—— ах =
2 . П7Г 1 . П7Г 4X П7ГХ
= —sin— sin-— + -5-5 cos-—•
П7Г 2 П7Г 2 П27Г2 2
птгх .
cos —— ах =
Z
1
1 . птг 8 4 птг 8 птгх
= Sin —- Н 7T—z COS ПТГ тг-Ъ COS — «~~q sin "1Г~
птг 2 nznz nznz 2 п6тг6 2
l
1 . П7Г 8 , 4TI 4 П7Г 8 . П7Г
= —sin—- + -9-9 (-1) r~2 COS"TT + -3-3 sm"TT-
П7Г 2 П^ТГ2 П27Г2 2 nd7TJ 2
Аналогично с помощью формул (3.45) вычисляем и
коэффициенты Фурье Ьп:
'п = 2У ^(x)sin"2~dx=2 / Sm"7" 2 / 2
. птгх ,
sin —- ах =
-2
1 птгх
= cos-—-
птг 2
-1
-1
х' птгх
cos -—-
птг 2
1
2
ПТГХ .
х cos —— dx =
—4 1 птг 4х птгх
= —совптгН cos —+ о oxsin—--
птг птг 2 п^тг^ 2
9 2
2 4 ? .
! П2ТГ2 У
. птгх ,
sin —— ах =
Zt
. ПТГ 8
+

296
3. РЯДЫ ФУРЬЕ
Таким образом, тригонометрический ряд Фурье функции
/(х), заданной на отрезке [—2, 2], имеет вид
13
8(-l)"-4cOS^x пжх
n=i
nn
~o~ 4 . nn Л ч cos"o"
9~~9 SHI —- + 8 «-^ *-
n2nz 2 n^TT'5
График суммы S(x) этого ряда представлен на рис. 3.10.
3.9. Разложение четных и нечетных функций
Напомним, что если функция f(x) определена на отрезке
[а, —а] и является четной (т.е. для всех х £ [—а, а] выполняется
а а
равенство f(x) = /(—х)), то / f(x)dx = 2ff(x)dx, а если явля-
-а 0
ется нечетной (т.е. для всех х G [—а, а] выполняется равенство
а
f(x) = — /(—х)), то / f(x)dx = 0. Легко проверить также, что
—а
произведение четной функции на четную или нечетной на
нечетную является четной функцией, а четной на нечетную есть
нечетная функция.

3.9. Разложение четных и нечетных функции 297
Пусть на отрезке [—тг, тг] задана четная кусочно непрерывная
функция f(x). Тогда при любом натуральном п
произведение f(x)smnx является нечетной функцией, а произведение
f(x)cosnx является четной функцией, и верны равенства:
тг тг
/ f(x)cosnxdx = 2 / f(x)cosnxdx, n = 0,1, 2 ...;
о
f(x)smnxdx = 0, n = 1, 2 ...
Поэтому все коэффициенты Ьп тригонометрического ряда
Фурье (3.14) функции f(x) равны нулю, все коэффициенты ап
определяются с помощью удвоенных интегралов на отрезке
[О, тг], а сам тригонометрический ряд Фурье четной на отрезке
[—тг, тг] функции принимает следующий вид:
оо
2 Г
п = — / /(x
к J
n=l
(3.48)
n = 0,1,...
Если же кусочно непрерывная функция f(x) определена на
[—тг, тг] и нечетна, то при любом натуральном п
произведение f(x)cosnx является нечетной функцией, а произведение
/(x)sinnx — четной функцией, и верны равенства
тг
/ f(x)cosnxdx = 0, п = 0,1, 2 ...;
-тг
тг тг
/ f(x)sinnxdx = 2 / f(x)smnxdx, n = 1, 2 ...

298
3. РЯДЫ ФУРЬЕ
Поэтому все коэффициенты ап тригонометрического ряда
Фурье (3.14) функции f(x) равны нулю, все коэффициенты Ьп
определяются с помощью удвоенных интегралов на отрезке
[О, тг], а сам тригонометрический ряд Фурье нечетной на
отрезке [—тг, тг] функции принимает следующий вид:
п=1
2 f
= — /(x)sinnxdx, n = l,2,...
я J
(3.49)
Аналогично, если функция f(x) определена на отрезке [—/, /],
кусочно непрерывна и является четной, то изложенные выше
рассуждения приводят к тому, что тригонометрический ряд
Фурье (3.43) этой четной функции с коэффициентами,
вычисляемыми по формулам (3.44), (3.45), принимает следующий вид:
lCOS-
ПТГХ
п=1
l '
(3.50)
ПТГХ
(x) cos-—-ax, n = 0,1,
Если же кусочно непрерывная функция определена на [—/, I] и
является нечетной, то ее тригонометрический ряд Фурье (3.43)
с коэффициентами, вычисляемыми по формулам (3.44), (3.45),
принимает следующий вид:
(3.51)
п=1
I
2 [
1J
n =
Наконец, пусть функция f(x) задана на отрезке [а, а+ 21],
где а = kl — некоторое кратное числа / > 0 (k G Z),
кусочно непрерывна и является четной относительно середины от-

3.9. Разложение четных и нечетных функции
299
резка разложения (рис. 3.11), т.е.
f{x) = f(2(a+l)-x), x e [а, а+ 2/]. У
Тогда периодическое продолжение
этой функции с периодом 21 на всю
действительную прямую R будет
четной функцией на R и, в
частности, на отрезке [—/, /]. Используя О
формулы (3.47), с помощью
рассуждений, аналогичных
приведенным выше, получаем, что тригонометрический ряд Фурье
(3.43) этой функции принимает вид
a+l
Рис. 3.11
a+2l
i COS
nnx
n=l
I
a+l
(3.52)
cos-
nnx
n = 0,1, 2,...
В том случае, если кусочно непрерывная на отрезке [а, а + 2/]
(а = kl) функция f(x) нечетна относительно середины
отрезка (рис. 3.12), т.е. f(x) = -f(2(a+l)-x)} x e [а, а + 2/] (при
этом верно равенство f(a+l) = 0),
то тригонометрический ряд
Фурье (3.43) этой функции принимает
следующий вид:
птгх
п=1
. 2 f
ТУ
In = 1,2,
(3-53)
Рис. 3.12
Действительно, в этом случае периодическое с периодом 21
продолжение функции f(x) на всю числовую прямую R будет

300
3. РЯДЫ ФУРЬЕ
нечетной функцией на R и, в частности, на [—/, /]. С помощью
рассуждений, аналогичных приведенным выше, получаем, что
все коэффициенты Фурье ап (см. формулы (3.47)) будут равны
нулю, а все коэффициенты Фурье Ьп будут равны удвоенным
интегралам по половине отрезка разложения, т.е. получаем
(3.53).
Пример 3.6.
Разложим в ряд Фурье на отрезке [—1,1]
функцию f(x) = e'xl. График этой
функции изображен на рис. 3.13.
Функция е'х1 непрерывна на отрезке
[—1,1], дифференцируема на интервале
(—1,1), кроме точки х = 0, где
существуют левая и правая производные, и
является четной на отрезке [—1,1].
Следовательно, ее тригонометрический ряд
Фурье имеет вид (3.50) при / = 1, причем
в силу непрерывности раскладываемой
функции f(x) этот ряд будет сходиться к f(x) в каждой
точке отрезка [—1,1]. Найдем коэффициенты Фурье этого ряда.
Имеем
1
Рис. 3.13
= 2 Л
Для вычисления остальных коэффициентов ап дважды
применим интегрирование по частям:
ап = 2 ех cosmrxdx = 2ex cosnnx
exsmnnxdx =
}
-2п27Г2 /
о J
excosnnxdx =
= 2(-l)ne-2-nVan.

3.10. Разложение в ряды Фурье по синусам и по косинусам 301
Таким образом, an = 2(-l)ne - 2 - п2тг2ап, откуда находим
_2(-1)пе-2
1 + П2ТГ2
Итак, тригонометрический ряд Фурье функции е'х1,
заданной на отрезке [—1,1], имеет следующий вид:
eN^ -I y>2(-l)ne-2
+ 2-j 1 + п2тг2
n=l
График суммы S(x) этого ряда изображен на рис. 3.14.
3.10. Разложение функций в ряды
Фурье по синусам и по косинусам
Рассмотрим функцию /(ж), заданную на отрезке [0, тг] и
удовлетворяющую на нем условиям теоремы 3.17 или теоремы
3.18. Поставим себе задачу разложения этой функции на
отрезке [0, тг] в тригонометрический ряд Фурье. В такой
постановке задача не имеет однозначного решения, так как она
многовариантна.
В самом деле, во-первых, эту функцию можно разложить
в тригонометрический ряд Фурье на отрезке [0, тг], как на

302 3. РЯДЫ ФУРЬЕ
произвольном отрезке вида [а, а + 21] с а = 0 и / = тг/2, используя
формулы (3.47). В этом случае сумма S(x) полученного ряда
будет тг-периодической функцией.
Во-вторых, можно доопределить данную функцию в
полуинтервале [—тг, 0) произвольным образом, лишь бы полученная
функция на отрезке [—тг, тг] продолжала удовлетворять
условиям теоремы 3.17 или теоремы 3.18. Разложим эту функцию в
тригонометрический ряд Фурье на отрезке [—тг, тг] и,
рассмотрев сумму данного ряда только на отрезке [0, тг], получим еще
одно представление исходной функции f(x) на отрезке [0, тг] в
виде тригонометрического ряда Фурье. В этом случае сумма
S(x) полученного ряда будет 2тг-периодической функцией.
Наконец, в-третьих, можно доопределить данную функцию
на произвольном отрезке [—Z, /], содержащем отрезок [—тг, тг],
так, чтобы полученная функция продолжала удовлетворять
на отрезке [—/, I] условиям аналогов теорем 3.17 или 3.18,
разложить доопределенную функцию в тригонометрический
ряд Фурье на отрезке [—/,/] и рассматривать его сумму только
на отрезке [0, тг] С [—М]- Сумма этого, третьего, варианта
тригонометрического ряда Фурье функции f(x) на отрезке
[0, тг] будет 2/-периодической функцией, причем 21 > 2тг.
Приведенные варианты разложений определенной на
отрезке [0, тг] функции f(x) в тригонометрический ряд Фурье, во-
первых, имеют различные периоды своих сумм, а во-вторых,
зависят от того, каким образом функция f(x) доопределяется
на отрезке [—тг, тг] или отрезке [—/, /], содержащем отрезок [0, тг].
Поэтому, чтобы получить для функции f(x) не просто какое-
то разложение в тригонометрический ряд Фурье, а разложение
со специальными свойствами (разложение специального вида),
необходимо, во-первых, уяснить требуемую периодичность
суммы ряда Фурье (и, следовательно, определить отрезок
разложения — [0, тг], [—тг, тг] или [—/, I] Э [0, тг]), а во-вторых, подобрать
такое продолжение функции f(x) на [—тг, тг] или [—/, /] Э [0, тг],
с помощью которого можно получить желаемый результат.

3.10. Разложение в ряды Фурье по синусам и по косинусам 303
Итак, пусть функция f(x) задана на отрезке [0, тг] и
удовлетворяет на нем условиям теоремы 3.17 или теоремы 3.18.
Рассмотрим два специальных разложения функции f(x) в 2тг-пе-
риодические (т.е. полученные с помощью разложения на
отрезке [—тг, тг]) тригонометрические ряды Фурье. Первое
разложение — это разложение в 2тг-периодический тригонометрический
ряд Фурье, не содержащий членов с синусами, т.е. в ряд, у
которого все коэффициенты Фурье Ьп равны нулю. Такое
разложение функции называют разложением в
тригонометрический ряд Фурье по косинусам кратных дуг (или по
косинусам). Второе разложение — это разложение в 2тг-пе-
риодический тригонометрический ряд Фурье, не содержащий
свободного члена и членов с косинусами, т.е. в ряд, у
которого все коэффициенты Фурье ап равны нулю. Такое разложение
функции называют разложением в тригонометрический ряд
Фурье по синусам кратных дуг (или по синусам).
Как показано в 3.9, такие разложения имеют четные и
нечетные на отрезке [—тг, тг] функции соответственно. Поэтому
для разложения функции /(ж), определенной на отрезке [0, тг],
по косинусам кратных дуг (и с 2тг-периодической суммой ряда
Фурье) необходимо продолжить функцию f(x) на промежуток
[—тг, 0) по четности, т.е. положить
/(*) = /(-*), *е[-тг,о).
Построим на отрезке [—тг, тг] тригонометрический ряд Фурье
полученной четной функции (см. (3.48)) и, рассмотрев его
сумму только на отрезке [0, тг], получим разложение исходной
функции f(x) на отрезке [0, тг] по косинусам. Для разложения
функции /(ж), определенной на отрезке [0, тг], по синусам
кратных дуг (и с 2тг-периодической суммой ряда Фурье) необходимо
продолжить функцию f(x) на промежуток [—тг, 0) по
нечетности, т.е. положить
f(x) = -f(-x), *€[-тг,О).

304
3. РЯДЫ ФУРЬЕ
При этом, возможно, потребуется переопределить значение
функции в нуле, поскольку для всякой нечетной функции /(0) =
= 0. Это никак не повлияет на ряд Фурье функции f(x).
Построим на отрезке [—тг, тг] тригонометрический ряд Фурье
полученной нечетной функции (см. (3.49)) и, рассмотрев его
сумму только на отрезке [0,тг], получим разложение исходной
функции f(x) на отрезке [0, тг] по синусам.
Аналогично можно разложить функции, заданные на
произвольном отрезке [0, Z], в 2/-периодические тригонометрические
ряды Фурье, содержащие только косинусы или только синусы.
В первом случае функцию необходимо доопределить в
промежутке [—/, /] до четной функции и воспользоваться формулами
(3.50). Во втором случае функцию следует доопределить до
нечетной на [—/, /] функции и применить формулы (3.51).
Пример 3.7. Разложим по косинусам и синусам функцию
0 ^ х ^ тг/2;
Доопределим сначала
функцию f(x) на отрезке [—тг, тг] до
четной функции/ч(х) (рис. 3.15):
9 тг/2, -тг ^ х < -тг/2;
-ж, -тг/2 ^ х < 0;
я, 0 ^ х < тг/2;
k тг/2, тг/2 ^ х ^ тт.
Рис. 3.15
Функция /ч(#) на отрезке [—тг, тг] удовлетворяет условиям
теоремы 3.15, поскольку она непрерывна, в любой точке
интервала (—тг, тг) имеет левую и правую производные, в точке
х = —тг имеет правую производную (/£+(—тг) = 0) и в точке
х = тг имеет левую производную (Д_(тг)=О). Кроме того,
/ч(—тг) = /ч(тг) = /ч(—тг+О) = /ч(тг—0) = тг/2. Поэтому,
согласно формулам (3.48), получаем следующие коэффициенты Фурье

3.10. Разложение в ряды Фурье по синусам и по косинусам 305
для четной функции
тг
/2 Ti
2 ( Г 1
0 ^
2
тг
/ 2
а 2 ( /zcosnz.
ТГ
2
2 f ' и
птг У
0
/ч
г
2
1
1
Or):
rf.T J =
)
ТГ
ТГ
2
sinnx
П
1 .
..*±
тг
тг
2
О
cosnx с
7Г
тг
2
птг
1
п
2
\
J
. птг
зш 2
2 /
Зтг
4 '
2xsinnx
птг
2
1 ЛЛ1
тг
О
тг
птг
2
П
Поскольку функция fH{x) непрерывна на отрезке [—тг, тг] и,
кроме того, /ч(—тг+О) = /ч(тг—0) = тг/2, то в силу теоремы 3.17
для любого х G [0, тг] верно разложение
Зтг
2
f{x) = /ч(ж) = s(x) = y + a^^vcosT"
n=l
cosnx'
График суммы ряда Фурье 5(ж), определенной на всей
числовой прямой, представлен на рис. 3.16.
-2я -^
« -f
У
я
2
\,
0
/1 1 К/
Я я ?2 2я х
2 2
Рис. 3.1в

306
3. РЯДЫ ФУРЬЕ
л
2
Рис. 3.17
л
Разложим функцию f(x) в ряд
Фурье по синусам, доопределив
ее до нечетной на отрезке [—тг, тг]
функции /н(гг) (рис. 3.17):
-тг/2, -тг^Ж-тг/2;
ж, -тг/2 *$z^ тг/2;
тг/2, тг/2<я^тг.
Вычислим коэффициенты Фурье функции fH{x) по формулам
(3.49):
ТГ
2 ч
2а; cos па;
Ьп = — / xsmnxdx+ / — smnxdx = —
тг \ 7 У 2 у
птг
cosnx
n
1 птг 2 .
= — cos —— Н—5~- sin па;
п 2 п^тг
1 1 птг 2 . птг (-1)п
cos птг + — cos — = —5— sin — , n € N.
n n 2 п2тг 2 n
Функция /н(я) на отрезке [—тг, тг] также удовлетворяет
условиям теоремы 3.17 и является непрерывной, поэтому для
любого х G [0, тг) имеем
f{x) = /н(ж) = S(x) =
2
n=l
smnx.
Поскольку
0| IM_t
то в точке ж = тг сумма ряда Фурье не совпадает со значением
функции f(x).

3.10. Разложение в ряды Фурье по синусам и по косинусам 307
График суммы S(x) ряда Фурье изображен на рис. 3.18.
Рис. 3.18
Пример 3.8. Разложим в тригонометрические ряды по
косинусам и по синусам на отрезке [0, 2] функцию
1,
Четная функция (рис. 3.19)
О, -2<ж<-1;
О, К х ^ 2,
У,
: 1
i
1 >!
-2 ^1 0
Г 2 х
Рис. 3.19
определена на отрезке [—2, 2] так, что f(x) = /ч(ж), х G [0, 2].
Используя формулы (3.50) при / = 2, получаем
а0
ап
1 1
= / f4{x)dx = / cbc = 1,
о о
2 ]
/. П7ГЖ Г
/4(x)cos-y-dx= /
П7ГГГ _
cos —-— ax =
2 П7ГГГ
= — sin ——
П7Г 2
2 . птг
= —sin-—, n G N.
П7Г 2

308 3. РЯДЫ ФУРЬЕ
Поскольку функция /ч(я) непрерывна во всех точках интервала
(0, 2), кроме точки х = 1, то, согласно аналогу теоремы 3.17 для
отрезка [—2, 2], получаем
^f [0,1)U(1, 2].
П=1
В точке разрыва х = 1 имеем
1-о) о+
в то время как /(1) = 1. Следовательно, сумма полученного
тригонометрического ряда Фурье в точке х = 1 отличается от
значения функции в этой точке.
График периодической с периодом Г = 4 функции S(x),
являющейся суммой ряда Фурье, представлен на рис. 3.20.
1
1
1
-3*
1
1
♦ -
1
-1
У-
1
1/2
0
i
■
:
3 х
Рис. 3.20
Для геометрической иллюстрации свойства сходимости
последовательности {5п(ж)},
2 . ктг ктгх
2^kY2
частичных сумм тригонометрического ряда Фурье функции
/ч(ж) на рис. 3.21 представлены графики частичных сумм у =
= 5п(ж), х G [-2, 2], с номерами п = 1, 3,5,10, 20 и 100. Из
рисунка ясно, что во всех точках отрезка [—2, 2],
являющихся точками непрерывности функции /(#), последовательность

3.10. Разложение в ряды Фурье по синусам и по косинусам 309
-2
к^. , J
1 2х -2 -1 0
-2 -1 О
1 2х
Рис. 3.21
{5п(я)} сходится к функции /(#), а в точках разрыва (точках
х = — 1 и ж = 1) такой сходимости нет.
Итак, функция f(x) на отрезке [0, 2] в ряд по косинусам
разложена. Разложим f(x) в ряд по синусам. Функция (рис. 3.22)
ш =
нечетная и определена так, что f(x) = /н(я), х G (0, 2].
Отметим, что кусочно постоянная на отрезке [—2, 2]
функция fH(x) удовлетворяет аналогу теоремы 3.17 для отрезка
о,
-1,
о,
1,
о,
-2
-1
х =
0<
К
0
X
X
X
X
;
<
<
1
2
-1;
0;
;
У:
1
-1
-2 **; 0
1
Рис.
1
1
Г 2х
-1
3.22

310 3. РЯДЫ ФУРЬЕ
[—2, 2] (/ = 2). Используя формулы (3.51) при / = 2, получаем
2 1
f f ППХ — f ' П7ГХ А —
n = J /H(z)sin— x = Jsm— х =
о о
2 птгх
= cos
птг 2
= —fl-cos^V nG
птг V 2 /
Поскольку функция /н(я) непрерывна во всех точках интервала
(0, 2), кроме точки х = 1, то в силу аналога теоремы 3.17 для
отрезка [—2, 2]) при всех х G (0,1) U (1, 2) получаем
2 (л П7Г\ • П7ГХ
(1 J sin — .
хг \ х ( \ at \ V^ 2 (л П7Г\ •
f{x) = /н(х) = ад = 2^ — (^1 -cos— J si
n=l
В точке разрыва х = 1 и на концах ж = 0 и ж = 2 отрезка
[0, 2] имеем
1-0) 0 + 1 1
S(2) =
-
/н(2-0) = 0 + 0
в то время как /(1) = 1, /(0) = 1, /(2) = 0. Следовательно, сумма
полученного тригонометрического ряда Фурье совпадает со
значением исходной функции f(x) в точке х = 2 и не совпадает
в точках х = 0 и х = 1.
График периодической с периодом Г = 4 функции S(x) —
суммы тригонометрического ряда Фурье функции fH(x) —
изображен на рис. 3.23.
Пример 3.9. Разложим функцию f(x) = х2 в ряды Фурье
по косинусам и по синусам в интервале (1, 2). Разложение
построим так, чтобы сумма S(x) получившегося ряда Фурье
имела наименьший период.

3.10. Разложение в ряды Фурье по синусам и по косинусам 311
-3 !
У-
1
0
->
<->
-1
>
Рис. 3.23
Для того чтобы разложить функцию f(x) в ряды по
синусам или косинусам, ее необходимо продолжить до нечетной
или четной на каком либо отрезке [—/, /]. Это можно сделать
многими способами, но сумма S(x)
ряда Фурье будет иметь
наименьший период, равный 2, только в том
случае, если доопределить функцию
f(x) так, чтобы функция f(x + 1)
стала четной или нечетной на
отрезке [-1,1]. Период функции S(x) при
этом будет равен 2.
Сначала разложим функцию f(x)
по косинусам, доопределив ее в
интервале (0,1) до четной
относительно х = 1 (см. 3.9) функции /ч(#)
(рис. 3.24):
{/т_о\2 о<т<1-
Коэффициенты Фурье четной относительно х = 1 функции
/ч(х) можно вычислить по формулам (3.52) при 1 = 1. Сперва
находим коэффициент clq:
Рис. 3.24
14

312
3. РЯДЫ ФУРЬЕ
а-п
4s
П27Г2
COSTITTX
9 l
-—I
! П27Г2./
Остальные коэффициенты вычисляем двукратным
интегрированием по частям:
2 о 2
/2х2 4 /*
х cosrnrxdx = sinriTrz / xs\nnnxdx =
ТПГ -I Т17Г J
1 х 1
И. I £+ I Z, I I I I
neN.
7Tznz
1
Поскольку f(x) = /ч(х), х G (1, 2), и функция /ч(#)
удовлетворяет аналогу теоремы 3.18 для отрезка [0,2] (является
непрерывной и кусочно монотонной на этом отрезке), и, кроме того,
/ч(0) = /ч(2) (значения на концах отрезка разложения
совпадают), то функция f(x) = х1 на всем отрезке [1, 2] может быть
представлена своим тригонометрическим рядом Фурье,
который имеет вид
г2_,^_о,_л_7,^4(2-(-1)П)
7
х2 = Д(а) = S{x) = {
п=1
График суммы S(x) этого ряда, определенной на всей
числовой прямой R и периодической с периодом Т = 2, изображен на
рис. 3.25.
-3 -2
-1 0
Рис. 3.25

3.10. Разложение в ряды Фурье по синусам и по косинусам 313
Разложим данную функцию /(х) = х2 на
отрезке [1,2] в ряд по синусам. Для этого
доопределим ее в интервале [0,1) до
нечетной относительно точки х = 1 функции /н(х)
(рис. 3.26):
-(х-2)2,
X
о,
2
х = 1;
К х
У-
4
1
0
-1
1*/* 2 *'•• х
i
2.
Функция fH(x) отличается от f(x) в точке
х = 1, но это не влияет на разложение этих
функций в ряд Фурье. Используя формулы (3.53) при / = 1,
вычисляем коэффициенты Фурье функции /н(я)'.
6n = 2|x2si
1
2(4 -(-
2х2
= cosnTrx
П7Г
П7Г
Н
2(4-(-l)n)
I xcosnnxdx =
1
2
sinnTrxdx =
.1
2
9^ 9 / ^1Г
! П27Г2 У
П7Г
Н
П°
П7Г
пз7Гз
Поскольку /(х) = /н(х) при х G (1,2), а /н(х) — кусочно
монотонная и кусочно непрерывная на отрезке [0, 2] функция
(Те- удовлетворяет аналогу теоремы 3.18 на отрезке [0,2]),
причем непрерывная в интервале (1, 2), то тригонометрический
ряд Фурье функции f(x) = х2 в каждой точке интервала (1, 2)
сходится к ней самой. Таким образом, разложение функции
f{x) = х2 в тригонометрический ряд Фурье в интервале (1, 2)

314
3. РЯДЫ ФУРЬЕ
имеет вид
П=
П7Г
sinnTrx, х Е (1, 2).
В точках х = 1 и х = 2, согласно аналогу теоремы 3.18 для
отрезка [0, 2], имеем
(2-0) = -4 + 4
в то время как /(1) = 1 и /(2) =
= 4. Поэтому сумма
полученного тригонометрического
ряда Фурье в точках х = 1 и х =
= 2 не совпадает со значением
исходной функции f(x) = х2 в
этих точках.
График суммы S(x) этого
ряда, определенной на всей
числовой прямой R и
периодической с периодом Т = 2,
изображен на рис. 3.27.
3.11. Вычисление сумм числовых
рядов с помощью рядов Фурье
В этом параграфе рассмотрено несколько примеров, в
которых показано, как можно использовать разложение функций в
тригонометрические ряды Фурье для вычисления сумм
некоторых числовых рядов. Если выше (см. 1) мы в основном касались
вопросов сходимости числовых рядов, то теперь можем найти
и суммы некоторых из них.

3.11. Суммирование числовых рядов с помощью рядов Фурье 315
Пример 3.10. Вычислим суммы следующих числовых
рядов:
к
|\7l+l °° 1
В примере 3.2 функция f(x) = #, х Е (—тг, тг), была разложена в
тригонометрический ряд Фурье
/1 1 (-l)n+1 \
х = 2(sinz — -sin2x+ -sin3z — ... + sinnz + ...).
V 2 о n /
Если положить в данном равенстве х = тг/2, то получим
т.е.
2n-l
n=l
Для вычисления суммы второго ряда можно использовать
равенство Парсеваля (3.18) для ряда Фурье функции f(x) = х:
00
71=1
Отсюда находим
00
n2 4тг 3
n=l
* ^2
Пример 3.11. Разложим функцию f(x) = х2 в промежутке
[—7г, тг] в ряд Фурье. Функция является четной, следовательно,

316
3. РЯДЫ ФУРЬЕ
в соответствии с формулами (3.48) имеем:
ао = - / x2dx = —,
тг у о
о
2 / 2 , 2х2 . * 4 Г .
ап = — х созпхах = sinnx / xsinnxax =
тгу птг 0 птгу
о о
тг
4х
= —т;—COSnx
cosnxdx =
nz
n°
n^
Поскольку функция х2 дифференцируема на [—тг, 7г] и ее
значения на концах этого отрезка совпадают, имеем разложение
, хе[-тг,тг].
п=1
Положив в этом равенстве х = 0, найдем
п=1
п=1
„2
Если же записать равенство Парсеваля для данного
разложения функции х2, то получим формулу
п=1
Следовательно,
4 4 4
Г4 7Г4 _ ТГ4
2 + 40 " 90'

3.11. Суммирование числовых рядов с помощью рядов Фурье 317
Пример 3.12. Вычислим суммы рядов
1_1_J_ J_ J__ 11111
1 + 5~7~11 + 13 + 17~'"' 5 + 7~11 + 13~17 + '"
различающихся лишь знаками своих членов. Для этого
используем разложение функции f(x) = тг/4 в интервале (0, тг) в
тригонометрический ряд Фурье по синусам. Такое
разложение можно получить, если в тригонометрический ряд Фурье на
отрезке [—тг, тг] раскладывается функция, полученная из f(x)
путем ее продолжения на [—тг, тг] до нечетной (см. формулы
(3.49)). Поскольку функция f(x) = тг/4 дифференцируема в
интервале (0, тг), то ее разложение в тригонометрический ряд
Фурье по синусам имеет вид (см. теорему 3.17)
ж ^ (1-(-1)п) .
71=1
Действительно, в соответствии с (3.49) имеем
тг
~ тгУ 4
2 Г тг 1
Ьп = — / -—sinnxete = — — cosnx
2n
2n
nGN.
о
Положив х = тг/2 в равенстве (3.54), получим
4 3 5 7 9' л ... .
п=1
оо
Умножим ряд ]£ (-1)п+1/(2п~1) на 1/3 и добавим к нему
п=1
нули следующим образом:
Согласно свойствам 1.4 и 1.5 числовых рядов, этот ряд сходится
и его сумма равна тг/12.

318 3. РЯДЫ ФУРЬЕ
Сложим этот ряд с рядом, из которого он был получен:
(0+ ^ + 0 + 0-^+0 + 0+ -L + 0 + 0 + ...
О Т 11 Lo IT 1У
Согласно свойству 1.6 числовых рядов, сумма последнего ряда
равна 7г/12 + 7г/4.
Итак,
Положим х = тг/3 в равенстве (3.54):
i ZZ zr ~ tz г
4^^ 2п 3 2 2-5 2-7 2-11
п=1
2-13 2-17 2 V 5 7 И 13 17
Тогда
1 1___1_ _!___]_ ?
5 + 7"ТГ+13""Т7 + ""
Раскладывая в тригонометрические ряды Фурье (в общие
или по синусам, или по косинусам) другие (кусочно
непрерывные) функции /(х), выписывая для них равенство Парсеваля и
подставляя в полученные соотношения различные конкретные
значения х = хо, можно найти суммы и других числовых
рядов. Данный способ вычисления сумм числовых рядов требует
определенного искусства и, вообще говоря, применим не для
всех рядов.

3.12. Дискретное преобразование Фурье 319
3.12. Дискретное преобразование Фурье.
Быстрое преобразование Фурье
Пусть функция f(x) с периодом 21 = Т непрерывна на всей
числовой прямой и имеет кусочно непрерывную на R
производную. Тогда она удовлетворяет условиям аналога теоремы 3.13
для 2/-периодических функций (см. 3.8) и ее можно разложить
в тригонометрический ряд Фурье на всей числовой прямой. Ее
ряд Фурье сходится в каждой точке х € R к значению функции
/(я). Итак, для любой точки х Е R имеет место равенство
ikx
*=-00
где г — мнимая единица, а коэффициенты разложения с& можно
вычислить, используя следующие формулы:
Т/2 Г
1 Г 2nikx 1 Г 2nikx
Ск = т j f{x)e—T-dx=-Jf(x)e—T-dx, keZ. (3.56)
-Т/2 О
Здесь мы использовали запись тригонометрического ряда
Фурье для 2/-периодической (2/ = Г) функции в комплексной
форме (см. 3.2 и 3.8) и свойства определенных интегралов
от периодических функций (см. 3.7). Кроме того, поскольку
функция f(x) имеет кусочно непрерывную на R производную,
то, согласно аналогу теоремы 3.13 для 2/-периодических
функций (см. 3.8), ряд Фурье функции f(x) сходится абсолютно и
равномерно на R, причем
+ОО +ОО
к=-оо k=l
Зафиксируем некоторое натуральное число N и рассмотрим
значения функции f(x) на сетке из действительных точек

320 3. РЯДЫ ФУРЬЕ
Xj=jT/N,j = 0,N-l:
+00 +00
, J=MT=T. (3.57)
fc=-oo k=-oo
Так как ряд Фурье функции f(x) сходится абсолютно в
каждой точке, то его члены можно переставлять любым способом,
сохраняя при этом сумму (см. теорему 1.11). Это
обстоятельство позволяет в ряде (3.57) привести подобные члены, т.е.
сложить члены с одинаковым значением экспоненты e2mki'N
Если fci — &2 = miV, где т Е Z, то число k\Xj/T — k^x^jT =
= mNxj/T = mj является целым. А поскольку функция e2mt =
= cos2?rt+ isin27rt, t G R, имеет период, равный единице, то для
всех j = 0, N—1
e2niklXj/T = е2тгг*2х,/Т? fci _ ^ = ^ m g z
Так как любое целое число fc можно единственным образом
представить в виде fc = / + mN, где / G {0,1,...,N—1}, т G Z,
и е2тгг(/+тЛ0х,/Г = е2тгг/х,/Т для всех ;- = Q, ЛГ-1 И ГП G Z, ТО
получаем
f(Xj) =
ЛГ-1 -Не» ЛГ-1 +оо
E
J=0 m=—oo 1=0 m=—оо
ЛГ-1 +оо N-1
= Ee27ri'Xj/T E
где
+оо
5= X) Ci+-^' 1 = 0,ЛГ-1, (3.58)

3.12. Дискретное преобразование Фурье 321
и коэффициенты ц+т# вычисляются по формуле (3.56). Итак,
если f(x) — произвольная 2/-периодическая функция,
непрерывная на R и имеющая на Ш кусочно непрерывную
производную, то ее значения в точках Xj = jfT/iV, j = 0, iV—1, могут
быть представлены в виде суммы, коэффициенты Ъ\ в которой
определяются формулой (3.58):
/(*;) = Х>27Г^/Т (3.59)
Несмотря на то что формула (3.59) задает представление
функции f(x) только на конечной сетке точек
Т 2Т
г Т 2Т (АГ-1)Г1
ее коэффициенты, вычисляемые по формулам (3.58) и (3.56),
определяются значениями функции f(x) на всем отрезке [О, Г],
а в конечном счете — на всей числовой прямой. Однако для
представления функции f(x) в виде суммы (3.59) на конечной
сетке точек совершенно не обязательно знать значения
функции f(x) на всей числовой прямой, а достаточно знать лишь ее
значения в точках самой сетки.
В самом деле, пусть функция f(x) определена не на всей
прямой R, а лишь в узлах сетки {О, T/N, 2Т/ЛГ, ..., (N-1)T/N}
(такую функцию называют сеточной). Тогда
представление в виде суммы (3.59) для нее можно получить, например,
следующим образом. Доопределим сначала сеточную
функцию f(x) на отрезке [О, Т] до непрерывной, кусочно линейной
функции, удовлетворяющей условию /(Г) = /(0). Графиком
этой функции на отрезке [0, Г] является ломаная с
вершинами в точках {xj]f(xj)), j = 0, iV-1, а также в точке (Т;/(0)).
Продолжим затем полученную функцию периодически на всю
числовую прямую с периодом 21 = Т. В итоге получим
непрерывную на множестве Ш 2/-периодическую функцию, имеющую

322 3. РЯДЫ ФУРЬЕ
кусочно непрерывную производную. Для такой функции имеет
место разложение (3.55), а в точках xj =jT/N, j = 0, ЛГ-1, —
представление (3.59).
Отметим, что тригонометрический полином
SN(x) = X>2-'*/T
из правой части (3.59) является интерполяционным для
сеточной функции /(#), т.е. обладает свойством
j) = /(*j)i J = 0, ЛГ-1.
Представление сеточной функции в виде суммы (3.59),
полученное с помощью непрерывной, кусочно линейной
интерполяции имеет существенный недостаток: для вычисления N ее
коэффициентов разложения с/, I = 0, N—1, необходимо
предварительно вычислить бесконечное число коэффициентов Q+mw,
т € Z. Однако должен существовать алгоритм расчета
коэффициентов с/ без предварительного вычисления коэффициентов
cl+mN- Этот алгоритм действительно есть, и его называют
дискретным преобразованием Фурье. Переходим к его
изложению.
Итак, рассмотрим линейное пространство Djq комплексных
сеточных функций, определенных в узлах сетки Xj = jT/N,
j = 0, N—1, где N — фиксированное натуральное число. Это
iV-мерное комплексное линейное пространство. Отображение,
которое всякой функции / Е Dn ставит в соответствие вектор
ее значений
/ = (/Ы /On) /(*n-i))tgCn,
устанавливает изоморфизм между линейным пространством
Dn сеточных функций и комплексным линейным
арифметическим пространством CN.

3.12. Дискретное преобразование Фурье 323
Введем в этом комплексном линейном пространстве
скалярное умножение
(3.60)
где черта сверху означает операцию комплексного сопряжения.
Аксиомы скалярного умножения для комплексных линейных
пространств те же, что и для действительных линейных
пространств (см. 3.1), за исключением аксиомы коммутативности,
которую заменяют следующей: (/, д) = (д, /). Комплексные
линейные пространства со скалярным умножением называют
унитарными пространствами. Нетрудно проверить, что
все четыре аксиомы для введенного выше скалярного
умножения выполняются. Таким образом, линейное пространство
Dn становится унитарным пространством. Система сеточных
функций
где х принимает значения jT/N, j = 0, TV—1, является ортонор-
мированным базисом в унитарном пространстве
Действительно, для любых целых кит имеем
j
- N-l Л N-l
При к = т получаем (<£>m, (pm) = 1 для всех целых чисел т.
Если кфт, то, используя формулу для вычисления суммы N
первых членов геометрической прогрессии со знаменателем q =
= e2ni(k-mVN (q^l при кфт)ъ первым членом Ъх = 1 (см. 1.1),
получаем
так как e27ri(fc~m) = 1 для любых целых кит.

324 3. РЯДЫ ФУРЬЕ
Таким образом, система сеточных функций {<pi}$Lol
представляет собой ортонормированный базис в унитарном
пространстве Dn.
Для любой функции / G Djq имеет место представление
(3.59). Учитывая введенное обозначение <pi{xj) = е2пг1х^т, I =
= О, TV—1, представление (3.59) можно переписать так:
ЛГ-1 N-1
/=0 /=0
Иными словами, для всякой функции / G D^ имеет место
разложение
4 x = 3—,j = 0,N-l. (3.61)
Это означает, что представления (3.59) и (3.61) являются
разложениями сеточной функции / G Dn по ортонормированному
базису {ifi}ii^1 унитарного пространства Dn, а коэффициенты
разложения q, I = 0, iV—1, — координатами функции (вектора)
f в этом ортонормированием базисе, т.е.
j=0
Следовательно, коэффициенты q не зависят от способа
продолжения сеточной функции на всю числовую прямую до
Т-периодической, определяются лишь значениями функции в
узлах сетки.
Соотношение (3.61) обычно называют дискретным
(конечным) рядом Фурье сеточной функции / Е Dn, а
коэффициенты Q — ее дискретными коэффициентами Фурье.
Разложение сеточных функций в дискретный ряд Фурье
(3.61) определяет линейное отображение Т\ D^ —> CN, которое

3.12. Дискретное преобразование Фурье 325
каждой функции / из унитарного пространства Dn, т.е.
сеточной функции /, определенной на сетке Xj = jT/N, j = О, ЛГ-1,
ставит в соответствие комплексный вектор
c = Hf) = (3> * cN-i)TeCN
Координатами этого вектора являются дискретные
коэффициенты Фурье функции /. Так как для любой функции / Е Dn
вектор с ее координат в ортонормированием базисе {<fi}^1
унитарного пространства Dn определяется однозначно, и,
наоборот, каждый вектор координат с Е CN однозначно
определяет функцию f(EDpj [IV], то отображение Т является
взаимно однозначным отображением Dn на С^ Таким образом,
отображение Т\ Dn —>• CN является невырожденным линейным
оператором, действующим из iV-мерного унитарного
пространства Dn в Cn Линейный оператор Т называют прямым
дискретным преобразованием Фурье.
Пусть в пространстве Dn выбран базис из сеточных
функций {efc(rr)}^=1, где для любого к = 1, N выполняются условия
ek(xj) = 0 при j = О, N—1, j'ф к — 1, и ek{xk-i) = 1. Для любой
сеточной функции / € Dn имеем разложение
N т
f{xk.l)ek{x), xj = J—, j = 0,W-l.
Столбец координат сеточной функции / G Dn в ортонормиро-
ванном базисе {ek{x)}£=i унитарного пространства Dn имеет
вид
f(xi) f(x2) f(xN-i)f
Согласно формулам (3.62), в стандартном базисе
арифметического пространства С^ столбец с координат образа сеточной
функции / при отображении Т (вектор дискретных
коэффициентов Фурье функции /) можно представить следующим обра-

326
3. РЯДЫ ФУРЬЕ
зом:
с =
со N
С2
\CN-l)
лг
лг-1
'JV
е т е т
27TJ1XQ 27TJ1-X1
е т е т
T
i=i \
27rt(N-l)gQ 2тгг(ЛГ-:
е т е т
2nilxN_1
е т
2ni2-xN_1
е т
2*i(N-l)xN_l
(/ы
\f(xN-i)J
ИЛИ
где / = {f{x0) f{xi) f{x2) f{xN-i)f Матрицу F
называют матрицей прямого дискретного преобразования
Фурье. Учитывая равенства Xj = jT/N, j = 0, iV—1, и вводя
параметр q = e~2irt/N, матрицу F прямого дискретного
преобразования Фурье можно записать в виде
/1
1
1
1
я"-1
\
,
(3.63)
Так как линейный оператор Т взаимно однозначно
отображает унитарное пространство Dn на С^, то существует
обратный к нему оператор Т~х: CN -¥ Dn- Линейный
оператор Т~1 каждому комплексному вектору с € С^ ставит в

3.12. Дискретное преобразование Фурье
327
соответствие сеточную функцию / £ Dn, для которой
координаты вектора с являются дискретными коэффициентами Фурье
функции /. Отображение Т~1 называют обратным
дискретным преобразованием Фурье. Оно определяется
формулами (3.59), которые эквивалентны следующему матричному
равенству: / = F~lc. Матрицу F"1 называют матрицей
обратного дискретного преобразования Фурье. Из
формул (3.59) следует, что матрица обратного дискретного
преобразования имеет вид
/1
1
1
1
,-1
1
г2
,-4
7
(3.64)
Обратимся теперь к вычислительным аспектам
осуществления прямого и обратного дискретных преобразований Фурье.
Выполняя прямое или обратное преобразование Фурье, нам
приходится умножать квадратную матрицу F или F"1
порядка N на столбец из N чисел. При этом для определения
всех дискретных коэффициентов Фурье сеточной функции /
из унитарного пространства Dn требуется порядка N2
арифметических операций* (матрицы F и F~l считаются
вычисленными заранее). Однако если N является составным числом,
то количество выполняемых арифметических операций
можно значительно сократить. Существует алгоритм вычисления
дискретных коэффициентов Фурье сеточных функций,
называемый быстрым дискретным преобразованием Фурье,
который позволяет уменьшить число производимых
арифметических операций до порядка N(N\ +N2 + ... + Nm), где N =
= N\ N2... Nm — разложение числа N на простые сомножители.
*Под арифметической операцией понимается умножение двух
комплексных чисел с последующим сложением.

328 3. РЯДЫ ФУРЬЕ
Рассмотрим идею быстрого преобразования Фурье на
примере вычисления прямого преобразования Фурье функции /
из унитарного пространства D^ в случае, когда N = N\N2-
Перепишем формулы (3.62) для вычисления дискретных
коэффициентов Фурье в следующем виде:
j=o
где q = e~2irt/N Обратим внимание на то, что qmN = 1 для всех
ra€Z.
Отметим, что любой номер I = О, N—1 можно представить в
виде I = l\ N\ + Jo, где 1\ < N2 и /q < N\ — неотрицательные
целые числа. Также любой номер j = О, N—1 можно представить
в виде j = j\ N2 + jo, где j\ < N\ и j0 < N2 —
неотрицательные целые числа. С учетом этих представлений для любых
/? j = О, N—1, имеем
lj = l{ji N2 + jo) = ljiN2 +1 jo = {hNi + lo)jiN2 +1 jo =
= hj\NiN2 + I0J1N2 +1 jo = hjiN + hj\N2 +1 jo,
и, следовательно,
Отсюда для любого I = 0, N—1 получаем
л N2-l
)* 4E
jo=0 v x ji=0 7 Z jo=0
jo=0 v x ji=0 7 Z j

3.12. Дискретное преобразование Фурье 329
где введено обозначение:
1 л=о
При известной матрице F дискретного преобразования
Фурье, т.е. при известных значениях ql°ilN2/N\, для вычисления
каждого коэффициента c(IqJq) требуется N\ арифметических
операций. Общее число таких коэффициентов N1N2 = N.
Таким образом, для вычисления всех коэффициентов с(/о, jo)
необходимо порядка N\N арифметических операций. Далее, при
известных коэффициентах c(/o,jo)> jo = 0, N2—1, и величинах
qli°/N2 для вычисления каждого коэффициента q требуется
осуществить порядка N2 операций. Всего таких
коэффициентов TV, значит, следует добавить еще N2N операций.
Следовательно, для вычисления всех коэффициентов дискретного
преобразования Фурье необходимо NN2 + N\N операций. Так
как N(N\ + N2) < N2 при N > 4, то получаем более выгодный
способ вычисления дискретного преобразования Фурье.
Экономия в количестве вычислений стала возможной благодаря
выделению коэффициентов c(Jo,io)> которые используются для
вычисления нескольких различных коэффициентов с/.
В общем случае, когда N = NiN2...Nm, удается
аналогичным образом выполнить дискретное преобразование Фурье
всего за N(N\ + N2 +... + Nm) операций. Более подробно
остановимся на случае, когда N является степенью числа 2, т.е.
ЛГ = 2т, тпеК
Разложим числа I = 0, N—1 и j = 0, N—1 по степеням числа
2, т.е. представим их в виде
т— 1 т— 1
/=5>2*, ;=]>>2Г, (3.65)
fc=0 r=0
где все коэффициенты 1^ и jr принимают одно из двух значений:
0 или 1. Для произвольной сеточной функции / G Dn положим

330 3. РЯДЫ ФУРЬЕ
/(O)O'o,...,jm-i) = /(zj), где j имеет разложение (3.65).
Коэффициент Фурье С[ с произвольным номером I равен
= ^t t E/(o)Cio.-..,i»-i))9«. (3.66)
jm-l=0jm-2=0 jo=0
Заметим, что q = е-2пг/2т Поэтому для любого целого р верно
равенство д2Шр = 1.
Рассмотрим теперь произведение целых чисел Ij. С учетом
представления (3.65) имеем
гТП— 1
/ Jb
=
\ /m~l
; 11 / 3r<
m—lm—r—l
E E <*•
r=0 A;=0
m—lm—г—1
- V V Ui 2k
r=0 A:=0
m-1
ч m—lm—1
^ A:=0 r=0
m—1 m—1
r=0 fc=m-
m—1 m—1
r=0 fc=m-i
m—r—1
т—1
r=0 fc=0 г=0
где
т—г—1 т—1 т—1
ar=a(l0,...,lm-r-x)= Е '*2*. S=E E
А:=0 r=0 k=m-r
Учитывая, что qNs = (qN)3 = 1, получаем
m—I m—1
r=0 r=0

3.12. Дискретное преобразование Фурье 331
Тогда, используя (3.66), имеем
j = ^ Е
jm-l
л 1 1
= ^гЕ Е М
j=0 jm-l=0 jO=0 Г=0
1 1 m-1
J0=0 jm-l=0 Г=0
|*>вв"4 E ^m-l2m"lam-1/(O)(jo,..,Jnl-i). (3.67)
.70=0 im-l=0
Если ввести следующие обозначения:
jm-1=0
.70=0
то процесс вычисления дискретных коэффициентов Фурье q
по формуле (3.67) сведется к быстрому алгоритму вычислений
с использованием следующих рекуррентных формул:
С(к)(/о,...,h-U J0, • • •, jm-k-l) =
\ ,...,t-2,j0l...,im-*), (3.68)
Jm-fe=0
где
r=0

332 3. РЯДЫ ФУРЬЕ
Начальными значениями (fc = 0) для этих формул являются
значения функции / Е Dn в узлах сетки Xj = jT/N, j = 0, TV—1:
m-l
r=0
а конечными значениями (к = m) — искомые дискретные
коэффициенты Фурье функции /:
m-l
Определим количество арифметических операций,
необходимых для вычисления дискретных коэффициентов Фурье с
использованием описанного алгоритма. На каждом fc-м шаге для
вычисления одного коэффициента c^(Iq, ... ,/fc-i, jo, • • • Jm-k-i)
при известных коэффициентах с^"1) требуется выполнить две
арифметические операции (как и выше, считаем, что
значения ^'m-*2m~ um-fc/2 известны заранее). Таких коэффициентов
насчитывается 2т. Поэтому на fc-м шаге совершается 2т 2
арифметических операций, а всего за т шагов нужно
выполнить 2т • 2га = 27Vlog2N операций.
Рассуждая аналогично, приходим к рекуррентным
формулам быстрого алгоритма обратного преобразования Фурье:
С{к) (/о,... Л-ЬЛЬ • • • Jm-k-l) =
1
= V^ Q~^m-k2m~karn-kC^k~lHlc\ lie 1 7П 7 -к) (3 69)
3m-k=0
где
r=0

3.12. Дискретное преобразование Фурье
333
Начальными значениями (к = 0) для этих формул являются
значения дискретных коэффициентов Фурье сеточной функции
feDN:
r=m—l
3=
r=0
а конечными значениями (к = га) — значения функции / G
в узлах сетки х\ = IT/N, I = 0, N—1:
k=m-l
l=
k=0
Итак, вместо необходимых N2 операций при использовании
обычного алгоритма преобразования Фурье, приведенный
алгоритм быстрого (прямого и обратного) преобразования Фурье
требует вьшолнения всего порядка 2iVlog2N арифметических
операций, давая тем самым не только существенный выигрыш
в затратах машинного времени (при реализации этого метода
на компьютере), но и увеличивая надежность вычислений.
Отметим, что процедура последовательного вычисления
величин c(*)(Zi,...,^_i,jo,...,Jm-A:-i) по рекуррентным
формулам (3.68) эквивалентна процедуре последовательного
вычисления 2т-мерных комплексных векторов
/с(*)(0,0,0,...,0)\
к = 0, m,
с помощью линейных отображений

334 3. РЯДЫ ФУРЬЕ
Таким образом, матрицу F (прямого или обратного)
дискретного преобразования Фурье (см. (3.63)) можно представить в
виде произведения т квадратных матриц порядка 2т:
F = FmFm-i... F2F\.
Матрицы i*\, i*2, ..., Fm замечательны тем, что каждая из них
имеет лишь по два ненулевых элемента в каждой строке (и
каждом столбце). За счет отбрасывания (не выполнения)
операций умножения на нули этих матриц и достигается выигрыш в
необходимом числе операций при выполнении дискретного
преобразования Фурье по быстрому алгоритму.
Можно показать, что элементы каждой матрицы Fn = (/jj* ),
п = 1,га, имеют следующий вид. Пусть 0^fc<2m~n,
параметр а имеет значение 0 при вычислении прямого
дискретного преобразования Фурье, и значение 1 при вычислении
обратного дискретного преобразования Фурье. Тогда:
/Jj) = l при j = k2n + v + l, I = k2n~l+v + l или j = k2n +
при j = k2n + 2""1 + v + 1, / = 2™"1 +
f*y = 0 в остальных случаях.
Численную реализацию прямого и обратного дискретных
преобразований Фурье можно проводить в соответствии со
следующим алгоритмом.
Алгоритм быстрого прямого (обратного)
дискретного преобразования Фурье
1. Входные данные: N — 2т — количество узлов; A(N),
B(N) — TV-мерные массивы действительных и мнимых частей
комплексного ЛГ-мерного вектора X(N). Вектор X(N) в случае

3.12. Дискретное преобразование Фурье 335
вычисления прямого дискретного преобразования Фурье
является вектором значений сеточной функции в узлах О, T/7V,
(N - 1)T/N. Вектор X(N) в случае вычисления обратного
дискретного преобразования Фурье является вектором
дискретных коэффициентов Фурье некоторой сеточной функции,
которую и необходимо восстановить. Параметр о принимает
значения: о = 0 для прямого дискретного преобразования
Фурье и a = 1 для обратного дискретного преобразования Фурье.
2. п = 1.
3. fc = 0.
4. v = 0.
5. j = k2n+v + l,l = k2n-l+v + l,p = 7rv/2n-1.
6. Если a = 0, то s = sinp, если a = 1, то 5 = — sinp.
7. с = cosp.
8. I1=2rn-l+l,jl=j + 2n~1.
9. AA{j) = A(l) + A{h)c + B{h)s, BB{j) = B{1) - A{h)s +
-B(h)c.
10. v =
11. Если v — 2n~l < 0, то вернуться к шагу 5, если v — 2n~1
^ 0, то перейти к шагу 12.
12. fc = fc + l.
13. Если к - 2m~n < 0, то вернуться к шагу 4, если к - 2m~n
^ 0, то перейти к шагу 14.
14. A ТТ
15. п =
16. Если п — m ^ 0, то вернуться к шагу 3, если п — m > 0,
то перейти к шагу 17.
17. Если a = 1, то перейти к шагу 18. Если о = 0, то АА(1) =
= AA(l)/N, ВВЦ) = BB{l)/N, I = TTlV, и перейти к шагу 18.
18. Выходные данные: j4j4(7V), BB(N) — ЛГ-мерные
массивы действительных и мнимых частей комплексного вектора
Y(N), полученного путем применения прямого или обратного
дискретного преобразования Фурье к вектору X(N).

336 3. РЯДЫ ФУРЬЕ
Дополнение 3.1. Доказательство леммы
Римана для определенных интегралов
Докажем теорему 3.10 (лемму Римана). Нам необходимо
показать, что для всякой кусочно непрерывной на отрезке [а, Ь]
функции f(x) имеют место следующие соотношения:
Ь ь
Km f(x)cos£xdx = 0, lim f(x)sin£xdx = 0.
Пусть сначала f(x) — кусочно постоянная
(ступенчатая) функция. Это означает, что существует такое разбиение
отрезка [а, Ь] точками хо, х\, ..., хп, а = xq < х\ < < хп = Ь,
что f(x) = Ck, если х G (zjt-i, х^), к = 1, п, где Ck G IR —
некоторые постоянные. Тогда имеем следующие равенства:
f A f
f(x)cos£xdx = 2^ / f(x)cos(£x) dx =
Поскольку синусы ограничены по модулю единицей, то при
£ -> оо получаем
1 •
/ f(x)
cos£xdx
Заметим, что значения функции /(х) в самих точках
разбиения хо, xi, ..., хп в доказательстве не используются и могут
быть произвольными.
Пусть теперь f(x) — произвольная кусочно непрерывная на
отрезке [а, Ь] функция. Покажем, что для любого числа е > О

Д.3.1. Доказательство леммы Римана 337
найдется такая ступенчатая функция д(х), что
\Т \ X) —д\^)\ ^ ^ С \CL% и\ш \ О. I U)
Выберем произвольное число е > 0. Из кусочной
непрерывности функции f(x) на отрезке [а, Ь] следует, что на [а, Ь] можно
указать конечное число точек a = j/o < 2/1 < • • • < Vn — Ь, таких,
что в интервалах (j/j-i, j/j), j = 1, iV, функция f(x) непрерывна
и существуют конечные пределы
= lim /(x) и /(ад-0)= lim /(x).
x->yji+0 х—fyj—0
Прежде всего определим функцию д(х) в точках j/j, j = 0, ЛГ,
положив
Для каждого номера j = 1, N рассмотрим отрезок [j/j-i, j/j] и
определенную на этом отрезке функцию fj{x), равную f(x) в
интервале (j/j_i,j/j), а на концах отрезка доопределенную по
непрерывности:
{
Все функции /j(x) на своих отрезках [j/j-i, j/j] являются
непрерывными. Следовательно, каждая такая функция равномерно
непрерывна на своем отрезке [1-5.9]. Поэтому для каждого
j' = 1, TV найдется число Sj(e) > 0, такое, что для любых
точек х1 и х" из отрезка [j/j-bj/j], удовлетворяющих условию
\х' — х"\ < 6j(e), верно неравенство
ф-у (3.71)

338 3. РЯДЫ ФУРЬЕ
Подберем такие натуральные числа fcj, чтобы выполнялись
неравенства
Разбив интервал (j/j-i, j/j) на полуинтервалы
Ijm = (l/j-i + (т-1)Д,-, 2/j-i + mAj], m = l,fcj-l,
и интервал J^. = (2/j_i + (fcj-l)Aj, 2/j-i + fcjAf), определим в
интервале (j/j_i,j/j) функцию у(х) следующим образом. На
каждом промежутке Ijm, т = 1, Ау, эта функция постоянная и
совпадает со значением fj(yj-\ +mAj) функции fj(x) в правом
конце промежутка Ijm. Функцию д(х) определим указанным
образом на всех интервалах (j/j-i, j/j). Тогда она в силу (3.71)
в каждом интервале (j/j-i, j/j) удовлетворяет неравенству
Поскольку f(x) = fj(x) при х € (j/j-i, J/j), то
|/(х)-5(х)|<^-^, xebj-uvj), (3.72)
и это верно для каждого интервала (j/j-i, j/j). Учитывая, что в
точках уо = а, уь 2/2, •. •, UN = Ь ранее положили g(yj) = /(2/j),
заключаем, что неравенство (3.72) выполняется для всех точек
х Е [а, 6]. Таким образом, существование кусочно постоянной
функции д(х), удовлетворяющей неравенству (3.70), доказано.
Продолжим доказательство леммы Римана. Согласно
доказанному ранее, для всякой ступенчатой функции д(х) верно
равенство
ь
lim / g(x)cos£xdx = 0.
а
Поэтому найдется такое £о > 0, что при |£| > £о будет выпол-
I b
няться неравенство \fg(x)cos£xdx < е/2. Учитьгоая это, а

Д.3.2. О достаточных признаках сходимости
339
также неравенство (3.70), при |£| > £о получаем
ь
f(x)cos£xdx =
о о
/ (f{x)—g(x))cos£xdx+ / g(x)cos£xdx
ь ь
; / \f(x)-g(x)\ \cos£x\dx+\ / g(x)cos£xdx
Это означает, что lim f f(x)cos£xdx = 0. Аналогично доказы-
вается и второе равенство lim f f(x)sm£xdx = 0. ►
Дополнение 3.2. О достаточных
признаках сходимости ряда Фурье
Теорема 3.11 является следствием более общей теоремы.
Сформулируем эту теорему.
Теорема 3.19 (признак Дини). Пусть функция f(x)
определена на R, имеет период 27Г и является кусочно
непрерывной на отрезке [—7г, тг]. Если в точке х еШ при некотором
значении S > 0 существует (конечен) интеграл
о
и
■du,
то тригонометрический ряд Фурье функции / сходится в
точке х к значению (f(x+0) + /(z-0))/2. #

340 3. РЯДЫ ФУРЬЕ
Нетрудно показать, что любая функция, удовлетворяющая
условиям теоремы 3.11, также будет удовлетворять и условиям
признака Дини (для любой точки х Е R). Таким образом,
теорема 3.11 действительно является следствием признака Дини.
Признак Дирихле (см. теорему 3.12) также является
следствием другой общей теоремы. Прежде чем сформулировать
эту теорему, введем следующее понятие. Функцию /(ж),
заданную на отрезке [а, 6], называют функцией с ограниченным
изменением, если существует такая постоянная М > 0, что,
каково бы ни было разбиение отрезка [а, Ь] точками а = xq <
< х\ < < хп = 6, справедливо неравенство
Всякая функция, монотонная на отрезке [а, 6], имеет
ограниченное изменение, причем сумма, стоящая в последнем неравенстве
слева, не зависит от выбора точек разбиения и всегда равна
\f(b) — f(a)\. Ограниченная кусочно монотонная на отрезке
функция также имеет на этом отрезке ограниченное изменение.
Теорема 3.20 {признак Жордана). Пусть функция
f(x) определена на М, имеет период 2п и является кусочно
непрерывной на отрезке [—7г, 7г]. Если точка х Е Ш такова, что
при некотором значении S > 0 функция f(x) имеет
ограниченное изменение на отрезке [х — rf, x + rf], то
тригонометрический ряд Фурье функции / сходится в точке х к значению
(/(х+0) + /(х-0))/2. #
Из этой теоремы, в частности, следует, что если 27г-пе-
риодическая и кусочно непрерывная на отрезке [—7Г, тг]
функция имеет на этом отрезке ограниченное изменение, то ее
ряд Фурье будет сходиться в любой точке х G Ш к значению
Покажем, что признаки Дини и Жордана не сводятся один
к другому, т.е. существуют функции, которые подпадают под
один признак, но не подпадают под другой.

Д.3.2. О достаточных признаках сходимости
341
Рассмотрим кусочно монотонную и непрерывную на
отрезке [-7Г, 7Г] фуНКЦИЮ
/(*) =
2тг
О,
, яе[-7г,0)и(0,тг];
= 0.
Покажем, что эта функция удовлетворяет условиям
признака Дирихле (а значит, и условиям признака Жор дана), но не
удовлетворяет условиям признака Дини в точке х = 0.
Действительно, эта функция непрерывна в любой точке х ф 0 на
отрезке [—тг, тг]. В точке х = 0 она тоже непрерывна, так как
lim
х-Ю
2тг
= —=0.
оо
Функция /(я), как нетрудно заметить, не убывает на интервале
(0, тг) и не возрастает на интервале (—тг, 0), а потому кусочно
монотонна на отрезке [—тг,тг]. Значит, она удовлетворяет
условиям признака Дирихле (в формулировке теоремы 3.18). Ее
ряд Фурье сходится к самой функции всюду на отрезке [—тг, тг]
(отметим, что /(—тг) = /(тг)), и в частности в точке х = 0.
Однако условия признака Дини в точке х = 0 не выполняются,
поскольку для любого 5>0, 0 < 5 < тг, имеем
о
I
U
du = \
и
2тг
= -21n
2тг
ы±
2тг
+ 2 lim In
u->+0
и
l2^
= +oo.

342 3. РЯДЫ ФУРЬЕ
Рассмотрим другую 2тг-периодическую функцию (р{х),
которая на отрезке [—тг, тг] определена следующим образом:
ф) = 11? -*, о) и (о,*];
\ О, х = 0.
Функция (р(х) дифференцируема в каждой точке х ф птг, п £ N,
а в точках х = птг, п ф 0, она имеет односторонние производные.
Функция <р(х) также дифференцируема и в точке х = 0:
(Ад;)2 cos
(Ад;) cos 2
у/(0)= lim Л [ ] = lim Дясоз
Дх->0 Дж Дх->0
Поэтому функция (р(ж) удовлетворяет условиям теоремы 3.11,
а значит, и условиям признака Дини. Ее ряд Фурье
сходится в любой точке х Е М к значению функции в этой точке.
Однако функция (р(х) не имеет ограниченного изменения на
отрезке [—а, а] при любом а > 0. В данном случае
достаточно рассмотреть отрезок [0, а], причем можно считать, что
а < тт. Пусть к — произвольное натуральное число,
большее 1/а2. Выберем некоторое натуральное число т и
рассмотрим разбиение 0 = хо < х\ < < хт+2 = о* отрезка [0, а]
точками Xi = l/\/fc + m + 1 — г, г = 1, т + 1, которые являются
точками экстремума функции cos(n/x2). При этом <p(xi) =
_^ Следовательно,
M*t+i)-
поскольку значения функции (р(х) в соседних точках Х{
противоположны по знаку. Суммируя, находим
m
P
1=1 1=1
l=k+l

Вопросы и задачи 343
Используя это соотношение заключаем, что
m+l т k+m-l
i=0 i=l l=k+l
+00
Поскольку рлд ^ 1 /l расходится, как остаток гармоническо-
i=k+i
го ряда, то последовательность его частичных сумм стремится
к +оо. Следовательно, для любого числа М > О можно выбрать
fc+m-l
такой номер т, что £) 1// > М/2. Для выбранного номера
m справедливо неравенство
771+1
г=0
Итак, функция (р(х) на отрезке [0, а] не является функцией
с ограниченным изменением, поскольку такое т можно
подобрать для всякого числа М > 0. Таким образом, в точке х = О
признак Жордана не применим. Тем более не применим и
признак Дирихле.
Вопросы и задачи
3.1. Найдите ряд Фурье в комплексной форме функции
3.2. Выясните, являются ли следующие тригонометрические
ряды рядами Фурье каких-либо функций евклидова
пространства £7О[~7Г, тг]:
оо . оо оо . Л оо
а)
п=1 п=1 п=1 п=1
оо
п=1

344 3. РЯДЫ ФУРЬЕ
3.3. Не вычисляя коэффициенты Фурье функции f(x) =
= тгх — х\х\, выясните, сходится ли ряд Фурье этой функции на
отрезке [—тг,тг] равномерно. Постройте графики сумм
продифференцированного и дважды продифференцированного ряда
Фурье данной функции.
3.4. Почленным интегрированием разложения
n=l
получите ряды Фурье функций ж2, ж3 и ж4.
3.5. Разложите в ряд Фурье на отрезке [—тг, тг] заданную
функцию /(я), постройте графики функции f(x) и суммы ее
ряда Фурье; найдите сумму ряда Фурье в указанной точке xq:
' -тг < я ^-тг/2;
_7г/2<^7Г? *о = 2тг;
{-1, -тг ^ я < -тг/2;
ж-тг/3, -тг/2 < ж < тг/2; ж0 = тг/3;
7Г —Ж, 7г/2 ^ Ж ^ ТГ,
д) /(ж) =ех,хе [-7Г, тг], ж0 = -тг.
3.6. Разложите в ряд Фурье заданную функцию /(ж) в
указанном промежутке; постройте графики функции f(x) и
суммы ее ряда Фурье:
alfWJ«. -т/2 < х < тг/2; /тг Зтгу
ajnj~\6, тг/2 < х < Зтг/2, I 2' 2/'
б) /(*) = х3, (0, 2тг); в) /(х) = |х - тг|, (0, 2тг).

Вопросы и задачи 345
3.7. Разложите в ряд Фурье функцию f(x) в промежутке
[—/, I] и постройте графики функции f(x) и суммы ее ряда
Фурье:
{ 0 < х <Г ' " * б>
3.8. Разложите в ряд Фурье функцию /(я), периодически
продолженную на всю числовую ось с периодом 3, постройте
графики функции f(x) и суммы ее ряда Фурье:
1, Кх<2;
3-х, 2^ж<3.
3.9. Найдите комплексную форму ряда Фурье
периодической с периодом тг функции
_ Г cosrr, 0 < х < тг/2;
и сумму полученного ряда в точке х = тг.
3.10. Разложите в ряд Фурье в комплексной форме
периодическую с периодом 3 функцию
(1/2 т —0-
1/9 т = 1-
О, К Ж 3.
3.11. Разложите в ряд Фурье следующие функции на
отрезке [--тг, тг]; постройте графики функций и сумм их рядов Фурье:
a) sin2ж; б) хcosx\ в) ж2.

346 3. РЯДЫ ФУРЬЕ
3.12. Разложите в ряд Фурье следующие функции на
отрезке [—/, /]; постройте графики функций и сумм их рядов Фурье:
а) я3, / = 1; б) shx, / = 2; в) chx, / = 2.
3.13. Разложите в ряд Фурье на отрезке [а, Ь] функцию /(ж),
постройте графики функции и суммы ряда Фурье:
а)/(х) = |х-2|,а = 1,Ь = 3; б) f(x) = (rr-2)3, а = 0, 6 = 4.
3.14. Разложите в ряд Фурье заданную функцию.
Постройте графики функции и суммы ее ряда Фурье:
а) f(x) = < ' . ^ I л в интервале (0, тг) по синусам;
^ U, тг/z < х < тг,
[ 2, (Кя^2;
б) f(x) = < —2, 2 < х ^ 3; на отрезке [0, 4] по синусам;
{ О, 3<х^4,
{О 0<ж<1-
1-х, 1 < х < 3; на отрезке [0, 6] по косинусам;
-2, 3 < х ^ 6,
Г х 0 < х < 1*
г) /(ж) = < ' ^ ^ 9' на отрезке [0, 2] по косинусам;
д) /(х) = < х — 1, 1 ^ х < 2; в интервале (0, 3) по синусам;
I 1 О < г <? %
е) /(х) = х в интервале (тг/2, тг) по косинусам.
3.15. Разложите функцию /(х) = sinax, 0 ^ х ^ тг, в ряд
Фурье по косинусам.
3.16. Разложите функцию /(х) = еах, 0 < х < тг, в ряд Фурье
по косинусам и в ряд Фурье по синусам.
3.17. Докажите, что
Зх2 — бтгж + 2тг2
й -
П=1

Вопросы и задачи 347
00 1 тг2
3.18. Докажите равенство Т] 7—■—тт- = —, используя ра-
п=1(2п-1)2 8
венство Парсеваля для функции
—тг/4, — тг ^ х < 0;
тг/4 0 < т < тг
00 3 — f—l)n 7тг2
3.19. Докажите равенство }2 — 2 = -т«-, используя раз-
п=1 п 12
ложение в ряд Фурье функции
00 1 1
3.20. Докажите равенство £) -——- = -, используя разло-
п=14п -1 2
жение в ряд Фурье функции f(x) = |sinx|.
3.21. Используя сумму ряда Фурье функции f(x) = \х\,
х Е (—1,1), вычисленную в точке xq = 1/4, докажите тождество
f i)n 2п~1 = _^_
^J ; (4n-3)2(4n-l)2 32v^'
3.22. Используя разложение по синусам функции f(x) =
= х(х — тг) в интервале (0, тг), докажите равенство
32'

4. ИНТЕГРАЛ ФУРЬЕ
При изучении рядов Фурье речь шла о представлении
действительных периодических функций, определенных на всей
числовой прямой (или функций, заданных на отрезке),
тригонометрическим рядом вида
оо
— + 2_] {ak c°s wkx + bk sin w kx),
где w — константа, обратно пропорциональная длине отрезка
разложения. В этой главе изучается интеграл Фурье, который
можно считать обобщением ряда Фурье на случай
непериодической действительной функции, определенной на всей числовой
прямой, при котором операция суммирования по
дискретному параметру к Е N заменяется операцией интегрирования по
непрерывному параметру А Е М. Интеграл Фурье, впервые
введенный в 1822 г. Ж. Фурье в книге „Аналитическая теория
тепла" для решения некоторых задач математической физики,
в настоящее время широко используют в прикладной
математике.
4.1. Определение интеграла Фурье
Действительную функцию f{x), заданную на бесконечном
промежутке Xct, называют абсолютно интегрируемой
на X, если она интегрируема на любом конечном отрезке [а, Ь] С
С X, и сходится несобственный интеграл
\f(x)\dx.
X

4.1. Определение интеграла Фурье 349
В качестве промежутка можно взять, например, бесконечный
полуинтервал [а, +оо) или всю числовую ось (—оо, +оо). В
последнем случае также говорят, что функция абсолютно
интегрируема на числовой оси. Заметим, что абсолютно
интегрируемые на R функции являются непериодическими* Для
абсолютно интегрируемой на R функции f(x) рассмотрим
следующие несобственные интегралы с параметром А ^ 0:
+ ОО +ОО
а(А) = - [ f(t)cos\tdt, Ь(А) = - [ f{t)sin\tdt. (4.1)
7Г У 7Г J
-оо
Формулы (4.1), по которым вычисляют функции а(А) и Ь(А),
А ^ 0, называют формулами Фурье.
Поскольку для всех A Е [0, +оо) и х Е R верны оценки
\f(x)coS\x\ < |/(x)|, |/(x)sinAx| < |/(х)|,
+ОО
и интеграл f \f(x)\dx сходится, то на основании признака
—оо
Вейерштрасса равномерной сходимости интеграла по
параметру [VI] несобственные интегралы (4.1) также сходятся,
причем абсолютно и равномерно по параметру А на полуинтервале
[0, +оо). Поэтому функции а(А) и Ь(А) корректно определяются
формулами (4.1) для любого А Е [0, +оо).
Функции а(Х) и Ь(А) непрерывны в промежутке [0, +оо).
Это вытекает из следующего утверждения.
Теорема 4.1**. Пусть функция f(x) абсолютно
интегрируема на R, функция двух переменных р(ж,А) непрерывна на
множестве
Р = R х [а, Ь] = {{х, А) Е R2: х Е R, А Е [а, Ь]}
*3а исключением вырожденных функций, почти всюду на К равных
нулю (см. 7.1).
**Доказательство теоремы см. Д.4.1.

350 4. ИНТЕГРАЛ ФУРЬЕ
и ограничена на нем, т.е. существует такое число М > 0, что
\д{х, А)| ^ М для всех (я, Л) G Р. Тогда функция
+оо
= J g(x,\)f(x)dx
непрерывна на отрезке [а, Ь]. #
Поскольку функции двух переменных cosArr и sinArr
непрерывны и ограничены на R2, значит, и на всяком множестве
Р = Кх[а,Ь], а функция f(x) абсолютно интегрируема на R, то
на основании теоремы 4.1 функции а(А) и Ь(А) являются
непрерывными на всяком отрезке [а, Ь] С [0, +оо), а следовательно, в
любой точке промежутка [0, +оо).
Для абсолютно интегрируемой на числовой прямой R
функции f(x) в соответствии с формулами (4.1) построим
непрерывные на [0, +оо) функции а(А) и Ь(А). Поскольку функция
a(A)cosArc + b(A)sinArc, как функция от А, непрерывна на
множестве [0, +оо) и, значит, интегрируема на любом конечном
отрезке [0, А] С [0, +оо), то можно рассмотреть следующий
несобственный интеграл:
+ОО
ф(х)= (a(\)cos\x + b(\)sin\x)d\, xeR, (4.2)
о
который в зависимости от значений параметра х может как
сходиться, так и расходиться.
Определение 4.1. Пусть f(x) — произвольная
абсолютно интегрируемая на R функция и функции а(Х) и Ь(А), А ^ О,
определены формулами Фурье (4.1). Несобственный интеграл
(4.2), являющийся функцией параметра хЕШ, называют
интегралом Фурье функции f(x).
Не касаясь пока вопроса сходимости интеграла Фурье,
представим его подынтегральную функцию в другом, более удоб-

4.2. Представление функции интегралом Фурье 351
ном виде. Для этого вместо функций а(А) и Ь(А) используем их
выражения из (4.1):
a(A)cosAx + b(A)sinAx =
+00 + ОО
= -( / f(t)cosXtdt) cosAx+-( / f(t)sinXtdt) sinAx =
*\J J *\J J
—oo —oo
+oo +00
= — / /(£)(cosA£cosAx+sinA£sinAxj6fe = — / f(t)cos\(t — x)dt.
-oo
Используя это представление, интеграл Фурье можно
записать в виде
+ОО +ОО
ф(х) = - f d\ f f{t)cos\(t-x)dt. (4.3)
О -oo
4.2. Представление функций интегралом Фурье
Как и в теории рядов Фурье, основной задачей в теории
интегралов Фурье является выявление условий сходимости
интеграла Фурье абсолютно интегрируемой функции /(х) к ней
самой. Для интегралов Фурье верна теорема, аналогичная
теореме 3.11 для рядов Фурье. Упрощая дальнейшее изложение,
будем говорить, что функция f(x) кусочно непрерывна на
бесконечном промежутке X, если эта функция кусочно
непрерывна на любом отрезке [о, Ь] С X.
Прежде чем приступить к обсуждению условий сходимости
интеграла Фурье, докажем следующее утверждение.
Теорема 4.2 (лемма Римана для несобственных
интегралов). Если функция /(х) кусочно непрерывна в
полуинтервале [а, +оо) и абсолютно интегрируема в этом полуинтер-

352
4. ИНТЕГРАЛ ФУРЬЕ
вале, то
+ОО +ОО
lim / f(x) cos(£x) dx = 0, lim / f(x) sin(£x) dx = 0.
f->+oo J ?->+oo J
Выберем произвольное е > 0. Так как функция f(x) абсо-
+00
лютно интегрируема, т.е. интеграл J \f(x)\dx сходится [VI],
+00
то найдется такое число А = А(е) > а, что / \f(x)\dx < е/2.
А
Для любого £ G М имеем
+ОО
f (x) cos(£x) dx
+ОО
f\f{x)\dx<E-.
Согласно лемме Римана для определенных интегралов
(теорема 3.10), примененной на отрезке [а, А], заключаем, что
А
lim f fix) cos(£x) dx = 0. Поэтому найдется такое число В > О,
*+°° А I
f()(£)d\ < |.
а
что при £ > В будет верным неравенство / f(x)cos(£x)dx
'а
Теперь для всякого числа £ > В имеем
+оо . А
f(x)cos(£x)dx
/ f (x) cos(£x) dx
e e
+00
+ ||/(z)cos(£z)dz
A
+00
Это и означает, что lim / f (x) cos(£x) dx = 0.
?-►+<» a
+00
Равенство lim / f(x)sm(£x)dx = 0 доказывается
аналогично. ►

4.2. Представление функций интегралом Фурье 353
Теорема 4.3. Пусть функция f(x) удовлетворяет
следующим условиям:
1) f(x) абсолютно интегрируема на М;
2) f(x) кусочно непрерывна на R;
3) в каждой точке х Е М существуют конечные обобщенные
правая и левая производные.
Тогда для любого х G М интеграл Фурье (4.3) функции f(x)
сходится и имеет место равенство
+00 +00
/(g-O) = 1 Г dx Г
к J J
О -оо
А Для любого положительного числа А рассмотрим
определенный интеграл, зависящий от параметра х:
А +оо
Ф{х,А) = - fd\ f f{t)cos\{t-x)dt.
О -оо
Несобственный интеграл Фурье (4.3) в точке х сходится, если
существует конечный предел lim Ф(х,А), который и будет
значением интеграла Фурье: ~* °°
Ф(х)= lim Ф(х,А). (4.5)
Л->"+оо
Зафиксируем число А > 0. Поскольку для всех £, х и А
и функция f(t) абсолютно интегрируема на R, то, согласно
признаку Веиерштрасса равномерной сходимости интеграла по
+оо
параметру [VI], несобственный интеграл / f (t) cos\(t—x)dt
-оо
сходится в любой точке х G Ш равномерно по параметру А на
отрезке [0, -Ьоо). Это по определению означает, что для любой
точки х G К и любого е > 0 найдется такое число Во(х, е) > 0, что
для всех В\ < —Во(х,е), B<i > Во(х,е) и A G [0, +оо) выполняется

354
4. ИНТЕГРАЛ ФУРЬЕ
неравенство
+00
+оо В2
I f(t)cos\(t-x)dt- If(t)cos\{t-x)dt
<!■
Для таких В\ и B<i имеем
А +оо А В2
fd\ f f(t)cos\{t-x)dt- fd\ f f(t)cos\{t-x)dt
0 -oo
A +00
A +00 B2 A
^ I d\ / f{t)cos\(t-x)dt- I f(t)cos\(t-x)dt ^ ?-d\ = e.
0 -oo B\ 0
Это означает, что для любого х Е М существует предел
А в2
lim - d\ I f(t)cos\{t-x)dt =
B1-+-oo ft J J
A +oo
= - [d\ f f{t)cos\{t-x)dt = Ф{x,A). (4.6)
0 —oo
Выберем произвольные числа В\ < 0 и #2 > 0. Разобьем
отрезок [Si, B2] на конечное число таких отрезков, на каждом
из которых функция /(ж) непрерывна, за исключением, быть
может, концов отрезков. Такое разбиение возможно, поскольку
/(ж) кусочно непрерывна на [J3i, #2]- Пусть [6i, 62] — один из
таких отрезков. Переопределим (если необходимо) значения
функции f(x) на концах этого отрезка так, чтобы функция
f(x) была непрерывна и в этих точках, а значит, и на всем
отрезке [bi, 62]- Это сделать можно, поскольку по определению
кусочно непрерывная функция f(x) может иметь разрывы
только первого рода. Причем при таком переопределении

4.2. Представление функции интегралом Фурье 355
(в конечном числе точек) интегралы не изменятся. Тогда
функция f(t)cos\(t — x) непрерывна на множестве
[bi, Ь2] х [О, А] = {(*, А) е М2: t е [6Ь 62], A е [О, А}}
и можно изменить порядок интегрирования в повторном
интеграле [VI]:
А Ь2 Ь2 А
fd\ I f{t)cos\{t-x)dt= fdt I f(t)cos\(t-x)d\ =
0 bi 61 0
62 A b2
= / dtf(t) / cos\(t-x)d\= / f{t) - '-dt. (4.7)
J J J t—x
61 0 61
Заметим, что
A ( sinA(t — x)
'cos\{t-x)d\=\ ~x ' l*X' (4.8)
{ A, t = x.
Поскольку lim ——-—— = А для любых a, A G 1, то интеграл
A *-*a
f cos \(t—x)d\ является непрерывной функцией переменных t
о
и х при всех значениях этих переменных, в том числе и при
t = х. Эта непрерывная функция, которая имеет вид (4.8), в
t? sin Alt — x)
обозначении входит в подынтегральное выражение в
ь ^~ х
правой части равенства (4.7).
Далее, учитывая свойство аддитивности определенного
интеграла, для всего отрезка [Bi,!^] получаем аналогичное
равенство:
в2 в2
fd\ff{t)co8\(t-z)dt=
^

356
4. ИНТЕГРАЛ ФУРЬЕ
На основании равенства (4.6) имеем
А +оо
Ф(х,А) = - fd\ f f(t)cos\{t-x)dt =
О -оо
В2
В2 +оо
= Bi™ool-[f(t)shiA{!-x)dt=1- [f(trAi*-x)dt=
B2->+oo B
замена переменного
t = и + x, dt ^ du
(x постоянно)
—oo
+OO
-i/
7Г J
sm Аи
-oo
+00
Во втором интеграле сделаем замену и = —v переменного
интегрирования:
0 +00
/., .sinAu , f ,, xsinj
f(u + x) du= / f(x-v)
и J v
sinAv
dv.
Используя это равенство, получаем следующее представление
функции Ф (х, А):
+00
и
+оо
+00
ч\ sin Аи
))
du. (4.9)
Выберем произвольную точку х G Ш. Согласно условию
теоремы, существуют конечные пределы /(ж+0) и /(х—0).

4.2. Представление функций интегралом Фурье 357
+00
sin Аи , тг
Используя интеграл Дирихле
и " 2' Л' v'
о
дробь (/(х+0) + /(х—0))/2 можно представить в виде
2 тг J Vv ' ^v Ч и
о
(4.10)
Вычитая (4.10) из (4.9), находим
Ф(х,А)-^
2
+00
= - / lf(x+u) + f{x-u)) du -
тг J \ /и
о
+оо
-- / f/(^
du =
и
о
Заметим, что функция
при всех х G К является кусочно непрерывной функцией
переменного и в промежутке [0, +оо). Действительно, функции
f{x + и) и f(x — и) кусочно непрерывны на М, так как кусочно
непрерывна функция f(u). Поэтому функция д(х,и) кусочно
непрерывна в интервале (0,+оо), и остается проверить
существование конечного правостороннего предела этой функции в

358 4. ИНТЕГРАЛ ФУРЬЕ
точке и = 0. Но это утверждение, как легко заметить,
эквивалентно существованию во всех точках х Е Ш конечных
обобщенных левых и правых производных
/i-ц-о
что гарантируется условиями теоремы. Однако применить
лемму Римана (см. теорему 4.2) к полученному несобственному
интегралу нельзя, поскольку не известно, является ли функция
д{х,и) абсолютно интегрируемой по переменному и в
промежутке [0, +оо).
Выберем произвольное положительное число S и представим
полученный интеграл в виде суммы трех интегралов:
+оо
Г
+
(д-0) = 1 Г д^и)si
7Г J
где
s
h
1 г
= — / g(x,u)sinAudu,
к J
о
+OO
_ 1 [ f(x+u) + f(x-u) .
(У
+оо
_ /(х+О) + /(х—0) /* sinAw
/3 = / du.
7Г J U
Рассмотрим эти три интеграла. Поскольку функция g(x,u)
кусочно непрерывна в промежутке [0, +оо) и, следовательно,

4.2. Представление функции интегралом Фурье
359
на отрезке [0, <5], то, согласно лемме Римана для определенных
интегралов, интеграл 1\ стремится к нулю при А —> +оо.
Функция (р{х,и) = (f(x+u) + f(x-u))/u в интеграле h при
каждом фиксированном х £ Ш является кусочно непрерывной
функцией переменного и в полуинтервале [5, +оо). Поскольку
для любых и Е [£, +оо) верна оценка
и I д
и функции f(x+u) и f(x—u) абсолютно интегрируемы по
переменному и на IR, то функция (р(х,и) является абсолютно
интегрируемой по переменному и во всем промежутке [5, +оо),
S > 0. Поэтому в силу теоремы 4.2 интеграл /2 стремится к
нулю при А —► +оо.
Наконец, для интеграла /з имеем
+оо
/sin;
11
sinAu
du=
замена
и = t/A,
+ОО +ОО
/Asint dt f sint
-ta = j —dt
И, следовательно,
lim (^i
-►+00 У U
+00 +00
f sinAu
hm / du = hm
Л-++00 J U Л-++00
6 SA
+00
+00
f smt
/ dt = 0,
J t
поскольку интеграл Дирихле / ^-dt сходится (равен тг/2).
о *
Значит, интеграл /з также стремится к нулю при А -* +оо.
Таким образом, учитывая полученные пределы для
интегралов Д, /2 и /з, приходим к следующему выводу:
(Ф(х,
ИЛИ

360 4. ИНТЕГРАЛ ФУРЬЕ
Это означает (см. (4.5)), что при всех х Е R несобственный
интеграл Фурье сходится и равен полученному значению:
+ОО +ОО
Ф(х) = i
О -оо
Заметим, что если х является точкой непрерывности
функции /(ж), то
2 2 /W
и равенство (4.4) принимает вид
+ОО +ОО
/(ж) = - f d\ f f(t)cos\(t-x)dt. (4.11)
О —оо
Следствие 4.1. Если функция /(ж) кусочно
дифференцируема в каждом конечном промежутке числовой прямой М и
абсолютно интегрируема на R, то ее интеграл Фурье (4.3) в
любой точке х G Ш сходится и
+ОО +ОО
л г г f(x
- d\ f(t)cos\(t-x)dt=±±-
-оо
Следствие 4.2. Если функция /(ж) дифференцируема и
абсолютно интегрируема на М, то ее можно представить своим
интегралом Фурье:
+ОО +ОО
f(x) = - f dX I f(t) cos \(t - x) dt, x£R.
Сформулируем еще один часто применяемый на практике
достаточный признак сходимости интеграла Фурье,
аналогичный признаку Дирихле для рядов Фурье.

4.2. Представление функции интегралом Фурье 361
Теорема 4.4. Пусть функция f(x) кусочно непрерывна и
кусочно монотонна в каждом конечном промежутке числовой
прямой R (т.е. удовлетворяет условиям Дирихле на
бесконечном промежутке (—оо, +оо)) и абсолютно интегрируема
на Ш. Тогда в любой точке х Е Ш ее интеграл Фурье сходится
и имеет место равенство
-foo -foo
- [ d\ f f{t)coB\(t-x)dt=^
Пример 4.1. Представим функцию
f(x\ _ J > х \ >
JK ' \ О, х > О
интегралом Фурье. График функции изображен на рис. 4.1.
Функция /(#) имеет
единственную точку разрыва первого
рода х = 0, в промежутке (—оо, 0]
монотонно возрастает, а в
промежутке (0, +оо) постоянна.
Следовательно, в каждом конечном
промежутке числовой прямой R
функция /(#) интегрируема, кусочно непрерывна и кусочно
монотонна.
Проверим абсолютную интегрируемость функции /(#):
-foo 0
[\f(x)\dx= fexdx = ex\°
J J l-<
Таким образом, функция f(x) удовлетворяет условиям
теоремы 4.4 (отметим, что /(#) удовлетворяет и условиям
теоремы 4.3). Поэтому интеграл Фурье функции f(x) в каждой

362 4. ИНТЕГРАЛ ФУРЬЕ
точке х eR сходится к значению (/(#+0) + /(х—0))/2:
+ОО +00
/(0)
-foo О
= - f d\ f e'cosA(*-x)dt.
-оо
-оо -оо
О
Для получения интеграла Фурье в явном виде вычислим
внутренний интеграл, применяя для этого два раза метод
интегрирования по частям:
о о
,х) = I etcos\{t-x)dt = cos\(t-x)det =
-
О
- / e
-оо J
-оо
О О
/ ег8тХ(г-х)(И = со8\х + Х / sin\(t-x)det =
оо -оо
О
— x)\ — А / е*й(втА(^ — х)) =
1-ОО У
^^-x)) =cosAx +
-оо
= cos Ax
' l-oo
—oo
0
= cosAx — AsinAx — A2 / е*cos\(t—x)dt =
—оо
= cos Ах — A sin Ax — А2/(А,х).
Итак, /(А,х) = cos Ах — A sin Ах — А2/(А,х) и, следовательно,
cos Ax — AsinAx

4.2. Представление функции интегралом Фурье 363
Таким образом, для всех х Е R
+00
[ cosAx-AsinAx JX ,, 1ОЧ
dA (4Л2)
И, наконец, поскольку все точки жЕМ, кроме х = 0,
являются точками непрерывности функции /(ж), т.е.
то на множестве R \ {0} функцию /(х) можно представить
следующим образом:
+ОО
., х 1 /* cos Ах — AsinAx ,л
О
причем для всех х G (—оо, 0)
+ОО
1 f cos Ax —AsinAx
о
а для всех х Е (0, +оо)
+оо
1 f cos Ax —AsinAx
-аА = U.
1 I" cos Ах
^У Г
+ А2
о
В точке х = 0 формула (4.12) сводится к следующему:
+оо
/(0+0)+ /(0-0) = 1 _ 1 Г d\
2 ~ 2 ~ тг У 1 + А2'
о
Значение интеграла Фурье 1/2 отличается от значения
функции /(0) = 1.

364 4. ИНТЕГРАЛ ФУРЬЕ
4.3. Интеграл Фурье в случае
четных и нечетных функций
Пусть абсолютно интегрируемая на Ш функция /(х)
является четной:
Д-х) = /(х), а; е (-оо,+оо).
Тогда при любом A Е Ш функция /(х) cos Ах переменного х
является четной на R, а функция /(х) sin Ах — нечетной на R.
Это обстоятельство приводит к следующим формулам для
вычисления функций а(А) и Ь(А) (см. (4.1)):
-foo -foo
а(А) = - / f{t)cos\tdt = - f f{t)cos\tdt, A e R;
7Г J 7Г J
—оо О
-foo
6(A) = - [ f{t)sm\tdt = O.
к J
— 00
В соответствии с определением 4.1 интеграл Фурье четной
функции /(х) принимает вид
-foo
Ф(х) = / (a(A)cosAx + 6(A)sinAx)dA =
о
-foo -foo
= - f cosAxdA I f {t) cos Xtdt, x e R. (4.13)
Если четная функция /(х) удовлетворяет условиям теоремы 4.3
или 4.4, то верно равенство
-foo -foo
2 Г Г /(х+0) + /(х-0)
- / cosAxdA / f{t)cos\tdt=JK 'I K -, xGR.
к J J 2
о о

4.3. Интеграл Фурье в случае четных и нечетных функции 365
Пример 4.2. Представим функцию
f(x) = е
х е (-оо, +оо),
интегралом Фурье. График
функции изображен на рис. 4.2.
Функция f(x) является четной и
дифференцируемой на Ш. Нетрудно
убедиться в том, что она абсолютно
интегрируема:
+оо +оо
Г \f{x)\dx = 2 f e~x2dx<2 f °° el
6 О
На основании следствия 4.2 функцию /(#) = е~х всюду на
R можно представить своим интегралом Фурье, который для
четной функции f(x) = e~x задается формулой (4.13):
f(x) = е
-foo -foo
= - / cosXxdX / e"*2
cosXtdt,
Представим этот интеграл Фурье в явном виде, т.е.
вычислим его внутренний интеграл
+ОО
I(\) = f е~*2 cos \t dt.
Для этого, используя дифференцирование несобственного
интеграла по параметру, составим дифференциальное уравнение,
решением которого является функция /(А). Подынтегральная
функция <p{t,\) = e~* cos At, а также ее частная производная
4>'\{tj\) = — te~t2sinXt непрерывны в области Р = [0, +оо) х R.

366 4. ИНТЕГРАЛ ФУРЬЕ
Кроме того,
И*, А)| ^ в"'2 \<ffx{t, А)| ^ te~t2 (*, A) б Р,
и интегралы от мажорирующих функций е~1 и £е~* сходятся:
-foo +00
[
о о
-foo -foo
+ОО
Поэтому на основании признака Веиерштрасса равномерной
сходимости интеграла по параметру [VI] несобственные
интегралы
+ОО +ОО
/ е~* cosXtdt и / te~l smXtdt
о о
сходятся равномерно по параметру А на всей числовой
прямой М. Следовательно, несобственный интеграл
+ОО +ОО
J(A)= f tp(t,\)dt= Г e~t2cos\tdt
о
является непрерывной и дифференцируемой функцией на R
[VI], а ее производная /'(А) непрерывна на R и определяется
формулой
-foo -foo
' smXtdt.
0
'(A)= f <p'x{t,\)dt = - Г te~t2s

4.3. Интеграл Фурье в случае четных и нечетных функций 367
Применим к интегралу /'(А) формулу интегрирования по
частям:
-foo +00
f +
J'(A) = - f te-t2sin\tdt=^ f s
о
-foo -foo
\ I е~'2 d(sinM) = -5 / е~'2 cosxtdt = -^
Итак, функция /(А) является решением следующего
линейного однородного дифференциального уравнения первого
порядка [VIII]: /'(А) + 1>1{Х) = 0. Это уравнение можно решить
разделением переменных. Имеем
dl A
T = "2dA-
Проинтегрировав обе части уравнения, находим
где С — любая константа, не равная нулю. Последнее
уравнение можно преобразовать к виду / = Се~Л*/4, в котором С
уже может принимать любые значения, так как значение С = О
соответствует решению /(А) = 0, потерянному при разделении
переменных.
Учитывая начальное условие
-foo
(это интеграл Эйлера — Пуассона), находим постоянную
интегрирования С = %/тг/2. Окончательно получаем
/(А) = ^

368 4. ИНТЕГРАЛ ФУРЬЕ
Подставляя найденное выражение для функции /(А) в
интеграл Фурье функции /(х) = е~х , заключаем, что эта функция
имеет следующее представление:
+оо -foo
о ' о
+оо -foo
= - / J(A)cosAxdA = -7= / e"A2/4cosAxdA, x e R. #
я* У V?r У
Пусть абсолютно интегрируемая на действительной
числовой прямой R функция /(х) является нечетной:
j у—х) = — J\x), a;t jr.
Тогда при любом А Е М функция /(х) cos Ах переменного х
является нечетной на R, а функция /(х) sin Ах — четной на R.
Формулы (4.1) для вычисления функций а(А) и 6(А) сводятся к
следующим:
+ОО
а(А) = - Г f(t)cos\tdt = 0;
к У
—оо
-foo -foo
Ь(А) = - [ f{t)sin\tdt=- [ f{t)sin\tdt, A € R.
7Г У 7Г У
-оо О
Интеграл Фурье нечетной функции /(х) принимает вид
-foo
Ф(х) = / (a(A)cosAx + b(A)sinAx)dA =
о
-foo -foo
= - f sinAxdA I f(t)sin\tdt, x € R. (4.14)
о о
Если функция удовлетворяет условиям теоремы 4.3 или 4.4,
то
-foo -foo
2 Г Г /(х+0) +/(х—0)
— / sinAxdA / f(t)sin\tdt = , х G R.
тг У У 2

4.3. Интеграл Фурье в случая четных и нечетных функций 369
Пример 4.3. Представим функцию
/(х) = e~|x|sinx, хеШ,
интегралом Фурье. График функции изображен на рис. 4.3.
Рис. 4.3
Функция /(х) является нечетной и дифференцируемой
всюду на Е. Действительно, во всех точках х ф О функция /(х)
дифференцируема как произведение дифференцируемых
функций е~1х' и sinx, а дифференцируемость в точке х = 0 можно
проверить непосредственно:
w/лч I- e"lAxlsinAx-0 .. _.д,| .. sin Ах
/ (0) = hm = hm e |Ax| hm — = 1.
Дж-»0 Дх Лх->0 Лх-^0 Ах
Кроме того, |e~lxlsinx| ^ e~lxl, x G R, т.е. функция f(x) no
модулю оценивается сверху функцией е~'х1, являющейся
интегрируемой на Ш:
+оо -foo
/г
в dx-2Je
+ 00
= 2.
Поэтому на основании признака сравнения для несобственных
интегралов [VI] функция /(х) = e""lx'sinx является абсолют-

370
4. ИНТЕГРАЛ ФУРЬЕ
но интегрируемой на числовой прямой R и ее, согласно
следствию 4.2, всюду на R можно представить своим интегралом
Фурье, который в данном случае задается формулой (4.14):
+ОО +ОО
f{x) = e"|x|sinx = - I sinAxdA / e"1*1 sin*sinXtdt, iER.
о о
Чтобы представить этот интеграл Фурье в явном виде,
нужно вычислить его внутренний интеграл
+ ОО +ОО
-1*1 . j. • x*jj. f _tCos(l-A)«-cos(l+A)«
dt =
+
f -1*1 . j. • x*jj. f
о о
-boo +oo
о о
Для этого найдем интеграл
+оо
J(6,a)= I e~btcosatdt, aGK, Ь>0,
о
применив дважды формулу интегрирования по частям:
+ОО +ОО
J(6,o)= f e~btcosatdt = ~ f cos at de~bt =
+oo
= \-^ [ e-btsi
b b J
+oo
sinatdt =
+OO
b 62 J
о
о
b b2
о
+OO
-% e"btdsinat =
b1 J
+OO
/

4.3. Интеграл Фурье в случае четных и нечетных функции 371
Из полученного равенства находим
) = -±_.
Таким образом,
+оо
о
+оо
О
И
+оо +оо
I e"wsmtsmXtdt = - \ e"*cos(l - X)tdt-
+оо
О
1 2А
Итак, функцию e~lxl sinrr на всей прямой R можно
представить следующим образом:
+оо
f 2AsinArr
о
+ОО
AsinAa:
Интеграл Фурье был определен для функций, заданных на
всей числовой прямой R. Однако интеграл Фурье четных и

372 4. ИНТЕГРАЛ ФУРЬЕ
нечетных функций можно вычислить, используя значения этих
функций только на положительной полуоси [0, +оо). Очевидно
также, что интеграл Фурье можно определить и с помощью
значения этих функций только на отрицательной полуоси (—оо, 0].
Это наводит на мысль, что интегралом Фурье можно
представить и функции, определенные только на положительной (или
отрицательной) полуоси. Функции, заданные только на одной
полуоси, например на [0, +оо), можно доопределять на другой
полуоси (—оо, 0) любым способом. Вообще говоря, можно
доопределять произвольно (например, нулем), однако, учитывая
простоту выражений интегралов Фурье четных и нечетных
функций (см. (4.13) и (4.14)), более естественным способом
является доопределение функции до четной или нечетной. При
этом в интеграле Фурье для полученной четной или нечетной
функции остается ограничиться рассмотрением того
полуинтервала (—оо, 0] или [0, +оо) значений аргумента гг, в котором
определена исходная функция f(x).
Рассмотрим, например, функцию /(ж), заданную только
на положительной полуоси [0, +оо). Пусть f(x) абсолютно
интегрируема в этом промежутке.
Продолжим функцию f(x) на отрицательную часть
числовой оси так, чтобы полученная функция стала четной, т.е. для
всех х < 0 положим
/(*)=/(-*)■
Доопределенная таким образом функция f(x) задана на всей
числовой прямой R, четна и абсолютно интегрируема на R.
Поэтому ее интеграл Фурье можно вычислить по формуле
(4.13). Если функция f(x) в полуинтервале [0, +оо)
удовлетворяет условиям теоремы 4.3 или 4.4 (кусочно непрерывна,
обладает односторонними производными или кусочно монотонна
на каждом отрезке), то, очевидно, доопределенная на Ш
функция f(x) удовлетворяет условиям теоремы 4.3 или 4.4 на всей
прямой R, и, следовательно, для функции f(x) при х Е [0, +оо)

4.3. Интеграл Фурье в случае четных и нечетных функции 373
выполняется соотношение
+оо +оо
f{x+0) + f(x-0)
= - I cosXxdX I f(t)cos\tdt. (4.15)
(рассмотрены точки х Е [0, +оо), поскольку исходная функция
f(x) определена только на [0, +оо)). В точке х = 0
доопределенная четная функция f(x) имеет, очевидно, равные
односторонние пределы /(+0) = /(—0), поэтому в точке х = 0 это
разложение исходной функции f(x) в интеграл Фурье можно
уточнить следующим образом:
/(+0) = - I dX f f{t) cos Xtdt
о о
Пример 4.4. Представим интегралом Фурье функцию
f(x) =
0,
1
-1 0 1 х
доопределив ее до четной функции
в интервале (—оо, 0). График до- Рис' 4'4
определенной функции изображен на рис. 4.4.
Запишем ее интеграл Фурье
+ОО +ОО +ОО 1
ф(х) = — / cosAxdA / f(t)cosXtdt=— / cos XxdX cos Xtdt
oo oo
и вычислим внутренний интеграл:
sin A
(4.16)

374 4. ИНТЕГРАЛ ФУРЬЕ
1
Поскольку lim(sinA)/A =1, то интеграл f cos Xtdt является
непрерывной функцией от А при всех значениях A G R. Для
краткости функцию (4.16) обозначим (sin А)/А. Тогда интеграл
Фурье доопределенной на R функции f(x) принимает вид
+ОО
_, ч 2 С sinA % 1%
Ф(х) = - / ——cosAzdA,
7Г J А
Доопределенная функция f(x) кусочно непрерывна, кусочно
монотонна на каждом отрезке и абсолютно интегрируема на R,
т.е. удовлетворяет условиям теоремы 4.4, следовательно, верна
формула (4.15). Учитывая, что все точки х Е R, кроме х = — 1 и
х = 1, являются точками непрерывности доопределенной
функции /(#), а также то, что исходная функция f(x) задана только
на положительной полуоси [0, +оо), получаем следующее
представление исходной функции f(x) интегралом Фурье:
/(*) = - /^cosAxdA, xe[0,l)U(l,+oo).
7Г J Л
О
В точке х = 1 интеграл Фурье (4.15) равен
+ОО
2 Г sinA
W "Г
А 2 2
о
и не совпадает со значением исходной функции (/(1) = 1). #
Функцию /(ж), определенную первоначально только на
положительной полуоси (0, +оо) (и абсолютно интегрируемую на
ней), на отрицательную полуось (—оо, 0] можно продолжить до
нечетной, положив
0, х = 0.

4.3. Интеграл Фурье в случае четных и нечетных функций 375
Если первоначально функция f(x) была определена в точке х = О
и имела в этой точке ненулевое значение, то в этой точке ее
придется переопределить, положив /(0) = 0. Доопределенная
таким образом функция f(x) задана на всей числовой прямой
(—оо, +оо), нечетна и абсолютно интегрируема на R.
Поэтому ее интеграл Фурье можно вычислить, используя формулу
(4.14). Если функция f(x) в интервале (0, +оо) удовлетворяет
условиям теоремы 4.3 или 4.4 (кусочно непрерывна, обладает
односторонними производными или кусочно монотонна на
каждом отрезке), то доопределенная функция f(x) удовлетворяет
условиям теоремы 4.3 или 4.4 на всей прямой R. Следовательно,
для функции f(x) при х е (О, +оо) выполняется соотношение
]] (4.17)
(рассмотрены точки х G (0, +оо), поскольку исходная функция
f(x) определена только на (0, +оо)). Заметим, что в точке
х = 0 доопределенная нечетная функция f(x) имеет
противоположные односторонние пределы /(-0) = -/(+0), а разложение
(4.17) представляет собой тривиальное тождество 0 = - / OdA.
* о
Пример 4.5. Представим интегралом Фурье функцию
доопределив ее при х ^ 0
нечетным образом. При этом необхо- у
димо изменить ненулевое значение
функции в точке х = 0 (/(0) = 1), ;~
положив /(0) = 0. График
доопределенной на R нечетной функции
f(x) изображен на рис. 4.5. Рис. 4.5
О
1
-1

376 4. ИНТЕГРАЛ ФУРЬЕ
Запишем ее интеграл Фурье
+оо +оо +оо 1
Ф(х) = - / sinXxdX / f(t)sinXtdt = - / sin XxdX sin Xtdt
о
и вычислим внутренний интеграл:
1 Г 1-cos A
sinXtdt=l A ' ^ ' (4.18)
о I 0, A = 0.
l
Поскольку lim(l — cos A)/A = 0, то интеграл f sin Xtdt
является непрерывной функцией переменного А при всех значениях
A G М. Функцию (4.18) для краткости обозначим (1 — cosA)/A.
Тогда получим
+оо
-cosA .
-sin Ах а А,
+
/ \ 2 / 1
(ж) = - /
тг J
А
о
Доопределенная функция f(x) кусочно постоянна и абсолютно
интегрируема на R, следовательно, удовлетворяет условиям
теоремы 4.3, а значит, верна формула (4.17). Учитывая, что все
точки х Е R, кроме х = 0, х = — 1 и х = 1, являются точками
непрерывности доопределенной функции /(х), а также то, что
исходная функция /(х) определена только на положительной
полуоси (0, +оо), с помощью интеграла Фурье получаем
следующее представление исходной функции /(х):
+оо
1 cos A
■sinXxdX, же (0,1)11(1,+00). (4.19)
Л
0
В точке х = 1, согласно (4.17), имеем
+оо
2> (4-20)
-hoc
«■>-§/

4.3. Интеграл Фурье в случае четных и нечетных функций 377
т.е. значение интеграла Фурье в этой точке не совпадает со
значением исходной функции (/(1) = 1). В точке х = О, как
отмечалось выше, равенство (4.17) вырождается:
0=- / OdA.
о
Значение интеграла Фурье и в этой точке не совпадает со
значением /(ж), поскольку /(0) = 1. #
С помощью интегралов Фурье можно находить значения
некоторых несобственных интегралов. Вычислим, например,
интегралы
J -rdt и j
shrt cost
at.
Первообразные подынтегральных функций этих интегралов не
являются элементарными функциями, поэтому
рассматриваемые интегралы не могут быть вычислены прямым способом (с
помощью формулы Ньютона — Лейбница).
Для вычисления первого интеграла используем функцию из
примера 4.5 и ее представление интегралом Фурье (4.19):
+оо +оо
/1\ 2 fl-cosA . AJX 2 Г
= /(-) = - / sin-dA=~ /
J V2/ 7Г J A 2 n J
замена переменного
A = 2*, *e(0, +cx)),
■5Л
+оо
откуда
!*.J.

378
4. ИНТЕГРАЛ ФУРЬЕ
Второй интеграл можно получить, если воспользоваться
значением интеграла Фурье той же самой функции в точке
х = 1 (см. (4.20)):
+<х>п • 2 А
f2sm
1 2 ri-cosA. AJX 2 f2sinon. А А_,л
- = — / г smAaA = — / —г—-2sm — cos — dX =
2 тг jг А тг У А 22
_8 TsinH
замена переменного
А = 2*, *е(0, +оо),
d\ = 2dt
8 /" sin31cost
о
В результате находим
+ ОО
/
о
sin tcost
it
4.4. Комплексная форма интеграла Фурье
Для дальнейшего изложения рассмотрим некоторые
свойства комплексных функций действительного
переменного, т.е. отображений, область определения которых
является подмножеством R, а область значений — подмножеством
С. Для краткости такие функции будем называть комплекс-
позначными функциями. Отметим, что комплекснозначную
функцию можно рассматривать как частный случай функции
комплексного переменного, у которой и область определения, и
область значений включаются в С.
Всякую комплекснозначную функцию /(х), хЕК, можно
представить в виде f(x) = и(х) + iv(x), где действительные
функции действительного переменного и(х) и v(x)
представляют собой действительную часть Ref(z) и мнимую часть
Im/(z) комплекснозначной функции f(x).
Комплекснозначную функцию f(x)=u(x)+iv(x)
называют ограниченной на множестве X С R, если на этом

4.4. Комплексная форма интеграла Фурье 379
множестве ограничена действительная функция
действительного переменного |/(х)| = y/u2(x) + v2(x), т.е. существует такое
число М > 0, что для всех х Е X выполняется неравенство
|/(х)| ^ М. Очевидно, что действительная и мнимая части
ограниченной комплекснозначной функции являются, в свою
очередь, ограниченными действительными функциями, и
наоборот.
Комплексное число с = a + ib называют пределом
комплекснозначной функции f(x) При X —> Xq И ПИШуТ
lim /(x) = с,
X—»Х()
если действительная функция действительного переменного
|/(х) — с\ является бесконечно малой при х —> хо, т.е.
Ve > 0 36 = 6(е) > 0 Vx e R:
0<|х-х0|<£ => |/(х)-с|<е.
Предел функции /(х) = и(х) + iv(x) при х —> xq существует
и равен с = a + ib тогда и только тогда, когда существуют
пределы lim и(х) = а и lim v(x) = 6. Действительно, так как
X—►Хо X—УХО
то из условия |/(х) — с| —>• 0 при х —> xq следует, что \и(х) —а\—>0
и |v(x) — 6| —> 0 при х —> хо- А это и означает существование
указанных пределов у функций и(х) и v(x). Наоборот, если
lim и(х) = а и lim v(x) = 6, то функции \и(х) — а\ и \v(x) — b\
являются бесконечно малыми при х —> xq. Следовательно,
функция /(х) — с также будет бесконечно малой при х —> хо,
так как
-с\ = v/(u(x)-a)2 + (t;(x)-6)2 ^ \и(х) -а\ + \v(x) - Ь\

380 4. ИНТЕГРАЛ ФУРЬЕ
(здесь мы использовали неравенство Vа2 + Ь2 ^а + b, верное для
любых а, Ь > 0).
Основные свойства пределов действительных функций
(предел суммы, разности, произведения, частного)
распространяются и на комплекснозначные функции.
Комплекснозначную функцию f(x) = u(x) + iv(x)
называют непрерывной в точке xq E R, если lim f(x) = /{xq).
X-tXQ
Из сказанного выше следует, что комплекснозначная функция
f(x) = u(x) +iv(x) непрерывна в точке xq тогда и только тогда,
когда в этой точке непрерывны действительные функции и(х)
и v(x).
Комплекснозначную функцию называют кусочно
непрерывной в некотором промежутке, если кусочно
непрерывными в этом промежутке являются и действительная, и мнимая
части этой функции. Производной комплекснозначной
функции f(x) = u(x) + iv(x) х в точке xq E R называют
предел (если он существует)
х-*хо х — Xq
Из свойств пределов следует, что f'{x) = u'(x) +iv'(x), причем
производная функции f(x) в точке xq существует тогда и
только тогда, когда в этой точке существуют производные
функций и{х) и v(x).
Пусть комплекснозначная функция f(x) = u(x) +iv(x)
определена на отрезке [а, Ь] числовой прямой. Говорят, что ком-
плекснозначнал функция f(x) интегрируема на
отрезке [а, 6], если на этом отрезке интегрируемы ее действительная
и мнимая части и(х) и v(x). При этом определенным
интегралом от комплекснозначной функции f(x) по отрезку
[а, Ь] называют число
ь ь ь
/ f(x)dx= / u(x)dx + i / v(x)dx.

4.4. Комплексная форма интеграла Фурье 381
Аналогично вводят понятие несобственного
интеграла от комплекснозначной функции, рассматривая
несобственные интегралы действительной и мнимой частей этой
+00
функции. Несобственный интеграл f f(x)dx от ком-
а
плекснозначной функции f(x)=u(x) + iv(x), определенной
на промежутке [а, +оо), называют сходящимся, если сходятся
несобственные интегралы
+00 +00
/ u(x)dx и / v(x)dx.
При этом полагают, что
+ОО +ОО +ОО
/ f(x)dx= I u(x)dx + i I v(x)dx.
На определенные и несобственные интегралы от комплекс-
нозначных функций распространяются основные свойства
интегралов от действительных функций. Например,
несобственный интеграл обладает свойством линейности
+ОО +ОО +ОО
/ (af(x)+0g(x))dx = a / f{x)dx + 0 / g(x)dx,
J J J
a a a
где a, /3 e С Кроме того, для обоих типов интегралов имеет
место свойство, связанное с операцией комплексного
сопряжения:
+ОО +ОО
+
f(x)dx= jj(x)dx.

382 4. ИНТЕГРАЛ ФУРЬЕ
Действительно,
+ +
/ u(x) + iv(x)dx = / u(x)dx + i / v(x)dx =
а а а
+ОО +00 +ОО
= / u(x)dx-i / v(x)dx= / (u(x)-iv(x))dx.
+оо
+
Несобственный интеграл J f(x)dx от комплексно-
а
значной функции f(x) = u(x) + iv(x), определенной на
промежутке [а, +оо), называют абсолютно сходящимся, если
сходится несобственный интеграл от действительной функции
+ ОО +00
[ \f(x)\dx= I у/иЦх) + v2(x)dx < +оо.
а а
+оо
Интеграл / f(x)dx от комплекснозначной функции f(x) =
а
= u(x) +iv(x) абсолютно сходится тогда и только тогда, когда
+ ОО +ОО
абсолютно сходятся интегралы J u(x)dx и f v(x)dx от ее
а а
действительной и мнимой частей. Это следует из очевидных
неравенств
|и(яО| < 1/(^)1, \v(x)\ < |/(аО|, \f(x)\ < \и(х)\ + \v(x)\,
которые уже были использованы при обсуждении пределов, и
признаков сходимости несобственных интегралов от
действительных функций [VI].
Как и в случае действительных функций, если
несобственный интеграл от комплекснозначной функции сходится
абсолютно, то он сходится. При этом
+00 +ОО
f(x)dx
J\f(x)\dx.

4.4. Комплексная форма интеграла Фурье 383
Пусть действительная функция f(x) определена на всей
числовой оси R. В случае, когда несобственный интеграл от этой
функции по бесконечному промежутку (—оо, +оо) расходится,
часто используют главное значение этого несобственного
интеграла. Напомним, что так называют предел
+оо А
V.p. Г f(x)dx= lim [ f(x)dx.
J A->+oo J
-оо -A
Символы V.p., указывающие на то, что используется
главное значение несобственного интеграла, берут свое начало от
начальных букв французского выражения valeur principal
(главное значение). Если этот предел существует, то говорят о
несобственном интеграле, сходящемся в смысле
главного значения.
Отметим, что если несобственный интеграл сходится, то
он сходится и в смысле главного значения, причем обычное
значение несобственного интеграла и его главное значение
совпадают. Поэтому для сходящихся интегралов понятие
главного значения на самом деле не дает ничего нового. Главное
значение несобственного интеграла позволяет расширить круг
используемых интегралов, вовлекая в оборот часть расходя-
+00
щихся интегралов. Например, несобственный интеграл f xdx
—оо
сходится в смысле главного значения, так как
7 Аг г*2 +А\
V.p. / xdx= lim / xdx= lim I — 1=0.
J A->+oo J A->+oo V 2 _AJ
-oo -A
Однако в обычном смысле этот интеграл расходится, поскольку
О +оо
расходятся оба интеграла f xdx и f xdx.
-оо О
Пусть комплекснозначная функция f(x) = и(х) + гv(x)
определена на всей числовой оси и интегрируема на любом отрезке

384 4. ИНТЕГРАЛ ФУРЬЕ
[а, Ь]. По определению полагаем, что
+00 +00 +00
V.p. / f(x)dx = V.p. / u(x)dx + iV.p. / v{x)dx,
— OO —00 —00
при этом будем говорить, что несобственный интеграл от ком-
плекснозначной функции сходится в смысле главного значения,
если сходятся в смысле главного значения несобственные
интегралы от действительной и мнимой частей комплекснозначной
функции.
Нетрудно убедиться в том, что и для комплекснозначной
функции понятие сходимости несобственного интеграла в
смысле главного значения расширяет понятие его обычной
сходимости: если несобственный интеграл от комплекснозначной
функции сходится, то он сходится и в смысле главного
значения, причем к тому же самому числу.
Понятие главного значения несобственного интеграла
необходимо для того, чтобы представить интеграл Фурье в
комплексной форме.
Теорема 4.5. Пусть действительная функция f(x)
абсолютно интегрируема на числовой прямой R, а также
удовлетворяет всем остальным условиям теоремы 4.3 или 4.4. Тогда
для всех х € R имеет место равенство
+ОО +ОО
/(х-0) = 1 Г dx Г те-щ^)dt (421)
2тг J J
-00 -00
< Поскольку функция f(x) удовлетворяет условиям теоремы
4.3 или 4.4, то интеграл Фурье (4.3) функции f(x) сходится и
имеет место разложение
+О
к J
+ОО +ОО
dX I f(t) cos X(t—x)dt, x 6 R. (4.22)
о

4.4. Комплексная форма интеграла Фурье 385
Зафиксируем х G R и рассмотрим следующие функции
переменного А е R:
+00 +00
<PxW= I f{t)cos\{t-x)dt, Vx(A)= f f(t)sin\{t-x)dt.
Функция f(x) является абсолютно интегрируемой на R, а
функции vx(t,А) = cosA(£—x) и /ix(t,A) = sinA(t—ж) при всех
х Е R непрерывны и ограничены по совокупности переменных
t и Л в R2, так как
|cosA(t —х)| < 1, |sinA(*-z)| < I, (t, A) GK2.
Согласно теореме 4.1, при всех х G R функции <рх(А) и фх{^)
являются непрерывными в каждой точке A G R и,
следовательно, интегрируемыми на каждом конечном отрезке [А, В].
Кроме того, функция <^х(А) четная:
+
(рх(-Л)= I f{t)cos{-X(t-x))dt =
—оо
+00
= f
—оо
а функция V*x(A) нечетная:
+оо
фх(-\)= f f(t)sin(-\(t-x))dt =
—оо
+оо
= - f f{t
-оо

386 4. ИНТЕГРАЛ ФУРЬЕ
Формула (4.22) означает сходимость (при всех х € R) несоб-
+00
ственного интеграла J ^x(A)dA, причем
о
^/(а?+0) + /(*-0)
2
Так как функция (рх{\) является четной, то ее несобственный
о +оо
интеграл f (px(\)d\ сходится и равен интегралу / <рх
-оо О
Следовательно, при х G R
+оо 0 +оо
( | |
-оо О
+00 +OO
= \v.V. I <px{\)d\. (4.23)
-oo —oo
Для нечетной непрерывной функции ^х(А) при всех А>0
интеграл по симметричному отрезку [—А, А] существует и
равен нулю:
А
[фх{\)с1\ = 0.
-А
Поэтому для всех a;ER сходится в смысле главного значения
+оо
несобственный интеграл f фх (A) dA, причем
—оо
+оо А
V.p. [ фх(\)<1\= lim [фх{\)<1\ = 0. (4.24)
У А->+оо У
-оо -А
+оо
(Заметим, что несобственный интеграл f фх(Х)с1Х в обычном
—оо
смысле может расходиться.)

4.4. Комплексная форма интеграла Фурье 387
Учитывая (4.23) и (4.24), находим
О
+оо m +оо
= ^V.p. I <px(\)d\- ^V.p. I
— 00 —OO
+00
-OO
+OO +OO
f f
= — V.p. I dX J f{t)(cosX(t-x)-ismX{t-x))dt =
— OO —OO
+OO +OO
—OO —OO
При переходе к последнему равенству использована формула
Эйлера [X], согласно которой
cos (-A(t-z)) +isin(-\{t-x)) = e"iA(t"x), А,*,ж е R.
Таким образом, формула (4.21) доказана. ►
Определение 4.2. Интеграл
+ОО +ОО
Ф(х) = 1- V.p. f dX f /(«)е"а('-х) dt, x€R, (4.25)
— OO —OO
входящий в правую часть равенства (4.21), называют
интегралом Фурье в комплексной форме функции f{x),
абсолютно интегрируемой на R.

388 4. ИНТЕГРАЛ ФУРЬЕ
Замечание 4.1. Следует обратить внимание на то, что
формула (4.25) определяет не какой-то новый интеграл Фурье,
а лишь другую, комплексную, форму его записи.
Действительная часть интеграла Фурье в комплексной форме совпадает с
интегралом Фурье в обычной (действительной) форме (4.3), а
его мнимая часть равна нулю.
Замечание 4.2. Как видно из хода доказательства
теоремы 4.5, необходимость использования главного значения
несобственного интеграла в формулах (4.21) и (4.25) возникает
+оо
только потому, что несобственный интеграл f rpx(X)d\ может
—00
расходиться. Если же этот интеграл сходится, то интеграл
Фурье в комплексной форме (4.25) также сходится, и в этом случае
можно вместо (4.21) использовать формулу
+00 +00
-0) 1 Гах (/(()e-gMd(i e€R (426)
2тг J J
-00 -ОО
Кроме того, в силу замечания 4.1 при выполнении условий
теоремы 4.5 действительная часть интеграла Фурье в комплексной
форме всегда сходится. Поэтому при проверке возможности
представления функции интегралом Фурье в соответствии с
формулой (4.26) достаточно проверить сходимость (в обычном
смысле) мнимой части комплексной формы интеграла Фурье.
Замечание 4.3. При получении формулы (4.21) интеграл
(4.24), равный нулю, можно было не вычитать из интеграла
(4.23), а, наоборот, добавлять. Равенство при этом не
нарушается. Это изменение приведет лишь к тому, что в экспоненте
интеграла Фурье в комплексной форме показатель изменит
знак, т.е. в комплексной форме интеграла Фурье показатель
можно выбирать как со знаком минус, так и со знаком плюс.
Общепринятой является формула со знаком минус, т.е.
формула (4.25).

4.4. Комплексная форма интеграла Фурье
389
Пример 4.6. Представим интегралом Фурье в комплексной
форме функцию
У*
f(x)
\0, |*|>f,
l
Рис. 4.6
график которой изображен на
рис. 4.6.
Функция f(x) абсолютно
интегрируема и кусочно постоянна на R, следовательно, она
удовлетворяет условиям как теоремы 4.3, так и теоремы 4.4.
Поэтому ее можно представить интегралом Фурье в
комплексной форме:
+ОО +ОО
f(x+O) + f(x-O)= 1
2 2тг F
d\
—оо —оо
+ОО
-00 -/
В этом интеграле вычислим внутренний интеграл:
e-iA(*-x) /
-Г
-I
Поскольку
e-iX(t-x)
2/,
А = 0.
eiAa:(eiA'
(eiA' -
to
t
iX
2eiXx sin XI
(4.27)
21,
A = 0.

390 4. ИНТЕГРАЛ ФУРЬЕ
Заметим, что
.. 2eiAxsinA/ iXx sinXl OJ
lim = 21 hm etAx hm —-r— = 21.
\->o A a->o a->o XI
Поэтому интеграл (4.27) (а также его действительная и мнимая
части) как функция от А является непрерывной функцией при
всех значениях А Е R. Для краткости обозначим эту функцию
(2егХх sin А/)/А. Тогда с учетом этого обозначения получаем
следующее представление функции f(x):
+00 „
/(аН-0) + /(а;-0)_ 1 ЛТ [ 2etXx sinXI
XI
— ОО
\ + f(x-O)= 1 у Г
2 2тг РУ
+О0
= ^V.p. J^eiXxdX, xeR. (4.28)
-oo
Как мы уже отмечали, интегралы, сходящиеся в смысле
главного значения, могут, вообще говоря, и не сходиться в
обычном смысле при всех значениях х Е К или хотя бы при
некоторых. Поэтому необоснованная замена главного значения
интеграла его обычным значением может привести к ошибке.
Рассматриваемая функция как раз является примером такого
рода: существуют точки х Е М, в которых замена
несобственного интеграла в смысле главного значения несобственным
интегралом в обычном смысле недопустима.
Покажем, что при всех х ф ±/ можно утверждать, что
несобственный интеграл в формуле (4.28) сходится не только в
смысле главного значения, но и в обычном смысле, в то время
как в точках х = ±Z интеграл (4.28) сходится только в смысле
главного значения, т.е. в обычном смысле расходится.
Действительно, согласно замечанию 4.2, достаточно рассмотреть
и исследовать на сходимость мнимую часть интеграла (4.28) —

4.4. Комплексная форма интеграла Фурье 391
интеграл
+00
sin XI sin Хх „ tA ЛЛЧ
-г rfA. (4.29)
7Г J
-oo
Как отмечалось выше, подынтегральная функция непрерывна
при всех А 6 R. Следовательно, для всякого е > 0 существует
определенный интеграл
е
1 fsinXlsinXx,.
— / ^ «А.
тг у А
Исследуем на сходимость несобственный интеграл
+00 +00
1 /1sinA/sinA£ 1 [ cosX(l-x)-cosX(l + x) JX
— / ^^ ал=— / г ал. (4.оО)
тг У А 2тг J X v '
е е
Если х ф ±Z, то этот интеграл представляет собой разность
двух сходящихся несобственных интегралов вида [VI]
+
2тг У
+оо
cosAA
Следовательно, интеграл (4.30) сходится. И в силу нечетности
подынтегральной функции интеграл (4.29) также сходится.
Поэтому при всех хф±1 символы V.p. в формуле (4.28) можно
опустить и рассматривать сходимость интеграла в обычном
смысле.
Если х = / или х = — Z, то интеграл (4.30) представляет
собой разность двух несобственных интегралов, один из которых
+г°сов2А/.. - +r°lj\
вида J —-— dX сходится, а второй вида J -г аХ расходится.
е А е А
Отсюда вытекает, что интеграл (4.30) расходится и, значит,

392
4. ИНТЕГРАЛ ФУРЬЕ
расходится интеграл (4.29). Таким образом, при х = ±1
интегралы (4.29) и (4.28) сходятся только в смысле главного
значения. Итак,
+00
[
7Г J А
-оо
+оо
f
+
1 __ f sin A/ iXx _- . ,
-V.p. / ——-elAxdA, x = ±L
7г У А
Учитывая, что функция f(x) непрерывна всюду на числовой
оси, кроме точек х = ±Z, получаем следующее представление
функции f(x):
+ОО
т.е.
и
+00
. 1 f sinXl iXx , i ,
0=- / —— e%Xxd\, \x\>l,
7Г J A
+oo
f
n J A
—оо
, \x\<l.
В точках х = —I и х = 1 интеграл Фурье рассматриваемой
функции принимает значения
Iv.P.
7Г
+00
2
-оо
которые отличаются от значений функции f(x).

4.5. Преобразование Фурье 393
4.5. Преобразование Фурье
Как показано в примере 4.6, интеграл Фурье в комплексной
форме функции f(x) приводит к представлению этой функции
в виде несобственного интеграла
+ОО
g(X)e dX
-оо
+о<
с некоторой константой С и некоторой функцией з(Л). При
этом функция д(Х) выражается через функцию f(x)
аналогичным интегралом.
Если для комплекснозначной функции f(x) несобственный
интеграл
+ОО
/(А) = ^V.p. I f(t)e-iMdt (4.31)
-ОО
сходится в смысле главного значения при любом Л 6 К, то
определяемую этим интегралом комплекснозначную функцию
/(А) называют прямым преобразованием Фурье функции
f{x). Аналогично функцию
+оо
(4.32)
которая определена на К, если несобственный интеграл
сходится в смысле главного значения при любом Л 6 К, называют
обратным преобразованием Фурье функции f(x).
Отметим также, что прямое и обратное преобразования
Фурье очень близки друг к другу и их можно поменять
местами. Выбор знака минус в показателе экспоненты прямого
преобразования Фурье и знака плюс в показателе экспоненты
обратного преобразования Фурье условный и является лишь
данью традиции.

394 4. ИНТЕГРАЛ ФУРЬЕ
Если комплекснозначная функция f(x) абсолютно
интегрируема наК, то в силу оценок |/(*)е"ш| ^ |/(i)|, |/(*)еш| ^ |/(t)|,
£, А 6 R, несобственные интегралы в формулах (4.31) и (4.32)
сходятся абсолютно при любом Л 6 К и, следовательно,
сходятся. Поэтому в этих формулах можно снять символы главного
значения. В результате формулы прямого и обратного
преобразований Фурье примут вид
+00 +ОО
"x>dt' 7(л) -
Прямое и обратное преобразования Фурье фактически
являются отображениями, область определения и область значений
которых являются некоторыми множествами функций,
определенных на всей числовой оси. Функции выступают как
аргументы преобразований, но в свою очередь имеют аргумент.
Поэтому удобно прямое преобразование Фурье функции f(x)
обозначать через F[/](A), где в квадратных скобках указан
аргумент преобразования Фурье, т.е. функция /, а в круглых
скобках — аргумент функции, которая является образом f(x)
при преобразовании Фурье. Аналогично обозначают и
обратное преобразование Фурье: F"1[/](A).
Бели интеграл Фурье Ф(х) действительной абсолютно
интегрируемой на R функции f(x) сходится в каждой точке я, то
его можно представить в виде композиции прямого и обратного
преобразований Фурье:
+ОО +ОО
Ф(х) = ^-V.p. f d\ !
—оо —оо
+ОО +ОО
Вообще говоря, обратное преобразование Фурье не
является обратным отображением к прямому преобразованию Фурье,

4.5. Преобразование Фурье 395
так как область определения обратного преобразования Фурье
и область значений прямого преобразования Фурье не
совпадают: даже если функция f(x) абсолютно интегрируема, то для
ее преобразования Фурье /(А) обратное преобразование Фурье
^1~1[/]> определяемое формулой (4.32), может и не
существовать. Кроме того, равенство f(x) = F"1 [F[f]] = f означает,
что функция f(x) совпадает со своим интегралом Фурье во всех
точках х 6 К. Но из теоремы 4.4 следует, что существуют
функции, которые в некоторых точках (точках разрыва)
отличаются от своего интеграла Фурье. Тем не менее, если ограничить
область определения прямого преобразования Фурье,
например, абсолютно интегрируемыми непрерывными функциями,
удовлетворяющими условиям Дирихле, то, согласно теореме 4.4,
будем иметь f(x) = F~l [F[/]](z), т.е. отображение, обратное
прямому преобразованию Фурье будет обратным
преобразованием Фурье. Это объясняет, почему два преобразования так
названы.
Описанная связь между прямым и обратным
преобразованиями Фурье позволяет получить для этих преобразований
формулы обращения, т.е. формулы, по которым можно
восстановить функцию по ее прямому (обратному) преобразованию
Фурье.
Теорема 4.6 (теорема обращения преобразования
Фурье). Пусть действительная функция f(x) абсолютно
интегрируема на числовой прямой R, удовлетворяет условиям
теоремы 4.3 или 4.4 и, кроме того, во всех своих точках разрыва
удовлетворяет условию
/(*+0) + /(*-0), (4.зз)
Тогда верна формула обращения прямого
преобразования Фурье
+ ОО
f(x) = -±= V.p. f /(A) eiXx dX, x G R,
v2tt J
-oo

396 4. ИНТЕГРАЛ ФУРЬЕ
а также формула обращения обратного преобразования
Фурье
+00
/(*) = -Lv.p
— 00
^ Формула обращения прямого преобразования Фурье
вытекает из теоремы 4.3 или 4.4 (в зависимости от условий, которым
удовлетворяет функция f{x)). Действительно, если функция
f(x) удовлетворяет условиям теоремы, то, согласно теореме
4.5, ее интеграл Фурье Ф(х) сходится всюду на R, причем
ф(х) = /(ж), х 6 К. Но, как показано выше, Ф(х) = F~l [F[f]] (x).
Поэтому f(x) = F~l [F[f]] (x) = F"1[/(A)](x), что и дает
формулу обращения прямого преобразования Фурье.
Докажем справедливость формулы обращения обратного
преобразования Фурье.
Пусть
+оо
J f(x)eiXxdx, XeR.
+
J
Тогда
+ОО +ОО
I
Это означает, что функция /(А) является прямым
преобразованием Фурье /(ж), т.е. /(А) = /(А). Используя формулу
обращения прямого преобразования Фурье, получаем
+оо
Следовательно,
+00 +ОО
f{x) =Ш= -j= V.P-/ 7(A)e^dA = -1= V.p.y /(A)e-iAxdA.
—оо

4.5. Преобразование Фурье 397
Это доказывает справедливость формулы обращения и для
обратного преобразования Фурье. ►
Теорема 4.6 верна для комплексных функций
действительного переменного (см. 4.7).
Пусть функция f(x) удовлетворяет условиям теоремы
обращения преобразования Фурье. Функцию
+00
= ±J f(t)e-iMdt
называют спектральной функцией исходной функции f(x).
С точки зрения механики функция егХх есть аналитическое
представление гармонического колебания. Поэтому формулу
обращения прямого преобразования Фурье
+оо
/ а(\\л\х.
S(X)etAxd\
-оо
можно понимать как разложение механического движения,
описываемого функцией /(ж), в суперпозицию бесконечного числа
независимых колебаний с различными частотами, а
спектральную функцию 5(Л) — как меру интенсивности отдельных
колебаний, соответствующих различным значениям частот Л.
Пример 4.7. Найдем преобразование Фурье функции (см.
пример 4.6)
JK ' \0, \х\>1.
Поскольку функция f(x) абсолютно интегрируема на К,
ее преобразование Фурье выражается несобственным
интегралом, сходящемся в обычном смысле. Поэтому
+ ОО I
-I

398
4. ИНТЕГРАЛ ФУРЬЕ
Вычислим интеграл при А/0 и преобразуем его, используя
формулу Эйлера:
/(А) = -
1 е
-i\x
\/2тт г\
-I
При Л = 0 получаем
2 sin XI
7Г ^*
2l
Итак,
-I
JsinA/
Л = 0.
Заметим, что функция /(Л) непрерывна при всех Л 6 К.
Вычислим обратное преобразование Фурье функции /(А).
Так как функция f(x) удовлетворяет, например, условиям
теоремы 4.3, а композиция прямого и обратного преобразований
Фурье есть интеграл Фурье, то
Заметим, что образ функции f(x) при последовательном
применении прямого и обратного преобразований Фурье, т.е.
функция F~l [F[f]\ (ж), не во всех точках совпадает с исходной
функцией f(x). Причина этого очевидна — для функции f(x)
не во всех точках выполняется условие (4.33).

4.6. Косинус-преобразование и синус-преобразование Фурье 399
4.6. Косинус-преобразование
и синус-преобразование Фурье
Рассмотрим действительные функции действительного
аргумента. Как показано в 4,3, интегралы Фурье четных и
нечетных действительных функций приводят к
представлениям исходной функции вида
+00 +ОО
С I р(\)соз\х<1\ и С I 7(A)sinAsdA
с некоторой константой С и некоторыми функциями /3(Л) и
7(А). Эти функции выражаются через исходную функцию
интегралами того же вида. Поэтому здесь, как и в случае
интеграла Фурье в комплексной форме, можно ввести прямые
и обратные преобразования, а интеграл Фурье рассматривать
как композицию прямого и обратного преобразований.
Бели действительная функция f(x) абсолютно
интегрируема в промежутке [0, +оо), то определяемые несобственными
интегралами функции
/С(Л) = )jl [ f(x)cos\xdx (4.34)
л— +ОО
Л(А) = у \ J f(x)sin\xdx, (4.35)
о
заданные в промежутке [0, +оо), называют
косинус-преобразованием Фурье и синус-преобразованием Фурье
функции f(x). Для косинус-преобразования Фурье и
синус-преобразования Фурье также используют обозначения FC[/](A) и

400 4. ИНТЕГРАЛ ФУРЬЕ
В силу абсолютной интегрируемости функции f(x) и оценок
\f(t) cosAt| ^ |/(t)|, \f(t) sinAt| ^ |/(t)|, t E [0, +oo), A E R,
несобственные интегралы в (4.34) и (4.35) сходятся абсолютно при
любом А 6 К.
Отметим следующую очевидную связь между
преобразованием Фурье и косинус- и синус-преобразованиями Фурье.
Преобразование Фурье четной действительной функции /(ж),
абсолютно интегрируемой на К, совпадает с
косинус-преобразованием Фурье функции /(ж), рассматриваемой на луче [0, +оо):
+00
— ОО
-1-00 +00
1 +
= —7= / f{x)cos\xdx — i —= / /(x)si
у2тг У v2тг У
—oo —00
+00
= -jL J f(x)cMXxdx = Fc[f]{\), AE[0,+oo)
(здесь использованы свойства четности функции f(x)cos\x и
нечетности функции f(x)sm\x на R). Аналогично
преобразование Фурье нечетной действительной функции /(ж),
абсолютно интегрируемой на R, равно синус-преобразованию Фурье
этой функции, умноженному на комплексное число —г:
+оо
-ОО
+00 +ОО
If I f
= —= I f(x)cos\xdx — i—=z / f(x)sin\xdx =
у2тг У v2тг J
—00
0
f{x)sm\xdx = -iF5[/](A), A 6 [0, +00)
—00
+00
о

4.6. Косинус-преобразование и синус-преобразование Фурье 401
(здесь использованы свойства нечетности функции /(х) cos Ах
и четности функции /(х) sin Ах на Е).
Рассмотрим функцию /(х), определенную в полуинтервале
[0, +оо). Ее можно продолжить на всю числовую прямую R до
четной, положив /(х) = /(—х), х G (—оо, 0), или до нечетной,
положив /(х) = —/(—х), х G (—оо, 0) (во втором случае, возможно,
необходимо переопределить функцию в нуле: /(0) = 0). Если
функция /(х) в промежутке [0, +оо) удовлетворяет условиям
теоремы 4.3 или 4.4, то с помощью этих продолжений и
формул (4.15), (4.17) можно получить разложения функции /(х) в
интеграл по косинусам и по синусам:
+ОО
о
Наконец, если функция /(х), кроме условий теоремы 4.3
или 4.4, во всех своих точках разрыва удовлетворяет условию
(4.33), то для нее верны формула обращения косинус-
преобразования Фурье
г—+ОО
f(x) = yJ\ f /c(A)cos AxdA, x G (0, +oo) (4.36)
0
(в точке х = 0 формула обращения верна, если /(0) = /(+0)) и
формула обращения синус-преобразования Фурье
г—+ОО
f(x) = J1 J £(A)sinAxdA, x G (0, +оо) (4.37)
о
(в точке х = 0 формула обращения верна, если /(0) = 0). Эти
формулы обращения кратко можно записать так:
Fc[Fc[/]]=/ и Fs[Fs[f])=f.

402 4. ИНТЕГРАЛ ФУРЬЕ
Пример 4.8. Функция
/(х) = е"Ьх, ze[0,+oo)
при Ь > 0 абсолютно интегрируема в промежутке [0, +оо).
Поэтому в соответствии с определением косинус-преобразование
функции /(х) имеет вид
I— Н-оо .— +00
FC[/](A) = J- f f{x)cos\xdx= J- f e'bxcos\xdx.
о о
В примере 4.3 был вычислен интеграл
+оо
1(Ъ,а) = / e-bxcosaxdx=T£—г' aGR' Ь>0>
о
С помощью этого интеграла получаем
У| У|^ А€[0,+оо).
Аналогично синус-преобразование функции /(х) имеет вид
(см. формулу (4.35))
. +ОО , +ОО
Fs[f](X) = \ - / f(x)sin\xdx= \ - / e~"5xsinAxdx.
V 7Г J V 7Г J
О О
Используя интеграл I(b,a), для всех a G 1R и Ъ > 0 находим
+ОО +ОО
J(b,a) = / e"5xsinaxdx = -- / sinaxde"bx =
о о
1 +оо 1 +?°
= -rsinaxe"6x +т / e~bxdsmax =
Ь о b J
о
+оо
= ± Г e-bxCQSaxdx="I(ba) = ^_
b J b b "\~cl

4.6. Косинус-преобразование и синус-преобразование Фурье 403
Таким образом,
yf /f^, A€[0,+oc).
Функция f(x) = e 6x, b > О, абсолютно интегрируема в
промежутке [0, +оо), непрерывна в этом промежутке и
дифференцируема в интервале (0, +оо), а в точке х = 0 имеет обобщенную
производную. Таким образом, функция f(x) удовлетворяет
условиям теоремы 4.3. Непрерывность функции означает и
выполнение условия (4.33). Поэтому для нее верны формулы
обращения косинус-преобразования Фурье
I— +оо +оо
-ьх /2 Г ^/хч Л ,Л 2 Г bcosXx f. r_ ч
е и* = а — I /c(A)cosAxaA= — / -75—г^-aA, xGlO,+00),
V тг у тг J и2 ' Х2
о о
и синус-преобразования Фурье
I— +оо
~ь*=v \ I ^
+оо +оо
(в точке х = 0 разложение не выполняется, поскольку функция
f(x) = еГЬх в нуле не равна нулю).
Заметим, что с помощью этих разложений можно вычислить
интегралы Лапласа:
cos ах , тг _аЬ
+оо
У ЬЧх2™~2Ь
о
dx = — е~а\ а > О, Ь > 0;
7
х sin ax тг _аЬ
ix = -е аЬ, а > О, Ь > 0.
Для этого достаточно в полученных выше разложениях
положить х = а и заменить (переобозначить) переменное
интегрирования А на х.

404 4. ИНТЕГРАЛ ФУРЬЕ
4.7. Свойства преобразования Фурье
Отметим некоторые свойства преобразования Фурье.
Теорема 4.7 (теорема о линейности преобразования
Фурье). Если комплекснозначные функции / и д определены и
абсолютно интегрируемы на числовой прямой R, то для любых
комплексных чисел а и /3 справедливо равенство
Ч Очевидно, что из абсолютной интегрируемости функций
/ и д следует абсолютная интегрируемость функции а/ + (Зд
для любых а Е С и /3 Е С. Вычислим преобразование Фурье
этой функции, используя свойство линейности несобственного
интеграла [VI]:
+оо
F[af + (3g}(\) = -^= I {af(t) + /3g(t))e-iXtdt =
+оо
-OO
, A€R. ►
Следует заметить, что аналогичным свойством обладает и
обратное преобразование Фурье.
Покажем, что теорема 4.6 обращения прямого и обратного
преобразований Фурье, доказанная для действительных
функций, верна и для комплексных функций. В самом деле, если
комплексная функция f(x) = u(x) +iv(x) удовлетворяет
условиям теоремы 4.6, то этим же условиям будут удовлетворять
действительные функции и(х) и v(x). Следовательно, для них
справедливы формулы
F-1[F[u]}=u, F-l[F[v]] = v, F[F-l[u]]=u, 1

4.7. Свойства, преобразования Фурье 405
Отсюда в силу доказанной линейности преобразований
Фурье имеем
= F-1 [F[u + iv}] = F'1 [F[u] + iF[v]] =
= F'l[F[u]] + iF'l[F[v]] = ti + iv = /,
Теорема 4.8. Бели комплекснозначная функция f(x)
определена и абсолютно интегрируема на числовой прямой R, то
ее преобразование Фурье /(А) является непрерывной и
ограниченной функцией на R. Кроме того, если функция f(x) кусочно
непрерывна на прямой R, то выполняется равенство
lim /(A)= lim /(A)=0.
Л—>+оо Л—>—оо
Ч Докажем сначала теорему для действительной функции f{x).
Непрерывность функции
+00
-00
+ОО +ОО
= -^= [ f{t)cos\tdt-i-l= [ f(t)sin\tdt
у2тг J V2tt J
— 00 —OO
на R непосредственно следует из теоремы 4.1, поскольку
функция f(t) абсолютно интегрируема на R, а функции cos Xt и sin At
непрерывны на R2 по переменным А и t и ограничены на R2
(|cosAt|<l, |sinAt|<l, A,teR).
Стремление к нулю на бесконечности функции /(А), т.е.
условие
lim /(A) = О,
Л->оо

406 4. ИНТЕГРАЛ ФУРЬЕ
в силу кусочной непрерывности функции f(t) вытекает из
теоремы 4.2 (леммы Римана для несобственных интегралов).
Ограниченность функции /(А) на R следует из оценки
+00
j=
f{t)e~iXtdt
—00
+ОО
-L
+оо. (4.38)
Пусть теперь /(х) = u(x) + iv(x) — комплексная функция.
Бели /(х) абсолютно интегрируема на R, то в силу оценок
функции и(х) и v(x) также абсолютно интегрируемы на R.
Кроме того, из кусочной непрерывности функции /(х) = и(х) +
+ iv(x), согласно определению, следует кусочная непрерывность
функций и(х) и v(x). В этом случае действительные функции
и(х) и v(x) удовлетворяют условиям данной теоремы и,
следовательно, их преобразования Фурье подчиняются доказанным
выше свойствам непрерывности, ограниченности и стремления
к нулю на бесконечности. Воспользуемся этими свойствами.
Во-первых, на основании теоремы 4.7
F[f)(X) = F[u + iv](\)=F[u)(X) + iF[v](X)
и, следовательно, функция /(А) = F[f](X) непрерывна как
сумма двух непрерывных функций F[u](A) и iF[v](A).
Во-вторых,
lim F[f]{\) = lim F[u + iv](\) =
А-юо А-*оо
= lim (F[u]{\) + iF[v](\j) = lim F[u](X) + i lim FM(A)=O,
A-*oo\ / A-foo A->oo
т.е. функция /(А) = F[/](A) стремится к нулю на бесконечности.
Ограниченность /(А) на R можно доказать с помощью той
же оценки (4.38) для интегралов, которая справедлива и для
комплексной функции f(t). ►

4.7. Свойства преобразования Фурье 407
Замечание 4.4. Можно показать, что доказанное для
абсолютно интегрируемой кусочно непрерывной функции f(t)
равенство lim /(A) = 0, вообще говоря, верно и для функций
А-*оо
), обладающих липш свойством абсолютной
интегрируемости. #
Часто в прикладных задачах приходится вычислять
преобразования Фурье не от самой функции /(х), а от ее
производных. Оказывается, существует простая взаимосвязь между
преобразованиями Фурье функции f(x) и ее производных.
Прежде чем перейти к изучению данного вопроса, докажем лемму.
Лемма 4.1. Пусть действительная функция /(х), а также
ее производная f'(x) непрерывны и абсолютно интегрируемы
на R. Тогда функция f(x) на бесконечности стремится к нулю:
/()
z-юо
4 В силу формулы Ньютона — Лейбница имеем
хек.
Поскольку функция f'(t) абсолютно интегрируема на R, то
+оо О
несобственные интегралы f \f'(t)\dt и f \f'(t)\dt сходятся,
О +оо -оо О
а значит, сходятся и интегралы / f(t)dt и J f'(t)dt [VI].
О —оо
Таким образом, существуют конечные пределы
+оо О
lim /Ы = /(0)+ I f'{t)dt и lim /(х)=/(0)- / f'(t)dt.
z-*+oo J х->-оо J
О —оо
Докажем, что оба эти предела равны нулю. Допустим, что
хотя бы один из них не равен нулю, например первый:
lim /(ж) = С, С т^О.

408 4. ИНТЕГРАЛ ФУРЬЕ
Тогда, согласно теореме о сохранении функцией знака своего
(ненулевого) предела [1-8.4], найдется такое число М > 0, что
для всех х > М выполняется неравенство f(x) ^ С/2 > 0 (С > 0)
или f(x) ^ С/2 < 0 (С < 0). Другими словами, для всех х > М
выполняется неравенство
Отсюда на основании признака сравнения для несобствен-
+00
ных интегралов [VI] получаем J \f(t)\dt = +оо. Следователь-
м
но,
+оо М +оо
/ I I
\f(t)\dt= I \f(t)\dt+ I \f(t)\dt = +оо,
-oo -oo M
что противоречит условию абсолютной интегрируемости
функции / на прямой R.
Рассуждая аналогично, получаем противоречие и в случае,
когда не равен нулю второй предел. Таким образом,
предположение неверно и действительно оба предела равны нулю:
lim /(ж) = 0, lim /(x) = 0. ►
Теорема 4.9 (теорема о преобразовании Фурье
производной). Если комплекснозначная функция / и ее
производные до n-го порядка включительно существуют, непрерывны и
абсолютно интегрируемы на числовой прямой R, то
справедливы следующие равенства:
F[f{k)) = (iX)kF[f\, k=T^i. (4.39)
< Докажем теорему для случая п = 1. Пусть функция f(t) и ее
производная первого порядка ff(t) определены, непрерывны и
абсолютно интегрируемы на всей числовой прямой R.
Рассмотрим случай, когда функция f(t) действительная.
Вычислим преобразование Фурье от производной /'(х),
применяя метод интегрирования по частям для несобственного

4.7. Свойства преобразования Фурье 409
интеграла:
+ОО +ОО
//
—оо
+оо
—оо
+оо
Здесь использованы равенства
е-ш/()+°°
/(*)+°°= _ип^(е"ш/(*))- И™ (с"ш/(*)) =0-0 = 0,
которые выполняются, поскольку функция е~*Л* ограничена по
модулю, а функция /(£) в силу леммы 4.1 стремится к нулю на
бесконечности:
lim /(*) = 0, lim f(t) = O.
Пусть функция /(t) является комплекснозначной, т.е. f(t) =
= u(t) +iv(t), где u(t) и v(t) — действительные функции. Тогда,
согласно теореме 4.7 и формуле (4.39), для действительных
функций имеем
F[f'] = F[u' + iv'] = F[u'] + iF[v'] = i\F[u] + i(t A) F[v] =
= i\(F[u] + %F[v]) = i\F[u + iv] = i\F[f].
Итак, теорема для случая п = 1 доказана. Справедливость
формулы (4.39) для произвольного n G N можно доказать с
помощью метода математической индукции. ►
Пример 4.9. Найдем преобразование Фурье функции

410 4. ИНТЕГРАЛ ФУРЬЕ
Поскольку знаменатель 62+х2 рациональной функции /(х) =
= 1/(Ь2+х2) ни при каком х G R не обращается в нуль, то эта
функция непрерывна и бесконечно дифференцируема на всей
числовой прямой R. В частности, ее первые шесть производных
существуют и также непрерывны на R. Кроме того, функция
/(х) абсолютно интегрируема на R:
+00
О "| X j \s \ <ju ■* v v ' I — OO
-00 -00
Нетрудно показать, что производная n-го порядка функции
/(х) = 1/(Ь2 + х2) при х -¥ оо эквивалентна функции 1/х2+п.
Следовательно, все производные (в том числе первые шесть)
также абсолютно интегрируемы на Ш [VI]. В силу теоремы 4.9
имеем
Вычислим преобразование Фурье функции /(х). Поскольку
эта функция является четной, то ее преобразование Фурье
совпадает с косинус-преобразованием Фурье:
Полученный интеграл, являющийся интегралом Лапласа,
был вычислен ранее (см. пример 4.8):
+ОО
о > 0.
Поэтому
+оо
caa\\\t , [2 тг _

4.7. Свойства преобразования Фурье 411
Окончательно получаем
F[<p}(\) = (i\)6F[f](X) = (гА)6У|^ = _y|£e-W\ A € R.
Теорема 4.10. Бели комплекснозначная функция / и ее
производные до n-го порядка включительно существуют,
непрерывны и абсолютно интегрируемы на числовой прямой R,
то ее преобразование Фурье /(А) = .F[/](A) удовлетворяет
условию
Функция / удовлетворяет условиям теоремы 4.9, поэтому
№] = (i\)nF[f], откуда заключаем, что
д Л/о.
Следовательно,
()|^, А^О. (4.40)
Поскольку по условию функция /(п)(ж) непрерывна и абсолютно
интегрируема на R, то в силу теоремы 4.8 lim F[f^](X) = 0,
или lim |-Р[/(п)](А)| =0. С учетом этого равенства из (4.40)
А-юо
получаем, что
oo.
Теорема 4.11. Если комплекснозначная функция f(x)
непрерывна на R, а функции /(ж), ж/(ж), ..., xnf(x) абсолютно
интегрируемы на R, то преобразование Фурье F[f](X) имеет на
R производные до n-го порядка включительно, причем
= (-i)kF[xkf(x)](X), Л = М. (4.41)

412 4. ИНТЕГРАЛ ФУРЬЕ
Ч Докажем теорему для случая п = 1 и действительной
функции. Пусть действительная функция f(x) непрерывна на
числовой прямой R и функции f(x) и xf(x) абсолютно интегрируемы
на R. В силу абсолютной интегрируемости функции f(x)
существует ее преобразование Фурье F[f](\), причем, согласно
теореме 4.8, функция F[f](X) непрерывна на R. Докажем,
что она дифференцируема на R. Функции двух переменных
f(t)e~iXt и А(/(*)е"ш) = -itf(t)e'iXt непрерывны на R2.
Кроме того, в силу равенства
и абсолютной интегрируемости функции £/(£), а также
признака Вейерштрасса равномерной сходимости интеграла по па-
+оо
раметру [VI] несобственный интеграл f tf(t)etdt сходится
—оо
равномерно по параметру Л на R. Поэтому, согласно теореме
о дифференцировании несобственного интеграла по параметру
[VI], функция F[f](X) является дифференцируемой на R,
причем для всех А Е R
+оо
+оо ;
—оо
+оо
-00
tf{t)e-iMdt = -iF[xf{x)]{\).
Пусть функция f(t) является комплекснозначной, т.е. f(t) =
= u(t) + iv(t)j где u(t) и v(t) — действительные функции. Тогда
на основании теоремы 4.7 и полученной выше формулы для

4.7. Свойства преобразования Фурье 413
действительных функций имеем
= -iF[xu{x)](\) + i(-%F[xv
= -iF[xu(x) + ixv{x)](X) = -iF[xf(x)](\), A € R.
Итак, теорема для случая п = 1 доказана. Справедливость
формулы (4.41) для произвольного n Е N можно доказать с
помощью метода математической индукции. ►
Пример 4.10. Найдем преобразование Фурье функции
ф)=х2е~\х\у хеШ.
Функция f(x) = e"lxl непрерывна на R, а функции же"Iх' и
я2е~'х' абсолютно интегрируемы на R. Поэтому в силу теоремы
4.11 верно равенство
И/](А))" = (-i)2F[x*f(x))(\) = -
Отсюда
Функция /(х) = е~1х', rr G R, является четной, поэтому ее
преобразование Фурье ^[/](А) совпадает с ее
косинус-преобразованием в промежутке [0, +оо). Учитывая результаты
примера 4.8, получаем
I— +о° I—
= yjlj e~*cos\xdx = yj± ^1^, A e R
Следовательно,

414 4. ИНТЕГРАЛ ФУРЬЕ
Таким образом, окончательно имеем
г, AeR. #
При решении многих задач, связанных с
дифференциальными уравнениями, часто приходится рассматривать
специальную операцию над функциями. Сверткой функций /ид,
заданных на R, называют функцию
+00
f*g(x)= j f(t)g(x-t)dt,
при условии, что интеграл справа сходится при всех х Е R.
Теорема 4.12. Если функции f и д непрерывны,
ограничены и абсолютно интегрируемы на всей прямой R, то свертка
/ * 9 функций / и д также непрерывна, ограничена и абсолютно
интегрируема на всей прямой М, причем
F[f*g] = VtoF[f]F\g]. #
Таким образом, преобразование Фурье свертки функций /
и д есть произведение преобразований Фурье функций /ид.
Дополнение 4.1. Некоторые свойства
несобственных интегралов с параметрами
Пусть действительная функция <р(я,А) двух переменных
определена на множестве
Р={{х, \)еШ2:х(ЕХ, Л ЕЛ},
где X и Л — некоторые числовые промежутки. Функцию
(/?(£, А) называют равномерно сходящейся по переменному

Д.4.1. Несобственные интегралы с параметрами 415
х на множестве X к функции гр(х) при стремлении Л -> Ао,
Ао Е Л, если
Ve>0 3<J = <J(e)>0 УАбЛ VsEX:
0<|А-А0|<<* => \<р(х,\)-ф(х)\<е.
Равномерная на множестве X сходимость функции (р{х,\)
к ф(х) при А -> Ао отличается от сходимости <р(х,\) к ф(х)
в каждой точке х Е X тем, что величина <$, существование
которой декларируется в определении сходимости, зависит
только от е и не зависит от х Е X (т.е. одинаковая для всех
х € X), в то время как при сходимости в каждой точке х Е X
эта величина зависит от е и, вообще говоря, от х Е X. Факт
равномерной на множестве X сходимости функции <р{х,\) к
функции ф(х) при А -> Ао обозначают следующим образом:
<p{x,\)=*il>(x), A-»A0.
л
Напомним, что сходящийся в каждой точке А Е Л С R не-
+оо
собственный интеграл / (p(x,\)dx называют равномерно схо-
а
дящимся по параметру А на множестве Л [VI], если
+00
УАеЛ: / <p(x,\)dx
А
<е
(т.е. величина А(е) одинаковая для всех А Е Л). Понятие
равномерной сходимости несобственного интеграла естественным
образом можно свести к понятию равномерной сходимости
+00
функции двух переменных: интеграл / <p(x,\)dx сходится
а
равномерно на множестве Л тогда и только тогда, когда
t +00
, А) = I <p(x, \)dx=Z I <p(x, A) dx, t -» +оо.

416 4. ИНТЕГРАЛ ФУРЬЕ
Теорема 4.13 (теорема о предельном переходе под
знаком несобственного интеграла). Пусть функция <р(х,А)
определена на множестве Р = {(я, Л) Е К2: х ^ а, А Е Л}, где
ЛсМ, функция ф(х) — в промежутке [а, +оо) и функция
у>(я,А) сходится к функции ф(х) при Л —> Ло равномерно по
переменному х на любом конечном отрезке [а, Л], Ао Е Л:
(р{х,\)£ф{х).
[а,А]
+оо
Кроме того, пусть несобственный интеграл f tp(x,\)dx схо-
а
дится равномерно по параметру Л на множестве Л; на каждом
конечном отрезке [а, А] функция ф(х) интегрируема и несоб-
+00
ственный интеграл f ф(х)(1х сходится. Тогда
а
-t-oo -t-oo +оо
lim / ip(x,\)dx= / ф(х)<1х= / ( lim (p(x,\))dx.
А->Ло J J J \A->Ao /
< Выберем произвольное е > 0. В силу определения равно-
+оо
мерной сходимости несобственного интеграла / <p(x,\)dx по
а
параметру Л на множестве Л найдется такое число Д = Д (е) ^ а,
что для любого числа А > Д(е) и любого Л Е Л выполняется
неравенство
+оо
ф,\)ёх
(4.42)
А +оо
+
Из условия сходимости несобственного интеграла f \p(x)dx
а
следует, что существует такое число До = До(^) ^ а>
любого числа А > До(^) верно неравенство
+оо
\j){x)dx
(4.43)

ДАЛ. Несобственные интегралы с параметрами
417
Выберем А > тах(Д(е), До(е)). Тогда справедливы оба
неравенства (4.42) и (4.43), причем (4.42) выполняется для всех
Л £ Л. Согласно условию теоремы, на отрезке [а, А] имеет место
равномерная сходимость:
), А->А0.
[а, Л]
В частности, это означает, что для е = е/(3(А—а)) > 0 найдется
такое число 5(е) > 0, что для любого Л Е Л, удовлетворяющего
неравенству 0 < |А — Ло| < S(s), и любого х Е [а, А] выполняется
соотношение
\ср{х,\)-ф(х)\<ё =
З(А-а)"
(4.44)
Используя арифметические свойства и свойства оценок по
модулю несобственных интегралов [VI], для всех Л Е Л,
удовлетворяющих неравенству 0 < |Л — Ло| < S(e), имеем
+оо
+оо
— / \))(x)dx
a
+00
А +
= / (p(x,\)dx+ / (p(x,\)dx- ip(x)dx- / ip(x)dx
a A a A
A +oo +oo
< \j(y(x,\)-x/>(x)) dx+\J <p(x,\)dx + I J 4>(x)dx
a A A
A +oo H-oo
^ l\ip{x,\)-il)(x)dx dx+ / (p(x,\)dx +\ / fp(x)dx
A A
e e
- + -

418 4. ИНТЕГРАЛ ФУРЬЕ
(в последнем неравенстве учитывались оценки (4.44), (4.42) и
(4.43)). Полученная оценка означает, что, согласно определе-
+00 +ОО
нию предела по Копш, lim / (p(x,\)dx = / i/>(x)dx. ►
А>Ао
Докажем теорему, из которой следует теорема 4.1.
Теорема 4.14. Пусть выполняются условия:
1) действительная функция /(я) абсолютно интегрируема
на [0, +оо);
2) действительная функция р(я,А) двух переменных
непрерывна на множестве Р = {(я, А) Е R2: я ^ О, А Е [а, Ь]};
3) функция </(я,А) ограничена на множестве Р, т.е.
существует такое число М > О, что для всех (я, А) Е Р выполняется
неравенство |</(я,А)| ^М.
Тогда функция
+ОО
^р(Х)= J g(xJ\)f(x)dx (4.45)
о
непрерывна на отрезке [а, Ь].
< Докажем, что в каждой точке Ао Е [а, Ь]
lim <р{\) = ip(^o)i
А->Ао
или
+ ОО +ОО
lim g(x,\)f(x)dx= g(x,\0)f(x)dx.
А->А0 J J
О О
Проверим, что для функций у>(я,А) = р(я,А)/(я) и ф(х) =
= р(я,Ао)/(я) выполняются условия теоремы 4.13 о предельном
переходе под знаком несобственного интеграла. Во-первых,
функция (р(х, А) определена на множестве Р, а функция ф(х) —
при я ^ 0. Во-вторых, абсолютная интегрируемость функции
/(я) на [0, +оо) предполагает ее интегрируемость на всяком

ДАЛ. Несобственные интегралы с параметрами 419
конечном отрезке [О,-А], а значит, и ограниченность [VI].
Поэтому
ЗКА>0 Ухе [0, A): \f(x)\^KA. (4.46)
Функция двух переменных д(х,\) непрерывна на множестве
Р. Следовательно, она непрерывна и на прямоугольнике Ра =
= {(ж, Л) Е R2: х Е [О, А], А Е [а, 6]}сР, где А — произвольное
положительное число. Прямоугольник Ра является
компактным множеством в R2 [1-5.6]. Поэтому функция р(ж,А),
непрерывная на компакте Рд, равномерно непрерывна на нем.
Следовательно, для всякого е > 0 найдется такое 6 = 6(е) > О,
что для любых (ж, Л) Е Ра и (ж;, Л;) Е Рд, удовлетворяющих
условию
выполняется неравенство
где константа А'д взята из (4.46). В частности, для
произвольного х е [О, А] и любого А Е [а, Ь], удовлетворяющего условию
|А — Ао| < <5(е), имеем
|ff(z, А)-<,(*, Ао)|<-^, (4.47)
так как в этом случае р((х, A), (rr, Aq)) = |А — Ао| < 8(е).
Выбрав произвольное е > 0, определяем, как указано выше,
число S = 6(е) > 0. В результате с учетом соотношений (4.46) и
(4.47) получаем, что для любого А Е [а, Ь], |А — Ао| < 6{e)i и для
всех х Е [0, А] выполняется неравенство
Их, А) - г!>(х)\ = \g(x,\)f(x) -g(x,\0)f(*)\ =
YlKA=t. (4.48)

420 4. ИНТЕГРАЛ ФУРЬЕ
Соотношение (4.48) и определяет равномерную на отрезке [0, А]
сходимость функции tp{x,\) к функции ф(х) при Л ->- Ао. А это
есть второе условие теоремы 4.13.
Наконец, поскольку
\g(x,\)f(x)\<M\f(x)\, (x,X)eP,
и, в частности,
\g(x,X0)f(x)\^M\f(x)l xG[
а функция Mf(x) абсолютно интегрируема на [0, +оо), то,
согласно признаку Вейерштрасса [VI] равномерной сходимости
несобственных интегралов, интеграл (4.45) сходится
равномерно по параметру Л на множестве Л = [а, Ь], функция ф(х)
интегрируема на каждом конечном отрезке [0, А] и несобственный
+оо
интеграл J i/>(x)dx сходится.
о
Итак, для функций <р{х,\) =g(x,\)f(x) и ф(х) = g(x,\0)f{x)
выполняются все условия теоремы 4.13 о предельном переходе
под знаком несобственного интеграла. На основании этой
теоремы для любой точки Ао Е [а, Ь] имеем
+00
lim <р(\) = lim / g(x,\)f{x)dx =
Л—>Ло А->Ао J
О
+ОО +ОО
= I (\im^g(x,\) /(rr)) dx = I g(x,\0)f{x)dx =
что и означает непрерывность функции <р(\) на [а, Ь]. ►
Покажем, что из доказанной теоремы вытекает теорема 4.1.
Пусть функции f(x) и д(ж, А) удовлетворяют условиям теоремы
4.1, т.е. функция f(x) абсолютно интегрируема на R, а функция

Вопросы и задачи 421
д(х,\) непрерывна и ограничена на множестве Р = R x [а, 6].
Имеем
+оо 0 +оо
= f 9{x,\)f{x)dx = Jg(x,\)f{x)dx + fg(x,X)f{x)dx =
—oo —oo 0
= J g(-x,\)f(-x)dx + J g{x,\)f(x)dx
Функции /(ж), д(х,\) и /(—я), д(—я, А) удовлетворяют условиям
теоремы 4.13. Поэтому функции <£i(A) и <£2(А) непрерывны на
[а, 6]. Следовательно, непрерывна на [а, Ь] и функция <р(А).
Вопросы и задачи
4.1. Представьте функцию f(x) интегралом Фурье:
— 1 1 < х < 2'
а) /(*) = { 2,' -0<*<'l; б) /(*) =—1_, а / 0;
в) № = ( n w > ч5 г) •^(rr) = e"e|x| cos6a:' а > 0;
^ U, \Х\ ^ О,
о
д) /(ж) = sgn(:r-a) - sgn(z-b), a < 6; е) /(ж) = хе~~х
4.2. Представьте интегралом Фурье функцию /(ж),
продолжив ее четным образом на интервал (—сх), 0):
о, x>i; 6)/w={T ЛТ
5
1, 0^ж^1;
2, 1<я^2;
0, ж > 2.

422 4. ИНТЕГРАЛ ФУРЬЕ
4.3. Представьте интегралом Фурье функцию /(ж),
продолжив ее нечетным образом на интервал (—оо, 0):
ч ., ч f cosrz, О^я^тг; х\ г, \ J 1 ^ /о
1 U' Ж>7Г' [О, х>2.
4.4. Представьте функцию f(x) интегралом Фурье в
комплексной форме:
х<0| а>0.
4,5. Найдите преобразование Фурье функции f{x):
в) /(ж) = е * /2cosaz; з) f(x) = | ^ j^j J ^
г) /(ж) =же-2'х1; и) /(ж) = x2e-Nsinba:;
д) /(я) = (ze-2l*l)'; к) /(х) = 2e"l2/2 + Заге"2^!.
4.6. Найдите косинус-преобразование Фурье и
синус-преобразование Фурье функции /(ж):
2, (К а: О; Г cos2x, 0<я<£;
0, х>2; { °' х>2-
4.7, Докажите справедливость следующих равенств:
б) F[eito/(x)](A) = F[/(x)](A - 6), 6 е К;

Вопросы и задачи 423
в) F[/(x - 6)](А) = e-"AF[/(x)](A), 6 € К;
г) ^[созбх/(„](Л, = n/W1(A-*) + nrWl(A + »i 46„.
Л ГНп6х/(х)](Л) = ПГ(.)](**)ПА(«)1(Л + *)| 6€R.
4,8, Найдите преобразование Фурье функции

5. РЯДЫ В НОРМИРОВАННЫХ
ПРОСТРАНСТВАХ
Понятия линейного и евклидова пространств известны
читателю из курса линейной алгебры [IV]. Введение в линейном
пространстве нормы элемента позволяет наделить это
линейное пространство структурой метрического пространства [I].
При наличии же метрики можно распространить на
нормированные пространства такие метрические (т.е. требующие
умения определять „близость" элементов) понятия, как сходимость
последовательностей, непрерывность и дифференцируемость
функций и др. В частности, на линейные пространства с
нормой переносится и теория рядов: можно определить понятие
ряда, а при наличии нормы (и, значит, метрики) поставить и
проанализировать важнейшие вопросы их сходимости.
5.1. Нормированные пространства
Действительное (комплексное) линейное пространство L
называют нормированным пространством, если в этом
пространстве задана норма, т.е. функция, которая каждому
элементу х е L ставит в соответствие действительное число ||ж|| и
которая удовлетворяет аксиомам нормы:
1) ||гег|| ^ 0, причем равенство ||х|| = 0 возможно только при
х = О*
3) ||я + у|| ^ Ikll + IMI (неравенство треугольника).
Из неравенства треугольника вытекает следующее полезное
неравенство:
Н*-у||, х,уеь. (5.1)

5.1. Нормированные пространства 425
Иногда в одном линейном пространстве рассматривают
несколько норм, вводя таким способом несколько нормированных
пространств. В этом случае разные нормы различают с
помощью индекса. Часто в качестве индекса используют
обозначение соответствующего нормированного пространства, т.е.
норму элемента х в нормированном пространстве L
записывают в виде \\x\\l.
Если в нормированном пространстве L ввести функцию
то нетрудно показать, что эта функция удовлетворяет
аксиомам метрики. Таким образом, любое нормированное
пространство можно рассматривать как метрическое пространство с
указанной метрикой (ее при этом называют метрикой,
индуцированной нормой).
Отметим, что не всякая метрика в линейном
пространстве является индуцированной некоторой нормой, т.е. линейное
пространство с метрикой не обязательно есть нормированное
пространство. Дело в том, что если метрика р индуцирована
нормой ||ж||, то верно равенство ||ж|| = р(х,0). Однако функция
f(x) = р(х)0) может и не удовлетворять аксиомам нормы, и в
этом случае метрика р не может индуцироваться какой-либо
нормой. Например, в действительном линейном пространстве
Ш метрике
соответствует функция
\х\
'<*•<»=гщ-
которая не удовлетворяет аксиомам нормы (аксиома 2 не
выполняется).

426 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Определение 5.1. Последовательность {xn}%Lx
элементов нормированного пространства L называют
сходящейся по норме к элементу х е L (сходящейся в
нормированном пространстве L), если числовая последовательность
{||хп -хЦ}^.! является бесконечно малой, т.е.
При этом элемент х Е L называют пределом
последовательности {хп}^=1^ сходящейся по норме в нормированном
пространстве L, и обозначают lim хп = х или хп -> я, п -> +оо.
п-юо
Бели последовательность {хп}^=1 элементов
нормированного пространства L сходится по норме к элементу х G L, то в
этом случае говорят о сходимости по норме (сходимости
в нормированном пространстве).
Как и для числовых последовательностей, предел
сходящейся последовательности в нормированном пространстве
единственный. Бели последовательность в нормированном
пространстве сходится, то всякая ее подпоследовательность также
сходится, причем к тому же самому пределу. Кроме того,
нетрудно показать, что если последовательности {хп}^=1 и {yn}£Li
элементов нормированного пространства L сходятся по норме,
заданнной в L, а последовательность {Хп}^=1 является
сходящейся числовой последовательностью, то последовательности
{хп ± 2/n}£Li и {Хпхп}^=1 также сходятся по норме в L и верны
равенства:
lim (хп±уп) = lim xn± lim yn, lim (Хпхп) = lim An lim xn.
n-юо п->оо п-юо n-юо n-»oo n-»oo
Понятие сходимости последовательностей определено и для
произвольных метрических пространств [I]. Напомним, что
элемент х метрического пространства X с метрикой р является
пределом последовательности {#n}£Li элементов из X, если
lim р(хП)х) = 0.
п-юо

5.1. Нормированные пространства 427
В силу равенства р(хп,х) = ||хп — х\\ для метрики,
индуцированной нормой в нормированном пространстве L, сходимость
по норме всякой последовательности {хп} элементов из L к
элементу х G L эквивалентна сходимости этой последовательности
к элементу х по метрике р.
Наличие индуцированной метрики в нормированных
пространствах позволяет перенести в нормированные
пространства важнейшие понятия метрических пространств, а именно:
ограниченность, замкнутость и компактность множеств,
ограниченность и непрерывность функций и т.д. Проиллюстрируем
это на примере некоторых понятий.
Множество М нормированного пространства L называют
ограниченным, если
Точку х нормированного пространства L называют предельной
точкой множества X С I/, если
Ve>0 3x£eX: 0<\\х-хе\\^е.
В нормированном пространстве L точка х является предельной
точкой множества X С L тогда и только тогда, когда
существует последовательность {zn}£Li отличных от х элементов из X,
сходящаяся к элементу х по норме в L.
Множество X нормированного пространства L
называют замкнутым, если оно содержит все свои предельные
точки. Отображение (функцию) (р: L\ -> L<i нормированного
пространства L\ с нормой || • ||i в нормированное пространство L*i
с нормой || • ||2 называют непрерывным в точке а Е Li, если
Ve > О 3S = 5(е) > 0 Va: G L\:
||z-a||i<* => \\<p(x)-tp(a)\\2<e.
Отображение ср: L\-±L<i, непрерывное в каждой точке
нормированного пространства Li, называют непрерывным на
нормированном пространстве L\.

428
5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Напомним, что нормированное пространство L называют
n-мерным, если оно n-мерно как линейное пространство, и
называют бесконечномерным, если оно бесконечномерно как
линейное пространство [IV].
Рассмотрим примеры некоторых конкретных
нормированных пространств.
Пример 5.1. Евклидово пространство Е можно
рассматривать как нормированное пространство, если в нем ввести
евклидову норму
В частности, нормированным пространством является
арифметическое евклидово пространство Шп с евклидовой нормой
х =
\
Аналогично в комплексном линейном пространстве Сп
всевозможных упорядоченных совокупностей z = (zi, ..., zn)
комплексных чисел, которое является унитарным пространством
со скалярным произведением
(ж, y) =
= (УЬ ..-, Уп),
норму можно задать формулой
\\z\\ =
\
k=\
\
Эту норму называют унитарной.
Пример 5.2. Рассмотрим линейное пространство С[а,Ь]
функций, непрерывных на отрезке [а, Ъ]. В этом линейном

5.1. Нормированные пространства 429
пространстве определим норму следующим образом:
||х||= max|*(t)|, xeC[a,b].
Поскольку любая непрерывная на отрезке функция
достигает своего наибольшего значения [1-9.5], определение нормы
корректно. Проверка первых двух аксиом нормы не вызывает
затруднений. Выполнение третьей аксиомы следует из свойств
модуля действительного числа. Действительно, для любого
фиксированного t Е [а, Ь] имеем
\*(t) + V(t)\ < \x(t)\ + \y(t)\ ^ max \x(t)\ + max \y(t)\.
te[a,b] te[a,b]
Выбрав в качестве t то значение, в котором непрерывная
функция \x(t)+y(t)\ на отрезке [а, 6] достигает максимума,
заключаем, что
max |ж(£)+у(£)| ^ max |ж(£)|+ max \y(t)\.
t€[a,b] t6[a,6] i£[a,6]
Это и есть неравенство треугольника, так как с помощью
нормы оно записывается в виде ||я + у|| ^ ||ж|| + ||у||.
Таким образом, линейное пространство непрерывных на
отрезке [а, Ь] функций с введенной нормой становится
нормированным пространством. Это нормированное пространство
имеет стандартное обозначение С[а,Ъ).
Последовательность элементов нормированного
пространства С[а,Ь] фактически является функциональной
последовательностью. Покажем, что сходимость по норме в С[а,Ь]
совпадает с равномерной сходимостью функциональной
последовательности на отрезке. Пусть последовательность
из С[а,Ь] сходится по норме к функции х G С[а,6]. Тогда
\\хп - х\\ = max \xn(t) - x(t)\ -> 0, n -> оо.
Поскольку
sup \xn(t) — x(t)\ = max \xn(t) — x(t)\,
te[a,b] te[a,b]

430 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
то в силу теоремы 2.2 имеем равномерную сходимость
функциональной последовательности {xn(i)}^_1 к функции x(t) на
отрезке [а, 6]. Согласно теореме 2.2, верно и обратное
утверждение: если последовательность {xn(t)}^Li функций из С[а,Ь]
равномерно на [а, Ь] сходится к функции ж(£), то эта
последовательность сходится и по норме в С[а,Ь].
Пример 5.3, Множество ограниченных числовых
последовательностей является линейным пространством относительно
операций почленного сложения последовательностей и
почленного умножения последовательностей на числа. В этом
линейном пространстве зададим норму формулой
Поскольку числовое множество, состоящее из членов
последовательности {#*}£?_!, ограничено, то, согласно теореме о
существовании точных верхней и нижней граней [1-2.7], величина
sup|xfc| конечна, следовательно, норма задала корректно. Не-
трудно доказать, что аксиомы нормы выполняются. При этом
неравенство треугольника можно доказать, как и в примере
5.2, используя свойства модуля действительного числа.
Нормированное пространство ограниченных последовательностей
обычно обозначают через т.
Изучим сходимость по норме в нормированном
пространстве т. Пусть имеется последовательность {х^}^=1
элементов нормированного пространства т, т.е. для каждого
номера п Е N элемент х^ = {ж^}]^ — ограниченная числовая
последовательность. Предположим, что последовательность
{x^}%Li сходится по норме в m к ограниченной числовой
последовательности х = {#*}£?_!, т.е.
- х\\ = sup|4n) - хк\-+ 0, п -> оо.

5.1. Нормированные пространства 431
Поскольку для любого номера к е N имеет место неравенство
то при каждом фиксированном значении к Е N
последовательность {|яд. — Xk\}%Li является бесконечно малой при п —>• оо.
Значит, числовая последовательность {я^ }£LX, состоящая из
к-х членов последовательностей х^п\ сходится к числу я* —
fc-му члену последовательности х Е т. Отметим, что эта
сходимость является равномерной* по переменному &, так как все
числовые последовательности {\х^ — s*|}£Li имеют
мажорирующую бесконечно малую последовательность {зир|я^ — я*|}.
Пример 5.4. Пусть р — некоторое число, причем р ^ 1.
Рассмотрим множество последовательностей действительных
00
чисел х = {я*}0;0^, таких, что ряд ^ \xk\p сходится. Это мно-
к=1
жество обозначим символом £р. В множестве £р введем
почленные операции сложения последовательностей и умножения их
на числа. Очевидно, что для любого А Е К. последовательность
Хх = {Xxk}^-i также принадлежит множеству £р. Для
доказательства того, что сумма любых двух последовательностей
из 1р также принадлежит 1Р, воспользуемся неравенством
Минковского для рядов (см. Д.5.1)
I
р
=1 ' 4=1 ' 4=1
верным при р ^ 1 для любых последовательностей \х\^_х и
{2/fc}jfe^i> принадлежащих множеству £р. В этом неравенстве из
сходимости рядов справа следует сходимость ряда слева, а это
и доказывает, что последовательность {я* + y^^Li входит в
* Последовательность {x^}^=i можно рассматривать как
функциональную последовательность, определенную на множестве N (к = 1, 2,...).

432 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
множество £р. Итак, относительно рассмотренных операций
множество £р является линейным пространством.
Введем в £р норму, используя формулу
(5.2)
4=1
Выполнение первых двух аксиом нормы очевидно. Как и ранее,
выполнение третьей аксиомы следует из неравенства Минков-
ского. Таким образом, £р является нормированным
пространством.
Аналогично можно определить комплексные нормированные
пространства £р, состоящие из последовательностей комплекс-
оо
ных чисел {£a:}?Li> таких> чт0 S \zn\p < °°. Норма в этом
п=1
линейном пространстве определяется формулой
Ые=1УМП (5-3)
5.2. Банаховы пространства
Выделим один важный класс нормированных пространств.
Этот класс появляется в результате попытки перенести на
нормированные пространства критерий Коши сходимости
числовой последовательности [1-6.4], который звучит так: числовая
последовательность сходится тогда и только тогда, когда она
фундаментальна.
Понятие фундаментальной последовательности без труда
переносится на произвольные метрические пространства.
Метрические пространства, в которых любая фундаментальная
последовательность сходится, называют полными. Понятия
фундаментальной последовательности и полноты можно
ввести и в нормированных пространствах, которые можно считать
частным случаем метрических пространств.

5.2. Банаховы пространства. 433
Определение 5.2. Последовательность {xn}%Li
элементов нормированного пространства L называют
фундаментальной, если выполняется следующее условие:
Ve>0 3N(e)eN Vn>N(e) VfceN: \\xn-xn+k\\ <e.
Теорема 5.1. Если последовательность {хп}^=1 элементов
нормированного пространства L сходится по норме к
некоторому элементу хо € L, то эта последовательность является
фундаментальной.
Ч Поскольку последовательность {sn}JJLi сходится по норме к
хо € L, то lim ||xn — хо|| = 0, т.е. в соответствии с определением
пюо
п—юо
предела
3N(e)eN Vn>N(e):
Возьмем произвольные числа п > N(e) и к € N. Тогда, согласно
свойству нормы, имеем
11*11 - *п+А:|| ^ \\ХП -Х0\\ + \\ХО - Хп+к\\ < - + - = С,
т.е. последовательность {хп}^=1 фундаментальна. ►
Обратное теореме 5.1 утверждение, вообще говоря, неверно:
существуют нормированные пространства, в которых не всякая
фундаментальная последовательность сходится. Однако имеет
место следующая теорема.
Теорема 5.2. Если последовательность {хп}^>=1 элементов
нормированного пространства L фундаментальна и некоторая
ее подпоследовательность {хПт }J£=i сходится по норме (к
некоторому элементу iGl), то последовательность {яп}{£=1 также
сходится по норме (к тому же элементу х).
А Сходимость подпоследовательности {^nm}m=i означает, что
lim ||яПт-я|| = 0, т.е.
т—юо
Ve>0 3M(e)€N Vm > М(<г): \\хПт -х\\ < J.

434 5, РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Используя ту же величину е, в силу фундаментальности
последовательности {хп} получаем
3N(e)eN Vn>JV(e) Чпт>п: \\хПт -хп
Зададим натуральное число К(е) по формуле
Выбирая любой номер п > К(е), находим какой-нибудь номер
пт>п (при этом, очевидно, т > М(е)). Тогда
II*» - *И < 11*« - *пт II + \\хПт - х\\< \ + | = е.
Окончательно имеем
GN Vn>K(e): ||ж„-а:||<е,
что означает lim ||xn — x|| = 0, т.е. последовательность {хп}
сходится к х € L по норме в L. ►
Приведем пример нормированного пространства и
фундаментальной последовательности в нем, не сходящейся ни к
одному элементу этого нормированного пространства.
Пример 5.5. Рассмотрим нормированное пространство
Со [0,1] многочленов с нормой
b()l, p€Co[O,l]. (5.4)
Это нормированное пространство является подмножеством
нормированного пространства С[0,1] функций, непрерывных на
отрезке [0,1], причем норма в Со[0,1], заданная
соотношением (5.4), совпадает с нормой в С[0,1]. Поэтому сходимость
последовательностей многочленов по норме (5.4) эквивалентна
равномерной сходимости этих последовательностей на отрезке

5.2. Банаховы пространства. 435
[0,1]. Покажем, что последовательность {pn(^)}^Li
многочленов
t2 tn
pn(t) = l + i + _ + ... + — nGN,
является фундаментальной, но не сходится по норме (5.4) ни
к какому многочлену. Последовательность {pn(*)}JJLii являясь
последовательностью частичных сумм ряда Тейлора функции
е*, сходится к непрерывной функции е* равномерно на
отрезке [0,1] (см. 2.5), а значит, и по норме (5.4) в нормированном
пространстве С[0,1]. Согласно теореме 5.1, эта
последовательность фундаментальна в нормированном пространстве С[0,1],
и, следовательно, в нормированном пространстве Со [0,1].
Однако последовательность {pn(t)} в нормированном
пространстве Со [0,1] не имеет предела, так как такой предел будет
пределом этой последовательности и в С[0,1]. Но в этом
нормированном пространстве пределом последовательности является
функция е*, не принадлежащая Со [0,1] (не является
многочленом). #
Выделим класс нормированных пространств, в которых
фундаментальность последовательности означает и ее
сходимость.
Определение 5.3. Нормированное пространство L
называют полным, или банаховым пространством*, если
в нем любая фундаментальная последовательность сходится.
Примером нормированного пространства, не являющегося
полным, является линейное пространство многочленов из
примера 5.5. Приведем примеры банаховых пространств.
Пример 5.6. Нормированное пространство R с нормой
||х|| = |х|, х € К, является банаховым в силу критерия Коши
сходимости числовых последовательностей [1-6.5].
*С. Банах (1892-1945) — польский математик, один из создателей
современного функционального анализа.

436 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Пример 5.7. Нормированное пространство Rn с
евклидовой нормой
х =
\
A;=l
также является банаховым, поскольку сходимость в Rn
эквивалентна покоординатной сходимости, причем в Кп верен
критерий Коши сходимости последовательностей [V].
Пример 5.8. Нормированное пространство С[а,Ь] (см.
пример 5.2) также является банаховым пространством, так как
сходимость по норме этого нормированного пространства —
это равномерная сходимость функциональных
последовательностей, а для равномерной сходимости функциональных
последовательностей верен критерий Копш, который можно
сформулировать следующим образом. Функциональная
последовательность {un(i)}, i€[a, ft], сходится равномерно на отрезке [a, ft]
тогда и только тогда, когда для любого е > О существует такой
номер N = -/V(e), что для любых номеров п,т> N(e) и
любого числа t Е [a, ft] верно неравенство \un(t) — um(t)\ < е.
Действительно, любая функциональная последовательность {un(i)},
£€[a,fc], может рассматриваться как последовательность
частичных сумм некоторого функционального ряда (см. 2.1).
Поэтому критерий Коши равномерной сходимости
функциональной последовательности можно свести к критерию Коши
равномерной сходимости функционального ряда.
Отметим также, что равномерный предел функциональной
последовательности, состоящей из непрерывных функций,
согласно теореме 2.11, является непрерывной функцией.
Следовательно, если функциональная последовательность из элементов
нормированного пространства С[а,Ь] сходится на [a, b]
равномерно, то предельная функция принадлежит С[а,Ь], т.е.
функциональная последовательность сходится в С[а,Ь] по норме. #
Не доказывая, отметим, что банаховыми являются также
нормированные пространства m и £р (см. примеры 5.3 и 5.5).

5.3. Подпространства, нормированных пространств 437
5.3. Подпространства
нормированных пространств
Обсудим некоторые свойства конечномерных
нормированных пространств. Значительная часть материала будет в
равной степени относиться и к действительным, и к комплексным
нормированным пространствам. Чтобы упростить изложение,
условимся далее обозначать n-мерное нормированное
пространство через Fn, понимая под этим как действительное
нормированное пространство Rn, так и комплексное нормирование
пространство Сп. Любое суждение о Fn на самом деле есть два
высказывания, первое — о Кп, а второе — о Сп. Условимся
также вместо F1 писать просто F, что подразумевает и R, и С.
Теорема 5.3. Пусть L — произвольное n-мерное
действительное (комплексное) нормированное пространство, в котором
выбран некоторый базис oi, 02, ап. Если Т\ L -> Fn —
линейное отображение, ставящее в соответствие элементу х =
= £ifli + £2^2 + + £nO>n £ L вектор-столбец его координат
F(x) = (£ь &> •••> £n) € Fn? то существуют такие
положительные числа аиД что для любого х Е L верно неравенство
гДе II IIь — норма в L, а || ||п — норма в Fn (евклидова в
действительном нормированном пространстве и унитарная —
в комплексном).
4 Отметим, что отображение Т является линейным и взаимно
однозначным [IV]. Для любого х € L, используя свойства нормы
и неравенство Коши — Буняковского [IV], получаем
г=1 " г=1
\
12
г=1
\
(5.5)
г=1

438 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Гп ~
= \ Yl ||fli||^ —
V i=i
Гп
где Р = \ Yl ||fli||^ — постоянная, не зависящая от х. Итак,
V
справедливость правого неравенства доказана.
Докажем справедливость левого неравенства. С этой
целью рассмотрим функцию д: ¥п —> R, определенную следующим
образом:
п
= T"l
где х = ^2 Zidi = T"l(x) E L. Покажем, что отображение д не-
прерывно на нормированном пространстве ¥п. Действительно,
для любых векторов х и у, используя неравенства (5.1) и (5.5),
получаем
* - »IL < i9||^(x - y)|U = fl|Я*) -^(У)11п = /9P- у||
||„,
где х = ^~1(x), у = ^~1(y). Выберем х 6 Fn и произвольное
e > 0. Положим 5 = е//?. Тогда для любого у € Fn,
удовлетворяющего условию ||х —у||п < J, выполняется неравенство
Это и означает, что функция д непрерывна в любой точке
хе¥п.
Отметим, что из равенства д(х) = 0 вытекает равенство х =
= 0, так как по определению д(х) = Ц^7"1^))^- Но НЯ"1^!^ =
= 0 только лишь при Т"1(х) = 0, а последнее равносильно
равенству х = 0.
Рассмотрим функцию д на единичной сфере Sn~~l в Fn, т.е.
на множестве S71"1 = {х Е Fn: ||x||n = 1}. На этом множестве
функция д не обращается в нуль, т.е. д(х) > 0 при х £ 5П"1.
Множество Sn-1 является ограниченным и замкнутым
подмножеством в Fn и, значит, компактным множеством [1-5.6].

5.3. Подпространства нормированных пространств 439
Действительная непрерывная функция g на компактном
множестве Sn~l достигает своей точной нижней грани [1-5.7], т.е.
существует такая точка хо, что значение а в этой точке
является наименьшим в S71"1:
min g(x) = g(xo) = a > 0.
В соответствии с определением минимума получаем
Поэтому для любого ненулевого элемента х £ L и
соответствующего вектора х = Т(х) € Fn в силу очевидных соотношений
имеем следующую оценку:
Итак, теорема доказана. ►
Следствие 5.1. Отображение Т, определенное в теореме
5.3, и обратное к нему отображение Т~1 являются
непрерывными отображениями L на Fn и Fn на L соответственно.
< Из теоремы 5.3 следует, что для всех х € L верно неравенство
||^(х)||п < -||£||L. Используя это неравенство, покажем, что
отображение Т непрерывно на нормированном пространстве L.
Выберем х € L, произвольное число е > 0 и положим S = ае.
Тогда для всех у € Ь, таких, что ||х — y||L < S = ае, имеем
< \ \\*-у\\ь < ~ « = е.
Это означает, что функция ^ непрерывна в точке х, а в
силу произвольного выбора х е L — на всем нормированном
пространстве L.

440 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Из теоремы 5.3 также следует неравенство ||x||l ^ Р\\Г(х)\\п,
xGL, которое равносильно неравенству ||^7~1(x)||l ^ /?||?||п?
JE Fn. Используя это неравенство, можно установить
непрерывность отображения Т~1 так же, как была доказана
непрерывность Т. ►
Следствие 5.2. Любые две нормы || ||i и || Ц2 в
конечномерном линейном пространстве L эквивалентны, т.е. для
некоторых положительных а и /3
А Нормы || • ||i и || • ||2 определяют два конечномерных
нормированных пространства L\ и L2, элементами которого являются
элементы одного и того же линейного пространства L. Выбрав
в L некоторый базис, зададим тем самым отображение Т из L
(а значит, из L\ и L2) в нормированное пространство Fn.
Согласно теореме 5.3, найдутся положительные константы ai, /3i
и с*2, /%, такие, что для всех х eL выполняются неравенства:
сч\\Г(х)\\п < \\x\U <
Отсюда для всех х € L имеем
1М|2 ^ All^Wlln ^ -Ыъ \\xh
Обозначая a = ot2lfi\ и /3 = /Зг/ai, получаем требуемые
неравенства. ►
Пусть L — линейное пространство. Непустое множество
Lq С L называют линейным многообразием, если вместе с
любыми своими элементами xi, £2, •••? #п (в любом конечном
числе) множество Lo содержит и всякую линейную комбинацию
этих элементов:
..., An€F :
г=1

5.3. Подпространства нормированных пространств 441
В частности, само линейное пространство L является линейным
многообразием.
Отметим, что определение линейного многообразия
сводится к определению линейного подпространства, которое
вводится в курсе линейной алгебры [IV]. Определение в линейной
алгебре ориентировано на конечномерные линейные
пространства, а в бесконечномерном случае различают линейное
многообразие (линейное подпространство по терминологии линейной
алгебры) и линейное подпространство, которое представляет
собой линейное многообразие с дополнительными свойствами.
В конечномерном случае оба понятия совпадают.
В нормированных пространствах большую роль играют
вопросы, связанные со сходимостью последовательностей.
Поэтому, выделяя множества, замкнутые относительно линейных
операций, т.е. линейные многообразия, естественно
дополнительно требовать, чтобы эти множества были замкнуты и
относительно сходимости последовательностей элементов этих
множеств, т.е. представляли собой замкнутые множества в
метрическом пространстве.
Определение 5.4. Подпространством
нормированного пространства L называют замкнутое линейное
многообразие в L, т.е. линейное многообразие, которое содержит все
свои предельные точки.
Теорема 5.4. Всякое конечномерное линейное
многообразие нормированного пространства L является его
подпространством, т.е. замкнуто в L.
< Пусть Lq — n-мерное линейное многообразие
нормированного пространства L и элемент хЕ L является предельной точкой
линейного многообразия Lq. Тогда найдется
последовательность {xk}^-i элементов из Lq, сходящаяся по норме в L к
элементу х. Согласно теореме 5.1, последовательность {xk}(j£=1
фундаментальна в L.
Линейное многообразие Lq можно рассматривать как п-мер-
ное нормированное пространство с той же нормой, что и в

442 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
нормированном пространстве L, т.е. ||y||Lo = ||y||L, у е Lq.
Выбрав в Lq некоторый базис, построим отображение Т\ Lq -> Fn,
ставящее в соответствие каждому элементу у 6 Lq столбец его
координат в выбранном базисе. В силу теоремы 5.3 найдутся
положительные константы а и /?, такие, что верны неравенства
<*\\Ну)\\п < IIj/IL < /3|№)lln, у е lq. (5.6)
Для определенной выше последовательности {хк}(^=1
элементов из Lq рассмотрим соответствующую ей последовательность
векторов {хк}™=1 из Fn, где хк = Р{хк), к Е N. Так как
последовательность {xfc}(^Ll фундаментальна, т.е.
Ve>0 3N{e)eN 4k>N{e) VmEN: \\xk -xk+m\\ < е,
то в силу неравенств (5.6) заключаем, что
Ve>0 3N(e)eN Vk>N{e) VmEN: \\xk -xk+m\\n < -.
Следовательно, последовательность {х^}^?=1 является
фундаментальной в Fn. Поскольку Fn является банаховым
пространством, эта последовательность имеет некоторый предел х* в
Fn. Это означает, что
Уе>0 3M{e)eN Vfc>M(e): \\xk -x*\\n < е.
Отсюда, учитывая (5.6), имеем
Ve>0 3M{e)eN Vfc>M(e): \\xk -z,||L <(3e,
где ж* = F~l(x*) E Lq. Полученное утверждение означает,
что lim xk = я*. Однако напомним, что последовательность
fc-юо
^_г уже имеет предел х Е L. Учитывая единственность
предела последовательности в нормированном пространстве,
получаем х = х+ Е Lq. Итак, всякая предельная точка
конечномерного линейного многообразия Lq принадлежит ему же.
Следовательно, Lq замкнуто. ►

5.4. Сепарабельные пространства 443
Из теоремы 5.4, в частности, следует, что в конечномерном
случае понятия линейного многообразия и линейного
подпространства совпадают, так как все линейные многообразия
конечномерного нормированного пространства являются
конечномерными, а потому замкнутыми. Таким образом, введенные
нами понятия не противоречат определению линейного
подпространства из курса линейной алгебры.
Бесконечномерные линейные многообразия в отличие от
конечномерных могут не быть замкнутыми. Например, в
нормированном пространстве С[0,1] (см. пример 5.2) линейное
многообразие всех многочленов Со [0,1] является
бесконечномерным. Как было показано в примере 5.5, существует
последовательность многочленов, сходящаяся по норме в С[0,1]
к непрерывной функции, не принадлежащей Со [0,1] (не
являющейся многочленом). Следовательно, линейное многообразие
Со [0,1] не является замкнутым в С[0,1].
5.4. Сепарабельные пространства
Пусть L — нормированное пространство. Множество,
полученное путем объединения множества Y С L с множеством
всех его предельных точек, называют замыканием
множества Y в L и обозначают Y Операция замыкания множества
обладает следующими свойствами:
1) ADA;
2) А = А, т.е. замыкание множества является замкнутым
множеством;
3) ЖГВ=^АиВ;
4) 0 = 0;
5)I = L.
Теорема 5.5. Замыкание М линейного многообразия М
в нормированном пространстве L является подпространством
нормированного пространства L.

444 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
-4 Поскольку М является замкнутым множеством в L, то,
согласно определению подпространства нормированного
пространства, достаточно доказать, что множество М есть
линейное многообразие в L.
Любой элемент х Е М можно рассматривать как предел
последовательности {хп}™=1 элементов, принадлежащих М.
Действительно, условие х Е М означает, что либо х Е М, либо х
является предельной точкой множества М, В первом случае
х является пределом постоянной последовательности с общим
членом хп = я, а во втором случае х является пределом
некоторой последовательности в М в силу определения предельной
точки множества.
Рассмотрим произвольные элементы а; и у из М.
Существуют последовательности {хп} и {уп} элементов М, сходящиеся
к х и у. Поскольку М является линейным многообразием в L,
то для любых а,/3 Е F имеем ахп + /Зуп е М, п Е N.
Последовательность {ctxn + /3yn} сходится по норме в нормированном
пространстве L (см. 5.1), причем
lim (ахп + /Зуп) = a lim хп + /3 lim уп = ах + /Зу.
п—>оо п—юо п—юо
Однако предел последовательности {ахп + /Зуп} элементов
множества М принадлежит М. Следовательно, ах + (Зу Е М.
Мы показали, что линейная комбинация произвольных
элементов х и у из М принадлежит этому множеству.
Рассуждения можно повторить с произвольным количеством элементов.
Это доказывает, что множество М является линейным
многообразием в нормированном пространстве L. ►
Определение 5.5. Множество Y в нормированном
пространстве L называют всюду плотным, если Y = L.
Другими словами, множество Y С L является всюду
плотным в L, если для всякой точки х Е L в любом открытом шаре
U(x,e) = {у Е L: \\х — у\\ < е} содержится хотя бы один элемент
из У.

5.4. Сепарабельные пространства 445
Определение 5.6. Нормированное пространство L
называют сепарабелъным, если в нем существует счетное
всюду плотное подмножество.
Напомним, что множество называют счетным, если
существует взаимно однозначное соответствие между этим
множеством и множеством натуральных чисел. Счетное множество
можно записать как последовательность. Поэтому
нормированное пространство L сепарабельно тогда и только тог^а, когда
существует последовательность {хп}^_1 элементов из L, для
которой верно утверждение
VxeL Ve>0 3fceN: \\xk-x\\<e
То же самое можно сформулировать иначе: в сепарабель-
ном нормированном пространстве L существует
последовательность {хп}™=1, такая, что всякий элемент х Е L либо совпадает
с одним из членов этой последовательности, либо является
пределом некоторой ее подпоследовательности.
Пример 5.9. Множество рациональных чисел Q является
счетным всюду плотным множеством в нормированном
пространстве R с нормой \\x\\ = |х|, iGK. Действительно, для
любого жЕКи любого числа е > О интервал (х — £, х + е)
содержит хотя бы одно рациональное число: достаточно выбрать
натуральное число q > l/(2e) и тогда расстояние между
соседними рациональными числами вида m/q будет равно 1/q < 2б,
так что хотя бы одно такое число попадет в любой интервал
длины 2е.
Множество действительных чисел М с нормой ||я|| = \х\
является банаховым пространством, сходимость по норме
которого совпадает с обычной сходимостью числовых
последовательностей. В этом банаховом пространстве множество Q является
счетным всюду плотным. Значит, М является сепарабельным
банаховым пространством.

446 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Пример 5.10. Банахово пространство Мп с евклидовой
нормой
х =
Е|т.|2 гр — (грл Т \
|xl| ? х — \xli • • • > хп)
г=1
также является сепарабельным. Счетным всюду плотным
множеством в этом банаховом пространстве будет, например,
множество
Теорема 5.6 {теорема Вейерштрасса)*. Для любой
непрерывной на отрезке функции существует последовательность
многочленов, сходящаяся к данной функции равномерно на
данном отрезке.
Пример 5.11. Теорема Вейерштрасса позволяет доказать,
что банахово пространство С[а,6] непрерывных на отрезке [а, Ь]
функций является сепарабельным. Счетным всюду плотным
множеством в С[а,Ь] является множество многочленов с
рациональными коэффициентами. Покажем это.
Согласно теореме Вейерштрасса, для любой непрерывной
на отрезке [а, Ь] функции x(t) существует последовательность
многочленов, которая равномерно на [а, Ь] сходится к я(<), т.е.
для любого числа е > 0 найдется многочлен p(t), такой, что
ье[а>ь\
Пусть p(t) = antn + an-\tn~l +... + a\t + «о? где а* Е К, г = О, п, —
коэффициенты многочлена р(£). Положим с = тах{|а|, |Ь|}.
Поскольку Q = R, для каждого коэффициента е^, г = 0, п, можно
*См., например: Г.М. Фихтенгольц.

^ 5.4. Сепарабельиые пространства 447
выбрать такое рациональное число г», что
Оценим модуль разности многочленов p(t) и ро(*) =
+ rn-\tn~l +... + го на отрезке [а, Ь]:
i=0 i=0 i=0
е
<
Из этой оценки вытекает, что
||р-ро|| = max \p(t)-po{t)\ < ^.
Оценим расстояние от функции x(t) до многочлена ро(*) в
нормированном пространстве C[a,b]:
Ik-Poll = max|a;(t)-po(*)l<
te[a,b]
< max |rr(t) — p(*)| + max \p{t) -po(t)| < ^ + | = e.
Итак, для любого элемента х G C[a,b] существует такой
многочлен ро с рациональными коэффициентами, что \\х — ро|| < е.
Значит, множество всех многочленов с рациональными
коэффициентами всюду плотно в C[a,b]. Это множество счетно,
так как является счетным объединением (по степеням
многочленов) счетных множеств Rq многочленов с рациональными
коэффициентами степени п. Каждый многочлен из множества
Rq однозначно определяется своими коэффициентами, т.е.
набором из п +1 рационального числа, и поэтому соответствует
некоторому элементу множества Qn+1. Поэтому множество
счетно, так как находится во взаимно однозначном
соответствии с некоторым подмножеством счетного множества Qn+1.

448 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Пример 5.12. Покажем, что банахово пространство m
ограниченных последовательностей (см. пример 5.3) не
является сепарабельным. Доказательство проведем от противного.
Предположим, что в m существует счетное всюду плотное
множество Eq. Для каждого элемента х Е Eq рассмотрим
множество
Так как Eq всюду плотно, то для любого элемента z Е m
найдется такой элемент х Е Eq, что \\х — z\\ < 1/3, т.е. z Е Кх
для некоторого х Е Eq.
Поскольку Eq счетно, его можно записать в виде
последовательности: Eq = {x(n)}. Пусть последовательность х^ имеет
вид х^ = {х^ }^=1, п Е N. Для каждого п Е N выберем число zn
на отрезке [0,1], которое отличается от Хп не менее чем на 1/3.
Это можно сделать, так как интервал (яп —1/3, Яп +1/3)
имеет длину 2/3 и не накрывает отрезок [0,1].
Последовательность z = {zn} принадлежит т, так как все ее члены
принадлежат отрезку [0,1], и потому последовательность ограничена по
модулю числом 1. Однако эта последовательность не попадает
ни в одно из множеств Кх, х Е Eq. Действительно, для любого
nEN
4n)| ^ \zn-x^\ > \
3
и z £ Кх при х = х^п\ Но выше, исходя из того, что множество
Eq всюду плотно, мы пришли к выводу, что каждый элемент
z E m принадлежит хотя бы одному из множеств Кх. Тем
самым получено противоречие, которое доказывает, что в m
нет счетных всюду плотных множеств и что это банахово
пространство является несепарабельным.

5.5. Сходимость рядов в банаховых пространствах 449
5.5. Сходимость рядов
в банаховых пространствах
Пусть {хп}™=1 — некоторая последовательность элементов
нормированного пространства L. По аналогии с числовыми рл-
оо
дами выражение вида х\ + Х2 +... + хп +..., или J2 хп, называ-
п=1
ют рлдом элементов нормированного пространства L.
Рассмотрим последовательность частичных сумм данного
ряда, т.е. последовательность {Sn}^=1 элементов Sne L вида
-\ h Хп, П Е N.
оо
Определение 5.7. Ряд 5Z хп элементов нормированного
п=1
пространства L называют сходящимся по норме в L, если
в L сходится последовательность {Sn}^Ll его частичных сумм.
В этом случае предел S E L последовательности частичных
L °°
сумм называют суммой данного ряда и пишут S = Y1 хп, или
оо п=1
S = Y1 хп, если из контекста понятно, в каком нормированном
п=1
пространстве (по какой норме) рассматривается сходимость
ряда.
оо
Таким образом, ряд Y1 хп элементов нормированного про-
п=1
странства L сходится к элементу S E L тогда и только тогда,
когда
lim Sn = 5, или lim \\Sn - S\\L = 0.
n-юо n-юо
Теорема 5.7 (необходимый признак сходимости ря-
оо
да). Если ряд £) хп элементов нормированного пространства
п=1
L сходится, то последовательность {хп} этих элементов
сходится к нулевому элементу О Е L.

450 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
оо
Ч Ряд 5Z хп сходится, следовательно, существует предел по-
п=1
следовательности его частичных сумм: lim Sn = S. Поэтому
n-юо
n = lim (5n-5n-i) = lim Sn- lim 5n-i = S-S = O. ►
n*oo n*oo n*oo
Пусть теперь L — банахово пространство. Для рядов в
банаховых пространствах, так же как для числовых и
функциональных рядов, имеет место следующий критерий сходимости.
Теорема 5.8 (критерий Коти сходимости ряда в
банаховом пространстве). Пусть L — банахово простран-
00
ство. Для того чтобы ряд 5Z хп элементов из L сходился в L,
п=1
необходимо и достаточно, чтобы для него было верным
утверждение
Ve>0 3N{e)eN Vn>N(e) VpGN: | ]Г хЛ<е.
k=n+l
оо
^ Сходимость ряда 5Z хп эквивалентна сходимости последова-
п=1
тельности его частичных сумм {S'fJJJLx. В банаховом
пространстве сходимость последовательности эквивалентна ее
фундаментальности:
\/е>0 3N(e)eN 4n>N{e) VpEN ||5n+p-5n|| < e.
II n+p II
Поскольку ||Sn+p - 5n|| = 5Z xk\U т0 получаем требуемое. ►
Для рядов в банаховых пространствах имеет место
следующий достаточный признак сходимости.
оо
Теорема 5.9. Пусть Ylxn — ряд элементов банахова
п=1
пространства L, причем выполняются условия: 1) ||zn|| < ап,

5.5. Сходимость рядов в банаховых пространствах 451
00 00
n e N; 2) числовой ряд J^ an сходится. Тогда ряд J2 хп также
71=1 71=1
сходится.
00
<4 Заметим, что числовой ряд ^2 an состоит из
неотрицательна
ных слагаемых, так как an ^ ||жп|| ^ 0, n G N. Поскольку этот
числовой ряд сходится, то, согласно критерию Коти
сходимости числового ряда (см. теорему 1.3), имеем
GN Vn>N{e)
Для всех n> N(e) и p G N, используя аксглолсы «орлсы, получаем
... + an+p < e.
Итак, выполнено условие критерия Копш сходимости ряда
из элементов банахова пространства. Следовательно, этот ряд
сходится. ►
Замечание 5.1. Теорема 5.9 в применении к банахову
пространству С[а,Ь] соответствует признаку Веиерштрасса
равномерной сходимости функциональных рядов. Обратим
внимание на то, что этот признак можно использовать для
произвольных функциональных рядов. В случае же применения
теоремы 5.9 к нормированному пространству C[a,b] можно
доказать признак Веиерштрасса только для функциональных
рядов, состоящих из непрерывных функций.
00
Следствие 5.3. Пусть $^ хп — ряд элементов из банахова
71=1 00
пространства L. Если числовой ряд ^ \\хп\\ сходится, то ряд
ОО 71=1
X) хп также сходится в L.
п=1

452 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
М Полагал ап = ||a:n||, n Е N, получаем сходящийся числовой ряд
00
^2 ап, причем \\хп\\ ^ ап, п Е N. Таким образом, выполняются
71=1 ОО
условия теоремы 5.9, следовательно, ряд 2^ хп сходится. ►
71=1
ОО
Определение 5.8. Пусть J2 хп — РЯД элементов нормиро-
71=1 ОО
ванного пространства L. Если сходится числовой ряд ]Г) \\хп\\,
ОО 71=1
то ряд ]Г хп называют абсолютно сходящимся.
71=1
Согласно следствию 5.3, в банаховом пространстве всякий
абсолютно сходящийся ряд является также сходящимся.
Оказывается, что сходимость абсолютно сходящихся рядов —
отличительный признак банаховых пространств.
Теорема 5.10. Если в нормированном пространстве L
каждый абсолютно сходящийся ряд сходится, то нормированное
пространство L является банаховым.
< Необходимо доказать полноту L, т.е. показать, что любая
фундаментальная последовательность в L сходится. Пусть
{хп}™=1 — произвольная фундаментальная последовательность
в L. Это значит, что верно утверждение
Ve>0 3N{e)eN Vn>N{e) Vm>n: \\xm-xn\\<e. (5.7)
Для е = 1/2 найдется такой номер N\, что \\хт — хп\\ < 1/2 при
п> N\ и т > п. Выберем какой-нибудь номер щ > N\. Тогда
\\хт ~ хП11| < 1/2 при т>щ.
Положим е = 1/22. В силу утверждения (5.7) найдется такой
номер 7^2, что \\хт — хп\\ < 1/22 при п > N2 и т > п. Выберем
номер n2 > max{7V2, щ}. Тогда \\хП2 - хП1 \\ < 1/2 и \\хт -хП2\\ <
< 1/22 при т > П2-
Продолжая так и далее, на fc-м шаге для е = 1/2* определяем
такой номер 7V)t, что \\хт — хп\\ < 1/2* при п > Nk и т > п.
Затем выбираем номер n* > max{7Vfc, n^—1}. При таком выборе

5.5. Сходимость рядов в банаховых пространствах 453
будем иметь ||a;nfc -Snfc_J < 1/2*""1 и ||жт - хПк\\ < 1/2* при
m > fife- В результате получим подпоследовательность {xnk}^-i
последовательности {sn}{JLij такую, что
HJ< keK (58)
Составим следующий ряд элементов из L:
Хщ + {ХП2 - *щ) + (^713 - *П2) + • • • + {Хпк + 1 ~ ХПк) +
Этот ряд абсолютно сходится, поскольку числовой ряд
к=1
почленно мажорируется сходящимся числовым рядом
Так как всякий абсолютно сходящийся ряд, согласно условию
00
теоремы, сходится, то сходится и ряд хП1 + $^(#71*+! ~хпк)-
к=\
Обозначим сумму этого ряда £, S G £, и найдем частичные
суммы этого ряда:
771-1
Sm = ХП1 + ^2 (Ж"*+1 "Хпк) =
к=1
= хП1 + хП2 — ггП1 + хПг — хП2 + ... + ж^ — хПт_х = rr^yyj.
Итак, для всех т G N справедливо равенство: Sm = rr7lm.
Сходимость ряда к элементу 5GL означает, что
последовательность {Sm} = {хПт} его частичных сумм сходится к
элементу S по норме в L. Таким образом, подпоследовательность
{xnm}m=i фундаментальной последовательности {хп}™=1
сходится (к элементу S G L). Согласно теореме 5.2,
последовательность {хп}™=1 также сходится (к тому же элементу SeL).
Поскольку последовательность {хп}™=1 произвольная,
нормированное пространство L является банаховым. ►

454 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
5.6. Банаховы пространства
со счетным базисом
В конечномерном нормированном пространстве всякая
максимальная линейно независимая система является его базисом
[IV], т.е. всякий элемент нормированного пространства
единственным образом можно представить в виде линейной
комбинации элементов этого базиса. Распространение понятия
базиса на бесконечномерное нормированное пространство
неизбежно приводит к бесконечным (по крайней мере, счетным)
системам элементов этого нормированного простралства и к
рядам в нем.
Определение 5.9. Пусть L — бесконечномерное банахово
пространство. Последовательность {ek}^=i элементов банахова
пространства L называют счетным базисом в L, если для
любого элемента х Е L существует единственный ряд вида
00
£) хк^к, %к £ F) сумма которого равна х:
к=1
(5.9)
k=i
При этом числа xi, x<i, ..., #&, называют координатами
элемента х банахова пространства L в базисе {е*}]^,
а представление (5.9) — разложением элемента х в ряд
по базису
Обратим внимание на то, что базис {e^^-i — это не просто
множество элементов нормированного простралства L, для
которого при некотором упорядочивании выполняется свойство
(5.9), а последовательность элементов {е*}0^ с данным,
зафиксированным порядком элементов в ней. Изменение порядка
элементов в последовательности {e^}^ изменяет
последовательность, и приводит к другому базису. Более того,
измененная таким образом последовательность может вообще не быть

5.6. Банаховы пространства со счетным базисом 455
базисом* в L. Отметим также, что не во всяком банаховом
пространстве существует счетный базис. Примеры будут
приведены ниже.
Пусть {вк}^=1 — счетный базис банахова пространства L.
Тогда {efc}^_1 является линейно независимой системой,
т.е. линейно независимой является всякая конечная подсистема
ее элементов. Это следует из единственности разложения
элементов банахова пространства L по базису. Действительно,
если какая-нибудь конечная подсистема е^, е*2,..., е*п элементов
базиса {е*}^ банахова пространства L линейно зависима, то
можно найти такие коэффициенты Ai, Л2, ..., А^,
одновременно не обращающиеся в нуль, что 0 = Aie^ + А2в*2 Н 1- А^е^.
В этом случае нулевой элемент банахова пространства будет
иметь два разных разложения по базису {е^}]^ (второе
разложение имеет только нулевые коэффициенты). А это
противоречит определению базиса.
Отметим, что в отличие от конечномерного линейного
пространства, где всякая максимальная линейно независимая
система является базисом, в бесконечномерном банаховом
пространстве счетная линейно независимая система, вообще
говоря, не обязательно является базисом. Действительно, во всяком
бесконечномерном банахобом пространстве всегда существует
счетная линейно независимая система, а базис, как отмечалось
выше, существует не всегда.
Пример 5.13. Рассмотрим банахово пространство £р,
р^1 (см. пример 5.4), и счетную систему {е^}]^ элементов
этого банахова пространства, где е* — последовательность, у
которой к-и член равен единице, а остальные равны нулю, т.е.
efc = {0, 0,..., 0,1, 0, 0,...}. Покажем, что последовательность
k-i
b=i является базисом в £р.
* Базисы банахова пространства L, которые остаются базисами при
любой перестановке его членов, называют безусловными базисами. Известно,
что, например, в банаховом пространстве С[о,6] безусловных базисов нет.

456 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Всякий элемент х Е £р — это числовая последовательность
оо
{я*}, для которой ]Г) \хк\р < оо. При этом норма элемента
х задается формулой \\x\\ = [J2\xk\p)P Покажем, что х =
ОО 71
= J2 хк^к- Частичная сумма Sn= J2 хкек этого ряда пред-
k=l ^ Jfc=l
ставляет собой последовательность {zi,Z2,-.-,zn,0,0,...}, в ко~
торой первые п членов совпадают с первыми п членами
последовательности ж, а остальные равны нулю. Поэтому
последовательность х — Sn имеет вид {0,..., 0, х^+ъ #п+2> - - -} и,
следовательно,
оо
Поскольку числовой ряд ]Г) \хп\р сходится, то последова-
71=1
оо
тельность сумм Rn= J2 \xn+k\p его п-х остатков стремится
к нулю при п —> оо (см. свойство 1.3). Поэтому
lim \\х - Sn\\ = lim R]/p = О,
71-ЮО 71-ЮО
а это означает, что элемент х Е 1Р является суммой ряда
00
*=1
Покажем, что полученное разложение элемента х по системе
{ejk}^°=1 единственно. Действительно, пусть существует другой
00 ОО ОО
ряд Е 2/fcefc> для которого х = ^2 Укек- Тогда ряд J2 zkek-> гДе
к=\ к=\ к=\
zk = хк — j/fc, A; E N, сходится к нулевому элементу в ^р, т.е. к
последовательности, составленной из одних нулей. Покажем,
что все коэффициенты zk ряда равны нулю, или хк = ук, к Е N.
00
Фиксируем некоторый номер га. Поскольку ряд ^ zkek cxo-
к=1
дится, для любого е > 0 можно выбрать такой номер N(e), что

5.6. Банаховы пространства со счетным базисом 457
II °° II
при п > N(e) будем иметь J2 zk^k\\ < £• Из равенства 0 =
= Sn + Rn, где 0 — сумма ряда J^ 2jfcejfc, Sn — его n-я частичная
_ оо А:=1
сумма, a i?n = J^ а^е* — сумма n-го остатка, заключаем,
что ||Sn\\ < е при п > N(e). Но Sn представляет собой
последовательность {zi, Z2,..., zn, 0, 0,...}, а норма этой
последовательности равна
-
Из этого представления находим, что \zm\ ^ ||5П|| при п>т.
Выбрав п > max{m, N(e)}, заключаем, что \zm\ < е. Поскольку
е > О выбиралось произвольно, то на самом деле |zm| = 0, а так
как и т — произвольно выбранный номер, то все
коэффициенты zm равны нулю. #
Банаховы пространства со счетным базисом обладают
следующим важным свойством.
Теорема 5.11. Банахово пространство со счетным базисом
сепарабелъно.
< Ограничимся доказательством для случая действительного
банахова пространства. Пусть в банаховом пространстве L
имеется счетный базис {е*}]^. Множество М всевозможных
линейных комбинаций элементов базиса с рациональными
коэффициентами, т.е. множество
М:
= < г Е L: r= J2 r^, г^ЕО, А; = 1, п >
является счетным как счетное объединение счетных множеств.
Докажем, что М = L, т.е. М всюду плотное множество в L.
Выберем произвольный элемент х Е L. Поскольку система
00
^_х — базис, то имеет место разложение х = J2 хк^кч где

458 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Xk — координаты элемента х в базисе {ejfcjj^. Из сходимости
ряда следует, что
lim Их — iS^II = lim ж —y^rrjfcejfc =0.
71—ЮО 71—Юо|| ^—' II
Следовательно, для произвольного е > 0 можно выбрать такой
номер п, что будет выполняться неравенство
||| (5.10)
Так как множество рациональных чисел Q всюду плотно
в М (см. пример 5.9), для каждого числа ж*, Л = 1,п, можно
выбрать рациональное число г^, при котором будет справедливо
неравенство
При таком выборе имеем
*=1
k=l к=
Используя неравенства (5.10) и (5.11), получаем
p| ||
jfc=l ik=l A:=l fc=l
Таким образом, для любого числа е нашелся такой элемент
71
г = ^2 rjfcejk, принадлежащий множеству М, что ||ж — г\\ < е, а
А:=1
это означает, что множество М является всюду плотным в L.
Следовательно, банахово пространство L сепарабельно. ►

5.6. Банаховы пространства со счетным базисом 459
Отметим, что любое конечномерное банахово пространство
является сепарабельным.
Как отмечалось выше, существуют банаховы пространства,
не имеющие счетного базиса. Такими, например, являются все
несепарабельные банаховы пространства. В частности,
банахово пространство m ограниченных последовательностей не
имеет счетного базиса, поскольку не является сепарабельным.
Итак, счетный базис могут иметь только сепарабельные
банаховы пространства, однако не все сепарабельные
пространства имеют счетный базис. Сепарабельное банахово
пространство, не имеющее счетного базиса, в 1972 г. построил М. Энфло.
Для банаховых пространств введем следующее понятие,
тесно связанное с понятием базиса.
Определение 5.10. Систему Q элементов банахова
пространства L называют замкнутой, если ее линейная оболочка
<Q>=lxeL: x =
I
J
является всюду плотным множеством в L.
Отметим, что для нормированных пространств со
скалярным умножением (евклидовых пространств) понятие
замкнутой системы уже было введено (см. определение 3.2).
Замкнутость системы Q в банаховом пространстве L
означает, что для каждого элемента х Е L можно указать
такой набор элементов <pi,<£>2> •••> 4>n Е Q и такой набор чисел
^ъ ^2> • • • j An E F, что справедливо неравенство
II
Другими словами, всякий элемент из L можно сколь угодно
точно (по норме банахова пространства L) приблизить линейными
комбинациями элементов системы Q.

460 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Теорема 5.12. Всякий счетный базис банахова
пространства является замкнутой системой.
< Пусть {е*}]^ — счетный базис банахова пространства L.
Тогда всякий элемент х Е Н является суммой некоторого ряда
00
по системе {е*}0^, т.е. х = ^ х^е^. Это означает, что после-
fc=l n
довательность частичных сумм Sn= Y!, хк^к-> принадлежащих
к=\
линейной оболочке системы {е*}]^, сходится по норме в L к
элементу х Е L. Иначе говоря, элемент х можно сколь угодно
точно приблизить линейными комбинациями элементов базиса.
Поэтому линейная оболочка системы {е*}^ всюду плотна в L,
а сама система {ek}^=1 замкнута. ►
Согласно теореме 5.12, понятия базиса и замкнутой
системы тесно связаны между собой. Однако они полностью не
совпадают — не всякая замкнутая счетная линейно
независимая система является базисом банахова пространства. Так,
например, счетная линейно независимая система одночленов 1,
£, t71, замкнута в банаховом пространстве С[0,1],
поскольку в С[0,1] всюду плотно множество всех многочленов (см.
пример 5.11), а это множество представляет собой линейную
оболочку рассматриваемой системы одночленов. Однако
система одночленов {tk}<^=l не является базисом в С[0,1], так как это
предположение означало бы, что любую непрерывную на
отрезке [0,1] функцию можно представить равномерно сходящимся
степенным рядом. Но тогда любая непрерывная функция
являлась бы аналитической и, в частности, дифференцируемой, что
неверно — примеров непрерывных недифференцируемых
функций можно привести множество.
Тригонометрическая система 1, cosx, sinx, cosnrr,
sinnx, также является линейно независимой и замкнутой
в подпространстве С*[—тг,тг] нормированного пространства
С[—7г,тг], состоящем из таких непрерывных на отрезке [0,1]
функций, что х(—тг) = ж(тг). Действительно, сходимость по
норме в нормированном пространстве С*[—тг,тг] равносильна

5.7. Базисы в пространстве непрерывных функции 461
равномерной сходимости на отрезке [—тг, тг]. Согласно теореме
3.6 любая непрерывная на [—тг, тг] функция x(t) является
равномерным пределом последовательности тригонометрических
полиномов
п
Рп (t) = aOn + ]Р (akn cos kx + bkn sin kx).
k=i
Однако тригонометрическая система не является базисом в
банаховом пространстве С*[—тг,тг]. Действительно, это
предположение означает, что любую функцию из С*[—тг,тг] можно
представить равномерно сходящимся к ней на отрезке [—тг, тг]
тригонометрическим рядом, который, согласно теореме 3.9,
будет совпадать с ее рядом Фурье (см. 3.1). Но это неверно, так
как существуют непрерывные функции, ряды Фурье которых
расходятся хотя бы в одной точке. На самом деле
существуют непрерывные функции, ряды Фурье которых расходятся
на всюду плотном в [—тг, тг] множестве, на множестве
мощности континуума, а также существуют примеры непрерывных
функций, ряды Фурье которых сходятся всюду на [—тг, тг], но
неравномерно в любом интервале, лежащем в отрезке [—тг, тг].
Все эти примеры достаточно сложны, их подробное описание
можно найти в специальной литературе*
5.7. Счетные базисы в пространстве
непрерывных функций
Первым примером счетного базиса в банаховом
пространстве С[0,1] является система Фабера — Шаудера, построенная
Г Фабером в 1910 г. Эта система представляет собой
простейший базис в семействе базисов банахова пространства С[0,1],
открытом в 1927 г. Ю. Шаудером.
*См., например: Бари Н.К.

462
5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Определим две начальные функции системы Фабера —
Шаудера (рис. 5.1):
= l и
= t при t€[0, 1].
(5.12)
1 t О
Рис. 5.1
1 t
Для построения остальных функций системы определим на
отрезке [0,1] функцию
2-2t,
которая обращается в нуль на концах отрезка [0,1], а на
отрезках [0,1/2] и [1/2,1] является линейной (рис. 5.2).
Для каждой пары чисел к = 0,1, 2,... и / = 1, 2,..., 2к
рассмотрим функцию g(2kt — (I—1)), определенную на отрезке
[(/ — 1)/2*, 1/2к]. Эта функция является композицией линейной
функции
x = 2kt- {l-l) = 2k(t- (l-l)/2k),
взаимно однозначно отображающей отрезок [(/ — 1)/2*, //2*] на
отрезок [0,1]), и функции д(х). График функции g(2kt— (/—1))
при некоторых значениях к и / представлен на рис. 5.3.
Очевидно, что любое натуральное число п ^ 2 можно
однозначно представить в виде
(5.13)

5.7. Базисы в пространстве непрерывных функций
463
о м ± it
Рис. 5.3
где fc — неотрицательное целое число, а г — натуральное число,
не превосходящее 2*, т.е. 1 ^ г < 2к. Например, 2 = 2°+1,
3 = 21+1, 4=2*+2, 5=22+1 и т.д. Вводя для функций системы
Фабера — Шаудера с номерами n ^ 2 двойную нумерацию
<Pn{t) = <рк; (*), где n=2k+i, определяем эти функции следующим
образом:
(5.14)
Рассмотрим подробнее несколько первых функций щ (t).
Функция if2{t) = щ (t) совпадает с функцией g(t) (см. рис. 5.2).
Функции <ps(t) = <p{i]{t) (3 = 21 + 1, к = 1, г = 1) и V4(t) = <Р?(*)
(4 = 21 + 2, fc = 1, г = 2) задаются формулами:
о,
g(2t),
Графики функций </?з(£) и </?4(^) представлены на рис. 5.4.
Заметим, что функции </?з(*) и </?4М — это функции,
которые в двойной нумерации имеют индекс fc = 1. Функций
системы, имеющих в двойной нумерации индекс fc = 2, будет четыре:

464
5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
о1 $ 4 i "t oi j | l -t
Рис. 5.4
Графики этих функций представлены на рис. 5.5.
13 1
4 8 2
1 t
l t
Рис. 5.5
Обратим внимание на то, что для любой пары индексов к и
г (к = 0,1, 2,..., г = 1, 2к) верны равенства
а на отрезках [(г - 1)/2*, (2г - 1)/2*+1] и [(2г - l)/2*+1, t/2*]
функция (ру (t) линейна. Кроме того, построенные по формуле
(5.14) функции <pn(t) непрерьюны на всем отрезке [0,1].

5.7. Базисы в пространстве непрерывных функции
465
Определение 5.11. Систему Ф = {</?n(£)}£L0 непрерывных
на отрезке [0,1] функций, определенных формулами (5.12) (при
п = 0,1) и (5.14) (при п ^ 2), называют системой Фабера —
Шаудера.
Теорема 5.13. Система функций Фабера — Шаудера
является базисом в банаховом пространстве С[0,1].
А Пусть функция f(t) непрерывна на отрезке [0,1].
Рассмотрим последовательность кусочно линейных функций {flfcW}^'
графики которых представляют собой ломаные, вписанные в
график функции /(£), так, что
для всех г = О, 2**1, где к = О, 1, 2,
(рис. 5.6). Последовательность {<Jk(t)}
равномерно на отрезке [0,1] сходится к
функции /(£), т.е.
* * I
Рис. 5.6
oo.
Действительно, так как функция f(t) непрерывна на отрезке
[0,1], то она равномерно непрерывна на этом отрезке [1-5.9],
т.е. для произвольного числа е > 0 существует такое число
5(е), что для любых ti, ti G [0,1], удовлетворяющих условию
1*1 ■" М < £(£)> выполняется неравенство |/(*i) — /(<г)| < е-
Зафиксируем е и выберем такое натуральное число if, что
l/2*+1 < б(е). Тогда |/(*x) - f{t2)\ < e, если |<i -12\ < l/2*+1 и
к Ж.
Пусть к> К. Выберем произвольную точку t € [0,1]. Для
этой точки найдется номер г, 1 ^ г ^ 2*+1, при котором t €
2*+15

466 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Так как ak(t) на каждом отрезке [ti-\,k, Uik] является линейной
функцией, то
ak(t) = 2k+1 (f(tiyk) - fiti-i*))(t - ti-i,*) + f(ti-i,k) (5.15)
при t E [*t-i,/b> U9k]> Поскольку для точек отрезка [<i-i,Jb Uyk]
верна оценка \t — ^_i^| < l/2*+1, то в силу выбора fc получаем
< 2fc+1 \f(titk) - f(ti_l>k)\ \t - ti<k\ + \f(ti-hk) - f(t)\ <
< \f(ti,k) - f(ti-i,k)\ + \f(ti-x,k) - /(01 <e + e = 2e.
Поскольку t — произвольная точка отрезка [0,1], а число
К зависит только от выбора числа е > 0, полученное
неравенство означает равномерную сходимость последовательности
{°k (*)}£Lo к Функции f(t) на отрезке [0,1], т.е.
max \ak(t) - f(t)\ -► 0, к -► оо.
оо
Поэтому и функциональный ряд ao{t) + ^ (^(^) — ^A;-i(0) Рав~
А;=1
номерно на отрезке [0,1] сходится к функции /(£), поскольку
его m-я частичная сумма равна am(t):
Итак, в С[0,1] имеет место разложение
k=i
Для произвольных индексов fc G N и i = 0, 2k выполняются
равенства <Tk(U,k-i) = °k-i{U,k-i) (рис. 5.7). Поэтому на отрезке

5.7. Базисы в пространстве непрерывных функции
467
[ti_i,jb-i, *»,fc-i], г = 1, 2*, разность (ak{t) -ak-i{t)) можно
представить следующим образом:
2i-\
2»-l
где (ру (t) — функция системы Фабера — Шаудера.
0 t-1 2г-1
Рис. 5.7
Для вычисления значения функции ak-i{t) в точке t
(2г—1)/2А;+1 воспользуемся формулой (5.15):
Отсюда при к ^ 1 для < € [(г-1)/2*, t/2*], * = 1, 2к, получаем
<rk(t)-<Tk-i(t) = Bkj<p®(t), (5.16)
где константы

468
5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
не зависят от последовательности функций о>(£), а
определяются исходной функцией f(t).
При фиксированном к ^ 1 всякая точка t E [0,1]
попадает в один из отрезков вида [(г—1)/2*, г/2*] с некоторым
номером г, 1 ^ г ^ 2*. Следовательно, выполняется равенство
(5.16). Согласно определению функций Фабера — Шаудера, для
остальных номеров j = 1, 2к, j'ф г, значение функций Фабера —
Шаудера в этой точке t будет нулевым:
Поэтому при к
)> tG[O,l]. (5.17)
Функцию ao(t) с индексом fc = 0 можно
представить в виде
где a(t) = /(0) + (/(l)-/(0))t -
функция, определяющая хорду АВ кривой
/(t), t е [0,1], с точками А = (0;/(0)) и
В = (1;/(1)) (рис. 5.8). Используя вид
можем записать
функций (fo(t) и
Кроме того, из соотношений ао(О) = а(0), ао(1) = а(1) и из
определения функции Фабера — Шаудера (f2{t) следует, что

5.7. Базисы в пространстве непрерывных функций 469
Поэтому
- /(О) «М (() )
(5.18)
где коэффициенты Во = /(0), Вг = /(1) - /(0) и В2 = /(1/2) -
— (/(0)+/(1))/2 зависят только от исходной функции f{t).
Используя формулы (5.17) и (5.18), получаем следующее
разложение функции f(t) на отрезке [0,1]:
причем функциональный ряд в правой части этого равенства
сходится равномерно на отрезке [0,1]. Членами ряда в
правой части равенства (5.19) являются суммы последовательных
оо
членов ряда Л Bnipn(t), Bn = BkJ, n = 2k+j, n ^ 2, сгруп-
n=0
пированных по признаку равенства индекса А: в их двойной
нумерации. Поэтому только разложения функции f(t) в ряд
по формуле (5.19), вообще говоря, еще не достаточно для
доказательства истинности разложения
BnVn{t), *е[0,1], (5.20)
n=O
в банаховом пространстве С[0,1].
Докажем, что из равномерной сходимости на [0,1] ряда
(5.19) к f(t) следует также и равномерная сходимость на [0,1] к

470 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
f(t) ряда (5.20). Действительно, частичные суммы ряда (5.20)
с номерами 2m, m ^ 2, имеют вид
пт
S2m (t) = J2 Bn4>n(t) = B0<f0{t) +
n=0
m-\ , 2k v
где Sm-i(t) — частичная сумма ряда (5.19) с номером га—1,
га ^ 2. Частичные суммы с номерами 2m+l, I = I, 2m, будут
следующими:
Всякая точка t из отрезка [0,1] попадает в некоторый
отрезок [(г — 1)/2т, г/2т], где номер г = 1, 2т зависит от точки t.
В соответствии со свойствами функций Фабера — Шаудера
имеем
О, Кц
Следовательно,
&.«(*)« (^W-^lW' /<i; (5.21)
Учитьшая представление (5.21), для любого n = 2m+/, m > 2,
/ = 1, 2т, имеем
l|5n-/||<||5n-5m_i|| + ||5m_1-/||<
<||5т-5т_1|| + ||5т_1-/||. (5.22)

5.7. Базисы в пространстве непрерывных функции 471
Разложение (5.19) означает, что последовательность {Sm(t)}
сходится к функции /(*) по норме банахова пространства
С[0,1], т.е. lim ||5m_i-/|| = 0. Разность Sm(t)-5m-i(«) явля-
m—юо
ется m-м членом сходящегося ряда (5.19). Согласно
необходимому признаку сходимости ряда в нормированном
пространстве, общий член ряда (5.19) сходится по норме в С[0,1] к нулю,
т.е. lim ||5m-5m_i|| =0. Из (5.22) следует, что
т—юо
lim||5n-/||=0,
п—юо
и разложение (5.20) доказано.
Итак, всякую непрерьгоную функцию f(t) можно
представить в виде равномерно сходящегося на отрезке [0,1] ряда по
системе Фабера — Шаудера. Докажем, что такое
представление единственно.
оо оо
Пусть имеются два различных ряда ^ сьпфп^) и S bn<Pn(t)
п=0 п=0
по системе Фабера — Шаудера, которые равномерно сходятся
на отрезке [0,1] к одной и той же функции f(t) E С[0,1]. Тогда
найдется такой номер N ^ 0, что ап = Ьп, п = 0, N—1, ho
(если ао ф Ьо, то N = 0). Для всякого т = 0, N— 1 получаем
m m
n=0 n=0
Учитывая, что для всякого N ^ 2 имеет место разложение
N = 2* + г, А; ^ 0, i = 1, 2* (см. (5.13)), полагаем
={ 2t-l
2*+i ' " -- г*^~.
В силу свойств функций системы Фабера — Шаудера при
любом N верно равенство <pN(tN) = 1. Поэтому aN<pN(tN) Ф
Ф bN(pN(tN) при aN фЬ„. Следовательно,
N N
п=0 п=0

472 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
т
Заметим, что J2 ап<£п(*лг) = 0 для всякого номера m>N,
поскольку для любого п > 2к + % в соответствии со свойствами
функций Фабера — Шаудера <рп{№ - l)/2fc+1) = 0. Значит,
m>N.
т
n=0
Аналогично получаем
N
\ — V^
n=0
N
^ri(tN), m>N.
n=0 n=0
oo с»
Из равномерной сходимости рядов J^ an^n(^) и S bn<Pn(t)
п=0 п=0
к функции /(£) следует их сходимость к f(t) в каждой точке
*е [0,1]. Поэтому
т N
f(t]y) = lim / fln¥?n(^iv) =
171—►ОО^—'
п=0 п=0
171
/(*лг) = lim У^Ьп<£п(*лг) lim
171—►ОО^—' 171—УОО
п=0 п=0
TajcHM образом,
N N
n=0 n=0
что противоречит неравенству (5.23). Следовательно, пред-
оо
положение о существовании различных рядов ^3 an<Pn(t) и
оо
S bn<Pn{t) по системе Фабера — Шаудера, сходящихся равно-
71=0
мерно на [0,1] к одной и той же функции f(t) e С[0,1], неверно
и разложение (5.20) единственно.

5.7. Базисы в пространстве непрерывных функций
473
В силу существования разложения (5.20) для любой
непрерывной функции из С[0,1] и единственности этого разложения
система Фабера — Шаудера является базисом в банаховом
пространстве С[0,1]. ►
В банаховом пространстве С[0,1] можно построить
системы, аналогичные системе Фабера — Шаудера, которые также
будут базисами в С[0,1]. Покажем, как это можно сделать.
Пусть действительная последовательность а\ с двойной
нумерацией (к = 0, 1,..., г = 0, 2к) удовлетворяет следующим условиям:
Пусть также
А* = max (ак
0, к
оо.
(5.25)
С помощью точек последовательности {агк} определим на
отрезке [0,1] систему типа Фабера — Шаудера. Положим
= t, te[o,i].
Для n > 2 с разложением n = 2k + г, к = 0,1, 2,
г = 1, 2*,
и
1 a\]-
определим функцию (pn{t) = y>jj.(i), которая:
1) равна единице при t = a^V^1;
2) равна нулю вне интервала (а]^1,агк);
3) линейна и непрерывна на отрезках [а£~\
Теорема 5.14*. Система функций {<pn}%Lo типа Фабера —
Шаудера, построенная с помощью последовательности
действительных чисел {aj.}, удовлетворяющих условиям (5.24) и (5.25),
является базисом в банаховом пространстве С[0,1]. #
*См., например: Кашин Б.С> Саакян А.А.

474 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Дополнение 5.1. Неравенства
Минковского и Гельдера
Теорема 5.15 (неравенство Гельдера для конечных
сумм). Для любых комплексных чисел #i, ..., ят и yi, ..., ут,
произвольных действительных р > 1 и q > 1, удовлетворяющих
условию - + - = 1, справедливо неравенство
— s ТП
(5.26)
М Докажем вспомогательное неравенство
ab<— + -9 (5.27)
р q
верное для любых а^О, Ь^О, р>1 и g > 1, для которых
В силу того, что функция lnx в промежутке (0, +оо)
выпукла вверх, для всяких х > 0, у > 0 и любого a G (0,1) верно
неравенство
Пусть а > О, Ь > 0, а числа р > 1, q > 1 связаны равенством
- + - = 1. Используем выпуклость логарифма, полагая в
неравенстве а = 1/р (при этом 1 — а = 1/g), x = ар и у = bq. В
результате получим
1п(-ар + -Ь9) > -1пар + -lnb* = Ina + lnb = \nab.
\р q ) p q
Поскольку функция lnx возрастает в области определения, то
из записанного неравенства вытекает неравенство (5.27) при

Д.5.1. Неравенства Минковского и Гель дера 475
а > 0 и Ь > О. Справедливость неравенства (5.27) при a = 0 или
6 = 0 проверяется непосредственной подсталовкои.
Вернемся к неравенству Гельдера. Введем обозначения:
п=1
=1
Если А = 0 или /л = 0, то неравенство Гельдера очевидно, так
как в этом случае либо х\ = ... = хт = 0, либо у\ = ... = ут = 0.
Пусть А > 0 и /х > 0. Полагаем
а =]£п| ъ =Ы П = Г-^
А ' п /i
Тогда, используя неравенство (5.27) для неотрицательных
чисел ап и Ьп, получаем серию неравенств
А/х ^
Умножая эти неравенства на A/z и суммируя их, а также
учитывая (5.28), находим
n=l 4i^ n=l ^^ n=l
Теорема 5.16 (неравенство Гельдера для рядов).
Пусть действительные числа р > 1 и q > 1 связаны равенством
1 1 оо оо
- + - = 1. Если числовые ряды X) \хп\р и X) \Уп\я сходятся, то
Р « n=i n=i
справедливо неравенство
(ЕУ (е)9 (5-29)
п=1 4=1 ^ 4=1 '

476 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
< Воспользуемся неравенством Гельдера для конечных сумм.
В условиях теоремы при любом т Е N справедливо неравенство
(5.26). Следовательно,
гг, п 1 ^ !
771 /ОО \ Т / ОО \ "Г
П=1 ЧП=1
ОО
так как частичные суммы знакоположительных рядов ]Г] \хк\р
оо п=1
и ^ \ук\р не превосходят сумм этих рядов. Из этого неравен-
п=1
ства видно, что последовательность частичных сумм знакопо-
оо
ложительного ряда ^ |^А;2/А;| ограничена сверху, а потому этот
п=1
ряд сходится (см. 1.4). Переходя в последнем неравенстве к
пределу при т -> +оо, получаем неравенство (5.29). ►
Теорема 5.17 (неравенство Минковского для
конечных сумм). Для произвольных комплексных чисел х\% Х2,
%т и Уь У2ч •• •) Ут и любого р ^ 1 справедливо неравенство
(т
n=l
При р = 1 неравенство (5.30) очевидно, поскольку
Пусть р > 1. Тогда имеет место очевидное неравенство:
п=1 п=1
m m
п=1 п=1

Д.5.1. Неравенства Минковского и Гель дера 477
«■ 1 Л 1
Полагая - = 1 —, к первой сумме в правой части неравенства
(5.31) применим неравенство Гельдера для конечных сумм:
4=1
(Y\\ip-l)q)
) (
71=1 4=1 ' 4=1
(
)
n=i ' 4=1
Здесь мы использовали тождество (р— 1)д = р. Аналогично
— • 171 ч —
)(
n=i 4=1 / 4=1
Учитывая эти неравенства в (5.31), находим
?7l
()(^(
п=1 4=1 7 V n=l п=1
m
При J^ \хп +уп\р = 0 неравенство Минковского очевидно.
п=1
m
При ^ |жп + Уп|р 7^ 0 разделим обе части предыдущего неравен-
п=1
(171 ч — -I •»
S 1жп + Уп|р ) 9 Учитывая, что 1 = -, приходим к
п=1 ' ЯР
неравенству (5.30). ►
Теорема 5.18 (неравенство Минковского для рядов).
т т
Пусть р ^ 1. Если ряды X) kn|p и X) |Уп|р сходятся, то
п=1 п=1
справедливо неравенство
f )p (f )
(f; i*»r)p + (f; |упг) р . (5.32)

478 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
<4 Доказательство теоремы опирается на неравенство Минков-
ского для конечных сумм. В условиях теоремы для любого
натурального т верно неравенство (5.30). Заменяя в правой
т
части этого неравенства частичные суммы рядов ^ 1хп|р и
771 п=1
Л \Уп\р суммами этих рядов, получаем
n=1 ill
- / оо v ■=• /оо v ■=•
il
ЧП=1 ' \l=l ' 4=1 7
Следовательно, частичные суммы знакоположительного ряда
оо
]С 1жп + Уп|р ограничены в совокупности, а потому этот ряд
п=1
сходится (см. 1.4). Переходя в неравенстве (5.30) к пределу
при т -т +оо, получаем неравенство Минковского для рядов. ►
Вопросы и задачи
5.1. Докажите, что в любом нормированном пространстве
L справедливо неравенство
11*-у||, х,уеь.
5.2. Докажите, что если в нормированном пространстве
последовательности {хп} и {уп} сходятся по норме к элементам
х и у, а числовая последовательность {Ап} сходится к числу Л,
то последовательности {хп + уп} и {ХпУп} сходятся по норме к
элементам х + у и Лх.
5.3. Докажите, что если в нормированном пространстве
последовательность {хп} сходится по норме к элементу х, то
5.4. Докажите, что функция
является нормой в Еп.

Вопросы и задачи 479
5.5. Выясните, сходится ли в нормированном пространстве
m последовательность {ж^}, где х^ = {x^}^_v если:
б) w. N
, к>щ б)^ -^ A;€N'
5.6. Докажите, что следующие функции являются нормами
в арифметическом пространстве Шп:
) iggj
5.7. Выясните, являются ли заданные функции нормами
в линейном пространстве непрерывно дифференцируемых на
отрезке [а, Ь] функций, и если да, то определите, является ли
соответствующее нормированное пространство банаховым:
a) max \x(t)\; б) |я?(а)| + max \x'(t)\;
te[a,b] te[a,b]
b
в) max>'(<)|; г) [\x(t)\dt+ max\x'(t)\;
te[a,b] J Ье[а,Ь]
д)И)()|+|()|
te[a,b]
5.8. Докажите, что линейные пространства £р, m, С[а,Ь]
являются бесконечномерными.
5.9. Докажите, что любое конечномерное линейное
многообразие нормированного пространства является его
подпространством.
5.10. Выясните, являются ли подпространствами
нормированного пространства С[0,1] множества следующих функций:
а) монотонные функции;
б) четные функции;
в) многочлены степени не выше к;
г) непрерывно дифференцируемые функции;

480 5. РЯДЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
д) функции x(t), удовлетворяющие условию х(0) = 0;
1
е) функции ж(<), удовлетворяющие условию / x(t)dt = 0.
-1
5.11. Докажите, что любая фундаментальная
последовательность метрического пространства ограничена.
5.12. Докажите, что нормированные пространства m и £р
являются полными.
оо оо
5.13. Пусть ^2 хп и ^2 Уп — ряды в нормированном про-
п=1 п=1
странстве L, а элементы х Е L и у Е L — их суммы. Докажите,
что
оо оо
Ххп) = Ая, А € R (А <Е С).
п=1 п=1
оо оо
5.14. Докажите, что если ряды ^ хп и ^ уп в нормиро-
п=1 п=1
ванном пространстве L абсолютно сходятся, то для любых а и
оо
/5 ряд S (ажп +РУп) также сходится абсолютно.
п=1
5.15. Докажите, что в подпространстве С*[—тг,тг]
нормированного пространства С[—тг,тг], которое состоит из функций
ж(£), удовлетворяющих условию ж(—тг) =х(тг), система 1, cosrr,
cos2rr, ..., cosnrr, не является замкнутой.
5.16. Докажите, что в подпространстве нормированного
пространства С[0,тг/2], состоящем из тех функций x(t),
которые удовлетворяют условию х(0) =0, система sinrr, sin3rr, ...
sin (2n + 1), ... замкнута.

6. ОРТОНОРМИРОВАННЫЕ
СИСТЕМЫ В ГИЛЬБЕРТОВЫХ
ПРОСТРАНСТВАХ
Гильбертовы пространства, представляющие собой
частный случай банаховых пространств, гармонично сочетают в
себе характеристики как банаховых, так и евклидовых
пространств. Это дает ряд замечательных свойств, выделяющих
их и из банаховых, и из евклидовых пространств.
Гильбертовы пространства составляют наиболее распространенный и
широко используемый в приложениях класс бесконечномерных
линейных пространств.
6.1. Гильбертовы пространства
Ранее (см. 3.1) были рассмотрены бесконечномерные
евклидовы пространства и некоторые их свойства. Введение в
евклидовом пространстве евклидовой нормы превращает его
в нормированное пространство. Тем самым на евклидовы
пространства распространяется все, что было сказано о
нормированных пространствах. В частности, можно говорить о
полном евклидовом пространстве, которое
(относительно евклидовой нормы) является полным нормированным, или
банаховым, пространством. В дальнейшем, говоря об
евклидовых пространствах как о нормированных пространствах, мы
будем иметь в виду норму, индуцированную скалярным
произведением.
Отметим, что наряду с евклидовыми пространствами, т.е.
действительными линейными пространствами со скалярным
умножением, можно рассматривать и комплексные линейные
пространства со скалярным умножением, которые называют

482 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
унитарными пространствами. В унитарном
пространстве U скалярное умножение (х, у) удовлетворяет тем же
аксиомам, что и в евклидовом пространстве, за исключением
аксиомы коммутативности, которая заменяется следующей:
(я, У) = (У, х), x,yeU.
Определение 6.1. Бесконечномерное полное евклидово
(унитарное) пространство называют действительным
(комплексным) гильбертовым пространством*
Другими словами, гильбертово пространство — это
бесконечномерное банахово пространство, норма в котором
индуцирована скалярным умножением. Приведем пример гильбертова
пространства.
Пример 6.1. Рассмотрим действительное нормированное
пространство l<i (см. пример 5.4 для случая р = 2). Покажем,
что в этом нормированном пространстве можно ввести
скалярное умножение таким образом, чтобы норма в ^2> определяемая
формулой (5.2), была индуцирована этим скалярным
умножением. Зададим скалярное умножение в £2 следующим образом:
для любых двух элементов х = {ж*}]^ и у = {ук}^1 этого
нормированного пространства положим
хпУп- (6Л)
п=1
оо
Это определение корректно, поскольку числовой ряд 1С хпуп
п=1
сходится, причем абсолютно. Это следует из сходимости ря-
оо оо
дов 2 |яп|25 ]С \Уп\2 и неравенства Гельдера для рядов при
п=1 п=1
2^\ХпУп\ ^ л
п=1 \
п=1
\
п=1
*Д. Гильберт (1862-1943) — крупнейший немецкий математик конца
XIX — начала XX в.

6.1. Гильбертовы пространства 483
Выполнение же аксиом скалярного умножения для функции
(я, у) очевидно.
Индуцированная скалярным умножением (6.1) норма в 1ъ
задается следующим образом:
\\x\\ = у/(х, х) =
\
п=1
т.е. совпадает с нормой, заданной в нормированном
пространстве ^2-
Как отмечалось ранее (см. 5), все нормированные
пространства £р, р ^ 1, полны, т.е. являются банаховыми.
Следовательно, бесконечномерное нормированное пространство ^2 со
скалярным произведением (6.1) является гильбертовым
пространством. Это гильбертово пространство, как и
соответствующее нормированное пространство, обозначают символом
Так же можно ввести комплексное гильбертово
пространство t*i, состоящее из комплексных последовательностей z —
оо
х, гп G С, n G N, таких, что Yl \zn\2 < оо. В этом
линейном пространстве скалярное произведение двух
последовательностей z = {zk}kLi nw = {wk}kLi определяют формулой
n=l
Индуцированная таким скалярным умножением норма также
совпадает с нормой, действующей в ^ которая задается
формулой (5.3). #
Бесконечномерное евклидово пространство не является
гильбертовым, если оно не полное. Приведем пример такого
евклидова пространства.

484 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
Пример 6.2. Рассмотрим бесконечномерное евклидово
пространство i?o[a,b] кусочно непрерывных функций.
Скалярное умножение в нем задается формулой
6
(ж, у) = fx{t)y{t)dt, x,ye Е0[а,Ь].
а
Можно показать, что относительно нормы, индуцированной
этим скалярным умножением, евклидово пространство Ео[а,Ь]
не является полным и, следовательно, гильбертовым
пространством. #
Приведем два важных свойства произвольных евклидовых
(унитарных) пространств, которые будут использованы в
дальнейшем. Следующая теорема фактически утверждает, что
скалярное умножение, как функция двух переменных, непрерывно
относительно нормы, индуцированной скалярным
произведением.
Теорема 6.1. Пусть последовательности {хп} и {уп}
элементов произвольного евклидова (унитарного) пространства Н
сходятся к элементам хеНиуеН по норме, индуцированной
скалярным умножением в Н. Тогда числовая
последовательность скалярных произведений {(хп, уп)} сходится к
скалярному произведению (х, у).
< Так как lim xn = х, числовая последовательность {||хп — х||}
п—юо
сходится к нулю и, следовательно, является ограниченной. В
силу свойств нормы для всякого n E N имеем
Значит, последовательность {||хп||} также ограничена.
Используя неравенство Коти — Бунлковского, получаем
I (яп, Уп) ~ (х, у) | = | (ж„, уп) - (ж„, у) + (х„, у) - (ж, у) | =
(Хп-Х, у) | < | (Ж„, Уп -У) | + | (Хп -X, у) \ ^
*ь\\хп\\\\уп-у\\ + \\*п-

6.1. Гильбертовы пространства 485
Каждая из последовательностей {||жп||||уп-у||} и {||жп-ж|
является бесконечно малой как произведение бесконечно малой
на ограниченную [1-7.5]. Поэтому
|(*п, Уп)-(я, V) |-+0, п-юо,
например, в силу теоремы о „зажатой" последовательности
[1-6.5]. Отсюда сразу следует, что числовая последовательность
{(яп, Уп)} сходится к числу (х, у), т.е.
lim (жп, уп) = (х, у). ►
п—юо
Теорема 6.2. Во всяком евклидовом (унитарном)
пространстве Н справедливо равенство параллелограмма
\\х + У\\2 + \\х - у\\2 = 2\\х\\2 + 2||у||2, х, у € Я.
•4 Используя определение нормы и свойства скалярного
умножения, получаем
= (х, х) + (у, х) + (ж, у) + (у, у) + (х, х) - (у, х) - (х, у) + (у, у) =
►
Замечание 6.1. Равенство параллелограмма важно
потому, что дает критерий для норм, которые являются
индуцированными некоторым скалярным умножением. В самом деле,
если норма ||х|| индуцирована скалярным умножением, то,
согласно теореме 6.2, для этой нормы справедливо равенство
параллелограмма. Пусть норма ||х|| в нормированном
пространстве L удовлетворяет равенству параллелограмма. Тогда
можно показать, что функция, которая в действительном
случае определяется равенством

486 б. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
а в комплексном случае — равенством
(Д)У)-11* + у112-||*-у112 , .\\x + iy\\2-\\x-iy\\^
является скалярным умножением, причем это скалярное
умножение индуцирует норму ||х||. Тем самым нормированное
пространство L превращается в евклидово (унитарное)
пространство. #
Пример 6.3. Покажем, что в нормированном пространстве
С[0,1] нельзя ввести скалярное умножение, которое индуцирует
его норму. Для этого достаточно показать, что норма в С[0,1]
не удовлетворяет равенству параллелограмма.
Норма в С[0,1] определяется следующим образом:
|||||()|,
Рассмотрим, например, функции x(t) = £ и y(t) = l — t. Для этих
функций имеем
|
|* + (l-t)| =
||y|||()|
Прямой проверкой легко установить, что равенство
параллелограмма для функций x(t) и у(t) не выполняется.
6.2. Расстояние до подпространства
Пусть Н — гильбертово пространство, М — его
подмножество. Тогда для любого хЕН расстоянием от элемента
х до множества М называют число
р(х,М)= inf ||s-u||.

6.2. Расстояние до подпространства 487
Отметим, что если х G М, то р(х,М) = inf \\х — и\\ = \\х — х\\ =
= 0. В каких еще случаях расстояние от элемента до множества
равно нулю?
Лемма 6.1. Пусть Н — гильбертово пространство.
Расстояние от элемента х G Н до множества М С Н равно нулю
тогда и только тогда, когда х принадлежит М или является
предельной точкой этого множества, т.е.
р(х,М)=0 <=» хе~М.
<4 Пусть р(х,М) = 0, т.е. inf \\х — и\\ = 0. Если х G М, то в силу
ием
свойства замыкания х G М С М. Если же х £ М, то,
согласно определению точной нижней грани, для любого числа е > 0
можно указать элемент и G М, ифх, для которого ||и — х|| < £.
То же самое можно сказать по-другому: любая е-окрестность
Ue(x) = {и€ Н: \\и — х\\ < е} содержит точки u G М\ {х}. Это
значит, что элемент х является предельной точкой
множества М.
Доказательство обратного утверждения аналогично. ►
Следствие 6.1. Если М — замкнутое подмножество
гильбертова пространства Н и х £ М, то р(х,М) > 0.
Пусть х и у — элементы действительного (комплексного)
линейного пространства L. Множество
[х, у] = {z G L: z = (l-a)z + ay, a G IR, 0 ^ a ^ 1}
назовем отрезком, соединяющим точки х и у. Множество
М линейного пространства L называют выпуклым, если оно
вместе с любыми своими точками х\ и Х2 содержит и весь
отрезок, соединяющий эти точки, т.е. для любых х\,х% G М
naGlR, 0<а<1, имеем (1—а)х\ + ах<2 G М.
Теорема 6.3. Пусть М — замкнутое выпуклое множество
в гильбертовом пространстве Н и х G Н. Тогда существует,

488 б. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
причем единственный, элемент у G М, такой, что
р(х,М) = \\х-у\\. (6.2)
М Если х G М, то р(х,М) = 0 = р(х,х) = ||х — ж||, т.е. в качестве
у Е М можно взять сам элемент х. Единственность у очевидна,
поскольку для любого z G Н, отличного от х, имеем \\х — z\\ > 0.
Пусть х £ М. Так как М замкнуто, то d = р(х,М) > 0.
По определению d = р(х,М) = inf \\х — и\\. Значит, согласно
ием
свойствам точной нижней грани, для всякого п G N можно
выбрать такой элемент ип G М, что
d ^ р{х,ип) = \\х - ип\\ <d+-. (6.3)
п
Докажем, что последовательность {ип} является
фундаментальной. Выберем два произвольных элемента ип и ит этой
последовательности и для элементов х — ип их — ит
гильбертова пространства Н запишем равенство параллелограмма:
\\(x-un) + (x-um)\\2 + ||(*-«„) - (x-um)||2 =
Отсюда находим
||«„ " «mil2 = 2||z - txn||2 + 2||х - um\\2 - \\2х -un- um||2 =
2 (6.4)
Так как M — выпуклое множество, а элементы ип и ит
принадлежат М, то (un+um)/2 G М. Следовательно, согласно
определению числа d, имеем
р А (6.5)

6.2. Расстояние до подпространства 489
Используя неравенства (6.3) и (6.5), из (6.4) получаем
п пг mm1
Возьмем произвольное е > 0 и выберем N = N(e) так, чтобы
N > (8d+4)/e2. Тогда при п > N и m > N имеем
<п т/ N
Таким образом,
Ve>0 3N = N{e)eN Vn>N Vm>iV:
что и означает фундаментальность последовательности {ип}.
Далее, поскольку Н — гильбертово пространство и,
значит, полно, существует предел у Е Н фундаментальной
последовательности {ип}. Покажем, что элемент у удовлетворяет
требуемым условиям. Во-первых, у Е М, так как {ип} С М и
М замкнуто. Во-вторых, учтем, что на основании теоремы о
предельном переходе в скалярном произведении
Переходя к пределу в неравенстве (6.3) при п —>• оо, получаем
т.е. ||ж-у|| =d.

490 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
Наконец, установим единственность элемента у Е М, для
которого выполняется условие (6.2). Пусть некоторый элемент
у* Е М также удовлетворяет условию (6.2), т.е. \\х — у*\\ = d.
Запишем равенство параллелограмма для элементов х — у и
х-у*:
Отметим, что у, у* Е М и, следовательно, (у + у*)/2 Е М, так
как множество М выпуклое. Поэтому \\х — (у+у*)/2|| ^ d.
Учитывая это, находим
Таким образом, 0 ^ ||у — у* ||2, что возможно лишь при \\у — у* \\ =
= 0, откуда у = у**>
Напомним, что гильбертово пространство Я в то же время
является и нормированным пространством. Множество L С Н
называют подпространством гильбертова
пространства if, если оно является подпространством нормированного
пространства Н.
Следствие 6.2. Для любого подпространства L
гильбертова пространства Н и произвольного элемента х Е Н
существует, причем единственный, элемент у Е L, такой, что
М Согласно определению, подпространство гильбертова
пространства замкнуто. Кроме того, подпространство выпукло,
что следует из определения линейного многообразия. Значит, к
подпространству гильбертова пространства можно применить
теорему 6.3. ►

6.3. Ортогональность 491
6.3. Ортогональность
Напомним, что элементы х и у евклидова (унитарного)
пространства Я называют ортогональными (мы будем
обозначать это так: х J_ у), если (я, у) = О [IV]. Элемент z Е Я
называют ортогональным подпространству L С Я, если
z -1 ж для всех ж Е L, что будем обозначать z J_ L.
Теорема 6.4. Если L — подпространство гильбертова
пространства Я, то множество 1Л = {z Е if: z J_ L} также
является подпространством Я.
«4 Выберем произвольные элементы 2:1,2:2 E I/-1-. В силу
определения множества lA для всех х Е L справедливы равенства
(zi, ж) = 0, (z2, х) = 0. Поэтому для любых чисел ai,c*2 E F
имеем
(OC\Z\ + QL2Z2, X) = OL\ (2:1, x) + OL2 {Z2, x) = 0, X E L.
Следовательно, ot\Z\ -\-0t2Z2 E L^, т.е. L1- — линейное
многообразие.
Докажем, что множество ZA замкнуто. Пусть
последовательность {zn} элементов множества L1- сходится по норме
гильбертова пространства Я к некоторому элементу z(zH.
Поскольку (zn, х) = 0, х Е L, для всех п Е N, то, согласно теореме
6.1 о предельном переходе в скалярном произведении, имеем
(z, х) = lim (zn, x) = 0, х Е L.
п—>оо
Следовательно, zEL1. Так как любая предельная точка
множества L1- является пределом некоторой последовательности
элементов из L-1-, то ZA = ZA и множество L1- является замкнутым.
Итак, множество L1- — замкнутое линейное многообразие, т.е.
подпространство гильбертова пространства Я. ►
Подпространство L1- называют ортогональным
дополнением к подпространству L в гильбертовом пространстве Я.

492 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
Отметим, что L П ZA = 0, поскольку для любого х Е ЬП lA по
определению множества ZA имеем (я, х) = О, откуда х = 0.
Теорема 6.5. Пусть L — подпространство гильбертова
пространства Я, х Е Я, а элемент у — тот элемент из L, для
которого p(x,L) = \\х-2/||. Тогда х-у€ lA
«* Необходимо доказать, что (х — у, К) = 0 для всех h € L.
Возьмем в L произвольный элемент h ф 0. Так как элемент
у, согласно условию теоремы, также принадлежит L, a L —
подпространство, тоу — XhEL для любого числа Л Е F. Значит,
\\x-(y-\h)\\>p(x,L) = \\x-y\\.
Возведем полученное неравенство норм в квадрат и запишем с
помощью скалярного произведения:
(х - у + АЛ, х - у + \h) ^ (х-у,х-у).
Преобразуем неравенство, используя свойства скалярного
умножения:
, x-y)+J{x-y, h) + X\{h, h) ^ (x-y, x-y).
Упростив неравенство, находим
\(h,x-y) + \(x-y, /i) + |A|2||/i||2^0. (6.6)
Учитывая, что /i/Ои, следовательно, \\h\\ ф 0, полагаем
л _ (х ~ 2/> *0 т_ (hx~y)
1№ И
После подстановки этих значений в (б.б) приходим к
неравенству
\(h,x-y)\2 1(Л,*-у)|а |(Л, *-у)|2
+ U
которое сводится к неравенству \(h, х — у) |2 < 0, справедливому
для любого элемента h E L. Но так как левая часть этого не-

6.3. Ортогональность 493
равенства всегда неотрицательна, то (Л, х — у) = 0 для любого
heL, т.е. x-yeL1. ►
Теорема 6.6. Пусть L — подпространство гильбертова
пространства Н. Тогда для любого элемента х Е Я найдутся
такие элементы j/ELh^eL1, что будет справедливым
разложение
причем это разложение единственно.
<4 Пусть х Е Н. Выберем, согласно следствию 6.2, элемент
у Е L, для которого \\х — у\\ = p(x,L). Тогда по теореме 6.5
имеем я — у Е ZA. Положив z = х -у, получим ж = у + z, где
у Е L и z E ZA. Докажем, что это представление единственно.
Допустим, что существуют два разложения элемента ж, т.е.
х = ух + z\ = у2 + ^2> 2/i, 2/2 € Z/, а^ь^Е ZA. Из равенства двух
сумм находим у\ — 2/2 = ^2 — ^1, причем yi — 2/2 € L и Z2 — 21 Е L1,
поскольку L и L1- — подпространства. Выше было отмечено,
что L П ZA = 0. Значит, yi — 2/2 = ^2 — 21 = 0 и yi = У2, 2i = 2:2. Мы
пришли к выводу, что два произвольных разложения элемента х
совпали. Поэтому элемент х имеет единственное разложение. ►
В разложении х = у + z, у Е L, zE ZA элемент у в
подпространстве L гильбертова пространства Н называют
ортогональной проекцией элемента х на подпространство L.
Теоремы 6.4 и 6.6 переносят на бесконечномерные
евклидовы пространства аналогичные утверждения из линейной
алгебры [IV]. Используя понятие прямой суммы, утверждение
теоремы 6.6 можно сформулировать следующим образом:
гильбертово пространство Н можно представить в виде прямой
суммы произвольного подпространства L и его
ортогонального дополнения LL: H = L®L±. Это утверждение верно
для любого конечномерного евклидова пространства [IV], но
если евклидово пространство бесконечномерно, то
утверждение сохраняет силу лишь при дополнительных требованиях:
пространство должно быть полным, а подпространство (в тер-

494 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
минологии бесконечномерных пространств — линейное
многообразие) — замкнутым. В конечномерных пространствах оба
дополнительных требования выполняются автоматически.
В дальнейшем прямую сумму Н = L © L1 в гильбертовом
пространстве Н будем называть ортогональной суммой.
Теорема 6.7. Линейное многообразие М гильбертова
пространства Н всюду плотно в Н тогда и только тогда, когда
единственным элементом жЕЯ, ортогональным М, является
нулевой элемент:
Л = Н <=^ (х±М =^ я? = 1
^Необходимость. Пусть линейное многообразие М всюду
плотно в Н (т.е. М = Н) и х J_ M. Тогда существует
последовательность {уп} элементов из М, сходящаяся к х по норме в
Н. Поскольку х _!_ М, то (я, уп) = О, п Е N. Значит, согласно
теореме 6.1 о предельном переходе в скалярном произведении,
lim (ж, уп) = (ж, х) = 0, откуда х = 0.
п—юо
Достаточность. Пусть в if единственным элементом,
ортогональным всем элементам из М, является нулевой
элемент. Множество М является подпространством гильбертова
пространства Н (см. теорему 5.5). Рассмотрим его
ортогональное дополнение М Если z Е М , т.е. z _!_ М, то z JL М. В
этом случае по условию теоремы z = 0. Следовательно, М =0.
Выберем произвольный элемент х Е Я. Согласно теореме 6.6,
имеет место разложение ж = у + z, где y€M,z€M =0. Таким
образом, х = у € М, и if = М. ►
6.4. Ортонормированные системы и ряды Фурье
Рассмотрим базисы в гильбертовых пространствах (о
базисах в банаховых пространствах см. 5.5).
Определение 6.2. Произвольное множество Е (не
обязательно счетное или конечное) ненулевых элементов гильбертова

6.4. Ортонормированные системы и ряды Фурье 495
пространства Н называют ортогональной системой, если
любые два различных элемента этого множества
ортогональны: (еь ег) = 0 при ei, в2 Е Е и е\ ф в2.
Определение 6.3. Ортогональную систему Е элементов
гильбертова пространства Н называют ортонормироеанной
системой, если норма каждого элемента этой системы равна
единице: ||е|| = 1, е Е Е.
Отметим, что понятие конечной ортогональной (ортонор-
мированной) системы введено в [IV], а счетной системы — в
3.1. Ив том и в другом случае ортогональная (ортонормиро-
ванная) система понимается как упорядоченный набор
элементов (конечная или бесконечная последовательность элементов).
Поэтому и в общем случае такую систему следует считать
упорядоченной и записывать как „несчетную последовательность"
{ea}a£i, где I — некоторое множество индексов.
Мы ограничимся только счетными ортогональными и орто-
нормированными системами. В этом случае / = N, а систему
можно записать как последовательность:
Пример 6.4. В действительном гильбертовом
пространстве ^2 (см. пример 6.1) со скалярным умножением (6.1) орто-
нормированной является, например, такая система
последовательностей:
п-1
В этой системе еп = {х£ /j^p где Хп = 1, п Е N и ж^ = 0 для
всех кфп. Ортонормированность этой системы очевидна.

496 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
Пример 6.5. В бесконечномерном евклидовом
пространстве Ео[—тг, тг] кусочно непрерывных функций на отрезке [—тг, тг]
со скалярным умножением
тг
, 9) = J f{x)g{x)dx, f,g
e Е0[-7г,
ортонормированнои системой является тригонометрическая
система
1 cos ж sinх cosnx sinnx
Это доказано в 3.1. #
Если {enJ^Lj — счетная ортонормированная система
гильбертова пространства if, то произвольная числовая
последовательность {afc}^!, c*fc E F, k Е N, позволяет составить ряд по
оо
этой системе вида ^ &кек-> представляющий собой ряд элемен-
к=1
тов нормированного пространства Н.
Определение 6.4. Пусть Н — гильбертово пространство
и {e^^Lj — счетная ортонормированная система в Н. Для
любого элемента х Е Н числа Ск = (ж, е&), к Е N, называют
коэффициентами Фурье элемента х по ортонормированнои
оо
системе {еп}^=1^ а ряд ^ c^e*, построенный с помощью этих
коэффициентов, — рядом Фурье элемента х по этой
ортонормированнои системе.
п
Определение 6.5. Частичную сумму ^ c^e/t ряда Фурье
элемента х Е Н по ортонормированнои системе {en}^L1
называют многочленом Фурье n-го порядка элемента х.
Основная цель этой главы — изучение рядов Фурье в
гильбертовых пространствах. Выясним предварительно некоторые
свойства многочленов Фурье.

6.4. Ортонормировалные системы и ряды Фурье 497
Нетрудно доказать, что любой конечный набор элементов
ортогональной (ортонормированной) системы {enJ^Lj является
линейно независимой системой. Следовательно, для всякого
nEN линейная оболочка Ln = (ei, ..., еп) является п-мерным
линейным многообразием, которое замкнуто (см. теорему 5.4),
а потому является n-мерным подпространством в Я. При
этом система элементов ei, в2, еп составляет базис в Ln.
Всякий элемент u€Ln можно единственным образом разложить
по этому базису, т.е. представить в виде
к=\
где коэффициенты разложения ак определены однозначно.
Согласно теореме 6.3, для любого элемента х G Н существует,
п
причем единственный, элемент w* = ^ а%ек € Ln, такой, что
Следующая теорема показывает, что представляют собой
элемент w* и его коэффициенты а£.
Теорема 6.8. Пусть Н — произвольное гильбертово
пространство, {ei,..., еп} — конечная ортонормированная система
в Н и Ln = (ei, ..., еп) — линейная оболочка этой системы.
Тогда для любого элемента х Е Н верны формулы
(6.7)
к=1
и
~ " (6-8)
где с* = (х, вк), к = 1,п, — коэффициенты Фурье элемента х.

498 б. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
п
М Выберем произвольный элемент и = ^ ак^к € Ln и рассмо-
трим скалярный квадрат элемента х — и:
\x-u\\2 = k-X)
k=l fc=li=l
n n n
Здесь Ck = (x, e/t), к = 1, п. Для любых двух комплексных чисел
с** и Ck верны соотношения
\ск - оск\2 = (ск - ак) (ск - ак) = (ск - ак) (ск - ак) =
= скс£ - ЯШ - Щск + акЩ = \ск\2 - акс£ - Щск + \ак\2,
из которых находим
-акс£- Щск + \ак\2 = \ск - ак\2 - \ск\2
Учитывая это тождество в правой части равенства (6.9),
получаем
|
к=1 к=1 к=1
п
Очевидно, что сумма ^ \ск — ак\2 достигает своего минималь-
к=1
ного значения, равного нулю, при ак = ск, к = 1, п. Значит,
и минимальное значение ||гс — гх||, uEL, достигается при этих
условиях, т.е. когда числа ак являются коэффициентами Фурье
элемента х. Это доказывает соотношение (6.7). Согласно опре-

6.4. Ортонормированные системы и ряды Фурье 499
делению расстояния от элемента до подпространства, имеем
II П II2 п II2 П
p2{x,Ln) = min U-VWJ Uy]
что совпадает с равенством (6.8). ►
Таким образом, элементом подпространства Ln = (е\, ..., еп)
гильбертова пространства if, реализующим расстояние от
элемента х G Н до Ln, является многочлен Фурье порядка п
элемента х по ортонормированной системе {еп}™=1.
Следствие 6.3. Пусть Н — гильбертово пространство,
{еп}™=1 — счетная ортонормированная система в Я. Тогда
к=1 к=1
где с* = (ж, ед;), fc E N, — коэффициенты Фурье элемента х по
системе {en}^Ll.
Ч Из теоремы 6.8 следует, что
т п
где Ln = (eb ..., en) и Lm = (eb ..., em). Поскольку Ln С Lm
при m > n, то
p{x,Ln) = min||z-u|| ^ min ||ж-w|| =/9(a?,LTO). ►
Теорема 6.9. Пусть Н — гильбертово пространство и
(en}£Li — счетная ортонормированная система в Я. Тогда для
любого элемента х€ Н верно неравенство Бесселя:
где Cfc = (х, е*), fc G N, — коэффициенты Фурье элемента х по
системе {еп}£°=1.

500 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
М Неравенство Бесселя является следствием равенства (6.8),
и его доказательство дословно совпадает с доказательством
неравенства Бесселя для бесконечномерных евклидовых
пространств (см. теорему 3.2). ►
Отметим, что теоремы 6.8 и 6.9 верны для произвольных
бесконечномерных евклидовых и унитарных пространств, а не
только для полных (т.е. гильбертовых).
6.5. Ортонормированные базисы
Все сказанное о счетных базисах в банаховых
пространствах (см. 5.5) относится и к гильбертовым пространствам,
являющимся частным случаем банаховых пространств.
Однако, как и в конечномерных евклидовых пространствах, нал-
больший интерес представляют счетные базисы, относящиеся
к ортогональным (ортонормированным) системам. Такие
базисы обладают рядом важных свойств, среди которых следует
отметить простоту процедуры разложения элементов
гильбертова пространства по этим базисам. Кроме того, для проверки
базисности ортонормированных систем существуют простые и
эффективные критерии.
Определение 6.6. Счетный базис {еп}^=1 гильбертова
пространства Н, являющийся ортогональной (ортонормиро-
ванной) системой, называют ортогональным (ортонорми-
рованным) базисом в Н.
Теорема 6.10. Счетная ортонормированная система {еп}
в гильбертовом пространстве Н является ортонормированным
базисом тогда и только тогда, когда любой элемент х Е Н
является суммой своего ряда Фурье по этой системе:
_ (6.11)
где Cfc = (x, е&), keN.

6.5. Ортонормированные базисы 501
<4 Необходимость. Пусть система {en}^=i является ор-
тонормированным базисом в гильбертовом пространстве Н.
Тогда всякий элемент хеН единственным образом можно пред-
оо
ставить в виде сходящегося ряда: х = £) &кек. Покажем, что
fc=i
коэффициенты ак, к Е N, являются коэффициентами Фурье
элемента х. Для этого заметим, что в силу ортонормированности
системы {еп}^-^ при всех п> к верно равенство
п п
) ат (еш, ек) = ак.
ra=l m=l
Согласно теореме 6.1 о предельном переходе в скалярном
произведении, имеем
оо п
оо п
ск = (х, ек) = ^ ^2 атет, ек) = yirn^ ^ атет, ек) =
771=1 771=1
П
= lim ( У2 атет, ekj = lim ak = ак, ке N. (6.12)
1
Ш=1
Достаточность. Пусть {еп}^=1 — ортонормированная
система и всякий элемент х G Н является суммой своего ряда
Фурье (6.11). Ряд Фурье элемента х представляет собой
разложение этого элемента по системе {en}^=i, что доказывает
существование разложения всякого элемента х Е Н по системе
{еп}^=1. Осталось доказать, что для всякого элемента х Е Н
разложение единственно.
оо
Пусть х— J2 ак^к — разложение элемента х по ортонор-
к=1
мированной системе {^n)^Li' Повторяя вычисления в
соответствии с равенствами (6.12), получаем ск = ак, к Е N, т.е.
произвольно взятое разложение элемента х по системе {еп}^_1
совпадает с рядом Фурье элемента х по этой системе. ►
Отметим, что в теореме 6.10 доказано более общее
утверждение: если {еп}^=1 — произвольная ортонормированная си-

502 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
стема (не обязательно являющаяся базисом) гильбертова
пространства Я и элемент хеН является суммой некоторого ряда
по этой системе, то этот ряд есть ряд Фурье элемента х Е Я по
системе {еп}^=1.
Для любой ортонормированной системы в гильбертовом
пространстве Я вьгаолняется неравенство Бесселя (см.
теорему 6.9). Если ортонормированная система является базисом в
Я, то это неравенство становится равенством.
Теорема 6.11. Для того чтобы ортонормированная
система {еп}^=1 гильбертова пространства Я была его базисом,
необходимо и достаточно, чтобы для любого элемента х Е Я
выполнялось следующее равенство Парсевалл:
к=1
где Cfc = (х, efc), к Е N, — коэффициенты Фурье элемента х по
системе
<4 Необходимость. Пусть {en}'^L1 — ортонормирован-
ный базис гильбертова пространства Я. Тогда для любого
х Е Я в силу теоремы 6.10 имеем представление х = J2 ск^к->
к=1
где Cfc = (ж, efc), к Е N. Сходимость этого ряда к элементу х
означает сходимость к х последовательности его частичных
71
II II
сумм X) ск^к по норме в Я, т.е. lim х— ]Г) CfceJ = 0. Учиты-
k=i n^ooN *=i !|
вая формулы (6.7) и (6.8), получаем
что и доказывает справедливость равенства Парсеваля.
Достаточность. Пусть {вп}^-! —
ортонормированная система гильбертова пространства Я, для любого элемента

6.5. Ортопормировалные базисы 503
оо
х Е Н числовой ряд ^ |с*|2 сходится и, кроме того, выполняет-
*=1 оо
ся равенство Парсеваля ||я||2 = £ |с*| , где с* = (ж, е*), fc 6 N, —
коэффициенты Фурье элемента х по системе {вп}^-!- Тогда,
используя соотношения (6.7) и (6.8), получаем
^n2 - 1С Iе*!2) = и^и
к1
|ГtJ&O )
к=1 к=1 к=1
оо
Это означает, что ряд ]Г) скек сходится к элементу х 6 Я по
к=1
норме в Я. Таким образом, элемент х € Н является суммой
своего ряда Фурье. Поскольку х — произвольный элемент
гильбертова пространства Я, то, согласно теореме 6.10, ор-
тонормированная система {еп}™=1 является базисом в Я. ►
В силу теоремы 5.12 любой базис {en}%Li банахова
пространства В является замкнутой системой, т.е. линейная
оболочка этой системы всюду плотна в В. Однако в произвольном
банаховом пространстве не всякая замкнутая система является
базисом. Следующая теорема показывает, что в гильбертовом
пространстве понятия базисности и замкнутости для ортонор-
мированных систем эквивалентны.
Теорема 6.12. Ортонормированная система {еп}^=1
гильбертова пространства Н является базисом тогда и только
тогда, когда она замкнута в Я.
< Замкнутость всякого, в том числе ортонормированного,
базиса в гильбертовом пространстве следует из теоремы 5.12.
Докажем обратное. Пусть линейная оболочка L системы {еп}^=1
является всюду плотным множеством в Н. Покажем, что
{еп}^°=1 — ортонормированный базис в Я. Условие плотности
L в Я означает, что для любого элемента х Е Я и любого
числа е > 0 можно указать такой элемент хе Е L, что \\х — хе\\ < е
(см. 5.4). Элемент хе принадлежащий линейной оболочке L,

504 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
является линейной комбинацией элементов системы {е^}, т.е.
N
хе = J2 акек для некоторых чисел о^, k = l,N. Согласно тео-
реме 6.8, примененной к конечной ортонормированнои системе
ei, ..., ejy, заключаем, что
N N
J
к=1 к=1
где с* = (ж, ек), к Е N, a LN = (ei, ..., едг). Отсюда в силу
следствия 6.3 получаем
п N
|z-]T/fceJ ^ k-JZ^eA: <e, n>N.
к=1 к=1
Таким образом, для произвольного х G Н установлена
истинность следующего утверждения:
п
= N(e)eN Vn>AT: |UJ
и II
что означает существование предела lim \\x — ^ скеЛ = 0.
оо п-^оо|| к=1 ||
Следовательно, х= Ylckek- Согласно теореме 6.10, система
к=1
{еп}™=1 является ортонормированным базисом в Я. ►
Доказанное утверждение можно перенести на произвольные
ортогональные системы, т.е. условие нормированности
элементов системы в этом случае несущественно.
Теорема 6.13. Ортогональная система {ч>п)™=\ в
гильбертовом пространстве Н является счетным базисом в Н тогда и
только тогда, когда она замкнута в Н.
< Замкнутость всякого базиса в гильбертовом пространстве,
в том числе ортогонального, следует из теоремы 5.12.
Докажем обратное. Пусть {<pn}%Li — замкнутая ортогональная

6.5. Ортонормированные базисы 505
система в Я. Поскольку элементы <рп ортогональной
системы отличны от нуля, то ее можно пронормировать, полагая
еп = <Рп/\\<Рп\\> п € N. В результате получим ортонормирован-
ную систему {en}JJL1? которая является замкнутой в Я, так
как линейные оболочки систем {у?п} и {еп} совпадают.
Значит, ортонормированная система {еп} является базисом в Я.
Поэтому любой элемент х Е Я единственным образом можно
оо
представить сходящимся рядом х = J2 °пеп — рядом Фурье
этого элемента. Но этот ряд легко преобразовать в ряд по
системе {<рп}:
Очевидно, что любой ряд по ортогональной системе {<рп}
преобразуется в ряд по системе {еп}. Значит, предъявленное
разложение х по системе {<рп} единственно.
Итак, любой элемент х € Н имеет разложение по системе
{у>п}, и притом единственное. Следовательно, эта система —
счетный базис в Н. ►
Рассмотрим еще одну характеристику ортонормированных
систем. Как и в случае бесконечномерных евклидовых
пространств (см. определение 3.3), ортонормированную систе-
МУ (en}£Li гильбертова пространства Н называют полной,
если единственным элементом в Я, ортогональным всем
элементам системы {еп}^=1, является нулевой элемент.
Теорема 6.14. Для того чтобы ортонормированная систе-
ма (en}£Li гильбертова пространства Н была базисом в Я,
необходимо и достаточно, чтобы она была полной в Я.
Ч Эта теорема — простое следствие теорем 6.7 и 6.12.
Действительно, на основании теоремы 6.12 ортонормированная система
{en}™-i является базисом тогда и только тогда, когда она
замкнута, т.е. линейная оболочка L этой системы всюду плотна

506 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
в Н. В свою очередь, согласно теореме 6.7, линейное
многообразие L всюду плотно в Н тогда и только тогда, когда
единственным элементом в Я, ортогональным всем элементам
линейного многообразия L, является нулевой элемент. Нам
остается показать, что если х ± е^, к Е N, то х _L L, так как
элемент, ортогональный L, ортогонален всем элементам в L, в
том числе и элементам системы {еп}.
Пусть х — элемент из Н, ортогональный всем элементам
системы {еп}, т.е. (ж, е*) =0, к Е N. Любой элемент у Е L
является линейной комбинацией элементов системы {еп}, т.е.
п
у = XI алеА; Для некоторых ctk- Поэтому
(х, у)= (z, ^afcefcj =^afc(z, e*) = ^Гак -0 = 0.
Это означает, что элемент х ортогонален L. ►
Пример 6.6. В гильбертовом пространстве £2 (см. пример
6.1) ортонормированная система последовательностей
п-1
является ортонормированным базисом. Действительно, как
показано в примере 5.13 (случай р = 2), эта система является
счетным базисом в банаховом пространстве ^2> норма в котором
индуцирована скалярным умножением гильбертова
пространства. Нетрудно увидеть, что эта система является ортонор-
мированной, а потому — ортонормированным базисом. В том
же примере показано, что последовательность х = {х^}^=1 Е ^2
оо
имеет разложение х = Y1 хп^п по заданной системе. Согласно
теореме 6.10, этот элемент имеет разложение в ряд Фурье по

6.6. Ортогонализация и существование ортогонального базиса 507
заданной системе. В силу единственности разложения элемен-
оо
та по базису ряд х = ^ хпеп является рядом Фурье элемента
х по ортонормированной системе {еп}, а члены Хк
последовательности х е #2 — коэффициентами Фурье элемента х по этой
системе.
6.6. Ортогонализация и существование
ортогонального базиса
Как показано в 6.5, если счетная система в гильбертовом
пространстве является ортогональной (ортонормированной),
то проверка того, является ли эта система базисом, заметно
упрощается. Поэтому в гильбертовых пространствах важно
уметь строить именно ортогональные (ортонормированные)
системы. Обычно не составляет труда указать в
гильбертовом пространстве какую-нибудь счетную линейно независимую
систему элементов. Ортогональную систему можно строить,
отталкиваясь от такой линейно независимой системы. Широко
известен алгоритм преобразования произвольной линейно
независимой системы в ортонормированную систему, называемый
процессом ортогонализации Грама — Шмидта (или процессом
ортогонализации Шмидта). Этот алгоритм применяется для
построения ортонормированных базисов в конечномерных
евклидовых пространствах [IV], но без изменений переносится
и в бесконечномерные евклидовы и унитарные пространства.
Суть процесса ортогонализации Грама — Шмидта состоит в
том, что исходную систему {дк]^-\ заменяют
эквивалентной ей ортонормированной системой {е^}^, т.е. такой, что
любой элемент е* является линейной комбинацией элементов gi
с номерами г ^ к и, наоборот, любой элемент gk является
линейной комбинацией элементов е* с номерами г ^ к. Существование
для произвольной счетной линейно независимой системы
эквивалентной ей ортонормированной системы утверждает
следующая теорема, однако заметим, что в данном случае важна

508 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
не столько формулировка этой теоремы, сколько ход ее
доказательства, так как именно в доказательстве раскрываются
детали процесса Грама — Шмидта.
Теорема 6.15. Пусть {gk}(kLl — произвольная линейно
независимая система элементов гильбертова пространства Н.
Тогда в Н существует ортонормированная система элементов
> связанная с системой {дк} соотношениями
+ ак2д2 + ... + аккдк, к Е N;
(O.lo)
19к = bfciei + bk2e2 + ... + bkkek, к Е N,
в которых ак{, bki Е F, i = 1, fc, к Е N, причем акк ^0и Ькк ф 0,
кек
< Доказательство удобно проводить в два этапа. На первом
этапе мы построим ортогональную систему, удовлетворяющую
соотношениям вида (6.13) (построение такой системы и есть
собственно процесс ортогонализации Грама — Шмидта). На
втором этапе мы пронормируем каждый элемент
ортогональной системы так, чтобы все элементы имели единичную норму.
Итак, построим ортогональную систему {Л}^, для
которой выполняются соотношения
bit = Ai/i + /W2 + • • ■ + АлЛ, * e N,
где ajtjt 7^ 0, pkk ф О, А; Е N. Отметим, что элементы Д
определяются с точностью до числового множителя, так как умножение
этих элементов на число не нарушает ни вида соотношений
(6.14), ни условий их взаимной ортогональности. Поэтому мы
можем считать, что ркк = 1, к Е N, и строить элементы Д
исходя из второй группы соотношений (6.14), т.е. искать Д в
соответствии с формулой
fk=9k- Pkifi - • • • - Ркк-ifk-i, кеК (6.15)

6.6. Ортогонализация и существование ортогонального базиса 509
Для к = 1 находим, что Д = д\. При этом ац = 1^0. Для
к = 2 в силу уравнений (6.15) элемент Д следует искать в виде
причем этот элемент должен быть ортогонален уже найденному
элементу Д. Следовательно,
о = (/2, Д) = (ю-Ai/i, /i) = (й, /i) -Ai(Л, Л).
Отсюда находим, что
(оо, fi)
№1~(л7л)
и
. (д^Д). (д2? Д)
ш» Д) l/ij Д)
т.е. верно первое соотношение (6.14) в случае к = 2, причем
а22 = 1^0 (второе соотношение, напомним, равносильно
равенству (6.15), исходя из которого и был построен элемент Д).
Далее мы можем построить элемент /з = дз ~ /%i/i ~~ /%2/2>
используя для определения коэффициентов /?3i и ^Зз2 условия
ортогональности /3 -L Д и /3 -L Д.
Продолжая процесс ортогонализации в соответствии с
методом математической индукции, полагаем, что построены
первые п — 1 попарно ортогональных элементов Д, Д,
/n_i G Я, удовлетворяющих условиям (6.14) при к = 1, п—1.
Построим элемент fn £ Н вида (6.15) при к = п, ортогональный
элементам Д, /2, /n_i. Условие Д ± /п (& < п) означает,
что
0 = (/п, Л) = (»п - ^Zfinjfj, fk) =
3=1
n-l
= (9п, fk) -yZPnj (fj, fk) = (9n, fk) - Pnk (fk, fk) •

510 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
Это позволяет найти все коэффициенты (3nk, к = 1, п—1. В
результате получаем
П-1/ - ч
Iffn? Jk) { (ала\
Из этого соотношения, а также из соотношений (6.14) при к =
= 1, п—1 заключаем, что выполняется первое соотношение (6.14)
при к = п. Действительно, в представлении (6.16) в правой
части достаточно заменить каждый элемент Д линейной
комбинацией элементов gi, g<i, ..., Qk, ^то возможно в силу первого
соотношения (6.14). В результате получим представление
элемента fr в виде линейной комбинации элементов gi, gn,
причем коэффициент при дп равен единице, т.е. в первом
соотношении (6.14) при к = п имеем апп = 1^0. Отметим, что из
этого представления вытекает, что fn ф 0, так как этот элемент
является линейной комбинацией линейно независимой системы
элементов и в этой линейной комбинации есть ненулевые
коэффициенты.
Итак, если ненулевые элементы Д, ..., /n_i попарно
ортогональны и удовлетворяют соотношениям (6.14) для к = 1, п—1,
то существует элемент fn ф 0, определяемый формулой (6.16),
такой, что система элементов Д, /п ортогональна и для
нее верны равенства (6.14). Согласно методу математической
индукции, существует счетная ортогональная система {Л}^,
удовлетворяющая условиям (6.14). Тем самым первая часть
теоремы доказана. Элементы Д. определяются последовательно
по возрастанию номеров с помощью формулы (6.16).
Чтобы завершить доказательство теоремы, требуется
построить не просто ортогональную систему элементов, а орто-
нормированную систему. Поскольку все элементы Д
ненулевые, то для этого достаточно их пронормировать:
е= кеК (6Л7)

6.6. Ортогонаишзация и существование ортогонального базиса 511
Построенная ортонормированная система {е*}^ является
искомой, поскольку с учетом (6.17) равенства (6.14) можно
записать в виде (6.13), если положить
Из доказательства теоремы 6.15 вытекает, что каждый
очередной элемент строящейся ортонормированной системы
определяется с точностью до множителя ±1. Таким образом,
элементы любой другой такой системы будут отличаться от
элементов построенной системы только знаком. Отметим
также, что для исходной линейно независимой системы {g^^i и
эквивалентных ей ортогональной { Д }£?_! и ортонормированной
{efc}jfcLi систем линейные оболочки систем ei, ..., еп, Д, ..., fn
и gi, ..., дп совпадают для любого натурального п:
(ей ...,еп) = (Д, ...,/n) = (ffi, ...,ffn). (6.18)
Теорема 6.15 позволяет получить следующий важный
результат.
Теорема 6.16. В гильбертовом пространстве Н
существует счетный ортонормированный базис тогда и только тогда,
когда Н является сепарабельным пространством.
<4 Необходимость. Поскольку гильбертово пространство
является банаховым, сепарабельность гильбертова
пространства со счетным ортонормированным базисом следует из
теоремы 5.11.
Достаточность. Пусть Н — сепарабельное
гильбертово пространство. Докажем, что в нем существует счетный
ортонормированный базис. Из сепарабельности Н следует,
что в этом гильбертовом пространстве существует
последовательность элементов М = {<7fc}jfcLi> являющаяся всюду плотным
множеством. Не ограничивая общности рассуждений, будем
считать, что первый элемент д\ отличен от нуля (иначе нужно
изменить нумерацию элементов М).

512 б. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
Обозначим ф\ = д\ и рассмотрим последовательность
оставшихся элементов {дк}^=2- Пусть дк — первый элемент в этой
последовательности, линейно независимый с ф\ = gi, т.е. дк ф \д\
ни при каком А Е F. Такой элемент дк существует,
поскольку иначе последовательность {дк}^1 являлась бы
подмножеством одномерного подпространства (gi) гильбертова
пространства Н (см. теорему 5.4). Поскольку подпространство
гильбертова пространства — замкнутое множество, то в этом
случае выполнялось бы включение М С (gi), откуда (д\) = Я, и
Н было бы одномерным пространством. Но это противоречит
определению гильбертова пространства.
Обозначим *02 = дк и снова рассмотрим последовательность
оставшихся элементов gfc+ь <7fc+2> Пусть д\ — первый
элемент в этой последовательности, линейно независимый сф\=д\
иф2= дк- Такой элемент д\ найдется, поскольку иначе
гильбертова пространство Н будет совпадать с линейной оболочкой
(ф\, Ф2), т.е. являться двумерным, что противоречит
определению гильбертова пространства. Обозначим фг=д1-
Продолжая процесс, построим бесконечную линейно
независимую систему элементов {V>n}£Li С М. Такая система будет
бесконечной, поскольку для построенных N линейно
независимых элементов ф\,ф2, -•-, Фи в оставшейся части системы {дк}
можно найти элемент gs, линейно независимый с элементами
-01, ф2, ..., фмч так как иначе гильбертово пространство Н
совпадало бы с линейной оболочкой (-01, -02? •••> Фм) и являлось
бы конечномерным линейным пространством, что
противоречит определению гильбертова пространства. Система {Фп}™=1
линейно независима, т.е. любая конечная ее подсистема фП1,
фП2, ..., фПкч п\ <П2 < <Пк, является линейно независимой,
поскольку линейно независима система -01, ф2, ..., фПк [IV].
Кроме того, любой элемент дь либо совпадает с одним из
элементов фП) либо является линейной комбинацией элементов
Ф\, Ф2ч •••> Фп-1 Для некоторого номера п. Следовательно,
множество М = {gk}*kLi является подмножеством линейной
оболочки элементов -01, -02? •••> Фт ••• Значит, замыкание линей-

6.7. Иэоморфность гильбертовых пространств 513
ной оболочки элементов ф\, ф2, Фт содержит в себе
множество М = Н, а построенная система {Фп}^=1 является
замкнутой счетной линейно независимой системой элементов
гильбертова пространства Н.
Применим к системе {фп}™=\ процесс ортогонализации Гра-
ма — Шмидта. В результате получим эквивалентную ортонор-
мированную систему {вп}^!, т.е. такую, что
(еь е2, ..., еп) = (фи ф2, ..., Фп), n€N.
Следовательно, линейные оболочки систем {еп} и {фп} также
совпадают. Поскольку линейная оболочка системы {фп} всюду
плотна в Н, то и линейная оболочка системы {еп} всюду плотна
в Я. Согласно теореме 6.12, ортонормированная система {еп}
является счетным ортонормированным базисом сепарабельного
гильбертова пространства Н. ►
Следствие 6.4. Применение процесса ортогонализации
Грама — Шмидта к произвольной замкнутой счетной
линейно независимой системе элементов сепарабельного гильбертова
пространства Н позволяет получить счетный ортонормирован-
ный базис в Н.
6.7, Изоморфность гильбертовых
сепарабельных пространств
Напомним, что линейные пространства L\ и Ь2
называют изоморфными, если существует биективное отображение
(р: L\ -> Z/2, сохраняющее алгебраические операции, т.е.
удовлетворяющее следующим условиям:
1) (р(х + у)= (р{х) + ip(y), x,ye Li;
2) <р(\х) = \<р{х), xeLu A 6 F.
При этом само отображение <р называют изоморфизмом
линейных пространств L\ и Z/2.
Определение 6.7. Гильбертовы пространства Н\ и
Нч со скалярными произведениями (•, -)Hl и (•, -)Яг называют

514 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
изоморфными, если существует такое биективное
отображение (р: Н\ —> #2, что верны равенства:
1) <р(х + У)= Ч>{?) + 4>{у), *, у Е #i;
2) <р(\х) = \tp{x), х Е Яь Л б F;
3) {<p{x),<p{y))H2 = {x,y)Hl, x,yeHi.
При этом отображение (р называют изоморфизмом
гильбертовых пространств Н\ и Яг.
Изоморфизм гильбертовых пространств сохраняет не
только алгебраические операции этих гильбертовых пространств,
но и их скалярные произведения.
Теорема 6.17. Всякое действительное (комплексное) сепа-
рабелъное гильбертово пространство Я изоморфно
действительному (комплексному) гильбертову пространству £2-
Ч Пусть Н — сепарабельное действительное (комплексное)
гильбертово пространство. Тогда, согласно теореме 6.16, в
Н существует некоторый счетный ортонормир о ванный базис
{efc}jfcLi- Всякий элемент х Е Н единственным образом можно
разложить в ряд по ортонормированной системе {е^}: х =
оо
Yl ck£k, О: = (#ь ек)ч к Е N (ряд Фурье элемента х по этой
системе). При этом имеет место равенство Парсеваля \\x\\2 =
оо
^2 |cfc|2. Согласно этому равенству, последовательность
к=г
съ 02, ..., Стг, коэффициентов Фурье любого элемента х Е Н
принадлежит гильбертову пространству H<i.
Зададим отображение (р: Н —> £2 следующим образом:
каждому элементу х Е Н поставим в соответствие числовую
последовательность х = {cfc}^ его коэффициентов Фурье по ор-
тонормированной системе {е^}. Докажем, что отображение (р
биективно.
Пусть х и у — два произвольных различных элемента
гильбертова пространства Я, т.е. х — у ф 0. Поскольку система
\е>к\ является ортонормированным базисом в Я, то она полна

6.7. Иэоморфность гильбертовых пространств 515
в Н (см. теорему 6.14). Следовательно, найдется такой номер
fcGN, что (х-у, ек) ф 0. Отсюда (х, ек) Ф (у, е&), т.е.
коэффициенты Фурье с номером к для элементов х и у различны и
двум разным элементам гильбертова пространства Н
соответствуют две разные последовательности коэффициентов Фурье
по системе {е^}. Таким образом, отображение <р представляет
собой инъекцию.
Убедимся, что отображение (р является сюръекцией, т.е.
множеством его значений является все гильбертово
пространство #2- Для этого докажем, что любой элемент х = {хк} гиль-
оо
бертова пространства £2 является образом элемента х=
гильбертова пространства Н. k=1
оо
Так как х Е £2, то ряд ^ \хк\ сходится. Значит, последова-
А;=1
тельность частичных сумм этого ряда фундаментальна, т.е.
= N{e)eN Vm>N Уп>тп: ]Г \хк\2<е.
k=m+l
00
Для последовательности {Sn} частичных сумм ряда ^ Xkek B
А:=1
силу того, что система {еп} ортонормированная, имеем
k=m+l
\
n>m.
k=m+l
Отсюда следует, что последовательность {Sn}
фундаментальна, так как
N{e)eN Vn,m>N: \\Sn - 5m|| < y/e.
В силу полноты гильбертова пространства последовательность
с»
{Sn) сходится. Значит, и ряд ^ %kek сходится к некоторому
элементу х Е Н.

516 б. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
Так как система {е^} — ортонормированный базис, то
любой элемент в Н, в том числе и элемент я, можно разложить
в ряд Фурье по этой системе (см. теорему 6.10). В силу
единственности разложения элемента по счетному базису ряд
оо
^2 хк^к и есть ряд Фурье элемента х, т.е. последовательность
к=\
{хк} является последовательностью коэффициентов Фурье
элемента х. Поэтому, согласно определению отображения (р,
последовательность х = {xk} E h является образом элемента х Е Н:
х = (р(х). Таким образом, отображение <р является инъектив-
ным и сюръективным, а значит, биективным.
Докажем, что отображение <р сохраняет алгебраические
операции гильбертова пространства Н. Пусть х и у —
произвольные элементы гильбертова пространства Я, а их
разложения в ряд Фурье имеют вид
к=\ к=\
Тогда
, Л € F.
Это значит, что элементу х + у € Н соответствует
последовательность {хк +ук} € ^2? а элементу Хх — последовательность
{Ххк} G ^2- Поэтому, согласно определению отображения <р,
имеем
<р{х + у) = {хк + ук} = {хк} + {ук} = (р
<р{\х) = {Ххк} = \{хк} = \ф), Л € F.
Наконец, установим соответствие скалярных произведений.
С одной стороны, по определению скалярного произведения в
с»
гильбертовом пространстве h для произвольных х = J2 хкек и

6.7. Иэоморфность гильбертовых пространств 517
оо
у = Е Ук^к имеем
оо
{ip(x), tp{y))l2 = (ж, y)h = Y^xkVk-
k=l
С другой стороны, в силу теоремы 6.1 о предельном
переходе в скалярном произведении и вследствие попарной
ортогональности элементов системы {е^} получаем
оо оо п п
(х, у)н = ( )0
А;=1
п оо
= lim ^хкЩ = У^хкЩ.
/ n-юо*—* *—^
k=l k=l k=l k=l
В результате приходим к равенству
(tp{x), (p{y))h = (х, у)н , х,у G Я.
Итак, биективное отображение (р: Н —>> £2 сохраняет
алгебраические операции и скалярные произведения гильбертова
пространства Я, а потому является изоморфизмом
гильбертовых пространств Я и ^2- ►
Следствие 6.5. Любые два действительных (комплексных)
сепарабельных гильбертовых пространства изоморфны.
< Пусть Ях, Яг — произвольные сепарабельные гильбертовы
пространства и {е^}^, {g^^kLi —некоторые ортонормирован-
ные базисы в Н\ и Яг соответственно. Зададим изоморфизмы
<р: Н\ -^ £2 и ф: Я2 -> ^2, как в теореме 6.17. Тогда отображение
ф-1о(р:Н1-^Н2, (6.19)
оо
ставящее в соответствие каждому элементу е = Yl ckek из Н\
оо fc=l
элемент д = ^ с^^А: из Яг, является изоморфизмом сепарабель-
А:=1
ных гильбертовых Hi и Яг- ►

518 б. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
Изоморфизм (6.19) назовем естественным
изоморфизмом сепарабельных гильбертовых пространств Hi и #2 с
выделенными в них ортонормированными базисами {ejt}^_1 и
{9к}™=1 соответственно. Естественный изоморфизм
гильбертовых пространств Hi и Нч сохраняет все коэффициенты Фурье
соответствующих друг другу элементов из Hi и #2 по
выделенным в них ортогональным базисам.
Всякие два ортогональных (не обязательно ортонормиро-
ванных) базиса {eic}(^=l и {gk}*kLi гильбертовых пространств
Яь и Яг также порождают изоморфизм этих гильбертовых
пространств. Действительно, ортогональным базисам {е^} и
{9к} соответствуют ортонормированные базисы {efc/||efc||} и
{fffc/llfffcll}? которые порождают изоморфизм ср гильбертовых
пространств. При этом
(00
^
^
Изоморфизм (6.20) назовем естественным
изоморфизмом сепарабельных гильбертовых пространств Нi и #2 с
выделенными в них ортогональными базисами {е^} и {дк}-
Если при естественном изоморфизме гильбертовых
пространств Hi и Нч с выделенными в них ортогональными базиса-
оо
ми {ek}^=i и {9к}™=1 элементу е = X) скек из Hi соответствует
оо _ fc=l _
элемент д = ^ ^к9к из Нч, то между коэффициентами с^ и Ck
разложений элементов е и д по базисам {е^} и {дк}, согласно
(6.20), имеет место следующая связь:
с„

6.7. Иэоморфность гильбертовых пространств 519
Верно и обратное утверждение: если некоторое
отображение ip: Н\ -> Н.2 гильбертовых пространств Н\ и H<i с
выделенными в них ортогональными базисами {е^}^ и \9kYk=\
оо
всякому элементу е = ^ с^е^ из Н\ ставит в соответствие такой
00 ~ k=l
элемент д = ^ ^к9к из ^2> что коэффициенты Ск и qt связаны
к=\
соотношениями (6.21), то отображение <р является
естественным изоморфизмом гильбертовых пространств Н\ и Н2-
Таким образом, (6.21) является характеристическим свойством
естественного изоморфизма гильбертовых сепарабельных
пространств с выделенными в них ортогональными базисами.
В заключение приведем теорему, справедливую для
произвольных (не обязательно сепарабельных) гильбертовых
пространств.
Теорема 6.18 (теорема Рисса — Фишера). Пусть
{^Pn}^=i — произвольная ортонормированная система в
гильбертовом пространстве Н и числа Cn E F, n E N, таковы, что
оо
ряд ^2 l^l2 сходится. Тогда справедливы утверждения:
71=1
ОО
1) РЯД S СпФп сходится и является рядом Фурье
некоторого1 оо
го элемента х Е Я, т.е. х = ^2 СпФт сп = (х, фп), n E N;
2) 1И2 = Е Ы2.
71=1
< Последовательность {сп}<^>=1 в соответствии с условием
теоремы является элементом гильбертова пространства ^2-
Рассмотрим в гильбертовом пространстве Н подпространство
Hq, полученное путем замыкания линейной оболочки ортонор-
мированной системы {фп} (см. теорему 5.5). Подпространство
#о является сепарабельным гильбертовым пространством, а
система {ipn} — счетным ортонормированным базисом в нем.
Согласно теореме 6.17, подпространство Hq изоморфно гиль-

520 б. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
бертову пространству £2, причем этот изоморфизм (см.
доказательство теоремы 6.17) ставит в соответствие каждому
оо
элементу х = ^2 хпФп из Щ последовательность {хп} G^? и
наоборот. Следовательно, любой последовательности {сп} при
оо
этом изоморфизме соответствует элемент Y1 спФп = х из Но (a
п=1
значит, и из if). Поскольку {фп} — счетный ортонормирован-
ный базис в гильбертовом пространстве Но, то для найденного
элемента х выполняются требуемые условия: 1) Сп = (х, фп),
оо
71=1
Вопросы и задачи
6.1. Докажите, что евклидово пространство Ео[а,Ь] не
является полным.
6.2. Докажите, что в нормированном пространстве £р, р ^ 1,
при р ф 2 нельзя ввести скалярное умножение, индуцирующее
норму этого нормированного пространства.
6.3. В гильбертовом пространстве £2 найдите расстояние
от элемента у Е £2 до ортогонального дополнения L1- к
подпространству L, если:
n=l
6.4. Докажите, что если в действительном нормированном
пространстве L для всех х, у Е L выполняется равенство
параллелограмма ||х + у||2 + ||х - у||2 = 2||х||2 + 2||у||2, то функция

Вопросы и задачи 521
является скалярным умножением в L, индуцирующим норму
в1.
6.5. Докажите, что если в комплексном нормированном
пространстве L для всех х,у £ L выполняется равенство
параллелограмма \\х + у\\2 + \\х - у\\2 = 2\\х\\2 + 2||y||2, то функция
, fv lk + y||2-||a:-y||2 .Ax + iv\\2-\\x-iy\\2 _
{x> У) = ^ +г ^ , x.yeL,
является скалярным умножением в L, индуцирующим норму
bL.
6.6. Пусть {VVi}£Li — ортогональная система в гильберто-
СХ)
вом пространстве Н. Докажите, что ряд ^ *фп сходится в Н
п=1 ^ оо
тогда и только тогда, когда сходится числовой ряд J^ HVVill •
n=l
6.7. Пусть {ви}^! — ортонормированная система в
действительном (комплексном) гильбертовом пространстве Я, а
{^n}£Li — последовательность действительных (комплексных)
с»
чисел. Докажите, что ряд ^ Апеп сходится в Н тогда и только
оо п=\
тогда, когда £} |АП|2 < +оо.
п=1
6.8. Докажите, что для того чтобы элемент х гильбертова
пространства Н был ортогонален подпространству L С Я,
необходимо и достаточно, чтобы для любого элемента у G L
выполнялось неравенство ||ж|| < \\х — у\\.
6.9. Докажите, что в гильбертовом пространстве 1ч
множество
является линейным многообразием, всюду плотным в ^2-
6.10. Докажите, что при фиксированном n E N множество
fc=i

522 6. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
является подпространством гильбертова пространства ^-
Найдите ортогональное дополнение к Мп в &2-
6.11. Приведите пример бесконечномерных подпространств
М is. N гильбертова пространства 1<п для которых li^
6.12. Докажите, что линейная оболочка последовательности
^х(п)joo^ элементов гильбертова пространства ^> где х^ =
= {2"n(*l"1)}g?=1, n e N, всюду плотна в ^2-
6.13. Докажите, что если евклидово пространство является
сепарабельным, то всякая его ортогональная система не более
чем счетна.
6.14. Пусть {en}n<Ll — произвольная ортонормированная
оо
система элементов гильбертова пространства Ни ^ спеп =
п=1
= хо — сумма ряда Фурье элемента х £ Н. Докажите, что
разность х — хо ортогональна всем элементам системы {еп}.
6Л5. Пусть {^nj^zi — линейно независимая система в
бесконечномерном евклидовом пространстве Е, a {/n}£Li —
ортогональная система в Е, которая связана с системой {фп}
равенствами
Фп = dnlfl + . • • + CLnnfn, П в N;
где апп ^0 и Ьпп ^0, п G N. Докажите, что если другая
ортогональная система {ffn}£Li в Е связана с системой {фп}
теми же равенствами, то при всех п G N элемент дп отличается
от элемента fn только постоянным множителем.

7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ
СИСТЕМАМ В L2[a,b]
Важнейшими нормированными пространствами являются
различные функциональные пространства, т.е. линейные
пространства, элементами которых являются функции. К такого
рода линейным пространствам относится, например,
бесконечномерное евклидово пространство Ео[а,Ь] кусочно непрерывных
на отрезке [а, Ь] функций. В этих линейных пространствах
норма задается с помощью определенного интеграла. Однако если
^ля этого использовать интеграл Римана, то получаются
нормированные пространства, не являющиеся полными (пример —
уже упомянутое евклидово пространство Ео[а,Ь]). Обеспечить
полноту функциональных пространств можно, расширив класс
интегрируемых функций. Для этого нужно пересмотреть
понятие определенного интеграла и вместо интеграла Римана
ввести другой тип интеграла — интеграл Лебега. Интеграл
Римана можно использовать только для непрерывных
функций или функций, имеющих „не слишком много" точек
разрыва. Интеграл Лебега применим к значительно более широкому
классу функций, который, в частности, включает
неограниченные функции. Класс интегрируемых по Лебегу функций
настолько широк, что построение неинтегрируемой функции
становится весьма сложной задачей.
В этой главе определен интеграл Лебега и с его помощью
введены гильбертовы пространства 1/2[а, Ь] и 1,2 ([а, Ь], д). В этих
линейных пространствах рассмотрены различные
ортогональные и ортонормированные системы и ряды по ним.
В интеграле Лебега интегральные суммы строятся на
основе разбиения отрезка интегрирования, но не на смежные
промежутки, как в интеграле Римана, а на множества весьма общего

524 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[a,Ъ]
вида. В связи с этим возникает необходимость в развитой
теории измерения таких множеств, так как в интегральных
суммах длины смежных отрезков в случае интеграла Римана
становятся мерами множеств разбиения в случае интеграла
Лебега.
7.1. Мера Лебега
На числовой прямой меру можно вводить множеством
способов. Мы определим одну из возможных мер — меру Лебега.
Эта мера обобщает понятие длины отрезка. Поэтому
естественно назвать мерой Лебега отрезка его длину. Более того,
назовем мерой Лебега произвольного конечного промежутка с
концами о и Ь длину этого промежутка, т.е. число b — а:
т([а, Ь]) = т((а, Ь)) =т([а, Ь)) =т((а, Ь]) = Ь — а.
Отметим, что в этом случае мера любой точки (точнее,
множества, состоящего из одной точки) равна нулю, поскольку точку
можно рассматривать как отрезок с совпадающими концами.
Также естественно считать равной нулю меру пустого
множества.
Введем для всех промежутков с концами в точках о и 6,
т.е. для отрезка [а, ft], интервала (о, ft) и полуинтервалов [о, ft)
и (a, Ь], общее обозначение (а,Ь). Для промежутка а = (й, Ь)
имеем
т(а) = т((а, ft)) = ft — a.
Можно доказать, что мера Лебега на множестве промежутков
обладает счетной полуаддитивностью:
(с, d) С (J (оп, Ьп) =Ф m((c,d»<5^m((on,ftn>,
(п) (п)
где объединение и сумма берутся либо по конечному набору
индексов п = 1, к, либо по счетному набору п = 1, 2,...

7.1. Мера Лебега 525
Рассмотрим произвольное множество Е С К. Конечное
или счетное множество промежутков* ап = (ап, Ьп) назовем
системой промежутков, накрывающей множество Е,
если
(п)
Для всякого ограниченного множества Е CR всегда
существует хотя бы одна накрывающая его система промежутков.
Такая система может состоять, например, из одного отрезка
Д = [ао,Ьо]- Сумма длин промежутков Ylm(an) каждой на-
(п)
крывающей Е системы {&п} есть величина неотрицательная
(она равна неотрицательному числу, или +оо).
Следовательно, непустое множество всех возможных значений таких сумм,
соответствующих различным системам промежутков,
накрывающим данное множество Е, ограничено снизу и потому имеет
конечную точную нижнюю грань. Эту точную нижнюю грань,
зависящую только от множества Е, называют внешней мерой
множества Е и обозначают т*(Е)\
т*(Е)= inf
Внутренней мерой т*(Е) ограниченного множества Е С
С R называют разность между длиной отрезка А = [ао, Ьо],
накрывающего Е, и внешней мерой дополнения к Е в Д, т.е.
m*(JE?) = ш(Д) -т*{А\Е), ЕС Д.
Нетрудно показать, что значение внутренней меры не зависит
от выбора накрывающего отрезка Д.
Рассмотрим некоторые свойства внешней и внутренней мер.
"Для удобства дальнейшего изложения будем допускать, что в системе
могут быть пустые промежутки вида (а, а).

526 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В Ь2[а,Ь]
1° Внешняя и внутренняя меры неотрицательны:
т*(Е) ^ 0, m*(E) ^ О, BcR.
< Так как сумма длин произвольной системы промежутков,
накрывающей Е, является неотрицательной, то и точная
нижняя грань сумм длин по всем таким системам — внешняя мера
множества Е — неотрицательна. Пусть отрезок Д
накрывает множество Е. Тогда система из одного отрезка Д является
накрывающей для множества Д \ Е. Следовательно, согласно
определению внешней меры, т*(Д \Е) < т(Д), откуда в силу
определения внутренней меры т* {Е) = т( Д) — га* (Д \ Е) > 0. ►
2° Внутренняя мера любого ограниченного множества
ЕсКне превышает его внешнюю меру: т*Е ^ т*Е.
Ч Пусть отрезок Д накрывает множество Е. Так как по
определению т+(Е) = т(Д) — т* (Д \Е), доказываемое неравенство
эквивалентно следующему:
т*{Е) +т*(Д\Я) ^ т(Д).
Пусть е > 0 — произвольное число. Выберем такую систему
{ап} промежутков, накрывающую -Б, что
() <т*Е + е.
(п)
Это возможно, так как по определению верхняя мера
множества есть точная нижняя грань таких сумм. Выберем также
систему {/Зп} промежутков, накрывающую множество Д \ Е,
для которой
(п)
Тогда
(7.1)
(п) (п)

7.1. Мера Лебега 527
Поскольку Д = EU(A \Е) С ((J ^n)U(U Pn), то в силу свой-
(п) (п)
ства счетной полуаддитивности меры Лебега на множестве
промежутков имеем
(п) (п)
В результате из неравенства (7.1) получаем
Так как е — произвольное положительное число, то последнее
неравенство верно для любого е > О только при т(Д) ^ т*(Е) +
+ т*(Д\Я). ►
3° Внешняя и внутренняя меры обладают следующим
свойством монотонности: если Е\ С i?2> где Е\ и Е2 —
произвольные ограниченные множества в R, то т*Е\ ^ т*Е2 и
m*^! ^ т*£;2.
^ Докажем монотонность внешней меры. Любая система
промежутков, накрывающая множество #2, накрывает и
множество £?i. Это значит, что множество А сумм длин промежутков
для всех систем, накрывающих Е\ включает в себя множество
В сумм длин промежутков для всех систем, накрывающих i?2>
т.е. AD В. Следовательно,
т*{Ег) = in£A < inf В = т*{Е2).
Пусть отрезок Д накрывает множество Е2. Тогда он
накрывает и множество Е\, причем (Д \Е2) С (Д \Е\). Согласно
доказанному свойству монотонности внешней меры, имеем
Отсюда получаем монотонность внутренней меры:

528 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[a,Ь]
4° Внепшяя мера обладает свойством
полуаддитивности:
к
Ec\jEn
п=\ п=\
< Пусть е > О — произвольное число. Для каждого множества
Еп, п = 1, А;, выберем систему {с*^ } промежутков,
накрывающую Еп, для которой
Тогда объединение этих систем накрывает множество (J Е^ а
значит, и множество £7. Поэтому n=1
к к
т*(Е) < ^^m(ajn)) ^ ^m*(^) +с.
n=i (г) n=i
Так как е > 0 — произвольное число, заключаем, что
к
т*(ЯК £>*(#„). ►
п=1
5° Если ограниченное множество Е С Е является
объединением конечного числа попарно не пересекающихся проме-
к
жутков, т.е. i? = (J ^п> гДе ^п = (лп?Ьп), то его внешняя и
п=1
внутренняя меры совпадают и равны сумме длин промежутков,
составляющих это множество:
к к
т*(Е) = т*(Е) = ^En = J>n - an).
п=\ n=l
Ч Совокупность промежутков Еп представляет собой систему
промежутков, накрывающих Е. Поэтому, согласно
определению внешней меры множества, имеем
к
n=l

7.1. Мера Лебега 529
Докажем, что на самом деле это неравенство является
равенством.
Выберем произвольную систему {сц} промежутков,
накрывающих множество Е. Для каждой пары индексов I и п
положим а\п' =сцС\Еп. Тогда
U а\п) = U at ПЕп = (U а,) ПЕп = Еп,
(I) (I) (I)
т.е. для фиксированного п система промежутков cq1'
накрывает промежуток Еп. Согласно свойству счетной
полуаддитивности меры на системе промежутков, имеем
т(а!П))' п = 1Л (7.2)
(О
При фиксированном I промежутки щ , n = l,fc, попарно
не пересекаются, так как а^ С Еп,, п = 1, А:, и ЕП1 П ЕП2 = 0
при п\ ф П2- Все эти промежутки содержатся в промежутке оц.
Поэтому
к
£m(ain)Km(aj). (7.3)
n=l
Комбинируя неравенства (7.2) и (7.3), заключаем, что
n=l n=l (I) (I) n=l (I)
Поскольку полученное неравенство верно для любой системы
{cty}, накрывающей Е, а точная нижняя грань — это
наибольшая нижняя грань, то
к
n=l
Итак, мы доказали, что внешняя мера множества Е равна
сумме длин составляющих его промежутков. Так как Е
ограничено, существует отрезок А, включающий в себя Е: Е С А.

530 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В Ь2[а, Ь]
Множество А\Е представляет собой конечное объединение
промежутков, а потому его внешняя мера равна сумме длин
составляющих его промежутков. Но сумма длин промежутков,
составляющих Е, и длин промежутков, составляющих А \ Е,
равна длине отрезка А. Отсюда следует, что внутренняя мера
множества Е равна сумме длин промежутков Еп,
составляющих Е. ►
Из последнего свойства вытекает, что внешняя и
внутренняя меры промежутка совпадают с его длиной, или мерой
Лебега.
Понятие меры обобщает понятие длины промежутка и
ассоциируется с такими понятиями, как площадь, объем. Поэтому
мера должна обладать свойством аддитивности: при
объединении непересекающихся множеств их меры должны
складываться. С помощью установленных свойств внутренней и внешней
мер можно показать, что внешняя мера (как и внутренняя)
обладает свойством аддитивности в классе множеств,
являющихся объединением конечного числа промежутков. Однако
это свойство теряется, если внешнюю меру использовать для
произвольных множеств. Возникает задача: выявить класс
множеств, в котором сохраняется свойство аддитивности, но
при этом этот класс множеств должен быть максимально
широким.
Ограниченное множество Е С Ш называют измеримым
по Лебегу, или просто измеримым, если его внешняя и
внутренняя меры совпадают: т+Е = т*Е. При этом общее
значение мер т*Е и т*Е называют мерой Лебега (лебеговой
мерой, или просто мерой) измеримого множества Е.
Лебегову меру множества Е будем обозначать т(Е). Таким образом,
т{Е)=т*{Е)=т*{Е).
Отметим, что из измеримости множества Е, включенного
в отрезок А, следует измеримость множества А\Е. В самом
деле, если Е измеримо, то т(Е) = т*(Е) = т(А) — тп*(А\Е) и

7.1. Мера Лебега 531
т*(А\Е)=т(А)-т{Е). Однако т*(А\Е) = т(А) -т*(Е) =
= т(А) - т(Е) и, следовательно, га* (А \ Е) = га* (А \ 2?), т.е.
множество А \ i£ измеримо.
Без доказательства отметим некоторые основные свойства
измеримых по Лебегу множеств и самой меры Лебега.
1. Если множества Е\ и Е2 измеримы, то измеримы и
множества Е\ U Е2, Е\ П Е2, Е\ \ Е2.
2. Любое подмножество измеримого множества, имеющего
меру нуль, измеримо, и его мера равна нулю.
3. Мера Лебега обладает свойством аддитивности: если
множества Е\ и Е2 измеримы и не пересекаются, то
m(Ei U Е2) = m{Ei) + m(E2).
оо
4. Объединение Е = (J Еп счетного набора измеримых мно-
п=\
жеств {Еп}^=1, являющееся ограниченным множеством, есть
множество измеримое.
5. Мера Лебега обладает свойством счетной
аддитивности (или а-аддитивности): если {Еп}™=1 —
последовательность попарно непересекающихся (т.е. Е{ HEj = 0, i ф j)
измеримых множеств, объединение которых является
ограниченным множеством, то
Ч1|Яп)=1>(Яп).
ОО
6. Пересечение Е = |°| Еп счетного набора измеримых мно-
п=1
жеств {Еп}™=1 есть также множество измеримое.
7. Пусть на отрезке А задана монотонно неубывающая
последовательность измеримых множеств {Еп}™=1, т.е.
последовательность, удовлетворяющая условию Еп С Еп+\ С А,
п G N. Тогда
т(\\Еп) = lim m(En).

532 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2 [о, Ь]
8. Пусть задана монотонно невозрастающал
последовательность измеримых множеств {J3n }£?_!, т.е.
последовательность, удовлетворяющая условию Еп D En+\, n Е N.
Тогда
ml Г\Еп) = lim m(En).
\' ' ) п—юо
Свойства 7 и 8 называют непрерывностью меры.
Рассмотрим простейшие примеры измеримых множеств.
Всякий промежуток (а, Ь) является измеримым по Лебегу
множеством, причем его мера совпадает с длиной (длина
промежутка уже была названа его мерой). Пустое множество
измеримо, и его мера равна нулю. Любое множество, состоящее из
конечного числа точек, измеримо, и его мера равна нулю.
Любое ограниченное счетное множество в R также измеримо, и его
мера равна нулю. Множество иррациональных чисел на отрезке
А измеримо и имеет меру т(А), так как является
дополнением к счетному множеству рациональных чисел этого отрезка,
которое является измеримым и имеет лебегову меру нуль.
Из теории действительных чисел известно*, что всякое
открытое множество на числовой прямой R является
объединением конечного или счетного числа попарно непересекающихся
интервалов (конечных или бесконечных). Следовательно,
всякое ограниченное открытое множество, будучи объединением
конечного или счетного набора попарно непересекающихся
конечных интервалов а^ = (а^, Ь^), является измеримым по Лебегу
множеством, и его мера равна сумме длин этих интервалов
(п)
В заключение приведем понятие, которое понадобится в
дальнейшем. Говорят, что некоторое свойство С, зависящее
от параметра х Е Е С R, выполнено на Е почти всюду,
если мера множества точек iGB, для которых это свойство
не выполняется, равна нулю.
*См.: Колмогоров Л.Я., Фомин СВ.

7.2. Измеримые функции 533
7.2. Измеримые функции
Определение 7.1. Пусть Е С Ш — измеримое по Лебегу
множество. Функцию /:Е—>Ш называют измеримой на
Е, если для любого числа A G R прообраз интервала (А, +оо),
т.е. множество f~l((A,+oo)) = {x G E: f(x) > А}, измерим по
Лебегу.
Приведем без доказательства основные свойства измеримых
функций.
1. Всякая функция, определенная на множестве меры нуль,
измерима.
2. Если функция /, определенная на измеримом множестве
Е С IR, измерима, то измеримыми являются прообразы любых
промежутков, т.е. множества, заданные следующими
соотношениями: l)f(x)^A; 2)f{x)<A\ 3)f(x)^A- 4)B<f(x)<
<A- 5) B^ f(x) <A; 6) В < f(x) < A; 7) В < f(x) < A;
8) f(x) = А. Кроме того, верно и обратное утверждение:
если измеримы все множества хотя бы одного из первых семи
указанных здесь типов, то функция / измерима на Е.
3. Сумма, разность и произведение двух измеримых на
Е функций измеримы на Е. Частное измеримых функций
измеримо, если знаменатель нигде на Е не обращается в нуль.
4. Композиция g°f{x) =g(f(x)) измеримой на Е функции
f(x) и непрерывной на R функции д(у) является измеримой
функцией на Е.
5. Если / и д — измеримые функции на множестве Е, то
множество, заданное неравенством f(x) <g(x), измеримо.
6. Пусть для любого х е Е существует предел lim fn(x) =
п—>оо
— fix). Если все функции /п(я) измеримы на Е, то и предельная
функция f(x) также измерима на Е.
7. Если функция f(x) измерима на Е и f(x) = д(х) почти
всюду на Е, то функция д(х) также измерима на Е.
Отметим, что все использующиеся на практике функции
являются измеримыми. Например, все непрерывные, кусочно

534 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2 [а, Ь]
непрерывные и интегрируемые по Риману на отрезке [ао, Ьо]
функции являются измеримыми на этом отрезке. Класс
неизмеримых функций связан с неизмеримыми множествами. Если
функция / не является измеримой на ограниченном множестве
Е, то для некоторого числа А множество {х Е Е: f(x) > А} не
является измеримым. Наоборот, если М — неизмеримое по
Лебегу ограниченное множество, содержащееся в ограниченном
промежутке Д, то функция
1, хеМ;
o, хеА\м
(функция-индикатор множества М) не является измеримой на
множестве М, так как не является измеримым множество
{х G Д: f(x) = 1} = М. Пример ограниченного неизмеримого
множества построить непросто*
7.3. Интеграл Лебега
Как и интеграл Римана, интеграл Лебега зависит от двух
составляющих — интегрируемой функции и области
интегрирования. Областью интегрирования в интеграле Лебега
является измеримое множество, а интегрируемой функцией —
измеримая функция. Отличительной особенностью интеграла
Лебега является то, что при составлении интегральных сумм
разбиение строится не в области определения функции, а в
области ее значений. Интеграл Лебега будем вводить в
несколько этапов, последовательно расширяя класс функций. Сначала
определим интеграл Лебега от ограниченных измеримых
функций.
Итак, пусть действительная измеримая функция f(x)
определена и ограничена на ограниченном измеримом множестве Е,
т.е. выполняются неравенства А^ f(x) ^ В, iGB, где А и В —
* Пример неизмеримого множества см., например: Колмогоров А.Н.,
Фомин СВ.

7.3. Интеграл Лебега 535
некоторые числовые константы. Выберем некоторое разбиение
г отрезка [А, В], т.е. множество точек
А = УО < У\ < У2 < < Уп-l <Уп = В,
которое разделяет отрезок на меньшие непересекающиеся
промежутки
[Л Vl), [Vl, W)i [Vn-2, Уп-l), [Уп-U В]-
Напомним, что величину
а(т) = jnax (ю+i - yi)
называют диаметром разбиения г.
Пусть
Ei = {xe E: yi < f(x) < j/i+i} , t = 0, n-2;
En_i = {ieB: уп-i < /(x) < yn} •
Сумму
n-l
i=0
где m{Ei) — мера Лебега множества Е{, называют
интегральной суммой Лебега для функции f(x) при заданном
разбиении т.
Определение 7.2. Интегралом Лебега от
ограниченной измеримой функции f(x) на измеримом множестве Е
называют предел
f(x)dx= lim 5T(/)
q(t)->0
интегральных сумм Лебега ST(f) при стремлении диаметра
разбиения а(т) к нулю, если этот предел существует.
Функцию /(х), для которой определен интеграл Лебега, называют
интегрируемой по Лебегу на множестве Е.

536 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В Ь2[а,Ь]
Для интеграла Лебега используют общепринятое
обозначение интеграла. Однако в тех случаях, когда необходимо
подчеркнуть, что записанный интеграл следует понимать как
интеграл Лебега, перед знаком интеграла ставят специальное
обозначение (L). Итак, интеграл Лебега от функции f(x) на
множестве Е обозначают следующим образом:
(L) I f(x)dx или I f{x)dx.
Е Е
Если множество Е есть промежуток (а, Ь), то часто используют
обозначение интеграла Лебега с двумя индексами:
ъ ъ
{L)ff{x)dx или f f(x)dx.
а а
Теорема 7.1*. Всякая ограниченная функция /(х),
измеримая на ограниченном измеримом множестве Е интегрируема
по Лебегу на Е.
Пример 7.1. Функция Дирихле
( . _ Г 1, х рационально;
\ 0, х иррационально,
не интегрируема по Риману [VI] ни на каком отрезке [а, Ь] С R.
Однако, согласно теореме 7.1, эта функция интегрируема по
Лебегу на любом отрезке числовой оси. Вычислим интеграл
Лебега от функции Дирихле, например, на отрезке [0,1]. Для
этого выберем произвольное разбиение г отрезка [0,1]
точками уо = 0, уи У2, ..., Уп-и Уп = 1 (отрезок [0,1] содержит все
значения функции D(x)). Тогда при п > 2 прообразы
промежутков [уь, 2/fc+i)5 k = 1, п—2, являются пустыми множествами,
прообраз промежутка [уо,У\) есть множество [0,1] \ Q меры
*См.: Вулих Б.З.

7.3. Интеграл Лебега 537
га([О,1] \ Q) = 1, а прообраз промежутка [уп-ь Уп] есть
множество [0,1] П Q меры нуль. Поэтому
5Tp)=0-m([0,l]\Q)+yn_1-m(QD[0,l])=yn-i-0 = 0.
Значит,
1
(L)[D(x)dx= lim ST(D) = 0. #
J а(т)->0
о
Отметим без доказательства некоторые свойства интеграла
Лебега от ограниченных измеримых функций, которые
понадобятся в дальнейшем.
1. Если / — неотрицательная ограниченная измеримая
функция на ограниченном измеримом множестве Е) то
2. Если / и д — ограниченные измеримые функции на
ограниченном измеримом множестве Е и f(x) ^ д(х), х G Е, то
(L)Jf(x)dx<(L)Jg(x)dx.
Е Е
3. Если / и д — ограниченные измеримые функции на
ограниченном измеримом множестве J3, то для любых
действительных чисел а и /3 верно равенство
J
ЕЕ
В отличие от интеграла Римана интеграл Лебега можно
определить и для неограниченных функций, хотя и не для всех.
Введем интеграл Лебега от неотрицательных неограниченных
функций.

538 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В La [о, Ь]
Пусть f(x) ^ 0, х 6 £7. Для всякого натурального ЛГ
рассмотрим функцию /лг(я) = min{/(a;), ЛГ}, являющуюся измеримой
ограниченной функцией. При этом /w(z) < /м+\(х), N G N, и
im /дг(ж) =/(*), zGS.
>oo
Для функций /iv(x) в силу теоремы 7.1 существует интеграл
Лебега. Последовательность интегралов (L) J ffq{x)dx не убы-
Е
вает и поэтому имеет предел (конечный или бесконечный) при
ЛГ-юо.
Определение 7.3. Конечный предел последовательности
интегралов (Ь) f f]y(x)dx при N —> +оо называют интегра-
Е
лом Лебега от неотрицательной измеримой функции f(x) по
измеримому множеству Е:
(L) [f(x)dx=lim (L) [fN(x)dx. (7.4)
J N->+oo J
E E
Как и выше, функции, для которых определен конечный
интеграл Лебега, называют интегрируемыми по Лебегу, или
суммируемыми функциями.
Рассмотрим произвольную измеримую функцию /(ж),
заданную на ограниченном измеримом множестве Е. Для этой
функции введем две функции f+{x) = max{/(x), 0} и f-(x) =
= max{—/(ж), 0}. Нетрудно показать, что обе введенные
функции измеримы на Е и неотрицательны. Кроме того, они
связаны с функцией f(x) равенством f(x) = f+(x) — /_(rr), x e E.
Определение 7.4. Измеримую функцию f(x) называют
интегрируемой по Лебегу, или суммируемой, если
суммируемы функции f+(x) и f-(x). При этом число
= (L)Ju(x)dx-(L)Jf.(x)dx (7.5)
Е Е Е
называют интегралом Лебега от функции f(x).

7.3. Интеграл Лебега 539
Замечание 7.1. Если для неотрицательной измеримой
функции предел (7.4) бесконечен, то можно считать, что
функция имеет бесконечный интеграл Лебега, равный +оо. Для
знакопеременной функции f(x) также можно расширить понятие
интеграла Лебега, считая, что он равен +оо, если /_(я)
суммируема, а /+(я) не является суммируемой (имеет бесконечный
интеграл Лебега). Аналогично в случае, когда /+(я)
суммируема, a f-(x) не является суммируемой, интегралу Лебега от
функции f(x) можно приписать значение — оо. При такой
расширенной трактовке интеграла Лебега интегрируемыми
следует считать в том числе и функции, имеющие бесконечный
интеграл Лебега. Смысл термина „суммируемая функция" при
этом не изменяется: он означает, что функция имеет конечный
интеграл Лебега. #
Итак, введение интеграла Лебега завершено и охватывается
тремя определениями 7.2, 7.3 и 7.4. Остается проверить, что
эти определения не противоречат друг другу.
Пусть измеримая на Е функция f(x) ограничена и
неотрицательна. Построим последовательность /лг(я) в соответствии
с определением 7.3. Так как f(x) ограничена, то существует
такой номер К, что f(x) < К, х G Е. Поэтому при N > К имеем
fN(x) = min{/(i), N} = /(я), хеЕ, т.е. функции fN(x),
начиная с некоторого номера, совпадают с функцией f{x). Значит,
последовательность интегралов (L) J fjsf{x)dx с некоторого но-
Е
мера становится постоянной и имеет своим пределом интеграл
(L) J f(x) dx, вычисленный согласно определению 7.2. Пусть из-
Е
меримая функция f(x) неотрицательна на Е. Тогда f-(x) = О
и определение 7.4 сводится к определению 7.3. Если измеримая
функция f(x) ограничена на J5, то функции /+(я) и f-{x) также
ограничены. Значит, интегралы от этих функций в равенстве
(7.5) можно понимать в смысле определения 7.2. В этом
случае равенство (7.5) превращается в одно из свойств интеграла
Лебега от ограниченных функций.

540 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[а, Ь]
Приведем без доказательства основные свойства интеграла
Лебега. Все рассматриваемые ниже множества и функции
будем считать измеримыми.
1. Суммируемая на Е функция почти всюду конечна на Е.
2. Функция, суммируемая на Е, суммируема на всяком его
измеримом подмножестве.
3. Если т(Е) = 0, то J f(x)dx = 0 для любой функции f(x).
Е
4. Если т(Е) > 0, f(x) > 0 и J f(x)dx = 0, то f(x) = 0 почти
Е
всюду на Е.
5. Если f(x) и д(х) суммируемы на Е, то при любых а, /3 G R
функция af(x) + /Зд(х) также суммируема на, Е и
[(
Е ЕЕ
6. Если А < f(x) < В почти всюду на Е, то
Г
f(x)dx^Bm(E).
E
В частности, если f(x) > О почти всюду на множестве Е, то
ff(x)dx>0.
Е
7. Если функции f(x) и д(х) суммируемы на Е и f(x) ^ д(х)
почти всюду на Е, то
Jf{x)dx^Jg(x)dx.
Е Е
8. Интеграл от постоянной функции по измеримому
множеству Е равен произведению значения функции на меру
множества Е:
/ cdx = с-т(Е).
Е

7.3. Интеграл Лебега 541
9. Пусть Е = U Еп — конечное или счетное объединение
(п)
попарно непересекающихся измеримых множеств, являющееся
ограниченным множеством, и функция f(x) измерима на Е.
Тогда
Е Уп)Еп
10. Если f(x) =g{x) почти всюду на JS, то
/ f(x)dx = / g(x)dx.
Е Е
11. Если |/(х)| < д(х) почти всюду на Е и функция д(х)
суммируема на Е, то функция f(x) также суммируема на Е и
J\f(x)\dx^Jg(x)dx.
Е Е
Кроме того, имеет место следующий критерий
суммируемости функции.
Теорема 7.2. Для того чтобы измеримая на Е функция
f(x) была суммируемой на £?, необходимо и достаточно, чтобы
суммируемой на Е была функция |/(х)|. При этом выполнятся
неравенство
Наконец, приведем две теоремы*, устанавливающие связь
между интегрируемостью по Риману и Лебегу.
Теорема 7.3. Если функция f{x) интегрируема по Риману
на отрезке [а, Ь], то она интегрируема по Лебегу (суммируема)
"Доказательство теорем см., например: Натансон И.П.

542 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[a,Ь]
на отрезке [а, Ь], и соответствующие интегралы равны:
ь ъ
(L)Jf(x)dx = (R)Jf(x)dx. #
а а
Функция Дирихле (см. пример 7.1) показывает, что
функция, интегрируемая по Лебегу, может быть неинтегрируемой
по Риману, даже если она ограничена. Известная теорема
Лебега* утверждает, что, для того чтобы определенная на отрезке
[а, Ь] действительная функция была интегрируемой по Риману,
необходимо и достаточно, чтобы она была ограниченной и
почти всюду на [а, Ь] непрерывной. Класс измеримых функций,
для которых существует интеграл Лебега, значительно шире.
Напомним, что интеграл Римана существует только для
ограниченных функций [VI]. На неограниченные функции он
переносится с помощью несобственного интеграла.
Принципиальное различие между несобственным интегралом и
интегралом Лебега состоит в том, что первый можно определить лишь
для функций, имеющих конечное число точек, в достаточно
малой окрестности которых функция не является ограниченной, в
то время как интеграл Лебега может существовать для
функции, которая является неограниченной в сколь угодно малой
окрестности каждой точки.
Теорема 7.4. Пусть f(x) — неограниченная на отрезке
ь
[а, Ь] функция и несобственный интеграл (К) f f(x) dx сходится.
а
Функция f(x) является суммируемой на отрезке [а, Ь] тогда
ь
и только тогда, когда несобственный интеграл (R)ff(x)dx
сходится абсолютно. При этом а
о о
{L)jf{x)dx = {R)Jf{x)dx.
*См.: Натансон И.П.

7.4. Банахово пространство Li[a,b] 543
7.4. Банахово пространство Li[a,b]
Рассмотрим некоторую измеримую функцию /(х),
заданную на измеримом множестве Е. Обозначим через CeU) класс
всех измеримых функций, почти всюду на Е равных
функции f{x). Согласно свойствам суммируемых функций (см. 7.3),
функции, равные почти всюду на JS, с точки зрения
суммируемости и интеграла Лебега не различаются: они одновременно
суммируемые или несуммируемые, и их интегралы Лебега
равны. Кроме того, нетрудно видеть, что выполнение одних и тех
же арифметических операций (сложение и умножение на
число) над различными представителями классов CeU) и Се{я)
приводит к одному и тому же классу функций:
(7.6)
Это позволяет при рассмотрении функций, суммируемых на
множестве JS, отождествлять все функции одного класса, т.е.
считать одной функцией любые две функции, равные почти
всюду на Е. В частности, все функции, отличные от нуля
лишь на множестве меры нуль, можно считать одной и той же
нулевой функцией.
Множество всех функций, суммируемых на отрезке [а, Ь] (с
отождествлением функций, равных почти всюду на этом
отрезке), образует линейное пространство относительно обычных
операций сложения функций и умножения функции на число.
Это линейное пространство называют пространством
суммируемых на [a, b] функций и обозначают L\[a,b].
Введем в линейном пространстве L\ [a, b] норму, полагая
= J\f(x)\dx,
В силу теоремы 7.2 функция \f(x)\ суммируема, поэтому
определение нормы функции / корректно. Нетрудно показать, что

544 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[a,6]
все аксиомы нормы выполнены. В частности, выполнение
первой аксиомы (а именно ||/|| = 0 <*=*► / = 0) обеспечено тем, что
в Li[a,6] отождествлены все функции, равные почти всюду на
[а, 6]. Следовательно, линейное пространство Za[a,6] является
нормированным пространством.
Сходимость последовательности функций {Д} в
нормированном пространстве Li[a,6] к некоторой функции /, т.е.
сходимость последовательности элементов нормированного
пространства L\[a,b] no норме, введенной в Li[a,6], означает, что
ь
J
\fk(x)-f{x)\dx->0,
Такую сходимость называют сходимостью в среднем.
Имеет место следующая теорема.
Теорема 7.5*. Нормированное пространство L\[a,b]
суммируемых на отрезке [а, Ь] функций является сепарабельным
банаховым пространством. #
Отметим, что всюду плотным подмножеством в
нормированном пространстве Ь\[а,Ъ] является, например, множество
непрерывных на отрезке [a, b] функций, а счетным всюду
плотным подмножеством в Li[a,6] — множество многочленов с
рациональными коэффициентами.
7.5. Гильбертово пространство L2[a,b]
Для многих приложений функционального анализа более
существенную роль по сравнению с пространством суммируемых
функций играет другое функциональное пространство,
являющееся евклидовым (а не только нормированным)
пространством.
* Доказательство см.: Колмогоров Л. Я., Фомин СВ.

7.5. Гильбертово пространство Ьг[а,Ъ] 545
Определение 7.5. Измеримую на отрезке [а, Ь] функцию
/: [а, Ь] —► R называют функцией, суммируемой с
квадратом на отрезке [а, Ь], если на [а, Ь] суммируема функция f2{x).
Множество всех функций (с отождествлением любых двух
функций, равных почти всюду), суммируемых с квадратом на
отрезке [а, Ь], образует линейное пространство, которое
называют пространством функций, суммируемых с
квадратом, и обозначают L2[a1b]. Таким образом,
f(x)eL2[a,b] » /2(x)GLi[a,6].
Докажем, что L2[a,b] действительно является линейным
пространством. Из свойств интеграла Лебега и очевидного
неравенства
хе[а,Ь],
следует, что произведение f{x)g(x) двух суммируемых с
квадратом функций f(x) и д(х) является суммируемой функцией.
Отсюда, положив д(х) = 1, заключаем, что всякая
суммируемая с квадратом функция f(x) является суммируемой, т.е.
L2[a,b] С Ьг[а,Ь].
Из равенства
(/(*) +д(х))2 = /2(х) + 2f(x)g(x) +g\x)
и свойства линейности интеграла Лебега следует, что сумма
двух суммируемых с квадратом функций также является
функцией, суммируемой с квадратом. Очевидно, что если f(x)
суммируема с квадратом, то и функция fc/(x), k E R также
суммируема с квадратом. Это доказывает, что множество
L2[a,b] замкнуто относительно операций сложения функций и
умножения функции на число. Нетрудно проверить, что эти
операции удовлетворяют аксиомам линейного пространства и
что L2[a,b] является линейным пространством. Отметим, что

546 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2 [а, Ь]
линейное пространство 1*2 [а?Ь] бесконечномерное, поскольку в
нем имеются бесконечные линейно независимые системы
элементов. Например, система одночленов 1, х, х2, хп,
принадлежащих Ь2[а,Ь], линейно независима.
Зададим в линейном пространстве 1/2[а,Ь] скалярное
умножение, положив
ь
(/,<?) = jf(x)g(x)dxJ /,5
Выполнение аксиом скалярного умножения проверить
несложно. Отметим, что выполнение аксиомы (/, /) = О <=> / = О
обеспечивается тем, что в 1/2[й>Ь] отождествлены все функции,
равные почти всюду на [а, Ь]. В частности, в качестве нулевого
элемента („нуля") линейного пространства 1>2[а,Ь] можно
использовать не только функцию f(x) = 0, но и любую функцию,
равную нулю почти всюду на [а, Ь]. Таким образом, линейное
пространство 1*2 [а>4 является бесконечномерным евклидовым
пространством.
В L2[a1b], как и во всяком евклидовом пространстве,
выполняется неравенство Коши — Буняковского, которое для 1*2 [а, Ь]
принимает вид
f f2{x)dx f
ь
2
92{x)dx.
Норма, индуцированная этим скалярным умножением в
определяется формулой
\
ь
P{x)dx, f€L2[a,b].
a
Сходимость функциональной последовательности {Д}^=1 к
функции f(x) в 1/2[й,Ь], т.е. сходимость последовательности

7.5. Гильбертово пространство 1*2 [а, Ь] 547
элементов {Д} нормированного пространства L2[a,b] к
элементу / по норме в 1>2[а,Ь]> означает, что
Такую сходимость назьшают сходимостью в среднем
квадратичном.
Теорема 7.6*. Евклидово пространство 1<2[а,Ь] полно, т.е.
является гильбертовым. #
Гильбертово пространство L2[a,b], как и банахово
пространство L\[a,b], является сепарабельным, т.е. обладает
счетным всюду плотным подмножеством. Таким подмножеством
для 1,2 [а, Ь] является множество многочленов с рациональными
коэффициентами.
Напомним, что числовую функцию f(x), заданную на
отрезке [а, Ь], называют кусочно постоянной (также
ступенчатой), если отрезок [a, b] можно разбить на конечное число
таких отрезков [a, ai], [ai,a2], ..., [an-i,an], [ап,Ь], внутри
которых (т.е. в интервалах (a*, a*+i), i = 1, п) функция f(x)
постоянна.
Теорема 7.7**. Каждое из перечисленных ниже множеств
функций, заданных на отрезке [а, Ь], является всюду плотным
множеством в гильбертовом пространстве L2[a,b]:
1) множество измеримых ограниченных функций;
2) множество непрерывных функций;
3) множество многочленов;
4) множество кусочно постоянных функций;
5) множество функций, принимающих на [a, b] конечное
число значений.
* Доказательство см.: Колмогоров А.Н., Фомин СВ.
**Доказательство см.: Натансон И.П.

548 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[a, Ъ]
Кроме того, класс тригонометрических полиномов,
заданных на отрезке [—тг, тг], является всюду плотным
подмножеством в гильбертовом пространстве 1*2[—я",тг]. #
Поскольку для различных отрезков [а, Ь] гильбертовы
пространства 1,2[а>Ь] сепарабельны, то, согласно теореме 6.17, все
они изоморфны гильбертову пространству ^2> и, следовательно,
изоморфны между собой.
Для любого отрезка [а, Ь] в сепарабельном гильбертовом
пространстве 1*2[й>Ь]> согласно теореме 6.16, существует
счетный ортонормированный базис. Если {ч>п}™=\ — некоторый
счетный ортонормированный базис в L2[a,b], то в соответствии
с общими результатами (см. 6) каждую функцию / Е 1*2 [а>Ь]
можно единственным образом разложить в ряд по этому
базису. Этим рядом является ряд Фурье функции / по системе
x) = Ylcn<Pn(x), Cn = (f, (рп)= / f(x)(pn(x)dx, n
n=i i
Для функции / G 1<2[а5Ь] и ее коэффициентов Фурье с„ по
системе {y>n}£Li вьшолняется равенство Парсеваля:
b
2
п=1
=[f2(x)dx.
7.6. Тригонометрическая система
Рассмотрим гильбертово пространство L2[~тг,тг] функций,
суммируемых с квадратом на отрезке [—тг, тг].
Тригонометрическая система
1 cosx sinx cosnx sinnx

7.6. Тригонометрическая система 549
является ортонормированной системой в сепарабельном
гильбертовом пространстве 1*2 [—7г?тг]- Действительно, ортонорми-
рованность этой системы была установлена, когда она
рассматривалась в евклидовом пространстве Eq[—тг,тг], скалярное
произведение в котором то же, что и в L^\a^ b] (различие в типах
интеграла не в счет: интегралы Римана и Лебега от кусочно
непрерывных функций совпадают).
Теорема 7.8. Тригонометрическая система (7.7) является
счетным ортонормированным базисом в гильбертовом
пространстве 1/2 [—Я",7Г].
< В силу теоремы 6.12 для доказательства утверждения
теоремы достаточно доказать замкнутость тригонометрической
системы (7.7). Иными словами, достаточно доказать, что
линейная оболочка системы (7.7), т.е. множество Т всех
тригонометрических полиномов вида
п
Р(х) = ар + У^ (flfe cos kx + bk sin kx),
k=\
является всюду плотным в Li2[—'n,'n\. Доказательство этого
утверждения проведем в два этапа: произвольную функцию
f(x) из 1/г[—7г>тг] аппроксимируем непрерывной функцией д{х),
затем функцию д(х) аппроксимируем непрерывной функцией
h(x) с равными значениями на концах отрезка [—тг, тг].
Применив к функции h(x) теорему Вейерштрасса, придем к
утверждению теоремы.
Итак, пусть f(x) — произвольная функция из L2[—k1k]. Так
как множество всех непрерывных на отрезке [—тг, тг] функций
всюду плотно в L2[—тг,тг] (см. теорему 7.7), то для любого числа
е > 0 найдется непрерывная на отрезке [—тг, тг] функция р(х),
такая, что
II/-511 =
\
71
J\f(x)-g(x)\*dx<£-.

550 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2 [а, Ь]
Непрерывная на отрезке [—тг, тг] функция д(х) ограничена на
нем, т.е. для некоторого числа М >
> 0 верно неравенство
В
\д{х)\<М, х<Е[-тг,тг].
Выберем положительное число
-л
Рис. 7.1
и рассмотрим непрерывную на
отрезке [—тг, тг] функцию (рис. 7.1)
г), —тг ^ х ^ тг—5;
-(х-тг) +д{—тг), тг — S < х ^ тг.
График функции /i(x) на промежутке [тг — 6, тг],
представляет собой отрезок прямой, соединяющий точки В(тг;д(—тг)) и
А(тг — 6;д(п — 6)). Из построения следует, что функция h(x)
ограничена, причем той же константой, т.е. \h(x)\ < М, х Е
G [—тг, тг]. Оценим расстояние в гильбертовом пространстве
1/2[—тг,тг] между функциями д(х) и h(x):
7Г 7Г
\\9-h\\2 = J\g(x)-h(x)\2dx=J\g(x)-h(x)\2dx<
7Г-5
(х)| \д(х)\ + \h(x)\2) dx <
1Г-6
е2 е2
36М2 9 '
Значит, \\д - h\\ < е/3.

7.6. Тригонометрическая система 551
Поскольку функция h(x) непрерывна и h(—тг) = Л(тг), то,
согласно теореме Вейерштрасса, существует
тригонометрический полином Р(х), такой, что
^, Х€[-7Г,7Г].
Оценим расстояние между функцией h(x) и этим полиномом
Р{х) в Ь2[-1Г,1г):
\\h-Pf = f\h{x)-P{x)\4x< f
* 2 Л
Следовательно, \\h — P\\ < е/3.
Теперь, наконец, получаем
<\\f-9\\ + \\9-h\\ + \\h-P\\<- + ^ + - = e,
т.е. во всякой е-окрестности функции f(x) G Li2[—тг,тг] есть хотя
бы один тригонометрический полином Р(х). Это означает,
что множество Т всех тригонометрических полиномов всюду
ПЛОТНО В L<2{—7Г,7Г]. ►
Поскольку тригонометрическая система (7.7) является
базисом в L2[—7г,тг], то любую функцию / Е L,2[—тг,7г] можно раз-
ложить в ряд Фурье по этому базису:
+£ № ^Р+с2) SJW)(г-8)
где нулевой коэффициент Фурье со функции / по базису (7.7)
в соответствии с общей теорией вычисляется по формуле

552 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[a,Ь]
а остальные коэффициенты с4' и <4' — по формулам
7Г
cosnx\ 1
—
nE
Отметим, что равенство функции f(x) сумме своего ряда
Фурье — равенство (7.8) — следует понимать как равенство
элементов в гильбертовом пространстве 1/2 [—тг,тг]. Кроме того,
сходимость ряда в правой части равенства (7.8) к своей сумме
также нужно понимать не в смысле поточечной сходимости
функционального ряда, а в смысле сходимости в гильбертовом
пространстве L2[—тг,7г], т.е. в среднем квадратичном:
Обозначая
/2
получаем разложение функции / Е L2[—тг,тг] в
тригонометрический ряд Фурье:
00
/(х) = —+ ^ancosnx + bnsinnx, (7.9)
71=1
где коэффициенты ап и Ьп определяются формулами:
ап = - f(x)cosnxdx, n = 0,1,...
я" У
— 7Г
7Г
Ьп = — I f(x)sinnxdx, n = 1, 2,...

7.6. Тригонометрическая система 553
При этом равенство (7.9) и сходимость ряда в правой его части
по-прежнему следует понимать не в смысле поточечного
равенства и поточечной сходимости, а в смысле равенства элементов
в 1/2[—7г,тг] и сходимости ряда в среднем квадратичном.
Поскольку тригонометрическая система (7.7) является ор-
тонормированным базисом в 1/2 [—тг,тг], то для всякой функции
f(x) Е I/2[—7г,тг] выполняется равенство Парсевалл:
= и/и2,
\ 1
71=1
которое, используя коэффициенты ап и Ьп и вид нормы
1/2[—тг,7г], можно переписать так:
Верно и обратное утверждение: если действительные числа
00
ап, Ьп, n Е N, таковы, что ряд ]Г) (а^ + Ь^) сходится, то, согласно
71=1
теореме Рисса — Фишера, тригонометрический ряд
00
— + ^ an cos nx + Ъп sinnx (7.10)
71=1
сходится по норме в 1/2[—тг,тг] к некоторой функции f(x) этого
гильбертова пространства, причем ряд Фурье функции f(x)
по тригонометрической системе (7.7) будет совпадать с этим
тригонометрическим рядом.
Можно показать, что из сходимости в среднем
квадратичном следует сходимость в среднем. Поэтому для любой
функции / G 1/2[—тг,7г] ее ряд Фурье сходится к функции f(x) не
только в среднем квадратичном, но и в среднем. Несмотря
на то что нормированное пространство Ь\[—тг,тг] не
является линейным пространством со скалярным умнооюением (в том

554 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В Ь2 [а, 6]
смысле, что норма в L\[—тг,7г] не индуцируется никаким
скалярным умножением), тригонометрический ряд вида (7.10) для
любой функции из L\[—7г,7г] формально составить можно,
поскольку все интегралы Лебега, используемые при вычислении
коэффициентов ап и Ьп, существуют. Однако утверждать, что
ряд Фурье по тригонометрической системе (7.7) для любой
функции из L\[—7г,тг] будет сходиться в L\[—тг,7г] к ней самой
уже нельзя. Это показывает следующее утверждение.
Теорема 7.9*. Тригонометрическая система (7.7) не
является базисом в L\[—7г,тг]. #
Таким образом, формально составленные ряды Фурье
функций из L\[—тг,7г] могут и не сходиться к раскладываемой
функции в L\[—7г,тг]. Более того, существуют функции из L\[—тг,тг],
ряды Фурье которых расходятся почти всюду на [—тг, тг].
Первый пример такого рода был построен в 1923 г. А.Н.
Колмогоровым**, когда ему не было еще и двадцати лет. В его примере
частичные суммы ряда являются почти всюду
неограниченными. Позднее И. Марцинкевич построил суммируемую функцию,
ряд Фурье которой расходится почти всюду на [—тг, тг], а
частичные суммы ограничены.
Обратимся теперь к проблеме сходимости рядов Фурье от
непрерывных функций. Ранее мы отмечали, что
тригонометрическая система (7.7) не является базисом в С[—тг,тг].
Теоремы 3.17, 3.18 (признак Дирихле), 3.19 (признак Дини) и 3.20
(признак Жордана) дают лишь достаточные признаки
сходимости ряда Фурье непрерывной функции, удовлетворяющей
дополнительным условиям типа дифференцируемости или
ограниченного изменения. Если на непрерывные функции не
накладывать дополнительные ограничения, то, вообще говоря, нет
оснований полагать, что ряды Фурье этих функций будут схо-
* Доказательство см.: Кашин Б. С, Саакян А. А.
"Колмогоров Андрей Николаевич (1903-1987) — выдающийся русский
математик.

7.7. Многочлены Лежалдра 555
диться. И действительно, в 1873 г. П. Дюбуа-Реймон установил,
что существуют непрерывные в точке функции, ряды Фурье
которых в этой точке расходятся. Вплоть до 1966 г. не было
известно, сходится ли ряд Фурье каждой непрерывной функции
хотя бы в одной точке.
Эта проблема была решена в 1966 г., когда Л. Карлесон
доказал следующую теорему.
Теорема 7.10 (теорема Карлесона). Для любых дей-
оо
ствительных чисел ао? ап, Ьп, п Е N, таких, что ряд J2 (ап + ^п)
сходится, тригонометрический ряд n=1
оо
— + у. ап cos пх + bn sinnx
п=1
сходится почти всюду на отрезке [—тг, тг]. #
Из теоремы Карлесона следует, что ряды Фурье (7.10) по
тригонометрической системе (7.7) сходятся почти всюду на
отрезке [—тг, тг] для всякой функции из 1/2 [—тг,тг], и в частности
для всякой непрерывной функции.
7.7. Многочлены Лежандра
Наряду с тригонометрической часто используют и другую
систему элементарных функций — систему многочленов.
Построим, например, базис гильбертова пространства L>2[—1,1],
состоящий из многочленов. Для этого рассмотрим
последовательность одночленов 1, #, х2,..., ж71, как систему элементов
гильбертова пространства Ьг[—1,1]. Линейной оболочкой этой
системы является множество всех многочленов, которое по
теореме 7.7 всюду плотно в Ьг[—1,1]. Это значит, что система
одночленов {xk}^L0 является замкнутой системой в 1*2[—1,1].
Однако замкнутая система может и не быть базисом в
гильбертовом пространстве.

556 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В Ь2 [а, 6]
Теорема 7.11. Система одночленов {xk}%L0 не является
базисом в гильбертовом пространстве L^— 1,1].
М Пусть f(x) — произвольная функция из 1*2 [—1,1]. Если
предположить, что система {xk}^L0 является базисом в 1/2[— 1Д]5 то
функция f(x) должна иметь единственное разложение в ряд по
этой системе, т.е.
/(z)^2f>**, (7.11)
к=0
причем сходимость ряда здесь необходимо понимать по норме
гильбертова пространства Ьг[—1,1], т.е. в среднем
квадратичном. Это значит, что последовательность частичных сумм
п
Sn = ]Г) CkXk в среднем квадратичном сходится к функции f(x):
dx -» 0, n -> +00.
^
Из сходимости последовательности в среднем квадратичном
следует сходимость этой последовательности в среднем.
Поэтому
0, n->+oo. (7.12)
Согласно свойствам интеграла Лебега, функция /(ж), сулс-
мируемал с квадратом на [—1,1], является суммируемой на
[—1,1] и, следовательно, является суммируемой на любом
измеримом подмножестве отрезка [—1,1]. В частности, на любом
отрезке [а, /3] С [—1,1] существует конечный интеграл Лебега
от функции f(x). Введем интеграл Лебега с переменным верх-

7.7. Многочлены Лежалдра
557
ним пределом, полагая
при s ^ 0 и
о
Jf(x)dx = (L) J f(x)dx
О [0,5]
5
Jf(x)dx = -(L) J f(x)dx
0 [3,0]
при s < 0. Рассмотрим функцию
s
F(s) = Jf(x)dx, e 6 [-1,1]
о
и функциональную последовательность {Fn(s)}%Ll с общим
членом
Fn(s)= (£ckxk)dx, в 6 [-1,1],
{ k=0
где коэффициенты с^ те же, что и в равенстве (7.11).
Докажем, что если для функции f(x) верно разложение
(7.11), то функциональная последовательность {Fn(s)}
сходится поточечно на отрезке [—1,1] к функции F(s).
Действительно, используя свойства интеграла Лебега и сходимость
(7.12), для всех s G [—1,1] получаем
\Fn(s)-F(s)\<
о л=и
п
- jf(x)dx
A:=0
A:=0
при п -> oo, откуда и следует поточечная сходимость
последовательности {Fn(s)}. Из этой сходимости с учетом линейных

558 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В Ь2[а,Ь]
свойств интеграла Лебега и его связи с интегралом Римана при
s Е [— 1,1] имеем
fc=o
/с=и 0
Таким образом, если система одночленов {хк}^0 является
базисом в 1/2 [— 1,1], то для всякой функции / Е L<^\—1,1]
построенную по ней функцию F(s) на отрезке [—1,1] можно
представить степенным рядом, сходящимся к F(s) поточечно на
этом отрезке. Но тогда функция F(s) является
действительной аналитической функцией на отрезке [—1,1] и, в частности,
бесконечно дифференцируемой в интервале (—1,1) (см. теорему
2.19). Однако можно привести примеры функций из 1/2[—1,1],
для которых функция F(s) не будет аналитической на отрезке
[—1,1]. Например, для функции f(x) = sgn(x) в силу
ограниченности принадлежащей 1/2 [—1,1] функция
5
F(s) = fsgn(x)dx = И, s Е [-1,1],
о
не дифференцируема в нуле. Полученное противоречие
доказывает, что система одночленов {хк}(£_0 не является базисом в
1Д]. ►
Нетрудно показать, незначительно изменив доказательство
теоремы 7.11, что система {хк}^_0 не является базисом ни в
каком другом гильбертовом пространстве 1/2[а,Ь].
Хотя система {хк}^_0 не является базисом в
гильбертовом пространстве Z/2[~~1>1]> он^, как мы отмечали ранее, есть
замкнутая линейно независимая система в Ьг[—1,1], т.е.
замыкание ее линейной оболочки совпадает с 1/2 [—1,1]. Для таких

7.7. Многочлены Лежалдра 559
систем имеется простой способ получения на их основе
базисов гильбертова пространства — процесс ортпогонализации
Грама — Шмидта. Применим к системе одночленов {xk}<j£=0
процесс ортогонализации, в результате которого получим ор-
тонормированный базис
Qo(x), Qi(x), Qk(x), (7.13)
в сепарабелъном гильбертовом пространстве 1/2[—1,1] (см.
следствие 6.4). Заметим, что наряду с системой (7.13) орто-
нормированным базисом будет и любая другая система,
члены которой отличаются от соответствующих членов системы
(7.13) только знаком. В соответствии с процессом
ортогонализации каждый элемент Qk(x) полученного ортонормированного
базиса является линейной комбинацией первых к + 1 элементов
1, х, х2, ..., хк исходной системы, т.е. является многочленом
степени к. Таким образом, ортонормированный базис (7.13)
состоит из многочленов.
Учитывая вид скалярного произведения в 1/2[— 1,1],
вычисляем в явном виде несколько первых членов ортонормированного
базиса (7.13):
Qo(x) = 1;
1
/ xdx
J dx
-l
1 1
J x2dx J
-1 1 -1 2 1
j l--j x = x --■
J dx J x2 dx
-l -l

560 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[a,Ь]
JxAdx
- . 1-=i—
/ dx / x2 dx
-l -l
l
М2л V 3
(X2 _ 1 \ = Ж3 _ 3x
Продолжая вычисления, в принципе можно вычислить в
явном виде любой член Qk(x) ортонормированного базиса (7.13).
Однако этот путь технически сложен, сопряжен с громоздкими
вычислениями и не приводит к легко устанавливаемому
явному представлению многочлена Qk{x). Как отмечалось, точные
выражения для Qfc(x) не обязательны. Достаточно построить
систему, члены которой совпадали бы с членами системы (7.13)
с точностью до постоянного числового множителя. Тогда,
пронормировав эту систему, получим требуемый ортонормирован-
ный базис. Покажем, что всякий многочлен Qfc(x), к — 0,1,...,
с точностью до постоянного множителя совпадает с
многочленом
(при к = 0 считаем, что Ro{x) = 1). Причем докажем это
утверждение не путем явного вычисления многочленов -Rfc(x),
а используя только свойства системы функций {^fc(x)}^=0'
Теорема 7.12. Система функций {Як(х)}^о является
ортогональной системой в гильбертовом пространстве L<^—1,1].
< Для всякого А; функция Rk(x) является многочленом fc-й
степени, т.е. непрерывной функцией, не равной тождественно

7.7. Многочлены Лежалдра
561
нулю на отрезке [—1,1]. Таким образом, при любом к функция
Rk{x) не является нулевым элементом в 1*2[—1,1].
Докажем, что
=/
dx = 0, кфп.
Пусть для определенности к < п. Тогда вследствие того, что
многочлен (х2 — 1)п = (х — 1)п(х + 1)п имеет корни —1 и +1
кратности п, производная порядка т <п этого многочлена будет
иметь корни —1 и +1 кратности п — т ^ 1. Следовательно,
dx
г<*2-
х=-\
= о,
(Г
dxm
(х2 -1)"
Х=1
= 0
для всех* т = 0, п—1. Учитывая эти равенства, проинтегрируем
по частям** скалярное произведение функций Rk{x) и Rn(x):
-1
-1
-1
-1
-1
"Напомним, что „нулевой" производной от функции считается сама
функция.
** Интегрирование по частям возможно, поскольку интеграл Лебега для
многочленов совпадает с интегралом Римана.

562 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[a,b]
Повторяя процесс интегрирования по частям п раз, получаем
Л
-1
2 — 1)к
Многочлен (х2 — 1)к степени 2к имеет нулевую производную
порядка к + п > 2к. Поэтому и интеграл в последнем равенстве
справа равен нулю, т.е. (Д^, Rn) = 0 при к < п. ►
Сравним теперь системы {Qk(x))kLo и {^k(x)}kLo- Всякая
функция Rk{x) = -гт(х2 ~~ 1)*» будучи к-и производной
многочлена степени 2fc, сама является многочленом степени А;, т.е.
принадлежит подпространству, порожденному первыми к + 1
элементами системы {xk}^L0. Наоборот, любой одночлен хк
принадлежит подпространству, порожденному первыми к + 1
элементами системы {Rk(x)}. Поэтому две ортогональные
системы многочленов {Qk(x)} и {Rk(x)} связаны с системой
одночленов {хк} следующим образом (см. теорему 6.15): к-е
элементы обеих систем принадлежат линейной оболочке
элементов 1, х, хк системы {хк}. Отсюда следует, что два
к-х элемента систем {Rk(x)} и {Qk{x)} могут отличаться как
элементы гильбертова пространства 1/2 [—1,1] только
постоянным числовым множителем. Поскольку Rk(x) и Qfc(x) являются
многочленами (непрерывными функциями), то они как
функции различаются только постоянным множителем.
Чтобы из ортогональной системы {Rh(x)} получить орто-
нормированную, нужно элементы этой системы
пронормировать. Применяя уже использовавшийся прием многократного
интегрирования по частям, получаем
\\Rkf = | ^
-1 -1
-1 -1

7.7. Многочлены Лежалдра 563
Вычислим интегралы
1
Ik = J(x2-l)kdx, * = 0,1,...
-1
используя рекуррентные формулы.
1
При к = 0 получаем /о = / (#2 — 1)° dx = 2. А при к ^ 1 имеем
-1
1 1
4 = Лх2 - \)kdx = f(x2 - I)*" V - l)dx =
-1
1
= |(а:2 - I)*"
-^-1 = 1^ j xd(x2 -l)k -1^ =
-1 -1
1 1
-1 -1
1
2-l)k
X{x2-l)
-1
-1
Отсюда заключаем, что
2к
Применяя полученную формулу п раз, находим
(2n)(2n-2)...2
/n = ("1) (2n + l)(2nl)3/°-(-1)
где по определению (2k + 1)!! = 1 • 3 • 5 •... • (2k + 1).
С помощью найденного интеграла вычисляем норму
многочлена Rk(x):
IIR II2 - (

564 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В Ь2[а,Ь]
где (2к)\\ = 2 • 4 •... • (2к). Таким образом,
к = м'2'
а система пронормированных многочленов имеет вид
Rk(x)_
_ni2 (714)
и представляет собой ортонормированный базис в
гильбертовом пространстве Ьг[—1,1].
Обычно в качестве базиса в L2[—1,1] используют не ор-
тонормированную систему многочленов (7.14) с громоздким
/pi, I -I
радикалом л/—-—, а более простую ортогональную (но не ор-
тонормированную) систему многочленов
Многочлены Pk{x) называют многочленами Лежандра*, а
их представление (7.15) — формулой Родрига.
Многочлены Лежандра попарно ортогональны, однако их
нормы не равны единице:
\ ( 0, кфщ
Pk{x)Pn{x)dx={ 2
-1
Поскольку система {Лк(#)}£^о является ортогональным
базисом в гильбертовом пространстве £/2[—1>1]> то каждую функ-
*Лежандр Адриен Мари (Legendre A.M.) (1752-1833) — французский
математик.

7.7. Многочлены Лежандра 565
цию f(x) Е 1/2 [— 1,1] можно однозначно представить своим
рядом Фурье по системе многочленов Лежандра:
к=0
где сходимость ряда справа рассматривается относительно
нормы в 1^2[—1,1], т.е. в среднем квадратичном, а равенство
выполняется почти всюду на отрезке [—1, 1]. Коэффициенты
Фурье Ck определяются по формулам
2к +
-1
1
-Jf(x)Pk(x)dx, A; = 0,1,2,...
Как производные четных функций (х2 — 1) /(к\2к),
многочлены Лежандра являются попеременно четными и нечетными
функциями. Поэтому в силу симметричности отрезка
интегрирования [—1,1] четные функции из 1/2 [—1>1] можно разложить
в ряд Фурье по многочленам Лежандра с четными номерами:
m=0
где
1
4m+ 1
2
-l
Jf(x)P2m(x)dx =
1
= (4m + l) I f{x)P2m(x)dx, rn = 0,1,...
0
Нечетные функции из 1*2[~1>1] имеют ряд Фурье по
многочленам Лежандра с нечетными номерами:
оо
m=0

566 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В Ь2[а,Ь]
где
С2т+1 =
4т+ 3
-1
1
J f(x)P2m+i{x)dx, m = 0,1,2,...
100,
-1,
-500,
1,
300,
х =
-1
х =
0<
х =
<
0
X
1
-1;
X
<
<0;
1;
Пример 7.2. Разложим в ряд Фурье по многочленам Ле-
жандра в гильбертовом пространстве L2[—1,1] функцию
/(*) =
В £/2[—1>1] любую функцию можно произвольно изменить на
множестве меры нуль, сохраняя ее неизменной как элемент
этого гильбертова пространства. Учитывая это, заменим
заданную функцию более простой:
д(х) =
Функции f(x) и д(х) представляют собой один и тот же
элемент гильбертова пространства 1лг[—1,1]. Поэтому их ряды
Фурье по ортогональному базису в 1^2 [—1,1], состоящему из
многочленов Лежандра, совпадают. Функция д(х) нечетна на
симметричном отрезке [—1,1], поэтому она имеет ряд Фурье по
многочленам Лежандра с нечетными номерами:
L2
m=0

7.7. Многочлены Лежандра
567
где
1
C2m+i = (4т + 3) / д(х) P2m+i (я?) dx =
Используя формулы Родрига, находим
4т + 3
(2т+ 1)12*
4т +
/
(2m+l)!22m+1
где
Вычислим значения Fm(l) и Fm(0). При
дифференцировании многочлена кратность всякого его корня уменьшается на
единицу. Поэтому при (2т)-кратном дифференцировании
многочлена (х2 — \)2т+1 с корнем х = 1 кратности 2га+1 получим
многочлен, для которого число 1 является корнем кратности 1.
Следовательно, Fm(l) = 0.
Для вычисления значения Fm(0) используем равенство
d2'
™
dx2m
=
(2k)\ = (2m)!,
0,
т = к;
т > к.

568 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[a,Ъ]
Из этого равенства следует, что значение функции (х2Л;)(2т) в
точке х = 0 отлично от нуля только при т = к, причем в этом
случае оно равно (2т)! Учитывая это и применяя к многочлену
(х2 — i)2m+! формулу бинома Ньютона, получаем
х=0
Jim
к
к=0
х=0
2m)!-(-
Следовательно,
(4m + 3)(2m)!
Так как функции д(х) и /(х) представляют собой один и
тот же элемент гильбертова пространства 1/2 [—1>1] и их ряды
Фурье по многочленам Лежандра совпадают, то функция f(x)
имеет следующее разложение в ряд Фурье по многочленам
Лежандра в 1*2 [—1,1]:
( iw 2m)!
("1) rn!(m + l)!2
где сходимость ряда справа рассматривается относительно
нормы в L2["~1>1]> т.е. в среднем квадратичном. #

7.8. Многочлены Чебышева 569
В заключение приведем несколько первых многочленов Ле-
жандра в явном виде:
Ро(*) 1, Р3(х)(5х
Pi (ж) = ж, Р4 (ж) = I (35х4 - ЗОх2 + 3),
о
Р2(х) = \(Зж2 - 1), Рь{х) = I(63x5 - 70х3 + 15s),
Z о
(сравните с первыми многочленами системы
7.8. Многочлены Чебышева
Пусть ц>(х) — некоторая фиксированная неотрицательная
суммируемая на отрезке [—1,1] функция, не являющаяся на
[—1,1] почти всюду равной нулю. Рассмотрим на [—1,1]
измеримые функции, суммируемые с квадратом и весом
ip(x), т.е. такие функции /(х), для которых интеграл Лебе-
1
га / f2(x)(p(x)dx конечен. Совокупность всех таких функции
-1
/(х), с условием отождествления функций f(x) и д(х), для
которых функции f{x)y/(p(x) и д(х)у/<р(х) совпадают почти всюду
на отрезке [—1,1], обозначим через 1/2 ([—1,1]> ¥>)• Очевидно,
что
Легко видеть, что множество 1*2([—1,1], ф) является
действительным линейным пространством. Оно бесконечномерно,
поскольку содержит бесконечную линейно независимую систему
элементов 1, ж, х2, ..., хп, ... Кроме того, из неравенства Ко-

570 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[a,Ъ]
ши — Буняковского для 1/2 [—1,1] следует, что
1 1
/ f(x)g(x)(p(x)dx = I \J(x)y/<p(x)) (g(x)y/<p(x)) dx
-l
-l
\
/ f2(x)<p{x)dx / g2(x)<p(x)dx.
-l A-i
Следовательно, для любых функций /, д € L2([—1,1], <р)
существует и конечен интеграл f f(x)g(x)(p(x)dx. Положим
-1
f,g G
-l
Нетрудно показать, что для (/, д) выполнены все аксиомы
скалярного умножения. Таким образом, линейное
пространство Z/2 ([—1,1], у) становится евклидовым пространством.
Индуцированная скалярным умножением норма в этом
евклидовом пространстве определяется равенством
\
1
J f2(x)<p(x)dx,
-l
Теорема 7.13*. Бесконечномерное евклидово
пространство £/2[~1>1] является гильбертовым пространством.
Система всех многочленов, определенных на отрезке [—1,1]? является
его всюду плотным подмножеством. #
*Эта теорема является следствием полноты гильбертова пространства
(,/) при X = [—1,1] и мере /л, которая для любого измеримого
множества Е С [—1,1] определена формулой р{Е) = J\p(x)dx. См.:
Колмогоров А.Н., Фомин СВ. Е

7.8. Многочлены Чебышева 571
Рассмотрим систему одночленов
1, х, х2, ..., хк, ...,
как счетную линейно независимую систему элементов
гильбертова пространства Lt2([—1,1], (р). Подвергнув эту систему
процессу ортогонализации, получим некоторую замкнутую
ортогональную или ортонормироеанную (по желанию) систему
{Qk{x)}^LQ многочленов в L2Q—1,1], ¥>)? т.е. базис этого
гильбертова пространства. Условие ортонормированности системы
{Як{х)}^-0 в 1^2([—1,1], (р) в этом случае определяется
формулами
' фт\
= га.
-1
Неотрицательную суммируемую на отрезке [—1,1]
функцию <р(х), не являющуюся на этом отрезке почти всюду
равной нулю, с помощью которой определяют гильбертово
пространство L>2([—1,1], <р), называют весом, или весовой
функцией, а функции, ортогональные в гильбертовом
пространстве 1*2([— 1,1], ¥>), — ортогональными с весом (р{х).
Система одночленов {xk}<£LQ в результате процесса орто-
гонализации в гильбертовом пространстве Ьг([—1,1], ^) для
различных весовых функций (р(х) приводит к различным
системам ортогональных многочленов. В частности, если в качестве
весовой взять функцию
<p{x) = -=L=t хб(-1,1),
то процесс ортогонализации системы одночленов {xk}^LQ в
Хг2([—1,1], <^) приводит к ортогональной системе, элементы
которой с точностью до постоянного множителя совпадают с
многочленами Чебышева
То (я?) = 1, Тп(х) = —zrcos(narccosx), n e N. (7.16)

572 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В Ь2[а,Ь]
Многочлены Тп(х) впервые были получены П.Л. Чебыше-
вым* при решении задачи об отыскании среди всех
приведенных (т.е. с коэффициентом 1 при старшей степени) многочленов
п-й степени такого многочлена, который на отрезке [—1,1]
имеет наименьшую максимальную абсолютную величину. Че-
бышев показал, что решением поставленной задачи являются
многочлены (7.16), в дальнейшем названные его именем.
Приведем несколько первых многочленов Чебышева в явном
виде:
= 1, Тг{х)=х,
Теорема 7.14. Система многочленов Чебышева является
ортогональной с весом (р{х) = 1/\/1 — х2 системой элементов в
<4 Покажем, что многочлены Тп(х) принадлежат гильбертову
пространству L2Q—1,1], Ч>) с весом (р(х) = 1/л/1 — х2, т.е.
< +оо, п = 0,1, 2,... (7.17)
Интегралы (7.17) следует рассматривать как интегралы
Лебега. Но подынтегральная функция каждого такого интеграла
непрерывна и неотрицательна на (—1,1), а поэтому сходимость
интеграла Лебега равносильна сходимости несобственного
интеграла Римана от той же функции (теорема 7.4). Многочлены
*Чебышев Пафнутий Львович (1821-1894) — один из крупнейших
русских математиков XIX в.

7.8. Многочлены Чебышева 573
Т%(х) являются непрерывными ограниченными функциями на
отрезке [—1,1], а несобственный интеграл на этом отрезке от
весовой функции сходится:
1
/dx . I1 7Г / 7Г\
, = arcsinx = — — ( —— 1 = 7г < -foo.
-1
Следовательно, при любом п несобственный интеграл (7.17)
сходится в силу признака сравнения для несобственных
интегралов:
Г Т2(тЛ Г М-
+оо,
где Мп= maxT2(z).
Теперь покажем, что многочлены Чебышева попарно
ортогональны с весом (р{х) = 1/\/1 — х2, т.е.
пфт. (7.18)
VI — X*
-1
Интеграл в равенстве (7.18), понимаемый как интеграл Лебега,
можно рассматривать и как несобственный интеграл Римана.
Это следует из того, что подынтегральная функция
представляет собой произведение непрерывной на отрезке [—1,1]
(следовательно, ограниченной) функции на интегрируемую на этом
отрезке в несобственном смысле неотрицательную функцию
<р(х). Несобственный интеграл Римана от такой функции
сходится абсолютно, а интеграл Лебега конечен (см. теорему 7.4),
причем оба интеграла равны.
Чтобы вычислить несобственный интеграл Римана,
используем представление (7.16) для многочленов Чебышева:
1 1
Тт(х)Тп(х) J 1 f cos(marccosx) cos(narccosx)
dx.
f
J
-1 -1

574 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2 [a, 6]
В интеграле справа выполним замену переменного х = cost,
t E [0,7г] (при этом dx = — sintdt и sint > 0 при t Е [0,7г]):
cos(marccosx) cos(narccosx)
dx =
7Г
— Г
-2 /
cosmtcosnt .
7—и—; si
sint
2ТП+П-2
cos mt cos ntdt.
о о
Вычисляя последний интеграл с использованием формул для
произведения косинусов, находим
_
122Й=Г' m = n-
(7.19)
Полученные формулы верны для натуральных значений m
и п. Если же т = 0, то аналогично получаем
}адад 1 ? го, п>о;
У ^Г^2 2*"1 У \тг, п = 0.
-1 О
Из выполненных вычислений следует, что система {Тп(х)} в
гильбертовом пространстве 1,2([—1,1], 1/л/1 — #2)
ортогональна. ►
Из формул (7.19) при т = п определяем нормы многочленов
Чебышева в гильбертовом пространстве Ьг([—1,1], 1/Vl — х2):
(7.20)
\
Норму многочлена Tq(x) легко вычислить непосредственно:
(7.21)
-1
\
-1

7.8. Многочлены Чебышева 575
Всякая функция из Хгг([—1,1], 1/\/1 — х2) может быть
разложена в ряд Фурье по ортогональному базису из многочленов
Чебышева:
= £сТ(х) (7.22)
п=0
где коэффициенты Фурье Сп определяются формулами
а сходимость ряда в (7.22) следует понимать как сходимость
по норме гильбертова пространства 1,2([—1,1], 1/>/1 — я2)? т.е.
сходимость равносильна условию
2
jf(x) - Sm(x)Y J _
m-юо
-l
где Sm(x) — частичные суммы ряда Фурье функции f(x) по
многочленам Чебышева.
Многочлены Чебышева являются попеременно четными и
нечетными функциями, так как для любого п G N
Тп(—х) = cos(narccos(—х)) = _х cos(n7r — narccosx) =
= 2^T(-l)ncos(narccosx) = (-l)nTn(x), x G [-1,1].
Поэтому четные на [—1,1] функции имеют ряд Фурье по
многочленам Чебышева с четными номерами, а нечетные функции —
с нечетными номерами.
Пример 7.3. Разложим в ряд Фурье по многочленам
Чебышева функцию
/Ог) = и, ж 6 [-1,1].

576 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[a,Ь]
Это четная функция, поэтому ее ряд Фурье по многочленам
Чебышева содержит слагаемые только с четными номерами:
ь2
m=0
где
№т\?
m = 0,1,...
При m = О имеем
2 f х л 2 Гл 2
со = — / —7= ах = у 1 ~ #
7Г у у 1 — х2 тг
О 7Г
Если же т > 0, то
24т
22т+1 г х cos(2m arCCOS x)
Т2т(х) , 22m+1 /'a;cos(2marc
, ах = / ,
1 _ Т2 7Г / л/1 —Т
Полученный интеграл можно вычислить с помощью уже
применявшейся подстановки х = cost, t G [0,7г/2]:
1 тг/2
22m+i /*:rCos(2marccosz) , 22m+1 / п ±J
/ -dx= / cosicos2miat =
о о
тг/2
2 / / \
= / fcos(2m-l)i-fcos(2m+l)tjdi =
o / . (2т-
22m ^ sm ^
7Г
2m-l
2m+ 1
/ (_i
7Г V 2m-1
• +
22m+1
тг(4т2 -1) '

7.8. Многочлены Чебышева
577
Таким образом, разложение функции |х| на отрезке [—1,1] в
ряд Фурье по многочленам Чебышева имеет следующий вид:
где сходимость ряда следует понимать как сходимость по норме
гильбертова пространства Lt2([— 1,1], 1/\/1 — ж2). #
Тригонометрическая система {cosnt}™=0 является
ортогональным базисом в гильбертовом пространстве L2[0,7r].
Следующая теорема устанавливает связь между гильбертовыми
пространствами 1/2([—1,1], 1/\/1 — я2) и 1/2[0,7г] с выделенными
в них ортогональными базисами {Тп(х)} и {cosnt}.
Теорема 7.15. Замена х = cos* независимого
переменного функций определяет естественный изоморфизм между
гильбертовым пространством 1,2([—1,1], 1/л/1 — х2) с
ортогональным базисом {Тп(х)}£?_0 и гильбертовым пространством
L2[0,7t] с ортогональным базисом {cosnt}™=Q.
< Замена переменного х = cos t определяет отображение,
которое каждой функции /(х), определенной на отрезке [—1,1],
ставит в соответствие функцию ф(г) = /(cosi), определенную
на отрезке [0, тг]. Покажем, что это отображение функции
/ G 1^2([—1,1], 1/лЛ—х2) ставит в соответствие функцию гр G
G 1г2[0» ^l» те- может рассматриваться как отображение из
одного гильбертова пространства в другое. Чтобы не усложнять
изложение дополнительными фактами из теории интеграла
Лебега, докажем это утверждение лишь для тех функций, которые
интегрируемы по Риману.
Если функция f(x) e L2([-l,l], 1/Vl-z2) интегрируема по
Риману, то для функции /(cosi) получаем
7Г
/■
t = axccosrc,
я =€[-1,1],
d
+оо,

578 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[а,Ь]
т.е. неотрицательная функция ip2(t) = /2(cost) интегрируема по
Риману в несобственном смысле, а потому ф(г) G L2[0,7r].
Теперь покажем, что при отображении f(x) -> /(cost)
коэффициенты Сп Фурье функции f(x) по системе {Тп(х)} и
коэффициенты Сп Фурье функции xp(t) = /(cost) по системе {cosnt}
связаны соотношениями (6.21). Это и будет означать, что такое
отображение является естественным изоморфизмом
гильбертовых пространств.
Нормы многочленов Чебышева вычисляются по формулам
(7.20) и (7.21). Нормы функций cosnt G L2[0,7г] таковы: ||1|| =
= у/п, || cosnt|| = л/тг/2, n G N. Поэтому необходимо доказать,
что
|1 ~ ~
НВД||2
(7.23)
— *
,
С
п
где || • ||х и || • ||2 — нормы в гильбертовых пространствах 1/2[0,7г]
и If2([—1,1], l/y/l—x2). Докажем соотношения (7.23). Пусть
функция / G L2([—1,1], 1/\/1—х2) интегрируема по Риману.
Тогда для нулевых коэффициентов Фурье имеем
X = COSt,
*е[о,тг],
dx = - sintdt,
7Г
= — / /(cost)dt = co-
Для остальных коэффициентов также используем замену
переменного. В результате для всех п G N имеем
/(x)cos(narccosx)
22п-х Г/(гс)Тп(гс) _, 2n /*
= / —t ax = — /
к J у/1-х2 к J
-1 -1
[я? = cost, tG[0,7r],l 2n f !„
= , ' L ' J4 =— / /(cost)cosntdt = 2n xcn.
[ dx = -smtdt J 7Г J

7.9. Система Хаара 579
Отображение f(x) -* /(cosi) является естественным
изоморфизмом гильбертовых пространств £г([—1,1], 1/Vl — x2) и
L2[0,7r] с ортогональными базисами {Тп(х)}™=0 и {cosnt}™=0.
Следовательно, замена
оо
в ряде Фурье £ СпТп{х) функции f(x) e L2([-l,l], l/y/l-x2)
n=0 oo
приводит к ряду Фурье Yj ^пcosnt функции /(cost) G £/2[0,тг]
п=0
(см. 6.7). Это позволяет свести анализ рядов по
многочленам Чебышева к анализу соответствующих рядов по более
изученной тригонометрической системе {cosn£}£°_0. А
поскольку замена х = cos* является непрерывно дифференцируемой,
то на ряды по системе многочленов Чебышева переносятся
дополнительные свойства, касающиеся различных видов
сходимости (сходимость почти всюду, равномерная сходимость,
сходимость в Li[0,7r], и т.д.) и которые могут быть доказаны
оо
ДЛЯ РЯДОВ 5Z Сп COS nt В 1^2 [0,7Г].
п=0
7.9. Система Хаара
Рассмотрим теперь гильбертово пространство Z/2[0,1].
Одной из простейших полных ортонормированных систем
(базисов) в 1^2 [0,1] является система Хаара. Эту систему впервые
построил и начал изучать А. Хаар в 1909 г. в связи с задачей
построения ортонормированной системы функций, ряды Фурье
непрерывных функций по которой сходились бы равномерно на
[0,1]. Простота и естественность системы Хаара объясняют ее
широкое применение в теории функций, теории вероятностей
и вычислительной математике.
Система Хаара состоит из кусочно постоянных на [0,1]
функций и определяется следующим образом. Как и для функ-

580 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В Ь2[а,Ь]
ций системы Фабера — Шаудера, для функций системы Хаара
наряду с одинарной (порядковой) нумерацией удобно ввести и
двойную нумерацию с помощью представления натурального
числа п^2в виде п = 2т + к, где га — неотрицательное
целое число, а к — натуральное число, не превосходящее 2т (см.
(5.9)). С помощью представления 1 = 2° + 0 (т.е. га = 0, к = 0)
двойную нумерацию получит и первая функция системы Хаара.
Таким образом, для каждой функции Хаара будут использова-
ны два равноценных обозначения Хп(#) и Хт (#), где числа п,
тик связаны соотношением п = 2т + к.
Первая функция системы Хаара постоянна:
а вторая имеет вид
0 х — -•
' — 2'
Эти две функции представлены на рис. 7.2 и 7.3
1 х
У)
1
0
»
1
2
ДО»)
| 1 х
Рис. 7.2
Рис. 7.3

7.9. Система, Хаара 581
Последующие функции Xm (x) системы Хаара с номерами
• определяются равенством
/fc-1 fc-l/2y
х Е 2т ' 2т /'
fc-1/2 i
В точках разрыва х = {к - 1)/2т (А; ф\), х = {к- 1/2)/2т и
ж = k/2m (к ф 2т) функция Хт (х) доопределяется как
полусумма односторонних пределов, а в крайних точках отрезка х = 0 и
ж = 1 — как соответствующий односторонний предел. Графики
функций Хт (я) при m = 1, 2 представлены на рис. 7.4.
Теорема 7.16. Система Хаара является счетным ортонор-
мированным базисом в гильбертовом пространстве 1/2[0,1].
< Сперва докажем, что у всех функций системы Хаара норма
в 1/2 [0,1] равна единице. Для первых двух функций Хо (х) и
Хо (я) это очевидно, а для остальных имеем
1 k/2m
Теперь покажем, что функции системы Хаара попарно
ортогональны. Ортогональность первых двух функций Хо (х) и
Хо (я) ко всем остальным функциям очевидна.
Рассмотрим произвольные функции Хт (#) и Хт {я) с одним
и тем же индексом m ^ 1 и различными индексами i и j. Их
произведение Xm(x)Xm (х) всюду на отрезке [0,1], кроме, быть

582 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В Ь2[а,Ъ]
У
*
1 X
-V2
yi
2
0
1
2
—>
1
<
1 X
>
-2
-1
-2
1 5
2 ЁГ
3.
1 X
У-
2
1
0
-2
........... ...... .^£^
i
i
I
A
T
1
1
3 7
T 18
lj x
Рис. 7.4

7.9. Система Хаара 583
может, одной точки, равно нулю. Следовательно,
1
о
Рассмотрим функции Хп{х) и Хт(х) с различными
индексами т^1ип^1и произвольными индексами г и j.
Для определенности считаем, что п > т. В этом случае из
определения функций системы Хаара следует, что интервал
((г — 1)/2п, г/2п), в котором функция Хп (х) отлична от нуля,
целиком лежит в интервале, в котором функция Хт{х)
постоянна и равна некоторой константе А (в зависимости от значений
индексов г и j А = 0 или А = ±л/2™). С учетом этого имеем
= A
(г-1)/2п
| /
= А f y/¥dx-\ f
Таким образом, ортонормированность системы функций Хаара
установлена.
Докажем замкнутость системы функций Хаара. Для этого
сначала произвольную функцию из Li [0,1] аппроксимируем
непрерывной функцией, а затем для этой непрерывной функции
подберем многочлен по системе Хаара, приближающий ее по
норме гильбертова пространства Z/2[0,1].
Пусть (р(х) — произвольная функция гильбертова
пространства 1/2 [0,1]. Поскольку множество непрерывных на отрезке
[0,1] функций всюду плотно в 1/2[0,1] (см. теорему 7.7), то
для всякого числа е > 0 найдется непрерывная на отрезке [0,1]

584 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[a,Ь]
функция д(х), такая, что
Покажем, что для непрерывной функции д(х) найдется
многочлен по системе Хаара
f(x) =
такой, что
(7-26)
Для этого рассмотрим множество -Dm+i всех таких функций из
1/2[0,1], которые постоянны в каждом (в отдельности) из
интервалов ((/ - l)/2m+1, f/2m+1), / = 1, 2, 3,..., 2m+1. При этом
значения функций на концах этих интервалов могут быть
произвольными, поскольку в гильбертовом пространстве 1/2 [0 > 1]
пары функций, отличающиеся на множестве меры нуль,
отождествлены. Поэтому на значения функций из Dm+i в точках
разрыва (на концах указанных интервалов) обращать внимание
не будем. Множество Dm+i является, очевидно, линейным
пространством. Каждой функции f(x) из Dm+i можно поставить в
соответствие арифметический вектор (f\, /2*1+1) G K2m ее
значений в интервалах постоянства (количество интервалов
постоянства равно 2m+1). Нетрудно заметить, что такое
отображение Dm+i на R2m является изоморфизмом двух линейных
пространств. Таким образом, Dm+i является
подпространством в 1/2[0)1] размерности 2m+1.
Все функции Хп(#) системы Хаара с порядковыми номерами
п от 1 до 2m+1 включительно (т.е. все функции х\ ix) c
номерами i = 0, т и к = О, 2Ш) принадлежат подпространству Dm+i-
Конечная система этих функций Хаара ортонормирована,
линейно независима (потому что ортонормирована), состоит из
2m+1 функций (что равно размерности подпространства An+i)
и потому является ортонормированным базисом в
подпространстве -Dm+i гильбертова пространства 1/2[ОД]- Поэтому всякую

7.9. Система Хаара 585
функцию f(x) из -Dm+i можно представить в виде линейной
комбинации функций Xi(z), Х2(я), -., Хп(я), где п = 2m+1.
Таким образом, для того чтобы подобрать многочлен по
системе Хаара с условием (7.26), достаточно найти функцию
f(x) из Ап+1, удовлетворяющую тому же условию (7.26). Так
как функция д(х) непрерывна на отрезке [0,1], то она также и
равномерно непрерывна на этом отрезке [1-5.9], т.е.
Ve>0 36 = 6{e)>0 Vxu x2 е [0,1]:
\Xl-x2\<6 =» \g(xi)-g(x2)\<l. (7.27)
Для заданного числа е > О на основании (7.27) подберем
соответствующее S = 6(е) > 0. Возьмем тп G N настолько
большим, чтобы выполнялось неравенство l/2m+1 < (J, и рассмотрим
функцию /(я), определенную на отрезке [0,1], полагая, что
Значения функции в концах интервалов роли не играют и
могут быть выбраны произвольно. Функция f(x) принадлежит
подпространству Дп+ь Покажем, что она удовлетворяет
условию (7.26). Если хе{{1- l)/2m+\ l/2m+1), то
Z-1
х —
2ТП+1
и с учетом (7.27) имеем
Поскольку интервалы ((I - l)/2m+1, l/2m) накрывают весь
отрезок [0, 1], за исключением конечного числа точек (концов

586 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ BL2[o,Ъ]
интервалов), то почти всюду на [0,1] выполнено неравенство
\g(X)-f(X)\<i.
Используя свойства интеграла Лебега, отсюда для функции
f(x) получаем условие (7.26).
Из оценок (7.25) и (7.26) окончательно находим
Итак, в любой е-окрестности всякого элемента <р{х) Е1/2 [0,1]
существует элемент
f{x) = aixi(x) + а2Х2{х) + ... + апхп(х), a, G R, г = Т7п,
принадлежащий линейной оболочке системы Хаара. А это
означает замкнутость системы Хаара в гильбертовом пространстве
1,2[0,1]. Поскольку система Хаара ортонормирована, то в силу
теоремы 6.12 она является счетным базисом в 1/г[0,1]. ►
Так как система Хаара является базисом гильбертова
пространства 1/2 [0,1], то всякая функция ср(х) G1/2 [0,1] может быть
разложена в ряд Фурье по системе Хаара:
n=l m=0k=l
с коэффициентами Фурье
и
1 = 0,1,2,..., fc =

7.9. Система, Хаара 587
Равенство элемента ср(х) £ 1/2[0,1] своему ряду Фурье надо
понимать как равенство почти всюду на [0,1], а сумму ряда
Фурье — как сумму ряда в гильбертовом пространстве 1/2[0,1],
сходящегося в среднем квадратичном.
Рассмотрим теперь банахово пространство Li[0,1]
суммируемых на отрезке [0,1] функций. Хотя 1а [0,1] и не является
гильбертовым пространством, но формально составить ряды
Фурье по системе Хаара можно для любой суммируемой
функции (р(х) Е Li [0,1], поскольку все интегралы Лебега для
вычисления соответствующих коэффициентов Фурье существуют в
силу суммируемости ср(х) Е 1а [0,1] и ограниченности (а значит,
и суммируемости) любой функции Хп(#) системы Хаара.
Напомним, что аналогичная операция формального
распространения рядов Фурье по тригонометрической системе (7.7) с
функций из L2[—7г,тг] на функции из L\[—7г,тг] не дает ничего
хорошего, так как тригонометрическая система (7.7) не
является базисом в L\[—7г,тг] (см. теорему 7.9). Ряд Фурье функции
из 1а [—тг,7г] по тригонометрической системе (7.7) может не
сходиться к функции в банаховом пространстве L\[—тг,тг] (т.е.
в среднем). Более того, этот ряд может расходиться почти
всюду на [—тг, тг]. В отличие от тригонометрической
системы (7.7) система Хаара обладает следующими замечательными
свойствами.
Теорема 7.17*. Система Хаара является счетным базисом
банахова пространства 1а [0,1]. Для любой суммируемой на
[0,1] функции (р(х) Е 1а [0,1] ее ряд Фурье по системе Хаара
сходится в среднем на [0,1] к самой функции (р{х).
Теорема 7.18. Ряд Фурье по системе Хаара любой
суммируемой на [0,1] функции <р(х) Е 1а [0,1] сходится к функции
<р{х) почти всюду на [0, 1].
* Доказательства этой и следующих двух теорем см.: Кашин Б. С, Саа-
клн А.А.

588 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В Ь2[а,Ь]
Теорема 7.19. Ряд Фурье по системе Хаара любой
непрерывной на [0, 1] функции ср(х) Е С[0,1] равномерно на [0,1]
сходится к функции (р(х). #
Заметим, что равномерная сходимость на отрезке [0,1]
совпадает со сходимостью по норме в банаховом пространстве
С[0,1] непрерывных на отрезке [0,1] функций. Поэтому данное
утверждение можно было бы считать утверждением о том, что
система Хаара является базисом банахова пространства С[0,1].
Но функции системы Хаара разрывны, и поэтому система
Хаара не может рассматриваться как базис в С[0,1].
В заключение отметим, что, проинтегрировав функции
системы Хаара
X
<рп(х) = Jxn(t)dt, х е [О, 1], п = 0,1,...,
получим с точностью до постоянного множителя функции
системы Фабера — Шаудера. Напомним, что система Фабера —
Шаудера является базисом в банаховом пространстве С[0,1]
непрерывных на отрезке [0,1] функций.
Система Фабера — Шаудера, если ее рассматривать как
систему элементов в гильбертовом пространстве Ьг[0,1], не
является ортонормированной системой. Однако она
является линейно независимой, и к ней можно применить процесс
ортогонализации. В результате получим некоторую полную
ортонормированную систему (базис) в 1/2 [0,1], которую
называют системой Франклина. Система Франклина состоит из
непрерывных функций и обладает теми же свойствами, что и
система Хаара: является базисом в Li[0,1], всякий ряд Фурье
по системе Франклина для функции из 1а [0,1] сходится к ней
почти всюду на [0,1]. Кроме того, система Франклина
является базисом в нормированном пространстве С[0,1], поскольку
состоит из непрерывных функций. Эта система была построе-

7.10. Системы Радемахера и Уолша 589
на Ф. Франклином в 1928 г. Исторически она является первым
примером ортонормированного (в 1/2 [0,1]) базиса в линейном
пространстве непрерывных функций.
7.10. Системы Радемахера и Уолша
Система Хаара, обладая рядом замечательных свойств,
обладает и существенным с точки зрения некоторых
приложений недостатком — ее функции, будучи ограниченными в
отдельности, в совокупности неограниченно растут (не являются
равномерно ограниченными). Кроме того, для многих
приложений (вычислительной математики, теории кодирования,
цифровой обработки сигналов и т. д.) важным требованием
является простота (т.е. конечность множества значений) функций
ортонормированных систем. В этом параграфе
познакомимся с двумя системами функций в гильбертовом пространстве
1/2[0,1], свободными от указанного недостатка и обладающими
указанным достоинством.
Первая из этих систем — система Радемахера —
строится на основе системы Хаара Хт (#) путем сложения и
нормирования функций Хаара с одинаковыми нижними индексами:
(728)
k=i
где i € (0,1). Поскольку для функций гильбертова
пространства Li [0,1] не существенно, как они определены в любом
конечном числе точек, то для определенности положим
rm(0) = rm(l) = 0, m = 0,1,2,...

590 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2 [а, Ъ]
Нетрудно видеть, что определенные таким образом функции
системы Радемахера гт(х) с номерами га ^ 1 имеют вид
{х) =
т.е. на интервалах вида ((fc — l)/2m, fc/2m) попеременно
принимают значения +1 и — 1, а во всех точках разрыва равны нулю.
Все функции Радемахера, в том числе и функцию го(я), можно
задать одной компактной формулой:
rm(x) =sgn(sin2m7ra;), же [0,1], т = 0,1,2,...
где
Система функций {гт(#)}ш=о была построена Г Радемахером
в 1922 г.
Выясним свойства системы Радемахера. Во-первых, в
силу равенств (7.28), выражающих функции Радемахера через
функции Хаара, из ортогональности системы Хаара
следует ортогональность системы Радемахера, так как скалярное
произведение функций Радемахера с различными номерами
есть конечная сумма скалярных произведений функций
Хаара с различными номерами. Во-вторых, поскольку г^(х) = 1
почти всюду на [0,1] для всех номеров т, то функции
Радемахера в 1/2 [0,1] имеют нормы, равные 1. Таким образом, система
Радемахера является ортонормированной.
Однако система Радемахера не является полной системой
и, следовательно, не является базисом в 1/2 [0,1]. В самом деле,

7.10. Системы Радемахера и Уолта
591
нетрудно видеть, что для всех m = 0,1, 2,... верно равенство
(г
1
= /
rm(x)ri(x)r2(x)dx =
-1
rx(x)r2{x)
т.е. функция д(х) = г\(х)г2{х), являясь ненулевым элементом
гильбертова пространства 1*2 [0,1] (она не является функцией,
равной нулю почти всюду на [0,1], — см. график этой
функции на рис. 7.5), ортогональна всем
функциям системы Радемахера.
Поэтому система Радемахера не
полна. Согласно теореме 6.14, система
Радемахера не является базисом в
/>2[0,1]. Следовательно, ряд Фурье
функции f(x) из />2 [0,1] по системе
Радемахера даже в случае его
сходимости в гильбертовом
пространстве />г[0,1] (т.е. в среднем
квадратичном) не всегда представляет
исходную функцию f(x). Тем не менее система Радемахера
обладает рядом интересных свойств.
оо
Теорема 7.20. Если числовой ряд ^2 <4i сходится, то ряд
оо ш=1
S стгт{^) по системе Радемахера сходится почти всюду на
m=l
отрезке [0,1].
< Положим
£ = 172^.
Рис. 7.5
(к) _
оо 2я
Тогда ряд 52 £ (cm ) сходится, поскольку
т=1к=1
оо 2т
EEi
m=lk=l
оо 2т
m=lk=l
< +00.
т=1

592 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2 [а, Ь]
Так как система Хаара {Хт (я)} ортонормирована, то в силу
оо 2т (к) (к)
теоремы Рисса — Фишера ряд Фурье ^2 52 dm Хт (х) по си"
m=lfc=l
стеме Хаара сходится в гильбертовом пространстве 1>2[0,1] к
некоторой функции f(x) E L2[0,l]. Согласно теореме 7.18, этот
ряд сходится к f(x) почти всюду на [0,1]. Но, учитывая
представление (7.28) функций системы Радемахера через функции
системы Хаара, для всех точек х Е [0,1], в которых сходится
оо 2т (к) (к)
РЯД J2 J2 4xmW, т.е. почти всюду на [0,1], имеем
fe
m=lk=l m=l v k=l ra=l
oo
Следовательно, ряд по системе Радемахера ^2 стгт{х) также
m=l
сходится почти всюду на отрезке [0,1]. ►
Сходимость ряда £ °т из квадратов коэффициентов ЯВЛЯ-
ется критерием сходимости ряда по системе Радемахера почти
всюду на [0,1], т.е. при нарушении этого критерия ряд по
системе Радемахера уже не будет почти всюду сходящимся. Более
того, в отличие от рядов по системе Хаара, для рядов по
системе Радемахера верно следующее утверждение.
оо
Теорема 7.21*. Если числовой ряд ^2 °т расходится,
оо т=\
то ряд 52 Cra^mfe) по системе Радемахера расходится почти
771=1
всюду на отрезке [0,1]. #
С помощью функций системы Радемахера можно построить
еще одну ортонормированную систему в 1*2 [0,1]> о которой шла
речь в начале параграфа.
* Доказательство см., например: Алексич Г.

7.10. Системы Радемахера и Уолша 593
Положим
wo(x) = l, xe [0,1]. (7.29)
Заметим, что всякое натуральное число п ^ 1 может быть
единственным способом разложено по возрастающим степеням
числа 2:
п = 21/1+21/2 + ... + 2^, (7.30)
где 0 ^ i/i < v2 < ... < vp. Например, 1=2°, 2 = 21, 3 = 2°+21,
4 = 22, 5 = 2°+22ит.д.
Для номера п^1 с разложением (7.30) положим
(z) ...tvp+i(z), xe [0,1], (7.31)
где r^+i(ж), i = 1, p, — функции системы Радемахера. Систему
{iun(z)}£L0 Функций, определенных формулами (7.29) и (7.31),
называют системой Уолша. Она впервые была введена
Дж. Уолшем в 1923 г.
Докажем, что функции системы Уолша в гильбертовом
пространстве 1*2 [0,1] попарно ортогональны. Для различных
номеров пи/, имеющих разложения п = 2"1 + 2172 + +2^,
где 0 ^ i/i < i/2 < < ^Р, и / = 27*1 + 2*2 + ... + 2^, где 0 < щ <
< 7/2 < ... < 7/9, находим
1
= / wn(x)wi(x)dx =
о
о
Преобразуем подынтегральное выражение. Сначала из
произведения
вычеркнем (удалим) все пары функций с одинаковыми
номерами. Такое вычеркивание не изменит интеграла, поскольку

594 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2 [а, Ъ]
квадрат любой функции Радемахера равен единице почти
всюду на [0,1]. Оставшиеся функции в произведении переставим
таким образом, чтобы их номера возрастали. В итоге получим
= rh(x)rJ2(x)...rjk(x),
где 1 ^ ji < J2 < • • • < j/fej и равенство выполняется почти всюду
на отрезке [0,1].
В соответствии с определением функций системы
Радемахера произведение функций Радемахера с меньшими номерами
rji(x)rj2(x)'"rjk-i(x) является кусочно постоянной функцией
со значениями А =<Я. или А = — 1, каждый ее интервал
постоянства Е{ = (а,-, Ь{) разбивается функцией rjk(x) с большим
номером на четное число интервалов равной длины, на которых
функция rjk(x) попеременно принимает значения +1 и —1.
Поэтому для любого интервала Е{ = (а*, Ь{) постоянства функции
Гп (*) rh (x) • • • ri*-i (x) имеем
Просуммировав эти равенства по всем интервалам постоянства
Ei = (a», б»), получим
l
Jrjl(x)rj2(x)...rjk(x)dx =
Ji (х)Тп(х)'"rJk-i (x))rjk (x)dx = О-
(О i
Следовательно, для всех п
1 1
= / wn(x)wi(x)dx= I rh(x)rJ2{x)...rjk{x)dx = 0.

7.10. Системы Радемахера и Уолша 595
Поскольку квадрат любой функции Радемахера равен
единице почти всюду на [0,1], то
почти всюду на [0,1]. Значит, для всех п = 0,1, 2,...
IKII =
\
X
Jwl(x)dx = l.
Итак, система Уолша {wn(x)}^LQ является ортонормиро-
ванной системой функций в 1*2 [0,1]- Как нетрудно заметить,
система Радемахера является подмножеством и
подпоследовательностью системы Уолша, а именно
rm+i(x) = w2m (z), х е [О,1], m = 0,1, 2,...
Однако, в отличие от системы Радемахера, система Уолша
полна.
Теорема 7.22. Система функций Уолша является
счетным ортонормированным базисом в гильбертовом
пространстве L2[0,l].
<4 Доказательство базисности системы Уолша аналогично
доказательству базисности системы Хаара (см. теорему 7.16).
Во-первых, из определения функций Уолша следует, что
все функции Уолша wn(x) с номерами 0 ^ п < 2т постоянны
в каждом из интервалов
:-1 к
Поэтому все эти функции wn(x) с номерами 0 ^ п < 2т
принадлежат подпространству Dm С Ьг[0,1] (см. доказательство
теоремы 7.16) функций, постоянных в каждом из интервалов

596 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2[a,Ъ]
((к - 1)/2т, к/2т), 1 ^ к ^ 2т. Подпространство Dm имеет
размерность 2т, и функции wn(x), 0 ^ п < 2т, как раз составляют
ортонормированный базис в подпространстве Dm.
Во-вторых, учитывая, что множество всех непрерывных
функций является всюду плотным в Ьг[0,1], для любого е > 0 в
е-окрестности всякой функции (р(х) Е L<i [0,1] можно найти
непрерывную функцию д(х), а в е-окрестности функции д(х) —
функцию f(x) из Dm (см. доказательство теоремы 7.16),
являющуюся многочленом по системе Уолша, т.е.
2m-l
f(X)=
Функция f(x) принадлежит линейной оболочке системы Уолша.
Это доказывает замкнутость системы Уолша в гильбертовом
пространстве L2[0,l]. И, наконец, поскольку система Уолша
ортонормирована, то, согласно теореме 6.12, она является
счетным базисом в L2[0,l]. ►
Итак, система Уолша, как и система Хаара, является
счетным базисом в гильбертовом пространстве L2[0,l]. Однако
свойства сходимости рядов Фурье по системе Уолша не так
хороши, как соответствующие свойства рядов по системе Хаара.
Теорема 7.23*. Система Уолша не является базисом в
банаховом пространстве Li[0,l]. #
Кроме того, существуют, например, непрерывные функции,
ряд Фурье которых по системе Уолша расходится в некоторой
точке отрезка [0,1], чего не может быть в случае рядов Фурье
по системе Хаара (см. теорему 7.19). Существуют также
суммируемые на отрезке [0,1] функции, ряд Фурье которых по
системе Уолша всюду на отрезке [0,1] расходится (сравните с
теоремой 7.18). Однако для рядов Фурье по системе Уолша
справедлива следующая теорема.
* Доказательства этой и следующей теорем см.: Кашин Б. С, Саакян А. А.

Вопросы и задачи 597
Теорема 7.24. Для любой функции f(x) G £2 [0,1] ее ряд
Фурье по системе Уолша сходится к самой функции f(x) почти
всюду на [0,1]. #
Как видим, свойства системы Уолша во многом аналогичны
свойствам тригонометрической системы.
Вопросы и задачи
7.1. Докажите, что банахово пространство Iq[0,1] не
является евклидовым, т.е. в Zq[0,1] не существует скалярного
умножения, индуцирующего норму этого банахова пространства.
7.2. Докажите, что для любых функций f(x) и д(х) из
гильбертова пространства />2[а,Ь] выполняется неравенство
л
\
7.3. Докажите, что для любой функции f(x) Е L<i[a, b]
выполняется неравенство
где || • ||li и || • ||l2 — нормы в банаховых пространствах Li[a,6]
и L2[a,6].
7.4. Докажите, что если последовательность {Д(х)}
функций банахова пространства Li[a,b] сходится в среднем к
суммируемой на отрезке [а, 6] функции /(я), то она сходится к f(x) и
по мере Лебега, т.е.
Ve>0: limm{ze[a,6]: \fk(x) - f(x)\ > е} = 0,
где m — мера Лебега.

598 7. РЯДЫ ПО ОРТОГОНАЛЬНЫМ СИСТЕМАМ В L2 [а, Ь]
7.5. Докажите, что если последовательность {Д(х)}
функций банахова пространства 1*2 [а, 6] сходится к функции }(х) в
среднем квадратичном, то она сходится к }{х) и в среднем.
7.6. Приведите пример функции, принадлежащей Li[0,1], но
не принадлежащей 1*2 [0, !]•
7.7. Докажите, что если последовательность {Д(я)}
функций банахова пространства L2[a,b] сходится равномерно на
отрезке [а, 6], то она сходится и в среднем квадратичном.
7.8. Приведите пример последовательности {Д(х)}
функций из Li[0,1], сходящейся к некоторой функции f(x) G Iq[0,1]
в среднем, но не сходящейся к f(x) почти всюду на отрезке
[0,1].
7.9. Приведите пример последовательности {//к(я)}
функций из Li[0,l], сходящейся к некоторой функции f(x) Е 1а [0,1]
почти всюду на [0,1], но не сходящейся к f(x) в среднем.
7.10. Докажите, что функция f(x) = \j\fx не является
пределом в среднем квадратичном на отрезке [0,1] никакой
последовательности непрерывных функций.
7.11. Докажите, что последовательность функций /п(я) =
= п2хе~пх, х Е [0,1], сходится к функции f(x) = 0 в каждой
точке отрезка [0,1], но не сходится к ней в гильбертовом
пространстве L2[0,l].
7.12. Найдите угол между элементами x(t) = sint и y(t) =t
гильбертова пространства 1/2[0,тг].
7.13. Докажите, что множество многочленов p(t), для
которых р(1) = 0, является выпуклым всюду плотным множеством
в гильбертовом пространстве Ьг[0,1].
7.14. Осуществите ортогонализацию системы элементов
xo(t) = 1, x\(t) = t, X2(t) = t2, xs(t) = t3 гильбертова
пространства 1г2[—1,1].

Вопросы и задачи 599
7.15. Докажите, что система функций 1, cost, cos2t, ...,
cosnt, образует ортогональный базис в L2[0,tt], а в L<i\—тг,тг]
является ортогональной системой, но не базисом.
7.16. Докажите, что система функций
[2 [2 [2
\1 — sint, \ — sin2t, \ — sinnt,
V тг V тг V я*
образует ортонормированный базис в 1г2[0,тг], а в Ьг[—тг,тг]
является ортогональной системой, но не базисом.
7.17. Пусть /п и gn — коэффициенты Фурье функций f(x)
и д(х) гильбертова пространства L2[a,b] по некоторой полной
ортонормированной системе в L2[a,b]. Докажите равенство
о
!■
00
п=\
7.18. В гильбертовом пространстве Ьг[—1,1] разложите
функцию f(x) = \x\ в ряд Фурье по системе многочленов
Лежандра.
7.19. Докажите, что многочлены Лежандра Рк(х)
удовлетворяют дифференциальному уравнению
{1-х2)РЦ(х) - 2хР^(х) + к(к + 1)Рк(х) = 0.
7.20. Докажите, что многочлены Чебышева Тп(х)
удовлетворяют дифференциальному уравнению
(1 - х2)Т£(х) - хЩх) + п2Тп(х) = 0.
7.21. В гильбертовом пространстве Z^O, 1] разложите
функцию f(x) = х в ряд Фурье по системе Хаара.

СПИСОК РЕКОМЕНДУЕМОЙ
ЛИТЕРАТУРЫ
Учебники и учебные пособил
Воробьев Н.Н. Теория рядов: Учеб. пособие для втузов. М.: Наука,
1986. 408 с.
By лих Б.З. Краткий курс теории функций вещественной переменной:
Учеб. пособие для вузов. М.: Наука, 1973. 304 с.
Зорин В.А. Математический анализ: Учеб. для студентов
университетов, обучающихся по специальностям „Математика" и „Механика": В 2 т.
Т. 2. М.: Наука, 1984. 640 с.
Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ:
Продолжение курса / Под ред. А.Н. Тихонова. М.: Изд-во МГУ, 1987.
358 с.
Карташев Л.Я., Рождественский Б.Л. Обыкновенные
дифференциальные уравнения и основы вариационного исчисления: Учеб. пособие для
студентов вузов. М.: Наука, 1986. 272 с.
Колмогоров А.Н., Фомин СВ. Элементы теории функций и
функционального анализа: Учеб. для студентов математических специальностей
университетов. М.: Наука, 1976. 496 с.
Люстерник Л.А., Соболев В.И. Краткий курс функционального
анализа: Учеб. пособие для студентов университетов, обучающихся по
специальности „Математика". М.: Высш. шк., 1982. 271 с.
Люстерник Л.А. Соболев В.И. Элементы функционального анализа.
М.: Наука, 1965. 520 с.
Математический анализ / И. И. Ллшко, А.К. Болрчук, Я. Г. Гай,
А.Ф. Калайда: Учеб. для студентов математических специальностей
университетов: В 3 т. Т. 2. Киев: Вища школа, 1985. 551 с.
Натансон И. П. Теория функций вещественной переменной: Учеб.
пособие для вузов. М.: Наука, 1974. 480 с.
Никольский СМ. Курс математического анализа: Учеб. для вузов: В
2 т. T.I. M.: Наука, 1990. 528 с; Т.2. М.: Наука, 1991. 544 с.
Пугачев В. С. Лекции по функциональному анализу: Учеб. пособие для
студентов втузов: М.: Изд-во МАИ, 1996. 744 с.

601
Садовничий В.А. Теория операторов: Учеб. для студентов,
обучающихся по специальности „Математика". М.: Изд-во МГУ, 1986. 368 с.
Толстое Г.П. Ряды Фурье. М.: Наука, 1980. 382 с.
Треногин В. А. Функциональный анализ: Учеб. пособие для вузов. М.:
Наука, 1993. 440 с.
Уваренков И.М. Маллер М.З. Курс математического анализа: Учеб.
пособие для физ.-мат. фак. пединститутов: В 2 т. Т. 2. М.: Просвещение,
1976. 479 с.
Фихтпенгольц Г.М. Основы математического анализа: В 2 т. Т. 2. М.:
Наука, 1968. 464 с.
Монографии
Алексин Г. Проблемы сходимости ортогональных рядов / Пер. с англ.
М.: Изд-во иностр. лит., 1963. 360 с.
Бари Н.К. Тригонометрические ряды. М.: Физматгиз, 1961. 936 с.
Дей М.М. Нормированные линейные пространства / Пер. с англ. М.:
Изд-во иностр. лит., 1961. 232 с.
Зигмунд А. Тригонометрические ряды / Пер. с англ. В 2 т. Т. 1. М.:
Мир, 1965. 611 с.
Канторович Л. В., А кило в Г.П. Функциональный анализ. М.: Наука,
1977. 744 с.
Качмаж С, Штейнгауз Г. Теория ортогональных рядов. М.:
Физматгиз, 1958. 507 с.
Кашин Б.С, Саакян А.А. Ортогональные ряды. М.: Наука, 1984. 496 с.
Рисе Ф., Секефалъви-Надь Б. Лекции по функциональному анализу
/ Пер. с франц. М.: Мир, 1979. 587 с.
Суетин П.К. Классические ортогональные многочлены. М.: Наука,
1976. 328 с.
Эдварде Р. Ряды Фурье в современном изложении / Пер. с англ. В 2 т.
T.I. M.: Мир, 1985. 264 с; Т. 2. М.: Мир, 1985. 400 с.
Справочные издания
Александрова Н.В. Математические термины: Справочник. М.: Высш.
шк, 1978. 190 с.
Бронштейн И.Н., Семендлев К.А. Справочник по математике для
инженеров и учащихся втузов. М.: Наука, 1986. 544 с.

602 СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Градштейн И. С, Рыжик И.М. Таблицы интегралов, сумм, рядов и
произведении. М.: Наука, 1971. 1108 с.
Дороговцев А.Я. Математический анализ: Справочное пособие для
преподавателей математики, инженерно-технических работников и
студентов. Киев: Вища школа, 1985. 528 с.
Математический энциклопедический словарь / Гл. ред. Ю.В. Прохоров.
М.: Сов. энцикл., 1988. 848 с.
Задачники
Виноградова И.А. Олехник С.Н., Садовничий В.А. Математический
анализ в задачах и упражнениях (числовые и функциональные ряды). М.:
Факториал, 1996. 477 с.
Данко П.Е., Попов Л.Г., Кожевникова Т.Я. Высшая математика в
упражнениях и задачах: В 2 т. Т. 2. М.: Высш. шк., 1986. 415 с.
Демидович Б.П. Сборник задач и упражнений по математическому
анализу. М.: Наука, 1977. 528 с.
Дороговцев А.Я. Математический анализ: Сборник задач. Киев: Вища
школа, 1987. 408 с.
Задачи и упражнения по математическому анализу для втузов / Под
ред. Б.П. Демидовича. М.: Наука, 1970. 472 с.
Избранные задачи по вещественному анализу / Б.М. Макаров, М.Г. Го-
Лузина, А.А. Лодкин, А.Н. Подкорытов. М.: Наука, 1992. 432 с.
Кириллов А.А. Гвишиани А.Д. Теоремы и задачи функционального
анализа. М.: Наука, 1988. 398 с.
Сборник задач по математике для втузов. Ч. 2. Специальные разделы
математического анализа: Учеб. пособие для втузов / Под ред. А.В.
Ефимова, Б.П. Демидовича: М.: Наука, 1986. 368 с.
Сборник задач по математическому анализу. Интегралы. Ряды / Под
ред. Л.Д. Кудрявцева. М.: Наука, 1986. 528 с.
Сборник задач по математическому анализу. Функции нескольких
переменных / Под ред. Л.Д. Кудрявцева. М.: Наука, 1995. 496 с.
Треногий В. А., Писаревский Б.М., Соболева Т. С. Задачи и упражнения
по функциональному анализу. М.: Наука, 1984. 256 с.
Шмелев П.А. Теория рядов в задачах и упражнениях. М.: Высш. шк.,
1983. 176 с.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аддитивность меры 531
- счетная 531
Аксиомы нормы IV, 424
Амплитуда колебания 249
Базис ортогональный 500
- ортонормированный IV , 500
- сметный 454
Бином Ньютона 1-86
Вес 571
Гармоника 248
Диаметр разбиения VI, 535
Дифференцирование почленное
функционального ряда 156
Дополнение ортогональное IV, ±91
Замыкание множества 443
Значение главное несобственного
интеграла VI, 383
Изоморфизм естественный 518,
518
- пространств гильбертовых 514
- линейных IV, 513
Интеграл Дирихле VI, 557
- Лапласа 403
- Лебега 535, 538
- несобственный от
комплекснозначной функции 381
сходящийся 381
абсолютно 382
Интеграл несобственный
сходящийся в смысле главного
значения 383
- определенный от комплексно-
эначной функции 380
- Римана VI
- Фурье 350
- в комплексной форме 387
- Эйлера — Пуассона VI, 367
Интегрирование функционального
ряда почленное 154
Интервал сходимости 171
Интерполяция II
Инъекция 1-74
Квадрат скалярный IV
Колебания гармонические 248
Композиция функций 1-76
Координаты вектора IV
- элемента банахова пространства
в базисе 454
Косинус-преобразование Фурье 399
Коэффициенты степенного ряда 157
- Фурье 244, 496
- дискретные 324
Кратность нуля аналитической
функции X, 216
Критерий Коши равномерной
сходимости функционального
ряда 146
-- сходимости ряда в банаховом
пространстве 450
функционального 121
числового 40

604
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Критерий суммируемости функции
541
Круг сходимости 162
Лемма Римана 264
- - для несобственных интегралов
351
Мажоранта числовая 137
Матрица дискретного
преобразования Фурье обратного 327
прямого 326
Мера 530
- внешняя 525
- внутренняя 525
- Лебега (лебегова) 530
Метрика 1-177
- индуцированная нормой 425
Многообразие линейное 440
Многочлен Фурье 496
Многочлены Лежандра 564
- Чебышева II, 571
Множество всюду плотное 444
- выпуклое 487
- замкнутое 1-186, 427
- измеримое 530
- - по Лебегу 530
- ограниченное 1-183, 427
Монотонность меры 527
Непрерывность меры 532
Неравенство Бесселя 246, 499
- Гельдера для конечных сумм 474
рядов 475
- Коши — Буняковского IV
- Минковского для конечных сумм
476
рядов 431, 477
Неравенство треугольника IV, 424
Норма IV, 424
- евклидова IV, 241
- унитарная 428
Нуль аналитической функции X,
216
Область значений 1-70
- определения 1-70
-- функциональной
последовательности 115
- сходимости функционального
ряда 118
-- функциональной
последовательности 116
Остаток ряда функционального 120
- числового 34
Отображение 1-70
- биективное 1-74
- непрерывное на нормированном
пространстве 427
- (функция) непрерывное в точке
1-191, 421
Отрезок 1-47, 487
Подпространство нормированного
пространства 441
Полином тригонометрический 251
-- интерполяционный 322
Полу аддитивность внешней меры
528
- меры счетная 524
Порядок тригонометрического
полинома 251
Последовательность множеств
монотонно невозрастающая 532
неубывающая 531
- сходящаяся в нормированном
пространстве 426
- по норме 426

605
Последовательность
фундаментальная 1-232
- функций 115
- функциональная 115
-- расходящаяся в точке 116
-- сходящаяся в точке 116
на множестве 116
неравномерно 130
поточечно 116
равномерно 129
- элементов множества 1-71, 115
Предел комплексноэначной
функции 379
- последовательности, сходящейся
по норме 426
- функциональной равномерный
129
Преобразование Абеля 102
- Фурье дискретное 322
быстрое 327
обратное 327
прямое 325
- обратное 393
- прямое 393
Признак Абеля 105
- Абеля — Дирихле 103
- Даламбера 63
- предельный 60
- Дини 339
- Дирихле 269, 280
- Жордана 340
- Коши интегральный 50
-- радикальный 68
предельно й ^6
- Лейбница 80
- равномерной сходимости
функционального ряда
Вейерштрасса 138
необходимый 136
Признак сравнения 44
-- предельный 46
- сходимости ряда необходимый
32, 449
Пример Коши 179
Принцип локализации Римана 268
Проекция ортогональная IV, ^93
Произведение ряда на число 37
- рядов 87
- - в форме Коши 90
Производная комплексноэначной
функции 380
- кусочно непрерывная 270
- левая обобщенная 264
- правая обобщенная 264
Пространства гильбертовы
изоморфные 513
- линейные изоморфные IV, 513
Пространство банахово 435
- гильбертово 482
- евклидово арифметическое IV,
428
- полное 481
- метрическое 1-177
-- полное 1-314, 432
- нормированное IV, 424
- полное 435
- сепарабельное 445
- суммируемых функций 543
- унитарное 323, 482
- функций, суммируемых с
квадратом 545
Процесс ортогонализации Грама —
Шмидта IV
Равенство параллелограмма 485
- Парсеваля 249, 502
Радиус сходимости 162, 171
Разбиение отрезка VI, 535

606
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Разделение переменных VIII
Разложение в степенной ряд в
окрестности точки 178
- стандартное 191
- функции в сумму гармонических
колебаний (гармоник) 249
- по косинусам кратных дуг 303
синусам кратных дуг 303
- элемента банахова пространства
в ряд по базису 454
Расстояние 1-177
- от элемента до множества 486
Расходимость ряда числового 24
Ряд абсолютно сходящийся 452
- биномиальный 190
- гармонический 41
- геометрический 28
- Дирихле 33, 53
- энакоотрицательный 42
- знакопеременный 70
- знакоположительный 42
- знакочередующийся 80
- мажорирующий 137
- Маклорена 177
- по ортонормированной системе
244
- степеням z — zq 157
- с неотрицательными членами 42
- неположительными членами 42
- степенной действительный 170
- комплексный 157
- обобщенный 210
- сходящийся абсолютно 70
- по норме 244, 449
- условно 72
- Тейлора 177
- тригонометрический в
комплексной форме 254
-- общий 253
Ряд функциональный 118
-- расходящийся в точке 118
- сходящийся в точке 118
на множестве 118
абсолютно 121
неравномерно 132
равномерно 132
условно 121
поточечно 118
- Фурье 243, 496
- в комплексной форме 256
- дискретный (конечный) 324
- тригонометрический 247
- числовой действительный 20
- комплексный 20
-- расходящийся 24
-- (ряд) 19
- сходящийся 22
- элементов нормированного
пространства 449
Свертка функций 414
Свойство, выполняющееся почти
всюду 532
Сетка VIII
Синус-преобразование Фурье 399
Система замкнутая 459
- линейно независимая 455
- ортогональная 495
- ортонормированная 242, 495
- замкнутая 249
-- полная 250, 505
- промежутков, накрывающая
множество 525
- Радемахера 589
- тригонометрическая 242
- Уолша 593
- Фабера — Шаудера 465
- Франклина 588

607
Система Хаара 579
Системы эквивалентные 507
Сумма интегральная VI
- - Лебега 535
- ортогональная 494
- прямая IV
- ряда 449
- функционального 120
мастичная 119
- числового 23
частичная 22
- рядов 37
- частичная 244
Суммирование рядов почленное 37
Сходимость в нормированном
пространстве 426
- среднем 544
квадратичном 547
- по норме 426
- ряда числового 23
- функционального ряда
неравномерная 132
поточечная 118
равномерная 132
- функциональной
последовательности
неравномерная 130
поточечная 116
равномерная 129
- числового ряда абсолютная 71
условная 73
Сюръекция 1-73
Теорема Абеля 157
- Вейерштрасса 252, 446
- Дирихле 269
- Карлесона 555
- Коши 87
- Мертенса 90
Теорема обращения преобразования
Фурье 395
— о линейности преобразования
Фурье 404
— непрерывности суммы
равномерно сходящегося ряда
151
— перестановке членов абсолютно
сходящегося ряда 76
— почленном дифференцировании
ряда 155
интегрировании ряда 153
— предельном переходе для
функциональных рядов 149
под знаком несобственного
интеграла 416
-- преобразовании Фурье
производной 408
— равномерной сходимости
тригонометрического ряда 260
— Римана 79
— Рисса — Фишера 519
Точка множества предельная 1-185,
427
Узел сетки VIII
Умножение скалярное IV, 239
Условия Дирихле 269
— на бесконечном промежутке 361
Фаза начальная колебания 249
Формула обращения
косинус-преобразования Фурье
401
-- преобразования Фурье
обратного 396
прямого 395
— синус-преобразования Фурье
401

608
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Формула Родрига 564
- Стирлинга 69
Формулы Фурье 349
- Эйлера X
Функции ортогональные с весом
571
- элементарные 1-131
- основные 1-126
Функция абсолютно интегрируемая
348
- бесконечно дифференцируемая
174
- весовая 571
- действительная 1-71, 115
-- аналитическая 177
- Дирихле VI, 536
- измеримая 533
- интегрируемая по Лебегу 535
Риману VI
- комплексная X, 115
- действительного переменного
378
- комплексного переменного X
- комплекснозначная
интегрируемая на отрезке 380
- кусочно непрерывная 380
- непрерывная в точке 380
- кусочно дифференцируемая 267
- монотонная 269
-- непрерывная 239
-- постоянная 336
- мажорирующая VI
- непрерывная равномерно на
множестве 1-206
- ограниченная на множестве 378
- предельная 116
Функция сеточная 321
- с ограниченным изменением 340
- спектральная 397
- ступенчатая 336, 547
- суммируемая 538
- с квадратом 545
и весом 569
- сходящаяся равномерно на
множестве 414
Центр степенного ряда 157
Частота колебания циклическая
(круговая) 249
Часть действительная
комплексноэначной функции 378
- мнимая комплексноэначной
функции 378
Член остаточный в форме
интегральной 188, 230
Лагранжа II, 182
-- формулы Тейлора II
- ряда 19
- общий 20
-- функционального 118
- функциональной
последовательности 115
Элемент ортогональный
подпространству 491
- функциональной
последовательности 115
Элементы ортогональные 241, 491
Ядро Дирихле 262
а-аддитивность меры 531

ОГЛАВЛЕНИЕ
Предисловие 5
Основные обозначения 11
1. Числовые ряды 19
1.1. Основные определения 19
1.2. Необходимый признак сходимости рядов 31
1.3. Свойства сходящихся рядов 34
1.4. Знакоположительные ряды. Признаки сравнения . . 42
1.5. Интегральный признак сходимости Коши 50
1.6. Признак Даламбера 60
1.7. Радикальный признак Коши 66
1.8. Абсолютная и условная сходимости 70
1.9. Знакочередующиеся ряды 80
1.10. Умножение рядов 85
1.11. Оценки сумм рядов 90
Д. 1.1. Доказательство теоремы Римана об условно
сходящихся рядах 94
Д. 1.2. Признаки сходимости Дирихле и Абеля 102
Вопросы и задачи 108
2. Функциональные ряды 115
2.1. Сходимость функциональных последовательностей и
рядов 115
2.2. Равномерная сходимость функциональных
последовательностей и рядов 127
2.3. Свойства равномерно сходящихся рядов 148
2.4. Комплексные степенные ряды 157
2.5. Действительные степенные ряды 170
2.6. Ряд Тейлора 177
2.7. Разложение элементарных функций в ряд Тейлора . 184
2.8. Применение рядов в приближенных вычислениях . . 199
2.9. Интегрирование обыкновенных дифференциальных
уравнений с помощью рядов 209
Д.2.1. Остаточный член формулы Тейлора в интегральной
форме 230
Вопросы и задачи 232

610 ОГЛАВЛЕНИЕ
3. Ряды Фурье 238
3.1. Ортонормированные системы и ряды Фурье 238
3.2. Комплексная форма записи тригонометрического ряда
Фурье 253
3.3. Ряды Фурье по тригонометрической системе .... 256
3.4. О порядке малости коэффициентов Фурье 270
3.5. Дифференцирование и интегрирование
тригонометрических рядов Фурье 275
3.6. Разложение функций в тригонометрические ряды
Фурье на отрезке [—тг, тг] 278
3.7. Сдвиг отрезка разложения 286
3.8. Разложение функций в тригонометрические ряды
Фурье на отрезке [—Z, I] 290
3.9. Разложение четных и нечетных функций 296
3.10. Разложение функций в ряды Фурье по синусам и по
косинусам 301
3.11. Вычисление сумм числовых рядов с помощью рядов
Фурье 314
3.12. Дискретное преобразование Фурье. Быстрое
преобразование Фурье 319
Д.3.1. Доказательство леммы Римана для определенных
интегралов 336
Д.3.2. О достаточных признаках сходимости ряда Фурье . 339
Вопросы и задачи 343
4. Интеграл Фурье 348
4.1. Определение интеграла Фурье 348
4.2. Представление функций интегралом Фурье 351
4.3. Интеграл Фурье в случае четных и нечетных функций 364
4.4. Комплексная форма интеграла Фурье 378
4.5. Преобразование Фурье 393
4.6. Косинус-преобразование и синус-преобразование
Фурье 399
4.7. Свойства преобразования Фурье 404
Д.4.1. Некоторые свойства несобственных интегралов с
параметрами 414
Вопросы и задачи 421

611
5. Ряды в нормированных пространствах 424
5.1. Нормированные пространства 424
5.2. Банаховы пространства 432
5.3. Подпространства нормированных пространств . . . 437
5.4. Сепарабельные пространства 443
5.5. Сходимость рядов в банаховых пространствах .... 449
5.6. Банаховы пространства со счетным базисом 454
5.7. Счетные базисы в пространстве непрерывных функций 461
Д.5.1. Неравенства Минковского и Гельдера 474
Вопросы и задачи 478
6. Ортонормированные системы в гильбертовых
пространствах 481
6.1. Гильбертовы пространства 481
6.2. Расстояние до подпространства 486
6.3. Ортогональность 491
6.4. Ортонормированные системы и ряды Фурье 494
6.5. Ортонормированные базисы 500
6.6. Ортогонализация и существование ортогонального
базиса 507
6.7. Изоморфность гильбертовых сепарабельных
пространств 513
Вопросы и задачи 520
7. Ряды по ортогональным системам в L2[a,b] 523
7.1. Мера Лебега 524
7.2. Измеримые функции 533
7.3. Интеграл Лебега 534
7.4. Банахово пространство L\ [а, Ь] 543
7.5. Гильбертово пространство Z/2[a,b] 544
7.6. Тригонометрическая система 548
7.7. Многочлены Лежандра 555
7.8. Многочлены Чебышева 569
7.9. Система Хаара 579
7.10. Системы Радемахера и Уолша 589
Вопросы и задачи 597
Список рекомендуемой литературы 600
Предметный указатель 603

Учебное издание
Математика в техническом
Выпуск IX
Власова Елена Александровна
РЯДЫ
Редактор Г. А. Нилова
Художник С. С. Водчиц
Корректор Е.В. Авилова
Оригинал-макет подготовлен в издательстве
МГТУ им. Н.Э. Баумана
под руководством А. Н. Канатников а
Санитарно-эпидемиологическое заключение
Xi 77.99.02.953.Д.005683.09.04 от 13.06.2004 г.
Подписано в печать 20.06.2006. Формат 60x88 1/16.
Печать офсетная. Бумага офсетная.
Усл. печ. л. 38,5. Уч.-изд. л. 38.
Тираж 3000 экз. Заказ № 728.
Издательство МГТУ им. Н.Э. Баумана,
105005, Москва, 2-я Бауманская, 5.
Отпечатано с готовых диапозитивов
Издательской группой «Логос»
на базе ООО «Печатный Дом «Современник»
105318, Москва, Измайловское ш., 4.
445043, г. Тольятти, Южное шоссе, 30.
ISBN 5-7038-2884-8
9|785703||828847

Издательство МГТУ им. Н.Э.Баумана
предлагает серию учебников для студентов
высших технических учебных заведений
«Математика в техническом университете»
21 выпуск
В. Д. Морозова
Введение в анализ (Вып. I)
Е. Е. Иванова
Дифференциальное исчисление функций одного переменного
(Вып. II)
А. Н. Канатников, А. П. Крищенко
Аналитическая геометрия (Вып. III)
А. Н. Канатников, А. П. Крищенко
Линейная алгебра (Вып. IV)
А. Н. Канатников, А. П. Крищенко, В. Н. Четвериков
Дифференциальное исчисление функций многих
переменных (Вып. V)
В. С. Зарубин, Е. Е. Иванова, Г. С. Кувыркин
Интегральное исчисление функций одного
переменного (Вып. VI)
B. Р. Гаврилов, Е. Е. Иванова, В. Д. Морозова
Кратные и криволинейные интегралы.
Элементы теории поля (Вып. VII)
C. А. Агафонов, А. Д. Герман, Т. В. Муратова
Дифференциальные уравнения (Вып. VIII)
Е. А. Власова
Ряды (Вып. IX)
В.Д.Морозова
Теория фунцкций комплексного переменного (Вып. X)

И. К. Волков, А. Н. Канатников
Интегральные преобразования и операционное
исчисление (Вып. XI)
Л. К. Мартинсон, Ю. И. Малов
Дифференциальные уравнения математической
физики (Вып. XII)
Е. А. Власова, В. С. Зарубин, Г. С. Кувыркин
Приближенные методы математической физики (Вып. XIII)
А. В. Аттетков, С. В. Галкин, В. С. Зарубин
Методы оптимизации (Вып. XIV)
В. И. Ванько, Г. С. Кувыркин, О. В. Ермошина
Вариационное исчисление и оптимальное
управление (Вып. XV)
А. В. Печинкин, О. И. Тескин и др.
Теория вероятностей (Вып. XVI)
В. Б. Горяинов, И. В. Павлов, Г. М. Цветкова и др.
Математическая статистика (Вып. XVII)
И. К. Волков, С. М. Зуев, Г. М. Цветкова
Случайные процессы (Вып. XVIII)
А. И. Белоусов, С. Б. Ткачев
Дискретная математика (Вып. XIX)
И. К. Волков, Е. А. Загоруйко
Исследование операций (Вып. XX)
В. С. Зарубин
Математическое моделирование в технике (Вып. XXI)
Адрес: 105005, Москва, 2-я Бауманская ул, д. 5
Тел: (495)263-6798 Факс: (495)261-4597
E-mail: press@bmstu.ru Веб-сайт: http://www.press.bmstu.ru