А. В. Паншина, В. М. Чуркин
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
В РЕШЕНИЯХ ЗАДАЧ
ИЗ СБОРНИКА
И. В. МЕЩЕРСКОГО
Аналитическая
механика
URSS
МОСКВА

ББК 22.21
Паншина Алла Викторовна,
Чуркин Валерий Михайлович
Теоретическая механика в решениях задач из сборника И. В. Мещерского:
Аналитическая механика. — М.: Книжный дом «ЛИБРОКОМ», 2012. — 200 с.
Пособие содержит решения 96 задач из главы XI «Аналитическая механика»
книги И. В. Мещерского «Задачи по теоретической механике» и предназначено
для самостоятельной работы над курсом теоретической механики. Подробное
изложение решения задач предваряют краткие сведения из теории, которые можно
использовать в качестве дополнительного справочного материала.
Книга может быть полезна преподавателям и студентам университетов
и технических вузов, а также всем, кто изучает теоретическую механику.
Издательство «Книжный дом "ЛИБРОКОМ"».
117335, Москва, Нахимовский пр-т, 56.
Формат 60x90/16. Печ. л. 12,5. Зак. № ЖО-49.
Отпечатано в ООО «ЛЕНАНД».
117312, Москва, пр-т Шестидесятилетия Октября, 11А, стр. 11
ISBN 978-5-397-02458-7
© Книжный дом «ЛИБРОКОМ», 2011
НАУЧНАЯ И УЧЕБНАЯ ЛИТЕРАТУРА
URSS
E-mail: URSS@URSS.ru
Каталог изданий в Интернете:
http://URSS.ru
Тел./факс (многоканальный):
+ 7 (499) 724-25-45
5472 Ю 64346
Все права защищены. Никакая часть настоящей книги не может быть воспроизведена или
передана в какой бы то ни было форме и какими бы то ни было средствами, будь то
электронные или механические, включая фотокопирование и запись на магнитный носитель,
а также размещение в Интернете, если на то нет письменного разрешения владельца.

Содержание
Предисловие
Введение
8.1 Задачи на принцип возможных перемещений
8.2 Задачи на общее уравнение динамики
8.3 Задачи на уравнения Лагранжа 2-го рода
8.4 Задачи на интегралы движения,
канонические уравнения Гамильтона,
уравнение Якоби—Гамильтона
Глава 1. Принцип возможных перемещений (§46, [1])
Глава 2. Общее уравнение динамики (§47, [1])
Глава 3. Уравнения Лагранжа 2-го рода (§48, [1])
Глава 4. Интегралы движения,
канонические уравнения Гамильтона,
уравнение Якоби—Гамильтона (§49, [1])
Литература

Предисловие
Настоящее пособие предназначено для самостоятельной работы над
курсом теоретической механики. Пособие содержит решения 96 задач
главы XI «Аналитическая механика» «Сборника задач по теоретической
механике» И. В. Мещерского.
Материал пособия разбит на пять основных разделов: «Введение»,
«Принцип возможных перемещений», «Общее уравнение динамики»,
«Уравнения Лагранжа 2-го рода» и «Интегралы движения, канонические
уравнения Гамильтона, уравнения Якоби—Гамильтона». В разделе «Введение»
приводятся краткие сведения из теории, которые можно использовать
в качестве дополнительного справочного материала при изучении
решений представленных в пособии задач.
В главах 1 и 2 нумерация решений повторяет нумерацию задач в
сборнике [1]. Порядок следования задач в главах 3 и 4 отличается от
расположения задач в «Сборнике задач» И. В. Мещерского. Задачи
имеют двойную нумерацию: первое число означает номер задачи данного
пособия, число в скобках — номер задачи из «Сборника задач» И. В.
Мещерского любого издания, начиная с 36-го (1986 г.). Перед главой 3
приводится таблица, позволяющая по номеру задачи из «Сборника задач»
И. В. Мещерского быстро находить ее решение в данном пособии.
Решение каждой задачи пособия составлено таким образом, чтобы
можно было его изучать, не обращаясь к решениям предыдущих задач
подобного типа.
Отметим, что некоторые условия задач и ответы к ним в [1] не
являются достаточно полными. В этих случаях авторы позволили себе сделать
соответствующие замечания и дополнения. Кроме того, в части задач
ответы, полученные авторами, не совпадают (или не совсем совпадают)
с ответами сборника [1]. Это связано либо с точностью вычислений,
либо с использованием других (более современных) обозначений, либо
с иными обстоятельствами, ответственность за которые лежит на авторах
настоящего пособия.
Авторы надеются, что пособие будет полезно преподавателям и
студентам университетов, втузов, школьникам старших классов, а также всем
желающим самостоятельно изучить методы решения задач теоретической
механики.

Введение
Термин «аналитическая механика» использован в сборнике И. В.
Мещерского для объединения задач, при решении которых применяется
универсальный аналитический аппарат исследования равновесия и движения
сложных механических систем. Решение задач этого раздела построено
на применении общих принципов механики, уравнений Лафанжа 2-го
рода и основ гамильтоновой механики.
В.1. Задачи на принцип возможных перемещений
Принцип возможных перемещений — это общий принцип
аналитической статики. Согласно этому принципу данное положение
механической системы будет положением равновесия, если в этом положении
сумма работ приложенных к системе активных сил на любом возможном
перемещении равна нулю. Аналитически принцип описывается
равенством, которое называют общим уравнением аналитической статики:
y*Tf(Vk,6rk) = 0. (В.1)
к
Здесь Ffc — активная сила, приложенная к fc-й точке системы, &**> —
возможное перемещение fc-й точки системы. (Векторы будут обозначаться
не стрелкой сверху, как в [7,8], а жирным шрифтом, как в [9].)
Возможным перемещением fc-й точки системы называется
воображаемое бесконечно малое перемещение, которое можно сообщить fc-й точке
в данный момент времени, не нарушая наложенных на систему связей.
При решении задач на принцип возможных перемещений
сначала устанавливают число степеней свободы рассматриваемой системы.
Затем выбирают соответствующее число независимых координат,
определяющих данное положение системы, и сообщают системе возможные
перемещения, при которых эти координаты получают приращения. Для
этих перемещений составляются уравнения работ (В.1), дополняемые
равенствами, которые связывают зависимые и независимые координаты
системы. Из полученных уравнений формируются условия равновесия
системы, к которой приложены заданные силы, или определяются силы,
под действием которых система находится в равновесии.
Принцип возможных перемещений формулируется для систем со
стационарными, удерживающими и идеальными связями. Для идеальных

6
Введение
связей на любом возможном перемещении системы сумма работ сил
реакций Rfc равна нулю, т. е. выполняется следующее равенство
к
Если на систему наложены неидеальные связи, то их реакции
включают в число активных сил. В число активных сил включают и реакции
идеальных связей, когда по условию задачи эти реакции подлежат
определению.
В.2. Задачи на общее уравнение динамики
Общее уравнение (аналитической) динамики записывается в виде
^2(¥к+Фк)Ьк = 0, (В.2)
к
где Фк — сила инерции fc-й точки системы
Фк = -ткак,
тк — масса fc-й точки системы, а* — ускорение fc-й точки системы.
Уравнение (В.2) выражает общий принцип аналитической динамики
(принцип Даламбера—Лагранжа), согласно которому при движении
механической системы в любой момент времени сумма работ приложенных
к системе активных сил и сил инерции на любом возможном перемещении
равна нулю. Уравнение справедливо для систем с идеальными связями.
Как и при исследовании равновесия с помощью принципа возможных
перемещений, для решения задач на общее уравнение динамики
необходимо определить число степеней свободы рассматриваемой системы
и выбрать соответствующее число независимых координат,
определяющих положение системы в данный момент времени. Затем сообщаются
системе возможные перемещения, при которых эти координаты получают
приращения. На этих перемещениях составляются уравнения работ (В.2),
дополняемые равенствами, связывающими зависимые и независимые
координаты системы.
Полученные таким образом уравнения в зависимости от постановки
задачи используются либо для определения ускорений звеньев,
составляющих рассматриваемую систему, либо в качестве дифференциальных
уравнений, описывающих движение системы.
Общее уравнение динамики применяют и для нахождения реакций
наложенных на систему связей. В этом случае искомые реакции
включаются в число активных сил.

Введение
7
В.З. Задачи на уравнения Лагранжа 2-го рода
Уравнения Лагранжа 2-го рода — это общее уравнение динамики,
записанное в обобщенных координатах. Для голономных систем уравнения
Лагранжа записываются в виде
d(dT\ дТ „ ,. t ч /п„
где Г — кинетическая энергия системы; ф — г-я обобщенная координата
системы, Qi — г-я обобщенная сила системы; s — число степеней свободы
системы.
Согласно уравнениям Лагранжа, движение механической системы,
имеющей s степеней свободы, описывается системой из s
обыкновенных дифференциальных уравнений 2-го порядка. Для составления этих
уравнений необходимо сначала определить число s, а затем установить,
какие из координат системы принимаются за обобщенные координаты.
Далее находятся кинетическая энергия Г, ее производные в соответствии
с равенствами (В.З) и обобщенные силы Q*.
Механическая система в большинстве рассматриваемых задач
представляется плоским или пространственным механизмом. Кинетическая
энергия такого механизма определяется суммой
з
где Tj — кинетическая энергия j-ro звена механизма, который движется
и имеет массу.
Звеном механизма может служить материальная точка или твердое
тело. В последнем случае выражение для 7} записывается в зависимости
от того, к какому виду движения твердого тела относится движение
данного звена механизма. Так, например,
• если звено массы га,- движется поступательно со скоростью Vj, то
Tj = 2mJV?>
• если звено вращается вокруг неподвижной оси с угловой
скоростью Vj, то
Ч = \j&
где Jj — момент инерции звена относительно оси вращения;
• если движение звена массы щ плоское, то

8
Введение
где Vj — скорость центра масс звена, Jj — момент инерции звена
относительно оси, проходящей через его центр масс, u)j — угловая
скорость звена;
• если звено вращается вокруг неподвижной точки, совпадающей с его
центром масс, то
Tj=-Jxuj2x + -Jyu2y+-Jzui
где Jx,Jy,Jz — моменты инерции звена относительно главных
центральных осей х, у, z; шх, шу, uz — проекции угловой скорости звена
на оси х, у и z.
Один из наиболее распространенных способов подсчета обобщенных
сил Qi состоит в следующем. Системе сообщают такое возможное
перемещение, при котором приращение получает только координата ф, т.е.
при котором
Sqi Ф О, 8qx=... = Sq^ = 5qi+x = ... = Sqs = 0.
На этом перемещении подсчитывается сумма элементарных работ
действующих на систему сил 2_^ ОД(^), а искомая обобщенная сила
к
находится по формуле
к °*
При движении системы в потенциальном силовом поле удобнее
использовать другую форму уравнений Лагранжа:
fdL\ дЬ л . f
d_(dh
It
(В.4)
Здесь L — функция Лагранжа
L = Т - П,
П — потенциальная энергия системы.
В.4. Задачи на интегралы движения,
канонические уравнения Гамильтона,
уравнение Якоби-Гамильтона
В общем случае функция Лагранжа L является функцией времени t,
всех обобщенных координат $ и всех обобщенных скоростей &
L = L(t,q\,... ,<7в,<7ь ... ,qs).

Введение
9
Однако в конкретной задаче может оказаться, что функция Лагранжа
не зависит явно от времени или каких-либо обобщенных координат. В этих
случаях можно упростить задачу исследования динамики рассматриваемой
системы, записав интегралы движения.
Если функция Лагранжа не зависит явно от времени, то имеет место
обобщенный интеграл энергии, который описывается выражением
ASL. г
> —Ф - L = const.
Если функция Лагранжа не зависит явно от п обобщенных
координат, называемых циклическими, то для рассматриваемой системы можно
записать п циклических интегралов вида
—-=ct (Z = 1,... ,п).
oqi
При переходе от лагранжевых переменных ф, ф к каноническим
переменным qi,pi уравнения движения системы принимают форму уравнений
Гамильтона
. дН дН , ч , ч
где Н — функция Гамильтона
8
Pi — г-й обобщенный импульс системы
8L
Исследование функции Я, как и в случае с функцией L, позволяет
определить возможность записи интегралов движения — обобщенного
интеграла энергии и циклических интегралов.
Интегрирование системы обыкновенных дифференциальных
уравнений, составленных с помощью уравнений Гамильтона (В.5), можно
свести к нахождению полного интеграла следующего уравнения в частных
производных
9W тт!\ dw dw\ л
■вГ + Ч*;* *;eST в57)=0- (в*6)
называемого уравнением Якоби—Гамильтона. Здесь W —
характеристическая функция.

10
Введение
Согласно теореме Якоби, если W(t; q\,..., qs\ ol\ ,..., as) — полный
интеграл уравнения Якоби—Гамильтона (В.6), содержащий s
произвольных постоянных а\,..., а5, то решение уравнений (В.5) находится из
соотношений
8W dW Л ,.
oqi oai
где Pi — произвольные постоянные.
Таким образом, если найдена функция W, удовлетворяющая
уравнению (В.6), то по теореме Якоби канонические переменные qi и pi
определяются как функции времени и 25 произвольных постоянных

Глава 1
Принцип возможных
перемещений (§46, [1])
Задача 1.1 (46.1). Груз Q поднимается с помощью домкрата,
который приводится в движение рукояткой О А = 0,6 м. К концу рукоятки,
перпендикулярно ей, приложена сила Р = 160 Н. Определить
величину силы тяжести груза Q, если шаг винта домкрата h = 12 мм.
РИС. 1.1.1
Ответ: Q и 50,2 кН.
М^ Решение. Воспользуемся принципом возможных перемещений
(принципом Лагранжа).
Предположим, что система находится в равновесии. Дадим рукоятке
О А возможное угловое перемещение Sip в сторону действия силы Р. Тогда
груз Q получит возможное перемещение вверх
с h-6(p
ds= ——.
27Г
Сумма элементарных работ будет:
Р-ОА-6(р- QSs.
Приравняв ее нулю и выразив £s через 5<р, получим:
P-OA-6<p-Q—6<p = 0.
27Г

12
Глава 1. Принцип возможных перемещений
Так как равенство должно иметь место при любых значениях возможного
перемещения 5<р, то
откуда
Р-ОЛ-0—=0,
27Г
Q = Р—2тг « 50,2 кН.
а
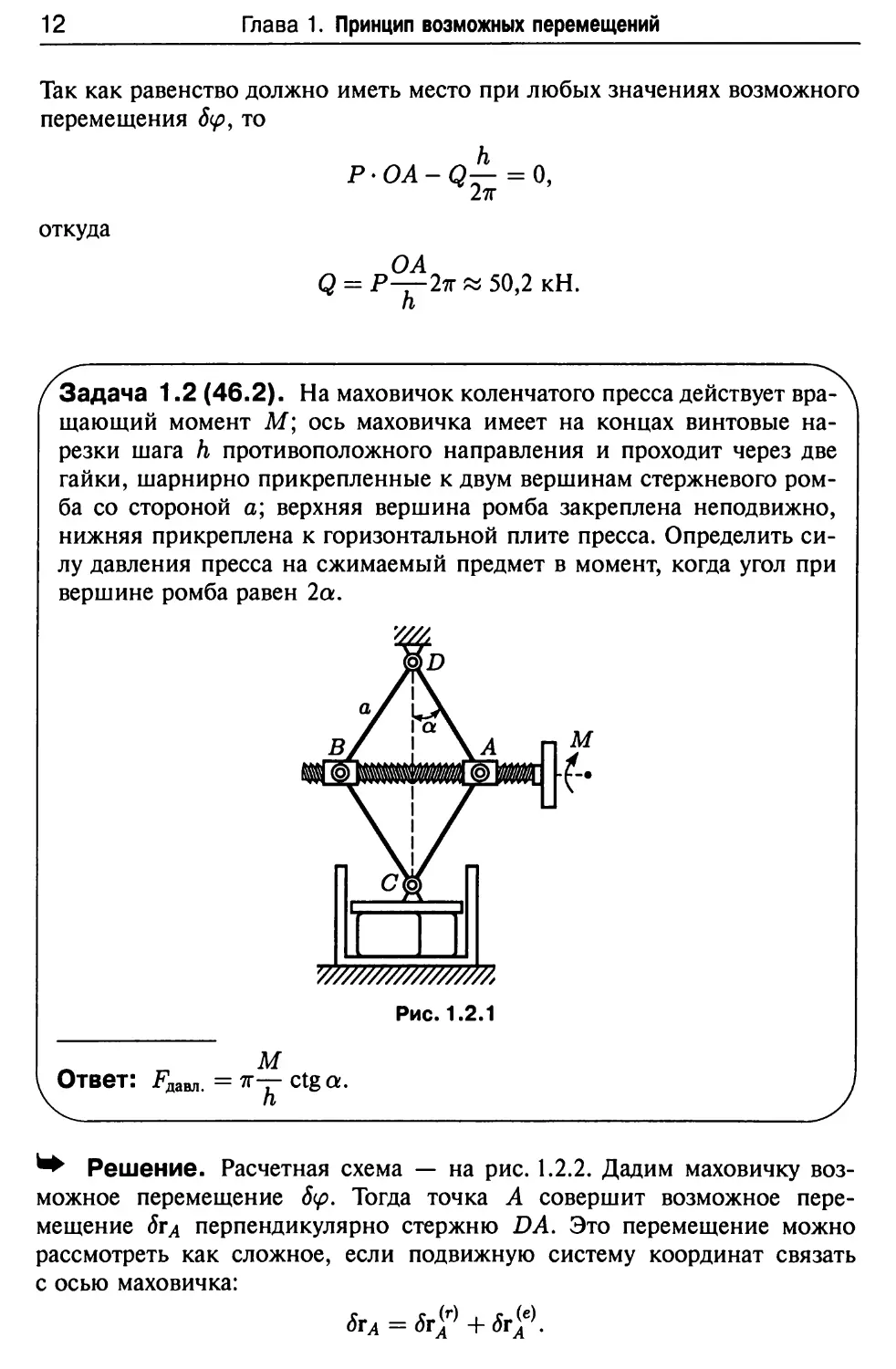
Задача 1.2 (46.2). На маховичок коленчатого пресса действует
вращающий момент М; ось маховичка имеет на концах винтовые
нарезки шага h противоположного направления и проходит через две
гайки, шарнирно прикрепленные к двум вершинам стержневого
ромба со стороной а; верхняя вершина ромба закреплена неподвижно,
нижняя прикреплена к горизонтальной плите пресса. Определить
силу давления пресса на сжимаемый предмет в момент, когда угол при
вершине ромба равен 2а.
Рис. 1.2.1
М
Ответ: ^давл. = 7г— ctg а
■Ф" Решение. Расчетная схема — на рис. 1.2.2. Дадим маховичку
возможное перемещение 5ц>. Тогда точка А совершит возможное
перемещение Sta перпендикулярно стержню DA. Это перемещение можно
рассмотреть как сложное, если подвижную систему координат связать
с осью маховичка:
Stj
=*«+*«

Глава 1. Принцип возможных перемещений
13
6<р м
Относительное возможное перемещение выразим через элементарное
угловое перемещение 5<р:
(r) _ hS(p
а-1:' =
2тг
Поэтому
SrA =
6г{
.М
cos а 27Г cos а
S(p.
Для определения возможного перемещения точки С (пресса)
воспользуемся равенством проекций возможных перемещений точек А и С
на прямую АС (точки А и С принадлежат одному стержню АС):
6га cos (90° - 2а) = 5гс cos а.
Отсюда
бгс = 2 sin а • 6га = 2 sin а 5<р = h Sip.
27г cos а 7г
Составим теперь уравнение равновесия системы в форме принципа
возможных перемещений:

14
Глава 1. Принцип возможных перемещений
MSip - P6rc = 0 => MSip - Р- tg а • Sip = О.
7Г
Так как равенство должно иметь место при любых значениях Sip, то
М - Р- tg а = 0.
7Г
Поэтому сила давления пресса
М
^давл. = -Р = 7Г— Ctg а.
Задача 1.3 (46.3). Определить зависимость между модулями сил Р
и Q в клиновом прессе, если сила Р приложена к концу рукоятки
длины а перпендикулярно оси винта и рукоятки. Шаг винта равен ft.
Угол при вершине клина равен а.
Ответ: Q = Р
2тга
htga'
■* Решение. Зададим возможное угловое перемещение Sip винту в
направлении момента, создаваемого силой Р. Тогда клин получит возможное
перемещение
6r{ = -Sip,
направленное влево. В результате пресс совершит вверх возможное
перемещение <5г2.
Рассмотрим перемещение пресса как сложное: Sr2 = &"2 + 5г2
(рис. 1.3.2). Так как
6г? = 6г\ = —Sip*
то
(е) Л
or2 = or2 tg а = — tg а • Sip.
Z7T

Глава 1. Принцип возможных перемещений
15
Применим теперь принцип возможных
перемещений:
Pa-5y>-Q6r2 =0
Поэтому
Pa-S(f-Q— tga-Sip = 0.
Z7T
Q = P
2тга
htga'
Рис. 1.3.2
Задача 1.4(46.4). Рисунок представляет схему машины для
испытания образцов на растяжение. Определить зависимость между
усилием X в образце К и расстоянием х от груза Р массы М до его
нулевого положения О, если при помощи груза Q машина
уравновешена так, что при нулевом положении груза Р и при отсутствии
усилия в К все рычаги горизонтальны. Даны расстояния l\, 12 и е.
Ответ: X
Mg—.
el2
lj
■* Решение. Расчетная схема — на рис. 1.4.2. Пусть рычаги
незначительно отклонены от горизонтального положения (это предположение
не влияет на окончательный ответ). Дадим рычагу, на котором
расположен груз Р, возможное угловое перемещение Sip. Тогда груз Р совершит
возможное перемещение 5гр = 5ip-(x + ОВ + 12), Q совершит возможное
перемещение
х йгА 6гв
8rQ = — -DQ= —
DQ=l-^DQ,

16
Глава 1. Принцип возможных перемещений
«г.
mJTc
iSU
6(р
0 iBC АЛ
'ШШШ//Ш////Ж
G
'Г
t*JT
Рис. 1.4.2
/&-
6ТГ
\6rQ
образец К совершит возможное поступательное перемещение
SrK = 6rG = —^ • EG = —- • EG = -=-*- • CD .
K G EN EN lx EN
С помощью несложных преобразований можно убедиться, что
EN = CD и EG = NG - NE = (CD + e)-CD = e.
Запишем уравнение равновесия системы с помощью принципа
возможных перемещений:
Р8гР - QSrQ - XSrK = 0.
Подставим сюда возможные перемещения, выраженные через
произвольно заданное угловое возможное перемещение 8у>\
Р5ф + OB +12) - QSip-f- DQ-X- Sip^ e = 0.
(о
Запишем теперь уравнение равновесия системы с помощью принципа
возможных перемещений при нулевом положении груза Р, когда х = 0
Рб<р(ОВ + 12) - QSiff- DQ = 0.
(2)

Глава 1. Принцип возможных перемещений
17
Из уравнений (1) и (2) получим:
Рх + Р(ОВ + l2) -Q-±DQ-X^e = 0,
h
P(OB + h)-QrDQ = Q
Px-X-^e = 0
Х = Р— =Mg—.
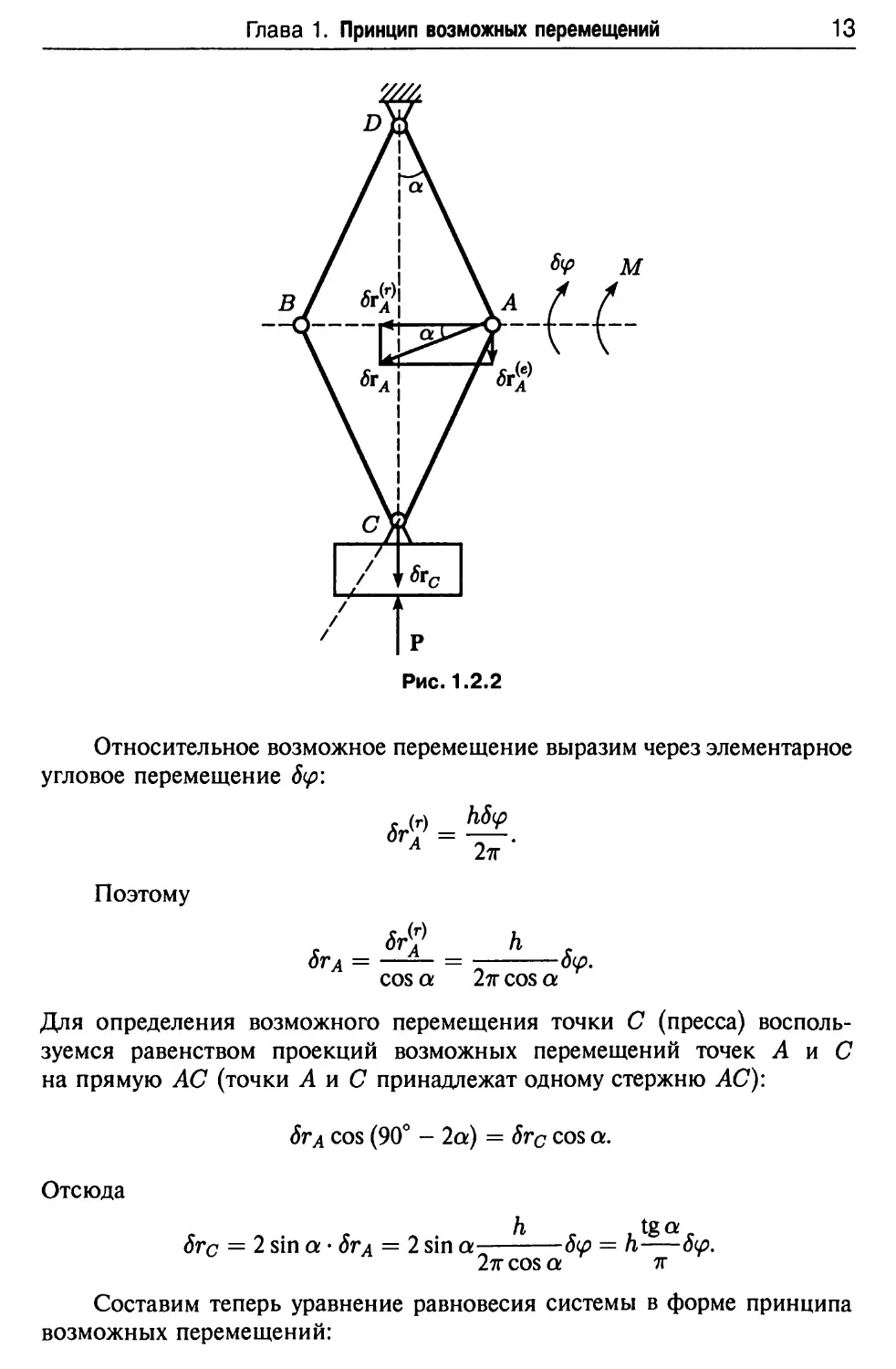
Задача 1.5 (46.5). Грузы КиЬ, соединенные системой рычагов,
изображенных на рис. 1.5.1, находятся в равновесии. Определить зависимость
ВС 1 ON 1 DE 1
между массами грузов, если дано:
i
АС 10' ОМ 3' DF 10'
\\\\\\\\\\\\у
Ц м ' '
Ас в
Г?
S7
О L
Рис. 1.5.1
Ответ: Mh = —MK.
Решение. Расчетная схема — на рис. 1.5.2.
Рис. 1.5.2

18
Глава 1. Принцип возможных перемещений
Дадим рычагу MN возможное угловое перемещение Sip (рис. 1.5.2).
Тогда точки системы получат следующие возможные перемещения:
SrE ОМ • DF
5гм = ОМ • Sip, 5rE = 6rM, SrL = SrF= — -DF = Sip———,
5rN = ON • Sip, SrA = SrN, SrK = 5rB = — -BC = Sip———.
Приравняв нулю сумму элементарных работ активных сил,
приложенных к системе, на заданном произвольном ее возможном перемещении,
получим уравнение равновесия:
Mug • 6rL - MKg • 6rK = 0.
Распишем величины SrL и £r#:
OM-DF c ON-BC c
Mbg———Sip - MKg Ac Sip = 0.
Отсюда получаем зависимость между массами:
Задача 1.6(46.6). Определить модуль силы Q, сжимающей
образец А, в рычажном прессе, изображенном на рис. 1.6.1. Дано: F= 100 Н,
а = 60 см, 6=10 см, с = 60 см, d = 20 см.
тЩ
тжж?жжжм
Рис. 1.6.1
Ответ: Q = 1800 Н.
■*• Решение. На рис. 1.6.2 изобразим силы, работа которых на
возможных перемещениях системы отлична от нуля: приложенная сила F
и реакция со стороны образца A Q'.
Дадим верхнему рычагу возможное угловое перемещение Sip. Тогда
р с с р t с с °~гс , bd
orD = aSip, ore = or в = о • Sip, Sr& = d = —Sip.
с с

Глава 1. Принцип возможных перемещений
19
'//////////////.
Рис. 1.6.2
Из уравнения равновесия FSr^ - Q'Sta = 0 получаем:
,bd
FaSip - Qi—Stp = 0.
с
Отсюда
ас
Q = Q' = F — = 1800 Н.
bd
Задача 1.7(46.7). На платформе в точке F находится груз массы М.
Длина АВ = а, ВС = 6, CD = с; IK = d; длина платформы EG = L.
Определить соотношение между длинами Ь, с, d, I, при котором
масса т гири, уравновешивающей груз, не зависит от положения его
на платформе, и найти массу гири т в этом случае.
■ a i Ь . с |
Ц ►р*—»l< »1
№mD
\т
®L
И* Щ jiK
'7777777777777777777777777777777777777,
Рис. 1.7.1
6+С 1 Ь п.
Ответ: —-— = -, т= - М.
о а а

20
Глава 1. Принцип возможных перемещений
^ Решение. Запишем принцип возможных перемещений для
системы. Для этого зададим рычагу AD угловое возможное перемещение S(p
(рис. 1.7.2). Тогда возможные перемещения точек системы выразятся через
заданное перемещение 5<р следующим образом:
8rm = 5rA = aS(p, SrE = Src = bScp;
5rH = 5rD = (b + c)6ip, 8rG
*-&*■
b + c
d- Sip.
Для определения возможного перемещения точки приложения
силы тяжести груза массы М, а значит точки F, запишем соотношения,
вытекающие из построения на рис. 1.7.2:
SrE _EG + GP
~5^~ GP
=> GP
b + c
SrG
dSy>
SrM = SrF =
8rE — Src
SrG
L =
b + c
bSip — dS(p
(b + c)dL
bl-(b + c)d;
(FG + GP) = 6rG-(\ + ^p)
GP
(b + c)ds
I
(b + c)d
I
<
Щ \+FG:
+ FG-
(b + c)dL
bl-(b + c)d
bl-(b + c)d
)■
IL
6<p.
St,
Al,.---6<p
Ы
Ф
mg
♦*.
д
*,
c.,-
<5rr
'<&^&-XD
SrE*
6tk
(St.f.
6t,
м%
H I
-7777777777777777777777777777777777777777)
Рис. 1.7.2
P

Глава 1. Принцип возможных перемещений
21
Запишем уравнение равновесия системы:
mg • Srm - Mg • 6rM = О
или
mgaS(p - Mg
(b + c)d+pG bl-(b + c)d
I
IL
6<p = 0.
(1)
Чтобы масса m гири, уравновешивающей груз М, не зависела от
положения груза на платформе, следует в уравнении (1) коэффициент при
расстоянии FG приравнять нулю:
U-(b + c)d
IL
= 0.
Отсюда получаем искомое соотношение между заданными длинами:
Ь + с _ I
~b~ = d'
С учетом найденного условия определим из (1) массу т груза:
(Ь + с) d
mgaSip - Mg Sip = 0
(b + c)d b
m = — M = - M.
al a
Задача 1.8 (46.8). К ползуну А механизма эллипсографа
приложена сила Р, направленная вдоль направляющей ползуна к оси
вращения О кривошипа ОС. Какой вращающий момент надо приложить
к кривошипу ОС, для того чтобы механизм был в равновесии в
положении, когда кривошип ОС образует с направляющей ползуна
угол у?? Механизм расположен в горизонтальной плоскости, причем
ОС = АС = СВ = I
Ответ: М = 2Р1 cos ip.

22
Глава 1. Принцип возможных перемещений
■Ф" Решение. Расчетная схема — на рис. 1.8.2.
Так как механизм расположен в горизонтальной плоскости и
подчинен идеальным связям, то в уравнение равновесия, составленное с
помощью принципа возможных перемещений,
войдут лишь сила Р и момент М. Зададим
кривошипу ОС возможное угловое
перемещение S(p. Тогда точка С совершит
возможное перемещение 5гс = ОС Sip = 15<р.
Ползуны А и В переместятся вдоль
своих направляющих. Точка Е (рис. 1.8.2)
есть мгновенный центр вращения звена АВ.
Поэтому можно записать соотношения:
Src СЕ АЕ 2/cosy?
^А = АЁ=>6ГА = 6ГСсё = 1б1Р~Т~ =
= 2lcos<p-8(p.
Выпишем уравнение равновесия:
MSip- Р5га = 0 => М5<р- P2lcos(p-Sep = 0.
Отсюда
М = 2Р1 cos (р.
6<р можно было вь
у а = 21 sin (р => 6уА = 21 cos (р • 6(р, 6га = 6уА = 21 cos ip • 8<р.
Замечание. Связь между 6га и 6<р можно было выписать, используя координатный
способ:
Задача 1.9(46.9). Полиспаст состоит из
неподвижного блока А и из п подвижных блоков. Определить
в случае равновесия отношение массы М
поднимаемого груза к силе Р, приложенной к концу каната,
сходящего с неподвижного блока А.
Рис. 1.9.1
Ответ:
Mg
= 2п.
W Решение. Расчетная схема — на рис. 1.9.2.
Так как связи идеальные и массой блоков пренебрегаем, то принцип
возможных перемещений имеет вид:
Р • 6т + Mg. SrM = 0.
(1)

Глава 1. Принцип возможных перемещений
23
У////////////////////
Ех
КУ[
Чту*
\jy
6т
В\
В,
лВп
Mg
Рис. 1.9.2
1 <5г
Дадим концу каната, к которому приложена сила Р, возможное
перемещение 8т вертикально вниз. В силу нерастяжимости каната точка i?i
(точка схода каната с 1-го подвижного блока) совершит вертикально вверх
возможное перемещение 8rBl = 5г.
Так как канат не проскальзывает вдоль обода блока, то точка Е\
(точка неподвижной части каната) является мгновенным центром
вращения (мгновенным центром скоростей) 1-го подвижного блока. Поэтому
перемещение центра масс С\ этого блока равно
Src{ = -&*£, = -5г.
Перемещение точки В2 (точка схода подвижной части каната с обода 2-го
подвижного блока) в силу нерастяжимости каната равно перемещению

24
Глава 1. Принцип возможных перемещений
точки С\:
6гв2 = SrCl = -5г.
Проделав аналогичные рассуждения для всех п подвижных блоков,
получим выражение для возможного перемещения груза М:
6гм = 5гСп = -5гВп_х = ( - J 5г.
Распишем уравнение (1)
PSr-Mg(-) Sr = 0.
Mg
Отсюда получим искомое отношение: -— = 2П.
Задача 1.10(46.10). В кулисном механизме при качании рычага
ОС вокруг горизонтальной оси О ползун А, перемещаясь вдоль рычага
ОС, приводит в движение стержень АВ, движущийся в вертикальных
направляющих К. Даны размеры: ОС = R, ОК = I. Какую силу Q
надо приложить перпендикулярно кривошипу ОС в точке С для того,
чтобы уравновесить силу Р, направленную вдоль стержня АВ вверх?
Рис. 1.10.1
Ответ: Q =
Р1
R cos2 ^
■* Решение. Расчетная схема — на рис. 1.10.2.
Дадим рычагу ОС из рассматриваемого положения равновесия
угловое возможное перемещение Sip. Тогда точка С совершит перемещение

Глава 1. Принцип возможных перемещений
25
Рис. 1.10.2
8гс = ОС • 8(р = RS(f (см. рис. 1.10.2). Для нахождения возможного
перемещения точки В рассмотрим перемещение точки А (ползуна) как
сложное.
Тогда St а = бтд + Ад (подвижную систему связали с рычагом ОС).
Из векторного треугольника имеем:
6гА = —^~
COSip
Переносное возможное перемещение
8г(?] = ОА-6<р =
COS(p
-Sip.
Поэтому
SrB = 8га = —T-fy-
COS2 if
Распишем уравнение равновесия системы:
I
Р5гв - QSrc = 0
COS2 if
6<p-Q- RScp = 0.
Отсюда
PI
У "* Rcos2(p'

26
Глава 1. Принцип возможных перемещений
Задача 1.11 (46.11). Кулак К массы М\ находится в покое на
гладкой горизонтальной плоскости, поддерживая стержень АВ массы М2,
который расположен в вертикальных направляющих. Система
находится в покое под действием силы F, приложенной к кулаку К
по горизонтали направо. Определить модуль силы F, если боковая
поверхность кулака образует с горизонтом угол а. Найти также
область значений модуля силы F в случае негладкой горизонтальной
плоскости, если коэффициент трения скольжения между основанием
кулака К и горизонтальной плоскостью равен /.
Рис. 1.11.1
Ответ: F = M2g tg а,
M2g tg а - f(M{ + M2)g ^ F < M2g tg a + f(Mx + M2)g.
■► Решение. Расчетная схема — на рис. 1.11.2.
Зададим кулаку К поступательное возможное перемещение 5тк
вправо. Тогда точка А стержня АВ совершит возможное перемещение
8та, равное сумме переносного перемещения 5тд (вместе с кулаком К
^^^^Ж^^^^^^
Mlg
N
Рис. 1.11.2

Глава 1. Принцип возможных перемещений
27
и потому равного 6тк) и относительного бгд (вдоль наклонной
поверхности кулака):
Из параллелограмма, построенного для возможных перемещений точки Л,
получаем:
5гА = 5гд tga = SrK tg а.
Поэтому поступательное возможное перемещение стержня АВ имеет вид:
8гав = йгд = 8гк • tg а.
Рассмотрим теперь два случая:
1. Горизонтальная поверхность — гладкая, т.е. Fw = 0. Запишем
уравнение равновесия с помощью принципа возможных перемещений:
F • Srk + Mig • 6rk + M2g • SrAB = 0 =>
==> FJrjfc - М^5гк tg a = 0.
Отсюда F = M2g tg a.
2. Горизонтальная поверхность — шероховатая, т. е. FTp ф 0. Запишем
уравнение равновесия:
F • <5г* + М, g • Srk + F^ • 6тk + М2 g • ftr^ = 0 =Ф
=Ф Ftfr* - FjpSrk - M2g • (Jr* tg a = 0.
Выразим отсюда силу трения скольжения:
FW = F-M2gtg(x.
Воспользуемся условием отсутствия скольжения IF^I ^ Fnpe}Kt, где
предельное значение силы трения скольжения Fnpejx, = fN.
Нормальная реакция N при покое складывается из сил тяжести
звеньев системы: N = M\g 4- M2g. В результате получаем неравенство
относительно силы F:
\F - M2gtga\ < f(Mx + M2)g.
Раскрываем знак модуля:
-/(Mi + M2)g ^F-Mtftga^ /(M, + M2)g.
Отсюда получаем область значений модуля силы F, обеспечивающую
равновесие при негладкой поверхности:
M2gigot - f(Mx + M2)g < F ^ M2gtga + /(M| + M2)g.

28
Глава 1. Принцип возможных перемещений
Задача 1.12(46.12). Круговой кулак К массы М\ и радиуса R
стоит на негладкой горизонтальной плоскости. Он соприкасается
с концом А стержня АВ массы М2, расположенного в вертикальных
направляющих. Система находится в покое под действием силы F,
приложенной к кулаку по горизонтали направо. При этом AM = h.
Найти область значений модуля силы F, если коэффициент трения
скольжения кулака о горизонтальную плоскость равен /.
Рис. 1.12.1
y/R2-h2 y/R2-h2
Ответ: M2g-f(Ml+M2)g^F^ M7g+f(Ml+M2)g.
■► Решение. Расчетная схема — на рис. 1.12.2.
Зададим возможное поступательное перемещение кулаку К &•#.
Точка А стержня АВ совершит возможное перемещение
бгА = бг%) + бт{;\
М
где переносная составляющая перемещения 5т^ = 8тк-
Поступательное возможное перемещение стержня АВ
г г г (е) г г V^2 " h2
отав = orА = 5rV tg а = 6rk tg а = 8rk .
п
Запишем принцип возможных перемещений для системы:
F • 6тк + Mig • 5тк + M2g • 6тАВ + F^ • 5тк = 0 =*
VR2 - h2
FSrk - M2g г Srk - FrpSrk = 0.
Сила трения скольжения

Глава 1. Принцип возможных перемещений
29
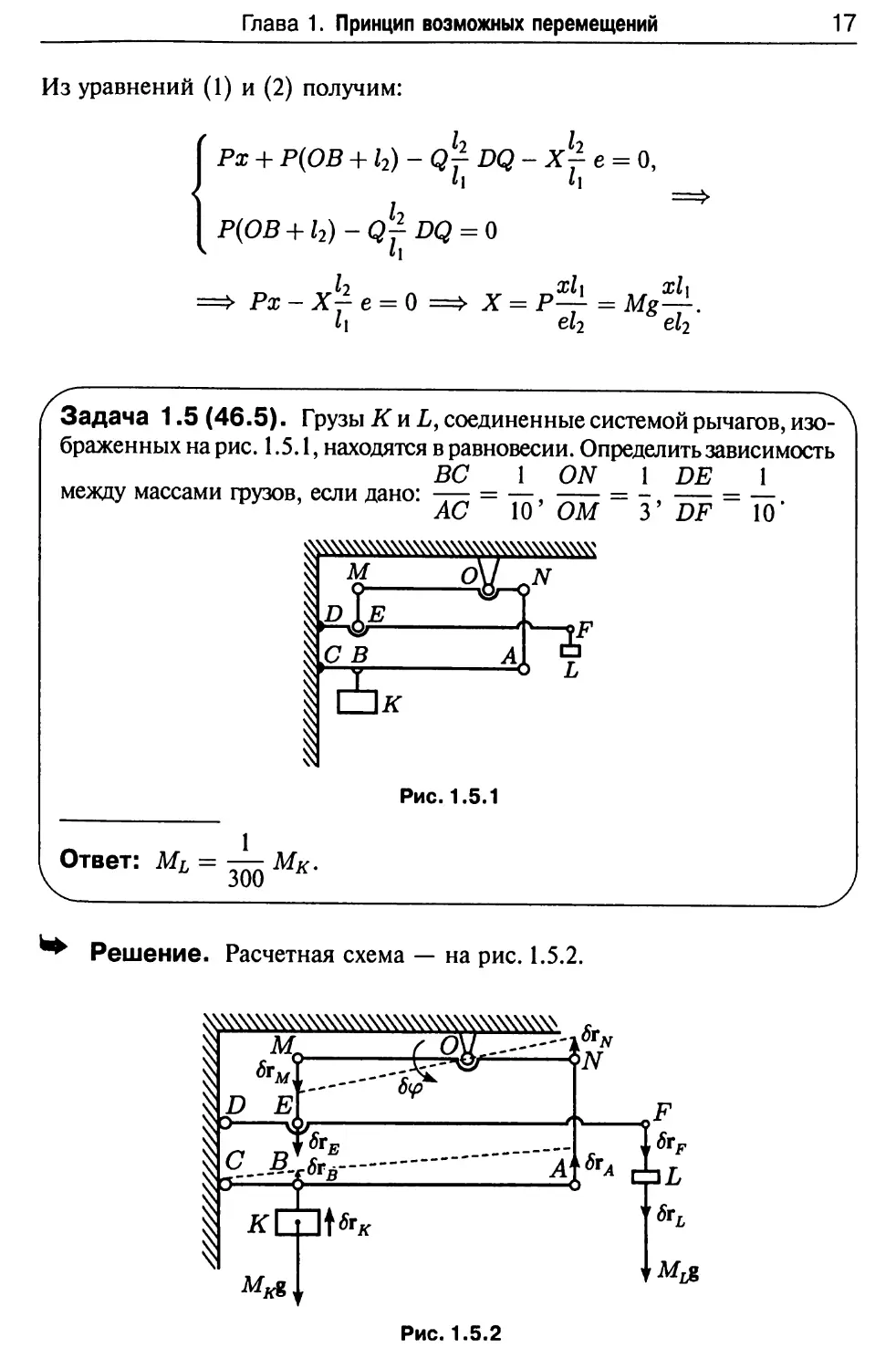
Составим условие отсутствия скольжения кулака К:
VR2 - Л2
\Frpl < F,
пред.
F-Mtf-
</ЛГ {N = Mxg + M7g).
Отсюда получаем:
VR2 - h2
M2g - ДМ, + M2)g ^F^ -^- M2g + f(M] + M2)g.
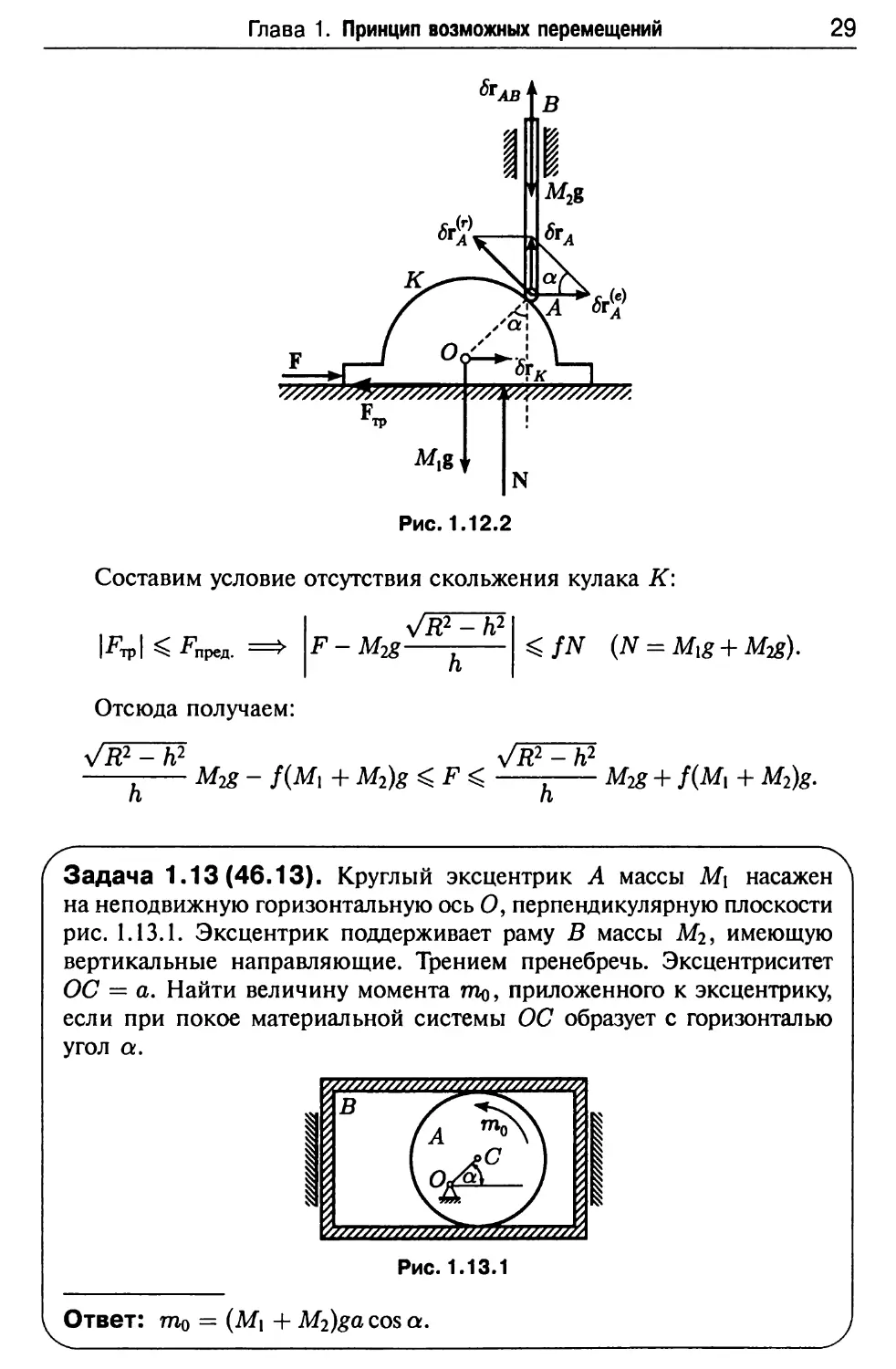
Задача 1.13(46.13). Круглый эксцентрик А массы M\ насажен
на неподвижную горизонтальную ось О, перпендикулярную плоскости
рис. 1.13.1. Эксцентрик поддерживает раму В массы М2, имеющую
вертикальные направляющие. Трением пренебречь. Эксцентриситет
ОС = а. Найти величину момента то, приложенного к эксцентрику,
если при покое материальной системы ОС образует с горизонталью
угол а.
'/SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSj
Рис. 1.13.1
Ответ: гао = (Mi + M2)ga cos а.

30
Глава 1. Принцип возможных перемещений
8I
ш
I*
«
Лг *g frM
У////////М///Я^///////7777Л
У;/////;;;;;;;/ф;;/7/;;///777УЛ
х
rM2g
Рис. 1.13.2
^ Решение. Расчетная схема — на рис. 1.13.2.
Если эксцентрику А задать возможное угловое перемещение 8а, то
центр масс С получит возможное перемещение
5гс = ОС • 8а = а • 6а,
а точка касания эксцентрика с рамкой (точка D) получит возможное
перемещение
г ^^ г ОС cos а _ cos а.
otd = OD • да = —;—-—да = а——-да.
sin р sin р
Составим уравнение равновесия:
т05а + Mjg • 8rc + M2g • &*д = 0,
COS Cfc
ra0<fa + Mxga8a cos (180° - a) + M2ga-7—/-8a cos (90° + /?) = 0 =>
sinp
cos a
=> moda - Mjga cos a- 8a — Miga sin /38a = 0 =>
sinp
или
Поэтому
m0 - Miga cos a - M2ga cos a = 0.
mo = (Mi -f M2)ga cos a.

Глава 1. Принцип возможных перемещений
31
Задача 1.14 (46.14). В механизме домкрата при вращении
рукоятки А длины R начинают вращаться зубчатые колеса 1, 2, 3, 4 и 5,
которые приводят в движение зубчатую рейку В домкрата. Какую силу
надо приложить перпендикулярно рукоятке в конце ее для того, чтобы
чашка С при равновесии домкрата развила давление равное 4,8 кН?
Радиусы зубчатых колес соответственно равны: г\ = 3 см, т-i = 12 см,
гз = 4 см, Г4 = 16 см, г$ = 3 см, длина рукоятки R = 18 см.
Рис. 1.14.1
Ответ: Р = 50 Н.
Решение. Расчетная схема — на рис. 1.14.2.
1

32
Глава 1. Принцип возможных перемещений
Если рукоятке А вместе с зубчатым колесом «1» задать углово^
возможное перемещение 6ip\, то будем иметь следующие соотношения
для возможных перемещений звеньев механизма:
7*1 7*1 7*з Т\ 7*1
5гР = R-6<p\, 5<р2,з = S(f\ — 9 8ipAyS = 8ip\ , SrBc = S<P\ r5.
7*2 7*2 7*4 r2 r4
Уравнение равновесия механизма домкрата имеет вид:
7*17*37*5
Поэтому
P-R-8ipx -Q-!-^6<pi = 0.
Г2Г4
r2uR
Задача 1.15(46.15). Дифференциальный ворот состоит из двух
жестко связанных валов Aw В, приводимых во вращение рукояткой С
длины R. Поднимаемый груз D массы М прикреплен к подвижному
блоку Е9 охваченному канатом. При вращении рукоятки С левая ветвь
каната сматывается с вала А радиуса г\, а правая ветвь наматывается
на вал В радиуса т*2 (т*2 > г\). Какую силу Р надо приложить
перпендикулярно рукоятке в конце ее для того, чтобы уравновесить груз D,
если М = 720 кг, г\ = 10 см, г2 = 12 см, R = 60 см?
Ответ: Р= 118 Н.
■* Решение. Расчетная схема — на рис. 1.15.2.
Дадим угловое возможное перемещение Sip вороту. Тогда 5гс = R5<p,
Stl = г25(р, 6tn = r\5ip.
Так как К есть мгновенный центр возможных вращений блока Е, то:
5rL
SrN
KN'
(О

Глава 1. Принцип возможных перемещений
33
Радиус блока Е равен гз = (п + г2)/2. Поэтому из соотношения (1)
получаем:
Г2&4>
г\5(р
г3 + ОК гз - ОК
Следовательно
■ о*=Г^1" !!zl!
Г\ +г2
гз
SrD = Sro = jj£ ' ^К = —^—fy-
Распишем принцип возможных перемещений системы:
Ъ -г,
отсюда
р.8гс- MgSrD - 0 => PRStp - Mg-L—Ls<p = О,
Г2 - Ti
p~M8~1jC = ll8 н-

34
Глава 1. Принцип возможных перемещений
Задача 1.16 (46.16). В механизме антипараллелограмма ABCD
звенья АВ, CD и ВС соединены цилиндрическими шарнирами Б и С,
а цилиндрическими шарнирами А и D прикреплены к стойке AD.
К звену CD в шарнире С приложена горизонтальная сила Fc.
Определить модуль силы ¥в, приложенной в шарнире В
перпендикулярно звену АВ, если механизм находится в равновесии в
положении, указанном на рис. 1.16.2. Дано: AD = ВС, АВ = CD,
A ABC = ZADC = 90°, ZDCB = 30°.
Ответ: FB = 2FC.
Рис. 1.16.1
■► Решение. Расчетная схема — на рис. 1.16.2.
Дадим звену CD угловое возможное перемещение 5(р. Тогда точка С
получит возможное перемещение 5гс = CD • 5<р. Рассмотрим звено ВС.
Точка В получит перемещение 8тв, перпендикулярное звену АВ, так как
она принадлежит звену АВ, которое может вращаться вокруг неподвижной
оси, проходящей через точку А.
Проведем перпендикуляры через точки В и С к их возможным
перемещениям. Получим точку К, которая является центром возможных
Рис. 1.16.2

Глава 1. Принцип возможных перемещений
35
вращений звена ВС (мгновенным центром скоростей). Поэтому имеет
место соотношение (1):
Src _ 8гв
КС~КВ'
Отсюда
6гв = 5rcj77; = CD- 5(РВСвс30 = CD sin 30°Sip = \CD5ip'
cos 30°
Запишем уравнение равновесия:
Отсюда
FcSrc - FBSrB = 0, или Fc • CDSip - FB-CD5<p = 0.
FB = 2Fq.
Задача 1.17 (46.17). Криюшипно-ползунный механизм ОАВ связан
в середине шатуна АВ цилиндрическим шарниром С со стержнем CD.
Стержни CD и DE соединены цилиндрическим шарниром D. Определить
зависимость между модулями сил F^ и F^, соответственно
перпендикулярных стержням О А и DE, при равновесии механизма в положении,
указанном на рис. 1.17.1. Дано: Z.DCB =150°, Z.CDE = 90°.
Ответ: FD = 4FA.
Рис. 1.17.1
Решение. Расчетная схема — на рис. 1.17.2.
Пусть Sip — возможное перемещение кривошипа ОА. Тогда
5га = О А • <fy.

36
Глава 1. Принцип возможных перемещений
Рассмотрим шатун АВ. Возможное перемещение ползуна В
направлено вдоль горизонтальной прямой. Построив перпендикуляры в точках А
и Б к их возможным перемещениям, видим, что они пересекаются в
точке В. Значит, в данном положении механизма бгв = 0. Следовательно,
точка В есть мгновенный центр вращения стержня АВ. Поэтому:
6гс = SrA— = -8rA = -OASip.
АВ 2 2
Рассмотрим звено DC. Перемещение бт^ направлено перпендикулярно
DE (так как точка D принадлежит звену DE), т.е. вдоль DC. Точка К,
которая является мгновенным центром вращения (МЦС) звена DC, лежит
на прямой ОАВ. Имеем соотношения:
-ОА6<р sin 30° = -ОА -Sip.
КС~ KD^ Td~ ГсКС "
2 DC
cos 30°

Глава 1. Принцип возможных перемещений
37
Запишем уравнение равновесия:
FASrA - FDSrD = О =>
Отсюда
FA • OAS(f - FD • - ОЛ • S(p = 0.
*Ъ = 4i^.
Задача 1.18(46.18). Колодочно-бандажный тормоз вагона
трамвая состоит из трех тяг АВ, ВС и CD, соединенных шарнирами В
и С. При действии горизонтальной силы F тормозные колодки К
и L, соответственно прикрепленные к тягам АВ и CD, прижимаются
к колесу. Определить силы давления N# и Nx, колодок на колесо.
Размеры указаны на рис. 1.18.1. Вагон находится в покое.
[
1
1 ^
►
{
\
V
\
h
У
1*1
48
y
1
*°
т
Ответ: NK
a + b
Рис. 1.18.1
a(b + d)
bd
Ъф Решение. Для определения сил давления N# и NL колодок на
колесо освобождаем систему от связей (убираем колесо) и вводим силы
реакций Rk и Rj, на колодки со стороны колеса в качестве активных
сил (Rk = -N#, RL = -NL в силу закона равенства сил действия и
противодействия).
Разобьем решение задачи на две части.
1. Дадим стержню АВ угловое возможное перемещение <$</? (рис. 1.18.2).
При этом возможные перемещения других элементов системы
равны нулю. Имеем:
6rA = ABS<p = (а + b)5(p, 8rK = KBSip = Ь5ц>, 5гк = 0.
уравнение равновесия, записанное с помощью принципа возможных
перемещений, принимает вид:
F • (а + Ь)5<р - RKbSip = 0.

38
Глава 1. Принцип возможных перемещений
А & a F
-*i—►
6(р
К
6тк
щ.
В
/////
Рис. 1.18.2
в
Рис. 1.18.3
Поэтому
NK = RK = F
а + Ь
Т""
2. Мысленно заменив шарниры В и С жесткими заделками, дадим
стержню CD (а значит и всей системе как твердому телу) угловое
возможное перемещение 6ф (рис. 1.18.3) вокруг неподвижной оси шарнира D.
Тогда возможные перемещения точек приложения сил будут следующими:
SrL = DL-6tp = d5ip,
SrA = DASiP = [(а + Ъ)-(Ъ + d)] -J—Sj; = —-5ф,
L J sin a sin a
SrK = DK-&I>= \(b + d) - b] —^(ty = -Д:ЭД.
L J sin p sin p
Уравнение равновесия примет вид:
RLSrL + F6rA cos (90° + a) + RKSrK cos (90° + /?) = 0,
или
a — d d
Rl dSip - F 5ф sin a - Rk ~5ip sin /3 = 0.
sin a sin p
Отсюда выражаем:
a-d „ „a-d „a+ 6 a(b + d)
Rl = F—r- + Rk = F—t- + F—— = F- }
Поэтому
NL = RL = F
d b
a(b + d)
bd
bd

Глава 1. Принцип возможных перемещений
39
Задача 1.19(46.19). На рисунке 1.19.1 изображена схема коло-
дочно-бандажного тормоза вагона трамвая. Определить зависимость
между а, Ь и с, при наличии которой колодки А и В под действием
силы F прижимаются с одинаковыми по модулю силами к
бандажам колес С и D. Найти также величину этой силы. Колеса считать
неподвижными.
F
_ а a+b+c п
Ответ: - = , RA = RB = F-
ос 2о
■* Решение. Расчетная схема — на рис. 1.19.2.
Освободим систему в точках А и В от связей и введем реакции R^
и Rq в качестве активных сил. Заметим, что достаточно рассмотреть лишь
нормальные реакции, так как колеса по условию задачи неподвижны
и потому силы трения скольжения равны нулю.

40
Глава 1. Принцип возможных перемещений
Дадим левому стержню угловое возможное перемещение <fy?. В
результате остальные точки системы получат следующие возможные
перемещения:
8гс = (а + b)5ip, 6га = bSip, SrD = сбр, 5гк = йгп,
6гк са
огв = ; а = ; 6<р.
а+Ъ+с а+о+с
Запишем принцип возможных перемещений:
-F5rc + RaSva + RBSrB = 0.
Или
ас
-F(a + b)5ip + RAb5(p + RB бр = 0 =>
a + 6 + с
ас
=»• -F(a + b) + RAb + Rb—t-t- =0. (1)
a + o + с
Нетрудно видеть, что эта система статически неопределенная, так как
число неизвестных реакций больше, чем число независимых уравнений
равновесия, которые можно составить (соответственно 7 и 6). Поэтому
для нахождения соотношения между a, b и с, при котором силы Ra и Rb
равны по величине, добавим условие равенства элементарных работ этих
сил на рассмотренном возможном перемещении.
Итак,
ас
RAb = Rb
Но так как Ra = Rb, то
а-\-Ь + с
ас
или
При таком
условии
из
а
Ь "
уравнения
а + Ъ + с
о + Ь + с
с
(1) получаем:
26 '

Глава 1. Принцип возможных перемещений
41
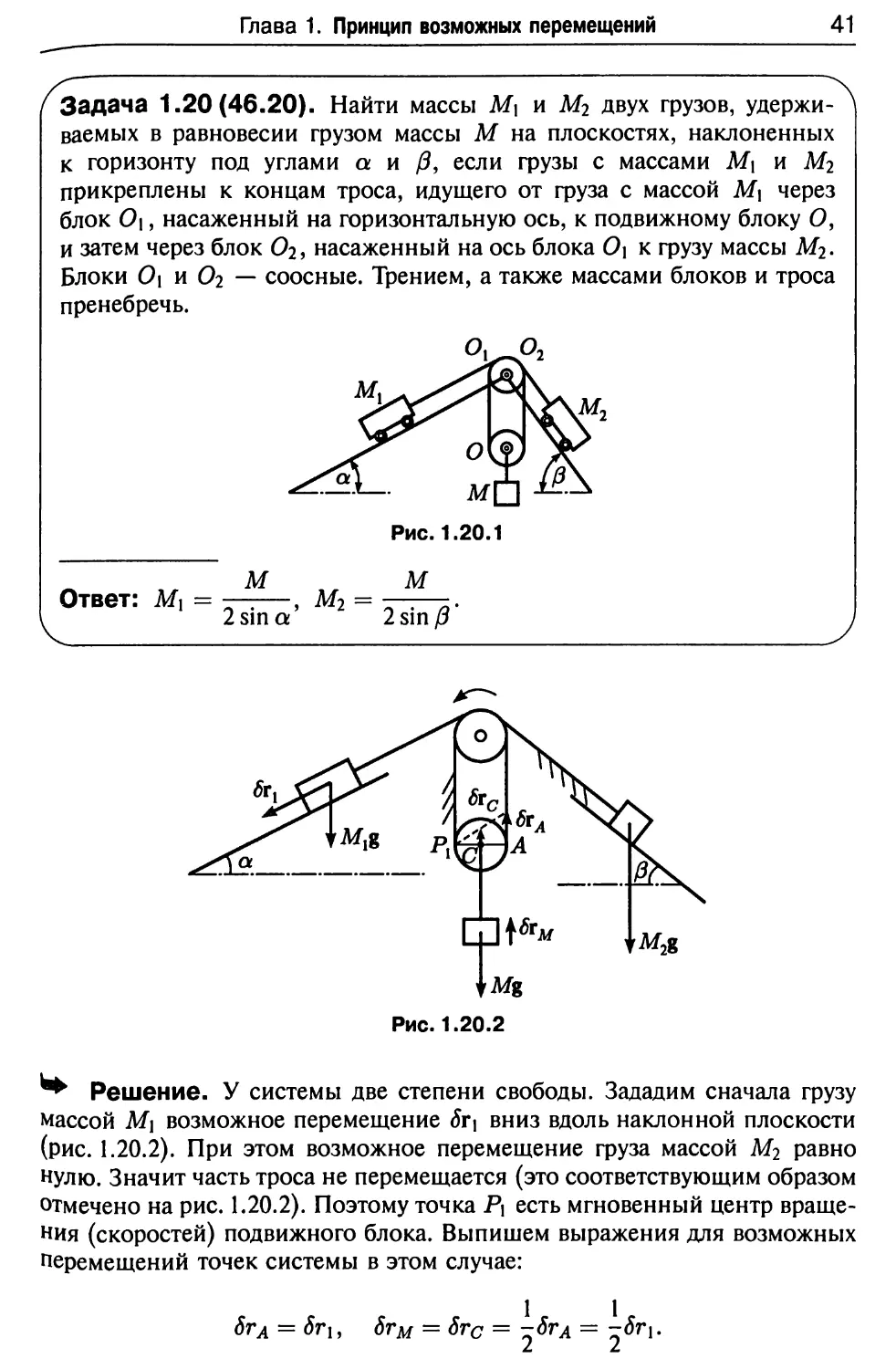
Задача 1.20(46.20). Найти массы М\ и М2 двух грузов,
удерживаемых в равновесии грузом массы М на плоскостях, наклоненных
к горизонту под углами а и /?, если грузы с массами М\ и М2
прикреплены к концам троса, идущего от груза с массой М\ через
блок 0\, насаженный на горизонтальную ось, к подвижному блоку О,
и затем через блок 02, насаженный на ось блока 0\ к грузу массы М2.
Блоки 0\ и 02 — соосные. Трением, а также массами блоков и троса
пренебречь.
Ответ: М. =
М
2 sin а
, М2
м
2 sin/?
■► Решение. У системы две степени свободы. Зададим сначала грузу
массой М\ возможное перемещение &*i вниз вдоль наклонной плоскости
(рис. 1.20.2). При этом возможное перемещение груза массой М2 равно
нулю. Значит часть троса не перемещается (это соответствующим образом
отмечено на рис. 1.20.2). Поэтому точка Pi есть мгновенный центр
вращения (скоростей) подвижного блока. Выпишем выражения для возможных
перемещений точек системы в этом случае:
бгл = Sr\, SrM = Src = -6га = -8г{.

42
Глава 1. Принцип возможных перемещений
Выпишем сумму элементарных работ всех активных сил (связи
идеальные) на заданном возможном перемещении системы:
Mig-&ri +Mg-SrM = 0,
или
M\gSr\ cos (90° - а) - Mg-6r\ = 0.
Отсюда масса груза
Mi =
М
2 sin а
Теперь зададим системе второе независимое возможное
перемещение: грузу массой М2 дадим перемещение 6т2 вниз по наклонной
плоскости (рис. 1.20.3). В этом случае возможные перемещения точек системы
имеют вид:
5гв = 5г2,
5гм = Src = -5гв = -5г2.
Сумма работ на этом перемещении будет:
M2g • 5r2 + Mg • 5тм = 0,
или
Откуда
M2g8r2 cos (90° -0)- Mg-8r2 = 0.
М2 =
М
2 sin/?'

Глава 1. Принцип возможных перемещений
43
Задача 1.21(46.21). К концам нерастяжимой нити привязаны
грузы А и £? одинаковой массы. От груза А нить проходит параллельно
горизонтальной плоскости, огибает неподвижный блок С,
охватывает подвижный блок D, затем огибает неподвижный блок Е, где
к другому концу нити привязан груз В. К оси подвижного блока D
подвешен груз К массы М. Определить массу М\ каждого из грузов А
и Б и коэффициент трения скольжения / груза А о
горизонтальную плоскость, если система грузов находится в покое. Массой нити
пренебречь.
Рис. 1.21.1
Ответ: М\
М 1 М
1.
Mg
Рис. 1.21.2
^ Решение. У системы две степени свободы. Сначала зададим грузу А
возможное перемещение 8т а (рис. 1.21.2). Тогда для точек системы имеем:
8r0l = SrA, 8rK = 8rc = jbrox = -z^a

44
Глава 1. Принцип возможных перемещений
///
А
мАш
6ти
к
в
Mg
Рис. 1.21.3
(так как точка Р\ — мгновенный центр вращений подвижного блока D
на заданном возможном перемещении системы). Силу трения Еф
включим в число активных сил.
Уравнение равновесия примет вид:
-FwSrA + Mg-SrA = 0.
Приравняв нулю коэффициент при 5га, получим:
Яр = \ms.
При предельном равновесии F^ = Fnpea = /Na- Нормальная
реакция Na в данном случае равна Мае. Поэтому получаем соотношение:
fMAg = -Mg.
0)
Теперь зададим системе другое независимое возможное перемещение:
8тв грузу В (рис. 1.21.3). Для точек системы имеем:
6го2 = SrB, SrK = Src = 2^Гв'
Уравнение равновесия примет вид:
MBgSrB - Mg-5rB = 0.
Отсюда
Мв
М

Глава 1. Принцип возможных перемещений
45
Так как Мд = Мв, то искомая масса грузов равна М\ = М/2. Теперь
из соотношения (1) определим коэффициент трения скольжения /:
, 1 М
Задача 1.22(46.22). Составная балка AD, лежащая на трех опорах,
состоит из двух балок, шарнирно соединенных в точке С. На балку
действуют вертикально силы, равные 20 кН, 60 кН, 30 кН. Размеры
указаны на рис. 1.22.1. Определить реакции опор А, В и D.
,,п „ б0кН |30кН
20 кН \ п
ffik а
V
а
а
аЖ
к 1а
1а *
-« Р-
Рис. 1.22.1
Ответ: RA = 10 кН, RB = 105 кН, RD = -5 кН.
■Ф* Решение. Для определения реакции скользящего шарнира А
«отбросим» эту связь и заменим ее действие силой реакции R^, направленной
вдоль вертикали (рис. 1.22.2).
Стержень АС получил возможность вращаться вокруг оси шарнира С.
Зададим стержню возможное перемещение Sip. Тогда
8га = АС5(р = 2aS(p, 8гех = Е\С5ц> = aSip.
Уравнение равновесия системы на заданном возможном перемещении
принимает вид:
Ra2<i6(p - F\a6ip = 0.
*л+"
^ ^
Е{
If,
^
в.
в
Рис. 1.22.2

46
Глава 1. Принцип возможных перемещений
А\ SrA Ех
6ТГ.
Е2 В
Рис. 1.22.3
SrE2 Л--"~'~6т
*3
Отсюда
RA = — = 10 кН.
2
Реакция направлена вертикально вверх.
Теперь определим реакцию скользящего шарнира В. Для этого его
воздействие заменим силой реакции RB (рис. 1.22.3). Стержень CD
получил возможность поворачиваться вокруг оси шарнира D, а стержень
АС получил возможность совершать плоские движения. Пусть 6ф —
возможное угловое перемещение стержня CD. Тогда
Srfy = 5а<^, 5rEi = 2а5ф,
8гв = 4а<^, 8rc = 6a5ip.
Рассмотрим перемещение стержня АС. Так как возможные
перемещения точки А происходят вдоль горизонтали, то нетрудно увидеть, что
в данном положении системы точка А является мгновенным центром
вращения (скоростей) (5га = 0). Поэтому
8гех = -г— • а = Ъад'ф.
2а
Уравнение равновесия системы на заданном ее возможном
перемещении имеет вид:
Fi • 3a5ip + F2 • SaSip - RB • 4а5ф + F3 • 2а5ф = 0.
Приравняв нулю коэффициент при 5ф, получим
RB = -(3F, + 5F2 + 2F3) = 105 кН.
Реакция в точке В направлена вертикально вверх.

Глава 1. Принцип возможных перемещений 47
v„t
w
^х
бтг.
ej:
Рис. 1.22.4
бтп
tF3
Определим реакцию шарнира D. Вначале заменим его шарниром,
который может скользить вдоль вертикального направления, добавив
реакцию Y^ (рис. 1.22.4).
Зададим точке D вертикально вверх возможное перемещение йг^.
Точка В имеет возможность перемещаться лишь по горизонтали.
Строим мгновенный центр вращения стержня CD. Он оказался в точке В
(5гв = 0). Поэтому имеем:
6гс 8rD а 1
огЕ, = — • а = — • 2а— = -drD,
2а 4а 2а 4
SrD
8гео = ~г~ ' а — l^rD
4а
SrD
8ге, = —А— 2а — -5rD.
4а
Уравнение равновесия:
Отсюда
YDSrD - F3-6rD + F2-SrD + F{-5rD = 0.
1Ь = ^з-^2-^, = -5кН.
А 6тл
Et
C- E> » B^ 6ZD
6t
* О
Еъ fir
Si
*i
*j
El
|F2
^3
-¥ ►
бТг

48
Глава 1. Принцип возможных перемещений
Теперь заменим неподвижный шарнир D шарниром, который
может скользить вдоль горизонтального направления, добавив реакцию Хд
(рис. 1.22.5). Зададим точке D горизонтальное возможное
перемещение Std- В силу наложенных связей вся система поступательно
переместится вместе с точкой D:
5т а = 5т Ei = StЕ2 = St в = &*#3 = St о-
Уравнение равновесия в данном случае примет вид:
XD5rD = 0.
Поэтому Xd = 0. Следовательно, реакция шарнира D направлена
вертикально вниз и равна
RD = YD = -5 кН.
Задача 1.23 (46.23). Определить вращающий момент, который
надо приложить на участке BD к балке AD, рассмотренной в
предыдущей задаче, для того чтобы опорная реакция в D равнялась нулю.
. Ответ: М = -20а кНм.
*+ Решение. Воспользуемся рис. 1.22.4 из задачи 1.22 (46.22).
Если точке D задать возможное перемещение Std то стержень CD
совершит угловое возможное перемещение
6ip= —
4а
(против направления часовой стрелки).
Запишем уравнение равновесия, добавив работу вращающего
момента М и учитывая, что YD = 0:
М^- + Fi -SrD + F2-SrD - F3-SrD = 0.
4a 4 4 2
Отсюда
M = a(-F, - F2 + 2F3) = -20a кНм.
Момент следует направить по часовой стрелке.

Глава 1. Принцип возможных перемещений
49
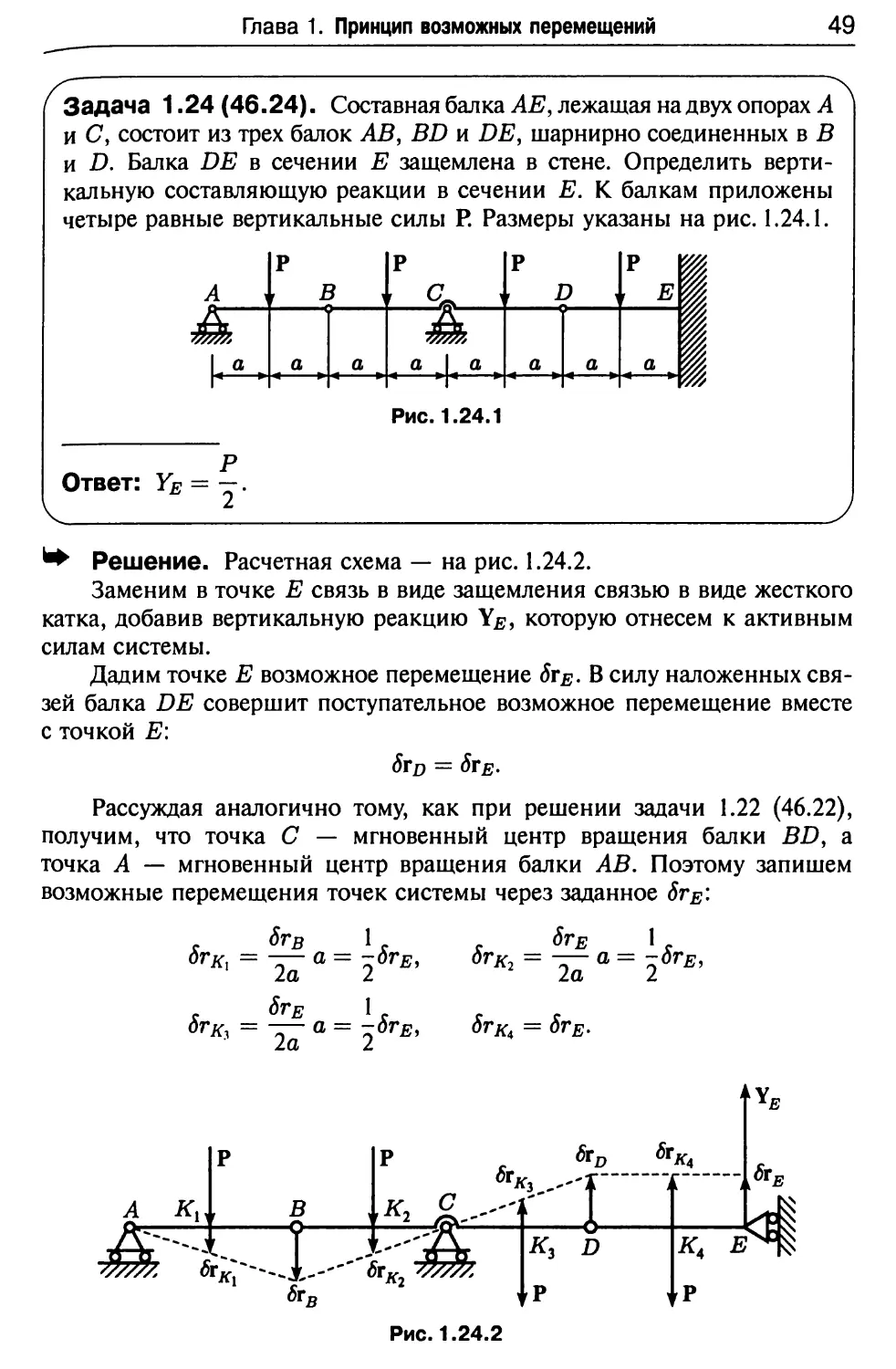
Задача 1.24 (46.24). Составная балка АЕ, лежащая на двух опорах А
и С, состоит из трех балок АВ, BD и DE, шарнирно соединенных в В
и D. Балка DE в сечении Е защемлена в стене. Определить
вертикальную составляющую реакции в сечении Е. К балкам приложены
четыре равные вертикальные силы Р. Размеры указаны на рис. 1.24.1.
В
—о—
3*
D
—О—
Рис. 1.24.1
Ответ: YE
Р
2~'
*Ф Решение. Расчетная схема — на рис. 1.24.2.
Заменим в точке Е связь в виде защемления связью в виде жесткого
катка, добавив вертикальную реакцию Y#, которую отнесем к активным
силам системы.
Дадим точке Е возможное перемещение 8те- В силу наложенных
связей балка DE совершит поступательное возможное перемещение вместе
с точкой Е:
5td = 8тЕ-
Рассуждая аналогично тому, как при решении задачи 1.22 (46.22),
получим, что точка С — мгновенный центр вращения балки BD9 а
точка А — мгновенный центр вращения балки АВ. Поэтому запишем
возможные перемещения точек системы через заданное <Jr#:
х 5гв 1 х
х 6ге 1х
Sr
5rK2 = —a=-28rE,
6гк4 = SrE.
А Кх
6тп Sr
к4
♦ Y.
*«

50
Глава 1. Принцип возможных перемещений
Запишем уравнение равновесия системы:
PzSrE + Р-6гЕ - Р-6гЕ - P6rE + YE6rE = 0.
Отсюда получим:
Вертикальная реакция направлена вверх.
Задача 1.25(46.25). Определить момент МЕ пары, возникающей
в заделке балки DE, рассмотренной в предыдущей задаче.
Ответ: МЕ = 0.
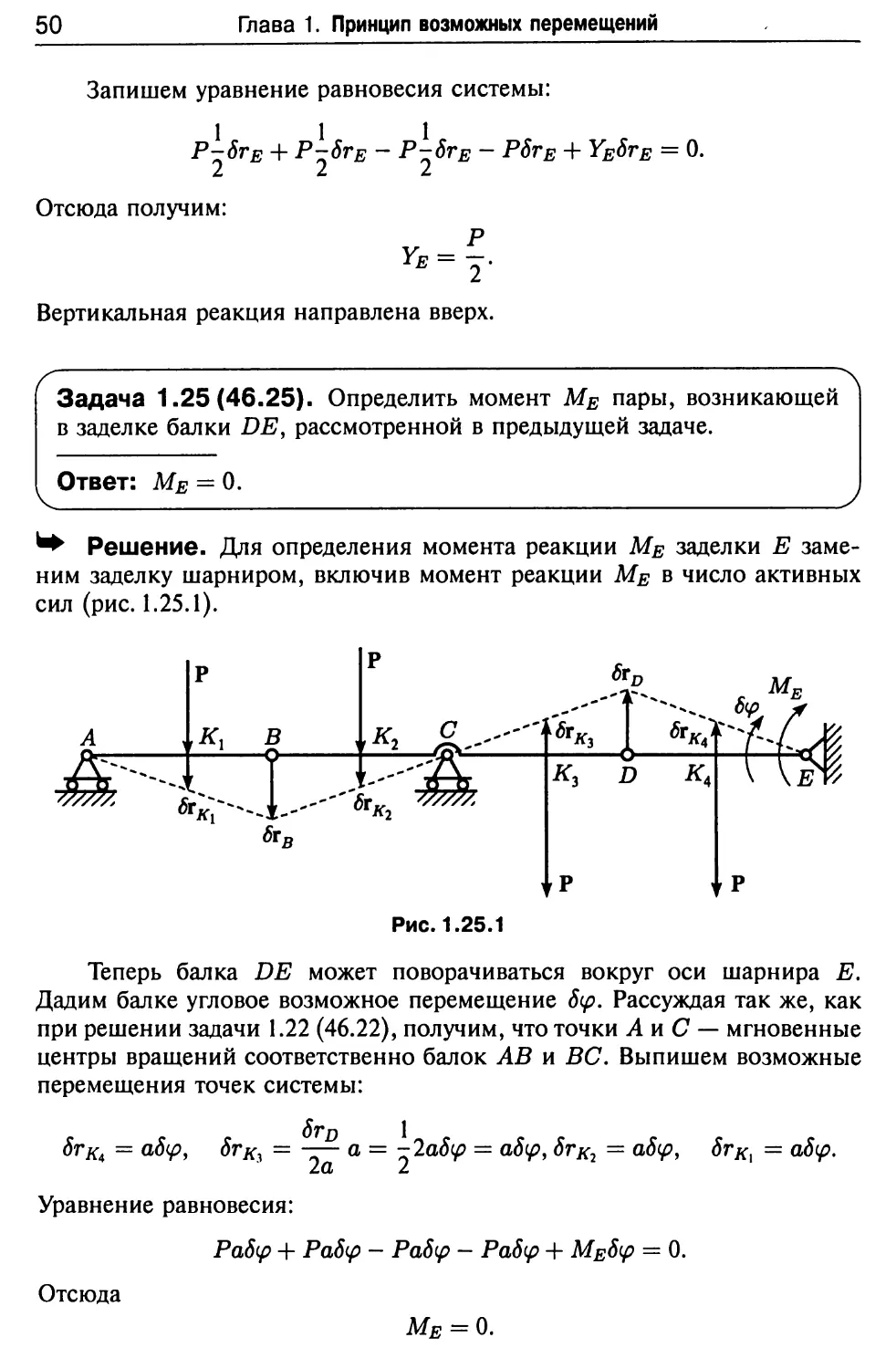
■► Решение. Для определения момента реакции МЕ заделки Е
заменим заделку шарниром, включив момент реакции МЕ в число активных
сил (рис. 1.25.1).
бтп
Мк
1 ^*~'\
%
У
;*|Г,
Кг
Р
D
**'
к,
1
\Н<
\ \\
гР
6тц
Рис. 1.25.1
Теперь балка DE может поворачиваться вокруг оси шарнира Е.
Дадим балке угловое возможное перемещение 5(р. Рассуждая так же, как
при решении задачи 1.22 (46.22), получим, что точки А и С — мгновенные
центры вращений соответственно балок АВ и ВС. Выпишем возможные
перемещения точек системы:
$гкА = абр, 5гКу = — а = -2а8ф = aSip, 8rKl = aS(p, 6rKl = a6(p.
Уравнение равновесия:
PaSip + PaSip - PaSip - PaSip + MESip = 0.
Отсюда
ME = 0.

Глава 1. Принцип возможных перемещений
51
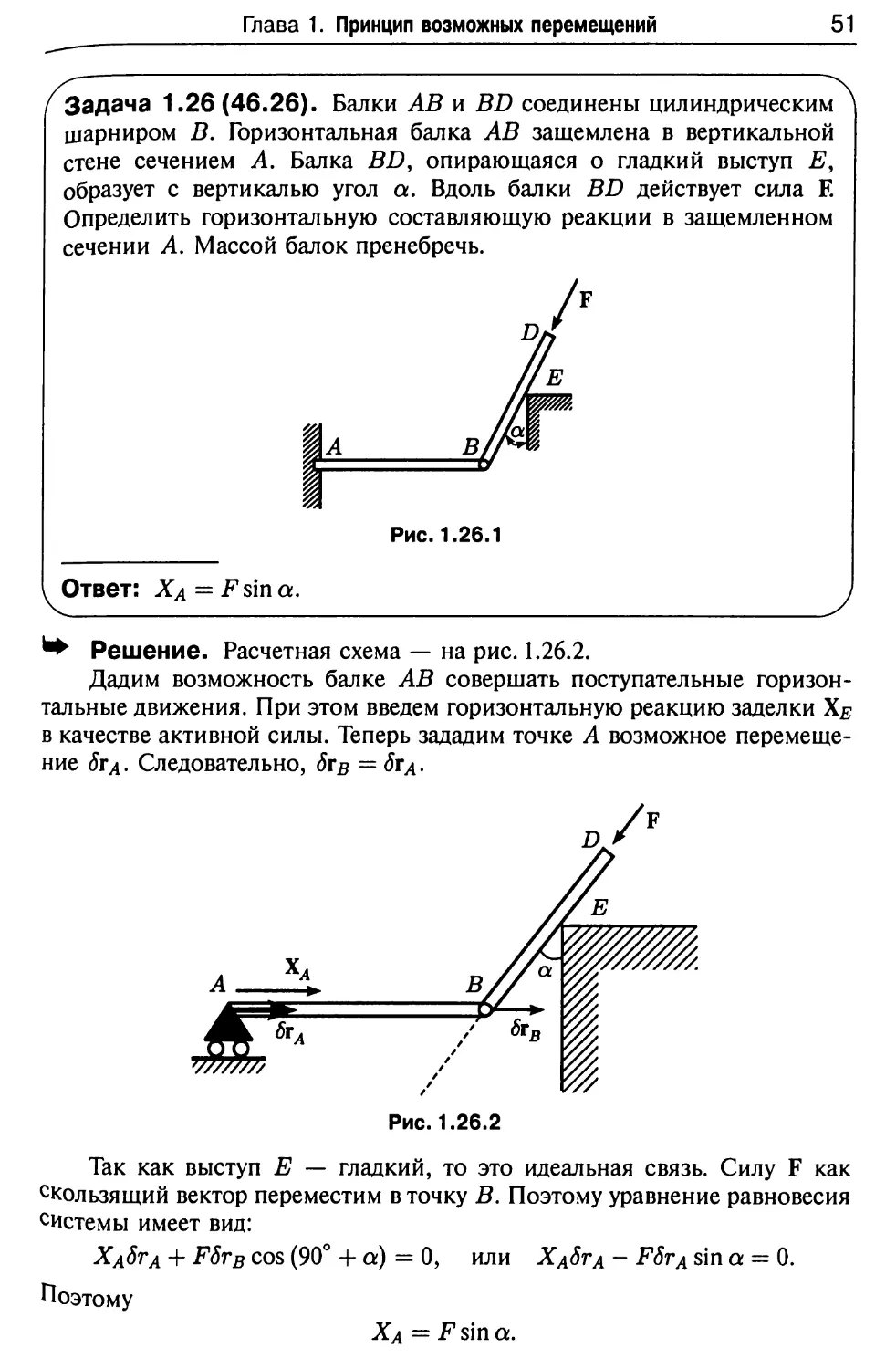
Задача 1.26(46.26). Балки АВ и BD соединены цилиндрическим
шарниром В. Горизонтальная балка АВ защемлена в вертикальной
стене сечением А. Балка BD, опирающаяся о гладкий выступ Е9
образует с вертикалью угол а. Вдоль балки BD действует сила Е
Определить горизонтальную составляющую реакции в защемленном
сечении А. Массой балок пренебречь.
Рис. 1.26.1
Ответ: ХА = Fsina.
■► Решение. Расчетная схема — на рис. 1.26.2.
Дадим возможность балке АВ совершать поступательные
горизонтальные движения. При этом введем горизонтальную реакцию заделки Хе
в качестве активной силы. Теперь зададим точке А возможное
перемещение 8га- Следовательно, 5тв = 6та-
—►
*а
Рис. 1.26.2
Так как выступ Е — гладкий, то это идеальная связь. Силу F как
скользящий вектор переместим в точку В. Поэтому уравнение равновесия
системы имеет вид:
Ха$га + F5rB cos (90° + а) = 0, или Ха6га - FSrA sin а = 0.
Поэтому
Ха = F sin а.

52
Глава 1. Принцип возможных перемещений
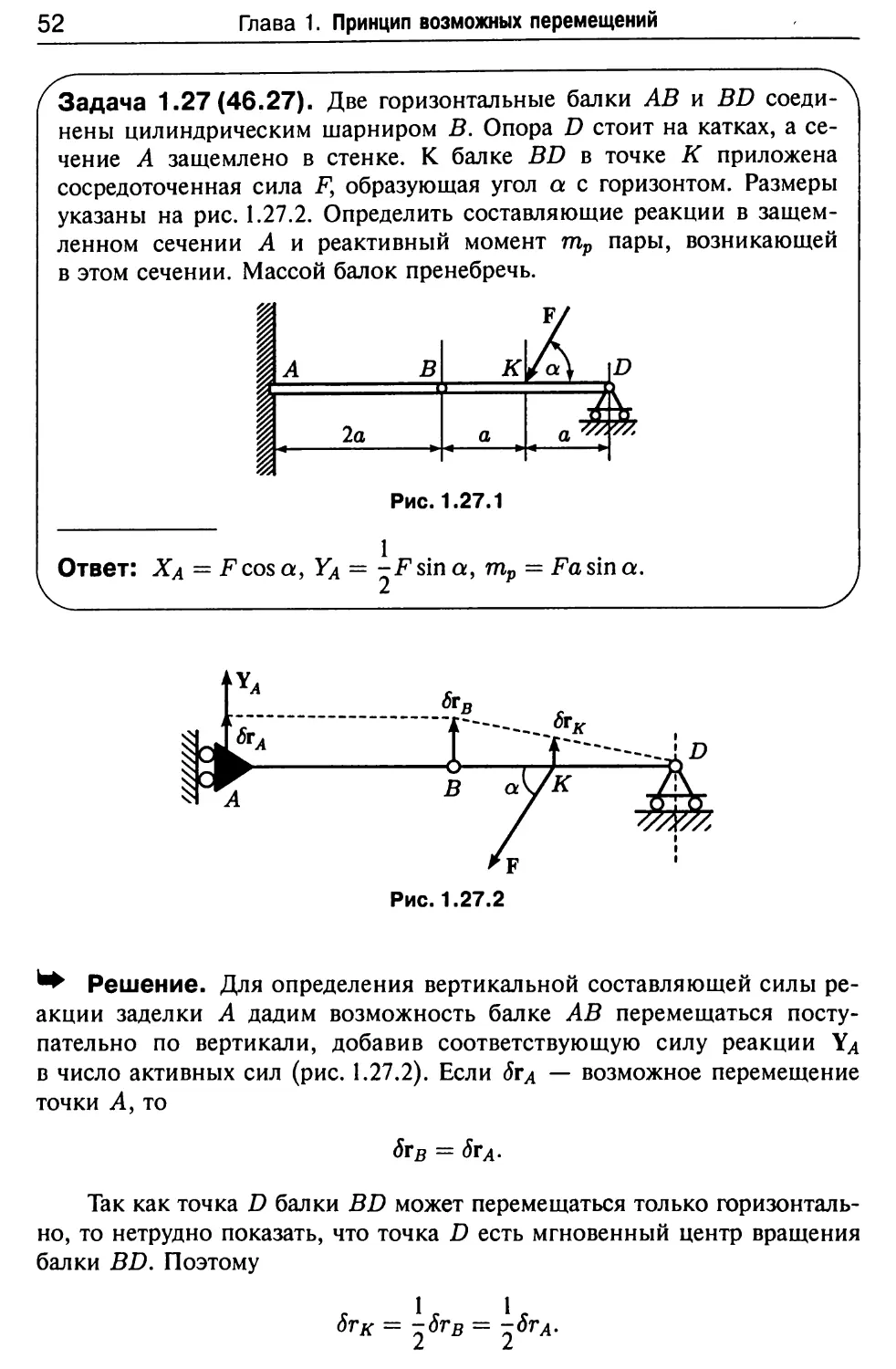
Задача 1.27(46.27). Две горизонтальные балки АВ и BD
соединены цилиндрическим шарниром В. Опора D стоит на катках, а
сечение А защемлено в стенке. К балке BD в точке К приложена
сосредоточенная сила F, образующая угол а с горизонтом. Размеры
указаны на рис. 1.27.2. Определить составляющие реакции в
защемленном сечении А и реактивный момент тр пары, возникающей
в этом сечении. Массой балок пренебречь.
1
I
I
I-
2а
К
Рис. 1.27.1
Ответ: Ха = Fcosa, Уд = -Fsina, тр = Fa sin a.
IY.
W
Рис. 1.27.2
■* Решение. Для определения вертикальной составляющей силы
реакции заделки А дадим возможность балке АВ перемещаться
поступательно по вертикали, добавив соответствующую силу реакции Ya
в число активных сил (рис. 1.27.2). Если 8гА — возможное перемещение
точки А, то
6т в = 5тА.
Так как точка D балки BD может перемещаться только
горизонтально, то нетрудно показать, что точка D есть мгновенный центр вращения
балки BD. Поэтому
5гк = -5гв = -&гА>

Глава 1. Принцип возможных перемещений
53
6тл
\4
Рис. 1.27.3
Уравнение равновесия имеет вид:
YA6rA + F6rA- cos (90° 4- а) = 0.
Отсюда
У А
1
-Fsina.
Для определения горизонтальной составляющей силы реакции
заделки А дадим балке АВ возможность перемещаться поступательно
горизонтально, добавив соответствующую силу реакции Х^ в число активных
сил (рис. 1.27.3). Если 8тА — возможное перемещение точки А, то в силу
наложенных связей имеем: 5тА = 8тв = 8тк = 8то-
Уравнение равновесия имеет вид:
XA8rA + F8rA cos (180° - а) = 0.
Отсюда ХА = F cos а.
МА
=4
6tp
Рис. 1.27.4
Для определения момента реакции заделки А дадим возможность
балке АВ поворачиваться вокруг оси, проходящей через точку А, добавив
момент реакции МА в число активных сил (рис. 1.27.4). Если Sip — угловое
возможное перемещение балки АВ, то
8гв = 2а8(р, 8гк = -8гв = а8<р.
Уравнение равновесия имеет вид: MA8ip + FaSip cos (90° + а) = 0.
Отсюда
rrip = МА = Fa sin а.

54
Глава 1. Принцип возможных перемещений
Задача 1.28(46.28). Железнодорожный кран опирается на рельсы,
укрепленные на двух горизонтальных двухпролетных балках с
промежуточными шарнирами. Кран несет груз Р = 30 кН, сила тяжести
крана Q = 160 кН. Определить момент реактивной пары в заделке
в положении крана, указанном на рис. 1.28.1.
0,60 м
Рис. 1.28.1
Ответ: МА = -210 кНм.
■* Решение. Рассмотрим по отдельности равновесие двух систем:
система балок (рис. 1.28.2) и кран с грузом (рис. 1.28.3).
В первой системе балке AD дадим возможность поворачиваться
вокруг горизонтальной оси шарнира А, которым заменили заделку А
(при этом добавили момент реакции заделки А Ма в качестве активной
нагрузки). В точках К и Е на систему действуют силы давления со стороны
крана. Зададим балке AD возможное угловое перемещение 6ф. Тогда
6rD = ADSip.
Так как наложенные связи позволяют точкам В и С перемещаться
лишь горизонтально, то несложно убедиться, что эти точки являются
мгновенными центрами вращения соответственно балок ТУТ и ТС. Поэтому
**-£■**■
AD-BK
DB
6<р, 8ге =
бгт
ТС
„„ AD-BT-EC,
ЕС = 6и>.
DB-TC у
6тс
%AJ Sip D
В К
Fi
*Е *£
StK
Рис. 1.28.2

Глава 1. Принцип возможных перемещений
55
N.
^ЩгЕХ1_
N,
Рис. 1.28.3
I
-г-
I
I
Уравнение равновесия системы балок имеет вид:
AD-BK с AD-BT-EC е
МА-6(р + F| ———6<р + F2— —6(р = 0.
DB
DB-TC
Выразим отсюда
МА
"С
AD-BK AD'BT-EC
DB
DB-TC
) = "(0,
9F, + 1,2F2). (1)
Рассмотрим теперь вторую систему (кран с грузом).
Нормальные реакции в точках касания с балками согласно закону
равенства сил действия и противодействия удовлетворяют условию: Fi = -N|,
F2 = -N2.
Заметим, что силы трения скольжения в точках касания (как
реакции идеальных связей) не учитываются, так как нет движения крана
относительно балок.
Зададим крану следующее возможное перемещение: 5гк ф 0, 6ге = 0
(рис. 1.28.3). Тогда точка L, через которую проходит линия действия силы
тяжести крана Q, совершит перемещение
Точка (f, через которую проходит линия действия силы тяжести груза Р,
совершит перемещение
Запишем уравнение равновесия в этом случае:

56
Глава 1. Принцип возможных перемещений
Отсюда получим:
Для определения нормальной реакции N2 зададим крану другое
(независимое) возможное перемещение: 5гЕ ф 0 (вверх), 5гк = 0. Тогда
Уравнение равновесия примет вид:
KL КС
N2SrE - Q&rE— - -Р^— = 0.
Отсюда получим:
2 VK# tf# V2,4 2,4 ' Ч
Вернемся к формуле (1). Так как F\ = N\9 F2 = N2, то
M^ = ~[0,9(0,75Q-2P) + 1,2(0,25Q+3P)]=-210kH-m.
Задача 1.29 (46.29). Каркас платформы состоит из Г-образных рам
с промежуточными шарнирами С. Верхние концы рам жестко
защемлены в бетонную стену, нижние — опираются на цилиндрические
подвижные опоры. Определить вертикальную реакцию защемления
при действии сил Pi и Р2.
lPl
гл \ С
Ответ: YA = Pl- Р2
I
Рис. 1.29.1

Глава 1. Принцип возможных перемещений
57
\Ф Решение. Расчетная схема — на рис. 1.29.2.
Освободим стержень АС частично от связи, т.е. дадим ему
возможность перемещаться поступательно по вертикали, добавив вертикальную
составляющую реакции заделки A YA к числу активных сил.
Пусть 5тА — возможное перемещение точки А. Тогда
5тс = 6тА = 8тЕ.
В силу наложенных связей точка В может совершать лишь
горизонтальные перемещения. Поэтому точка К, лежащая на пересечении
перпендикуляров, восстановленных в точках В и С стержня ВС к их
возможным перемещениям, есть мгновенный центр вращения стержня
ВС. Следовательно,
SrN = — KN = 8rA-.
Принцип возможных перемещений имеет вид:
Отсюда
YA6rA-P{5rA + P2-5rA = 0.
YA = Pl-P2-.
*л*
Я^ А6тл
6тЕ 6тс
Е
Pi
К
**/*
^fli-
N Pj
Рис. 1.29.2

58
Глава 1. Принцип возможных перемещений
Задача 1.30(46.30). Две балки ВС и CD шарнирно соединены
в С, цилиндрическим шарниром В прикреплены к вертикальной
стойке АВ, защемленной в сечении А, а цилиндрическим
шарниром D соединены с полом. К балкам приложены горизонтальные
силы Pi и Р2. Определить горизонтальную составляющую реакции
в сечении А. Размеры указаны на рис. 1.30.2.
Рис. 1.30.1
Ответ: ХА = -Р, - -Р2.
■* Решение. Расчетная схема — на рис. 1.30.2.
Дадим стойке АВ возможность перемещаться поступательно в
горизонтальном направлении. Горизонтальную составляющую реакции
заделки Ха включим в число активных сил системы.
Пусть 5та — возможное перемещение точки А. Тогда 5тв = 6т а.
Балка CD может поворачиваться вокруг оси неподвижного
шарнира D. Поэтому возможное перемещение 5тс ортогонально CD. Так как
Stв \\Src, то перпендикуляры в точках В и С к их возможным
перемещениям параллельны, и потому балка ВС совершает из данного положения
возможное поступательное перемещение. Значит, SrL = 6тв = &•<;.
Рис. 1.30.2

Глава 1. Принцип возможных перемещений
59
И, следовательно,
6ГК = {КН=26ГА-
Уравнение равновесия имеет вид:
Отсюда
ХАйгА + Р1&гА + -ЪбгА = 0.
ХА = -Рх - -Р2.
Горизонтальная составляющая реакции заделки А направлена влево.
Задача 1.31 (46.31). Определить момент тпА реактивной пары,
возникающей в заделке А стойки АВ, рассмотренной в
предыдущей задаче.
Ответ: МА
=(p,+Hj
■* Решение. Расчетная схема — на рис. 1.31.1.
Заменим заделку в точке А цилиндрическим шарниром с
неподвижной осью, добавив момент заделки МА к числу активных сил. Дадим
стойке АВ угловое возможное перемещение 8<р. Точка В совершит
перемещение 8гв = hSip.
Рис. 1.31.1

60
Глава 1. Принцип возможных перемещений
Воспользовавшись решением задачи 1.30 (46.30), выпишем
соотношения:
SrL = SrB = hSip, 8гк = -hSip.
Уравнение равновесия:
-МА5(р + P\h&y + P2-h8<p = 0.
Поэтому
МА
"(Р, + 5Р2)Л'
Задача 1.32 (46.32). Две фермы I и II, соединенные шарниром D,
прикреплены стержнями III и IV с помощью шарнира С к земле;
в точках А и В они имеют опоры на катках. Ферма I нагружена
вертикальной силой Р на расстоянии а от опоры А. Найти реакцию
катка В.
Ответ: RB
тельно точки С2)
Рис. 1.32.1
aDC2 ,
Рт-=г^г \Ь = С2В cos /? — плечо реакции RB относи-
Указание. Предварительно определить положение мгновенных центров скоростей
С\ и Сг ферм I и II.
^ Решение. Расчетная схема — на рис. 1.32.2.
Освободим систему от связи в точке В. Реакцию Rb,
направленную перпендикулярно плоскости скольжения катка В, включим в число
активных сил (рис. 1.32.2).
Зададим точке А возможное перемещение 6гА (по горизонтали
направо). Точка Е фермы I принадлежит также стержню III (ЕС). Поэтому
возможное перемещение 6те ортогонально ЕС. Мгновенный центр
скоростей С\ фермы I лежит на пересечении продолжения стержня ЕС
и перпендикуляра к Sta в точке А. Возможные перемещения точек К и D
ортогональны соответственно отрезкам С\К и C\D.

Глава 1. Принцип возможных перемещений
61
Рис. 1.32.2
Рассмотрим ферму II. Точка N, являясь общей точкой тел II и IV,
имеет возможное перемещение, ортогональное CN. Мгновенный центр
скоростей фермы II находится на пересечении прямых CN и C\D.
Перемещение точки В Stb ортогонально С2В. Поэтому
Уравнение равновесия имеет вид:
P8rK cos (180° - а) + RBSrB cos /3 = 0,
или
„с C\Kcosa ^г DC{-C2Bcos/3
АС\
АСХ • DC2
Отсюда получаем:
Rb = P
aDC2
bDCi9
где а = С\Кcos a, b = С2Вcos /3 (b — плечо реакции RB относительно
точки С2).

Глава 2
Общее уравнение динамики (§47, [1])
Задача 2.1 (47.1). Три груза массы М каждый соединены
нерастяжимой нитью, переброшенной через неподвижный блок А. Два груза
лежат на гладкой горизонтальной плоскости, а третий груз
подвешен вертикально. Определить ускорение системы и натяжение нити
в сечении аЬ. Массой нити и блока пренебречь.
№ШШ)/
шШАушшш/ААг
Рис. 2.1.1
Ответ: a=-g,T=- Mg.
Ъ+ Решение. Расчетная схема — на рис. 2.1.2.
Воспользуемся при составлении дифференциального уравнения
движения системы общим уравнением динамики (принципом Даламбера—
Лагранжа):
к
При движении механической системы в любой момент времени сумма
элементарных работ всех активных сил, реакций неидеальных связей и сил
инерции точек системы равна нулю на любом возможном перемещении системы.
На систему действуют из активных сил только силы тяжести грузов.
Связи, наложенные на систему, — идеальные (гладкая поверхность, нерастяжимая
нить, гладкий шарнир). Поэтому реакции связей не изображаем на рисунке.
Груз «3» движется поступательно вертикально вниз с ускорением а.
Поэтому равнодействующая сил инерции точек груза «3» имеет вид:
Фз = -М3а = -Ма.

Глава 2. Общее уравнение динамики
63
ф1
77/
1&-, Ф,
/7/
а1 = *2
мх%
мг%
i
|Ф3
*Г3
M3g
Рис. 2.1.2
В силу нерастяжимости нити ускорения грузов «1» и «2», которые
движутся поступательно, равны по величине ускорению груза «3». Поэтому
Ф, = ф2 = Ма.
Рассмотрим произвольный момент времени t, когда система
занимает некоторое положение, изображенное на рисунке. Зададим грузу
«3» произвольное возможное перемещение Jr3 из этого положения. Для
определенности направим его вниз. Тогда, в силу нерастяжимости нити,
грузы «1» и «2» совершат возможные перемещения 6т\ = 5т2, по величине
совпадающие с бгз:
8г\ = 8г2 = 5гз.
Запишем сумму элементарных работ всех сил, изображенных на
рисунке, на заданном возможном перемещении системы и приравняем ее
нулю:
MigSri - Фзбгз - Ф\5г\ - Ф25г2 = О,
или
MgSr3 - Ма8г3 - Мабгз - Мабгз = 0.
Приравняв коэффициент при (5г3 нулю, получим:
Mg - Ма - Ма - Ма = 0.
Отсюда
1
а =5*
Для определения натяжения нити в сечении аЬ рассмотрим движение
лишь груза «1», заменив отброшенную связь (нить) силой натяжения
нити Т (рис. 2.1.3).

64
Глава 2. Общее уравнение динамики
Ф.
/7/
6т{ Т ai
—> > **
Рис. 2.1.3
Зададим грузу возможное перемещение 8т\ и запишем общее
уравнение динамики:
Т6г{ — Ф,<5п = 0.
Отсюда получаем:
Т5г{ - Ма5г{ = 0 =» Г = Ма = - Mg.
Задача 2.2 (47.2). Решить предыдущую задачу с учетом массы блока,
считая, что при движении грузов блок А вращается вокруг неподвижной
оси. Масса блока — сплошного однородного диска — равна 2М.
Ответ: а
-g, Т = - Mg.
4 4
■*■ Решение. Расчетная схема — на рис. 2.2.1.
Воспользуемся решением задачи 2.1 (47.1). Здесь блок А обладает
массой. Так как блок однородный, то его центр масс лежит на
неподвижной оси вращения Oz. Поэтому после приведения сил инерции точек
блока к его центру масс мы получим лишь главный момент сил инерции,
Ф,
77/
*1 Ф2
Mlg
6т,
M2g
A >,V$
ад
Ш
|M3g
I.
Рис. 2.2.1

Глава 2. Общее уравнение динамики
65
направленный вдоль оси вращения:
LOz = -JozGz = z—б = ~MRa (так как МА = 2М).
2 К
Если грузу «3» задать возможное перемещение 5г3, то блок совершит
угловое возможное перемещение
Запишем общее уравнение динамики системы:
MigSri - Ф3£г3 - |^н)|^ — Ф^Г| — Ф25г2 = О,
или
8т$
MgSr^ - Мабгз - MRa— - MaSr^ - MaSr^ = 0.
К
Отсюда получаем ускорение:
1
a=-g.
Сила натяжения нити в сечении ab:
Т = Ф, = Ма = - Mg.
4
Задача 2.3 (47.3). Два груза массы М\ и М2
подвешены на двух гибких нерастяжимых нитях, которые
навернуты, как указано на рис. 2.3.1, на барабаны,
имеющие радиусы г\ и т2 и насаженные на общую
ось; грузы движутся под влиянием силы тяжести.
Определить угловое ускорение е барабанов,
пренебрегая их массами и массой нитей.
Ответ: е =
М2г2 - М\Т\
Mir? 4- М2т\
•8-
Рис. 2.3.1
*► Решение. Расчетная схема — на рис. 2.3.2.
Активными силами, приложенными к системе, состоящей из грузов,
Невесомых барабанов и нитей, являются силы тяжести грузов. Реакции
связей не изображаем, так как связи идеальные.

66
Глава 2. Общее уравнение динамики
Рис. 2.3.2
Равнодействующие сил инерции точек грузов:
Ф1 = — М\&\, Ф2 = —Мга2.
Выразим величины ускорений грузов через угловое ускорение е
барабанов:
CL\ = Г\€, 0,2 = 7*2£.
Поэтому величины сил инерции имеют вид:
Ф\ = М\Г\Е, Ф2 = М2Г2б.
Зададим барабанам угловое возможное перемещение Sip (из произвольного
текущего положения). Поэтому
8s\ = r\8ip, 8s2 = Г25(р.
Составим общее уравнение динамики системы:
-M\gSs\ - Ф\8з\ + M2gSs2 - Ф2Л52 = 0.
Подставим величины возможных перемещений и сил инерции:
-M\gr\S(p - М\Г\ег\5(р + M2gr2S(p - М2Г2ЕГ25(р = 0.
Приравняв нулю коэффициент при 5<р, получим угловое ускорение
барабанов:
М2Г2 — М\Г\
Мхг\ + М2г\
£•

Глава 2. Общее уравнение динамики
67
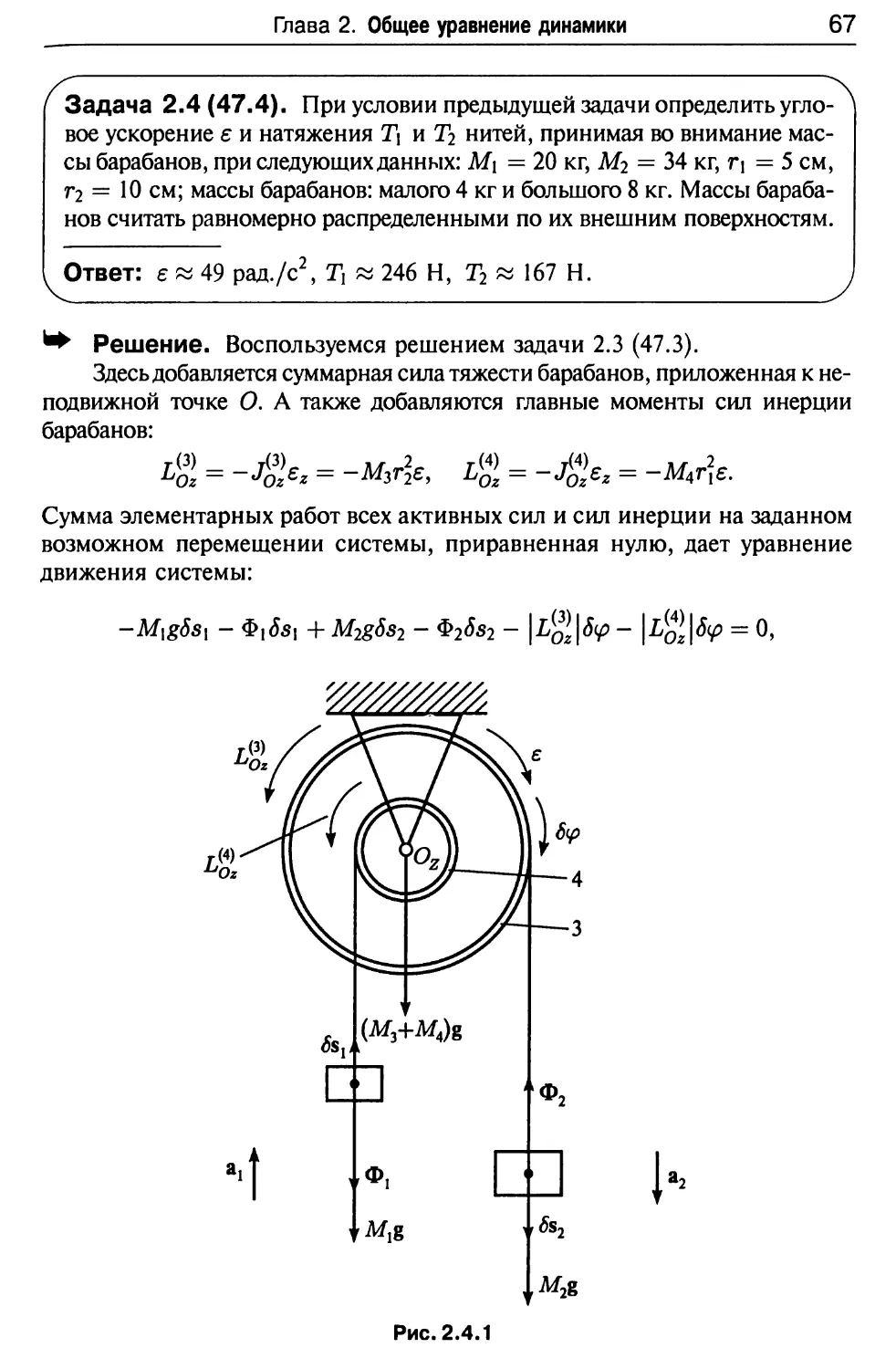
Задача 2.4(47.4). При условии предыдущей задачи определить
угловое ускорение е и натяжения Т\ и Т2 нитей, принимая во внимание
массы барабанов, при следующих данных: М\ = 20 кг, М2 = 34 кг, т\ = 5 см,
Г2 = 10 см; массы барабанов: малого 4 кг и большого 8 кг. Массы
барабанов считать равномерно распределенными по их внешним поверхностям.
Ответ: е и 49 рад./с2, Т{ « 246 Н, Т2 « 167 Н.
^ Решение. Воспользуемся решением задачи 2.3 (47.3).
Здесь добавляется суммарная сила тяжести барабанов, приложенная к
неподвижной точке О. А также добавляются главные моменты сил инерции
барабанов:
г.Р>
-J{3)e
JOz£z
-M3r2e,
г(4)__7(4)
-M4r{e.
"Oz - uOz°z - -'«3'2*, ^Oz - uOzc*
Сумма элементарных работ всех активных сил и сил инерции на заданном
возможном перемещении системы, приравненная нулю, дает уравнение
движения системы:
-Mlg5s{ - Фхб8Х + M2gSs2 - Ф28з2 - \1%я\8<р - |bJ2|fy> = 0,
rWl
Рис. 2.4.1

68
Глава 2. Общее уравнение динамики
+ Ф,
'M,g
Ф2
► I
r6s2
'M2g
Рис. 2.4.2
или
-M\gr\8(p - М\Г\ег\5<р + M2gr25y> - M2r2er25<p - Мзг2е8(р - М^ебр = 0.
Приравняв нулю коэффициент при Sip, вычислим угловое ускорение
барабанов:
М2г2 -Мхг\ Асл 2
£ = г](М1 + М4) + гЦМ2 + М3)8 * 49 Рад"/С •
Для определения сил натяжения Tj и Т2 нитей, рассмотрим отдельно
движение грузов, добавив силы натяжения (рис. 2.4.2).
Зададим грузам соответствующие произвольные возможные
перемещения <5si и <5s2 и запишем для каждого груза общее уравнение динамики:
T\6s\ - M\gSs\ - M\r\e8s\ = 0, -T26s2 + М^5в2 - M2r2e8s2 = 0.
Отсюда получаем:
Г, = Mxg + Mxrxe = Mx(g + ne) « 246 H,
T2 = M2g - M2r2e = M2(g - r2e) « 167 H.
Задача 2.5 (47.5). К системе блоков,
изображенной на рис. 2.5.1, подвешены грузы: М\ массы
10 кг и М2 массы 8 кг. Определить ускорение а2
груза М2 и натяжение нити, пренебрегая массами
блоков.
Ответ: а2«2,8м/с2, Г «56,1 Н.

Глава 2. Общее уравнение динамики
69
//////////////////////////у
\ 'Ф
Ф1
Рис. 2.5.2
♦ Ф,
^ Решение. К системе (два груза, 2 блока и нить) приложены в
качестве активных сил силы тяжести грузов (рис. 2.5.2). Пусть груз массой Mi
движется ускоренно вниз. Тогда сила инерции
Ф = -М\&2
направлена вверх. Точка Р есть мгновенный центр скоростей подвижного
блока. Поэтому
1
а,
= ао = -а2.
И груз массой М\ при нашем предположении движется вертикально
вверх. Величина силы инерции этого груза
<3>i = М\
а2
Заметим, что связи, наложенные на систему, идеальные.
Задав грузу «2» из произвольного текущего положения системы
возможное перемещение 5т (см. рис. 2.5.2), получим возможные перемещения

70
Глава 2. Общее уравнение динамики
4т
to,
i* j,
остальных точек системы:
5гв = Sr9
5г\ = 5го = -5гв
-5г.
2
M2g
Рис. 2.5.3
Общее уравнение динамики системы:
M2g5r - Ф25г - M\gSr\ - Ф\5г\ = 0.
Распишем это уравнение:
M2g5r- M2a2Sr- M\g-Sr — М\---бг = 0.
Приравняв нулю коэффициент при 6г, вычислим ускорение 2-го груза:
о2
хм Ml
М2- —
М2 + —
4
^-Я«2,8(м/с0.
Так как величина а2 получилась положительной, то предположение
о направлении движения верно.
Для определения силы натяжения нити рассмотрим отдельно
движение груза массой М2 (рис. 2.5.3), добавив силу натяжения нити в число
активных сил. Общее уравнение динамики для этого груза имеет вид:
MjgSr - Ф25г - TSr = 0.
Приравняв нулю коэффициент при <$г, получаем:
Г = M2g - Ф2 = M^g - М2а2 = M2(g - а2) « 56,1 Н.
^D
j QB
ЬЫ
Рис. 2.6.1
Задача 2.6 (47.6). К нижнему шкиву С подъемника
приложен вращающий момент М. Определить
ускорение груза А массы М\, поднимаемого вверх, если масса
противовеса В равна М2, а шкивы С и D радиуса г
и массы М3 каждый представляют собой однородные
цилиндры. Массой ремня пренебречь.
Ответ: а
М
— + (M2-M{)g
г
м, + м2 + м3

Глава 2. Общее уравнение динамики
71
а, 4
■* Решение. На рисунке 2.6.2 изобразим активные силы, приложенные
к системе (силы тяжести и вращающий момент), и силы инерции точек
звеньев системы, которые приводятся к силам
Ф! = -М\&\ и Ф2 = -М2а2
для грузов А и В и главным моментам L^"' и L^1"' для шкивов D и С.
Распишем величины:
Ф1 =Af|Oi,
Ф2 = М2а2,
(ин) | _ M3r2 0±
2 г'
1^1 = 1^
Задав грузу А возможное перемещение 6т\, распишем уравнение динамики
системы:
1Л\т Q,\ $Т\ 0Т\
-M\gSr\ - M\d\8r\ + M2gSr\ - M2a\5r\ - 2 h М— = 0.
2 г г г
Отсюда получим:
М
а =
+ (M2-M,)g
/
м1+м2 + м3

72
Глава 2. Общее уравнение динамики
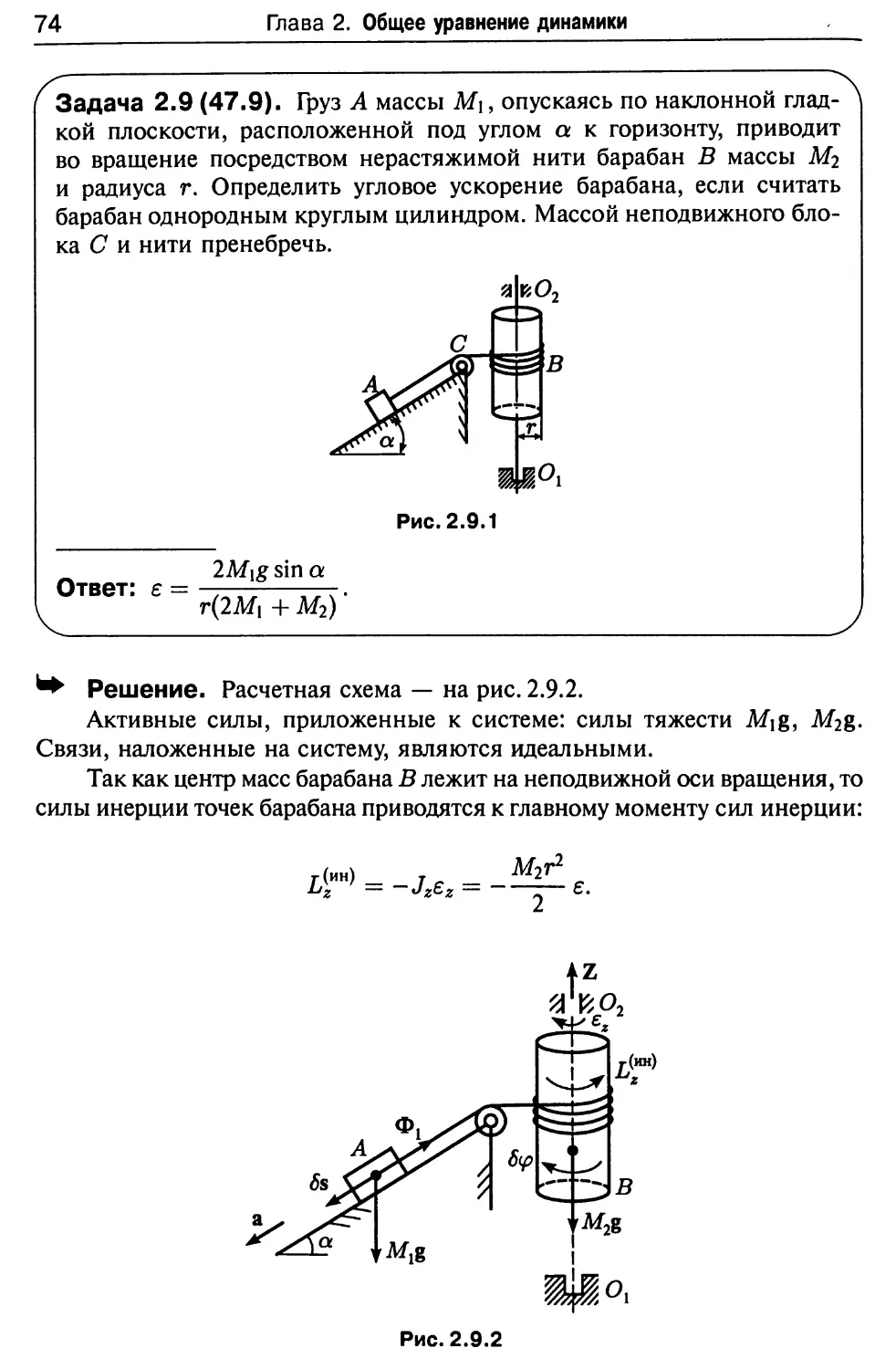
Задача 2.7(47.7). Вал кабестана — механизма для передвижения
грузов — радиуса г приводится в движение постоянным вращающим
моментом М, приложенным к рукоятке АВ. Определить ускорение
груза С массы га, если коэффициент трения скольжения груза о
горизонтальную плоскость равен /. Массой каната и кабестана пренебречь.
А^=
\Т
=?в
77777777777777Я
WW»
Рис. 2.7.1
Ответ: а2 =
М - fmgr
тг
■* Решение. Изобразим на рис. 2.7.2. силы, приложенные к системе:
сила тяжести груза rag, вращающий момент М, реакция шероховатой
поверхности — сила трения
Fw = fN = fmg9
главный вектор сил инерции поступательно движущегося груза
Ф = -та (равнодействующая).
1
////
7777777777/.
Г
N
////
fmg
Рис. 2.7.2

Глава 2. Общее уравнение динамики
73
Если Ss — возможное перемещение груза, то угловое возможное
перемещение вала
6(р — —.
г
Запишем общее уравнение динамики для системы:
М5у - Фбв - FjpSs = 0.
Распишем величины:
Ss
Mi maSs - fmgSs = 0.
г
Приравняв нулю коэффициент при Ss, получим искомое ускорение груза:
М - fmgr
а2 =
тг
Задача 2.8 (47.8). Решить предыдущую задачу с учетом массы
кабестана, момент инерции которого относительно оси вращения равен J.
^ г(М - fmgr)
Ответ: а = -Ц- г—-.
J + mrl
■► Решение. Воспользуемся решением задачи 2.7 (47.7).
Здесь добавится сила тяжести кабестана. Но ее работа на возможных
перемещениях системы равна нулю, так как предполагается, что центр
масс лежит на неподвижной оси вращения. Также добавится главный
момент сил инерции точек кабестана:
Общее уравнение динамики примет вид:
MSip - |4ин)\S<P ~ $Ss ~ F^Ss = 0,
или
Js raSs с .
М J maSs - fmgSs = 0.
г г г
Тогда ускорение груза равно:
r(M - fmgr)
а — — z—.
J + mrz

74
Глава 2. Общее уравнение динамики
Задача 2.9 (47.9). Груз А массы Мь опускаясь по наклонной
гладкой плоскости, расположенной под углом а к горизонту, приводит
во вращение посредством нерастяжимой нити барабан В массы М2
и радиуса г. Определить угловое ускорение барабана, если считать
барабан однородным круглым цилиндром. Массой неподвижного
блока С и нити пренебречь.
Рис. 2.9.1
Ответ: е
2M\g sin а
r(2Mx + М2)'
■* Решение. Расчетная схема—на рис. 2.9.2.
Активные силы, приложенные к системе: силы тяжести Mig, M2g.
Связи, наложенные на систему, являются идеальными.
Так как центр масс барабана В лежит на неподвижной оси вращения, то
силы инерции точек барабана приводятся к главному моменту сил инерции:
Г(ИН)
М2Г2
-J2£z = — е.
Рис. 2.9.2

Глава 2. Общее уравнение динамики
75
Для груза, движущегося поступательно, имеем равнодействующую
сил инерции
Ф| = М\а = M\sr.
Пусть 5<р — возможное угловое перемещение барабана. Тогда груз А
получает возможное перемещение
Ss = г8(р.
Запишем общее уравнение динамики для системы:
MxgSacos(90° + а)-Ф16в- \L{^H)\6ip = 0=>
==> -M\g sin а rSp - М\€г25(р е6<р = 0.
Отсюда
е =
2M\g sin а
г{Жх+М2у
Задача 2.10(47.10). Человек толкает тележку, приложив к ней
горизонтальную силу Е Определить ускорение кузова тележки, если масса
кузова равна М\, Mi — масса каждого из четырех колес, г — радиус
колес, /к — коэффициент трения качения. Колеса считать сплошными
круглыми дисками, катящимися по рельсам без скольжения.
F-J-(Ml+4M2)g
Ответ: а = ^7—ттт •
Мх + 6М2
■► Решение. Расчетная схема — на рис. 2.10.1.
Активные силы, приложенные к системе: силы тяжести кузова
тележки и четырех колес, а также сила Е
M2g
Рис. 2.10.1

76
Глава 2. Общее уравнение динамики
Колеса не проскальзывают, поэтому из реакций связей следует учесть
лишь моменты трения качения колес га& (г = 1, 2, 3,4).
Пусть а — ускорение кузова тележки. Тогда для кузова имеем силу
инерции
Ф = -Mia.
Силы инерции точек каждого колеса приводим к соответствующему
центру масс Ci (i = 1, 2, 3,4) и получаем главный вектор сил инерции
Ф» = -М2ас, = -М2а,
который приложен к точке Q, и главный момент сил инерции
г(ин) _ ,
bCiZ — ~JCiz£z,
где
Мгг1 а
2 г
Зададим кузову тележки возможное поступательное перемещение 6s.
Тогда центры масс колес получат такие же возможные перемещения Ss,
а сами колеса — угловые возможные перемещения
л Ss
так как качение колес происходит без проскальзывания.
Распишем общее уравнение динамики для тележки на заданном
возможном перемещении:
Л^о* a os ^ и s
FSs - M{aSs - 4M2aSs - 4— } ты— = 0. (1)
t=i
Рассмотрим сумму элементарных работ моментов трения качения:
4 S S
- Y, ш*- = -(Л^ + Л^2 + fkN3 + fkN4)- =
.—Г r Т
1=1
= -h(Nl+N2 + N3 + N4)5s = -^ (Mlg + Шя)8з.
г г
Поэтому из уравнения (1) получаем:
Л
F - — (М, 4- 4M2)g
а= Т- .
Mi + 6М2

Глава 2. Общее уравнение динамики
77
Задача 2.11 (47.11). Каток А массы М\, скатываясь без скольжения
по наклонной плоскости вниз, поднимает посредством нерастяжимой
нити, переброшенной через блок В, груз С массы Mi. При этом
блок В вращается вокруг неподвижной оси О, перпендикулярной его
плоскости. Каток А и блок В — однородные круглые диски одинаковой
массы и радиуса. Наклонная плоскость образует угол а с горизонтом.
Определить ускорение оси катка. Массой нити пренебречь.
ас
Рис. 2.11.1
^ М\ sin а - Mi
Ответ: а = g.
2М\ 4- М2
^ Решение. На рис. 2.11.2 изобразим активные силы, приложенные
к системе, — силы тяжести тел А, В и С — и силы инерции. Связи
идеальные, поэтому реакции не изображаем.
Рассмотрим силы инерции.
Силы инерции точек катка А, движущегося плоскопараллельно,
приведем к его центру масс (точка О). Получим главный вектор
Фл = —Mia
Рис. 2.11.2

78
Глава 2. Общее уравнение динамики
Jaz
г(ин)
LAz - "
М{т2
'JAz^Azi
. £а =
а
—»
г
(где a — ускорение оси катка, т.е. точки О), приложенный к точке О,
и главный момент сил инерции
где
так как качение без скольжения). Силы инерции точек блока В приведем
к его центру масс, расположенному на неподвижной оси вращения.
Поэтому получим главный момент сил инерции
ьВг — —Jbz£b>
где
Mir2 а
Jbz = ^ > 6в = Sa = у
Для поступательно движущегося груза С получим равнодействующую
силу инерции
Фс = -М2*с (где ас = а).
Пусть Sso — возможное перемещение центра масс катка А. Тогда
угловое перемещение катка, в силу отсутствия скольжения, равно
, Ss0
г
Угловое возможное перемещение блока В равно
, Ssq
6<Рв = —,
г
линейное возможное перемещение груза С, в силу нерастяжимости нити,
равно Ssc = Sso.
Составим общее уравнение динамики системы:
MigSso cos (90° - а) - Фл^о - \L^ \&<Ра - \1*в? \S(Pb - Mtg&sc - Фс&*с = 0.
Распишем входящие сюда величины:
п, • х *• х МУабво M^aSso %ж , ., г
Mxg sin adso - M{adso M2gds0 - M2ads0 = 0.
ATT ITT
Приравняв нулю коэффициент при Sso, получим уравнение, из которого
выразим искомое ускорение:
Mi sin a — М2
d = я.
2M{+M2 *

Глава 2. Общее уравнение динамики
79
Задача 2.12(47.12). Груз В массы М\ приводит в движение
цилиндрический каток А массы М2 и радиуса г при помощи нити,
намотанной на каток. Определить ускорение груза В, если каток
катится без скольжения, а коэффициент трения качения равен /к.
Массой блока D пренебречь.
Рис. 2.12.1
Ответ: а =
8*(м,-£м2)
шх + зм2
^ Решение. На рис. 2.12.2 изображены активные силы, приложенные
к системе (силы тяжести Mig и Mig), реакция неидеальной связи (момент
трения качения катка гак) и силы инерции: сила инерции груза
Фв = -М,а,
главный вектор сил инерции катка
Фл = -М2ас
и главный момент сил инерции катка
г(ин) _ j
Шу° Js. //&
i
в\~
\
\
[i
Фв
П
t 6s
rMjg
Рис. 2.12.2

80
Глава 2. Общее уравнение динамики
Здесь, в силу отсутствия скольжения катка А,
1 а
ас =
Момент инерции катка
ас=2а> £=2т
М2г2
Jcz = —Z~-
Пусть 5s — возможное перемещение груза В. Тогда центр масс С
катка А переместится на 5sc = Ss/2, а сам каток повернется на элементарный
угол Sip = Ss/(2r).
Составим общее уравнение динамики системы:
M\g5s - Фвбв - Фа^с - mK5ip - |l^" |<fy> = 0. (1)
Момент трения качения
тк = fKN = fKM2g,
так как центр масс С катка движется горизонтально.
Распишем все величины в уравнении (1):
a Ss 5s М2Г2 a 5s
Mlg5s - Mxa5s -M2--- fKM*- - ~^YtYt = °'
Приравняв нулю коэффициент при возможном перемещении 6s, получим
уравнение, из которого определим искомое ускорение:
8g
а = —
(м, - £м2)
8М, + ЗМ2
Задача 2.13(47.13). Стержень DE массы М\ лежит на трех
катках А, ВнС массы М2 каждый. К стержню приложена по горизонтали
вправо сила F, приводящая в движение стержень и катки. Скольжение
между стержнем и катками и также между катками и горизонтальной
плоскостью отсутствует. Найти ускорение стержня DE. Катки считать
однородными круглыми цилиндрами.
D Е F
Ответ: а =
Рис. 2.13.1
8F
8Afi + 9М2

Глава 2. Общее уравнение динамики
81
ф1
1
1
Ф2 ( Oj*p\fj
A^f
/ / / /
У
' Б
им
г(ин)
rM2g
К
11""^
Рис. 2.13.2
а ^
?".
—-
г
F
■Ф* Решение. Расчетная схема — на рис. 2.13.2.
Активные силы, приложенные к системе (стержень и 3 катка): сила
F, сила тяжести стержня M\g и три силы тяжести катков, равные M2g
и приложенные к соответствующим центрам масс.
Связи, наложенные на систему, — идеальные.
Пусть а — ускорение стержня. Тогда, в силу отсутствия
проскальзывания, ускорения центров всех трех катков равны
оо = ",
и угловые ускорения катков равны
2г
Так как стержень движется поступательно, то для него сила инерции
Ф1 = -Mia.
Так как катки одинаковы и движутся одинаково (плоскопараллельно), то
для каждого из них получаем главный вектор
Ф2 = -М2а0
и главный момент сил инерции катка
г(ин)
bOz
-Joz^z
(*■-¥)•
Зададим стержню из произвольного текущего положения возможное
перемещение Ss. Центры масс катков получат возможные перемещения
5s0 = Ss/2. Угловые перемещения катков равны Stp = Ss/(2r).
Составим общее уравнение динамики системы:
FSs -Ф{8з- ЗФ2*50 - 3|Z#2H) \6ip = 0.

82
Глава 2. Общее уравнение динамики
Распишем величины:
a Ss Mir2 a 5s
FSs - Mxa8s - ЗМ2-- - 3-2- — — = 0.
2 2 2 2r2r
Поэтому искомое ускорение:
8F
а =
8Afi -f 9М2
Задача 2.14 (47.14). Определить ускорение груза М2,
рассмотренного в задаче 47.5, с учетом массы блоков — сплошных однородных
дисков массы 4 кг каждый.
. Ответ: а2 « 0,7 м/с2.
■Ф* Решение. Расчетная схема — на рис. 2.14.1.
Воспользуемся решением задачи 2.5 (47.5). Здесь добавятся сила
тяжести неподвижного блока, приложенная к неподвижной точке, и сила
тяжести подвижного блока, приложенная к подвижной точке О.
Угловое ускорение £з неподвижного блока равно
а2
е3 = —.
Г"*
Угловое ускорение £4 подвижного блока равно
а2
Ускорение центра масс О подвижного блока и груза «1» равны
1
2'
Для неподвижного блока имеем главный момент сил инерции
U0 = й\ = ~02-
Art" = "^3^3* ( Лз = —Т— ) •
Для подвижного блока имеем главный вектор
Ф0 = -М3а0
и главный момент сил инерции
LZ4 = -Jz4^4z ( JzA = -~Z~ ) •

Глава 2. Общее уравнение динамики
83
///////////////////////////
Пусть Ss2 — возможное перемещение груза массой Mi. Тогда:
5^2 с 1 с с Ss2
д(р3 = —, 6s{ = 6s0 = -ds2, ova = -г-.
г 2 2т
Общее уравнение динамики системы принимает вид:
г ж X ъж X Мзг2 а2 SS* лж SS* лж а2 6s2
1 Г Г 2 2 2
ъж SS* лж fl2 Ss2 М^ а2 SS2 .
- M3g— - М3 — — — — = 0.
2 2 2 2 2r 2г
Приравняв нулю коэффициент при <fe2> получим уравнение, из
которого определим искомое ускорение:
а2
(м2- -М\ - -M3)g
Л _ _ L- -0 7
1 _ 7 U'7
м/с2.
AM{+M2 + - M3
4 8

84
Глава 2. Общее уравнение динамики
Задача 2.15(47.15). Груз А массы М\, опускаясь вниз,
посредством нерастяжимой нити, переброшенной через неподвижный блок D
и намотанной на шкив В, заставляет вал С катиться без
скольжения по горизонтальному рельсу. Шкив В радиуса R жестко насажен
на вал С радиуса г; их общая масса равна Мг, а радиус инерции
относительно оси О, перпендикулярной плоскости рис. 2.15.1, равен
р. Найти ускорение груза А. Массой нити и блока пренебречь.
Рис. 2.15.1
Mx{R-rf
ТВеТ" а Ml(R-r)2 + M2(r2 + p2)8'
■Ф" Решение. Расчетная схема — на рис. 2.15.2.
Связи, наложенные на систему, — идеальные, поэтому изображаем
лишь активные силы (силы тяжести M\g и Mig) и силы инерции: для
груза силу
Ф] = — М\&,
для шкива с валом главный вектор сил инерции
Ф2 = -М2ао
и главный момент сил инерции
Лин) _ _ т
bOz ~ JOz£z-
Так как вал катится без скольжения, то в точке его касания Р с
неподвижной опорой находится мгновенный центр скоростей. Поэтому
имеем соотношения:
ак = а
(так как нить нерастяжимая);

Глава 2. Общее уравнение динамики
85
|Mlg
Рис. 2.15.2
Следовательно,
Ф1 = Mi а, <&2 = М2а
\№\ = м2Р2 а
R-r9
R-r
Если 5s — возможное перемещение груза А, то
5s0 = 5s- , 5(р=- .
R-r R-r
Запишем общее уравнение динамики системы:
MigSs - Фхбв - Ф2550 - |1^н)|5<р = О,
или
Г Г 2 1
M\g5s - M\aSs - М2а——-5s т;—z ~ ^iP ат^ ~^s — О-
'R-r~~ R-r ~"'r ~(R-r)2
Приравняв нулю коэффициент при 5s, определим ускорение груза А:
Mx(R-r)2
а =
М,(Я-г)2 + М2(г2 + р2)
g-

86
Глава 2. Общее уравнение динамики
Задача 2.16 (47.16). Центробежный регулятор вращается вокруг
вертикальной оси с постоянной угловой скоростью и. Определить
угол отклонения ручек О А и ОВ от вертикали, принимая во внимание
только массу М каждого из шаров и массу М\ муфты С, все стержни
имеют одинаковую длину I.
Ответ: cos (р ■■
М + Мх
М1Ш2 '
■* Решение. Расчетная схема — на рис. 2.16.2.
Связи, наложенные на систему — идеальные. К активным силам
относятся три силы тяжести.
Найдем силы инерции шаров А и В и муфты С, которые считаем
материальными точками. Так как регулятор вращается равномерно, то
угол <р не меняется. Поэтому муфта С неподвижна, а шары А и В имеют
только нормальные составляющие ускорения:
ас = 0, а\ = а# = сЛ sin <р.
Следовательно для сил инерции точек А9 В и С имеем:
Фа = Ма!д = Мш21 sin <р,
Фв = Мав = Мш21 sin <р,
Фс = Мае = 0.
Из произвольного текущего положения системы дадим стержням АО
и ВО возможное угловое перемещение 5<р вокруг оси, проходящей через
точку О перпендикулярно плоскости стержней, что наложенные связи
позволяют. Тогда точки А и В совершат возможные перемещения
6га = 8гв = lS<p.

Глава 2. Общее уравнение динамики
87
Ош
Sip*
Ч>
6тл
_^Д fc
1 dip
бТп
• V^**^
в
6тс/ \м%
*в
Mlg
Рис. 2.16.2
Для определения возможного перемещения 5гс точки С
построим мгновенный центр вращения стержня АС (точка Р на рис. 2.16.2).
Поэтому имеем:
бгд 18<р
fire = -=-т PC = — 21 sin (р = 21 sin ipSip.
г л i
Составим общее уравнение динамики регулятора:
MgSrA cos (90° -f (р) + Фа^га cos ip +
+Mg5rB cos (90° -f <p) + Фв<5г5 cos y? - M\g5rc = 0.
Или
-2Mg sin (p • W<p + 2Mu?l2 sin (p cos ip - 5(p- M\g2l sin (p- Sep = 0.
Приравняем нулю коэффициент при <5<р:
-2Mgl sin <р + 2Mw2l2 sin (pcoscp - 2M\gl sin <£> = 0.
Так как sin ^ ^ 0, то получаем:
M + M,
cosy? =
Mlu2
-g-

88
Глава 2. Общее уравнение динамики
Задача 2.17 (47.17). Центробежный регулятор
вращается с постоянной угловой скоростью и).
Найти зависимость между угловой скоростью
регулятора и углом а отклонения его стержней
от вертикали, если муфта массы М\
отжимается вниз пружиной, находящейся при а = О
в недеформированном состоянии и закрепленной
верхним концом на оси регулятора; массы шаров
равны М2, длина стержней равна /, оси подвеса
стержней отстоят от оси регулятора на
расстоянии а; массами стержней и пружины пренебречь.
Коэффициент жесткости пружины равен с.
Ответ:
Ь)
(М{ + M2)g + 2lc(\ - cos а)
M2(a + l sin а)
tga.
■► Решение. Расчетная схема — на рис. 2.17.2.
Действие пружины, как неидеальной связи, заменим силами
упругости Fynp в точке С и F^np в точке D.
Причем
ГуПр — Fynp — ел.
Деформацию А сжатия пружины найдем, используя условие, что при
а = 0 пружина недеформирована:
А = 2(Z — /cos а).
Используя решение задачи 2.16 (47.16), выпишем силы инерции точек А,
В и С:
Фа = MidUX = М2и)2(а +1 sin a),
Фв = М2ав = M2u2(a + I sin a),
Фс = M\(Lc = 0.
Задав возможное угловое перемещение 5а стержням AD\ и BD2f
получим следующие возможные перемещения точек А, В и С:
5гА = бгв = 15а,
5гс = 21 sin аба,
5rD = 0.
Распишем общее уравнение динамики системы:
2М^5гА cos (90° + а) + 2ФA5rA cos а - Mxg5rc - Fyup5rc = 0 =>

Глава 2. Общее уравнение динамики
89
Рис. 2.17.2
=> -2M2gsina-l6a+2M2u)2(a+lsma) cosa-15а-2M\glsma* 5а-
-2d(l-cosa)-2Zsina-(Ja = 0=^-M2^sinQ: + M2a;2(a + Zsina)cosa-
-Migsina-2d(l-cosa)sina = 0==^
=> -M2g+M2W2(a+ls\na)ctga-M\g-2cl(\ -cosa) = 0,
так как, очевидно, sin а Ф 0.
Отсюда получаем:
2 (Mi + M2)g + 2Zc( 1 - cos a)
a; = — — tga.
M2\a + Ism a)

90
Глава 2. Общее уравнение динамики
Задача 2.18(47.18). Центробежный
пружинный регулятор состоит из двух грузов А
и В массы М каждый, насаженных на
скрепленный со шпинделем регулятора гладкий
горизонтальный стержень муфты С массы
Mi, тяг длины I и пружин, отжимающих
грузы к оси вращения; расстояние
шарниров тяг от оси шпинделя равно е, с —
коэффициент жесткости пружин.
Определить угловую скорость регулятора при угле
раствора а, если при угле а0, где а0 < а, пружины находятся в
ненапряженном состоянии; массой тяг и трением пренебречь.
Ответ: ш
I M\g tg а + 2cZ(sin а - sin а0)
2М(е + I sin а)
■* Решение. Расчетная схема — на рис. 2.18.2.
Пружины, как неидеальные связи, заменим силами упругости Fy^
и Fynp£. Причем Fynp.4 = FynpB = сА. Деформации А сжатия пружин
найдем из условия, что они недеформированы при угле ао < а:
А = /sinа - / sin а0 = /(sinа - sinа0).
А SrA aj
Рис. 2.18.2

Глава 2. Общее уравнение динамики
91
Выпишем величины сил инерции точек А, В и С:
Фа = Ма\ = Ми2(е + / sin а),
Фв = М2ав = Мш2{е + I sin а),
Фс = M\dc = 0.
Пусть 5тс — возможное перемещение муфты С. Тогда, построив
мгновенный центр вращения стержня АС (точка Р на рис. 2.18.2), найдем
возможное перемещение точки А:
8rc I cos а
PC I sin а
В силу симметрии бгв = 5га.
Выпишем общее уравнение динамики системы:
M{g5rc - Фа&га + FynpA • 6гА - Фв5гв + FynpB • SrB = 0, или
M\g5rc - 2Ми2(е + I sin a) ctg а • бгс + 2c/(sin а - sin а0) ctg а • <$гс = 0.
Отсюда получаем:
LJ :
(Mig tg а + 2cZ(sin а - sin а0)
2М(е + / sin а)
Задача 2.19(47.19). В регуляторе четыре груза одинаковой массы
М\ находятся на концах двух равноплечих рычагов длины 21, которые
могут вращаться в плоскости регулятора вокруг конца шпинделя О
и образуют с осью шпинделя переменный угол <р. В точке Л, на-
хощейся от конца шпинделя О на расстоянии
ОА = а, со шпинделем шарнирно соединены
рычаги АВ и АС длины а, которые в точках
В и С в свою очередь сочленены со стержнями
BD и CD длины а, несущими муфту D. В
точках В и С имеются ползунки, скользящие вдоль
рычагов, несущих грузы. Масса муфты равна
М2. Регулятор вращается с постоянной угловой
скоростью и). Найти связь между углом и
угловой скоростью ш в равновесном положении
регулятора.
Ответ: и =
2M2ga
Md2 *

92
Глава 2. Общее уравнение динамики
Рис. 2.19.2
■Ф Решение. Расчетная схема — на рис. 2.19.2.
Активные силы, приложенные к системе, — это силы тяжести грузов
(точек К\, К2, Кз и К4), равные M\g, и сила тяжести муфты D, равная
Mig. Связи, наложенные на систему идеальные.
При равновесном положении регулятора, когда и = const и угол
<р = const, ускорение муфты D равно нулю, а грузы в точках К{ (г = 1,2,3,4)
имеют лишь нормальные составляющие ускорений, равные
ап = u2l sin (р
и направленные перпендикулярно в сторону вертикальной оси вращения.
Поэтому величины сил инерции в точках следующие:
Фя = M2aD = О,
Ф#. = М\ап = М\и I sin (p.
Дадим системе возможное перемещение: повернем рычаги на
элементарный угол 8ip. Грузы К{ получат возможные перемещения Ssi = IScp

Глава 2. Общее уравнение динамики
93
(г = 1,2,3,4). Для определения возможного перемещения точки D
рассмотрим сначала перемещение ползуна В как сложное перемещение:
Ssb = Ssse + SsBr
(см. рис. 2.19.2).
Абсолютное возможное перемещение Ssb перпендикулярно стержню
АВ. Переносное возможное перемещение перпендикулярно рычагу ОКз
и равно по величине
Ssse = OBSip = 2а cos ip • Sip.
Относительное возможное перемещение 8sbv направлено вдоль рычага
(Жз- Из векторного треугольника нетрудно вычислить:
Ssse 2а cos if • Sip
Ssb = = = 2aSip.
cos ip cos (p
Теперь построим мгновенный центр вращения Р стержня BD. Он
находится на пересечении перпендикуляра в точке D к вектору Ssd и
продолжения стержня АВ.
Поэтому
PD ADiglip
SsD = Ssb— = ЛврдГдА =
. AD-tg2<p 2acos2<p-tg2ip .
= osb—jt; = 2a- dip = 4a sin 2</? • dip.
AU _ BA 2a cos 2ip
cos2^ cos2y? ~a
Общее уравнение динамики регулятора:
2M\gSs\ cos (90° - <p) + 2<I>i<5si cos ip +
+ 2Mig(5s3 cos (90° + ip) + 2Ф3 J53 cos <p - M2g • <5$я = 0.
Распишем входящие сюда величины:
2M\gsinip-lSip + 2M\u?lsinipcosip-l-Sip- 2M\gsinip-l5ip +
+2M\u2lsinipcosip-l-Sip- M2g• 4asin2ip-5ip = 0.
Приравняем нулю коэффициент при &р:
4Mia>2Z2 sin ip cos (р- AM^ga sin 2<p = 0.
Отсюда получаем:
/2M2ga
W = V Mr?"'

Таблица соответствия номеров задач
из «Сборника задач» И. В. Мещерского и глав 3, 4 данного пособия
№задач
«Сборника задач»
И. В. Мещерского
1 48.1
48.2
1 48.5
48.6
48.7
| 48.9
| 48.10
48.13
48.14
48.17
48.19
48.23
48.24
48.26
48.27
48.28
48.29
48.30
48.31
48.33
48.34
48.35
48.37
глав 3, 4
данного пособия
3.1
3.2
3.3
3.4
3.5
3.6
3.7 |
3.8 |
3.9 |
3.14 |
зло 1
3.11 |
3.12
3.15 |
3.16 |
3.22 |
3.23 1
3.17 |
3.18 |
3.19 |
3.20 |
3.21
3.24 |
«Сборника задач»
И. В. Мещерского
1 48.38
1 48.39
| 48.40
1 48.41
| 48.42
1 48.43
48.44
J 48.48
1 48.49
| 49.1
49.2
| 49.3
1 49.4
| 49.5
49.7
1 49.8
49.11
49.12
49.13
49.14
49.15
49.16
глав 3, 4
данного пособия
3.31
3.28
4.5
3.27
3.13
3.25 1
3.26 1
3.29 1
з.зо 1
4.1 |
4.2 |
4.3 |
4.4 1
4.6 1
4.7
4.8 1
4.9 1
4.10 |
4.11 1
4.12 1
4.13 |
4.14 |

Глава 3
Уравнения Лагранжа 2-го рода (§48, [1])
Задача 3.1 (48.1). Передача вращения между двумя валами
осуществляется двумя зубчатыми колесами, имеющими соответственно z\ и z2
зубцов, моменты инерции валов с насаженными на них колесами
соответственно равны J\ и J2. Составить уравнение движения первого
вала, если на него действует вращающий момент М\, а на другой вал —
момент сопротивления М2. Трением в подшипниках пренебречь.
Ответ: (J{ + i2J2)(p = Мх - iM2.
■* Решение. Система имеет одну степень свободы. Если принять в
качестве обобщенной координаты угол поворота первого вала щ, то угол
поворота второго вала определяется из равенства (рис. 3.1.1)
22<Р2 = 21</>1. (О
Уравнение движения первого вала составим с помощью уравнений
Лагранжа 2-го рода. Для рассматриваемой системы имеем
£(—\ - — -п
сИ\дф\/ дф\
где Г — кинетическая энергия системы, Q — обобщенная сила системы.

96
Глава 3. Уравнения Лагранжа 2-го рода
Система состоит из двух твердых тел, которые вращаются вокруг
неподвижных осей. Поэтому
T=-Jx<p\ + -J2<p\,
или с учетом равенства (1)
Далее находим
T=-{Jx+i2J2)<p2u где г=-.
1 Z2
d (дТ\ . .2 т. .. дТ л
dt \дф\)
д<Р\
Обобщенная сила системы определяется приложенными моментами
М\ и М2. Подсчитывая работу 5А, которую совершают моменты М\ и М2
на возможном перемещении 5<р\, находим
SA Мх8ух - М28(р2 __ ....
Q = т— = с =МХ- гМ2.
о<Р\ 6<pi
В результате получаем искомое уравнение движения первого вала
(Ji + i2 J2)<£ = Mi - iM2.
rife*»
Задача 3.2(48.2). Барабане
центрифуги приводится во
вращение электродвигателем ЭД
через двухступенчатый редуктор.
Заданы момент инерции J0
электродвигателя, момент инерции
J2 барабана, момент инерции J\
промежуточного вала
редуктора, передаточные числа щ и i\2
ступеней редуктора (рис. 3.2.1).
К ротору электродвигателя
приложены вращающий момент Мо
и момент сопротивления Mq,
к валу редуктора и к барабану —
моменты сил сопротивления М[
и М2, соответственно. Составить дифференциальное уравнение
вращения барабана центрифуги.
Рис. 3.2.1
Ответ: (J0toi*i2 + ^1*12 + Зг)Ф = (М0 - MjJMu - Мл*\2 - М2.

Глава 3. Уравнения Лагранжа 2-го рода
97
^Ф Решение. Система имеет одну степень свободы. Приняв в качестве
обобщенной координаты угол поворота барабана центрифуги </?, представим
<А) = *01^1 = io\i\2<P-
Уравнение движения барабана центрифуги составим с помощью
уравнений Лагранжа 2-го рода
£(—\ - — -О
М\дф) d<p~Q'
где Г — кинетическая энергия системы, Q — обобщенная сила системы.
Рассматриваемая система состоит из трех твердых тел
(электродвигателя, вала редуктора и барабана центрифуги), которые вращаются вокруг
неподвижных осей. Поэтому
или с учетом равенств (1)
r=-(Jo^,i?2 + J,i?2 + J2)02.
Обобщенная сила системы определяется вращающим моментом М0
и моментами сопротивления М'0, М[ и Мг2. Подсчитывая работу 5А,
которую совершают моменты М0, Mf0, М[ и М2 на возможном перемещении
5(р, находим
SA (М0- Щ)8<рр - M[6<pi - M'26ip
Sip 5<р
= (Mo - M'0)io\i\2 - M[i\2 - M*2.
Учитывая полученные выражения, записываем
dt
/ йгГ\ f¥P
и составляем искомое уравнение вращения барабана центрифуги
(Jo*oi*?2 + J\in + Ji)4> = (мо ~ М'0)ц\Ц2 - M\iX2 - М2.

98
Глава 3. Уравнения Лагранжа 2-го рода
Задача 3.3(48.5). Определить движение
груза массы т, висящего на однородном тросе
массы гп\ и длины / (рис. 3.3.1). Трос
навернут на барабан радиуса а и массы Ш2.
Ось вращения горизонтальна. Трением
пренебречь. Массу барабана считать равномерно
распределенной по его ободу. В начальный
момент t = О система находилась в покое,
длина свисавшей части троса Iq.
Ответ: х
ml
+
ТП\
(lo+^)ch\f
m\g
(m + 771] + ТП2)1
t.
■► Решение. Система имеет одну степень свободы и находится в
потенциальном силовом поле. Запишем уравнение движения груза с помощью
уравнений Лагранжа 2-го рода, приняв х в качестве обобщенной координаты:
\ дх ) дх
d_(dL
Jt
О,
где L — функция Лагранжа
L = Т - П,
Г — кинетическая энергия системы, П — потенциальная энергия системы.
Система состоит из груза, тяжелого троса и барабана. Поэтому
_ 1 2 1 2 1 2
Т = -тпх + -ТП\Х + -Ju) .
2 2 2
Учитывая, что
получаем
т 2 х
J = тг& , и = —,
а
1 ,*
Т = -(тп + ГП\ + тп2)х .
Потенциальную энергию определяют силы тяжести груза и свисающего
с барабана троса
тт f m» л m*8 2
П = -mgx - / —ж ах = -mgx —х .
о
I
21

Глава 3. Уравнения Лагранжа 2-го рода
99
Таким образом, находим
К \ .2 т\8 2
L = -(га + гп\ + т2)х + mgx + ~^гх >
— = (га+га,+га2)±, —I — 1 =(ra + mi + ra2)x, — = rag+raigy,
и уравнение движения груза принимает следующий вид
m\g
х —
-х •
= 0.
(га + ТП[ + ra2)Z (га + тп\ + га2)
Интефируя это уравнение в пределах, указанных условием задачи, получим
ml / raZ\ /
7П\ \ Ш\) V
™>\g
(га + raj + га2)/
*.
Задача 3.4(48.6). В
эпициклическом механизме бегающая
шестеренка радиуса г\ насажена на
кривошип с противовесом, который
вращается вокруг оси неподвижной
шестеренки под действием
приложенного момента М(рис. 3.4.1).
Определить угловое ускорение
вращения кривошипа и окружное
усилие S в точке касания шестеренок,
если расстояние между осями
шестеренок равно I, момент инерции
кривошипа с противовесом
относительно оси вращения кривошипа
равен J0, масса бегающей
шестеренки гп\, момент инерции
шестеренки относительно ее оси J\. Трением пренебречь; центр масс
шестеренки и кривошипа с противовесом находится на оси вращения
кривошипа.
Рис. 3.4.1
Ответ: е ■
М
I
J0+m{l2 + Jxl7
F'5 = Ji30.
■► Решение. Для определения углового ускорения вращения
кривошипа используем уравнения Лафанжа 2-го рода. Рассматриваемая
система имеет одну степень свободы, и если принять в качестве обобщенной

100
Глава 3. Уравнения Лагранжа 2-го рода
координаты угол <р, то уравнение движения кривошипа можно
представить в следующей форме:
dt\d<p) d<p~Q'
(1)
где Т — кинетическая энергия системы, Q — обобщенная сила системы.
Учтем, что система состоит из двух движущихся твердых тел
(кривошипа с противовесом и бегающей шестеренки). Причем кривошип
с противовесом вращается вокруг неподвижной оси, а движение
бегающей шестеренки — плоское. Поэтому
1
1
1
где V\ — скорость центра масс бегающей шестеренки (точки 0\)
V, = ф19
и\ — угловая скорость бегающей шестеренки.
Бегающая шестеренка находится в зацеплении с неподвижной
шестеренкой. Следовательно, в точке касания шестеренок (К на рис. 3.4.2)
находится мгновенный центр скоростей бегающей
шестеренки. Поэтому
Vi , .1
С учетом полученных выражений для V\ и ш\ будем иметь
р
Jo + m\lz + J\-
Рис. 3.4.2
и, следовательно,
r=-fj0 + m1/24-Ji^J^2,
dfdT\ / ;2 Р\ ОТ л
(2)
В условии задачи предполагается, что обобщенную силу системы определяет
только приложенный к кривошипу момент М Подсчитывая работу 8А,
которую совершает этот момент на возможном перемещении 5<р, находим
8 A MS(p
(3)
Подставив выражения (2), (3) в уравнение (1), определяем угловое
ускорение вращения кривошипа
М
ч>-
J0 + mi/2 +Ji-j

Глава 3. Уравнения Лагранжа 2-го рода
101
Окружное усилие находим, приравняв момент от окружного усилия
Sr\ моменту от сил инерции бегающей шестеренки J\U\\
Задача 3.5 (48.7). В планетарном механизме колесо с осью 0\
неподвижно (рис. 3.5.1). К рукоятке 0\Оз приложен вращающий момент М.
Механизм расположен в горизонтальной плоскости. Определить
угловое ускорение рукоятки, считая колеса однородными дисками с
одинаковыми массами га и радиусами г и пренебрегая массой рукоятки.
Рис. 3.5.1
Ответ: е\ =
М
22тг2'
Рис. 3.5.2
■* Решение. Расчетная схема — на рис. 3.5.2.
Угловое ускорение рукоятки определим с помощью уравнений
Лагранжа 2-го рода. Рассматриваемая система имеет одну степень свободы. Выберем
в качестве обобщенной координаты угол поворота рукоятки (р и представим
уравнение движения системы в следующей форме:
dt\d<p) dip
Q,
(1)
где Т — кинетическая энергия системы, Q — обобщенная сила системы.

102
Глава 3. Уравнения Лагранжа 2-го рода
Система состоит из двух движущихся и имеющих массу твердых тел
(колес с центрами в точках 02 и Оз). Поэтому
Т = Т2 + Т3, (2)
где Т — кинетическая энергия системы; Г2,Т3 — кинетические энергии
колес с центрами в точках 02 и Оз, соответственно.
Движение колеса с центром в точке 02 плоское. Следовательно,
1 ? 1 9
Т2 = ~mV{ + -М,
где V2 — скорость центра масс колеса; и2 — угловая скорость колеса; J —
момент инерции колеса относительно оси, проходящей через точку 02:
J = -mr2.
2
Точка 02 является общей для колеса и рукоятки, которая вращается вокруг
точки 0\ с угловой скоростью ф. Поэтому (рис. 3.5.2)
V2 = фО\02 = 2фг.
Колесо с центром в точке 02 находится в зацеплении с неподвижным
колесом. Следовательно, в точке К касания колес находится мгновенный
центр скоростей колеса с центром в точке 02. Поэтому
Уг ..
и2 = — = 2ф.
г
Таким образом, выражение для кинетической энергии колеса с центром
в точке 02 принимает вид
Т2 = Зтпг2ф2.
Прежде чем находить кинетическую энергию колеса с центром в точке
Оз, выясним, к какому виду движения твердого тела относится движение
этого колеса. Определим скорости его точек Оз и N. Полагая, что точка
Оз принадлежит рукоятке, а точка N — колесу с центром в точке 02,
находим
Vz = фО\Оз = 4фг,
Vn = u2KN = 4фг.
Как видно, скорости точек Оз и N равны по величине и направлению.
Это означает, что колесо с центром в точке Оз, которому принадлежат
точки Оз и N, движется поступательно. Следовательно,
Г3 = -mV2 = Ътг2ф2.

Глава 3. Уравнения Лагранжа 2-го рода
103
Возвращаясь к равенствам (1) и (2), будем иметь
, л d /дТ\ , ОТ
В условии задачи предполагается, что обобщенную силу системы
определяет только приложенный к рукоятке момент М. Определяя работу 5А,
которую совершает момент М на возможном перемещении 6<р, находим
SA М5<р
8(р 5(р
(4)
Подставляя выражения (3) и (4) в уравнение (1), получим угловое
ускорение вращения рукоятки
М
Задача 3.6(48.9). Груз М массы 101 кг поднимает
с помощью полиспаста груз М\, который вместе с
подвижной обоймой имеет массу 320 кг (рис. 3.6.1). Всех
блоков четыре, большие блоки имеют массу по 16 кг,
малые — по 8 кг, радиусы больших блоков равны г,
радиусы малых равны г\. Определить ускорение груза М.
При определении энергии блоков предполагаем, что
массы их равномерно распределены по окружности.
Ответ: а = 0,lg.
Рис. 3.6.1
■► Решение. Расчетная схема — на рис. 3.6.2.
Определим ускорение груза М с помощью уравнений Лагранжа 2-го рода.
Система имеет одну степень свободы и находится под действием сил тяжести
грузов My М\ и подвижных блоков. Приняв в качестве обобщенной
координаты перемещение х\ груза М, запишем уравнение движения
рассматриваемой системы в виде
d/ST
dt \дх
Ь\) дх\
(о
где Т — кинетическая энергия системы, Q — обобщенная сила системы.

104
Глава 3. Уравнения Лагранжа 2-го рода
б)
г)
Рис. 3.6.2
Так как система состоит из шести движущихся твердых тел (двух
фузов, двух подвижных и двух неподвижных блоков), представим ее
кинетическую энергию суммой
6
где Т\, Т2 — кинетические энергии фузов М и М\\ Г3, Г4 — кинетические
энергии малого и большого подвижных блоков; Ts,T(> — кинетические
энергии малого и большого неподвижных блоков.
Грузы М и М\ движутся поступательно. Поэтому
Г, = \mxVl Т2
\m2Vl
где тп\, V\ — масса и скорость фуза М; mi, V2 — масса и скорость фуза М\.
Движение подвижных блоков плоское, а неподвижных —
вращательное вокруг неподвижных осей. Следовательно,
1
1
1
1
1
1
Г3 = -m3V3z + -J3ui, Т4 = -mAVt + -JAul Т5 = -J5ui, Т6 = -J6lS6,

Глава 3. Уравнения Лагранжа 2-го рода
105
где шз, га4 — массы малого и большого подвижных блоков; J3, J4, «/5, «/б —
моменты инерции подвижных и неподвижных блоков относительно их
осей вращения: J3 = J5 = m^r], J4 = Je = m^2, V^V^ — скорости
центров масс малого и большого подвижных блоков; о^оч, ^5,^6 — угловые
скорости вращения подвижных и неподвижных блоков.
Учтем, что (рис. 3.6.2)
Топ,
г,=
ъ--
Ть--
^3
w3 = — =
да
1 .2
= -77111!,
1 .2
= 32W3X| +
1 2х]
= 2тзГ|4^
4ri'
-ТПзГ,
v,=
W4 :
1 .2
= -m3Xi,
= я?ь
ЗУ4
г
^2 = ^з =
3±i
Аг '
т2=
1 .2 m
= T7m3x\> -М =
т6=
= ^4
U5 =
1
"32
1
"32
1
ГП2Х\,
ТП4Х\ +
1 2х]
*1
^6
16г2"
= -т4хь
- *1
10
32
7714^1,
Т=—(16mi+m2+2m3 + 10m4+4m3+16m4)a;i =—(16mi+m2+29m4)i?.
I(i;) = ii(,6mi+m2+29m^" fr°- (2)
Подсчитывая работу 5А, которую совершают силы тяжести грузов М,
Mi и подвижных блоков на возможном перемещении 6х\, находим
обобщенную силу системы
6А u^-(m2 + -m4)g6x4 3 W (3)
~- I m2 + -m4 j
dxi ox\ V 2 у 4
Подстановка выражений (2) и (3) в уравнение (1) дает
—(16mi + ™>2 + 29m4)£i = raig - ( m2 + -m4 J -.
Отсюда, подставив численные значения масс грузов и блоков, определяем
ускорение груза М
а = х\ = Q,\g.

106
Глава 3. Уравнения Лагранжа 2-го рода
Рис. 3.7.1
Задача 3.7(48.10). В машине для
статического уравновешивания роторов
подшипники наклонены под углом а к вертикали
(рис. 3.7.1). Ротор, помещенный в
подшипник, имеет момент инерции J (относительно
своей оси) и несет неуравновешенную
массу т на расстоянии г от оси. Написать
дифференциальное уравнение движения ротора
и определить частоту малых колебаний около
положения равновесия.
Ответ: ф +
mgr sin а
J + mr2
(f = 0, к-
i
mgr sin a
J + mr2
■* Решение. Система имеет одну степень свободы и находится в
потенциальном силовом поле. Уравнение движения ротора запишем с помощью
уравнений Лафанжа 2-го рода, приняв угол поворота ротора ip в качестве
обобщенной координаты
±[дЬ\ _дЬ_()
где L — функция Лагранжа
L = T-U,
Т — кинетическая энергия системы, П — потенциальная энергия системы.
Представим
Г = Г,+Г2,
где Т\ — кинетическая энергия ротора
1 2
Т2 — кинетическая энергия неуравновешенной массы
То = тГПГ ф .
2
Таким образом, получаем
Т= -(j + rar2)<£2.
Потенциальную энергию системы определяет сила тяжести
неуравновешенной массы
П = -mgr sin a cos (p.

Глава 3. Уравнения Лагранжа 2-го рода
107
Далее находим
£ = х(«7 + тг2)ф2 + mgr sin a cos у?,
dfdL\ . 2ч..
— = -Щ£Г sin a sin и?,
и записываем уравнение движения ротора
(J + тг2)ф + mgr sin a sin </? = 0.
В случае малых колебаний уравнение (1) можно заменить следующим:
mgr sin а
(1)
<р +
-<р = 0.
J + тг2
Уравнение (2) — уравнение гармонических колебаний с частотой
(2)
/mgr sin а
~ V J + ™,г2 '
Задача 3.8(48.13). Записать уравнение
движения маятника, составленного из
материальной точки М массы т, подвешенной на нити,
навернутой на неподвижный цилиндр
радиуса а (рис. 3.8.1). Длина свисающей в
положении равновесия части нити равна I. Массой
нити пренебречь.
Ответ: (I + ав)в + ав2 + g sin в = 0.
Рис. 3.8.1
■* Решение. Расчетная схема — на рис. 3.8.2.
Для записи уравнения движения маятника воспользуемся
уравнениями Лафанжа 2-го рода. Рассматриваемая система имеет одну степень
свободы и находится в потенциальном силовом поле. Принимая в качестве

108
Глава 3. Уравнения Лагранжа 2-го рода
обобщенной координаты угол 0, записываем
dt\de) дв " '
l + ав Где L —- функция Лагранжа
L = T-U,
Т — кинетическая энергия маятника (рис. 3.8.2),
Т = -mV2 = -т(1 + а0)2Р,
П — потенциальная энергия маятника,
П = -mg(AB - AC) = -mg [(I + ав) cos в - a sin 0].
Таким образом, имеем
3L
L= -m(l + ав)2в2 + mg [(I + ав) cos в - a sin 0],
m(l + а0)20, 31 ( — ) = 2ma(l + ав)62 + ™>(1 + ^в)2в,
— = ma(l + а0)02 - mg(l + а0) sin у>,
и искомое уравнение движения принимает вид
m(l + а0)20 -f ma(l + а0)02 + rag(/ 4- а0) sin 0 = 0,
или
(Z + a0)0 + a02+gsin0 = O.
Задача 3.9(48.14). Записать уравнение движения маятника,
составленного из материальной точки массы т, подвешенной на нити,
длина которой изменяется по произвольно заданному закону / = l(t).
I g
Ответ: ф + 2-ф+ - sinip = 0.
6 i
■* Решение. Расчетная схема — на рис. 3.9.1.
Для записи уравнения движения маятника используем уравнения
Лафанжа 2-го рода. Рассматриваемая система имеет одну степень свободы

Глава 3. Уравнения Лагранжа 2-го рода
109
и находится в потенциальном силовом поле. Выбирая /,
в качестве обобщенной координаты угол ip отклонения q
маятника от вертикали, будем иметь
d/9L\ dL_
Ш\дф) ~ду~'
где L — функция Лагранжа
L = Т - П,
Г — кинетическая энергия маятника, П —
потенциальная энергия маятника.
Вводя систему координат хОу, находим (рис. 3.9.1)
Рис. 3.9.1
Учтем, что
Т = -mV2 = -m(x2 + у2), П = -mgl cos ip.
х = / cos ip,
x = I cos ip- 1ф sin (p,
y = ls\n v?,
у = l! sin (p + 1ф cos (p.
Тогда
T=l-m(P + l2<p2)y
L = -m(l + 1 ф ) + mgl cos ip,
dL j2. d fdL\ „ .. |2.. dL
— = ml ip, — I — = Imllip + ml <p, — = -rag/ sin y>,
cfy? at \dip/ dip
и искомое уравнение движения маятника записывается в виде
12-
2тп11ф + ml <р + mgl sin ip = О,
или
' g
ф + 2-ф + -sinip = 0.

110
Глава 3. Уравнения Лагранжа 2-го рода
Задача 3.10 (48.19). Концы однородного тяжелого стержня АВ
длины 2а и массы М скользят без трения по горизонтальному и
вертикальному стержням рамки, вращающейся с постоянной угловой
скоростью и вокруг вертикальной стороны (рис. 3.10.1). Составить
уравнение движения стержня и определить положение его
относительного равновесия.
Рис. 3.10.1
4 2" 4 2 2
Ответ: -Ма в - -Ма и sin в cos в- Mga sin в = 0 — уравнение
движения стержня, в положении равновесия 0 = 0.
■* Решение. Расчетная схема — на рис. 3.10.2.
Уравнение движения стержня составим с помощью уравнений
Лагранжа 2-го рода. Рассматриваемая система имеет одну степень свободы
и находится в потенциальном силовом поле. Принимая в качестве
обобщенной координаты угол 0, записываем
dt\d6j " дв " '
где L — функция Лагранжа
L = T-Il,
Т — кинетическая энергия стержня, П — потенциальная энергия стержня.
Учитывая, что стержень вращается вместе с рамкой вокруг
неподвижной оси и совершает плоское движение относительно рамки, представим
■L = ■'пер ~г -*отн>
где Гпер — кинетическая энергия вращения стержня вокруг неподвижной оси

Глава 3. Уравнения Лагранжа 2-го рода
111
Jx — момент инерции стержня относительно оси у*
вращения рамки (рис. 3.10.2).
J, = ^2 ткх\ = ^2 mk(xc + х*к) =
к к
2
= Мх\ + ^2 mkal sto2 0 = тМа2 sin2 0,
к 3
Готн — кинетическая энергия плоского движения
стержня относительно рамки
гот„ = l- Je2 + \mv\
J — момент инерции стержня относительно центра Рис. 3.10.2
масс
J=\Ma\
V — скорость центра масс стержня
V2 = x2c + y2c = (a0cos в)2 + (-од sin в)2 = а2в1.
Таким образом, будем иметь
Г = -MaW sin2 0 + -Ма2в2 = -Ма2(и2 sin2 0 + в1).
3 3 3х '
Потенциальную энергию стержня определяет его сила тяжести:
П = mga cos 0.
В результате получаем
L = -Ma2(u;2 sin2 0 + в2) - Mga cos 0,
d_fdL\ _4
)
2л
-Ма'в,
дЬ
= -Ма ш sin 0 cos 0 + Mga sin 0,
dt\dej Увл~"9 дв 3"
и записываем искомое уравнение движения стержня
4 -4
-Ма2в Ма2и2 sin 0 cos 0 - Mga sin 0 = 0.
3 3
Для определения положения относительного равновесия стержня
составим выражение измененной потенциальной энергии W
W = U-T0i

112
Глава 3. Уравнения Лагранжа 2-го рода
где Г0 — составляющая кинетической энергии, которая не зависит от
обобщенной скорости в (энергия центробежных сил инерции),
Следовательно,
2
Г0 = -Ма2и2 sin2 в.
3
W = Mga cos в - -Ма2и2 sin2 в.
Положение стержня будет положением относительного равновесия при
выполнении условия
0W 2 2 2
-тт- = -Mga sin 9 - -Ma и sin в cos в = 0.
дв 3
Отсюда находим, что в положении равновесия 0 = 0. Для того чтобы это
положение было устойчивым, необходимо выполнение неравенства
d2W
дв
>0.
В данном случае при в = О
d2W
дв2
= -Mga.
Это означает, что условие устойчивости положения равновесия при в = О
не выполняется.
Задача 3.11 (48.23). Материальная точка М
движется под действием силы тяжести по
прямолинейному стержню АВ, который вращается с
постоянной угловой скоростью и вокруг
неподвижной вертикальной оси (рис. 3.11.1). Стержень АВ
образует угол а с горизонталью. Найти закон
движения точки.
Рис.3.11.1
Ответ: r = ClewtcoSQ
, Г* -иЛ COSQ , 8sin &
+ bit +
J2
cos* a

Глава 3. Уравнения Лагранжа 2-го рода
113
^ Решение. Расчетная схема — на рис. 3.11.2.
Для того чтобы найти закон движения
точки, воспользуемся уравнениями Лагранжа 2-го
рода. Данная система имеет одну степень
свободы и движется в потенциальном силовом поле.
Приняв в качестве обобщенной координаты
перемещение г точки вдоль стержня, запишем
dt\df J дг
где L — функция Лагранжа
L = Т - П,
Г — кинетическая энергия системы, П —
потенциальная энергия системы. Представим
(рис. 3.11.2)
где
*а = Vnep + Voth»
V'nep = W COS Q, Кгн = Г.
В результате будем иметь
р
Т= — (u;V cos2 а + г2).
Потенциальную энергию системы определяет сила тяжести точки М,
П = Рт sin а.
Далее находим
±(
dt\
L = — (u2r2 cos2 а + г2) - Pr sin а,
дЬ\ _ Р..
дг) ~ /'
dL PU2 2
— = г cos а - Р sin а,
0r g
и составляем уравнение движения системы
г - (и2 cos2 a)r + g sin а = 0.
Интегрируя это уравнение, получим
г = Схё
wt cos а
+ С2е
-Wt COS Q
gsma
ш2 cos2 a *

114
Глава 3. Уравнения Лагранжа 2-го рода
Задача 3.12 (48.24). Материальная точка массы т движется по
круговой рамке радиуса г, которая вращается с постоянной угловой
скоростью ш вокруг вертикального диаметра АВ (рис. 3.12.1). Составить
уравнение движения точки и определить момент М, необходимый для
поддержания постоянства угловой скорости.
Рис. 3.12.1
Ответ:
ф+ ( — и2 cos (р J sin <p = 0 — уравнение движения точки,
М = 2тг и>ф sin ip cos (р.
■*■ Решение. Расчетные схемы — на рис. 3.12.2, 3.12.3.
Уравнение движения точки составим с помощью уравнений Лагранжа
2-го рода. Данная система имеет одну степень свободы и движется в
потенциальном силовом поле. Приняв в качестве обобщенной координаты
угол (р, записываем
= 0,
d fdL"
dt\d<p/ dip
где L — функция Лагранжа: L = Т- П, Т — кинетическая энергия точки,
П — потенциальная энергия точки. Для материальной точки имеем
T=\mV?,
где (рис. 3.12.2)
vr — vneD + va
Vnep = ur sin <p, VmH = гф.

Глава 3. Уравнения Лагранжа 2-го рода
115
Рис. 3.12.2
Таким образом, получаем
Г = -mr2(u2 sin2 <р + ф2).
Потенциальную энергию точки определяет ее сила тяжести,
П = -mgr cos <р.
Поэтому
1
L = -mr (и sin ip + ф ) + mgr cos tp,
d /6L\ 2 dL 2 2
— I —- J = mr <p, — = mr и sin (p cos ip - mgr sin y>,
а1\оф/ dip
и искомое уравнение движения точки принимает вид
ф + ( — о;2 cos (р J sin у? = 0.
При определении момента М, необходимого для поддержания
постоянства угловой скорости круговой рамки, обратимся к уравнению
относительного движения точки
таохн = F + N + Фпер + Фкор.
Учитывая выражения для силы инерции Кориолиса Фкор и ускорения
Кориолиса акор (рис. 3.12.3)
Фкор = -7Пакор, акор = 2[и, Vqth],

116
Глава 3. Уравнения Лагранжа 2-го рода
приходим к выводу о том, что только силаФКор, направленная
перпендикулярно плоскости круговой рамки, способна создавать момент,
необходимый для поддержания постоянства угловой скорости рамки. Определяя
плечо такого момента, находим
М = ФКОрГ sin (р = 2тг2иф sin ip cos <р.
Задача 3.13 (48.42). Однородный диск радиуса Д, имеющий
массу М, вращается вокруг горизонтальной оси О с постоянной угловой
скоростью и (рис. 3.13.1). К диску на нити АВ длины I подвешена
материальная точка массы га. Составить уравнение движения
материальной точки.
Рис. 3.13.1
Ответ: ф - —и2 sin (art - ф) + у sin ф = 0.
*+ Решение. Расчетная схема — на рис. 3.13.2.
Система имеет одну степень свободы и находится в потенциальном
силовом поле. Выбирая в качестве обобщенной координаты угол ф,
запишем уравнения Лагранжа 2-го рода
Л\дф) дф~ '
где L — функция Лагранжа
L = T-II,
Т — кинетическая энергия системы, П — потенциальная энергия системы.
Найдем кинетическую энергию системы, составленной из двух тел
(диска и материальной точки):
Г = Г! + Г2.

Глава 3. Уравнения Лагранжа 2-го рода
117
Рис. 3.13.2
Здесь Tj — кинетическая энергия диска
г, = I М
J — момент инерции диска относительно оси вращения
J = ^MR\
Тг — кинетическая энергия материальной точки
Т2 = \mV\
V — абсолютная скорость материальной точки (рис. 3.13.2),
V = мугн "г Vnep.
Учтем, что
Уотн = ф1, Viep = ШК
Тогда
V1 = Г^ + Bruf + URipw cos ((p - 1>)9
T2 = -rn[l2tp2 + R2u2 + URipu cos (ip - ip)],
T= -(M+ 2га)ДV + -га[l2ip2 + URtpucos (tp - ip)].
Потенциальная энергия системы определяется силой тяжести
материальной точки:
П = -mg(R cos ip + l cos ip).

118
Глава 3. Уравнения Лагранжа 2-го рода
В результате находим
L = -(M+2m)R2v2+-m[12ф2 + 2Шфи cos (ip - ф)] +mg(R cos ip +I cos ф),
— =ml2ip+mlRwcos((p-il/)9 — I —г ) =ml2$-mlRw(u--'ip)sin(u>-'il>),
дф dt\dil>/
■— =mlRw^s\n{(p-ij))-mghmxl).
дф
Таким образом, искомое уравнение движения точки записывается в виде
т12ф - mlRw2 sin (ip - ф) + mgl sin ф = О,
или, с учетом того что <р = ut,
ф —-и2 sin (иЛ - ф) + - sin ф = 0.
/
/
Задача 3.14(48.17). Кривошипный механизм состоит из поршня
массы т\, шатуна АВ массы т2, кривошипа ОВ, вала и махового
колеса (рис. 3.14.1). J2 — момент инерции шатуна относительно его
центра масс С\ Jz — момент инерции кривошипа ОВ, вала и махового колеса
относительно оси; О, — площадь поршня, р — давление, действующее
на поршень, I — длина шатуна; s — расстояние между точкой А и центром
масс шатуна; г — длина кривошипа OB; М — момент сопротивления,
действующий на вал. Составить уравнение движения механизма, считая
угол поворота шатуна ф малым, т.е. полагая sin^ = ф и cosф = 1.
В качестве обобщенной координаты взять угол поворота кривошипа (р.
Механизм расположен в горизонтальной плоскости.
V777777,
Рис. 3.14.1
Ответ:
+
(mi + m2)r2 sin2 ip + (J2 + m2s2)-j cos2 <p + J3
r2
(mi + m2)r2 - (J2 + m2s2) ' ~2 ~:
Ф +
ф sin ip cos ip = pQr sin ip — M.

Глава 3. Уравнения Лагранжа 2-го рода
119
Рис. 3.14.2
^ Решение. Расчетная схема — на рис. 3.14.2.
Уравнение движения механизма составим с помощью уравнений
Лагранжа 2-го рода. Данная система имеет одну степень свободы. Выбирая
в качестве обобщенной координаты угол (р, записываем
(И\дф) dip Чу v;
где Г — кинетическая энергия системы, Q — обобщенная сила системы.
Механизм состоит из трех движущихся и имеющих массу твердых
тел (поршня, шатуна и кривошипа, жестко связанного с валом и маховым
колесом). Поэтому
Т = Г1+Г2 + Гз,
где Т\ — кинетическая энергия поршня, Т2 — кинетическая энергия
шатуна, Гз — кинетическая энергия кривошипа с валом и маховым колесом.
Поршень движется поступательно. Следовательно,
Г, = X-mxVl
где V\ — скорость поршня
Представим (рис. 3.14.2)
х\ =lcosip + r cos <р « I + г COS (f.
Тогда
V\ = -r<p sin <р, Т\ = -т\г2ф2 sin2 (р.
Для шатуна, совершающего плоское движение, имеем
1 7 1 2
Т2 = -m2V{ + -J2u/2,
где V2 — скорость центра масс шатуна, и2 — угловая скорость шатуна.

120
Глава 3. Уравнения Лагранжа 2-го рода
Согласно рис. 3.14.2 находим
V} = x\ + yl
#2 = Х\ - s cos ф « I - s + г cos (р, х2 = -тф sin <р,
2/2 S S . 5 .
—-— = 7» 2/2 = тг sm ¥>> 2/2 = -тг<р cos <р,
V2 = г2 f sin2 <p + -у cos2 tp J 02,
u;2 =tk
r sin <p = s sin ^ « 5^,
^ = -фсоыр.
Таким образом, получаем
1 / s2 \ 1 r2
T2 = -m2r2 f sin2 y> + p" cos2 V ) Ф2 + 2Jl~P^2 ^ ^'
Кривошип с валом и маховым колесом считаются одним твердым телом,
которое вращается вокруг неподвижной оси. Поэтому
Г3 = - J3J3 = -ъф2.
В результате будем иметь
«2.2 -2
Г = -т\г ф sin (р + -Ш2Г'
/.2 ^ 2 \ . 2
I sin <р + -у cos </?!</>
+
дТ
дф
±(дТу
dt
1 г2 1
+ 2J2^2cos2</?+-J3<£2,
г2
(mi + Ш2)Г Sin </? + (J2 + Ш25 ) J} C0S У + ^3
(I)
г2
(mj + m2)r2 sin2 <p + («/2 + ™>2s2) -^ cos2 </? + J3
/2
r2
/2
Ф +
+ 2
9Г
(mj + m2)r2 - (J2 + m252) ^
(m, + m2)r2 - ( J2 + m2s2 J -j
ф2 sin tp cos <p.
<£2 sin ip cos <p.

Глава 3. Уравнения Лагранжа 2-го рода
121
Для определения обобщенной силы системы сначала подсчитываем
работу 5А, которую совершают на возможном перемещении 5(р сила
давления, действующего на поршень, и момент сопротивления на валу
механизма
5А = рШх\ - MSip = pQ,r5<p sin <р - М5(р.
Затем находим
Q = — = рЫг sin ip- М.
dip
Подставив полученные выражения в уравнение (1), записываем искомое
уравнение движения кривошипного механизма
Ф +
0 0 Ш О 1 9^ О I
(mi + гп2)г sin (р -f ( J2 + rri2S J -^ cos (p + J3
+ (mi + m2)r2 — (J2 + ™>is2) -J2\ ф2 s*n(P cos ^ = P^r s*n 4>- M.
Задача 3.15(48.26). Однородная нить, к концу которой привязан
груз А массы т, огибает неподвижный блок Б, охватывает подвижный
блок С, поднимается вверх на неподвижный блок D и проходит
параллельно горизонтальной плоскости, где к ее концу привязан
груз Е массы m (рис. 3.15.1). К оси блока С прикреплен груз К массы
гп\. Коэффициент трения скольжения груза Е о горизонтальную
плоскость равен / При каком условии груз К будет опускаться
вниз, если начальные скорости всех грузов равнялись нулю. Найти
ускорение груза К Массами блоков и нити пренебречь.
Рис. 3.15.1
Ответ: При условии mi > m(l + /); ускорение а = g
mi -m(l + /)
mi + 2m

122
Глава 3. Уравнения Лагранжа 2-го рода
Рис. 3.15.2
■* Решение. Расчетные схемы — на рис. 3.15.2, 3.15.3.
Для определения ускорения груза К используем уравнения Лагранжа
2-го рода. Рассматриваемая система имеет две степени свободы. Выбирая
в качестве обобщенных координат перемещение х\ груза Е и перемещение
#2 груза А, записываем
d (дТ\ дТ „ ,. t ^
7t[wJ-^rQi (г=1'2)'
(О
где Т — кинетическая энергия системы, Qi — обобщенная сила системы,
соответствующая г-й обобщенной координате.
Система состоит из трех грузов, которые движутся поступательно.
Поэтому
1 ,2 1 .2 1 .2
Т = -тпх\ + -тпх? Н—тп\х .
2 2 2
Здесь х — скорость груза К
Учитывая последнее выражение, находим
Г = -гп(х] + х\) + -т\(х\ + х2)2,
d(dT\ .. 1 ,.. . ОТ л
3l(zr) =mx, + -m1(sl+a:2), — = О,
(2)
<*/«Г\ .. 1 . ...
dt\W2)=mX2-{-4m{X]+X2)>
дхх
от
дх:
= 0.
Для подсчета обобщенных сил сообщим системе возможные
перемещения, при которых координаты Х\ и х2 получат приращения 6х\

Глава 3. Уравнения Лагранжа 2-го рода
123
и 6x2 > и составим выражения для элементарных работ 8Ai (i = 1,2)
действующих на систему сил. При 8х\ Ф О, 5х2 = О имеем (рис. 3.15.2)
5А\ = -F5x\ 4- m\g5x,
где F — предельная сила трения скольжения, приложенная к грузу Е,
F = fN,
N — нормальная реакция, приложенная к грузу Е,
N = mg,
8х — приращение координаты х при данном возможном перемещении
8х = —5х\.
2
Следовательно,
Q\ = -^- = 2#(mi - 2fm)-
При Sx2 Ф 0, 8х\ = О (рис. 3.15.3)
5А2 = -mg8x2 4- m\g8x,
2
Q2 = j^ = -g(m{ - 2m).
Подставляя полученные выражения в уравнения (1), записываем
уравнения движения системы
тх\ 4- -тх(х\ 4- х2) = -g(mi - 2/га),
тх2 4- -mi(xi 4- х2) = -g(m\ - 2т).
Решая эту систему относительно х\, х2 и учитывая, что согласно
равенству (2)
.. 1,.. ...
а = х= -(х\ 4-я2),
находим ускорение а груза К
mi -т(1 4-/)
а = g .
т\ 4- 2т

124
Глава 3. Уравнения Лагранжа 2-го рода
Груз К будет опускаться вниз, если а > О, т. е. если
т\ - га(1 + /) > 0, или mi > тп(\ + /).
Задача 3.16 (48.27). Два груза D и Е массы га каждый привязаны
к концам нерастяжимой нити (рис. 3.16.1). Эта нить от груза Е идет
через неподвижный блок А, затем охватывает подвижный блок В,
возвращается вверх на неподвижный блок С, соосный с блоком А,
проходит параллельно гладкой наклонной плоскости, где к концу нити
привязан груз D. Наклонная плоскость образует угол а с горизонтом.
К подвижному блоку В прикреплен груз К массы т\. Коэффициент
трения скольжения груза Е о горизонтальную плоскость равен /.
Массами блоков и нити пренебречь. Выяснить условие, при котором
груз К будет опускаться. Найти ускорение этого груза. В начальный
момент скорости всех грузов равнялись нулю.
Е
%
w//);////;;//w/№l
Ответ: При условии т\ >ra(/+sina), ускорение a=g
rai-ra(/+sina)
т\+ 2га
■* Решение. Расчетные схемы — на рис. 3.16.2, 3.16.3.
Для определения ускорения груза К используем уравнения Лагранжа
2-го рода. Рассматриваемая система имеет две степени свободы. Выбирая
в качестве обобщенных координат перемещение х\ груза Е и перемещение
Х2 груза D, записываем
d (дТ\ дТ „ ,. t ^
7A^J-^rQi (г = 1'2)'
(1)
где Т — кинетическая энергия системы, Qi — обобщенная сила системы,
соответствующая г-й обобщенной координате. Система состоит из трех

Глава 3. Уравнения Лагранжа 2-го рода
125
тел (грузов А, К и D), которые движутся поступательно. Поэтому
m 1 .2 1 .2 1 .2
Т = -77lXi Н ТПХэ Н 77liX .
2 2 2
Здесь х — скорость фуза К
*= -(±i+±2).
Учитывая последнее выражение, находим
Т = -тп(х] + ±г) + -mi(±i + х2)2,
dfdT\ .. 1 . . ОТ л
Л \0±:
9xi / 4 9xj
1 = ТПХ2 + ТШ1(Х1 + Х2),
dfdT\ .. 1 . .. ч ОТ л
аг2
(2)
При подсчете обобщенных сил сообщим системе возможные
перемещения, при которых координаты xi и хг получат приращения 5х\
и 6x2, и составим выражения для элементарных работ SAi (i = 1,2)
действующих на систему сил.
При 6х\ Ф О, 8x2 = 0 имеем (рис. 3.16.2)
5А\ = -FSx\ + m\gSx,
где F — предельная сила трения скольжения, приложенная к грузу Еу
F = fN,

126
Глава 3. Уравнения Лагранжа 2-го рода
IM
WWWW//MAHA
Рис. 3.16.3
N — нормальная реакция, приложенная к грузу Е,
N = mg,
6х — приращение координаты х при данном возможном перемещении
1
Следовательно,
5х = -5х\.
Q\ = -jrf- = -jg{™,\ ~ 2/m).
При 6x2 Ф 0, 6х\ = 0 (рис. 3.16.3)
5А2 = -mg5x2 sin а + m\g6x,
Sx = -8x2*
2
&М 1 ,
Q2 = ^— = -g(m\ - 2m sin a).
Подставляя полученные выражения в уравнения (1), записываем
уравнения движения системы:
тхх + -тх{х\ + х2) = -g(m\ - 2/m),
тх2 + —77ii(xi +Х2) = -g(m\ - 2т sin a).
Решая эту систему относительно х\, х2 и учитывая, что согласно равенству (2)
.. 1,..
а = х= -(а?1 + х2),

Глава 3. Уравнения Лагранжа 2-го рода
127
находим ускорение а груза К
гп\ - m(f + sin а)
а = g .
Ш\ + 2га
Груз К будет опускаться вниз, если а > О, т. е. если
гп\ > ra(/ + sina).
Задача 3.17(48.30). Через блоки Л и Б с неподвижными осями
переброшен шнур, поддерживающий подвижный блок С (рис. 3.17.1).
Части шнура, не лежащие на концах, вертикальны. Блок С нагружен
гирей массы га = 4 кг, к концам шнура прикреплены грузы
массы mi = 2 кг, 7П2 = 3 кг. Определить ускорения всех трех грузов,
пренебрегая массами блоков и шнура и трением на осях.
Ответ: о = — g, а,
Рис. 3.17.1
" и8' а2 = и8'
^ Решение. Расчетные схемы — на рис. 3.17.2, 3.17.3.
Для решения задачи используем уравнения Лагранжа 2-го рода.
Рассматриваемая система имеет две степени свободы. Выбирая в качестве
обобщенных координат перемещение х\ гири массы т\ и перемещение
х2 гири массы 77i2, записываем
d (дТ\ ОТ „ ,. 1 ^ч
йЫ-йг* (г=1,2)'
(о

128
Глава 3. Уравнения Лагранжа 2-го рода
где Т — кинетическая энергия системы, Qi — обобщенная сила системы,
соответствующая г-й обобщенной координате.
Система состоит из трех тел, которые движутся поступательно.
Поэтому
.2 • 2 «2
Т = -rri\X\ + -TtiiXi + -тпх .
Здесь х — скорость гири массы тп
. 1,. . ч
Учитывая последнее выражение, находим
„, ' .2 1 .2 1 ,. -ч2
Г = -mjX! + -га2я2 + ^m(^i + х2) ,
дТ
дх[
(2)
dfdT\ .. 1 . . _ л
d(dT\ .. 1 . .. ч ет А
^№;=т2Х2+4т(Х1+Ж2)' ^=0-
Для подсчета обобщенных сил сообщим системе возможные
перемещения, при которых координаты х\ и х2 получат приращения 5х\
и (Jx2, и составим выражения для элементарных работ SAi (г = 1,2)
действующих на систему сил. При 6х\ ф О, 6х2 = О имеем (рис. 3.17.2)
Рис. 3.17.2

Глава 3. Уравнения Лагранжа 2-го рода
129
где 5х — приращение координаты х при данном возможном перемещении
Следовательно,
5х = -5х\.
2
^ SA\ * /„
Q, = — = -g(2ml - m).
При Sx2 ф 0, 5х{ = О (рис. 3.17.3)
8А2 = rri2g5x2 - mgSx,
2
Ql = ~5х"2 = 2^2m2 " Ш^
Подставляя полученные выражения в уравнения (1), записываем
уравнения движения системы
1 g
тп\Х\ + -тп{х\ Н- хг) = -(2гп\ - га),
1 m m g
^2^2 + Tm(^i + ^2) = т (2ш2 — га).
У////////////////////Ш<///Л
КЛ
О
т
m2g
1^2
Рис. 3.17.3

130
Глава 3. Уравнения Лагранжа 2-го рода
Решая эту систему относительно х\, х2, подставляя численные значения
масс и учитывая, что согласно равенству (2)
1
находим
а = х= -(х{ +х2),
а = ТТ*' а' = -7Т*' a2=ng'
Задача 3.18 (48.31). Грузы М\ и М2 одинаковой массы т
движутся по двум наклонным направляющим О А и ОВ, расположенным в
вертикальной плоскости под углами а и /3 к горизонту (рис. 3.18.1).
Нить, соединяющая эти грузы, идет от груза М\ через блок О,
вращающийся около горизонтальной оси, охватывает подвижный шкив Q,
несущий груз М массы тп\, и затем через блок 0\, надетый на ту же
ось, что и блок О, идет к грузу М2. Блоки 0\ и О соосные. Определить
ускорение а груза М, пренебрегая трением, а также массами блока,
шкива и нити.
Рис. 3.18.1
Ответ: а = g
тп\ -m (sin а + sin (3)
тп\ -f 2m
■* Решение. Расчетные схемы — на рис. 3.18.2, 3.18.3.
Для определения ускорения груза М используем уравнения Лагранжа
2-го рода. Рассматриваемая система имеет две степени свободы. Выбирая
в качестве обобщенных координат перемещение х\ груза М\ и
перемещение X2 груза М2, записываем
Jt{dFj-^rQi (г = 1'2)'
(1)

Глава 3. Уравнения Лагранжа 2-го рода
131
Рис. 3.18.2
где Т — кинетическая энергия системы, Q» — обобщенная сила системы,
соответствующая i-й обобщенной координате.
Система состоит из трех тел (грузов М, М\ и М2), которые движутся
поступательно. Поэтому
m 1 .2 * .2 1 .2
Т = -ma?! -f -ТПХ2 + -ttiiX .
Здесь х — скорость груза М
. 1,.
Учитывая последнее выражение, находим
(2)
Г = -гп(х] + ±г) + -mi(zi + х2)2,
дх]
дТ
дх~2
= 0.
При подсчете обобщенных сил сообщим системе возможные
перемещения, при которых координаты х\ и Х2 получат приращения 5х\
и 6x2 у и составим выражения для элементарных работ 5А( (i = 1,2)
действующих на систему сил. При
имеем (рис. 3.18.2)
5хх ф О, 8х2 = О
SA\ = —mg5x\ sin а + migSx,

132
Глава 3. Уравнения Лагранжа 2-го рода
L -L-'rr^g
Рис. 3.18.3
где Sx — приращение координаты х при данном возможном перемещении,
1
Следовательно,
Sx = -Sx\.
Q\ = -г— = -g\m\ - 2т sin а).
ох\ 2
При 5х2 ф О, Ьх\ = О (рис. 3.18.3)
8Аг = -mg5x2 sin /3 + m\gSx,
Следовательно,
Sx = -Sxi.
2
Qi = £jr = 2^(mi ~ 2m sin/3).
Подставляя полученные выражения в равенства (1), записываем
уравнения движения системы
тх\ + -mi(xi +xi) = -g(m\ - 2т sin а),
тх2 + -mi(xi + я2) = -£(mi - 2msin/?).
Решая эту систему относительно Х\, &2 и учитывая, что согласно равенству (2)
а = я = 2^! + ^2^

Глава 3. Уравнения Лагранжа 2-го рода
133
находим
a=g-
т\-т (sin а + sin /?)
гп\ + 2га
Задача 3.19 (48.33). Дана система из двух
блоков, неподвижного А и подвижного В, и трех
грузов Мь М2 и М3, подвешенных с помощью
нерастяжимых нитей, как показано на рис. 3.19.1
Массы грузов соответственно равны гп\, m-i и га3>
при этом т\ < гп2 + газ. Массами блоков
пренебречь. Найти, при каком соотношении масс гп\,
77i2 и шз груз М\ будет опускаться в том случае,
когда начальные скорости грузов равны нулю.
Ответ: тп\ >
4ГП2ТПЗ
7712 + 771з
■* Решение. Расчетные схемы — на рис. 3.19.2, 3.19.3, 3.19.4.
Для ответа на поставленный в задаче вопрос используем уравнения
Лагранжа 2-го рода. Рассматриваемая система имеет две степени свободы.
Выбирая в качестве обобщенных координат перемещение х\ груза М\
и перемещение х2 груза Mi относительно блока В, записываем
d /дТ\ ОТ
dt \ d±i) dxi
Qi (i =1,2),
(О
где T — кинетическая энергия системы, Qi — обобщенная сила системы,
соответствующая г-й обобщенной координате.
Система состоит из трех тел (грузов М\, М2 и М3), которые движутся
поступательно. Поэтому
Т = -m{V? + -ш2У22 + -m3Vl
Учитывая, что (рис. 3.19.2)
V\=X\, V2 =±i+±2, Уз=Х\-Х2,

134
Глава 3. Уравнения Лагранжа 2-го рода
получим
Т = -(ТП\ + ТП>2 + ТПз)Х\ + (7712 — ТП^)Х\Х2 +
+ r(m2 + m3)x2,
-г: I уст- ) = (mi + m2 + m3)2;i + (т2 - т3)я2,
— ( 77Т- 1 = (т2 - m3)xi + (т2 + т3)х2,
Рис. 3.19.2
ОТ
дх~2
0.
При подсчете обобщенных сил сообщим системе возможные
перемещения, при которых координаты х\ и х2 получают приращения 5х\
и 5х\, и составим выражения для элементарных работ ОД (г = 1,2)
действующих на систему сил. При 6х\ Ф О, 6x2 = 0 находим (рис. 3.19.3)
8А\ = (mi — m2 — m3)g&ci,
dxi
При 5x2 Ф 0, (fa, = 0 (рис. 3.19.4)
6А2 = (m3 - m2)g<fo2,
0X2
Таким образом, уравнения движения системы записываются в виде
(mi + m2 + m3)^i + (m2 — m3)x2 = (mi — m2 — m3)g,
(m2 - m3)x, + (m2 + m3)z2 = (m3 - m2)g.
Полученные уравнения разрешаем относительно ускорения груза М\:
mi(m2 + m3) — 4m2m3
mi(m2 + m3) 4- 4m2m3
При выбранном направлении перемещения х\ груз Mi будет опускаться
в том случае, когда а\ > О, т.е. когда
mj(m2 + m3) - 4m2m3 > О,

Глава 3. Уравнения Лагранжа 2-го рода
135
или
ГП\ >
477127713
7712 Н~ ^3
Задача 3.20(48.34). Найти ускорение тележки, по платформе
которой катится без скольжения круглый цилиндр, если сама тележка
скатывается тоже без скольжения по плоскости, наклоненной к
горизонту пол углом а и параллельной платформе тележки. Образующие
цилиндра перпендикулярны линиям наибольшего ската платформы.
Масса тележки без колес М, масса всех колес га, масса цилиндра М\,
колеса считать однородными сплошными дисками.
Ответ: а =
6М + 6га + 2М,
6М + 9га + 2МХ
gsina.
■* Решение. Расчетные схемы — на рис. 3.20.1-3.20.5.
Ускорение тележки определим с помощью уравнений Лагранжа 2-го
рода. Система имеет две степени свободы и находится в потенциальном
силовом поле. Выбирая в качестве обобщенных координат
перемещение х\ центра масс цилиндра относительно тележки и перемещение х
платформы тележки, записываем (рис. 3.20.1):
гЫ-йГ* (г=1'2)-
со

136
Глава 3. Уравнения Лагранжа 2-го рода
Рис. 3.20.1
где Г — кинетическая энергия системы, Qi — обобщенная сила системы,
соответствующая г'-й обобщенной координате.
Представим
Г = Г, +Г2 + Г3, (2)
где Т\ — кинетическая энергия платформы тележки, Т2 — кинетическая
энергия колес, Т3 — кинетическая энергия цилиндра.
Платформа тележки движется поступательно со
скоростью V\ = х. Следовательно,
1
1
Рис. 3.20.2
Г, = -MVf = -Их2.
2 2
Движение колес — плоское. Поэтому
Г2 = 1мУ22 = I J2ul
где Vi — скорость центра масс колеса (рис. 3.20.2), J2 — момент инерции
колеса относительно оси, проходящей через его центр масс, и2 — угловая
скорость вращения колеса.
Учитывая, что колеса считаются однородными сплошными дисками
радиуса г, что катятся они по наклонной плоскости без скольжения, а их
оси соединены с платформой тележки, находим:
V2 = x9
X
и2 = -,
J2 = -mr ,
Т2 = -mx4
1 2(Х\2 3 .2
+ -mr ( - ) = -mx
4 \r J 4

Глава 3. Уравнения Лагранжа 2-го рода
137
Поскольку цилиндр также совершает
плоское движение и также катится без скольжения
по платформе тележки, то
Гз = 1М1У32 + ^,
где V3 — абсолютная скорость центра масс
цилиндра (рис. 3.20.3)
V3 = VmH + УПер,
РИО. 3.20.3
Кгн, Кер — относительная и переносная скорости центра масс цилиндра,
•чэтн == #1 > Miep = #>
J3 — момент инерции цилиндра относительно оси, проходящей через его
центр масс,
J3 = x-mxr\
R — радиус цилиндра, и>з — угловая скорость вращения цилиндра,
Х\
Таким образом, будем иметь
1
Ъ = ^М1(х1+х)2 + -М1х2и
Т = -Мх1 + -тпх2 + -Mi(±i + if + -Mix],
d (дТ\ / 3 \
дг_
дх
d ( дТ\ 3
dt{dx-J = 2M^ + Mi*
дТ
dxl~°'
Для подсчета обобщенных сил сообщим системе возможные
перемещения, при которых координаты х и Х\ получат приращения 6х и Sxi,
и составим выражения для элементарных работ ОД (г = 1,2) действующих
на систему сил.

138
Глава 3. Уравнения Лагранжа 2-го рода
При
имеем (рис. 3.20.4):
Следовательно,
При
имеем (рис. 3.20.5):
Рис. 3.20.4 Рис. 3.20.5
6х ф 0, 6х\ - О
5А\ =(М + М\+ m)gSx sin а.
Mi
Q, = — - (М + М\ +m)gma.
6х
6xi ФО, Sx = 0
5А2 = M\gSx\ sin а,
Qi = -=— =M\gsma.
0Х\
В результате получаем следующие уравнения движения системы
( М + -га + Mi J х + М\Х\ = (М + Mi + m)g sin a,
-x\ +x = gsina.
Отсюда находим ускорение тележки
6М + 6га + 2М|
a = х = е sin а.
6М + 9га + 2М,

Глава 3. Уравнения Лагранжа 2-го рода
139
Задача 3.21 (48.35). Составить уравнения движения
эллиптического маятника, состоящего из ползуна М\ массы т\, скользящего
без трения по горизонтальной плоскости, и шарика М2 массы m2i
соединенного с ползуном стержнем АВ длины / (рис. 3.21.1). Стержень
может вращаться вокруг оси А, связанной с ползуном и
перпендикулярной плоскости рисунка. Массой стержня пренебречь. Определить
период малых колебаний эллиптического маятника.
Рис. 3.21.1
И Г -1
Ответ: — [(т\ + т2)у + т21ф cos(p\ = О, 1ф + у cos (р + g sin <р = 0 —
Сии
уравнения движения; т=2жл
ТП\1
(m\+m2)g
— период малых колебаний.
■* Решение. Расчетная схема — на рис. 3.21.2.
Уравнения движения маятника запишем с помощью уравнений
Лагранжа 2-го рода. Система имеет две степени свободы и находится в
потенциальном силовом поле. Выбирая в качестве обобщенных координат
перемещение у ползуна и угол <р отклонения стержня АВ от вертикали,
записываем
d (dL\ 3L л ,. f ^ч
т \-г- " тг- =0 (г = 1,2),
где L — функция Лагранжа
L = Т - П,
Т — кинетическая энергия системы, П — потенциальная энергия
системы, g, =у, q2= ip.
Кинетическую энергию системы представим суммой
Т = Т1+Т2,

140
Глава 3. Уравнения Лагранжа 2-го рода
гпд
Рис. 3.21.2
где Т\ — кинетическая энергия ползуна
Г, = -тпху\
Ti — кинетическая энергия шарика
1 2
Ti = -rn2V2,
V2 — абсолютная скорость шарика (рис. 3.21.2)
▼2 = мэтн "г Vnep.
Учитывая, что
^отн = ф1, Vnep = у,
находим
Vl = ф212 + у2 + 21фу cos <р,
Т = -(ttij + m2)y2 + -гп212ф2 + тп21уф COS (f.
Потенциальную энергию системы определяет сила тяжести шарика:
П = -rri2gl cos (p.
Таким образом, будем иметь
L= -(гп\+ т2)у2 + -т212ф2 + т21(уф + g) cos tp,
—- = (mj + m2)y + m2ltp cos tp, — = 0,
oy oy

Глава 3. Уравнения Лагранжа 2-го рода
141
dL ,2. ,. 9L ,, х .
— = т21 <р + m2ly cos (р, — = -т21 (у<р + g) sin <р,
оф oip
d fdL\ 2
— (—-)= ^Ы Ф + mily cos (р - т21уф sin <р.
аЬ\дф/
В результате получаем уравнения, описывающие движение
рассматриваемой системы:
— [(mi + т2)у + т21ф cos if] = О,
1ф + У cos у> +g sin tp = 0.
В случае малых колебаний эти уравнения вырождаются в следующие:
(mi + т2)у + m2Z£ = О,
1ф + y + g<p = o,
или
м _ т21 (т\ +т2\ _
Из последнего уравнения находим период малых колебаний маятника
Т — 27Гч
ТП\1
(гп\ +m2)g'
Задача 3.22(48.28). Призма А массы m скользит по гладкой
боковой грани призмы В массы тп\, образующей угол а с горизонтом
(рис. 3.22.1). Определить ускорение призмы В. Трением между
призмой В и горизонтальной плоскостью пренебречь.
Рис. 3.22.1
Ответ: а =
mg sin 2а
2(гп\ + m sin2 а)'

142
Глава 3. Уравнения Лагранжа 2-го рода
Рис. 3.22.2
^ Решение. Расчетная схема — на рис. 3.22.2.
При определении ускорения призмы В используем уравнения
Лагранжа 2-го рода. Система имеет две степени свободы и находится в
потенциальном силовом поле. Выбирая в качестве обобщенных координат
перемещение х\ призмы В и перемещение х2 призмы А относительно
призмы В, записываем
где L — функция Лагранжа
L = Т - П,
Г — кинетическая энергия системы, П — потенциальная энергия системы.
Найдем кинетическую энергию системы. Система состоит из двух
призм, которые движутся поступательно. Поэтому
T=l-mlV?+l-mV\
где V\ — скорость призмы В; V2 — абсолютная скорость призмы А.
Учитывая, что (рис. 3.22.2)
V\ =х]9 V2=VOTH+Vnep,
Кэтн = %2> ''пер == Я'Ь
получаем:
Т = -(т + гп\)х] + -т(х2 - 2х\ cosа)х2.
Потенциальную энергию системы определяет только сила тяжести
призмы А:
П = -mgx2 sin а.

Глава 3. Уравнения Лагранжа 2-го рода
143
Таким образом, находим
L = -TTiiXj + -т(х\ + ±2 — 2x1X2 cos а) + rngxi sin а,
гп\Х\ + т(х\ - Х2 cos а),
dtydxj ~
d(dL\
дь
дх:
= mg sin а,
и записываем уравнения движения системы:
(т + т\)х\ - 7ПХ2 cos а = О,
#2 - xi cos а - д sin а = 0.
Отсюда определяем ускорение призмы В:
mg sin 2а
а = Х\ =
2 (т\ +msin2 а)'
Задача 3.23(48.29). На гладкой горизонтальной плоскости
помещена треугольная призма ABC массы т, которая может скользить без
трения по этой плоскости (рис. 3.23.1). По грани призмы АВ катится
без скольжения однородный круглый цилиндр массы т\. Определить
ускорение призмы.
Рис. 3.23.1
Ответ: а =
m\g sin 2а
3(m + гп\) - 2гп\ cos2 а'

144
Глава 3. Уравнения Лагранжа 2-го рода
Рис. 3.23.2
^ Решение. Расчетная схема — на рис. 3.23.2.
Ускорение призмы определим с помощью уравнений Лагранжа 2-го
рода. Система имеет две степени свободы и находится в потенциальном
силовом поле. Выбирая в качестве обобщенных координат перемещение
х\ призмы и перемещение х2 центра масс цилиндра относительно призмы,
записываем
!(£)-£-<'-•'>. <»
где L — функция Лагранжа
L = Т - П,
Т — кинетическая энергия системы, П — потенциальная энергия системы.
Представим
Г = Г,+Г2,
где Т\ — кинетическая энергия призмы, Т2 — кинетическая энергия
цилиндра.
Призма движется поступательно, а движение цилиндра — плоское.
Поэтому
Ti = \mVl
1 , 1 2
T2 = -mlV2 + -Ju2,
где V\ — скорость призмы (рис. 3.23.2)
V — скорость центра масс цилиндра,
» = ^отн "Г ''пер»
J — момент инерции цилиндра относительно его центра масс, ш —
угловая скорость цилиндра.

Глава 3. Уравнения Лагранжа 2-го рода
145
Учитывая, что
будем иметь
Г = -raxf +
Кугн = х2>
Miep = %\>
7 '™ -2
«/= 2mir >
х2
w= —,
г
-77li(Xi + а?2 — 2xi;
1
-J-
Потенциальную энергию системы определяет только сила тяжести
цилиндра:
П = -m\gX2 sin а.
Таким образом, находим
1 .2 1 /.2 .2 ^. . \ 1 .2
L = -mxi + -mi I Xi + x2 - 2xiX2 cos a) + -m\x2 + migX2 sin a,
d/МЛ „ , „
-7-1 t— 1 = mxi + m\ (x\ - X2 cos a),
dt \dx\ t
d ( dL\ /3..
I I = 777.1 I — Т.л — :
dV
;(S=m,(r2-^,cosa)'
dL
— = raisin a
ax2
и записываем уравнения движения системы:
(m + mi)xi - 7П1Х2 cos a = 0,
3x2 - 2xi cos a - 2<7 sin a = 0.
Отсюда определяем ускорение призмы
77iigsin2a
a = xi
3(m + m\) - 2m\ cos2 a'

146
Глава 3. Уравнения Лагранжа 2-го рода
Задача 3.24(48.37). По неподвижной призме А, расположенной
под углом а к горизонту, скользит призма В массы Ш2 (рис. 3.24.1).
К призме В посредством цилиндрического шарнира О и
спиральной пружины с коэффициентом жесткости с присоединен тонкий
однородный стержень OD массы гп\ и длины I. Стержень совершает
колебания вокруг оси О, перпендикулярной плоскости рисунка.
Положения призмы В и стержня OD определены посредством координат s
и (р. Написать дифференциальные уравнения движения материальной
системы, состоящей из призмы В и стержня OD, пренебрегая
силами трения. Определить период малых колебаний стержня OD, если
m\gl cos2 а < 2с.
тттжштшт*щ^*
Рис. 3.24.1
Ответ: -тп\12ф - -m\ls cos (if + а)
1
-miglsimp- ар,
1 1 2
(mj +7712)5- -m\l(pcos(<p + a) + -m\l(p s\n(<p + a) = (m\+m2)gsina —
2 2
^ _ 7П\[т\(1 +3sin2a) + 4ra2]
2m \ I—— : — ^ период
уравнения движения, г
^малых колебаний.
6(m\ + га2)(2с - m\gl)
^ Решение. Расчетные схемы — на рис. 3.24.2, 3.24.3.
Система имеет две степени свободы (обобщенные координаты s
и (р заданы условием задачи). Для записи уравнений движения системы
используем уравнения Лагранжа 2-го рода в виде
d(dT\ дТ „ ,.
о»
где Т — кинетическая энергия системы, Qi — обобщенная сила системы,
соответствующая г-й обобщенной координате, q\ = (р, д2 = з.
Представим
Г = Г,+Г2, (2)

Глава 3. Уравнения Лагранжа 2-го рода
147
ШЛШШШШ^ЖШЩ^Й^»
Рис. 3.24.2
где Т\ — кинетическая энергия стержня, Г2 — кинетическая энергия
призмы В.
Движение стержня — плоское. Следовательно,
Tx=l-mxV2+l-Ju\
где V — скорость центра масс стержня, J — момент инерции стержня
относительно центра масс, и — угловая скорость стержня.
Находим (рис. 3.24.2)
1
v = vneD+v(
Miep — 89 *чп
:*&
V2 = s2 + -12ф2 - 1ёф cos (у? + a), J = —ml2, и> = ф,
12'
Т\ = -m\
s2 + -12ф2 - 1ёф cos ((р + а)
1 i2 .2
Призма В движется поступательно. Поэтому
Гг = -m2s
В результате получаем
1
Т = ^(mi + Ш2)52 + -тп\12ф2 - -тп\1ёф cos (tp + а).
2 6 2
Находим
ет ' ,2. > ,. /
тгт = -wM ф- -m\lscos((p + a),
аф 3 2
I — 1 = -тп\1 ф - -m\ls cos (</? + а) + -mi/s<£sin (<р + а),
d/ЯГ
dt

148
Глава 3. Уравнения Лагранжа 2-го рода
шшшшшшш
Рис. 3.24.3
—- = -m\ls(p sin (ф + а),
dip 2
ет / ч. * ,. /
—- = (m, +7n2)5- -m\lipcos((p + a),
os 2
dt\ds) ~
ОТ
-z- =0.
(m\ +m2)5 - -mi/<£cos(<p + a)-miZ<£2sin(<p + a),
При подсчете обобщенных сил сообщим системе возможные
перемещения, при которых координаты (риз получат приращения 6<р и 6s,
и составим выражения для элементарных работ SAi (г = 1,2) действующих
на систему сил. При Sip Ф О, 8s = О будем иметь (рис. 3.24.3)
5А\ = m\g- sin <р - ар] Sip, Q\ = -=— = rrt\g- sin ip - ар.
V 2 ) S^p 2
При Sip = 0, 5s ^ О
SAy
5А2 = (тп\ + Tri2)gSs sin a, Q2 = -т— = (mi + mi)g sin a.
Подставляя полученные выражения в уравнения (1), записываем
искомые дифференциальные уравнения движения системы
-т\12ф- -m\lscos (ip + а) = -m\gls\r\ip- ар,
(3)
(mi +m2)s- -miJ<£cos(<p + a) + -mi/<£2sin(<^ + a) = (mi +77i2)gsina, (4)

Глава 3. Уравнения Лагранжа 2-го рода
149
В случае малых колебаний уравнения (3), (4) заменяются следующими:
2т\12ф - 3m\ls cos а = 3(m\gl - 2с)(р,
2(тп\ + 7712)5 - гп\1ф cos а = 2(тп\ + rrt2)g sin а.
Отсюда, исключая s, получим
6(тп\ + гп2}(2с - m\gl) 3(m\ + 77i2)g sin 2а
rrai/2(mi + 4ш2 + Ъгп\ sin2 а) /(raj + 4m2 + Ътп\ sin2 а)
Отсюда определяем период малых колебаний стержня
_ 1 гп[12(гп\ + 4га2 + Ъгп\ sin2 а) _ m\[m\(\ + 3 sin2 а) + 47712]
у 6(т\ + тп2)(2с - m\gl) у 6(т\ + Ш2)(2с - m\gl)
\
Задача 3.25 (48.43). Составить уравнения движения
математического маятника массы га, подвешенного на упругой нити. Длина нити
в положении равновесия Z, ее жесткость равна с. Найти движение
маятника для случая малых колебаний. В качестве обобщенных
координат взять угол (р отклонения маятника от вертикали и относительное
удлинение нити z.
Ответ: (I + х)ф + 2хф + g sin у> = О,
х - (1+ х)<£ +#(1 - cos <р) Н х = 0 — уравнения движения;
m
ip = Bsin I л/yt + /3), z = A sin ( \/—t + а ) — для случая малых
v колебаний.
■* Решение. Расчетные схемы — на рис. 3.25.1, 3.25.2.
В задаче требуется найти зависимости от времени t угла <р и
относительного удлинения z, где
* = 7; (1)
х — абсолютное удлинение нити.
Однако удобнее сначала составить уравнения движения маятника,
используя абсолютное удлинение х, а затем с помощью равенства (1)
переписать полученные уравнения через относительное удлинение z.

150
Глава 3. Уравнения Лагранжа 2-го рода
Маятник имеет две степени свободы и
находится в потенциальном силовом поле. Приняв в
качестве обобщенных координат угол <р и удлинение я,
I ^ . запишем уравнения движения маятника с помощью
■ ^ уравнений Лагранжа 2-го рода
d (dL\ дЬ л ,.
*\m)-h-q (, = ,'2)>
oral-" у где q\ = <р9 q2 = х, L — функция Лагранжа
Рис. 3.25.1 1, = Г-П,
Т — кинетическая энергия маятника
T=\mV\
V — абсолютная скорость маятника (рис. 3.25.1):
V = Vnep+VOT„, Viep =ф(1 + х)9 VmH=X,
Т=]-7П[(1 + Х)2ф2 + Х2],
П — потенциальная энергия маятника, определяемая
силой тяжести маятника и силой упругости пружины
(рис. 3.25.2):
1 2
П = mg(l + х)(\ - cos <р) + -сх .
Таким образом, будем иметь
L = -m[(l + x) ф +х \ - mg(l + x)(\ - cos<p) - -ex ,
dL 2 dL
—- = m(l + х) ф, — = -mg(l + х) sin tp,
оф U(f
d fdL\ /, ч2- . /, х- • d /9L>i
d^V^J =m(Z + x)^ + 2m(/ + ф<р, - {-) = mx,
dL
dz
= m(l -f- rr)<£ - mg(\ - cos y>) - ex.
В результате получаем следующую систему уравнений, описывающих
движение маятника:
(/ + х)ф + 2xф-\-g sirup = О, х- (1 + х)ф2 +g(\ - COS if) Н X = 0.
m

Глава 3. Уравнения Лагранжа 2-го рода
151
Учитывая равенство (1), выполняем замену абсолютного удлинения х
на относительное z:
(1 + z)<p + 2гф+- sin if = О, (2)
z - (1 + z)ip2 + f (1 - cos tp) + -* = 0. (3)
( m
Уравнениям (2), (3) соответствуют следующие уравнения малых
колебаний маятника:
g с
ф+-:(р = 0, Z-\ Z = 0,
I т
с решениями
(р = В sin I а I у t -f /J j, z = Л sin f 4 /—t + a 1,
где А, В,а,(3 — постоянные интегрирования, определяемые из начальных
условий.
Задача 3.26(48.44). Один конец нерастяжимой тонкой нити
обмотан вокруг однородного круглого цилиндра радиуса R, второй
конец прикреплен к неподвижной точке О (рис. 3.26.1). Цилиндр,
разматывая нить, опускается вниз, одновременно раскачиваясь вокруг
горизонтальной оси, проходящей через точку подвеса нити.
Пренебрегая массой нити, составить дифференциальные
уравнения движения цилиндра.
Рис. 3.26.1
Ответ: р-фЯ- -рф2- -gcos<p = 0, р2ф + 2фрр-В,рф2+gp$\xnp = 0.

152
Глава 3. Уравнения Лагранжа 2-го рода
Рис. 3.26.2
*+ Решение. Расчетная схема — на рис. 3.26.2, 3.26.3.
Система имеет две степени свободы и находится в потенциальном
силовом поле. Выбирая в качестве обобщенных координат расстояние р
от точки О до точки схода нити с цилиндра, измеренное вдоль нити,
и угол у отклонения нити от вертикали, запишем уравнения Лагранжа
2-го рода
где L — функция Лагранжа
L = Т - П,
Г — кинетическая энергия системы, П — потенциальная энергия системы,
Я\ =Р, qi = <Р.
Движение цилиндра плоское. Поэтому
T=l-mV2+l-Ju;2, (2)
где V — скорость центра масс цилиндра; J — момент инерции цилиндра
относительно центра масс; ш — угловая скорость цилиндра. Представим
(рис. 3.26.2)
V = Vnep+VOTH) Цкр = фОС, OC = y/R2 + fi, VOTH = p,
V2 = (p2(R2 + р2) + р2- 2рфл/Я? + р2 cos а.
Учитывая, что
R R

Глава 3. Уравнения Лагранжа 2-го рода
153
Рис. 3.26.3
окончательно получаем
V2 = ф2(Я2 + р2) + р2 - 2рфК (3)
Подставив в равенство (2) выражение (3) и приняв во внимание, что
J = -mR , и= — -<р=--<р,
будем иметь
Т = -т|>2(Д2 + р2) + р2 -2рфВ\ + -шД2
(И
(4)
Потенциальную энергию системы определяет только сила тяжести
цилиндра (рис. 3.26.3):
П = -mg (р cos if - R sin ф).
Используя выражения (4), (5), находим
;,2/D2 , л2\ , 1_/^2 1Al.D\ , *_/л d,v\2
(5)
£=г тпф2(Я2+р2)+-m(p2 - IpipR)+-m(/j- ВфУ+mg(pcos<p- Rs\t\(p),
r\r Г 1
— =m\p-<pR+-(p-Ilp)
d(dL\ 3 . .
diUJ = 2m(^V'ii)*
— =m{pp +gcosy>),
op

154
Глава 3. Уравнения Лагранжа 2-го рода
— = т ^p(R2 + р2) -pR- -R(p - Rip)
It (P) = \m№3R2 + 2p2) ~~ VpR + 4^'
dL
dip
-mg(p sin <p + R cos <p).
После подстановки полученных выражений в равенства (1) искомые
уравнения движения цилиндра принимают следующий вид:
3
-т(р - RCp) - т(рф2 + g cos <р) = О,
(1я2 + р2)ф-
■Rp + 2фрр + g(p sin у? + R cos <р) = О,
или
.2
p-<pR- -рф - -gcos <р = О,
р2<р + 2<ррр - #р<£2 -f gp sin <р = 0.
Задача 3.27(48.41). Однородный диск радиуса Д, имеющий
массу М, может вращаться вокруг горизонтальной оси О (рис. 3.27.1).
К диску на нити АВ длины I подвешена материальная точка
массы га. Составить уравнения движения системы.
Рис. 3.27.1
1
Ответ: -(М + 2т)R ф + тШф cos (<р-ф) + тШф sin ((р-ф) +
+ mgRsin <р = О, 1ф + ifrp cos (у>- ф) - R1^ sin (ip-ifr) +g sin ф = 0.

Глава 3. Уравнения Лагранжа 2-го рода
155
Рис. 3.27.2
^ Решение. Расчетная схема — на рис. 3.27.2.
Система имеет две степени свободы и находится в потенциальном
силовом поле. Выбирая в качестве обобщенных координат углы риф,
запишем уравнения Лагранжа 2-го рода:
d fdL\ dL л . л ^
ъЫ~тгя (г=,,2)'
где L — функция Лагранжа
L = T-U,
Т — кинетическая энергия системы, П — потенциальная энергия системы,
Найдем кинетическую энергию системы, составленной из диска и
материальной точки:
Т = Т{+Т2,
где Т\ — кинетическая энергия диска
г, = \зф\
J — момент инерции диска относительно оси вращения
1 2
J=-MR\
2
Т2 — кинетическая энергия материальной точки
Т2 = l-mV\

156
Глава 3. Уравнения Лагранжа 2-го рода
V — абсолютная скорость материальной точки (рис. 3.27.2),
V = Уотн + Упер*
Учитывая, что
Vm = Ф1 Кер = фЯ, V2 = 12ф2 + ЯУ + ЯПФФ COS (tp - ф),
получаем
Г2 = -га [12ф2 + RУ + 2/Д# cos (tp - ф)},
Г = -(М + 2га)дУ + -га[/У + 2Ш# cos (<р - ф)].
Потенциальная энергия системы определяется силой тяжести
материальной точки:
П = -mg(R cos <р - I cos ф).
По известным выражениям для Г и П находим:
Ь=-(М+2т)Я2ф2 + -т[12ф2 + 2Шфф cos ((р-ф)] + mg(Rcos^p + lcosф),
dL \ <>
— = -(М +2т)Я'ф + т1Яфсо$((р - ф),
— ( — ) = - (М+2тп)Я2ф + тШфсоь ((р-ф)- тШф(ф - ф) sin ((р-ф),
а1\оф/ 2
dL
— = -тШфф sin (<р - ф) - mgRsirup,
д(р
dL 2 .
—7=ml ф + mlRфcos((p-ф)t
дф
d /dL\ 2~
-j-1 —г ) =ml ф-\-mlRфcos(lp-ф) -тШф(ф-ф)sm(^p-ф),
at \дф/
dL
— = тШфф sin ((р-ф)- mgl sin ^.
В результате, искомые уравнения движения системы принимают
такой вид:
1 2 -2
— (М + 2т) R ф + raZify cos {(р-ф) Л- тШф sin ((р-ф) + га#Я sin <р = О,
i$ + Я<£ cos (ip- ф) - R^ sin (ip - ф) + g sin ф = 0.

Глава 3. Уравнения Лагранжа 2-го рода
157
Задача 3.28 (48.39). Материальная точка А массы т\ движется
в вертикальной плоскости по внутренней гладкой поверхности
неподвижного цилиндра радиуса I (рис. 3.28.1). Материальная точка В
массы гаг, присоединенная к точке А посредством стержня АВ
длины /, может колебаться вокруг оси А, перпендикулярной плоскости
рисунка. Положения точек А и В определены с помощью углов
а и у?, отсчитываемых от вертикали. Составить дифференциальные
уравнения движения системы. Написать дифференциальные
уравнения малых колебаний системы. Массой стержня АВ пренебречь.
Рис. 3.28.1
Ответ: (mi + rri2)la + т-Дф cos ((р - а) - т-Дф sin (ip- а) +
+ (mi + m2)g sin а = О,
wi2^2 [ф + # cos (ip - а) + a2 sin ((р - a)] -f rri2gl sin (р = О — уравнения
движения;
(mi + rri2)la + milCp + (mi + tn-^ga = О, 1ф + la + g<p = О — уравнения
\малых колебаний системы. У
^ Решение. Расчетная схема — на рис. 3.28.2.
Система имеет две степени свободы и находится в потенциальном
силовом поле. Выбирая в качестве обобщенных координат углы а и у>,
запишем уравнения Лагранжа 2-го рода:
где L — функция Лагранжа
L = T-n,
Т — кинетическая энергия системы, П — потенциальная энергия системы,
q\ = a, qi = Ч>-

158
Глава 3. Уравнения Лагранжа 2-го рода
Рис. 3.28.2
Кинетическую энергию системы представим суммой Г = Т\ +Т2, где Т\ —
кинетическая энергия точки А
Тх = -тпх12а\
Т2 — кинетическая энергия точки В (рис. 3.28.2)
Г2 = X-m2V\
V — абсолютная скорость точки В,
» = ▼пер "h Voth.
Учтем, что Vnep = to, ^от„ = 1ф. Тогда
у2 = 12а2 + 12ф2 + II2 аф cos (<р-а),
Г = -(mi + m2)l2a2 + -m2l2[ф2 + 212афcos (р - а)].
Потенциальная энергия системы определяется силами тяжести точек А и В:
П = -m\gl cos а - ra^cos а + cos <р).
В результате будем иметь
L = -(тп\ + тп2)12а2 + -т2/2 [ф2 + 2d<£ cos (у? - а)] + m\gl cos а +
+ rri2^Z(cos а + cos <р),
dL
да
= (гп\ + m2)Z а + m2l ф cos (<р - а),

Глава 3. Уравнения Лагранжа 2-го рода
159
(0L\ 2 2 2
( — J =(m\+m2)l a+m2l (pcos((p-a)-rri2l ф(ф-а)$т(<р-а),
d_
dt
—-=rri2/2d0sin((^-a)-(mi4-m2)^/sina,
да
— =m2/2|V>+acos(y?-a)],
— I — J =m2Z2[^+acos(^-a)-o:(0-Q:)sin(^-a)],
a r
— = -m,2l a(psm(ip—a)-'m2glsinip.
dip
После подстановки полученных выражений в равенства (1)
записываем уравнения движения системы
(mi + гп2)/о: + m2Z<£ cos ((р - а) - Ш21ф2 sin (ip-a) + (m\ + rri2)g sin а = О,
mil2 [ф + ol cos (ip - a) + a2 sin (ip - a)] + rri2gl sin <p = 0.
В случае малых колебаний эти уравнения заменяются следующими:
(mj -f 7П2)/о: + т21ф -f (mi + rri2)ga = О, 1ф + la + gip = 0.
Задача 3.29(48.48). Механизм робота-манипулятора состоит из
колонны для вертикального перемещения, устройства для горизонтального
перемещения, состоящего из звеньев 1 и 2, и выдвигающейся
горизонтальной руки со схватом 3 (рис.3.29.1). Массы звеньев механизма mi, Ш2
и тпз. Движущие силы, создаваемые приводами в поступательных
парах, равны соответственно Fq\, F\2 и F23. Составить
дифференциальные уравнения движения механизма. Трением пренебречь.
i_
V
Рис. 3.29.1
Ответ: (mi + 7712 + rn-^z = Fo\ - (m\ -f m2 + тз)#,
(m2 + m3)y = F12, m3x = F23.

160
Глава 3. Уравнения Лагранжа 2-го рода
*■* Решение. Система имеет три степени свободы (обобщенные
координаты z, у и х заданы условием задачи). Для записи уравнений движения
системы используем уравнения Лагранжа 2-го рода в виде
dt
(£)-£-* «-™- <■>
где Т — кинетическая энергия системы, Qi — обобщенная сила системы,
соответствующая i-й обобщенной координате,
9i = z, q2 = у, q3 = х.
Представим кинетическую энергию системы суммой
T = Ti+T2 + T3,
где Tj — кинетические энергии звеньев 1, 2 и 3. Все звенья движутся
поступательно. Поэтому
Т\ = -miz ,
T2 = -m2(z2 + y2),
T3 = -m3(z2 + y2 + x2),
Т= -(mi+m2 + m3)z + -(m2 + m3)y + -m3x .
Далее находим
d(dT\ . . дТ n
Tt{Tz)={mi+m2 + m3)z; Tz=°'
dt{-dy-)={m2 + mi)y' "°'
dy
dt\dx)
дТ л
m3x; - = 0.
При подсчете обобщенных сил сообщаем системе возможные
перемещения, при которых координаты z, у и х получат приращения 6z, Sy
и 6х, и составляем соответствующие выражения для элементарных работ
SAi (г = 1, 2, 3) действующих на систему сил.
При Sz Ф О, Sy = 6х = О будем иметь
5А\ = Fq\Sz - (mi + гаг -f m^)g5z.

Глава 3. Уравнения Лагранжа 2-го рода
161
Следовательно,
8А\
(?, = — = Foi - (mi + m2 + m3)g.
При Sy Ф 0, Sz = Sx = О
&42
5A2 = Fl2Sy, Q2 = -r± = Fl2.
При Sx Ф 0, fo = Sy = 0
<fy
<L43
M3 = F23(Jx, Q3 = ^ = ^23.
Подстановка полученных выражений в уравнения (1) дает:
(mi + m2 + m3)z = F0i - (mi + m2 + m3)g,
(m2 + m3)j/ = F\2, тзх = F23.
Задача 3.30 (48.49). Механизм робота-манипулятора состоит из
поворотной колонны 1, устройства для вертикального перемещения 2
и выдвигающейся руки со схватом 3 (рис. 3.30.1). Момент инерции
звена 1 относительно оси поворота J\\ масса звена 2 т2, момент
инерции относительно оси поворота J2; масса выдвигающейся руки
со схватом тз, расстояние от оси поворота до центра масс р, момент
инерции относительно центральной оси J3. К оси поворота приложен
момент М, движущие силы, создаваемые приводами в поступательных
парах, равны соответственно F\2 и F23. Составить дифференциальные
уравнения движения механизма. Трением пренебречь.
Рис. 3.30.1
d
Ответ: -r[{J\+J2 + Jz+mip2)ip\ =М, (т2+т3)2=^12-(т2+т3)£,
m3(p-p<£2) = F23.

162
Глава 3. Уравнения Лагранжа 2-го рода
W Решение. Система имеет три степени свободы (обобщенные
координаты у>, z и р заданы условием задачи). Для записи уравнений движения
системы используем уравнения Лагранжа 2-го рода в виде
г(я)-5-» «='•»>• <•>
где Г — кинетическая энергия системы, Qi — обобщенная сила системы,
соответствующая г-й обобщенной координате,
Я\ =<Рз Q2 = z, q3 = р.
Представим
Г = Г, +Г2 + Г3,
где Т\ — кинетическая энергия звена 1 (поворотной колонны), Г2 —
кинетическая энергия звена 2 (устройства для вертикального перемещения),
Гз — кинетическая энергия выдвигающейся руки со схватом.
Звено 1 вращается вокруг неподвижной оси с угловой скоростью <р.
Следовательно,
1 2
Звено 2 движется поступательно вдоль оси вращения звена 1
(относительное движение) и вращается вокруг этой оси (переносное движение).
Таким образом,
J-2 = -^2отн "Т -*2пер>
где
1 .2
•*2отн = ym1Z »
^2пер = у^Ф •
Движение выдвигающейся руки со схватом также складывается из
относительного движения (поступательного вдоль оси выдвижения руки
со схватом) и переносного движения (вращательного вокруг оси
вращения звена 1 и поступательного вдоль этой оси). Поэтому
-*3 = -*Зотн "Г -*3пер>
где
Тзотн = -ТПзР ,
Тзпер = - (J3 + т3р2)ф2 + -га3£2.

Глава 3. Уравнения Лагранжа 2-го рода
163
В результате получаем
Т = -J\<p2 + -m2z2 + -J2ip2 + -тгр2 + -(J3 + т3р2)ф2 + -m3i2,
или
Т = -(Ji + J2 + Jz + m3p2)02 + -(m2 + m3)i2 + -m3p2.
Далее находим
l(i) = lf(Jl+j2+j3+m3^'
—-0
д<р
d(dT\ .
diUJ=(m2+m3)2'
яг
dt\dp
dT .2
(^)=™зА
- = тзР¥> .
Для определения обобщенных сил сообщим системе возможные
перемещения, при которых координаты <p,z и р получат приращения 8(р,
5z и 5р, и составим соответствующие выражения для элементарных работ
5Ai (г = 1, 2, 3) действующих на систему сил.
При Stp^O, 8z = 5р = О будем иметь:
5А\ = М5фу
При 6z^09 Sip = 5p = Q
5A2 = FnSz - (m2 + m3)gSz9
SA2
Qi = -j- = F\2 ~ (m2 + m3)g.

164
Глава 3. Уравнения Лагранжа 2-го рода
При 6р ф 0, S(p = 5z = 0
6А3 = F235p,
Q3 = -т-2 = F23.
5р
Подставляя полученные выражения в уравнения (1), записываем искомые
уравнения движения механизма:
jt [(J\ +J2 + J3 + гп3р2)ф] = М,
(т2 + m3)z = F12 - (т2 + m3)g,
m3(p- рф2) = F23.
Задача 3.31 (48.38). Призма А массы тп3 движется по гладкой
горизонтальной плоскости (рис. 3.31.1). По призме А скользит
призма В массы ш2. К призме В посредством цилиндрического шарнира О
и спиральной пружины с коэффициентом жесткости с присоединен
тонкий однородный стержень OD массы тп\ и длины I.
Стержень совершает колебания вокруг оси О, перпендикулярной
плоскости рисунка. Положения призм А, В и стержня OD
определены посредством координат я, s и (р. Написать дифференциальные
уравнения движения материальной системы, состоящей из призм А,
В и стержня OD, пренебрегая силами трения.
шшшшшшшш^З
Рис. 3.31.1
1 ,2.. 1 ,- / v 1 ,.. 1 .
Ответ: -тп\1 ф - -m\lscos ур + о) - -гп\1х cos р = m\g- s\np- ср,
1 1 2
(m\+m2)s--m\lpcos(p + a) + -m\ty s\n(<p + а) + (m\ +m2)xcosa =
= (тп\ +m2)g sin а,
1 2
(mi +7712 + m3)x + (гп\ -f ra2)s cos а + -тп\1(ф simp- фсоьр) = 0.

Глава 3. Уравнения Лагранжа 2-го рода
165
Рис. 3.31.2
^ Решение. Расчетные схемы — на рис. 3.31.2, 3.31.3.
Система имеет три степени свободы (обобщенные координаты х, 5
и (р заданы условием задачи). Для записи уравнений движения системы
используем уравнения Лагранжа 2-го рода в виде
l(S)-s-* <—>■
где Г — кинетическая энергия системы, Qi — обобщенная сила системы,
соответствующая г-й обобщенной координате,
Ч\ =<р, Чг = s, д3 = х.
Представим
Т = Т1+Т2 + Т3,
где Т\ — кинетическая энергия стержня, Тг — кинетическая энергия
призмы Ву Гз — кинетическая энергия призмы А.
Движение стержня — плоское. Следовательно,
1 2 1 2
где J — момент инерции стержня относительно оси, проходящей через
его центр масс
ш — угловая скорость стержня
ш = ф,
V\ — абсолютная скорость центра масс стержня (рис. 3.31.2),
Vj = Vqth i Vnep,

166
Глава 3. Уравнения Лагранжа 2-го рода
VOTH — относительная скорость центра масс стержня
V™ = 21(Р>
Упер — переносная скорость центра масс стержня.
Переносное движение центра масс стержня, в свою очередь,
складывается из поступательного движения призмы В относительно призмы А
со скоростью V2 и поступательного движения призмы А относительно
горизонтальной плоскости со скоростью V3 (рис. 3.31.2). Поэтому
Vnep=V2+V3,
где Vi = 5, V3 = х.
Таким образом, находим:
V\x = scosa+x- -1фсоьф,
V\y = -ss\na- -tysimp,
Vj =s +x + -1 ф -Zs<£cos(</?+a)+(2scosa-/<£cos<p),
T\ = -mi
£2+х2 + -12ф2-1&фсо$((р+а)+(2£соза-1фсо$ф)х
1 ,2.2
Для призм В и А, которые движутся поступательно, записываем:
Тг = -ТП2Уп2ер = -гаг (s2 + х2 + 2sx cos a),
1 .2
Т3 = -тп-кх •
2
В результате получаем
Т=-т{
s2 + х2 + -12ф2 - 1&ф cos ((р + a) + (2i cos а-1ф cos <p)x
+
+ — m\l ф +-тпг\ё +x + 2sxcos a) +-тпз± ,
l_
24'
ет ' ,2. 1 ,. / ч 1 ,.
— = -mit ф —m\lscos (<p + a) - -milxcosy,
dip 3 2 2
d /0T\ 1 ,2„ 1 ,.. .
dt{dj) = 3miltp-2mlSCOS{(p + a) +
+ -miZ^sin (y? + a) - -m\l(x cos ip- хф sin ip),

Глава 3. Уравнения Лагранжа 2-го рода
167
дТ 1 ,.. , . 1
— = -m\ls<psm((p+a) + -m\lx<psm(py
— = (m\+m2)s—mi^cos((^+a) + (mi+m2)a;cosa,
as 2
dfdT\ . . 1 . .
— ( — l=(m1H-rn2)5--mi/^cos(^+a) +
1
+ -гп\1ф sin(</?+a) + (mi+m2)xcosa,
дТ л
вГ0«
/У7"1 1
-— = (mi+m2+тз)а;+-mi (2scosa-^cos^)+m25COsa,
ox 2
— ( — J =(mi+m2+m3)x+-mi(25COsa-^cos(^+Z(^2sinv?)+m25COsa,
at \ ox J 2
дТ _
~дх~
Для определения обобщенных сил сообщим системе возможные
перемещения, при которых координаты (р, s и х получат приращения <fy>,
Ss и Sx, и составим соответствующие выражения для элементарных работ
5А{ (г = 1, 2, 3) действующих на систему сил (рис. 3.31.3).
При 5(p^Q> Ss = 6х = 0 будем иметь
/ 1 \с „ 5А\ 1 .
&Ai = I mig- sm ip- cip ) д(р, Q\ = — = rriig- sin tp - op.
При <Js ^ 0, 5<p = Sx = 0
<L42 = (mi + m2)gSs sin a, Q2 = ~г~ = (mi + mi)s sin a.

168
Глава 3. Уравнения Лагранжа 2-го рода
При 8х Ф О, Sep = 6s = О
5АЪ = О, д3 = 0.
Подставив полученные выражения в уравнения (1), записываем
дифференциальные уравнения движения рассматриваемой системы:
1 |2- 1 ,- / ч * ,~ ' •
-mj/ ф — -m\ls cos (<р + а) - -mi/#cos<p = m\g- sin у?- ар,
1 1 2
(mi + тг)5 - -m^cos (у? + a) + -т\1ф sin (<p 4- a) +
+ (mi + m2)x cos a = (mi + mi)g sin a;
1 2
(mi 4-m2 + тз)х + (mi + m2)scosa f- -т\1(ф sin у?- <£cosy?) = 0.

Глава 4
Интегралы движения,
канонические уравнения Гамильтона,
уравнение Якоби-Гамильтона (§49, [1])
Задача 4.1 (49.1). Трубка АВ вращается с
постоянной угловой скоростью и вокруг
вертикальной оси CD, составляя с ней угол а
(рис. 4.1.1). В трубке находится пружина
жесткости с, один конец которой укреплен в точке А.
Ко второму концу пружины прикреплено
тело М массы га, скользящее без трения внутри
трубки. В недеформированном состоянии длина
пружины равна АО = I. Приняв за обобщенную
координату расстояние х от тела М до точки О,
определить кинетическую энергию Г тела М и
обобщенный интеграл энергии.
Ответ: Т=-т[х +cj2(Z-fx)2sin2a] —
кинетическая энергия тела М;
х - и (I + х) sin aj + 2mgx cos a + ex
интеграл энергии.
const — обобщенный
■* Решение. Расчетная схема — на рис. 4.1.2.
Тело М считается материальной точкой. Поэтому
1 ,
где V — абсолютная скорость тела М,
» = М)ТН ~г Vnep.
Учитывая, что (рис. 4.1.2)
V'oth = я, Кер = и{1 + х) sin а,

170 Глава 4. Интегралы движения, канонические уравнения Гамильтона
Рис. 4.1.2
находим
V2 = x2 + u2(l + x)2sin2a,
Т = -m[x2 + u2(l + х)2 sin2 а].
Рассматриваемая система имеет одну степень свободы. Следовательно,
обобщенный интеграл энергии определяется выражением
dL. г
—x-L = const.
ох
Здесь L — функция Лагранжа
L = Т - П,
П — потенциальная энергия системы.
В данном случае потенциальная энергия системы равна сумме
потенциальных энергий силы тяжести тела М и силы упругости
деформированной пружины:
1 2
П = mgx cos а + -сх .
Таким образом, функция Лагранжа и соответствующий ей обобщенный
интеграл энергии записываются в виде
L = -m[x2 + u2(l + х)2 sin2 а] - mgx cos а - -сх2,
m [х2 - и2{1 + х)2 sin2 а] + 2mgx cos а + сх2 = const.

Глава 4. Интегралы движения, канонические уравнения Гамильтона 171
Задача 4.2 (49.2). Найти первые интефалы движения
сферического маятника длины Z, положение которого определяется углами в и ф
(рис. 4.2.1).
Ответ: т12ф sin2 в = С\ — циклический интефал сферического
маятника;
в1 + ф2 sin2 в - 2- cos в = С2 — обобщенный интефал энергии
сферического маятника.
■► Решение. Расчетная схема — на рис. 4.2.2.
Для того чтобы найти первые интегралы движения маятника,
составим его функцию Лафанжа L
L = Т - П,
где Т — кинетическая энергия маятника, П — потенциальная энергия
маятника.
Учитывая, что положение маятника определяется углами в и ф,
находим (рис. 4.2.2):
T=X-mV\
» = *отн "Г »пер>

172 Глава 4. Интегралы движения, канонические уравнения Гамильтона
V'nep = Ф1 Sin 0,
V2 = l2(9t + ftsin20),
Т = ^(в2 + ф2 sin2 в).
Потенциальная энергия определяется силой тяжести маятника
П = -mgl cos в.
Таким образом, функция Лагранжа маятника описывается следующим
выражением:
L = -ml2^ + ф2 sin2 в) + mgl cos 0.
Как видно, составленная функция L явно не зависит от координаты ф
и времени t. Поэтому для сферического маятника можно записать два
первых интеграла движения: циклический интеграл, соответствующий
координате ф, и обобщенный интеграл энергии. Циклический интеграл
сферического маятника представляется выражением
dL t • о
—г = тпгф sin2 в = С{.
дф
Рассматриваемая система имеет две степени свободы. Поэтому выражение
для обобщенного интеграла энергии записывается в виде
Учитывая, что
— = ы1%
дв
находим обобщенный интеграл энергии сферического маятника
e2 + V>2sin2e-2yCos0 = C2.

Глава 4. Интегралы движения, канонические уравнения Гамильтона 173
Задача 4.3(49.3). Гироскопический тахометр установлен на
платформе, вращающейся с постоянной угловой скоростью и вокруг оси £
(рис. 4.3.1). Определить первые интегралы движения, если
коэффициент жесткости спиральной пружины равен с, моменты инерции
гироскопа относительно главных центральных осей х, у, z соответственно
равны А, В и С, причем В = А. Силы трения на оси z
собственного вращения гироскопа уравновешиваются моментом, создаваемым
статором электромотора, приводящим во вращение гироскоп. Силами
трения на оси прецессии пренебречь.
Рис. 4.3.1
Ответ: С (и sin в + ф) = п — циклический интеграл;
- [(Сф2 + Ав2) - (Си2 sin2 в + Аи2 cos2 в)] + -св2 = h- обобщенный
интеграл энергии.
■► Решение. Расчетная схема — на рис. 4.3.2.
Для того чтобы определить первые интегралы уравнений движения
тахометра, составим функцию Лагранжа L: L = Т - П, где Г —
кинетическая энергия тахометра, П —- потенциальная энергия тахометра.
Представив, что тахометр — это твердое тело, вращающееся вокруг
неподвижной точки, записываем
Т=1-А(и2х + Ш2у)+1-Ыг.
Здесь cjx, иу, и2 — проекции угловой скорости тахометра на оси х, у> z.
Учтем, что (рис. 4.3.2) их = и cos в, иу = 6,иг = и sin 0 + ф. Тогда
Г = - А(и2 cos2 в + в2) + -С(и sin в + ф)2.

174 Глава 4. Интегралы движения, канонические уравнения Гамильтона
Рис. 4.3.2
Потенциальную энергию тахометра определяет момент спиральной пружины
2
В результате получаем
L = -А(и2 cos2 в.+ в2) + -С(и sin в + ф)2- -с в2.
(О
Исследуя полученную функцию Лагранжа, отмечаем, что она не
зависит от угла <р и времени t. Следовательно, для рассматриваемого тахометра
можно составить два первых интеграла движения: циклический интеграл
и обобщенный интеграл энергии.
Циклический интеграл, соответствующий координате <р,
записывается в виде
9L „t л ч
— = С (и sin в 4- ф) = п.
оф
(2)
Обобщенный интеграл энергии в данном случае определяется выражением
dL . 8L. т .
—tp+ —$-L = h,
дфУ дв
или с учетом выражений (1), (2)
- \(Cip2 + Ав2) - (Си2 sin2 в + Аи2 cos2 б)] + ]-с в2 = h.

Глава 4. Интегралы движения, канонические уравнения Гамильтона 175
Задача 4.4 (49.4). Материальная точка М соединена
с помощью стержня ОМ длины I с плоским шарниром О,
горизонтальная ось которого вращается вокруг
вертикали с постоянной угловой скоростью и (рис. 4.4.1).
Определить условие устойчивости нижнего
вертикального положения маятника, период его малых
колебаний при выведении его из этого положения и
обобщенный интеграл энергии. Массой стержня пренебречь.
Ответ: g/l > и — условие устойчивости нижнего
вертикального положения маятника;
2тг
ч/^Д^
Рис. 4.4.1
ф2 - и2 sin2 tp-2- cos (р
период малых колебаний маятника;
h — обобщенный интефал энергии.
■* Решение. Расчетная схема — на рис. 4.4.2.
Рассматриваемая система имеет одну степень свободы. Обобщенная
координата у?, показанная на рис. 4.4.1, определяет положение маятника
в любой момент времени (угол поворота маятника
относительно вертикальной оси находится по заданной
угловой скорости и).
Для определения условия устойчивости нижнего
вертикального положения маятника составим
выражение измененной потенциальной энергии системы W
W=U-T0,
где П — потенциальная энергия маятника, Г0 —
составляющая кинетической энергии, которая не
зависит от обобщенной скорости ф (энергия
центробежных сил инерции).
Чтобы найти Го, запишем выражение
кинетической энергии маятника. Рассматривая маятник как
материальную точку, будем иметь
Т = \mV2.
2
.---V,
Рис. 4.4.2
Здесь V — абсолютная скорость точки М (рис. 4.4.2),
V = Vot„ + Vnep, V0TH = ф1, Кер = U)l Sin if.

176 Глава 4. Интегралы движения, канонические уравнения Гамильтона
Таким образом, получаем
V2 = 12(ф2 + и1 sin" <р), Т = ^гп1\ф* + и? sin" tp).
Потенциальная энергия маятника определяется силой тяжести
материальной точки М: П = -mgl cos tp. Следовательно,
W = П - То = -mgl cos <р - -ml2v2 sin2 <p.
Нижнее вертикальное положение маятника будет устойчивым при
выполнении условия
д<р2
>0.
(р=0
В данном случае это условие переписывается в виде mgl - ml2u2 > О, или
I *ш
Чтобы определить период малых колебаний маятника, составим его
уравнение движения, используя уравнения Лагранжа 2-го рода
(И\дф) д<р~ '
где L — функция Лагранжа
1 = Г-П.
Учитывая полученные ранее выражения для Г и П, находим
L = -т12(ф2 + и/ sin2 ф) + mgl cos tp,
— I —- ) = т12ф, — = ml2u2 sin (p cos ip - mgl sin (p\ 0)
at \дф J dip
<£ - ш sin у? cos <p H- у sin tp = 0.
В случае малых колебаний уравнение (1) заменяется следующим:
♦+(?-4
Отсюда период малых колебаний
2тг

Глава 4. Интегралы движения, канонические уравнения Гамильтона 177
Обобщенный интеграл энергии для системы с одной степенью свободы
представляется выражением
-—</?- L = п.
дф>
Для рассматриваемого маятника оно принимает вид
-ml (ф -и sin у)-mglcosy = h, или <£ -и sin tp-2- cosip = h.
Задача 4.5(48.40). Шероховатый цилиндр массы га и радиуса г
катится без скольжения по внутренней поверхности полого цилиндра
массы М и радиуса R> способного вращаться около своей
горизонтально расположенной оси О (рис. 4.5.1). Моменты инерции цилиндров
относительно своих осей равны mr2/2 и MR2. Составить уравнения
движения системы и найти их первые интегралы.
7 m2(R-r) m Л .. Я .. 2g
Ответ: V'-tttttt v£V = 0» V^TiT* ч^+ттт; rsin<£ = 0 —
2М(М + га)Я"
3(Д-г)г З(Д-г)
1
уравнения движения системы; MR2ij> + -mR[Rtp - (R - г)ф] = Cj,
-MR2ip2+-т[Щ - (Я - г)<£]2+-га(Д - r)2ф2-mg(R - г) cos у> = С2.

178 Глава 4. Интегралы движения, канонические уравнения Гамильтона
Рис. 4.5.2
*■► Решение. Расчетная схема — на рис. 4.5.2.
Система имеет две степени свободы
(обобщенные координаты (риф заданы условием
задачи) и находится в потенциальном силовом
поле. Для записи уравнений движения системы
используем уравнения Лагранжа 2-го рода в виде
d fdL\ dL
где L — функция Лагранжа
L = T-II,
Т — кинетическая энергия системы, П — потенциальная энергия системы,
Ч\ =Ф, qi = Ч>-
Представим
T = Tl+T2f
где Т\ — кинетическая энергия цилиндра массы М, Т2 — кинетическая
энергия цилиндра массы т.
Полый цилиндр массы М вращается вокруг неподвижной оси и,
следовательно,
Г, = \М2 = l-MR2i>\
Движение цилиндра массы т плоское. Он катится по внутренней
поверхности полого цилиндра без скольжения. Поэтому
Т2 = -mV2 + -J2uf,
где V — скорость центра масс цилиндра массы т (точки 0\ на рис. 4.5.2)
V = <p(R-r),
и — угловая скорость вращения цилиндра массы т относительно точки 0\.
Обозначим в — угол поворота цилиндра массы т относительно
точки 0\. Тогда
Вт = ip(R - г) - ярЯ,
"=0=^(-^J-v>-.
Учитывая, что
j2 = -таг ,

Глава 4. Интегралы движения, канонические уравнения Гамильтона 179
окончательно получаем
Т2 = ^га[3(Д - г)2ф2 - 2Д(Д - г)фф + (Яф)2],
Г = ]-MR2i)2 + X-m{Z(R - г)2ф2 - 2Д(Д - г)фф + (Яф)2].
Потенциальную энергию системы определяет только сила тяжести
цилиндра массы га:
П = mg(R - r)(l - cos ф).
Таким образом,
£=-МД2^Ч-га[3(Д-г)У-2Д(Д-^^
(О
Находим
— = MR2i> + -тП[Иф - (Д - г)ф],
dip 2
&L Л
— (^J = Af Л2^ + -mR[W -(R- г)ф],
— = -га(Д - г)V - -тД(Д " r)tf,
9L ,п ч •
—- = -гадД - г) sin <р,
В результате получаем следующие уравнения, описывающие движение
рассматриваемой системы:
1 3 1
МД^+-га[Д0-(Д-г)<£] =0, -(Д-г)уЗ- -Д^ + gsin^ = 0,
или
й Н т— Ф = 0,
^ 2М(М + га)Д^
^"з(д^^+з(д^)8Ш^а

180 Глава 4. Интегралы движения, канонические уравнения Гамильтона
Для записи первых интегралов уравнений движения исследуем функцию
Лафанжа рассматриваемой системы. Как видно из выражения (1), функция L
явно не зависит от координаты ф и времени t. Следовательно, в данном случае
можно записать циклический интеграл, соответствующий координате ф:
(2)
и обобщенный интеграл энергии
(3)
Подставляя в равенства (2), (3) выражения для функции L и ее
производных, находим
1
МЯ2ф+ -mR[Rip-(R-r)4>] =Си
-MR2ф2 + Jm[Rф-(R-r)ф]2 + -m(R-r)2ф2-rng(R-r)cos^p=C2^
Задача 4.6(49.5). Уравновешенный
гироскоп в кардановом подвесе движется по
инерции (рис. 4.6.1). Определить кинетическую
энергию системы и первые интегралы
уравнений движения, если момент инерции
внешней рамки относительно неподвижной оси
вращения £ равен «7^, моменты инерции
внутренней рамки относительно главных
центральных осей х, у, z равны J*, J*, J*,
а соответствующие моменты инерции
гироскопа — JX, Jy, JZ (JX = Jy),
Ответ:
T = \ { [JZ + Jz + № + Jx - J*z ) COS2 в] ф2 +
Рис.4.6.1 +(JX + Jy)? + <?г(Ф sin 0 + ф)2}
—кинетическая энергия;
(фьтв + ф) =n, [j£ + J*+(Jx + Jx - Jz) cos2 в]ф + J2ns\r\6 = ni —
циклические интегралы,
[J* + J*z + (Jx + Jx - J*z) cos2 в] ф2 + (Jx + J*)? = h - обобщенный
интеграл энергии.

Глава 4. Интегралы движения, канонические уравнения Гамильтона 181
^ Решение. Расчетная схема — на рис. 4.6.2.
Кинетическую энергию системы
представим суммой
Т = Тг + Т1+Т2,
где Тр — кинетическая энергия гироскопа,
Т\ — кинетическая энергия внешней рамки,
Г2 — кинетическая энергия внутренней рамки.
Гироскоп — это твердое тело,
вращающееся вокруг неподвижной точки. Следовательно,
Tr = -Jx(<4 + u2y) + -Jzu22,
где (jX9 иу, uz — проекции угловой скорости
гироскопа на оси х, у, z.
В данном случае (рис. 4.6.2)
Рис. 4.6.2
их = tp COS 0,
иу = вУ
Поэтому
Гг = -J^cos2 в + в2) + -J,(V>sin<9 + ф)2.
Принимая во внимание, что внешняя рамка вращается вокруг
неподвижной оси Of, а внутренняя рамка — вокруг пересекающихся осей Of и Оу,
находим
Г, = I Jrf9 Т2 = 1-Гхф2 cos2 в + ]-Гув2 + ]-ГЛфйп в + ф)2,
T=U[Js + J*z+ (J* + JX- Jt) cos2 в]ф2 +
+ (Jx + Jj)# + J,(^SH10 + 0)2
Чтобы записать первые интегралы уравнений движения гироскопа,
составим выражение для функции Лагранжа L
L = T-U9
где П — потенциальная энергия гироскопа. Так как рассматриваемый
гироскоп уравновешенный,
П = 0.
И
■

182 Глава 4. Интегралы движения, канонические уравнения Гамильтона
Таким образом,
Исследуя полученную функцию Лагранжа, отмечаем, что она не
зависит от углов <р, ф и времени t. Следовательно, в данном случае можно
составить три первых интеграла уравнений движения: два циклических
интеграла и обобщенный интеграл энергии.
Циклические интегралы, соответствующие координатам (риф,
записываются в виде
9L ,. л ч
— = (фыпв + ф) = п,
оф
or
-у = [J{ + J*z + (J* + JX- fz) cos2 в]ф + J2nsme = щ.
оф
Обобщенный интеграл энергии определяется выражением
dL dL . dL. г ,
—ф + —г^ + —гв - L = h,
дфУ дф* дв
или
[Jt + fz + (Гх + Jx - Jj) cos2 0]^2 + (Л + fy)? = ft.
Задача 4.7 (49.7). Составить функцию Гамильтона и канонические
уравнения движения для математического маятника массы т и
длины I, положение которого определяется углом ц> отклонения его
от вертикали. Проверить, что полученные уравнения эквивалентны
обычному дифференциальному уравнению движения математического
маятника.
Р2 Р
Ответ: Н=-—-j - mgl cos <^, ф=—-j, р= -mgl sin <р.
^ Решение. Рассматриваемая система имеет одну степень свободы.
Поэтому функция Гамильтона записывается в виде
H = pq-L,
где р — обобщенный импульс системы
dL

Глава 4. Интегралы движения, канонические уравнения Гамильтона 183
q — обобщенная скорость системы, L — функция Лафанжа: L = Г - П,
Г — кинетическая энергия системы, П — потенциальная энергия системы.
Согласно условию задачи q = ф. Поэтому
1
(1)
Т = -ml ф , П = -mgl cos у>,
L = -гп12ф2 + mgl cos ip,
2 Р2
p = ml ф9 Н = -—- - mgl cos (p.
2ml1
Составляем канонические уравнения движения маятника, т. е. уравнения
движения в виде системы
• -НЕ -__^
др' д(р
Учитывая выражение (1), получаем
^=mP' P=~mSlsin(P' (2)
Переписывая систему (2) в лафанжевых переменных, будем иметь
гп12ф = -mgl sin у?,
или
ф + у sin (р = 0.
Задача 4.8(49.8). Материальная точка массы т
подвешена с помощью стержня ОМ длины / с плоским
шарниром О, горизонтальная ось которого вращается
вокруг вертикали с постоянной угловой скоростью и
(рис. 4.8.1). Составить функцию Гамильтона и
канонические уравнения движения. Массу стержня не учитывать.
р ml 2 2
Ответ: Н = -—-г —и sin ю - mgl cos u>,
2ml1 2
p 2 2
ф = —-г, p = ml и simp cos tp - mgl sin (p.
ml1
Рис. 4.8.1

184 Глава 4. Интегралы движения, канонические уравнения Гамильтона
Рис. 4.8.2
■* Решение. Расчетная схема — на рис. 4.8.2.
Рассматриваемая система имеет одну степень
свободы. Поэтому функция Гамильтона записывается
в виде
Н = рф - L,
где р — обобщенный импульс системы
8L
p=Tf
q — обобщенная скорость системы, L — функция
Лагранжа
L = Т - П,
Г — кинетическая энергия системы, П —
потенциальная энергия системы.
Находим
T=l-mV\
где V — абсолютная скорость точки М (рис. 4.8.2),
» = муш ~г Vnep,
Кггн = ф1,
Vnep = ul sin <р,
V2 = l2&2+u2s\n2ip),
Т = -гп12(ф2 + и2 sin2 (р).
Потенциальную энергию системы определяет сила тяжести точки М:
П = -mgl cos (p.
Таким образом, получаем
L = T-Il,
L = -пй2(ф2 + и2 sin2 (р) + mgl cos <p,
p = ml ф,
H
(1)
P2 rnl2 2 . 2
-—tz —u sin (p - mgl cos (p.
2ml1 2

Глава 4. Интегралы движения, канонические уравнения Гамильтона 185
Составляем канонические уравнения движения системы
*=w
он
дН
р = -
V
которые с учетом выражения (1) принимают следующий вид:
V
<р =
ml2'
i2. 2
р = ml и sirup cos ip - mgl sin ip.
Задача 4.9 (49.11). Положение оси симметрии z волчка,
движущегося относительно неподвижной точки О под действием силы тяжести,
определяется углами Эйлера, углом прецессии яр и углом нутации в
(рис. 4.9.1). Составить функцию Гамильтона для углов яр, в и ср (угол
собственного вращения) и соответствующих импульсов, если т —
масса волчка, I — расстояние от его центра масс до точки О, С —
момент инерции относительно оси z, А — момент инерции
относительно любой оси, лежащей в экваториальной плоскости, проходящей
через точку О.
Рис. 4.9.1
Л тт ! \ (Рф - Рш cos в)2 2
р2
+ т~ + mgl COS 0.
2G

186 Глава 4. Интегралы движения, канонические уравнения Гамильтона
Рис. 4.9.2
^ Решение. Расчетная схема — на рис. 4.9.2.
Волчок имеет три степени свободы. Углы Эйлера ф,0 и(р определяют
положение волчка в любой момент времени. Поэтому функция Гамильтона
представляется выражением
з
где pi — обобщенный импульс системы, соответствующий г-й
обобщенной координате
8L
qi — обобщенная скорость системы, соответствующая г-й обобщенной
координате, L — функция Лагранжа: L — Т - П, Г — кинетическая
энергия системы, П — потенциальная энергия системы.
Полагая, что q\ =ф9 q2 = в, q$ = <р, находим кинетическую энергию
волчка, как твердого тела, вращающегося вокруг неподвижной точки
Т=^А{ш2х + и?у)+1-Си2г,
и>х =ф sin в sin ср + 0 cos <р,
шу = ф sin в cos (р - в sin (р,
u>z = ф + ф cos 0,
T = Х-А{ф2 sin2 в + в2) + l-C^cosO + ip)2.

Глава 4. Интегралы движения, канонические уравнения Гамильтона 187
Потенциальная энергия волчка определяется его силой тяжести
(рис. 4.9.2):
7Г = mgl cos в.
Таким образом, получаем
L = -А(в2 + ф2 sin2 0) + -С(ф + ф cos в)2 - mgl cos в.
Отсюда
Тогда
or
р{ =рф= — = Аф sin2 в + C(ip cos 6 + ф),
дф
dL .
Рз = Ру> = ^т = C(ipcos в + ф).
. _ р^ - рф cos 0
^~ Л sin2 в '
<£:
А9
Рф РФ - Рф cos в
С A sin Мдв
Подставив эти выражения в равенство (1), будем иметь
5 л • г * Г (p^-Ptf COS 0)2 2
Я=^+р^+руу-£= —^ j^fl +р^
Р2
+ -p; + mgZcos0.
2G
Задача 4.10 (49.12). В условиях предыдущей задачи составить
канонические уравнения движения волчка.
~ ; РФ - Рф cos 0 . р0
Ответ: Ф= * А .2л , Pv = 0> #=т>
Л sin2 0 А
(Рф - Рф COS 0)(Ру, - Рф COS 0)
Р0 = —, . Л + ragisin0,
A sin3 0
Р</> ~ Рф COS в Рш .
* = - AtJsM +S' ^ = °-

188 Глава 4. Интегралы движения, канонические уравнения Гамильтона
■* Решение. Для системы с тремя степенями свободы канонические
уравнения движения записываются в виде
дН
dpi
дН
Й = --сГ (*= 1>2,3)..
Используя функцию Гамильтона, полученную в предыдущей задаче,
находим
, Рф-Русоьв . ре
A sin2 в А
(РФ - Р<р cos в) fa-рф cos 6)
Ре = -- /. з а + m8l sm в>
A sin3 в
. _ Рф~ Р<р cos 0 р^
*~ Atgf^ne~ + 'cf
Рч> = 0.
Задача 4.11 (49.13). Свободная точка единичной массы движется
в вертикальной плоскости ху под действием силы тяжести.
Составить дифференциальное уравнение в частных производных Якоби—
Гамильтона и найти его полный интеграл (ось направлена вертикально
вверх).
Ответ:
\У = Ы + Ь2Х± ^-J(-2gy - 26, - Ъ22)3 + с.
\ 31_ J
^ Решение. Для рассматриваемой точки дифференциальное
уравнение в частных производных Якоби—Гамильтона записывается в виде
dW
/ aw dw\ Л
HV'x'y'-te'-b)= °'
где W — характеристическая функция;
_/ dw dw\
HV'X'V--&'-*)
— функция Гамильтона.

Глава 4. Интегралы движения, канонические уравнения Гамильтона 189
Представим
H = p{x + p2y-L,
где pi (i = 1,2) — обобщенные импульсы
дЬ дЬ
L — функция Лагранжа
L = T-U,
Т — кинетическая энергия, П — потенциальная энергия.
Для точки единичной массы находим
Т = ~{х2 + у2), 11= gy, L = ~(х2 + у2) - я/,
Р\=х, р2 = У, Н= -(р2\ + р22) + gy.
В результате уравнение Якоби—Гамильтона переписывается таким образом:
0W 1Г/0ИЛ2 fdW\2]
Учитывая, что координата х циклическая, полный интеграл
уравнения (1) будем искать в виде
W = blt + b2x + F(y), (2)
где 61,62 — произвольные постоянные.
Подстановка выражения (2) в уравнение (1) дает
2Ь,+^+(^г) +2gy=0'
F{y) = ±j^{-2gy-2bx-b\Y + C
или
Отсюда
и, следовательно,
W = bit + Ь2х ± ^-yj{-2gy - 26, - Ъ\У + С.
3*

190 Глава 4. Интегралы движения, канонические уравнения Гамильтона
Задача 4.12(49.14). Пользуясь результатами, полученными при
решении предыдущей задачи, и свойствами полного интеграла уравнения
Якоби—Гамильтона, найти первые интегралы уравнений движения точки.
Ответ: t+ -\J-2gy- 26, -Ь\ = а,, х+ -\J-2gy- 26, - Ь\ = а2,
о о
Ъг = х, yj-2gy - 26, - b\ = у.
ч '
^ Решение. Согласно теореме Якоби первые интегралы уравнений
движения точки записываются в виде
dW dW dW dW
— =au —=аъ — =p„ — =P2f
где a\,a,2 — произвольные постоянные.
Подставляя в эти равенства выражения полного интеграла W и
обобщенных импульсов р\,Р2, полученных при решении предыдущей задачи, имеем:
t+ -y/-2gy-2bi-% = оь
х + — y-2gy - 26, - b\ = а2,
Ъ2 = х, \j-2gy - 26, -Ц = у.
Задача 4.13 (49.15). Физический маятник массы М вращается
вокруг неподвижной оси. Момент инерции маятника относительно этой
оси равен J, расстояние от центра масс маятника до оси равно I.
Составить дифференциальное уравнение Якоби—Гамильтона, найти его
полный интеграл и первые интегралы движения маятника (нулевой
уровень потенциальной энергии взять на уровне оси маятника).
0W 1 fdW\2 1Ж ,
0твет: -K+Tj\-di) -м*1«"<р = 0-
W = bt±V2J Г y/Mgl cos <р - b d<p,
<P
^\/^ / / =Q> ±y/2Jy/Mgl cos(p-b = Зф.
\ 2 J JMgl cos ip - b
cos <p - 0

Глава 4. Интегралы движения, канонические уравнения Гамильтона 191
■► Решение. Физический маятник — это система с одной степенью
свободы. Угол ip отклонения маятника от вертикали определяет
положение маятника в любой момент времени. Поэтому дифференциальное
уравнение Якоби—Гамильтона для маятника записывается в виде
где W — характеристическая функция,
H(t,<p,
д<р)
— функция Гамильтона.
Представим
H = p<p-L,
где р — обобщенный импульс
0L
Р==дф>
L — функция Лагранжа
L = T-Il,
Т — кинетическая энергия, П — потенциальная энергия. Для физического
маятника находим
1 2 1 2
Г = -J(fг, П = -Mgl cos (р, Ъ—-Зф + Mgl cosy?,
P2
p = Jip, H = — - Mgl cos tp.
В результате уравнение Якоби—Гамильтона переписывается таким образом:
0W 1 (dW\2 ,r ,
Полный интеграл уравнения (1) будем искать в виде
W = bt + F(<p), (2)
где Ь\ — произвольная постоянная.
Подстановка выражения (2) в уравнение (1) дает
2Jb + ( -^ j - 2JMgl cos у> = О,

192 Глава 4. Интегралы движения, канонические уравнения Гамильтона
или
dip
Отсюда
-^ = ±yJlJ(Mgl cos ip-b).
F(<p) = ±\/2J f л/Щ cos ip - bdip
и, следовательно,
W = bt± V2J Г у/Mgl cos ср-Ь dtp. (3)
Согласно теореме Якоби первые интегралы уравнений движения
маятника записываются в виде
dW dW
-дъ=а> ^=р' (4)
где а — произвольная постоянная.
Подставив в равенства (4) выражение (3), получим
Г~ ^
<=F\/t / > t = = а, ±\flJy/Mg\cosip-b = Зф.
V 2 У \/MgZ cos у? - о
Задача 4.14 (49.16). Движение волчка, имеющего одну
неподвижную точку О, определяется углами Эйлера ip, в и <р. Пользуясь
результатами решения задачи 4.9 (49.11), составить уравнение в частных
производных Якоби—Гамильтона и найти его полный интеграл.
dW 1
0твет:1п+й
1
..(
dW 3W \2 /dW\2]
Lsin20V"' " "~V| ' 1 лл f ■+
1 /dW\2
+ — (— J + mg/cos0 = O, W = M + M> + b3¥> +
// A62 1
W -2Ab{ --w-- -T-r7i(b2 - Ьз cos в)2 - lAmgl cos в d6.
у С sin20

Глава 4. Интегралы движения, канонические уравнения Гамильтона 193
■^ Решение. Для системы с тремя степенями свободы уравнение
Якоби—Гамильтона записывается в виде
где
9W I' , л dW dW dW\
-+H^,^,^,-,-,-j
/ , л dW dW dW\
(о
— функция Гамильтона; W — характеристическая функция.
При решении задачи4.9 (49.11) для волчка была получена следующая
функция Гамильтона:
1
Н=2А
, - р9 COS в)2 г
+ Рв
sin2 в
Р2
+ т^; + mgl cos в.
2G
Поэтому уравнение (1) принимает такой вид:
dW J_
dt+2A
l fdw dw Л2 /aw\2i
+M^) +mgicos9=°- w
Учитывая, что координаты ф и <р циклические, полный интеграл
уравнения (2) будем искать в форме
w = b{t + b2ip+b3<p + F(e),
где Ь\, &2,6з — произвольные постоянные.
Подстановка выражения (3) в уравнение (2) дает
(3)
>+и
*ф-ь-?+Ш
+ -pj + mgl cos в = О,
2G
или
^ = J-2Abx - ^ - -г^(Ь2 - Ь3 cos в)2 - 2Amgl cos в.
Отсюда
F{$) = Г J-2Abi -ф-- -гт2(Ь2 - Ьз cos0)2 - 2Amgl cos в d.6

194 Глава 4. Интегралы движения, канонические уравнения Гамильтона
и, следовательно,
W = b\t + b2ip + h(p +
+ / \l-2Abx --zr- -т-тт; (h - h cos в)2 - lAmgl cos в d6.
У у С sin2 в

Литература
1. Мещерский И. В. Задачи по теоретической механике: Учебное пособие.
44-е изд., стер. / Под ред. В. А. Пальмова, Д. Р. Меркина. СПб.: Лань,
2005. 448 с. (См. также предыдущие изд. данного задачника с 1986
по 2004 г.)
2. Лурье Л. И. Аналитическая механика. М.: Физматлит, 1963.
3. Журавлев В. Ф. Основы теоретической механики. М.: Физматлит, 2001.
319 с.
4. Никитин Н. Н. Курс теоретической механики: Учебник для
машиностроительных и приборостроительных специальностей вузов. 6-е изд.,
перераб. и доп. М.: Высш. шк., 2003. 719 с.
5. Курс теоретической механики: Учебник для вузов / В. И. Дронг,
В.В.Дубинин, М.М.Ильин и др.; Под общ. ред. К. С.
Колесникова. М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. 736 с. (Сер. «Механика
в техническом университете». Т. 1)
6. Neuber И. von. Losungen zur aufgabensummlung Mestschersri. Berlin: VEB
Deutscher Verlag der Wissenschaften, 1961. 464 s.
7. Козлова 3. Я., Паншина А. В., Розенблат Г. М. Теоретическая
механика в решениях задач из сборника И. В. Мещерского: Динамика
материальной точки / Под ред. Г. М. Розенблата. Изд. 2-е, стер. М.:
КомКнига/URSS, 2007. 312 с.
8. Козлова 3. Я, Паншина А. В., Розенблат Г. М. Теоретическая механика
в решениях задач из сборника И. В. Мещерского: Динамика
материальной системы: Учебное пособие / Под ред. Г. М. Розенблата. Изд. 2-е,
стер. М.: Книжный дом «JIh6pokom»/URSS, 2009. 432 с.
9. Чуркин В. М. Теоретическая механика в решениях задач из сборника
И. В. Мещерского: Кинематика: Учебное пособие. М.: Книжный дом
«J1h6pokom»/URSS, 2010. 384 с.
10. Чуркин В. М. Теоретическая механика в решениях задач из
сборника И. В. Мещерского: Устойчивость равновесия. Малые
колебания. Устойчивость движения: Учебное пособие. М.: Книжный дом
«J1h6pokom»/URSS, 2010. 136 с.
11. Веселовский И. Н. Сборник задач по теоретической механике. М.:
ГИТТЛ, 1955. 500 с.
12. Бать М.И., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика
в примерах и задачах: Учебное пособие для втузов. Т. 1-3. 9-е изд.,
перераб. М.: Наука. Гл. ред. физ.-мат. лит., 1990.

196
Литература
13. Кирсанов Л/. Н. Решебник. Теоретическая механика / Под ред. А. И.
Кириллова. 2-е изд., стер. М: Физматлит, 2008.
14. Арсеньев О. //., Степаненков О. С, Шаповалов Л. В. и др. Теоретическая
механика: Руководство к решению задач / Под общ. ред. С. К. Слез-
кинского. СПб.: Политехника, 2007. 487 с.