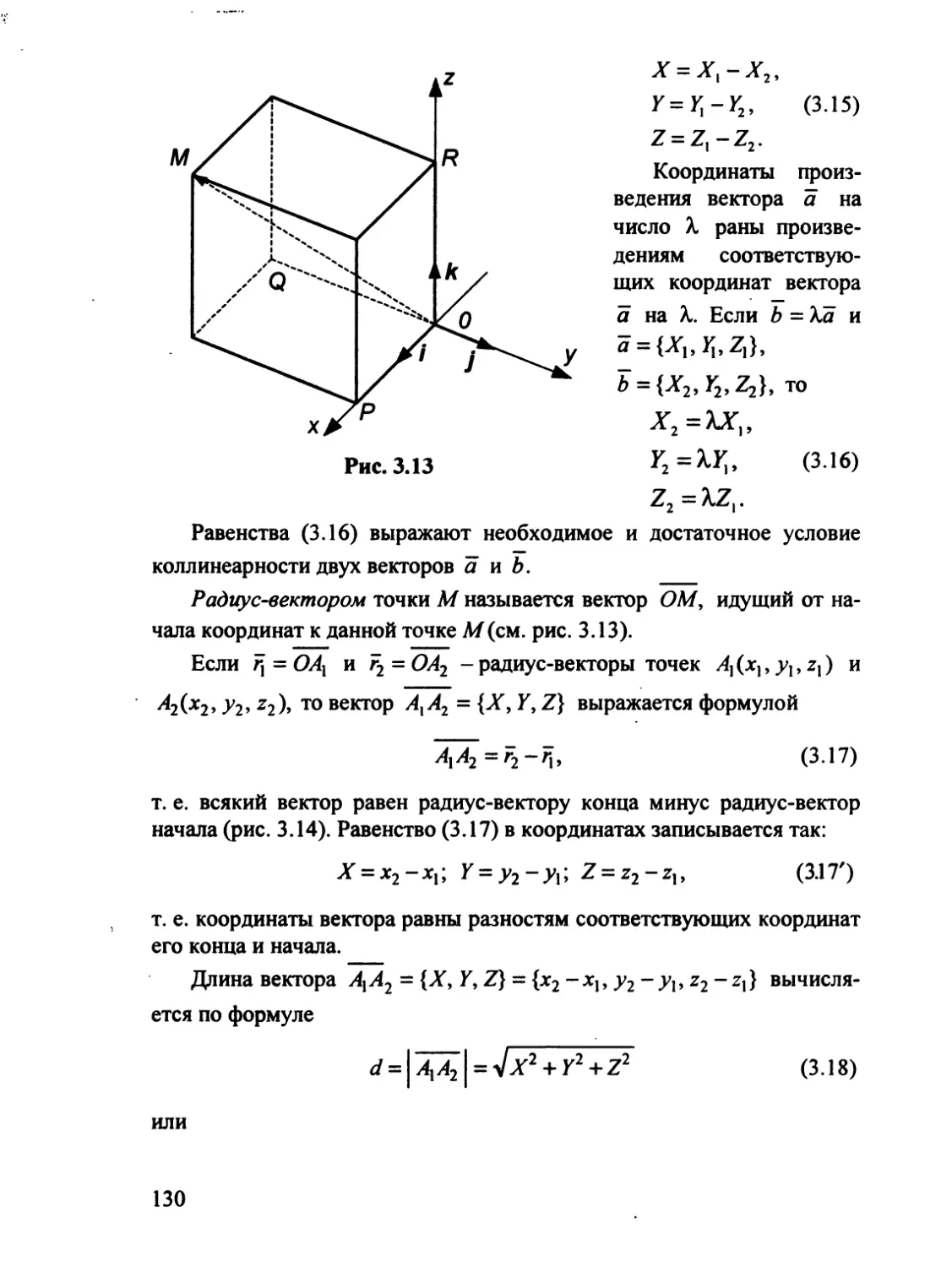
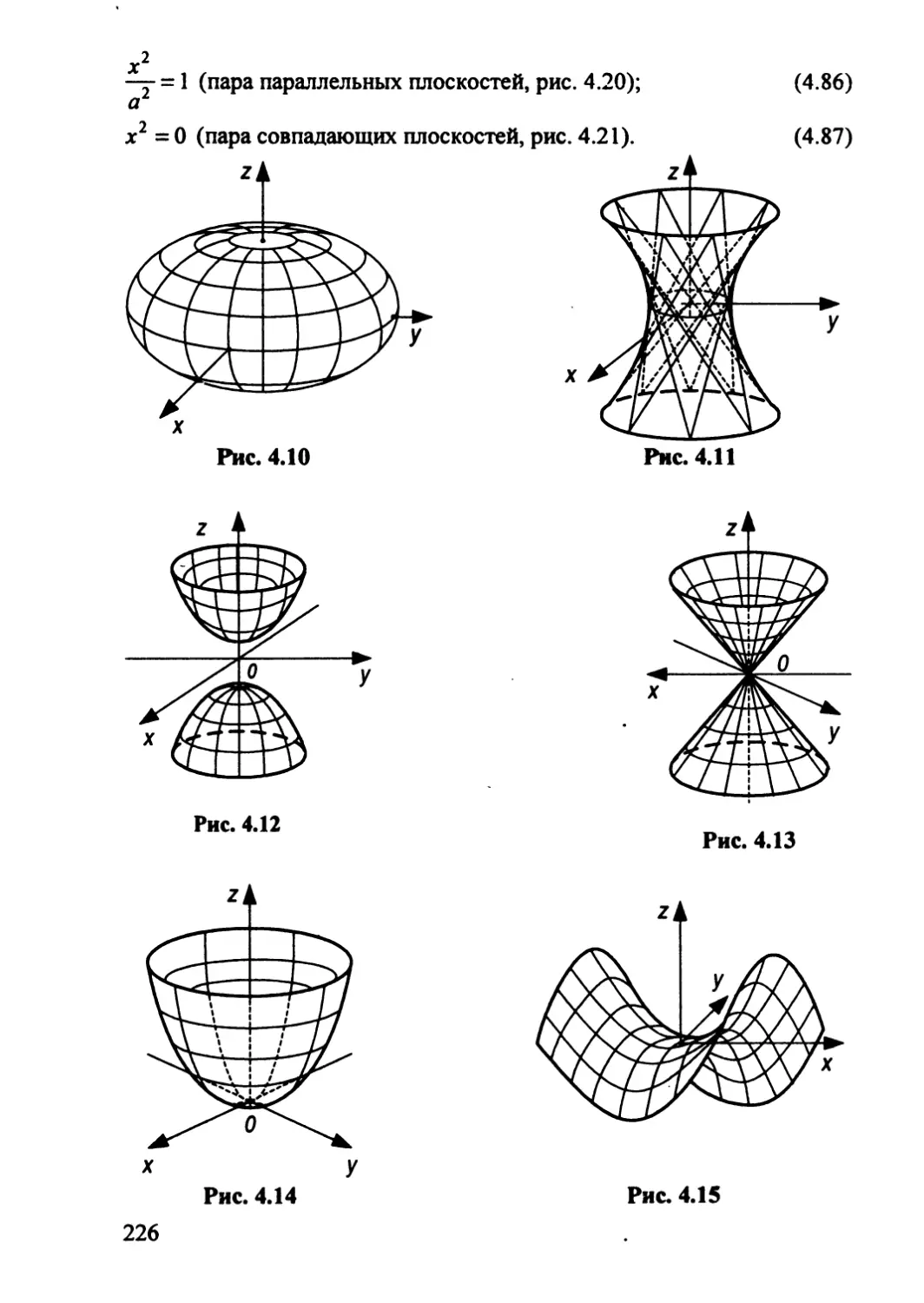
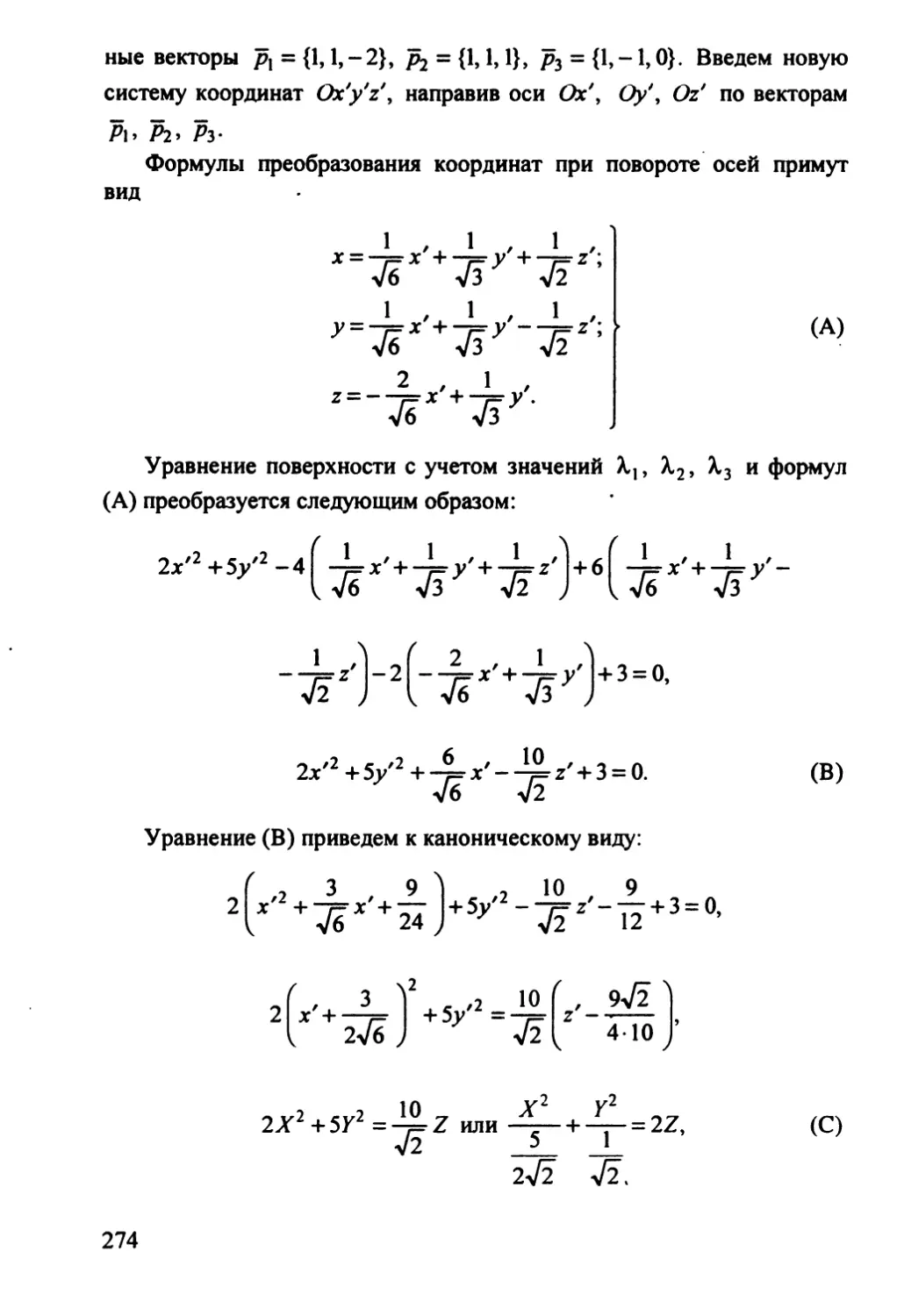
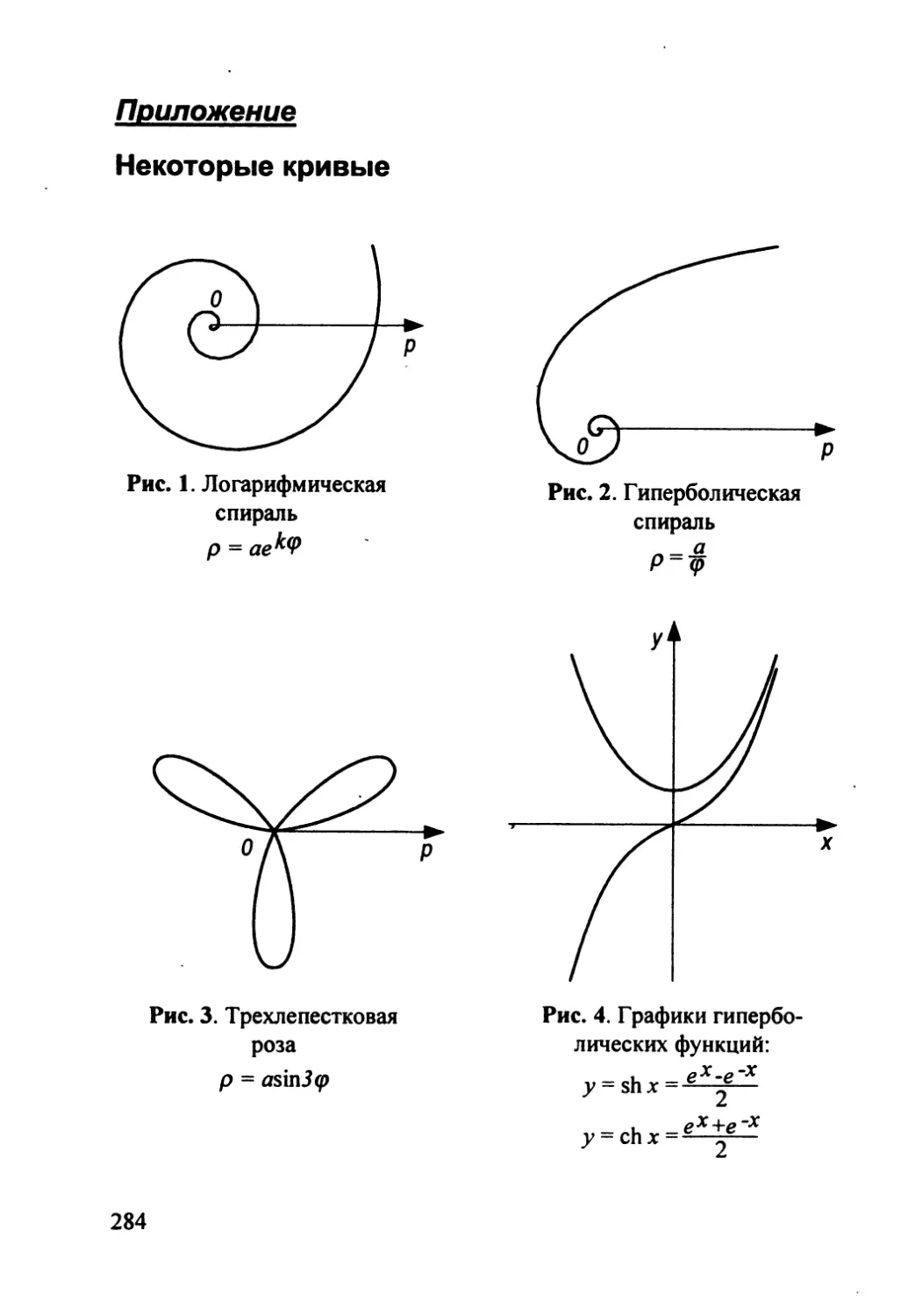
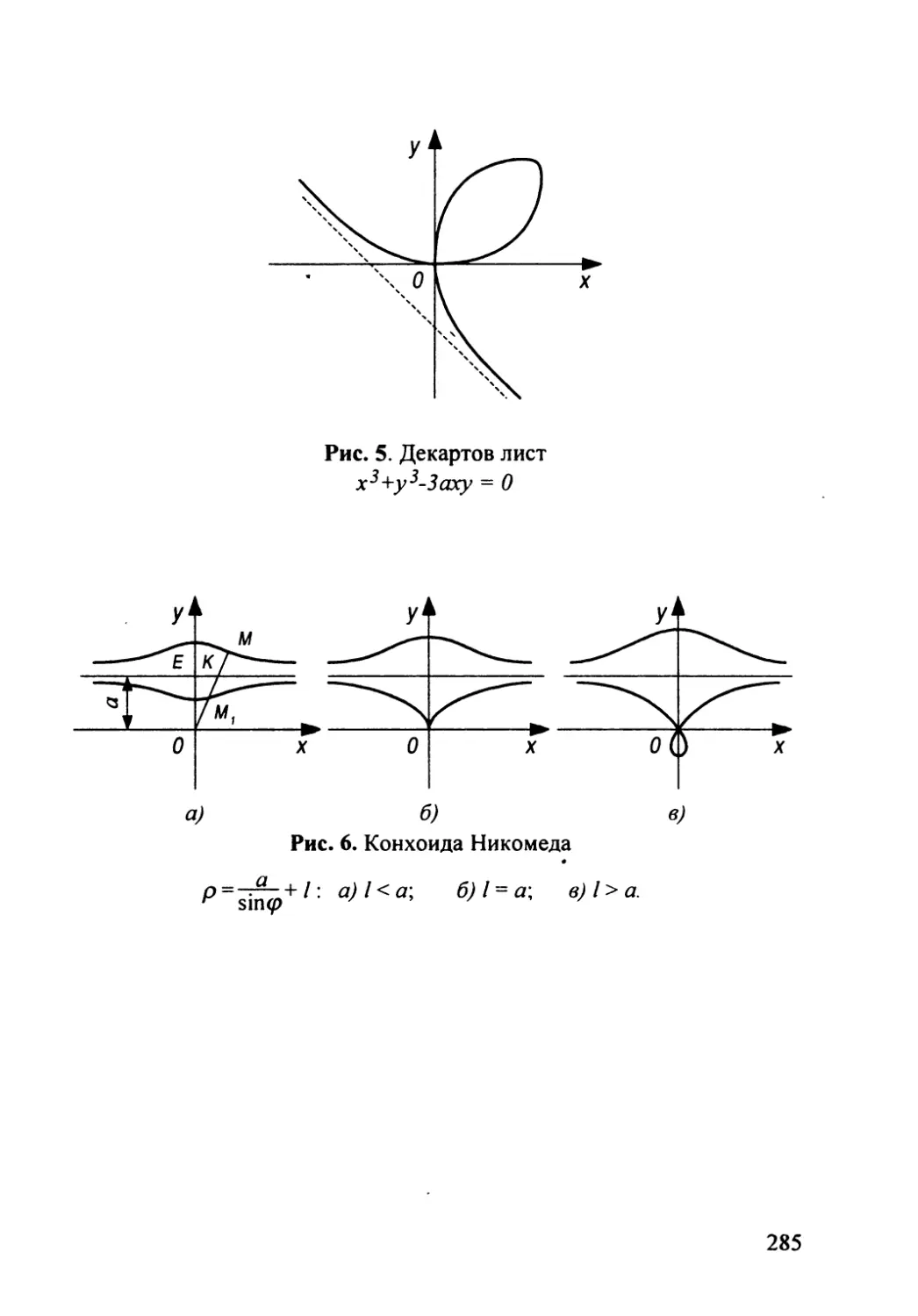
Автор: Гусак А.А.
Теги: математика высшая математика решение задач справочное пособие пособие для вузов
ISBN: 985-6317-52-5
Год: 1998
Текст
А.А.Гусак
СПРАВОЧНОЕ
ПОСОБИЕ К
РЕШЕНИЮ ЗАДАЧ
АНАЛИТИЧЕСКАЯ
ГЕОМЕТРИЯ
И
ЛИНЕЙНАЯ
АЛГЕБРА /
А.А. Гусак
СПРАВОЧНОЕ ПОСОБИЕ
К РЕШЕНИЮ ЗАДАЧ:
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
И ЛИНЕЙНАЯ АЛГЕБРА
МИНСК
ТетраСистемс
1998
УДК 51(076.1)
ББК 22.11я73
Г 96
Автор:
кандидат физико-математических наук, профессор А.А. Гусак
Рекомендовано к изданию:
кафедрой общей математики и информатики
механико-математического факультета
Белорусского государственного университета.
Гусак А.А.
Г 96 Справочное пособие по решению задач: аналитиче-
ская геометрия и линейная алгебра. -
Мн.: ТетраСистемс, 1998.-288 с.
ISBN 985-6317-52-5
Справочное пособие включает следующие разделы: аналитиче-
ская геометрия на плоскости и в пространстве, векторная алгебра,
определители и системы линейных алгебраических уравнений, матри-
цы. Пособие содержит определения основных понятий, соответствую-
щие формулы, около 300 базовых, ключевых примеров с подробными
решениями. В конце каждого параграфа помещены задачи для само-
стоятельного решения, приведены ответы, к некоторым задачам даны
указания.
Предназначается студентам и преподавателям вузов.
УДК 51(076.1)
ББК 22.11я73
ISBN 985-6317-52-5
© НТООО "ТетраСистемс",
1998
ВВЕДЕНИЕ
Справочное пособие к решению задач по высшей математики
издается в трех частях:
• Аналитическая геометрия и линейная алгебра.
• Математический анализ и дифференциальные уравнения.
• Теория вероятностей.
Данная книга посвящена решению задач по аналитической
геометрии и линейной алгебре и включает в себя следующие разде-
лы: аналитическая геометрия на плоскости и в пространстве, векторная
алгебра, определители и системы линейных уравнений, матрицы.
Пособие имеет следующую структуру. В начале каждого пара-
графа приводятся соответствующие теоретические сведения (опреде-
ления основных понятий, уравнения, формулы, правила, признаки, ме-
тоды). Затем следуют примеры решения типовых задач различной сте-
пени трудности. Далее предлагаются задачи для самостоятельного ре-
шения. Ко всем задачам даны ответы, а к некоторым - и указания. По-
собие снабжено иллюстративным и справочным материалом. В посо-
бии содержатся система замечаний учебно-методического характера,
полезных для студентов, изучающих курс высшей математики.
Рекомендуемая литература
Боревич З.И. Определители и матрицы. - М.: Наука, 1988.
Бугров С.Я., Никольский С.М. Элементы линейной алгебры и аналитической
геометрии. -М.: Наука, 1984.
Бугров С.Я., Никольский С.М. Задачник. - М.: Наука, 1984.
Гусак А.А. Высшая математика: В 2т. - Мн.: ТетраСистемс, 1998.
Гусак А.А. Задачи и упражнения по высшей математики: В 2т. - Мн.:
Выш. шк., 1988.
Гусак А.А., Гусак Г.М., Бричикова Е.А. Справочник по высшей математике.
-Мн.: ТетраСистемс, 1998.
Ефимов Н.В. Краткий курс аналитической геометрии. - М.: Наука, 1975.
Ильин В.А., Позняк Э.Г. Линейная алгебра. - М.: Наука, 1974.
Мантуров О.В., Матвеев Н.М. Курс высшей математики. - М.: Высш, шк.,
1986.
Тышкевич Р.И., Феденко А.С. Линейная алгебра и аналитическая геометрия.
- Мн.: Выш. шк., 1976.
Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре.
- М.: Наука, 1988.
3
Аналитическая геометрия,
векторная алгебра, определители, матрицы
Гпава 1.
Аналитическая геометрия на плоскости
§ 1.1. Система прямоугольных декартовых координат
на плоскости. Простейшие задачи
Прямоугольными декартовыми координатами точки М на плоско-
сти называются расстояния от этой точки х = ML, у = MN (рис. 1.1)
до координатных осей Оу и Ох, измеренные одной и той же единицей
длины и взятые с соответствующими знаками. Если точка расположена
справа от оси Оу, то абсцисса х данной точки положительна, если сле-
ва - отрицательна; если точка лежит выше оси Ох, ее ордината у по-
ложительна, если ниже оси Ох - отрицательна (при указанном на
рис. 1.1 выборе положительных направлений осей, обозначенных
стрелками). Для точек, лежащих на оси Оу, х = 0; для точек, лежащих
на оси Ох, у = 0. Запись М (х, у) означает, что точка М имеет коор-
динаты хи у.
у 1. Расстояние между двумя точками
м М}(х},ух) и М2(х2, у2) вычисляется по
L х М формуле
d = J(x2 -х,)2 + (у2 -yt)2. (1.1)
У
2. Координаты точки М(х,у), деля-
щей отрезок МХМ2, где Мх(хх,ух),
® N х М2(х2,у2), в данном отношении
рис. и МХМ\ ММ2 = / (при /# -1), определяют-
ся формулами:
, = (1.2)
1+/ у 1+/
3. Координаты середины отрезка МХМ2 вычисляются по форму-
лам:
4
Xi+X2 У1+.У2 /,
x = ---L\ v = ——(1.3)
2’2
4. Площадь треугольника с вершинами Р(х1,у1), £?(х2,у2),
/?(х3, у3) равна
5 = ±|[(х2-Х1)(Уз-у1)-(хз-х,)(у2-у1)], (1.4)
где знак минус следует брать, когда выражение в квадратных скобках
отрицательно, знак плюс - когда оно положительно.
Замечание. Формула (1.4) может быть написана в виде
5 = ^1 (Х2 -xJtVj -yJ-tXj -Х,)(у2 -у,) |, (1.4')
где двумя вертикальными чертами обозначена абсолютная величина
(арифметическое значение) выражения, стоящего в квадратных скобках. Абсо-
лютная величинах определяется так:
. . f х, если х > 0;
х = <
[-Х, еслих<0.
Например, 141 = 4, | - 61 = 6.
Пример 1. Построить точку М (2,3). Найти точки, симметричные
точке М относительно координатных осей, (биссектрис координатных
углов и начала координат.
Замечание. Выражение «найти точки» означает найти координаты
этих точек.
Решение. Построим сначала точку М (2, 3). Отложив на оси Ох
(вправо) от начала координат отрезок ОМХ =2 (рис. 1.2), восставим в
точке перпендикуляр к оси Ох. Отложив на оси Оу кверху) от нача-
ла координат отрезок ОМ2 = 3, восставим в точке Л/2 перпендикуляр
к оси Оу. Точка М пересечения указанных перпендикуляров является
искомой. (Эту точку можно построить и другим способом: на перпен-
дикуляре к оси Ох, проходящем через точку (Ц,отложить отрезок
М = 3 кверху от оси Ох.)
Проводя последующие построения, пользуемся определением то-
чек, симметричных относительно данной прямой (это точки, лежащие
на одном перпендикуляре к прямой, на одинаковых расстояниях и по
разные стороны от нее).
Построим точку N, симметричную точке М, относительно оси Ох.
5
Координаты этой точки xN = ОМХ, yN =- MXN (точка N справа от
оси Оу, поэтому х > 0 и ниже оси Ох, поэтому у < 0). Но ОМХ = хм,
MXN = МХМ = ум, следовательно, xN =хм, yN = -ум- Так как из
условия хм = 2, ум = 3, то N (2, -3).
Для точки L, симметричной
точке М относительно оси Оу,
находим:
х£ = -ЬМ2 = -М2М = -хм,
yL= LS = МХМ = ум, поэтому
L (-2,3).
Построим теперь точку Р,
симметричную точке Л/ относи-
тельно биссектрисы / и /// коор-
динатных углов.
Координаты ее хР = ОРХ и
уР = РРХ выразим через коорди-
наты точки М. С этой целью рас-
смотрим равнобедренные тре-
угольники МАР и ОАМХ (А -
точка пересечения МХМ и биссектрисы). Так как ОМХ = МХА и
МХА = РХР, то РХР = ОМХ, т. е. уР = хм. Далее, поскольку
АМ = АР=МХРХ, МХМ= МХА + АМ, ОР} = ОМХ + МХРХ, ~то
МХМ = ОРХ, т. е. хР- ум. Таким образом, получим Р (3, 2).
Построим точку Q, симметричную точке М относительно биссек-
трисы // и IV координатных углов. Из равных прямоугольных тре-
угольников OQQX и ОРРХ (OQ = OP, Z QOQX = Z РОРХ) находим,
что OQX=OPX, QQ\=PP\- Так как ОРХ = МХМ и РРХ=ОМХ, то
OQX = МХМ, QQ = ОМХ. Следовательно, xQ=-yM, Уо~~хм и
Q (-3,-2) (координаты точки Q отрицательны, так как она лежит
ниже оси Ох и слева от оси Оу).
Построив точку R, симметричную точке М относительно начала
координат, и рассмотрев равные прямоугольные треугольники ORS и
ОМХМ ( OR = ОМ, Z SOR = ZMXOM), получим OS = ОМХ,
SR-МХМ, поэтому xR = -хЛ/, yR = -yM и 7?(—2, — 3).
Ответ: W(2,-3), £(-2,3), Р(3,2), £(-3,-2), /?(-2,-3).
6
Замечание. Координаты точек N, £, Л Q, R, симметричных
точке Л/(2, 3) относительно соответственно оси Ох, оси Оу, биссек-
трисы / и III координатных углов, биссектрисы II и IV координатных
углов, начала координат, можно получить с помощью следующих
формальных действий:
1) для точки N - изменить знаку, оставивх прежним;
2) для точки L - изменить знак х, оставив прежним у;
3) для точки Р - поменять местами х и у;
4) для точки Q - поменять местами х и у, изменив их знаки;
5) для точки R - изменить знаки х и у.
Пример 2. Доказать, что треугольник с вершинами 7Э(—2, —1),
(2(6,1), R (3,4) - прямоугольный.
Решение. Зная стороны а, Ь, с треугольника, с помощью теоремы
Пифагора можно установить, является ли данный треугольник прямо-
угольным {а1 +Ь2 = с2), остроугольным (с2 < а2 +/>2) или тупо-
угольным (с2 > а2 + 62).
Найдем длины сторон данного треугольника, пользуясь формулой
(1.1). Вычислим вначале длину PQ, подставляя в формулу (1.1) коор-
динаты точек Р и Q Xj = -2, ух = -1, х2 = 6, у2 ='1:
PQ = J[6-(-2)f+0-H)f = V82 + 22 = 768.
Для вычисления PR подставим в формулу (1.1) значения х1 = -2,
У| = -1, х2 = 3, у2 = 4:
PR = 7[3-(-2)]2 + [4-(-1)]2 = л/52 + 52 = л/50.
Аналогично для 3-ей стороны х, = 6, у1 = 1, х2 = 3, у2 = 4:
QR = 7(3-6)2 + (4-1)2 = J(-3)2 + 32 = -Л!
Квадраты длин сторон будут соответственно равны:
PQ2 =68; PR1 =50; QR2 = 18,
откуда
PQ2 = PR2 + QR2 .
Последнее равенство означает, что треугольник прямоугольный.
7
Замечание. Формула (1.1) не изменится, если в ней поменять местами
Х| и х2, у, и у2 (так как (х,-х2)2 - (х2-х,)2, - у2)2 = (у2 - у^)2.
При использовании этой формулы первой точкой (т. е. имеющей координаты
X], ft ) можно считать любую из данных двух точек, оставшаяся точка будет
второй (т. е. имеющей координаты х2, у2 )•
Пример 3. Вычислить длины медиан треугольника с вершинами
/>(-3,2), 0(5,4), 2?(7,-2).
Решение. Найдем вначале основания медиан, являющиеся середи-
нами сторон треугольника. Пусть Z, Л/, N- соответственно середины
сторон PQ, QR, PR. Координаты точки L определяем по формулам
(1.3). В данном случае Xj = -3, у1 = 2, х2 = 5, у2 = 4. Обозначая ко-
ординаты точки L через xL и yL, получим:
-3+5 2+4
xl = —у- = 1; У/. = -^- = 3; а (1,3).
Аналогичным образом находим:
= = «(Я);
Вычислим длину медианы LR. Подставляя в формулу (1.1) коорди-
наты точек L и R, т. е. значения х, = 1, У] = 3, х2 = 7, у2 = - 2, полу-
чим
LR = ^(7—I)2+(—2 —З)2 = д/б2 + (-5)2 = ТбТ.
По формуле (1.1) находим длины медиан МР и NQ:
МР = 7[6-(-3)]2+(1-2)2 = л/92+(-1)2 = -J82.
NQ = 7(5-2)2 + (4-0)2 = л/з2+42 = 5.
Замечание. Формулы (1.3) не изменятся, если в них поменять места-
ми X] и х2, у} и у2. При использовании этих формул первой точкой (т. е.
имеющей координаты Х|, ух) можно считать любую из двух данных точек.
Пример 4. Даны две смежные вершины параллелограмма
8
A (1,-2), В (3,2) и точка N (5,-1) пересечения его диагоналей. Най-
ти две другие вершины параллелограмма.
Решение. Так как диагонали параллелограмма в точке пересечения
делятся пополам, то N- середина BD и середина АС, где D и С-две
другие вершины. Формулы (1.3) для данного случая примут вид:
откуда
хс = 2xn ~хА’Ус = 2Уы-УA, xi> = 2xn~xb, Уй = 2Уы~Ув-
Подставляя в эти формулы координаты точек А, В и N найдем вершины
С (9,0), 0(7,-4).
Пример 5. В треугольнике с вершинами Р (2,3), Q (6,3),
R (6,-5) найти длину биссектрисы QL.
Решение. Из элементарной геометрии известно, что биссектриса
угла треугольника делит противоположную сторону на части, пропор-
циональные прилежащим сторонам. Найдем длины этих сторон. По
формуле (1.1) имеем:
PQ = 7(6-2)2 + (3-3)2 = 4,
QR = 7(6-6)2 +(-5-3)2 = 8.
Следовательно,
PQ.QR = 4:8 = 1:2 и PL.LR = 1:2,
где L (х, у) - точка пересечения биссектрисы угла Q со стороной PR.
Координаты точки L определим по формулам (1.2). В данном случае:
поэтому:
3+ 2 * 5) _ 1 <10 l j
1+1 =5; 1з'з)'
2
По формуле (1.1) вычисляем длину биссектрисы QL.
9
п, 10У (> О2 8 —
К 3) I з) з
Замечание. В формулах (1.2) нумерация точек имеет существенное
значение. При использовании этих формул нужно различать начало и конец
отрезка. В данном примере можно было бы рассматривать отношение
RL.LP= 2:1, тогда точку R нужно считать первой (т. е. Xj = 6, ух = -5),
точку Р - второй (х2 = 2, у2 = 3), число / в этом случае уже будет другим, а
именно / = 2. (Убедитесь в том, что постановка этих значений в формулы
(1.2) дает прежний результат. Сделайте чертеж.)
Рис. 1.3
Пример 6. Отре-
зок, определяемый
точками A/j(-6,7),
М2 (- 2, 3), разделен
на 4 равные части.
Найти точки деления
А, Л/, N, До какой точ-
ки Р нужно продол-
жить отрезок МХМ2,
чтобы его длина увели-
чилась в 3 раза?
Решение. По усло-
вию отношения, в ко-
торых точки Л, Л/, N и
Р (рис. 1.3) делят отре-
зок М2 соответст-
венно равны:
M{L 1 МХМ 2
1} = ЬМ2 = 3 ’ li= ММ2 ~ 2
, =_^=з = г / = ^. = _2
3 NM2 1 ’ 4 РМ2 2
(в последнем случае нужно взять знак минус, так как отрезки М}Р и
РМ2 имеют противоположные направления). Координаты точек A, N и Р
определим по формулам (1.2), координаты точки М-по формулам (1.3).
Определяем координаты точки L. Поставив в формулы (1.2) значе-
10
ния Х| = -6, у} = 7, х2 = -2, у2 = 3.1 = получим:
— 6+ —(—2) 7+--3
хЛ =-----2-j---= -5; yL =-----= 6; £ (-5, 6).
1 + - 1 + -
3 3
Так как М- середина отрезка Мх Л/2, то по формуле (1.3) имеем:
-6 + (-2) 7+3
хм =-----2-----= -4; Ум = ~2~ = 5; М (-4, 5)'
Подставляя в формулы (1.2) координаты точек Ц и Л/2 и /3 = 3,
находим точку N:
-6+3(-2) „ 7 + 3-3 .
—^ = -3;Л = —= 4;«(-3.4>.
Аналогично находим точку Р ( принимая во внимание, что
Р(6,-5).
Пример 7. Даны две точки Л (3,5) и М (6, -2). На оси Оу найти
такую точку N, чтобы площадь треугольника LMN равнялась 15 квад-
ратным единицам.
Решение. Пусть N (0, у) - искомая точка (х = 0, так как точка
лежит на оси Оу). В формулу (1.4) подставим значения
S = 15, *! = 3, у j= 5, х2 = 6, у2 = -2, х3 = 0, уз = у.
Получаем
15 = ±|[(6-3)(у-5)-(0-3)(-2-5)] =
11
= ±—(3v —36).
2 '
отсюда
15 = ^(3y-36), 15 = -1(3^-36).
Решая полученные уравнения относительно у, находим
У1 = 22, у2 = 2.
Следовательно, условию задачи удовлетворяют две точки:
^(0,22), TV2(0,2).
Пример 8. Найти точку, одинаково удаленную от осей координат и
отточки М(1,8).
Решение. Пусть N (х, у) - искомая точка, ее координаты пока
неизвестны. Так как по условию точка равноудалена от осей коорди-
нат, то у = х или у = -х (см. определение прямоугольных декарто-
вых координат, стр. 4).
Рассмотрим первый случай (у = х). Выразим расстояние между
точками М (1,8) и ЛЦх, у) через их координаты. По формуле (1.1)
получаем
MN = д/(х-1)2 + (х-8)2.
По условию это расстояние равно | х |, следовательно,
д/(х-1)2+(х-8)2 =|х|.
Освобождаясь от радикала, получим квадратное уравнение
х2-18х + 65=0,
корни которого Xj = 5, х2 = 13. Поскольку у = X, ТО У! = 5, у2 = 13.
Следовательно, получены две точки, удовлетворяющие условию
задачи: 2V, (5, 5), TV2 (13,13).
Примечание. Второй случаи (у = — х) условию задачи не удовле-
творяет.
Пример 9. Найти центр и радиус окружности, проходящей через
точки L (0, 0), М (3, -1), N (8,4).
Решение. Пусть С (а, Ь) - центр окружности и R - ее радиус. Най-
12
дем неизвестные числа а, b и R. Согласно условию CL = R, СМ = R,
CN = R. Определим длины CL, CM, CN по формуле (1.1) и подставим
их выражения в последние три равенства. Получим:
7(0-a)2 +(0-Z>)2 = R или а2 + Ь2 = В2; (А)
д/(3-а)2 + (-1-г>)2 = /? или (3 - а)2 + (1 + b)2 = R2; (В)
7(8 - а)2 + (4-6)2 = R или (8 - а)2 + (4 - b)2 = R2. (С)
Раскрывая скобки в левых частях уравнений (В) и (С), используя
уравнение (А), приводя подобные члены и сокращая соответственно на
2 и 8, находим:
5-3a + Z>=0;l
10-2a-Z>=0. J
Решая эту систему, получаем: а = 3, b = 4, С (3, 4). Из уравнения
(А) находим, что R = 5.
Задачи
1. Построить точки: Л/^1,4), Л/2(—2,3) Л/3(-4,-5), Л/4(2,-7),
Л/5(0,1), Л/6(4, 0), М7(0,-6), Л/8(-8,0), Л/9(0,0).
2. Найти точки, симметричные точке М (-1, 5) относительно оси
Ох, оси Оу, начала координат, биссектрис координатных углов.
3. Найти точки, симметричные точке М (а, Ь) относительно ко-
ординатных осей, начала координат, биссектрис координатных углов.
4. Дан прямоугольник ABCD со сторонами АВ- 2, AD = 6. Оп-
ределить координаты вершин прямоугольника, приняв:
1) за оси координат две непараллельные стороны его и точку их
пресечения за начало координат;
2) точку пересечения диагоналей за начало координат, за оси ко-
ординат две прямые, параллельные сторонам прямоугольника.
5. Вычислить периметр треугольника с вершинами А (3,4),
В (3,8), С (6, 4).
6. Доказать, что треугольник с вершинами Р (3,4), Q (7,7),
R (4,3) - равнобедренный.
7. Установить, будет ли треугольник PQR с вершинами В (2,2),
Q (1, 6), R(7, -1) остроугольным, тупоугольным или прямоугольным.
13
8. Дана середина отрезка L (5.2) и один из его концов М (2, -1).
Найти второй конец.
9. Даны середины сторон треугольника Л (-1,5), Л/(1,1),
N (4, 3). Найти его вершины.
10. Отрезок, определяемый точками A/j(—8, — 9), Л/2(-3,-4) раз-
делен на пять равных частей. Найти точки деления. До какой точки
нужно продолжить отрезок чтобы его длина увеличилась в 4
раза?
11. Дан треугольник с вершинами А (- 7, 7), В (3, 2), С (-1, -1).
Найти точки, в которых сторона АВ делится биссектрисами внутренне-
го и внешнего углов при вершине С.
12. Найти точку пересечения медиан треугольника, вершины кото-
рого Л(-2,1), В(2, — 1), С(4,3).
13. Вычислить площадь треугольника с вершинами В (0,-2),
2(4,5), В (6,-4).
14. Даны вершины А (2,1), В (-2,-2), С (-8, 6) треугольника
АВС. Найти длину высоты, опущенной из вершины В.
15. Доказать, что точки А (-3, -4), В (1, 4), С (0, 2) лежат на од-
ной прямой.
16. Даны две точки L (4, 2), и М (6, -2). На оси Ох найти такую
точку N, чтобы площадь треугольника LMN была равна 8 квадратным
единицам.
17. Вычислить площадь четырехугольника с вершинами А (-3, 2),
В (3,4), С (6,1), £>(5,-2).
18. Найти центр тяжести треугольника с вершинами Я (1,-2),
В (4,1), С (7,-2).
19. На оси Оу найти точку, одинаково удаленную от начала коор-
динат и от точки Л/ (4, 5).
20. На координатных осях найти точки, удаленные от точки
М (4, 3) на 5 единиц.
Ответы
2. /V (-1,-5), £(1,5), В(1,-5), Р(5,-1), £(-5,1). Указание.
См. пример 1. 3. N L(—a,b\ R(—a,—b), P(b,a),
Q (-b.-a). 4. 1) Я (0, 0), В (0, 2), С (6, 2), D (6, 0). В качестве поло-
жительного направления оси Ох взято направление от А к D, 2) А (-3, — 1),
В(-3,1), С(3,1), £>(3,-1). 5.12. 7. Тупой угол при вершине Р.
14
9. N (8,5). 9. A (-4,3), В (2,7), С (6,-1). 10. £,(-7,-8),
£^-6,-7), £з(-5,-6), £4(-4,-5), Р(12,11). Указание.
4
l2 = |> Z3 = T> ^4 = 4, /5 = -^. 11. kJ—К2(13,-3)- Указа-
•Э £ Э у Э Э /
н и е. АС = 10, ВС = 5, /| = — = -, 12 = --. 12. 7V( -, 1 ). 13.25 кв. ед.
АС 2 2 3
14. Л = 2^5. Указание. Вычислить площадь S и длину АС.
15. Указание. Убедиться в том, что SMBC = 0. 16. 7^(1, 0), N2(9> 0).
17. 26 кв. ед. 18. ДГ (4, -1). Указание. Центр тяжести треугольника сов-
падает с точкой пересечения медиан. 19. 7V (0; 4,1). 20. 0), Л/2(0, 6),
Л/3(8, 0).
§ 1.2 Уравнение линии в прямоугольных декартовых
координатах
Линия на плоскости задается как некоторое геометрическое место
точек, т. е. совокупность точек, обладающих некоторым свойством,
исключительно им присущим.
Уравнением линии на плоскости называется уравнение относитель-
но переменных хну, которому удовлетворяют координаты любой точ-
ки данной линии и только они.
В общем виде уравнение линии на плоскости в прямоугольных де-
картовых координатах записывается так:
F(x,y)=0. (1,5)
Из определения уравнения линии вытекает, что если при подста-
новке координат точки в данное уравнение получаем тождество, то
точка лежит на соответствующей линии; если тождество не получается,
то точка не лежит на этой линии.
Чтобы составить уравнение линии, как некоторого геометрическо-
го места точек, необходимо:
1) взять произвольную точку линии с текущими координатами
X, у;
2) записать общее свойство точек данного геометрического места
в виде равенства;
3) выразить входящие в это равенство величины с помощью коор-
динат.
Точки пересечения двух линий ^(х, у)=0 и F2(x,y)=Q находят
15
(1.6)
из системы уравнений:
^(х,у)=О;
F2(x, у)=0.
Если система (1.6) имеет действительное решение, то линии пере-
секаются. Число точек пересечения равно числу решений системы.
Если действительных решений нет, то линии общих точек не имеют.
Пример 1. Составить уравнение геометрического места точек,
равноудаленных от двух данных точек М}(-2,4), М2(6, 8).
Решение. Пусть М (х, у) - произвольная точка данного геометри-
ческого места. По условию
МХМ=М2М. (А)
С другой стороны, по формуле расстояния между двумя точками
получаем:
Мх М = 7(х + 2)2 + (j-4)2; М2 М = 7(х-6)2 + (у-8)2.
Подставляя эти выражения в равенство (А), находим уравнение
данного геометрического места:
7(х+2)2 + (у-4)2 = 7(х-6)Г+(у-8)2.
Упростим полученное уравнение. Возведя в квадрат обе части уравне-
ния и раскрывая скобки в подкоренных выражениях, находим
< х2 + 4х + 4 + у2 -8у+16 = х2 -12х + 36 + у2 -16у + 64.
Перенося все члены в левую часть, приводя подобные и сокращая на 8,
получим уравнение
2х + у-10 = 0. (В)
Таким образом, координаты любой точки данного геометрического
места удовлетворяют уравнению (В).
Покажем теперь, что если точка не принадлежит нашему геомет-
рическому месту, то ее координаты не будут удовлетворять уравнению
(В). В самом деле, пусть N (х, у) - такая точка. Тогда выполняется
одно из двух неравенств:
< M2N\ > M2N
или в координатах:
16
7(х + 2)2+(.у-4)2 < 7(х-6)2 + (>-8)2;
7(х+2)2 + (у-4)2 >А/(х-6)2+(у-8)2.
Первое из этих неравенств приводит к виду
2х + у-10< О,
а второе к виду
2х + у-10> 0.
Следовательно, координаты точки N уравнению (В) не удовлетворяют.
Итак, уравнение данного геометрического места точек есть
2х + у-10 = 0.
Это уравнение является уравнением прямой линии (из элементарной
геометрии известно, что геометрическим местом точек, указанных в
условиях задачи, будет прямая, перпендикулярная к отрезку М} М2 и
проходящая через его середину).
Замечание. Если точка N (х', у') не лежит на прямой
2х + у - 10 = 0, то при подстановке ее координат в данное уравнение полу-
чаем либо 2х' + у' —10 < 0, либо 2х' + у' —10 > 0.
Пример 2. Написать уравнение окружности радиуса R = 4 с цен-
тром в начале координат. Лежат ли на этой окружности точки А (4, 0),
В (2,3), С (4,3), D (3,-77), Е(1,2), Г (0,5)?
Решение. Пусть М (х, у) - произвольная точка данной окружно-
сти (геометрического места точек, удаленных от начала координат на 4
единицы). По определению окружности имеем ОМ = 4.
Длина отрезка ОМ по формуле (1.1) равна
ОМ = ^jx2 + у2.
Следовательно, уравнение окружности имеет вид
-Jx2 + у2 = 4.
Возведя в квадрат обе части уравнения, получим
х2 + у2 = 16.
Выясним, лежат ли на данной окружности указанные точки. Под-
ставляя координаты точки А в уравнение окружности, получаем тожде-
17
ство
42 + 02 = 16.
Таким образом, точка А лежит на окружности.
Для точки В получается неравенство
22 + 32 < 16,
поэтому точка В окружности не принадлежит. (Заметим, что точка В
лежит внутри круга радиуса R = 4, ибо ее расстояние до начала коор-
динат ОВ = 722 + 32 = л/Гз < 4.)
Подстановка в уравнение координат точки С (4, 3) приводит к не-
равенству
42 + 32 > 16,
следовательно, точка С также не лежит на окружности. (Заметим, что
точка С лежит вне круга радиуса R = 4, так как ее расстояние до нача-
ла координат ОС = л/42 +32 = 5 > 4.)
х Аналогичным образом убеждаемся, что точка D лежит на окруж-
ности, а точки Е и F ей не принадлежат.
Замечание 1. Если R— а, где а - положительное число, то уравне-
ние окружности радиуса /? = а с центром в начале координат запишется так:
х2 + у2 = а2.
Замечание 2. Координаты любой точки, лежащей внутри круга ра-
диуса R— а, удовлетворяют неравенству
2 2 9
х +у < а~,
для координат любой точки, лежащей вне этого круга, выполняется неравенст-
во
х2 + у2 > а2.
Пример 3 . Точка М движется так, что в любой момент времени ее
расстояние до точки А (6,0) втрое больше расстояния до точки
<2
ВI —, 0 I. Найти уравнение траектории движения точки М.
Решение. Текущие координаты точки М обозначим через х, у, т. е.
М (х, у). По условию задачи МА = ЗМВ.
18
Выразим расстояния МА и МВ через координаты точек:
ЛМ = 7(*-6)2+(у-О)2; МВ =
+ (У-О)2.
Подставляя эти выражения в предыдущее равенство, получим
уравнение траектории движения точки М:
л/(х - 6)2 + / = 3j( х - |j + у2.
Упрощая это уравнение, находим
х2 + у2 = 4.
Получено уравнение окружности радиуса R = 2 с центром в начале
координат (см. замечание 1 к примеру 2).
Пример 4. Найти геометрическое место точек, для которых раз-
ность квадратов расстояний до двух данных точек есть величина по-
стоянная.
Решение. Пусть F} и F2 - две данные точки (рис. 1.4). Расстояние
между ними обозначим через 2а, где а - некоторое число. Начало ко-
ординат поместим в середине отрезка FXF2, в качестве положительно-
го направления оси Ох возьмем направление от точки F} к точке F2
Рис. 1.4
за ось Оу примем прямую, перпенди-
кулярную к отрезку FxF2 и проходя-
щую через его середину. При таком
выборе системы координат точки Fx
и F2 будут иметь координаты
Xj = - а, у1 = 0, х2 = а, у2 = 0, т. е.
Л(-«,0), F2(a,0).
Согласно условию, получаем
MF2 - MF2 = 4с,
где через 4с обозначена данная постоянная величина.
Подставляя в это равенство выражения
MF2 = (x+a)2 + (y-0)2; MF22 =(х-а)2 + (у-0)2,
19
получим
(х + а)2 + у2-[(х-а)2 + у2] = 4с, 4ах = 4с,
т. е. х = — или х = Ь, где b = — - постоянная.
а а
Замечание. Уравнение х = Ь, где b - постоянная, является уравне-
нием прямой, параллельной оси Оу и отсекающей на оси Ох отрезок, равный Ь.
В самом деле, если точка М лежит на этой прямой, то ее координата х = b. С
другой стороны, если х = Ь9 то точка лежит на указанной прямой.
Пример 5. Составить уравнение геометрического места точек,
произведение расстояний которых до двух данных точек F} и F2 есть
величина постоянная, равная а2, где а-половина расстояния между
точками Fx и F2. (Эта линия называется лемнискатой Бернулли.)
Решение. Начало координат выберем в середине отрезка F}F29
длина которого обозначена через 2а. Ось Ох направим вдоль FXF2.
Координаты точек F} и F2 при указанном выборе координатной сис-
темы будут соответственно равны: Xj = - а, у} = 0, х2 = а, у2 = О,
т. е. Fx(-a, 0), F2(a, 0). Если М (х, у) - произвольная точка геомет-
рического места, то по условию
FxMF2M = a2.
Подставляя в это равенство выражения
ЛЛ/ = Л/(х+а)2+О'-0)2; F2М = 7(x-a)2+(y-O)2,
получим искомое уравнение данного геометрического места
-](х+а)2 + у2 ^(х-а)2 + у2 = а2.
Дальнейшие выкладки имеют целью получить уравнение лемнискаты
Бернулли в более простом виде. Возводя в квадрат обе части уравнения
и группируя члены, находим
[ (х2 + у2 + а2)+ 2ах} [ (х2 + у2 + а2)- 2ах] = а4,
отсюда
[(х2 + у2)+а2]2 -4а2х2 = а4.
Преобразуя последнее уравнение, получаем
20
(X2 + у2)2 + 2а2(х2 + у2)+ а4 - Да2х2 = а4,
(х2 +у2)2 +2а2(у2 -х2) = 0
или в окончательном виде
(х2 + у2)2-2а2(х2 -у2)= 0.
Пример 6. Найти точки пересечения линий:
х2 + у2 = 25; х+7у-25 = 0.
Решение. Решим систему уравнений данных линий. Определим х
из последнего уравнения
х = -7у+25 (А)
и подставим его в первое уравнение:
49у2 -350у+625+/ = 25.
После упрощения получим
/-7у+12 = 0,
откуда ух =4, у2 = 3. Подставляя эти значения в уравнение (А), най-
дем Xj = - 3, х2 = 4. Следовательно, линии пересекаются в двух точ-
ках: ^(-3,4), Л/2(4, 3).
Пример 7. Найти точки пересечения окружности х2 + у1 = 36 с
координатными осями.
Решение. Для любой точки, лежащей на оси Ох, ордината у равна
нулю (по определению прямоугольных декартовых координат точки на
плоскости). Обратно, если у = 0, то точка лежит на оси Ох. Следова-
тельно, ось Ох имеет уравнение у = 0. Аналогично можно показать,
что уравнение оси Оу есть х = 0.
Чтобы получить точки пересечения данной окружности с осью Ох,
необходимо решить систему уравнений:
х2 + у2 = 36;
, = <4
Подставляя значение у в первое уравнение, получим х2 = 36, от-
21
куда jq = 6, х2 = -6. Таким образом, данная окружность пересекает
ось Ох в двух точках: Л/, (6,0), М2 (- 6, 0).
Решим систему уравнений:
х2 + у2 = 36;
х = 0,
получим ух = 6, у2 = -6. Следовательно, точки ^(0,6), TV2(0,-6)
являются точками пересечения окружности с осью Оу.
Пример 8. На окружности х2 + у2 = 25 найти точки с ординатой
у = 4 и точки с абсциссой х = х0.
Решение. Подставляя значение у = 4 в уравнение окружности,
получим
х2 +42 = 25 или х2 = 9,
откуда Х| = 3, х2 = -3. Таким образом, первому условию задачи удов-
летворяют две точки A/j(3,4), Л/2(-3, 4).
Найдем точки данной окружности, для которых х = х0. Подставляя
это значение х в уравнение окружности, получим х02 + у2 = 25, откуда
/ = 25-х02, у = ±д/25-х02.
Из последнего равенства видно, что у принимает действительные
значения лишь в случае, когда подкоренное выражение неотрицатель-
но, т. е. когда 25-х02 > 0 или х02 < 25. Это соотношение выполняется
при х0, для которых -5<х0<5. Следовательно, при условии
- 5 х0 < 5 существуют две точки:
^(х0,725-Хо2), JV2(x0,-^25-х02).
Задачи
1. Найти уравнение геометрического места точек, равноудален-
ных от начала координат и от точки М (2, 6). Принадлежат ли этому
геометрическому месту точки А (7,1), В (2, 5), С (1,3), £)(-2,4)?
2. Определить траекторию движения точки М в каждом из сле-
дующих случаев:
1) расстояние до оси Оу равно а единицам;
2) расстояние до оси Ох равно Ь единицам;
22
3) расстояния до координатных осей равны между собой.
3. Написать уравнение линии, по которой движется точка Л/, оста-
ваясь втрое дальше от оси Оу, чем от оси Ох.
4. Составить уравнение геометрического места точек, удаленных
от начала координат на 6 единиц. Лежат ли на данной линии точки
А (6,0), В (3,4), С (7,2), Г>(5,-ч^Т)?
5. Точка М движется так, что ее расстояние от точки А (4, 0)
вдвое меньше расстояния от точки В (16, 0). Найти уравнение траекто-
рии движения точки Л/.
6. Определить траекторию точки М, которая движется так, что ее
расстояние от точки А (8,0) в четыре раза больше расстояния от точки
7. Найти точки пересечения линии 3x + 4j/-12 = 0 с координат-
ными осями.
8. Составить уравнение геометрического места точек, равноуда-
ленных от точек пересечения линий:
х2 + / = 25, 4х-3^ = 0.
9. Найти уравнение геометрического места точек, одинаково уда-
ленных от оси Ох и от точки F (0,2). В каких точках эта линия пере-
секает координатные оси?
10. Дана окружность диаметра О А = 2а и касательная к ней в точ-
ке А. Через точку О проведен луч ОС и на нем отложен отрезок ОМ,
равный отрезку ВС, заключенному между окружностью и касательной.
Если луч ОС будет вращаться около точки О, то точка М опишет кри-
вую, называемую циссоидой Диокпеса. Составить уравнение этой кри-
вой и построить ее.
Ответы
1. х + Зу —10 = 0. Точки А, С и D принадлежат линии. 2. 1) х = а,
х = —а (прямые, параллельные оси Оу); 2) у = Ь, у — —Ь (прямые, парал-
лельные оси Ох); 3) у = х (биссектриса первого и третьего координатных
углов), у=~х (биссектриса второго и четвертого координатных углов).
3. у = ±-~ х. 4. Окружность х2 4- у2 = 36. На окружности лежат точки А и
D, точка В - внутри окружности, точка С - вне ее. 5. х2 + у2 = 64.
6. Окружность х2 + у2 = 4. 7. М (4, 0), N (0, 3). 8. Зх + 4у = 0.
9. >’ = -- +1. М (0,1) -точка
4
пересечения с осью Оу. Ось Ох ли-
ния не пересекает.
10. х3 = у2(2а-х). Указа-
ние. Начало координат поместить
в точку (9, ось Ох направить вдоль
ОА (рис. 1.5), тогда
ОМ = ,.р + у2,
АС2 = ОС' ВС, откуда:
АС2
ВС=^ ^C = 2atg<p =
у 2Л z.ayix -ту
= 2а—; ОС =--------=------------. Подставить выражения ОМ и ВС в
х costp х
равенство ОМ = ВС.
§ 1.3 Прямая линия на плоскости
Положение прямой линии на плоскости относительно системы ко-
ординат можно задать различными способами. Например, прямая од-
нозначно определяется двумя точками, точкой и направлением, отрез-
ками, отсекаемыми на осях координат, и т. д. В зависимости от способа
задания прямой рассматривают различные виды ее уравнения.
1.3.1. Уравнение прямой с угловым коэффициентом.
Общее уравнение прямой. Уравнение прямой в отрезках
Угловым коэффициентом прямой называется тангенс угла, образо-
ванного ею с положительным направлением оси Ох прямоугольной
декартовой системой координат. (Положительные углы отсчитываются
в направлении «против часовой стрелки» от оси Ох до прямой.)
Уравнение прямой с угловым коэффициентом имеет вид
y=kx + b, (1.7)
где £ - угловой коэффициент; b - отрезок, отсекаемый ею на оси Оу.
Уравнение вида
Ах + Ву + С=0, (1.8)
где А и В одновременно в нуль не обращаются (т. е. А2 + В2 Ф 0) назы-
24
вается общим уравнением прямой. Частные случаи этого уравнения:
1) Ах + By = 0 (С = 0) - прямая, проходящая через начало коор-
динат;
С
2) Лх + С=0 или х = я, где а =-(В=0,А*0) - прямая, па-
24
раллельная оси Оу;
3) Ах = 0 или х = 0 (В = 0, С = 0) - ось Оу;
С
4) Ву + С=0 или у = Ь, где Ь---(А = 0, В* 0) - прямая, па-
В
раллельная оси Ох;
5) By = 0 или у = 0 (А = 0, С = 0) - ось Ох.
Уравнение прямой в отрезках:
где а9Ь - длины отрезков, отсекаемых на осях координат, взятые с
соответствующими знаками. Если а или Ь отрицательно, то это зна-
чит, что прямая пересекает соответствующую отрицательную полуось.
Если прямая не параллельна оси Оу (т. е. В * 0), то ее общее урав-
нение, разрешая относительно у, можно привести к уравнению с угло-
вым коэффициентом:
у = кх + Ь,
, A L С
где к-—=—-.
В В
Если прямая не проходит через начало координат (т. е. С * 0) и не
параллельна ни одной из координатных осей, то ее общее уравнение
путем деления на - С можно привести к уравнению в отрезках
V.I,
-С -С а b
С , С
где а =—=—-.
А В
Пример 1. Написать уравнение прямой, параллельной биссектрисе
первого координатного угла и отсекающей на оси Оу отрезок, равный
четырем единицам.
Решение. Искомая прямая, как и биссектриса первого координат-
ного угла, образует с осью Ох угол а = 45°, поэтому A = tg45° = l.
25
Подставляя в уравнение y=Ax + Z> значения к = 1 и £ = 4, получим
искомое уравнение у = х + 4.
Пример 2. Построить прямые:
1) у=Зх + 2;
3)f-f=,; 4)2х-3=0;
2) Зх - 4у = 0;
5) 2у + 5 = 0.
Решение. Для по-
строения прямой доста-
точно выбрать две ее
произвольные точки. Ко-
ординаты этих точек на-
ходят из уравнения пря-
мой. Одной из координат
приписывают любое зна-
чение, тогда другая одно-
значно определяется
уравнением прямой.
Построим прямую
у = Зх + 2. В уравнении
прямой положим х = 0,
тогда у =30+ 2, у = 2.
Получили точку М (0,2).
Полагая
^ = 5.
ЛГ (1,5).
M,N и через них проводим прямую (рис. 1.6).
Построим прямую Зх-4у = 0. Так как коэффициент С=0, то
прямая проходит через начало координат. Это можно получить и непо-
средственно: полагая х = 0, получаем у = 0. Положим х = 4, тогда
3-4-4у = 0, откуда у=3; вторая точка £(4,3). Прямая, проходящая
через точку L и начало координат, является искомой.
Х У 1
Уравнение у - у = 1 можно переписать в виде
уравнение прямой в отрезках, причем а = 5, b = - 2.
отрезки, получим точки Р (5, 0), Q (0,-2). Через точки Р и Q прово-
х = 1, получим
Вторая точка
Строим точки
= Это
5 -2
Откладывая эти
дим прямую.
26
Уравнение 2х-3 = 0 перепишем так: х = —. Это прямая парал-
3
лельна оси Оу и отсекает на оси Ох отрезок, равный —, справа от оси
Прямая 2у + 5 = 0 или у = -^ параллельна оси Ох, отсекает на
оси Оу отрезок, равный
—, книзу от оси Ох.
Замечание. Для нахождения координат точек из уравнения прямой
можно придавать любые значения х или у, а потом из уравнения определить
у или х. (Например, если х = — 2, то для прямой у = Зх + 2 у = -4, если
у = — 1, то х = — 1.) Геометрически это означает, что прямую можно постро-
ить по любым двум ее точкам.
Пример 3. Построить прямую Зх-4у-12=0. Где лежат точки,
для которых: 1) Зх-4у-12>0; 2) Зх-4у-12<0?
Решение. Чтобы построить прямую, достаточно фиксировать две
ее произвольные точки. Пусть например, Xj = 0, тогда
30-4у-12=0, -4^-12 = О, ^=-3.
Получили точку ^(0,-3). Положим у2 =0, тогда
Зх2-40-12= 0, х2 = 4.
Вторая точка М2(4, 0). Построим точки и М2 и проведем че-
рез них прямую. Прямая М2 и будет искомой (рис. 1.7).
Возьмем три точки плоскости А^Хо, уД MQ(xQ, yQ),
из которых точка Мо лежит на прямой Зх-4у-12=0, а точки и
N2 по разные стороны от нее. Так как все три точки имеют одну и ту
же абсциссу, то они лежат на прямой, перпендикулярной оси Ох. Пусть
для определенности У\<Уъ<У2> т. е. лежит «ниже» прямой, а
N2 - «выше». Подставляя координаты этих точек в уравнение прямой
найдем:
Зх0- 4yj -12> 0;
Зх0 -4у2 -12 < 0;
27
3x0 -4у0 -12 = 0.
Таким образом, если точка N2 лежит выше прямой
Зх-4у-12 = 0, то при подстановке ее координат в это уравнение по-
лучаем отрицательное число; для точки лежащей ниже этой пря-
мой, - положительное число. Обратное также верно.
Следовательно, для
точек одной полуплоско-
сти, определяемой прямой
Зх-4у-12 = 0, имеем
Зх-4у-12>0, для точек
второй полуплоскости
Зх-4у-12<0.
Замечание. Послед-
нее утверждение
любой прямой.
Ах + By 4- С = 0
плоскость на две полуплоско-
сти, для точек одной из них
Ах + By + С > 0, для точек
уравнении прямой С < 0 и
верно для
Прямая
делит
другой Ах 4- By + С < 0. Причем, если в
Ах} + Ву} 4- С < 0, то точка Л/j (jq, у}) и начало координат лежат по одну
сторону от прямой; если С < 0 и Ах2 + Ву2 + С > 0, то точка M2(x2i у2) и
начало координат расположены по разные стороны от прямой
Ах 4- By + С = 0.
Пример 4. Определить параметры к и b прямых: 2х + 5у-10=0;
Зу+7=0; 4х-9у = 0.
Решение. Разрешив первое уравнение относительно у, получим
2 10 2
у =— х + — или у = — х + 2.
5 5 5
2
Сравнивая это уравнение с уравнением у = кх + Ь, находим ,
1^=2.
Разрешив два других уравнения относительно у, получим:
7 7
У = - у ’ откуда *2 = 0, *2 =
28
4 4
У = -х, откуда к3 = = 0.
Пример 5. Найти отрезки, отсекаемые на осях координат прямы-
ми:
7х + 2у-14 = 0; 2х-Зу-6 = 0; 4х + 5>>+8 = 0.
Решение. Разделим первое уравнение на 14, второе на 6, третье
на - 8 и перенесем свободные члены в правые части. Сравнивая полу-
ченные уравнения с уравнением (1.9), находим соответственно:
- + ^ = 1, а, =2, Ь=7; - + -^- = 1, а2 = 3, Ь, = -2;
27 1 и 3-2 2
х у . , 8
~;+~ё = 1’ аз = -2> =
-2 5
5
Замечание. В последнем случае после деления на - 8 получим
Чтобы определить а и Ь, данное уравнение нужно привести к виду уравнения
(1.9), т. е. написать его так, чтобы в правой части была единица, первое сла-
гаемое левой части в числителе содержало только х, второе-в числителе
только у.
Пример 6. Даны точки Л(-6, 0) и N (0, 8). Через середину отрез-
ка LN провести прямую, отсекающую на оси Ох отрезок втрое боль-
ший, чем на оси Оу.
Решение. Определяя координаты середины отрезка по формулам
(1.3), получим точку М (-3, 4). Уравнение прямой ищем в виде
По условию а = ЗЬ. Следовательно, уравнение примет вид
A+Z=1.
зь ь
Ддя определения b используем условие прохождения искомой прямой
через точку М (-3,4). Так как точка М лежит на искомой прямой, то
ее координаты удовлетворяют уравнению прямой, т. е.
29
------1— = 1,
3b b
откуда b=3. Подставляя это значение в равенство а = ЗЬ, получим
а = 9. Таким образом, уравнение искомой прямой запишется так:
—+ — = 1 илих + Зу-9=0.
9 3
Задачи
1. Написать уравнения прямых, параллельных биссектрисе второ-
го координатного угла и отсекающих на оси Оу отрезки = 3,
(,.-4. Ь3 = |.
2. Составить уравнения прямых, отсекающих на оси Оу отрезок
b = 2 и наклоненных к оси Ох соответственно под углами cq = 30°,
а2=45°, а3 = 0, а4 = 135°.
3. Написать уравнения прямых, проходящих через начало коорди-
нат и образующих с осью Ох соответственно углы а! = 30°, а2 = 45°.
а3 = 60°, а4 = 135°.
4. Уравнения прямых:
Зх-у + 2 = 0; 4х + 2у-5 = 0; 2х + 7>> = 0;
Зу-8 = 0; 5х + 9 = 0
привести к виду уравнений с угловыми коэффициентами.
5. Найти углы, образуемые прямыми:
х + у-2=0; х-у + 5 = 0; 2у-3= 0; 4х + 7=0;
Зх-2у = 0
с осью Ох.
6. Найти отрезки, отсекаемые на осях координат прямыми:
d^=i; N) I 11 * и
4 3 5 2
3) 2x + 3j-6 = 0; 4) Зх-2^ + 12 = 0;
5) j>=4x-2; 6) у = 6-Зх.
7. Построить прямые, заданные уравнениями:
30
у=-2х + 5; --- = 1; 2x-3y + 6 = 0;
У 3 4
4х + 5у - 20 = 0; Зх - 2 у = 0; 4х + 5у = 0;
5х + 9 = 0; Зу+5 = 0.
8. Вычислить площадь треугольника, заключенного между осями
координат и прямой 2х +1 у -14 = 0.
9. Диагонали ромба, равные 10 и 12 единицам, приняты за оси ко-
ординат. Найти уравнения сторон ромба.
10. Какая должна быть зависимость между коэффициентами а и
х у
Ь, чтобы прямая — + — = 1 была наклонена к оси Ох под углом
а b
ф = 45°?
11. При каких значениях С прямая 2х + Зу + С=0 отсекает на оси
Оу отрезки 5j = 4, = -6?
12. Найти значения В, при которых прямая 2х + Ву-6=0 обра-
зует с осью Ох углы (pj = 45°, ф2 = 135°.
13. При каких значениях А прямая Ях + 5у-40=0 отсекает на
координатных осях равные отрезки?
14. Определить параметр Ь, при котором прямая у = 2х + Ь отсе-
кает на оси Ох отрезок а = 3.
Ответы
5 7з
1. у = -х + 3, у = -х-4, у=-х+—. 2. у = —х + 2,
у = х + 2, у = 2, у = -х + 2. 3. Зу->/Зх = О, у = х, у = л/Зх. у = -х.
5 2 8 9
4. у=Зх + 2, у = -2х + —, у =— х, у = —, х =—. 5. aj=135°,
3
a2 = 45°, a3 = 0, a4=90°, a5 = arctg-. 6. 1) a = 4, 5=3; 2) 67 =-2,
5=5; 3)67 = 3, 5=2; 4) 67 =-4, 5=6; 5) a = ±, 5=-2; 6)67 = 2,
b=6. 8. 5 = 7кв. ед. 9. —+ —= 1, -^=1, -±-^ = 1, *-* = L
56 56 56 56
10. a=-b. 11. C] = -12, C2 = 18. 12. =-2. B2 = 2. 13. A - 5.
14. b= -6.
31
1.3.2 Угол между двумя прямыми. Условия параллельности и
перпендикулярности прямых. Пересечение двух прямых
Тангенс угла между двумя прямыми:
= + (А)
у = к2х + Ь2 (В)
определяется формулой
к2 -к,
= (110)
Условие параллельности прямых (А) и (В) имеет вид
^ = ^2, (1.11)
а условие их перпендикулярности
= (1.12)
Если прямые заданы общими уравнениями:
А}х + В^у + С| = О’ (С)
А2х + В2у+С2 = О, (D)
то тангенс угла между ними вычисляется по формуле
tg(p= (j 13)
А1А2 + В1В2
Условие параллельности прямых (С) и (D)
Л2 Вг
Условие их перпендикулярности
А1А2 + В1В2 = 0. (1.15)
Для нахождения общих точек прямых (С) и (D) необходимо
решить систему уравнений:
32
А}х + Ду+Cj = 0;
Л2х + В2У + С2 = 0,
(1.16)
причем при
(1.17)
имеется единственная точка пересечения, при
А2 &2 С2
прямые не имеют общей точки (они параллельны), при
а2 в2 с2
(1.18)
(1.19)
прямые имеют бесконечное множество общих точек (они совпадают).
Пример 7. Найти угол между прямыми:
2 3 2
у =— х + 3; у = — х + — .
5 У 7 7
2 3
Решение. Подставляя в формулу (1.10) значения кх = -у, k2 =
получим
Пример 8. Найти угол между прямыми:
6х + 8у + 5 = 0; 2х - 4у - 3 = 0.
Решение. Пользуемся формулой (1.13). Подставляя в нее значения
4 = 6, В] = 8, А2 = 2, В2 = -4, находим
6(-4)-2-8 -24-16 -40 п
tgcp =----------=----------=----= 2, ф = arctg2.
6-2+8(-4) 12-32 -20 v
Замечание к примерам 7 и 8. Формулы (1.10) и (1.13)
определяют тангенс одного из двух углов между прямыми, сумма которых
2 Зак. 1816
33
равна 180°. Меняя нумерацию прямых, получим второе значение для тангенса
угла, отличающееся от первого только знаком. Если в примере 7 считать
2 3 2
второй прямую у = - — х + 3, тогда к2=- — . По формуле (1.10)
находим, что tg(p = — 1, откуда (р = 135°. (Сделайте чертеж.)
Пример 9 . Указать, какие из следующих прямых:
1) Зх-15у + 16=0; 2) Зх + 15у-8 = 0;
3) 6х-30у + 13=0; 4) 30х + 6у+7 = 0
параллельны и перпендикулярны.
Решение. Первая и третья прямые параллельны, так как
выполняется условие (1.14). В самом деле: 4=3; Д = -15; А2 = 6;
& = -зо- А = 2 = 1. A = z!5=l. А = А
’ Я2 6 2’ #2 -30 2’ Л2 В/
Третья и четвертая прямые перпендикулярны, ибо выполняется
условие (1.15). Действительно,
А^ + В^ = 6-30 + (-30) 6 = 0.
Первая и четвертая прямые также перпендикулярны.
Замечание 1. Условие (1.14) означает, что если прямые
параллельны, то коэффициенты при текущих координатах одной прямой
можно получить из соответствующих коэффициентов другой путем
умножения их на одно и то же число. Например, коэффициенты первой
1
прямой получены умножением на —
коэффициентов третьей прямой, с другой
стороны, коэффициенты третьей прямой получены из коэффициентов первой
прямой умножением на 2.
Замечание 2. Из условия (1.15) вытекает, что если прямые
перпендикулярны, то коэффициенты при х и у одной из них получаются из
соответствующих коэффициентов другой переменой их мест и изменением
знака одного из коэффициентов. Например, прямые Ах + By + С = 0,
Вх - Ау + С] =0 перпендикулярны.
Пример 10. Вычислить площадь треугольника, стороны которого
лежат на прямых, заданных уравнениями:
х-Зу + 11 = 0; 5х + 2у-13=0; 9х+7у-3=0.
Решение. Искомую площадь вычислим по формуле (1.4), для чего
вначале найдем координаты вершин треугольника.
Решая систему уравнений
34
x-3y + ll = 0; 1
5х4-2у-13 = 0, J
находим вершину Р (1,4).
Решая систему
5х4-2у-13 = 0;
9х + 7 у - 3 = О,
получим вторую вершину Q (5, - 6).
Наконец, из системы
x-3j4-ll = 0;
9х+7у-3 = О
получим третью вершину R (-2, 3).
С помощью формулы (1.4) находим, что 5 = 17 кв. ед.
Пример 1 1 . Через точку М (1,-2) провести прямую,
параллельную прямой 4х + 7 у - 3 = 0, и прямую, перпендикулярную
данной прямой.
Решение. Уравнение прямой, параллельной данной, ищем в виде
4х + 7у+С‘= О,
где С - пока неизвестный коэффициент (см. замечание 1 к примеру 9).
Так как искомая прямая проходит через точку Л/(1,-2), то
координаты последней должны удовлетворять уравнению прямой.
Подставляя координаты точки в искомое уравнение, получим
4-14-7 (-2)4-С= О,
откуда С = 10.
Следовательно, уравнение искомой прямой имеет вид
4x4-7^4-10= 0.
Уравнение прямой, перпендикулярной данной, будем искать в виде
7х-4у4-С= 0
(см. замечание 2 к примеру 9).
Определим С из условия, что прямая проходит через точку
М (1,-2). Подставляя ее координаты в уравнение, получим
35
71-4(-2)+С=0,
откуда С = -15.
Таким образом, прямая, перпендикулярная данной, имеет
уравнение
7х-4у-15=0.
Пример 12. Найти длины сторон треугольника и его внутренние
углы, если известно, что стороны лежат на прямых:
х-6у + 5=0; 5х-2у-3=0; х + у-9=0.
Решение. Чтобы вычислить длины сторон треугольника,
необходимо знать его вершины. Найдем их. Решая систему уравнений
первых двух прямых
х-6у + 5 = 0;
5х-2у-3=0,
получим вершину А (1,1).
Система уравнений первой и третьей прямой
х-6у + 5 = 0;
х+у-9= 0
определит вторую вершину В (7, 2).
Из системы уравнений второй и третьей прямой
5х-2у-3=0;
х + у-9 = 0
А
находим вершину С (3, 6).
По формуле (1.1) вычисляем длины сторон:
АВ = -J(7 —I)2+(2 —I)2 = 737;
ВС = л/(3-7)2 +(6-2)2 = л/32;
АС = д/(3-1)2 + (6-1)2 = л/29.
36
Так как
АВ2 < ВС2 + АС2,
где АВ - наибольшая сторона, то треугольник АВС остроугольный (см.
пример 2 § 1.1).
Таким образом, ни один из внутренних углов треугольника на
является тупым, а поэтому ни один из тангенсов этих углов не может
— Z Л Я» X
быть отрицательным (tg(р < 0, если — < <р < тс).
Переходя к нахождению углов треугольника, заметим, что
рассматривая прямые, на которых лежат его стороны, и пользуясь
формулами (1.10) или (1.13), мы получаем тангенс внутреннего или
внешнего угла при данной вершине (см. замечание к примерам 7 и 8
настоящего параграфа). Чтобы различить эти углы, будем
руководствоваться следующими соображениями. Формулы (1.10) и
(1.13) должны давать для тангенсов внутренних углов не более одного
отрицательного числа (так как треугольник не может содержать более
одного тупого внутреннего угла). Если тангенс одного из углов
оказался отрицательным, нужно проверить является ли треугольник
тупоугольным (аналитически, с помощью неравенства с2 > а1 + Ь2).
По формуле (1.13) определяем тангенсы углов треугольника
(внутренних или внешних пока неизвестно):
tg<Pl =
1 (—2)— 5(-6) _ -2+30 = 28
1-5 + (—6)(—2) “ 5 + 12 ”17’
tg<P2 =
11-1 (-6)1 + 6 7
11 + 1 (-6) ” 1-6” 5’
51-1(- 2) 5 + 2 7
tg4>3- 1-5 + 1(-2)" 5-2“ 3’
Буквами ср},<р2 и Фз обозначены внутренние или внешние углы
соответственно при вершинах Я, В и С. Таким образом, тангенс одного
из углов оказался отрицательным. Это означает, что или треугольник
тупоугольный, или угол ф2 является внешним углом при вершине В.
Поскольку выше было показано, что треугольник АВС остроугольный,
то верно второе предположение. Меняя нумерацию прямых,
пересекающихся в точке В (первой будем считать прямую
37
х + у-9=0, второй-х-6у+5 = 0), по формуле (1.13) получаем
1(-6)-1.| = -6-1 = -7=7
1-1 + Ц-6) 1-6 -S S
Так как tgcp) > 0 tgcp3 > 0, то cpj = ZA, ф3 = ZC. Тангенсы
внутренних углов определены, величины углов можно найти по
таблицам.
Ответ: АВ = 4з7, ВС = ,]32, АС = 419, tgA = —, tgB = ~,
Замечание 1. При нумерации прямых, противоположных принятым
здесь, мы получили бы
28 7 7
tg<Pi = -—, tg<p2 = -, tgcp3 = --.
Этот результат не удовлетворяет условиям задачи (двух тупых внутренних
углов в треугольнике быть не может).
Замечание 2. В некоторых аналогичных задачах может оказаться
tgcpt < 0, tg<p2 < 0, tg<p3 < 0.
Этот случай надо отбросить (трех тупых внутренних углов в треугольнике
быть не может). Нужно изменить нумерации на противоположные в каждой
паре прямых.
Замечание 3. Если окажется
tgcp, > 0, tg<p2 > 0, tgq>3 > 0,
то нужно проверить еще, нет ли тупого угла среди внутренних углов
треугольника. Если такой угол имеется, нужно изменить нумерацию в
соответствующей паре прямых (определяющих данную вершину).
Задачи
15. Найти углы между прямыми:
1) • Г 2 у = — х-7; Л 3 у = 5х + 9; 2) [ 1 т У=4*-3> х - 4у + 7 = 0;
3) < з у = — х - 2; У 7 7х + Зу + 5 = 0; 4) 1* 2х - 4у + 9 = 0; 6х-2у-3=0;
38
f 4x-5y + 2=0; ( 6x-3y+5=0;
[5x + 4y-3 = 0; 6) [ 2x-6y-3 = 0;
16. Составить уравнения прямых, проходящих через начало
координат, если известно:
1) прямая параллельна прямой 2х - Зу + 5 = 0;
2) перпендикулярна прямой у = Зх + 5;
3) образует угол 45° с прямой у = 2х- 3.
17. Найти внутренние углы треугольника, стороны которого лежат
на прямых:
4х-3>> + 3=0; Зх + 4>> + 4=0; х-7>> + 18 = 0.
18. Через точку пересечения прямых Зх + 5у - 8 = 0;
4х - Ту + 3 = 0 провести прямую, перпендикулярную первой из них, и
прямую, параллельную прямой 2х + бу - 2 = 0.
19. Даны две стороны параллелограмма: х - у +1 = 0,
Зх + 2у -12 = 0 и точка Е (6,4) пересечения его диагоналей.
Написать уравнения двух других сторон параллелограмма.
20. Найти-длины сторон и внутренние углы треугольника, стороны
которого лежат на прямых:
4х-3>> + 7=0; Зх +2^-16 = 0; х-5у + 6=0.
Ответы
, п л п п п 3 л
15. <Р1 = -, <р2 = 0, <Рз = у, 4>4 = р 95=2’ Фб = дЯ, Ф7=д-
16. 1) 2х-Зу = 0; 2) у = -|х; 3) у = -3х, у = |х. 17.90°, 45°, 45°.
18. 5х —Зу —2 = 0, 2х + 6у — 8 = 0. 19. х-у-5 = 0, Зх + 2у-40=0.
Указание. Определить точку пересечения двух данных сторон,
являющуюся одной из вершин параллелограмма. Вторая вершина находится из
условия, что точка Е - середина отрезка. Через эту вершину провести
прямые, параллельные данным. 20. АВ = 5, ВС = V13, АС = л/26,
39
1.3.3. Уравнение прямой, проходящей через данную точку в
данном направлении. Пучок прямых. Уравнение прямой,
проходящей через две данные точки
Уравнение прямой, проходящей через данную точку М}(хи ) в
данном направлении,
У~У\ =к(х-х1), (1.20)
где k = tga (a - угол, образуемый этой прямой с осью Ох).
Если в уравнении (1.20) считать, что к принимает все
действительные значения, то это уравнение будет уравнением пучка
прямых, т. е. совокупности прямых, проходящих через данную точку
(центр пучка). Уравнение пучка прямых, проходящих через точку
пересечения двух прямых
Ах + Ву+С = 0;
Ахх + Ду + Q = 0,
имеет вид
а(Ях + Ву + С)+р(Я1х+Ду+С1) = О, (1.21)
где а и Р принимают всевозможные действительные значения.
Уравнение прямой, проходящей через две точки М}(хиух) и
М2(х2>У2^
У = ~ (х2 * Х1 ’ У2 * У1 )• (1 -22)
У2-У1 *2-*1
Угловой коэффициент этой прямой определяется формулой
*= У2~У| (х2 *xt). (1.23)
x2-xi
Замечание. Уравнение (1.20) не может выражать прямую пучка,
параллельную оси Оу.
Пример 13. Написать уравнение прямой, проходящей через точку
М (-2,3) и параллельной биссектрисе второго координатного угла.
Решение. Искомая прямая, как и биссектриса второго
координатного угла, образует с положительным направлением оси Ох
угол ф = 135°, поэтому к = tgl35° = -1. Так как точка М дана, то
xt=-2, у1 = 3.
40
Уравнение (1.20) при к = -1, jq = - 2, yt = 3 принимает вид
У_3 =-1 [х —(—2)], у—3=-х-2
или
х + у - 1 = 0.
Пример 14. Составить уравнение пучка прямых, проходящих
через точку М (4, -5). Среди пучка прямых выбрать прямую,
параллельную прямой 2х - Зу + 6 = 0, и прямую, перпендикулярную
ей.
Решение. Так как координаты точки М известны, т. е.
х, = 4, у! = - 5, то уравнение
у + 5= к (х-4),
где к может принимать любые действительные значения, является
уравнением пучка прямых, проходящих через точку М.
При каждом фиксированном значении к получаем вполне
определенную прямую. Среди этого множества прямых выберем ту,
которая параллельна прямой 2х - Зу + 6 = 0. Разрешив последнее
уравнение относительно у, получим
у = -х + 2,
3
2
откуда к = где к -угловой коэффициент данной прямой. Искомая
2
прямая будет также иметь угловой коэффициент к = —.
Подставляя это значение к в уравнение пучка, находим уравнение
искомой прямой:
2
у + 5 = -(х-4); Зу + 15 = 2х-8
или окончательно
2х-Зу-23 = 0.
Прямая, перпендикулярная прямой 2х - Зу + 6 = 0, получается из
3
уравнения пучка при к = — (это значение к найдено из условия
41
перпендикулярности ^ = -—). Следовательно, вторая искомая
*2
прямая определяется уравнением
3
^ + 5 = --(х-4) -
или
Зх + 2у-2 = 0.
(Решение задачи по отысканию прямых, параллельных или
перпендикулярных данной прямой, сравните с решением примера 11.)
Пример 15. Составить уравнение прямых, проходящих через
середины сторон треугольника с вершинами А (3,4), В (3,2),
С (-1,2).
Решение. Середины сторон АВ, ВС, СА обозначим соответственно
через D, Е, F. По формулам (1.3) находим, что D(3,3), Е(1,2),
F(l,3).
Подставляя в уравнение (1.22) координаты точек D и Е, т. е.
значения xj =3, у} = 3, х2 = 1, у2 = 2, получим уравнение прямой
DE:
у-3_х-3 у-3_х-3
или
х-2>^ + 3=0.
Подстановка координат точек Е и F в уравнение (1.22) приводит к
соотношению
у-2 _ х —1
' 3-2 " ЬЙ’
лишенному смысла, так как знаменатель правой части обратился в
нуль. Но в данном случае уравнение прямой, проходящей через точки
Ей F можно получить и непосредственно. Так как абсциссы точек Е и
F равны единице, то отрезок EF будет параллелен оси Оу и расположен
справа от оси Оу на расстоянии d = 1 от нее. Уравнение прямой EF как
прямой, параллельной оси Оу и отсекающей на оси Ох отрезок d = 1,
имеет вид
х = 1 или х -1 = 0.
42
Это уравнение формально можно получить и с помощью формулы
(1.22), если считать, что соответствующий числитель также равен
нулю, т. е. х -1 = 0.
Поскольку ординаты точек D и F равны трем, то отрезок DF будет
параллелен оси Ох и отстоять от нее на расстоянии d = 3.
Следовательно, уравнение прямой DF, как параллельной оси Ох и
отсекающей на оси Оу отрезок 6=3, таково:
у = 3 или ^-3=0.
Пользуясь уравнением (1.22) получаем тот же результат. В самом
деле, подставляя в него координаты точек DuF, находим
х-3^ j-3
1-3 “ 3-3’
откуда
у-3=0.
Замечание. Если при подстановке координат точек в уравнение (1.22)
один из знаменателей обращается в нуль, то искомое уравнение получается
приравниванием нулю соответствующего числителя. (Оба знаменателя
одновременно в нуль обратиться не могут, так как это означало бы, что
Xj = х2, У\ = _у2, т- е- 470 точки Afj и М2 совпадают, а их, естественно,
считают различными).
Пример 16. Написать уравнение сторон и высот треугольника с
вершинами Р (-4,3), Q (2,5), R (6, -2).
Решение. Напишем уравнение стороны PQ. Для этого подставим в
уравнение (1.22) следующие значения: х} = -4, = 3, х2 = 2, у2 = 5.
Получаем
у-3_х + 4
5^1" 2 + 4
или
У =
х 13
— + —.
3 3
Из этого уравнения вытекает, что kPQ = р
где через кРО обозначен
угловой коэффициент прямой PQ.
Чтобы получить уравнение прямой QR, необходимо подставить в
уравнение (1.22) значения: х} = 2, ^ = 5, х2 = 6, у2 = -2. Тогда
43
получим
у-5 _х-2
-2-5“ 6^2
или
7 17
Л 4 2
7
откуда угловой коэффициент прямой kQR = - —.
Аналогичным образом найдем уравнение прямой PR. Имеем
у-3 х + 4 1
----=-----, у =— х + 1,
-2-3 6 + 4 Л 2
^2 = кР0 = -). Подставляя эти значения в
откуда
к --1
kPR- 2-
Высота, опущенная из точки Я (6,-2) на сторону PQ,
определяется уравнением (1.20). В данном случае: Xj = 6, ^ = -2,
Л = -3 (значение к получено из условия перпендикулярности двух
f 1
прямых: к} =------
к2
уравнение (1.20), получим
у + 2 = -3(х-6) или Зх + у-16=0.
Уравнение высоты, опущенной из вершины Q (2, 5), определяется
следующими данными: х}=2, у} = 5, к = 2 (так как ^=-")-
Подставим полученные значения в уравнение (1.20), тогда
у-5=2(х-2), 2х-у + 1 = 0.
Аналогично найдем уравнение третьей высоты:
4
у-3 = у(х + 4), 4х-7у + 37=0.
Замечание. При составлении уравнений прямой, проходящей через
две данные точки, любую из них можно считать первой (т. е. имеющей
44
координаты Убедитесь в том, что уравнение прямых PQ, QR, PR
останутся прежними и для иной нумерации точек. Например, при составлении
уравнений прямой PQ считайте, что Xj = 2, = 5, х2 = — 4, у2 = 3.
Пример 17. Написать уравнение прямой, проходящей через точку
М пересечения прямых 5х - у +10 = 0, 8х + 4у + 9 = 0, и параллельной
прямой х + Зу = 0 (не находя точки Л/).
Решение. Уравнение пучка прямых, проходящих через точку М, в
соответствии с уравнением (1.21), имеет вид
а(5х-у + 10)+р(8х + 4у + 9) = О
или
(5а + 8р) х + (4р - а) у + (1 Оа + 9р) = 0. (А)
Записывая условие параллельности (формула (1.14)) для данного
случая, получим
5а + 8Р _ 4Р~а
i з ’
отсюда
16а = -20р.
Можно взять а = -5, Р = 4. Уравнение (А) при этих значениях
примет вид
7х + 21у-14 = 0 или х + Зу-2 = 0.
Задачи
21. Стороны треугольника заданы уравнениями: 7х-6у + 9=0;
5х + 2у - 25 = 0; Зх +1 Оу + 29 = 0. Найти координаты вершин и
уравнения высот треугольника.
22. Дан треугольник с вершинами Р (-4, 0), Q (0, 4), R (2, 2).
Написать уравнения его медиан.
23. Даны вершины треугольника: Р(6,0), 0(0,6), R (-4,4).
Составить уравнения сторон треугольника, вершинами которого
являются середины сторон данного треугольника.
24. Найти точку пересечения медиан треугольника с вершинами
Р(2,1), 0(0,7), Я (-4,-1).
25. Написать уравнение прямой, проходящей через начало
координат и точку пересечения медиан треугольника, стороны
45
которого лежат на прямых, заданных уравнениями: у = 4х + 4;
у = -х + 4; 4у = х + 1.
26. Найти точку, равноудаленную от трех данных точек: L (4, -1),
М (8,1), ЛГ(9,4).
27. На прямой х-2у + 2 = 0 найти точку, равноудаленную от
точек Л/^-2,3), Л/2(2,-1).
28. Найти точку, симметричную точке М (5,5) относительно
прямой х + у - 3 = 0.
29. Найти проекцию точки М (- 5,4) на прямую х - у - 5 = 0.
Ответы
21. Р(-3,-2), 6(3,5), Я(7,-5), 6х + 7у-7 = 0, 2х-5у-4 = 0,
10х-Зу-15 = 0. 22. Зх —5у +12 = 0, Зх-у + 4 = 0, у = 2.
( 2 7^
23. х-2у + 3 = 0, х+у-3=0, 2х+5у-21 = 0. 24. ЛЧ—,-.
25. 5х-2у = 0. 26. # (4, 4). 27. N (0,1). 28. N (—2, -2). 29. N (2,-3).
1.3.4. Нормальное уравнение прямой. Расстояние
от точки до прямой
Нормальное уравнение прямой имеет вид
xcosa + ysina-p = 0, (1-24)
где р - длина перпендикуляра, опущенного из начала координат на
данную прямую; a - угол, образуемый этим перпендикуляром и осью
Ох.
Расстоянием от точки до прямой называется длина
перпендикуляра, опущенного из этой точки на данную прямую.
Расстояние от точки Мх(хьух) до прямой (1.24) вычисляется по
формуле
</ = |xj cosa+yjsina-р|. (1.25)
Общее уравнение прямой
Ях + Ву + С=0 (1.26)
умножением на нормирующий множитель
46
знак которого противоположен знаку С, приводится к нормальному
виду’
Ах + Ву+С
±^а2 + в2
(1.28)
Расстояние от точки до прямой (1.26) определяется
формулой
d =
Ах} + Ву} +С
4а2+в2
(1.29)
Пример 18. Написать уравнение прямой, если известно, что
расстояние ее от начала координат равно 72 и что перпендикуляр,
опущенный на нее из начала координат, составляет с осью Ох угол
ф = 45°.
Решение. По условию задачи р = ^2, а = 45°, поэтому
cosa = sma = >/^/ Подставляя эти значения в уравнение (1.24),
получим
72 72 г-
х- — + у------у2 = 0,
2 У 2
откуда
х + у-2 + 0.
Пример 19. Определить длину перпендикуляра, опущенного из
начала координат на прямую х - у + 3 = О, и угол, образуемый этим
перпендикуляром с осью Ох.
Решение. Уравнение прямой приведем к нормальному виду, для
чего найдем нормирующий множитель. Из уравнения прямой следует,
что А = 1, В = -1. По формуле (1.27) найдем
1 _________1_
V2-
Умножая уравнение прямой на нормирующий множитель ц = —т=,
получим
47
1 1 з л
1
откуда cosa = --7=
sin a = -т=-, р = —?=. Следовательно, a = 135°,
Пример 20. Дан треугольник с вершинами Р (0, 5), Q (- 3,1),
R (-1, -2). Найти длину высоты, опущенной из точки R.
Решение. Задача сводится к определению расстояния от точки R до
прямой PQ. Напишем уравнение этой прямой. На основании уравнения
(1.22) имеем
х _ у-5
1-5 -3-0’ -3 -4
или
4х-Зу + 15 = 0.
Расстояние точки R (1,-2) до этой прямой вычислим по формуле
(1.29)
d =
4 1-3 (-2)+15
>/42+(-3)2
= 5.
Следовательно, длина высоты равна 5.
Замечание. Эту задачу можно было бы решить и другими способами.
Например, длину искомой высоты можно вычислить, зная площадь
треугольника PQR и длину основания PQ. Эта же длина определяется как
расстояние между двумя точками R и М, где М-основание высоты,
опущенной из точки R на основание PQ. В свою очередь координаты точки М
можно найти, решая систему уравнений стороны PQ и высоты RM. (Решите
задачу указанными способами и сравните с данным решением.)
Пример 21. Написать уравнения биссектрис углов, образуемых двумя
пересекающимися прямыми:
4*+ В|>>+ Сх = 0; А2х + В2У + С2 = 0.
Решение. Пусть Л/0(х0,у0) - фиксированная точка биссектрисы.
Расстояние этой точки до первой прямой определится формулой
48
Л^о + Ауо + G
расстояние d2 до второй прямой - формулой
j _ ^2Х0 + ^2Уо + ^2
А2 + В22
Так как точка MQ одинаково удалена от сторон угла, то
4хо + В^у0 + Cj
Л2Хр + В2у0 + С2
-Ja22 + B22
Это равенство имеет место для любой точки Л/ (х, у) биссектрисы,
поэтому
/^х + В^у+С!
742 + в/
_ Л2х + В2У+С2
//122+b/
Последнее равенство можно записать так:
^x + Bjy + q Л2х + В2у+С2
Полученные уравнения являются искомыми.
Пример 22 Найти точку М пересечения биссектрис внутренних
углов треугольника PQR, стороны которого заданы уравнениями:
Зх + 4у + 12 = 0 (Р0;
4х + Зу-12 = 0 (0Я);
Зх-4у-12 = 0 (PR).
Решение. На основании формулы (1.30) уравнения биссектрис
углов, образуемых сторонами PQ и QR, запишутся так
4х + Зу -12 _ Зх + 4у +12
л/42+32 л/з2 + 42
49
или
4х + Зу-12 = ± (Зх + 4у +12),
отсюда:
4х + Зу-12-(Зх + 4у + 12)=0;
4х + Зу-12 + (Зх + 4у+12)=0.
Таким образом, уравнения биссектрис следующие:
х - у - 24 = 0;
х + у = 0.
Одно из этих уравнений будет уравнением биссектрисы
внутреннего угла Q треугольника PQR, второе - уравнением
биссектрисы внешнего угла. Так как вершины Р и Q лежат по одну
сторону от биссектрисы внешнего угла Q, то при подстановке их
координат в уравнение этой биссектрисы получим числа одного знака
(см. пример 3). Вершины Р и R расположены по разные стороны от
биссектрисы внутреннего угла Q, поэтому подстановка координат
точек Р и R в уравнение этой биссектрисы дает числа разных знаков.
Два последних утверждения дают способ отличить биссектрису
внутреннего угла от биссектрисы внешнего угла треугольника.
Найдем вершины треугольника PQR. Из уравнений
Зх + 4у +12 = 0; 1
Зх-4у-12 = 0 J
получаем Р(0,-3).
Решая систему уравнений
Зх+4у + 12 = 0; 1
4x + 3y-12 = 0, J
находим 0(12,-12).
Аналогичным образом определим точку R (3,36; -0,48).
Подставляя координаты точек Р(0,-3) и R (3,36; -0,48) в
уравнение х-у-24=0, находим:
50
0 + 3-24<0;
3,36+0,48-24 <0.
Получены числа одного знака, следовательно, уравнение
х-у-24=0 является уравнением биссектрисы внешнего угла Q.
Подставляя координаты этих же точек в уравнение х + у = 0, получим:
0+(-3)<0;
3,36+ (-0,48) >0.
Следовательно уравнение биссектрисы внутреннего угла Q
треугольника PQR имеет вид
х + у = 0.
Аналогичным образом найдем уравнение биссектрисы внутреннего
угла R. На основании формулы (1.30) уравнения биссектрис углов,
образованных прямыми PR и QR, будут
4х + Зу-12 _ ± Зх —4у-12
д/42 + 32 ” 7з2+42
отсюда
4х + Зу-12 = ±(Зх-4у-12)
или
7х - у - 24 = 0, х - 7 у = 0.
Подставляя в первое из этих уравнений координаты двух вершин
^(0,-3), 0(12,-12), получим:
7 0-(-3)-24< 0;
712-(-12)-24> 0.
Таким образом, уравнение
7х —у —24=0
будет уравнением биссектрйсы внутреннего угла R.
Прямые PR и PQ, пересекающиеся в точке Л образуют два угла,
биссектрисы которых имеют уравнения
51
Зх + 4у + 12 _ Зх - 4у -12
л/32+42 л/з2+(-4)2
ИЛИ
у+3 = 0, х = 0.
Подставляя в первое из этих уравнений координаты точек Q (12, -12),
R (3,36; -0,48), получим:
-12+ 3 < 0;
-0,48 +3>0.
Следовательно,
у+3 = 0
является уравнением биссектрисы внутреннего угла Р.
Чтобы определить точку М пересечения биссектрис внутренних
углов треугольника PQR, достаточно найти точку пересечения двух из
найденных биссектрис. Возьмем, например, биссектрисы QM и RM,
уравнения которых
х + у = 0; 7х - у - 24 = 0.
Решая систему из двух последних уравнений, найдем, что точка М
пересечения биссектрис имеет координаты х = 3, у = -3. Задача
решена. (Сделайте чертеж.)
Задачи
30. Даны уравнения прямых:
1) 5х + 7у-9 = 0; 2) -х + у-3 = 0;
4
,ч 2 3 е л 12 5 „ л
3) —х+—у-6 = 0; 4)—х-----у-7 = 0;
5 4Z 13 13
5) —Х-—у-2 = 0; 6) — х+—у-4 = 0.
5 5 3 3 л
Какие из этих уравнений являются уравнениями в нормальном виде?
31. Привести к нормальному виду уравнения следующих прямых:
1) 5х + 12у-26 = 0; 2) Зх-4у + 10 = 0;
3) 2х + 2у + 7 = 0; 4) у = Зх + 5;
52
5) y = kx + b2; 6)-+- = l.
a b
32. Написать уравнение прямой, параллельной данной прямой
4х + Зу -15 = 0 и отстоящей от нее на расстоянии d = 2.
33. Найти расстояние между параллельными прямыми:
5х-12у-26 = 0; 5х-12у-65 = 0.
34. Даны уравнения оснований трапеции:
Зх-4у-15 = 0; Зх-4у-35 = 0.
Вычислить длину ее высоты.
35. Написать уравнение прямой, проходящей через точку A/j (1,5)
на расстоянии пяти единиц от начала координат.
36. Написать уравнения биссектрис углов, образованных прямыми:
4х-Зу-10 = 0; 9х-12у-7 = 0.
37. Составить уравнение биссектрисы внутреннего угла В
треугольника с вершинами: Л (3,2), В (-1,-1), С (7,7).
38. Найти точку, равноудаленную от точек М (-3,1), 7V(5,7) и
отстоящую от прямой Зх- 4у + 38 = 0 на расстоянии d = S.
39. Даны центр квадрата N (4,3) и уравнение стороны
х - у - 5 = 0. Написать уравнения остальных трех сторон.
40. Дано уравнение одной из сторон угла 4х-Зу + 9 = 0 и
уравнение его биссектрисы х-7у + 21 = 0. Написать уравнение другой
стороны угла.
Ответы
30 Уравнения 4), 5). 31.
5 12 „ л 3 4 _
1)—х + —у-2 = 0; 2)—х + —у-2 = 0;
13 13 5 5
—. —— = 0. 32. 4х + 3 у — 25 = 0, 4х + Зу-5 = 0.
Указание. Уравнение искать в виде 4х + Зу + С = 0. Воспользоваться
формулой (1.29). 33. rf = 3. Указание. Определить д и р^, взять их
53
разность. Второй способ. Взять произвольную точку на одной прямой и
определить ее расстояние до второй прямой. 34. h = 4. 35. 5х + 12у — 65 = О,
у - 5 = 0. Указание. Уравнение прямой искать в виде
У~~У\ = (х - Xj). Определить к из условия, что прямая отстоит от начала
координат на d = 5. 36. Зх + Зу-23 = 0; 21х-21у-37 = 0.
37. 7х-у + 6 = 0. 38.ЛГ(1,4), Л/(-5,12). 39. х-у + 3 = 0; х + у-3 = 0; .
х + у-11 = 0. 40. Зх + 4у-12 = 0.
§ 1.4. Линии второго порядка
Линия называется линией (кривой) второго порядка, если она
определяется уравнением второй степени относительно текущих
координат х иу, т. е. уравнением вида
Ax2 + By2 + Cxy+Dx + Ey+F = 0. (1.31)
При соответствующем выборе системы координат уравнение
линии второго порядка можно привести к простейшему виду.
1.4.1. Окружность
Уравнение окружности радиуса R с центром в точке N (а, Ь) имеет
вид
(х-а)2 +(у-Ь)2 = Л2. (1.32)
Уравнение
Ах2+ Ау2+ Dx + Ey+F = Q (1.33)
путем дополнения до полных квадратов можно привести к виду
(х-а)2+(у-Ь)2 =с. (1.34)
При с>0 уравнение (1.34) определяет окружность радиуса
R = Jc\ при с = 0 уравнению удовлетворяют координаты
единственной точки N (а, 6); при с < 0 уравнению не удовлетворяют
координаты ни одной точки плоскости.
Пример 1. Написать уравнение окружности радиуса R = 6 с
центром в точке N (2, - 3).
Решение. После подстановки значений а = 2, b = -3, R = 6 в
уравнение (1.32) получаем
54
(х-2)2 + (у+3)2 =36.
Пример 2. Найти координаты центра и радиуса окружности
х2 +у2 -6х + 10у-15 = 0.
Решение. В данном уравнении выделим полные квадраты,
прибавляя и вычитая соответствующие числа. Получаем
(х2-6х+9)+(/ + 10/+25)-9-25-15 = 0,
(х-3)2 +(у+5)2 = 49.
Сравнивая это уравнение с уравнением (1.32), находим
а = 3, 6 =-5, Я = 7.
Пример 3. Найти координаты центра и радиус окружности
Зх2+Зу2-4х + 9у+4 = 0.
Решение. Разделим обе части уравнения на 3:
з 2 4 о 4
х +у -у х + Зу+у = 0.
Дополняя до полных квадратов, находим
( 2 о 2 4W 2 3
х-2-х + - + у +2 —
I 3 2
= 0
или
( 3^
+W
49
36'
Сравнивая полученное уравнение с уравнением (1.32), заключаем, что
2 » 3 7
а = —, Ь = —, 7? = —.
3/2 6
Пример 4. Какое геометрическое место точек определяется
уравнением
4х2+4/+8х-12^+13 = 0?
55
Решение. Разделив обе части уравнения на 4, находим
2 2 о 13
х + у +2х-3у + — = 0.
4
Дополняя до полных квадратов, получим
z 2 ( 2 3 9^1 9 13 Л
(х2+2х + 1)+ у2-2—V + --1 — + — = 0
С 2Л 4у 4 4
или
2 ( зУ
(х + 1)2+1 у--\ =0-
Этому уравнению удовлетворяют координаты лишь одной точки, а
именно:
Пример 5. Написать уравнения касательных к окружности
х2 +у2 +4х-8у + 2 = 0,
проходящих через начало координат.
Решение. Уравнение касательной ищем в виде у = кх (Ь = 0, так
как прямая проходит через начало координат).
Касательная к окружности имеет с ней одну общую точку (две
точки пересечения сливаются в одну). Чтобы найти точки пересечения
прямой и окружности, необходимо решить систему уравнений:
х2 + у2 +4х-8у+2 = 0;
у = кх.
Подставляя второе уравнение в первое, получаем
(1 + Л2)х2+(4-8Л)х + 2 = 0.
Это уравнение имеет два равных корня, когда дискриминант его
равен нулю, т. е.
(4-8А)2-8(1 + А2) = 0
или
56
7Л2-8А + 1 = 0,
откуда k{ = 1, £2 = —
Следовательно, уравнения искомых касательных
1
запишутся в виде у = х, у = у х.
Задачи
1. Написать уравнение окружности, проходящей через точку
N (7, -2), центр которой находится в точке S (3, -5).
2. Даны две точки М (4,2) и 7V (12,8). Составить уравнение
окружности, диаметром которой служит отрезок MN.
3. Найти координаты центра и радиус окружности:
1) х2 + у2-4х + 8>>-16 = 0;
2) Зх2+Зу2-6х + 8^-у = 0;
3) х2 + у2+7х = 0;
4) 5х2 +5у2 +9 у = 0.
4. Написать уравнение окружности, касающейся осей координат и
проходящей через точку # (8,9).
5. Найти уравнение окружности, центр которой находится в точке
N (2, -3) и которая касается прямой 4х + Зу - 19 = 0.
6. Написать уравнение окружности, проходящей через три точки
1(2,1), Л/(6,3), #(9,2).
7. Определить угол между радиусами окружности
х2 +у2 -10х-6у + 16 = 0, проведенными в точки пересечения ее с
осью Ох.
8. Написать уравнение прямой, проходящей через центры двух
окружностей:
х2 + у2 - 4х + 8>>-16 = 0, х2 +у2 +8х + 12у-14 = 0.
9. Найти уравнение общей хорды окружностей:
х2 +у2 -2х-6>> + 6 = 0, х2 + у2 -6х-10у+ 30 = 0.
10. Составить уравнение окружности, касающейся оси Ох и
проходящей через точки L (0, 8), М (7,1).
57
Ответы
1. (х-3)2+(> + 5)2 =25. 2. (х - 8)2 + (>• - 5)2 = 25. 3. 1)С(2,-4),
f 4 А г~
R = 6; 2) С 1,— , Я = 76;
I 3/
4)С(0;-0,9), R = 0,9.
4. (х-5)2 +(у-5)2 = 25,
(х-29)2+(у-29)2 = 841.
Указание. Уравнение искать в
виде (х-а)2 + (у-а)2 = а2.
5. (х-2)2+(у + 3)3 = 16.
Указание. Радиус искомой окружности равен расстоянию данной точки до
прямой. 6. (х — 6)2 + (у + 2)2 = 25. 7. <р = 90°. 8. х-Зу-14 = 0.
9. х + у—6 = 0. 10. (х-4)2+(у-5)2 = 25; (х-12)2+(у-13)2 = 169.
1.4.2. Эллипс
Эллипсом называется геометрическое место точек, сумма
расстояний которых до двух данных точек (фокусов) есть величина
постоянная (эта постоянная больше расстояния между фокусами).
Каноническое уравнение эллипса:
X2 V2
—+7Г = 1, (1.35)
а о
где а = ОА - большая; Ь=ОВ - малая полуось (рис. 1.8). Координаты
фокусов: /*i(-c, 0), Г2(с, 0), где
с = 4а2-Ь2. (1.36)
Эксцентриситетом эллипса называется отношение фокусного
расстояния 2с к большой оси 2а:
с
е = — (е < 1, так как с < а). (1.37)
а '
Расстояния точки М (х, у) эллипса до фокусов (фокальные
радиусы) определяются формулами:
58
7i=a+£x; r2=a-£x. (1.38)
Директрисами эллипса называются прямые, уравнения которых
а
х = ±—, где е - эксцентриситет.
£
Пример 6. Найти полуоси, фокусы и эксцентриситет эллипса
4х2 +9у2 = 16.
Решение. Разделив на 16 обе части уравнения, получим
16
х
~4
или
,2
2
4 £6 = L
9
Сравнивая это уравнение с уравнением (1.35), находим:
2 А ,2 16 „ L 4 2 2 . 16 20
а =4, b -—, а = 2, b-—, c=a-b=4-= —,
9 3 9 9
2V5
с =--,
3
с V?
Е = —= .
а 3
Таким образом, имеем:
Пример 7. Написать простейшее уравнение эллипса,
симметричного относительно координатных осей и проходящего через
точки Ь(Зу/2,2у/2), 7V (6, 0).
Решение. Простейшее уравнение указанного эллипса имеет вид
2 2
^+4
а b
= 1.
Определим а2 и Ь2 из условия принадлежности эллипсу точек L
59
и N. Подставляя координаты этих точек в данное уравнение, получим:
18 8 , 36 0
2 + > г ~ I’ г + > г
а о а о
Из второго уравнения находим, что а2 =36. Подставляя найденное
2
значение а в первое уравнение, получаем
18 8 ,
—।—г L
36 ь2
откуда Ь2 = 16.
Таким образом, искомое уравнение будет
36 16
Пример 8. На эллипсе 16х2 +25у2 = 400 найти точку, расстояние
которой от правого фокуса в четыре раза меньше расстояния от левого
фокуса.
Решение. Разделив обе части уравнения на 400, находим
25 16
откуда
з
а2 = 25, 62 = 16, а = 5, Ь = 4, с2 = 25-16 = 9, с = 3, Е = -
5
В силу формул (1.38) расстояние до фокусов выразятся так:
с 3 3
л = 5 + — х; а = 5 — х.
1 5 2 5
По условию г, =4г2; следовательно,
с 3 /с 3
5+—х=4 5—х ,
5 I 5 )
ч
откуда х = 5. Подставляя это значение в уравнение эллипса, получим
у = 0. Искомая точка М (5, 0).
Пример 9. Доказать, что отношение расстояний любой точки
эллипса до фокуса и соответствующей директрисы есть величина
60
Рис. 1.9
Решение. Пусть
М (*> у) ~ произвольная точка
эллипса (рис. 1.9).
d2 = MN
директрисы
формулой
По
точки
Расстояние
М до
выразится
а
---х.
Е
второй из формул
(1.38) г2 =а-£х, поэтому
^2
а
е
2L-
d2
а-Ех
----= £,
а
----х
Е
что и требовалось доказать.
Пример 10. Найти эксцентриситет и директрисы эллипса
х2+3у2 =6.
Решение. Напишем уравнение эллипса в виде
2 2
±-+2L=i.
6 2
Сравнивая полученное уравнение с каноническим уравнением
(1.35), заключаем, что а1 = 6, Ь2 = 2. Следовательно,
с1 = а2-Ь2 =6-2 = 4,
, с 2
откуда с = 2, Е = —= —т=-.
a V6
Уравнения директрис в общем виде:
а а2
х=±—=±—
Е С
2 6
Подставим сюда значения а и с, получим х = ±—= ±3. Уравнения
61
директрис: х = 3, х = -3.
Задачи
11. Составить простейшие уравнения эллипсов, зная что:
1) полуоси эллипса соответственно равны 7 и 6;
2) расстояние между фокусами равно 24 и большая ось 26;
3) большая полуось равна 5 и расстояние между фокусами 8.
12. Найти канонические уравнения эллипсов по следующим
данным:
1) большая полуось равна 10 и эксцентриситет равен 0,8;
2) малая полуось равна 12 и эксцентриситет равен
3) эксцентриситет равен 0,6, расстояние между фокусами 6;
4) сумма полуосей равна 18 и расстояние между фокусами 12.
13. Определить длины осей, координаты фокусов и
эксцентриситеты эллипсов, заданных уравнениями:
1) 9х2 * * * * + 25/ = 225; 2) 9х2 + / = 36.
14. Дан эксцентриситет эллипса е. Найти отношение его полуосей.
Как величина эксцентриситета характеризует форму эллипса?
15. Известно, что прямая х - Зу -12 = 0 касается эллипса
2 2
X у
—+— = 1. Найти точку касания.
36 12
х2 у2
16. Сколько касательных можно провести к эллипсу — + — = 1 из
н 7 20 16
каждой точки L (1,2), М (0,4), N (5,3)?
X2 у2
17. Написать уравнения директрис эллипса += 1.
2 2
X у
18. Найти длину диаметра эллипса — + —= 1, направленного по
12 6
биссектрисе второго координатного угла. (Диаметром эллипса
называется хорда, проходящая через центр-точку пересечения его
осей.)
19. Найти уравнение эллипса, расстояние между его фокусами
которого равняется 8 и расстояние между директрисами - 24.
20. Дан эллипс х2 +2у2 = 8. Через точку М (1,1) провести хорду,
делящуюся в этой точке пополам.
21. Отрезок постоянной длины скользит своими концами по
сторонам прямого угла. Определить кривую, описываемую любой
62
точкой Л/, лежащей на этом отрезке.
Ответы
х2 У2 ,
и. 1) —+—= 1;
49 36
2 2
X У
12.1)—+—=1; 2)
100 36
х2 у2
2)---+ —= 1;
169 25
2 2 2
. — = 1; з)^- = 1:
169 144 25 16
.2
х2 у2 1
3) — + —= 1.
25 9
х2 у2
4)-----+ —= 1.
100 64
13. 1) а = 5, 6 = 3, с = 4, е = 0,8, F|(-4,0), F2(4,0); 2) а = 2, 6=6,
с = 4л/2, 7*J(0,-4>/2), 7^(0,4>/2). Указание. Если а<Ь, то фокусы
находятся на оси Оу, при этом c = yb2 — а2 , £ = —. 14. — = V1— Е2 • Если
b а
b
£ = 0, то — = 1, b = а (эллипс превращается в окружность). Если £ близко к
а
нулю, то b незначительно отличается от а (эллипс вытянут). Если £ близко
к единице , то Ь мало по сравнению с а (эллипс сжат). 15. М (3, -3). 16. Из
точки М можно провести одну касательную, из точки jV - две, из точки L - ни
одной. У казание. Выяснить, где лежат точки L, М, N по отношению к
Г- X2 у2
эллипсу. 17. х = 25, х = -25. 18. iZ = 4V2. 19.-----I-—= 1.
л 48 32
20. х + 2у - 3 = 0. Указание. Уравнение прямой искать в виде
у — 1 = k (х —1). Коэффициент к определить из условия, что точка М (1,1)
является серединой отрезка LN, где L и точки пересечения этой прямой с
эллипсом. 21. Эллипс. Указание. За оси координат принять стороны
прямого угла. Ввести в рассмотрение угол (р, образуемый данным отрезком с
осью Оу. Исключить параметр (р из полученных выражений для х и у.
1.4.3. Гипербола
Гиперболой называется геометрическое место точек, разность
расстояний которых до двух данных точек (фокусов) есть величина
постоянная (указанная разность берется по абсолютному значению;
требуется также, чтобы она была меньше расстояния между фокусами
и отлична от нуля).
Каноническое (простейшее) уравнение гиперболы
2 А2 1
а о
(139)
где а = ОАХ = ОАг - действительная; Ъ = ОВХ = ОВг - мнимая полуось.
Фокусы гиперболы:
63
fi(-c,O), F2(c, 0),
где
c = Ja2 + b2. (1.40)
Эксцентриситетом гиперболы (1.39) называется отношение
с
£ = — (е>1, так как с>а). (1.41)
а
Асимптоты гиперболы (1.39):
Гиперболы
у = +-х. (1.42)
а
Расстояния точки
М(х, у) гиперболы
(рис. 1.10) до ее фокусов
определяются формулами:
т\ = |£х + а|; г2 =|ех~а|.(1.43)
Прямые
х = ±- (1.44)
£
называются директрисами
гиперболы.
х__у_ = 1 _1_+21 =
2 >2 2 + >2
а о а о
называются сопряженными.
Гипербола с равными полуосями (а = Ь) называется
равносторонней, ее уравнение
х2-у2=а2. (1.39х)
Пример 11. Найти полуоси, координаты фокусов, эксцентриситет,
уравнения асимптот и директрис гиперболы
9х2-16/ = 144.
64
Решение. Приведем данное уравнение к каноническому виду, для
чего необходимо разделить обе части его на 144. Выполняя деление,
получим
--^- = 1
16 9
Сравнивая это уравнение с уравнением (1.39), заключаем, что
а2 = 16, Ь2 =9. Таким образом, а = 4 есть действительная полуось,
6 = 3 - мнимая полуось. Далее с = 4а2 +b2 = V16 + 9 = 5, фокусы:
с 5
6](-5, 0), F2(5,0). Эксцентриситет £ = — = —. Подставляя значения
а 4
а и b в формулу (1.42), получим уравнения асимптот:
В соответствии с формулой (1.44) находим уравнение директрис:
16
х = ±—.
5
Пример 12. Составить простейшее уравнение гиперболы,
симметричной относительно координатных осей, пересекающей ось Оу
и проходящей через две точки: М (24, 5^/5), N (0, 5). Найти фокусы
этой гиперболы.
Решение. Уравнение гиперболы ищем в виде
Так как точки М и N лежат на гиперболе, то их координаты
удовлетворяют уравнению гиперболы.
Подставляя координаты данных точек в это уравнение, получим
125 242 25 _
>2 2 ~ / 2 “ L
D a D
Решая полученную систему, найдем:
Ь2 = 25, а2 = 144.
Таким образом,
65
3 Зак. 1816
25 144
есть искомое уравнение.
Определим с по формуле (1.40). Имеем c = V144 + 25 =13.
Фокусы данной гиперболы лежат на оси Оу: 7^(0,-13), F2(0,13).
Пример 13. Доказать, что произведение расстояний любой точки
гиперболы до асимптот есть величина постоянная.
Решение. Уравнение асимптот гиперболы
г2 v2
Х У -1 A2v2 „2„2-z.2A2
—-----у = 1 или о х —ay = a b
о
имеют вид
b
y = ±— x или bx±ay = Q. (A)
a
Пусть M (x, у) - произвольная точка гиперболы. Ее расстояния до
асимптот (А) по формуле (1.29) выразится так:
Ьх-ау
>1а2+Ь2
Ьх + ау
Ja2 +Ь2
J ^2 =
откуда
4^2 ~
Ь2х2-а2у2
а2+ Ь2
а2Ь2
с2
что и требовалось доказать.
Задачи
22. Составить простейшие уравнения гиперболы, зная, что:
1) расстояние между фокусами равно 10, а расстояние между
вершинами 8;
2) действительная полуось равна 5 и эксцентриситет 2,6.
23. Написать канонические уравнения гипербол, если известно,
что:
1) расстояние между фокусами равно 10 и эксцентриситет
2) действительная полуось равна V20 и гипербола проходит
через точку N (-10,4).
66
24. Найти длины осей, координаты фокусов и эксцентриситеты
гипербол, заданных уравнениями:
'1) 144х2 -25/ = 3600; 2) 9/ -16х2 = 144.
25. На гиперболе —----— = 1 взята точка, абсцисса которой рав-
на 3. Вычислить фокальные радиусы этой точки.
х2 у2
26. Дан эллипс — + — = 1. Найти уравнение гиперболы, вершины
15 6
которой находятся в фокусах, а фокусы - в вершинах данного эллипса.
27. Найти зависимость между эксцентриситетом гиперболы и
углом между ее асимптотами. Как величина эксцентриситета влияет на
форму гиперболы?
28. Составить уравнение гиперболы, зная, что расстояние между ее
директрисами равно 4, а расстояние между фокусами 16.
29. Найти эксцентриситет гиперболы, если известно, что
расстояние между ее директрисами в четыре раза меньше расстояния
между фокусами.
30. Доказать, что отношение расстояния любой точки гиперболы
до фокуса к расстоянию ее до соответствующей директрисы есть
величина постоянная, равная эксцентриситету.
Ответы
2)|^-^-=1. 24. 1)а = 5, 6=12, с = 13, Л (-13,0), F2(13,0),
13 _ „ х2 у1 а
Е =—. 25. Г =2, А =8. 26.-— = 1. 27. E COS—= 1.
5 1’2 9 6 2
28.-----= 1. 29. Е = 2. 30. Указание. См. 1.4.2, пример 9.
16 48
1.4.4. Парабола
Параболой называется геометрическое место точек, одинаково
удаленных от данной точки (фокуса) и данной прямой (директрисы).
Уравнение параболы, симметричной относительно оси Ох и
проходящей через начало координат (рис. 1.11), имеет вид
у2 =2рх. (1.45)
67
Уравнение директрисы
Парабола (1.45) имеет фокус
FlpOL Фокальный радиус точки
М (х, у) параболы выражается формулой
г = х+Л (1.47)
Парабола симметричная относительно оси Оу и проходящая через
начало координат (рис. 1.12), имеет уравнение
х2 = 2ру. (1.48)
Уравнение директрисы этой параболы:
у = -^- (1.49)
(
Фокусом параболы (1.48) является точка FI 0, у I.
Фокальный радиус точки М (х, у) параболы (1.48)
г = (1-50)
Пример 14. Найти координаты фокуса и уравнение директрисы
параболы у2 = 12х. Определить расстояние точки М (3, 6) до фокуса.
68
Решение. Сравнивая уравнение у2 = 12х с уравнением (1.45),
получаем 2р = 12, откуда р = 6, = 3. Следовательно, уравнение
директрисы х = “3, фокус находится в точке F (3, 0). Точка М (3, 6)
лежит на параболе у2 = 12х, так как ее координаты удовлетворяют
уравнению параболы. Расстояние точки М (3,6) до фокуса
определяется по формуле (1.47). Подставляя в эту формулу значения
х = 3 и р = 6, получаем г = 3+3 = 6.
Пример 15. Найти координаты фокуса и уравнение директрисы
параболы х2 = 8у. Определить расстояние точки N (4,2) до фокуса.
Решение. Из уравнения (1.48) и х2=8у заключаем, что 2р = 8,
р
р = 4, 2 = 2- Таким образом, уравнение директрисы запишется в виде
У = -2, фокусом является точка F (0, 2). Фокальный радиус точки
2V(4,2) равен г = 2 + 2 = 4.
Пример 16. Составить уравнение геометрического места точек,
одинаково удаленных от точки F (0, 3) и прямой у = -5. Определить
точки пересечения этой кривой с осями координат.
Решение. Искомым геометрическим местом будет парабола.
Напишем ее уравнение. Пусть Л/ (х, у) - произвольная точка
геометрического места. По условию MF=MN, где N- основание
перпендикуляра, опущенного из точки М на прямую у = -5. Так как
MF = yjx2+(y-3)2 и MN = 7 (д'-(-5))2,
ТО
7*2 + (у-3)2 =7 (у+5)2,
откуда
х2 + у2 - бу+ 9 = у2 + 10у + 25.
Приводя подобные члены, получим уравнение параболы
х2 = 16у + 16.
Для определения точек пересечения с осью Ох необходимо решить
69
систему уравнений:
х2 = 16у + 16;
у = 0 (уравнение оси Ох).
Имеем X! = -4, х2 = 4. Таким образом, 0), Л/2(4, 0) - две точки
пересечения с осью Ох. Полагая в уравнении параболы х = 0
(уравнение оси Оу), получим у = ~1. Парабола пересекает ось Оу в
точке Л/3(0,-1). 1
Пример 17. Написать уравнение параболы, симметричной
относительно оси Оу и проходящей через точки пересечения прямой
х + у = 0 и окружности х2 + у2 + 8 у = 0.
Решение. Найдем точки пересечения прямой и окружности, для
чего решим систему уравнений
х + у = 0; 1
х2+>>2+ 8>> = 0. J
Определяя х из первого уравнения и подставляя его во второе, получим
(-у)2+/ + 8у = 0
или
2/ + 8у = 0, 2у(у+4) = 0,
откуда
У) =0, у2 =-4.
Так как х = -у, то Xj = 0, х2 = 4. Следовательно, О (0, 0),
М (4, -4) - искомые точки пересечения.
Уравнение параболы, симметричной относительно оси Оу и
проходящей через начало координат, имеет вид
х2 = 2ру.
Определим параметр р из условия, что парабола проходит через
точку М (4, -4). Подставляя координаты этой точки в уравнение
параболы, получим
42 = 2р(-4),
70
откуда
2р = -4.
Следовательно, искомое уравнение параболы имеет вид
х2 = -4у.
Пример 18. Дана парабола у2 = 6х. Через точку N (4,1) провести
такую хорду, которая делилась бы в этой точке пополам.
Решение. Уравнение искомой хорды запишем в виде
у-1 = Л(х-4) или у = Л(х-4)+1.
Для нахождения точек пересечения хорды с параболой необходимо
решить систему
= 6х;
у = *(х-4)+1.
Подставляя второе уравнение в первое, получим
Л2(х2-8х+16)+2Л (х-4)+1 = 6х
ИЛИ
к2х2 - 2 (4к2 - к+3) х +1 6к2 - »к+1 = 0.
Это уравнение можно переписать так:
2_2(4А2-*+3) х 16А:2-8Л+1 _Q
Х к2 Х+ к2 ~ '
По теореме Виета для корней х, и х2 этого уравнения находим
Так как N (4,1) - середина хорды, то
fi±^ = 4
2
71
Следовательно,
4jt2-*+3 ,
—Г~=4'
откуда
£ = 3.
Таким образом, получаем следующее уравнение искомой хорды
у-1 = 3(х-4)
или
Зх-у-11 = 0.
Пример 19. Написать уравнение касательной к параболе у1 = 4х,
проведенной через точку N (-3, 2).
Решение. Уравнение касательной ищем в виде
у-2 = Л(х + 3)
или
у = Л(х + 3)+2.
Точки пересечения последней прямой с параболой найдем из
системы:
у1 = 4х;
у = *(х + 3)+2.
Для касательной точки пересечения сливаются в одну, поэтому k
определяется из условия, что система имеет единственное решение.
Подставляя второе уравнение системы в первое, получим
Л2(х2+6х+9)+4Л (х + 3)+4 = 4х
ИЛИ
к2х2 +(6к2 +4А-4) х+9к2 +12Л+4 = 0.
Это уравнение имеет два равных корня, когда его дискриминант
равен нулю, т. е.
72
(6k2+4k- 4)2 - 4*2 (9k2 +12k + 4) = 0.
Преобразуя последнее уравнение (раскрывая скобки, производя
умножение и приводя подобные члены), получим
-48*2 -32*+ 16 = 0
ИЛИ
Зк2 + 2к -1 = 0,
откуда
= У’ ^2 ~ “1-
Таким образом, уравнения касательных будут
у-2 = -1(х + 3);
>,-2 = |(х + 3)
или
х + у + 1 = 0;
х-Зу + 9 = 0.
Задачи
31. Написать уравнение параболы, зная, что:
1) парабола симметрична относительно оси Ох, проходит через
точку N (-3, 6) и начало координат;
2) парабола симметрична относительно оси Оу, проходит через
точку N (6,3) и начало координат.
32. Составить уравнение параболы, зная, что:
1) фокус находится в точке F(5,0), директриса будет осью
ординат и ось симметрии - осью абсцисс;
2) фокус находится в точке F (0,5), директриса служит осью
абсцисс и ось симметрии - осью ординат.
33. Найти координаты фокусов и уравнение директрисы параболы,
заданной уравнением:
1) у2 =6х; 2) у2 = -6х;
73
3) х2 = 4у\ 4) х2 = -4у.
34. На параболе у2 = 16х найти точку, фокальный радиус которой
равен 5.
35. Написать уравнение параболы, зная, что вершина ее лежит в
начале координат, направление оси симметрии совпадает с
отрицательным направлением оси Оу, а параметр р равен расстоянию
от фокусов гиперболы 9х2 -4у2 -36 = 0 до асимптот.
36. Дана парабола х2 = 16у. Через точку N ^2, — j провести хорду,
делящуюся в ней пополам.
37. Найти касательные к параболе х2 = 4у, проходящие через
точку W(0,-1).
38. Дана парабола х2 = 4у. Определить длину ее хорды,
проходящей через точку (2,3) и параллельной прямой
х-2у+5 = 0.
39. Осевое сечение зеркала прожектора имеет форму параболы.
Определить положение фокуса, если диаметр зеркала 80 см, а глубина
его 40 см.
40. Найти уравнение параболы и ее директрисы, если парабола
проходит через точки пересечения прямой у-х = 0 и окружности
х2 + у2 + 8х = 0 и симметрична относительно оси Ох.
Ответы
31.1) / =-12х; 2) х2 = 12у. 32.1) у2 = 10х-25; 2) х2 = 10у-25.
34. М (1,4), АГ (1,-4). 35. х2 = - бу. 36. х-4у+8 = 0. 37. х+у+1 = 0;
х - у — 1 = 0. 38. d = 3-У5. 39.10 см от вершины. 40. у2 = —4х.
74
§ 1.5. Преобразования прямоугольных координат
Координаты (х, у) точки М в прямоугольной декартовой системе
координат Оху (старой) и ее координаты {X, Y) в другой прямо-
угольной системе OyXY (новой) связаны формулами:
Рис. 1.13
при параллельном переносе
(рис. 1.13)
х = Х + а,
y=Y+b
X = х-а, 1
или , ( (1-51)
Y = у - о, J
где (а, Ь) - координаты нового начала
Оу в старой системе координат;
при повороте осей вокруг начала
координат на угол а (рис. 1.14)
х = JVcosa- У sin а,
у = ^sinon- Kcosa.
Уравнение
у = Ах2 +Вх + С
(1.53)
выделением полного квадрата приводится к уравнению
у = А(х-а)2 + Ь, (1.54)
которое с помощью преобразования (1.51) можно записать так:
Y=AX2. (1.54')
Последнее уравнение является уравнением параболы с вершиной в
начале новой системы координат и осью симметрии, совпадающей с
осью OY.
Аналогичным образом уравнение
х = Ау2+Ву + С (1.55)
преобразуется к виду
X=AY2. (1.55')
75
и
Уравнения
(х-х0)2 , (У-Уо)2
„1 А2 “ 1
а о
(1.56)
= 1
(1.57)
с помощью формул (1.51)
приводятся соответст-
венно к уравнениям:
X2 Y2 ,
а о
X2 Y2 ,
2 12
а о
(156')
(15Г)
Следовательно, урав-
нение (1.56) определяет
эллипс, оси которого па-
раллельны координатным
осям и центр находится в
О1(х0, Уо)> а уравнение (1.57) - гиперболу (с теми же особенно-
точке
стями расположения относительно системы координат).
Уравнение равносторонней гиперболы
2 2 2
х -у =а
с помощью преобразования (1.52) при а = 45° приводится к виду
XY = c. (1.58)
Уравнение
ху + Ах + Ву + С = 0 (1.59)
с помощью формул (1.51) приводится к уравнению (1.58), где
Х = х + А, Y = y + B, с=АВ-С, (1.60)
и, следовательно, определяет гиперболу, асимптоты которой являются
координатными осями новой системы координат с началом в точке
76
Ох(-А,-В).
Пример 1. Уравнение кривой у = х2 + 4х + 5 привести к канониче-
скому виду. Построить эту кривую.
Решение. Преобразуем правую часть уравнения, выделяя полный
квадрат:
у = (х2 + 4х + 4) +1, у = (х + 2)2 + 1.
Последнее уравнение можно записать так:
>>-1 = (х + 2)2.
Полагая
>>-1=Г, х + 2 = %,
получим
Y- X2.
Это уравнение определяет параболу с вершиной в начале новой
системы координат и осью симметрии, совпадающей с осью OXY.
Найдем координаты нового начала в старой системе. Так как но-
вые координаты нового начала равны нулю, т. е.
Jf = O, У=0,
то из формул преобразования (X = х + 2, Y = у-l) получаем
х + 2 = 0, у-1 = О,
откуда х = - 2, у = 1. Таким образом определена точка О] (-2,1).
Строим старую и новую системы координат и кривую относитель-
но новой системы по ее каноническому уравнению Y = X2 (рис. 1.15).
Тем самым кривая построена и по отношению к старой системе коор-
динат.
Пример 2. Упростить уравнение кривой у = 2х2 + 8х +12, опреде-
лить ее вид и расположение на плоскости.
Решение. Преобразуем правую часть уравнения, выделяя полный
квадрат:
у = 2(х2 +4х+6) = 2[(х2 + 4х+4)+2] = 2[(х+2)2 +2],
77
у = 2 (х+2)2+4, у-4 = 2(х + 2)2.
Это уравнение можно записать в
виде Y = 2X2, где Y = y-4,
Х = х + 2. Оно определяет параболу,
симметричную относительно оси
б?! У, с вершиной в начале новой сис-
темы координат. Найдем старые ко-
ординаты вершины. Подставляя ее
новые координаты (0, 0) в формулы
преобразования: Y = у-4, Х = х + 2,
получаем 0 = у-4, 0 = х + 2, откуда
х = -2, у = 4.
Следовательно, данная кривая является параболой, вершина кото-
рой находится в точке О1(-2,4), а ее
ось симметрии параллельна оси Оу
(рис. 1.16).
Пример 3. Уравнение кривой
х = - 4у2 + бу - 3 привести к про-
стейшему виду.
Решение. Преобразуя правую
часть уравнения, получаем
7 ( 7 6 3
х = -4у + 6у-3 = -4| у У + ~
14 4
2^3 9)9 3
у -2- — у + —-+ —
4 z 16; 16 4
Последнее уравнение перепишем так:
% = -4У2,
78
3 3
где X = х+—, Y = у—. Оно определяет параболу с вершиной в точ-
4 _4
( 3 з^
ке О| —, — и осью симметрии, параллельной оси Ох (рис. 1.17).
14 4;
Рис. 1.17
Пример 4. Упростить урав-
нение кривой
(х-2)2 t (у+З)2
25 16
и определить ее параметры.
Решение. Вводя новые коор-
динаты по формулам X = х - 2,
Y = у + 3, получаем уравнение
эллипса
25 16
с полуосями а = 5, 6 = 4.
Из формул преобразования Х-х-2, Y = y+3 находим коорди-
наты центра эллипса: х = 2, у = -3 (рис. 1.18).
Пример 5. Определить вид кривой и ее расположение на плоско-
сти по уравнению
9х2 + 4у2 - 54х - 32у+109 = 0.
Решение. Выделяя полные квадраты, преобразуем левую часть
уравнения:
9(х2-6х+9)+4(/-8^+16)-81-64+109 = 0,
9(x-3)2+4(j>-4)2-36 = 0.
Разделим обе части уравнения на 36
(х-З)2 (>’-4)2
-------+-------= 1.
4 9
Вводя новые координаты по формулам % = х - 3, У = у - 4, запишем
уравнение в виде
79
Это уравнение эллипса с по-
луосями а = 2, 6 = 3 ис цен-
тром в точке Of (3,4).
Пример 6 Определить вид
и расположение на плоскости
линии
4x2-9j2-8x-36j/-68 = 0.
Решение. Преобразуем
левую часть уравнения, выде-
ляя полные квадраты:
4 (х2-2х + 1)-9 (у2 +4у+4)-4+36-68 = О,
4(x-1)2-9(j+2)2-36 = 0.
Разделим обе части уравнения на 36:
(х-1)2 (у+2)2
9 4
Вводим новые координаты по формулам Аг = х-1, У = у + 2. Уравне-
ние примет вид
9 4 “ ‘
Оно определяет гиперболу с центром в точке Ох(\,-2) и полуосями
а = 3, 6 = 2 (рис. 1.19).
Пример 7. Определить вид и расположение линии
ду-2х-у + 6 = 0.
Решение. Применяя тождество
ху + Ах + Ву+С = (х + В)(у+ Л)-ЛВ+С,
80
преобразуем левую часть
уравнения
ху-2х-у + 6 =
= (x-1Xj-2)-2+6.
Следовательно, уравне-
ние можно переписать
так:
(х-1)(у-2) = -4.
Вводя новые координаты
по формулам х -1 = X,
у-2= У, получаем
уравнение ЛТ = -4. Это уравнение является уравнением гиперболы,
асимптоты которой служат осями новой системы координат (рис. 1.20).
Центр гиперболы находится в точке Ц(1,2).
Пример 8. Определить вид
и расположение линии
Решение. Данное уравне-
ние перепишем в виде
у (х-3) = 9-х
или
ду-Зу+х-9 = 0.
Преобразуя левую часть
уравнения, получаем
лу-Зу+ х-9 = (х-3) (у + 1)-(-3 1)-9 =
= (х-3)(у + 1)-6.
Следовательно, уравнение линии можно записать так:
(х-3)(у+1) = 6
81
или
АУ = 6,
где
Jf = x-3, Y = y+\.
Уравнение определяет гиперболу с центром в точке О|(3,-1),
асимптоты ее служат осями новой системы координат.
Задачи
Уравнение линии привести к каноническому виду, построить ли-
нию:
1. у = х2-5х + 7.
3. у = -Зх2+6х-5.
5. х = 5/-10у+6.
7 (х~2)2 , (-V+4)2 t
16 25
9 (х-3)2
9 16
11. 9х2+4/-18х-8у-23 = 0.
12. 4х2+9/2+16х + 18у-11 = 0.
13. х2-4/+6х+16у-11 = 0.
14. 9х2-4у2+18х + 8у-31 = 0.
15. ху-Зу + 4х-20 = 0.
2.
4.
6.
8.
10.
у = 4x2 +8x+7.
х = -2д»2 + 8^-3.
(x+1)2 (У~3)2_1
36 25
(x + 5)2 (y+2)2
9 4
16. xy+2y-x+2 = 0.
.o 2x+9
18. y =---.
Ответы
1. Y = X2, 2- Y = 4X2, Of(-1,3). 3. Y = -3X2,
O|(l,-2). 4. X=Y2, 5- X = 5Y2, 0,(1, 1). 6. X = -2Y2,
y2 y2 v-2 у2
0.(5,2). 7.^-+— = 1, 0.(2,-4). 8.—+— = 1, O,(-l, 3).
10 23 JO 2 J
v-2 у2 Y2 y2 Y2
9.—- = 1, Q(3,2). И,——I, O.(-5,-2). 11.—+
82
y2 у 2 у2 у 2 у2
+— = 1, 0.(1,1). 12.--+— = 1, О (-2,-1). 13.------------=1,
9 1 9 4 1 4 1’
V2 у2
С\(-3,2). 14.-------= 1, Ц(-1,1). 15. АТ = 8, 0(3,-4). 16. XY =
4 9
= -4, Ох(-2,\). 17. АТ = 2, ^(1,-3). 18. АТ = -1, СЦ-4,2).
§ 1.6. Полярные координаты
Полярными координатами точки М на плоскости называются по-
лярный радиус р = ОМ и полярный угол ф = Z.POM, отсчитываемый
от полярной оси ОР к отрезку ОМ (рис. 1.21) против движения часо-
вой стрелки.
Прямоугольные декартовы и по-
лярные координаты точки М при соот-
ветствующем выборе координатных
систем (рис. 1.21) связаны формулами:
х = рсозф; j/ = psincp; (1.61)
p = ->jx2+y2-, tg<p = —. (1.62)
X
Уравнение линии на плоскости в
Рис. 1.21 полярных координатах следующее:
^(р,ф) = О. (1.63)
Пример 1. Найти уравнение окружности^ проходящей через по-
люс, центр окружности лежит на полярной оси, а радиус равен а.
Решение. Соединим отрезками прямой точку М с полюсом и с ко-
нечной точкой D диаметра, проходящего через полюс О (рис. 1.22).
Координатами точки М будут угол ф и длина р отрезка ОМ. Из
прямоугольного треугольника OMD получаем искомое уравнение
р = 2а cos ф.
Пример 2. Точка М равномерно движется по прямой ON, равно-
мерно вращающейся вокруг точки О. Траектория точки М называется
спиралью Архимеда. Составить уравнение спирали Архимеда и по-
строить ее.
83
Рис. 1.22
л Рис. 1.23
Решение. Примем точку О
(рис. 1.23) за полюс системы, начальное положение ОР прямой ON -
за полярную ось. Пусть в начальный момент движения точка М нахо-
дится в полюсе. Расстояние ОМ = р, пройденное точкой М вдоль пря-
мой ON, и полярный угол ф возрастают в силу равномерности движе-
ния пропорционально времени. Следовательно, они пропорциональны
друг другу, т. е.
Р = аф,
(А)
где а - коэффициент пропорциональности.
Уравнение (А) и является уравнением спирали Архимеда. В декар-
товой системе координат:
Jx2+y2 =aarctg—.
х
(Последнее уравнение получено из уравнения (А) с помощью формул
(1.62).)
Построим кривую по ее уравнению (А). Придавав значения ф и оп-
ределяя соответствующие значения р, составим таблицу:
ф 0 п ~6 п 4 л Т л 2 2 — л 3 3 — л 4 5 — л 6 л 5 — п 4 4 — л 3 3 — л 2 7 — л 4 2л
р 0 п — а 6 л — а 4 л — а 3 л — а 2 2 —па 3 3 —па 4 5 — па 6 па 5 —па 4 4 —па 3 3 —па 2 7 —па 4 2 ла
Построив соответствующие точки, получим искомую кривую
(см. рис. 1.23).
Пример 3. Отрезок АВ постоянной длины 2а своими концами
скользит по осям декартовых координат. Из начала координат на АВ
84
опущен перпендикуляр ОМ. Геометрическое место точек М называет-
ся четырехлепестковой розой. Написать ее уравнение, построить кри-
вую.
Решение. Из треугольника ОМА (рис. 1.24) определим
р = ОМ= CMcoscp.
Из треугольника АВО получаем
О А = A8sin ф = la sin ф,
поэтому
р = 2а sin ф cos ф.
Таким образом, искомое уравнение
имеет вид
р = азт2ф.
Кривая изображена на рис. 1.25.
Пример 4. Из точки О на окружность радиуса а проводится луч
ОК (рис. 1.26), от точки L пересечения его с окружностью отклады-
вается отрезок LM = 2а по направлению луча ОК. Линия, описывае-
мая точкой М при вращении луча, называется кардиоидой. Составить
уравнение кардиоиды.
Решение. Выберем полярную
систему координат, как показано на
рис. 1.26. Непосредственно из черте-
жа получаем
p = OL + LM.
Так как
£Л/ = 2а, OL = ОВсозф = 2ясозфу
то
р = 2а (1 + со$ф).
Полученное уравнение и является искомым. Когда ф пробегает проме-
жуток (-л, л), кардиоида описывается полностью.
Пример 5. На окружности радиуса а фиксирована точка О. Луч
Ох вращается около точки О, при этом он пересекает окружность в
некоторой точке W. На прямой ON от точки N в направлении луча
85
Ох откладывается отрезок NM = b. Когда луч Ох совершит полный
оборот, точка М опишет кривую,
называемую улиткой Паскаля. Со-
ставить уравнение этой кривой и
построить ее. Показать, что при
b = 2а получается кардиоида
(см. пример 4).
Решение. Примем точку О за
полюс, а полярную ось совместим с
диаметром О А (рис. 1.27). Непо-
средственно из чертежа находим
р = ОЛ/ = ОЛГ + МИ.
Подставляя в это равенство выраже-
ния
ON = 2acos<p, NM = fe,
получим уравнение улитки Паскаля в
полярных координатах
р = 2acos<p + fe,
Исходя из определения кривой, легко
построить ряд ее точек. Форма кри-
вой зависит от соотношения между
постоянными 2а и Ь. Если Ь<2а,
кривая имеет вид, изображенный на рис. 1.27. На рис. 1.28 изображена
кривая для случая Ь>2а.
Если Ь = 2а, то уравнение
улитки Паскаля примет вид
р = 2а (l + cos(p).
Это уравнение кардиоиды, рас-
смотренной в предыдущем приме-
ре (см. рис. 1.26).
В декартовых прямоугольных
координатах уравнение улитки
Паскаля таково:
(х2 + у2 - 2ах)2 - Ь2 (х2 + у2) = 0.
Следовательно, улитка Паскаля является алгебраической кривой чет-
86
вертого порядка.
Примечание .В области техники улитка Паскаля находит, в частно-
сти, применение в кулачковых механизмах . Она используется как линия для
вычерчивания профиля эксцентрика, если требуется, чтобы скользящий по
профилю стержень совершал гармоническое колебание. В самом деле, посту-
пательное перемещение S точки М(рис. 1.29) определится по формуле
S = р = 2а cos ОУ+Ь = 2а sin
л ] t
ОУ+— +5,
2j
где О) - угловая скорость эксцентрика.
Рис. 1.29
Одна из составных частей в механизме для
поднятия и опускания семафора очерчена по
улитке Паскаля.
В швейной машине форму кардиоиды име-
ет кулачок, под воздействием которого колеб-
лется толкатель, подающий нитку на шпульку .
Пример 6. Написать уравнение лемни-
скаты Бернулли в полярных координатах и
построить ее.
Решение. В примере 5 § 1.2 было по-
лучено уравнение лемнискаты Бернулли в
прямоугол ьных декартовых координатах:
(х2 + у2 )2 = 2а2 (х2 - у2 ).
Так как х и у входят в это уравнение только в четных степенях, то
лемниската симметрична относительно координатных осей (если точка
Л/(х, у) принадлежит лемнискате, то точки Л/^-х, у), Л/2(х,-у),
М3(-х,-у) также ей принадлежит (см. замечание к примеру 1 § 1.1)).
Поскольку
• 2 2 2
x = pcos<p, ^ = psmq>, х +у = р ,
то уравнение лемнискаты в полярных координатах примет вид
р4 = 2а2р2 (cos2 ф - sin2 ф)
или
р2 = 2а2 соэ2ф.
Из этого уравнения видно, что р = а<2 при ф = 0. Если ф увеличив а-
87
ется от ф = О до ф = —, то р уменьшается от р = до р = 0. Если
4
п п
— <ф< —
4 v 2
то р принимает мнимые значения, т. е. на лемнискате нет
точек, для которых ф меняется в указанных пределах. Следовательно,
мы можем построить часть лемнискаты, расположенную в первой чет-
(
верти для 0 < ф < — , и поэтому в силу симметрии кривой всю ли-
k 4)
НИЮ.
Построение лемнискаты по точкам можно также осуществить сле-
дующим образом. Переписывая уравнение лемнискаты в виде
р2 = с2(2соз2ф-1),
Рис. 1.30
( Я 1
мую под углом ф ф < — к
к 4)
где с2 = 2я2, заключаем, что по-
лярный радиус ее произвольной
точки является катетом прямо-
угольного треугольника, гипотену-
за которого равна cjl созф, а дру-
гой катет равен с. На оси абсцисс
от точки О отложим отрезки
ОА = ОА' = с (рис. 1.30), на оси
ординат - отрезок ОВ = с, радиу-
сом АВ = сл/2 описываем окруж-
ность с центром в начале коорди-
нат. Через точку О проводим пря-
Ох, пересекающую окружность в
точках N и 2V'. Из точки N опустим перпендикуляр ND на ось Ох,
из точки А радиусом, равным OD, засекаем на ОВ точку С. Тогда
ОС2 = АС2 - ОА2 = OD2 - ОА2 = (ON coscp)2 - ОА2 =
= (с^2 coscp)2 - с2,
откуда и следует, что катет ОС определяет длину полярного радиуса
точки лемнискаты, соответствующей углу ф. На прямой NN' из точки
О радиусом ОС засекаем точки М и Л/', принадлежащие лемниска-
88
те. Повторяя указанное построение при других значениях ср, получим
вторую пару точек и т. д.
Примечание. В технике лемниската применяется, в частности, в ка-
честве переходной кривой на закруглениях малого радиуса, как это имеет ме-
сто на железнодорожных линиях в горной местности и на трамвайных путях.
Уравнение лемнискаты встречается впервые в математической литературе
в статье Я. Бернулли опубликованной в «Acta eruditorum» в 1694 г.
Пример 7. Написать уравнение конического сечения в полярных
координатах. (Сечением любого круглого конуса плоскостью, не про-
ходящей через его вершину, определяется кривая, которая может быть
лишь эллипсом, гиперболой или параболой.)
Решение. Пусть АВС (рис. 1.31) - дуга конического сечения
(эллипса, гиперболы или параболы), В - вершина, F - фокус, DN -
соответствующая директриса. Примем точку F за полюс, прямую
BFP за полярную ось, выбрав на ней направление от фокуса F в сто-
рону, противоположную директрисе. Пусть Л/о - точка дуги ВС ко-
нического сечения, лежащая на перпендикуляре к полярной оси, про-
ходящем через полюс F. Назовем фокальным параметром р = FMQ.
Пусть М (р, ф) -
произвольная точка кривой.
Найдем зависимость между
полярными координатами р, ф
и данными числами р и е, где
е -эксцентриситет. По обще-
му свойству всех точек кониче-
ского сечения (см. определение
параболы, пример 9 и зада-
чу 30 §1.4) имеем
FM
MN
Далее,
ГЛ/ = р, MN = 7У0Л/0+рсозф.
Так как
-^- = е, FM0 = p,
N0M0
то
89
Следовательно,
8
р
MN =—+pcosq).
е
(В)
Равенство (А) с учетом (В) перепишем в виде
—= е,
р
—+pCOS(p
е
откуда
1 —£COS(p
(С)
Уравнение (С) будет определять эллипс, если е < 1, параболу при
е = 1, гиперболу, когда е > 1.
В уравнении (С) величина р для параболы имеет прежнее значе-
ние (т. е. то же, что в уравнении у2 = 2рх), так как р = ГЛ/0 = Л/0У0
есть расстояние от фокуса до директрисы. Выразим р для эллипса и
гиперболы. Подставляя координаты точки Л/0(-с, р) эллипса в урав-
нение
^+/=|
а о
получаем
+р2 -1
откуда
„2 2 д2
р а — с о
~7Т~ Р
о а а
2 Ь4 Ь2
’ =— р=—
а а
Подставляя координаты точки гиперболы Л/0(с, р) в ее уравнение,
находим
90
1
а2 Ь2
р2 с2-а2 Ь2
ИЛИ --------7
Ь2 а2
откуда
а2
b2
р = —
а
Таким образом, уравнения эллипса, гиперболы и параболы в по-
лярных координатах (при указанном выборе полюса и полярной оси)
имеют одинаковый вид:
l-ecoscp’
ь2
где р = — для эллипса и гиперболы.
а
Пример 8. Прямая х = а пересекает ось Ох в точке А и произ-
вольный луч ОВ в точке В. На луче от точки В по обе стороны отло-
жены отрезки ВМХ и ВМ2, равные АВ. Написать уравнение геомет-
рического места точек и М2 в полярных и прямоугольных декар-
товых координатах. (Кривая эта называется строфоидой.)
Решение. Из чертежа (рис. 1.32) получаем
р = ОВ+АВ.
Так как
ОВ =——, ^B = atgq>,
COS(p
то
_ а (1 ± sin ф)
СОБф
В декартовых координатах это уравнение примет вид
2 = х(х-а)2
2а-х
91
Задачи
1. В полярной системе координат
(р, <р) построить точки: А (2,0),
„Л, я А
я з, — L
V 4 J
„( Зя А
Е 2, — L
I 4 J
c 1,-L
I 2/
D (4, я),
F(-2,0),
G -3,- ,
I 4 J
( л
А (4,-л), МI -2, —
к н,--],
I 2/
2. Написать в полярных коорди-
натах уравнения линий:
!) =
2)
3)
3.
xcosa + ysina-p = 0;
у - 2х = 0;
Построить линии:
4)
x2 + у2 = 2ay.
1)
Р = Я;
2)
а
3) р=--------;
coscp
л
Ф = у
5) p = 2(l + 2coscp).
р = а (1 —- coscp);
Написать в декартовых координатах уравнения линий и постро-
ить линии:
1)
5.
1)
4)
4.
2)
3)
4)
6.
1)
7.
psin<p = b; 2) p2cos2(p = a2;
Построить линии:
р = еф (логарифмическая спираль);
a z • _
р = — (гиперболическая спираль);
Ф
p = asin3cp (трехлепестковая роза);
. зФ
р = a sin —.
3
Написать канонические уравнения кривых второго порядка:
16 _ 16 5
р =---------; 2) р =---------; 3) р =--------.
5-3coscp 3-5cos<p 1-coscp
тт
Через точку £1 а, — I проведена прямая, параллельная поляр-
ной оси. Произвольный луч ОК пересекает эту прямую в точке К. На
92
3) p = acostp.
луче по обе стороны от точки К отложены отрезки КМХ = КМ = /.
Геометрическое место точек М и Мх называется конхоидой Никомеда.
Составить уравнение конхоиды и построить ее.
8. Написать уравнение геометрического места точек, произведе-
ние расстояний которых до двух данных точек Fx(-b, 0), F2(fe, 0) есть
величина постоянная, равная а* 2 *. Построить кривую (овалы Кассини;
при Ь = а получаем лемнискату Бернулли).
Ответы
1.Указание. Отрицательные углы ф отсчитываются по часовой стрел-
ке, отрицательные значения р откладываются не на луче, наклоненном к по-
лярной оси под углом ф, а на его продолжении за полюс (т. е. на луче, обра-
зующем с полярной осью угол (р +л). 3. 1) окружность радиуса R; 2) прямая,
проходящая через начало координат под углом (р = 60° к оси Ох; 3) прямая
х = а; 4) кардиоида; 5) улитка Паскаля. 4. 1) у = Ь; 2) х2 - у2 = а2;
о 7 X2 у2 X2 у2
3) х +у = ах. 5. См. приложение. 6-1)~+~=:1; 2) —----------— = 1;
3) у2=10х. 7. р= а +1.
sin ср
См. приложение. 8. р =
в декартовых координатах:
Указания.1. Из условия
имеем MFX • MF2 = а2, откуда
J(x + b)2+y2 yltx-b)2 + у2 = а2.
2. Построение овалов Кассини мож-
но осуществить следующим образом.
Зная параметры а и Ь, находим
положение фокусов Fx и F2 и вер-
шин Ах и А2 (рис. 1.33). Проводим
р । из точки ^2 ЛУ4’ который пересечет
окружность, описанную из начала
координат радиусом, равным Ь, в точках Nx и N2. Если теперь из фокусов
и F2 описать окружности радиусами, равными A2NX и A2N2, то точка
М их пересечения будет принадлежать овалу. Действительно,
93
MFi • MF2 = A2N\ • A2N2 = const в силу известной теоремы о произведении
секущей на ее внешнюю часть. Меняя направление луча A2N2N}9 можно по-
строить любое число точек овала Кассини.
§ 1.7. Параметрические уравнения линии
Параметрическими уравнениями линии на плоскости называются
уравнения вида
* = Ф1(0; 1
-У = <р2(О, /
(1.64)
где cpiO)» ФгСО - функции переменной t.
Пример 1. Написать параметрические уравнения окружности ра-
диуса R с центром в начале координат.
Решение. Пусть М (х, у) -
произвольная точка окружности
(рис. 1.34). Тогда
х = Я cos/;
у = 7?sin t.
Полученные уравнения и будут
искомыми. Исключая параметр t
из этих уравнений (для чего нужно
возвести в квадрат оба уравнения и
почленно сложить), получим урав-
нение окружности в прямоуголь-
ных координатах:
х2 +у2 = Л2.
Пример 2. Окружность радиуса а катится по оси абсцисс. Найти
параметрические уравнения линии, описываемой при указанном дви-
жении той точки окружности, которая при начальном положении ок-
ружности находилась в начале координат. (Описываемая линия назы-
вается циклоидой.)
Решение. Пусть М (х, у) - произвольная точка циклоиды
(рис. 1.35). Тогда
х = OP = OQ-PQ = MQ- PQ = at - a sin Г = a (t - sin/),
94
Рис. 1.35
где t = Z.MCQ - угол пово-
рота окружности,
у = PM = QN = QC - NC =
= а - a cost = а (1 - cos t).
Итак, получены параметриче-
ские уравнения циклоиды:
х = a (t-sint); 1
у = а (1 - cost). J
Пример 3. Прямоугольник, две стороны которого совпадают с
осями координат, изменяется так, что его диагональ сохраняет посто-
янную величину а. Линия, описываемая основанием перпендикуляра,
опущенного из вершины прямоугольника, противоположной началу
координат, на его диагональ, называется астроидой. Найти ее уравне-
ние.
Рис. 1.36
Решение. Пусть OLAN -один
из прямоугольников, для которых
LN = а (рис. 1.36). Введем в рас-
смотрение угол t = ZALN, . тогда
AMAN-t, AMNP = t.
По определению координат
имеем:
х = OP = QM, у = МР.
Подставляя в эти равенства вы-
ражения для QM и Л/Р, получае-
мые из треугольников LQM, LMA
и LAN, находим:
х = QM = LMcost = {LA cost) cost = LA cos21 =
= {LN cost) cos21 = a cos31;
у = MP- MNsint = {ANsint)sint = /47Vsin2t =
= {LN sin t) sin21 = a sin31.
95
Следовательно, получены параметрические уравнения астроиды
х = a cos3 /; 1
y = asin3/. J
Исключая параметр t (для чего нужно извлечь сначала корень ку-
бический из обеих частей уравнения, а потом возвести их в квадрат),
получим уравнение астроиды в прямоугольных декартовых координа-
тах
2 2 2
х3 + у3 = а3.
Пример 4. По окружности х2 + у2 = а2 перемещается прямая, на-
чальное положение которой х = а. Определить траекторию точки пе-
ремещающейся прямой, принимая за начальное ее положение точку
А (а, 0). (Кривая называется разверткой окружности.)
Рис. 1.37
Решение. Возьмем произволь-
ную точку N данной окружности
(рис. 1.37). Введем угол t = Z-AON.
В силу условия задачи длина дуги
NA равна длине отрезка Ж/, где
М- точка искомой траектории, на-
чальное положение которой совпа-
дало с точкой А. Координаты точки
М через угол t и радиус а выра-
зятся следующим образом:
х = OP = ОК + КР = OK + QM =
= acos/ + WA/sin/ =
= acos/ + a/sin/;
y = MP = QK = NK-NQ = as\nt-
- MN cos t = a sin t - at cos t.
Таким образом, получены следующие параметрические уравнения
развертки окружности:
x = a(cos/ + /sin /);
у = a (sin/-/cos/).
Пример 5. Окружность радиуса г катится без скольжения по ок-
ружности радиуса R. Написать параметрические уравнения кривой,
96
описанной фиксированной точкой катящейся окружности. (Эта кривая
называется эпициклоидой, при г - R эпициклоида обращается в кар-
диоиду, см. пример 4 §1.6.)
УД
Рис. 1.38
Решение. Поместим на-
чало координат в центр не-
подвижной окружности.
Считаем, что в исходном
положении вычерчивающая
точка совпадает с точкой А,
в которой производящая ок-
ружность касается непод-
вижной, и ось абсцисс на-
правим через точку А
(рис. 1.38).
Угол MOXN между ра-
диусами, проведенными в
вычерчивающую точку про-
изводящей окружности и в
точку касания ее с неподвижной окружностью, обозначим через Л
Рассмотрим отношение радиусов окружностей т = г: R, которое на-
зывается их модулем. Так как качение производящей окружности
предполагается совершающемся без скольжения, то AN = MN или
R /.NOA = rt, откуда
ZNОA ~ — t = mt.
R
Из чертежа получаем:
х = OP = OD+DP = OD + EM = (R +г) cos mt +
+rsmZ-MOxE\
у = MP= OXD-(\Е = (/?+r) sin/и/ -г cos АМС\Е.
Так как
sinZAW1E = sin (r-ZO(91D) = sin
( л
/ —----
\2
4 Зак. 1816
97
= -cos(Z + mZ);
cosZA/^£ = sin (Z + mZ)
и, кроме того, г = mR, то параметрические уравнения эпициклоиды
запишутся так:
х = (/?+ mR) cos mt - mR cos (t + mt); 1
у = (R+mR) sin mt - mRsin (t + mt). j
Задачи
1. Построить кривую
x = t2, y = 3t.
2. Даны параметрические уравнения линии:
х = acosz, у = 6 sinZ.
Написать уравнение линии в прямоугольных координатах.
3. Линия задана пара-
метрическими урав-
нениями:
Составить ее уравнение в
прямоугольных декартовых
координатах.
4. Декартовым листом
называется кривая, парамет-
рические уравнения которой
3at 3at2
х=—г; у-—г-
1+г3 1 + /3
Написать уравнение кривой в прямоугольных координатах.
5. Окружность радиуса г катится без скольжения по окружности
радиуса R>r внутри ее. Составить параметрические уравнения кри-
вой (гипоциклоиды), описанной точкой М катящейся окружности (при
2 2 2
7? = 4г гипоциклоида обращается в астроиду х3 + у3 = а3,
см. пример 3).
98
6. Дана окружность диаметра ОС = а и касательная в точке С.
Произвольный луч ОЕ пересекает в точках D и Е окружность и ка-
сательную. Через эти точки проведены прямые, параллельные соответ-
ственно оси Ох и оси Оу до пересечения в точке М. Геометрическое
место точек М называется локоном Аньези. Составить параметрические
уравнения кривой и построить ее.
Ответы
2 2 2 2
1. у2=9х. 2. ^г+^г = \. 3. = 4. х3+у3-Заху = 0.
а2 Ь2 а2 Ь2
5. x = (7?-/w7?)cosZ/wZ + /w7?cos(Z-/wZ); у = (R-mR)
xsin(/-w/). 6. x = actgZ; y = asin2Z; у (x2 + a2) = а3. (См. рис. 1.39.)
99
Гпава 2.
Определители и системы линейных
алгебраических уравнений
§ 2.1. Определители второго и третьего порядка, их
свойства
Пусть задана квадратная таблица из четырех чисел а2,
th
(А)
Число а|^-а2А называется определителем второго порядка, соот-
ветствующим таблице (А). Этот определитель обозначается символом
а\
а2
. Таким образом,
а\
«2
- 01^2 “^2^-
(2.1)
Числа а}, а2, называются
элементами определителя (2.1). В опре-
ai
делителе различают первый столбец ,
а2
второй столбец , а также первую
th
строку axt\ и вторую строку а2 1%.
Пара чисел образует главную диагональ, пара а2 - вторую
диагональ.
Знаки перед произведениями, стоящими в правой части формулы
(2.1), расставляются по схеме, указанной на рис. 2.1.
Пусть дана квадратная таблица из девяти чисел ах, а2, а3, Ь\,
Ь^, сх, с2, с3
100
«1
а2
< а3
А Ъ
Ь с2
^3 с3 >
(В)
Определителем третьего порядка, соответствующим таблице (В),
называется число, находимое по формуле
а, Ьх
«2 *2
а3 Ь3
С2
= а}Ь2с3 + Ьхс2а3 + а2Ь3с} - сДя3 - b}а2с3 - afafy.
(2.2)
сз
Числа ах, а2, а3, й^, b$9 cl9 с2, с3 называются элементами
определителя. В определителе третьего порядка различают три столбца
и три строки.
Числа аъ й^, с3 образую главную диагональ, числа cl9 fy, а3 -
вторую диагональ.
Чтобы запомнить, какие произведения в правой части формулы
(2.2) брать со знаком + и какие со знаком полезно следующее пра-
вило.
Один из. трех членов определителя,
входящих в его выражение (2.2) со зна-
ком +, является произведением элемен-
тов главной диагонали, два других члена
- произведением элементов, стоящих на
параллелях к главной диагонали, и эле-
мента из противоположного угла. Члены,
входящие со знаком -, строятся таким
же образом, но относительно второй диагонали.
Схематически правило изображено на рис. 2.2.
Минором какого либо элемента называется определитель, полу-
чаемый из данного определителя вычеркиванием той строки и того
столбца, на пересечении которых стоит данный элемент.
Замечание.
В определителе второго порядка
a, bi
а2 *2
минором
элемента ах является элемент его можно считать «определителем первого
порядка». Элемент получается из определителя второго порядка вычерки-
ванием первой строки и первого столбца. Аналогично минором элемента а2
является элемент й| и т. д.
101
Алгебраическим дополнением элемента называется его минор, взя-
тый со своим или противоположным знаком, согласно следующему
правилу: если сумма номеров столбца и строки, на пересечении кото-
рых стоит элемент, есть число четное, то минор берется со своим зна-
ком, если нечетное - то с противоположным.
Определитель третьего порядка равен сумме произведений эле-
ментов какой-либо строки (столбца) на их алгебраические дополне-
ния.
Например:
О1 6,
а3 65
с2 =а.
с2 к °2
А
с3 а3
С2 t а2
+ q
с3 а3
^2
(2.3)
Формула (2.3) определяет разложение определителя по элементам
первой строки.
Свойства определителей
1. Величина определителя не изменится при замене всех его строк,
соответствующими столбцами.
2. При перестановке двух столбцов (или строк) определитель ме-
няет знак.
3. Определитель с двумя одинаковыми столбцами (или строками)
равен нулю.
4. Множитель, общий для элементов некоторого столбца (или
строки), можно выносить за знак определителя.
5. Определитель равен нулю, если все элементы некоторого
столбца (или строки) равны нулю.
6. Величина определителя не изменится, если к элементам неко-
торого столбца (строки) прибавить элементы другого столбца (строки),
предварительно умножив их на один и тот же множитель.
Указанные свойства позволяют упростить вычисление определите-
лей третьего порядка, а именно, каждый определитель можно разло-
жить по элементам любой строки (столбца), обратив в нули два эле-
мента этой строки (столбца).
2.1.1. Некоторые приложения определителей к аналитической
геометрии
1. Площадь треугольника с вершинами А(хиух)9 В(х2,У2)>
С (х3, у3) вычисляется по формуле
102
У\ 1
*2 У2 ।
«з Уз 1
(2.4)
где знак выбирается одинаковым со знаком определителя.
2. Условие, при котором три точки A/^Xj,^), Л/2(х2, у2),
Л/3(х3, Уз) лежат на одной прямой:
*1 У1 1
*2 У2 1
*3 Уз 1
(2.5)
3. Уравнение прямой, проходящей через две данные точки
Ч(*1,У|Х М2(х2,у2):
У 1
У, 1
У2 I
4. Условие, при котором три прямые
+ Q = 0, А2х + В2У + С2 = 0, А3х + В3у + С3 = 0
пересекаются в одной точке:
Л;
А-
3
02
в.
с.
(2.6)
(2.7)
Пример 1. Вычислить определитель
4 3
-5 6 '
Решение. По формуле(2.1) получим
4 3
= 4-6—(—5)3 = 39.
-5 6
103
Пример 2. Вычислить определитель
4-2 4
10 2 12
1 2 2
Решение. Прибавляя удвоенный второй столбец к первому, затем к
третьему столбцу и применяя формулу (2.3), найдем
4 -2 4 0 -2 4 0 -2
10 2 12 = 14 2 12 = 14 2
1 2 2 5 2 2 5 2
0
16
6
= 2(84 - 80) = 8.
= -(-2)
14 16
5 6
Замечание. Определитель можно было бы вычислить, разлагая его,
например, по элементам третьей строки, предварительно обратив в нули два ее
элемента.
Тот же результат можно получить непосредственно по формуле (2.3):
4 -2
10 2
1 2
4
12
2
12
2
-(-2)
10 12
1
+4
10 2
1 2
= 4
2
2
2
= 4 (4 - 24)+2 (20 -12)+4 (20 - 2) = - 80+16 + 72 = 8.
Пример 3. Вычислить определитель
3 -38 4
5 -35 2
2 -49 3
Решение. Разложим этот определитель по элементам третьего
столбца, обратив предварительно в нули два его элемента. Прибавляя к
первой строке вторую, умноженную на -2, и к третьей - вторую,
3
умноженную на —, находим
104
3 -38 4
5 -35 2
2 -49 3
-7 32
5 -35
11 7
’ 2 2
32
7
2
= -(-49 + 352) = -303.
Пример 4. Определить х из уравнения
х 1 1
1 х 1
1 1 х
= 0.
Решение. По формуле (2.2) получаем
Решим это кубическое уравнение. Разлагая на множители левую
часть уравнения, находим
х3-Зх+2 = х3-х-2х+2 = х(х2-1)-2(х-1) =
= (х-1)[х(х + 1)-2] = (х-1)(х2+х-2).
Следовательно,
(х-1)(х2+х-2) = 0,
откуда Х| =1, х2 = 1, х, = -2.
Пример 5. Вычислить площадь треугольника с вершинами
Л (1,-1), В (2,3), С (4,5).
Решение. Вычислим определитель, входящий в формулу (2.4),
пользуясь формулой (2.2):
1 -1 1
Д= 2 3 1 =3-4+10-12+2-5 = -6.
4 5 1
105
Так как Д < О, то в формуле (2.4) нужно взять знак минус:
S = -1Д = (-1 j (-6) = 3 (кв. ед.).
Пример 6. Упростить выражение
О 0 1
cosa sin£ 1
sin a cosp 1
Решение. Разлагая определитель по элементам первой строки, по-
лучаем
О 1
О
cosa
sin a
sin£
cos£
= 1-
cosa
sin a
sin£
cos£
= cosa cos £-sin a sin £ =
1
1
= cos (a + p).
Задачи
Вычислить определители:
-3
-5
4
8
b
a
cosa
sin a
-sin a
cosa
Вычислить определители, разложив их по элементам первой стро-
ки:
2 3 -5 1 -ь -1
7. -1 4 1 8. b 1 ь
6 -2 -7 1 ь 1
Вычислить определители:
1 -3 1 -2 0 2
9. 0 1 3 10. 2 -1 -2
0 -1 3 1 -2 1
106
6 4 2
11. 7 5 1
3 2 4
1
cos а
cosа cosp
1 cos (а + Р)
cosP cos(a + p) 1
Решить уравнения:
18. Лежат ли точки Л (1,1), В (-2, 7), С (0,3) на одной прямой?
19. Даны точки Л (1,-1), В (2,4). На прямой у = 2х-4 выбрать
точку С так, чтобы площадь треугольника АВС была равна 4 квад-
ратным единицам.
20. Написать уравнение прямой, проходящей через точки
^(0,-2), А/2(“5,3). Проходит ли прямая МХМ2 через точку пере-
сечения прямых: х-3<у-2 = 0, 2х + 5>> + 7 = 0.
Ответы
1.3 . 2.-4. 3.2. 4. а2+Ь2. 5. 1. 6.0. 7.55. 8. 2(1-Z>2). 9.6. 10.4. 11.6.
12.-6. 13.27. 14.0. 15. (x-y)(_y-z)(z-x). 16. х(=-1, х2 = 2.
ПО 8^
17. X] = 1, х2=2. 18. Да. 19. М^-2,8), Л/21 —I, 20. х + у + 2 = 0.
Проходит.
§ 2.2. Решение систем линейных алгебраических
уравнений с помощью определителей
Система двух линейных алгебраических уравнений с двумя неиз-
вестными
aix+biy = ci;
a2x + b2y = c2
(2.8)
107
имеет единственное решение
q bf
с2____^2.
"1 th
аг Ьг
а2
"1
а2
С1
А
*2
(2.9)
при условии, что определитель системы отличен от нуля, т. е.
Система трех линейных уравнений с тремя неизвестными
axx + t\y + cxz = dj;
+ + c2z = d2; (2.11)
a3x + b^y + c3z = d3
имеет единственное решение
где Ах = 4 </2 d> А Ь2 Ьз <2 % Дх х = —у = ^_ Д ’ ; Дг = «1 а2 «3 А bi Ьз dy d2 ^3 (2.12) ,(2.13)
Д а\ °2 °3 д di rf2 rf3 ci Ъ сз
при условии, что определится А = ь системы О] bl Cl t?2 а3 by с3 (2.14)
Однородная система двух уравнений с тремя неизвестными
axx + t\y + cxz = 0;
a2x + ^2>' + c2z = 0
(2.15)
имеет решение
108
q О]
c2 a2
q Z>|
a2 Z>2
(2.16)
z — k
где к - произвольный множитель, если хотя бы один из определителей
отличен от нуля. В случае, когда все определители равны нулю система
(2.15) сводится к одному уравнению.
Однородная система трех уравнений с тремя неизвестными
a^x + b^y + c^z = 0;
а2х + + C2Z ~ Ъ
а3х + b^y + c3z = 0
(2.17)
имеет решение, отличное от нулевого (х = 0, у = 0, z = 0 - нулевое
решение системы), когда определитель системы равен нулю, т. е.
а\ с\
& — Д2 Ь} С2 — 0.
Ь$ с3
(2.18)
Пример 1. Решить систему уравнений
4х + у = 5;
Зх-2>> = 12.
Решение. В данном случае: ^=4, ^=1, q=5, а2=3, /^=-2,
с2 = 12.
4 1
3 -2
ваться формулами (2.9). Получаем
5 1
12 -2
Х~ 4 1
3 -2
Определитель системы
Ф 0, поэтому мы можем пользо-
-10-12 -22 2
-8-3 “ -11 “ ’
109
У =
4 5
3 12
4 1
3 -2
”=-3.
-11
Пример 2. Решить систему уравнений
2х 4- 4у + z = 4;
3x4-6^4-22 = 4;
4х - у - 3z = 1.
Решение. Вычислим определители, входящие в формулы (2.12):
О
= 9(4-3) = 9;
= 1 (-44+26) =-18;
-4
13
= 1 (-13+40) = 27;
4
6
-1
4
4
Так как определитель системы А Ф 0,
значения в формулы (2.12), находим
= 9(8-12) = -36.
то подставляя полученные
Ах -18 „ А 27 , Дг -36
— =----= _2; у = ^- = — = 3; z = —=------= -4.
А 9 А 9 А 9
ПО
Пример 3. Решить систему
2х - Зу + 4z = 0;
Зх + у - 2z = 0.
Решение. Составим таблицу из коэффициентов данной системы:
2
3
-3
1
4
-2
Вычеркивая поочередно столбцы, получим определители:
(во втором определителе меняем порядок столбцов).
По формулам (2.16) находим решение системы:
х = 2*, у = 16*, z = 11*,
где к - произвольный множитель.
Пример 4. Решить систему
x + 2y-3z = 0;
2x + 4y-6z = 0.
Решение. Составляя таблицу из коэффициентов
f 1 2 -3"
<2 4 -6,
и вычеркивая поочередно столбцы, получаем:
2
4
2
4
= 0.
Данная система приводится к одному уравнению
х + 2у - 3z = 0,
в чем можно убедится непосредственно, сокращая на 2 второе уравне-
ние.
В1
Решение системы будет
где х и z могут принимать произвольные значения.
Пример 5. Решить систему
x-3y + 2z = 0;
x-y + z = 0; ►
2x + y-3z = 0.
Решение. Определитель системы
1 -3 2
1 -1 1
2 1 -3
= -7*0.
Следовательно, данная система имеет единственное нулевое реше-
ние: х = 0, у = 0, z = 0.
Пример 6. Решить систему
x + y + z = 0;
3x-y + 2z = 0;
х - Зу = О.
Решение. Определитель системы
Минор этого определителя
отличен от нуля. Следовательно, третье уравнение данной системы
есть следствие двух первых. Решая эти уравнения по формулам (2.16),
получим
112
где к - произвольный множитель.
Пример 7. Решить систему
x + y-z = 0;
4x + 4y-4z = 0;
5х + 5у - 5z = 0.
Решение. Определитель системы
= 0.
Все миноры определителя А тоже равны нулю. Система приво-
дится к одному уравнению, что непосредственно видно, если сократить
второе уравнение на 4 и третье на 5. Чтобы найти решение системы,
достаточно разрешить лишь первое уравнение, например, относитель-
но у. Находим
у = z —х,
где х и z могут принимать любые значения.
Пример 8. Решить систему
х + у - z = 3;
x + y + z = 1;
х + у = 1.
Решение. Определитель системы
но среди его миноров есть отличный от нуля, например,
Среди определителей третьего порядка таблицы
113
Ч 1 -1 3'
11 11
J 1 0 1,
имеется определитель, отличный от нуля, например,
1 -1 3
1 1 1 = -2.
1 0 1
Данная система несовместна (не имеет решения), что видно если
сложить первые два уравнения и сравнить результат с третьим уравне-
нием.
Пример 9. Решить систему
х + у - z = 3;
x + y + z = 1;
х + у = 2.
Решение. Определитель системы Д = 0, но среди его миноров есть
отличные от нуля. Определители третьего порядка таблицы
Ч 1 -1 з"
11 11
4’02,
все равны нулю. Данная система приводится к двум уравнениям, что
становится ясным, если сложить первые два уравнения. Решая совме-
стно, например второе и третье уравнения, получим:
х + у = 2, z = -l или х = 2-у, z = -l,
где j; может принимать любые значения.
Пример 10. Решить систему
x + 2y + 3z = 1;
2x + 4>> + 6z = 3; >
3x + 6y + 9z = 2.
114
Решение. Определитель системы
Все его миноры также равны нулю. Среди определителей второго
порядка таблицы
' 1 2 3 Г
2 4 6 3
,3692,
есть отличные от нуля, например,
Данная система несовместна, в чем убеждаемся непосредственно,
умножив первое уравнение на 2 или на 3.
Пример 11. Решить систему
x + 2y + 3z = 1;
, 2x + 4y + 6z = 2; >
3x + 6y + 9z = 3.
Решение. Определитель системы тот же, что и в предыдущем при-
мере, значит А = 0. Все его миноры тоже равны нулю. Определители
второго порядка таблицы
f 1 2 3 Г
2 4 6 2
,3693,
равны нулю. Данная система приводится к одному уравнению, в чем
непосредственно убеждаемся, если сократим второе уравнение на 2, а
третье (на 3. Остается решить первое уравнение, чтобы получить реше-
ние данной системы. Таким образом, находим
х = l-2y-3z,
где у и z произвольны.
115
Задачи
Решить с помощью определителей системы уравнений:
5х + 3у = 21; Г 6х4-5у = 1;
2х + 7 у = 20. ’ [ 8х + Зу = 5.
9х + 2у = 8;
4х + у = 3.
2х 4- Зу = 9;
5х 4- 2у = 6.
х 4- 2у = 4;
Зх4-у = 12.
(14- а) х - ay = 14- а\
ах + (\-а)у = а-\.
Решить системы уравнений:
7. • x + 2y 4- 3z = 6; 4x + y + 4z = 9; 3x + 5y + 2z = 10.
9. 2x 4- у + 3z = 3; 4x + 2y + 5z = 5; 3x + 4y + 7z = 2.
11. 3x 4- 4y 4- 2z - 8 = 0; x + 5y + 2z-5 = 0; 2x + 3y + 4z-3 = 0.
13. x + 3y + 2z-4 = 0; 2x4-6y4-z = 2; 4x + 8y-z-2 = 0.
j x4-2y-3z = 0;
* 1 3x-4y4-z = 0.
х 4- у 4- z = 0;
8. <! 2x-3y4-4z = 0;
4х-1 ly 4-10z = 0.
x + y + z = 0;
10. s 2x-3y + 4z = 0;
5x-7y + 8z = 0.
x4-y4-z = 2;
2x-3y + 4z = 3;
4x-l ly 4-10z = 5.
(x —y4-z —1 = 0;
x + y-z-2 = 0;
5x + y-z-7 = 0.
( 2x + 3y-z = 0;
* [ x-2y + 2z = 0.
Ответы
1. x = 3, у = 2. 2. x = 1,
y = -l. 3. x = 2, y = -5. 4. x = 0, у = 3.
5. x = 4, у = 0. 6. x = 1 - а, у = - (14- a). 7. x = 1, у = 1, z = 1.
8. x = 7£, у ——2k, z = -5k. 9. x = 1, y = -2, z = 1. 10. x = у = z = 0.
11. x = 2, y = l, z = -l. 12. x = --(9-7z), y = j(l + 2z). 13. x = 3,
y = -l, z = 2. 14. Система несовместна. 15. x = -10A, y = — 10Л,
z =-10k. 16. x = 4k, у--5k, z--7k.
116
Гпаеа 3.
Векторная алгебра
§ 3.1. Основные понятия
Различают величины векторные и скалярные. Скалярная величина
может быть охарактеризована одним числом, выражающим отношение
этой величины к соответствующей единице измерения. Примеры ска-
лярных величин: длина, площадь, объем, время, угол, температура,
плотность, сопротивление проводника, электроемкость, работа и др.
Векторная величина характеризуется числом и направлением.
Примеры векторных величин: сила, скорость, ускорение, напряжен-
ность электрического или магнитного поля и др. Всякая векторная ве-
личина может быть изображена с помощью прямолинейного отрезка, у
Вектором называется на-
правленный отрезок. Вектор
вполне характеризуется сле-
дующими элементами:
1) начальной точкой («точкой
приложения»);
2) направлением', 3) длиной
(«модулем вектора»). Если
начало вектора есть М, а его
конец N(рис. 3.1), вектор обо-
значается символами MN
или MN. Иногда вектор обо-
значают одной буквой жирного шрифта а, b и т. д. или такой же бук-
вой светлого шрифта с черточкой наверху а, Ь и т. д.
Длина вектора MN обозначается через | MN |, вектора а - через
|а| или просто а.
Единичным вектором называется вектор, длина которого равна
единице.
Нулевым вектором называется вектор, начало и конец которого
совпадают. Нуль-вектор обозначается символом 0.
Векторы, лежащие на параллельных прямых (или на одной и той
же прямой), называются коллинеарными. Коллинеарные векторы могут
117
иметь одно и то же направление (равнонаправленные векторы;
рис. 3.1, а, векторы а.Ь) или противоположные направления
(рис. 3.1, а, векторы b и d, с и 6, а и сГ).
Два вектора называются равными, если они коллинеарны, направ-
лены в одну и ту же сторону и имеют равные дйины (другими словами
равными векторами называются равнонаправленные векторы с одина-
ковыми длинами; а = Ь).
Векторы, противоположно направленные и имеющие равные дли-
ны, называются противоположными (векторы b и d, векторы MN и
NM). Вектор, противоположный вектору а, обозначается через -а.
Суммой двух векторов а и b назы-
вается третий вектор с, определяемый
следующим построением: 1)от произ-
вольной точки О пространства отклады-
вается вектор ОА = а\ 2) от его конца А
откладывается вектор АВ-Ь\ 3) начало
первого вектора соединяется с концом
второго; полученный вектор ОВ есть
вектор-сумма с (см. рис. 3.1. б).
Сумма двух векторов обладает
свойством переместительности
(рис. 3.2).
a+b=b+d (3.1)
и свойством сочетательности (рис. 3.3)
{а + Ь) + с = а + (£ + с). (3.2)
Сумма противоположных векторов рав-
Рис. 3.3 на нуль-вектору.
Суммой п векторов
d},d2,a3,... ,ап называется вектор, начало которого совпадает с нача-
лом вектора а конец-с концом вектора ап, при условии, что точ-
ка приложения каждого последующего вектора совпадает с концом
предыдущего. На рис. 3.4 изображена сумма 5 векторов
а}, а2, а3, а4, а5. Сумма п векторов обладает свойством сочетательно-
сти (слагаемые можно группировать как угодно).
118
Рис. 3.4
Разностью двух векторов а и
Ь называется такой вектор d, ко-
торый при сложении с вектором Ь
дает вектор а:
b+d = а, a-b -d.
Построение вектора d можно
осуществить следующим образом.
От произвольной точки пространст-
ва О откладывается вектор ОА = а
и вектор ОВ = Ь, тогда вектор
d = ВА, т. е. начало его совпадает с концом вычитаемого вектора 6, а
конец его-с концом уменьшаемого вектора а (рис. 3.5). Другой спо-
соб: вектор d равен сумме двух векторов а и -Ь (рис. 3.5).
Произведением вектора а на
число X называется новый вектор
Ха, длина которого равна | X11 а |,
а направление совпадает с направ-
лением вектора а при Х>0 и
противоположно ему при X < 0.
На рис. 3.6 изображены векторы
а, За, -2а.
Свойства произведения векто-
ра на число:
1) Х(ца) = (Хц)а;
2) (-Х) а = X (-а) = - (Ха);
3) (Х + ц)а = Ха + ца;
4) X(а+ £) = Ха+XZ>;
5) Ха = 0, если X = 0 или а = 0.
Всякий вектор а может быть представлен в виде а = а01 а |, где
а0 - единичный вектор направления вектора а.
Если а и b - два коллинеарных вектора, то всегда можно найти
такой скаляр X, что
119
b=\a. (3.3)
а Число X называется отношением вектора b к
коллинеарному ему вектору а (а Ф 0):
33 А
— = X или b : а = X.
* я
-2а
---------- Условие, необходимое и достаточное для
коллинеарности двух векторов а и Ь, выража-
Рис. 3.6 ется равенством (3.3) или в более общем виде
равенством
оса+Р*=0. (3.4)
Векторы, параллельные одной и той же плоскости (или лежащие в
одной плоскости), называются компланарными. Если а и b не колли-
неарны, то любой вектор с, компланарный с векторами а и Ь, мож-
но единственным образом представить в виде
c=oca+pz>. (3.5)
Условие, необходимое и достаточное для компланарности трех
векторов d,b,c выражается равенством (3.5) или в более общем виде
ota+P6+yc=0, (3.6)
где числа а, Р и у одновременно в нуль не обращаются.
Если даны три некомланарных вектора а, Ь, с, то всякий четвер-
тый вектор d можно однозначно разложить по векторам d,b,c\
d = оса+р/> + ус. (3.7)
Между любыми четырьмя векторами a, b;c,d существует линей-
ная зависимость, т. е.
аа+рб + yc+bd =0, (3.8)
где а, Р, у, 5 не равны нулю одновременно.
Линейной комбинацией векторов oj, а2, а3,..., называется вы-
ражение
120
ос1а1+а2а2 + ---+а,,а„,
(3.9)
где ab a2,..., a„ - произвольные числа.
К линейной комбинации векторов можно применять все правила
преобразований, установленные в алгебре для многочленов первой
степени.
Пример 1. В параллелограмме ABCD (рис. 3.7) АВ-р, AD = q.
Выразить векторы ВС, CD, AC, СА, BD, DB через р и q.
Решение. Коллинеарные векто-
ры ВС и AD имеют равные длины
(противоположные стороны парал-
лелограмма равны и параллельны) и
одинаково направлены. В соответст-
вии с определением равенства векто-
ров получаем BC=AD. Так как
AD = q, то ВС = q.
Векторы CD и АВ противопо-
ложно направлены и имеют равные
длины. По определению противопо-
ложных векторов получаем
CD = -DC = -АВ = -р, т. е. CD = -p.
Вектор АС является суммой векторов АВ и ВС, но ВС = AD,
поэтому AC = p + q.
Далее, СА = - АС = ~(p + q) = ~p~q- (Этот результат можно по-
лучить и другим способом: СА = CD + DA, CD = - DC = - АВ = -p,
DA = - AD = -q, поэтому CA = -p - q.)
По определению разности двух векторов получаем: BD = AD-АВ
или BD -q-~p, так как AD -q, АВ- р.
Аналогичным образом находим, что DB -'p-q.
Ответ: BC = q, CD--p, AC = p + q, CA = -p-q, BD-
= q-p, DB = p-q.
121
Замечание. Ели даны два неколлинеарных вектора р и q, то их
сумма и разность являются диагональными векторами параллелограмма, по-
строенного на векторах jp ид.
Пример 2. При каких условиях векторы ~p+q и "p-q коллинеар-
ны?
Решение. В силу замечания к примеру 1, если векторы р и q не
коллинеарны, то на них можно построить параллелограмм, диагональ-
ные векторы которого Jp + q и ~p~q во всяком случае не коллинеар-
ны. Следовательно, коллинеарность векторов p + q и р-g может
иметь (и действительно имеет) место, тогда и только тогда, когда р и
q коллинеарны.
Пример 3. Показать на чертеже, что (р+q)+(q - р) = 2q.
Решение. Как известно (см. примеры 1 и 2), р + g и (д-р) -
диагонали параллелограмма, построенного на векторах р и q. По-
строим СЕ = BD (рис. 3.7). Так как
ЯС=р + д, CE-BD-q-p, АЕ = AD+ DE -q + q = 2q
и 7е = ЛС+СЕ,
то 2q = (p + q)+(q-p).
Замечание. Алгебраически равенство проверяется раскрытием ско-
бок.
Пример 4. В параллелепипеде ABCDA'B'C'D' (рис. 3.8) АВ-р,
AD = g, АА' = F. Выразить векторы AC, D'B', AC', В'С, D'B,
DB' через р, q, г.
Решение. По определению суммы векторов получаем:
~АС = ~АВ+~ВС = ~АВ+ ~AD = р + q-
АС' = АВ + ВС + СС' = АВ + AD+ А А' = р + g + г.
По определению разности двух векторов находим:
Z/ZT = ~АГВ'-~A^D' = ~AB-~AD = p-q\
122
Так как
то
B'C=BC-BB' = AD-AA' = q-r.
D'B = D'D+DA +АВ и D'D = -АА' = -г,
DA = -q, АВ = р,
D'B= p-q-r.
то
Поскольку
DB' = DA + АВ+ВВ' и
DA = -q, АВ = р, В В' =
DB' = p-q +г.
Пример 5. Доказать, что при любом
расположении точек А, В, С
формула АВ л- ВС л-С А = 0.
Решение. Вектор ВС
вектор СА - от конца вектора ВС,
справедлива
отложен от
конца вектора АВ,
вектора С А совпадает с началом вектора А В. Следовательно, сумма
АВ + ВС + СА является вектором, начало и конец которого совпадают.
Такой вектор по определению есть нуль-вектор, т. е. АВ + ВС + СА = 0.
Пример 6. На сторонах треугольника
АВС построены произвольные параллело-
граммы ABML, BCPN, ACQR
Доказать, что из отрезков RL,
можно составить треугольник
при этом направление каждого отрезка).
Решение. Из чертежа (рис. 3.9) непо-
средственно получаем
тогда конец
(рис. 3.9).
W, PQ
(сохраняя
LM + MN + NP + PQ+QR+ RL = 0;
с другой стороны,
123
LM+NP + QR-AB + BC + CA = O (см. пример 5).
Следовательно,
Л47У + Р£?+яЕ = О.
Последнее равенство означает, что ломаная, построенная на трех дан-
ных векторах Л/TV, PQ и RL, должна замкнуться, а это и требовалось
доказать.
g D Пример?. Дан треугольник
4^ /7 АВС, в котором АВ = р, ВС = q
о/ \ у'' / (рис. 3.10). Выразить векторы А К,
кл \/' / BL, СМ, где K,L,M -
/ \ / основания медиан, через векторы
Az / Решение. Пользуясь опреде-
-----LA--лением суммы двух векторов, по-
А Г С лучаем
Рис. 3.10 ~лк = 7в+вк.
Так как
~вк=-вс
2
(это следует из определения произведения вектора на число и опреде-
ления медианы) АВ = р, ВС = q, то
— _ 1 _
AK = p+-q.
Далее,
вЕ = вс+сг, cl = --~ac
2
(векторы CL и АС противоположно направлены), AC=p + q, поэто-
му
BL = g-y(p+g) = y(g-p).
124
Аналогично находим, что
CM = ^p-(p.+ q) = -q-^p.
Замечание. Эти выражения для АК, BL и СМ можно получить и
по-другому. Например, достроив треугольник АВС до параллелограмма
ABDC, получим
~АК = | ~AD = | (АВ+ BD) = у (АВ + АС) =
1 г_ _ч. _ 1 _
= ^[р+(р+ч)]=р+-Я-
Пример 8. Показать, что |а + 6 |<|а|+|б |. В каком случае в этом
отношении имеет место знак равенства?
Решение. Если векторы а и b не коллинеарны, то, построив их
сумму, получим треугольник, длины сторон которого соответственно
равны | а |, | b | и | а + b |. Неравенство
|а+6 | <|а| + |й |
вытекает из того, что в треугольнике одна сторона меньше суммы двух
других. Равенство
|а + 6 | = |а | + |б |
имеет место тогда и только тогда, когда векторы а и b одинаково
направлены.
Пример 9. В равностороннем треугольнике АВС (рис. 3.11) М
есть середина стороны ВС, О - центр тяжести треугольника. Имеет
ли смысл каждое из выражений: 1) АО: AM, 2) МО: АО, 3) ОА : ОВ?
В случае утвердительного ответа найти значение соответствующего
выражения.
Решение. Так как векторы АО и AM коллинеарны, то отношение
АО: AM имеет смысл. Найдем значение этого отношения. Поскольку
центр тяжести треугольника совпадает с точкой пересечения его меди-
ан и эта точка делит каждую медиану в отношении 2:1 (считая от
125
вершины), то
| лл7| = з | ом\, |ло| = 2|ол7|,
следовательно,
_______________2 ОМ у
АО : AM = -==- = —.
3 ОМ 3
Л -1- Отношение МО : АО также имеет
Рис. 3.11 ___ ______
смысл, ибо векторы МО и АО колли-
неарны. Так как эти векторы противоположно направлены, то
Отношение ОА: ОВ смысла не имеет, ибо векторы О А и ОВ не
коллинеарны.
Пример 10. Упростить выражение
4а-26 +5с 4а-46-3с 2а-206+Зс
----------------------Р----------_
2 6 3
Решение. Приводим данное выражение к общему знаменателю,
получим
4а-26+5с 4а-46-Зс 2а-206+Зс
---------- — ————— 4--------------—
2 6 3
12a-6b + 15c—4a+4b + 3c + 4a-40b + 6c
6
12а-42Ь+24с
6
= 2а — 7Ь+ 4с.
Задачи
1. Дан прямоугольник ABCD. Коллинеарны ли векторы AD и
СВ\ ~AD-~AB и Ш-DC; Ш + ЛВ и BC+CD?
2. Даны две различные точки А и В окружности радиуса R с
126
центром в точке О. Равны ли векторы ОА и ОВ1
3. Дан ромб ABCD. Равны ли векторы AD и DC, AD и ВС, АВ
и CD? _________________________________________________
4. В правильном восьмиугольнике ABCDEFGH даны АВ-а,
ВС-Ь, CD-с, DE-d. Выразить каждый из векторов BF, BG,
FD, DG, DH, CG, СА через векторы a,b,c,d.
5. Дана точка О пересечения диагоналей параллелограмма
ABCD и векторы АВ = р, AD - q. Выразить через р и q следующие
векторы: ВС, СВ, CD, AC, BD, DB, АО, СО, ВО.
6. Проверить на рисунке следующие формулы:
z— уч z— Тх а ~~ b — а + Ь
(a + b)-(a-b) = 2b; —-—+ 6 =—-—.
7. Показать, что
|«1 +а2 + ••• +а„ | <. | а, |+|а21+••• +| а„ |.
В каком случае в этом отношении имеет место знак равенства?
8. В треугольнике АВС АВ = р, ВС = q, СА = F. Выразить че-
рез р, q, г векторы АК, BL, СМ, где K,L, М - середины сторон
треугольника.
9. Четырехугольник ABCD - параллелограмм, О - точка пересе-
чения его диагоналей, М- произвольная точка, отличная от О. Можно
ли выразить числом отношение (МА + МВ + Л/С+ MD): ЛЮ?
10. Упростить выражения:
1) 2(3а-46+5с)-3(а+26-3с)+5(2а+36-4с);
_ 2d - ЗЬ + 4с 5а-66-2с а-2Ь-6с
2) +---------------------------------.
2 3 4
Ответы
1. Векторы AD и СВ коллинеарны; векторы DA + АВ = DB и ВС+
+ CD = BD также коллинеарны 2. ОА * ОВ. 3. AD Ф DC, AD = ВС,
AB*CD. 4. BF = b + c + d-d; BG = -a + d + c; FD-a-d\
DG = d-a-b\ DH=d-d-b-c\ CG = c + d-d-b; CA = -a-b.
5. BC = q\ CB = -q; CD = -p\ AC = p + q; BD = -~p + q',
127
DB = p-q\ AO = ^(p + q) = ^p + ^q-, CO = -^(p + q\, BO =
1 , _ _x
= —(~p + ^). 7. Указание. Отрезок прямой короче ломаной, проведенной
между его концами. Знак равенства имеет место в том и только в том случае,
когда направления векторов ах , а2, • • •, ап совпадают. 8. АК = p + ^q,
BL = q + ±r, СМ = г+-^р. Другие выражения: АК=-^(р-г),
BL = ^(q - р), СМ = ± (г- q). 9. Да, отношение равно 4. 10. 1) 1 За +
- _ 5 _ 7 _
+Z> -с, 2)--а+—с.
12 6
§ 3.2. Координаты вектора. Простейшие действия над
векторами, заданными своими координатами
Осью называется прямая, на которой установлено положительное
направление. Ось Ои вполне определяется единичным вектором
ё = ОЁ (рис. 3.12).
Проекцией точки А на ось Ои называется точка Ах пересечения
этой оси с плоскостью, проходящей через данную точку А перпенди-
кулярно Ои (рис. 3.12, а).
Рис. 3.12
Проекцией вектора АВ на ось Ои называется алгебраическая ве-
личина отрезка АХВ\ (рис. 3.12, б), где АХ9ВХ - проекции точек А и В
на данную ось (т. е. длина отрезка АХВХ9 взятая со знаком +, когда на-
правление отрезка совпадает с положительным направлением оси Ои,
и со знаком - в противном случае).
128
Если q> - угол между вектором а и осью Ои, то проекция вектора
а на ось Ои равна произведению длины вектора на косинус угла ф:
пр^а = |a|cos<p. (3.10)
Свойства проекции вектора на ось Ои
I • npcCaj + а2 + • •• + а„ ) = пр^ + пр^ + • • • + пр^а»;
2 . прОи(аа) = апрОиа.
Прямоугольными координатами точки М в пространстве называ-
ются числа х, у, z выражающие алгебраические величины отрезков
OP, OQ, OR (рис. 3.13), где P,Q,R- проекции этой точки на взаимно
перпендикулярные координатные оси: ось Ох (ось абсцисс), ось Оу
(ось ординат), ось Oz (ось аппликат).
Координатами вектора а относительно прямоугольной системы
координат Oxyz называются проекции X, У, Z вектора а на оси ко-
ординат. Обозначение:
a = {%,r,Z} или a {X,Y,Z}. (3.11)
Если z, j,k -орты координатных осей Ох, Оу, Oz, то вектор
а {X, Y, Z} можно представить в виде
a = Xl+Yj + Zk. (3.12)
Векторы
ах = Xi, ау = YJ, az = Zk (3.13)
называются составляющими или компонентами вектора
a = X~i + Yj + Zk.
Координаты суммы векторов равны суммам соответствующих ко-
ординат слагаемых. Если ax{Xx,Yx,Zx}, a2-{X2,Y2,Z2},...,
ап = {Xn,Yn,Zn}, и а1+52 + ---+5Л = я, где а {X, Y,Z}, то
х = аг1+х2 + --+%л, у = у1+у2+---+1;„ z=zi+z^ + -+zw. (з.14)
Координаты разности векторов равны разностям соответствующих
координат. Если ах-а2=а и ах= {Xx,Yx,Zx}, а2 = {X2,Y2,Z2},
а {X, Y,Z}, то
5 Зак. 1816
129
x = xt-x2,
Y=Y,-Y2, (3.15)
z = z,-z2.
Координаты произ-
ведения вектора а на
число X раны произве-
дениям соответствую-
щих координат вектора
а на X. Если b = Ха и
a = {Xl,Yi,Zi},
b = {X2,Y2,Z2}, то
%2=ХГ,,
Г2=Х^ (3.16)
z2=xz,.
Равенства (3.16) выражают необходимое и достаточное условие
коллинеарности двух векторов а и Ь.
Радиус-вектором точки М называется вектор ОМ, идущий от на-
чала координат к данной точке М(см. рис. 3.13).
Если Fl=OAl и г2 = ОА2 -радиус-векторы точек А}(х}, у}, zx) и
Л2(х2, у2, z2), то вектор АХА2 = {X, У, Z} выражается формулой
(3.17)
т. е. всякий вектор равен радиус-вектору конца минус радиус-вектор
начала (рис. 3.14). Равенство (3.17) в координатах записывается так:
% = х2-х1; Y = y2-yl; Z = z2-zit (3.17')
т. е. координаты вектора равны разностям соответствующих координат
его конца и начала.
Длина вектора А}А2 = {X, Y, Z} = {х2 -xb у2 - ух, z2 - zj вычисля-
ется по формуле
d = \A^\ = Jx2 + Y2+Z2 (3.18)
или
130
d = | A{A21 = J(x2 - x, )2 + ( j2 - Ji )2 + (z2 - Zj )2 •
(3.19)
Рис. 3.14
Формулой (3.19) определяется
также расстояние между двумя точка-
ми пространства 4 (х,, , zx),
Л(х2> У2> z2)-
Направляющими косинусами век-
тора Л А = {X, Y, Z} или
44 = {x2-x1,y2-y1,z2-zl} назы-
ваются косинусы углов а, Р, у, обра-
зованных этим вектором с осями коор-
динат Ох, Оу, Oz\
cosa =
cosa = . - X1 X1 ; (3.20)
V(*2 “ *1 )2 + (У2 - УI )2 + (Z2 “ Zl )2
о Y
COS В = I
Jx2 + y2+z2
cos ft = У1 ; (3.21)
7(*2-*i)2+ (Уг “ Уi У + (Z2 “ zi )2
Z
cosy = / ,
Jx2+y2+z2
cosy = . = z2 zi . (3.22)
7(x2 - x, )2 + (y2 - у, )2 + (z2 - z1 )2
cos2 a + cos2 P + cos2 у = 1. (3.23)
Координаты всякого вектора а = {X, Y, Z} через направляющие
131
косинусы выражаются формулами:
Jf = |a|cosa; y = |a|cosp; Z = |a|cosy. (3.24)
Координаты единичного вектора е равны его направляющим ко-
синусам:
ё = {cos a, cosP, cosy}. (3.25)
В частности координаты единичных векторов /, j,k координат-
ных осей выражаются следующим образом:
1 = {1,0,0}, j = {0,1,0}, к = {0,0,1}. (3.26)
Радиус-вектор точки М (х, у, z), делящей данный отрезок МХМ2,
где Afj(xb у}9 z,), Л/2(х2, У2> 2г)> в Данном отношении к = т1:т2
выражается формулой
г = или г = J—-% (3.27)
/И| + m2 1 + Л
Если М-середина отрезка МХМ2,
то:
y = (3.29)
2 2 2
Пример 1. Дан вектор а, образующий с осью Ои угол ф! = 60°, и
вектор Ь9 образующий с той же осью угол ф2 = 120°. Найти проекцию
суммы a + ft + c, где с = 3а, на ось Ои, если известно, что |а| = 6,
|*| = 4
132
Решение. Так как проекция суммы векторов равна сумме их про-
екций, необходимо найти проекцию каждого слагаемого на ось Ои. В
соотвествии с формулой (3.10) получаем:
проиЛ = |а | с°8ф1 = 6cos60°=6~ = 3;
проиб = | b | cos<p2 = 4cosl20°=4
По свойству 2 находим проекцию вектора с = За:
проиё = прбЬ(За) = Зпр^а = 3-3 = 9.
По свойству 1 находим:
пРои(^+^+ё) = проЛ+пРоЛ+пРоиё = 3+(-2)+9 = 10.
Пример 2. Дан вектор а = {3, -4,5}. Написать разложение вектора
а по координатным ортам. Чему равны составляющие вектора а ?
Решение. В соответствии с формулами (3.11) и (3.12) разложение
вектора а по координатным ортам имеет вид
a = 3i-4j + 5i.
По формулам (3.13) находим составляющие вектора а:
ax=3i, ay=-4j, az=5k.
Пример 3. Найти координаты и составляющие вектора
а =2/+6/-7£.
Решение. Вектор а имеет следующие координаты:
% = 2, Г =6, Z = -7
и составляющие (или компоненты):
ах=2/, 5^ = 6/, az=-7k.
Пример 4. Даны векторы а = {1,-2,3}, b={2,1,-4}. Найти век-
торы: с = a+b, d-a-b, p = 3a+2b, q = 5a-4b.
133
Решение. Пользуемся формулами (3.14), (3.15). В данном случае
имеем:
X1=l, y;=-2, Zj=3, Х2=2, У2=1, Z2=-4.
По формулам (3.14) получаем координаты вектора с:
Аг = 1 + 2 = 3; У = -2+1 = -1; Z = 3+(-4) = -l; с = {3,-1,-1}.
С помощью формул (3.15) находим координаты вектора d:
Jf = l-2 = -l; У = -2-1 = -3; Z = 3-(-4) = 7; J = {-l,-3,7}.
Координаты векторов За и 26 определяем по формулам (3.16):
За = {3 1,3 (-2), 3 3} = {3, -6,9};
26 = {2 2,21,2 (-4) } = {4,2, -8}.
Снова используя формулы (3.14), получаем координаты вектора р:
jf = 3+4 = 7; У = -6+2 = -4; Z = 9+(-8) = l; р = {7,-4,1}.
Аналогичным образом находим координаты вектора q:
X = 51-4-2 = -3; У = 5(-2)-41 =-14;
Z = 5-3-4(-4) = 31; ^={-3,-14,31}.
Пример 5. Даны векторы: ^={2,4,-6}, а2 = {-1,-2,3},
а3 = {4,8, -12}, а4 = {6,0,0}, а5 = {0, -5, 0}, а6 = {0,0,2},
а7 = {0,1,3}, а8 = {2,0,—1}, а9 = {3, -4,0}. Какие из этих векторов кол-
линеарны, параллельны координатным осям, параллельны координат-
ным плоскостям?
Решение. Так как координаты векторов а} и а2 пропорциональ-
ны, т. е.
то векторы ах и а2 коллинеарны. Поскольку
а2
1 _
-“ а15 то векторы
ах и а2 противоположно направлены. Векторы ах и а3 также колли-
134
неарны, ибо
4 = 2-2, 8 = 2-4, -12 = 2(-6).
Векторы ах и а3 одного направления, так как а3 = 2ах.
Сравнивая координаты векторов а4, а5, а6 с координатами век-
торов f, J,k (формулы (3.26)), заключаем, что вектор а4 параллелен
оси Ох, вектор а5 - оси Оу, вектор а6 - оси Oz (а4 и i коллинеарны,
так как а4 = 6i; а5 и J коллинеарны, ибо a5=-5J; а6 и к также
коллинеарны, ибо а6 = 2к).
Поскольку у вектора а7 координата х = 0, т. е. проекция на ось Ох
равна нулю, то вектор а7 перпендикулярен оси Ох и, следовательно,
параллелен плоскости Oyz. Аналогичным образом заключаем, что век-
тор а8 параллелен плоскости Oxz, а вектор а9 - плоскости Оху.
Замечание 1. Если одна из координат вектора равна нулю, то вектор
перпендикулярен соответствующей координатной оси.
Замечание 2. Если вектор имеет только одну отличную от нуля коор-
динату, то он параллелен соответствующей координатной оси.
Пример 6. Даны две точки Ах(2, -5,1), Л2(3,4, -6). Найти коор-
динаты и компоненты вектора а = АХА2.
Решение. Искомые координаты находим по формулам (3.17'). В
данном случае имеем: х, =2, ух = -5, zx =1, х2 = 3, у2 =4, z2 = -6.
Подставляя эти значения в указанные формулы находим:
Х = 3-2 = 1, У = 4-(-5) = 9, Z = -6-l = -7.
Следовательно, а = {1,9,-7}; компоненты ах = i, ау = 9J, а2 = -7 к.
Пример 7. Даны проекции силы F на координатные оси: X = 4,
Y = 4, Z = -4л/2. Найти величину силы F и направление ее действия.
Решение. Вектор АВ- F по условию имеет координаты X = 4,
К = 4, Z = -4a/2. Величина силы F равна модулю вектора F, кото-
рый можно вычислить по формуле (3.18):
| F | = 7%2 + r2+Z2 = ^42+ 42+(-4>/2)2 = 8.
Направляющие косинусы вектора F определим по формулам
135
(3.20)-(3.22):
4 1 о 4 1 -4^2 -V2
cosa = —= —; cosp = — = —; cosy =----=-----.
8 2 * 8 2 ' 8 2
Следовательно, сила F = 8 действует в направлении вектора, обра-
зующего с координатными осями углы: a = 60°, Р = 60°, у = 135°.
Пример 8. Вычислить периметр треугольника АВС с вершинами
Я (8,0,7), В (10,2,8), С (10,-2, 8).
Решение. Найдем длины сторон треугольника по формуле (3.19).
Подставляя координаты соответствующих точек в эту формулу, полу-
чим:
АВ = д/(10—8)2 +(2-0)2 +(8-7)2 = 722+22+12 = 3;
ВС = J(10-10)2+(-2-2)2 +(8-8)2 = J(-4)2 = 4;
АС = 7(10 - 8)2 + (-2 - О)2 + (8 - 7)2 =
= ^22+(-2)2+ 12 =3.
Следовательно, периметр треугольника Р = 4 + 3 + 3 = 10.
Пример 9. Вектор а составляет с осью ординат и осью аппликат
углы в 60°. Найти угол между вектором а и осью абсцисс.
Решение. Воспользуемся формулой (3.23). В данном случае
COS Р = cos у = ^-.
р = у = 60°,
поэтому
Подставляя эти значения в
формулу (3.23), получим
2 1 1 1 2 1
cos a+—+— = 1 или cos a = —
4 4 2
откуда
1 1 1
cosa = ±-7=, cosai=“7=, cosa? =—т=-
V2 v2 V2
Следовательно, o^ =45°, a2 =135°.
Пример 10. Даны вершины A (2,2,2), В(6,5,0), С(0,3, 8) па-
раллелограмма ABCD. Найти вершину D.
136
Решение. Пусть О - точка пересечения диагоналей параллело-
грамма. Так как О - середина отрезка АС, то по формулам (3.29) по-
лучим:
2 + 0 , 2+3 5
х =----= 1, у —------= —,
2 2 2
2+8 с 5
----= 5, О 1,-
2 ( 2
z =
С другой стороны, О - середина BD. Координаты точек В и О
известны, координаты точки D определим по тем же формулам (3.29).
Имеем:
6+х 5 _ 5 + у 0+z
2” 2 ’
откуда х = - 4, у = 0, z = 10. Следовательно, D (-4,0,10).
Пример 11. Отрезок АВ, где А(3, -5,2), В (5,-3,1), точками С
и D разделен на три равные части. Найти координаты точек С и D.
Решение. По условию АС: СВ = 1:2, AD: DB = 2:1. Подставляя в
формулы (3.28) значения Xj=3, ^=-5, Zj=2, х2=5, у2=-3,
z2 = 1, X = —, получим координаты точки С:
3 + 2 5 И 5+2( 3) 13
—^~=v; у=—-а—=~^
Координаты точки D находятся с помощью тех же формул при 1 = 2:
3+2-5 13 -5+2 (-3) 11
1 + 2 ” 3 ’ У~ 1 + 2 “ 3
2+2-1 4
Z“ 1 + 2 “ 3‘
13 11 4Л
3 ’ 3’3/
Следовательно, С —,-----, — , D
V 3 3 3}
Задачи
1. Даны векторы а = {2, -5,3}, £={1,3,-7}. Найти векторы
с = 4а + 3£, rf = 5<7-2£.
137
2. Сила F = 6Н действует в направлении вектора, образующего с
координатными осями углы а = Р = 120°, у = 45°. Найти проекции
вектора силы и его составляющие.
3. Даны точки Л(1,-3,-2), 5(8, 0,-4), С (4,8,-3). Найти та-
кую точку D, чтобы четырехугольник ABCD был параллелограммом.
4. Вершины четырехугольника находятся в точках Я (2,0,4),
5(7,-15,16), С (-1,-1,11), D (-14,28, -6). Показать, что ABCD
есть трапеция.
5. Найти координаты концов отрезка, который точками С (7, 0,3)
и D (- 5,0,0) разделен на три равные части.
Ответы
1. с = {11,-11,-9}, d = {8,-31,29}. 2.х = -3, у = -3, 2 = 3^2;
Fx=—3i, Fy=—3j, Fz = 3i/2k. 3. D(— 3,5, — 1). ^Указание. Убе-
литься в том, что среди векторов АВ, ВС, CD, AD есть два коллинеарных.
5. Л (19, 0, 6), В (-17,0,-3).
§ 3.3. Скалярное произведение
Скалярным произведением двух векторов называется число, равное
произведению их длин на косинус угла между ними. Скалярное произ-
ведение векторов а и Ь обозначается одним из символов ab, или
а Ь, или (ab):
аЬ = |а| | & | cos (55)- (3.30)
Учитывая равенство (3.10), формулу (3.30) можно записать так:
ab = |а| прдб или ab =|б | пр^я. (3.31)
Из формулы (3.30) следует, что аЬ>$, если угол ф = (57>) -
острый; ab < 0, если угол ф - тупой; ab = 0, если угол ф - прямой или
один из векторов равен нулю.
Свойства скалярного произведения:
1. ab = Ьа (свойство переместительности);
2. а (Ь + с) = аЬ + ас (свойство распределительности);
138
3. X (ab) = (Ха ) b = a (kb) (свойство сочетательности).
Скалярное произведение оа называется скалярным квадратом
вектора а и обозначается символом а2. "Из формулы (3.30) следует,
что скалярный квадрат лектора равен квадрату его длины, т. е.
а2=|а|2. (3.32)
Если векторы а и b заданы своими координатами
a = {Xx,Yx,Zx}, b = {X2,Y2,Z2},
то их скалярное произведение выразится формулой
ab = X^ + Jf^+Z^, (3.33)
угол между ними - формулой
ab XxX2 + Y}Y2+ZxZ2
cos {ab) = = "7---7.........(3.34)
I a H b | ДММ +
а необходимое и достаточное условие их перпендикулярности примет
вид
Jf1%2 + ^r2+Z1Z2=0.
(5.35)
Пример 1. Найти скалярное произведение двух векторов а и Ь,
для которых |а| = 8, =5 в каждом их следующих случаев:
ф1 =60°, ф2=90°, ф3 = 120°, ф4 =180°, где ф = (аЬ).
Решение. По формуле(3.30) находим:
1) ab =|а| |б|со8ф1 = 8-5cos60°=20;
2) ab = |а|-|б |соэф2 = 8-5cos90°= 0;
3) ab =|а | |б | созфз = 8-5cosl20°=-20;
4) ab =|а||б |созф4 = 8-5cosl80°=-40.
Пример 2. Доказать,' что вектор р-а-
b(ba)
Ь2
перпендикулярен
вектору Ь.
139
Решение. Умножаяскалярно вектор Ь на вектор р, получим
т-т- bb(ba) -г b2(ba) -
bp = оа---=2— = (Ьа)----—— = {ba)-x—j—z— =
4 4 н
(6а)-(£а) = 0.
Так как Ьр = 0, то Ыр.
Пример 3. Какому условию должны удовлетворять векторы р и
q, чтобы вектор p + q был перпендикулярен вектору p-q*!
Решение. Если (р + <?)± (р-(/), то (р + ^)(р-^) = 0. Раскрывая
скобки в последнем равенстве (что можно сделать в силу свойства 2),
получим
(Р + ?)(Р-?) = ЯР-Р?+?Р-<7?=О-
Принимая во внимание свойство 1, формулу (3.32), находим
|р|2_И12=0’
откуда |р| = |д|.
Обратное также верно. Если |р| = |^|, то (p+q) A.(p-q). Какой
геометрический смысл имеет данное условие? (См. замечание к при-
меру 1 §3.1.)
Пример 4. Даны три вектора: a=4/-3j, b = 12/-4к,
с — 2i—j + 2k. Вычислить выражение 5а2 -fe2 +7с2.
Решение. Найдем вшнале скалярные квадраты данных векторов.
Если а = {Хь ZJ, то из формул (3.18) и (3.32) следует, что
a2 = Xj + Y?+Z}. (3.33')
Подставляя координаты данных векторов в формулу (3.33'), полу-
чим:
а2 = 42 +(-3)2 +02 = 25; Ь2 = 122 +02 +(-4)2 = 160;
с2 =22+(-1)2+22 =9.
140
Следовательно, 5а2 - b 2 + 1с 2 = 5:25 -160 + 7 • 9 = 28.
Пример 5. Даны два вектора: а = {1,-2,2}, 6= {2,-2,-1}. Найти
их скалярное произведение и угол между ними. Чему равно выражение
2а2 - 4а6 + 56 2 ?
Решение. Подставляя в формулу (3.33) координаты векторов а и
Ь, находим
ab = 1-2 + (-2)(-2)+2 (-1) = 4.
Так как
| а | = д/12+(-2)2+ 22 = 3 и | b | = ^22 +(-2)2 +(-1)2 = 3,
то по формуле (3.34) получим
Поскольку а2=|а|2=32=9и62=|б| = 32 =9, то
2а2-4а6+562 = 2-9-4-4 + 5-9 = 47.
Пример 6. Вычислить, какую работу производит сила
F = {2,-1,-4}, когда точка ее приложения, двигаясь прямолинейно,
перемещается из положения М (1, -2, 3) в положение 7V (5,-6,1).
Решение. В соответствии с определением работы и скалярного
произведения получаем
А = Fs,
где А - работа; F - вектор действующей силы; s - вектор пути.
Найдем вектор s = MN. По формулам (3.17') получаем:
5 = {5-1,-6-(-2), 1-3}, s = {4,-4,-2}.
С помощью формулы (3.33) находим
А = Fs = 2 • 4 + (-1) (- 4)+(- 2) (-4) = 20 (ед. работы).
Пример 7. Дан треугольник с вершинами А (-3, 5, 6), В (1, -5, 7),
С (8, -3, -1). Найти внутренний угол при вершине А и внешний угол
141
при вершине С.
Решение. Внутренний угол треугольника при вершине А равен
углу между векторами АВ и АС, а внешний угол при вершине С ра-
вен углу между векторами СВ и АС (сделайте чертеж).
По формулам (3.17х) находим координаты указанных векторов:
7&={4,-10,1}, ЛС = {11,-8,-7}, СД={-7,-2,8}.
С помощью формулы (3.34) находим косинусы углов:
4.Ц + (-10)(-8)+1(-7)
COS (Di = COS (АВ- АС) = - ----7—.............=
742+(-10)2+12а/ЙГ+ (“ »)2 + (- 7)2
(-7)11+(-2)(-8)+8(-7)
V(-7)2 +(-2)2 +82 д/112 +(~8)2 +(-7)2
-117 ___1_
~7п7л/234 ~ VT
Следовательно, (pi =45°, ф2=135°.
Пример 8. Показать, что четырехугольник с вершинами
А (-5,3,4), В (-1, - 7, 5), С (6, - 5, -3), D (2, 5; -4) есть квадрат.
Решение. По формулам (3.1 Т) находим векторы
Тв={4,-10,1}, 5С={7,2,-8}, DC = {4,-10,1}, AD = {7,2,-8}.
Сравнивая координаты векторов АВ и DC, ВС и AD, заключа-
ем, что
AB=DC, BC=AD.
Так как
|йв| = 742+(-10)2+12 =л/Н7, |вс| = ^72 +22 +(-8)2 =ТП7,
142
то
|1b|=|bc|=|dc| = |7d|.
Поскольку
~АВ ^С = 4-7 + (-10)2 + 1(-8) = 0,
то ~АВ ± ~ВС.
Следовательно, четырехугольник ABCD есть квадрат.
Пример 9. При каком значении X векторы а = 4i + X/ + 5к и
b = X/ + 2j - 6к взаимно перпендикулярны?
Решение. Условие перпендикулярности (3.35) в данном случае
запишется так:
4Х + 2Х + 5(-6) = 0 или 6Х-ЗО = О,
откуда X = 5.
Пример 10. Найти вектор х, коллинеарный вектору а = {1,2,-3}
и удовлетворяющий условию х а = 28.
Решение. Принимая во внимание условие коллинеарности двух
векторов (3.16), заключаем, что
х = {Х, 2Х,-ЗХ},
где X- пока неизвестный коэффициент. Так как х а = 28, то в соответ-
ствии с формулой (3.33) находим
1Х + 2-2Х + (-3)(-ЗХ) = 28 или 14Х = 28, откуда Х = 2.
Следовательно, х = {2,4,-6}.
Пример 11. Даны три вектора а = /-2/+2Л, Z>=2z+j-2A,
с = 10/ + 4j + 2k. Найти np^Z>, np^(fe+c), пр-+^с, пр^(2а-3с).
Решение. Применим формулу
прг* = |^г, (3.3 Г)
н
получающуюся из первой формулы (3.31): ab = | а | пр^б.
Подставляя условия примера в формулу (33 Г), получим
143
т_аЬ__ 12+(-2) 1 + 2 (-2) _ 4
P° l«| 712+(-2)2 + 22 3
Для нахождения остальных проекций определим векторы:
Ь+с =(2/+J-2l)+(10i+4j+2jt) = 12i+5j;
a + b =(i-2j + 2k)+(21+j-2k) = 3i-j;
2а-Зс = 2(7-2}+2k)-3(l0i+4j + 2k) = -2Si-}6j-2k.
В соответствии с формулой (33 Г) находим:
m гьжтп °(Ь+с) 112+(-2)5+20 2.
пр5(* + с) = —pq— = , =
_ (а + Ь)с
П?а+ЬС= i- гГ
310+(-1)4+0-2 26
д/з2 +(-1)2 +02 V10 ’
Ь{2а-3с) 2(-28)+1(-16)+(-2)(-2)
прг(2а - Зс) =-|Y|---=-----—г=— --------------=
* V2 + 1 +("2)
3 ‘
Замечание. Проекцию вектора b на вектор а можно найти и по
формуле
прг6 = 6а0,
где а0 = гт - единичный вектор направления а. В данном случае
н
_ Г1 2 21 — — _ 4
а0 = <—, —, — >, поэтому пр5о = о а0 = —.
144
Задачи
1. Известно, что |а| = 6, |ft| = V2. Найти скалярное произведе-
ние векторов а и b в каждом из следующих случаев:
coscp] = 45°, cos(p2 = 90°, cos(p3 = 135°, cos<p4 = 180°.
2. Доказать, что вектор р = с (ba)-a (Ьс) перпендикулярен век-
тору Ь.
3. Вычислить скалярное произведение векторов а и Ь, заданных
своими координатами, и углы между ними:
1) а = {3,-4}, Ь = {5,12};
2) а = {2,-3,2}, Ь = {4,2,-1}.
4. Даны три силы: ^ = {2,-5,1}, Г2={1,2,-6}, Г3 = {-4,-3,3},
приложенные в одной точке. Вычислить, какую работу производит
равнодействующая этих сил, когда точка ее приложения, двигаясь
прямолинейно, перемещается из точки Л/(4,2, -8) в точку
У (3,-2,-5).
5. Найти внутренние углы треугольника с вершинами А (5,2, -4),
В (9,-8,-3), С(16,-6,-11).
6. Даны два вектора: а = {1, -2,4}, ft={3,1,-5}. Найти вектор
х, зная, что он перпендикулярен оси Оу и удовлетворяет условиям:
ха = -3, хЬ = 8.
7. Даны три вектора: а = {2,-1, 3}, ft = {4,3,-5}, с = {7,-2,-6}.
Найти вектор х, удовлетворяющий условиям: ха =8, xft=0,
хс = 10.
8. Найти проекцию вектора а = {4,3, - 7} на ось вектора
ft = {1,-2,-2}.
Ответы
/- - 33 _-
1.6; 0; -6; -6V2. 3.1)aft =-33, cos<p = -—; 2)aft = 0. 4.19.
5. (р, =(р2; (р3=90°. 6. х = {1, 0,-1}. 7. х = {2,-1,1}. 8.4.
145
§ 3.4. Векторное произведение
Пространственным репером называется совокупность трех не-
компланарных векторов, приложенных в одной точке и заданных в оп-
Репер а = ОА, b = ОВ,
с = ОС называется правым
(рис. 3.16, а), если кратчай-
ший поворот вектора ОА к
вектору ОВ совершается
против часовой стрелки для
наблюдателя, глаз которого
находится в точке С.
Если же указанный пово-
рот совершается по часовой
стрелке (рис. 3.16, б), то ре-
пер называется левым.
Если даны два репера и
каждый из них правый или
каждый левый, то говорят, что эти реперы имеют одинаковую ориен-
тацию', если же один репер правый, а другой - Левый, то реперы име-
ют противоположную ориентацию.
Векторным произведением двух векторов а и Ь называется тре-
тий вектор с (рис. 3.17), удовлетворяющий условиям:
1) вектор с перпендикулярен каждому из векторов а и Ь\
2) модуль вектора с равен произведению модулей векторов а и
Ь на синус угла между ними, т. е.
| с | = | а |-| Ь | sin (afe); (3.36)
3) реперы а,Ь,с и i, j,k (i, J,k - координатные орты) имеют
одинаковую ориентацию.
Векторное произведение с векторов а и Ь обозначается одним
из символов:
с = [я/>] или c-axb. (3.37)
Из формулы (3.36) следует, что модуль векторного произведения
146
[aft] равен площади S параллелограмма,
построенного на векторах а и Ь :
|[a*]| = S. (3.38)
Векторное произведение может быть
выражено формулой
[ab] = Se, (3.39)
Рис. 3.17 гДе е - орт направления [afe].
Векторное произведение ненулевых век-
торов ровно нулю тогда и только тогда, когда векторы а и b колли-
неарны:
В частности
[а6] = 0, или а = ХЬ.
[а а] = 0.
(3.40)
(3.40')
Свойства векторного произведения:
1- [ab] = -[6a],
2. [a+b, d] = [ad]+[bd],
3. [Xa,6] = [a,Xfc] = X[afe].
Если векторы а и b заданы своими координатами
а = {Xx,Yx,Zx}, b = {X2,Y2,Z2},
то
или
- ( Y, Zx
r2 z2
j к
Уу А
z(
z2
Xi
(3-41)
(3.42)
%2 Y2 Z2
y2
147
Площадь треугольника, построенного на этих векторах, выражает-
ся формулой
а синус угла между ними - формулой
Замечание. Формула (3.42) означает, что координаты векторного
произведения можно получить следующим образом. Выписываем таблицу из
координат векторов (соблюдая порядок):
1*2 >2 Z2J'
Закрывая первый столбец этой таблицы, получаем определить, являющей-
ся первой координатой. Закрывая второй столбец и беря полученный опреде-
литель со знаком минус, найдем вторую координату. Закрывая третий столбец,
получим определитель, являющийся третьей координатой векторного произ-
ведения [afe].
Пример 1. Найти векторные произведения
М. L/Й [И], [Д], М, [7*],
где z, у, к - орты правой системы координат.
Решение. Найдем вначале [(/]. Пользуясь определением вектор-
ного произведения, заключаем:
1) вектор [zy] коллинеарен к, так как он перпендикулярен векто-
рам z и у;
2) вектор [zy] является единичным, так как площадь параллело-
грамма, построенного на векторах / и у, равна единице
(параллелограмм в данном случае представляет собой квадрат AOBD
со стороной, равной единице, см. рис. 3.18).
148
z к Из полученных утверждений
следует, что вектор [Z/] равен
либо к, либо -к. Вторую воз-
С можность нужно отбросить, так
а как репер i, j,-k является ле-
к _ _
вым. Следовательно, [//] = к.
О j Аналогичным образом нахо-
/ дим, что [Д]= f, [ki] = J.
/ D При нахождении вектора
х г [/7] утверждения 1) и 2) остают-
Рис. 3.18 ся верными. Заключение будет
другим: так как репер j,i,-к
является правым, то [ji] = ~k. Аналогично получаем [kj] = -i и
Замечание. Три последних результата можно получить из трех пер-
вых, пользуясь свойством 1.
Пример 2. Даны векторы а и Ь, для которых |а| = 6, |b | = 4.
Найти векторные произведения в каждом из следующих случаев:
<р1=0, ф2=ЗО°, ф3=90°, ф4 = 150°, где ф = (ай).
По формуле (3.36) находим модули векторных произведений:
1) |[а*]| = |а| |sin0 = 0; 2) |[afe]| = |a| |fe|sin30°=6-4-^ = 12;
3) |[a£]| = |a| |£|sin90°=6-4 = 24; 4) |[а£]| = |а| |£| sinl50°=
= 6-4—=12.
2
Решение. По формуле (3.39)получаем:
l)[aF] = 0; 2)[а6] = 12ё; 3) [а6] = 24ё; 4)[afe] = 12e, где ё-
единичный вектор направления [5Ь].
Пример 3. Найти векторное произведение векторов
a-2i-3j + 5Л, ft=4f+2j-6i.
Решение. Пользуясь формулой (3.40'), свойствами векторного
произведения и результатами примера 1, получаем
149
[ab ] = [(2i - 3 J+5к) x (4/ + 2 J - 6k)] =
= 8R / ] + 4[<7J-12[7F] -12[Ji] - О +18[Jk] + 20[£7] +10[£] - 30[Й] =
= Ф7] - 12[/Л ] - 12[J7] +18[JI] + 20[Л7] +10[kj] =
= 16 [lj]- 8 [£/]+32 [£7] = 87 + 32j +16k.
Пример 4. Упростить выражение [(За-2b) (2a + 5b)].
Решение. Пользуясь формулой (3.40') и свойствами векторного
произведения, получаем
[(3a-2F)(2a+5F)] = [3a2a] + [3a5F] + [(-2F) 2а]+[(-2Ь) 5й] =
= 6 [аа]+15 [aF]-4 [Fa]-10 [bb] = 15 [ай]+4 [JF] = 19 [aF].
Пример 5. Показать, что векторы [ай] и [2а(3а-5й)] коллине-
арны.
Решение. Упростим второе векторное произведение:
[2а (За -5b) ] = [2a3a ]+[2а (-5Ь) ] = 6 [aS]-10 [aF] =
= -10[aF].
Векторы [ай] и -10 [ай] коллинеарны.
Пример 6. Даны векторы а, b 9 с, удовлетворяющие условию
а + й+ +с = 0. Доказать, что [ай] = [йс] = [са].
Решение. Умножим векторно а на а+Ь +с = 0. Получим
[аа] + [ай] + [ас] = 0 или [ай] = -[ас] = [са].
Умножая векторно а+й+с = 0 на й, находим
[aft] + [FF] + [cF] = 0 или [JF] = -[FF] = [FF].
Из двух равенств [ай] = [са] и [ай] = [йс] следует доказываемое
равенство.
Замечание. Векторы а,Ь,с образуют треугольник. Все векторы
[ай], [йс], [са] направлены в одну сторону, а модуль каждого из них равен
удвоенной площади треугольника, построенного на векторах а,Ь,с.
150
Пример 7. Доказать, что
[аЬ]2+(аЬ)2 = а2 Ь2.
Решение. По определению векторного и скалярного произведения
имеем:
|[а&]| = |а | |b | sin (ab)9 аЬ = |а|-|&| cos(aZ>).
Возводя в квадрат обе части каждого равенства и складывая по-
членно, получим
|[й]|2+(а6)2 =|а|2|б|2.
Так как квадрат длины вектора равен его скалярному квадрату, то
полученному равенству можно придать вид
[ab]2+(ab)2=a2b2.
Пример 8. Даны векторы
а = {1,-2,2}, b = {3,0,-4}.
Найти их векторное произведение, синус угла между ними и площадь
параллелограмма, построенного на этих векторах.
Решение. Составим таблицу из координат векторов
1 -2 2 Л
3 0-4/
Закрывая поочередно первый, второй, третий столбцы и рассмат-
ривая полученные определители (причем второй-со знаком минус),
получаем
или [ай] = {8,10,6}.
[«*] =
По формуле (3.38) находим площадь параллелограмма
s = | [а6]| = л/82 + 102 + 62 = V200 = 1 oV2.
С помощью формулы (3.44) определяем синус угла между данны-
151
ми векторами
*- |м»]| 7в2+ю2+б2
* • 6 ф2+(-2)2+22 ^32+(-4)2
IO-s/2 2^2
3-5 3
Пример 9. Вычислить площадь треугольника с вершинами
Я (-1,0,2), В (1,-2,5), С (3,0,-4).
Решение. Находим сначала координаты векторов а = АВ и
Ь=~АС:
а = {2,-2,3}, Ь ={4,0,-6}.
Координаты векторного произведения [ab ] определяем по форму-
ле (3.42), предварительно выписав таблицу
2 -2 3 А
4 0 -6 j
Получаем
[й] =
-2 3
0 -6
2 3
4 -6
2 -2
4 0
или [ад] = {12,24,8}.
С помощью формулы (3.43) находим площадь треугольника
5 = у | [ аЬ ] | = у V122+242+82
2
2
•7784 =
= — = 14 (кв. ед.).
Пример 10. Три силы /*[={2,4,6}, F2 = {1,-2,3}, F3 = {1,1,-7}
приложены в точке Я(3,-4, 8). Определить величину и направляю-
щие косинусы момента равнодействующей этих сил относительно точ-
ки В (4, -2,6).
152
Решение. Если вектор F изображает силу, приложенную в точке
Л/, а вектор а = NM, то вектор [aF] представляет собой момент силы
F относительно точки N.
Найдем сначала равнодействующую трех данных ил
F = 6j+F2+F3.
Так как координаты суммы векторов равны суммам соответст-
вующих координат слагаемых, то
F = {2 + 1 + 1,4 + (-2)+1, 6 + 3 + (-7)}, F = {4,3,2}.
По координатам конца и начала определяем координаты вектора а:
а = £4 = {3-4,-4-(-2), 8-6}, а = {-1,-2,2}.
С помощью формулы (3.42) находим координаты [aF]:
[Z7F] =
-2 2
3 2
-1 2
4 2
-1 -2
4 3
[aF] = {-10,10,5}.
Следовательно, величина момента равнодействующей равна
225 = 15.
Направляющие косинусы момента силы определим по формулам
(3.20)-(3.22):
-10 2 о Ю 2 5 1
cosa =-----= —, cosp = — = —, cosy = —= —.
15 3 15 3 15 3
Задачи
1. Найти векторное произведение векторов а = i - 3j + 2k и
b = 6/ + 5j-4£.
2. Показать, что векторы [6 а] и [36 (4а+ 56)] коллинеарны.
3. Упростить выражения: 1) [(2а-36)(а+46)], 2) [(4а-
-6+2с)(а+36-2с)], 3) [(37-4J-5I)(2/ + 6J-A)].
4. Векторы a,b,c,d связаны соотношениями [a6] = [ct/],
• [at/] = [6rf]. Доказать, что векторы (a-J) и (6-с) коллинеарны.
153
5. Даны векторы я = {-4,-8, 8}, 6={4,3,2}. Найти их вектор-
ное произведение, синус угла между ними, площадь параллелограмма,
построенного на этих векторах.
6. Дан треугольник с вершинами Я (4, -14, 8), В (2, -18,12),
С (12, -8,12). Найти длину его высоты, опущенной из вершины С на
сторону АВ.
7. Даны две силы /*[={4,1,3}, F2 = {-2,2,1}, приложенные в
точке А (6, -6,-3). Определить величину и направляющие косинусы
момента равнодействующей этих сил относительно: 1) начала коорди-
нат; 2) точки В (5, - 8, - 5).
8. Доказать «тождество Лагранжа»:
а2
а\ + b\ + cf аха2 + + С1С2
+ с}с2 al+b^+cl
9. Даны векторы а = {3,1,2}, /> = {2,7,4}, с = {1,2,1}. Найти
[[ай] с] и [а [Ас]].
Ответы
1. [56] = 2/ + 16J+23A. 3. 1) 11[а6]; 2) 13[а6]-10[ас]-4[6с];
3) 34/-7j+26A. 5. [a/>]= {—40,40,20}, S = 60, 81п<р = -^
V29
6. А = 10. 7. 1) F = Ft +F2 = {2,3,4}, а = ОА = {6,-6,-3}, |[aF]| =
1 2 2 — _ —
= 45, cosa = -—, cosP = ——, cosy = у; 2)F = {2,3,4}, a = BA =
= {1,2,2}, |[af]| = V5, cosa = -^=, cos|J = 0,
8. Указание. Воспользоваться тождеством
9. [[aft], с] = {-46,29,-12}, [a [£c]]= {-7, 7, 7}.
-1
cosy = -yy.
примера 7.
§ 3.5. Смешанное произведение. Двойное векторное
произведение
Смешанным произведением трех векторов а,Ь,с называется чис-
ло, равное векторному произведению [5Ь], умноженному скалярно на
вектор с. Смешанное произведение векторов а,Ь,с обозначается
154
символом abc.
Верны следующие равенства:
abc = [аб] с = а [6 с]. (3.45)
Смешанное произведение abc равно объему параллелепипеда, по-
строенного на векторах а, 6, с, взятому со знаком плюс, когда реперы
а,Ь,с и i, j, к имеют одинаковую ориентацию, и со знаком минус -
в противном случае. Равенство
abc = 0 (3.46)
является необходимым и достаточным условием компланарности трех
векторов а, 6, с.
Свойства смешанного произведения:
1. abc =bca-cab, abc = — (bac) = - (cba) = - (acb)\
2. a (b+d)c = abc+adc, ab (с+d) = abc+abd;
3. a (X6)c =a6 (Ac) = X(a6c).
Если векторы d,b,c заданы своими координатами
a = {Xl,Yi,Zl}, b = {X2,Y2,Z2}, с = {X3,Y3, Z3},
то их смешанное произведение вычисляется по формуле
*1 у, Z,
abc = ?2 Z2
Хз Уз Z3
(3.47)
а объем параллелепипеда, построенного на этих векторах, определяет-
ся формулой
V = |а6с| = ±
хх rx Zi
^2 У2 Z2
*3 Уз Z3
(3.48)
в которой знак берется одинаковым со знаком определителя.
Двойным векторным произведением \\jdb] с] называется векторное
произведение вектора [аб] на вектор с. Умножая вектор а векторно
на [6с], получим двойное векторное произведение [а [6с]]. В общем
155
случае
[а [6с]]* [[аб] с]. (3.49)
Пример 1. Векторы а,Ь,с удовлетворяют условию
\ab ]+[6 с ]+[с а ] = 0. Доказать, что эти векторы компланарны.
Решение. Умножим скалярно вектор а на вектор
[я6]+[6с]+[с я] = 0. Получим
а.[а6]+а [6с] + а [са] = 0 или aab + abc + аса = 0. (А)
Так как векторы а,а,Ь и а, с, а компланарны, то в силу условия
(3.46) заключаем, что
aab = 0, аса = 0. (В)
Равенство (А) с учетом равенств (В) принимает вид
abc = 0.
В силу того же условия (3.46) заключаем, что векторы а, b и с
компланарны.
Замечание. Смешанное произведение трех векторов, среди которых
имеется два равных, равно нулю.
Пример 2. Доказать тождество ab (с+ аа +Р6) = abc, где а и р -
произвольные числа.
Решение. Принимая во внимание свойства смешанного произве-
дения и замечание к примеру 1, получаем
ab (с + oZz + $b) = abc + aaba +$abb -abc.
Пример 3. Найти смешанное произведение трех векторов
а = {1,1,2}, b = {2,1,1}, с = {1, -2,3}. Какой репер образуют векторы
а,Ь,с1 (Координатный репер - правый.)
Решение. По формуле (3.47) находим
abc = 1 2 1 1 2 1 1 0 1 -1 (N СП 1 -1 -3 = -10.
1 -2 3 0 -3 1 -3 1
Так как смешанное произведение отрицательно, то реперы а,Ь,с
156
и z, j,k имеют противоположную ориентацию, т. е. а,Ь9с - левый
репер.
Пример 4. Доказать, что векторы а = {1, 2, - 2}, b = {1, - 2,1},
с = {5, -2,-1} компланарны.
Решение. Найдем
формуле (3.47):
смешанное
произведение этих
векторов по
-2
-2
аЬс =
-2
-1
= -2
2 -1
-2
-1
-3
6 -3
= 0.
1
1
5
2
1
1
2
2
О
6
о
Следовательно, выполнено условие (3.46). Это и означает, что век-
торы а,Ь,с компланарны.
Пример 5. Найти объем тетраэдра ABCD с вершинами в точ-
ках А B(x2,y2,z2), С (х3, y3,z3), D (х0, у0, z0).
Решение. Найдем векторы трех ребер тетраэдра, исходящих из
какой-либо его вершины, например вершины D.
a = DA = {Х| -х0, У1~у0, zx -z0), b = DB={x2 -x0, y2-y0, z2-z0},
c = DC={x3-x0,y3-y0,z3-z0}. (A)
Построив параллелепипед на векторах а, b, с, примем за его осно-
вание параллелограмм ABCL, построенный на векторах а = DA и
b = DB. За основание тетраэдра примем грань АВС. Площадь этой
грани равна половине площади S параллелограмма ABCL.
s,=|s. (В)
Так как высота у параллелограмма и тетраэдра одна и та же, то
обозначив ее через Л, получим:
Vy = X-sxh- (С)
V = Sh, (D)
где V - объем параллелепипеда.
157
Из формул (В) - (D) следует, что
(Е)
Принимая во внимание равенство (А) и формулу (3.48), получим
И
6
х1-*о У1-Уо
*2-*0 У2-У0 z2~z0
(3.50)
y3-yQ z3-zQ
Пример 6. Даны вершины тетраэдра: Л(0,-2,5), В(6, 6,0),
С (3,-3,6), D (2, -1,3). Найти длину его высоты, опущенной из вер-
шины С.
Решение. Найдем сначала объем тетраэдра ABCD. По формуле
(3.50) получаем
У\
6
0-2
6-2
3-2
-2-(-1)
6-(-1)
-з-(-1)
Так как определитель равен отрицательному числу, то в данном
случае перед формулой нужно взять знак минус. Следовательно,
Г1 = -1(-1-411) = —= —.
1 6 6 2
Искомую величину h определим из формулы V = Sh, где S -
площадь основания. Определим площадь В:
5 = ||[aF]|,
где a = ~DA = {-2,-1,2}; b = DB= {4,7,-3}.
158
то
Поскольку
Р»] =
-12 -22
7 -3 ’ “ 4-3
[а6] = {-11,2,-10},
-2 -1
4 7
11[й>]| = |7(-11)2+22+(-10)2 Л./225 =у.
Подставляя в формулу V = — Sh значения V = — и 5 = полу-
чим Л = 3.
Пример 7. Показать, что точки Л(3,-4,1), В (2,-3,7),
С (1, -4,3), D (4, -3,5) лежат в одной плоскости.
Решение. Если точки A (xb у}, z0, B(x2,y2,z2), С (x3,y3,z3),
£>(х0, Ж 2о) лежат в одной плоскости, то объем тетраэдра ABCD
равен нулю. Из формулы (3.50) получаем необходимое и достаточное
условие компланарности четырех точек:
*1"*0 •Vi-J'o Zi -z0
х2-х0 У2-У0 Z2 ~Z0 = 0.
х3-х0 Уз-Уо z3 ~ zo
(3.51)
Подставляя координаты точек А, В, С, D в определитель, стоя-
щий в правой части формулы (3.50), получаем
3-4
2-4
1-4
4-(-3) 1-5
З-(-З) 7-5
4-(-3) 3-5
-1 -1 -4
-2 0 2
-3 -1 -2
— 1
-2
-2
0 2 =-(-1)
0 2
= 0.
2
2
159
Рис. 3.19
Пример 8. Доказать тождест-
во [[а6]с] = b (ас)-а (Ьс).
Решение. Векторы а,Ъ,с
приведем к общему началу. Вве-
дем прямоугольную систему коор-
динат следующим образом. Нача-
ло координат поместим в точке
приложения векторов а, b, с
(рис. 3.19). Вектор i направим
вдоль вектора а, вектор j выбе-
рем в плоскости векторов а, Ь,
тогда вектор к определится условием, что репер i, j,k - правый. При
таком выборе системы координат имеем: .
a = {Xi,0,0}; Ь = {х2> у2,0}; с = {х3, y3,z3}. (А)
По формуле (3.42) получаем
[а/>] = {0,0, х,у2} и [[а*] с] = {-хху2у3, j2x3,0}. (В)
С другой стороны:
ас = XjX3, Ь (ас) = {xjx2x3, х^2х3, 0},
be = х2х3 + у2у3, а (Ьс) = {Х!Х2Х3+х,у2^3,0,0},
откуда
b (ас)-a (bc) = {-xly2y3,x}y2x3,0}. (С)
Сравнивая формулы (В) и (С), получим
[[аб]с] = Ь (ас)-а (be). (3.52)
Пример 9. Доказать тождество
[а [6 с]] = Ь (ас)-с (ab). (3.53)
Решение. Для доказательства используем свойства векторного
произведения и формулу (3.52), полученную в примере 8:
160
[a [6 с]] = - [[Л с ] а} = - {с (ab ) - b (ас )} = b (5с) - с (ab).
Замечание. Результатам, содержащимся в формулах (3.52) и (3.53)
можно дать следующую формулировку: двойное векторное произведение рав-
но среднему (по занимаемому месту) вектору, умноженному на скалярное про-
изведение двух крайних, минус другой вектор внутренней скобки, умножен-
ный на скалярное произведение двух остальных.
Пример 10. Доказать тождество
[»][?</] =
ас ad
be bd
(3.54)
Решение. Скалярное произведение векторных произведении [56]
и [с 5] можно рассматривать как смешанное произведение трех векто-
ров 5, b и [с</]. Принимая во внимание формулу (3.45), получим
[56 ] [сd] = 56 [с J] = а [6 [с J]]. (А)
В силу замечания к примеру 9 имеем
[6[cJ]]=c(65)-J(6c),
поэтому
5[6 [с 7]] = а {с (bd)-d (be) } =
= (ae)(bd)-(ad) (bc) =
Из равенств (А) и (В) получаем соотношение (3.54).
Замечание. В случае, когда а = с, 6 = d, получаем тождество при-
мера 7 § 3.4, или в координатах «тождество Лагранжа» (см. задачу 8 § 3.4).
Задачи
1. Доказать тождество (5+6)(6+ с)(с+5) = 256с.
2. Найти смешанное произведение трех векторов: 5={7,-1,4},
6 = {-4,5, -6}, с = {6, 8,-3}. Какой репер образуют векторы а,Ь,с1
3. Вычислить объем параллелепипеда, построенного на векторах
5 = {3,4, 6}, 6 ={4,1,1}, с = {2,0,3}.
4. Показать, что векторы 5={1,5,4}, 6 = {6, -4,4}, с =
= {10,-1,10} компланарны.
6 Зак. 1816
161
5. Проверить, что точки А (5,-1,-1), В (4,2, 2), С (5,3,1),
D (8,0, -5) лежат в одной плоскости.
6. Вычислить объем тетраэдра, вершины которого находятся в
точках Л (5,2,2), В (-8,-2, 5), С (6,3,0), D(9,3,2).
7. Даны вершины тетраэдра А (4,5, -3), В (6,3,0), С (8, 5, -9),
D (-3, -2, -10). Найти длину его высоты, опущенной из вершины D.
8. При каких условиях [[аб] с] = [а [6с]].
9. Показать, что [а [6 с ]] + [6 [са ]]+[с [аЬ ]] = 0.
10. Доказать тождество [ab ] [сd]+[ас ] [db ]+\ad ] [6 с ] = 0.
Ответы
2. 31. Векторы d,b,c образуют правый репер. 3.43. 6. 0,5. 7. Л = 11.
8. Векторы а и с должны быть коллинеарны или вектор b должен быть
перпендикулярен векторам а и с. 9. Указание. Воспользоваться замеча-
нием к примеру 9. 10. У к а з а н и е . К каждому слагаемому применить форму-
лу (3.54).
162
Гпава 4.
Аналитическая геометрия в пространстве
§ 4.1. Плоскость в пространстве
Плоскость в пространстве относительно прямоугольной системы
координат может быть задана различными способами. Например,
плоскость однозначно определяется точкой и вектором, ей перпенди-
кулярным; тремя точками; отрезками, отсекаемыми на осях координат
и т. п. В зависимости от способа задания плоскости рассматривают
различные виды ее уравнения.
4.1.1. Общее уравнение плоскости. Уравнение в отрезках.
Составление уравнения плоскости по различным ее
заданиям
Уравнение плоскости, проходящей через данную точку
Л/0(х0, Л’о» zo) и перпендикулярной вектору п = {А, В, С}, в вектор-
ном виде записывается так:
и(г-го) = О, (4.1)
где г0 - радиус-вектор точки MQ(xQ, yQ, z0); г - радиус-вектор произ-
Рис. 4.1
вольной точки Л/(х, у,z) данной плоскости.
Уравнение (4.1) выражает условие перпендику-
лярности векторов п и r-r0 = MQM (рис. 4.1),
имеющее место для любой точки плоскости.
Это уравнение можно записать в виде
Hr + D = 0, где D = -(nrQ). (4.2)
Так как п = {А, В, С} и
r-rQ = {х-xQ, у-yQ, z-zQ}, то в соответствии
с формулой (3.33) уравнение (4.1) примет вид
л (х-х0)+ В {у-у0)+ с (z - z0) = О
(43)
или
Ax + By+Cz+D = О,
(4.4)
163
где
7) = -(Ях0 + Ду0 + Сг0).
Уравнение (4.3) называется уравнением плоскости, проходящей
через данную точку, а уравнение (4.4) - общим уравнением плоскости.
Замечание. В уравнениях (4.3) и (4.4) коэффициенты Я, В, С одно-
временно в нуль не обращаются (так как вектор п не является нуль-векто-
ром).
Частные случаи общего уравнения плоскости:
1. Свободный член равен нулю, т. е. D = 0:
Ах + By + Cz = 0 (плоскость проходит через начало координат). (4.5)
2. Один из коэффициентов при текущих координатах равен нулю
и
a) D Ф 0, тогда плоскость параллельна соответствующей коорди-
натной оси:
А = 0, By + Cz + D = 0 (плоскость параллельна оси Ох); (4.6)
В = 0, Ах + Cz + D = 0 (плоскость параллельна оси Оу); (4.7)
С = 0, Ах + By + D = 0 (плоскость параллельна оси Oz); (4.8)
б) D = 0, тогда плоскость проходит через соответствующую коор-
динатную ось:
А = 0, By + Cz = 0 (плоскость проходит через ось Ох); (4.9)
В = 0, Ах + Cz = 0 (плоскость проходит через ось Оу); (4.10)
С = 0, Ах + By = 0 (плоскость проходит через ось Oz). (4.11)
3. Два коэффициента при текущих координатах равны нулю и
a) D Ф 0, тогда плоскость параллельна соответствующей коорди-
натной плоскости:
В = 0, С = 0, Ях + £> = 0 (плоскость параллельна плоскости Oyz); (4.12)
А = 0, С = 0, By + D = 0 (плоскость параллельна плоскости Oxz); (4.13)
А = 0, В = 0, Cz + D = 0 (плоскость параллельна плоскости Оху); (4.14)
б) D = 0, тогда плоскость совпадает с соответствующей коорди-
натной плоскостью:
В = 0, С = 0, Ах = 0 илих = 0 (уравнение плоскости Oyz); (4.15)
А = 0, С = 0, By = 0 или у = 0 (уравнение плоскости Oxz); (4.16)
А = 0, В = 0, Cz = 0 или z = 0 (уравнение плоскости Оху). (4.17)
Если ни один из коэффициентов общего уравнения (4.4) не равен
нулю, то оно может быть преобразовано к виду
164
(4.18)
D - D D
vjiq a = ~~~^9 = c = -—-алгебраические величины направ-
ленных отрезков, отсекаемых на осях координат. Уравнение (4.18) на-
зывается уравнением плоскости в отрезках.
Пример 1. Составить уравнение плоскости, перпендикулярной
вектору л = {2,-1,4} и проходящей через точку Л/о(5,2,-3). Лежат
ли на этой плоскости точки Р (1,2, -1), Q (4,5,1) и /?(— 6,2, -3)?
Решение. Подставляя в уравнение (4.3) значения А = 2, В = -1,
С = 4, х0 = 5, у0 = 2, zQ = -3, получим
2 (х-5)-(у-2)+4 (z + З) = 0.
Раскрывая скобки и приводя подобные члены, находим искомое
уравнение плоскости
2x-y + 4z + 4 = 0.
Выясним, лежат ли точки Р, Q и R на данной плоскости. Под-
ставляя последовательно координаты этих точек в левую часть послед-
него уравнения, получим:
21-1-2 + 4 (-1)+4 = 0; 2-4-1-5+41 + 4 > 0;
2(-6)-1-2 + 4(-3)+4<0.
Следовательно, точка Р лежит на данной плоскости. Точки Q и
R плоскости не принадлежат. Они находятся по разные стороны от нее
(в результате подстановки их координат в уравнение плоскости полу-
чены числа разных знаков).
Замечание.* Плоскость Ах +By+ Cz + D = 0 разбивает пространство
на два полупространства, для точек одного из них Ах + By + Cz + D < 0, для
точек другого Ах + By + Cz + D > 0.
Пример 2. Составить уравнения плоскостей по следующим дан-
ным:
1) плоскость перпендикулярна оси Oz и проходит через точку
Р(1, -2,3);
2) плоскость проходит через ось Оу и точку 6(4,2,-5);
3) плоскость параллельна оси Ох и проходит через две точки
165
R (1,1,2) и S (5,3,-2).
Решение.
1) Плоскость, перпендикулярная оси Oz, параллельна координат-
ной плоскости Оху и ее уравнение (см. уравнение (4.14)) имеет вид
Cz + D = 0.
Подставляя в это уравнение координаты точки Л получим
С • 3 + D = 0, откуда D = - ЗС. Следовательно, Cz - ЗС = О,
С (z - 3) = 0, но С Ф 0, значит получим уравнение z - 3 = О или z = 3.
2) Так как плоскость проходит через ось Оу, то ее уравнение
(см. уравнение (4.10)) ищем в таком виде:
Ах + Cz = 0.
Подставляя в это уравнение координаты точки Q, получим
5
А -4 + С (-5) = 0, откуда А = — С. Таким образом, плоскость имеет
4
уравнение — Cx + Cz = 0 или С|— x + z| = 0, но С^О, значит
4 \4 у
5x+4z = 0.
3) Поскольку плоскость параллельна оси Ох, то ее уравнение не
содержит члена с х (см. уравнение (4.6)), т. е/ имеет вид
By + Cz + D = 0.
Так как плоскость проходит через две точки Р и 5, то их коорди-
наты удовлетворяют уравнению. Подставляя координаты этих точек в
данное уравнение, получим
B+2C+D = 0; 3B-2C+D = 0,
D D
откуда B =---, С =----. Следовательно, уравнение принимает вид
2 4
D D
---у----z + D = 0 или 2y + z-4 = 0.
2 Л 4
Пример 3. Определить отрезки, отсекаемые плоскостью
2х - Зу + 8z - 4 = 0 на осях координат.
Решение. Переписав уравнение в виде 2х - Зу + 8z = 4 и разделив
обе части его на 4, получим
166
х 3 _ • , х у z .
----y+2z = l или —l—=4-+т = 1.
2 4 2 _4 1
3 2
Сравнивая последнее уравнение с уравнением (4.18), находим:
„ . 4 1
а = 2, Ь = —, с = —.
3 2
Пример 4. Построить плоскости:
1) 3x+4y-6z-12 = 0; 2) z+y-2 = 0;
3) z + y = 0; 4) Зу-7 = 0.
167
Решение. 1) Определив отрезки а = 4, b = 3, с = -2, осекаемые
на осях координат, получим три точки А (4,0, 0), В (0,3,0),
С(0,0,-2), в которых плоскость пересекает координатные оси
(рис. 4.2, а).
2) Вторая плоскость параллельна оси Ох (см. уравнение (4.6)).
Полагая у = 0, из уравнения z + у - 2 = 0 получим z = 2. Следова-
тельно, плоскость пересекает ось Oz в точке С (0,0, 2). Аналогично
находим, что точка В (0,2,0) есть точка пересечения с осью Оу
(рис. 4.2, б).
3) Плоскость z + y = 0 проходит через ось Ох (см. уравнение
(4.9)). Она делит пополам угол между координатными плоскостями
Oxz и Оху (рис. 4.2, в),
4) Плоскость Зу - 7 = 0 параллельна плоскости Oxz
(см. уравнение (4.13). Она отсекает на оси Оу отрезок б = —
7
(рис. 4.2, г) (значение Ъ получено из уравнения у = у).
Пример 5. Составить уравнение плоскости, проходящей через три
данные точки Мх(xj, ух, zx), М2(х2, у), М3(х3»Уз-> 2з)• Написать
уравнение для случая A/j(l,3,-2), М2(4,-5,6), Л/З(~3,1,2).
Рис. 4.3
т. е.'
Решение. Пусть М -
произвольная точка плоскости
(рис. 4.3) и гх = ОМу, г2 = ОМ2,
r3 = ОМ3, F = ОМ - радиус-
векторы точек Му, м2, м3, м.
Введем в рассмотрение векторы:
МУМ2 = г2-г}, M}M2=r3-t\,
М}М — г .
Поскольку эти три вектора ле-
жат в одной плоскости, то их сме-
шанное произведение равно нулю,
('•-r1)(r2-r1)(r3-rI) = 0.
(4.19)
Уравнение (4.19) является искомым. В координатной форме оно
168
имеет вид
X —Xj
X2-Xj
Хз-Xj
У~У1
У2-У1
Уз~У1
z-zx
z2-zl
= 0.
(4.20)
Уравнение плоскости, проходящей через точки Л/|(1,3,-2),
Л/2(4, -5, 6), М3(-3,1,2) в соответствии с (4.20), запишется так:
х-1 у-3 z + 2 х-1 у-3 z + 2
4-1 -5-3 6+2 = 0 или 3 -8 8 = 0.
-3-1 1-3 2+2 -4 -2 4
Разлагая последний определитель по элементам первой строки^по-
лучим
(х-1)
или
8x + 22y + 19z-36 = 0.
Пример 6. Составить уравне-
ние плоскости, проходящей через
две данные точки Мх (х1, ух, zx),
Л/2(х2, У2> *2) параллельно данно-
му вектору а = {ах, а2, а3}. Векто-
ры а и МХМ2 - неколлинеарны.
Решение. Отложим вектор а
от точки Мх (рис. 4.4). Пусть
М (х, у, z) произвольная точка
плоскости и rj = ОМХ, г2 = ОМ2,
F = ОМ - радиус-векторы точек
Мх, М2, М. Введем в рассмотре-
ние векторы
МхМ2=г2-гх, МХМ = г-гх.
Векторы а, МХМ2, М}М лежат в одной плоскости, поэтому их
169
смешанное произведение равно нулю, т. е.
(г-^)(г2-Г|)п = 0.
(4.21)
В координатной форме это уравнение примет вид
X — X] У-У] z-zx
Х2-Х! Уг~У\ z2-Zi = 0. (4.22)
«1 а2 а3
Пример 7. Показать, что плоскости 5x-3y-26z-3 = О,
10x + 3y + llz- -42 = 0, 20x-39y-23z + 96 = 0,
10x + 21y + 2z + 21 = 0 образуют тетраэдр. Лежит ли внутри этого тет-
раэдра точка Е (1,1,2)?
Решение. Четыре плоскости образуют тетраэдр, если каждая трой-
ка их пересекается в одной точке и среди четырех точек пересечения
нет совпадающих.
Решая систему уравнений
5x-3^-26z-3 = 0;
10х + 3>> + 1 lz-42 = 0; >
20x-39y-23z + 96 = 0,
получим точку А (3,4,0).
Из системы уравнений
5x-3y-26z-3 = 0;
10x + 3y + l lz-42 = 0; >
10x + 21y + 2z + 21 = 0
получим вторую точку В (4, -3,1).
Система уравнений
5x-3y-26z-3 = 0;
20x-39y-23z + 96 = 0; >
10x + 21y + 2z + 21 = 0
дает третью точку С (-4,1,-1).
Наконец, решая систему
170
10x + 3y + l к-42 = 0;
20x-39y-23z + 96 = 0; >
10x + 21y + 2z + 21 = 0,
получим четвертую точку D (-1, -1,5).
Так как полученные точки различны, то данные плоскости образу-
ют тетраэдр, вершинами которого являются точки А, В, С, D.
Выясним теперь, лежит ли точка Е внутри тетраэдра ABCD. Если
Е лежит внутри тетраэдра, то она и каждая вершина его располагают-
ся по одну сторону от противоположной грани. Далее, если две точки
пространства находятся по одну сторону плоскости, то при подстанов-
ке их координат в левую часть уравнения этой плоскости получаем
числа одного знака (см. замечание к примеру 1). Рассмотрим точки А
и Е. Для точки А противоположной является грань, лежащая в плос-
кости 10x + 21y + 2z + 21 = 0. Подставляя координаты точек А и Е в
левую часть уравнения этой плоскости, получим
10-3 + 21-4 + 2-0 + 21 > 0, 101 + 21-1 + 2-2 + 21 > 0.
Следовательно, точки А и Е лежат по одну сторону от грани
BCD.
Для точки С противоположной будет грань, лежащая в плоскости
10х + Зу + 1 к-42 = 0. Подставляя координаты точек С и Е в левую
часть последнего уравнения, получим
10 (—4)+3 • 1 +11 (—1)—42 < 0, 10-1 + 3-1 + 11-2-42 <0.
Таким образом, точки С и Е лежат по одну сторону от грани
ABD.
Так как
20-4-39(-3)-23 1 + 96> 0, 20 1-39-1-23-2 + 96 > 0,
то точки В и Е находятся по одну сторону от грани ACD. Аналогич-
ным образом убеждаемся, что точки D и Е лежат по одну сторону от
грани АВС.
Следовательно, точка Е лежит внутри тетраэдра ABCD.
Пример 8. Составить уравнение плоскости, проходящей через точ-
ки Мх(1, -2,6), М2(5, -4, -2) и отсекающей равные отрезки на осях
Ох и Оу.
171
Решение. Уравнение плоскости ищем в виде
X у Z ,
abc
По условию а = Ь9 поэтому уравнение можно записать так:
х у z ,
а а с
Подставляя координаты точек и М2 в последнее уравнение, полу-
чим
1-26,5-4-2, 1612,
—+—+— = 1, —+—+— = 1 или —+ —= 1,--------= 1.
а а с а а с ас ас
Решая полученную систему уравнений, находим с = 2, а = Следо-
вательно, искомое уравнение имеет вид
X у Z ,
“Г" + — + — = 1
112
2 2
или
4x + 4y + z-2 = 0.
Задачи
1. Составить уравнение плоскости, проходящей через точку
М (2, -1,-4) и перпендикулярной вектору п = {3, -6,1}, в векторной
и координатной формах.
2. Написать уравнение плоскости в каждом из следующих случа-
ев:
1) плоскость перпендикулярна оси Ох и проходит через точку
Р (4,-7,6);
2) плоскость параллельна оси Оу и проходит через точки
0(1,2,-1), Я(2,-3,-4);
3) плоскость проходит через точку S (6, -7, 5) и ось Oz.
3. Определить отрезки, отсекаемые на осях координат плоскостя-
ми:
1) 2x-3y + 4z-24 = 0; 2) 4x + y-3z-2 = 0.
172
4. Построить плоскости:
1) 2x + 3y-4z-12 = 0; 2) 2x-3y-6 = 0;
3) 4х + 5у = 0; 4) 4х + 9 = 0.
5. Написать уравнение плоскости, проходящей через точку
М (4, -3, 5) и отсекающей на осях координат равные отрезки.
6. Написать уравнение плоскости, проходящей через три точки:
£(-2,4,1), М (0,2,-1), N (2,0,-1).
7. Грани тетраэдра лежат в плоскостях: x + y + z-l = 0; х-у-
-1 = 0; х - z -1 = 0; z - 2 = 0. Лежит ли начало координат внутри это-
го тетраэдра?
8. Составить уравнение плоскости, проходящей через точку
?Ц(Х], У], Zj) и параллельной двум неколлинеарным векторам
а = {al9 а2, а3}9 b - {b[9b19b3}. Написать уравнение в случае, когда
М}(29-1,3), а = {1,-1,2}, b = {2,1,-3}.
Ответы
1. лг-8 = 0; 3x-6y + z-8 = 0. 2.1)х-4 = 0; 2)3x + z-2 = 0;
1 2
3)7х + 6у = 0. 3.1) а = 12, 6 =-8, с = 6; 2) а = —, Ь = 2, с = -у.
5. х + у + z-6 = 0. 6. х + у-2 = 0. 7. Не лежит. 8. (г-r\)ab = 0,
Х-Х] У~У\ Z — Z] х-2 у+1 z-3
«1 а2 о3 = 0, 1 -1 2 = 0,
А ft. 2 1 -3
или x + 7y + 3z-4 = 0.
173
4.1.2. Нормальное уравнение плоскости.
Расстояние от точки до плоскости
Нормальным уравнением плоскости называется уравнение вида
xcosa + ycosP + zcosy- р = 0, (4.23)
где cosa, cos0, cosy - направляющие косинусы перпендикуляра, опу-
щенного из начала координат на данную плоскость, ар- его длина.
Общее уравнение плоскости (4.4) умножением на нормирующий
множитель
1
л1а2 + в2+с2
(4.24)
знак которого противоположен знаку D, можно привести к нормально-
му виду (4.23).
Расстояние точки (jq, , z}) до плоскости (4.23) вычисляется
по формуле
d = | Xj cosa + ух cosP + zx cosy - p |,
(4.25)
а до плоскости (4.4) - по формуле
| Лхх + Вух + Cz} + D |
у1а2 + В2+С2
(4.26)
Отклонением точки от плоскости называется число (+</), если эта
точка и начало координат лежат по разные стороны от данной плоско-
сти, и число (-rf), если они лежат по одну сторону от данной плоско-
сти.
Отклонение 8 точки Л/0(х0, у0, z0) от плоскости (4.23) определя-
ется формулой
8 = ±(х0 cos a + yQ cos P + z0 cos у - p), (4.27)
а от плоскости (4.4) - формулой
5 = ±^xQ + By0+Cz0 + D^ (4 28)
Ja2+b2+c2
где знак следует выбрать противоположным знаку D.
174
Очевидно,
(4.29)
Пример 9. Найти направляющие косинусы и длину перпендикуля-
ра, опущенного из начала координат на плоскость
10х-2у-1 к + 45 = 0.
Решение. Уравнение плоскости приведем к нормальному виду.
Найдем сначала нормирующий множитель. В данном случае Л = 10,
В = -2, С = — 11, D = 45. Поскольку D>0, то в формуле (4.24) нуж-
но взять знак минус. Получаем
1 . 1
Ц =-—=----------.
71O2 + (-2)2 +(-11)2 15
Умножая обе части данного уравнения плоскости на нормирующий
множитель, получим нормальное уравнение
10 2 11 45 л
— х +— у + —z--= 0
15 15Л 15 15
или
2 2 11 „ л
— х +—у +— z-3 = 0.
3 15 15
Сравнивая последнее уравнение с уравнением (4.23), находим:
2 о 2 11
cosa = —, cosp = —, cos у =—, р = 3.
3 н 15 1 15
Пример 10. Вычислить расстояние точек М}(3,4,-7),
Л/2(2,4,9), Л/3(5,1,0) до плоскости 2x-j> + 2z-9 = 0.
Решение. По формуле(4.26) получаем:
|2-3-4 + 2 (~7)~9| |~21L7.
1 J?2 4-Г-П2 4-9 2 3
d |2-2-4 + 2-9-9L|9|_? J2 5-1 + 2 O-9| _р
2 ./о2 д-Г-П2 + 72 3 ’ 3
3
175
Следовательно, точка М3 лежит на данной плоскости.
Пример 11. Дан тетраэдр с вершинами А (2,-1,3), В(1,-3,5),
С (6,2,5), D (3, -2, -5). Найти длину высоты, опущенной из вершины
D на грань АВС.
Решение. Искомая высота равна расстоянию от точки D до плос-
кости, проходящей через точки Л, В, С. Составим уравнение этой плос-
кости:
х-2 у + 1 z-3 х-2 j> + 1 z-3
1-2 -3+1 5-3 = 0, -1 -2 2 = 0
6-2 2 + 1 5-3 4 3 2
или
2x-2y-z-3 = 0.
По формуле (4.26) находим расстояние точки D до плоскости:
у_|2-3-2(-2)-(-5)-3| |12|=1
д/22 +(-2)2 +(-1)2 3
Пример 12. На оси Ох найти точку, равноудаленную от точки
Л(9,-2,2) и от плоскости Зх-бу + 2z-3 = 0.
Решение. Пусть М (х, 0,0) - искомая точка (у = 0, z = 0, так как
точка лежит на оси Ох). Находим расстояние этой точки до данной
плоскости и точки Л:
Зх-6 0 + 2 0-3
j32+(-6)2+22
I _|3лг-3|
7
d2 = МА = д/ (9-х)2 +(-2)2 +22.
В соответствии с условием имеем dx = d2, поэтому
7(9-х)2+8 = 1ЗХ~3! или 7д/х2-18х + 89 = 31х-11.
Возведя в квадрат обе части последнего уравнения и приводя по-
добные члены, получим
5х2-108х + 544 = 0.
176
Решая это квадратное уравнение, находим Xj =8, х2 = 13,6. Следо-
вательно, условию задачи удовлетворяют две точки:
Л/1(8,0,0)иЛ/2(13,6; 0; 0).
Пример 13. На оси Oz найти точку, равноудаленную от двух плос-
костей:
2x-2y + z-3 = 0; x + 2y-2z + 12 = 0.
Решение. Пусть М (0,0, z) - искомая точка. Расстояние этой точ-
ки до данных плоскостей определяется соответственно формулами:
d |2 0-2 0+z-3| |z-3|
' ^2г+(-2)2+? 3
d _|10+2 0-2z + 12| _|-2z+12|
2 Jl2 + 22 +(-2)2 3
По условию d} = d2, поэтому
|z-3| l-2z+12|
-—откуда z-3 = ±(-2z+12).
Решая уравнения
z-3 = -2z+12 и z-3 = -(-2z + 12),
получим z, = 5, z2 = 9. Таким образом, условию удовлетворяют две
точки A/j (0,0,5) и Л/2(0,0,9).
Пример 14. Составить уравнение плоскостей, делящих пополам
двугранные углы между пересекающимися плоскостями:
А}х + Вху + Qz + Dj = 0; А2х + В2у + C2z + D2 = 0.
Решение. Каждая из искомых плоскостей является геометриче-
ским местом точек, равноудаленных от двух данных плоскостей. Пусть
М (х, J, z) - произвольная точка искомой плоскости, тогда:
J^+B^+q2
| А2х + В2у + C2z + D2 J
А2 + В2 4- С2
177
Так как по условию d} = d2, то
| А}х + В}у + C}z + Dx | _ | A2x + B2y + C2z + D21
7л2 +B12+C,2 Ja2 + b22+c2
откуда получаем уравнения искомых плоскостей:
Ахх + В}у + C\z + Dx _ А2х + В2у + C2z + D2
^А2 + В2 + С2 -Ja^+B^+C^
В частности, если даны плоскости 5х- 10y + 10z-6 = 0,
1 Ох + 2у -1 к + 4 = 0, то уравнения плоскостей, делящих пополам дву-
гранные углы между ними, запишутся следующим образом:
5x-10y + 10z-6 _+ 10х + 2у-1к + 4
^52 + (-10)2 +102 J}02+22 +(-П)2
Следовательно,
5x-10y + 10z-6 = ±(10x + 2y-lk + 4),
откуда
1) 5х-10у + 10z-6 = (10х + 2у-1 к + 4)
или 5х + 12у-2к + 10 = 0;
2) 5x-10y+10z-6 = -(10x + 2y-lk + 4)
или 15x-8y-z-2 = 0.
Пример 15. Определить, лежат ли точка Л/(1,1,-9) и начало
координат по одну или по разные стороны от плоскости
2х-2у+ z+12 = 0.
Решение. Уравнение плоскости приведем к нормальному виду.
Так как D > 0, то в формуле (4.24) нужно взять знак минус, т. е.
_________1 _ _ 2
g jl2+(-2)2+12 3
Умножая обе части уравнения на нормирующий множитель, получим
178
Подставляя координаты точки М в последнее уравнение, находим
отклонение 8
2 2 1
8 = -- + - —-(-9)-4<0.
3 3 3
Поскольку 8 < 0, то точка М и начало координат лежат по одну
сторону от данной плоскости.
Пример 16. Определить, лежат ли точки М(1,-1,2) и
N (-2,1,-3) в одном, в смежных или вертикальных углах, образован-
ных при пересечении двух плоскостей:
1) 3x-2j> + 4z-10 = 0,x + 3y-5z + 6 = 0;
2) 2x + 4y-z-5 = 0, х-у-z-3 = 0;
3) 5х - бу + 2z + 7 = 0, х + у - 3z + 8 = 0.
Решение. Если две точки лежат в одном двугранном углу, образо-
ванном двумя плоскостями, то они расположены по одну сторону от
каждой плоскости.
Если две точки находятся в двух смежных углах, то они располо-
жены по разные стороны от одной из них и по одну сторону от другой.
Если точки находятся в вертикальных углах, то они расположены
по разные стороны каждой из данных плоскостей. Для каждого из этих
трех утверждений обратное также верно.
1) Найдем отклонения точек М и;У от первой плоскости
3 1-2С-0+4 2-10 3(-2)-2 1 + 4(-3)-10
О] =-----7-------=---->0; о7 =---------------------<0
V9+4+16 V9+4 + 16
и от второй плоскости
5;
1 + 3 (-1)-5-2 + 6 Л
----, —>0;
-V1 + 9 + 25
-2 + 31-5(-3) + 6
52 =-----1________< °-
Так как 8] и 82 разных знаков, то точки М и N расположены по
разные стороны от первой плоскости, по той же причине они находятся
по разные стороны и от второй плоскости. Следовательно, точки M»N
179
лежат в вертикальных углах.
2) Находим отклонения точек М и N от первой плоскости
= 2-1 + 4 (-l)-2-S <0. 5 = 2(-2)->41-(-3)-5 е„
V4 + 16+1 ‘ т/4 + 16+1
и от второй плоскости
Следовательно, точкиMhN находятся в одном углу.
3) Поскольку
51-6(-1) + 2-2 + 7 5(-2)-61+2(-3) + 7
di =----, =— <0; о7 =-----------. =-----> 0;
- 725 + 36 + 4 - 725 + 36 + 4
1 + (_1)_3.2 + 8 1(_2) + 1-3(-3) + 8
О] =-----. .... — <0; о7 =---, . ------<0,
-71+1 + 9 -71 + 1 + 9
то точки М и N лежат по разные стороны от первой плоскости и по
одну сторону от второй. Следовательно, они расположены в смежных
двугранных углах.
Задачи
9. Определить, какие из уравнений являются нормальными:
п 3 6 2 о Л 2 1
1) —х—у + —2 + 3 = 0; 2) —х—у +
7 7 7 3 3
1 Л Л 1 * 3 2 2 Л
+—z-2 = 0; 3) —х—у + —2-2 = 0.
3 3 3 3
10. Найти направляющие косинусы и длину перпендикуляра, опу-
щенного из начала координат на плоскость 2х - Зу - 62 -14 = 0.
11. Определить расстояния точек Р (4,3, - 2), Q (0,6,0) и
R (15,0,0) до плоскости 2х +10>> -1 к -15 = 0.
12. Дан тетраэдр с вершинами А (3,4,0), В (4, - 3,1),
С (-4,1,-1), £>(—1, — 1,5). Найти длину высоты, опущенной из вер-
шины D.
13. На оси Оу найти точку, равноудаленную от двух плоскостей
180
x + y-z + l = 0, x-y + z-5 = 0. .
14. Написать уравнение плоскости, проходящей через точку
Р (5,2,0) и удаленной от точки Q (6,1, -1) на расстояние 1 и от точки
R (0,5,4) на расстояние 3.
15. Составить уравнение плоскостей, делящих пополам двугранные
углы между плоскостями х + 2у - 2z - 3 = 0, 2х - у + 2z - 9 - 0.
16. Доказать, что плоскость 5х - Зу + 4z - 2 = 0 пересекает отрезок,
соединяющий начало координат с точкой М (1,2,3).
Ответы
9. Уравнение 3. Указание. Если уравнение является нормальным, то
выполняются два условия: 1) свободный член отрицателен; 2) сумма квадратов
2
коэффициентов при текущих координатах равна единице. 10. cosa = y,
cos0 = -y, cosy =-у; р = 2. 11. dx=3, J2=3, d3=\.
135
12. Л = -7=. 13. M(0,-3,0). 14. x + 2>> + 2z-9 = 0, >>-2 = 0.
V710
15. x-3>> + 4z-6 = 0, Зх + >>-12 = 0. 16. Указание. Показать, что
< 0,32 > 0.
4.1.3. Угол между двумя плоскостями. Условия параллельности
и перпендикулярности двух плоскостей
Угол между двумя плоскостями
Ахх + Вху + Cxz + Dx = 0, (4.30)
А2х + В2у + C2z + D2 =0 (4.31)
определяется формулой
COS(p =
А} А2 + BtB2 + CjC2
В2 +c,2 Ja22 + b22+c22
(432)
Необходимое и достаточное условие параллельности плоскостей
(4.30) и (4.31):
л2 в2 с2 d2
(4.33)
181
или
А^ — , В2 — , С*2 — , Z?2 A«Z)|
(коэффициенты при текущих координатах пропорциональны).
Необходимое и достаточное условие совпадения плоскостей (4.30)
и (4.31)
A=A=£l=A (434)
л2 в2 с2 d2
(все соответствующие коэффициенты пропорциональны).
Условие перпендикулярности плоскостей (4.30) и (4.31):
АхА2 + ВХВ2 + CtC2 = 0. (4.35)
Пример 17. Найти угол между двумя плоскостями
1 lx - 8j> - 7z + 5 = 0, 7х + 2у - 8z - 3 = 0.
Решение. Подставляя в формулу (4.32) значения А} = 11, В} = - 8,
С\=-7, А2=7, В2=2, С2 =-8, получим
_ 1Ь7 + (-8)2 + (-7)(-8) _ 117 _ 1
C0S<₽ ~ V121 + 64 + 49 V49 + 4 + 64 ” V234 VT17 ” VI ’
Следовательно, (р = 45°.
Замечание. Формула (4.32) определяет один из двух неравных между
собой углов, сумма которых равна 180°. Если уравнение второй плоскости
написать в виде -7x-2>> + 8z + 3 = 0, то по формуле (4.32) получим
cos(p = —1=-, откуда ф = 135°.
V2
Пример 18. Через точку N (2, -1,-3) провести плоскость, парал-
лельную плоскости 5х - 4у + 6z - 3 = 0.
Решение. В соответствии с условием (4.33) уравнение плоскости
ищем в виде
5Хх - 4ку + 6Az + D = 0.
Подставляя в это уравнение координаты точки N, находим
5Х-2-4Х (-1) + 6Х (-3) + D = 0 или -4Х = -£>,
откуда D = 4Х. Подставляя значение D в искомое уравнение и полагая
182
X = 1, получим
5х - 4у + 6z + 4 = 0.
Замечание. Уравнение плоскости, параллельной плоскости
Ах + By + Cz + Dj =0, можно искать в виде Ах + By + Cz + D = 0.
Пример 19. Составить уравнение плоскости, параллельной плос-
кости 4х - 4у + 2z - 3 = 0 и отстоящей от нее на 5 единиц.
Решение. Уравнение искомой плоскости запишем так:
4x-4y + 2z + D = 0.
Найдем расстояние между плоскостями, для чего возьмем произ-
вольную точку первой плоскости и определим ее расстояние до второй.
3
Положив х = 0, у = 0, из уравнения 4х - 4у + 2z - 3 = 0 найдем z = ~;
( ЗА
получим точку Л/l 0,0, — J. Расстояние этой точки до плоскости
4х - 4у + 2z + D = 0 определяется формулой
Так как по условию d = 5, то для определения D имеем уравнение
|3+£>|
5 = -!——1 или 30 = ±(3 + D),
откуда
Dx =27, D2 = -33.
Подставляя в искомое уравнение найденные значения D получим
две плоскости:
4x-4y + 2z + 27 = 0 и 4х-4у+ 2z-33 = 0.
Пример 20. Написать уравнение плоскости, параллельной плоско-
сти х + 2у - 2z + 7 = 0 и удаленной от точки М (4,3, - 2) на расстоя-
ние d = l.
183
Решение. Уравнение искомой плоскости ищем в виде
х + 2у - 2z + D = 0.
Расстояние точки М до этой плоскости выразится формулой
d_ |4 + 2-3-2(-2)+D| _ 114 +£)|
V1 + 4 + 4 ~ 3
Так как по условию d-1, то для определения D получим уравне-
ние
114+ D\
7 = ^—-—L или 21 = ±(14 + D),
откуда Dx = 7, D2 = -35.
Таким образом, условию задачи удовлетворяют две плоскости
x + 2y-2z + 7 = 0, x + 2y-2z-35 = 0.
Первая плоскость совпадает с данной плоскостью.
Пример 21. Через начало координат провести плоскость, перпен-
дикулярную плоскости 5x-2^ + 5z-10 = 0 и образующую с плоско-
стью x-4>>-8z +12 = 0 угол (р = 45°.
Решение. Поскольку искомая плоскость проходит через начало
координат, то ее уравнение имеет вид
Ах + By + Cz = 0.
Коэффициенты А, В, С одновременно в нуль не обращаются (это
координаты вектора, перпендикулярного плоскости). Предполагая, что
А * 0, уравнение перепишем в виде
х + by + cz = 0,
где
t В С
Ь =—, с =—.
А А
Условие перпендикулярности (4.35) для плоскостей x + 6y + cz = 0
и 5х - 2у + 5z -10 = 0 запишется так:
5-26 + 5с = 0. (А)
184
Угол между плоскостями x-4y-8z + 12 = 0 и x + fcy + cz = 0 оп-
ределится формулой (4.32):
cos<p =
1-46-8с
Vl + 16+64 Vl + Z>2 + c2
Так как (р = 45°, то для определения коэффициентов b и с имеем
второе уравнение
1_ 1-46-8с
/2 л/вТл/и-б2 +с2
(В)
Решим систему уравнений (А) и (В). Определяя b из уравнения (А),
г 5(1 + с)
подставляя полученное выражение Ь = —— в уравнение (В) и ос-
вобождаясь от радикалов, находим
81 1 + 25(1 + С>2
4
+ с2 = 2 [1-10(1 + с)-8с]2
или
81 -у
— (29с2 + 50с + 29) = 2 • 92 (-1 - 2с)2,
4
откуда
29с2 + 50с+29 = 8 +32с+32с2.
Приводя подобные члены и сокращая на 3, получим квадратное урав-
нение
с2-6с-7 = 0,
„ , „ , , 5(1 +с) ,
его корни С] = 7, с2 = -1. По формуле b = —-— находим Ь} = 20,
*2=0.
Следовательно, условию задачи удовлетворяют две плоскости
x + 20y + 7z = 0 и x-z = 0.
Замечание. При решении задачи был исключен случай А = 0. Это
исключение оправдано, так как предположение А = 0 приводит к несовмест-
ной системе уравнений относительно В и С.
185
Пример 22. Составить уравнение плоскости, проведенной через
точку A/0(x0,y0,z0) перпендикулярно к двум пересекающимся плос-
костям Ахх + Вху + Cxz + Dx = 0, А2х + В2у + C2z + D2 = 0. Написать
уравнение плоскости для случая, когда М (2,-3,1) и плоскости зада-
ны уравнениями 3x-y + 2z-l = 0, 4x + 5y-3z + 2 = 0.
Решение. В общем уравнении плоскости Ах + By + Cz + D = 0 ко-
эффициенты при х, у и z - координаты вектора п = {А, В, С}, перпен-
дикулярного к плоскости.
Так как вектор пх = {Ах, Вх, Сх} перпендикулярен плоскости
Ахх + Вху + Cxz + Dx = 0, а вектор п2 = {А2, В2, С2} перпендикулярен
плоскости A2x+B2y + C2z + D2 =0, то задача сводится к составлению
уравнения плоскости, проходящей через данную точку и параллельной
двум неколлинеарным векторам (см. задачу 8).
Пусть М (х, у, z) - произвольная точка плоскости, F = ОМ ее ра-
диус-вектор, Fq = OMq -радиус-вектор данной точки Л/о, тогда век-
торы F-FQ,nx и п2 компланарны и их смешанное произведение равно
нулю:
(r-r0)"i л2=0.
Это уравнение и является искомым векторным уравнением плоско-
сти. В координатах оно принимает вид
У-Уо z~zo
В, С} = 0.
В2 С2
Для данного конкретного случая, когда х0 = 2, у0 = -3, z0 = 1,
Ai=3, С|=2, Л2=4, В2=5, С2=-3, последнее уравне-
ние запишется так:
х-2 у+3
3 -1
4 5
z— 1
2
-3
= 0 .
или
7x-17y-19z-46 = 0.
186
Пример 23. Доказать, что параллелепипед, грани которого лежат в
плоскостях 7х -11>> + 9z -14 = О, 4х + 5у + 3z + 6 = О,
78х -15у - 79z + 3 = 0, является прямоугольным.
Решение. Составляем выражение АХА2 + ВХВ2 + СХС2 для каждого
случая:
1) 7-4 + (-11)5+9-3 = 0; 2) 4-78+5(-15) + 3(-79) = 0;
3) 7 78 + (-11) (-15) + 9 (-79) = 0.
Так как выполняется условие (4.35) для каждой пары плоскостей, то
плоскости попарно перпендикулярны. Это и означает, что параллеле-
пипед является прямоугольным.
Задачи
-1 lx + 8>>+7z + 5 = 0;
4x-3>> + 2z + 7 = 0;
3x + 6j>-9z-2 = 0;
x + 2^ + 2z-4 = 0.
17. Найти угол между двумя плоскостями:
1) 4х-10y+z-3 = 0,
2) 2x + 6y + 5z-9 = 0,
3) x + 2j>-3z-6 = 0,
4) 2x-3y + 6z + 8 = 0,
18. Составить уравнение плоскости, проведенной через точку
К (1,5,2) параллельно плоскости, проходящей через три точки
£(4,-3,1), М (3,4,0), 7V (-1, -1,5).
19. Дана вершина параллелепипеда Р (3,2,4) и уравнения плоско-
стей, в которых лежат его три непараллельные грани:
x + 2>> + 3z-12 = 0, 3x-y + 2z-6 = 0, 2x + 3>>-z-18 = 0.
Написать уравнения плоскостей, в которых лежат три другие грани.
20. Составить уравнение плоскости, проведенной через точки
Р (1,-1,2), 0(3,1,2) перпендикулярно к плоскости
4x-5y + 3z-2 = 0.
21. Написать уравнение плоскости, проведенной через точку
Р (2,1,-3) перпендикулярно к двум плоскостям:
2x-3y + z-5 = 0; x + 4^-2z + 3 = 0.
22. Найти плоскость, параллельную плоскости x-2j> + 2z-7 = 0 и
отстоящую от точки Р (4,1,-3) на расстоянии d = 2.
23. Составить уравнение плоскости, проведенной через точку
187
Mq (x0 , yQ, zQ ) параллельно вектору a = {a}, a2, a3} и перпендикулярно
плоскости Ax + By + Cz+ D = 0.
Ответы
17. (р^Ш0, Ф2=90°, ф3=0°, ф4=78°28'.
18. 10x + 3j>+1 lz-47 = 0. 19. x + 2j> + 3z-19 = 0, 3x-y + 2z-15 = 0,
2x+3y-z-8 = 0. 20. 7x+lly + 9z-14 = 0. 21. 2x + 5.y+1 lz + 24 = 0.
22. x-2y + 2z+10 = 0, x-2y + 2z-2 = 0.
х-х0 У~Уо z-z0
23. «1 а2 «3 = 0.
А В С
§ 4.2. Прямая в пространстве
Прямая в пространстве относительно прямоугольной декартовой
системы координат может быть задана различными способами. На-
пример, прямая однозначно определяется точкой и параллельным ей
вектором, двумя точками и т. п. В зависимости от способа задания
прямой рассматривают различные виды ее уравнений.
4.2.1. Параметрические уравнения прямой. Канонические
уравнения прямой. Уравнения прямой, проходящей через
две точки
Уравнение прямой, проходящей через данную точку
Л/о(хо,уо>^о) параллельно вектору а = {/,/«, л}, в векторном виде
записывается так
r = r0 + at9 (4.36)
где г -радиус-вектор любой точки
Af(x,y,z) прямой (рис. 4.5), rQ -
радиус-вектор точки Л/о, t-
параметр, принимающий всевоз-
можные действительные значения.
Вектор а называется направляющим
вектором прямой. Его координаты
пропорциональны направляющим
косинусам прямой.
Уравнение (4.36) в координатах примет вид:
188
х = х0 + It; y = yQ+mt; z = z0 + nt. (4.37)
Уравнения (4.37) называются параметрическими уравнениями
прямой. Если параметр t рассматривать как время, а уравнения (4.37)
как уравнения движения точки М, то эти уравнения будут определять
прямолинейное и равномерное движение точки М. При t = 0 точка М
совпадает с точкой Л/о. Скорость точки М постоянна и определяется
формулой
v = a//2 + т2 +п2. (4.38)
Исключая из уравнений (4.37) параметр t, получим канонические
уравнения прямой
= У~Уо = (439)
t т п
Уравнения прямой, проходящей через точки Mx(xuyX9zx) и
Л/2 (х2 , У2 ’ z2 ) имеют вид
(4.40)
*2-*1 У2-У\ *2"*1
Пример 1. Составить параметрические уравнения прямой, прохо-
дящей через точку Л/о(1, -2,3) и параллельной вектору а = {2,4,-5}.
Найти точку Р прямой, которой соответствует значение t = 2.
Решение. Пользуемся формулами (4.37). Так как в данном случае
х0 = 1, Уо=”2, z0=3, Z = 2, w = 4, л =-5, то параметрические
уравнения прямой имеют вид
х=1 + 2/, y = -2 + 4r, z = 3-5r
При t = 2 получаем
х = 1 + 2-2 = 5; _у = -2 + 4-2 = 6; z = 3-5-2 = -7.
На прямой фиксированная точка Р (5,6, - 7).
Пример 2. Составить параметрические уравнения прямых, прове-
денных через точку Л/о(5, -1,-4) в каждом из следующих случаев:
1) прямая параллельна прямой х = 3 + 6t, y = 2-4t, z-l-t;
2) прямая параллельна оси Ох;
3) прямая перпендикулярна плоскости x + 2y+3z-5 = 0.
189
Решение. 1) Так как прямая параллельна прямой х = 3 + 6/,
у = 2 - 4r, z = 7 -t, то они имеют один и тот же направляющий вектор
а = {6, -4, -1}. Подставляя значения х0 = 5, = -1, z0 = -4 и коор-
динаты вектора а в формулы (4.37), получим параметрические урав-
нения прямой
x = 5 + 6r, y = -l-4r, z=-4-r
2) Вектор, параллельный оси Ох, имеет координаты у = 0, z = О
(координата х равна длине вектора, взятой с соответствующим знаком).
В качестве направляющего вектора можно взять вектор а = {1,0,0},
совпадающий с ортом 7, поэтому x = 5 + f, у = -1, z = -4.
3) Поскольку вектор п = {1,2,3} перпендикулярен плоскости
х + 2у + 3z - 5 = 0, то в силу условия он будет параллелен прямой. Сле-
довательно, параметрические уравнения прямой примут вид
х = 5+Г, у = -1 + 2/, z = -4 + 3r
Пример 3. Написать параметрические уравнения прямой, прове-
денной через начало координат перпендикулярно плоскости
4x-3y + 5z-7 = 0.
Решение. Вектор п = {4,-3,5} нормали к плоскости является на-
правляющим вектором прямой. Так как прямая проходит через начало
координат, то х0 = у0 = z0 = 0. Таким образом,
x = 4r, y = -3r, z = 5/.
Пример 4. Составить канонические уравнения прямой, проведен-
ной через точку Л/0(6,2,-3) параллельно вектору а = {4,-5,7}. Ле-
жат ли на этой прямой точки Р (2,7,-10), £2(10,-3,5), /£(3,4,7)?
Решение. Применяем формулы (4.39). Так как х0 = 6, yQ = 2,
z0 = - 3, I = 4, т = -5, п = 7, то канонические уравнения примут вид
х —6 _ у-2 _ z+3
-5
Подставляя в эти уравнения координаты точек Р, Q, R, соответст-
венно находим
190
2-6 7-2 -10+3 , 10-6 -3-2 5 + 3
= = = -1, = * ,
4-----------------------------------5-7-4--5-7
3-6 4-2 7 + 3
---* *
4-5---------7
Следовательно, точка Р лежит на прямой, а точки Q и R на прямой
не лежат.
Пример 5. Составить канонические уравнения диагоналей парал-
лелограмма, три вершины которого находятся в точках А (2,4,6),
В (-3,5,4), С (8,-6,2).
Решение. Задача сводится к составлению уравнения прямой, про-
ходящей через две точки. Напишем уравнение диагонали АС. По фор-
муле (4.40) получаем
х-2 у-4 z-б х-2 у-4 z-6
= = , = =----или
8-2----------------------------------6-4-2-6-6--10--4
х-2 _ у-4 _ z-6
~3~“'^5~“^2”‘
Поскольку точка D не дана, то уравнения диагонали BD напишем
как уравнения прямой, проходящей через точки В и S, где S-точка
пересечения диагоналей. Так как S является серединой отрезка АС, то
ее координаты равны полусуммам соответствующих координат кон-
цов, т. е. 5 (5, -1,4). Уравнения диагонали BD принимают вид
х + 3 у-5 z-4 х + 3 у-5
----= — = или = -
5 + 3 -1-5 4-4 4 -3
z-4 = 0.
Замечание. Если при подстановке координат точек в уравнения (4.40)
один или два знаменателя обращаются в нуль, то нужно приравнять нулю со-
ответствующий числитель. (Все три знаменателя не могут быть равны нулю
одновременно, так как точки и Л/2 различны.)
Пример 6. Даны вершины треугольника Р(6,-2,2), Q(4, -5, -4),
Я (-2,-17,0). Составить параметрические уравнения биссектрисы его
внутреннего угла при вершине Q.
Решение. Найдем вначале точку N пересечения биссектрисы со
стороной PR. Из элементарной геометрии известно, что биссектриса
внутреннего угла треугольника делит противоположную сторону на
i9i
части, Пропорциональные прилежащим сторонам. Так как
QP = 7(4 - 6)2 + (- 2 + 5)2 + (2 + 4)2 = 7;
QR = 7(- 2-4)2 +(-17+5)2 +42 = 14,
то 1= PN:NR = QP.QR = 7:14, т. е. / = ^.
По формулам (3.28) находим точку N:
6+|(-2) 10 -2+1 (-П)
V- ___£____Л,-_________к_____-_7-
Z
4° 4
,1 3
2
Напишем канонические уравнения прямой, проходящей через точ-
ки Q и N:
х-4 у+5 z + 4 х-4 у + 5 z + 4
— = — = — или —— = - = ——.
12-4 "7 + 5 4+4 _2 -2 16
3 3 3 3
Умножая все знаменатели на —,
получим канонические уравнения
биссектрисы внутреннего угла при вершине Q:
х-4 _ у + 5 _ z + 4
Обозначая буквой t равные отношения и выражая х, у, z через г, по-
лучим параметрические уравнения той же биссектрисы:
х = 4-Г, у = -5-3/, z = -4 + 8/.
Пример 7. Даны уравнения движения точки A/(x,y,z): х = 3 + 6г,
у = 5 - 2r, z = - 8+Зл Определить ее скорость.
192
Решение. В соответствии с формулой (4.38) получаем
v = V36+4+9 = 7.
Пример 8. Даны уравнения движения точки A/(x,y,z): х = 2+2/,
у = -2 - 2/, z = 1 +1, Вычислить расстояние, пройденное точкой М за
промежуток времени от = 1 до /2 = 6.
Решение. Определим начало и конец прямолинейного пути точки
М. При t = 1 находим
х = 2 + 21 = 4, у = -2-21 = -4, z = l + l = 2.
Итак, получили точку Мх (4,-4,2). При / = 6 получаем вторую точку
Л/2(14,-14,7).
Пройденное расстояние равно длине отрезка МхМ2:
d=M]M2 = 7(14“4)2 +(-14+4)2 +(7-2)2 = ^225 = 15.
Пример 9. Точка M(x9y9z) движется равномерно и прямолиней-
но из начального положения Л/0(2,12,-5) в направлении, противопо-
ложном вектору b = {-1,2,-2} со скоростью v = 12. Составить урав-
нения движения точки М и определить точку, с которой она совпадет в
момент времени / = 4.
Решение. Определим сначала координаты направляющего вектора
а. По условию а = - 16, X > 0, т. е. а = {X, -21,21}. Далее,
|a| = v = 12, поэтому -J12 + (-21)2 +(21)2 = 12 или 31=12, откуда
1 = 4. Следовательно, а = {4,-8,8}. Уравнения движения точки М
примут вид
х = 2 + 4/, у =12-8/, z = -5+8z.
Полагая в этих уравнениях t = 4, получим точку N (18,-20,27).
Задачи
1. Составить параметрические уравнения прямых, проведенных
через точку Л/о (5,-3,8) в каждом из следующих случаев:
1) прямая параллельна прямой х = 1-3/, у = 4+2/, z = 5-6/;
2) прямая параллельна оси Оу;
3) прямая параллельна оси Oz;
4) прямая перпендикулярна плоскости 4х+7у - 8z - 3 = 0.
2. Написать канонические уравнения прямой, проходящей через
7 Зак. 1816
193
точку Л/о(5,-3, л/2) и параллельной вектору, образующему с коорди-
q ТС тс w
натными ортами углы а = у ’ Р = у, Y = у- Лежат ли на этой прямой
точки Р(1, -2,3), 0(4,-4,0)?
3. Составить канонические уравнения сторон треугольника с вер-
шинами Р (2, -4,3), Q (4,6,7), R (5,2,-8) и уравнения его медианы,
проведенной из вершины R.
4. Дан треугольник с вершинами А (4,1, -1), В (7,4, - 5),
С (-5,13,8). Написать параметрические уравнения биссектрисы внеш-
него угла при вершине А.
5. Составить уравнения траектории точки М (х, у, z), движущейся
прямолинейно и равномерно в направлении вектора b = {2,-2,1} из
начального положения Л/0(4,6,-7) со скоростью v = 15.
6. Написать уравнения траектории точки M(x,y,z), которая,
двигаясь прямолинейно и равномерно, прошла расстояние от точки
A/j(l,7,-5) до точки Л/2(21,-48,45) за промежуток времени от
Г, = 0 до t2 = 5.
Ответы
1. 1) x = 5-3r, y = -3 + 2t, z = 8-6t; 2) х = 5, у = -3 + Г, z = 8; 3)
х — 5
х = 5, у = -3, z = 8 + f; 4) x = 5 + 4r, y = -3 + 7r, z = 8-8f. 2.—— =
у + 3 z-<j2 ~ х-2 у + 4 z-3
=----= —р=—. На прямой лежит точка О. 3.-=-=-;
1 41 *15 2
х-4 _ у-6 _ z-7 x-2_y+4_z-3 х-5 _ у-2 z+18
1 ~ -4 “"-15’ ~Т~6~ ~УТ’ -1 13
4 х-4 = j^-1 = z+l 5 х = 4+10/ _y = 6-10r, z = -7+5f
6-17
6. x = l+4r, y = l-\\t, z = -5+10r.
4.2.2. Прямая как линия пересечения двух плоскостей.
Взаимное расположение двух прямых в пространстве
Прямая как линия пересечения двух плоскостей определяется со-
вместным заданием двух уравнений первой степени:
194
Atx + Bxy + C,z + D\ = 0;
A2x+ B2y+C2z+D2 = 0,
(4.41)
при условии, что коэффициен-
ты Л|, В,, С, первого не про-
порциональны коэффициен-
там А2,В2,С2 второго
За направляющий вектор
прямой (4.41) можно принять
векторное произведение
а=[«1й2], где
Л1 = {^i, Яр С|},
й2 = {А2, В2, С2 } - векторы
нормалей к соответствующим
плоскостям (рис. 4.6):
л, с(
л2 с2
-4|
Л2
5,
в2
. (4.42)
Канонические уравнения прямой (4.41) имеют вид
л Ao
в, с,
в2 с2
У-Уо
А, Сх
^2 ^2
(4-43)
а ее параметрические уравнения запишутся так:
х = х0 +
В\ С,
в2 С2
С У = Уо-
4 С,
л2 с2
Г, z = z0 +
By
В2
t.
(4.44)
At Bi ’
Л2 В2
4)
Л
Даны две прямые своими параметрическими уравнениями:
х = Xj + lxt, y = yx+mxt, z = zx + nxt\ (4.45)
x = x2 + y = y2+ z = z2 +
(4.46)
195
Рассмотрим определитель
/, /И! И,
д = /2 тг П2 х2~х\ У2-У1 Z2-Z!
(4.47)
составленный из коэффициентов, входящих в уравнения (4.45), (4.46).
I. Равенство
А »») «1
/2 т2 «2
*2-*1 z2"zl
= 0
является необходимым и достаточным условием принадлежности двух
прямых одной плоскости.
1. Если в определителе (4.47) все строки пропорциональны, т. е.
Z2 = 1Z], т2 = Ати,, п2 = АЛ], х2- х} = ц/,, у2 - у} = pjWj,
22-21=^,
(4.48)
то прямые (4.45) и (4.46) совпадают.
2. Если пропорциональны только первые две строки, т. е.
/2 = Ц, т2 = Ajwj , п2 = A/jj (4.49)
то прямые (4.45) и (4.46) параллельны.
3. Если А = 0, но условие (4.49) не выполнено, то прямые (4.45) и
(4.46) пересекаются.
II. Если А 0, то прямые (4.45) и (4.46) скрещиваются.
Пример 10. Написать канонические и параметрические уравнения
прямой:
3x-4>> + 5z-10 = 0;
6x-5y + z-17 = 0.
Решение. Чтобы воспользоваться формулами (4.43) и (4.44) необ-
ходимо найти координаты направляющего вектора а. Для этого удоб-
но поступить следующим образом. Составим таблицу из коэффициен-
тов при текущих координатах в данных уравнениях:
196
3 -4 5>
6 “5 1)
Закрывая поочередно один столбец этой таблицы, вычислим полу-
ченные определители и возьмем второй определитель со знаком минус.
Получим координаты направляющего вектора а:
1 =
-4
-5
= 21; /и = -
= 27; и =
-4
-5
= 9.
5
1
3 5
6 1
3
6
Возьмем теперь какую-нибудь точку данной прямой. Для этого
нужно придать конкретное значение одной из координат, значение
двух других определятся системой уравнений. Положим, например,
2 = 0, тогда исходные уравнения примут вид:
Зх-4у-10 = 0; 6х-5у-17 = 0.
Решая эту систему, получим х0 = 2, yQ = -1. Следовательно на
прямой фиксирована точка Л/0(2, -1,0). Уравнения (4.43) запишем
так:
х-2 у+1 z х-2 у +1 2
----= -----= — или------------=—.
21 27 9 7 9 3
Параметрические уравнения (4.44) принимают вид:
х = 2 + 7г; у = -1 + 9г; 2 = 3г.
Замечание. Точку Л/о на прямой можно выбрать произвольно, по-
этому в уравнениях (4.43) и (4.44) при разных выборах Л/о окажутся различ-
ные числа х0,у0,20 для одной и той же прямой. Координаты направляющего
вектора определяются с точностью до постоянного множителя.
Пример 11. Составить уравнения оси Ох.
Решение. Ось Ох можно рассматривать как линию пересечения
двух плоскостей Oxz и Оху. Уравнение плоскости Oxz есть у = 0, а
уравнение плоскости Оху -2 = 0, поэтому ось Ох имеет следующие
уравнения:
у = 0; 2 = 0.
197
Пример 12. Привести уравнения прямой
2x-y+2z-5 = 0;
2x+y-4z-7 = 0
к уравнениям в проекциях на координатные плоскости Oxz, Oyz.
Решение. Одну и ту же прямую можно представить множеством
разных систем двух уравнений первой степени.. В частности, прямую
(4.41) можно рассматривать как линию пересечения двух плоскостей,
проходящих через нее и перпендикулярных двум координатным плос-
костям.
Представим данную прямую как линию пересечения двух плоско-
стей, проходящих через нее и перпендикулярных плоскостям Oxz и
Oyz. Плоскость, перпендикулярная плоскости Oxz, параллельна оси Оу,
поэтому в ее уравнении коэффициент при у равен нулю. Исключая у
путем почленного сложения двух данных уравнений, получим
4x-2z-12 = 0 или z = 2x-6.
Исключая х путем почленного вычитания второго уравнения из
первого, получим
Следовательно, уравнения прямой в проекциях на плоскости Oxz и
Oyz, имеют вид:
о 11*
z = 2x-6; z = — у—.
3Л 3
Пример 13. Найти уравнение проекции прямой
х-2 у+1 z-5
"У” —"7"
на плоскость
x-3y + 2z-7 = 0.
Решение. Проекция прямой на плоскость представляет собой ли-
нию пересечения этой плоскости и плоскости, проходящей через дан-
ную прямую перпендикулярно данной плоскости.
Составим уравнение плоскости, проходящей через прямую
198
х-2 _ у+1 _ z-5
перпендикулярно плоскости x-3y + 2z-7 = 0. Пусть M(x9y9z) -
произвольная точка искомой плоскости, Л/0(2, — 1,5) -
принадлежащая ей точка прямой, тогда векторы
Л/0Л/= {х-2,у+1,z-5}, а = {6,-5,4}, Я={1,-3,2} лежат в одной
плоскости, поэтому их смешанное произведение равно нулю, т. е.
Л/о М • а • п = 0 или в координатах
х-2 у+1 z-5
6 -5 4 =0.
1 -3 2
Упрощая это уравнение, получим 2x-8y-13z + 53 = 0. Таким об-
разом, искомая проекция определяется уравнениями:
x-3y + 2z-7 = 0; 2х-8у- 13z + 53 = 0.
Пример 14. Исследовать взаимное расположение двух прямых в
каждом из следующих случаев:
1) х — 1 — 2/, у = 2 + St, z = -3 + 4t и
х = -4 + Зг, у = 2-Г, z = 5-2r;
2) х = 2 + Г, у = -3 - 2r, z = 4 - 2t и
х = 7 + 5г, у = 8-Юг, z = 9-10r;
3) х = 6 + 2/, у = 5 - /, z = 3 + 2/ и
x = 10 + 4f, у = 3-2t, z = 7 + 4/;
4) x = l + 2r, y = 7 + t, z = 3 + 4r и
x = 6 + 3r, у = -l-2r, z=-2+L
Если прямые пересекаются, найти их точку пересечения.
199
Решение.
1) Определитель (4.47) в данном случае принимает вид
д=
5
-1
4
-2
-2
3
-4-1 2-2 5-(—3)
Вычислим этот определитель:
Д =
-2
3
-5
5
-1
О
4
-2
8
13
3
-5
О
-1
О
-6
-2
8
= (-1)
13
-5
-6
8
= -74.
Так как Д * 0, то прямые скрещиваются.
2) Определитель (4.47) имеет вид
1
5
7-2
-2 -2 1 -2 -2
-10 -10 = 5 1 -2 -2 = 0.
8+3 9-4 5 11 5
Поскольку Д = 0 и только первые две строки пропорциональны, то
прямые параллельны.
3) Так как в определителе
2
4
Д =
10-6
-1 2
-2 4
-2 4
все строки пропорциональны, то прямые совпадают.
4) Так как определитель равен нулю, т. е.
7
9
9
21
27 7
= 0,
и первые две его строки не пропорциональны, то прямые пересекают-
ся.
200
Найдем общую точку этих прямых. Уравнение второй прямой за-
пишем в виде:
х = 64-35; у = -1-25; z = -2 + 5,
где 5 - параметр. Приравнивая соответствующие координаты, получим
систему уравнений
1 + 2/ = 6+35, 7-ьг = -1-25, 3 + 4/ = -2 + 5.
Исключая t из первых двух уравнений, получим 75 = -21, откуда
5 = -3. Из первого уравнения находим г = -2. (Третье уравнение сис-
темы при найденных значениях t и 5 обращается в тождество.) Под-
ставляя значение t в уравнения первой прямой или значение 5 в урав-
нения второй прямой, получим точку пересечения N (-3,5,-5).
Замечание. Одни и те же координаты точки пересечения двух прямых
получаются, как правило, при различных значениях параметра, входящего в их
уравнения. При отыскании общей точки пересекающихся прямых целесооб-
разно обозначить параметры в их уравнениях различными буквами.
Задачи
7. Составить параметрические уравнения прямых:
x4-y-6z-4 = 0;l 2x-y+3z-7 = 0;
1) Ч 2)
7 3x-y-5z-8 = 0;J 4x + 5y-6z-10 = 0.
8. Привести уравнения прямой
2x-3y + z-10 = 0;l
2x-y-z-6 = 0 j
к уравнениям в проекциях на координатные плоскости Оху, Oyz.
9. Составить уравнения проекции прямой
х = х0 + 7/, y = y0+m/, z = z0+«f
на плоскость Ах + By+Cz+ D =
10. Написать уравнения проекции прямой
x = 2 + 4f, у=1-/, z = 3-2/
на плоскость 3x-y+2z-7 = 0.
11. Составить уравнения: 1) оси Оу\ 2) оси Oz.
12. Исследовать взаимное расположение следующих пар прямых в
пространстве; если прямые параллельны, написать уравнение плоско-
сти, проходящей через них; если прямые пересекаются, найти их об-
201
щую точку и написать уравнение содержащей их плоскости:
1) х = 9/, y = 5t, z=-3+r и х = 27-9/, у = 15-5/, z = -r;
2) х = /, у = 8-4/, z = -3-3r и x + y-z = 0, 2x-y + 2z = 0;
2х + 3<у = 0;1 x + z-8 = 0; 1
3) > и >
z-4 = 0 J 2у + 3z-7 = 0;J
x + z-l = 0; 1 3x+y-z+13 = 0;l
4) > и >
x-2y + 3 = OJ y + 2z-8 = 0. J
Ответы
7. 1)х = 3+11/, ^=1+13/, z = 4r; 2)
x = -9t, у = 8, z = 5+14r
Ax + By + Cz +
+ D = 0. 10. 4x+14y + z-25 = 0, 3x-y + 2z-7 = 0. 11. l)x = 0, z = 0;
2)x = 0, >> = 0. 12. 1) совпадают; 2) параллельны и лежат в плоскости
12х-3>> + 8z = 0; 3) скрещиваются; 4) пересекаются в точке У(-3,0,4) и
лежат в плоскости Зх + 4у+5z -11 = 0.
4.2.3. Угол между двумя прямыми. Расстояние от точки до
прямой. Кратчайшее расстояние между двумя прямыми
Углом между прямой и координатной осью называется угол между
направляющим вектором прямой и ортом оси.
Углом между двумя прямыми называется угол между направляю-
щими векторами этих прямых.
Косинус угла между двумя прямыми
х = х1+/1Г, у = У) z = zl+n]t; (4.50)
х = х2+/2/, у = У2 +^2^ z = z2+n2t;
определяется формулой
AZ, +7И./И, +п,п>
COS(p = . -2 .
-y/j2+7Hj2 + Л]2 • + m2 + n?
Условие перпендикулярности прямых (4.50) и (4.51):
ZjZ2 + тхт2 + пхп2 = 0.
(4.51)
(4.52)
(4.53)
Расстояние от точки А/о(хо>.Уо>2о) Д° прямой (4.50) вычисляется
202
по формуле
W — X Л-Уо zi-*o ОТ! п{ 2 + Х]-Х0 Zj — Zo А "1 2 + *1-*0 У1~Уо li т} 2
у//2 + т2 +п,2 (4-54)
или в векторной форме
^^7[(Л-ГО)Д]2
где и г0 - радиус-векторы точек Мх и Л/о;
вектор (рис. 4.7).
Рис. 4.8
Кратчайшее расстояние между прямыми (рис. 4.8)
Рис. 4.7
Г =Tj +Я]/, г =г2
определяется формулой
|[«1 Л2]|
а - направляющий
(4.56)
или в координатной форме
203
Х2~ХУ У2-У1 z2~zl
А т1 »1
d = ±
12 т2 п2
(4.57)
где знак плюс берется в случае, когда определитель третьего порядка
положителен и знак минус - в противном случае.
Пример 15. Найти углы между координатными осями и прямой,
проходящей через две точки Л/^3,-4, V2), Л/2(4,-5,2>/2).
Решение. В качестве направляющего вектора можно взять вектор
д = Л/,Л/2 = {4-3>-5-(-4),2^—J2} =
= 0,-1, 5^}.
Направляющие косинусы этого вектора определяются формулами
(3.20)-(3.22):
1 1 « 1 &
cosa= , =—, cosp = —, cosy = —.
Vi+T+2 2 H 2.2
Следовательно, прямая образует с координатными осями углы
а = 60°; р = 120°; у=45°.
Замечание. В качестве направляющего вектора можно взять и вектор
М2 М} = {-1,1,- V2}, тогда получим углы eq = 120°, р1 = 60°,
Yj =135°, дополняющие углы а, £, у до 180°.
Пример 16. Определить направляющие косинусы прямой
х = 4+2/, у = -3-Г, z = 5-2r.
Решение. Направляющий вектор прямой есть вектор
а = {2,-1, -2}. По формулам (3.20)-(3.22) получаем направляющие
косинусы прямой:
2 2 q 1 2
V4+1+4 3 3 3
204
Пример 17. Найти угол между двумя прямыми:
x-5_y+3_z-6 х-2_у-4_z+1
-8
Решение. Первая прямая имеет направляющий вектор
oj = {7,2,-8}, а вторая а2 = {11,-8,-7}. В соответствии с формулой
(4.52) получаем
cos <р = ^11 + 2(-8)+(-8)(-7) = 117 = 1
/49+4+64 /121 + 64+49 /П7/234 /2 ‘
Следовательно, ф = 45°.
Пример 18. Составить уравнение прямой, проведенной через точ-
ку Л/0(2,-3,5) перпендикулярно двум данным прямым:
х—1 у-3 z+5 z-2 у+1 z+7
-1 ~ 2 ” 2 ’ 6 " 3 ~ -2 ‘
Решение. Уравнение прямой ищем в виде
х-2 _ у+3 _ z-5
I т п
Коэффициенты Z, т, п, определяемые с точностью до постоянного
множителя, в силу условия (4.53) должны удовлетворять системе двух
уравнений:
(-1)/+2ш+2л = 0;|
6/+З/и-2и = 0.J
Складывая и вычитая почленно эти уравнения, получим
5Z+5/w = O;l
3Z-2« = 0,J
2
откуда Z = -т, 1 = — п. Полагая, например, п = 3, получим Z = 2, т = -2.
Следовательно, уравнение прямой принимает вид
х-2 _ у + 3 _ z-5
2 ~ -2 “ 3 *
205
Пример 19. Найти расстояние от точки Л/о(1,-2,3) до прямой
x = 9-2r, y = 4-4r, z = 7 + 4r.
Решение. Пользуемся формулой (4.54). Так как х0 = 1, у0 = -2,
z0=3, Xj=9, У! =4, Zj=7, Zj=-2, Wj=-4, ^=4, то
4-(-2) 7-3 2 9-1 7-3
-4 4 + -2 4
2)2+(-4)2+42
9-1 4-(-2)
-2 -4
2 +402 -ь(—20)2 = УзбОО _ 10
•74+16+16 ” у/36
Итак, расстояние равно 10.
Пример 20. Вычислить расстояние между скрещивающимися
прямыми
х = 3+2/, у = 7-2/, z = l+3t;
х = 5+4/, у = 8, 7 = 2-6/.
Решение. Прежде всего можно убедиться, что прямые являются
скрещивающимися. В самом деле, определитель (4.47) отличен от ну-
ля, т. е.
5-3
2
4
8-7 2-1 2 1
-2 3=2-2
0 -6
1 2
3=6
-6 4
1 1
0 5
0 -6
= 56.
4 0
Так как определитель положителен, то по формуле (4.57) нужно
взять знак плюс. Подставляя соответствующие значения в эту формулу,
получим
5-3 8-7 2-1
2-2 3
2 1 1
2-2 3
4 0-6
7122 +(-24)2 +82
206
56
28
= 2.
Задачи
13. Найти направляющие косинусы прямых
х-5 _ у + 4 _ z-1 2x-2z + 3 = 0; 1
-2 2) 10х-12y+4z-5 = 0.J
14. Определить углы между осями координат и каждой из следую-
щих прямых:
х-4 _у + 6 _z-7 Зх-4<у = 0;1
’ V2 1 -1 ’ } 5x-3z = 0.J
15. Найти угол между двумя прямыми в каждом из следующих
случаев:
1Ч х-1 у+2 z-7 х-4 у + 5 z-6
1) = ---=----- и ----= ---=------;
4 -10 1 -11 8 7
х + у-4 = 0; 1 х-у = 0; 1
) V2y-z-l = 0j Лу-z-V2 = O.j
16. Вычислить расстояние от точки Л/0(7,-2,3) до каждой из
следующих прямых:
1) х = 3 —/, у = -5-2/, z=l + 2/;
2) х = 6+10/, у = -3+11/, z = 2 + 2/.
17. Вычислить кратчайшее расстояние между двумя прямыми:
х-3 у+1 z х + 2 z-3
1) -----= — и ---=-----, у-4 = 0;
-6 4 1 3 -1
2) х = 3 + /, y=\-t, z = 2 + 2/ и х = -/, у = 2 + 3/, z = 3/.
18. Найти расстояние между параллельными прямыми:
1 ) х = 5-4/, у = 2 +7/, z=l + 4/ и х = 8/, у-3-14/, z = 4-8/;
х-2 у+1 z х-7 у-1 z-3
7 3 4 2 3 4 2
19. Найти кратчайшее расстояние между диагональю куба и непе-
ресекающей ее диагональю грани, если ребро куба равно 1.
20. Составить уравнение прямой, проведенной через точку
Л/0(4,7,-5) перпендикулярно двум данным прямым
х = 3 + 2/, у = 8-/, z = -l + 4/ и х=1 + 3/, у = -5 + /, z = 6+r.
207
21. Составить уравнение общего перпендикуляра к двум непарал-
лельным прямым
г = + axt, г = r2 + a2t.
Ответы
6 Л 2 3 6 Л 7
13. l)cosa = y, cosp = ——, cosy = у; 2) cosa =—, cosp =—,
cosy = ^-. 14. l)a = 45°, 0 = 60’, y = 120’; 2)a = 118°41', 0 = 68’54',
y = 36’52'. 15. l)(p = 135°; 2)<p = 60°. 16. 1) d = 5; 2)d = ^-. 17.
1) —; 2) -Д=. 18. 1) -V146; 2) 3. 19. 20. = =
13 VnO 3 V6 -12 1
21. (r-r1)a1a=0, (r-r2)a2a=0, где а=[а]9а2].
§ 4.3. Прямая и плоскость в пространстве
Угол между прямой
x = x0+Z/, у = Уо + т!, z = z0+nt (4.58)
и плоскостью
Ах+ By+Cz+ D = 0
определяется формулой
I Л/+В/и + Сл|
>1 А2 + В2 +С2 ^12 +т2 +п2
(4.59)
(4.60)
Координаты точки пересечения прямой (4.58) и плоскости (4.59)
находится из системы уравнений (4.58) и (4.59).
Условие параллельности прямой (4.58) и плоскости (4.59):
Al + Bm + Cn = Q. (4.61)
Условие, при котором прямая (4.58) лежит на плоскости (4.59):
Al + Bm+Cn = 0, Axq + ByQ+CzQ + D = 0. (4.62)
Условие перпендикулярности прямой (4.58) и плоскости (4.59):
208
ARC
— = — = — или Л = М, В = Л/и, С = Хл, Л,*о. (4.63)
I т п
Пучком плоскостей называется совокупность плоскостей, прохо-
дящих через данную прямую.
Уравнение пучка плоскостей, проходящих через прямую:
Aix + Bly+Ciz+Di=O,'\
> (4.04)
А2х +B2y + C2z+D2 =0]
имеет вид
a (Ахх + Вху+Cxz + Dx) + Р (А2х + В2у + C2z + D2) = 0, (4.65)
где аир принимают всевозможные действительные значения
(а2 +р2 *0).
Уравнение (4.65) можно записать так:
Ахх + Вху+Cxz + Dx + X ( А2х + В2у + C2z + D2) = 0, (4.65')
i Р Л
где Л = —, а^О.
а
Пример 1. Найти угол между прямой x = 5+f, у = -3 + /, z = 4-2r
и плоскостью 4х - 2у - 2z+7 = 0.
Решение. Применяем формулу (4.60). Так как М, т=1, п = -2,
А = 4, В = -2, С = -2, то
. |4-1 + (-2)1 + (-2) (-2)| 6 _1
Sm<₽ Vl+1 + 4 V16+4 + 4 4вЛд 2'
Следовательно, <р = 30°.
Пример 2. Найти точку пересечения плоскости
3x-4y+5z+16=0 ипрямой х = -6+2г, у = 7-Г, z = 8-3r
Решение. Решим совместно систему уравнений прямой и плоско-
сти. Подставим выражение для х, у, z в уравнение плоскости
3 (-6+20-4(7-0 + 5(8-30 + 16 = 0.
После упрощения получим
-5Г+10 = 0,
откуда t = 2. Из уравнения прямой при t = 2 находим координаты точки
209
пересечения х = -2, у = 5, z = 2.
Таким образом, искомой точкой пересечения является точка
N (-2,5,2).
Пример 3. Найти проекцию точки Р (3,2, -1) на плоскость
x-5y + 4z-31 = 0.
Решение. Задача сводится к отысканию основания перпендикуля-
ра, опущенного из точки Р на данную плоскость. Напишем уравнение
этого перпендикуляра (см. § 4.2, пример 3):
х = 3 + /, y = 2-5r, z = -l + 4r.
Находим точку пересечения перпендикуляра и данной плоскости:
(3 + Г)-5(2-5О + 4(-1 + 4г)-31 = 0, 42г-42 = 0, Г = 1.
Следовательно, проекцией точки Р на плоскость является точка
6(4,-3,3).
Пример 4. Найти проекцию точки Р(5,-6,7) на прямую
х=7-2/, y=l + 3r, z = 4 + f.
Решение. Искомая проекция является точкой пересечения данной
прямой и плоскости, проведенной через точку Р перпендикулярно этой
прямой. Составим уравнение указанной плоскости (см. §4.1, пример
1):
-2(x-5) + 3(y + 6) + (z-7) = 0 или 2x-3y-z-21 = 0.
Находим точку пересечения данной прямой и полученной плоско-
сти:
2(7-20-3(1 + Зг)-(4 + 0-21 = 0, -14г-14 = 0,
Г = -1.
Итак, точка (2(9, -2,3) является проекцией точки Р на данную
плоскость.
Пример 5. Найти точку, симметричную точке Р(2,7,1) относи-
тельно плоскости х - 4у+z4- 7 = 0.
Решение. Искомая точка Q является вторым концом отрезка PQ,
для которого серединой будет точка R - проекция точки Р на данную
плоскость. Найдем точку R. Уравнение перпендикуляра к плоскости,
проведенного через точку Р, имеет вид
210
x = 2 + r, y = 7-4r, z = l + L
Решим совместно систему уравнений перпендикуляра и данной плос-
кости
(2 + /)-4(7-4/) + (1 + /) + 7 = 0 или 18,-18 = 0, / = 1.
Следовательно, R (3,3,2) - точка пересечения. По формулам
(3.29), которые в данном случае целесообразно представить в виде
х2 =2х-х}, у2 = 2у-у}, z2 = 2z-z,,
находим точку Q (4, -1,3).
Пример 6. При каком значении п прямая
х = 2+5/, у = -3+2/, z=5+zrt параллельна плоскости
2x + 4y-6z + 7 = 0.
Решение. Обращаемся к условию (4.61) параллельности прямой и
плоскости. Подставляя соответствующие значения в это уравнение,
получим
2-5+4-2 + (-6)л = 0 или 18-6и = 0,
откуда п = 3.
Пример 7. При каких значениях В и D прямая
х-1 _ у + 2 _ z-4
-з
лежит в плоскости 4x+By-2z+D = 0?
Решение. Подставляя в уравнения (4.62) соответствующие значе-
ния, получим систему уравнений
4-5+В (-3) + (-2) 7 = 0, 4-1 +В (-2) + (-2) 4 +D = 0,
из которой определяем В = 2 и D = 8.
Пример 8. При каких значениях т и А прямая
х = 3 + 2/, у- -5 + mt, z=A + 6t перпендикулярна плоскости
y4x-2y + 3z-5 = 0?
Решение. Условие (4.63) в данном случае примет вид
= -2 = _3
2 т 6’
211
т. е — = — и — = —, откуда А = 1, т = -4.
2 2 m2
Пример 9. Составить уравнение плоскости, проходящей через точ-
ку Р(4,-1,1) и прямую
2x-3y+5z-7 = 0;l
4x + 2y-6z-5 = 0.J
Решение. Напишем уравнение пучка плоскостей, проходящих че-
рез данную прямую. В соответствии с уравнением (4.65’) получаем
(2х - Зу + 5z - 7) + X (4х + 2у - 6z - 5) = 0.
Подставляя в это уравнение координаты точки Р, будем иметь
[2-4-3(-1) + 5 1-7]+Х[4-4 + 2 (-1)-6 1-5] = 0,
9 + 31 = 0, Х = -3.
Из уравнения пучка при X = - 3 находим уравнение искомой плос-
кости
10x + 9y-23z-8 = 0.
Задачи
1. Найти угол между прямой
х = 8-2г, у = 7-2/, z = 9+4/
и плоскостью
6x-3y-3z+l = 0.
2. Найти проекцию точки Р(1,2,-3) на плоскость
6x-y + 3z-41 = 0.
3. Найти точку, симметричную точке Р(2,-4,5) относительно
прямой
x = l-3r, y = -3 + r, z = 3-4/.
4. Провести через точку пересечения плоскости x+y+z-l=0 с
прямой у=1, z+l = 0 прямую, лежащую в этой плоскости и перпен-
дикулярную данной прямой.
212
5. При каком значении / прямая
х-3 у + 2 z-5
"Т""”4"”~6~
параллельна плоскости 2х - 5у+3z - 7 = 0.
6. Составить уравнение плоскости, которая проходит через пря-
мую
3x-y + 2z + 9 = 0, x+z-3=0 и:
1) через точку W (4,-2,-3);
2) параллельно оси Ох\
3) параллельно оси Оу\
4) параллельно оси Oz.
Ответы
1. Ф = 30Г. 2. 0(7,1,0). 3.0^,—,-^J 4. x+y + z-l = 0,
x-l = Q. 5. / = 1. 6. I) 23х —2y + 21z-33 = 0; 2)y+z-18 = 0;
3) x+z —3 = 0; 4) x-y+15 = 0.
213
§ 4.4. Поверхности в пространстве. Сфера. Поверхности
вращения. Цилиндрические и конические поверхно
сти
Поверхностью в пространстве называется геометрическое место
точек, координаты которых удовлетворяют уравнению
F(x,y,z) = 0. (4.66)
Линия в пространстве как пересечение двух поверхностей опреде-
ляется двумя уравнениями:
Fx(x,y,z) = (y, 1
F2{x,y,z) = Q. J
(4.67)
Уравнение
(x-o)2+(y-Z>)2+(z-c)2 = R2 (4.68)
определяет сферу радиуса R с центром в точке S(a, b, с). Если
а = Ь = с = 0, получаем уравнение сферы радиуса R с центром в начале
координат:
x2+y2+z2=R2. (4.69)
Уравнение
Ax2 + Ay2 + Az2 + Bx + Cy+Dz+E = 0 (4.70)
с помощью дополнения до полных квадратов можно привести к виду
(x—a)2+(y — b)2+(z — c)2 = d.
(4.71)
Если > 0, то уравнение (4.71) определяет сферу радиуса R = y/d.
Если б7 = О, то уравнению (4.71) удовлетворяют координаты единст-
венной точки 5 (а, Ь, с). Если J<0, то уравнению (4.71) не удовле-
творяют координаты ни одной точки пространства.
Поверхность, образованная вращением линии /
* = <Pi(z); 1
У = Ф2(*) J
(4.72)
вокруг оси Oz (рис. 4.9), определяется уравнением
X2 +у2 = <p12(z) + (p22(z). (4.73)
214
Рис. 4.9
Цилиндрической поверхностью называ-
ется поверхность, описываемая прямой
(образующей), параллельной данному на-
правлению и пересекающей данную линию
(направляющую).
Уравнение цилиндрической поверхно-
сти, образующие которой параллельны оси
<9z, имеют вид
F(x,^) = 0. (4.74)
Уравнения направляющей цилиндриче-
ской поверхности (4.74):
Г(х,у) = 0;1
Z = 0. J
(4.75)
Конической поверхностью называется поверхность, описываемая
прямой, проходящей через данную точку (вершину конуса) и пересе-
кающей данную линию (направляющую конуса).
Пример 1. Составить уравнение сферы, если известно, что точки
Л/^4,-3,7), Л/2(2,1,3) являются концами одного из ее диаметров.
Лежат ли на этой сфере точки Л/3(4,-2,+7), Л/4(5,-3,4),
Л/5(7,2,3)?
Решение. Центром искомой сферы является середина отрезка
Мх М2, а ее радиус равен половине длины отрезка Мх М2. Координаты
середины отрезка МХМ2 находим по формулам (3.29), получаем точку
С (3, -1,5). По формуле (3.19) находим радиус сферы
R = СМ2 = 7(2-З)2 + (1 + 1)2 + (3-*5)2 = 3.
Подставляя в формулу (4.68) значения а = 3, Ь = -1, с = 5, R = 3,
получим уравнение сферы:
(х - З)2 + (у +1)2 + (z - 5)2 = 9.
Выясним, лежат ли точки Л/3, Л/4, М5 на этой сфере. Подставляя
координаты точек в уравнение сферы, находим:
(4-3)2+(-2+1)2+(7-5)2 = 1 + 1+4 = 6<9;
(5-3)2+(-3+1)2+(4-5)2 =4+4 + 1 = 9;
215
(7-З)2 +(2 + 1)2 + (3-5)2 = 16+9 + 4 = 29>9.
Следовательно, точка Л/4 лежит на сфере, точки Л/3 и М5 на
сфере не лежат.
Замечание. Точка Л/3 лежит внутри сферы, ибо ее расстояние до
центра сферы меньше радиуса; точка М5 лежит вне сферы, так как ее рас-
стояние до центра сферы больше радиуса.
Пример 2. Написать уравнение сферы, проходящей через четыре
точки Мх(1,1,0), М2(7,-11,0), Л/3(10,1,9), Л/4(-2,-11, + 9).
Уравнение сферы ищем в виде
(x-a)2+(y-b)2+(z-c)2 =R2.
Решение. Подставляя координаты точек М}, М2, Л/3, Л/4 в это
уравнение, получим систему четырех уравнений относительно четырех
неизвестных а,Ь,с и R:
(1 —а)2 +(1-6)2 +(0-с)2 = Я2;
(7-а)2+(-11-6)2+(0-с)2 = Я2; ’
(10-а)2 +(1-6)2 +(9-с)2 = Я2;
(-2-а)2+(-ll-Z>)2+(9-с)2 = Я2.
Решая эту систему уравнений, находим: а = 4, Ь = -5, с = 6,
Я = 9.
Следовательно, уравнение сферы имеет вид
(х - 4)2 + (у+5)2 + (z—6)2 =81.
Пример 3. Найти центр и радиус сферы
2х2 + 2у2 + 2? - 12х- 10у+8z+1 = 0.
Решение. Данное уравнение обладает следующей особенностью:
коэффициенты при квадратах координат равны между собой, уравне-
ние не содержит членов с произведениями координат. Это уравнение
можно привести к виду (4.71). Разделив обе части уравнения на 2, по-
лучим
х2 +у2 + z2 -6x-5y+4z + y = 0.
Дополним левую часть уравнения до полных квадратов:
216
(х2 -6х+9)+(/ -2-j/+yj+(z2 +4z+4)-9-y- 4 + ^- = 0
ИЛИ
( 5 A2 7с
(х-3)2+ у-- + (z+2)2=-^.
V 2) 4
Сравнивая полученное уравнение с уравнением (4.68), находим:
Пример 4. Найти точку пересечения сферы
(х-4)2 +(у+5)2 +(z-6)2 =81
и прямой х = 3-Г, у = -3 + 2/, z = 4-2r.
Решение. Чтобы найти точку пересечения сферы и прямой, необ-
ходимо решить совместно систему их уравнений. Подставим выраже-
ния для х, у, z через параметр t в уравнение сферы:
(-1 - О2 + (2+2/)2 + (-2 - 202 =81.
Раскрывая скобки и приводя подобные члены, получим
9/2 + 18f-72 = 0 или f2+2r-8 = 0.
Решая последнее уравнение, находим =-4, t2 =2. Из уравнений
прямой при = -4 получаем точку пересечения Мх (7, -11,12), при
t2 = 2 - точку М2 (1,1,0).
Пример 5. Какую поверхность определяет уравнение
х2+/=25?
Решение. Данное уравнение не содержит членов с координатой z.
В соответствии с формулой (4.74) заключаем, что уравнение
х2 + у2 = 25 определяет цилиндрическую поверхность с образующей,
параллельной оси Oz. В плоскости Оху уравнение направляющей этой
цилиндрической поверхности будет х2 + у2 =25. Это окружность ра-
диуса R = 5. Эта же линия в пространстве в соответствии с формулами
(4.75) определяется уравнениями:
217
х2 +у2 =25;
z = 0.
Следовательно, данное уравнение определяет прямой круговой ци-
линдр.
Пример 6. Дан эллипс
х2 Z2
а с
у = 0.
Вращая этот эллипс вокруг оси Oz, получим поверхность, называемую
эллипсоидом вращения. Составить ее уравнение.
Решение. Уравнения эллипса приведем к Ьиду (4.72), т. е. выразим
х и у как функции переменной z, найдем квадраты х и у:
( Г2А
х2=а2 1—y
I с )
/=0.
В соответствии с формулой (4.73) получим уравнение эллипсоида
вращения:
( т2
х2 +у2 =а2 1—у
I с )
или
Пример 7. Составить уравнение однополостного гиперболоида
вращения, полученного вращением гиперболы:
а2 с2 ’
у = 0
вокруг оси Oz.
218
Решение. Из уравнений гиперболы имеем
( т2>1
х2 =а2 I + -5- :
у2=0.
Складывая почленно эти уравнения, получаем искомое уравнение
однополостного гиперболоида:
(
х2+у2=а2 1+-у
I с )
или
х2 у2 z2
~5 + ~^~~5 =
а а с
1.
Пример 8. Дана ось круглого цилиндра
х = 9-Г, у = 4-2r, z = 7 + 2r и точка Л/0(1,-2,3) на его поверхности.
Составить уравнение цилиндра.
Решение. Пусть М (х, у, z) - произвольная точка данного кругло-
го цилиндра. Расстояние этой точки до оси цилиндра равно расстоя-
нию точки Л/о до той же оси. Найдем эти расстояния. По формуле
(4.54) получаем:
4+2 7-3
-2 2
д/202+202+ (—10)2 V900
V1 + 4+4 “ 79
4-у 7-z 2 9-х 7-z 2 9-х 4-у
-2 2 + -1 2 + -1 -2
7(-1)2 +(-2)2 + 22
219
7(2(4 —у)+ 2(7 —z)]2 + [2(9 —х)+(7 —z)]2 + [-2 (9-x) + (4-y)]2 _
7(22 - 2 y - 2z)2 + (25 - 2x - z)2 + (2x - у -14)2
V9
Так как dQ = d, то уравнение круглого цилиндра имеет вид
7(22 - 2у - 2z)2 + (25 - 2х - z)2 + (2х - у -14)2 = V900.
Упрощая это уравнение, получим
8х2 + 5у2 + 5z2 -4jy+4xz + 8.yz-156x-60y-138z+405 = 0.
Пример 9. Составить уравнение конуса, описанного около сферы
х1 + у2 + z2 = 4, если вершина конуса находится в точке 5 (0,0,8).
Решение. Напишем параметрические уравнения прямой, прохо-
дящей через точку S (0,0,8):
x = lt, у-mt, z = 8 + nt. (А)
Найдем точки пересечения этой прямой со сферой и потребуем,
чтобы эти точки совпадали, т. е. чтобы прямая касалась сферы. Под-
ставляя уравнения (А) в уравнение сферы, получим квадратное уравне-
ние относительно t
(It)2 +(mt)2 +(Z+nt)2 =4
ИЛИ
(/2+/и2+и2)/2+16л/ + 60 = 0. (В)
Уравнение (В) имеет равные корни, когда его дискриминант равен
нулю, т. е.
64л2 — 60 (Z2 + /и2 +и2) = 0
или
п2 -15(/2 +ги2) = 0. (С)
Итак, координаты направляющего вектора прямой, проходящей
через точку 5 и касающейся данной сферы, удовлетворяют уравнению
(С). Подставляя в это уравнение выражения Z, т, п из уравнений (А),
220
получим
(z-8)2-15(х2 +у2) = 0.
Следовательно, уравнение конуса имеет вид
15 (х2 +>»2)-(z-8)2 =0.
Пример 10. Направляющая конуса задана уравнениями
X2 Z2
—+ — = 1, у = 0,
9 25
вершина находится в точке S (0, -3,4). Составить уравнение конуса.
Решение. Напишем уравнения образующей конуса как прямой,
проходящей через точку S и произвольную точку N (х, у, z) направ-
ляющей. Если М (X, У, Z) - любая точка образующей и тем самым
любая точка конуса, то уравнение образующей примет вид
Х-0 y+3 = Z-4
х-0 у+3 z-4
илиХ = хГ, У+3 = (у + 3)Г, Z-4 = (z-4)r.
Из последних уравнений определим х, у, z:
X У+З-Зг Z-4 + 4/
х =—; у =------; z =-----
t t t
и подставим их выражения в уравнения направляющей. Так как у = 0,
У+3
то t =----. Исключая t из первого уравнения направляющей, получа-
ем
2
Z-4 + 4
25
или
X2 (3Z+4Y)2 (У+3)2
9 + 9-25 9
Раскрывая скобки, приводя к общему знаменателю и приводя по-
добные члены, получим уравнение конуса
25Х2 - 9Г2 + 9Z2 + 24ZY -150У- 225 = 0.
221
Замечание. Если направляющая конической поверхности задана
уравнениями F} (х, у, z) = О, F2 (х, у, z) = 0, то уравнения образующих этой
поверхности можно записать в виде
Х-х0 __ Y-y0 _ Z-z0
х-хр у-ур Z-Zp ’
где х, у z - координаты точки, принадлежащей направляющей; х0, у0, z0 -
координаты вершины конуса; X,Y,Z - текущие координаты точки кониче-
ской поверхности. Исключая х, у, z из данных четырех уравнений, получим
искомое уравнение конической поверхности.
Пример 11. Написать уравнение цилиндрической поверхности,
направляющая которой дана уравнениями 4
х2 +у2 =25, z = 0,
а образующая составляет равные углы с осями координат.
Решение. В силу условия уравнения образующей можно записать
так:
Х-х _ Y-y _Z-z
l ~ l ~ l
или
X = x + lt9 Y = y + lt, Z = z + lt,
где X, У, Z - координаты любой точки образующей; х, у, z-
координаты точки направляющей; 1=т=п9 так как образующая состав-
ляет равные углы с осями координат.
Выразим из последних уравнений х, у, z:
х = Х-/г, у=У-/Г, z-Z-lt
и подставим их в уравнение направляющей.
Так как z=0, то Z = /г, следовательно,
x = X-Z, y=y-Z,
поэтому уравнение цилиндрической поверхности примет вид
(%-Z)2+(y-Z)2 = 25
ИЛИ
X2 + Y2 + 2Z2-2AZ-2XZ-25 = 0.
222
Замечание. Если уравнение направляющей искомой цилиндрической
поверхности заданы в виде F} (х, у9 z) = О, F2 (х, у, z) = 0, то уравнения об-
разующей этой поверхности можно записать так:
X-x Y-y Z-z
I т л
где х, у, z - координаты точки направляющей; Z, т, п- координаты направ-
ляющего вектора образующей; X, У, Z - текущие координаты точки обра-
зующей, или точки цилиндрической поверхности.
Исключая из этих уравнений х, у, z, получим искомое уравнение цилиндриче-
ской поверхности.
Задачи
1. Составить уравнение сферы в каждом из следующих случаев:
1) сфера проходит через точку Л/о(3,-1,4) и имеет центр
С (1,-3,5);
2) сфера имеет центр С (4,2,3) и касается плоскости
6x-3y+2z + 4 = 0;
3) сфера проходит через три1 точки A/j (3, — 1,9), Л/2(7,-2,6),
М3(4,2,5) и ее центр лежит в плоскости x+y+z-7 = 0.
2. Найти центр и радиус сферы Зх2 + 3/ + 3z2 -12x + 15>>-9z +
+ 33 = 0. Лежат ли на этой сфере точки (3, — 2,1), М2 (1,0,0),
Л/3(2,1,3)?
3. Имеет ли общие точки сфера х2 + у1 + z1 - 2х - 4у+8z - 28 = 0
с каждой из следующих прямых:
1) x = 7 + 6f, j> = -l-3f, z = -2 + 2f; 2) x = 2-t, y = 5-2t,
z = -l-2r
4. Составить уравнение сферы, проходящей через точку
N (3,-2,2) и окружность x2+y2+z2 =9, 2x + y-z + 2 = 0.
5. Какие поверхности определяются уравнейиями:
1) х2 +у2 = 9; 2) у2 +Z2 = 16; 3) х2 +z2 = 25.
6. Составить уравнение двуполостного гиперболоида вращения,
полученного вращением гиперболы:
X2 Z2
у = 0
а с
вокруг оси Oz.
223
7. Составить уравнение параболоида вращения, полученного вра-
щением параболы
х2 = 2z, у = О
вокруг оси Oz,
8. Написать уравнение круглого цилиндра, если даны уравнения
его оси
x = t, у =1 + 2/, z = -3-2/
и точка У (1,-2,1) на его поверхности.
9. Написать уравнение конуса с вершиной в точке S (1,2,4), обра-
зующие которого составляют с плоскостью 4x + 4y+2z-3 = 0 углы
<р = 45°.
10. Направляющая конуса задана уравнениями:
2 2
—+—=!, z=0,
16 9
вершина конуса находится в точке S (5,0,3). Составить уравнение ко-
нуса.
11. Написать уравнение круглого цилиндра, образующие которого
касаются сферы х2 +у2 +z2 = 1 и составляют равные углы с осями
координат.
12. Составить уравнение круглого цилиндра, описанного около
двух сфер:
(х -1)2 * (у - 2)2 + (z+2)2 = 36; х2 + у2 + z2 = 36.
Ответы
1. 1) (х-1)2+(у+3)2+(z-5)2 = 9;
2) (х — 4)2 + (у - 2)2 +(z — 3)2= 16. Указание. Радиус сферы равен рас-
стоянию от центра сферы до плоскости. 3) (х-1)2 + (у+4)2 +(z-3)2
2 }2
М2 (— 5,5,-6); 2) общих точек
= 49.
лежит точка
М}.
нет.
мож-
2. о = 2, 6 = --,
2
3.1) A/j(7, — 1,-2),
4. х2 + у2 + z2 - 4х - 2у + 2z -13 = 0. Указание. Уравнение сферы
но искать в виде х2 + у2+z2 —9 + Х (2x + y-z+2) = 0. 5. 1) круглый ци-
линдр с образующей, параллельной оси (?z; 2) круглый цилиндр с образую-
щей, параллельной оси Ох, 3) круглый цилиндр с образующей, параллельной
224
X2 у2 Z2 2 2
оси Оу. 6. —r-+^-z-Г = “1- 7. х2+у = 2z.
а а с
8. 8х2 + 5у2 + 5z2 -4xy+8yz + 4xz+16x+14y+22z-39 = 0. 9. х2 + у2 +
+ 7z2- 16xy-8xz-8yz + 62x + 44y-32z-ll = 0. 10. 9ЛГ2+ 16У2+9Z2 +
+30AZ+96Z-144 = 0. 11, x2+y2+z2-xy-yz-xz = ^. 12. 117x2 +
+18/ +1 Sz2 + 32xy - 32jz -1458 = 0.
§ 4.5. Поверхности второго порядка
Поверхностью второго порядка называется поверхность, опреде-
ляемая уравнением второй степени относительно текущих координат х,
У,z-
При соответствующем выборе прямоугольной декартовой системы
координат в пространстве уравнение поверхности второго можно привести к одному из видов: порядка
2 2 2 х у Z —+^у+—= 1 (эллипсоид, рис. 4.10); 2 2 2 х у Z — + - = 1 (однополостный гиперболоид, рис. 4.11); а Ь с х2 у2 z2 - у+ г- = -1 (двуполостный гиперболоид, рис. 4.12); а Ь с х2 у1 z2 , — 4~ Г = 0 (конус, рис. 4.13); х2 у2 — +-J- = 2z (эллиптический параболоид, рис. 4.14); а1 о X2 у2 — —= 2z (гиперболический параболоид, рис. 4.15); a1 Ь X2 у2 - у+^у = 1 (эллиптический цилиндр, рис. 4.16); а Ь X2 у2 — у~^у=1 (гиперболический цилиндр, рис. 4.17); а Ь у2 =2рх (параболический цилиндр, рис. 4.18); х2 у2 — = 0 (пара пересекающихся плоскостей, рис. 4.19); а b (4.76) (4.77) 4.78) (4.79) (4.80) (4.81) (4.82) (4.83) (4.84) (4.85)
8 Зак. 1816 225
—г = 1 (пара параллельных плоскостей, рис. 4.20); (4.86)
а
Рис. 4.15
226
227
Уравнения (4.76) - (4.87) называются каноническими уравнениями
поверхностей второго порядка.
Уравнения второй степени могут выражать, кроме поверхностей в
собственном смысле, и другие образы, которые лишь условно можно
назвать поверхностями.
Общее уравнение второй степени относительно х, у, z может быть
приведено к одному из уравнений (4.76) - (4.87) или к одному из сле-
дующих уравнений:
х2 у2 z2
—+^2“+”у = 0 (мнимый конус);
х2 у2
—= 0 (пара мнимых пересекающихся плоскостей);
а b
2 2 2
х у Z
-у + £у + -у = -1 (мнимый эллипсоид);
а Ь с
х2 у2
—+= -1 (мнимый эллиптический цилиндр);
а* 1г
х2
—у = -1 (пара мнимых параллельных плоскостей).
а
Уравнению (4.88) удовлетворяют координаты единственной точки
0(0,0,0), уравнению (4.89) - координаты точек, лежащих на прямой
х = 0, у = 0. Уравнениям (4.90) - (4.92) не удовлетворяют координаты
ни одной точки пространства.
Поверхности, образованные движением прямой, называются ли-
нейчатыми^ а прямые, целиком лежащие на поверхности, называются
прямолинейными образующими.
Однополостный гиперболоид (4.77) имеет два семейства прямоли-
нейных образующих:
(4.88)
(4.89)
(4.90)
(4.91)
(4.92)
lx z} ( у 1
Р-----=<7 1—г ;
V0 с) V о)
(х z
я -+~
I а с
(4.93)
bj
Р \ = я 1+Т Ь
\а с) V b J
(х z\ ( 1А
<7 ~+“ = Р •
\ а с J \ о J
> (4.94)
Гиперболический параболоид (4.81) имеет также два семейства об-
разующих:
228
(4.95)
(4.96)
Формулы преобразования прямоугольной декартовой системы ко-
ординат в прямоугольную декартовую систему:
при параллельном переносе координатных осей:
х = % + а, у = Г + 6, z = Z + c (4.97)
или
Х = х-а, Y = y-b, Z = z-c, (4.98)
где х, у, z - координаты некоторой точки в старой системе координат
Oxyz\ X,Y,Z - координаты той же точки в новой системе координат
O'XYZ; a,b,c - координаты нового начала О' в старой системе коор-
динат;
при повороте координатных осей:
х = X cos»! + Kcosa2 + Zcosa3;
у = JTcosPj + KcosP2 +Zcosf$3;
Z = X cosy! + Y cosy 2 + Z cosy 3,
(4.99)
где a19a2,a3 - углы, образуемые осью Ox соответственно с новыми
осями OX, OY, OZ\ Р1,Р2»Рз’ Y1» Уг» Уз -углы’ образуемые соответ-
ственно осью Оу и осью Oz с новыми осями (или eq,У1 -углы,
образуемые новой осью ОХ соответственно со старыми осями Ох, Оу,
Ozht. д.).
Пример 1. Уравнение поверхности
9x2 + 16/+36z2-18x+64y-216z+253 = 0
привести к каноническому виду и определить вид поверхности.
Решение. Преобразуем левую часть уравнения, дополняя соответ-
ствующие члены до полных квадратов:
9(х2 -2х + 1) +16(/ +4y+4) + 36(z2 -6z+9)-9-64-
-324 + 253 = 0,
9(х-1)2+ 16(j+2)2+36(z-3)2 = 144.
229
Разделив обе части уравнения на 144, получим
(х-1)2 t (у+2)2 | (z-З)2
16 9 4
Вводя новые координаты по формулам (4.98)
% = х-1, У = у+2, Z = z-3,
последнее уравнение перепишем в виде
Сравнивая это уравнение с уравнением (4.76), заключаем, что дан-
ная поверхность - эллипсоид с полуосями а = 4, b = 3, с = 2.
Следовательно, исходное уравнение также определяет эллипсоид с
указанными параметрами и центром в точке О' (1, -2,3).
Замечание. Если а = Ь то уравнение (4.76) определяет эллипсоид
вращения. При a = b = с= R уравнение (4.76) является уравнением сферы
радиуса R с центром в начале координат.
Пример 2. Какую поверхность определяет уравнение
4х2 - 9/ + 36z2 -16х - 54у - 72z - 65 = 0.
Решение. Преобразуем левую часть уравнения:
4(х2-4х+4)-9(у2 + 6j+9)+36(z2-2z+l)-16+81-
-36-65 = 0
или
4 (х-2)2-9(у+3)2 +36(z-l)2 =36.
Разделив обе части уравнения на 36 и введя новые координаты по
формулам
% = х-2, Г = у+3, Z = z-1,
получаем
Изучим форму этой поверхности с помощью метода сечений. Най-
дем главные сечения. В сечении поверхности плоскостью OXY полу-
чим гиперболу
230
X2 Y2
9 4
= 1, Z = 0;
в сечении плоскостью OYZ - гиперболу
Y2 Z2
-----+ — = 1, % = 0;
4 1
в сечении плоскостью OXZ - эллипс
y2 Z2
—=1, Г = 0.
9 1
параллельная плоскости OXY, пересекает поверхность
Плоскость,
по гиперболе
Плоскость,
по гиперболе
Плоскость,
по эллипсу
X2 г2_. Л2
--------— 1---, Z — п.
9 4 1
параллельная плоскости OYZ, пересекает поверхность
4 1 9
параллельная плоскости OYZ, пересекает поверхность
V2 Z2 , Л2 v ,
—+— = 1+—, У = й.
9 1 4
Анализируя сечения, заключаем, что данная поверхность является
однополостным гиперболоидом.
х2 у2 Z2 х2 у2 Z2
Замечание. Уравнения —-----—=1,---------jn+—+ —=1 0ПРе"
а о с2 а о с
деляют однополостные гиперболоиды. Эти уравнения того же типа, что урав-
нение (4.77). В правой части все эти уравнения содержат единицу, в левой
части-только квадраты всех координат, причем два коэффициента положи-
тельны, один - отрицателен.
Пример 3. Определить вид поверхности
Зх2 - 4/ + 6z2 + 24х+iy - 36z+122 = 0.
Решение. Упрощая уравнение, получим
3(х2 + 8х + 16)-4(у2-2y+l)+6(z2-6z+9)-48+4- 54 + 122 = 0,
231
3(х+4)2-4 (у-1)2 +6(z-3)2 =-24,
(х + 4)2 (у-1)2 , (z-З)2 =
8 6 4’
Это уравнение можно записать так:
X2 Y2 Z2
+— = -1,
8 6-4
где Х = х+4, Y = y-l, Z = z-3.
С помощью метода сечений можно убедиться в том, что уравнение
определяет двуполостный гиперболоид.
х2 у2 z2 х2 у2 z2
Замечание. Уравнения —---^-4—= —2"+ —+— = -!
а о с а о с1
являются уравнениями двуполостных гиперболоидов. Эти уравнения, как и
уравнение (4.78), в правой .части содержат отрицательную единицу, в левой
части - два положительных и один отрицательный коэффициент при квадратах
координат. Уравнение (4.78) можно записать в виде
2 »2 2
abc
где в правой части стоит единица, но в левой части только один коэффициент
положителен, два других - отрицательны.
Пример 4. Уравнение поверхности
4х2 - 9/- 8х - З6.у - 72z+184 = О
привести к каноническому виду. Определить, какую поверхность пред-
ставляет это уравнение.
Решение. Преобразуем левую часть уравнения:
4(х2-2х+1)-9(у2 +4j+4)-72z-4 + 36+184 = 0,
4 (х-1)2 -9 (у+2)2 = 72 (z-3).
Разделив обе части уравнения на 36, получим
(£zl)i_(z±2)i=2(z_3)
9 4
или
232
где % = х-1, Г = у+2, Z = z-3.
Сравнивая полученное уравнение с уравнением (4.81), заключаем,
что данная поверхность является гиперболическим параболоидом, для
которого а = 3, 6 = 2.
у2 Z2 X2 Z2
Замечание. Уравнения —т---у- = 2х, —----Y = определяют
о с а сг
гиперболические параболоиды. Каковы особенности их расположения относи-
тельно системы координат?
Пример 5. Какую поверхность представляет уравнение
X2 +4у2-6х + 16у+9 = 0?
Решение. Преобразуем левую часть уравнения:
(х2 -6х+9)+4(у2 +4у+4)-16 = 0, (х-3)2 +4(у+2)2 = 16,
(х-з)21 (у+2)2 r l
16 4 ’ 16 4
где Х = х-3, У = у+2. Принимая во внимание уравнение (4.82), за-
ключаем, что данное уравнение представляет эллиптический цилиндр,
для которого а = 4, b = 2.
X2 Z2 у2 Z2
Замечание. Уравнения —у + —=1, Т + —определяют зл-
ят с2 о с
липтические цилиндры с образующей параллельной-соответственно оси Оу,
оси Ох.
Пример в. Определить вид поверхности
у2-4х-6у+17 = 0.
Решение. Преобразуя данное уравнение, получим
(/-6j>+9)-4x-9 + 17 = 0, О>-3)2 =4(х-2).
Введем новые координаты У = у - 3, X = х-2, получим
Y2 = 4Х.
Следовательно, данная поверхность является параболическим ци-
линдром, для которого р = 2 (см. уравнение (4.84)).
233
Замечание. Уравнения у2 = 2pz, х2 =2pz определяют параболиче-
ские цилиндры с образующей, параллельной соответственно оси Ох, оси Оу.
п
Пример 7. Доказать, что урав-
нение z = ху определяет гиперболи-
ческий параболоид.
Решение. Перейдем к новой
системе координат OXYZ, получен-
ной из системы Oxyz путем вращс-
ния ее вокруг оси Oz на угол ф = —.
4
Воспользуемся формулами преобра-
зования координат при повороте
осей. Так как (рис. 4.22) 0^=—,
3 п Q п Q п
«2 = 4*. «3=-, р,=-. ₽2=-,
п
Yi = 2’ Y2 = 2> Уз
= 0, то формулы (4.99) примут вид
2
Подставляя выражения для х, у, z в уравнение z = ху, получим
л/9 -J9 1
Z = ^(X-Y)~-(X + Y) = ±(X2 -Г2)
или X2-Y2 =2Z.
Это уравнение получается из уравнения (4.81) при а = 6=1. Так
как уравнение (4.81) определяет гиперболический параболоид, то
уравнение z = ху является уравнением гиперболического параболоида.
Пример 8. Найти угол между прямолинейными образующими ги-
X2 у2
перболического параболоида---— = 2z, проходящими через точку
16 4
ЛГрД-).
I 8;
Решение. Прежде всего точка N лежит на данном гиперболиче-
ском параболоиде, так как ее координаты удовлетворяют его уравне-
нию:
234
16 4 8*
Преобразуем уравнение к виду
4 2JV4 2J
= 2z.
Два семейства прямолинейных образующих определяются систе-
мами уравнений:
Подставляя координаты точки У в эти уравнения, находим:
(4 П 3
Р\----=а-—;
<4 2) ч 8’
(4 О п
г2*
,(4 11 > -
U 2) 4
,(4 П , 3
q —+— = р —.
\4, 2) i
4 ' л '
откуда q = — р, р =4q .
Следовательно, уравнения прямолинейных образующих примут
вид
И 2)
4(1+/| = 2.3;
и 2)
или
3x-6j-16z = 0;
х + 2у-6 = 0;
х-2у-2 = 0;
x + 2^-16z = 0.
Первая прямая имеет направляющий вектор = {8,-4,3}, вторая
а2 = {8,4,1}, поэтому
51
COS<P = ^89-
235
Задачи
1. Какие геометрические образы представляются уравнениями:
X2 V2 Z2 V2 X2 V2 X2
о 2) Tr-2r=2z; 3> ТГ-—=1?
а Ь с b а Ь а
2. Какие поверхности определяют уравнения:
1) х2 = 2ру; 2) z2 = 2ру; 3) z2 =2рх?
В задачах 3-10 привести уравнения к каноническому виду и опре-
делить вид поверхности:
3. 2х2-бу2 + 3z2-12x-24y-24z+30 = 0.
4. —х2 +2у2 +3z2-4x+4y-24z+52 = 0.
5. x2 + 2y2-3z2-2x+8y+27z-18 = 0.
6. x2 + 2y2 +6x-18y-8z+49 = 0.
7. x2-3y2 +8x+6y+10=0.
8. x2 +4x-6y+22 = 0.
9. z2-2z-8x-7 = 0.
10. z2+4z+6y-20=0.
11. Доказать, что уравнение z2 =xy определяет конус.
12. Найти прямолинейные образующие однополостного гипербо-
лоида
проходящие через точку (4,-3,-2).
Ответы
1. 1) конус, 2) гиперболический параболоид, 3) гиперболический ци-
линдр. 2. 1)-3) параболический цилиндр. 3. Однополостный гиперболоид.
4. Двуполостный гиперболоид. 5. Конус. 6. Эллиптический параболоид.
7. Гиперболический цилиндр. 8. Параболический цилиндр. 9. Параболический
цилиндр. 10. Параболический цилиндр. 11. Указание. Повернуть систему
координат вокруг оси Oz на угол ф = ~ (см. пример 7).
4
3x + 4y-6z-12 = 0; 1 у + 3 = 0;
12. > и
3x-4y + 6z-12 = 0 J x + 2z = 0.
236
Гпава &
Матрицы и их применение
§ 5.1. Матрицы, основные действия над ними
Матрицей называется система тп величин, расположенных в пря-
моугольную таблицу из т строк и п столбцов. Величины, из которых
составлена матрица, называются её элементами. Элемент матрицы,
стоящий на пересечении строки с номером к (номера считаются сверху
вниз) и столбца с номером I (номера считаются слева направо) обозна-
чается через ак1. Числа к, I называются индексами элемента.
Матрица обозначается одним из символов: .
а\ 1 а12 а13
а21 а22 а23
а\п
а2п
< ат2 ат$
или
атп >
«11 «12 «13 . «1л
а21 а22 «23 •• «2л
ат1 «л>2 «m3 • атп
.(5.1)
Квадратной матрицей n-го порядка называется матрица, имеющая
п строк и п столбцов:
<а\\ ап а13 ••• а1п
а21 а22 а23 ••• а2п
к &п2 &пЗ ••• &пп >
Определителем квадратной матрицы называется такой определи-
тель, у которого элементы те же, что и у матрицы и стоят на тех же
местах.
Главной диагональю квадратной матрицы называется диагональ ее,
составленная из элементов ах,, агг,..., апп.
Симметрической матрицей называется квадратная матрица, у ко-
торой элементы, расположенные симметрично относительно главной
диагонали, равны друг другу, т. е.
аН = alk • (5
Диагональной матрицей называется квадратная матрица, у которой
все элементы, не находящиеся на главной диагонали, равны нулю.
Единичной матрицей называется диагональная матрица, у которой
237
каждый элемент, находящийся на главной диагонали, равен единице.
Нулевой матрицей называется матрица, все элементы которой рав-
ны нулю.
Суммой матриц А и В, имеющих одинаковое число строк и оди-
наковое число столбцов
Л =
а11 а12 а13
^21 а22 а23
а2п
^11 ^12 ^13
^21 Ь22 ^23
(5.4)
< ат\ ат2 атЗ
атп >
h.
fill
Ьт2 Ьтз
Ь/ПП )
В =
^2п
называется третья матрица С
СП С12
С21 С22
С13
С23
С\п
С2п
(5.5)
к Ст\ Ст2 СтЗ ••• Стп >
каждый элемент которой равен сумме соответствующих элементов
слагаемых матриц, т. е.
Сн=ан+Ьк1 (А = 1,2, ...,ти;/ = 1,2, ...,л). (5.6)
Сумма матриц А и В обозначается так:
С=А + В. (5.7)
Аналогично определяется разность матриц А и В
С=А-В, (5.8)
где
ckl ~ akl "~^к1‘
(5.9)
Произведением матрицы А на число X называется матрица В, ко-
торая получается из матрицы А умножением всех ее элементов на X:
Обозначение:
Ьц -
В = кА.
(5.Ю)
(5.Н)
238
Матрицы А и В называются равными
А = В, (5.12)
если они имеют одно и то же число строк и одно и то же число столб-
цов и если при этом каждый элемент ак1 матрицы А равен соответст-
вующему элементу Ьи матрицы В.
Произведением АВ двух квадратных матриц А и В одного по-
рядка называется третья квадратная матрица С того же порядка, со-
ставленная по следующему правилу: элемент ckh стоящий в матрице
С на пересечении £-й строки с Z-м столбцом, есть сумма произведений
элементов Л-й сроки матрицы А на соответствующие элементы 1-го
столбца матрицы В:
Ск1 = + а*2^2/ + ajH^/+---+ahA/- (5.13)
Определитель произведения АВ квадратных матриц А и В равен
произведению их определителей:
DAB=DADB. (5.14)
Определение произведения можно распространить и на неквадрат-
ные матрицы, у которых число столбцов матрицы множимого А рав-
но числу строк матрицы множителя В. При соблюдении этого усло-
вия множимое А может иметь любое число (т) строк, а матрица В -
любое число (л) столбцов. Матрица С = АВ будет иметь т строк и п
столбцов, ее элементы вычисляются по формуле (5.13).
Основные свойства действий над матрицами:
1. А + В = В+А\
2. Л + (В + С) = (Л + В) + С;
3. Х(Л + В) = М + ХВ;
4. (Х+р.) А = ЛЛ + цЛ;
5. Л(ВС) = (А8)С;
6. А(В+С) = АВ+АС.
239
Пример 1. Найти сумму матриц:
Я =
f 2
7
, -1
-3 4^ < -1
6 -5 , В = -7
8 9j [ 1
3 -4'
-5 5 .
-8 -8у
Решение. Обе матрицы имеют одинаковое число строк (три) и
одинаковое число столбцов (три). Такие матрицы можно складывать.
По формуле (5.6) получаем
-3+3 4+(-4)Л
6+(-5) -5+5
8 +(_8) 9+(-8)>
О
О
О О
1 О
О 1
Сумма матриц оказалась единичной матрицей.
Пример 2. Даны три матрицы:
' 1
А = 3
<2
О 2 Л ( 1
-4 5 ,В= 2
\ -3J V 1
-1 0> ( 3
3 4 , С= I
-5 б)
4 5Л
-3 2 .
6 -7,
Найти матрицу ЗЛ+4Д-2С.
Решение. По определению произведения матрицы на число, полу-
чаем:
' 3 о
ЗА= 9 -12
<6 3
6 1 '
15 , 45 =
-9J
4 -4 0"
8 12 16
4 - 20 24,
( 6 8
2С= 2 -6
16 12
10'
4 .
-14,
240
На основании формул (5.6) и (5.9) находим
( 3+4-6
f 3+4-6 0-4-8
ЗЛ+4В-2С = 9+8-2 -12 +12 - (-6)
6+0-10
15+16-4
6+4-16 3+(-20) —12 -9+24-(-14))
r 1 -12 -4 4
15 6 27
к-6 -29 29,
Пример 3. Найти произведение АВ двух квадратных матриц
Решение. Обе матрицы являются квадратными матрицами второго
порядка. Такие матрицы можно умножать. Применим формулу (5.13).
Эта формула имеет следующий смысл: чтобы получить элемент мат-
рицы произведения АВ, стоящий на пересечении строки к и столбца I,
нужно взять сумму произведений элементов строки к матрицы А на
соответственные элементы столбца I матрицы В («скалярное произве-
дение» строки к матрицы А на столбец I матрицы В).
В соответствии с формулой (5.13) элемент сн получается как
сумма произведений элементов первой строки матрицы А на элемен-
ты первого столбца матрицы В, элемент с21 - как сумма произведений
элементов второй строки матрицы А на элементы первого столбца
матрицы В:
сп = 1-3 + 2-7 = 17, с21 = 5-3 + (-6) 7 =-27.
Аналогично определяются элементы с12 и с22:
С}2 = 1 (-4) + 2 • 8 = 12, с22 = (“4) 5+(-6) 8 = -68.
Следовательно,
17 12
-27 -68
241
Пример 4. Найти произведения АВ и ВА матриц
-1 3'
-2 -6
0 3>
Решение. По формуле (5.13) получаем элементы си матрицы АВ:
сп = 5-4+3-4 + (-7)2 = 18; с21 = (-1)4+6-4 + (-3)2 = 14;
с31 = 2-4+(-4)4 + 1-2 = -6;
с12 =5(-1)+3(-2)+(-7)0 = -11; с22 = (-!)(-!) +
+6(—2)+(—3)0 = -11; с32 = 2(-1) + (-4)(-2)+10 = 6;
с13 = 5 • 3+3 (-6) + (-7) 3 = -24; с23 = (-1) 3+6 (-6) +
+ (-3) 3 = -48; с33 = 2 • 3+(-4) (-6)+1-3 = 33.
Итак,
г 18 -11 -24' -
АВ = 14 -11 -48 .
<“б 6 33 >
По той же формуле (5.13) находим элементы си матрицы ВА.
Меняя местами матрицы А и В, умножая последовательно первую,
вторую, третью строки матрицы В на первый столбец матрицы А,
получим элементы первого столбца матрицы ВА:
с'1} = 4-5+(-1)(-1) + 3-2 = 27; c2i = 4-5+(-2)(-1)+
+ (-6)2 = 10; с3| = 2• 5+0(—1) + 3• 2 = 16.
Аналогично вычисляются элементы второго столбца:
с'2 = 4-3+(-1)6+3(-4) = -6; с22 =4-3 + (-2)6+
242
+ (-6) (-4) = 24; с32 = 2-3+0-6+3(-4) = -6
и элементы третьего столбца матрицы ВА:
q'3 = 4 (-7) + (-1) (-3) + 31 = -22; с'23 = 4 (-7) + (-2) (-3) +
+(-6) 1 = -28; с33 = 2 (-7)+0 (-3) + 3 • 1 = -11.
Следовательно,
( 27 -6 -22 Л
ВА = 10 24 -28 .
к 16 -6 -11,
Сравнивая матрицы АВ и ВА и пользуясь определением равенст-
ва матриц, заключаем, что АВфВА.
Замечание 1. Умножение матриц не подчиняется закону перемести-
тельности.
Замечание 2. Для проверки правильности результатов, полученных
при умножении квадратных матриц, можно воспользоваться равенством (5.14).
Так как
dab ~
18 -11 -24
14 -11 -48
-6 6 33
= 132,
то равенство (5.14) действительно выполняется.
Замечание 3. Из формулы (5.14) следует равенство
&ва - Dа *&в-
В данном примере можно непосредственно убедиться, что DBA =132, следо-
вательно, указанное равенство выполняется.
Пример 5. Найти произведения АВ и ВА двух матриц
1 0 2 -П 1
, В =
3102/ 3
<4
Г
о
-2
243
Решение. Число столбцов матрицы А равно числу строк матрицы
В, поэтому можно умножать матрицу А на матрицу В. По формуле
(5.13) находим:
сн =1-2 + 01 + 2-3 + (-1)4 = 4;
с21 = 3-2 + 11 + 0-3 + 2-4 = 15;
с12 =11 + 00 + 2 (-2) + (-1) (-1) = -2;
с22 = 31 + 10+0(-2) + 2(-1) = 1.
Следовательно,
АВ =
4
15
-2
1
Число столбцов матрицы В равно числу строк матрицы А> по-
этому можно умножать матрицу В на матрицу А:
f 5 1 4 (Г
1 0 2 -1
ВА = -3 -2 6 -7
< 1 -1 S
Пример 6. Систему двух уравнений с двумя неизвестными
2х} + Зх2 = -5;
7Х|~4х2=26
(А)
записать в матричном виде.
Р е'ш е н и е. Систему эту можно представить так:
2х, + Зх2 f “ 5
7Xj -4х2 J 26 J’
Действительно, согласно определению, равенство двух матриц
имеет место в том и только в том случае, когда их соответственные
элементы равны. Поэтому последнее равенство имеет тот же смысл,
что и исходная система. Матрицу, стоящую в левой части равенства
(В), можно представить в виде произведения АХ двух матриц
244
(2 3 \ х,
.4= н!= 1
7 -4 J х2
Уравнение (А) принимает вид
( -5 )
АХ = В, где В = I.
I 26 I
Задачи
1. Даны матрицы
( 2
4
5
А-
1
-2
6
1
-7
Составить матрицу ЗА + 2В.
Найти произведения
2.
АВ и ВА двух квадратных матриц
-3) (6 I
L я=
5 Г 17—2
3.
Найти произведение АВ двух матриц
( о 1 А ( 1 о А
л = L в=
I о о г о о,
4.
Вычислить определитель матрицы произведения двух матриц
2 3 4
-5 6 7.
2 -3 -4 ,
В-
О
-1
6
-5
3
5. Найти произведение АВ двух матриц
-1
1
4
1
2
1
4
О
-3
-1
Можно ли умножать матрицу В на матрицу
А?
( 4
Л =
I 2
А =
А =
г 3
2
. 1 -з
1
О
2
— 1
О
, в =
3
2
О
1
5
2 Л
-4 .
6 ,
1
1
В =
245
6. Записать в матричной форме систему уравнений
5jq + 2х2 = 11;
7х) - 6х2 = 9.
Ответы
Г 8
-5^
-4
-5
28
( 3
4. DAB =396. 5. АВ =
Матрицу В на матрицу А умножать нельзя, так как число столбцов В не
равно числу строк А.
6. АХ = В, где< А =
( 5 2 ( Xi > ( 11
k 7 - 6 J Vx2 7 I
§ 5.2. Линейные преобразования на плоскости и в
пространстве. Аффинные преобразования.
Собственные векторы матрицы
Если каждой точке М плоскости (пространства) поставлена в со-
ответствие определенная точка А/' той же плоскости (пространства),
то говорят, что задано преобразование плоскости (пространства).
Если плоскость (пространство) подвергнуть некоторому преобра-
зованию Л, потом преобразованию В, то в результате возникает но-
вое преобразование, которое называется произведением преобразова-
ния А на преобразование В и обозначается символом ВА,
Преобразование, которое каждой точке М ставит в соответствие
точку М совпадающую с Л/, называется тождественным.
Если произведение ВА преобразования А на преобразование В
является тождественным, то преобразование В называется обратным
по отношению к А.
Преобразование плоскости, выражаемое формулами вида
х' = аих + апу + ап\
(5.15)
246
называется линейным.
Матрица
*п
*21
*12
*22 У
(5.16)
составленная из коэффициентов при х и у, называется матрицей линей-
ного преобразования (5.15), а ее определитель - определителем ука-
занного преобразования.
Линейное преобразование плоскости (5.15) называется аффинным,
если его определитель отличен от нуля, т. е.
*п
*21
0,2 #0.
*22
(5.17)
Аффинное преобразование плоскости вполне определяется задани-
ем трех неколлинеарных точек, в которые должны перейти три данные
неколлинеарные точки.
Линейное преобразование пространства определяется формулами
xz = а] хх + al2y + a13z+а14;
у' = а2хх + а22у + ^23z + *24»
z' = а31х + а32у + a33z + а34.
(5.18)
Линейное преобразование (5.18) называется аффинным преобразо-
ванием пространства, если его определитель отличен от нуля, т. е.
ап «12 «13
а21 а22 «23
«31 «32 а33
(5.19)
Аффинное преобразование пространства вполне определяется за-
данием четырех некомпланарных точек, в которые должны перейти
четыре данные некомпланарные точки.
При аффинных преобразованиях плоскости:
1) прямые линии переходят в прямые;
2) параллельные прямые преобразуются в параллельные прямые;
3) сохраняется простое отношение трех точек;
4) линии второго порядка преобразуются в линии второго порядка
(причем эллипс переходит в эллипс, гипербола - в гиперболу, парабо-
ла - в параболу);
5) сохраняется отношение ориентированных площадей соответст-
247
венных фигур, это отношение равно определителю преобразования
(5.17).
При аффинных преобразованиях пространства:
1) прямые переходят в прямые, плоскости - в плоскости;
2) сохраняется параллельность прямых и плоскостей;
3) сохраняется простое отношение трех точек;
4) поверхности второго порядка преобразуются в поверхности
второго порядка (причем сохраняется тип поверхности);
5) сохраняется отношение ориентированных объемов соответст-
венных тел, это отношение равно определителю преобразования (5.19).
Ненулевой вектор р называется собственным вектором квадрат-
ной матрицы Л, если линейное преобразование с матрицей А перево-
дит вектор р в коллинеарный ему вектор /Г, т. е.
р’ = ^-
(5.20)
Число X называется собственным числом (или «собственным значе-
нием») матрицы А, соответствующим собственному вектору р.
Координаты /, т собственных векторов матрицы (5.16) находят-
ся из системы уравнений
XZ = aH/ + a12m;
Хт = а2\1 + о22т
или
(яц -Х)/ + а12ти = 0;
a21Z + (a22 -Х)/и = 0,
(5.21)
(5.22)
где X - корень характеристического уравнения для матрицы А:
а11“^ а12
а21 а22 “
= 0.
(5.23)
Собственные векторы матрицы
' аи ап а\3
А = а2| ^22 а23 (5.24)
< а31 а32 а33 >
находятся из системы уравнений
248
(#H - X)/4-#12ти4-#13и = 0;
4*21/ + (#22 ” М т + а23п = 0; •
#31/ + а32т+(а33 - X) п = 0,
(5.25)
где X - корень характеристического уравнения
ан -1 «12 «13
«21 «22 «23 = 0. (5-26)
«31 «32 «зз -1
Если матрица А - симметрическая, то все корни ее характеристи-
ческого уравнения действительны.
Собственные векторы, соответствующие двум различным корням
характеристического уравнения, взаимно перпендикулярны.
Для всякой симметрической матрицы (5.24) существует тройка
взаимно перпендикулярных векторов.
Пример 1. Найти преобразование, переводящее точки М} (0,1),
Л/2(1,0), Л/3(1,1) в точки Л//(2,-1), Л//(1,4), Л/3 (5,6). В какую
точку переходит при этом преобразовании точка N (-1,2)? Какая
точка преобразуется в точку L' (-2, - 3) ?
Решение. Задача сводится к определению коэффициентов линей-
ного преобразования:
х' = апх+апу+ахз;\
, . . f (А)
у = а21х+а22.У+«2з]
Подставляя координаты соответственных точек и в эти урав-
нения, получим
2 — #i ] ’ 0 + С1\2 ’1 + #|3, — 1 — #21 * 0 4* ^22 * 1 + ^23 •
/
Подстановка координат точек М2 и М2 приводит к уравнениям
1 •— #| । • 1 + #|2 * ^13 ’ 4 — #21 ’ 1 + @22 * ^23 *
Подставляя координаты точек М3 и лу/ в уравнения (А), находим
5 — #| । • 1 + #|2 ’ 1 + #]з 9 6 — #21 * 14" #22 * 14" #23.
Итак, для определения шести неизвестных коэффициентов получено
249
шесть уравнений:
а12+л13-2; л22+а23 аи+а13-^ а21 + а23 -•4» 1
а11 + а12 + а13 = ^21 + а22 + а23 = 6- J
Решая эту систему (для чего можно, например, из первого и пятого
уравнения вычесть третье, из шестого - второе и четвертое), получим
=3, 6Z|2 = 4> «13 = —2, «21 ~ @22 = «23 = —3.
Следовательно, формулы данного преобразования имеют вид
х, = Зх + 4у-2;1
у' = 7х + 2у-3. j
Это преобразование является аффинным, так как его определитель от-
личен от нуля.
Найдем, в какую точку переходит при данном преобразовании точ-
ка 7V(-1,2). Подставляя ее координаты в формулы преобразования,
находим:
х'= 3(-1) + 4 2-2 = 3; / = 7(-1) + 2-2-3 = -6.
Итак, точка 7V(-1,2) переходит в точку N'(3,-6).
Подставляя координаты точки L' в эти формулы, получим:
-2 = Зх + 4у-2; -3 = 7х + 2у-3;
Зх + 4у = 0; 7х + 2у = 0,
откуда х = 0, у = 0. Следовательно, в точку L' (-2, - 3) переходит точ-
ка L (0,0).
Пример 2 Найти преобразование, обратное линейному преобразо-
ванию
х' = 2х + Зу-7; 1
z 4 (А)
/ = Зх + 5у-9. J v 7
Решение. Это преобразование является аффинным, так как его
определитель отличен от нуля. Если данное преобразование переводит
точку Л/(х,у) в точку Л/' (х^у'), то обратное ему преобразование
переводит точку М' (х^у') в точку Л/(х,у). Чтобы решить задачу,
250
нужно выразить х и у через х', у'. Так как определитель преобра-
зования отличен от нуля, то система (А) разрешима относительно х и
у. Решение можно найти с помощью определителей или способом
исключения одного из неизвестных.
Умножая первое уравнение на 5, второе на -3, складывая по-
членно, получим 5х' - Зу' = х - 8, откуда х = 5х' - Зу' + 8.
Умножая первое уравнение на -3, второе на 2 и складывая по-
членно, получим -Зх' + 2у' = у + 3, откуда у = - Зх' + 2у' - 3.
Следовательно, обратное преобразование имеет вид
x = 5x,-3j' + 8; 1
у = -3x, + 2y'-3. J
Пример 3 Найти собственные числа и собственные векторы матри-
цы
Решение. Характеристическое уравнение (5.23) в данном случае
принимает вид
5-Х 2
2 8-Х
Раскрывая определитель, получим
X2-13X4-36 = 0,
откуда
Xj=4, Х2=9.
Система уравнений (5.22) для определения координат собственных
векторов при Х| = 4 запишется так:
(5-4)/+2/и = 0; 1 /+2ти = 0;
2/+(8-4)/и = 0 J н™ 2/+4/и = 0.
Второе уравнение является следствием первого. Из первого урав-
нения находим отношение координат собственного вектора
/: т = 2: -1. Получен собственный вектор р} = {2, -1}.
251
При Х2 = 9 получаем систему уравнений
(5-9)/+2т = 0;1
2/+(8-9)/и = 0 J н™
-4Z+2m = 0;
2/-ти = 0,
откуда находим второй собственный вектор р2 = {1,2}.
Как и следовало ожидать, рх ± р2, ибо рхр2 = 2 • 1 + (-1) • 2 = 0.
Замечание. Зная один собственный вектор, мы тем самым знаем бес-
численное множество других, ибо всякий вектор, коллинеарный с собствен-
ным, сам является собственным и имеет то же самое собственное число. На-
пример, при Aq = 4 собственными являются векторы qx = {20,10},
f 2 11
Пример 4 Найти собственные значения и собственные векторы
матрицы
1 3^
5 1 .
1 L
Решение. Характеристическое уравнение (5.26) в данном случае
запишется так:
1-Х 1 3
1 5-Х 1
3 1 1-Х
= 0.
Применяя правило, определяемое формулой (2.2), находим
(1-Х) (5-Х)(1-Х)+3+3-9(5-Х)-(1-Х)-(1-Х) = 0.
Раскрывая скобки и приводя подобные члены, получим кубическое
уравнение
Х3-7Х2+36 = 0. (А)
Чтобы решить это уравнение, поступим следующим образом. Ме-
тодом проб найдем один из корней уравнения разделив потом ле-
вую часть уравнения на и приравняв к нулю результат, получим
квадратное уравнение, Корень Х1 ищем среди делителей свободного
члена уравнения (А). Для уравнения третьей степени имеет место тео-
рема Виета, в соответствии с которой произведение корней равно сво-
252
бедному члену. Нетрудно убедиться, чтоХ, = 3 есть корень уравнения
(А). Так как
(X3 - 7Х2 + 36): (X - 3) = X2 - 4Х -12,
то для определения двух других корней получим квадратное уравнение
Х2-4Х-12 = 0, откуда Х2 =6, Х3=-2.
Найдём собственный вектор рх, соответствующий собственному
значению Xj = 3. Система уравнений (5.25) примет вид
(1 - 3) /+/и+Зл = 0; - 2/ + ти+3/? = 0;
/+(5-3)>и+и = 0; ► или / + 2ти+л = 0;
3/+>и+(1-3)и = О J 3/+ти-2и=0.
Из последней системы находим
/:т:л = 1:-1:1, ^ = {1,-1,!}.
Аналогично определяем
р2 = {1,2,1}, р3 = {1,0,-1}.
Легко видеть, что
А ±Р2> Р2 Р1 -*-Рз-
Пример 5 Найти собственные значения и собственные векторы
матрицы
г 5 -2 -Г
Л= -2 2 -2
-2 5,
Решение. Характеристическое уравнение
5-Х -2 -1
-2 2-Х -2
-1 -2 5-Х
= 0 или X3 - 12Х2+36Х = 0,
т.е. Х(Х2 - 12Х + 36) = 0,
имеет корни X, = Х2 = 6, Х3 = 0.
253
Система уравнений (5.25) при Х3 = О запишется так:
5/-2т-л = 0;
-2/+2т-2л = 0; ►
-/-2ти+5л = 0.
Отсюда находим отношение координат собственного вектора
/:ш:л=1:2:1, рх ={1,2,1}.
При = Х2 = 6 система уравнений
(5-6)/-2m-п = 0; -/-2т-л = 0;
-2/+(2-6)т-2л = 0; > или -2/-4т-2л = 0; ►
-/-2т+(5-6)и = 0 -/-2т-л=0
сводится к одному уравнению /+2т+л = 0, поэтому отношение коор-
динат собственных векторов однозначно определить нельзя. Собствен-
ному значению X = 6 соответствует бесчисленное множество неколли-
неарных собственных векторов, перпендикулярных к вектору
~рх = {1,2,1}. Из этих векторов можно произвольным образом выбрать
два ортогональных вектора. Например, в качестве р2 возьмем вектор с
координатами /2 = 1, т2 = -1, п2 = 1 (они удовлетворяют уравнению
/+2т + п = 0). Тогда координаты собственного вектора
Рз = &> шз> лз)> ортогонального рх и р2, определятся уравнениями
/3+2т3+л3=0, /3 1 + т3(-1) + л3 1 = 0,
откуда
/3 = 1, т3 = 0, «з = -1.
Итак, получено три взаимно перпендикулярных собственных вектора:
А ={1,2,1}, р2 = {1,-1,1}, р3 = {1,0,-1}.
Задачи
1. Найти преобразование, переводящее точки A/f (0,0,0),
М2 (1,0,0), Л/3 (0,1,0), Л/4 (0,0,1) в точки Л/{(6, - 5,2),
М2 (8, -1,3), М3 (4, - 2,5), Л/4 (1, - 3, - 5). В. какую точку перейдет при
этом точка У (2,3,1)? Какая точка преобразуется в точку L' (1,4,-1)?
254
2. Найти преобразование, обратное данному преобразованию:
х' = х+2у-5; 1
у' = 2x + 3y-4. J
В задачах 3-9 определить собственные значения и собственные
векторы матрицы:
<2 2
6. 2 2
<1 1
< 7
8. А = -2
< 0
-8 10Л
11 2 .
2 2,
П
1 .
3 >
-2 О"
6 -2 .
-2 5,
Ответы
1. х'= 2x-2y-5z + 6, у'= 4x+3y + 2z-5, z'= x + 3y-7z + 2;
ЛГ(-1,14,6), £(1,1,1). 2. х = 2у’-Зх'-7, у = 2х'-у' + 6. 3. X, =
= 8, Х2 = 18, = {1, -1}, р2 = {1,1}. 4. X, =9, Х2 = -1, рх = {1,3},
р2 = {3, — 1}. 5.Нет собственных значений. 6. Х|—2, Х2=5, Х3=0,
р{ ={1,1,-2}, р2 ={1,1,1}, р3={1,-1,0}. 7. Х( =3, Х2=6, Х3=0,
Pj={l, 1,-1}, р2 = {1,-2,-1}, ={1,0,1}. 8. X! =3, Х2=6, Х3=9,
р1={1,2,2}, р2={2,1,-2}, р3 = {2,-2,1}. 9.Х]=9, Х2=18,
Х3 = -9, р} = {1,2,2}, р2 = {-2,2, -1}, ft = {2,1, -2}.
§ 5.3. Приведение общего уравнения линии второго
порядка к каноническому виду
Общее уравнение второго порядка относительно х и у
aitx2 + а22у2 + 2al2xy + 2ai3x + 2а23у + а33 = 0 (5.27)
255
с помощью преобразований прямоугольной системы координат
х = x'cosa-y'sina; 1 Аг = х,~хп;] , , >(5.28) и °Ч у — х sina + y cosa J у = у -у$ J (5.29)
приводится к одному из канонических уравнений:
X1 Y2 —у + — = 1 (эллипс); а о X1 Y2 (5.30)
— 1 (гипербола); а а Y2 = 2рХ (парабола); X2 Y2 — = 0 (две пересекающиеся прямые); а о X2 = а2 (две параллельные прямые); (531) (5.32) (5.33) (5.34)
X2 = 0 (две совпадающие прямые); (5.35)
X2 Y2
—у + — = -1 (мнимый эллипс); а и X2 Y2 —у + — = 0 (две мнимые пересекающиеся прямые); а b X2 = -а2 (две мнимые параллельные прямые). (5.36) (5.37) (5.38)
Если координатные оси новой системы Ох'у' направить по двум
взаимно перпендикулярным собственным векторам матрицы
1 _ ( а12 _ 1 л » Л21 “а12> V ^21 а22 7 (5.39)
составленной из коэффициентов уравнения (5.27), то члены второго
порядка
Ф (х, у) = а, ]Х2 + а22у2 + 2апху (5.40)'
преобразуются в* члены второго порядка
Ф' (х', у') = Х|Х/2 + Х2у'2, (5.41)
где Xj, Х2 - корни характеристического уравнения этой матрицы.
256
Полученное уравнение
Х^х'2 +Х2у'2 +2а1,3х/+2а23у'+а33 =0 (5.42)
с помощью преобразования параллельного переноса (5.29) приводится
к каноническому виду, т. е. к одному из уравнений (5.30) - (5.38).
Пример 1. Определить вид, параметры и расположение линии по
ее уравнению
13х2+10ху+13у2-72 = 0.
Решение. Выпишем коэффициенты уравнения: Оц=13,
2я12 = 10, а12 = 5, а22 = 13, а33 = -72, а13 = 0, а23 = 0 и составим
матрицу
Матрица А имеет собственные значения Xj=8, Х2=18 и собст-
венные векторы р] = {1,-1}, р2 = {1,1}. Вектор р, образует с осью
Ох угол а, определяемый равенствами (см. 3.20):
1 1
cosa = —т=; sina =—
V2 V2
Следовательно, a = -45°. Повернем систему Оху вокруг начала на
угол a = -45° (т. е. направим ось Ох' по вектору рх, ось Оу' - по
~р2 )• В новой системе Ох'у' уравнение линии в соответствии с форму-
лой (5.41) принимает вид
8х'2 + 18/2=72.
Разделив обе части уравнения на 72, получим
х'2 у'2
— + ^—=1.
9 4
Это уравнение эллипса с полуосями а = 3, b = 2.
Пример 2. Определить вид, параметры и расположение линии
5х2 + 4ху+8/ - 32х -56у+80 = 0.
9 Зак. 1816
257
Решение. Матрица А, составленная из коэффициентов при стар-
ших членах и ее характеристическое уравнение соответственно примут
вид
5-Х 2
2 8-Х
= 0.
Характеристическое уравнение
Х2-13Х + 36 = 0
имеет корни Х1 =4, Х2 =9.
Находим собственные векторы: р} = {2, -1}, р2 = {1,2}. Вектор рх
образует с осью Ох угол а, определяемый равенствами:
cosa = -7=; sina = —7=
V5 V5
(A)
Повернем систему Oxy на данный угол а, т. е. совершим преобразо-
вание координат (5.28):
В соответствии с формулой (5.41) члены второй степени преобра-
зуются следующим образом:
5х2 + 4ху + Зу2 = 4х'2 + 9/2.
Подставляя выражения для х и у из формулы (В) в оставшиеся
члены уравнения, получим
-32х-56у + 80 = -32
+ ^=у' |+80 = --^х'-^-у+80.
4$ ) V5 V5
Следовательно, исходное уравнение примет вид
258
ч & 144
4х'2 + 9/2 —т= х'-=- у'+80 = 0.
V5 75
Преобразуя это уравнение, получим
4 x'2-2-j=x'+-
I 75 5
+ 9 у'2
16 , • 64 1 4
~7=у +— —
75 5 J 5
z \2 / \2
_JL*J. + 80 = 0, Лх'—+9^'—М =36.
5 I 75 J I 75 J
(С)
Совершим теперь преобразование параллельного переноса по форму-
лам
(D)
Уравнение (С) перепишем в виде
V 2 у2
4Аг2+9У2 = 36 или---+ — =1. (Е)
9 4.
Следовательно, исходное уравнение является уравнением эллипса с
полуосями а = 3, 6 = 2.
Вид кривой и ее параметры а и b определены. Чтобы выяснить
расположение линии, найдем точку, в которой находится начало новой
системы координат (УХУ. Так как для точки (У (начало системы
1 8
(УХУ) Х = 0, У = 0, то из формул (D) определим х' = , у' = -^=-,
а из формул (В) найдем х = 2, у = 3. Итак, началом системы (УХУ
служит точка О'(2,3).
Построив в старой системе координат Оху точку О' (2,3), отло-
жив от нее векторы р} = {2, -1}, р2 = {1,2} и направив по ним коор-
динатные оси О'Х, О'У, построим эллипс (Е) в новой системе О'ХУ.
Тем самым определено расположение эллипса относительно старой
системы координат Оху.
259
Пример 3. Определить вид, параметры и расположение линии
7х2-24ху-38х + 24д'+175 = 0.
Решение. Характеристическое уравнение матрицы А, составлен-
ной из коэффициентов при старших членах,
7-Х -12
-12 0-Х "°
имеет корни X] =-9, Х2 = 16. Этим собственным значениям соответ-
ствуют собственные векторы Р]={3,4}, р2 = Вектор рх обра-
зует с осью Ох угол а, определяемый равенствами:
3 4
cosa = —; sma = —.
5 5
Повернем систему координат Оху на угол а. Формулы преобразова-
ния (5.28) запишутся так:
Исходное уравнение линии примет вид
о о ( 3 4 А (4 3
-9х/2 + 16у'2-38 -х'-у’ + 24 -х'+-у’ +175 = 0
I 5 5 ) U 5Z )
или
,2 ,, ,2 18 , 224 f _ _ _
-9xz + 16y х +—j-+175 = 0.
Преобразуя это уравнение, получим
п( л 2 , 1 > ,2 14 , 49 Л 1
-9 х + —х +— + 16 у +—у +— +9---------
( 5 25 ) V 5 25 J 25
49
-16—+ 175 = 0
25
или
260
или 9Х2-16У2-144 = 0,
У2
( 11 ( 7 Y
-9 х' + - + 16 /+— +144 = 0. (В)
V 5 ) V 5 )
После преобразования параллельного переноса
Х = х'+±, Y = y’+1- (С)
уравнение (В) запишется так
-9.Y2+ 16У2+ 144 = 0
откуда
X1
16 9
Уравнение (D) определяет гиперболу с полуосями а = 4, 6 = 3.
Найдем точку, в которой находится начало системы O'XY. Так как для
этой точки X = 0, Y = 0, то из формул (С) и (А) находим х = 1, у = -1.
Построив точку О' (1, -1) относительно старой системы Оху, отложив
из этой точки векторы рх = {3,4}, р2 = {4,-3} и направив по ним ко-
ординатные оси О'Х, O'Y, построим гиперболу (D) в новой системе
O'XY.
Пример 4. Определить вид, параметры и расположение линии
х2 + 2xy+j2 -8х+4 = 0.
Решение. Характеристическое уравнение
= 0 или (1-Х)2 — 1 = 0
имеет корни X, =2, Х2 = 0. Им соответствуют собственные векторы
Pi = {1,1}, Р2 = {“1, П- Вектор рх образует с осью Ох угол а, опре-
деляемый равенствами:
1.1
cos а = —==; sin а = —?=. (А)
& &
Повернем систему Оху на угол а, т. е. совершим преобразование
1-Х 1
1 1-Х
261
(В)
В новой системе Ох'у' уравнение кривой примет вид
2х,2-8| -J^x'—Ц у'1+4 = 0.
I V2 J2 J
Преобразуя это уравнение, получим
( 2 18
2 х'2-2 -==х' + 2 + -£=/-4 + 4 = 0,
I V2 J V2
С помощью преобразования параллельного переноса
X = x'-j2;
г=/
последнее уравнение приводится к каноническому виду
Х2 =—Y.
V2
<С)
(D)
Уравнение (D) определяет параболу с параметром р = -= = v2.
V2
Из уравнений (С) и (В) находим точку О' (1,1) - начало новой системы
координат O'XY. В этой точке находится вершина параболы.
Пример 5. Определить форму и расположение линии
х2 +у2 -2ху-х+у-2 = 0.
Решение. Характеристическое уравнение
1-Х -1
-1 1-Х
= 0 или (1-Х)2 -1 = 0
262
имеет корни X, = 2, Х2 = 0. Этим собственным значениям соответст-
вуют собственные векторы р} = {1,-1}, р2 = {1,1}. Вектор р} образует
с осью Ох угол а, определяемый равенствами:
cosa =
7
sina = -
Формулы преобразования координат при повороте осей на угол а
запишутся так:
1,1,
х = —7=Х +—7= у ,
42 42
1,1,
>> =—’
42 42
Уравнение линии в новой системе координат примет вид
„ ,2 ( 1 , 1 ,1 Г 1 , 1 ,К л
2х - —г=х +-7=-у + —у -2 = 0,
V V2 42 ) \ 42 42 )
2х'2—^х'-2 = 0, х'1—^х'-1 = 0.
V2
Преобразуем последнее уравнение:
х'2-2—I
I I I 1 л I , I
—---------1 = 0, х--------
8 J 8 I 2>/2
’ = 0
8
или
2 = 9
8 ’
где
1
2-Л”
3
Уравнение (В) определяет пару прямых X = -^=-
(А)
(В)
(С)
3
2-У2 ’
параллельных новой координатной оси О'Х.
Напишем уравнения этих прямых в старой системе координат
263
Оху. Из уравнений (А) находим
, V2 . .
х =—(х-у);
, V2,
У =—(х+у).
(D)
Из формул (С) и (D) получаем
(Е)
Уравнение (В) приводится к виду
(х-у-2)(х-у+1) = 0,
откуда получаем уравнения прямых:
х-у-2 = 0; х-у+1 = 0.
Замечание 1. Линия второго порядка, состоящая из двух прямых, на-
зывается распадающейся. Необходимое и достаточное условие распадения
линии (5.27) выражается равенством А = 0, где
Д =
«11 «12
а2\ а22
«31 «32
«13
«23
«33
Замечание 2. Установив, что линия распадающаяся, уравнения со-
ставляющих ее прямых можно найти приведением многочлена к сумме квадра-
тов по способу Лагранжа. Применим этот способ к данному уравнению. Вы-
пишем все члены, содержащие х, дополним их до полного квадрата, прибав-
264
ляя и вычитая соответствующие члены:
( 1 f 2
"Н+2 I '
+у2+у-2 = x-L-Д
п2
2 1 2 п
_/_у +/+>,_2 =
4
откуда Х“-у-2 = 0, х-у+1 = 0.
Пример 6. Доказать, что линия 2х2 -4у2-2ху-х-4у-1 = 0 рас-
падается на пару пересекающихся прямых. Найти уравнения этих пря-
мых с помощью способа Лагранжа.
Решение. Выпишем коэффициенты данного уравнения
а„=2, =-!,»„ =-4.«„=-l,aa=-2, «„=-> » сос»»м
определитель:
2
2
2
-4 -2
-2 -1
Так как Д = 0 (вторая и третья строки пропорциональны), то дан-
ная линия распадается на пару прямых (см. замечание 1).
Найдем уравнения этих прямых с помощью способа Лагранжа:
2х2-4у2 -2ху-х-4у-1 = 2 х2-ху--^-х -4у2-
—4у—\ = 2 х2
Г 1 И
+ — у+ —
I 2Z 4 J
У+
1 V Г
— I -4у2-4у-1 = 2 х-
1 П Т Г 1 2
265
1 1 1 t 2 . . -J 1 1 V 9 2
+—уч -4y-4y-l = 2x— у— —у -
4 16 J I 2 4 J 2
9 1 , J 1 1 У 9f 2 1
--у 1 = 2 x у у +2—y +
2z 8 I 2 4 J 2Y 2Z
1
+ —
4
= 0,
( i i r ( i Y
4 lx-у----9ly+- =0,
I 2Л 4 ) Y 2 J
J 1 1 ) J 1
2 x--у----3 У+ —
I 2Z 4 J Y 2
J 1 1 1 J 1
I 2Z 4 J Г 2
= 0,
L И з V, i о з
2x-y---3y 2x-y + 3y+— =0,
V Z 2 Z 2 Д Л 2 Z 2 J
(2x-4y-2) (2x + 2y+l) = 0,
2x-4<y-2 = 0, 2x + 2y+l = 0.
Итак, уравнения прямых имеют вид
х-2у-1 = 0, 2х + 2у+1 = 0.
Пример 7. Доказать, что уравнение
х2+4у2 +4ху-2х-4у+1 = 0
определяет пару совпадающих прямых. С помощью способа Лагранжа
найти уравнения прямых.
Решение. Так как
1 2 -1
то линия - распадающаяся.
266
Найдем уравнения прямых с помощью способа Лагранжа:
х2 +4у2 +4ху-2х-4у+1 = [х2 +2х(2у-1)+(2у-1)2 ]-
-(2у-1)2 +4у2— 4у + 1 = [х + (2у—I)]2-(4_у2 -4у + 1) +
+ 4у2-4у+1 = (х+2у-1)2 = 0.
Следовательно, прямые определяются уравнениями:
х + 2у-1 = 0, х+2у-1 = 0.
Замечание. С помощью способа Лагранжа можно определить вид
любой кривой второго порядка.
Пример 8. Пользуясь приведением многочлена второй степени к
сумме квадратов по способу Лагранжа, определить вид кривой
4х2 -4ху+у2 -8х+6у-2 = 0.
Решение. Преобразуя левую часть уравнения, получим
4х2 -4ху+у2 -8х + 6у-2 = 4 (х2 -ху-2х)+у2 +6у-2 =
= 4 х2-2х
л( 1 ,У 2 £
—41 —у+11 +у +6у-
-2=4 х —
-у+11
2 )
( 1 , \ 2
-4 —у +у+1 +у +6у-
\4 J
( 1 Г
-2 = 4lx--y-ll +2у-6 = 0,
( 1 У
41 х-^у-11 =-2(у-3),
(А)
267
Вводя новые переменные по формулам
Х = х-—у-1;
2Z
У = У-3,
уравнение (А) перепишем в виде
X2=--Y.
2
(В)
(С)
Уравнение (С) является уравнением параболы. Формулы (В) опре-
деляют аффинное преобразование. При аффинном преобразовании
парабола переходит в параболу. Следовательно, исходное уравнение
также определяет параболу.
Задачи
Определить вид линии, пользуясь приведением многочлена второй
степени к сумме квадратов по способу Лагранжа:
1. X2 + 5у2-2ху+2х+14у+13 = 0.
2. х2-Зу2-2ху+2х-18у-19 = 0.
3. х2 +у2 +2ху-2х-8_у+7 = 0.
4. 5х2+5у2-26ху-10х+26у+5 = 0.
5. х2 +у2 +2ху+2х+2у-3 = 0.
6. х2 +4у2-4ху+2х-4у+1 = 0.
7. 5х2+5у2-26ху-10х+26у-41 = 0.
8. х2+5у2-2ху+2х+14у+17 = 0.
9. 13х2+ 13у2-Юху-26х+10у+49 = 0.
10. 2х2 +2у2 +4ху+2х+2у+5 = 0.
Определить вид, параметры, расположение линий второго порядка
и построить их:
11. 17х2+ 17у2-16ху = 250.
12. Зх2 + Зу2 + Юху = 8.
13. 9х2 + 24ху +1бу2 +120х - 90у = 0.
14. 5х2+6ду+5у2 - 16х — 16у—16 = 0.
15. 5х2+ 12ху-22х-12у-19 = 0.
16. 4х2 -4ху + у2-2х-14у + 7 = 0.
268
17. x2-2y2-xy+3y-\ = 0.
18. 4x2 +y2-4лу+4х-2у+1 = 0.
Ответы
1. Эллипс. 2. Гипербола. 3. Парабола. 4. Пара пересекающихся прямых.
5. Пара параллельных прямых. 6. Пара совпадающих прямых. 7. Гипербола.
8. Пара мнимых пересекающихся прямых. 9. Мнимый эллипс. 10. Пара мни-
X2 Y2
мых параллельных прямых. 11. Эллипс -^- + -^- = 1, & (®»0), tga = l.
X2 Y2
12. Гипербола-----= 1, О'(0,0), tga = l. 13. Парабола; р = 3,
1 4
4 X2 Y2
О'(0,0), tga = y. 14. Эллипс -^- + -£-=1, tga = -l.
X2 Y2 , 2
15. Гипербола - — =1, О (1,1), tga = —. 16. Парабола;
3 ( 1 3 А
р = -у=-, О' tga = 2. 17. Пара прямых х-2у + 1 = 0,
х + у — 1 = 0. 18. Пара совпадающих прямых 2х — у +1 = 0.
§ 5.4. Приведение общего уравнения поверхности
второго порядка к каноническому виду
Общее уравнение второго порядка относительно х, у, z
апх2 + а22У2 + a33z2 + 2а]2ху + 2а13хг + 2а2зУ?+2а14х + 2а24у +
+2a34z + a44 =0
(5.43)
с помощью преобразований прямоугольной декартовой системы коор-
динат (4. 97) и (4. 99) можно привести к каноническому виду, т. е. к
одному из уравнений (4. 76) - (4. 92).
Если новые координатные оси Ох', Оу', Oz' направить по трем
взаимно перпендикулярным собственным векторам симметрической
матрицы
«21
«31
Я =
«12 «13
«22 «23
«32 «33 у
Ц, =а,,),
(5.44)
269
составленной из соответствующих коэффициентов уравнения (5.43), то
члены второго порядка
Ф (х, у, z) = яих2 +а22у2 + a33z2 + 2ai2xy + 2al3xz + 2a23yz (5.45)
преобразуются в члены второго порядка
Ф' (х\ у', z') = Xjx'2 + Х2У2 + X3z'2, (5.46)
где Х2, Х3 - корни характеристического уравнения данной мат-
рицы.
Уравнение (5.43) преобразуется при этом в уравнение
Л^х'2 + Х2у'2 + X3z'2 +2а1,4х/ + 2а'24у' + 2a34z'+а44 =0, (5.47)
коэффициенты а'}4, я24, а34 которого определяются с помощью фор-
мул (4. 99).
Уравнение (5.47) с помощью преобразования параллельного пере-
носа
X = х'-а;
Г = /-А; >
Z = z' -с
(5.48)
приводится к каноническому виду.
Пример 1. Определить вид, параметры и расположение поверхно-
сти по её уравнению
5х2 +1 ly2 + Iz1 -1 Ьху+20xz+4jnz = 18.
Решение. Данное уравнение не содержит членов с первой степе-
нью х, у, z, поэтому для его упрощения достаточно найти собствен-
ные значения Xj, Х2, Х3 матрицы А, составленной из коэффициен-
тов при членах второго порядка: =5, а22 =11, ауз =2,
а12=~8, а13 = 10, я23=2.
Матрица Я и ее характеристическое уравнение примут вид:
( 5 -8 10" 5-Х -8 10
А = -8 11 2 -8 11-Х 2 = 0
< ю 2 2> 10 2 2-Х
(при составлении матрицы принято во внимание, что а21=а]2,
270
a3i = а1з» a3i = а2з )• Характеристическое уравнение X3 -18Х2-
—8IX ч-18 81 = О имеет корни Xt = 18, Х2=9, Х3=-9. Найдем соб-
ственные векторы, соответствующие данным собственным значениям.
При Х| = 18 система (5.25) запишется так:
(5-18)/-8т+10и = 0;
-8/+(11-18)/л+2л = 0;
10/+2ти+(2-18) л = О
-13/-8/и+Юл = 0;
или -8/-7/и+2л = 0;
10/ + 2/и-16л = 0.
Отсюда находим р} = {-2,2,-1}. Аналогично получаем собствен-
ные векторы р2 = {1,2,2}, р3 = {2,1,-2}.
Перейдем к новой системе координат Ox'y'z' с началом в той же
точке, оси которой Ох', Оу', Oz' направлены соответственно по век-
торам р}, р2, р3. В соответствии с формулами (5.45) и (5.46) все чле-
ны второго порядка исходного уравнения преобразуются в члены вто-
рого порядка 18х'2 + 9у'2 -9z'2, а уравнение (5.47) примет вид
18x'2 + 9/2-9z'2 =18.
Разделив обе части этого уравнения на 18, получим
Сравнивая полученное уравнение с уравнением (4. 77), заключаем, что
данная поверхность является однополостным гиперболоидом с пара-
метрами а = 1, b = 41, с = V2.
Пример 2. Определить вид, параметры и расположение поверхно-
сти
7х2 +6у2 + 5z2 -4xy-4>>z-6x-24y+18z + 30 = 0.
Решение. Матрица А, составленная из коэффициентов при стар-
ших членах уравнения =7, а22 =6, а33 =5, а12 =-2, а13 =0,
а23 = -2, и ее характеристическое уравнение запишутся так:
-2 0
6-Х -2
-2 5-Х
= 0.
271
Характеристическое уравнение
13-1812+991-162 = 0
имеет корни Xj =3, Х2 = 6, = 9* Им соответствуют собственные
векторы матрицы р} = {1,2,2}, р2 = {2,1,-2}, р3 = {2, - 2,1}.
Перейдем к новой системе координат Ox'y'z\ оси которой направ-
лены по векторам д, р2, Рз> а начало остается прежним. Формулы
преобразования координат (4. 99) примут вид
1,2,2,
x = — x+—у+ — z ;
3 3 3
2 , 1,2,
3 3Z 3
2,2,1,
3 3Z 3
х = у (х' + 2у' + 2z');
или у = у (2x,+y,-2z/);
z = |-(2x'-2/+z')
(А)
/ 1 о 2
(так как cosa( = —, cospi = — ,
2 а .
д; cosa2 = у, cosp2 = —, cosy2 = -
2 o
p2; cosa3 = —, cosp3 = -
вектора
косинусы
2
cosyj =у -направляющие косинусы
1 2
fz у -направляющие
2 1
у, cos у3 = у - направляющие
вектора р3). Исходное уравнение с учетом значений
косинусы
Xj, Х2, Х3 и формул (А) запишется в виде
3x'2 + 6/2 + 9z'2 - 6 • | (x'+2y’+2z') - 24 • (2x'+У - 2z')+
+ 18|(2x'-2y+z')+30 = 0
ИЛИ
Зх'2 + бу'2 + 9z'2 - 6x' - 24/+18z'+30 = 0.
Преобразуя это уравнение, получим
3(х'2-2х' + 1)+6(/2-4y'+4) + 9(zz2 +2z' + l)-3-24- 9 + 30 = 0
или
272
3(х'-1)2 +6(/-2)2 +9(z' + l)2-6 = 0.
(В)
Применяя еще одно преобразование координат, а именно, преобра-
зование параллельного переноса
% = х'-1;'
Г = /-2; ►
Z = z' + 1,
(С)
уравнение (В) приведём к виду
vr2 у2 у2
ЗХ2+6Y2+9Z2 =6 или--+ —+ ±-=1. (D)
2 12 2
Уравнение (D) определяет эллипсоид с параметрами
а =
V2,
6=1,
Чтобы определить расположение эллипсоида относительно старой
системы координат, необходимо найти точку О' - начало системы
O'XYZ. Новые координаты этой точки равны нулю, т.е.
X = 0, Y = 0, Z = 0. Из формул (С) и (А) находим координаты этой
точки в старой системе: х = 1, у = 2, z = -1.
Пример 3. Определить каноническое уравнение и расположение
поверхности
2х2 +2у2 + 3z2 + 4xy + 2xz + 2<yz-4x + 6y-2z + 3 = 0.
Решение. Составим матрицу Л и ее характеристическое уравне-
ние
г2 2
А= 2 2
J 1
1'
1 ;
3,
2-1 2 1
2 2-1 1 =0.
1 1 3-1
Характеристическое уравнение
13-712+ 101 = 0 или 1(12-71 + 10) = 0,
имеет корни 1| =2, 12 = 5, 13 = 0, которым соответствуют собствен-
273
ные векторы рх = {1,1, -2}, = О, 1> П> Рз = П, -1,0}. Введем новую
систему координат Ox'y'z', направив оси Ох', Оу', Oz' по векторам
Р\, Рг> Рз-
Формулы преобразования координат при повороте осей примут
вид
(А)
Уравнение поверхности с учетом значений Xj, Х2, ^з и формул
(А) преобразуется следующим образом:
„ ,2 г ,2 J 1 , 1 , 1 ,1 J 1 , 1 z
2х +5у -4 —=х + —=у +~r=z + 6 —г=х + -₽у -
VV6 43 -J2 ) V V6 V3
1 ,] J 2 , 1 ,1 , Л
---7=z -2----=Х +-7=у + 3 = 0,
V2 J I V6 V3 )
2х'2 +5у'2 + -==-x'--^z'+3 = 0.
V6 J2
Уравнение (В) приведем к каноническому виду:
( , 3 9 , 10 , 9
2\ х'2 +—т=х +— + 5у 2-~i=2 - — + 3 = 0,
I V6 24 I z V2 12
, з У г ,2 ю
2 х + —+ 5у = -==
I 2V6 J V2
, 9>/2 '
Z 4-10 ’
10 X2
2X2+5Y2 =^t=Z или —т- + —= 2Z,
V2 _L _L
2>/2 л/2.
(В)
(С)
274
где X = х' + Ц=, Y=y', Z = z'-?-=-. (D)
2-Уб 40
Уравнение (С) определяет эллиптический параболоид, для которо-
го а2 = , Ь2 = ~7=г. Началом новой системы O'XYZ является точ-
2V2 V2
„,( 1 19 И
ка О I- — , у I, ее координаты определяются из равенств
% = 0, К = 0, Z = 0 и из формул (D), (А). В этой точке находится вер-
шина эллиптического параболоида.
Пример 4. Определить каноническое уравнение и расположение
поверхности
2х2 +5у2 +2z2 -2ху+ 2>>z-4xz + 2x-10y-2z-1 = 0.
Решение. Составим матрицу
Л и ее характеристическое уравне-
ние:
( 2 -1 -2
А= -1 5 1
2-Х -1
-1 5-Х
-2 1
-2
1
2-Х
= 0.
Характеристическое уравнение
X3-9А.2+ 18Х = 0
имеет корни X] =3, Х2 = 6, = 0, которым соответствуют собствен-
ные векторы
Л = {1,1,-1}, рг = {\,-2,-\}, р3 = {1,0,1}.
Оси новой системы Ox'y'z' направим по векторам рх, р2, р3. Форму-
лы преобразования координат при повороте осей примут вид
1 , 1 , 1 ,
Х = —Т=Х + —=у +—=z\
V3 V6 V2
(А)
275
Уравнение поверхности с учетом значений Я,, и формул
(А) преобразуется следующим образом:
Зх'2+6у'2+2| -4=x'+-L y'+-!=z' |-10| -т=х
I V3 V6 V2 J I V3
или Зх'2 + 6_у'2 —7= х' + у’ -1 = 0.
V3 V6
Уравнение (В) приводим к каноническому виду:
з\ х'2 -~у=х' + — | + 6| у'2 +-^=у' + — |-1-4-1 = 0,
I 7з 3 ) Г - Тб 6 I
1,1) |,2)
3 х—+6 / + -т= =6,
I л/з; I >/б j
ъг2 у2
ЗА'2+6Г2 =6 или------+ —= 1,
2 1
(В)
(С)
v , 1 v , 2
где X = х —, У = У + “г •
V3 V6
Следовательно, данное уравнение определяет эллиптический ци-
линдр с параметрами а = V2, b = 1. Ось цилиндра коллинеарна вектору
р3 = 0,0,1}.
Пример 5. Определить вид поверхности
х2 + 4у2 +9z2 +6xz-12yz-x + 2y-3z-6 = 0.
Решение. Составим матрицу А и ее характеристическое уравне-
ние:
( 1 -2 3^
Я= -2 4 -6
<3-6 9>
1-Х -2 3
-2 4-Х -6
3 -6 9-Х
= 0.
276
Характеристическое уравнение
Х3-14Х2 =0
имеет корни Х|=14, Х2=0, Х3=0. Корню Х1 = 14 соответствует
собственный вектор pf = {l,-2,3}. Двойному корню Х = 0 соответст-
вует бесчисленное множество собственных неколлинеарных векторов,
ортогональных вектору рх. Среди них выберем два взаимно перпенди-
кулярных, например, р2 = {1,-1,-1}, р3= {5,4,1}. Перейдем к новой
системе координат Orj/z', оси которой коллинеарны ч векторам
Р1> Рз> Рз-
Формулы преобразования при повороте осей примут вид
(А)
Уравнение поверхности с учетом значений Х2, Х3 и формул
(А) преобразуется следующим образом:
э 14
14х'2—£=х'-6 = 0.
V14
(В)
Приведем к каноническому виду уравнение (В):
14 х'2
-14 -—6 = 0,
56
i4fx'——
I 2VT4
277
- — = 0, 14Х2- — = 0, X2= —,
4 4 56
v / 1 xz v2 25
где X = x-----• Уравнение X = — определяет пару параллель-
2714 56
ных плоскостей. Уравнения этих плоскостей в старой системе коорди-
нат можно найти с помощью способа Лагранжа. Выписывая вначале
все члены уравнения поверхности, содержащие х, дополняя их до
полного квадрата, получим:
х2 -4xy+6xz-x + 4y2 + 9z2 - 12yz + 2y-3z-6 = Jx2 -
( i \ / Il f
-2x1 2y-3z+y l+l 2y-3z + y I -I 2y-3z + — I +4y2 +
+ 9z2 -12yz+2y-3z-6 =
x-f2y-3z+^
+ 9z2 + — -12yz + 2y-3z |+4y2 +9z2 -12yz + 2y-3z-
4 J
( 1 V 25
-6= x-2y + 3z-- - — = 0,
I 2 ) 4
x-2y+3z--“-
x-2y + 3z-y
(x-2y-h3z-3)(x-2y + 3z + 2>=0.
Следовательно, уравнения плоскостей:
x-2y+3z-3 = 0, x-2y + 3z + 2 = 0.
Замечание. Уравнения этих плоскостей можно было найти и другим
способом. Разрешая уравнения (А) относительно х' и у', выражая X = х' -
278
1 V2 25
----₽= через x и v и подставляя в уравнение л = —, получим
2V14 56
if _ , 1 А2 25
— I x-2y + 3z-= —, откуда и следуют уравнения плоскостей.
14 V 2 J 56
Пример 6. Пользуясь приведением левой части уравнения к сумме
квадратов по способу Лагранжа, определить вид поверхности
х2 +y2-3z2 -2xy-6xz-6yz + 2x + 2y + 4z = 0.
Решение. Преобразуя левую часть уравнения, получим
х2 -2xy-6xz + 2x+y2 -3z2 -6yz + 2y + 4z = [x2 -2х(у +
+ 3z-l) + (j + 3z-l)2 ]-(y + 3z-l)2 +/-3z2-6yz +
+ 2y+4z = [x-(j + 3z-l)]2 -^2 +9z2 + l + 6^z-2y-
-6z)+y2 ~3z2 -6yz + 2y+4z = (x-y-3z+1)2 - 12z2 -
-12^z+10z + 4y-l = (x-y-3z + l)2-12 z2+2z( ~У~
5 W 1 5 A2
— + ~У —
12 J I 2Z 12 J
+ +4y-\ = (x-y-
7 ( 1 5 V 7
+ 4y-l = (x-y-3z + l)-12lz + —у-— I +3y2 -y +
+ -J| = (x-^-3z+l)2-12fz + y^--j|-l +з(/-|у+
279
3 13
36
36 + 12 ’
1
Следовательно, уравнение приведено к виду
(х-у-Зг+1)2 -V2\z+^y-~
2 ( 1У
+ 3 у-- +1 = 0.
\ 6 J
(А)
Введем новые координаты по формулам
X = x-y-3z+l;
Z = z+-y- — .
2 12
(В)
Уравнение (А) перепишется так:
у2 у2 у2
X2 +3Y2 -12Z2 =-1 или —+ А—А- = -1. (С)
1 b 1
3 12
Полученное уравнение определяет двуполостный гиперболоид.
Линейное преобразование (В) является аффинным (его определи-
тель отличен от нуля). Так как при аффинном преобразовании двупо-
лостный гиперболоид переходит в двуполостный гиперболоид, то ис-
ходное уравнение тоже определяет двуполостный гиперболоид.
Пример 7. С помощью способа Лагранжа определить вид поверх-
ности
4xy+2x + 4y-6z-3 = 0.
Решение. Левая часть уравнения не содержит членов с квадратами
координат. Положим х = х'+у', у = х'-у\ z = z\ тогда уравнение
перепишется так
4(х'+у') (х'-у')+ 2 (х'+у')+4 (х'-y')-6z'-3 = 0
или
4х'2 - 4у'2 + 6х' - 2у' - 6z' - 3 = 0.
280
Преобразуя это уравнение, получим
л ( ,2 6 , л ( / 2 1 , 1^9 1 n z" л
I 4 16 J I 2Л 16 ) 4 4
или
( 3 У ( 1 У ( 5 А
4 х'+- -4 у'+ — =6 z + - .
V 4 ) (/ 4 ) V 6 )
Вводя новые координаты по формулам
X = x' + — ;Y = y'+ — ;Z = z+—,
4 4 . 6
получим уравнение гиперболического параболоида
2 2 X1 У2
4JT2 -4Y2 =6Z; 4;—4r = 2Z.
2 2
4 4
Пример 8. Определить вид поверхности
у2 +2xy+4xz+2yz-4x-2y = 0.
Решение. Преобразуем левую часть уравнения:
у2 ^2xy+2yz-2y+4xz-4x = ^y2 +2у (x+z-l)+(x +
+z-l)2 ]-(x+z-l)2+4xz-4x = [y+(x+z-l)]2 -
~(х2 +z2 +l + 2xz-2x-2z)+4xz-4x = (y+x+z-l)2 -
-х2 +2xz-z2 -2x + 2z-l = (y+x+z-l)2 -(x-z +
+ l)2=[(j+x+z-l)-(x-z + l)][(y+x + z-l) + (x-
-z + l)] = (y+2z-2)(y + 2x) = 0.
281
Следовательно, уравнение определяет две пересекающиеся плос-
кости
y+2z-2 = 0, 2х + у = 0.
Задачи
Определить вид поверхности, пользуясь приведением левой части
ее уравнения к сумме квадратов по способу Лагранжа:
1. 2x2+3y2+12z2-4xy + 4yz-8z+l = 0.
2. х2+2у2-4z2-2xy + 4yz + 8z-2 = 0.
3. 8x2+9y2-12z2-16xy+4yz+12z-4 = 0.
4. 2х2 +у2-12z2 -4xy-4yz+8z-3 = Q.
5. lx2+ly2-2xy-2z+2 = 0.
6. xy + xz+yz + 2x + 2y-2z = 0.
7. x2 -2y2 +z2 + 4xy- lOxz + 4yz + 2x + 4y- lOz-1 = 0.
8. x2 +y2 + 4z2 + 2xy + 4xz + 4^z-»6z+l = 0.
9. 4x2 + 49y2 + z2 -28xy + 4xz-14yz + 8x-28y + 4z + 3 = 0
10. x2 +4y2 + 9z2 -4xy + 6xz-12yz-2x + 4y-6z + l = 0
Определить каноническое уравнение и расположение поверхности:
11. х2 -2у2 +z2 + 4xy-8xz-4yz-14x-4y + 14z + 16 = 0
12. 2х2 +2/-5z2 +2xy-2x-4y-4z + 2 = 0.
13. 5х2 -у2 + z2 + 4xy + 6xz + 2x + 4y + 6z-8 = 0.
14. 2х2 +у2 + 2z2 -2xy+2yz + 4x-2y = 0.
15. х2 -2у2 + z2 +4jy-10xz + 4^z + 2x + 4y-10z-l = 0.
16. х2 + у2 + 4z2 + 2xy + 4xz + 4<yz-6z+l = 0.
Ответы
1. Эллипсоид. 2. Конус. 3. Однополостный гиперболоид. 4. Двуполостный
гиперболоид. 5. Эллиптический параболоид. 6. Однополостный гиперболоид.
7. Гиперболический цилиндр. 8. Параболический цилиндр. 9. Пара параллель-
ных плоскостей. 10. Пара совпадающих плоскостей. 11. Конус X2 +
+ K2-9Z2=0. Корни характеристического уравнения Х1=Х2=-3,
Х3=6, вершина в точке О' (1,1,-1); ось конуса коллинеарна вектору
282
_ X2 Y2 Z2
р3 = {2,1, - 2}. 12. Двуполостный гиперболоид + —------— = -1. Кор-
5 Й 25
ни характеристического уравнения Xq =1, Х2 = 3, А3 = -5. Ось коллинеар-
на вектору р3 = {0,0,1}. 13. Гиперболический параболоид
7Х2 -2Г2 -2d — Z = 0.
Корни характеристического уравнения
Xj — 7, Х»2 — —2, Х»з — 0.
р2 = {-1,2,1},
____________________
I 24 28 56
Собственные векторы pt = {4,1,2},
р3 = {1,2,-3}, вершина находится в точке
123 X2 Y2
I. 14. Эллиптический цилиндр —— + —— = 1. Корни
2
характеристического уравнения X) =3, Х2 = 2, Х3 = 0. Собственные векто-
ры р} = {-1,1,1}, р2 = {1,0,1}, р3 = {1,2,-1}. 15. Гиперболический ци-
линдр X2 - Y2 = |. 16. Параболический цилиндр Y = л/З X2.
283
Приложение
Некоторые кривые
Рис. 1. Логарифмическая
спираль
р = ае^Ф
Рис. 2. Гиперболическая
Рис. 3. Трехлепестковая
роза
р = asinJtp
спираль
Рис. 4. Графики гипербо-
лических функций:
. ех-е’х
y = shx=e £—
к ех+е~х
у = chx=-—
284
Рис. 5. Декартов лист
х3+у1-Заху = О
Рис. 6. Конхоида Никомеда
р=^>+1- а)1<а' б)1=а' в)1>а-
285
Оглавление
Введение.................................................3
Глава 1. Аналитическая геометрия на плоскости............4
§1.1. Система прямоугольных декартовых координат
на плоскости. Простейшие задачи........................4
§ 1.2 Уравнение линии в прямоугольных декартовых
координатах...........................................15
§ 1.3 Прямая линия на плоскости.......................24
1.3.1. Уравнение прямой с угловым коэффициентом. Общее
уравнение прямой. Уравнение прямой в отрезках........24
1.3.2 Угол между двумя прямыми. Условия
параллельности и перпендикулярности прямых.
Пересечение двух прямых........................32
1.3.3. Уравнение прямой, проходящей через данную точку
в данном направлении. Пучок прямых. Уравнение
прямой, проходящей через две данные точки............40
L3.4. Нормальное уравнение прямой. Расстояние от
точки до прямой.................................46
§ 1.4. Линии второго порядка..........................54
1.4.1. Окружность...................................54
1.4.2. Эллипс.......................................58
1.4.3. Гипербола....................................63
1.4.4. Парабола.....................................67
§ 1.5. Преобразования прямоугольных координат.........75
§ 1.6. Полярные координаты............................83
§ 1.7. Параметрические уравнения линии................94
Глава 2. Определители и системы линейных
алгебраических уравнений...............................100
§ 2.1. Определители второго и третьего порядка,
их свойства..........................................100
2.1.1. Некоторые приложения определителей к
аналитической геометрии.............................102
§ 2.2. Решение систем линейных алгебраических
уравнений с помощью определителей....................107
Глава 3. Векторная алгебра.............................117
§3.1. Основные понятия..............................117
§ 3.2. Координаты вектора. Простейшие действия над
векторами, заданными своими координатами........128
§ 3.3. Скалярное произведение........................138
286
§ 3.4. Векторное произведение.........................146
§ 3.5. Смешанное произведение. Двойное векторное
произведение..........................................154
Глава 4. Аналитическая геометрия в пространстве.........163
§ 4.1. Плоскость в пространстве.......................163
4.1.1. Общее уравнение плоскости. Уравнение в отрезках.
Составление уравнения плоскости по различным
ее заданиям.........................................163
4.1.2. Нормальное уравнение плоскости.
Расстояние от точки до плоскости....................174
4.1.3. Угол между двумя плоскостями. Условия
параллельности и перпендикулярности двух
плоскостей..........................................181
§ 4.2. Прямая в пространстве...........................188
4.2.1. Параметрические уравнения прямой. Канонические
уравнения прямой. Уравнения прямой, проходящей
через две точки.....................................188
4.2.2. Прямая как линия пересечения двух плоскостей.
Взаимное расположение двух прямых в
пространстве........................................194
4.2.3. Угол между двумя прямыми. Расстояние от
точки до прямой. Кратчайшее расстояние между
двумя прямыми.......................................202
§ 4.3. Прямая и плоскость в пространстве...............208
§ 4.4. Поверхности в пространстве. Сфера. Поверхности
вращения. Цилиндрические и конические
поверхности......................................214
§ 4.5. Поверхности второго порядка....................225
Глава 5. Матрицы и их применение........................237
§ 5.1. Матрицы, основные действия над ними............237
§ 5.2. Линейные преобразования на плоскости и в
пространстве. Аффинные преобразования.
Собственные векторы матрицы...........................246
§ 5.3. Приведение общего уравнения линии второго
порядка к каноническому виду..........................255
§ 5.4. Приведение общего уравнения поверхности второго
порядка к каноническому виду..........................269
Приложение..............................................284
287
Справочное издание
Гусак Алексей Адамович
Справочное пособие к решению задач:
аналитическая геометрия и линейная алгебра
Редактор С.В. Процко.
Дизайн обложки С.А. Демидовой.
Ответственный за выпуск А.Ф. Мясников.
Подписано в печать 02.07.98.
Формат 60x84 1/16. Бумага для офсетной печати. Гарнитура Таймс.
Печать офсетная. Печ.л. 18. Усл.печ.л. 30,24. Тираж 7000 экз.
Заказ 1816.
НТООО «ТетраСистемс» (Лицензия ЛВ № 76 от 19.11.97. до 19.11.2002).
220036, Минск, пер.Домашевский, НА-508.
Качество печати соответствует качеству представленных
издателем диапозитивов.
Отпечатано с готовых диапозитивов заказчика
в типографии издательства «Белорусский Дом печати».
220013, Минск, пр. Ф. Скорины, 79.
ISBN-985-6317-52-5
9 789 8 56 3 17 5 24 >