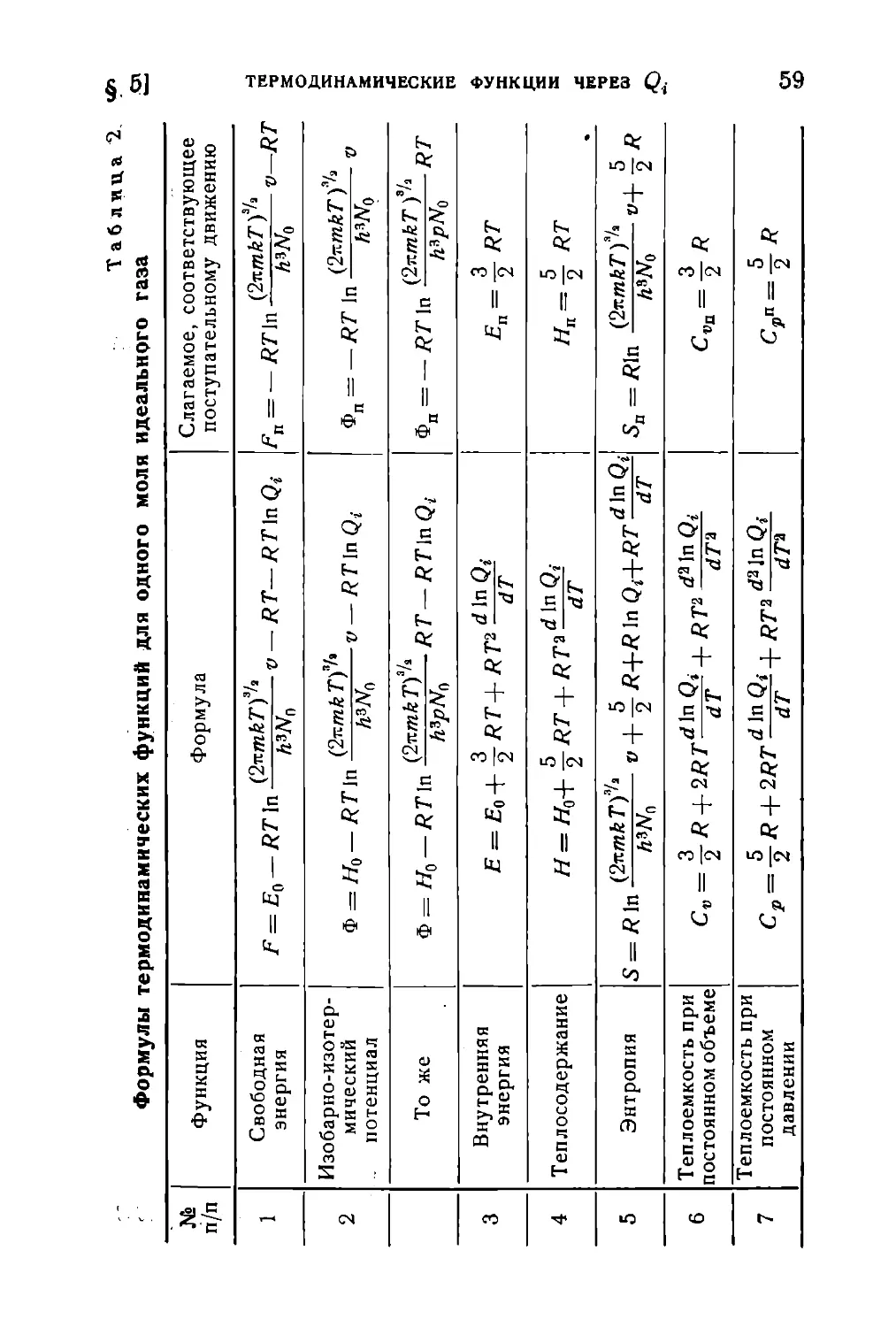
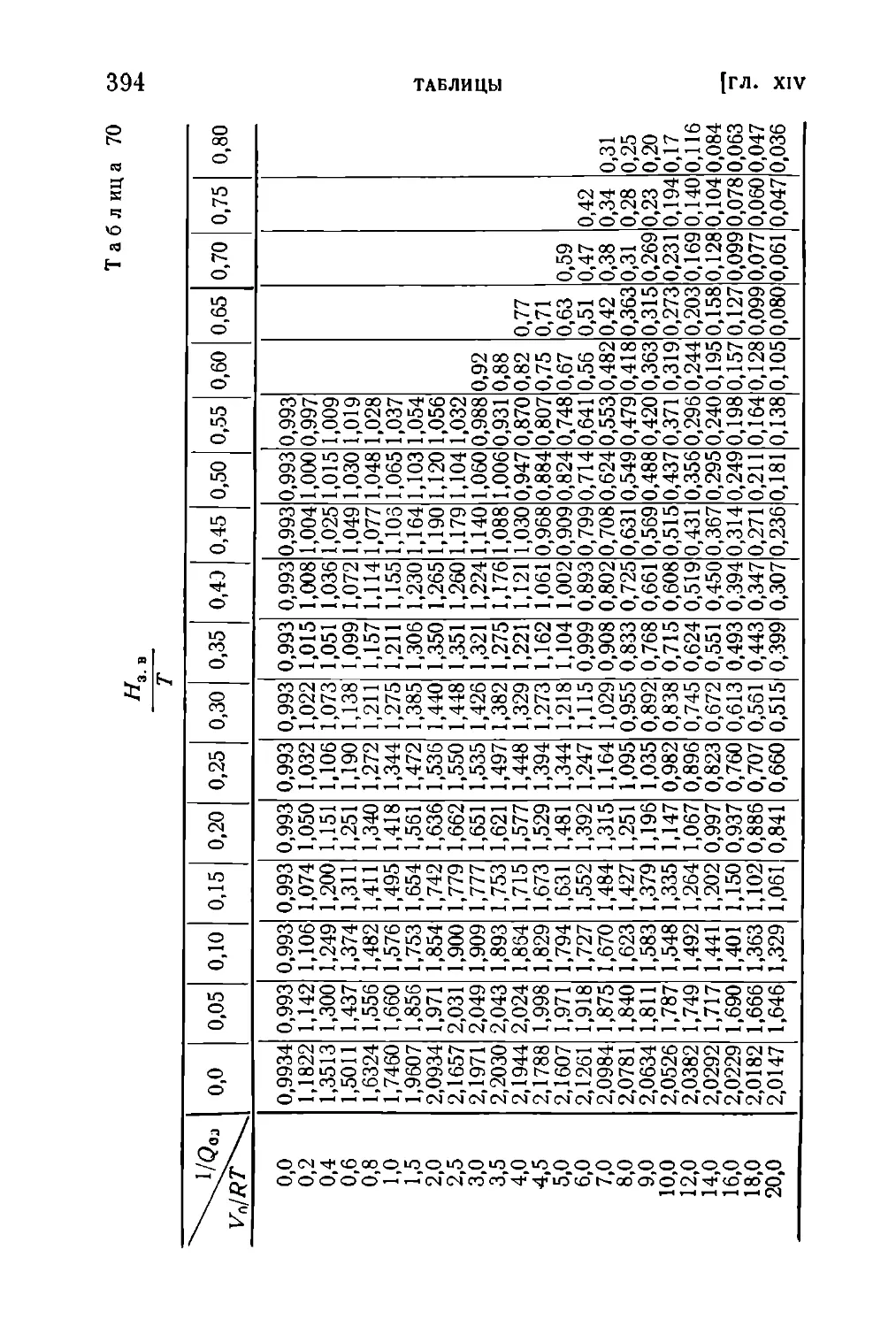
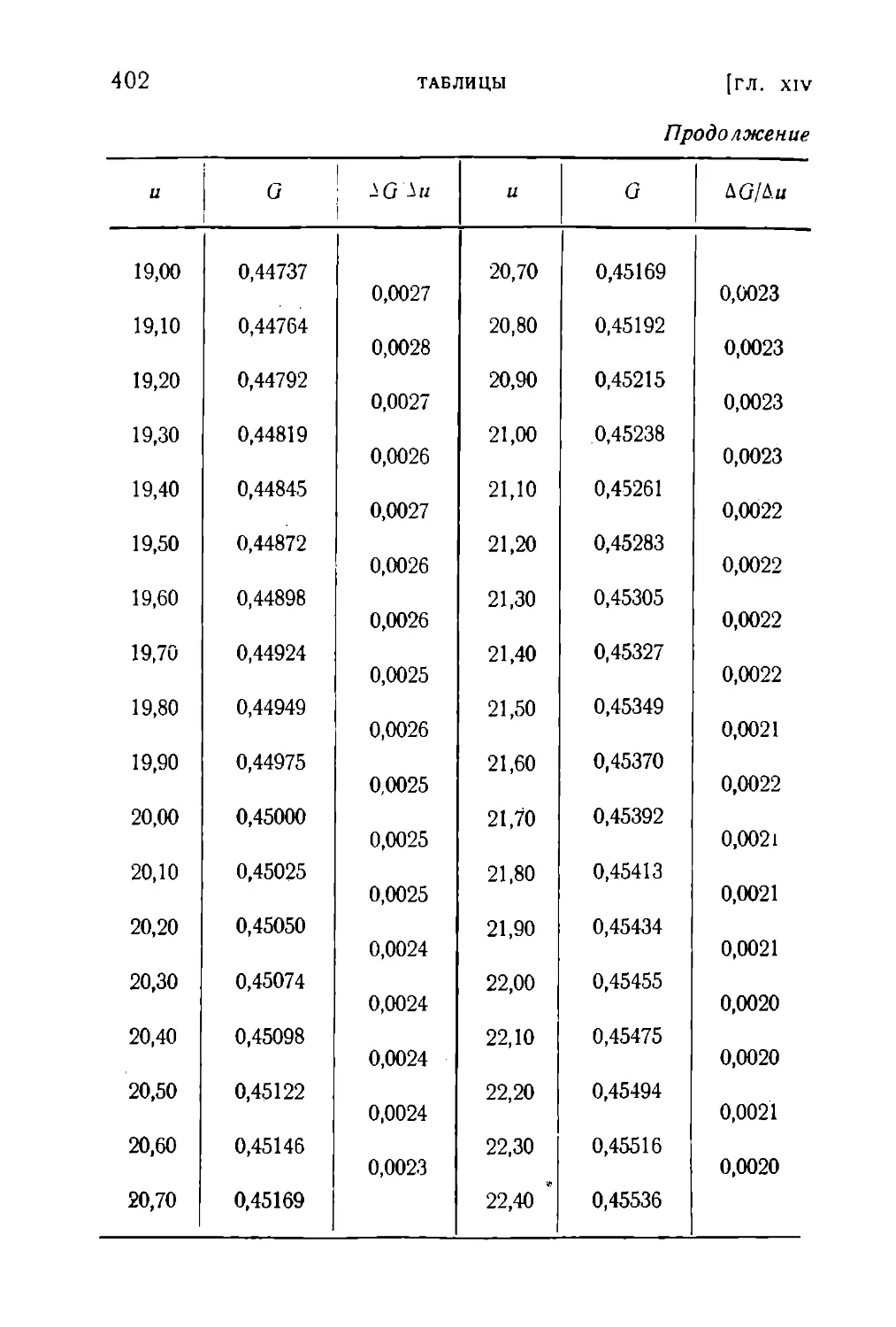
Текст
И. Н. ГОДНЕВ
ВЫЧИСЛЕНИЕ
ТЕРМОДИНАМИЧЕСКИХ
ФУНКЦИЙ
по молекулярным
ДАННЫМ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1956
13-5-4
АННОТАЦИЯ
В монографии излагаются элементы статисти-
ческой термодинамики и их применение к вычисле-
нию термодинамических функций газов и частично
жидкостей и твердых тел, а также методы расчета
химических равновесий и реакций изотопного
обмена. Параллельно с вопросом вычисления
термодинамических функций рассмотрены необхо-
димые молекулярные данные (состояния и уровни
энергии).
Книга предназначена для студентов старших
курсов физико-химических специальностей, аспи-
рантов, инженеров и научных работников, имею-
щих дело с термодинамикой и ее применениями.
СОДЕРЖАНИЕ
Предисловие ................................ 9
Введение .................................... И
Глава I. Основные формулы статистической термодина-
мики ................................... 1G
§ 1. Статистическая физика, статистическая механика и
статистическая термодинамика (16). §2. Макроскопическое
описание состояния (18). § 3. Микроскопическое описание
состояния при применении к изучаемой системе классиче-
ской механики (19). § 4. Особенности описания состояния
квантовомеханических систем (21). § 5. Квантовомеханиче-
ское описание микросостояния (29). § 6. Вычисление сред-
них. Формула для свободной энергии (31). § 7. Сумма по
состояниям системы (34). § 8. Выражение для термодина-
мических функций системы через сумму по состояниям Z
(39). § 9. Нулевая энергия (42). § 10. Пример (43).
Глава II. Применение общих формул статистической
термодинамики к идеальным газам.......................... 46
§ 1. Выражения для термодинамических функций идеаль-
ного газа через сумму по состояниям молекулы (46). § 2. Об-
щие выражения для энергии молекулы (48). § 3. Фор-
мулы для термодинамических функций идеального газа
при выделении нулевой энергии (51). § 4. Вычисление
суммы по состояниям для поступательного движения (53).
§ 5. Выражения для термодинамических функций идеаль-
ного газа через сумму по состояниям Qj (56). § 6. Фор-
мулы для вычисления термодинамических функций при
применении метода непосредственного суммирования (60).
§ 7. Случай разделения энергии (61). § 8. Формулы для
химического потенциала (65). § 9. Термодинамические фун-
кции смеси газов (66).
1*
4
СОДЕРЖАНИЕ
Глава!!!. Термодинамические функции одноатомных
газов................................................. 70
§ 1. Сумма по состояниям молекулы одноатомного газа
(70). § 2. Электронные состояния атома и вычисление Q{
(72). § 3. Формулы для вычисления термодинамических
функций одноатомного газа без учета влияния второго и
высших электронных уровней (78). § 4. Учет второго и
высших электронных уровней (81). § 5. Общие формулы
и сводная таблица (84). § 6. Эффект изотопии '(86).
§ 7. Сравнение с опытными данными (89).
Глава IV. Уровни энергии и состояния двухатомных
молекул............................................... 91
§ 1. Волновая функция молекулы в случае разделения
энергии (91). § 2. Простейшая модель двухатомной моле-
кулы: жесткий ротатор — гармонический вибратор (92).
§ 3. Электронные уровни двухатомных молекул (97).
§ 4. Учет ангармоничности колебаний (101). § 5. Примене-
ние модели нежесткий ротатор — ангармонический вибра-
тор (103). § 6. Применение модели колеблющийся рота-
тор (104). § 7. Учет симметрии полной волновой функции
молекулы (106). § 8. Формулы для весов уровней энергии
вращения двухатомных молекул (112).
Глава V. Вычисление термодинамических функций двух-
атомных газов.........................................115
§ 1. Разложение суммы по внутренним состояниям
на множители при применении модели жесткий ротатор —
гармонический осциллятор (115). § 2. Сумма по электрон-
ным состояниям двухатомной молекулы при разделении
энергии (116). § 3. Вычисление <2колеб (И7). § 4. Вычисле-
ние QBp жесткой двухатомной гетеронуклеарной моле-
кулы (117). § 5. Вычисление QBp для жесткой молекулы
с одинаковыми ядрами (120). §6. Сумма по внутренним со-
стояниям Qi при применении модели жесткий ротатор —
гармонический осциллятор (123). § 7. Электронные слагае-
мые термодинамических функций двухатомной молекулы
для случая, если 5ЭЛ = р0 (124). § 8. Слагаемые термо-
динамических функций, соответствующие гармоническому
колебанию в двухатомной молекуле (124). § 9. Слагаемые
СОДЕРЖАНИЕ
5
термодинамических функций, соответствующие вращатель-
ному движению жесткой двухатомной молекулы (127).
§ 10. Формулы для. вычисления термодинамических функ-
ций двухатомной молекулы в предположении жесткого
вращения и гармонического колебания (127). § 11. Эффект
изотопии в случае двухатомных газов (132). § 12. Вычи-
сление QDp при применении модели нежесткого рота-
тора (135). § 13. Применение метода непосредственного
суммирования (138). § 14. Метод Гордона и Барнеса (140).
§ 15. Метод Касселя (146). § 16. Сравнение вычисленных
значений с опытными данными (150).
Глава VI. Классификация и симметрия многоатомных
молекул ...............................................
§ 1. Введение (152). § 2. Классификация многоатомных
молекул применительно к вычислению термодинамических
функций (153). § 3. Элементы симметрии молекулы (160).
§ 4. Операции симметрии (163). § 5. Группы симметрии
молекулы (165). § 6. Группа вращений и число сим-
метрии (171).
Глава VII. Уровни энергии вращения и колебания квази-
твердых молекул .......................................
§ 1. Введение (174). § 2. Уровни энергии вращения
линейной молекулы (174). § 3. Энергия вращения сим-
метричного волчка (175). § 4. Уровни энергии вращения
молекулы типа сферического волчка (181). § 5. Энергия
вращения молекулы типа асимметричного волчка (182).
§ 6. Число степеней свободы колебательного движения
в молекуле (185). § 7. Колебания в молекуле с точки зре-
ния классической механики (186). § 8. Симметрия нормаль-
ных колебаний (194). § 9. Вековое уравнение для опре-
деления частот колебаний (195). § 10. Квантовомеханиче-
ское рассмотрение колебаний (199). § 11. Влияние ангар-
моничности колебаний на уровни энергии (204). § 12. Экспе-
риментальные основания определения частот колеба-
ний (207). § 13. Характеристические частоты (209).
§ 14. Веса уровней энергии квазитвердых молекул (212).
§ 15. Вычисление весов уровней энергии с помощью
теории групп (217). § 16. Определение симметрии ядер-
ных спин-функций (219), § 17. Определение симметрии
152
174
6
СОДЕРЖАНИЕ
волновых функций, описывающих вращение молекулы (222).
§ 18. Построение таблиц умножения и определение веса
уровня (222).
Глава VIII. Вычисление термодинамических функций
квазитвердых молекул.................................226
§ 1. Введение (226). § 2. Вычисление Qap для жесткой
линейной несимметричной молекулы (228). § 3. Вычисле-
ние Q для жесткой несимметричной молекулы типа сим-
метричного волчка (228). § 4. Вычисление QBp для жест-
кого сферического волчка (231). § 5. Вычисление QBp для
жесткой молекулы типа асимметричного волчка (232).
§ 6. Влияние симметрии и спина (235). § 7. Сумма по коле-
бательным состояниям (238). § 8. Формулы для вычисле-
ния термодинамических функций жесткой молекулы в пред-
положении гармонического характера колебаний (240).
§ 9. Вычисление моментов инерции (246). § 10. При-
мер (250). § 11. Учет ангармоничности и других отступле-
ний от модели жесткой по отношению к вращениям моле-
кулы с гармоническими колебаниями (251).
Глава IX. Термодинамические функции газов в случае
свободного вращения..................................253
§ 1. Общие замечания (253). § 2. Вычисление суммы по
состояниям вращательного движения в общем виде для
случая свободного вращения (254). § 3. Вторая общая
формула для QBp (261). § 4. Случай симметричных волч-
ков (264). § 5. Пример (270). § 6. Случай асимметричных
волчков (276). § 7. Вычисление термодинамических функ-
ций в случае свободного вращения (279).
Глава X. Вычисление термодинамических функций газов
в случае заторможенного внутреннего вращения ... 281
§ 1. Потенциальный барьер внутреннего вращения.
Поворотные изомеры (281). § 2. Приближенный метод
Питцера (288). § 3. Определение уровней энергии волчка
с заторможенным вращением (294). § 4. Первые таблицы
Питцера (298). § 5. Пример (300). § 6. Приближенный
метод Питцера для случая нескольких симметричных
волчков (302). § 7. Пример — вычисление энтропии
СОДЕРЖАНИЕ
7
этана (304). § 8. Пример — вычисление термодинамических
функций ацетона при 500° К (307). § 9. Метод Кроу-
форда (312). § 10. Новые таблицы Питцера и Гвинна (315).
§ 11. Метод П. Г. Маслова (318). § 12. Практические фор-
мулы (320).
Глава XI. Вычисление термодинамических функций
реальных газов, жидкостей и твердых тел по термо-
динамическим функциям в идеальном газовом со-
стоянии ...............................................
§ 1. Вычисление термодинамических функций реаль-
ных газов (322). § 2. Вычисление термодинамических
функций жидких и твердых тел (325). § 3. Пример (328).
Глава ХП. Расчет химических равновесий.................
§ 1. Введение (330). § 2. Общие формулы для констант
равновесия газовых реакций (331). § 3. Вычисление кон-
станты равновесия с помощью таблиц приведенного
изобарно-изотермического потенциала (334). § 4. При-
меры (335). § 5. Детализация формул для вычисления
констант химического равновесия через сумму по состоя-
ниям в случае диссоциации двухатомной молекулы (338).
§ 6. Детализация формул для константы равновесия при
применении к многоатомным газам. Компенсация ядерного
спина (341). § 7. Применение таблиц прироста изобарно-
изотермического потенциала реакций образования (343).
§ 8. Применение «комбинированных термодинамических
функций» (347).
Глава XIII. Расчет констант равновесия реакций изотоп-
ного обмена . . . .....................................
§ 1. Введение (350). § 2. Вычисление констант равно-
весия реакции изотопного обмена А2~- B2^t2AB (350).
§ 3. Расчет константы равновесия типичной обменной
реакции (355). § 4. Вспомогательные таблицы для вычисле-
ния f (361). § 5. Примеры (363). § 6. Более общий случай.
Поправка на ангармоничность (365). § 7. Влияние эффекта
изотопии при расчете химических реакций (366).
Глава XIV. Таблицы.....................................
§ 1. Общие замечания (370). § 2. Таблица физических
постоянных (370). § 3. Таблицы термодинамических функ-
322
330
350
370
8
СОДЕРЖАНИЕ
ций гармонического осциллятора (370). § 4. Таблицы для
вычислений по способу Гордона и Барнеса (371). § 5. Пер-
вые таблицы Питцера (371). § 6. Новые таблицы Питцера
и Гвинна (372). § 7. Таблица Бигелейзена и Майер (372).
§ 8. Таблица литературных источников значений термо-
динамических функций (372).
Литература ...........................405
Наиболее важные обозначения............414
ПРЕДИСЛОВИЕ
Данная монография посвящена рассмотрению статисти-
ческих методов вычисления термодинамических функций по
молекулярным данным *). Широкое применение этих методов
при расчетах технологических и энергетических процессов
и их интенсификации и усовершенствовании, а также при
решении других задач делает актуальным составление дан-
ной монографии. Хотя статистические методы вычисления
термодинамических функций частично освещены в ряде учеб-
ников и монографий, является целесообразным дать систе-
матическое изложение этого вопроса, доступное достаточно
широкому кругу студентов физико-химических специаль-
ностей, аспирантов, инженеров и научных работников,
имеющих дело с термодинамикой и ее разнообразными при-
менениями.
В монографии излагаются необходимые сведения по ста-
тистической термодинамике, исходные молекулярные данные
и методы вычисления термодинамических функций газов и
отчасти жидкостей и твердых тел, а также рассматривается
вопрос о расчете химических равновесий.
В качестве основного положения, из которого выводятся
необходимые для вычисления термодинамических функций
формулы, в монографии использовано известное соотношение
между свободной энергией и суммой по состояниям системы,
причем доказательство этого соотношения не приводится.
Последнее сделано по двум соображениям: во-первых,
достаточно строгое доказательство значительно увеличило бы
*) Краткое изложение этого вопроса дается в ряде учебни-
ков, монографий и справочников [5,22,32, 19, 20, 3, 11, 29, 10, 12,
70,72]. См. также А. И. Бродский [4], В. М. Грязнов
и А. В. Фрост [26], Г десстон[24] и обзорные работы [63,
49, 94].
10
ПРЕДИСЛОВИЕ
объем монографии, а приведение элементарных доказа-
тельств, например доказательств, основанных на известной
формуле Больцмана, едва ли было бы целесообразно, так
как они после появления работ Фаулера и А, Я. Хинчина
заслуживают многочисленных упреков; во-вторых, к настоя-
щему времени появился ряд руководств по статистической
термодинамике, рассматривающих указанный вопрос более
детально.
В монографии используются только элементарные сведе-
ния из классической и квантовой механики. Если читатель
совершенно незнаком с этими сведениями, рекомендуется
прочитать главы V, IX—XII учебника Э. В. Шпольского
«Атомная физика» [84]. Места, не являющиеся необходи-
мыми, а также некоторые места, требующие большой под-
готовки, выделены мелким шрифтом.
Автор выражает благодарность проф. М. А. Ельяшевичу,
рецензировавшему данную монографию и сделавшему ряд
ценных указаний, а также аспирантам Г. А. Зайцеву и
Р. А. Гудовой, прочитавшим рукопись в процессе ее под-
готовки. Автор благодарит также редактора издательства
М. В. Копытину за большую работу цо подготовке книги
к изданию и редактирование.
Автор будет весьма признателен за критические замеча-
ния и предложения по устранению недостатков, которые
будут сообщены ему читателями.
ВВЕДЕНИЕ
Статистические методы вычисления термодинамических
функций и расчета химических равновесий приобрели к на-
стоящему времени очень большое значение. Высокая точ-
ность и простота этих методов открывают широкие воз-
можности для их дальнейшего применения при решении
ряда теоретических и практических задач.
Вычисление термодинамических функций статистическими
методами оказалось возможным благодаря возникновению и
развитию статистической термодинамики, установившей
связь молекулярных состояний с макроскопическими свой-
ствами системы. Значительному прогрессу статистической
термодинамики способствовало возникновение квантовой ме-
ханики, позволившей более точно установить связь возмож-
ных состояний молекул и термодинамических функций.
Выяснилось, что для определения последних нужно знать
допустимые состояния молекул и соответствующие им уровни
энергии ер е2, s3, . . ., еге, ...
Квантовая механика показала, как находить эти состоя-
ния и эти уровни энергии из спектроскопических и молеку-
лярных данных.
Задача вычисления термодинамических функций оказалась
сравнительно простой для идеальных газов и некоторых
других систем, например одноатомных твердых тел. В этих
простых случаях нужно найти выражение
Б
_______________________________п
п
где k — постоянная Больцмана, Т—абсолютная температура,
а индекс п означает возможное состояние молекулы. Сум-
мирование в этой формуле проводится по всем возможным
квантовым состояниям.
12
ВВЕДЕНИЕ
Величина Q получила название суммы по состояниям
молекулы. Зная Q и две ее первые производные по темпе-
ратуре, можно найти все основные функции состояния:
внутреннюю энергию Е, энтальпию (теплосодержание) Н,
энтропию S, свободную энергию F и изобарно-изотермиче-
ский потенциал Ф.
Напомним кратко определение этих функций (см. [29,48,
42,27]).
Внутренней энергией Е называется энергия системы,
являющаяся функцией ее состояния и характеризуемая тем,
что ее приращение равно сообщенному системе количеству
теплоты Q, сложенному с работой внешних сил W:
e2-e1==q^w.
Энтальпией (теплосодержанием) называется функция со-
стояния, определяемая равенством
H = E + pv.
Энтропией называется такая функция состояния, дифа
ференциал которой равен элементу теплоты, подведенному
обратимо, деленному на абсолютную температуру тел-
fl момент подведения этого элемента теплоты:
dS = ^-.
Свободной энергией называется функция состояния, опре-
деляемая равенством
F = E—TS.
Наконец, изобарно-изотермический потенциал (термоди-
намический потенциал Гиббса) определяется с помощью
формулы
Ф = Н — TS = E-\-pv — TS.
Все эти функции являются характеристическими [29]. Че-
тыре из них (£, Н, F и Ф) представляют собой так назы-
ваемые термодинамические потенциалы [29].
Перечисленные выше функции состояния нашли очень
большое применение как при рассмотрении теоретических
ВВЕДЕНИЕ
13
вопросов, так и при решении практических задач. Составле-
ние тепловых балансов, проектирование котлов, компрес-
соров, тепловых и холодильных машин, расчет химических
равновесий, расчет химической аппаратуры, проблемы ин-
тенсификации и рационализации технологических процессов
и многие другие задачи (см., например, [И]) требуют
знания термодинамических функций. Все это придает
очень большую ценность статистическим методам их вычи-
сления.
На развитие статистических методов и их применение
оказало существенное влияние изучение свойств и строения
молекул. Большую роль при этом сыграли классические
работы А. М. Бутлерова [7], построившего теорию хими-
ческого строения молекул. Чрезвычайно полезным оказалось
изучение оптических, электрических и других свойств мо-
лекул. Обширный экспериментальный материал по спектрам,
накопленный к тридцатым годам нашего столетия, позволил
в период 1926—1934 гг. выполнить точное вычисление
термодинамических функций двухатомных и простых много-
атомных газов (например, НС1, Н2, D2, HD, О2, N2, СО,
С1.2, NO, СО2, Н2О, N2O, HCN и некоторых других) *).
Найденные значения функций состояния позволили провести
точный расчет ряда химических равновесий.
Очень большое значение в применении статистических
методов, особенно к многоатомным молекулам, имело от-
крытие комбинационного рассеяния света Г. С. Ландсбергом
и Л. И. Мандельштамом в Москве и Раманом в Калькутте.
Изучение спектров комбинационного рассеяния позволило
находить частоты нормальных колебаний, необходимые для
определения колебательных состояний молекул.
Это открытие, нашедшее ряд широких применений [31,
90, 20, 19, 81, 13], способствовало дальнейшему прогрессу
в определении состояний многоатомных молекул. В изучении
спектров комбинационного рассеяния многоатомных молекул
выдающееся место занимают работы отечественных ученых
А. И. Бродского, Я- К. Сыркина, М. В. Волькенштейна,
П. А. Бажулина, П. П. Шорыгина, Е. Ф. Гросса, В. М. Та-
тевского и др. (см. [20, 12, 13]).
*) См. обзорные работы А. В. Фроста [198], Я. И. Г е р а с и-
м о в а [113], С. Глесстона [114], Касселя [236], Цензе [267].
14
ВВЕДЕНИЕ
Применение электронографических данных (см. [22]) и
результатов по изучению спектров комбинационного рассея-
ния и инфракрасных спектров (см. [20, 82]) сделало воз-
можным вычисление термодинамических функций большого
числа многоатомных молекул. Одним из первых, использо-
вавших методы статистической термодинамики для расчета
функций состояния и равновесия многоатомных газов, был
А. В. Фрост [199, 200].
К 1940 г. были произведены вычисления термодинами-
ческих функций около 120 газов и паров (см. обзорные
работы Касселя [236], Цейзе [268] и Вильсона [264]). В пе-
риод 1940—1946 гг. были получены данные еще примерно
для 150 соединений,
Применение статистических методов и их развитие были
обусловлены дальнейшими успехами в изучении строения и
свойств многоатомных молекул и их электронных, колеба-
тельных и вращательных состояний.
Существенный прогресс в изучении колебаний много-
атомных молекул был достигнут в работах советских ученых.
М. А. Ельяшевич и Б. И. Степанов разработали удобный
метод вычисления частот колебаний многоатомных молекул
и рассмотрели ряд его применений *).
М. В. Волькенштейн и М. А. Ельяшевич построили тео-
рию интенсивности и поляризации колебательных спек-
тров **). Л. С. Маянц [163] разработал теорию характери-
стических частот.
Значительную помощь в изучении строения многоатомных
молекул оказало измерение дипольных моментов (см. [57]).
Обширные исследования в этой области были выполнены
Я. К. Сыркиным, В. Г. Васильевым, Е. Н. Гурьяновой,
А. Н. Шидловской, Е. А. Шотт-Львовой и др.
Большое значение для вычисления термодинамических
функций имели электронографические измерения (см. [22]),
позволившие определить расстояния между ядрами в мо-
лекулах и по ним найти значения моментов инерции. За
последнее время для определения моментов инерции и изу-
*) См. обзорную работу М. А. Ельяшевича [137], а также
М. В. Волькенштейн, М. А. Ельяшевич и Б. И. Степа-
нов [12].
**) См. обзорную работу М. В. Волькен штейна [107], см.
также [12] и [13].
ВВЕДЕНИЕ 15
чения структуры молекул нашла широкое применение
радиоспектроскопия (микроволновая спектроскопия) (см. об-
зорную работу Вильсона [266] и монографию [89]).
Успехи в изучении свойств и строения молекул, которые
достигнуты к настоящему времени, а также ожидаемый
прогресс в этой области, увеличивают актуальность стати-
стических методов вычисления термодинамических функций.
Несомненно, что эти методы найдут широкое применение
при решении ряда важнейших практических задач.
ГЛАВА I
ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ
ТЕРМОДИНАМИКИ
§ 1. Статистическая физика, статистическая механика
и статистическая термодинамика
Статистическая физика изучает системы, построенные из
очень большого числа корпускул: молекул, ионов, электро-
нов и т. д. При этом статистическая физика исходит из
свойств и законов движения микрочастиц, составляющих
данную систему, и ставит своей основной задачей определе-
ние по ним макроскопических свойств изучаемых объектов.
Такая постановка задачи вытекает из реальности микро-
частиц (молекул, атомов, ионов, электронов, протонов, ней-
тронов и др.), существование которых твердо установлено
и не вызывает ни малейших сомнений.
Основоположником статистической физики следует счи-
тать М. В. Ломоносова, разработавшего впервые [46, 45,
44, 47] начала кинетической теории вещества и, в ча-
стности, кинетической теории газов. Кинетическая теория
вещества получила дальнейшее развитие во второй поло-
вине XIX века в работах Максвелла, Клаузиуса и Больц-
мана в виде кинетической теории газов, а затем в работах
Больцмана [210,2], Гиббса [21] и Михельсона [51] были
разработаны общие принципы классической статистической
физики.
Важным этапом в развитии статистической физики яви-
лось введение в нее квантовых представлений. Возникнове-
ние в XX веке квантовой механики и применение ее законов
способствовало дальнейшему глубокому развитию кинетиче-
ской теории вещества.
СТАТИСТИЧЕСКАЯ ФИЗИКА
17
§ ч
Основой для создания классической статистической фи-
зики послужили начала статистической механики, разрабо-
танные главным образом Гиббсом [21].
Особенностью систем, построенных из очень большого
числа частиц, является отсутствие знания начальных условий,
под которыми в классической механике понимаются значения
координат и скоростей частиц в начальный момент времени.
Действительно, в случае таких систем невозможно даже
выписать начальные условия, не говоря уже об их экспери-
ментальном определении. Интегрирование уравнений движе-
ния без знания начальных условий оказывается невозмож-
ным. Поэтому статистическая физика базируется на законах
статистической механики — механики, изучающей системы,
начальные условия которых не полностью известны *).
Применение статистической механики к системам, по-
строенным из большого числа частиц, оказалось чрезвы-
чайно плодотворным, особенно при изучении систем в со-
стоянии термодинамического равновесия. В частности, ме-
тоды статистической физики позволили обосновать основные
положения термодинамики. Возникшая таким образом дис-
циплина получила название статистической термодинамики.
Статистическая термодинамика является частью статистиче-
ской физики. Другой составной частью последней является
статистическая кинетика **), изучающая скорости процес-
сов во времени в системах, построенных из большого числа
частиц.
Методы статистической термодинамики на основании
свойств и законов движения корпускул, из которых построена
данная система (например, газ, кристалл), позволяют про-
изводить вычисление различных физических величин в состо-
янии термодинамического равновесия. Эти методы дают воз-
можность найти статистическое истолкование основных тер-
модинамических величин: температуры, энтропии, свободной
энергии и т. д.
*) Статистическая механика оказывается полезной и при изу-
чении систем с небольшим числом степеней свободы (см. Т о л-
мен [95]). В литературе часто не проводят различия между ста-
тистической физикой и статистической механикой.
**) В. Г. Л е в и ч [40] дает слишком узкое определение стати-
стической физики, отождествляя последнюю со статистической тер-
модинамикой. С этим нельзя согласиться (см., например,
М. А. Леонтович [41]).
2 Зак. 835. И. Н. Годнее
18 ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ (гл. i
§ 2. Макроскопическое описание состояния
В классической (феноменологической) термодинамике со-
стояние системы описывается с помощью небольшого числа
параметров, доступных непосредственному измерению. Опыт
показывает, что в случае системы, находящейся при опре-
деленных внешних условиях, задаваемых координатами внеш-
них тел и условиями теплового обмена с окружающими телами,
макроскопические свойства системы приобретают значения,
которые практически не меняются с течением времени. В этом
случае говорят, что система находится в состоянии термо-
динамического равновесия *). Это равновесие называется
устойчивым, если при произвольных небольших изменениях
внешних условий система после устранения этих изменений
возвращается в первоначальное состояние.
Процесс достижения состояния термодинамического рав-
новесия происходит постепенно. По мере достижения состоя-
ния термодинамического равновесия макроскопические свойства
системы меняются, принимая через достаточно большой про-
межуток времени определенные практически постоянные зна-
чения **).
Макроскопическое состояние такой системы, находящейся
в условиях термодинамического равновесия, может быть
описано значениями внешних параметров at, а2, а„, ... и
температурой окружающей среды или значениями парамет-
ров at, а.2, а3, . .. и внутренней энергии системы Е. Так,
например, состояние газа, построенного из одинаковых мо-
лекул, с макроскопической точки зрения может быть задано
температурой и объемом (последний является внешним пара-
метром) или энергией и объемом.
В случае более сложных систем, построенных из моле-
кул разного рода, макроскопическое состояние системы может
быть описано концентрациями компонентов, температурой и
объемом. Но число таких параметров даже в случае слож-
ной, многофазной системы будет невелико.
*) Предполагается, что это состояние не поддерживается с по-
мощью какого-нибудь внешнего процесса.
**) Эти равновесные свойства с течением времени претер-
певают небольшие колебания около средних значений — флукту-
ации.
КЛАССИЧЕСКОЕ ОПИСАНИЕ МИКРОСОСТОЯНИЯ
19
§ 31
§ 3. Микроскопическое описание состояния
при применении к изучаемой системе классической
механики
Макроскопическое описание состояния, широко приме-
няющееся в классической термодинамике, оставляет вне рас-
смотрения молекулярное строение системы. Реальное суще-
ствование молекул и других частиц, из которых построены
окружающие нас тела, делает возможным, по крайней мере
принципиально, применять наряду с макроскопическим опи-
санием состояния так называемое микроскопическое описание,
которое характеризует систему с помощью величин, опре-
деляющих возможно более детально состояние каждой ча-
стицы. Это описание будет различным в зависимости от
того, можно ли применять к частицам системы законы клас-
сической механики или поведение частиц системы нужно
рассматривать с точки зрения квантовой механики. Первые
работы по статистической механике были выполнены при
описании микросостояния с помощью классической механики,
причем был получен ряд ценных результатов, но вскоре
выяснилось, что применение последней оказывается законным
только в предельных случаях. Более общие результаты,
хорошо оправдывающиеся на опыте, получаются при при-
менении квантовой механики. Статистическая физика, осно-
ванная на применении классической механики, оказывается
частным случаем статистической физики, основанной на при-
менении квантовой механики.
Рассмотрим сначала описание микросостояния с точки
зрения классической механики.
Пусть система состоит из N одинаковых частиц, из ко-
торых каждая обладает тремя степенями свободы. Для опи-
сания движения одной частицы нужно знать три координаты
частицы xit yit и три составляющие скорости vxi, vyi, vzi
или три координаты xit yit и три импульса рж{ = m.vxi,
pyi = tnvyi, pzi = mvzi. Для описания всей системы нужно
задать 3/V координат и 3N импульсов. Все эти величины и
будут описывать микросостояние системы. В более общем
случае, если каждая частица имеет г степеней свободы,
нужно задать l = rN обобщенных координат qv q2, qfj, ...,
ql и 1 — rN обобщенных импульсов pt, р.2, p;i, . . ., рг. Так,
например, микросостояние 1 г-моля идеального двухатомного
2*
20 ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ термодинамики (гл. I
газа, молекула которого будет иметь г = 5 степеней сво-
боды, если можно пренебречь колебательным движением
ядер, мы будем описывать совокупностью 5N0 обобщенных
координат и 5N0 обобщенных импульсов, где No— число
Авогадро. Если система состоит из нескольких сортов частиц,
например частиц с степенями свободы, Д/2 частиц
с г2 степенями свободы, то для описания микросостояния
системы нужно задать I = Nlr1 -f- N2r2 обобщенных коор-
динат и столько же обобщенных импульсов.
Микросостояние системы удобно изображать точкой
в 2/-мерном евклидовом пространстве, построив 21 осей и
откладывая на них значения координат и импульсов. Это
пространство получило название фазового пространства,
а точка, изображающая микросостояние, — фазовой точки.
С течением времени состояние системы будет изменяться,
и фазовая точка будет описывать в фазовом пространстве
линию, которая получила название фазовой траектории.
Следует подчеркнуть, что движение частиц происходит
в обычном пространстве, а фазовое пространство применяется
для графического изображения микросостояния системы.
Изменение микросостояния с течением времени может быть
представлено уравнениями классической механики, например урав-
нениями Гамильтона [8, 62, 43], которые в случае сил, обладающих
потенциалом, имеют вид
• _дН
Pi~~dqi’
где z = 1, 2, 3.I и Н(р, q, t) — функция Гамильтона.
В случае систем, изучаемых в статистической термоди-
намике, фазовое пространство имеет очень большое число
измерений. Так, в случае одного моля одноатомного газа,
состояние которого определяется 3% координатами и ЗА/0
импульсами, фазовое пространство будет иметь 6Af0, т. е.
'—'36 -1023 измерений. Естественно, что для таких систем
нельзя ни определить экспериментально положение фазовой
точки (микросостояние) в данный момент времени, ни проин-
тегрировать дифференциальные уравнения механики. Это
и вызывает необходимость применения особых методов ста-
тистической механики, которые заключаются в рассмотрении
§ 4] ОПИСАНИЕ СОСТОЯНИЯ КВАНТОВОМЕХАНИЧЕСКИХ СИСТЕМ 21
множества микросостояний, совместимых с заданными внеш-
ними условиями, и вычислений по этому множеству средних
значений физических величин. ,
§ 4. Особенности описания состояния
квантовомеханических систем
Выше мы предполагали, что частицы, из которых по-
строены системы, изучаемые в статистической термодина-
мике, подчиняются законам классической механики. Однако
это предположение в общем случае оказывается несостоя-
тельным. Вместо классической механики мы должны приме-
нять квантовую механику — науку о свойствах и движении
микрочастиц *). Свойства микрочастиц (электронов, прото-
нов, атомов, молекул и т. д.) резко отличаются от свойств
тел, рассматриваемых в классической механике.
При изучении квантовомеханических систем мы сталки-
ваемся со следующими особенностями (сначала будем пред-
полагать, что система состоит из небольшого числа частиц
и число степеней свободы системы I невелико):
а) Энергия (в случае системы, занимающей конечный
объем т/) и некоторые другие величины, например момент
количества движения, не могут принимать произвольных
значений, но имеют только дискретные значения. Так, ока-
залось, что энергия атома или молекулы, находящихся
в конечном объеме v, может принимать только определен-
ный ряд значений ер г2, е3, ..., ек, . . ., причем не су-
ществует состояний с промежуточными значениями. Ана-
логично линейный гармонический осциллятор, колеблющийся
с частотой V, имеет состояния с энергиями
h'> 3h't 5Иу 7 fi'/ 9/гч
“2 ’ -g-, -у, -у........и т. д,
где h — постоянная Планка.
Состояния с определенными значениями энергии sv е2,
г3....гк, . . . получили название стационарных, а сами
значения энергии были названы уровнями энергии.
*) Элементарное изложение основ квантовой механики см.
Э. В. Шпольский [84]; более подробное изложение см. Д. И. Б л о-
Хинцев [1], Л, Ландау и Е. Лифшиц [37], В. А. Фок [67].
О смысле волновой функции см. дискуссию [97, 197, 101], а также
работы Бома [209].
22 ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ [гл. I
В квантовой механике каждой физической величине А может
быть поставлен в соответствие линейный эрмитов оператор А.
Значения, принимаемые физической величиной, оказываются соб-
ственными значениями оператора А. Они могут быть найдены при
решении уравнения
= (1.2)
Набор собственных значений at, а2, а3, ... называется спектром
физической величины А. Некоторые величины (например, импульс,
координаты) имеют непрерывный спектр. В частности, энергии соот-
ветствует оператор энергии Н, и собственные значения (уровни
энергии) определяются при решении уравнения
ЯФ = еФ, (1.3)
которое называется уравнением Шредингера для стационарных
состояний или волновым уравнением стационарных состояний.
Ь) При изучении квантовомеханических систем, как пока-
зывает опыт, необходимо ввести новые переменные, не имею-
щие себе аналогов в классической механике. Такими пере-
менными являются «спиновые» переменные, описывающие
поведение собственного момента количества движения частиц —
спина. По этой причине элементарная квантовомеханическая
частица, обладающая спином, например электрон, будет
иметь не три, а четыре степени свободы движения.
Величина квадрата спинового момента (собственного момента
количества движения частицы) оказывается равной
№
П-4)
где 5 — квантовое число может быть либо целым числом, включая
значение 0, либо полуцелым. Для данной элементарной частицы
квантовое число s или, как кратко говорят, спин имеет только одно
фиксированное значение. При этом оказывается, что проекция спи-
нового момента на неподвижную ось может принимать только дис-
кретные значения
= (1-5)
где квантовое число т8 пробегает значения s, s— 1....—s, всего
2s+1 значений. В случае электрона квантовое число s равно 1/2.
Квантовое число ms у электрона принимает только два значения:
ms = 1/2 и тя = — 1/2. Для дейтона $ = 1, а допустимые значения
те будут -|- 1, 0, — 1.
§ 4] ОПИСАНИЕ СОСТОЯНИЯ КВАНТОВОМЕХАНИЧЕСКИХ СИСТЕМ 23
с) Состояние квантовомеханической системы с I степенями
свободы не может быть задано набором I координат qr,
q2, q; и I импульсов pv р.2< pt. Вместо этого оно
описывается функцией
Ф = Ф(^, q.2.....qt, t) (1.6)
одних только координат или функцией
Ф = Ф(Р1, р.2, .... р„ t) (1.7)
одних только импульсов *). Такое описание состояния свя-
зано со статистическим характером утверждений квантовой
механики. Оказывается, что, зная состояние системы, мы не
можем, вообще говоря, с достоверностью предсказать ре-
зультат измерения данной физической величины, но можем
только найти вероятность **) того, что данная величина М
получит значение т, лежащее в интервале (а, Ь), т. е.
вероятность неравенства а < т < Ь. Квантовая механика
дает формулы, по которым можно вычислить эту вероят-
ность, если известна функция Ф (q, t). В частности, по квад-
рату модуля этой функции может быть найдена вероятность
того, что з момент времени t координаты системы лежат
в интервале
от qr до qr-±~dqv
от q.2 до q2-\-dq2.
от qi ДО q^dq^
Эта вероятность будет равна
|4r|2cty1<ty.2 ... dqv
(1-8)
Таким образом, заданием функции Ф определяются не зна-
чения физических величин, а законы их распределения. Функ-
ция Ф(q, t), обычно называемая волновой функцией, удо-
влетворяет дифференциальному уравнению, так называемому
*) Достаточно задать одну из этих функций, так как другая
может быть найдена по заданной.
**) Здесь имеется в виду общий случай. В некоторых частных
случаях вероятность того, что данная величина примет определенное
значение, может быть равна единице,
24 ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ [г,1. I
уравнению Шредингера или волновому уравнению, которое
показывает, как меняется состояние по времени.
В стационарных состояниях, т. е. в состояниях с задан-
ной энергией гк, система может быть описана функцией
Чк<41> Ч-2> • • •• 4i)> (!-9)
которая не зависит от времени. Эту функцию называют
волновой функцией стационарного состояния. Она удовле-
творяет дифференциальному уравнению Шредингера, не со-
держащему времени, т. е. волновому уравнению для стаци-
онарных состояний. При этом оказывается, что каждому
уровню энергии соответствует одна или несколько функций.
В последнем случае говорят, что уровень энергии вырожден,
а число линейно независимых функций, соответствующих
данному уровню энергии, называется весом уровня или сте-
пенью вырождения. В случае вырождения мы будем иметь
следующую схему состояний:
_____Ч______
'i'll- '^12- •••- W
1 2 ах
_________________________________________________________________________________________________________________________________________________________________
'?21- '?22...................................................... • • •; 'At- $к-2’ • • •> '^кап>
—|— 1 #2 —1 , . • . , fl.-J .................................................................
fl2 ак
(1-Ю)
Уровню гх будет соответствовать аг функций — ф1Р б12, .. .,
и вес уровня будет ар вес уровня е2 будет а.2 и т. д.
Волновое уравнение, которому удовлетворяет функция W (^1(
• • • Яъ описывающая состояние системы, имеет вид
= <U1)
где Н—оператор энергии.
Это уравнение по своей роли аналогично системе уравнений
механики, например системе уравнений Гамильтона (1.1). В случае
§ 4] ОПИСАНИЕ СОСТОЯНИЯ КВЛНТОВОМЕХАНИЧЕСКИХ СИСТЕМ 25
стационарных состояний уравнение (1.11) может быть непосред-
ственно проинтегрировано. Мы будем иметь:
Ч;И<7, (М2)
Подставляя решение (1.12) в уравнение (1.11), мы получим уравне-
ние (1.3), т. е. уравнение Шредингера для стационарного состоя-
ния
= (1-13)
с помощью которого можно найти и собственные значения энергии
(уровни энергии) еъ е2..е.у, ..., и соответствующие им волновые
функции стационарных состояний (собственные функции оператора
энергии). Произвольная волновая функция Ф (q, t), описывающая
некоторое состояние, может быть разложена в ряд по собственным
функциям стационарных состояний ф;(^). Это разложение будет
иметь вид
Ч’(<7, 0 = (1-14)
к
Для описания состояния вместо функции Д’ (q, t) можно применить
совокупность всех коэффициентов ct с<> с-, ... с,>с ..., входящих
в (1.14).
d) Важной особенностью квантовомеханического описа-
ния состояния системы, содержащей несколько одинаковых
частиц, является наличие определенных условий симметрии,
накладываемых на волновые функции.
Пусть система состоит из N одинаковых частиц, из кото-
рых каждая имеет г степеней свободы. Общее число степе-
ней свободы будет Nr — I. Пусть система находится в ста-
ционарном состоянии, описываемом функцией
7?........................(1-15)
принадлежащей уровню с энергией гк. Обозначив совокуп-
ность всех г координат j-й частицы через запишем функ-
цию (1.15) в виде
(1.16)
Функция (1.16) является решением волнового уравнения Шре-
дингера. Но этому уравнению будет удовлетворять и функция
'Ш- Ъ............^). (1-17)
полученная перестановкой всех координат первой частицы
со всеми координатами ;2 второй частицы, а также все другие
26 ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ [ГЛ. I
функции, возникающие из функции (1.16) при других пере-
становках координат £р $2, • •, Всего таких перестано-
вок существует (NI). Если уровень энергии был первона-
чально невырожденным и если все функции, полученные
перестановками, будут линейно независимыми, мы вместо
одной функции (1.16) будем иметь NI линейно независимых
функций. Так, в случае N = 3 в результате 3! = 6 пере-
становок получаются следующие функции:
(123), ^(132), '
^(213), Ы231),
(1-18)
6ft(312), ^(321),
где совокупности координат частиц ;2 и £3 обозначены
цифрами 1, 2, 3. На первый взгляд может показаться, что
все такие состояния будут физически различными и уровень
энергии гк, бывший первоначально невырожденным, станет
вырожден ДЛ кратно. Однако в действительности это не так.
Опыт показал, что волновые функции, описывающие ре-
альные состояния системы, должны удовлетворять еще осо-
бым требованиям симметрии. Полные волновые функции,
т. е. функции, содержащие все координаты системы, должны
быть или симметричными или антисимметричными по отно-
шению к перестановкам координат одинаковых частиц.
Симметричной функцией называется такая функция, кото-
рая при любой перестановке координат $2, ..., оди-
наковых частиц остается неизменной *):
Р<Ь = 6, (1.19)
где Р<Ь означает функцию, полученную из 6 перестановкой
координат одинаковых частиц.
Антисимметричной функцией называется такая функция,
которая при перестановке координат двух частиц (при транс-
позиции) меняет знак на обратный **):
ТЬ = — <р. (1.20)
*) В дальнейшем при применении термина «перестановка» мы
не будем указывать особо, что речь идет о перестановках коорди-
нат $!, .....%N, т. е. «обмене частиц».
**) Символ Р означает любую перестановку, а символ Т —
транспозицию,
§ 4] ОПИСАНИЕ СОСТОЯНИЯ КВАНТОВОМЕХАНИЧЕСКИХ СИСТЕМ 27
Здесь следует подчеркнуть, что определение антисимме-
тричной функции, установленное для транспозиции, не тре-
бует, чтобы при всякой перестановке функция меняла знак.
Если перестановка, например, состоит из двух транспози-
ций, антисимметричная функция изменит знак на обратный
два раза, вследствие чего функция при такой перестановке
останется неизменной.
Примером симметричной функции для N= 2 будет функция
6(12) + 6(21),
которая при применении к ней перестановки обращается в
ф(21) + 6(12),
т. е. остается неизменной. С другой стороны, для N=2
функция
6(12)-ф(21),
как легко убедиться, будет антисимметричной.
Симметричные и антисимметричные функции обладают
важным свойством: при выполнении любой перестановки ко-
ординат одинаковых частиц квадрат их модуля остается не-
изменным. Это приводит к тому, что в системах, описывае-
мых такими функциями, в результате перестановок не воз-
никают новые состояния. Любая перестановка координат
одинаковых частиц приводит к тому же состоянию, т. е.
состояния, полученные при обмене частиц, оказываются не-
различимыми. Из ЛП возможных функций, соответствующих
невырожденному уровню энергии, реализуется только одна —
симметричная или антисимметричная.
При данном еЛ в силу линейности уравнения Шредингера (1.13)
ему будут удовлетворять не только рассмотренные выше М функ-
ций, но и любая их линейная комбинация. Может случиться, что ни
одна из ЛП функций, полученных перестановками координат одинако-
вых частиц, не является ни симметричной, ни антисимметричной. Но,
построив надлежащим образом линейные комбинации, мы можем по-
лучить одну симметричную и одну антисимметричную функцию *).
Кроме таких функций можно построить линейные комбинации более
сложной симметрии. Например, для W=3 из _3! = 6 функций (1.18)
можно построить одну симметричную
ф (123) + 6 (132) + ф (213) + 6 (231) + 6 (312) + 6 (321), (1.21)
*) Все 2V! функций предполагаются линейно независимыми.
28 ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ [гл. 1
одну антисимметричную и четыре функции более сложной симме-
трии. Аналогично для = 4 при отсутствии вырождения и усло-
вии что все NI = 4! = 24 функции являются линейно независимыми,
мы можем построить одну симметричную функцию, одну антисим-
метричную и 22 функции, имеющие более^ сложную симметрию ).
Однако квадрат модуля функции сложной симметрии не остается
неизменным при перестановках, и такие состояния не были обна-
ружены в природе.
были обна-
Таким образом, из всех возможных типов симметрии
полных волновых функций реализуются только два: класс
симметричных функций и класс антисимметричных функций.
В природе существуют двоякого рода системы, построенные
из одинаковых частиц:
1) системы, состоящие из частиц, описываемых полными
антисимметричными волновыми функциями. Такие частицы
называются частицами, подчиняющимися статистике Ферми —
Дирака;
2) системы, состоящие из частиц, описываемых полными
симметричными волновыми функциями. Такие частицы назы-
ваются частицами, подчиняющимися статистике Бозе — Эйн-
штейна. К частицам первого рода принадлежат, например,
электроны, протоны, нейтроны. К частицам второго рода
принадлежат, например, дейтоны. Частицы, полные волно-
вые функции которых удовлетзоряли бы другим условиям
симметрии, в природе не обнаружены *) **).
Условия симметрии полных волновых функций (случаи
симметричных или антисимметричных функций) сложных ча-
стиц, например ядер, могут быть определены с помощью
следующего простого правила:
если сложная частица состоит из четного числа элемен-
тарных частиц, подчиняющихся статистике Ферми— Ди-
рака,— протонов, нейтронов, электронов,—то она описы-
*) Волновые функции по своей симметрии могут быть разде-
лены на классы симметрии. В случае четырех частиц Ай = 4! = 24
функции распределяются на пять классов. К классу А (симметрич-
ных функций) принадлежит одна функция, к классу В (антисимме-
тричных функций) — одна функция, к классу Е (первый тип слож-
ной симметрии) — четыре, к классу 7\ (второй тип сложной симме-
трии) —девять, к классу Т2 (третий тип сложной симметрии) — девять.
**) Между спином и статистикой элементарных частиц имеется
связь: частицы с полуцелым спином подчиняются статистике Ферми—
Дирака: частицы с целым спином, включая значение нуль, — стати-
стике Бозе — Эйнштейна.
§ 5] КВАНТОВОМЕХАНИЧЕСКОЕ ОПИСАНИЕ МИКРОСОСТОЯНИЯ 29
вается симметричными волновыми функциями; если сложная
частица состоит из нечетного числа таких частиц, то она
описывается антисимметричными волновыми функциями.
Необходимость этого правила доказывается очень просто.
Пусть сложная частица состоит из b элементарных частиц.
Перестановка двух сложных частиц производит одновременную
перестановку стольких пар элементарных частиц, сколько их со-
держится в сложной частице, т. е. производит перестановку b пар.
При перестановке одной пары знак меняется на обратный; следо-
вательно, полная волновая функция после перестановки двух слож-
ных частиц будет умножена на (—I)6, т. е. при b четном она со-
хранит знак и изменит его при b нечетном.
Так, например, ядро гелия 2Не4 состоит из двух прото-
нов и двух нейтронов, b — 4, откуда следует, что ядра
гелия будут описываться симметричными волновыми функ-
циями. Аналогично для ядер 8О17 мы имеем Ь= 17, откуда
следует, что эти ядра будут описываться антисимметричными
волновыми функциями.
§ 5. Квантовомеханическое описание микросостояния
Изложенные выше особенности квантовомеханических си-
стем должны быть приняты во внимание при микроскопиче-
ском описании систем, изучаемых в статистической термодина-
мике. В этом случае мы будем иметь дело с квантовомеханиче-
ской системой, обладающей очень большим числом степеней
свободы. В отличие от классической статистики, где состоя-
ние определялось совокупностью всех I координат и I им-
пульсов, микросостояние системы будет описываться волно-
вой функцией
q2> • Чк (1.22)
удовлетворяющей условиям симметрии *). Если рассматри-
ваемая система будет изолирована, она будет находиться
в одном из своих стационарных состояний с энергией Еп,
которое описывается функцией tyn(qlt qit , qi), соответ-
ствующей этому уровню энергии.
Так же как и в случае применения классической меха-
ники, микросостояние системы остается для нас практически
*) Взаимодействие системы с окружающими телами предпола-
гается слабым и медленным (квазистатическим).
30 ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ [гл. I
неизвестным. Мы не можем указать, в каком именно из допу-
стимых микросостояний находится система в данный момент
времени. Однако мы можем найти множество стационарных
микросостояний, совместимых с заданными внешними усло-
виями. Рассмотрение множества допустимых микросостояний и
вычисление по ним средних величин и позволяют решить основ-
ные задачи статистической термодинамики. Описание микро-
состояния с помощью функции (1.22) вместо набора коор-
динат qv q2, . . ., qt и импульсов pv р.2, .... pt является
весьма существенным отличием квантовомеханическбго опи-
сания от описания микросостояния, применяемого в классиче-
ской механике. Другой важной особенностью микросостояния
являются условия симметрии, накладываемые на волновые
функции, описывающие эти микросостояния.
В зависимости от условий симметрии при вычислении
средних различают две статистики: статистику Бозе — Эйн-
штейна и статистику Ферми — Дирака.
При применении таких статистик мы сталкиваемся с ре-
ализацией меньшего числа микросостояний всей системы,
совместимых с внешними условиями, по сравнению с числом
состояний, подсчитанных при отсутствии условий симметрии.
Так, в разобранных выше простых случаях из N! возмож-
ных состояний реализуется только одно (симметричное или
антисимметричное). Однако существуют системы, у которых
требования симметрии не снижают числа возможных микро-
состояний. При подсчете последних мы можем не учитывать
требований симметрии. Такие системы получили название
локализованных. К ним относятся системы, построенные из
частиц, положение которых фиксировано. Примером локали-
зованной системы являются ато-
мы твердого тела, образующие
кристаллическую решетку.
Рассмотрим несколько подроб-
нее простой пример локализован-
ной системы, состоящей из двух
электронов, из которых каждый
принадлежит определенным ато-
мам А и В (черт. 1). Такой случай
осуществляется,например, в твердом теле с неметаллической ре-
шеткой. Каждый электрон оказывается локализованным, например
электрон первый у атома А, электрон второй у атома В. Пусть
электрон первый находится в k-м энергетическом состоянии, электрон
ВЫЧИСЛЕНИЕ СРЕДНИХ
31
§ 6]
второй — в Z-м состоянии. Состояние системы описывается волновой
функцией
^(1)^(2). (1.23)
Переставляя состояния электронов k и I, получим вторую вол-
новую функцию
<^(1)^(2), (1.24)
которая также будет решением волнового уравнения. Таким обра-
зом, мы получим АП = 2! состояний, которые удовлетворяют волно-
вому уравнению. В этих состояниях электроны остаются локализо-
ванными (электрон 1 принадлежит А, электрон 2 принадлежит В).
Функции (1.23) и (1.24) не удовлетворяют условиям симметрии.
Однако из каждой такой функции можно построить по одной
антисимметричной комбинации, переставляя координаты электро-
нов. Мы получим:
= (1)^(2)-^(2)^(1) (1-25)
я
ф2 = ^ (П^(2) -^(2)^(1). (1.26)
Таким образом, из двух функций получаем две, и условие сим-
метрии не снижает число допустимых состояний. Если бы мы имели
два нелокализованных электрона, то из двух функций, возникаю-
щих в результате перестановок, можно было бы построить только
одну антисимметричную комбинацию, и учет симметрии снизил бы
число допустимых состояний. Более общим примером локализован-
ных систем является система, состоящая из N электронов, из кото-
рых каждый фиксирован у определенного атома твердого тела.
Аналогично система, состоящая из N гармонических осцилляторов,
пространственное положение которых является фиксированным,
также является локализованной системой.
В случае локализованных систем число линейно незави-
симых волновых функций, полученных перестановками, сов-
падает с числом линейно независимых функций, удовлетво-
ряющих условиям симметрии. При подсчете числа возможных
состояний и вычислении средних мы можем игнорировать усло-
вия симметрии. Мы получаем квантовую статистику без учета
условий симметрии. Такая статистика носит название полной
квантовой статистики.
§ 6. Вычисление средних. Формула для свободной энергии
Важнейшей задачей статистической термодинамики является
обоснование законов термодинамики на базе молекуляр-
ных представлений о строении вещества. Вместе с тем,
32 ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ (гл. I
статистическая термодинамика должна дать формулы, по-
зволяющие вычислять термодинамические функции системы
по молекулярным состояниям *).
Решение этих основных задач требует рассмотрения мно-
жества микросостояний, совместимых с внешними условиями,
в которых находится система. Такое рассмотрение является
необходимым, так как заданному микросостоянию, т. е. усло-
виям, в которых находится система, соответствует, вообще
говоря, бесчисленное множество микросостояний, с помощью
которых это макросостояние реализуется. Задавая условия,
в которых находится, например, 1 моль идеального газа,
объемом и температурой (его макросостояние), мы с микро-
скопической точки зрения будем иметь дело с бесчисленным
множеством микросостояний, удовлетворяющих заданным
условиям.
Естественно, что при заданном макроскопическом состо-
янии мы не можем указать, в каком именно микроскопиче-
ском состоянии находится система, и статистическая тер-
модинамика для решения своих задач должна применять
теорию вероятностей, т. е. ее метод, как показывает и на-
звание, должен быть статистическим. Естественно допустить,
что наблюдаемые на опыте величины могут быть найдены
как средние величины, вычисленные по множеству допусти-
мых микросостояний **). Этим именно путем и идет стати-
стическая термодинамика. В зависимости от внешних усло-
вий, в которых находится изучаемая система, в статистиче-
ской термодинамике применяется вычисление двух видов
средних:
а) микроканонических средних, вычисляемых при усло-
вии, что энергия системы постоянна (замкнутая система);
б) канонических средних, т. е. средних, вычисляемых при
условии, что температура системы постоянна (система в тер-
*) Изложение основ статистической термодинамики см. В. Г. Л е-
вич [40], А. Г. Самойлович [56], Майер и Майер [49],
Л. Ландау и Е. Лифшиц [38]. См. также Фаулер и Г у г-
г е н г е й м [63], Т о л м е н [95] и Я. И. Френкель [68].
**) Кроме таких средних («средне пространственных») воз-
можно вычисление так называемых «временных средних», т. е.
средних величин, вычисленных при рассмотрении эволюции данной
системы во времени. Проблема связи этих двух средних получила
название «эргодической проблемы» (см. М. А. Леоитович [41]
и А. Я. X инчин [74], ср. А. Я- X и н ч и н [75]).
§ 6] ВЫЧИСЛЕНИЕ СРЕДНИХ 3
мостате). При этом предполагается, что система находите
в состоянии термодинамического равновесия.
Следует подчеркнуть, что указанные выше условия являютс
идеализацией, так как в действительности не существуе
абсолютно замкнутых систем или систем с абсолютно по
стоянной температурой, но эта идеализация вполне допу
стима, так же как допустимо, например, в механике при
менение абсолютно твердого тела и построение механик
неизменяемых твердых тел.
Оба метода вычисления средних, впервые введенны
Гиббсом [21], нашли большое применение.
Математически строгое рассмотрение вопроса о вычислени
микроканонических средних было проведено Дарвином и Фаулеро!
(см. Фаулер [88], Фаулер и Гуггенгейм [63]) и А. Я. Хинчиным [74,75
применившим для обоснования классической и квантовой статистик
предельные теоремы теории вероятностей. А. Я. Хинчиным бы,
также выяснен вопрос об условиях применения канонически:
средних.
При квантовомеханическом рассмотрении вопроса о вычисле
нии средних нужно иметь в виду, что в данном микросостоя
нии физическая величина может принимать ряд значений, приче!
квантовая механика дает вероятности этих отдельных значений
Поэтому нужно сначала вычислять «квантовомеханическое сред
нее», а затем уже находить микроканоническое или каноническо!
среднее *).
При приближенном вычислении средних (квазиклассическа:
статистика) можно пользоваться фазовым пространством, полагая
что каждому микросостоянию (волновой! функции) соответствуе1
ячейка объемом Аг.
Применение методов средних дает возможность получит!
формулы, позволяющие вычислить термодинамические функ
ции по микросостояниям системы, а также обосновать законь
термодинамики **).
При этом для свободной энергии системы, занимающей
объем v и находящейся при температуре Т, получаете!
*) Такое двойное вычисление средних в общем случае произ'
водится с помощью так называемой матрицы плотности (см. Т о Л'
мен [95] и Л. Ландау и Е. Лифшиц [38]).
**) Для обоснования законов термодинамики возможен еще
Другой путь—путь обобщения /7-теоремы Больцмана (см. Н. Н. П и-
рогов [167], Тол мен [95], Борн и Грин [87]), рассматрИ'
Вающий состояние термодинамического равновесия как частный
случай.
3 Зак. 835. И. H. Годнее
34 ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ [гл. I
следующее фундаментальное выражение *):
F = — kT\nZ, (1.27)
где k — постоянная Больцмана и Z-—так называемая сумма
по состояниям системы, зависящая от микросостояний си-
стемы п и соответствующих им уровней энергии Еп'.
(1.28)
п
Суммирование в (1.28) производится по всем допустимым
микросостояниям системы п. Каждое состояние при сум-
мировании берется один раз. Соотношение (1.27) является
справедливым для любой системы (газа, твердого тела),
построенной из взаимодействующих частиц.
§ 7. Сумма по состояниям системы
Сумма по состояниям системы (1.28) играет большую
роль в разнообразных практических применениях статисти-
ческой термодинамики. При помощи соотношения (1.27)
через сумму по состояниям устанавливается связь свободной
энергии, а следовательно, и других термодинамических функ-
ций, с допустимыми микросостояниями. При этом сумма
по состояниям сама является термодинамической функцией
состояния, т. е.
Z = Z(v, T} = Z(p, Г). (1.29)
Для вычисления Z, как это следует из (1.28), нужно
знать допустимые состояния **) и уровни энергии. При сум-
мировании, как мы указывали выше, каждое состояние
считается отдельно. Если уровни энергии системы вырождены,
при суммировании в (1.28) появятся одинаковые слагаемые,
причем, если уровень энергии вырожден о>4 раз, появится <ui
одинаковых слагаемых е~Е4кТ. Поэтому выражение (1.28)
можно записать в виде
Z = ^i^ie кт, (1.30)
*) Мы приводим здесь это выражение без доказательства. Эле-
ментарное доказательство можно найти в книге Планка [55] или
Шредингера [85]; см. также М. А. Леонтович [41],
В. Г. Левич [40], Л. Ландау и Е„Лифшиц [38].
**) В дальнейшем, где это не вызывает недоразумений, вместо
слова «микросостояние» мы будем употреблять термин состояние.
§ 7] СУММА ПО СОСТОЯНИЯМ СИСТЕМЫ 35
причем суммирование в (1.30) производится уже не по
состояниям, а по уровням энергии.
Приведем простой пример, показывающий, как надлежит
пользоваться формулами (1.28) и (1.30). Пусть схема состоя-
ний (см. (1.10)) имеет вид
Номера Ео % Ел 'hi 'Ьг 'ha д2 (1.31)
^21 '^22 'Ьз 'hl <?2Б' • •
состояний 1 2 3 4 5 6 7 8 9
Применяя формулу (1.28), мы будем иметь:
Eq El Е1 Е, Ед
z = е~ + е~ е~ w + е~ w -ф-
_____ Е$ ___ Е^ — Ед Ед
_|_е" ат____-ре'лг .
Такой же результат получается с помощью формулы (1.30):
Eq El Ед
z= 1Г*зг + Зе"'*2’-|-5е"*57+ ...
Следует подчеркнуть, что сумма по состояниям Z зависит
от допустимых микросостояний изучаемой системы. Значе-
ние Z в случае идеального газа при точном вычислении
будет разным в зависимости от рода статистики [41], так
как множество допустимых состояний системы в зависимости
от условий симметрии будет различным. Иное выражение
для Z получится в случае локализованной системы, например
системы гармонических осцилляторов.
Отметим одно важное свойство Z — ее «мультипликатив-
ность» в случае, если система состоит из независимых
частей. Пусть последняя состоит из двух таких частей А
и В. Энергия системы будет:
Еав = ЕаЛ-Ев. (1-32)
Для суммы по состояниям ZAb мы получим:
Ед +^В ^A+^B
Еав= 2 е = 2 2 е
соот. АВ сост. А ооот. В
Вынося е~Ел/кТ за знак суммы по состояниям В, мы будем
иметь:
Zab-ZaZb- (1.33)
3*
36 ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ [гЛ. t
Вычисление Z оказывается в общем случае делом весьма
сложным. Простое выражение для Z получается при изуче-
нии сравнительно несложных систем, например системы
гармонических осцилляторов или идеального газа при не очень
низких температурах. В этих случаях сумму по состояниям
можно выразить через так называемую сумму по состояниям
молекулы (частицы). Энергия упомянутых выше простых
систем будет складываться из энергии отдельных частиц
£ = si + s2+---+^- (!-34)
Значение уровня энергии Еп всей системы в состоянии п
будет зависеть от состояний, в которых находятся отдельные
частицы. Мы получим:
— i2, .... iN = + %+•• + siN- (1 -35)
Для системы, состоящей из М гармонических осцилляторов
(каждый из них локализован, и нам не требуется принимать
во внимание условий симметрии), мы будем иметь:
n+iW'"
Z0C4= 2 е кт . (L36)
n=ii,, г2, i„ ...)
Суммирование в (1.36) надо выполнить по всем допустимым
состояниям системы п (разным набором состояний iv i2,
Z3, ...). Состояния Zv Z2, Z3, . . . можно считать независи-
мыми, так что результат суммирования по можно вынести
за знак остальной суммы, т. е.
Так же будет обстоять дело и с суммированием по i.2, is,...
При этом суммы по состояниям Zx, Z2, ... будут одина-
ковыми.
В результате мы получим:
' •. N
(1.38)
§ 7] СУММА ПО СОСТОЯНИЯМ СИСТЕМЫ 37
Заметим, что формулу (1.38) можно получить непосред-
ственно, применяя соотношение мультипликативности (1.33)
к N независимым осцилляторам.
Аналогично решается задача вычисления Z для идеаль-
ного газа, если исключить область малых объемов и очень
низких температур. В этом случае мы имеем дело с не-
локализованной системой. При суммировании нужно учесть,
что состояния, полученные перестановкой частиц, не будут
различимы. Число различных состояний будет в /V! меньше.
Вместо (1.38) получим*):
/ —
Дгаза — —~ yyi (1-39)
Мы видим, таким образом, что в рассмотренных случаях
для вычисления Z нужно найти выражение
*з
(2 = 2е_/сТ, (1.40)
з
где суммирование производится по всем состояниям моле-
кулы /. Эта сумма получила название суммы по состояниям
молекулы (частицы). Для ее вычисления нужно знать допу-
стимые состояния и уровни энергии молекулы.
Сумма по состояниям молекулы может быть записана
также в виде
Ч
(1.41)
к
В отличие от формулы (1.40), где суммирование про-
изводится по всем состояниям /, в формуле (1.41), где gk
уровней энергии гк объединены в одно слагаемое, мы сум-
мируем по различным уровням энергии гк.
*) В случае достаточно разреженного газа можно сказать, что
каждая молекула занимает один из уровней энергии гк. Если бы
не было требований симметрии, мы получили бы для Z выраже-
ние (1.38). Однако число состояний требуемой симметрии будет
в М меньше, так как из А! состояний получается одно симметрич-
ное и одно антисимметричное. Отсюда и получается выраже-
ние (1.39),
38 ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ [гл. I
Сумма по состояниям молекулы в случае, если энергия
последней состоит из нескольких независимых частей, обла-
дает свойством мультипликативности. Повторяя рассуждения,
которые привели нас к формуле (1.33), мы получим:
•а+'в
— QaQb- (1.42)
А, В
Возвращаясь теперь к выражениям (1.38) и (1.39), пере-
пишем последние в окончательном виде
ZOCU = Q-V (1.43)
и
ON
Лаза = -^-. (1-44)
Следует заметить, что последняя из этих формул не может
быть применена к идеальному газу при очень низких темпе-
ратурах. Хотя в последнем случае и имеет место фор-
мула (1.34), строгий учет условий симметрии приводит
к выражениям для Z, зависящим от рода статистики и отлич-
ным от (1.44). (Вычисление Zra3a в случае статистик Ферми —
Дирака и Бозе — Эйнштейна см. М. А. Леонтович [41].)
При решении некоторых задач статистической термоди-
намики иногда бывает нужно найти приближенное выражение
суммы по состояниям молекулы, которое получается при
применении классической механики. Пусть молекула имеет
г степеней свободы. Элемент объема фазового пространства
молекулы будет dt. — dq^ ... dqrdpt. . . dpr. Заменяя сум-
му (1.40) интегралом и применяя для s формулы классической
механики, мы получим:
в
Q™ = с J . . . J е кт dqt ... dqr dpt . . . dpr, (1.45)
где С — множитель, компенсирующий размерность йл (Q—ве-
личина безразмерная). Однако формула (1.45) не учитывает
существования дискретных квантовых состояний.
Принимая во внимание, что
dqdp — h
(см. [84, 1]), естественно допустить:
C = h~T.
§ 8] ВЫРАЖЕНИЕ ДЛЯ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ 39
Таким образом; мы получим:
Qs-ч ~ . J е d'K. (1-46)
Формула (1.46), естественно, оказывается приближенной.
Она хорошо оправдывается при высоких температурах.
§ 8. Выражение для термодинамических функций
системы через сумму по состояниям Z
Основное выражение для свободной энергии (1.27) при
применении известных термодинамических соотношений позво-
ляет получить также формулы для вычисления по Z всех
остальных термодинамических функций системы. К таким
функциям относятся изобарно-изотермический потенциал Ф,
внутренняя энергия Е, теплосодержание Н, энтропия S,
теплоемкости Ср и Cv и некоторые другие. Свободная энер-
гия и первые три из указанных выше функций (Ф, Е и Н)
представляют так называемые термодинамические потенциалы
(см. [29]). Все они имеют размерность энергии, и по ним
при соблюдении соответствующих условий может быть вычи-
слена максимально полезная работа соответствующего про-
цесса. Вместе с тем, они являются также и характеристиче-
скими функциями (см. [29]), к которым принадлежит также
и энтропия, не являющаяся, однако, термодинамическим
потенциалом.
По характеристической функции (например, свободной
энергии) и ее производным легко найти термодинамические
свойства системы. Этим свойством свободной энергии мы
и воспользуемся для получения формул, выражающих термо-
динамические функции системы через сумму по состояниям Z.
Найдем прежде всего давление. Мы имеем*):
(1-47)
Подставляя в выражение (1.47) значение свободной энергии
из формулы (1.27), получим:
(,-48)
*) См. М. X. Карапетьянц [29] или Д. Партингтон
и А, Раковский [54].
4Q ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ [гл. I
Формула (1.48) позволяет найти уравнение состояния системы,
если известна сумма по состояниям Z. Умножая правую
и левую части равенства (1.48) на объем системы v,
получим:
/dlnZ\
Pv = kTv\-^-)T
(1-49)
или
(1.50)
Для вывода формул, определяющих остальные теормодина-
мические функции, мы можем воспользоваться известными
соотношениями
Ф = F -ф- pv, (1-51)
*--(£).=- (Я (1.52)
e=F~T&\- (1.53)
-*-Я (1-54)
<•=- 'дЕ\ <dTk' (1.55)
\дТ)р‘ (1.56)
Таким образом, заменяя Р и pv в выражении (1.51) из (1.27)
и (1.50), мы будем иметь:
Ф = — kT In Z + kT
1 \o In v) )T
(1-57)
или
Ф= kT
(1.58)
Дифференцирование свободной энергии по температуре
в силу формулы (1.52) позволяет получить следующее выра-
жение для энтропии:
S = 4[lnZ+7(^)J. (1.59)
§ 8] ВЫРАЖЕНИЕ ДЛЯ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ 41
Имея это выражение и значение F из формулы (1.27), мы
найдем для внутренней энергии
E = F-]-TS = — kT\nZ + kT\nZ + kT2{^Pj ,
т. е.
Е="2(^),- (>•«»
Аналогично получается выражение для теплосодержания
с помощью формулы (1.54). Это выражение можно получить
также из определения H = E-\-pv.
Таблица 1
Сводка формул, выражающих термодинамические функции
через сумму по состояниям системы
№ Термодинами- ческая функция Обо- значен- ние Формула
1 Свободная энергия F /•’ = — kTlnZ
2 Изобарно-изотер- мический потенциал Ф . ,_.[7dlnZ\ , -т] Ф — kT II -v, 1 — InZ [у о In V JT J
3 Внутренняя энергия Е E = kT^(d^\ \ дТ )v
4 Теплосодержание И г),]
5 Энтропия S
6 Теплоемкость при постоянном объеме cv с.=да+а,]
ti = kT
Таким образом,
dlnZ\ . _/dInZ\ ~1
d In v )T~I- \ dT /„J
(1.61)
42 ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ [гл. I
или
]• С1-62)
[\ д In г/ )т 1 \<7 In Т v '
Для определения теплоемкости Cv продифференцируем вы-
ражение для внутренней энергии (1.60). Мы получим:
т. е.
С, = йгГ2(^Д) (1.63)
L \ и* /г» \ /vj
Полученные формулы целесообразно представить в виде
таблицы (см. табл. 1).
Заметим, что все эти формулы являются общими. Из
этих общих формул и соотношения мультипликативности
(1.33) вытекает аддитивность термодинамических функций,
если система состоит из нескольких независимых частей,
находящихся в термодинамическом равновесии.
§ 9. Нулевая энергия
При применении выведенных формул нужно установить
способ отсчета энергии. Пусть при наименьших значениях
квантовых чисел энергия системы будет Ео. Мы будем иметь:
Д„ = £о + £;- ' (1.64)
f
где Еп-—энергия системы, отсчитанная от уровня с наи-
меньшими квантовыми числами (т. е. низшего энергетического
уровня). Сумма по состояниям Z будет иметь вид
Z = кт =2* кТ (1.65)
п п
ИЛИ
Е„ Еп
Z = e кТ кТ . (1.66)
п
Из формул (1.27) и (1.66) следует:
F = E0 — kTlnZe'kT (1.67)
§ 10] пример 43
или, если суммировать по уровням энергии,
Г
F = E0 — kTln кТ (1-68)
i
Записывая последнюю из этих формул в развернутом виде,
мы получим:
f f
_Е^
F = E0 — ftrin(o>0 + (o1e'"^ + w9e_*TH-...), (1.69)
_Ч_
так как множитель е кТ для низшего энергетического уровня
обратится в единицу (этому уровню соответствует энер-
гия Еп, равная нулю).
При Т-> 0 все слагаемые, кроме первого, в сумме под
знаком логарифма в (1.69) будут стремиться к нулю, т. е.
выражение, стоящее под знаком логарифма, будет конечной
величиной и, следовательно,
(Пг=0 = £0- (1-70)
С другой стороны, используя определение свободной
энергии
F = E—TS
и замечая, что энтропия при Т = 0 также является конечной
величиной, мы будем иметь:
(Е)т_й = (Р)т_й —Е . (1.71)
По этой причине величина Ео получила название нулевой
энергии.
Таким образом, нулевая энергия имеет двоякое истолко-
вание: с одной стороны, она является энергией системы
при наименьших значениях квантовых чисел, с другой сто-
роны, она равняется энергии системы при Т=0. При тер-
модинамических вычислениях нужно указывать, от какого
состояния отсчитывается энергия Ео (см. § 2 главы II).
§ 10. Пример
Приведем в заключение этой главы пример вычисления суммы
по состояниям Z. Пусть изучаемая система состоит из локализо-
ванных гармонических осцилляторов. Мы имеем в силу фор-
мулы (1.38)
Z=QN,
(1-72)
44 ОСНОВНЫЕ ФОРМУЛЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ [гл. I
где Q — сумма по состояниям молекулы:
___________________________________
Q = ^e кт. (1.73)
Как известно, уровни энергии гармонического осциллятора опреде-
ляются выражением *)
+ vh\ (1.74)
где v = 0, 1, 2, 3,...
Уровни энергии (1.74) являются простыми. При v = 0 осцилля-
тор имеет нулевую энергию е0 = уДм. В силу формул (1.73) и (1.74)
мы будем иметь:
h'l(’,+ 2') 1 Йу 3 ftv 5 Av
Q = kT =e 2 2 + г 3 лт+ . (175)
V
i '°
Вынося e 2 kT = e кт за знак суммы, мы получим убывающую
ftv
Ъ гр
геометрическую прогрессию с знаменателем х = е и первым чле-
ном, равным единице.
Таким образом,
в и hv 2hv
Q~e кт-\-е АГ
или
1 ftv
Q =-----• (1-76)
1-е кт
Из формул (1.72) и (1.76) следует:
(1 ftv . N
/шт \
-------- (177)
1—е~кт /
Подставляя Z в формулу (1.27), получим для свободной энергии
hv
Л = уй^+^7’!п(1 — е кТ)
♦) См., например, Э. В. Шпольский [84], § 44, § 149.
ЙЙИМЁЁ
45
или
f = ЛГе0 4- kNT In (1 — е~ кт
Аналогично из формул (1.60) и (1.77) получается выражение для
энергии
hi
1 , е'кТ
2 т" hv
1-е'кТ
Заметим, что при 7 = 0, как это и следует ожидать, формулы (1.78)
и (1-79) дают:
(Пт=о = (£)т=о = ^о = 7Уу •
Е = Nh't
h't
.. . Nh'te kT
= o +-------ГК
1-e kT
(1-78)
(1-79)
(1-80)
Для энтропии из (1.59) и (1.77) получается:
-ht/kT n( е
S = Nk
_kT 1— e
Наконец, для теплоемкости системы мы будем иметь
мулу (1.63)):
(1-81)
(см. фор-
h№Ne~h'ilkT
Cv ЛГ2(1 — е-^1^
(1.82)
ГЛАВА II
ПРИМЕНЕНИЕ ОБЩИХ ФОРМУЛ СТАТИСТИЧЕСКОЙ
ТЕРМОДИНАМИКИ К ИДЕАЛЬНЫМ ГАЗАМ
§ 1. Выражения для термодинамических функций
идеального газа через сумму по состояниям молекулы
В главе I были выведены общие формулы, выражающие
значения термодинамических функций системы через сумму
по состояниям Z, которая определяется соотношением
Z = Se *т (2.1)
п
(см. формулы (1.28) и (1.30)).
В настоящей главе мы рассмотрим применение получен-
ных общих формул к идеальным газам, причем исключим
из рассмотрения случай очень низких температур и малых
объемов (т. е. исключим случай вырождения газов).
Для идеального газа, состоящего из N молекул одного
сорта, в главе I мы нашли соотношение между Z и Q
ON
Z = (2-2)
которое будет иметь место при указанных выше условиях.
Теперь, применяя общее выражение для свободной энер-
гии (1.27)
F = — ATlnZ (2.3)
и подставляя в него Z из (2.2), получим для свободной энер-
гии идеального газа
F = — k TN 1 n Q -|- k T1 п /V!
(2-4)
1] ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ИДЕАЛЬНОГО ГАЗА 47
После применения формулы Стирлинга
1пх! = х1пх — х (2.5)
формула (2.4) принимает вид
F = — kTN\n^ — kTN (2.6)
или
F = — nRTln-^ — nRT, (2.7)
где п — число молей и R — Nok— универсальная газовая
постоянная.
Для изобарно-изотермического потенциала Ф мы будем
иметь:
$ = F+pv = F + nRT (2.8)
и, следовательно,
Ф = —fcTWln-2- (2.9)
или
Ф = — nRTln-^ (2.10)
Используя далее общие термодинамические соотношения
(1.52)—(1.56), мы получим формулы для вычисления основ-
ных термодинамических функций идеального газа.
Так для энтропии получим:
5 = = <2J1)
или
s=-(£).=4NI“y+^^).+‘w- (2-12)
Используя (1.53), получим:
E = NkT2(^ty . (2.13)
Тогда для 5 можно написать:
S = ^ + n/?ln^ + n/? = y + n/?ln %. (2.14)
4Й
ПРИМЕНЕНИЕ ОБЩИХ ФОРМУЛ К ИДЕАЛЬНЫМ ГАЗАМ [ГЛ. it
Аналогично из формул (1.54), (1.55), (1.56) получаются
выражения для остальных термодинамических функций иде-
ального газа:
H=NkT2(^^ , (2.15)
(2.16)
<2J7>
Следует заметить, что сумма по состояниям молекулы Q
есть функция объема и температуры или давления и тем-
пературы, и для производных In Q, как это следует из
равенств (2.11) и (2.12), справедливо соотношение
I д In Q \ / д In Q \ [ 1
~Т-
(2.18)
§ 2. Общие выражения для энергии молекулы
Из изложенного в § 1 следует, что для определения
термодинамических функций идеального газа необходимо
знать дискретные уровни энергии и допустимые состоя-
ния молекулы, по которым производится суммирование. Эти
уровни и эти состояния известны очень точно для многих
двухатомных и простых многоатомных молекул. Достаточно
хорошо изучен и класс квазитвердых многоатомных моле-
кул, т. е. молекул, не имеющих внутренних вращений и
внутренних перегруппировок. Менее благополучно обстоит
дело в случае более сложных молекул, которые нельзя
отнести к таким простым классам. Классификация таких
молекул будет подробно обсуждена в главе VI.
Пусть дана многоатомная молекула идеального газа,
занимающего объем v при температуре Т. Молекула
состоит из а электронов и b ядер (например, для моле-
кулы метана СН4 с =10, Ь = 5). Каждый электрон имеет
три степени свободы поступательного движения и одну
степень свободы, ' соответствующую спину, т. е. имеет
всего четыре степени свободы. Точно так же ядро, обла-
дающее спином, если не рассматривать внутренних движе-
ний в ядре, будет иметь четыре степени свободы. Таким
§ 2] ОБЩИЕ ВЫРАЖЕНИЯ ДЛЯ ЭНЕРГИИ МОЛЕКУЛЫ 49
образом, при рассмотрении молекулы мы имеем дело со
сложной системой, имеющей 4а4£> степеней свободы. Если
в задаче о молекуле можно пренебречь движением электро-
нов и не учитывать электронный и ядерный спин, молекулу
можно рассматривать как систему, имеющую 3£> степеней
свободы.
В общем случае энергию молекулы можно разделить на
две части: энергию поступательного движения гп и энергию,
соответствующую всем остальным степеням свободы. Это
утверждение в случае классической механики вытекает из
известной теоремы Кенига (см., например, [43, 8[); анало-
гичный результат получается при квантовомеханическом рас-
смотрении (см., например, [1, 92]). Разделение энергии на
части позволяет описывать состояние всей молекулы с по-
мощью волновой функции
Ф = Ш (2.19)
где функция фп характеризует поступательное движение
молекулы, а описывает остальные движения молекулы.
При определении энергии молекулы необходимо указать
способ ее отсчета. Мы видели (см. § 9 главы I), что
система обладает нулевой энергией. Нужно теперь найти
истолкование нулевой энергии молекулы.
Пусть за нуль энергии мы приняли некоторое определен-
ное состояние, отстоящее от минимума потенциальной энер-
гии молекулы на s'. В качестве такового состояния можно
принять состояние диссоциированной молекулы или некото-
рое другое определенное состояние.
Можно записать:
г = < + < + <• (2-20)
где е' и s'— выражения для поступательной энергии и
энергии внутренних движений. Значения энергий е' и е'
определяются с помощью квантовой механики, которая уста-
навливает вид зависимости их от квантовых чисел. При
наименьших значениях квантовых чисел е' обращается в нуль,
но е' оказывается отличной от нуля. Разобьем ej на две
части
< = < + (2.21)
4 Зак. 835. И. Н. Годней
50
ПРИМЕНЕНИЕ ОБЩИХ ФОРМУЛ К ИДЕАЛЬНЫМ ГАЗАМ [ГЛ. II
где e.i означает энергию внутренних движений молекулы,
отсчитанную от уровня при наименьших квантовых числах,
а г"— часть энергии, не зависящую от квантовых чисел.
Таким образом, мы получим:
® — £o + So+En + Si-
Обозначая сумму первых двух слагаемых через е0:
8о = ео~Ь s0
и опуская штрих у е', мы можем написать:
8 = Bo~hsn~hsi- (2.22)
Величина г0 получила название нулевой энергии молекулы.
Величину е', являющуюся частью е0, можно рассматривать
как химическую нулевую энергию.
Рассмотрим смысл величины е0 на примере двухатомной
молекулы (черт. 2). Пусть за нуль энергии принято значе-
ние, изображаемое линией AM, отстоящей от минимума
потенциальной энергии вниз на расстояние Тогда е' изо-
бразится отрезком ВС. Принимая во внимание, что фор-
мулы квантовой механики дают энергию г(, отсчитываемую
от состояния минимума энергии (точки С), уровень энергии
при наименьших квантовых числах изобразится линией DN.
Тогда е" изобразится отрезком CD. Этот отрезок дает
§ 3] ВЫДЕЛЕНИЕ НУЛЕВОЙ ЭНЕРГИЙ 51
нулевую колебательную энергию . Величина з0 изобра-
зится отрезком MN.
Во многих случаях энергия внутренних движений с до-
статочной точностью может быть разложена на три сла-
гаемых: электронную энергию гэл, энергию колебаний ядер
гКолеб И энергию вращения гвр.
si —- £эл Н- -колеб —гвр (2.23)
Состояние такой молекулы мы можем описать функцией
Ф = = 7п'т'эл7колеб%р'т|я. е> (2.24)
где ^эл, ФКОлеб, %р соответственно означают волновые функ-
ции, описывающие электронное, колебательное, вращатель-
ное движение молекулы. Функция 6Я. 0 описывает ядерный
спин. Электронный спин мы включаем в 6ЭЛ.
§ 3. Формулы для термодинамических функций
идеального газа при выделении нулевой энергии
Применяя выражение (2.22) к вычислению суммы по
состояниям молекулы (1.40), мы получим:
°o+en+ef
Q = кТ , (2-25)
з
где J означает совокупность квантовых чисел поступатель-
ного движения и квантовых чисел внутренних движений.
Величина е~,<зкТ может быть вынесена за знак суммы.
Выполняя суммирование по квантовым числам поступатель-
ного движения и вынося результат за знак второй суммы,
будем иметь:
ед ______j.
Q = e кТ{^е кТ)(£е кТ)
п i
ИЛИ
еп
Q = e~kTQnQi, (2.26)
где
_2п
= к? (2.27)
п
4*
52
ПРИМЕНЕНИЕ ОБЩИХ ФОРМУЛ К ИДЕАЛЬНЫМ ГАЗАМ [ГЛ. it
— сумма по состояниям поступательного движения, а
(2.28)
i
— сумма по состояниям внутренних движений. Обозначив
произведение Qn и Q.; через q,
q = QnQi, (2,29)
мы можем представить сумму по состояниям молекулы
в виде
_ 9°
Q = e кТ - q. (2.30)
Если возможно дальнейшее разделение энергии внутрен-
него движения на электронную энергию еэл, энергию вра-
щения евр и энергию колебания ядер гколеб, то
Qi — Qan Qso_ie6 Q
вр-
(2-31)
Выбрав уровень отсчета энергии, можно выразить основ-
ные термодинамические формулы через сумму по состоя-
ниям q. Подставляя выражение (2.30) в формулы (2.6),
(2.9), (2.13) и (2.15), получим *):
F — Ео = — kTN In 3L — kTN, (2.32)
Ф — Ео = — ATWln^,
(2.33)
(2.34)
(2.35)
где Eq, равное Ns0, означает нулевую энергию всего газа.
*) Заметим, что для идеального газа Ео = Нп, как это следует
изопределения энтальпии (Н = Е-[ pv = ЕnRT). В формулах
(2.33) и (2.35) величину Ей часто заменяют равной ей величиной /70.
§ 4]
ВЫЧИСЛЕНИЕ Q,
53
Для энтропии и теплоемкости мы будем иметь:
5 = ^1п^ + ^т(-^-)/ (2.36)
Cv - NkT* (^)v + WkT, (2.37)
<2-38)
Из изложенного следует, что значения внутренней энергии Е,
теплосодержания Н, свободной энергии F и изобарно-изо-
термического потенциала Ф будут зависеть от способа отсчета
энергии, а значения энтропии S и теплоемкостей Cv и Ср
зависеть не будут.
§ 4. Вычисление суммы по состояниям
для поступательного движения
Вычислим Qn — сумму по состояниям поступательного
движения молекулы. Для этого найдем сначала уровни
энергии sn.
Волновое уравнение, описывающее поступательное движение
молекулы, будет иметь вид
^ + -^Р-(*п--т = 0, (2.39)
где Л — оператор Лапласа, V—потенциальная энергия (У = 0
внутри сосуда и V — оо на стенках). Пусть газ находится в сосуде,
имеющем форму куба с ребром а. Совместим оси координат
с ребрами. Собственная функция ф, удовлетворяющая условиям
конечности, однозначности и непрерывности, должна обращаться
в нуль на поверхности сосуда. Положим
ф = Х(х)У(_у)7(г). (2.40)
Уравнение (2.39) после подстановки ф принимает вид X" , Y" , Z" , 8лЗ/пеп п (2.41)
X 1 Y 1 Z 1 h? ~U' Это последнее разделяется на три:
X v (2.42)
У *2’ Z” , 9 (2.43)
-z=-^ (2.44)
54
ПРИМЕНЕНИЕ ОБЩИХ ФОРМУЛ К ИДЕАЛЬНЫМ ГАЗАМ [ГЛ. II
ИЛИ
х" + k2X = 0, (2.45)
y" + k*Y=0, (2.46)
z" + k2Z = 0. (2.47)
Характеристическое уравнение первого из этих уравнений будет
иметь вид Ь2 + k2 = 0,
откуда b = + krl.
Следовательно, X = cos krx -|- Bt sin ktx. (2.48)
Аналогично получается:
Y = A2 cos k2y + B2 sin k2y, (2.49)
Z = A3 cos k2z -f- B2 sin k2z. (2.50)
Граничные условия
Ф = 0 ДЛЯ x—y=Z=4
И = 0 для x=y = z = a
дают: /i ==z A2 == -Дд 0 (2.51)
и ^1 = ~, a (2.52)
k2=^, a (2.53)
5 a ’ (2.54)
где «J, п2, л3 —целые числа.
Из этих равенств и (2.40), (2.48), (2.49) и (2.50) следует:
4 = BrB2B2 sin х sin —^~У sin г. (2.55)
Подставляя kv й2 и й3 в (2.41), получим:
8z2men л2
—^2— = («1 + п2 + лз)- (2.56)
откуда получаются собственные значения энергии
sn = 8а?гп № + П2 + ’ (2.57)
§ 41
ВЫЧИСЛЕНИЕ Q,
55
В формуле (2.57) квантовые числа nt, и2 и п8 прини-
мают значения 0, 1, 2, 3, 4, ... Низший уровень энер-
гии равен нулю при nt = 0, п2 = 0, п3 = 0.
Зная уровни энергии гп, мы можем теперь вычислить
сумму по состояниям поступательного движения. Подставляя еп
в формулу“(2.27), будем иметь:
СО СО СО о о О
Qn= 2 2 S е~(га1+п2+”з) (2.58)
П, = 0 па = о П3 = 0
или
<?П= (2 е" S"»1’*3’} . (2.59)
При вычислении суммы, стоящей в скобках, которую обо-
значим через В,
со h’n’
в = 2 8и,о2А2,,
о
суммирование можно заменить интегрированием *). Обозначив
с — SmaflkT
и п через х, будем иметь:
я-
Таким образом,
„ / 2nmkT \'1‘
В-НН °
и, следовательно,
„ / 2r.mkT \s/‘
где v = а* * * 8— объем газа.
(2.60)
*) При применении формулы Эйлера]—Маклорена мы полу-
чили бы (см. [236]):
D /2кткТ\'1г . 1
В = \~~й^~) а±2'
Непосредственное суммирование показывает, что мы можем пре-
небречь 1/" по сравнению с первым слагаемым.
56 ПРИМЕНЕНИЕ ОБЩИХ ФОРМУЛ К ИДЕАЛЬНЫМ ГАЗАМ [ГЛ. II
Обозначив коэффициент перед объемом в последней фор-
муле через D,
D = (2.61)
h3 '
мы получим:
Qn = W. (2.62)
§ 5. Выражения для термодинамических функций
идеального газа через сумму по состояниям Q{
Результаты, полученные в предыдущем параграфе, по-
зволяют вывести формулы, выражающие термодинамические
функции газа через сумму состояний по внутренним дви-
жениям молекулы
Из формулы (2.29) следует:
q = QnQi = DvQi = vQ{. (2.63)
Таким образом, сумма по состояниям молекулы Q прини-
мает вид (см. (2.30))
Q = e-'»/krDwQj. (2.64)
Заменяя q в формулах (2.32), (2.33), (2.34) и (2.35), мы
получим:
F = Ео — kTNIn /Д v — kWin Qi — kTN, (2.65)
Ф=Н0 —STTVln -v — kTN\nQi (2.66)
или, принимая во внимание
pv • NkT,
^=H0 — kTN\n-^^^-kT~kTN\nQi. (2.67)
Далее
E = E0+^NkT+NkT*^Q-, (2.68)
H = H0 + ~NkT-trNkT’2-^^-. (2.69)
Вторые слагаемые этих формул представляют значения тер-
модинамических функций, соответствующие поступательному
движению.
§ 5] ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ЧЕРЕЗ Q; 57
Для энтропии будем иметь (см. (2.36)):
_ «.к™ (2тслг£7’)3/3 . , ... _ .
5 — kN In -jpN----v -|- kN In Qi -|-
+ ^kN+kNT-^±, (2.70)
t. e.
S = 5n + fe/VIn + kNT d, (2.71)
где Sn— известное выражение Закура-Тетроде для энтро-
пии поступательного движения,
5д=^1п (2^)3/Д v + ^-kN. (2.72)
Исключая из формулы (2.70) объем с помощью уравнения
состояния pv = NkT, мы получим зависимость энтропии газа
от давления и температуры
с (Ir.mkT^^kT . .... „ ।
5 = kN In ----—----------k kN In Qi 4-
Np 1 г 1
+1 АЛГ—|— kNT d . (2.73)
Формула для Sn, если выразить массу молекулы через
молекулярный вес и число Авогадро (т = M/Nq) и подста-
вить значения постоянных, примет вид для одного моля
Sn = |/?1п Т+/? 1п о +1/? In Ж — 11,069. (2.74)
Исключая объем с помощью уравнения Менделеева—Кла-
пейрона и выражая давления в атмосферах, мы получим:
Sn = -| /?1п Т—/?1пр + -|-/?1пМ — 2,313 (2.75)
или
SD = /?(-|-lnT— 1пр + -|>пМ— 1,164). (2.76)
Для теплоемкостей аналогично получается:
Cv = ^Nk-h 2NkT d -\-NkT2 d2^', (2.77)
Cp = ^Nk + 2NkT^^^NkT2^^. (2.78)
58 ПРИМЕНЕНИЕ ОБЩИХ ФОРМУЛ К ИДЕАЛЬНЫМ ГАЗАМ [ГЛ. II
3 5
Выражения у Mi и у Додают значения теплоемкостей, соот-
ветствующие поступательному движению.
Из этих формул при N = Мо легко получаются выра-
жения термодинамических функций для одного моля. Такие
формулы сведены в таблицу 2, где в последнем столбце
приведены слагаемые, соответствующие поступательному
движению. Выделяя эти слагаемые, мы получим для одного
моля идеального газа:
F = f0 + Fn — RTlnQi, (2.79)
Ф=//0-|-Фп — RTlnQi, (2.80)
Е = Е0 + Еп + ЯТ2^К (2.81)
/7 = #о + Нп + Я7’а^-^-, (2.82)
5 = + (2.83)
Cv = ^-R-\-2RT^-^^-RTi (2.84)
Cp = ^R+2RT^^-\-RT*^Q-. (2.85)
При расчетах химических равновесий вместо Н — Ео и
Ф со обычно пользуются функциями --—— = Y~
/ . Ф — Еп Ф — Нп ,
(приведенная энтальпия) и —?—1 ?—- (приведенный
изобарно-изотермический потенциал)*).
Из формулы (2.69) для одного моля (N = jV0) мы получим:
= Н~Н° . (2.86)
Далее из (2.66) следует для одного моля
= = -(2jX^/a —/?lnQj(2.87)
*) См. примечание на стр. 52.
иг*
СП
Т а б лица 2.
Формулы термодинамических функций для одного моля идеального газа
№ п/п Функция Формула Слагаемое, соответствующее поступательному движению
1 Свободная энергия f = £о — In ’’ v-RT-RT\n г„- , RT
2 Изобарно-изотер- мический потенциал Ф = Я0-/?Т1п (2™kJ}l' v-RTln Qi
То же Ф = я0 -/? rm/? г -г In (?z Л р1У(\ *п- RT
3 Внутренняя энергия £ = £o+f RT4-RT2^-^ £ го |сч II е 1
4 Теплосодержание Н = Яо+ у RT + R П Я„ = | RT
5 Энтропия S = R In (2ТСХГ)Л v + 4 R+R In Qi+RT с _ о, (btmkT)^ . 5 п Sn R П AW0 v+ 2 R
6 Теплоемкость при постоянном объеме Cv = ^-R + 2RT^^i + RT2 £ U 1 И1 C — — P v Гд — 2
7 Теплоемкость при постоянном давлении Cp = ^R + 2RT^^ + RT2^^- QJ ro [cm II c e, Cj 1
сл
l£>
ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ЧЕРЕЗ
60
ПРИМЕНЕНИЕ ОБЩИХ ФОРМУЛ К ИДЕАЛЬНЫМ ГАЗАМ [ГЛ. Ц
ИЛИ
n = ~^ = ^=^ = — R\n^^-,RT—RlnQi. (2.88)
Для поступательного движения, если подставить численные
значения постоянных, получим:
'ЦД) = — — -|-/?1пТ+/?1пр4-7,280. (2.89)
При вычислении термодинамических функций в таблицах
обычно вместо Н — Но и Ф — Но приводятся значения функ-
„ Н-Нс, Ф-Нь
ЦИЙ ----- И --уГ—.
§ 6. Формулы для вычисления термодинамических
функций при применении метода
непосредственного суммирования
Найденным формулам можно придать другой вид, удоб-
ный для вычисления термодинамических функций, методом
непосредственного суммирования, при котором сумма по со-
стояниям и ее производные вычисляются суммированием по
уровням энергии молекулы. Мы имеем:
— 8 .
__J
Qi=^Sj^T, (2.90)
з
где суммирование производится по уровням энергии.
Дифференцирование In Qi дает:
-в ./ST
1
In С4 ___ 3
dT ~~ Q{kT*
„, 0 ЫГ* ± 2 2
a* In Qi______Ki j_____________
~йТГ - Q^T*
— e ./kT
J__________
Q{kTs
dT
ъ 2 ~^кТ
2___________
Qik2Ti
~ Q2k‘iT4 * (2-91)
§71
СЛУЧАЙ РАЗДЕЛЕНИЯ ЭНЕРГИЙ
61
Положим £ . = 5^/ = 2 j e 2^M* j j (2.92) (2.93) (2.94)
формулы для производных теперь примут вид
dlnQi— 1 (2.95)
dT kT^A’
(Р In Qi 1 2е 2 2B 1 (2.96)
dT2 A kT^A \^а) •
Подставляя эти значения в формулы (2.79) — (2.85), мы по-
лучим:
F = E04-Fn — RTln'Z А, (2.97)
Ф = ЯО+ФП —/?Т1п2д, (2.98)
R У.В
Е = Е0 + Еп+-^~ (2.99)
А 2^А
R У.В
Н = НО + НП + -^- (2.100)
* Z 1
5 = Sn + Я In 2 Д + R 2В *72^’ (2.101)
R г2с (2.102)
’ 2 ' *272 L2 А V2^J’
5 lA[2c _fS£\3i (2.103)
СР — 2 К Н *272 Щ А \2^J’
§ 7. Случай разделения энергии
Выведем формулы для вычисления термодинамических
Функций идеального газа в случае, если возможно разделе-
ние энергии молекулы е4 на электронную энергию, энергию
62 ПРИМЕНЕНИЕ ОБЩИХ ФОРМУЛ К ИДЕАЛЬНЫМ ГАЗАМ [ГЛ. II
колебаний и энергию вращения (см. формулу (2.23)). Мы
будем иметь:
’эл+’колеб+’вр
Qi= 2 г^=2 2 So •
эл. сост, волеб. сост, эл. колеб. вр.
вр. сост сост сост сост
(2.104)
При суммировании по вращательным квантовым числам можно
’эл+’колеб
е кТ вынести за знак суммы. Получим:
’эл+’колеб ’вр
Qi= 2 2 е 2 (2.105)
эл. сост волеб. вр. сост
сост
Обозначив
евр
2 e'~^=QBp, (2.Ю6)
вр.сост
мы можем вынести ее за знак двойной суммы по электрон-
ным и колебательным состояниям. Таким образом,
8эл+®волеб
<?| = <2вр2 2 е (2.107)
вл. волеб.
сост сост
Далее, применяя аналогичный метод, получим:
• эл ’волеб еэл
Qi=Q»p2e кТ 2е кТ =QbpQSo.™6 2 е * *r’(2.io8)
эл. колеб. эл. сост
оост оост
где
’колеб
Околеб — 2 е кТ (2.109)
колеб. 4
оост
получило название суммы по колебательным состояниям или
колебательной суммы состояний.
Окончательно мы получим:
Qi = Qap Фколеб Qэл> (2.110)
где
<?эд= 2 е~^ (2.111)
эл. оост
§ 71
СЛУЧАЙ РАЗДЕЛЕНИЯ ЭНЕРГИИ
63
___сумма по электронным состояниям (электронная сумма
СОСТОЯНИЙ).
Подставляя выражение из формулы (2.110) в фор-
мулы (2.79)-—(2.85), легко видеть, что каждая термодина-
мическая функция будет представлена суммой слагаемых,
которые будут зависеть только от электронных или коле-
бательных, или вращательных состояний молекулы *).
Действительно, подставляя Q{ в формулы (2.79) и (2.80),
мы получим:
F = £0H-Fn —ЯПпфэл — ЯПпфколеб —ЯЛпфвр (2.112)
и
Ф = Но 4- Фп — RTIn QM — RTIn QKone6 — RT in QBp (2.113)
или
F — Рал 4~/"колебН- fspi (2.114)
ф =-^oH-ФиЧ-Фэл Н-ФколебН-Фвр. (2.115)
где
/7ЭЛ=ФвЛ= — /?Пп(?эл. (2.116)
^"колеб= Фколеб — RTltl (2.117)
Гвр = фвр = —/?TlnQ,p. (2.118)
Аналогично для энергии и теплосодержания при подста-
новке Qi из формулы (2.110) в формулы (2.81) и (2.82) по-
лучаются выражения
3 dlnQ.,
Е = До+ з /?Т+ RT*+
+ /?Г2 d 1П ^оле6 + /?Га —^вр (2.119)
и
5 d In Q.j.
H = H^^RT+RT^-^ +
+ /?Т2^1П^одеб . (2.120)
*) To-есть при наличии мультипликативности суммы по состоя-
ниям Qi (ср. (2.110) с (1.42)) будет иметь место аддитивность термо-
динамических функций.
64 ПРИМЕНЕНИЕ ОБЩИХ ФОРМУЛ К ИДЕАЛЬНЫМ ГАЗАМ [ГЛ. II
образом,
Таким
Е = RTДэл Дколеб ~|~Д вр* (2.121)
Н = Hq-|- RT Езд Дколеб ~Ь Д вр» (2.122)
где d 1П Сэл ДЭл = Нэл= (2.123)
р 1_г птз In Фколеб С колеб — колеб — , (2.124)
d In Q Езр = Hvp = RT2. (2.125)
Далее из формулы (2.110) и формулы (2.83) следует:
д = дп+ d 1п Сэл R 1п Сэл + R Т + R In Сколеб +
+ П^олеб + R 1п + RT (2.126)
или
причем •S — 5д-|- 5эл ~Ь дколеб н~ 5вр, d In Сэл 5эл = Я1пСэл+Я7’^7^, (2.127) (2.128)
Дколеб = R 1П Сколеб + RT 9 (2.129)
d 1п Сип ДВр = /?1пСвр + /?Д-^Е. (2.130)
В этих последних выражениях, принимая во внимание фор- In Q.,„ мулы (2.123), (2.124), (2.125), мы можем исключить —-=—,
tfln <?волеб dT d In Свр р И —dT ’ выРазив их чеРез Е»л, ^колеб И Двр-
Мы получим: Е Дэл = Я1пСэл (2.131)
Дколеб — R 1П Сколеб Ч- у , (2.132)
Е Дир = Я1пСвр + -^. (2.133)
§ 81
ФОРМУЛЫ ДЛЯ ХИМИЧЕСКОГО ПОТЕНЦИАЛА
65
Наконец, подстановка Qj из формулы (2.110) в формулы
(2.84) и (2.85) для теплоемкостей газа дает:
cv ср = R Ч- Сэл Ч~ Сколеб -|- Св;:, = у /? + Сэл Ч- Сколеб Ч-Сцр, (2.134) (2.135)
где Сэл = <Z In 2RT dT + rf2 In пто ЭЛ K dT‘i ’ (2.136)
Сколеб г, Сколеб dT 1 rj-po^2 Сколеб + я?2 d-n > (2.137)
Свр = d In Q & In C.„ RT2 - . aT* (2.138)
Следует подчеркнуть, что все формулы для термодинами-
ческих функций, выведенные в настоящем параграфе, будут
иметь место только при условии разделения энергии si на
еэл, е»р и гКолеб. Такое разделение в большом числе случаев
действительно оправдывается, но оно является приближенным.
При более точных вычислениях нужно учитывать взаимо-
действие между электронными, колебательными и враща-
тельными состояниями. В этом случае нужно применять
общие формулы, выведенные в §§ 5—6.
§ 8. Формулы для химического потенциала
Найдем в заключение выражение для химического по-
тенциала через сумму по состояниям Qt. Мы имеем:
/дР\ /дФ \
(2.139)
Дифференцирование равенства (2.7) по п при постоянных
объеме и температуре или равенства (2.10) по п при по-
стоянных давлении и температуре с учетом зависимости Q
от объема дает
и = —= —7?Т1п-%- (2.140)
‘ /v nN0 v '
Или
и —N0so—RTla-^-, (2.141)
5 Зак. 835. И. Н. Годнее
66 Применение оЬЩИХ формул К идеальным газам [гл. и
или
Н = Ч®о — RT\n^^. (2.142)
Применение выведенных в этой главе формул к расчетам
химических равновесий будет рассмотрено в главе XII.
Сравнивая формулу (2.142) с выражением для изобарно-
изотермического потенциала (2.67), мы заметим, что по-
следний может быть представлен в виде
Ф = п[1. (2.143)
§ 9. Термодинамические функции смеси газов
Рассмотрим теперь вопрос о вычислении термодинами-
ческих функций смеси идеальных газов. Пусть в сосуде
объемом v находится при температуре Т смесь из двух
газов, содержащая молекул первого газа и N% молекул
второго. Рассмотрение вопроса о смеси двух газов легко
может быть обобщено на случай смеси любого числа газов.
Будем предполагать температуру газа Т не очень низкой,
а объем v достаточно большим, так что случай вырожде-
ния газов, имеющий место при низких температурах и
малых v, исключается.
Для энергии всей системы мы можем написать:
^ = г1 + га+---+Ч + < + <+-”+41- (2.144)
где gj, г.,, .... s^.—энергии молекул первого газа,
а г', .... e'v—энергии молекул второго газа. Для суммы
по состояниям всей системы будем иметь:
9l + 9j+sW, + 9l + ••+еУ3
Z= 2 е кТ = 2 е кТ (2.145)
все сост. к все сост
Выполняя суммирование по состояниям первого газа, полу-
чим:
‘1 + 92+"-+9Яа
Z = Zt 2 « кТ (2.146)
все сост.
а-го газа
или
Z = ZtZ2. (2.147)
§ 9] ТЕРМОДИНАМИЧЕСКИЙ ФУНКЦИИ СМЕСИ ГАЗОВ 67
Заметим, что вычисление каждой из сумм по состояниям
выполняется для данного объема v. Таким образом, мы
можем записать:
Z(Ni + N2, v, T)^Z^NV v, T)Z2(N2, v, Т) (2.148)
' или
lnZ(Ni+^2,f. Т) = 1пZ^N^v, Z2(N2, v, T). (2.149)
Обращаясь к общим формулам главы I, определяющим
термодинамические функции системы через сумму по состоя-
ниям Z (см. формулы (1.48), (1.60), (1.59), (1.63)), мы на
основании формулы (2.149) получим:
Р(^ + ^, v, T) = P1(NV v, T)-\-p2{N2, v, Т), (2.150)
+ v, T) = Ei(N1, v, T) + E2(N2, v, Т), (2.151)
S(Nt + N2, v, T) = S1(N1, v,'T)-[-S2(N2, v, T), (2.152)
CJ/Vt + ^2) v, T) = CM,v, T)+Ct,(N2, v, T). (2.153)
Первая из этих формул представляет закон Дальтона о ра-
венстве общего давления смеси Р сумме парциальных да-
влений, а вторая и четвертая формулы выражают аддитив-
ность энергии и теплоемкостей. Из формулы (2.152) следует,
что энтропия смеси равняется сумме энтропий составляющих
газов, причем энтропии компонентов вычисляются в предпо-
ложении, что данный газ занимает при той же темпера-
туре Т весь объем смеси v. В этом случае каждый газ на-
ходится под своим парциальным давлением Таким образом,
мы можем написать:
S(NX + ^, Р, T) = Sl(N1, Pl, Л + р2, Г). (2.154)
Однако энтропия смеси не будет равна сумме энтропий
составляющих газов, если их вычислять при давлениях, рав-
ных общему давлению смеси Р. В самом деле, используя
зависимости энтропии от давления (см. формулу (2.73)),
будем иметь:
Si(Nv Р, Т) — 5г(^, pt, T) = kN1ln^-, (2.155)
S2 (N2, P, T) — S2(V2, p2, T) = kN2 In , (2.156)
5*
68
ПРИМЕНЕНИЕ ОБЩИХ ФОРМУЛ К ИДЕАЛЬНЫМ ГАЗАМ [ГЛ. 11
откуда
МА/р pt, T) = S1(N1, Р, Т) — ЙА/Jn^-, (2.157)
S2(/V2, Р2> T) = S2(V2, Р, Т) — fe/VJn^-. (2.158)
Подставляя значения 5Х(^, pv Г) и S2(iV2, р2, Т) в фор-
мулу (2.154), получим:
5(^ + ^, Р, T) = SM, Р, Т) +
H-S2(N2) Р, Т)— — fc/V2ln^. (2.159)
Применяя уравнение состояния pv = NkT к отдельным газам
и к смеси, мы можем написать:
ptv = NJtT,
p2v = N2kT,
Pv = (Nt + N2)kT,
откуда
Pt = Nt
P Nt + N2 ’
Pi _ N2
P Wj + Wa '
Подстановка этих отношений в формулу (2.159) дает:
S = (^ + ^, Р, T) = St(Nt, Р, Л +
+ S2 (N2, Р, Т) — kNt In 7У1.. Ш In . (2.163)
1 24 2 ' 1 jVj-j-jVa 2 + !
Последние два слагаемых в формуле (2.163) получили на-
звание энтропии смешения
-----(2.164)
Таким образом, будем иметь:
S = Sx^t, Р, T) + S2(N2, Р, П + ^ем. (2.165)
Легко видеть, что полученные формулы обобщаются на слу-
чай смеси любого числа а газов.
(2.160)
(2.161)
(2.162)
ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ СМЕСИ ГАЗОВ
69
§ 9]
Мы получим:
AScm = — AjATj 1 n Ni+Ni+\ "+Na — Жг In Ni+N2+\ . .+дго~ • • •
' ’ ' — kNa ,n Л\ +/У2+ ДГа ’ (2•166)
Выражения, стоящие под знаком молярные доли компонентов । логарифма, , представляют (2.167)
''•*-м1+лг3+.. • + Na‘
Окончательно будем иметь:
Д-$'ОМ=—k 2 Ni In (2.168)
или д$см =— i n-i In xit (2.169)
если выразить числа молекул через число молей tip
ГЛАВА III
ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ
ОДНОАТОМНЫХ ГАЗОВ
§ 1. Сумма по состояниям молекулы одноатомного газа
В предыдущей главе нами были выведены общие фор-
мулы для вычисления термодинамических функций газов.
Рассмотрим теперь применение этих формул к решению
одной из самых простых задач статистической термодина-
мики— определению термодинамических функций одноатом-
ных газов, например Не, Аг, Кг, Хе и др.
Для решения этой задачи, как было показано в главах
I и II, нужно найти сумму по состояниям молекулы
е.
<3 = 2^. (з.1)
i
Вычисление этой суммы оказывается особенно простым
в случае одноатомных газов, энергия молекул которых г — s0
состоит только из двух слагаемых *)
г — s0 —гпН~£эл, (3.2)
где гп — энергия поступательного движения и еэл — электрон-
ная энергия молекулы.
Если ядро молекулы одноатомного газа не имеет ядер-
ного спина, состояние ее в соответствии с формулой (3.2)
задается функцией, представляемой произведением двух
множителей
*> *) Энергией вращения молекулы (атома) одноатомного газа
можно пренебречь.
§ 1] СУММА ПО СОСТОЯНИЯМ МОЛЕКУЛЫ ОДНОАТОМНОГО ГАЗА 71
из которых первый — фп описывает поступательное движение
молекулы, а фэл—электронные состояния, включая и элек-
тронно-спиновые состояния. В случае, если спин ядра моле-
кулы (атома) будет отличен от нуля, волновая функция (3.3)
должна быть умножена на функцию ядерного спина ф ,
т, е. состояние молекулы будет описываться функцией
Ф = Ф 6 ф
I 1 Д 1 ЭЛ 'Я. с
(3.4)
Для ядра со спином s существует *)
« = 2у-Н (3.5)
спиновых состояний, отличающихся ориентацией вектора
ядерного спина. Все эти 2s-|-1 состояний имеют практи-
чески одинаковую энергию, и при суммировании по уровням
энергии мы можем их объединить в одно состояние с ве-
сом а. Выполняя суммирование по уровням энергии посту-
пательного движения, мы получили в главе II общее выра-
жение
Q = e'^QnQit (3.6)
где Qn — сумма по состояниям поступательного движения,
е0 — нулевая энергия и — сумма по внутренним состоя-
ниям молекулы (см. формулы (2.26), (2.27), (2.28)). В нашем
случае внутренняя энергия молекулы е{, как это следует из
сравнения формул (2.22) и (3.2), представится только элек-
тронной энергией, т. е.
б{=еэл. (3.7)
Для суммы по состояниям Qi мы имеем:
= = 2 (3.8)
i все внутр. сост.
молекулы
где суммирование необходимо выполнить по всем возможным
внутренним состояниям молекулы, которые в нашем случае
состоят из последовательности электронных состояний, и
в случае наличия ядерного спина — из последовательности
*) См. Э. В. Шпольский [84], т. II, гл. 18, см. также
г. Г е р ц б е р г [18].
72 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ОДНОАТОМНЫХ ГАЗОВ [ГЛ. III
спиновых состояний ядра, причем каждому электронному
состоянию соответствует 2s-|- 1 состояний, имеющих одина-
ковую энергию. При суммировании, как это было указано
выше, мы можем объединить спиновые состояния ядра и
приписать состоянию вес о, равный 2s-|- 1. Мы получим:
6ЭЛ ®эл
Qi— 2 ае кТ=а е кТ. (3.9)
ЭЛ. СОСТ ЭЛ. сост
Сумма по электронным состояниям молекулы нами была
названа электронной суммой состояний
«ЭЛ
2 е кТ. (З.Ю)
ЭЛ. сост
Таким образом, будем иметь:
<?{ = а£эл. (З.И)
Если ядерный спин отсутствует (s = 0), я равно 1 и Qi
равняется
§ 2. Электронные состояния атома и вычисление Qi
Электронные состояния атомов в настоящее время хорошо
изучены *).
Состояние атома задается, во-первых, указанием его
электронной конфигурации и, во-вторых, указанием кван-
товых чисел, характеризующих результирующие движения
электронов.
Пусть z' означает число электронов в атоме. Для ней-
трального атома z' равно порядковому номеру элемента z
в периодической системе Д. И. Менделеева, для х-кратно
ионизированного атома z' — z — х.
Состояние каждого электрона в атоме можно прибли-
женно описать с помощью его главного квантового числа п.
Далее, движение электрона в атоме приближенно характе-
ризуется его орбитальным моментом 1{ и спиновым момен-
*) См. Г. Герцберг [18]. См. также В. Н. Кондратьев [32],
С. Э. Ф р и ш [69], А. Н. Теренин [60], М. А. Ельяшевич [28].
Таблицы уровней энергии см. Моор [91].
§ 2] ЭЛЕКТРОННЫЕ СОСТОЯНИЯ АТОМА И ВЫЧИСЛЕНИЕ Qt
73
том s^. Величины этих моментов определяются соответ-
ственно квантовыми числами / и $, а величины их проек-
ций— квантовыми числами и ms. При данном п квантовое
число I может принимать значения 0, 1.........(ге—1); кван-
товое число $ имеет фиксированное значение 1/2. Всего для
характеристики электрона в атоме требуется четыре кванто-
вых числа: п, I, т,, ms.
Величины квадратов векторов 1(- и s(- определяются формулами
+ D (3.12)
и
2 / I i\ А3 1 3 21„
si- 4^2 1) — 4l-2 2 2 ’ (3-13)
где 1ns — соответствующие квантовые числа. Эти формулы являются
частным случаем общей формулы квантования момента количества
движения. Если вектор момента количества движения К задан кван-
товым числом К, величина квадрата этого момента определяется
выражением
-£-/<(/<+1). (3.14)
Возможные значения проекции вектора К на неподвижную ось
будут:
4-^. (3.15)
где квантовое число Alt принимает значения от К до —К через
единицу (всего 2/С-|- 1 значений).
В частном случае допустимыми значениями квантового числа /пг
являются значения 1, 1—1,..., О,..., —/ (2/-|- 1 значений),
а допустимыми значениями т8 будут только 1/г и — */2 (два зна-
чения).
Электронная конфигурация атома определяется заданием
квантовых чисел и Ц всех z' электронов атома. Она
обозначается символом
«1/?; п/г; пЛ .... (3.16)
где а — число электронов с квантовыми числами nt и lv
b-—число электронов с квантовыми числами п.2 и 12 и т. д.
Значения квантового числа I обозначаются буквами, как это
Указано в таблице 3.
74 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ОДНОАТОМНЫХ ГАЗОВ [ГЛ. III
Таблица 3
Обозначения квантовых чисел
Значения квантового числа 1 Обозначения дан- ного значения квантового числа Значения квантового числа L Обозначения данного значе- ния квантового числа
Z = 0 5 S
Z = 1 р L = \ р
Z = 2 d L = 2 D
Z = 3 f L=3 F
Z = 4 g L = 4 G
Данной электронной конфигурации соответствует одно
или несколько состояний атома, возникающих при сложении
орбитальных и спиновых движений электронов *).
В случае так называемой нормальной связи ** ***)) (электро-
статические взаимодействия электронов велики по сравнению
с магнитными взаимодействиями орбитального движения и
спинов) векторы дают полный орбитальный момент коли-
чества движения
L = 21i> (3-17)
а векторы st—полный спиновый момент
S = 2Si. (3.18)
Величины этих векторов определяются квантовыми чис-
лами L< и S.
Полный момент количества движения всего атома бу-
прФ *
J = L + S. (3.19)
*) Для определения всех состояний, соответствующих задан-
ной электронной конфигурации, может быть применена векторная
схема (см. М. А. Ельяшевич [28]).
**) Другие типы связей см. Г. Г е р ц б е р г [18] и М. А. Елья-
шевич [28].
***) Если не учитывать спин ядра, которому соответствует спи-
новый момент ядра. При учете последнего полный момент полу-
чается геометрическим сложением спинового момента ядра с век-
тором J.
§ 2] ЭЛЕКТРОННЫЕ СОСТОЯНИЯ АТОМА И ВЫЧИСЛЕНИЕ Q4 75
Вектору J соответствует квантовое число J, принимаю-
щее при заданных L и S значения
L-\-S, L-]-S— 1, L-j-S —2, ... \L — S|.
При L^> S таких значений существует *)
2S4-1=M (3.20)
Например, при £ = 3, S = 2 допустимыми значениями J
будут 5, 4, 3, 2, 1.
Для определения возможных состояний атома, соответ-
ствующих заданной электронной конфигурации, находят
сначала возможные значения квантовых чисел L и 5. При
этом принимаются во внимание требования симметрии, со-
гласно которым волновая функция атома должна быть анти-
симметричной по отношению к перестановкам координат
электронов (принцип Паули).
Заданным значениям квантовых чисел L и 5 соответ-
ствует (2S —|— 1)(2L-|- 1) состояний. При отсутствии взаимо-
действия между векторами L и S все эти состояния имели бы
одинаковую энергию и уровень энергии атома при заданной
электронной конфигурации и заданных квантовых числах
L и S был бы вырожден (27.1)(2Л>—|— 1)-кратно. Однако
взаимодействие векторов L и S приводит к расщеплению
такого уровня, т. е. состояния с разными J имеют разную
энергию. Таким образом, для описания уровня энергии кроме
электронной конфигурации нужно задать еще квантовые
числа L, S и J. Такой уровень в силу квантования проек-
ции вектора J на неподвижную ось будет вырожден
2J+ 1 = р (3.21)
-кратно.
Группа уровней энергии, соответствующая заданным
квантовым числам L и S, но отличающаяся значением J, по-
лучила название терма (см. М. А. Ельяшевич [28])**). Вели-
*) При S^>L квантовое число J будет иметь значения L + S,
£ + S — 1, ..., S — L, всего 27. -|- 1 значений.
**) Часто термом называют просто значение энергии атома,
Взятое с обратным знаком.
76 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ОДНОАТОМНЫХ ГАЗОВ [ГЛ. III
чина М, определяемая формулой (3.20), получила название
мультиплетности терма. Терм обозначается символом *)
ML, (3.22)
в котором М означает максимальную мультиплетность терма,
a L означает величину квантового числа L, записываемую
в виде буквы, как это указано в таблице 3. По мульти-
плетности М можно найти квантовое число 5 (см. фор-
мулу (3.20)). Терму соответствует (2Л —J— 1)(2Л> —|— 1) состоя-
ний. Например, при L=\, 5=1 в терм SP входят
(2 —|— 1) (2 —1) = 9 состояний. Этим состояниям соответ-
ствуют три уровня с J=2, 1, 0, из которых первый вы-
рожден пятикратно, второй трехкратно, а третий невыро-
жден. Всего мы получаем, как и следует ожидать, 5 -)- 3 -|~
-[-1=9 состояний.
В соответствии с изложенным выше уровень энергии
атома в случае нормальной связи обозначается символом
«1/?; n2ll, ti-fi, •••; 11 Lj, (3.23)
где nf; nf; nf\ . . . означает электронную конфигурацию
атома, а символ MLj дает значения квантовых чисел 5, L, J.
Так, нормальное состояние атома Na, имеющего 11 элек-
тронов, представляется формулой
ls22s22p63s25i/a, (3.24)
показывающей распределение электронов по состояниям в обо-
лочке атома, причем буква 5 указывает, что L = 0, а ин-
декс 1/2,— чт0 J=lk-
В общем случае, как это было указано выше, заданной
электронной конфигурации соответствует ряд состояний
(термов)**). В случае так называемых заполненных оболочек
необходимо получается L = G, 5 = 0 и 7=0. Для таких
заполненных ***) оболочек одной электронной конфигурации
соответствует один терм, состоящий из одного состояния ’50,
*) Для так называемых нечетных термов справа вверху у сим-
вола квантового числа L ставится еще индекс и, например 3Р°.
**) Таблицы термов, возникающих из заданной электронной
конфигурации, см. М. А. Ельяшевйч [28] и Моор [91].
***) Заполненная оболочка, соответствующая заданным чис-
лам гаи/, содержит 2 (2/-|- 1) электронов.
2] ЭЛЕКТРОННЫЕ СОСТОЯНИЯ АТОМА И ВЫЧИСЛЕНИЕ Qt 77
которому соответствует, следовательно, один невырожденный
уровень энергии. Такая заполненная оболочка получается,
например, для нормального состояния атома Не. В таб-
лице 4 в качестве примера приведены основные электрон-
ные состояния нескольких атомов с указанием р0 — веса
основного электронного уровня.
Таблица 4
2 Атом Основное состояние Po
1 н 1$ 2S,;2 2
2 Не 1s31So 1
3 Li ls22s2S„, 2
4 Be 1№ 2s2’So 1
5 В ls22s32p3P,\ 2
6 С ls22s32p22P0 1
7 N ls22s22p3 4S°^ 4
8 0 Is2 2s3 2/И 3P2 5
9 F U22s22p52/^/a 4
17 С1 4
Примем за начало отсчета электронной энергии уровень
основного состояния атома. В этом состоянии по определе-
нию принимаем еэл равным нулю. Мы получим:
<?эл = Гое АТ + Р1е А7, + Р2е кТ + •••==
= Po + Pt« кТ + Р2е АТ+ • • •
(3.25)
Электронные уровни энергии в атоме отстоят, вообще говоря,
довольно далеко друг от друга, так что в очень большом
числе случаев мы можем пренебречь при средних темпера-
турах уже вторым слагаемым. В этом случае получим:
Сэл = ?о- (3.26)
Подставив это значение электронной суммы по состояниям
в формулу (3.11), будем иметь:
Qi=«Po-
(3.27)
78 теймОДИнамйчёскйё функций одноатомных газов [гл. Ш
Таким образом, для суммы по состояниям q (см. формулу
(2.63)) мы получим:
q = QnQi == *—k:) wpo- (3.28)
Однако формулы (3.27) и (3.28) могут быть применены не
всегда, и для некоторых одноатомных газов при вычислении
суммы по электронным состояниям мы должны принять во
внимание слагаемые, следующие за первым.
Так, для хлора вблизи основного электронного состоя-
ния находится уровень 2Р‘/а, отстоящий *) от первого
на 0,109eV = 881 см~1-. Веса состояний 2А/а и 2Л/а, как это
следует из формулы (3.21), будут 4 и 2. Таким образом,
сумма по электронным состояниям для одноатомного хлора
будет:
881ЙС
<уэл = 4 + 2е кТ • (3.29)
Аналогично для кислорода мы имеем три первых уровня SP2,
3Pt и '6Рй, из которых два последних отстоят от первого
соответственно на 159 см-1 и 227 см~1. Следовательно,
_ 15' he 227he
QM = 5 + 3e~“^+le" •
(3.30)
§ 3. Формулы для вычисления термодинамических
функций одноатомного газа без учета влияния второго
и высших электронных уровней
Если можно не принимать во внимание второго и следую-
щих электронных уровней энергии, формулы для вычисления
термодинамических функций одноатомного газа будут иметь
очень простой вид. В этом случае мы имеем (см. формулу
(3.27)):
Qi = apo = const. (3.31)
Для вычисления термодинамических функций, как это было
„ d In Qs
показано в главе П, нужно найти производные и
*) См. Моор [91].
ВЫЧИСЛЕНИЕ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
79
§ 3]
Мы получим на основании формулы (3.31)
dT*
дЦп Q/__, d- In Qz- _« zq QO\
dT ~ dT* ~U’ (0.02)
Подставляя значение Qi из (3.31) в общие формулы для
свободной энергии и изобарно-изотермического потенциала
F = £0 + Fn — /?Г1пОй ]
Ф = НО+ФП —tfTInQ; } (3’33)
(см. формулы, приведенные в таблице 2, стр. 59), мы будем
иметь для одного моля газа
F = E0 — /?Г1п (2Kg^)Z> Р-/?Т-7?Т1п ар0 (3.34)
и
Ф = Н0 —/?7Чп (2^Г)'\ —/?Пп «р0. (3.35)
Таким образом,
F = £'04-fn — RTln а — /?Ппр0, (3.36)
Ф = ЯО + ФП —/?Т1па —/?Т1пр0 (3.37)
или
F = Е0 — ЯТ1П (2Т*.Р ’ Ч-о — RT— RTln а, (3.38)
v ЛЧ/Vo
Ф= Но - RT In (2тсХ7 " ~ 1П ”• (3-39)
п d In Qi d* In Qi ,
Принимая во внимание, что и обращаются
в нуль, для энергии и теплосодержания одного моля газа
на основании общих формул (см. табл. 2)
Е = £о +(3.40)
Н = + (3>41)
мы будем иметь;
£ = Е0 + |/?Г, (3.42)
H=Hb+^RT. (ЪАЪ
80 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ОДНОАТОМНЫХ ГАЗОВ [ГЛ. III
Теплоемкости одноатомного газа будут (см. формулы (2.77)
и (2.78)):
CV = ^R, (3.44)
Cp=^R. (3.45)
Наконец, общая формула энтропии
S = Sa + R]nQi + RT1^^ (3.46)
применительно к одному молю идеального одноатомного газа
примет вид
S = /? In -(2кХ7'/а + I /? + А? Ь ар0 (3.47)
или
5 = 5д + R 1п р0 + R In а. (3.48)
Подставляя в (3.48) значение 5П из формулы (2.72). мы
получим:
5 = | R In Г-}- R In 1» + у R In M + C+R In p0+R In a, (3.49)
где
c = «'"^ + 4
Таким образом,
5 = у R In Т+ R In v + 4 R In М — 1 1,069 + R In p0+R In a.
(3.51)
Исключая объем с помощью уравнения Менделеева — Кла-
пейрона и выражая давление в атмосферах, будем иметь
(см. (2.75)):
S = |rIhT- Rln/^ + ^Rln М+4+RInpo + Rlna (3.52)
или
S = -|-RlnT—Rln/> + |-Rln /И —2,313 + R lnp0 + Rlna.
(3.53)
Величина Rina получила название энтропии ядерного спина.
§ 4J УЧЕТ ВТОРОГО И ВЫСШИХ ЭЛЕКТРОННЫХ УРОВНЕЙ 81
Мы видим, что для вычисления энтропии одноатомного
газа в заданном состоянии (р, Г) или (v, Т) надо знать
только молекулярный вес, вес низшего электронного уровня
(См. табл. 4) и спин ядра.
При расчетах химических равновесий при средних и высо-
ких температурах, как увидим далее, энтропия спина R 1п а
может быть опущена, так как это слагаемое при вычисле-
ниях сокращается. Поэтому при вычислении энтропии, сво-
бодной энергии и изобарно-изотермического потенциала мы
можем опустить слагаемые /?7’1па и /?1па.
Термодинамические функции (S, F и Ф), вычисленные
без учета энтропии ядерного спина и некоторых других
факторов (см. § 6 этой главы), получили название практи-
ческой энтропии, практической свободной энергии и практи-
ческого изобарно-изотермического потенциала. Заметим, что
значения других функций — энергии, теплосодержания и
теплоемкостей одноатомного газа не зависят от спина ядра,
т. е. от а.
Для практических энтропий и изобарно-изотермического
потенциала мы будем иметь:
S = |/?ln Т— /?1пр + | /?1пМ — 2,313 + /? in о0 (3.54)
и
Ф=Н0— ^ЯПп М— у /?Г1п 7’+/?Г1п/?+7,2807’— /?Т1пр0.
(3.55)
Последняя формула получается из формулы (3.39) при под-
становке численных значений постоянных и отбрасывании
слагаемого ДПпа. Вместо Ф, как было указано выше (см.
Ф__е
формулы (2.87) и (2.88)) применяется часто функция ——.
Из формулы (3.55) следует:
П = ^=Д = —|/?1п М—|/?1п ?+/? In р+7,280—/? In рс.
(3.56)
§ 4. Учет второго и высших электронных уровней
Все выведенные в предыдущем параграфе формулы для
вычисления термодинамических функций были получены
в предположении, что мы можем пренебречь учетом второго
И следующих электронных уровней.
6 Зак. 835. И. Н. Годнее
82 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИЙ ОДНОАТОМНЫХ ГАЗОВ [гл. lit
Если второй электронный уровень энергии атома лежит
близко к основному, электронная сумма по состояниям не
будет равна р0 и мы Должны выполнить вычисление термо-
динамических функций, пользуясь общим выражением для Q3!I
(см. формулу (3.10)).
Выведем формулы для вычисления термодинамических функций
одноатомного газа для случая, когда можно ограничиться учетом
второго электронного уровня. Примером такого газа являются пары
таллия. Мы будем иметь:
<2эл=Ро+Р1‘?’еЛЛ <3-57)
Для Qi в силу формулы (3.11) получим:
Qi = “(Po + (3.58)
И
In Qi = In a -|- In (pn -|- p1e-8‘/AI’)- (3.59)
_ d In Qi rf3 In Qi
Вычислим производные —и —, знание которых необхо-
димо для вычисления термодинамических функций. Дифференцируя
выражение (3.59), получим:
d In Qi _ рхе Е‘/кт et
dT ~^+^‘,kT'kT2
(3.60)
ДГ2 —
(t: Л-B g-‘/kT) в e~^kT £1 d (Pn+Pie~ed>cT)
JPa+Plg )- ~dT ~Ple -------dT
(Po + Pi*-*’'*2)2
= P1 km __ kn pig km _
Po+Pi^-e,/A:2T Pn+p<8,/*J' (pn + P<ej/AT)2 ~
-(Po+p^-'./*2’)2 f0+pie-8^ ‘ (3'61)
Подставляя In Qi из формулы (3.59) в общие формулы, определяю-
щие свободную энергию и изобарно-изотермический потенциал, мы
вместо формул (3.36) и (3.37) получим:
6|
F = Eo-L- Fn — RTln a — RT In (p0 -f- pre kT). (3.62)
§ 4] учет второго И высших электронных Уровней
83
и
ф = нп +*ьл — /?ппа — тггin (р0 + рг<? кТ)- (3.63)
Выражения для энергии и теплосодержания, определяемые общими
формулами (3.40) и (3.41), теперь будут иметь вид
£ — fn 4- — RT 1 — eip'e е/кТ £ co-f- 2 KJ -f- й Po+Pi^ 1Z (3.64) (3.65)
И Н= На + - RT + — - 1Ptg *‘1кТ . 2 Ф k ро + р<^’
т. е.
Е — Eo + 'q- RT + £эл, (3.66)
Н=На+^ЯТ + Еэл. (3.67)
Для энтропии получим на основании общей формулы (3.46)
S = Sn + Л In а R In (р0 + рхе —_е /кТ-, (3.68)
kT Pn + Pi^ J
S = Sn + 'n а + ^эл (3.69)
[см. (2.128)].
d In Qi In Qi
Наконец, для теплоемкости, подставляя —и ——в фор-
ат dT2 т
мулы (2.84) и (2.85), мы получим:
с 3 л । 2/? №'‘‘1кт *
”“2 + kT Po + p<e‘/M1
£1РоР1е~с,/кТ 2Repe~B‘/kT
<3-™>
т. е.
С — v — 3 -/? + 2 R е?р (3.71)
- йз/’2 (Ро + pie~BilkT)1
и С — р — 5 -я+ 2 R ^йРхе~"'1кТ (3.72)
^72 ( Mp^kTf
Для вычисления практических функций в формулах для S, F и Ф
слагаемое энтропии ядерного спина 7? In а и У?? In а, как было ука-
зано выше, опускается.
6*
84 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ОДНОАТОМНЫХ ГАЗОВ [гЛ. Ill
§ 5. Общие формулы и сводная таблица
Если нужно учесть три и более электронных уровней,
удобно пользоваться общими формулами вида (2.97)—(2.103),
содержащими SC. Вычисляя эти выражения для
электронных состояний, мы получим:
<2эл = ро + Р1« кТ -1- р2е *г+--- (3.73)
0H-s1P1e лт (3.74)
O + sjpie кТ -1- г2р2е кТ + .. . (3.75)
На основании общих формул главы II (см. формулы (2.97) —
(2.103)), а также формул (2.1 16), (2.123), (2.128), (2.136)
мы можем написать:
Дэл = — (3.76)
Дэл нэл= - А (3.77)
<>ЭЛ ~— R 1п 1 kT 5 А (3.78)
И Сэл R 2 С /1Ж' (3.79)
Для термодинамических функций мы получим, если опустить
выражения, зависящие от ядерного спина,
Р = До “Г Fп дэл> (3.80)
Ф = : Фп ~Ь Фэл, (3.81)
Е = До + 4^Д+Дэл. (3.82)
И = НоЧ’4^Д+Дэл, (3.83)
s = СпД- Зэл> (3.84)
|я+сэл, (3.85)
ср== ~2 Я ~Ь Сэл- (3.86)
сл
Таблица 5
Таблица формул для вычисления термодинамических функций одноатомного газа
№ п/п Функция Общая формула Значение электронного слагаемого при учете только одного осн. ЭЛ. уровня
1 Энергия £эл = 0
2 Теплосодержание ^эл = £эл = 0
3 Энтропия S=-|/?ln7 + -|lnAl — /? 1пр — 2,313 + 5ЭЛ 5эл = я In Ро
4 Приведенная свободная энергия -|- R In Л4--|/?1п Т’+/?1пр4-5,293+^ ^*эл о . —?г- = — Я In р0
5 Приведенный изобарно- изотермический потенциал 5=^=— | /? In М— T+R In р+7,280+ ~ Ф»Л п . у, 1П р0
6 Теплоемкость при постоянном объеме с„ = |/? + сэл ^»эл = £"эз 0
7 Теплоемкость при постоянном давлении с^ = 4/? + сэл С —С — 0 ^рэл — ^эл — v
00
сл
ОБЩИЕ ФОРМУЛЫ И СВОДНАЯ ТАБЛИЦА
86 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ОДНОАТОМНЫХ ГАЗОВ [ГЛ. III
Эти формулы для термодинамических функций одноатомного
газа являются самыми общими. В таблице 5 мы приводим
сводку практических формул, причем в последнем столбце
даны значения электронных слагаемых для случая, когда
нужно учитывать только один электронный уровень.
§ 6. Эффект изотопии
Все формулы, которые были выведены в этой главе,
а также в главе II, относятся к газам, молекулы которых
тождественны по своим свойствам (имеют одинаковый моле-
кулярный вес, одинаковый ядерный спин). В действительности
большинство одноатомных и многоатомных газов предста-
вляет смесь молекул различных изотопов. Так, одноатомный
хлор с химическим молекулярным весом 35,47 представляет
смесь атомов с атомным весом 35 и 37, причем первого
изотопа в газе содержится 75,4% и второго 24,6%. Ана-
логично молекулярный С1.3 представляет смесь молекул трех
сортов:
С115'35, С1Г’37 И С1|5,:’7.
Естественно возникает вопрос, как скажется существование
смеси изотопных молекул в газе на его термодинамических
функциях.
Мы перейдем теперь к рассмотрению этого так назы-
ваемого эффекта изотопии для одноатомных газов.
Прежде всего заметим, что ядра различных изотопов
имеют разный ядерный спин. Классическим примером этого
являются изотопы водорода Н и D, из которых первый
имеет спин s, равный 1/2, а у второго $=1. Однако при
вычислении практических энтропий, свободной энергии и изо-
барно-изотермического потенциала при средних и высоких тем-
пературах мы можем не принимать во внимание, как это было
упомянуто в §§ 3, 4 настоящей главы и как это будет пока-
зано далее, энтропию ядерного спина. С другой стороны,
вместо однородного газа, который рассматривался до сих пор
при выводе формул для вычисления термодинамических функ-
ций, мы будем иметь смесь различных газов с разными
молекулярными весами. Поэтому вычисление энтропии газа,
представляющего смесь молекул различных изотопов, нужно
было бы производить по формулам, выведенным в § 9
ЭФФЕКТ ИЗОТОПИИ
87
главы II для смеси газов. Мы видели, что энтропия смеси
газов равняется сумме энтропий компонентов, если энтропия
каждого компонента вычисляется при заданной температуре,
причем данный компонент занимает весь объем смеси, т. е.
находится под своим парциальным давлением. Заменяя в фор-
муле (2.152) числа молекул числами молей, мы можем
написать:
5 = 5^^, v, D + S2(«2> v, 7’) + S3(n3, v, Г), (3.87)
где «j, и2, пз— числа молей первого, второго и третьего
изотопов газов в смеси. Если энтропию каждого газа вычи-
слить при общем давлении смеси Р, мы получим:
S = Si(ni< Р, T) + S.2(n.2, Р, Т) +
_|_£3(п3, Р, Г) — (n^in x1-\-n2R\n х2-\-плР\п х3), (3.88)
где xv х2, х3— молярные доли газов, построенных из моле-
кул первого, второго и третьего изотопов (см. § 9 главы II).
Применяя формулу для энтропии (2.73), легко усмотреть,
что при данном давлении и данной температуре энтропия
газа пропорциональна числу молекул или молей. На осно-
вании формулы (2.73) мы можем написать:
St(nt, Р, T) = n1S1(n=\, Р, Г), '
S2(n2, Р, T) = n2S2(n=1, Р, Т), (3.89)
S3(n3, Р, T) = n2S2(n = l, Р, 70,
где 54(п=1, Р, Т) означает энтропию при температуре Т
и давлении Р одного моля газа, построенного из молекул
данного изотопа.
Выполняя подстановку значений энтропии из фор-
мул (3.89) в (3.88), получим:
S = nrSl(n=l, Р, T) + n2S2(n=--\, Р, ?) +
+ п35’3 (п = 1, Р, Т)—(3.90)
г
Найдем теперь энтропию одного моля смеси. Для одного
моля числа nt, п2, пй совпадут с молярными долями xt, х2,
xs('ii = xi), причем л’г+х2 + х3 = 1.
Для энтропии одного моля одноатомного газа нами была
Выведена формула (3.52). Выражая энтропию с помощью
88 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ОДНОАТОМНЫХ ГАЗОВ [ГЛ. III
этой формулы и подставляя в (3.90), получим:
= X! R In T—R In R4-1R In M^Q+Rln ax+^)+
4~x2 R In T — R In P-|- -% R In Л12-|- Cr -]- R In a2 -|- 5ЭЛ) +
+ х3(|я1пГ-Я1пР-|-|/?1пМ}+С1 + Я1па3+.$эл) —
— RSxJnx^ (3.91)
Выполняя приведение подобных членов, мы будем иметь:
5n=i = (Xi Ч~ ха -|- Хд) R In Т— (xt-|-x2 Ч~х3) R In Р-|-
Ч- (Х1 Ч- х2 Ч- ХЧ Qt + (Х1 4“ Х2 Ч- Хз) ^ЭЛ 4“ Х1 ~2 В 1° 4“
Ч-х2 R In М2Ч-х3у R In M34-xtR In ах -x2RIn a2-|-
-|-x3Rlnot3— RSxJnx^ (3.92)
или, так как xt x2 + x3 = 1,
5;M=1==|RlnT— «1пР + С1 + 5Эл + х1-|/?1пМ14-
x2-|- R In M24-x3 у R In Mg-f-XiRIn <z1-|-x2R In a2-|-
+ x3Rlna:(—RSxJnx^ (3.93)
Если бы мы считали смесь изотопных молекул однородным
газом с молекулами, масса которых равна M/No, где
М — химический молекулярный вес и a — спиновый вес пре-
обладающего изотопа, мы получили бы вместо (3.93)
5 = 4 Rin Г—RlnR + C( + ^4-| RlnM4-Rlna. (3.94)
Таким образом, существование смеси изотопов в одноатом-
ном газе приведет к увеличению энтропии по сравнению
с энтропией, определяемой формулой (3.94), на величину
S™ ! — S = Xt-| R In Л^ + х.21 R In М3 + х3| R In Л43 +
xtR In ax + x2R In pt2 4- x3R In a3 —
— RSx^lnxi — -^-RlnAl—Rina, (3.95)
4
СРАВНЕНИЕ С ОПЫТНЫМИ ДАННЫМИ
§7]
формУлУ (3.95) можно переписать так:
3 af’a*
89
!а~3
------R^X; 1П X;
а 1 г
(3.96)
ИЛИ
3 а^‘а^аХз
^/?1п 1 Л 3 -j-A>ln-j-?-j-
2 М 1 а
Таким образом, влияние существования
к увеличению энтропии на величину
Д$изот=-у^'п лл 3+^1п ^Г^-
«SxJnXj. (3.97)
изотопов приводит
Rlx^nx^ (3.98)
М
Оказывается, что три последних слагаемых формулы (3.97)
или ДЗизот компенсируются при расчете обычных химических
реакций*). Таким образом, как и при рассмотрении энтро-
пии ядерного спина, мы можем не принимать во внимание
этих слагаемых формулы и рассчитывать энтропию одно-
атомного газа по формуле (3.94). Аналогичный результат
получается, как легко видеть, для свободной энергии и изо-
барно-изотермического потенциала. Что касается энергии,
теплосодержания и теплоемкостей, то они, как это следует
из формул (3.82), (3.83), (3.85), (3.86), будут одинаковы
для всех одноатомных изотопов данного элемента. Поэтому
для практических вычислений термодинамических функций
одноатомного газа мы можем использовать формулы, при-
веденные в таблице 2.
Заметим, что первое слагаемое в (3.98) обычно бывает
мало. Так, для обычного хлора с М = 35,47 оно соста-
вляет — 0,00069.
§ 7. Сравнение с опытными данными
Приведем в заключение этой главы некоторые данные,
показывающие совпадение вычисленных и опытных значений
термодинамических функций для одноатомных газов. Обще-
известно, что опытные молекулярные теплоемкости С„ одно-
5 з Р
атомных газов весьма близки к -^R, a Cv— к R, как это
) См. § 6 главы XII и § 7 главы XIII,
90 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ОДНОАТОМНЫХ ГАЗОВ [ГЛ. III
следует из элементарной классической теории и из фор-
мул (3.44) и (3.45). Отношение CpfCv = 7 для одноатомных
газов должно быть равно Б/3= 1,667, и это наблюдается
в действительности. Так, для паров ртути при темпера-
туре 548—629°К у равна 1,666, для аргона при 284°К
Т аб л и ц а 6
Одноатомные газы ^выч С опытные
Аргон 36,99 36,8—37,1
Ксенон 40,54 40,7±0,3
Неон 34,96 35,0±0,1
Криптон 39,20 39,0±0,3
Магний (газ) . . 35,51 35,3
7=1,66. Хорошее совпадение получается и для энтропий
и других термодинамических функций. В таблице 6 приве-
дены значения опытных и вычисленных энтропий при 298,1°К
(см. [3]).
ГЛАВА IV
УРОВНИ ЭНЕРГИИ и состояния ДВУХАТОМНЫХ
МОЛЕКУЛ *)
§ 1. Волновая функция молекулы в случае
разделения энергии
В предыдущей главе мы рассмотрели вычисление термо-
динамических функций одноатомных газов. Эта задача ока-
залась простой, так как внутренние движения сводились
к электронным движениям, учет которых не оказывает зна-
чительного влияния на значения термодинамических функций.
В случае двухатомных, трехатомных и более сложных мо-
лекул мы должны кроме электронных движений принять во
внимание колебания ядер и вращение молекулы в целом.
Кроме того, при рассмотрении возможных состояний моле-
кулы нужно учитывать также ядерный спин.
В первом приближении можно рассматривать электронные
колебательные и вращательные движения молекулы не зави-
сящими друг от друга. В этом случае для молекулы, не
имеющей ядерного спина, мы можем написать (см. фор-
мулу (2.19)):
Фг = 'т'эл'^колеб'т'вр (4 • 1)
И
si == гэл ~|“ еколеб ~И ®вр• (4.2)
Функцию, учитывающую электронный спин, мы включаем
В %Л.
Таким образом, для полной энергии молекулы получаем:
г = г0 + ®11 “Ь г1 = £оЧ~ гпЧ" гэл+ ®колебЧ-£вр- (4-3)
. *) Для более подробного изучения см. В. Н. Кондратьев [32],
’ Герцберг [19], А. Г ейдон [16], А. Н. Теренин [60].
92 УРОВНИ ЭНЕРГИИ И СОСТОЯНИЯ ДВУХАТОМНЫХ МОЛЕКУЛ [гл. IV
При наличии ядерного спина мы учитываем его волновой
функцией <ря. 0, которая добавляется как сомножитель в
Таким образом,
’г1» == '^эл ‘ '['колеб ‘ фвр ‘ '[я, с- (4-4)
Полная волновая функция, учитывающая все движения моле-
кулы, будет:
'^ = 'Ш (4.5)
или
Ф == '[п'т'эл'['колеб7вр|['я. с- (4-6)
Если молекула содержит одинаковые ядра, то функция б
должна удовлетворять условиям симметрии по отношению
к перестановкам координат одинаковых ядер, т. е. она
должна быть в зависимости от статистики, которой под-
чиняются эти ядра, или симметричной или антисимме-
тричной.
Разделение внутренней энергии молекулы si на слагаемые
(см. (4.2)) является приближенным, но это приближение
хорошо оправдывается в ряде случаев *).
§ 2. Простейшая модель двухатомной молекулы:
жесткий ротатор — гармонический вибратор
Рассмотрим подробно вопрос об уровнях энергии и со-
стояниях двухатомной молекулы. Простейшей моделью ее
является модель, в которой при рассмотрении вращения рас-
стояние между ядрами считается постоянным, а колебания
ядер принимаются гармоническими. Масса молекулы пред-
полагается сосредоточенной в ядрах, которые рассматри-
ваются как материальные точки. Такая модель получила
название модели «жесткий ротатор — гармонический вибра-
тор».
При применении этой модели, естественно, предпола-
гается разделение внутренней энергии молекулы на электрон-
ную энергию, энергию вращения и энергию колебания ядер-
Таким образом, при использовании рассматриваемой модели
выполняется формула (4.2).
*) См, Г, Г ерцберг [19], глава IV,
93
§ 2] жесткий ротатор — Гармонический вибратор
Пусть ядра молекулы с массами тх и т2 находятся на
расстоянии г (черт. 3). Обозначим через О центр инерции.
Z7z
г*
с Г1 * 4 'г
О
Черт. 3.
2
Момент инерции относительно оси, проходящей через
центр инерции и перпендикулярной к линии, соединяющей
ядра, будет:
(4-7)
Определяя координаты центра инерции, мы будем иметь:
Г =
1 т^-}- т2
(4-8)
и
г - mi
2 т1-\-т2
Подставляя эти значения rt и г2 в
} = т1т2
тг 4- т2
(4-9)
формулу (4.7), получим:
(4.Ю)
Выражение —та1?2_
лекулы р.:
было названо приведенной массой мо-
(4.Н)
Таким образом,
/ = рг2. (4.12)
• Рассматривая решение уравнения Шредингера для вра-
щательных состояний жесткой двухатомной молекулы, мы
Получим следующие уровни *) энергии:
_AV(J+1)
Sb1’ — 8^1
(4.13)
*) См. К. В. Никольский [53], стр. 251; Э. В. Ш п о л ь-
с,сий [84], стр. 89, т. 11; см. также [92].
94 УРОВНИ ЭНЕРГИИ И СОСТОЯНИЯ ДВУХАТОМНЫХ МОЛЕКУЛ [гл. IV
где h — постоянная Планка, а / — момент инерции, опреде-
ляемый формулой (4.12). Квантовое число J, получившее
название вращательного квантового числа, может принимать
значения 0, 1, 2, 3, 4, 5, . . . Оно определяет момент ко-
личества движения молекулы, равный
/7(7+1)-^«7^. (4.13а)
Если двухатомная молекула не имеет одинаковых ядер,
мы не должны принимать во внимание требований симме-
трии, накладываемых на волновую функцию по отношению
к перестановкам ядер, и 7 действительно принимает указанные
выше значения 0, 1, 2, 3, 4, 5, . .. Сложнее обстоит дело,
как мы увидим далее, если двухатомная молекула имеет
одинаковые ядра.
Уровни энергии, определяемые формулой (4.13), оказы-
ваются вырожденными, причем вес уровня равен 27+ 1.
Вращательные уровни жесткой двухатомной молекулы, не
-----------------------------3=ВИЗ)
--------------------------3=5(11/
---------------------------3=4(9/
---------------------------3=3(7)
---------------------------3=2(5/
---------------------------3=1(3/
-----------------------------
Черт. 4.
имеющей одинаковых ядер, представлены на чертеже 4, где
числа в скобках означают квантовые веса этих уровней.
Если энергию вращения выражать в см+ мы получим;
= +1(1+ I) = BJ(J + 1). (4.14)
где величина
В = о ~9~Г
+гЗс1
(4.15)
называется вращательной постоянной.
2] ЖЕСТКИЙ РОТАТОР------ГАРМОНИЧЕСКИЙ вибратор 95
Перейдем теперь к рассмотрению колебаний. Предпо-
лагая, что сила, возвращающая ядра в их положение равно-
весия, пропорциональна смещению, мы можем написать на
основании второго закона Ньютона соответственно для пер-
вого и второго ядер
т1-^Г = — k(r — ге), (4.16)
m2^- = ~k<r — re\ (4-17)
где ге — равновесное расстояние между ядрами, г — расстоя-
ние в данный момент, a rt и г2 — расстояния обоих ядер от
центра инерции (см. черт. 3). Дифференцируя дважды по
времени выражения (4.8) и (4.9), будем иметь:
= (4.18)
dt* nii ntz dt* v 7
= —T-S-- (4-19)
dfi -|- m2 dt2 v '
Подставляя эти значения в уравнения (4.16) и (4.17), полу-
чим два тождественных уравнения
= (4’2°)
d^f*
Коэффициент перед является приведенной массой р. За-
мечая, что ге — величина постоянная, мы можем под знаком
производной заменить г через г — ге, тогда получим урав-
нение колебаний
9-rf2(Slre) =-^r~re). (4.21)
Это — уравнение колебаний для гармонического осциллятора
с массой т, равной приведенной массе молекулы р, и сме-
щением х, равным г — ге.
Как известно, классическая частота колебаний гармони-
ческого осциллятора будет *):
(4.22)
*) См., например, Э. В. Шпольский [84], т. I, § 44.
96 УРОВНИ ЭНЕРГИИ И СОСТОЯНИЯ ДВУХАТОМНЫХ МОЛЕКУЛ [гл. IV
При рассмотрении гармонического осциллятора с точки
зрения квантовой механики для уровней энергии получается
выражение *)
гколеб = h'< (и ’ (4-23)
где колебательное квантовое число v принимает значения О,
1, 2, 3, . .. Диаграмма уровней энергии представится серией
равноотстоящих линий. Все эти уровни невырождены, и
у. каждый имеет вес, рав-
---------------------------- ный 1. Наиболее низкий
уровень энергии полу-
чается при v = 0. В этом
состоянии энергия моле-
кулы, как это следует
из формулы (4.23), не
равна нулю, но имеет
значение г (0) = у h'i.
Подставляя значения еколеб
и гвр в формулу (4.2),
для модели жесткий рота-
тор— гармонический ос-
циллятор мы получим:
гг = $эл + h'i [v -|- j -ф-
----—--------------2
---------------z
A ------------------------0
Черт. 5.
<4-24)
Схема уровней энергии
двухатомной молекулы
в предположении приме-
нимости формулы (4.24)
представлена на черте-
же 5. Здесь даны колебательные и вращательные уровни
двух электронных состояний А и В молекулы.
В реальной молекуле наиболее далеко отстоят друг от
друга электронные уровни. Каждому электронному уровню
соответствует свой набор колебательных и вращательных
*) См., например, Э. В. Шпольский [84], т. 1, § 149.
3] Электронные уровни двухатомных Молекул 97
уровней. Расстояния между электронными уровнями имеют
поряДок нескольких десятков тысяч см-1, расстояния между
колебательными уровнями — 1000 см'1, а между вращатель-
ными— только несколько си-1.
§ 3. Электронные уровни двухатомных молекул
В рассмотренной нами в § 2 модели предполагалось, что вра-
щательные и колебательные состояния не зависят от электронного.
В действительности, как это обнаруживается при более точном
рассмотрении, электронное, колебательное и вращательное движе-
ния влияют друг на друга. Однако в первом приближении целесо-
образно рассмотреть электронные состояния двухатомной молекулы
независимо от вращений и колебаний.
При таком рассмотрении нужно предполагать ядра молекулы
неподвижными. Движение электронов в двухатомной молекуле про-
исходит в достаточно сильном электрическом поле двух ядер, обла-
дающем осевой симметрией. Орбитальные моменты количеств дви-
жения электронов складываются в результирующий момент коли-
чества движения L, а спиновые движения электронов — в резуль-
тирующий электронный спин S.
Величины векторов L и S, как и
в атоме, соответственно опреде-
ляются квантовыми числами L и S.
Рассмотрение вопроса о движе-
нии электронов показывает, что
у достаточно обширного класса
молекул вектор L совершает пре-
цессию вокруг оси молекулы, так
что проекция его в направлении
этой оси при отсутствии внеш-
них воздействий остается постоянной (черт. 6). Эта проекция имеет
величину
где
квантовое
число принимает одно из
ь 2п
значений L, L — 1, L — 2, ..., — L. Оказывается, что знак кванто-
вого числа ML не влияет на величину энергии, так как два со-
стояния электрона, отличающиеся направлением вращения отно-
сительно оси молекулы, будут иметь одинаковую энергию. Абсо-
лютная величина квантового числа ML обозначается обычно
буквой А,
А = I ML |.
(4.25)
В соответствии с квантовым числом А можно построить
вектор Д, направленный по оси молекулы, равный по вели-
чине А —.
7 Зак. 835. И. Н. Годнее
ЙЙ УРОВНИ ЭНЕРГИИ И СОСТОЯНИЯ ДВУХАТОМНЫХ МОЛЕКУЛ [гл. IV
Классификация электронных состояний для большой группы
двухатомных молекул производится по значениям *) квантового
числа А. При заданном Z, как это следует из допустимых значе-
ний М^, квантовое число А может принимать значения 0,1,2,...,/..
Уровни электронной энергии двухатомных молекул оказываются
зависящими прежде всего от квантового числа А.
Соответственно положительным и отрицательным значениям ,
при которых молекула имеет одинаковую энергию, уровни с А=/=0
будут вырождены двукратно. Молекулярные электронные состоя-
ния с разными значениями А обозначаются большими греческими
буквами.
Для А = 0 принято обозначение 2,
» А = 1 » » П.
» А = 2 » » Д и т. д.
При дальнейшей классификации электронных состояний моле-
кулы нужно принять во внимание спин электронов.
Вектор S, представляющий результирующий спин электронов
и определяемый квантовым числом S, оказывается квантованным
г, , „ h
в пространстве. Его проекция на ось молекулы будет равна 2 • .
где квантовое число 2 принимает значения **) через единицу от -|-S
до —S (всего 2S -1- 1 значений). По величине этой проекции можно
построить вектор 2, направленный, как и вектор А, по оси моле-
„ „ h.
кулы и равный
Полный момент количества движения электронов относительно
оси молекулы получится сложением векторов А и 2, направленных
по оси молекулы, так что оказывается возможным ввести алгебраи-
ческим сложением квантовых чисел А и 2 квантовое число 2, опре-
деляющее результирующий электронный момент количества движе-
ния относительно оси молекулы 2:
Q = А + 2. (4.26)
Как и в случае атома, спиновое движение электронов оказы-
вает влияние на положение уровней электронной энергии молекулы.
Значение электронной энергии поэтому будет зависеть не только
от квантового числа А, но и от квантовых чисел S и й. Влияние
последнего обусловлено взаимодействием орбитального и спинового
движений электронов, что приводит, вообще говоря, к расщепле-
*) Следует заметить, что квантовое число А, как и вводимое
ниже квантовое число 2, имеет смысл не для всех двухатомных
молекул. Поэтому рассматриваемая ниже классификация электрон-
ных состояний не является общей. Она, однако, оказывается при-
менимой к достаточно большой группе двухатомных молекул. См.
В. Н. Кондратьев [32], Г. Г ерцберг [19].
**) Квантовое число 2 не следует смешивать с символом 2, при-
меняемым для обозначения состояния с А = 0.
§ 3] ЭЛЕКТРОННЫЕ УРОВНИ ДВУХАТОМНЫХ МОЛЕКУЛ 99
нию*) вырожденного уровня энергии, который соответствовал бы
данным значениям Л и S, на 2S-|-1 близких уровней, различаю-
щихся величиной квантового числа 12. Так, например, при Л = 2,
5=1 (S = — 1, 0, 4-1) уровень энергии распадается на три близ-
ких уровня со следующими значениями 11:
Ut = 2 — 1 = 1,
1>3 = 2 4- 0 = 2,
12,, = 2^1=3.
Группа близких уровней энергии, соответствующих заданным
значениям квантовых чисел Л и S, получила название электронного
терма двухатомной молекулы **).
Электронный терм обозначается символом
25+1 {А}, (4.27)
где величина Л задается в виде букв (3, П, Д, ... см. выше). Ве-
личина 2S 4~ 1 = как и в случае атома, получила название муль-
типлетности терма.
Уровень энергии обозначается символом (4.27) с указанием
внизу справа квантового числа 12. Например, символ зп2 означает
уровень энергии с А = 1, М = 3 (следовательно, S = 1) и 12 = 2.
В рассмотренном выше примере состоянию с А = 2, S = 1 соот-
ветствует терм зд, который состоит из трех компонентов: 3ДЬ 3Д2
и ЗД9 (12 = 1, 12 = 2, 12 = 3).
Дальнейшая более подробная характеристика электронных тер-
мов двухатомных молекул связана с характером симметрии элек-
тронных волновых функций. Если электронная функция при отра-
жении от плоскости, проведенной через ядра, остается неизменной,
состояние, ей соответствующее, называется симметричным и обозна-
чается символом + (например, S+); если электронная функция ме-
няет знак на обратный, состояние называется антисимметричным
и обозначается символом - (например, 2~).
Для молекул, имеющих два одинаковых ядра, например О2, или
молекул с ядрами, несущими одинаковый заряд, например О!®О’8,
электронные термы различаются далее по четности и нечетности.
Состояние называется четным, если электронная волновая функция
остается симметричной (не меняющей знак) при изменении знака
координат всех электронов. Такое состояние обозначается индек-
сом д внизу символа терма, например 2д, Если волновая функ-
ция меняет знак на обратный при изменении знака координат элек-
тронов, состояние называется нечетным и обозначается значком и,
например 2„, П„.
В таблице 7 мы приводим несколько примеров основных (нор-
мальных) состояний двухатомных молекул.
*) При А = 0 такое расщепление не имеет места.
**) Часто в литературе термин «терм» применяется для значе-
ния энергии (иногда взятого с обратным знаком), ср. примечание
На Стр. 75.
7*
100 УРОВНИ ЭНЕРГИЙ Й СОСТОЯНИЙ ДВУХАТОМНЫХ МОЛЕКУЛ [гл. IV
До сих пор мы рассматривали ядра молекулы неподвижными.
Если принять во внимание вращение молекулы, предполагая послед-
нюю жесткой, то вопрос об определении уровней энергии и состоя-
ний значительно осложнится. При вращении молекулы будет иметь
Таблица 7
Основные состояния некоторых
двухатомных молекул
Молекула Состояние Равновесное расстояние в А
Н3 iv+ ^9 0,741
СО 1,128
О2 1 cs 1,208
n2 1,095
NO % 1,150
-
место сложение различных моментов количества движения — элек-
тронного спина S, электронного орбитального момента L и момента
вращения ядер ш. Мы встретимся *) с различными типами связи,
которые были разобраны и классифицированы Хундом (слу-
чаи а, Ь, с и d). Наибольший практический интерес представляют
случаи а и Ь.
Случай а соответствует тем предположениям, которые были
введены выше при классификации электронных термов. Здесь взаи-
модействие L и S преобладает над взаимодействием L и ш. Век-
тор Q, направленный по оси молекулы, складывается с моментом
количества движения ядер m и образует результирующий момент
количества движения J. Энергия вращения молекулы в первом при-
ближении оказывается равной
евр = hcB[J(J+ 1) - Q2J.
(4.26а)
Здесь квантовое число J не может принимать значений, меньших Й.
Мы имеем поэтому
/=й, Й4-1, й + 2, ... (4.266)
*) См. В. Н. Кондратьев [32], глава IV; Г. Герцберг
[19], глава V; Л. Ландау и Е. Лифшиц [37].
§ 4] УЧЕТ АНГАРМОНИЧНОСТИ КОЛЕБАНИЙ 101
ттля 12 состояний 2 = 0, так как Д=0 и 2 = 0. Формула (4.26а)
яля этого случая совпадает с формулой (4.14) и J принимает зна-
чения 0, 1, 2, 3......
В случае b взаимодействие векторов L и m преобладает над
взаимодействием L и S. Случай b является в известном смысле
обратным случаю а, где взаимодействие (L, S) преобладает над
л in). Векторы Лиш дают результирующий вектор К, последний
де с вектором S дает J. В этом случае квантовое число 2, а также
и Q теряют смысл.
Энергия вращения в случае b оказывается зависящей в первую
очередь от квантового числа К, определяющего вектор К. Кванто-
вое число К принимает значения Л, Л-|-1, Л-j-2 и т. д.
Каждый уровень энергии с данным К состоит из 25Д-1 компо-
нентов, различающихся значением квантового числа J, которое при
принимает значения, отличающиеся на единицу и лежащие
в интервале от f(-\- S до К-— S. В случае 5 = 0 (одиночные состоя-
ния) А' = J и случаи а и b совпадают.
Следует заметить, что случаи Хунда, из которых мы рассмо-
трели только а и Ь, являются предельными случаями взаимодей-
ствия моментов количества движения. В реальных молекулах воз-
можен переход от одного случая к другому. Примером переходного
случая от а к b является молекула О2, имеющая основное состоя-
ние •
§ 4. Учет ангармоничности колебаний*)
Рассмотренная нами в § 2 модель молекулы является
приближенной, так как в действительности колебания в мо-
лекуле являются не гармоническими, а допущение о независи-
мости вращений, колебаний и электронных состояний нуждается
в уточнении. Первой поправкой, которая может быть введена,
является учет ангармоничности колебаний. Допуская разде-
ление энергии, мы можем применить модель жесткий рота-
тор— ангармонический осциллятор. Учет ангармоничности
колебаний состоит в применении для потенциальной энергии
вместо квадратичной зависимости
V = k{r-reY, (4.28)
соответствующей гармоническим колебаниям, выражения, со-
держащего третью и более высокие степени изменения рав-
новесного расстояния ге:
V= Л(г —ге)2 —d(r — ге)8-|-... (4.29)
р . *) Для более подробного рассмотрения вопросов §§ 4, 5, 6 см.
• Герцберг [19], глава Ши К. В. Никольский [53].
102 УРОВНИ ЭНЕРГИИ И СОСТОЯНИЯ ДВУХАТОМНЫХ МОЛЕКУЛ [гл. IV
Постоянная d, учитывающая ангармоничность колебаний,
оказывается значительно меньше k. Уровни энергии ангар-
монического осциллятора не представляются системой равно-
отстоящих уровней. Расстояние между ними при переходе
к более высоким энергиям уменьшается. В случае малой
ангармоничности d <<^ k получается выражение
гколеб = j) — ^ехе У ) “Ь
+ ЧЛ(^ + |)3+--- (4.30)
Здесь ^ехр, чрур— постоянные, зависящие от k и d. По-
стоянная '>ехе значительно меньше '>р, а чруе— значительно
меньше '>ехе. Переходя к частоте колебания, представленной
в виде волнового числа (т. е. частоте, выраженной
в ел-1), мы получим:
гколеб ~~ hC(X>e (v —I- -yj hCtilpXp (v
+ + y)3 + • • (4.31)
Индекс e, которым снабжена частота, указывает на отсчет
энергии от минимума потенциальной энергии.
Аналогично случаю гармонического осциллятора здесь
также имеется нулевая энергия, которая определяется из
формул (4.30) и (4.31) при v = 0:
he [д сое — 1 + (4.32)
Если производить отсчет от уровня энергии с v = 0, то
у.клеб — г0 = he — шрхр + j v —
— (“Л —• • •) ^ + («ел+ • • .)^3+ • • • ] (4.33)
ИЛИ
-колеб — го — he [coq'V — WqXoV ' И-('-о.УгУ9 ~Ь • • • ], (4.34^
§ 5] НЕЖЕСТКИЙ РОТАТОР — АНГАРМОНИЧЕСКИЙ ВИБРАТОР 103
где коэффициенты перед степенями v, как это следует из
сравнения двух предыдущих выражений, имеют значения
U)o = t°e —(иехе + ^-‘иеЛ+ • • • > (4-35)
шсхо = wexe у шеуе + . • • . (4.36)
шоУо ~ “е-УеЧ- • • (4-37)
Таким образом, при учете ангармоничности колебаний сле-
дует различать частоты и <о0. Так, для НС1 ше=2989 см-1,
<м0 = 2937 см-1. Первая из этих частот (шр) представляет
частоту, которую имел бы ангармонический осциллятор при
бесконечно малой амплитуде *).
Применяя модель жесткий ротатор — ангармонический ос-
циллятор, мы получим для энергии двухатомной молекулы
si — гэл + he [we (у -yj — шехе (у
^8^7(7+!). (4.38)
Однако и это выражение является приближенным, так как
в действительности расстояние между ядрами при вращении не
остается постоянным.
§ 5. Применение модели
нежесткий ротатор — ангармонический вибратор
Мы получим еще лучшее приближение к действитель-
ности, если применим модель нежесткого ротатора, т. е.
ротатора с изменяющимся расстоянием. Момент инерции
такого ротатора будет зависеть от квантового числа J.
*) См. Г. Герцберг [19]. Кроме этих двух частот для ха-
рактеристики колебаний двухатомной молекулы иногда применяется
так называемая наблюдаемая основная частота равная частоте
испускаемого излучения при переходе от состояния v =1 к со-
стоянию v = 0. Легко показать при помощи формулы (4.31), что
эта частота будет равна
У = си/ = с [we — 2<uexe] + .,.
104 УРОВНИ ЭНЕРГИИ И СОСТОЯНИЯ ДВУХАТОМНЫХ МОЛЕКУЛ [гл. IV
Квантовомеханическое вычисление показывает, что уровни
энергии нежесткого ротатора можно представить в виде
евр = gj [1 - uJ(J+ 1)] J (J+ 1) + . . . (4.39)
sBp = ftcB[l — zzJ(J+1)]J(J+1)+ .... (4.40)
где В—постоянная вращения, определяемая формулой (4.15),
а и — коэффициент, малый по сравнению с единицей.
Формулу (4.40) можно написать иначе:
eBp = Ac[BJ(J-)-l) —BwJ2(J+l)2]+ . . . (4.41)
или, обозначив Ви через D, мы получим:
8ВР = he [В J (J + 1) — DР (J + 1 )2 + . . . ]. (4.42)
Формула (4.42) нашла применение в спектроскопической
практике, причем часто в ней учитывается третье слагаемое
fJ£(J+l)3.
Применяя модель ангармонический осциллятор — не-
жесткий ротатор, мы получим для энергии молекулы г{:
гг — гэл + he [<»е (^ + "2 ) — шехе + у) 4“ • • j +
+ Ac[BJ(J+l) — Z)/2(J+1)2+. . .]. (4.43)
Это выражение также является приближенным, так как мы
не учли взаимодействия колебательных и вращательных со-
стояний. В самом деле, при колебаниях меняется расстояние
между ядрами, а поэтому изменяются момент инерции и по-
стоянные В и D. Взаимная связь колебаний и вращений
учитывается в более точной модели, которая получила на-
звание «колеблющегося ротатора».
§ 6. Применение модели колеблющийся ротатор
Пусть равновесное расстояние между ядрами будет ге.
Этому равновесному расстоянию соответствует вращательная
постоянная В (см. формулу (4.15)). Отмечая эту постоянную
§ 6] ПРИМЕНЕНИЕ МОДЕЛИ КОЛЕБЛЮЩИЙСЯ РОТАТОР 105
индексом е, мы будем иметь:
Ве = -^-г^ (4.44)
е 8~.^с/е v 7
где
= (4.45)
Для колеблющегося ротатора постоянные В и D зависят от
квантового числа v. С достаточно удовлетворительным при-
ближением можно принять:
Вс = Ве-«е(г/+1)+...> (4.46)
где постоянная ае мала по сравнению с Ве, и
^. = ^ + 3^ + 1)+..., (4.47)
где 9е мало по сравнению с De. Для вращательной энергии
в данном колебательном состоянии, описываемом квантовым
числом v, мы можем написать:
звр = he [£W+ О - D,:P (J + 1)2+ ... J. (4.48)
Таким образом, при применении модели колеблющийся ро-
татор энергия молекулы будет:
8 — 8эл + he р)е fu + --<DeXe (v + + • • • j +
+MW 0 - I)9 + • • (4.49)
Выражение (4.49) нашло применение при вычислении термо-
динамических функций двухатомных газов. При точных вы-
числениях приходится принимать во внимание зависимость
энергии колебания и вращения от электронных состояний.
Это достигается определением постоянных ше и шехе для
каждого электронного уровня, а также введением поправок
в энергию вращения (см. Герцберг [19]).
Приведем теперь сводку уровней энергии, соответствую-
щих различным моделям двухатомной молекулы (см. табл. 8).
Рассмотренные формулы могут быть непосредственно
Применены к молекулам, основное электронное состояние
Которых является ^-состоянием.
106 УРОВНИ ЭНЕРГИИ И СОСТОЯНИЯ ДВУХАТОМНЫХ МОЛЕКУЛ [гл. IV
Таблица 8
Формулы для уровней энергии двухатомной молекулы
№
п/п
Модель
£ -4- £ г
вр I кэлеб
Жесткий ротатор—
гармонический
осциллятор
Жесткий ротатор—
2 ангармонический
осциллятор
3 Нежесткий рота- тор — ангармони- ческий осциллятор ftc[BJ(J+ 1) —ОЛ(У-г 1)3-Ь ... ] + + Ас + у j — шехе г у j + • • • j
4 Колеблющийся ротатор he + 1) - Dc J2 (J + I)2 J- . . . ] -b + he pe (y 4- xK (y 4- j j + ... j
§ 7. Учет симметрии полной волновой функции
молекулы
При определении допустимых состояний молекулы весьма
существенным оказываются требования симметрии, которым
должна удовлетворять полная волновая функция, представ-
ленная в первом приближении в виде произведений сомно-
жителей 6ЭЛ, <Ьволе6, 6Dp, бя.(см. формулу (4.6)). Дей-
ствительно, полная волновая функция 6 должна быть сим-
метричной или антисимметричной по отношению к переста-
новкам координат одинаковых ядер в зависимости от типа
статистики (Бозе — Эйнштейна или Ферми — Дирака), кото-
рой подчиняются ядра. Эти условия симметрии естественно
отпадают, если молекула не имеет одинаковых ядер.
Пусть дана двухатомная молекула, построенная из оди-
наковых ядер, обладающих спином 5. Спин у, каждого из
§ 7] УЧЕТ СИММЕТРИИ ПОЛНОЙ ВОЛКОВОЙ ФУНКЦИИ МОЛЕКУЛЫ 107
ядер может принимать 2s-j- 1 значений, так что всего
будет (2s -|- 1 )3 спин-состояний, соответствующих с доста-
точной степенью точности одинаковой энергии молекулы.
Например, для протонов s=l/2, тогда для молекулы Н,
существуют четыре спин-состояния одинаковой энергии; для
дейтонов s = 1, а поэтому в случае молекулы D2 будет су-
ществовать (2- 1 -(- 1)- = 9 спин-функций. Для молекулы Н.2
эти четыре спин-функции будут *):
а(1)а(2),
«(1)?(2),
а (2) ,3(1), ।
;3(1) 3(2), J
(4.50)
где символ а означает, что для данного ядра ms=l/2,
а символ !?, — что т3~—1/2.
Применяя линейные комбинации этих функций, мы по-
лучим четыре функции вида
а(1) «(2),
а (1)3 (2)+ «(2) ,3(1),
(4-51)
3(1).3(2)
И
а (1),3(2)-а (2) 3(1).
(4-52)
Три функции (4.51) будут симметричными относительно
перестановок координат ядер (1) и (2), а функция (4.52) —
антисимметричной. Полная волновая функция (4.6) будет:
'Y = '/п'Ьэ,.|^колеб7вр'/я.
Функция бп не зависит от координат одинаковых ядер и
поэтому всегда является симметричной. В основном состоя-
нии для большинства молекул, например Н.2, D.2 и др., Сэл
также является симметричной. Симметрия 6волеб зависит от
квантового числа но в основном состоянии и эта функция
тоже будет симметричной. Произведение Сп • 6ЭЛ • бк0.ТСб
будет, таким образом, симметричной функцией, и симметрия
*) См, Э. В, 111 п о л ь с к и й [84], П а у л и н г и Вильсон [92].
108 УРОВНИ ЭНЕРГИИ И СОСТОЯНИЯ ДВУХАТОМНЫХ МОЛЕКУЛ [гл. IV
всего произведения (4.6) для основного состояния будет
определяться последними двумя сомножителями 6вр и бя.с.
В качестве примера применим эти рассуждения к моле-
куле Н2. Полная волновая функция для этой молекулы
должна быть антисимметричной, так как ядра молекулы Н2
(протоны) подчиняются статистике Ферми — Дирака. Прини-
мая во внимание, что симметрия определяется двумя по-
следними множителями функции (4.6), мы придем к заклю-
чению, что полная антисимметричная функция может быть
осуществлена следующим образом:
Ф — (^вр)сим (’+ с)аптиоим,
Ф — (%р)антисим ' ('т'я. с)сим-
Другие комбинации типа
б — (%р)сим ’ ('^я.с)сим>
== (%р)антисим ’ (Фя. с)антисим
(4.53)
(4.54)
не будут удовлетворять требованиям симметрии, ибо в этом
случае полная волновая функция будет симметричной по
отношению к перестановкам координат одинаковых ядер,
что не может иметь места, так как протоны подчиняются
статистике Ферми — Дирака. Принимая во внимание, что
Существуют Три фуНКЦИИ (^я.с)СИм (4.51), а (6Я. о)антИсИМ —
одна (4.52), мы получим, что вес уровня энергии, соответ-
ствующий (%р)антисНМ. будет:
Pi = 3(27+1),
а вес уровня — (%Р)сим примет обычное значение
р2 = (27+1).
(4.55)
(4.56)
Исследование показывает, что при четных значениях
вращательного квантового числа J функция 6вр будет сим-
метрична по отношению к перестановкам координат оди-
наковых ядер, а при нечетных—-антисимметрична. Таким
образом, при 7=0, 2, 4, 6, .... которым в силу фор-
мулы (4.53) соответствует антисимметричная ядерная спин-
функция, квантовый вес уровня будет (27+1); при 7 =
7] УЧЕТ СИММЕТРИИ ПОЛНОЙ ВОЛНОВОЙ ФУНКЦИИ МОЛЕКУЛЫ 109
₽=!, 3, 5, 7, ... вес уровня энергии будет 3(2J-|-1).
Диаграмма уровней энергии молекулы водорода предста-
влена на чертеже 7,. где указаны симметрии %р и ^я.е и
вес энергетического уровня.
J=5— opmo Симметрия Фер х Фя с антисим. * сим. Вес энергетического уровня 11*3 = 33
J=4— пара сим.*антисим. 9*1 = 9
J=3— орто антисим. *сим. 7 *3=21
J--2 — пара сим. * антисим. 5*1 = 5
J=1— орто антисим. *сим. 3*3=9
J=O — пара сим. *антисим. 1*1=1
Черт. 7.
Состояния двухатомной молекулы, в которых ядерные
спин-функции оказываются симметричными, получили назва-
ние орто-состояний, а состояния с антисимметричными ядер-
ными спин-функциями — пара-состояний. Таким образом,
в случае водорода четным J соответствуют пара-состояния
(%р симметрично), нечетным J—орто-состояния (бвр анти-
симметрично).
В случае более высокого спина (s > 1/2) также будет
иметь место разделение спин-функций на симметричные и
антисимметричные. Для одного ядра существует
а = 2у-Н (4.57)
спин-функций, а для всей молекулы
а2 = (2s 4-1)2. (4.58)
Из этих спин-функций
gs= a(g + 1)=(2s+W+l) (4.59)
110 УРОВНИ ЭНЕРГИИ И СОСТОЯНИЯ ДВУХАТОМНЫХ МОЛЕКУЛ [гл. IV
функций будут симметричными по отношению к переста-
новкам координат одинаковых ядер и
1)=х(2х+1) (4.60)
— антисимметричными *).
9.3
Так, для водорода х = 1/2, а = 2, поэтому ^=—9- = 3
2-1 2
и Sa~~2~ = 1 ’ как мы и получили ранее.
Для дейтона мы имеем s=l, так что для каждого
ядра молекулы D2 существует а = 2s-)- 1 = 3 спин-функции,
а для всей молекулы 3-3 = 9 спин-функций. Из этих функ-
„ 3-4 '
ций мы можем построить gs = —= 6 симметричных спин-
3 • 2
функций и ga — —= 3 антисимметричные.
Как показывает квантовомеханическое рассмотрение
этого вопроса, переходы между состояниями «пара» и
«орто» в обычных условиях могут происходить лишь очень
редко **). Это приводит в случае двухатомных газов при
*) Эти формулы для и ga получаются из следующих сооб-
ражений. Пусть спиновые функции первого ядра будут ut,U2.и,,
спиновые функции второго ядра vb v2...v* (каждое ядро имеет
а = 2s 1 функций). Среди этих функций будет тождественно
с »t, и2 — с v2, .... — с Рассмотрим, как мы можем по-
строить симметричные функции молекулы. Во-первых, такими функ-
циями будут функции вида urV\, u2v2....UjVj....ибо пе-
рестановка ядер между тождественными функциями дает функцию,
равную первоначальной. Таких функций будет а. Во-вторых, мы
можем построить симметричные функции вида (напри-
мер, функцию UjV2 U2t»t), из которых каждая после выполнения
над ней перестановки координат одинаковых ядер дает функцию,
равную первоначальной. Таких функций будет столько, сколько
а (а — 1)
можно выполнить сочетании из а индексов по два, т. е. ———-
а(а—1)
Столько же, т. е. ——можно построить антисимметричных
функций вида и,»;—Таким образом, всего мы будем иметь
, а (а—1) а (а —1) а (а—1)
£s = a+—~~2—~ = ~ симметричных и ga = —------------
антисимметричных ядерных спин-функций. Сумма чисел ge и ga
дает общее число функций, т. е. а2, так как функций других типов
симметрии для случая двух ядер не существует.
**) См. § 14 главы VII, см. также Г. Герцберг [19],
стр. 103.
§ 7] УЧЕТ СИММЕТРИЙ ПОЛНОЙ ВОЛНОВОЙ ФУНКЦИИ МОЛЕКУЛЫ 111
наличии ядерного спина к существованию молекул двух
сортов — «орто» и «пара», т. е. двухатомный газ пред-
ставляет смесь двух модификаций, которые получили на-
звание спин-модификаций. Так, например, водород Н2 при
средних и высоких температурах представляет смесь пара-и
орто-водорода в соотношении 1 :3. При низких темпера-
турах устойчивым является пара-водород, и его удалось
получить в чистом виде *).
Рассмотрим в качестве второго примера орто-и пара-
сОстояний вращательные уровни молекулы D2. Дейтоны,
как мы видели в главе I, подчиняются статистике Бозе —
Эйнштейна, поэтому полная функция должна быть симме-
тричной. Функции такой симметрии получаются перемноже-
нием симметричных вращательных функций (четные J, как
и в случае Н2) на симметричные ядерные спин-функции или
антисимметричных вращательных (нечетные J) на антисим-'
метричные ядерные спин-функции. Из 9 спин-состояний, как
мы установили выше, шесть будут описываться
J=5 Симметрия th x Твр <яс антисим. * антисим L.u 0=3 =33 Состояние пара
J-4 сим * сим 9*Б=59 орто
J=3 антисим < антисим 7*3=21 пара
3=2 сим.«сим. 5*6=30 орто
3=1 3=0 антисим. к антисим сим. * сим Черт. 8. 3*3=9 1*6=6 пара Орто
ядерными симметричными функциями и три (£„ = 3) будут
описываться антисимметричными. Таким образом, уровню
энергии с четным J будет соответствовать (2J—[— 1) 6 различ-
ных полных функций, т. . е. вес уровня с четным J будет
(2У—|—1)6. Аналогично вес уровня с нечетным J будет
3(2J—1). Диаграмма вращательных уровней молекулы D2
представлена на чертеже 8, где указаны симметрии враща-
*) См. С. Глесстон [22], где указана также литература по
этому вопросу.
112 уровни энергии и состояния двухатомных молекул [гл. iv
тельных и ядерных функций, а также веса энергетических
уровней.
Состояния, в которых ядерные спин-функции оказы-
ваются симметричными, мы назвали орто-состояниями, а со-
стояния с антисимметричными ядерными спин-функциями—
пара-состояниями. Теперь в молекуле D.2 орто-состояниям
будут соответствовать уровни энергии с четными J, а пара-
состояниям— уровни с нечетными J.
Подчеркнем, что найденные здесь значения весов уровней
энергии орто-и пара-состояний молекул Н2 и D2 относятся
к основным колебательным и электронным состояниям,
в которых бколеб и 6ЭЛ симметричны. Для возбужденных
уровней энергии значения весов состояний определяются
аналогичным образом с учетом симметрии бколеб и бэл.
Если молекула состоит из двух одинаковых ядер, не
имеющих спина*), например молекула О16, требования сим-
метрии полной волновой функции также сказываются на
допустимых состояниях молекулы. В этом случае в зависи-
мости от симметрии %л в основном состоянии отпадают со-
стояния с четными или нечетными значениями квантового
числа J (или К), как это и подтверждается анализом спек-
тров. Так, для молекулы О26 в спектре отсутствуют состояния
с четными значениями квантового числа К.
§ 8. Формулы для весов уровней энергии вращения
двухатомных молекул
Выведем теперь общие формулы, определяющие веса
уровней энергии вращения двухатомных молекул. В преды-
дущем параграфе такая задача нами была решена для мо-
лекул Н2 и Г)2.
Мы видели, что положение уровней энергии вращения
двухатомной молекулы определяется квантовым числом J
или К**). Если бы не было требований симметрии к полной
волновой функции и ядра молекулы не имели бы спина, вес
уровня энергии был бы равен
p=2J-j-l, (4.61)
*) При s = 0 ядра подчиняются статистике Бозе — Эйнштейна.
Для случая связи Хунда «6».
§ 8] ЙЕСА УРОВНЕЙ ЭНЕРГИИ ВРАЩЕНИЯ 113
так как каждому значению J, как мы видели, соответствует
2J-|-1 состояний равной энергии. Это действительно и
имеет место для гетеронуклеарных молекул с ядерным
спином, равным нулю. Если оба ядра гетеронуклеарной
молекулы обладают спинами $х и s.2> которым соответствует
а1 = 2$1-|-1, (4.62)
a2 = 2sa+l (4.63)
спин-состояний, отличающихся пространственной ориентацией
вектора спина, число состояний равной энергии будет
в аха2 раз больше. Действительно, в этом случае требова-
ния симметрии отпадают и все эти состояния реализуются.
Таким образом, квантовый вес уровня энергии sBp для гете-
ронуклеарных молекул будет:
Р = (2J+ 1) = (2/ + 1) (2st + 1) (2у2 +1)- (4.64)
В случае молекулы с одинаковыми ядрами и спином s
существование а2 = (2s-|-1 )2 состояний, если бы отсут-
ствовали требования симметрии, привело бы также к уве-
личению веса уровня в а2 раз, т. е. вес был бы
р = (2/+1)а2. (4.64а)
Однако из-за требований симметрии не все эти состояния
будут допустимы при данном значении квантового числа J.
Будем предполагать, как мы это делали ранее и как это
имеет место для большинства двухатомных молекул, что
функция бэл, описывающая основное состояние молекулы,
симметрична по отношению к перестановкам координат оди-
наковых ядер. Рассмотрим сначала случай ядер, подчиняю-
щихся статистике Ферми — Дирака. Полная волновая функ-
ция (4.6) в этом случае должна быть антисимметричной
относительно перестановки координат одинаковых ядер. Сим-
метричным состояниям 6вр (четные J) в силу указанного
выше требования симметрии будут соответствовать, как и
в рассмотренном выше примере с Н2, только состояния
с антисимметричными ядерными спин-функциями, так как
только перемножение таких функций дает полную антисим-
метричную функцию (произведение '^п'^л'-колеб будет сим-
метричным). Мы видели, что таких антисимметричных ядер-
ных функций существует только ga (см. формулу (4.60)).
9 Зак. 835. И. Н. Годней
114 УРОВНИ ЭНЕРГИИ И СОСТОЯНИЯ ДВУХАТОМНЫХ МОЛЕКУЛ [гл. IV
Таким образом, вес уровня энергии с четным J будет:
рчет = (2J+ l)ga = (2J+ l)s(2s + 1). (4.65)
Для нечетных J аналогичным образом мы получим:
рнеч = (2J + 1) g, = (2J+ 1) (2s + 1) (у + 1). (4.66)
Если ядра молекулы подчиняются статистике Бозе — Эйн-
штейна, для симметричного электронного состояния мы будем
иметь обратное соответствие:
Рчет = (2 J+ 1) gs = (2 J + 1) (2s 4- 1) (s + 1) (4.67)
и
рнеч = (2J+ 1) ga = (2J+ 1) s (2s + 1). (4.68)
Из этих формул легко усмотреть, что при s = 0 (в этом слу-
чае ядра подчиняются статистике Бозе — Эйнштейна (рнеч = О
для симметричного электронного состояния. Для антисим-
метричного электронного состояния при s = 0 будет иметь
место*) рчет = 0.
*) Этот случай реализуется у молекулы О^6.
ГЛАВА V
ВЫЧИСЛЕНИЕ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
ДВУХАТОМНЫХ ГАЗОВ
§,1. Разложение суммы по внутренним состояниям
на множители при применении модели
жесткий ротатор — гармонический осциллятор
В предыдущей главе нами были рассмотрены энергети-
ческие уровни двухатомных молекул. Применим теперь эти
данные к вычислению термодинамических функций двух-
атомных газов. В зависимости от степени точности, с кото-
рой производится вычисление этих функций, мы можем
использовать каждую из моделей, обсужденных в предыду-
щей главе.
Самым простым случаем вычисления будет применение
модели жесткий ротатор — гармонический осциллятор.
Для энергии молекулы в этом случае будем иметь:
е = гп + £Эл + + у j + •/(•/+ 1). (5.1)
Выделяя нулевую энергию колебаний мы можем
написать:
h2
s^ + sn + ^ + b^ + ^JG/H-l). (5.2)
Сумма по состояниям молекулы будет (см. формулу (2.30)):
Q = е' q, (5.3)
где
q = QaQi- (5.4)
Здесь Q| — сумма состояний по внутренним движениям, а
8*
116 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [ГЛ. V
Qa — сумма по состояниям поступательного движения, кото-
рая была вычислена нами ранее.
По определению Qi мы можем написать:
•эл+Лто+‘§^5у J
Qi= S е (5-5)
□о всем
внутр. СОСТОЯНИЯМ
ИЛИ
•эл h'jv т/ти»
Qi = { 2 ^)( 2 2 e-^J(J+1’),(5.6)
вое эл. все колеб. все в ащ.
СОСТ сост сост
так как при применении нашей модели электронные, коле-
бательные и вращательные состояния можно считать неза-
висимыми. Таким образом, сумма по состояниям Qi предста-
вится в виде произведения трех сомножителей. Эти сомно-
жители, как мы видели в главе II, получили название
электронной, колебательной и вращательной сумм состояний
(см. § 7 главы П). Мы имеем:
8ЭЛ
<2эл= 2 (5.7)
эл.сост
hw
<2колеб = 2 (5.8)
колеб.
сост
Ла
QBp= 2 (5.9)
В| ащ.
сост
§ 2. Сумма по электронным состояниям
двухатомной молекулы при разделении энергии
Во многих случаях при вычислении достаточно учи-
тывать один электронный уровень, если следующие за ним
уровни лежат достаточно высоко. Мы имеем:
О 8| еа
<2эл = Ро^ + р1^*Т + р2^^+ • • • (5.10)
Если можно пренебречь вторым и следующими слагаемыми,
то получим:
Сэл = Ро- (5.11)
Для многих молекул (основное состояние XS) р0 = 1, так что
<?8Л=1. (5.12)
§ 4] QBp ЖЕСТКОЙ ГЕТЕРОНУКЛЕАРНОЙ МОЛЕКУЛЫ
117
Однако Ро не всегда равно единице. Для молекулы кисло-
рода О2, имеющей основное состояние 82, вес р0 = 3. В мо-
лекуле NO, вблизи основного состояния которой 2П1/Э лежит
уровень 2Пуа, нужно учитывать оба эти состояния, причем
каждое из них вырождено двукратно. Для NO мы будем
иметь:
0эл = 2 + 2е"^+.. ., (5.13)
где гх — энергия уровня 2Пу,, отсчитанная от 2П1/а.
§ 3. Вычисление QKOaee
Колебательная сумма по состояниям вычисляется просто.
Здесь вес каждого уровня равен единице, так что мы будем
иметь:
= + + . (5.14)
Это выражение представляет убывающую бесконечную reo-
ftv
метрическую прогрессию со знаменателем е кТ и первым
о
членом екТ = \. Мы получим:
Фволеб — • (5.15)
§ 4. Вычисление Q„p жесткой двухатомной
гетеронуклеарной молекулы
Вычисление вращательной суммы по состояниям несколько
сложнее. Принимая во внимание, что для двухатомной моле-
кулы, состоящей из разных ядер, не имеющих спина, вес
вращательного уровня равен (2J-(-l), мы можем написать:
ftV(Z+n о, hv^+n
QBp = 2 е =2(2J-H)e ^1кТ . (5.16)
вращ. j_0
оост
Положив № ___/к 17\
8т:2 kT — 4 Р-*/)
получим:
оо
Qbp= S (2J-H 1) e_T‘Zt'Z+1’- (5.18)
д=о
118 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [ГЛ. V
При малых температурах выражение (5.16) легко можно
вычислить непосредственным суммированием. Для высоких
температур и больших значений момента инерции I можно
суммирование в формуле (5.16) заменить интегрированием
QBp=j* (2J+l)rxJ(J+1)dJ. (5.19)
о
Этот интеграл легко вычисляется при помощи подстановки
TJ(J+l) = x,
откуда
dx = T(2JH-l)dJ
или
aj ~ т (2/4-1)’
Подстановка дает:
оо оо
QBl— [ (2JH-l)e“xJ(J+1)dJ = l [ e-°>dx = ±
о о
или
_ 8iMkT
Vbi ~ •
(5.20)
(5.21)
(5.22)
(5.23)
(5.24)
Однако выражение (5.24) является приближенным. Оно мо-
жет быть получено также с помощью формулы (1.46), если
в последней вместо г подставить значение энергии ротатора,
которое дает классическая механика. Условием его приме-
ра /j2
нимости является 1 или -о 1, т. е. о .... Т.
Ят.ЧкГ
Для более точного вычисления вращательной суммы со-
стояний необходимо применить методы, разработанные Мул-
холандом [245] и другими*). Эти авторы показали, что
сумма вида
5= 2 (2J+l)e"AJlJ+1) (5.25)
может быть представлена рядом
к
s=//4 [4+2игл)!+М ’ (5-26)
П = 0
*) См., например, Кассель [235].
§ 41 QBp ЖЕСТКОЙ ГЕТЕРОНУКЛЕАРНОЙ МОЛЕКУЛЫ
119
где Bt = ~, B9 = -^r, В3 = ^-— так называемые числа Бер-
о ои г*
нулли. Выписывая первые слагаемые, мы будем иметь:
S~ ["Л _^Т2”^ 480 8064 ’ •]• (5‘27)
Применение этой формулы к сумме (5.18) дает:
QBr — ^ + т2 + 48О'Т-1_ 8064 ‘ ‘(5-28)
Если разложить ет/4 в ряд и произвести умножение, QBp можно
представить в виде
4 + 1+1^+з^2+- <5-28а)
Подставляя т из формулы (5.17) в формулы (5.28) и (5.28а)
мы получим:
1 й’
о _е4жГ^1+_1_+2____________+
VsP [ Л2 12 480
+«(«?)’+•] <5-29>
и
_№IkT , 1 | 1 ft2 . 4 / Л2 у. ,т
Vsp— д2 “Г 3 “г 15 8-2IkT г 315 \8^1кт) ' ' ‘
h2
Если выполнено условие g^^y <С^ 1, эти формулы переходят
в формулу (5.24), соответствующую применению классиче-
ской механики и справедливую при высоких температурах и
больших /.
Формула для QBp была получена нами в предположении
отсутствия ядерного спина. Если оба ядра гетеронуклеарной
молекулы будут иметь спины st и у2, число допустимых
состояний молекулы будет больше в ata.2=(2sl-1-1) (2^2—j—1) раз,
так как все спиновые состояния будут реализоваться (см.
§ 8 главы IV). Мы получим:
Qap— Д2 а1а2- (5.31)
1 20 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [гл. V
§ Б. Вычисление Опр для жесткой молекулы
с одинаковыми ядрами
Если двухатомная молекула имеет два одинаковых ядра,
мы должны поинять во внимание условия симметрии, на-
кладываемые на полную волновую функцию. Эти условия
в случае спина, равного нулю, приведут, в зависимости от
симметрии ''эл в основном состоянии, к допустимым враща-
тельным состояниям только с четными или нечетными значе-
ниями квантового числа J (см. § 8 главы IV). В случае анти-
симметричной 4ЭЛ в основном состоянии мы будем иметь:
Q,p= S (2J+ (5.32)
<Г=1, 3, 5, 7, . . .
Если при s — 0 функция 6ЭЛ симметрична, то:
<2bF= 2 (2J+ l)e“’J(J+1). (5.33)
<7=0, 2, 4, . . .
Величина т здесь определяется формулой (5.17). При сред-
них и высоких температурах можно принять:
5 (2J+l)e"Tj(J’+n^ 5 (27+ l)e"xJ(J’+1'^
<7-1, 3, 6, ... <7=0, 2, 4,...
S (27+l)e-Tj(J+1). (5.34)
<7=0, 1,2, 3,4,. . .
Таким образом, в случае одинаковых ядер получим в силу
формулы (5.23):
или
где
_ 1 _8^Т_0кл
— 2т — h* — ~
(5.35)
8^rkT О
(5.36)
о = 2.
Это число о, равное в случае двухатомных молекул 2, по-
лучило название числа симметрии. Оно было введено впер-
§. 5] <2вр ДЛЯ ЖЕСТКОЙ МОЛЕКУЛЫ С ОДИНАКОВЫМИ ЯДРАМИ 121
вые еще Гиббсом *), а затем Эренфестом и Тркалом [217].
С геометрической точки зрения а представляет число экви-
валентных положений молекулы, которые могут быть пере-
ведены друг в друга ее вращением. Так, для двухатомной
молекулы с двумя одинаковыми
ядрами таких положений существует
два (черт. 9).
Для молекулы, построенной из
разных ядер, очевидно, число сим-
метрии а = 1.
Если одинаковые ядра молекул
имеют спин s, требования симметрии,
/ 2 2 1
* < »- — —
Черт. 9.
как мы видели в предыдущей главе, приводят при дан-
ном J к реализации только части спин-состояний. Для
весов уровней энергии вращения в силу требований сим-
метрии нами были получены формулы (4.65)—(4.68), кото-
рые мы запишем теперь в виде
/’чет = (27+ 1) ^чет’
(5.37)
/’неч —<27+ ^неч’
(5.38)
где Ки g л в зависимости от рода статистики даются
чет ® неч А
формулами
= ( go = s(2s+l),
чет I gs = (2s+W+D.
f gs = (2s+W+l).
I,M I go = s(2s+l).
Здесь верхняя строка относится к случаю статистики Ферми —
Дирака, а нижняя — к случаю Бозе-—Эйнштейна. В обоих
случаях
^чет + ^еч) = «2 = (2^1)9- (5-41)
При вычислении вращательной суммы по состояниям в силу
существования разных весов рчет и /?неч необходимо прово-
дить суммирование отдельно по четным и нечетным J. Мы
*) См. Дж. В. Гиббс [21], глава XV.
122 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [ГЛ. V
получим:
QB=g4eT S (2J+1)^J(J+1' +
BP °ЧвТ J^o, 2.4, ...
+ gHe4 S (27+ l)e~T<J+1)< (5.42)
J=l, 3, Б, . . .
Для средних и высоких температур будем иметь в силу
формулы (5.34)
<?вр = ^е4 S (27+D<+J,J+1) +
J=0, 1, 2. 3,...
+ 2 (27+ l)e-’JlJ+1’ =
J = 0, 1, 2, 3,...
= y(g,eT+^He,) S (27+l)e-^‘J+11. (5.43)
J=l, 2, 3,...
Сумма, входящая в это выражение, при сделанных допуще-
3vVkT „ .
ниях, как мы видели, равна —. 1 аким образом, по-
лучим:
1 . . . 8л2ГА7' - ...
Q,p =-2 (^чет + ^им)^-' (5‘44)
ИЛИ
_ +ет + 8"2^7’ £чет + ^неч^ zj- в с ч
Qsp— - дз — - ч?кл, (5.45)
где с—число симметрии, равное 2.
Заменяя (£чет + £неч) из формулы (5.41), будем иметь
окончательно:
Фвр
Л 2а
(25+ I)2
8тг2/АГ »
------- 'У.
ft2a
аа.
(5.46)
Сравнивая это выражение с выражением (5.24), мы видим,
что влияние симметрии и ядерного спина приводит к по-
явлению множителя а2/а.
Заметим, что формулы (5.31) и (5.46) могут быть запи-
саны в виде одной общей формулы
_ 8^IkT
Фвр — а1а‘2’
(5.47)
где ах и а2-—веса спиновых состояний ядер, определяемые
формулами (4.62) и (4.63). В случае., гомонуклеарной моле-
кулы a1 = a2 = 2s+l, а число симметрии о равно 2. Для
гетеронуклеарной молекулы а = 1.
§ 6] Qi ЖЕСТКОГО РОТАТОРА----ГАРМОНИЯ. ОСЦИЛЛЯТОРА 123
§ 6. Сумма по внутренним состояниям Q4 при применении
модели жесткий ротатор — гармонический осциллятор
Значения сумм по состояниям фэл, QK1Me6, <2вр> найден-
ные в предыдущих параграфах для модели жесткий рота-
тор — гармонический осциллятор, позволяют теперь легко
получить соответствующие выражения для термодинамиче-
ских функций двухатомых газов. С этой целью найдем
сумму по состояниям Qi-
Пусть возбужденные электронные уровни молекулы лежат
достаточно высоко. Мы видели, что в этом случае Q3JI
равняется весу основного электронного уровня р0 (см. (5.11)).
Для молекул с основным состоянием р0 = 1.
Мы имеем (см. (5.6)):
Qi = ФэлФколебФвр (5.48)
или, если применить формулы (5.11), (5.15) и (5.47),
. / 1 \ 8~4kT
(5.48а)
Подставляя это значение Qj в формулу (2.63), получим вы-
ражение для суммы по состояниям д:
Ч— QnQi
(iTzmkT)^ WIkT , i -
(5.49)
которое нам понадобится впоследствии при расчете хими-
ческих равновесий.
Для получения формул, выражающих термодинамические
функции через молекулярные данные, найденное значение
нужно подставить в формулы (2.79)—(2.85). Другой воз-
можностью является подстановка Q3.b. Фколеб. QBp в фор-
мулы § 7 главы II, выведенные в предположении разделе-
ния энергии молекулы на еэл, sK0JieS и sBp. В нашем случае
применения модели жесткий ротатор — гармонический ви-
братор такое предположение оправдывается, и мы найдем,
что каждая термодинамическая функция будет суммой сла-
гаемых, соответствующих поступательному, электронному,
124 ТЕРМОДИНАМИЧЕСКИе ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [гл. V
колебательному и вращательному состояниям. Мы получим:
Ф — ФдЧ- Фэл Ч- Фколеб 4“ Фвр.
г, | 3 „
И =но +1 Еэл + £КОлеб + £»р.
S = 5п + 5ЭЛ -|- Сколеб Ч- 5Вр,
с„ = *2 R + Сэл ~Ь Сколеб Ч- СВр,
(5.50)
§ 7. Электронные слагаемые термодинамических функций
двухатомной молекулы для случая, если Q3a = р0
Для электронных слагаемых мы будем иметь (см. фор-
мулы (2.116), (2.123), (2.128) и (2.136)):
Дэл = Фэл — RTln Q3]l = — RT In p0, (5.51)
d In Q,»
E3a=H33l=RT2-4^ = Q, (5.52)
rf In Q.
5Эл = Л1пСЭл+/?Т-77Л = /?1пр0, (5.53)
d ln <2ЭЛ , d2 In Q
CM = 2RT—~^-\~RT2—-^- = 0, (5.54)
ибо Сэл в принятом нами приближении постоянно.
§ 8. Слагаемые термодинамических функций,
соответствующие гармоническому колебанию
в двухатомной молекуле
Для вычисления слагаемых, соответствующих колеба-
тельному движению, мы воспользуемся формулой (5.15).
Дифференцируя 1п СК0Леб. получаем:
1П Q олеб _ 1 '
dT en‘lkT—\ kT^ ‘
§ 8] ГАРМОНИЧЕСКИЕ ЧАСТИ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ 125
и
d3 1П 9колв5
dfi
‘Mlv МТЛ. 2h4 / hi \2 bi/kT
• kT3 -------• (5-56)
Применяя формулу (2.117), мы будем иметь:
Ftonti — Фжолеб— RTIn QяoлtS — RT1П -j-----—hi/кТ
Ъм
= ЯПп(1 — e~^). (5.57)
Эту формулу можно переписать в виде
F _ *1
-^ = /?1п(1— г.
Далее на основании формулы (2.124) мы найдем:
^волеб — ^колеб — RT^
d 1п <?<олеб
dT
Или
= /?7’2 —
kT*
R —
1 К k
eh'>/kT__ j = etolkT __ j
d!EL
K kT
T~ ~ е^'кТ_1
р
^колеб
(5.58)
(5.59)
(5.60)
Подставляя (?КОлеб и d 1П^олеб в формулу (2.129), получаем:
5колеб = R 1П Околеб + RT Ск°Леб
h't
= —Я1п(1 —
dT
* kT
ghi/hT_ j
(5.61)
Наконец,
^1п9Волеб
' dT*
d In Околеб
для теплоемкости подстановка ------------- и
dj
из формул (5.55) и (5.56) в формулу (2.137) дает:
Г* OD7< In Околев I In <2кг)леб
''волФб —। К * dT'&
Rl<S^ew
<5-“)
156 ТЕ^МОЛиНДМЙЧЕСКИе ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [гл. V
Полученные выражения совпадают, как легко убедиться,
с формулами § 10 главы I, если последние применить
к одному молю и исключить нулевую энергию. Мы видим,
что все величины — Р«олей/Т, Еколец/Т, энтропия и теплоем-
кость— являются функциями одной переменной hvIkT, а по-
этому их вычисление может быть выполнено по таблицам
этих функций. Такие таблицы были составлены рядом
авторов *). Параметром этих таблиц обычно служит величина
где
= (5.64)
Если частота выражена в см-1, мы имеем:
0=^= 1,4385 ш. (5.65)
В таблицах, приведенных в учебнике Тейлора и Глес-
стона [94], вместо применен параметр у , что упрощает вы-
числения. В приложении приведена такая таблица (см. табл. 50
в конце книги). Величины Сколев> -к^л-6- и в^ле- определяются
из них непосредственно. Для вычисления энтропии можно при-
менить соотношение
5 = -у+7’ <5-66>
которое следует из
энергию:
формулы, определяющей свободную
F = E — TS.
(5.67)
*) Таблицы этих функций, которые получили название функ-
ций Эйнштейна, приведены во многих руководствах. Таблицы для
трехмерного гармонического осциллятора см. В. Н е р н с т [52],
Н. А. Колосовский [30]; для одномерного гармонического
осциллятора см. В. М. Г р я з н о в и А. В. Ф р о с т [26], М. X. Кара-
пет ья нц [29], Д. О. ЧернобаевиА. Г. Животовский [79],
Тейлор и Глесстон [94], а также справочник [72]. Недавно
Торкингтон [260] составил таблицы, определяющие термодина-
мические функции одномерного осциллятора по двум параметрам
(частоте и температуре).
16] ЖЕСТКОВ ВРаЩЁНЙЕ Й ГАРМОНЙЙЕСкОЕ КОЛЁБАЙЙЕ 127
§ 9. Слагаемые термодинамических функций,
соответствующие вращательному движению жесткой
двухатомной молекулы
Для вычисления слагаемых, соответствующих вращатель-
d In QBp dalnQ
ному движению, нужно найти производные—- и—.
Мы будем иметь на основании формулы (5.47)
d In QBp _ i
dT ~ T’
(5.68)
daln<?Bp 1
dT* 7a ’
(5.69)
Применяя формулы (2.118), (2.125), (2.130), (2.138), по-
лучим:
FBp =Фвр = — /?TInQBp (5.70)
d In Q„n
E,t=Hvl,=R’n—^- = RT, (5.71)
d In Qnn WIkT
5вр=/?1п^вр+/?Т^Л = /?1п-7йа-а1а9 + /?, (5.72)
d In QB d2 In Qm
Cat = 2RT-^--}-RTi—~^=2R — R = R. (5.73)
§ 10. Формулы для вычисления, термодинамических
функций двухатомной молекулы в предположении
жесткого вращения и гармонического колебания
Мы вычислили слагаемые термодинамических функций,
соответствующие электронному, колебательному и враща-
тельному движениям молекулы. Подставим теперь их в фор-
мулы (5.50). Тогда для теплоемкостей получим:
с.=|*+ ,ДС1|а +r°4r+X4_,),^ (5^)
с*Чд+ • <5-75>
128 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ (ГЛ. V
Для энергии и теплосодержания мы будем иметь:
3
Д = Д0 + 4/?Т + -к^Дт + /?7' =
5
= g0 + T^+-M;_f, (5.76)
5
Н = Но + 1Rт + t + Rт =
7
-=H^RT+-^^:-T. (5.77)
Формула для энтропии
X — Хп -|- Хэл Н- ХКолеб 4“ X
вр
после подстановки Хп из формулы (2.72), Хэл из формулы
(5.53), ХКОлеб из формулы (5.61) и Хвр из формулы (5.72)
примет вид
$=7?1п дзд); -^ + -2 Я + Я1пРо
R —
К kT
gh'i/kT__ j
— Rln(l — e и’) + Я1п?^-а1а2 + /? (5.78)
или
X - - у /?+ R|п - -----
' ‘ ° i 2 ~
+ л/»*_1~'?"1(1~е к1)’ (5-79)
т. е.
с 7 п . п. (2тсй)Я|,а8кЗй I 5 п. _ . 3 п. .. , n. I
X — /? + 7? In — , 5,-(--у /? In Т-|--у R In Л4-|- R In ,и-^
2 h2 • 2
-ф- R In I — R In а —|- R In pQ —f- R In Ядй2 —|- Хволеб. (5.80)
§ 10] ЖЕСТКОЕ ВРАЩЕНИЕ И ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ 129
Подставляя численные значения постоянных, мы получим:
5= 166,538 +у Я In ?+ R In ®+| R In Л4 +
+ R In I — R In з —|— R In pQ —R In 5колеб- (5.81)
Если исключить объем с помощью уравнения Менделеева —
Клапейрона и выразить энтропию как функцию температуры
и давления, выраженного в атмосферах, то получим:
5= 175,293+ у Rin Г — R 1п/> +R In/И +
—R 1п / — R In з —|— R In pg R In -|— <5>волеб- (5.82)
Слагаемое R In 7ta2 представляет энтропию ядерного спина.
При практических применениях энтропии при высоких темпе-
ратурах его можно не принимать во внимание (см. главу XII,
§ 6). Энтропия, вычисленная без учета спина, как было ука-
зано выше, получила название практической («виртуальной»
энтропии). Мы получим:
Sni.aKT= 175,293 + у/?1п7’~/?1пр + -|/?1пМ +
—|- R In I — R In з + R In pg + 5Колеб‘ (5.83)
Для давления в 1 атмосферу формула (5.83) примет вид
£практ = 175,293 +-|+1п7+4 Rin М +
+ RlnZ — R In з + R In po + 5Колеб- (5.84)
Наконец, подставив значеня Рзл, f+еб, RBp из формул (5.51),
(5.57) и (5.70) в первые две из формул (5.50), мы получим
. соответственно выражения для свободной энергии и изобарно-
изотермического потенциала:
F = Ео - RT’ln (2тсХ+‘- v - R Т - RT ‘П ‘° +
+ RT In (1 — —RT’ln ^^7^2, (5.85)
. Ф = Ho - RT In v-RT\n^
I + RTIn (1—е"?‘',/и’) —RT’ln ^^ata2 (5.86)
9 Зак. 835. И. H. Годнее
130 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [ГЛ. V
ИЛИ
г р пт rm (ZitmkT'fr&i&IkT ।
Т = Fo - RT - RT In h^Ki - W7xa2 +
+ RT In (l—e~h'llkT) (5.87)
и
л rr „г, (2T.mkT)3/^IkT .
Ф = Ho - RT In vW2 +
+ ЯТ1п(1 — (5.88)
Последняя из этих формул может быть записана в виде
Ф = Н0 — RTln ^^^ — ^RTlnT — ^RTlnM —
и hbN^‘ 2 2
— RT 1 n I — RT In г» + RT Ins — RTln p0 — RTln агя2 +
+ RT In (1 — r№T). (5.89)
Исключая объем v и выражая его через Т и давление в ат-
мосферах, получим:
Ф = н0-р RTIn р — у RT In М — у RT In Т — RТIn Ро -ф-
+ RTln z — RTln <7^2 — RTln /+ Фколе6 — 168,340 Т. (5.90)
Аналогично для свободной энергии будем иметь:
F = £04-RTIn/? —|/?Т1пМ —yRTln Т—RTlnp0 —
— RTln/+RTln s — RTln — 170,327Т. (5.91)
При практических вычислениях слагаемое RTinata2, обусло-
вленное существованием ядерного спина, опускают. Мы по-
лучаем практическое значение изобарно-изотермического по-
тенциала:
Ф = Я0 + /?Г1пр —-|-RTln Л1 — у RTln Т— RTlnp0 +
+ RTln а — RTln 7+Фколеб — 168.340Т. (5.92)
В таблице 9 сделана сводка полученных результатов.
Подчеркнем, что приведенные здесь формулы являются при
ближенными, применимыми при средних и высоких темпера
§ 10] ЖЕСТКОЕ ВРАЩЕНИЕ И ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ 131
турах. Для вычисления термодинамических функций с помо-
щью этих формул нужно знать только молекулярный вес,
момент инерции, частоту колебаний и вес основного элек-
тронного уровня.
Таблица 9
Формулы для вычисления термодинамических функций двух-
атомных газов при применении модели жесткий ротатор —
гармонический осциллятор
№ п/п Термодинамиче- ская функция Практическая формула
1 Энергия Е-Еп £-£0 = 4/?7’ + 5колев
2 Теплосодержание н-нй я-н0 = 1/?г+£колеб
3 Энтропия S S=^-/?ln7'-/?lnp+|/?lnAf + + R In I — R In о -|- 7? in p0 -f- SK0Jle6 -|- 4- 175,293
4 Приведенная сво- бодная энергия Е-Еп Т = R 1 n p - у R In T - R In M - — R In 14- R In a — R In p0 4- 4- — 170,327
5 Приведенный изобарно-изотер- мический потен- циал Ф = П П = Ф ~ Яп = 7? Inp-ytflnr- Q —R hi M — R In 14- R In a — R In роД- + _ 16g,340
6 Теплоемкость Cv с1) = 4/?4-Сколеб
7 Теплоемкость Ср Cp — + ^«ОЛеб
9*
132 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [гл. V
Приведем в качестве примера вычисления термодинами-
ческих функций СО при 600° К. Основным состоянием этой
молекулы является 1Е+-состояние, так чтор0=-1. Равно-
весное расстояние ядер ге=1,128А (см. табл. 7 в гла-
ве IV). Частота колебаний ше = 2167 см-1, о/= 2143 сл-1.
Число симметрии а равно 1. Момент инерции будет р.г2, где
и. — приведенная масса, равная — • • Мы получим
/ = 14,49 • 1О-40 г • см2. Вычисления дают:
Sn~)~SBp = 52,05
Дколеб = 0,07
S = 52,12 кал!град • моль.
Заметим, что при вычислениях колебательных функций лучше
брать не <ое, а ш' (наблюдаемую основную частоту) *). По-
следняя дает лучшее приближение.
Для теплоемкости мы получим:
7
С„ = -£/? = 6,95
Сколе б — 0,31
Ср = 7,26 кал/град моль.
Эти значения оказываются близкими к точным значениям,
вычисленным Джонстоном и Дэвисом [233],
5 = 52,254 кал/град • моль
и
Ср — 7,279 кал{град моль.
§ 11. Эффект изотопии в случае двухатомных газов
При выводе формул для термодинамических функций
двухатомного газа мы предполагали, что молекулы тожде-
ственны по своим свойствам, т. е. имеют одинаковый моле-
кулярный вес, одинаковый момент инерции, одинаковую ча-
стоту колебаний и одинаковый ядерный спин. В действи-
тельности большинство двухатомных газов представляет
смесь молекул разных изотопов, а поэтому нам нужно рас-
смотреть влияние эффекта изотопии' на значение термодина-
*) См. примечание на стр. 103.
§ 11] ЭФФЕКТ ИЗОТОПИИ В СЛУЧАЕ ДВУХАТОМНЫХ ГАЗОВ 133
мических функций. Для одноатомных газов такая задача уже
была решена нами в § 6 главы III.
Допустим, что элемент имеет два изотопа с атомными
весами At и А2. В этом случае будет существовать три сорта
молекул А4', А^2 и ХА'ХЛ‘2 с молекулярными весами Mv
М2 и М,, и газ Х2 следует рассматривать как смесь моле-
кул трех сортов. В § 6 главы III мы приводили пример
с хлором С1.?, который представляет смесь молекул трех
сортов — С1^5'35, С1Г7 и С1Г7. Молекулы ХА', и ХА'ХЛ-
кроме разных молекулярных весов будут иметь разные мо-
менты инерции и частоты колебаний. Они будут отличаться
также числами симметрии и значениями ядерных спинов.
Будем обозначать величины, относящиеся ю молекулам ХА
ХА* и ХА1ХАг, соответственно индексами 1, 2 и 3. Для чи-
сел симметрии мы будем иметь:
ot = 2, а.3 = 2 и = 1.
Пусть молярные доли изотопных молекул в равновесной
смеси будут _у,, у2 и
Для энтропии смеси газов в § 6 главы III нами была
выведена формула (3.90), которая для одного моля смеси
примет вид (см. также § 9 главы II)
$см = («1 = 1 - Р< T)+y-2S-2 («2 = 1, Т) 4“
+№% («в = 1 • р> T)-R^ yi In Л- (5.93)
Подставляя в эту формулу энтропии отдельных изотопных
молекул [см. формулу (5.82)], будем иметь:
5CM=yt[c + l/?lnT —+ + —
— R In Cj -|- R In р0-(- R In («1^2)1 4“ Сколеб (ш1)^ 4~
+ у2 [ с —|— | R In Т— R In Р +1R In М2 + R In I2 — R 1п з2+
4~ Р 'п Ро 4“ Р In («t®.>)2 4~ Сколеб (ш2)^ 4“
4-л[с4-4/?1пГ — ^,пР + 4/?,пМз + /?1п/з“/?1паз+
4- Р in Ро 4- Р I" (at с/.’)з 4- Сколеб (шз)^
— Р1У11«л+л In у2 4-J31пЛЬ (5-94)
134 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [ГЛ. V
Принимая во внимание, что уг-[-у.2-[-Уз = 4 получим:
SCM = с + у /? In Г — Я In Р + Я In Ро + | Я In +
+ R In — я In aj/‘4M,1+ Я In (ata2)i‘ (Мг)*’ (ЛгЧ
~Ь Ун^колеб (ш1)Ч“У2^колеб (“о) + У Околев (шз) —
— Я[л1пл + -У21пУ2 + .Уз1г1 Уз1- (5-95)
Если рассматривать газ Х2 состоящим из однородных моле-
кул Х2, которые построены из одинаковых атомов со сред-
ним атомным весом и спиновым весом а, и если приписать
молекуле Х2 средний момент инерции / и среднюю ча-
стоту ш, то энтропия такого газа будет:
5 = с4-уЯ1п Т — Я1пР + у Я1пЛ1 + Я1пр0 +
+ Я In/—Я In □ +Я In а2-|-5колеб (ш). (5.96)
Как и в случае одноатомного газа, эффект изотопии пред-
ставится разностью энтропий, определяемых формулами (5.95)
и (5.96),
А5ИЭОТ
= |я1п
+-Я1п
м
7
сУ’а^а^3 (a,a.,)?1 (а.я.,)^ (ар)’^
— я in —k R-- - - - - - +
о 1 a* J
4“ Узколоб (Ш1)4-У2^|'колеб (ш2)~Ь Уз^колеб (“з) —
~ Зколеб (ш) — Р 1У11П У( + уа 1 п уа + Уз 1П Уз! • (5.97)
Молярные доли yt, у.2, у3, вообще говоря, не являются ве-
личинами постоянными, но могут меняться с температурой,
так как в смеси ХА‘, ХАг, XAlXA1 с изменением температуры
смещается равновесие реакции изотопного обмена
Xfl + XA1 # 2ХА‘ХА\ (5.98)
Подробное рассмотрение вопроса, выполненное Джоки
и Оверстритом [219] для смеси изотопных молекул хлора,
показало, что при расчете химических реакций можно не учи-
тывать *) эффект изотопии, так как АДИЗОТ оказывается пра-
*) См. § 7 главы XIII.
§ 12] QB1, для модели нежесткого ротатора 135
ктически постоянным. Таким образом, мы можем не учиты-
вать эффект изотопии, если возможно пренебречь смещением
равновесия реакции изотопного обмена с температурой. По-
этому практическая энтропия двухатомных газов вычисляется
с помощью формулы (5.83) при применении средних вели-
чин. Это подтвердилось также сравнением практической эн-
тропии с опытными значениями, полученными по измерениям
теплоемкостей и скрытых теплот при низких температурах.
Так, для С12 экспериментальная энтропия при 298,2°К оказа-
лась равной 53,32 кал/град • моль, тогда как вычисленная по
формуле (5.83) — 53,31 кал/град • моль.
Заметим, что в отличие от одноатомного газа теплоем-
кость, энергия и другие функции отдельных газов, постро-
енных из одинаковых изотопных молекул, будут несколько
отличаться друг от друга и от термодинамических функций
смеси.
§ 12. Вычисление QB1, при применении модели
нежесткого ротатора
До сих пор мы рассматривали вычисление термодинами-
ческих функций паи применении простейшей модели жесткий
ротатор — гармонический вибратор. Перейдем теперь к изу-
чению более точных методов вычисления термодинамических
величин. В первую очередь рассмотрим вычисление QBp для
нежесткого ротатора. Уровни энергии последнего, как мы
видели в предыдущей главе, даются формулой (4.42). Пере-
пишем последнюю здесь в виде
sBp = he [BJ(J+ DP (J+ I)3], (5.99)
изменив знак у коэффициента D и прибавив еще одно сла-
гаемое FJ3(J4-1)3. Положим
J-lrL = ttli (5.100)
Исключая J из формулы (5.99) и вводя новые коэффициенты
В', D' и F', получим:
евр = he (B'nt1 D'm4 F'nft + . ..) —
136 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [ГЛ. V
где
= + (5.102)
D' = D — у, (5.103)
F' = F.
(5.103а)
Заметим, что до возникновения квантовой механики форму-
ла вида (5.101) использовалась в спектроскопии для пред-
ставления уровней энергии (без последнего члена, содер-
жащего квадратные скобки). Переходя к вычислению Qni,,
будем иметь:
<?вр= 5(2J+l)c-e»r/ftr
j=
(5.104)
или, если ввести число т,
<?.„ = 2 (6Л05)
т = 1/2
Положив
= (5.106)
получим:
ИсЬ. со
QBn = е кТ 5 %те
III = 1/2
he , he , he .
kT B ^-kTD mi-kTF m
(5.107)
D'heint Vhcm”
Разлагая e kT и e kT в ряд, будем иметь:
п V о D'hcm* ।
QBp — ekT 2j 2/ne kT 1 — — k
114 = 1/2
+4m’+->
х[>-^чня+...]. <5-io8>
§ 121
Q„p ДЛЯ МОДЕЛИ НЕЖЕСТКОГО РОТАТОРА
137
Перемножение скобок дает:
со hr*
„ ТГ Ч? о ~рр-в'т°Г1 D'hcnit F'hcnfi ।
<?»₽= 1 2me [1-----------------^- +
ж = 1/2
। 1 /D'hcmA\? । D'hcmt F'hcnfi ,
+ 2! V kT ) + ~kT kT Г-
+!(“/+•]• <5-109>
Далее мы получим:
hcb„ “ he a
= e kT | 2me kT M 4-
m=l/2
“ he
i V1 о _й’‘В’”’’Г D'hcmA F'hcmfi । 1 (D'hcmi'fl
+ Zi [ kT kT 2! \ kT )
m = 1/2
D'ticmS Phctrfi , 1 {Ffh,cnfi\p . 11 c
+ + (5-
Применяя к вычислению первой суммы формулу *) (5.26) и
ограничиваясь двумя первыми членами, будем иметь;
hebg
QB1, = екТ
kT
hcB'
kT
B'hcnfi
kT
СО Т, Л
ц+ V 2me-^"-[
m = l/2
1 /D'hcm^ । D'hcm* F'hctrfi
2f\ kT ) FT kT~
(5.111)
D'/icm*
Остальные суммы в (5.111) можно заменить интегралами
вида
Г _B_hcm* 1ЬТ\К+1
J 2^+!е • (5.112)
о
*) Следует учесть, что показатели уев (5.25) имеют
вид Л7(/+1), а в первой сумме в (5.110) — А , вслед-
ствие чего множитель еА^ сократится.
138 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [гл. V
Таким образом, окончательно получим *):
Q =е^ — [1 +—— 2!^(—) —Е
1 B'hA № B'2\hc/
, D'2 f kT\2 . , Р'Л'ЛЩ31
K 2! Bri \ he) ’ B'° \hc) J
(5.113)
Эта формула была получена Джоки и Оверстритом [219).
Она позволяет легко получить первую и вторую производные
In QBp по температуре, необходимые для вычисления термоди-
намических функций.
В случае применения модели колеблющегося ротатора
коэффициенты В', D' и F' будут зависеть от квантового
числа v. При вычислении QD|, для данного колебательного
уровня мы будем иметь:
kT г В he
QU1 „ = е кТ Н—v—
1 В he L 12£Г
(5.114)
- ~ (-У + 5! (—У I.
2! в В'° 'he/ J
V V
Эта формула может быть непосредственно применена к мо-
лекулам, имеющим электронное основное состояние Здесь
величина bOv будет определяться формулой (5.106), где по-
стоянные В, D и F относятся к данному колебательному
уровню v, т. е.
§ 13. Применение метода непосредственного
суммирования
Для очень точного вычисления термодинамических функ-
ций двухатомных газов может быть применен метод непо-
средственного суммирования, заключающийся в вычислении
2 я, 2 В и 2е (см. § 6 главы П) путем суммирования
по всем дискретным значениям энергии si, найденным из
анализа спектров.
________________ W
*) Следует заметить, что величина hcb^kT не является нулевой
энергией, деленной на kT.
§ 13]
МЕТОД НЕПОСРЕДСТВЕННОГО СУММИРОВАНИЯ
139
Основными формулами, служащими для определения тер-
модинамических функций по этому методу, являются фор-
мулы (2.97)—(2.103), часть которых мы приведем здесь:
5 Я У В
H = (5.116)
„ Я У В
S = Sn + /?ln^X + -^-, (5.117)
kT 21А
Ф — НОФП _
——Я1п2л (5.118)
5 R Г У с /УвУ
С. = -/?Н--------. (5.119)
1 2 детЧул \уд/
Способ непосредственного суммирования нашел широкое
применение в конце двадцатых — начале тридцатых годов
нашего века, когда были вычислены термодинамические
функции ряда двухатомных газов, например, О2, Н2, СО,
N2, S2 и других. Он особенно удобен при вычислениях для
сравнительно низких температур, когда для отыскания 2^>
и У С требуется немного термов. При средних и
высоких температурах по этому методу необходимо затра-
тить большой труд, так как приходится принимать во вни-
мание очень много слагаемых. Значительное сокращение вы-
числений может быть достигнуто с помощью рекуррентных
формул Джонстона и Чапмена [232]. Эти формулы могут
быть [115] представлены в виде
= (5.120)
Z Л-
(SM+1 = ^кТ [(ZM+MSAL (5-121)
(SС)с+1 = [(2с)„ + 2ЛГ (2 B)v + д:(2 Д], (5.122)
где Д„ есть разность колебательных энергий двух соседних
колебательных уровней
* колеб колеб /р» 1 oq\
^•0 — £v+l —• (O.lzoj
Величины (SA- (2Д и (2c)„ относятся здесь к дан-
ному колебательному уровню.
140 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [ГЛ. V
Другой модификацией метода непосредственного сум-
мирования является способ Джонстона и Дэвиса [233],
позволяющий значительно упростить вычисления с помощью
формул, по которым можно вычислить сумму состояний
и ее производные для данного колебательного уровня. Эти
формулы могут быть получены с помощью выражения Джоки
и Оверстрита [219].
§ 14. Метод Гордона и Барнеса
Метод непосредственного суммирования, несмотря на
некоторые упрощения, введенные рядом авторов, оказывается
очень трудоемким. Поэтому в практике вычисления термо-
динамических функций нашли применение другие методы,
требующие меньшей затраты труда. К ним относятся метод
Гордона и Барнеса [222], метод Касселя [235] и др. Рас-
смотрим сначала метод Гордона и Барнеса применительно
к молекулам с основным электронным состоянием. Он
основан на применении формулы Джоки и Оверстрита
и представлении константы Bv, определяющей энергию вра-
щения данного колебательного уровня, с помощью выражения *)
, В'о
В _ ._______2_____
v 1 + + М3 ’
Эта формула была применена Гордоном и Барнесом вместо
(4.46). Коэффициенты ]3.2 должны быть определены по
зависимости Bv от квантового числа V. Для энергии колеба-
ния Гордон и Барнес использовали выражение (4.31), прини-
мая колебания ангармоническими и ограничиваясь в (4.31)
двумя слагаемыми. Для суммы по внутренним состояниям
мы имеем:
6колеб+евр
и'~ • (5.125)
V J
Вес основного электронного состояния р0 для молекул
равен 1. В этой формуле предполагается, что энергия коле-
баний отсчитывается от состояния ^ = 0. Если отсчитывать
*) Мы обозначаем коэффициенты* Bv со штрихом, так как
в методе Гордона и Барнеса для энергии вращения применяется
формула (5.101).
.§ 141
МЕТОД ГОРДОНА И БАРНЕСА
141
энергию от минимума потенциальной энергии, применяя при
вычислениях формулу (4.31), как это делают Гордон и Бар-
нес, то получим:
= ’ кТ
V J
*0 %+ВВр
= кТ -
V J
(5.126)
где ев означает энергию колебаний, вычисляемую по фор-
муле (4.31). Здесь st дается формулой (4.32). В нашей
модели колеблющийся ротатор — ангармонический вибратор
предполагается, что энергия колебаний не зависит от J,
а поэтому мы получим:
е' с % евп
Qi--='2lA = ehT'£i L kT^Pje кТ
V I J
s> e
____ _ v
V
(5.127)
Для данного колебательного уровня v на основании (5.114)
будем иметь:
kT
Q^v=ekT W
Bvh.c
B'vhc
I" 12£Г
4! D* IkT^ D'vF'v ,kT^
2! BAkc) W
(5.128)
Величина /z01) дается формулой (5.115). Гордон и Барнес
пренебрегли в ней двумя последними слагаемыми, а также
зависимостью Bv от г», положив
~ ~4~ — &о-
(5.129)
142 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [гл. V
Введем теперь обозначения
00 = kT Bohc (5.130)
Q-o kT B'vhc' (5.131)
dv = ™'v B', (5.132)
в' 4v (5.133)
В новых обозначениях QBpv примет вид
QBp« = e <7„(1 +^± + ^ + з4+Л + .-.). (5.134)
Заменяя в формуле (5.131) B'v его значением из фор-
мулы (5.124) и принимая во внимание формулу (5.130),
получим:
^ = ?о(1 +iV + ?2®2)- (5.135)
Теперь Qbpd будет иметь вид
QBP „ = (1 + X
X (1 + 12 3^-Ь^и Н- ' ‘' )• (5-136)
Выражая Ьо, определяемое формулой (5.129), через q0,
мы получим:
hcbn 1 Bohc 1
ЙГ = Т kT = 1^7
(5.137)
Таким образом,
1
Qbp V = е iq“q0 (1 + + ?2^2) X
X (l + Г2^ + d” + 3^ + /” + • • •)• <5-138)
В последней скобке формулы (5.138) оказалось возможным
пренебречь зависимостью коэффициентов от V, приняв их
равными q0, d0 и /0.
МЕТОД ГОРДОНА И БАРНЕСА
143
§ 14]
Мы получим:
<2вр v = elq Я о (1 Ч- Чг 1 + у2^ + ^о+ Зс?о+/о
(5.139)
Подставляя это значение QBp „ в формулу (5.127), будем иметь:
= ем-е4?1 +1 +d +3d9+/„) е-/т(i + +
V
Гордон и Барнес ввели функции
*у
Qv = ^e кт =ft(x, w),
V
sv
v--= —Q-----= /2(x, -w),
ev
^e'kT
v2 = ^—qv---=/3^- ™)>
где
(5.140)
(5.141)
(5.142)
(5.143)
(5.144)
и x— постоянная в константе <оех, определяющей ангар-
моничность колебаний. Взяв натуральный логарифм 2-^
и принимая во внимание, что для малых у
f In (1-|-_у) я=:_у, (5.145)
получим *):
i'"2-4 = ^+l"«-+4;+ln”+w+
~Ьdo3do—|-/оЧ--|- р'-з'У2- (5.146)
*) В формулу (5.146) можно ввести поправку —^"^о’ как эт0
сделали Гордон и Барнес, вследствие чего коэффициенты при d2
'в (5.149) и (5.155) будут соответственно равны 15/2 и 15.
144 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [ГЛ. V
Гордон и Барнес составили удобные таблицы, по которым
можно найти v и v'2 как функции w и х.
Найденное значение In У, А по уравнению (5.118) позволяет
„ Ф —
найти —
Для вычисления энтропии мы имеем уравнение (2.83),
которое перепишем в виде
VI д In У А
5 = 5п + ^1п + . (5.147)
Для энтропии колебаний и вращений, деленной на R, мы
будем иметь:
^колеб. + lnJ2 А . (5.148)
Дифференцируя (5.146) по Т и подставляя найденную про-
изводную в (5.148), получим:
= In Qv + + In q0+ 1 + +
Н-?2$2“|~2d 9dg--1-3/о> (5.149)
где
Величины
lnQ. + Г^
(5.150)
(5.151)
(5.152)
и s.2, как функции х и w, определяются по таблицам,
составленным Гордоном и Барнесом. Наконец, обозначив
часть теплоемкости, зависящую от температуры и соответ-
ствующую колебательным и вращательным движениям моле-
кулы, через СКолеб. вр> напишем:
колеб.
(5.153)
_ R
§ 14] МЕТОД ГОРДОНА И БАРНЕСА 145
Применение известного термодинамического соотношения
к Сколеб, вр дает:
СКолеб,вр = Г—кувр . (5.154)
Из (5.154) и (5.149) получается:
колеб, вр ^*^колеб, вр
К ~ ~R дТ =
= ^ + 1 + + 2rf0 + 18do + 6/о. (5.155)
Здесь
Cv=Td-^, (5.156)
<ц = 7^, (5.157)
с.2=Тд^. (5.158)
С
Значения , ct и с2 определяются также по таблицам Гор-
дона и Барнеса.
В приложении нами воспроизведены таблицы для вычи-
слений по методу Гордона и Барнеса (см. табл. 51—61)*).
Каждое из значений + и находится по двум
к1 К К
таблицам: сначала для значения ге» их = 0 (табл. 51),
а затем к найденной величине вводится поправка по табли-
цам 52, 53 и 54. Значения функций v, slt ct, v2, s.2 и c.2
приведены в таблицах 55, 56, 57, 59, 60 и 61.
В качестве одного из примеров вычисления термодина-
мических функций по этому методу Гордон и Барнес при-
водят вычисление термодинамических функций СО при
i3000°K. Этот пример мы приведем здесь**).
Мы имеем <ие = 2167,4 см~\ шехе= 12,70, b'v =
£= 1,843—0,020г», о' = —5,453- 10'6—6,9 • 10'%. Из этих
*) Недавно для вычислений по способу Гордона и Барнеса
И. В. Смирновой и А. В. Фростом [171] были составлены
Дополнительные таблицы.
**) В этом примере -использованы старые значения физиче-
ских постоянных. Кроме того, при интерполяции Гордон и Барнес
Допустили незначительную ошибку, которую мы оставили без
Исправления.
10 Зак. 835. И. Н. Гйднев
146 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [ГЛ. V
данных получается: -ш== 1,0347, х = 0,00586, <7О=1136,5,
°1=0,0 1 09, ,32=1,2 • 10-4, do=0,00673. По таблицам мы на-
ходим In + = 0,4390 + 0,0107 = 0,4497 (табл. 51
и 52), = 1,0092 + 0,0237 (табл. 51 и 53), ^=0,9154+
+ 0,0251 (табл. 51 и 54), v = 0,573, и3= 1,26, ух=1,508,
s.2 = 4,40, ct = 2,072, с2= 10,000. Далее по уравнению
(5.146) мы находим In 2 А = 7,4989. Точное вычисление
дает 1п 2 Д = 7,4991.
Наконец, уравнения (5.149) и (5.155) дают:
^К0Лр ’ вр = 9,0994,
/\
с
колеб, вр _ । 979
что совпадает с значениями, найденными непосредственным
суммированием (9,0997 и 1,980).
В качестве второго примера см. [116], где проведено
вычисление термодинамических функций молекулы Р2.
Метод Гордона и Барнеса легко может быть распро-
странен не только на молекулы, находящиеся в состоянии 1S,
но и на молекулы в других состояниях, а также на простые
многоатомные молекулы, например Н2О, N.2O, HCN и др.
(см. [222—225]).
§ 15. Метод Касселя*)
Метод Касселя, как и метод Гордона и Барнеса, позво-
ляет значительно сократить труд при вычислении термоди-
намических функций. Он является более точным, чем способ
Гордона и Барнеса, но менее удобным, так как требует
большей затраты труда.
Вычисление термодинамических функций двухатомной молекулы
без ядерного спина с >21 основным состоянием по этому методу
производится следующим образом.
Пусть коэффициенты, определяющие уровни энергии враще-
ния, представлены в виде
Bv = Во + av + ₽i>2, (5.159)
Dv = Dq + ~(v. .. (5.160)
*) См. [235, 236].
§ 15] метод клссЁЛй 147
Сумма состояний по вращательным уровням QBp (v), соответствую-
щая данному колебательному квантовому числу V, после разложе-
ния в ряд множителей, учитывающих отклонения от твердого *)
ротатора, может быть представлена с помощью формулы типа Мул-
холанда следующим образом:
QBpW = /Co + ^ + ^v3 + /<3V3+ (5.161)
Общая сумма состояний будет:
хп —^,(ш„г + ш1,Я!г>2+ ...)
<?< = 2Л= кТ (5.162)
D = 0
После разложения е по степеням v2 и перемноже-
ния полученного многочлена на QBp(v) формула (5.162) прини-
мает вид
оо йсш» v
^A=^P(v)e кт , (5.163)
и=о
,где
P(v) = P0 + /’1v4-P2v2 + P3^+ (5.164)
Кассель не дает явных выражений для Кр Ki......QBp (v) и P(v).
'Вид этих функций должен быть найден каждый раз после подста-
новки численных значений коэффициентов. Пусть
hew»
/ \ е kT — z. (5.165)
В этом случае
о»=2л= S (/>o+p1t'+p2v2+p3t'3+...)^ (5.166)
'Или
00
f Qi=^A = P0 S^ + Л s +
/у. t’=0 t = 0
+ ?2 2 + рз 2 + • • (5.167)
S, с- О 1) = 0
“^Первое слагаемое формулы (5.167) представляет убывающую гео-
метрическую прогрессию. Следовательно,
со
(5-168)
*) При фиксированном v.
1 10*
148 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИЙ ДВУХАТОМНЫХ ГАЗОВ [гЛ. V
Дифференцирование этого сходящегося ряда дает:
QO
VZ®~1 =
Г' = 0
1
(1-г)2 •
Отсюда после умножения на z получается:
00
у^ =_______г-__.
АА (1-г)3
Г = 0
(5.169)
Дифференцирование этого ряда и умножение на z позволяет про-
суммировать третий ряд
со
y^=*(1+z).
U (1-г)* •
г! = 0
Аналогично
СО
У = /(1+4z + z2)
(1—2)4
D = 0
со
У - --(1+ 112+llz2 + z3)
(1-г)*
l) = 0
и T. Д.
В общем случае получается:
оо
2 ^ = (1-2)-1Д
г = 11
где даются формулами
/о=1,
А = г(1 — г)-1,
/3 = z(l J- г)(1—г)"'2,
f?, = г (1 + 4z + г3) (1 — г) +
/4 = z(l J-llz+llz2 + 23)(l-z)-4,
/5 = 2 (1 + 26г + 66г3 + 26г" + z<) (1 — z)-'\
A = 2 (1 + 57г + 302г3 + 302г^ + 57г* + г^) (1 - г)"с,
А = г (1 + 120г + 1191г3 + 24162’’’+ 1191г< +
+ 120г5 + г®)(1 — г)-7.
(5.170)
(5.171)
(5.172)
(5.173)
(5.17-1)
§ 15] МЕТОД КАССЕЛЯ 149
Теперь применение (5.173) к (5.167) дает:
Qi = 2 А = (' - pifi- (5.175)
Если вынести за знак суммы множитель kTI^Bah.c, входящий в
то окончательно получается:
5л=,’<-т1Б(1~2,’‘2/'гг‘' <5,76)
Эту формулу Кассель приводит в своей обзорной работе
в 1936 г. [236].
Здесь первый множитель представляет сумму по состояниям
для твердого ротатора, множитель (1—z)~l— ее значение для
гармонического вибратора, а — число симметрии. Ряд fag, оце-
нивает все отклонения реальной молекулы от идеальной модели —
твердый ротатор в соединении с гармоническим вибратором.
Найденное значение суммы по состояниям позволяет опреде-
лить изобарно-изотермическии потенциал или —— по формуле
(5.118). Вычисляя производные можно найти и другие термо-
динамические формулы.
Формула (5.117), служащая для вычисления энтропии, может
быть представлена в виде
S= Sn + /? [in Q — ± • ^1, (5.177)
L * V J
где через Q' обозначено дифференцирование по у. Функция Q'
может быть найдена дифференцированием (5.176).
Аналогичным образом можно поступить при вычислении тепло-
емкости. Мы получим:
Здесь, как и в (5.177), штрихи у Q означают дифференцирование
По -1-.
Т
Для определения Q' и Q" Кассель в обзорной работе 1936 г.
Приводит таблицу производных f i и /„. Пусть
л = <5-179)
тогда
= (5-180)
И
Л" =S(/i^ + 2/^+Z>p.
(5.181)
150 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ДВУХАТОМНЫХ ГАЗОВ [ГЛ. V
Производные g\ и g'^, как и Pit надлежит находить в каждом
случае отдельно, что является довольно неудобным.
Дифференцирование (5.176) при применении (5.180) и (5.181)
делает возможным вычисление остальных термодинамических функ-
ций. Метод Касселя может быть обобщен для вычисления функций
состояния некоторых трехатомных и многоатомных газов*). Неудоб-
ством этого метода является применение неявных формул для
QBp(w), Р^ gi и т. д. Можно построить [25] метод вычисления А,
устраняющий эти недостатки, а также недостатки метода Гордона
и Барнеса.
Полезные таблицы для вычислений термодинамических
функций двухатомных газов были построены недавно
М. П. Вукаловичем, В. Н. Тимофеевым и другими [15], раз-
работавшими удобный метод вычисления этих функций и
выполнившими критический пересмотр термодинамических
свойств ряда двухатомных и многоатомных газов.
§ 16. Сравнение вычисленных значений
с опытными данными
Таблица 10
Практическая энтропия двух-
атомных газов при 298,2° К
и р = 1 атм
Газ с '-'вычисл Q ^калории
N3 45,79 45,9
о2 49,03 49,1
НС1 44,66 44,5
НВг 47,48 47,6
HJ 49,36 49,5
Наличие очень точных спектроскопических данных для
двухатомных молекул позволяет выполнить вычисления их
термодинамических функций с
гораздо большей точностью,
чем это достигается при экспе-
риментальных измерениях.
С другой стороны, экспери-
ментальные измерения тепло-
емкости наталкиваются в ряде
случаев на очень большие
трудности. Это обстоятельство
вместе с высокой точностью
вычислений термодинамических
функций придает статистиче-
ским методам определения их
большое значение.
Экспериментальные данные
по теплоемкости, полученные
надежными методами, хорошо совпадают с вычисленными [79].
Статистические методы вычисления теплоемкости позволили
) См. также Пеннингтон и Коб [248].
§ 16] СРАВНЕНИЕ С ОПЫТНЫМИ ДАННЫМИ 151
устранить большие расхождения между вычисленными и
экспериментальными значениями по методу скорости звука.
Причиной такого расхождения являлось отсутствие состоя-
ния равновесия при экспериментальных измерениях (см. [63]).
Хорошее согласие вычисленных и найденных эксперимен-
тальных значений получилось также и для энтропии. Наблю-
давшиеся в некоторых случаях, например для Н2, D2, СО
и других газов, отклонения в настоящее время хорошо вы-
яснены [63]. В таблице 10 приведено сравнение вычисленных
И найденных калориметрических энтропий.
ГЛАВА VI
КЛАССИФИКАЦИЯ И СИММЕТРИЯ МНОГОАТОМНЫХ
МОЛЕКУЛ
§ 1. Введение
Прежде чем переходить к рассмотрению задачи о вычи-
слении термодинамических функций многоатомных газов,
целесообразно установить классификацию многоатомных мо-
лекул и рассмотреть их квантовые состояния. Простейшим
типом многоатомных молекул являются так называемые квази-
твердые молекулы, т. е. молекулы, в которых отсутствуют
внутренние вращения и другие внутренние движения с боль-
шими амплитудами. К ним относятся, например, молекулы
СН4, Н2О, SO2, С2Н2 и др. Такие молекулы обладают пра-
ктически единственной устойчивой конфигурацией ядер.
Однако существует очень много молекул, имеющих вну-
тренние движения со сравнительно большими смещениями
(внутреннее вращение, внутренние перегруппировки), и их
нельзя рассматривать в виде квазитвердых. Так, в молекуле
этана имеет место внутреннее вращение группы СН3 отно-
сительно другой группы СН3, в молекуле ацетона СН3СОСН3
имеют место вращения двух групп СН3 относительно осталь-
ной части молекулы (остова). В упомянутых выше молекулах
вращение ограничено наличием потенциального барьера, так
что его нельзя рассматривать как свободное вращение. Воз-
можно существование молекул, где барьер оказывается ма-
лым. К ним принадлежит молекула диметилацетилена
СН3С=С—сн3.
Кроме молекул с внутренними вращениями существуют
молекулы с внутренними перегруппировками, представи-
телем которых является молекула NH3. В ней имеет место вну-
§ 2] КЛАССИФИКАЦИЯ МНОГОАТОМНЫХ МОЛЕКУЛ 153
тренняя перегруппировка ядра азота, переходящего из
равновесного положения, расположенного по одну сторону
плоскости, проведенно.й через ядра водорода, в равновесное
положение, лежащее по другую сторону этой плоскости*).
Молекула обладает, таким образом, двумя равновесными
конфигурациями. Переход ядра азота не является свобод-
ным, так как оно должно преодолеть барьер, составляющий
2076 см~1, т. е. 5,933 ккал)моль. В молекуле AsCl3 этот
барьер должен быть значительно больше, так что практи-
чески молекула находится в единственной устойчивой кон-
фигурации. Для молекулы NH3 время перехода из одной
конфигурации в другую примерно в 1000—700 раз больше
периода самого медленного колебания ядер около положения
равновесия **).
§ 2. Классификация многоатомных молекул применительно
к вычислению термодинамических функций
Классификация многоатомных молекул применительно
к вычислению термодинамических функций представлена
в приведенной ниже таблице И. Классификация была по-
строена по принципу учета внутренних смещений и величины
барьера, ограничивающего внутренние смещения. Величина
внутренних смещений, принятая во внимание при построении
классификации, отнесена к средним температурам. Следует
иметь в виду, что такая классификация является в некоторой
мере условной, так как при повышении температуры вели-
чины внутренних смещений увеличиваются, и молекулы, кото-
рые мы рассматривали в первом приближении при средних
температурах как квазитвердые, при очень высоких темпе-
ратурах не могут быть отнесены к этому классу. Однако
в процессе вычисления термодинамических функций и сравне-
ния результатов с опытными данными можно убедиться
в пригодности данной модели молекулы и законности отне-
сения этой молекулы к данному классу.
Все молекулы разделены на восемь классов. Разделение
на подклассы проведено с целью выделения простых случаев.
Наиболее простым является упомянутый выше класс
*) Здесь речь идет об относительном смещении ядра азота;
В действительности перемещаются ядра водорода, как более легкие.
**) Колебания >г.
164 КЛАССИФИКАЦИЯ И СИММЕТРИЯ МНОГОАТОМНЫХ МОЛЕКУЛ [ГЛ. VI
Таблица 11
Классификация многоатомных молекул по характеру
внутренних движений
№ класса Характеристика класса № подклас- са, на кото- рый разде- лен класс Характеристика подкласса Примеры
I II III Квазитвердые молекулы Молекулы, имею- щие внутрен- ние перегруп- пировки типа колебаний с большой ампли- тудой Молекулы, пред- ставляемые в виде остова, несущего сим- метричные волчки 1-1 1-2 1-3 1—4 1-5 III—1 III—2 Двухатомные мо- лекулы Линейные много- атомные моле- кулы Многоатомные молекулы типа сферического волчка Многоатомные молекулы типа симметричного волчка Многоатомные молекулы типа асимметричного волчка Движение волч- ков практиче- ски свободно Движение волч- ков затормо- жено* СОа,СН=СН СН4, SF, СН3С1 С2Щ NH3 Диметилаце- тилен СН3С=ССН3 Этан, пропан, ацетон
§ 2]
КЛАССИФИКАЦИЯ МНОГОАТОМНЫХ МОЛЕКУЛ
155
Продолжение
|№ класса Характеристика класса № подклас- са, на кото- рый разде- лен класс Характеристика подкласса Примеры
IV Молекулы, пред- ставляемые в виде остова, несущего асим- метричные волчки IV—1 IV—2а IV—2b IV—3 IV—4 Молекула имеет один волчок с почти свобод- ным вращением Молекула имеет один волчок с заторможенным вращением, центр тяжести волчка лежит на оси враще- ния или близок к ней Молекула имеет один волчок с заторможенным вращением, центр тяжести волчка лежит сравнительно далеко от оси вращения Молекула имеет несколько асим- метричных волчков со сво- бодным враще- нием Молекула имеет несколько асим- метричных волчков с за- торможенным вращением (об- щий случай) CII2DC=CCH2D СН CI, сн2=сн— —ch2d
156 КЛАССИФИКАЦИЯ И СИММЕТРИЯ МНОГОАТОМНЫХ МОЛЕКУЛ [ГЛ. VI
Продолжение
№ класса Характеристика класса № подклас- са, на кото- рый разде- лен класс Характеристика подкласса Примеры
V VI Молекулы, пред- ставляемые в виде остова, несущего сим- метричные и асимметричные волчки Молекулы, пред- ставляемые в виде остова, несущего волч- ки на волч- ках V—1 V—2 V—3 V—4 Молекула имеет один асимме- тричный и не- сколько симме- тричных волч- ков со свобод- ным вращением Молекула имеет один асимме- тричный волчок со свободным вращением и несколько сим- метричных с заторможенным вращением Молекула имеет один асимме- тричный волчок с заторможен- ным вращением и несколько(п) симметричных волчков Общий случай 1-бутен, п = 1 н. бутиловый спирт СНаСНаСНаСН2ОН
§ 2]
КЛАССИФИКАЦИЯ МНОГОАТОМНЫХ МОЛЕКУЛ
157
Продолжение
। № класса Характеристика класса № подклас- са, на кото- рый разде- лен класс Характеристика подкласса Примеры
VII VIII Молекулы с вну- тренним враще- нием групп, ограниченным барьерами сло- жного вида с несколькими сравнительно глубокими ми- нимумами раз- ной глубины (случай пово- ротных изоме- ров) Молекулы с вну- тренними дви- жениями более сложного типа 1,2 дихлорэтан, CF2Br • CF2Br, дивинил
квазитвердых молекул. Ко второму классу отнесены молекулы,
имеющие внутренние перегруппировки типа колебаний с боль-
шой амплитудой, как это имеет место в молекуле аммиака.
Классы HI, IV, V и VI охватывают важные типы внутреннего
вращения. Подразделение на подклассы проведено для клас-
сов I, III, IV и V с целью выделения более простых случаев,
причем некоторые подклассы являются частными случаями
других подклассов. Для классов II, VI и VII такое под-
разделение не приведено, так как эти случаи почти не
изучены и дальнейшая классификация их усложнила бы
таблицу.
Разделение на подклассы для квазитвердых молекул вы-
полнено по форме остова молекулы и соотношениям между
ее главными моментами инерции.
158 классификация и симметрия многоатомных молекул [гл. vi
Как известно, моментом инерции твердого тела относи-
тельно оси называется выражение
(6.1)
где — кратчайшее расстояние материальной точки mi от
оси. Моменты инерции, вычисленные относительно осей, про-
ходящих через центр масс (центр тяжести), называются цен-
тральными. В механике доказывается, что существуют для
всякой точки тела такие три взаимно перпендикулярных на-
правления, для которых моменты инерции будут максималь-
ными или минимальными. Эти направления называются глав-
ны ми осями инерции, а соответствующие им моменты
инерции — главными моментами инерции. Если
главные моменты инерции определены для центра масс, то
они называются главными центральными момен-
тами инерции. Если вычислить момент инерции 1г отно-
сительно произвольной оси /, проходящей через данную
точку О, и отложить в направлении I величину т0 мы
получим поверхность в виде эллипсоида, который называется
эллипсоидом инерции. Оси этого эллипсоида совпа-
дают с главными осями инерции.
Для вывода уравнения эллипсоида инерции поместим в точку О
начало прямоугольной системы координат хуг.
Момент инерции тела относительно прямой /, проходящей через
точку О и имеющей направляющие косинусы X, р, в системе хуг,
как легко убедиться, будет (см. [8]):
h — Ixx*-2 + IyyV-2 + 4г'<2 — — ^ху^> (6.2)
где 1ЯХ, Iyy, 1гг — моменты инерции тела относительно осей,
/а:а:=5я1»о1+г1). '
iyy = +
=Smi<xi+yi)- .
(6.3)
a Ix& I&y — так называемые произведения инерции,
^хз “ *
(6.4)
§ 2]
КЛАССИФИКАЦИЯ МНОГОАТОМНЫХ МОЛЁКУЛ
15&
Откладывая на прямой Z от начала
мы получим точку, имеющую координаты
1
координат отрезок — ,
V h
. X р. ч
х = , У = ~7= > z = ~Р^ •
УЛ Vh Vh
(6.5)
Определяя из этих формул X, р, \ и подставляя их в выраже-
ние (6.2), мы получим геометрическое место точек, являющихся
1
концами отрезков , отложенных по всевозможным направле-
ниям от точки О.
Уравнение построенной таким образом поверхности будет:
ЬяХ'2 + 1ууУ'2 + 4Z2 — ^угУ'г' — ^xzX'z' — сМхух'у' = 1, (6.6)
т. е. будет уравнением поверхности эллипсоида. Если в качестве
осей координат выбрать оси эллипсоида инерции, а новые коорди-
наты обозначить через $, т; и С, уравнение (6.6) примет вид
4^ + 4^ + ^= 1. (6.7)
Из уравнения (6.7) следует, что произведения инерции и
обращаются в нуль, а /Т1) и будут главными моментами
инерции.
Если точка О совпадает с центром масс, эллипсоид инерции
называется центральным. В последующем главные центральные
моменты инерции мы будем обозначать 1Х, 1у, 1г или /1( 1%, /3.
Молекулу, имеющую три различных главных централь-
ных момента инерции (/t Ф /2 =£ 1&), по отношению к ее
^вращениям называют молекулой типа асимметричного волчка,
уа иногда просто асимметричным волчком. Если два главных
центральных момента инерции будут равны (/х =# /2 = /3),
^'молекула называется молекулой типа симметричного волчка
^.(или симметричным волчком). Эллипсоид инерции такой мо-
лекулы представляет эллипсоид вращения. Никонец, если
Нравны все три главных центральных момента инерции
= 12 = /3), молекула представляет сферический волчок.
'В этом случае эллипсоид инерции будет сферой.
5 Разделение квазитвердых молекул на подклассы прове-
рено с учетом этих трех случаев, причем особо выделен
/Подкласс линейных молекул и подкласс двухатомных моле-
кул. Следует заметить, что случай линейных молекул можно
^рассматривать как предельный случай симметричного волчка,
|Для которого один из главных центральных моментов инерции
160 КЛАССИФИКАЦИЯ И СИММЕТРИЯ МНОГОАТОМНЫХ МОЛЕКУЛ (гл. VI
равен нулю или очень мал, тогда как два других равны
между собой (/t -> 0, /2 = /3).
Случаи внутреннего вращения внутримолекулярных групп
предусмотрены классами III, IV, V и VI. Наиболее простым
типом является наличие вращающихся групп, которые можно
рассматривать в виде симметричных волчков, как это имеет
место, например, для метиловых групп СН3. В этом случае
центр масс волчка лежит на оси вращения и эллипсоид
инерции вращающейся группы (волчка) относительно ее
центра масс представляется эллипсоидом вращения, причем
ось вращения волчка совпадает с осью его эллипсоида инер-
ции. Если одно из этих требований или все не выполняются,
волчок (вращающаяся группа) называется асимметричным.
§ 3. Элементы симметрии молекулы
Существенную помощь в изучении состояний многоатом-
ных молекул оказывает учет свойств симметрии их равно-
весных конфигураций. Как известно, симметрией называется
свойство геометрических фигур переходить при различных
положениях в совмещение с первоначальным положением *).
Таким свойством обладают очень многие молекулы, напри-
мер СН4, СН3С1, SF6 и др. Описание симметрии молекулы
производится путем описания сим-
метрии ее равновесной конфигу-
рации.
Существование симметрии свя-
зано с наличием определенных
элементов симметрии—
плоскостей симметрии, осей сим-
метрии или центра симметрии.
Так, молекула S0.2, имеющая пло-
скую равновесную конфигурацию,
имеет две плоскости симметрии
и одну ось второго порядка
(черт. 10).
Плоскостью симметрии называется плоскость, при отра-
жении от которой соответствующие точки фигуры совме-
щаются друг с другом. Так, при .отражении молекулы S0.2
*) См. [64] и [65].
§ 3]
ЭЛЕМЕНТЫ СИММЕТРИИ МОЛЕКУЛЫ
161
в плоскости В (черт. 10) ядро О(1) переходит в ядро О(2)
в наоборот. При отражении в плоскости симметрии фигура
преобразуется в фигуру, которую нельзя отличить от пер-
воначальной. Плоскость симметрии обычно обозначается
буквой а.
Вторым элементом симметрии является центр симме-
трии или центр инверсии. Центром симметрии называется
точка, обладающая тем свойством, что линия, проведенная
через нее и любую точку фигуры, встретит при своем про-
должении в другую сторону от нее соответствующую точку
на таком же расстоянии. Например, плоская молекула
%2F2Z2, изображенная Haj чертеже 11 щимеет£центр симме-
Черт. 11. Черт. 12.
трии С, ибо ZtC = CZ2, УгС = СУ2, ХГС = СХ2. Легко видеть,
что молекула SO2 не имеет центра симметрии. Центр сим-
метрии обычно обозначается символом г или С.
Третьим элементом симметрии является поворотная
ось симметрии, т. е. прямая, при вращении вокруг ко-
торой на углы, кратные от определенной части 360°, фигура
совмещается сама с собой. Если при вращении на 360° сов-
мещение имеет место два раза (при повороте на 180° и
ha 360°), ось симметрии называется осью второго порядка.
Если такие совмещения имеют место р раз (при вращениях
Ua 360° _ 360° ОСАО\
на углы , 2 , ..., 360 j , ось называется осью
Симметрии порядкар. Примером молекулы, имеющей
ось симметрии третьего порядка, является молекула СН3С1,
равновесная конфигурация которой изображена на черте-
же 12. Действительно, при вращении этой молекулы вокруг
беи СС1 на углы 120°, 240° и 360° молекула совмещается
11 Зак. 835. И. Н. Годнее
162 КЛАССИФИКАЦИЯ И СИММЕТРИЯ МНОГОАТОМНЫХ МОЛЕКУЛ [ГЛ. VI
сама с собой. Легко видеть, что молекула SO2 имеет ось
симметрии второго порядка, которой является прямая SK
(черт. 10). Для обозначения оси симметрии порядка р
принят символ Ср. Заметим, что всякая фигура имеет ось
симметрии первого порядка Сх, так как очевидно, что при
вращении на 360° фигура совместится сама с собой. В мо-
лекулах возможно существование осей 2, 3, 4, 5, 6 и
более высокого порядка. Этим симметрия молекул отли-
чается от симметрии кристаллов, где возможно существова-
ние только осей симметрии 2, 3, 4 и 6 порядка. Кроме
того, молекулы могут иметь ось симметрии бесконечного
порядка. Такая ось симметрии имеется у всех линейных,
в частности двухатомных, молекул. Ядра этих молекул
в равновесной конфигурации лежат на одной прямой, по-
этому при вращении на произвольный угол молекула совме-
щается сама с собой. Примером таких молекул являются
СО2, HCN, НС=СН и другие. Ось симметрии бесконечного
порядка обозначается символом С^_.
Наконец, в молекулах, как и в кристаллах, возможно
существование и четвертого элемента симметрии — зеркально-
поворотной оси порядка р, обозначаемой буквой Sp. Моле-
кула (фигура), обладающая этим элементом симметрии, пре-
образуется сама в себя при выполнении поворота на угол
360°
вокруг оси с последующим отражением в плоскости,
перпендикулярной к оси. В случае наличия зеркально-
„ 360°
поворотной оси при простых поворотах на углы ? ,
2-^-, ..., 360° молекула, вообще говоря, еще не совме-
щается сама с собой. Совмещение наступает при последую-
щем отражении от плоскости, перпендикулярной к оси.
Примером зеркально-поворотных осей в молекуле X.2Y2Z2
будут прямые АВ и Х±Х2 (черт. И). Действительно, при
вращении вокруг оси АВ на 180° и последующем отражении
от плоскости, перпендикулярной к этой оси (эта плоскость
будет перпендикулярной к чертежу и будет проходить
через ХГХ2), молекула совмещается сама с собой.
При наличии нескольких элементов симметрии некоторые
из них не всегда являются независимыми: существование
одних приводит к появлению других. Так, легко видеть, что
§ 4]
ОПЕРАЦИИ СИММЕТРИИ
163
существование двух взаимно перпендикулярных плоскостей
симметрии приводит к оси симметрии второго порядка.
Такой осью является линия пересечения этих плоскостей.
Заметим, что наличие элементов симметрии, например
осей симметрии, значительно упрощает определение положе-
ния главных осей в молекуле. В самом деле, оси симметрии
всегда являются главными осями, вследствие чего уже при
наличии только одной оси симметрии мы можем определить
положение одной из главных центральных осей, которая
будет совпадать с осью симметрии. С другой стороны, пло-
скость симметрии будет перпендикулярна к главной оси.
Можно показать также, что при наличии оси симметрии
третьего или более высокого порядка молекула будет
являться симметричным волчком. В этом случае моменты
инерции относительно двух осей, лежащих в плоскости,
перпендикулярной к оси симметрии, будут равны друг другу
и эллипсоид инерции обращается в эллипсоид вращения.
Заметим, что из наличия оси симметрии второго порядка
нельзя делать заключения о равенстве моментов инерции
относительно двух перпендикулярных к ней осей. Заметим
также, что наличие осей симметрии порядка выше третьего
является достаточным, но не необходимым признаком: моле-
кула может быть симметричным волчком при наличии оси
симметрии второго порядка и даже при отсутствии элемен-
тов симметрии.
Если молекула имеет две или несколько осей симметрии
третьего или более высокого порядка, она будет иметь рав-
ными все три главных момента инерции и будет обяза-
тельно сферическим волчком. Разумеется, молекула может
быть сферическим волчком и при отсутствии этих признаков.
§ 4. Операции симметрии
Существование элементов симметрии позволяет, как мы
видели, выполнять операции, которые переводят данную
фигуру в положение, совпадающее с первоначальным. Эти
операции получили название операций симметрии. Так, по-
воротной оси симметрии Ci соответствуют четыре операции,
переводящие при поворотах фигуру саму в себя: вращение
на угол 90°, вращение на угол 180°, вращение на угол 270°
и вращение на угол 360°. В общем случае существование
164 КЛАССИФИКАЦИЯ И СИММЕТРИЯ МНОГОАТОМНЫХ МОЛЕКУЛ [гл. VI
Таблица 12
Элементы и операции симметрии
Элементы симметрии Соответствующие операции симметрии
условное обозна- чение название вид операции число опера- ций симмет- рии (включ.Сх)
G — плоскость симметрии с — отражение от плоскости, а2= Cj 2
i — центр симметрии 1 — отражение в центре, 2
Сп — поворот- ная ось сим- метрии п-го порядка Сп — поворот на угол Cfl— поворот на угол 2- — , z-з о 2л — поворот на угол 3* —, С™—1 — поворот на угол (п-1)—= - —, с^ = сх ' п П 9 п 1 п
€ > Sn — зеркаль- но-поворотная ось симметрии п-го порядка (для четных п) о 2г Sn—поворот на угол — с отражением в перпендику- лярной плоскости, с2 ~2 п 2л = — поворот на угол 2 • —, а 2ТС — поворот на угол 3* —, с отражением —поворот на угол (п — 1) -^-с отражением, S” = п
§ 5] ГРУППЫ СИММЕТРИИ МОЛЕКУЛЫ 165
поворотной оси С„ приводит к наличию р операций сим-
н 360° о 360° ос„о
метрии — вращений на углы , 2............... 360 .
Эти операции симметрии обозначаются соответственно
Ср, Ср, Ср, . . ., Ср. В число операций симметрии включается
и операция покоя, которую в литературе до сих пор было
принято обозначать буквой Е или /. М. В, Волькенштейн,
М. А. Ельяшевич и Б. И. Степанов [12] применили для
обозначения этой операции естественный символ Сх. Послед-
него обозначения будем придерживаться и мы. Очевидно,
что СРр эквивалентно выполнению операции Ct.
Плоскости симметрии соответствует операция отражения
от плоскости, обычно обозначаемая также буквой а. После-
довательное выполнение двух операций отражения, т. е. а2,
эквивалентно операции Сх, так что можно написать:
о2 = Сг (6.8)
Для обзора элементов и операций симметрии мы приведем
таблицу 12, которая заимствована нами из монографии
Волькенштейна, Ельяшевича и Степанова [12]. Заметим, что
при подсчете числа операций симметрии, соответствующих
разным элементам симметрии, операция считается только
один раз.
При изучении молекул и вычислении термодинамических
функций очень большое значение имеет применение числа
симметрии а, которое было введено впервые Гиббсом [21]
(см. также [217]). Числом симметрии называется число опе-
раций симметрии, представляющих чистые вращения моле-
кулы, т. е. общее число вращений молекулы, переводящих
ее в тождественное положение. Например, для молекулы
СН3С1 (черт. 12) число симметрии а равняется трем, так как
существуют три операции вращения на углы 120°, 240° и
360° вокруг оси СС1, переводящие молекулу саму в себя
(более подробно о числе симметрии см. § 6 этой главы).
§ 5. Группы симметрии молекулы
При исследовании совокупности операций симметрии,
Переводящих молекулу в тождественное положение, оказы-
вается, что эта совокупность с математической точки зрения
166 КЛАССИФИКАЦИЯ И СИММЕТРИЯ МНОГОАТОМНЫХ МОЛЕКУЛ [ГЛ. VI
представляет группу *). Операции симметрии являются эле-
ментами группы, причем единичный элемент группы (е)
представляется операцией симметрии Ct.
Как известно, группой называется совокупность элемен-
тов a,b,c,d, . . ., удовлетворяющих следующим постулатам:
1) Существует такая операция (умножение), при выпол-
нении которой двум элементам, а и Ь, соответствует третий
элемент совокупности
ab — c. (6.9)
2) Для операции умножения выполняется ассоциативный
закон
а(Ь • с) = (а • Ь) • с. (6.10)
3) Среди элементов совокупности существует единичный
элемент е, для которого
ае = еа -- а, (6-11)
где а — произвольный элемент совокупности.
4) Совокупность содержит наряду с элементом а и об-
ратный элемент а-1, для которого
аа-1 = а~1а = е. (6.12)
Заметим, что умножение, вообще говоря, не обладает
свойством коммутативности, т. е.
ab^= Ьа. (6.13)
Однако существуют группы, для которых это свойство
выполняется, так что
ab = ba. (6.14)
Такие группы называются абелевыми.
Число элементов группы называется ее порядком. При-
мерами групп являются группа перестановок и группа ли-
нейных преобразований.
Рассмотрим еще в качестве примера совокупность опе-
раций симметрии молекулы СН3С1 (черт. 12). Таких опера-
ций, соответствующих одной оси симметрии третьего по-
рядка (прямая СС1) и трем плоскостям симметрии, проходя-
щим через каждое из ядер водорода и ось, существует шесть:
*) См. О. Ю. Шмидт [83], Вигнер [96], Б. Л. Ван-дер-
Верден [9], Л. Ландау и Е. Лифшиц [37], А. Г. К у р о ш
[35], Розенталь и Мурфи [256].
§ 5] ГРУППЫ СИММЕТРИИ МОЛЕКУЛЫ 167
1) операция — покой или вращение на угол 0°, или
вращение на 360° вокруг оси симметрии;
2) операция С3— вращение вокруг оси СС1 на 120°;
3) операция С»— вращение вокруг оси СС1 на 240°;
4) отражение в плоскости симметрии Н(1)СС!;
5) отражение в плоскости симметрии Н(2)СС1;
6) отражение в плоскости симметрии Н(3)СС1.
Легко видеть, что эти шесть операций образуют группу.
Последовательное выполнение двух операций симметрии эк-
вивалентно выполнению одной операции, причем выполняется
требование 2) приведенного выше определения. Единичному
элементу е соответствует операция Cv Для каждой опера-
ции симметрии существует обратная операция, например эле-
ментом, обратным С.л, будет вращение на 120° в противопо-
ложном направлении, совпадающее с вращением на 240°,
т. е. элемент С3. Таким образом, группа симметрии мо-
лекулы СН3С1 содержит шесть элементов, т. е, она является
группой шестого порядка. Эта группа не является абе-
левой. Число симметрии молекулы СН3С1, как было указано
выше, будет равно трем, так как существуют три враще-
ния (Сх, С3 и С3), переводящие молекулу в тождественное
положение.
Симметрию молекулы (ее равновесной конфигурации)
целесообразно описывать группой симметрии, образованной
ее операциями симметрии. Группы симметрии молекул отно-
сятся к так называемым точечным группам симметрии, т. е.
к группам симметрии, операции которых оставляют непо-
движной по крайней мере одну точку в пространстве.
Точечные группы симметрии обозначаются обычно жир-
ными буквами, соответствующими элементам симметрии.
Если молекула имеет только ось симметрии порядка р, соот-
ветствующая группа симметрии обозначается Ср; если моле-
кула имеет ось симметрии порядка р и р плоскостей сим-
метрии, проходящих через эту ось, соответствующая груп-
па симметрии обозначается *) Cpv. Так, группа симметрии
*) Обычно при определении симметрии принято ось симметрии
наиболее высокого порядка считать вертикальной. Плоскости симме-
трии в этом случае будут вертикальными, отсюда и произошел сим-
вол V. Такие плоскости обычно обозначаются символом Гори-
зонтальная плоскость симметрии обозначается символом ид.
168 КЛАССИФИКАЦИЯ И СИММЕТРИЯ МНОГОАТОМНЫХ МОЛЕКУЛ [ГЛ. VI
Таблица 13
Обозначение групп симметрии молекул
№ п/п Наличие элементов симметрии Соответ- ствующая группа симметрии Примечание
1 Нет С,
2 Плоскость симметрии Cs 1
3 Центр симметрии Ci
4 Ось симметрии порядка р ср
5 Зеркально-поворотная ось поряд- ка р Sp Для четных р\ для нечетных $р ~ cph
6 Ось симметрии порядка р и р плоскостей симметрии, про- ходящих через ось Cpv
7 Ось симметрии порядка р и р осей второго порядка, пер- пендикулярных к оси Ср и об- разующих между собой равные углы Dp
8 Ось симметриии порядка р и плоскость симметрии, перпен- дикулярная к этой оси С ph Группы С2П И имеют центр сим- метрии
9 Ось симметрии порядка р и р осей симметрии второго по- рядка, перпендикулярных к оси Ср, и, кроме того, р верти- кальных плоскостей симме- трии делящих пополам угол между двумя соседними осями второго порядка и проходящих через ось симметрии Ср Dpd
§ 5J
ГРУППЫ СИММЕТРИИ МОЛЕКУЛЫ
169
Продолжение
№ п/п Наличие элементов симметрии Соответ- ствующая группа симметрии Примечание
10 Ось симметрии порядка р и р вертикальных плоскостей симметрии ст,,, проходящих че- рез эту ось Ср, образуя между . о 360° собой углы , и, кроме то- го, горизонтальная плоскость симметрии перпендикуляр- ная к оси Ср. Следствием этих элементов является наличие р осей симметрии второго по- рядка Dph При четных р имеется центр симметрии Z и зеркально- поворотная ось поряд- ка р
11 Три взаимно перпендикулярные оси симметрии второго поряд- ка и четыре оси симметрии третьего порядка, причем оси второго порядка делят попо- лам углы между осями третьего порядка т
12 Три взаимно перпендикулярыые оси симметрии второго поряд- ка, четыре оси третьего порядка и шесть плоскостей симме- трии та Оси симметрии С% являются зеркально- поворотными осями четвер- того порядка
13 Элементы симметрии группы Т и центр симметрии. Следствием этих элементов является нали- чие трех плоскостей симме- трии ал Тп Четыре оси С3 являются зер- кально-пово- ротными ося- ми шестого порядка
170 КЛАССИФИКАЦИЯ И СИММЕТРИЯ МНОГОАТОМНЫХ МОЛЕКУЛ [гл. VI
Продолжение
№ п/п Наличие элементов симметрии Соответ- ствующая группа симметрии Примечание
14 Три взаимно перпендикулярные оси симметрии четвертого по- рядка, четыре оси симметрии третьего порядка, шесть осей симметрии второго порядка О
15 Элементы симметрии группы О и центр симметрии. Следствием этих элементов является нали- чие девяти плоскостей симме- трии Oh Оси симметрии С4 являются одновременно зеркально- поворотными осями симме- трии четвер- того порядка, а оси симме- трии С3—зер- кально-пово- ротными ося- ми шестого порядка
молекулы СН3С1, имеющей ось третьего порядка и три
плоскости симметрии, проходящие через эту ось (черт. 12),
представляется символом C.iv. Для молекулы SO2 (черт. 10)
симметрия будет С.2в. Если молекула не имеет совсем
элементов симметрии, ей соответствует группа из одного
элемента (Сх); такая группа обозначается Q, При нали-
чии единственной плоскости симметрии или центра симме-
трии группы симметрии обозначаются соответственно через
Cs и Сг.
Для групп симметрии, обусловленных существованием оси
симметрии Ср порядка р и плоскости симметрии, к ней пер-
пендикулярной (ай), применяется символ Cph. Примером мо-
лекулы с симметрией C.2h является молекула X2Y2Z2, изобра-
женная на чертеже 11. Группа симметрии этой моле-
кулы состоит из четырех элементов: Clt С2, ah и инвер-
сии I.
§ 6j ГРУППА ВРАЩЕНИЙ И ЧИСЛО СИММЕТРИИ 171
Другими группами симметрии являются группы Dp, Dpd,
Dph, Т, Td, О и Oh*).
Характеристика важнейших групп симметрии приведена
в таблице 13.
Заметим, что симметрия молекул не совпадает с симме-
трией кристаллов, например случаи молекулярной симметрии
Соощ, ^5t>’ ^7f> ^7h’ C8v и некоторые другие не
принадлежат тридцати двум кристаллическим классам.
§ 6. Группа вращений и число симметрии
Изучение симметрии молекул имеет чрезвычайно большое
значение при определении электронных, колебательных, вра-
щательных и спиновых состояний молекулы. Применение
теории групп при рассмотрении этих состояний оказалось
очень полезным, так как позволило просто решить ряд важ-
ных задач классификации состояний. Дело в том, что с сим-
метрией молекул тесно связана и симметрия их волновых
функций. Так, рассмотрение группы симметрии молекулы
позволяет классифицировать колебания молекулы и волновые
функции, описывающие эти колебания.
При изучении вращательных состояний существенную по-
мощь оказало рассмотрение группы вращений R, являю-
щейся подгруппой группы симметрии. Как известно, подгруп-
пой называется часть элементов группы, образующая также
группу, вообще говоря, более низкого порядка. Подгруппа
обязательно должна содержать единичный элемент группы.
Так, подгруппой группы симметрии C.iv является группа С,,
состоящая из элементов Ct, С3 и С|. Подгруппой группы С2/г
является группа С2, содержащая два элемента — и С2.
Назовем группой симметрии вращения (группой /?) сово-
купность всех операций симметрии, представляющих чистые
вращения молекулы. Порядок этой группы, очевидно, будет
равен числу симметрии молекулы а, т. е. он будет равен
числу вращений молекулы, переводящих ее в тождественное
положение. Число симметрии оказалось очень важным при
вычислении термодинамических функций (см. § 5 главы V,
§ 6 главы VIII, см. также главы IX и X).
*) См. подробнее М. В. В о л ь к е н ш т е й н, М. А. Е л ь я-
Шевич и Б. И. Степанов [12] и Г. Герцберг [20].
172 КЛАССИФИКАЦИЯ И СИММЕТРИЯ МНОГОАТОМНЫХ МОЛЕКУЛ [гл. VI
Рассмотрим в качестве примера определение числа сим-
метрии молекулы ВС13. Равновесная конфигурация этой мо-
лекулы имеет вид равностороннего плоского треугольника
с ядром В в центре (черт. 13). Симметрия этой молекулы
описывается группой D.3h, имеющей 12 элементов. Эта
молекула имеет шесть операций симметрии, выполняемых
вращением: покой, два вращения на 120° и на 240° от-
носительно оси, проходящей через ядро В и перпендику-
лярной к плоскости молекулы, и три вращения на 180° от-
носительно осей С1(1) —Ь, С1(2) —с и С1(3) —а. Таким
образом, число симметрии этой молекулы будет 6. Заме-
тим, что указанные выше операции симметрии образуют
группу Р3.
Точно так же можно убедиться в том, что молекула
метана, равновесная конфигурация которой является пра-
вильным тетраэдром (черт. 14), имеет число симметрии 12.
Для молекулы Н2О или SO2 <з будет равно 2 (черт. 10).
Для молекул, не имеющих элементов симметрии вращения
(группы Cj, Cs, С^, число симметрии равно единице.
Каждой группе симметрии молекулы соответствует своя
подгруппа вращения R (группа симметрии вращения). Так,
группе С2„ молекулы Н2О соответствует группа С2, группе
С3„— группа С3. Порядок группы симметрии вращения равен
числу симметрии а. В таблице 14 приведены наиболее важ-
ные случаи симметрии молекул с указанием их подгрупп
вращения. В ней даны также соответствующие числа сим-
метрии (для квазитвердых молекул).
§ б] ГРУППА ВРАЩЕНИЙ И ЧИСЛО СИММЕТРИИ 173
В случае внутреннего вращения группа R приобретает
дополнительное число элементов, вызванных вращениями
внутри молекулы. Это приводит к увеличению числа сим-
метрии. Так, у молекулы этана число симметрии оказывается
равным 18 (вместо 6). Этот вопрос будет рассмотрен позднее
(см. § 2 главы IX).
Таблица 14
Числа симметрии я для молекул
разной симметрии
Группа симметрии Под- группа R G
^1» ^8» c, 1
Cit C2ft c2 2
Cg, Csv, C3h c3 3
C4v, C4 4
^'>v> C5 5
^6и» ('Gh C6 6
D2 = V, Did, Vh V 4
Di, D3d, D3 6
Dit Did, Dih Di 8
D6 12
s0 Cg 3
Ct 1
C2 2
T, Td T 12
Oh 0 24
ГЛАВА VII
УРОВНИ ЭНЕРГИИ ВРАЩЕНИЯ И КОЛЕБАНИЯ
КВАЗИТВЕРДЫХ МОЛЕКУЛ
§ 1. Введение
Рассмотрим сначала вопрос об уровнях энергии квази-
твердых молекул. В первом приближении, как это имело
место и для случая двухатомных молекул, вращательные
и колебательные движения в молекуле можно рассматривать
отдельно, пренебрегая всеми видами взаимодействия. В таком
случае
®i == ®эл ~Н ®колеб ~Н ®вр- (7.1)
Выражения для энергии вращения будут зависеть от под-
класса, к которому принадлежит молекула, т. е. эти выра-
жения будут различными для линейных молекул, молекул
типа симметричного волчка, молекул типа асимметричного
волчка и молекул типа сферического волчка.
При определении энергии вращения и энергии колебания
мы будем предполагать центр инерции молекулы неподвиж-
ным. Допустимость такого рассмотрения вытекает из воз-
можности отделения поступательного движения от других
видов движений.
§ 2. Уровни энергии вращения линейной молекулы
Для линейной многоатомной молекулы выражение энергии
вращения получается таким же, как и для двухатомной моле-
кулы. В первом приближении мы имеем:
да
(7-2)
или
zsl = hcBJ{J+ 1). (7.3)
§ 3] ЭНЕРГИЯ ВРАЩЕНИЯ СИММЕТРИЧНОГО ВОЛЧКА 175
Здесь 1в означает момент инерции относительно оси, пер-
пендикулярной к оси молекулы и проходящей через центр
масс. Величина 1в вычисляется с помощью формулы (6.1). При
вычислении момента инерции суммирование в формуле (6.1)
производится по ядрам и не производится по электронам.
Связанная с этим незначительная ошибка отчасти компенси-
руется применением вместо массы ядер массы нейтральных
атомов т^. Ошибка, допускаемая таким приближением, зна-
чительно меньше ошибки, связанной с современными мето-
дами определения моментов инерции.
Классическими примерами многоатомных линейных моле-
кул являются молекулы СО2, ацетилена С2Н2 и др.
Формула (7.3) получается в предположении, что много-
атомная линейная молекула может быть представлена моделью
жесткого ротатора. При применении
модели нежесткого ротатора мы полу-
чим, как и в случае двухатомной мо-
лекулы,
евр=/гс[Ш(/+1)— 4---------------
-DJ2(J+ 1)2 + ...]. (7.4)
Член DJ- (J-f- I)2 характеризует в 3-------—-----
первом приближении влияние центро-
бежной силы, приводящей при враще- 2-------1—------
нии молекулы к незначительному уве- 1 - - |- 1 -
личению расстояния между ядрами. На О
чертеже 15 показана схема вращатель- ц 15
ных уровней энергии линейной много-
атомной молекулы. Как и в случае двухатомных молекул,
квантовое число J определяет момент количества движения
молекулы, равный
(7.5)
§ 3. Энергия вращения симметричного волчка
Перейдем к рассмотрению уровней энергии вращения
молекул типа симметричного волчка. Примером таких мо-
лекул являются СНУС1, СНС13, AsCl3 и др. В этом случае
Два главных центральных момента инерции равны между
собой и эллипсоид инерции представляется эллипсоидом
176
УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ
[ГЛ. VII
вращения. Мы будем обозначать каждый из двух равных
главных моментов инерции через 1в, а третий момент инер-
ции через 1а- Ось, соответствующая этому третьему мо-
а) 1а<1в, т. е.
ственной оси меньше каждого из двух равных моментов инер-
ции (вытянутый симметрич-
ный волчок);
Ь) 1а > т- е. момент
инерции относительно соб-
ственной оси больше каж-
дого из двух равных момен-
тов инерции (сплющенный
симметричный волчок).
Рассмотрим вращение
симметричного волчка с точ-
ки зрения классической ме-
ханики. С этой целью по-
строим вектор Р (черт. 16),
представляющий общий мо-
мент количества движения
молекулы. Этот вектор бу-
дет образовывать некоторый
угол с собственной осью.
Составляющую вектора Р в направлении оси волчка обозна-
чим через Рг, а угол между этими векторами — через 0.
менту инерции, обычно на-
зывается собственной осью
симметричного волчка.
Если молекула имеет
ось симметрии порядка вы-
ше второго, то эта ось
будет являться собственной
осью симметричного волч-
ка, так как в этом слу-
чае моменты инерции от-
носительно осей, перпен-
дикулярных к ней, будут
равны.
При изучении вращений
симметричного волчка сле-
дует различать два случая:
момент инерции относительно соб-
§ 31 ЭНЕРГИЯ ВРАЩЕНИЯ СИММЕТРИЧНОГО ВОЛЧКА 177
Исследование движения симметричного волчка с непо-
движным центром тяжести методом классической механики
показывает, что угол 6 остается постоянным, причем вектор Р
по закону сохранения момента количества движения непо-
движен в пространстве (для случая свободного движения
между столкновениями). Движение молекулы (волчка) со-
стоит из двух движений: вращения волчка относительно
своей оси (по этой оси направлен вектор Pz) и вращения
(прецессии) оси молекулы (вектора Pz) вокруг вектора Р
(см. черт. 17, где молекула изображена в виде цилиндра
и С представляет центр тяжести молекулы).
Частота первого из этих движений зависит от моментов
инерции /А и 1в и абсолютной величины вектора Pz, частота
второго определяется моментом инерции 1в и абсолютной
величиной вектора Р.
Представление о движении молекулы можно получить путем
построения двух конусов: неподвижного с осью Р (черт. 18), имею-
щего вершину в центре масс молекулы С, и подвижного конуса,
который закреплен в молекуле
и ось которого совпадает с осью
молекулы (вектором Pz). Угол
раствора второго конуса 2<Ь опре-
деляется соотношением
1А
(7.6)
Для вытянутого симметричного
волчка (случай а), 1А<^1в) Угол ®
будет больше ф; для сплющенного
симметричного волчка (случай Ь),
1д>1в) Угол в будет меньше
угла <р- На чертеже 18 конусы
построены для случая а). Дви-
жение молекулы в пространстве
'Представится качением второго конуса по первому (неподвижному)
Конусу без скольжения и с постоянной скоростью. Линия касания
будет мгновенной осью вращения. Обе оси — мгновенная ось вра-
щения и ось Р (неподвижная в пространстве), как это видно из
чертежа 18, будут менять свое положение относительно оси моле-
кулы. Описанное вращение молекулы будет иметь место между
Столкновениями молекул.
Вычислим кинетическую энергию вращения. Пусть через центр
(Масс волчка мы провели три взаимно перпендикулярные оси х,
У, г, неизменно связанные с волчком. Обозначим проекции угловой
^скорости на эти оси координат через р, q и г.
12 Зак. 835. И. Н. Годпев
178 УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ [гл. VII
Кинетическая энергия вращающегося волчка Т будет *):
27 = 1ХхР2 + Iyyq2 + 4Z2 — Ъ1у3дг — 21хгрг — 2Ixypq, (7.7)
где 1ХХ, 1уу и 1гг— моменты инерции, а Iyg, 1ХЗ, 1ху — произведе-
ния инерций относительно осей х, у, г, т. е.
Ixx = ^mi (У2г +
Iyy = 2 mi (xi + -
Izz = 2 mi (xi ’
bxy — M-i
lyz — 2 mi yi2i'
f coz = mi
(7.8)
Если за оси x, у, z взять главные оси инерции (которые
в нашем случае будут главными центральными), то кинетическая
энергия будет:
27’ = ^Х + /^ + /Л (7.9)
где 1Х, 1у, /г—главные моменты инерции и шх, шу и <ог — проек-
ции угловой скорости на главные оси. Пусть главная ось инерции z
направлена по собственной оси волчка. Тогда
2^ = М + /В(^ + ^)- (7.Ю)
Для проекций момента количества движения мы будем иметь:
рх = 7®“®, |
ру = 7г/ш«/> } (7.П)
pz = 73“г- J
Исключая Шд., и>у и шг из формулы (7.9), получим:
р2 р-2
л 'р _ t______?/ ।__£
/ “г Г “Г Г
Л(В *у lz
или
т J П 19)
1 — 1 2/я х> V •1~/
Перейдем теперь к определению уровней энергии вращения.
Для этой цели мы должны составить волновое уравнение, восполь-
*) См., например, Н. И. Бухгольц [8].
§ 3]
ЭНЕРГИЯ ВРАЩЕНИЯ СИММЕТРИЧНОГО ВОЛЧКА
179
зовавшись найденным значением классической энергии вращения.
Потенциальная энергия V здесь равна нулю, так как мы рассма-
триваем свободное движение. Однако решение волнового уравнения
довольно сложно *), поэтому мы приведем полуклассический вывод.
Из чертежа 16, движения Р с оси z, следует, сумму векторов определяющего связь полного момента количества его составляющей Рг, направленной по главной что вектор N будет представлять геометрическую Ра, и Ру. Таким образом, мы имеем: р^ + р2=№ = р2-р2. (7.13)
Подставляя эти значения в формулу (7.12), получим: Р2 р‘2 pi Т==^-^2Г-2Г' (7'14) -‘a ~'в .в
т. е. р2 р2( 1 1 \ г=2г + т\г~~г Г (7Л5) 27в 2 \ ‘а ‘в/
Полный момент количества движения Р и его проекция Рг на ось г
оказываются квантованными. Мы имеем:
P=V 7(7+1)^, (7.1б)
^ = /<2^, (7-17)
где квантовое число J пробегает значения 0, 1, 2, 3, ..., квантовое
число К принимает целые значения, лежащие между + J и —I.
Подставляя значения Р2 и Р2 из соотношений (7.16) и (7.17) в фор-
мулу (7.15), получим:
й2 /г3 / 1
г--.-8^7</+1> + да'<,(т7
г- , (7.18)
в /
т. е.
_ А2 Г7(7+ 1) , 1
вр 8л2 [ 1В
1 \]
{в /]
(7.19)
Если К = 0, выражение для евр приводит к ранее полученному
выражению (7.2) для линейного ротатора
• Л2 1
£bp = 8^V(''+1)-
(7.20)
*) См. Паулин г и Вильсон [92]; см. также Денни-
сон [215], Л. Ландау и В- Лифшиц [37].
12*
180
УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ
[гл. VII
Введем постоянные
о h
№clB ’
А —
(7.21)
(7.22)
постоянных выражение для
энергии
(7.23)
При применении этих
вращения имеет вид
sBp = he [BJ(J+ \) + К2(А — В)].
Уровни энергии симметричного волчка оказываются выро-
жденными. Строгое квантовомеханическое решение показы-
вает, что данным значениям J и К соот-
ветствует 27Д- 1 значений квантового чис-
ла М, определяющего проекцию полного
момента количества движения относитель-
но произвольной оси, закрепленной непо-
движно в пространстве. Энергия вращения
не зависит от М, а также не зависит от
знака К, как это следует из формулы
(7.19). Поэтому уровень энергии с/<=0
будет вырожден 2J—[— 1 -кратно, а уро-
вень энергии с К =#= 0 будет вырожден
2 (2J-[-1)-кратно, так как каждому зна-
чению J соответствуют два уровня с кван-
товым числом ±К, имеющих одинако-
вую энергию. Диаграмма уровней симме-
тричного волчка для случая вытянуто-
го симметричного волч-
ка (случай а)) предста-
влена на чертеже 19,
где сбоку указаны зна-
чения квантовых чисел
J и К.
Выведенные формулы относятся к жесткому симметрич-
ному волчку. При рассмотрении нежесткого симметричного
волчка нужно добавить поправочные члены, аналогичные по-
правочному члену, содержащему коэффициент D в формуле
(7.4). Формула для вращательной энергии нежесткого сим-
метричного волчка была получена Славским и Деннисо-
ном [257].
г
— 55
----5 4
------53
--------52 5/
- 5 50
----4С
------47
-------424/
- 40
------33
_______32
3- 30
гг21
=-=20
=¥-]О
Иг?!,)
Черт. 19.
§ 4] ЭНЕРГИЯ ВРАЩЕНИЯ МОЛЕКУЛЫ СФЕРИЧ. ВОЛЧКА 181
§ 4. Уровни энергии вращения молекулы
типа сферического волчка
Если квазитвердая молекула имеет три равных главных
момента инерции, она является сферическим волчком. В ка-
честве примера можно привести молекулы СН4, СС14, SF6
и другие. Обычно к подклассу типа сферического волчка
принадлежат молекулы, обладающие высокой симметрией
(молекулы тетраэдрической или октаэдрической структуры).
Возможно существование молекул типа сферического волчка
и более низкой симметрии.
При 1Я = 1у = /г = /, как это следует из формулы (7.11), для
квадрата полного момента количества движения мы получим:
^ = ^+^+^=/2(4+4+^)=/2“2> <7-24)
т. е. вектор Р будет пропорционален вектору угловой скорости и,
следовательно, они будут иметь одинаковое направление. Поэтому
мгновенная ось вращения будет совпадать с направлением полного
момента количества движения. Молекула совершает простое вра-
щение вокруг неподвижной оси, которая может иметь любую ори-
ентацию по отношению к молекуле.
Уровни энергии вращения сферического волчка можно
получить из уровней энергии симметричного волчка (7.23)
или (7.19), если положить 1А = 1В = 1.
Мы получим:
в»р = 8^А-/+1). <7-25)
Таким образом, для уровней энергии вращения сферического
волчка получается выражение, аналогичное выражению для
простого жесткого ротатора.
Формула (7.25) относится к жесткому сферическому
волчку. Для нежесткого сферического волчка в выражение
энергии нужно ввести поправочный член вида — Z9J2 (У—{— 1 )2.
В случае симметричного волчка все уровни с различными
по абсолютной величине квантовыми числами К были отлич-
ными. Теперь эти уровни, как следует из формулы (7.25),
будут совпадать. Каждому значению J соответствует 2J-\- 1
значений квантового числа К и 27Д- 1 значений квантового
числа М. Поэтому вес уровня будет (2J-j- l)(2J-j~ 1) =
= (2J+1)2.
182
УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ
[гл. VII
Следует заметить, что выражения весов уровней энергии
для симметричного и сферического волчков, равные соответ-
ственно 2(27+1) при К + О и (27+ I)2, еще не дают пол-
ного статистического веса уровня энергии молекулы. Если
бы на волновую функцию молекулы, содержащей одинако-
вые ядра, не накладывалось никаких требований симметрии
(полная волновая функция должна быть симметричной или
антисимметричной по отношению к перестановкам координат
одинаковых ядер в зависимости от типа статистики, которой
подчиняются ядра, см. § 4 главы I и § 7 главы IV), то для
получения статистического веса нужно было бы эти выра-
жения просто умножить на число спин-состояний, соответ-
ствующих данному уровню энергии. В действительности при
вычислении весов мы должны учитывать эти условия сим-
метрии, вследствие чего точный вес уровня нельзя вычислить
с помощью такого простого правила. Однако эта задача
сравнительно легко может быть решена методом теории
групп (см. далее, § 14 и 15 этой главы).
§ 5. Энергия вращения молекулы
типа асимметричного волчка
Молекула с тремя различными главными моментами
инерции по отношению к вращению является асимметрич-
ным волчком. К этому подклассу принадлежит большое
число многоатомных молекул, например Н2О, SO2, С2Н4,
Н2СО и др.
Вращательное движение асимметричного волчка с точки
зрения классической механики имеет более сложный харак-
тер, чем движение симметричного волчка. Для случая сво-
бодного движения (движения между столкновениями) полный
момент количества движения Р остается постоянным по ве-
личине и направлению, однако в молекуле нет более такого
направления, вдоль которого составляющая вектора Р
имела бы постоянное значение (для симметричного волчка
составляющая вектора Р вдоль собственной оси молекулы Р;
имеет, как мы видели выше, постоянное значение). Таким
образом, в общем случае не существует связанной с моле-
кулой оси, которая совершала бы простое вращение вокруг
вектора Р. Вращательное движение асимметричного волчка
можно представить как вращение относительно наибольшей
§ 5] ЭНЕРГИЯ ВРАЩЕНИЯ МОЛЕКУЛЫ АСИММЕТРИИ. ВОЛЧКА 183
или наименьшей оси инерции, причем ось эллипсоида опи-
сывает вокруг вектора Р сложную коническую поверхность,
которая не является замкнутой (о наглядном представлении
такого движения см. Герцберг [20]).
Пусть 1Л, 1В, 1С означают главные центральные моменты
инерции, расположенные в порядке возрастания (/а<//;</с).
Для энергии вращения будем иметь:
1 \ (Р\ Pr Р^\
еВ)> = 2 = У уЦ<7-26)
Задача определения уровней энергии асимметричного
волчка оказалась очень сложной. Решение этой задачи по-
казало, что уровни энергии не могут быть представлены
в явном виде формулой, аналогичной формуле (7.19).
Вопросу об определении уровней энергии было посвящено
много работ (см. М. А. Ельяшевич [126]). Для энергии
вращения асимметричного волчка Ванг [261] получил выра-
жение
tan
евг-^[^(^+1) + ^1, (7.27)
где J—вращательное квантовое число, a D и R — выраже-
ния, зависящие от главных центральных моментов инерции
/в, 7с.
°-г~Цгв+тУ (’.ЭД
«=я>(^+Й- <7-29’
Величина представляет сложную функцию от 1а, /д, !с
и J, значения которой могут быть определены из соответ-
ствующих вековых уравнений. Каждому значению J соот-
ветствует 2У —|— 1 значений wT, отмечаемых квантовым чис-
лом т, которое при данном J принимает 2J-\-1 значений.
Естественно, что степень вырождения уровня энергии в слу-
чае асимметричного волчка понижается по сравнению с сим-
метричным волчком. Для асимметричного волчка остается
пространственное вырождение вращения и степень вырожде-
ния уровня sjT составляет 2У—1 [вместо 2(274-1) или
(27+ 1)2].
184
УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ
[ГЛ. VII
Для обозначения уровней энергии асимметричного волчка
вместо квантового числа т можно применять пару квантовых
чисел Ka = K_i, Kc = K+i соответственно двум возможным
предельным случаям перехода от асимметричного волчка
к симметричному (вытянутый и сжатый волчок), причем
квантовое число т являет-
Таблица 15 ся разностью этих чисел:
Обозначение уровней энергии .асимметричного волчка т = (7.30)
Обозначение уровней
Уровень Обозначе- Обозначе- энергии асимметричного
ние уровня ние уровня волчка в зависимости от
энергии '4 к, J и т или J и пары
и д+1 представлено в тао-
Е0 % %, 0 лице 15, а вид этих уров-
Е1 1-1 1о, 1 ней —на чертеже20. Нуж-
Еа 1о 11,1 но заметить, что при дан-
Еэ Ч 11,0 ном J энергия возрастает с ростом т. Если ввести
ч 2-2 2q( 2 вместо моментов инер-
ч 2-! 21,2 ции их обратные величины
Е« 2о 2ы 1
е7 2t 2'2,1 а 1а
е8 22 2а, о Ь=ТВ- (7.31)
е9 З-з Зо,з
и т. д. и т. д. 1 С==Т' *0
то выражение для уровней энергии, как это следует из
формулы (7.27), примет вид
г«Р = £ {J(J+ 1) Ф+ [« -Ф] ’ (7.32)
К сожалению, это выражение не является явной формулой
для определения уровней энергии, так как нельзя выра-
зить в виде явной функции квантовых чисел и моментов
инерции, и эта величина должна быть определена из соот-
ветствующих уравнений. Последние, для первых значений J
были составлены рядом авторов. Такие уравнения до J=6
включительно приведены в монографии Герцберга [20]. Об-
§ 6] СТЕПЕНИ СВОБОДЫ КОЛЕБАТЕЛЬН. ДВИЖЕНИЯ В МОЛЕКУЛЕ 185
стоятельное исследование уровней энергии и других свойств
асимметричного волчка было предпринято Кингом, Хайне-
ром и Кроссом [239, 213, 240, 227] *). В этих работах
Приведены полезные таблицы. Вместо величины для
во/t чок
волчок
Черт. 20.
определения уровней энергии указанные авторы применяют
величину гт, связанную с -г»т простым соотношением.
Соответствие уровней энергии асимметричного волчка
с двумя предельными случаями (вытянутого и сжатого) сим-
метричного волчка представлено на чертеже 20.
§ 6. Число степеней свободы колебательного
движения в молекуле
Перейдем теперь к рассмотрению колебательных движе-
ний молекулы. В первом приближении мы будем предпо-
лагать, что эти колебания происходят независимо от других
движений, как это допускается при применении формулы (7.1).
В случае квазитвердых молекул амплитуды колебательных
*) См. также Голден [221].
186
УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ
[ГЛ. VII
движений оказываются очень малыми по сравнению с рас-
стояниями между ядрами. Для таких малых смещений мы
можем ввести предположение о гармоническом характере
колебаний.
Пусть молекула имеет N ядер. Для описания полного
движения их нужно применить 3Af координат, из которых
три описывают поступательное движение всей молекулы
в целом и три — вращение всей молекулы, если молекула
нелинейна. Таким образом, для описания колебательного
движения в случае нелинейной молекулы требуется ЗЛ7—6
координат и молекула имеет 3N— 6 колебательных степеней
свободы. В случае линейной многоатомной молекулы, вра-
щательное движение которой определяется только двумя
координатами, для описания поступательного и вращатель-
ного движения требуется пять координат. Следовательно,
линейная многоатомная молекула будет иметь 3N — 5 ко-
лебательных степеней свободы. Так, молекула С0.2, пред-
ставляющая трехатомную линейную молекулу, будет иметь
3-3 — 5 = 4 колебательные степени свободы. Моле-
кула СС14, принадлежащая к подклассу сферического волчка
и не являющаяся линейной молекулой, будет иметь
3-5 — 6 = 9 колебательных степеней свободы.
Если многоатомная молекула не является квазитвердой,
число колебательных движений, близких к гармоническим,
будет меньше 3N—6, так как часть степеней свободы
в этом случае соответствует внутренним движениям большой
амплитуды.
§ 7. Колебания в молекуле с точки зрения
классической механики
Рассмотрим сначала колебательные движения многоатом-
ной квазитвердой молекулы с точки зрения классической
механики. Задача расчета колебательного движения сво-
дится к определению формы и частот колебаний ядер в мо-
лекуле.
Для описания колебательных движений целесообразно
ввести естественные колебательные координаты, как это
было предложено М. А. Ельяшевичем [127, 131, 137], ко-
торый показал, что такие естественные колебательные коор-
динаты обладают рядом преимуществ. Описание равновесной
§ 7] КОЛЕБАНИЯ В МОЛЕКУЛЕ 187
конфигурации ядер в молекуле можно выполнить заданием
расстояний между ядрами и углов между связями. Число
таких независимых параметров, очевидно, будет равно числу
внутренних степеней свободы, т. е. оно будет равно ЗМ—6
для нелинейной молекулы и 3/V—5 для линейной. Так, на-
пример, для нелинейной трехатомной молекулы XYZ (черт. 21)
число независимых параметров
равно трем. В качестве таких пара-
метров можно выбрать два рас- /\
стояния XY и XZ и угол YXZ. / \
В процессе колебательных дви- / \
жений равновесные расстояния si / \
между ядрами и равновесные / \
углы будут изменяться. У z
В качестве естественных ко- q(.pT 21
лебательных координат, как по-
казал М. А. Ельяшевич, целесообразно выбрать изменения
равновесных расстояний si и равновесных углов Эти
изменения мы будем обозначать через Число таких ко-
лебательных независимых координат будет п = 3N—6 для
нелинейной многоатомной молекулы и n = 3N—5 для ли-
нейной. Если молекула находится в состоянии равновесной
конфигурации, естественные координаты qv q2, q3, ...
и т. д. будут равны нулю. Заданием этих независимых коле-
бательных координат полностью определяется изменение
равновесной конфигурации при колебаниях. Существенно
отметить, что естественные колебательные координаты не
зависят от положения и ориентации молекулы как целого.
Для малых колебаний, которые мы рассматриваем, мы
можем разложить потенциальную энергию V в ряд Тейлора
У(7Р q2, .... qn) =
= yo+2(^)o^+l•••’ (7-33)
г i.j
где индекс 0 указывает, что значения производных вычис-
ляются при = О, ?2 = 0....Если отсчитывать величину
потенциальной энергии от значения ее в равновесной кон-
фигурации (V = 0 при qy = 0, <?2 = 0, <73 = О, . . .), то вели-
чина Vq будет равна нулю. С другой стороны, в положении
равновесия (в равновесной конфигурации) потенциальная
188 УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ [гл. V11
энергия должна быть минимальна. Необходимым условием
равновесия является:
(В = ° <'=>. 2. 3.............») <7-34>
Таким образом, в формуле (7.33) первое и второе слагае-
мые обращаются в нули.. Положив
и ограничиваясь членами второй степени, мы получим:
(7.36)
i.j
т. е. потенциальная энергия представится в виде квадратич-
ной формы. Величины kij получили название силовых по-
стоянных или динамических коэффициентов. Они характери-
зуют силовую структуру молекулы. Из формулы (7.35)
следует, что = т. е. квадратичная форма будет сим-
метричной. Так, для молекулы XYZ в качестве естественных
координат мы можем выбрать изменения q2 и q2 двух связей
XY и XZ и изменение q.A угла между ними. Потенциальная
энергия молекулы XYZ будет:
V = J 4“ У *12?1?2 + у ^1зМз +
+ у ^21?2?1 + у *22?! + ~2 ^ЧчЧчЧч +
+ 4 + 4 ^32^2 + 4 (7-37)
или, принимая во внимание, что такая квадратичная форма
симметрична, т. е. что kij = kji, мы будем иметь:
V = 4 ku4* + 4 k^4'l + 4 + k12qyq.2 +
+ ^n4t Яч + ^ччЧчЧч- (7.38)
Частным случаем естественных координат являются ва-
лентно-силовые координаты, в качестве которых берутся
изменения расстояний между атомами, связанными химически
(т. е. изменения длин связей), и изменения валентных углов
§ 7] колебания в молекуле 189
между ними *). В еще более частном случае мы получим
так называемую модель чисто валентных сил, при примене-
нии которой в выражении потенциальной энергии пренебре-
гают всеми слагаемыми, кроме содержащих квадраты ва-
лентно-силовых координат. Так, потенциальная энергия мо-
лекулы XYZ при применении модели чисто валентных сил
будет иметь вид
<7-39)
Потенциальную энергию молекулы можно представить
также в виде (см. [189, 163, 139, 12])
2V = S^/iZ (7.36а)
где fi и fj — обобщенные силы, a k*j — так называемые
коэффициенты влияния.
Значения сил /,• можно найти дифференцированием (7.36). Мы
получим:
, дУ V а
fi ~ dq{ ~
3
Л. С. Маянц [163] показал, что коэффициенты влияния обладают
специфической инвариантностью, состоящей в том, что элементы
матрицы этих коэффициентов, относящиеся к данным координатам,
однозначно определяются выбором этих координат и не зависят от
выбора других координат **)
Обстоятельное изучение коэффициентов влияния было
проведено П. Г. Масловым [139—145, 98, 146, 151], при-
менившим их к изучению оптических и термодинамических
свойств органических молекул (см. § 11 главы X).
Для решения задачи определения частот и формы ко-
лебаний ядер в молекуле необходимо знать кинетическую
энергию молекулы. Хотя задача о малых колебаниях системы
Материальных точек рассматривалась многократно и ее ре-
*) Кроме валентно-силовых координат иногда используются
Центральные координаты, в качестве которых применяются измене-
ния расстояний между атомами. Частным случаем применения та-
ких координат является так называемая «модель центральных сил»
(см. М. А. Ельяшевич [137]), а также М. В. Волькен-
штейн, М. А. Ельяшевич и Б. И. Степанов [12].
**) Таким же свойством, как показал Л. С. Маянц, обладают и
Элементы матрицы, обратной матрице кинетической энергии.
190
УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ
[ГЛ. УЦ
шение в общем виде было известно давно *), применительно
к молекулам до недавнего времени не было создано удо-
влетворительных методов расчета колебаний. М. А. Ельяше-
вич и Б. И. Степанов вместо прежних малоудовлетворитель-
ных методов дали простой и удобный способ решения этой
задачи и рассмотрели ряд важных применений [127—136,
172—181).
Преимуществом этого способа является возможность прак-
тически быстро определить коэффициенты кинетической энер-
гии, выраженной через импульсы, и получить уравнения,
в которых неизвестные частоты входят только в диагональ-
ные члены.
Пусть естественные колебательные координаты будут qr,
q2,..., qn. Обозначим через qt, q2,..., qn скорости изме-
нения обобщенных координат по времени. Кинетическая
энергия, выраженная через qv q2,.. ., qn, представится
квадратичной функцией
7’=IS7’^W (7-40)
i. i
Обычный метод решения задачи о малых колебаниях состоит
в применении уравнений Лагранжа (см. [8, 39])
(г = 1, 2, 3,.. ., п). (7.41)
dt d4i dqt
Таких уравнений существует столько, сколько имеется сте-
„ , D дТ dV .
пеней свободы, т. е. п. Вычисляя -г- и — из формул (7.40)
dqi dqi
и (7.36) соответственно, мы получим:
<7-42)
d4i j
и
= (7-43)
j
*) См. учебники динамики, например: Л. Ландау и Л. Пяти-
горский [39]; Л. Г. Л о й ц я н с к и'й и А. И. Л у р ь е [43],
т. II; ср. Р. Курант и Д. Гильберт [34]; векторный метод
решения предложен Л. С. Маянцем [158], [163].
§71
КОЛЕБАНИЯ В МОЛЕКУЛЕ
191
Подставляя эти выражения в уравнения (7.41), получим
И уравнений вида
(7.44)
з з
или
2(^; + М>) = 0- (7-45)
з
Так, для нелинейной молекулы XYZ с тремя колебательными
степенями свободы мы получим три уравнения:
+ Т'зчЯч + 71з?з+^пЯ1 + + ^1з9з = °>
Т'чхЯх + Т^Яч + ?ыЯл + ^2171 + ^22^2 + ^23^3 = О,
ТмЯг + + Т 33(?3 4- ^3i?i + &з2?2 + ^зз'Уз = 0.
(7-46)
Решая систему уравнений (7.45), мы можем найти зави-
симость координат от времени.
Уравнения движения (7.45) приняли бы очень простой
вид, если бы нам удалось от естественных колебательных
координат перейти к таким координатам, при применении
которых все коэффициенты Т^- и Лу равнялись бы нулю
при i+j, т. е. выражения для потенциальной и кинетической
энергии содержали бы только члены с чистыми квадратами.
Если бы существовали такие координаты Qt, Q2,..., Qn,
мы имели бы:
Т = 4(ГиЙ+4$+... + Т™^) (7.47)
и
1^—"2 (&nQi~Ь&22Q2^rmQn). (7-48)
При применении уравнений Лагранжа к расчету движения
в таких координатах мы получили бы вместо уравнений (7.45)
совсем простые уравнения
TiiQi + k'aQ^O, 1 = 1, 2, 3,..., п. (7.49)
Для нелинейной молекулы XYZ с тремя степенями свободы
эти уравнения имели бы вид
T’nQi -ф- knQi — О,
T’aaQa -1— A22Q2 =: О,
T’aaQi -f~ ^ззФз = 0.
(7.50)
192 УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ [гл. VII
Можно показать *), что такие координаты существуют
при условии, если кинетическая и потенциальная энергии
системы выражаются в виде (7.36) и (7.40). В частном слу-
чае эти координаты можно выбрать так, чтобы кинетиче-
ская и потенциальная энергии имели вид
Г =4 ($ + $+• • + <?»). (7.47а)
И = 4(М?! + ^ + -.- + М2»). (7.48а)
В этом случае коэффициенты перед квадратами в формуле
кинетической энергии обращаются в единицы. Обобщенные
координаты, при применении которых потенциальная и кине-
тическая энергии имеют вид (7.47а) и (7.48а), т. е. не содер-
жат членов вида QiQj и Qfij при /=#/, и коэффициенты
перед квадратами в формуле кинетической энергии равны
единице, получили название нормальных координат **).
Переход от естественных координат к нормальным мы
можем осуществить путем линейных преобразований
= (7-51)
i
где Bki — постоянные коэффициенты. Это вытекает из ли-
нейности уравнений движения (7.45) ***). Легко видеть, что
уравнения движения при введении нормальных координат
решаются сразу. Действительно, подставляя в уравнения
Лагранжа выражения (7.47а) и (7.48а), мы получим
+ Ш = 0 (/ = 1,2,3........п). (7.52)
Заметим, что уравнения (7.52) получаются из уравне-
ний (7.49), если ввести
k'-
= (7.53)
* а
*) См. Е. Т. Уиттекер [62].
**) Иногда нормальным координатам дается несколько более
общее определение, чем приведенное выше. Под нормальными ко-
ординатами понимают такие координаты, в которых выражение энер-
гии имеет вид 7= — и V = ^iQi< где — постоянная.
i i.
***) См. М. В. Волькенштейн, М. А. Ельяшевич и
Б. И. Степанов [12].
§ 7] КОЛЕБАНИЯ В МОЛЕКУЛЕ 193
решение каждого из уравнений (7.52) можно представить
в виде
С^С?51п(/^4-о4). (7.54)
Таким образом, каждая из нормальных координат Qi совер-
шает гармоническое колебание с циклической частотой
= (7.55)
и начальной фазой о^.
Обычная частота v (число колебаний в единицу времени)
будет:
Теперь мы можем вернуться к естественным координатам.
Подставляя решения (7.54) в формулу (7.51), получим:
9/£ = S5A.iQ?sin(coi!? + Si), (7.57)
г
т. е. реальное движение в молекуле (изменение естественных
координат со временем) может быть получено суперпози-
цией (наложением) простых гармонических колебаний
вида (7.54). Эти простые колебания получили название нор-
мальных колебаний.
Для системы с п колебательными степенями свободы мы
в общем случае получили п различных частот: ш2.....<оп.
Они называются частотами собственных колебаний молекулы
или просто частотами колебаний. В частном случае может
получиться, что среди этих п частот некоторые оказываются
равными. Тогда мы говорим о вырождении колебаний. Если
частоты = <о2 = ... = <ок = а, говорят, что данное коле-
бание с частотой а вырождено А-кратно. Так, например,
для молекулы метана СН4 обладающей высокой симметрией,
мы имеем следующие значения девяти частот:
— 2085 см-1,
ч2 = = 1054 см-1,
= м6 — ч6 = 2258 см-1,
— \п --- 996 см-1.
В этом примере частота 1054 см-1 вырождена двукратно,
а частоты 2258 см-1 и 996 см-1 вырождены трехкратно.
Частота 2085 см-1 невырождена (вырождена однократно).
13 Зак. S35. И. Н. Годнее
194 УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ [гл. VII
Для определения вида смещений, соответствующих одному
нормальному колебанию (вида нормального колебания), по-
ложим в частном случае, что все Q° = 0, за исключением
одного. Так, для определения вида первого нормального
колебания положим, что все ($ = 0, кроме Q}. В этом слу-
чае из уравнения (7.57) мы будем иметь:
^B^sin^ + Sj). (7.58)
Мы видим, что при осуществлении первого нормального ко-
лебания все ядра будут смещаться из положения равновесия
с частотой шх. Амплитуды смещения будут разными в зави-
симости от коэффициентов Вк1. На чертеже 22 изображен
Черт. 22.
вид нормальных колебаний молекулы Н2О, причем величина
стрелок пропорциональна действительным смещениям. Реаль-
ное движение в молекуле, как указано выше, получается
суперпозицией (наложением) нормальных колебаний.
§ 8. Симметрия нормальных колебаний
При изучении колебаний большое значение имеет определение
симметрии нормальных колебаний. Симметрия характеризует пове-
дение смещений нормального колебания при преобразованиях сим-
метрии молекул. Так, при выполнении всех операций симметрии
молекулы НгО (симметрия С^) смещения колебаний и (см.
черт. 22) преобразуются сами в себя. Такие нормальные колебания
получили название симметричных. Поведение колебания ч3 по от-
ношению к операциям симметрии оказывается более сложным:
при операциях Cj и отражении в плоскости молекулы оно пре-
образуется само в себя, а при выполнении остальных двух опера-
ций симметрии меняет знак.
По отношению к заданной операции симметрии нормальное
колебание может вести себя трояким образом: оно может преобра-
'§ 91
ВЕКОВОЕ УРАВНЕНИЕ
195
зоваться само в себя, может изменить знак смещений или может
претерпеть более сложные изменения. Симметрия колебания за-
дается его поведением по отношению ко всем операциям симметрии.
'Симметричное колебание остается неизменным при всех операциях
симметрии. Такое колебание обычно обозначается буквой А. Другие
случаи симметрии обозначаются буквами В, Е, Т с индексами, при-
чем имеются таблицы *), характеризующие поведение данного ко-
лебания по отношению ко всем операциям симметрии. Так, колеба-
ние ч9 молекулы Н2О оказывается имеющим симметрию Каждой
группе симметрии молекулы соответствует определенное число таких
случаев симметрии.
Классификация всех нормальных колебаний задается обычно
формулой вцда
D — -|- b1Bi -]- ..., (7.58а)
показывающей, сколько и каких колебаний имеет данная молекула.
.Если колебание вырождено (симметрия таких колебаний обозна-
чается символами Е и Т), при подсчете числа колебаний нужно
учесть степень вырождения. Например, для молекулы Н2О фор-
мула (7.58а) имеет вид
0 = 24 + ^. (7.58b)
Это означает, что молекула Н20 имеет три нормальных колебания
две симметрии и одно — Bt. Для колебаний молекулы метана
получается:
П=Д1 + Д + 27’2, (7.58с)
откуда следует, что из ЗА— 6 = 9 колебаний существуют одно
'.симметричное колебание Alt одно двукратное вырожденное коле-
бание типа Е и два трижды вырожденных колебания типа Т2.
| § 9. Вековое уравнение для определения
| частот колебаний
fc Для вычисления термодинамических функций нужно знать ча-
Йстоты колебаний молекулы <о2, ..., ып. Однако для их опреде-
ления не требуется обязательно отыскивать переход к нормальным
ККоординатам и приводить уравнения движения к виду (7.49). Про-
Кцесс перехода к нормальным координатам, т. е. вычисление коэф-
фициентов преобразования (7.51), представляет дело далеко не
Вйростое **).
К, Для определения частот <л2, .... ч>п мы можем получить
Вуравнение n-й степени следующим образом. Пусть мы приме-
нили естественные координаты qb q->.....qn. Уравнения движения
с *) См. Г. Герцберг [20[. Это — таблица так называемых
|Нрактеров неприводимых представлений групп симметрии моле-
кулы. Вместо символа Т часто применяется символ Е.
fc **) См. М. В. Волькенштейн, М. А. Ельяшевич и
₽• И. Степанов [12].
|л 13*
196 УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ [гл. Vii
в этих координатах, как мы нашли в предыдущем параграфе,
имеют вид (см. уравнения (7.45))
S(M‘j + W = ° (/=1, 2 3, ..., л). (7.59)
Частное решение этого уравнения, как это следует из формулы
(7.57), мы можем представить в виде
qj = 7” sin (со/6). (760)
Подставляя в уравнения (7.59) значение производных
4j = q°ju> cos (mf + о) ]
и „ ) (7-61)
qj = ~4j “3 sin + 8) = — j
получим:
= 0 (7.62)
3
2 (kij - ^Ttj) qj^O (I = 1, 2............n). (7.63)
J
В развернутом виде эти п уравнений будут иметь вид
(+1 — “3Л1) 71 + (^12 — 7г+- • -+(^m — ш) Яп — 0>
(+t — "^Т’гх) 71 + (^22 — ш27"22) 7г+- • -+№п — 0>3Т'2п) Яп = 0,
(^ni — u)37’nl) 71+ (+2 — 0)3Т’п2) 7г + • • • +
+ (knn — ^Тпп) qn = 0.
(7.64)
= 0. (7.65)
Условием разрешимости этой системы п однородных уравнений,
как известно, является равенство нулю определителя *)
^11 — ТЦщ3 ^12 — Т12ф3 • • • — 7" 1ПО>3
&21— Т'2гш3 ^22 — Т'22'Ь3 ... k}n— Т'чпи^
knl 7'п1ш2 kn2 ТпДРР • • knn 7'пп<о2
Этот определитель, который может быть сокращенно записан
в виде
I ^j - | = 0, (7.66)
будет содержать к = шЗ в л-й степени. Уравнение (7.66) (так назы-
ваемое вековое уравнение) будет иметь л корней kj, k2..., k„.
Решая его, мы найдем искомые частоты (Dj, ..., <яп (некоторые
из них могут быть равными в случае вырождения). Однако это
*) См. А. Г. К у р о ш [36].
ВЕКОВОЕ УРАВНЕНИЕ
197
, § 9]
уравнение обладает весьма существенным недостатком: неизвестное
X = <с2 входит, вообще говоря, в каждый элемент определителя и
решение этого уравнения будет громоздким.
М. А. Ельяшевич [127—132] разработал общий удобный метод
составления векового уравнения, при применении которого веко-
вое уравнение содержит неизвестное X только в диагональных
членах *). Такое уравнение может быть составлено, если исходить
не из коэффициентов 7,-у в выражении (7.40), а из коэффициентов
матрицы (A(-ft), обратной матрице (Ту). Для вычисления коэффи-
циентов A4-ft М. А. Ельяшевичем [131, 137, 12] были составлены
удобные таблицы; такие таблицы получаются при непосредствен-
ном составлении уравнений движения в векторном виде в естест-
венных координатах. Эти коэффициенты А{к получили название
коэффициентов кинематического взаимодейстия, или кинематиче-
ских коэффициентов. Преимуществом метода М. А. Ельяшевича
является также возможность простого перехода от естественных
координат к так называемым координатам симметрии (см. ниже),
благодаря чему вековое уравнение еще более упрощается.
Для упрощения векового уравнения, следуя М. А. Ельяшевичу,
введем коэффициенты Ац, удовлетворяющие условию **)
= (7.67)
i
где
. _ ( 1 при /=у,
( 0 при l=pj-
Умножая каждое из уравнений движения (7.59) на соответствую-
щий элемент Ац и суммируя по I, получим:
2 Au + М? = 0 (1 = 1, 2, 3..п). (7.68)
i.3
В силу соотношения (7.67) каждое из уравнений движения теперь
принимает вид
41 + 2 = °- (7'69)
Подстановка решения в виде (7.60) дает (см. также формулу (7.61):
- +2 A= 0 (/ = 1, 2, 3..п) (7.70)
i.j
ИЛИ
а = 0 (/=1,2,3........и). (7.71)
i j
*) Эквивалентный, но менее удобный метод был предложен
Вильсоном [265]. Вопрос о разных формах векового уравнения
был рассмотрен В. М. Татевским [189], а также Л. С. Маян-
ием [163].
**) To-есть мы вводим матрицу (А) с элементами Ац, которая
(обратна матрице (Г). Уравнение (7.67) в матричной форме озна-
чает (А) (Г) = £,
198
УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ
[гл. VII
Введем коэффициенты
Dy = 2 Auky. (7.72)
i
Эти коэффициенты получили название коэффициентов полного
взаимодействия. Следует заметить, что Dy #= Dji, т. е. эти коэф-
фициенты не являются симметричными относительно индексов I и j.
Теперь, как это следует из (7.72), мы будем иметь:
S Dy4j - = 0 (/ = 1, 2, 3...п) (7.73)
з
Выпишем эти уравнения в раскрытом виде, придавая / значения
1, 2, 3...п. Мы получим:
D^q^ + -01272 + • • • + Dlnqn — ей?! = 0, )
Oai7i + O2272 + • • + О^пЯп — <&qz = Q, у (7 74)
0,1,71 + Dn2<j2 + ... + Dnnqn — <i>2qn = 0 ]
или
(0ц — ы3) 7t ~ О127г + • • + Dinqn — О,
01271 +(-Das — ю3) 7з + • • • + О2п7>1 — 0, (7 75)
Oni7i + D^q^ + ... + (Dnn — w2) qn — 0.
Из условий разрешимости [уравнений (7.75) (равенства нулю опре-
делителя) следует:
Dll— “3 f>12 • • в1п
Z)22 — • D^n = 0. (7.76)
Ont О,,2 ... Dnn
Это уравнение получило название естественного векового уравне-
ния. Неизвестное \ = и& входит в него только в диагональные
элементы определителя. Из него могут быть определены частоты
колебаний wt, «>2, ш3..о>п. Подставляя в (7.75) первый корень wt,
затем второй корень нт. д. и решая соответственно системы
уравнений (п-систем), мы можем определить изменение естествен-
ных координат при выполнении 1-го, 2-го и т. д. колебаний. Так
может быть найдена форма колебания. Следует заметить, что
решение таких однородных уравнений позволяет определить только
относительные значения амплитуд.
Решение уравнения (7.76), представляющего уравнение л-п
степени относительно неизвестного /. = о>3, является при больших
степенях п довольно сложным и громоздким. Поэтому большое
значение приобретает' упрощение этого уравнения. В том случае,
если молекула обладает симметрией" вековое уравнение (7.76)
можно привести к совокупности нескольких уравнений низших
степеней путем введения координат симметрии. Вопрос о введении
§ 10] КВАНТОВОМЕХАНИЧЕСКОЕ РАССМОТРЕНИЕ КОЛЕБАНИЙ 199
координат симметрии был подробно рассмотрен М. А. Ельяшеви-
чем *), который составил таблицы коэффициентов симметрии, позво-
ляющие легко произвести переход к координатам симметрии и об-
легчить составление векового уравнения.
При применении координат симметрии вековое уравнение
принимает вид
(7.77)
где заштрихованные блоки представляют вековые уравнения мень-
ших степеней с неизвестным X — входящим в диагональные
элементы определителя. Таким образом, вековое уравнение сте-
пени п распадается на ряд вековых уравнений меньших степеней
л1( Иг...пк, причем п = nj-J-ng-h. • .-]-Пк- Степени nt, п2, .лд
зависят от симметрии молекулы **).
При изучении колебаний многоатомных молекул возникают
двоякого рода задачи: определение постоянных потенциальной
энергии (динамических коэффициентов и коэффициентов влияния)
по экспериментально наблюдаемым частотам и вычисление частот
колебаний по известным значениям постоянных потенциальной
энергии. Значительные успехи в решении этих задач были сделаны
М. А. Ельяшевичем, Б. И. Степановым, М. В. Волькенштейном и
другими советскими исследователями (см. [12, 50]).
§ 10. Квантовомеханическое рассмотрение колебаний
Рассмотрим теперь колебания многоатомной квазитвердой
молекулы с точки зрения квантовой механики. Наиболее простое
решение задачи о колебаниях получится при применении нормаль-
ных координат.
Волновое уравнение для колебательных движений в естествен-
ных координатах qt (п степеней свободы) будет иметь вид
НЬ = еф, (7.78)
: где ф (qb 72.Qn) — волновая функция естественных координат,
Н—оператор энергии и е — собственное значение энергии. Вид
*) См. М. А. Ельяшевич [132, 135, 137]; см. также
ГМ. В. Волькенштейн, М. А. Ельяшевич и Б. И. Сте-
i панов [12]. Новый способ учета симметрии разработан недавно
Л. С. Маянцем [164].
;; **) См. Г. Герцберг [20], М. В. Волькенштейн,
f М. А. Ельяшевич и Б. И. Степанов [12].
200
УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ
[ГЛ. VII
оператора энергии при применении естественных координат легко
найти, использовав классическое выражение для энергии и метод
соответствия классических формул формулам квантовой механики.
Этот оператор будет иметь простой вид, если использовать
нормальные координаты Qb Q2, ..., Qn. При применении нормаль-
ных координат потенциальная и кинетическая энергии будут иметь
вид (см. § 7 этой главы)
(7-79)
к
T = (7.80)
к
Выше мы показали, что коэффициент Ьк равен (см. формулу
(7.55)). Таким образом,
(7.81)
к к
Обобщенные импульсы при применении нормальных координат Qk
будут:
= <7.82)
oQk
Запишем теперь выражение энергии в классической механике через
координаты и импульсы. Мы получим:
= + (7-83)
к к
Для получения оператора энергии Н в формуле (7.83) выражения
для координат и импульсов нужно заменить соответствующими опе-
раторами. Для координат таким оператором будет оператор умно-
жения, а для импульса имеем:
' _ Л д
P^Wl’dQ^’
Подставляя эти значения в выражение (7.83), получим:
или
(7.84)
(7.85)
(7.86)
к к
"=2
Л
А2 д2 ’ 1
Втг2 dQl+ 2
§ 10] КВАНТОВОМЕХАНИЧЕСКОЕ РАССМОТРЕНИЕ КОЛЕБАНИЙ 201
Волновое уравнение (7.78) примет вид
S(- к № дзф \ 8л2 dQ2kl 1 + ~ 0>lQ& = Ч (7.87)
или ут даф + ^(е Л2 \ to 1. •—* -G- 11 р (7.88)
В уравнении (7.88) волновая функция ф является функцией нор-
мальных координат Qlt Q.,.Qn. Положим
b = MQJW---MQn)- (7.89)
При применении выражения (7.89) волновое уравнение распадается
на п уравнений, из которых каждое имеет вид
причем
e = 2efc' (7.91)
Уравнение (7.90) представляет, как легко видеть, уравнение для
одномерного гармонического осциллятора. Решая его, мы получим;
Ч&к (7.92)
^(Qk) = Nvle 2
и
Ч = (v/c + у) A'jfe, (7.91a)
где 2?ru>fc ак = — (7.93)
и 'fc 2тг (7.94)
— классические частоты нормальных колебаний, а и* — соответствую-
щее квантовое число, причем 0^ = 0, 1, 2, 3, ..., п.
Таким образом,
г=2(^+4)^- <7-95)
< к
Из выражения (7.95) следует, что уровень энергии опреде-
ляется набором п квантовых чисел и1, v.2.vn. Такой
Уровень энергии целесообразно обозначать символом s(w1,
......Наинизшим уровнем будет уровень с = О,
202 УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ [гл. VII
-и2 = 0, vn = 0. Этому уровню соответствует нулевая
колебательная энергия
го = 2~ у ^2 + ••• (7.96)
В многоатомной молекуле она, как это следует из формулы
(7.96), может в некоторых случаях достигать значительной
величины. Соседними (не обязательно самыми близкими)
с нулевым уровнем энергии будут уровни, для которых одно
из квантовых чисел равно единице, а остальные — нули. Та-
кими уровнями энергии будут е(1, 0, ..., 0), е(0, 1.......
0).....е(0, 0, .. ., 1). Схема части уровней колебательной
энергии молекулы SO2 (^ = 1151 см'1, ч.2 — 519 см'1,
v3= 1361 см'1) изображена на чертеже 23.
В зависимости от величины частот возможен случай, когда
уровень е(0, 1, 1, .. ., 0) лежит ниже уровня s (1, 0, . .., 0)
(см. черт. 23).
. Следует заметить, что частота испускаемого кванта энер-
гии при переходе молекулы из возбужденного состояния
в другое, как это следует из известного соотношения
= —(7.97)
§ 10] КВАНТОВОМЕХАНИЧЕСКОЕ РАССМОТРЕНИЕ КОЛЕБАНИЙ 203
вообще говоря, не будет совпадать ни с одной из нормаль-
ных частот колебаний молекулы. Однако в частном случае
при переходе, когда одно из квантовых чисел vk изменяется
на единицу, причем другие остаются постоянными, частота
испускаемого излучения будет равна частоте молекулы чк.
Действительно, в этом случае мы имеем:
Ч- (ук + 1 + у) h'ik-ф- .. . j — +
4“ (^‘2 Ч- у) ^-2 + 4“ [vk + у) (7.98)
откуда
(7.99)
Волновая функция, описывающая колебательное движение
молекулы, как это следует из формулы (7.89), будет про-
изведением функций (7.92), описывающих движение каждого
из осцилляторов.
Формула (7.95), определяющая энергию молекулы, в слу-
чае вырождения частот может быть записана иначе. Пусть
частота с номером k вырождена /и^-кратно. Энергия, соот-
ветствующая этому колебанию, будет:
слагаемых
= h^k + v-2 + 4“ • • • Ч- Vm Ч- у ) •
Вводя квантовое число
^ = •^1 + ^+ • •
(7.100)
(7.101)
описывающее состояние вырожденного колебания, мы получим:
Зк = ^к + у)-
(7.102)
Для энергии всей молекулы будем иметь:
г = h'>k (vk Ч~ у) •
к
(7.103)
204 УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ [гл. VII
Суммирование в этой формуле производится только по коле-
баниям различных частот, т. е. каждое вырожденное коле-
бание считается только один раз. В случае вырождения ча-
стот уровень энергии будет, вообще говоря, вырожденным.
Степень вырождения уровня зависит от кратности выро-
ждения частоты и квантового числа vk, определяемого фор-
мулой (7.101). Можно показать, что степень вырождения
уровня энергии, если колебания являются строго гармониче-
скими, будет (см. [20], [12]) для двукратно вырожденного
колебания
^2 = ^4-1. (7.104)
Для трехкратно вырожденного колебания
g3 = j(^+ !Ш + 2). (7.105)
Легко видеть, что для нулевого колебания (vA = 0) выро-
жденной частоты степень вырождения будет равна единице,
т. е. вырождение энергии для этого уровня отсутствует.
§ И. Влияние ангармоничности колебаний
на уровни энергии
До сих пор мы предполагали, что колебания в молекуле
являются гармоническими. В действительности такое пред-
положение приближенно. Понятие нормальных колебаний
было введено нами при условии, что потенциальная энергия
представляется квадратичной формой, т. е. что в выражении
потенциальной энергии (7.33) можно ограничиться только
квадратичными членами. При более точном расчете надле-
жит учесть кубические члены и члены более высоких сте-
пеней. В этом случае колебания ядер в молекуле мы не
имеем права рассматривать как гармонические и надлежит
учесть влияние ангармоничности.
Разлагая в ряд выражение потенциальной энергии как
функции естественных координат qt, q2, .... qn, мы теперь
в отличие от (7.36) будем иметь:
2V= S 2 fijk4i4j4k~\~
i, j i, j, к *
+ 2 ё^кгЯгЧзЧкЧгА- ••• (7.106)
», /, к, 1
ВЛИЯНИЕ АНГАРМбЙИЧНбСТЙ КОЛЕБАНИЙ
205
§ И)
В случае ангармонических колебаний как при примене-
нии классической, так и квантовой механики полная энергия
ТV не может быть представлена в виде суммы энергий
независимых, хотя бы и ангармонических колебаний.
Переход к нормальным координатам, которые надлежит
определить как координаты, в которых кинетическая энергия
приводится к виду (7.47) и квадратичные члены потенциаль-
ной энергии к виду (7.48), не позволяет устранить все пе-
рекрестные члены (при применении нормальных координат
остаются слагаемые третьей и более высоких степеней).
Волновое уравнение в нормальных координатах уже не
распадается на несколько независимых выражений.
Для уровней энергии молекулы, не имеющей вырожден-
ных частот, получается выражение
6 = к + у) + ^хкк (?к + у) +
к к
+ hxkt [vk + у) (т»г + у) -|- .. ., (7.107)
1>к
в котором постоянные хкк и хк1 учитывают влияние ангар-
моничности. Они обычно малы по сравнению с частотами
нормальных колебаний чк. Так, для трехатомной молекулы
й случае отсутствия вырожденных частот выражение (7.107)
принимает вид
е = h'<x (®t + 4) + (®2 + у) + (v-s + 4) +
-\-hXlt (®l + y) + ^x22 (®2 + у) + yj +
+ hx1<2 у) + у) + (^I + у) (^з + y) +
+ Ax23^2 + y) ^3~l_4)_|_ (7-108)
Нулевая энергия молекулы, как это следует из формулы
(7.107), будет:
<7-109>
к к 1>к
Если отсчитывать колебательную энергию не от миниму-
ма поверхности потенциальной энергии, как это сделано
206
УРОВНИ ЭНЕРГИЙ КВАЗИТВЕРДЫХ МОЛЕКУЛ
[гл. Vn
в формуле (7.107), а от наиболее низкого колебательного состо-
яния = 0, v2 — 0, . . ., vk — 0, . . .), в котором молекула
имеет энергию (7.109), мы будем иметь:
s^, u2, vA, ...) —г(0, 0, ..., 0) =
— htiV! • • • Ч~ h'inVn -|- hXiiVi -|-
-|- hx22V2 -|- hx^vl -|- ... -|- hxnnvn-\- h 2 xki'vkvi’ (7. ИО)
1>к
где x°ik = xik (если мы ограничимся рассмотрением вторых
степеней квантового числа V) и
। । 1 V11’ ''l — Д + Х11 + у 1>к хкГ
0 1 1 1 V(2) — ';2 Ч~ Х22 ~Г 9~ Zj г>к Хк1
0_ | .1 V(3) чз —''з+^зз+у 1>к Хк1
(7.1П)
Таким образом, в случае • многоатомных молекул, как и
в случае двухатомных, следует различать частоты \2,
у3, ..., уп и Mi, v2, ...уп. Первые из них соответствуют
частоте че или ше, а вторые — частоте v0 или ш0 двухатом-
ной молекулы. Частоты v2.........уп можно назвать часто-
тами при бесконечно малых амплитудах. Обычно разности
частот ук и Vfc не очень велики. Однако для колебаний,
связанных с атомами водорода, это различие довольно зна-
чительно. Так, для молекулы Н2О мы имеем:
-^ = 3825,3 см~1, у2 = 1653,9 см'1, — 3935,6 см~1,
'^ = 3693,9 см-1, м°= 1614,5 см~1, = 3801,8 см~1.
Легко видеть, что частота испускаемого кванта энергии
при переходе из состояния vk — 1 в состояние vk — 0 при
всех других квантовых числах, равных нулю, уже не будет
совпадать с частотой ук, как это имело место для гармони-
ческих колебаний (см. формулу (7.99)). Для частоты испу-
§ 12] ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧАСТОТ КОЛЕБАНИЙ 207
скаемого кванта -»'к, как это следует из формулы (7.97) и
значений энергии (7.107) и (7.110), получается:
ук — '*к + хкк = 'Jk + ^хкк + ~2 Х}1- (7.112)
1>3
Эти частоты м' иногда называются основными наблюдаемыми
частотами. В случае Н2О они имеют следующие значения:
м'== 3651,7 см~1, v'= 1595,0 см-1, ч'= 3755,8 см-1.
Выведенные формулы относятся к молекулам, не имеющим
вырожденных колебаний. В случае наличия вырожденных
колебаний формула.для энергии (7.107) заменяется несколько
более сложной (см. Герцберг ]20]).
§ 12. Экспериментальные основания определения
частот колебаний
В предыдущих параграфах мы видели, что для опреде-
ления уровней энергии многоатомных молекул необходимо
знать частоты нормальных колебаний ч2> • • • • vn- Исклю-
чительно важное значение для анализа состояний многоатом-
ных молекул, в особенности их колебательных состояний,
имеет открытие комбинационного рассеяния света, сделан-
ное Л. И. Мандельштамом и Г. С. Ландсбергом [138]
в Москве в 1928 г. и одновременно Раманом в Калькутте.
Благодаря этому открытию стало возможным с помощью
сравнительно простой аппаратуры найти частоты колебаний
молекул (см. [20]). Другим источником наших сведений
so частотах колебаний являются инфракрасные спектры *).
I настоящему времени накоплен обширный эксперименталь-
1й материал, особенно по спектрам комбинационного рас-
яния. Оба метода — изучение спектров комбинационного
юсеяния и изучение Инфракрасных спектров — взаимно до-
•лняют друг друга. Дело в том, что не всегда все коле-
ния будут активными в спектре комбинационного рассеяния
инфракрасном спектре, может быть так, что данное коле-
ние разрешено в спектре комбинационного рассеяния и
♦) Обзоры по инфракрасным спектрам и их применениям
. [205] и [226], где приведена обширная литература.
208
УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ
[гл. vit
запрещено в инфракрасном и наоборот. Возможны колебания,
которые запрещены в обоих спектрах. Поэтому наилучшие
результаты по определению колебаний дает совместное при-
менение обоих спектров.
Очень большую помощь при определении частот нормаль-
ных колебаний имеет изучение спектров изотопических мо-
лекул, например Н2О, D.2O и HDO, обладающих практиче-
ски одинаковыми потенциальными энергиями. Сравнение спек-
тров таких изотопических молекул позволяет выполнить
правильное отнесение наблюдаемых в спектре частот к тому
или иному нормальному колебанию молекулы, а также вы-
полнить определение силовых постоянных.
Существенную помощь при изучении колебаний изотопи-
ческих молекул оказывает правило произведений, устана-
вливающее зависимость между произведениями частот коле-
баний данной симметрии двух изотопических молекул [255] *).
Для колебаний данной симметрии правило произведений
имеет вид
Г f I
Уг • • •
• • • ->d
(7.113)
где Л1 и М' — массы двух изотопических молекул, Iv, I.
и Ixlylz—главные центральные моменты инерции, а
ч2, ..., и ч', ч'....-/— соответствующие частоты коле-
баний данной симметрии **). Применительно к произведению
всех п частот колебаний правило произведений принимает вид
f ! /
• • • ''п
V2 • • ‘‘п
лГW. (7.114)
F V”l/ \тз/ VW V / 7 я///
В формуле (7.114) т2, ..., и rn'i, /п2.......т'н озна-
чают соответственно массы атомов двух изотопических
молекул, содержащих по N атомов. Заметим, что в правило
*) Недавно Л. М. Свердлов [168, 169] вывел правило сумм
и некоторые другие полезные соотношения между частотами изо-
топических молекул.
**) Значения остальных символов см. Г. Герцберг [20], где
имеются удобные таблицы для вычисления я, [1...t,
§ 13] ХАРАКТЕРИСТИЧЕСКИЕ ЧАСТОТЫ 209
произведений следует подставлять частоты при бесконечно
малых амплитудах.
Для определения колебаний могут быть в некоторой сте-
пени использованы спектры поглощения в видимой и ультра-
фиолетовой области, а также спектры флуоресценции *).
Большое значение при определении частот колебаний
приобретают также методы вычисления их, разработанные
Ельяшевичем и Степановым [127—133, 135, 136, 172, 173,
179—181]. Б. И. Стёпанов [174—181] выполнил расчет
частот колебаний большого числа молекул.
Анализ колебательных состояний многоатомных молекул
приобрел к настоящему времени очень большое значение
как для определения структуры молекул, природы химиче-
ской связи, природы жидкого и твердого состояний, так
и для анализа углеводородов. В изучении колебательных
спектров и их применений выдающееся место занимают ра-
боты советских ученых: Г. С. Ландсберга, П. А. Бажулина,
Е. Ф. Гросса, М. В. Волькенштейна, П. П. Шорыгина,
М. И. Батуева, А. И. Бродского, В. М. Чулановского,
В. М. Татевского и др. **).
§ 13. Характеристические частоты
При определении частот колебаний многоатомных моле-
кул весьма существенную помощь оказывает наличие так
называемых характеристических частот. Действительно, изу-
чение колебательных спектров многоатомных молекул по-
казало, что спектры молекул, обладающих одними и теми же
характерными химическими группами или связями, очень
часто имеют некоторое число весьма близких частот. Такие
частоты получили название характеристических. К их
числу относятся, например, частоты, сопровождающие связи
С—Н, С=С, С=С, С=О, С—С1 и другие. Теория харак-
теристических частот была построена недавно Л. С. Маян-
цем сначала для отдельных связей [159], а затем им была
дана общая теория этого вопроса [163]. Л. С. Маянц
*) См. А. Н. Т е р е н и н [61]; Б. С. Н е п о р е н т и Б. И. С те-
па н о в [165].
**) Подробную сводку этих работ см. Г. Герцберг [20]
(дополнения редактора); М. В. Волькенштейн, М. А. Е л ь я-
Шевич и Б. И. Степанов [12] и М. В. Волькенштейн [13],
где дан обстоятельный список литературы.
14 Зак. 835. И. Н. Годнее
210 УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ [гл. VII
показал, что следует различать характеристичность формы и
характеристичность частоты колебания. Им были разрабо-
таны специальные методы расчета частот характеристических
колебаний[160—163].
В качестве примера в таблице 16 приведены некоторые
характеристические частоты (полную таблицу характеристи-
ческих частот см. [12]).
Влияние структуры молекул на характеристические ча-
стоты связей было исследовано Я. К. Сыркиным и сотруд-
никами [182—184, 104, 170, 202], получившими ценные
результаты.
Таблица 16
Группа Характеристи- ческие частоты, в см~г Характер колебаний
*с-н 3300 Валентный
&С-Н . 3020
>с-н 2960 2>
>С = 0 1720
-ос- 2050
>с=с< 1650 »
>с-с< 900
>C-F 1049
> С-Cl 648
>С-0Г 647—563
>C-J 593—502
^с-н 700 Деформационный
1100
,н
•‘СгН 1000
н
г>н "с>н 1450
C = N 1665—1658
о-н 3400—3300
Изучение характеристических частот привело к введению
понятия о валентных и деформационных колебаниях. Приме-
нение естественных координат, в частном случае валентно-
§ 13] ХАРАКТЕРИСТИЧЕСКИЕ ЧАСТОТЫ 211
силовых координат, оправдывает это. В самом деле, хотя
при каждом нормальном колебании и изменяются все коле-
бательные координаты, но часто можно выделить группу
координат, которые преимущественно изменяются при дан-
ном колебании. Таким образом, существуют колебания, при
которых преимущественно изменяется длина данной связи,
например СП. Такие колебания получили название валент-
ных. Деформационные колебания состоят в изменении вели-
чин углов между связями. Однако следует заметить, что
применение терминов валентное колебание или деформа-
ционное колебание является приближенным, причем степень
приближения бывает различной в разных случаях. Такое
разделение колебаний возможно не всегда, так как в неко-
торых случаях нельзя выделить преимущественное изменение
длин связей или углов. При наличии характеристических
деформационных и валентных частот возможно довольно
значительное изменение и некоторых других координат.
Так, в валентном колебании метана с частотой 3022 см~г,
как показал Б. И. Степанов [174], углы меняются довольно
сильно. Деформационные колебания, как правило, имеют
значительно меньшую частоту, чем валентные.
Деформационные колебания (частоты), связанные с изме-
нением углов внутри данной группы атомов, например
группы СН3 или СН2, получили название внутренних дефор-
мационных колебаний. Другим типом деформационных ко-
лебаний являются внешние деформационные колебания, при
которых углы между связями в группе остаются неизмен-
ными, но изменяются углы, определяющие ориентацию
группы в целом по отношению к соседним связям.
При описании валентных и деформационных колебаний
принято указывать, к каким связям и углам они относятся.
Поэтому говорят о валентном колебании С—С, валентном
колебании С=С, валентном колебании С—С1, деформацион-
ном колебании угла С—С—С или Н—С—Н и т. д.
Пусть дана N-атомная разветвленная нелинейная моле-
кула, которая не содержит замкнутых колец атомов, и
пусть возможна классификация колебаний на валентные и
Деформационные. Такая молекула имеет N—1 связей. Сле-
довательно, она будет иметь W—1 валентных колебаний.
; Остальные координаты будут деформационными. Таких ко-
лебаний будет (3N— 6)—(N—1)=2М—5. Например, для
14*
212 УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ [гл. VII
молекулы СС14, имеющей девять колебаний, существует
четыре валентных колебания и пять деформационных.
Многие авторы обозначают валентные колебания симво-
лом у, а деформационные — символом 3. Особое место
среди колебаний занимают так называемые крутильные,
характеризующие повороты групп вокруг связей, соединяю-
щих части молекулы. Они часто обозначаются символом т.
§ 14. Веса уровней энергии квазитвердых молекул
Выше мы указывали (см. § 4 этой главы), что вес уровня
энергии вращения молекулы, вообще говоря, не определяется
простыми формулами, выведенными для весов уровней жест-
ких волчков. Причиной этого является существование тре-
бований симметрии, накладываемых на волновые функции,
описывающие состояние молекул.
Рассмотрим теперь вопрос об определении весов уровней
энергии. Как и в случае двухатомных молекул, мы можем
в первом приближении представить волновую функцию
в виде произведения
Ф — ф'п • фэл ' Фколеб • фвр " фи. с» (7.115)
где фп, фэл> фколеб, фвр описывают соответственно поступа-
тельное, электронное, колебательное и вращательное дви-
жения. Функция фя.0 описывает спин ядер. Электронный
спин предполагается включенным в фэл.
Пусть молекула содержит N одинаковых ядер. В зави-
симости от рода статистики, которой подчиняются одинако-
вые ядра, волновая функция (7.115), как это мы видели
в главе I, должна удовлетворять требованиям симметрии:
для ядер, содержащих четное число нуклонов, она должна
быть симметричной относительно перестановок координат
одинаковых частиц, для ядер, состоящих из нечетного числа
нуклонов, — антисимметричной. Так, волновая функция,
описывающая состояние всей молекулы метана СН4, содер-
жащей четыре ядра Н, должна быть антисимметричной по
отношению к перестановкам координат этих одинаковых
ядер, ибо ядро Н состоит только из одного протона. Ядро
дейтерия (дейтон) состоит из двух нуклонов, а поэтому
состояние молекулы CD4 должно описываться симметричными
волновыми функциями.
§ 14] ВЕСА УРОВНЕЙ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ 213
Вес уровня энергии молекулы надлежит определять как
число линейно независимых волновых функций, соответ-
ствующих данному уровню энергии и удовлетворяющих
требованиям симметрии. Волновые функции фэл, фкч.тоб,
фвр и дя.с, соответствующие данному уровню энергии,
вообще говоря, являются вырожденными. Общее число ли-
нейно независимых функций, соответствующих данному
уровню энергии, будет:
g = ёэл^колеб^вр^я. с, (7.116)
где £-эл, gколеб, gbp, ga.e означают соответственно степень
вырождения электронных, колебательных, вращательных и
спиновых состояний. В частном случае некоторые из мно-
жителей (7.116) могут быть равны единице, например для
основного электронного состояния обычно g3!l = 1, анало-
гично и для основного колебательного состояния §’Колеб = 1-
Выполняя перестановки одинаковых ядер, мы получим Nig
функций, соответствующих данному уровню энергии. Однако
не все эти функции будут линейно независимыми. С другой
стороны, эти функции не удовлетворяют требованиям сим-
метрии. Из них нужно построить такие независимые линей-
ные комбинации, которые удовлетворяли бы требованиям
симметрии. Число таких функций и будет представлять вес
уровня энергии *).
Можно показать, что при определении симметрии вол-
новых функций мы можем не исследовать все возможные
перестановки ядер (их будет 7V!, если молекула содержит
один сорт ядер, и Nx! • N2l для случая двух сортов), но
можем ограничиться изучением перестановок, эквивалентных
чистым вращениям молекулы [262, 121]**). Число таких пере-
становок, как мы видели в § 6 главы VI, представляет число
*) Следует подчеркнуть, что требование о симметричном (ан-
тисимметричном) характере относится к полной волновой функции,
т. е. функции, описывающей все движения, которую в первом при-
ближении можно представить в виде (7.115). Множители, входящие
в состав полной волновой функции, могут иметь характер сим-
метрии, отличной от одномерного (симметричного и антисимме-
тричного), ибо при умножении и таких функций может получить-
ся симметричная (антисимметричная) полная волновая функция
(см. Деннисон [215]).
**) Т. е. ограничиться определением симметрии по отношению
к группе R.
214 УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ [гл. VII
симметрии молекуы о. Определение веса уровня упрощается
тем обстоятельством, что определение симметрии произве-
дения ^п'т'эл'1'колеб%14л.с может быть выполнено путем опре-
деления симметрии каждого из сомножителей и исследова-
ния, какие множители дадут функции требуемой симметрии.
В отличие от случая двухатомных молекул (N=2), где
каждая ИЗ функций фэл, фколеб, '^вр, фя-с могла быть только
симметричной или антисимметричной по отношению к пере-
становкам координат одинаковых ядер, при определении
симметрии волновых функций многоатомной молекулы мы
встретимся с более сложными случаями симметрии. Типы
симметрии волновых функций обозначаются, как и типы
симметрии нормальных колебаний (см. § 8 этой главы), бук-
вами А, В, Е, Т с индексами, и для их характеристики
применяются таблицы, о которых упоминалось в § 8 *).
Для определения веса уровня энергии нужно найти от-
дельно симметрию электронных функций, отдельно симме-
трию колебательных функций, симметрию вращательных
функций и симметрию спиновых функций, а затем опреде-
лить, какую симметрию будут иметь функции, являющиеся
их произведением. Такое определение симметрии произве-
дения функций выполняется также с помощью особых таб-
лиц, по которым легко найти, сколько существует полных
функций требуемой симметрии, число которых и дает вес
уровня энергии. При определении симметрии мы можем
не принимать во внимание волновую функцию 6П, описы-
вающую поступательное движение молекулы, ибо она не
зависит от внутренних координат и поэтому является все-
гда симметричной. Точно так же 6ЭЛ обычно бывает симме-
тричной для основного состояния. Так же обстоит дело
И с Сколеб. которая симметрична для основного состояния
*) Определение симметрии произведения ФпФэлФколсбФврФя с
значительно упрощается при применении теории групп, которая
оказывается очень полезной при исследовании состояний молекулы.
С точки зрения теории групп совместные перестановки ядер, вы-
полняемые вращением молекулы, образуют группу, о которой
говорилось в § 6 главы VI и которая является подгруппой гпуппы
всех перестановок. Симметрия волновых функций описывается не-
приводимыми представлениями, матрицы которых определяют закон
преобразования волновых функций при'выполнеиии операций груп-
пы R. Для обозначения симметрии функций и применяются сим-
волы неприводимых представлений.
§ 14] ВЕСА УРОВНЕЙ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ 215
(У1==0, v2—0,..., vn = 0). В этом случае для определения
веса уровня энергии нужно исследовать симметрию произ-
ведения вращательных и спиновых функций.
Рассмотрим в качестве примера значения весов уровней
энергии молекулы СН3С1 *). Эта молекула представляет сим-
метричный волчок и имеет симметрию Cav. Возможными ти-
пами симметрии по отношению к перестановкам координат
ядер, выполняемым вращением, являются А, Ег и Е2. Функ-
ции симметрии А — симметричные функции**). Основное
электронное состояние этой молекулы является невырожден-
ным и симметричным (симметрия Д). Основной колебатель-
ный уровень невырожден, а соответствующая волновая функ-
ция будет тоже симметричной (симметрия Л). Уровень энергии
вращения при К Ф 0 будет вырожден 2 (2J-|-1)-кратно.
Этому уровню соответствует 23 спин-функций ядер
протонов, если пренебречь взаимодействием спинов. Таким
образом, если бы на волновые функции (7.115) не накла-
дывались требования симметрии, уровень энергии был бы
вырожден 23 • 2 (2У—|— 1)-кратно. Однако в действительности
вес уровня будет меньше, так как полная волновая функция
должна быть симметрии А ***).
Определение симметрии фвр приводит к тому, что она
зависит от числа К. При АГ=.О волновая функция имеет
симметрию А (всего 2J-|-1 функций); при |/(|, кратном
трем, симметрия будет тоже А [всего 2(2J-|-1) функций];
при | /С|, не делящемся на три, симметрия будет типа Et-|-E2
[всего 2(2J—|— 1) функций]. Из восьми спиновых функций
этой молекулы четыре имеют симметрию А, две — Et и
две — Е2.
Определяя симметрию произведения этих функций и от-
брасывая волновые функции непригодной симметрии (волно-
вая функция должна иметь симметрию Л), мы получим следую-
щие значения весов уровней энергии: при ^=0 уровень
энергии будет вырожден 4(2J-|- 1)-кратно; при |/С|, кратном
*) Подробнее см. §§ 15—18 этой главы.
**) Эти функции удовлетворяют в нашем случае требованиям
как статистики Ферми — Дирака, так и Бозе — Эйнштейна, так как
все перестановки симметрии вращения С3 являются четными.
***) Протоны подчиняются статистике Ферми—Дирака, но в на-
шем случае, как. было указано выше в примечании, симметрия А
соответствует обеим статистикам.
216
УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ
[гл. VH
трем, —8 (27+ 1)-кратно и при [/С|, не делящемся на
три, —4 (2J—1)-кратно. Эти результаты представлены в та-
блицах 17 и 18*).
Таблица 17
Общая таблица для определения весов уровней энергии
молекулы СН3С1
Значение К Вес уровня энергии Вес, соответствую- щий спин-состоя- ниям симметрии А Вес, соответствую- щий спин-состоя- ниям симметрии Е = Ei + £2
К = о 4(27+1) 4(27+1) 0
| к | не делится на три 4(27+1) 0 4(27+ 1)
. АП делится на ' три, К + 0 8(27+ 1) 8(27+1) 0
Таблица 18
Веса уровней энергии молекулы СН3С1
№ п/п Кванто- вое число 7 Кванто- вое число К Вес уровня Симметрия спин-состояний данного уровня энергии
1 0 0 4 (27+1) = 4 А
2 1 0 4(27+ 1) = 12 А
3 1 (1,-1) 4(27+ 1) = 12 Е
4 2 0 4 (27+1) = 20 Е
5 2 (1,-1) 4 (27+1) = 20 Е
6 2 (2,-2) 4(27+1) = 20 Е
7 3 0 4(27+1) = 28 А
8 3 (1,-1) 4(27+0 = 28 Е
9 3 (2,-2) 4(27+ 1) = 28 Е
10 3 (3,-3) 8(27+0 = 56 А
И и т. д.
При определении весов уровней энергии мы заметим, что
полная волновая функция, удовлетворяющая требованиям сим-
метрии, может иметь разную симметрию ядерных спин-
функций. Действительно, четыре спин-функции симметрии А
*) В веса уровней не включен множитель веса спии-состоянин
ядра С1.
§ 15] ВЫЧИСЛЕНИЕ ВЕСОВ УРОВНЕЙ ЭНЕРГИИ 217
при перемножении с вращательными волновыми функциями
симметрии А дают функцию требуемой симметрии (А); с дру-
гой стороны, четыре спин-функции симметрии E = £'t-|-£,2
при перемножении с волновыми функциями такой же симметрии
тоже дают функции требуемой симметрии. Таким образом,
получаются два рода уровней энергии. Вес уровня энергии,
относящийся к данной симметрии ядерных спин-функций,
указан в последних двух столбцах таблицы 17 и в предпо-
следнем столбце таблицы 18. Оказывается, что переходы
между такими уровнями энергии весьма мало вероятны. Та-
ким образом, газ, состоящий из молекул СН3С1, предста-
вляет смесь двух сортов молекул. Эти модификации полу-
чили название спин-модификаций [121]. Аналогичные резуль-
таты получаются и для молекулы СЭдА'. Однако вес уровней
будет другим, так как спин D = 1 (ядра D подчиняются
статистике Бозе — Эйнштейна).
В случае молекулы СХ3У, ядра которой не имеют спина,
мы получим, что некоторые уровни энергии из-за требова-
ний симметрии будут отсутствовать, как это имело место
в случае двухатомных молекул без ядерного спина. Такими
уровнями будут уровни с |/С|, не делящимся на три, т. е.
примерно будут отсутствовать 2/3 возможных уровней и
будет реализоваться 1/3. Это соответствует введению числа
симметрии о = 3. Аналогично обстоит дело и в случае
молекул, ядра которых обладают спином. Например,
у молекулы СН3С1 осуществляется только д~з=1/з возмож-
ных состояний. Этот результат будет верен и в общем слу-
чае— симметрия вращения приводит к реализации в сравни-
тельно широкой области вращательных уровней ~1/з части
мыслимых состояний (см. [242]).
§ 15. Вычисление весов уровней энергии
с помощью теории групп *)
Рассмотрим подробнее, как вычисляются веса уровней энергии
молекул. Пусть молекула имеет N одинаковых ядер, обладающих
спином 5. Для определения веса уровня энергии нужно найти,
сколько волновых функций требуемой симметрии можно построить
из всех волновых функций, соответствующих данному уровню энер-
*) Изложение теории групп см. О. Ю. Шмидт [83], Ви-
гнер [96], А. Г. К у р о ш [35].
218
УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ
[ГЛ. VII
гии без учета симметрии. Число таких функций дано формулой
(7.116). Мы уже указали, что симметрия волновых функций может
быть определена по отношению к группе R — группе перестано-
вок, соответствующих чистым вращениям молекулы. При этом мы
можем не учитывать вырождения, обусловленного перестановками *).
Симметрия волновых функций описывается неприводимыми пред-
ставлениями, по матрицам которых преобразуются волновые функ-
ции при выполнении преобразований группы.
Пусть основной электронный уровень молекулы невырожден
и описывается, как обычно, симметричной волновой функцией.
Найдем вес уровня вращательной энергии для основного колеба-
тельного состояния (^ = 0, v2 = 0> ••), в котором фколеб будет
также симметрична. В этом случае мы будем иметь ^Э1=1.
£,колеб = 1- Нашему уровню энергии будет соответствовать (см.
формулу (7.16))
линейно независимых волновых функций. Значение £вр будет зави-
сеть от типа молекулы. Для сферического волчка мы имели (см. §§ 3,
4, 5 этой главы)
^вр = (27+1)2; (7.118)
для симметричного волчка
( 2(27+1), 1 А7|=#0;
£вр j (27+1), |R|=0;
для асимметричного волчка
^вр = (27+ 1).
(7.119)
(7.120)
Этомуже уровню энергии соответствуют (2$+1)ге = ап линейно
независимых спин-функций. Вес уровня энергии без учета требо-
ваний симметрии был бы равен
£вр-“п- (7-121)
При выполнении операций группы R gB[l волновых функций будут
подвергаться линейным преобразованиям. Матрицы этих преобра-
зований образуют приводимое представление **) группы R, которое
мы обозначим £>вр. Разлагая это представление на неприводимые
представления группы R, получим искомую симметрию вращатель-
ных волновых функций
71 вр ~ а1^1 + + • • • + ап^п- (7.122)
Это разложение будет показывать, в каком количестве и какой
симметрии существуют вращательные волновые функции. При этом
*) См. Вильсон [262], И. Н. Г о д н е в [121].
**) См. Вигнер [96], Розенталь и Мурфи [256].
§ 16] ОПРЕДЕЛЕНИЕ СИММЕТРИИ ЯДЕРНЫХ СПИН-ФУНКЦИЙ 219
коэффициент перед одномерными представлениями будет давать
непосредственно число функций данной симметрии. Если предста-
вление двумерно, для получения числа функций коэффициент перед
ним нужно умножить на два, если трехмерно — на три.
При выполнении операции группы R также произойдут линей-
ные преобразования ядерных спин-функций. Матрица этих пре-
образований образует приводимое аге-мерное представление груп-
пы R, разложение которого определяет симметрию ядерных спин-
функций
Da. c = Mi+W+- + Mn- (7-123)
Для определения симметрии волновых функций, получаемых пере-
множением вращательных и спиновых функций, нужно построить
прямое произведение представлений
Г>яс-Пвр. (7.124)
Разложение этого представления на неприводимые представления
группы R
Вя. о ’ 75вр = + • • + спАп (7.125)
покажет, какой симметрии и в каком количестве получаются резуль-
тирующие полные волновые функции. Из этих функций б зависи-
мости от рода статистики будут реализоваться в природе только
функции симметрии и А%. Коэффициент перед ними
в формуле (7.125) и дает вес уровня. Иногда обе статистики соот-
ветствуют одному представлению Аг (см. пример с СХ3К, стр. 217
и 224). Если уровень колебательной энергии вырожден, нужно
найти симметрию колебательных волновых функций путем построе-
ния и разложения соответствующего представления Околей. Построив
прямое произведение
Т^ко.теб ‘ 75Вр Da G, (7.126)
мы получим искомую симметрию всех функций. Такое произведе-
ние нужно построить и в том случае, если колебательный уровень
невырожден, но волновая функция имеет симметрию, отличную
от Аг (тождественного представления). В этом случае Е>колеб будет
одномерным. Таким же образом, т. е. путем построения и разло-
жения представления
Т^эл ' Т^колеб ’ 7\р 7)я е (7.127)
учитывается симметрия электронных волновых функций.
§ 16. Определение симметрии ядерных спин-функций
Рассмотрим теперь определение симметрии ядерных спин-функ-
ций. Это определение может быть выполнено разными методами.
Вильсон [262] применял метод непосредственного вычисления сле-
дов (суммы диагональных элементов) матриц представления Da 0.
220 УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ [гл. VII
Его способ основан на том обстоятельстве, что если данная пере-
становка (элемент группы R) преобразует спиновую функцию
в функцию, отличную от первоначальной, диагональный элемент
матрицы будет равен нулю; если перестановка оставляет спиновую
Черт. 24.
функцию неизменной, диагональ-
ный элемент матрицы будет равен
единице. Поэтому след матрицы,
соответствующей данной переста-
новке, равен числу спиновых функ-
ций, остающихся неизменными при
этой перестановке. Зная следы
матриц представления и применяя
таблицу характеров неприводимых
представлений, легко выполнить
разложение представления Da 0 и
получить искомую симметрию ядер-
ных спин-функций. Приведем при-
мер применения метода Вильсона.
Пусть дана молекула СН3х,
имеющая симметрию C3v (черт. 24).
Группа R — группа перестановок
одинаковых ядер при чистых вра-
щениях молекулы — будет изоморфна с группой С3, состоящей из
трех элементов: покоя — С\ или вращения на 360°, вращения на 120°
вокруг оси Ох (С3) и вращения на 240° вокруг этой же оси (С3).
Неприводимые представления группы С3 приведены
где
в таблице 19,
2тсг
о> = е 3 .
Таблица 19
Молекула СН3С1 имеет 23 = 8 спин-
функций. Эти спин-функции в зависи-
мости от значения квантового числа та
будут *):
ut = a(l)a(2)a(3),
И2 = а(1)Я(2)₽(3),
U3 = а (1) 8 (2) а (3),
u4 = Р (1) а (2) я (3), I (7 128)
ц5 = ₽(1)И2)«(3), |
и6 = р(1)я(2)₽(3),
ц7 = я(1)Н2)₽(3),
«8 = 8 (1) [5 (2) ₽ (3),
Неприводимые пред-
ставления группы С3
Ci C'l
А 1 1 1
I £1 1 О) 0)3
1 в2 1 0)3 О)
Для определения следов матриц нужно определить, какие из этих
функций будут оставаться неизменными при операциях группы.
Элемент С\ (покой) оставит все восемь функций неизменными, по-
этому -л (Cj) = 8. Элемент С3—вращение молекулы на 120° вокруг
*) Смысл символов а и р см. стр. 107.
§ 16] ОПРЕДЕЛЕНИЕ СИММЕТРИИ ЯДЕРНЫХ СПИН-ФУНКЦИЙ 221
оси ОХ, — эквивалентный перестановке которую можно
представить в виде цикла (132), оставит без изменений две функ-
ции иг и zz3. Поэтому х (С3) = 2. Аналогично получается х(С3) = 2.
Следы матриц представления Оя а приведены
в таблице 20.
Для разложения представления Dx 0 на
неприводимые мы можем, использовать извест-
ную формулу (см. [96, 9])
(7-129)
д
где /г — порядок группы, S(g')— след матри-
цы приводимого представления для элемента g,
— характер неприводимого предста-
вления для элемента g и аг. — кратность этого
Таблица 20
Следы матриц
представления
Оя 0 для СН3 X
с3 С2
8 2 2
представления. Так
как следы и характеры, соответствующие элементам группы, при-
надлежащим к одному классу сопряженных элементов, одинаковы,
то формулу (7.129) можно записать так:
(7.130)
к
где bjt — число элементов в данном классе. Черта над х означает
взятие комплексного сопряженного числа.
Разложение представления Dtt с с помощью формулы (7.129)
дает *) аг = 4, а2 = 2, ая = 2, т. е.
£)Я.О=4А + 2(Е1 + £2) = 4А + 2Е (7.131)
Аналогично производится определение симметрии ядерных спин-
функций и для других молекул. Определение симметрии ядерных
спин-функций возможно и другим общим методом **), позволяющим
установить также соответствие между симметрией их по отно-
шению к полной группе перестановок и результирующим спи-
ном ***).
Заметим, что следы матриц представления Da с могут быть
вычислены в общем виде с помощью формулы
$(£) = < (7.132)
где v — число циклов данной перестановки (элемента группы /?).
Так, для СН3С1 мы имеем: = (1) (2) (3), С3 = (1 3 2), С3 = (12 3).
Первый элемент (С\) имеет три цикла, v = 3, вторые два имеют
о=1. Таким образом, S (CJ = 23 = 8, S (С3) = S (С3) = 21 = 2
(см. табл. 20).
*) См. Вигнер [96].
**) И. Годнее [119, 120].
***) И. Годнее и В. Сорокин [124]. •
222 УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ [гл. VII
§ 17. Определение симметрии волновых функций,
описывающих вращение молекулы
Для определения симметрии волновых функций, описывающих
вращение молекулы, существует также несколько методов. Одним
из методов является вычисление следов матриц представления Г>вр
примененное Вильсоном [262]. Другим методом [122] является раз-
ложение представлений так называемой внутренней группы вра-
щений (internal rotation group), который позволяет составить таб-
лицы симметрии волновых функций для всех важных случаев
группы R (случаи, когда группа R изоморфна с группами О, Т,
De, С6, £>5, С5, Z>4, С4, О3, С3, Z?2> Сз). Так, применяя эти таблицы
для молекулы СН3С1, являющейся симметричным волчком, мы по-
лучим (табл. 8 в работе [122]):
DBp = (2J+l)A
DBp = (2J+ 1)£,
Двр = (2/+1)2Д,
/С=0,
[ К | не делится на 3,
|/С1 кратно трем.
(7.133)
Точно так же для молекулы BF3, имеющей симметрию /)зЛ, группа R
будет изоморфна с группой £)3. Таблица 7, приведенная в указан-
ной выше работе, дает:
Т^вр = (2/+1)А, К =0, J четное,
•°вр = (27+1)Д2, = (2J+ 1)Д, К = 0, J нечетное, (7.134)
°вр | КI не делится на 3,
= (2J +1)(А + А2), 1 /С| делится на 3.
§ 18. Построение таблиц умножения й определение
веса уровня
Построение прямого произведения Оар • Da с и его разложе-
ние может быть выполнено с помощью таблиц, дающих разложе-
ние прямых произведений на неприводимые представления. Такие
таблицы можно легко построить, используя известное правило вы-
числения характеров прямого произведения. Характер матрицы
прямого произведения равен произведению характеров соответ-
ствующих матриц, т. е.
'(g) = ^i(g)^k(g)- (7-135)
Поэтому для построения «таблицы умножения» нужно по фор-
муле (7.135) вычислить характеры, а затем произвести разложение.
§ 18] ТАБЛИЦЫ УМНОЖЕНИЯ И ОПРЕДЕЛЕНИЕ ВЕСА УРОВНЯ 223
Таблица 21
Произведение С1 С'1
ЛХ А 1 1 1
А X Et = Ej X А 1 О) 0)2
А ХЕ2 = Е2 ХА 1 0)2 0)
е1хе2 = е2хе1 1 «Д= 1 шЗ = 1
X 1 0)2 0)4 = 0)
е2 х е2 1 0)4 = о) 0)2
Построим в качестве примера «таблицу умножения» представлений
группы С3. Перемножая характеры представлений (см. табл. 19)
по формуле (7.135), мы по-
лучим значения характе-
ров, приведенных в та-
блице 21. Из этой таблицы
мы непосредственно полу-
чим «таблицу умножения»
(таблица 22).
Легко видеть, что зна-
чение произведения пред-
ставлений не зависит от
порядка сомножителей, по-
этому можно приводить
только половину таблицы.
Эта таблица может быть
применена для перемно-
жения и суммы предста-
влений, которые перемно-
жаются по обычным правилам. Вычислим, например, произведение
(E1 + E2)(E1 + E2). (7.136)
Мы будем иметь:
(Е1 + Еа) (Е1 + Е2) =
= Ej X “Ь Ej X ЕаЕ'з X EjЕа X Еа- (7.137)
Применяя таблицу 22, получим:
(Ех-|- Еа) (Ej-j- Е2) = Е2 + Л + Л Ех = 2Л -|- Ei + Е2. (7.138)
Таблица 23
Таблица 22
Таблица умножения Характеры неприводимых
неприводимых пред- представлений группы
ставлений группы С3 т, w =
А Ei е2 Т зс2 4С3
А А Et е2 А 1 1 1 1
Е\ 0)2
Ег Ег е2 А 1 1 0)
е2 1 1 0)2 0)
е2 е2 А Et Т 3 — 1 0 0
Аналогичным образом строятся таблицы умножения представле-
ний других групп. Приводим в качестве примера таблицу непри-
224 УРОВНИ ЭНЕРГИИ КВАЗИТВЕРДЫХ МОЛЕКУЛ [гл. VII
водимых представлений группы Т (табл. 23) и таблицу умножения
(табл. 24).
С помощью таких таблиц легко осуществляется разложение
^я. сХ -Одр X ^колеб.
Рассмотрим в качестве примера вычисление весов уровней
энергии молекулы СН3С1. Протоны подчиняются статистике
Таблица 24
Таблица умножения представлений
группы Т
Ферми—Дирака и полные волновые функции должны иметь симме-
трию Л*). Мы имеем (см. формулу (7.131)):
Е>я с = 4А + 2 (fj Е2). (7.131а)
Симметрия вращательных функций дается формулой (7.133). Пере-
множение представлений нужно выполнить для каждой строки фор-
мулы (7.133) отдельно (с помощью табл. 22).
Для случая К = 0 мы получим:
DBf XDB с = (2/+ 1) А • [4А + 2 (Et + Д2)] =
= 4 (2J + 1) АА + 2 (2J + 1) A (Et + Е2) =
= (27+‘1)[4Д + 2(£1 + £2)]. (7.139)
Из этой формулы мы видим, что могут существовать 4 (2У —|— 1)
полных волновых функций симметрии А, 2 (2J-|- 1) функций сим-
метрии Ег и 2(27Д- 1) функций симметрии Е2. Последние два сорта
функций не удовлетворяют требованиям симметрии, и мы должны
их отбросить. Таким образом, уровню с /С=0 соответствует 4 (27-|-1)
функций и вес уровня энергии будет 4 (2/-)- 1). как это указано
в таблице 17.
*) Эту же симметрию должны иметь функции и для молекулы
С Ла У, если ядра X подчиняются статистике Бозе — Эйнштейна
В этом случае функции симметрии А, как это было указано выше,
удовлетворяют требованиям обеих статистик.
§ 18] ТАБЛИЦЫ УМНОЖЕНИЯ И ОПРЕДЕЛЕНИЕ ВЕСА УРОВНЯ 225
Для ] К|, которое не делится на три, мы получим:
Dtf X Е)я с = (27 + 1) (Et + £2) [4А + 2 (Et + £2)] =
== 4 (27+1) AEr + 4 (27+ 1) AE2 + 2 (27 + 1) (£x + £2) (£x + E2) =
== 4 (27+ 1) Er + 4 (27+ 1) E2 + 2 (27+ 1) E1E1 + 4 (27+ 1) ErE2 +
+ 2 (27+1) £2£2 = 4 (27+1) £x +4 (27+1) £2+ 2 (27+1) £2 +
+ 4 (27 + 1) A + 2 (27+ 1) £x = (27+ 1) [4A + 6 (£x + £2)J. (7.140)
Из формулы (7.140) следует, что вес этого уровня энергии будет
4(27+1).
Наконец, для | /(|, которые делятся на три, мы получим:
Лвр X ол. с = 2 (27+ 1) А • (4Д + 2 (£х + £2)] =
= (27+ 1) (8А + 4АЕГ + 4А£2) =
= (27+1)[8А + 4(£х + £2)], (7.141)
откуда вес этого уровня энергии получается равным 8(27+1)
(см. табл. 17). Из вычислений видно, что первому и третьему из этих
серий уровней энергии соответствует симметрия спиновых функ-
ций А, придающих весам уровней множители 4 и 4, во второй серии
(|/С| не делится на три) реализуются спиновые состояния симметрии
£х + £2 = £ с множителем 2. Эти состояния соответствуют двум
некомбинирующим состояниям А и £ (спин-модификациям).
15 Зак. 835. И. II. Годнее
ГЛАВА VIII
ВЫЧИСЛЕНИЕ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
КВАЗИТВЕРДЫХ МОЛЕКУЛ
§ 1. Введение
Одним из первых исследователей, применивших методы
статистической механики к вычислению термодинамических
функций многоатомных молекул, был А. В. Фрост [199, 200].
С тех пор многими авторами было выполнено большое
число работ *), посвященных вычислению термодинамических
функций квазитвердых молекул. Большая часть таких вычи-
слений была сделана в предположении о разделении энергии
(см. (7.1)) и пренебрежении ангармоничностью колебаний. При
этом оказалось, что для подавляющего числа многоатомных
молекул можно не принимать во внимание возбужденные
электронные уровни энергии, так как эти уровни лежат
высоко над основным состоянием. Можно пренебречь учетом
6t
даже первого из этих уровней, так как выражение е кт,
где — энергия первого электронного уровня, оказывается
очень малым. Кроме того, в большинстве случаев основное элек-
тронное состояние невырождено, т. е. вес его равен единице.
Таким образом, имеем:
<?эл=2^"^= 1+г^+ ... «1. (8.1)
г
Исключение из этого правила составляет небольшое число
молекул с мультиплетным основным состоянием, к которым
относятся NO2, С1О2, а также свободные радикалы.
*) См. обзорные работы А. В. Фроста [198], Я. И. Гераси-
мова [113], Касселя [236], Ц е и з е [267, 268], Вильсона [264].
ВВЕДЕНИЕ
227
§ 11
Наиболее точные значения термодинамических функций
мы можем получить, как это было указано выше (см.
главы II, III и V), при применении точных выражений для зна-
чений уровней энергии и применении метода непосредствен-
ного суммирования. Однако для многих многоатомных моле-
кул постоянные этих точных выражений, например постоян-
ные ангармоничности колебаний, еще неизвестны. С другой
стороны, метод непосредственного суммирования отнимает
много труда. Значительное упрощение вычислений получается
при условии, что можно применить предположение о раз-
делении энергии. Оказалось, что это предположение удо-
влетворительно оправдывается для очень большого числа
многоатомных молекул. В этом случае мы имеем:
Qi = Сэл ’ Сколеб ’ Qbp- (8-2)
Для электронных состояний большинства квазитвердых
молекул, как указано было выше, Сэл = 1, следовательно,
Qi — Сколеб ‘ Qsp-
(8-3)
Дальнейшее упрощение получится при допущении гармо-
нического характера колебаний. В этом случае для энергии
молекулы имеем следующие выражения:
для линейной молекулы
8«р И- гколеб —
+ (8.4)
для молекулы типа симметричного волчка
Д , , Л3 IW +1) 1 \1 I
;-вр-1-гколеб— 8я2 [ \/д
( + 2 ^к [vk + g’j > (8.5)
к
для молекулы типа сфеоического волчка
j ®вр + гколеб = J (•/+ 1) + h')k (vk у j . (8.6)
15*
228 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ КВАЗИТВЕРД. МОЛЕКУЛ [ГЛ. VIII
§ 2. Вычисление Qul> для жесткой линейной
несимметричной молекулы
Рассмотрим сначала вычисление Qnp. Как видно из фор-
мул (8.4)—(8.6), статистическая сумма по вращательным
состояниям будет зависеть от типа молекулы (линейная мо-
лекула, молекула типа сферического волчка и др.). Будем
сначала предполагать, что молекула не имеет осей симме-
трии (s = 1) и что ядра молекулы не имеют спина.
Для линейной молекулы при применении жесткой модели,
как и в случае двухатомных молекул, мы получим для вы-
соких температур
Вр СО
QBp= = (8-7)
i J = n
(см. формулу (5.24)).
Для более точного вычисления можно применить фор-
мулу (5.30), которая была рассмотрена при вычислении тер-
модинамических функций двухатомных газов.
§ 3. Вычисление Qap для жесткой несимметричной
молекулы типа симметричного волчка
Для молекулы типа симметричного волчка мы имеем:
(8.8)
Уровни энергии волчка, как это было показано в главе VII,
определяются формулой
Г^(У+ 1)
L !в
—
— 8^2
Н2(^- Т-У1- (8.8а)
\'а ‘в/i
Вес уровня энергии волчка будет равен 2(27-1- 1) для
К ¥= 0 и (27+1) для /<=0. Суммирование в (8.8) нужно
производить по 7 от 0 до оо и значениям К от —7 до +7.
Рассматривая оба уровня с + К и'—К как два отдельных
уровня (но с равной энергией), мы можем приписать каж-
дому уровню вес (27+1).
§ 3| Qn),. НЕСИММЕТРИЧ. МОЛЕКУЛЫ ТИПА СИММЕТРИИ. ВОЛЧКА 229
Таким образом,
СО K=+J № ( / 1__TV
J=0K=-J
Положив, как и в главе V,
WkTIB ~~ T1
и
/гз ( 1 1 \
8тМТ\1а 1бГ'~’
мы получим:
ОО К= +J
Q„v = 5 2 (2J+ l)e-JV+tK-.E-%
J=<> K=-J
(8.9)
(8.10)
(8.И)
(8.12)
Для высоких температур будем иметь:
д<С1
Т2
1.
(8.13)
В этом случае суммы, входящие в выражение (8.12), можно
заменить интегралами. Мы будем иметь:
QBp = J" (2J-H)e-J<'z+l^dJ J e~K^dK (8.14)
-j
или
QBp = J (2J+V)e-J(J+^dJ 2 j e~^SidK, (8.15)
о
так как функция под знаком второго интеграла четная.
Для вычисления интеграла применим метод интегрирования по
частям. Положим
2(2/+ \)e-J{J+1}z‘dJ = du, '
J
J" е dK = v.
о
тогда
dv = e~'2j2dJ
И }
+ _ __ 2 + I
)
u = 2 | (27+1)
(8.16)
(8.17)
230 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ КВАЗИТВЕРД. МОЛЕКУЛ [ГЛ. VIII
Интегрирование по частям дает:
00
qbj==2_ j*
1 о
(8.18)
Наши вычисления выполняются в предположении, что и т2 малы,
поэтому основное значение интеграла определяется областью боль-
ших значений числа J, так что J (7+ 1) можно заменить на J2 в той
области интегрирования, где подинтегральное выражение значи-
тельно отличается от нуля.
Мы получим:
СО
= (8.19)
1 о
Как известно,
(8.20)
Таким образом, приближенное значение суммы по вращательным
состояниям будет:
^вр т,
7С
(8.21)
Подставляя значения и х% из (8.10) и (8.11), получим:
. Л2 1
Т1 + 8iMT * 1А
И
8rfkTIB „ (8rMTI.\'h-
Q —_________£ тг'/г I __)
7вр ла \ ла ) *
(8.22)
(8.23)
Таким образом,
(8.24)
Это выражение можно записать и в таком виде:
Свр
2r.kT/B\'/2 / 2r.kTIB\'1г / Ir.kTI
) \ h? J V-ла-
(8.25)
(2пкТ1в^
в котором выделены два равных множителя I——) > со-
ответствующих двум равным моментам инерции /д == /д,
§ 4] Qsp ДЛЯ ЖЕСТКОГО СФЕРИЧЕСКОГО ВОЛЧКА 231
При рассмотрении выражения (8.25) естественно предпо-
ложить, что в случае асимметричного волчка для QBp мы
должны получить такое же выражение, но с заменой одного
из /в на 1С.
Подчеркнем еще раз, что выражение (8.25) является
приближенным. Точно такое же выражение получится для
суммы по вращательным состояниям, если применить фор-
мулу (1.46) и использовать для энергии волчка выражение,
которое дает классическая механика. Заметим также, что
формула (8.23) выведена в предположении, что число сим-
метрии о=1.
§ 4. Вычисление Qnp для жесткого
сферического волчка
Из формулы (8.24) или (8.25) при 1В — 1А мы можем
найти приближенное значение суммы по вращательным со-
стояниям для жесткого сферического волчка
ѻР= 8кз(-2^у/д. (82б)
Этот же результат может быть получен заменой суммы
QHp = S (2J+1)%-Z(’/+1)T (8.27)
J=o
интегралом, где (2J-1- I)2 — вес вращательного уровня и
Мы получим:
СО
QBp = J (2J-\-Vpe-j(j+iUdJ (8.29)
О
или *)
оо
( 4J2e-^dJ = ^ = 8K2(2^)3/’. (8.30)
о
При этих вычислениях попрежнему предполагалось, что
а = 1.
' 1
*) Точное вычисление интеграла (8.29) дает
232 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ КВАЗИТВЕРД. МОЛЕКУЛ [ГЛ. VIII
§ 5. Вычисление QBP для жесткой молекулы
типа асимметричного волчка
Для молекулы типа асимметричного волчка, как было
указано выше (см. § 5 главы VII), не существует явных
формул, позволяющих вычислить уровни энергии по задан-
ным значениям квантовых чисел. Однако уровни энергии
могут быть найдены путем решения соответствующих веко-
вых уравнений *). Таблицы уровней энергии были составлены
недавно Кингом, Хайнером и Кроссом [239, 240, 227].
Для точного вычисления суммы по вращательным состояниям
следует применить метод непосредственного суммирования.
В этом случае мы будем иметь:
№ е(<7, w I
(8.31)
7 = 0 W_
где (2У—f— 1) — вес уровня, а та. — корень соответствующего
векового уравнения, входящий в выражение энергии (7.32)
<8-32>
Для приближенного вычисления суммы по состояниям
для высоких температур мы можем аппроксимировать после-
довательность корней выражением т2, где т пробегает целые
значения от —J до 4-7, и заменить в первом приближении
b 4" с л
—— близким к нему в условиях реальных молекул значе-
нием У Ьс. Мы получим:
Q., = 2 ’ 2,(W+ (8,33)
7 = 0 -. = -J
Заменяя далее сумму интегралом, имеем:
Q„= f \ d-.=
О _ -J
СО fol _ J fol _
- f (27+1)Г««Т/,-'И”'',“л/2 (8,34)
о о
*) См., например, Ванг [261]; см. также М. А. Ельяше-
вич [126].
§ 5] Qnp ДЛЯ ЖЕСТКОЙ МОЛЕКУЛЫ ТИПА АСИММЕТРИЯМ. ВОЛЧКА 233
так как функция под знаком второго интеграла четная.
Применяя метод интегрирования по частям, изложенный
в § 3, и обозначая
= <835>
^gf (a-VS> = -i. (8.36)
мы получим, как и в § 3,
Quj> _ 1 — / / тс
V (<+
т. е. Q14' №1гТ 1 -]/"
h- \Тс у /г2я
или Сир — 8 т:2 — (kT)’1' 1
/г3 У abc
Принимая во внимание (см. формулу (7.31)), что
мы получим:
(8.37)
(8.38)
(8.39)
(8.40)
(8.41)
как и следовало ожидать на основании формулы (8.25).
Формула (8.41) получается также при применении формулы
(1.46) и выражения для энергии асимметричного волчка, ко-
торое дает классическая механика.
Мы рассмотрели приближенное вычисление суммы по со-
стояниям, применимое в области высоких температур. Для
более точного вычисления вращательной суммы по состоя-
ниям можно применить метод, разработанный Касселем [235].
Этот метод основан на применении известной формулы
234 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ КВАЗИТВЕРД. МОЛЕКУЛ [ГЛ. VIII
Эйлера—Маклорена, с помощью которой можно показать, что
сумма
5=2 2 (2АГ+ (8.42)
К=0 п = — к
может быть представлена в виде (см. [235])
S = ir'W/4(;3 + 1)"1/а Г1 +1(3 + I)-1 а + . .. 1. (8.43)
Применение этой формулы к симметричному волчку
(см. формулы (8.9) — (8.11)) при
= а, 1
?а = т2 J
(8.44)
дает:
(8.45)
ИЛИ
а, = Аг’М‘ । +1, (£ _ i) (I)’1.
(8.46)
Руководствуясь соответствием с симметричным волчком,
Гордон [223] показал непосредственным суммированием, что
аналогичная формула хорошо оправдывается и для асимме-
тричного волчка. Этот результат может быть получен при
применении приближенного значения уровней энергии асим-
1 етричного волчка (см. [117]).
Действительно, полагая в формуле (8.33)
а==^кТ^Ьс = ^УЬс' (8Л7)
(8.48)
~^=-1
Y Ьс
и применяя формулу (6.43), получим:
(8,49)
§ 6] ВЛИЯНИЕ СИММЕТРИИ И СПИНА 235
откуда
£ _3_ a, VbC _1_
4 (айс) 2 X
X [1 + “а•••]*)• (8.50)
Если ограничиться первым членом в разложении (8.50),
мы будем иметь:
?'Уьс _ /2пкТТлЛ /2^kT/„\^ /2izkTI„\~
QBp 1 £ *
Следует заметить,
арУЬс
тель е 4 близок
8Л-^)Л-г)Л-гУ- (8-51)
что при высоких температурах множи-
и алмнипр. **Y
§ 6. Влияние симметрии и спина
При выводе формул для QU|1 в §§ 2—5 этой главы мы
предполагали, что число симметрии молекулы равно единице,
а также, что ядра молекулы не обладают спином. Рассмо-
трим теперь вычисление суммы по вращательным состояниям
при а > 1. Будем сначала предполагать, что ядерный спин
отсутствует. При рассмотрении двухатомных молекул, содер-
жащих два одинаковых ядра, мы выдели, что наличие тре-
бований симметрии, которым должны удовлетворять волновые
функции, приводит к реализации приблизительно половины
вращательных состояний. Аналогично обстоит дело и с много-
атомными молекулами. Если число симметрии не равно еди-
нице, при высоких температурах реализуется только 1/а часть
возможных вращательных состояний (см. § 14 главы VII),
а поэтому сумма по состояниям оказывается в а раз меньше.
Так, для молекулы СН3Х с симметрией С31) (этот при-
мер был рассмотрен в § 14 главы VII) о = 3 и реализуется
*) Формула, несколько отличная от (8.50), была получена не-
давно Стриппом и Кирквудом [259], применившими метод
вычисления суммы по состояниям, который не требует знания уров-
ней энергии (ср. И. Халатников [201]).
**) Необходимо еще раз подчеркнуть (см. примечание на
«оо\ % "г бС ° о
стр. 168), что величина —— не является нулевой энергией, де-
ленной на kT.
236 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ КВАЗИТВЕРД. МОЛЕКУЛ [ГЛ. VIII
только 1/з состояний. Таким образом, для молекул, имеющих
число симметрии, отличное от единицы, мы получим:
Овр(°=1)
(8.52)
где QBp(a= 1) вычисляется по формулам, выведенным в пре-
дыдущем параграфе. Значения чисел симметрии приведены
в таблице 14 (глава VI).
Подставляя вместо QBp(c = 1) его значения из формул (8.7),
(8.25), (8.41) и (8.26), получим:
а) для линейной молекулы
п _ 8^kTI
Упр— аЛ2 ;
б) для молекулы типа симметричного волчка
8т2 /2и^Т/в\’/г /2ккТ1в\\!? i2izkTIA\'h
^Вр = ~ ( ДЗ ) Д2 ) \ Д2 ) ’
в) для молекулы типа асимметричного волчка
8к2 /2TtkTIAV!i /2тсА7'/в\’/гp.tikTIfj'JIt
^вр ~ Т (, Л2 ) \ /г2 / \ /г3 ) ’
г) для молекул типа сферического волчка
„ _ 8-з (2тгкТ1^
М Л2 / *
(8.53)
(8.54)
(8.55)
(8.56)
Такой способ учета симметрии оказывается законным для
средних и высоких температур. Он хорошо оправдывается
при комнатных температурах и выше *). Однако такой метод
учета требований симметрии не применим к газам при низких
температурах. В этом случае надлежит выполнить вычисле-
ние весов уровней энергии и применить метод непосред-
ственного суммирования.
Теперь допустим, что ядра молекулы обладают спином.
Пусть молекула имеет nt одинаковых ядер со спином
п.2 ядер со спином s.2, п3 ядер со спином д3. Проекция спи-
на s на ось z может принимать 2s —|— 1 значений, так что
всего будет существовать
а = (2$х+ 1)"‘(2у2+ 1)"2(2у3+ Г)"’ (8.57)
*) Для большинства молекул этот способ применим до темпе-
ратур больше 200° К (исключение — На, Da и некоторые др.).
§ 6] ВЛИЯНИЕ СИММЕТРИИ И СПИНА 237
спин-состояний. Так, для молекулы C6H3D3 мы имеем = О
(спин ядер углерода), s2 — х/2 (протоны) и s3 = 1. Общее
число спин-состояний будет:
ос = 16 . 23 • З3 = 216. (8.58)
Все эти а состояний, описываемых а линейно независи-
мыми спин-функциями, можно классифицировать по симме-
трии, как это было изложено в §§ 14—16 главы VII.
Оказывается, что каждому спин-состоянию данной сим-
метрии можно найти сомножитель в виде вращательной функ-
ции, который дает полные волновые функции требуемой
симметрии, так что все спин-состояния реализуются в моле-
кулах газа. Однако и при наличии спина осуществляются не
все вращательные состояния, а только I/а часть их. Таким
образом, при наличии спина у ядер мы получим, что вра-
щательная сумма по состояниям должна быть при средних
и высоких температурах больше в раз (см. §§ 14—16
главы VII, см. также [242]).
Мы получим:
QBp=A(° = 12a. (8.59)
Таким образом, при учете спина при высоких темпера-
турах правую часть формул (8.53) — (8.56) следует умножить
на а. Однако, как будет показано далее (см. § 6 главы XII),
при расчете химических равновесий при средних и высоких
температурах влияние спина может не учитываться.
Легко видеть, что учет этого множителя, как это сле-
дует из формул главы II и как это было сделано в главах III
и V, привел бы к появлению слагаемого вида
/? In а = R In (2sx + 1 )"* (25.2 + 1)”’(2s3 + I)”3 =
= nl/?In(2s1+ l) + n2/?ln(2s.2+ 1)-1- n3R In (2s3-1- 1), (8.60)
t. e. слагаемого вида
/?1п(2$+ 1)
на каждый атом, ядро которого обладает спином $. При
вычислении практической энтропии, приведенного изобарно-
изотермического потенциала и приведенной свободной энер-
гии слагаемое А! In а по указанным выше соображениям не
учитывается.
238 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ КВАЗИТВЕРД. МОЛЕКУЛ [ГЛ. VIII
§ 7. Сумма по колебательным состояниям
Найдем сумму по колебательным состояниям. Будем пред-
полагать колебания гармоническими. В этом случае, как мы
получили в главе VII,
гколеб = h^k (^'к + y)’ (8.61)
к
Будем отсчитывать энергию от низшего колебательного
состояния vr = 0, т>2 = 0, v., — 0, ...
Нулевую энергию колебаний, определяемую формулой
(7.96), включим в состав г0. Таким образом,
еколеб — 2 ^к^к‘ (8.62)
к
Суммирование в формуле (8.62) производится по всем
колебаниям. В случае вырожденных колебаний в формуле
(8.62) получаются одинаковые слагаемые, каждое из кото-
рых будем рассматривать отдельно. Тогда
еколеб
Отлеб = 2 в кТ —
®|, 1>2,
Лч,®, + Лм!1>3+... + Лчv
= 2 е . (8.63)
vt, 1>п
Выполняя суммирование по квантовому числу vv получим:
n4iv,+h'>„va+...+h'>nvn
<?Волеб = 2^"^ 2 е . (8.64)
V,....Vn
Продолжая этот процесс суммирования по квантовым
числам v2, f3, ... vn, будем иметь:
Гколеб = QtQa • • Qn> (8.65)
где каждая из сумм по состояниям Qk имеет вид
Qk = 2 (8.66)
vk
В формуле (8.65) в случае вырожденных частот будут одинако-
вые сомножители.
§ 7] СУММА ПО КОЛЕБАТЕЛЬНЫМ состояниям 239
Сумма (8.66) представляет геометрическую прогрессию,
для которой мы получили (см. формулу (5.15)):
0,1=1_ A"- <8-б7)
Таким образом,
_hv. _hy
Сколеб = (!—* ^)-\1— е ^...(l-e ЛТ)'1 (8.68)
ИЛИ n *>к
Сколеб = II (1-е" (8.69)
/с=1
В случае гармонических колебаний для вычисления суммы
по колебательным состояниям нужно знать только частоты
нормальных колебаний. Если частоты будут вырождены, в фор-
муле (8.69) появятся одинаковые произведения. Формулу (8.69)
для случая вырожденных частот можно будет поэтому пере-
писать в виде т п,к
Сколеб = П(1-^)А (8-7°)
fc=l
где dk — степень вырождения частоты
Частоты нормальных колебаний, которые нужно знать
для вычисления Сколеб! как было указано выше, определяются
из инфракрасных спектров и спектров комбинационного рас-
сеяния. При этом для вычисления Сколеб по формуле (8.69)
или (8.70), если известны постоянные ангармоничности, сле-
дует использовать наблюдаемые основные частоты а не
частоты при бесконечно малых амплитудах *), так как при
применении первых получается лучшее приближение.
Приведем в заключение этого параграфа выражение для
суммы по состояниям q рассмотренной нами модели квази-
твердой молекулы. Мы имеем:
q = СпСг — СпСэлСврСколебСя. с •
Заменяя значения сомножителей, получим:
_ (InmkT)^ 8л2 /2^7’/л\7. / 2тгй7’/б\‘А
q~ № V а \ № ) hT~) \ ha ) Х
п ^к
X П Роа. (8.71)
к = 1
*) См. § 4 главы IV, § 11 главы VII.
240 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ КВАЗИТВЕРД. МОЛЕКУЛ /ГЛ. VII-
В дальнейшем мы будем опускать у Q; и q множители ро
и а, так как множитель а не входит в выражение для прак-
тической энтропии и других функций, а р0 равно 1 для
большинства многоатомных молекул. В случае, если р0 не
равно единице, легко ввести соответствующие поправки
в формулы последующего параграфа.
§ 8. Формулы для вычисления термодинамических
функций жесткой молекулы в предположении
гармонического характера колебаний
Мы нашли приближенные значения сумм по состояниям
QB]1, Фколеб и q. При подстановке этих значений в общие
формулы, выведенные в гл. II, получатся явные выражения
для вычисления термодинамических функций. Если
Qru ро I >
мы имеем:
Qi QBp * Сколеб
и, следовательно (см. формулы табл. 2 в главе II),
Е = Ео-\-^-RT-\-RT2 4-^Г2—^олеб , (8.72) ‘ ai 4
Н = Яо + |/??+/?Г2 RT2 £1п^|,теб , (8.73)
F = — RTlnQB[l— RT In QKo.4e6, (8-74)
Ф = 7/о4-Фц—/?Г1п Qnp — RTIn QKC)^6, (8.75)
5 = rf In Q Sn+/?InQBr + /?7’-^ d In QL.„, - + /?1пОКОлоб+ RT—.
(8.76)
с» = 3 d In Q»n 4 R + 2RT- + RT2 2 al 1 rf2|nQBp . d'nQK0Jie(i rfP | -A' dT 1 Ч-/?/2^1^0-406. (8.77)
Ср — 5 d In Q jR^2RT—RT2 dJ In QB|. I n D-p Ен Фколеб ! dT'i 1 dT “1 rf2 In Q .й + /№ • (8-78?
§ 8] ВЫЧИСЛЕНИЕ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ 241
Таким образом, при разделении энергии можно от-
дельно вычислить слагаемые, соответствующие вращательному
и колебательному движениям молекулы. Мы будем иметь:
п* ______ г г _____ пт} ^колеб
сколеб — Л Колеб — К ‘ ,
Fколеб == Фколеб == RFln Сколеб.
^олеб = R 1П фколеб + RT
(8.79)
(8.80)
(8.81)
Сколеб = 2RT ^1п^одеб 4- RT2 -1п^оле6. (8.82)
Подставляя значения <?КОлеб
(см. § 8 главы V):
из формулы (8.69), получим
Дколеб — 7/колеб — R /;
к е к
1
_ч.
Fколеб = Фколеб — RT 2^(1 — в )(
к
(8.83)
(8.84)
*>к
5Колеб = /?^-й^й----R 2 1п(1 - е~ ™ ), (8.85)
к е ~ 1 к
Сколеб — R
к
^к_
(РГ‘‘Т
, h'ldlcT - *
(е — I)2
(8.86)
Для вычисления этих величин, как было указано выше,
имеются удобные таблицы (см. табл. 50). В отличие от
двухатомных молекул, где имеется только одна частота
колебаний, при применении формул (8.83)—(8.86) необходимо
производить вычисления для каждой частоты отдельно, а затем
выполнить суммирование слагаемых, найденных по таблицам.
В случае вырожденных частот появляются одинаковые
слагаемые, что можно учесть умножением их на степень
вырождения частоты. В этом последнем случае суммирова-
ние, разумеется, нужно производить только по численно
‘различным частотам, которых будет меньше чем ЗЛА—6.
16 Зак. 835. И. Н. Годнее
242 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ КВАЗИТВЕРД. МОЛЕКУЛ [гл. VIII
В качестве примера рассмотрим вычисление колебательной
теплоемкости СН3С1 при Т =400° К- Эта молекула имеет
шесть частот колебаний, из которых три вырождены дву-
кратно. Эти частоты приведены в таблице 25 с указанием
их симметрии и степени вырождения. В последних столбцах
приведены вычисленные теплоемкости.
Таблица 25
Часто- ты Сим- мет- рия Значение частоты Степень вырож- дения Табличные зна- чения тепло- емкости Значение колебательной теплоемкости
л Аг 2966’сл-* 1 0,0052 • 1 0,0052
At 1355 с 1 1 0,3659 • 1 0,3659
'^3 Ai 732 см~' 1 1,1493-1 1,1493
Е 3042 см~1 2 0,0042 - 2 0,0084
ч Е 1455 ‘с м 1 2 0,3502 • 2 0,7004
*в Е 1015/xf"1 2 0,7240 2 1,4480
Сколеб = 3,677
Выражения для слагаемых термодинамических функций,
зависящих от вращательной энергии, как это следует из
данных §§ 2—6, будут зависеть от типа молекулы.
Для линейной молекулы мы будем иметь:
следовательно,
Евр = Явр = Я7*?^^==ЯГ2у ~ RT, (8.88)
FBp = Фвр = - RTIn Qap = -RTln^^-, (8.89)
d In Q WIkT
SBp = /?lnQBp-[-/?7’-^^ = /?ln—+ Я (8.90)
и
d In Qaa . da In Q
СВр = 2/?7'-?^ + /?Г3—~^L = 2R—R = R. (8.91’
Подставляя найденные значения слагаемых вращательного
движения в формулы (8.72)—(8.78), получим для линейных
многоатомных молекул при средних и высоких температурах
§ 8] вычисление термодинамических функций 243
следующие формулы:
Д — ДоЧ“ ~2 RT^колеб. (8.92)
77 = -% RT-|-НКолеб> (8.93)
F = Ео + Fn - R Т In - ГКОЛеб, (8.94)
Ф = Но + Фп - RT In - Фколеб, (8.95)
$ = Sn + R In + R H-£колеб, (8.96)
С® ~2 ft ~Н^колеб> (8.97)
Ср = -% R Сколеб- (8.98)
Для вычисления Sn, Fn и Фп мы имеем формулы, при-
веденные в таблице 2 (см. главу II; см. также формулы
(2.74), (2.75), (2.89)).
Мы видим, что для линейных молекул получаются выра-
жения, совпадающие с выражениями для вычисления термо-
динамических функций двухатомных молекул.
Сводной таблицей этих формул является таблица 9, по-
строенная нами для двухатомных молекул, но относящаяся
ко всем линейным молекулам. Отличие линейных много-
атомных молекул от двухатомных проявляется лишь в суще-
ствовании нескольких частот колебаний (вместо одной), что
^надлежит учесть при вычислении слагаемых Дколеб. 5К0лвб>
!йголеб> Fколеб-
Рассмотрим теперь вывод формул для вычисления термо-
динамических функций нелинейных молекул при средних и
Высоких температурах.
к Выражение для QBp асимметричного волчка (8.41) в част-
|ном случае дает формулы для QBp симметричного и сфери-
ческого волчков, поэтому нам будет достаточно рассмотреть
^Случай молекулы с тремя неравными моментами инерции.
|Мы имеем на основании формул (8.59) и (8.55), если опу-
стить множитель а,
Ял2 / 2~kTI. \7« / 2nkTIn\'lt j
й.=т(тг) Ь^) • <8-")
16»
244 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ КВАЗИТВЕРД. МОЛЕКУЛ [гл. VIII
d In Q d? In QBn
Вычисляя производные —-т~. - и — , мы получим:
tfinQBp dT _11 ~~ 2 T (8.100)
И ^Ш(?вр dT2 2 j_ 2 p • (8.101)
Таким образом, для нелинейной многоатомной молекулы
будем иметь:
d In Qnn 3
Евр = Нвр = RT* | RT, (8.102)
FBI, = Фвр= — RTln QBp=—RTln— --------, (8.103)
d In Q„n
SBp = /?lnQBp + /?T-^^ =
8-2 (2гйЛа/а , 3
= R m —-------J ° + (8-104)
И
CBP = 2RT ^^-RT* --1” ^°P =2/? I R = | R. (8.105)
Подстановка этих значений в формулы (8.72)—(8.78)
дает:
f — Eо -|- 3RT4“ Сцолеб, (8.106)
77 = H0-{-4RT -j-7/колеб, ' (8.107)
8л2 (2лйГ)'1/а (I J Jr.)'1' F =Ea + Fn—RT\n — AB0> - Н^колеб! (8.108)
ф=н0+фп- /гтчп ——-h\-A B c> - an6 ЬЛсолеб, (8.Ю9)
Q - Q _L. 3 D । p 1„ 8^(2^7)V4WC)7a , Л Sn + -2 R + R In ^3 [ -Зколеб, (8.1Ю)
Cr — ЗЯ 4-СК0леб, (8.111)
Ср = 4R СЕ0Леб. (8.112)
§ 8]
ВЫЧИСЛЕНИЕ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
245
Таблица 26
Формулы для вычисления термодинамических функций
нелинейных квазитвердых молекул
№ п/п Термодинамиче- ская функция Практическая формула
1 Энергия Е — Ео~ 3RT + EsojkS
2 Энтальпия H-H0 = 4RT + /7коле6 = 4RT + Еколеб
3 Энтропия 5=/?^1пЛ44-41п Т + ^lnIAfBr0—\np~ - Ina + 133,520)+ 5К0Леб
4 Приведенная сво- бодная энергия = я( - | In М - 4 In Т — — 7|п !лгв'с +ln Р +|п ’ — 130,52о) + +(т) х /колеб
5 Приведенный изо- барно-изотерми- ческий потен- циал п = 5-=-^° = R ( - In М - 4 In Г— — у In In р 4- In о — 129,520j -f- О ' ‘ 'колвв
6 Теплоемкость С„ = зя + сколеб
7 Теплоемкость Ср Ср ~ 4“ ^колеб
Выражения (8.103) и (8.104), если в них подставить значе-
ние постоянных, примут вид
FBp = Фвр = — RT (1п---------------Н 133,185}, (8.113)
5вр = Я|1п—--------------р 134,685]. (8.114)
Если заменить в формулах (8.108), (8.109), (8.110)
246 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ КВАЗИТВЕРД. МОЛЕКУЛ [ГЛ. V1H
Fn, $п и их значениями и подставить численные зна-
чения постоянных, мы получим:
F = E0 — ЯГ (in-------+ 130,520} И-FK0Je6, (8.115)
М31'ТЧ1 г 1 )1, 2
Ф = /70 — AJT {1п-----129,520}+^коле6, (8.116)
s = /?|ln----------------Ь 133,520} +5К0Леб. (8.117)
Из формулы (8.116) следует:
П = ? ° = — R (1п-------- * в —h 129,520} +
Эти формулы являются общими для нелинейных жестких
по отношению к вращению молекул.
При 1В — 1С они будут применимы для молекул типа
симметричного волчка, при /А = Iв = Iс—для молекул
типа сферического волчка. В заключение дадим сводку прак-
тических формул для вычисления термодинамических функ-
ций жестких молекул при средних и высоких температурах
(см. табл. 26).
§ 9. Вычисление моментов инерции
Рассмотрим теперь, как вычисляются главные централь-
ные моменты инерции многоатомных молекул. Непосредст-
венное определение их методами оптической спектроскопии
возможно для сравнительно небольшого числа молекул *).
Поэтому для определения моментов инерции используются
электронографические данные, дающие основные расстояния
равновесной конфигурации молекулы **).
*) См. Хиббен [90], глава II.
**) В последнее время для определения моментов инерции
молекул начала находить широкое применение радиоспектроскопия
(микроволновая спектроскопия), методы которой позволяют более
непосредственным образом находить моменты инерции. Радиоспек-
троскопические измерения последних позволяют провести также
достаточно точное вычисление междуядарных расстояний. При этом
существенную помощь оказывает изучение изотопических молекул
(см. обзорную работу В ильсона [266] и монографию [89]).
§ 9]
ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
247
Если молекула обладает симметрией, определение поло-
жения главных осей инерции, как было указано выше, упро-
щается, так как уже ось симметрии второго порядка является
главной, а плоскость симметрии всегда перпендикулярна
к главной оси. Наличие элементов симметрии упрощает также
и определение центра инерции молекулы.
Для определения главных центральных моментов инерции
прежде всего необходимо найти положение центра инерции.
Пусть мы выбрали произвольную систему координат х',
у', z', жестко связанную с молекулой. Пользуясь основными
расстояниями между ядрами, мы можем вычислить коорди-
наты ядер в этой произвольной системе. Пусть массы ядер
будут mv т2........ тп, координаты их xlt ylt zb ха ,
4, • • •
Обозначив координаты центра инерции через х0, yQ, z0,
получим: = (8.120) = <8Л21)
Перенося, начало Координат в центр инерции молекулы,
мы от координат х', у', z' можем перейти к центральным
координатам с осями х, у, z,
х = х' — х0, (8.122)
У = У'—Уо, (8.123)
z — zr — z0. (8.124)
Оси х, у, z, вообще говоря, не являются главными осями
инерции. Вычислим моменты инерции и произведения инер-
ции относительно центральных осей х, у, z. Квадрат рас-
стояния от оси х произвольной точки с массой mi будет:
(8.125)
248 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ КВАЗИТВЕРД. МОЛЕКУЛ [гл. VIII
Поэтому для моментов инерции мы получим:
Цх — A — + г (8.126)
lyy^B^^nti (x2i + z2i), i (8.127)
Цг — С = ^nti (Xj + yi). i (8.128)
Произведения инерции будут:
Ixy -F = 2 пцхгУг, i (8.129)
IX, = E = ^ i (8.130)
fyz ” “ S • i (8.131)
В системе координат х, у, z, которая является централь-
ной, произведения инерции 1ху, /жг, 1уг, вообще говоря, от-
личны от нуля, и поэтому оси х, у, z не являются глав-
ными, для которых, как известно, произведения инерции
должны обращаться в нуль *). Заметим, что при выборе
произвольной системы координат х', у', z' при конкретных
расчетах надлежит руководствоваться соображениями сим-
метрии, так чтобы хоть часть произведений инерции обра-
тилась в нуль.
Для определения главных центральных моментов инерции из
Лвэ> Iyy< Ц» Ixy< Ixz> lyz необходимо составить, как это доказы-
вается ' в курсах теоретической механики . (см. [8]), следующее
уравнение:
Л-Х — F —Е
— F В — Х — D = О, (8.132)
—Е — D С—Х
корни которого Xt = 1А, Х„ = IB, XS = IC и являются главными
центральными моментами инерции.
*) См. Н. Н. Бухгольц [8].
ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
249
§ 9]
Заметим, что произведение корней векового уравнения
(8.132) равно*) детерминанту
А
— F
— Е
At^2X3 = IaIb!c =
— F — Е
В —D
— D С
(8.133)
вычисляя который, мы можем непосредственно определить
произведение (JaIbIc)!*’ которое только и требуется для
вычисления вращательных слагаемых термодинамических
функций, как это следует из формул § 8. Поэтому при
вычислении термодинамических функций можно и не опре-
делять значений главных центральных моментов инерции,
ограничившись вычислением детерминанта (8.133).
Величины А, В, С, D, Е, F можно выразить через коор-
динаты ядер в произвольной (нецентральной) системе коор-
динат. Так, для А — 1ХХ, заменив yi и из формул (8.123)
и (8.124), мы получим:
Л = 2 "Ц (yai + z|) = 2 "Ч (y'i — У о)2 + 2Х (z'i—Zq)2 (8.134)
i i i
ИЛИ
4 = 2 — 2y0 5 ^y • +/02«i+
г i i
+ —+ 2 (8.135)
i i i
Исключая из этих выражений _у0 и г0 с помощью формул
(8.120) и (8.121) и замечая, что ^lmi = М—масса всей мо-
лекулы, имеем:
л = ^ityi+Zi) — 7j(SOTiZ*)8, (8‘136)
i i i
Аналогичным образом можно получить выражения для
В, С, D, Е и F. Применяя такие выражения, можно и не
*) См. А. Г. К у р о ш [36].
250 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ КВАЗИТВЕРД. МОЛЕКУЛ [ГЛ. VIn
определять координаты центра тяжести. Мы получим:
^(^П ~ (8Л37)
i i i
с = +х'^ ~ Jf (2 т*у'$ ~ i (2 miX'^’(8-138)
г i i
г=2 т*х'*у* ~ (2 (2т^) ’ (8-139)
i i i
E = 2 mix'iz'i — (2 mix'^) (2 т^'1) ’ (8.140)
i i i
2т^~^(2т^)(2т^)' (8.141)
i i i
§ 10. Пример
В качестве примера приведем вычисление моментов инер-
ции молекулы кетена Н2С = С = О. Молекула кетена имеет
плоскую конфигурацию симметрии C.2v (черт. 25). Размеры
молекулы характеризуются следующими данными:
г1 = (С = С)= 1,35 А,
г, = СН= 1,07 А,
/3 = СО = 1,17'А,
^НСН— 118°.
§11] УЧЕТ АНГАРМОНИЧНОСТИ 251
Поместив начало координат в точку, лежащую посре-
дине между атомами С и направляя ось х вдоль оси С = С
(ось у' проведем в .плоскости чертежа), мы можем легко
найти значение координат ядер (табл. 27).
Таблица 27
Атом Координаты в исходной системе Координаты в центральной системе
хг У' X У
с(1) 0,675 0 1,318 0
С(2) — 0,675 0 — 0,032 0
О — 1,845 0 —1,202 0
н(1) 1,226 + 0,917 1,869 + 0,917
Н(2) 1,226 — 0,917 1,869 — 0,917
Из данных таблицы получается положение центра тяжести
по формулам (8.119) и (8.120)
а = — 0,643, Ь = 0.
Переходя к центральной системе координат, найдем
центральные координаты ядер, которые мы приводим во вто-
ром столбце таблицы 27. Легко видеть, что система коор-
динат ху является центральной и главной, так как ось х
является осью симметрии второго порядка.
Мы получим:
А = 2771 (У2Ч-2'2) = 2,82 • 1О~40 г • см2,
В = 2»г(^2 + ^) = 84,74 • Ю-40 г • см2,
С = 2"г(^ + У2) = 87,55 • 1О~40 г • см2.
Все произведения инерции обращаются в нуль.
§ 11. Учет ангармоничности и других отступлений
от модели жесткой по отношению к вращениям молекулы
с гармоническими колебаниями
Для более точных вычислений термодинамических функций
многоатомных молекул, если известны постоянные ангармо-
ничности и другие коэффициенты, учитывающие отступления
ОТ модели жесткой по отношению к вращениям молекулы
252 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ КВАЗИТВЕРД. МОЛЕКУЛ [ГЛ. VIII
с гармоническими колебаниями, могут быть применены спо-
собы Гордона и Барнеса и Касселя (см. §§ 14, 15 главы V).
Такие расчеты были выполнены для линейных молекул HCN,
СО2 и др., а также некоторых нелинейных молекул (см.,
например, Гордон [223—225]). Для этих вычислений Гордон
составил дополнительные таблицы [225]*).
Удобный метод учета ангармоничности для случая двух-
атомных и многоатомных газов был разработан недавно
М. П. Вукаловичем и сотрудниками [15]**).
Вопрос о влиянии центробежного растяжения при вра-
щении молекул на термодинамические свойства был обсужден
Вильсоном [263].
Нужно заметить, что необходимые постоянные известны
для сравнительно небольшого числа молекул. Поэтому
в практике вычисления термодинамических функций часто
ограничиваются вычислениями по формулам, приведенным
в предыдущем параграфе, тем более, что эти формулы дают
достаточно удовлетворительные результаты. Так, для Н.2О при
Т= 1000°К точные вычисления дают 5=55,598 кал/град• моль,
тогда как приближенная модель дает 5=55,52 кал/град-моль.
*) См. также И. В. Смирнова и А.-В. Фрост [171].
**) См. также Пеннингтон и Коб [248].
ГЛАВА IX
ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ГАЗОВ
В СЛУЧАЕ СВОБОДНОГО ВРАЩЕНИЯ
§ 1. Общие замечания
В главе VI при рассмотрении классификации молекул
было указано, что существует большое число соединений,
в молекулах которых имеет место внутреннее вращение.
К таким соединениям принадлежат этан, пропан, ацетон,
диметилацетилен и др. В большинстве случаев внутреннее
вращение не является свободным и существует потенциаль-
ный барьер, ограничивающий вращение групп внутри молекул.
Однако есть молекулы, где вращение оказывается практически
свободным.
В настоящей главе мы рассмотрим в общем виде вычи-
сление термодинамических функций газов в случае сво-
бодного вращения групп. Хотя молекул со свободным вра-
щением существует очень мало, рассмотрение этого случая
необходимо для решения задачи о вычислении термодинами-
ческих функций в случае заторможенного вращения. Приме-
ром газа с почти свободным вращением внутри молекул
является диметилацетилен (СН3—CsC—СН3).
Пусть дана многоатомная молекула, имеющая t волчков,
вращение которых происходит свободно. Например, в слу-
чае СН3—СО—СН3 t = 2, так как имеет место вращение
двух групп СН3 относительно остова молекулы. Такая моле-
кула будет иметь три степени свободы вращательного дви-
жения и t степеней внутреннего вращения. Наличие этих £-|-3
степеней свободы естественно приводит к уменьшению числа
степеней свободы колебательного движения. Если бы не
было внутреннего вращения, мы имели бы 3N — 6 нормаль-
ных колебаний, как это имеет место в квазитвердых моле-
кулах.
254 СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ [гл. IX
Теперь число колебательных степеней свободы будет:
п' — 32V—(3-[-3 + 0 = 3/V — 6 — t, (9.1)
т. е. будет на t степеней свободы меньше. Будем пред-
полагать в первом приближении, что энергия этих 3.V—6—Г
колебательных степеней свободы может быть отделена от
энергии вращательных степеней свободы. В этом случае
сумма по состояниям Qit как это следует из предположения
о разделении энергии (см. главу II), может быть предста-
влена в виде произведения
Qi = QtcrweS ’ Qsp " Qs.t (9-2)
Будем предполагать, как и в случае квазитвердых молекул,
что электронная сумма по состояниям
QM=1. (9.3)
Мы будем иметь для таких молекул
Qi = Сволеб • Qbp- (9.4)
§ 2. Вычисление суммы по состояниям вращательного
движения в общем виде для случая свободного вращения
Рассмотрим вычисление QDI. Это вычисление мы проведем,
пользуясь выражением для энергии, которое дает классическая
механика. В этом случае, как об этом сообщалось в § 7
главы I, мы должны применить формулу (1.46) (см. также
§ 3 и § 5 главы VIII)
Qo = | • • • J е кТ dqx ... dqadpxdp2 ... dpa, (9.5)
где s означает число степеней свободы рассматриваемой
системы (оно равно Г+3), qv q.2, ..., qs — обобщенные
координаты и рх, р2, ..., ps — обобщенные импульсы.
При применении этой формулы к вращательным степеням
свободы необходимо учесть наличие числа симметрии. Число
симметрии квазитвердой молекулы определялось как число
вращений молекулы (число элементов группы /?), переводя-
щих ее в тождественное положение (см. § 6 главы VI).
Легко видеть, что внутреннее вращение приводит к увели-
чению числа симметрии. Рассмотрим, например, молекулу
§ 21
ВЫЧИСЛЕНИЕ QBp
255
этана. Если бы не было вращения группы СН3 относительно
.другой группы СН3, то эта молекула имела бы число сим-
метрии 6 (вращательная симметрия ZJ3, см. табл. 14).
Однако группа СН3 может занимать три положения,
полученные одно из другого ее вращением. Эти три враще-
ния можно соединить с каждым из шести вращений всей
молекулы в целом, всего получится 3-6 = 18 вращений,
и число симметрии молекулы этана будет 18. В общем слу-
чае, если обозначить число симметрии при отсутствии вну-
треннего вращения через <з0, а число симметрии волчков
через ot, а2, .... а{, то мы будем иметь:
а = а0.а1.а2 .. . at. (9.6)
Для иллюстрации в таблице 28 приведены числа сим-
метрии некоторых молекул с внутренним вращением.
Т а б л и ц а 28
Числа симметрии молекул с внутренним вращением
256 СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ [гл. IX
Деление фазового интеграла на число симметрии про-
исходит из-за требований симметрии, приводящих к реали-
зации 1/а части состояний.
В качестве независимых переменных qv q.2, .... qa можно
выбрать три эйлеровых угла 0, ф и о, определяющих про-
странственную ориентацию молекулы в целом, и углы
ар а2....аг, описывающие положения волчков относительно
остова при вращении их вокруг своих осей.
В случае свободного вращения потенциальная энергия
будет равна нулю и поэтому
е = Т+У= Т,
т. е. кинетическая энергия равна полной энергии.
Для вычисления кинетической энергии применяется не-
сколько различных методов. Кинетическую энергию можно
представить в виде положительно определенной *) квадра-
тичной функции обобщенных скоростей
Т = ^а^к=Т{д, q). (9.9)
i, к
Квадратичной функции (9.9) соответствует матрица из s строк
и $ столбцов, которую мы обозначим через
ап а1-2 • • • ats
(Д) = Я21 й22 • • ‘ а2з , (9.Ю)
\ав1 аз2 • • ‘ азз'
причем эта матрица будет симметричной, т. е. aik = aki.
Детерминант этой матрицы обозначим через [Д[,
«И й12 • • а18
и -- а-21 а22 • ‘ • а2з (9.11)
аз1 аз2 • • ass
*) Квадратичная функция называется положительно определен-
ной, если ее значение всегда больше нуля для значения перемен-
ных, отличных от нуля. Это свойс!во для кинетической энергии
вытекает из физических соображений, ибо кинетическая энергия
не может быть отрицательной.
§ 2]
ВЫЧИСЛЕНИЕ Qsp
257
Вычисление интеграла (9.8) показывает, что (QBp оказы-
вается зависящей от детерминанта [Л].
Для QBp получается следующая формула:
QBp = -lr(2^7’)a/aJ... ... dqs. (9.12)
ai %
Для доказательства этой формулы заметим, что интегрирование
в формуле (9.8) производится по координатам и импульсам,
а поэтому нам нужно выразить е (q, q) через импульсы. Обобщенный
импульс pi по определению будет (см., например, [8])
dT(q:q) • (9.13)
Дифференцируя выражение энергии (9.9), мы получим:
Pl = аМ.Я1 + а12?2 + • • • + а1вЯв>
Да = а2191 + ^22^2 + • • • + й2в<7«> (9.14)
Рв — ав1Я1 + as2<?2 + • • • + аввЯв- .
Если решить уравнения (9.14) относительно обобщенных ско-
ростей, то получится:
<71 = ^11Р1 + ^12Р2 + ... + bitp8, )
?2 = ^21Р1 + ^22^2 + • • • + Ьъара, I (9.15)
Я в — Vi + btf,p% Ц- • • + bggPa. J
Легко видеть, что матрица (В), составленная из коэффициен-
тов Ь(к, будет обратна матрице (Л)
(В) = (6й) = (Л)-1. (9.16)
Обозначив через [Л] и [В] детерминанты матриц (Л) и (В),
мы из соотношения (9.16) будем иметь:
J [В] = [Л]“1. (9.16а)
; Подставляя значения q{ в выражение для кинетической энергии,
^случим:
7’ = у ^ikpiPk. (9.17)
i,Tt
17 Зак. 835. И. Н. Годнее
258
СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ
[гл. IX
Действительно, мы можем записать формулу (9.9) в виде про-
изведения трех матриц
• \
I
. . (9.18)
. /
Ча/
Уравнение (9.15) в матричном виде мы можем записать, так:
/чЛ /Р1\
!=(/)-( К2 . (9.19)
\'Ча/ \р8/
Выполняя в равенстве (9.19) операцию транспонирования, которая,
как известно, обладает свойством *)
(АВ)' = (В)'(Д)', (9.20)
получим:
= (9.21)
так как (Л) = (Д)'.
Подставляя значение матрицы строки ... qa) из уравнения
(?1\
: I из уравнения (9.19) в ра-
Ча/
венство (9.18), пОлучим:
/Д1\ 1Р1\
2Г=(Р1...р8)(Д)-1(Л)М)-1 : =(Р!...д8)(Л)-1 : =
\Рв1 \psl
/Р1\
= (Р1 • • • Ра) (В) : I. (9.22)
\Ра/
откуда и следует равенство (9.17).
Выразив энергию как функцию импульсов, мы могли бы теперь
подставить выражение (9.17) в формулу (9.8), определяющую QBp.
Однако, прежде чем это делать, целесообразно привести выраже-
ние для энергии к диагональному виду. Это возможно выполнить
с помощью ортогонального линейного преобразования импульсов,
так как кинетическая энергия представляет положительно опреде-
ленную квадратичную форму **).
*) См. И. М. Г е л ь ф а н д [17].
**) Там же.
§ 2]
ВЫЧИСЛЕНИЕ QBp
259
Перейдем к новым импульсам p1p.i ... ра с помощью линейного
ортогонального преобразования
Pl = сцР1 + с1зР2 + • • • + ciap's >
P-i = сцР1 4“ с2^Р-1 + • • • + ciaPs > (9.23)
Ps = CslPl + Cs2Pi + • • • + casPs
с матрицей
Ccll c12 • • • cle \
C21 C22 • • • C2e ). (9.24)
Cs2 . . . Css '
В силу ортогональности преобразования (9.23) матрица (С)
будет ортогональной.
При этом мы выбираем матрицу (С) так, чтобы кинетическая
энергия в новых координатах приняла диагональную форму
s
Т = | Dip-. (9.25)
i = l
При линейном преобразовании координат, как известно, матрица
в новых координатах примет вид (см. [36, 17])
(С)'(В) (С), (9.26)
где (С) — матрица преобразования и (С)' — транспонированная
матрица. Применяя эту формулу к нашему преобразованию, при-
водящему квадратичную форму (9.17) к диагональному виду, мы
получим:
(Dj 0 ...Ок
О D2 ...О \
О OD3...O =(С)'(В)(С), (9.27)
о о о ... dJ
причем в силу ортогональности матрицы (С) детерминанты [С] и
[С]' будут равны единице. Таким образом,
[D] = [С]' [В] [С] (9.28)
или
ад ... D„ = [В], (9.29)
или, используя соотношение (9.16а),
ад...£18 = [В] = [Л]-1. (9.30)
Теперь посмотрим, какой вид примет интеграл (9.8) при пере-
ходе от переменных рь р^,..., ра к pv р2.........ра. Переходя
17*
260
СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ
(ГЛ. IX
к новым переменным, мы получим:
<?вР= -^7 J ••• J е 2кТ dPl...dpsdqr...dqs =
[Я] е ЫТ dp\ ... dp'sdqt ... dq., (9.31)
ij-
где [Я] означает определитель Остроградского (якобиан преобра-
зования) *), который в нашем случае будет
[Я] = dPi dp't dpi дрг др\ dPi др-2 .. dp'2 ” dPt dPs дрч dp's (9.32)
В силу формулы (9.23) мы dPs dps др{ др^ получим: 7П С12 . . . dps дР'з
[Я] = C2t С22 cs2 . .. Cag • • С88 = [С]. (9.33)
Мы видели, что детерминант [С] матрицы (С) равен единице и
поэтому
[Я] = 1. (9.34)
Таким образом,
<?вр ( • • • ( в dPi dPsdqi... dqs. (9.35)
G ll v и
Теперь мы можем выполнить интегрирование по импульсам. Мы
будем иметь:
QBI, =-^ | ••• I [ j е 2кТ 'dPr J е 2кт 2 dPi---
вц а — со —со
+ “ D* ,2
j е 2кТ Ps rfp'j dqt... dqs. (9.36)
— 00
*) См. Г. М. Фихтенгольц [66] или А. Я. Хин чин [76].
§ 3]
ВТОРАЯ ОБЩАЯ ФОРМУЛА для QBp 261
Как известно,
(9.37)
Применяя эту формулу к каждому интегралу в (9.36), получим:
Используя формулу (9.30), мы имеем окончательно:
₽. Р8
(?Dp = -L (2^7)3/3 J ... ( [A]^dq,... dqs. (9.40)
Формула (9.40) была впервые получена Эдинофом и Астоном [218].
Мы нашли таким образом общее выражение для QDp.
Вообще говоря, детерминант [Л] является функцией ко-
ординат qv q.2, . . ., qs и поэтому в общем случае его
нельзя выносить за знак интеграла.
§ 3. Вторая общая формула для QBp
Если в качестве обобщенных координат выбрать три
эйлеровых угла 0, б и ф и указанные выше углы av а2,.... at,
то полученное в предыдущем параграфе выражение для QBp
может быть несколько упрощено при выполнении интегри-
рования по эйлеровым углам *).
Пусть кинетическая энергия молекулы выражена че-
рез проекции угловой скорости вращения остова ч>у,
<ог и производные углов, определяющих ориентацию
I *) Это впервые было показано Касселем [237]; см. также
262
СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ
[ГЛ. IX
волчков, а1, <х2....af. В этом случае кинетическая энер-
гия также представится в виде квадратичной функции
где /i означает одну из величин <оу, шг, а1, а2, аг.
Проекции угловой скорости ш2 могут быть, как изве-
стно, выражены через эйлеровы углы и их производные *):
и>х ='ф sin 0 sin <р -|- 0 cos if,
<1>У = ф sin 6 cos <р — 0 sin } (9.42)
<ог = ф cos 0 у. J
Заметив, что при нашем выборе координат в квадратичную форму
(9.9) войдут производные эйлеровых углов 0, ф и <? и производные
а1: а2... о(, а в квадратичную форму (9.41) входят — и>х, о^, шг
и вр и2....“ti мы получим уравнения преобразования
1Г = Шд, = ф sin 0 sin tf 0 cos
/2 = и>у = ф sin 0 cos v — 0 sin 4>,
ls — 0>г = ф COS 0 -ф- 'f,
li = «1.
4 = а2.
4 = at
(9.43)
с матрицей (Р), равной
/ COS <f> sin 0 sin у 0 0 . . 0 1
— Sin У Sin 0 COS ? 0 0 . . 0
0 COS 0 1 0 . . 0
(Р) = 0 0 0 1. . 0
(9.44)
О 0 0 0 ... 1
*) См. Н. Н. Бухгольц [8], ч. П или Л. Г. Л о йц я некий
и А. И. Лурье [43], т. I,
§ 3] ВТОРАЯ ОБЩАЯ ФОРМУЛА ДЛ? QBp 263
Детерминант матрицы (Р) будет:
cos <р sin в sin <р 0 0 . . 0
— Sin ' sin fl cos f 0 0 . . 0
0 cos 0 1 0 . . 0
н = 0 0 0 1 . . 0 = sin 0.
(9.45)
О 0 0 0... 1
Матрицы квадратичных форм (9.9) и (9.41) связаны соотношением
(см. формулу (9.26))
(Л) = (Р)'(5)(Р), (9.46)
гд'е (Р)' — транспонированная матрица, a (S) = (s^) матрица квад-
ратичной формы (9.41).
В силу формулы (9.46) для детерминантов матриц (Л) и (S)
мы получим:
[Л] = [SJ [Р]2 (9.47)
или
[Л] = [S] Sin2 fl = Sln2 6. (9.48)
Подставляя значение [Л] из формулы (9.48) в выражение для QBp
(см. формулу (9.40)) и принимая во внимание выбор первых трех
координат (^ — 0, 72 = ф, q3 = <р, q-a = а2, ..qs = а(), мы
будем иметь:
QbP = 4- (2™Г)8/3 X
<shs
тс 2тс 2тс 2тс 2тс
X |*... f f j f [«»&]’2 sin 6 dt) й?ф dy darda2 ... dat. (9.49)
0 0 0 0 0
Выполняя интегрирование, получим (s = ^-|-3)
। £+3
2г. 2я
X 8z2 j .. . ... dat. (9.50)
о о
Если детерминант [sifc] не зависит от углов at, «2......a(,
как это имеет место в случае симметричных волчков, его
можно вынести за знак интеграла, вследствие чего получается:
t+з
= 2 М/!(2*А (9.51)
264
СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ
[ГЛ. IX
Напомним, что в формуле (9.51) означает детерминант
матрицы, соответствующей квадратичной форме (9.41), т. е.
детерминант матрицы кинетической энергии молекулы, выра-
женной через <х>х, <йу, <1>г, at. a2, ..., at.
§ 4. Случай симметричных волчков
Рассмотрим, какой вид примет формула для QBf в случае
молекул, имеющих вращающиеся группы в виде симметрич-
ных волчков. Примерами таких молекул являются СН3С=ССН.>,
СН3СОСН3, СН3СН2СН3 и др. *). В таких молекулах цен-
тральный эллипсоид инерции каждого волчка является эллип-
соидом вращения и ось волчка совпадает с осью вращения
эллипсоида инерции.
Пусть МС-». ;ула имеет t симметричных волчков. Будем
предполагать, что оси волчков, как это имеет место для
многих молекул, не пересекаются в одной точке. Проведем
через центр тяжести молекулы, который при вычислении
энергии вращения мы будем предполагать неподвижным,
*) Вращение СН3 групп в СН3СОСНЭ, СН3СН2СН3 не является
свободным (см. главу X),
§ 4] СЛУЧАЙ СИММЕТРИЧНЫХ волчков 265
оси х, у, z, жестко связанные с остовом молекулы. В случае
молекул с симметричными волчками моменты инерции и произ-
ведения инерции всей молекулы относительно осей х, у, z
не будут меняться при изменении углов ар а2..at, опре-
деляющих положение волчков относительно остова молекулы.
Для вычисления детерминанта от которого зависит, как
мы видели в предыдущем параграфе, QBp, нужно найти явное
выражение кинетической энергии вращения всей молекулы
через а>х, <иу, <в2 и at, a2, ..., af.
Проведем через центр тяжести z-ro волчка, лежащий на
его оси, Координатные оси х', у', z', параллельные х, у, z
(черт. 26). Обозначим косинусы углов, образованных осью
z’-ro волчка с осями х, у, z через лг,
Энергия вращения молекулы будет:
Т — еост-|--|-г2-|- ... —Sf—[— . . . —se, (9.52)
где е, означает энергию z-го волчка.
Движение остова молекулы представляет собой вращение отно-
сительно центра тяжести с угловой скоростью ш. Для остова можно
написать *):
-4л о , ^?л 2 । б*л О — г, ип,
Еост = у + У “у + у "2 — — Еошхшг — 'o'W (9.53)
Чтобы вычислить энергию Z-ro волчка, перенесем угловую ско-
рость »> в точку В (вектор в>', черт. 26). Волчок относительно непо-
движной системы координат будет совершать вращательное движе-
ние с угловой скоростью ш + а,- и поступательное движение со ско-
ростью V/ = <adit где df означает длину перпендикуляра, опущен-
ного из центра тяжести волчка на линию, вдоль которой лежит
вектор о». Кинетическая энергия волчка будет:
Ч = ^i(wa; + Xi“i)3 +у B’i<my + Mi)4|c'iK+Vi)2-
— I4«j) (“г+ ¥i)~ ^(%+Ч’г) (0,г+ ЧЧ> —
— F'i (“a: + ЧЧ) (“у + Ч°Ч> + у Mivl <9-54)
где А'-, в'-, С';, D;, Eit F; означают моменты инерции и произведе-
*) См. Н. Н. Бухгольц [8].
266 СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ [ГЛ. IX
ния инерции волчка в системе координат х,^ yi, Подставляя еост
и выражения для энергии каждого волчка в формулу (9.52) и сум-
мируя, мы получим:
2Е = Л'4 + во'4 + Со4 — — 2Епыхи\ ~ 2Eowxmy +
+ 5?1i(“a! + Xiai)3+Sfii (0)г/ + Mi)3 + SCi (0)z+ —
— 25 Di(°y+ Mi) ('%+ ^’г)-22£4<“;г + Х4“г)(“г+\“г) —
(“y+ Mi) 0-55)
Пользуясь теоремой Штейнера, можно написать:
М=Ли>-Л«>'. (9-56)
где 7?;ш—момент инерции Z-ro волчка относительно оси <о и
Лш' '— момент инерции волчка относительно оси о/. Направляющие
косинусы параллельных векторов ы и ы' в системе х, у, z будут
“г
— , —- , — , так что
СО <0 <Й
Лш = (л1г“ж + 5г“г/ + ^г“г ~ 2О»м«вг —
2Ег^х^у) ^2»
, , , , ” > (9.57)
= (4“® + В о^ + С оЛ- «, -
I W ' V Ц/ 1 b tf 1 Ь 4 h у Z
-^VH^iVj) i-
Из формул (9.55), (9.56), (9.57) следует:
27 = (Ло + £ Л) + (В„ + В.) <о3 + (Со + 2 СО -
- 2 (Do + 2 Di) - 2 (£0 + 2 Ci) -
- 2 (Do + 2 pi) + 2 (4х? + B'iA + С?? - 2D^Pi -
2^/^p.^) 2 [2 (^iAi a i] шх 4"
. +2[S(-4Xi + B^-4'4>4K +
+ 2 [S (— E'iKi — Di^i + c'ivi) “г] “г- (9.5S)
Выражение
+ B'Ai + CiA - 2Г)МЧ - V-fyi'i - 2E'№i = (9.59)
§ 4] СЛУЧАЙ СИММЕТРИЧНЫХ волчков
267
представляет момент инерции l-го волчка относительно оси враще-
ния. Можно показать, что в случае симметричных волчков выраже-
ния, входящие в (9.58),
+ j (9-60)
равны соответственно *) K^i и K^i-
Таким образом, мы будем иметь:
2Т = (+ + 2 А) + (в0 + 2 А) шг/ + (+ + 2 А) ‘“г—
- 2 (£>0 + 2 - 2 (Ео + 2 Е{) -
— 2 (Fo + 2 А) шж“г/ + 2 Aai + 2 (2к?4аг)ша: +
+ 2(2 ) ф, + 2 (2 X) ®г. (9.61)
Выражения < cq Q Q tti й, II II II И И II + <хГ СТ Q сц ьГ Zl Н /1 И +1 И + + + + + + о о о о , о о ч; aq Q Ci 9j ь. (9.62)
представляют моменты инерции и произведения инерции всей
молекулы в системе х, у, z. Мы получим окончательно:
2Т — Аш~х -4- Вш~,, -I- Со>г — 2£>фмф, — 2Е<п„а>^ — 2Гш.Ёа>и -I-
‘"I У I * fj 4 Uz ff I
+ 2 +ai + 2 (2 ) “ж +
+ 2(2^Мг)<«г, + 2(2^л)«’г- (9.63)
*) Для этого нужно выразить моменты инерции и произведения
инерции УЦ, Bit Ср Dp Ei и через главные центральные мо-
менты инерции волчка (формулы преобразования см. Уитте-
кер [62]). Равенство величин KiPi и Ki4 и выражений (9.60)
будет иметь место также и для случая, когда волчок не симметри-
чен, но ось вращения является главной.
Для произвольного волчка имеют место более сложные соот-
ношения.
268
СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ
[ГЛ. IX
Сравнивая выражение кинетической энергии (9.63 лой (9.41), получим: । с форму-
0 0 К-2 0 0 . 0 . . 0 KA KA- K-^2 K-2<2
= 0 0 0 . • • Kt KA Kf?t Kt'>t (9.64)
ка . . Kt\t A — F — E
К&1 к^.2 Kt\it — F В — D
к^ . .. K^t — E — D C
Введем обозначения
л = 2 (у1++2 =
В = 2 m-i (?i + x<)=2 + 5 mix‘i =
c = 2 mi (x2i + _yb=S mix2i + 2 "ЧУ2 =
D = '£lmiyizi = <yz},
E (xz],
F = '£imixiyi = {xy}
'.^}+',yy\. ((9 65)
и
[u} = 2>X
i = l
Ж = 2 АгА,
и T. Д.
{ХУ/ + {zz} -
[zz] + [xx],
(9.66)
Умножая последовательно первый, столбец детерминан-
та (9.64) на Aj, у-р \ и вычитая соответственно из трех послед-
них столбцов, затем повторяя аналогичную операцию со вто-
§ 4I СЛУЧАЙ СИММЕТРИЧНЫХ волчков
269
рым столбцом (умножение на л2, и2) и т. д., получим:
= К, ...Kt X
<УУ } 4- {ZZ} — {А/-}
- Uy} - {М
— {xz} — {Ь}
— <-*У } — {Хр-} — {xz} — {Ь}
{хх} + {zz} — {№} — {у г} — {р.ч}
— {у^ —W U*} + {yy}~ W
(9.67)
Например, в случае одного волчка (детерминант четвертого
порядка) мы будем иметь:
1^.1 =
кх Ktf't K^.r Kt\
K^t A —F — E
— F В — D —
Кг\ — E —D C
Kt 0 KtV-i Kt\
Kt'-t A — K^t —F — E
KtVt В K^t В — D
Kt't в К.к^, —D C
Kt 0 0 Kt\
Kt\ — F — Ki^t^ t в
Kt\H — B~ Kt'^t B- -Kt^t — D
Kt\ -E-K^ — D — KlU.t'' t c
Kt 0 0 0
Kt'^t A — Kt'^i -E-Kt\\
в K^^y — D — Kt^t
Kt\ В K^'t't — D — Kt\H\ C-KtA
A — K^t
—В—K^t
— В — K^t
в-кгА
— D — K^i
— Е —
— D —
C — KtA
.(9.68)
Если бы у нас было два волчка, мы вместо детерминан-
та (9.68) получили бы детерминант, содержащий элементы
А— KjKi — K^i, —F — и т- Д- Рассмотре-
ние общего случая приводит к формуле (9.67).
270
СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ
(ГЛ. IX
Величины, входящие в детерминант (9.67), в случае сим-
метричных волчков не будут зависеть от углов а1( а2, ..., а4.
Следовательно, можно применить формулу (9.51). Подставляя
в нее значение детерминанта (9.67), мы получим окончательно:
t+з
<2вр - v (^ж) 2 х
Ы-Н^} —(U)
— {*у} —
— {xz} — М
— {*у} — Uh}
(хх) + {zz} — Ы
— {yz} — {р}
— {xz} — {av)
— {yz} — M
{xx)+(jj}—И
'1г
Эта формула была выведена Касселем [237].
(9.69)
§ 5. Пример
Рассмотрим пример вычисления [sift]. Пусть дана молекула
диметилацетилена (черт. 27), у которой атомы С лежат на
одной прямой. Эту молекулу можно представить состоящей
из остова Н3СС = С и симметричного волчка СН3 *).
*) Может показаться, что в молекуле диметилацетилена имеется
два волчка СН3, вращающихся относительно линейного остова
С = С. Однако в этом случае положение волчков относительно ли-
нии остова С = С остается неопределенном, а поэтому молекула
диметилацетилена (подобно двухатомной молекуле, которая имеет
не три, а две степени свободы вращения) будет иметь не пять,
а четыре степени свободы вращательного движения.
ПРИМЕР
271
§ 5]
Проведем через центр тяжести молекулы оси координат,
причем ось х направим по линии С — С = С — С, вдоль ко-
торой лежит также ось волчка, а ось z расположим так,
чтобы проекция одного из атомов водорода (Н(4|) на пло-
скость zOy лежала на оси z.
Для междуядерных расстояний применим обозначения
(CsC) = D1, (С —С) = О2, (С —H) = d,
а массы атомов Н и С обозначим через т и М соответ-
ственно. Моменты инерции и произведения инерции всей
молекулы, как это было указано выше, не будут зависеть
от положения волчка (метиловой группы) относительно остова.
Поэтому при вычислении мо-
ментов инерции можно рас-
положить волчок любым обра-
зом. Мы выбираем такое
положение волчка, при ко- / \
тором проекция одного ато- / \
ма водорода (Нщ) на пло- / \ у
скость yQz лежит на оси z, / \------*-
т. е. выбираем положение, /s'
при котором СН3 является ।tУ'_______________
зеркальным изображением ос-
това (по отношению к пло- Черт. 28.
скости zOy). Проекция ато-
мов волчка на плоскость zOy изображена на чертеже 28.
Проекция расстояния СНц) на ось z будет r = Jsina,
где a — угол НСх (см. черт. 27). В случае тетраэдри-
ческого строения метиловой группы cos(CCH) = — 1/3 и
2 ъл2~
cos (НСх) — 1/э. Для sin а мы получим sin a = ——, а сле-
2d /2 „
довательно, г =—— . Проекции линии СН(2) на оси у и z
будут соответственно рг — г cos р и р.2 — — г sin 8 (3 = 30°,
cos р —2~ , sin р — Заменяя значения г и р, мы най-
d /6 d У 2
дем pt — ——, р.2 =--------—. Из структуры молекулы
и этих данных легко можно найти координаты ядер. Эти
координаты приведены в таблице 29.
№ п/п Атом X
1 C(i) = + + °2)
2 С(2) х _ , Dt Х2~ + ~Т
3 с (9) Хз- 21
4 С (4) X.—(^ + рг)
5 Н(О £>1 , , d . L х5= -2L+D2 + rfcosa = -g +-?
6 И (2) х. (3+°*+^)
7 Н(9) U + °'+d0
8 н (4) Хц~ (2 +П2+ 3 )
9 Н(5) x9 = -(4i+D2+dr) \ z. 0 f
10 Н(6) *1о = ~(^ + П2 + 4)
Таблица 29
У Z
У1 = ° + = 0
у2 = 0 г3 = 0
Уз = ° z3 = 0
у4 = о г4 = 0
7 +О2 у5 = 0 4d /“2 3
1 о d Уб = + г cos р = z.=-rSI„P=_qp О
о d у, = — г cos р = d V~b Z! = —r Sin P = — IT о
у8 = 0 2d У~2 z ~r~ 3
a d V~6 у9 = Г COS р = g r d /“2 2 3
г d "/”6 У ю = — г cos р = д— r d Zv' “ 2 — 3
СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ [ГЛ. IX
§ 5]
ПРИМЕР
273
Из данных таблицы 29 легко видеть, что выбранные оси
являются центральными, так как для координат центра
инерции
Ло
J] m{yi _ (9.70)
20 =
Момент инерции метиловой группы относительно оси х будет:
8
„ V 2 q «4</22 8md2 п
= = 3 • —9—=-3-• (9-71)
i = l
Направляющие косинусы оси волчка будут Л= 1, р = О,
м = 0.
Вычислим моменты инерции и произведения инерции. Мы
будем иметь:
{хх} = ^/п;хг?= 2М^у1+О.2у + 2Л1^у +
+ 6/п(^ + О2 + 4)9;
{МУ} = S = 4ffl (Чг“) = 4т V = 4 т<12'
{zz} = 2 тг2^ = 2тг<2 + 4/П (^У= 2/И/’2 + 4/и =
= 3^ = 3/п(^)2 = |^;
1*У) = S miXiyi ^m(j~>r^ + D^r C0S Р +
+т (4+т+°2)r cos *S)+
+m [~(4+т+/?2)гсо!5‘9]+
+ot[ _(4+t+d-2) (—/’cos13)]=°-
(9.72)
18 Зак. 835. И. H. Годней
274
СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ
[ГЛ. IX
Аналогично получается (см. табл. 29):
(9.72)
Таким образом, оси х, у, z являются главными централь-
ными осями. Моменты инерции всей молекулы будут:
4а = S + У + М =
= 2 • 4 md? = 2К',
о
lvy = М + № = 2М + Д2)2 + 2М (ф)3 +
+ 6/п D.2 yj -|- уrnd*',
= М + Ы = 2А1 (у1+а2у + 2 м +
-j_6m(^-1 + a2 + 4) +4md'-
(9.73)
Выражение {Ал] будет состоять из одного сла-
гаемого, так что
{АА} = 1 • К,
{ни} =о>
Н = 0,
М=0. <9-74*
{А\) = о,
Н = о.
§ 5| пример 275
Детерминант [sift] для диметилацетилена принимает вид
{хЯ + М - 0 0
[Sid = к 0 {хх} + {zz} 0 . (9.75)
0 0 {хх} + {уу}
Подставляя значения моментов инерци, мы получим:
= К
чк—к
о
о
о
1уу
О
(9.76)
О
о
т. е.
l^id = № [2М + О2)2 + 2Л4 (^)2 +
-4- 6/п + D.2 + 1 /nd2]2. (9.77)
Принимая расстояния Z?1 = 1,20А, D.2 = (С — С) = 1,47А,
d — (С — Н)=1,09А, находим:
/C = -|-/nd2 = | 6 0200]8023 • 1-092, 10-16 = 5,30 • 1О“40 г • см2;
JXX = 2K = 10,6 • 10~4° г • см2,
/22 = /w= 2М(^ + О2у+2Л1(^У +
+ 6/n + D2 + 4? +1 md2 = 250 • Ю"40 г • см ,
\ Z, о J и
откуда
[^d = К21уу • /22 = 176 • IO"166 г4 • cms.
Число симметрии диметилацетилена будет:
о — <s03t = 6-3=18.
18*
276
СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ
[ГЛ. IX
Для диметилацетилена мы получим (см. формулу (9.51) или
(9.69)):
=
= т? Ст)2 (2л) ’5,30'250 ’ 1(г80-
§ 6. Случай асимметричных волчков
В §§ 4 и 5 мы рассмотрели применение общей формулы
(9.50) к вычислению суммы по состояниям QBp для молекул,
имеющих симметричные волчки. В случае молекул, пред-
ставленных в виде остова с асимметричными волчками,
а также в других более общих случаях задача вычисле-
ния детерминанта [sijt] оказывается более сложной. Дело
в том, что при наличии асимметричных волчков, напри-
мер группы вида CH2X центр инерции волчка не лежит на
его оси.
При вращении волчка меняется положение центра инер-
ции всей молекулы относительно осей координат, неизменно
связанных с остовом, а это значительно усложняет задачу
вычисления детерминанта для случая свободного вра-
щения.
Можно показать, как это было сделано Касселем[237],
что детерминант входящий в формулу (9,50), может
быть представлен в виде
Kll *12- Dt Ft
Ktl . . •• Ktt Dt Ft
ы = Dv . . • Dt {yy} 4- {zz} — {xy} ~~{xz}
. . • Et — {xy} {xx} + {zz} —
Fr • Ft — {xz} — M {xx} + {yy}
(9.78)
где {хх), {уу} и т. д. даются формулами (9.65), а коэф-
фициенты Kij, Dit Ег и Fi удовлетворяют соотношениям
§ 6] СЛУЧАЙ АСИММЕТРИЧНЫХ волчков 277
(см. [237])
.V t t _ _
к—I i=lj-1
N ' . (
2 (ул — ?ьУк) = 2 °л.
. (9-79)
S mk(..zkxk — xaza) = 2 fyi<
k = l i=l
N . . f
S mk (xkyk — ykxk) = 2 F^i.
k=i i = l
При применении формулы (9.78) к молекуле с симметрич-
ными волчками в частном случае получается формула (9.67).
Коэффициенты детерминанта (9.78), вообще говоря, являются
функциями углов at, я2......я4. Поэтому величину [5Й]
нельзя выносить за знак интеграла. Вычисление QBp выпол-
няется в этом случае с помощью формулы (9.50).
Для случая одного асимметричного волчка, вращающегося
относительно остова, детерминант [уй] имеет вид (см. [103])
лл№
К-^ГГ'2 ^M"(y0a3-z0^
+ М" Ооя3 — z0a2)
&з + М" (zoat — х0я3)
kj + M"(*oa2 — JV-O
^ху
6.2 + М" (zoat — х0я3) Ьй + М" (х0я2 — ^oat)
lyx Izx
lyy ^гу
hjz ^zz
(9.80)
где М — масса молекулы, М" — масса волчка, К—момент
инерции волчка относительно оси его вращения, 1ХХ, 1уу,
Iyz> ^zx’ hty — моменты инерции и произведения инер-
ции всей молекулы относительно соответствующих осей
системы координат х, у, z, проходящих через центр
278
СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ
[ГЛ. IX
инерции молекулы и параллельных осям системы х', у', z',
неизменно связанных с остовом, х0, у0, z0— координаты в
системе х, у, z точки О, лежащей на оси волчка, через кото-
рую проведено начало координат осей х’, у', z'.
Величины blt b2, b.it «2, а3 определяются формулами
—— 77 х' х’ ' Р-7х' У' Хг Z' > I
b2 — 77у'х' -1- р7у'у' ч/у’г' , J
Ь'2 = 7/&х' Р-7 z'y' z'z' > J
ai = p.C —УТ],
a2 = у* —
а3 = 7т] — p,«,
(9.81)
(9.82)
(9.83)
где 5, 7] и Z — координаты центра инерции волчка по отно-
' ' Г п п // П /Z
шению К осям X , у , Z , а lx'x’> Iy'y’> ‘z'z'< Ix'y^ ly'z',
Ix'z' — моменты инерции и произведения инерции волчка
относительно соответствующих осей системы х', у', z'.
Для центрального волчка, т. е. волчка, у которого центр
инерции лежит на оси вращения, получается:
тс T’t b.
Sift] = bl b2 7а?а: Ary lyx ^УУ 7гж 1?у (9.84)
Т’з ^xz lyz Izz
Подчеркнем в заключение, что рассмотренное решение
задачи о вычислении QBp для случая асимметричных волчков
является весьма приближенным, так как вращение рассматри-
валось независимо от колебаний, причем предполагалось,
что энергия вращения может быть найдена для молекулы,
в которой отсутствуют колебания. При вращении асимме-
тричных волчков, вообще говоря, будут иметь место сме-
щения центра инерции молекулы относительно остова. Учет
этого смещения должен быть выполнен вместе с рассмотре-
нием колебаний (см. § 10 главы X). С другой стороны, нами
не был принят во внимание потенциальный барьер, ограничи-
вающий вращение волчков.
§ 7] ВЫЧИСЛЕНИЕ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ 279
§ 7. Вычисление термодинамических функций
в случае свободного вращения
Вычисление термодинамических функций для молекул
со свободным вращением выполняется так же, как и для
квазитвердых молекул при предположении о разделении энер-
гии, с тем только отличием, что число колебательных сте-
пеней свободы уменьшается на t степеней свободы, где
t — число волчков.
Мы будем иметь (см. формулы § 7 главы II):
f — /п + /вр + /колеб । (9.85)
где /—любая из термодинамических функций (свободная
энергия, энтропия, теплосодержание, теплоемкость и т. д.).
Так, для энергии мы будем иметь:
3 d In Q
E^E^ + ^RT+RT^— +£К0Леб. (9.86)
При дифференцировании логарифма выражения для QBp
(9.50) по температуре получим:
dlnQB„ /4-3d In Г /4-3 1
= <9-87>
так как остальные слагаемые, входящие в выражение QBp,
при дифференцировании дадут нуль. Следовательно,
£ = £0+|/?7’4-/?^Ц^)т’-4-£колеб (9.88)
или
Е = Е0 + ЗЯ7’+|/?7’+£колеб. (9.89)
Таким образом, каждый волчок с одной степенью сво-
боды дает для энергии слагаемое RT, как и следовало
ожидать из классической теории о равномерном распреде-
лении энергии по степеням свободы, применимой при высо-
ких температурах.
Величина £Колеб вычисляется для n'= ЗМ — 6 — t колеба-
ний по таблицам для функций Эйнштейна. Например, для
диметилацетилена мы имеем N=10, /=1. Число колеба-
280 СЛУЧАЙ СВОБОДНОГО ВРАЩЕНИЯ [гл. IX
ний п' равняется 23, а не 24, как это было бы в случае
отсутствия внутреннего вращения.
Для теплоемкости Cv, дифференцируя выражение (9.89),
мы получим:
Сс = 3/? + /4 + Сволеб. (9.90)
Далее для энтропии будем иметь:
d In QBn
S = 5n+/?lnQBp+/?r—-р + ^колеб (9.91)
или
5 = 5п+/?1п(?вр + /?Ц^ + 5Колеб. (9.92)
или
t+3
S = Sn+ R In {е 2 • QBp}-|-Зколеб- (9.93)
Таким образом, в случае свободного вращения задача
вычисления термодинамических функций оказывается про-
стой, если найден детерминант Для определения термо-
динамических функций требуется знание структуры молекулы
и ti' = 3N—6 — t частот нормальных колебаний.
Однако при применении формул, выведенных для свобод-
ного вращения, к реальным молекулам, например этану,
пропану и др., выяснилось, что между опытными значениями
термодинамических функций и вычисленными значениями при
применении гипотезы о свободном вращении оказалось зна-
чительное расхождение. Это привело к пересмотру гипотезы
о свободном вращении.
ГЛАВА X
ВЫЧИСЛЕНИЕ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
ГАЗОВ В СЛУЧАЕ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО
ВРАЩЕНИЯ
§ 1. Потенциальный барьер внутреннего вращения.
Поворотные изомеры
Гипотеза о свободном вращении в молекулах, как пока-
зало изучение этана и других веществ, оказалась несостоя-
тельной. При вычислении термодинамических функций мы
должны принять во внимание наличие потенциального барьера,
ограничивающего вращение волчков. Вся совокупность опыт-
ных фактов (спектры, дипольные моменты, опытные термо-
динамические данные, электронограммы) показывает, что
вращение в молекулах оказывается заторможенным.
Причиной этого является взаимодействие атомов волчка
с атомами остова. Движение волчка будет иметь более
сложный характер, чем простое вращение. Только при высо-
ких температурах, когда средняя энергия, приходящаяся на
вращение волчка, значительно больше работы преодоления
барьера, вращение можно считать практически свободным.
При низких температурах, когда кинетическая энергия вну-
треннего вращения оказывается меньше работы преодоления
барьера, вместо вращения будут иметь место црутильные
колебания около положения равновесия.
Одной из первых молекул, для которой был приближенно
определен потенциальный барьер, является молекула этана.
В ней при вращении одной из групп СН3 (волчка) относи-
тельно другой группы (остова) будут осуществляться после-
довательно две конфигурации: транс-конфигурация а, при
которой атомы Н одной группы сдвинуты на 60° против
атомов другой, и цис-конфигурация Ь, при которой атомы Н
находятся друг против друга. Эти конфигурации изображены
282 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
на чертеже 29, где показан их вид, если смотреть вдоль
оси С—С, а также их боковой вид. Первая из этих конфи-
Черт. 29.
и три минимума, как это
где min отмечен буквой а,
гураций имеет симметрию Dad,
вторая— D3h.
Если допустить, что атомы
водорода отталкиваются друг
от друга, транс-конфигурация
будет устойчивее *), и при
переводе молекулы из конфи-
гурации а в конфигурацию b
(поворот на 60°) нужно затра-
тить работу, т. е. преодолеть
потенциальный барьер высо-
той Vo. Принимая во внимание,
что при полном повороте груп-
пы СН3 три раза осущест-
вляется конфигурация а и три
раза конфигурация b (симме-
трия вращения), мы придем к
выводу, что кривая барьера
будет иметь три максимума
изображено на чертеже 30,
a max — буквой Ь. Отрезок 1b
V
О'а 7 а а 2л
Черт. 30.
на чертеже 30 изображает высоту потенциального барьера.
Аналогично обстоит дело и в случае других молекул,
содержащих группу СН3, например СН3ОН или CH3SH.
*) Вопрос об устойчивости цис- и транс-конфигурации этана
нельзя считать окончательно решенным. Повидимому, взаимодей-
ствие электронных облаков отдельных связей СН происходит так,
§ 1] ПОТЕНЦИАЛЬНЫЙ БАРЬЕР ВНУТРЕННЕГО ВРАЩЕНИЯ 283
В этих молекулах вследствие симметрии группы СН3 кривая
барьера должна иметь также три максимума и три минимума.
В более общем случае симметричных волчков с симметрией
Сп мы будем иметь п. максимумов и п минимумов *).
Для несимметричных волчков кривая потенциального
барьера должна иметь более «ложный вид. Например, у мо-
лекулы СН2С1СН2С1 при вращении группы СН2С1 (волчка)
относительно другой группы СН2С1 (остова) возникают по-
следовательно конфигурации a, b, с, d, е, f, изображенные
на чертеже 31, где показан их вид для наблюдателя, смот-
рящего вдоль оси С — С. За начальное положение избрана
транс-конфигурация, соответствующая наибольшему расстоя-
нию ядер хлора.
Имеющиеся в настоящее время данные говорят в пользу
наибольшей устойчивости транс- конфигурации а, которой
соответствует минимум потенциальной энергии **).
Цис-конфигурация d, наоборот, является наименее устой-
чивой. Этой конфигурации соответствует максимум
что оно проявляется как бы в отталкивании атомов водорода.
Поэтому более правдоподобна большая устойчивость транс-конфи-
гурации. Это подтверждается также спектроскопическими данными
Смита [258].
*) Такой случай, когда число симметрии волчка аг- совпадает
с числом максимумов или минимумов п, не является самым общим.
Существуют симметричные волчки, у которых сг уг п. Так, напри-
мер, у нитрометана CH3NO2 о£ = 3, а п = 6.
**) М. В. В о л ь к е н ш т е й н, М. А. Е л ь я ш е в и ч, Б. И. С те-
па н о в [12].
284 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
потенциальной энергии. Кривая потенциального барьера для
1,2-дихлорэтана изображена на чертеже 32. Кривая имеет
максимумы неодинаковой высоты и минимумы разной глу-
бины, что вызвано разными условиями взаимодействия элек-
.0
60 120 180 240 300 360
a b cd в f д
Черт. 32.
тронных облаков в разных
конфигурациях.
Наличие минимумов
потенциальной энергии
разной глубины в моле-
кулах, подобных 1,2-ди-
хлорэтану, приводит к
новому виду изомерии —
поворотной изомерии *).
Существование поворот-
ной изомерии прежде
всего проявляется в ко-
том, что время существо-
в
лебательных спектрах. Дело
вания поворотных изомеров, разделенных значительным барь-
ером, много больше времени колебания ядер, так что моле-
кула, прежде чем перейти из одной конфигурации в другую,
успеет проколебаться несколько сотен раз, что приводит
к появлению определенных колебательных частот, соответ-
ствующих данному поворотному изомеру. В случае 1,2-ди-
хлорэтана существуют три изомера: трансизомер и два
изогнутых изомера («гош»), соответствующих конфигурациям
сие. Эти два последних изомера, как легко видеть из чер-
тежа 31, являются зеркальными изображениями друг друга и,
следовательно, должны иметь разную оптическую активность.
Равновесие поворотных изомеров дигаллоидопроизводных
этана было детально изучено О. Ароновым, В. Татевским,
А. Фростом путем рассмотрения изменения соответствующих
линий в колебательных спектрах **).
Разные поворотные изомеры галлоидопроизводных этана
должны иметь также и разные дипольные моменты ***).
*) Обзор свойств поворотных изомеров см. М. В. Волькен-
штейн [105], [108]. См. также М.В. Вол ькенштейн, М. А. Е л ь я-
шевич, Б. И. Степанов [12].
**) О. Аронов, В. Татевскийи А. ф р о с т [99], [100]; см.
также [243, 244] и [166].
***) См. М. В. В о л ь к е н ш т е й н, М. А. Е л ь я ш е в и ч,
Б. И. Степанов [12].
§ 1 ] ПОТЕНЦИАЛЬНЫЙ БАРЬЕР ВНУТРЕННЕГО ВРАЩЕНИЯ 28 5
Вопрос о форме потенциального барьера до настоящег о
времени остается невыясненным даже хля случая симметрич-
ных волчков. Обычно для случая потенциальной кривой с zz
минимумами одинаковой глубины допускалась зависимость
вида
V = у (1 — cos га о). (10.1)
Эта зависимость соответствует разложению барьера в рял
Фурье
V(a) = X + Bcosna + Ccos2na-|- ... (10.1а)
и применению первых двух слагаемых Барьер является чет -
ной функцией угла а, так как 1/(а)=1/( — а) и в разло-
жение войдут только члены с косинтсами. Для метиловой
группы п = 3, и формула (10.1) принимает вид
V=^°(l— cos За. (10.110
Для определения высоты потенцгального барьера до
настоящего времени использовались главным образом опыт-
ные термодинамические данные (энтрпия и теплоемкость)-
Попытки квантовомеханического расчта величины барьера
оказались малоудовлетворительными *).
Приближенные значения барьера дл некоторых молекул
приведены .в таблице 30 **). Недавно были предприняты ра-
боты по определению барьера с поющью микроволновой:
спектроскопии ***). Для метилового сшрта барьер получился:
в 1086 кал!моль, для CF3CH3— 350 кал!моль, для
СН3СНО—2600 кал!моль ****).
Следует заметить, что при примекнии микроволнового
метода определяется не сама величина барьера Уо, но раз-
ность энергетических уровней, по котсрой вычисляется вели-
чина барьера при допущении определеной его формы.
*) Об этих и других попытках вычиаения барьера см. об-
зорную работу [105]; см., например, [241], tp. [247]; см. также [254,
204].
**) Более полные таблицы данных до 194 г. см. Я. К. С ы р-
кин и М. Е. Дяткина [58], М. j. Волькенштейн,
М. А. Ел ьяшевич, Б. И. Степанов 12], В. М. Грязнов
и А. В. Фрост [26], см. также [204, 254].
***) См. Вильсон [266], Горди и др. 89], Дейли [214].
****) См. Дейли [214].
286 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ (ГЛ. X
Таблица 30
Молекула Связь п Величина барьера в кал!моль
более старые данные микро- волновые данные данные новых обзоров Питцера [254] и Астона [204]
Этан СН3СН3 . . С-С 3 1 3150 2750 — 2875 ±125 [254]
Пропан СН3СН2СН3 . . С-С 3 1 3300 3400 — 3400[254]
Изобутан СН(СН3)3 . . . С-С 3 3800 3620[254]
Тетраметилметан С(СН3)4 .... С—С 3 4500 — 4300 [254]
Пропилен СН3СНСНа . . С—С 2100 — 1950(254]
Диметилацетилен СН3С==СН3 . . С—С 3 500 — 0[204]
1,1,1-трихлорэтан СН3СС13 .... С—С 3 2700 — —
1,1,1-трифторэтан CHgCFg .... С—С 3 3450 3350 —
Разные
Метанол СН3ОН . С-0 3 1 данные от 6400 до 1340 1086 1350[204]
Ацетальдегид СН3СНО . . . С—с 3 2100 2600 —
Ацетон СН3СОСН3 . . С-С 3 1000 — 560—1240 [204]
Метилмеркаптан CH3SH .... С—S 3 1460 — 1460[204]
Метиламин ch3nh2 .... C-N 6*) 1500 — 1520(204]
Нитрометан CH3NO2 .... С—N 6*) 1 800 500 (см. [234']) 6**) —
§ 1] ПОТЕНЦИАЛЬНЫЙ КАРЬЕР ВНУТРЕННЕГО ВРАЩЕНИЯ
287
Продолжение
Величина барьера в киломоль
Молекула Связь n более старые данные микро- волновые данные данные новых обзоров Питцера [254] и Астона[204]
Толуол С6Н5СН3 . С-С 6* **)) 500 500 ± 500 [254]
CH3SiH3 С—Si 3 — 1 1190[214] 1310[89] —
CH3SiF3 С—Si 3 -1 1200[214] 1170[89] —
Силан Si2He . . . Si—Si 3 0 — —
Тетрометил-силан (CH3)4Si .... Si—С 3 1300 — 1100—1500(204]
Перекись водо- рода Н2О2 . . . 0—0 21 У1=10000 F2=16000 — —
Естественно, что результаты, основанные на термодина-
мических данных и базирующиеся на применении форму-
лы (10.1), также являются весьма приближенными. Недавно
Блейдом и Кимболом [208] был предпринят пересмотр высоты
барьера, определяемого из термодинамических данных. Учи-
тывая возможность влияния формы барьера, Блейд и Кимбол
вычислили границы, в которых должен лежать барьер. Для
этана оказалось, что Уо лежит в интервале от 1550 до
2700 кал/моль ***), для 1, 1, 1-трифторэтана—от 2300 до
8300 кал!моль, для метанола — от 800 до 3000 кал)моль.
Из этих данных следует, что величины барьера, приведенные
в таблице 30, являются ориентировочными и в известной
мере условными. Тем не менее, значения барьеров, опреде-
ленных из экспериментальных термодинамических данных,
*) Значение п = 6 обусловлено комбинацией симметрии вра-
щения остова С2 с симметрией волчка С3.
**) См. РЖ Хим, 1955, 31049.
***) Этот результат вызвал возражения со стороны Питцера [254],
считающего, что интервал ошибки в случае этана должен быть зна-
чительно меньше.
288 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
позволяют выполнить приближенное вычисление термодина-
мических функций в практически достаточном интервале
температур. Следует только помнить, что величины этих
барьеров оценены условно при применении простой формы
барьера (10.1).
§ 2. Приближенный метод Питцера
Задача вычисления термодинамических функций в слу-
чае заторможенного внутреннего вращения была приближенно
решена Питцером [249] в 1937 г., использовавшим резуль-
таты Нильсена [246] об уровнях энергии вращения молекулы,
состоящей из двух коаксиальных симметричных волчков *).
В этих работах для потенциального барьера было применено
выражение (10.1).
Рассмотрим прежде всего приближенный метод Питцера,
позволивший удовлетворительно рассчитать значения термо-
динамических функций ряда углеводородов, например этана,
пропана и др.
Допустим сначала, что молекула состоит из остова и
симметричного волчка, имеющего момент инерции К отно-
сительно оси вращения. Такая молекула имеет / = 4 степе-
ни свободы вращения. Предположим сначала, что для вычи-
сления суммы по состояниям мы применили приближенную
формулу (1.46)
Qka = [ • • • j е kTdPt ... dpsdql... dqs, (10.2)
которая для нашего случая примет вид
QbP. кл = J • • • J е kTdpi dp.2 dp3 dpt dq2 dq2 dq3 dqi.
(10.3)
В отличие от случая свободного вращения полная энер-
гия теперь состоит из двух слагаемых
e = (Ю-4)
где V(д) — потенциальная энергия. ,
*) Случай двух асимметричных волчков см. [211].
§ 2] ПРИБЛИЖЕННЫЙ МЕТОД ПИТЦЕРА 289
Выбирая в качестве независимых переменных три эйле-
ровых угла 6, и ® и угол поворота волчка а, мы полу-
чим:
<?вр. Ki=-^4 I ••• J е кТ dPtdP‘AdP‘AdP>.dtid''id^da.
(10.5)
Применяя метод Эдинофа и Астона, рассмотренный в пре-
дыдущей главе (см. § 2 главы IX), мы можем выполнить
интегрирование по импульсам. Последнее дает:
к 2г. 2г,
J J J [A]V^0d6d®da, (10.6)
ООО.
где [Л]—детерминант коэффициентов кинетической энергии.
Мы видели (см. формулу (9.48)), что
[А] = [S] sin2 0, (10.7)
где [5] — детерминант кинетической энергии, выраженный
через проекции угловых скоростей а>х, шг и производ-
ную угла а.
Таким образом,
х 2п 2к 2к У( 1
<?вр. M = 4-4(2irfeT)2 f f f f Sin 0 [sik]‘ke~~^dbd^d^da.
J St S (10.8)
В случае симметричных волчков детерминант яв-
ляется величиной постоянной, и мы можем [s^|/а вынести за
знак интеграла. Выполняя интегрирование по эйлеровым
<углам (см. § 3 главы IX), получим:
г 2^-
' . п Vo (1-COS па)
( Свр.вл = ^(2^7’)281:2[5й]1/а] е 2 ™ da. (10.9)
[ °
IПредставим детерминант следующим образом:
[$Й] = АВС-/Л1ив, (10.10)
где А, В и С — главные центральные моменты всей моле-
кулы, а /прив— так называемый приведенный момент инерции.
!
19 Зак. 835. И. Н. Годнее
£90 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
Формула (10.10) может служить определением приведен-
ного момента инерции одного волчка. Таким образом,
/n₽HB = jgL (10.10а)
Для молекул, у ко-
торых ось волчка являет-
ся главной и централь-
ной осью всей молекулы,
мы можем, выбрав ее за
ось х, провести две дру-
гие оси у и z так, чтобы
они также являлись глав-
ными и центральными.
В этой системе (черт. 33)
произведения инерции будут равны нулю, а направляющие
косинусы будут А = 1, р. = 0 и v = 0. Детерминант [sife] для
нашего случая примет вид (см. формулу (9.67))
1^1 = К
1ХХ — К 0 о
0 1уу 0
0 О 1гг
= К(1ХХ-К)
(10.11)
Из формулы (10.10) мы будем иметь:
. __ __________ К{1ХХ К(1ХХ К)
'прав — 7 7 7 7 7 7 = 7 • (10.12)
1хх‘уу‘гг 1хх1уу‘гг 1хх ,
Величина 1ХХ— К представляет момент инерции остова
(части молекулы за исключением волчка) относительно оси
вращения волчка. Обозначив его через В', получим:
1ХХ-К = В' (10.13)
и
1ХХ = К+В'. (10.14)
Подставляя 1Х!В в формулу (10.12), будем иметь:
/пгив = у^7. (10.15)
Так, для молекулы этана, состоящей из двух метильных
групп, момент инерции 1ХХ относительно оси волчка будет
2К, где К—момент инерции метильной группы (волчка) отно-
сительно оси вращения. Момент В' будет равен 2К — К=К,
§ 2] ПРИБЛИЖЕННЫЙ МЕТОД ПИТЦЕРА 291
и мы получим:
г _ к-к __К
при — К+К — '2К 2‘
(10.16)
Из общей формулы (10.10а), являющейся определением
приведенного момента инерции одного волчка, легко полу-
чить формулу для случая, если ось волчка не является глав-
ной центральной осью молекулы. Пусть в молекуле проведены
главные центральные оси, и ось волчка образует с ними
углы, косинусы которых мы обозначим X, р., -л Так как оси
координат являются главными, произведения инерции (см.
формулу (9.65)) {ху}« (xz)> [yz] равняются нулю.
На основании (10.10а) и (9.67) мы будем иметь:
Лц ив —
Л —/Саз
— К'-у-
— К^ч
— К'кч
— Куч
— К>-у
В —Ку-2
— Куч С — Кч2
~АВС
(10.16а)
К
Разлагая детерминант по элементам первой строки, полу-
чим:
А — ЮУ
— KA[i
— Ккч
—Кку —К^ч
В —Ку2 —Ку-ч
— Куч С — Кч2
= (Л — КА2)
В —Ку2
— Куч
— Куч —К^-у —Куч
—|- К Ар.
С — Кч2 —КХч С — Кч2
— Кку В —Ку2
— Ккч
= АВС — К(ЛВу24-ЛСр.2-|-ВСА2), (10.16b)
откуда
^. = КЛВС-У(Л8^С^+?С^. (10.16с)
Эта формула была применена Кроуфордом при более
Строгом рассмотрении задачи о симметричных волчках
(см. § 9 этой главы). Формулу (10.16с) можно записать
19*
292 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [гЛ. X
следующим образом:
3
/и„ = К-№(| + е+^) = /<-№2^ =
1=1
3
= (10.16d)
1=1 ъ
Заменяя [$^] в формуле (10.9), получим:
QBP. кл =^(2^Т)28т:2(ЛВС)1/7^и0)г^ da. (10.17)
Входящее в формулу (10.17) а означает число симметрии
с учетом внутреннего вращения. Оно может быть представ-
лено в виде (см. формулу (9.6))
о = а0о< — Соп,
(10.18)
где <зг есть число симметрии волчка. Это число af обычно со-
впадает *) с числом п, входящим в формулу барьера (10.1).
Выражение (10.17) мы можем теперь переписать следую-
щим образом:
п _ 8л2 pr.kTAx11 12ккТВ\’г (ZrdiTC^
Увр. кл-ао\ Л2 / \ Л2 / \№) Х
Множитель
х±нн'-р
о
Vo (1 —COS Па)
2 кт da.
8л2 (2itkTA\,b{2пкТВ\'/а {2nkTC\^ _
сД Л2 м Л2 ) \ Л2 ) —Уж- вр
(10.19)
(10.20)
представляет сумму по состояниям жесткой (замороженной)
молекулы (см. формулы (8.55) или (8.99)). Таким образом,
мы можем написать:
1 (2пй77П1)П1|),/,а f _ У» О
(2вр.Кл = (?ж.вр-^-------] е da- <10-21)
о
*) Здесь и далее рассматривается случай = п. Если эти два
числа не совпадают, то к энтропии и приведенной свободной энер-
гч . п
гии нужно ввести поправку R \п —.
§ 2] ПРИБЛИЖЕННЫЙ МЕТОД ПИТЦЕРА
293
Если бы вращение волчка было свободным, Уо равнялось бы
нулю, и интеграл (10.21) был бы просто равен 2тг. Мы
получили бы:
_ 1 (2^Т/прив)^ >
Qbj. вл. своб — Qat. вр п 2it. (10.22)
Записывая последнее выражение в виде
Qep. кл. своб — Qat. Bp.QcB,
(10.23)
где Q0B есть сумма по состояниям волчка в случае свобод-
ного вращения, получим:
1 (2^^првв)‘/а
(10.24)
Возвращаясь к формуле (10.21), полученной в случае при-
менения выражения для энергии, которое дает классическая
механика, мы видим, что множитель у QM. вр можно рас-
сматривать как сумму по состояниям волчка, вычисленную
приближенно для случая заторможенного вращения.
Мы можем записать:
1 cir.kTi г ч~соа па^
Сволчка,вл.мех=- ------\ е (10.25)
6
Теперь формула (10.21) будет иметь вид
Qep. кл = Qat. врфволчка, кл. мех- (10.26)
Естественно предположить, как это и было сделано Питцером
в первой работе, что и при применении выражения для энер-
гии, которое дает квантовая механика, имеет место соот-
ношение, аналогичное (10.26), т. е.
Qep — Qat. bjiQb. в, (10.27)
где Q3. в — сумма по состояниям волчка, вычисленная для
случая заторможенного вращения при применении квантово-
механических уровней энергии
(10.28)
Г
294 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
Соотношение (10.27), как это следует из общих формул
главы II, позволяет выполнить вычисление термодинамических
функций с помощью правила аддитивности.
Мы получим:
/вр = /ж. вр+/э.в. (10.29)
где /ж. вр'—слагаемое термодинамической функции, вычи-
сленное для вращения «замороженной» молекулы, а /э. в—сла-
гаемое термодинамической функции, соответствующее дви-
жению волчка.
Питцер [249] составил удобные таблицы для вычисления
слагаемых f3 в применительно к теплоемкости С3 в, приве-
Н, в
денной энергии (теплосодержания) —у- , энтропии 5Э. в и при-
F3 в
веденной свободной энергии -у-. Последние две величины
не приводятся в таблицах непосредственно, но легко могут
быть найдены по табличным данным (см. § 4 этой главы).
§ 3. Определение уровней энергии волчка
с заторможенным вращением
Для определения Q3 в нужно знать уровни энергии ег. Их
можно найти из соответствующего волнового уравнения, опреде-
ляющего стационарные состояния волчка с заторможенным вра-
щением.
Уравнение Шредингера для одномерного ротатора
+ = ° <10-30)
в нашем случае примет вид
8тга/ г 1 л
2 ^(1-созла)|ф = °. (10.31)
Введя новую переменную
мы будем иметь: X па (10.32)
da? ’ Па dx? 4 (10.33)
Уравнение (10.31) примет вид
^Ф(х) 1-32^/ 1ч
dx* л2*3 v 2Vn)
i6^/nrHBv0
nW C0S 2х
(10.34)
§ 3]
УРОВНИ ЭНЕРГИИ ВОЛЧКА
295
Обозначив
32^/пгив
изда 1
в_8*а4гивП
“ П2Д2
«г =
мы получим уравнение
+ \аг 4- 29 cos 2х] ф (х) = О,
(10.35)
(10.36)
(10.37)
которое обычно называется уравнением Матье.
Решения этого уравнения, удовлетворяющие физическим тре-
бованиям*), существуют при дискретных значениях ап, аь а%, а3,...,
являющихся собственными значениями этого уравнения. По значе-
ниям аг, для которых имеются таблицы, можно найти собственные
значения энергии ег, знание которых позволяет с помощью фор-
мулы (10.28) вычислить Q3 в. Уровни энергии оказываются невы-
рожденными. При вычислении суммы по состояниям суммирование
производится по значениям г с учетом требований симметрии **).
Частным случаем уравнения (10.31) или (10.34) будет случай
свободного вращения, имеющий место при — 0. Мы получим
fl = 0, и вместо (10.31) будет иметь место уравнение
^,8кЗ/пгив
daa "Г Л2 Ег
или в переменных х
^J + MU) = 0, (10.39)
определяющее уровни энергии свободного плоского ротатора.
Другим частным случаем является случай больших Уп. При
наличии большого барьера ротатор (волчок) проводит большую часть
времени внутри потенциальных ям, где он совершает колебания (так
называемые крутильные колебания). В этом случае угол а можно
считать малым, так что sin па можно принять равным па.
Разлагая cos па в ряд, мы получим:
cos z = 1 — у + — ... , (10.40)
т. е.
я2нг2
cos па =1--ДЛ_. (10.41)
*) См. М. В. Волькенштейн, М. А. Ельяшевич,
Б. И. Степанов [12].
**) Возможные значения: г = 0, +1, +2, ±3,... В случае
наличия симметрии волчка (и = a^l) часть значений г отпадает.
При этом оказывается, что при суммировании, независимо от тре-
бований симметрии, приходится использовать одинаковые эначе-
< ния аг (для данного 6). Но эти значения аг соответствуют в каждом
\ Случае симметрии срорму набору г,
296 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
Подставляя значение cos па в уравнение (10.31), имеем:
, ^а/прив
da? + h?
ф = 0
или
./в^прив 2теЗ/ ^3,3.
-------АЗ----Р = 0-
(10.42)
(10.43)
Это — уравнение гармонических колебаний с потенциальной энергией
и постоянной k, равной
V = ly„„2a3
^Von?=k.
(10.44)
(10.45)
Собственные значения энергии будут:
(10.16)
где v0 — частота колебаний — определяется формулой
(10.47)
или
1 п
2 те
(10.48)
Эта формула устанавливает в случае больших барьеров связь между
высотой барьера Уо и частотой крутильных колебаний.
Из изложенного следует, что собственные значения уравнения
Матье при малых значениях г оказываются близкими к уравнениям
гармонического осциллятора.
При больших г мы будем иметь приближение к уравнениям
свободного ротатора. Собственные значения аг для разных 0 и г
приведены в таблице 31 *).
*) Значения аг (для данного 0) при разных случаях симметрии
волчка (числа л) соответствуют разным» наборам чисел г. Поэтому
в таблице 31 значения г не указаны. Для п — 1 строки таблицы
соответствуют значениям г = 0, —1, Д-1, —2, 4-2, —3, -|-3. Для п = 2
эти строки соответствуют г = 0, —2, —4, -j-4, —6, 4~6.
§ 3)
УРОВНИ ЭНЕРГИИ ВОЛЧКА
297
Таблица 31*)
Значения а? для разных 0 и г
0 = 0 1 2 3 4 5 6
0,0000 — 0,4551 — 1,5140 - 2,8344 — 4,2805 - 5,8000 — 7,3688
4,0000 3,9170 3,6722 3,2769 2,7469 2,0995 1,3518
4,0000 4,3713 5,1727 6,0452 6,8291 7,4491 7,8701
16,0000 16,033 16,128 16,273 16,452 16,648 16,845
16,0000 16,034 16,141 16,339 16,650 17,097 17,689
36,0000 36,014 36,057 36,129 36,229 36,359 36,517
36,0000 36,014 36,057 36,129 36,230 36,361 36,523
0 = 7 8 9 10 12 14 16
— 8,9737 —10,607 — 12,262 — 13,937 — 17,332 — 20,776 — 2 ,259
0,5175 0,3894 —1,3588 — 2,3822 —4,5635 — 6,8907 - 9,3341
8,0866 8,1152 7,9828 7,7174 6,8787 5,7363 4,3712
17,027 17,183 17,303 17,381 17,395 17,207 16,819
18,417 19,253 20,161 21,105 22,972 24,651 26,009
36,704 36,917 37,157 37,420 38,006 38,648 39,315
36,715 36,94 37,21 37,51 38,24 39,16 40,22
0 = 18 20 24 28 32 36 40
— 27,773 — 31,313 — 38,459 -45,673 -52,942 — 60,256 — 67,606
— 11,873 —14,491 — 19,923 — 25,562 -31,365 — 37,303 — 43,352
2,8331 1,1543 — 2,5398 — 6,5881 — 10,914 —15,467 — 20,208
16,242 15,494 13,553 11,121 8,2947 5,1467 1,7300
26,988 27,595 27,885 27,283 26,062 24,379 22,325
39,972 40,590 41,606 42,225 42,394 42,118 41,433
40,93 42,1
*) Чертой в таблице отмечен переход от «колебательных» уров-
ней к «вращательным», имеющий место при квантовом числе г0
(см. стр. 313).
298 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
§ 4. Первые таблицы Питцера
Как уже было указано выше, Питцер [249] в 1937 г.
составил удобные таблицы для вычисления термодинамических
функций симметричного заторможенного волчка. Для эн-
F
тропии и приведенной свободной энергии вместо S3. в и —~
F — F
о г. ‘ 3. в ' св
он ввел величины осв — о3. в и -у----, представляющие
разности между соответствующими термодинамическими
функциями свободного волчка и волчка заторможенного. Эти
величины, которые можно рассматривать как поправки на
заторможенное вращение по сравнению со свободным вра-
щением, оказываются функциями двух переменных
к т
и 10~38 ” . Значения этих величин как функций
•'приз1'О “Г
и 10-зв ---у-, где Уо выражено в кал)моль и /прив в г • см1,
'прив*'О
приведены в таблицах 62 и 63. Для теплоемкости и энергии
Питцером были также составлены таблицы, причем в табли-
Нз в „
цах даны и С3, в как функции тех же двух параметров
(см. табл. 64 и 65). Принимая во внимание, что S3. в можно
представить в виде
S3.B = SCB — (Sob — Ss.b), (10.49)
где 5св — слагаемое энтропии, соответствующее свободному
вращению волчка, мы получим в соответствии с форму-
лой (10.29)
SBp = вр ~Н So. в = Sac. вр Ц- SCB (SCB — S3. в). (10.50)
Величина SB. вр может быть вычислена по формуле (8.104),
слагаемое S0B легко определить по значению суммы по
состояниям Qob- Используя соотношение
d In
SCB— RlnQaB-\-RT(10.51)
(см. § 7 главы II) и формулу (10.24), мы получим:
SCB = R In
B)V>
1 (2гй77 )/а d ln ---j,---* 2ir
' ТТрИВ' Q I DT1
й --------^+RT—------------------
(10.52)
§ 4]
ПЕРВЫЕ ТАБЛИЦЫ ПИТЦЕРА
299
или
SCB = R (—0,775 + -Jin Т+ | In /пряв • 10*0 —Inn). (10.53)
Таким образом, в силу формулы (10.49) получается:
S9.в = R (—0,775 +1 In Т+ у 1п/пг,вв • 10*0 — Inn) —
— (S0B —$з.в). (Ю.54)
Для свободной энергии волчка со свободным вращением
на основании формул (10.24) и (2.118) мы получим:
_^ = r(— 1,275-1-1- in 7’+|1п/прив 10«> —Inn).
(10.55)
Представляя приведенную свободную энергию, взятую
с обратным знаком, в виде суммы двух слагаемых, как это
было сделано в случае энтропии (см. (10.49)), мы будем
иметь:
F /F F —F \
1 Э. В ( 1 СВ I 1 э. в 1 св \
— т J ~
F F —F Ф
л СВ * * 4 * * * 3. В ' СВ 3. В /1 л
=-----Т-------?-----=-----уг- (10.56)
или
Ф F
3. В 3. в
+ —т ~
= R (— 1,275 +1 In Т+ 11 /црив • 1040 — In «) —
— Fa-B~F°\ (10.57)
Последние слагаемые формул (10.54) и (10.57) вычис-
ляются с помощью таблиц Питцера по параметрам и
10-36 П2//прив . уо.
В силу предположения о разделении энергии ei моле-
кулы на энергию колебания и вращения мы получим для
любой термодинамической функции
f = /п + /вр + /колеб. (10.58)
Таким образом,
£ = Si, + -SBp + 5К0лее. (10-^9)
300 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
Используя выражение (10.50) для SBp, полученное выше,
будем иметь:
•$ = Sn-|-Вр53. в-|-«$ВОлеб- (10.60)
Аналогичным образом получим:
Заметим, что последние три
и (10.61а) попарно равны, т. (
: (10’61а)
4 ' / ' ‘ /колеб
(^)+(т) • <10-62)
' * ' ' * /колеб
слагаемых формул (10.61)
Исключая и
\ 7 /п ' 1 /ж. вр
иметь:
^^ = 4/?
из формулы (10.62), мы будем
+ . (10.63)
' Т \ 1 /колеб
Для теплоемкости получим:
Ср— 4/?-j-C3. в 4“ Сколеб- (10.64)
§ 5. Пример
Рассмотрим пример на применение таблиц Питцера. Пусть
Ф
требуется вычислить при Т = 400° К' S3. в. и 5вр моле-
кулы, содержащей группу СН3 с приведенным моментом
/прИВ ^=4,52 • 10’40 г . см2 и барьером Vo = 2100 кал]моль.
ПРИМЕР
301
§ 51
Пусть Sok. вр = 22,57 кал/град моль. Для группы СН3
число минимумов (число симметрии вращения) п — 3. По
формулам (10.53) и (10.55) получим:
5СВ = 1,986 (—0,775 + 1 • 2,303 1g 400 —
+ у • 2,303 lg4,52 — 2,3031gз) = 3,73,
— ~ = 1,986 (— 1,275 + у • 2,303 1g 400 +
+ у 2,303 Ig4,52 — 2,3031g з) = 2,73.
Далее, для применения таблиц Питцера мы вычисляем зна-
чения параметров
Уп _ 2100 _
RT~ 1,986-400 ’
и
„2 9
10-36 /пГив'Ло= 10-36 4,52-10-^-2100 = 9’48’
Из таблиц Питцера (см. табл. 62 и 63), применяя интерпо-
лирование, находим Зсв— 53.в = 0,61 кал)град • моль
и
Р — F Ф — Ф
л 3. В J СВ 3. В СВ 1 1
—т—=—7—=1,16.
Полученные данные позволяют найти энтропию и свобод-
ную энергию, соответствующие заторможенному вращению.
Мы получим:
$з. в = 5СВ — (5СВ — 5з. в) = 3,73 — 0,61 =
= 3,12 кал/град • моль,
ф ф ф — ф
----= — -----------3-*т е° =2,73 —1,16 =
= 1,57 кал]град • моль,
5Вр = 5ж. Вр + 53. в = 22,57 —|— 3,12 =
= 25,69 кал!град • моль.
302 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ X
§ 6. Приближенный метод Питцера для случая
нескольких симметричных волчков
Приближенный метод, рассмотренный нами в предыду-
щем параграфе, был применен Питцером для случая несколь-
ких симметричных волчков и даже для случая асимметрич-
ных волчков с небольшой асимметрией.
Пусть молекула имеет t волчков. В этом случае мы бу-
дем иметь s = t-1- 3 вращательных степеней свободы. Фор-
мула для QBp. кл будет иметь вид
if f _ *fc4 v а‘’ Яа...at}
Qvp. кл = J • • • | e kT dPt dp% • • •
... dp8dqx... dqs. (10.65)
После интегрирования по импульсам мы получим:
...
QB?. кл = ± (2*kT)e,i j .. . J [A^e ™ dqS'
(10.66)
Выполняя далее интегрирование по трем первым пере-
менным (эйлеровым углам), мы, как и в § 3 главы IX
(ср. (9.50)), найдем:
2* 2г- ..............
С»р.кл = ^(2^Г)8/281г2 j .. . J da, ... dat.
о о
(10.67)
Для симметричных волчков [уй] является величиной по-
стоянной. Если пренебречь потенциальной энергией взаимо-
действия волчков друг с другом и применить к каждому
волчку формулу типа (10.1), то получим:
t
V0(l — cosrtOTaJ. (10.68)
и»=1
Выражение (10.68), естественно, является грубым прибли-
жением. Другое допущение, которое было введено Питце-
ром, состоит в предположении, что детерминант [si/t] можно
представить в виде
= АВС1щт) 1 • 7Прив 2- • • /прав t- (10.69)
§ 6] МЕТОД ПИТЦЕРА ДЛЯ СИММЕТРИЧНЫХ волчков 303
Действительно, для ряда молекул такое предположение оправ-
дывается, однако формула (10.69) не является общей.
При этих допущениях мы приближенно получим:
1 i+З I/
<2вр.к.п = (2tckT) а 8л2(ДВС/Прив 1Л1рив 2 • • • ^прив t) 2 X
p2 Koi (I—003 та,»,) ^ot^~cos ntat^
X e 2ZeT . .. I e 2kT dat.
о 0
(10.70)
Представляя число симметрии в виде а0 • nt ... nt,
будем иметь:
_ 8л2 (2тгй7Л),/г (2лЛ7В)’'2 (2vkTC)'ls
Увр. кл — ао • h • h • h X
(2,1^7’/пгив m)7a
г” ,
j е~ daj. (10.71)
Сравнивая это выражение с выражением QBp. для одного
волчка (10.26), мы видим, что
Qep. вл — QiK. BpQl кл. MexQa кл. мех ••• Ф(кл.мех- (10.72)
Так же как и в случае одного волчка, естественно сделать
допущение о сохранении соотношения типа (10.72) и при
применении квантовой механики. Мы будем иметь:
t
Qep — Qx. вр U (Qa. в)тп>
т = 1
(10.73)
где (Q3. в)то — сумма по состояниям m-го волчка. Из фор-
мулы (10.73) и общих формул главы II получим для сла-
гаемого термодинамической функции, соответствующего вра-
щательному движению,
t
/вр=/ж.вр+ S (/э.в)т. (10.74)
т = 1
Мы видим, что для вычисления термодинамических функ-
ций нужно вычислить соответствующие слагаемые для каж-
дого волчка, а затем сложить их с выражениями для жест-
кой молекулы. Таким образом, аналогично формулам (10.60)—
304 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ (ГЛ.
(10.64) мы получим:
t
(10.76)
^=^ = 4/?+V(^) 4 (-£) , (10.77)
1 47 ' т ' J /колеб
VI = 1
t
Ср = 4/? —|— 2 (Cj. вХпН-^килеб- (10.78)
т = 1
/ф \
Слагаемые (S3. в)т, (-4^) и т. д. вычисляются для каж-
дого волчка по формулам типа (10.54) и (10.57) с помощью
таблиц Питцера, как это было изложено в предыдущем
параграфе.
§ 7. Пример — вычисление энтропии этана
Рассмотрим в качестве примера вычисление энтропии
этана СН3СН3 при температуре 298,1°К и р = 1 атм. Одна
из групп СН3 является остовом, а другая представляет сим-
метричный волчок. Центр тяжести молекулы лежит в середине
линии С — С (точка О, черт. 34). Проведем через точку О оси
координат, причем ось х направим по линии С — С, а ось z
расположим так, чтобы проекция одного из атомов водо-
рода (T/(L)) на плоскость zOy лежала на оси z. Построенные
§ 7] ПРИМЕР— ВЫЧИСЛЕНИЕ ЭНТРОПИИ ЭТАНА 305
оси координат будут, как легко видеть, главными централь-
ными осями инерции. Обозначим расстояние С — С через D
и расстояние С—-Н через d. Как и в случае диметилацети-
лена (см. § 5 главы IX), примем углы ССН тетраэдриче-
скими, cos ССН = —1/3. Из этих данных получим коорди-
наты атомов (см. табл. 32). „ о
Если подставить величины D = 1,55А и d = 1,09А, мы
получим численные значения координат, приведенные соот-
ветственно во вторых столбцах таблицы 32.
Таблица 32
Атом X У 2
с(1) ~ 0,775 0 0 0 0
С(2) ~4 -0,775 0 0 0 0
н(1) 4+4 1дз8 0 0 ?-^d 1,028 О
Н(з) 4+4 11138 у “б d-^-d 0,890 О У “2 —0,514 О
Н(з) 4+4 мЗв У “б —0,890 и У "2 —0,514 О
Н(4) -(5-+|)-1.|зв 0 0 ь028 и
н(б) -(т+т)-".™ У"б d-^-d 0,890 О —0,514
Н(в) -(т+4)-изв —0,890 О —0,514 О
Из данных этой таблицы легко вычислить моменты инер-
ции, для которых получаются следующие значения:
А = = 10,61 • 10~<0 г • см\
i
В = = 42,26 • 10-4° г-см2, . (Ю.79)
С = 2"Ч (*?-+-/) = 42,26 • IO-40 г-см2. |
* * ) 20
20 Зак. 835. И. Н. Годнее
306 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
Используя эти данные, получим, что АВС= 18950- 10-120г3-си6.
Произведения инерции ^imixizi> оказы-
ваются равными нулю.
Детерминант для этана принимает вид
А — К 0 0
[«id = К
0
0
В
0
0
С
= К(А — К)ВС, (10.80)
g
где величина К, равная у md2, представляет момент инерции
группы СН3 относительно оси вращения. Учитывая, что А = 2К,
Таблица 33 и подставляя значение детерминан- та [si4] в выражение приведенного
Частоты Слагаемое -1 С см °волеб момента инерции (10.12), получим: . _К(А-К)В-С __ Уприв— - АВС —
827 (2) 0,375 993 0,096 1170(2) 0,094 1375 0,020 1380 0,020 1460(2) 0,028 1465 (2) 0,028 2925 (2) 0 2960(2) 0 2980 (2) 0 =4= 2-65,10-40 г-см<2- Из этих данных легко вычис- лить энтропию вращения (см. фор- мулу (10.50)). Для этана п=3, Уо = 2750 кал/моль, -^=4,64, 10-36и2 -гут = 12,35. Из таблиц Пит- ^(Нп! ив
$Коле6=0.661 цера мы находим 6'ев — S3. в =
____________________ =1,15 кал/град • моль. Далее,
Sgb = 2,90 кал)град • моль (фор-
мула (10.53)), вр = 16,31 кал/град • моль (см. формулу
(8.114), в которой надо подставить о = 6). Следовательно,
= Sjk.bp + Scb—(Sub—S3. B) = 18,06 колорад• моль. (10.81)
Применяя формулу (2.75), получим:
SD = 36,12 кал/град • моль.
Вычисление колебательной энтропии приведено в таб-
лице 33.
§ 8] ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ АЦЕТОНА ПРИ 500° К 307
Таким образом,
S = $„ 4- SBp + 5колеб = 36,12 + 18,06 + 0,66 =
= 54,84 кал!град • моль.
Экспериментальное определение энтропии этана дает:
S = 54,85 кал)град моль.
§ 8. Пример — вычисление термодинамических
функций ацетона при 500е К
В качестве второго примера рассмотрим вычисление термоди-
намических функций ацетона при 500°К и />=1 атм. Молекула ацетона
СН3СОСН3 состоит из остова (СО) и двух волчков. Выберем систему
координат, связанную с молекулой, начало которой совместим
с атомом углерода С(1) (черт. 35) и ось х которой лежит в плоскости
(С—С—С), а ось у делит угол С—С—С пополам. Эта система
координат не является центральной.
Обозначим расстояние С—С через D, С—Н через d и С—О
через Dv Углы между связями (Z С—С—С, z Н—С—Н), как и
в рассмотренных выше примерах, будем считать тетраэдрическими.
Координаты атомов для случая, когда проекции атомов и Н'т
на плоскость хОу лежат на осях волчков, представлены в таб-
лице 34. Заметим, что моменты инерции всей молекулы не будут
зависеть от положения волчков относительно остова, так как волчки
являются симметричными.
20*
SOS СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЁННЕГО ВРАЩЕНИЯ [ГЛ. X
Таблица 34
Атом X У z
О 0 -Dt 0
С(1) 0 0 0
С(2) D / 6 3 0
С(2) D У"б 3 0
Н(1) (°+W (D+J)? 2/2 3 d
Н(э) Qi 3
Н(з) (a + W+4* /2 3 d
Н(1) -(»< (°+4)? 0
Н(2) L\ о / о о j \ 0 / 0 0
Н('з) (я+Ят+г'
§ 8] ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ АЦЕТОНА ПРИ 500° К 309
Для координат центра тяжести по известным формулам будем
иметь:
а = ------= 0,
V—=0>
• (10.82)
b=^~---
2 /ЗЛ(^-+ m) + j yr3md-M1D1
где M, ,M[ и m означают соответственно массы атомов углерода,
кислорода и водорода. Из формул (10.82) следует, что для пере-
хода к центральной системе координат нужно координаты х и z
оставить без изменения, а из координаты у вычесть величину Ь.
Принимая D = 1,54 A, d = 1,10 А и Dx = 1,24 А, вычислим моменты
инерции, для которых получаются следующие значения:
А = S = 91-6'10 40 2 • см2>
i
B = '£mi (х? + z?) = 94,6 • 10 -40 2
i
С = 2 (-*4 + У2г) = 175,4 • 1О-40 г • сМ
i
(10.83)
Произведения инерции 2 т{Х(У{, 2 тгУЛ и S равны
г i г
нулю, т. е. выбранные нами центральные оси являются главными.
Произведение АВС оказывается равным 1 519 900 • 1О~120 г3-еж6.
Детерминант [s^j для ацетона принимает вид
А-~К
О
ибо
[Sa] = №
о о
2
В-=гК 0
О
о с
(10.84)
с
Мг + ЗЛ14- бте
0
о
2 Wi = = К (cos2 ₽ + cos2 р) = +± К
310 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
И
'S = К (COS3a + COS2a) = К Д- А) = К-
Здесь р означает угол хС(1)С(2) а а означает угол С^2)С(11у
( а <6 /3 \
I COS 3 = , COS а — 1.
Детерминант [s./Д на основании формулы (10.69) можно пред-
ставить в виде
= (10.85)
откуда
прив (ЛВС)'2 (АВС)1'1
По данным моментов инерции для /прив получается 5,09 • Ю-40 г • ел2.
Для группы СН3в молекуле ацетона п = 3, Vo = 1000 кал/моль.
Из таблиц Питцера находим для одного волчка:
(Scn — S3 в) = 0,11 ка.г/град • моль,
С3 в = 1,20 кал/град моль
и
F — F
3,в у,—— = 0,52 кал/град • моль.
Применяя формулы (10.54), (10,57), (2.75) и (2.89), получим со-
ответственно:
53 в = 3,96 кал/град • моль,
/ Ф3 в \
— г j-~ I = 2,56 кал/град моль,
Sa = 40,66 кал!град - моль
и
— ('У') = 35,69 кал/град • моль.
Для двух волчков получим:
S3 в = 7,92 кал/град • моль,
С3 в = 2,40 кал/град • моль
и
— I 3 в ) = 5,12 кал/град • моль.
§ 8] ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ АЦЕТОНА ПРИ 500°К 311
Вычисление дает:
и
Тогда
и
5Ж вр = 24,34 кал/град моль
У вр j = 21,36 кал!град моль.
SBp = 32,26 кал1град • моль
/Ф\
ууj = 26,48 кал/град • моль.
Вычисление слагаемых термодинамических функций, соответ-
ствующих колебаниям, приведено в таблице 35, где указаны значе-
ния 22 частот нормальных колебаний.
Таблица 35
Частота *) см-1 Слагаемое г колеб Слагаемое ^о)колеб т Слагаемое ^п)иолеб Т
391 1,791 1,077 0,783
488 1,688 0,905 0,556
531 1,643 0,843 0,488
787 1,321 0,524 0,219
900 (2) 2,338 0,836 0,310
1066 0,959 0,298 0,095
1070 0,953 0,295 0,094
1220 0,778 0,215 0,060
1350 0,643 0,162 0,041
1353 0,638 0,160 0,041
1420 0,577 0,139 0,034
1423 0,573 0,138 0,033
1430 0,568 0,136 0,033
1438 0,559 0,133 0,032
1710 0,357 0,072 0,015
2930(6) 0,186 0,024 0,002
СКолеб=15,57 5,956 2,836
5КОЛеб = 8’79 кал/град • моль
*) Цифра в скобках означает приближенную крат-
ность частоты.
312 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
Таким образом,
Сдолеб =•= 15,57 кал!град • моль,
5колеб = 8'7^ кал{град моль
и
/Ф\
) = 2,84 кал!град • моль.
Окончательные результаты вычислений термодинамических функ-
ций ацетона приведены в таблице 36.
Таблица 36
Т° к S кал)град‘молъ С кал!град»моль - ( Ф ) кал/град-моль
500 81,7 25,9 65,0
§ 9. Метод Кроуфорда
Более строгое решение задачи о вычислении термодинамиче-
ских функций молекулы, состоящей из остова и нескольких сим-
метричных волчков, было дано Кроуфордом [212].
При решении этой задачи он допустил, что потенциальная
энергия молекулы аддитивно складывается из энергий отдельных
волчков, причем потенциальная энергия каждого волчка представ-
ляется формулой типа (10.1). Таким образом,
t
V = | Voi (1 - cos пЛ). (10.87)
4=1
Определяя виц матрицы энергии вращения для всей молекулы,
Кроуфорд показал, что сумма по состояниям QBp, вычисленная при
применении метода возмущений с точностью до второго порядка,
может быть представлена в виде произведения
= <10-88)
где QeBp— сумма по состояниям жесткой молекулы, a Qb Qz,...
..., Qt — соответственно суммы по состояниям внутреннего затор-
моженного вращения первого, второго и т. д. волчков,- Вели-
чина (?жвр может быть найдена по формуле (8.55) или (8.99) при
условии, что при ее вычислении берется число симметрии сг0, т. е.
число симметрии жесткой молекулы. Так[ для этана а0 = 6, для
метилового спирта »0=1. Формула (10.88) позволяет выполнить
аддитивное вычисление термодинамических функций каждого
§ 9]
МЕТОД КРОУФОРДА
313
волчка. Уровни энергии, знание которых необходимо для вычис-
ления сумм по состояниям Qt, Qz....Qt>
_ *mr
Qm = ^e kT
r
(10.89)
как показал Кроуфорд, определяются из уравнения Матье
+ (amr + 20m cos 2х) ф = 0, (10.90)
где
= ^т~т- (10.91)
и г — квантовое число, принимающее значения*) 0, +1, ±2,...
(ср. с формулой (10.36)). Здесь Кт означает момент инерции т-го
волчка относительно оси вращения, а множитель определяется
формулой
ато = 1-/<4^г + тг + тН’ (10>92)
I zi Lj V» J
где А, В, С — главные центральные моменты инерции всей моле-
кулы, \т, р.то, '/т — направляющие косинусы углов, образованных
осью m-го волчка с главными осями инерции. Выражение
можно рассматривать как приведенный момент инерции т-го
волчка (см. формулу (10.16d)):
X3 3 ^3
кт^л = Ахрив = - к?т + 4] • <10'93)
Уровни энергии волчка, зависящие от собственных значений атг
уравнения Матье, знание которых необходимо для вычисления суммы
по состояниям (10.89), можно разделить на два типа. При малых атг
(нижние уровни) они оказываются близкими к уровням энергии
крутильных колебаний. Верхние уровни приблизительно соответ-
ствуют вращательным уровням уравнения (10.39). При вычислении
суммы по состояниям оказалось целесообразным выполнить сум-
мирование по двум типам уровней отдельно, причем для «враща-
тельных» уровней, как показал Кроуфорд, необходимо ввести
поправочный множитель. Переход от «колебательных» уровней
к «вращательным», имеющий место при квантовом числе г0, пока-
зан в таблице 31 чертой. Таким образом, при г<^г0 вычисляется
сумма по состояниям, соответствующая «колебательным» уровням,
априг>г0 — сумма, соответствующая «вращательным» уровням.
*) При вычислении сумм по состояниям надлежит учесть усло-
вия симметрии, приводящие к отбору допустимых значений кван-
товых чисел (см. примечания на стр, 295, 296).
314 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
Первая из этих сумм в дальнейшем обозначена индексом V, а вто-
рая — индексом /?.
Положим 1 9 2 h п,п Ymr~ 32n2KmtlmRT amr' (I0'94)
где R— универсальная газовая постоянная. Сумма по состоя-
ниям Qm оказалась равной
+ (10.95)
где = (Ю.96) Gv = ^e~Tmr (10.97)
И Од = 2e-s’"r"i''. (l0-98) R
Сумма (10.97) вычисляется по «колебательным» уровням, и поэтому
она снабжена индексом V, а сумма (10.98) вычисляется по «враща-
тельным» уровням (индекс /?).
Выражения для слагаемых термодинамических функций, соот-
ветствующих /п-му волчку, имеют вид S3 в = /?[шо+^-], (Ю.99) F = R [q - In О], (Ю.Ю0) = + (Ю.Ю1) Г J / Н \2 1 Сз.в = л|-^- . (10.102)
При вычислении термодинамических функций соответствующие
выражения нужно прибавить к выражениям для внешнего враще-
ния. В соотношениях (10.99)—(10.102) G, Н и 'J определяются
формулами G = ^Gr + Gv, (10.103) = 2'^+4,. . (10.104) = + 4 (Ю.105)
§ 10] НОВЫ! Е ТАБЛИЦЫ ПИТЦЕРА И ГВИННА 315
где Gr и Gv даются равенствами (10.97) и (10.98), а
М — V V 1 *v — 1 mre > V (Ю.Ю6)
w — 2 Y j-rn у о y p nlr *‘R — mr » R (Ю.Ю7)
T — V y2 p~Yvir (10.108)
7 O] и (Ю.Ю9)
Для вычисления по методу Кроуфорда имеются удобные таб-
лицы (см. [94]).
§ 10. Новые таблицы Питцера и Гвинна*)
В работе Кроуфорда для потенциальной энергии волчков
было применено выражение (10.87), в основе которого лежит
предположение о возможности представить эту энергию
в виде суммы слагаемых типа (10.1). Более общей формой
потенциала, чем (10.1), является выражение
СО
V=2|v0Hl-cosfcna), (10.110)
к = 1
представляющее периодическую функцию угла а.
Рассмотрение задачи определения уровней энергии
молекулы с симметричными волчками, имеющей барьер
типа (10.110), было предпринято Питцером и Гвинном [252]
в предположении аддитивности потенциальной энергии волчков
(10.111)
Ш = 1
При этих предположениях оказывается возможным вы-
полнить вычисление уровней энергии каждого волчка с по-
мощью уравнения Хилла, а сумма по состояниям с доста-
точной точностью представится произведением
Qnp — Q-к. вр QjQa • • Qf (10.112)
*) Ср. работы Хальфорда [228—230] и их применение к вы-
числению термодинамических функций метилового спирта [231].
316 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
В этой же работе Питцер и Гвинн составили новые та-
блицы для вычисления термодинамических функций затормо-
женного волчка с потенциалом обычного типа, представляе-
мого формулой (10.1). Эти таблицы оказываются пригодными
и для вычисления термодинамических функций в случае не-
скольких волчков, если допустить аддитивность их потен-
циальной энергии.
В качестве переменных в этих новых таблицах выбраны
Vo 10-39 я2 Vo 1 „
вместо и 10 -г--------J7- величины и тг-• гДе Qob —
К* К* Vcb
сумма по состояниям волчка со свободным вращением, кото-
рая определяется формулой (10.24). Если в формулу (10.24)
подставить числовые значения постоянных, получится:
(1038Z гй
QCB = 2,793 -------
я
(10.113)
Приведенный момент инерции для одного волчка, как и
в работе Кроуфорда, определяется выражением (10.16d)
или (10.93).
Если имеется несколько волчков, приведенный момент
может быть приближенно вычислен с помощью этой же фор-
мулы или в более точном приближении с помощью формулы
1 V
Г _____ ,0 1 тт'
7прив — *прив “Jo
т'фт т'
где /° дается формулой (10.16d) или (10.93), а
X _ к к V ЧМ
лтт — у----•
г = 1
(10.114)
(10.115)
Здесь Ц означает главный центральный момент инерции от-
носительно оси I (I = х, у, z), а Ат и X г означают напра-
г
вляющие косинусы осей m-го и т'-го волчков с главными
центральными осями инерции (I = х, у, z).
В приложениях дано шесть таблиц Питцера и Гвинна:
р
таблица 66 для приведенной] свободной энергии------,
§ 10] НОВЫЕ ТАБЛИЦЫ ПИТЦЕРА й гвйнна 317
р — F.
таблица 67 для —, таблица 68 для S3. в, таблица 69
Н3 в
для SCB — S3. в. таблица 70 для —и таблица 71 для С3. в.
В качестве примера применения новых таблиц Питцера
выполним вычисление энтропии этана при Т=298,1°К-
При потенциале Уо = 2750 кал/моль и п = 3 мы имеем
/иРив = 2,65 • Ю-40 г см2.
Из этих данных легко вычислить = = 4,64 и = 0,38.
К! Мов
По новым таблицам Питцера находим:
S3. в = 1,76 кал/град моль.
Воспользовавшись данными, полученными нами для
Sn = 36,12 кал/град • моль,
5Ж. Вр = 16,31 кал!град моль
и
^’колеб = 0.66 кал/град • моль
в § 7 этой главы, вычислим полную энтропию этана, кото-
рая будет:
S = Sn + Sb. вр + S3. в + Зколвб = 54,85 кал/град • моль.
Применение старых таблиц дает S = 54,84 кал/град • моль,
что хорошо согласуется с предыдущими данными.
В более поздней работе [253] Питцер представил ряд
аргументов, показывающих, что при предположении потен-
циального барьера в виде (10.1) его таблицы, составленные
для случая симметричных волчков, могут быть использованы
для приближенного вычисления термодинамических функций
молекул с асимметричными волчками *), если несколько иначе
определить приведенные моменты инерции. При таких вычи-
слениях, если число симметрии волчка от не совпадает
с числом минимумов пт в формуле для барьера, нужно
ввести поправку к энтропии и свободной энергии.
Следует заметить, что предположение о применимости
формы барьера (10.1) к случаю асимметричных волчков
*) Доказательство этого дано Питцером лишь для случая мо-
лекул, частоты колебаний которых возбуждены классически
(Ам <С kT).
318 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ |ГЛ. X
является весьма грубым приближением. Однако для волчков
с малой асимметрией метод Питцера может дать удовлетво-
рительные результаты *).
Так, для CH2D • CH.2D, принимая одну из групп за остов,
а другую за асимметричный волчок, можно применить для
вычисления термодинамических функций таблицы Питцера,
положив, что число минимумов иот=3. Однако в этом слу-
чае число симметрии волчка = 1, а поэтому мы должны
ввести поправку к энтропии и свободной энергии /?1ппт=
= R 1п 3, которая должна быть прибавлена к энтропии
Р
и —уг (см. [253]). В еще более поздней работе Кильпат-
рик и Питцер [238] рассмотрели вопрос о вычислении термо-
динамических функций в случае молекул с волчками на
волчках **).
Заметим, однако, что все эти методы не могут быть
непосредственно применены к барьерам сложной формы
с максимумами и минимумами неодинаковой высоты и глу-
бины. Изучение таких газов, представляющих смесь пово-
ротных изомеров, было начато рядом исследователей
[106, 123] (см. также [12])***).
§ 11. Метод П. Г. Маслова
Указанные выше трудности делают актуальной разра-
ботку новых методов, с помощью которых можно было бы,
хотя бы приближенно, провести вычисление термодинамиче-
ских функций без знания потенциального барьера и его
формы.
Существенный прогресс в этом направлении был дости-
гнут в работах П. Г. Маслова, изучившего коэффициенты
*) Для молекул, к которым не применимо предположение
о форме барьера (10.1), Питцером была начата разработка при-
ближенного метода (см. последний раздел работы [252], см. так-
же [250]).
**) См. также работу М. Е. Дяткиной [125], где проведено
вычисление термодинамических функций нормальных пропилового
и бутилового спиртов и этиленгликоля, молекулы которых принад-
лежат к этому классу (классу VI).
***) Изучение поворотной изомерии сказалось также полезным
при построении теории линейных полимеров [109, 111] (см. обзор-
ные работы [110, 112]).
§ 111 МЕТОД П. Г. МАСЛОВА 319
влияния большого ряда молекул [139—145, 98, 146, 151, 50]
и применившего их к вычислению термодинамических функ-
ций паров органических соединений [50]. Используя коэф-
фициенты влияния, П. Т. Маслов разработал методику при-
ближенной количественной оценки роли различных взаимо-
действий внутри молекулы и сформулировал обобщенный
принцип аддитивности [149] (ср. [59]).
Применение этого принципа позволило П. Г. Маслову
получить ряд общих полуэмпирических формул, определяю-
щих термодинамические функции (Ср, ДФ, Д/7, ДЗ) паров
различных классов органических соединений в достаточно
широком интервале температур (250—1600°К) [147, 148,
150, 152—157, 50] (ср. [59]). Так, для теплоемкостей
«-алканов, n-алкенов и «-алкинов П. Г. Маслов получил
общую формулу [152, 50]
__ & । (2« — 2 — т) (2« — т) । (т—2п—2) (2«—2—т) ।
^(«г —2« —2) (2п — те) g, (101i6)
где п — число атомов углерода, т — число атомов водорода
в молекуле, а а, 3, 7, 8 — определенные функции темпера-
туры и числа п (8 зависит также от т).
Применительно к «-алканам формула (10.116) примет
вид [153, 50]*)
Ср = — 1,8413 + 8,2720 • Ю-3? — 15,97 • 10"7Т^ —0,116 X
X 10-9Т3+ (0,43026 +21,14- 10"3 7’— 116,950 • 10'7Т2+
+ 2,5018- 10“97'3) « +294,7926 rt"1(2n + 2)-2e_0’0071’.
(10.117)
Закономерности, найденные П. Г. Масловым, позволяют
находить термодинамические свойства целых классов орга-
нических соединений без знания их структуры, барьера и
колебательного спектра, если известны термодинамические
свойства одного или максимум двух представителей данного
класса.
*) В работе [148] для некоторых коэффициентов формулы
(10.117) П. Г. Маслов дал несколько отличные значения.
320 СЛУЧАЙ ЗАТОРМОЖЕННОГО ВНУТРЕННЕГО ВРАЩЕНИЯ [ГЛ. X
§ 12. Практические формулы
В заключение этой главы приведем табличную сводку
практических формул, применяемых при вычислении термо-
динамических функий молекул с заторможенным вращением
(табл. 37).
Таблица 37
| № п/п | Величина Практическая формула
1 Энтропия посту- пательного дви- жения 5Ц = in 7 —lnp+ in М— U64)
2 Приведенный изо- барно-изотер- мический потен- циал поступа- тельного дви- жения - Пп = 7? In Т - In р + In М — 3,664j
3 Энтропия враща- тельного дви- жения = Я (у in 7 + у In АВС — 1па+134,685)
4 Приведенный изо- барно-изотер- мический потен- циал враща- тельного дви- жения -Пя, В1 ,=7? In 7+| in ЛВС-In а+133,185)
5 Энтропия свобод- ного вращения SCB=/?(-0,775 +1 Ш7 + 1 In7ПГИВ • 10«-Inn)
6 Приведенный изо- барно-изотер- мический потен- циал свобод- ного вращения -Псв=7? (-1,275+11п7+|1п/п1ШВ • Ю40—In
7 Энтропия газа по способу Пит- цера 5 = Sn + 5ж. вр+5коле«+2 [SCB—(S0B—S3 в)]
§ 12]
ПРАКТИЧЕСКИЕ ФОРМУЛЫ
321
Продолжение
1 № п/п. | Величина Практическая формула
8 Приведенный изо- барно-изотер- мический потен- циал по спо- собу Питцера п Пп Пж Вр Пколеб — 2 [Пев + (Пз. в — Псв)]
9 Энтропия газа по способу Кроуфорда t 5 = 5д + 5ж. вр + 5колеб + S Si i
10 Приведенный изо- барно-изотер- мический потен- циал по спо- собу Кроуфорда t ~ П = — пп — Пж вр — пколеб — 2 Щ i
11 Энтропия газа по новым таб- лицам Питцера t S = Sn+ Sx. вр + 5колеб + 2 5’з. в i
12 Приведенный изо- барно-изотер- мический потен- циал по новым таблицам Пит- цера t U ‘ Пд вр ^колеб S П;'з, д i
21 Зак. 835. И. И. Годней
ГЛАВА XI
ВЫЧИСЛЕНИЕ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
РЕАЛЬНЫХ ГАЗОВ, ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
ПО ТЕРМОДИНАМИЧЕСКИМ ФУНКЦИЯМ
В ИДЕАЛЬНОМ ГАЗОВОМ СОСТОЯНИИ
§ 1. Вычисление термодинамических функций
реальных газов
Рассмотренные нами методы позволяют выполнить вычи-
сление термодинамических функций в идеальном газовом
состоянии. Это не снижает практической ценности статисти-
ческих методов, так как по значениям термодинамических
функций в идеальном газовом состоянии могут быть най-
дены термодинамические функции реальных систем.
Для перехода от идеального газового состояния к реаль-
ному можно использовать уравнение состояния и известные
термодинамические соотношения [29, 48]
Интегрирование этих уравнений может быть выполнено
с помощью ряда уравнений состояния, предложенных к на-
§ 1] ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ РЕАЛЬНЫХ ГАЗОВ
323
стоящему времени *). При умеренных давлениях можно при-
менить уравнение состояния Д. Бертло, нашедшее широкое
применение при введении поправок на неидеальность,
[p + ^)(v-t>) = RT. (11.5)
Постоянные а и b этого уравнения связаны с критиче-
скими величинами соотношениями
27 Г3
a=-R^,
64 Ркр
. 1
4 fKp.
(И-6)
(11.7)
Приближенно уравнение состояния Д. Бертло может быть
представлено в виде
pv = RT
I / Гкр
' 128ркрГ \ Л
(11.8)
находящем ряд применений.
С помощью уравнения (11.8) могут быть найдены по-
правки на неидеальность газа. Так, для вычисления энтро-
пии реального газа из уравнения (11.8) мы имеем:
(dV\ I 277?Гкр
; \дт)р- р “^зг^гз-
f Теперь соотношение (11.3) дает:
L tdSx _ R 27 RT^
\др)т р 32 ркрГ3 •
(Н-9)
(11.10)
Для идеального газа, который подчиняется уравнению Мен-
делеева— Клапейрона pv = RT, аналогичным образом по-
лучается:
< др /т р ‘
(И.И)
*) См. О. Д. Хвольсон [73], т. Ill; М. П. Вукалович
и И. И. Новиков [14].
21*
324
ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ РЕАЛЬНЫХ ТЕЛ [ГЛ. XI
Заменяя в равенстве (11.10) —— его значением из равен-
ства (11.11), будем иметь:
р$реалън\ =
\ др ) т \ др / т 32 ркрГ3
или
д (^реальн *^ид) ___7?Твр
др ~ — 32 ^рГз •
Интегрирование от р = 0 до р дает:
_ 27 RT^
^реальн 5пд — р рз Р’
отсюда
27 /?7±
(В-12)
(11.13)
(П-14)
(11.15)
Аналогичным образом вычисляется поправка на теплоем-
кость. Дифференцируя равенство (11.9) второй раз, мы по-
лучим: д*и 81 (11.16) дЛ 32 р 74
Подставляя найденное значение производной в общее
термодинамическое соотношение (11.4), будем иметь:
дСД _81 /?7*р
др )т 32 ркрЛ-
(П-17)
Интегрирование этого равенства дает:
81
СР -Ср = (11.18)
^реальн .ид oz pKJ/°
отсюда
81 RT*
сР =ср +^^г^р- (Н-19)
™реальп Лтд о 2
vr
Для вычисления поправки на теплосодержание мы исполь-
зуем соотношение (11.1). Подставляя в него объем из урав-
§ 2] ТЕРМОДИНАМИЧ. ФУНКЦИИ ЖИДКИХ И ТВЕРДЫХ ТЕЛ 325
нения Бертло и из формулы (11.9), мы получим после
приведения подобных членов
М 162/;
\ др)т~ К 128/>кр 128 *р^Л-
(11.20)
После интегрирования в пределах от р — 0 до р будем
иметь:
Дифференцирование этого равенства по температуре, как
это и должно быть в силу соотношения
'»~\дТ)р
(11.22)
дает формулу (11.19).
Вычитая из формулы (11.21) значение pv, мы можем
получить выражение для внутренней энергии.
Таким образом, используя уравнение состояния Бертло,
можно найти термодинамические функции реального газа.
Подчеркнем, что полученные формулы могут быть исполь-
зованы лишь при умеренных давлениях. Для более высоких
давлений надлежит применять более точные уравнения состоя-
ния или экспериментальные данные р — v—Т*).
Решение такой задачи выполняется аналогичным образом
путем применения общих термодинамических соотношений
(11.1) — (11.4) к данному уравнению состояния.
§ 2. Вычисление термодинамических функций
жидких и твердых тел
По значениям термодинамических функций в идеальном
газовом состоянии могут быть найдены термодинамические
функции жидких и твердых тел, если известны соответ-
ствующие скрытые теплоты парообразования и плавления и
значения теплоемкостей.
Пусть известна скрытая теплота парообразования жидко-
сти при температуре кипения Тк для давления, равного 1 атм,
*) См., например, М. X. Карапетьянц [29].
326 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ РЕАЛЬНЫХ ТЕЛ [ГЛ. XI
и пусть требуется найти энтальпию НЯ(Т) и энтропию жидкого
вещества 8Я(Т) при температуре Т < Тк.
Нагревая один моль жидкости до температуры кипения
и превращая его в пар при постоянном давлении, равном
1 атм, мы будем иметь:
тк
Нп*Р(Тк)—Нж(Т)= ^CpdT+k, (11.23)
т
тк
fC dT X
(11.24)
J 1 к
T
где 8Я(Т) и НЯ(Т) означают энтропию и теплосодержание
жидкости при давлении в 1 атм. Заметим, что зависи-
мостью энтропии и теплосодержания жидкости от давления
обычно можно пренебречь.
Из равенств (11.23) и (11.24) получим:
тк
Hx(T) = Hmr(Tk)— ^CpdT-\ (11.25)
т
и
тк
f C„dT
sx (7) = Snap (Tk) - A _ . (11.26)
1 к ' 1
T
Выполняя вычисление теплосодержания и энтропии при
температуре кипения Тк и р = 1 атм в идеальном газовом
состоянии и вводя поправку на неидеальность, найдем:
Нт^Тк)-НК^Тк) = а, (11.27)
^’пар(7’л) — 8„л(Тк, р = 1 атм) — Ь. (11.28)
Из равенств (11.27) и (11.28) следует:
//паР(ТА) = а + /7ид(Тй), (11.29)
Snap (Tj;) = .$Яд (7\, р = 1 атм). (11.30)
Заменяя в формулах (11.25) и (11.26) НПаР(7\) и Snap (Л)
из равенств (11.29) и (11.30), мы получим:
Тк
Нж(Т) = Нид(Т’А)+а- J CpdT-k (11.31)
т
§ 2] ТЕРМОДИНАМИЧ. ФУНКЦИИ ЖИДКИХ И ТВЕРДЫХ ТЕЛ 327
и
тк
Г С dT \
S*(T) = S^(Tk, р= \ атм) + ь— ----------------(11.32)
J 1 к
Т
Следует заметить, что это соотношение между 5Ж и 5ИД
часто используется для вычисления энтропии идеального газа
по экспериментально найденной энтропии жидкости.
Мы видим, однако, что оно может быть использовано
также для вычисления энтропии жидкости, если последняя
неизвестна.
Если известна скрытая теплота парообразования при
температуре Т, для вычисления энтропии и теплосодержания
можно поступить иначе.
Пусть давление паров, насыщающих пространство при тем-
пературе Т, будет р. Мы будем иметь:
//пар (р, Г) = Нж (р, Г) + Г, (11.33)
Snap (Р, Т) = $ж(р, Т) + у. (11.34)
Пренебрегая зависимостью энтропии и теплосодержания
жидкости от давления, получим:
Япа„(р, Т) = Нж(7') + л', (11.35)
Snap (р> Т) = 5«(.Т)+у, (11.36)
где Нж (Т) и 5Ж (Г) означают, как это было указано выше,
теплосодержание и энтропию жидкости при температуре Г
и давлении в 1 ашм.
Выполняя вычисление энтропии и теплосодержания в иде-
альном газовом состоянии при давлении р и температуре Т
и вводя поправки на неидеальность, мы найдем *):
//дар (Г, р) = Нид (Г) + а', (11.37)
Snap (7) р) — S№(T, p)-\-b'. (11.38)
*) Нил не зависит от давления, а поэтому мы опустили сим-
вол р у величины Ния в формулах (11.37) и (11.40).
328 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ РЕАЛЬНЫХ ТЕЛ [ГЛ. XI
Величина 5КД (Т, р) может быть найдена по энтропии 5 (Т, р =
= 1 атм) с помощью равенства (см. формулу (2.73))
S(T, p) = S(T, р = 1) — /?1пр. (11.39)
Из равенств (11.35) — (11.38) следует:
Нж(7') = Нид(Т)+а/ — //, (11.40)
5Ж(Т) = 3ИД(Т, p) + b'-^. f (11.41)
Аналогичным образом можно выполнить вычисление тер-
модинамических функций твердых тел *) по значениям тер-
модинамических функций в идеальном газовом состоянии.
Для этого надо рассмотреть процесс перехода:
тв. тело при температуре Т, р = 1 атм ид. газ (Т, р).
(11.42)
§ 3. Пример
Рассмотрим в качестве примера вычисление энтропии
жидкого H.2S при температуре плавления 187,6°К-
Температура кипения H2S при р = 1 атм равна 212,8°К;
скрытая теплота парообразования [220] л = 4463 кал/моль.
Выполняя вычисление энтропии в идеальном газовом со-
стоянии при р = 1 атм и Тк = 212,8° К, мы найдем 5ИД. Газа =
= 46,31 кал/град • моль. Поправка на идеальность при
7’=212,8°К и р = 1 атм по уравнению (11.15) составляет:
д — •Spetuibti *^ид — 0,1 кал/град,
откуда
1 атм) = 46,21 кал/град • моль.
Прирост энтропии жидкого H>S при нагревании от тем-
пературы плавления 187,6° К до температуры кипения 212,8° К
*) Здесь мы не рассматриваем статистических методов вычи-
сления термодинамических функций твердых тел (кристаллов). Этим
методам посвящено много работ, о которых см. Р. Фаулер и
Э. Гуггенгейм [63], Л. Ландауи Е. Лифшиц [38]; см. так-
же В. В. Тарасов [185—188].
§ 3]
ПРИМЕР
329
можно найти графически по кривой теплоемкости. Вычисле-
ние даст:
213,8 „ „
/• Ср dT
—=г- = 2,05 кал!град • моль.
187,6
Применяя формулу (11.32), мы получим:
S»(187,6°K) =
= 46,31 —0,10 — 2,05 — = 23,18 калорид-моль.
212,0
Этот результат хорошо согласуется с экспериментальным
определением [220] энтропии жидкого H2S по теплоемкости
твердых фаз H2S и теплотам фазовых превращений, которое
дает (187,6°К) = 23,25 кал!град • моль.
ГЛАВА XII
РАСЧЕТ ХИМИЧЕСКИХ РАВНОВЕСИЙ
§ 1. Введение
Статистические методы, примененные в предыдущих главах
к вычислению термодинамических функций, позволяют просто
и точно выполнить расчет химических равновесий. В настоя-
щей главе мы рассмотрим вопрос о расчете констант равно-
весий химических реакций газов.
Для химической реакции
аА-\-ЬВ тМ (12.1)
мы имеем:
= const (12.2)
при постоянной температуре. Здесь ал, ав, aL и ам озна-
чают активности реагирующих веществ.
Выражение (12.2) известно под именем обобщенного за-
кона действия масс. При газовой реакции активности равны
летучестям, так что закон действия масс принимает вид
П2 31
К-71Л' <12'3)
В случае идеальных газов летучести равны парциальным
давлениям, следовательно,
КОНСТАНТЫ РАВНОВЕСИЯ ГАЗОВЫХ РЕАКЦИЙ
331
§ 2]
Для вычисления константы равновесия разработан ряд ме-
тодов *). Здесь мы рассмотрим только статистические методы
расчета химических равновесий.
§ 2. Общие формулы для констант равновесия
газовых реакций
Вычисления констант равновесия статистическими мето-
дами могут быть выполнены как с помощью таблиц термо-
динамических функций, так и непосредственно при примене-
нии формул, определяющих суммы по состояниям реагирую-
щих веществ.
Пусть дана химическая реакция в газовой фазе
аА + ЬВ И-\-тМ. (12.5)
Как известно, в состоянии равновесия при постоянном
давлении и постоянной температуре
ДФ = 0. (12.6)
В формуле (12.6). как и в последующих формулах, символ Д
означает прирост данного рассчитываемого свойства при реак-
ции, т. е.
^f=lfL + mfM-afA-bfB, (12.7)
где fL, fA, fB — значения этого свойства для веществ
L, Л1, А и В, отнесенные к одному молю.
Подставляя в (12.6) вместо изобарно-изотермического по-
тенциала каждого вещества его значение через химический
потенциал (ф = пр.), мы получим:
ДФ =/а тА-тчм — аи.—Z>un = 0 (12.8)
‘ Ь 1 ‘ JU 1 А 1 х '
ИЛИ
= О2-9)
Для химического потенциала в § 8 главы II нами были
получены выражения
= (12.10)
*) Г. Льюис и М. Рендалл [48], М. X. Карапетьянц [29],
Р. Веннер [11]; см. также М. И. ТемкиниЛ. А. Шварц-
ман [196].
332
РАСЧЕТ ХИМИЧЕСКИХ РАВНОВЕСИЙ
[ГЛ. XII
= Noeo —RTln (12.11)
Для веществ А, В и т. д. мы имеем:
= (12.12)
Qn
= (12.13)
и т. д.
Подставляя эти выражения в равенство (12.9), получим:
— aRTln^—= — IRTln^—mRTln^ (12.14)
na nb nl nm
или ^anb ~ QaQb ~ = const = Kn- (12.15)
состояниям Q в § 3 главы II была предста-
Сумма no
влена в виде
Q = е kTq,
(12.16)
где е0—нулевая энергия, a q— сумма по состояниям, вы-
численная по энергиям, отсчитанным от нулевого состояния.
Если заменить суммы по состояниям Qa, Qb и т. д. в фор-
муле (12.15) их выражениями через q, константа равнове-
сия Kn примет вид
Kn »А»В QaQb
— е а Ъ ’
Яа^в
(12.17)
где Де0 — прирост нулевой энергии при реакции (12.5),
Де0 — 1г -[- тгом ^sob' (12.18)
От выражения для константы равновесия Kn мы можем
легко перейти к константам равновесия Кс и Кр.
§ 2]
КОНСТАНТЫ РАВНОВЕСИЯ ГАЗОВЫХ РЕАКЦИЙ
333
В самом деле, для концентраций веществ Сл, Св и т. д.
имеем: с л v Ntf>' (12.19)
NB (12.20)
и т. д.,
откуда Na = CaNqv, (12.21)
Nb = CbNov (12.22)
и т. д.
Подставляя числа молекул NA, NB, NL, NM в формулу
(12.17), мы получим после элементарных преобразований
г — б в -^\NovJ\NovJ (Чв\ \NovJ \Nov/ (12.23)
Наконец, применив уравнение состояния
pv = NkT, (12.24)
будем иметь:
PAV NA~~kf’ (12.25)
pnv В kT (12.26)
и т. д.,
где рА, рв и т. д.—парциальные давления реагирующих
веществ. Подстановка чисел NA, Nb и т. д. в формулу (12.17)
после элементарных преобразований дает:
(kT')l+m'a~b = Кр. (12.27)
Таковы общие выражения для констант равновесия Кц, Кс
и Кр газовой реакции. Мы видим, что для расчета константы
равновесия нужно знать Де0 и суммы по состояниям qA, qB,
Qm-
334
РАСЧЕТ ХИМИЧЕСКИХ РАВНОВЕСИЙ
[ГЛ. XII
§ 3. Вычисление константы равновесия
с помощью таблиц приведенного
изобарно-изотермического потенциала
При наличии таблиц термодинамических функций для вы-
числения константы равновесия может быть применен простой
метод, основанный на использовании известного соотношения
ДФ° = — RT\nKp, (12.28)
которое определяет прирост изобарно-изотермического потен-
циала реакции при стандартных условиях.
Пусть имеются таблицы термодинамических функций, со-
ставленные по молекулярным и спектроскопическим данным,
в которых для стандартных условий = 1) даны значения
приведенного изобарно-изотермического потенциала П°,
ф° —£0_ф° —/7»
— т ? ,
(12.29)
для каждого реагирующего вещества, а также значения тепло-
содержания, отсчитанного от абсолютного нуля,
/г° = //° — Е? = Н° — Но. (12.30)
В этих формулах индекс °, поставленный вверху, указывает,
что все величины относятся к стандартным состояниям, при
которых давления (точнее летучести) равны 1 атм. Вычисляя
прирост приведенного изобарно-изотермического потенциала П°
при реакции (12.5), получим:
откуда
ДФ гззДНо+Т’ЛП0. (12.32)
Теперь сопоставление формул (12.28) и (12.32) дает:
ЛЯ° ДП
1п^ = -^г—/Г’ <12-33)
Таким образом, для вычисления Кр необходимо знать ДП9
и ДНо- Первая из этих величин определяется по табличным
значениям П°, а вторая — может быть вычислена по тепло-
§ 4] примеры 335
вому эффекту реакции Qp при комнатной температуре. В са-
мом деле, на основании формулы (12.30) мы имеем:
Н0 = (12.34)
откуда
ДН° = Д^ + Д/г°. (12.35)
Пусть дан тепловой эффект реакции при 298° К. Тогда
Qaoe = — ДН2<18 (12.36)
и
Д/^298 — Д 77о —|— ДЙ298, (12.37)
откуда
ДН0 = -С298 —Д^98. (12.38)
Таким образом, для вычисления Кр мы должны найти &Hq
по формуле (12.38), а затем по формуле (12.33) найти Кр.
§ 4. Примеры
Приведем два примера, иллюстрирующих вычисление кон-
стант равновесия.
а) П р и м е р 1. Пусть дана реакция
СО(г) + Н2О(г) СО2(г) + Н2(г). (12.39)
Константа равновесия будет:
к _ Рсо/н,
Р PeQPUfi
В таблице 38 приведены термодинамические функции
реагирующих веществ при 7' = 298,2°К, 600°К и^800°К-
Тепловой эффект реакции (12.39) при 298,2°К равен
9838 кал!моль. Мы имеем на основании таблицы 38 при
298,2°К
Дй° = 2 А0 — 2 А° = — 176 кал!моль.
обр исч
Формула (12.38) дает:
ДНо = — 9662 кал!моль.
336
РАСЧЕТ ХИМИЧЕСКИХ РАВНОВЕСИЙ [ГЛ. XII
Таблица 38
т° к Функция со2 Н2 СО Н2О
298,2 Л» Ф° — Я® П’ = уГ—- 2238 — 43,555 2024 — 24,423 2073 — 40,350 2365 — 37,172
600 я с II в S- 1 о <= ч 1 1 о © 5322 — 49,238 4129 — 29,203 4210 — 45,222 4873 — 42,768
800 до Ф°— Н° П« = ^-1 7689 — 51,895 5537 — 31,186 5699 — 47,254 6666 — 45,131
Зная ДЯ° по формуле (12.33), мы можем вычислить 1п/Ср
при любой температуре, если известны П° для каждого ве-
щества. Для 298,2°К на основании таблицы 38 мы имеем:
ДП° = 2 П° — S П° = 9,544
обр исч
И
1g /Ср = 4,9965,
откуда
Кр = 9,92 • 10*.
Для 600°К получим:
ДП° = 2П° —2П° = 9,549
обр исч
И
1g/Ср = 1,4325,
откуда
/С =27,07.
Для 800°К имеем:
ДП° = 2 Пэ — 2 П° = 9,304
обр исч
§ 4]
ПРИМЕРЫ
337
и
откуда
1g Кр = 0,6062,
Кр — 4,038.
Эти значения констант равновесия хорошо согласуются
с опытными данными (см. табл. 39).
Таблица 39
т° к Ig/G, ° 'вычисл 1g Кр ^опытн
298,2 4,997
600 1,433 1,54—1,42
800 0,606 0,70—0,60
Ь) Пример 2. Рассмотрим теперь реакцию
2С2Н-ОН (г) ^=± Н2 (г) + 2Н2О (г) + С4Н6 (г). (12.40)
Тепловой эффект реакции (12.40) при 298,2° К можно
найти по теплотам образования Н2О (г), С2Н5ОН (г) и С4Н6 (г),
значения которых приведены в таблице 40 вместе с вели-
чинами й° для температуры 298,2° К-
Таблица 40
Вещество q (кал) при 298,2° К
Н2О (г) 57 814 2362
Н2 (г) 0 2024
С4Н6 (г) — 26 748 3620
С2Н5ОН (г) 56 300 3274
Теплота образования воды Н2О (г) вычисляется по те-
плоте образования Н2О (ж) и скрытой теплоте испарения;
теплота образования спирта колеблется в пределах 56 201 —
56 625; нами принято значение 56 300 кал.
Применяя для вычисления теплового эффекта формулу
= ^с,н. “Ь 2^н2о ,
мы получим:
Q298 = — 2 3 7 2 0 кал!моль.
22 Зак. 835. И. Н. Годнее
S38 Насчёт1 хЙмйческйх равйовЁсйй [ёл. kii
Таблица 41
Приведенные изобарноизотермические потенциалы Пи
т° к С2Н5ОН С4Н6 нао н2 дп°
400 — 58,98 — 58,546 — 39,513 — 26,438 — 46,054
600 — 64,95 — 65,308 — 42,765 — 29,218 — 50,156
1000 — 75,07 — 76,835 — 46,999 — 32,752 — 53,445
На основании таблицы 40
Дй° = /г° — 2 h° = 3820 кал!моль.
обр исч
Применяя теперь формулу (12.38), получим:
Таблица 42 ДЯо — 19 900 кал)моль. Приведенные изобарно-изотермиче-
Т° К кр ские потенциалы П° даны в табли- це 41 вместе с значениями ДП°. Подставляя значения ДН° и ДП° в формулу (12.33), найдем константы равновесия при соответствующих температурах. Результаты предста- влены в таблице 42.
400 600 1000 0,156 51,4-102 21,3-106
§ 5. Детализация формул для вычисления констант
химического равновесия через сумму по состояниям
в случае диссоциации двухатомной молекулы
В § 2 мы вывели общие формулы для вычисления кон-
стант химических равновесий через суммы по состояниям.
Рассмотрим теперь, какой вид примут эти формулы, если
в них подставить явные выражения для QA, QB и т. д. Сна-
чала разберем простой случай диссоциации двухатомной
молекулы.
Пусть дана реакция .
АВ = ААГВ.
(12.41)
§ 5] СЛУЧАЙ ДИССОЦИАЦИИ ДВУХАТОМНОЙ МОЛЕКУЛЫ 339
(12.42)
Мы будем иметь на основании общей формулы (12.17)
„ ~^ЧаЯв
™АВ ЧАВ
В главе III для суммы по состояниям одноатомного газа q
мы получили выражение (3.28)
(2r.mkT)^
Я — рРо«-
(12.43)
где т — масса молекулы, v — объем, р0 — вес основного элек-
тронного состояния и
a = 2s+l (12.43а)
— вес, обусловленный существованием ядерного спина $. Это
выражение справедливо для случая, если можно пренебречь
всеми электронными уровнями, кроме первого. Мы имеем:
(2лчпАкТ')1г
Я А = ---ДЗ-----WaA-
(2~mBkT)i'‘
Яв = ьз vPoBaB-
(12.44)
(12.45)
Для двухатомной молекулы АВ мы получили при средних
и высоких температурах (см. формулы (5.4), (5.48) и (5.49))
ЧАВ = Qn • «вр • «колеб • Р0АВ • «лв (12.46)
_ ^mABkT)3\ WIkT аАВ
Я АВ № VPoaB h‘i а фколеб- (12.47)
Здесь т.Ав = тА~!гтв— масса молекулы АВ, /—момент
инерции и
“AB = (2si+l)(252+l) = aAaB (12.48)
— вес ядерного спина.
Подставляя эти выражения для qA, qB и д АВ в фор-
мулу (12.42), получим:
NaNb
Kn~ ^ав
(2лтлтвАГ)1'» Л2 1 рПАр0В
-е V'^kTQ^ Р0АВ
(12.49)
v
22*
340
РАСЧЁТ ХИМИЧЕСКИХ РАВНОВЕСИЙ
[ГЛ. XII
Заметим, что веса спиновых состояний сокращаются при
средних и высоких температурах и потому не входят в фор-
мулу (12.49).
Если провести аналогичным образом вычисления Кс
(см. формулу (12.23)), получим:
_ 1 р,)Ар0В
^IkTQKOXe6 Рлв (
При применении формул (12.49) и (12.50) кроме молеку-
лярных данных нужно знать изменение нулевых энергий s0 при
химической реакции. Это изменение для реакции типа (12.41)
может быть найдено и из чисто спектроскопических данных.
Следует подчеркнуть, что при вычислении Де0 должно
быть применено одно и то же энергетическое состояние, от
которого отсчитываются уровни энергии атомов и молекул
(см. § 2 главы II). Этот нулевой уровень может быть выбран
при расчете Кд- для на-
шей реакции (12.41) мы
можем отсчитывать энер-
гию молекулы от энергии
системы, находящейся в
состоянии полной диссо-
циации на атомы, или от
энергии низшего кванто-
вого состояния молекулы
АВ (при v = 0).
Пусть мы выбрали в
качестве точки отсчета
энергии состояние мини-
мума потенциальной энергии молекулы АВ (черт. 36). Энер-
гия атомов А-\-В изобразится отрезком Cd, равным
soa4~£ob> а энергия молекулы еоЛВ — отрезком fg. Изме-
нение нулевой энергии при реакции будет:
Д£о = £°д “Ь — голв> (12.51)
т. е. при реакции диссоциации произойдет увеличение нуле-
вой энергии на отрезок ab, равный Ле0 (см. черт. 36). Так,
например, для реакции
произвольным образом: например,
-> 2J
§ 6] МНОГОАТОМНЫЕ ГАЗЫ. КОМПЕНСАЦИЯ ЯДЕРНОГО СПИНА 341
мы имеем по кривой диссоциации энергию гол-|-гов =
= 35 860 кал, а =пЛВ = 310 кал. Изменение Дг0 будет
35 860 — 310 — 35 550 кал. Если в качестве точки отсчета
принять верхний уровень кривой диссоциации, будем иметь
год + гов = 0> а энергия молекулы АВ (при v = 0) будет
равна -—35 550 кал.
Следовательно, As0 — 0 — (— 35 550) = 35 550 кал, т, е.
мы получим прежний результат.
§ 6. Детализация формул для константы равновесия
при применении к многоатомным газам.
Компенсация ядерного спина
Найдем теперь выражение для константы равновесия ре-
акции с участием многоатомных квазитвердых молекул. Бу-
дем предполагать, что расчет производится при средних
и высоких температурах, когда мы можем применить с до-
статочной точностью формулы, выведенные в §§ 1—7 главы VIII.
При этих условиях имеем:
Ч ~~ Qn ' Qs:i ' Qnp ’ С?колеб ‘ Qn. с (12.52)
или
_ (2ктА7’)“л 1 8-2(l-kT)'1-
Q № V с № (JaIbIc)11 X
ХП (1_Д-.^> (|2 И)
Будем далее предполагать, что низший электронный уровень
имеет вес р0, равный 1 для всех молекул, участвующих
в реакции. Точно так же предположим, что остальные уровни
электронной энергии лежат достаточно высоко для всех мо-
лекул.
В случае реакции (12.5) будем иметь:
„ I ~ ™
Кс = vN,i . . (12.54)
ГЧА\а(Чв\Ь
I A J I D I
''vNq'
Подставляя выражения сумм по состояниям q и снабжая
нужные величины соответствующими индексами L, М, А и В,
342
РАСЧЕТ ХИМИЧЕСКИХ РАВНОВЕСИЙ [ГЛ. ХИ
получим:
K2*mLkT/ 2тсОТмй7'\’/Лт
с Г/ 2пт.А1гТ \эМаГ
Lv^o ) J L\ АГ0 / J
У/ Фвр дФвр Af Сколеб Д^колеб Л aLalt Q2 55)
Сколеб лРколеб В аАаВ
Легко видеть, что при средних и высоких температурах
множитель
? „т
_ aLaM
д ~ г,аг,Ь
аАаВ
(12.56)
обратится в единицу. В самом деле, пусть в молекулу А
входит at атомов первого рода с ядерным спином st, а2—
второго рода с ядерным спином s2 и as — третьего рода
с ядерным спином $3; положим в молекуле В числа этих
атомов соответственно будут bt, b2 и bs. Для молекул М
и L обозначим эти соответствующие числа через mt, т2, т3
и /х, /2, /3. Например, в реакции
N2-|-ЗН2-> 2NH3 (12.57)
мы имеем для молекул N2: аг = 2, д2 = 0, а3 = 0; для Н2:
Ьг = 0, Ь2 = 2, £3 = 0; для NH3: тг = 1, т2 = 3. Далее,
a—i, b = 3, т = 2 и / = 0. При обычных химических ре-
акциях имеет место сохранение атомов, а поэтому можно
написать:
aat + bbr = llt + mmv j
aa2-\-bb2 = ll2-\-mm2, !• (12.58)
лй3 —[— bb3 ll3 —|— J
Мы будем иметь (см. формулу (8.57)):
аА = (2^ + 1 )“ (2s2 + 1 )О1 (2s3 + 1)“’, ’
aB = (2S1+ 1)6'(2^+ 1)\2я3+ 1)\ । 9)
а ь = (2st + 1 )г'(2s2 + 1(2s3 + 1А
адг = (2$х + 1 )m\2s2 + 1 )m’(2s3 + 1Г •
§ 7]
ПРИМЕНЕНИЕ ТАБЛИЦ
343
Подставляя эти значения в выражение (12.56), получим:
Л г,т
___ aLaM ___
г.аг,Ь
аАаВ
_ (2st + (2s2 4- 1)^+"»»о (2$34- 1)»з+»»»>3
~ (2st4- l)aa‘+b6' (2s2+ l)aCTa+bb2(2s34- 1)ааз+ьг,= ’ ( ’ '
откуда, принимая во внимание соотношения (12.58), мы ви-
дим, что 5 равняется 1.
Теперь выражение для Кс (12.55) примет вид
Qbp lQbf 31 . Фколеб дОколеб 31
Qnp А*^вр В ^колеб А*2колеб В
(12.61)
Таким образом, при средних и высоких температурах
при расчете химических реакций мы можем не принимать во
внимание ядерный спин. Этим и объясняется введение прак-
тической энтропии, не содержащей ядерного спина (см. § 3
и § 4 главы III, § 10 главы V, § 6 главы VIII).
Подчеркнем еще раз, что формула (12.61) в отличие от
общей формулы (12.23) является приближенной*). Заметим,
что при расчете обычных химических реакций формулами
типа (12.23) или (12.61) обычно не пользуются, так как
изложенный выше метод (см. § 3 этой главы) гораздо удоб-
нее. Однако выражение (12.61) применяется при расчете ско-
ростей химических реакций **).
§ 7. Применение таблиц прироста изобарно-
изотермического потенциала реакций образования
Расчет химических равновесий на основании спектроско-
пических и молекулярных данных может быть выполнен
*) Удобный приближенный метод расчета констант равновесий,
основанный на применении правила произведений, предложен
В. М. Татевским и А. В. Фростом [190].
**) См. Г. Э й р и н г, Дж. Уолтер, Дж. Кимбалл [86],
см. [23], а также М. И. Темкин [192—195].
344
РАСЧЕТ ХИМИЧЕСКИХ РАВНОВЕСИЙ
[ГЛ. XII
также с помощью таблиц, содержащих величину ДФ“, т. е.
прирост изобарно-изотермического потенциала реакции об-
разования при стандартных условиях, а также таблиц, со-
держащих так называемые «комбинированные термодинами-
ческие функции».
В самом деле, на основании спектроскопических и моле-
кулярных данных и данных теплот образования можно соста-
вить таблицы величин ДФ°. В литературе эти величины не
совсем удачно получили название «свободных энергий реак-
ции образования».
Пусть дано газообразное соединение АВС при стан-
дартных условиях, т. е. при летучести, равной 1 атм (да-
вление равно 1 атм). Для его реакции образования имеем:
A-i-B + C^ABC, (12.62)
где А, В, С означают элементы, из которых построено
вещество АВС, в их стандартных состояниях.
Пусть нам известна величина приведенного изобарно-
изотермического потенциала IP для каждого из элементов.
Мы имеем:
Ф9 — Н°
1Р =-----(12.63)
откуда
Ф° = П1о + /Уо0. (12.64)
Для реакции образования мы получим:
ДФ“= 7ДП®_|_ДНО°Л (12.65)
Величина может быть найдена с помощью уравне-
ния (12.35), если известен тепловой эффект реакции образо-
вания (теплота образования) q, равный приросту теплосо-
держания ДЯ/' с обратным знаком:
<? = — \Н°Г. (12.66)
Применяя уравнение (12.35), будем иметь:
ДН;=ДН7-|-Д^,, (12.67)
откуда
Д//о/ = ЬН°Г—(12.68)
ПРИМЕНЕНИЕ ТАБЛИЦ
345
§ 71
Подставляя значение из (12.68) в формулу (12.65),
получим окончательно:
ТДЦ^ Mf. (12.69)
При вычислении «свободной энергии образования» ДФ^
органических соединений нужно иметь таблицы термодина-
мических функций твердого углерода в виде графита или
алмаза. Такие таблицы составлены на основании тщательных
экспериментальных исследований, и величина ДФ£ известна
для многих органических веществ *). Величины ДФ; для не-
которых простейших углеводородов приведены в таблице 43.
Значения ДФ^ позволяют легко найти константу равновесия
химической реакции.
Пусть дана реакция
AB-\-CD = AC-\-BD. (12.70)
Для прироста изобарно-изотермического потенциала мы имеем:
Аф° = ф^ + ф^_ф^_ф^. (12.71)
Это выражение не изменится, если прибавить и вычесть зна-
чения изобарно-изотермических потенциалов элементов в их
стандартных состояниях, т. е. представить АФ° в виде
ДФ° = [Ф°ло - (Ф^+ ФЬ)] -|~ [ф’е - (Ф^ + Фр)] -
- [фдв - (фд + Фв)1 - [Фст - (Фо + Фр)]. (12.72)
Каждое выражение, стоящее в квадратных скобках, озна-
чает прирост изобарно-изотермического потенциала данного
*) См. А. Введенский [10], В. Коробов и А. Фрост [33],
см. также [71, 72]. Большая работа по вычислению углеводо-
родов была проведена В. М. Татевским [59], выполнившим об-
стоятельное изучение химического строения углеводородов и за-
кономерностей в их физико-химических свойствах. Методы вычисле-
ния ДФ«, констант равновесия реакции образования и других
величин были разработаны, как это указывалось выше, П. Г. М а с-
ловым [50], получившим обширный цифровой материал для многих
органических соединений. См. также справочник Россини
и др. [93].
346
РАСЧЕТ ХИМИЧЕСКИХ РАВНОВЕСИЙ
[ГЛ. XII
Таблица 43
Прирост изобарно-изотермического потенциала ДФ^ для
реакции образования
Вещество 298,16° К 400° К 500° К 600° к
Метан —12,140 —10,048 — 7,481 — 5,49
Этан — 7,860 — 3,447 + 1,168 + 5,97
Пропан — 5,614 + 1,191 + 8,230 + 15,50
Бутан-и — 3,754 + 5,435 +14,868 + 24,59
Этилен +16,282 4- 17,675 + 19,245 + 20,918
Пропилен .... + 14,990 + 18,610 + 22,450 + 26,46
Ацетилен .... + 50,000 + 48,577 + 47,196 + 45,835
Бензол + 30,989 + 35,008 + 39,242 + 43,663
Толуол + 29,228 + 35,390 + 41,811 + 48,477
^Вещество 700° К 800° К 900° К 1000°К
Метан — 3,05 — 0,55 + 2,01 + 4,61
Этан +10,90 + 15,92 + 21,00 + 26,13
Пропан + 22,93 + 30,45 + 38,05 + 45,68
Бутан-п + 34,50 + 44,50 + 54,59 + 64,71
Этилен + 22,676 + 24,490 + 26,354 + 28,249
Пропилен .... 4- 30,59 + 34,81 + 39,10 + 43,43
Ацетилен .... + 44,498 + 43,178 + 41,882 + 40,604
Бензол + 48,211 + 52,838 + 57,537 + 62,270
Толуол + 55,306 + 62,236 + 69,255 + 76,320
соединения из его элементов при стандартных условиях
ФдР------------------(Фр -|- Фр) = №fBD,
Фда — (Фд + Фс) = (12.73)
и т. д.
Таким образом,
ДФ° = ДФ^рр ДФ^дс — ДФ/дв — АФ/сл • (12.74)
Найденное правило вычисления ДФ° легко обобщить на слу-
чай реакции с числами молекул реагирующих веществ, от-
§ 8] «КОМБИНИРОВАННЫЕ ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ» 347
личными от единицы. В этом случае значения Дф£ нужно
брать с соответствующими коэффициентами.
Так, для реакции
ЗС2Н2 (г) —> С6Н6 (г) (12.75)
мы будем иметь:
А Ф° = ДФ^н„ - 3АФ^.н, (12.76)
Рассмотрим в качестве примера вычисление константы
равновесия реакции
СН3СН2СН3#СН4 + С2Н4 (12.77)
при 600° К.
Мы получим (см. табл. 43):
АФ° = — RT In Кр = АФд;н4 + АФ^сан( — A$fCH3CH,CH3
или
Дфо — -5,494-20,918— 15,50 = —0,072,
откуда
Кр = 1,00.
В качестве второго примера рассмотрим реакцию
СН3СН3 = С2Н2 4- 2Н2. (12.78)
Величина АФ^ для водорода равняется нулю, так как моле-
кулярное состояние водорода Н2 принято за исходное стан-
дартное состояние, а поэтому все величины, входящие
в уравнение (12.65), будут равны нулю.
Мы получим:
ДФ° = ЛФд^н, 4-0 — АФд;н3СН3-
При 800° К на основании данных таблицы 43 будем
иметь:
Дф° — 43,18— 10,90 = 32,28 кал!моль.
§ 8. Применение «комбинированных термодинамических
функций»
При расчете химических реакций также применяются так назы-
ваемые «комбинированные термодинамические функции», которые
могут быть составлены с помощью значений /7° и Ф°, определен-
ных по молекулярным и спектроскопическим данным. Отнесем
начало отсчета функций № и Ф° не к состоянию соединения при
348
РАСЧЕТ ХИМИЧЕСКИХ РАВНОВЕСИЙ
[ГЛ. XII
7' = 0°К, а к состоянию элементов в их стандартных состояниях
при 0°К- При изменении точки отсчета этих термодинамических
функций мы должны прибавить к табличным значениям Ф°—И
Н°—Н” прирост этих функций в процессе синтеза при абсолют-
ном нуле данного соединения из элементов в их стандартных
состояниях. Этот прирост будет для обеих функций равен Д77°, т. е.
ДЯ0° = IH«Tj + тН°0Ы - аНпйА - ЬНп0В.
Мы получим:
//2= HO-rtf+Mtf,
(12.79)
(12.80)
(12.81)
Эти функции, получившие название «комбинированных термо-
динамических функций», нашли применение в ряде работ *).
Для элементов в их стандартном состоянии Д/7д равняется
нулю и
/7»(эл) = Н —77°, (12.82)
фО(эл) = Ф — Н”. (12.83)
При составлении таблиц комбинированных функций вместо функ-
ции, определяемой уравнением (12.81), обычно применяется вели-
Фк
чина----.
Мы получим:
Ф° /70° — Ф° ДТ/J
-у- = у-.
(12.84)
В таблице 44 приведены значения «комбинированных термодинами-
ческих функций» нескольких простых углеводородов.
Расчет равновесий с помощью этих функций производится ана-
логично способу, рассмотренному в § 3. В самом деле, из уравне-
ния (12.28) следует:
ДФ° ДФ" ^|/ Ф°ч
Я1пК7, =-----_ = ---(12.85)
/ фк\
где при суммировании величина I-----^-1 для продуктов реакции
берется со знаком плюс, а для исчезающих веществ — со знаком
минус. При этом необходимо учитывать коэффициенты, входящие
в уравнение реакции. *
*) См., например, Астон [203]; см. также [71], [251].
§ 8] «КОМБИНИРОВАННЫЕ ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ»
349
Таблица 44
«Комбинированные термодинамические функции» простых
углеводородов
т° к -Ф«/7- = 1 ® о ; £ 1 11 1 >° ДЯ® Т
метан этан пропан метан этан пропан
298,16 90,08 100,65 118,07 — 13,59 — 13,66 — 15,97
400 78,83 89,51 105,19 —12,66 — 12,23 —13,92
600 69,04 80,60 95,40 —10,44 - 8,51 — 8,56
800 65,19 77,92 93,09 — 7,67 — 3,77 — 1,71
1000 63,64 77,60 93,58 — 4,43 1,75 6,19
1500 63,50 80,45 98,84 5,14 17,94 29,16
примера рассмотрим вычисление при 1000° К ДФ°
В качестве
реакции
Мы имеем:
2СН4 (г) = С2Н0 (г) + Н2 (г).
Ф® Н" - Ф°
Комбинированная функция-------=-------f----для водорода Н2, сов-
падающая с обычным значением приведенного изобарно-изотерми-'
ческого потенциала (ДН® = 0), при 1000° К равна 32,1^кал!град моль.
Из данных таблицы 44 мы получим:
ДФ®
----------------уД = 77,60 + 32,74 — 2 • 63,64 = — 16,94,
откуда
ДФ° = ДФ° = 16940 кал)моль.
ГЛАВА XIII
РАСЧЕТ КОНСТАНТ РАВНОВЕСИЯ РЕАКЦИЙ
ИЗОТОПНОГО ОБМЕНА
§ 1. Введение
Среди химических реакций особое место занимают реак-
ции изотопного обмена, находящие в настоящее время боль-
шое практическое применение (см. [6, 77, 78]).
Примерами таких реакций являются:
H2O + D2-^D2O + H2,
2СО16+ СО28# 2СО18+ СОз6,
D2O + T2O^±2DTO
(13-1)
(13.2)
(13.3)
и многие другие.
В настоящей главе мы рассмотрим расчет констант равно-
весия подобного типа реакций.
§ 2. Вычисление констант равновесия реакции
изотопного обмена А2-\- В.2^2АВ
Рассмотрим сначала вычисление констант равновесия реак-
ций с участием двухатомных изотопных молекул. Пусть дана
реакция вида
А2 + В2^2АВ, (13.4)
где А и В — символы двух изотопов одного элемента.
Примерами таких реакций являются:
и
H2 + D2;j>2HD
11б + С1Г^2СГбСГ7
(13.5)
(13.6)
§ 2] КОЙСТАЙФЫ ЙАВЙОВЁСЙЯ РЁАкЦЙЙ ЙЗбТ'ОЙЙО^б 6ЁЙЕЙА 351
Реакция типа (13.4) не охватывает всех возможных случаев
реакций двухатомных молекул с участием изотопов. Так,
реакция
H2+2DJ^> D2-|-2HJ (13.7)
не является частным случаем процесса (13.4), однако метод
его расчета легко может быть обобщен на случай этой и дру-
гих реакций.
Для константы равновесия реакции типа (13.4) мы имеем
(см. формулу (12.17)):
х/2 Д®.э 2
„ _ "АВ V АВ _ ~кт ЧаВ
N “ XaNB1 ~ Qa2Qb2 “ е Ча2Чв2 '
Прирост нулевой энергии Де0 будет:
Де0 = 2е0 дв — ео а2 — ео В2-
(13.8)
(13.9)
Разность нулевых энергий для изотопических молекул,
имеющих одинаковую энергию диссоциации, сведется к раз-
ности нулевых энергий колебаний у.
Мы получим:
д®0=2 4 ^ав—4 —4 =
2 Ь^ав ^а, '‘в)'
(13.10)
Будем предполагать, что температура, для которой про-
изводится расчет равновесия, не является слишком низкой.
Тогда (см. § 3 главы II и главу V)
Ч QnQi == СпСвр ' Сколеб • QsjQh. с. = QnQBpQKOje6po®. (13.11)
Следовательно,
(2e0A£-s0 A2-s0 В.? п2
к кт . АВ АВ у
N QnA2QuB2Q»VA2QvB*
Околеб АВ Р" АВ аАВ . q.
/\ 75-----75------------------. (13.12)
'«колеб Да'*колеб В2 Ро АаРоВа аА2аВ2
Применяя выражение (2.60) для сумм по состояниям по-
ступательного движения Qn, получим:
Qu АВ __ (Л^АвУ Мав _ (тА + тв)3 ,. о .
QuaQuB ~~ М^в ~ ^Амв ~ 1 '
Д Д -Dj zig Лд .Од ' А' ' JJ'
352 КОНСТАНТЫ РАВНОВЕСИЯ РЕАКЦИЙ ИЗОТОПНОГО ОБМЕНА (ГЛ. XIII
Отношение сумм по состояниям для вращательных дви-
жений, как это следует из формулы (5.36), примет вид
2 > (—У
QbP АВ _ IАВ . \°АВ/ !АВаА°В2 о . .
Овр А,^вр Д Лг/д Zj_W_L\ IaJb?AB
\zaJ \sbJ
Числа симметрии молекул А2, В2 и АВ будут соответ-
ственно 2, 2 и 1. Мы получим:
ФарАВ _ I АВ л
<?вРЛд~ <7д ‘ (13.15)
Для колебательных состояний имеем:
Оволеб АВ
Qколеб А2^колеб Д
1_____\ /____1_____'
_e-h'lA^T)
(1_г-^АВ/^)2
(13.16)
При низких температурах это выражение близко к еди-
нице, так как h'>'^>kT.
Наоборот, при достаточно высоких температурах, когда
h't<s^kT, выражение для QK0.TC6 принимает классическое зна-
чение kl'lh'i.
Таким образом, при достаточно высоких температурах
имеем:
колеб АВ А^В*
^колеб Д^колеб Д * АВ
(13.17)
Электронные состояния изотопических молекул А2, В.2
и АВ можно считать идентичными. Мы получим, что мно-
житель рз лд/р0 А Ро в будет равен единице. Наконец, для
2
спиновых множителей ------- также цолучим единицу (см. §6
главы XII).
§ 2] КОНСТАНТЫ РАВНОВЕСИЯ РЕАКЦИИ ИЗОТОПНОГО ОБМЕНА 353
Подставляя найденные значения множителей в форму-
лу (13.12), будем иметь:
M'/Mb I. IR
(l g-^r)(l-g-^r'
(13 18)
Для частных случаев при
чим соответственно
М-ав
Кя=4-^:
KN = 4 • -
1
АВ
АВ
Лм полу-
• е кТ,
(13.19)
р кТ
Лв
(13.20)
-^2
Если допустить, что силы, действующие в изотопических
молекулах, практически не изменяются с изменением масс
молекул, то можно выразить моменты инерции и частоты
двух изотопических молекул через момент инерции и частоту
колебаний одной из них. Действительно, мы можем к каждой
из молекул применить формулы (4.22) и (4.12)
2к V [л ’
/ =
(13.21)
(13.22)
где у. — приведенная масса молекулы (см. формулу (4.11))
и г — расстояние между ядрами.
На основании формулы (4.11) получим:
_тА
2 ’
__тв
Нв3— 2 >
_ тлтв
^АВ тА + т.в*
(13.23)
Следовательно,
ла
'‘в,
АВ
= . тАтв
~ 2 ‘ 2 ‘ +
(13.24)
(”^В\-'/2 . ( тАтВ
\ 2 ) \ 2 ) • \тА + тв
\ - ’/2
) . (13.25)
23 Зак. 835. И. Н. Годнее
354 константы Равновесия Реакций изотопного Обмена [гл. xhi
Мы будем иметь:
, , Мяв
'А> - 1ав 2тв
1вг— АВ
тл+тв
2тА
_ ( Ъпв \</г
\тА + тв) ^АВ’
— ( 2тА \1/г
— \тА + тв) ^-В-
(13.26)
(13.27)
(13.28)
(13.29)
Разность нулевых энергий Де0 теперь может быть найдена
по одной частоте и значению масс молекул. Подставляя зна-
чения частот из (13.28) и (13.29) в формулу (13.10), найдем:
Део-2[_2^в Ua+'bJ + U ^АВ.
= h'AB
/ 2 т^ + гп^ j
2 (тА + mB)'/2J
(13.30)
Если теперь в (13.19) и (13.20) подставить значения мо-
ментов инерции и частот, определяемых формулами (13.26) —
(13.29), и заменить отношение молекулярных весов отноше-
нием масс, то получим:
Kn = ‘2- ' -г^е кТ (kT<g-hy) (13.31)
и
KN = 4-e ьт (kT^h'i). (13.31а)
Если Ле0 незначительно, как это имеет место, например, при
реакции
C132b+C1F^2C13bC131,
при средних и высоких температурах Kn будет близко к 4.
К этому же заключению можно придти и непосредственно,
записав закон действия масс в виде (13.8) и подставив при-
ближенные значения сумм по состояниям. Действительно, при-
нимая во внимание числа симметрии, доы имеем:
Qa^Qb,^^. (13.32)
§ 3] КОНСТАНТА РАВНОВЕСИЯ ТИПИЧНОЙ ОБМЕННОЙ РЕАКЦИЙ 355
Подставляя эти значения в выражение (13.8), получим
при малом Де0
в Q а в
<13'32а)
2 ‘ 2
Для реакции
H2 + D2^2HD
при температурах 273 — 741° К, как показывают вычисления,
оказывается применимым уравнение (13.31) (мно = 3770 сл-1).
Значения константы Kn приведены в таблице 45, где они
сравниваются с опытными данными. Следует отметить хоро-
шее совпадение.
Таблица 45
т° к 273 298 383 543 670 741
^выч 3,18 3,26 3,46 3,67 3,77 3,81
^опытн 3,24 3,28 3,50 3,85 3,8 3,70
§ 3. Расчет константы равновесия типичной
обменной реакции
Перейдем теперь к рассмотрению более общего случая
обменных изотопных реакций. Типичную обменную реакцию
можно записать в виде
aCy-YbD^aC^bD^ (13.33)
где Cv С2, Dt и О2 —молекулы, содержащие один общий
элемент, причем индексы 1 и 2 указывают, что молекула
содержит соответственно только легкий или тяжелый изотоп.
Примером такой реакции будет:
О264-2Н2О18^Оа8 + 2Н2О16. (13.34)
В этом случае Cj = О26, Д2 = Н2О18, С2 = О28 и Dr = Н2О16.
Другим примером является реакция
С1О26+ 2Н2О18 -» СЮ28+ 2Н2О16. (13.35)
23*
356 КОНСТАНТЫ РАВНОВЕСИЯ РЕАКЦИЙ ИЗОТОПНОГО ОБМЕНА [ГЛ. XIII
На основании общей формулы (12.15) имеем:
QcQd
(13.36)
Из формулы (13.36) видно, что для вычисления константы
равновесия реакции типа (13.33) требуется вычислить отно-
шения сумм по состояниям изотопических молекул С.2 и Сг,
D2 и Dv Обозначим суммы по состояниям данной пары изо-
топических молекул через Qt и Q2.
Для двухатомных молекул на основании формул главы V
мы получим для средних и высоких температур
Ог _ -Ч^^п)2 «?вР)2 (Околеб>2
Ql (^п)1 (QBp)i (<?Колеб)1
«03—Вп
е кТ
Ср 4 /МЛ*1’ (I - e-hl‘/kT)
а2 (1 — е-ъ^кт~У
(13.37)
Здесь ох, а2, /х, /2, 7ИХ и Л12 означают соответственно
числа симметрии, моменты инерции и молекулярные веса изо-
топических двухатомных молекул Сх и С2.
Разность нулевых энергий двух изотопических молекул,
например
С.2 и Сх или D-2 и Dt,
будет определяться, как и в случае молекул, рассмотренных
в § 2, разностью нулевых энергий колебаний.
Мы получим для двухатомных молекул:
^Vp /1 о о оч
е02 — soi — • (13.38)
Подставляя эту разность в формулу (13.37), получим:
Ог _ £1 А (Мг\3/а e~h^kT
Qi сг/рХМр/ (l-e"W7cT)
e-htJzkT
(13.39)
§ 3] КОНСТАНТА РАВНОВЕСИЯ ТИПИЧНОЙ ОБМЕННОЙ РЕАКЦИИ 357
или, если ввести переменные
kT’
и
U'2 kT ’
Оз = Д Л /Л^\3/а е 2 (1-£"“)
Ot ViW (1—<Г“2)
е 2
(13.40)
(13.41)
(13.42)
Для многоатомных молекул, имеющих несколько частот
нормальных колебаний, мы получим, применяя формулы (2.30)
и (8.71),
Q2 _ „ Е ^е" — — кТ <?! д(л2в3с2),/а /мд'72тт (i-g ft^/fcT) .
Здесь Mlt, д2 xxi, . .. означают частоты первой изо-
топической молекулы, а ч21, м22, ..., \2i, ...—частоты вто-
рой. Для разности нулевых энергий, как и в предыдущем
случае, будем иметь:
_ . _____V, V
е02 е01 — Zj ~2 Zj ~2~ ’
г г
(13.44)
т. е. эта разность сводится к нулевой энергии колебаний.
Подставляя выражение (13.44) в формулу (13.43), по-
Оз = Д М2ВзС2у'2 ТТ / e-ftW2,cr х (1 _e~h\i/kT)
Qi а2 U151CJ XAfj/ -U- ( -Пч„,1кт) . -т» /2кТ •
г — g а ! (g и )
(13.45)
Вводя переменные uli и zz2i (приведенные частоты), опре-
деляемые формулами
= <13-46)
(13-47)
мы получим:
@2___gi \'/г/М2\/г-j-j-/ е \/1—г 1г\ л ч ДЯХ
358 КОНСТАНТЫ РАВНОВЕСИЯ РЕАКЦИЙ ИЗОТОПНОГО ОБМЕНА [ГЛ. XIH
Выражения (13.42) и (13.48) можно упростить, восполь-
зовавшись правилом произведений, о котором мы говорили
в § 12 главы VII. Это правило позволит исключить моменты
Qi
инерции и вычислить отношение — на основании значений
VI
частот.
Пусть п означает число атомов изотопного элемента,
входящих в каждую из молекул данной пары и обмениваю-
щихся при реакции (13.33)*).
Применяя правило произведений ко всем f частотам
многоатомных молекул 2 и 1 (см. формулу (7.114)), по-
лучим **):
уц^12 .. _ Г/т2\зп /МДЗ / Л^СЛ
^21^22 • • • ';2г • • • ;2f ' \^1/ \2Vf2/ \ А^В^С^ /
Из формулы (13.49) следует:
п
i
= №\п/2 Z^A3/7 ABiCi\1/2
\т1/ мИ2/ \ А2В2Р2 /
или
(тА3п/7Л12\% ( Л2В2С2 \’/2
^24 \«2/ \А11/ \ /
(13.50)
(13.51)
Вводя вместо и 42i соответственно uti и a2i, мы получим:
П«14/т_Л3п/7Л12\а/’/ Л2В2С2_
«24 \^2/ U1) \ А1В1С1 /
i
Из (13.52) следует:
// Л2В2С2 \’/г __ /т^п/2тт «24
\Л11/ \AjBiCi) \«11/ АА «и
(13.52)
(13.53)
Подставляя это выражение в формулу (13.48), мы будем
*) По условиям реакции (13.33) предполагается, что все эти
атомы обмениваются в реакции.
**) В нашем случае в изотопические молекулы входит только
один изотоп, а поэтому в правило произведений войдет множитель
§ 3] КОНСТАНТА РАВНОВЕСИЯ ТИПИЧНОЙ ОБМЕННОЙ РЕАКЦИИ 359
иметь:
Qa _ ^1 /{Иа\3”/2 тт и-це
Qi ^\mj JLL (j _е~иц)
uKg
-“i?2
(13.54)
(1 — g “«)
Для двухатомных изотопических молекул получим анало-
гичным образом
(тх\п/2 uie~u^2 . (1 — g~“Q . 1 „ р. с
Qi ’а \«1/ (1— е~и‘) '
Определив отношение с помощью формул (13.54) или
vi
(13.55), мы можем далее на основании соотношения (13.36)
легко найти /Су.
Теория приближенного вычисления констант равновесия
реакций изотопного обмена была разработана В. М. Татев-
ским [191], Бигелейзеном и Майер [206] и др. (ср. [190]).
Вычисление константы равновесия реакции (13.33) можно
<?2
упростить, если вместо ввести произведение
VI
Оз /^1\ЗП/2
Qi
(13.56)
Легко показать, что константа равновесия реакции (13.33)
может быть найдена по отношению величин f в соответ-
ственных степенях.
В самом деле, пусть в реакции (13.33) в молекулах Ct
и С2 содержится (обменивается) пх атомов, а в молекулах £)а
и п2 атомов данного изотопа. Общее число обмениваю-
щихся атомов в реакции (13.33) будет:
п1а = п2Ь. (13.57)
Так, для реакции (13.34), в которой имеет место обмен
изотопов О16 и О18, мы имеем nt = 2, а = 1, п2 = 1, b = 2.
На основании формулы (13.56), определяющей величину /,
имеем:
2^/«1\ЗП1/2
Q01 \т2/
и
(13.58)
(13,59)
360 КОНСТАНТЫ РАВНОВЕСИЯ РЕАКЦИЙ ИЗОТОПНОГО ОБМЕНА [ГЛ. XIII
У<* Q
Определяя из этих выражений ° и 77-1 и подставляя
Ус; Уд
их в формулу (13.36), получим:
к НЭТ" . "ПЭТ НЭТ” (13.60)
откуда в силу равенства (13.57) /г — КN — ръ • (13.61)
Нетрудно убедиться, что величина /, определяемая фор-
мулой (13.56), представляет отношение констант равновесия
образования изотопических молекул из атомов в газообраз-
ной фазе.
Действительно, пусть изотопические молекулы (например,
Су и С2, Dy и £)2) образуются из п атомов *) изотопного эле-
мента и г атомов другого элемента /?:
nAr-\- rR = Cv 1 /1^2 “I- ГR —- ^2’ J (13.62)
Константы равновесия этих реакций будут соответственно:
К Qi 1 Qa.Qr ’ K2 = g2 . QnA,QrB (13.63) (13.64)
Разделив формулу (13.64) на (13.63), мы получим:
к2_у2/ЭТге Ki QAQaJ ' (13.65)
Qa
Отношение , представляющее отношение сумм по со-
Уд,
стояниям одноатомных газов, будет равно отношению масс
*) Для молекул Cj И Сд п равно п\, для молекул Dy и £>з
ц равно
§ 4] ВСПОМОГАТЕЛЬНЫЕ ТАБЛИЦЫ ДЛЯ ВЫЧИСЛЕНИЯ / 361
изотопных элементов Аг и А.-> (см. формулы (3.6) и (3.28)):
<?да \т2/
(13.66)
Подставляя, это отношение в формулу (13.65), по-
лучим:
? = (13'67)
Al V1 \т2'
Из сравнения с формулой (13.56) следует:
(13.68)
Явное выражение для f мы получим на основании фор-
мулы (13.56). Вводя в нее величину , определяемую фор-
V1
мулой (13.54), будем иметь:
Ti l I u2ie 2 (1 —е 18)
°* 11 (l-^V) ’
(13.69)
§ 4. Вспомогательные таблицы для вычисления f
Бигелейзен и Майер [206] *) составили таблицу значений
функции G, по которым может быть вычислена функция /**).
Обозначим приведенные частоты колебаний в молекуле
с тяжелым изотопом, которые ранее были обозначены w2i,
через uit а частоты в молекуле с легким изотопом обозначим
(см. формулы (13.46) и (13.47)). Мы будем иметь:
«24 =
«1г = мг + Дмг-
(13.70)
(13.71)
Величина Az/j будет положительной, так как uti > u.2i.
Подставляя значения u2i и uti в формулу (13.69), по-
лучим:
(13.72)
*) См. также В. М. Татевский [191].
**) Таблицы для вычисления изменений термодинамических
функций (AS, А/7, АСр) при изотопном замещении см. [207],
362 КОНСТАНТЫ РАВНОВЕСИЯ РЕАКЦИЙ ИЗОТОПНОГО ОБМЕНА [ГЛ. XIII
Далее
г 1 е
(13.73)
или
1п/=1п!1+уГ^_1п(^+^1-1п—
J а3^^|_2 \
(13.74)
Если Д«4 мало, что имеет место для всех изотопов за
исключением изотопов водорода, то можно логарифмические
функции, входящие в формулу (13.74), разложить в ряд
по Ди1( ограничиваясь первым слагаемым. Мы получим:
|n(i±Ab) = |„(i+Ab)ai^i (,3.75)
= --£2^74»< = —4“<- <13-ге>
1 — е < е l— 1
Подставляя эти значения логарифмов в формулу (13.74),
будем иметь:
1п/=1п9А+£(±-1 + —1—W (13.77)
°2 ' 2 и» е <_1 /
Положим
° = |-|+is=T <13J8>
тогда
in/=1п^+д««- <1з-79>
Значения функции G, составленные Бигелёйзеном и Майер,
приведены в таблице 72 (см. таблицы в конце книги).
§ 5]
ПРИМЕРЫ
363
§ 5. Примеры
Ниже приводятся примеры расчета константы равновесия
с помощью таблиц Бигелёйзена и Майер.
Пример 1. Пусть требуется найти при 600° К кон-
станту равновесия реакции
СО™+ 2Н2О18 СО™ + 2Н2О™. (13.80)
Мы имеем на основании (13.36)
^со’8
^со™
^=/О~ (13-81)
или на основании формулы (13.61)
^ = ^2- (13.82)
Значения частот колебаний молекул СО™, СО26, Н2О16
и Н2О18 приведены в таблицах 46 и 47. В этих же табли-
цах выполнено вычисление величин ui и Дм^
В последнем столбце таблиц 46 и 47 приведены значе-
ния Oj, найденные по таблицам Бигелейзена и Майер *).
Числа симметрии для всех молекул равны двум.
Таблица 46
СО™ СО™ Диг Gi для СО™
Ч{ СМ-1 и( + Диг см-1
1342 3,219 1266 3,037 0,182 0,22128
667 1,600 657 1,576 0,024 0,12649
667 1,600 657 1,576 0,024 0,12649
2355 5,650 2320 5,566 0,084 0,32435
*) При вычислениях с целью приближенного учета ангармонич-
ности использованы наблюдаемые основные частоты (а не нулевые
частоты). Они приведены в таблицах 46, 47 и 48.
364 КОНСТАНТЫ РАВНОВЕСИЯ РЕАКЦИЙ ИЗОТОПНОГО ОБМЕНА [ГЛ. XIII
Таблица 47
H30te Н2О>8 Gt для H3Ot8
ел/-1 и, + \ см~1 “г
3650 8,756 3642 8,737 0,019 0,38574
1595 3,826 1590 3,814 0,012 0,26018
3756 9,011 3740 8,972 0,039 0,38864
Применяя формулу (13.79) и данные таблицы 46, по-
лучим:
/' = 1,076.
Аналогично на основании (13.79) и данных таблицы 47
/"2 = 1,053.
Подставляя /' и /"2 в формулу (13.82), имеем:
Kn = 1,023.
Пример 2. В качестве второго примера рассмотрим рас-
чет константы равновесия при 500°К и 1000°К реакции
Na4+2N15O#N25+2NWO. (13.83)
Константа равновесия будет (см. формулу (13.36)):
Qn15
2
QN14
(13.84)
W№<0
Исходные данные и значения Д« и G для каждой пары
изотопных молекул приведены в таблице 48.
Вычисления, аналогичные вычислениям первого примера,
для f' и f"2 дают соответственно 1,0$ I и 1,062 для 500° К
и 1,026 и 1,019 для 1000° К.
§ 6] ОБЩИЙ СЛУЧАЙ. ПОПРАВКА НА АНГАРМОНИЧНОСТЬ
365
Таблица 48
Моле- Число симме- трии а У см~1 Т = 500° К Т = 1000° к
кула Ди G Ди G
N1/ 2 2 2332 ] 2254 j 0,224 0,34744 0,112 0,23211
1WO N15O 1 1 1877 ) 1844 ) 0,095 0,31668 0,047 0,19866
Из этих данных получаются значения констант
и
^=1,018 при 500° К
KN= 1.007 при 1000° К.
§ 6. Более общий случай.
Поправка на ангармоничность
В §§ 4 и 5 был рассмотрен расчет константы равновесия
реакции изотопного обмена в предположении, что изотопные
молекулы Сг и С2 и Dt и D2 содержат только один сорт изо-
топов. Легко видеть, что методы расчета, рассмотренные
в §§ 4 и 5, могут быть обобщены на случай содержания
нескольких изотопов в молекуле.
Пусть дана реакция
аСЫ) — аСbD, (13.85)
где С и С, D и D — изотопные молекулы. Будем предпола-
гать, что молекулы С и С, D и D содержат несколько изо-
топов.
Мы будем иметь:
(13.86)
366 КОНСТАНТЫ РАВНОВЕСИЯ РЕАКЦИЙ ИЗОТОПНОГО ОБМЕНА [ГЛ. ХП1
Применение правила произведения для этого более об-
щего случая приведет к выражению
«fc Q/9 .
Ог _ I I /w2fc\ тI u2ie (1 — g “) (13.87)
Qi °2 11 wJ 11 (1—e~u2i) ulie~Ulil3 '
где пк означает общее число атомов данного изотопного
элемента, содержащихся в молекуле.
Обобщая формулу (13.56), получим:
<13-88)
к
В частном случае изотопов одного сорта произведение
(т./Д - 1тЛп .
обратится в и мы получим опять фор-
мулу (13.56). В рассматриваемом более общем случае для
константы равновесия получается:
f/a \
KN = f-b. (13.89)
При точных расчетах необходимо ввести поправки на
ангармонические члены в колебательной энергии и другие
поправки. Методы вычисления суммы по состояниям для этого
случая были рассмотрены в главе V. Расчет таких реакций
можно выполнить с помощью общих методов (см. §§ 2 и
3 главы XID. Следует заметить, что в огромном боль-
шинстве случаев такими поправками можно пренебречь*).
Исключение представляют реакции обмена изотопа водорода.
§ 7. Влияние эффекта изотопии при расчете
химических реакций
Рассмотрим теперь влияние эффекта изотопии на значе-
ния констант равновесия химических реакций. Эффект изо-
топии был обсужден нами в § 6 главы III и § 11 главы V.
Мы указывали, что эффект изотопии компенсируется при
расчете обычных химических реакций и его можно не при-
нимать во внимание в подавляющем большинстве случаев.
*) Результаты по расчетам реакций изотопного обмена см.
сборник [77], где есть сводка литературы.
§ 7] ЭФФЕКТ ИЗОТОПИИ ПИИ РАСЧЁТЕ ХИМИЧЕСКИХ РЕАКЦИЙ 367
Покажем это на примере реакций с двухатомными мо-
лекулами.
Пусть элемент А Имеет два изотопа: А' и Л". Такой
элемент будет иметь три сорта двухатомных молекул:
А', Л" и А'А". Пусть нужно выполнить расчет равновесия
реакции
Л2Н-Н2#2НЛ (13.90)
для средних и высоких температур.
В случае двух изотопов элемента Л мы будем иметь три
реакции:
Л2 + Н2#2НЛ', (13.91)
Л2 + Н2^±2НЛ", (13.92)
А'А" + Н2^НА' + НА". (13.93)
В качестве конкретного примера можно привести реакцию
с участием хлора, имеющего два изотопа: С135 и С137.
В этом случае будем иметь:
С12-|-Н2 —> 2НС1, (13.94)
С126 + Н2->2НС135, (13.95)
С1Г + Н2^2НС137, (13.96)
С1збС137+н2 нсг36+но37. (13.97)
Мы видим, что при реакциях (13.91) — (13.93) обра-
зуются две изотопные молекулы: НЛ' и НА". В газовой
фазе будут присутствовать молекулы Л', Л", А'А", НА'
и НА". Обозначим числа этих молекул соответственно через
N.', N.«, Nvr. и А/„.„, а суммы по состояниям —
АА А П’л ИЯ *
через Qa>, Qa», Qa,a„, QilA, и <2ИД„. Общее число моле-
кул Л2 будет:
,. (13.98)
Аа ^2 А> A'A" v '
Аналогичным образом:
Мы = АТцд' + Мы"-
(13.99)
368 КОНСТАНТЫ РАВНОВЕСИЯ РЕАКЦИЙ ИЗОТОПНОГО ОБМЕНА [ГЛ. XIII
Применяя закон действия масс в форме (12.15) к реак-
циям (13.91) — (13.93), получим:
Сна' _ ^НА' (13.100)
> •
Сд'Сн2 МцМг,
Сна" _ nha« (13.101)
Qa'^ ~ *Vh2 ’
СнА'СнА" MlA'MiA" (13.102)
Са’А"Сн2 NA'A"Nh2
Найдем из этих выражений Л/нд' + Mia" = Mia, т. е.
общее число молекул НЛ. Для этого умножим последнее
равенство на два, определим из него произведение 2Mia' • Мд"
и сложим с значениями Mia' и Nha". найденными из ра-
венств (13.100) и (13.101). Мы получим:
М1А = (MlA' + Л^НА"Г =
<131М)
Н2 ' Л Л /
Если бы мы пренебрегли
нили бы закон действия масс
бы написать:
эффектом изотопии и приме-
к реакции (13.90), то могли
Сна Mia
(13.104)
<?а2Сн2
Здесь предполагается, что Qha и Qa2 вычислены для мо-
лекул со средним химическим молекулярным весом и обыч-
ными числами симметрии. Из выражения (13.104) следует:
9 Мтт Q и д
МнА = 7^-т?И-Л/Аа. (13.105)
*А3
Это выражение отличается от выражения (13.103), полу-
ченного с учетом существования изотопов. Однако легко
видеть, что если молекулы изотопа незначительно отличаются
друг от друга по своим свойствам, как это имеет место,
например, для хлора и других элементов (исключение соста-
§ 7] ЭФФЕКТ ИЗОТОПИИ ПРИ расчете химических реакций 369
вляет водород), то формула (13.103) в частном случае пере-
ходит в формулу (13.105).
Действительно, при сделанных выше предположениях
можно положить (см. формулу (13.32)):
Qha' ~ Qua" <?ид,
Qa" ~ QA2-
(13.106)
(13.107)
Для молекулы А'А", имеющей число симметрии, равное
единице, мы будем иметь:
Qa'a" — ^Qa2-
(13.108)
Подставляя эти значения в формулу (13.103), получим:
(13.109)
Отсюда (13.98): следует, если принять во внимание равенство v-T = • (13.110) <?H2Qa2 V
Это выражение совпадает с (13.104), написанным без учета
эффекта изотопии.
Аналогичный результат получится при рассмотрении
более сложных реакций.
Таким образом, мы видим, что при расчетах обычных
химических реакций при средних и высоких температурах
мы можем не принимать во внимание эффекта изотопии.
При составлении таблиц термодинамических функций
поэтому опускаются слагаемые, обусловленные эффектом
изотопии, Д5,.м и др. (см. § 6 главы 111 и §11 главы V).
24 Зак. 835. И. Н. Годнее
ГЛАВА XIV
ТАБЛИЦЫ
§ 1. Общие замечания
В заключение приведем ряд таблиц, сказывающихся по-
лезными при вычислении термодинамических функций. Такими
таблицами являются: таблица физических постоянных, та-
блицы термодинамических функций гармонического осцил-
лятора, таблицы Гордона и Барнеса, таблицы Питцера, таб-
лицы Питцера и Гвинна, таблицы для расчета реакций изо-
топного обмена и таблица литературных источников значений
термодинамических функций.
§ 2. Таблица физических постоянных
Значения физических постоянных, применяемых в настоя-
щей монографии, приведены в таблице 49. Эти значения
основаны на новых данных Бэрджа [102]. Они отклоняются
очень незначительно от старых значений Бэрджа, применен-
ных Герцбергом [20] и др., и новых значений 1952 г. [216],
опубликованных в 1953 г. Последние приведены в третьем
столбце таблицы 49.
§ 3. Таблицы термодинамических функций
гармонического осциллятора
В таблице 50 приведены слагаемые теплоемкости С, при-
веденной энергии и приведенной свободной энергии
с обратным знаком — -—для колебательного движения
гармонического осциллятора в функции от приведенной ча-
стоты ш/Т, выраженной в см-1 град*1. Значения функций
даны в кал/град • моль. Величина энтропии может быть най-
§ 5] ПЕРВЫЕ ТАБЛИЦЫ ПИТЦЕРА 371
дена по формуле
+ (14.1)
Для вычислений термодинамических функций гармониче-
ского осциллятора может быть использована также таблица 51
(см. ниже).
§ 4. Таблицы для вычислений по способу
Гордона и Барнеса (табл. 51—61)*)
В первой из этих таблиц (см. таблицу 51) приведены:
логарифм суммы по колебательным состояниям, SJR и C,.JR
для гармонического осциллятора в функции от параметра
то — hc^JkT. Таблица 52 содержит поправки к сумме по
колебательным состояниям в зависимости от то и х.
Слагаемые г0/йТ в обозначении величин, содержащихся
в таблицах 51 и 52, вызваны тем, что при вычислении Qv
энергия отсчитывается от минимума потенциальной энергии.
Таблица 53 служит для вычисления поправки к энтро-
пии SJR, а таблица- 54 — поправки к теплоемкости Cv/R
в зависимости от то и х. Таблицы 55, 56, 57, 59, 60, 61
содержат v, st, ct> ц2, s2 и с2 как функции то и х. Опре-
деление этих величин см. в § 14 главы V. Таблица 58 со-
держит v, s( и ct для то > 4 при х = 0. Пример примене-
ния таблиц 51—61 см. § 14 главы V.
§ 5. Первые таблицы Питцера (табл. 62—65)
В таблицах 62 и 63 приведены значения З’св— S3, в и
р ____р пч
33—— как функции V0/RT и 10-36у-------------(см. § 4
' 7п|'ив '/о
главы X). Здесь Уо означает высоту потенциального барьера,
Т—абсолютную температуру, R — универсальную газовую
постоянную, /П[)ИВ— приведенный момент инерции, выражен-
ный в г • см2, и п—число минимумов или максимумов кри-
вой барьера.
В таблицах 64 и 65 приведены НЗ Ъ1Т и Сэ. в. Примеры
применения этих таблиц см. в §§ 5, 7, 8 главы X.
*) Дополнительные таблицы для значений то от 0,2 до 0,6
см. И. В. С м и р н о в а и А. В. Фрост [171].
24*
372
ТАБЛИЦЫ
|гл. Xtv
§ 6. Новые таблицы Питцера и Гвинна
Таблицы 66, 67, 68, 69, 70, 71 служат для более точ-
ного вычисления термодинамических функций волчка с за-
торможенным вращением (новые таблицы Питцера и Гвинна).
Параметрами этих таблиц являются V0/RT и 1/QC1), где
Vo — высота барьера, Т — абсолютная температура, /? —
универсальная газовая постоянная и Qcn— сумма по состоя-
ниям волчка со свободным вращением. Величина QC1) дается
формулой (10.24) или (10.113).
В таблице 66 даны значения приведенной свободной энер-
гии с обратным знаком —F3. В/Т; таблица 67 содержит
величины 3’в у.—--; таблица 68 дает значения 5'3. в; та-
блица 69 содержит разность 50В—Sa в; таблицы 70 и 71
И, В
служат соответственно для вычисления и С3. в. Пример
применения таблиц см. в § 10 главы X.
(14.2)
§ 7. Таблица Бигелейзена и Майер
В таблице 72, составленной Бигелейзеном и Майер, при-
ведены значения функции
с _ 1 1 , 1
2 и ' еи — 1 ’
которая применяется при расчете констант равновесия реак-
ций изотопного обмена (см. §§ 4—6 главы XIII).
Параметром таблицы является величина
h'<
U ~ kT'
вычисленная для молекулы с тяжелым изотопом. В таблице 72
приведены также значения &G/&U.
(14.3)
§ 8. Таблица литературных источников значений
термодинамических функций
Таблица 73 служит для отыскания литературных источ-
ников, в которых можно найти численные значения термо-
динамических функций. В первой графе таблицы 73 указан
тип соединения, а во второй — ссылки на литературу, где
можно найти табличные значения термодинамических функ-
ций, или ссылки на оригинальные работы.
Таблица 49 к
Значения физических постоянных
Постоянная Значения постоянных, применен- ных в книге Новые значения 1952 г.
Заряд электрона еп . . . . 4,8025-Ю-10 CQSE 4,8029 -ПГ10 CGSE
Масса электрона т ... . 9,1066- 10-38 г 9,1085- 1034 г
Постсушная Планка h . . . 6,624 • 10-37 эрг сек 6,625 -К)'27 эрг-сек
Скорость света с 7/16 массы атома кисло- рода М1 2,99776 10tu CMjceK 1,6599- 10г 2,99793 • 101“ см!сек
Число Авогадро Nn . . . . ^„(хям. шв) = 6,0228-1023 (г- моль)'1 N (физ. шк) =6,0247-1023(2- мольГ1
Постоянная Больцмана k . Газовая постоянная R (па моль) 1,3804 - 10“10 эрг'град ( 1,9865 кал)град • моль 1 8,3144 • 107 эрг'град • моль 1,3804 • 10 1е эрг!град 8,3166 • 107 эрг':град • моль
ТАБЛИЦЫ 373
Таблица 50
Таблица для вычисления термодинамических функций гармонического осциллятора
Ш/Т" Е — Е-. С Е — Еп (Е-Еп)
С Т Т Т Т
0,10 1,9834 1,8473 3,9942 0,65 1,8481 1,2007 0,9905
0,11 1,9827 1,8338 3,8186 0,66 1,8441 1,1908 0,9722
0,12 1,9819 1,8203 3,6596 0,67 1,8398 1,1810 0,9545
0,13 1,9810 1,8068 3,5143 0,68 1,8357 1,1711 0,9370
0,14 1,9801 1,7935 3,3807 0,69 1,8315 1,1614 0,9200
0,15 1,9791 1,7801 3,2572 0,70 1,8272 1,1517 0,9033
0,16 1,9780 1,7670 3,1428 0,71 1,8227 1,1420 0,8870
0,17 1,9768 1,7538 3,0361 0,72 1,8184 1,1325 0,8713
0,18 1,9756 1,7407 2,9362 0,73 1,8140 1,1230 0,8557
0,19 1,9744 1,7276 2,8424 0,74 1,8093 1,1135 0,8405
0,20 1,9731 1,7147 2,7542 0,75 1,8047 1,1041 0,8256
0,21 1,9717 1,7018 2,6710 0,76 1,8002 1,0948 0,8110
0,22 1,9703 1,6890 2,5920 0,77 1,7955 1,0856 0,7968
0,23 1,9687 1,6763 2,5142 0,78 1,7908 1,0764 0,7828
0,24 1,9671 1,6636 2,4662 0,79 1,7863 1,0674 0,7692
0,25 1,9655 1,6510 2,3786 0,80 1,7813 1,0582 0,7558
0,26 1,9638 1,6384 2,3140 0,81 1,7765 1,0492 0,7437
0,27 1,9620 1,6260 2,2525 0,82 1,7716 1,0403 0,7299
0,28 1,9601 1,6135 2,1935 0,83 1,7667 1,0314 0,7174
0,29 1,9583 1,6012 2,1372 0,84 1,7618 1,0226 0,7052
0,30 1,9563 1,5889 2,0831 0,85 1,7568 1,0138 0,6931
0,31 1,9542 1,5767 2,0311 0,86 1,7517 1,0050 0,6812
0,32 1,9521 1,5645 1,9813 0,87 1,7466 0,9964 0,6697
0,33 1,9500 1,5525 1,9333 0,88 1,7415 0,9878 0,6583
0,34 1,9178 1 \ 1,5101 1 1,8872 0,89 1,7361 0,9793 / 0,6473
374 ТАБЛИЦЫ [гл. XIV
0,35 0,36 0,37 0,38 0,39 1,9454 1,9430 1,9406 1,9381 1,9356 1,5285 1,5167 1,5048 1,4931 1,4814 1,8427 1,7998 1,7584 1,7185 1,6799 0,90 0,91 0,92 0,93 0,94 1,7312 1,7259 1,7206 1,7154 1,7099 0,9708 0,9620 0,9541 0,9458 0,9377 0,6363 0,6256 0,6151 0,6049 0,5948
0,40 1,9330 1,4698 1,6425 0,95 1,7045 0,9295 0,5848
0,41 1,9303 1,4583 1,6063 0,96 1,6991 0,9212 0,5751
0,42 1,9275 1,4468 1,5713 0,97 1,6935 0,9132 0,5657
0,43 1,9247 1,4354 1,5374 0,98 1,6882 0,9051 0,5563
0,44 1,9218 1,4240 1,5045 0,99 1,6826 0,8971 0,5471
0,45 1,9188 1,4128 1,4726 1,00 1,6770 0,8893 0,5382
0,46 1,9159 1,4016 1,4416 1,01 1,6714 0,8815 0,5294
0,47 1,9128 1,3904 1,4117 1,02 1,6658 0,8737 0,5208
0,48 1,9097 1,3793 1,3826 1,03 1,6601 0,8659 0,5123
0,49 1,9066 1,3682 1,3543 1,04 1,6544 0,8582 0,5040
0,50 1,9033 1,3573 1,3267 1,05 1,6487 0,8507 0,4959
0,51 1,9001 1,3464 1,3001 1,06 1,6429 0,8430 0,4877
0,52 1,8966 1,3354 1,2741 1,07 1,6371 0,8355 0,4800
0,53 1,8933 1,3248 1,2488 1,08 1,6312 0,8281 0,4722
0,54 1,8898 1,3140 1,2242 1,09 1,6254 0,8207 0,4647
0,55 1,8863 1,3034 1,2001 1,10 1,6196 0,8133 0,4572
0,56 1,8827 1,2929 1,1766 1,11 1,6137 0,8060 0,4499
0,57 1,8791 1,2823 1,1539 1,12 1,6077 0,7988 0,4426
0,58 1,8754 1,2719 1,1316 1,13 1,6017 0,7916 0,4357
0,59 1,8718 1,2616 1,1099 1,14 1,5957 0,7845 0,4287
0,6? 1,8680 1,2513 1,0887 1,15 1,5897 0,7774 0,4218
0,61 1,8641 1,2411 1,0681 1,16 1,5837 0,7703 0,4151
0,62 1,8602 1,2308 1,0481 1,17 1,5776 0,7634 0,4086
0,63 1,8562 1,2207 1,0284 1,18 1,5715 0,7564 0,4021
0,64 1,8522 1,2107 1,0093 1,19 1,5653 0,7495 0,3957
К § 3] ТАБЛИЦЫ 375
Продолжение
ш/Т С Е-Еа (г — £<,) Т ш/Г С Е — Еп (Е-Еу) Г
Т Т
1,20 1,5592 0,7427 0,3894 1,75 1,2018 0,4391 0,1672
1,21 1,5531 0,7359 0,3832 1,76 1,1952 0,4348 0,1647
1,22 1,5468 0,7292 0,3773 1,77 1,1887 0,4304 0,1622
1,23 1,5406 0,7225 0,3713 1,78 1,1822 0,4262 0,1599
1,24 1,5343 0,7159 0,3656 1,79 1,1756 0,4219 0,1575
1,25 1,5281 0,7093 0,3598 1,80 1,1690 0,4177 0,1551
1,96 1,5217 0,7027 0,3542 1,81 1,1625 0,4135 0,1528
1,27 1,5156 0,6963 0,3486 1.82 1,1559 0,4096 0,1505
1,28 1,5091 0,6898 0,3432 1,83 1,1493 0,4053 0,1484
1,29 1,5030 0,6834 0,3379 1,84 1,1428 0,4011 0,1461
1,30 1,4966 0,6771 0,3326 1,85 1,1363 0,3972 0,1440
1,31 1,4902 0,6708 0,3275 1,86 1,1298 0,3932 0,1418
1> 1,4839 0,6646 0,3225 1,87 1,1233 0,3893 0,1397
1,33 1,4774 0,6585 0,3175 1,88 1,1167 0,3855 0,1377
1,34 1,4710 0,6523 0,3126 1,89 1,1102 0,3816 0,1356
1,35 1,4646 0,6462 0,3078 1,90 1,1038 0,3777 0,1336
1,36 1,4583 0,6402 0,3030 1,91 1,0973 0,3739 0,1316
1,37 1,4520 0,6342 0,2983 1,92 1,0909 0,3701 0,1297
1,38 Г,4455 0,6283 0,2937 1,93 1,0845 0,3665 0 1278
1,39 1,4390 0,6223 0,2893 1,94 1,0780 0,3627 0,1259
1,40 1,4324 0,6164 0,2848 1,95 1,0716 0,3591 0,1240
1,41 1,4259 0,6107 0,2804 1,96 1,0653 0,3554 0,1222
1,42 1,4194 0,6049 0,2761 1,97 1,0589 0,3518 0,1205
1,13 1,41'29 0,5998 0,2719 1,98 1,0525 0,3482 0,1187
1,44 1,4065 0,5935 0,2677 1,99 1,0461 0,3446 1 0,1169
376 ТАБЛИЦЫ [ГЛ. XIV
1,46 1,3934 0,5823 0,2595
1,47 1,3868 0,5768 0,2556
1,48 1,3802 0,5713 0,2518
1,49 1,3736 0,5658 0,2471
1,50 1,3671 0,5604 0,2441
1,51 1,3605 0,5550 0,2404
1,52 1,3538 0,5493 0,2367
1,53 1,3473 0,5445 0,2332
1,54 1,3406 0,5392 0,2297
1,55 1,3340 0,5340 0,2262
1,56 1,3274 0,5288 0,2227
1,57 1,3208 0,5238 0,2193
1,58 1,3143 0,5187 0,2161
1,59 1,3077 0,5138 0,2129
1,60 1,3010 0,5088 0,2097
1,61 1,2943 0,5039 0,2065
1,62 1,2878 0,4988 0,2034
1,63 1,2812 0,4942 0,2004
1,64 1,2746 0,4893 0,1974
1,65 1,2680 0,4847 0,1944
1,66 1,2613 0,4799 0,1914
1,67 1,2547 0,4753 0,1885
1,68 1,2481 0,4706 0,1858
1,69 1,2415 0,4659 0,1830
1,70 1,2349 0,4613 0,1802
1,71 1,2283 0,4568 0,1775
1,72 1,2217 0,4523 0,1749
1,73 1,2151 0,4478 0,1723
1,74 1,2086 0,4435 0,1698
Ж" 2,02 2,04 2,06 2,08 ’ПЖ” 1,0272 1,0146 1,0020 0,9897 0,3342 0,3275 0,3208 0,3142
2,10 0,9772 0,3077
2,12 0,9649 0,3014.
2,14 0,9526 0,2952
2,16 0,9405 0,2891
2,18 0,9284 0,2832
2,20 0,9161 0,2773
2,22 0,9041 0,2716
2,24 0,8921 0,2659
2,26 0,8799 0,2605
2,28 0,8682 0,2551
2,30 0,8570 0,2497
2,32 0,8455 0,2445
2,34 0,8339 0,2394
2,36 0,8225 0,2344
2,38 0,8112 0,2295
2,40 0,8000 0,2246
2,42 0,7885 0,2198
2,44 0,7778 0,2151
2,46 0,7669 0,2106
2,48 0,7560 0,2061
2,50 0,7453 0,2017
2,52 0,7346 0,1974
2,54 0,7240 0,1932
2,56 0,7135 0,1891
2,58 0,7031 0,1850
o.f Y 52
0,1118
0J023
0,0992
0,09640
0,09362
0,09091
0,08828
0,08576
0,08326
0,08084
0,07850
0,07622
0,07402
0,07189
0,06982
0,06780
0,06585
0,06395
0,06213
0,06032
0,05859
0,05690
0,05526
0,05370
0,05217
6,05065
0,04919
ТАБЛИЦЫ 377
Продолжение
«/Г с £ —£о (/•'-£») о>/7" с £ — (Е-Еп) Т
Т Т Т
2,60 0,6928 0,1810 0,04778 5,00 0,0775 0,01074 0,00150
2,62 0,6826 0,1771 0,04640 5,10 0,0697 0,00948 0,001290
2,64 0,6725 0,1732 0,04507 5,20 0,0628 0,00836 0,001116
2,66 0,6625 0,1695 0,04379 5,30 0,0563 0 00740 0,000965
2,68 0,6527 0,1656 0,04253 5,40 0,0506 0,00652 0,000837
2,70 0,6429 0,1622 0,04131 5,50 0,0454 0,00575 0,000727
2,72 0,6332 0,1587 0,04014 5,60 0,0409 0,00507 0,000629
2,74 0,6236 0,1553 0,03901 5,70 0,0367 0,00447 0,000545
2,76 0,6140 0,1519 0,03788 5,80 0,0330 0,00393 0,000472
2,78 0,6046 0,1483 0,03679 5,90 0,0295 0,00347 0,000409
2,80 0,5953 0,1454 0,03572 6,00 0,0265 0,00305 0,000353
2,82 0,5862 0,1422 0,03471 6,10 0,0236 0,00269 0,000306
2,84 0,5771 0,1391 0,03371 6,20 0,0212 0,00236 0,000266
2,86 0,5680 0,1361 0,03275 6,30 0,0189 0,00208 0,000231
2,88 0,5591 0,1331 0,03181 6,40 0,0169 0,00183 0,000200
2,90 0,5502 0,1301 0,03089 6,50 0,0151 0,00161 0,000173
2,92 0,5417 0,1272 0,03003 6,60 0,0134 0,00142 0,000151
2,94 0,5331 0,1244 0,02917 6,70 0,0120 0,00125 0,000131
2,96 0,5246 0,1216 0,02834 6,80 0,0107 0,00110 0,000114
2,98 0,5163 0,1189 0,02752 6,90 0,00960 0,000962 0,0000993
3,00 0,5080 0,1162 0,02673 7,00 0,00852 0,000845 0,0000865
3,05 0,4876 0,1099 0,02486 7,10 0,00758 0,000742 0,0000750
3,10 0,4680 0,1038 0,02311 7,20 0,00674 0,000651 0,0000651
3.1 5 0,4189 0,0981 0,02150 7,30 0.00600 0,000571 0,0000565
3/20 \ 0,4305 \ 0,0927 0,02000 7,40 0,005.М 0,000502 у 0,0000491
378 таблицы [гл. XIV
3725 ' 0,4127 " Г 0,0875 0,61861 ’ 7,50 6,00474 0,000441 0,0000427
3,30 0,3956 0,0826 0,01731 7,60 0,00423 0,0003868 0,0000369
3,35 0,3787 0,0780 0,01608 7,70 0,00376 0,0003497 0,0000320
3,40 0,3627 0,0736 0,01498 7,80 0,00332 0,0002979 0,0000278
3,45 0,3471 0,0696 0,01393 7,90 0,00298 0,0002618 0,0000241
8,00 0,00265 0,0002292 0,0000209
3,50 0,3323 0,0656 0,01297
3,55 0,3177 0,0619 0,01207 8,10 0,00234 0,0002008 0,0000181
3,60 0,3038 0,0584 0,01124 8,20 0,00208 0,0001759 0,0000156
3,65 0,2903 0,0550 0,01045 8,30 0,00185 0,0001542 0,0000135
3,70 0,2775 0,0519 0,00972 8,40 0,00164 0,0001352 0,0000117
8,50 0,00145 0,0001187 0,0000101
3,75 0,2651 0,0489 0,00904
3,80 ’ 0,2532 0,0461 0,00842 8,60 0,00129 0,0001038 0,0000088
3,85 0,2417 0,0435 0,00783 8,70 0,00113 0,0000908 0,0000077
3,90 0,2307 0,0410 0,00729 8,80 0,00101 0,0000795 0,0000067
3,95 0,2201 0,0387 0,00678 8,90 0,00089 0,0000696 0,0000058
9,00 0,000792 0,0000610 0,0000050
4,00 0,2099 0,0364 0,00631
4,10 0,1907 0,0322 0,00547 9,10 0,000701 0,0000535 0,0000043
4,20 0,1732 0,0986 0,00473 9,20 0,000620 0,0000466 0,0000037
4,30 0,1571 0,0253 0,00409 9,30 0,000549 0,0000408 0,0000032
4,40 0,1424 0,0225 0,00354 9,40 0,000486 0,0000357 0,0000028
9,50 0,000431 0,0000312 0,0000024
4,50 0,1286 0,0200 0,00306
4,60 0,1166 0,0176 0,00265 9,60 0,000380 0,0000273 0,0000021
4,70 0,1054 0,0156 0,00230 9,70 0,000335 0,0000239 0,0000018
4,80 0,0952 0,0138 0,00199 9,80 0,000297 0,0000209 0,0000016
4,90 0,0859 0,0122 0,00173 9,90 0,000262 0,0000184 0,0000014
10,00 0,000232 0,0000161 0,0000012
X
с^э
со
ТАБЛИЦЫ
380
ТАБЛИЦЫ
[ГЛ. XIV
ТАБЛИЦЫ ДЛЯ ВЫЧИСЛЕНИЙ ПО СПОСОБУ ГОРДОНА
И БАРНЕСА (табл. 51—61)
Таблица 51
w = hcu>elkT, х = 0
(In Q„ + enlkT) S„IR Cv/R w (In Qv + eo/kT) Sv/R Cv/R
0,55 0,8603 1,6103 0,9752 2,60 0,0772 0,2858 0,5859
0,60 0,7959 1,5257 0,9705 2,70 0,0696 0,2641 0,5631
0,65 0,7382 1,4482 0,9655 2,80 0,0627 0,2440 0,5405
0,70 0,6863 1,3769 0,9602 2,90 0,0566 0,2255 0,5182
0,75 0,6394 1,3108 0,9544 3,00 0,0511 0,2083 0,4963
0,80 0,5966 1,2494 0,9483 3,10 0,0461 0,1923 0,4747
0,85 0,5576 1,1921 0,9419 3,20 0,0416 0,1776 0,4536
0,90 0,5218 1,1384 0,9351 3,30 0,0376 0,1640 0,4330
0,95 0,4890 1,0881 0,9281 3,40 0,0339 0,1513 0,4129
1,00 0,4587 1,0407 0,9207 3,50 0,0307 0,1396 0,3933
1,05 0,4307 0,9959 0,9130 3,60 0,0277 0,1288 0,3743
1,10 0,4048 0,9536 0,9050 3,70 0,0250 0,1188 0,3558
1,15 0,3807 0,9136 0,8967 3,80 0,0226 0,1096 0,3380
1,20 0,3584 0,8756 0,8882 3,90 0,0205 0,1010 0,3207
1,25 0,3376 0,8395 0,8794 4,00 0,0185 0,0931 0,3041
1,30 0,3182 0,8052 0,8703 4,20 0,0151 0,0791 0,2726
1,35 0,3001 0,7725 0,8610 4,40 0,0124 0,0670 0,2436
1,40 0,2832 0,7414 0,8515 4,60 0,0101 0,0568 0,2170
1,45 0,2673 0,7117 0,8418 4,80 0,0083 0,0481 0,1928
1,50 0,2525 0,6833 0,8319 5,00 0,0068 0,0407 0,1708
1,55 0,2386 0,6562 0,8217 5,20 0,0055 0,0344 0,1508
1,60 0,2255 0,6303 0,8114 5,40 0,0045 0,0290 0,1329
1,65 0,2132 0,6055 0,8010 5,60 0,0037 0,0245 0,1168
1,70 0,2017 0,5817 0,7904 5,80 0,0030 0,0207 0,1025
1,75 0,1909 0,5590 0,7796 6,00 0,0025 0,0174 0,0897
1,80 0,1807 0,5371 0,7687 6,40 0,0016 0,0123 0,0682
1,85 0,1711 0,5162 0,7577 6,80 0,0011 0,0087 0,0516
1,90 0,1620 0,4962 0,7466 7,20 0,0007 0,0061 0,0387
1,95 0,1535 0,4769 0,7354 7,60 0,0005 0,0043 0,0289
2,00 0,1454 0,4584 0,7241 8,00 0,0003 0,0030 0,0215
2,10 0,1306 0,4236 0,7013 8,40 0,0002 0,0021 0,0159
2,20 0,1174 0,3916 0,6783 8,80 0,0002 0,0015 0,0117
2,30 0,1056 0,3620 0,6552 9,20 0,0001 0,0010 0,0086
2,40 0,0951 0,3346 0,6320 9,60 0,0001 0,0007 0,0062
2,50 0,0857 0,3092 0,6089 10,00 " 0,0000 0,0005 0,0045
i
к § 4]
ТАБЛИЦЫ
381
Таблица 52
(In Qv + *nlkT\i>,iD — (In Qv + как функция щ» = Лс<ое/АГ и х
W х=0,005 0,010 0,015 0,020 0,025
0,6 0,0169 0,0358 0,0576 0,0837 0,1133
0,7 0,0143 0,0299 0,0474 0,0677 0,0913
0,8 0,0123 0,0255 0,0401 0,0566 0,0755
0,9 0,0107 0,0222 0,0347 0,0485 0,0640
1,0 0,0095 0,0196 0,0304 0,0422 0,0553
1,1 0,0084 0,0174 0,0269 0,0372 0,0485
1,2 0,0076 0,0156 0,0241 0,0332 0,0430
1,3 0,0069 0,0141 0,0217 0,0298 0,0385
1,4 0,0062 0,0127 0,0196 0,0269 0,0346
1,5 0,0057 0,0116 0,0178 0,0244 0,0314
1,6 0,0052 0,0106 0,0163 0,0222 0,0285
1,7 0,0048 0,0097 0,0149 0,0203 0,0260
1,8 0,0044 0,0089 0,0136 0,0186 0,0238
1,9 0,0040 0,0082 0,0125 0,0171 0,0219
2,0 0,0037 0,0075 0,0115 0,0157 0,0201
2,2 0,0031 0,0064 0,0098 0,0134 0,0171
2,4 0,0027 0,0055 0,0084 0,0114 0,0145
2,6 0,0023 0,0047 0,0072 0,0098 0,0124
2,8 0,0020 0,0040 0,0061 0,0084 0,0107
3,0 0,0017 0,0034 0,0053 0,0072 0,0092
3,2 0,0014 0,0030 0,0045 0,0062 0 0079
3,4 0,0012 0,0025 0,0039 0,0053 0,0068
3,6 0,0011 0,0022 0,0033 0,0045 0,0058
3,8 0,0009 0,0019 0,0028 0,0039 0,0050
4,0 0,0008 0,0016 0,0024 0,0033 0,0043
4,2 0,0007 0,0014 0,0021 0,0029 0,0037
4,4 0,0006 0,0012 0,0018 0,0024 0,0031
4,6 0,0005 0,0010 0,0015 0,0021 0,0027
4,8 0,0004 0,0009 0,0013 0,0018 0,0023
5,0 0,0004 0,0007 0,0011 0,0015 0,0020
5,2 0,0003 0,0006 0,0010 0,0013 0,0017
5,4 0,0003 0,0005 0,0008 0,0011 0,0014
5,6 0,0002 0,0004 0,0007 0,0009 0,0012
5,8 0,0002 0,0004 0,0006 0,0008 0,0010
6,0 0,0002 0,0003 0,0005 0,0007 0,0009
382
ТАБЛИЦЫ
|гл. XlV
Таблица 53
(Sv!R)WtX — (SvIR)w 0 как функция w = hv»eikT и х
ЦО х = 0,005 0,010 0,015 0,020 0,025
0,6 0,0357 0,0778 0,1317 0,2000 0,2695
0,7 0,0302 0,0649 0,1069 0,1598 0,2206
0,8 0,0263 0,0557 0,0899 0,1318 0,1822
0,9 0,0232 0,0488 0,0777 0,1124 0,1534
1,0 0,0207 0,0434 0,0685 0,0975 0,1318
1,1 0,0187 0,0390 0,0613 0,0863 0,1153
1,2 0,0171 0,0355 0,0554 0,0775 0,1026
1,3 0,0157 0,0325 0,0505 0,0703 0,0923
1,4 0,0145 0,0299 0,0464 0,0643 0,0840
1,5 0,0135 0,0277 0,0428 0,0592 0,0770
1,6 0,0125 0,0258 0,0397 0,0548 0,0710
1,7 0,0117 0,0241 0,0370 0,0509 0,0658
1,8 0,0110 0,0225 0,0347 0,0475 0,0612
1,9 0,0103 0,0211 0,0325 0,0445 0,0572
2,0 0,0097 0,0199 0,0305 0,0417 0,0536
2,2 0,0086 0,0177 0,0270 0,0369 0,0473
2,4 0 0077 0,0158 0,0241 0,0329 0,0420
2,6 0,0069 0,0141 0,0216 0,0294 0,0376
2,8 0,0062 0,0127 0,0194 0,0263 0,0336
3,0 0,0056 0,0114 0,0174 0,0236 0,0301
3,2 0,0050 0,0102 0,0156 0,0212 0,0270
3,4 0,0045 0,0092 0,0140 0,0190 0,0242
3,6 0,0040 0,0082 0,0125 0,0170 0,0217
3,8 0,0036 0,0073 0,0112 0,0152 0,0194
4,0 0,0032 0,0066 0,0100 0,0136 0,0174
4,2 0,0029 0,0059 0,0090 0,0122 0,0155
4,4 0,0025 0,0052 0,0080 0,0108 0,0138
4,6 0,0022 0,0046 0,0071 0,0096 0,0123
4,8 0,0020 0,0041 0,0063 0,0085 0,0109
5,0 0,0018 0,0036 0,0055 0,0076 0,0097
5,2 0,0016 0,0032 0,0049 0,0067 0,0086
5,4 0,0014 0,0028 0,0043 0,0059 0,0076
5,6 0,0012 0,0025 0,0038 0,0052 0,0067
5,8 0,0011 0,0022 0,0033 . 0,0046 0,0059
6,0 0,0009 0,0019 0,0029 0,0040 0,0052
к § 4]
Таблицы
383
Таблица 54
(CVIR)W, х — (CV/.R)W> о как функция w — hc<ae/kT и х
W х = 0,005 0,010 0,015 0,020 0,025
0,6 0,0384 0,0936 0,1852 0,2868 0,3213
0,7 0,0324 0,0752 0,1416 0,2331 0,3058
0,8 0,0278 0,0631 0,1128 0,1863 0,2658
0,9 0,0244 0,0544 0,0940 0,1515 0,2235
1,0 0,0219 0,0480 0,0809 0,1263 0,1871
1,1 0,0198 0,0430 0,0713 0,1083 0,1585
1,2 0,0182 0,0391 0,0639 0,0950 0,1364
1,3 0 0168 0,0358 0,0580 0,0850 0,1195
1,4 0,0157 0,0332 0,0533 0,0772 0,1068
1,5 0,0147 0,0310 0,0494 0,0708 0,0969
1,6 0,0139 0,0292 0,0462 0,0658 0,0888
1,7 0,0132 0,0276 0,0435 0,0615 0,0822
1,8 0 0126 0,0262 0,0412 0,0579 0,0770
1,9 0,0121 0,0251 0,0392 0,0549 0,0726
2,0 0,0116 0,0241 0,0376 0,0523 0,0691
2,2 0,0110 0,0224 0,0348 0,0481 0,0628
2,4 0,0104 0,0211 0,0326 0,0449 0,0582
2,6 0,0098 0,0200 0,0309 0,0424 0,0547
2,8 0,0094 0,0192 0,0294 0,0403 0,0517
3,0 0,0090 0,0184 0,0282 0,0384 0,0492
3,2 0,0087 0,0177 0,0271 0,0368 0,0470
3,4 0,0084 0,0170 0,0260 0,0353 0,0450
3,6 0,0080 0,0163 0,0249 0,0338 0,0430
3,8 0,0077 0,0156 0,0238 0,0323 0,0411
4,0 0,0073 0,0149 0,0227 0,0308 0,0392
4.2 0,0070 0,0142 0,0216 0,0293 0,0372
4,4 0,0066 0,0135 0,0205 0,0278 0,0353
4,6 0,0063 0,0127 0,0194 0,0262 0,0333
4,8 0,0059 0,0120 0,0182 0,0247 0,0314
5,0 0,0055 0,0112 0,0171 0,0231 0,0294
5,2 0,0051 0,0104 0,0159 0,0216 0,0275
5,4 0,0048 0,0097 0,0148 0,0201 0,0256
5,6 0,0044 0,0090 0,0137 0,0186 0,0237
5,8 0,0041 0,0083 0,0127 0,0172 0,0219
6,0 0,0037 0,0076 0,0116 0,0158 0,0202
384
ТАБЛИЦЫ
[гл. XIV
_ Таблица 55
v как функция w = hcu>elkT и х
W х = 0,00 0,005 0,01 0,015 0,02
0,6 1,216 1,279 1,353 1,461 1,611
0,7 0,986 1,031 1,083 1,152 1,248
0,8 0,816 0,849 0,888 0,936 0,999
0,9 0,685 0,711 0,741 0,776 0,821
1,0 0,582 0,603 0,627 0,654 0,687
1,1 0,499 0,516 0,536 0,557 0,583
1,2 0,431 0,445 0,461 0,479 0,499
1,3 0,375 0,386 0,400 0,415 0,432
1,4 0,327 0,338 0,349 0,362 0,375
1,5 0,287 0,296 0,306 0,317 0,328
1,6 0,253 0,261 0,269 0,279 0,289
1,7 0,224 0,231 0,238 0,246 0,255
1,8 0,198 0,204 0,211 0,218 0,225
1,9 0,176 0,181 0,187 0,193 0,200
2,0 0,157 0,162 0,167 0,172 0,178
2,2 0,125 0,128 0,133 0,137 0,142
2,4 0,100 0,103 0,107 0,110 0,114
2,6 0,080 0,083 0,086 0,089 0,092
2,8 0,065 0,067 0,069 0,072 0,074
3,0 0,053 0,054 0,056 0,058 0,060
3,2 0,043 0,044 0,046 0,048 0,049
3,4 0,035 0,036 0,037 0,039 0,040
3,6 0,028 0,029 0,030 0,032 0,033
3,8 0,023 0,024 0,025 0,026 0,027
4,0 0,019 0,020 0,020 0,021 0,022
Таблица 5G
как функция w = ficu>eikT и х
12) х = 0,000 0,005 0,010 0,015 0,020
0,6 2,834 3,023 3,283 3,706 4,280
0,7 2,358 2,494 2,670 2,930 3,318
0,8 2,001 2,104 2,231 2,403 2,661
0,9 1,724 1,804 1,901 2,024 2,201
1,0 1,503 1,567 1,643 1,736 1,861
1,1 1,322 1,375 1,436 1,509 1,602
1,2 1,171 1,216 1,266 1,325 1,397
1,3 1,044 1,081 1,124 1,173 1,230
1,4 0,936 0,968 1,004 1,045 1,092
1,5 0,842 0,870 0,901 0,936 0,975
1,6 0,760 0,785 0,812 0,842 0,876
1,7 0^88 0,711 0,734 0,760 0,789
к § 4]
ТАБЛИЦЫ
385
Продолжение
i V W х = 0,000 0,005 0,010 0,015 0,020
1,8 0,625 0,645 0,666 0,689 0,714
1,9 0,569 0 586 0,605 0,625 0,648
2,0 0,519 0,534 0,551 0,569 0,589
2,2 0,433 0,446 0,459 0,474 0,490
2,4 0,363 0,374 0,385 0,398 0,411
2,6 0,306 0,315 0,324 0,334 0,345
2,8 0,258 0,266 0,274 0,283 0,292
3,0 0,218 0,225 0,231 0,239 0,247
3,2 0,184 0,190 0,196 0,203 0,210
3,4 0,156 0,161 0,166 0,172 0,178
3,6 0,132 0,137 0,141 0,146 0,151
3,8 0,112 0,116 0,120 0,124 0,129
4,0 0,095 0,098 0,102 0,106 0,110
Таблица 57
Q как функция w = hc<s>ejkT и х
w х = 0,000 0,005 0,010 0,015 0,020
0,6 3,332 3,734 4,426 5,791 , 6,966
0,7 2,854 3,142 3,577 4,396 5,512
0,8 2,496 2,712 3,013 3,526 4,355
0,9 2,217 ' 2,384 2,606 2,947 3,528
1.0 1,992 2,126 2,297 2,540 1 2,935
1,1 1,808 1,918 2,054 2,236 2,515
1,2 1,654 1,745 1,856 1,999 2,203
1,3 1,522 1,599 1,692 1,807 1,963
1,4 1,409 1,475 1,553 1,647 i 1,771
1,5 1,310 1,367 1,433 1,512 ; 1,613
1,6 1,222 1,272 1,330 1,397 ! 1,481
1,7 1,144 1,188 1,238 1,297 1,367
1,8 1,073 1,112 1,157 1,208 1,269
1,9 1,009 1,044 1,084 1,129 . 4,184
2,0 0,951 0,982 1,018 1,058 ' 1,104
2,2 0,847 0,874 0,902 0,934 0,970
2,4 0,758 0,780 0,804 0,831 0,861
2,6 0,680 0,699 0,719 0,742 0,766
2,8 0,611 0,627 0,645 < 0,664 0,685
3,0 0,548 0,563 0,578 ; 0,595 ; 0,613
3,2 0,492 0,505 0,519 0,534 0,550
3,4 0,441 0,453 0,466 0,478 . 0,493
3,6 0,395 0,406 0,417 0,429 . 0,442
3,8 0,353 0,363 0,373 0,384 0,396
4,0 0,316 0,324 0,334 ‘ 0,343 : 0,354
25 Зак. 835. И. Н. Годнее
386 ТАБЛИЦЫ [гл. XIV
Таблица 58
v, и Ci для больших значений w, w = hc<oe/kT, x = О
W 4,4 4,8 5,2 5,6 6,0 6,4 6,8 7,2 7,6 8,0
V 0,012 0,008 0,006 0,004 0,002 0,002 0,001 0,001 0,001 0,000
S1 0,068 0,048 0,035 0,025 0,017 0,012 0,009 0,006 0,004 0,003
0,250 0,196 0,153 0,118 0,090 0,069 0,052 0,039 0,029 0,022
Таблица 59
v3 как фунция w = hcu>e/kT и х
W х = 0,000 0,005 0,010 0,015 0,020
0,6 4,18 4,66 5,34 6,58 8,44
0,7 2,93 3,22 3,61 4,22 5,23
0,8 2,15 2,33 2,57 2,92 3,47
0,9 1,62 1,75 1,91 2,12 2,44
1,0 1,26 1,35 1,46 1,60 1,79
1,2 0,80 0,85 0,91 0,98 1,07
1,4 0,53 0,57 0,61 0,65 0,69
1,6 0,38 0,40 0,42 0,45 0,48
1,8 0,28 0,29 0,30 0,32 0,34
2,0 0,21 0,22 0,23 0,24 0,25
2,4 0,12 0,12 0,13 0,14 0,14
2,8 0,07 0,07 0,08 0,08 0,09
3,2 0,05 0,05 6,05 0,05 0,05
к § 4]
ТАБЛИЦЫ
387
Таблица 60
s2 как функция w = hcwe)kT и х
W х = 0,000 0,005 0,010 0,015 0,020
0,6 13,66 15,70 19,03 25,86 34,43
0,7 9,71 10,94 12,75 16,10 21,44
0,8 7,20 8,00 9,08 10,88 13,99
0,9 5,51 6,05 6,76 7,82 9,64
1,0 4,32 4,71 5,20 5,87 6,96
1,2 2,82 3,03 3,29 3,62 4,07
1,4 1,94 2,08 2,23 2,42 2,65
1,6 1,40 1,49 1,58 1,69 1,83
1,8 1,04 1,10 1,16 1,24 1,33
2,0 0,80 0,83 0,87 0,92 0,99
2,4 0,49 0,51 0,54 0,56 0,59
2,8 0,32 0,33 0,35 0,36 0,38
3,2 0,21 0,22 0,23 0,24 0,25
Таблица 61
с2 как функция w = hcts>e[kT и х
w jc = 0,000 0,005 0,010 0,015 0,020
0,6 30,0 36,7 50,6 80,8 101,3
0,7 21,6 25,6 32,6 48,4 70,0
0,8 16,3 18,9 22,8 31,1 44,8
0,9 12,6 14,4 16,9 21,5 30,2
1,0 10,0 11,3 13,0 15,8 21,0
1,2 6,7 7,4 8,3 9,5 11,6
1,4 4,7 5,2 5,7 6,3 7,3
1,6 3,5 3,8 4,1 4,5 5,0
1,8 2,7 2,9 3,1 3,3 3,7
2,0 2,1 2,2 2,4 2,5 2,8
2,4 1,3 1,4 1,5 1,6 1,7
2,8 0,9 1,0 1,0 1,1 1,1
3,2 0,7 0,7 0,7 0,8 0,8
25*
388
ТАБЛИЦЫ
[гл. XIV
ПЕРВЫЕ ТАБЛИЦЫ ПИТЦЕРА (табл. 62-65)
Таблица 62
(Scb — S3 в) кал/град • моль
V0/RT IO'36 п2//пгив
0 1 2 4 8 16 32 64 128
0,0 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00
0,5 0,03 0,03 0,03 0,03 0,03 0,03 0,03 0,03 0,03
1,0 0,12 0,12 0,12 0,12 0,12 0,11 0,11 0,10 0,09
2,0 0,42 0,41 0,41 0,41 0,40 0,38 0,36 0,29 0,21
3,0 0,79 0,77 0,76 0,75 0,74 0,68 0,62 0,47
4,0 1,13 1,11 1,Ю 1,08 1,05 0,97 0,84 0,61
5,0 1,42 1,39 1,37 1,35 1,29 1,18 0,98
6,0 1,66 1,62 1,60 1,57 1,49 1,34 1,08
7,0 1,87 1,82 1,79 1,74 1,63 1,44 1,12
8,0 2,04 1,98 1,95 1,88 1,74 1,50 1,12
9,0 2,19 2,11 2,07 1,98 1,81 1,54
10,0 2,32 2,21 2,16 2,06 1,86 1,55
12,0 2,53 2,37 2,32 2,17 1,91 1,53
14,0 2,69 2,51 2,42 2,23 1,91 1,46
16,0 2,83 2,63 2,50 2,27 1,89 1,36
р ______р ф — ф
J 3. в 1 СВ 3. в св
Таблица 63
Ю'36 л2//привУ0
Vn/RT 0 1 2 4 8 16 32 64 128
0,0 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00
0,5 0,47 0,40 0,38 0,36 0,32 0,29 0,23 0,16 0,08
1,0 0,87 0,77 0,73 0,68 0,61 0,53 0,42 0,28 0,12
2,0 1,52 1,35 1,28 1,18 1,04 0,86 0,63 0,35 0,11
3,0 1,98 1,73 1,63 1,49 1,29 1,03 0,70 0,32
4,0 2,33 1,99 1,85 1,67 1,43 1,10 0,70 0,26
5,0 2,60 2,18 2,00 1,78 1,50 1,11 0,65
6,0 2,81 2,30 2,10 1,85 1,52 1,08 0,58
7,0 2,98 2,39 2,16 1,88 1,51 1,03 0,49
8,0 3,13 2,45 2,20 1,89 1,48 0,96 0,38
9,0 3,26 2,50 2,22 1,89 1,45 0,88
10,0 3,38 2,53 2,24 1,88 1,40 0,82
12,0 3,57 2,57 2,23 1,83 1,31 0,69
14,0 3,72 2,59 2,21 1,76 1,20 0,57
16,0 3,86 2,59 2,18 1,68 1,08 0,43
к § 5]
ТАБЛИЦЫ
389
Таблица 64
Н3. JT
V.IRT 0 1 2 4 8 16 32 64 128
0,0 0,99 0,99 0,99 0,99 0,99 0,99 0,99 0,99 0,99
0,5 1,43 1,36 1,34 1,32 1,28 1,25 1,19 1,12 1,04
1,0 1,74 1,64 1,60 1,55 1,48 1,41 1,30 1,17 1,02
2,0 2,09 1,93 1,86 1,76 1,63 1,47 1,26 1,05 0,89
3,0 2,18 1,95 1,86 1,73 1,54 1,34 1,07 0,84
4,0 2,19 1,87 1,74 1,58 1,37 1,12 0,8-5 0,64
5,0 2,17 1,78 1,62 1,42 1,20 0,92 0,66
6,0 2,14 1,67 1,49 1,27 1,02 0,73 0,49
7,0 2,10 1,56 1,36 1,13 0,87 0,58 0,36
8,0 2,08 1,46 1,24 1,00 0,73 0,45 0,25
9,0 2,06 1,38 1,14 0,90 0,63 0,33
10,0 2,05 1,31 1,07 0,81 0,53 0,26
12,0 2,03 1,19 0,90 0,65 0,39 0,15
14,0 2,02 1,07 0,78 0,52 0,28 0,10
16,0 2,02 0,95 0,67 0,40 0,18 0,06
Таблица 65
г
3. В
VoIRT 10-38 п2//привУ0
0 1 2 4 8 16 32 64 128
0,0 0,99 0,99 0,99 0,99 0,99 0,99 0,99 0,99 0,99
0,5 1,06 1,06 1,06 1,06 1,06 1,06 1,06 1,05 1,04
1,0 1,22 1,22 1,21 1,21 1,21 1,20 1,19 1,17 1,14
2,0 1,69 1,68 1,68 1,67 1,65 1,61 1,54 1,43 1,22
3,0 2,10 2,08 2,07 2,05 2,01 1,91 1,73 1,47
4,0 2,29 2,27 2,25 2,21 2,13 1,98 1,73 1,34
5,0 2,33 2,30 2,27 2,23 2,12 1,89 1,56
6,0 2,32 2,26 2,22 2,16 2,01 1,70 1,31
7,0 2,27 2,19 2,12 2,05 1,85 1,52 1,09
8,0 2,22 2,11 2,04 1,92 1,68 1,34 0,91
9,0 2,18 2,05 1,94 1,80 1,53 1,19
10,0 2,15 1,99 1,86 1,68 1,39 1,03
12,0 2,11 1,89 1,73 1,45 1,15 0,77
; 14,0 2,08 1,81 1,61 1,24 0,93 0,55
16,0 2,06 1,75 1,51 1,06 0,72 0,34
НОВЫЕ ТАБЛИЦЫ ПИТЦЕРА И ГВИННА (табл. 66—71)
Таблица 66
— в (кал1гРад моль)
0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80
0,0 0,2 0,4 0,6 0,8 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 6,0 7,0 8,0 9,0 10,0 12,0 14,0 16,0 18,0 20,0 2,754 2,710 2,623 2,518 2,406 2,296 2,040 1,819 1,630 1,473 1,340 1,225 1,133 1,053 0 919 2,392 2,359 2,296 2,208 2,106 2,004 1,770 1,563 1,389 1,240 1,117 1,013 0,925 0,849 0,728 2,086 2,061 2,014 1,944 1,856 1,764 1,548 1,360 1,197 1,059 0,943 0,847 0,764 0,696 0,586 1,821 1,803 1,765 1,708 1,636 1,559 1,370 1,193 1,043 0,914 0,802 0,713 0,637 0,577 0,477 1,587 1,574 1,543 1,498 1,442 1,379 1,210 1,052 0,912 0,793 0,694 0,613 0,543 0,483 0,393 1,377 1,368 1,342 1,309 1,266 1,214 1,069 0,927 0,802 0,695 0,603 0,527 0,463 0,408 0,325 1,188 1,182 1,160 1,134 1,100 1,059 0,938 0,817 0,709 0,612 0,528 0,456 0,397 0,347 0,272 0,53 0,46 0,40 0,35 0,30 0,23 0,34 0,29 0,25 0,19 0,22 0,16 0,14 0,08
0 819 0^636 0,503 0,402 0,325 0,267 0,218 0,183 0,15 0,12 0,10
0 735 0,564 0,440 0,346 0,275 0,221 0,178 0,146 0,119 0,10 0,08 0,06
0 667 0^504 0,388 0,300 0,235 0,186 0,149 0,119 0,096 0,079 0,06 0,05
0 610 0Д56 0,345 0,264 0,203 0,159 0,125 0,099 0,079 0,064 0,051 0,04
0 521 0^380 0^280 0,209 0,157 0,120 0,092 0,071 0,055 0,043 0,033 0,027
0 452 0^321 0,232 0,169 0,124 0,092 0,069 0,052 0,038 0,030 0,022 0,018
0 396 0^276 0,195 0,139 0,100 0,072 0,053 0,039 0,028 0,021 0,016 0,012
0 351 0^240 0,166 0,117 0,082 0,058 0,042 0,030 0,022 0,016 0,012 0,009
0,315 0^211 0,144 0,098 0,068 0,047 0,033 0,024 0,017 0,012 0,009 0,006
390 таблицы [гл. XIV
ж
с^>
О>
Таблица 67
св
— (кал/град • моль)
Уо//?Г\ 0 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55
0,0 0,0000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000
0,2 0,1937 0,154 0,117 0,085 0,061 0,044 0,033 0,025 0,018 0,013 0,009 0,005
0,4 0,3776 0,326 0,274 0,225 0,176 0,131 0,096 0,072 0,056 0,044 0,035 0,026
0,6 0,5516 0,489 0,424 0,361 0,298 0,236 0,184 0,142 0,113 0,089 0,068 0,054
0,8 0,7161 0,640 0,566 0,493 0,420 0,348 0,286 0,230 0,185 0,145 0,111 0,088
1,0 0,8711 0,784 0,699 0,617 0,537 0,461 0,389 0,322 0,262 0,208 0,163 0,129
1,5 1,2200 1,114 1,010 0,909 0,809 0,714 0,622 0,538 0,451 0,375 0,308 0,250
2,0 1,5182 1,395 1,276 1,159 1,045 0,935 0,829 0,726 0,628 0,535 0,450 0,371
2,5 1,7724 1,635 1,501 1,371 1,246 1,124 1,004 0,889 0,778 0,675 0,575 0,479
3,0 1,9893 1,839 1,693 1,552 1,415 1,282 1,152 1,027 0,907 0,794 0,682 0,576
3,5 2,1756 2,013 1,856 1,704 1,557 1,414 1,275 1,143 1,019 0,893 0,774 0,660
4,0 2,3366 2,163 1,996 1,833 1,676 1,525 1,379 1,239 1,108 0,974 0,850 0,732
4,5 2,4772 2,293 2,117 1,945 1,780 1,621 1,467 1,322 1,184 1,044 0,914 0,791
5,0 2,6012 2,408 2,221 2,042 1,868 1,703 1,543 1,392 1,244 1,104 0,969 0,841
6,0 2,8108 2,599 2,396 2,202 2,015 1,836 1,664 1,500 1,344 1,194 1,052 0,916
7,0 2,9833 2,755 2,537 2,328 2,129 1,936 1,757 1,583 1,418 1,262 1,111 0,971
8,0 3,1294 2,886 2,653 2,432 2,220 2,020 1,828 1,646 1,474 1,312 1,157 1,011
9,0 3,2563 2,998 2,753 2,520 2,298 2,087 1,888 1,698 1,520 1,351 1,192 1,039
10,0 3,3686 3,097 2,839 2,594 2,362 2,144 1,936 1,741 1,557 1,383 1,219 1,063
12,0 3,5602 3,263 2,982 2,718 2,468 2,233 2,013 1,806 1,612 1,429 1,258 1,096
14,0 3,7205 3,400 3,099 2,816 2,551 2,303 2,071 1,854 1,651 1,462 1,285 1,119
16,0 3,8584 3,517 3,197 2,897 2,618 2,358 2,116 1,891 1,682 1,486 1,305 1,135
18,0 3,9793 3,618 3,280 2,965 2,674 2,403 2,152 1,920 1,704 1,505 1,319 1,146
20,0 4,0872 3,707 3,353 3,024 2,720 2,440 2,181 1,942 1,722 1,519 1,331 1,155
со
ТАБЛИЦЫ
- — — Т а б л и ц а 68
S3 в (кал/град моль) •’
0,25 0,30 0,35 0,40 0,45 0,50 0,55' 0,60 0,65 0,70 0,75 0,80
0,0 3,748 3,386 3,079 2,814 2,580 2,371 2,181
0,2 3,743 3,382 3,076 2,811 2,578 2,369 2,179
0,4 3,730 3,370 3,065 2,801 2,568 2,359 2,171
0,6 3,709 3,347 3,043 2,780 2,547 2,340 2,153
0,8 3,679 3,318 3,013 2,750 2,519 2,315 2,128
1,0 3,638 3,279 2,974 2,714 2,485 2,279 2,095
1,5 3,512 3,156 2,854 2,600 2,376 2,173 1,992
2,0 3,355 3,004 2,709 2,458 2,241 2,048 1,873
2,5 3,180 2,836 2,548 2,303 2,091 1,907 1,741
3,0 3,008 2,667 2,380 2,138 1,933 1,756 1,600 1,45
3,5 2,838 2,500 2,218 1,978 1,782 1,610 1,459 1,34
4,0 2,678 2,343 2,069 1,834 1,643 1,475 1,326 1,22 1,10
4,5 2,528 2,199 1,926 1,698 1,511 1,348 1,204 1,10 1,00
5,0 2,396 2,068 1,798 1,579 1,392 1,233 1,095 0,97 0,88 0,81
6,0 2,166 1,844 1,585 1,370 1,192 1,040 0,913 0,79 0,70 0,63 0,56
7,0 1,983 1,665 1,411 1,204 1,033 0,891 0,770 0,665 0,57 0,50 0,44 0,39
8,0 1,830 1,519 1,272 1,071 0,906 0,770 0,656 0,564 0,482 0,41 0,36 0,31
9,0 1,703 1,397 1,156 0,962 0,804 0,674 0,569 0,482 0,411 0,348 0,29 0,25
10,0 1,593 1,295 1,060 0,872 0,719 0,596 0,495 0,418 0,352 0,295 0,245 0,21
12,0 1,417 1,125 0,904 0,728 0,588 0,476 0,388 0,315 0,258 0,212 0,173 0,143
14,0 1,275 0,994 0,783 0,620 0,492 0,388 0,309 0,247 0,196 0,158 0,126 0,102
16,0 1,157 0,890 0,688 0,533 0,414 0,322 0,251 0,196 0,155 0,120 0,094 0,075
18,0 1,058 0,801 0,609 0,464 0,353 0,270 0,205 0,158 0,121 0,093 0,072 0,056
20,0 0,975 0,727 0,542 0,405 0,303 0,228 ' 0,170 0,129 0,097 0,073 0,056 0,042
392 таблицы [гл. XIV
Т а б л и ц а 6& я
5св — 5з. в (кал^рад моль)
\Шв ИП/7?Г\ 0,0 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55
00 0 0000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000
0 2 0^0049 0,005 0,004 0,004 0,004 0,004 0,004 0,003 0,003 0,002 0,002 0,002
0 4 00198 0,020 0,018 0,018 0,018 0,018 0,016 0,014 0,013 0,012 0,012 0,010
06 0 0440 0,044 0,043 0,043 0,040 0,039 0,039 0,036 0,034 0,033 0,031 0,028
0 8 00771 0,077 0,077 0,075 0,072 0,069 0,068 0,066 0,064 0,061 0,056 0,053
1 0 01185 0,118 0,117 0,115 0,112 0,110 0,107 0,105 0,100 0,095 0,092 0,086
15 0,2527 0,252 0,250 0,248 0,242 0,236 0,230 0,225 0,214 0,204 0,198 0,189
20 0’4182 0,417 0,415 0,410 0,402 0,393 0,382 0,370 0,356 0,339 0,323 0,308
2 5 0’6001 0,599 0,594 0,585 0,577 0,568 0,550 0,531 0,511 0,489 0,464 0,440
3,0 0J856 0,783 0,777 0,768 0,757 0,740 0,719 0,699 0,676 0,647 0,615 0,581
3,5 0^9660 0,964 0,957 0,944 0,929 0,910 0,886 0,861 0,836 0,798 0,761 0,722
4,0 1,1356 1,133 1,126 1,111 1,094 1,070 1,043 1,011 0,980 0,937 0,896 0,855
4,5 1’2918 1,289 1,280 1,265 1,244 1,220 1,187 1,153 1,116 1,069 1,023 0,977
5,0 1 '4339 1,431 1,421 1,404 1,380 1,352 1,318 1,281 1,235 1,188 1,138 1,086
6,0 1,6781 1,674 1,662 1,643 1,616 1,582 1,542 1,494 1,444 1,388 1,331 1,268
7,0 1,8783 1,874 1,860 1,837 1,807 1,765 1,721 1,668 1,610 1,547 1,480 1,411
8,0 2,0447 2,040 2,024 1,998 1,962 1,918 1,867 1,807 1,743 1,674 1,601 1,525
9,0 2,1864 2,180 2,163 2,134 2,095 2,945 1,989 1,923 1,852 1,776 1,697 1,612
10,0 2’3095 2,303 2,284 2,252 2,208 2,155 2,091 2,019 1,942 1,861 1,775 1,686
12 0 2,5155 2,508 2,485 2,447 2,394 2,331 2,261 2,175 2,086 1,992 1,895 1,793
14^0 2,6847 2,676 2,650 2,607 2,547 2,473 2,392 2,296 2,194 2,088 1,983 1,872
16 0 2,8289 2,819 2,788 2,740 2,674 2,591 2,496 2,391 2,281 2,166 2,049 1,930
18,0 2^9545 2,943 2,910 2,855 2,781 2,690 2,585 2,470 2,350 2,227 2,101 1,976
20’0 3,0659 3,054 3,017 2,956 2,872 2,773 2,659 2,537 2,409 2,277 2,143 2,011
§ 6] таблицы 393
Т а б л иц a 70
и со
^з.в **
т
^\V<2OJ Уп/7?7\ 0,0 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,4Э 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80
0,0 0,9934 0,993 0,993 0,993 0,993 0,993 0,993 0,993 0,993 0,993 0,993 0,993
0,2 1,1822 1,142 1,106 1,074 1,050 1,032 1,022 1,015 1,008 1,004 1,000 0,997
0,4 1,3513 1,300 1,249 1,200 1,151 1,106 1,073 1,051 1,036 1,025 1,015 1,009
0,6 1,5011 1,437 1,374 1,311 1,251 1,190 1,138 1,099 1,072 1,049 1,030 1,019
0,8 1,6324 1,556 1,482 1,411 1,340 1,272 1,211 1,157 1,114 1,077 1,048 1,028
1,0 1,7460 1,660 1,576 1,495 1,418 1,344 1,275 1,211 1,155 1,105 1,065 1,037
1,5 1,9607 1,856 1,753 1,654 1,561 1,472 1,385 1,306 1,230 1,164 1,103 1,054
2,0 2,0934 1,971 1,854 1,742 1,636 1,536 1,440 1,350 1,265 1,190 1,120 1,056
2,5 2,1657 2,031 1,900 1,779 1,662 1,550 1,448 1,351 1,260 1,179 1,104 1,032
3,0 2,1971 2,049 1,909 1,777 1,651 1,535 1,426 1,321 1,224 1,140 1,060 0,988 0,92
3,5 2,2030 2,043 1,893 1,753 1,621 1,497 1,382 1,275 1,176 1,088 1,006 0,931 0,88
4,0 2,1944 2,024 1,864 1,715 1,577 1,448 1,329 1,221 1,121 1,030 0,947 0,870 0,82 0,77
4,5 2,1788 1,998 1,829 1,673 1,529 1,394 1,273 1,162 1,061 0,968 0,884 0,807 0,75 0,71
5,0 2,1607 1,971 1,794 1,631 1,481 1,344 1,218 1,104 1,002 0,909 0,824 0,748 0,67 0,63 0,59
6,0 2,1261 1,918 1,727 1,552 1,392 1,247 1,115 0,999 0,893 0,799 0,714 0,641 0,56 0,51 0,47 0,42
7,0 2,0984 1,875 1,670 1,484 1,315 1,164 1,029 0,908 0,802 0,708 0,624 0,553 0,482 0,42 0,38 0,34 0,31
8,0 2,0781 1,840 1,623 1,427 1,251 1,095 0,955 0,833 0,725 0,631 0,549 0,479 0,418 0,363 0,31 0,28 0,25
9,0 2,0634 1,811 1,583 1,379 1,196 1,035 0,892 0,768 0,661 0,569 0,488 0,420 0,363 0,315 0,269 0,23 0,20
10,0 2,0526 1,787 1,548 1,335 1,147 0,982 0,838 0,715 0,608 0,515 0,437 0,371 0,319 0,273 0,231 0,194 0,17
12,0 2,0382 1,749 1,492 1,264 1,067 0,896 0,745 0,624 0,519 0,431 0,356 0,296 0,244 0,203 0,169 0,140 0,116
14,0 2,0292 1,717 1,441 1,202 0,997 0,823 0,672 0,551 0,450 0,367 0,295 0,240 0,195 0,158 0,128 0,104 0,084
16,0 2,0229 1,690 1,401 1,150 0,937 0,760 0,613 0,493 0,394 0,314 0,249 0,198 0,157 0,127 0,099 0,078 0,063
18,0 2,0182 1,666 1,363 1,102 0,886 0,707 0,561 0,443 0,347 0,271 0,211 0,164 0,128 0,099 0,077 0,060 0,047
20,0 2,0147 1,646 1,329 1,061 0,841 0,660 0,515 0,399 0,307 0,236 0,181 0,138 0,105 0,080 0,061 0,047 0,036
ТАБЛИЦЫ [ГЛ. XIV
Таблица 71
С3 в (кал/град • моль)
\VQ0B 0,0 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80
0,0 0,9934 0,993 0,993 0,993 0,993 0,993 0,993 0,993 0,993 0,993 0,99 0,99
0,2 1,0033 1,003 1,003 1,002 1,001 1,000 0,999 0,998 0,998 0,998 1,00 1,00
0,4 1,0326 1,033 1,032 1,030 1,028 1,025 1,024 1,021 1,019 1,017 1,02 1,01
0,6 1,0799 1,080 1,079 1,076 1,073 1,068 1,065 1,060 1,056 1,051 1,05 1,04
0,8 1,1433 1,143 1,141 1,138 1,133 1,128 1,121 1,114 1,106 1,099 1,09 1,08
1,0 1,2201 1,219 1,217 1,212 1,206 1,199 1,190 1,180 1,169 1,157 1,14 1,13
1.5 1,4506 1,449 1,444 1,435 1,423 1,408 1,391 1,370 1,348 1,324 1,30 1,27
2,0 1,6975 1,69.5 1,687 1,673 1,655 1,632 1,606 1,574 1,541 1,505 1,469 1,43
2,5 1,9211 1,917 1,908 1,888 1,866 1,840 1,801 1,756 1,717 1,670 1,623 1,58
3,0 2,0986 2,095 2,082 2,062 2,033 1,996 1,952 1,900 1,846 1,794 1,738 1,68 1,7
3,5 2,2223 2,218 2,204 2,180 2,146 2,106 2,054 1,995 1,934 1,869 1,803 1,74 1,7
4,0 2,2986 2,294 2,276 2,249 2,213 2,168 2,110 2,048 1,980 1,907 1,834 1,76 1,69 1,6
4,5 2,3354 2,330 2,312 2,280 2,238 2,190 2,129 2,062 1,990 1,911 1,832 1,75 1,67 1,6
5,0 2,3443 2,338 2,318 2,285 2,241 2,186 2,120 2,056 1,972 1,890 1,808 1,719 1,62 1,55 1,4
6,0 2,3155 2,307 2,283 2,245 2,192 2,130 2,059 1,979 1,893 1,803 1,711 1,616 1,51 1,43 1,33 1,2
7,0 2,2647 2,256 2,228 2,185 2,126 2,055 1,973 1,883 1,787 1,688 1,588 1,491 1,394 1,30 1,21 1,12 1,0
8,0 2,2157 2,205 2,174 2,125 2,058 1,979 1,888 1,788 1,684 1,576 1,468 1,362 1,260 1,159 1,07 0,99 0,91
9,0 2,1759 2,164 2,130 2,074 1,999 1,909 1,808 1,699 1,587 1,474 1,362 1,252 1,149 1,049 0,955 0,86 0,79
10,0 2,1454 2,133 2,094 2,033 1,951 1,854 1,745 1,630 1,507 1,382 1,262 1,151 1,047 0,949 0,853 0,762 0,68
12,0 2,1050 2,089 2,043 1,972 1,877 1,763 1,636 1,502 1,365 1,233 1,107 0,989 0,877 0,774 0,683 0,600 0,519
14,0 2,0810 2,063 2,009 1,923 1,814 1,686 1,546 1,400 1,254 1,112 0,978 0,855 0,744 0,644 0,555 0,476 0,408
16,0 2,0654 2,044 1,983 1,887 1,764 1,622 1,468 1,311 1,156 1,009 0,873 0,749 0,639 0,542 0,457 0,384 0,321
18,0 2,0544 2,031 1,961 1,853 1,717 1,562 1,397 1,232 1,070 0,919 0,780 0,657 0,549 0,456 0,378 0,312 0,256
20,0 2,0462 2,020 1,944 1,827 1,678 1,510 1,333 1,158 0,991 0,837 0,701 0,580 0,477 0,389 0,316 0,256 0,207
со
CD
СЛ
ТАБЛИЦЫ
О)
396
ТАБЛИЦЫ
[ГЛ. XIV
Таблица 72
Значения функции G = —-------1------
2 а еи — 1
и G ДО/Аи и G ДС/Д«
0,00 0,00000 1,00 0,08198 0,0790
0,05 0,10 0,004165 0,008415 1,05 1,10 0,08593 0,08987 0,0788
0,0782
0,15 0,01265 1,15 0,09378
0,0780
0,20 0,01671 1,20 0,09768 0,0774
0,25 0,02075 ч 1,25 0,10155 0,0770
0,30 0,02496 1,30 0,10540 0,0764
0,35 0,02910 0,0832 1,35 0,10922 0,0760
0,40 0,03326 0,0824 1,40 0,11302 0,0756
0,45 0,03738 0,0824 1,45 0,11680 0,0750
0,50 0,04150 0,0822 1,50 0,12055 0,0746
0,55 0,04561 0,0818 1,55 0,12428 0,0738
0,60 0,04970 1,60 0,12797 0,0734
0,0818
0,65 0,05379 1,65 0,13164 0,0728
0,0816
0,70 0,05787 1,70 0,13528 0,0722
0,0812
0,75 0,06193 1,75 0,13889 0,0716
0,0808
0,80 0,06597 1,80 0,14247
0,0804 0,0712
0,85 0,06999 0,0804 1,85 0,14603 0,0704
0,90 0,07401 1,90 0,14955 0,0700
0,0798
0,95 0,07800 1,95 0,15305
0,0796 0,0694
1,00 0,08198 2,00 0,15652
к § 7)
ТАБЛИЦЫ
397
Продолжение
и G ' ДО/Ди и G ЬО/Ьи
2,00 0,15652 0,0688 3,05 0,22184 0,0550
2,05 0,15996 3,10 0,22459 0,0544
0,0678
2,10 0,16335 3,15 0,22731 0,0536
0,0674
2,15 0,16672 3,20 0,22999 0,0530
0,0668
2,20 0,17006 3,25 0,23264 0,0524
0,0662
2,25 0,17337 3,30 0,23526 0,0518
0,0654
2,30 0,17665 3,35 0,23785 0,0512
0,0648
2,35 0,17989 3,40 0,24041 0,0506
0,0642
2,40 0,18310 3,45 0,24294 0,0500
0,0636
2,45 0,18628 3,50 0,24544 0,0492
0,0630
2,50 0,18943 3,55 0,24790 0,0484
0,0620
2,55 0,19253 3,60 0,25032 0,0478
0,0616
2,60 0,19561 3,65 0,25271 0,0474
0,0610
2,65 0,19866 3,70 0,25508 0,0466
0,0604
2,70 0,20168 3,75 0,25741 0,0462
0,0594
2,75 0,20465 3,80 0,25972 0,0456
0,0592
2,80 0,20761 3,85 0,26200 0,0450
0,0580
2,85 0,21051 3,90 0,26425 0,0444
0,0576
2,90 0,21339 3,95 0,26647
0,0572 0,0438
2,95 0,21625 4,00 0,26866 0,0432
0,0562
3,00 0,21906 4,05 0,27082 0,0426
0,0556
3,05 0,22184 4,10 0,27295
398
ТАБЛИЦЫ
[гл. XIV
Продолжение
и. G AG/Ди и G AG/Au
4,10 0,27295 0,0420 5,15 0,31168 0,0318
4,15 0,27505 0,0414 5,20 0,31327
0,0314
4,20 0,27712 0,0408 5,25 0,31484
0,0308
4,25 0,27919 0,0402 5,30 0,31638
0,0304
4,30 0,28119 5,35 0,31790
0,0398 0,0300
4,35 0,28318 5,40 0,31940
0,0394 0,0296
4,40 0,28515 5,45 0,32088
0,0388 0,0292
4,45 0,28709 5,50 0,32234
0,0384 0,0288
4,50 0,28901 5,55 0,32378
0,0378 0,0284
4,55 0,29090 5,60 0,32520
0,0372 0,0280
4,60 0,29276 5,65 0,32660
0,0368 0,0276
4,65 0,29460 0,0362 5,70 0,32798
0,0272
4,70 0,29641 5,75 0,32934
0,0358 0,0268
4,75 0,29820 5,80 0,33068
0,0354 0,0264
4,80 0,29997 5,85 0,33200
0,0350 0,0260
4,85 0,30172 5,90 0,33330
0,0342 0,0256
4,90 0,30343 5,95 0,33458
0,0338 0,0250
4,95 0,30512 0,0334 6,00 0,33583
0,0252
5,00 0,30679 6,10 0,33831
0,0330 0,0244
5,05 0,30844 6,20 0,34075
0,0326 0,0236
5,10 0,31007 6,30 0,34311
0,0322 0,0230
5,15 0,31168 6,40 0,34541
К § 71
ТАБЛИЦЫ
399
Продолжение
и G ДО/Ди и G ДО/Ди
6,40 0,34541 0,0225 8,50 0,38255 0,0135
6,50 0,34766 0,0218 8,60 0,38390
0,0133
6,60 0,34984 8,70 0,38523
0,0214 0,0128
6,70 0,35198 8,80 0,38651
0,0208 0,0127
6,80 0,35406 0,0202 8,90 0,38778
0,0123
6,90 0,35608 0,0197 9,00 0,38901
0,0121
7,00 0,35805 9,10 0,39022
0,0193 0,0118
7,10 0,35998 0,0188 9,20 0,39140
0,0116
7,20 0,36186 9,30 0,39256
0,0183 0,0114
7,30 0,36369 0,0178 9,40 0,39370 0,0111
7,40 0,36547 9,50 0,39481
0,0175 0,0109
7,50 0,36722 0,0170 9,60 0,39590 0,0107
7,60 0,36892 9,70 0,39697
7,70 0,37058 0,0166 0,0105
9,80 0,39802
0,0162 0,0102
7,80 0,37220 9,90 0,39904
0,0159 0,0101
7,90 0,37379 10,00 0,40005
0,0155 0,0098
8,00 0,37534 0,0150 10,10 0,40103 0 0097
8,10 0,37684 10,20 0,40200
0,0148 0,0094
8,20 0,37832 0,0145 10,30 0,40294
0,0094
8,30 0,37977 0,0140 10,40 0,40388
0,0091
8,40 0,38117 10,50 0,40479
0,0138 0,0089
8,50 0,38255 10,60 0,40568
ЛОО
ТАБЛИЦЫ
[ГЛ. XIV
Продолжение
и G AG/Au и G SG/bu
10,60 0,40568 0,0088 12,70 0,42126 0,0061
10,70 0,40656 0,0087 12,80 0,42187
0,0061
10,80 10,90 0,40743 0,0085 12,90 0,42248
0,0060
0,40828 0,0083 13,00 0,42308
11,00 0,0058
0,40911 0,0082 13,10 0,42366
11,10 0,0058
0,40993 0,0079 13,20 0,42424
11,20 0,0057
0,41072 0,41151 0,0079 13,30 13,40 0,42481 0,42537
11,30 0,0056
11,40 0,0078 0,0056
0,41229 0,0076 13,50 0,42593
0,0054
11,50 11,60 0,41305 0,0075 13,60 0,42647
0,0054
0,41380 0,0074 13,70 0,42701
0,0053
11,70 0,41454 0,0072 13,80 0,42754
0,0052
11,80 0,41526 0,0072 13,90 0,42806
0,0051
11,90 0,41598 0,0070 14,00 . 0,42857
0,0051
12,00 0,41668 0,0068 14,10 0,42908
0,0050
12,10 0,41736 0,0067 14,20 0,42958
0,0049
12,20 0,41803 0,0067 14,30 0,43007
0,0049
12,30 0,41870 0,0065 14,40 0,43056
0,0047
12,40 0,41935 0,0065 14,50 0,43103
0,0048
12,50 0,42000 0,0063 14,60 0,43151
0,0046
12,60 0,42063 0,0063 14,70 14,8& 0,43197
0,0046
12,70 0,42126 0,43243
К § 71
ТАБЛИЦЫ
401
Продолжение
и G и G AG/Ди
14,80 0,43243 0,0046 16,90 0,44083 0,0035
14,90 0,43289 0,0044 17,00 0,44118
0,0034
15,00 0,43333 0,0044 17,10 0,44152
0,0034
15,10 0,43377 17,20 0,44186
0,0044 0,0034
15,20 0,43421 17,30 0,44220
0,0043 0,0033
15,30 0,43464 0,0042 17,40 0,44253 0,0033
15,40 0,43506 0.0042 17,50 0,44285 0,0032
15,50 0,43548 0,0042 17,60 0,44318 0,0032
15,60 0,43590 17,70 0,44350 0,0032
0,0041
15,70 0,43631 17,80 0,44382
0,0040 0,0031
15,80 0,43671 0,0040 17,90 0,44413
0,0031
15,90 0,43711 18,00 0,44444
0,0039 0,0031
16,00 0,43750 0,0039 18,10 0,44475 0,0030
16,10 0,43789 0,0038 18,20 0,44505 0,0031
16,20 0,43827 0,0038 18,30 0,44536
0,0029
16,30 0,43865 18,40 0,44565
0,0037 0,0030
16,40 0,43902 0,0037 18,50 0,44595 0,0029
16,50 0,43939 18,60 0,44524
0,0037 0,0028
16,60 0,43976 0,0036 18,70 0,44652 0,0029
16,70 0,44012 0,0036 18,80 0,44681
0,0028
16,80 0,44048 18,90 0,44709
0,0035 0,0028
16,90 0,44083 19,00 0,44737
26 Зак. 835. И. Н. Годнее
402
ТАБЛИЦЫ
[гл. xiv
Продолжение
и G дс д« и G ДО/Ди
19,00 0,44737 0,0027 20,70 0,45169 0,0023
19,10 0,44764 0,0028 20,80 0,45192 0,0023
19,20 0,44792 0,0027 20,90 0,45215 0,0023
19,30 0,44819 0,0026 21,00 0,45238 0,0023
19,40 0,44845 0,0027 21,10 0,45261 0,0022
19,50 0,44872 0,0026 21,20 0,45283 0,0022
19,60 0,44898 0,0026 21,30 0,45305 0,0022
19,70 0,44924 0,0025 21,40 0,45327 0,0022
19,80 0,44949 0,0026 21,50 0,45349 0,0021
19,90 0,44975 0,0025 21,60 0,45370 0,0022
20,00 0,45000 0,0025 21,70 0,45392 0,0021
20,10 0,45025 0,0025 21,80 0,45413 0,0021
20,20 0,45050 0,0024 21,90 0,45434 0,0021
20,30 0,45074 0,0024 22,00 0,45455 0,0020
20,40 0,45098 0,0024 22,10 0,45475 0,0020
20,50 0,45122 0,0024 22,20 0,45494 0,0021
20,60 0,45146 0,0023 22,30 0,45516 0,0020
20,70 0,45169 22,40 ' 0,45536
К § 71
ТАБЛИЦЫ
403
Продолжение
и G AG/Ди и G AG/Ди
22,40 0,45536 0,0020 23,70 0,45781 0,0017
22,50 0,45556 0,0019 23,80 0,45798 0,0018
22,60 0,45575 0,0020 23,90 0,45816 0,0017
22,70 0,45595 0,0019 24,00 0,45833 0,0018
22,80 0,45614 0,0019 24,10 0,45851 0,0017
22,90 0,45633 0,0019 24,20 0,45868 0,0017
23,00 0,45652 0,0019 24,30 0,45885 0 0017
23,10 0,45671 0,0019 24,40 0,45902 0,0016
23,20 0,45690 0,0018 24,50 0,45918 0,0017
23,30 0,45708 0,0018 24,60 0,45935 0,0016
23,40 0,45726 0,0019 24,70 0,45951 0,0017
23,50 0,45745 0,0018 24,80 0,45968 0,0016
23,60 0,45763 0,0018 24,90 0,45984 0,0016
23,70 0,45781 25,00 0,46000
404
ТАБЛИЦЫ
[ГЛ. XIV
Т а б лица 73
Таблица литературных источников значений
термодинамических функций*)
№ п/п Тип соединения Ссылки Примечание
1 Простейшие соединения Н2> О2, Н2О, СО2, СН4 и т. д. [3], [33],[ 79], [80], [15] Литературные источники см. также в обзорн. ра- боте [236]
2 Неорганические соеди- нения [3[, [33] См. обзорн. работы Виль- сона [264] и Цензе [267]. [268], где можно найти ссылки
3 Углеводороды [33], [10], [70], [71], [72], [15]
4 Другие органические соединения [33] См. [264], [237], [2E8J
*) См. также справочник Россини и др. [93].
ЛИТЕРАТУРА
1. Книги, монографии, справочники
1. Блохинцев Д. И., Основы квантовой механики, 2-е изд.,
Гостехиздат, 1949.
2. Больцман Л., Лекции по теории газов, ч. I, II, Гостехиздат,
1953.
3. Брицке Э. В., К а п у с т и н с к и й А. Ф., В е с е л о в с к и й Б. К.,
Шамовский Л. М., Ченцова Л. Г., Анваер Б. И.,
Термические константы неорганических веществ, изд. АН СССР,
1949.
4. Б р о д с к и й А. И., Вычисление термодинамических функций,
Металлургиздат, 1947.
5. Бродский А. И., Физическая химия, т. I, II, Госхимиздат,
1948.
6. Бродский А. И., Химия изотопов, Изд. АН СССР, 1952.
7. Бутлеров А. М. Избранные работы, Изд. АН СССР, 1951.
8. Бу х г о л ь ц Н. Н., Основной курс теоретической механики,
ч. I, II, Гостехиздат, 1945.
9. В а н-д е р-В е р д е н Б. Л., Метод теории групп в квантовой
механике, ГНТИУ, 1938.
10. В в е д е н с к и й А. А., Термодинамические расчеты процессов
топливной промышленности, Гостоптехиздат, 1949.
И. Веннер Р., Термохимические расчеты, ИЛ, 1950.
12. Волькенштейн М. В., Ельяшевич М. А. и Степа-
нов Б. И., Колебания молекул, т. I и II, Гостехиздат, 1949.
13. В о л ь к е н ш т е й н М. В., Молекулярная оптика, Гостехиздат,
1951.
14. В у к а л о в и ч М. П. и Новиков И. И., Уравнение состояния
реальных газов, Госэнергоиздат, 1948.
15. В у к а л о в и ч М. П., Кириллин В. А., Р е м и з о в С. А.,
С и л е ц к и й В. С., Тимофеев В. Н., Термодинамические
свойства газов, Машгиз, 1953.
16. Г ей дон А., Энергии диссоциации и спектры двухатомных
молекул, ИЛ, 1949.
17. Гельфанд И. М., Лекции по линейной алгебре, Гостехиздат,
1-е изд. 1948; 2-е изд., 1951.
18. Герцберг Г., Атомные спектры и строение атомов, ИЛ, 1948.
19. Герцберг Г., Спектры и строение двухатомных молекул,
ИЛ, 1949.
27 3». 8СВ. № М. Мхй»
406 ЛИТЕРАТУРА
20. Герцберг Г., Колебательные и вращательные спектры много-
атомных молекул, ИЛ, 1949.
21. Гиббс Дж. В., Основные принципы статистической механики,
Гостехиздат, 1946.
22. Г лесс тон С., Успехи общей химии, Госхимиздат, 1941.
23. Г л е с с т о н С., Л е й д л е р К., Э й р и н г Г., Теория абсолют-
ных скоростей реакций, ИЛ, 1948.
24. Глесстон С., Теоретическая химия, ИЛ, 1950.
25. Годнее И. Н., К вычислению термодинамических функций по
спектроскопическим данным, диссертация, Физ.-хим. институт
им. Карпова, 1937.
26. Г р я з н о в В. М. и Фрост А. В., Статистические методы
расчета термодинамических величин, Москва, 1949.
27. Г у г г е н г е й м Э. А., Современная термодинамика, изложенная
по методу Гиббса, Госхимиздат, 1941.
28. Е л ь я ш е в и ч М. А., Спектры редких земель, Гостехиздат,
1953.
29. К а р а п е т ь я н ц М. X., Химическая термодинамика, Госхим-
издат, 1-е изд., 1949; 2-е изд., 1953.
30. К о л о с о в с к и й Н. А., Химическая термодинамика, Госхим-
техиздат, Ленинградское отд., 1932.
31. Ко ль pay ш К., Спектры комбинационного рассеяния, ИЛ,
1952.
32. К о н д р а т ь е в В. Н., Структура атомов и молекул, Изд.
АН СССР, 1946.
33. Коробов В. В. и Фрост А. В., Свободные энергии органи-
ческих соединений, Москва, 1949.
34. Курант Р. иГильбертД., Методы математической физики,
т. I, Гостехиздат, 1951; т. II, Гостехиздат, 1945.
35. Курош А. Г., Теория групп, Гостехиздат, 1944.
36. Курош А. Г., Курс высшей алгебры, 2-е изд. Гостехиздат,
1949.
37. Ландау Л. и ЛифшицЕ., Квантовая механика, ч. I, Гостех-
издат, 1948.
38. Ландау Л. и Лифшиц Е., Статистическая физика, Гостех-
издат, 1951.
39. Ландау Л. и Пятигорский Л., Механика, Гостехиздат,
1940.
40. Левич В. Г., Введение в статистическую физику, Гостехиздат,
1950.
41. Л е о н т о в и ч М. А., Статистическая физика, Гостехиздат, 1944.
42. Л е о н т о в и ч М. А., Введение в термодинамику, Гостехиздат,
1950.
43. Л о й ц я н с к и й Л. Г. и Лурье А. И., Курс теоретической
механики, ч. I и II, Гостехиздат, 1948.
44. Ломоносов М. В., О составляющих природные тела нечув-
ствительных физических частицах, в которых заключается доста-
точное основание частных качеств, Поли. собр. соч., т. I, 279,
Изд. АН СССР, 1950.
45. Л о м о н о с о в М. В., Прибавление к размышлениям об упруго-
сти воздуха, Поли. собр. соч., т. II, 145, Изд. АН СССР, 1951.
ЛИТЕРАТУРА
407
46. Л омоносов М. В., Размышления о причине теплоты и холода,
Поли. собр. соч., т. II. 7, Изд. АН СССР, 1951.
47. Ломоносов М. В., Опыт теории упругости воздуха, Поли,
собр. соч., т. II, 105, Изд. АН СССР, 1951.
48. Льюис Г. Н. и Рендалл М., Химическая термодинамика,
ОНТИ, 1936.
49. Майер Дж. и Майер М. Г., Статистическая механика, ИЛ,
1952.
50. Маслов П. Г., Диссертация, Ленинград, 1953.
51. Михельсон В. А., Собр. соч., т. I, Кооп. изд. Акад,
им. К. А. Тимирязева «Новый агроном», Москва, 1930.
52. Н е р н с т В., Теоретические и опытные основания нового тепло-
вого закона, ГИЗ, 1929.
53. Никольский К. В., Квантовая механика молекулы, ГТТИ, 1934.
54. Партингтон Дж. Р. и Раковский А. В., Курс химиче-
ской термодинамики, ГНТИ, 1932.
55. Планк М., Теория теплового излучения, ОНТИ, 1935.
56. Самойлович А. Г., Термодинамика и статистическая физика,
Гостехиздат, 1953.
57. С майе Ч., Диэлектрическая постоянная и структура молекул,
ОНТИ, 1937.
58. Сыркин Я. К. и Дяткина М. Е., Химическая связь и
строение молекул, Госхимиздат, 1946.
59. Татевский В. М., Химическое строение углеводородов и
закономерности в их физико-химических свойствах, Изд. МГУ,
1953.
60. Т е р е н и н А. Н., Введение в спектроскопию, Изд. ЛГУ,
1933.
61. Теренин А. Н., Фотохимия красителей, Изд. АН СССР
1947.
62. Уиттекер Е. Т., Аналитическая динамика, ОНТИ, 1937.
63. Фаулер Р. и Гуггенгейм Э., Статистическая термодина-
мика, ИЛ, 1949.
64. Ф е д о р о в Е. С., Сокращенный курс кристаллографии, 1910.
65. Федоров Е. С., Симметрия кристаллов, Изд. АН СССР, 1949.
66. Фихтенгольц Г. М., Курс дифференциального и инте-
грального исчисления, т. I, Гостехиздат, 1947; т. II, 1948; т. III,
1949.
67. Фок В. А., Начала квантовой механики, Изд. ЛГУ, 1932.
68. Ф р е н к е л ь Я. И., Статистическая физика, Изд. АН СССР,
1948.
69. Фриш С. Э., Атомные спектры, ГТТИ, 1934.
70. Физико-химические свойства индивидуальных углеводородов,
под ред. М. Д„ Тиличеева, вып. I, Гостоптехиздат, 1945.
71. Физико-химические свойства индивидуальных углеводородов,
под ред. М. Д. Тиличеева, вып. II, Гостоптехиздат, 1947.
72. Физико-химические свойства индивидуальных углеводородов,
под ред. М. Д. Тиличеева, вып. II, Гостоптехиздат, 1951.
73. X в о л ь с о н О. Д., Курс физики, т. I — V, ГИЗ, 1923.
74. X и н ч и н А. Я., Математические основания статистической
механики, Гостехиздат, 1943.
27*
408
ЛИТЕРАТУРА
75. X и н ч и н А. Я., Математические основания квантовой стати-
стики, Гостехиздат, 1951.
76. X и н ч и н А. Я., Краткий курс математического анализа, Гос-
техиздат, 1953.
77. Химия изотопов, сборник № 1, ИЛ, 1948.
78. Химия изотопов, сборник, № 2, ИЛ, 1948.
79. Ч е р н о б а э в Д. О. i Ж и в о т о в с ь к и й А. Г., Теплосмшсть
газ!в, КиТв, 1938.
80. Чернобаев Д. О. i Животовський А. Г., Константи
р1вноваги газових реакщй, КиТв, 1939.
81. Чулановский В. М., Введение в молекулярный спектраль-
ный анализ, Гостехиздат, 1951.
82. Шефер К. и Матосе и Ф., Инфракрасные спектры, ОНТИ,
1935.
83. Шмидт О. Ю., Абстрактная теория групп, ГТТИ, 1933.
84. Ш п о л ь с к и й Э. В., Атомная физика, 3-е изд., Гостехиздат,
т. I, 1950; т. II, 1951.
85. Шредингер Э., Статистическая термодинамика, ИЛ, 1948.
86. Э й р и н г Г., Уолтер Дж. и Кимбалл Дж., Квантовая
химия, ИЛ, 1948.
87. Born М. and Green Н. S., A General Kinetic Theory of Liquids,
Cambridge, 1949.
88. Fowler R. H., Statistical Mechanics, 2 edit., Cambridge, 1936.
89. Gordy W., Smith W. V. and T r a m b a r u 1 о R. F., Micro-
wave Spectroscopy, 1953 (см. перевод, Горди В., Смит В., Трам-
баруло Р., Радиоспектроскопия, Гостехиздат, 1955).
90. Н i b b е n J. Н., The Raman Effect and its Chemical Applications,
New York, 1939.
91. Moore С. E., Atomic Energy Levels, Circ. Nat. Bur. Stand. 467,
Washington, v. 1, 1949; v. Il, 1952.
92. P a u 1 i n g L. and Wilson E. B., Introduction to Quantum
Mechanics, McGraw Hill Book Comp., 1935.
93. Rossini F. D., W a g m a n D. D., Evans W. H., LevineS.
and Jaffe 1., Selected Values of Chemical Thermodinamic Pro-
perties, Circ. Nat. Bur. Stand. 500, Washington, 1952.
94. Taylor H. S. and Glasstone S., A Treatise on Physical
Chemistry, Third Edit., v. I, New York, 1945.
95. Tolman R. C., The Principles of Statistical Mechanics, Oxford,
1938.
96. Wigner E., Gruppentheorie und ihre Anwendung auf die
Quantenmechanik der Atomspektren, 1931.
2. Работы, опубликованные в периодической печати
97. Александров А. Д., ДАН СССР 85, 291 (1952).
98. А н т и п и н а С. А. и Маслов П. Г., ЖЭТФ 22, 705
(1952).
99. А р о н о в О. Л., Т а т е в с к и й В. М. и Ф р о с т А. В., Вест-
ник МГУ, № 1, 125, (1948); № 2, 45 (>1948).
100. Аронов О. Л., Татевский В. М. и Ф рост А. В., ДАН
СССР 60, 387, 1177, 1343 (1948).
ЛИТЕРАТУРА
409
101. Блохинцев Д. И., Вопросы философии, № 6, 171 (1952).
102. Бэрдж Р. Т., УФН 26, 74 (1944).
103. Власов Н. А. и Годнее И. Н., Сборник научно-исследова-
тельских работ ИТИ 4, 92 (1947).
104. В о л ь к е н ш т е й н М. В. и Сыркин Я. К., Журн. физ.
химии 12, 677 (1938).
105. Во л ь к е н ш т е й н М. В., Успехи химии 13, 234 (1944).
106. Волькенштейн М. В., ДАН СССР 49, 111 (1945).
107. Волькенштейн М. В., УФН 29, 54 (1946).
108. Волькенштейн М. В., Изв. АН СССР (сер. физ.) 14, 466
(1950).
109. Волькенштейн М. В., ДАН СССР 78, 879 (1951).
ПО. Волькенштейн М. В., УФН 43, 485 (1951).
111. В о л ь к е н ш т е й н М. В. и Птицын О. Б., ДАН СССР 86,
677 (1952).
112. Волькенштейн М. В. и Птицын О Б., УФН 49, 501
(1953).
113. Герасимов Я. И., Успехи химии 2, 475 (1933).
114. Глесстон С., Успехи химии за 1935 г. (ежегодник англий-
ского хим. общ.), ОНТИ 32, 68 (1937).
115. Г о дне в И. Н. и Свердлин А. С., ЖЭТФ 5, 864 (1935).
116. Г о д н е в И. Н. и Свердлин А. С., Журн. физ. хим. 8, 904
(1936).
117. Годнее И. Н., Титов М. Е. и Шишаков П. А., Труды
ИХТИ, 3, 28 (1940).
118. Годнее И. Н., П а ю х и н а А. И. и С у ш к и н И. В., ЖЭТФ
11, 122 (1941).
119. Го дне в И. Н„ ДАН СССР 43, 202 (1944).
120. Годнев И. Н„ ДАН СССР 48, 264 (1945).
121. Годнев И. Н., Журн. физ. хим. 19, 637 (1945).
122. Годнев И. Н., Журн. физ. хим. 20, 897 (1946); 21, вып. 3
(1947).
123. Годнев И. Н. и Морозов В. П., Журн. физ. хим. 21, 799
(1947).
124. Годнев И. Н. и С о р о к и н В. С., ДАН СССР 58, 1931 (1947).
125. Дяткина М. Е., Журн. физ. хим. 28, 377 (1954).
126. Ельяшевич М. А., Труды ГОИ 12, вып. 106 (1938).
127. Е л ь я ш е в и ч М. А., ДАН СССР 28, 605 (1940).
128. Ельяшевич М. А., Журн. физ. хим. 14, 461 (1940).
129. Ельяшевич М. А., Журн. физ. хим. 14, 488 (1940).
130. Ельяшевич М. А., Журн. физ. хим. 14, 1381 (1940).
131. Ельяшевич М. А., Журн. физ. хим. 15,847 (1941).
132. Ельяшевич М. А., Журн. физ. хим. 15, 831 (1941).
133. Ельяшевич М. А. и Степанов Б. И., Изв. АН СССР
(сер. физ.) 5,. 155 (1941).
134. Ельяшевич М. А. и Степанов Б. И., ДАН СССР 32, 481
(1941).
135. Ельяшевич М. А., ЖЭТФ 13, 65 (1943).
136. Ельяшевич М. А. и Степанов Б. И., Журн. физ. хим.
17, 145 (1943).
137. Ельяшевич М. А., УФН 28, 482 (1946).
410
ЛИТЕРАТУРА
138. Ландсберг Г. С. и Манд е льштам Л. И., ЖРФХО (часть
физ.) 60, 335 (1928).
139. Маслов П. Г., ДАН СССР 67, 819 (1949).
140. Маслов П. Г., ДАН СССР 70, 985 (1950).
141. Маслов П. Г., ДАН СССР 71, 867 (1950).
142. Маслов П. Г., Учен. зап. Лен. горн, ин-та 24, 185 (1950).
143. Маслов П. Г. и Антипина С. А., Журн. физ. хим. 25, 594
(1951).
144. Маслов П. Г., Журн. физ. хим. 25, 803, 814 (1951).
145. Маслов П. Г. иАнтипинаС. А., ЖЭТФ 22, 164, 172 (1952).
146. Маслов П. Г., ЖЭТФ 23, 736 (1952).
147. Маслов П. Г., ДАН СССР 84, 993 (1952).
148. Маслов П. Г., ДАН СССР 84, 1187 (1952).
149. Маслов П. Г., Журн. физ. хим. 26, 1311 (1952).
150. Маслов П. Г., ДАН СССР 86, 767, 981 (1952).
151. Маслов П. Г., ЖЭТФ 22, 716, 729 (1952).
152. Маслов П. Г., Журн. физ. хим. 27, 505 (1953).
153. Маслов П. Г., Журн. физ. хим. 27, 69 (1953).
154. Маслов П. Г., Журн. физ. хим. 27, 237 (1953).
155. Маслов П. Г., Журн. физ. хим. 27, 243 (1953).
156. Маслов П. Г., Журн. физ. хим. 27, 509 (1953).
157. Маслов П. Г., Журн. прикл. хим. 26, 388, 543, 749, 868 (19531.
158. Маянц Л. С., ДАН СССР 32, 120 (1941).
159. Маянц Л. С., Изв. АН СССР (сер. физ.) 5, 158 (1941).
160. Маянц Л. С., ДАН СССР 48, 334 (1945).
161. Маянц Л. С., ДАН СССР 50, 121 (1945).
162. Маянц Л. С., ДАН СССР 54, 27 (1946).
163. Маянц Л. С., Трупы Физ. инет. АН СССР 5, 63 (1950).
164. Маянц Л. С., ЖЭТФ 25, 393 (1953).
165. НепорентБ. С. и Степанов Б. И., УФН 43, 380 (1951).
166. Пентин Ю. А., БобовичЯ. С., ГуревичД. Б. иТатев-
ский В. М„ ДАН СССР 89, 435 (1953).
167. Пирогов Н. Н., ЖРФХО 18, вып. 9, физический отдел, 307
(1886).
168. Свердлов Л. М., ДАН СССР 78, 1115 (1951); 86, 513
(1952).
169. Свердлов Л. М., ДАН СССР 88, 249 (1953).
170. Словохотова Н. А., Сыркин Я. К. и Волькен-
штейн М. В, ДАН СССР 35, 161 (1942).
171. Смирнова И. В. и Фрост А. В., Учен. зап. МГУ, № 164,
145 (1953).
172. Степанов Б. И., Журн. физ. хим. 14, 474 (1940).
173. Степанов Б. И., Журн. физ. хим. 15, 78 (1941).
174. Степанов Б. И., Журн. физ. хим. 15, 865 (1941).
175. Степанов Б. И., ДАН СССР 40, 296 (1943).
176. Степанов Б. И., ДАН СССР 45, 61 (1944).
177. Степанов Б. И., Журн. физ. хим. 19, 497 (1945).
178. Степанов Б. И., ЖЭТФ 15, 43 (1945).
179. Степанов Б. И., Журн. физ. хим. 20, 917 (1946).
180. Степанов Б. И., Acta Physicochimica URSS 22, 238 (1947).
181. Степанов Б. И., Изв. АН СССР (сер. физ.) 11, 357 (1947).
ЛИТЕРАТУРА
411
182. Сыркин Я. К. иВолькенштейнМ. В., Acta Physico-
chimica URSS 2, 303 (1935).
183. Сыркин Я. К. и Волькенштейн М. В., Acta Physico-
chimica URSS 2, 308 (1935).
184. Сыркин Я. К., Изв. АН СССР (сер. физ.) 4, 103 (1940).
185. Тарасов В. В., ДАН СССР 46, 22, 117 (1945).
186. Тарасов В. В., ДАН СССР 54, 803 (1946).
187. Тарасов В. В., ДАН СССР 58, 577 (1947).
188. Тарасов В. В., Журн. физ. хим. 24, 111 (1950).
189. Татевский В. М., ЖЭТФ 15, 445 (1945).
190. Татевский В. М. и Фрост А. В., Вестник МГУ 12, 113
(1947).
191. Татевский В. М., Журн. физ. хим. 25, 261 (1951).
192. Темкин М. И., Журн. физ. хим. 11, 169 (1938).
193. Темкин М. И., Уч. зап. ЛГУ, № 38 (сер. физ.), вып. 5, 74
(1939).
194. Темкин М. И., Журн. физ. хим. 14, 1054 (1940).
195. Темкин М. И., Журн. физ. хим. 15, 296 (1941).
196. Темкин М. И. и Шварцман Л. А., Успехи химии, 17, 259
(1948).
197. Ф о к В. А., Вопросы философии, № 4, 170 (1952).
198. Фрост А. В., Успехи химии 2, 445 (1933).
199. Фрост А. В., ДАН СССР 4, 158 (1933).
200. Фрост А. В., ЖОХ 4, 124 (1934).
201. Халатников И., ДАН СССР 87, 539 (1952).
202. Ш и г о р и н Д. Н. и Сыркин Я. К., Изв. АН СССР (сер.
физ.) 9, 225 (1945).
203. Aston J. О., Ind. Eng. Chem. 34, 514 (1942).
204. Aston J. О., Disc. Farad Soc. 10, 73 (1951).
205. Barnes R. B. and Gore R. C., Analyt. Chem. 21, 7 (1949).
206. Bigeleisen J. and Mayer M. G., J. Chem. Phys. 15, 261
(1947).
207. Bigeleisen J., J. Chem. Phys. 21, 1333 (1953).
208. Blade E. and Kimball G., J. Chem. Phys. 18, 630 (1950).
209. Bohm D., Phys. Rev. 85, 166, 180 (1952); 89, 458 (1953).
210. Boltzmann L., Sitzb. d. Wiener Akad. (II) 63, 397, 679 (1871).
211. Burkhard D. G., J. Chem. Phys. 21, 1541 (1953).
212. Crawford B. L„ J. Chem. Phys. 8, 273 (1940).
213. Cross P. C., Hainer R. M. and King O. W., J. Chem. Phys.
12, 210 (1944).
214. Dailey В. P., Annals New York Acad. Sc. 55, 915 (1952).
215. Dennison D. M., Rev. of Mod. Phys. 3, 280 (1931).
216. Du Mon d J. W. M. and Cohen E. R., Rev of Mod. Phys.
25, 691 (1953).
217. Ehrenfest P. and Trkal V., Ann. d. Phys. [4] 65, 609
(1921).
218. Eidinoff M. L. and Aston J. Q., J. Chem. Phys. 3, 379
(1935).
219. Giauque W. F. and Overstreet R., J. Am. Chem. Soc. 54,
1731 (1932).
220. G i a u q u e W. F. and В 1 u e R. W., J. Am. Chem. Soc. 58, 831 (1936).
4 12
ЛИТЕРАТУРА
221. Golden S„ J. Chem. Phys. 16, 78, 250 (1948).
222. Gordon A. R. and Barnes C., J. Chem. Phys. 1, 297 (1933).
223. Gordon A. R., J. Chem. Phys. 2, 65 (1934).
224. Gordon A. R„ J. Chem. Phys. 2, 549 (1934).
225. Gordon A. R., J. Chem. Phys. 3, 259 (1935).
226. Gore R. C„ Analyt. Chem. 22, 7 (1950); 23, 7 (1951); 24, 8
(1952); 26, 11 (1954).
227. Hainer R. M., Cross P. C. and К i n g O. W., J. Chem. Phys.
17, 826 (1949).
228. Halford J. O., J. Chem. Phys. 15, 645 (1947).
229. Halford J. 0., J. Chem. Phys. 16, 410, 560 (1948).
230. Halford J. 0., J. Chem. Phys. 18, 444 (1950).
231. Halford J. 0., J. Chem. Phys. 18, 361, 1051 (1950).
232. Johnston H. L. and Chapman A. T., J. Am. Chem. Soc. 55,
153 (1933), см. стр. 160.
233. Johnston H. L. and Davis C. O., J. Am. Chem. Soc. 56,
271 (1934).
234. Jones W. M. and Giauque W. F., J. Am. Chem. Soc. 69,
983 (1947).
235. Kassel L. S., J, Chem. Phys. 1, 576 (1933).
236. Kassel L. S., Chem. Rev. 18, 277 (1936).
237. Kassel L. S., J. Chem. Phys. 4, 276 (1936).
238. Kilpatrick J. E. and P i t z e r K. S., J. Chem. Phys. 17, 1064
(1949).
239. King O. W., Hainer R. M. and Cross P. C., J. Chem. Phys.
11, 27 (1943).
240. King G. W., J. Chem. Phys. 15, 820 (1947).
241. Lassettre E. N. and Dean L. B., J. Chem. Phys. 17, 317
(1949).
242. Mayer J. E., Brunauer S. and M а у e r M. G., J. Am. Chem.
Soc. 55, 37 (1933).
243. Mizushima S., Morino Y., Watanabe I., SimanoutiT.
and Yamaguchi S,. J. Chem. Phys. 17, 591 (1949).
244. Mizushima S., Shimanouchi T., Nakagawa I. and
Miyake A., J. Chem- Phys. 21, 215 (1953).
245. Mulholand H. P., Proc. Camb. Phil. Soc. 24, 280 (1928).
246. Nielsen H. H., Phys. Rev. 40, 445 (1932).
247. Oosterhoff L. J., Disc. Farad Soc. 10, 79 (1951).
248. Pennington R. E. and Kobe K. A., J. Chem. Phys. 22, 1442
(1954).
249. Pitzer K. S., J. Chem. Phys. 5, 469, 473 (1937).
250. Pitzer K. S„ J. Chem. Phys. 8, 711 (1940).
251. Pitzer K. S., Chem. Rev. 27, 39 (1940).
252. P i t z e r K. S. and Gwinn W. D., J. Chem. Phys. 10, 428 (1942).
253. Pitzer K. S., J. Chem. Phys. 14, 239 (1946).
254. Pitzer K. S., Disc Farad Soc. 10, 66 (1951).
255. Redlich O., Zs. f. physik. Chem. В 28, 371 (1935).
256. Rosenthal J. E. and Murphy G. M., Rev. Mod. Phys. 8,
317 (1936).
257. Slawsky Z. I. and Dennison D. M., J. Chem. Phys. 7,
509 (1939).
ЛИТЕРАТУРА
413
258. Smith L, 0., J. Chem. Phys. 17, 139 (1949).
259. Stripp K. F. and Kirkwood J. O., J. Chem. Phys. 19, Ц31
(1951).
260. Torkington P., J. Chem. Phys. 18, 1373 (1950).
261. Wang S. C„ Phys. Rev. |2], 34, 243 (1929).
262. Wilson E. B., J. Chem. Phys. 3, 276 (1935).
263. Wilson E. B„ J. Chem. Phys. 4, 526 (1936).
264. Wilson E. B., Chem. Rev. 27, 17 (1940).
265. Wilson E. B, J. Chem. Phys. 7, 1047 (1939); 9, 76 (1941).
266. Wilson E. B., Disc. Farad Soc. 9, 108 (1950).
267. Z e i s e H„ Zs. f. Elektrochem. 39, 758, 895 (1933); 40, 662, 885
(1934).
268. /eise H., Zs. I. Elektrochem. 47, 380, 595, 644 (1941); 48, 425
476 (1942).
НАИБОЛЕЕ ВАЖНЫЕ ОБОЗНАЧЕНИЯ
а, Ь, с — величины, обратные соответствующим глав-
ным центральным моментам инерции моле-
кулы 1А, 1В, 1С, расположенным в возрастаю-
щем порядке 1А 1В < 1С.
А, В, С — моменты инерции молекулы в центральной
системе координат.
А — оператор.
[А] — детерминант квадратичной формы кинетиче-
ской энергии вращения, выраженной через
обобщенные скорости.
В — постоянная вращения двухатомной моле-
кулы.
В, D, В—коэффициенты, определяющие энергию вра-
щения нежесткого ротатора.
Bv, Dv, Fv — коэффициенты, определяющие энергию вра-
щения колеблющегося ротатора.
с — скорость света.
Ср — теплоемкость при постоянном давлении.
Съ — теплоемкость при постоянном объеме.
Ср — поворотная ось симметрии порядка р.
С3ч>, Z>3h и т. д. — обозначения групп симметрии молекулы.
D — выражение, определяемое формулой
_ _ (2nmkT)^a
h? ’
D, Е, F—произведения инерции молекулы в централь-
ной системе координат.
Е—энергия системы (газа).
Ер — нулевая энергия системы (газа).
Еп, Е( — дискретные значения энергии (уровни энер-
гии) системы (газа).
ДЕ — прирост энергии.
Al • • — обобщенные силы.
F—свободная энергия.
g— вес уровня энергии частицы.
h — постоянная Планка.»
Н—энтальпия (теплосодержание).
Но — нулевая энтальпия.
НАИБОЛЕЕ ВАЖНЫЕ ОБОЗНАЧЕНИЯ
415
Н — оператор энергии.
Д/7—прирост энтальпии.
—прирост энтальпии при реакции образования.
I — центр симметрии.
/— момент инерции.
/Пр„в — приведенный момент инерции.
/д, /в, 1С—главные центральные моменты инерции, рас-
положенные в возрастающем порядке 1А<^
1 с-
1Х, 1у, 4 — главные центральные моменты инерции.
Jyyi — моменты инерции.
4г. lyz — произведения инерции.
J—квантовое число полного момента количества
движения атома.
J—квантовое число момента количества движе-
ния молекулы, определяющее величину энер-
гии вращения (вращательное квантовое
число).
k — константа Больцмана.
k^j — динамические коэффициенты.
Ац — коэффициенты влияния.
К—момент инерции волчка относительно оси
вращения.
К—квантовое число, определяющее энергию
вращения двухатомной молекулы в случае
Хунда «Ь».
К—второе квантовое число, определяющее
энергию вращения симметричного волчка.
К, К$, Кс, Кр — константы равновесия.
I — число степеней свободы системы.
I — азимутально квантовое число электрона.
L — квантовое число результирующего орбиталь-
ного момента количества движения всех
электронов.
L — результирующий орбитальный момент коли-
чества движения электронов.
т — масса молекулы (частицы).
та — квантовое число, определяющее проекцию
спинового момента частицы.
М—мультиплетность терма.
Af — молекулярный вес.
п — число молей.
п — число минимумов потенциального барьера
молекулы, обладающей внутренним враще-
нием.
п—главное квантовое число электрона.
п — число колебательных степеней свободы ква-
зитвердой молекулы.
416
НАИБОЛЕЕ ВАЖНЫЕ ОБОЗНАЧЕНИЯ
п' — число колебательных степеней свободы мо-
лекулы с внутренним вращением.
N— число молекул (частиц).
N — число атомов, входящих в состав молекулы.
Аго — число Авогадро.
р — давление.
р—вес энергии вращения молекулы.
Pi< Р2’ Рз— парциальные давления.
Рь Р2> Рз> • • • — обобщенные импульсы.
Р—общее давление смеси газов.
П — приведенный изобарно-изотермический по-
тенциал.
АП — прирост приведенного изобарно-изотермиче-
ческого потенциала.
ДПу—прирост приведенного изобарно-изотермиче-
ского потенциала в реакции образования
соединения.
q — сумма по состояниям молекулы при отсчете
энергии от уровня с наименьшими кванто-
выми числами.
Яъ Яъ, Яз< • • —обобщенные координаты.
Q — сумма по состояниям молекулы (Q = e~e^kTq).
Qii Qz< •••> Qn — нормальные координаты.
Qi— сумма по состояниям внутренних движений.
Q„— сумма по состояниям поступательного дви-
жения.
<2КОлеб — сумма по состояниям колебательных движе-
ний.
— сумма по состояниям вращательного движе-
ния.
(?эл — сумма по электронным состояниям молекулы.
QK7 — сумма по состояниям молекулы, вычисленная
при применении классической механики.
г — число степеней свободы одной частицы.
г — квантовое число при вычислении собственных
значений уравнения Матье.
ге—равновесное расстояние между ядрами двух-
атомной молекулы.
R—универсальная газовая постоянная,
s—квантовое число спинового момента частицы
(спин).
s — число степеней свободы вращательного дви-
жения.
sz — проекция спинового момента частицы.
— спиновый момент электрона.
[л^/с] — детерминант квадратичной формы кинетиче-
ской энергии вращения, выраженной через
проекции угловой скорости «>х, ш;/, шг и
угловые скорости вращения волчков.
НАИБОЛЕЕ ВАЖНЫЕ ОБОЗНАЧЕНИЯ
417
S— квантовое число результирующего спина
электронов.
S — энтропия.
Sn—'зеркально-поворотная ось симметрии га-го
порядка.
AS — прирост энтропии.
S — вектор результирующего спина электронов.
t — число волчков в молекуле в случае внутрен-
него вращения.
Т — абсолютная температура.
Т — кинетическая энергия.
v — объем.
v—колебательное квантовое число.
V—потенциальная энергия.
1/0— высота потенциального барьера.
хь х2, х3 — молярные доли.
х, у, г — координаты.
{ хх }, {уу }, { zz } — суммы вида т(у2{, £ mizl
г i i
{ху}, {xz}, {yz}— произведения инерции молекулы в централь-
ной системе координат.
z— порядковый номер элемента в периодической
системе Д. И. Менделеева.
Z — сумма по состояниям системы.
а = 2s 1 — число спиновых состояний частицы со спи-
ном s.
и(1), ^(1), ... —спиновые функции частицы.
е — энергия молекулы (частицы).
е>- — значения энергии молекулы в состоянии у.
е0 — нулевая энергия молекулы.
X, |х, ч — направляющие косинусы оси волчка в си-
стеме координат, жестко связанной с моле-
кулой.
А — квантовое число, описывающее электронные
состояния двухатомной молекулы.
{ Хрь} — выражение, определяемое формулой {Хр} =
t
= S
i = l
|j. — химический потенциал.
р — приведенная масса молекулы.
че — частота колебаний двухатомной молекулы,
соответствующая бесконечно малой ампли-
туде (нулевая частота).
"*0 — частота колебаний двухатомной молекулы,
соответствующая отсчету энергии от v = 0.
ч' — наблюдаемая основная частота двухатомной
молекулы, соответствующая переходу от
v = 1 к v = 0.
ч — частота.
418
НАИБОЛЕЕ ВАЖНЫЕ ОБОЗНАЧЕНИЯ
*1» ^2» •••> '‘п — частоты нормальных колебаний многоатом-
ной молекулы при бесконечно малых ампли-
тудах.
Чр ч®, — частоты нормальных колебаний многоатом-
ной молекулы, соответствующие частоте ш0
двухатомной молекулы.
м2, ..., vn — наблюдаемые основные частоты.
р —• вес электронного уровня.
р0 — вес основного электронного уровня.
а — число симметрии.
— плоскости симметрии.
S — символ электронного состояния двухатомной
молекулы с А = 0.
S — квантовое число, определяющее проекцию
результирующего спинового момента элек-
тронов двухатомной молекулы.
т — второе квантовое число, определяющее энер-
гию вращения асимметричного волчка.
т, ^ii т2 — параметры при вычислении QBp.
Ф — изобарно-изотермический потенциал.
ДФ — прирост изобарно-изотермического потен-
циала.
ДФ^—прирост изобарно-изотермического потен-
циала при реакции образования соединения.
0, ф, <Р —• эйлеровы углы.
ф = Ф (<j) — волновая функция, зависящая от координат.
Ф = Ф (q, t) — волновая функция, зависящая от координат
и времени.
фп —волновая функция, описывающая поступа-
тельное движение.
Фэл—волновая функция, описывающая электрон-
ное движение.
'Рколеб — волновая функция, описывающая колебатель-
ное движение.
Фвр — волновая функция, описывающая вращатель-
ное движение.
шг-—-вес уровня энергии системы.
и>е — частота колебаний двухатомной молекулы
при бесконечно малой амплитуде (нулевая
частота), выраженная в см~1.
шехе — постоянная ангармоничности двухатомной
молекулы.
<о0 — частота колебаний двухатомной молекулы,
соответствующая отсчету энергии от v = 0
и выраженная в см~1*
WJ, ш2, шп— циклические частоты колебаний многоатом-
ной молекулы.
НАИБОЛЕЕ ВАЖНЫЕ ОБОЗНАЧЕНИЯ
419
Примечания. 1. Индекс 0 вверху справа у термодинамиче-
ской величины означает отнесение этой величины к стандартному
состоянию, например: S.0 означает энтропию в стандартном состоя-
нии, ДФ° —прирост изобарно-изотермического потенциала при
стандартных условиях.
2. Индексы П1 ЭЛг колеб) вр означают соответственно отнесение
данной величины к поступательному, электронному, колебательному
и вращательному движениям.
3. Индексы ов и 3 в означают соответственно свободное вра-
щение и заторможенное вращение волчков в молекуле, индекс ж вр
(жесткое вращение) означает случай вращения молекулы при
жестко заторможенных волчках.
Годнев Иван Николаевич
Вычисление термодинамических функций
по молекулярным данным
Редактор /И. В. Копытина
Техн, редактор Н. А. Тумаркина
Корректор А. С. Каган
Сдано в набор 12/XII 1955 г.
Подписано в печать 21/11 1956 г.
Бумага 84x108/32. Физ. печ. л. 13,13
Условн. печ. л. 21,58 Уч.-изд. л. 22,92
Тираж 4 000 экэ. Т-02408 Цена 13 р. 45 к. Зак. 835.
Государственное издательство
технико-теоретической литературы
Москва. В-71, Б. Калужская, 15.
Министерство культуры СССР. Главное
управление полиграфической промышленности.
4-я типография им. Евг. Соколовой.
Ленинград, Измайловский пр., 29.
ОПЕЧАТКИ
Стр. Строка Напечатано Следует читать
12 17 св. дифа диф-
12 19 » тел- тела
59 Таблица 2, 4 столбец, 1 стр. сн. СрП с ^ри
114 5 сн. (Рнеч = 0
220 19 св. СН3Х СН3Х
220 25 » Ох ох
262 v 4 » 'at
280 9 » sn
Зак. 835.